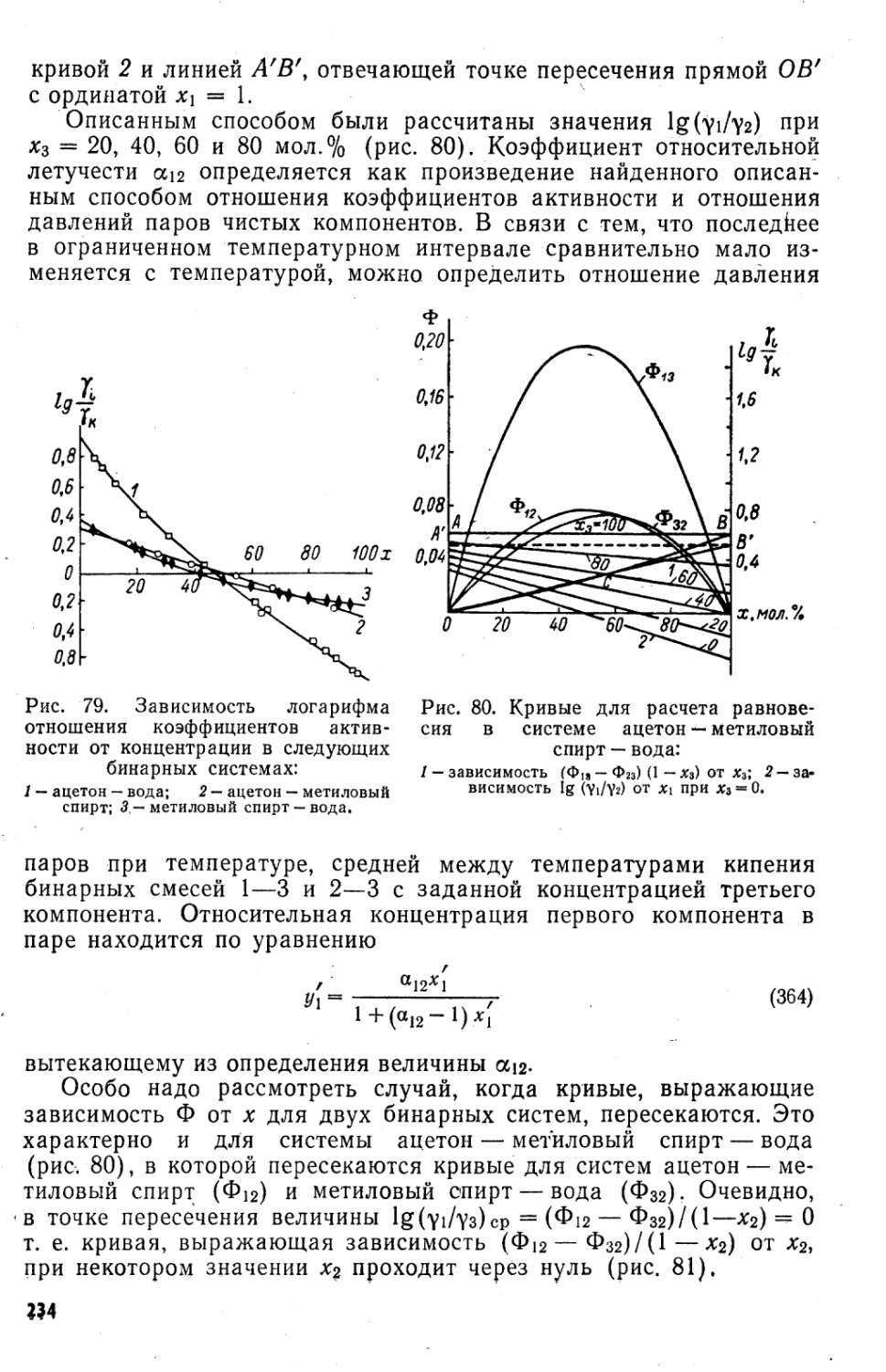
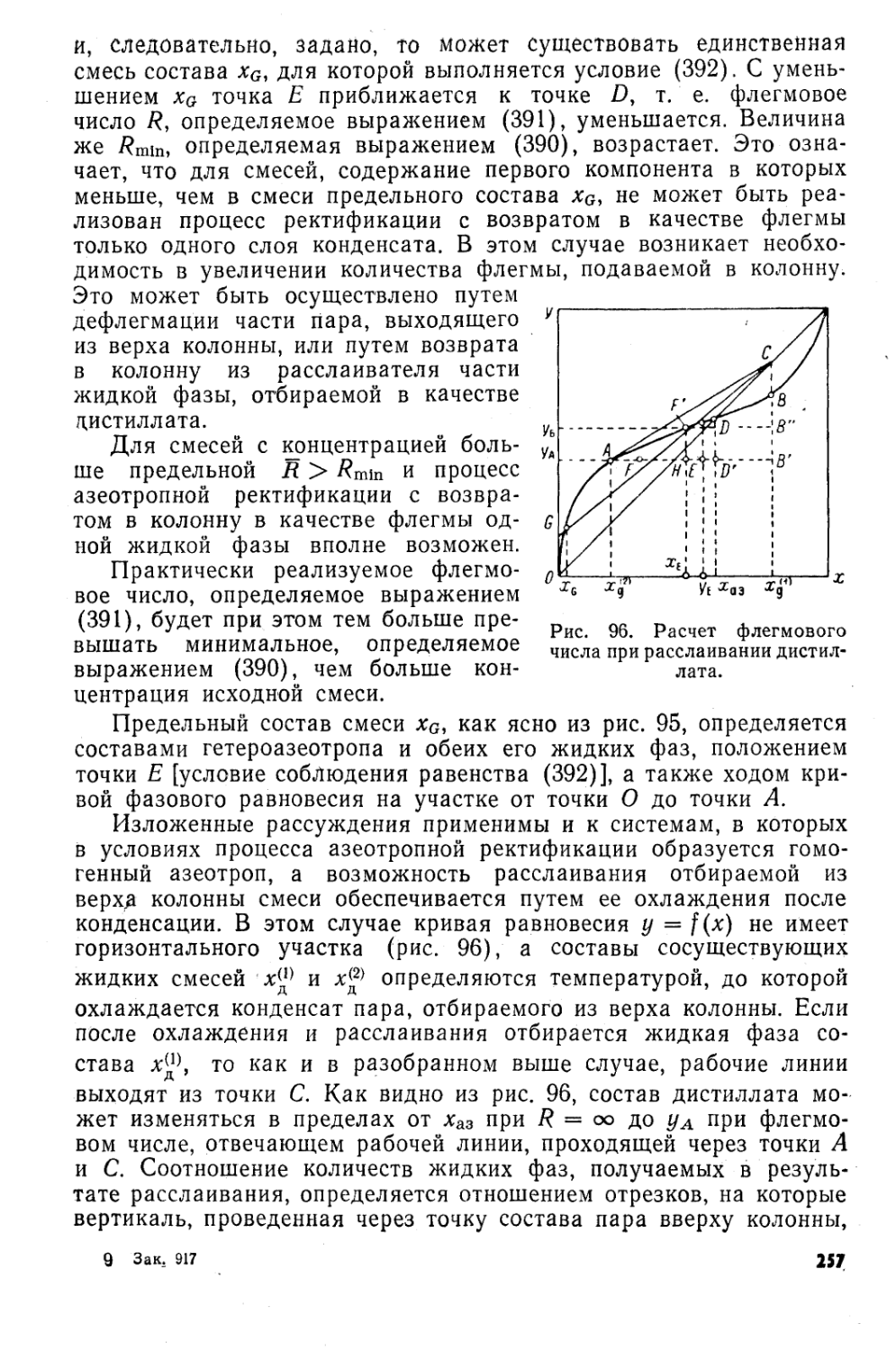
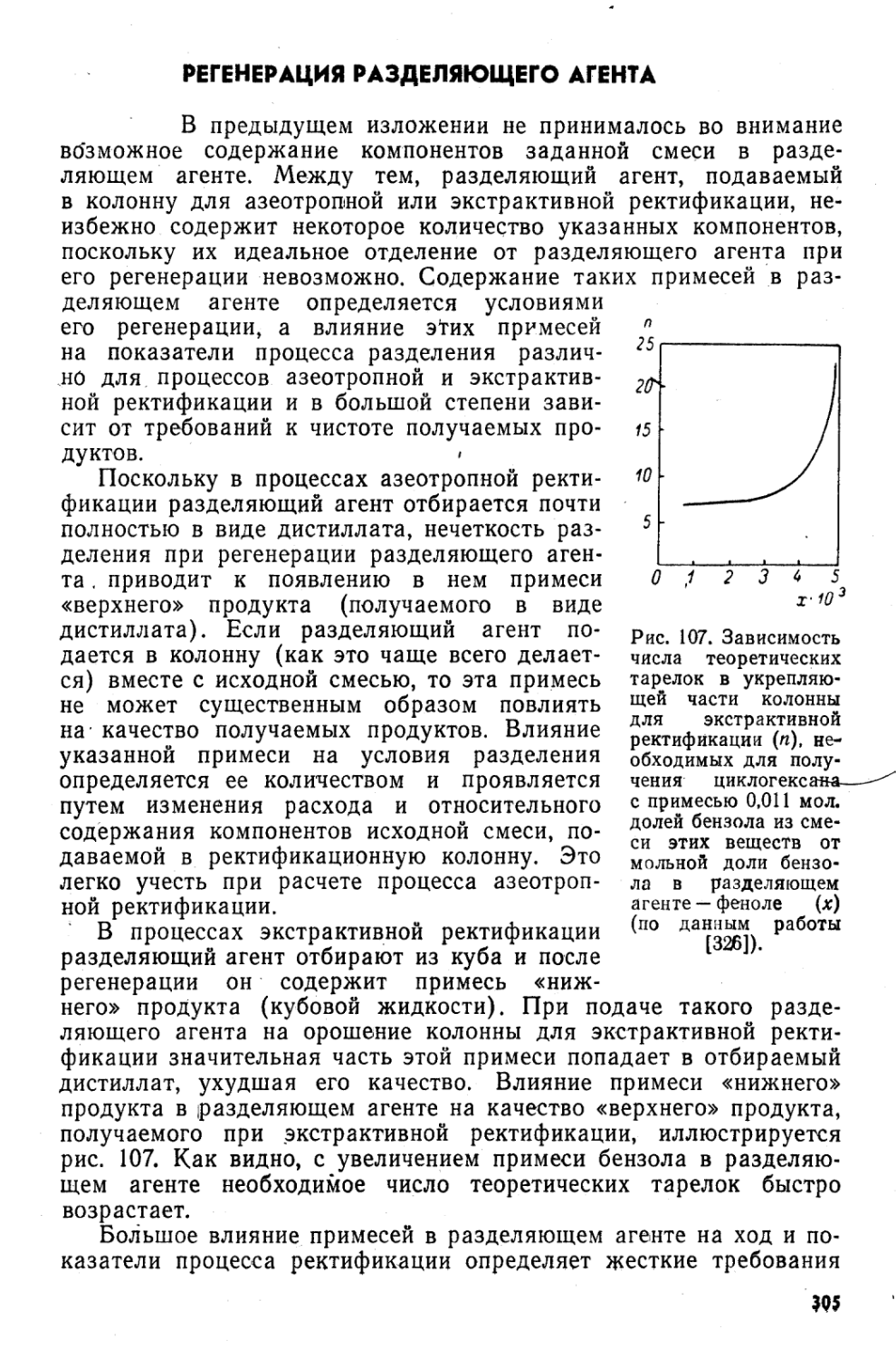
Автор: Коган В.Б.
Теги: химическая технология химическая промышленность химия ректификация
Год: 1971
Текст
В. 6. К0ГАН
АЗЕОТРОПНАЯ
И
ЭКСТРАКТИВНАЯ
РЕКТИФИКАЦИЯ
Издание 2-е
переработанное и дополненное
/Щ\
ИЗДАТЕЛЬСТВО «ХИМИЯ»
Ленинградское отделение
,1971
В. Б. Коган. Азеотропная и экстрактивная ректи¬
фикация. Изд. 2-е доп. и пер. Изд-во «Химия».
JL, 1971, стр. 432, табл. 46, рис. 118.
Книга является вторым переработанным и
дополненным изданием монографии, вышедшей
в 1961 г. В книге освещается теория и практиче¬
ское применение методов азеотропной и экстрак¬
тивной ректификации для разделения различных
смесей. Подробно рассматриваются физико-хими¬
ческие основы, расчет, технологическое оформление
и применение этих методов. Описываются совре¬
менные методы выбора селективных разделяю¬
щих агентов для процессов азеотропной и экс¬
трактивной ректификации.
Книга предназначена для инженерно-техниче¬
ских и научных работников химической, нефтехи¬
мической и других отраслей промышленности,
в которых применяется разделение жидких сме¬
сей, а также для преподавателей, аспирантов и
студентов, специализирующихся в области химиче¬
ской технологии, нефтепереработки и в смежных
областях.
2-5-2
132—70
ВЛАДИМИР БОРИСОВИЧ КОГАН
АЗЕОТРОПНАЯ И ЭКСТРАКТИВНАЯ РЕКТИФИКАЦИЯ
Издательство «Химия», Ленинградское отделение,
Невский пр., 28
С. 432
Редактор Е. А. Подгорная
Техн. редактор 3. Е. Маркова
Переплет художника Ю. Н. Васильева
Корректор М. 3. Басина
Сдано в набор 6/1 1971 г. Подписано к печати 2/IN 1971 г. Формат 60X90 1/16. Бумага № 2,
Печ. л. 27. Уч.-изд. л. 29,55. M-28054. Тираж 3500 экз. Цена 2 р. 13 к. Заказ 917.
Ордена Трудового Красного Знамени
Ленинградская типография NS 2 имени Евгении Соколовой Главполиграфлрома
Комитета по печати при Совете Министров СССР, Измайловский пр., 29
Посвящаю памяти отца
ПРЕДИСЛОВИЕ
Методы азеотропной и экстрактивной ректификации иг¬
рают важную роль в решении выдвигаемых современной
химией задач по разделению сложных смесей. Это открыло новые
перспективы перед химической технологией и привлекло внимание
инженеров и исследователей к этим методам.
За сравнительно короткое время после выхода первого издания
настоящей монографии (1961 г.) в разработке теории и техники
азеотропной и экстрактивной ректификации достигнуты значитель¬
ные успехи. Нуждается в систематизации и обобщении опыт при¬
менения рассматриваемых методов с учетом вышедшей за это
время литературы. Так, в последнее время опубликована моногра¬
фия автора «Гетерогенные равновесия» [3], освещающая проблему
расчета условий фазового равновесия, монография-справочник
«Равновесие между жидкостью и паром» [31], в которой описаны
методы экспериментального исследования и проверки данных
о равновесии между жидкостью и паром, а также приведен экспе¬
риментальный материал, опубликованный в мировой литературе
до 1966 г. Появилась, наконец, монография «Солевая ректифика¬
ция» [142], излагающая теоретические основы и вопросы прак¬
тического применения метода экстрактивной ректификации с
применением солей в качестве разделяющих агентов.
Изложенные обстоятельства потребовали существенного допол¬
нения и переработки книги при подготовке 2-го издания. В пер¬
вую очередь, представлялось необходимым дополнить книгу изло¬
жением новых методов выбора разделяющих агентов для процес¬
сов азеотропной и экстрактивной ректификации. В разработке этой
центральной для указанных методов задачи достигнуты опре¬
деленные успехи. Дополнены разделы, посвященные методам
I*
з
предсказания свойств азеотропных смесей, закономерностям ди¬
стилляции и ректификации неидеальных смесей, а также расчету
ч процессов азеотропной и экстрактивной ректификации. Коренным
образом переработаны и дополнены разделы, освещающие практи¬
ческие применения методов азеотропной и экстрактивной ректифи¬
кации. Некоторые разделы книги переработаны и сокращены с уче¬
том наличия в отечественной литературе указанных выше моно¬
графий.
Автор выражает благодарность Б. К. Кричевцову, В. В. Кафа-
рову, JI. А. Серафимову и Л. С. Кофману за ценные замечания
при подготовке 2-го издания книги, а также Л. В. Утробиной
и Т. Г. Романовой за большую помощь в подготовке рукописи
к печати.
Автор
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
а — активность:
Aik — коэффициент, характеризующий величину отклонений компонен¬
та i бинарной системы i—k от закона Рауля;
D — расход пара в колонне;
f ■— летучесть;
£ — теплосодержание пара;
L — расход жидкости в колонне;
т — положительный азеотроп;
M — отрицательный азеотроп;
п — число компонентов в системе;
N — число молей;
Я —общее давление;
P1 —давление паров чистого компонента;
р—парциальное давление;
G — расход разделяющего агента;
q — энтальпия жидкости;
Q — количество тепла;
R — флегмовое число;
S-энтропия;
t, T температура;
У —часть общего расхода пара в колонне, приходящаяся на долю
компонентов заданной смеси;
W — часть общего расхода жидкости, приходящаяся на долю компо¬
нентов заданной смеси;
\УК —расход или количество кубового остатка;
Wc- расход или количество исходной смеси;
х — молярная концентрация компонента в жидкости;
Xp-молярная концентрация разделяющего агента в жидкости;
X1 ‘ т
~ относительная концентрация компонента I в жидкости;
-Xp
а — коэффициент относительной летучести;
Y — коэффициент активности.
ВВЕДЕНИЕ
I f ак известно, метод ректификации, широко применяемый
■I в технике для разделения жидких смесей, основан на
массообмене между паром и жидкостью. Движущей силой про¬
цесса является различие химических потенциалов компонентов во
взаимодействующих фазах, обусловленное разной относительной
летучестью компонентов. Величина движущей силы определяется
условиями равновесия между жидкостью и паром в системе, под¬
вергаемой разделению, а также технологическим режимом процес¬
са— в первую очередь, соотношением расходов парового и жидко¬
стного материальных потоков.
Условия фазового равновесия зависят от физико-химической
природы компонентов заданной смеси, температуры и давления.
Последнее в процессах ! ректификации практически постоянно и
выбирается по технологическим соображениям. Поэтому при задан¬
ном давлении условия равновесия между жидкостью и паром
оказываются физико-химической характеристикой разделяемой сис¬
темы и не могут быть изменены без введения в нее новых компонен¬
тов. Возможности изменения движущей силы процесса ректифика¬
ции за счет изменения соотношения расходов материальных пото¬
ков также лимитируются технико-экономическими соображениями.
Поэтому возможности интенсификации процессов разделения сме¬
сей с помощью обычной ректификации ограничиваются примене¬
нием высокоинтенсивной аппаратуры и организацией оптималь¬
ной технологии разделения, обеспечивающей наиболее рациональ¬
ную последовательность выделения отдельных компонентов или
фракций из исходной многокомпонентной смеси. Необходимо так¬
же иметь в виду, что обычная ректификация, как правило, приме¬
6
няется для разделения систем, компоненты которых не образуют
азеотропных смесей.
В принципе, путем обычной ректификации можно разделять
и азеотропные смеси, проводя процесс при двух различных давле¬
ниях. При этом используется изменение состава азеотропной смеси
с изменением температуры. Как будет показано ниже, это измене¬
ние тем больше, чем больше различаются теплоты испарения
компонентов заданной смеси. Обычно существенно различаются
теплоты испарения у веществ различной химической природы. Не¬
обходимо также помнить, что возможный интервал изменения да¬
влений ограничен температурами хладагентов, используемыми для
конденсации паров в дефлегматорах, и теплоносителей, применяе¬
мых в кубах ректификационных установок. В рилу указанных при¬
чин метод ректификации при двух различных давлениях получил
ограниченное практическое применение для разделения азеотроп¬
ных смесей.
Качественно изменились возможности техники ректификации
с появлением методов азеотропной и экстрактивной ректификации.
Эти методы основаны на увеличении движущей силы процесса
разделения за счет изменения условий равновесия между жидко¬
стью и паром, достигаемого путем добавления к заданной смеси
специально подобранных веществ — разделяющих агентов.
Метод азеотропной ректификации заключается в проведении
процесса ректификации с разделяющими агентами, образующими
с одним или несколькими компонентами исходной системы азео¬
тропные смеси, которые при ректификации отбираются в виде
дистиллата. Такие разделяющие агенты должны, следовательно,
быть летучими веществами. Обычно процессы азеотропной ректи¬
фикации проводятся так, чтобы вводимый в колонну разделяю¬
щий агент практически полностью выводился с дистиллатом. В виде
кубовой жидкости можно получить один компонент или смесь не¬
скольких компонентов с минимальным содержанием разделяю¬
щего агента.
Метод экстрактивной ректификации заключается в проведении
процесса ректификации с практически нелетучими разделяющими
агентами, или имеющими значительно меньшую относительную ле¬
тучесть, чем компоненты заданной смеси. В процессах экстрактив¬
ной ректификации практически весь разделяющий агент отводится
с кубовой жидкостью, а в дистиллат обычно попадает в очень не¬
больших количествах. Разделяющий агент подается в ректифи¬
7
кационную колонну на некотором расстояний от Ce верха и стекает
вместе с флегмой. Образование азеотропных смесей разделяющим
агентом с компонентами исходной смеси нежелательно во избежа¬
ние загрязнения дистиллата разделяющим агентом.
Однако в некоторых случаях для экстрактивной ректификации
применяются разделяющие агенты, образующие азеотропную смесь
с компонентом, отбираемым в виде дистиллата. Такой процесс
называется азеотропно-экстрактивной ректификацией.
В соответствии с описанными особенностями процессов азео¬
тропной и экстрактивной ректификации они различаются по техно¬
логическому оформлению. Это обусловлено, в первую очередь, раз¬
личием условий регенерации разделяющего агента, необходимых
для организации его рецикла. В процессах экстрактивной ректи¬
фикации регенерация разделяющего агента чаще всего не пред¬
ставляет затруднений. В связи с большим различием относительной
летучести компонентов заданной смеси и разделяющего агента
его регенерация легко осуществляется путем обычной ректифика¬
ции, в процессе которой он отбирается в виде кубовой жидкости
и вновь подается в колонну для экстрактивной ректификации. Ти¬
пичная схема установки для экстрактивной ректификации пока¬
зана на рис. I.
Поскольку в процессах азеотропной ректификаций разделяю¬
щий агент выводится из системы в виде азеотропных смесей, его
регенерация представляет значительно большие трудности. В связи
с этим для процессов азеотропной ректификации наиболее жела¬
тельны разделяющие агенты, обладающие ограниченной взаимной
растворимостью в компонентах, отбираемых в виде дистиллата.
В этом случае рецикл разделяющего агента может быть осущест¬
влен путем расслаивания охлажденного конденсата, отбираемого
из верха ректификационной колонны, и отбора в качестве дистил¬
лата слоя, обогащенного целевым компонентом. Содержащийся
в этом растворе разделяющий агент может быть отогнан в регене¬
рационной колонне в виде азеотропа, также подвергаемого рас¬
слаиванию после конденсации и охлаждения.
Практически чистый целевой компонент получается в регене¬
рационной колонне в виде кубовой жидкости. Типичная схема
установки для азеотропной ректификации с разделяющим агентом,
ограниченно смешивающимся с отгоняемыми компонентами, изо¬
бражена на рис. 2,
8
Рис. I. Схема установки для экстрактивной ректификации:
I — экстрактивно-ректификационная колонна; 2 —отгонная колонна;
3 — насос*
HD <Щ>.
Исходная смесь
^разделяющий
агент
Низкокипящиа
компонент
Рис. 2. Схема установки для азеотропной ректифи¬
кации;
I —колонна для азеотропной ректификации; 2 — регенерацион¬
ная колонна; 3 - холодильник, ί-расслаиватель.
Несмотря на принципиальные технологические различия ме¬
тодов азеотропной и экстрактивной ректификации они имеют об¬
щую физико-химическую основу, которая заключается в изменении
условий фазового равновесия в системе, подвергаемой разделению
с помощью разделяющих агентов. Поэтому теоретической основой
методов азеотропной и экстрактивной ректификации является уче¬
ние о фазовом равновесии.
Глава I
ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ УЧЕНИЯ
О ФАЗОВОМ РАВНОВЕСИИ
ЖИДКОСТЬ —ПАР
ОСНОВНЫЕ
ТЕРМОДИНАМИЧЕСКИЕ ЗАКОНОМЕРНОСТИ
Движущая сила процесса ректификации, как и всех мас¬
сообменных процессов, обусловлена различием истин¬
ных составов взаимодействующих паровой и жидкой фаз от рав¬
новесных. Состояние равновесия этих фаз—.естественное начало
отсчета движущих сил в процессах ректификации. Кроме того,
условия фазового равновесия являются основой для технологиче¬
ских расчетов. Отсюда вытекает определяющая роль условий рав¬
новесия между жидкостью и паром для процессов ректификации.
Термодинамические основы учения о гетерогенном равновесии
были заложены Гиббсом [I].
Условия фазового равновесия, в частности, в системах
жидкость — пар подробно рассмотрены в монографиях [2, 3]. По¬
этому рассмотрим лишь некоторые положения, без которых невоз¬
можно понимать физико-химические основы процессов азеотроп¬
ной и экстрактивной ректификаций.
При соприкосновении жидкости и пара между ними происходят
процессы массо- и теплообмена, обусловливающие изменение всех
свойств фаз. Конечным результатом этих процессов будет состоя¬
ние динамического равновесия, которое характеризуется равенст¬
вом чисел молекул каждого компонента, переходящих из одной ,
фазы в другую. Изменения, происходящие в такой системе, сопро¬
вождаются соответствующими изменениями ее энергетического со¬
стояния. Последние заключаются в переходе энергии от среды к си¬
стеме или в обмене энергией между отдельными частями системы.
Согласно закону сохранения энергии, все энергетические изме¬
нения в изолированной системе заключаются в переходе энергии
из одной формы в другую. Обозначив работу через Л, количество
тепла через Q и внутреннюю энергию через I), условие, выражае¬
мое первым законом термодинамики, для бесконечно малого про¬
цесса можно записать в виде уравнения:
6Q + 6A-dU = Q (I)
Физический смысл этого уравнения заключается в том, что
общий запас энергии изолированной системы является величиной
постоянной, а разница между механической и тепловой энергией
11
расходуется на изменение внутренней энергии системы. В зависи¬
мости от характера процесса внутренняя энергия системы может
увеличиваться или уменьшаться.
Необходимо отметить, что в противоположность работе и теп¬
лоте, само понятие о которых предполагает взаимодействие ме¬
жду системой и средой, внутренняя энергия не связана со средой,
а зависит только от состояния, системы, т. е. является функцией ее
состояния. При переходе от одного состояния к другому внутрен¬
няя энергия изменяется на определенную величину, зависящую
только от начального и конечного состояний и, в противополож¬
ность работе ц теплоте, не зависящую от пути перехода. По этим
причинам функцию U можно рассматривать как характеристиче¬
скую, определяющую энергетическое состояние системы. Таким об¬
разом, для конечного процесса из уравнения (I) получаем:
AC/= AQ+ АЛ (2)
Если единственной силой, действующей на систему, является
давление, т. е. если исключить из рассмотрения силы тяжести,
центробежную и другие, то механическая энергия системы выра¬
жается произведением давления на объем PV. Для этого случая
уравнение(2) можно переписать следующим образом:
AtZ = AQ-A(PK) (3)
При этом за положительное направление теплового потока при¬
нято направление от среды к системе.
Все процессы, с которыми приходится иметь дело на практике,
могут быть разделены на три группы.
Первая группа — самопроизвольно протекающие процессы: теп¬
лообмен, диффузия и другие процессы, приближающие систему
к состоянию равновесия.
Вторая группа — передача тепла от более холодного к более
теплому телу, совершаемая в холодильных машинах, подъем тяже¬
стей и др. Для осуществления этих процессов необходим подвод
энергии от внешнего источника.
Третья группа — обратимые процессы, занимающие промежу¬
точное положение между процессами, относящимися к первым
двум группам. Под обратимым понимается такой процесс, в кото¬
ром переход системы в прямом и обратном направлениях совер¬
шается через непрерывную серию состояний равновесия. Подобно
тому как температура определяет направление теплового потока,
направление процесса может быть определено по значению энтро¬
пии S, являющейся функцией, характеризующей состояние системы.
Согласно второму закону термодинамики, все самопроизвольные
процессы протекают в направлении увеличения энтропии. Если
бесконечно малый процесс сопровождается поглощением системой
из среды тепла dQ, то
где T — наивысшая температура в системе.
лг
Знак равенства в приведенном соотношении относится к обра¬
тимому процессу^ Изменение энтропии в конечном обратимом про¬
цессе можно рассматривать как сумму изменений в большом
числе бесконечна малых процессов, на которые можно разбить
рассматриваемый конечный процесс. Тогда:
Если обратимый процесс является изотермическим, то
Изменение внутренней энергии системы в обратимом процессе
с помощью уравнений (3) и (6) может быть выражено следую¬
щим образом:
MJ=TAS-Ib(PV) (7)
Принимая во внимание, что во всех .случаях мы оперируем
лишь разностями таких энергетических функций, как U и S, знач¬
ки Δ можно опустить. Тогда
Если в серии обратимых изменений система возвращается в на¬
чальное положение (круговой процесс), то ее энергетическое со¬
стояние в результате не изменяется. Следовательно, для обрати¬
мого кругового процесса:
Как указывалось, при рассмотрении равновесия в гетерогенных
системах, в качестве параметров состояния обычно принимают
давление, температуру и состав. При таком выборе параметров
состояния в качестве характеристической энергетической функции
удобно пользоваться введенной Гиббсом [I] функцией Ζ, называе¬
мой изобарным потенциалом и определяемой уравнением:
Подобно UnS функция Z зависит только от состояния си¬
стемы. Следовательно, в обратимом круговом процессе dZ = 0.
Другая важная особенность функции Z, как и других энергетиче¬
ских функций, заключается в том, что она является величиной
экстенсивной, т. е. значение Z для системы — сумма значений Z
для отдельных ее частей.
Каждый процесс происходит под действием определенной дви¬
жущей силы. В результате изменений, вызываемых самопроизволь¬
ным процессом, движущая сила в изолированной системе непре¬
рывно убывает. Предельным состоянием, к которому стремится
система в результате такого процесса, оказывается состояние рав¬
новесия. Последнее может быть охарактеризовано как такое
(5)
U = TS-PV
HU = 0 и HS = О
(9)
Z = U-TS+ PV
(10)
13
состояние, в котором между отдельными частями системы отсут¬
ствует движущая сила для передачи энергии в любой ее форме.
Это условие может быть выражено следующим образом:
dT = 0 (Ila)
dP = 0 (116)
dZ = 0 (Ив)
Равенство (Ila) формулирует условие термического равнове¬
сия, равенство (116)—условие механического равновесия, а ра¬
венство (11в) выражает условие отсутствия движущей силы для
передачи энергии в любой ее форме. Выражение (11 в)—более об¬
щий критерий равновесия, чем (Ila) и (1*16), так как теплота и
механическая работа являются частными видами энергии.
Условие dZ = 0 формально может быть интерпретировано как
отвечающее экстремальной точке на кривой зависимости Z от со¬
става. Поскольку процесс установления фазового равновесия само¬
произволен, в нем должно иметь место уменьшение Z до значения,
отвечающего состоянию равновесия. Следовательно, экстремум на
кривой зависимости Z от состава должен быть минимумом. Физи¬
чески это означает, что в состоянии равновесия «потенциальная»
энергия системы минимальна. Согласно условиям экстремума,
точке минимума на кривой отвечают условия
"-O (12)
дх
Q2Z
> о (13)
дх2
где X — состав, мол. доли.
Неравенство (13) называется условием устойчивости равно¬
весия.
УРАВНЕНИЯ РАВНОВЕСИЯ
Если в качестве параметров состояния приняты давле¬
ние, температура и состав фаз, то изобарный потенциал каждой
фазы Zf может быть представлен в виде функции этих величин
z' = qp(p, T9 Nflt Nf2 ...Nfn) (14)
где Nfv Nf2 ... Nffl — количества молей I, 2 ... п-го компонентов;
п — число компонентов в системе.
По правилам дифференцирования функции нескольких пере¬
менных имеем
,нр+т л т .. (.5)
I дР Ir, N, V дТ Jpt N \ AV1- V г .V ^ V, *
•i I I
где индексы Tt Nfi; Pt Nfi и Pt Tt Nf ф Nfi означают, что част¬
ные производные берутся соответственно при постоянных темпера¬
туре и составе, давлении и составе, а также при постоянных дав¬
14
лении, температуре и числах молей всех компонентов, за исклю¬
чением компонента, по которому производится дифференциро¬
вание.
Если рассматриваемая фаза находится в равновесии с другими
фазами, то все энергетические изменения состояния фазы яв¬
ляются обратимыми. При постоянных составе и температуре изме¬
нение изобарного потенциала фазы может происходить только за
счет совершения работы рассматриваемой фазой над другими фа¬
зами системы, или наоборот. Следовательно
где V' — объем рассматриваемой фазы.
При постоянных составе и давлении единственной формой об¬
мена энергией между отдельными частями системы является пере¬
дача тепла.
где S'— энтропия рассматриваемой фазы.
С учетом выражений (16) и (17) уравнение (15) запишется
следующим образом:
к одному молю изменение изобарного потенциала за счет измене¬
ния количества рассматриваемого компонента при постоянных Р,
T и количествах всех других компонентов. Эти величины были на¬
званы Гиббсом химическими потенциалами:
Рассмотрим систему, состоящую из двух фаз, находящихся
в равновесии при заданных P и Т. Предположим, что вследствие
бесконечно малого процесса dNt молей компонента i переходит из
фазы I в фазу II. Тогда изменения изобарных по*енциалов фаз
будут:
(16)
Значит
(17)
П
dZ'-V'dP-Sd'T
(18)
Частные производные
(19)
Таким образом:
f fZ
dZ'~V'dP-S'dT + 2 ^dNri
П
(20)
i — I
dZf = — dNι й dZ” — μ" UNi
(21)
15
Поскольку система находится в равновесии, то dZ?=dZ' + dZ”=0.
Отсюда следует:
μί~μΓ (22)
Уравнение (22) может быть применено к любому компоненту
и к любым двум фазам многофазной системы, находящейся в рав¬
новесии. Условие, выражаемое уравнением (22), является общим
для всех многофазных систем. Таким образом, химический по¬
тенциал произвольного компонента системы, находящейся в рав¬
новесии, во всех фазах одинаков.
Как уже отмечалось, Z— линейная функция массы. Поэтому
из определения химического потенциала, выражаемого уравне¬
нием (19), следует, что μ не зависит от массы, т. е. является вели¬
чиной интенсивной.
При условии постоянства P и T из уравнения (20) имеем:
dZ~ 2 μί dN'i (23)
Поскольку химические потенциалы компонентов не зависят от
количества компонентов, уравнение (23) может быть легко проин¬
тегрировано. Физический смысл интегрирования заключается при
этом в увеличении количества каждого компонента от величины
dN\ до Nfi без изменения состава фазы. Получаем
п
Zr-Zr0= 2 N'l (24)
ί« 1μ£
где Zq-значение функции Z' в состоянии, принятом за начало
отсчета.
Условимся в дальнейшем рассматривать I моль фазы. Тогда
количества молей компонентов будут выражать их молярные
доли х:
2 Xi - 1 И Xn = I - 2 XI (25)
ί-ι _ ί-i
Заменяя числа молей молярными долями в уравнении (24),
имеем
Zr-Z0= 2 (μί-μή)*ί + и* (26)
*<= I
Κ + Ζ'-Ζ'0-Σ(μ'-μ'η)χ' (27)
/«I
После замены dN'( в уравнении (20) величинами dxu прини-
п— I
мая во внимание, что dxn= — 2 dxh получаем:
1
п—I
dZ' = Vr dP -S' dT+Σ (μ; - μ;) dx\ (28)
' ' 1
I*
Дифференцирование уравнения (27) дает:
dv-'n ~dZ' — 2 x'id M - μ·«) - 2 (ι*ί - μ«) dxI
I-1 (-I
Величину dZ' в уравнении (29) можно заменить с помощью
уравнения (28). Тогда
п—\
άμ'η -V'dP-S'dT-Σ x'td (μί - μ^) (30)
/-I
Равенство (30) может быть отнесено к любой фазе многоком¬
понентной системы. Обозначая индексом " величины» относящиеся
к паровой фазе, а индексом ' — к жидкой фазе, можно записать:
dv-n - V" dP - s" dT -ΣνιΊ (μΓ - νΟ
ή-ϊ (з,)
d^-V'dP-S'dT-S Xid(ri-/n)
I = I
где у\ и Χχ — молярные доли компонента i в паре и жидкости.
Согласно уравнению (22):
ί/μ'=ί/μ" (32)
Поэтому из уравнений (31) получаем:
п— I
(V" - V') dP - (S" -SOdr+ 2 (Vi-xI)d^i- μ„) (33)
г-ι
Выражение (33) — уравнение равновесия многокомпонентной
двухфазной системы. При числе фаз, равном трем или более, урав¬
нения типа (33) могут быть написаны для любой пары фаз. Сле¬
довательно, число независимых уравнений типа (33), выражающих
условия равновесия многокомпонентной многофазной системы, все¬
гда на единицу меньше числа фаз в системе.
Уравнению состояния равновесной двухфазной системы можно
придать иной вид. Для бинарной двухфазной системы Ван-дер-
Ваальс [4] получил следующее уравнение состояния:
[у. V - С-,) Щ ^P-
А. В. Сторонкин[2] распространил это уравнение на многокомпо¬
нентные двухфазные рпотемы. Уравнении Состояния таких систем,
состоящих из равновесной жидкой и паровой фаз, имеют вид:
Нижние индексы хф Xi и у фу{ означают, что соответствую¬
щие производные берутся при постоянных концентрациях всех ком-
(34) — (36) выражаются через химические потенциалы компонен¬
тов следующим образом:
В приведенных уравнениях состояния множитель при dP вы¬
ражает изменение объема, происходящее при изобарно-изотермиче¬
ском образовании одного моля паровой фазы из такого большого
количества жидкой смеси, что ее состав при этом не изменяется.
Следуя А. В. Сторонкину, обозначим этот множитель через V<12>.
Множитель при dT выражает изменение энтропии, происходя¬
щее в результате такого процесса, равное дифференциальной мо¬
лярной теплоте испарения, деленной на температуру. Обозначим
этот множитель через QW/T.
Тогда уравнениям состояния (33) и (35) можно придать сле¬
дующий вид:
* 'р.т, х+ X1
dT +
п—\ п-I
(35)
и
(36)
в уравнениях
(37)
(38)
и
^ * !Т, Р, хфх(
дифференциал
(39}
' I* Tt Pt хфх{
по составу при T = const и P = const·
Величина D — полный
— полный
* Tt Р*
ИЗОБАРНЫЙ
И ХИМИЧЕСКИЕ ПОТЕНЦИАЛЫ
ИДЕАЛЬНЫХ И РЕАЛЬНЫХ ФАЗ.
ЛЕТУЧЕСТЬ, АКТИВНОСТЬ
И КОЭФФИЦИЕНТ АКТИВНОСТИ
, Уравнения равновесия, приведенные выше, включают
изобарный и химические потенциалы, которые не поддаются непо¬
средственному определению. Поскольку эти функции являются
энергетическими, на их значения влияет энергия взаимодействия
компонентов друг с другом, которая, в свою очередь, зависит от
физико-химических свойств системы. Определение интенсивности
взаимодействия компонентов в растворе выходит за пределы воз¬
можностей термодинамики. Однако в некоторых простейших слу¬
чаях, а именно для идеальных фаз, представляется возможным
выразить изобарный и химические потенциалы через параметры
состояния.
Паровая фаза. Согласно уравнению (18), для однокомпонент¬
ной фазы имеем:
ClZ = VdP-SdT (40)
dZ=VdP (при T = const) (41)
Если рассматриваемая фаза является идеальным газом, то
связь между объемом, давлением и температурой выражается урав¬
нением Клапейрона
V = jTT (42)
где R — универсальная газовая постоянная.
С учетом уравнения (42) из выражения (41) получаем
dZ = RTlnP
и
Z-Zo = RT In -^r
где Z0 и P0—изобарный потенциал и давление в состоянии, при¬
нятом за начало отсчета.
Аналогично уравнению (44) для компонента газовой смеси
μ/ - и·? - 1п 4сг (45)
где μ° — химический потенциал в состоянии, принятом за начало
отсчёта; ρι — парциальное давление; PJ -давление компонента
в состоянии, принятом за начало отсчета.
Если газ не является идеальным, то связь между объемом,
давлением и температурой выражается более сложными
зависимостями, чем уравнение (42). Соответственно усложняется
19
(43)
(44)
определение изобарного потенциала через параметры состояния.
Для сохранения формы уравнения (43) в этих случаях Льюис [5]
ввел специальную функцию /, названную летучестью и определяе¬
мую уравнением:
С помощью определения (46) из уравнения (41) для неидеаль¬
ного газа получаем
где 7° и P0 — летучесть и давление в состоянии, принятом за на¬
чало отсчета. _ ■
Из сравнения уравнений (44) и (47) легко видеть, что лету¬
честь идеального газа равна его давлению. Летучесть и давление
реального газа или пара, вообще говоря, не равны друг другу.
Однако при низких давлениях (до нескольких атмосфер) разницей
между ними для практических целей в большинстве случаев мож¬
но пренебречь.
При рассмотрении любых процессов приходится иметь дело
с изменениями, а не с абсолютными значениями изобарного и хи¬
мических потенциалов, поэтому летучести всегда входят в урав¬
нения равновесия в виде отношения. Отношение летучести в рас¬
сматриваемом состоянии к летучести в стандартном состоянии, по
Льюису, называется активностью:
С учетом этого определения из уравнения (47) для однокомпо
нентной системы следует:
Летучесть и активность Cii компонента i раствора или газо¬
вой смеси определяются выражениями, аналогичными (48) и (49)
где f( и /J-летучести компонента i в смеси и в состоянии, при¬
нятом за начало отсчета.
Так как химические потенциалы компонентов в фазах, находя¬
щихся в равновесии, одинаковы [см. уравнение (22)], то, согласно
определению (50), должны быть одинаковы и их активности. Из
сопоставления уравнений (45) и (50) очевидно, что для идеаль¬
ного газа:
RTd In f^VdP
(46)
P
(47)
I
f0
(48)
Z — ZQ — RT In а
(49)
(50)
(51)
20
Жидкая фаза. Расчет изобарного и химических потенциалов
для раствора представляет большие трудности, чем для газа, так
как в растворе молекулы компонентов взаимодействуют друг
с другом более интенсивно. Важным частным случаем раствора,
для которого можно выразить изобарный и химические потенциалы
через параметры состояния, является идеальный раствор. Под
последним принято принимать такой раствор, который при всех
концентрациях подчиняется закону Рауля, выражаемому уравне¬
нием:
Pi - P0iXi (52)
Из сравнения уравнений (51) и (52) следует, что активность
компонента идеального раствора равна его концентрации:
сIi = Xi (53)
Поэтому химические потенциалы компонентов идеального рас¬
твора определяются значениями их концентрации:
Р/ ~~ Ц? — ЯГ Ifl xI (54)
В реальных растворах зависимость активности и химических
потенциалов компонентов от концентрации усложняется из-за про¬
исходящего в этих растворах взаимодействия компонентов.
Отклонение поведения компонентов реальных смесей от идеаль¬
ного выражается количественно с помощью коэффициентов актив¬
ности:
aI
Y i = ~r (55)
Xi
Используя это определение и уравнение (51) для реальных
растворов, можно получить выражение, аналогичное уравнению
закона Рауля ’ -
Pt = P0IaI = P0IxCii = (Pj)uYf (56)
где (рг)ид — парциальное давление компонента I над идеальным
раствором того же состава, что и рассматриваемый реальный
раствор.
Удобство применения коэффициентов активности заключается
в дом, что по их значению легко судить о характере и величине
отклонений'от идеального поведения компонентов. Для идеальных
систем у г = I. Если уг* > I, то парциальное давление компонента i
превышает величину, следующую из закона Рауля. Такие откло¬
нения от закона Рауля называются положительными. При Yi < I
парциальное давление компонента i меньше, чем над идеальным
раствором. Такие отклонения от закона Рауля называются отрица¬
тельными.
21
Из изложенного выше вытекает следующее выражение для оп¬
ределения химических потенциалов компонентов- реального рас¬
твора:
Pt -μ? = %т ln*tYi (57)
В случае, когда паровую фазу можно рассматривать как иде¬
альный газ, а молярным объемом жидкости по сравнению с мо¬
лярным объемом пара можно пренебречь, коэффициенты активно¬
сти просто выражаются через составы равновесных фаз. Из
определений (51) и (55) следует:
Yi = T^- (58)
HiXi
Парциальное давление компонента может быть выражено че¬
рез общее давление и его молярную долю с помощью закона
Дальтона:
Pi = Pyi (59)
Отсюда:
Pyl
Y I = Tcif- (5°)
^ixI
,Необходимо отметить, что величина коэффициента активности
каждого компонента определяется совокупным взаимодействием
всех компонентов. Поэтому коэффициенты активности зависят не
только от физико-химических свойств смеси, но и от ее состава.
При этом абсолютные значения коэффициентов активности зави¬
сят от состояния, принимаемого за начало отсчета и называемого
стандартным. Выбор его, вообще говоря, произволен. При рассмот¬
рении равновесия в системах жидкость — пар обычно в качестве
стандартного принимается состояние чистого компонента при тем¬
пературе системы.
Неидеальность паровой фазы при расчете коэффициентов ак¬
тивности может быть учтена, если вместо давлений пользоваться
летучестями, определяемыми уравнением (46). Для расчета лету¬
чести .необходимо знать зависимости V = ^(P)t которые могут
быть выражены графически или аналитически с помощью уравне¬
ний состояния. Соответственно, летучесть находят путем графиче¬
ского или аналитического интегрирования уравнения (47).
При термодинамической обработке данных о равновесии ме¬
жду жидкостью и паром обычно не прибегают к непосредствен¬
ному использованию летучестей, а вводят поправки, учитывающие
неидеальность паровой фазы и объем жидкости. Наиболее рас¬
пространен метод расчета этих поправок, предложенный Скетчар-
дом и Раймондом [6].
22
Этот метод основан на следующих допущениях.
I. Для паровой фазы справедливо уравнение состояния в форме
П
Vn =
I-1
SMfc+-T-) да)
где Vn — объем паровой смеси; β{— некоторая функция темпера¬
туры и давления для компонента I.
2. Объемы в жидкой фазе аддитивны
Vm-JjNiVi (62)
/-1
где Уж — объем жидкой смеси; V*— молярный объем жидкого
компонента L
3. Объем жидкости не зависит от давления:
я,
J VndP -F* (P1-P) (63)
4. За стандартное принято состояние чистых компонентов при
температуре системы.
С учетом этих допущений коэффициент активности определяет¬
ся уравнением:
Необходимо отметить, что указанные выше допущения прием¬
лемы при давлениях, не сильно отличающихся от атмосферного.
Неидеальность паровой фазы и объем жидкости учитываются
поправкой:
■...--fr-ffi'-» ю
Вычисление величины β обычно производят по уравнению
Бертло
где Tltp и Pkp — критические температура и давление.
Из уравнения (65) видно, что величина поправки зависит от
разности между общим давлением и давлением паров чистого ком¬
понента при температуре системы. Эта разность возрастает с уве¬
личением разницы температур кипения компонентов.
23
ЧАСТНЫЕ СЛУЧАИ РАВНОВЕСИЯ
При T — const и P — const изменения энергетического
состояния системы обусловлены только взаимодействием компо¬
нентов. Для этого случая из уравнения (33) следует:
Σ (УI-·xi)dO1i-Iin)-0 (67>
i- I
ИЛИ
п п
S S (68)
г-1 г-ι
При T = const и P = const изобарный потенциал одного моля
фазы, согласно уравнению (24), равен
п
Z-Zqziss ^ μ .х I (69)
i-1
а его дифференциал, в соответствии с уравнением (20) равен:
п
dZ~2M*i (70)
i-1
По правилам дифференцирования функции нескольких пере¬
менных из уравнения (69) получаем:
п п
dZ=> 2 Vidxi + 2 xi dVi (71)
/-I i-i
В состоянии равновесия, согласно условию (11в), dZ = 0.
С учетом этого из уравнений (70) и (71) следует:
2 μ,***-0 (72)
i-i
И
2 * I ^ise0 (73)
«-I
Уравнение (73), называемое уравнением Гиббса — Дюгема,
справедливо для любой фазы, находящейся в равновесии.
Технологические процессы, с которыми приходится иметь дело
на практике, редко протекают при изобарно-изотермических усло¬
виях. Чаще имеет место T — const или P = const. Для простоты
при выводе условий равновесия в этих частных случаях ограни¬
чимся рассмотрением бинарных систем. Из уравнений (33) при
T — const получаем:
(ν"-ν')άΡ = (ΰ-χ)ά(μι-μ2) (74)
Если пренебречь молярным объемом жидкости по сравнению
с молярным объемом пара и рассматривать последний, как иде*
альный газ, ίο ИЗ уравнения (74), с yHetoM уравнения (42), полу¬
чаем:
RTd In P = (у — х) d (μι - μ2) (75)
Для идеального газа, согласно уравнению (45):
άμ^ RTd In pt (76)
Подставляя значения άμ\ и άμζ в уравнение (75), имеем:
d In P — (у — х) d In -^- (77)
P 2
для идеального газа ух — pj (р\ + Р2)· С учетом этого из урав¬
нения (77) после элементарных преобразований, вытекает
xd In pi + (\ — х) d In р2*=0
или
Tl
J ^xi(Hnpi=Zl) (78)
Уравнение (78) называется уравнением Дюгема — Маргулеса.
Оно выражает условия равновесия двухфазной системы при T =
= Const и сделанных выше допущениях.
Если от парциальных давлений с помощью закона Дальтона
перейти к составу паровой фазы, то уравнению (78) можно придать
другой вид:
din P= yr*dy (79)
5 у(\-х) *
При давлениях, не очень сильно отличающйхся от атмосфер¬
ного, молярный объем пара обычно в сотни раз превышает моляр¬
ный объем жидкости. Для бензола, например, при атмосферном
давлении отношение молярных объемов составляет около 300.
Отклонение поведения паров от законов идеальных газов при этих
условиях также обычно невелико. Поэтому при небольших давле¬
ниях погрешности, вызываемые допущениями, лежащими в основе
уравнения Дюгема — Маргулеса, для технических целей «в боль¬
шинстве случаев не имеют практического значения.
Необходимо подчеркнуть, что в отличие от уравнения Гиббса —
Дюгема, относящегося к одной фазе, уравнение Дюгема — Маргу¬
леса относится к двум фазам.
Уравнению Дюгема — Маргулеса можно придать другую фор¬
му, если парциальные давления компонентов выразить через ак¬
тивности и коэффициенты активности с помощью уравнения (56):
П
2 Vln «1-0 (80)
<=1
Для идеального раствора:
П
2 xid 1п ^ss0 (so
/-1
25
С учетом уравнения (81) из уравнения (80) следует:
^Xjd Inyi=-O * (82)
i-1
Рассмотрим условия равновесия при P = const. Из уравнения
(33) для этого случая получаем:
п—I
(S" - S') dT + 2 Oi- *,) d (μ, - μ ) (83)
* = I
Изменение энтропии при фазовом превращении ΔS==S" — Sf
выражается через изменение объема AV уравнением Клаузиуса —
Клапейрона:
с- £3 /34\
dr AF
Если пренебречь (как это было сделано при выводе уравнения
равновесия при T = const) молярным объемом жидкости по срав¬
нению с молярным объемом пара и допустить, что последний ведет
себя как идеальный газ, то из уравнений (42), (83) и (84), для би¬
нарной системы получается уравнение (75), из которого вытекает
уравнение Дюгема —Маргулеса. Следовательно, уравнение Дю¬
гема— Маргулеса приближенно выражает условия равновесия как
при T = const так и при P = const. При применении уравнения
Дюгема—Маргулеса в последнем случае теплота смешения не при¬
нимается во внимание, исходя из допущения, ч$о она мала по
сравнению с теплотой испарения. Это важное обстоятельство не¬
обходимо иметь в виду, так как теплота смешения иногда бывает
весьма значительной. Из этого следует, что уравнение Дюгема —
Маргулеса является более строгим для случая равновесия при
T = const, чем при P = const.
Уравнения равновесия могут быть получены, исходя из рас¬
смотрения изменения энергии при смешении компонентов раствора.
В процессе смешения количество каждого компонента остается
неизменным, а изобарный и химические потенциалы изменяются.
Для процесса смешения при P = const и T = const это положение
может быть выражено уравнением (для одного моля смеси):
п
dZ — 2 ·*ί^» (®*)
г-ι
Выражая химические потенциалы через активности, согласно
определениям (50) и (55), получаем после интегрирования:
Z-ZO = RTiyiXi In*,+2 *г lnY/) Ч86)
Vi-I г-ι /
Для идеального раствора уг = I, поэтому:
П
Z - Z0« RT 2 Xi In Xi (87)
i-1
26
Сопоставляя уравнения (86) и (87), легко Ьидеть, что измене¬
ние энергии системы при образовании реального раствора склады-
ft
вается из двух частей. Величина RT ^jXilnxi выражает изме-
*-1
нение энергии за счет перехода вещества от упорядоченного рас¬
пределения до смешения к неупорядоченному распределению, ха-
п
рактерному для жидких смесей. Величина RT 2 я* In Yt выражает
изменение энергии за счет взаимодействия компонентов друг с дру¬
гом и зависит от свойств системы и ее состава. Эта величина,
называемая в иностранной литературе избыточной свободной энер¬
гией смешения, является неидеальной долей изобарного потенциа¬
ла смешения. Избыточные термодинамические функции были вве¬
дены в теорию растворов Скетчардом [6] и Киреевым [7].
В последнее время широко применяется функция
ф - 2 χι 1S V/ 1 <88)
ί = I
связанная с неидеальной долей изобарного потенциала смешения
ΔΖΗΘид очевидным соотношением:
ф = А? неид, (89}
2,303# Г К }
Для бинарной системы:
Φ-xIgYi + O-х) Igy2 (90)
Величины, стоящие в правой части уравнения (88), формально
можно рассматривать как независимые переменные. Тогда по пра¬
вилам дифференцирования функции нескольких переменных полу¬
чаем:
dO - xd Ig Vi + (I - X) dig Y2 + Ig Yi dx - Ig γ2 dx (91)
Согласно уравнению Дюгема—Маргулеса, сумма первых двух
членов правой части этого уравнения равна нулю. Поэтому:
d<b**\g^-dx (92)
По определению ф — функция состояния. Поэтому интеграл άΦ
равен разности значений Ф в точках, соответствующих пределам
интегрирования. При х = I, γι = I, а при х = 0 γ2 = I. В обеих
этих точках Ф= 0, в чем легко убедиться из уравнения (88). Та¬
ким образом, интегрируя (92) от х = 0 до х— I, получаем:
j-
^Ldx= 0 (93)
Y2
27
Уравнение (93) было выведено Херингтоном [8] и Редлихом и
Кистером[9] независимо друг от друга. Поскольку при выводе этого
уравнения использовано уравнение Дюгема — Маргулеса, оно при¬
менимо при тех допущениях, на которых основано уравнение Дю¬
гема— Маргулеса. Эти допущения были рассмотрены выше. Сле¬
дует, однако, отметить, что по условиям вывода уравнения (93)
несоблюдение этих допущений должно сказываться только в виде
поправочного члена xd\nyi + (I— x)d Igy2 = O. Поэтому примене¬
ние уравнения Редлиха и Кистера связано, по-видимому, с мень¬
шей погрешностью, чем уравнения Дюгема — Маргулеса.
ИДЕАЛЬНЫЕ И РЕАЛЬНЫЕ СИСТЕМЫ.
ХАРАКТЕР ИЗМЕНЕНИЯ
КОЭФФИЦИЕНТОВ АКТИВНОСТИ
И ОТНОСИТЕЛЬНОЙ ЛЕТУЧЕСТИ
В БИНАРНЫХ СИСТЕМАХ
Простейшим типом систем являются идеальные. Они
определяются как системы, в которых жидкая фаза во всем диа¬
пазоне концентраций подчиняется закону Рауля, а паровая фаза —
закону Дальтона. Для идеальных систем можно рассчитать состав
пара, зная давление паров чистых компонентов. По закону Даль¬
тона:
УГ^Р—Р- (M)
2 Pi
(-1
Подстановка значения pt из уравнения (52) дает:
P0iXt
У I-<95>
2 P°lxi
/и I
Обычно уравнению (95) придают несколько иную форму, выра¬
жая у в зависимости не от абсолютных значений, а от отношения
давлений паров чистых компонентов. При этом чаще всего берут
отношение давлений паров всех компонентов к давлению пара са¬
мого высококипящего компонента. Тогда:
β αίηΧ1 /gg4
У%9Л αΐιΛ + α2«*2+ ·■· +cWfI+-" + aU-l)*V-l+ V
Величины а называются коэффициентами относительной лету¬
чести.
28
Для бинарной системы:
(97)
. + Jt (а — I)
L-IzJL
jc * I — jc
(98)
Уравнение (98) показывает, что величина а определяет отно¬
сительное распределение компонентов между жидкостью и паром.
Чем больше величина а, тем сильнее различаются составы пара
и жидкости и тем легче разделяется смесь путем ректификации.
Коэффициент относительной летучести идеальной системы яв¬
ляется постоянной величиной только при постоянной температуре.
Поскольку температуры кипения смесей при постоянном давлении
зависят от их состава, то при расчете составов равновесных фаз
для случая P = const нужно принять во внимание изменение а
с температурой [10, 11].
В практике ректификации наиболее распространены системы,
жидкая фаза которых представляет собой реальный раствор, а па¬
ровая фаза может рассматриваться как идеальный газ. Пользуясь
коэффициентами активности, состав пара в таких системах можно
рассчитать по уравнению (96), в котором коэффициенты относи¬
тельной летучести выражаются соотношениями:
Zi Zl
‘ Yn
(99)
Как уже указывалось, значения у зависят от интенсивности
взаимодействия компонентов раствора. Вычислить их по данным
о свойствах компонентов для любой системы при современном со¬
стоянии теории растворов не представляется возможным. Поэтому
значения коэффициентов активности определяют по опытным дан¬
ным. Однако с помощью выведенных выше уравнений представ¬
ляется возможным установить некоторые общие закономерности,
определяющие характер изменения коэффициентов активности в
бинарных системах.
Уравнение Дюгема — Маргулеса для бинарной системы можно
записать следующим образом:
dig Yi _ I -* ANgy2
dx х ' dx
Из этого уравнения видно, что кривые lgyi = cp(x) и lgy2 = <p(-x:)
должны иметь обратный наклон. На рис. 3, а показана зависимость
-коэффициентов активности компонентов от состава для системы
с положительными отклонениями от закона Рауля. При кон¬
центрации любого компонента, равной единице, коэффициент
активности его, в соответствии с выбором стандартного состояния,
равен единице, a Igy = O. По мере уменьшения концентрации
29
рассматриваемого компонента величина γ возрастает. Если коэф¬
фициент активности одного компонента больше единицы во всем
диапазоне концентраций, то, как следует из уравнения (100), коэф¬
фициент активности второго компонента также должен быть больше
единицы во всем диапазоне концентраций. Расположение кривой
Igy = φ(χ) для одного компонента выше, а для другого ниже оси
абсцисс противоречило бы законам термодинамики, формулируе¬
мым уравнением . (100). Это относится также к системе с отрица¬
тельными отклонениями от идеального поведения, характер изме¬
нения коэффициентов активности от состава в которых показан на
рис. 3,6. Из (100) следует, что при наличии на кривой Igv = φ(·^)
О 6 в
Рис. 3. Характер зависимости коэффициентов активности и их
отношения от состава в бинарных системах:
я —с положительными отклонениями от закона Рауля; б —с отрицательными
отклонениями от закона Рауля; б —с экстремальными точками на кривых
Ig Y * Ф (х)·
для одного компонента максимума или минимума при опре¬
деленном значении х на аналогичной кривой IgY = φ(*) для дру¬
гого компонента при этом же значении х должна быть экстремаль¬
ная точка противоположного значения, т. е. максимуму на кривой
Igy1 = ф(х) соответствует минимум на кривой IgY2 = <p(*)
(рис, 3, в).
Необходимо отметить, что системы с экстремальными точками
на кривых lgY = <p(x) встречаются на практике сравнительно ред¬
ко. Наиболее распространены системы, для которых зависимости
IgY = Cp(X) имеют вид, представленный на рис. 3, а и б.
Отмеченные закономерности в изменении коэффициентов актив¬
ности определяют характер изменения их отношения в зависимо¬
сти cfc состава раствора. Из рис. 3, й видно, что в системах с поло¬
жительными отклонениями от закона Рауля отношение Ig Υι/Υ2>0
в области малых концентраций первого компонента. В точке пере¬
сечения кривых IgYi = φ(*) и lgY2=<p(*) отношение γι/γ2 = E
а при концентрациях больших, чем соответствующая точке пере¬
сечения, γι/γ2<1. В системах с отрицательными отклонениями от
идеального поведения наблюдается обратная зависимость γι/γ2 от
концентрации.
30
В системах с экстремальными точками на кривых IgYi = φ(χ)
и Igy2 = Cp (я) они дважды пересекаются. Следовательно, кривая
IgYiZy2 = ф(х) дважды пересекает ось абсцисс (рис. 3, б).
Характер зависимости Ig(YiZY2) = ср(х) определяет характер из¬
менения коэффициентов относительной летучести бинарных си¬
стем от состава раствора. В системах с положительными отклоне¬
ниями от идеального поведения, в соответствии с уравнением (99)
и изложенными выше закономерностями, а в области малых кон¬
центраций низкокипящего компонента больше, чем величина, по¬
лученная на основании закона Рауля. В области же больших кон¬
центраций низкокипящего компонента а
меньше, чем для идеальной смеси. В си¬
стемах с отрицательными отклонениями
от идеального поведения имеет место
обратная зависимость. Этим опреде¬
ляется ход зависимости составов равно¬
весных пара и жидкости для систем раз¬
ного типа (рис. 4). Для идеальных
систем кривая # = φ(*) является равнобо¬
кой гиперболой, как это видно из урав¬
нения (97). В системах с положитель¬
ными отклонениями от идеального пове¬
дения при малых значениях х величина у
превышает значение у для идеальной
смеси, а в области больших х — мень¬
ше их.
Следовательно, наличие положитель¬
ных отклонений от закона Рауля улуч¬
шает, по сравнению с идеальной смесью,
условия разделения путем ректифика¬
ции в области малых и ухудшает в области больших значений х.:
В системах с отрицательными отклонениями от закона Рауля, на¬
оборот, условия разделения по сравнению с идеальной смесью
ухудшаются в области малых и улучшаются в области больших
значений х.
Описанный характер зависимости а от л: в реальных дистемах
диктуется общими термодинамическими закономерностями. Дей¬
ствительно, согласно уравнению Редлиха и Кистера (93), алгеб¬
раическая сумма площади, ограниченной кривой Ig Υ1/Υ2 = φ (лг),
осью абсцисс и ординатами х = 0 и х=1, должна быть равна
нулю. Следовательно, если в определенной области концентраций
γι/γ2 > I и, соответственно с этим, а больше, чем для идеальной
смеси, то должна быть область концентраций, в которой γι/γ2 < I
и а меньше, чем для идеальной смеси. Из уравнения (93) выте¬
кает, что а реальной смеси не может быть больше или меньше а
идеальной смеси во всем диапазоне концентраций.
При определенных условиях кривая α = φ(χ) может пересекать
ось абсцисс. Согласно уравнению (98), в этой точке составы
Рис. 4. Зависимость между
составами равновесных па¬
ра у и жидкости я:
I — идеальная система; 2 — си¬
стема с положительными откло¬
нениями от идеального поведе¬
ния; 3 — система с отридатель-
ными отклонениями от идеаль¬
ного поведения.
31
жидкости и пара одинаковы, т. е. эта точка являетси азео¬
тропной.
Из изложенных выше положений следует, что вероятность об¬
разования азеотропа тем больше, чем ближе друг к другу давления
паров чистых компонентов и чем больше
отклонения в системе от идеального поведе¬
ния (рис. 5).
Если отношение давлений паров чистых
компонентов меньше предельного значения
отношения V1/Y2. то в, системе азеотроп не
образуется. Если PfyPfI превышает пре¬
дельное значение νι/Υ2> то азеотроп в си¬
стеме образуется.
Азеотропы, образующиеся в системах
с отрицательными отклонениями от за¬
кона Рауля, характеризуются наличием
максимума температуры кипения. Азеотро¬
пы, образующиеся в системах с положи¬
тельными отклонениями от закона Рауля,
имеют минимум . температуры кипения.
В процессах азеотропной ректификации чаще всего приходится
иметь дело с азеотропами последнего типа.
ЗАКОНЫ КОНОВАЛОВА И ВРЕВСКОГО
Некоторые важные закономерности, устанавливающие
связь между параметрами состояния бинарных систем при рав¬
новесии, могут быть выведены из уравнения Ван-дер-Ваальса (34).
Если производные объема, энтропии и изобарного потенциала
взять соответственно по составам паровой и жидкой фаз, то урав¬
нения Ван-дер-Ваальса запишутся следующим образом:
(101)
[v -V'- (у-х) dP - [s" -S'-(y-x) (-g-)] dT - (у - X) -Ц- dx (102)
При температуре и давлении, достаточно удаленных от кри¬
тических, величины V" — V' и S" — S' превосходят соответственно
величины (у - х) и (у- х) (·||-). Следовательно, коэффициен¬
ты при dP и dT в уравнениях (101) и (102) — величины положи¬
тельные. По условию устойчивости равновесия (13) d2Z/dx2> 0.
При T = const из уравнения (102) следует:
Рис. 5. Соотношения
P^lP0l (пунктирная ли¬
ния) и Y1Zy2 (сплошная
линия) в бинарных си¬
стемах, имеющих и не
имеющих азеотропную
точку.
dP . Q2Zjdx2
- W X) у* _ ψ _ _ х) (dV/dx)
(ЮЗ)
На основании изложенного выше, дробь, стоящая в правой
части уравнения (103), положительна. Поэтому знак производной
dP/dx определяется знаком разности у— х.
паровая фаза относительно богаче жидкой тем компонентом, при¬
бавление которого к жидкости вызывает повышение общего дав¬
ления. Это положение составляет содержание первого закона Ко¬
новалова [12].
Принимая T = const и разделив правые и левые части уравне¬
ний (101) и (102) друг на друга, получаем:
Левая часть уравнения (105) —величина положительная. По¬
этому:
К аналогичному выводу можно прийти, принимая P = const.
Неравенство (106) ,показывает, что с увеличением концентра¬
ции любого компонента бинарной смеси в жидкой фазе концентра¬
ция его в паровой фазе всегда возрастает. Это положение известно
как второй закон Коновалова.
Из уравнения (103) следует, что в точке равных составов
жидкости и пара (х = у) dPjdx = 0, т. е. на кривой P = φ(χ) в
этой точке имеется экстремум. Рассматривая равновесие при
P = const, из уравнения (100) получаем:
Из этого уравнения видно, что при у — х dT/dx = 0, кривая
T = <р(х) в этой точке также имеет экстремум. Значит экстремуму
на кривых температуры кипения или давления паров смесей отве¬
чает равенство составов жидкости и пара (третий закон Конова¬
лова). Эта закономерность соблюдается в системах с любым
числом компонентов.
Вревским [13] были установлены важные закономерности, оп¬
ределяющие характер изменения свойств систем с температурой.
Согласно первому закону Вревского, при повышении темпера¬
туры раствора заданного состава его пар обогащается тем ком¬
понентом, парциальная молярная теплота испарения ,которого
больше. г
Второй закон Вревского определяет направление изменения
состава азеотропа с изменением температуры: при повышении
При у >х -jj > о
(104)
(105)
(106)
(107)
2 Зак. 917
33
температуры растворов кривая давления пара которых имеет
максимум (минимум), в нераздельно кипящей смеси возрастает
относительное содержание того компонента, испарение которого
требует большей (меньшей) затраты энергии.
Третий закон Вревского устанавливает, что при изменении
температуры раствора, кривая давления пара которого имеет мак¬
симум, состав пара раствора и состав нераздельно кипящей смеси
изменяются в одном и том же направлении. При изменении темпе¬
ратуры раствора, кривая давления пара которого имеет минимум,
состав пара раствора и состав нераздельно кипящей смеси изме¬
няются в противоположных направлениях.
Вопрос о применимости законов Коновалова и Вревского
к многокомпонентным системам был исследован Сторонкиным, по¬
казавшим, что первый и второй законы Коновалова в многоком¬
понентных системах могут не соблюдаться [3, 14].
Глава Il
ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ
МЕТОДОВ АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ
АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Общие закономерности, устанавливающие влияние разде¬
ляющего агента на коэффициент относительной летуче¬
сти заданной бинарной смеси, могут быть выведены [15] на осно¬
вании анализа свойств функции Ф [см. уравнение (88)], пропор¬
циональной неидеальной доле изобарного потенциала смешения.
'Для трехкомпонентной системы, состоящей из компонентов I и 2'
заданной смеси и разделяющего агента («р»):
Ф = Ig Yi + Xi Ig V2 + Jtp Ig Yp (108)
Дифференцируя уравнение (108), получаем:
άΦ - Xi d Ig Y1 + X2 d Ig у2 + Xpd Ig γρ + Ig γ, dx j + Ig γ2 dx2 + Ig γρ dxp (109)
Сумма первых трех членов правой части уравнения (109), со¬
гласно уравнению Дюгема — Маргулеса ■(82), равна нулю. Следо¬
вательно:
ί/φ = Ig γ, dxi + Ig γ2 dx2 + Ig Yp dxp (HO)
Молярные доли компонентов I, 2 и «р» связаны между собой
условием:
X1 + х2 + Xp =· I (111)
Примем, что Xp = const. Тогда
dxi + dx2 — 0 (112)
и уравнение (HO) перепишется следующим образом:
-Ig-Jj-d*i (113)
Заменим абсолютные концентрации первого и второго компо¬
нентов их относительными концентрациями:
S *. .. (П4)
Xli-X2 I-Jfp 2 I-Jfp
35
Из определения (114) следует:
<**,«( \-χν)άχ[ (115)
После замены dx\ в уравнении (113), получаем:
-Kdx' (П6)
Уравнение (116) проинтегрируем теперь в пределах от х[ = 0
до Xrl= I. При этом состав смесей будет изменяться от бинарной
смеси 2 — р до бинарной смеси I — р с выбранной постоянной кон¬
центрацией разделяющего агента. Поскольку Ф является функцией
состояния системы, интеграл άΦ равен разности значений функции
Ф в точках конца и начала интегрирования
I
1 Φιο-Φ2
. Yi . / Φιρ-Φ2ρ
1Sr-rfiI г—;— (И?)
У2 1 Xp
О
где Ф1р и ФгР — значения функции Ф для бинарных смесей I — р
и 2 — р с заданной концентрацией разделяющего агента.
По мере уменьшения хр составы смесей I—р и 2 — р, соответ¬
ствующие пределам интегрирования, приближаются к чистым ком¬
понентам I и 2, .для которых Ф = 0. В частном случае, когда
хр = 0, система становится бинарной, и уравнение (117) превра¬
щается в уравнение Редлиха и Кистера (93).
Принимая во внимание, что для бинарной системы I" lg— dx =
J Y2
=0 (93) и °
Yi* P2
ΐ-V <"8>
уравнения (117) и (93) можно переписать следующим образом:
Г I j ' ^ip - , , rf3I ,, (П>
I Ig ар dxi = P Р -Hg —о (119)
о ‘“*р 2
г P0
JlgadJC=Ig-^ (120)
0 2 '
'V
Здесь ар — коэффициент относительной летучести первого и вто¬
рого компонентов в присутствии разделяющего агента.
Легко видеть, что левые части уравнений (119) и (120) выра¬
жают среднее значение коэффициента относительной летучести
первого и второго компонентов во всем диапазоне их концентраций
соответственно в присутствии (ар)ср и в отсутствии аср разделяю¬
щего агента. С учетом этого, уравнения (119) и (120) преобра¬
зуются так:
ф. -ф0 р?
Ig (Op)cp = —^+Ig (121)
И
P01
Igacp = Ig^ (122)
*2
Вычитая из уравнения (121) уравнение (122), получаем:
(ар)ср Φιρ — Фгр
Ocp I — ^p
Величина
5 ^ар^ср
~ Ocp
выражающая среднее увеличение коэффициента относительной ле¬
тучести компонентов рассматриваемой бинарной смеси, обуслов¬
ленное присутствием разделяющего агента, называется селектив¬
ностью.
Из уравнения (123) следует, что селективность разделяющего
агента определяется его концентрацией и значениями функций Ф
для бинарных систем, состоящих из компонентов заданной смеси
и разделяющего агента. Для увеличения относительной летучести
первого компонент^ необходимо соблюдать следующее условие:
Φιρ — Фгр > О (125)
Из определения функции Ф (88) нетрудно заключить, что при
положительных отклонениях от идеального поведения в бинарных
системах I —р и 2 — р (γι > I и γρ > I) Φιρ > О и Фгр > 0, а ве¬
личина Φίρ или Ф2Р тем больше, чем больше отклонения от идеаль¬
ного поведения. Для идеальной системы (γι = γρ = I) Φ = 0. В би¬
нарной системе с отрицательными отклонениями от идеального по¬
ведения (γι < I и γΡ < I) Ф<0, причем с увеличением степени
неидеальности системы величина Ф уменьшается. В соответствии
с этим из неравенства (125) следует, что для увеличения относи¬
тельной летучести одного из компонентов заданной смеси нужно,
чтобы в бинарной системе, образованной разделяющим агентом
и этим компонентом, были большие положительные (или меньшие
отрицательные) отклонения от идеального поведения, чем в си¬
стеме, образованной разделяющим агентом и вторым компонентом.
Установленная связь между относительной летучестью в мно¬
гокомпонентной системе со свойствами (степенью неидеальности)
бинарных систем базируется на самых общих термодинамических
положениях. Сделанные при выводе допущения обусловлены лишь
ограничениями, лежащими в основе уравнения Дюгема — Маргу¬
леса. Эти ограничения, как известно, заключаются в постоянстве
(123)
(124)
17
температуры и в возможности пренебречь молярным объемом
жидкости по сравнению с молярным объемом пара. Второе допу¬
щение делает доказательство строгим только для области не очень
больших давлений, где оно и является общепринятым. Условие
постоянства температуры не уменьшает строгости вывода. Наобо¬
рот, это условие является необходимым, так как исключает из рас¬
смотрения изменения отношения давлений паров с температурой
и дает возможность выявить изменение относительной летучести
только за счет взаимодействия компонентов. Это и лежит в основе
методов азеотропной и экстрактивной ректификации.
Уравнение (123) имеет важное значение для теории процессов
азеотропной и экстрактивной ректификации, так как оно не только
доказывает возможность выбора разделяющих агентов на основе
оценки степени неидеальности бинарных систем, но позволяет так¬
же термодинамически точно определять среднее увеличение коэф¬
фициента относительной летучести, вызываемое разделяющим
агентом, по данным о равновесии в бинарных системах.
МЕХАНИЗМ ДЕЙСТВИЯ
РАЗДЕЛЯЮЩИХ АГЕНТОВ
И КРИТЕРИИ ИХ ВЫБОРА
Уравнение (123) определяет условие, которому должен
удовлетворять разделяющий агент для того, чтобы он увеличивал
коэффициент относительной летучести заданной смеси. Это урав
нение не позволяет, однако, установить, распространяется ли это
увеличение на весь диапазон концентраций компонентов заданной
смеси. Кроме того, оно не отражает влияния свойств и состава
смеси, подвергаемой разделению, на степень изменения ее коэффи¬
циента относительной летучести. Для решения этих вопросов сле¬
дует выяснить механизм действия разделяющих агентов. С этой
целью необходимо обратиться ц анализу имеющихся опытных дан¬
ных σ равновесии между жидкостью и паром в трехкомпонентных
системах.
Из рассмотрения этих данных ясно, что влияние третьего ком¬
понента на распределение компонентов заданной смеси между
жидкой и паровой фазами возрастает с увеличением его концент¬
рации. Кроме того, при этом уменьшается влияние концентрации
компонентов заданной смеси на их коэффициент относительной ле
тучести. Эти закономерности наблюдаются во всех исследованных
трехкомпонентных системах. Для иллюстрации этих положений на
рис. 6 и 7 приводятся кривые равновесия двух бинарных смесей
а на рис. 8 — зависимости ар от х[ для этих систем при постоян
ных значениях %р и различных концентрациях третьего компонента
В количественной форме влияние третьего компонента на рав¬
новесное распределение двух других компонентов между жидко¬
стью и паром можно установить с помощью рассматриваемых
ниже уравнений, описывающих условия равновесия в трехкомпо-
38
I
HeHfHbix системах. Эти уравнения выражают условия равновесия
в зависимости от свойств бинарных смесей, образованных компо¬
нентами рассматриваемой тройной системы, и величин, учитываю-
Рис. 6. Кривые равновесия смесей
ацетона и метилового спирта при
разных концентрациях воды.
/ /
#2 и — относительные концентрации
ацетона в жидкости и паре, мол. %.
О ^ 20 40 SO 80 100
Xi
Рис. 7. Кривые равновесия смесей
ацетона и хлороформа при разных
концентрациях метилизобутилке-
тон а.
/ /
xI и относительные концентрации
ацетона в жидкости и паре, мол. %.
ар
4
щих совместное взаимодействие всех компонентов друг с другом.
Имеющиеся опытные данные свидетельствуют о том, что основное
влияние на условия равновесия в трех¬
компонентных системах оказывают
свойства бинарных смесей. Если при¬
нять, что кривые зависимости коэффи¬
циентов активности от состава для би¬
нарных систем имеют симметричный
ход, а влиянием совместного взаимо¬
действия всех компонентов можно
пренебречь, то коэффициент относи¬
тельной летучести бинарной смеси в
присутствии третьего компонента (раз¬
деляющего агента) может быть выра¬
жен приближенным уравнением *)
Ί
О 20 40 60 80
too
Xi
Ig α0 * Ig
Я?'
Рис. 8. Зависимость ар от X1:
+
2 /Т·,
ацетон (I) — метиловый спирт
(2)— вода (р); ацетон (I) —
хлороформ (2) — метилизобутилке-
тон (р).
+ *Р К - Af2р) + Arl2 (I - хр) (I - 2*0 (126)
где T3- температура кипения трехкомпонентной, смеси; А\р —
T(^ip ^p sr Y (^2р ^рг)> Аг = Y (Аг ^21) и ^ik ^sz Y*
Cm. уравнение (358) в табл. 31.
39
йрй X1 = 0 и xk =» I (i и k — индексы, обозначающие комйбнён^
I, 2 или „р“).
Константы A'ik входящие в уравнение (126), являются мерой
неидеальности соответствующих бинарных систем. Они принимают¬
ся равными средним арифметическим значениям логарифмов коэф¬
фициентов активности обоих компонентов при бесконечно малой
их концентрации в растворе. Уравнение (126) было сопоставлено
с опытными данными для ряда систем Розеном [16], Гарнером
и Эллисом [17] и автором [18].
Для бинарной смеси (при Xp = 0) из уравнения (126)
Igoc= igf +А'12( 1-2*,) (127)
\ *2 'T2
где Гг — температура кипения бинарной смеси.
Если отношение давлений паров чистых компонентов мало
изменяется с температурой; то из уравнений (126) и (127) при
Xi = Xi следует:
1S = *р К-A'2p-A'l2 (I -2х[)] (128)
Из уравнения (128) видно, что степень увеличения коэффи¬
циента относительной летучести разделяющим агентом зависит от
свойств и состава заданной смеси. Для возрастания коэффициента
относительной летучести во всем диапазоне концентраций необхо¬
димо, чтобы
л[р-4,-|42|>0 (129)
где J Aj21 — абсолютная величина Arl2.
Разумеется, выполнение условия (129) возможно лишь при со¬
блюдении неравенства
Aip — А2р > 0 (130)
• эквивалентного неравенству (125).
Из изложенного следует, что для увеличения коэффициента от¬
носительной летучести заданной смеси во всем диапазоне концент¬
раций условие, формулируемое неравенствами (130) и (125), яв¬
ляется необходимым, но не достаточным; достаточное условие вы¬
ражается неравенством (129). Если условие (129) не соблюдается,
то в разделяемой бинарной системе с положительными отклоне¬
ниями от идеального поведения (Л{2>0) в области малых относи¬
тельных концентраций первого компонента (0 < х( < х'), добавляе¬
мое вещество будет ухудшать условия разделения по сравнению
с условиями разделения исходной бинарной системы в той же
области концентраций. Примером такой системы является система
метилэтилкетон — гептан —толуол, данные о равновесии в которой
приведены на рис. 9. При отрицательных отклонениях от закона
Рауля в заданной бинарной системе ухудшение условий ее разде¬
40
ления при несоблюдении неравенства (129) происходит в обла¬
сти относительно больших концентраций первого компонента
(*2<*i<l). Эти положения непосредственно вытекают из урав¬
нения (128).
Выше указывалось, что коэффициент относительной летучести
бинарной системы зависит от степени ее неидеальности, характе¬
ризуемой в уравнениях (127) и (128) величиной Arxv а также от
отношения давлений паров ком¬
понентов и состава раствора. Об¬
ращает на себя внимание, что
члены АХ2(1—2хх') и Arl2(I — 2х()
входят соответственно в уравне¬
ния (127) и (128) с разными зна¬
ками. Следовательно, разделяю¬
щий агент в наибольшей степени
увеличивает коэффициент отно¬
сительной летучести заданной
смеси в том диапазоне концен¬
траций, в котором в отсутствие
разделяющего агента он имеет
наименьшее значение. В области
концентрации, соответствующей
наибольшим значениям коэффи-
цента относительной летучести
в отсутствие разделяющего аген¬
та, прибавление последнего уве¬
личивает а в минимальной сте¬
пени (см. рис. 8).
Из уравнения (126) следует,
что с увеличением Xv до единицы,
Я0
Ig «р стремится к величине Ig + (Л' — А'2Л, постоянной при
Р2
любых относительных концентрациях компонентов заданной смеси.
Однако, как это вытекает из свойств реальных систем, отклонение
коэффициента относительно летучести бинарной системы от по¬
стоянной величины тем меньше, чем меньше степень неидеальности
рассматриваемой системы. Следовательно, в отношении изменения
коэффициента относительной летучести в зависимости от концент¬
рации компонентов исходной смеси влияние разделяющего агента
заключается как бы в уменьшении степени неидеальности бинар¬
ной системы, подвергаемой разделению. Отмеченное действие раз¬
деляющего агента объясняется тем, что при его прибавлении
уменьшается концентрация компонентов исходной смеси, а это
вызывает ослабление взаимодействия между ними.
Таким образом, действие разделяющего агента обусловлено
двумя факторами;
Рис. 9. Кривые равновесия смесей
метилэтилкетона и гептана при раз¬
личных полярных концентрациях то¬
луола в жидкости.
/ /
χχ и ух — относительные концентрации ме¬
тилэтилкетона , мол. %,
41
1) изменением относительной летучести компонентов вслед¬
ствие разной интенсивности их взаимодействия с разделяющим
агентом [в уравнении (126) этот фактор учитывается членом
*рКр-лу];
2) уменьшением интенсивности взаимодействия компонентов
рассматриваемой системы друг с другом за счет разбавления рас¬
твора разделяющим агентом [в уравнении (126) этот фактор учи¬
тывается членом Afl2 (I — а: )(I —2*!)].
На основании уравнения (128) получаем, что при разделении
бинарной системы с большими отклонениями от закона Рауля
третий компонент в определенном диапазоне концентраций может
действовать как разделяющий агент при Aflp--A2р <0. Из уравне¬
ния (126) вытекает, что эффективное действие таких разделяю¬
щих агентов возможно в тех случаях, когда отношение давлений
паров компонентов заданной бинарной системы достаточно велико.
Указанные разделяющие агенты могут быть применены, в частно¬
сти, для разделения систем, компоненты которых, несмотря на
большую разницу температур кипения, образуют азеотропы или
в определенной области концентраций имеют состав пара, мало
отличающийся от состава жидкости. Отсюда вытекают положения,
на основании которых следует производить выбор разделяющих
агентов.
1. Наиболее желательными разделяющими агентами являются
такие, которые удовлетворяют условию (129), так как они позво¬
ляют увеличить коэффициент относительной летучести компонентов
заданной смеси во всем диапазоне концентраций.
2. При разделении систем с относительно небольшими отклоне¬
ниями от закона Рауля и близкими температурами кипения ком¬
понентов фактором, определяющим благоприятное действие разде¬
ляющего агента, является разная интенсивность его взаимодей¬
ствия с компонентами заданной смеси. Роль фактора разбавления
в таких случаях мала.
3. При разделении систем с большими отклонениями от закона
Рауля благоприятное действие разделяющего агента в той области
концентраций, в которой разделение исходной смеси путем обыч¬
ной ректификации затруднительно или невозможно, может обус¬
ловливаться главным образом влиянием разбавления исходной
смеси.
Приведенные выше представления о механизме действия разде¬
ляющих агентов и возникающие из них следствия являются об¬
щими для процессов азеотропной и экстрактивной ректификации
Таким образом, при выборе разделяющих агентов для процес¬
сов азеотропной и экстрактивной ректификации должны учиты
ваться свойства системы, подлежащей разделению. Прежде всего,
на основании данных о равновесии между жидкостью и паром
в исходной системе должны быть определены требования, предъ¬
являемые к разделяющему агенту. Затем на основе этого должен
4?
быть произведен ориентировочный выбор предполагаемых разде¬
ляющих агентов. Следующая стадия — определение данных о рав¬
новесии между жидкостью и паром в бинарных системах, состоя¬
щих из компонентов заданной смеси и разделяющих агентов,
с целью ориентировочного определения эффективности последних.
Такое определение может быть произведено приближенно по урав¬
нению (128). Наконец, для получения данных, необходимых для
расчетов, связанных с проектированием, должны быть определены
условия равновесия между жидкостью и паром в многокомпонент¬
ной системе, состоящей из компонентов заданной смеси и раздел
ляющего агента.
В заключение необходимо остановиться на допущениях, лежа¬
щих в основе приближенного уравнения (126). Легко видеть, что
влияние указанных выше двух факторов, определяющих механизм
действия разделяющих агентов, должно проявляться во всех си¬
стемах. Несоблюдение допущений может привести лишь к откло¬
нению истинных значений коэффициентов относительной летучести,
а также величин, характеризующих каждый из этих факторов, от
значений, вытекающих из уравнения (126). Принимая во внимание
приближенный характер уравнений (126) и (128), они могут быть
использованы лишь для ориентировочной количественной оценки
эффективности разделяющих агентов. Возможность такого исполь¬
зования этих уравнений вытекает из сопоставления расчетов по
уравнению (126) с экспериментальными данными для ряда трех¬
компонентных систем [16—18].
ВЫБОР РАЗДЕЛЯЮЩИХ АГЕНТОВ
Разделяющие агенты, используемые в процессах азео¬
тропной и экстрактивной ректификации, должны удовлетворять
требованиям общего характера [19—30]. Важнейшими из них яв¬
ляются следующие:
1) изменение относительной летучести компонентов заданной
смеси в желательном направлении;
2) легкость регенерации из смесей с компонентами системы,
подвергаемой разделению;
,-3) безопасность в обращении, доступность и дешевизна;
4) инертность по отношению к компонентам заданной смеси,
неспособность вызывать коррозию аппаратуры или разлагаться
при нагревании.
Вопросы, связанные с удовлетворением требований, изложен¬
ных в пунктах 2, 3 и 4, относятся к числу обычных технологиче¬
ских вопросов. Их решение определяется в основном свойствами
системы, подвергаемой разделению. Наиболее сложной задачей
является выбор разделяющих агентов, удовлетворяющих первому
требованию.
Все. известные методы выбора разделяющих агентов можно
разделить на две группы:
43
1) методы, основанные на использовании данных о свойствах
растворов, образуемых компонентами заданной смеси и предпола¬
гаемыми разделяющими агентами;
2) методы, использующие данные о свойствах компонентов.
Рассмотренный в предыдущем разделе механизм действия раз¬
деляющих агентов является общим для процессов азеотропной
и экстрактивной ректификации. Поэтому во всех случаях для опре¬
деления применимости того или иного вещества в качестве разде¬
ляющего агента следует исходить из оценки степени неидеальности
бинарных систем, образованных этим веществом и компонентами
заданной смеси. Как указывалось, специфика разделяющих аген¬
тов, применяемых в процессах азеотропной ректификации, заклю¬
чается в том, что они должны образовать азеотропы с компонен¬
тами исходной смеси. В связи с этим дополнительно приходится
'определять наличие и свойства азеотропов.
МЕТОДЫ ВЫБОРА РАЗДЕЛЯЮЩИХ АГЕНТОВ
ПО ДАННЫМ О СВОЙСТВАХ РАСТВОРОВ
Выбор разделяющих агентов по данным о равновесии
между жидкостью и паром.
Выбор разделяющих агентов с помощью данных о рав¬
новесии между жидкостью и паром заключается в сравнении на
основании этих данных величины отклонений от закона Рауля
в бинарных системах, образован¬
ных предполагаемым разделяющим
агентом и каждым компонентом за¬
данной смеси. По уравнениям (60)
или (64) с помощью данных о рав¬
новесии можно рассчитать коэф¬
фициенты' активности или их отно¬
шение, что дает возможность опре¬
делить значения функций Ф для
бинарных систем. Далее по уравне¬
нию (123) можно найти среднее
увеличение коэффициента относи¬
тельной летучести, вызываемое
прибавлением рассматриваемого
вещества. Таким образом, по дан¬
ным о равновесии между жидко¬
стью и паром можно дать не только
качественную, но и количественную
оценку эффективности предполагае¬
мого разделяющего агента.
На рис. 10 изображены рассчитанные по данным о равновесии
коэффициенты активности в бинарных системах, образованных
ацетоном, метиловым спиртом и водой, откуда следует, что в си¬
Рис. 10. Коэффициенты актив¬
ности в бинарных системах аце¬
тон — вода (γι, yQ и метиловый
спирт — вода (у", у^) и зависи¬
мость величины ctp/α от молярной
концентрации воды хр.
44
стеме ацетон — вода коэффициенты активности компонентов зна¬
чительно выше, чем в системе метиловый спирт — вода. Поэтому
прибавление воды к системе метиловый спирт — ацетон должно вы¬
зывать увеличение относительно летучести последнего. Зависи¬
мость степени увеличения коэффициента относительно летучести -
ацетона и метилового спирта от концентрации воды, рассчитанная
по уравнению (123) с помощью коэффициентов активности, также
приведена на рис. 10.
Данные о равновесии между жидкостью и паром, опубли¬
кованные в мировой литературе до 1965 г., систематизированы
в книге [31].
Применяя данные о равновесии для выбора разделяющих аген¬
тов, можно использовать общеизвестные особенности взаимодей¬
ствия в гомологических рядах соединений.
Как показывает анализ имеющихся опытных данных, опреде¬
ляющее влияние на степень неидеальности бинарных систем, обра¬
зованных каким-нибудь веществом и членами гомологического
ряда, оказывает характер функциональных групп компонентов.
Влияние же величины углеводородного радикала в молекулах чле¬
нов гомологического ряда сильно сказывается только на началь¬
ных членах ряда. Основываясь на этих положениях, можно вы¬
бирать разделяющие агенты по данным о равновесии в системах,
образованных гомологами как компонентов заданной смеси, так
и разделяющего агента.
Как видно из табл. I, значения αρ/α для систем циклогексан —
бензол и метилциклогексан — толуол в присутствии различных ве¬
ществ, являющихся гомологами, весьма близки.
T а б л и ц а I
Сопоставление значений αρ/α для систем
циклогексан — бензол и метилциклогексан — толуол
в присутствии различных веществ
Вещество
Концентра¬
ция, мол. %
Циклогексан —
бензол '
Метилциклогек¬
сан — толуол
Ацетон
66
2,07
1,9
Пиридин
66,8
1,86
1,9
Анилин
66
2,16
1,9
Фенол
66
2,05
2,0
Нитрометан
68
3,0
3,0
Несмотря на большое число опубликованных работ, в настоя¬
щее время условия равновесия между жидкостью и паром иссле¬
дованы недостаточно. В связи с трудностью экспериментального
исследования равновесия важнейшее значение для выбора разде¬
ляющих агентов имеют рассматриваемые ниже методы, основан¬
ные на использовании данных о свойствах растворов, легко опре¬
деляемых экспериментальным путем.
4$
Выбор разделяющих агентов
по данным о температурах кипения смесей
Давление пара реальной бинарной системы с помощью
коэффициентов активности выражается уравнением:
P sss^iYi +^2 О -*ι)Υ2 (131)
Из этого уравнения следует, что с увеличением коэффициентов
активности давление пара возрастает (температура кипения по¬
нижается). Поэтому, сравнивая давления паров или температуры
кипения идеальной и заданной смесей одинакового состава, можно
определить характер и оценить величину отклонений последней от
закона Рауля. Зависимости температур кипения смесей от со¬
става для основных типов систем при¬
водятся на рис. 11. Для идеальной си¬
стемы наклон кривых возрастает с
уменьшением концентрации низкоки¬
пящего компонента. Для системы с по¬
ложительными отклонениями от зако¬
на Рауля кривая во всем диапазоне
концентраций располагается ниже, а
для системы с отрицательными откло¬
нениями от закона Рауля — выше кри¬
вой I. Чем больше расстояние между
кривыми I п 2 или I и 3, тем больше
степень неидеальности рассматривае¬
мых систем. Сопоставляя температуры
кипения смесей, образованных разде¬
ляемыми веществами и предполагае¬
мым разделяющим агентом, можно
оценить пригодность последнего. Из
рис. 11 видно, что разность температур кипения реальной и иде¬
альной смесей изменяется с изменением состава. Поэтому имеет
значение, при каком составе производятся определения темпера¬
тур кипения.
Фенске с соавторами [32] в качестве критерия выбора разде¬
ляющего агента предложили определять температуры кипения
эквимолекулярных смесей исходных компонентов и предполагае¬
мого разделяющего агента. Часто компоненты смесей, разделяе-
мыхг путем азеотропной и экстрактивной ректификации, имеют
близкие температуры кипения. При этом выбор разделяющего
агента сводится к сравнению температур кипения одинаковых по
составу смесей исходных компонентов с веществом, которое испы¬
тывают в качестве предполагаемого разделяющего агента.
Для примера рассмотрим использование описанного метода с целью выявле¬
ния возможности применения воды в качестве разделяющего агента для системы
этиловый спирт — метилэтилкетон. Эквимолекулярные смеси воды с этиловым
спиртом и метилэтилкетоном имеют, соответственно, температуры кипения 80 и
73,5° С. Значительно более высокая температура кипения смеси воды с этиловым
Рис. 11. Характерные кривые
зависимости температур ки¬
пения смесей от состава:
/ — идеальная система; 2 — система
с положительными отклонениями от
закона Рауля; 3 — система с отри¬
цательными отклонениями от закона
Рауля; 4 — система с положительным
азеотропом; 5 —система с отрица¬
тельным азеотропом.
46
спиртом, чем с метилэтилкетоном, показывает, что последний в смеси с водой
имеет большие положительные отклонения от идеального поведения, чем этило¬
вый спирт. Следовательно, в присутствии воды должна возрастать относитель¬
ная летучесть метилэтилкетона. Имеющиеся [33] указания о применении воды для
разделения метилэтилкетона и этилового спирта путем экстрактивной ректифи¬
кации подтверждают это положение.
Метод сравнения температур кипения смесей может быть при¬
менен, разумеется, также для выбора разделяющих агентов для
процессов азеотропной ректификации.
Сравнение температур кипения эквимолекулярных смесей дает
возможность лишь качественно оценить степень неидеальности би¬
нарных систем, образованных
компонентами заданной смеси и
предполагаемым разделяющим
агентом. Для количественного
определения эффективности раз¬
деляющих агентов по температу¬
рам кипения Херингтон [34] пред¬
ложил следующее приближенное
уравнение для определения сред¬
него значения OCp при атмосфер¬
ном давлении
Ig ctP * γ [AT42I + (АГ2р — AT4lp) Xp]
Xp I
(132)
где AT2x -T2 -Tх\ АТ2р — T2p — T2,
Arlp = Tlp-TY, T = V2(T2p^rlp);
Tlp и Г2р — температуры кипения
смесей первого и второго компо¬
нентов с разделяющим агентом
при концентрации последнего хр\
Ti и T2 — температуры кипения
первого и второго компонентов.
Применимость уравнения
(132) была проверена [34] путем
сопоставления рассчитанных и
экспериментальных значений
Для семи различных систем, для которых эта величина
изменялась в пределах 0,05—0,44. Среднее отклонение опытных
и расчетных величин составило ~10%.
Из уравнения (132) видно, что наиболее эффективным разде¬
ляющим агентом является тот, который при одинаковом значении
Xp дает наибольшее значение (AT2p — ATxp)/Т.
Гарнер и Эллис [17] проанализировали опытные данные о
равновесии между жидкостью и паром в 9 Трехкомпонентных
системах. Оказалось, что между коэффициентом относительной ле¬
тучести бинарной системы и разностью температур кипения AT
одинаковых по составу смесей разделяющего агента с исходными
Oip
Рис. 12. Зависимость ар от Δ7:
I — ^mm Χ\ίΧ2 ""
Δ — этиловый спирт — бензол — декан;
Q — этиловый спирт — бензол — нитробензол;
# —этиловый спирт —бензол— фенол;
□ — метилциклогексан — толуол—фурфурол;
X — метилциклогексантолуол — фенол;
+ - гептан—метилциклогексан—фурфурол;
А — гептан — толуол — фурфурол.'
47
компонентами при постоянном отношении концентрации последних
имеется линейная зависимость (рис. 12). Как видно, опытные точ¬
ки для разных систем при постоянных значениях х\/х2 группируют¬
ся около прямых линий. Наклон прямых линий и точка нх пере¬
сечения с ординатой hJ = 0 определяется степенью неидеальности
системы, образованной низкокипящим компонентом заданной сме¬
си и разделяющим агентом. Мерой неидеальности является лога¬
рифм коэффициента активности компонента I в системе I—р при
бесконечно малой концентрации этого компонента (Л !р). При
XlIx2 = I величина ар определяется уравнением:
Ctp ^ Alp(0,1 ΔΓ- 0,95) + 1,5 * (133)
О соответствии рассчитанных по уравнению (133) и найденных
экспериментально величин а можно судить по приводимому
в табл. 2 сопоставлению этих величин для ряда трехкомпонентных
систем.
Таблица 2
Сопоставление расчетных и опытных значений ар
-
Состав, мол. доли
ΔΓ
0
tP
Система
Xl
*2
xP
А1р
расчет¬
ная
опытная
Этиловый
0,335
0,335
0,33
0,55
7,8
1,40
1,38
спирт (I) —
0,25
0,25
0,50
0,55
14,8
1,79
1,80
бензол (2) —
нитробензол
(P)
0,15
0,15
0,70
0,55
26,2
2,41
2,44
Метилцикло¬
0,30
0,30
0,40
0,73
15,9
2,00
1,99
гексан (I) —
0,25
0,25
0,50
0,73
18,4
2,15
2,21
толуол (2) —
фурфурол (р)
0,15
0,15
0,70
.0,73
24,8
2,64
2,69
Этиловый
0,35
0,35
0,30
0,90
10,9
‘ 1,63
1,63
спирт (I) —
0,25
·■ 0,25
0,50
0,90
20,6
2,51
2,57
бензол (2) —
декан (р)
0,075
0,075
0,85
0,90
53,3
5,45
5,45
Величина Aip, входящая в уравнение (133), может быть опре¬
делена по данным о равновесии в системе I — р. Для выявления
зависимости Aip от температуры кипения смесей веществ I и «р»
были сопоставлены значения Alp и AT'-Tip-Ti (Tip и T1 — тем¬
пературы кипения эквимолекулярной смеси веществ I и «р» и чи¬
стого компонента I). Значения Aiv, AT' и IgAF для ряда систем
приводятся в табЛ. 3.
Зависимость Aip от IgAF' прямолинейна (рис. 13) и выражает¬
ся уравнением:
Л,р = (1,38 -IgAr) 0,96 (134)
48
Таблица 3
Значения Axpy ΔΓ и Ig ΔΓ' для различных систем
Система
Л1Р
ΔΓ'
Ig ΔΓ'
Этиловый спирт — декан
0,90
2,7
0,43
Этиловый спирт — нитробензол
0,55
7,4
0,87
Бензол — декан
0,04
22,0
1,34
Бензол — нитробензол
0,15
20,0
1,30
Толуол — фурфурол
0,31
12,4
1,03
Бензол — фурфурол
0,20
17,8
1,25
Метилциклогексан — фенол
0,65
4,5
0,65
Изооктан — фурфурол
0,92
2,7
0,43
Этиловый спирт — этилбензол
0,75
3,6
0,56
Уравнение (134) может быть несколько уточненр, если в него
ввести член, учитывающий разность температур кипения разде¬
ляющего агента и компонента заданной
смеси, Tp — Т\:
А 1р = (1,38 - Ig ΔΓ) 0,96 + 0,8 Ig (Гр - T1) - 1,95]
(135)
Гарнер и Эллис показали, что вели¬
чина A ip может быть'приближенно опре¬
делена также по уравнению
^р-О'7[''9-|г(-г)„0.»] (|36)
где (dT/dx)x=o,5 — наклон кривой темпе¬
ратур кипения смесей компонентов I и р
в точке х = 0,5.
Если система,, подлежащая разделе¬
нию, близка к идеальной, то величина ар
мало меняется с изменением относитель¬
ной концентрации исходных компонен¬
тов. В этом случае для оценки эффек¬
тивности разделяющего агента руковод¬
ствуются величиной, вычисленной по уравнению (133). Если же си¬
стема, подлежащая разделению, сильно отклоняется от закона
Рауля, то величина ар при Xilx2 = I, определяемая уравнением
(133), не равна ар при других отношениях концентраций компо¬
нентов исходной смеси. Для определения ар при значениях Xifx2,
отличающихся от единицы, можно получить:
при XiIx2 =J
Ctp — j4jp (0,1 ДГ 0,95) -4-1 »5 -H AipAjy (13*)
При Xilx2 =J
ар = Aip (0,1 ΔΓ- 0,95) + 1,5 -*41рЛ12 (13*)
4?
Рис. 13. Зависимость Axp
от Ig Mf для бинарных си¬
стем.
В этих уравнениях величина AI2 является мерой неидеальности
разделяемой системы.
Для оценки применимости уравнений (137) и (138) в тайл. 4
приводится сопоставление опытных и расчетных значений сср для
ряда систем. Как видно из табл. 4, среднее расхождение этих
значений составляет около 5%, хотя отдельные точки и разли¬
чаются примерно на 20%. Приведенное сопоставление показывает
возможность использования уравнений (133), (137) и (138) для
приближенной оценки эффективности разделяющего агента.
Таблица 4
Сопоставление опытных и расчетных значений аР
Система
Xl
Х2
*р
^lP
Al 2
AT
0E
расчет-
( ная
I
ОПЫТ'
ная
Этиловый спирт (I) —
0,49
0,21
0,30
0,55
0,8
7,8
0,96
0,86
бензол (2)— нитробен¬
0,35
0,15
0,50
0,55
0,8
14,8
1,35
1,40
зол (р)
0,21
0,09
0,70
0,55
0,8
26,2
2,00
2,04
0,105
0,045
0,85
0,55
0,8
39,5
1,90
2,00
0,21
0,49
0,30
0,55
0,8
7,8
1,84
1,90
0,15
0,35
0,50
0,55
< 0,8
14,8
2,23
2,22
0,09
0,21
0,70
0,55
0,8
26,2
2,85
2,80
0,045
0,105
0,85
0,55
0,8
39,5
2,77
2,73
Метилциклогексан (I) —
0,49
0,21
0,30
0,73
0,12
15,9
1,91
1,70
толуол (2) — фурфу-
0,35
0,15
0,50
0,73
0,12
18,4
2,07
2,15
рол (р)
0,21
0,09
0,70
0,73
0,12
24,8
2,56
2,70
0,105
0,045
0,85
0,73
0,12
28,0
2,96
3,10
0,21
0,49
0,30
0,73
0,12
15,9
2,08
1,90
0,15
0,35
0,50
0.73
0,12
18,4
2,23
2,25
0,09
0,21
0,70
0,73
0,12
24,8
2,72
2,75
0,045
0,105
0,85
0,73
0,12
28,0
3,14
3,00
Этиловый спирт (I) —
0,49
0,21
0,30
0,9
0,8
10,9
0,91
1,00
бензол (2) — декан (р)
0,43
0,15
0,50
0,9
0,8
20,6
1,79
1,60
0,105
0,045
0,85
0,9
0,8
53,3
4,73
4,70
0,21
0,49
0,30
0,9
0,8
10,9
2,35
2,57
0,15
0,35
0,50
0,9
0,8
20,6
3,23
3,87
0,045
0,105
0,85
0,9
0,8
53,3
6,17
6,10
Выбор разделяющих агентов
по данным о растворимости
Растворимость и относительная летучесть однозначно
связаны термодинамически, поскольку они зависят от молекуляр¬
ных свойств компонентов растворов.
Чем больше различие свойств компонентов раствора, тем, как
правило, больше отклонение парциальных давлений от величин,
соответствующих идеальным растворам, и тем более вероятна
ограниченная взаимная растворимость компонентов. Связь между
50
отклонениями от идеального поведения и взаимной растворимо¬
стью в бинарных системах была рассмотрена Гильдебрандтом [35],
показавшим, что с увеличением отклонений от идеального поведе¬
ния возрастает тенденция к расслаиванию.
Рассмотрение связи между растворимостью и относительной
летучестью в многокомпонентных системах [36], на основании тер¬
модинамических соображений и анализа имеющихся опытных дан¬
ных, показало, что в этих системах, как правило, возрастает по
сравнению с бинарными относительная летучесть тех компонентов,
которые обладают наименьшей взаимной растворимостью.
Доказательство этой закономерности может быть получено пу¬
тем анализа уравнения (123). Выше было показано, что относи¬
тельная летучесть первого компонента бинарной системы при при¬
бавлении к ней третьего компонента возрастает, если соблюдается
неравенство Ф13 > Фгз. Бинарной системе с меньшей взаимной рас¬
творимостью должно отвечать большее значение функции Ф. Пре¬
дельным случаем будет система, состоящая из полностью несме-
шивающихся компонентов. В такой системе активности компонен¬
тов равны единице, а коэффициенты активности Y1 = — и
Х\
Y2 = -T-!—. Поэтому значение функции Ф определяется выраже-
1 — Xx
нием:
O=-X1IgXi-(I-X1)Ig(I-Xi) (139)
Если составы сосуществующих жидких фаз близки к чистым
веществам, то поведение компонента, являющегося растворителем,
мало отклоняется от идеального. В связи с этим активность
компонента в области существования двух жидких фаз может быть
принята равной концентрации этого компонента в фазе, по отно¬
шению к которой он является растворителем. В этом случае коэф-
Xf
фициенты активности компонентов равны соответственно Yi = “ и
I — Xrf
Y2 = -j , а функция Ф определяется выражением:
Ф = — х Ig х — (I — х) Ig (I — х) + х' Ig х' + (I - х") Ig (I - х”) (140)
Сравнивая значения функции Ф для двух систем I—3 и 2—3
с ограниченной взаимной растворимостью компонентов, получаем:
013~023 = [x'lgx' + (l-x")ig(l~x")]i3-[^]gx'+(l-xOlg(l-^)]23 (HI)
Легко видеть, что Ф13 > Ф23, если взаимная растворимость в си¬
стеме I—3 меньше, чем в системе 2—3. Иными словами, прибавле¬
ние к бинарной системе третьего компонента увеличивает отно¬
сительную летучесть того вещества, которое обладает меньшей
взаимной растворимостью с добавляемым (рис. 14 и 15). Из рас¬
смотрения рис. 14 и 15 следует, что в обоих случаях с увеличением
концентрации метилэтилкетона или нитрометана, ограниченно рас¬
творимого в воде, относительная концентрация последней в паро¬
вой фазе возрастает.
51
Эта закономерность обосновывает возможность выбора разде¬
ляющих агентов, используемых в процессах азеотропной и экстрак¬
тивной ректификации, по данным о растворимости. Впервые эта
возможность была отмечена Кольборном и Шенборном [22], кото¬
рые базировались на представлениях об аналогии между процес¬
сами экстракции и экстрактивной ректификации.
Удобство метода выбора разделяющих агентов по данным
о растворимости обусловливается чрезвычайной легкостью ее экс¬
периментального определения. Применяя для выбора разделяю¬
щего агента данные о растворимости, нужно, однако, учитывать,
что последняя обычно сильно изменяется с температурой. Если
Рис: 14. Кривые равновесия системы
ацетон — вода при различных кон¬
центрациях метилэтилкетона в жидко¬
сти [37].
Рис. 15. Кривые равновесия системы
пропиловый спирт — вода при различ¬
ных концентрациях нитрометана
в жидкости [38].
оба компонента заданной смеси обладают ограниченной взаимной
растворимостью с предполагаемым разделяющим агентом, то рас¬
творимость следует сравнивать при одинаковой температуре.
Для выбора разделяющих агентов по растворимости полезны
некоторые эмпирические закономерностй. Так, взаимная раствори¬
мость уменьшается по мере удаления друг от друга членов следую¬
щего ряда: вода — низшие жирные кислоты — гликоли — амиды —
низшие спирты — низшие амины — низшие кетоны — низшие аль¬
дегиды — нитропроизводные углеводородов — эфиры — галогенза-
мещенные углеводороды — углеводороды [39].
Фрэнсис [40, 41] представил растворимость различных веществ
в виде диаграммы (рис. 16). При выборе разделяющих агентов4
диаграмма Фрэнсиса может быть распространена на классы сое¬
динений, представителями которых являются вещества, указанные
на рис. 16.
Кроме данных о растворимости для выбора разделяющих аген¬
тов можно использовать данные о критических температурах
52
Гептан
Вода
эфир
Рис. 16. Диаграмма растворимости по Фрэн¬
сису [40]:
Растворимость; полная; значительная;
• · «слабая.
растворения, основываясь на том, что более высокому значению
последней чаще всего отвечает меньшая взаимная растворимость.
Данные о критических температурах растворимости углеводородов
в различных растворителях систематизированы Фрэнсисом [40, 41],
который показал, что аро¬
матические углеводороды
значительно лучше раство¬
ряются в полярных веще¬
ствах, чем неароматические.
Отсюда вытекает возмож¬
ность применения полярных
веществ для улучшения раз¬
деления смесей углеводоро¬
дов. Например, гептан и ме¬
тилциклогексан, критиче¬
ские температуры раствори¬
мости которых в анилине
равны соответственно 70 и
41° С, могут быть разделе¬
ны путем экстрактивной
ректификации с использо¬
ванием анилина в качестве
разделяющего агента.
Сводка данных о растворимости имеется в ряде справочников
[42, 43].
Выбор разделяющих агентов
по данным о свойствах азеотропных смесей
Метод выбора разделяющих агентов с помощью данных
о свойствах азеотропных смесей [44] — дальнейшее развитие идей,
лежащих в основе рассмотренных способов выбора "разделяющих
агентов по данным о температурах кипения, а также предложений
[23] о применении в качестве разделяющего агента гомолога менее
летучего компонента исходной смеси. Это предложение основы¬
вается на том факте, что отклонения от идеального поведения в
системах, состоящих из членов гомологического ряда, невелики.
Поэтому применение гомолога одного из компонентов заданной
смеси в качестве разделяющего’ агента обеспечивает увеличение
относительной летучести другого компонента.
Однако, по экономическим или технологическим соображениям,
применение в качестве разделяющего агента гомолога одного из
компонентов заданной смеси может оказаться нецелесообразным.
В этом случае выбор может быть осуществлен следующим обра¬
зом. По таблицам азеотропных смесей [45] выбирается вещество
(промежуточный разделяющий агент), которое дает, положитель¬
ный азеотроп с низкокипящим компонентом и не дает азеотропа
с высококипящим компонентом. Выбранное таким образом веще¬
ство нежелательно применять в качестве разделяющего агента
53
в процессе экстрактивной ректификации, так как оно образует
азеотроп с одним из компонентов. В качестве разделяющего агента
следует применить такой высококипящий гомолог этого вещества,
который не дает азеотропов с компонентами заданной смеси. При
этом принимается, что при такой замене степень отклонения по¬
ведения компонентов смеси от закона Рауля мало изменяется.
Применение изложенного метода можно проиллюстрировать на примере вы¬
бора разделяющего агента для системы метиловый спирт — бензол. Рассмотрим
применимость органических соединений, близких к бензолу, в частности аромати¬
ческих галогензамещенных. Анализируя ряды галогенпроизводных бензола и
спиртов, легко убедиться, что они образуют системы с большими положитель¬
ными отклонениями от закона Рауля. В частности, фторбензол (т. кип. 85,2°С)
образует положительные азеотропы с метиловым, этиловым, изопропиловым,
грег-бутиловым и пропиловым спиртами, несмотря на довольно большую раз¬
ницу температур кипения этих веществ. Хлорбензол (т. кип. 131,9° С) дает азео¬
тропы со спиртами, кипящими выше 97° С, а бромбензол (т. кип. 156,2° С)—с
изоамиловым и другими более высококипящими спиртами. Вместе с тем анализ
данных о равновесии между жидкостью и паром в системах бензол — ароматиче¬
ские галогенпроизводные показывает незначительной отклонение от идеального
поведения. Поэтому в качестве разделяющих агентов для системы метиловый
спирт — бензол можно использовать галогенпроизводные бензола. По соображе¬
ниям технологии для этой цели наиболее подходящим веществом является хлор¬
бензол.
Другой возможный вариант использования данных о свойствах
азеотропной смеси для выбора разделяющих агентов заключается
в следующем. Если два близкокипящих компонента образуют,
каждый в отдельности, азеотропную смесь с минимумом темпера¬
туры кипения с третьим веществом (предполагаемый разделяю¬
щий агент), то компонент, температура кипения азеотропа с кото¬
рым ниже, будет иметь большие отклонения от закона Рауля. От¬
носительная летучесть этого компонента будет возрастать также
при прибавлении гомолога предполагаемого разделяющего агента.
При выборе йоследнего с помощью изложенного метода резуль¬
таты тем надежнее, чем меньше разница температур кипения раз¬
деляемых компонентов.
При значительном различии температур кипения компонентов
может быть рекомендован следующий метод. Подбирается система
из двух близкокипящих компонентов, аналогичная заданной. Ана¬
логия должна быть сохранена в характере функциональных групп,
поэтому новую систему надо подбирать из гомологических рядов
разделяемых компонентов. К выбранным таким образом компонен¬
там подбирается вещество, образующее азеотропную смесь с ми¬
нимумом температуры кипения с каждым из них, но с различной
величиной понижения температуры кипения. В качестве разделяю¬
щего агента для первоначальной смеси принимается либо выбран¬
ное вещество, либо его гомолог.
Как пример использования описанного метода, рассмотрим вопрос о приме¬
нимости воды в качестве разделяющего агента для системы ацетон — метиловый
спирт.
В табл. 5 сопоставлены температуры кипения членов гомологических рядов
компонентов этой системы, а также температуры кипения их азеотропов с во¬
54
дой. Анализ данных табл. 5 позволяет заключить, что AT в ряду кетонов значи¬
тельно больше, чем в ряду спиртов. Например, этиловый спирт и метилэтилкетон
имеют почти одинаковые температуры кипения, а значение AT у метилэтилкетона
во много раз превышает значение AT для этилового спирта.
Таблица 5
Свойства членов гомологических рядов
кетонов и спиртов, а также их азеотропов с водой
Спирт
Температура
кипения, 0C
AT
Кетон
Температура
кипения, 0C
AT
спирт
азео¬
троп
кетон
азео¬
троп
Метиловый
64,7
Ацетон
56,4
Этиловый
78,3
78,2
0,1
Метилэтилкетон
79,6
73,5
6,1
Пропиловый
97,2
87,4
9,8
Метилизопропил-
кетон
95,4
79,0
15,5
грег-Амиловый
101,7
87,3
14,4
Диэтилкетон
101,7
82,9
18,9
втор-Амиловый
119,3
92,5
25,7
Метилизобутил-
кетон
117,0
87,9
29,1
Примечание: AT — разность температур кипения спирта (или кетона) и его азеот¬
ропа с водой (понижение температуры кипения).
Для пропилового спирта AT = 9,8°, а у близкого к нему по температуре ки¬
пения метилизопропилкетона AT = 15,5°.
Таким образом, члены гомологического ряда спиртов дают с водой меньшие
отклонения от идеального поведения, чем соответственные члены гомологиче¬
ского ряда кетонов. Поэтому в системе метиловый спирт — ацетон вода будет
увеличивать относительную летучесть последнего. Соответственно с этим в про¬
цессе экстрактивной ректификации в виде дистиллата будет получаться ацетон,
а в качестве кубовой жидкости — водный раствор метилового спирта.
На основании анализа данных о понижении температур кипения азеотроп¬
ных смесей оказывается возможным выбирать разделяющий агент даже для си¬
стем, компоненты которых являются членами одного гомологического ряда. При¬
мером такой системы является система этиловый спирт — изопропиловый спирт.
Несмотря на незначительное различие температур кипения этих веществ, их азео¬
тропы с водой довольно значительно отличаются по температурам кипения.
Для' изопропилового спирта AT = 82,5—80,38 = 2,12°, тогда как для этилового
спирта AT всего 78,3 — 78,15 = 0,15°. Это показывает, что в системе этиловый
спирт — вода отклонения от закона Рауля меньше, чем в системе изопропило¬
вый спирт — вода. Поэтому присутствие воды в жидкой фазе способствует обо¬
гащению паровой фазы изопропиловым спиртом, что объясняет имеющиеся в ли¬
тературе сведения о возможности разделения смесей этилового и изопропило¬
вого спиртов путем экстрактивной ректификации с применением воды в качестве
разделяющего агента [46].
Применение метода газо-жидкостной хроматографии
для выбора разделяющих агентов
Метод газо-жидкостной хроматографии, как известно,
заключается в разделении смеси веществ в колонке с «активной»
насадкой, по-разному взаимодействующей с компонентами задан¬
ной смеси. Разделяемую смесь небольшими порциями вводят
55
в колонку и смесь быстро испаряется. Перемещение смеси по
длине колонки относительно насадки, необходимое для достиже¬
ния эффективного разделения, осуществляется потоком газа-носи¬
теля. Селективное действие насадки обеспечивается нанесением на
частицы твердого носителя соответствующим образом подобран¬
ного разделяющего агента (неподвижной фазы).
Очевидно, что по аппаратурно-технологическому оформлению
процессы экстрактивной ректификации и газо-жидкостной хрома¬
тографии сильно различаются. Так, при экстрактивной ректифи¬
кации разделяемую смесь вводят в колонку не отдельными пор¬
циями, а непрерывно; движутся обе фазы (жидкая и паровая),
а не одна (газовая); насадка (или другие внутренние устройства
в колонне) предназначена только для развития поверхности кон¬
такта фаз и не играет активной роли,* как в хроматографии.
Однако по своим физико-химическим основам рассматриваемые
процессы аналогичны — в обоих используется различие во взаимо¬
действии разделяющего агента с компонентами заданной смеси.
Так, Херингтон [47] нашел, что это определяет возможность ис¬
пользования газо-жидкостной хроматографии для решения вопро¬
сов, связанных с практическим применением метода экстрактивной
ректификации. Кроме того, использование этой возможности, осно¬
ванное на количественных закономерностях процесса хроматографи¬
ческого разделения, было исследовано многими авторами [48—53].
При введении в поток инертного газа-носителя пробы иссле¬
дуемой смеси, образующие ее компоненты распределяются между
газовой и жидкой фазами. Последняя представляет собой раствор
заданных компонентов в веществе, использованном в качестве не¬
подвижной фазы. При перемещении пробы с газом-носителем
вдоль колонки непрерывно происходит взаимодействие газовой и
неподвижной фаз, заключающееся в абсорбции каждого компо¬
нента из газовой в неподвижную фазу и последующей десорбции
из нее в газовую фазу. За счет многократно повторяемых по длине
колонки актов абсорбции и десорбции и осуществляется разделе¬
ние смеси. Очевидно, что некоторая доля любого компонента, вве¬
денного в колонку с пробой, в произвольный момент времени на¬
ходится в газовой, а остальное количество—*в неподвижной фазе.
Поскольку обычно количество пробы весьма мало, она лока¬
лизована в небольшой зоне по длине колонки, причем газовая
и жидкая фазы могут рассматриваться как бесконечно разбавлен¬
ные растворы. Поведение каждого компонента в таких растворах
не зависит от присутствия других составных частей пробы. Ско¬
рость движения вдоль хроматографической колонки зоны, в кото¬
рой находится рассматриваемый компонент, зависит от скорости
движения газа-носителя и свойств раствора, образуемого этим ком¬
понентом и неподвижной фазой. Исследованию количественной
связи между указанными параметрами посвящен ряд работ
[53—60]. К наиболее обоснованному выводу, учитывающему кине¬
тические факторы, пришел Бреслер [60]. Согласно кинетической
5Ф
f£opMM, ё любом сечении зоны, ё которой находится проба, бДйб-
временно происходят как абсорбция, так и десорбция. Так как
процессы перехода вещества из газовой фазы в жидкую и в про¬
тивоположном направлении протекают с конечными скоростями,
концентрация распределяемого вещества в жидкой ’фазе —перед¬
няя по ходу потока часть зоны — меньше той, которая отвечает со¬
стоянию равновесия с газовой фазой. Это является следствием
того, что в передней части зоны преобладающее значение имеет
процесс абсорбции вещества из газовой фазы. Наоборот, у заднего
фронта зоны концентрация вещества в жидкой фазе больше рав¬
новесной, поскольку преобладает процесс десорбции. Очевидно,
что в некотором сечении зоны газовая и жидкая фазы находятся
в равновесии. Скорость движения фронта, отвечающего состоянию
равновесия, рассматриваемая как скорость движения зоны,7 такая
же, как если бы фазовое равновесие в пределах всей зоны устанав¬
ливалось мгновенно. Выбирая систему координат, движущуюся со
скоростью перемещения зоны н, можно выразить расход вещества
в колонке /, как сумму потоков в газовой и жидкой фазах, каждый
из которых, в свою очередь, складывается из двух составляющих —
конвективной и диффузионной
/ = Fr[(-iL-„)Cr-Z,r^] + F}lt(_„ClK-D«^f-) (142)
где Fr и Fm - площади поперечного сечения соответственно газо¬
вой и жидкой фаз; υ — объемный расход газа-носителя; сг и сж —
концентрации вещества соответственно в газовой и жидкой фазах,
выраженные числами молей в единице объема; / — произвольная
координата по длине колонки, Dv и Dm — коэффициенты диффузии
соответственно в газовой и жидкой фазах.
Очевидно, что количество вещества Q, заключенное в некоторый
момент времени τ в единице объема колонки, может изменяться
только за счет перемещения с газом-носителем. Условие мате*
риального баланса для этого процесса выражается равенством:
dQ dl^ .
~ΊΓ~Ίΰ (143)
В принятой подвижной системе координат величина I является
функцией времени и выражается равенством
I *=ζ +их (14$)
где ζ — расстояние от начала колонки и τ —время.
С помощью выражения (142) условие (143) выражается сле¬
дующим образом:
п дсг , Р дсж р ( о Л дст д% „ дсж п дгсж /1яг,
~ёх + ж Ir rIТ7~ I ~Ш~ + FrDv IiF *1п ж ж IiT
В соответствии с изложенным выше уравнение (145), выведен¬
ное для зоны, может быть отнесено к сечению колонки, в котором
SI
Жйдкая и газовая фазы находятся в равновесии. При этом нужно
иметь в виду, что изменение равновесных концентраций во вре¬
мени, обусловленное «размывом» хроматографической зоны, пере¬
мещающейся по длине колонки со скоростью и, может происходить
только за счет диффузионных процессов. Следовательно
дсж ^2°γ д2сж
• Fr-^ + F^^FrDr-^ + F^-^- (146)
где Сж и С? — равновесные концентрации рассматриваемого веще¬
ства в жидкой и газовой фазах.
С учетом (146) уравнение (145) приобретает вид:
θ<φ
-W = up^ ~дГ (147>
•ά-)
Условия фазового равновесия в конкретной системе в области
разбавленных растворов зависят только от температуры. Если она
постоянна, то концентрация компонента в одной фазе является
только функцией его концентрации в другой фазе. Поэтому
дс del, dcP del
—SL =—— _ —* .—L (148)
dl dl del dl
Используя это выражение для преобразования уравнения (147),
получаем:
■
F'+F*^t
Условия фазового равновесия для разбавленных растворов вы¬
ражаются с помощью закона Генри
dc^fdcV = К (150)
где К — коэффициент распределения компонента между жидкой
й газовой фазами.
При постоянном расходе газа-носителя скорость последнего по
длине колонки меняется за счет изменения давления вследствие
гидравлического сопротивления. Обычно это учитывают путем вве¬
дения поправки к скорости, вычисленной без учета гидравличе¬
ского сопротивления колонки. Скорость движения пробы уо длине
колонки равна
u = L/x (151)
где L — длина колонки; τ — время, за которое рассматриваемый
компонент проходит колонку.
Подставляя это выражение в формулу (149), получаем
VR = vx = L(Fr + F^)=V,+ VmK (152)
58
где Vr — удерживаемый объем, т. е. объем газа-носителя, который
должен пройти через колонну до появления максимума концентра¬
ции рассматриваемого компонента на выходе из колонки;
V0 = FrL — объем газа в колонке (ее свободный объем); Vm — объ¬
ем, занятый неподвижной фазой.
Величины V0 и Vm зависят от конструкции хроматографической
колонки (ее длины, диаметра, размера насадки) и для определен¬
ной колонки они постоянны. Следовательно, уравнение (152) уста¬
навливает линейную зависимость удерживаемого объема от ко¬
эффициента распределения. Это уравнение является основным
в теории распределительной хроматографии. ОнЬ дает возмож¬
ность рассчитать коэффициент распределения компонента между
движущейся и неподвижной фазами по значению удерживаемого
объема, т. е. определить условия фазового равновесия для низких
концентраций рассматриваемого компонента.
Из уравнения (152) имеем
где — исправленный приведенный удерживаемый объем, т. е.
объем пропущенного газа-носителя, приходящийся на единицу
объема неподвижной фазы.
Связь коэффициента распределения вещества между газовой
и жидкой фазами с коэффициентом активности этого вещества в
растворе исследована в работах [58—61]. Парциальное давление
Pi летучего компонента i над раствором в неподвижной фазе в со¬
ответствии с выражением (56) равно Pi = P0iXiVf, где Xi — моляр¬
ная доля компонента ί в неподвижной фазе; yj°— его коэффициент
активности в бесконечно разбавленном растворе; Р9 — давление
паров чистого компонента при заданной температуре.
Поскольку молярная доля компонента i в неподвижной фазе
весьма мала и раствор близок к бесконечно разбавленному, вели¬
чина Xi может быть выражена как
где Nm — число молей вещества, нанесенного на насадку, в еди¬
нице ее объема.
Из. этих выражений вытекает следующее уравнение:
С другой стороны, парциальное давление пара компонента i
может быть выражено с помощью закона Дальтона (в предполо¬
жении, что газовая фаза подчиняется законам идеальных газов)
(153)
(155)
Pi = pVi
(156)
59
где P — общее давление; yt — молярная доля компонента i в газо¬
вой фазе.
Величина tji может быть представлена как
у I=а; ('57)
где JVr — число молей газа-носителя в единице объема.
В соответствии с этим:
ср
Pi -P -щ = RTc* ! (158)
Сопоставляя выражения (155) и (158), получаем:
ср RTNm
1,т
Обычно разделение с помощью газо-жидкостной хроматогра¬
фии производится при давлениях, незначительно отличающихся от
атмосферного, поэтому предположение о подчинении газовой фазы
законам идеальных газов оправдывается с достаточной для прак¬
тических целей точностью. (При необходимости неидеальность
газовой фазы может быть учтена путем введения поправок, мето¬
дика расчета которых описана в работе [3]).
Сочетая выражения (153) и (159), получаем формулу для оп¬
ределения коэффициента активности летучего компонента I в бес¬
конечно разбавленном растворе
оо RTNxVx ώ
*
где Vm — исправленный приведенный удерживаемый объем компо¬
нента i.
Вследствие изменения давления газа по длине колонки объемы
газа-носителя приводятся к среднему давлению в колонке, которое
рассчитывается [62] по уравнению
_2 (P1IP2Y-1
ср ~ 3 (Р\1Рг)г — I (16,)
где Pi и Рг — давления газа соответственно на входе и выходе из
колонки.
С учетом выражения (161) получаются расчетные формулы
~ 2 (Р,/Р2)3 -I RT2NkVkH)
1 3 (Pi/P2f ~ I Pty
Рис. 17. Хроматограмма.
где W — объемный расход газа-носителя, слР/мин, определяемый
на выходе из колонки при давлении P2 и температуре T2; T — тем¬
пература, при которой происходит хроматографическое разделе¬
ние; Ah — расстояние на хроматограмме между максимумами
пиков рассматриваемого компонента и воздуха (рис. 17) и ω —
скорость движения бумажной ленты, на которой записывается
хроматограмма.
Таким образом, по данным газо-жидкостной хроматографии
представляется возможным рассчитывать коэффициенты активно¬
сти компонентов в бесконечно разбавленных растворах. Это имеет
очень важное практическое значе¬
ние, поскольку эти величины весь¬
ма затруднительно определять дру¬
гими методами. Нужно, однако, учи¬
тывать, что в изложенных" выше
рассуждениях рассматривается си¬
стема газ — носитель — летучий
компонент — неподвижная фаза, на¬
несенная на насадку, т. е. пред¬
полагается, что твердый носитель
является инертным и не оказывает
никакого влияния на фазовое рав¬
новесие в указанной системе. Как
показывает практика, это условие
не всегда выполняется. На поверх¬
ности носителя возможна адсорбция компонентов исследуемых
смесей, оказывающая большое влияние на условия их равновес¬
ного распределения между газовой и неподвижной фазами. Это
приводит к существенным отклонениям коэффициентов активностей
летучих компонентов в бесконечно разбавленных растворах в ма¬
лолетучих растворителях, найденных по данным газо-жидкостной
хроматографии, от значений, определенных другими методами.
Наибольшее влияние адсорбции на поверхности носителя обнару¬
живается при использовании для хроматографических эксперимен¬
тов жидких фаз, полярность которых значительно меньше поляр¬
ности исследуемых летучих веществ. Это влияние проявляется
в асимметричности хроматографических пиков {появление адсорб¬
ционных «хвостов»), а также в изменении удерживаемого объема
с изменением величины вводимой пробы. Отмеченные явления
обусловлены нелинейностью изотерм адсорбции на твердых по¬
верхностях и обнаруживаются при использование обычно приме¬
няемых носителей — кизельгура, огнеупорного кирпича, силика¬
геля, окиси алюминия, целита, пористого тефлона.
Адсорбционная активность большинства носителей обусловлена
наличием на поверхности гидроксильных групп, а также микропо¬
ристостью. Поэтому уменьшение адсорбции может быть достиг¬
нуто путем химической модификации поверхности носителя веще¬
ствами, вступающими в реакцию с гидроксильными группами
*1
/
[63—66]. Большое значение имеет уменьшение пористости носите¬
лей. Значительные успехи в этом направлении достигнуты в рабо¬
тах советских ученых [67—69]. Для исключения адсорбции предло¬
жено использовать в качестве носителей насадку из мелких метал¬
лических спиралей, изготовленных из тонкой проволоки [70],
а также кристаллы хлорида натрия [71], не имеющие на своей по¬
верхности гидроксильных групп. Распространенный метод подавле¬
ния адсорбции заключается в нанесении на носитель достаточно
большого количества неподвижной фазы. Обычно при небольших
относительных количествах последней время выхода максимумов
пиков на хроматограммах изменяется с увеличением количества
неподвижной фазы. При содержании последней выше определен¬
ного уровня (обычно 10—15% от веса носителей, например, огне¬
упорного кирпича, диатомита, целита) время выхода максимума
пиков при прочих равных условиях остается постоянным.
Для выбора разделяющих агентов экстрактивной ректификации
нет необходимости в определении коэффициентов активности
каждого компонента. Достаточно определить отношение коэффи¬
циентов активности двух компонентов, поскольку, в соответствии
с формулой (99), величиной этого отношения определяется значе¬
ние коэффициента относительной летучести рассматриваемых двух
компонентов. Для определения отношения γ?°/γ~ из формулы (163)
получается очень простое выражение:
Таким образом, отношение коэффициентов активности двух ком¬
понентов при бесконечно малой их концентрации в неподвижной
фазе обратно пропорционально расстояниям на хроматограмме
максимумов пиков этих компонентов от максимума пика воздуха
(см. рис. 17). Необходимо отметить, что отношение γ?°/γ* опреде¬
ляется с большей точностью, чем каждый коэффициент активности
в отдельности, поскольку при расчете значения .γ£°/γ“, по данным
хроматографического эксперимента, погрешности в определении
Y Г и Y* > обусловленные указанными выше причинами, в значитель¬
ной мере исключаются.
Так как в разбавленном растворе взаимодействие компонентов
ink друг с другом практически не проявляется, величина Yf/γ*
выражает предельно возможную селективность разделяющего
агента (неподвижной фазы) по отношению к этим компонентам:
(164)
(165;
В соответствии с выражением (164) получаем:
(166)
62
Это coofHomeHne и лежит в основе применения газо-жидкостной
хроматографии для выбора разделяющих агентов в процессах
экстрактивной ректификации. Из простого по технике и непродол¬
жительного по времени хроматографического эксперимента полу¬
чается количественная оценка максимально возможной селектив¬
ности разделяющего агента.
Техника эксперимента заключается в следующем. Испытуемое
в качестве разделяющего агента вещество наносят на носитель
в количестве, достаточном для подавления влияния адсорбции, и
полученная насадка загружается в хроматографическую колонку.
В поток газа-носителя, движущегося через колонку, вводят неболь¬
шую пробу заданной смеси и на регистрирующем приборе записы¬
вается хроматограмма. Если * вещество, наносимое в качестве не¬
подвижной фазы, при температуре хроматографического разделе¬
ния обладает значительной летучестью, то газ-носитель перед
входом в колонку целесообразно предварительно насыщать парами
этого вещества. Предпочтительнее использовать в таких случаях
метод циркуляционной хроматографии, который заключается в цир¬
куляции в системе газа-носителя с помощью специального насоса
[72]. Однако это связано со значительными техническими трудно¬
стями. Обрабатывая хроматограмму в соответствии с формулой
(166), определяют значения коэффициентов относительной лету¬
чести компонентов. Детали техники хроматографических экспери¬
ментов описаны в работах [59, 73, 74].
Поскольку коэффициент относительной летучести двух компо¬
нентов зависит от температуры, хроматографические эксперименты
желательно проводить при температуре, близкой к температуре
проведения экстрактивной ректификации. Если это невозможно, то
следует учитывать изменение отношения коэффициентов актив¬
ности с температурой (см. [3]). Чтобы избежать трудностей при
эксперименте, связанных с большой относительной летучестью ис¬
пытываемого разделяющего агента, иногда прибегают к следую¬
щему приему. В качестве неподвижной фазы наносят на насадку
Таблица 6
Сопоставление значений ν° г найденных с помощью
газо-жидкостной хроматографии (ГЖХ) и по давлению паров
Неподвижная
фаза
Летучее
вещество
Температура,
0O
Значения V0
ГЖХ
по давлению
паров
Трихлорбензол
Гексан
30
2,93
2,90
Гекеадекан
Метиловый спирт
25
71,5
75,1
То же
40
45
43,3
Ацетон
25
6,3
6,11
»
40
5,1
5,19
Метилэтилкетон
25
3,8
3,57
То же
40
3,1
3,15
63
ВЫсококипящий гомолог исследуемого вещества, й получаемые ре¬
зультаты экстраполируют на интересующее вещество с учетом
влияния длины углеводородного радикала на взаимодействие чле¬
нов рассматриваемого гомологического ряда с компонентами за¬
данной смеси.
В ряде работ показано хорошее совпадение значений коэффи¬
циентов активности и относительной летучести, определенных по
данным газо-жидкостной хроматографии и другими методами. Для
иллюстрации в табл. 6 сопоставлены значения коэффициентов ак¬
тивности нескольких веществ по данным работ [61, 75], а в табл. 7
приведены значения коэффициентов относительной летучести, най¬
денные по данным о фазовом, равновесии и получение из хрома¬
тограмм [51]. к
Таблица7
Сопоставление значений а® при 20 0Cr
найденных с помощью газо-жидкостной хроматографии (ГЖХ)
и по данным Of фазовом равновесии
(по результатам работы [51]).
Неподвижная
фаза
Бинарная система
* Значения а®
компонент I
компонент 2
гжх
фазовое
. равновесие
Нитрометан
Изопентан
Изопрен
6,50
5,9
2-Мет илбутен-2
3,64
3,1
2-Метилбутен-2
Изопрен
1,78
1,5
Ацетонитрил
Изопентан
»
5,0
5,1
2-Метилбутен-2
3,05
2,7
2-Метилбутен*2
Изопрен
1,63
1,3
Диметилформамид
Изопентан
6,52
6,2,
2-Метилбутен-2
3,55
3,5
2-Метилбутен-2
Изопрен
1,83
1,9
ВЫБОР РАЗДЕЛЯЮЩИХ АГЕНТОВ
ПОДАННЫМ
О СВОЙСТВАХ КОМПОНЕНТОВ РАСТВОРОВ
Влияние разделяющих агентов на относительную лету¬
честь компонентов смеси определяется свойствами образующихся
растворов, которые обусловлены свойствами чистых компонентов,
а также межмолекулярным взаимодействием.
Выяснению природы растворов, изучению их свойств и выявле¬
нию закономерностей, описывающих их поведение, посвящено боль¬
шое количество работ, однако до сих пор не существует единой
теории растворов. Теоретическое обобщение имеющегося огром¬
ного экспериментального материала затрудняется многообразием
и сложностью факторов, определяющих поведение веществ в рас¬
64
творах. Одна из причин этого заключается в том, что межмолеку-
лярное взаимодействие, будучи гораздо более слабым, чем внутри¬
молекулярное, труднее поддается точному учету. Первая попытка
количественной оценки сил межмолекулярного взаимодействия
принадлежит Ван-дер-Ваальсу [76]. В предложенном им широко из¬
вестном уравнении состояния газов и жидкостей влияние этих сил
учитывается эмпирическими коэффициентами.
В настоящее время принято считать, что в общую энергию меж¬
молекулярного взаимодействия вносят вклад пять основных состав¬
ляющих:
Ориентационный эффект, обусловленный взаимодей¬
ствием молекул за счет наличия постоянных диполей, строго
ориентированных в пространстве [77]. Энергия взаимодействия двух
молекул выражается формулой
ор “ 3 kTrQ ( *
где μι и Ц2 — дипольные моменты взаимодействующих молекул;
г — расстояние между центрами диполей, см\ k — постоянная
Больцмана, эрг/град; T — температура, °К.
Индукционный эффект, обусловленный взаимодействием
неполярных или слабо полярных молекул, вследствие их поляри¬
зации под действием постоянных диполей. В результате поляриза¬
ции возникают силы, аналогичные электростатическим, определяю¬
щим ориентационный эффект [78]. Энергия взаимодействия за счет
индукционного эффекта поляризуемой молекулы I с молекулой 2,
имеющей постоянный диполь, выражается как
2μ|α,
7?ИНД = Jq (168)
где μ2 — момент постоянного диполя, αι — поляризуемость моле¬
кулы I, см3.
Вклад взаимодействия этого вида относительно невелик и со¬
ставляет 5 10% от общей энергии Межмолекулярного взаимодей¬
ствия. Поэтому учетом индукционного эффекта часто пренебре¬
гают.
Дисперсионный эффект, учитывающий взаимодействие
молекул за счет сил притяжения мгновенных виртуальных диполей,
которые образуются благодаря движению электронов около ядер
[79]. Энергия такого взаимодействия двух молекул, обладающих
поляризуемостями αι и аг и дисперсионными частотами Vi и V2,
определяется выражением
ЯДИС SiO1Oj. A_V£i_ (169)
4 г6 η+ V2
где h — постоянная Планка, эрг-сек.
3 Зак. 917
65
Дисперсионный эффект присущ всем молекулам, тогда как
ориентационный и индукционный — только полярным и поляризуе¬
мым. Общая квантовомеханическая теория межмолекулярного
взаимодействия, развитая Лондоном, приводит к выводу, что при¬
рода всех составляющих одна и та же — электростатическое при¬
тяжение молекул.
Водородная связь —особый тип взаимодействия, осуще¬
ствляемого ковалентно связанным атомом водорода с каким либо
атомом в той же или другой молекуле, обладающим неподеленной
парой электронов, т. е. такими спаренными электронами, которые
не использованы для образования химической связи и принадле¬
жат только данному атому. Донорами электронов являются атомы
фтора, кислорода, азота и некоторых других элементов. Из-за
своих малых размеров водород настолько близко приближается
к атому-донору, что образуется подобие химической связи, локали¬
зованной в пространстве. Энергия взаимодействия за счет водо¬
родной связи составляет 5—10 ккал/моль, тогда как средняя энер¬
гия кулоновского межмолекулярного взаимодействия равна
2—3 ккал/моль.
π-связь в комплексах дает соединения, образуемые ато¬
мом водорода с π-электронами двойной связи [80]. В качестве до¬
норов в я-комплексах выступают соединения, в молекулах которых
имеются электроны, занимающие я-орбитали. Таковы, в частности,
непредельные углеводороды. Акцепторами электронов могут быть
некоторые неорганические вещества (галогены, двуокись серы, че-
тырехокись азота, соли серебра, меди и ртути), а также различные
органические вещества, содержащие полярные группировки, спо¬
собные оттягивать электроны. Степень смещения электронов
в я-комплексах намного меньше, чем в соединениях, образуемых
за счет ковалентных связей. Как правило, стабильность я-ком-
плексов, образуемых углеводородами, повышается с ростом нена¬
сыщенное™ последних [81].
Энергия этого вида межмолекулярного взаимодействия может
приближаться к энергии водородной связи [82].
Энергетическое состояние молекул компонентов раствора обус¬
ловлено совместным действием всех указанных составляющих меж¬
молекулярного взаимодействия. Их количественный учет представ¬
ляет чрезвычайно большие трудности. Применительно к требова¬
ниям теории азеотропной и экстрактивной ректификации задача
может быть сведена к оценке степени неидеальности бинарной си¬
стемы по данным о свойствах компонентов.
Долецалек [83] попытался количественно объяснить отклонения
от закона Рауля химическими реакциями в растворах. Отрицатель¬
ные отклонения от закона Рауля он объясняет ассоциацией ком¬
понентов друг с другом, а положительные отклонения — диссоциа¬
цией в растворе ассоциированных комплексов одного из компонен¬
тов. Однако, эта теория, по-видимому, справедлива лишь для
ограниченного класса растворов.
66
, С идеями Долецалека в значительной мере связаны попытки
предсказания поведения систем, образованных неполярным рас¬
творителем и полярными веществами — членами одного гомологи¬
ческого ряда, базирующиеся на рассмотрении изменения степени
ассоциации полярного компонента в растворе [84—86].
Одна из первых теорий неидеальных растворов была предло¬
жена Ван-Лааром [87], исходившим из идей Ван-дер-Ваальса. Ван-
Лаар получил для количественной оценки степени неидеальности
бинарной системы следующее выражение:
где Atfсм — теплота смешения компонентов; ах и bXi а2 и Ь2— кон¬
станты в уравнениях состояния Ван-дер-Ваальса соответственно
для первого и второго компонентов; Х\ и X2 — молярные роли ком¬
понентов в растворе.
Следовательно, равенство CLjb2l = a2fb\, являющееся условием
идеальности системы, означает равенство критических давлений
компонентов. Степень же отклонения поведения системы от идеаль¬
ного должна определяться различием критических давлений. Это
весьма редко согласуется с действительностью. Попытки автора
усовершенствовать эту теорию не привели к положительным ре¬
зультатам.
Для описания свойств неидеальных систем Гильдебрандт пред¬
ложил теорию регулярных растворов [35], основанную на допуще¬
ниях о сферической форме и симметричном строении молекул.
Кроме того, принималось, что энтропии смешения реального и
идеального растворов одинаковы. В соответствии с этой теорией
теплота смешения двух компонентов
где V) и V2 молярные объемы компонентов, смъ!моль\ AEx и
AE2 — энергии испарения компонентов, кал/моль.
Величина AEiIvii имеющая смысл энергии испарения, приходя¬
щейся на единицу объема компонента, или «плотности энергии»
была названа Гильдебрандтом внутренним давлением. Член
(170)
Из этого выражения следует, что Atf0M = O при == α!(2/δ2.
Ho, как известно, из уравнения состояния Ван-дер-Ваальса сле¬
дует:
pKP--Ir--Sr . <171>
(171)
(172)
(173)
3*
67
При этом степень неидеальности системы определяется вели¬
чиной
Л2 = (δι - 62)2 (174)
характеризующей энергию взаимодействия молекул первого и вто¬
рого компонентов. Величина Ai2 является коэффициентом в урав¬
нениях. описывающих зависимость коэффициентов активности ком¬
понентов регулярного раствора от его состава
Ig Yi =A12 (I-Xi)2 и Ig V2 = A12X21 (175)
Теория Гильдебрандта хорошо оправдывается для растворов
веществ, межмолекулярное взаимодействие которых определяется
дисперсионными силами. Для растворов, содержащих полярные
компоненты, наблюдается расхождение этой теории с практикой.
Для иллюстрации этого положения сопоставим приводимые ниже данные
о внутреннем давлении различных веществ с известными сведениями [31] о ха¬
рактере отклонений от закона Рауля в бинарных системах, образованных этими
веществами:
(Д£г/°г)0’5,
(калДшз)0,5
Ацетон 9,74
Бензол 9,00
Хлороформ 8,93
Толуол 8,32
Октан 7,50
Этиловый спирт 7,45
Гептан . 7,35
Системы этиловый спирт — октан и этиловый спирт — гептан характери¬
зуются большими положительными отклонениями от закона Рауля, хотя внутрен¬
ние давления образующих их компонентов почти одинаковы. Система ацетон —
хлороформ с небольшой разностью внутренних давлений компонентов
(0,81 кал°»5/см1*5) имеет большие отрицательные отклонения от идеального пове¬
дения, тогда как система бензол — толуол с примерно такой же разностью вну¬
тренних давлений компонентов практически идеальна, а в системе ацетон — бен¬
зол наблюдаются большие положительные отклонения от идеального поведения.
Причина отмеченных противоречий заключается в ограниченной примени¬
мости допущений, лежащих в основе теории Гильдебрандта.
По Гильдебрандту, основная причина отклонения поведения ре¬
альных растворов от регулярных заключается в притяжении одина¬
ковых или разнородных молекул, обусловленном их полярностью.
За счет взаимного притяжения молекул полярного компонента мо¬
жет происходить выталкивание молекул другого — неполярного
компонента. Результатом этого являются, положительные отклоне¬
ния от закона Рауля. При большой разнице полярностей компо¬
нентов, как, например, в системах, образованных метиловым спир¬
том и парафиновыми углеводородами, компоненты по изложенной
выше причине могут оказаться ограниченно взаимно раствори¬
мыми. Большее притяжение разнородных, чем однородных моле¬
кул обусловливает отрицательные отклонения от идеального по¬
ведения.
68
Чтобы учесть силы взаимодействия молекул за счет ориента-
щионного эффекта Ван-Аркель предложил [88] рассчитывать кон¬
станту Aj2 по формуле
Ai2 = -δ2)2 +(CO1-CD2)2 (176)
где (ύι = YaE0P/vc — потенциал межмолекулярного взаимодей¬
ствия; AjEop — энергия взаимодействия диполей.
Теория Ван-Аркеля проверялась в работе [89], причем она была
модифицирована в отношении более точного определения потен¬
циала межмолекулярного взаимодействия со*. При этом использо¬
валась предложенная недавно зависимость последнего от критиче¬
ских констант индивидуальных веществ [90]. Однако эта теория
не получила большого практического применения, и на практике
для качественных предсказаний используются представления
о связи между отклонениями от идеального поведения компонен¬
тов и различием их полярности. Последняя характеризуется вели¬
чиной дипольных моментов, значения которых для ряда веществ
при 20° С следующие:
μ.-ιοί»
μ -1018
э. с, е.
э. с.е.
Гексан (C6H14)
0
Бромбензол (C6H5Br) ....
1,43
Гептан (C7H16)
0
Анилин (C6H5NH2)
1,51
Октан (C8H18)
0
Хлорбензол (C6HrCl)
1,56
Циклогексан (C6H12)
0
Двуокись серы (SO2) . .
1,61
Бензол (C6H6) . . ......
0
Йодистый этил (C2H5I) . . .
1,66
’Сероуглерод (CS2)
0
Октиловый спирт (C8H17OH)
1,68
Четыреххлористый углерод
Метиловый спирт (CH3OH) .
1,68
(CCl4)
0
Этиловый спирт (C2H5OH) . .
1,70
п-Дихлорбензол (C6H4Cl2) . .
0
Фенол (C6H5OH)
1,70
л-Ксилол (C8H10)
0
Бромистый этил (C2H5Br) , .
1,83
Нафталин (C10H8)
0
Вода (H2O)
1,85
Толуол (C7H8) .
0,4
Этилацетат (CH3COOC2H5) .
1,86
Бромоформ (CHBr3)
1,0
о-Дйхлорбензол (C6H4Cl2) . .
2,24
Хлороформ (CHCl3)
1,05
Ацетальдегид (CH3CHO) . . .
2,46
Дифениловый эфир [(C6H3)2O]
1,14
Ацетон [(CH3)2CO]
2,8
Нодбензол (C6HI)
1,30
Ацетонитрил (CH3CN) ....
3,2
Этиламин (C2H5NH2) . . . .
1,3
Нитрометан (CH3NO2) ....
3,42
Диметиловый эфир [(CH3)2O]
1,32
Нитробензол (C6H5NO2) . . .
4,19
м-Дихлорбензол (C6H4Cl2) . .
1,48
Для выбора разделяющих агентов на основании представлений
о связи между полярностью молекул и характером отклонений от
идеального поведения в образуемых ими системах последние было
предложено [20] разделять на следующие группы: I) высокополяр¬
ные, 2) неполярные, 3) один компонент полярный, другой неполяр¬
ный и 4) оба компонента с умеренной полярностью. К первой
группе относятся, например, системы ацетон — метиловый спирт,
вода — уксусная кислота и вода — этиловый спирт. Для первой из
этих систем подходящими разделяющими агентами являются, на¬
пример, дихлорметан [91] — неполярное вещество и вода [92],
4?
имеющая резко выраженную полярность. Разделение смесей уксус¬
ной кислоты и воды облегчается при проведении ректификации
в присутствии таких полярных веществ, как эфиры уксусной
кислоты или неполярных углеводородов и их хлорпроизводных [93].
Разделяющими агентами для системы вода — этиловый спирт
являются неполярное вещество — бензол [94], а также полярные
вещества — высшие жирные спирты, например амиловый [95], или
фенол [96].
Примерами систем второй группы являются различные смеси
углеводородов. Для них в качестве разделяющих агентов исполь¬
зуются полярные вещества, например, спирты (жирные и фенол),
кетоны (ацетон) и амины (анилин).
Если один компонент заданной смеси полярный^ а другой непо¬
лярный, то в. качестве разделяющего агента могут быть использо¬
ваны как полярные, так и неполярные вещества. Например, для
разделения смеси метиловый спирт — бензол применимы в каче¬
стве разделяющих агентов ксилол (неполярное вещество) и хлор¬
бензол (вещество с умеренной полярностью), увеличивающие от¬
носительную летучесть метилового спирта [44]. С другой стороны,
для разделения смесей спиртов и углеводородов, например, бути¬
лового спирта и углеводородов парафинового ряда, путем азеотроп¬
ной ректификации можно в качестве разделяющего агента приме¬
нять воду (сильно полярное вещество) [97], увеличивающую отно¬
сительную летучесть углеводородов.
При выборе разделяющих агентов для систем этой группы
можно руководствоваться следующими положениями. Если жела¬
тельно увеличить относительную летучесть полярного компонента,
то в качестве разделяющего агента следует применить неполярное
вещество. Наоборот, при желании увеличить относительную лету¬
честь неполярного компонента подходящим разделяющим агентом
окажется полярное вещество, по химической природе близкое
к полярному компоненту.
Для систем, оба компонента которых имеют умеренную поляр¬
ность, подходящими разделяющими агентами могут оказаться как
сильно полярные, так и неполярные вещества. При выборе разде¬
ляющих агентов для систем этого типа Шейбл [23] рекомендует
применять высококипящие гомологи менее летучего компонента.
Дикс и Карлсон [98] предложили использовать в качестве разде¬
ляющих агентов вёщества, образованные присоединением поляр¬
ной группы к менее летучему компоненту.
Приведенное выше разделение смесей на группы является ко¬
нечно чрезвычайно условным, а рекомендации выбора разделяю¬
щих агентов на основе изложенных представлений — весьма ориен¬
тировочными.
Можно привести много примеров, когда вещества с близкими
дипольными моментами образуют системы с большими отклоне¬
ниями от идеальных, и наоборот, — компоненты с сильно отличаю¬
щимися дипольными моментами образуют смеси, близкие к идеаль¬
на
ным. В частности к сильно отличающимся от идеальных можно
отнести системы*:
Этиловый спирт (1,70) —этилацетат (1,86)
Этиловый спирт (1,70) —вода (1,85)
Этилацетат (1,86)—вода (1,85)
Бромистый этил (1,83) —вода (1,85)
Бромистый этил (1,83) — этиловый спирт (1,70) ’
Компоненты данных систем обладают мало отличающимися ди¬
польными моментами.
Примером систем, близких к идеальным, но образованных ком¬
понентами с разными дипольными моментами, являются:
о-Дихлорбензол (2,24) — четыреххлористый углерод (0)
Бензол (0) — хлорбензол (1,56)
Попытки объяснить отклонения от идеального поведения только
полярностью молекул были цодвергнуты критике Юэлом, Гарри¬
соном и Бергом [99], которые предложили для решения этого во¬
проса исходить из представлений о водородной связи. Эти пред¬
ставления основываются на способности атома водорода распола¬
гаться между двумя атомами кислорода, азота или фтора, а также
между одним из этих атомов-доноров и углеродным атомом, если
к нему присоединены электроотрицательные атомы или группы.
В зависимости от атомов, между которыми располагается водо¬
род, водородные связи разделяются на сильные и слабые:
Сильные Слабые
ОН N HN
HCCl2
N HO О, N
О HN
HCCl-CCl
HCNH2
HCCN
На основе этих представлений органические вещества можно
разделить на пять групп.
I группа. Вещества, способные образовывать трехмерные сетки
сильных водородных связей (например, вода, этиленгликоль, гли¬
церин, аминоспирты, гидроксиламин, оксикислоты, полифенолы,
амиды).
II группа. Вещества, содержащие активный водород и атом-до-
нор (О, N или F) — спирты, кислоты, фенолы, первичные и вторич¬
ные амины, оксимы, нитросоединения и нитрилы с атомом водо¬
рода в α-положении, аммиак, гидразин, фтористый водород, циа¬
нистый водород и др.
III группа. Вещества с атомом-донором в молекуле, но не
имеющие активного атома водорода. Таковы эфиры, кетоны, аль¬
дегиды, сложные эфиры, третичные амины, нитросоединения и
нитрилы, не имеющие атома водорода в а-положении.
* В скобках указаны значения дипольных моментов μ* IO18 э. с. е. при 20°С.
71
IV группа. Вещества, имеющие активный атом водорода, но без
атома-донора. Таковы, в частности, хлорпроизводные углеводоро¬
дов, у которых хлором замещены два или три атома водорода
у углерода, крайнего в цепочке, или один атом водорода у угле¬
рода, находящегося в середине цепочки, например, хлороформ, ди¬
хлорметан, I, I-дихлорэтан, 1,2-дихлорпропан, 1,2,3-трихлорпропан
и 1,1,2-трихлорэтан,
V группа. Вещества, не имеющие ни атома-донора, ни актив¬
ного водорода, в частности, углеводороды, сероуглерод, меркап¬
таны, галогенпроизводные углеводородов, не относящиеся к IV
группе и др.
Системы, образованные веществами, относящимися к различ¬
ным группам, по-разному отклоняются от закона Рауля (табл. 8).
Хотя в табл. 8 отсутствует сравнение интенсивности отклонений от
закона Рауля, а лишь указан их характер, она весьма полезна для
выбора разделяющих агентов.
Таблица 8
Характер отклонений от идеального поведения
в бинарных системах,
образованных различными группами соединений
Группы
Отклонения
от закона Рауля
Изменение водородной
связи при смешивании
компонентов
Примеры
I+V
II + V
III+V
I+ IV
II+ IV
Ι+Ι
Ι + ΙΙ
Ι + ΙΙΙ
ΙΙ + ΙΙ
ΙΙ + ΙΙΙ
ΙΙΙ + ΙΠ
III+IV
IV+IV
IV+V
V +V
Всегда положительные.
Часто ограниченная
взаимная раствори¬
мость
Всегда положительные
Всегда отрицательные
Всегда положитель¬
ные. Часто огра¬
ниченная взаимная
растворимость
Всегда положитель¬
ные
Обычно положитель¬
ные, в некоторых
случаях отрицатель¬
ные, сложные группы
Системы, близкие к
идеальным, отклоне¬
ния от закона Рауля
всегда положитель¬
ные
Всегда нарушается
Всегда нарушается
Всегда образуется
Нарушается и обра¬
зуется, но прева¬
лирующее влияние
оказывает диссо¬
циация комплек¬
сов, образованных
веществами I и II
классов
Образуется и нару¬
шается
He играет роли
Этиленгликоль — на¬
фталин, положи¬
тельный азеотроп
Этиловый спирт—бен¬
зол, положительный
азеотроп
Хлороформ — ацетон,
отрицательный азе¬
отроп
Дихлорэтан — вода,
положительный азе¬
отроп. Этиловый
спирт — бензол, по¬
ложительный азео¬
троп
Этиловый спирт — во¬
да, положительный
азеотроп. Гидра¬
зин — вода, отрица¬
тельный азеотроп
Ацетон — гексан, по¬
ложительный азео-
/ троп. Бензол—цик¬
логексан, положи¬
тельный азеотроп
72
Отличительная особенность всех описанных предложений — по¬
пытка установить связь степени неидеальности свойств компонен¬
тов растворов с каким-нибудь одним свойством или одним видом
межмолекулярного взаимодействия. Такой подход дает полезные
результаты, когда компоненты заданной смеси сильно различаются
по химическому строению и свойствам. В более сложных случаях
необходимо учитывать различные составляющие межмолекуляр¬
ного взаимодействия.
Методы выбора разделяющих агентов,
основанные на оценке отдельных составляющих
межмолекулярного взаимодействия
Идея раздельного учета отдельных составляющих меж¬
молекулярного взаимодействия при выборе разделяющих агентов
для процессов экстрактивной ректификации была выдвинута в ра¬
боте Прауснитца и Андерсона [100]. Авторы исходили из того, что
изменение свободной энергии за счет смешения компонентов при
постоянном давлении AGp обусловлено изменением внутренней
энергии Δί/Ρ,-объема ДУР и энтропии Sp
AGp = Шр + P AKp - T ASp (177)
Изменения внутренней энергии и энтропии при P = const по
Скотту [101] можно выразить через изменение этих функций при
V = const следующим образом
Δί/ρ-Δί/ν + [-7·(^-ρ]Δν+... (178)
и
= + (Wjy ··· (179)
Пренебрегая членами высших порядков и подставляя выраже¬
ния (178) и (179) в уравнение (177), получаем:
AGp = AUy-TkSv (180)
Изменение энергии молекулы в результате смешения можно
разделить на две части: I) изменение потенциальной энергии
Δί/ποτ, обусловленное поведением ближайшего окружения рассма¬
триваемой молекулы в растворе и 2) изменение ротационной и
вибрационной составляющей энергии Δί/ροτ молекулы в растворе
по сравнению с чистым веществом. Следовательно
Wv = МП0Т +MJpot (181)
Принимаются следующие два допущения.
I. Избыточная энтропия определяется изменением вращатель¬
ной и колебательной составляющих энергии
IbSv = Wff0r (182)
к
2. Потенциальная энергия смеси является квадратичной функ¬
цией молярных объемов
2 2 xIxIv^icц
~ У пот«“ !—■ (183)
- 2 xPl
где Vi — молярный объем компонента i\ Cij — константа, выра¬
жающая энергию взаимодействия компонентов i и /, приходя¬
щуюся на единицу объема.
Для бинарной смеси из уравнений (180)—(183) следует
у ^CZiiot = (λγι Vri-Ь лг21^2) (184)
где Φι и Ф2 — объемные доли компонентов в растворе; А12 =
= Cu -f С22 — 2Ci2 — изменение энергии раствора, отнесенное
к единице объема.
Чтобы использовать уравнение (184) для выбора разделяющих
агентов, необходимо сравнить различные значения констант Cij1
характеризующих силы межмолекулярного взаимодействия. Рас¬
смотрим раствор, состоящий из полярного (I) и неполярного (2)
компонентов. Величина Сц обусловлена действием дисперсионных
сил и полярным взаимодействием. Значение же С22 обусловлено
только дисперсионными силами. Константу Ci2 можно рассматри¬
вать как сумму двух членов: первого, учитывающего дисперсион¬
ное взаимодействие, и второго, учитывающего взаимодействие ин¬
дуцированного диполя молекулы второго компонента с полярной
молекулой первого компонента. Соответственно с этим, пользуясь
определением параметра растворимости (173), константы С можно
выразить следующим образом:
(185)
С*-(^р)2-6* (186)
AU^ni AUlicn2 У/> ξα
+ -ϊ-ΰ—б1н0г+|12 (187)
ViV2 ) (V1V2)'!'
И
Λΐ2 = δ?Η + δ?π + δ!-2[δΐΗδ2 + Μ (188)
Здесь ЛЯисп и Δί/исп — неполярная и полярная составляющие
энергии испарения; ξι2— константа, пропорциональная индукцион¬
ной составляющей энергии взаимодействия, приходящейся на еди¬
ницу объема.
Если первый компонент также неполярный, то
п ~ %i2 ~ 0 (189)
и уравнение (163) приобретает вид:
Λΐ2 = (δι-δ2)2 (190)
74
Энергия индукционного взаимодействия между двумя поляр¬
ными молекулами мала по сравнению с энергией взаимодействия,
обусловленного полярностью, и поэтому включается в значение διπ·
Уравнения (184) и (188) дают возможность рассчитать селек¬
тивность разделяющего агента. Если обозначить индексами I и 2
компоненты бинарной смеси, подлежащей разделению, то для рас¬
чета селективности при бесконечном разбавлении S012 получаем:
Для количественного использования приведенных соотношений
необходимо ввести некоторые условия относительного расчета зна¬
чений δ 1н, δ In И Ii2.
Чтобы найти δ 1н и δ in, необходимо разделить энергию испаре¬
ния на неполярную и полярную части. Для этого можно использо¬
вать гомоморфный метод, предложенный Бонди и Симкиным [102].
В соответствии с этим методом неполярная часть энергии испаре¬
ния полярной молекулы равна энергии испарения ее неполярного
аналога при той же приведенной температуре. Например, аналогом
ацетонитрила является этан. Хотя этот метод неточен, он дает при¬
емлемые полуколичественные результаты.
Член Ii2 в уравнении (188) учитывает энергию всех видов взаи¬
модействия между молекулами первого и второго компонентов за
исключением взаимодействия за счет лондоновских дисперсионных
сил. Можно предполагать, что определяющее влияние на селектив¬
ность оказывает энергия индукционного взаимодействия Δί/инд. По¬
этому, если полярный, разделяющий агент притягивается за счет
индукционного эффекта с большой энергией к одному компоненту
и с малой — к другому компоненту заданной смеси, то он обладает
селективным действием.
При подстановке уравнения (188) в уравнение (191) получается
следующее выражение для определения селективности:
RT In S02 = δ2π (F1 - V2) + [F1 (δρΗ - δ,)2 - F2(δρΗ - δ2)2] + (2F2|p2 - 2F1?pl) (192)
Три слагаемых в правой части этого уравнения выражают
вклад в селективность соответственно полярного, дисперсионного
и индукционного эффектов. Уравнение (192) можно записать сле¬
дующим образом
RT InS0l2 = P+ D + I (19?)
где
P = O2pn(F1-F2) (194)
D=Vi (δΡΗ — δι)2 -F2 (δρΗ — б2)2 (195)
I = 2F2ip2 — 2F ι|ρ1 (196)
Уравнения (193)—(196) не пригодны для расчета равновесия
между жидкостью и паром. Однако они приводят к важным
JS
заключениям относительно селективного действия разделяющих
агентов. Рассмотрим их применение к разделению смесей угле¬
водородов.
Как отмечалось выше, энергии индукционного взаимодействия
для различных неполярных веществ, в частности углеводородов,
мало различаются. Поэтому при отсутствии химического взаимо¬
действия индукционная составляющая не должна оказывать опре¬
деляющего влияния на селективность. Полярный эффект пропор¬
ционален разности молярных объемов разделяемых углеводородов.
Если Vi и V2 различаются значительно, то полярная составляющая
селективности играет доминирующую роль. Если подставить экс¬
периментальные величины в уравнения (193) — (196), то, как пра¬
вило, член P значительно превышает сумму DnI. При равенстве
молярных объемов компонентов член P исключается. Определяю¬
щее влияние разности молярных объемов компонентов на вели¬
чину P вытекает из предположения, что потенциальная энергия
смеси является функцией объемных, а не молярных долей компо¬
нентов. Это значит, что чем больше молекула углеводорода, тем
больше ее способность к взаимодействию с полярным веществом.
Следовательно, полярная составляющая должна обусловливать
большие положительные отклонения от закона Рауля углеводоро¬
дов большего размера. Это положение находится в соответствии
с общеизвестным фактом повышения относительной летучести па¬
рафиновых углеводородов по сравнению с нафтеновыми и послед¬
них по сравнению с ароматическими при одном и том же числе
атомов углерода в молекулах углеводородов.
В табл. 9 приводятся найденные экспериментально значения
селективности для ряда систем при бесконечном разбавлении,
а также рассчитанные по экспериментальным данным значения
энергии индукционного взаимодействия полярного вещества с каж¬
дым углеводородом. Углеводород, молекула которого по размеру
больше, во всех случаях имеет большую относительную летучесть.
Однако количественной связи селективности с энергией индукцион¬
ного взаимодействия нет.
Если углеводород большего размера образует, а малого — не
образует комплекс с полярным веществом, то уравнение (194) не
может быть использовано. Например, коэффициент активности
этилбензола (V = 123 смг/моль) в разбавленном растворе в феноле
при 25°С равен 5,3, а циклогексана (V — 109 см?/моль)—11,8
[103]. В результате образования полярным веществом комплексов
с ароматическим углеводородом его коэффициент активности ока¬
зывается, несмотря на больший молекулярный объем, меньше ко¬
эффициента активности циклогексана. Следовательно, относитель¬
ная летучесть ароматического углеводорода понижается.
В тех случаях, когда углеводород меньшего размера образует,
а большего не образует комплексы с полярным веществом, урав¬
нение (194) для качественной оценки применимо. Уравнение (194)
не только учитывает различие размеров молекул компонентов, но
76
Таблица 9
Влияние размеров молекул на селективность
S ,
о о л
(Я <5*
OfflOO
Oonsj
о
S-м
я §
H
О
О
>1 *
O O
3 н
Cu O
B OJ
я о -
о. а «
OJ сх CQ
OJ ^ _
ё §
в * *
S
£ 4*4
Sgbs*
|§8 8
pI 5 ΛI SJ
S
CQ
S
Eh
W
CL)
Энергия И]
ЦИОННОГО I
действия,
кал1моль
O ^
3 CJ
с η
I о S
H и 3
° S о
о Cf
S OSo
<1*1 υρ,
CJ
О
Метилэтилке¬
25
Гептан -f толуол
147
2,84
1,150
тон
107
1,230
Гептан + бензол
147
89
3,92
1,150
1,220
Декан + гептан
196
1,39
1,070
147
1,150
Ацетон
45
Гексан 4- бензол
136
89
4,27
1,400
1,450
Фенол
25
Г ептан 4- цикло¬
147
1,72
2,010
гексан
109
1,560
Циклогексан 4-
109
4,06
1,560
бензол
89
1,570
Г ептан 4- толуол
147
5,1
2,010
107
1,650
Фурфурол
25
Этилциклогексан +
143
1,99
1,890
циклогексан
109
1,800
Фурфурол
25
Циклогексан 4-
109
4,35
1,760
бензол
89
1,800
Гептан 4- бензол
147
12,5
2,140
89
1,800
Гептан 4- бутан
147
2,5
2,140
101
1,850
также показывает, что при разделении смесей углеводородов, мо¬
лекулы которых имеют различные размеры, селективность сильно
зависит от полярной составляющей параметра растворимости. Зна¬
чит, эффективность разделяющего агента зависит от его поляр¬
ности, которая должна быть большой, и от его молярного объема,
который должен быть небольшим. Например, уравнение (194) по¬
зволяет предсказать, что для выделения циклогексана из смеси
с бензолом ацетон является лучшим разделяющим агентом чем
метилэтилкетон, а ацетонитрил превосходит фенол. Из уравнения
(194) вытекает также, что когда молярные объемы разделяемых
углеводородов близки, то для достижения одинаковой селектив¬
ности полярный параметр растворимости разделяющего агента
должен быть больше, чем в случае заметно различающихся моляр¬
ных объемов углеводородов. В предельном случае равенства мо¬
лярных объемов полярная составляющая становится равной нулю.
При этом уравнение (195) приобретает вид:
D = 2F [брн - -i- (6, + δ2) j (δ2 - δ,)
(197)
77
В этом случае дисперсионный член D пропорционален разности
параметров растворимости двух разделяемых углеводородов. Для
двух углеводородов одинакового размера (и с примерно равными
давлениями паров) эта разность мала и, следовательно, диспер¬
сионный эффект не может обусловливать значительную селектив¬
ность. Значит, для компонентов с молекулами одинакового размера
нельзя ожидать селективного действия разделяющего агента за
счет его полярности или физического взаимодействия (например,
за счет дисперсионных сил). В таких случаях селективность мо¬
жет обусловливаться силами химического взаимодействия, приво¬
дящими к увеличению индукционной составляющей энергии.
Так, хотя молекулы углеводородов C4 близки по размерам, их
молярные объемы несколько различаются вследствие того, что
двойная связь C==C несколько короче одинарной связи С—С. По¬
этому, при большом значении полярного фактора растворимости
разделяющего агента может быть обеспечена его селективность.
Однако при малом различии молярных объемов все же превали¬
рующее значение приобретает достижение селективности за счет
химического взаимодействия, вызывающего изменение индукцион¬
ной составляющей внутренней энергии.
С химической точки зрения, , неидеальное поведение компонен¬
тов растворов обусловлено ассоциацией и сольватацией. При этом
в растворе находятся агрегаты одинаковых (ассоциаты) или раз¬
нородных (сольваты) частиц. Индукционная энергия не учитывает
специфические силы, приводящие к комплексообразованию. Од-
. нако, как было отмечено выше, непредельные углеводороды'—
бензол, этилен или их производные —г могут образовывать ком¬
плексы с различными веществами, например, с иодом, двуокисью
серы, нитросоединениями, цианидами и др. Эти комплексы обра¬
зуются в результате взаимодействия кислотно-основного типа. При
этом вещество, способное' быть донором электронов, проявляет
основные свойства, а являющееся акцептором электронов — кис¬
лотные. Поскольку π-электрон в ненасыщенных углеводородах
сильно поляризован, ароматические, олефиновые и некоторые аце¬
тиленовые углеводороды обладают основными свойствами, а пара¬
финовые углеводороды этих свойств не имеют. Поэтому во многих
случаях селективность разделяющих агентов обусловлена их спо¬
собностью образовывать комплексы разной степени устойчивости
с разделяемыми углеводородами. Углеводород, образующий более
стабильный комплекс, имеет меньшую относительную летучесть.
Существует ряд методов получения информации о стабильности
комплексов. Некоторые из них описаны в работе [82]. Относительно
простой способ основан на использовании данных спектроскопиче¬
ских исследований в видимой или ультрафиолетовой области
[82, 104]. Генкин [105] предложил для этой цели метод, основан¬
ный на использовании газо-жидкостной хроматографии. Во
многих случаях качественным показателем комплексообразованйя
является появление окрашивания, Так, иод образует синие рас-
78
творы с гептаном и четыреххлористым углеродом и коричневые
растворы с веществами, способными проявлять основные свой¬
ства — толуолом, ксилолом, мезитиленом.
В ряде работ были предложены полуэмпирическке методы оп¬
ределения влияния различных веществ на поведение компонентов
растворов. Так, в работе [53] предложено рассматривать избыточ¬
ную парциальную молярную энергию при бесконечном разбавлении
(RT In у0) как сумму отдельных членов, каждый из которых свя¬
зан с наличием характеристических групп в молекулах растворен¬
ного вещества и растворителя. Для монофункционального раство¬
ренного вещества RX в монофункциональном растворителе RfX'
(R h R7 — углеводородные радикалы, а X и X7 — функциональные
группы) возможны шесть попарных взаимодействий между входя¬
щими в эти молекулы группами, как это видно из приводимой
схемы:
Изменение составляющих, характеризующих каждое из этих
взаимодействий, в пределах гомологических рядов определяется
систематическим изменением групп RhX рассматриваемых пар
компонентов. Так, в простейшем случае, когда оба компонента —
углеводороды R-H и R7—Н, члены, учитывающие взаимодействия
а, Ь, с, е и f, равны нулю или очень малы. Описанная групповая
модель раствора предполагает, что вклад каждого взаимодействия
между двумя группами не зависит ни от других частей молекул,
ни от концентрации молекул, включающих эти группы, ни от лю¬
бых других молекул, присутствующих в растворе. Например, со¬
гласно групповой модели, среда гептилового спирта как раствори¬
теля равноценна эквимолекулярной смеси метилового спирта и
гексана. Исходя из этих допущений, для гомологических рядов
получено уравнение:·
igy^A + BJh. + £. + D {ni-n2)2 + L (I98)
ΛΪ2 ” I fl 2
где П\ и п2 — число атомов углерода в радикалах R и R7; А — ко¬
эффициент, зависящий от природы функциональных групп X и X7;
В — коэффициент, зависящий только от природы функциональной
группы растворителя X7; С — коэффициент, зависящий только от
природы функциональной группы растворенного вещества X; D —
коэффициент, не зависящий ни от X, ни от X7; F -1- коэффициент,
существенно зависящий только от природы функциональной группы
растворителя (буквенные обозначения коэффициентов соответ¬
ствуют обозначениям типов взаимодействий на приведенной выше
схеме).
79
Среднее отклонение расчетных значений от экспериментальных
для 44 исследованных серий составило 8%. Максимальные откло¬
нения коэффициентов активности углеводородов в таких полярных
веществах как фенол, фурфурол, этиловый спирт достигают 30—
50%. Особенно ненадежен метод Пьеротти для полифункциональ-
ных соединений. Причина этого заключается в несоблюдении прин¬
ципа аддитивности избыточной свободной энергии смешения
в таких случаях, а также в том, что не учитывается энтропийный
фактор.
Длй оценки коэффициентов активности по приведенному урав¬
нению необходимо экспериментально определить пять констант,
что является серьезным недостатком метода Пьеротти.
Дил показал [106], что если оценивать не коэффициенты актив¬
ности, а коэффициенты распределения углеводородов между по¬
лярным растворителем и гептаном, то вся исследуемая серия мо¬
жет быть охарактеризована с помощью не пяти, а трех эксперимен¬
тально определяемых констант. Кик отмечают Карлсон и Стюарт
[107]* уравнение Дила приводит к менее точным результатам, чем
уравнение Пьеротти. В работе [108] предложено учитывать не
только взаимодействие структурных групп, но и энтропийную со¬
ставляющую коэффициентов активности, для определения которой
рекомендовано уравнение Флори-Хаггинса [109]. Однако это урав¬
нение применимо ,лишь к системам со слабым взаимодействием
молекул. Для систем, содержащих полярные компоненты, оно при¬
водит к значительным погрешностям [110].
К полуэмпирическим методам определения коэффициентов ак¬
тивности относятся сравнительные методы, основанные на идеях,
развитых Карапетьянцем [111]. Эти методы были применены Са¬
харовым [112—114] для расчета величин удерживаемых объемов
в газо-жидкостной хроматографии с помощью зависимости
Ig Vi — P Ig Устанд + В (199)
где Vi — удерживаемый объем рассматриваемого вещества;
^станд — удерживаемый объем стандартного вещества на той же
неподвижной фазе; р и В — коэффициенты, постоянные для рас¬
сматриваемого компонента i.
Уравнение (199) дает возможность рассчитать удерживаемые
объемы рассматриваемого вещества на различных неподвижных
фазах, если известны удерживаемые объемы этого вещества на
двух неподвижных фазах и удерживаемые объемы стандартного
вещества на всех исследуемых неподвижных фазах. Для получе¬
ния точных результатов по этому методу нужно, чтобы стандарт¬
ное вещество по химической природе было по возможности ближе
к рассматриваемому.
Все рассмотренные полуэмпирические методы не отличаются
высокой точностью. Их ценность снижается также в связи с тем
что они могут быть применены лишь к частично исследованным
разделяющим агентам.
во
Корреляция селективности
с помощью уравнений Гаммета — Тафта
Бренстед и Педерсон [115], исследуя связь между ката¬
литическими константами кислот &на и их константами ионизации
/Сна, получили следующую зависимость
*НА“Л(*НА)в (200)
где А и а — константы, характеризующие каталитическую реак¬
цию.
Как известно, логарифм константы равновесия реакции пропор¬
ционален происходящему в ходе реакции изменению свободной
энергии:
Д(?нд AGtt д
1п*на =-~кГ и lnicHA (201)
Соответственно с этим
δ<^ηα “*а A^ha + cons^ (202)
т. е. изменение свободной энергии активации является линейной
функцией изменения энергии ионизации. Уравнения такого типа
получили название принципа линейности свободных энергий. Гам-
мет [116] применил аналогичную зависимость к различным реак¬
циям с участием мета- и пара-производных бензола, представив
ее в виде
In Zfe=Infc0 + р In ' (203)
Ao
где k и A0 — константы скорости или равновесия реакций соответ¬
ственно для замещенной и незамещенной бензойных кислот; К и
K0 — константы диссоциации замещенной и незамещенной бензой¬
ных кислот в воде; р — константа, учитывающая чувствительность
реакционной серии к влиянию заместителей.
Обозначив
Гп = σ (204)
Ao
можно преобразовать уравнение (203) к виду
Ig k = Igk0 + ρσ (205)
или
= ρσ (206)
где σ — константа Гаммета, учитывающая природу заместителя.
Выражение (206) называется уравнением Гаммета. В качестве
стандартной реакции Гамметом была выбрана реакция диссоциа¬
ции бензойных кислот в воде при 25° С. Для этой реакционной
серии было принято р = I, и уравнением Гаммета для стандартной
серии является выражение (204). В качестве стандартного заме¬
стителя был принят незамещенный фенил (^ΟβΗ3 = 0) и по извест¬
ным константам диссоциации мета- и пара-бензойных кислот рас¬
считаны соответствующие значения констант Гаммета σΜ и σπ
различных заместителей в мета- и пара-положениях. Константы
заместителей, по Гаммету, являются мерой изменения электронной
плотности на атоме углерода бензольного кольца, связанном с бо¬
ковой цепью, в которой находится реакционный центр.
Границы применимости принципа линейности свободных энер¬
гий были значительно расширены Тафтом [117], выдвинувшим сле¬
дующие два принципа: I) изменение свободной энергии реакции
аддитийно полиотношению к отдельным составляющим, учитываю¬
щим строение молекул (индукционный эффект, различные виды
сопряжения, стерические факторы и др.); 2) принцип линейности
свободных энергий должен применяться не ко всему изменению
свободной энергии, а к каждой составляющей. В общем виде урав¬
нение Тафта имеет вид
Ig k/kQ = ρ*σ* + 6 Es + h Δ/г 4- ψ (207)
где σ* — индукционные константы заместителей; р* — константа,
учитывающая чувствительность рассматриваемой реакции к индук¬
тивному влиянию заместителей; Es — стерические константы заме¬
стителей; б — коэффициент чувствительности реакции к стериче-
скому влиянию заместителей; h — параметр реакционной серии,
учитывающий гиперконъюгацию*; Δ/г — разность участвующих
в гиперконъюгации чисел атомов водорода в рассматриваемом и
стандартном заместителях; ψ — вклад π-электронного сопряжения
с реакционным центром. Уравнения Гаммета (206) и Тафта (207)
получили широкое применение для корреляции не только данных
о реакционной способности органических соединений, но также
многих химических и физико-химических свойств [119]. Если прева¬
лирующее значение имеет индукционный эффект, то уравнение
(207) переходит в уравнение Гаммета (206). Как показывает прак¬
тика [119], различные химические и физико-химические свойства
органических веществ хорошо коррелируются при использовании
индукционных констант Тафта а*, найденных-по данным о кине¬
тике щелочного и кислотного гидролиза сложных эфиров. Можно,
следовательно, полагать, что эти константы универсальны и харак¬
теризуют свойства заместителей, независимо от природы осталь¬
ной части молекул. В качестве стандартного заместителя выбрана
метильная группа, следовательно, о£н =0.
Поскольку электроотрицательные заместители ускоряют щелоч¬
ной гидролиз сложных эфиров, то более электроотрицательные за¬
местители имеют большие положительные значения а*, и наоборот.
* Гиперконъюгация— образование сопряжения между связями С—H и двой¬
ными связями C = C, тройными связями C=C или бензольным кольцом (а, π-со¬
пряжение), обусловленное смещением электронов в одинарных связях (см. [118]).
82
Таблица 10
Полярные (индукционные) константы σ * Тафта
Заместитель
Заместитель
(CH3)3N+
NO2
CH3SO2
CN
F
Cl
COOH
Br
CCl3
CF3
C3H5O
I
FsCH
CH3OOC
Cl2CH
(CH3)3
O2N-CH=CH
CH3CO
HO
CH3O
C3H5-CsC
HOOCCH2
ClCH2
HOOC-CH=CH
BrCH2
CF3CH2
Cl-CH=CH2
Cl2CH-CH=CH2
C3H5CO-N
/CH2-CH2
44CH2
-CH2
C3H5OCH2
ICH2
N=C-(CH2)2
C3H5-(OH)CH
CH2=CH
C2H5OCO-N;
CH2-CH2
4CH2-CH2
/CH2-CH2
°\
4CH2-CH2
CH3-CO-CH2
5,3*
3,9*
3,7*
3.6*
3,1 *
2,9*
2,9*
2,8*
2.65
2.6*
2,38
2,36*
2.05
2,00
1,940
1,90
1,704
1.65
1,55*
1,45*
1,35
1.05
1.05
1,012
1,000
0,92
0,900
0,882
0,86
0,850
0,85
0,80
0,765
0,653 **
0,70
0,67
0,60
C3Hs
HOCH2
R-CsC
CH3SO2CH2
NCCH2
Cl3C-CH=CH
FCH2
Cl(CH2)2
CH3CH=CH
CF3(CH2)2
NC(CH2)3
C3H5CH2
CH3CH = CH-CH2
CF3(CH2)3
C3H5(CH3)CH
H2C
I /CH
H2Cx
C3H5(CH2)2
NC(CH2)4
C3H5(C2H5)CH
C3H5(CH2)3
CH3+
CH3OCH2
O2N(CH2)2
H
C3H5CH=CH
(C3H3)2CH
Циклогексил
(CH3)3C-CH2
CH2-CH2
/
V
CH4
4 -CH2-CH2
(CH3)2CH
Циклопентил
C2H5(CH3)CH
(C2H5)2CH
/CH2
\г
CH,
4 CH2
CH2-CH2
CH2-CH2
0.600
0.555
1,30
1,32
1,300
1,188
1.10
0,385
0,360
0,32
0,30
0,215
0,13
0,12
0,11
0,11
0,080
0,06
0,04
0,02
0,000
0,520
0,50
0,490
0.410
0,405
-0,15
-0,165
-0,18
-0,190
-0,200
-0,210
-0,225
-0,24
-0,26
* Вычислено по формуле σ^·-2,8σ·.
** Эта величина для заместителя CH2-CH, по*видимому, несколько завышена Если
вычислить величину σ* для указанного заместителя путем комбинирования правил затухания
и аддитивности индукционного эффекта, получится величина 0,40.
83
Продолжение
Заместитель
σ *
I Заместитель
σ'*
(CH3)3SiCH2
XH2-CH24
сн/ ;сн—сн2
Xch2-Ch2/
CN(CH2)5
-0,26
-0,06
-0,06
C2H5+
H-C3H7
H-C4H9
H-C4H3
(CH3)3C-(CH3)CH
(CH3)3C
-0,100
-0,115
-0,125
-0,130
-0,28
-0,300
Так как выбор стандартного заместителя произволен, то численные
значения о* и даже их знак зависят от выбранного стандарта срав¬
нения. Зависимость величин σ* от строения заместителей характе¬
ризуется двумя закономерностями — правилом аддитивности и за¬
коном затухания индукционного эффекта. Правило аддитивности
может быть записано следующим образом:
* * *
orXiX2X3C = orX1CH2 + orX2CH2 + cfX3CH2 (208)
где Xi, X2 и Хз — заместители, связанные с атомом углерода.
В большинстве случаев правило аддитивности выполняется
весьма точно. Наблюдаются отклонения от аддитивности, особенно
при введении третьего заместителя, если Xb Х2» Хз — сильно элек¬
троотрицательные заместители, например, хлор или фтор.
Согласно закону затухания индукционного эффекта, введение
углерода (группы CH2) между электроотрицательным заместите¬
лем X и реакционным центром уменьшает влияние индукционного
эффекта первого на последний примерно в 2,8 раза:
orXCH2 β 0Xzt (209)
Если X — водород или предельный углеводородный радикал, то:
0XCH2 °»100 + 0X ± (21°)
Значения индукционных констант Тафта приведены в табл. 10.
Применение уравнения Гаммета (206) подробно рассмотрено
в работе [120], где приведен также обширный фактический мате¬
риал. В табл. 11 представлены заимствованные из работы [121]
сведения о значениях констант заместителей в мета-(ом) и пара-
(σπ) положениях. Практика показывает, что константы заместите¬
лей σ при наличии полярных эффектов сопряжения между заме¬
стителем и реакционным центром не всегда дают удовлетвори¬
тельную корреляцию опытных данных. В связи с этим возникает
необходимость специального учета указанного фактора. Соответ¬
ствующие опытные данные приведены в работе [121]. Для приме¬
нения уравнения Гаммета имеют существенное значение некоторые
84
Таблица 11
Константы заместителей в уравнении Гаммета
crM
σπ
Заместитель
по дан¬
ным
работы
Г120]
по дан¬
ным
работы
[122]
по дан¬
ным
других
работ
по дан¬
ным
работы
[120]
по дан¬
ным
работы
[122]
по дан¬
ным
Других
работ
CH3
—0,069
-0,069
-
-0,170
‘ -0,170
От-0,080
ДО-0,170
C2H5
-0,043
-0,07
—
-0,151
-0,151
—
C3H7
—
—
-0,126
__
—
CH(CH3)2
—
—
—
-0,151
-0,151
—
C4H9
—
—
-0,161
—
—
CH2CH(CH3)2
—
—
—
-0,115
—
—
CH(CH3)C2H5
—
—
—
-0,123
—
—
C(CH3)3
-0,120
-0,10
—
-0,197
-0,197
—
(CH2)2CH(CH3)2
—
—
—
0,225
—
—
C(CH3)2C2H5
—
—
— ■
-0,190
—
—
CF3
0,415
0,43
—
0,551
0,54
—
CCl3
—
0,407
—
—
0,454
CH2Cl
- —
' —
0,184
—
—
CHCl2
—
0,185
—
—
0,212
CH2CN
—
—
0,007
—
—
CH2CH2COOH
-0,027
—
-0,066
—
—
он
-0,002
0,121
-0,357
-0,37
—
OCH3
0,115
0,115
—
-0,268
-0,268
-0,361
OC2H5
0,150
0,1
—
-0,250
-0,24
—
OC3H7
—
0,1
—
-0,286
-0,25
—
OCH(CH3)2
—
0,1
—
-0,286
-0,45
—
OC4H9
—
0,1
—
-0,320
-0,32
—
OC5H11
—
0,1
—
-0,340
-0,34
—
O(CH2)5CH(CH3)2
—
—
-0,265
—
—
OCH2C5H5
—
—
-0,415
—
—
OC5H5
—
0,252
—
-0,028
-0,320
—
0“
-0,708
_
-0,519
—
—
OCOCH3
—
0,39
—
0,31
—
NH2
-0,161
-0,16
—
0,660
-0,66
—
NHCH3
-0,302
—
-0,592
-0,84
—
NHC2H5
-0,240
_ м
—
—
—
NHC4H9
-0,344
-
—
—
—
N(CH3)2
-0,211
—
-0,600
-0,83
—
NHCOCH3
—
0,21
—
-0,015
0,00
—
NHCOC6H5
0,217
■ —
0,078
—
—
NHNH2
-0,020
—
-0,550
—
—
NHOH
-0,044
—
—
-0,339
—
—
NH9
0,634
—
—
—
—
—
NH2CHj
0,958
—
—
—
—
—
NH2C2Hj
0,958
—
—
—
—
—
N(CH3)J
0,904
0,88
0,67
0,859
0,82
0,66-г· 1,11
Nj
-
—
1,7
—
. —
1,8 ±0,5
GOOH
0,355
0,37
_
0,265
0,45
___
COOCH3
0,315
__
0,436
COOC2H5
0,398
0,37
—
0,522
0,45
85
Продолжение
Заместитель
0M
σπ
по дан¬
ным
работы
[120]
по дан¬
ным
работы
[122]
по дан¬
ным
других
работ
по дан¬
ным
работы
1120]
по дан¬
ным
работы
[122]
по дан¬
ным*
других
работ
CONH2
0,280
—
CHO
0,355
—
0,382
0,216
—
—·
COCH3
0,306
0,376
0,306
0,516
0,502
—
COC6H5
—
—
0,459
—
—
CN
0,678
0,56
0,52
0,628
0,660
0,65
СОСГ
0,104
-0,1
—
0,132
0,0
—
NO2
0,710
0,710
—
0,778
0,778
—
NO
—
—
—
0,123
—
—
F
0,337
0,337
—
0,062
0,062
—
Cl
0,373
0,373
—
0,227
0,227
—
Br
0,391
0,391
—
0,232
0,232
—
I
0,352
0,352
—
0,276
0,18
0,27
IO2
0,70
0,70
—
0,76
0,76
—
SCH3
0,144
0,15
—
-0,047
0,0
—
SOCH3
0,551
0,52
—
0,567
0,49
0,73
SO2CH3
0,647
0,60
0,56
0,728
0,72
0,68
SCN
—
—
—
0,699
0,52
—
SeCN
—
—
—
0,664
—
—
B(OH)2
0,006
' —
—
0,454
—
—
Si(CH3)3
-0,121
—
-0,072
-0,07
—
Si(C2H5)3
_
—
—
—
0,0
—
CH2Si(CH3)3
-0,16
—
—
-0,21
—
C6H5
0,218
0,06
—
0,009
-0,01
—
N = N-C6H5
—
—
—
0,640
—
—-
CH=CH-C6H5
0,141
—
—
—
—
—
A5O3H
—
—
—
-0,019
-0,02
—
PO3H-
0,228
0,2
—
0,238
0,26
—
SO2
—
—
0,381
—
—
SO2NH2
—
0,46
0,55
0,621
0,57
0,62
S0"
—
0,05
0,31
-
0,09
0,37
3,4-(СН2)з
—
—
-
-0,259
-
—
3,4-(СН2)4
—
—
—
-0,477
—
—*
3,4-(СН)4
—
—
—
0,170
0,042
3,4-СН202
—
—
—
-0,159
—
—
Ge(CH3)3
—
—
—
’ —
0,0
—
Ge(C2H5)3
—
—
—
—
0,0
—
Sn(CH3)3
—
—
—
—
0,0
—
Sn(C2H5)3
—
—
—
—
0,0
—
SeCH3
—·
0,1
—
—
0,0
—
SC2H5
—
—
—
—
0,03
—
SCH(CH3)2
—
—
—
—
0,07
—
SH
—
0,25
—
—
0,15
—
SCOCH3
—
0,34
—
—
0,44
—
S(CH3)J
-
1,0
—
—
0,90
—
2-СН3СаН5
—
—
—
—
—
—0,016
2-НОСвН4
—
• —
—
—
—
0,003
2-СН3ОС3Н4
—
—
—
—
—
0,012
2-С1С3Н4
Л
0,047
86
Продолжение *
cfM
σπ
Заместитель
по дан¬
ным
работы
[120]
по дан¬
ным
работы
11221
по дан¬
ным
других
работ
по дан¬
ным
работы
[120]
по дан¬
ным
работы
[122]
по дан¬
ным
Других
работ
HC=C-
0,281
CH3CH = CH-
—
—
—
—
-0,043
%+н
-
2,1
-
-
2,3
\ю+н
-
2,3
-
-
-
правила аддитивности. Если в бензольном ядре имеется несколько
заместителей в мета- и пара-положениях или с реакционным цент¬
ром связаны симметрично несколько бензольных ядер, то может
быть использовано соотношение
IgWo-рЦ* (211)
т. е. в рассматриваемых случаях константы Гаммета для замести¬
телей складываются. Если несколько бензольных ядер связаны
с реакционным центром несимметрично, то
ig k/k0=2 Pff <212)
Интерполяционное уравнение Гаммета — Тафта было приме¬
нено Лейтманом и Гайле [123] для корреляции селективности орга¬
нических веществ по отношению к углеводородам различных клас¬
сов. Авторы исходили из расчленения селективности на физиче¬
скую и химическую составляющие. Физическая составляющая
учитывает действие ван-цер-ваальсовых сил. Химическая составляю¬
щая обусловлена образованием ненасыщенными углеводородами
я-комплексов с полярными веществами. Для выделения химиче¬
ской составляющей селективности введено понятие о гипотетиче¬
ском насыщенном углеводороде, физическое взаимодействие кото¬
рого с молекулами разделяющего агента такое же, как рассматри¬
ваемого ненасыщенного углеводорода. Логарифм коэффициента
активности последнего можно представить выражением
IgYa=IgYrH-X (213)
где Ya — коэффициент активности ненасыщенного углеводорода;
Υγη— коэффициент активности соответствующего ему гипотетиче¬
ского насыщенного углеводорода; X == Δ Igya-изменение коэффи*
циента активности ненасыщенного углеводорода, обусловленное
образованием я-комплексов.
Поскольку величина Algya является мерой изменения свобод¬
ной энергии при образовании я-комплекса к ней может быть
87
применено уравнение Гаммета — Тафта, и, поэтому, в результате
можно написать
где Σσ— сумма констант заместителей в молекуле разделяющего
агента.
Химической составляющей селективности является величина
lgYrn/Ya, которая в соответствии с соотношениями (213) и (214)
является линейной функцией суммы констант Гаммета для рас¬
сматриваемого ряда разделяющих агентов. Справедливость этого
была доказана [123] путем обработки опытных данных о найден¬
ных с помощью метода- газо-жидкостной хроматографии коэффи¬
циентах активности 10 углеводородов различных классов в смесях
со 100 различными полярными веществами. При расчете физиче¬
ской и химической составляющих селективности за гипотетический
насыщенный углеводород принимали нафтеновый углеводород,
имеющий такой же молярный объем, как и входящий в рассматри¬
ваемую систему ненасыщенный углеводород.
6 — метилциклогексан; 7 — этил-
циклогексан; 8 — бензол; 9 — то¬
луол; 10 — JK-KC и лол.
В качестве примера рассмотрим определение составляющих селективности
2,4-дихлорнитробензола в системе гексан — бензол.
Как видно из рис. 18, для углеводородов одного класса наблюдается линей¬
ная зависимость коэффициента активности углеводородов от его молярного объ¬
ема. Очевидно селективность 2,4-дихлорнитробензола по отношению к гексану в
Δ lgA = const -f σ
(214)
OJi
90 110 130 150 170 190
V1
ο as is
Рис. 18. Зависимость коэф¬
фициентов активности угле¬
водородов при бесконечном
разбавлении в 2,4-динитро-
хлорбензоле , от молярных
объемов углеводородов (Vi)
Рис. 19. Корреляция хими¬
ческой составляющей селек-
I— гексан; 2 —гептан; 3 —октан;
4 — нонан; 5—циклогексан;
при 60° С:
тивности 1ш{Угн1Уб) ПР0ИЗ"
водных бензола с электро-
фильными заместителями
константами Гаммета (Σσ).
Цифрами обозначены производ¬
ные бенаола в соответствии
с табл. 12.
системе гексан — бензол равна отрезку ас. Коэффициент активности гипотетиче¬
ского нафтенового углеводорода, имеющего такой же молярный объем как бен¬
зол отвечает ординате точки Ь, лежащей на прямой линии, изображающей зави¬
симость Ig v5 = f (V ι) для нафтеновых углеводородов. Химическая составляющая
селективности равна длине отрезка ab, а физическая составляющая—длине от¬
резка Ьс. Следует отметить, что различие коэффициентов активности парафино¬
вых и нафтеновых углеводородов, соответствующее отрезку Ьа (рис. 18) об¬
условлено различием в ван-дер-ваальсовых взаимодействиях этих углеводородов
с полярным веществом, главным образом, за счет индукционного эффекта. При
корреляции опытных данных химическую составляющую селективности сопостав¬
ляли с максимальным значением суммы констант Гаммета. Рис. 19 иллюстри¬
рует зависимость химической составляющей селективности различных производ¬
ных бензола с электрофильными заместителями от суммы констант Гаммета.
Определение суммы констант Гаммета поясним следующими примерами. В мо¬
лекуле нитробензола (на рис. 19,5) заместителем является группа NO2, для ко¬
торой в мета-положении σΜ = 0,710, а в пара-положении On= 0,778 (см. табл. 11).
Для корреляции принимается большее значение. В молекуле о-хлорнитробензола
имеются два заместителя ΝΟ2 и Cl. Для первого принято наибольшее значение
(Хп *= 0,778, отвечающее пара-положению, а для второго — σΜ = 0,373, отвечаю¬
щее мета-положению, что дает Σδ = 1,151. Для 2,4,6-тринитроэтилбензола при¬
нято для каждой из трех нитрогрупп σπ = 0,778, а для этильной группы σ =
= —0,07. Следовательно, Σσ = 3 · 0,778 — 0,07 = 2,264.
В табл. 12 приведены значения химической и физической со¬
ставляющих селективности различных производных бензола с элек¬
трофильными заместителями при 65° С по отношению к системам,
образованным бензолом соответственно с гексаном, гептаном и
октаном. Указанные величины сопоставлены с максимальными
значениями сумм констант Гаммета длй соответствующих замести¬
телей. В соответствии с изложенным выше, в системах, образован¬
ных определенным полярным веществом, бензолом и различными
парафиновыми углеводородами, химическая составляющая селек¬
тивности одинакова, а физические составляющие селективности
возрастают с увеличением размеров молекул парафиновых угле¬
водородов.
Возможность использования уравнения Тафта для корреляции
селективности алифатических разделяющих агентов была показана
в работе автора, выполненной совместно с Зарецким, Кононовым
и Подольняк [124], на примере системы тиофен — бензол. В каче¬
стве разделяющих агентов были испытаны этиленгликоль, диэти¬
ленгликоль, этилцеллозольв, метилцеллозольв и тетрагидрофурфу-
риловый спирт.
В алифатическом ряду полярные эффекты чаще всего являются
только индуктивными (в отличие от ароматических соединений).
Поэтому константы а* Тафта для заместителей потенциально
имеют более общий характер, чем константы σ Гаммета. Это отно¬
сится, в частности, к алифатическим гликолям с небольшим чис¬
лом метиленовых групп между группами ОН и к их простым эфи¬
рам, На реакционный центр этих соединений может оказывать
влияние, в основном, только индукционный эффект заместителей.
Влиянием других факторов внутримолекулярного взаимодействия
(стерический эффект, полярное и неполярное сопряжения,
89
Таблица 12
Селективность производных бензола по отношению к бинарным системам, образованным бензолом
с гексаном, гептаном и октаном, при 65°С
Соединение
Химиче¬
ская
составля¬
ющая
Y0
. ггн
ls~r
Бензол — гексан
Ig-
физиче-
ск ая
составля¬
ющая
доля
физиче¬
ской
составля¬
ющей,
%
Бензол — гептан
физиче¬
ская
составля
ющая
доля
физиче¬
ской
составля¬
ющей,
%
Бензол — октан
Ig ·
физиче¬
ская
состав¬
ляющая
доля
физиче¬
ской
состав¬
ляющей,
%
Нитромезитилен .
Бензофенон ....
Ацетофенон . . .
о-Нитроэтилбензол
я-Нитроэтилбензол
о-Нитротолуол . .
я-Нитротолуол . .
Нитробензол . . .
jw-Нитроанизол . .
о-Нитрохлорбензол
2-Метнл-6-этил-Н-окись
пиридина ....
N-Окись пиридина
2.4-Динитробенз альдегид
2.4-Динитрохлорбензол .
2,4,6-Тринитроэтилбензод
0,200
0,459
0,502
0,708
0,708
0,709
0,709
0,778
0,893
1,151
1,341
1,480
1,911
1,929
2,264
0,341
0,360
0,414
0,390
0,418
0,416
0,423
0,442
0,485
0,495
0,590
0,640
0,699
0,725
0,767
0,482
0,634
0,612
0,550
0,573
0,595
0,581
0,638
0,701
0,669
0,916
1,178
0,968
1,023
1,074
0,141
0,274
0,198
0,160
0,155
0,179
0,158
ОД 97
0,216
0,174
0,326
0,538
0,269
, 0,298
0,307
29.2
43.2
32.3
29,1
27.0
30.1
27.2
30,9
30.8
26,0
35.6
45.6
27.8
29,1
28,5
0,517
0,692
0,654
0,584
0,602
0,640
0,623
0,677
0,759
0,704
1,005
1,307
1,030
1,098
1,180
0,176
0,322
0,240
0,194
0,184
0,224
0,200
0,235
0,274
0,209
0,415
0,667
0,331
0,373
0,413
34.0
48.0
36,7
33.2
30.6
35.0
32.1
34.7
36.1
29.7
41.3
51.0
322
34.0
35.0
0,550
0,755
0,691
0,616
0,632
0,682
0,661
0,711
0,812
0,738
1,059
1,454
1,084
1,173
1,282
0,209
0,395
0,277
0,226
0,214
0,266
0,238
0,269
0,327
0,243
0,469
0,814
0,385
0,448
0,515
38.0
52.3
40.1
36.7
33.8
39.0
36.0
37.8
40.3
33.0
44.3
56.0
35,5
38.2
40.1
гиперконъюгация и др.) для этих соединений можно пренебречь.
Это относится также к влиянию внутримолекулярных водородных
связей, так как для алифатических гликолей и их простых эфиров
с небольшим числом связей С—С и С—О между гидроксильными
группами внутримолекулярные водородные связи довольно слабы
и для рассматриваемых в настоящей работе соединений равноцен*
ны [125].
Для примера рассмотрим систему бензол — тиофен. Разность молекулярных
объемов бензола и тиофена при 70 С составляет V б — Vt = 7,5 смъ1моль или
~8,0 объемн.%, т. е. молярные объемы достаточно близки, что позволяет пре¬
небречь энтропийным вкладом в селективность.
В системах тиофен — бензол — полярный растворитель вклад индукционной
и ориентационной составляющих ван-дер-ваальсового взаимодействия в селектив¬
ность незначителен, так как тиофен и бензол имеют близкие по величине диэлек¬
трические проницаемости εχ «= 2,76 и Be = 2,28, и при отсутствии дипольного мо¬
мента у бензола дипольный момент тиофена невелик — μτ ** 0,53£>. Вклад дис¬
персионной составляющей ван-дер-ваальсового взаимодействия в селективность,
в основном, определяется разницей в поляризуемости молекул разделяемых ком¬
понентов. Величина поляризуемости на единицу объема, рассчитанная по урав¬
нению Клаузиса — Мосотти, для тиофена составляет L1 = 11,9· IO-26 саг3, а для
бензола аб = 12,1 · IO-26 см~г. В связи с тем, что поляризуемости тиофена и бен¬
зола очень незначительно отличаются друг от друга, вкладом дисперсионной со¬
ставляющей в селективность можно пренебречь.
Таким образом, в системах тиофен — бензол — полярное вещество можно
полностью пренебречь различием в физическом взаимодействии разделяемых
компонентов с полярным веществом и оценить его селективность, исходя из хи¬
мических сил взаимодействия.
Компоненты рассматриваемой системы — и бензол, и тиофен — имеют во внеш¬
ней электронной оболочке π-электроны, которые способны поляризоваться при
введении соединений с электрофильными группами, образуя при этс&т π-ком¬
плексы различной стабильности. Следовательно, в данной системе селективность
алифатических растворителей определяется стабильностью π-комплексов.
Селективность полярных веществ сравнивалась по величинам логарифма от-,
ношения предельных значений коэффициентов активности разделяемых компо¬
нентов, которые определялись экстраполяцией приведенных в работе [126] дан¬
ных о фазовом равновесии жидкость — пар в трехкомпонентных системах.
Для корреляции селективности разделяющих агентов были использованы
значения индукционных констант о* Тафта для соответствующих заместителей.
В качестве реакционного центра для каждого из рассматриваемых разделяющих
агентов принималась группа —О—(CH2)2—ОН, а вся оставшаяся часть моле¬
кулы рассматривалась как заместитель.
Для тетрагидрофурфурилового спирта индукционный , эффект заместителя
оценивался как для алифатического соединения, что допустимо, учитывая его
строение.
/х·
При наличии нескольких заместителей типа —С—X2 индукционные константы
4X3
Тафта рассчитывались по правилу аддитивности (208). В тех случаях, когда ме-
*ду заместителем и реакционным центром находится группа —CH2—, индук-
шонные константы рассчитывались по правилу затухания индукционного эф¬
фекта (209). Значения индукционных констант а*, а также величины Igy
для соответствующих полярных растворителей приведены в табл. 13. График
зависимости Ig у™/у™ — f (в*) приведен на рис. 20.
Как видно из рис. 20, точки хорошо ложатся на прямую линию. Коэффи¬
циент корреляции г = 0,98,
91
Таблица 13
Предельные значения селективности разделяющих агентов
при 70° С и вычисленные индукционные константы от *
Тафта Для соответствующих заместителей
в системе бензол тиофен
Разделяющий агент
Предельные
значения
селективности
S00 = Y
OO
I Υ6
Ig
Υ°°
yT
о *
Этиленгликоль
1,62
0,21
+0,49
Диэтиленгликоль
1,55
0,19
+0,198
Этилцеллозольв
1,48
0,17
— 0,1
Метилцеллозольв .
1,49
0,174
0
Тетрагидрофурфуриловый спирт . .
1,44
0,158
-0,24
Адекватность модели проверена с использованием F-критерия Фишера.
Среднеквадратичное отклонение экспериментальных значений от вычисленных по
данному уравнению составляет Si = 0,0143. Эта величина незначительно превы-
« шает среднее значение среднеквадратичных по-
Ig It грешностей эксперимента, равное S2 = 0,01415.
У τ , Следовательно, корреляция выполняется впол¬
не удовлетворительно.
Как видно из данных таблицы 13, наиболь¬
шую величину селективности из рассматривае¬
мых алифатических соединений имеет этилен¬
гликоль (S°° = 1,62). Селективность диэтилен-
гликоля меньше и равна S00 = 1,55.
Принимая во внимание, что потенциал
ионизации тиофена (основность) (I1 = 8,95 эв)
несколько меньше, чем бензола (Iб — 9,245 эв),
можно предполагать, что тиофен дает с по¬
лярными веществами, содержащими электро-
фильные группы, более стабильные комплексы,
чем бензол. Это предположение дает возмож¬
ность объяснить уменьшение относительной ле¬
тучести тиофена в тройных системах тиофен—
бензол — полярный растворитель по сравнению
с относительной летучестью тиофена в бинар¬
ных системах с бензолом.
В связи с вышеизложенным следует счи¬
тать, что тиофен дает с этиленгликолем более
стабильные комплексы, чем с диэтиленгликолем. Если учесть, что индукционные
константы а* Тафта для соответствующих заместителей, влияющих на реак¬
ционный центр гликолей, составляют для этиленгликоля — 0,49, а для диэтилен-
гликоля— 0,198, то вполне очевидно, что константы о* Тафта характеризуют
сродство к электрону (кислотность) разделяющих агентов. ,
Следовательно, при оценке селективности полярных разделяю¬
щих агентов для системы, состоящей из двух компонентов с π-элек¬
тронами во внешней электронной оболочке, необходимо исходить
из донорно-акцепторного механизма (или кислотно-основйого ха¬
рактера) межмолекулярного взаимодействия, причем этот специ¬
фический тип взаимодействия отвечает образованию комплексов
между указанными соединениями.
0,1-
-0,3 -0,1 О 6,1 0,3 OS
σ*
Рис. 20. Корреляция селектив¬
ности Ig (Υβ/γ?) некоторых ве¬
ществ по отцошению к системе
бензол — тиофен константами
Тафта:
I — этиленгликоль; 2 — дизтиленгли-
коль; 3 — этилцеллозольв; 4 — метил¬
целлозольв; 5 — тетрагидрофурило-
вы й спирт.
92
ПРИМЕНЕНИЕ МИНЕРАЛЬНЫХ ВЕЩЕСТВ
В КАЧЕСТВЕ РАЗДЕЛЯЮЩИХ АГЕНТОВ
ПРИ ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
В процессах экстрактивной ректификации наиболее
удобно применять в качестве разделяющих агентов вещества, яв¬
ляющиеся при обычных условиях жидкими. Поэтому в практике
наибольшее распространение получили жидкие органические раз¬
деляющие агенты, и из неорганических веществ — вода и в значи¬
тельно меньшей степени аммиак, двуокись серы и некоторые дру¬
гие соединения. Однако не во всех случаях удается подобрать
подходящие разделяющие агенты. Например, в качестве последних
в процессах абсолютирования этилового спирта путем азеотропной
ректификации используются вещества (углеводороды или их про¬
изводные) , повышающие относительную летучесть не спирта,
а воды, причем в такой степени, что в процессе ректификации она
становится более летучим компонентом. Между тем температура
кипения воды значительно выше температуры кипения этилового
спирта. Поэтому весьма желательно изыскание таких разделяющих
агентов, которые повышали бы его относительную летучесть.
Однако подобрать жидкий разделяющий агент, удовлетворяющий
этому требованию, не удается. Подобные обстоятельства побудили
исследователей обратиться к изысканию твердых растворимых
веществ, улучшающих разделение смесей методами дистилляции
и ректификации.
Давно уже известно применение некоторых солей для выделе¬
ния органических веществ из растворов путем высаливания, т. е.
уменьшения растворимости. Явление высаливания изучалось боль¬
шим числом исследователей. Выяснилось, что соли могут не
только понижать, но и повышать растворимость органических ве¬
ществ, т. е. наряду с высаливанием может происходить и
всаливание вещества. Такое влияние твердых растворимых ве¬
ществ на поведение компонентов растворов предопределяет воз¬
можность их применения в процессах дистилляции и ректифика¬
ции. Процессы экстрактивной ректификации, в которых исполь¬
зуются твердые разделяющие агенты, в частности соли, получили
название процессов солевой ректификации.
Возможность практического использования метода солевой ректификации от¬
мечалась в литературе Марийе [127, 128], Логиновым и Дзиркалом [129] и дру¬
гими [123—134]. Испытывалось главным образом применение солей для процесса
абсолютирования этилового спирта [128, 129, 131, 132, 134—140]. В последнее
время интерес к методу солевой ректификации резко возрос благодаря ее успеш¬
ному применению для решения ряда сложных практических задач. Существенно
расширились и области применения этого метода. Систематическое изложение
современного состояния теории и практического использования солевой ректифи¬
кации содержится в монографии [141]. Поэтому здесь ограничимся лишь рас¬
смотрением наиболее важных вопросов, связанных с выбором твердых веществ
в качестве разделяющих агентов.
Прежде всего необходимо отметить связь, существующую ме¬
жду растворимостью и относительной летучестью компонентов
93
растворов. Применительно к системам, образованным неэлектро¬
литами, эта связь была исследована в работе [36], в которой пока¬
зано, что при прибавлении к бинарной смеси вещества, ограничен¬
но смешивающегося с компонентами этой смеси, возрастает
относительная летучесть компонента, имеющего меньшую взаим¬
ную растворимость с добавляемым веществом. Аналогичная зако¬
номерность распространяется на тройные и многокомпонентные
системы, одним из компонентов которых является твердое веще¬
ство. Связь между растворимостью и относительной летучестью
вытекает также из полной аналогии закономерностей, описываю¬
щих влияние соли на растворимость и относительную летучесть
компонентов. Влияние твердого вещества на растворимость выра¬
жается известным уравнением Сеченова
lg^" - (215'
где С и Cp — концентрации высаливаемого компонента в насыщен¬
ном растворе соответственно без соли и с солью; хр — молярная
доля твердого вещества в растворе; Ke— константа.
Как показано в работе [142], а также следует из имеющихся
опытных данных [141], влияние твердого растворимого вещества
на относительную летучесть бинарного растворителя выражается
уравнением
Ig-^- = Atfp (216)
где Otp и а — коэффициенты относительной летучести компонентов
(при их одинаковом относительном содержании) соответственно
в присутствии и в отсутствие растворенного твердого вещества;
А — константа.
На рис. 21 и 22 зависимость (216) иллюстрируется на примере
систем муравьиная кислота — вода, а также пиридин — вода с раз¬
личными неорганическими соединениями.
Из сопоставления уравнений (215) и (216) можно заключить,
что увеличению относительной летучести одного из компонентов
растворителя соответствует уменьшение его растворимости в ре¬
зультате прибавления к смеси твердого вещества.
Линейная зависимость Igap/a от л;р между прочим, вытекает
из уравнения (128) при условии постоянства относительного содер¬
жания летучих компонентов раствора (х\ == const) или при усло¬
вии, ЧТО А12 <С Aip.
Детальное исследование показывает, что не всегда соль, ха¬
рактеризующаяся большим различием растворимости в компонен¬
тах заданной смеси, обусловливает большее изменение их относи¬
тельной летучести. Так, И. Н. Ципарис [142] выяснил следующую
последовательность увеличения растворимости указанных ниже
соединений в уксусной кислоте: (CaHg^NI <CHaCGONa<
<СНзСО0К<НС0О1С.
94
Ё соответствий с этим следовало ожидать увеличений относи¬
тельной летучести уксусной кислоты в водных растворах от пер¬
вого члена этого ряда к последнему. Однако по данным о равно¬
весии между жидкостью и паром указанные соединения распола¬
гаются в ряд: (C2H5)4NI<CH3COOK<HCOOK<CN3COONa.
Несмотря на отсутствие прямой количественной связи между
растворимостью твердого вещества в компонентах растворителя
и его влиянием на относительную летучесть последних, данные
о растворимости весьма удобны для выбора разделяющих агентов.
Ig Zs
3 Ot
Рис. 21. Данные о равновесии
между жидкостью и паром в
системах, образованных му¬
равьиной кислотой, водой и
солями:
Xr — относительная концентрация
муравьиной кислоты (без учета
соли), мол. %: / — MgCI2, Xf ** 8,9:
2 -CaCI2, JCi «8,9; 3 - NaCI, xf - Ъ,7\
4 -NaHCO3, х'«8,9.
Hs'
XptMOA. %
Рис. 22. Данные о равновесии между
жидкостью и паром в системах, обра¬
зованных пиридином, водой и неорга¬
ническими* веществами:
1 - · - K2SO4; ▲ - LI2SO4; О - Na2SO4;
2 -A-MgSO4; X-(NH4)2SO4; 3 - ® - CaCl2;
4-0 -NaCl; S-M-MgCI2.
При этом нужно руководствоваться правилом, что при прибавле¬
нии к раствору твердого вещества возрастает относительная лету¬
честь того компонента, в котором это вещество хуже растворимо.
При выборе твердых веществ в качестве разделяющих агентов
полезны данные о температурах кипения растворов рассматривае¬
мого вещества в компонентах заданной смеси. Если раствор
твердого вещества в одном компоненте имеет более высокую тем¬
пературу кипения, чем раствор такого же состава во втором
компоненте, то относительная летучесть последнего при прибавле¬
нии этого твердого вещества будет ^увеличиваться. Это связано
с тем, что большему повышению температуры кипения раствора
по сравнению с растворителем соответствуют большие отрицатель¬
ные (или меньшие положительные) отклонения от идеального по¬
ведения.
95
* Влияние твердого растворенного вещества (например, соли) на
поведение составных частей растворителя зависит от многих фак¬
торов: от химической природы и размеров анионов и катионов,
образующих соль, от природы и состава компонентов смешанного
растворителя, от температуры и т. д.[142].
На основании анализа можно сделать следующие рекоменда¬
ции о выборе твердых веществ в качестве разделяющих агентов.
1. По свойствам заданной смеси и ее составу с учетом требо¬
ваний к чистоте продуктов разделения выясняется, какого типа
разделяющий агент целесообразно использовать — высаливатель
или всаливатель менее полярного компонента смеси.
2. При использовании высаливателя выбирают соли с наиболь¬
шим значением энергии сольватации ионов. В качестве всаливате-
лей выбирают соли, ионы которых имеют большие размеры, низ¬
кую валентность и малую энергию сольватации. Желательно, чтобы
в состав соли входил радикал одноименный со всаливаемым ком¬
понентом (например, для всаливания муравьиной кислоты HCOOH
можно применять муравьинокислый калий НСООК).
3. Сопоставляя соли с ионами одинаковой валентности и ана¬
логической электронной структуры, предпочтение следует отдавать
высаливателям с наибольшими значениями Э = Z2Ir и Э/К' (где
2 — валентность иона; г — его радиус; К! — величина ковалентости,
равная разности потенциала ионизации атома и энергии гидрата¬
ции иона).
4. При выборе высаливателей (всаливателей), в первую оче¬
редь, следует остановиться на той соли, которая хуже (лучше)
растворяется в высаливаемом (всаливаемом) менее полярном
компоненте разделяемой смеси.
5. В качестве разделяющего агента следует выбирать ту соль,
температура кипения раствора которой в менее летучем компо¬
ненте разделяемой смеси при одинаковой молярной концентрации
соли наиболее высокая.
6. При сопоставлении разделяющих агентов необходимо учи¬
тывать требования технологии: стоимость, доступность, коррозион¬
ную активность, условия регенерации соли и др.
Технологическое оформление процессов экстрактивной ректи¬
фикации с применением твердых разделяющих агентов рассмат¬
ривается далее (см. стр. 247).
СВЯЗЬ МЕЖДУ РАСТВОРИМОСТЬЮ
И ЭФФЕКТИВНОСТЬЮ РАЗДЕЛЯЮЩИХ АГЕНТОВ.
ВЫБОР КОМБИНИРОВАННЫХ
РАЗДЕЛЯЮЩИХ АГЕНТОВ
ДЛЯ ПРОЦЕССОВ ЭКСТРАКТИВНОЙ ректификации
При выборе разделяющих агентов для процессов экст¬
рактивной ректификации часто приходится сталкиваться с тем, что
испытуемые вещества ограниченно смешиваются с одним или не¬
сколькими компонентами заданной смеси.
96
В некоторых случаях ограниченная взаимная растворимость
компонентов заданной смеси и разделяющего агента является
следствием добавок к последнему вещества, плохо смешивающе¬
гося с компонентами исходной смеси. Например, для разделения
смесей углеводородов с помощью экстрактивной ректификации
в качестве разделяющих агентов используются смеси полярных
органических веществ с водой. Этим достигается понижение темпе¬
ратуры разделяющего агента и повышение его селективности.
Вопрос о связи между растворимостью и эффективностью разде¬
ляющих агентов рассмотрен в работе [143]. Пользуясь уравнением
(123) был проанализирован ход зависимости величины Ig αρ/α
от концентрации разделяющего агента для характерных случаев
его ограниченной взаимной растворимости с одним или обоими
компонентами исходной бинарной системы. Для бинарных систем
с ограниченно смешивающимися компонентами весь концентра¬
ционный интервал разделяется на три области:
1) область гомогенных растворов с преимущертвенным содер¬
жанием первого компонента;
2) область гомогенных растворов с преимущественным содер¬
жанием второго компонента;
3) область совместного существования двух фаз.
При расчете функций Ф для таких систем по данным о раство¬
римости принималось, что в первой и второй областях зависимости
коэффициентов активности компонентов от состава смесей симмет¬
ричны, т. е. растворы ведут себя IfaK регулярные.
Зависимости lgap/a — f(xp) для систем различных типов при¬
ведены на рис. 23. Кривая I (рис. 23, а) соответствует гипотетиче¬
скому случаю, когда разделяющий агент образует с одним из ком¬
понентов заданной смеси идеальную систему, а с другим не сме¬
шивается. Кривая 2 отвечает сочетанию идеальной и регулярной
систем, кривые 3 и 3'—регулярной с бесконечно малой взаимной
растворимостью компонентов, а кривые 4 и 4' — двум регулярным
системам с различной степенью неидеальности. Для систем с огра¬
ниченной взаимной растворимостью компонентов возможно множе¬
ство вариантов с различными границами расслаивания. Резуль¬
таты расчетов для нескольких характерных случаев представлены
на рис. 23, бив. Как видно, получаются различные зависимости
Ig ap/a=f(Xp) для систем разных типов. Если один или оба ком¬
понента образуют с разделяющим агентом расслаивающуюся си¬
стему (рис. 23,6 и в), эта зависимость имеет характерный S-образ¬
ный ход. В этих случаях в области средних концентраций разде¬
ляющего агента его селективность изменяется мало, а в области
больших концентраций — резко возрастает. Если же разделяющий
агент образует с компонентами заданной смеси системы с одно¬
родной жидкой фазой, то указанная зависимость имеет ход, близ¬
кий к линейному (рис. 23, а, кривые 2, 4 и 4'). Очевидно, наиболь¬
шее увеличение относительной летучести имеет место в том слу¬
чае, когда разделяющий агент образует с компонентами заданной
4 Зак, 917
97
смеси бинарные системы, наиболее отличающиеся друг от
друга.
С уменьшением взаимной растворимости прогиб кривых
Igotp/α =/(Яр) увеличивается, захватывая все большую область
концентраций. Соответственно с этим значительное увеличение от¬
носительной летучести наблюдается в области все более высоких
концентраций разделяющего агента (рис. 23, в, кривые 2—4).
вающаяся — регулярная
(Л =0,5), 3' — расслаиваю¬
щаяся— регулярная (Л= I);
4 — регулярная (Л « Не¬
регулярная (Л =0,5), 4
регулярная (Л = I) — ре¬
гулярная (А = 0,8).
б — Системы: I — расслаи¬
вающаяся — регулярная
(Л= I); 2 — с ограничен¬
ной взаимной раствори-
(/ //
xI =* 0,035; Jtj =*
= 0,965) — регулярная
(Л = I); 3 — с ограниченной
взаимной растворимостью
(л I = 0,05; = 0,9δ) — ре¬
гулярная (Л= I); 4—с огра¬
ниченной взаимной ра¬
створимостью = 0,05;
О I о
Xp. МОЛ %
■ 0,965
и-;·
0,10;
■ 0,80); 3 - то же
Xp4 МОЛ Ус
Рис. 23. Зависимость
эффективности разде¬
ляющего агента
Ig (сЕр/α) от его со¬
держания в смеси Xp
для тройных систем
с различными соче¬
таниями бинарных си¬
стем: компонент за¬
данной смеси —раз¬
деляющий агент.
а —Системы: / — расслаи¬
вающаяся — идеальная;
2 — регулярная (Л = I) —
идеальная; 3 — расслаи-
»0,9θ) -
- 0,035; х
0,035;
0,965) - (х[ =
0,965
0,05; х
регулярная
(Л= I); 5 —с ограничен¬
ной взаимной растворимо¬
стью =>0,10; Xj=0,90) —
регулярная (Л=>1); 6 — с
ограниченной взаимной
растворимостью *=0,10;
X1 = 0,8θ) — регулярная
(Л= I).
в — Системы: I — расслаи¬
вающаяся регулярная
(Л = I); 2 — обе системы с
ограниченной взаимной
растворимостью ^x^=0,035;
δ) — (jCj =°,1°; xi = 0,9°); 4-1
0,92).
Рассмотренным вариантам различных сочетаний бинарных си¬
стем с некоторой степенью приближения отвечают реальные си¬
стемы, встречающиеся в практике экстрактивной ректификации.
Рассмотрим несколько углеводородных систем с полярными разделяющими
агентами. Линейная зависимость lgap/a = /(xp) наблюдается в системах три-
метилэтилен — изопрен — разделяющий агент, когда в качестве последнего ис¬
пользуется ацетонитрил или диметилформамид, которые полностью смешиваются
с обоими углеводородами. Эти системы соответствуют сочетанию 4 на рис. 23, а.
Вогнутые кривые получаются в системах изопентан — триметилэтилен — разде¬
ляющий агент, в которых последний ограниченно смешивается с изопентаном.
98
Весьма характерно изменение селективности диметилформамида при прибав¬
лении к нему воды по отношению к смесям углеводородов: изопентан — триметил-
этилен и триметилэтилен — изопрен. Сопоставление данных о взаимной раствори¬
мости ,углеводородов и водного диметилформамида с данными о равновесии ме¬
жду жидкостью и паром показывает, что по мере увеличений содержания воды
и обусловленного этим уменьшения взаимной растворимости углеводородов и
разделяющего агента форма кривых Ig αρ/α ~ дхр) все больше отклоняется от
линейной. При этом прогиб кривых возрастает, захватывая все большую область
концентраций разделяющего агента. Селективность последнего по мере увеличе¬
ний добавок воды понижается в области средних и повышается в области высо¬
ких концентраций.
Изложенные закономерности могут быть использованы для
выбора комбинированных разделяющих агентов и определения
условий их применения в процессах экстрактивной ректификации.
В тех случаях, когда основной компонент комбинированного
разделяющего агента полностью смешивается со всеми вещества¬
ми, подлежащими разделению, или область ограниченной взаим¬
ной растворимости с некоторыми из них мала, добавка к нему
компонента с малой растворимостью в указанных веществах, на¬
пример воды, повышает эффективность разделяющего агента в
области высоких концентраций, обычно применяемых в процессах
экстрактивной ректификации. Если же взаимная растворимость
основного компонента разделяющего агента и веществ, образую¬
щих заданную смесь, относительно мала, то добавка к нему ком¬
понента с еще меньшей растворимостью с указанными веществами
нецелесообразна.
СРАВНИТЕЛЬНАЯ ОЦЕНКА
МЕТОДОВ ВЫБОРА РАЗДЕЛЯЮЩИХ АГЕНТОВ
И НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ УКАЗАНИЯ
Как было показано, методы выбора разделяющих аген¬
тов основываются на сравнительной оценке степени неидеальности
бинарных систем, образованных компонентами заданной смеси
и предполагаемым разделяющим агентом. Следовательно, наибо¬
лее надежными надо считать те методы, которые позволяют с наи¬
большей достоверностью судить о характере и величине отклоне¬
ний от закона Рауля в указанных бинарных системах. Предпочти¬
тельны методы, базирующиеся на использовании свойств
растворов, в первую очередь таких, как температуры кипения сме¬
сей, составы и температуры кипения азеотропов и растворимость.
Как будет показано ниже, по значениям этих свойств можно не
только дать сравнительную оценку степени неидеальности соответ¬
ствующих бинарных систем, но также приближенно рассчитать
условия равновесия в них.
Весьма эффективен и удобен выбор разделяющих агентов с по¬
мощью газо-жидкостной хроматографии в связи с широким при¬
менением этого метода в исследовательских и заводских лабо¬
раториях.
4*
99
Сопоставляя различные методы выбора разделяющих агентов,
необходимо иметь в виду, что все свойства растворов взаимосвя¬
заны и их значения определяются свойствами компонентов и ин¬
тенсивностью их взаимодействия друг с другом. Поэтому о харак¬
тере отклонений от идеального поведения можно судить не по од¬
ному, а по ряду свойств. Так, к заключению о пригодности воды
в качестве разделяющего агента для системы этиловый спирт —
этилацетат можно прийти, основываясь на том, что смеси этилаце¬
тата и воды имеют более низкие температуры кипения, чем такого
же состава смеси этилового спирта и воды. К этому же выводу
можно прийти, основываясь на том, что азеотроп этилацетат —
вода имеет более глубокий минимум температуры кипения, а так¬
же принимая во внимание наличие ограниченной взаимной раство¬
римости в системе этилацетат — вода, в противоположность систе¬
ме этиловый спирт — вода. Все методы выбора разделяющих аген¬
тов по свойствам растворов практически равноценны. Выбор того
или иного метода в каждом конкретном случае определяется
степенью полноты имеющихся данных о свойствах растворов и
трудностью их экспериментального определения.
Учитывая, что при современном состоянии теории растворов за¬
труднительно судить о величине отклонений бинарных систем от
закона Рауля по свойствам образующих их отдельных веществ,
методы выбора разделяющих агентов по’ свойствам компонентов
могут использоваться лишь для ориентировочных качественных
предсказаний.
Для выбора разделяющего агента может быть рекомендован
следующий путь. Прежде всего нужно рассмотреть данные о свой¬
ствах компонентов смеси, подлежащей разделению, а также усло¬
вия равновесия между жидкостью и паром, чтобы выяснить огра¬
ничения относительно химической совместимости разделяющих
агентов, и определить основные требования к ним с учетом степени
неидеальности заданной смеси. Затем следует проанализировать
данные о равновесии между жидкостью и паром [31], об азеотроп¬
ных смесях [45].и растворимости [42, 43] в системах, образованных
компонентами заданной смеси или их гомологами и различными
веществами. Такое рассмотрение часто позволяет выявить критерии
сравнительной оценки степени неидеальности в системах, образо¬
ванных рядом соединений, которые представляют интерес в каж¬
дом конкретном случае. Таким путем были установлены некоторые
важные в практическом отношении закономерности, например, что
полярные вещества в наибольшей степени увеличивают относи¬
тельную летучесть углеводородов с наибольшим отношением ато¬
мов H : С в молекуле. Если соответствующие данные о свойствах
растворов отсутствуют или их недостаточно, то, руководствуясь
представлениями о. полярности, о водородной связи или образова¬
нии π-комплексов, следует наметить классы соединений, которые
интересно испытать в качестве предполагаемых разделяющих аген¬
тов. Это испытание заключается в определении одного или не¬
100
скольких свойств растворов исходных компонентов и намеченных
к испытанию веществ. В качестве такого свойства желательно при¬
нять растворимость или температуру кипения, весьма удобные
в экспериментальном отношении. В некоторых случаях, особенно
при выборе разделяющего агента для процесса азеотропной рек¬
тификации, прибегают к определению свойств азеотропов. По по¬
лученным данным производится сравнительная оценка испытанных
веществ. Следует отметить, что такая оценка на основании указан¬
ных данных может быть достаточно достоверной лишь в тех слу¬
чаях, когда компоненты заданной смеси достаточно сильно разли¬
чаются по химической природе. Если же это отличие мало, необхо¬
димо дополнительно определить равновесие между жидкостью и
паром в нескольких точках бинарных систем, состоящих из компо¬
нентов заданной смеси и предполагаемого разделяющего агента,
или определить значения а заданной смеси в присутствии послед¬
него.
Для выбора и предварительной оценки эффективности разде¬
ляющих агентов всегда желательно определить методом газо¬
жидкостной хроматографии коэффициенты относительной летучести
для разбавленных растворов компонентов заданной смеси в разде¬
ляющем агенте. Методика такого определения была описана выше.
При сравнительной оценке различных разделяющих агентов
учитываются, естественно, технико-экономические факторы — стои¬
мость, доступность, пригодность в коррозионном отношении, токсич¬
ность, пожароопасность и др. Кроме того, разделяющие агенты
должны образовывать азеотропы с компонентами, которые в про¬
цессе ректификации отгоняются в виде дистиллата.
АЗЕОТРОПНЫЕ СМЕСИ
УСЛОВИЯ ОБРАЗОВАНИЯ
И ХАРАКТЕРИСТИКА АЗЕОТРОПНЫХ СМЕСЕЙ
Образование азеотропов оказывает определяющее влия¬
ние на условия разделения жидких смесей методами дистилляции
и ректификации. В связи с этим явление азеотропии явилось объек¬
том многочисленных экспериментальных и теоретических исследо¬
ваний. Характеристика, номенклатура и1 классификация различных
азеотропных смесей подробно описаны в книге Свентославского
[144]. Поэтому в настоящей работе эти вопросы рассматриваются
лишь в той степени, в какой это необходимо для понимания даль¬
нейшего изложения.
Свойства бинарных азеотропных смесей в самом общем виде
устанавливаются законом Коновалова. Согласно этому закону точ¬
кам максимума или минимума на кривых, изображающих зависи¬
мость давления паров смесей от их состава, отвечают растворы,
состав которых одинаков с составом равновесного пара. Сторонкин
101
показал [14, 145], что этот закон соблюдается не только в бинар¬
ных, но и в многокомпонентных системах, а экстремуму темпера¬
туры всегда соответствует противоположный экстремум давления.
Однако равенство составов равновесных паровой и жидкой фаз не
обязательно соответствует экстремуму температуры или давления,
как это имеет место в бинарных системах. Это обусловлено гораздо
более сложными соотношениями между парциальным и общим
давлениями паров и составами фаз в многокомпонентных системах
по сравнению с бинарными.
Связь между числом и типом особых точек в трехкомпонентных
системах в общем виде определяется так называемым правилом
азеотропии [146], подробно рассматриваемым ниже. Это правило
устанавливает взаимосвязь числа вершин, отвечающих чистым ком¬
понентам, а также бинарных и тройных азеотропных точек в зави¬
симости от характера поверхности, давления паров или температур
кипения в рассматриваемой системе. Ясно, что с увеличением
числа компонентов в системе, такая взаимосвязь существенно
усложняется.
Необходимо иметь в виду еще одно обстоятельство. Во всех
прогнозах обычно принимается, что в бинарной системе возможен
один азеотроп — положительный или отрицательный. Соответ¬
ственно с этим принимается, что и в тройной системе может обра¬
зовываться один азеотроп. Между тем, недавно появилось сообще¬
ние [147] о бинарной системе бензол — перфторбензол, в которой
имеются два азеотропа — положительный и отрицательный. Как
показывает анализ такое положение возможно при условии S-об¬
разной формы зависимости неидеальной доли изобарного потен¬
циала смешения от состава бинарных смесей, обусловливающей
наличие экстремальных точек на кривых зависимости коэффициен¬
тов активности компонентов от состава. При этом в тройной си¬
стеме, включающей такую бинарную, должно быть более одного
тройного азеотропа. Такие системы на практике редки, но воз¬
можны. Поэтому установление строгих закономерностей, опреде¬
ляющих условия образования азеотропных смесей, особенно много¬
компонентных, представляет большие трудности.
Бинарные системы
Выше было показано, что образование азеотропа яв¬
ляется следствием отклонения системы от идеальности. Характер
зависимости температуры кипения и состава пара от состава
жидкости в бинарных системах, имеющих положительный и отри¬
цательный азеотропы, иллюстрируется рис. 24. Жидкость, состав
которой находится в области до азеотропной точки, в системах
с положительными азеотропами находится в равновесии с паром,
содержащим больше (чем раствор) того компонента, концентра¬
ция которого принята в качестве независимой переменной. В об¬
ласти концентраций, лежащих за азеотропной точкой, пар относи¬
102
тельно богаче вторым компонентом. В системах с отрицательными
азеотропами наблюдается обратная зависимость.
В соответствии с рассмотренным характером зависимости коэф¬
фициентов активности компонентов бинарных систем от состава,
чем меньше различие давлений паров чистых компонентов, тем при
меньших отклонениях от закона Рауля возможно образование азео¬
тропа и тем ближе его состав к эквимолекулярной смеси.
С увеличением разницы давлений паров компонентов точка по¬
ложительного азеотропа смещается в область больших концентра¬
ций низкокипящего, а отрицательного азеотропа — в область боль¬
ших концентраций высококипящего компонента. Чем больше сте¬
пень неидеальности системы, тем больше отклоняется от прямой
6
Рис. 24. Зависимость давления (а) и состава
пара (б) от состава жидкости в бинарных си¬
стемах с положительным (т) и отрицательным (M)
азеотропами:
/ — система с положительным гомогенным азеотропом;
2 — система с отрицательным азеотропом; 3 — система
с гетероазеотропом.
линии кривая зависимости давления пара от состава (при T =
= const) и тем более резко выражен экстремум на этой кривой.
При больших положительных отклонениях от закона Рауля
в системе могут образоваться две жидкие фазы. ,По правилу фаз
двухкомпонентная система, имеющая три фазы (две жидкие и
одну паровую), при постоянных температуре или давлении нон-
вариантна. Следовательно, в области существования двух жидких
фаз температура кипения и состав пара должны быть постоянны.
Характерные кривые для систем этого типа приведены на рис. 24.
Особенности поведения бинарных систем, имеющих две жидкие
фазы, будут подробно рассмотрены ниже.
Трехкомпонентные системыг
образованные полностью смешивающимися веществами
Если откладывать концентрации компонентов в растворе на
сторонах равностороннего треугольника, а давление (или темпе¬
ратуру) по оси, перпендикулярной к плоскости треугольника, то
103
зависимость давления (или температуры) от состава будет изо¬
бражаться поверхностью (рис, 25).
В зависимости от свойств системы характер поверхности дав¬
ления (при T = const) различен. В идеальной системе она яв¬
ляется плоскостью. В системах с положительными отклонениями
от закона Рауля поверхность давления располагается выше, а в
системах с отрицательными отклонениями — ниже этой плоскости.
Наличие азеотропных точек в бинарных системах, входящих
в трехкомпонентную, обусловливает появление на поверхности
давления выступов или впадин. Характер поверхности давления
в трехкомпонентной системе еще осложняется влиянием совокуп¬
ного взаимодействия всех компонентов друг с другом. Точка трой¬
ного аз.еотропа, отвечающая экстремуму давления, геометрически
Рис. 25. Зависимость давления пара от состава жидкости в трех¬
компонентных системах:
а —три бинарных (ти Шз, Щ) и один тройной (т) азеотропы; б— два бинар¬
ных азеотропа, порождающих хребет на поверхности давления; в — два по¬
ложительных, один отрицательный (M) и седловинный (S) тройной азеотропы.
определяется как точка касания поверхности давления и плоско-
сти, параллельной плоскости концентрационного треугольника.
Рассекая поверхность давления плоскостями, параллельными пло¬
скости треугольника составов, получаем в сечении линии — изо¬
термы — изобары, которые должны быть замкнутыми вблизи точки
тройного азеотропа (рис. 25,а). Поверхность давления может
иметь такой вид лишь при наличии бинарных азеотропов.
Рассмотрение имеющихся данных о свойствах азеотропных сме¬
сей показывает, что при наличии трех одинаковых по характеру
бинарных азеотропов в большинстве случаев образуется тройной
азеотроп. Случаи образования тройного азеотропа при наличии
лишь двух бинарных или отсутствия тройного азеотропа, когда
имеются три бинарных, — относительно редки.
При наличии в трехкомпонентной системе двух бинарных азео¬
тропов одинакового характера (положительных или отрицатель¬
ных) между азеотропными точками на поверхности давления про¬
ходит хребет или лощина (рис. 25, б).
Большой интерес представляют системы, в которых имеются
как положительные, так и отрицательнее бинарные азеотропы.
Два положительных азеотропа или , положительный азеотроп и
низкокипящий компонент, не входящий в состав этого азеотропа,
104
порождают образование хребта на поверхности давления. Два от¬
рицательных азеотропа или один отрицательный азеотроп и высо-
кокипящий компонент, не входящий в состав этого азеотропа,
обусловливают появление впадины. При одновременном наличии
в тройной системе хребта и впадины может получиться седловина
на поверхности давления (рис. 25,в). В этом случае к поверхности
давления можно провести параллельную концентрационному тре¬
угольнику касательную плоскость. Точка касания отвечает седло¬
винному или положительно-отрицательному азеотропу. В соответ¬
ствии с геометрической природой седловины давление (или тем¬
пература) в точке седловинного азеотропа не должна быть ни
самым большим, ни самым малым в системе. Следовательно, сед¬
ловинные азеотропы не имеют экстремума температуры или дав¬
ления. Такой азеотроп впервые был обнаружен Райндерсом и
де Минье [148] при исследовании системы ацетон — хлороформ -
вода.
Трехкомпонентные системы,
образованные ограниченно растворимыми веществами
Трехкомпонентные системы, образованные веществами
с ограниченной взаимной растворимостью, при постоянных темпе¬
ратуре или давлении имеют, согласно правилу фаз, в области
существования паровой и жидкой фаз две степени свободы, а в
области существования двух жидких
фаз — одну. Следовательно, при переходе
от одной области к другой форма поверхно¬
сти давления (или температуры) должна
изменяться. В гомогенной области характер
зависимости давления или температуры от
состава такой же, как для систем, компо¬
ненты которых полностью растворимы
друг в друге.
В гетерогенной области пар находится
в равновесии с обеими жидкими фазами.
Следовательно, давление и состав пара
должны быть одинаковы для всех валовых
составив жидкой фазы, фигуративные точ¬
ки которых в концентрационном треуголь¬
нике лежат на прямой линии, соединяющей
точки составов равновесных жидких фаз (ноде). Рассекая по¬
верхность давления вертикальной плоскостью* проходящей через
ноду BC (рис. 26), получим линию пересечения ABCD, которая
на участке BC является прямой, а на участках AB и CD — кривой.
Из изложенного следует, что поверхность давления в области су¬
ществования двух жидких фаз искривлена лишь в одном направ¬
лении. Если в такой системе образуется азеотроп, состав которого
изображается точкой, лежащей в области ограниченной взаимной
растворимости (гетероазеотроп), то максимальное давление
Щ
Рис. 26. Зависимость да¬
вления пара от состава
жидкости в трехкомпо¬
нентной системе, обра¬
зованной ограниченно
растворимыми вещества-^
ми.
должны иметь все смеси, состав которых отвечает ноде, проходя¬
щей ч.ерез точку состава гетероазеотропа. Таким образом, в систе¬
мах, имеющих гетероазеотропы, касание поверхности давления
в горизонтальной плоскости происходит не в точке, как в случае
систем гомогенных в жидкой фазе, а по отрезку прямой — ноде.
Все известные трехкомпонентные гетероазеотропы являются
положительными азеотропами с наименьшей температурой кипения
в системе. Таковы, в частности, гетероазеотропы, образованные
этиловым, изопропиловым, пропиловым и изобутиловыми спир¬
тами, углеводородами с температурами кипения до IOO0C и водой.
В тройных системах, компоненты которых обладают ограниченной
взаимной растворимостью, могут образовываться седловинные
азеотропы. Такие азеотропы имеются, например, в системах аце¬
тон — хлороформ — вода и муравьиная кислота — вода — дихлор¬
этан [149]. Однако во всех известных случаях точка седловинного
азеотропа лежит в гомогенной области.
Для процессов азеотропной ректификации особый интерес пред¬
ставляют азеотропные смеси, образованные ограниченно раствори¬
мыми веществами. Применяя разделяющие агенты, дающие такие
азеотропы, можно весьма просто технологически оформить про¬
цесс, так как регенерация разделяющего агента осуществляется
в этом случае путем расслаивания. Слой, обогащенный разделяю¬
щим агентом, возвращается в ректификационную колонну в виде
флегмы. Азеотропные смеси, компоненты которых ограниченно
растворимы, имеют особо важное значение. Поэтому рассматри¬
ваются некоторые их свойства.
ПРЕДСКАЗАНИЕ АЗЕОТРОПИИ
Бинарные системы. В настоящее время отсутствуют об¬
щие методы предсказания азеотропии. Для этой цели можно
использовать эмпирические обобщения различных авторов. Юэл
Гаррисон и Берг [99] использовали развитые ими представления
о водородной связи для некоторых качественных предсказаний.
Были, в частности, весьма подробно систематизированы группы
веществ, образующих отрицательные азеотропы. К ним относятся:
1) вода с сильными кислотами, например, с HCl, HBr, HI,
HNO3;
2) вода с некоторыми ассоциированными жидкостями, напри¬
мер, с муравьиной кислотой, гидразином и этилендиамином;
3) вещества с атомами-донорами с жидкостями, имеющими
подвижный водородный атом, например, ацетон — хлороформ, цик-
логексанон — бромоформ и бутилацетат—1,1,2-трихлорпропан;
4) органические кислоты с аминами, например, уксусная кис¬
лота с триэтиламйном и пропионовая кислота с пиридином;
5) фенолы с аминами, например, фенол с анилином и о-крезол
с диметиланилином;
106
6) органические кислоты с веществами-донорами, содержа¬
щими кислород, например, муравьиная кислота с диэтилкетоном
и масляная кислота с цйклогексаноном;
7) фенолы с веществами-донорами, содержащими кислород,
например, фенол с метилгексилкетоном и о-крезол с этилокса-
латом;
8) фенолы со спиртами, например, фенол с октанолом и о-кре-
зол с этиленгликолем.
Имеющиеся указания об условиях образования положительных
азеотропов, к сожалению, весьма неконкретны.
Наиболее общие уравнения получены лишь для простейшей
группы неидеальных систем — регулярных растворов [150, 151].
Для таких растворов условие образования азеотропа (а= I)
имеет вид:
А (I -2хаз) = Ig (Р°/Jfy (217)
где хаз — молярная доля первого компонента в азеотропе; А — ко¬
эффициент, являющийся мерой неидеальности системы. Образова¬
ние азеотропа и его состав могут быть предсказаны по этому
уравнению, если по каким-либо данным известен или может быть
найден коэффициент А.
Условия образования бинарных гетероазеотропов для случая
одинаковой взаимной растворимости компонентов были исследо¬
ваны Стецким [152], который вывел уравнения
'“-г^ ,2|8)
и
P^(P°i + Pl)x\xp[A(l-xy/Rr] (219)
где г/аз —- молярная доля второго компонента в гетероазеотропе;
х* — растворимость одного компонента в другом.
Ввиду ограниченной применимости теории регулярных растворов
важное значение для выбора разделяющих агентов, используемых
в процессах азеотропной ректификации, имеют эмпирические ме¬
тоды предсказания азеотропии [45, 153—158], а также опытные
данные о свойствах азеотропных смесей, собранные в справочнике
Хорсли [45].
Лека, опубликовавший большое число экспериментальных дан¬
ных о свойствах азеотропных смесей, пришел к выводу, что опре¬
деляющее влияние на их свойства оказывают функциональные
группы в молекулах компонентов. Азеотропы, образованные ка¬
ким-либо веществом и компонентами с одинаковой функциональ¬
ной группой, названы им гомофункциональными азеотропами.
Азеотропные системы, в которых вещества с одинаковой функцио¬
нальной группой являются членами одного гомологического ряда,
были названы Свентославским [159] полиазеотропными системами.
I о;
Таблица 14
Температуры кипения азеотропных смесей,
образованных этиловым спиртом
и некоторыми углеводородами
Углеводород
Температура
кипения, 0C
углеводо-
род
азеотроп
Углеводород
Температура
кипения, 0C
углеводо¬
род
азеотроп
Толуол . .
1,2,4-Триметил-
циклопентан .
2,2,3-Триметил-
пентан .
110,63
109,29
109,84
77,63
74.3
74.3
Бензол . . .
2.3-Диметилпен-
тен . . j* . . -
2.4-Диметилпен-
тан ....
80,10
84,2
80,50
68 Д
67,1]
64,6
Предложены различные эмпирические методы предсказания
свойств азеотропов в полиазеотропных системах.
Метод Мэйра, Глазго и Россини. Авторы работы [153]
исследовали свойства азеотропных смесей различных углеводоро¬
дов и пришли к выводу,
что в азеотропах, обра¬
зованных каким-нибудь
веществом и парафино¬
выми, циклическими, оле-
финовыми, диолефино-
выми и ароматическими
углеводородами с одина¬
ковыми температурами
кипения, отклонение пар¬
циальных и общего дав¬
лений от значений, соот¬
ветствующих идеальным
смесям, уменьшается для
этих углеводородов в при¬
веденной последователь¬
ности. Самую низкую
температуру кипения име¬
ет азотропная смесь, об-
Рис. 27. Зависимость между температурами . рНЗОВанная парафиновым
Кипения углеводородов и составами и темпе¬
ратурами кипения азеотропов, образуемых
ими с этиловым спиртом:
/ — метилбуТен-3; 2 — изопентан; 3 — мет и л бутадиен-2;
4 — пентан; 5 — метйлбутен-2; 5—гексадиен-1; 7 — гек¬
сан; 8 — циклогексан; 5 —бензол; 10 — гептан; // — ме¬
тилциклогексан; 12 — толуол; 13 — октан; 14 — метил-
гептан.
углеводородом, и наи¬
высшую — ароматиче¬
ским углеводородом. Этот
вывод ил л юстр ир уется
данными табл. 14. '
На рис. 27 показана
зависимость температур
кипения углеводородов и составов от температуры кипения азео¬
тропов, образуемых ими с этиловым спиртом. Прямые линии
108
соединяют точки, соответствующие температурам кипения чистых
углеводородов, с точками, отвечающими температурам кипения и
составам азеотропов этих углеводородов. Из рис. 27 видно, что
содержание этилового спирта в азеотропе возрастает с увеличе¬
нием температуры кипения углеводорода. Точки состава и темпера¬
туры кипения азеотропов этилового спирта с парафиновыми угле¬
водородами ложатся на плавную кривую (пунктир). Это может
быть использовано для определения температуры кипения и соста¬
ва азеотропов, образуемых этиловым спиртом и другими членами
гомологического ряда парафиновых углеводородов. Для этого на оси
ординат отмечается точка
кипения углеводорода, из
которой проводится прямая
с углом наклона, средним
между углами наклона со¬
седних прямых. Точка пере¬
сечения проведенной таким
образом прямой с пунк¬
тирной кривой определяет
температуру кицения и со¬
став азеотропа. Такое по¬
строение на рис. 27 приве¬
дено для 3-метилгептана.
Соответствующая прямая
линия проведена пунктиром.
Полученный состав азео¬
тропа (0,815 мол. доли эти¬
лового спирта) удовлетво¬
рительно согласуется с най¬
денным опытным путем [45]. Точки для углеводородов других клас¬
сов располагаются над линией для парафиновых углеводородов
примерно в следующем порядке: циклические углеводороды, моно-
олефины, диолефины и ароматические углеводороды. Из этого
следует, что различные по химической природе углеводороды с при¬
мерно одинаковыми температурами кипения образуют с каким-
либо веществом азеотропные смеси, температуры кипения которых
повышаются при переходе в указанном ряду углеводородов от
парафиновых к ароматическим.
Зависимости, аналогичные рассмотренным, получаются для
азеотропных смесей, образованных углеводородом и рядом поляр¬
ных веществ.
На рис. 28 приведены данные о составах и температурах ки¬
пения азеотропных смесей, образованных бензолом и спиртами.
Пунктирные кривые соединяют точки составов и температур
кипения азеотропных смесей спиртов различного строения. Самая
нижняя кривая относится к азеотропным смесям с первичными
спиртами, следующая, расположенная над ней — к азеотропам
с вторичными и самая верхняя — к третичным спиртам. Это
Рис. 28. Данные о свойствах азеотропных
смесей бензола и спиртов, обработанные
по методу Мэйра, Глазго и Россини:
/ — метиловый спирт; 2 —этиловый спирт; 3 — изо*
пропиловый спирт; 4 — грег-бутиловый спирт;
5 — пропиловый спирт; 6 — фторбутиловый спирт;
7 — изобутиловый спирт.
<09
свидетельствует о том, что наибольшие отклонения от идеального
поведения имеются в системах, состоящих из углеводорода и пер¬
вичных спиртов, и наименьшие — в системах, содержащих третич¬
ные спирты *.
Метод Мейснера и Гринфильда. Авторы работы [154]
обработали данные о температурах кипения и составах бинарных
азеотропных смесей, образованных различными углеводородами,
галогензамещенными углеводородами, спиртами, карбоновыми
кислотами, кетонами, альдегидами, а также эфирами одно- и двух¬
основных кислот. Общим компонентом рассмотренных серий азео¬
тропов являлись углеводород или галогензамещенный углеводо¬
род. По опытным данным
находилась зависимость
молярной концентрации
углеводорода от величи¬
ны Y=TS(TH — Ts) или
Y = T2s(Tff-Ts)- Ю~Ё, где
Th и Ts — температуры
кипения углеводорода и
второго компонента аЗео-
тропа (в °К).
На рис. 29 приводятся
данные для серий азео¬
тропов спиртов с углево¬
дородами и галогензаме¬
щенными углеводородами.
Как видно из рис. 29,
экспериментальные точки
группируются около пря¬
мой линии, выражаемой
уравнением
-0,915· IO-6T2s(Th-Ts) (220)
где χΆ3 — молярная кон-
центрация углеводорода
в азеотропе.
На рис. 30 представлены данные об азеотропных смесях, обра¬
зованных альдегидами, фенолами, крезолами и кетонами с угле¬
водородами (за исключением терпеновых), а также фенолами и
крезолами с галогензамещенными углеводородами. Прямая, около
которой группируются точки, представленные на рис. 30, описы¬
вается уравнением
JCa3 = 50-0,915-IO-6Ts(Th-Ts) v (221)
* Сводка данных об азеотропах различных углеводородов и полярных ве¬
ществ имеется в работе [160].
Рис. 29. Данные о свойствах азеотропных
смесей спиртов с углеводородами и галоген¬
замещенными углеводородами, обработанные
по методу Мейснера и Гринфильда:
Гд — температура кипения углеводорода или галоген-
замещенного углеводорода, °К; Т§ — температура ки¬
пения спирта, 0K: С) ~ азеотропы с углеводородами;
0 — азеотропы с галогензамещенными углеводородами.
HO
Уравнения типа (220) и (221) были применены [161] для обра¬
ботки данных об азеотропах в системах, образованных различ-
* ныМи классами соединений. Сводка уравнений, определяющих
составы азеотропов, приводится в табл. 15. Состав азеотропа вы¬
ражается в молярных процентах компонента того класса, назва¬
ние которого в первом столбце
таблицы стоит в начале.
Приведенные уравнения по¬
лучены в результате обработ¬
ки опытных данных для боль¬
шого числа систем. Наилуч¬
шие результаты получаются
для азеотропов, образованных
углеводородами и галогенза¬
мещенными углеводородами с
жидкостями, имеющими атом-
донор (кетонами и сложными
эфирами), и с ассоциирован¬
ными жидкостями первого
класса по классификации
Юэла, Гаррисона и Берга, а
также двумя углеводородами.
Для этих систем среднее от¬
клонение истинных составов
азеотропов от рассчитанных
составляет ±8%. Для других
классов соединений эти откло¬
нения еще больше.
Данные для систем, не
включенных в табл. 15, не под¬
даются обработке по методу
Мейснера и Гринфильда. Та¬
ковы, например, системы, об¬
разованные карбоновыми кис¬
лотами и углеводородами. Ре¬
зультаты обработки опытных
данных для этих систем, приведенные на рис. 31, показывают, что
экспериментальные точки ложатся не на прямую, а на кривудо
линию.
Для определения температуры кипения азеотропов получено
[91] следующее эмпирическое уравнение:
Δ7' = A-Bz (222)
где AT— разность температур кипения компонентов; А и В — кон¬
станты, значения которых приводятся в табл. 16; г = Tl — Газ для
азеотропов с минимумом температуры кипения иг== Газ—Tl для
азеотропов., с максимумом температуры кипения; Газ — темпера¬
тура кипения азеотропа; Tl — температура кипения низкокипящего
компонента.
Рис. 30. Данные о свойствах азеотроп¬
ных смесей альдегидов, фенолов, кре-
золов и кетонов с углеводородами,
а также фенолов и крезолов с галоген¬
замещенными углеводородами, обрабо¬
танные по методу Мейснера и Грин-
ф иль да:
Th и Tg — температуры кипения углеводорода
и второго компонента азеотропа, °К: V — угле¬
водороды + кетоны; ▼ — углеводороды + альде¬
гиды; □ — углеводороды + фенолы или крезолы;
■ — галогензамещенные углеводороды + фенолы
или крезолы.
Таблица 15
Сводка уравнений
для определения состава азеотропов,
образованных различными классами соединений
Классы соединений,
образующих азеотроп
JCa3, мол. %
Литера¬
тура
Углеводороды — спирты . . .
Галогензамещенные углеводо¬
роды-спирты .
Углеводороды — альдегиды . .
Углеводороды (за исключени¬
ем терпенов) — фенол (кре¬
золы и кетоны) ... . . .
Г алогензамещенные углеводо¬
роды — фенолы (крезолы)
Г алогензамещенные углеводо¬
роды — карбоновые кислоты
Углеводороды, галогензаме-
щенные ,углеводороды —
’ эфиры одноосновных кар¬
боновых кислот (кроме му¬
равьиной)
Углеводороды, галогензаме¬
щенные углеводороды —
эфиры двухосновных кислот
и муравьиной
Г алогенз амещенные углево¬
дороды — углеводороды . .
Г а логензамещенные углеводо¬
роды — галогензамещенные
углеводороды
Галогензамещенные углево¬
дороды — вода
Г алогензамещенные углево¬
дороды — гликоль
Г алогензамещенные углево¬
дороды — кетоны (сложные
эфиры) . . .
Кетоны — сложные эфиры не¬
карбоновых кислот . . . .
Углеводороды — углеводороды
Вещества 5 класса (по клас¬
сификации Юэла) — вода,
(2-аминоэтанол)
Вещества 5 класса— гликоль
(глицерин)
55—0,915 Y
/55—0,915 Y
50—0.915 7
50-0,915 Y
50-0,915 Y
50-1,25 Y
*0-3 Y
50-1,7 Y
23-1,87 7
50-1,25 7
35 — 0,58 Y
35-0,438 7
52,1 + 1,18 7
49,7-1,187
50-0,5 Y
50-0,5 7
50-0,5 7
tI(Th-Ts)I О"6
T2s(THrTs)W~*
Ts(Tfi-Ts) ю-«
Ts (Th-Ts) ΙΟ'6
TS (TH~Ts) 10"6
Ts(Tfi-Ts) иг6
Ts (Tn-Ts)W
Ts (Th-Ts) 10'
Ts(Th-Ts)IO
-5
Ts(TH-Ts)W-7
T2s(Th-Ts)IO-5
T2s(Th-Ts)IO-5
(Th-Ts)(Th+Ts)-Ts-
■ 10-ί
(th-ts)(th + ts)t2s.
• 10 7, а при
TH-TS> I и
Tfi+rS-> 1000
(тн - Ts) Ts - 10-7
(th-ts)(th + ts)tI.
10
T2s(Th-Ts)IO-5
T —Т
H S
[147]
[147]
[147]
[147]
[147]
[147]
[147]
[147]
[154]
[154]
[154]
[147J
[147]
[147]
[147]
[147]
[147]
112
Приведенные уравнения могут быть применены для предсказа¬
ния свойств азеотропов в системах, образованных рассмотренными
классами химических соединений. Например, для системы пропи¬
ловый спирт (T8 = 370)—бензол (Гн = 353) получаем с помощью
уравнения (220) состав азеотропа хаз = 76 мол. %.
Температура кипения, рассчитанная по уравнению (222), равна
Газ = 346,4° К или ^аз = 73,4° С. Соответствующие эксперименталь¬
ные величины равны хаз = ■
= 79,4 мол.% и ^a3 ==77,Г С.
Таким образом, рассчитан¬
ные величины удовлетвори¬
тельно согласуются с опыт¬
ными. Необходимо, однако,
иметь в виду, что в некото¬
рых случаях из приведен¬
ных выше уравнений выте¬
кает наличие азеотропов в
системах, для которых в
справочнике Хорсли [45]
имеется указание, что они
неазеотропны; или, наобо¬
рот, — отсутствие азеотро¬
пов в системах, в которых
они обнаружены [161]. Это
накладывает определенные
ограничения на применение
метода Мейснера и Грин¬
фильда.
Метод С к о л н и к а.
Для установления законо¬
мерностей в изменении
свойств азеотропных смесей,
образованных каким-нибудь
веществом и членами гомо¬
логического ряда, Сколник
[155] для большого числа
систем рассмотрел зависи¬
мости между: I) логариф¬
мом концентрации компонента; общего для рассматриваемой се¬
рии азеотропов, и температурой их кипения; 2) температурой ки¬
пения азеотропа и температурой кипения компонентов; 3) темпе¬
ратурами кипения компонентов и логарифмов концентрации азео¬
тропа.
Было обнаружено, что в координатах логарифм молярной кон¬
центрации общего компонента серии азеотропов хаз— темпера¬
тура кипения азеотропа Ta3 экспериментальные точки ложатся на
прямые линии. На рис. 32 эта закономерность показана на при¬
мере азеотропных смесей бензола и парафиновых углеводородов.
UO 60
МОЛ %
Рис. 31. Данные о свойствах азеотропных
смесей карбоновых кислот с углеводоро¬
дами (О) и галогензамещенными углево¬
дородами (·), обработанные по методу
Мейснера и Гринфильда:
для кривой I по оси абсцисс отложена молярная
концентрация кислоты, а для прямой 2 —галоген*
замещенного водорода.
11?
Таблица 16
Значения констант А и В в уравнении (222)
Система
Класс
по Юэлу
л
в
Углеводороды — спирты
5-2
40
3,5
Углеводороды — кислоты
5-2
30
3,5
Углеводороды — муравьиная кислота ......
5-2
65
3,5
Углеводороды — фенолы
5-2
25
3,5
Углеводороды — кетоны
5-3
25
3,5
Галогензамещенные углеводороды — спирты , .
4-2
40
5,0
Углеводороды — углеводороды
Углеводороды — сильно ассоциированные жид¬
5-5
10
3,5
кости . г
5-1
75
4,0
Углеводороды — аминоспирты .........
Г алогензамещенные углеводороды — жидкости
5-1
35
2,0
с атомом-донором
Г алогензамещенные углеводороды — углеводо¬
4-3
15
4,0
роды, сульфиды
Г алогензамещенные углеводороды — сильно ас¬
4-5
20
3,0
социированные жидкости
5— I
55
3,0
Таблица 17
Значения констант А и В
в уравнении (223] (155, 156]
Общий компонент
полиазеотропной системы
Гомологический ряд
л
в
Бензол
Парафиновые углеводороды
0,1108
-37,14
Циклические »
0,1054
-35,22
Парафиновые углеводороды
с разветвленной цепью
0,07091
-23,05
Первичные спирты
0,01752
-4,232
Вторичные »
0,02145
-5,628
Третичные »
0,02329
-6,287
Этанол
Парафиновые углеводороды
0,02525
-6,875
Циклические »
0,02524
-6,872
Циклические моноолефины
0,02755
— 7,681
Циклические диолефины
0,02591
-7,105
Ароматические углеводороды
0,03422
. -10,03
Олефины
0,02804
-7,856
Этантиол
Парафиновые углеводороды
0,049
-13
Пропантиол-1
То же
0,072
-22,4
Нафтеновые углеводороды
0,131
-43
Пропантиол-2
Парафиновые »
0,066
-19,6
Нафтеновые »
0,084
-27
Бутантиол-1
Парафиновые »
0,087
-30
Нафтеновые »
0,101
-35
Бутантиол-2
Парафиновые »
0,084
-28
Нафтеновые »
0,111
-38
2-Метилпропантиол-1
Парафиновые »
0,097
-33
Нафтеновые »
0,117
-40
2-Метилпропантиол-2
Парафиновые »
0,095
-30
114
Связь между Igxaa и taз может быть выражена уравнением
IgXa3 = л (273,1 +/аз) + В (223)
где А и ZJ- константы для рассматриваемой серии азеотропов.
Значения констант AnB для некоторых полиазеотропных систем
приводятся в табл. 17.
Линейный характер зависимости между Igxa3 и ta3 позволяет
легко определять состав азеотропов членов гомологического ряда
по температурам кипения и составам азеотропов двух соедине¬
ний, принадлежащих к этому ряду.
Для сравнительной оцен¬
ки различных полиазеотроп¬
ных систем, особенно при
выборе разделяющих аген¬
тов для процессов азеотроп¬
ной ректификации, жела¬
тельно знать интервал тем¬
ператур членов гомологиче¬
ского ряда, в котором они
образуют азеотропы. Эта
величина* равная разности
абсцисс точек прямой I (см.
рис. 32) при х = 0 и X =
= 100%, определяется углом
наклона этой прямой. Чем
он меньше, чем больше ин¬
тервал температур членов
гомологического ряда, обра¬
зующих азеотропы, и тем,
следовательно, больше от¬
клонения от идеального по¬
ведения в полиазеотропной
системе. Таким образом, на¬
клон прямой I может рас¬
сматриваться как мера отклонений от закона Рауля. Сравнитель¬
ная оценка способности различных систем к образованию азео¬
тропов может быть получена путем определения относительного
азеотропного эффекта, равного отношению коэффициентов А рас¬
сматриваемых систем к угловому коэффициенту для системы, при¬
нятой за эталон для сравнения*. Ниже приводятся значения
относительного азеотропного эффекта для ряда систем. За эта¬
лонную принята полиазеотропная система бензол — нормальные
парафиновые углеводороды.
* В развитие этих представлений Дести и Фидлер [157] предложили опреде¬
лять относительный азеотропный эффект как I/Л, В их работе приводятся зна¬
чения А и \/А для азеотропных систем, состоящих из соединений, которые со¬
держат серу и углеводороды.
Рис. 32. Данные о свойствах азеотропных
смесей бензола и парафиновых углеводо¬
родов, обработанные по методу Сколника:
I — зависимость логарифма молярной концентрации
бензола от температуры кипения азеотропа: Il — за¬
висимость логарифма молярной концентрации бен¬
зола от температуры кипения парафинового угле¬
водорода; 1,1' — 2,2,4-триметилпентан; 2,2'—2,3-диме-
тилпентан; 3,3' — 2,4-диметилпентан; 4,4' —2,2,3-три-
метилбутан.
115
Пропанитиол-!·*~ нафтеновые углеводороды . 0,β5
2-Метилпропантиол-1 — нафтеновые углеводороды ..... 0,95
Бензол — парафины ^ 1,00
Бутантиол-2 — нафтеновые углеводороды 1,0
Бензол — циклические углеводороды . 1,05
Бутантиол-1 — нафтеновые углеводороды . . . 1,10
2-Метилпропантиол-1 — парафиновые углеводороды 1,14
2-Метилпропантиол-2 — парафиновые углеводороды . .... 1,17
Бутантиол-1 — парафиновые углеводороды 1,27
Пропантиол-2 — нафтеновые » 1,32
Бутантиол-2 — парафиновые » . 1,32
ГТропантиол-1 — парафиновые » 1,54
Бензол — парафины с разветвленной цепью 1,56
Пропантиол-2 — парафиновые углеводороды ........ 1,68
Этантиол — парафиновые » 2,26
Этанол — ароматические » 3,23
Этанол — олефиновые » 3,95
Этанол — циклические мойоолефины 4,02
Этанол — циклические диолефины 4,28
Этанол — циклические углеводороды 4,39
Этанол — парафиновые » 4,39
Бензол — третичные спирты 4,76
Бензол — вторичные » 5,17
Бензол — первичные » 6,32
Приведенные данные дают возможность судить о величине от¬
клонений от идеального поведения в различных системах. Они
показывают, в частности, что в системах, образованных углеводо¬
родами и спиртами, степень неидеальности возрастает при пере¬
ходе от третичных спиртов к первичным.
Зная величину относительного азеотропного эффекта, можно
ПрОВесТИ Прямую ЛИНИЮ, выражающую ЗавИСИМОСТЬ IgXaa от /аз
по данным о свойствах азеотропа, образованного членом гомо¬
логического ряда. Для предсказания состава азеотропов с по¬
мощью этой прямой следует, однако, предварительно определить
их температуры кипения. Это можно сделать, используя тот факт,
что зависимость между логарифмом концентрации общего компо¬
нента полиазеотропной системы и температурой кипения членов
гомологического ряда выражается плавной кривой (см. рис. 32,
кривая 2). Предсказание свойств азеотропа сводится к нахожде¬
нию на этой кривой точки с абсциссой, равной температуре кипения
интересующего члена гомологического ряда, и последующему опре¬
делению на прямой I точки с такой же ординатой. Координаты
этой точки дают значения температуры и состава азеотропа. Однако
для построения кривой 2 требуется несколько экспериментальных
точек, что снижает практическую ценность описанного способа.
Чтобы устранить этот недостаток, Скол ник попытался установить
связь между температурами кипения членов гомологических ря¬
дов и образуемых ими азеотропов. В результате получено эмпи¬
рическое уравнение
116
Ig(D-U3) = E- F (273,1+0
(224)
где £), £ и P— константы, значения которых для некоторых Пблй-
азеотропных систем приведены в табл. 18; t — температура кипе¬
ния члена гомологического ряда, 0C.
130
§
<1110
<5>
40
I 90
I
£ 70
■ I
I 50
I
I 30
^O к там
χ 2, 5 Диметилгексан
Толуол \ Метилциклогексан
" Гептан
\Щ^Цинлогексен
Бензол *£К^циН/}0генсан,
Цишгешдиен^Щгексан
\р\*Гексадиен
3
3 - Метилбутадиен -1.2
2-Метил Вутен -T^ffeнтан
Изопрен ' Метил бутан
10
О,
З-Метилбутен - 2
i ί 1 I 1 1 1 -J *—
0,8 ГО 1,2 1,4 1,6 1,8
lg(67,6 ~ tаз)
2J)
Рис. 33. Зависимость между температурами кипения
углеводородов и азеотропов, образуемых ими с эти¬
ловым спиртом:
/ — парафины и олефины; 2 — циклические углеводороды;
3 — циклические моноолефины; 4 — циклические диолефины;
5 — ароматические углеводороды.
Вытекающая из уравнения (224) линейная зависимость
Ig (D- ί*3) от I иллюстрируется рис. 33.
T а б ли ц а 18
Значения констант Dr E и F в уравнении |224)
Система
D
E
-F
Этанол — парафиновые углеводороды .
37
9,8
0,029
Пропантиол-1 — парафиновые углеводороды . . .
69
13,9
0,039
Пропантиол-2 — парафиновые »
. . .
55
12,0
0,034
Бутантиол-1 — парафиновые »
. . .
ιοα
15,9
0,041
Бутантиол-1 — нафтеновые »
. . .
101
15,7
0,040
Б^ таьтлол-2 — парафиновые »
. . .
88
13,5
0,036
Бутантиол-2 — нафтеновые »
2-Метилпропантнол-1 — нафтеновые
углеводо-
87
18,3
0,049
роды
2-Метилпропантиол-1 — парафиновые
углеводо-
90
17,0
0,045
роды
2-Метилпропантиол-2 — парафиновые
углеводо-
92
13,7
0,036
роды
67
15.0
0,042
117
Метод.Деньера, Фидлера и Лоури. Недостаток ме¬
тода обработки и предсказания данных о свойствах азеотропов,
образующих полиазеотропную систему, предложенного Сколни-
ком, заключается в сложности определения температуры кипения
азеотропа по температурам кипения компонентов. Для того чтобы
исключить эти трудности, Деньер, Фидлер и Лоури [156] предло¬
жили использовать зависимость температуры кипения, членов го¬
мологического ряда от молярной концентрации компонента, об¬
щего для полиазеотропной систе¬
мы. Эта зависимость для каждой
полиазеотропной системы являет¬
ся прямой для азеотропов, обра¬
зуемых парафиновыми углеводо¬
родами с бензолом и этиловым
спиртом [162].
На рис. 34 приводятся дан¬
ные для систем, образованных
тиоспиртами и углеводородами.
Как видно из рис. 34, для каж¬
дой полиазеотропной системы по¬
лучается линейная зависимость.
Аналогичные зависимости для
некоторых других систем пред¬
ставлены на рис. 35.
Интересно отметить, что во
всех случаях температура кипе¬
ния общего компонента полиазео¬
тропной системы лежит вблизи
точки с абсциссой 51 мол.% с от¬
клонением ±3%. Точки пересе¬
чения прямых линий с ордина¬
тами х\ = 0 и = 100% дают
минимальную и максимальную
температуры кипения членов гомологического ряда углеводородов,
образующих азеотропы с рассматриваемым веществом. Опреде¬
ляемый таким образом интервал температур кипения зависит от
угла наклона прямых и характеризует степень неидеальности рас¬
сматриваемых систем.
Из приведенных на рис. 34 и' 35 опытных данных следует, что
интервал температур кипения углеводородов, которые образуют
азеотропы с соединениями, содержащими серу, убывает с увели¬
чением числа атомов углерода в молекулах последних. Для одного
и того же соединения, содержащего серу, этот интервал темпера¬
тур кипения для парафиновых углеводородов больше, чем для
нафтеновых, а для последних больше, чем для олефиновых.
Использование линейной зависимости температур кипения
членов гомологического ряда от состава образуемых ими азеотро¬
пов весьма облегчает предсказание свойств последних.
Рис. 34. Зависимость температуры
кипения углеводорода от молярной
концентрации тиоспирта в образуе¬
мых ими азеотропах:
□ — парафины; О “ парафины с разветвлен¬
ной цепью; ф — нафтены; / — бутандйол-1;
2—2 метилпропантиол-1; 3 — бутантиол-2;
4 — пропантиол-1; 5 — 2-метилпропантиол-2;
6 — пропэ нтиол; 7 — этантиол.
118
Для установления этой зависимости достаточно двух экспери¬
ментальных точек. Состав азеотропа, образуемого каким-нибудь
членом гомологического ряда, можно определить по температуре
кипения последнего путем линейной интерполяции. По найден¬
ному составу азеотропа его температура кипения определяется
Рис. 35. Зависимость температуры кипения упеводорода от мо¬
лярной концентрации серусодержащего соединения в образуе¬
мых ими азеотропах:
О — парафины с разветвленной цепью; □ — парафины; # — нафтены; X — оле¬
фины; I — тиопентан-2; 2 — 3-метил-2-тиобутан-2; 3 — тиобутан; 4 — тиопентан-2;
5 — дитиогексан-3,3; 6 — тиоциклопентан; 7—дитиобутан-2,3; 8 — метилтиофен-3;
9 — метилтиофен-2; 10 — тиофен.
с помощью предложенного Сколником графика зависимости тем¬
пературы кипения азеотропа от логарифма его состава.
Для проверки описанного метода последний был применен к полиазеотроп-
ным системам, образованным бутиловым и метиловым спиртами с парафиновыми
углеводородами [163] для определения свойств азеотропов октана (т. кип.
125,8° С) по данным для азеотропов с гептаном (т. кип. 98,45° С) и нонаном
(т. кип. 150,5°С). Азеотропы гептана со спиртом содержат соответственно
72,8 мол.% метилового спирта и 22,4 мол.% бутилового спирта (т. кип. азеотро¬
пов соответственно 58,8 и 93,85°С), а нонана — 95,3 мол.% метилового спирта и
81,3 мол.% бутилового спирта (т. кип. азеотропов соответственно 64,1 и 115,9°С).
Путем линейной интерполяции находим для азеотропа октана с метиловым спир¬
том
*м=wZ-Sf(95,3 “72,8)+72,8=84,6 мол‘%
и с бутиловым спиртом
Хб = ||о,5 - 98.45 (81'3- 22’4) + 22>4 = 53·4 мол-%
119
Температуры кипения азеотропов, найденные по методу Сколника, равны
соответственно для азеотропов с метиловым спиртом:
/м - 58,8 + 95^’i7g 72,8 (lg 84’6 ~ 72’8) " 61'-7° С
и бутиловым спиртом:
I I К Q — Q4 SR
^аз « 93,85 + (Ig 53,4 - Ig 22,4) - 108,95° С
Эти величины удовлетворительно согласуются с опытными величинами: кон¬
центрации метилового спирта 88,1 мол.% и бутилового спирта 54,1 мол.%, т. кип.
соответственно 62,75° и 108,45°. При использовании для расчета в качестве ис¬
ходных данных свойств азеотропов более удаленных членов ряда углеводоро¬
дов, например гексана и нонана, получается меньшее соответствие расчетных и
опытных данных.
Метод Шора. Обработав опытные данные для 600 бинар¬
ных систем, Шор [158] сопоставил составы серий азеотропных сме¬
сей, образованных общим компонентом и со¬
единениями одного класса. Оказалось, что
для двух серий, образованных одним классом
соединений и двумя разными общими ком¬
понентами, наблюдается линейная зависи
мость содержания соединений указанного
класса в одной серии азеотропов от содержа¬
ния тех же соединений в другой серии. На
рис. 36 такая зависимость иллюстрируется
на примере азеотропных серий, образованных
карбоновыми кислотами соответственно с
α-терпеном и изоамиловым эфиром. Абсцис¬
са каждой экспериментальной точки на этом
рисунке соответствует содержанию опреде¬
ленной карбоновой кислоты в азеотропной
смеси с α-терпеном, а ордината — содержа¬
нию той же кислоты в азеотропной смеси
с изоамиловым эфиром. В класс соединений
для двух сопоставляемых серий включаются
группы родственных соединений. Так, класс
алкилгалогенов включает хлориды, бромиды,
иодиды. Класс углеводородов включает али¬
фатические, ароматические и олефиновые со¬
единения. В класс спиртов входят также спир-
тоэфиры.
На рис. 37 приведены экспериментальные данные для серий
азеотропов, образованных галогеналкилами с метиловым и этило¬
вым спиртами. Как видно, экспериментальные точки группируются
около прямой линии. Отклонение от линейной зависимости может
быть обусловлено не только неточностью корреляции, но и погреш¬
ностью экспериментальных данных из-зд применения недостаточ¬
но чистых исходных веществ.
х Г вес. %
Рис. 36. Корреляция
опытных данных о со¬
ставах азеотропных
смесей, образован¬
ных карбоновыми ки¬
слотами с α-терпеном
и изоамиловым эфи¬
ром:
х' — содержание (вес. %)
карбоновой кислоты в
азеотропной смеси с тер¬
пеном; Xflr- содержание
(аес. %) карбоновой ки¬
слоты в азеотропной Сме¬
си с изоамиловым эфи¬
ром.
w
Ta б л и ца 19
Сводка опытных данных о составах азеотропов,
обобщаемых зависимостью
х" = тх' + b
Класс
соединений
Первый общий
компонент
Второй общий
компонент
Число
использо¬
ванных
систем
т
ъ
Сложные эфи¬
Гептан
Вода
18
0,12
83
ры
Метиловый спирт
12
1,62
-81
Этиловый спирт
12
М4
-26
Вода
Фенол
19
-4,35
196
Этиловый спирт
Пропиловый
11
1,05
31,5
То же
спирт
Аллиловый спирт
8
1,22
17
Вода
16
0,12
84
Изопроциловый
PTT MtTT
11
2,25
-75
Галогенсодер¬
I
Вода
19
0,24
75
жащие ал¬
килы
Метиловый спирт
45
1,37
—38
Пропиловый
31
0,82
22
спирт
Аллиловый спирт
17
0,82
24,5
Бутиловый спирт
24
0,64
51
Изопропиловый
22
0,72
37
спирт г
вгор-Бутиловый
17
0,99
13
спирт
грег-Бутиловый
20
1,85
-69
спирт
грет-Амиловый
16
2,50
-69
Галогенсодер¬
Сероуглерод
спирт
Муравьиная ки¬
17
0,21
82
жащие ал-
килы
Этиловый
слота *
То же
25
0,41
42
спирт
Метиловый
He при¬
Углеводороды
спирт
Этиловый
Вода
.13
менима
, 0,28
72
спирт
То же
Метиловый
38
0,80
8
» »
спирт **
Пропиловый
Λ ГГ МПФ
29
1,13
6
Этиловый
LIliipi
Аллиловый спирт
17
1,06
8,5
спирт
То же
Изопропиловый
л rt Mt4IT*
32
1,09
-8
» »
LHiip 1
Этиленгликоль '
25
0,21
86
* Применимы до х —80 вес. Ht
** Применимы до х —81 вес. Ht
ш
Продолжение
Класс
соединений
Первый общий
компонент
Второй общий
компонент
Число
использо¬
ванных
систем
т
b
Спирты
Бензол
Толуол
23
0,87
38
Толуол
т-Ксилол-
19
1.14
37
Гептан
Вода
16
0,89
44,5
Бромхлорметан
Нитрометан
12
1,13
35
Тетрахлорэти-
»
19
1,29
-11,5
Карбоновые
лен
а-Терпинен
Изоамиловый
5
1,75
-27,5
кислоты
»
эфир
Бромоформ
6
0,58
-20,5
Описанным способом обработаны опытные данные для шести
различных классов органических веществ. Сводка полученных
результатов, представленных в виде зависимости x/f = mxf + b, при¬
водится в табл. 19. Входящие в при¬
веденную формулу величины имеют
следующие значения: Xf и х" — весовые
проценты соединения в азеотропах соот¬
ветственно с первым и вторым общими
компонентами, т и b — эмпирические
константы.
Тройные системы. Условия образова¬
ния тройного азеотроца определяются
равенствами
(■Щ*
или
ш„г-(^г-° <*»>
Согласно закону Коновалова, в точке
экстремума температуры или давления
составы жидкости и пара одинаковы. По¬
этому условием образования тройного
азеотропа является равенство единице
коэффициентов относительной летучести
всех компонентов, т. е.
Ct 12 — Ctj з “ ®2з I (227 )
Эти равенства действительны для азеотропов всех возможных
типов — положительного, отрицательного и положительно-отрица¬
тельного (седловинного). Из термодинамического анализа, выпол¬
ненного Хаазе [164], следует, что тип азеотропа определяется зна¬
чениями частных производных коэффициентов относительной ле-
х ''вес 7·
Рис. 37. Корреляция опыт¬
ных данных о составах азео¬
тропных смесей, образован¬
ных галогеналкилами с ме¬
тиловым и этиловым спир¬
тами:
xf — содержание (мол. %) гало-
геналкила в азеотропной смеси
с этиловым спиртом; х" —содер¬
жание (мол. %) галогеналкила
в азеотропной смеси с метило¬
вым ςρ-ΗρτοΜί # — хлориды;
S- бромиды; X - иодиды;
— смешанные галогеналкилы.
122
гучести в азеотропной точке β33, баз и еаз, определяемых равен¬
ствами
(д Inai3Na3 . / д In ааз)аз / din Ct23\аз ,ппо.
баз=1 -шг)Х] и еаз=1 -шг)Х2 (228)
Условия образования положительного азеотропа (с максиму¬
мом давления пара) выражается неравенствами
Раз®аэ-«2з>0. Раз<0 И баз<0 (229)
отрицательного азеотропа (с минимумом давления пара)—нера¬
венствами
РаАз-ен>0· Раз>° и Раз>° (230)
а положительно-отрицательного азеотропа — неравенством
Раз^аз — еаз < 3 (231)
равенства (225)—(227) и неравенства (229)—(231) могут быть
использованы для предсказания возможности образования и типа
тройного азеотропа, если известна зависимость коэффициентов
активности компонентов от состава смесей. Простейшей формой
зависимости является такая, которая получается при условиигчто
зависимость коэффициентов активности компонентов от состава
в бинарных системах, входящих в состав тройной, выражается
уравнением теории регулярных растворов (с одной константой),
а совместное взаимодействие всех трех компонентов друг с другом
отсутствует. В этом случае зависимости коэффициентов относи¬
тельной летучести от состава тройных смесей выражаются урав¬
нениями, аналогичными уравнению (126), а условия образования
тройного азеотропа определяются соотношениями
рО рО
Ig «13 - Ig -Hf + 1S — = “7^· + [^13 (I ~ 2ДГ! ~ х2) + (A12 - ^23) х2] = 0 (232)
рз Тз рз
и
Yo p^
Ig Й23= Ig-Tn-+ lg— = Ig -jj- + И23 (I -Jcl - Sjc2) + (Л12 - Л,з) jc,] = O
Рз Уз рз
при решении которых совместно, получаем следующие уравнения
для определения состава азеотропа:
рз° Л . (, Р°з
\/\\2 ~ ^13 ~ П2ъ) “
~аз _
Хл ~
(Ai2 — Л13 ~ ^23) ^lg 2^23J ^23 ^ S’ ~^о— j^13
1 (Ai2 — А !з — A2 з)2 — 4Л1зЛ23
(ЛJ2 — Л]3 — Л2з) I Ig ~q Ais) + 2Л]3 fig —--— /
х™ = 1 ' 1 1 · С23з\
2 (Л12 — л13 - л23)2 - 4Л,зЛ23 (аМ)
123
Если при заданной температуре для Jtj3 и xf получаются зна¬
чения, лежащие в интервале между 0 и I, и сумма χψ и χψ не
превышает единицы, то в системе образуется азеотроп. Давление
пара в экстремальной точке Pa3 определяется уравнением:
*** Л13 (-^f3)2 + A23 (*|а)2 + (^1з + A23 ~ ^12) χ\3χ23 (234)
3
Рассчитав величину Pa3 по уравнению (234), можно опреде¬
лить тип азеотропа, образующегося в рассматриваемой системе.
Для этого можно воспользоваться также неравенствами (229),
(230) и (231). При принятой зависимости коэффициентов актив¬
ности от состава величины β, б и ε выражаются через константы Л
уравнениями:
β = — 2 АI з; δ — — 2Л2з и BsssA^-Ai3— Л2з (235)
Подставив эти величины в неравенства (229) — (231), получаем
следующие условия для определения типа экстремума: для азео-
"тропа с максимумом давления пара
44l3^23 ~ {А\2 — А\3 — ^2з)2 0» ^!З'^О И Л23>0 (236)
для азеотропа с минимумом давления пара
' . 4Л13Л23 — (А\2 — Ai3 — Л2з)2 > 0; Л]з<0; Л2з<0; (237)
и для седловинной точки
4Л13Л23 — (Al 2 — Ai3- Л2з)2<^0 (238)
Поскольку нумерация компонентов произвольна, константы A12
и Л13, а также A12 и Л2з могут взаимно заменять друг друга. От¬
сюда следует, что тройной азеотроп с максимумом давления пара
может образовываться лишь в том случае, если все константы
А > 0, т. е. во всех бинарных системах, входящих в состав рас¬
сматриваемой тройной системы, имеют место положительные от¬
клонения от закона Рауля. Соответственно с этим, тройной азео¬
троп с минимумом давления пара может образоваться лишь при
наличии отрицательных отклонений от закона Рауля во всех би¬
нарных системах, состоящих из компонентов заданной тройной
системы. Если константа А для бинарных систем имеют разные
знаки, то, в соответствии с неравенствами (236) —(238), един¬
ственным типом азеотропа, который может образовываться в трой¬
ной системе, является седловинный.
Предсказание азеотропии в трехкомпонентных системах
с помощью выведенных соотношений производится следующим
образом. По данным о равновесии или о составе азеотропа рассчи¬
тывают константы А для трех бинарных систем, состоящих из рас¬
сматриваемых компонентов. По найденным константам с помощью
уравнений (233) определяют значения Jtj3 и χψ. Далее, поль¬
зуясь неравенствами (236) — (238), находят тип экстремума и по
124
уравнению (234) вычисляют давление пара в экстремальной
точке.
Для экспериментальной проверки уравнений (233) и (234),
а также неравенств (236) — (238) были выбраны системы, для
которых можно допустить применимость уравнений (232).
Сопоставление результатов расчетов с опытными данными
[45, 165, 166] приведено в табл. 20.
t Из табл. 20 следует, что в количественном отношении рассчи¬
танные и экспериментальные величины сильно расходятся, каче¬
ственное же соответствие имеет место для всех систем, кроме си¬
стемы бензол — циклогексан — метиловый спирт. Это, возможно,
объясняется неточностью опытных данных, использованных для
расчетов. *
Из сопоставления очевидна возможность предсказания нали¬
чия и вида тройного азеотропа в системах, компоненты которых
образуют бинарные системы с симметричным ходом зависимости
коэффициентов активности от состава. Однако это условие сильно
ограничивает возможность применения метода Хаазе.
Иной подход был применен для предсказания возможности об¬
разования и свойств тройного азеотропа в работе [167]. Равнове¬
сие между жидкостью и паром в трехкомпонентной системе при
постоянном давлении графически представляется, как известно,
в виде двух поверхностей T = f(xux2) и T = <р(у\; у2), изображаю¬
щих зависимость температур кипения от состава жидких смесей
и точек росы от состава пара. Эти поверхности касаются друг дру-
.га в точке тройного азеотропа. Предлагаемый способ основан на
допущении, что поверхность T =' φ(ί/ι; Уг) может быть аппрокси¬
мирована уравнением второй степени
T * ^20*I С\]Х\Х2 4" 6*02*2 4~ ^10*1 4“ ^Q\x2 4“ ^OO (239)
где T — температура конденсации; Xi и лг2 — молярные доли пер¬
вого и второго компонентов в паре; Cmn — эмпирические коэффи¬
циенты.
В индексе «тп» т — показатель степени при хх и п — показа¬
тель степени при х2.
Для определения эмпирических коэффициентов Cmn исполь¬
зуют условия экстремума в бинарных системах
dTjdxj = 0 при X2 — 0 (система I —3)
dT/dx2 = 0 при Xi — 0 (система 2—3) (240)
dTfdXi^O при X3* 0 (система 1—2)
с помощью которых из уравнения (239) получают следующие со¬
отношения
2См*(,1а, + С10-0 · (241).
2С02423) + С01=0 (248*
2 (C2Q — Сц + Сщ) ·*ί * + (^ii — 2С02 + С|0 — Coi) = 0 (243)
12S
Таблица 20
Сопоставление расчетов по уравнениям (233) и (234)
и неравенствам (236) — (238) с опытными данными
Вид экстремума
температуры
Свойства j
азеотропа
рассчитанные
экспериментальные
Система
расчет¬
ный
экспе-
римен-
таль-
ный
Х\
Х2
Хз
*аз
Xl
Х2
хз
^аз
Пентан — триметилэтилен — диэтиловый эфир
Отс.
Отс.
—
—
—■
30
—
__
-
_
Бензол — циклогексан — метиловый спирт
Мин.
0.20
0,21
0,59
50
-
-
-
-
Бензол — циклогексан — пропиловый спирт
»
Мин.
0,37
Oy 50
0,13
70
-
-
-
<74
Циклогексан — метиловый спирт — ацетон
»
0.24
0,16
0,60
50
0,28
0,29
0,43
-
Циклогексан — метиловый спирт — метилацетат
»
»
0,13
0,32
0,55
50
0,24
0,35
0,41
50,8
Г ексан — этиловый спирт — хлороформ
»
*
0,64
0,03
0,33
58
-
-
-
58,3
Сероуглерод — ацетон — метилацетат
Отс
Отс.
-
-
-
40
-
-
-
-
Ацетон — метиловый спирт — метилацетат
Мин.
Мин.
0,35
0,21
0,44
50
-
-
-
53,9
Ацетон — метиловый спирт — хлороформ
Седл.
Седл.
0,13
0,47
0,40
58
0,32
0.45
. 0,28
57,5
Ацетон — хлороформ — изопропиловый эфир
Отс.
Отс.
60
Примечание. Мин. — минимум температуры кипения: Седл. — седловинная точка: Отс. — тройной азеотроп не образуется.
В этих выражениях величины х^к) обозначают молярную долю
компонента i в бинарном азеотропе, образованном компонентами
ink.
Еще три уравнения получаются при подстановке в уравнение
(239) данных о температурах кипения компонентов.
Для определения состава тройного азеотропа используют усло¬
вия (225), применение которых к уравнению (239) дает:
2C2oXi3 + Сц^|3 = — Cjq (244)
C11X1 + 2С02х| = — Cq1 (245
Совместным решением этих уравнений определяют величины
Xf3 и х33. Затем по уравнению (239) находят температуру кипе¬
ния тройного азеотропа.
Однако описанный метод не получил практического примене¬
ния из-за существенных ограничений, связанных с формой интер¬
поляционного уравнения (239), которое не может отразить все
возможное разнообразие форм поверхностей температур конден¬
сации (или кипения) в тройных системах.
В дальнейшем развитие методов предсказания возможности
образования и свойств тройных азеотропов происходило в направ¬
лении использования более сложных интерполяционных уравнений
для описания зависимости коэффициентов активности от состава
смесей.
В работе [168] предложен 'способ предсказания возможности
образования и свойств азеотропной смеси в многокомпонентной
системе, базирующийся на использовании зависимости коэффици¬
ентов активности компонентов от состава раствора. Она основана
на допущении, что изменение энергии при смешении обуслов¬
лено попарным взаимодействием молекул, и энергия взаимодей¬
ствия любой пары молекул не зависит от других видов взаимодей¬
ствий
W In Yi -S (I -Xi) XpAtp- 2 W4P? (246)
P-1 Р. р-1
где Apq — константы, учитывающие энергию взаимодействия моле¬
кул компонентов р и q.
Первая сумма в правой части уравнения (246) берется при
условии ρφϊ, а вторая — при условиях рФц, ρφϊ и q Ф i. Для
бинарных систем из уравнения (246) получаются уравнения тео¬
рии регулярных растворов (175). В азеотропной точке, согласно
уравнению (60), коэффициент активности компонента i выра¬
жается формулой:
Vi = PIP0I (247)
127
Если принять, что зависимости InP-/(1/Г) и InP0i = J(IlT)
в ограниченном интервале температур имеют одинаковые угловые
коэффициенты, то можно написать
/? In Yi =* (1/Г (248)
где ΔHi — энтальпия испарения чистого компонента i; T и T0i-
температуры кипения раствора и компонента i при заданном дав¬
лении, соответственно.
Если отношение HHiIT0i заменить изменением энтропии
то из уравнений (246) и (248) получим следующие уравнения для
компонентов i и /:
ASi(Tl- J) =2 0-*i) xPaIP- Σ ХРХ0АР
P=I Р.
ASi (г® - Τ’) = 2 0 - xl) xPaIP - Σ
Р, Q** I
ХРХ0АРЧ
(249)
(250)
[η η Ύ
Σ ХРХ0АР0
P = I Р, Q-1 J
п
Σ (1-*/) ХРА
XnXrtAnn
P я PQ
P = I
pt q=I
(251)
Легко видеть, что правая часть уравнения (251) имеет мак¬
симальное значение при Xi = 0 и Jtp = Xj = I и минимальное при
*ί = I и Xp = Xj — 0. Следовательно, условие образования азео¬
тропной смеси может быть выражено неравенствами:
Aif
ASj
< Г, - Г, <
aH
ASi
(252)
Такие неравенства можно написать для всех попарных комби¬
наций компонентов рассматриваемой многокомпонентной системы.
Решение системы уравнений для различных пар компонентов, по¬
зволяет рассчитать состав азеотропной смеси. Для тройных си¬
стем получается уравнение:
/Ii2A = Af (253)
где
Af =
(I-AT1)X2 — *2*3 (I — Xl) Хз
(I-X2)X1 (I-X2)X3 -XiXs
-XiX2 (I-X3)X2 (I-X3)Xi
AH1(I-TITV) _Х2Хз X3
AH2(I-TITV) (I-^2)X3 -X1X3
Atf3 (I-777·“) (I-X3)X2 (I-^)X1
128
Решая совместно два уравнения (253), написанные для двух
пар компонентов, можно найти состав азеотропа. Если при этом
получается Xi = О или Xi = I, то азеотроп разрушается.
Для сцстем, у которых два компонента общих, а третий при¬
надлежит к одному гомологическому ряду, значения А12 близки.
Поэтому должна получиться линейная зависимость между вели¬
чинами M и Δ. Рис. 38 и 39 иллюстрируют это положение на при-
M
Рис. 38. Зависи¬
мость M от Δ для
тройных азеотропных
смесей, образованных
водой с бензолом (О),
четыреххлористым
углеродом (#) и спир¬
тами:
/ — этиловый спирт; 2—
изопропиловый спирт;
3-трет-бутиловый спирт;
4 — пропиловый спирт;
5—аллиловый спирт;
6 — фторбутиловый спирт;
7 — гексиловый спирт.
Af
1 О/
70
h
SO
J3
50
L·
UO
I 5
30
- /
20
- У
10
-/
0 1 2 3 (IO i)
Δ
I
Рис. 39. Зависи¬
мость M от Δ для
азеотропных смесей,
образованных цикло-
гексаном, водой и
спиртами:
I — этиловый спирт; 2—
изопропиловый спирт;
3-трет-бутиловый спирт;
4 — аллиловый спирт;
5 — пропиловый спирт.
мере азеотропных смесей, образованных водой и спиртами соот¬
ветственно с четыреххлористым углеводородом, бензолом и цик-
логексаном.
В работе [169] для предсказания возможности образования и
свойств тройного азеотропа по экспериментальным данным о свой¬
ствах бинарных систем предложено использовать зависимость
коэффициентов активности компонентов тройных смесей от со¬
става последних: [см. уравнение (355) на стр. 229].
Ig Yi
I
Ir +* Al4-X AlV
[х' + х*1й7 + х* A1J
'[x^a 12 йг)
+ Bi) + [Ап +Аи~ А32 - Jfj ] (254>
5 Зак. 917
129
Аналогичные уравнения можно написать для Igy2 и Igy3, изме-
1
нив индексы в уравнении (254) по схеме Д(т· е. запи¬
сывая это уравнение для Igу2, надо индекс I заменить на 2,
2 на 3 и 3 на I, в выражении для Igy3 следует индекс I заменить
на 3, 2 на I и 3 на 2). Как указывалось, в азеотропной точке коэф¬
фициенты активности компонентов определяются выражением
Ацетон
JMl IMk
1.щ IM Ь?6
/-.V Л
1Θ38Λ023 1.032 твшв ~
/.V V у
1,096 1,057 1,048 1.009 1,174 1,155
/ у у у \
1.ШЛ116 1081 Imk t.ISS.I, W W3
/ уVY у\
iMijo5,i.m Ws IJse IMdmm
/.V V V V V \
1,530 l,33i.1.?IS 1.1*8 φο Μ87Λ3221,3*3
1Ш 1,516027 1^97 1191. 1^29 1^5 1,347 1 3801405
/.VVV Л/ \/ \/ \/ \
2,7771,7801.482 1,265 1224 1244 1288 1,344 1,403 1,433/445.
/-V V V V V V V V \
2,94^2.154^1,475 1,354 1,270 1,267 1298 045 098 1,454 14821,605
$4-2,40^1,630 \fjl2 \fj96 \±?82 \tJo6 \j348 \/зв \$1 \,505
Л A A JV Л .Д
2,94^2.154^1,475 1,354 1,270 1,267 1,798 1,345 098 1,454 14821§05
$4-2,40^1,630 \фв \lj282 \tJo6 \j348 \$1 \,505
4 -fi / / / / i / / #>/
Циклогексан Метиловый спирт -
Рис. 40. у-Карта для ацетона в системе ацетон — метиловый спирт—
циклогексан при 50° С.
(247). Идея предлагаемого способа обнаружения и определения
свойств тройного азеотропа заключается в том, что, рассчитывая
значения коэффициентов активности компонентов по уравнениям
типа (254), выясняют путем графической интерполяции получен¬
ных данных, имеется ли смесь такого состава, для которой
равенство Xi + Хг + хз = I и условия (247) выполняются одновре¬
менно для всех компонентов. Анализ осуществляется в следую¬
щей последовательности. [Для наглядности изложение иллю¬
стрируется данными для системы ацетон (I)—метиловый спирт
130
(2) — циклогексан (3)]. Вначале по данным о равновесии между
жидкостью и паром или по иным данным определяют константы
Aik для бинарных систем, входящих в состав рассматриваемой
тройной системы. Затем по уравнениям (254) рассчитывают зна¬
чения коэффициентов активности для такого числа смесей, чтобы
можно было бы построить так называемые γ-карты для всех трех
компонентов. На рис. 40 представлена такая γ-карта для ацетона.
Далее для нескольких температур определяют коэффициенты
активности компонентов по
формуле (247) и для каждой
температуры на треугольную
диаграмму наносят линии по¬
стоянных коэффициентов ак¬
тивности («изогаммы») всех
компонентов. При построении
изогамм значения коэффициен¬
тов активности определяют по
данным γ-карт путем линей¬
ной интерполяции. В пределах
небольших интервалов такая
интерполяция допустима. Для
системы ацетон — метиловый
спирт —циклогексан такая ди¬
аграмма изображена на
рис. 41, показывающем ход
изогамм при 50, 52 и 54° С.
Из рис. 41 следует, что с
повышением температуры кри¬
вая для γι перемещается
вверх, γ2 — вправо, a γ3 — вле¬
во. При SO0C точки пересече¬
ния изогамм Ajtt В и С ограничивают область ABCi которая при
повышении ^температуры до 53° С уменьшается до размера, отве-»
чающего положению точек DEF. Очевидно, что точка пересечения
всех трех изограмм, отвечающая несколько большей (52° С) тем¬
пературе, должна находиться внутри области DEF. При 54° С
происходит обращение взаимного расположения изогамм. Сле¬
довательно, температура кипения тройного азеотропа лежит в ин¬
тервале между 52 и 54° С.
На рис. 42 изображены изогаммы компонентов при 53° С. Вид¬
но, что область, ограничиваемая изогаммами, уменьшается до
размеров, близких к точке. Дальнейшее уточнение, учитывая не¬
избежные погрешности, связанные с использованием интерполя¬
ционных уравнений (254) и с определением констант, не имеет
смысла.
Результаты, получающиеся с помощью описанного метода, ил¬
люстрируются сопоставлением расчетных и опытных величин для
ряда систем в табл. 21.
Рис. 41. Линии постоянных коэффи¬
циентов активности компонентов (изо¬
гаммы) системы ацетон (I) — метиловый
спирт (2) — циклогексан (3) при 50, 52 и
54° С:
Yt; Y2; —* Y8.
5*
131
Таблица 21
Сопоставление расчетных [169] и экспериментальных свойств
тройных азеотропов
Система
Расчетные данные
Экспериментальные данные
№ по
пор.
компонент I
компонент 2
компонент 3
содержание компонентов,
вес. %
£кип* °с
содержание компонентов,
вес. %
/ °с
КИП’
I
2
3
I
2
3
I
Ацетон — метиловый спирт — цикло¬
47,5
14,0
38,5
53
43,5
16,0
40,5
51.1
гексан
2
Изопропиловый спирт -
- вода — ни-
64,5
8,5
27,0
78
62,0
6,0
32,0
78,0
трометан
3
Этиловый спирт — этилацетат — вода
11,0
82,5
6,5
70
8,4
82,6
9,0
70,23
4
Хлороформ
— этиловый спирт — вода
96,5
1.0
2,5
55
92,5 .
4,0
3,5
55,4
5
Этиловый спирт — бензол — вода
27,0
71,0
2,0
68
18,5
74,1
7,4
64,86
6
Ацетон — хлороформ — метиловый
42,5
38,5
19,0
56
30,0
47,0
23,0
56,4
спирт
7
Четыреххлористый углерод — этило¬
вый спирт — бензол
Тройного азеотропа нет
Тройного азеотропа ;
нет
8
Г ептан — 2-бутанон — толуол
То
I же
То же
Системы, приведенные в табл. 21, относятся к различным ти¬
пам. Первая система характеризуется наличием трех бинарных
гомогенных азеотропов с минимумом температуры кипения. В сле¬
дующих четырех системах имеется по два бинарных положитель¬
ных гомогенных азеотропа и один гетероазеотроп. Шестая система
содержит два гомогенных положительных и один отрицательный
бинарный азеотроп. Из двух неазеотропных систем седьмая со¬
держит две бинарные си¬
стемы с положительными
гомогенными азеотропами
и одну неазеотропную
систему. В восьмой си¬
стеме имеется только од¬
на азеотропная бинарная
с гомогенным положи¬
тельным азеотропом. Во
всех случаях расчетные и
экспериментальные ве¬
личины качественно со¬
гласуются, однако рас¬
хождение в ряде систем
относительно велико.
Расчеты с помощью
уравнений (254) можно
легко упростить, приме- Циклогексан Метиловый спирт
НЯЯ ЭВМ. Рис. 42. Изогаммы компонентов системы аце-
Использованию интер- тон—метиловый спирт — циклогексан при 53° С.
ПОЛЯЦИОННЫХ уравнений, (Обозначения те же, что на рис. 41.)
выражающих зависи¬
мость коэффициентов активности компонентов тройных систем от
состава смесей для предсказания свойств азеотропов, посвящены
работы [170, 171].
В работе [171] для решения фассматринаемой задачи предло¬
жено использовать уравнения Вильсона [172], с помощью кото¬
рых зависимость отношения коэффициентов активности компо¬
нентов тройных смесей от состава выражается соотношениями
In JiL In + х2Л32 + Хз· ^ Xi (^1з ~ I)
Уз xI + Х2^12 Н“ Хз^13 Xi + X2^j2 + Х3Л13
-L *2 (Л23 ~~ ^2l) , Хз (I ~ ^3t) (255)
Х1Л21 + Х2 + Хз^23 Х1-4з1 + Х2^32 + Хз
In Yl«In *i4n· +*2^32-Мз + Xi (An-An) +
Y3 " X1A21 H- X2 H- X3A23 X1 H- X2A12 + X3A13
+ HsltJ.) + *■ — (256)
X1A21 -f- X2 H- х3Л23 X1A31 H- х2Л32 H- X3
где Aih — константы, определяемые по опытным данным для би¬
нарных систем.
133
Используется условие образования тройного азеотропа в фор¬
ме (227). Коэффициенты относительной летучести рассчитывают
по формулам (99), а входящие в них отношения коэффициентов
активности — по формулам (255) и (256). Расчеты выполняют
с помощью ЭВМ, причем для выявления азеотропной точки ис-
«.— I
пользуют метод минимизации функции 2 (ty* — I), которая
для тройной системы имеет вид:
/-(<*13-I)+ (α,,- 1) (257)
По данным о свойствах чистых компонентов и бинарных систем
находят давления паров чистых компонентов P0i и константы Виль¬
сона для бинарных систем Aik. Затем задается шаг Δ** изменения
величин Xi. Для сокращения времени рекомендуется выполнять
расчет в два этапа: на первом этапе с шагом Δχ* = 3 мол. % для
нахождения области расположения азеотропной точки и на вто¬
ром этапе — с шагом Ал:г* — 0,1 мол.% для нахождения состава
азеотропа. Признаком наличия азеотропа является близость к
нулю функции /, определяемой выражением (257). Для. увеличе¬
ния надежности расчетов рекомендуется выполнять их для всех
возможных вариантов нумерации компонентов, чтобы затем усред¬
нить результаты по методу наименьших квадратов.
Для проверки были сопоставлены результаты расчетов для
одной четверной и девятнадцати тройных систем. Системы были
отобраны по признакам надежности данных о составе тройного
азеотропа, точности данных для бинарных систем, используемых
для определения констант Вильсона и однородности жидкой фазы
(при наличии двух жидких фаз уравнения Вильсона непригодны).
Выполненные расчеты показали отсутствие азеотропов в четы¬
рех тройных системах. Для остальных систем расхождение рас¬
четных и экспериментальных значений концентраций компонентов
в азеотропах не превышало 2 мол.%.
Следует отметить, что прием, основанный на отыскании мини¬
мума функции /, может быть использован при выражении зави¬
симости коэффициентов активности от состава смесей не только
с помощью уравнений Вильсона, но и других уравнений, исполь¬
зуемых как для тройных, так и для многокомпонентных систем.
Очевидно, точность результатов, получаемых любыми расчет¬
ными методами, прежде всего зависит от точности используемых
исходных данных. Для рассматриваемой задачи такими данными
являются давления паров чистых компонентов и сведения о фазо¬
вом равновесии в бинарных системах. Константы, характеризую¬
щие условия фазового равновесия в бинарных системах, должны
определяться при той температуре, для которой выполняются рас¬
четы для тройной или многокомпонентной системы. В противном
случае может возникнуть погрешность, обусловленная изменением
коэффициентов активности компонентов с температурой. Это из¬
134
менение тем больше, чем больше теплоты смешения компонентов.
Необходимо иметь это в виду при использовании констант, харак¬
теризующих условия фазового равновесия в бинарных системах,
косвенных данных — температур кипения смесей, найденных на
основании косвенных данных о свойствах азеотропов, о раствори¬
мости и др.
СВОЙСТВА АЗЕОТРОПНЫХ СМЕСЕЙ,
ОБРАЗОВАННЫХ КОМПОНЕНТАМИ
С ОГРАНИЧЕННОЙ ВЗАИМНОЙ РАСТВОРИМОСТЬЮ
Бинарные системы. При совместном существовании двух жид¬
ких и паровой фаз бинарная система, согласно правилу фаз, имеет'
одну степень свободы. Следовательно, при постоянных темпера¬
туре или давлении такая система становится нонвариантной, а со¬
став и давление пара (или температура кипения) остаются по¬
стоянными при любых относительных количествах жидких фаз.
Такие системы разделяются на две основные группы. К первой
Рис. 43. Кривые фазового равновесия бинарных систем,
образованных компонентами 'с ограниченной взаимной
растворимостью.
а — Зависимость P «* f (х); б — зависимость у « φ (х): I — системы пер¬
вой группы; 2 —системы второй группы; 3 —системы третьей группы.
группе относятся системы, в которых при постоянной температуре
давления пара в области существования двух жидких фаз превы¬
шает давление паров чистых компонентов. В этих системах
образуются гетероазеотропы с минимумом температуры кипения,
состав которых является промежуточным между составами жид¬
ких фаз. Ко второй группе относятся системы, в которых давление
пара при совместном существовании двух жидких фаз имеет про¬
межуточное значение между давлениями паров компонентов,
а состав пара не является промежуточным между составами
жидких фаз. В этих системах гетероазеотропы не образуются. Кри¬
вые фазового равновесия для указанных групп систем представ¬
лены на рис. 43.
135
Из диаграмм состав пара — состав жидкости, приведенных на
рис, 43, видно, что системы, имеющие гетероазеотропы, не могут
быть разделены на чистые компоненты в процессе ректификации,
тогда как для систем, не образующих гетероазеотропов, это вполне
возможно. Поэтому определение принадлежности систем к одной
из этих групп имеет важное практическое значение.
Если пары ведут себя как идеальные газы, то общее давление
равно сумме парциальных давлений компонентов и тогда для си¬
стем первой группы
P ~ р2> Р\> Р\ (258)
для систем второй группы
где Р, pi и р2 — общее и парциальные давления компонентов в об¬
ласти существования двух жидких фаз.
Из неравенств (258) и (259) получаем соответственно:
В области совместного существования двух жидких фаз пар¬
циальные давления паров компонентов постоянны и с помощью
формулы (56) могут быть выражены как
где Xj и х" — молярные доли; и у" — коэффициенты активно¬
сти первого и второго компонентов в фазах, обогащенных соответ¬
ственно первым и вторым компонентами.
Заменяя с помощью формул (262) р\ и Р2 в неравенствах (260)
и (261), можно придать последним следующий вид:
Если взаимная растворимость компонентов относительно неве¬
лика, то коэффициент активности компонента, являющегося рас¬
творителем по отношению к компоненту, концентрация которого
мала, в каждой из фаз близок к единице (поскольку за стандарт¬
ное принимается состояние чистого компонента). Поэтому для ка¬
чественной оценки принадлежности систем рассматриваемого типа
к одной из указанных групп можно принять γ( γ" I. Тогда из
неравенств (263) и (264) получаем
р\<р<рЧ
(259)
p0I-Pi <Pi
р\ — Pi Pi
(260)
(261)
гчО f f nO ff ft
PI =^lYl И Р2~Р2Х2Ч2
(262)
и
(264)
(263)
136
для систем первой группы
E = Л
рО г‘
Г2 х2
P0 г
Я—зг—1г< I (265)
и для систем второй группы
Е ” P0 ж
^ 2 *2
Sr·—>! (266)
где л;'— молярная доля второго компонента в фазе, обогащенной
первым компонентом.
Таким образом, вероятность образования гетероазеотропа мо¬
жет определяться значением величины E1 связывающей давления
паров и взаимную растворимость компонентов. Из неравенства
(265) следует, что вероятность образования гетероазеотропа тем
больше, чем меньше различаются давления 'паров компонентов
и чем меньше их взаимная растворимость.
Применимость неравенств (265) и (266) для предсказания типа
систем иллюстрируется табл. 22, в которой приведены рассчитан¬
ные значения E1 а также указана группа, к которой относится
каждая система. Данные о наличии и составах гетероазеотропов,
необходимые для определения принадлежности систем к той или
иной группе, заимствованы из литературы [45, 173, 174].
Для первых шести систем фактор E значительно больше еди¬
ницы, что указывает на отсутствие гетероазеотропов в этих систе¬
мах. Действительно, пар, образующийся при кипении двухфазных
жидких систем никотин—вода и фенол—вода, содержит соответ¬
ственно 0,28 мол.% никотина [173] и 2,6 мол.% фенола [174], т. е.
меньше, чем его содержание в обеих жидких фазах. В системе
гексан—анилин гетероазеотроп также не образуется [45]. Системы
4—6, относительно состава пара которых данные обнаружить не
удалось, вероятно, не должны образовывать гетероазеотропы.
В системах 9—15, для которых E < I, как и следовало ожидать,
образуются гетероазеотропы [45], характеризующиеся наличием ми¬
нимума температуры кипения и составом пара, промежуточным
между составами жидких фаз.
Таким образом, приведенное сопоставление подтверждает воз¬
можность использования неравенств (265) и (266) для определе¬
ния вероятности образования гетероазеотропа в бинарной системе.
Особый интерес представляют системы, для которых E & I. Из
перечисленных в табл. 22 — это системы диэтиловый эфир—вода
и этилметилкетон—вода, где имеет место весьма четко выражен¬
ный минимум температуры кипения при наличии двух жидких фаз.
Так, при атмосферном давлении двухфазная смесь диэтиловый
эфир—вода кипит при 34,2° С (т. кип. эфира 34,6°), а смесь этил-
метилкетона и воды — при 73,45° С (т. кип. этилметилкетона 79,6°).
По этому признаку указанные системы следовало бы считать
1)7
Таблица 22
Результаты применения неравенств (265) и (266)
к бинарным системам
с ограниченной взаимной растворимостью компонентов
№ по
пор.
Компоненты ,
*КИП’ °С
Р\,
MM PT. СТ.
Р2>
MM PT. ст.
X2.
мол. %
/У
*2,
мол. %
E
Группа,
к которой
относится
система
I
2
I
Вода
Никотин
100
760
7,66
0,84
32,4
2,57
II
2
*
Фенол
62,5
167,6
5,0
4,45
18,3
8,2
II
3
Г ексан
Анилин
50
408
2,4
20,4
78,7
44,1
II
4
Бензол
Ацетамид
100
1344
8
5,22
88,5
9,9
II
5
Метиловый спирт
T етраэтилсилан
70
927
30
15
79
5,9
II
6
Двуокись серы
Г ексан
-10
760
26
3
65,7
1,34
II
, 7
Диэтиловый эфир
Вода
34,6
760
41,3
5,52
98,78
1,02
IH
8
Этилметилкетои
>
70
548,7
234
40,1
95,4
0,987
III
9
Вода
Фурфурол
97,9
704
92,2
4,06
49,7
0,623
I
10
Пропионитрил
Вода
80
430
355
37,8
94,6
0,48
I
11
Вода
Анилин
75
289
14,4
1,06
70,0
0,304
I
12
*
Циклогексанол
100
760
72
0,78
49,3
0,165
I
13
*
Бутиловый спирт
92
567
269
2,1
35,3
0,125
I
14
Двуокись серы
Бутан
-18
525
399
6,3
67
0,124
I
15
Вода
Диэтилкетон
80
355
309
0,69
79,7
0,1
I
принадлежащими к первой группе. Однако состав пара в обеих си¬
стемах не будет промежуточным между составами жидких фаз, что
указывает на отсутствие гетероазеотропа и является характерным
признаком систем второй группы. Следовательно, эти системы
(Е я* I) занимают промежуточное положение между первой и вто¬
рой группами и должны быть отнесены к самостоятельной третьей
группе. Как показывает рассмотрение опытных данных, в этих си¬
стемах образуется гомогенный азеотроп в области концентраций,
примыкающей к низкокипящему компоненту. Так, азеотропы ди¬
этиловый эфир—вода и метилэтилкетон—вода содержат при атмо¬
сферном давлении соответственно 5,15 и 33 мол.% воды.
Состав и давление пара можно выразить с помощью уравнений
(94) и (56). Получаем
где у' и у" — коэффициенты активности первого и второго компо¬
нента в фазах, обогащенных этими компонентами.
Условия, определяющие принадлежность бинарных систем к от¬
меченной выше промежуточной группе, с учетом уравнений (267)
и (268) могут быть выражены следующими неравенствами:
Следовательно, для принадлежности систем к третьей группе
необходимо наличие в них положительных отклонений от закона
Рауля, которые и имеются в системах с ограниченной взаимной
растворимостью.
Представляет интерес выяснить возможность наличия бинар¬
ных систем, имеющих в области существования двух жидких фаз
состав пара, промежуточный между составами последних, и
(267)
и
(268)
(269)
И
(270)
Из неравенств (269) и (270) следует:
(2/1)
139
давление, промежуточное между давлениями паров чистых ком¬
понентов. Если выразить эти условия с помощью уравнений (267)
и (268), то получим:
P0
Г Г х 2 // ^ I M7о\
Yl < ATiYl+ —5- Υ2 < 1 (272)
Следовательно, для образования таких систем необходимо на¬
личие в них отрицательных отклонений от закона Рауля. В настоя¬
щее время неизвестно ни одной бинарной системы с отрицатель¬
ными отклонениями от идеального поведения, компоненты которой
имели бы ограниченную взаимную растворимость. Исходя из пред¬
ставлений о связи между растворимостью и отклонениями от за¬
кона Рауля [35], существование таких систем представляется не¬
возможным.
Из изложенного вытекает следующая классификация бинарных
систем, имеющих две жидкие фазы:
I группа (Е < I)-—системы, образующие гетероазеотропы.
В этих системах имеется минимум температуры кипения при сов¬
местном существовании двух жидких фаз, а состав пара — проме¬
жуточный между составами последних;
II группа (E > I) —системы, не образующие гетероазеотропов.
В этих системах отсутствует минимум температуры кипения при
совместном существовании жидких фаз, а состав пара не является
промежуточным между составами последних.
III группа (E « I) —системы, занимающие промежуточное по¬
ложение между системами I и II групп. В этих системах имеется
минимум температуры кипения при совместном существовании
двух жидких фаз, но состав пара не является промежуточным ме¬
жду составами последних.
Характер кривых фазового равновесия для указанных групп
изображен на рис. 43.
Рассмотрение свойств систем, относящихся к различным груп¬
пам, показывает, что в качестве разделяющих агентов для процес¬
сов азеотропной ректификации могут применяться вещества, обра¬
зующие с отгоняемыми компонентами системы второй и третьей
групп. В первом случае расслаивание разделяющего агента и
отгоняемого компонента может производиться при температуре ки¬
пения гетероазеотропа. Если разделяющий агент дает с отгоняе¬
мым компонентом систему третьей группы, то дистиллат представ¬
ляет coj6oft гомогенный азеотроп, разделение которого путем рас¬
слаивания возможно лишь за счет использования уменьшения
взаимной растворимости с понижением температуры. В этом слу¬
чае конденсат пара, выходящего из верха колонны, необходимо
подвергать дополнительному охлаждению.
Трехкомпонентные системы. Выше было показано, что при до¬
бавлении к многокомпонентной системе вещества, обладающего
ограниченной взаимной растворимостью с некоторыми компонен-
140
Таблица 23
Сопоставление относительного содержания компонентов в тройных и бинарных азеотропах
Компоненты
Состав тройного
азеотропа, мол. %
Содержание
А в бинар¬
ных
азеотропах,
мол. %
о,
^ H
<1 EQ
*
к
к
XQ
CU
H
ш.
Si
^ о
<1 CQ
* I*
А
Б
в
xA
xB
xB
xAB
*АВ
< EQ
*
<! CO
* I*
Этиловый спирт
Вода
Дихлорэтан
25,7
19,4
54,9
89,7
55,7
1,32
8,7
0,468
1,26
Бромистый пропил
21,5
22,8
55,7
89,7
40,8
0,943
8,7
0,386
0,69
Этилацетат
12,4
28,4
59,2
89,7
46,0
0,437
8,7
0,21
0,852
»
Диэтилформаль
23,0
38,7
38,3
89,7
60,8
0,594
8,7
0,601
1,55
Этиленхлоргидр ид
Дихлордиэтило- 1
вый эфир
Вода
' 9,1
4,5
86,4
90,9
23,2
2,02
10,0
0,105
0,302
Пропиловый спирт
Вода
Йодистый аллил
27,6
36,9
35,5
43,2
53,7
0,748
0,762
0,777
1,16
»
Пропилацетат
15,7
56,2
28,1
43,2
63,0
0,280
0,762
0,558
1,70
»
Нитрометан
18,45
40,4
41,15
43,2
56,4
0,457
0,762
0,448
1,29
»
Бензол
8,9
28,3
62,8
43,2
20,9
0,314
0,762
0,142
0,264
Изопропиловый спирт
Циклогексан
21,8
25,3
52,9
68,5
44,5
0,862
2,17
0,412
0,802
Диизопропиловый
эфир
Трихлорэтилен
8,3
14,8
76,9
68,5
24,9
0,561
2,17
0,108
0,392
Аллиловый спирт
13,0
27,7
59,3
44,7
48,7
0,469
0,808
0,219
0,95
»
Диаллиловый эфир
9,2
41,8
49,0
44,7
42,0
0,22
0,808
0,188
0,724
Ацетонитрил
»
Трихлорэтилен
35,4
25,2
39,4
71,3
61,7
1,404
2,48
0,899
1,61
Метилэтилкетон
Четыреххлористый
углерод
32,1
17,4
50,5
66,9
84,0
1,84
2,02
0,636
5,25
Пропиловый спирт
»
Трихлорэтилен
41,3
20,3
38,4
89,7
51,4
2,03
8,7
1,075
1,06
Аллиловый спирт
»
Г ексан
6,2
19,6
74,2
44,7
6,53
0,316
0,808
0,084
0,070
Изопропиловый спирт
Гексиловый спирт
»
Нитрометан
Берзол
54,6
5,6
17,6
5,5
27.8
88.9
68,5
5,5
69,3
Нет
3.1
1.02
2,17
0,058
1,96
2,26
тами, возрастает относительная летучесть тех из них, которые
имеют наименьшую взаимную растворимость с этим веществом.
Эта закономерность [175] может быть применена [168] и к трех¬
компонентным азеотропным смесям. Если три компонента А, Б и В
образуют азеотроп, а компоненты Б и В имеют наименьшую взаим¬
ную растворимость, то, в соответствии с указанной закономер¬
ностью, тройной азеотроп должен содержать относительно больше
компонентов Б и В, чем бинарные азеотропы АБ и AB. Это поло¬
жение подтверждается имеющимися экспериментальными дан¬
ными. В табл. 23 сопоставлены отношения концентраций компонен¬
тов В ТРОЙНОМ (Ха/х б) тр И (Ха/Хв) тр И В бинарНЫХ {Ха/хб) бин и
(*а/*в)6ин азеотропах для некоторых систем, одним из компонен¬
тов которых является вода.
Как видно из табл. 23, в большинстве случаев относительное
содержание компонента А, обладающего наибольшей взаимной
растворимостью с двумя другими, в тройной азеотропной смеси
меньше, чем в бинарных.
Это соответствует указанной выше закономерности, вытекаю¬
щей из связи между растворимостью и относительной летучестью.
Несоблюдение этой закономерности для некоторых систем (четыре
из них приведены в конце табл. 23) ставит под сомнение правиль¬
ность данных о составах азеотропных смесей.
Для систем пропиловый спирт — вода — трихлорэтилен, аллило¬
вый спирт — вода — гексан, изопропиловый спирт — вода — нитро¬
метан и гексиловый спирт — вода — бензол автором были экспери¬
ментально определены составы азеотропных смесей [176] (табл. 24).
Таблица 24
Сопоставление литературных [45] и опытных данных [169]
Система
Пропиловый спирт .
Аллиловый спирт . .
Изопропиловый спирт
Гексиловый спирт . .
Трихлорэтилен
Гексан
Нитрометан
Бензол
Подтверждением правильности полученных опытных данных
о составе азеотропов является их соответствие приведенной выше
закономерности, устанавливающей связь между составами бинар¬
ных и тройных азеотропов (табл, 25).
142
Таблица 25
Сопоставление составов тройных и бинарных азеотропов
Система
r xK \
< *Б /тр
ί—)
\ *Б /бин
(Щ
\ xB /тр
\ /бин
0,339
0,759
0,208
1,857
0,517
0,827
0,159
0,223
1,308
2,17
1,343
2,25
Пропиловый
спирт
Аллиловый спирт
Изопропиловый
спирт
Вода
»
»
Трихлорэти¬
лен
Г ексан
Нитрометан
Таким образом, рассмотрение имеющихся экспериментальных
данных подтверждает, что трехкомпонентные азеотропные смеси,
образованные веществами с ограниченной взаимной раствори¬
мостью, содержат по сравнению с соответствующими бинарными
азеотропами относительно больше тех компонентов, которые хуже
растворяются друг в друге.
Эта закономерность может использоваться для выбора разде¬
ляющих агентов в процессах азеотропной ректификации. Как пока¬
зывают рассмотренные примеры, она может применяться также
для качественной проверки данных о составах азеотропных смесей.
Практическое применение этой закономерности иллюстрируется на
примере процесса разделения смесей, получающихся в производ¬
стве жирных спиртов С7—C9 (см. гл. 3).
о составах азеотропных смесей
Состав тройного азеотропа, вес. %
Содержание А в бинарном азео-
тропе, вес. %
по справочнику [45]
по данным работы
[169]
по справочнику
[45]
по данным
работы [169]
А
Б
в
А
Б
в
АБ
AB
АБ
AB
12
7
81
8,1
7,1
84,8
28,3
17
28,3
17,1
5
5
90
5,1
8,5
86,4
72,3
4,5
12,5
62
6
32
51,5
11.7
36,9
87,9
69
—
5,6
5,5
88,9
Тройного азеотропа не дает
Экспериментальное определение свойств азеотропных смесей
При использовании метода азеотропной ректификации на
практике неизбежно приходится сталкиваться с необходимостью
экспериментального определения свойств азеотропов, образуемых
143
компонентами заданной смеси и разделяющим агентом. Методика
этого исследования описана в работе [144]. Чаще всего для этой
цели используют метод ректификационного анализа, сущность ко¬
торого заключается в "разгонке смесей рассматриваемых веществ
на колонке с возможно большей эффективностью и последующем
анализе отобранных проб. Для разгонки используют обычные ла¬
бораторные ректификационные колонки [177, 178]. В процессе раз¬
гонки контролируется температура кипения дистиллата. Во избе¬
жание экспериментальных ошибок исходные вещества должны
быть предварительно очищены.
Критерием чистоты является постоянство температуры кипения
и других физических св.ойств (например, показателя преломления,
удельного веса) в процессе разгонки исходного вещества на ко¬
лонке.
Техника определения наличия и свойств бинарного азеотропа
заключается в следующем. В куб колонки загружают смесь, вклю¬
чают обогрев куба и колонку выводят на режим работы без отбора
дистиллата («на себя»). По достижении установившегося режима
для удаления возможных низкокипящих примесей медленно отби¬
рают небольшую порцию дистиллата (2—5% от загрузки). После
этого колонка вновь в течение 0,5—I ч работает «на себя». Нали¬
чие азеотропа определяется, прежде всего, по показаниям термо¬
метра, установленного в верху колонки. Если температура в верху
колонки ниже температур кипения компонентов, значит образуется
положительный азеотроп.
По истечении указанного выше времени отбирается проба ди¬
стиллата, после чего колонка вновь работает «на себя». Таким
путем отбирается несколько проб, которые затем анализируются.
Для подтверждения правильности полученного результата по¬
лезно сделать контрольное определение, заключающееся в раз¬
гонке смеси, состав которой отвечает найденному составу азео¬
тропа. В этом случае всю загруженную смесь следует перегонять
при постоянной температуре, а пробы кубовой жидкости и дистил¬
лата должны иметь одинаковый состав в течение всего процесса
разгонки.
Наличие отрицательного азеотропа может быть установлено по
появлению в процессе разгонки искусственной смеси фракции
с температурой, превышающей температуры кипения компонентов.
Температуру кипения и состав этой фракции устанавливают в ре¬
зультате ряда последовательных определений; температуру же ки¬
пения и состав азеотропа уточняют путем контрольной разгонки
смеси, состав которой найден в предыдущих определениях.
Методика определения наличия и состава трехкомпонентных
азеотропов, в принципе, аналогична методике исследования азео-
тропизма в бинарных системах. Различие заключается в том, что
трехкомпонентные смеси при ректификации разделяются на боль¬
шее число фракций, чем бинарные. Это, однако, может вызвать
некоторое усложнение только при определении свойств седловин-.
144
ного и отрицательного азеотропов. Наличие и свойства положи¬
тельных тройных азеотропов, с которыми наиболее часто прихо¬
дится сталкиваться на практике, устанавливаются также, как для
бинарных положительных азеотропов. Разумеется, температуру
в верху колонки следует в этом случае сравнивать с температу¬
рами кипения бинарных азеотропов.
Усложнение определения наличия седловинных и отрицатель¬
ных тройных азеотропов обусловливается необходимостью отбора
фракций с более низкими температурами кипе¬
ния перед взятием проб этих азеотропов. Для
уменьшения возникающих при этом трудностей
целесообразно провести несколько последова¬
тельных опытов, определяя вначале примерные
температуру кипения и состав азеотропа, а за¬
тем уточнить эти характеристики повторными
опытами по разгонке смесей, состав которых най¬
ден в предыдущих экспериментах.
Примеры определения седловинных азеотро¬
пов методом ректификационного анализа приве¬
дены ниже. Тройные отрицательные азеотропы,
по-видимому, крайне редки (в настоящее время
не известно ни одного такого азеотропа).
Для систем с двумя жидкими фазами тре¬
буется некоторое уточнение описанной методики,
поскольку бинарные трехфазные системы при
постоянном давлении нонвариантны, методика
определения свойств бинарного гетероазеотропа
чрезвычайно упрощается. Для этого достаточно
загрузить компоненты в дистилляционную колбу
в произвольном соотношении, но так, чтобы
при кипении имелись две жидкие фазы, и в
процессе дистилляции фиксировать температуру
отгонки. Состав азеотропа определяют путем
анализа проб конденсата пара, отгоняемого в
процессе дистилляции.
Исследование азеотропии в трехкомпонентных системах, имею¬
щих две жидкие фазы, производят с помощЪю колонки. Необхо¬
димы особые предосторожности, чтобы уменьшить погрешности,
связанные с расслаиванием отбираемых проб азеотропа.
Для этого отбор проб дестиллята надо производить из паро¬
вой фазы, а не из жидкой. В качестве пробы должен использо¬
ваться весь полученный при этом конденсат. Если необходимо
исследовать часть пробы, то она раньше должна быть гомогенизи¬
рована путем добавки к отвешенному количеству пробы опреде¬
ленного количества гомогенизирующего вещества, не препятствую¬
щего последующему анализу. Колонка должна быть снабжена го¬
ловкой, обеспечивающей удобный отбор проб из паровой фазы.
Для ,этой цели пригодна обычная головка, изображенная на
W
Рис. 44. Головка
ректификационной
колонки:
/ — кран; 2 —конден¬
сатор; 3 — холодиль¬
ник.
рис. 44. Во время опыта кран I находится в закрытом положении,
а проба пара отбирается путем уменьшения расхода охлаждаю¬
щей воды, поступающей в конденсатор 2. Этот пар конденсируется
в холодильнике 3, к которому присоединяется пробоотборник..
ВЛИЯНИЕ ДАВЛЕНИЯ
НА СОСТАВ И ТЕМПЕРАТУРУ КИПЕНИЯ
АЗЕОТРОПНЫХ СМЕСЕЙ
Уравнение состояния многокомпонентной двухфазной си¬
стемы (39) для азеотропной смеси, в силу равенства Xi = у и пре¬
образуется к виду:
Это уравнение, известное под названием уравнения Клапейро¬
на — Клаузиуса, является уравнением состояния однокомпонент¬
ной системы. Таким образом, в отношении взаимосвязи между
температурой и давлением азеотропная смесь ведет себя подобно
ч чистому веществу.
Связь между температурой и давлением, согласно уравнению
(273), определяется объемным К<12> и тепловым Q<12) эффектами фа¬
зового перехода. При давлениях, достаточно удаленных от крити¬
ческого, величины К<12> и Q(12) имеют одинаковый знак, следова¬
тельно, повышение давления приводит к повышению температуры
кипения азеотропной смеси. Поскольку между этими параметрами
состояния существует простая связь, устанавливаемая уравнением
(273), вместо влияния давления на состав азеотропных смесей
можно рассматривать влияние температуры.
Бинарные системы. Влияние температуры и давления на состав
азеотропной смеси выявляется путем анализа уравнения Ван-дер-
Ваальса, являющегося уравнением состояния двухкомпонентной
двухфазной системы. После ряда преобразований (см. [3]) полу¬
чаются уравнения
где хаз — молярная доля в азеотропной смеси компонента, обозна¬
ченного индексом «I»; Li и Li— молярные теплоты испарения ком¬
понентов из растворов (парциальные молярные теплоты испарения
компонентов); V[ и V2 — парциальные молярные объемы компо¬
нентов в жидкой фазе.
dP_ q(12)
dT “ γ№)τ
(273)
(274)
и
(275)
146
При температурах и давлениях, достаточно удаленных от кри-
1 моль смеси из жидкой фазы в паровую значительно превышает
разность парциальных молярных объемов компонентов в жидкой
фазе. Уравнения (274) и (275) можно переписать следующим об¬
разом:
Из этих уравнений очевидно, что знак производных (dx/dT) аз
и (dx/dP)аз, характеризующих влияние температуры и давления на
состав бинарного азеотропа, определяется знаком частной произ¬
водной (<Э In yi/dxi)T, р, а также знаком разности L1— Li. Анализ
показывает [3], что для систем с положительными отклонениями от
идеального поведения в точке экстремума температуры и давления
а для систем с отрицательными отклонениями от идеального пове¬
дения '
Эти неравенства являются математической формулировкой вто¬
рого закона Вревского (см. стр. 43). k
Сторонкину и Морачевскому [179] удалось привести уравнения
(276) и (277) к более, удобному для практического использования
виду. Они основывались на том, что в состоянии равновесия хими¬
ческие потенциалы любого компонента в сосуществующих фазах
одинаковы. Для случая идеальной паровой фазы это условие за¬
писывается как
где μ^' и μ," — химические потенциалы первого компонента в жид¬
кой и паровой фазах и стандартном состоянии.
тических, У(12> > V1 — Уг, так как изменение объема при переходе
(276)
и
dx \
dP) аз
(277)
/ а In у, \ ‘ RT ' Qdад
\ dXi )т, р
(d InYiM(C1)7. р<0
(278)
(д In Υι/<5*ι)Γ р>0
Поэтому для положительных бинарных азеотропов
dхa3ldT > 0 и dxα3/άΡ > 0
(279
(280)
при La >Li
а для отрицательных бинарных азеотропов
dx HnIdT < 0 u dXasIdP < 0 при Li>L2
(281)
μ?' + RT Injc1 + RT lnYl = μ^ + RT In P + RT In ух
(282)
Дифференцирование этого равенства при постоянных значениях
T и P дает соотношение
(HRIl) = 1 \(дУЛ*3 _ Л
I dxi )т,р Хаз WdxlJrtP. J
►го уравненй
/ dx \ __ хаз
i dT /аз j I
(283)
с помощью которого уравнения (276) и (277) преобразуются
к виду:
•^аз U ~~ Хаз) L2
ду_\аз
дх/т, р
RT2
(
dx \ __ X3L3Q-Xas) V{12)
dP ) аз
^idyV3
\ дх )т, P
L\ — L2
RT ' Qi 12)
(284)
(285)
В этих формулах производные (<ду/дх)“® р выражают наклон
кривых фазового равновесия у = f(x) в азеотропной точке. Из
уравнений (284) и (285) следует, что при прочих равных условиях
влияние температуры и давления на состав
азеотропной смеси тем больше, чем ближе
ее состав к эквимолекулярному, поскольку
при этом увеличивается произведение
Хаз(I—Хаз). Это имеет место при уменьше¬
нии разницы температур кипения компо¬
нентов. Наклон кривой равновесия в азео¬
тропной точке (ду/дх)™р определяется раз¬
личием составов жидкости и пара (рис. 45).
Чем меньше различаются составы равно¬
весных фаз, тем ближе к единице значение
Рис. 45. Влияние степени производной. Различие составов равновес-
неидеальности бинарной ны* Фаа, согласно определению коэффи¬
циента относительной летучести (99), об¬
условлено значениями давлений паров
компонентов при заданной температуре и
степенью неидеальности системы. При
определенных, например одинаковых дав¬
лениях паров компонентов, различие соста¬
вов равновесных фаз тем больше, а значение производной
(dy/dx)T,p тем меньше, чем больше степень неидеальности системы
(см. рис. 45). Поэтому при прочих равных условиях влияние тем¬
пературы и давления на состав азеотропной смеси тем больше,
чем меньше различаются температуры кипения компонентов и чем
меньше отклонения от закона Рауля в рассматриваемой системе.
Использование формул (284) и (285) осложняется тем, что зна¬
чения парциальных молярных теплот испарения компонентов из¬
вестны или могут быть вычислены для сравнительно небольшого
числа систем. В связи с этим еще Вревский рекомендовал вместо
парциальных молярных теплот испарения компонентов ислользо-
системы на значение
производной (dy/dx)f3p:
I — небольшие отклонения от
идеального поведения; 2—боль¬
шие отклонения от идеального
поведения.
148
вать значения теплот Испарения чистых компонентов. Связанная
с этим погрешность тем меньше, чем больше различие теплот испа¬
рения компонентов и меньше теплота их смешения. Эти положения
иллюстрируются табл. 26, заимствованной из работы [172].
Таблица 26
Различные и экспериментальные данные
о влиянии температуры на состав азеотропа
Система
f, 0C
(dx/dT)as-IQ2t град~1
Расчетные
величины
Экспери¬
ментальные
данные
по парциальным
молярным тепло-
там испарения
по теплотам
испарения чистых
компонентов
Бензол—циклогексан
70
0,08
0,08
0,09
Бензол—изопропиловый
70
0,37
0,39
0,365
спирт
55
0,38
0,40
0,365
40
0,35
0,39
0,365
Циклогексан — изопропи¬
70
0,33
0,35
0,37
ловый спирт
55
0,35
0,36
0,37
40
0,36
0,38
0,37
Чтобы рассчитать значение производной {ду/дх)Р3р по уравне¬
ниям (284) и (285) нужны данные о равновесии между жидкостью
и паром.
В связи с тем, что такие данные не всегда имеются, представ¬
ляют интерес приближенные методы расчета влияния давления на
температуру кипения и состав азеотропной смеси [180—188]. Допу¬
ская симметричную форму зависимости неидеальной доли изобар¬
ного потенциала смешения от состава раствора (т. е., предполагая,
что последние ведут себя как^ регулярные), Киреев [180, 181] полу¬
чил следующие выражения, устанавливающие связь между давле-.
нием, составом и температурой кипения азеотропа
P- V(IgP02-IgPa3)KigP0l-IsPli3) + 1 (286)
(2*аз-D = (£)* (2<3 - 0 - L'~/·- [(-ψ)2 ~ Р] (287)
где Раз — давление пара азеотропной смеси; Li и L2 — молярные
теплоты испарения компонентов; хаз и х'з—молярные доли низко¬
кипящего компонента в азеотропе при температурах Г и Т'\ kf —
константа, значение которой определяется уравнением:
к' = ,ΡΡ, τ [In Pa3 - (I - хйз) In P01 - х'аз In P20] (288)
*аз Ч хаз)
149
Уравнение (287) позволяет определить состав азеотропа при
температуре T по известному составу азеотропа при темпера¬
туре Г'. Связь между давлением и составом азеотропа выражается
уравнением (288). Однако, как указывает Киреев, это уравнение
не может быть рекомендовано для расчета величины Р&3, так как
она очень чувствительна к точности исходных данных.
Отмер и Тен-Эйк [178] предложили метод расчета влияния дав¬
ления на температуру кипения и состав бинарных и тройных азео¬
тропов, основываясь на допущении, что зависимость парциального
давления компонента азеотропа от температуры выражается урав¬
нением, аналогичным уравнению Клаузиуса — Клапейрона
dpf dT
Lf3Pf3 RT2 *289^
аз -
где pi —парциальное давление первого компонента в азеотропе;
Lf3-MonHpHaH теплота испарения первого компонента из рас¬
твора.
Сочетая это уравнение с уравнением Клаузиуса — Клапейрона
для азеотропной смеси, получаем
d IgpT1 Lf3
d Ig Pa3 “ La3 (29°)
где Paa — давление паров азеотропа и
Las-молярная теплота испарения азеотропа.
Если принять Li3/La3= const, то, произведя интегрирование
уравнения (290) и заменяя парциальное давление с помощью за¬
кона Дальтона, получаем
La3 — La3
ig ^?3 = -lX;—Ig **?+с (291)
где xf3 — молярная доля первого компонента в азеотропе;
L1- молярная теплота испарения первого компонента;
С —константа интегрирования.
Аналогичным путем получается уравнение, выражающее связь
между давлениями паров азеотропа и чистого компонента:
Ig Pa3 = !g P0I + С (292)
Согласно уравнениям (291) и (292), имеет место линейная за¬
висимость Igjcf3 и IgPa3 от IgP?. Это подтверждено опытными
данными (рис. 46) для 9 систем с положительными и 4 — с отри¬
цательными бинарными азеотропами, а та^же для тройных гетеро¬
азеотропов бензол — пропиловый спирт — вода и трихлорэтилен —
этиловый спирт — вода.
150
Прямые, выражающие зависимость IgArf3 от IgPi и IgPa3 от
IgP?, можно провести по данным о свойствах азеотропа при
двух давлениях. Если известны свойства только при атмосферном
давлении, то теплоты испарения рассчитывают, пренебрегая тепло¬
той смешения, которая для систем, состоящих из органических
жидкостей, обычно весьма мала по сравнению с теплотой испаре¬
ния. При этом допущении молярная теплота испарения азеотропа
определяется по правилу аддитивности.
Рис. 46. Экспериментальная проверка метода Отмера и Тен-
Эйка.
I — пропиловый спирт — вода; 2 — ацетонитрил — вода; 3 - метиловый
спирт — бензол; 4— метиловый спирт — метилэтилкетон; 5 — ацетон — вода;
6 — этилацетат-этиловый спирт; 7 — β-пиколин-фенол; 8 — х лоро форм-эти ло«
вый спирт; 9 — γ-пиколин — фенол; 10 — хлористый - водород— вода;
II — бромистый водород — вода; 12 — метилэтилкетон — вода; 13 — этило¬
вый эфир — вода; 14 — бензол — пропиловый спирт — вода (а — мол. % бен¬
зола, б —мол. % пропилового спирта); /5 —трихлорэтилен — этиловый
спирт — вода (мол. % этилового спирта xf3, мол. % низкокипящего ком¬
понента в азеотропе).
Для систем 10 и —шкала давлений должна быть помножена на 10“*»
а д$я системы 13 — на 10~2.
Описанные методы определения влияния давления на свойства
азеотропов являются приближенными, но благодаря простоте,
удобны для технических расчетов.
Тройные системы. Гомогенные азеотропы. Термодина¬
мически строгое решение вопроса о влиянии температуры на со¬
став тройного азеотропа дано в работе [189]. Вывод основывается
на условии равенства химических потенциалов компонента в сосу¬
ществующих фазах. Для трехкомпонентной системы химический
потенциал является функцией температуры, давления и молярных
долей двух компонентов. Исходя из равенства полных диф¬
ференциалов химического потенциала первого компонента в рав¬
новесных фазах и принимая во внимание физический смысл его
частных производных по указанным переменным, можно получить
151
уравнение
-L1 Κ-νη«"Ί
(dx I \
Ur Ja
(дуЛ^ (дхЛ
V <5x2 Ir, p, X11 dT Ia
I _ MiMa3
\ Jr1 Λ x,
(293)
где индекс «аз» указывает на то, что соответствующие производ¬
ные берутся в азеотропной точке.
Разность парциальных молярных объемов первого компонента
в паровой и жидкой фазах V" — V\ практически равна изменению
объема при образовании I моль пара из жидкой смеси И12>. По¬
этому для первого компонента можно написать:
U - Qil2y ' I дуА*3 (dx2\
\ дх2 )т, Р, Xx I dT Ja3
(dxI \
Ur Ja
X1
RT2
I
дхI /г, P1 Xi
(294)
Аналогичное уравнение может быть получено для второго ком¬
понента
L2-Qil2y
( ду2 \аз / dxi \
I dxt Jr. P1 хА dr Ja
(dx2\ 4?Г* V дх\ /г. Р. хЛ <4? /аз
UrJa3
I <Эх2 /Г, Р. ж,
Из уравнений (294) и (295) следует, что как и в бинарных си¬
стемах, изменение состава азеотропной смеси с температурой за¬
висит не только от значений парциальных молярных теплот испаре¬
ния компонентов, но и от условий равновесия между жидкостью и
паром, учитываемых производными (OyJdx2)1-' р> Х} и (Oy2Idxl)r р .
Уравнения (294) и (295) могут быть решены совместно относи¬
тельно производных (dxJdT) и (dxJdT)аз, выражающих изменение
состава азеотропа с температурой. Для этого им удобно придать
вид
Выполненный в работе [189] анализ данных об изменении состава тройных
азеотропов в системах, образованных бензолом и циклогексаном с изопропило¬
вым и пропиловым спиртами, а также в системе циклогексан — этилацетат — эти¬
ловый спирт показывает, что при повышении температуры во всех случаях воз¬
растает содержание спиртов, имеющих большие, чем у других компонентов, теп¬
лоты испарения.
Содержание же бензола и этилацетата в азеотропах при повышении темпе¬
ратуры резко уменьшается, а циклогексана — остается практически постоянным,
хотя теплоты испарения этих веществ близки. Это объясняется тем, что измене¬
ние состава тройных азеотропных смесей с температурой обусловливается не
только теплотами испарения компонентов, но в большой степени зависит от усло¬
вий равновесия между жидкостью и паром.
Гетероазеотропы. Отличительная особенность гетеро¬
азеотропов— равенство состава пара и валового состава жидкости,
фактические составы которых отличаются от состава пара. Изме¬
нение температуры влечет за собой изменение составов всех фаз,
однако между ними существует линейная зависимость, которая
объясняется тем, что смесь, имеющая состав паровой фазы, может
быть получена смешением жидких фаз в определенном соотноше¬
нии. Иначе говоря, в треугольной диаграмме составы жидкой и па¬
ровой фаз лежат на одной ноде. Вопрос о влиянии температуры
на состав тройного гетероазеотропа исследован в работе [190]. Рас¬
сматривая химический потенциал каждого компонента как функ¬
цию температуры, давления и молярных долей двух компонентов
и производя преобразования, аналогичные сделанным выше, можно
получить расчетные уравнения
я"(Ш,+А"Шгв·»MHs-L+MttL-* (298>
в которых коэффициенты А и -В имеют следующие значения:
;л12=-(^-Г ;л21=-(|а)аз
\dxJp,T, х, Xdx2IpjTtXi Xdxijp.T.x,
- A в -,аз, 5(,)· в _жа 3jlzSl,S<r)
Лг2 Xdx2JptTtXl' ‘ ‘ RT* +Ь\> B2-X2 ^r-+ S2
ыг) I *Ух Y3 (dJLИ , ( ЛУх Y3 (dxP)
1 VxP Ir. xf ' dT IXu Хг I dX2 Ir, /р V dT Ixit Хг
^ /rfMa3 ' (dxV) , (dU2 γ (dXp\
\ dxi))T x<f) \ dT )Xit Xi dx2 J JTt x(r) \ dT )Χι χ>
Верхний индекс «(г)» означает, что соответствующие величины
относятся к первой или ко второй жидкой фазе. Величина LiP озна¬
чает парциальную молярную теплоту испарения компонента i из
первой или из второй жидкой фазы, нижним индексом «аз» обо¬
значены производные, отвечающие условию сохранения азеотро¬
пии. Верхний индекс «аз» указывает на частные производные,
«3
которые берутся в точке состава азеотропа или в точке на бйно-
дали * отвечающей азеотропной ноде.
.Из рассмотрения уравнений (298) следует, что изменение со¬
става тройного гетероазеотропа с температурой определяется не
только соотношением парциальных молярных теплот испарения
компонентов Lf\ дифференциальных теплот испарения жидких
фаз Q<r), и условиями равновесия между жидкостью и паром, но
также зависимостью взаимной растворимости компонентов от тем¬
пературы. Влияние этого фактора учитывается в уравнениях (298)
величинами Sjr) и SiP. £сли взаимная растворимость компонентов
не зависит от изменения температуры, то Siri = S^ = O и уравне¬
ния (298) становятся аналогичны уравнениям (296) и (297), опи¬
сывающим влияние температуры на состав тройных гомогенных
азеотропов.
Для практического применения уравнений (298) необходимы
данные о парциальных молярных теплотах испарения компонентов
и дифференциальной теплоте испарения одной из жидких фаз, дан¬
ные о равновесии между паром и расслаивающейся жидкостью,
а также данные о равновесии жидкость — пар для гомогенных рас¬
творов при изотермических условиях для области концентраций,
близкой к ноде, проходящей через точку тройного гетероазеотропа.
Анализ уравнений (298) показывает, что неравенства
(dxi/dT)a3^ 0, если LiP — Q(r) ^ 0, определяющие характер измене,
ния состава бинарных азеотропных смесей с максимумом темпе¬
ратуры кипения, для тройных гетероазеотропов могут и не соблю¬
даться. Вероятность несоблюдения этих неравенств тем больше,
чем меньше разность Lf — Q(r) по абсолютной величине.
Сопоставление расчетов по уравнениям (298) с опытными данными было
выполнено [190] на примере системы пропилацетатпропиловый спирт — вода.
Таблица 27
Сопоставление расчетных и экспериментальных данных
о влиянии температуры на состав
гетероазеотропа пропилацетат — пропиловый
спирт —вода [{dxi/dT)a3· 100 град~х]
Результаты расчетов
Производная
Опытные
данные
по уравнениям (298)
по уравнениям (298)
при 0
г* I
г«2
г*» I
г-2
(dXi/dT)&3
{dXifdT)^
-0,32
0.16
-0,29
0.12
I
Op
-0,77
0,52
-0,37
0.25
* Бинодаль — линия в треугольной диаграмме, являющаяся геометрическим
местом конечных точек нод.
154
Опытные данные удовлетворительно согласуются с величинами, рассчитанными
по уравнениям (298). Расчеты показали, что несмотря на незначительное влия¬
ние температуры на взаимную растворимость компонентов, величины SP имеют
такой же порядок, как и калорические слагаемые в выражениях для Bi. По¬
этому пренебрежение величинами SP приводит к ухудшению результатов рас¬
четов, как это видно из табл. 27.
ДИСТИЛЛЯЦИЯ
ТРЕХКОМПОНЕНТНЫХ СМЕСЕЙ
В бинарных системах в ходе процесса дистилляции при
отсутствии в системе азеотропной точки состав смеси всегда изме¬
няется в направлении обогащения высококипящим компонентом.
В случае образования компонентами азеотропной смеси весь
интервал концентраций делится на две части: I) от одного чистого
компонента до азеотропа и 2) от азеотропа до другого чистого
компонента. Направление изменения состава жидкости при дистил¬
ляции в каждом из этих интервалов концентраций определяется
характером азеотропа. Если он положительный (минимум темпе¬
ратуры кипения при постоянном давлении), то составы жидкости
меняются в направлении обогащения чистыми компонентами.
В случае образования отрицательного азеотропа (максимум тем¬
пературы кипения при постоянном давлении) составы жидких сме¬
сей при дистилляции изменяются в направлении к азеотропу/
Количественные закономерности процесса дистилляции выяв¬
ляются путем применения к нему закона сохранения вещества
(условия материального баланса). Условие материального баланса
за бесконечно малый отрезок времени имеет вид
d(Wx) + ydW = 0 или d\nW = jyd~x)
откуда
In*/-
W2 J у-X
Xl
где W\ Vi Х\ — количество и состав исходной жидкости; W2 я X2-
количество и состав жидкости в произвольный момент времени;
у— состав пара, образующегося при дистилляции бинарной рмеси.
Если образующийся при дистилляции пар находится в равно¬
весии с жидкостью, то связь между количеством жидкости и ее
составом определяется условиями фазового равновесия y = f(x).
Для трехкомпонентных систем закономерности процесса дистил¬
ляции значительно сложнее. Основы теории процессов простой дис¬
тилляции трехкомпонентных смесей были разработаны Шрей-
немакерсом [191]. Кривые изменения состава тройных растворов
при простой дистилляции в треугольнике Гиббса были названы
Шрейнемакерсом дистилляционными линиями. Дифференциаль¬
ное уравнение дистилляционной линии получается из уравнения
(299)
(300)
15 5
материального баланса процесса дистилляции за бесконечно ма¬
лое время. Если из W молей смеси, содержащей Xi (молярные
доли первого компонента) и X2 (молярные доли второго компо¬
нента) отгоняется dW молей пара состава у\, у2, то уравнения ма¬
териального баланса по первому и второму компонентам будут
yxdW = d (Wxi) и y2dW=*d (Wx2) (301)
ИЛИ
W dxx = dW (t/ι — Χι) (302)
W dx2 =*dW (у2 — x2) (302a)
Разделив уравнение (302) на (302a), получаем:
dX\ β у I - Xi
dX2 Ш У2~*2
(303)
Очевидно, что это уравнение справедливо для процесса дистил¬
ляции, как при постоянном давлении, так и при постоянной темпе¬
ратуре. Для каждой конкретной системы молярные доли компо¬
нентов в паровой фазе являются функциями состава раствора и
поэтому уравнение дистилляционной линии (303) будет уравнением
кривой в треугольнике составов жидкой фазы.
Очевидно, что каждой дистилляционной линии соответствует ли¬
ния пара, изображающая изменение состава паровой фазы в про¬
цессе дистилляции.
Левая часть уравнения (303) —тангенс угла наклона касатель¬
ной к дистилляционной линии в точке Xu ^2, а правая — характе¬
ризует направление воды, ее наклон.
Таким образом, нода, проведенная из произвольной точки дис¬
тилляционной линии, всегда касательна к этой линии. Следова¬
тельно, кривая пара всегда расположена с выпуклой стороны
дистилляционной линии (рис. 47).
Ход дистилляционных линий в трехкомпонентных системах изу¬
чали многие исследователи [2, 148, 191, 193]. Было показано [191,
192—194], что дистилляционные линии могут выходить или закан¬
чиваться только в вершинах треугольников составов или в точках,
соответствующих азеотропам. В трехкомпонентной системе, не
имеющей азеотропов, все дистилляционные линии кончаются
в точке, соответствующей вершине самого высококипящего компо¬
нента, т. е. последняя капля кубового остатка, который получается
при простой дистилляции любой смеси, приближается по составу
к чистому высококипящему компоненту. Другой предельной точкой
дистилляционных линий будет вершина, соответствующая низкоки-
пящему компоненту. Таким образом, в трехкомпонентной системе,
не имеющей азеотропов, есть одно семейство дистилляционных ли¬
ний, предельными точками которых являются вершины низкокипя¬
щего (А) и высококипящего (С) компонентов (рис. 48).
Рассматривая поведение трехкомпонентных смесей при дистил¬
ляции становится очевидным, что ход дистилляционных линий свя¬
зан с ходом изотерм-изобар. Последние представляют собой линии,
156
соединяющие точки составов растворов с одинаковыми темпера¬
турами кипения при постоянном давлении. Щрейнемакерс [191] на¬
шел, что дистилляционные линии всегда идутгв направлении воз¬
растания температур кипения раствора. Отсюда следует, что
дистилляционная линия не может дважды пересекать изотерму-
изобару с одним и тем же значением температуры. Это положение
определяет связь между ходом изотерм-изобар и дистилляцион¬
ных линий в концентрационном треугольнике. Рис. 48 показывает,
в
8
Рис. 47. Взаимное располо¬
жение дистилляционной ли¬
нии (I) и линии пара (2)
в тройной системе.
Пунктиром изображены ноды.
Рис. 48. Изотермы-изобары
(сплошные линии (пунктирные)
в трехкомпонентной системе,
не имеющей азеотроцов*
что одному семейству изотерм-изобар в трехкомпонентной системе,
не имеющей азеотропов, соответствует одно же семейство дистил¬
ляционных линий.
Образование азеотропов в трехкомпонентной системе обуслов¬
ливает усложнение зависимости температуры кипения смесей от
состава. На поверхности температур кипения появляются вмятины
или возвышения, могущие вызвать образование нескольких се¬
мейств изотерм-изобар.
В качестве примера рассмотрим систему дихлорметан (А) — ацетон (B) —■
метиловый спирт (С), ход изотерм-изобар и дистилляционных линий в которой
изображен на рис. 49. B этой системе имеются два бинарных азеотропа с мини¬
мумом температуры кипения: дихлорметан — метиловый спирт гп\ (^Кип = 39,2° С)
и ацетон — метиловый спирт т2 (^кип = 54,6° С). Наличие азеотропов порождает
распадение изотерм-изобар на два семейства. Одно из них примыкает к стороне
AB, а другое к вершине С. Соответственно с этим, в рассматриваемой системе
ход процесса дистилляции будет зависеть от того, каков состав начальной смеси.
Вследствие этого на поверхности температур кипения образуется лощина, конеч¬
ными точками которой являются точки т\ и т2, а изотермы-изобары выходят на
стороны AB и AC. Лощинная линия' mim2 делит изотермы-изобары на две ча¬
сти, поэтому ход процесса дистилляции в рассматриваемой системе зависит от
состава начальной смеси.
Самая низкокипящая смесь в системе азеотроп m\, который и должен быть
предельной точкой дистилляционных линий. Как мы уже видели при рассмо¬
трении хода дистилляционных линий в системах, не имеющих азеотропов,
друг'ой предельной точкой этих линий является высококипящий компонент.
В рассматриваемой системе таким компонентом будет метиловый спирт, однако
157
дистилляционная линия для" смеси, состав которой изображается точкой приле¬
гающей к стороне AB, не может подходить к вершине Ct так как для этого она
должна была бы дважды пересекать одну и ту же изотерму-изобару (см. рис. 49).
Следовательно, для таких смесей конечной точкой дистилляционных линий может
быть только вершина В. Наоборот, дистилляционные линии, проходящие в обла¬
сти, примыкающей к вершине С, не могут кончаться в точке В.
Таким образом, в соответствии с ходом изотерм-изобар в системе дихлорме¬
тан — ацетон — метиловый спирт имеются два семейства дистилляционных линий
(рис. 49,6). Начальной точкой линий обоих семейств является точка т\, а ко¬
нечной точкой для одного семейства *—точка Ct для другого — точка В. Из при¬
веденных рассуждений ясно, что из смеси, состав которой лежит на дистилля¬
ционной линии одного семейства, не может быть получен кубовый остаток, ха¬
рактерный для дистилляционных линий другого семейства.
А
41,5· А
Рис. 49. Изотермы-изобары (а) и дистилляционные
линии (б) в системе дихлорметан (А) —ацетон (В) —
метиловый спирт (С).
Часть треугольника составов, занятая дистилляционными линиями одного
семейства, называется дистилляционной областью. Линии, отделяющие, дистилля¬
ционные области друг от друга, называются разделяющими линиями дистилля¬
ции. В системе дихлорметан — ацетон — метиловый спирт имеются две дистилля¬
ционные области, отделенные друг от друга разделяющей линией, которая
проходит через точки т\ и т2.
В соответствии с физической природой процесса дистилляции
разделяющая линия должна соединять точки составов смесей
с наинизшими температурами кипения, т. е. она должна проходить
по лощине на поверхности T = φ(χι, Хг)·
Из изложенного ясно, что для образования двух дистилляцион¬
ных областей необходимо в системе иметь хотя бы один азеотро^
Однако наличие азеотропов не во всех случаях вызывает образо¬
вание двух дистилляционных областей.
На рис. 50 показан ход изотерм-изобар и дистилляционных ли¬
ний в системе сероуглерод (А) —ацетон (В) —хлороформ (С).
В этой системе имеется один азеотроп с максимумом температуры
кипения ацетон — хлороформ — M (tKт — 64,5° С) и один азеотроп
с минимумом температуры кипения сероуглерод — ацетон — т
(/кип = 39,2°С). Несмотря на наличие азеотропов в этой системе
имеется одно семейство изотерм-изобар (рис. 50, а) и, соответ-
158
ственно с этим,одно семейство дистилляционных линий (рис. 50, б).
Последние начинаются в точке т и кончаются в точке М.
Бушмакин и Киш показали [193], что ход дистилляционных ли¬
ний в трехкомпонентных системах и возможность распадения
треугольника составов на несколько дистилляционных областей
определяются взаимным расположением изотерм-изобар, вершин
в
56.*'
Рис. 60. Изотермы-изобары (а) и дистилляционные
линии (б) в системе сероуглерод (А) — ацетон (В) —
хлороформ (С).
концентрационного треугольника и азеотропных точек. Вершины
треугольника и азеотропные точки могут быть расположены по
отношению к изотермам-изобарам двояким образом.
Рис. SI. Изотермы-изобары, не пересекающие вершины треугольника со¬
ставов или азеотропные точки.
Сплошные линии —изотермы-изобары, пунктирные-дистилляционные линии.
Изотермы-изобары могут проходить так, что ни одна из них
не пересекает вершину или азеотропную точку. На рис. 51 показан
такой ход изотерм-изобар вблизи вершины треугольника А
(рис. 51,а), вблизи бинарного азеотропа с минимумом (т) или
максимумом (M) температуры кипения (рис. 51,6) и вблизи трой¬
ного азеотропа (т или M) (рис. 51, в). Из рис. 51 следует, что ни
одна изотерма-изобара конечной протяженности не пересекает
1S9
точки А, т или М. Эти точки образуют выродившуюся «точеч¬
ную» изотерму-изобару. Поскольку дистилляционные линии всегда
пересекают изотермы-изобары, точки А или M являются конце¬
выми точками дистилляционных линий.
Другой возможный ход изотерм-изобар и дистилляционных ли¬
ний вблизи вершины A1 азеотропной точки т или M и седловин¬
ной точки 5 показан на рис. 52.
Отличие хода изотерм-изобар от рассмотренного выше заклю¬
чается в том, что через точки A1 т или M проходят изотермы-изо¬
бары конечной протяженности. В этом случае точки A1 mf M и S
не1 могут быть концевыми точками дистилляционных линий, так
Рис. 52. Изотермы-изобары, пересекающие вершину треуголь¬
ника составов или азеотропные точки.
(Обозначения те же, что на рис. 51).
как при этом, по крайней мере, одна дистилляционная линия дол¬
жна была бы вблизи этих точек совпасть с проходящей через них
изотермой-изобарой, но как указывалось, дистилляционные линии
всегда пересекают изотермы-изобары. Следовательно, вблизи то¬
чек A1 Yn1 M и 5, лежащих на изотермах-изобарах конечной про¬
тяженности, дистилляционные линии могут иметь только гипербо¬
лический ход, как показано на рис. 52.
Будет ли вершина концентрационного треугольника или азео-
тропная точка точечной изотермой-изобарой или через нее пройдет
изотерма-изобара конечной протяженности, зависит от соотноше¬
ния температур кипения компонентов системы и азеотропов. Из
очевидных геометрических соображений следует, что вершина кон¬
центрационного треугольника является точечной изотермой-изо¬
барой, если вблизи нее по сторонам треугольника концентраций
кривые температур кипения обеих бинарных смесей имеют наклон
одинакового знака, т. е. температуры кипения возрастают или
убывают по направлению к вершине. В этом случае часть поверх¬
ности температуры кипения вблизи вершины поднята или опу¬
щена и концевые точки линии пересечения этой поверхности с го¬
ризонтальными плоскостями (T = const) будут лежать на сторо¬
нах, сходящихся в вершине. Это хорошо видно на рис. 48—50, на
которых изображены изотермы-изобары и дистилляционные ли¬
нии для ряда трехкомпонентных систем. Если вблизи вершины
160
кривые температур кипения имеют разные наклоны, то через эту
вершину проходит изотерма-изобара конечной протяженности.
Легко видеть, что через точки тройных азеотропов с максиму¬
мом или минимумом температуры кипения не могут проходить
изотермы-изобары конечной протяженности, так как температура
системы в этих точках максимальная или минимальная. Следо¬
вательно, тройные азеотропы всегда являются точечными изотер¬
мами-изобарами и концевыми точками дистилляционных линий.
Этим же свойством обладают точки бинарных азеотропов, если
их температура кипения в системе минимальная или максимальная
64,6·
с с
Рис. 53. Изотермы-изобары (а) и дистилляционные
линии (б) в системе метилацетат (А) — хлоро¬
форм (В) — метиловый спирт (С).
(например, точки т и M на рис. 50 и точка πΐ\ на рис. 49). Если
температура кипения бинарного азеотропа не является ни макси¬
мальной, ни минимальной в тройной системе, то, как следут из
геометрических соображений, через такую азеотропную точку про¬
ходит изотерма-изобара конечной протяженности (например, точ¬
ка т2 на рис. 49).
Выше указывалось, что через седловинную точку трехкомпо¬
нентной системы проходят изотермы-изобары конечной протяжен¬
ности. Соответственно с этим дистилляционные линии вблизи этой
точки имеют геперболический ход.
Для иллюстрации закономерностей, имеющих место в системах
с седловинной точкой, на рис. 53 изображены изотермы-изобары
(рис. 53, а) и дистилляционные линии (рис. 53, б) в системе ме¬
тилацетат (А)—хлороформ (В)—метиловый спирт (С). Из
рис. 53 следует, что наличие седловинной точки порождает обра¬
зование четырех семейств изотерм-изббар и дистилляционных ли¬
ний. Интересно отметить, что все три азеотропные точки (ть т2
и Λί) являются в этом случае точечными изотермами-изобарами.
Следовательно, для распадения концентрационного треугольни¬
ка на дистилляционные области и появления разделяющих линий
дистилляции необходимо, чтобы в системе имелась седловинная
6 Зак, 917
161
точка или образовывался бинарный азеотроп с такой темпе¬
ратурой кипения, которая не была бы ни максимальной, ни
минимальной в системе. Как видно из рис. 53, при наличии седло¬
винной точки в системе появляются четыре дистилляционные
области.
Разделяющие линии дистилляции могут быть двух типов [193].
Линии первого типа разделяют семейства дистилляционных линий
с разными исходными точками. Таковы разделяющие линии ме¬
жду дистилляционными областями I и 2, а также 3 и 4 (рис. 53).
Такие разделяющие линии соответствуют хребту на поверхности
температур кипения.
Разделяющие линии второго типа разграничивают семейства
дистилляционных линий с разными конечными точками. Эти раз¬
деляющие линии соответствуют лощине на поверхности температур
кипения. К таким линиям можно отнести разделяющие линии HilS
и Sm2 между дистилляционными областями I и 3, а также 2 и 4
(рис. 53) и т\т2 (рис. 49). В общем случае лощинная и хребтовая
линии являются кривыми. Следовательно, разделяющие линии ди¬
стилляции также будут кривыми.
ПРАВИЛО АЗЕОТРОПИИ
Связь между ходом дистилляционных линий и числом
особых точек в тройных системах в общем виде исследована в ра¬
ботах [146, 195]. Особыми точками тройной системы на треуголь¬
ной диаграмме, как это ясно из изложенного выше, будут вершины
треугольника, а также точки составов бинарных и тройных азео¬
тропных смесей. Особые . точки, являющиеся точечными изотер¬
мами-изобарами и, следовательно, конечными точками дистилля¬
ционных линий (см. рис. 51), называются узлами. Узлом может
быть вершина треугольника, точка бинарного или тройного
азеотропа. Другой тип особых точек — концевые точки изотерм-
изобар (см. рис. 52). Дистилляционные линии не проходят через
такие точки, а имеют вблизи них гиперболический ход. Такие осо¬
бые точки называются седлами. Седлом может быть вершина
компонента, азеотропная точка с температурой кипения, не являю¬
щейся ни наивысшей, ни наинизшей температурой в системе,
а также точка тройного седловинного азеотропа. Выполненный
Гуриковым [146] анализ приводит к соотношению
2С3 + C2 + 2= 2У3 -h N2 + Ni (304)
где Nz— число тройных особых точек, являющихся узлами; N2 —
число бинарных азеотропных точек, являющихся узлами; N\ —
число вершин концентрационного треугольника, являющихся уз¬
лами; C3 и C2- числа тройных и бинарных азеотропных точек,
являющихся седлами.
Это соотношение получено для тройных двухфазных систем,
исходя из следующих условий:
162
1) устойчивости относительно непрерывных изменений состоя¬
ния каждой из двух сосуществующих фаз;
2) непрерывности термодинамических функций;
3) наличия всех компонентов в обеих фазах;
4) возможности образования двумя компонентами только
одного азеотропа.
Закономерность, выражаемая формулой (304), была названа
«правилом азеотропии», поскольку она устанавливает связь между
числами бинарных и тройных азеотропных смесей в тройных си¬
стемах*. Необходимо обратить внимание на то, что в этой фор¬
муле фигурируют числа всех бинарных и тройных азеотропов, яв¬
ляющихся в треугольной диаграмме как узлами, так и седлами,
тогда как из трех вершин треугольной диаграммы в формуле
(304) фигурирует только число вершин, являющихся узлами.
В справедливости правила азеотропии легко убедиться на примере
систем, для которых диаграммы изотерм-изобар и дистилляцион*
ных линий были приведены выше. Так, для системы дихлорметан —
ацетон — метиловый спирт (см. рис. 49) V3 = O, Сз = 0, A^=I,
C2 = I и Ni = 2. Подставляя эти числа в формулу (304), получаем
2*0 + I + 2 = 2*0 + I +2. Аналогично для системы сероуглерод —
ацетон — хлороформ (см. рис. 50) V3= C3 = 0, N2 = 2, C2 = 0 и
N 1=0, т. е. 2 · 0 + 0 + 2 = 2 · 0 + 2 + 0. Для системы метилаце¬
тат— хлороформ —метиловый спирт (см. рис. 52) Ns ~0, C3 = I,
N2 — 3, C2 — 0 и Ni = I и 2*1+0 + 2 = 2*0 + 3+1.
Формула (304) основа для классификации тройных систем
по характеру расположения на треугольной диаграмме дистилля¬
ционных линий. Гуриков [146] предложил разделять тройные си¬
стемы на четыре группы по числу бинарных азеотропов, образуе¬
мых компонентами тройной системы.
I группа — системы, компоненты которых не образуют азео¬
тропов (М = 0);
II группа — сйстемы с одним азеотропом (M = I);
III группа — системы с двумя азеотропами (M = 2);
IV группа — системы с тремя бинарными азеотропами (М = 3).
. В основу Классификации положено также условие, что в трой¬
ной системе может существовать только один тройной азеотроп.
Принцип классификации ясен из табл. 28 и рис. 54, заимство¬
ванных из книги Сторонкина [2].
Согласно приведенной классификации* возможны 16 типов си¬
стем, различающихся ходом процессов открытого испарения, реа¬
лизующихся в 22 вариантах.
Выясним, при каких физических предпосылках реализуется тот
или иной тип тройной системы.
* Правило азеотропии было распространено на четверные системы Серафи¬
мовым [ЖФХ, 42, 252 (1968)] и на системы с произвольным числом компонентов
Жаровым [ЖФХ, 43, 2784 (1969); Вестн. ЛГУ № 10, вып. 2, 155 (1969)].
а* 163
Тип 1
т
Тип 3
Тип 2а
д
Тип Ua
Тип 46
Тип 5
Тип 86 Тип 8в
Рис. 54. Классификация тройных систем
H
О
η
Тип Ют
Тип 11
Тип 14 б
8 соответствии с правилом азеотропии.
T а б л и ц а 28
Классификация тройных систем
в соответствии с правилом азеотропии
Группа
Тип
Значения коэффициентов в формуле (304)
Cs
' C2
Ns
N2
Ni
0
I
0
0
0
0
2
2
0
I
I
0
I
т
3
0
I
0
0
3
1
4
0
0
0
I
I
5
I
0
0
I
3
6
0
2
I
0
2
7
0
I
I
I
0
II
8
0
I
0
I
2
9
0
0
0
2
0
10
I
0
0
2
2
11
0
3
I
0
3
12
0
2
I
I
I
ΪΤΤ
13
0
2
0
I
3 ,
111
14
0
I
0
2
I
15
I
I
0
2
3
16
I
0
0
3
I
Пусть, как и в приведенных выше примерах, А — компонент
с наинизшей, a G — с наивысшей температурой кипения
(^a < < ^c)- Рассмотрим возможные типы тройных систем с од¬
ним положительным бинарным азеотропом. Если такой азеотроп
образуют компоненты А и В, то температура кипения азеотропа
будет в тройной системе наинизшей. В этом случае азеотропная
точка и противолежащая стороне AB вершина С являются конце¬
выми точками дистилляционных линий. Ход последних в треуголь¬
ной диаграмме показан на рис. 55, а. Как видно из рисунка, в си¬
стеме такого типа имеется одно семейство дистилляционных ли¬
ний. Вершины А и В являются седлами, а вершина С и точка т —
узлами. Следовательно, C3 = C2 = N3 = 0; N2= I и Ni = I. Рас¬
смотренная система принадлежит к группе I тип 4 (табл. 28).
Если положительный азеотроп образуют компоненты А и С, то
температура его кипения, как и в рассмотренном выше случае,
является наинизшей в системе. Азеотропная точка т и вершина
высококипящего компонента С являются концевыми точками един¬
ственного семейства дистилляционных линий, соединяющих точки
т и С. Такая система также принадлежит к группе I тип 4
(табл. 28, рис. 55,6). Если бинарный азеотроп т образуют компо¬
ненты В и С, то возможны два случая: I) когда tm > tA, т. е. тем¬
пература кипения компонента А — наинизшая в системе; 2) когда
tm < т. е. наинизшую температуру в системе имеет азеотроп.
В процессе дистилляции предельной точкой состава дистиллата,
а, следовательно, и дистилляционных линий, является точка (азео¬
троп или компонент) с наинизшей температурой кипения. Соответ¬
ственно с этим дистилляционные линии в первом случае (/т>^л)
В
В в
е z
Рис. 55. Ход изотерм-изобар (сплошные линии) и дистилляцион¬
ных (пунктирные) линий в тройных системах с одним бинарным
положительным азеотропом т, образованным:
а —компонентами А и В; б — компонентами А и С; в — компонентами B и G
при fm > а —компонентами В и С при *т < *А-
распадаются на два семейства (рис. 55, в). Начальной точкой
обоих семейств является вершина А, а конечной точкой — соответ¬
ственно вершины В и С. Следовательно, в такой системе все вер¬
шины будут узлами, а точка т — бинарным седлом. Таким обра¬
зом, Cz = Nz = 0\ Сг = I, Л^2 = 0 и = 3, и система принадлежит
к группе I тип 3.
Системы такого типа часто встречаются на практике. Грани¬
цей между двумя семействами дистилляционных линий является
лощина на поверхности температуры кипения, выходящая из вер¬
шины А на сторону BC в точку т. Если tm < tA, то точка т дол¬
жна быть концевой точкой дистилляционных линий, а между
167
точками А и т на поверхности температур кипения должна про¬
стираться лощина. Представляется естественным, что наличие
последней должно приводить к появлению в треугольной диаграм¬
ме двух семейств дистилляционных линий, начинающихся в точке
т и заканчивающихся соответственно в вершинах В и С. Предпо¬
лагаемый ход дистилляционных линий и отвечающее ему распо¬
ложение изотерм-изобар показано на рис. 55, г, из которого видно,
что две вершины треугольника являются узлами (Ni = 2). Узлом
C2H5COOH
Рис. 56. Ход изотерм-изобар (сплошные линии), до¬
линной ( ) и хребтовой (— · —) линий в си¬
стеме этилформиат — ацетон — метилацетат.
будет и точка т (Л^=1). При отсутствии тройного азеотропа
Nz = Cz = О и равенство (304) в рассмотренном случае не выпол¬
няется
2-0 + 0 + 2=^2-0-Н+2
Таким образом, описанный ход дистилляционных линий про¬
тиворечит условию (304). Чтобы это условие выполнялось, в си¬
стеме должен быть седловинный азеотроп. Поскольку точка такого
азеотропа не может быть концевой точкой дистилляционных ли¬
ний и является тройным седлом (C3 = I), для выполнения равен¬
ства (304) необходимо, чтобы все вершины треугольника, а также
точка бинарного азеотропа, были узлами (Л^ = 3 и Af2=I). Ход
дистилляционных линий при этом должен соответствовать изобра¬
женному на рис. 54 для системы группы I тип. 5. Система такого
типа например ацетон — метилацетат — этилформиат, исследована
в последнее время Серафимовым с сотрудниками [195]. Ход изо-
терм-изобар для этой системы, а также расположение особых
точек в треугольной диаграмме показаны на рис. 56. Как видно,
через вершину низкокипящего компонента — этилформиата — и
точку азеотропа, образованного ацетоном и метил ацетатом, проход
168
дит долинная линия, а вершины, соответствующие двум послед¬
ним компонентам, соединяет хребтовая линия. Наличие лощины
и хребта на поверхности температур кипения порождает образо¬
вание тройного седловинного азеотропа с температурой кипения
55,61° С.
Изложенные соображения относятся и к тройным системам
с одним отрицательным бинарным азеотропом М. Если последний
образуется компонентами В и С или А и С, то ход изотерм-изобар
и дистилляционных линий аналогичен показанному соответственно
на рис. 55, а и б. Только в первом случае начальной точкой дистил¬
ляционных линий является вершина А, а конечной — точка азео¬
тропа с максимумом температуры кипения, лежащая на стороне
SC, во втором случае начальной точкой — вершина А, а конеч¬
ной— точка азеотропа, лежащая на стороне AC (рис. 57).
В в
a f б
Рис. 57. Ход изотерм-изобар (сплошные линии) и ди¬
стилляционных (пунктирные) линий в тройных си¬
стемах с одним бинарным отрицательным азеотропом:
а — образованным компонентами В и С; б — образованным
компонентами А и С.
Если бинарный отрицательный азеотроп образуют компоненты
А и В (причем tm<tc), то в системе имеются два семейства ди¬
стилляционных линий, и их ход аналогичен показанному на
рис. 55, в. Если tm < tc, то между вершиной С и азеотропной точ¬
кой проходит хребтовая линия и в азеотропной точке заканчи¬
ваются дистилляционные линии. Такая система относится к груп¬
пе I тип 5, характеризующейся наличием тройного седловинного
азеотропа.
Диаграммы дистилляционных линий, изображенные на
рис. 54, б и б, отвечают системам, в которых образуется тройной
положительный (или отрицательный) азеотроп при наличии од¬
ного бинарного положительного (или отрицательного азеотропа).
Такие системы возможны, но, видимо, крайне редки.
Системы с двумя бинарными азеотропами относятся к числу
наиболее распространенных в практике азеотропной ректифи¬
кации. Наличие в тройной системе двух бинарных положительных
азеотропов порождает образование на поверхности температур
169
кипения лощины, и, как следствие, появление двух семейств ди¬
стилляционных линий. Ход изотерм-изобар и дистилляционных
линий при различных соотношениях температур кипения компонен¬
тов и бинарных азеотропов (при отсутствии тройного) показан на
рис. 58.
При соотношениях температур кипения компонентов и азео¬
тропов, показанных на рис. 58, а — г образуются системы типа
В
Рис. 58. Ход изотерм-изобар (сплошные линии) и дистилляционных
(пунктирные) линий в тройных системах с двумя положительными
бинарными азеотропами при различных соотношениях температур ки-
* пения азеотропов и компонентов:
а ~~ *mi < *mj ^ *А: б — ^m1 < *А < *т2: 9"" *п
8в (см. рис. 54), для которых характерно расположение узловой
азеотропной точки напротив стороны, которой принадлежат узло¬
вые вершины концентрационного треугольника.
Если компоненты В и С или А и С образуют бинарный азео¬
троп с наинизшей температурой .кипения в' системе, то все три
узловые точки (азеотропные точки начала дистилляционных ли¬
ний и вершины — концы дистилляционных линий) лежат на одной
стороне концентрационного треугольника (рис. 58,5 и е). Такие
системы относятся к группе II тип 86.
Аналогичные соотношения получаются при наличии в тройной
системе двух бинарных отрицательных азеотропов. Возможные
сочетания температур кипения компонентов и азеотропов в таких
17Q
системах и связанные с ними типы диаграмм температур кипения
и дистилляционных линий Показаны на рис. 59. Если азеотроп Мг,
С
С А
в
Рис. 59. Ход изотерм-изобар (сплошные линии) и дистилляцион¬
ных (пунктирные) линий в тройных системах с двумя отрица¬
тельными азеотропами:
« - ^m1 < tC < *м*·· 6-tc< ^m1 < *мг» в - tQ < *м, < *м,·
-В
В
В
С
С
с
Рис. 60. Ход изотерм-изобар (сплошные линии) и дистилляционных (пунк¬
тирные) линий в тройных системах с одним положительным и одним
отрицательным бинарными азеотропами:
а~*т <*А< tQ <*С< tW 6-*m < tA < tB < tC < tW в - tA > *т < tB < tC < *т;
β-ίΑ < *т </в < iM < iCi д~*А <tm<tB< tQ-tW e~tm < *А < *В < iM < tC·
образованный компонентами В и С имеет наивысшую в тройной
системе температуру кипения, то система относится к типу 8в.
Если же все узловые точки лежат на одной стороне (рис. 61,в),
171
т. е. наивысшая в тройной системе — температура кипения азео¬
тропа JMb то система относится к типу 86.
На рис. 60 представлен характер диаграмм изотерм-изобар
и дистилляционных линий для тройных систем с одним положи¬
тельным и одним отрицательным бинарными азеотропами при раз¬
личных сочетаниях температур кипения компонентов и азеотро¬
пов. Если температура кипения положительного азеотропа — наи-
низшая, а отрицательного — наивысшая в системе (рис. 60, а и б),
то последняя относится к типу 9. Во всех
других случаях система относится к ти¬
пу 8а (рис. 60, в — е).
Согласно приведенной классифика¬
ции, в тройных системах возможно обра¬
зование тройных — положительного, от¬
рицательного или седловинного — азео¬
тропов при наличии двух бинарных
(группа II, типа 6, 7 и 10).
Очевидно, для образования тройного
седловинного азеотропа необходимо со¬
четание лощины и хребта на поверхно¬
сти температур кипения. Таковы, напри¬
мер, системы, относящиеся к типу 10.
Соответственно расположению лощин и
хребтов, а также седловинной точки S
на поверхности температур кипения кон¬
центрационный треугольник разделяется
на четыре области, ход дистилляционных линий в каждой из ко¬
торых показан на рис. 54, о и а.
Чтобы получилась система типа 106, на поверхности темпера¬
тур кипения должен быть хребет, порожденный наличием двух
отрицательных бинарных азеотропов, и лощина, проходящая от
одной вершины к другой внутри концентрационного треугольника,
или лощина, обусловленная двумя положительными бинарными
азеотропами, и хребет, расположенный внутри треугольника кон¬
центраций между вершинами В и С.
При наличии в тройной Системе трех бинарных положительных
азеотропов, как правило, образуется тройной положительный
азеотроп. Такие широко распространенные системы относятся
к группе III, тип 11 (рис. 54,/?). В них все вершины концентра¬
ционного треугольника и точка тройного азеотропа являются уз¬
лами, а все точки бинарных азеотропов — седлами. Изотермы-изо¬
бары внутри концентрационного треугольника изображаются замк¬
нутыми линиями (рис. 61). Антиподом рассмотренной системы
является система с тремя бинарными и тройным отрицательными
азеотропами, пока не встречавшаяся в практике.
Система типа 12 (см. рис. 54, с) может получиться, если би¬
нарный азеотроп, являющийся узлом, противоположен по знаку
двум другим бинарным и тройным азеотропам. Если, например,
В
Рис. 61. Ход изотерм-изо¬
бар (сплошные линии) и ди¬
стилляционных (пунктир¬
ные) линий в тройных си¬
стемах с тремя бинарными
и одним тройным азеотро¬
пами одинакового знака.
172
тройной азеотроп — положительный, то бинарный азеотроп, обра¬
зующий узловую точку, может быть только отрицательным. Таким
образом, для систем этого типа характерно образование положи¬
тельного или отрицательного тройного азеотропа при наличии в
системе трех бинарных азеотропов разного знака. Эксперимен¬
тальных данных о наличии таких систем пока нет.
Весьма редки в практике азеотропной и экстрактивной ректи¬
фикации системы, в которых имеется три бинарных азеотропа и
отсутствует тройной (группа III, типы 13 и 14, рис. 54, т и у).
Наличие в тройной системе бинарных азеотропов противопо¬
ложного знака чаще всего порождает образование на поверхности
температур кипения как лощин, так и впадин, что обусловливает
образование седловинного тройного азеотропа. Так, системы
типа 16 могут получаться, если между двумя азеотропными точ¬
ками на поверхности температур кипения расположены лощина,
порожденная двумя положительными бинарными азеотропами,
и хребет, простирающийся от точки третьего бинарного азеотропа
(он должен быть отрицательным) к противолежащей ему вершине,
или, если между двумя точками отрицательных азеотропов прохо¬
дит хребет, а между третьим — положительным бинарным азео¬
тропом и противолежащей ему вершиной — лощина. В обоих слу¬
чаях имеется четыре семейства дистилляционных линий, располо¬
жение которых показано на рис. 54, ц. В таких системах все точки
бинарных азеотропов и лишь одна вершина концентрационного
треугольника являются узлами.
Однако для образования тройного седловинного азеотропа на¬
личие бинарных азеотропов разного знака не обязательно. Так,
система типа 15 (см. рис. 54, х) имеет три узловые вершины и
одну точку бинарного азеотропа, не являющуюся узловой. Следо¬
вательно, температура кипения этого азеотропа должна быть про¬
межуточной между температурами кипения каждого из образую¬
щих его компонентов и его азеотропа с третьим компонентом
рассматриваемой тройной системы.
Возможны два варианта: I) через точки двух бинарных азео¬
тропов гп\ и m2 и седловинную точку S проходит хребет и, следо¬
вательно, эти азеотропы отрицательные; 2) через указанные точки
проходит лощина и тогда ограничивающие ее бинарные азео¬
тропы— положительные. В первом случае между третьим би¬
нарным азеотропом (т3) и противолежащей ему вершиной
на поверхности температур кипения должна располагаться
лощина. Это может быть лишь в том случае, если азеотроп т3—
положительный. Ho тогда его температура кипения — наи-
низшая в системе, и точка т3 должна быть концевой точкой
двух семейств дистилляционных линий. Тогда мы приходим к си¬
стеме типа 16 (см. рис. 54, у), рассмотренной выше. Во втором
случае точка т3 не может отвечать отрицательному азео¬
тропу, температура кипения которого выше температуры кипения
образующих его компонентов, так как в этом случае получилась
Ш
бы система типа 16. Очевидно, что для удовлетворения условий
tm,<tm,<tA (ИЛИ /«,>/«,>/А) И Ц < tm, < *С (ИЛИ tms>tms>tC)
нужно, чтобы все бинарные азеотропы были одного знака — поло¬
жительные или отрицательные. "
Следует подчеркнуть, что правило азеотропии и вытекающая
из него классификация тройных систем основана на том, что
в бинарной системе возможен один азеотроп, а в тройной «,си¬
стеме— лишь один тройной азеотроп. Между тем, термодинамика
не исключает образование двух азеотропов в бинарной системе [2].
Как упоминалось, в последнее время экспериментально показано
наличие двух бинарных азеотропов в бинарной системе бензил —
перфторбензол [147]. Наличие двух бинарных азеотропов может
порождать образование в тройной системе двух тройных азеотро¬
пов (из них один, очевидно, должен быть седловинный), что
должно чрезвычайно усложнять ход изотерм-изобар и процесс
простой дистилляции. Однако детальное рассмотрение этого воп¬
роса в рамках настоящей работы представляется нецелесооб¬
разным.
РЕКТИФИКАЦИЯ
ТРЕХКОМПОНЕНТНЫХ СМЕСЕЙ
При четкой ректификации сложных систем, в которых
не образуется азеотропов, получается столько фракций, сколько
компонентов имеется в системе, и каждая фракция представляет
собой практически чистый компонент. При наличии азеотропов
в системе, подвергаемой разделению, положение усложняется, так
как результат ректификации зависит от свойств системы' и отно¬
сительного содержания компонентов в исходной смеси. Наиболее
подробно поведение системы при ректификации может быть вы¬
явлено на основании данных о равновесии между жидкостью и
паром. Трудность получения этих данных заставила обратиться
к поискам иных путей определения условий разделения сложных
смесей.
Весьма эффективным средством решения этой задачи ока¬
зался метод ректификационного анализа, принципы которого были
определены Юнгом [196] и развиты в работах ряда исследовате¬
лей [9, 149, 165, 192—194, 197, 198]. С помощью этого метода были
получены интересные теоретические и практические результаты.
Метод ректификационного анализа основан на том, что при
отгонке от заданной смеси чистого вещества или смеси постоян¬
ного состава, состав кубовой жидкости в концентрационном тре¬
угольнике, в соответствии с метрическими свойствами последнего,
изменяется по прямой линии, которая проходит через точки со¬
ставов исходной смеси и дистиллата. Подвергая ректификации на
колонке, возможно более близкой к идеальной *, ряд смесей, точки
* Под идеальной понимается колонка с бесконечно большим разделительным
действием и задерживающей способностью, равной нулю.
174
состава которых лежат в различных областях концентрационного
треугольника, и, анализируя получающиеся кривые разгонки, вы¬
ражающие зависимость между количествами и температурой ки¬
пения дистиллата, можно получить представление об условиях
разделения системы путем ректификации.
Чтобы уяснить круг вопросов, решаемых методом ректифика¬
ционного анализа, рассмотрим простейший случай разделения
трехкомпонентной системы с одним положительным бинарным азео*
тропом, температура кипения которого является наинизшей темпе¬
ратурой в системе. В соответствии с общими закономерностями
процесса ректификации в качестве первой
фракции при разгонке исходных смесей любо¬
го состава получается бинарный азеотроп. Од¬
нако ход процесса ректификации смесей раз¬
ного состава окажется различным. В этом
легко убедиться при рассмотрении рис. 62.
При ректификации исходной смеси I по
мере отгонки азеотропа m состав кубовой
жидкости будет перемещаться по прямой ml
до пересечения ее в точке N со стороной тре¬
угольника SC. По достижении точки N весь
компонент А, содержавшийся в смеси I, бу¬
дет отогнан в виде азеотропа т, а оставшаяся
кубовая жидкость будет представлять собой
бинарную смесь компонентов В и С. При
дальнейшей ректификации этой смеси в качестве дистиллата полу¬
чается чистый компонент В, а в кубе — компонент С.
При ректификации исходной смеси 2 в качестве первой фрак¬
ции, вместе с которой удаляется компонент В будет отгоняться
азеотроп ш, в качестве второй фракции — компонент А, и в кубе
останется компонент С.
Таким образом, при ректификации смесей I и 2 получаются
различные фракции. Это указывает на то, что в рассмотренном
случае треугольник концентраций распадается на две области.
В пределах каждой из них ход процесса ректификации изобра¬
жается пересекающимися прямыми линиями mN и BC или тК
и AC. Отдельные площади в треугольной диаграмме, в пределах
каждой из которых получаются одинаковые фракции в одной и
той же последовательности, называются областями ректификации.
Легко видеть, что в рассмотренном случае линией, разделяющей
области ректификации, оказывается секущая тС. То, что эта ли¬
ния — прямая, является геометрической интерпретацией факта
получения в качестве первой фракции азеотропа ш при разгонке
любых трехкомпонентных смесей. Поскольку точка т — концевая
точка линий ректификации mN и тК, изображающих ход про¬
цесса ректификации смесей произвольного состава и относящихся
к разным областям, эти линии не могут пересекать разделяющую
линию тС,
в
Рис. 62. Линии ректи¬
фикации в трехкомпо¬
нентной системе с од¬
ним положительным
бинарным азеотропом
(*А < *в < *c)v
17$
Большую группу систем разных типов исследовали методом
ректификационного анализа Юэл и Велч [91]. На колонке с эф¬
фективностью, равной 75 теоретическим тарелкам (при полном
возврате флегмы), они исследовали следующие типы тройных
систем:
1) с двумя бинарными положительными азеотропами (си¬
стема дихлорметан — ацетон — метиловый спирт);
2) с одним бинарным отрицательным азеотропом для случая,
когда третий компонент имеет наинизшую (система дихлорме¬
тан— ацетон — хлороформ) и наивысшую температуры в системе
(система ацетон — хлороформ — бензол);
3) с двумя положительными и одним отрицательным бинар¬
ными азеотропами (система ацетон — хлороформ — метиловый
спирт);
4) с двумя отрицательными и одним положительным бинар¬
ными азеотропами (система ацетон — хлороформ — изопропило¬
вый эфир).
РЕКТИФИКАЦИЯ СИСТЕМЫ
С ДВУМЯ ПОЛОЖИТЕЛЬНЫМИ БИНАРНЫМИ АЗЕОТРОПАМИ
(СИСТЕМА ДИХЛОРМЕТАН — АЦЕТОН — МЕТИЛОВЫЙ СПИРТ]
Система дихлорметан — ацетон — метиловый спирт пред¬
ставляет практический интерес с точки зрения изучения условий
разделения смесей ацетона и метилового спирта с помощью азео¬
тропной ректификации. В этой системе имеется два бинарных
положительных азеотропа: ацетон — метиловый' спирт (т. кип.
54,6°С; 86,5 мол.% ацетона) и дихлорметан — метиловый спирт
(т. кип. 39,2°С; 94 мол.% дихлорметана). Система дихлорметан —
ацетон неазеотропна. Температуры кипения азеотропов и ком¬
понентов показаны на треугольной диаграмме (рис. 63). Точки I
и 2. на треугольной диаграмме изображают составы смесей,
изучавшихся путем ректификационного анализа. Кривые ректифи¬
кации этих двух смесей приведены на рис. 63, под треугольной
диаграммой. Эти кривые свидетельствуют об отсутствии тройного
азеотропа в рассматриваемой системе. Из рис. 63 следует, что
ход ректификации в этой системе относительно прост. Разгонка
смесей, состав которых изображается точками в треугольнике
Amim2 дает следующие фракции: I) азеотроп дихлорметан — ме¬
тиловый спирт; 2) азеотроп ацетон — метиловый спирт; 3) мети¬
ловый спирт; 3) метиловый спирт (рис. 63,7). При ректификации
смесей, состав которых изображается точками в треугольниках
Mim2B и т{ВС, получаются фракции, отвечающие вершинам со¬
ответствующих треугольников. Таким образом, наличие двух поло¬
жительных бинарных азеотропов в тройной системе порождает
появление трех ректификационных областей в концентрационном
треугольнике. Разделяющие линии ректификации между всеми
тремя областями — прямые. Это подтверждается тем, что при
т
разгонке смеси 2, точка состава которой лежит на прямой т\В,
получаются две фракции — азеотроп дихлорметан — метиловый
спирт и ацетон, как это видно из рис. 63,2. Поэтому для разде¬
ления азеотрвпа ацетон —· метиловый спирт к нему необходимо
41,5
Рис. 63. Ход процесса ректификации в системе
дихлорметан (С) — метиловый спирт (А) — аце¬
тон (В).
Состав системы (С—А—В), мол. %: / — 20—40—40;
2 — 68—4,5—27,5; V —объем дистиллата, мл.
добавить такое количество дихлорметана, чтобы точка состава
полученной тройной смеси лежала на линии гп\В. При ректифика¬
ции этой смеси метиловый спирт в соответствии с рис. 63,2 отго¬
няется в виде азеотропа с дихлорметаном, а в качестве второй
фракции получается ацетон.
РЕКТИФИКАЦИЯ СИСТЕМ
С ОДНИМ ОТРИЦАТЕЛЬНЫМ БИНАРНЫМ АЗЕОТРОПОМ
(СИСТЕМЫ ДИХЛОРМЕТАН — АЦЕТОН — ХЛОРОФОРМ
И АЦЕТОН — ХЛОРОФОРМ — БЕНЗОЛ)
В системе дихлорметан — ацетон — хлороформ (рис. 64)
имеется один отрицательный азеотроп ацетон — хлороформ
(т. кип. 64,6°С; 79,5% хлороформа). Компонент, противолежащий
177
стороне ацетон — хлороформ, имеет наинизшую температуру ки¬
пения в системе. Следовательно, первой фракцией при ректифика¬
ции любых смесей будет дихлорметан, второй фракцией — ацетон
или метиловый спирт и третьей — азеотроп — ацетон — хлороформ.
На рис. 64,1 и 64,2 приведены характерные кривые разгонки сме¬
сей, состав которых изображается в треугольнике концентраций
61,2'
С
ГС
65 г
45 -
35O 40 80 120 160 200 240 280 0 40 80 120 160 200 240 280
V V
Рис. 64. Ход процесса ректификации в системе дихлор¬
метан (А) — хлороформ (С) — ацетон (В).
Состав системы (А—С—В), мол. %: /—48,7—41,0 — 10,3; 2 — 48,8—30,8—20,4;
V — объем дистиллата, мл.
точками / и 2. Анализ опытных данных показывает, что в рас¬
сматриваемой системе имеются две области ректификации. Раз¬
деляющей линией между ними оказывается прямая, соединяющая
вершину дихлорметана с азеотропной точкой. Система ацетон —
хлороформ — бензол отличается от рассмотренной выше системы
дихлорметан — ацетон — хлороформ тем, что компонент, противо¬
лежащий отрицательному азеотропу, имеет наивысшую темпера¬
туру кипения в системе. Это должно породить образование хребта
на поверхности температуры. На рис. 65 показаны точки составов
исходных смесей, подвергавшихся ректификации, и приведены
178
соответствующие кривые ректификации. Характерная особенность
большинства из них — понижение температуры дистиллата в про¬
цессе разгонки. Типичной кривой ректификации для этой системы
61,20
С
Рис. 65. Ход процесса ректификации в системе бензол (В) — хлоро¬
форм (С) — ацетон (А).
Состав системы (В — С—А), мол. %: / — 10,0—22,5—67,5; 2— 15—50—35; 8— 30—40—30;
4 -65-25-10; 5-75-15-10; 5- 10-70-20; 7-20-65-15; 5 V- 25—60—15; 2-40-48-12;
/5 — 55— 36 — 9; // — 25—70—5; V — объем дистиллата. мл.
является кривая 2 (рис. 65). Из рис. 65 видно, что первой фрак¬
цией при разгонке будет ацетон, второй — азеотроп ацетон — хло¬
роформ. После отгонки большей части этого азеотропа температура
179
вверху колонки падает до величины, близкой к температуре
кипения хлороформа. Удаление небольшого количества послед¬
него в качестве дистиллата вновь приводит к повышению темпе¬
ратуры дистиллата, в виде которого отгоняется азеотроп ацетон —
хлороформ. Последняя фракция будет состоять из бензола. Та¬
ким образом, в процессе ректификации получаются не три, как
обычно, а четыре фракции, причем третья имеет более низкую
температуру кипения, чем вторая и четвертая.
Для выяснения причин такого поведения рассматриваемой си¬
стемы интересно сопоставить составы и количества исходных сме¬
сей с количеством отогнанного из них ацетона. Оказывается, что
после отгонки последнего составы смесей выражаются точками на
кривой линии, проходящей от азеотропной
точки к вершине бензола. Эта линия — разде¬
ляющая линия ректификации. Она разделяет
концентрационный треугольник на две обла¬
сти. В области, ограниченной кривой BMi сто¬
роной AB и отрезком AM, в качестве первой
фракции получается ацетон, а в области, ог¬
раниченной кривой BM1 стороной BC и отрез¬
ком CM — хлороформ.
Чтобы выяснить причины получения че¬
тырех фракций при разгонке, рассмотрим
несколько подробнее процесс ректификации
смеси 2. По мере отгонки ацетона состав ку¬
бового остатка будет перемещаться по секу¬
щей, проходящей через точку 2, в направ¬
лении разделяющей линии. По достижении последней отгонка
ацетона прекращается, и начинает отгоняться азеотроп ацетон —
хлороформ. При этом состав кубовой жидкости будет изменяться
по прямой, соединяющей точку пересечения указанной выше се¬
кущей и разделяющей линии К с азеотропной точкой M в направ¬
лении, противоположном последней. Поскольку разделяющая ли¬
ния— кривая, вогнутая по отношению к вершине ацетона, такое
изменение состава кубовой жидкости приведет к тому, что точка
этого состава окажется за пределами разделяющей линии в дру¬
гой ректификационной области, где первой фракцией является
хлороформ. После отгонки некоторого количества последнего,
точка состава кубовой жидкости вновь возвращается на разде¬
ляющую линию.
При дальнейшей разгонке вновь будет отогнано некоторое
количество азеотропа ацетон — хлороформ, а точка К опять пе¬
реместится в область ректификации BCM. Наглядно описанный
процесс поясняется ступенчатым ходом линии ректификации
(рис. 66). Чем больше разделительное действие колонны и меньше
ее задерживающая способность, тем мельче ступени на линии
ректификации. При идеальных условиях линия ректификации сли¬
вается с кривой BM. При этом в процессе ректификации должен
С
Рис. 66. Ход процес¬
са ректификации сме¬
си, состав которой
изображается точкой
на кривой разделяю¬
щей линии ректифи¬
кации.
180
получаться дистиллат переменного состава. По мере приближения
состава кубовой жидкости к бензолу состав дистиллата будет из¬
меняться от азеотропа ацетон — хлороформ до хлороформа, а тем¬
пература вверху колонны соответственно понижаться от 64,5° С
до 61,2° С. Поэтому при ректификации смесей, состав которых
изображается точками в области ABM, должны, строго говоря,
получаться три фракции: первая фракция — ацетон, вторая фрак¬
ция переменного состава, представляющая собой смесь ацетона
и хлороформа с концентрацией последнего более 79,5 мол.% и
третья фракция — бензол. Описанное выше ступенчатое пониже¬
ние температуры третьей фракции и появление четвертой фракции
объясняются влиянием задержки жидкости в колонне, а также
трудностью четкого разделения в связи с близостью составов
равновесных фаз вблизи хребта на поверхности температур ки¬
пения.
Таким образом, появление фракции переменного состава об¬
условлено наличием в системе кривой разделяющей линии ректи¬
фикации, которая может быть пересечена, если точка состава
кубовой жидкости приближается к ней с вогнутой стороны.
РЕКТИФИКАЦИЯ СИСТЕМ
С ПОЛОЖИТЕЛЬНЫМИ И ОТРИЦАТЕЛЬНЫМИ
БИНАРНЫМИ АЗЕОТРОПАМИ
В системах, имеющих положительные и отрицательные
бинарные азеотропы, ход процесса ректификации еще более сло¬
жен, чем в описанных выше случаях.
В качестве примера рассмотрим системы ацетон — хлоро¬
форм— метиловый спирт и ацетон — хлороформ — изопропиловый
эфир. В системе ацетон—хлороформ — метиловый спирт имеются
два положительных азеотропа: ацетон — метиловый спирт
(т. кип. 54,6° С, 86,5% ацетона) и хлороформ — метиловый спирт
(т. кип. 53,5°С; 87,5 мол.% хлороформа) и отрицательный азео¬
троп ацетон — хлороформ. Температуры кипения компонентов и
азеотропов обозначены на треугольнике концентраций, изобра¬
женном на рис. 67. На сторонах AB и AC имеются точки с мини¬
мумом температуры кипения, что вызывает образование на по¬
верхности температуры лощины между точками гп\ и т2. Точка M
на стороне BC и противолежащая этой стороне вершина метило¬
вого спирта соответствуют точкам с наивысшими температурами
кипения в системе. Это порождает образование на поверхности
температуры кипения хребта, простирающегося от точки M к вер¬
шине А. Наличие хребта и лощины вызывает образование на
поверхности температуры седловины, в которой поверхности
жидкости и пара сближаются друг с другом. Точке касания этих
поверхностей отвечает точка седловинного азеотропа S. Состав
этого азеотропа выявляется кривой разгонки (рис. 67,/), смеси /,
точка состава которой лежит на прямой Sm2. Первая фракция
181
при ректификаций, как следует т рис. 67, I — азеотроп
ацетон — метиловый спирт. Вторая фракция, кипящая при
57,5° С, по составу приближается к седловинному азеотропу, тем-
61,2'9
С
64J0 т, 54.6° 56Л9
54рГг* , , Vr . ■ .
О 20 40 60 80 100 120 140
V
Рис. 67. Ход процесса ректификации в системе метиловый спирт (А) —
ацетон (В) — хлороформ (С).
Состав системы (А—В—С), мол. %: I — 18—57—25; 2 — 32—38—30; 3 — 32—23—45;
4 — 60,2—15,0—24,8; 5 — 55,5—24,5—20,0; 3-16-24-60; 7- 10,3 -23,1-66,6; 3-6-22-16;
, 2— 17,9—34,7—47,4; /3-10-42-48.
пература которого является ни наивысшей, ни наинизшей в трой¬
ной системе. Из анализа кривой ректификации (рис. 67,1) сле¬
дует, что вторая фракция содержит 21,8% метилового спирта,
32,2% ацетона и 46,0% хлороформа. При приближении к точке
182
седловинного азеотропа с разных направлений определяемые экс¬
периментально составы азеотропа различаются на несколько про¬
центов. Это показывает, что поверхности жидкости и пара вблизи
азеотропной точки весьма близки друг к другу. Средний состав
седловинного азеотропа ацетон — хлороформ — метиловый спирт,
найденный по экспериментальным данным, следующий: 30% аце¬
тона, 47% хлороформа и 23% метилового „спирта.
Кривые ректификации смесей 2 и 3 (рис. 67,2 и 67,5) анало¬
гичны друг другу, за исключением первой фракции. Для смеси 2
первой фракцией является азеотроп ацетон — метиловый спирт,
а для смеси 3 азеотроп хлороформ — метиловый спирт. Второй и
третьей фракциями в обоих случаях будут соответственно седло¬
винный азеотроп и чистый метиловый спирт. Такие же фракции,
но в других соотношениях, получаются при ректификации сме¬
сей 4 и 5 (см. рис. 67,4 и 67,5). Таким образом, через точку
седловинного азеотропа и вершину метилового спирта проходит
разделяющая линия ректификации, которая делит треугольник кон¬
центраций на две части: одну, примыкающую к стороне хлоро¬
форм— метиловый спирт, и другую — к стороне ацетон — метило¬
вый спирт. Хотя азеотроп метиловый спирт — хлороформ имеет
наинизшую температуру кипения в системе, он не может полу¬
чаться при ректификации смесей, состав которых лежит в той
части треугольника концентраций, которая примыкает к стороне
ацетон — метиловый спирт.
Положение* разделяющей линии ректификации ^SM опреде¬
ляется путем расчета состава смесей, остающихся после отгонки
первой фракции. Эти составы изображаются на рис. 67 остриями
стрелок на линиях, показывающих направление изменения состава
смеси при ректификации. Часть разделяющей линии ректифика¬
ции между точками седловинного азеотропа и вершиной метило¬
вого спирта является почти прямой. Это следует из того, что при
ректификации смесей 2—5 по достижении жидкостью состава,
изображаемого точкой на линии ASM или вблизи нее, получаются
седловинный азеотроп и метиловый спирт.
Иное положение на участке разделяющей линии ректифика¬
ции SM. Как показывает анализ кривых ректификации смесей
6—10 линия SM сильно искривлена. Подтверждением этого яв¬
ляется наличие характерного понижения температуры на кривых
ректификации этих смесей (см. рис. 67, кривые 6—10) и образо¬
вание четырех фракций; механизм этого явления выше был уже
рассмотрен. При ректификации смесей 6—8 первой фракцией яв¬
ляется азеотроп —хлороформ — метиловый спирт, второй фрак¬
цией— седловинный азеотроп. Третья фракция по составу при¬
ближается к азеотропу ацетон — метиловый спирт, и четвертая
фракция — азеотроп ацетон —хлороформ. При ректификации сме¬
сей 9 и 10 первая и третья фракции представляют собой азеотроп
ацетон — метиловый спирт, а вторая и четвертая — аналогичны
фракциям, получающимся при ректификации смесей 5—8.
183
Из рис. 67 следует, что в системе ацетон — хлороформ — ме¬
тиловый спирт имеются шесть областей ректификации: Am\S,
trixSM, Arrt2Si Hi2SMi т\СМу т2ВМ. Области ArrtiS и Am2S раз¬
личаются первыми фракциями (соответственно азеотропы mi
и ш2). Вторая и третья фракции для них одинаковы. Фракции,
получающиеся при ректификации смесей, принадлежащих к обла¬
стям Sm1M^cMecn 6—8) и Sm2M (смеси 9 и 10), были рассмот¬
рены выше. Процесс ректификации в областях т\СМ и т2ВМ
аналогичен этому процессу в трехкомпонентной системе, не имеющей
азеотропов, — получающиеся фракции отвечают вершинам соответ¬
ствующих областей.
В системе ацетон — хлороформ — изопропиловый эфир, концен¬
трационный треугольник и кривые ректификации для которой изоб¬
ражены на рис. 68, имеются два отрицательных бинарных азео¬
тропа: ацетон — хлороформ M1 и хлороформ — изопропиловый
эфир M2 (т. кип. 70,5° С; 36,5% хлороформа) и положительный
азеотроп ацетон — изопропиловый эфир т (т. кип. 54,2° С; 61%
ацетона). Наличие двух отрицательных азеотропов порождает об¬
разование хребта, положение которого определяется кривой M1M2.
Площадь концентрационного треугольника разделяется линией
M1M2 и прямыми тМ\ и тМ2 на четыре области ректификации
mCM2, AmMu тМ\М2 и SM1M2. Кривая разгонки, изображенная
на рис. 68, Ii иллюстрирует типичную кривую ректификации для
области тСМ2. Поскольку эта область ограничивается прямыми
линиями, при разгонке должны получаться три фракции, доответ-
ствующие угловым точкам — азеотропу ацетон — изопропиловый
эфир, чистому изопропиловому эфиру и его азеотропу с хлорофор¬
мом. На рис. 68, I имеются три горизонтальных участка, соответ¬
ствующих этим фракциям. Аналогично протекает процесс ректифи¬
кации смесей в области AmM1. Как видно из рис. 68,2, в этой
области получаются три фракции: азеотроп ацетон — изопропило¬
вый эфир, чистый ацетон и азеотроп ацетон — хлороформ. Области
.тМхМ2 и BM1M2 разделяются хребтом. Поэтому ректификация
смесей, точки состава которых лежат в этих областях, сопровож¬
дается характерным понижением температуры в процессе раз¬
гонки, подробно рассмотренным на примере предыдущих систем.
Ход процесса ректификации в области mMiM2 иллюстрируется кри¬
выми разгонки смесей 3—5, изображенными на рис. 68,3—5. Пер¬
вой фракцией является азеотроп ацетон — изопропиловый эфир,
второй — азеотроп ацетон — хлороформ, отгонка которого приводит
к понижению температуры. Последней фракцией станет отрица¬
тельный азеотроп хлороформ — изопропиловый эфир.
Ректификация смесей, принадлежащих области SM1M2, дает
в качестве первой фракции хлороформ. Второй фракцией будет
азеотроп ацетон — хлороформ, отгонка которого приводит к пони¬
жению температуры, хорошо заметному на кривых ректификации,
изображенных на рис. 68,6 и 68,7. Последней фракцией оказы¬
вается азеотроп хлороформ — изопропиловый эфир.
184
61.2*
В
ГС
74
66
58
50
О 40 80 120 160 200 240
74 '
CC О 4 0 80 120 160 200 240 66
74
66
58
58
50
J4Q 40 80 120 160 200
6
ГС о 40 80 120 160 200 240
74
66
58
50
66
58
74
66
SS1
О 40 80 120 160 200
7
О 40 80 120 160 200 240 О 40 80 120 160 200
V V
Рис. 68. Ход процесса ректификации в системе изо¬
пропиловый эфир (С) — хлороформ (В) —ацетон (А).
Состав системы (С — В—А), мол. %: /—65—15—20; 2-20—20—60;
3 — 40—40—20; 4-20-60-20; 5- 10-20-70; 6-10-80-10;
7-15-8-5.
РАЗДЕЛЯЮЩИЕ ЛИНИИ РЕКТИФИКАЦИИ
Разделение концентрационного треугольника на ряд об¬
ластей и существование разделяющих линий, соединяющих азео-
тропные точки с вершинами треугольника, впервые рассмотрено
Оствальдом [199], назвавшим их линиями непереходимости. Он
считал, что эти линии всегда прямы и не могут пересекаться
при ректификации. Проведенное выше рассмотрение поведения
различных систем при' ректификации показывает, что образова¬
ние разделяющих линий ректификации обусловлено наличием
в системе азеотропов. При этом разделяющие линии ректификации
могут быть как прямыми, так и кривыми. Если в системе имеются
только положительные азеотропы, то разделяющие линии — прямые.
Прямые разделяющие линии ректификации не обязательно свя¬
заны с наличием лощин на поверхности температуры. Их образо¬
вание обусловлено, в сущности, метрическим свойством концентра¬
ционного треугольника, которое заключается в том, что при отгонке
из заданной смеси фракции постоянного состава, состав получаю¬
щегося раствора изменяется по прямой, проходящей через точки
составов исходной смеси и отгоняемой фракции. Прямые разде¬
ляющие линии не могут быть пересечены в процессе ректификации,
так как это противоречило бы указанному свойству треугольника
концентраций.
Кривые;разделяющие линии ректификации получаются при на¬
личии в системе хребта на поверхности температуры, обусловлен¬
ного образованием в системе отрицательных азеотропов. Как уже
было показано, хребет может проходить между двумя точками от¬
рицательных бинарных азеотропов (например, в системе ацетон —
хлороформ — изопропиловый эфир) или между точкой отрицатель¬
ного бинарного азеотропа и противолежащей вершиной, если она
соответствует компоненту с наивысшей температурой кипения (на¬
пример, в системе ацетон — хлороформ — бензол). Характерная
особенность систем с кривой разделяющей линией заключается
в том, что при ректификации смесей, точки состава которых лежат
в областях, ограниченных этой кривой, вторая фракция представ¬
ляет фракцию переменного состава, и ее отгонка сопровождается
понижением температуры в верху колонки. Кривая разделяющая
линия, в противоположность прямой, не является линией неперехо¬
димости. Это очевидно из того, что при ректификации смесей, точки
состава которых лежат с вогнутой стороны разделяющей линии,
получаются фракции переменного состава с точками состава, рас¬
положенными с выпуклой стороны разделяющей линии.
Таким образом, кривая разделяющая линия ректификации мо¬
жет быть пересечена, если состав смеси, подвергаемой разгонке,
изображается точкой, лежащей с вогнутой стороны этой линии.
Было предложено [194] различать следующие типы разделяю¬
щих линий ректификации. Линии типа I (см. рис. 63—69) отделяют
ректификационные области, заключающие смеси, которые при рек-
186
тификации дают разные первые фракции. Таковы разделяющие
линии BM на рис. 65, AS, SM на рис. 67 и MiM2 на рис. 68. Линии
типа 2 отделяют ректификационные области, растворы которых
дают при разгонке разные вторые фракции, например, разделяю¬
щие линии Bmi на рис. 63, AM на рис. 64, т\М и т2М на рис. 67,
а также тМ2 и mMv на рис. 68. Линии типа 3 отделяют ректифи¬
кационные области, растворы которых дают разные третьи фрак¬
ции (кубовые остатки). Таковы разделяю¬
щие линии Hiim2 на рис. 63 и MiS и m2S
на рис. 67.
Кроме того, в отдельную группу выделя¬
ются разделяющие линии типа 2—3, разгра¬
ничивающие ректификационные области,
растворы которых дают разные вторые и
третьи фракции, причем состав второй фрак¬
ции одной области одинаков с составом тре¬
тьей фракции другой области. Примером
такой разделяющей линии является линия
Cm на рис. 69, на котором показаны обла¬
сти ректификации в системе сероуглерод
(Л)—ацетон (S)—хлороформ (C)-. В об¬
ласти ACm при ректификации в качестве
первой фракции получается азеотроп серо¬
углерод— ацетон (т), в качестве второй — сероуглерод и в каче¬
стве третьей — хлороформ. В области CmM первой фракцией яв¬
ляется азеотроп сероуглерод — ацетон, второй — хлороформ и тре¬
тьей— азеотроп ацетон — хлороформ (Al). Линии типа I могут
быть прямыми или кривыми. Линии остальных типов всегда пря¬
мые. Из рассмотренных примеров следует, что в одной и той же
системе могут быть разделяющие* линии разных типов.
Между разделяющими * линиями ректификации и дистилляции
имеется следующая связь. Разделяющая линия ректификации
типа I существует при наличии разделяющей линии дистилляции,
соответствующей хребту на поверхности температур кипения. Раз¬
деляющая линия ректификации типа 2 не имеет соответствующей
ей разделяющей линии дистилляции. Она выходит всегда из ка¬
кой-либо исходной точки дистилляционных линий, и заканчивается
в конечной точке этого же семейства дистилляционных линий. Раз¬
деляющая линия типа 3 проходит там, где идет разделяющая ли¬
ния дистилляции, соответствующая лощине на поверхности темпе¬
ратур кипения. Разделяющая линия ректификации типа 2—3 не
имеет соответствующей ей разделяющей линии дистилляции. Она
выходит из исходной точки какого-либо семейства дистилляцион¬
ных линий и заканчивается в вершине или азеотропной точке, не яв¬
ляющейся ни исходной, ни конечной точкой дистилляционныхлиний.
Из изложенного следует, что число ректификационных обла¬
стей может совпасть с числом дистилляционных областей или пре¬
вышать последнее. Число ректификационных областей в концен¬
56,4*
8
Рис. 69. Области ректи¬
фикации в системе серо¬
углерод (А) — ацетон
(В) — хлороформ (С).
187
трационном треугольнике возрастает с увеличением числа азеотро¬
пов. Если в системе имеются только бинарные азеотропы, то число
ректификационных областей на единицу больше числа этих азео¬
тропов. Тройной азеотроп — положительный, отрицательный или
седловинный — увеличивает число ректификационных областей
еще на два. Таким образом, максимальное их число в трехкомпо¬
нентной системе равно шести.
ПРИМЕНЕНИЕ ПРИНЦИПОВ
РЕКТИФИКАЦИОННОГО АНАЛИЗА
К АЗЕОТРОПНОЙ РЕКТИФИКАЦИИ
При выборе разделяющих агентов в процессах азеотроп¬
ной ректификации весьма важно заранее определить примерный
ход процесса. Для этого можно успешно использовать принципы
ректификационного анализа.
С практической точки зрения, наибольший интерес представ¬
ляют тройные системы, которые могут встречаться при разделении
методом азеотропной ректификации бинарных смесей с положи¬
тельным или отрицательным азеотропом. Рассмотрим различные
системы, придерживаясь классификации Молоденко и Бушмакина
[149], предложивших различать пять групп систем соответственно
типу и числу азеотропов в них. Поведение систем различных групп
может быть выявлено с помощью диаграмм, приводимых на
рис. 70. Система, подвергаемая разделению, на этих диаграммах
изображается стороной AB.
Первый треугольник показывает характер расположения изо¬
терм-изобар, зависящий от соотношения температур кипения ком¬
понентов и азеотропов. Второй треугольник представляет собой
диаграмму, иллюстрирующую ход процесса ректификации в си¬
стеме. Строится он следующим образом. На треугольнике отме¬
чается положение всех бинарных и тройной азеотропных смесей,
а также примерный ход хребтовой линии. Затем проводится секу¬
щая, соединяющая азеотропную точку (или другую точку) си¬
стемы, подлежащей разделению, с вершиной, соответствующей раз¬
деляющему агенту. Эта секущая является геометрическим местом
точек состава смесей, получающихся при прибавлении разделяю¬
щего агента к заданной смеси. Количество разделяющего агента,
которое нужно добавить для проведения процесса азеотропной
ректификации, определяется точкой пересечения этой секущей с со¬
ответствующей разделяющей линией ректификации. Рассмотрим
применение принципов ректификационного анализа к разным си¬
стемам.
На рис. 70,1 приведены диаграммы для I группы систем, имею¬
щих по два положительных бинарных азеотропа. Системы этой
группы могут быть двух типов — без тройного азеотропа
(рис. 70, I, а) и с ним (рис. 70,1,6). Соответственно с этим мопут
получаться различные ректификационные диаграммы, При отсут^
tea
ствии в системе тройного азеотропа в качестве первой фракции из
тройных смесей отгоняется во всех случаях бинарный азеотроп
с наинизшей температурой т\. Добавим к заданной смеси т2 та¬
кое количество разделяющего агента, чтобы состав полученной
смеси выражался точкой О, являющейся точкой пересечения секу¬
щих т2Р и гп\В. Ректифицируя эту смесь после отгонки всего со¬
держащегося в ней компонента А в виде азеотропа ти получим
компонент В в чистом виде. Если исходной смесью является не
азеотроп т2, а смесь /С, то количество разделяющего агента, тре¬
бующееся для проведения процесса азеотропной ректификации,
определяется точкой пересечения 0' секущих KP и Вгп\. В обоих
случаях смесь разделяется на две фракции — азеотроп mi и ком¬
понент В. Соотношение этих фракций, в соответствии с метриче¬
скими свойствами концентрационного треугольника, определяется
правилом рычага. Например, для смеси, состав которой изобра¬
жается точкой G, отношение количеств, получающихся при раз¬
гонке азеотропа гп\ и компонента В, равно OB : Omx. Из ректифи¬
кационной диаграммы, приведенной на рис. 70, I, а, легко видеть,
что это отношение возрастает с увеличением концентрации разде¬
ляющего агента в азеотропе т\. Это, конечно, не означает умень¬
шения выхода выделяемого из азеотропа т2 компонента В, а свя¬
зано только с увеличением количества разделяющего агента, от¬
гоняемого с компонентом А. Количество же выделяемого в чистом
виде компонента В определяется количеством и составом исходного
азеотропа т2. При этом принимается, что-процесс ректификации
проводится на идеальной колонке.
Системы paccMOipeHHoro типа наиболее распространены в про¬
цессах азеотропной ректификации (например, рассмотренная выше
система дихлорметан — ацетон — метиловый спирт).
При наличии в системе двух бинарных и одного тройного азео¬
тропов с минимумом температуры кипения треугольник концентра¬
ций разделяется на пять ректификационных областей, в каждой из
которых первой фракцией будет тройной азеотроп. Количество раз¬
деляющего агента, которое следует добавить к азеотропу т2 для
его разделения, определяется в данном случае точкой пересече¬
ния О секущей т2Р и разделяющей линии ректификации тъВ
(рис. 70, 1,6). При ректификации смеси О получаются две фрак¬
ции— тройной азеотроп т3, с которым отгоняется весь компонент А,
содержащийся в исходной смеси, и компонент В. Количество этих
фракций пропорционально отношению отрезков ВО и Отъ: Легко
видеть, что, если тройной азеотроп имеет такое же относительное
содержание компонентов А и В, как азеотроп т2 (т. е. точка со¬
става тройного азеотропа лежит на секущей т2Р)у то выделение
компонента В в чистом вйде становится невозможно. Вещество,
которое дает с компонентами А и В такой тройной азеотроп, не¬
пригодно в качестве разделяющего агента. Сравнение рассмотрен¬
ных систем первой группы показывает, что наиболее желательным
разделяющим агентом для выделения компонента В путем
W
ж
P
ш
Рис. 70. Ректификационные диаграммы
для систем: / — первой группы; // — вто¬
рой группы; III — третьей группы;
IV—четвертой группы; 7—пятой группы.
азеотропной ректификации будет такое вещество, которое o6pa3yef
с отгоняемым компонентом только бинарный азеотроп.
Необходимо отметить, что системы, имеющие тройной азеотроп
при наличии только двух бинарных, являются относительно ред¬
кими [45], и поэтому их практическое значение для азеотропной
ректификации невелико.
К второй группе относятся системы, имеющие один отрицатель¬
ный бинарный азеотроп (в системе, подлежащей разделению) и
один положительный азеотроп, образуемый одним из компонентов
заданной смеси и разделяющим агентом. Диаграммы, изображаю¬
щие поведение разных типов систем этой группы приведены на
рис. 70,11. Первый тип — системы, в которых положительный
бинарный азеотроп имеет наинизшую температуру кипения
(рис. 70, И, а).*У таких систем имеются три области ректификации,
придем в каждой из них первая фракция — положительный бинар¬
ный азеотроп ш. Все разделяющие линии ректификации — прямые.
Легко видеть, что вещество, образующее систему такого типа,
вполне пригодно для разделения азеотропа М. Количество разде¬
ляющего агента, которое надо добавить к отрицательному азео¬
тропу M для его разделения, определяется точкой пересечения О
секущих Вт и MP. При ректификации смеси О отгоняются после¬
довательно азеотроп ш и чистый компонент В в соотношении
ВО : От. Примером системы такого типа является система серо¬
углерод —- ацетон — хлороформ [200].
Возможно существование систем второго типа, отличающихся
от рассмотренных тем, что наинизшую температуру кипения в си¬
стеме имеет компонент В. Ректификационная диаграмма систем
этого типа, изображенная на рис. 70,11,6, по форме аналогична
диаграмме для систем/первого типа. Различие между ними заклю¬
чается в том, что в областях ректификации тМВ и тВР первой
фракцией для систем второго типа оказывается не азеотроп ш,
а компонент В. Из рис. 70, 11,6 следует, что принципиально можно
выделить чистый компонент В из азеотропа M с помощью разде¬
ляющего агента, дающего систему второго типа. Однако практи¬
чески такой процесс трудно осуществить, так как компонент В и
азеотроп m в подобных системах имеют наинизшие температуры,
и, следовательно, различие их температур кипения должно быть
минимальным.
В еистемах третьего типа (рис. 70,11, в) компонент, добавляе¬
мый к бинарной смеси AB, имеет температуру кипения, превышаю¬
щую температуру кипения компонентов А и В. Это обусловливает
образование хребта на поверхности температуры между точками M
и Р. При прибавлении к азеотропу M компонента P получаются
смеси, точки состава которых лежат в области ректификации.тМР.
Как уже было показано, при ректификации таких смесей в каче¬
стве первой фракции отгоняется некоторое количество азеотропа
ш, вторая фракция является фракцией переменного состава,
191
а третьей фракцией — компонент P (если fa > ^м) или азеотроп M
(если fa < Ы) ·
Системы четвертого типа (см. рис. 70, II, г) в основном анало¬
гичны системам третьего типа. Их особенность заключается в на¬
личии седловинного азеотропа. В соответствии с этим фракция пе¬
ременного состава будет представлять собой смесь седловинного
азеотропа и компонента В.
Легко видеть, что вещества, дающие с заданной бинарной
смесью системы третьего или четвертого типов, неэффективны как
разделяющие агенты, так как при изменении состава жидкости
в процессе ректификации по хребтовой линии из этой жидкости
вновь получаются смесь исходных компонентов и разделяющий
агент, а количество компонента А, которое может быть выделено
в виде азеотропа m за счет кривизны хребтовой линии, относи¬
тельно мало.
К третьей группе относятся системы с тремя бинарными поло¬
жительными азеотропами (рис. 70,111). Системы этой группы мо¬
гут быть двух типов, — не имеющие и имеющие тройной азеотроп.
В первом случае (рис. 70, III, а) концентрационный треугольник
распадается на четыре области ректификации: Атхтъ, т\т2тг,
т\Вт2 и m2mzP. При добавлении к азеотропу тх разделяющего
агента состав получающейся смеси изменяется по прямой гп\Р,
проходящей через области ректификации т\т2тъ и т2тгР. Если
количество добавленного к азеотропу тх разделяющего агента та¬
ково, что точка состава полученной смеси лежит в треугольнике
т\т2тъ, то при ректификации получаются три фракции mi, т2 и Шз
в той последовательности, в которой возрастают температуры ки¬
пения азеотропов. Таким образом, часть заданной смеси вновь вы¬
деляется, а другая часть разделяется на смесь компонента А с раз¬
деляющим агентом (ш3) и смесь компонента В с разделяющим
агентом (т2).
Если состав смеси, полученной после .добавки разделяющего
агента, изображается точкой в треугольнике m2/n3P, то при ректи¬
фикации получаются фракции ш2, ш3 и Р, т. е. выделяется избыток
разделяющего агента, и смесь AB разделяется на компоненты, по¬
лучающиеся в смеси с разделяющим агентом. Отсюда следует, что
количество последнего, необходимое для разделения смеси п\\ опре¬
деляется точкой пересечения О секущей Ш\Р и разделяющей линии
ректификации m2m3. Примером систем этой группы является ис¬
следованная Бенедиктом и Рубиным [21] система метиловый
спирт — парафиновый углеводород (ίκип = IlO0C)—толуол.
При наличии трех бинарных и тройного азеотропов в системе
концентрационный треугольник распадается на шесть областей рек¬
тификации (рис. 70, III, б).
Секущая тхРу по которой изменяются составы смесей при при¬
бавлении разделяющего агента к азеотропу п%и проходит через
области ректификации ттхт2} mm2m3 и m2m3Ps
192
При ректификации смесей, составы которых изображаются точ¬
ками пересечения О и Of секущей m, P и разделяющих линий рек¬
тификации (m2m3 и тт2), должны получаться фракции, соответ¬
ствующие концам разделяющих линий. Так, при ректификации
смеси О' вначале отгонится тройной азеотроп, а затем бинарный
азеотроп ш2 разделяющего агента с компонентом В. Ректификация
смеси О даст фракции ш2 и т3. Таким образом, как и в предыду¬
щем случае, количество разделяющего агента, которое надо доба¬
вить к исходной смеси mi для выделения из нее каждого компо¬
нента в отдельности, определяется точкой пересечения О секущей
Ш\Р и разделяющей линии т2щ3.
Системы с двумя положительными и одним отрицательным би¬
нарными азеотропами, образующие седловинный азеотроп, отно¬
сятся к четвертой группе. В этих системах имеется шесть областей
ректификации, разграниченных разделяющими линиями MSPi
Mm2i Sm2i Smx и Mmx (рис. 70. IV). Как видно, секущая MP про¬
ходит через области ректификации MSm2 и m2SP вблизи хребтовой
линии. Добавив к смеси M разделяющий агент в количестве, соот¬
ветствующем точке пересечения секущей MP и линии m2S и про¬
изведя ректификацию смеси О, получим две фракции: седловинный
азеотроп и компонент А в виде азеотропа ш2 в соотношении
т20 : OS. Таким образом, количество компонента А, которое мо¬
жет быть выделено путем азеотропной ректификации, тем больше,
чем больше кривизна хребтовой линии. В рассмотренном случае
выделяется только часть компонента А. Основное его количество
отгоняется в смеси с компонентом В и разделяющим агентом
в виде азеотропа S, аналогично тому, как это имеет место для си¬
стем второй группы четвертого типа (рис. 70, II, г). Отсюда сле¬
дует, что разделение смеси AB в таких случаях практически не¬
возможно. Поэтому вещества, прибавление которых к смеси AB
дает системы четвертой группы, непригодны для разделения отри¬
цательных азеотропов путем азеотропной ректификации.
Иные соотношения получаются для систем этой группы, если
в качестве исходной взять смесь m2 компонентов А и Р, а в каче¬
стве разделяющего агента — компонент В. В этом случае, добавив
к смеси т2 разделяющий агент в количестве, соответствующем
точке пересечения секущей Bm2 и линии mxMf можно разделить
указанную смесь путем ректификации на компоненты А и P соот¬
ветственно в виде азеотропов тх и М.
Если исходной является смесь mi компонентов В и Р, а компо¬
нент А — разделяющий агент, то, прибавив такое его количество,
которое соответствует точке пересечения прямых тхА и Aim2 полу¬
чим чПри ректцфикации две фракции: азеотроп т2 и азеотроп М.
Таким образом, в системах четвертой группы эффективно может
протекать только процесс разделения бинарного положительного
азеотропа. Примером системы четвертой группы является рассмо¬
тренная выше система ацетон — хлороформ — метиловый спирт.
7 Зак. 917
193
Пятую группу образуют системы, в которых имеется два отри¬
цательных и один положительный бинарных азеотропа (рис. 70, V).
Между точками отрицательных азеотропов в этих системах прохо¬
дит хребтовая линия AliM2, вместе с прямым М\Ш и М2т разде¬
ляющая поле концентрационного треугольника на четыре ректифи¬
кационные области. Если прибавить к смеси Mi соответствующее
количество разделяющего агента, то полученную смесь О можно
путем ректификации разделить на смесь компонентов А и Р, отго¬
няемую в виде положительного бинарного азеотропа ш, и смесь
компонентов В и Р, образующих отрицательный азеотроп M2. Сле¬
довательно, вещества, дающие системы пятой группы, могут быть
разделяющими агентами для разделения отрицательных азеотро¬
пов. Примером системы этой группы является рассмотренная выше
система ацетон — хлороформ — изопропиловый эфир.
В предыдущих рассуждениях принималось, что исходная смесь
азеотропна, так как ее разделение наиболее затруднительно. Ра¬
зумеется все выводы остаются справедливыми, если исходная смесь
отличается по составу от азеотропа.
Рассмотрение поведения систем, относящихся к различным
группам, позволяет установить некоторые общие положения, имею¬
щие значение для применения метода азеотропной ректификации.
Из приведенных ректификационных диаграмм следует, что разде¬
лить положительные азеотропы проще, чем отрицательные. Наибо¬
лее желательны разделяющие агенты, образующие только бинар¬
ные азеотропы с одним или обоими компонентами заданной смеси.
В последнем случае азеотропы должны иметь достаточную разницу
температур кипения. В качестве агентов для разделения отрица¬
тельного азеотропа на компоненты наиболее целесообразно при¬
менять вещество с температурой кипения ниже температуры кипе¬
ния этих компонентов и образующее положительный азеотроп
с одним из них или положительный азеотроп с одним и отрица¬
тельный с другим. Применение в качестве разделяющих агентов
веществ, дающих с компонентами заданной смеси тройные азео¬
тропы (положительные, отрицательные и седловинные), менее це¬
лесообразно, хотя в ряде случаев и позволяет выделить один из
компонентов.
Выше рассматривались системы с одной жидкой фазой.
Имеются указания [149], что появление жидкой гетерогенной обла¬
сти не влияет на поведение системы при испарении. Поэтому при¬
веденные положения применимы и для систем с неполной взаимной
растворимостью компонентов.
ОПРЕДЕЛЕНИЕ РАВНОВЕСИЯ
МЕЖДУ ЖИДКОСТЬЮ И ПАРОМ
Для технологических расчетов, связанных с применением
методов азеотропной и экстрактивной ректификации, необходимо
располагать данными о равновесии между жидкостью и паром
194
в системах, образованных компонентами заданной смеси и разде¬
ляющим агентом. Эти данные составляют основу всех технологи¬
ческих расчетов, поэтому их определение является одним из важ¬
нейших этапов исследований, связанных с разработкой способов
разделения. Для решения этой задачи используются главным об¬
разом экспериментальные методы. Однако в последнее время, осо¬
бенно для трех- и многокомпонентных систем, все возрастающее
значение приобретают расчетные методы, основанные на использо¬
вании ряда закономерностей термодинамической теории гетероген¬
ного равновесия.
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
Экспериментальные методы исследования равновесия ме¬
жду жидкой и паровой фазами заключаются в установлении между
ними равновесия с помощью того или иного прибора, последующем
отборе проб каждой фазы и их анализе. Таким образом, опреде¬
ление условий равновесия состоит из нескольких последовательных
операций, в каждой из которых возможны экспериментальные по¬
грешности. Получение достаточно точных данных о равновесии,
несмотря на кажущуюся простоту, представляет значительные
трудности и требует соблюдения ряда специальных мер. Наиболее
опасны систематические погрешности, которые могут возникнуть
вследствие недостаточной чистоты применяемых веществ, а также
несовершенства приборов для исследования равновесия и методов
определения состава смесей.
Очистка исходных веществ
Применяемые для исследования вещества должны под¬
вергаться, по возможности, более тщательной очистке. Способ
очистки следует выбирать в зависимости от свойств примесей в'ис¬
ходных веществах. Очистку можно производить с помощью физи¬
ческих (перегонка, кристаллизация) или химических (например,
обезвоживание с помощью водоотнимающих средств) методов.
В большинстве случаев вещества очищают перегонкой на лабора¬
торных колонках. Для дальнейшей работы отбирается средняя
фракция, которая в случае необходимости может быть подвергнута
однократной или многократной повторной перегонке. Критерием
чистоты является постоянство физических1 свойств дистиллата
в процессе его отгонки, а также отсутствие или допустимо малое
количество примесей, устанавливаемое путем анализа. К числу
наиболее употребительных физических свойств вещества, контро¬
лируемых при его очистке, относятся температура кипения, пока¬
затель преломления и плотность. Могут, конечно, использоваться
и другие свойства — электропроводность, вязкость, температура
кристаллизации и пр. He все перечисленные свойства одинаково
изменяются в зависимости от концентрации примесей. Поэтому
7*
195
в каждом отдельном случае экспериментатор должен выбрать для
контроля чистоты такие свойства, которые наиболее чувствительны
к содержанию примесей.
Для контроля степени чистоты по температуре кипения Свенто-
славский [201] предложил измерять изменения температуры при
выкипании вещества в дифференциальном эбулиометре.
Для исследования равновесия следует применять вещества,
у которых эти изменения не превышают 0,1°.
В большинстве случаев измерение разности температур можно
заменить точным контролем температуры отгонки дистиллата при
ректификаций вещества, подвергаемого очистке. Постоянство этой
температуры является критерием чистоты. Если температура изме¬
ряется термометром с ценой деления 0,1°, то с помощью лупы
можно фиксировать постоянство температуры в процессе перегонки
с точностью до нескольких сотых долей градуса. Дополнительная
перегонка полученного при этом вещества с отбором средней фрак¬
ции— Добавочная гарантия его чистоты.
В ряде случаев^постоянство температуры в процессе перегонки
не может служить гарантией чистоты вещества. Так, при выделе¬
нии симметричного метилэтилэтилена (т. кип. 36,5° С) из смесей,
получающихся при дегидрировании изоамилового спирта, измере¬
ние температуры дистиллата не дает возможности судить об отсут¬
ствии примеси триметилэтилена (т. кип. 38,7° С),. В этом случае
более надежным критерием чистоты является постоянство показа¬
теля преломления дистиллата, которое можно контролировать с по¬
мощью рефрактометра ИРФ-23 при разностных отсчетах с точ¬
ностью 2—3 -10-5 (показатели преломления п® соответственно
1,3798 и 1,3878). Дополнительно чистота контролируется путем
анализа, осуществляемого при очистке углеводородов C5 методом
газо-жидкостной хроматографии.
Анализ на содержание примесей — необходимое условие кон¬
троля чистоты \веществ во всех случаях, когда примесь (часто,
вода) дает с компонентами исследуемой системы смеси, сильно от¬
клоняющиеся от закона Рауля. В присутствии большинства орга¬
нических веществ, особенно, углеводородов, галогензамещенных
углеводородов, эфиров и других относительная летучесть воды
резко возрастает, вследствие чего значительное количество ее мо¬
жет попасть в пробу конденсата паровой фазы, обусловливая этим
большую погрешность эксперимента. , .
Допустимое содержание примесей зависит от природы этих при¬
месей и требуемой степени точности экспериментальных данных.
При этом нужно руководствоваться тем, что чем ближе примесь
по химической природе к компонентам изучаемой системы, тем
больше допустимое ее содержание при одинаковой точности опыт¬
ных данных. Так, при изучении равновесия между жидкостью и
паром в системах, состоящих из углеводородов и бутилового
спирта [202], заметную погрешность вызывает присутствие в по¬
следнем воды в количестве — 0,05%. В противоположность этому
19*
примесь 1—2% метилэтилэтилена в триметилэтилене, используе¬
мом для исследования равновесия в системах, состоящих из три-
метилэтилена и полярных, веществ, оказывается вполне допустимой
для технических целей, так как указанные углеводороды — весьма
близкие по свойствам изомеры. Разумеется, требования к чистоте
веществ следовало бы сильно повысить, если бы задачей исследо¬
вания являлось выяснение различия в поведении разных изомеров.
Приборы для изучения равновесия
между жидкостью и паром
Основные методы, применяемые для исследования рав¬
новесия между жидкостью и паром при не очень высоких давле¬
ниях, можно разделить на следующие:
Г) метод однократного испаренця;
2) циркуляционный метод;
3) динамический метод.
Техника экспериментального исследования равновесия между
жидкостью и паром подробно описана в работе [31]. Поэтому
здесь приводятся только основные сведения.
Метод однократного испарения.
Этот метод исследования равновесия, являю¬
щийся, по-видимому, наиболее старым [203—
207], заключается в отгонке небольшого коли¬
чества дистиллата из такого большого коли¬
чества жидкости, что состав ее заметно не
изменяется. Установки, применяемые разными
исследователями, различаются конструктив¬
ным оформлением. Типичная установка для
исследования равновесия с помощью метода
однократного испарения (рис. 71) состоит из
колбы I и поворачивающегося в шлифе кон¬
денсатора 2, который может одновременно ра¬
ботать как обратный холодильник.
Достоинством метода является простота,
недостатком — необходимость применять
сравнительно большое количество смесей и
трудность исключить частичную конденсацию
пара на стенках испарителя, вызывающую
отклонение состава отбираемого пара от рав¬
новесного.
С появлением других методов исследова¬
ния способ однократного испарения почти совсем вышел из употреби
ления. Однако в последние годы он снова приобрел практическое
значение и в измененном аппаратурном оформлении применяется
для исследования равновесия в системах с неоднородной жидкой
фазой.
Рис. 71, Схема уста¬
новки для исследова¬
ния равновесия между
жидкостью и паром
методом однократно¬
го испарения:
/-колба; 2—конденсатор.
197
Циркуляционный метод. Этот метод основан на не¬
прерывном возвращении в кипятильник конденсата до установле¬
ния равновесия, по достижении которого отбирают для анализа
пробы жидкой фазы и конденсата. Типичный прибор такого
типа — прибор Отмера [208] (рис. 72).
Основная часть прибора — цилиндрический сосуд I с впаянной
по оси его трубкой 2, снабженной в нижней части отверстиями 3
для входа пара. Внутрь этой трубки встав¬
ляется термометр 4. Исходная смесь зали¬
вается в прибор через воронку 5. Нижняя
часть прибора обогревается нагревателем
6. Образующийся при кипении пар прохо¬
дит по трубке 2 и конденсируется в кон¬
денсаторе 7, из которого жидкость стекает
в приемник конденсата 8. Для контроля
скорости поступления конденсата служит
капельница 9. Постоянный уровень жидко¬
сти в приемнике 8 поддерживается с
помощью переливной трубки 10, по кото
рой конденсат паровой фазы возвращается
в прибор.
Равновесие достигается тогда, когда
состав пара, образующегося при кипении
жидкости, и состав конденсата, возвращае¬
мого в кипятильник, будут одинаковы.
Циркуляция конденсата производится до
установления равновесия, после чего пробы
жидкой и паровой фаз отбирают для ана¬
лиза с помощью кранов 11 и 12 (эти кра-
0 Wcm ны служат также для опорожнения при-
Рис.72. Циркуляционный бора). При помощи трубки 13 прибор сое-
прибор Отмера: диняется с маностатом.
I — цилиндрический сосуд; ПогрвШНОСТИ В рзбОТв ЦИркуЛЯЦИОННОГО
2-впаянная трубка; 3-шту- прибора МОГуТ ОбуСЛОВЛИВаТЬСЯ уНОСОМ
цер для входа пара; 4 — тер- г 1 j j j
мометр; 5-воронка; 6-на- ЖИДКОСТИ ПрИ КИПеНИИ ИЛИ КОНДеНСаЦИеИ
ковденсат^ пародойНСфазн; n3P3 Н3 СТвНКЭХ ПриборЭ. УнОС ЖИДКОСТИ
9 — капельница; /^-перелив- β Приборе Отмера устраняется блаГО-
ная трубка; 11, 12 — краны; 1
13 — трубка. даря большим размерам парового про¬
странства.
Погрешность же, вызываемая конденсацией пара, по возможности
исключается благодаря тепловой изоляции парового пространства
и нагревателя, который компенсирует потери тепла в окружающую
среду. Чтобы исключить перегрев парового пространства, следует
контролировать температуру в слое изоляции. Различными иссле¬
дователями было предложено большое число конструкций цирку¬
ляционных приборов [202, 209—248]. Приборы этого типа наиболее
распространены в практике исследования равновесия. Их исполь¬
зуют для исследований как под вакуумом, так и под давлением,
W
Из большего числа различных конструктивных вариантов цир¬
куляционных приборов остановимся лишь на приборе, предложен-
ном Бушмакиным [244], в котором исключена конденсация пара на
наружных стенках. Этот прибор схематически изображен на
рис. 73. Внутренняя трубка I выполнена в виде колокола, нижний
открытый конец которого погружается в жидкость. Часть пара,
образующегося при кипении жидкости, обо¬
греваемой нагревателем 2, направляется под
колокол, а часть — в кольцевое пространство
между колоколом и корпусом 4 прибора,
снабженным нагревателем 3 для компенсации
потерь тепла в окружающую среду. Оба по¬
тока пара охлаждаются в конденсаторах 5
и б, и конденсат возвращается в кипятильник.
Расход конденсата контролируется с по¬
мощью капельниц 7. Пробу конденсата отби¬
рают из приемника <§, а жидкости — из кипя¬
тильника. Для регулирования интенсивности
нагрева парового пространства проводится
холостой опыт, в процессе которого при вы¬
бранном режиме работы кипятильника опре¬
деляется зависимость количества конденсата,
поступающего из конденсатора б, от силы
или напряжения тока в обмотке нагревате¬
ля 3. При режиме работы нагревателя 3,
отвечающем^ условию компенсации потерь
тепла в окружающую среду, возрастание ин¬
тенсивности нагрева не приводит к увеличе¬
нию количества жидкости, вытекающей из
конденсатора б. Опыты проводятся при най¬
денном таким образом режиме обогрева на¬
ружных стенок прибора.
Джилеспи [245] предложил циркуляцион¬
ный прибор, в котором для исключения по¬
грешностей за счет конденсации пара и обеспечения точного изме¬
рения температур кипения использован иной принцип, чем в при¬
борах, описанных выше. Впоследствии был описан ряд видоиз¬
менений этого прибора [246—249]. Один из вариантов прибора
Джилеспи, испытанный автором, изображен на рис. 74.
Через один из конденсаторов исходную смесь заливают в при¬
бор в таком количестве, чтобы целиком заполнить колбу I. После
заполнения прибора, нижнюю часть колбы 7, на внутренней по¬
верхности которой для обеспечения равномерного кипения на¬
паяна стеклянная крошка, обогревают с помощью нагревателя (нД
рисунке не показан). Благодаря тому, что колба I целиком запол¬
нена, пар, образующийся при кипении, поднимаясь по трубке 2,
увлекает с собой жидкость. При этом пар и жидкость приводятся
в тесный контакт, и между ними устанавливается равновесие.
Рис. 73. Прибор, кон¬
струкции И. Н. Буш-
макина:
/ — внутренняя трубка; 2,
3 — нагреватели; 4 — кор¬
пус прибора; 5, 6 — кон¬
денсаторы; 7 — капельни¬
ца; 8— приемник; 9 — про¬
боотборник.
199
Паро-жидкостная смесь выбрасывается струей на термометриче*
ский карман 3, помещенный в головке прибора 4, которая обес¬
печивает разделение жидкой и паровой фаз. Жидкая фаза по
трубке 5, образующей гидравлический затвор, стекает в прием¬
ник б, из которого по переливной трубке 7,. пройдя через капель¬
ницу <5, возвращается в колбу I. Во избежание потерь от испаре¬
ния приемник 6 снабжен обратным холодильником 9. Верхняя
часть трубки 5 представляет собой цилин¬
дрическую воронку 10, кромка которой на
2—4 мм- не доходит до верхней стенки го¬
ловки. Пар, отделенный от жидкости, под¬
нимается вверх и по кольцевому каналу
между корпусом головки и воронкой 10
поступает в обратный холодильник 11, из
,которого конденсат направляется в прием¬
ник 12, устроенный так же, как прием¬
ник 6. Для выравнивания давления во
внутренней трубке приемника 12 выше пе¬
релива сделано отверстие 3. Конденсат по
трубке 13 через капельницу 14 возвращает¬
ся в колбу I. Пробы жидкости и пара от¬
бирают соответственно из приемников 6 и
12, снабженных кранами. В нижней части
прибора имеется кран 15 для слива жидко¬
сти. В зависимости от количества загру¬
женной смеси и интенсивности нагрева
колбы изменяется соотношение между фа¬
зами в паро-жидкостной смеси. С увеличе¬
нием количества жидкости в приборе (при
неизменной интенсивности нагрева) возра^
стает ее относительное содержание в паро¬
жидкостной смеси. Для установления же¬
лательного режима работы прибора в него
заливают несколько больше жидкости, чем
нужно, а избыток сливают после закипания
жидкости.
В описанном приборе обеспечивается
высокая точность измерения температуры
кипения, поскольку принцип измерения аналогичен используемому
в эбулиометрах (например, в эбулиометре Свентославского). По¬
грешности за счет частичной конденсации пара на стенках го¬
ловки сведены к минимуму благодаря ее малым размерам. Кроме
того, в силу конструктивных особенностей конденсация пара на
наружных стенках головки не может приводить к погрешностям.
При необходимости головка может быть, разумеется, снабжена
термоизоляцией и компенсационным нагревателем. Малые раз¬
меры головки, играющей роль сепаратора, увеличивают, конечно,
возможность погрешности за счет уноса капель жидкости паром.
Рис. 74. Циркуляцион¬
ный прибор Джилеспи:
I — колба; 2, 5, 13 — трубки;
3—термометрический карман;
4 — прибор; 5—приемник;
7 — переливная трубка; 8,
14 — капельница; 9,11 — обрат¬
ные холодильники; 10 — ци¬
линдрическая врронка; 12—
приемник; 15-кран для сли¬
ва жидкости.
200
Однако, как показывает практика, роль этого фактора весьма
мала. Опыт показывает, что в приборе Джилеспи обеспечивается
высокая точность получаемых результатов, не уступающая точ¬
ности данных, получаемых на лучших приборах других конст¬
рукций.
В работе [250] предложена конструкция циркуляционного при¬
бора, в основу которой положены прибор Бушмакина и принцип
измерения температуры кипения в эбулиометре Свентославского.
Приборы описанной конструкции, изготовленные из стекла,
пригодны для работы при атмосферном давлении и под вакуумом.
Заданное давление поддерживается маностатом.
Время установления равновесия в циркуляционных приборах
зависит оъ интенсивности кипения и соотношения объемов жидко-х
сти и конденсата. Объем загружаемой жидкости может варьиро¬
ваться в широких пределах (обычно от 70 до 150 мл). Объем
приемника конденсата зависит от количества жидкости, требую¬
щегося для анализа . (чаще всего от 5 до 15 мл). Чем меньше
объем приемника конденсата, тем быстрее достигается равнове¬
сие. Практически оно устанавливается за время, в течение кото¬
рого получается количество конденсата, в 4—5 раз превышающее
его объем в приемнике. В наиболее распространенных приборах
продолжительность работы до отбора проб I—2 ч.
Следует подчеркнуть, что приемники должны обеспечивать
хороший обмен жидкости. Для этого их лучше делать небольшого
диаметра, но высокими, и с внутренними трубками, расположен¬
ными возможно ближе ко дну.
Динамический метод. Динамический метод заклю¬
чается в насыщении инертного газа нарами исследуемых веществ
до состояния равновесия путем приведения этого газа в контакт
с исходной смесью. Затем определяют количество каждого ком¬
понента, унесенное определенным количеством газа.
В противоположность описанным выше методам, применяемым
для исследования равновесия при постоянном давлении, динами¬
ческий метод удобен для получения данных о равновесии при
постоянной температуре. Это несколько ограничивает примени¬
мость динамического метода, так как процессы ректификации
проводятся при практически постоянном давлении. Этот метод,
однако, весьма удобен, если желательно сравнить влияние различ¬
ных разделяющих агентов на коэффициент относительной лету¬
чести заданной смеси при одинаковой температуре.
Впервые динамический метод был применен Тамманом еще
в 1888 г.
Принципиальная схема установки для исследования равнове¬
сия между жидкостью и паром динамическим методом дана на
рис. 75. Основная часть установки — сатуратор /, помещаемый
в термостат, представляющий собой горизонтальную трубку дли¬
ной 1,2—2 м} выполненную обычно в виде змеевика и снабженную
патрубками для входа инертного газа и выхода паро-газовой
201
смеси. Сатуратор на V2 —2/з объема заливают жидкостью, над
которой с помощью аспираторов 2 просасывается инертный газ
(обычно высушенный воздух). Количество инертного газа, пропу¬
щенного через сатуратор, определяется путем взвешивания жидко¬
сти, выходящей из аспиратора, с учетом поправки на упругость
паров этой жидкости. Расход
инертного газа регулируется по
расходу вытекающей жидкости.
Насыщенную паро-газовую
смесь, выходящую из сатуратора,
пропускают через систему улав¬
ливания θ, в которой собираются
компоненты заданной смеси.
Улавливание производится погло¬
щением кислотой или щелочью
или вымораживанием. Выделен¬
ная смесь затем анализируется и
в ней определяется количество
каждого компонента. Их парциальные давления рассчитываются
обычно по закону Дальтона в предположении,- что паро'-газовая
смесь ведет себя как идеальный газ.
Исследование равновесия
между жидкостью и паром
в системах, образованных компонентами
с ограниченной взаимной растворимостью
При разработке методов азеотропной и экстрактивной
ректификации на практике часто возникает необходимость в ис¬
следовании равновесия между жидкостью и паром в системах,
компоненты которых обладают ограниченной взаимной раствори¬
мостью. В этом случае расслаивание жидкости или конденсата
затрудняет применение циркуляционного и динамического мето¬
дов в их обычном оформлении. Погрешности при этом вызваны
нарушением соотношения между жидкими фазами в приемниках
проб и недостаточным перемешиванием жидких фаз.
Во избежание этого жидкость в приемниках проб циркуляцион¬
ного прибора гомогенизируется энергичным размешиванием с йо-
мощью мешалок [251]. Однако чаще всего [252—257] для исследо¬
вания используется соответствующим образом измененный метод
однократного испарения. Непосредственная отгонка небольшого
количества пробы позволяет исключить погрешности, связанные
с расслаиванием. Обычно загружается такое количество жидко¬
сти, чтобы состав ее в результате отбора пробы существенно не
изменялся. В зависимости от количества отбираемой пробы за¬
грузка колеблется в пределах 150—500 мл. Изменение состава
жидкости в случае, необходимости рассчитывают по измеренным
количествам и составу начальной смеси и отобранной пробы; со¬
Рис. 75. Схема установки для иссле¬
дования равновесия динамическим
методом:
I - сатуратор; 2— аспиратор: 3 — система
улавливания.
202
став равновесной жидкости определяют как средйее арифметиче¬
ское начального и конечного составов. Для уменьшения этой по¬
правки во всех случаях желательно свести до минимума количе¬
ство отбираемой пробы. Это возможно, однако, лишь при наличии
падежных методов анализа, требующих малого количества проб.
Для перемешивания жидких фаз, находящихся в приборе, при¬
меняют мешалки [254, 255, 257]. Тот же результат достигается
часто при использовании выносного кипятиль¬
ника [253], обеспечивающего интенсивную цир¬
куляцию и перемешивание жидкости.
Для исследования равновесия жидкость —
пар при расслаивании жидкости могут при¬
меняться видоизмененные циркуляционные
приборы [256, 258].
На рис. 76 изображен прибор, используе¬
мый для указанной цели в лаборатории ав¬
тора [257]. Куб прибора I представляет собой
плоскодонную колбу, снабженную магнитной
мешалкой 2 и нагревателем 3. Сверху колба
снабжена подъемной трубкой 4, по которой
поднимается паро-жидкостная смесь, посту¬
пающая в сепаратор 5. Последний имеет та¬
кую же конструкцию, как в приборе Джи¬
леспи. Паро-жидкостная смесь орошает кар¬
ман для термометра 6 и разделяется на жид¬
кую фазу, стекающую по трубке 7 в куб, и
паровую фазу, которая по трубке 8 поступает
в конденсатор. Конденсат стекает по трубке,
к которой припаян двухходовой кран 9. До
установления равновесия кран приводится в такое положение,
чтобы конденсат, проходя через капельницу 10, по трубке 11 воз¬
вращался в куб. Когда прибор прогреется и установится равнове¬
сие, пробку крана 9 поворачивают в такое положение, чтобы весь
стекающий из холодильника конденсат по отводу 12 поступал
в охлаждаемый приемник.
Таким образом, в описанном приборе сочетаются принципы
циркуляционного метода и метода однократного испарения.
Исследование равновесия
между жидкостью и паром
с помощью газо-жидкостной хроматографии
Для определения состава смеси методом газо-жидкост¬
ной хроматографии требуется проба небольшого объема. Это от¬
крывает большие возможности перед техникой изучения равнове¬
сия между жидкостью и паром. Методы исследования, основанные
на использовании газо-жидкостной хроматографии, предложены
в работах [259—261]. На рис. 77 изображена схема установки,
Рис. 76. Прибор для
исследования равно¬
весия между паром
и двумя жидкими фа¬
зами [251].
(Пояснения см. в тексте.)
203
Предложенной Кофманом й .сотрудниками. Исходную сМесь За¬
гружают в ампулу /, снабженную нуль-манометром 2. Ампула и
нуль-манометр термостатируются. Проба пара из ампулы отби¬
рают в предварительно вакуумированную камеру 3 объемом
0,2—0,5 мл с запорным вентилем, предназначенным для отключе¬
ния камеры от ампулы. С помощью вентиля 4 ампула соединяется
с манометром. После отбора пробы -пара в камеру 3, последнюю
Рис. 77. Схема установки для исследования равновесия
жидкость—пар с помощью газо-жидкостной хроматографии.
(Пояснения см. в тексте.)
отключают от ампулы, открывают вентили 5 и 6, и, потоком газа-
носителя, проходящего предварительно через термостатируемую
емкость 7, проба пара транспортируется в хроматограф.
Описанный метод можно применять для исследования как. при
атмосферном, так и при повышенном давлениях, а также для
гомогенной и гетерогенной жидких фаз.
МЕТОДЫ ПРОВЕРКИ И ИСПРАВЛЕНИЯ
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
О РАВНОВЕСИИ МЕЖДУ ЖИДКОСТЬЮ И ПАРОМ
При экспериментальном определении условий равно¬
весия между жидкостью и паром возможны различные погреш¬
ности, которые могут быть разделены на две группы. К первой
группе относятся случайные, несистематические погрешности. Они
204
обусловлены неизбежной при экспериментальном исследовании
неточностью определения состава фаз, а также измерения темпе¬
ратур кипения и давлений. К второй группе относятся система¬
тические погрешности, вызываемые применением загрязненных
исходных веществ, несовершенством приборов для исследования
равновесия или ошибками в методе исследования. Отсюда выте¬
кает необходимость проверки экспериментальных данных о рав¬
новесии. Это в равной мере относится как к вновь получаемым
данным, так и к данным, уже имеющимся в литературе, так как
во многих работах, особенно выполненных до 1945—1950 гг., про¬
верка опытных данных не производилась.
Для качественной проверки и обнаружения несистематических
погрешностей применимы обычные методы графической интерпо¬
ляции, используемые во всех экспериментальных исследованиях
и основанные на непрерывности изменения свойств системы при
условии отсутствия скачкообразных изменений, связанных с ка¬
чественными превращениями. Эти методы, естественно, неприме¬
нимы для обнаружения систематических погрешностей, при нали¬
чии которых воспроизводимость опытов, часто расцениваемая
экспериментатором как критерий их достоверности, ничего не
говорит о точности получаемых данных.
Отсюда вытекает часто недооцениваемая важность применения
термодинамических методов проверки, позволяющих обнаружи¬
вать систематические погрешности.
Бинарные системы
Для обнаружения несистематических погрешностей
опытных данных о равновесии в бинарных системах эти данные
изображаются в виде диаграмм, выражающих зависимость со¬
става пара от состава жидкости (кривые у— х) и зависимость
температур или давлений при кипении и конденсации соответ¬
ственно от состава жидкости и пара (кривые t — х, у или P — х, у).
Разброс точек дает возможность судить о величине случайных
погрешностей. Для выявления несистематических погрешностей
Бущмакиным [262] был рекомендован способ представлять данные
в виде зависимости коэффициента относительной летучести а
от х. Достоинство этого метода заключается в чувствительности а
к колебаниям составов пара и жидкости. Однако для области
малой концентрации одного из компонентов это превращается
в недостаток, так как незначительные абсолютные погрешности
в определении составов фаз вызывают большое отклонение вели¬
чины а.
Классическим методом термодинамической проверки данных
о равновесии является проверка по уравнению Дюгема — Mapry-
леса [уравнения (78), (80), (82)]. Применение различных форм
этого уравнения было подробно рассмотрено Битти и Калингер-
том [263]. Для быстрой качественной проверки очень удобно
205
уравнение Дюгема — Маргулеса в виде:
jnp±,<npI_^_±z*_ (305)
dx / dx . х
Правая часть этого уравнения всегда отрицательна. Это озна¬
чает, что углы наклона кривых Igyi = φ(χ) и Igy2 = <р(*) должны
быть противоположны, т. е. увеличение коэффициента активности
одного компонента должно сопровождаться уменьшением коэф¬
фициента активности второго компонента. Выше уже указыва¬
лось, что при обычном выборе стандартного состояния коэффи¬
циенты активности компонентов в чистом виде равны единице.
Следовательно, если коэффициенты активности одного компо¬
нента во всем интервале концентраций больше единицы, то коэф¬
фициенты активности второго компонента также должны быть
всегда больше единицы. Иными словами, положительным откло¬
нениям от закона Рауля в поведении одного компонента всегда
отвечает такое же отклонение от закона Рауля для второго ком¬
понента. При наличии точки максимума (или минимума) на кри¬
вой зависимости коэффициента активности одного компонента от
состава на кривой для другого компонента при том же составе
смеси должна быть точка минимума (или максимума). По¬
скольку кривые γι = φ(χ) и у2 = φ(χ) выходят, соответственно,
из точек Х\ = I, γι == I и %\ = 0, у2 = I, то в этом случае по край¬
ней мере одна кривая γ = φ(χ) должна пересекать ось х в интер¬
вале между х = 0 и х= I. Несоблюдение этих условий, вытекающих
из уравнения (305), указывает на ошибочность эксперимен¬
тальных данных.
Характерный ход зависимости коэффициентов активности от
состава для систем с различными отклонениями от закона Рауля
показан на рис. 3. Количественная проверка может производиться
по уравнениям (78) или (305) и заключается в следующем.
По экспериментальным данным о равновесных составах жидко¬
сти и пара, температурах кипения и давлениях паров рассчиты¬
вают парциальные давления pi = Pyг или коэффициенты активно¬
сти по уравнениям (58) или (64), если возникает необходимость
в учете объема жидкости и неидеальности паровой фазы. Затем
строят графики зависимости Igyi и Igy2 от х или Igpi и Igp2
от х. К кривым, построенным по экспериментальным точкам, про¬
водят касательные при различных значениях х и определяют тан¬
генсы углов наклона этих касательных к оси х. Согласно урав¬
нениям (305) и (71), отношения тангенсов углов наклона каса¬
тельных к кривым Igyi = ф(х) и lgY2 = q>(*) или IgPi= у(х) и
lgp2 = cp(x), должно быть равно (— 1 χ *-j. Несоблюдение
этого условия указывает на неточность экспериментальных
данных.
Другой вариант проверки опытных данных с помощью уравне¬
ния Дюгема — Маргулеса заключается в следующем. По опытным
206
данным строят зависимость IgY2= ф( — 1 х с помощью кото¬
рой путем графического интегрирования по уравнению
Va
IgYi=J--^rflgY2 (306)
(где Yg — значение γ2 при' Xi = I), рассчитывают γι. Совпадение
рассчитанных и опытных значений γι указывает на точность по¬
следних; несовпадение же свидетельствует о наличии эксперимент
тальных погрешностей. Если расхождение не очень велико, то,
задаваясь новым положением кривой Ig Y2 = ф ( — -J--], путем
повторных пересчетов можно определить термодинамически
согласующиеся кривые γι = φ(χ) и Υ2=φ(*), наиболее соответ¬
ствующие опытным данным.
Описанные методы, основанные на непосредственном примене¬
нии уравнения Дюгема — Маргулеса, имеют существенный недо¬
статок. Поскольку в выражение для расчета коэффициентов актив¬
ности входят давления паров компонентов, отклонение расчетных
величин от истинных обусловливается не только погрешностями
в определении состава равновесных фаз, но и в определении тем¬
пературы кипения.
Таким образом, проверка по "уравнению Дюгема — Маргулеса
позволяет оценить термодинамическую согласованность данных
в целом. Между тем для практических целей в первую очередь
представляют интерес данные о составах равновесных фаз.
В этом отношении большое значение имеет метод Херингтона
[8] и Редлиха и Кистера [9], который в значительной мере позво¬
ляет исключить из рассмотрения влияние погрешностей в опреде¬
лении температур кипения. Этот метод основан на использовании
уравнения (93)
I
/
о
Поскольку в этом уравнении фигурирует отношение коэффи¬
циентов активности, влияние погрешностей измерения темпера¬
туры, согласно уравнению (60), может сказываться только в из¬
менении отношения РЦР], а не абсолютных величин P01 и Р\, как
при использовании уравнения Дюгема — Маргулеса. Изменением
же отношения РЦР\ в пределах ошибки измерения температуры
в подавляющем большинстве случаев можно пренебречь.
Проверка по методу Херингтона, Редлиха и Кистера произво¬
дится следующим образом. На основании экспериментальных
207
данных по уравнению
Il
Y 2
О-Ух)
P0I
(307)
рассчитывают отношение у\/у2 и строят график зависимости
lgYi/Y2 от х*. Затем путем графического интегрирования опреде¬
ляют площади, ограниченные кривой IgyiM = <р(*) и осями коор¬
динат. Согласно уравнению (93), площадь, ограниченная осями
координат и участком кривой Ig γι/γ2 = φ(*), лежащим выше
оси х9 должна быть равна пло¬
щади, ограниченной осями ко¬
ординат и участком кривой
IgYiM = чр(*), лежащим ниже
оси х. Для иллюстрации мето¬
да Херингтона, Редлиха и
Кистера на рис. 78 приводится
проверка опытных данных для
г % систем хлороформ — метилизо-
бутилкетон и метиловый
спирт —метилпропилкетон. Со¬
гласно уравнению (93), пло¬
щади ABC и AFG должны
быть равны, соответственно,
площадям CDE и GEH. Сопо¬
ставив площади AFG и GEH9
легко убедиться в том, что
они примерно равны. Это подтверждает правильность данных
о равновесии в системе хлороформ — метилизобутилкетон.
Как видно из рис. 78, для системы метиловый спирт—метил¬
пропилкетон экспериментальные точки хорошо ложатся на одну
прямую линию. Это указывает на то, что случайные погрешности
при исследовании были невелики. Тем не менее, опытные данные
для этой системы ошибочны, так как площадь ABC значительно
меньше площади CDE. Следовательно, данные для системы ме¬
тиловый спирт — метилпропилкетон противоречат условию (93).
Необходимо отметить, что критерием точности дайных яв¬
ляется не отношение разности абсолютных значений положитель¬
ной и отрицательной площадей к одному из них, как это иногда
считают, а абсолютное значение этой разности, которое выражает
среднюю во всем диапазоне концентраций погрешность в опреде¬
лении γι/γ2 и, соответственно, а. При этом следует помнить, что
погрешности возможны преимущественно в какой-нибудь ограни-
'0 70 80 90 100
х ,мол.
'2
Рис. 78. Проверка данных о равновесии
в системах хлороформ — метилизобутил¬
кетон (/) и метиловый спирт — метил¬
пропилкетон (2) по методу Редлиха и
, Кистера.
Если необходимо учитывать объем жидкости и неидеальность паровой
фазы, то γι/γ2 вычисляют по формуле
уравнения (64). )
Il = y(l~xi)pt .ii
Y2 х\{У-У\)р] V
вытекающей из
i
т
ченной области концентраций, где фактическая погрешность будет
больше средней. Неприменимость относительного различия пло¬
щадей в качестве критерия правильности данных вытекает из
того, что эта величина зависит от степени неидеальности рассмат¬
риваемой системы, и для идеальной системы при любой малой
погрешности данных о равновесии равна бесконечности.
Из изложенного очевидно, что метод Херингтона, Редлиха и
Кистера позволяет проверять данные о равновесных составах
фаз, не рассматривая влияние погрешностей в определении тем¬
пературы. Для полной проверки данных о равновесии рекомен¬
дуется одновременно использовать4 метод Херингтона, Редлиха и
Кистера и уравнение Дюгема — Маргулеса. Соответствие опытных
данных уравнению Херингтона, Редлиха и Кистера подтверждает
правильность составов равновесных фаз. Согласованность же
опытных данных с уравнением Дюгема — Маргулеса свидетель¬
ствует о правильности данных о температурах кипения или давле¬
нии паров.
В работах [264—266] рассматривается вопрос об определении
характера и оценке погрешности экспериментальных данных на
основе использования уравнений Дюгема — Маргулеса, а также
Херингтона, Редлиха и Кистера. Применяя описанные методы про¬
верки, следует иметь в виду, что уравнения Дюгема — Маргулеса
и Херингтона, Редлиха и Кистера йвляются строгими лишь при
условиях постоянства температуры, идеальности паровой фазы и
возможности пренебречь молярным объемом жидкости по срав¬
нению с молярным объемом пара.
При использовании описанных методов проверки изобарных
данных игнорируется изменение коэффициентов активности с тем¬
пературой в интервале температур кипения смесей. Однако, как
показали Карлсон и Колборн [267], при небольших теплотах сме¬
щения компонентов и не очень большом различии их температур
кипения, изменением коэффициентов активности с температурой
можно в большинстве случаев пренебречь. Это и позволяет реко¬
мендовать применение к изобарным данным уравнения Дюгема —
Маргулеса [3].
Трехкомпонентные системы
Методы проверки данных о равновесии между жидко¬
стью и паром в системах, содержащих три или более компонен¬
тов, основываются' на использовании закономерностей, аналогич¬
ных тем, которые лежат в основе методов проверки данных о
равновесии в бинарных системах. Штейнхаузер и Уайт [268]
применили уравнение Дюгема — Маргулеса в форме
x2dlg у2 + Xsd Ig Уз== 0 (308)
для проверки данных о равновесии между жидкостью и паром
р системе метилэтилкетон — гептан — толуол при изменении
Ϊ09
состава жидкости по изотермам — изобарам. Уравнение Дюгема —
Маргулеса не получило, однако, широкого практического приме¬
нения для проверки данных о равновесии в многокомпонентных
системах из-за трудностей, связанных с использованием этого
уравнения.
Наибольшее распространение получили методы проверки опыт¬
ных данных [269—271], основанные на использовании свойств
функции Ф, определяемой уравнением (88). Полный дифферен¬
циал этой функции по составу определяется выражением
Уравнение (310) можно проинтегрировать при любом способе
изменения состава смесей при известных по опытным данным за¬
висимостях lgYi/yn от состава, а также значениях функции Ф в
точках начала и конца интегрирования. Для тройной системы из
уравнении (310) следует
где х\9 Xf2 и Ф', х"9 X2 и Ф" — концентрации компонентов и зна¬
чения функции Ф в точках соответственно начала и конца инте¬
грирования.
В процессах экстрактивной ректификации концентрация одного
из компонентов (разделяющего агента) изменяется мало и часто
может быть принята постоянной. При X3 = const, т. е. при изме¬
нении состава смесей по сечению концентрационного треуголь¬
ника, из уравнения (311) получаем
где Φι3 и Фгз — значения функций Ф для бинарных смесей I—3
и 2—3 с заданной постоянной концентрацией х3. При введении
относительной концентрации первого и второго компонентов выра¬
жение (312) переходит в уравнение (117),
п
^ф== 2 1SY IdxI
(309)
где п — число компонентов в системе.
п — I
С учетом того, что dxn = — 2 dx{ выражение (309) преобра¬
зуется к виду:
(310)
№
tf
(311)
(312)
210
Различные варианты методов проверки опытных данных о рав¬
новесии между жидкостью и паром для систем различных типов
подробно описаны в работе [3].
МЕТОДЫ РАСЧЕТА РАВНОВЕСИЯ
МЕЖДУ ЖИДКОСТЬЮ И ПАРОМ
Методы расчета равновесия между жидкостью и паром
представляют большой практический интерес, так как позволяют
получить необходимые для технологических расчетов данные на
основании ограниченного экспериментального материала или по
результатам косвенных измерений.
Все известные методы можно разделить на следующие:
1) использующие частные решения дифференциального урав¬
нения фазового равновесия;
2) основанные на использовании интерполяционных выраже¬
ний для функции Ф;
3) эмпирические.
Во всех случаях методы расчета равновесия в сложных си¬
стемах основываются на использовании данных для входящих
в их состав более простых систем. Поэтому вначале рассмотрим
методы расчета равновесия между жидкостью и паром в бинар¬
ных, а затем в тройных и многокомпонентных системах.
Бинарные системы
Впервые Маргулес [272] предложил для описания усло¬
вий фазового равновесия в бинарной системе выразить коэффи¬
циенты активности компонентов в виде степенных рядов, коэффи¬
циенты в которых подбираются так, чтобы удовлетворялось урав¬
нение Дюгема — Маргулеса (82). В наиболее распространенной
форме полученные Маргулесом интерполяционные уравнения
с двумя эмпирическими коэффициентами имеют вид
Ig Y1 = (I -*i)2 [A + 2*ι (В -Л)] и Igy2 = *! [Я + 2(! — *ι) (Λ-θ)] (313)
Завидский [273], а затем многие другие исследователи путем
сопоставления расчетов с экспериментальными данными показали,
что интерполяционные уравнения Маргулеса хорошо передают
условия равновесия между жидкостью и паром в разнообразных
системах. Ван-Лаар [274] получил интерполяционные выражения
для коэффициентов активности с двумя константами иной формы.
Наиболее распространен следующий вид этих выражений:
- ,8Т"['+4'кгГ “ ,8V,>!-Vr <314)
Нетрудно убедиться, что константы А и В в уравнениях (313)
и (314) имеют простой физический смысл ^ = Igy1 лри Х\ = О,
211
а В = IgY2 при X2 = О (или х = I) и представляют собой, следо¬
вательно, значения логарифмов коэффициентов активности компо¬
нентов при бесконечном разбавлении.
При использовании приведенных интерполяционных уравнений
задача определения условий равновесия между жидкостью и па¬
ром сводится к нахождению двух констант. Для этого необходимы
два уравнения, которые могут быть составлены по данным о рав¬
новесии для раствора одного состава, т. е. по одной эксперимен¬
тальной точке.
Поскольку приведенные уравнения получены как частные ре¬
шения дифференциального уравнения при условии T = const,
были сделаны попытки, используя идеи Ван-Лаара, получить ви¬
доизмененные уравнения, которые учитывали бы влияние темпе¬
ратуры на коэффициенты активности компонентов [275—277].
Однако полученньщ уравнения содержат большее число констант,
и распространения He получили.
Наиболее общий метод получения расчетных уравнений заклю¬
чается в представлении функции Ф в виде интерполяционных
уравнений (с учетом того, что при Xi = 0 и X2 = О, Ф = 0) и по¬
следующем определении логарифмов коэффициентов активности.
Это делается на основе следующих выкладок. Дифференцируя
выражение Ф (88) для бинарной системы по правилам дифферен¬
цирования функции нескольких переменных, получаем:
ЛФ= IgYi dx, -Ig Y2 dXx +Xid Ig γι + (I -Xi) d In γ2 (315)
Сумма двух последних членов равна нулю в соответствии
с уравнением Дюгема — Маргулеса (82). Поэтому
= Ig Yi-Ig Y2-lg'^ (316)
Сочетая это выражение с определением· функции Ф (88),
имеем:
'"lgYi-0 + (l-*i)-!jp и ΐ8Υ2~Φ-*ι-3^ (317)
Эти выражения позволяют найти коэффициенты активности
компонентов по известной зависимости Φ = /(*ι). Известно боль¬
шое число различных уравнений, основанных на изложенных прин¬
ципах. Вооль [278] показал, что эти уравнения обобщаются одним
- - - Σ zIzIaH + Σ zIzIhaW +··· <318>
Σ <1ιχι " Ик
I-I
где qi — эффективный молярный объем компонента i; atj и Oijh—
• In '
эмпирические константы Zt = <7*х</S Янхк ~ эффективная моляр-
ная доля компонента i. Сумма 2 состоит из произведений эффек-
212
тйвных Молярных долей двух разнородных компонёнтов, а сумМй-
2 из членов, представляющих собой различные возможные ком-
Uk
бинации трех величин ζ для двух компонентов. Например, для
бинарной системы2ZiZjali = ZiZ2Cii2 + ζ2ζχα2\ = 2ζιΖ2α\29'ΣιΖιζ.ζι.αηι,^
if ijk 1 1
~ Z\Z2^ai\2 a\2l a2ll) Ζ\Ζ2 (^122 ^212 ^22ΐ) = ^\\^\Ζ2 \22Ζ1ΖΤ
Таким образом, если в выражении (318) ограничиться двумя
членами, то для Ф получается выражение
Ф - IglXl + q2x2)z{z2 (2а12 + San2Zi + Sai22Z2) (319)
которому после Введения констант А = q\(2ai2 + 3ai22) и
В = q2{2ai2 + Зап2) можно придать вид:
Ф - ZiZ2 ^xi + (I — х) j [А (I - Z1) + Bzl (320)
Сводка основных уравнений, исходя из представлений функции Ф
в виде интерполяционного уравнения, приводится в табл. 29.
Рядом авторов предложены эмпирические уравнения, выра¬
жающие в аналитической форме связь между составами равно¬
весных фаз. Сводка некоторых уравнений этого типа приводится
в табл. 30.
Было показано [289], что перечисленные- в табл. 30 уравнения,
кроме (325), обобщаются одним
__j/l__== Xi I +Дц* I
I-I-X1 я20 + Д21*2 + а22*2 ,
где а\и а20, Ci2i и а22 — эмпирические константы.
Сопоставление различных уравнений проведено в работе [3], где
читатель сможет более глубоко ознакомиться с рассматриваемым
вопросом. Здесь лишь отметим, что эмпирические уравнения, как
правило, используют для аналитической интерполяции данных, по¬
лученных экспериментально. Однако их не применяют для расчета
равновесия между жидкостью и паром по ограниченным или кос¬
венным экспериментальным данным, так как ни одно из предло¬
женных уравнений не является достаточно универсальным.
Для этой цели применяют уравнения, полученные термодинами¬
ческими методами, главным образом, перечисленные в табл. 29.·
Наибольшее распространение получили уравнения Маргулеса, Ван-
Jlaapa, а также предложенные сравнительно недавно уравнения
Вильсона.
Как указывалось, константы в интерполяционных уравнениях
можно рассчитать по ограниченному фактическому материалу, не¬
обходимому для составления стольких уравнений, сколько имеется
констант. Чаще, всего на практике используют интерполяцион¬
ные уравнения с двумя константами. Если известны температура
213
Таблица 29
Сводка уравнений для расчета коэффициентов активности компо
Авторы и ссылка
Связь между константами
г
Скетчард и Хамер [279]
42 V2
I
T+12 ι~χι
VI X1
Ван-Лаар [274]
Il=A
42 в
■В I-X1
A X1
Маргулес [272]
I
42
Xi
Бенедикт, Джонсон, Соло¬
мон, Рубин [280]
-
-
Редлих и Кистер [9]
-
-
Вильсон [172]
\
214
нентов бинарных систем
ф
Коэффициенты активности
Номер
уравне¬
ния
ζ (I — ζ)Χ
X JC1 + (I -jc,) Щх
Х[вг-{£ + Л(1.-г)]
Ig Y. = (I-Z)2 [а + 22 (в -л)]
Igγ2 = 22[β + 2(1-г) (л-^-β)]
(321)
J
2(1-2) Ax
х[*1 + (I ~*i) -j]
%v,-V('+e
>гъ-в/(1+А· „')
(314)
Jt1 (I — х{)Х
XfBjc1 +А (I -Jf1)]
IgYi = O-*!)2 И+ 2*, (В-Л)]
Ig Y2 = JCj [В + 2 (I - Jt1) (Л - В)]
(313)
Здфс2Ли2 + 3JC1Jf^ 122
Ig Yl = (б*[*2 — 6*1*2) 12 + (3*2 — 6*1*2) 122
Ig Y2 = (3*1 “ 6*1*2) ^ll2 + (б*1*2 - 62^2) A122
(322)
Jfl 0 -*ι)Χ
XfB + С (2л:,- I) +
+ D (2jc — I)2 + ...]
Ig = В (I — 2jt|) + C [6JC, (I — jc) — 1J +
+ В(I — 2jc,) [I — 8*] (I — Jf1)] + ...
(323)
- JC1 In (I — JC1JX
ХЛ12— (I -Jf1JX
Xln JfH2I
\
In γ, = — In jc, + (I — Jt1) A12] +
I П jf I Г Al2 А,л I
(324)
L*! + Л12 (I — *,) JfH21 + (I -Jf1) J
In Y2 = - In [(I - JC1) + JfH21] -
Г ^i2 ^2* I
' L*i + (I — *1) Ai2 *Иг1 + (I — *i)J
*15
Таблица 30
Сводка эмпирических уравнений,
связывающих составы равновесных фаз
Авторы и ссылка
Уравнение
Дон-
станты
Номер
урав¬
нения
Додж [281]
I ί\χ ~'ι —Χι exP (ь + 2cxI + 3dxD
Ь, с, d
(325)
Кларк [282]
-а* +6
I -yi X-Xi
а, b
(326)
Праль [283]
CxI (А — χχ)
Ш Cxi (Л-Jf1) + (I -Xi) (В +Xi)
A1 B1 С
(327)
Норриш и Тунг [284]
Mxi + С- In Г 2/1 · (1
L (I-Ifi)* *1 J
M1 С, k
(328)
Хирата [285]
I-уГа + т1* I-Xi
а, т
(329)
Майо и Льюис [286]
OXI -f X1X2
у =
Ox1 + 2*!*2 + QX2
O1 р
(330)
Спинер, Лю и Г рей-
дон [287]
У\ Х\ auXi+X2
I — Ух I — Х\ Ct21X2 + X1
«12> «21
(331)
Кретчмер и Вииб [288]
Ух _ х\ A + Bx1
А, В, С
(332)
I — у\ I — X1 (С -f- X1) (I — 2С + Cx1)
кипения бинарной смеси определенного состава и состав пара,нахо-
дящёгося в равновесии с этой смесью, то по формуле (60) можно
рассчитать коэффициенты активности обоих компонентов и соста¬
вить два уравнения, которые могут быть решены совместно отно¬
сительно констант. Помимо этой очевидной возможности, кон¬
станты, а следовательно и условия фазового равновесия, могут
быть рассчитаны по косвенным данным.
Расчет равновесия
по данным о давлении паров смесей
Завидский [273] показал возможность расчета констант
в уравнениях Маргулеса (313) по значениям тангенсов углов на¬
клона зависимости общего давления паров смесей от их состава
в концевых точках Xi = 0 и Х\ = I. Им получены следующие урав-
216
i
нения, расчет по которым показал хорошее согласие с эксперимен¬
тальными данными.
Недостаток этого метода заключается в неточности операции
графического дифференцирования на концах кривой P = f(xi).
Этот недостаток устранен в методе расчета констант в уравне¬
ниях Маргулеса, предложенном в работе [290]. По этому способу
вся область концентраций делится на три равные части и для со¬
ставления уравнений, необходимых для расчета констант, исполь¬
зуются опытные данные о давлениях паров чистых компонентов и
двух смесей, содержащих примерно по V3 и 2/з мол. доли каждого
компонента. Влияние погрешностей в измерении давления паров
смесей, равноудаленных от чистых компонентов, сказывается на
точности расчета констант в наименьшей степени. Как и в способе,
предложенном Завидским, принимается, что к пару можно приме¬
нить законы идеальных газов, в частности закон Дальтона. Выра¬
жая общее давление над смесью как сумму парциальных давле¬
ний, для двух смесей получаем два экспоненциальных уравнения,
которые содержат искомые константы в показателях степени. Эти
уравнения могут быть решены графически, методом подбора или
с помощью ЭВМ.'В работе [290] уравнения, составленные для двух
смесей по V3 и 2/з мол. доли каждого компонента, решены в виде
номограммы с бинарным полем. Подробно этот метод описан
в книге [3].
Л Карлсон и Кольборн предложили [261] рассчитывать константы
в уравнениях Маргулеса (313) или Ван-Лаара (314) по найденной
экспериментально зависимости давления паров смесей от их со¬
става, основанный на использовании выражений
вытекающих из закона Дальтона и формулы (60).
При приближении X2 к единице, у2 также стремится к единице.
Принимая последовательно у2 = I и γι = I, с помощью уравнений
(334) определяют приближенные значения соответственно γι и γ2.
Далее строят кривые Ig γι ==ф(λ:ι) и" Igγ2 = φ(ΛΓι), экстраполяцией
которых до значений Х\ = 0 и Х\ = I определяют константы А и В
в уравнениях Ван-Лаара или Маргулеса. По этим константам рас¬
считывают коэффициенты активности и давления паров, которые
сравнивают с опытными величинами. Если приемлемое совпадение
не достигается, то расчет повторяют, причем для определения γι
и у2 используют значения ^ и γι, найденные в первом приближении.
(333)
217
В качестве примера в табл. 31 приведены результаты расчета
равновесия в системе диоксан — вода при 80° С по опытным дан¬
ным Ховорка, Шефера и Дрейсбаха [291]. Экстраполяцией прибли¬
женных значений γι и γ2 до Xi = 0 и Xi = I получены величины
γι = 4,36 и γ2 = 7,4, которые соответствуют константам уравнения
Ван-Лаара: А = 0,64 и В = 0,87. В табл. 31 приведены рассчитан¬
ные по этим константам коэффициенты активности. По значениям
последних рассчитаны парциальные и общие давления. Хорошее
совпадение рассчитанных и опытных величин указывает на пра¬
вильность расчета.
Таблица 31
Расчет равновесия в системе диоксан — вода по методу Карлсона
Xi
P
*ОПЫТ’
MM PT. ст.
Р°х
I
Р®х
2 2
Р-Р%
P-P01XI
р°х> ■
«N
<Л
о.
0,1
476
35,5
345
3,69
1,27
0,2
526,5
71,0
307
3,08
1,48
0,4
571
142,1
229
2,40
1,87
0,6
575,5
213
153,5
1,98
2,36
0,8
550
284
76,6
1,67
3,47
0,9
501,5
319
38,3
1,45
4,78
Кричевский и Казарновский [292] предложили рассчитывать со¬
ставы равновесных пара и жидкости путем численного интегриро¬
вания уравнения Гиббса — Дюгема в форме (79) по методу Рун-
ге — Кутта. Достоинством этого метода [3] является то, что не
налагается никаких ограничений на форму зависимости коэффи¬
циентов активности компонентов от состава смесей. Однако, из-за
громоздкости расчетов этот метод широкого распространения не
получил.
Все описанные методы расчета основаны на использовании
опытных данных о давлении паров при постоянной температуре.
Между тем, процессы ректификации протекают при практически
постоянном давлении и переменной температуре. Если для расчета
условий равновесия при P = const принять значения коэффициен¬
тов активности, найденные при T = const, то возникает погреш¬
ность, связанная с изменением коэффициентов активности с тем¬
пературой. Эта погрешность тем меньше, чем меньше различаются
температуры кипения компонентов и чем меньше теплота их сме¬
шения. Последнее имеет место, если компоненты мало различаются
по химической природе. Вопрос о влиянии температуры на коэф¬
фициенты активности подробно рассмотрен в книге [3].
218
Расчет равновесия
по данным о температурах кипения смесей
В работе [293] предложен метод расчета условий равно¬
весия между жидкостью и паром при постоянном давлении. Урав¬
нение состояния бинарной смеси при P = const может быть запи¬
сано как
Xi d Ig Yi + (I - X1) d Ig Y2 =» — dT (335)
где Atf см — теплота смешения компонентов.
и Кольборна
Yi
Y2
Pu
Ръ
P
расч,
P —P
расч iOnbiT
. I пп
MM PT. ст.
MM PT. ст.
MM PT. ст.
р 1UU*
*опыт
3,51
1,012
124,5
358
482,5
-1,4
2,85
1,05
202
322
524
+ 0,5
1,94
1,24
276
285
561
+ 1,8
1,40
1,74
298
266
564
+ 2,0
1,10
3,06
312
234 ·
546
+ 0,7
1,025
4,52
328
173
501
+0,1
При известной зависимости AtfCM от состава смесей коэффи¬
циенты активности компонентов можно найти, решая уравнение
(335) совместно с уравнением
P -Pfc1Y1 +Pl (I -X1) V2 (336)
в котором и Р\ — известные функции температуры. Такой рас¬
чет дает значения коэффициентов активности компонентов с уче¬
том их изменения с температурой. Если исключить член, содержа¬
щий Atfсм» то уравнение (335) переходит в уравнение Дюгема —
Маргулеса, погрешности при применении которого в случае
T Ф const обсуждены выше.
Коэффициенты активности компонентов рассчитываются сле¬
дующим образом. По экспериментальным данным о температурах
кипения смесей определяют путем интерполяции значения темпе¬
ратур кипения через каждые 5—10 мол.% и находят давления па¬
ров чистых компонентов. Затем по уравнениям (334) рассчиты¬
ваются приближенные значения у^\ принимая в первом прибли¬
жении у<1)=1. По найденным таким образом значениям у\{)
строят кривую и путем'графического интегрирования
219
с помощью уравнений (335) или (82) находят значения γ® во
втором приближении. Так, при использовании для этого уравне¬
ния (82), получают:
Как показывает практика, численное интегрирование удобно за¬
менить нахождением конечных приращений AlgYf, и тогда
где индекс «ср» означает, что значение дроби *ι/(1—*ι) берется
для середины концентрационного интервала, соответствующего из¬
менению коэффициента активности первого компонента на вели¬
чину A Ig Yf10.
Полученные значения yf2) подставляют в формулу (336) и на¬
ходят зйачения коэффициентов активности первого компонента во
втором приближении. Описанную операцию повторяют до получе¬
ния в двух последовательных приближениях совпадающих значе¬
ний γι и Y2. Как показывает практика, уже второе приближение
обычно дает результаты, практически не отличающиеся от третьего.
Это дает возможность, зная температуру и состав азеотропной
смеси при определенном давлении, составить два уравнения, ко¬
торые могут быть решены относительно констант. Для определе¬
ния констант в уравнениях Ван-Лаара (314) получаются выражения
а для расчета констант в уравнениях Маргулеса (313) — выра¬
жения
(337)
(338)
Расчет равновесия
по данным о свойствах азеотропной смеси
Поскольку в азеотропной точке составы жидкости и
пара одинаковы, из формулы (60) получаем:
(340)
л *аа Q - 2*»з) Ig WPfjаз + 2(1" *«з)2 Ig №°)аз
Л =
Хаз (I — Хаз)2
2*аз Ig (PfPi)аз + 0 ~ *аз)(2*аз ~')'g
_____
(341)
\ MQ
Для регулярных растворов (при Л = В) значение константы
можно найти только по температуре кипения или по известному
составу азеотропа. В первом случае получаем формулу
Ig
которую можно решить относительно константы А. При известном
составе азеотропа имеем:
тенциалы каждого компонента одинаковы, в соответствии с фор¬
мулой (57) получаем условия
где штрихами обозначены величины, относящиеся к первой и вто¬
рой сосуществующим фазам. Если принять, что в обеих областях
концентраций гомогенных растворов зависимость коэффициентов
активности от состава смесей описывается интерполяционными
уравнениями с двумя константами, то для определения последних
можно на основе равенств (343) получить два уравнения. Для на¬
хождения констант в уравнениях Маргулеса (313) получаем фор¬
мулы:
А=_>#1
2хаз — I
(342)
Напомним, что во всех приведенных формулах хлз — молярная
доля первого компонента в азеотропе.
Расчет равновесия
по данным о взаимной растворимости
Поскольку в равновесных жидких фазах химические по-
> Г ГГ ГГ Г > ГГ H
jcIYl “ jcI Yl и ЧЪ = *2 Υ2
(343)
A-
■ 2KO- Af-*Г0 - AT] 1S уз
//
[(|-.у(1 —2,0—0 -«;? 0-*4)!
1 - xI
(344)
«I
Для расчета констант в уравнениях Ван-Лаара получаются
формулы:
Описанные методы расчета равновесия между жидкостью и па¬
ром, по данным о взаимной растворимости компонентов, основаны
на допущении, что свойства гомогенных растворов с преимуще¬
ственным содержанием как одного, так и другого компонента опи¬
сываются одними и теми же уравнениями. В работах [143, 294]
применен иной подход — принимается, что гомогенные растворы
ведут себя как регулярные, причем константы А\ и A2f характе¬
ризующие степень неидеальности для растворов с преимуществен¬
ным содержанием первого и второго компонентов, различные. Воз¬
можная погрешность, связанная с этим допущением, тем меньше,
чем меньше взаимная растворимость компонентов. Исходя из усло¬
вий (343), имеем следующую систему экспоненциальных уравнений
для расчета констант А\ и A2:
Расчеты селективности разделяющих агентов, выполненные
с помощью этих уравнений, хорошо согласуются с опытными дан¬
ными [143].
тическая точка растворимости характеризуется выполнением ра¬
венств:
х
Ai
В
(345)
х[ exp A1 (l — Xj)2 = хI exp A2 (l — х(')2
(I - х') exp A1 (x[f = (I - х'О exp A2 (x'{f
(346)
Расчет равновесия
по данным о критической точке растворимости
Исходя из условий устойчивости равновесия [2], [3], кри-
N
(347)
222
которые дают возможность составить два уравнений для расчета
двух констант в интерполяционных уравнениях, описывающих за¬
висимость коэффициентов активности компонентов бинарной смеси
от ее состава. Если выразить с помощью формулы (57) химические
потенциалы через коэффициенты активности, то, используя урав¬
нения Маргулеса (313) для выражения зависимости последних от
состава, производя дифференцирование согласно условиям (347)
и решая полученные уравнения, определяем формулы для расчета
констант
-Oxf-HSx1-I — Oxf-HlOx1-2
A = V/ Цг И Цг7 —νΓ (348)
13,8xf (I — Xi) 13,8xf (I — X1)
где — мол. доля первого компонента в смеси, отвечающей кри¬
тической точке растворимости.
Для нахождения значений констант в уравнениях Ван-Лаара
имеем выражения:
Л-· 5’8Г>(1-Г,)2л ■ Д-7—Ti— <349>
(2 — *ι) (' — *i) (1+*ι) (2- *ι)
Уравнения (348) и (349) могут быть использованы двояко [3]:
для расчета условий равновесия между жидкостью и паром и для
расчетного определения критической точки растворимости.
Расчет равновесия
по кривой открытого испарения
Изменение количества жидкости в процессе открытого
испарения, ее состав, а также состав равновесного пара законо¬
мерно связаны ’ между собой уравнением (299), поэтому можно
рассчитать условия равновесия между жидкостью и паром по дан¬
ным о ходе процесса открытого испарения. На такую возможность
впервые обратили внимание Ярым-Агаев и Коган [295]. Из уравне¬
ния (299) следует:
У~х== d in ψ (35°)
Следовательно, определив экспериментально зависимость х =
= f(Iri W) и построив соответствующую кривую, можно определять
составы равновесных фаз путем графического дифференцирования.
Как видно из уравнения (350), разность составов равновесных
пара и жидкости равна тангенсу угла наклона касательной к кри¬
вой х — f (In W). Величины, входящие в уравнение (350), могут
быть выражены в любых размерностях. При этом размерности ве¬
личин х, у и W должны быть согласованы. Так, если х и у выра¬
жены в мол. долях, то W — в числах молей; если х и у выражены
в масс.%, то W — в единицах массы. Точность результатов-, полу¬
чаемых по описанному методу, определяется точностью исходных
экспериментальных данных, которая зависит от точности анализов
223
и соблюдения условий равновесия в "ходе процесса дистилляции.
Наиболее важная предпосылка обеспечения этогс^ — соблюдение
адиабатичности в ходе экспериментов, чтобы исключить искажение
состава пара за счет частичной конденсации. Технические детали,
связанные с использованием этого метода, описаны в работе [3].
СРАВНИТЕЛЬНАЯ ОЦЕНКА
МЕТОДОВ РАСЧЕТА РАВНОВЕСИЯ
В БИНАРНЫХ СИСТЕМАХ
И НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
Как указывалось, наибольшее распространение в прак¬
тике получили методы расчета равновесия, основанные на исполь¬
зовании зависимости коэффициентов активности от ^состава, кото¬
рая выражается уравнениями Маргулеса, Ван-Лаара и Вильсона
с двумя константами, определяемыми экспериментально. Эти урав¬
нения используются двояко: для представления данных о равнове¬
сии в аналитической форме и для расчета условий равновесия по
неполным или косвенным данным. В первом случае задача иссле¬
дователя заключается в' определении таких значений констант,
которые приводят к наилучшему согласию экспериментальных дан¬
ных с соответствующей аналитической зависимостью. Это — обыч¬
ная интерполяционная задача, которая чаще всего решается с по¬
мощью метода наименьших квадратов.
При использовании интерполяционных уравнений для расчета
условий равновесия между жидкостью и паром, как было показано
выше, константы в этих уравнениях могут быть рассчитаны по
весьма ограниченным экспериментальным данным. Однако есте¬
ственное стремление к уменьшению объема необходимых экспери¬
ментальных исследований должно быть соразмерено с требова¬
ниями, предъявляемыми к точности данных о равновесии. Если эти
данные получаются одним из описанных расчетных методов, то не¬
обходимо принимать во внимание возможные источники погреш¬
ностей. Прежде всего, погрешность неизбежна вследствие того, что
принимаются априорные зависимости коэффициентов активности
компонентов от состава смесей. Такие зависимости могут быть
выражены применяемыми интерполяционными уравнениями. До
сих пор отсутствуют критерии выбора наиболее приемлемого
по форме уравнения для рассматриваемой конкретной ,системы.
К тому же часто выбор тбго или иного интерполяционного
уравнения бывает предопределен тем, 4ΐο с помощью этого урав¬
нения представлены данные о равновесии длй других систем, имею¬
щих отношение к рассматриваемому процессу разделения. Имеется
одно общее правило, которым следует руководствоваться: чем
меньше отклонения от идеального поведения в рассматриваемой
бинарной системе, тем меньше погрешности,^ связанные с исполь¬
зованием априорной зависимости коэффициентов активности ком¬
понентов от состава жидкости. Это относится ко всем без исключе-
224
йия интерполяционным уравнениям. Степень неидеальности си¬
стемы определяется различием химической природы и строения
молекул компонентов. На основании изложенных выше представ¬
лений о природе межмолекулярного взаимодействия и роли хими¬
ческих и структурных факторов, представляется возможным каче¬
ственно предсказать степень неидеальности бинарной системы. Ко¬
личественно ее можно оценить, используя данные, позволяющие
рассчитать коэффициент активности хотя бы одного компо¬
нента. Помимо методов, описанных выше, для этой цели можно
воспользоваться сопоставлением температуры кипения смеси
(или давления паров) с рассчитанной по закону Рауля. Если
на основании такой оценки выяснится, что степень неидеальности
системы невелика, то можно применять любое интерполяционное
уравнение, удобное для дальнейшего использования. Если же вы¬
ясняется, что отклонения от идеального поведения большие, то,
выбрав определенные интерполяционные уравнения и рассчитав
константы в них по одному из описанных методов, нужно убе¬
диться в адекватности полученного математического описания
условий фазового равновесия. Естественно, это невозможно сде¬
лать без привлечения дополнительного экспериментального мате¬
риала (любые данные, позволяющие рассчитать коэффициенты
активности компонентов).
Как показывает практика, наиболее надежно константы в ин¬
терполяционных уравнениях определяются по данным о равновесии
между жидкостью и паром, если они получены с достаточной точ¬
ностью и если состав жидкой смеси не очень близок к одному из
чистых компонентов. При использовании данных о равновесии для
одной жидкой смеси, желательно, чтобы ее состав не очень отли¬
чался от эквимолекулярного. Если константы определяются путем
усреднения по данным, о равновесии для двух смесей, то жела¬
тельно, чтобы они содержали примерно по 7з и 2/з мол. доли
каждого компонента. Примерно такой же точности данные полу¬
чают при расчете равновесия по давлению паров или температурам
кипения смесей. Нужно только помнить, что при использовании для
расчета уравнения Дюгема — Маргулеса приходится пренебрегать
влиянием температуры на коэффициенты активности, которое опре¬
деляется теплотой смешения и различием температур кипения ком¬
понентов. Это, впрочем, относится ко всем методам, основанным
на применении уравнения Дюгема — Маргулеса или его частных
решений.
При использовании данных о свойствах азеотропной смеси для
расчета констант нужно иметь в виду, что их значения весьма чув¬
ствительны к точности определения температуры кипения и состава
азеотропной смеси, особенно по мере удаления последнего от экви¬
молекулярного. Поэтому по мере приближения состава азеотроп¬
ной смеси к одному из компонентов точность расчетов понижается.
Чаще всего данные, получаемые этим методам, уступают до точ¬
ности данным, полученным методами, рассмотренными выше.
8 Зак/ 917
225
При расчете равновесия жидкость — пар по данным о раство¬
римости или о критической точке растворимости имеем менее точ¬
ные результаты, по сравнению с полученными на основании данных
о составах равновесных фаз, температурах кипения, давлении па¬
ров или о свойствах азеотропной смеси. Это обусловлено значи¬
тельным влиянием температуры на взаимную растворимость ве¬
ществ, а также тем, что допущение о применимости одного и того
же интерполяционного уравнения к обоим областям гомогенных
смесей, видимо, не всегда оправдывается. Поэтому эти методы
можно рекомендовать только для приближенных расчетов. Это же
относится к расчету равновесия по найденной экспериментально
кривой открытой дистилляции в связи с малой точностью операции
графического дифференцирования. К тому же экспериментальное
получение кривой открытого испарения в отношении трудоемкости
вряд ли имеет преимущества по сравнению с получением опытных
данных о равновесии между жидкостью и паром.
МЕТОДЫ РАСЧЕТА РАВНОВЕСИЯ
.МЕЖДУ ЖИДКОСТЬЮ И ПАРОМ
В МНОГОКОМПОНЕНТНЫХ СИСТЕМАХ
Аналитические методы
С увеличением числа компонентов в системе резко воз¬
растают трудности исследования равновесия между жидкостью и
паром из-за сложности определения состава многокомпонентных
смесей и необходимости проведения большого числа эксперимен¬
тов. Для наглядности изложения ниже рассматривается определе¬
ние равновесия в трехкомпонентных системах. Это оправдывается
тем, что принципы современных методов расчета равновесия яв¬
ляются общими для трех- и многокомпонентных систем.
В настоящее время наибольшее применение получили методы
расчета равновесия, основанные на использовании уравнения Дю¬
гема — Маргулеса и эмпирических зависимостей неидеальной доли
изобарного потенциала смешения от состава смесей [9, 16, 172, 275,
278, 280, 296—305]. Неидеальная доля изобарного потенциала сме¬
шения выражается при этом обычно в виде суммы неидеальных
долей изобарного потенциала смешения бинарных систем, обра¬
зованных веществами, входящими в многокомпонентную систему,
и дополнительных членов, учитывающих совместное взаимодей¬
ствие всех компонентов друг с другом. Эти члены включают эмпи¬
рические коэффициенты, которые определяются по данным о рав¬
новесии в трехкомпонентной системе. С помощью зависимости
неидеальной доли изобарного потенциала смешения от состава
жидкости коэффициенты активности определяются по уравнению
п—1
Σ δΦ
χι~δΓ (351)
I i
226
вытекающему из определения функции Ф (88) и уравнения Дю¬
гема— Маргулеса (82).
По найденным значениям коэффициента активности концентра¬
ция произвольного компонента в паре рассчитывается по уравне¬
нию:
Различные формы зависимости неидеальной доли изобарного
потенциала смешения от состава растворов были исследованы
Воолем [278], который получил для многокомпонентных систем
уравнения для определения коэффициентов активности компонен¬
тов, по форме аналогичные уравнениям Маргулеса и Ван-Лаара
для бинарных систем. Сводка уравнений, обобщаемых уравнением
Вооля [318], приведена в табл. 32. В табл. 33 дана сводка уравне¬
ний для расчета коэффициентов активности компонентов тройных
систем. Уравнения (255) и (256), предложенные Вильсоном [165]
были приведены выше.
Константы Aik и q в уравнениях, приводимых в табл. 32 имеют
то же значение, что и константы в уравнениях табл. 29. Взаимо¬
действие всех компонентов друг с другом в уравнениях табл. 32
учитывается константой С, а в уравнениях табл. 33 — констан¬
тами С, Dt и D2. В уравнениях (363) (табл. 33) Oi3 и Ф2з — значе¬
ния функций Ф для бинарных смесей I—3 и 2—3 с такой же
концентрацией'третьего компонента, как в тройной системе, Ф12 —
значение функции Ф для бинарной смеси I—2 с таким же относитель¬
ным содержанием компонентов, как в тройной смеси; ур, ур —
коэффициенты активности компонентов в соответствующих бинар¬
ных системах i — k. В уравнениях (362) <&ik — значение функции Ф
для бинарной системы i — k с таким же относительным содержа¬
нием компонентов, как в тройной системе. В табл. 32 и 33 приве¬
дены уравнения для определения коэффициента активности пер¬
вого и второго компонентов. Уравнения для определения коэффи¬
циентов активности других компонентов могут быть получены
путем замены индексов в указанных выше уравнениях по схеме
Легко видеть, что по принципу построения, уравнения, приве¬
денные в табл. 32 и 33, аналогичны соответствующим уравнениям
для бинарных систем. Методы определения констант для бинарных
систем были описаны выше. «Тройные» константы, учитывающие
совместное взаимодействие всех компонентов, определяются по
опытным данным для тройной системы. Число констант, учитываю¬
щих отклонение от закона Рауля в бинарных системах, а также
p0IxCh
(352)
,1
8г
227
Таблица 32
Уравнения для расчета коэффициента активности, обобщенных
Авторы и ссылка
Константы
2
Уол [278]
г,-
Xl + х2 — + X3 —
Яг Я\
X2
ql
X1 +Х2~- + Х3-^-
Я\ ЯI
* Si.
3 <7.
JCi + Jc2 — + JC3 —
<7ι ЯI
Скетчард [296, 297]
Я 2 У2
<7i V1
Q3 K3
ЯI “ V1
JCi
K2 j. K3
JC! + JC2 у- + AC3 у-
X
2 V1
Ζϊ V2 V3
JCi+Jc2-pr-+ Jc3-рт-
K3
"3TT
гз ~ K2 F3
JCl + AC2 -р- + JC3 у-
Уравнения типа урав¬
нений Ван-Лаара [278]
Я2 _ ^21
<7i Tl12
<7з Tl31
Я\ Tl13
Яг _ Tl32
Я2 Tl23
X1
г1 ~ , A2i , Л31
Х\ + X2 -д ь X3 -д—
А12 Zi13
Tl21
X2 -д
12
2 , Tl21 , Лз1
*1 + Х2 —д ь *3 -д
Ti 12 Ti13
г ^31
" 3 Tli3
3 - + * Aii Al ·
Xi т X2 -I г X3 —д
Αϊ2 Д13
Уравнения типа уравне¬
ния Маргулеса [278]
Я2 _ <7з _ _£з_ j
?I ?! ?2 “
Ζχ=Χ\
Z2 = X 2
гз = *3
228
уравнением (318]
Ig Yi
Номер
уравне¬
ния
Xi + х2 + *з ~~Г~) X
<7ι ЯI J
χ[ζ,ζ2 · [A2iZx + Ai2Z^ +
+ z,z3 ^31Z1 -^-+ -413z3j +
+ Z2Z3
\ ч з
Л‘- +
Я\
\ Яъ /
^3 [a32z2 -|i- + A23Z3 j!-j
+ Z1Z2Z3 ( A21 ~~~
\ Я 2
А
А ДI 3 + A32 — С j j
^A12 A 2zj (а.
lL
Я2
.)]■
+ Z*
[τΐ13 A2zj ^A31 A]3jj +
A Z2Z3 \^2ΐ ~ + Ai3 — A32 +2Z1X
L Я 2 Яъ
X^A3I —A13j Α2ζ3Χ
(353)
*1+A2-^-Aa3 Y^jX
X^z1Z2 * ^A2I · Z1 -γ- A A12Z2 j A
+ ZiZ3-< ^A31-Sr1 -ψ- A A13S3 j A
+ Z2Z3 · ^A32Z2 -pr- A A23Z3 -p—
+
■('
Zl
K2
+ Л,3 +/I32-Zl.-с)]
— Aio +
; ^A12 + 2z1 ^A21
+ 2з [Aj3 + 2^i (a31 ~y~ “ yA 13)]
A
A Z2Z3 j^A21 A A13 — A32 A
A 2Zi ^A31 — A13j A 2z3X
X ^A32 -y^ — A23 -yj —C (I — 2zl}]
(354)'
^iAT2A2I Aa1A3Asi A X2X3A23 ~A31
T*13
A21 A31
Xi+X2-T-+ X3-*-
Sl12 Si13
I
v -L v 21 -L v 31
Al A X2 —A l· X3 -j—
л12 Л13
X
X
A
[х2МШ+х1АЛ^к)
+ зд(л12 + Л,3-Л32·^-)
(355)
AT1AT2 (A21AT1 A A12AT2) А
A A1A3 (A31A1 A A13A3) А
A A2A3 (A32A2 A A23A3) А
A A1A2A3 (A21 A A13 A A32 “ С)
jkI И12 + 2*1 (^21 — ^12)] +
+ *3 Hl3 + 2*1 Из1 _ y4I3)] +
A A2A3 [A21 A A13 — A32 А
A 2xi (A31 — A13) А
А 2а3 (A32 — A23) — С (I — Sa1)]
(356)
229
Авторы и ссылка
Константы
j
Z
Симметричные уравне¬
ния, Уол [278]
?2 _ Яъ = Яъ __ j
Я\ Я\ = Я2
^21 в Л12
Л31 Л13, Л23 =* Л32
С ф 0
Z1 = X1
Z2 = X2
Z3 =*3
/
Симметричные уравне¬
Я 2 _ Яг_ _ _^з_ j
<7ι “ Я\ Яг
Л 21 β Л12, Л31 = Л13
Л23 = Л32> С =* 0
Z1 = X,
ния
Z2 = X2
Z3 = X3
' Таблица 33
Некоторые уравнения для расчета коэффициентов активности трех
Авторы и ссылка
Константы
Ф
Ли и Коул
[276]
Ьъ &2i ^3
&12> &13> &23
Редлих и Ки-
стер [9]
^12- C12 · · м
Bi3, C13 ..
^23» C23 ,
С, S1, D2 ...
X1X2 [S12 + C12 (X1 — х2) + ... ] +
+ X1X3 [S13 + C13 (X1 -X3) + ... ] +
+ X2^3 [S23 + C23 (X2 — X3) + . . . ] +
+ X1X2X3 (С + S1X1 + D2X2 + ...)
Бенедикт,
Джонсон,
Соломон,
Рубин [280]
^ 112» Л122>
23» Л133,
. Л223, Л233
2 3RT 0**1*2^112 + Зх1х2Л122 + ЗХ]Х3Л113 +
+ 3^133^1*1 + ^A123X1X2X3 + ЪА222х\хъ + Sx2X23A233)
Колер [302]
—
Фi2 (I — X3)2 + Ф23 (I — X1)2 + Ф31 (I — X2)2,
Жаров и Мо¬
рачевский
[305]
I Ф*1 yi_ х"з Ф23 +
+I·-,*”)/., (; ^ _ J
23Q
Продолжение
ф
IgYl
Номер
уравне¬
ния
XiX2 (X1 +X2) Al2 +
+ XiX3 (*i 4-*3) A13 +
+ *2*з {Х2 4~ Xz) А2з 4-
+ ΧγΧ2Χζ {А\2 4* А13 + A23 — С)
*2^12+ *3^13 +
+ *2*3 Ml2 А\$ ^23 ”” С (I — 2л:I)]
(357)
X1X2 (Xl +х2) Ai2 +
+ XiX3 (х\+х3) An +
+ X2X3 (Хг + х3) A23 4-
+ XiX2X3 (^4i2 4- ^41з + A23)
X22A12 + X23A13 + X2X3 (A12 + A13 - A23)
(358)
компонентных систем
Коэффициенты активности
Haoiep
уравне¬
ния
THgYi =
(I?) (Ir) '=+(Ir) (Ir) ^+[(Ir) (Ir)+ (Ir) (Ir) - w) '*'·
(359)
[ti fIft*+If tsI
Ig =B12 (х2-Xl) - Ct2 [(X1-X2)2-2Х!Х2] +
Y2
+ Xz 1з 4" ^ΐ3 (2*ι — X3) B23 — С2з (2*2 — -^з) 4- С (х2 — *1) 4-
4- £>1*1 (2х2 - х3) + D2X2 (х2 - 2*ι)]
(360)
RT In Yi = A112 (6*1*2 ~ 6*jх2) + A122 (з*| — §Х\Х2) 4-
+ А\\з (6*1*3 - 6х?*з) + Л,33 (ЗХ3 - βΛΓ,ΛτΙ) +
Н* ΑΙ23 {^χ2χ3 ~ \х2х'з) + Л223 ( —6JC2JC3) H- Л233 (—^Jc2Jc3)
(361)
Ig Vi = (I-JC3) Ig vl2H-(I-JC2) >g Yi* + Jc3(I — х3) Ф12 +
+ Jc2 (I — Jc2) Ф3] — (I — JCj)2®23
(362)
, 'Yi хз . Y(il3) Jc3 vf Jc, Y(f ,
S2 1-сс2 Sf I-X2 gYf I-Jc2 gYf +
Фз, Λ Yf , Yf V,'
+ Ig (-Vi VgYf gYfj 31
VYiT*,-1
(363)
231
взаимодействие всех компонентов друг с другом, в большинстве
методов можно выбирать в зависимости от требуемых степеней
точности расчетов и надежности исходных данных.
Большое практическое значение приведенных методов расчета
коэффициентов активности обусловливается тем, что влиянием
взаимодействия всех компонентов друг с другом в ряде случаев
можно пренебречь. При этом оказывается возможным рассчиты¬
вать равновесие в трехкомпонентной системе по данным для би¬
нарных систем.
Поскольку разные авторы предлагают весьма различные по
форме зависимости коэффициентов активности компонентов трой¬
ных смесей от их состава, для сравнительной оценки этих уравне¬
ний интересно сопоставить расчеты с опытными Данными. Такое
сопоставление результатов расчетов по уравнениям Бенедикта
с тремя константами для бинарных систем, Ван-Лаара — с двумя
константами для бинарных систем, Маргулеса — с двумя констан¬
тами для бинарных систем и одной для тройной системы, а также
по уравнениям Редлиха и Кистера с опытными данными для си¬
стемы метилэтилкетон — гептан — толуол [306], показало, что все
перечисленные расчетные методы дают близкие результаты.
Сопоставление результатов расчетов по уравнениям Вооля, Ван-
Лаара, Маргулеса и Редлиха и Кистера с опытными данными для
12 тройных систем [299] показало, что, как правило, лучшие ре¬
зультаты получаются при использовании уравнений, содержащих
только константы, определяемые по опытным данным для бинар¬
ных систем. Для большинства рассмотренных систем такие резуль¬
таты дают уравнения Ван-Лаара, Маргулеса и Редлиха и Кистера.
Эти методы получили наибольшее практическое применение. Кроме
того, в последнее время используют методы Колера и Вильсона,
которые для ряда систем дают хорошие результаты.
Графо-аналитические методы
Автором [297] предложен графо-аналитический метод
расчета равновесия в трехкомпонентных системах по данным для
бинарных систем, базирующийся на использовании уравнения
(117). Как показывает анализ имеющихся экспериментальных дан¬
ных, по мере прибавления третьего компонента к бинарной смеси
коэффициент относительной летучести образующих ее компонентов
все в меньшей степени изменяется с изменением их относительной
концентрации, стремясь к постоянной величине при X3 = I. При
увеличении X3 происходит также непрерывное изменение величины
(Φΐ3 — Ф2з)/(1 —*з), которая приобретает некоторое предельное
значение при X3 = I. Легко ридеть, что при X3 = I отношение γ±/γ2
постоянно и равно этой предельной величине. Последняя выражает
максимально возможное изменение относительной летучести пер¬
вого и второго компонентов, вызываемое третьим компонентом,
232
Таким образом, имея данные для трех бинарных систем, обра¬
зованных компонентами тройной системы, можно определить по¬
ложение линий, выражающих зависимость отношения коэффициен¬
тов активности любых двух компонентов от состава при концен¬
трациях X3 = 0 и X3 = I.
Кроме того, при помощи уравнения (115) можно найти зависи¬
мость среднего изменения ' отношения коэффициентов активности
lg(yi/y2)cp = (Фз — Ф23) / (I—хз) от концентрации третьего компо¬
нента. Изменение относительной летучести при произвольной кон¬
центрации третьего компонента можно рассматривать как долю
изменения при X3 = I. Предлагаемый метод расчета основан на до¬
пущении, что эта доля постоянна при любых относительных кон¬
центрациях первого и второго компонентов.
Ход расчета излагается ниже на примере системы ацетон —
метиловый спирт — вода.
На рис. 79 изображены зависимости логарифма отношения ко¬
эффициентов активности от концентрации компонента, стоящего
в названии системы первым, для систем ацетон — метиловый спирт
Ig(YiZy2) =cp(xi) ацетон — вода Ig(γι/γβ) = φι(Χι) и метиловый
спирт — вода Ig (Y2/Y3) = <р2(х2).
Путем графического интегрирования зависимостей логарифма
отношения коэффициентов активности компонентов от концентра¬
ции, изображенных на рис. 79, рассчитывают функции Ф. Послед¬
ние представлены для указанных бинарных систем на рис. 80, где
по оси абсцисс отложена концентрация компонента, индекс кото¬
рого стоит первым.
Далее по найденным значениям функций Φί3 и Ф23 определяют
величины Ig(YfZy2) = (Ф13 — Ф2з) АО—Хз), зависимость которых от
концентрации воды изображается на рис. 80 (кривая I). Путем
экстраполяции этой кривой до Хз = I определяется значение
Ig(YiZy2) в этой точке. В соответствии с изложенным выше, пря¬
мая ABy параллельная оси абсцисс и отвечающая предельному
значению Ig(YiZy2), выражает отношение коэффициентов актив¬
ности первого и второго компонентов X3 = I. При X3 ф I Ig(Υ1/Υ2)ср
составляет часть от значения Ig(γι/уа)ср при X3 = I. Следовательно,
кривые, выражающие зависимость Ig(YiZy2) от Xi, при разных зна¬
чениях X3 должны располагаться между линиями 2 и ABy отвечаю¬
щими X3 = 0 и X3 = I. Наиболее простые соотношения имеют ме¬
сто, если линия I — прямая. В этом случае значение Ig (γι/γ2) ср
при произвольной величине X3 составляет равную X3 часть от зна¬
чения Ig(YiZY2) при X3 = I.
При этом, в соответствии с указанным выше допущением, зави¬
симость Ig(YiZY2) от Xi при X3 Ф I может быть легко найдена, как
равная X3 часть расстояния от кривой 2 до прямой AS.
Если линия I — кривая, то каждую точку С этой кривой можно
рассматривать, как лежащую на прямой OBfy которая проходит
через эту точку и начало координат, а зависимость Ig(YiZY2) от Xi
при заданном X3 может быть найдена путем интерполяции между
из
кривой 2 и линией А'В\ отвечающей точке пересечения прямой OB'
с ординатой х\ = I.
Описанным способом были рассчитаны значения Ig(iYiM) ПРИ
хъ = 20, 40, 60 и 80 мол.% (рис. 80). Коэффициент относительной
летучести αΐ2 определяется как произведение найденного описан¬
ным способом отношения коэффициентов активности и отношения
давлений паров чистых компонентов. В связи с тем, что последнее
в ограниченном температурном интервале сравнительно мало из¬
меняется с температурой, можно определить отношение давления
OM
А'
60 80 100х 0г04
20 40
Xt мол.%
Рис. 79. Зависимость логарифма
отношения коэффициентов актив¬
ности от концентрации в следующих
бинарных системах:
I — ацетон — вода; 2 — ацетон — метиловый
спирт; Д— метиловый спирт —вода.
Рис. 80. Кривые для расчета равнове¬
сия в системе ацетон — метиловый
спирт — вода:
/ — зависимость (Ф^ — Фгз) (I — *з) от JC3; 2 — за¬
висимость Ig (Y1/Y2) от JCi при лса = 0.
паров при температуре, средней между температурами кипения
бинарных смесей I—3 и 2—3 с заданной концентрацией третьего
компонента. Относительная концентрация первого компонента в
паре находится по уравнению
/ ‘ «12*1
Ух — г (364)
!+(^i2-1K
вытекающему из определения величины αΐ2·
Особо надо рассмотреть случай, когда кривые, выражающие
зависимость Ф от х для двух бинарных систем, пересекаются. Это
характерно и для системы ацетон — метиловый спирт — вода
(рис. 80), в которой пересекаются кривые для систем ацетон — ме¬
тиловый спирт (Φι2) и метиловый спирт — вода (Ф32). Очевидно,
в точке пересечения величины Ig (Υ1/Υ3) ср = (Ф12 — Ф32) / (I—*2) = 0
т. е. кривая, выражающая зависимость (Ф12 — Ф32)/ (I—*2) от *2>
при некотором значении х$ проходит через нуль (рис. 81).
«4
Из рис. 81 следует, что при концентрациях метилового спирта
менее 40 мол.% величина (Ф12 — Фзг)/(1 — *2) отрицательна, а при
больших концентрациях — положительна.
В соответствии с изложенным, кривая Ig (γι/уз) = ф(#2) при X2 =
= 40 мол.% может быть найдена как геометрическое место точек,
отстоящих от кривой 2 (рис. 81) на 2/б расстояния ее от оси
абсцисс. Полученная кривая 3 для системы ацетон — метиловый
спирт — вода изображена на рис. 81.
Из геометрических соображений следует, что пересечение кри¬
вых Φ = φ(#) наиболее вероятно при мало отличающихся по ве¬
личине функциях Φι2 и Фз2. Ho при
этом в диапазоне концентраций X2,
на концах которого (Ф12 — Фзг)/(1—
—х2) = 0, значения (Ф12 — Ф32/О —
—х2) мало отличаются от нуля. Так,
в системе ацетон — метиловый
спирт — вода значение (Ф12 —
— Ф32)/(I — *2) при0<х2<40 мол.%
в экстремальной точке .составляет
всего — 0,012. Поэтому для техноло¬
гических расчетов можно пренебречь
этой величиной и считать, при
0 < х2 < 40 мол. % значение (Ф12 —
Ф32) /(I —*2) = 0. Максимальная от¬
носительная погрешность, вызывае¬
мая этим допущением, не может
превышать 3%. Указанное допуще¬
ние, по-видимому, может быть сде¬
лано во всех аналогичных случаях. При этом значения Ig (γι/γ3) в
интервале 0<#2<40 мол.% могут определяться линейной интер¬
поляцией между кривыми Ig (γι/уз) = φ/#ι при #2 = 0 и осью
абсцисс.
При помощи описанного выше метода могут быть рассчитаны,
независимо друг от друга, три относительные концентрации в паре:
первого компонента по отношению к сумме со вторым (у\2) и тре¬
тьим (tj\3) и второго по отношению к сумме с третьим (/13). При
этом для расчета состава пафа получаются четыре уравнения
с тремя неизвестными:
У\ 0 - У X2) β У2У\2> У2 0 ~ #23) ~ УзУ23
/, / \ / , (365)
УIV - У13) “ УзУ\$ у I + у2 + Уз = 1
Комбинируя последнее уравнение с любыми двумя, можно рас¬
считать по три значения уи у2, Уз* Небольшое расхождение вели¬
чин, рассчитанных по разным уравнениям, является критерием
правильности расчета. При очень малых или очень больших зна¬
чениях у' на конечном результате может сильно сказываться
Рис. 81. Зависимости:
1 “ Ig (YiZVa)cp “(Φίϊ- Ф32) (I - Хг) ОТ Хъ
2 — Xg (Y1/Y3) от JCi при JC2 = O; 3 - при
Хг *=40 мол. % для системы ацетон (/) —
метиловый спирт (2) — вода (3).
235
погрешность в йх определении. В таких случаях значения у' для
дальнейших расчетов применять не следует. ,
Практика показывает, что для получения наиболее достовер¬
ных значений уи У2> Уъ целесообразно определять по три величины
для у и затем брать среднее.
Сусарев и Горбунов [298] предложили графический способ рас¬
чета равновесия жидкость — пар в тройных системах, в которых
два компонента образуют систему с небольшими отклонениями от
идеального поведения. В практике экстрактивной ректификации
с такими системами приходит¬
ся иметь дело весьма часто.
Таковы, например, системы,
образованные двумя углево¬
дородами и полярным разде¬
ляющим агентом. Способ ос¬
нован на двух предположе¬
ниях: I) относительные изме¬
нения парциальных давлений
паров двух сходных компо¬
нентов при постоянном пар¬
циальном давлении третьего
компонента (на изопотенциале
третьего компонента) зависят
от их относительного содер¬
жания так же, как в бинар¬
ной системе, образованной
этими компонентами; 2) изо¬
потенциалы третьего компо¬
нента — в треугольной диаграмме прямые линии, соединяющие
точки составов бинарных смесей с одинаковыми парциальными
давлениями третьего компонента.
Расчет равновесия между жидкостью и паром по этому методу
состоит из следующих операций.
1. По данным о равновесии жидкость — пар в бинарных систе¬
мах при постоянной температуре строят графики парциальных дав¬
лений паров компонентов систем I—3 и 2—3 и график зависимости
активностей а* компонентов системы I—2 с малой степенью не¬
идеальности. На рис. 82 эти графики изображены на участках пло¬
скости, примыкающих к сторонам концентрационного треуголь¬
ника.
2. По указанным графикам находят составы смесей I—3 и 2—3
с одинаковыми парциальными давлениями третьего компонента
и найденные точки соединяют прямыми линиями. Получают в тре¬
угольной диаграмме сетку изопотенциал третьего компонента.
3. Для выбранной точки L треугольника составов путем интер¬
поляции находят изопотенциалу третьего компонента, проходящую
через эту точку, и для точек К и M на сторонах треугольника опре¬
деляют парциальные давления паров компонентов рь р2 и рз.
Рис. 82. Метод расчета фазового рав¬
новесия в тройной системе, предложен¬
ный Сусаревым и Горбуновым.
236
4. Построением секущей A3LN определяют активности первого
и второго компонентов в бинарном растворе N с таким же относи¬
тельным содержанием этих компонентов, как в тройной смеси L.
5. На основании первого предположения парциальные давления,
паров первого и второго компонентов над тройным раствором на¬
ходят как произведения парциальных давлений этих компонентов,
найденные в третьем этапе расчета, на значения их активности,
определенные в четвертом этапе расчета.
6. Суммированием найденных парциальных давлений опреде¬
ляют общее давление, а молярную долю каждого компонента
в паре определяют по закону Дальтона как частное от деления
парциального давления паров рассматриваемого компонента на
общее давление.
Глава III
ТЕХНОЛОГИЧЕСКОЕ
ОФОРМЛЕНИЕ ПРОЦЕССОВ
АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
ТЕХНОЛОГИЧЕСКИЕ СХЕМЫ ПРОЦЕССОВ
АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
ЛАБОРАТОРНЫЕ УСТАНОВКИ
ДЛЯ АЗЕОТРОПНОЙ РЕКТИФИКАЦИИ
Проведение лабораторных опытов по азеотропной и экст¬
рактивной ректификации — обязательная стадия иссле¬
дований, связанных с применением этих методов на практике.
Опыты по азеотропной ректификации проводят на обыкновен¬
ных лабораторных колонках, описанных в руководстве [178].
Исходную смесь и разделяющий агент загружают в куб, и про¬
изводят обычную разгонку, в процессе которой последовательно
отбирают небольшие порции дистиллата. При этом осуществляется
контроль за температурой отгонки и физическими свойствами
отобранных фракций (чаще всего показатель преломления или
плотность). После отделения разделяющего агента из фракций
дистиллата исследуют физические свойства или производят хими¬
ческий анализ выделенных веществ для определения их состава.
Границы фракций различных азеотропов и избытка разделяющего
агента определяют, как и при обычной разгонке. Для этого поль¬
зуются графиком зависимости температуры паров в верху колонки
от объемной доли отобранного дистиллата. Разделяющий агент
загружают в количестве, несколько превышающем необходимое
для отгонки компонентов, которые отбираются в виде дистиллата
азеотропа.
Как уже указывалось, наиболее желательными разделяющими
агентами в процессах азеотропной ректификации являются веще¬
ства, имеющие ограниченную взаимную растворимость с отгоняе¬
мыми компонентами. Специфика проведения опытов с такими раз¬
деляющими агентами связана с расслаиванием дистиллата. Если
необходимо, чтобы он имел состав азеотропа, то следует произво¬
238
дить отбор из паровой фазы по аналогии с опытами по определе¬
нию состава гетероазеотропов. Для отбора расслаивающегося ди¬
стиллата можно пользоваться также головкой с электромагнитным
клапаном [19, 307]. Один из конструктивных вариантов такой го¬
ловки изображен на рис. 83. В укрепленной на подвеске I пла¬
стинке 2 помещен сердечник из мягкого железа 3, заключенный
в стеклянную оболочку. С помощью электромагнита 4, связанного
с реле времени, пластинка с заданной периодичностью отклоняется
в направлении, обеспечивающем отбор стекающего конденсата.
Выступ 5 фиксирует положение пластинки 2.
Рис. 83. Схема головки Рис. 84. Головка с сепа-
с качающейся подвеской: ратором, предназначен-
/ —подвеска; 2 — пластинка; пая ДЛЯ отбора легкой
3 — сердечник; 4 — электромагнит; фазы:
5 —фиксатор; б — холодильник. , . „ о „
м I, 4 — конденсаторы; 2 — пере¬
ливная трубка; 4 — гидравли¬
ческий затвор; 5 — кран.
Расслаивание дистиллата создает возможность отбора только
одной жидкой фазы, обогащенной отгоняемым компонентом за¬
данной смеси. Если эта фаза является более тяжелой, то разгонку
можно производить на колонке с обычной головкой (см. рис. 44).
Чтобы обеспечить расслаивание погона в месте припайки крана
для отбора дистиллата следует сделать небольшое расширение.
Если желательно отбирать более легкую фазу, то головка колонки
должна быть дополнительно снабжена сепаратором, в котором про¬
исходит расслаивание жидкости, поступающей из конденсатора.
Головка с сепаратором схематически изображена на рис. 84. Сепа¬
ратор представляет собой сосуд диаметром 2—3 см, высотой 10—
15 см, в середину которого поступает конденсат из конденсатора I.
Легкую фазу отбирают по переливной трубке 2, а тяжелую фазу —
через гидравлический затвор 3. Верхние части сепаратора
т
и гидравлического затвора должны сообщаться с атмосферой при
проведении разгонки под атмосферным давлением или с вакуум¬
ной системой при работе под вакуумом. Положение границы раз¬
дела фаз в сепараторе определяется их плотностями и высотой гид¬
равлического затвора. Если допускают свойства перегоняемых ве¬
ществ, удобно делать гидравлический затвор на гибких соедине¬
ниях. Это обеспечивает легкую регулировку его высоты. Сепаратор,
аналогичный изображенному на рис. 84?- можно применять также
при отборе тяжелой фазьц В этом случае система его соединения
с ,колонной должна быть соответствующим образом изменена.
Конструкцию головки следует выбирать с учетом условий рас¬
слаивания. В тех случаях, когда расслаивание происходит при тем¬
пературе более низкой, чем температура конденсации, должно
быть обеспечено охлаждение конденсата перед его поступлением
в сепаратор.
Отбор при разгонке только фазы, богатой отгоняемым компо¬
нентом, дает возможность уменьшить загрузку разделяющего
агента. Она определяется количеством разделяющего агента в от¬
бираемом растворе и избытком, необходимым для поддержания
достаточной концентрации разделяющего агента по высоте ко¬
лонки. Этот избыток может быть отогнан в чистом виде, если раз¬
деляющий агент не образует азеотропов с компонентами, остаю¬
щимися при азеотропной ректификации в кубе. В противном случае
избыток разделяющего агента может быть удален в паровой фазе
в виде азеотропа с отгоняемым компонентом к концу его отбора.
Для обеспечения такой возможности предусматривается (рис. 84)
конденсатор 4, с помощью которого возвращается флегма при от¬
гонке паров азеотропа. Отбор последнего производят через кран 5,
служащий также для опорожнения сепаратора.
ЛАБОРАТОРНЫЕ УСТАНОВКИ
ДЛЯ ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Простейшая лабораторная установка периодического
действия для экстрактивной ректификации представляет собой
обычную колонку, снабженную градуированной емкостью для по¬
дачи разделяющего агента (рис. 85). Последний непрерывно по¬
дают в колонку в процессе разгонки. Некоторое количество разде¬
ляющего агента отбирают с отгоняемыми веществами. Основное
же его количество поступает в куб. Подачу разделяющего агента
прекращают по достижении желательной степени разделения. Ку¬
бовый остаток, представляющий собой смесь разделяющего агента
и неотогнанных компонентов заданной смеси, подвергается допол¬
нительной ректификации с целью отгонки последних. Отбор дистил¬
лата производят небольшими порциями, как при обычной разгонке.
Недостаток описанной установки заключается во все возрастаю¬
щем разбавлении кубовой жидкости разделяющим агентом по ходу
разгонки. Кроме того, из-за ограниченных размеров куба на такой
I4Q
установке можно разгонять лишь небольшие количества смесей
при относительно небольшой концентрации разделяющего агента.
Это ограничивает применение установок описанного типа. Их ис¬
пользуют для проведения опытов качественного характера или для
очистки и выделения небольших количеств веществ из смесей.
Более совершенна установка с непрерывным возвратом разде¬
ляющего агента, схема которой изображена на рис. 86. Установка
состоит из двух колонок, расположенных друг над другом. Исход¬
ную смесь загружают в куб верхней экстрактивно-ректификацион¬
ной колонки. В процессе разгонки колонка непрерывно орошается
разделяющим агентом, подаваемым с помощью насоса I или само¬
теком из емкости 2. По переливной трубе 3 раствор компонентов
заданной смеси в разделяющем агенте вытекает из куба верхней
колонны, поддерживая таким образом в нем постоянный уровень
жидкости, и поступает в верх исчерпывающей ректификационной
колонки 4, предназначенной для отгонки компонентов исходной
смеси и регенерации разделяющего агента. Эта колонка в дальней¬
шем будет называться отгонной. Полнота отгонки компонентов ис¬
ходной смеси, имеющая исключительно важное значение для
успешного проведения процесса, контролируется, как правило, по
температуре кипения жидкости в кубе 5. Надежность такого
Рис. 85. Лаборатор¬
ная установка перио¬
дического действия
для экстрактивной
ректификации.
Рис. 86. Лабораторная
установка периодиче¬
ского действия для экст¬
рактивной ректификации
с непрерывным возвра¬
том разделяющего
агента:
/—-насос; 2 — емкость; 3,6—
переливные трубки; 4 — рек¬
тификационная колонка.
241
контроля обусловливается обычно большим различием температур
кипения разгоняемых веществ и разделяющего агента. В случае
необходимости к показаниям термометра должна вводиться по¬
правка, учитывающая разницу давлений в кубе и атмосферного.
В кубе 5 поддерживается постоянный уровень с помощью перелив¬
ной трубки 6,. по которой разделяющий агент стекает в промежу¬
точную емкость 7. Из последней он насосом I подается в экстрак¬
тивно-ректификационную колонну. Транспортировку разделяющего
агента можно производить также путем его испарения в промежу¬
точной емкости и конденсации образующихся паров в конденсаторе,
расположенном над емкостью для разделяющего агента 2, в кото¬
рую поступает конденсат.
Взаимное расположение экстрактивно-ректификационной и от¬
гонной колонок в значительной мере определяет их конструкцию.
Колонки делают сравнительно небольшой высоты (экстрактивно¬
ректификационная 70—100 см и регенерационная 30—60 см), а для
обеспечения' достаточного разделительного действия используют
эффективную насадку, например проволочные трехгранные призмы
конструкции Левина [308].
Для опытов по экстрактивной ректификации, предназначенных
для определения технологических показателей, используют уста¬
новки непрерывного действия. Установки этого типа были описаны
разными авторами [20, 309—312]. Они различаются деталями уст¬
ройств для подачи разделяющего агента и исходной смеси, отбора
продуктов разделения и др. Установка для проведения процесса
экстрактивной ректификации под вакуумом была описана Кортю-
мом [312]. Кафаров и Гордиевский [309] применяли установку,
схема которой изображена на рис. 87.
Основная часть установки — колонка /, выполненная из труб¬
ки 2 (внутренним диаметром 18 мм, высотой 1460 мм). Устройство
куба 3 обеспечивало поддержание в нем постоянного уровня
жидкости. По накоплении последней в колбе За излишек перетекал
через отверстия 36 в чашку Зв, из которой он выводился через
холодильник 4. Приемником кубовой жидкости служила колба 5.
Нагрев куба производился нагревателем 6, выполненным в виде
двух разъемных полусфер из асбестовой массы, в которые была
вмазана спираль из нихромовой проволоки. Контролировали на¬
гревание куба с помощью амперметра, включенного в цепь подо¬
гревателя. Регулирование скорости испарения производилось рео¬
статом.
В качестве куба использовали трехгорлую колбу. В одно из
боковых горл вставляли термометр 7, ко второму боковому горлу
присоединяли водяной манометр 8 для измерения перепада давле¬
ния в колонне. В широкое горло куба вставляли колонку.
Для создания адиабатических условий работы колонны ее снаб¬
жали муфтами 9 и IO1 изготовленными из двух концентрических
стеклянных трубок, диаметром 40 и 50 мм. Каждая трубка была
снабжена нагревателем. Регулирование теплового режима осущест¬
*4*
вляли с помощью реостата. Для точного контроля температур ме*
жду муфтами и колонкой находились термометры 11. Муфты кре¬
пили к штативу 12 двумя металлическими фланцами, охватываю¬
щими текстолитовые крышки. В среднем фланце, являвшемся
Вис. 87. Схема установки непрерывного действия для экстрактивной ректифи¬
кации: ,
I—колонка; 2, 13 -трубки; 3-куб; 4 — холодильник; 5 —цриемная колба; 6, 27, 28 — на¬
греватели; 7, И, 16, 30, 31 - термометры; 3—манометр; 9, 10 — муфты; 12 — штатив;
14 - головка полной конденсации; 15 - регулятор; 17 — змеевиковый холодильник;
18 — ловушка; 19 — стакан со льдом; 20 — хлоркальциевая трубка; 21 — колба; 22 — холо¬
дильник; 23, 24 — мерные цилиндры; 25— насос; 26 — мотор; 29-карманы; 32-контакт¬
ный термометр; 33 —реле; 34— общий щит.
общим для обеих муфт, была сделана прорезь для вывода пат¬
рубка, по которому в колонку подавали исходную смесь.
Подачу разделяющего агента в колонку производили по
трубке 13. В верхний шлиф колонки вставляли головку полной
конденсации 14, снабженную, регулятором отбора дистиллата 15 и
термометром 16, предназначенным для контроля температуры па¬
ров, выходящих из колонки. Дефлегматором служил змеевиковый
243
холодильник 17, соединенный с ловушкой 18, помещавшейся в ста¬
кане со льдом 19. Ко второму отводу ловушки присоединяли
хлоркальциевую трубку 20. Приемниками дистиллата служила
колба 21. Воздушное пространство колбы было соединено с ловуш¬
кой /§. Дистиллат охлаждался в холодильнике 22.
Подачу разделяющего агента и исходной смеси из градуиро¬
ванных мерных цилиндров 23 и 24 осуществляли спаренным дози¬
рующим насосом 25, который приводился в движение мотором 26.
Максимальная производительность каждого цилиндра насоса
составляла 400 мл/ч, а минимальная — Ьмл/ч. Подача регулирова¬
лась изменением хода поршня. На линиях ввода в колонку разде¬
ляющего агента и исходной смеси были установлены подогрева¬
тели 27 и 28, мощностью по 600 вт каждый, в которых произво¬
дился подогрев жидкостей до заданных температур. На каждой
линии после подогревателей, в карманах 29, были установлены
термометры 30 и 31. Регулирование температуры исходной смеси
осуществлялось реостатом. Температура разделяющего агента ре¬
гулировалась автоматически с помощью контактного термометра 32
и реле 33, включенных в цепь нагревателя 28.
Всю установку монтировали на штативе 12. Электроприборы и
реостаты были вынесены на общий щит 34.
После пуска установки и достижения стабильного температур¬
ного режима колонки регулятор отбора дистиллата устанавливали
таким образом, чтобы отбор происходил с желательной скоростью.
Последнюю определяли экспериментально на основе сопоставления
результатов анализа кубовой жидкости и дистиллата при мед¬
ленно увеличивающемся отборе последнего. При максимальном
содержании легколетучего продукта в дистиллате отбор его фикси¬
ровался и оставался постоянным в течение всего времени раз¬
гонки. Необходимое флегмовое число подбирали опытным путем
с учетом количества и состава дистиллата, а также кубовой
жидкости. Изменение флегмового числа производилось изменением
скорости испарения. Количество подаваемых на разгонку исходной
смеси и разделяющего агента регулировалось изменением произ¬
водительности насоса 25 и контролировалось измерением времени,
в течение которого подавалось 100—200 мл жидкости из мерных
цилиндров 23 и 24.
ПРОМЫШЛЕННЫЕ УСТАНОВКИ
ДЛЯ АЗЕОТРОПНОЙ РЕКТИФИКАЦИИ
Технологическая схема установки для азеотропной рек¬
тификации определяется условиями проведения процесса (перио¬
дическим или непрерывным) и способом регенерации разделяю¬
щего агента. Установки периодического действия, используемые
для разделения относительно небольших количеств смесей, по прин¬
ципам устройства аналогичны рассмотренным выше лабораторным
установкам. Технологическая схема должна предусматривать реге-
244
нерацйю разделяющего агента (способ осуществления которой за¬
висит от свойств системы), а также необходимое количество ем¬
костей, снабженных соответствующими коммуникациями, для
приема отдельных фракций. При ограниченной взаимной раство¬
римости отгоняемых компонентов и разделяющего агента регене¬
рация последнего производится путем отгонки его из отобранного
дистиллата. В случае полной взаимной растворимости для регене¬
рации разделяющего агента чаще всего используют экстракцию.
Технологическое оформление периодических процессов азеотроп¬
ной ректификации сравни¬
тельно просто и поэтому
подробно не рассматривает¬
ся. В качестве одного из
типичных примеров ниже
описывается процесс разде¬
ления путем азеотропной
ректификации смесей, полу¬
чающихся в производстве
спиртов C7-C9.
Значительно сложнее схе¬
мы установок непрерывного
действия для азеотропной
ректификации. На рис. 88
изображена принципиаль¬
ная схема установки для
случая, когда разделяющий
агент образует бинарный ге-
тероазеотроп с отгоняемым
компонентом. Исходную
смесь подают в среднюю часть колонны У, из верха которой от¬
бирается близкий по составу к гетероазеотропу пар, поступаю¬
щий в конденсатор 2. Конденсат расслаивается в сепараторе 3,
из которого слой, богатый разделяющим агентом (на схеме более
легкий), возвращается в колонну У в виде флегмы. Слой жидкости,
бедный разделяющим агентом, полностью или частично отводится
в отгонную колонну 4, из куба которой получается в чистом виде
отогнанный компонент, а пар из верха колонны поступает в кон-,
денсатор 2.
Компонент, получаемый в виде кубовой жидкости колонны У,
может содержать некоторое количество разделяющего агента, от¬
гонка которого производится в колонне 5. Дистиллат этой колонны
присоединяется к исходной, смеси, поступающей в колонну У, а из
куба отбирается компонент, очищенный от разделяющего агента.
По описанной принципиальной схеме производится отгонка
воды из ее смесей с различными органическими веществами, на¬
пример с уксусной кислотой.
Близкая к описанной схема может быть применена при образо¬
вании разделяющим агентом тройного гетероазеотропа, как это
Рис. 88. Схема установки непрерывного
действия для азеотропной ректификации
при отгонке в качестве дистиллата бинар¬
ного гетероазеотропа:
I, 5 — колонны; 2 — конденсатор; 3 — сепаратор;
4 — отгонная колонна.
245
HMeet место, в частности, в процессах обезвоживания низкокипя¬
щих жирных спиртов, например этилового, путем азеотропной рек¬
тификации с бензолом как разделяющим агентом. Отличие в этом
случае состоит в том, что дистиллат отгонной колонны, как пра¬
вило, сильно отличается по составу от азеотропа, поэтому он дол¬
жен возвращаться не в конденсатор 2,
а в соответствующее сечение ко¬
лонны I.
Принципиальная схема процесса
азеотропной ректификации с регенера¬
цией разделяющего агента путем эк¬
стракции показана на рис. 89. Исход¬
ная смесь подается в колонну I1 из
куба которой отбирается высококипя-
щий компонент, подвергаемый очистке
от разделяющего агента в колонне 2.
Дистиллат колонны I для регенерации
разделяющего агента направляется в
экстракционную колонну 3, из которой
отбираются низкокипящий компонент,
подвергаемый очистке в ректифика¬
ционной колонне 4, и смесь применяе¬
мого дл5п экстракции растворителя
с разделяющим агентом, регенерируе¬
мым из этой смеси в ректификацион¬
ной колонне 5. Из колонны 5 разде¬
ляющий агент возвращается в колон¬
ну У, а растворитель, отбираемый из
куба, возвращается в экстракционную
колонну. По описанной схеме производится разделение смесей
близкокипящих ароматических и парафиновых углеводородов с ис¬
пользованием метилового спирта в качестве разделяющего агента.
Приведенные схемы, являющиеся типичными для процессов
азеотропной ректификации, не охватывают всего многообразия
возможных схем. Выбор рациональной схемы производится с уче¬
том свойств системы, подвергаемой разделению.
ПРОМЫШЛЕННЫЕ УСТАНОВКИ
ДЛЯ ЭКСТРАКТИВНОЙ! РЕКТИФИКАЦИИ
В процессах экстрактивной ректификации регенерация
разделяющего агента за редкими исключениями производится пу¬
тем ректификации, чему благоприятствует обычно большая раз¬
ница температур кипения разделяющего агента и компонентов за¬
данной смеси. Это обусловливает более простое технологическое
оформление этих процессов по сравнению с непрерывными процес¬
сами азеотропной ректификации. Для промышленных установок
экстрактивной ректификации типичной является принципиальная
Рис. 89. Схема процесса азео¬
тропной ректификации с реге¬
нерацией разделяющего агента
путем экстракции:
I — колонна для азеотропной ректи
фикации; 2 — ректификационная ко¬
лонна для очистки высококипящего
компонента от разделяющего агента;
ιί — экстракционная колонна; 4 — рек¬
тификационная колонна для очист¬
ки низкокипящего компонента;
5 —ректификационная колонна для
регенерации разделяющего агента.
246
схема, изображенная на рис. I. Отклонения от этой схемы возни¬
кают при образовании разделяющим агентом азеотропов с отго¬
няемыми компонентами. Связанные с этим усложнения техноло¬
гической схемы обусловлены необходимостью разделения ааеотро-
пов, способы осуществления которого были рассмотрены при
обсуждении процессов азеотропной ректификации. В качестве ти¬
пичного примера процесса экстрактивной ректификации ниже будет
описан метод выделения бутадиена из бутан-бутадиеновых смесей.
3
яд
Si
Дистиллат
№
-Кубовая "ϊ
жидкость
Дистиллащ
3
Кубовая
жидкость
Рис. 90. Схемы процесса экстрактивной ректифика¬
ции с минеральными разделяющими агентами:
а — С применением твердого минерального вещества; б — с при¬
менением раствора минерального вещества в компоненте, от¬
бираемом в качестве кубовой жидкости:
/—колонна; 2 — куб; 3 — подача исходной смеси; 4 — подача
разделяющего агента; 5-мешалка; 6 — дефлегматор, 7 —холо¬
дильник.
Обязательной частью промышленной установки для экстрактивной
ректификации является оборудование для очистки разделяющего
агента от примесей (смолы, продукты коррозии аппаратуры), обра¬
зующихся при длительной работе. Наиболее распространенный
прием такой очистки — дистилляция. '
Процессы экстрактивной ректификации с применением мине¬
ральных веществ в качестве разделяющих агентов. Специфика тех¬
нологического оформления процессов экстрактивной ректификации
с минеральными разделяющими агентами состоит в том, что боль¬
шинство из них является при обычных условиях твердыми веще¬
ствами, ограниченно растворимыми в компонентах заданной смеси.
, При растворении минерального вещества в бинарной жидкой
смеси принципиально возможны два различных случая: в первом
случае образующаяся при пересыщении раствора новая фаза
является твердой, во втором — жидкой. В соответствии с этим про¬
ведение процесса экстрактивной ректификации с минеральными
*47
разделяющими агентами принципиально возможно по двум вариан¬
там, схематически представленным на рис. 90.
По !первому варианту для создания достаточно высокой кон¬
центрации разделяющего агента по высоте колонки минеральное
вещество растворяется во флегме и исходной смеси.
По второму варианту колонка орошается раствором минераль¬
ного вещества в компоненте, отбираемом в процессе экстрактивной
ректификации в виде кубовой жидкости. При этом соотношение
материальных потоков может быть таким, что в верхней части ко¬
лонки будут образовываться две жидкие фазы. Регенерация разде¬
ляющего агента в обоих случаях осуществляется путем выпарки.
Технологическое преимущество второго способа перед первым
заключается в том, что все материальные потоки являются жидки¬
ми и для регенерации разделяющего агента нет необходимости в
выделении его в чистом виде. Однако при этом в колонку вводится
компонент, от которого должен быть освобожден дистиллат. По¬
этому применение процесса экстрактивной ректификации с исполь¬
зованием в качестве разделяющего агента раствора минерального
вещества возможно лишь для минеральных веществ, обладающих
высокой эффективностью. При разделении систем, имеющих азео-
тропную точку, важно чтобы в части ректификационной колонки,
работающей в присутствии разделяющего агента, получались пары
с большей, чем в азеотропе, концентрацией отгоняемого компо¬
нента.
Технологическое оформление и практическое применение про¬
цессов экстрактивной ректификации с использованием твердых ве¬
ществ в качестве разделяющих агентов подробно рассмотрено
в работе [142].
МАТЕРИАЛЬНЫЙ И ТЕПЛОВОЙ БАЛАНС
ПРОЦЕССА АЗЕОТРОПНОЙ РЕКТИФИКАЦИИ
ПЕРИОДИЧЕСКИЙ ПРОЦЕСС
По условиям проведения азеотропная ректификация ни¬
чем не отличается от обычной ректификации многокомпонентных
смесей. В периодическом процессе исходная смесь и разделяющий
агент загружаются в куб и производится обычная разгонка. Ма¬
териальный баланс этого процесса выражается следующими урав¬
нениями (см. рис. 91):
Dn+ i~~Ln = n (366) Dn+1 уп+ j — LnXn =* ПхА (367)
где Dn+1, L71 и П — мгновенные молярные расходы пара, жидкости
и дистиллата на произвольной тарелке; уп+и %п — молярные кон¬
центрации одного из компонентов в паре и жидкости, проходящих
через произвольное сечение колонны; хд—молярная концентрация
этого же компонента в дистиллате; ц —номер тарелки, считая
сверху вниз.
243
Отсюда получается обычное уравнение рабочей линии
R хя
Уп +I*
R+ I
R+ I
(368)
J5L
Os
0пГ7ТГГп
Уп + 11 fXn
где R = Ljn — флегмовое число укрепляющей чдсти колонны. Это
уравнение может быть написано относительно любого, компонента.
Следовательно, возможное число уравнений (368.) для рассматри¬
ваемой системы равно числу образующих ее компонентов. Однако
число независимых уравнений будет на единицу меньше. Так, если
исходная смесь является бинарной, а
разделяющий агент однокомпонент¬
ным (третий компонент), ход процесса
азеотропной ректификации описывает¬
ся двумя уравнениями (368). Оба эти
уравнения имеют одинаковые угло¬
вые коэффициенты [Rl(R + I)] и раз¬
личаются лишь величиной свободных
членов.
Как и при обычной ректификации,
изменение величины R по высоте ко¬
лонны обусловлено изменением эн¬
тальпий пара и жидкости.
Концентрация разделяющего аген¬
та по высоте колонны несколько из¬
меняется соответственно с изменением
состава кубовой жидкости во времени.
Однако определяющее влияние ока¬
зывают условия равновесия и состав
азеотропов, образуемых разделяющим
агентом с компонентами заданной смеси. Обычно кривые равно¬
весия бинарных систем, состоящих из разделяющего агента и
компонентов заданной смеси, в пределах между чистым компонен¬
том и азеотропом весьма выпуклы. Поэтому требуется сравни¬
тельно небольшое число тарелок для достижения концентрации
разделяющего агента, близкой к азеотропной. При малых содер¬
жаниях в жидкости всех компонентов заданной смеси, кроме
одного, концентрация разделяющего агента практически отвечает
составу его азеотропа с этим компонентом. Более высокая концен¬
трация разделяющего агента в периодическом процессе не может
быть достигнута.
' Изменение концентрации разделяющего агента во времени
сильно зависит от его начальной концентрации в смеси, загружен¬
ной в куб. Обычно загрузку разделяющего агента выбирают таким
образом, чтобы она несколько превышала количество, требуемое
для удаления из смеси всего отгоняемого компонента в виде азео¬
тропа. При меньшей загрузке часть этого компонента (если он об¬
разует азеотропы с другими компонентами заданной смеси) не
может быть выделена в чистом . виде, Значительный избыток
Рис. 91. Схема материальных
потоков в колонне периодиче¬
ского действия.
*
249
загруженного разделяющее агента вызывает дополнительный рас¬
ход тепла на его отгонку. Таким образом, загрузка разделяющего
агента определяется составами азеотропов, образуемых компонен¬
тами системы. Определение загрузки разделяющего агента было
рассмотрено выше.
Периодическую азеотропную ректификацию, как и обычную,
можно осуществлять двумя способами — с постоянным флегмовым
числом и переменным составом дистиллата и с постоянным соста¬
вом дистиллата и переменным флегмовым числом. Чаще всего про¬
цесс проводят по второму способу. Если начальное количество ку¬
бовой жидкости Wc молей, концентрация отгоняемого компонента
в ней хс, а содержание этого компонента в дистиллате хд, то зави¬
симость состава кубовой жидкости х от количества полученного
дистиллата П для этого способа проведения процесса легко полу¬
чить из уравнения материального баланса
Если отгонка целевого компонента прекращается, когда его кон¬
центрация в кубовой ^жидкости становится равна Xui количество
дистиллата, полученного за операцию, выражается уравнением:
Расход тепла определяется с помощью уравнения теплового ба¬
ланса
где i и q — энтальпия пара и жидкости; ηΆ —- энтальпия дистил¬
лата; Qa — мгновенный расход тепла, отводимого* в дефлегматоре.
Принимая во внимание уравнение (366), из уравнения (372)
получаем:
Это уравнение справедливо для любого сечения колонны. От¬
нося его к самому верхнему сечению, имеем
где гд = *д —<7Д— скрытая теплота испарения дистиллата.
Затрата тепла за операцию может быть рассчитана с помощью
уравнения (374). Согласно этому уравнению, количество тепла,
отводимого в дефлегматоре за время отгонки бесконечно малого
количества дистиллата άΠ, равно:
WcXc = Пх:д + (Wc - П) х
(369)
откуда:
СХС 77X д
Wc-II
(370)
(371)
ID = qL + <7д77 +
(372)
L (i — q) + П (i - <7Д) - Q11
(373)
Q11 = гд/7 (£+1)
(374)
dQ = qA(R+l)dH
(375)
250
Расход тепла, отводимого в дефлегматоре за операцию, равен
интегралу этого уравнения при изменении количества дистиллата
от 0 до П:
п
<2д“<7д { Rdn + ГьП (376)
О
Для расчета Qjl по этому уравнению необходимо знать зависи¬
мость R от Я. Эта зависимость может быть установлена путем рас¬
чета состава кубовой жидкости при разных флегмовых числах по
заданным составу дистиллата и числу тарелок в колонне и после¬
дующего нахождения по уравнению (371) количества дистиллата,
отвечающего расчетному составу кубовой жидкости.
НЕПРЕРЫВНЫЙ ПРОЦЕСС
В непрерывном процессе азеотропной ректификации ис¬
ходную смесь с заданным расходом подают в среднюю часть ко¬
лонны, а сверху и из куба отбирают соответственно дистиллат и
кубовую жидкость, которые представляют собой продукты разде¬
ления. Последние, кроме компонентов заданной смеси, всегда со¬
держат некоторое количество разделяющего агента. При расслаи¬
вании дистиллата большая часть разделяющего агента возвра¬
щается в колонну в виде флегмы. В противном случае весь
разделяющий агент, подаваемый в колонну, выводится с продук¬
тами разделения. В обоих случаях для проведения непрерывного
процесса азеотропной ректификации необходимо непрерывно по¬
давать в колонну разделяющий агент в количестве, равном отво¬
димому из системы. Разделяющий агент, вообще говоря, можно
подавать в различные части колонны. Так, его можно вводить в ко¬
лонну вместе с исходной смесью, в верх колонны или в любое про¬
межуточное сечение.
Чтобы определить целесообразное место ввода разделяющего
агента в колонну, необходимо рассмотреть факторы, определяю¬
щие его распределение в колонне.
Как и в периодическом процессе, концентрации разделяющего
агента в разных сечениях по высоте колонны зависят главным
образом от условий равновесия между жидкостью и паром. Су¬
щественное отличие заключается, однако, в том, что в непрерывном
процессе распределение концентраций постоянно во времени. По¬
скольку в этом случае количества подаваемого и возвращаемого
в колонну разделяющего агента одинаковы, распределение его кон¬
центраций по высоте зависит от количества разделяющего агента
в колонне и ее емкости, определяемой объемом жидкости на та¬
релке и числом тарелок. Так как в системе разделяющий агент —
отгоняемый компонент самую низкую температуру кипения имеет
азеотроп, образованный этими веществами, при ректификации со¬
став жидкости всегда стремится приблизиться к составу азеотропа.
251
32
^28
Г
% 20
116
I *
I 8
^ 4
Кйз
При малом количестве разделяющего агента в системе концентра¬
ция его, близкая к азеотропной, будет поддерживаться только на
верхних тарелках. С увеличением количества разделяющего агента
в системе число этих тарелок будет возрастать. При достаточном
увеличении количества · разделяющего агента его концентрация на
части тарелок может быть даже выше, чем в соответствующих
азеотропах. Если в точке подачи разделяющего агента его содер¬
жание ниже, чем в азеотропе, то на нижележащих тарелках будет
происходить уменьшение, а на вышележащих — увеличение кон¬
центрации разделяющего агента в на¬
правлении приближения к составу азе¬
отропа.
Если концентрация разделяющего
агента больше азеотропной, то он яв¬
ляется высококипящим компонентом и
должен концентрироваться на ниж¬
них тарелках. Обычно стремятся к то¬
му, чтобы концентрация разделяющего
агента на возможно большем числе
тарелок была близка к азеотропной
при минимальном содержании разде¬
ляющего агента в кубе. Чаще всего
это довольно легко осуществить вслед¬
ствие отмеченного выше большого раз¬
личия составов равновесных жидкой и
паровой фаз в системе, состоящей из
компонента заданной смеси и разде¬
ляющего агента. Характерным приме¬
ром в этом отношении является кри¬
вая (рис. 92), из которой следует, что от куба до второй тарелки
концентрация разделяющего агента резко возрастает от весьма ма¬
лой величины до величины, близкой к средней концентрации по
высоте колонны. EIa остальных 30 тарелках изменение концентра¬
ции разделяющего агента сравнительно невелико, хотя относитель¬
ная концентрация бутадиена резко изменяется. Отсюда следует,
что разделяющий агент можно подавать в любую точку колонны,
кроме области, прилегающей к кубу, так как это связано с опас¬
ностью повышения концентрации разделяющего агента жидкости,
находящейся в нем. Целесообразно подавать разделяющий агент
в колонну вместе с исходной смесью.
На рис. 92 показано также распределение температуры по вы¬
соте колонны. Изменение температуры зависит от концентрации
разделяющего агента. На тарелках 2—32 температура меняется
незначительно в соответствии с небольшим изменением концентра¬
ции разделяющего агента, а между кубом и второй тарелкой на¬
блюдается резкое изменение температуры. Из этого, между про¬
чим, вытекает возможность контроля концентрации разделяющего
агента по температуре на тарелке,, близкой к кубу.
0 20 4 0 60 80 10020 60 100
Вес % J кип
Рис. 92. Распределение темпе¬
ратур и концентраций разде¬
ляющего агента (NH3) и бута¬
диена в колонне для выделе¬
ния последнего из смесей
с бутиленами путем азеотроп¬
ной ректификации.
252
Если на ректификацию подается Wc моль/ч исходной смеси
с концентрацией рассматриваемого компонента хс, то связь между
количествами получаемых кубовой жидкости и дистиллата, а также
относительными концентрациями в них отдельных компонентов
определяется материальным балансом, который
для произвольного компонента имеет вид
WcXc = Л'х'д + (377)
и
Wc = If + W'K (378)
где TIr и W'K, χ'Ά и Xf — соответственно моляр¬
ные расходы и концентрации дистиллата и кубо¬
вого остатка без учета содержания в них разде¬
ляющего агента.
Условия материального баланса укрепляю¬
щей части колонны непрерывного действия ана¬
логичны рассмотренным выше для периодиче¬
ского процесса. Поэтому уравнение (378) яв¬
ляется также уравнением рабочей линии укреп¬
ляющей части колонны непрерывного действия
по произвольному компоненту.
Уравнение рабочей линии исчерпывающей ча¬
сти колонны получается на основании рассмотре¬
ния материального баланса произвольного нижнего участка ко¬
лонны, включающего куб (см. рис. 93)
VrVA-rV, <379)
Ln- Dn-.1 — Wk (380)
где Wk — расход кубового остатка; хк — молярная концентрация
рассматриваемого компонента в нем.
После преобразований получается следующее уравнение рабо¬
чей линии исчерпывающей части колонны
Уп-ι = R' ~ I Хп R'- I (381)
где Rf = LIWk флегмовое число исчерпывающей части колонны.
Уравнения (368) и (381) могут быть составлены для любого
компонента смеси.
Тепловой баланс колонны непрерывного действия без учета по¬
терь тепла в окружающую среду выражается уравнением
Qk + Wcqc + Ggp = Qa + TIq А + WKpK (382)
где Qk и Qfl — расходы тепла, подводимого в кубе и отводимого
в дефлегматоре; G — расход разделяющего агента, подаваемого
в колонну; qCy qv, qn и qK — энтальпия исходной смеси, разделяю¬
щего агента, дистиллата и кубовой жидкости.
Энтальпии материальных потоков зависят от того, при каких
условиях проводится процесс. Если исходная смесь и разделяющий
•Ш
I I ^n"1
Zn \ I Уп-1
Рис. 93. Схема ма¬
териальных пото¬
ков в исчерпываю¬
щей части колон¬
ны непрерывного
действия.
253
агент подаются в виде жидкостей, нагретых до температуры кипе¬
ния, а дистиллат и кубовый остаток отбираются в таком же со¬
стоянии, то можно принять, что
Wcqc Т* GijrP nqд + WKqK (383)
и, соответственно с этим:
Qk ^ Qz (384)
Этому уравнению можно придать и другой вид
Dr^Dr (385)
. к к в д v /
где Dk и Db — расходы пара, образующегося в кубе, и вверху ко¬
лонны; гк и гд — скрытые теплоты испарения кубовой жидкости и
дистиллата.
Из этого уравнения легко видеть, что расход пара по высоте
колонны изменяется в зависимости от изменения скрытой теплоты
испарения смесей с составом. Если гк > гд, то расход пара в ко¬
лонне возрастает снизу вверх. При гд > гк расход пара по мере
приближения к верху колонны убывает. Изменение расхода пара
вызывает соответствующее изменение количества _ жидкости, сте¬
кающей по высоте колонны. Из уравнений (366) и (380) следует,
что расход жидкости изменяется в том же направлении, что и рас¬
ход пара. Следовательно/при гк > гд расход стекающей жидкости
по мере приближения к кубу уменьшается, а при гк < гд воз¬
растает.
Поскольку дистиллат и кубовая жидкость существенно разли¬
чаются по составу, их теплоты испарения должны иметь еще боль¬
шее различие, чем для смесей промежуточного состава. Соответ¬
ственно с этим наибольшее различие расходов пара и жидкости
должно быть между верхом и низом колонны.
Если скрытые теплоты испарения дистиллата и кубового
остатка мало различаются, то материальные потоки в пределах
каждой части колонны (укрепляющей и исчерпывающей) практи¬
чески постоянны. *
Расход тепла на проведение процесса Qll определяется по урав¬
нению (382). Требующаяся для расчета величина Qa зависит от
количества отбираемого дистиллата и флегмового числа. Значе¬
ние Qa определяется уравнением (374). При подаче и отборе из
колонны всех материальных потоков в виде жидкости при темпе¬
ратуре кипения расход тепла на ректификацию, в соответствии
с условием (383), можно приближенно определить с помощью
выражения (384).
ОСОБЕННОСТИ РАСЧЕТА ПРОЦЕССОВ
АЗЕОТРОПНОЙ ректификации
С РАССЛАИВАНИЕМ КОНДЕНСАТА
В процессах азеотропной ректификации часто приме¬
няются разделяющие агенты, образующие гетероазеотроп или об¬
ладающие ограниченной взаимной растворимостью с отгоняемым
254
П, Xg
компонентом. Это представляет значительные технологические
удобства, так как разделение смеси отгоняемого компонента и раз¬
деляющего агента с целью его регенерации может быть легко осу¬
ществлено путем расслаивания и возвращения в колонну слоя,
обогащенного разделяющим агентом. Особенность такого процесса
заключается в том, что состав пара, выходящего из верха ректи¬
фикационной колонны, и состав отбираемого дистиллата различны.
Схема материальных потоков для такого процесса представлена
на рис. 94. В качестве дистиллата отбирают один из получающихся
в расслаивателе жидких слоев (на схеме ниж- 2
ний), обогащенный отгоняемым компонентом.
Рассмотрим наиболее простой и наглядный
случай, когда в процессе азеотропной ректи¬
фикации гетероазеотроп с разделяющим аген-
том образует один компонент, а содержание L χ Ii^wy
других компонентов столь мало, что в верхней n^Ln"1' п_|
части колонны практически происходит ректи- Y
фикация бинарной смеси. \ W
Условия материального баланса для та-, _!ЗЕ —
кого процесса выражаются уравнениями
Bn^yn .-LnXn +Пх{^ и Dn, =Ln + Я (386) Рис. 94. Схемы мате-
п 1п 1 п д я-i я риальных потоков в
из которых получается следующее уравнение процессе азеотропной
ректификации с рас-
рабочеи линии. слаиванием дистилла-
R Xi^ та:
У β" I 'I η х 4* Ti η (387) I - колонна; 2 — конденса-
Ita Ita тор; 3 — расслаиватель.
Если пренебречь изменением материальных потоков по высоте
колонны R = const, то уравнение (387) является уравнением пря¬
мой линии, проходящей через точку хна диагонали диаграммы
у = f(х) с угловым коэффициентом, равным R(I +/?).
На рис. 95 изображена кривая равновесия между жидкостью и
паром OGAEDBF и построение, обычно выполняемое при графи¬
ческом определении флегмового числа. Точка D1 лежащая на диа¬
гонали, отвечает составу гетероазеотропа, расслаивающегося на
две жидкие фазы, составы которых изображаются точками А и В.
Рабочие линии выходят из точки C1 отвечающей составу жидкой
фазы л;£>, отбираемой после расслаивания конденсата. Как и при
обычной ректификации, минимальное флегмовое число для смеси
состава Xg определяется положением рабочей линии, проходящей
через точку G (с абсциссой xG) на кривой равновесия у = }(х).
Очевидно, минимальное флегмовое число, по геометрическим сооб¬
ражениям, определяется из выражения
^min _ .
_ _ 1+/?min ш
где BC и BE — длины соответствующих отрезков на рис, 95,
US
Раскрывая физический смысл этого выражения, получаем
Rn
.(I).
I +Rn
е<»-:
(389)
где Xe — абсцисса точки пересечения рабочей линии CG с кривой
равновесия.
Из-соотношения (389) следует
D __ .
4min
BD
DB
(390)
т. е. минимальное флегмовое число равно отношению длин отрез¬
ков BD и ED на диаграмме, изображенной на рис. 95. Физический
смысл выполненного построения за¬
ключается в том, что при непрерывной
ректификации смеси состава xG в ко¬
лонне с бесконечно большим разде¬
ляющим действием можно получить
вверху колонны пар состава хЕ, после
конденсации которого получаются две
жидкие фазы, составы которых изоб¬
ражаются абсциссами точек А и В.
Рассмотрим теперь, при каких ус¬
ловиях можно проводить процесс, что¬
бы возвращать в виде флегмы только
одну жидкую фазу конденсата, а дру¬
гую* отбирать в качестве дистиллата.
Из метрических свойств диаграммы,
изображенной на рис. 95, очевидно,
что соотношение количеств жидких
фаз, соответствующих точкам А и В,
определяется положением точки E на прямолинейном участке
кривой равновесия ABi а именно: количество фазы А пропорцио¬
нально длине отрезка BE, а количество фазы В — длине отрезка
AE. Если в качестве флегмы возвращается в колонну фаза At
а фаза В отбирается в виде дистиллата, то флегмовое число равно:
_ Ш X^-Xe
R = -==-=— т=г (391)
Рис. 95. Расчет флегмового
числа при наличии в системе
гетероазеотропа.
AE
_ у{2)
Очевидно, прямая линия CG проходит через точку E только при
соблюдении равенства флегмовых чисел, определяемых выраже¬
ниями (390) и (391), т. е. при условии
xI ха
_ г
xA xE
X -*<2)
Xp Xjl
(392)
*Е xE'
Поскольку положение на диаграмме точек At Bt D обусловли¬
вается физико-химическими свойствами рассматриваемой системы
256
С
8"
/XX !'
I А \/ I 1 '
В'
Iy V I1I
Ψ А I I
/I Xi 1 *
I I / I ' t i
IV I Xe' M
VL—L771—Ii^j
L._.y
и, следовательно, задано, то может существовать единственная
смесь состава xGj для которой выполняется условие (392). С умень¬
шением Xq точка E приближается к точке Dj т. е. флегмовое
число Rj определяемое выражением (391), уменьшается. Величина
же Rmim определяемая выражением (390), возрастает. Это озна¬
чает, что для смесей, содержание первого компонента в которых
меньше, чем в смеси предельного состава xGj не может быть реа¬
лизован процесс ректификации с возвратом в качестве флегмы
только одного слоя конденсата. В этом случае возникает необхо¬
димость в увеличении количества флегмы, подаваемой в колонну.
Это может быть осуществлено путем
дефлегмации части пара, выходящего
из верха колонны, или путем возврата
в колонну из расслаивателя части
жидкой фазы, отбираемой в качестве
дистиллата.
Для смесей с концентрацией боль¬
ше предельной R > Rmm и процесс
азеотропной ректификации с возвра¬
том в колонну в качестве флегмы од¬
ной жидкой фазы вполне возможен.
Практически реализуемое флегмо¬
вое число, определяемое выражением
(391), будет при этом тем больше пре¬
вышать минимальное, определяемое
выражением (390), чем больше кон¬
центрация исходной смеси.
Предельный состав смеси Xqj как ясно из рис. 95, определяется
составами гетероазеотропа и обеих его жидких фаз, положением
точки E [условие соблюдения равенства (392)], а также ходом кри¬
вой фазового равновесия на участке от точки О до точки А.
Изложенные рассуждения применимы и к системам, в которых
в условиях процесса азеотропной ректификации образуется гомо¬
генный азеотроп, а возможность расслаивания отбираемой из
верхд колонны смеси обеспечивается путем ее охлаждения после
конденсации. В этом случае кривая равновесия у = f (x) не имеет
горизонтального участка (рис. 96), а составы сосуществующих
жидких смесей и х® определяются температурой, до которой
охлаждается конденсат пара, отбираемого из верха колонны. Если
после охлаждения и расслаивания отбирается жидкая фаза со¬
става χΜ, то как и в разобранном выше случае, рабочие линии
выходят из точки С. Как видно из рис. 96, состав дистиллата мо¬
жет изменяться в пределах от X8l3 при R = оо до уА при флегмо-
вом числе, отвечающем рабочей линии, проходящей через точки А
и С. Соотношение количеств жидких фаз, получаемых в резуль¬
тате расслаивания, определяется отношением отрезков, на которые
вертикаль, проведенная через точку состава пара вверху колонны,
К -Z03
Рис. 96. Расчет флегмового
числа при расслаивании дистил¬
лата.
9 Зак. 917
257
делит отрезок AB'. При расслаивании, например, охлажденного
конденсата азеотропной смеси отношение количества фазы, обо¬
гащенной отгоняемым компонентом (состава х®), к количеству
фазы, обогащенной разделяющим агентом (состава х®) равно от¬
ношению отрезков AD'/B'D'. Если смесь на тарелке питания имеет
состав Xg, то предельно возможный (при бесконечном разделитель¬
ном действии колонны) состав дистиллата соответствует орди¬
нате Уе точки E' пересечения кривой равновесия и рабочей ли¬
нии CO, проведенной через точку G на кривой равновесия с абс¬
циссой Xg. После охлаждения и расслаивания конденсата состава уЕ
отношение расходов фаз, в соответствии с выражением (391), опре¬
деляющее !флегмовое число, равно:
R = B7EfAE (393)
Из рассмотрения наклона гипотенузы. CF' треугольника B"CF'
получается следующее выражение для определения минимального
флегмового числа для составов исходной смеси xG и дистил¬
лата X®
Д
XtP-У р В'E
*п,ш- Д -W (394)
У В ~ xE ЕН
Из рассмотрения рис. 96 легко убедиться, что всегда #min > Я,
так как при равенстве числителей в выражениях (393) и (394)
всегда EH < AE. Это означает, что если при условиях процесса
азеотропной ректификации образуется гомогенный азеотроп, а кон¬
денсат пара для расслаивания нуждается в дополнительном охла¬
ждении, то во всех случаях можно отбирать в качестве дистиллата
лишь часть жидкой фазы, обогащенной отгоняемым компонентом.
Другая часть вместе с жидкой фазой, обогащенной разделяющим
агентом, должна возвращаться в колонну в качестве флегмы. Ка¬
кова эта часть, легко рассчитать, исходя из следующих соображе¬
ний. Числитель в выражениях (393) и (394) пропорционален ко¬
личеству фазы, обогащенной разделяющим агентом, а знаменатель
в выражении (393) — пропорционален количеству фазы, обогащен¬
ной отгоняемым компонентом. Нетрудно убедиться, что отношение
количества обогащенной отгоняемым компонентом фазы, отбирае¬
мой в качестве дистиллата, к возвращаемому, равное отношению
отрезков AF/EF, определяется положением точки F, которое нахо¬
дится из очевидного соотношения
(Ж)
min EH AF
с помощью которого может быть найдено отношение AFjEF. Как
следует из изложенного выше, это отношение зависит от условий
равновесия между жидкостью и паром в системе, подвергаемой
258
азеотропной ректификации, температуры, при которой произво¬
дится расслаивание жидких фаз и их равновесных составов,
а также от состава смеси на тарелке питания.
Изложенные рассуждения могут быть распространены на трех-
и многокомпонентные системы.
МАТЕРИАЛЬНЫЙ БАЛАНС ПРОЦЕССА
ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Отличие процесса экстрактивной ректификации от обыч¬
ной заключается в том, что в колонну, кроме исходной смеси и
флегмы, вводят разделяющий агент, причем его расход чаще всего
значительно превышает расходы других материальных потоков.
Это вызывает соответствующее изменение материального и тепло¬
вого балансов процесса ректификации.
Колонна для экстрактивной ректификации (рис. I) состоит из
следующих частей:
1) регенерационная, расположенная выше точки ввода разде¬
ляющего агента и предназначенная для очистки отбираемого ди¬
стиллата от разделяющего агента путем обычной ректификации;
2) укрепляющая, расположенная между точками ввода исход¬
ной смеси и разделяющего агента. В ней происходит обогащение
восходящего пара компонентами, отбираемыми в виде дистиллата;
3) исчерпывающая, расположенная ниже точки ввода исходной
смеси. Предназначена для выделения (исчерпывания) из истекаю¬
щей жидкости компонентов, отбираемых в виде дистиллата.
В точках ввода в колонну разделяющего агента и исходной
смеси происходит скачкообразное изменение расхода материаль¬
ных потоков жидкости или пара, или того и другого. Разделяющий
агент всегда вводят в колонну в виде жидкости, вследствие чего
ее расход в точке ввода изменяется. Если температура подавае¬
мого разделяющего агента отличается от температуры кипения
смеси, находящейся в этом сечении колонны, то одновременно мо¬
жет происходить изменение расхода парового потока за счет ча¬
стичной конденсации пара (если температура разделяющего агента
ниже температуры кипения смеси) или частичного испарения
жидкости (если температура разделяющего агента превышает тем¬
пературу кипения смеси).
Исходную смесь можно вводить в колонну в виде пара, жидко¬
сти или паро-жидкостной смеси. В зависимости от агрегатного
состояния вводимой в колонну смеси изменяются расходы пара,
жидкости или обеих материальных потоков.
Для произвольного сечения укрепляющей части колонны для
экстрактивной ректификации (рис. 97) условия материального ба¬
ланса выражаются равенством
Dn+l + G = Ln + n (395)
9*
2S9
где Dy Gi L и Π — молярные расходы пара, разделяющего агента,
жидкости и дистиллата; п — номер тарелки, считая сверху вниз.
Если подаваемый в колонну разделяющий агент не содержит
компонентов исходной смеси, то материальный баланс по произ¬
вольному компоненту выражается уравнением
(397)
°п+1Уп+1 =1пхп + П\
или
Уп+1
Ln
Di
Я+I
(398)
Уравнение (398) выражает зависимость между концентрациями
любого компонента в паре и жидкости, проходящих через произ¬
вольное сечение укрепляющей части колонны для экстрактивной
ректификации. В общем случае величины L
и D изменяются по высоте колонны, по¬
этому, если зависимость, выражаемую урав¬
нением (398), представить графически, то
для разных компонентов получается серия
-fiO
Рис. 97. Схема мате¬
риальных потоков в
укрепляющей части экст¬
рактивно-ректификацион¬
ной колонны.
дует из того, что коэффициенты при хп и
хд для всех компонентов одинаковы, а раз¬
личаются они лишь по величине хд.
Если от абсолютных концентраций пе¬
рейти к относительным концентрациям ком¬
понентов заданной смеси, то уравнение
(398) может быть переписано как
Уп+л [* (^p)n+l] “ Dn+i Χχί ^ ~
П
Di
Я + I
где (ί/ρ)η+ι, (*р)п И (Хр)д —концентрации
разделяющего агента в парах, выходящих
с (я + 1)-й тарелки, в жидкости, стекающей с н-й тарелки, и в
, Уп+\ , *Я , ЛГд
дистиллате; у' , = -т—7—г , х' = Ί—г-т- их' = Ί—р—г
I - (Ур)п+1 9 ■ п I - (*р)я д I - (Xp)Л
соответствующие относительные концентрации рассматриваемого
компонента.
В общем случае проходящие через колонну потоки жидкости
и пара состоят из разделяющего агента и компонентов заданной
смеси. Если на долю последних приходится часть жидкости Wt то
Ln —
Подставляя это выражение в уравнение (399), имеем:
^«+i I1 ~iyp)n+i]= On χη + рп+1 — (лр)д]
(400)
(401)
760
Обычно дистиллат, получаемый при экстрактивной ректифика¬
ции, практически не содержит разделяющего агента. Для этого
случая из уравнения (401) получаем:
Уп+1 - 7=77) [ητ1- х'п + ΊΓ~ хя) (402>
1 \Ур)п+1 \ип+1 п+1 I
Уравнение (402) — уравнение рабочей линии укрепляющей ча¬
сти экстрактивно-ректификационной колонны для произвольного
компонента. В частном случае, когда разделению подвергается би¬
нарная смесь/, изменение концентраций по высоте колонны описы¬
вается одним уравнением (402).
В общем случае величины Wt D и ур изменяются по высоте ко¬
лонны, и рабочие линии, описываемые уравнениями (402), яв¬
ляются кривыми.
Легко видеть, что произведение Dn+1 [I—(ί/ρ)η+ι] = Vn+i равно
молярному расходу части парового потока, приходящейся на долю
компонентов смеси, подвергаемой разделению. Поэтому уравне¬
ние (402) может быть переписано следующим образом:
г W п Ir . П г /ЛГ&\
Уп+1~ vn+l *п+vn+l х* ( *
Вследствие очевидного условия материального баланса
Vn+l = Wn + n (404)
уравнение (403) может быть преобразовано к виду
Уn+i" % + I %п + Τ+ΊΪ *405*
где R = Wjn — приведенное флегмовое'число в укрепляющей ча¬
сти колонны.
Уравнение (405) по форме совершенно аналогично уравнению
рабочей линии для процесса обычной ректификации. Из этого
уравнения видно, что ход рабочей линии процесса экстрактивной
ректификации определяется отношением частей расходов жидкости
и пара, приходящихся на долю компонентов заданной смеси.
Сопоставляя уравнения (399) и (403), нетрудно убедиться, что
отношение истинных расходов жидкости и пара в колонне для
экстрактивной ректификации LJDn+1 превышает отношение «при¬
веденных» материальных потоков WJVn+1. Действительно,
L (406)
Dn+ι Уя+ι I— (хр)п
Поскольку разделяющий агент имеет меньшую относительную
летучесть, чем компоненты заданной смеси, то ур < Xp и отноше¬
ние, стоящее в правой части уравнения (406), всегда больше
единицы. Следовательно, угловой коэффициент рабочей линии
в истинных концентрациях [см. уравнение (398)] всегда превышает
261
угловой коэффициент рабочей линии, выраженной в относительных
концентрациях [см. уравнение (405)]. - '
Уравнение материального баланса (399) применимо как
к укрепляющей, так и к регенерационной части колонны для экс¬
трактивной ректификации. Применяя его к сечению, расположен¬
ному над точкой ввода разделяющего агента и, принимая во вни¬
мание, что для этого сечения
D=- L + П (407)
где D и L — расходы пара и жидкости в регенерационной части
колонны, получаем
/ R I *р / I / I (Л'р)д
Уп+1“— -*п+·= *Л — (408)
n+1 R + I I-Pv nR + I л , I -
где R = L/Π — флегмовое число; ур — молярная доля разделяю¬
щего агента в паре, поступающем из укрепляющей части колонны
в регенерационную; хр — молярная доля разделяющего агента
в жидкости, стекающей из регенерационной части колонны в укреп¬
ляющую.
Состав материальных потоков в регенерационной части ко¬
лонны для экстрактивной ректификации изменяется в сравнительно
узких пределах, поскольку концентрация разделяющего агента
в паре, поступающем в эту часть колонны, как правило, невелика.
Вследствие этого изменение расходов пара и жидкости в этой ча¬
сти колонны можно не принимать во внимание. Поэтому практи¬
чески R = const.
Поскольку обычно концентрация разделяющего агента в дистил¬
ляте пренебрежимо мала, уравнение (408) для верхнего сечения
колонны переходит в уравнение рабочей линии обычного процесса
ректификации:
у-Д=* + -%=■ (409)
1+/? 1+/?
в котором R выражает отношение расхода жидкости, возвращае¬
мой, в колонну в качестве флегмы, к расходу отбираемого дистил¬
лата.
Сопоставляя уравнения (405) и (408), приходим к выводу, что
относительное флегмовое число, входящее в уравнение (405), зави¬
сит от концентрации разделяющего агента в паре и жидкости. На
это обстоятельство обращено внимание в работе [313]. В регенера¬
ционной части колонны величины ур, жр и (*р)д связаны очевидным
условием материального баланса:
D9V = Lip + я(*Р)д (41°)
Если (хр)д = 0, то
V-TTsiP <«■>
262
Так как Л/(I + j?) < I, то хр > ур. Принимая это во внимание
и сопоставляя уравнения (405) и (408), получаем:
— > I
I 4* R I +R I-JCp
(412)
Следовательно, флегмовое число Л превышает приведенное
флегмовое число R. Используя соотношение (41J^), получаем сле¬
дующее выражение, связывающее величины R и R в регенерацион¬
ной части колонны
личины RnR имеют тем большее различие, чем больше флегмо¬
вое число и концентрация разделяющего агента в паровой фазе,
зависящая от его концентрации в жидкой фазе и относительной
летучести.
Концентрация разделяющего агента в жидкой фазе может быть
найдена из условия материального баланса, составленного для
произвольного сечения укрепляющей части колонны (см. рис. 97)
Величина G = LnXv выражает расход разделяющего агента,
движущегося по колонне с потоком жидкости. Если (*Р)Д = 0, то
Таким образом, фактический расход разделяющего агента в ко¬
лонне для экстрактивной ректификации превышает расход разде¬
ляющего агента, поступающего в колонну на величину, равную
расходу последнего в потоке пара. Как видно из уравнения (416),
это различие тем больше, чем больше концентрация разделяющего
агента, т. е. чем больше его летучесть. Величину yv можно выра¬
зить через концентрацию разделяющего агента в жидкой фазе Jtp,
принимая, что между паром и жидкостью устанавливается равно¬
весие. Тогда в соответствии с уравнением (97)
(413)
из которого следует, что
АЯ = Я-Я = (1+Я)-^
I -У,
(414)
Dn+гУр + G = LnXр + П (JCp)i
(415)
G = Dyp + G
(416)
β*Ρ
(417)
Ур= I +(β — I) Jtp
М3
где β — коэффициент относительной летучести разделяющего
агента по отношению к разделяемой смеси, находящейся в рассма¬
триваемом сечении колонны.
Опуская в уравнении (415) индекс при D и заменяя Ln с по¬
мощью уравнения (396), а ур с помощью уравнения (417), после
преобразований получаем:
G — П (яр)д
(418)
(Z) + G) (I — β) — /7 11 — Я *рР
I -XoI
Если дистиллат не содержит разделяющего агента, т. е.
(JCp) д = о, то
*Р —< (419)
/ JCpP )
(Z) + G) (I —β) — Я 11 — Я -у—-
V * хр /
Из уравнений (418) и (419) следует, что, в соответствии с из¬
ложенным, при заданном молярном расходе разделяющего агента
его концентрация в жидкой фазе возрастает с увеличением коэф¬
фициента относительной летучести β.
При условии, что разделяющий агент подают в колонну при
температуре кипения смеси в соответствующее сечение колонны и
поэтому не происходит изменения расходов материальных потоков,
обусловленных процессами частичной конденсации или испарения,
уравнению (419) можно придать другую форму. В этом случае,
согласно материальному балансу для верхнего сечения колонны
D=W + n (420)
где W — количество флегмы, подаваемой в верхнее сечение ко¬
лонны.
Заменяя П в формуле (419), получаем после преобразований:
q
Xp = & (D-W)
(W + G) (I — β) — ■ J>-
I Лр
В частном случае применения нелетучего разделяющего агента
(β = °): о
xP = w + G (422)
Для произвольного сечения укрепляющей части колонны в про¬
цессе экстрактивной ректификации можно, в соответствии с изло¬
женным выше, записать уравнения материального баланса
Ln = Wn + Gn= G + Wn + Dyp (423)
и
D= Vn+Dyp (424)
264
из которых следует, что для нелетучего разделяющего агента
D = VnL = G + Wt а увеличение его расхода в паровой фазе за
счет испарения на величину Dy^ вызывает такое же увеличение
расхода в жидкой фазе. Повышение концентрации разделяющего
агента благоприятствует повышению коэффициента относительной
летучести. С другой стороны, с увеличением коэффициента относи¬
тельной летучести разделяющего агента уменьшается доля компо¬
нентов заданной смеси в потоках пара и жидкости и как следствие
уменьшается приведенное флегмовое число, определяющее ход про¬
цесса экстрактивной ректификации. Связь между угловыми коэф¬
фициентами рабочих линий, выражаемых в абсолютных концен¬
трациях уравнением (398) и в относительных концентрациях —
уравнением (405), для укрепляющей части колонны при экстрак¬
тивной ректификации имеет следующий вид:
LR R \-yO
— = rz-= (425)
D I +R- I +/? I — Xp
Связь между отношениями расходов жидкости и пара в произ¬
вольном сечении укрепляющей части колонны WnIVn и расходами
этих потоков вверху колонны DnW вытекает из уравнений мате¬
риального баланса (423) и (424) и выражается соотношением
Wn Rn W-Dyp
-vf-TTR-Г-ЩГ^) <426>
преобразование которого с учетом выражения (419) дает
bR = R-Rn = yP(\+R) (427)
где Δ/? — изменение флегмового числа в произвольном сечении
укрепляющей части колонны по сравнению с его значением вверху
колонны; R = W/Π — отношение расхода возвращаемой в колонну
флегмы к количеству отбираемого дистиллата (флегмовое число
вверху колонны); Rn = Wn/n— приведенное флегмовое число
в произвольном сечении укрепляющей части колонны.
Как и в регенерационной части колонны изменение флегмового
числа возрастает с увеличением его значения, а также с ростом
концентрации разделяющего агента в паровой фазе. Изменение
флегмового числа по высоте колонны можно учесть с помощью
уравнений (414), (427) и (417). Следует при этом иметь в виду,
что величина β изменяется с изменением состава смесей, как это
вообще имеет место для неидеальных систем. Если β изменяется
сравнительно немного (на 15—20%), то для инженерных расчетов
можно принять среднее значение этой величины.
Уравнение рабочей линии исчерпывающей части колонны для
экстрактивной ректификации получается способом, аналогичным
описанному выше.
265
Материальный баланс произвольного участка исчерпывающей
части колонны, включая куб, выражается уравнением (рис. 98)
• Dm-. I + G + Wk
(428)
где Wk — молярный расход компонентов заданной смеси, отбирае¬
мых в виде кубового остатка; т — номер тарелки (счет тарелок
снизу вверх).
Применяя уравнение (428) к произвольному компоненту, полу¬
чаем
Lmxm ^ ^т—\Ут—\ H- (С + U^K) (429)
где хк — молярная доля рассматриваемого компонента в кубовой
жидкости.
Переходя к относительным концентрациям и подставляя вместо
L его значение из уравнения (400), имеем
Ут~1 I - (</,
I / , __Гк_
\Dm-t т Dm-i Х«)
(430)
где х'т и х' — относительные концентрации рассматриваемого
компонента в жидкости, стекающей с m-й тарелки, и в кубовой
жидкости; Wk — доля заданной смеси, от¬
бираемая в виде кубовой жидкости.
Заменяя A„_i[(l — yi)m-\] = Vm-\, ана¬
логично тому, как это было сделано при
ние рабочей линии исчерпывающей части
колонны в следующей форме:
»' _ х' w« / ί43η
Ут—I у . хт у хк V4dl/
. Из условия материального баланса вы¬
текает:
(432)
Поэтому уравнению (431) можно при¬
дать форму обычного уравнения рабочей
линии исчерпывающей части колонны
г,/ /
R
У =
Я'+I
Rf-I
(433)
Рис. 98. Схема мате¬
риальных потоков в ис¬
черпывающей части экст¬
рактивно-ректифика¬
ционной колонны.
W
где /?/==-п7—приведенное флегмовое число исчерпывающей части
W к
колонны для экстрактивной ректификации.
Концентрация разделяющего агента в исчерпывающей части ко¬
лонны выражается уравнением (421). В случае подачи в колонну
исходной смеси в виде жидкости, нагретой до температуры тарелки
питания, величина W в уравнении (421) складывается из расходов
флегмы и исходной смеси. Легко видеть, что в кубе имеет место
Mt
скачкообразное возрастание концентрации разделяющего агента,
поскольку величина Wk всегда составляет лишь часть величины W
для произвольной тарелки.
В кубе концентрация разделяющего агента выражается следую¬
щим очевидным соотношением:
W--WSv (434)
При подаче в колонну исходной смеси в виде жидкости скачко¬
образное изменение концентрации разделяющего агента происхо¬
дит также на тарелке питания, как это следует из уравнения (421).
В этом случае концентрация разделяющего агента в укрепляющей
части больше, чем в исчерпывающей.
Соответственно с этим изменяются и
условия равновесия между жидкостью
и паром. На рис. 99 показан характер
кривых равновесия, выраженных в отно¬
сительных концентрациях < компонентов,
для случая, когда исходная сме'сь яв¬
ляется бинарной.
При питании колонны паровой смесью
равновесие выражается плавной кривой
во всей области концентраций, кроме
куба, в котором происходит скачок кон¬
центрации разделяющего агента. В слу¬
чае подачи в колонну исходной смеси
в виде жидкости, при прочих равных
условиях на участке от куба до точки по¬
дачи исходной смеси хс кривая равнове¬
сия располагается ниже, чем при пита¬
нии колонны паровой смесью.
Вопрос о влиянии агрегатного состояния исходной смеси в про¬
цессе экстрактивной ректификации подробно рассматривается
ниже.
В соответствии с рассмотренным характером распределения
концентрации разделяющего агента по высоте колонны изменяется
и температура. При подаче в колонну исходной смеси в виде пара
изменение температуры по высоте колонны аналогично показан¬
ному на рис. 92. Наивысшую температуру кипения имеет кубовая
жидкость с максимальной в ней концентрацией разделяющего
агента. Затем на ближайших к кубу тарелках температура резко
понижается и далее по мере приближения к точке ввода разде¬
ляющего агента температура продолжает медленно уменьшаться.
Обусловлено это, с одной стороны, понижением температуры ки¬
пения в связи с возрастанием концентрации отгоняемого компо¬
нента, с другой стороны, — уменьшением гидравлического сопро¬
тивления части колонны, находящейся выше рассматриваемого
сечения. Выше точки ввода разделяющего агента температура
Рис. 99. Характер равнове¬
сия при питании экстрак¬
тивно-ректификационной ко¬
лонны паровой (сплошная
линия) и жидкой (пунктир¬
ная) бинарной смесью.
267
резко понижается в связи с резким уменьшением его концентрации.
При подаче в колонну исходной смеси в виде жидкости вблизи
тарелки питания происходит резкое изменение температуры, обус¬
ловленное скачкообразным изменением концентрации разделяю¬
щего агента.
Характер распределения температур по высоте колонны для
этого случая показан на рис. 116 (стр. 326) на примере процесса
разделения смесей углеводородов C4 путем экстрактивной ректи¬
фикации.
ТЕПЛОВОЙ БАЛАНС
ПРОЦЕССА ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Для произвольной п-й тарелки колонны для экстрактив¬
ной ректификации уравнение теплового баланса записывается как
(см. рис. 97)
Dn+\ln+l + Ln-l<?n-l - Dnln + iA <435)
где i и ? - молярные энтальпии соответственно пара и жидкости.
С учетом уравнения материального баланса
Dn-и + Ln-I = Dn-\- Ln (436)
выражение (435) преобразуется к виду:
Dn+\{ ln+1 - Q - Ln-1 ('ln ~ Vn-1) - Ln ('« - О (437)
Энтальпии пара и жидкости в общем случае изменяются по
высоте колонны. Если пренебречь этим изменением, -как это чаще
всего принимается при расчетах процессов обычной ректификации,
то из уравнения (437) следует
Ln**. Ln-1 (438)
т. е. молярный расход жидкости не изменяется по высоте колонны.
При этом условии из уравнения (436) вытекает также постоянство
молярного расхода пара по высоте колонны:
Dn+Dn (439)
Легко видеть, что в рассмотренном случае рабочие линии про¬
цесса экстрактивной ректификации, выражаемые уравнением (402),
являются прямыми.
Существенное различие процессов обычной и экстрактивной
ректификации заключается, однако, в том, что в последних расход
жидкости значительно превышает расход пара. Поэтому энтальпия
жидкости при экстрактивной ректификации играет значительно
большую роль, чем в тепловом балансе процессов обычной ректи¬
фикации.
Уравнение рабочей линии укрепляющей части экстрактивно¬
ректификационной колонны с учетом изменения энтальпий пара и
жидкости по высоте колонны может быть получено сочетанием
268
уравнений материального баланса (396) и (397) для произвольной
тарелки с уравнением теплового баланса части колонны, располо¬
женной выше этой тарелки. Без учета потерь тепла в окружающую
среду это уравнение имеет вид
Dn + \ln+\^ g^ss (44°)
где <7р и <7Д — удельные энтальпии поступающего в колонну разде¬
ляющего агента и отбираемого дистиллата; Qx- расход тепла,
отводимого в дефлегматоре.
Если обозначить
-CTJi («')
то из уравнений (396) и (397) получаем:
Ln у п+1+ WXi
Dn+! хп +Wxi
(442)
Уравнению теплового баланса (440) может быть придана ана¬
логичная форма
Ln *„+1+®/
Dn+\ 4„ + ω/
(443)
где j = <7Д + QtJΠ — GqvIE
Сочетая уравнения (442) и (443), получаем после преобразо¬
ваний следующее уравнение рабочей линии:
уп+, = Λ+i t-cflL + ωΧΛ AtJ-Z-qJL- (444)
Яп + Щ Vft+ω/
Тепловой баланс произвольной секции исчерпывающей части
колонны, включая куб, без учета потерь тепла выражается урав¬
нением:
= Dm-\lm-\ + (G + Wk) ?к ^445)
Уравнению (445) с помощью уравнения (429) можно придать
форму, аналогичную уравнениям (442) и (443), Получаем соот¬
ветственно
Lm Ут—ι хк
&т — \ хт ~~ хк
Lm Im-1 £
(446)
(447)
Dm-1 Qm ^
где t = 4*—G%7·
Из уравнений (446) и (447) вытекает следующее уравнение
рабочей линии исчерпывающей части экстрактивно-ректификацион¬
ной колонны:
£'m “ E lm-\ ~
Уравнения (444) и (448) позволяют найти связь между кон¬
центрациями любого компонента в материальных потоках, прохо¬
дящих через произвольное сечение соответственно укрепляющей
или исчерпывающей частей колонны. Для этого необходимо знать
зависимость энтальпий пара и жидкости от состава.
Определение изменения энтальпий материальных потоков для
неидеальных систем осложняется наличием теплового эффекта при
смешении компонентов и неаддитивностью теплоемкости жидкости.
Наиболее существенно влияние теплот смешения, Данные по кото¬
рым часто отсутствуют. Теплоты смешения могут быть рассчитаны
по данным о равновесии между жидкостью и паром при несколь¬
ких температурах с помощью уравнения
rflnV -Ml (449)
d(l/T) R
где AL — дифференциальная теплота смешения компонентов.
Такой расчет был произведен Кольборном [24] для случая раз¬
деления смеси бутана и бутена-1 с применением фурфурола в ка¬
честве разделяющего агента. Равновесие между жидкостью и па¬
ром в системе, состоящей из этих компонентов, описывается урав¬
нениями Маргулеса (356). Для бесконечно разбавленного раствора
бутана (индекс I) в фурфуроле (индекс Р) Igyi = Aip, поэтому из
уравнения (449) следует
iID rf^lD
—— -- (450)
2,3R d (1/Т)
где Li1p — разность парциальной молярной теплоты испарения ком¬
понента в бесконечно разбавленном растворе и теплоты испарения
чистота компонента при той же температуре.
Аналогичное уравнение может быть написано для раствора бу¬
тена-1 (индекс 2) в фурфуроле:
UL dA0r.
—— = —— (451)
2,3R d(\/T) ^01'
Из данных о равновесии [314] следует, что в интервале 38—93° С
константы А примерно пропорциональны I/Т. Найденные по этим
данным значения парциальных молярных теплот смешения для
бесконечно разбавленных растворов равны (ккал/кмол): L% = 3180,
Lpi = 4700, L2p = 2400, Lp2 = 2000. Для бинарной смеси I — P
произвольной концентрации имеем:
1S Yi “4 Hip+ ? 0V_yV)*i] · (452>
Производя дифференцирование по l/Т при постоянном составе
2,3Rd Ig у, 2,3RdApi г0
и заменяя d ^^— = Lt и ~d ^^ = LPi с помощью уравне¬
ния (449), получаем
Li “ *р[^?р + 2 (^pi — ^?р) *ι] (453)
270
Аналогичным образом для трехкомпонентной системы с по¬
мощью уравнения (356) имеем:
L1 = X2 [L02 + 2xj (L021 - L012)] + 4 [L0ip + 2х{ (l°, - I°p)] +
+ X2Xp [4 + L0lp - L0p2 + 2хх (L0pl - L0p) + 2хр (L0p2 - L0p) - Lc (I - *,)] (454)
2 3R dC
где Z-C = -J^j-щ-\ С — константа в уравнениях Маргулёса для
тройной системы.
Смеси углеводородов близки к идеальным, поэтому L0H =* Ζ-21 “ 0.
С учетом этого для трехкомпонентной системы, состоящей из 0,2 мол. доли бу-
тена-1 и 0,8 мол. доли фурфурола (х\ *■ 0, X2 =* 0,2 и Xp = 0,8), по уравнению
(454) получаем Lx = 2190 ккал/кмол. С помощью аналогичного уравнения для
определения L2 для системы состава Х\ = 0,2, X2-O и хр 0,8 получаем L2 =*
« 1470 ккал/кмол. При 65° С скрытая теплота испарения бутана равна
7820 ккал/кмол, теплота же его испарения из трехкомпонентной смеси состава
X1 = о, X2 = 0,2 и х — 0,8 равна 7820 — 2190 * 5630 ккал/кмол. Это указывает
на важную, роль теплоты смешения в общем тепловом балансе. Различие рассчи¬
танных теплот смешения компонентов для бесконечно разбавленных тройных си¬
стем относительно невелико. Поэтому приближенно можно считать, что пар¬
циальные молярные теплоты смешения в рассмотренном случае зависят только
от концентрации разделяющего агента.
Расход тепла на проведение процесса экстрактивной ректифи¬
кации определяется с помощью уравнения теплового баланса всей
колонны:
0к + О?р + ^с-Сд + Я?д + (О + 1^«7к ' (455)
Обычно процессы экстрактивной ректификации проводятся при
концентрации разделяющего агента 70—90 мол.%. При этом доля
компонентов заданной смеси в общем потоке жидкости относи¬
тельно невелика. Если исходную смесь подают в колонну, а дистил¬
лат и кубовую жидкость отбирают из колонны в виде жидкостей,
нагретых до температуры кипения, то можно принять:
+ (456)
При этом из уравнения (321) следует:
Ск = «д+ 0K-^p) (457)
Так как температура кубовой жидкости выше температуры по¬
даваемого в колонну разделяющего агента, то количество тепла,
подводимого к кубу, всегда превышает количество тепла, отводи¬
мого в дефлегматоре. Из уравнения (457) следует
°Л = в/д + 0(4к-?р) (458)
где гк и гд — скрытые теплоты испарения кубовой жидкости и ди¬
стиллата.
Из этого уравнения следует, что изменение расхода пара
по высоте колонны зависит от теплот испарения дистиллата и
*71
кубовой жидкости, а также от разности энтальпий последней и по¬
ступающего в колонну разделяющего агента.
Аналогичное уравнение может быть написано для произволь¬
ного сечения колонны
Л'-ЯяГд+0(*-*р) №9)
где Dy г и q — соответственно расход пара, скрытая теплота ис¬
парения и энтальпия жидкости в произвольном сечении колонны.
Характер изменения скрытых теплот испарения смесей по вы¬
соте колонны может быть различен в зависимости от свойств раз¬
деляемой системы.
Если скрытые теплоты испарения компонентов близки, то из¬
менением скрытых теплот испарения смесей по высоте колонны
в некоторых случаях можно пренебречь. При этом условии расход
пара Ъ колонне понижается сверху вниз, как это следует из урав¬
нения (459), поскольку q > qv.
Из уравнений материального баланса (396) и (428) можно
видеть, что расход жидкости по высоте колонны изменяется в та¬
ком же направлении, как и расход пара. Следовательно, при ука¬
занном выше условии расход жидкости также уменьшается по мере
приближения к низу колонны.
Интересно выяснить, как изменяются по высоте колонны части
потоков пара V и жидкости Wt приходящиеся на долю компонен¬
тов исходной смеси. Величина V определяется выражением:
V = D(\-yp) (460)
В верху колонны пар, как правило, практически не содержит
разделяющего агента, поэтому Dn = Уд. При приближении к‘точке
подачи разделяющего агента концентрация последнего в парах воз¬
растает до величины, отвечающей условиям равновесия, и затем
к низу колонны несколько понижается вследствие уменьшения ко¬
эффициента относительной летучести разделяющего агента β. Влия¬
ние различных факторов на величину V выражается следующим
уравнением, вытекающим из уравнения (459) и определения (460):
V=^-TlIv/* + 6 (*-%)} (460
На основании изложенного и уравнения (461) следует, что наи¬
большее значение V достигается в части колонны выше точки
ввода разделяющего агента. Вблизи этой точки величина V умень¬
шается вследствие резкого увеличения г/р. При дальнейшем при¬
ближении к низу колонны величина V определяется двумя факто¬
рами, — изменением г/р, влияющим обычно в направлении увели¬
чения V, и увеличением г и q, влияющими в противоположном
направлении. Если относительная летучесть разделяющего агента
мала и влиянием изменения его концентрации в парах можно пре¬
небречь, то к низу колонны величина V уменьшается. В соответ¬
ствии с уравнениями материального баланса (404) и (432) вели-
т
чина W изменяется в том же направлении, что и V. Следовательно,
приведенные флегмовые числа для укрепляющей и исчерпывающей
частей колонны R и R' в случае близких скрытых теплот испаре¬
ния компонентов заданной смеси уменьшаются по высоте колон¬
ны по мере приближения к кубу. Однако это уменьшение чаще
всего весьма невелико. Поэтому расчет процессов экстрактивной
ректификации в большинстве случаев производят, принимая R
и Rf постоянными по высоте колонны.
Изложенные соображения справедливы, разумеется, и в слу¬
чае подачи исходной смеси в виде пара. При этом расход тепла,
которое необходимо подвести к кубу, выражается уравнением
Qk = + ПЧ + (G + Wk) Vk ~ ~ <462>
где Tc — энтальпия исходной паровой смеси.
В заключение надо остановиться на одном обстоятельстве,
имеющем исключительно важное значение для успешного про¬
ведения процесса экстрактивной ректификации. Во всех приве¬
денных выше рассуждениях принималось, что разделяющий агент,
подаваемый в колонну, не содержит компонентов заданной смеси.
Это условие выполняется при тщательной отгонке последних из
кубовой жидкости, отбираемой из колонны для экстрактивной
ректификации. Если эта отгонка произведена недостаточно тща¬
тельно, то вещества, остающиеся в возвращаемом на экстрактив¬
ную ректификацию разделяющем агенте, будут попадать в ди¬
стиллат, уменьшая четкость разделения. ,
ВЛИЯНИЕ АГРЕГАТНОГО СОСТОЯНИЯ
РАЗДЕЛЯЕМОЙ СМЕСИ
В ПРОЦЕССЕ ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Как отмечалось, при подаче исходной смеси в колонну
для экстрактивной ректификации в виде жидкости на тарелке пи¬
тания и ниже нее происходит уменьшение концентрации разделяю¬
щего агента по сравнению с его концентрацией в укрепляющей
части колонны. Это вызывает соответствующее уменьшение коэф¬
фициента относительной летучести компонентов заданной смеси
в исчерпывающей части колонны. Это неблагоприятное обстоя¬
тельство может быть исключено при подаче в колонну исходной
смеси в паровой фазе. Необходимо, однако, считаться с тем, что
при одинаковом коэффициенте относительной летучести в случае
питания колонны паровой смесью всегда требуется большее флег¬
мовое число, чем при подаче в колонну жидкости того же соста¬
ва. Увеличение же расхода флегмы обусловливает уменьшение
концентрации разделяющего агента, распространяющееся не толь¬
ко на исчерпывающую, но также и на укрепляющую части колон¬
ны для экстрактивной ректификации. Таким образом, как и в
большинстве технических задач, в рассматриваемом случае мы
173
сталкиваемся с двумя противодействующими факторами, что вы¬
двигает необходимость более подробного рассмотрения вопроса
о влиянии агрегатного состояния исходной смеси в процессе экс¬
трактивной ректификации.
Для достижения желательного значения коэффициента отно¬
сительной летучести требуется поддерживать в колонне опреде¬
ленную концентрацию разделяющего агента, которая определяет¬
ся, уравнением (421).
Чтобы концентрация разделяющего агента в исчерпывающей
части колонны оставалась одинаковой при питании колонны как
жидкой, так и паровой смесью, отношение удельных расходов
разделяющего агента, согласно уравнению (421), должно быть:
Gn H7n (I - β) О - *р) - β Фп - Wa)
Gx “ Wx (I т β) (I - Хр) ~ β Фж - Wx) ( )
Индексы «п» и «ж» в этом и следующих уравнениях озна¬
чают, что соответствующие величины относятся к случаю питания
колонны паром и жидкостью.
Величины W и D на тарелке питания можно выразитб через
флегмовое число R. В расчете на I кмол исходной смеси имеем:
Gx = II (Rx +1): Гж^ЛЯж-Н; Оп = Лфп+1)-1 и Wa=IIRa (464)
Примем, что исходная смесь является бинарной и минималь¬
ное флегмовое число определяется условиями фазового равнове¬
сия на тарелке питания. Примем далее, для простоты, что про¬
дукты разделения — практически чистые компоненты, т. е.:
хд » I и х'к~ О (465)
Такие условия разделения чаще всего и реализуются на прак¬
тике. При принятых допущениях флегмовые числа Rm и Rn вы¬
ражаются уравнениями
«к-KrO.,I
*с(ап- 0 ν '
где аж и ап — коэффициенты относительной летучести компонен¬
тов заданной смеси на тарелке питания; σ — коэффициент избыт¬
ка флегмы.
В общем случае коэффициент относительной летучести зави¬
сит не только от концентрации разделяющего агента, но также
от концентрации компонентов заданной смеси. Ранее было пока¬
зано, что влияние последнего фактора связано с неидеальностью
системы, подвергаемой разделению. Если степень неидеальности
невелика, то в пределах изменения состава жидкости на тарелке
питания для рассматриваемых вариантов, процесса можно вос¬
пользоваться средним значением коэффициента относительной ле*
274
тучести а. Тогда из уравнений (466) и (467) получается:
'Ж '
σ (468)
*■- it—(<69)
После подстановки значений W, D и R из уравнений (464),
(468) и (469) в уравнение (463) последнее преобразуется:
л(а-Ц-^+Яж)(1-р)(1-*Р) + рГк
(1+СЛЯж)(1-р)(1-Хр) + р\Гк
(470)
При допущении (465)
П — хс и IFk = I — лгс (471)
Подставив эти значения в уравнение (470), получаем:
Oa (XcRx+ I) (I - Р) (I - Хр) + P (I - Xe) + (а - ахс - I) (I - Р) (I - χν)
(472)
O3к (*с£ж+1)(1-Р)(1-*р) + Р(1-*с)
Из уравнения (472) следует, что GJGm ^ I при условии
(а-ахе-I) (I-P) (I-*Р)<0 (473)
Так как (I —β) >0 и (I—хс) > 0, то это условие равносиль¬
но неравенству:
(474)
Таким образом, при значениях хс, лежащих в интервале от
единицы до I — I/о, одинаковая концентрация разделяющего
агента в исчерпывающей части колонны в случае ее питания па¬
ровой смесью достигается при меньшем расходе разделяющего
агента, чем при подаче в колонну исходной смеси в жидкой фа¬
зе. Область концентраций, в которой GJGm < I тем больше, чем
меньше коэффициент избытка флегмы, т. е. чем ближе реальное
флегмовое число к минимальному.
Для количественной оценки величины GJGm несколько преоб¬
разуем уравнение (472), подставив в него значение Rm из урав¬
нения (468):
п а (—- {"■+ I - Xe) (I - Р) (I - *р) + P (I - Xe)
■р-= -Liz1 ^ : (475)
Gx 1 " '
(-^rr+ *) (! - Р) (‘ — *р> + P <! “ X^
Для «идеальной» колонны экстрактивной ректификации, под
которой понимается колонна с бесконечно большим числом таре¬
лок, работающая при минимальном флегмовом числе (о= I) и
с нелетучим разделяющим агентом (β = 0), из уравнения (475)
получаем:
Gn _а-хл(а-\) „
_ = K0 (476)
Из уравнения (476) следует, что в рассматриваемом предель¬
ном случае величина GnIGm изменяется при изменении Xi от
GnlGm = I при Xi = 0 до GnIGm = l/а при Xi = I9 а минимальное
значение отношения Gu/Gm (при Xi= I) тем меньше, чем больше
значение а. Из изложенного следует, что в идеальном процессе
экстрактивной ректификации (σ = I и β = 0) для поддержания
заданной концентрации разделяющего агента всегда требуется
меньший относительный расход его при подаче в колонну исход¬
ной смеси в виде пара, чем в случае подачи ее в· виде жидкости.
Таблица 34
Значения отношения Gn/Ож при дгр = 0,7, σ = 1,2 и переменных xCf
β ** 0,0
β 0,1
α
*с
1.2
1,5
2,0
3,0
5,0
1.2
1,5
2,0
3,0
5,0
0
1,03
1,06
1,09
1,13
1,15
0,96
0,99
1,02
1,06
1,09
10
1,00
1,03
1,04
1,05
1,06
0,99
0,99
1,01
1,03
1,04
30
0,98
0,95
0,93
0,90
0,88
1,02
0,99
0,96
0,93
0,91
50
0,94
0,88
0,82
0,75
0,69
1,01
0,95
0,87
0,80
0,67
70
0,91
0,81
0,71
0,60
0,51
0,97
0,87
0,76
0,64
0,54
90
0,87
0,74
0,60
0,45
0,32
0,90
0,76
0,64
0,47
0,33
100
0,86
0,71
0,55
0,37
0,23
0,86
0,71
0,55
0,37
0,23
В реальном процессе ректификации коэффициент избытка
флегмы больше единицы. При а ф I и β = 0 из уравнения (475)
получаем:
Ож
а [а — Xi (а — I)]
а — 1 + 4σ
(477)
Величина GnIGm, определяемая уравнением (477), может быть
представлена в виде произведения величины GnIGm =
ального процесса экстрактивной ректификации,
уравнением (476), и коэффициента
Ka-
ασ
α — I + cr
Нетрудно убедиться, что при а> I /С0>1. В
умножая обе части неравенства σ > I на а —
σ(α — I) > а— I, аа > а — I + а и
а σ
Ka =
а— I +а
>
Ко для иде-
выражаемой
(478)
самом деле,
I, получаем
(479)
276
Влияние летучести и концентрации разделяющего агента мож¬
но представить в виде коэффициента
Kp=I β(1 ~*с) t^'1 - (48°)
(I-P) (I-V+ „ с) ■
+ 1
а — I
который больше единицы при хс > I — 1/а и меньше единицы при
Xe < I — 1/а:
G ж
= K0KaK P (481)
Для количественной оценки влияния различных факторов на
величину GnIGm в табл. 34 приведены ее значения, вычисленные
по уравнению (481) при Xv = 0,7, σ = 1,2 и переменных хс> а и β.
аир
β = 0,3
β«0,5
1.2
1.5
2,0
3,0
5,0
1,2
1,5
2,0
3,0.
5,0
0,79
0,84
0,90
0,96
1,00
0,56
0,70
0,80
0,88
0,92
0,92
0,95
0,97
0,99
1.01
0,84
0,89
0,93
0,96
0,98
1.11
1,07
1,03
0,99
0,96
1,25
1,16
1,10
1,04
0,99
1.19
1,09
0,99
0,90
0,82
1,45
1,27
1,13
1,00
0,89
1.14
1,01
0,87
0,73
0,61
1,41
1,21
1,02
0,84
0,69
0,98
0,83
0,67
0,50
0,36
1,12
0,94
0,75
0,56
0,40
0,86
0,71
0,55
0,37
0,23
0,86
0,71
0,55
0,37
0,23
Из табл. 34 .следует, что характер зависимости GnIGm от раз¬
личных факторов весьма сложный. При изменении свойств систе¬
мы и технологических условий проведения процесса величина
GjJGm может изменяться в широких пределах. В рассмотренной
области значений переменных GJGm изменяется примерно от 0,3
до 1,5.
Таким образом, правильный выбор агрегатного состояния по¬
даваемой в колонну смеси имеет существенное значение для
уменьшения относительного расхода разделяющего агента в про¬
цессе экстрактивной ректификации. На практике редко приме¬
няют разделяющие агенты, коэффициент относительной летучести
которых превышал бы 0,3. Для таких разделяющих агентов из
табл. 34 следует, что, как правило, предпочтительным оказывает¬
ся питание колонны паровой смесью. Получаемое при этом со¬
кращение относительного расхода разделяющего агента возрастает
с увеличением коэффициента относительной летучести компонен¬
тов заданной смеси и с повышением в последней концентрации
277
Вещества, отбираемого в процессе экстрактивной ректификации
в виде дистиллата.
Составы жидкости на тарелке питания при подаче в колонну
жидкой и паровой смесей различны. В первом случае концентра¬
ция низкокипящего компонента больше, чем во втором. В связи
с этим коэффициенты относительной летучести ап и ат для двух
рассматриваемых вариантов подачи исходной смеси в колонну в
общем случае не равны друг другу. С учетом изменения а из
уравнений (463), (464), (466) и (467) следует:
На практике наиболее распространены системы с положитель¬
ными отклонениями .от закона Рауля. Для таких систем ап>ссж.
Из уравнения (482) видно, что при этом условии точка GnIGm =
= I смещается в сторону меньших концентраций низкокипящего
компонента.
В связи с отмеченным влиянием агрегатного состояния исход¬
ной смеси на удельный расход разделяющего агента в процессе
экстрактивной ректификации интересно выяснить целесообраз¬
ность предварительного испарения (или конденсации) исходной
смеси перед додачей ее в колонну. Из уравнений теплового ба¬
ланса процесса экстрактивной ректификации с учетом расхода
тепла в отгонной колонне следует, что при парообразном состоя¬
нии исходной смеси конденсация ее перед подачей в колонну во
всех случаях энергетически невыгодна. Наоборот, при высоких
концентрациях разделяющего агента, обычно применяемых на
практике, предварительное испарение исходной смеси может при¬
вести к экономии общего расхода тепла в процессе разделения.
Эта экономия тем больше, чем выше коэффициент относительной
летучести компонентов смеси, подвергаемой разделению.
иметь дело с неидеальными многокомпонентными системами, со¬
держащими, как минимум, два компонента исходной смеси и раз¬
деляющий агент. Условия фазового равновесия в таких системах
выражаются сложными зависимостями, а расчет процессов ректи¬
фикации представляет большие трудности вследствие того, чтомно-.
гокомпонентные системы обладают большим числом степеней сво¬
боды. В противоположность бинарным системам, для которых со¬
ставы продуктов разделения (дистиллата и кубовой жидкости)
однозначно определяются содержанием одного компонента, для
процессов разделения многокомпонентных смесей нельзя опреде-
0 + 1" Хс)(1 ~ β) (1 - *р) + β
(482)
РАСЧЕТ ПРОЦЕССОВ
АЗЕОТРОПНОЙ РЕКТИФИКАЦИИ
В процессах азеотропной ректификации приходится
278
лить состав этих материальных потоков без предварительных расче¬
тов. Дополнительные затруднения возникают часто из-за того, что
расходы жидкости и пара значительно изменяются по высоте рек¬
тификационной колонны вследствие различия теплот испарения
и большой теплоты смешения компонентов. Это характерно для
систем, компоненты которых различаются по химической природе.
Наиболее точным методом расчета процессов ректификации,
одинаково применимым как для идеальных, так и для реальных
систем, является известный метод расчета «от тарелки к тарел¬
ке». Поскольку расчет основан на методе последовательных при¬
ближений, объем вычислений весьма велик и резко возрастает
с увеличением числа компонентов. К тому же для точного расчета
требуется большое количество экспериментальных данных. По¬
этому еще совсем недавно, когда в инженерной практике исполь¬
зовали лишь простейшие средства вычислительной техники, метод
«от тарелки к тарелке» отпугивал своей трудоемкостью. В связи
с этим усилия многих ученых, работающих в области техники
разделения жидких смесей, были направлены на разработку упро¬
щенных методов расчета процессов ректификации многокомпо¬
нентных смесей. Естественно, всякие упрощения достигаются це¬
ной замены истинных закономерностей процесса приближенными
схемами. Этот путь позволяет получить результат более просто
и на основе использования неполных экспериментальных данных,
но зато с меньшей точностью.
В настоящее время, когда возможности вычислительной тех¬
ники в связи с широким распространением электронно-вычисли¬
тельных машин чрезвычайно возросли, многочисленные прибли¬
женные методы расчета используются во все уменьшающейся сте¬
пени. Наибольшее практическое значение, как наиболее точный,
приобретает метод расчета «от тарелки к тарелке». Различные
варианты расчетов по этому методу подробно рассмотрены в ра¬
ботах [315, 316]. Поэтому здесь ограничимся краткой характери¬
стикой этого метода.
Расчет «от тарелки к тарелке» заключается в совместном ре¬
шении уравнений материального й теплового баланса и уравне¬
ний, описывающих условия равновесия между жидкостью и па¬
ром. Метод в его наиболее распространенных формах основан
на использовании понятия теоретической тарелки, т. е. принима¬
ется, что жидкость на всей тарелке имеет одинаковый состав
(идеально перемешивается), а между покидающим тарелку па¬
ром и находящейся на ней жидкостью устанавливается, равнове¬
сие. Такой подход позволяет существенно упростить расчеты, хо¬
тя, в принципе, не является обязательным.
Одна из основных трудностей, с которыми приходится стал¬
киваться при расчете процессов ректификации многокомпонент¬
ных смесей — сложная зависимость состава продуктов разде¬
ления от условий проведения процесса и эффективности ректи¬
фикационной установки. Поэтому точные составы продуктов
279
разделения можно определить с помощью метода последователь¬
ного приближения. Для этого приходится задаваться составом
дистиллата или кубовой жидкости. Задавшись составом одного из
этих материальных потоков, мы тем самым однозначно определяем
состав другого материального потока, поскольку при заданном
расходе и составе исходной смеси расходы и составы дистиллата
и кубовой жидкости связаны условиями материального баланса
(377) и (378).
При каждом новом последовательном расчете принятый вна¬
чале состав одного из продуктов разделения корректируется та¬
ким образом, чтобы рассчитанный по методу «от тарелки к та¬
релке» состав другого продукта разделения с заданной точностью
совпал с вытекающим из условий материального баланса. Если
первоначально задаются составом кубовой жидкости, то расчет
«от тарелки к тарелке» производится в направлении от куба к
дефлегматору. Если задаются составом дистиллата, то расчет
выполняется в противоположном направлении.
Исходным составом дистиллата или кубовой жидкости зада¬
ются, исходя из требований к продуктам разделения. Если одним
из них является один из компонентов в практически чистом виде,
то обычно регламентируется сумма примесей или содержание
компонента ближайшего по относительной летучести. Этими сооб¬
ражениями определяются низко- и высококипящие ключевые ком¬
поненты.
Состав другого продукта разделения может быть при этом
определен с высокой точностью и может быть принят за начало
отсчета. Очевидно, нецелесообразно принимать за начало расчета
состав первого продукта разделения, так как содержание в нем
всех компонентов, кроме одного, мало, и трудно задаться кон¬
центрациями примесей с достаточной точностью. Это вызывает
неустойчивость решения, заключающуюся в несоблюдении усло¬
вий материального баланса и приводящую к необходимости вы¬
полнения большого числа последовательных приближений.
Если состав' одного из продуктов разделения, принятый за на¬
чало расчета, например состав кубовой жидкости, найден, то сле¬
дующим этапом расчета является определение температуры ее
кипения при выбранном давлении. Температуру кипения находят
методом итераций, так, чтобы давление паров, рассчитанное по
формуле
п
Р-Σ xZlyi (483)
г-1
совпадало с заданным.
Коэффициенты активности компонентов γ«, входящие в уравне¬
ние (483), являются сложными функциями температуры и соста¬
ва смесей. Зависимость величин у, от состава выражается с по¬
мощью одного из интерполяционных уравнений, как это описано
выше. Влияние же температуры на у; выражается уравнением
280
(449). В ограниченном температурном интервале изменение коэф¬
фициентов активности с температурой чаще всего не учитывается.
Величины P0i — функции температуры, которые могут быть пред¬
ставлены в аналитической форме, например, известным уравне¬
нием Антуана
Ig P = A + -^ (484)
в котором константы Л, β и С являются характеристиками рас¬
сматриваемого вещества.
Определив температуру кипения кубовой жидкости и значе¬
ние P0r можно рассчитать состав равновесного пара по уравне¬
нию (352). Для проверки правильности вычислений используют
п
условие 2 г/* = I, которое должно выполняться с заданной сте-
г = 1
пенью точности.
Затем, задавшись значением флегмового числа /?', можно с
помощью уравнения материального баланса (381) определить со¬
став жидкости, стекающей с тарелки, которая находится над ку¬
бом. Расход пара Ζ)κ, образующегося в кубе с учетом зависи¬
мости энтальпии материальных потоков от состава и температуры,
определяется из уравнения теплового баланса, составленного для
сечения колонны, находящегося над кубом (без учета потерь теп¬
ла)
Qk + <71 ~ AA + WKqK (485)
где qu tK и ίκ — энтальпия жидкости, стекающей с первой тарел¬
ки, пара, образующегося в кубе, и кубовой жидкости при темпе¬
ратурах кипения.
Из уравнения материального баланса
L1 = Dk + Wk (486)
Правильность найденного состава жидкости на тарелке про¬
веряется с помощью соотношения
п
г-ι
< δ (487)
где б — допустимая погрешность расчетов.
Расчет по описанной схеме производится последовательно для
каждой тарелки исчерпывающей части колонны вплоть до тарел¬
ки питания. Положение последней определяется, исходя из изве¬
стного условия
(488)
Хв, п xBi f хв, m
где хп,п и хв,п — молярные доли низкокипящего и высококипящего
ключевых компонентов на тарелке, расположенной над тарелкой
281
ййтаний; Xsttm й хв,т — молярные Доли тех же компонентов на
тарелке, расположенной под тарелкой питания; xnj и Xbj- мо¬
лярные доли тех же компонентов в смеси, поступающей на раз¬
деление.
При переходе через тарелку питания меняются условия мате¬
риального и теплового баланса. Принцип же расчета остается
тем же.
Расчет по описанной, схеме выполняется для ряда значений
флегмовых чисел, и на основании анализа полученной зависи¬
мости числа теоретических тарелок от флегмового числа опреде¬
ляются оптимальные условия прове¬
дения процесса ректификации.
Если описанный метод приме¬
няют для расчета процесса разделе¬
ния бинарной смеси с помощью
азеотропной ректификации, то опре¬
деление состава дистиллата и кубо¬
вой жидкости обычно не представ¬
ляет особых затруднений, так как
относительное содержание компо¬
нентов исходной смеси в продуктах
разделения обычно бывает задано,
а содержание разделяющего3 агента
в дистиллате близко к его кон¬
центрации в азеотропной смеси с
компонентом, отгоняемым в виде
дистиллата.
Кроме описанного аналитического метода в практике исполь¬
зуют различные графические методы расчета «от тарелки к та¬
релке». Эти методы основаны на' использовании графического
представления данных о фазовом равновесии. Для трехкомпо¬
нентных систем условия равновесия между жидкостью и паром
изображаются в виде треугольной диаграммы, использование ко¬
торой для расчета процесса азеотропной ректификации показано
на рис. 100.
Состав подаваемой в колонну смеси изображается точкой X0i
являющейся точкой пересечения секущей, выходящей из верши¬
ны, которая соответствует разделяющему агенту, к точке состава
исходной смеси и линии, соединяющей составы дистиллата хд, и
кубового остатка хк. Конец отрезка, проведенного из точки хк,
изображает состав пара ук, находящегося в равновесии с кубо¬
вой жидкостью. В соответствии с уравнениями материального
баланса (379) и (380) состав жидкости, стекающей с первой та¬
релки Xi7 изображается точкой, лежащей на отрезке х^Ук. Распо¬
ложение этой точки определяется соотношением расходов жид¬
кости и пара в колонне. Из уравнений (379) и (380) следует:
I
Рис. 100. Расчет процесса ректи¬
фикации трехкомпонентной смеси
в треугольной диаграмме.
282
·ν· loo
I
§
I
бинарная
'система
'уксусная кис-
Тлота-этилауе-
тат
20 40 60 80 100
Содержание уксусной кислоты в жидкости, мол, %
а
В равновесии с жидкостью состава Xif находится пар состава
Iji. Точка жидкости состава Xz9 стекающей с лежащей выше та¬
релки, лежит на прямой, которая соединяет точки хк и г/ь Поде¬
лив эту прямую в отноше¬
нии, вытекающем из уравне¬
ния (489), находим точку хь
Находящийся в равновесии
с ней пар имеет состав,
изображаемый точкой у2.
На прямой, соединяющей
точки г/2 и хКу находится
описанным выше способом
точка Xz9 соответствующая
составу жидкости, стекаю¬
щей с третьей от куба та¬
релки. Такое построение
продолжается для всех та¬
релок исчерпывающей части
колонШ. Для определения
числа тарелок в укрепляю¬
щей части колонны произво¬
дится аналогичное построе¬
ние. Различие заключается
только в том, что точки со¬
ставов жидкости на тарел¬
ках укрепляющей части ко¬
лонны находятся на прямых,
которые соединяют точки
состава пара с составом ди¬
стиллата хД.
Из приведенного описа¬
ния видно, что этот метод
представляет собой графи¬
ческую интерпретацию ме¬
тода расчета «от тарелки
к тарелке».
Чамберсом [317} был
предложен графический ме¬
тод расчета процессов' рек¬
тификации трехкомпонент¬
ных смесей, напоминающий
известный графический ме¬
тод Мак-Кэба и Тиле для
бинарных смесей.
По методу Чамберса число тарелок, необходимых для разде¬
ления заданной смеси, рассчитывают путем обычного графиче¬
ского построения числа ступеней в двух диаграммах у — х.
£Ж. 101 иллюстрирует этот метод на примере расчета колонны для
бинарная система
Рабочая линия
/укрепляющей части
бинарная система
этилацетат-
вода
Рабочая линия исчерпывающей части
20 40 60 80 100
Содержание воды в жидкости, мол, V*
б
Рис. 101. Расчет процесса азеотропной рек¬
тификации по методу Чамберса.
Цифры на кривых выражают содержание
(в мол. %) воды в жидкости (а) и уксус¬
ной кислоты в жидкости (б).
233
обезвоживания уксусной кислоты с использованием этилацетата
в качестве разделяющего агента.
На рис. IО I,а приведены кривые, выражающие зависимость
между концентрациями уксусной кислоты в жидкости и в паре
при различных концентрациях воды в жидкой фазе. Самая ниж¬
няя кривая (при концентрации воды, равной нулю) является
кривой равновесия бинарной системы уксусная кислота — этил-
ацетат, а самая верхняя — кривой равновесия бинарной системы
уксусная кислота — вода.
На рис. 101,6 изображены кривые, выражающие зависимость
между концентрациями воды в жидкости и в паре при различных
концентрациях уксусной кислоты. Нижняя кривая выражает усло¬
вия фазового равновесия в бинарной системе вода — этилацетат.
Другая граничная кривая — кривая равновесия бинарной системы
вода — уксусная кислота. Расчет производится следующим
образом.
На основании материального баланса определяют составы ку¬
бовой жидкости и дистиллата. Из точек на диагонали диаграммы
101,а и б, отвечающих составу кубовой жидкости, проводится ра¬
бочая линия с углом наклона, определяемым соотношением рас¬
ходов жидкости и пара на тарелке, расположенной над кубом.
Затем путем графического построения определяют концентрации
уксусной кислоты и воды. Концентрацию этилацетата находят по
разности. На ближайших к кубу тарелках концентрация этил¬
ацетата в рассматриваемом примере мала, поэтому концентра¬
ции уксусной кислоты и воды определяют ступенчатым построе¬
нием между рабочей линией и кривой равновесия для бинарной
системы уксусная кислота — вода. Начиная с пятой тарелки, со¬
держание этилацетата достигает величины, при которой он суще¬
ственно влияет на условия фазового равновесия. Соответственно с
этим изменяется характер построения. Как видно из рис. 101, кон¬
центрация уксусной кислоты по высоте колонны все время убы¬
вает. Концентрация же воды до восьмой тарелки возрастает,
а затем резко уменьшается, приближаясь к величине, отвечаю¬
щей составу азеотропа этилацетат — вода. На лежащих выше та¬
релках относительное содержание воды и этилацетата сохраняет¬
ся таким же, как в азеотропе, образуемом этими веществами.
Наиболее прост расчет по описанному методу, когда рабочая
линия является прямой. Как уже указывалось, это имеет место,
если скрытые теплоты испарения компонентов мало различаются.
При большом различии скрытых теплот испарения для каждой
тарелки проводится своя рабочая линия.
Для расчета процессов азеотропной ректификации можно ис¬
пользовать известные методы расчета процессов ректификации
многокомпонентных смесей, достаточно подробно рассмотренные
в работах [315, 316, 318—321].
При расчете процессов азеотропной ректификации важно знать
минимальное число тарелок, соответствующее работе колонны с
294
бесконечным флегмовым числом. Это определение можно произ¬
вести графическими методами. Расчет облегчается тем, что пар,
поступающий на произвольную тарелку, имеет такой же состав,
как стекающая с нее жидкость. Это обстоятельство упрощает и
аналитический расчет, который может быть произведен следую¬
щим образом.
Если известны концентрации двух компонентов разделяемой
смеси в кубе х'к и х", то отношение концентрации этих компо¬
нентов в парах над кубом определяется уравнением
г г
Ук / хк
<2(490)
Ук xK
где а[2— коэффициент относительной летучести рассматриваемых
компонентов при заданном составе кубовой жидкости.
Состав жидкости, стекающей с первой от куба тарелки, равен
составу поступающего на нее пара. Поэтому отношение концен¬
траций рассматриваемых компонентов в парах над этой тарелкой
определяется уравнением
/ /
— “а12«12— (491>
У\
где а'2 — коэффициент относительной летучести рассматриваемых
компонентов при отношении их концентраций XflJx" — tfK/у"· Повто¬
ряя этот расчет столько раз, сколько в колонне тарелок, получаем
...*ΐ2 (492)
хп хк
где Ctj2' ... CtJ12 — коэффициенты относительной летучести при со¬
ставе жидкости на тарелках от третьей до п.
Если состав дистиллата равен составу пара, поднимающегося
над самой верхней тарелкой, то:
-α ί2αίΧ''...α"+1^ (493)
Использование уравнения (493) осложняется, однако, тем, что
коэффициенты относительной летучести зависят от состава сме¬
сей. Если концентрации компонентов заданной смеси изменяются
в небольшом интервале, и концентрация разделяющего агента
может быть принята постоянной, то коэффициент относительной
летучести мало изменяется, и для расчета можно использовать
усредненное значение а. В этом случае минимальное число
285
тарелок определяется следующим приближенным уравнением
Это уравнение называется уравнением Фенске [322]. Прибли¬
женное значение среднего коэффициента относительной летучести
можно определить как среднее геометрическое значений а для
границ рассматриваемого интервала концентрации:
Следует подчеркнуть, что так рассчитывать значение аСр мож¬
но лишь в случае небольшого изменения а по высоте колонны.
Определение минимального флегмового числа для процесса
ректификации многокомпонентной смеси вообще и для процесса
азеотропной ректификации, в частности, является чрезвычайно
сложной задачей. Предложенные методы применимы, главным
образом, для случая ректификации идеальных смесей. Если в про¬
цессе азеотропной ректификации концентрация разделяющего
агента в укрепляющей части колонны мало изменяется, то мини¬
мальное флегмовое число может быть ориентировочно определено
по условиям равновесия на тарелке питания с помощью уравне¬
ния материального баланса (368), в котором вместо хп должна
быть подставлена концентрация отгоняемого компонента в жид¬
кости, а вместо #η+ι — концентрация этого компонента в равновес¬
ном паре.
При этом для оценки количества флегмы, которое надо пода¬
вать в колонну, необходимо учитывать изменение расхода жид¬
кости по высоте колонны в соответствии с изменением скрытых
теплот испарения смесей. С целью выбора рабочего флегмового
числа обычно графическим или аналитическим методом рассчи¬
тывают числа тарелок при различных флегмовых числах и на
основании этих расчетов выбирают оптимальные условия прове¬
дения процесса.
Для успешного проведения непрерывного процесса азеотроп¬
ной ректификации вджное значение имеет правильный выбор по¬
ложения тарелки питания.
Было предложено [323] при расчетах процессов азеотропной
ректификации определять положение тарелки питания по методу
Джиллиланда [324], согласно которому на тарелке питания долж¬
но выполняться условие, выражаемое неравенствами
(494)
откуда
/»+1 =
(495)
IgCtcp
aCP=Vai2O?+1
(49в)
где Xflxf — отношение концентраций компонентов заданной смеси
на тарелке питания; χ'ί+ι/χ"+1 — то же на тарелке выше тарелки
питания; x'cjx" — отношение концентраций этих компонентов в
исходной смеси.
Таблица 35
Составы исходной смеси и продуктов разделения
Компонент
*
Исходная смесь
Кубовая жидкость
Дистиллат
вес. %
мол. %
вес. %
мол. %
вес. %
мол. %
Уксусная кислота . .
Этилацетат
Вода .
7,80
84,65
7,55
4,50
66,46
29,04
99,86
0,0074
0,131
99,12
0,01
0,87
91,85
8,15
ю~10
69,7
30,3
В процессе азеотропной ректификации концентрация разде¬
ляющего агента может быть практически постоянна на большей
части высоты колонны, включая та¬
релку питания. При этом в процессе
разделения переменной величиной яв¬
ляется только относительное содержа¬
ние компонентов заданной смеси.
В этом случае положение тарелки пи¬
тания определяется так же, как при
ректификации бинарной смеси.
Рассмотрим, например, расчет не¬
прерывного обезвоживания уксусной
кислоты путем азеотропной ректифи¬
кации с применением этилацетата в
качестве разделяющего агента [325].
Составы исходной смеси, дистилла¬
та и кубовой жидкости, рассчитанные
по уравнениям материального балан¬
са, приведены в табл. 35.
Данные о фазовом равновесии в
системе вода — уксусная кислота —
этилацетат представлены на рис. 101.
По этим данным были рассчитаны
значения коэффициентов относительной летучести для каждой
пары компонентов. На рис. 102 в качестве примера изображены
интерполированные кривые зависимости коэффициента относи¬
тельной летучести воды и уксусной кислоты от относительного со*
держания этих веществ при разных концентрациях этилацетата
в жидкости. При расчете процесса азеотропной ректификации от
тарелки к тарелке состав пара, находящегося в равновесии
OLt2
Рис. 102. Зависимость коэффи¬
циента относительной летуче¬
сти воды и уксусной кислоты
при разных концентрациях
этилацетата в жидкости.
207
с жидкостью, рассчитывали по уравнениям
-Vi = :г T-; Уг = “21 УI И у3 = Ct3, ψ- у, (498)
I I Г1 3 I Л2 X1 X1
I + α31 — + α2ι —
Xj X1
где индексами I, 2 и 3 обозначены соответственно уксусная кис¬
лота, вода и этилацетат.
Скрытые теплоты испарения компонентов составляют
(в кал/кг): уксусной кислоты 96,75, этилацетата — 87,5 и воды—
540. Константы Трутона равны соответственно 14,8; 22,1 и 26,0.
Если принять, что в паровой фазе уксусная кислота присутствует
в виде димеров с молекулярным весом 120, то константа Трутона
для нее составит 29,6, что значительно ближе к значениям этих
констант для этилацетата и воды. Соответственно с этим были пе¬
ресчитаны данные о равновесии между жидкостью и паром. По¬
ложение тарелки питания определяли из условия (497). Исходя
из приведенных в табл. 35 составов материальных потоков, было
рассчитано изменение концентраций жидкости и пара на тарел¬
ках для бесконечного и нескольких конечных флегмовых чисел и
на основании этого найдено необходимое число тарелок. Для
иллюстрации полученных результатов в табл. 36 и 37 приводятся
рассчитанные концентрации (в мол. долях) для флегмовых чисел
R = оо и R = 0,333.
Таблица 36
Составы жидкости и пара на тарелках при R = оо
№
тарелки
Xl
Х2
*3
У\
У2
Уз
Куб
0,9912
0,0087
0,0001
0,982
0,01815
0,000291
I
0,982
0,01815
0,000291
0,962
0,0373
0,000843
2
0,962
0,0373
0,000843
0,923
0,0745
0,00242
3
0,923
0,0745
0,00242
0,852
0,141
0,0069
4
0,852
0,141
0,0069
0,737
0,244
0,0191
5
0,737
0,244
0,0191
0,577
0,370
0,0538
6
0,577
0,370
0,0538
0,382
0,465
0,153
7
0,382
0,465
. 0,153
0,16
0,456
0,384
’ 8
0,16
0,456
0,384
0,0224
0,332
0,6455
9
0,0224
0,332
0,6455
0,00135
0,299
0,6996
10
0,00135
0,299
0,6996
0,0000743
0,2995
0,7004
11
0,0000743
0,2995
0,7004
CO I
I
О
О
0,300
0,700
12
4,04· 10"!
0,300
0,700
2,2 · 10.
0,301
0,699
13
2,2· 1°"'
0,301
0,699
*·2 -10^o
0,302
0,698
14
1,2 · 10 ‘
0,302
0,698
6,53· 10" “
0,303
0,697
15
6,53· 10
0,303
0,697
3,55· 10
0,303
0,697
Из табл. 36 и 37 видно, что отношение концентраций уксусной
кислоты и воды приближается к отношению этих компонентов в
исходной смеси между восьмой и девятой тарелками при R=^oо
288
Таблица 3?
Составы жидкости и пара на тарелках при К=0,Ш
jSfa
тарелки
х\
*2
*3
Vi
' У2 :
УЗ
Куб.
0,9912
0,0087
0,0001
0,982
0,01815
0,000291
I
0,983
0,01785
0.000284
0,9624
0,0368
0,000821
2
0,9634.
0,0359
0,000797
0,926
0,0718
0,00228
3
0,930
0,0675
0,00221
0,865
0,129
0,00629 .
4
0,870
0,125
0,00609
0,7625
0,2202
0,0172
5
0,772
0,213
0,0166
0,615
0,338
0,046
6
0,629
0,327
0,0445
0,437
0,439
0,124
7
0,457
0,424
0,120
0,232
0,458
0,311
8
0,258
0,443
0,301
0,06
0,374
0,566
9
0,092
0,362
0,547
0,00828
0,303
0,689
10
0,042
0,293
0,666
0,00295
0,292
0,705
11
0,0118
0,257
0,732
0,000728
0,295
0,705
12
0,00291
0,269
0,732
0,000168
0,299
0,7008
13
0,000672 4
0,285
0,715
3,75·10“;|
0,302
0,698
14
1,5.101
0,296
0,704
8,4-10“"
0,303
0,697
15
3,29-10 I
0,303
0,697
1,77- 10“!
0,303
0,697
16
7,075 · 10 I
0,303
0,697
3,81 · 10 *
0,303
0,697
17
1,525-10 I
0,303
0,697
8,19-10“®
0,303
0,697
18
3,27-10 I
0,303
0,697
1,76-10“:
0,303
0,697
19
7,04-10 “®
0,303
0,697 .
3,78 - Ю“*
0,303
0,697
20
1,51 - 10“
0,303
0,697
8,12-10“ 0
0,303
0,697
21
2,95-IOI 0
0,303
0,697
1,59- КГ
0,303
0,697
22
3,3-10 10
0,303
0,697
10 1
0,303
0,697
и на десятой — при R = 0,333. Выше этих тарелок, в укрепляю¬
щей части, концентрации воды и этилацетата практически посто¬
янны и близки к концентрациям этих веществ в азеотропе этил¬
ацетат — вода. В укрепляющей части колонн происходит только
отделение уксусной кислоты, концентрация которой по мере при¬
ближения к верху колонны быстро уменьшается.
Влияние флегмового числа на число тарелок видно из табл. 38.
Число тарелок в исчерпывающей части сравнительно мало изме¬
няется с изменением флегмового числа.
T а б л и ц а 38
Изменение числа тарелок
в зависимости от флегмового числа
Флегмовое число
Число тарелок
в исчерпывающей
части
в укрепляющей
части
общее
0,233
10
12
22
0,177
10
15
25
0,12
11
17
28
-
10 Зак. 917
289
С уменьшением флегмового числа заметно возрастает коли¬
чество'тарелок только в укрепляющей части колонны. Представ¬
ляет интерес выяснить влияние состава исходной смеси на усло¬
вие ее разделения. В табл. 39 приводится материальный баланс
процесса из расчета на 100 кмоль исходной смеси с соотношением
концентраций воды и этилацетата большим, чем в азеотропе,
образуемом этими веществами.
T а б л и ц а 39
Материальный баланс
процесса азеотропной ректификации (в кмольJ
Компонент
Исходная смесь
Дистиллат
Кубовая жидкость
Уксусная кислота . .
5,4
9,45-KT9
5,4 4
Этилацетат
58,7
58,7
5,44· 10 *
Вода
35,9
35,86
4· IO-
Оказалось, что уменьшение отношения концентраций этилаце¬
тат и воды с 2,3 до 1,64 приводит к росту минимального флегмо¬
вого числа с 0,12 до 0,5.
Расчет от тарелки к тарелке
показывает, что при флегмо-
вом числе R = 0,95 для по¬
лучения тех продуктов раз¬
деления, которые указаны
в табл. 39, требуется ко¬
лонна с 18 тарелками. Точ¬
ка питания в этом слу¬
чае находится на девятой
тарелке. Значит, для умень¬
шения флегмового числа не¬
обходимо поддерживать в
колонне соотношение коли¬
честв разделяющего агента
и отгоняемого компонента,
Содержание уксусной кислоты в жидкости,мол % отвечающее составу азео¬
тропа.
Сопоставление результа¬
тов аналитического расчета
с расчетом по методу Чам¬
берса, приведенным на рис. 101, показывает применимость послед¬
него для расчета числа тарелок в исчерпывающей части колонны.
Для расчета числа тарелок в укрепляющей части колонны метод
Чамберса не может быть применен из-за малых концентраций
уксусной кислоты.
При малом изменении концентраций этилацетата и воды выше
точки питания, как в рассмотренном примере, число тарелок мож¬
Рис. 103. Расчет числа тарелок в укрепляю¬
щей части колонны для обезвоживания
уксусной кислоты.
290
но рассчитывать по видоизмененному методу Мак-Кэба и Тиле,
пользуясь диаграммой, выражающей зависимость логарифма кон¬
центрации высококипящего компонента заданной смеси в паре от
логарифма молярной концентрации этого компонента в жидкости.
Эта диаграмма для рассматриваемого процесса обезвоживания
уксусной кислоты приводится на рис. 103. Как было показано
в гл. I, при малой концентрации растворенного вещества, распре¬
деление его между жидкостью и паром описывается законом
Генри. Соответственно с этим связь между концентрациями уксус¬
ной кислоты в паре и жидкости (рис. 103) выражается прямой
линией. Число тарелок, найденное ступенчатым построением (см.
рис. 102), совпадает с рассчитанным аналитическим методом от
тарелки к тарелке.
Отличительной особенностью рассмотренных примеров являет¬
ся чрезвычайно низкая концентрация разделяющего агента в ку¬
бовой жидкости. Поэтому, в исчерпывающей части колонны кон¬
центрация разделяющего агента оказывается значительно ниже,
чем в азеотропе этилацетат — вода. С целью улучшения условий
разделения в исчерпывающей части колонны часто оказывается
целесообразным допускать большее содержание разделяющего
агента в кубовой жидкости. Примером такого процесса является
разделение смеси парафинового углеводорода и толуола путем
Таблица 40
Результаты расчетов разделения смесей
парафинового углеводорода с толуолом
путем азеотропной ректификации
Параметры режима
Номер варианта
I
2
3
4
5
6
Состав исходной смеси, мол. %:
метиловый спирт
70,0
70,4
78,1
78,1
78,1
70,7
парафин
15,0
14,8
11,7
11,7
11,7
15,7
толуол
15,0
14,8
10,2
10,2
10,2
13,6
Состав дистиллата, мол. %:
метиловый спирт
81,3
81,3
81,1
81,1
81,1
81,1
парафин . . .
17,6
17,6
18,1
18,1
18,1
18,1
толуол
Состав кубовой жидкости, мол. %:
1,1
1,1
0,8
0,8
0,8
0,8
метиловый спирт ...
10,0
10
72,5
72,5
72,5
1,1
парафин
1,0
0,1
0,2
0,2
0,2
0,8
толуол
89,0
89,8
27,3
27,3
27,3
98,1
Чистота толуола, мол. % ·
98,8
99,9
99,2
99,2
99,2
99,2
Выход толуола, %
93,8
93,8
95,2
95,2
95,2
95,2
Флегмовое число
OO
OO
1,85*
2,60
3,64
3,64
Общее число тарелок
14
18
45
28
30
Тарелка питания (счет от куба) ....
—
—
16
12
14
* Минимальное флегмовое число.
/
азеотропной ректификации с метиловым спиртом [280]. Последний
легко отделяется от углеводородов путем отмывки водой.
Влияние различных факторов в процессе азеотропной ректи¬
фикации иллюстрируется результатами расчетов, приведенными
в табл. 40.
Первые два расчета проведены при R = оо и концентрации ме¬
тилового спирта в кубовой жидкости 10 мол.%. При одинаковом
выходе толуола 93,8% для получения конечного продукта чисто¬
той 98,8% требуется 14 теоретических тарелок, а для получения
продукта чистотой 99,9% — 18 тарелок.
Изменение состава жидкости на тарелках для первого вариан¬
та расчета представлено кривой на рис. 104 (составы жидкости
на кривой обозначены круж¬
ками). На двух ближайших к
кубу тарелках концентрация
метилового спирта повышает¬
ся от 10 до 83 мол.%, а на
всех вышележащих тарелках—
превышает 80 мол.%. Из рис.
104 видно, что на двух бли¬
жайших к кубу тарелках то¬
луол отделяется от метилового
спирта, а на остальных тарел¬
ках происходит разделение
смеси парафина и толуола.
Варианты расчета 3—5 по¬
казывают связь между флег¬
мовым числом и числом таре¬
лок. Как и в рассмотренном
ранее процессе обезвоживания
уксусной кислоты, при увеличе¬
нии флегмового числа в основном уменьшается число тарелок
в укрепляющей части. Так, при увеличении флегмового числа от
2,60 до 3,64 число тарелок в исчерпывающей части колонны умень¬
шается всего с 16 до 12, а в укрепляющей части — с 29 до 16.
Выше уже отмечалась легкость отделения разделяющего аген¬
та от высококипящего компонента. Это дополнительно подтвер¬
ждается сравнением результатов двух последних вариантов рас¬
чета. Как видно из табл. 40, при прочих равных условиях для
уменьшения концентрации метанилового спирта в кубовой жид¬
кости с 72,5 мол.% до 1,1 мол.% требуются всего две дополни¬
тельные тарелки в исчерпывающей части колонны (варианты
5 и 6).
Выше рассматривался расчет непрерывного процесса азео¬
тропной ректификации. При расчете периодического процесса про¬
является дополнительное затруднение, связанное е изменением со¬
става кубовой жидкости по ходу разгонки в соответствии с уравне¬
нием (370).
Рис. 104. Изменение составов жидкости
по высоте колонны при разделении
смеси парафинового углеводорода и
толуола путем азеотропной ректифика¬
ции при R = оо.
292
Расчет процесса периодической азеотропной ректификации мо¬
жет производится следующим образом. По заданным составам и
количествам начальной смеси и отбираемого дистиллата с по¬
мощью уравнений (370) рассчитывают состав кубовой жидкости
к концу процесса. По найденному составу кубовой жидкости и
известному составу дистиллата с помощью описанных выше ме¬
тодов определяют число тарелок и флегмовое число, требующееся
для достижения заданной степени разделения в конце процесса.
Затем для нескольких флегмовых чисел, меньше найденных в пре¬
дыдущем расчете, по заданному составу дистиллата находят
состав кубовой жидкости, получающейся при ректификации в ко¬
лонне с найденным для конца процесса числом тарелок. Опи¬
санным способом устанавливают зависимость необходимого флег¬
мового числа от состава жидкости в кубе. Расчеты можно произ¬
водить аналитически («от тарелки к тарелке») или описанными
выше графическими методами.
РАСЧЕТ ПРОЦЕССОВ
ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Особенность процессов экстрактивной ректификации за¬
ключается в том, что они проводятся обычно при высокой концен¬
трации разделяющих агентов (70—90 мол.%), причем последние
чаще всего имеют значительно более высокие температуры кипе¬
ния, чем компоненты заданной смеси. Если в процессах обычной
и азеотропной ректификации расходы жидкости и пара имеют
незначительные различия, то в процессах экстрактивной ректифи¬
кации расход жидкости, как правило, значительно превышает рас¬
ход пара. Поэтому и количество тепла, переносимого потоком
жидкости, значительно больше, чем в процессах обычной и азео¬
тропной ректификации. Соответственно больше роль энтальпии
жидкости в тепловом балансе колонны. Вследствие этого даже от¬
носительно небольшое изменение температуры по высоте колонны,
обычно характерное для процессов экстрактивной ректификации,
может вызвать значительное изменение расходов пара и жид¬
кости. Это обусловливает изменение по высоте колонны флегмо¬
вого числа и концентрации разделяющего агента, а также в свою
очередь, усложняет определение условий фазового равновесия и
обусловливает криволинейный ход рабочих линий процесса рек¬
тификации. Разумеется, отмеченная особенность относится лишь
к той части колонны для экстрактивной ректификации, которая
расположена ниже точки ввода разделяющего агента. Часть ко¬
лонны, находящуюся выше точки ввода разделяющего агента,
рассчитывают как в обычных процессах ректификации. Поэтому
этот вопрос здесь не рассматривается.
Точный расчет процесса экстрактивной ректификации может
быть выполнен по описанному выше методу «от тарелки к тарел¬
ке» с помощью вычислительных машин. Принцип такого расчета^
аналогичен рассмотренному для азеотропной ректификации.
Трудность заключается в том, что не всегда имеются данные
о теплофизических свойствах растворов, в частности о теплотах
смешения. Пример расчета с помощью ЭВМ колонны для выде¬
ления бензола из углеводородной смеси путем экстрактивной
ректификации с фенолом как разделяющим агентом описан в ра¬
боте [326].
Для учета изменения энтальпий материальных потоков по вы¬
соте колонны для экстрактивной ректификации предложено [327]
рассчитывать процесс с помощью диаграммы энтальпия — со¬
став.
Во многих случаях, в частности при разделении смесей ве¬
ществ, близких по химической природе, например смесей углево¬
дородов, концентрация разделяющего агента и энтальпия жид¬
кости по высоте колонны изменяются мало. При этом роль
разделяющего агента может быть сведена только к изменению от¬
носительной летучести компонентов заданной смеси. Принимая со¬
ответствующие значения коэффициентов относительной летучести,
можно рассчитывать процесс экстрактивной, ректификации без
учета наличия разделяющего агента в смеси. Это чрезвычайно
упрощает задачу, поскольку, оперируя относительными концент¬
рациями компонентов заданной смеси, можно свести расчет про¬
цесса экстрактивной ректификации к расцету обычной ректифи¬
кации. Особенно упрощается задача, если подвергаемая разделе¬
нию смесь является бинарной. В этом случае могут применяться
обычные широко известные методы расчета процессов ректифи¬
кации бинарных смесей.
Другое существенное упрощение возникает в связи с поддер¬
жанием в процессе экстрактивной ректификации высокой кон¬
центрации разделяющего агента. В гл. II было показано, что
изменение коэффициентов относительной летучести компонентов
заданной смеси в зависимости от их относительного содержания
определяется двумя факторами: степенью неидеальности задан¬
ной смеси и концентрацией разделяющего агента, разбавляющего
эту смесь и, благодаря этому, уменьшающего относительное
влияние взаимодействия молекул компонентов заданной смеси.
С увеличением концентрации разделяющего агента коэффициент
относительной летучести компонентов исходной смеси все в мень¬
шей степени зависит от их относительного содержания и в этом
отношении смесь все больше приближается к идеальной. Благо¬
даря этому при больших концентрациях разделяющих агентов
в расчет могут приниматься средние значения коэффициентов от¬
носительной летучести, зависящие от концентрации разделяющего
агента в жидкости и не зависящие от соотношения количеств
исходных веществ в смеси. Связанная с этим допущением по¬
грешность тем меньше, чем меньше степень неидеальности задан¬
ной смеси. При разделении, например, таких блрзких к идеаль¬
ным смесей, как смеси углеводородов, это положение оправды-
294
бается с высокой степенью точности. При изложенных допуще¬
ниях процесс экстрактивной ректификации может рассчитываться
как обычная ректификация идеальных смесей.
Если разделению подвергается бинарная смесь, и коэффи¬
циент относительной летучести в достаточной степени точности
может быть принят постоянным, то минимальное число-тарелок
(при бесконечном флегмовом числе), необходимое для обеспече¬
ния разделения в заданных пределах, определяется по уравнению
Фенске (495). Как и для обычной ректификации, рабочие линии
укрепляющей и исчерпывающей частей колонны пересекаются
в точке состава исходной смеси. Это условие определяет положе¬
ние тарелки питания.
Если пренебречь изменением относительных расходов жид¬
кости W и пара V по высоте колонны (в этом случае рабочие
линии являются прямыми), то минимальное флегмовое число опре¬
деляется условиями равновесия на тарелке питания. Если исход¬
ная смесь подается в колонну нагретой до температуры кипения,
то минимальное флегмовое число выражается уравнением
где Xc — состав исходной смеси, мол. доли.
При питании колонны паровой смесью состава ус минималь¬
но е флегмовое число определяется по уравнению:
Рабочие флегмовые числа принимаются с избытком против
минимального. Следует подчеркнуть, что увеличение флегмового
числа в процессах экстрактивной ректификации связано с необ¬
ходимостью соответствующего увеличения расхода разделяющего
агента для поддержания желательной его концентрации в колон¬
не. В связи с этим обычно процесс проводится при небольших
коэффициентах избытка флегмы (против минимального), равных
Числа тарелок в укрепляющей и исчерпывающей частях ко¬
лонны при рабочих флегмовых числах могут быть найдены с по¬
мощью известных методов, применяемых для расчета процессов
обычной ректификации бинарных смесей. В работах по экстрак¬
тивной ректификации чаще всего используется графический ме¬
тод Мак-Кэба и Тиле, заключающийся в ступенчатом построении
между кривой равновесия и рабочими линиями в диаграмме у—х
[20, 21, 24, 325]. Для этой цели могут использоваться также ана¬
литические методы, например метод Гельперина [11].
На рис. 105, приводится графический расчет числа теоретиче¬
ских тарелок в экстрактивно-ректификационной колонне для раз¬
деления бутан-бутиленовых смесей с использованием водного
(499)
(500)
1,1-1,3.
295
ЙЦеФона в качестве разделяющего агента [325]. Для построений
кривой равновесия принято усредненное постоянное значение коэф¬
фициента относительной летучести ар = 1,36.
Исходная смесь подается в колонну в виде пара и содержит
0,586 мол. доли бутанов, отгоняемых в процессе экстрактивной
ректификации. Относительная концентрация бутанов в дистил¬
ляте принимается равной *' = 0,92 мол. доли, а в кубовой жид¬
кости *' = 0,09 мол. доли. Согласно уравнению (500), минималь¬
ное флегмовое число равно:
п . I М,36> 0,92 0,08 \ 4
^mln 1,35-1 I 0,586 0,414 j
Принятое для расчета флегмовое число /? = 5,13, что отвечает
коэффициенту избытка флегмы σ = = 1,16. Путем построе¬
ния ступенек легко найти, что
эффективность экстрактивно- .
0fS2 ректификационной колонны
должна составлять 30 теорети¬
ческих тарелок, а исходная
смесь должна подаваться ме¬
жду 15 и 16 тарелками.
Если коэффициент относи¬
тельной летучести и флегмовое
числ:о не могут быть при¬
няты постоянными, то кривая
равновесия строится с учетом
изменения ар, а рабочие ли¬
нии— с учетом изменения рас¬
ходов жидкости и пара, опре¬
деляемого уравнениями (408)
и (448).
Во многих случаях метод
экстрактивной ректификации
применяется для разделения
многокомпонентных смесей.
Таковы, например, обычно смеси углеводородов. По изложенным
выше причинам, коэффициенты относительной летучести компонен¬
тов таких смесей в процессе экстрактивной ректификации могут
быть приняты постоянными. Поэтому расчет может производиться
с помощью методов, применяемых для расчета процессов обычной
ректификации идеальных многокомпонентных смесей. Из числа
этих методов наиболее распространен приближенный метод Джил¬
лиланда [324], как самый простой. Аналитический метод расчета
процессов ректификации многокомпонентных идеальных смесей
был предложен Андервудом [328—331].
Метод Джиллиланда основан на определении минимальных
флегмового числа и числа теоретических тарелок с последующим
графическим определением рабочих значений этих величин. При
0 OJ Oj Oj OJ Oj
Содержание бутана $ жидкости ,мол.дом
Ряс. 105. Расчет экстрактивно-ректифи¬
кационной колонны для разделения
бутан-бутиленовых смесей по методу
Мак-Кеба и Тиле.
296
питании колонны жидкой смесью, нагретой до температуры кипе¬
ния, минимальное флегмовое число определяют по уравнению
*mtn = M(Ar + S +0-1)
(501)
где величины Mt Nt S и О — функции составов и коэффициентов
относительной летучести, определяемые следующими уравне¬
ниями:
где хл, д и хл, с — молярные концентрации легкого ключевого ком¬
понента в дистиллате и исходной смеси; хт, к, *т. с и хт, д — моляр¬
ные концентрации тяжелого ключевого компонента в кубовой
жидкости, исходной смеси и дистиллате; х*K — молярная концен¬
трация в' кубовой жидкости компонента ί более летучего, чем лег¬
кий ключевой компонент; Хщ — молярная концентрация в дистил¬
лате компонента j менее летучего, чем^ тяжелый ключевой ком¬
понент; ал. т — коэффициент относительной летучести легкого и
тяжелого ключевых компонентов; а<т — коэффициент относитель¬
ной летучести более летучего компонента, чем легкий ключевой, по
отношению к тяжелому ключевому компоненту; — коэффи¬
циент относительной летучести менее летучего компонента, чем
тяжелый ключевой, по отношению к последнему; П и Wk- мо¬
лярные расходы дистиллата и кубовой жидкости.
При расчете процессов экстрактивной ректификации все кон¬
центрации и расходы должны приниматься без учета содержания
разделяющего агента.
I I
Знаки суммы Σ и Σ. стоящие в первых частях выражений (504)
и (505), показывают, что суммирование производится соответ¬
ственно по всем компонентам, более летучим, чем легкий ключе¬
вой, и по всем компонентам, менее летучим, чем тяжелый клю¬
чевой.
Минимальное число тарелок люin определяется по уравнению
Фенске (495). Для нахождения рабочих значений флегмового чис¬
ла ^ и числа теоретических тарелок η используется эмпирическая
кривая (рис. (Об), представляющая функциональную зависимость:
(503).
(502)
α<τ*ίκ
■ «π г-®/.·
Л. T IT
(504)
(505)
Наиболее распространенная на практике область значений ве-
JD D .
личины —η ,~т~ отвечает средней части оси абсцисс рис. 106.
1 AT I
П П
Так, при коэффициенте избытка флегмы σ = 1,2 величина—
А ~Г I
равна соответственно 0,063 при Япнп = 0,5 и 0,154 при Rmin = 10.
В этой области кривая идет довольно полого, и значения
сравнительно мало отклоняются от 0,55. Поэтому для ориентиро¬
вочных расчетов можно принимать:
/t « 2,2 + I) (507)
Положение тарелки питания, по Джиллиланду, определяется
приведенными выше (неравенствами (497). Физический смысл этих
неравенств заключается в том, что от¬
ношение концентраций ключевых ком¬
понентов в исходной смеси должно
быть больше или равно отношению
концентраций этих компонентов на та¬
релке питания и меньше или равно
этому отношению для тарелки, распо¬
ложенной над тарелкой питания.
Необходимо подчеркнуть, что ме¬
тод Джиллиланда является прибли¬
женным. Однако его максимальная по¬
грешность, как правило, не превыша¬
ет 7%, что лежит в пределах обычной
погрешности определения к. п. д. таре¬
лок. Это и позволяет практически при¬
менять метод Джиллиланда.
Метод Андервуда основан на сов¬
местном решении уравнений мате¬
риального баланса и фазового равновесия для случая постоянных
флегмовых чисел и коэффициентов относительной текучести. Для
удобства расчетов компоненты нумеруют в порядке возрастаю¬
щей относительной летучести. Коэффициенты относительной ле¬
тучести берутся по отношению к первому — самому высококипя-
щему компоненту и, например, для пятикомпонентной системы,
обозначаются αι, аг, аз, ад и а$. При этом αι = I. Из уравнений
закона Рауля и рабочей линии (405) имеем для произвольного
компонента
/ aix\о
mxi0 + at = — (508)
2 aIxU
ί = 1
где m = R/(R + I), а% — XfiJiR + I) и х'0, х'п и х'д — относительный
молярные концентрации компонента i на тарелке, принятой за на-
298
n~nmin
П+2
0,в
0,4
0,2
OtI
OM
0,04
OMnn
0,010,02 0,04 OJ 0,2 0,4 0,61,0
R + 1
Рис. 106. График для расчета
рабочих флегмовых чисел та¬
релок по методу Джиллиланда.
S
S-- ■
X
чало отсчета (0), на соседней с нею тарелке (I) ив дистиллате;
k — число компонентов.
Уравнение (508) может быть написано для любого компонента.
Система этих уравнений выражает зависимость между составами
жидкости на соседних тарелках. При любом флегмовом числе на
двух соседних тарелках, бесконечно удаленных от точки ввода,
состав жидкости одинаков. Для этих тарелок уравнение (508) за¬
пишется следующим образом:
тх\ + Cii = -j 1 1— (509)
Σ aix'i
t = l
Обозначая Ф = т^а.х' получаем:
1 = 1
1 + ai f αίΦ
— = и χ. = (510)
Ф a^m т (ct£ — Ф)
п
В силу очевидного условия 2^=1 получается уравнение:
1 = 1
аа„ а. .а а,а. а.а,
Tl Tl , Illrtlj , 11, , 11 I I I \
- + -^ ITST + ··· + л + ··· + —(5П)
■ Ф а , — Ф “ * а. — Ф ’' * а, — Ф
/г—I I
или
а, х
1Л 1Д
Σα,-Φ
г = I 1
■Я+I (512)
В этом уравнении неизвестной величиной является Ф. Число
решений этого уравнения равно числу компонентов в системе. Пу¬
тем соответствующих преобразований система уравнений (508)
может быть приведена к уравнению
k f k f I k
V aiX‘0 _ ф Y* aiXil /V_ ' /С.оч
2j а.-Ф т 2j а.-Ф 2da‘Xil * *
ί=ι 1 г=1 1 I i=i
Подставлял последовательно значения Ф, являющиеся корнями
уравнения (512), в уравнение (513), получаем систему уравнений,
число которых равно числу компонентов. Так, для трехкомпонент¬
ной системы получаются три уравнения (513). Разделив, напри¬
мер, первое на второе, получаем:
/ F F F F F
«3*30 а2х20 «1*10 «3*31 . «2*21 , «1*11
α3-Φι
■ +
Ot2 - Φι
- +
а, - Ф,
F
«3*30
■ +
F
«2*20
- +
«1*10
O3- Φι
- + ■
«2 ~ Ф]
■ +
а, - Ф,
F
«3*31
- +
«2*21
- -+■
I F
«1*11
Ф · / FlF (514)
аз — Ф2 «2 Ф2 ctI — Фг «з — Ф2 «2 — Ф2 aI — Ф
299
Особенностью уравнения (514) является его симметричная
структура. Применяя его последовательно к соседним тарелкам,
получаем для S-й тарелки:
t t г / / f
X3X30 «2^20 , «1*10 α3 *3s - «2*2s , ctIjtIs
■ + +
α3 -- O1 α2 — Φ| αι — Φι / Φ
Q3X30 α2*20 , aIxIQ '
• +
α3 - Φ2 α2 ~ Φ2 αι ~ Φ2
«3*30 , α2χ20 , ctIjtIO
Ct3 — Фа Q2 — Φ2 Qi — Φ2
/ , / /
Cf3X3O t Ct2X2O , ctIjtIO
' Ί 3Γ г
Ct3 — Φι
■ +
a2 - Φι
+
Ql ·
-Φι
«3*3s
+
Q2X2s
+
a
I* Is
Q3 - Ф2
Q2 Φ2
Ql-
-Φ2
«3*3s
+
«2*2s
+
«1
[xIs
a3 “ Ф2
Q2 — Φ2
Qj -
-Φ2
«3*3s
+
Q2X2s
+
«I
[jtIO
(515)
~ ί g·1 ~-Ρ- (515a)
V фз / QoXo„ QnXn„ α,χ.η
Ct3 - Φ3 Q2- φ3 Cti — Фз Ct3 — Φ3 α2 — Φ3 αι - Φ
Аналогичные уравнения могут быть написаны для системы
с любым числом компонёнтов. Уравнения (515) позволяют опре¬
делить состав жидкости на произвольной тарелке укрепляющей
части колонны по известному составу смеси на нулевой тарелке.
В качестве последней удобно принять самую верхнюю тарелку,
изменив соответствующим образом нумерацию тарелок (счет
сверху вниз). Тогда в уравнения (515) должны быть подставлены
концентрации соответствующих компонентов в дистиллате. При
этом левые части уравнения (515) становятся равными единице
и эти уравнения приобретают вид:
a3*3s , Ct2X25 CtjXjs
Q3- Φ2
+
Q2 — Φ2
+
aI '
-Φ2
«3*3s
+
«2*25
+
«I
e
I
CO
O
Q2- Φΐ
α, ■
-Φ,
«3*3s
+
«2*25
+'
«I
IxIs
α3 - Φ3
Q2 - Φ3
Bi ■
-Фз
«3*35
■ +
«2*25
+
α
lxis
-№)‘
(516)
(516 а)
Q3 — Ф2 Q2 ■— Ф2 Ql — Ф2
Методом, аналогичным описанному выше, для исчерпывающей
части колонны может быть получено уравнение, подобное урав¬
нению (512)
S-spry—« <5,7)
i = l ‘
где х'1к — относительная молярная доля компонента i в кубовой
жидкости; ψ — величина для исчерпывающей части колонны, ана-
Л Р %n+qWc-WK / , ,
логичная величине Ф; S = - — (q — коэффициент, за-
Wk
висящий от агрегатного состояния исходной смеси).
300
Зависимость концентрации компонентов от номера тарелки в
исчерпывающей части колонны выражается уравнениями, анало¬
гичными уравнениям (516)
и
^ F · I \ O
Ψι \
Σ aIxIv /у aix'iv = ί Ψι Y
°ι-*1 I,, ai~b U3/
г = 1 V 1 I ί-ι
где V — номер тарелки исчерпывающей части колонны (счет та¬
релок от куба).
Значения ψ определяются по уравнению (517).
Минимальное флегмовое число может быть определено с по¬
мощью уравнения (512). Умножив обе части уравнения (512)
на Я, а уравнения (517) — на Wk и почленно сложив эти уравне¬
ния, получаем
ΥΊ CLtXfic
4 * iC =1-<7 (519)
Cki - ф
*=I 1
где Xic — относительная молярная концентрация компонента I
в исходной смеси. -
Коэффициент q == I при питании колонны жидкой смесью при
температуре кипения, и q = 0, если исходная смесь подается в ко¬
лонну в виде пара.
Решив уравнение (519) относительно Ф и подставив получен¬
ное значение в уравнение (512), находим Rmin. Уравнение (519)
имеет число решений, равное числу компонентов в системе. Для
расчета Яш1п используются значения Ф, лежащие в интервале зна¬
чений се для ключевых компонентов. Для примера рассмотрим не¬
сколько вариантов расчета ,Rmin при разделении шестикомпонеКт-
ной смеси, подаваемой в колонну в виде пара (q = 0). Состав
исходной смеси и коэффициенты относительной летучести имеют
следующие значения: Xic = 0,2; х2с = *зс = *4с = %ьс = 0,15;
х6с = 0,2; αι = I, а2 = 2, аз = 3, а4 = 4, аь = 5 и а6 — 6. J
По уравнению (519): ч ^
6-0,2 , 5‘0,15 , 4-0,15 , 3 - 0,15 , 2*0,15 , 0,2- . /КОЛ.
+ -FZTfT + "л— ДГ + -Q -I! гЪ " + "Г—ДГ +T-I ДГ 8=31 (52°)
6~Ф 1 5 — Ф 4-Ф 1 3- Ф 2 — Φ 1-Ф
Это уравнение используется для последующего расчета.
I вариант
Ключевые компоненты оказываются соседними по относитель¬
ной летучести — легким ключевым является четвертый компо¬
нент, а тяжелым — третий. Принимаем Хзд = х4к = 0,0001, Корень
301
уравнения Ф4 должен иметь значение, промежуточное между аз и
а4. Методом последовательного приближения находим Ф4 == 3,50.
Поскольку дистиллат содержит очень мало первого, второго и
третьего компонентов, его состав может быть принят равным
*бд = 0,4; Хбд = 0,3 и х4д = 0,3. По уравнению (512) находим
6 * ‘ + к5~Ъпп + "Л'" Ькл = Xmln + I ИЛИ ^fflIn - 3,36
6-3,50 5-3,50 1 4-3,50
IIi вариант
Ключевыми являются третий и пятый компоненты. Четвертый
компонент распределяется между дистиллатом и кубовой жид¬
костью. Задано х3д = х5к = 0,0001. В этом случае должны исполь¬
зоваться два решения уравнения (520) Ф4 и Ф3, лежащие между
а3 и а3. Значение Ф4 = 3,50 найдено ранее. Из уравнения (520)
следует, что Ф3 = 4,559. Состав дистиллата в рассматриваемом
случае неизвестен. Он содержит практически все количество пя¬
того и шестого компонентов, имеющееся в исходной смёси, и не¬
известное количество четвертого компонента. Имеем: хАд + х$д + аг6д =
0 15
= I и х5я/х6л = -for · Отсюда *зд = 0,429 (I — х4д) и х6д = 0,57 (I — х4д).
Для расчета Rm^ получаются два уравнения:
6 · 0,571 (I — х4д) 5 ■ 0,429 (I — х4д) 4х4д ^ ^
6 - 3,50 ~ + 5 - 3,50 + 4 - 3,50 = ^mln + 1
6-0,571 (I -х4я) 5-0,429 (1 -х4А) 4х
. (521)
4Д
6 - 4,559 + 5 - 4,559 + 4 - 4,559 ^mln + 1
Решая эту систему уравнений, находим лг4д = 0,2266 и Rmi„ =
= 2,978.
Полный состав дистиллата равен *6Д = 0,4415, х$я = 0,3318,
х4д = 0,2266 и х3д = 0,0001.
Отношение расходов дистиллата и исходной смеси JS- =*
W с
= *5С + *8С = 0,4526 и, соответственно, WjWc = 0,5474.
ХБ.Д 4" -^бД
По уравнению материального баланса находим состав кубо¬
вой жидкости *5к = 0,0001, X4k = 0,0866, х3к = χ2κ = 0,2739 и Xik =
= 0,3655.
III вариант
Ключевыми являются второй и пятый компоненты. Компоненты
третий и четвертый распределяются между дистиллатом и кубовой
жидкостью. Задано Хгд = *5к = 0,0001. В этом случае в расчет
должны приниматься три значения Ф, лежащие между а2 и а3.
Из уравнения (520) находим Ф3 = 2,441. Составляя уравнения,
302
как при расчете II варианта, получаем:
6 · 0,571(1— лг3д — лг4д) 5 · 0,429 (I — х1л - лг4д) 4х4д
“ 4 P—(V ; V"ι Ь “I г-,, г -f
6 — 2,441 5-2,441 ' 4-2,441
Злг3д Dll
+ 3-2,441 s=Rmia'hl
Еще два аналогичных уравнения получаем для Ф4 и Фя, най¬
денных выше. Решая эти три уравнения относительно х3д, ^4д и
RmIn, находим х3д = 0,1608, х4д = 0,2235 и RmIn = 1,548. Составы
дистиллата и кубовой жидкости рассчитывают также, как в ва¬
рианте II. По найденному значению Rmm выбирают рабочее флег¬
мовое число.
Концентрация компонента i на произвольной тарелке 5, укреп¬
ляющей части колонны при флегмовом числе, отличающемся от
минимального, будет
B1 + ■ -)?- B2 + ... Bn
Xis = ^\ — (522)
r=l г
D _ λ1Φ1 D _ λ2Φ2 D ληφη , 1 _ ΦΛ V1 aAtn
где B,- φ, , B1- φ| ... B, φ, κ R 2ijai_9rf ■
Зависимость концентрации произвольного компонента от но¬
мера тарелки V в исчерпывающей части колонны при R Ф Rmrn
выражается уравнением
—— - A1+ *1κ, A2+ ... + An
α. — 4). α. — ib0 α. — ib
Xiv ‘ 2 -η (523)
-(s+i)2m;
г —I - "
I _ (Q) П α Xf
где A1 — μ^+1, A2 = μ-2Φ2+1 · * · = IVK+1 и μ~ ^ "sTT Σ (α. - ψ )2 *
Γ * = 1 ν 1 τ}
Значения Φ и φ в этих уравнениях рассчитывают соответствен¬
но по уравнениям (512) и (517) для выбранного флегмового числа.
С помощью уравнений (522) и (523) получаются следующие
уравнения, связывающие числа тарелок в укрепляющей и исчер¬
пывающей частях колонны:
+ ■ Аз + ... + ~А{— +■■·+ — Λ- (524)
Фг-Ч>! Фг-ф2 Ф,~Ф3 Фг-Фг Φ,-Ψ« фг(фг
Vl aAic (S+l)\rK V, ,γ,
где ЦФ,) = 1 + q и P = — ^«ίΨί/Σ^Γ·
I-1 aI Vr Wc J=1 *_!
303
Число уравнений (524) равно числу компонентов системы. Их
легко получить, приравнивая последовательно Фг = Φι, Фг, Фз, . ·.
.... Ф п- Величину P можно исключить, разделив два уравнения
(524) друг на друга. Получаем:
А\ I Ag I I Aj I I All
Ф Г —Φι Ф г-ф2 ··’ Фг-^1 "· ф r-Φ» ФЛФк) (525)
A1 I л2 I I Al I I Л» ФУ(Фг)
Фк - ψι Фк - ф2 ' " Фк ~ фi * * ’ Фк ~ ф«
Уравнение (525) содержит в левой части величины Л, являю¬
щиеся функциями числа тарелок в исчерпывающей части колон¬
ны V, а в правой части — функции числа тарелок в укрепляющей
части s. Уравнению (525) могут удовлетворять различные значе¬
ния V и s. Решением этого уравнения является такое сочетание
значений v и Sf которое отвечает наименьшему общему числу та¬
релок в колонне п=* V + s. Это сочетание значений υ и s опреде¬
ляет оптимальное положение точки ввода исходной смеси.
Для примера рассмотрим влияние точки ввода исходной смеси на общее
число тарелок при ректификации пятикомпонентной смеси. Составы исходной
смеси, дистиллата и кубовой жидкости (в мол. долях), а также значения коэф¬
фициентов относительной летучести компонентов приводятся в табл. 41. Флегмо¬
вое число R принято равным 5 (Rmin = 3,08). Смесь подают в колонну в виде
жидкости при температуре кипения.
Таблица 41
Состав исходной смеси и продуктов разделения
Номер
компонента
а
*с
f
ХА
/
xK
5
5
0,3
0,6
4
4
0,2
0,39
0,01
3
3
0,2
0,1
0,39
2
2
0,2
—
0,4
I
I
0,1
0,2
Из приведенных ниже результатов расчетов по уравнению (525) следует, что
оптимальная точка ввода исходной смеси находится между 19 и 20 тарелками
от верха колонны:
s 24 23 22 21 20 19,1 18 17
V. . 16,3 16,8 17,5 18,3 19,1 20 21,6 23,3
п. 40,3 39,8 39,5 39,3 39,1 39,1 39,6 40,3
При этом минимальное общее число тарелок равно 39,1. Однако изменение
положения точки питания в пределах между 17—24 тарелками от верха колонны
очень мало сказывается на общем числе тарелок — увеличение числа тарелок
в укрепляющей части колонны приводит практически к такому же уменьшению
потребного числа тарелок в исчерпывающей части. Это свидетельствует о допу¬
стимости некоторых отклонений при выборе положения точки ввода исходной
смеси. Следует иметь в виду, однако, что с уменьшением коэффициента избытка
флегмы отклонение положения точки ввода о/ оптимального сказывается более
значительно.
104
РЕГЕНЕРАЦИЯ РАЗДЕЛЯЮЩЕГО АГЕНТА
В предыдущем изложении не принималось во внимание
возможное содержание компонентов заданной смеси в разде¬
ляющем агенте. Между тем, разделяющий агент, подаваемый
в колонну для азеотропной или экстрактивной ректификации, не¬
избежно содержит некоторое количество указанных компонентов,
поскольку их идеальное отделение от разделяющего агента при
его регенерации невозможно. Содержание таких примесей в раз¬
деляющем агенте определяется условиями
его регенерации, а влияние stnx примесей
на показатели процесса разделения различ¬
но для процессов азеотропной и экстрактив¬
ной ректификации и в большой степени зави¬
сит от требований к чистоте получаемых про¬
дуктов. *
Поскольку в процессах азеотропной ректи¬
фикации разделяющий агент отбирается почти
полностью в виде дистиллата, нечеткость раз¬
деления при регенерации разделяющего аген¬
та , приводит к появлению в нем примеси
«верхнего» продукта (получаемого в виде
дистиллата). Если разделяющий агент по¬
дается в колонну (как это чаще всего делает¬
ся) вместе с исходной смесью, то эта примесь
не может существенным образом повлиять
на' качество получаемых продуктов. Влияние
указанной примеси на условия разделения
определяется ее количеством и проявляется
путем изменения расхода и относительного
содержания компонентов исходной смеси, по¬
даваемой в ректификационную колонну. Это
легко учесть при расчете процесса азеотроп¬
ной ректификации.
В процессах экстрактивной ректификации
разделяющий агент отбирают из куба и после
регенерации он содержит примесь «ниж¬
него» продукта (кубовой жидкости). При подаче такого разде¬
ляющего агента на орошение колонны для экстрактивной ректи¬
фикации значительная часть этой примеси попадает в отбираемый
дистиллат, ухудшая его качество. Влияние примеси «нижнего»
продукта в разделяющем агенте на качество «верхнего» продукта,
получаемого при экстрактивной ректификации, иллюстрируется
рис. 107. Как видно, с увеличением примеси бензола в разделяю¬
щем агенте необходимое число теоретических тарелок быстро
возрастает.
Большое влияние примесей в разделяющем агенте на ход и по¬
казатели процесса ректификации определяет жесткие требования
п
Рис. 107. Зависимость
числа теоретических
тарелок в укрепляю¬
щей части колонны
для экстрактивной
ректификации (п), не¬
обходимых для полу¬
чения циклогексана—
с примесью 0,011 мол.
долей бензола из сме¬
си этих веществ от
мольной доли бензо¬
ла в разделяющем
агенте — феноле (х)
(по данным работы
[326]).
105
к процессу регенерации разделяющего агента, чаще всего осуще¬
ствляемому путем обычной ректификации.
Расчет процесса регенерации разделяющего агента — типичная
задача расчета процесса ректификации без каких-либо принци¬
пиально новых элементов. Необходимо иметь в виду, что повы¬
шение требований к чистоте продуктов разделения, получаемых
в стадии регенерации разделяющего агента, не приводит к уве¬
личению энергетических затрат, но требует применения ректифи¬
кационных колонн с достаточным разделительным действием, а
также применения методов контроля и регулирования процесса,
обеспечивающих достижение необходимых показателей.
МАССООБМЕН
В ПРОЦЕССАХ АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Процессы азеотропной ректификации с гомогенной жид¬
кой фазой по условиям массообмена совершенно аналогичны про¬
цессам обычной ректификации. Специфичны в этом отношении про¬
цессы гетероазеотропной и экстрактивной ректификации. Особен¬
ность первых заключается в том, что в ректификационной колонне
имеются, кроме паровой, две жидкие фазы, и эффективность разде¬
ления определяется условиями массообмена между всеми тремя
фазами. Особенность процессов экстрактивной ректификации за¬
ключается в том, что, в противоположность обычной, расход жидко¬
сти, как правило, в несколько раз превышает расход пара в ко¬
лонне. Присутствие больших количеств разделяющего агента,
отличающегося по свойствам от компонентов исходной смеси,
обусловливает уменьшение концентрации последних и резко изме¬
няет физические свойства раствора. В некоторых случаях в колонне
могут образовываться две жидкие фазы. Указанные факторы долж¬
ны оказывать влияние на эффективность массообмена.
В промышленности для проведения процессов экстрактивной
ректификации наибольшее применение получили тарельчатые ко¬
лонны. Влияние различных факторов на коэффициент полезного
действия колпачковых тарелок было исследовано Грозе с соавто¬
рами [332] на специально сконструированной установке. Основной
ее частью являлась колонна внутренним диаметром 330 мм, в кото¬
рой на расстоянии 600 мм друг от друга находились 10 тарелок
Каждая из них имела 13 круглых колпачков диаметром 42 мм
с трапецеидальными прорезями. Тарелки были моделью используе¬
мых в промышленных колоннах для экстрактивной ректификации
в производстве бутадиена. Исследование проводилось на примере
разделения смесей изобутана и бутена-1 с использованием в каче¬
стве разделяющего агента как безводного фурфурола, так и фур¬
фурола, содержащего до 9 вес.% воды. Концентрация углеводоро¬
дов в жидкости изменялась от 12 до 27 мол.%, температура от 44
до 66° С, избыточное давление от 2,8 до 7,1 ат, расход разделяю¬
306
щего агента — от 34 до 144 л/мин, высота барботажного слоя — от
74 до 94 мм.
Установка представляла собой модель исчерпывающей части
экстрактивно-ректификационной колонны. Отбираемый из верха
колонны пар конденсировали, конденсат смешивали с жидкостью,
отбираемой из куёа, и эту смесь подавали на верхнюю тарелку
колонны. При установившемся режиме измеряли расходы мате¬
риальных потоков и отбирали пробы жидкости и пара с каждой та¬
релки. Опытные данные обрабатывали графическим методом Мак-
Кеба и Тиле, поскольку исходная смесь являлась бинарной и отно¬
сительная летучесть разделяю¬
щего агента сравнительно ма¬
лой. Данные опытов показали,
что рабочая линия процесса
экстрактивной ректификации,
выраженная в относитель¬
ных концентрациях изобутана
в углеводородной смеси, во
всех случаях близка к пря¬
мой.
По опытным данным рас¬
считывали коэффициенты по¬
лезного действия Мэрфри и по
значениям последних опреде¬
ляли общие к. п. д. тарелок
[94]. Эти величины определя¬
лись как средние для 2-й — 5-й
тарелок, считая от куба. Верхние 5 тарелок не принимались в рас¬
чет, так как на них концентрация углеводородов изменялась не¬
значительно. Первая от куба тарелка не принималась в расчет
вследствие того, что температура на ней была значительно выше,
чем на других тарелках.
Результаты опытов приводятся на рис. 108 в виде зависимости
среднего к. п. д. от величины F = UYpn (где U—скорость пара
в свободном сечении колонны, м/сек\ рп — плотность пара, кг/мг.
Из рис. 108 следует, что найденные значения к. п. д. лежат в пре¬
делах 39—51%. Для одной серии опытов" эти значения различаются
па 7—11%. Изменение производительности в исследованных пре¬
делах мало влияет на к. п. д. тарелок. Небольшая тенденция к по¬
нижению к. п. д. тарелок с увеличением производительности наблю¬
дается для серии опытов с безводным фурфуролом при 60° С и
с водным фурфуролом при наличии одной жидкой фазы на тарел¬
ках (серии I и III), тогда как в опытах с безводным фурфуролом
при 43° С (серия II) и с водным фурфуролом при наличии двух
жидких фаз (серия IV) наблюдается некоторое увеличение к. п. д.
с ростом F. Уменьшение к. п. д. с повышением скорости пара обычно
обусловлено уносом жидкости и ухудшением ее контакта с паром.
Влияние этих факторов компенсировалось увеличением высоты
П п.
0,6
0,5
OA
*0,08 0,16 0,24 0,32 0,40 0,48 0,56 0,64 0,12
Рис. 108. Данные опытов по определе¬
нию к. п. д. колпачковой тарелки:
О — серия I (разделяющий агент — безводный
фурфурол; t = 60° С); Δ — серия II (разделяющий
агент — безводный фурфурол; f = 43°C); □ — се¬
рия III (разделяющий агент — фурфурол с
4 вес. % воды); О — серия IV (разделяющий
агент —фурфурол с 6 — 9 вес.% воды).
д
□<
Δ
о
о
Г
Δ
о
TV-
>
о
8'1 .
сУ
С
~Сг~
Cv
I
о
□
"I
U
□
I
307
барботажного слоя, сопровождавшим увеличение скорости пара.
Так, при Zr = OiIOe и F = 0,41 высота барботажного слоя равна
соответственно 74 и 94 мм. Влияние понижения температуры с 60
до 43° С практически не обнаруживается. По-видимому, ухудшение
массообмена, связанного с повышением вязкости жидкости, ком¬
пенсируется увеличением поверхности контакта фаз вследствие
соответствующего возрастания расхода пара, вызванного пониже¬
нием давления.
Из рис. 108 следует также, что добавка воды к фурфуролу не
влияет на к. п. д. тарелок. Действие этого фактора в условиях про¬
ведения опытов было аналогично влиянию температуры. Так, при
добавке к фурфуролу 4 вес.% воды вязкость раствора умень¬
шается примерно на 10%, но для поддержания принятой темпе¬
ратуры требуется поддерживать давление на 30% выше давле¬
ния, получающегося при применении безводного фурфурола. При
F = const это соответствует уменьшению объемного расхода пара
JHa 14%.
С целью выяснения относительного влияния сопротивлений
массопередаче в паровой и жидкой фазах Герстер и Кольборн
[333] исследовали процессы десорбции кислорода из воды, а также
увлажнения воздуха на тарелках описанной выше конструкции.
На основании полученных данных они пришли к заключению,
что zU сопротивления массопередаче при экстрактивной ректифи¬
кации смесей углеводородов C4 с фурфуролом приходится на долю
жидкой фазы.
Полученные в описанных исследованиях значения к. п. д. таре¬
лок удовлетворительно согласуются с результатами испытания про¬
мышленных колонн для разделения смесей углеводородов C4 путем
экстрактивной ректификации с водным фурфуролом как разделяю¬
щим агентом [334]. С учетом уточненных данных о равновесии меж¬
ду жидкостью и паром в системах углеводороды C4 — фурфурол
средние значения к. п. д. тарелок в промышленных колоннах состав¬
ляют примерно 40%.
Имеются результаты испытания колпачковых тарелок в про¬
мышленной колонне для выделения толуола из смесей с неарома¬
тическими углеводородами путем экстрактивной ректификации
с применением фенола в качестве разделяющего агента [335]. Ко¬
лонна диаметром 2,13 м имела 65 колпачковых тарелок, располо¬
женных на расстоянии 450 мм друг от друга. Из полученных опыт¬
ных данных следует, .что относительные расходы углеводородной
части пара и жидкости, а также концентрация разделяющего аген¬
та практически постоянны по высоте колонны. Это обусловлено
близостью температур кипения углеводородов и малой относитель¬
ной летучестью разделяющего агента. Среднее значение к. п. д. та¬
релки составляет 50%.
Гарнер, Эллис и Гренвил исследовали влияние различных фак¬
торов на эффективность массообмена в васадочной колонне при
обычной и экстрактивной ректификации смеси метилциклогексана
308
и толуола [336]. Опыты по экстрактивной ректификации проводи¬
лись с использованием фурфурола в качестве разделяющего агента.
Колонна диаметром 50 мм и высотой 6,7 м имела 8 секций, в каж¬
дой из которых находился слой колец Рашига 6X6мм высотой
530 мм. Зависимость высоты насадки, эквивалентной одной
теоретической тарелке
(ВЭТТ), от скорости пара
при экстрактивной ректи¬
фикации (рис. 109) имеет
такой же характер как и
при обычной ректифика¬
ции. В области малых
нагрузок увеличение рас¬
хода пара в колонне при¬
водит вначале к возрас¬
танию ВЭТТ, что связа¬
но с уменьшением вре¬
мени контакта жидкости
и пара. При дальнейшем
возрастании нагрузки
увеличивается задержка
жидкости на насадке и степень турбулизации пара и жидкости.
Это обусловливает улучшение условий массообмена и понижение
ВЭТТ. Оптимальные условия массообмена имеют место при таких
расходах пара и жидкости, когда эф¬
фективная смоченная поверхность на¬
садки максимальна. Скорость пара,
отвечающая этим условиям, может
быть названа скоростью оптимальной
нагрузки U0.
Найденная в опытах зависимость
эффективности массообмена от отно¬
шения скорости пара в колонне к ско¬
рости оптимальной нагрузки (считая
на свободное сечение колонны) при
различных концентрациях разделяю¬
щего агента в жидкой фазе представ¬
лена на рис. 110. По оси ординат отло¬
жена величина (ВЭТТ/т) (VIW)7 где
т — средний угол наклона кривой
равновесия, а У и W — углеводород¬
ные части расходов пара и жидкости.
Из рис. HO следует, что при значениях UjU0= I эффективность
массообмена практически не зависит от концентрации разделяю¬
щего агента в жидкой фазе. В противоположность этому при
U/Uq > I рост концентрации разделяющего агента вызывает рез¬
кое уменьшение эффективности колонны, вследствие увеличения
' задержки жидкости в насадке.
Рис. HO. Влияние концентра¬
ции разделяющего агента на
эффективность массообмена в
насадочной колонне.
Цифры на кривых означают моляр¬
ную концентрацию фурфурола в
жидкости.
В,мп
Рис. 109. Зависимость высоты насадки, экви¬
валентной теоретической тарелке, от удельного
расхода пара:
Л— удельный расход пара, кгЦм2 · ч); В —отношение
высоты насадки; эквивалентной теоретической тарелке,
к среднему углу наклона кривой равновесия.
309
Из анализа опытных данных следует, что основное значение
при экстрактивной ректификации имеет сопротивление массопере-
носу в жидкой фазе.
Получено следующее эмпирическое уравнение для определения
ВЭТТ при скорости оптимальной нагрузки
где d — определяющий размер насадки, см.
Очевидный недостаток этого уравнения заключается в том, что
оно не отражает влияния физико-химических свойств материаль¬
ных потоков на эффективность массообмена.
Исследование кинетики массообмена при экстрактивной ректи¬
фикации в насадочной колонне продолжено в работе [337].
Опыты проводились со смесями бензола и четыреххлористого
углерода в колонне диаметром 39 мм с насадкой из колец Рашига
5 X 5 X 1,5 мм высотой 1,03 м. Чтобы выявить влияние разделяю¬
щего агента на кинетику массопереноса и исключить его влияние
на фазЬвое равновесие применяли неэффективные разделяющие
агенты, практически не влияющие на условия распределения ком¬
понентов между жидкостью и паром. Было найдено, что такими
веществами являются фенол, анилин, фурфурол, нитробензол и
хлорбензол.
Выполнено восемь серий экспериментов в безотборном режиме
при постоянном расходе разделяющего агента и переменном [(от 2
до 20 кмоль/ (м2-ч)] расходах пара и жидкости, а также при по¬
стоянном расходе исходной смеси 1,8 кмоль/(м2 -ч) и переменном
[от 0 до 4,7 кмоль/(м2-ч)] расходе разделяющего агента.
На основании анализа полученных опытных данных сделано
заключение, что основное сопротивление массопереносу при
экстрактивной ректификации создается со стороны жидкости.
Зависимости высоты единицы переноса массы от расходов жидко¬
сти (и пара) и разделяющего агента представлены на рис. 111.
Как видно, каждая кривая состоит из двух ветвей — восходящей
и нисходящей. Граница между ними отвечает отношению скорости
пара в колонне к скорости, соответствующей оптим-альной на¬
грузке, равному 0,57. Данные о кинетике массообмена описы¬
ваются следующими уравнениями:
ВЭТТ = 11 md (VIW)
(526)
при U/Uо < 0,57
0,0005787
(527)
1+0,2421 (PIWfj85
при U/U& > 0,57
Sh.
I +0,3317 (Р/Г)0'795
0,0003573 р 1,245 о 0,6
оою/п/ГС7\0 795 ^ ж ж
(528)
где Shjii = ^ж^ж/ёУ^ж — критерий Шервуда для жидкости; Rem =
= 4/,/3,6йрж — критерий Рейнольдса; Scm = рж/уш^ш — критерий
Шмидта; Km — коэффициент массоотдачи в жидкой фазе,
кг/(м2-ч); μ^κ — динамическая вязкость жидкости, кг!{м-ч)\ ут—
плотность жидкости, кг/ж3; D'm—динамический коэффициент диф¬
фузии жидкости, кг/(м-ч); L — массовый расход жидкости,
кг/(ж2-ч); а — удельная поверхность насадки, м2\мъ\ Dm— кинема¬
тический коэффициент диффузии жидкости, м2/ч.
Эффективность ситчатых тарелок в условиях процесса экстрак¬
тивной ректификации была исследована в работах [338] и [339].
В работе [338] испытывалась колонна диаметром 100 мм с 26
тарелками с отверстиями диаметром I мм и живым сечением 16%.
Опытами по обычной ректификации смесей бензола с четыреххло¬
ристым углеродом и толуола с гептаном было установлено, что
м? час
Рис. 111. Зависимость высоты единицы переноса массы Hov, м, от мо¬
лярного расхода пара V и жидкости W (в безотборном .режиме V = Wt
кмоль/(м2 · ч) при различных расходах разделяющего агента Gt кмоль/(м2 · ч):
О-с =0,607; A-G = 0,930; D-G = Ijei; X-G= 1,556; #-G = 1,861; V-G= 2,324;
■ - G = 3,118; *--0 = 4,666.
при бесконечно большом флегмовом числе при расходах жидко¬
сти 800—3000 мл/ч к. п. д. тарелок равен соответственно 64—66 и
67—69%. При флегмовых числах 4—17 для системы толуол —
гептан к. п. д. тарелок колебался от 60 до 65%. Опыты по экстрак¬
тивной ректификации смесей толуола и гептана в присутствии фе¬
нола показали, что с увеличением концентрации последнего массо-
обмен ухудшается. Это приводит к понижению к. п. д. до 58,6%
при концентрации фенола в жидкой фазе 30 мол.% и до 41,6 мол.%
при концентрации фенола 75 мол.%. Главная причина уменьше¬
ния к. п. д. тарелок — повышение вязкости жидкости на тарелках
с ростом концентрации фенола. При концентрации последнего
60—88 мол.% к. п. д. тарелок составляет 50—40%.
311
КП.8t %
В работе [339] исследовался процесс ректификации расслаи¬
вающихся систем этиловый спирт — вода — хлорбензол и этило¬
вый спирт — вода — толуол в колонне диаметром 170 мм с шестью
ситчатыми тарелками с отверстиями диаметром 2 мм. Доля жи¬
вого сечения от общей площади тарелки составляла 9%. Опыты
проводили при бесконечном флегмовом числе и таких условиях,
чтобы на тарелках находились две жидкие фазы. Это особенно
интересно, поскольку часто .высокоэффективные разделяющие
агенты, применяемые в процессах
азеотропной и экстрактивной ректифи¬
кации, ограниченно смешиваются с
компонентами заданной смеси. Между
тем, по поводу применения таких раз¬
деляющих агентов в литературе
имеются противоречивые мнения.
В рассмотренной выше работе [332]
по изучению кинетики массопереноса
на колпачковых тарелках при экстрак¬
тивной ректификации смесей углево¬
дородов C4 с фурфуролом как разде¬
ляющим агентом часть опытов прове¬
дена при наличии на тарелках двух
фаз — водной и фурфурольно-углево-
дородной (серия IV, рис. 108). Срав-
Рис. 112. Зависимость к. п. д.
барботажной тарелки от кон¬
центрации бутилацетата в воде
при различной интенсивности
барботажа (в вт):
X-130; 0-180; Δ-200.
ными опытов III серии, проведенных
с гомогенными растворами на тарел¬
ках, показывает, что значения к. п. д.
тарелок практически одинаковы. Это
позволяет заключить, что при имевшем
место в проведенных опытах хорошем
диспергировании жидких фаз за счет
динамического воздействия парового потока, образование на тарел¬
ках двух жидких фаз не оказывает влияния на величину к. п. д.
тарелок. Этот вывод согласуется с данными Шенборна [340], полу¬
ченными при ректификации смесей толуола и трихлорэтилена
в присутствии и в отсутствие воды. При плохом перемешивании
жидкости образование двух жидких фаз на тарелках может при¬
водить к понижению к. п. д. тарелок [341].
Данные опытов по ректификации * смесей этилового спирта и
воды и хлорбензолом и толуолом в колонне с ситчатыми тарел¬
ками [339] показывают, что с увеличением скорости пара в ко¬
лонне коэффициент массоотдачи в паровой фазе увеличивается.
Величина его оказывается близкой к значению коэффициента
массоотдачи, при соответствующей скорости, при ректификации
бинарной смеси этиловый спирт — вода. Следовательно, наличие
двух жидких фаз на тарелке ректификационной колонны не ока¬
зывает существенного влияния на коэффициент массоотдачи в щ-
робой фазе. Опытные данные о KiiHefHke Масбойерёдачй на
тых тарелках при наличии двух жидких фаз описываются крите¬
риальным уравнением
Nun - 1,95 ReJ7 PrJ5 We"*0’38 (529)
где Nun = 22,4(βπΛ(ϊτ/Αι) —диффузионный критерий Нуссельта
для паровой фазы; Ren = Т^п/гстУж/9,81цп — критерий Рейнольдса
для паровой фазы; We == о//г^туж — критерий Вебера; βπ— коэффи¬
циент массоотдачи в паровой фазе, кмоль/{м2 · ч); Dn— средний
коэффициент диффузии в паровой фазе, м2/ч; Wn — скорость пара
в свободном сечении колонны, м/сек; Acт = APcт/уж— высота ста¬
тического слоя жидкости на тарелке, принятая за определяющий
линейный размер, м; АРСт — сопротивление статического слоя
жидкости, кг/м2; а — поверхностное натяжение, кг/м.
Влияние разделяющего агента в уравнении (529) учитывается
введением фиктивного коэффициента диффузии, рассчитываемого
по способу, описанному в работе [342]. Если его определение за¬
труднено, то рекомендуется [339] выражать критерий Нуссельта
в уравнении (529), пользуясь коэффициентом диффузии в бинар¬
ной системе Duq с помощью соотношения
Nun = 22,4 ■ ■ Pn-- · (530)
\-X9 Da6 '
где Xpмолярная доля разделяющего агента в жидкой фазе.
В работе [343] на основании исследования гидродинамического
режима в колонне при ректификации расслаивающихся смесей
показано, что даже такие взаимно нерастворимые вещества, как
циклогексан и вода, находятся в виде эмульсии и градиент кон¬
центраций по высоте слоя жидкости на тарелке отсутствует. Бла¬
годаря большой поверхности контакта фаз и их активному пере¬
мешиванию создаются благоприятные условия для маесопередачи.
Однако в соответствии с имеющимися в литературе сведения¬
ми, есть основание считать, что указанное выше положение спра¬
ведливо лишь при таких соотношениях количеств жидких фаз,
которые обеспечивают возможность развития достаточной меж-
фазной поверхности. Если количество одной из жидких фаз мило
по сравнению с количеством другой жидкой фазы, то эффектив¬
ность тарелки может понижаться. В этом отношении представ¬
ляют интерес данные работы [344] по исследованию кинетики
отгонки бутилацетата из разбавленных водных растворов при бар-
v ботаже через них водяного пара. При наличии двух жидких фаз
в системе бутилацетат — вода образуется гетероазеотроп, сод ер-
жащий 73 вес.% бутилацетата. Растворимость последнего в воде
при температуре кипения равна 0,67 вес.%. Следовательно,
при достижении равновесия между жидкими и паровой фазами
при валовой концентрации бутилацетата в жидкости более
0,67 вес.% пар во всех случаях должен был бы содержать 73 вес.%
313
бутилацетата. Эффективность барботажного устройства, испытан¬
ного в работе [344], оценивалась значением к. п. д., вычислявшегося
как отношение истинной концентрации бутилацетата в паре к рав¬
новесной. Полученные опытные данные представлены на рис. 112.
Кривые относятся к различной интенсивности барботажа, оцени¬
вавшейся электрической мощностью, подводимой к испарителю
для получения водяного пара, барботировавшего через слой смеси
бутилацетата и воды.
Как видно из рис. 112 к. п. д. тарелки уменьшается с убыва¬
нием концентраций бутилацетата в жидкости и увеличением ин¬
тенсивности барботажа. Приведенные данные могут быть интер¬
претированы следующим образом. Поскольку количество жидкой
фазы, богатой бутилацетатом, мало по сравнению с количеством
водной фазы, пар в основном находится в контакте с последней.
Убыль бутилацетата в водной фазе за счет его перехода в пар
компенсируется переносом из жидкой фазы, богатой бутилацета¬
том. При малых относительных количествах этой фазы лимити¬
рующим фактором является массоперенос между жидкими фазами
вследствие малой поверхности контакта между ними. При увели¬
чении этой поверхности с ростом валовой концентрации бутилаце¬
тата в жидкости относительное влияние массопереноса между
жидкими фазами уменьшается, и при некоторой концентрации
бутилацетата к. п. д. тарелки перестает зависеть от содержания
последнего. t
Приведенные данные показывают, что взаимная растворимость,
относительное содержание жидких фаз и кинетика массообмена
между ними могут оказывать существенное влияние на эффек¬
тивность ректификационных колонн при наличии двух жидких
фаз. Этот вопрос нуждается в более подробном исследовании.
СОПОСТАВЛЕНИЕ АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Из рассмотренных выше (гл. II) физико-химических
закономерностей следует, что как при экстрактивной, так и при
азеотропной ректификации определяющим фактором является из¬
менение относительной летучести компонентов заданной смеси за
счет изменения степени неидеальности системы, вызываемого при¬
сутствием разделяющего агента.
Мерой отклонения от идеального поведения являются коэффи¬
циенты активности, изменение отношения которых характеризует
эффективность разделяющих агентов, применяемых как в процес¬
сах экстрактивной, так и в процессах азеотропной ректификации.
Оба рассматриваемых процесса имеют, следовательно, одну
общую физико-химическую природу; отличие же между ними по¬
рождается различным соотношением температур кипения компо¬
нентов заданной смеси и разделяющего агента. Для азеотропной
ректификации последний выбирается так, чтобы он образовывал
314
азеотропные смеси с компонентами, которые желательно отогнать.
Наоборот, в процессах экстрактивной ректификации стремятся
к тому, чтобы разделяющий агент не образовывал азеотропов
с компонентами заданной смеси, так как в противном случае за¬
трудняется отделение последних от разделяющего агента.
Эти особенности процессов азеотропной и экстрактивной рек¬
тификации и составляют наиболее существенное различие между
ними. В процессах азеотропной ректификации возможно почти
весь разделяющий агент выделить в виде азеотропов в качестве
дистиллата, получив в кубе один или несколько компонентов за¬
данной смеси (высококипящие компоненты),, практически не со¬
держащие разделяющего агента. В процессах же экстрактивной
ректификации почти весь разделяющий агент отводится из куба
колонны вместе с высококипящими компонентами, а в практически
чистом виде выделяются один или несколько компонентов (низко-
кипящие компоненты), отгоняемых в качестве дистиллата. Однако
и в этом отношении между рассматриваемыми процессами нет рез¬
кой границы. Возможен промежуточный случай, когда высококи-
пящий разделяющий агент образует азеотропы с отгоняемыми
компонентами. При этом в процессе ректификации часть разде¬
ляющего агента отгоняется в составе азеотропов, а часть отби¬
рается в виде кубовой жидкости. Такие процессы сочетают в себе
признаки процессов азеотропной и экстрактивной ректификации
и поэтому могут быть названы процессами азеотропно-экстрактив-
ной ректификации. Они могут реализовываться при использовании
в качестве разделяющих агентов не только индивидуальных ве¬
ществ, но и смесей.
Легко видеть, что различие между азеотропной и азеотропно-
экстрактивной ректификацией обусловлено только различием в
соотношении расходов исходной смеси, флегмы и разделяющего
агента. Если относительный расход последнего таков, что практи¬
чески весь вводимый в колонну разделяющий агент отгоняется,
то мы имеем дело с азеотропной ректификацией. При увеличении
же расхода разделяющего агента последний будет частично по¬
падать в кубовую жидкость, т. е. будет иметь место процесс
азеотропно-экстрактивной ректификации. Следует подчеркнуть, что
существенным недостатком такого процесса является усложнение
технологического оформления за счет необходимости регенерации
разделяющего агента как из кубовой жидкости, так и из ди¬
стиллата.
В связи с тем, что азеотропы имеют при заданном давлении
вполне опоеделенный состав, появляется естественное ограничение
в концентрации разделяющего агента по высоте колонны, в кото¬
рой проводится процесс азеотропной ректификации. На сколько-
нибудь значительной высоте колонны эта концентрация не может
быть выше азеотропной, так как стремление перейти этот рубеж
за счет увеличения подачи разделяющего агента неизбежно долж¬
но привести к концентрированию разделяющего агента в кубе.
315
Это с очевидностью вытекает из того факта, что разделяющий
агент всегда имеет меньшую относительную летучесть, чем поло¬
жительные азеотропы, образуемые им с компонентами заданной
смеси. Таким образом, выбор веществ, пригодных в качестве раз¬
деляющих агентов, для азеотропной ректификации более ограни¬
чен, чем для экстрактивной, так как для последней отпадает огра¬
ничение в отношении температуры кипения, налагаемое условием
образования азеотропов. Благодаря применению в процессах эк¬
страктивной ректификации относительно высококипящего разде¬
ляющего агента его концентрация в колонне легко может изме¬
няться в широких пределах путем изменения расхода этого агента.
Как указывалось, роль разделяющего агента при экстрактив¬
ной и азеотропной ректификациях сводится только к изменению
относительной летучести компонентов заданной смеси. Отсюда
естественно стремление уменьшить расход тепла на испарение раз¬
деляющего агента. В процессах азеотропной ректификации иногда
! стремятся добиться этого, применяя в качестве разделяющих
агентов такие вещества, концентрация которых в образуемых ими
азеотропах мала. При этом, однако, упускают из вида, что" эф¬
фект, получаемый от присутствия разделяющего агента, возра¬
стает с его концентрацией. Поэтому, если концентрация разделяю¬
щего агента в азеотропах, а следовательно, и в колонне, мала, то
такой разделяющий агент7 не может сильно повышать коэффи¬
циент относительной летучести заданной смеси. В связи с этим
в процессах азеотропной ректификации чаще всего в качестве раз¬
деляющих агентов используют вещества, температура кипения
которых близка или ниже температуры кипения отгоняемых ком¬
понентов. Чем ниже температура кипения такого разделяющего
агента, тем больше его концентрация в азеотропах.
В результате сопоставления методов азеотропной и экстрак¬
тивной ректификации установлено, что первый метод имеет суще¬
ственные недостатки:
1) необходимость применения разделяющих агентов с большой
относительной летучестью, что сопряжено с расходом тепла на их
испарение;
2) более узкий выбор разделяющих агентов в связи с ограни¬
чениями, налагаемыми условиями образования азеотропов;
3) более сложное технологическое оформление процесса ввиду
необходимости регенерации разделяющего агента из азеотропов;
4) практическая невозможность варьировать концентрацию
разделяющего агента в колонне, так как-последняя определяется
составами образующихся азеотропов.
Такие значительные недостатки азеотропной ректификации мо¬
гут породить сомнение в целесообразности ее практического ис¬
пользования, поскольку часто разделение возможно как путем
азеотропной, так и путем экстрактивной ректификации. В послед¬
нем случае в качестве разделяющего агента применяют веще¬
ство с более высокой температурой кипения, чем аналогичное, ис-
316
пользуемое при азеотропной ректификации. Однако применение
азеотропной ректификации предпочтительно в следующих случаях:
1) при необходимости выделить в чистом виде «высококипя-
щие», а не низкокипящие компоненты;
2) при термической нестойкости одного или нескольких ком¬
понентов заданной смеси. В этом случае метод азеотропной ректи¬
фикации позволяет проводить процесс разделения при более низ¬
ких температурах, чем при использовании экстрактивной ректифи¬
кации;
3) при относительно малом количестве исходной смеси и
легкой регенерации разделяющего агента путем расслаивания бла¬
годаря образованию им гетероазеотропов с «низкокипящими»
компонентами;
4) при желательности в силу тех или иных условий периоди¬
ческого проведения разделения; метод экстрактивной ректифика¬
ции в периодическом оформлении чрезвычайно неудобен.
Кроме того, азеотропная ректификация удобна как метод
очистки целевого продукта от сравнительно небольшого количе¬
ства примесей, которые могут быть отогнаны в виде дистиллата.
Таков, например, метод получения безводного этилового спирта
путем отгонки воды с использованием в качестве разделяющего
агента бензола.
Для производств крупного масштаба, в которых требуется не¬
прерывное проведение процесса разделения и обеспечение макси¬
мально возможной экономии тепла, предпочтителен метод экстрак¬
тивной ректификации.
ПРИМЕНЕНИЕ МЕТОДОВ
АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
В настоящее время методы азеотропной и экстрактивной
ректификации находят применение для решения разнообразных
задач по разделению жидких смесей. Их используют не только
в тех случаях, когда неприменима обычная ректификация, но и
для интенсификации процессов разделения, которые могут осу¬
ществляться этим способом.
Появление методов азеотропной и экстрактивной ректифика¬
ции было обусловлено, в первую очередь, необходимостью разде¬
ления смесей близкокипящих углеводородов в связи с широким
развитием химического использования нефти и природных газов.
Эта огромная проблема остается одной из важнейших областей
применения методов азеотропной и экстрактивной ректификации.
Другое, важнейшее направлениё — выделение и очистка разнооб¬
разных продуктов органического синтеза. В рамках настоящей
книги не представляется возможным' рассмотреть все известные
многочисленные практические применения методов азеотропной и
317
экстрактивной ректификации. В таблице, приводимой в приложе¬
нии (стр. 341), дается аннотированная сводка работ по данному
вопросу. Указаны система, подвергаемая разделению, разделяю¬
щие агенты и ссылка на оригинальную работу, в которой можно
почерпнуть более полные сведения о процессе разделения *.
Здесь мы ограничимся лишь некоторыми общими положе¬
ниями.
Процессы азеотропной и экстрактивной ректификации почти
никогда не используются самостоятельно, а являются стадиями
технологических процессов разделения смесей. Естественно, по¬
этому, что эффективность и показатели процессов азеотропной и
экстрактивной ректификации в большой степени зависят· от пока¬
зателей предшествующих и последующих стадий. Так, для успеш¬
ного выделения путем азеотропной и экстрактивной ректификации
отдельных веществ из многокомпонентных смесей, например из
смесей углеводородов, важнейшее значение имеет предваритель¬
ное выделение узкой фракции, являющейся в указанных процес¬
сах исходной смесью. Состав этой функции определяется требова¬
ниями к целевому продукту, составом исходной смеси и особен¬
ностями процесса азеотропной и экстрактивной ректификации.
Так, экстрактивная ректификация широко применяется для выде¬
ления ароматических углеводородов из природных смесей. Послед¬
ние, кроме ароматических, содержат парафиновые и нафтеновые
углеводороды, отгоняющиеся при экстрактивной ректификации в
виде дистиллата. Наличие этих соединений с температурами, пре¬
вышающими температуру кипения ароматического углеводорода,
затрудняет разделение. Такие соединения должны быть, поэтому,
предварительно отделены, если возможно, путем обычной ректи¬
фикации. В связи с тем, что ароматические углеводороды обра¬
зуют положительные азеотропы с многими парафиновыми угле¬
водородами, фракция, выделенная путем обычной ректификации
и предназначенная для разделения путем экстрактивной ректифи¬
кации, имеет интервал температур кипения ниже температуры
кипения ароматического углеводорода. Так, например, для выде¬
ления толуола используется смесь с интервалом температур кипе¬
ния 95—IOS0C [345], а для выделения бензола — с интервалом
температур кипения 73—77°С [346]. Из этих фракций ароматиче¬
ские углеводороды выделяются путем экстрактивной ректифика¬
ции с применением полярных веществ в качестве разделяющих
агентов.
Выделение ароматических углеводородов производится по ти¬
пичной схеме непрерывного процесса экстрактивной ректифика¬
ции. В среднюю часть экстрактивно-ректификационной колонны
подают углеводородный концентрат, а на некотором расстоянии
от верха — разделяющий агент. В качестве дистиллата отбирают
* Сведения о практических применениях процессов солевой ректификации
приведены в работе [1411,
318
неароматические углеводороды, а из куба —раствор ароматиче¬
ского углеводорода в разделяющем агенте, подаваемый в сере¬
дину отгонной колонны. В последней в качестве дистиллата отби¬
рают ароматический углеводород, а из куба — разделяющий агент,
возвращаемый на орошение колонны для экстрактивной ректи¬
фикации.
Если смесь, подаваемая в колонну для экстрактивной ректифи¬
кации, недостаточно освобождена от неароматических углеводо¬
родов с температурами кипения выше, чем у ароматического
углеводорода, то последний получается с примесями этих высоко-
кипящих соединений. Для освобождения конечного продукта от
них требуется дополнительная очистка, которая может быть осу¬
ществлена с помощью обычной ректификации.
В процессах азеотропной и экстрактивной ректификации все
возрастающее применение находят комбинированные разделяю¬
щие агенты. Чаще всего одно из веществ, входящих в состав та¬
кого комбинированного разделяющего агента, ограниченно смеши¬
вается с одним или несколькими компонентами заданной смеси.
Как было показано выше, ограниченная взаимная растворимость
является проявлением больших положительных отклонений от
идеального поведения. Поэтому добавка вещества, ограниченно
смешивающегося с компонентами заданной смеси, позволяет по¬
высить селективность разделяющего агента. В процессах азеотроп¬
ной ректификации это позволяет, кроме того, упростить регене¬
рацию разделяющего агента. В процессах экстрактивной ректифи¬
кации применение таких комбинированных разделяющих агентов,
помимо благоприятного влияния на селективность, позволяет по¬
низить температуру кипения кубовой жидкости, что имеет суще¬
ственное значение, если температуры кипения компонентов задан¬
ной смеси и разделяющего агента сильно различаются. Так, при¬
меняемый для разделения смесей углеводородов С4 фурфурол при
атмосферном давлении кипит при 16ГС, а его смесь с 4 вес.%
воды — при 102° С. Использование фурфурола с добавкой воды
сильно облегчает технологическое оформление процесса экстрак¬
тивной ректификации, обеспечивая возможность применения в ка¬
честве теплоносителя водяного пара, а в качестве хладагента для
конденсации — воды.
ПРИМЕРЫ ПРИМЕНЕНИЙ
МЕТОДОВ АЗЕОТРОПНОЙ
И ЭКСТРАКТИВНОЙ РЕКТИФИКАЦИИ
Выделение бутадиена из смесей углеводородов C4. Вы¬
деление бутадиена из смесей углеводородов C4 — одна из крупных
промышленных проблем, решенных с помощью метода экстрактной
ректификации. Имеются два пути получения бутадиена на основе
использования метода экстрактивной ректификации. Первый
319
jftytb — йейосредственное выделение бутадиена из газов крекинга,
в которых он содержится в количестве ~0,5%. Второй путь — вы¬
деление бутадиена из смесей, получающихся при последователь¬
ном каталитическом дегидрировании бутана и бутиленов. В про¬
мышленности используют крупные установки по получению бута¬
диена обоими способами [334, 335].
По условиям разделения оба эти способа в принципе равно¬
ценны. В обоих случаях смеси, из которых выделяется бутадиен,
состоят из большого числа веществ. Различаются эти методы лишь
относительным содержанием компонентов в исходных смесях.
В дальнейшем рассматривается метод выделения бутадиена из
смесей, получающихся при двухстадийном каталитическом дегид¬
рировании бутана [347]. При этом отмечаются наиболее существен¬
ные отличия процесса, основанного на использовании газов кре¬
кинга в качестве исходного сырья.
Смеси, из которых выделяется бутадиен, содержат (после отде¬
ления низкокипящих компонентов — например, воДорода, метана,
этана) вещества, приведенные ниже в порядке возрастания тем¬
пературы кипения:
°с
Углеводороды C3:
пропилен —47,70
пропан —42,07
метилацетилен . '. —23,20
Углеводороды C4:
изобутан ....
изобутилен . . .
бутилен-1 . . .
бутадиен-1,3 . .
бутан
гра«с-бутилен-2
^нс-бутилен-2 .
винилацетилен .
этилацетилен . .
диацетилен . . .
диметилацетилен
Большое число компонентов, из которых многие незначительно
различаются по температурам кипения, определяет трудности раз¬
деления смесей.
Разделению смесей углеводородов C4 предшествует отгонка
низкокипящих примесей (углеводородов Сз), осуществляемая пу¬
тем обычной ректификации. Полученный при этом из катализата
процесса дегидрирования бутана концентрат состоит в основном из
бутилена-1, бутана и бутиленов, а концентрат катализата процесса
дегидрирования бутиленов содержит главным образом бутилен-1,
бутадиен-1,3, бутилены и некоторое количество бутана, иЗобутана
и изобутилена. Опыт показывает, что разделение смесей бутана и
бутиленов с помощью обычной ректификации хотя принципиально
и возможно, но невыгодно. Выделение же чистого бутадиена из
катализата дегидрирования бутиленов путем обычной ректифика-
-11,73
-6,90
-6,26
-4,41
-0,50
0,88
3,72
5,1
8.7
9.8
26,99
320
ции невозможно из-за того, что бутадиен с бутаном образует азео-
троп, который при давлении 8 ат содержит 21 мол.% бутана. Это
обстоятельство заставило обратиться к методу экстрактивной рек¬
тификации.
При выборе разделяющих агентов для смесей углеводородов С4
принималось во внимание, что в полярных веществах лучше всего
растворяются диолефины, а хуже всего — парафины. Моноолефи-
ны занимают промежуточное положение. Следовательно, полярные
вещества должны увеличивать летучесть парафинов и моноолефи-
нов по отношению к диолефинам. Принималась во внимание также
стабильность, доступность и стоимость полярных веществ. С уче¬
том этих требований на основе определения коэффициентов отно¬
сительной летучести смесей углеводородов в присутствии разных
веществ наилучшими разделяющими агентами были признаны
фурфурол, ацетон и фенол в смеси с водой.
В присутствии этих полярных веществ относительная летучесть *
отдельных углеводородов изменяется. В табл. 42 приведены зна¬
чения коэффициентов относительной летучести основных углеводо¬
родов С4 (по отношению к бутадиену-1,3) в отсутствие и в присут¬
ствии фурфурола, содержащего 4% воды [347].
Таблица 42
Коэффициенты относительной летучести углеводородов С4
в отсутствие и в присутствии водного фурфурола
Вещество
Коэффициент относительной летучести
в отсутствие разделяющего
агента
в присутствии фурфурола
с 4% воды
Изобутан
1,209
2,6
Изобутилен .
1,070
1,666
Бутилен·!
1,046
1,718
Бутадиен-1,3
1,000
1,000
Бутан
0,871
2,020
граяг-Бутнлен-2 .....
0,843
1,190
Час-Бутилен-2 ......
0,776
1,005
Рассмотрение данных табл. 42 показывает, что разделение бу¬
тана и бутиленов, а также бутана и бутадиена-1,3 с помощью
экстрактивной ректификации должно происходить сравнительно
легко. Разделение же бутана и бутилена-1 в присутствии водного
фурфурола затруднено. Поэтому в промышленном методе разде¬
ления смесей углеводородов С4 применяются как обычная, так и
экстрактивная ректификация.
Первая стадия процесса — выделение и очистка бутиленов, а
также получение практически чистого бутана, возвращаемого на
дегидрирование. Принципиальная схема этой стадии процесса
изображена на рис, ИЗ. Катализат дегидрирования бутана
11 Зак. 917
321
компримируется и из него удаляются водород и низкокипящие при¬
меси. Полученная в этой стадии процесса смесь в основном состоит
из бутана и трех изомеров бутилена. Бутадиен содержится в ма¬
лом количестве, достаточном, однако, чтобы было целесообразно
его выделение. Концентрации изобутана и изобутилена настолько
малы, что они не имеют значения при выделении бутилена.
Кроме перечисленных веществ, в смеси присутствуют также
небольшие количества соединений с .температурами кипения ниже
и выше, чем температуры кипения углеводородов C4. Эту смесь
Рис. 113. Схема процесса разделения бутан-бутиленовых смесей:
/ — ректификационная система; 2, 3, 5 — колонны; 4— система экстрактивной
ректификации.
подают в ректификационную систему /, состоящую из двух после¬
довательных колонн, по 50 тарелок в каждой. В этой системе
производится выделение бутилена-1 путем четкой ректификации.
Вместе с бутиленом-1 в виде азеотропа с бутаном отгоняется бу¬
тадиен. В дистиллате содержатся также в небольших количествах
углеводороды C3 и наиболее легкие углеводороды C4 изобутан и
изобутилен. Этот дистиллат подается в колонну 2 для отгонки
углеводородов C3. Полученная в этой колонне в виде кубовой (
жидкости смесь направляется в систему выделения бутадиена,
в которой бутилен-1 отгоняется в смеси бутиленов, направляемой
на вторую стадию дегидрирования.
Кубовая жидкость ректификационной системы I поступает в
колонну <?, имеющую 20 тарелок, для выделения пентана и других
высококипящих примесей, которые в процессе ректификации кон¬
центрируются в кубовой жидкости. Полученную в качестве дистил¬
лата смесь бутиленов и бутана подают в систему экстрактивной
322
ректификации 4, состоящую из двух последовательных колонн,
имеющих по 50 тарелок. В качестве разделяющего агента приме¬
няют фурфурол, содержащий ~6 вес.% воды. В виде дистиллата
в процессе экстрактивной ректификации получается бутан, воз¬
вращаемый на дегидрирование. Бутилены отводятся в смеси с раз¬
деляющим агентом из куба второй колонны. Эту смесь подают
в отгонную колонну 5 с 20 тарелками, в которой отгоняются бу-
бутилен -2
Рис. 114. Схема установки для выделения и очистки бутадиена.
тилены, а разделяющий агент отбирают из куба в промежуточную
емкость, из которой он возвращается в систему экстрактивной
ректификации.
При использовании в качестве исходного сырья для выделения
бутадиена газов крекинга бутилен-сырец содержит значительные
количества изобутана и изобутилена, которые отгоняются вместе
с бутиленом-1 [334]. Из этой смеси изобутилен удаляется путем
поглощения 65% серной кислоты на холоду с последующей поли¬
меризацией при нагревании. Оставшиеся же изобутан и бутилен-1
разделяются путем экстрактивной ректификации.
Вторая стадия процесса заключается в выделении и очистке
бутадиена, а также регенерации непревращенных бутиленов для
возвращения их ц стадию дегидрирования. Принципиальная схема
второй стадии процесса изображена на рис. 114. Получающаяся
при дегидрировании бутиленов смесь углеводородов комприми¬
руется и из нее удаляются водород и низкокипящие примеси ана¬
логично тому, как это делается в первой стадии процесса. Затем в
колонне I с 40 тарелками производится отгонка углеводородов C3
И*
323
от C4. При этом углеводороды C4 освобождаются также от основ¬
ной доли метилацетилена. Хотя температура кипения последнего
значительно выше, чем пропана, эти два вещества образуют поло¬
жительный азеотроп, содержащий при давлении 22,6 ат. 16 мол.%
метилацетилена. Это благоприятствует отгонке последнего. Кубо¬
вую жидкость колонны / отбирают в промежуточную емкость, от¬
куда она поступает в колонну 2, представляющую собой комбина¬
цию двух последовательно соединенных колонн, имеющих по 50 та¬
релок каждая. В колонне4 2 в качестве дистиллата отбирается
бутадиен, бутилен-1, часть бутилена-2 и бутана,"а также более ле¬
тучие углеводороды. В качестве кубовой жидкости — бутилены,
часть бутана, ацетиленовые углеводороды и высококипящие при¬
меси. Назначение этой операции — предварительное концентриро,-
вание бутадиена с целью уменьшения количества смеси, подавае¬
мой в колонну для экстрактивной ректификации, проводимой
с водным фурфуролом как разделяющим агентом. Получаемый
25% концентрат бутадиена подают в систему экстрактивной рек¬
тификации 3, состоящую из двух колонн, имеющих по 50 тарелок.
В процессе экстрактивной ректификации отгоняются изобутан,
изобутилен, бутан, бутилен-1 и часть бутиленов, которые возвра¬
щаются на дегидрирование бутиленов. В качестве кубовой жидко¬
сти отбираются растворенные в разделяющем агенте бутадиен и
часть бутиленов с примесью следов других углеводородов C4. Этот
раствор поступает в отгонную колонну 4, в которой отгоняются все
перечисленные углеводороды. Содержание бутадиена в получаю¬
щейся углеводородной смеси находится на уровне 85%. Отбирае¬
мый из куба отгонной колонны разделяющий агент возвращается
в процесс экстрактивной ректификации.
Следующий этап процесса — очистка бутадиена, осуществляе¬
мая в трех последовательных колоннах 5 с общим числом тарелок
120. В процессе ректификации бутадиен и следы соединений с бо¬
лее низкими температурами кипения (изобутан, изобутилен, бути¬
лен-1, бутан и метил ацетилен) удаляются в виде дистиллата.
Кубовая жидкость, содержащая бутилен-2, ацетиленовые углево¬
дороды C4 и высококипящие примеси, объединяется с кубовой
жидкостью колонны 2 и полученная смесь подается в колонну 6
с 20 тарелками. В этой колонне в качестве кубовой жидкости от¬
деляются углеводороды Cs и примеси с еще более высокими тем¬
пературами кипения. С целью очистки бутадиена от ацетиленовых
соединений, в частности от метилацетилена, не отогнанного в ко¬
лонне /, отбор бутадиена производится не со 120-й, а со 101-й та¬
релки. Как видно из табл. 43, при этом обеспечивается низкое
содержание ацетиленовых углеводородов в конечном продукте и
концентрирование этих примесей во флегме, отбирая небольшие
количества которой можно выводить из системы ацетиленовые уг¬
леводороды во избежание их накопления.
Как видно из приведенного описания, процессы экстрактивной
ректификации играют важнейшую роль в общем комплексе про-
324
Таблица 43-
C оста вы смесей в колонне очистки бутадиена (мол.%)
Смесь
Цис-бу¬
тилен-2
Бутан
Бута¬
диен
Бути¬
лен-1
транс-
Бути¬
лен-2
Изобу-
тален
Изобу¬
тан
Ацети¬
лен
Флегма
Жидкость
со 101-й
тарелки
0,02
0.11
0.06
0,06
95,7
98,70
1,30
0.12
0,14
0,87
0,47'
0,07
0,21
0,00
2,10
0,07
изводства бутадиена. Остановимся несколько подробнее на их
характеристике.
В обоих процессах экстрактивной ректификации углеводород- *
ную смесь подают на 50-ю тарелку, а разделяющий агент — на
96-ю, считая от куба. Оставшиеся 4 тарелки до верха колонны
обеспечивают удаление из дистиллата фурфурола, содержание ко¬
торого в углеводородных смесях должно быть минимальным. Регу¬
лирование процесса осуществляется следующим образом: устанав¬
ливаются постоянные расходы исходной смеси, флегмы и разде¬
ляющего агента и температура последнего, а регулируемым
параметром является нагрев куба. Соотношение расходов разде¬
ляющего агента и подаваемой смеси углеводородов составляет
около 12: I по объему. Надежным критерием для контроля про¬
цесса является состав углеводородной части смесей на тарелках,
промежуточных между кубами и тарелками, на которые подаются
исходные смеси углеводородов. Так, было найдено, что при 30—
35% кбнцентрации непредельных углеводородов в жидкости, отби¬
раемой с 30-й от куба тарелки колонны для разделения бутилена-2
и бутана, концентрация бутилена в бутане, получаемом в качестве
дистиллата, не превышает 3—4%, а бутилены получаются со сте¬
пенью чистоты 95—98%.
Контроль процесса экстрактивной ректификации в стадии раз¬
деления бутилен-бутадиеновых смесей производится по составу
углеводородов на 26-й тарелке. Было найдено, что при обычном
составе исходной смеси пары на 26-й тарелке должны содержать
40—50% бутадиена, что обеспечивает достаточно низкую концен¬
трацию его в дистиллате (~ 1%).
Распределение концентраций основных компонентов смесей уг¬
леводородов С4 по высоте экстрактивно-ректификационной колон¬
ны для разделения смесей бутана и бутилена-2 иллюстрируется
рис. 115, на котором состав выражен в относительных молярных
процентах углеводородов без учета наличия разделяющего агента.
Из этого рисунка видно, что наибольшее изменение концентрации
бутана и соответственно бутиленов происходит между 10 и 35-й
тарелками. В этой области и располагается точка контроля.
J25
Изменение важнейших параметров по высоте колонны экстрак¬
тивной ректификации для выделения бутадиена показано на
рис. 116. Изменение концентрации бутадиена по высоте колонны
выражается плавной кривой. Наибольшее изменение концентрации
имеет место в исчерпывающей части колонны, что показывает це¬
лесообразность расположения здесь точки контроля. Резкое изме¬
нение температуры наблюдается вблизи куба и выше точки ввода
разделяющего агента, что связано с резким изменением концентра¬
ции последнего в этих точках. Этим же объясняется некоторое из¬
менение температуры вблизи тарелки питания (50-я тарелка).
Рис. 115. Основные показатели ра- Рис. 116. Основные показатели ра¬
боты экстрактивно-ректификационной боты экстрактивно-ректификационной
колонны для разделения бутан-бути- колонны для выделения бутадиена,
леновых смесей.
По основной же части высоты колонны температура'изменяется
очень мало. Это изменение между 5 и 90-й тарелками составляет
всего около 12°, причем значительная доля перепада температур
обусловлена повышением давления от верха колонны к кубу, ко¬
торое, как видно из рис. 116, весьма существенно.
Особо следует остановиться на вопросах, связанных с длитель¬
ным использованием разделяющего агента. Хотя фурфурол яв¬
ляется термостойким веществом, но в присутствии воды, бутадиена
и других углеводородов при повышенных температуре и давлении
может происходить его полимеризация и взаимодействие с непре¬
дельными углеводородами, в частности с бутадиеном. Это вызы¬
вает потери фурфурола и необходимость удаления образующихся
продуктов реакции.
Другими источниками потерь являются утечки через неплотно¬
сти в вентилях и насосах, а также попадание фурфурола в про¬
326
дукты разделения. Общие потери, зависящие от температуры,
объема системы и концентрации углеводородов, весьма невелики
и составляют 0,01—0,02% от расхода циркулирующего фурфурола.
По данным заводских балансов, из этого количества ~60% при¬
ходится на полимеризацию, а 40%—на механические потери.
Очистка разделяющего агента от полимеров производится пу¬
тем дистилляции, которой подвергается I % от циркулирующего
количества его. При этом концентрация полимеров в разделяющем
агенте поддерживается ~1%. При выборе технологической схемы
процесса очистки разделяющего агента принималось во внимание,
что с повышением температуры, которое наблюдается при концен¬
трировании полимеров, возрастает скорость полимеризации и уве¬
личивается опасность отложения полимеров на греющих поверх¬
ностях. В связи с этим для очистки разделяющего агента был
принят метод перегонки с водяным паром. Схема установки для
очистки изображена на рис. 117,
Рис. 117. Схема установки для очистки разделяю¬
щего агента:
/, 2, 4— испарители; 3 — отстойник.
Перегонка производится в трехступенчатом противоточном ис¬
парителе. Водный фурфурол, подлежащий очистке, подается в
испаритель /, в котором он вступает в контакт с парами воды и
фурфурола, выходящими из испарителя 2. Пары, отбираемые из
испарителя Iy конденсируются, и конденсат в отстойнике 3 разде¬
ляется на два слоя. Нижний слой, богатый фурфуролом, содержа¬
щий от 4 до 6% воды, возвращается в систему экстрактивной рек¬
тификации. Водный слой содержит 9% фурфурола. Эта смесь вы¬
паривается и в виде пара подается в нижнюю часть третьей
ступени испарителя 4. Таким образом, вода, требующаяся для
очистки, циркулирует в системе, что способствует предотвращению
потерь фурфурола.
В испарителе I полимер концентрируется от I до 4%. Этот
раствор подается в испаритель 2У в котором концентрация поли¬
мера возрастает до 20%. Отсюда жидкость подается в колонну для
отгонки полимера 4У являющуюся третьей ступенью испарителя, в
которой производится окончательное отделение фурфурола от
полимера. Первые две ступени испарителя имеют греющие эле¬
менты и подачу острого пара. В третьей ступени греющий элемент
327
не установлен из-за возможности' отложения на нем полимера,
вследствие большой концентрации последнего в растворе.
Разделение смесей, получающихся в производстве жирных спир¬
тов C7—C9. При производстве жирных спиртов C7—C9 путем ката¬
литического гидрирования бутиловых эфиров жирных кислот
C7-C9 получаются сложные многокомпонентные смеси, состоящие
главным образом из бутилового спирта, спиртов C7—C9 парафино¬
вых углеводородов и воды. Углеводороды и вода — побочные про¬
дукты процесса, получающиеся за счет гидрирования спиртов. При
этом на одну молекулу углеводорода образуется молекула воды.
Задачей процесса разделения является получение конечного про¬
дукта — спиртов C7—C9, отгонка бутилового спирта, возвращаемо¬
го в стадию получения эфиров кислот C7—C9, и удаление побочных
продуктов.
Таблица 44
Свойства азеотропных смесей
бутилового спирта с углеводородами
Углеводород
Температура кипения
азеотропа, 0C
Содержание бутилового
спирта в азеотропе, мол. %
Гексан .
68,2
3,7
Гептан
93,85
22,4
Октан
108.45
54,1
Нонан
115,9
81,3
Опыт показал, что при ректификации исходных смесей полу¬
чаются фракции с температурами кипения ниже IOO0 С, расслаи¬
вающиеся после конденсации, что указывает на образование азео¬
тропных. смесей. В связи с этим прежде всего возникла необходи-
Таблица 45
Свойства трехкомпонентных азеотропных смесей, образованных
Углеводород
Температура
кипения
азеотропной
смеси, 0C
Объемы
слоя, мл
Плотность слоя d
4
верхнего
нижнего
верхнего
нижнего
Гексан
' * 61,5
69,4
2,3
0,666
0,991
Гептан
78,1
88,8
8,5
0,696
0,991
Октан .........
86,1
53,6
10,4
0,730
0,991
Нонан
90,0
20,3
6,1
0,765
0,991
328
мость исследовать свойства азеотропных смесей, образованных
нормальными парафиновыми углеводородами, спиртами и водой.
Поскольку самым низкокипящим спиртом в исходных смесях яв¬
ляется бутиловый спирт, возможные азеотропы его с углеводоро¬
дами и водой должны иметь самые низкие температуры кипения по
сравнению с азеотропами, образуемыми другими спиртами. Следо
вательно, при ректификации азеотропы, в состав которых входит
бутиловый спирт, должны отгоняться в первую очередь. Поэтому
следовало изучить свойства азеотропных смесей, образованных уг¬
леводородами (гексаном, гептаном, октаном и нонаном), бутило¬
вым спиртом и водой. Азеотропы с гексаном были включены в
число объектов исследования в связи с наличием примеси капро¬
новой кислоты СбН^Ог в исходной смеси кислот.
Определение наличия и состава азеотропных смесей бутилово¬
го спирта и углеводородов производилось [348] путем разгонки
смесей ,этих веществ на колонне с эффективностью, равной 40 тео¬
ретическим тарелкам, при прлном возврате флегмы (на смеси бен¬
зол— дихлорэтан). Результаты определения свойств азеотропных
смесей в системах бутиловый спирт—углеводород приводятся в
табл. 44.
Факт образования углеводородами и бутиловым спиртом азео¬
тропов с минимумом температуры кипения показывает, что при
ректификации смесей, получающихся в результате гидрирования
бутиловых эфиров жирных кислот, углеводороды должны выде¬
ляться во ,фракциях с температурой кипения ниже температуры
кипения бутилового спирта.
Опыты по ректификации показали, что перечисленные выше
углеводороды, бутиловый спирт и вода образуют тройные азеотро¬
пы. При определении их состава, во избежание погрешностей из-за
расслаивания, пробы отбирались из паровой фазы. Конденсат пара
расслаивали и определяли количества и составы слоев, по которым
затем рассчитывали валовой состав тройного азеотропа. Резуль¬
таты этих определений приведены в табл. 45.
бутиловым спиртом, водой и углеводородами
Содержание, вес. %
Состав азеотропа, мол. %
бутиловый спирт
вода
углеводород
в верх*
в ниж¬
в верх¬
в ниж¬
бутило¬
в верхнем
в нижнем
нем
нем
нем
нем
вый
вода
углеводо¬
слое
слое
слое
слое
слое
слое
спирт
род
3,0
' 2,0
Следы
97,0
97,0
1,0
2,9
19,2 .
77,9
9,6
2,5
0,4
96,4
90,0
1,1
7,6
41,4
51,0
26,4
1,6
1,4
96,8
72,2
1,6
14,5
60,0
25,5
44,1
2,3
4,3
36,0
51,6
1,7
18,3
69,9
11,8
W
Из полученных данных следует, что благодаря более высоким
температурам кипения бинарных азеотропов по сравнению с трой¬
ными, последние должны отгоняться в первую очередь. При этом
вначале отгоняются тройные азеотропы с нцзкокипящими углево¬
дородами, а затем — с имеющими более высокие температуры ки¬
пения. Так как углеводороды и вода содержатся в исходных смесях
в эквимолекулярных количествах, а молярная концентрация воды
в тройных азеотропах с бутиловым спиртом и соответственно окта¬
ном и нонаном больше концентрации последних, то в виде тройных
азеотропов может отгоняться только часть указанных углеводоро¬
дов. Остающиеся углеводороды следует отгонять в виде бинарных
азеотропов с бутиловым спиртом. В связи со значительным содер¬
жанием углеводородов в исходных смесях это должно приводить
к отгонке в виде азеотропов относительно большого количества
бутилового спирта. Так как последний должен возвращаться в тех¬
нологический процесс для получения эфиров жирных кислот
(а применение для этой цели смесей бутилового спирта и углево¬
дородов !невозможно), очевидна необходимость уменьшения до
минимума количества смесей бутилового спирта и углеводорода.
Из закономерности, характеризующей связь между свойствами
бинарных и тройных азеотропов, образованных компонентами с
ограниченной взаимной растворимостью, следует, что прибавление
воды к смесям бутилового спирта и углеводородов должно увели¬
чивать относительную летучесть последних, вследствие чего в трой¬
ных азеотропах содержание бутилового спирта по отношению к
углеводороду должно быть меньше, чем в соответствующих бинар¬
ных азеотропах. Сопоставление данных табл. 44 и 45 подтверждает
это положение.
Содержание бутилового спирта по отношению к октану и нона-
ну в тройных азеотропах оказывается соответственно примерно в
2 и 2,8 раза меньше, чем в бинарных азеотропах. Используя эту
закономерность, представляется возможным значительно умень¬
шить количество бутилового спирта, отгоняемого в смеси с угле¬
водородами. Для этого необходимо все углеводороды отгонять в
виде тройных азеотропов. Чтобы обеспечить возможность этого,
к исходным смесям необходимо добавлять некоторое количество
воды, зависящее от относительного содержания отдельных угле¬
водородов в исходных смесях. В производственных условиях воду
добавляют с небольшим избытком. Любопытно отметить, что для
выделения побочных продуктов — углеводородов и воды — в рас¬
сматриваемом случае оказывается в технологическом отношении
выгодным один из них— воду — добавлять к исходным смесям.
После отгонки побочных^продуктов остаются смеси спиртов с
небольшим количеством эфиров жирных кислот. Разделение этих
смесей легко осуществляется путем обычной ректификации.
С трехкомпонентными азеотропными смесями отгоняется зна¬
чительное количество бутилового спирта, который содержится
главным образом в верхнем слое, получающемся после конденса-
330
ции и расслаивания указанных азеотропных смесей. Кроме бути¬
лового спирта и углеводородов, в нем содержится небольшое ко¬
личество воды. Для выделения бутилового спирта из этих смесей
был применен метод "азеотропной ректификации. В качестве раз¬
деляющего агента выбран метиловый спирт, дающий почти идеаль¬
ные смеси с бутиловым спиртом и обладающий ограниченной
взаимной растворимостью с парафиновыми углеводородами. Бла¬
годаря этому метиловый спирт увеличивает относительную лету¬
честь углеводородов, которые отгоняются в виде азеотропов с ним.
В табл. 46 приведены экспериментальные данные о свойствах азео¬
тропных смесей метилового спирта и углеводородов.
Таблица 46
Свойства азеотропных смесей
метилового спирта и углеводородов
Углеводород
Температура кипения
азеотропной смеси, 0C
Содержание метилового спирта
в азеотропной смеси, мол. %
Г ексан
49,5
49,1
Г ептан
58,8
72,8
Октан
62,7
88,1
Нонан
64,1
95,3
Для последующего разделения смесей метилового спирта и
углеводородов было использовано резкое понижение растворимо¬
сти последних при прибавлении к смесям воды.
Исследование растворимости в трехкомпонентных системах
метиловый спирт — углеводороды — вода [349] показало, что при
добавлении ~15% воды к смесям метилового спирта и углеводо¬
родов последние выделяются практически в чистом виде в верхнем
слое, а нижний водно-спиртовой слой содержит очень мало угле¬
водородов.
На основании изложенных экспериментальных данных был
разработан используемый в промышленности метод разделения
смесей, получающихся в производстве жирных спиртов C7—Cg [97].
Принципиальная схема процесса разделения изображена на
рис. 118. Исходную смесь загружают в куб /, в который из мер¬
ника 2 добавляется требуемое количество воды. В колонне 3, снаб¬
женной парциальным дефлегматором 4, при атмосферном давле¬
нии отгоняются тройные азеотропы типа бутиловый спирт — угле¬
водород — вода, которые после конденсации в конденсаторе 5 и
охлаждения в холодильнике 6 поступают в расслаиватель 7. Из
последнего нижний водный слой направляется в емкость S, из ко- ,
торой перекачивается в отделение очистки сточных вод для выде¬
ления растворенных бутилового спирта и углеводородов. Верхний
слой поступает в емкость 9. После отгонки тройных азеотропов
вначале при атмосферном давлении, а затем под вакуумом,
331
отбирается в емкость 10 бутиловый спирт, возвращаемый в произ¬
водство. После этого отгоняются содержащиеся в исходной смеси
спирты Cs—Ce и целевой продукт — спирты C7-C9, которые через
промежуточные мерники 11 отбираются соответственно в емкости
12 и 13.
Из емкости 9 верхний слой, полученный в результате расслаи¬
вания тройных азеотропов, перекачивают в куб 14, куда из емко¬
сти 15 загружают требуемое количество метилового спирта, и в
Рис. 118. Схема процесса разделения смесей, получающихся
в производстве спиртов C7-C9:
I, 14 — кубы; 2, // — мерники; 3, 16 — колонны; 4 — дефлегматор; 5 —конден¬
сатор; 6 — холодильник; 7, 17 — расслаиватели; 8—13, 15, 18, 20—22 — емкости;
19 -приемник.
колонне 16 производят разгонку этой смеси. В первую очередь
отгоняют азеотропы метилового спирта с углеводородами, которые
поступают в расслаиватель 17 под слой воды, предварительно за¬
ливаемой из емкости 18, Затем в приемник 19 отгоняют избыток
метилового спирта, после удаления которого перегоняют в емкость
20 оставшийся в кубе метиловый спирт. Из расслаивателя 17
нижний слой, представляющий собой водный раствор метилового
спирта, сливают в емкость 2/, из которой насосом перекачивают
в куб 14 для получения безводного метилового спирта, отгоняемого
в приемник 19, Из последнего метиловый спирт передается в ем¬
кость 15 для повторного использования. Остающуюся в кубе воду
сливают. После удаления из расслаивателя нижнего слоя в ем¬
кость 22 сливают верхний слой, представляющий собой практи¬
чески чистые углеводороды.
ЛИТЕРАТУРА
1. I. W. G i b b s, The Scientific Papers, v. I, N. Y 1906.
2. А. В. C T σρ о и к и и, Термодинамика гетерогенных систем, Изд. ЛГУ, 1967.
3. В. Б. Коган, Гетерогенные равновесия, Изд. «Химия», 1968.
4. И. Д. В а н - д е р - В а а л ь с, Ф. К о н с т а м м, Курс термостатики, Химтео-
рет, 1936.
5. G. N. Lewis, Proc. Am. Acad. Arts Sci., 37, 49 (1901).
6. G. Scatchar d, С. L. Raymond, J. Am. Chem. Soc., 60, 1278 (1938).
7. В. А. Киреев, ЖФХ, 14, 1457 (1940).
8. Е. F. G. Heringt on, Nature (London), 160, 610 (1947).
9. О. Redlich, A. К. Kister, Ind. Eng. Chem., 40, 345 (1948).
10. А. Г. Касаткин, Основные процессы и аппараты химической промышлен¬
ности, Госхимиздат, I960.
11. Н. И. Гель перин, Дистилляция и ректификация, Госхимиздат, 1947.
12. Д. П. Коновалов, Об упругости паров растворов, Изд. АН СССР, 1928.
13. М. С. Вревский, Работы по теории растворов, Изд. АН СССР, 1953.
14. А. В. Сторонкин, Вестн. ЛГУ. Сер. хим., № 8, 187 (1953).
15. В. Б. Коган, ЖПХ, 30, 1863 (1957).
16. А. М. Розен, ДАН СССР, 81, 863 (1951).
17. F. Н. Garner, S. R. М. Ellis, Trans. Inst. Chem. Eng. (London), 29, 45
(1951).
18. В. Б. Коган, Хим. пром., Nb 6, 356 (1957).
19. Сб. «Физическая химия разделения смесей», вып. I, ИЛ, 1949.
20. Перегонка, под ред. А. Вайсбергера, ИЛ, 1954.
21. М. В е n е d i с t, L. С. Rubin, Trans. Am. Inst. Chem. Eng., 41, 353 (1945).
22. А. Р. С о I b и г η, Е. М. Shoenburn, ibid., 41, 421 (1945).
23. Е. G. Scheibe I, Chem. Eng. Progr., 44, 927 (1948).
24. А. Р. С о I b u г n, Canad. Chem. Proc. Ind., 34, 286 (1950).
25. G. Korttim, Chem. Ztg., 74, 151 (1950).
26. Η. Η. М. Jones, Chem. Proc. Eng., 33, 494 (1952).
27. Η. Η. М. Jones, ibid., 34, 350, 359 (1953).
28. Η. Н. М. Jones, ibid., 34, 381 (1953).
29. A. P a r i s, Ind. chim., 40, 91 (1953).
30. С. H. Обрядчиков, Производство моторных топлив, Гостоптехиздат,
1949.
31. В. Б. Коган, В. М. Фридман, В. В. Кафаров, Равновесие между
жидкостью и паром, Изд. «Наука», 1967,
32. М. R. Fenske, С. S. Carlson, D. iQuiggle, Trans. Am. Inst. Chem.
Eng., 43, 1322 (1947).
33. W. S. H а г η е у, S. S с h n е I d е г, пат. США 2511847, 1950.
34. Е. F. G. H е г i n g t о n, Nature, 170, 935 (1952).
35. Д. Г. Гильдебранд*, Растворимость неэлектролитов, Госхимиздат, 1938.
36. В/Б. Коган, ЖФХ, 29, Nb 8, 1470 (1955).
333
37. D. F. O t h m е г, М. М. Chudgar, S. L. Levy, Ind. Eng. Chem., 44, 8, 1872
(1952).
38. A. R. Fowler, Н. Hunt, ibid., 33, 90 (1941).
39. G r i g n a r d, Traite de Chimie organique, v. I, Paris, 1935.
40. A. W. Fr a nci s, Ind. Eng, Chem., 36, 764 (1944).
41. A. W. Francis, ibid., 36, 1096 (1944).
42. A. Seidel, Solubilities of Inorganic, Metallorganic and Organic Compounds,
New York, 1940.
43. В. Б. Коган, В. М. Фридман, В. В. К а ф а р о в, Справочник по раство¬
римости, т. I и 2, Изд. «Наука», 1962—1965.
44. В. В. К а ф а р о в, Л. А. Г о р д и е в с к и й, ЖПХ, 28, 176 (1956).
45. Л. Хорсли, Таблицы азеотропных смесей, ИЛ, 1951.
46. С. S. С а г I s о п, пат. США 2620294, 1952.
47. Е. F. G. Herington, Analyst, 81, 53 (1956).
48. Т. М. Reed, Anal. Chem,, 30, 221 (1958).
49. Н. R ot z sc he, Z. Anal. Chem., 175, 338 (1960).
50. С. К. Огородников, В. Б. Коган, ЖПХ, 35, 461 (1962).
51. С. К. Огородников, А. Н. Генкин, В. Б. Коган, М. С. Немцов,
Труды 2-й Всесоюзной конференции, Изд. «Наука», 1964, стр. 56.
52. Н. Rock, Chem. Ing. Techn. 7, 489 (1956).
53. G. J. Pierotti,'С. Н. Deal, Е.-L. Derr, Р. Е. Porter, J. Am. Chem.
Soc., 78, 2989 (1956).
54. A. J. P. Martin, R. L. М. Synge, Biochem. J., 35, 1358 (1941).
55. Е. Glukauf, Trans. Faraday Soc., 51, 34 (1955).
56. А. А, Ж у х о в и ц к и й, Н. М. T у р к е л ь т а у б, Усп. хим. 25, 859 (1956).
57. А. В. L i 111 е w о о d, С. S. G. Phillips, D. Т. Price, J. Chem. Soc., 1955,
1480.
58. Р. Е. Porter, С. Н. Deal, F' Н. Stros s, J. Am. Chem. Soc., 78, 2999
(1956).
59. А. К е й л е м а н с, Хроматография газов, ИЛ, 1959.
60. С. Е. Бресл ер, ЖФХ, 32, 628 (1958).
61. А. К в а и т е с, Г. P е й н д е р с, Газовая хроматография, Сборник докладов
на 2-м Международном симпозиуме в Амстердаме в 1958 г., под ред.
А. А. Жуховицкого и Η. М. Туркельтауба, ИЛ, 1960, стр. 120.
62. А. Т. J a m е s, A. J. P. M а г t i n, Biochem. J., 50, 679 (1952).
63. А. В. Киселев, Газовая хроматография, Труды 1-й Всесоюзной конферен¬
ции 1959 г., Изд. АН СССР, 1960, стр. 45.
64.'j. Bohemen, S. Н. Langer, R. Н. Perett, J. Н. Purnell, J. Chem.
Soc, 1960, 2444.
65. H. В. А к ш и н с к а я, А. В. Киселев, Ю. С. Никитин, Р. С. Пет¬
рова, В. К. Чуйкина, К. Д. Щербакова, ЖФХ, 36, 1121 (1962).
66. А. V. Kiselev, Gas Chromatography, Ed. М. van Swaay, London, 1962,
p. 34.
67. А. В. Киселев, Ю. С. Никитин, Η. K. Савинова, И. М. Савинов,
Я. И. Яшин, ЖФХ, 38, 2328 (1964).
68. С. П. Жданов, А. В. Киселев, Я. И. Яшин, Газовая хроматография,
Вып. I, изд. НИИТЭХИМ, 1964, стр. 5.
69. Д. П. Добычин, Н. В. П о р ш н е в а, Η. М. Тур кельта у б, Газовая
хроматография, Труды 2-й Всесоюзной конференции, Изд. «Наука», 1964,
стр. 69.
70. I. Sorensen, F. Soltoft, Acta chim. scand., 10, 1673 (1956).
71. I. Nelson, A. Milun, Chem. a. Ind. (London), № 23, 663 (1960).
72. R. S. Porter, J. F. Johnson, Ind. Eng. Chem., 52, № 8, 133 (i960).
73. Э. Байер, Хроматография газов, ИЛ, 1961.
74. С. Д. Ногаре, Р. С. Д ж у в е т, Газо-жидкостная хроматография, Изд.
«Недра», 1966.
75. A. Neckel, F. Kohler, Monatsh., 87; 176 (1956).
76. J. D. V a n d е г Waals, Die kontinuitat des gasformigen und flussigen
Zustandes, Amsterdam, 1881.
77. W. Н. Keesom, Phys. Z., 22, 129 (1921).
334
78. P. Debye, ibid., 21, 178 (1920),
79. P. London, Z. Phys., 63, 245, (1930).
80. M. J. S.Dewar, J. Chem. Soc., 68, 1727 (1946).
81. R. Anderson, R. Cambio, J. M. Prausnit z, Am. Inst. Chem. Eng. J.,
8, 66 (1962).
82. L. J. Andrews, Chem. Rev., 54, 713 (1954).
83. F. D о I e z a I e k, Z. phys. Chem., 64, 727 (1908). '
84. 0. R e d I i с h, A. Т. K i s t e r, J. Chem. Phys., 15, 849 (1947).
85. Я. Марек, Г. Ста н д a p т, Сборник чехословацких химических работ,
вып. 19, 1954, стр. 1047.
86. С. В. Kretscnmer, R. Wiebe, J. Chem. Phys., 22, 1697 (1954).
87. И. И. В а н - Jl а а р, Шесть лекций о термодинамическом потенциале, ОНТИ,
1938.
88. А. Е. Arkel, Trans. Faraday Soc., 42В, 81 (1946).
89. R. N. Finch, М. van Winkle, Am. Inst. Chem. Eng. J., 8, 455 (1962).
90. L. Rie del, Chem. Eng. Techn., 26, 83 (1954).
91. R. H. Ewell, L. M. Welch, Ind. Eng. Chem, 37, 1224 (1945).
92. J. Griswold, С. В. B u f f о r d, ibid, 41, 2347 (1949).
93. B. H. К о 3 л о в, С. Ф. К р ы л о в, ЖПХЛ26, 824 (1953).
94. S. Yong, J. Chem. Soc, 81, 707 (1902).
95. W. Е. Catterall, пат. США 2591671, 1952.
96. С. S. С а г I s о η, Р. V. S m i t h, пат. США 2583412, 1952.
97. В. Б. Коган, В. М. Фридман, И. В. Дейзенрот, авт. свид. 106651,
22 мая 1957 г.; Бюлл. изобрет, Лг9 5 (1957).
98. R. S. Diks, С. S. Carlson, Trans. Am. Inst. Chem. Eng, 41, 789 (1945).
99. R. H. E w e 11, J. M. Harrison, L. Berg, Ind. Eng. Chem, 36, 871 (1944).
100. J. M.Prausnitz, R. Anderson, Am. Inst. Chem. Eng. J, 7, 96 (1961).
101. R. L. Scott, Disc. Faraday Soc, № 15, 44 (1953).
102. A. Bondi, D. J. S i m k i n, Am. Inst. Chem. Eng. J, 3, 4^3 (1957).
103. G. J. P i e г о 11 i, С. H. Deal, E. L. Derr, Ind. Eng. Chem, 51, 95 (1959).
104. D. F. Booth, S. Dainton, K- J. Ivin. Trans. Faraday Soc, 55, 1293 (1959).
105. A. H. Генкин, Автореф. канд. дисс, НИФХИ им. Карпова, 1966.
106. С. Н. Deal, Е. L. Derr, М. N. Papadopoulos, Ind. Eng. Chem. Fun¬
dament, I, № I, 17 (1962).
107. С. S. Carlson, J. Stewart, Distillation, N. Y. — London, 1965, p. 423.
108. G. M. Wilson, С. H. Deal, Ind. Eng. Chem. Fundament, I, № I, 20 (1962).
109. E. A. G u g g e n h e i m, Mixtures, Oxford, 1952.
HO. S. H. Langer, JvH. Purnell, J. Phys. Chem, 67, 263 (1963).
111. М. X. K a p а п e т ь я н ц, Методы сравнительного расчета физико-химических
свойств, Изд. «Наука», 1965.
112. В. М. Сахаров, сб. «Газовая хроматография», вып. 2, изд. ГОСИНТИ,
1964, стр. 16.
113. В. М. Сахаров, Нефтехимия, 5, 762 (1965).
114. В. М. Сахаров, сб. «Газовая хроматография», Труды 3-й Всесоюзной кон¬
ференции по газовой хроматографии, Дзержинск, 1966, стр. 280.
115. В. J. N. Bronsted, К. J. Pederson, Z. Phys. Chem, 108, 185 (1924).
116. L. P. Hammett, J. Am. Chem. Soc, 59, 96 (1937).
117. Р. Тафт, в кн. «Пространственные эффекты в органической химии», ИЛ,
1960, гл. 13.
118. К. Д. Неницеску, Органическая химия, т. I, ИЛ, 1963.
119. В. А. Пальм, Основы количественной теории органических реакций, Изд.
«Химия», 1967.
120. Η. Н. J a f f е, Chem. Revs, 53, 191 (1953).
121. В. А. Пальм, Усп. хим, 30, 1069 (1961).
122. D. Н. McDamel, Н. С. Brown, J. Org. Chem, 23, 420 (1958).
123. А. А. Гайле, Автореф. канд. дисс, ЛТИ им. Ленсовета, 1968.
124. М. И. 3 а р е ц к и й, В. Б. Коган, Η. Ф. Кононов, В. Г. П о д о л ь н я к,
ЖПХ, 43, № 7, 1563 (1970).
125. Teijo YonezawafHazime Saito,Shinichi MatsuokafKemi-
che Fukui, Bull. Chem. Soc. Japan, 38, 143 (1^65); 39, 989 (1966).
335
126. М. И. Зар едкий, В. Б. К о г а ьд Η. Ф. Кононов, В. Г. Подольняк,
Ф. X. Толчинская, ЖПХ, 43, № 6, 1299 (1970).
127. Marilley, Distillation et rectification, Paris, 1925.
128. Marilley, Granger, франц. пат. 512653, 1919.
129. В. Логинов, В. Дзиркал, ЖПХ, 7, 572 (1934).
130. W. Н. Walker, W. К. Lewis, W. Н. McAdams, Е. R. Gilliland,
Principles of Chemical Engineering, New York — London, 1953.
131. R. R. Tur si, A. R. Thomson, Chem. Ing. Progr., 47, 304 (1951).
132. E. C. Novella, I. M. T a г г о s o, Anales real. soc. espan. у quim.,(Madrid),
488, 441 (1952).
133. I. Prosrt, G. К о 11 a r, Magyar kem. folyoirat, 60, HO (1954).
134. С. E. Morel I, E. R. Gilliland, канад. пат. 516100, 1955.
135. R. Shaw, I. A. V. Biftler, Proc. Roy. Soc., 129A, 811, 519 (1939).
136. A. Gyger, A. Gyger (jr.), В. K. John sen, Helv. chim. acta, 38, 108, 946
<1955).
137. L. Gar win, Κ. E. Hutchinson, Ind. Eng. Chem., 42, 727 (1950).
138. Э. Л. Черняк, ЖОХ, 8, 14—15, 1341 (1938).
139. R. M. Rieder, A. R. Thompson, Ind. Eng. Chem., 42, 379 (1950).
140. A. I. Johnson, W. E. F u r t e r, Canad. J. Techn., 34, 413 (1957).
141. И. H. Ципа^ис, Л. Л. Добросердов, В. Б. Коган, Солевая ректи¬
фикация, Изд. «Химия», 1969.
142. В. Б. Коган, С. Ф. Булушев, В. М. Сафронов, О. Ф. M о с к о в е ц,
ЖПХ, 32, 2409 (1959).
143. В. Б. Коган, Г. В. Бурова, М. С. Немцов, ЖПХ, 38, 128 (1965).
144. В. Свентославский, Азеотропия и полиазеотропия, Госхимиздат, 1938.
‘145. А. В. Сторонки н, А. Г. Морачевский, Вестн. ЛГУ, № 4, 69 (1956).
146. Ю. В. Гуриков, ЖФХ, 32, 1980 (1958).
147. W. J. Gaw, F. L. Swinton, Nature, 212, № 5059, 283 (1966).
148. W. Reinders, С. Н. de Minjier, Rec. irav. chim., 52, 207 (1940).
149. П. Я. Молоденко, И. Н. Бушмакин, Вестн. ЛГУ, JSfo ю, вып. 2, 68
(1957).
150. A. Munster, Z. phys. Chem., 195, 67 (1950).
151. W. Kuhn, Helv. chim. acta, 37, 1585 (1954).
152. J. S t e с k i, Roczn. Chem., 29, 954 (1955).
153. B. J. M air, A. R. Glasgow, F. D. Rossini, J. Res. Natl Bur. Stand.,
27, 39 (1941).
154. H. P. Meissner, S. H. Greenfi Id, Ind. Eng. Chem., 40, 438 (1948).
155. H. Sko Ini k, ibid., 40, 442 (1948).
156. R. L. Denyer, F. A. Fidler, R. A. Lowry, ibid. 41, 2727 (1949).
157. D. H. Des ty, F. A. Fidler, ibid., 43, 905 (1951).
158. L. M. Shorr, J. Appl. Chem., 14, 376 (1964).
159. W. Swietoslawsk i, Bull. Soc. chim. Belg., 62, 10 (1953).
160. Ф. Д. Россини, Б. Д. Мэйр, А. Д. С т p e й ф, Углеводороды нефти, Гое-
топтехиздат, 1957.
161. А. I. Johnson, J. A. Madonis, Canad. J. Chem. Eng., 37, 71 (1959).
162. R. F. Marschner, W. P. Cropper, Ind. Eng. Chem., 38, 262 (1946).
163. В. Б. Коган, В. М. Фридман, И. В. Дейзенрот, ЖПХ, 30, 1339
(1957).
164. R. Haase, Z. phys. Chem., 195, 362 (1950).
165. М. Lecat, L’azeotropisme, Brussel, 1918.
166. М. Lecat, Tables azeotropiques, Brussel, 1949.
167. I. К I e i n, Chem. Eng., 67( 233 (1960).
168. I. Yamada, Τ. Yoshida, O. Kawase, Bull. Chem. Soc. Japan, 32, 570
(1959).
Γ69. P. J. Horvath, Chem. Eng., 68, 159 (1961).
170. В. N. R a j u, M. N. R a о, Indian Chem. Eng., 8, № 2, 21 (1966).
171. Ю. B. Ap истов ич, Э. H. Степанова, ЖПХ, 43, JSfo 10 (1970).
172. G. М. W i I s о n, J. Am. Chem. Soc., 86, № 2, 127 (1964).
173. C.K.Smith, Ind. Eng. Chem., 34, 251 (1942).
174. F. А. Н. S с h г е i n е m a k е г s, Z. phys. Chem., 35, 459 (1900).
336
175. В. BvKoraHi ЖФХ, 29, 1984 (1955).
176. В. Б. К о г а н, Т. С. T о л с т о в а, Там же, 33, 277 (1959).
177. М. И. Розенгарт, Техника лабораторной перегонки и ректификации, Гос¬
химиздат, 1951.
178. Э. К р ель, Лабораторная техника в органической химии, Госхимиздат,
1941.
179. А. В. Сторонки н, А. Г. Морачевский, ЖФХ, 31, 42 (1957).
180. В. А. Киреев, там же, 14, 1469 (1940).
181. В. А. К и р е е в, там же, 15, 481 (1941).
182. О. Redlich, R. Schulz, J. Am. Chem. Soc., 66, 1007 (1944).
183. Е. Coulson, Е. F. G. Herington, J. Chem. Soc., 1947, 597.
184. Н. Skolnik, Ind. Eng. Chem., 43, 172 (1951).
185. D. F. Othmer, Е. Н. Ten Eyck, ibid., 41, 2897 (1949).
186. D. F. Othmer, R. Gi Imon t, ibid., 36, 858 (1944).
187. Н. S. Nutting, L. Н. Horsley, Anal. Chem., 19, 602 (1947).
188. T. Gopichan d, V. N. K. K. R a o, K* R. K. S a r m a, M. N. R a o, Trans.
Indian Inst. Chem. Eng., 6, 108 (1953—1954).
189. А. В. Сторонки и, А. Г. Морачевский, Л. С. Кудрявцева, ЖФХ,
31, 395 (1957).
190. Н. А. Смирнова, А. Г. Морачевский, А. В. Сторонкин, Вестн.
ЛГУ, No 10,72 (1960).
191. F. А. Н. Schreinemakers, Z. phys. Chem., 36, 413 (1901).
192. W. Reinders, С. Н. de Minjier, Rec. trav. chim., 59, 369, 392 (1940).
193. И. Н. Бушмакин, И. Н. Киш, ЖПХ, 30, 561 (1957).
194. R Haase, Z. Naturforsch., 4а, 342 (1949).
195. Л. А. Серафимов, ЖФХ, 42, 248 (1968).
196. S. Joung, Fractional Distillation, London, 1903.
197. Н. Lang, Z. Electrochem., 54, 438 (1950).
198. И. H. Бушмакин, И. H. Киш, ЖПХ, 30, 379 (1957).
199. W. Ostwald, Lehrbuch der allgemeine Chemie, Leipzig, 1896—1902.
200. Н. Д. Л и т в и н о в, ЖФХ, 26, 898 (1952).
201. W. Swietoslawski, Ebuliometric Measurements, New York, 1945.
202. В. Б. К о г а н, В. М. Ф р и д м а н, Т. Г. Романова, ЖФХ, 33, 1521 (1959).
203. Brown, Trans. Chem. Soc.,' 35, 547 (1879).
204. Н. R. С arveth, J. Phys. Chem., 3, 153 (1899).
205. A. E. T а у I о r, ibid., 4, 290 (1900).
206. Rauligh, Phil. Mag., (VI), 4, 521 (1902).
207. M. A. R о s a n о f f, C. W. Bacon, R. H. W h i t e, J. Am. Chem. Soc., 36, 1803
(1914).
208. D. F. Othmer, Ind. Eng. Chem., 20, 743 (1928).
209. J. S. S t о с k h a r d t, C. M. H u 11, ibid.: 23, 1438 (1931).
210. S. C. Lee, J. Phys. Chem., 35, 3558 (1931).
211. D. F. Othmer, Ind. Eng. Chem., Anal. Ed., 4, 232 (1932).
212. J. S. Carey, W. K. Lewis, Ind. Eng. Chem., 24, 882 (1932).
213. W. A. Wright, J. Phys. Chem., 37, 233 (1933).
214. R. M. Willey, E. H. Harder, Ind. Eng. Chem., Anal. Ed., 7, 349 (1935).
215. A. S. B r u n j e s, С. C. Furnas, Ind. Eng. Chem., 27, 396 (1935) .
216. Η. M. Trimble, W. Potts, ibid., 27, 66 (1935).
217. H. W. Schee line, E. R. Gilliland, ibid., 31, 1050 (1939).
218. E. Baker, R. О. H. Hubbard, I. H. Huguet, S. S. Michailowski,
Ind. Eng. Chem., 31, 1260 (1939).
219. W. R e i n d e r s, C. H. d e Minjier, Rec. trav. chim., 59, 369 (1940).
220. E. R. Gilliland, H. W. Schee line, Ind. Eng. Chem., 32, 48 (1940).
221. A. F. D u n I о p, D. F. T r i m b I e, ibid.'', 32, 1000 (1940).
222. Κ. E, Coulter, R. A. Lindsay, E. M. Baker, ibid., 33, 1251 (L941).
223. A. R. Fowler, H. Hunt, ibid, 33, 90 (1941).
224. В. А. Киреев, И. П. Ситников, Зав. лаб, 10, 509 (1941)г
225. R. York, R. С. Holmes, Ind. Eng. Chem.. 34, 345 (1942).
226. W. М. L and on, D. В. Keyes, ibid, 34, 938 (1942).
227. J Griswold, D. Andres, V. A. Klein, Petrol. Ref, 22, 171 (1943).
337
228. D. F. Othmer, Ind. Eng. Chem., 35, 614 (1943).
229. H. S t a g e, I. S. Baumgarten, 61 u. Kohlef 40, 126 (1944).
230. R. Gilmont, D. F. Othmer, Ind. Eng. Chem., 36, 1061 (1944).
231. D. F. Othmer, F. R. Mor ley, ibid., 38, 751 (1946).
232. E. S. Pe r r y, R. E. F u g u i 11, ibid., 39, 782 (1947).
233. D. F. Othmer, Ind. Eng. Chem., Anal. Ed., 20, 763 (1948).
234. F. E. Williams, Ind. Eng. Chem., 39, 779 (1947). ,
235. W. Schaffer, H. Stage, Chem. Ing. Techn., 21, 418 (1949).
236. Т. E. Smith, R. F. Bouner, Ind. Eng. Chem,, 41, 2867 (1949).
237. L. S i e g, Chem. Ing. Techn., 15, 322 (1950).
238. M. R. F e n s к e, H. S. Myers, D. Q u i g g I e, Ind. Eng. Chem., 42, 649
(1940).
239. D. F. Othmer, W. P. Moeller, S. W. E n g I u n g, K- G. Christop¬
her, ibid., 43, 707 (1951).
240. R. C. Shai r, W. F. Schuri g, ibid., 43, 1624 (1951).
241. М. B u к a b a, J. M a j e w s к i, Przem. Chem., 31, 551 (1952).
242. D. F. Othmer, S. j. S i I v i s, A. Spiel, Ind. Eng. Chem., 44, 1864 (1952).
243. G. Kort u m, H. J. F r e i e r, F. W о e r n e r, Chem. Ing. Techn., 3, 125 (1953).
244. И. H. Б у ш μ а к и и, ЖПХ, 32, 812 (1959).
245. D. Т. С. Gillespie,Ind. Eng. Chem., Anal. Ed., 18, 575 (1946).
246. R. T. F о I w e r, J. Soc. Chem. Ind., I, 131 (1949).
247. R. M. Rieder, A. R. Thompson, Ind. Eng. Chem., 41, 2905 (1949).
248. Г Brown, A. H. E w a I d, Austr. J. Sci. Res., Ser. A., 3, 306 (1950).
249. I. Brown, Austr. J. Sci. Res., Ser. A., 5, 530 (1952).
250. И. Я. Городецкий, В. М. О л e в с к и й, Труды ГИАП, вып. 10, 1959,
стр. 99.
251. В. В. Удовенко, JI. Г. Фаткуллина, ЖФХ, 26, 211 (1952).
252. W. Reinders, С. Н. de Minjier, Rec. trav. chim.,-66, 573 (1947).
253. А. N. С a m р b е 11, J. Am. Chem. Soc., 67, 981 (1945).
254. К. П. Андреев, Ю. А., Ц и р л и н, ЖПХ. 27, № 4, 402 (1954).
255. М. И. У с а н о в и ч, В. Ф. Сергеева, К. К. Хайрулина, ЖОХ, 25,
№ 13,2427 (1955).
256. Н. А. Смирнова, А. Г. Морачевский, Вестн. ЛГУ, № 10, вып. 2,
106 (1959).
257. С. К. Огородников, В. Б. Коган, М. С. Немцов, ЖПХ, 34, 841
(1961).
258. М. Neuman, С. В. Hayworth, R. Е. Treybal, Ind. Eng. Chem., 41,
' 2039 (1949).
259. Л. С. К о ф м а н, Л. А. Г а л а т а, Т. Н. Матвеева, Вестн. техн. и эко¬
ном. информ., № 12 (1961). ^
260. I. Wichterle, Е. Hala, Ind. Eng. Chem. Fundamentals, 2, 157 (1963).
261. Ё. Г. К о м а р о в а, В. Б. К о г а н, ЖПХ, 37, 1776 (1964).
262. И. Н. Бушмакин, Е. Д. Воейкова, ЖОХ, 19, 1615 (1949).
263. В. Н. Beattie, G. Calingaert, Ind. Eng. Chem., 26, 904 (1934).
264. В. Т. Жаров, А. Г. Морачевский, ЖПХ, 36, 2232 (1963).
265. В. Т. Жаров, А. Г. Морачевский, Там же, 36, 2397 (1963).
266. В. Т. Ж а р о в, А! Г. Морачевский, Там же, 37, 604 (1964).
267. Н. С. Carlson, А. P. Colburn, Ind. Eng. Chem., 34, 581 (1942).
268. Н. Н. Steinhauser, R. H. White, ibid., 41, 2912 (1949).
269. Ε. F. G, H e r i η g t ο η, Research, 3, 41 (1950).
270; V. V. G. Krishnamurt i, С. Venkata Ra о, J. Sci. Ind. Res., 14,
(В —C), 188 (1955).
271. В. Б. Коган, ЖФХ, 32, 1095 (1958).
272. M. Mar gules, Sitzungsber. Akad. Wiss. Wien, Math. Naturw., 104, 1243
(1895).
273. J. Z a w i d s k i, Z. phys. Chem., 35, 129 (1900).
274. J. J. V a n L a a r, ibid., 72, 723 (1910).
275. R. R. White, Trans. Am. Inst. Chem. Eng., 41, 546 (1945).
276. I. M. Li, J. Coul I, J. Inst. Petrol., 34, 692 (1948).
277. K. T. Ju, J. C ou 11, Chem. Eng. Progr. Simposium Ser., 48, № 2, 38 (1952).
338
278. К. Who I, Trans. Am. Inst. Chem. Eng., 42, 215 (1946).
279. С. Scatchar d, W. J. Hamer, J. Am. Chem. Soc., 57, 1805 (1935).
280. M. Benedict, C. A. Johnson, E. Solomon, L. C. Rubin, Trans. Am.
Inst. Chem. Eng., 41, 371 (1945).
281. Б. Ф. Додж, Химическая термодинамика в применении к химическим про¬
цессам и химической технологии, ИЛ, Д950.
282. А. М. Clark, Trans. Faraday. Soc., 41, 718 (1945).
283. W. Н. Prah I, Ind. Eng. Chem., 43, 1767 (1951).
284. R. S. Norrish, G. H. Twigg, ibid., 46, 201 (1954).
285. M. H i r a t a, Chem. Eng. (Japan), 13, 138 (1949).
286. F. R. Mayo, F. H. Lewis, J. Am. Chem. Soc., 66, 1594 (1944).
287. I. H. Spinner, B. C. Y. Lu, W. F. G г a у d ο n, Ind. Eng. Chem., 48, 147
(1956).
288. С. В. K re t s с h me г, R. Wiebe, J. Chem. Phys., 22, 1697 (1964).
289. Э. Хала, И. Пик, В.4 Ф р и д, О. В и л и м, Равновесие между жидкостью
и паром, ИЛ, 1962.
290. В. Б. Коган, В. М. Фридман, ЖФХ, 28, 1889 (1954).
291. F. Hovorka, R. A. Schaefer, D. Dreisbach, J. Am. Chem. Soc., 58,
2264 (1936).
292. И. Р. Кричевский, Я. Казарновский, ЖФХ, 5, 1222 (1934).
293. С. К. Огородников, В/ Б. Коган, М. С. Немцов, ЖПХ, 34, 323
(1961).
294. Н. Schubert, Z. phys. Chem., 217, 236 (1961).
295. Н. Л. Я рым-Агаев, Е. А. Коган, ЖФХ, 30, 2510 (1956).
296. G. Scatchard, Trans. Faraday Soc., 33, 160 (1937).
297. G. Scatchard, S. E. Wood, J. M. M о с h e I, J. Am. Chem. Soc., 68, 1960
(1946).
298. H. G. G i I m о n t, E. A. Weinman, F. Kramer, E. Miller, F. Hash·
mall, D. F. Othmer, Ind. Eng. Chem., 42, 120 (1950).
299. H. Д. Литвинов, ЖФХ, 26, 898 (1952).
300. E. F. G. Heringto n, J. Appl. Chem., 2, 11 (1952).
301. В. S. Edwards, F. H a s h m a 11, D. F. Othmer, Ind. Eng. Chem., 46, 194
(1954).
302. F. Kohler, Monatsh. Chem., 91, 738 (1960).
303. В. Б. К о г.а и, В. М. Сафронов, ЖФХ, 33, 1353 (1959).
304. М. П. Cycap ев, А. Н. Горбунов, Там же, 38, 583 (1964).
305. В. Т. Жаров, А. Г. Морачевский, сб. «Физико-химические свойства
растворов», Изд. ЛГУ, 1964, стр. 28.
306. Н. Buchholz, G. Kortiim, Angew. Chem., 63, 163 (1951).
307. F. С. Collins, V. Lantz, Ind. Eng. Chem., Anal. Ed., 18, 673 (1946).
308. А. И. Левин, Нефт. хоз., JSfb 10, 40 (1949).
309. В. В. Кафаров, Л. А. Гордиевский, ЖПХ, 28, 713 (1956).
310. J. Griswold, D. Andres, С. F. van Berg, J. E. Kasch, Ind. Eng.
Chem., 38, 66 (1946).
311. J. Griswold, C. F. van Berg, ibid., 38, 170 (1946).
312. G. Kortiim, A. B.ittel, Chem. Ing. Techn., 28, 40 (1956).
313. В. М. Барбой, Ю. H. Гарбер, И. H. Фельдман, ΤΟΧΤ, 4, JSib I, 115
(1970).
314. J. A. Gers ter, Т. S. Mertes, А. P. Colburn, Ind. Eng. Chem., 39, 797
(1947).
315. В. М. Платонов, Б. Г. Б e p г о, Разделение многокомпонентных смесей,
Изд. «Химия», 1965.
316. Ч. Д. Холланд, Многокомпонентная ректификация, Изд. «Химия», 1969.
317. J. М. Chambers, Chem. Eng. Progr., 47, 555 (1951).
318. R. J. Hengstebeck, Trans. Am. Inst. Chem. Eng., 42, 309 (1946).
319. R. J. Hengstebeck, Chem. Eng. Progr., 53, 243 (1957); Хим. и хим. тех-
нол., JVb 4, 176 (1958).
320. Е. W. Thiele, R. L. Geddes, Ind. Eng. Chem., 25, 289 (1933).
321. В. О. Рейхсфельд, Л. Н. Ep ко в а, Оборудование производств основ¬
ного органического синтеза и синтетических каучуков, Изд. «Химия», 1965.
339
- 322. M. R. Fenskel Ind. Eng. Chem., 24, 482 (1932).
323. S. R. M. Ellis, С. J. Pearce, Brit. Chem. Eng., 2, 648 (1957).
324. E. R. Gilliland, Ind. Eng. Chem., 32, 918, 1101, 1220 (1940).
325. G. T. Atkins, С. M. Boyer, Chem. Eng. Progr., 45, 553 (1949).
326. R. Henni g, Chem. Techn., 17, 77 (1965).
327. D. Ge I b i n, ibid., 11, 70 (1959).
328. A. J. V. Underwood, J. Inst. Petrol., 31, 111 (1945).
329. A. J. V. Underwood, ibid., 32, 598, 614 (1946).
330. A. J. V. U n d e r w о о d, Chem. Eng. Progr., 44, 603 (1948).
331. A. J. V. U n d e r w о о d, ibid., 45, 609 (1949).
332. E. W. G г о h s e, R. E. M с C a r t n e y, H. J. H a u e r, J. A. G e r s t e r,
A. P. Colburn, ibid., 45, 725 (1949)
333. J. A. G e r s t e r, A. P. Colburn, W. E. Bonnet, T. W. C a r m о d y, ibid.,
45, 716 (1949).
334. J. Happel a. oth., Trans. Am. Inst. Chem. Eng., 42, 189 (1946).
335. Й. G. Drickamer, H. H. Hummel, Trans. Am. Inst. Chem. Eng., 41,
607 (1945).
336. F. H. Garner, S. R. M. Ellis, W. H. Granville, J. Inst. Petrol., 42,
JSfe 389, 148 (1956).
337. M. Serwinski, S. MichaIowski, Chem. Stosow., 38, JSfe I, 67 (1966).
338. Чжан Юань-ци, Чэнь Хай-тао, РЖХим., 1958, 25386; Acta Focalia
sinica, 2, 63 (1957).
339. М. Р. Зяпаров, А. Н. Плановский, Теор. основы хим. технол., 2, Jsfe I,
35 (1968).
340. Е. М. S с h о е n b о г n, J. Н. Koffolt, J. Н. Withrow, Trans. Am. Inst.
Chem. Eng., 37, 997 (1941).
341. G. G. Brown, ibid., 37, 1019 (1941).
342. О. A. Hougen, К. M. Watson, Chem. Process Principles, Part 3, N. Y.,
1948.
343. И. Я. Городецкий, В; М. Олевский, Хим. пром., Jsfe 5, 350 (1961).
344. Я. Д. Авербух, Jl. Д. Березина, Труды Уральск, политехи, ин-та, сб.
152, 1966, стр. 140.
345. V. Berti, G^ Leidi, Rev. combust., 3, 255 (1949).
346. Англ. пат. 613867, 1948.
347. С. К. Buell, R. С. Boatright, Ind. Eng. Chem., 39, 695 (1947).
348. В. Б. Коган, В. М. Фридман, И. В. Дейзенрот, ЖПХ, 30, 1339
(1957).
349. В. Б. К о г а н, И. В. Дейзенрот, Т. А. К у л ь д я е в а, В. М. Фрид¬
ман, Там же, 29, 1387 (1956).
I
ПРИЛОЖЕНИЕ
СВОДКА ЛИТЕРАТУРЫ ПО ПРИМЕНЕНИЮ АЗЕОТРОПНОЙ И ЭКСТРАКТИВНОЙ
РЕКТИФИКАЦИИ
В начале приводятся системы, содержащие неорганические ве¬
щества. Органические компоненты перечисляются ,в порядке, соот¬
ветствующем принятой систематизации (см. ниже). Представители
одного класса соединений располагаются в порядке увеличения чи¬
сла атомов углерода в молекуле. Если из многокомпонентной си¬
стемы выделяется одно индивидуальное вещество, то оно приводится
первым (например, этиловый спирт — метиловый спирт, вода). Если
в названии системы содержится определенное химическое вещество
и представитель класса соединений, то вещества указывается первым
(например, гексан — близкокипящий нафтен, изопрен — амилены).
Органические соединения перечисляются следующим образом:
I) углеводороды (парафины, олефины, диолефины, ароматические
углеводороды, нафтены); 2) галогензамещенные углеводороды;
_) кислородсодержащие алифатические (спирты, многоатомные спир¬
ты, альдегиды, кетоны, кислоты, простые эфиры, сложные эфиры);
4) кислородсодержащие ароматические (фенолы, альдегиды, кетоны’
кислоты, простые эфиры, сложные эфиры); 5) азотсодержащие (ни"
тросоединения, амины, амиды, нитрилы); 6) серусодержащие; 7) фос"
форсодержащие; 8) кремнеорганические; 9) гетероциклические.
Порядок расположения разделяемых систем соответствует при-
веденной классификации органических соединений. Соединения од¬
ного класса перечисляются в порядке увеличения числа атомов угле¬
рода в молекуле. Если в названии системы указываются только
классы соединений, то такие системы помещаются в конце соответ¬
ствующего класса. Например, система парафины— олефины поме¬
щается после систем, содержащих конкретные парафиновые углево¬
дороды.
Разделяющие агенты для данной системы перечисляются со¬
гласно приведенной классификации.
Разделяющий агент
Разделяемая система
формула
Литера¬
тура
Неорганические соединения
Гидразин — вода
Метаборная кислота — вода
Моносилан — фосфин (арсин)
Трихлорсилан — треххлористый бор
Этиловый спирт + бензол
C2H5GH + C6H6
91
Бензол
C6H6
89
Ксилол
C6H4(CH3)2
89
Триэтоксисилан
(C2H5O)3SiH
18
Дипропиловый эфир
(C3H7)2O
37
Диизопропиловый эфир
(C3H7)2O
38, 51, 52*
53
Дибутиловый эфир
(C4H9)2O
51, 53
Диамиловый эфир
(C5H11)2O
37
Диизоамиловый эфир
, (C5H11)2O
37
Ацетонитрил
CH3CN
38, 52
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Трихлорсилан — хлорокись фосфора
Диизопропиловый эфир
Диамиловый эфир
(C3H7)2O
53
(C5Hh)2O
. 37
Диизоамиловый эфир
(C5Hn)2O
37
Трихлорсилан — треххлористый фос-
Диизопропиловый эфир
(C3H7)2O
53
фор
Дибутиловый эфир
(C4H9)2O
53
Диамиловый эфир
(C5Hn)2O
37
Трихлорсилан — четыреххлористый
Диизопропиловый эфир
(C3H7)2Q
52, 53
титан
Дибутиловый эфир
(C4H9)2O
51, 53
Тетрахлорсилан — треххлористый бор
Диизопропиловый эфир
(C3H7)2O
38, 52, 53
Дибутиловый эфир
(C4H9)2O
51, 53
Ацетонитркл
CH3CN
38, 52
Тетрахлорсилан — треххлористый
Диизопропиловый эфир
(C3H7)2O
53
фосфор
Дибутиловый эфир
(C4H9)2O
51, 53
Ацетонитрил
CH3CN
38
Тетрахлорсилан — четыреххлористый
Диизопропиловый эфир
(C3H7)2O
52, 53
титан
Дибутиловый эфир
(C4H9)2O
53
Органические соединения
Парафины
Пропан — сероводород
Легкое экстракционное масло
341
Бутан — изобутан
Метилмеркаптан
CH3SH
283
Фурфурол + вода
OCH=CH-CH=CCHO + H2O
I I
379
Бутан — бутен
Фурфурол
OCH=CH CH=CCHO
I I
33
Бутан — бутен ы
Метанол + вода
CH3OH + H2O
112
Ацетон
(CH3)2CO
112, 286.
Анилин + вода
C6H5NH2 + H2O
368
233
Ацето нитрил
CH3CN
139
Бутан — бутен — бутадиен
Бутан — бутадиен
Бутаны — бутены
Фурфурол
Фурфурол + о-ксилол
Фурфурол + 1,2,3-трихлорпропан
Фурфурол + ацетонилацетон
Фурфурол + метилдихлорацетат
Фурфурол 4- фенилацетонитрил
Фурфурол + пиридин
Фурфурол + вода
Диэтилфосфонат
Фосфонаты
Диэтилпропионилфосфонат
Д иэтшгоензо ил фосфон ат
а-Оксофосфонаты
Циклогексил-^^диметил-Р-метил-
фосфонамидат
Фосфон амидаты
[I - (Диэтоксифосфинил) этокси]три-
метилсилан
трис-[ I - (Диэтоксифосфинил) этокси]
метилсилан
Фосфинилалкоксисиланы
Метил-Ν,Ν-дибутил-Р-гексилфос-
фонамидат
Фосфонамидаты
Ν,Ν-Диметилформамид
Ацетонитрил
осн=снсн=ссно
135, 208,
I I
209, 369
ОСН=СНСН=ССНО + C6H5(CH3)2
95
ОСН=СНСН=ССНО + C3H5Cl3
I I
95
осн=снсн=ссно+
95
1 1 +(CH3COCH2)2
осн=снсн=ссно+
95
1 ! +ChCI2COOCH3
OCH-CHCH = CCHO +
95
1 ! +C6H5CH2CN
ОСН-СНСН-ССНО+ V
95
+ C6H5N (цикл.)
ОСН=СНСН=ССНО + H2O
I I
233, 438
H(OC2H5)2PO
156
Rr(OR)2PO1)
156
C3H7C(O) (OC2H5)2PO
154
C6H5C(O)(OC2H5)2PO
154
RrC(O)(OR)2PO2)
154
CH3(OC6Hn)[N(CH3)2]PO
153
R(ORrr) (NR2)PO з)
153
155
(CH3) 3SiOCH (CH3) PO (OC2H5) 2
CH3SifOCH (CH3) PO (OC2H5) 2]3
155
(R)mSifOCH(Rr)PO(ORrr)2Jn 4>
155
C6Hi3(OCH3)[N(C4H9)2]PO
153
R(ORrr) (NR2)PO 3>
153
HCON(CH3)2 ' .
75
CH3CN
75
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Пентан — изопентан
Пентан — изопентан — 2-метилбу-
тен-1 —2-метилбутен-2
Пентан — пентен-1
Диэтилметилфосфонат
Диизопропилметилфосфонат
Фосфон аты
Диэтилметилфосфонат
Фосфонаты
Бензол 4- β,β'-оксидйпропионитрил
Бензо^ 4 сульфолан
CH3(OC2H5)2PO
flCH3 (OC3H7)2PO
R7(OR)2PO о
CH3(OC2H5)2PO
R' (OR)2PO w
C6H6 H- (NCCH2CH2)2O
C6H6H-CH2(CH2)2CH2SO2
156
156
156
156
156
207
207
4
Метиловый спирт
Этиленхлоргидрин
Ацетон
Метилэтилкетон
Метилэтилкетон + у-бутиролактон
CH3OH
CH2OHCH2Cl
(CH3)2CO
CH3COC2H5
CH3COC2H5 4 OCH2CH2CH2CO
I I
207
207
207
174, 207
207
Диэтилкетон
Циклопентанон
2,4-Пентандион
Ацетонилацетон
Метилцеллозольв
Метилцеллоз.ольв 4 нитрометан
Метилцеллозольв 4- сульфолан
(C2H5)2CO
C5H8O
(CH3CO)2CH2
(СН3СОСН2)2
CH3OCH2CH2OH
CH3OCH2CH2OH 4 CH3NO2
CH3OCH2CH2OH4CH2(CH2j2CH2S02
207
207
174
174
174
207
207
Метилцеллозольв 4 вода
Метилкарбитол
Диэтилоксалат
у-Бутиролактон
CH3OCH2CH2OH 4 H2O
СН3ОСН2СН2ОСН2СН2ОН
(COOC2H5)2
OCH2CH2CH2CO
I I
207
207
207
174, 207
Зтиленкарбонат
CH2OC(O)OCH2
207
Пропиленкарбонат
Ch3CHOC(O)OCH2
207
Диэтилкарбонат
(C2H5O)2CO,
174, 207
Ацетофенон
CH3COC6H5
174, 207
Нитрометан
CH3NO2
174, 207
Этилендиамин
(CH2NH2)2
207
Ν,Ν-Диметилформамид
HCON(CH3)2
174, 207
Ν,Ν-Диметилацетамид
CH3CON(CH3)2
207
Ν,Ν-Диметилцианамид
NCN(CH3)2
207
Ацетонитрил
CH3CN
207
Пропионитрил
C2H5CN
207
β-Хлорпропионитрил
ClCH2CH2CN
207
Бутиронитрил
C3H7CN
207
Дибутилхлорметилфосфонат
ClCH2(OC4H9)2PO
156
Диэтилцианометилфосфонат
NCCH2(OC2H5)2PO
156
Фосфонаты
R7(OR)2PO*)
156
Диэтилпропионилфосфонат
C3H7C(O)(OC2H5)2PO
154
Диэтилкарбоэтоксифосфонат
C2H5OC(O) (OC2H5)2PO
154
Этилпропилкарбометоксифосфонат
CH3OC(O)(OC2H5)(OC3H7)PO
154
Метилэтилбензоилфосфонат
C6H5C(O) (OCH3) (OC2H5)PO
154
Диэтилбензоилфосфонат
C6H5C(O)(OC2H5)2PO
154
Этилизопропилциклогексаноилфос-
фонат
а-Оксофосфонат
C6H11C(O) (OC2H5) (OC3H7)PO
154
R7C(O)(OR)2PO 2>
154
Циклогексил-Н,Н-диметил-Р-метил-
CH3(OC6Hn)[N (CH3)2JPO
153
фосфонамидат
Метил^^-дибутил-Р-гексил-фос-
C6H13(OCH3)IN(C4H9)2JPO
153
фонамидат
Гексил-Н,Н-диметил-Р-этилфосфои-
C2H5(OC6H13)IN(CH3)2JPO
153
амидат
R (OR") (NR7)2PO 3>
Фосфонамидаты
153
[I - (Диэтоксифосфинил) этокси]-три-
(CH3) aSiOCH (CH3) PO (OC2H5) 2
155
метилсил^н
трис-[I - (Диэтоксифосфинил) этокси]-
CM3Si[OCH (CH3) PO (OC2H5) 2]з
155
метилсилан
Фоефинилалкоксисиланы
(R)mSiIOCH(R7)PO(OR77)2Jn 4>
155
ТетрагиДрофуран
CH2(CH2)2CH2O
I I
174, 207
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Пентан — пентен-1
Фурфурол
осн=снсн=ссно
I I
95, 207
Фурфурол + о-ксилол
ОСН=СНСН=ССНО + C6H4(CH3)2
1 I
95
Фурфурол 4- 1,2,3-трихлорпропан
ОСН=СНСН=ССНО + C3H5Cl3
I I
95
Фурфурол + ацетонилацетон
OCH=снсн=ссно+
95
Фурфурол + метилдихл ор ацетат
— 1 +(CH3COCH2)2
осн=снсн=ссно+
95
Фурфурол + пиридин
* +снс12соосн3
OCH=CHCH =CCH O + C5H5N
I I
95
Тетрагидрофурфуриловый спирт
OcH2(CH2)2CHCH2OH
174
Пирролидон
NhCOCH2CH2CH2
I I
174, 207
N -Метилпирролидон
Ch3NCOCH2CH2CH2
174, 207
Пиридин + γ-бутиролактон
C5H5N + OCH2CH2CH2CO
I j
207
Пиридин + β,β'-оксидипропионит-
P ил
Пиридин + вода
Ацетилпиперидин
C5H5N + (NCCH2CH2)2O
207
C5H5N + H2O
CH3CON(CH2)4CH2
I I
207
207
Пентан — пентен-1—2-метил бутен-I—
2-метилбутен-2 ✓
Диметилсульфолан
Д и эти л фосфон ат
Фосфон аты
(CH3)2C4H6SO2
H(OC2H5)2PO
R7(OR)2PO ·)
174, 207
156
156
Пентан — 2-метилбутен-1 — 2-метил
бутен-2 — изопрен
Пентан—2-метилбутен-1 —изопрен
Пентан—изопрен
Пентан—ацетон
Изопентан—пентен-1
Пентан—2-метилбутен-1—изопрен
Диметилфосфонат
H(OCH3)2PO
156
Фосфонаты
R7(OR)2POD
156
Диэтил бензоилфосфойат
C6H5C(O) (OC2H5)2PO
154
а-Оксофосфонаты
R7C(O)(OR)2PO2)
154
Циклогексил-Ν ,N-диметил-Р -метил-
CH3 (OC6Hn) [N (CH3) 2]Р0
153
фосфонамидат
Фосфонамидаты
R(OR") (NR )PO3)
153
трис-[\- (Диэтоксифосфинил) -этокси]-
CH3SifOCH (CH3) PO (OC2H5) J3
155
метилсилан
Фосфинилалкоксисиланы
(R) mSi[OCH(R7)PO (OR") Jn 4)
155
Диэтилпропианилфосфонат
C3H7C(O)(OC2H5)2PO
154
Диэтилбензоилфосфонат
C6H5C(O)(OC2H5)2PO
154
а-Оксофосфонаты
R7C(O)(OR)2PO 2)
154
Метил-Ν ,N - дибутил-Р -гексилфос-
фонамидат
Фосфонамидаты
C6H и (OCH3) [N (C4H9) JPO
153
R (OR") (NR2)PO3)
153
[I - (Диэтоксифосфинил) этокси]три-
(CH3) sSifOCH (CH3) PO (OC2H5) 2
155
метилсилан
Фосфинилалкоксисиланы
(R) mSifOCH (R') PO (OR") Jn 4>
155
Метилформиат
HCOOCH3
34
Вода
H2O
266
Ацетонитрил
CH3CN >
61
Циклогексил-Ν,Ν-диметил-Р-метил-
CH3 (OC6H ц) [N (CH3JJPO
153
фосфонамидат
Фосфонамидаты
R (OR") (NRO PO 3>
153
трис-[\- (Диэтоксифосфинил) этокси]-
CH3SifOCH (CH3) PO (OC2H5) J3
155
метилсилан
Фосфинилалкоксисиланы
(R) mSifOCH (R') PO (OR") 2]п 4)
155
Диэтилпропионилфосфонат
C3H7C(O) (OC2H5)2PO
154
Диэтилбензоилфосфонат
C6H5C(O) (OC2H5)2PO
154
а-Оксофосфонаты
R7C(O)(OR)2PO2)
154
Метил-Ν, Ν-дибутил-Р-гексилфос-
C6H13(OCH3) [N (C4H9)JPO
153
фонамидат
Фосфонамидаты
R (OR") (NRO PO 3>
153
[ I - (Диэтоксифосфинил) этокси]-три-
(CH3) 3Si[OCH (CH3) PO (OC2H5) J
155
метилсилан
Фосфинилалкоксисиланы
(R) mSifOCH (R') PO (OR") Jn 4>
155
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
' название
формула
Пентан—изопрен
Метилформиат
HCOOCH3
34
Пентан—ацетон
Вода
H2O
266
Изопентан—пентен-1
Ацетонитрил
CH3CN
61
Изопентан—пентен-2
Ацетонитрил
CH3CN
61
Изопентан—2-метилбутен-2
Нитрометан
CH3NO2
58, 59
Ν,Ν-Диметилформамид
HCON(CH3)2
58, 59
Ацетонитрил
CH3CN
61
Изопентан — олефины Cs
Метилформиат
HCOOCH3
34
Изопентан — изопрен
Нитрометан
CH3NO2
58, 59
Ν,Ν-Диметилформамид
HCON(CH3)2
58, 59
Ацетонитрил
CH3CN
61
Ацетонитрил + вода
CH3CN + H2O
4
Парафин C5 — олефин C5
Пёрфтортр иэтил ам ин
(C2F5)3N
64
Парафин C5 — диолефин C5
Метилформиат
HCOOCHs
34
Перфтортриэтиламин
(C2F5)3N
64
Г ексан—гептан
Вазелиновое масло
—
30
Этиленгликоль
(CH2OH)2
30
Диэтиленгликоль
(HOCH2CH2)2O
30
Триэтиленгликоль
(HOCH2Ch2OCH2)2
30
Динонилфталат
C6H4 (СООСэН 19) 2
30
Пропиленкарбонат
CH3CHOC(O)OCh2 *
30
Tp икрезил фосфат
(CH3C6H4O)3PO
30
Диметиланилин
C6H5N(CH3)2
30
Триэтаноламин
(HOCH2CH2)3N
30
Динитриладипат
(NCCH2CH2)2
30
Иминодипропионитрил
(NCCH2CH2)2NH
30
Дибутоксидиэтилсульфид
(C4H9OCH2CH2)2S
30
Силиконовбе масло
1 —
30
-
Пирролидон
NhCOCH2CH2CH2
I I
30
ш
Г ексан—2-метилбутен-2
Г ексан—гексен-1
Г ексан—2-метилпентен-1
Г ексан—4-метилпентен-1
Гексан—изопрен
Гексан—бензол
N -Метил пирролидон
Метилформиат
Вазелиновое масло
1,1,1-Трихлорэтан
1, 1,2,2-Тетрахлорэтан
1,2,3-Трихлорпропан
Трихлорэтилен
Тетрахлорэтилен
Вторбутиловый спирт
Метилэтилкетон
Диоксан
Целлозольв
Пропиленкарбонат
Трикрезилфосфат
Анилин
Диметиланилин
Ν,Ν-Диметилформамид
Динитриладипат
Иминодипропионнтрил
Пирролидон
N -Метилпиррол идон
Ν,Ν-Диметилформамид
Ν,Ν-Диметилформамид
Метилформиат
Вазелиновое масло
Пропиловый спирт
Этиленгликоль
Диэтиленгликоль
T риэтиленгликоль
Фенол
Динонилфталат
CH3ISiCOCH2CH2CH2
HCOOCH3
CCl3CH3
CHCi2CHCI2
СН2С1СНС1СН2С1
C2HCl3
C2Cl4
C4H9OH
CH3COC2H5
OCH2CH2OCh2CH2
L I
C2H5OCH2CH2OH
Ch3CHOC(O)OCH2
I 1
(CH3C6H4O)3PO
C6H5NH2
C6H5N(CH3)2
HCON(CH3)2
(NCCH2CH2)2
(NCCH2CH2)2NH
NhCOCH2CH2CH2
I J
Ch3NCOCH2CH2CH2
I I
HCON(CH3)2
HCON(CH3)2
HCOOCH3
C3H7OH
(CH2OH)2
(HOCH2CH2)2O
(HOCH2Ch2OCH2)2
C6H5OH
C6H4(COOC9Hi9)2
30
57
30
228
228
410
228
228
228
228
410
410
30
30
30
30
230
30
30
30
30
239
239
57
30
357
30
30
30
163
30
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Г ексан — бензол
Пропиленкарбрнат
Ch3CHOC(O)OCH2
30
Трикрез ил фосфат
Пер фтортр иэтил амин
Триэтаноламин
Этилендиамин
Г ексаметилендиамин
Анилин
Диметиланилин
Ν,Ν-Диметилформамид
Динитриладипат
Иминодипропионитрил
Дибутоксидиэтилсульфид
Диметилфосфонат
Фосфон аты
Силиконовое масло
Фурфурол
(CH3C6H4O)3PO
(C2F5)3N
(HOCH2CH2)3N
(CH2NH2)2
(C3H6NH2)2
C6H5NH2
C6H5N (CH3)2
HCON(CH3)2
(NCCH2CH2)2
(NCCH2CIi2)2NH
(CJ-I9OCH2CH2)2S
H(OCH3)2PO
R'(OR)2PO1)
осн=снсн=ссно
I I
30
64
30
30
30 -
30, 163
30
163
30
30
30
156
156
30
163
Пирролидон
NhCOCH2CH2CH2
I I
30
Ν-Метилпирролидон
Ch3NCOCH2CH2CH2
I I
30, 163
Сульфолан
CH2(CH2)2CH2SO2
I I
163
Г ексан—бензол—метилциклопентан
Метилсульфолан
Диметилсульфолан
Пропилсульфоланиловый эфир
Диметилфосфонат
Фосфон аты
Диэтилпропионилфосфонат
CH3C4H7SO2
(CH3)2C4H6SO2
(C3H7O)C4H7SO2
H(OCH3)2PO
R'(OR)2PO I)
C3H7C(O)(OC2H5)2PO
163
163
163
156
156
154
Гексан-
w
VSI
-метилциклопентан
Диэтилбензоилфосфонат
а-Оксофосфонат
Метил-Ν,N-дибутил-Р-гексил-фос-
фонамидат
Циклогексил-Ν,N-диметил-Р-метил-
фосфонамидат
Фосфонамидаты
[I - (Диэтоксифосфинил) этокси]три-
метилсилан
трис-[\- (Диэтоксифосфинил) этокси]-
метилсилан
Фосфинилалкоксисиланы
Вазелиновое масло
Диэтиленгликоль
Триэтйленгликоль
Динонилфталат
Пропиленкарбонат
Трикрезилфосфат
Триэтаноламин
Этилендиамин
Анилин
Диметиланилин
Ν,Ν-Диметилформамид
Ν,Ν-Диметилформамид + пропилен¬
карбонат
Динитриладипат
Иминодипропионитрил
Дибутоксидиэтилсульфид
Диметилфосфонат
Фосфон аты
Диэтилбензоилфосфонат
а-Оксофосфонаты
Метил-Ν,Ν-дибутил-Р-гексилфос-
фонамидат
Фосфонамидаты
трис-[\ - (Диэтоксифосфинил) этокси]-
метилсилан
C6H5C(O)(OC2H5)2PO
R'C(О) (OR)2PO2)
C6H13 (OCH3) [N (C4H9)2JPO
СН3(ОС6Нц)^(СН3)2]РО
RiOR'7) (NR2)PO3)
(CH3) 3SiOCH (CH3) PO (OC2H5) 2
CH3SitOCH (CH3) PO (OC2H5) 2]3
(R) mSi[OCH(R')PO(OR7')2]п 4>
(HOCH2CH2)2O
(HOCH2CH2OCh2)2
C6H4(COOC9H19)2
Ch3CHOC(O)OCH2
(CH3C6H4O)3PO
(HOCH2CH2)3N
(CH2NH2)2
C6H5NH2
C6H5N(CH3)2
HCON(CH3)2
HCON(CH3)2 + CH3CHOC(O)OCh2
! I
(NCCH2CH2)2
(NCCH2CH2)2NH
(C4H9OCH2CH2)2S
H(OCH3)2PO
R(OR7)2PO1)
C6H5C(O)(OC2H5)2PO
R7C(O)(OR)2PO2)
C6H13 (OCH3) [N (C4H9)2JPO
R(OR77) (NR2)PO3)
CH3Si[OCH (CH3)PO(OC2H5)2J3
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Г ексан — метилциклопентан
Фосфинилалкоксисиланы
(R) mSi[OCH (R7)PO (OR77)2Jn 4)
155
Силиконовое масло
—
30
Пирролидон
NhCOCH2CH2CH2
I I
30
N -Метилпирролидон
Ch3NCOCH2CH2CH2
I I
30
Г ексан — циклогексан
Вазелиновое масло
30
Диэтиленгликоль
(HOCH2CH2)2O
30
Триэтиленгликоль
(HOCH2Ch2OCH2)2
30
Динонилфталат
C6H4(COOC9Hi9)2
30
Пропиленкарбонат
CH3CHOC(O)OCh2
30
Трикрезилфосфат
(CH3C6H4O)3PO
30
Перфтортриэтиламин
(C2F5)3N
64
Триэтаноламин
(HOCH2CH2)3N
30
Анилин
CeHsNH2
30
Диметиланилин
C5H6N(CH3)2 .
30
Динитриладипат
(NCCH2CH2)2
30
Иминодипропионитрил
(NCCH2CH2)2NH
30
Дибутоксидиэтилсульфид
(C4H9OCH2CH2)2S
30
Диэтилпропионилфосфонат
C3H7C(O) (OC2H5)2PO
154
Диэтилбензоилфосфонат
C6H5C(O)(OC2H5)2PO
154
а-Оксофосфонаты
RO(O)(OR)2PO2)
154
Метил-Ν,Ν-дибутил-Р-гексилфос-
фонамидат
C6H13 (OCH3) [N (C4H9)2JPO
153
Циклогексил-Ν,N-диметил-Р-метил-
фосфонамидат
CH3 (OC6H„)[N (CH3)2JPO
153
Фосфонамидаты
R (OR") (NRS)PO3)
153
[I - (Диэтоксифосфинил) этокси]-три-
(CH3)3SiOCH(CH3)PO(OC2H5)2
155
метилсилан
12 Зак. 917
Гексан — метилциклогексан
Гексан — близкокипящие нафтены
Г ексан — углеводороды Ce
2,2-Диметилбутан — циклопентан
Диметилбутан — метилпентан
Парафины С5-б — олефины Cs-e
Гептан — толуол
Гептан— метилциклогексан ,
трис-[\ - (Диэтоксифосфинил) этокси]-
CH3SifOCH (CH3] PO (OC2H5) 2]з
155
метилсилан
Фосфинилалкоксисиланы
(R)mSifOCH (R')PO(OR")2]n 4>
, 155
Силиконовое масло
—
30
Пирролидон
NHCOCH2CHijCH2
I I
30
N -Метилпирролидон
Ch3NCOCH2CH2CH2
30
Диметил фосфон ат
H(OCH3)2PO
156
Фосфон аты
R7(OR)2PO *>
156
Треххлористый фосфор
PCl3
321
Трехбромистый фосфор
PBr3
321
Треххлористый фосфор + трехбро¬
PCl3 ~f~ PBr3
321
мистый фосфор
Метиловый спирт
CH3OH
414
Метилформиат
HCOOCH3
109
Анилин
C6H5NH2
215
Фурфурол
OCH=CHCH=CCHO
I I
109
Дихлорметан
CH2Cl2
100, 101
Tp иметил хл ор м етан
(CH3)3CCl
100, 101
НиТроэтанол
HOCH2CH2NO2
13
Нитропропанол
HOC3H6NO2
13
Нитробутанол
HOC4H8NO2
13
Нитроспирты
HOCnH2nNO2
13
Бутилцеллозольв
C4H9OCH2CH2OH
441
Фенол
C6H5OH
138
Анилин
C6H5NH2
33, 250
N,N - Д иметилформамид
HCON(CH3)2
441
Диметилсульфоксид
(CH3)2SO
441
Фурфурол
осн=снсн=ссно
I I
за
Сульфолан
CH2(CH2)2CH2SO2
I I
441
Парафиновое масло
370
Этиленгликоль
(CH2OH)2
370
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Г ептан — метилциклогексан
Бутиленгликоль
C4H8(OH)2
370
Анилин
C6H5NH2
168, 370
Хинолин
C9H7N
370
Гептан — гептановая нефтяная фрак¬
Р^'-Дихлордиэтиловый эфир
(ClCH2CH2)2O
220
ция
Фенол
C6H5OH
220
Нитробензол
C6H5NO2
220
Анилин
C6H5NH2
220
Фурфурол
ОСН=СНСН=ССНО
I I
220
Гептан — пропиловый спирт
Диэтиленгликоль
(HOCH2CH2)2O
434
2,3-Диметилпентан — бензол
Г ексафтортетр ах лор бутан
C4F6Cl4
270
2,3-Диметилпентан — циклогексан
Перфтортрибутиламин
(C4F9)3N
269
Г ексафтортетрахлорбутан
C4F6Cl4
270
2,3-Диметилпентан — близкокипящий
Перфтортрибутиламин
(C4F9)3N
270
Треххлористый фосфор
PCl3
321
нафтен
Трехбромистый фосфор
PBr3
321
Треххлористый фосфор + трехбро¬
мистый фосфор
PCl3 -Ь PBr3
321
2,3-Диметилпентан — моноамиламин
Перфторгептан
C7Fi6
143
2,4-Диметилпентан — бензол
Перфторметилциклогексан
C7Fi4
144
Г ексиленгликоль
C6H12(OH)2
408
Перфтордибутиловый эфир
(C4F9)2O
144
Перфтортрипропиламин
(C3F7)3N
144
Перфтортрибутиламин
(C4F9)3N
144
Анилин
C6H5NH2
408
Диметилфосфонат
H(OCH3)2PO
156
Фосфон аты
Rx(OR)2PO »
156
Фурфурол
ОСН=СНСН=ССНО
I I
408
2,4-Диметилпентан — бензол — цик¬
Диметилфосфонат
■ I
H(OCH3)2PO
156
логексан
Фосфон аты
Rx(OR)2PO1*
156
2.4-Диметилпентан — циклогексан
2.4-Диметилпентан — близкокипящий
нафтен
2,4-Диметилпентан — треххлористый
фосфор
Парафин С 6-7 — треххлористый фос¬
фор
Октан — октен-1
V»
Wi
Диэтилпропионилфосфонат
Диэтилбензоилфосфонат
а-Оксофосфонаты
Метил-Ν, N-дибутил-Р-гексилфос-
фонамидат
Циклогексил-Ν,Ν-диметил-Р-метил-
фосфонамидат
Фосфонамидаты
[I - (Диэтоксифосфинил) этокси]-три-
метилсилан
трис-[I - (диэтоксифосфинил) этокси]-
метилсилан
Фосфинилалкоксисиланы
Диметилфосфонат
Фосфонаты
Треххлористый фосфор
Трехбромистый фосфор
Треххлористый фосфор + трехбро¬
мистый фосфор
γ-Бутиролактон
γ-Валеролактон
Лактон алифатической кислоты
γ-Бутиролактон
γ-Валеролактон
Лактон алифатической кислоты
Диэтилбензоилфосфонат
а-Оксофосфонаты
Циклогексил-Ν,N -диметил-Р-метил-
фосфонамидат
Фосфонамидаты
C3H7C(O) (OC2H5)2PO
C6H5C(O)(OC2Hs)2PO
R7C(O) (OR)2PO 2>
C6H13 (OCH3) [N (C4H9MPO
154
154
154
153
CH3 (OC6Hn) [N (CH3)2JPO
153
R (OR77) (NR2)PO«)
(CH3)3SiOCH (CH3)PO(OC2H5)2
153
155
CH3Si[OCH (CH3) PO (OC2H5) 2]з
155
(R)mSi[OCH (R')PO (OR77)2Jn 4>
H(OCH3)2PO
R7(OR)2PO «
PCl3
PBr3
PCl3 + PBr3
155
156
156
321
321
321
OCH2CH2CH2CO
I I
323
CH3CHCH2CH2C(O)O
I I
323
O(CR2)nCO 5)
I I
323
OCH2CH2CH2CO
I I
323
CH3CHCH2CH2C(O)O
323
O(CR2)nCO5)
323
C6H5C(O) (OC2H6)2PO
R7C(O)(OR)2PO2)
CH3 (OC6Hi I) [N (CH3) 2]Р0
154
154
153
R (OR77I (NRi) PO 3)
153
П родолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Октан — октен-1
[I - (Диэтоксифосфинил) этоксц]три-
метилсилан
(CHahSiOCH (CH3) PO (OC2H5) %
155
Октан — этилциклогексан
Фосфинилалкоксисиланы
(R)mSi[OCH(R')PO(OR")2]n 4>
155
Изопропиловый спирт
изо· C3H7OH
356
Бутилцеллозольв
C4H9OCH2CH2OH
356
Изооктан — толуол
Анилин
C6H5NH2
33
Фурфурол
осн=снсн=ссно
I I
33
Диметилгексан — дипропиламин
Перфтортрипропиламин
(C3F7)3N
143
Нонан — о-ксилол
Уксусная кислота + пиридин
CH3COOH + C2H5N (цикл.)
456
Парафины С 7-9 — олефины С7-9
Ацетонитрил
CH3CN
116
Смесь парафинов
Ацетон
(CH3)2CO
316
Метилэтилкетон
CH3COC2H5
316
Диоксан
OCH2CH2OCH2Ch2
I I
316
Фенол + вода
C6H5OH + H2O
330
Ацетонитрил
CH3CN
316
Ацетонитрил + вода
CH3CN + H2O
316
Лактонитрил
CH3CHOHCn
316
Анилин + вода
C6HcMH2 + H2O
330
Морфолин
OcH2CH2NHCH2CH2
I I
316
Диметилсульфолан + вода
(CH3)2C4H6SO2 (цикл.) + H2O
330
Парафины — изопарафины
Перфторпарафины
Перфторсоединения
CnF2n+2
142
142
Парафины — олефины
Бензол + β,β'-оксидипропионитрил
C6H6 + (NCCH2CH2)2O
207
Бензол 4- сульфолан
C6H6 + CH2 (CH2) 2CH2S02
I I
207
Хлороформ
CHCl3 '
97
Метил хлористый
CH3Cl
97
Хлорбензол
C6H6Cl
3
Метиловый спирт
CH3OH
207
Этиловый спирт
C2H5OH
97
Этиленхлоргидрин
CH2OHCH2Cl
207
Изоамиловый спирт
мзо-СбНцОН
97
Ацетон
(CH3)2CO
163, 207
Ацетон + вода
(CH3)2CO + H2O
330
Метилэтилкетон
CH3COC2H5
207
Метилэтилкетон + γ-бутиролактон
CH3COC2H6 + OCH2CH2CH2CO
I I
207
Диэтилкетон
C2H6CO
207
Циклопентанон
C4H8CO
207
Пентандион
(CH3CO)2CH2
207
Ацетонилацетон
(CH3COCH2)2
207
Метилцеллозольв
CH3OCH2CH2OH
207
Метилцеллозольв + вода
CH3OCH2CH2OH + H2O
207
Метилцеллозольв + нитрометан
CH3OCH2CH2OH + CH3NO2
207
Метилцеллозольв + сульфолан
CH3OCH2CH2OH+
207
+CH2(CH2)2CH2SO2
Монометиловый эфир диэтиленгли-
коля
СН3ОСН2СН2ОСН2СН2ОН
207
1,4-Диоксан
OCH2CH2OCh2CH2
I I
97
Изопропилацетат
CH3COOC3H7
97
Диэтилоксалат
(COOC2H6)2
207
у-бутиролактон
OCH2CH2CH2CO
I - I
207
Этиленкарбонат
CH2OC(O)OCH2
I I
207
Пропиленкарбонат
CH3CHOC (O) OCH2
I I
207
Диэтилкарбонат
(C2H5O)2CO
207
Нитрометан
CH3NO2
163, 207
Этилендиамин
(CH2NH2)2
207
Анилин + вода
C6H5NH2 + H2O
233
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Парафины — олефины
Ν,Ν-Диметилформамид
Ν,Ν-Диметилформамид -I- гексан
Ν,Ν-Диметилформамид + гептан
Ν,Ν-Диметилформамид + бензол
Ν,Ν-Диметилацетамид
N,N-Д иметилцианамид
Ацетонитрил
Пропионитрил
β-Хлорпропионитрил
Бутиронитрил
Тетрагидрофур ан
HCON(CH3)2
HCON(CH3)2+ C6H14
HCON(CH3)2 + C7H16
HCON(CH3)2+ C6H6
CH3CON(CH3)2
NCN(CH3)2
CH3CN
C2H5CN
ClCH2CH2CN
C3H7CN
OCH2(CH2)2CH2
I I
207
374
374
374
207
207
163, 207
207
207
207
207
Фурфурол
осн=снсн=ссно
I I
207
Фурфурол -H вода
OCH=CHCH=-CCHo + H2O
I I
233
Тетрагидрофурфуриловый спирт
ОСН2(СН2)2СНСН2ОН
I I
207
Пирролидон
NhCOCH2CH2CH2
I I
207
N-Метил пир рол идон
Ch3NCOCH2CH2CH2
207
Ν-Метилпирролидон -H вода
Ch3NCOCH2CH2CH2 + H2O
I I
435
Пиридин -H убутиролактон
C5H5N + OCH2CH2CH2CO
I I
207
Пиридин -H β,β'-оксидипропионит-
р ил
Пиридин + вода
C6H5N + (NCCH2CH2)2O
207
C5H5N + H2O
207
Парафины — ненасыщенные углево¬
дороды
Парафины — ароматические углево¬
дороды
Парафины — нафтены
Олефины
Бутен-1 — цис· бутен-2
Бутен-1 — бутадиен
Ацетилпиперидин
Диметилсульфолан
фурфурол
Фурфурол + вода
Фурфурол -I- гидроокись кальция
Фенол
Трифторуксусная кислота
Гептафтормасляная кислота
Ν-Диметилкарбамат диметиламмо-
ния
N-Замешенные карбаматы алкил-
аммония
Хлороформ
Метил хлористый
Этиловый спирт
Изоамиловый спирт
Трифторуксусная кислота
Гептафтормасляная кислота
1,4-Диоксан
Изопропилацетат
Фенол + вода
Ароматические амины + вода
Треххлористый фосфор
Трехбромистый фосфор
Треххлористый фосфор -I- трехбро¬
мистый фосфор
Метиламин
Метиламин
Ch3CONCH2(CH2)3CH2
(CH3)2C4H6SO2
ОСН=СНСН=ССНО
I I
ОСН=СНСН=ССНО + H2O
I I
ОСН=СНСН=ССНО + Ca(OH)2
I I
C6H5OH
CF3CCH
C3F7COOH
(CH3)2NC(O)O- NH2(CH3)2
R2NC(O)O-NR417>
CHCl3
CH3Cl
C2H5OH
азо-CsHi ιΟΗ
CF3COOH
C3F7COOH
OCH2CH2OCH2Ch2
I I
CH3COOC3H7
C6H5OH + H2O
RNR'R" *) -I- N2O
PCl3
PBr3
PCl3 + PBr3
CH3NH2
CH3NH2
207
207
380, 433
380, 433
378
412
145
145
242
242
97
97
97
97
145
145
97
97
330
331
321
321
321
7
7
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Бутен-1—углеводороды C4
Фурфурол + вода
ОСН=СНСН=ССНО + H2O
I I
146
Цис- бутен-2 — грйяс-бутен-2
Метиламин
CH3NH2
7
Транс-6 утен-2 — бутадиен
Метиламин
CH3NH2
7
Бутен — парафины
Фурфурол 4- вода
ОСН=СНСН=ССНО + H2O
I I
380
Бутен —- бутадиен
Ацетон
(CH3)2CO
368
Метиламин
CH3NH2
8
Фурфурол
осн=снсн=ссно
I I
368
Пентен-1 — 2-метилбутен-1
Диэтил фосфон ат
H(OC2H5)2PO
156
Фосфон аты
R7(OR)2PO1)
156
Пентен-1 — 2-метилбутен-1 — 2-ме-
Диэтил фосфон ат
H(OC2H5)2PO
156
тилбутен-2
Фосфонаты
R7(OR)2PO I)
156
Пентен-1 — изопрен
Ацетон
(CH3)2CO
368
Ацетонитрил
CH3CN
61
Пентен-2 — 2-метилбутен-2
CH3CN
61
Пентен-2 — изопрен
Ацетон
(CH3)2CO
368
Ацетонитрил
CH3CN
61
2-Метил бутен-I — 2-метилбутен-2
Диэтилметилфосфонат
CH3(OC2H5)2PO
156
Фосфонаты
R7(OR)2PO υ
156
2-Метилбутен-1 — 2-метилбутен-2 —
Диэтилметилфосфонат
CH3(OC2H5)2PO
156
изопрен
Фосфонаты
R7(OR)2PO 1>
156
З-Метилбутен-1—углеводороды Cg-
Фурфурол + вода
ОСН=СНСН=ССНО 4- H2O
I I
146
2-Мет ил бутен-2 — изопрен
Диэтиленгликоль
(HOCH2CH2)2O
181
Метилформиат
HCOOCH3
57
Этцлоксалат
(COOC2H5)2
181
Нитрометан
CH3NO2
58, 59
Ν,Ν-Диметилформамид
HCON(CH3)2
58,59, 181
2-Метилбутен — изопрен
Олефин Cs — диолефин C5
4-Метилпентен-1 — 4-метцл пентен-2
/
Смесь олефинов C6
Олефины — диолефины
Ацетонитрил
CH3CN
181
Р, β'-Окси д ипропионитр uh
(NCCH2CH2)2O
181
Диметилфосфонат
H(OCH3)2PO
156
Фосфонаты
R7(OR)2PO1)
156
Диметилсульфоксид
(CH3)2SO
181
Ν,Ν-Диметилформамид
NCON(CH3)2
411
Метилформиат
HCOOCH3
34
Перфтортриэтиламин
(C2F5)3N
64
Ацетонитрил 4- вода
CH3CN 4- H2O
4
Дихлорметан
CH2Cl2
284
1,1,1-Трихлорэтан
CCl3CH3
284
1,1,2-Трихлорэтан
CHCl2CH2Cl
284
Тетрахлорэтилен
C2Cl4
284
Трихлорэтилен
C2HCl3
284
Дибромэтилен
C2H2Br2
284
Нитробензол
C6H5NO2
284
Триэтиламин
(C2H5)3N
284
Дихлорметан
CH2Cl2
284
1,1,1-Трихлорэтан
CCl3CH3
284
1, 1,2-Тр ихлорэтан
CHCl2CH2Cl
284
T етр ахлорэтилен
C2Cl4
284
Трихлорэтилен
C2HCl3
284
Дибромэтилен
C2H2Br2
284
Нитробензол
C6H5NO2
284
Триэтиламин
(C2H5)3N
284
Бензол 4- ρ,Ρ'-оксидипропионитрил
C6H6 4- (NCCH2CH2)2O
207
Бензол 4- сульфолан
C6H6 4- CH2(CH2)2CH2SO2
I I
207
Метиловый спирт
CH3OH
207
Этиленхлоргидрин
CH2ClCH2OH
207
Ацетон
(CH3)2CO
207
Метилэтилкетон
CH3COC2H5
207
Метилэтилкетон 4- γ-бутиролактон
CH3COC2H5 + OCH2CH2CH2CO
I I
207
Диэтилкетон
(C2H5)2CO
207
Циклопентанон
CH2(CH2)3CO
207
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Олефины — диолефины
2,4-Пентандион
(CH3CO)2CH2
207
Ацетон ил ацетон
(CH3COCH2)2
207
Метилцеллозольв
CH3OCH2CH2OH
207
Метилцеллозольв -F нитрометан
CH3OCH2CH2OH -F CH3NO2
207
Метилцеллозольв -F сульфолан
CH3OCH2CH2OH-F
-FCH2(CH2)2CH2SO2
I I
207
Метилцеллозольв -F вода
CH3OCH2CH2OH -F H2O
207
Монометиловый эфир диэтиленгли-
коля
СНзОСН2СН2ОСН2СН2ОН
207
Метиловый эфир ацетоуксусной
кислоты
СНэСОСНзСООСНз
187
Диэтилоксалат
(COOC2H5)2
207
у-Бутиролактон
OCH2CH2CH2CO
I I
207
Этиленкарбонат
CH2OC(O)OCH2
207
Пропиленкарбонат
CH3CHOC(O)OCh2
I I
207
Дизтилкарбонат
(C2H5O)2CO
207
Нитрометан
CH3NO2
207
Этилендиамин
(CH2NH2)2
207
Ν,Ν-Диметилформамид
HCON(CH3)2
207
Ν,Ν-Диметилформамид -F гексан
HCON(CH3)2 -F C6Hi4
374
Ν,Ν-Диметилформамид -F гептан
HCON(CH3)2-FC7Hi6
374
Ν,Ν-Диметилформамид + бензол
HCON(CH3)2-FC6H6
374
Ν,Ν-Диметилацетамид
CH3CON(CH3)2
207
N,N-Диметилцианамид
NCN(CH3)2
207
Ацетонитрил
CH3CN
207
Пропионитрил
C2H5CN
207
Олефин — алкин
Олефины — алкилмонобромнды
Олефины — нитрилы
Олефины (диолефины) — фракция Cs
Диолефины
Диолефин Сз-б — парафины Сз-6
(олефины Сз^б)
Бутадиен — бутан (бутены)
Бутадиен — бутан (изобутан, буте¬
ны)
ы
о*
β-Хлорпропионитрил
ClCH2CH2CN
207
Бутиронитрил
C3H7CN
207
Тетрагидр офуран
OCH2(CH2)2CH2
I I
207
Фурфурол
осн=снсн=ссно
I I
207
Тетрагидрофурфуриловый спирт
ОСН2(СН2)2СНСН2ОН
207
Пирролидон
NhCOCH2CH2CH2
I I
207
N -Метилпирролидон
Ch3NCOCH2CH2CH2 .
I I
207
Пиридин -Ь убутиролактон
C6H5N + OCH2CH2CH2CO
I I
207
Пиридин + р,р'-оксидипропионит-
рил
C5H5N 4- (NCCH2CH2)2O
207
Пиридин 4- вода
C5H5N 4- H2O
207
Ацетил пипер идин
CH3COiNCH2(CH2)3CH2
207
Диметилсульфолан
(CH3)2C4H6SO2
207
Ν,Ν-Диметилформамид
HCON(CH3)2
258
Ν,Ν-Диалкиламиды
RCONR'R" 7>
193
Метиловый спирт
CH3OH
420
Ацетонитрил + вода
CH3CN + H2O
4
N,N-Диметилформамид
HCON(CH3)2
394
Метиловый спирт + вода
CH3OH + H2O
113
Спирты + вода
ROH 9> + H2O
113
Ацетон + вода
(CH3)2CO + H2O
113
Ν,Ν-Диметилформамид
HCON(CH3)2
296
Аммиак
NH3
355
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Бутадиен — бутан (бутеновая фрак¬
ция)
β,β'-Дихлордиэтиловый эфир
β,β'-Дихлордиэтиловый эфир + ди¬
хлорэтан
, β,β'-Дихлордиэтиловый эфир + аце¬
тон
Целлозольв
Целлозольв + вода
Фурфурол
(ClCH2CH2)2O
(ClCH2CH2)2O + C2H4Cl2
(ClCH2CH2)2O + (CH3)5CO
C2H5OCH2CH2OH
C2H5OCH2CH2OH + H2O
осн=снсн=ссно
I I
19
19
10.
19
19, 22
22
Фурфурол + вода
0СН=СНСН=ССН0 + H2O
I I
19
Бутадиен^бутены
Ацетон+вода
Ацетонитрил
Ацетонитрил + вода
Пропионитрил + вода
Лактонитрил + вода
Фурфурол + вода
(CH3)2CO + H2O
CH3CN
CH3CN + H2O
C2H5CN + H2O
CH3CHOHCn + H2O
OCH=CHCH-CCHO + H2O
I I
229, 316
185
317
317
317
225, 229
Бутадиен-—бутен-2 (ацетилены С4)
Бутадиен—олефины (диолефины)
Бутадиен—винил ацетилен
Изобутан
Метиловый эфир ацетоуксусной кис¬
лоты
Ацетон
β,β'-Дихлордиэтиловый эфир
Диоксан
C4H10
СН3СОСН2СООСН3
(CH3)2CO
(ClCH2CH2)2O
OCH2CH2OCh2CH2
I
424
187
425
425
425
Фенол
Ν,Ν-Диметилформамид
Ацетонитрил
Фурфурол
C6H5OH
HCO(CH3)2
CH3CN *
осн=снсн=ссно
I I
425
425
425
425
165
Бутадиен — углеводороды C4
Бутадиен — углеводороды
Бутадиен (изопрен) — углеводороды
С4-5
Изопрен — 4-метилпентен-1 (цис-4-
метилпентен-2)
Изопрен — пентены
Изопрен — циклопентадиен
Изопрен — углеводороды Cs
Фурфурол -F- вода
Метиламин
Ν,Ν-Диметилформамид
Фурфурол
Ν,Ν-Диметилформамид
Ν,Ν-Диметилацетамид
Ацетонитрил
Ацетонитрил + вода
Дигексилсебацинат '
Tp икрез ил фосфат
Дибензиловый эфир
Дибутилфталат
Диизодецилфталат
Ацетон
Ацетон 4- вода
Амины
Амины + вода
Ацетонитрил
Фурфурол
Фурфурол + вода
Пиридин
Пиридин + вода
N,N -Диметил форм амид
Ацетонитрил
Спирты
Метилаль
Ацетон
Ацетон + вода
Кетоны
Окись пропилена
OCH=CHCH-CCHO + H2O
I I
425
CH3NH2
360
HCON(CH3)2
415
OCH=CHCH-CCHO
f I
360
HCON(CH3)2
454
CH3CON(CH3)2
150, 151
CH3CN
189, 371
CH3CN + H2O
118
[(CH2)4COOC6Hnb
166
(CH3C6H4O)3PO
166
(C6H5CH2)2O
166
C6H4(COOC4H9)2
166
C6H4(COOCioH2I)2
166
(CH3)2CO
344
(CH3)2CO + H2O
344
RNR7R" ®)
344
RNR7R" 8> + H2O
344
CH3CN
232
ОСН=СНСН=ССНО
I ' I
344
ОСН=СНСН=ССНО + H2O
I I
344
C5H5N (цикл.)
344
C5H5N (цикл.) + H2O
344
HCON(CH3)2
432
CH3CN
432
ROH9)
165
CH2(OCH3)2
373
(CH3)2CO
343
(CH3)2CO + H2O
79, 342
RCOR'10)
165
CH3CHCH2O
437
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Изопрен — углеводороды C5
Метилформиат
HCOOCH3
188
Амины
RNR7R"8)
165
Изопрен — углеводороды
Диметилсульфоксид
(CH3)2SO
84
Ν,Ν-Диметилформамид
HCON(CH3)2
35
Изопрен — фракция крекинг — ди¬
Ацетон
(CH3)2CO
234, 254
стиллата ·
Ацетонитрил
CH3CN
234, 254
Изопрен (гранс-пиперилен) — углево¬
дороды C5
Ацетон + вода
(CH3)2CO
79
Диолефин — парафины (олефин-1,
Метиловый спирт 4 вода
CH3OH + H2O
113
олефин-2)
Этиловый спирт + вода
ROH9) 4 H2O
113
Ацетон + вода
(CH3)2CO 4 H2O
113
Диолефины парафины (олефины)
Этаноламин + \,\-бис-трет-бутнл-
ΆίηίΜ/ О TTfTOU
H2NCH2CH2OH + (HSC4H8)2CHCH3
295
MCjJlla 111 Ciri
Этаноламин 4 паральдегид
NH2CH2CH2OH +
4- OCH (CH3) OCH (CH3) OCHCH3
I I
295
Анилин 4 паральдегид
Фенилгидразин + паральдегид
C6H5NH2 +
+OCH (CH3) OCH (CH3) OCH (CH) з
C6H5NHNH2 +
295
Фенилгидразин 4- \,\-бис-трет-6у-
тилмеркаптоэтанол
+ OCH (CH3) ОСНСНзОСНСНз
C6H5NHNH2 4- CH3C(C4H9)2SH
295
Ацетонитрил
CH3CN
185
Ацетонитрил + пропионитрил
CH3CN 4- C2H5CN
185
Пропионитрил
C2H5CN
185
Фурфур иловый спирт + паральде¬
гид
C4H3OCH2OH 4
+ OCH=CHCH =CCH2OH
I I
295
Диолефины — алкины
Ацетонитрил + вода
CH3CN + H2O
255
Диолефины — углеводороды
Ацетон
(CH3)2CO
316
Диоксан
OCh2CH2OCH2CH2
I I
316
Диоксан + вода
OCH2Ch2OCH2CH2 + H2O
I I
316
Ацетонитрил
CH3CN
316
Ароматические углеводороды
Бензол — парафины
Фенол
C6H5OH
288
Бензол — гептан (циклогексан, ме¬
Парафины
CnH2n +2
294
тилциклогексан)
Ацетон + вода
Вода
Полиэтиленгликоли
Бензол — гептан (метилциклогексан)
(CH3)2CO + H2O
H2O
Н[ОСН2СН2]пОН
404
404
Бензол — толуол (парафины Сб-7,
iIUi;
319
нафтены Сб-7)
Ацетон
(CH3)2CO
319
Ацетон Ч- вода
(CH3)2CO + H2O
319
Моноэфиры диэтиленгликоля
ROCH2CH2OCH2CH2OH9>
319
I
Моноглицериновые эфиры
—
319
)
Фенол
C6H5OH
319
Крезол технический
CH3C6H4OH
319
Резорцин
C6H4(OH)2
319
Алкилфенолы
CnH2n_7OH
319
Нитробензол
C6H5NO2
319
Диэтаноламин
(HOCH2CH2)2NH
319
Анилин
C6H5NH2
319
Ксилидин
(CH3)2C6H3NH2
319
Фурфуриловый спирт
OCH = CHCH - CCH2OH
I I
319
Фурфурол
осн=снсн=ссно
I I
319
Хинолин
C9H7N
319
Бензол — метилциклопентан
о-Этоксианилин
C2H5OC6H4NH2
291
Диметилфосфонат
H(OCH3)2PO
156
Фосфонаты
R7(OR)2PO1)
156
Бензол — циклогексан
Гексан
C6H14
117
Y
о
Парафиновое масло
370
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Бензол — циклогексан
Г ексафтортетрахлорбутан
C4F6Cl4
270
Метиловый спирт
CH3OH
429
Этиловый спирт
C2H5OH
429
Пропиловый спирт
C3H7OH
429
Изопропиловый спирт
USo-C3H7OH
429
Этиленгликоль
(CH2OH)2
6,370, 429
Бутиленгликоль
C4H8(OH)2
370
Ацетон
(CH3)2CO
429
Диацетоновый спирт
Ch3COCH2COH(CH3)2
429
Метилэтилкетон *
CH3COC2H5
173, 429
Метил изобутилкетон
CH3COC4H9
161
Уксусная кислота
CH3COOH
429
Ρ,Ρ'-Дихлордиэтиловый эфир
(ClCH2CH2)2O
429
1,4-Диоксан
OCH2CH2OCH2Ch2
I I
429
Целлозольв
C2H5OCH2CH2OH
429
Метилцеллозольв
CH3OCH2CH2OH
429
Диэтиленгликоль
(HOCH2CH2)2O
429
Карбитол
C2H5OcH2CH2OCH2CH2OH
429
Метилацетат
CH3COOCH3
320
Фенол
C6H5OH
412, 429
Нитрометан
CH3NO2
429
Нитробензол
C6H5NO2
429
Перфтортриэтиламин
(C2F5)3N
64
Перфтортрибутиламин
(C4F9)3N
270
Анилин
C6H5NH2
33, 250,
260, 354,
370, 429
Формамид
HCONH2
429
Ацетонитрил
Ρ,Ρ'-Оксидипропионитрил
CH3CN .
(NCCH2CH2)2O
429
6
Бензол — неароматические углеводо¬
роды
Бензол — близкокипящие углеводо
роды
•ензол — четыреххлористый углерод
Бензол — метиловый спирт
Диметилфосфонат
Фосфонаты
Фурфурол
Пиридин
Хинолин
Вода
Метилциклопентан
Циклогексан
Неароматический углеводород
Метиловый спирт
Метиловый спирт + вода
Этиловый спирт
Изопропиловый спирт
Ацетон
Ацетон + вода
Метилэтилкетон
Уксусная кислота
Ацетонитрил
Аммиак
β,β'-Оксидипропионитрил + бензо¬
нитрил
β,β'-Иминодипропионитрил + бен¬
зонитрил
Р,р7-Тиодипропионитрил 4- бензо¬
нитрил
Алифатический динитрил + арома¬
тический мононитрил
Алафитический динитрил + гетеро¬
циклический моноамин
Толуол
Ксилол
Хлорбензол
о-Дихлорбензол
Спирты
Ксилолы
Хлорбензол
Анилин
H(OCH3)2PO
156
R7(OR)2POD
156
осн=снсн-ссно
33, 392,
I ' I
429
C5H5N
429
C9H7N
370
H2O
429
C6H12
276
C6H12
83
—. ■
83
CH3OH
83, 158
CH3OH + H2O
444
C2H5OH
83, 158
C3H7OH
158
(CH3)2CO
83, 158,276
(CH3)2CO+ H2O
444
CH3COC2H5
83, 158
CH3COOH
158
CH3CN
83, 158,387
NH3
198
(NCCH2CH2)2O + C6H5CN
201
(NCCH2CH2)2NH + C6H5CN
201
(NCCH2CH2)2S + C6H5CN
201
NCRXR'CN ч> + CnH2n^7CN
201
NCRXR7CN + RNH 12)
201
C6H5CH3
236
C6H4(CH3)2
236
C6H5Cl
236, 391
C6H4Cl2
236
ROH »)
236
C6H4(CH3)2
24
C6H5Cl
24
C6H5NH2
24
П родолжение
Разделяемая система
Разделяющий агейт
Литера¬
тура
название
формула
Бензол —■ этиловый спирт
Декан
С10Н22
25
Нитробензол
C6H5NO2
25
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν-Этиламид гликолевой кислоты
HoCH2CONHC2H5
183
Парафиновое масло
—
370
Бензол *— тиофен
Этиленгликоль
(CH2OH)2
370
Бутиленгликоль
C4H8(OH)2
370
Анилин
C6H5NH2
370
Хинолин
C9H7N
370
Бензол — вода
Этиловый спирт
C2H5OH
235
Бензол — бензол содержащее сырье
Фенол
C6H5OH
282
Бензол (толуол) — неароматические
C6H5OH
281
углеводороды
Толуол — парафины
C6H5OH
351, 368
Толуол — парафины (олефины, наф-
Метиловый спирт
CH3OH
158
тены)
Этиловый спирт
C2H5OH
158
Изопропиловый спирт
C3H7OH
158
Ацетон
(CH3)2CO
158
Метилэтилкетон
CH3COC2H5
158
Уксусная кислота
CH3COOH
158
Триоксан
OCH2OCh2OCH2
I I
274
Толуол — метилциклогексан
Ацетонитрил
CH3CN
158
Метиловый спирт
CH3OH
362, 429
Этиловый спирт
C2H5OH
429
Пропиловый спирт
C3H7OH
429
Изопропиловый спирт
C3H7OH
429
Этиленгликоль
(CH2OH)2
429
Ацетон
(CH3)2CO
429
Метилэтилкетон
CH3COC2H5
429
Диацетоновый спирт
Ch3COCH2COH(CH3)2
429
Муравьиная кислота
Уксусная кислота
Ацеталь
1,4-Диоксан
Метилцеллозольв
Диэтиленгликоль
Фенол
Нитрометан
Анилин
Толуол — неароматические углеводо¬
роды С 7-8
Толуол ■— неароматические углево¬
дороды
Формамид
Ацетонитрил
Фурфурол
Пиридин
Пиперидин
Вода
Фенол + алкилфенол
Этилциклопентан
Метиловый спирт
Ацетон
Метилэтилкетон
Метилэтилкетон + вода
Ацетонилацетон
β,β'-Дихлордиэтиловый эфир
Фенол
Крезол
Нитробензол
Нитротолуол
Анилин
Ацетонитрил
Фурфурол
HCOOH
CH3COOH
CH3CH(OC2H5)2
OCh2CH2OCH2CH2
I I
CH3OCH2CH2OH
(HOCH2CH2)2O
C6H5OH
CH3NO2
C6H5NH2
HCONH2
CH3CN
осн=снсн-ссно
C5H5N
(CH2)5NH
H2O
C6H5OH + СпН271_7ОН
C7Hu
CH3OH
(CH3)2CO
CH3COC2H5
CH3COC2H5+ H2O
(CH3COCH2)2
(ClCH2CH2)2O
C6H5OH
CH3C6H4OH
C6H5NO2
CH3C6H4NO2
C6H5NH2
CH3CN
осн=снсн=ссно
I !
429
429
429
429
429
429
392, 429
429
33. 168,
197. 388,
429
429
429
33. 429
429
429
429
104
276
160
276
444
160. 339
179
179
179
179
179
179
179. 405
444
179
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Сульфолан
CH2(CH2)2CH2SO2
405 '
Диметилсульфолан
(CH3)2C4H6SO2
393, 405
Диметилсульфолан + кумол
(CH3)2C4H6SO2 + C6H5C3H7
405
Толуол — углеводороды
Метилэтилкетон H- вода
CH3COC2H5 + H2O
108, 199,
'
Уксусная кислота
CH3COOH
231, 272.
348, 363
280
Фенол
C6H5OH
5, 365
Толуол — газолин
Фенол H- триэтаноламин
C6H5OH + (HOCH2CH2)3N
352
Фенол + фенолят калия
C6H5OH + C6H5OK
349
Толуол—фракция бензина
Фенол
C6H5OH
105
Фенол + метиловый спирт
C6H5OH + CH3OH
105
Толуол — нефтяная фракция
Фенол
C6H5OH
42, 177
Толуол (ксилол) — ароматическая
Фенол + алкилфенолы
C6H5OH + CnU2n + он
104
нефтяная фракция
о-Ксилол — п-ксилол
Диметил фосфонат
H(OCH3)2PO
156
Фосфонаты
R7(OR)2PO 1>
' 156
0-Ксилол — ксилолы
β, β'-Тиодипропионитрил
(NCCH2CH2)2S
92
о-Ксилол — Λί-КСИЛОЛ — /1-КСИЛОЛ
Моногликоли
CnH2n (OH)2
275
Метилцеллозольв
CH3OCH2CH2OH
275
Монометиловый эфир ацетата эти-
СН3ОСН2СН2ОСОСН3
275
ленгликоля
Эфиры моногликолей
275
Хлористый алюминий
AlCl3
334
Бромистый алюминий
Пятифтористый мышьяк
AlBr3
334
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлоцистая сурьма
SbCl3
332, 334
Трехбромистая сурьма
SlBr3
334
о-Ксилол — стирол
л-Ксилол — л-ксилол
л-Ксилол — этилбензол
л-Ксилол — ароматические углеводо¬
роды C8
л-Ксилол — диметилдиоксан
Ксилол — стирол
ϊ
Ксилол—неароматические углево¬
дороды С 7-8
Ксилол — неароматические углево¬
дороды
Ксилолы — углеводороды
Ксилол — ароматическая нефтяная
фракция
Исследуется 28 растворителей 29>
Метилцеллозольв
Ν,Ν-Диметилформамид
N,N-Диметил форм амид -F вода
Ν,Ν-Диэтилформамид
Ν,Ν-Диизопропилформамид
Ν,Ν-Диалкилформамид -F вода
Октан
1.2-Дибромэтан
Бензиловый спирт
Нитробензол -F дихлорбензол
7,8-Бензохинолин
N-, S-, о-Замещенные антраценов
или фенантренов
Этиленгликоль
1.2-Пропил енгликоль
I ,З^Бутиленгликоль
Амид карбоновой кислоты
Бутиловый спирт
Изобутиловый спирт
Вода -F органическая соль цинка
или кадмия -F муравьиная кисло¬
та
Вода -I- органическая соль цинка
или кадмия -F уксусная кислота
Вода -F органическая соль цинка
или кадмия -F алифатическая кис¬
лота
Фенол -F алкилфенол
Триоксан
2,4-Диметилсульфолан
Метиловый спирт
Фенол
CH3OCH2CH2OH
HCON(CH3)2
HCON(CH3)2 -F H2O
HCON(C2H6)2
HCON(Oso-C3H7)2
HCON (CnH27l-H Ь
C8H18
C2H4Br2
C6H5CH2OH
C6H5NO2 -F C6H4Cl2
C13H9N
(CH2OH)2
СН2ОНСНОНСН3
СН2ОНСН2СНОНСНз
RCONR7R'7 >*>
C4H9OH
оз0-С4Н9ОН
H2O -F (RCOO)2M и) + HCOOH
H2O + (RCOO)2M к> 4- CH3COOH
H2O -F (RCOO)2M *4> -F RCOOH *>
C6H5OH + СпНап-гОН
OCH2OCH2OC
(CH3) 2C4H6S02 (цикл.)
CH3OH
C6H5OH
140
И
318
184
318
318
184
382
12
309
382
213
213
202
202
202
206
40
40
192
192 »4>
192
104
274
393
307
105
Продолжение
Разделяемая система
Разделяющий агент
Литера-
■ тура
название
формула
Ксилолы — фракция бензина (/кип =
Метиловый спирт
CH3OH
369
=* 120—150° С)
Фенол
C6H5OH
369
Крезолы
CH3C6H4OH
369
Ксиленолы
(CH3)2C6H3OH
369
Высшие фенолы
—
369
ксилолы — дистиллат рифоуминга
Фракция фенолов (/Кип = 200—
—
383
— 150° С)
Этилбензол —· ксилолы
Этилциклогексан
C8H16
39
Бензиновая фракция (/кип = 129 —
—
39
— 130° С)
Хлороформ
CHCl3
97
Метил хлористый
CH3Cl
97
Этиловый спирт
C2H5OH
97
Изоамиловый спирт
C3H7OH
97
Изопропилацетат
CH3COOC3H7
97
1,4-Диоксан
OCh2CH2OCH2CH2
I I
97
Этилбензол — стирол
Пропиловый спирт
C3H7OH
45
Изобутиловый спирт
ггзо-С4Н9ОН
45
Изоамиловый спирт
C5HuOH
45
Диэтилкарбинол
(C2H5)2CHOH
45
Уксусная кислота
CH3COOH
21, 45
Этиленкарбонат
CH2OC(O)OCH2
152
Вода + органическая соль цинка,
H2O + (RCOO)2M 15) + HCOOH
192
кадмия или ртути + муравьиная
кислота
Вода + органическая соль цинка,
H2O + (RCOO)2M 15) + CH3COOH
192
*
кадмия или ртути + уксусная
кислота
t
Этилбензол — стирол — фенил ацети¬
лен
Вода 4- органическая соль цинка,
кадмия или ртути 4- алифатиче¬
ская кислота
Диметилфосфонат
Фосфонаты
2-Пирролидон
14-Метил-2-пирролидон
1.5-Диметил-2-пирролидон
1Ч-Пропил-2-пирролидон
1Ч-Гексил-2-пирролидон
N-Метил-4-гексил-2-пирролидон
3.5-Диамил-2-пирролидон
Производные 2-пирролидон а
2-Пирролидон
^Метил-2-пирролидон
1.5-Диметил-2-пирролидон
^Пропил-2-пирролидон
Ν-Γ ексил-2-пирролидон
Ы-Метил-4-гексил-2-пирролидон
H2O + (RCOO)2M «*> + RCOOH 9>
H(OCH3)2PO
R'(OR)2PO »
NhCOCH2CH2CH2
I I
Ch3NCOCH2CH2CH2
I I
CH3NCOCH2CH2CHCH3
I !
Csh7NCOCH2CH2CH2
I I
C6H13NCOCH2Ch2CH2
I I
CH3NCOCH2Ch (C6H13) CH2
I I
NHCOCH(C5Hn)CH2CHC5H11
RNCOCHRCHRCHR ι6>
I I
NHCOCH2CH2CH2
I I
Ch3NCOCH2CH2CH2
! I
CH3NCOCH2CH2CHCH3
I I
C3H7NCOCH2CH2Ch2
I I
C6H13NCoCH2CH2CH2
I I
CH3NCOCH2Ch (C6H13) CH2
I I
192
156
156
157
157
157
157
157
157
157
157
157
157
157
157
157
157
Продолжение
Разделяемая система
'4
Разделяющий агент
Литера¬
тура
название
формула
3,5-Диамил-2-пирролидон
NhcocH(CsHii)CH2CHC5H11
I I
157
Производные 2-пирролидона
RNCOCHRCHRCHR ι6>
I I
157
Этилбензол -фен ил ацетилен
2-Пирролидон
NhCOCH2CH2CH2
I I
157
N -Метил-2-пирролидон
Ch3NCOCH2CH2CH2
I I
157
1,5-Диметил-2-пирролидон
Ch3NcoCH2CH2CHCH3
I I
157
Ы-Пропил-2-пирролидон
C3H7NCOCH2CH2Ch2
I I
157
]Ч-Гексил-2-пирролидон
C6Hi3NCOCH2CH2CH2
I I
157
Ы-Метил-4-гексил-2-пирролидон
Ch3NCOCH2CH (C6H13) CH2
I I
157
3,5-Диамил-2-пирролидон ν
NHCOCH (CsHii) CH2CHC5HiI
I
157
Производные 2-пирролидона
RNCOCHRCHRCHR *6>
I I
157
Этилбензол — ароматические углево¬
дороды C8
Этилбензол — ароматические углево¬
дороды
Этилбензол — этилциклогексан
Стирол — фенилацетилен
Ν,Ν-Диметилформамид
Ν,Ν-Диэтилформамид
Амид карбоновой кислоты
Трихлорбензол
Дихлорбензол
Г ексиленгликоль
2-Пирролидон
HCON(CH3)2 "
HCON(C2H5)2
RCONRfR" 13>
C6H3Cl3
C6H4Cl2
C6Hi2(OH)2
NhCOCH2CH2CH2
I I
206
206
206
81
'81
361
157
Стирол — близкокипящие углеводо¬
роды
Ароматические углеводороды Сб-8 —
парафины Сб-8 (нафтены Сб-8)
Ароматические углеводороды Се-8~
ненасыщенные углеводороды Сб-7
Ароматические углеводороды Се-8 —
неароматические углеводороды
М-Метил-2-пирролидон
1.5-Диметил-2-пирролидон
Ы-Пропил-2-пирролидон
Ν-Γ ексил-2-пирролидон
И-МетшМ-гексил-2-пиррол ид он
3.5-Диамил-2-пирролидон
Производные 2-пирролидона
Пропиленгликоль
Многоатомный спирт
Муравьиная кислота
Муравьиная кислота 4- вода
Уксусная кислота
Жирные кислоты С2-4
Метилцеллозольв
Целлозольв
Диэтиленгликоль
Метиллактат
Этиллактат
Моноацетат глицерина
Диацетат глицерина
Диэтиленгликоль 4- вода
Полиалкиленгликоля 4- вода
Фенол
Морфолин 4: вода
Ch3NCOCH2CH2CH2
! I
ch3ncoch2ch2chch3
C3H7NCOCH2CH2Ch2
I
C6H13NCOCH2CH2Ch2
I _J
CH3NCOCH2Ch (C6H13) CH2
I I
NHCOCH (C5Hn) CH2CHC5H11
!_ I
NRCOCHRCHRCHR
I [
C3H6(OH)2
HCOOH
HCOOH 4- H2O
CH3COOH
CnH2n+1COOH
CH3OCH2CH2OH
C2H5OCH2CH2OH
(HOCH2CH2)2O-
СНзСНОНСООСНз
СН3СНОНСООС2Н5
СН3СООСН2СНОНСН2ОН
(CH3COO)2C3H5OH
(HOCH2CH2)2O 4- H2O
Н[0 (CR2)nJmOH 4-H2O
C6H5OH
OcH2CH2NHCH2CH2 + H2O
I I
157
157
157
157
157
157
157
148
148
148
148
106
106
158, 150,
217
10
148
217
217
148
148
427
427 ·
290
271
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Пропилбензол-аллилбензол
V —
2-Пирролидон
NhCOCH2CH2CH2
I I
157
Ы-Метил-2-пирролидон
Ch3NCOCH2CH2CH2
I I
157
1,5-Диметил-2-пирролидон
CH3NCOCH2CH2CHCH3
I I
157
Ы-Пропил-2-пирролидон
C3H7NCOCH2CH2Ch2
I I
157
1^-Гексил-2-пирролидон
C6H13NCOCH2Ch2CH2
I I
157
N -Метил-4-гексил-2-пирролидон
Ch3NCOCH2CH (C6H13) CH2
I I
157
3,5-Диамил-2-пирролидон
NHCOCH (C5H10 CH2CHC5H11
157
Производные 2-пирролидона
RNCOCHRCHRCHR >6>
I I
157
Пропилбензол неароматические угле¬
Нитрометан
CH3NO2
301
водороды
Кумол неароматические углеводо¬
Нитрометан
CH3NO2
301
роды
Кумол — фенол
Вода
H2O
278
о-Этилтолуол — о-винилтолуол
2-Пирролидон
NhCOCH2CH2CH2
I I
157
Ы-Метил-2-пирролидон
Ch3NCOCH2CH2CH2
I А
157
1,5-Диметил-2-пирролидон
ch3ncoch2ch2chch3
I
157
N-Пропил-2-пирролидон
C3H7NCOCh2CH2CH2
I I
157
379
Ν-Γ ексил-2-пирролидон
C6Hi3NCOCH2CH2CH2
I I
157
N -Метил-4-гексил-2-пирролидон
Ch3NCOCH2CH (C6H13) CH2
I I
157
3,5-Диамил-2-пирролидон
NHCOCH (C5Hn) CH2CHC5Hn
I I
157
Производные 2-пирролидона
RNCOCHRCHRCHR
I I
157
Этилтолуолы — неароматические уг-
ТТРПП Л CiTlCi пы
Нитрометан
CH3NO2
301
лсьидириды
Смесь изомеров метилэтилбензола
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлористая сурьма
SbCl3
334
Псевдокумол — неароматические уг¬
Трехбромистая сурьма
SbBr3
334
Нитрометан
CH3NO2
301
леводороды
Мезитилен — неароматические угле¬
Нитрометан
CH3NO2
301
водороды
Смесь изомеров триметилбензола
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлористая сурьма
SbCl3
334
Смесь ароматических углеводородов
Cg
Трехбромйстая сурьма
SbBr3
334
Диалкиловый эфир ортофталевой
кислоты
C6H4(COOCnH2n-H) 2
82
Еутилбензол — 1-фенилбутен-1 — 1-
фенил-1,3-бутадиен
2-Пирролидон
NHCOCH2CH2CH2
I I
157
N-Метил-2-пиррол идон
Ch3NCOCH2CH2CH2
I I
157
1,5-Д иметил-2-пирролидон
CH3NCOCH2CH2CHCH3
I I
157
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула -
N-Пропил-2-пирролидон
C3H7NCoCH2CH2CH2
I I
157
Ν-Γ ексил-2-пирролидон
C6Hi3NCOCH2CH2CH2
I I
157
N -Метил-4-гексил-2-пиррол идон
CH3NCOCh2CH (C6H13) CH2
I I
157
3,5-Диамил-2-пирролидон
NHCOCH (CsHii) CH2CHCsH11
S I
157
Производное 2-пирролидона
RNCOCHRCHRCHR »б>
I I
157
Бутилбензол — I-фенил-1,3-бутадиен
2-Пирролидон
NhCOCH2CH2CH2
I I
157
N-MeTHA-2-nnppo л идон
Ch3NCOCH2CH2CH2
I I
157
1,5-Диметил-2-пирролидон
CH3NCOCHfcCH2CHCH3
I l
157
N-Пропил-2-пирролидон
C3H7NCOCH2Ch2CH2
I I
157
Ν-Γ ексил-2-пиррол идон
C6H13NCOCh2CH2CH2
f I
157
'
Ы-Метил-4-гексил-2-пирролидон
CH3NCOCH2Ch (C6H13) CH2
157
3,5-Диамил-2-пирролидон
NHCOCH (CsHu) CH2CHCgH11
I I
157
Производные 2-пирролидона
RNCOCHRCHRCHR »6>
I I
157
Цимол — а-метилстирол
2-Пирролидон
NhCOCH2CH2CH2
I I
157
Цимол — метилфенилацетилен
Смесь изомеров диэтилбензола
Ы-Метил-2-пирролидон
1.5-Д иметил-2-пирролидон
^Пропил-2-пирролидон
N-Г ексил-2-пиррол идон
Ы-Метил-4-гексил-2-пирролидон
3.5-Диамил-2-пирролидон
Производные 2-пирролидона
2*Пирролидон
N -Метил-2-пирролидон
1.5-Диметил-2-пирролидон
N-Пропил-2-пирролидон
Ν-Γ ексил-2-пирролидон
Ы-Метил-4-гексил-2-пирролидон
3.5-Диамил-2-пирролидон
Производные 2-пирролидона
Хлористый алюминий
Бромистый алюминий
Пятифтористый мышьяк
Треххлористый мышьяк
Ch3NCOCH2CH2CH2
I I
СНзЫСОСН2СН2СНСНз
I I
C3H7NCOCh2CH2CH2
I I
C6Hi3NCOCH2CH2CH2
I I
Ch3NCOCH2CH (C6Hi3) CH2
NHCOCH (C5Hu) CH2CHC5H1,
! I
RNCOCHRCHRCHR *6>
J I
nhcoch2ch2ch2
I j
Ch3NCOCH2CH2CH2
J I
ch3ncoch2ch2chch3
ι_ I
C3H7NCOCH2CH2Ch2
I I
C6Hi3NCOCH2CH2CH2
I I
Ch3NCOCH2CH (C6H13) CH2
I [
NHCOCH (C5Hn) CH2CHCsH х,
I \
RNCOCHRCHRCHR 16>
J !
AICl3
AIBr3
AsF5
AsCl3
157
157
157
157
157
157
157
157
157
157
157
157
157
157
157
334
334
334
334
Продолжение
Разделяющий агент
Литера¬
Разделяемая система
название
формула
тура
Индан — инден
Трехбромистый мышьяк
Треххлористая сурьма
Трехбромистая сурьма
2-Пирролидон
AsBr3
SbCl3
SbBr3
NhCOCH2CH2CH2
" I
334
334
334
157
Н-Метил-2-пирролидон
Ch3NCOCH2CH2CH2
I I
157
1,5-Диметил-2-пирролидон
ch3ncoch2ch2chch2
I I
157
Н-Пропил-2-пирролидон
C3H7NCOCH2CH2Ch2
I I
157
N-Г ексил-2-пирролидон
C6Hi3NCOCH2CH2CH2
I 1
157
Ы-Метил-4-гексил-2-пирролидон
CH3NCOCH2Ch (C6Hi3) CH2
I . I
157
3,5-Диамил — 2-пирролидон
NHCOCH (C5Hu) CH2CH (C5Hu)
157
Производные 2-пирролидона
RNCOCHRCHRCHR 1б>
I I
157
Инден — смесь углеводородов
Дифенил — индол
Длкилбифенилы Cj3—С17 — нефтяная
фракция (*кип — 275—305° С)
Нафталин — одноядерные аромати¬
ческие углеводороды Cio-12
Нафталин — 1-метилнафталин
Г ексанол
Этиленгликоль
Диэтиленгликоль
Триэтиленгликоль
Полиэтиленгликоли
Этиленгликоль
Пропиленгликоль
Этиленгликоль
Пропиленгликоль
C6H13OH
(CH2OH)2
(HOCH2CH2)2O
(HOCH2Ch2OCH2)2
Н[ОСН2СН2]пОН
(CH2OH)2
C3H6(OH)2
(CH2OH)2
C3H6(OH)2
389
202
202
202
453
386
386
386
386
Нафталин — 2-метилнафталин
Нафталин — 1,2,3,4-тетрагидронафта-
лин
Нафталин — парафины (алкилбензо-
лы, нафтены, алкилтетрагидронаф-
талины)
Нафталин — алифатические (цикло¬
алифатические, частично гидриро¬
ванные) углеводороды
Нафталин — производные бензола
(тетрагидронафталина, индена)
Нафталин — тетрагидронафталин
Нафталин *— углеводороды
Этиленгликоль
Пропиленгликоль
Этиленгликоль
Пропиленгликоль
N -Метилпирролидон
(CH2OH)2
C3H6(OH)2
(CH2OH)2
C3H6(OH)2
Ch3NCOCH2CH2CH2
I I
386
386
386
386
96
Ν-Алкилпирролидон
RnCOCH2CH2CH2
I ]
96
Малеиновый ангидрид
ососн=снсо
I I
363
Формиат гликоля
Бутиролактон
НСООСН2СН2ОН
OCH2CH2CH2CO
I I
304
302
2-Пирролидон
NhCOCH2CH2CH2
I I
157
N-Memn-2-пирролидон
Ch3NCOCH2CH2CH2
I I
157
1,5-Д иметил-2-пирролидон
Ch3NcoCH2CH2CHCH3
I I
157
1Ч-Пропил-2-пирролидон
C3H7NCOCH2CH2Ch2
I I
157
1Ч-Гексил-2-пирролидон
C6H13NCOCh2CH2CH2
I I
157
К-Метил-4-гексил-2-пирролидон
Ch3NCOCH2CH (C6H13) CH2
I I
157
3,5-Диамил-2-пирролидон
NHCOCH (C5Hi I) CH2CHC5H11
I I
157
Производные 2-пирролидона
RNCOCHRCHRCHR 16>
] ]
157
Малеиновый ангидрид
OCOCH-CHCO
I I
381
Бутиролактон
I I
OCH2CH2CH2CO
I I
381
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Формиат гликоля
НСООСН2СН2ОН
381
Моноэтаноламин
HOC2H4NH2
381
Ν-Метилформамид
HCONHCh3
381
Нафталин — углеводородные масла
Этиленгликоль
(CH2OH)2
403
Моноэтаноламин
HOC2H4NH2
403
Нафталин — фенол
Целлозольв + вода
C2H5OCH2CH2OH + H2O
15
Нафталин — тионафтен
Этиленгликоль
(CH2OH)2
202
1,2-Пропиленгликоль
СНаОНСНОНСНз
202
Диэтиленгликоль
(HOCH2CH2)2O
202
Нафталин—высококипящая фрак¬
Этиленгликоль
(CH2OH)2
445
ция каменноугольной смолы
Глицерин
СН2ОНСНОНСН2ОН
445
Тяжелое масло
—
413
Нафталин — примеси
Этиленгликоль
(CH2OH)2
133
Глицерин
СН2ОНСНОНСН2ОН
133
Бензиловый спирт
C6H5CH2OH
133
Вода
H2O
133
I-Метилнафталин-2-метилнафталин
Ундеканол
CnH23OH
195. 196
5-Этилнонанол-2
CnH23OH
195. 196
Монобутиловый эфир диэтиленгли-
коля
C4H9OcH2CH2OCH2CH2OH
195, 196
2-Аминопиридин
H2NC5H4N
195, 196
З-Аминопиридин
H2NC5H4N
195, 196
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
/
Треххлористая сурьма
SbCl3
334
2-Метилнафталин — нафталиновое
Трехбромистая сурьма
SbBr3
334
Хлоргидрат 2-пиколина
CH3C5H4N · HCl
401
масло
13 Зак. 917
Метилнафталин — парафины (алкил-
бензолы, нафтены, алкилтетрагид-
ронафталины)
Диметилнафталины — газойль
Изомеры диметилнафталинов
Алкилнафталины — алифатические
(циклоалифатические, частично
гидрированные) углеводороды
Алкилнафталины Ci3—Ci7 — нефтя¬
ная фракция (*„нп = 275—305° С)
Антрацен — фенантрен
Антрацен — карбазол
Фенантрен — карбазол
Ароматические углеводороды — аци¬
клические углеводороды
Смесь ароматических углеводоро¬
дов
ш
CO
Ul
Ν-Метилпирролидон
Ν-Алкилпирролидон
Диэтиленгликоль + вода
Хлористый алюминий
Бромистый алюминий
Пятифтористый мышьяк
Треххлористый мышьяк
Трехбромистый мышьяк
Треххлористая сурьма
Трехбромистая сурьма
Малеиновый ангидрид
Формиат гликоля
Полиэтиленгликоли
Триэтиленгликоль
»
Перфторметилциклогексан
Перфтордибутиловый эфир
Перфтортрипропиламин
Перфтортрибутиламин
Метилэтилкетон
Монометиловый эфир диэтиленгли
коля
2-Пирролидон
П-Метил-2-пирролидон
1,5-Д йметил-2-пирролидон
К-Пропил-2-пирролидон
RnCOCH2CH2CH2 >s>
I I
(HOCH2CH2)2O + H2O
AlCl3
AlBr3
AsF5
AsCl3
AsBr3
SbCl3
SbBr3
ососн=снсо
I !
HcOOCH2CH2OH
н[осн2сн21пОН
(HOCH2CH2OCh2)2
(HOCH2Ch2OCH2)2
(HOCH2Ch2OCH2)2
C7Fl4
(C4F9)2O
(C3F7)3N
(C4F9)3N
CH3COC2H6
СН3ОСН2СН2ОСН2СН2ОН
NhCOCH2CH2CH2
I I
Ch3NCOCH2CH2CH2
I I
CH3NCOCH2CH2CHCH3
! I
C3H7NCOCH2CH2Ch2
I I
90
90
447, 448,
449, 450
334
334
334
334
334
334
334
303
304
453
I
I
I
144
144
144
144
347
289
157
157
157
157
_ Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Смесь ароматических углеводородов
Ы-Гексил-2-пирролидон
CeHtaNCOCH2CH2CH2'
I I
157
N -Метил-4-гексил-2-пирролидон
CH3NCOCh2CH (C6Hi3)CH2
157
3>5-Диамил-2-пирролидон
NHCOCH(C5Hi1)CH2CHC5Hn
I |\
157
Производные 2-пирролидона
RNCOCHRCHRCHR W
I I
157
Ароматические углеводороды — па¬
2,3-Бутандиол + 2-этилгексанол
(CH3CHOH)2 + C8Hi7OH
107
рафины (нафтены)
Пропиленкарбонат
CH3CHOC(O)OCh2
I I
384, 385
Фурфурол
OCH-СНСН—CCHO
I I
86
Ароматические углеводороды — наф¬
Метиловый спирт
CH3OH
429
тены
Этиловый спирт
C2HsOH
429
Пропиловый спирт
C3H7OH
429
"
Изопропиловый спирт
OSO-C3H7OH
429
Этиленгликоль
(CH2OH)2
429
Ацетон , .
(CH3)2CO
429
Диацетоновый спирт
Ch3COCH2COH(CH3)2
429
Метилэтилкетон
CH3COC2H5
429
Муравьиная кислота
HCOOH
429
Уксусная кислота
CH3COOH
429
Трифторуксусная кислота
CF3COOH
145
Гептафтормасляная кислота
C3F7COOH
145
χβ,β'-Дихлордиэтиловый эфир
(ClCH2CH2)2O
429
Ацеталь
CH3CH(OC2H5)2
429
1,4-Диоксан
OCH2CH2OCh2CH2
I I
429
Метилцеллозольв
CH3OCH2CH2OH
429
Ароматические
ароматические
углеводороды — не¬
углево дор оды
Целлозольв
Диэтиленгликоль
Карбитол
Фенол
Нитрометан
Анилин
Формамид
Ацетонитрил
Фурфурол
Пиридин
Пиперидин
Вода
Парафины
Ароматические углеводороды
Нафтены
Метиловый спирт
Метиловый спирт + вода
Этиловый спирт
Пропиловый спирт
Гексафторизопропиловый спирт
Бутиловый спирт
Гексиловый спирт
ОдноатОмные спирты
Этиленгликоль
Двухатомные спирты
Ацетальдегид ^
Пропиональдегид
Ацетон
Ацетон + вода
Метилэтилкетон
C2H5OCH2CH2OH
(HOCH2CH2)2O
C2H5OcH2CH2OCH2CH2OH
C6H5OH
CH3NO2
C6H5NH2
HCONH2
CH3CN
ОСН==СНСН=ССНО
I I
C5H5N (цикл.)
HNCH2(CH2)3CH2
U I
H2O
СпН2п+2
CnH2n-B
С n H2 η
CH3OH
. CH3OH + H2O
C2H5OH
C3H7OH
C3HF6OH
C4H6OH
C6Hi3OH
ROH 9)
(CH2OH)2
C2H2n(OH)2
CH3CHO
C2H5CHO
(CH3)2CO
(CH3)2CO -μ H2O
CH3COC2H5
429
429
429
412
429
429
429
429
429
429
429
429
180
180
180
180
108, 199,
231, 272,
348, 363
180
180
245
180
180
306
180
306
180
180
180
108, 199,
231, 272,
348, 363
96, 180
Продолжение
Разделяемая система
Разделяющий агент -
Литера¬
название
формула
тура
Ароматические углеводороды — не¬
ароматические углеводороды
Метилэтилкетон + вода
Диэтилкетон
Дипропилкетон
Циклопентанон
CH3COC2H5 + H2O
(C2H5)2CO
(C3H7)2CO
CH2(CH2)3CO
I I
108, 199,
231, 272,
348, 363
180
180
180
Циклогексанон
CH2(CH2)4CO
I I
180
Муравьиная кислота
Уксусная кислота
Пропионовая кислота
Уксусный ангидрид
Диизопропиловый эфир
Дибутиловый эфир
Диоксан
HCOOH
CH3COOH
C2H5COOH
(CH3CO)2O
(C3H7)2O
(C4H9)2O
OCh2CH2OCH2CH2
I I
180
180
180
180
180
180
180
Триоксан
OCH2OCh2OCH2
I I
274
4-Метилдиоксолан
OCh2CH(CH3)OCH2
I I
216
Целлозольвы
Диэтиленгликоль
Дипропиленгликоль
Моноалкиловый эфир диэтиленгли-
коля
β,β'-Дихлордиэтиловый эфир
Фенол
ROCH2CH2OH 9>
, (HOCH2CH2)2O
(Ch3CHOHCH2)2O
CilH2^iOCH2CH2OCH2CH2OH
(ClCH2CH2)2O
C6H5OH
127
127, 180
127
180
180
176, 177,
179, 180,
273, 351,
365
Крезолы
CH3C6H4OH
273
Кснленол
(CH3)2C6H3OH
273
Резорцин
C6H5(OH)2
273
Алкилфенолы
СпН2п-7ОН
180
Фенолы (/кип до 230° С)
—
67
Бензиловый спирт
C6H5CH2OH
180
Дифениловый эфир
(C6H5)2O
180
Фенилцеллозольв
C6H5CH2CH2OH
127
Эфиры бензойной кислоты
C6H5COOR 9>
180
Эфиры фталевой кислоты
RoCOC6H4COOR' -19>
180
Нитрометан
CH3NO2
180
Нитроэтан
C2H5NO2
180
Нитробензол
C6H5NO2
180
Нитротолуол
CH3C6H4NO2
180
Нитроксилол
(CH3)2C6H3NO2
180
Алифатические первичные амины
Сз-8
RNH2 9)
180
Анилин
C6H5NH2
85, 180
Алкиланилины
—
180
Ацетонитрил
CH3CN
180, 212
Пропионитрил
C2H5CN
180, 407
Лактонитрил
CH3CHOHCn
180
Бутиронитрил
C3H7CN
180
Бензонитрил
C6H5CN
180
Тетрагидрофуран
OCH2(CH2)2CH2
162
Фурфуриловый спирт
OCH = CHCH - CCH2OH
I I
180
Фурфурол
осн-снсн-сно
I l
180
Пиридины
C5R5N (цикл) 5)
180
Хинолины
C9R7N (цикл.) 5>
180
Морфолин
OcH2CH2NHCH2CH2
I I
180
Сульфолан
CH2(CH2)2CH2SO2
I I
180, 186
390
Продолжение
Разделяемая система
Разделяющий агент
Литера1
тура
название
формула
Ароматические углеводороды — не¬
2-Метилсульфолан
CH2(CH2)2CH(CH3)SO2
180
ароматические углеводороды
I I
З-Метилсульфолан
CH2CH2CH(CH3)CH2So2
180
*
2-Этилсульфолан
CH2(CH2)2CH(C2H5)SO2
I I
180
2,5-Диметилсульфолан
CH3CH(CH2) 2СН (CH3) SO2
I I
180
2,4-Диметилсульфолан
CH2CH (CH3) CH2CH (CH3) SO2
I I
180
2-Метил-5-этилсульфолан
C2H5CH (CH2) 2СН (CH3) SO2
I I
180
2-Сульфолен
CH2CH2CH-CHSo2
I I
180
Метил-З-сульфоланилввый эфир
CH2CH2CH (OCH3) CH2SO2
I I
180
Пропил-З-сульфоланиловый эфир
CH2CH2CH (OC3H7) CH2SO2
I I
180
Аллил-З-сульфоланиловый эфир
CH2CH2CH (OCH2CH= CH2) CH2SO2
180
Металлил-З-сульфоланиловый эфир
СН2СН2СН[ОСН2С (CH3) = CH2ICH2SC
I I
h
180
Этил-З-сульфоланилсульфид
CH2CH2CH (SC2H5) CH2SO2
I I
180
T ретбутил-3-сульфоланилсульфид
CHiCH2CH(SC4H9)CH2SO2
I I
180
Металлил-З-сульфоланилсульфид
CH2CH2CHtSCH2CH (CH3) =CH2JCH2S
I
1O2
Г
180
Ароматический углеводород — ка¬
менноугольное масло
Нафтены
Метилциклопентан — близкокипящие
углеводороды
Метилциклопентан — углеводороды
Метилциклопентан — бензиновая
фракция
Диметилциклопентан — близкокипя-
щий парафин
Циклогексан — диметилпентаны
Циклогексан — близкокипящие угле¬
водороды
Сульфоланилсульфоны
Производные сульфолана
Вода
Полиалкиленгликоль
Полиалкиленоксид
Полиэфир алкиленгликоля с двух¬
основной кислотой
Полиамид
β,β'-Оксидипропионитрил 4- бензо¬
нитрил
β,β'-Иминодипропионитрил H- бен¬
зонитрил
β,β'-Тиодипропионитрил H- бензо¬
нитрил
Алифатический динитрил H- арома¬
тический мононитрил
Алифатический динитрил H- гетеро¬
циклический моноамин
Анилин
Фурфурол
У
Метиловый спирт
Этиловый спирт
Треххлористый фосфор
Трехбромистый фосфор
Треххлористый фосфор H- трехбро¬
мистый фосфор
Бензол
Треххлористый фосфор
Трехбромистый фосфор
Треххлористый фосфор H- трехбро¬
мистый фосфор
β,β'-Оксидипропиояитрнл + бензо¬
нитрил
RSO2C4H7SO2 ®>
H2O
Н[0 (CR2) *]*0Н 5>
[(CR2) «О (CR2) гДх 5>
Н0[ (CR2) n OCO (CR2) mC 00]*Н *)
[(CR2)nNHCO(CR2)tn]*
(NCCH2CH2)2O -f C6H5CN
(NCCH2CH2)2NH + C6H5CN
(NCCH2QH2)2S H- C6H5CN
NCRXR'CN" H- CnH2n-7CN
NCRXR'CN «) + RNH 12>
C6H5NH2
осн-снсн-ссно
! !
CH3OH
C2H5OH
PCl3
PBr3
PCl3 H- PBr3
C6H6
PCl3
PBr3
PCl3 H- PBr3
(NCCH2CHa)2O H- CeHsCN
)
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
β,β'-Иминодипропионитрил + бен¬
зонитрил
(NCCH2CH2) 2NH + C6H5CN
201
β,β'-Тиодипропионитрил + бензо¬
нитрил
(NCCH2CH2)S + C6H5CN
201
Алифатический динитрил+ арома¬
тический мононитрил
NCRXR'CN “> + CnH2n-6CN
201
Алифатический динитрил + гетеро¬
циклический моноамин ,
NCRXR'CN ") + RNH 12>
201
Циклогексан — циклогексановая
фракция бензина
Метиловый спирт
CH3OH
48
Циклогексан — углеводородная
Фенол
C6H5OH
141
фракция (лигроин)
CH3OH
Циклогексан — дихлорэтан
Метиловый спирт
200
Циклогексан — дихлорпропан
Метиловый спирт
CH3OH
200
Циклогексан — ацетон
Вода
H2O
266
Метилциклогексан — гептановая
Анилин
C6H5NH2
221
нефтяная фракция
CH3OH
Метилциклогексан — бензиновая
Метиловый спирт
49
фракция
Этиловый спирт
C2H5OH
49
Нафтены — парафины (изопарафи¬
ны)
Диоксолан + вода
OCH2CH2OCH2 + H2O
I I
322
1,3-Диоксан + вода
OCH2OCH2CH2Ch2 + H2O
I I
322
1,4-Диоксан + вода
OCH2CH2OCh2CH2 + H2O
I I
322
Триоксан + вода
OCh2OCH2OCH2 + H2O
I I
322
Смесь углеводородов (C2H4, C3H6,
Ацетон + вода
(CH3)2CO + H2O
118
C4H6, C6H6 и др.)
Акрилонитрил
CH2-CHCN
118
Фурфурол
OCH=CHCH-CCHO
I I
229
Смесь углеводородов С4
Смесь углеводородов С4_5
Смесь парафинов, олефинов, диоле-
финов C5
Смесь углеводородов C5
Ацетон
Ацетон + вода
Фенол + вода
Метиламин
Анилин
Ν,Ν-Диметилформамид
Ацетонитрил
Ацетонитрил -Ь вода
Фурфурол
Фурфурол + вода
Полярные вещества + вода
Вода
Ацетон
Ν,Ν-Диметилформамид
Ν,Ν-Диметилформамид + вода
Ν,Ν-Дифенилформамид
Ацетонитрил
Фурфурол
Этилендиамин
Пиридин
Бутират триэтиленгликоля
Нитрометан
Нитробензол
Анилин
Ν,Ν-Диметилформамид
Ν,Ν-Диметилформамид + вода
Ацетонитрил
Ацетонитрил + вода
Бензонитрил
Фурфурол
Фурфурол + вода
(CH3)2CO
115, 287
(CH3)2CO + H2O
115, 190
C6H5OH + H2O
329
CH3NH2
7
C6H5NH2
233
HCON(CH3)2
75
CH3CN
75
CH3CN
317
осн=снсн=ссно
115, 225,
I I
229, 239,
380
ОСН=СНСН = ССНО + H2O
115, 146,
I I
249, 446
Полярные вещества + H2O
446
H2O
115
(CH3)2CO
8
HCON(CH3)2
9
HCON(CH3)2 + H2O
9
HCON(C6H5)2
8
CH3CN
8,9
ОСН=СНСН = ССНО
I I
8
(CH2NH2)2
50
C5H5N (цикл)
50
C3H7Cooch2Ch2Och2CH2OCH2CH2OH I 14
CH3NO2
14
C6H5NO2
14
C6H5NH2
14
HCON(CH3)2
14, 55, 246
HCON(CH3)2 + H2O
246
CH3CN
14, 65, 66
246
CH3CN + H2O
246
C6H5CN
14
осн-снсн-ссно
I [
246
OCH = CHCH = CCHO + H2O
I I
246
Нродолжбние
Разделяемая система
Разделяющий агент
Литера¬
тура
*
название
формула
Ν-Метилпирролидон
Ch3NCOCH2CH2CH2
I I
66
Смесь углеводородов С5-6
Нитрозтанол
hoch?ch2no2
13
Нитропропанол
HOC3H6NO2
13
1
Нитробутаиол
HOC4H8NO2
13
Ациклические углеводороды Ce —
Фенол 4- гликоль
C6H5OH + HOROH 2°)
292
циклические углеводороды C6
Фурфурол + гликоль
ОСН-СНСН-ССНО + HOROH 2°)
I I
292
Смесь углеводородов C6
Анилин
C6H6NH2
219
β,β'-Оксидипропионитрил + бензо¬
нитрил
(NCCH2CH2)2O + C6H6CN
201
β,β'-Иминодипропионитрил + бен¬
зонитрил
(NCCH2CH2)2NH + C6H5CN
201
β,β/-TйoдшIpoπиoниτpил + бензо¬
нитрил
(NCCH2CH2)2S + C6H5CN
201
Алифатический динитрил + арома¬
тический мононитрил
NCRXR'CN “> + CnH2n-7CN
201
Алифатический динитрил + гетеро¬
циклический моноамин
NCRXR'CN i2> + RNH 13>
201»). и»
Углеводород С6_7 — галогенид фос¬
фора
Смесь алифатических углеводородов
Диалкилсульфоны
RSO2R'и».
324
Фурфурол + вода
ОСН = СНСН=ССНО + H2O
I I
225
Смесь парафинов, ароматических уг¬
леводородов, нафтенов
Тетрагидрофурфуриловый спирт
ОСН2(СН2)2СНСН2ОН
44
Алифатические углеводороды — цик¬
Метоксианилины з0>
CH3OC6H4NH2
291
лические углеводороды
Этоксианилины з0)
C2H5OC6H4NH2
291
Пропоксианилины
C3H7OC6H4NH2
291
Изопропоксианилины 30)
C3H7OC6H4NH2
291
Бутоксианилины 30>
C4H9OC6H4NH2
291
Втор, бутоксианилины
C4H9OC6H4NH2
291
Алифатические углеводороды — али
фатические и ароматические ами¬
ны
Парафины — олефины — ароматиче¬
ские углеводороды — нафтены
Парафины — олефины — диолефи-
ны — ароматические углеводоро¬
ды — нафтены
Трет, бутоксианилины30)
C4H9OC6H4NH2
291
Пентоксианилины 30>
C5H11OC6H4NH2
291
Г ексоксианилины30)
C6H13OC6H4NH2
291
Метилпентоксианилины 30I
C6H13OC6H4NH2
291
Г ептоксианилины 30>
C7H15OC6H4NH2
291
Октоксианилины 30J
C8H17OC6H4NH2
291
2-Этилгексоксйанилины 30)
C8H17OC6H4NH2
291
Перфторгептан
C7F16
143
Перфтор метилциклогексан
C7F14
143
Пер фтор дибутиловый эфир
(C4F9)2O
143
Перфтортрипропиламин
(C3F7)3N
143
Перфтортрибутиламин
(C4F9)3N
143
Неопентадиол + вода
C5H1O(OH)2 + H2O
244
Фенол + крезол
C6H5OH + CH3C6H4OH
409
Анилин
C6H5NH2
33
Анилин + диметиланилин
C6H5NH2 + C6H5N(CH3)2
409
Диметилфосфонат
H(OCH3)2PO
156
Диэтилфосфонат
H(OC2H5)2PO
156
Д иэтилметилфосфон ат
CH3(OC2H5)2PO
156
Диизопропилметилфосфонат
CH3(OC3H7)2PO
156
ДиметилхлорметилфосФонат
CICH2(OCh3)2PO
156
бис- (β-Хлорэтил) винилфосфонат
СН2~СН(ОСН2СН2С1)2РО
156
Диэтилцианометилфосфонат
NCCH2(OC2H5)2PO
' 156
Фенилбутилфосфонат
C4H9(OC6H5)(OH)PO
156
Дитолилфенилфосфонат
C6H5(OC6H4CH3)2PO
156
Дифенилцианоэтилфосфонат
NCC2H4(OC6H5)2PO
156
Фосфонаты
IT(OR)2PO1)
156
Диэтилпропионилфосфонат
C3H7C(O)(OC2H5)2PO
154
Этилпропилцарбометоксифосфонат
CH3OC (О) (OC2H5) (OC3H7) PO
154
Диэтилкарбоэтоксифосфонат
C2H5OC(O) (OC2H5)2PO
154
Этилбутилгексаноилфосфонат
C6Hi3C(O) (OC2H5) (OC4H9)PO
154
Метилэтилбензоилфосфонат
C6H5C(O)(OCH3)(OC2H5)PO
154
Д иэтил бензоил фосфон ат
C6H5C(O)(OC2H5)2PO
154
Этилпропилкарбонафтилоксифос-
фонат
Этилизопропилциклогексаноилфос-
фонат
C10H7C(O) (OC2H5) (OC3H7)PO
154
C6H11C(O) (OC2H5) (OC3Pi7)PO
154
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
а-Оксофосфонаты
R'C (0) (OR)2PO 2>
154
Г ексил-М,Ы-диметил-Р-этилфосфо-
намидат
C2H5(OC6H13)[N (CH3)2JPO
153
Метил-Ν,Ν-дибутил-Р-гексилфос-
фонамидат
C6H13 (OCH3) [N (C4H9)2JPO
153
Циклогексил-М,Н-диметил-Р-метил-
фосфонамидат
CH3(OC6H„)[N(CH3)2]PO
153
Фосфонамидаты
R (OR") (NR3)PO з)
153
[I - (Диэтоксифосфинил) этокси]-
триметилсилан
,(CH3)3SiOCH(CH3)PO(OC2H5)2
155
[ I - (Диэтоксифосфинил) этокси]три-
этилсилан
(C2H5) 3SiOCH (CH3) PO (OC2H5) 2
155
[I-(Диэтоксифосфинил) пропокси]-
трипропилсилан ,
бис-[I - (Дипропоксифосфинил) про-
покси]диэтилсилан
(C3H7)3SiOCH(C2H5)PO(OC2H5)2
155
(C2H5) 2Si[OCH (C2H5) PO (OC3H7) a]a
155
бис-[\-(Диэтоксифосфинил) буто-
кси]диметилсилан
(CH3) 2Si[OCH (C3H7) PO (OC2H5) 2]3
155
трис-[ I - (Диэтоксифосфинил) это-
кси]метилсилан
CH3Si[OCH(CH3)PO(OC2H5)2J3
155
трис-[I - (Диэтоксифосфинил) про-
покси]метилсилан
CH3Si[OCH (C2H5) PO (OC2H5) 2]3
155
Фосфинилалкоксисиланы
(R)mSi[OCH(R')PO(OR")2]„ «)
155
Фурфурол
OCH = CHCH=CCHO
I I
33
Углеводороды — алкилмоноброми-
ды
Неполярные вещества
Диалкиламиды жирных кислот
RCONR'R" 7>
193
Ацетон + этиленгликоль
(CH3)2CO + (CH2OH)2
330, 440
Галогензамещенные углеводороды
Диметилфталат
C6H4(COOCH3)2
330, 440
Четыреххлористый углерод — ацетон
Бензол
C6H6
409
Фтороформ — тетрафторэтилен
Дифторхлорметан — трихлорэтилен
(гексафторпропилен)
Хлороформ — ацетон
Дихлорметан — метиловый спирт
(ацетон, вода)
Метил бромистый — углеводороды
С4
1,1,1-Трихлорэтан — 1,1-дихлорэтан —
1,2-дихлорэтан — этил хлористый
Дихлорэтан — изопропиловый спирт
Четыреххлористый углерод
Перфторпропен
Пер фтор бутен
Пергалогенированный углеводород
Эфиры муравьиной кислоты
Эфиры уксусной кислоты
Метилизобутилкетон
Вода
Вода
Алифатические альдегиды
Алифатические кетоны
Ароматические кетоны
Алифатические амиды
Алифатические нитрилы
Алифатические сульфокиси
Бутилэтиловый эфир
Метилаллиловый эфир
2-Нафтилпропиловый эфир
1.3-Диоксолан
1.4-Диоксан
2,2-Диметилдиоксан
Монометиловый эфир диэтиленгли-
коля
Диметиловый эфир диэтиленглико-
ля
Дигептиловый эфир диэтиленглико-
ля
2,6-Диметоксифенол
п-Гептилоксифенол
п-Октилоксифенол
5-Амино-2-нитрофенол
л-Аминофенилмеркаптан
Дидецилфталат
CCI4
C3F6
C4F6
HCOOR9)
CH3COOR 9)
CH3COC4H9
H2O
H2O
RCHO 23>
RCOR'23)
RCOR'24)
RCONR'R" 23)
RCN 23)
RSO2R'23)
C2H5OC4H9
CH3OCH2CH = CH2
C3H7OCi0H7
OCH2OCH2CH2
I !
OCH2Ch2OCH2CH2
I - I
ОС (CH3)2CH2OCH2CH2
I I
СН3ОСН2СН2ОСН2СН2ОН
(CH3OCH2CH2)2O
(C7Hi5OCH2CH2)2O
(CH3O)2C6H3OH
C7Hi5OC6H4OH
C8Hi7OC6H4OH
H2N(NO2)C6H3OH
H2NC6H4SH
C6H4(COOCioH2I)2
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
I, 2-Дибромгексафторпропанбром
1,2-Дибромтетрафторэтан
СРзВгСРгВг
175
2-Бромпропан метиловый спирт
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν-Этиламид гликолевой кислоты
HoCH2CONHC2H5
183
Тетрафторэтилен трифторметан (ди-
Спирты
ROH 9)
фторметан, монохлорпентафтор-
Кетоны
RCOR' 10I
443
этан, дифторэтан)
Простые эфиры
ROR'10>
443
Сложные эфиры
RCOOR' 10>
443
Перфторпарафины
Бензол
C6H6
' 442
Перфторолефины (перфторциклопа-
Алкилбензолы
СпНгм-б
442
рафины) F-, Cl-, Вг:замещенные
Г алогензамещенные алифатические
—
442
углеводороды
углеводороды
Галогензамещенные бензолы .
СбН%Х6_п21>
442
Г алогензамещенные алкилбензолы
—
442
Фторбензол — изопропиловый спирт
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν-Этиламид гликолевой кислоты
HoCH2CONHC2H5
183
Хлористый бензил — бензилацетат
Вода
H2O
36
Хлорэтилбензол —
Этиловый спирт
C2H5OH
98
β-хлорстирол
Гексиловый спирт
C6Hi3OH
98
Псевдогексиловый спирт
C6Hi3OH
98
Диацетоновый спирт
Ch3COCH2COH(CH3)2
98
Ацетон ил ацетон
(CH3COCH2)2
98
Масляная кислота
C3H7COOH
98
Бутилцеллозольв
C4H9OCH2CH2OH
98
Бензальдегид
C6H5CHO
98
Фурфуриловьш спирт
ОСН=-СНСН=ССН2ОН
I I
- 98
Тетрагидрофурфуриловый спирт
OCH2(CHa)aCHCHaOH
98
Г алогенуглеводороды — галогенсо¬
Одноатомные спирты
ROH 9>
457
держащие ангидриды
Двухатомные спирты
(CR2) п (OH)2 9)
457
Ш
Кислородсодержащие соединения
углеводородов
Метиловый спирт — этиловый спирт
Метиловый спирт — альдегид (и при¬
меси)
Метиловый спирт — ацетон
Метиловый спирт — метилэтилкетон
Метиловый спирт — кетоны (нитри¬
лы)
Метиловый спирт — метилаль
Метиловый спирт — метилацетат
Метиловый спирт — винилацетат
Метиловый спирт — метил борат
Малеиновый ангидрид
Вода
/
Вода
Неароматический углеводород
Сз-п + ароматический углеводо¬
род Сб-8
Неароматический углеводород
Cs-n + галогенуглеводород Ci_4
Этиленгликоль
Пропиленгликоль
Ν,Ν-Диметилформамид
Ν,Ν-Диэтилформамид
Вода
Диэтилкетон
Ацетон
Этиленгликоль
Ν,Ν-Диметилформамид
Ν,Ν-Диметилацетамид
Ν-Этиламид
Вода
Целлозольв
Ν,Ν-Диметилформамид
Ν,Ν-Диэтилацетамид
Вода
у>
Октан
Декан
Ксилол
Дифенил
Дихлорбензол
Фенол
Крезол
Дифениловый эфир
молочной кислоты
ососн=снсо
I I
H2O
H2O
CnH2w-*
(CH2OH)2
CH20HCHOHCH3
HCON(CH3)2
HCON(C2H5)2
H2O
(C2H5)2CO
(CHa)2CO
(CH2OH)2
HCON(CH3)2
CH3CON(CH3)2
CH3CH OHCONHc2H5
H2O ,
C2H5OCH2CH2OH
HCON(CH3)2
CH3CON(C2H5)2
H2O
H2O
CsH,*
Ci^H22
QH4(CH3)2
(C6H5)2
C6H4Cl2
C6H5OH
CH3C6H4OH
(C6Hs)2O
457
457
134, 149
297
297
136
137
183
183
235, 368
359
367
182
183
183
183
240
265
183
183
419
336
298
298
298
298
298
298
298
298
400
П родолжение
Разделяемая система
Разделяющий агент
I Литера¬
название
формула
тура
Дифениловый эфир + дифенил
(C6H5)2O + (C6H5)2
298
Ν,Ν-Диметилформамид
HCON(CH3)2
183, 298
Ν,Ν-Диэтилформамид
HCON(C2H5)2
298
Ν-Метил ацетам ид
CH3CONHCH3
298
Ν,Ν-Диметилацетамид
CH3CON(CH3)2
298
Ν-Этиламид молочной кислоты
CH3CHOHCONHC2Hs
183
Алкил-И-замещенные амидов
RFCNC(O)R,"25)
298
Диметилсульфоксид
(CH3)2SO
298
Метиловый спирт — диэтиламин
Ν,Ν-Диметилформамид
HCON (CH3)2
183
Ν-Этиламид молочной кислоты
CH3CHOHCONHC2H5
183
Метиловый спирт — тетрагидрофуран
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν,Ν-Диэтилформамид
HCON(C2H5)2
'183
Метиловый спирт — органические
Вода + гидроокись натрия
H2O + NaOH
253
примени
Метиловый спирт — вода
Бензол
C6H6
222, 326
431
Метиловый спирт — примеси
Углеводороды
„
426
Этиловый спирт — метиловый спирт
Циклогексан
C6Hi2
366
(вода)
Метилциклогексан
C7Hu
366
Этиловый спирт — пропиловый спирт
Вода
H2O
256
Этиловый спирт — изопропиловый
Этилцеллозольв
C2H5OCH2CH2OH
425
спирт
Бутилцеллозольв
C4H9OCH2CH2OH
425
Фенол
C6H5OH
124
Вода
H2O
119, 256.
368
Этиловый спирт — изопропиловый
спирт — метилэтилкетон — этилаце-
Углеводороды (/Кип = 200—270° С)
310
тат
Этиловый спирт — амиловый спирт
Вода
H2O
256
Этиловый спирт — ацетальдегид
>
H2O
353
Этиловый спирт — пропионовый аль¬
дегид
»
H2O
353
Этиловый спирт — масляный альде¬
гид
Этиловый спирт — акролеин
Этиловый спирт — альдегиды
Этиловый спирт — адеталь
Этиловый спирт — метилпропиловый
эфир
Этиловый спирт — аллилформиат
Этиловый спирт — этилацетат
Этиловый спирт — метиловый эфир
акриловой кислоты
Этиловый спирт — триэтиламин (во¬
да)
Этиловый спирт — этокситриметил-
силан
Этиловый спирт — триэтилфосфит
Этиловый спирт тиофен
Этиловый спирт — вода
Ν,Ν-Диметилформамид
N,N-Диэтил а детамид
Ν,Ν-Диметилформамид
Ν-Этиламид гликолевой кислоты
Хлорбензол
Бутиловый спирт
Этиленгликоль
Диэтиленгликоль
Дибутилфталат
N,N - Диметил форм а м ид
Ν,Ν-Диэтилформамид
Вода
Ν,Ν-Диметилформамид
Ν-Этиламид гликолевой кислоты
Бензол
Нафтены
Алифатические углеводороды
Крезол
Этилнитрат
Ацетонитрил
Ν,Ν-Диметилформамид
Ν,Ν-Диэтилформамид
Бензол
Дихлорэтан
Изобутиловый спирт
Этиленгликоль
Глицерин
Глицерин + хлористый кальций
Глицерин + хлористый натрий
Глицерин + хлористый калий
H2O
353
H2O
353
H2O
353
H2O
353
HCON(CH3)2
183
CH3CON(C2H5)2
183
HCON(CH3)2
183
Ch2OHCONHC2H5
183
C6H5Cl
24
C4H9OH
24
(CH2OH)2
24
(HOCH2CH2)2O
434
C6H4(COOC4H9)2
434
HCON(CH3)2
183
HCON(C2H5)2
183
H2O
88
HCON(CH3)2
183
Ch2OHCONHC2H5
183
C6H6
94
CnH2n
94
—
94
CH3C6H4OH
94
C2H5NO3
94
CH3CN
94
HCON(CH3)2
183
HCON(C2H5)2
183
C6H6
23, 439*
455
C2H4Cl2
339
C4H9OH
47
(CH2OH)2
364
СН2ОНСНОНСН2ОН
368
СН2ОНСНОНСН2ОН + CaCl2
372, 451
СН2ОНСНОНСН2ОН + NaCl
372, 451
СН2ОНСНОНСН2ОН + KCl
372, 451
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Глицерин + азотнокислый натрий
СН2ОНСНОНСН2ОН + NaNO3
372. 451
Диэтиловый эфир
(C2H5)2O
439. 455
Пропилацетат
CH3COOC3H7
339
Бутилацетат
CH3COOC4H9
339
Пропиловый спирт — аллиловый
рттипт
Вода
H2O
240
Cllnp I
Пропиловый спирт — втор-бутило¬
Целлозольв
C2HsOCH2CH2OH
395
вый спирт
Бутилцеллозольв
C4H9OCH2CH2OH
395
Дифениловый эфир
(C6Hs)2O
131
Простые эфиры
ROR' 9>
122
Сложные эфиры
RCOOR' 10>
122
Сульфолан
CH2(CH2)2CH2SO2
I I
121
Пропиловый спирт—метилэтилкетон
Г ексан
C6Hj4
132
Бензол
C6H6
132
Углеводороды
132
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν,Ν-Диэтилацетамид
CH3CON(C2H5)2
183
Ν-Этиламид гликолевой кислоты
Ch2OHCONHC2H5
183
Пропиловый спирт — диэтилкетон
Диэтиленгликоль
(HOCH2CH2)2O
434
Диметилфталат
C6H4(COOCH3)2
434
Дибутилфталат
C6H4(COOC4H9)2
434
Дидецилфталат
C6H4(COOC10H21)2
434
Пропиловый спирт — ацеталь
Ν,Ν-Диметилформамид
HCON(CH3)2
183
N,N-Д иэтилацетамид
CH3CON(C2H5)2
183
Ν-Этиламид молочной кислоты
CH3CHOHCONHC2H5
183
Пропиловый спирт — диоксан
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν,Ν-Диэтилацетамид
CH3CON(C2H5)2
183
Ν-Этиламид гликолевой кислоты
Ch2OHCONHC2H5
183
Пропиловый спирт — пиридин
Г ексан
C6H14
132
Бензол
C6H6
132
Пропиловый спирт — пропил-аллило-
вая фракция
Изопропиловый спирт — смесь спир¬
тов С2-4
Изопропиловый спирт — вода
Аллиловый спирт — метилкарбонат
Аллиловый спирт — диэтилсульфид
Спирты Ci-з — вода
Бутиловый спирт — углеводороды
Бутиловый спирт — вода
Втор-бутиловый спирт — метилэтил¬
кетон
Втор-6утиловый спирт — вода
Спирты Cl—4 — кислородсодержащие
соединения Ci_s
2-Метилбутанол-1 —3-Метил бута-
нол-1
3-Метилбутен-З-ол-1 — 4,4-Диметил-
диоксан-1,3
2-Метилбутен-3-ол-2 — 4,4-диметил-
диоксан-1,3
Диметилвинилкарбинол — вода
Изопентенолы — 4,4-диметилдиок-
сан-1,3
Метилбутинол — ацетон
Углеводороды
132
Бензин
—
16
Гидроокись натрия + вода
NaOH + H2O
402
Бензол
C6H6
402
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν,Ν-Диэтилацетамид
CH3CON(C2Hs)2
183
Ν,Ν-Диметилформамид
HCON(CH3)2
183
Ν,Ν-Диэтилацетамид
CH3CON(C2H6)2
183
Бутиловый спирт
C4H9OH
128
Амиловый спирт
C5HnOH
128
Высокомолекулярный спирт
—
128
Метиловый спирт
CH3OH
27
Дихлорэтан
C2H4Cl2
339
Пропилацетат
CH3COOC3H7
339
Бутилацетат
CH3COOC4H9
339
Вода
H2O
69. 130,
230
Гептан
C7Hi6
452
Изооктан
WSO-C8Hi8
452
Метилциклогексан
C7Hh
452
Фракция газолина (*кип = 70—
90° С)
—
452
Углеводороды (£КИп « 200—270° С)
—
312
Спирты Cs
ROH 9)
312
Высшие спирты + углеводороды
—
312
2,3-Дихлорпропанол-1
СН2ОНСНС1СН2С
262
2,3-Дибромпропанол-2
CH3CBr(OH)CH2Br
262
Вода
H2O
77
Вода
H2O
77
Хлороформ
CHCl3
41
Метил-грет-бутиловый эфир
CH3OC4H9
41
Вода
H2O
77
Бензол
C6He
396
Продолжение
Разделяющий агент
Литера¬
Разделяемая система
название
формула
тура
Смесь спиртов Ci-s
Углеводороды
313
Фенол
C6H5OH
124
Спирты C3-S кислородсодержащие
Простые эфиры
ROR' 10>
122
соединения С3_5
Сложные эфиры
RCOOR' 10>
122
Гексанол — бутиловый спирт (ацета-
Этиленгликоль
(CH2OH)2
223
ли)
1,2-Пропиленгликоль
СН2ОНСНОНСН3
223
Глицерин
СН2ОНСНОНСН2ОН
223
Многоатомные спирты
—
223
Г ексанол — циклогексанол
Ксилолсульфонат натрия 4- вода
(CH3)2C6H3SO3Na + H2O
315
Г ептанол — 3-метилциклогексанол
Маслянокислый натрий + вода
C3H7COONa + H2O
315
/ι-Цимолсульфонат натрия + вода
CH3 (C3H7) C6H3SO3Na + H2O
315
сГОктанол-2 — /-октанол-2
с?-Лимонен
CioHi6
300
Октанол-2-дибутоксиметан
Ν-Этиламид гликолевой кислоты
CH2OHCONHC2Hs
183
Ν-Этиламид молочной кислоты
ch3chohconhc2h5
183
Жирные спирты С7-9
Вода
H2O
27
Спирты — вторичные спирты — тре¬
тичные спирты
H2O
119, 120.
178, 211,
311
395
Смеси спиртов · '
Целлозольвы
ROCH2CH2OH 9>
Сульфолан
CH2(CH2)2CH2SO2
121
Спирты — кетоны
Ароматические углеводороды
CnH2n- в
277
Спирты — кетоны (сложные эфиры)
Этиленгликоль
(CH2OH)2
267
T р иэтиленгликоль
(HOCH2Ch2OCH2)2
267
Гликольамин
CH2OHCH2NH2
267
Спирты — альдегиды — кетоны
Этилендиамин
(CH2NH2)2
267
Дифенил
(C6H5)2
122
Дифениловый эфир
(C6H5)2O
122
Простые эфиры
ROR' 10>
122
Сложные эфиры
RCOOR' *°>
122
Вода щелочная (pH — 7—12)
122
Спирты — эфиры
Спирты — соединения С3_6
Спирты — высокомолекулярные со¬
единения
Спирты — вода
Этиленгликоль — целлозольв
Этиленхлоргидрин — вода
Формальдегид — метиловый спирт
(вода и др. примеси)
Формальдегид — метиловый спирт
(метилаль)
Муравьиная кислота — вода (и при¬
меси)
Формальдегид — спирт (вода)
Формальдегид *** триоксан
Формальдегид — вода
Пропиленгликоль
Гликоли
Дифениловый эфир
Дифенил
Ароматические соединения
Бензол
Г азолин
Масла
Вода
Бензол
Толуол
Циклогексан
Четыреххлористый углерод
1,2-Дихлорэтан
Диизопропиловый эфир
Этилацетат
Ацетон + вода
Диоксан
Триоксан
Триоксан ■+* бензол
Ν,Ν-Диметилформамид
Ν,Ν-Диэтилформамид
Ν,Ν-Диэтилацетамид
Ν,Ν-Диэтиламид гликолевой кисло-
ты
Ν-Этиламид молочной кислоты
Амиды
Алкиленгликоли
Вода
Пентан
Г ексан
Г ептан
Октан
СН2ОНСНОНСН3
CnH2n (OH)2
(C6H5)2O
(C6H5)2
C6H6
H2O
C6H6
C6H5CH3
C6H12
CCU
CH2ClCH2Cl
(C3H7)2O
CH3COOC2H5
(CH3)2CO + H2O
OCh2CH2OCH2CH2
I I
OCH2OCh2OCH2
I I
OCh2OCH2OCH2 + C6H
I I
HCON(CH3)2
HCON(C2H5)2
CH3CON(C2H5)2
CH2OHCON(C2H5)2
CH3CHOHCONHC2H5
RCONR'2β)
CnH2n (ОН) 2
H2O
C5H12
C6H14
C7H16
C8H18
164
164
123
314
314
129
129
129
43
26
26
26
26
26
26, 56
26
210
172
172
172
183
183
183
183
183
183
416
416
62
62
62
62
Продолжение
Разделяющий агент
Литера¬
Разделяемая система
название
формула
тура
Парафины
СпН2п +2
62
Ароматические углеводороды
CnH2W-6
62
Нафтены
CnH2W
62
Бутир альдегид — изобутир альдегид
Вода
H2O
345
Смесь альдегидов С3-а
»
H2O
345
Ацетон — углеводород (пентан, цик-
Этиленгликоль
(CH2OH)2
268
логексены и др.)
Вода
H2O
266
Ацетон — галогенсодержащие соеди¬
Этиленгликоль
(CH2OH)2
268
нения
Адетон — спирты
Этиленгликоль
(CH2OH)2
268
Ацетон — спирт (вода)
Целлозольвы
ROCH2CH2OH ®>
350
Г идроксиламин
NH2OH
350
Ацетон — эфиры
Этиленгликоль
(CH2OH)2
268
Ацетон — кислородсодержащие со¬
Этиленгликоль
(CH2OH)2
268
единения
Вода
H2O
130
Ацетон — серусодержащие соедине¬
Этиленгликоль
(CH2OH)2
268
ния
Ацетон — сероуглерод
Вода
H2O
266
Метилэтилкетон — спирты (альдеги¬
Пентан
C5H12
126
ды, кетоны, вода)
Метилэтилкетон — ацетали
Вода
H2O
240
Метилэтилкетон — пиридин
Гексан
C6H14
132
Бензол
C6H6
132
Углеводороды
—
132
Метилэтилкетон — вода
Бутилцеллозольв
C4H9OCH2CH2OH
325
Кетоны — спирты (вода)
Целлозольвы
ROCH2CH2OH
350
Г идроксиламин
NH2OH
350
Кетоны — вода
Ароматические углеводороды
CnH2n-6
171
Нитрилы
RCN ®>
421
Фуран
ОСН=СНСН-СН
I I
HO
Муравьиная кислота — уксусная кис¬
лота
Муравьиная кислота — кислоты C2—
C3
Муравьиная кислота — вода
Муравьиная кислота — перекись во¬
дорода
Муравьиная кислота (уксусная кис¬
лота) — вода
Уксусная кислота — муравьиная кис¬
лота (вода)
Уксусная кислота — винилацетат
Уксусная кислота — подсмольная
вода
Уксусная кислота — вода
Уксусная кислота — вода (примеси)
Алкилфураны
Тетрагидрофур ан
Производные тетрагидрофурана
Хлороформ
1.2-Дихлорэтан
1-Хлорбутан
Хлорированные углеводороды
Толуол
Пентан — гексановая фракция
Фталевый ангидрид
Нитробензол + хлористый кальций
Нитробензол 4- хлористый натрий
Вода
Высшие эфиры
Петролейный эфир
Ацетальдегид
Вода
Углеводороды
1.2-Дихлорэтан
Пропил ацетат
Бутилацетат
Винилацетат
Эфиры уксусной кислоты
Диметиланилин
Г ексан
Г ептан
Октан
Нонан
OCR-CRCR=CR
I I
OCH2(CH2)2CH2
I I
CHCl3
CH2ClCH2Cl
C4H9Cl
C6H5CH3
“/CO
C6H4; ;о
xCOx
C6H5NO2 + CaCl2
C6H5NO2 + NaCl
H2O
HO
194, 328
194, 328
340
241
241
241
54
54
372:
372
372
169
241
CH3CHO
H2O
CH2ClCH2Cl
CH3COOC3H7
CH3COOC4H9
CH3COOCH=Ch2
CH3COOR 9>
C6H5N(CH3)2
C6Hi4
C7H16
C8H18
C9H2O
204
338
28
28, 339
339
28, 73„
339
80
28
205
257
257
257
257
П родолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Декан
С10Н22
257
Пропионовая кислота — вода
Толуол
C6H5CH3
72
Акриловая кислота — вода
Бензол
C6H6
399
Хлорбензол
C6H5Cl
399
о-Дихлорбензол
C6H4Cl2
399
Эфиры акриловой кислоты
CH2-CHCOOr9)
399
Эфиры метакриловой кислоты
CH2=C(CH3)COOR9)
399
Акрилонитрил
CH2-CHCN
399
Монокарбоновые кислоты Ci-з — во-
Tl Я
Диизопропиловый эфир
(C3Hy)2O
54
Да
Метакриловая кислота — вода
Г ексан
C6H14
60
Гептан
C7H16
60
Бензол
C6H6
60
Циклогексан
C6H12
60
Метилциклогексан
C7H14
60
Четыреххлористый углерод
CCl4
60
1,2-Дихлорэтан
CH2ClCH2Cl
60
Щавелевая кислота — вода
Метилэтилкетон
CH3COC2H5
74
Лимонная кислота — вода
Метилэтилкетон
CH3COC2H5
74
Карбоновые кислоты — вода
Ароматические углеводороды
CtiH2Ti-6
171
Нитрилы
RCN 9)
421
Фуран
осн-снсн-сн
I I
HO
Алкилфураны
OCR—CRCR-CR *7)
I I
HO
Тетрагидрофур ан
OCH2(CH2)2CH2
104, 328
Производные тетрагидрофурана
194, 328
Этиловый эфир— вода
Дихлорэтан
CH2ClCH2Cl
339
Пропилаиетат
CH3COOC3H7
339
Бутилацетат
CH3COOC4H9
339
Диизопропиловый эфир — изопропи¬
ловый спирт (вода)
Окись пропилена — метилаль
Окись пропилена — метилформиат
Триоксан — формальдегид (вода)
Метилаль — вода
Ацетали — спирты (вода)
Этил ацетат — этиловый спирт (аце¬
тон, вода)
Бутилацетат — фенол
Метилпропионат — акрилонитрил
Бутилакрилат — реакционная смесь
(акриловая кислота + бутиловый
спирт)
Алкиленкарбонаты — примеси
Эфиры — вода
S
Вода
Изооктан
Циклогексан
Керосин
Бензол
Дихлорметан
Дихлорэтан
Трихлорэтилен
Ν,Ν-Диметилформамид
Ν-Этиламид гликолевой кислоты
Этиленгликоль
1.3-Бутил енгликоль
Глицерин
Многоатомные спирты
Неполные простые эфиры гликолей
Этаноламин
Аминоспирты
Этилендиамин
Диэтилентриамин
1.2.3-Триаминопропан
Многоатомные амины
Бутилацетат
Вода
Четыреххлористый углерод
Вода
Нонан
Парафины Сц_1з
Ароматические углеводороды
Нитрилы
Фур а н
Алкилфураны
H2O
MSO-C8Hi8
C8Hi2
C6H6
C6H6
CH2Cl2
C2H4Cl2
CHCl-CCl2
HCON(CH3)2
Ch2OHCONHC2H5
(CH2OH)2
НОСН2СН2СНОНСН3
НОСН2СНОНСН2ОН
ROCnH2nOH »>
HOCH2CH2NH2
(CH2NH2)2
(H2NCH2CH2)2NH
H2NCH2CH (NH2) CH2NH2
CH3COOC4H9
H2O
CCl4
H2O
C9H2O
С n H2 η 4-2
CnH2n-S
RCN 9>
ОСН=СНСН=СН
I J
OCR==CRCR==Cr
I -I-
406
358
358
358
390
93
93
93
93
183
183
182
182
182
182
182
182
182
182
182
182
182
87
436
418
114
17
17
171
421
HO
110
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Фенол — оксиацетон (метил бензофу-
ран)
Фенол — оксикарбонильные соеди¬
нения
Фенол — вода
л*-Крезол — /г-крезол
Крезолы — алкилароматические уг¬
леводороды
Резорцин — алкилароматические уг¬
леводороды
Пирокатехин алкилароматические
углеводороды
Гидрохинон алкилароматические уг¬
леводороды
Пирогаллол алкилароматические уг¬
леводороды
ос-Нафтол — а-тетралон
α-Нафтол — тетралол, тетралон
Фенолы — нейтральные масла
Тетрагидрофуран
Производные тетрагидрофурана
Вода
»
1.2-Дихлорэтан + метиловый спирт
1.2-Дихлорэтан + этиловый спирт
1.2-Дихлорэтан + изопропиловый
спирт
1.2-Дихлорпропан + метиловый
спирт
1.2-Дихлорпропан + этиловый
спирт
1.2-Дихлорпропан + изопропило¬
вый спирт
Бензиловый спирт
Вода
»
»
Спирты (ίκππ = 200—300° С)
Додецилкарбинол
Алифатические спирты Ci_3
OCH2(CH2)2CH2
I I
H2O
H2O
CH2ClCH2Cl + CH3OH
CH2ClCH2Cl + C2H5OH
CH2ClCH2C + WSO-C3H7OH
СН2С1СНС1СНз + CH3OH
СН2С1СНС1СНз + C2H5OH
СН2С1СНС1СНз + НЗО-С3Н7ОН
C6H5CH2OH
H2O
H2O
H2O
H2O
H2O
ROH 9>
Ci3H27OH
ROH 27)
194, 328
194, 328
264
264
227
227
227
227
227
227
308
279
279
279
279
279
203
422
299
Фенолы — каменноугольное масло
Бензиловый спирт — бензилацетат
Диметилфенилкарбинол — ацетофе-
нон
Метилбензоат — линолевое масло
Этилбензоат—ментол-1
Этилсалицилат — сафрол
Камфора — линолевое масло
Азотсодержащие соединения
Нитрометан — высшие нитроалканы
Метиламин — диметиламин — три-
метиламин
Диизопропиламин — реакционная
смесь аммонолиза изопропилового
спирта
Триметиламин — метиламины (ам¬
миак)
Триметиламин — метиламины (ам¬
миак, вода)
Триметиламин — аммиак
Этилендиамин — вода
Гексаметилендиамин — 1,2-диамино-
циклогексан (гексаметиленимин,
адипонитрил)
Полиалкиленгликоль
Полиалкиленоксид
Полиэфир алкиленгликоля с
основными кислотами
Полиамид
Вода
Этиленгликоль
Бензоат натрия
Салицилат натрия
Бензоат натрия
Салицилат натрия
Фталат натрия
Гексан 4- вода
Циклогексан + вода
Алкан C6-в + вода
Аммиак + вода
Вода
Аммиак
Вода
»
Этиленгликоль
Пропиленгликоль
Алифатические диолы
N -Метилдиэтаноламин
Алифатические аминоспирты
Вода
HOf(CR2) П0]*Н ιό
333
[ (CR2) п0 (CR2) т\х, 17)
333
HOt(CR2)nOCO(CR2)wCOObH *7>
333
[(CR2)nNHCO(CR2)m]* 17>
333
H2O
36
(CH2OH)2
63
C6H5COONa
259
C6H5COONa
259
HOC6H4COONa
259
C6H5COONa
259
HOC6H4COONa
259
C6H4(COONa)2
259
C6Hi4 + H2O
423
C6Hi2 Η- H2O
423
СпН2п+2 H2O
423
NH3 + H2O
224
H2O
29
NH3
337
H2O
226
H2O
263
H2O
226, 247
(CH2OH)2
238
СН2ОНСНОНСНз
238
CnH2n(OH)2
238
CH3N(CH2CH2OH)2
238
—
238
H2O
20
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Анилин — метиланилин (диметил-
Парафиновое масло
261
анилин)
Глицерин
СНзОНСНОНСШЭН
261
Анилин — зтиланилин
Парафиновое масло
—
261
Этиланилин — диэтиланилин
—
261
Первичные, вторичные и третичные
—
261
ароматические амины
Ксилилендиамин — -и-цианбензил-
Глицерин
СН2ОНСНОНСН2ОН
430
амин
Алифатические полиолы
—
430
ж-Ксилилендиамин — изофталонит-
Глицерин
СН2ОНСНОНСН2ОН
430
р ил
Алифатические полиолы
—
430
Ксилилендиамины — ароматические
Глицерин
СН2ОНСНОНСН2ОН
430
нитрилы
Алифатические полиолы
—
430
Этиленимин — дихлорэтан (хлоргид-
Гексан
C6H14
147
раты аминов, вода, хлористый на¬
Алифатические углеводороды
—
147
трий)
(/кип = 50—80° С)
Цианистый водород — акрилонитрил
Вода
H2O
170
Ацетонитрил — трихлорацетонитрил
Углеводороды (/Кип = 35—115° С)
—
252
Ацетонитрил *—акрилонитрил
Этиленгликоль H- вода
(CH2OH)2 H- H2O
218
Полиоксисоединения + вода
+ H2O
218
Ацетилацетон + вода
(CH3CO)2CH2 H- H2O
397
Циклогексанон H- вода
C5Hi0CO H- H2O
397
Бензальдегид H- вода
C6H5CHO + H2O
397
Ацетофенон + вода
CH3COC6H5 + H2O
397
Фурфурол + вода
OCH = CHCH = CCHO H- H2O
I I
397
Ацетонитрил —- акрилонитрил — выс¬
Вода
H2O
398, 400
шие нитрилы
Ацетонитрил — метакрилонитрил
Вода
H2O
376
Силаны
Четыреххлористый кремний — диме-
Цимол
CH3C6H4C3H7
70
тилдихлорсилан
Четыреххлористый кремний — триме-
тилхлорсилан
Четыреххлористый кремний — метнл-
хлорсиланы
Декалин
I, I ,З-Трихлорпропан
1.4-Дихлорбутан
1.4-Дибромбутан
1.1.1.5-Тетрахлорпентан
1.5-Дибромпентан
Бромистый изоамил
1,9-Дихлорнонан
Хлорбензол
Хлористый бензил
Пер фтор масло
Ацетофенон
Хлористый бензоил
β,β'-Дихлордиэтиловый эфир
Диметилдиоксан
Анизол
Дибензиловый эфир
Этилмонохл ор ацетат
Метиловый эфир трихлоруксусной
кислоты
Диэтиловый эфир перфторглутаро-
вой кислсты
Изоамилбензоат
Диметилфталат
Диизобутил фталат
Хлорпропиленкарбонат
Триизобутилфосфат
Нитрометан
Нитробензол
Адипонитрил
Трифторпропилдиметилдисилоксан
Сульфолан
Ацетонитрил
Метилдихлорсилан
β,β'-Дихлордиэтиловый
эфир
CioHi8
CI2CHCH2CH2Ci
CICH2(CH2)2CH2Ci
BrCH2(CH2)2CH2Br
Cl3C(CH2)3CH2Cl
BrCH2(CH2)3CH2Br
C5HnBr
CICH2(CH2)7CH2Ci
C6H5Cl
C6H5CH2Cl
CH3COC6H5
C6H5COCl
(ClCH2CH2)2O
(CH5)2C4H6O2
CH3OC6H5
(C6H5CH2)2O
CICh2COOC2H5
CI3CCOOCh3
CF2(CF2COOC2H5)2
C6H5COOC5Hii
C6H4(COOCH3)2
C6H4(COOC4H9)2
C3H5ClCO3 (цикл.)
(изо-С4Н90)3Р0
CH3NO2
C6H5NO2
(NCCH2CH2)2
[C3H4F3(CH3)2SiJ2O
CH2(CH2)2CH2SO2
CH3CN
CH3SiHCl2
(ClCH2CH2I2O
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
32, 377
307
71
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
название
формула
тура
Четыреххлористый кремний—диалкил-
Дицианобутан
(NCCH2)2
285
дихлорсиланы
Адипонитрил
(NCCH2CH2)2
285
β,β'-Оксидипропионитрил
(NCCH2CH2)2O
285
Метилтрихлорсилан — диметилди-
динитрилы
NC (CR2) αΖ (CR2) bCN 28>
285
I, I ,З-Трихлорпропан
Ci2CHCH2CH2CI
70
хлорсилан
1,4-Дихлорбутан
(ClCH2CH2)2
70
1,4-Дибромбутан
(BrCH2CH2)2
70
1,1,1,5-Тетрахлорпентан
CbC(CH2)3CH2Cl
70
1,5-Дибромпентан
(BrCH2CH2)2CH2
70
Бромистый изоамил
C5HnBr
70
1,9-Дихлорнонан
CICH2(CH2)7CH2Ci
70
Хлорбензол
C6H5Cl
70
Хлористый бензил
C6H5CH2Cl
70
Перфтормасло
—
70
Ацетофенон
CH3COC6H6
70
Хлористый бензоил
C6H5COCl
70
β,β'-Дихлордиэтиловый эфир
(ClCH2CH2)2O
70
Диметилдиоксан
(CH3)2C4H6O2
70
Анизол
CH3OC6H5
70
Дибензиловый эфир
(C6H5CH2)2O
70
Этилмонохлораиетат
CICh2COOC2H5
70
Метиловый эфир трихлоруксусной
кислоты
CI3CCOOCh3
70
Диэтиловый эфир перфторглутаро-
вой кислоты
CF2(CF2COOC2H6)2
70
Изоамил бензоат
C6H5COOC5Hi1
70
Диметил фталат
C6H4(COOCH3)2
70
Диизобутилфталат
C6H4(COOC4H9)2
70
Хлорпропиленкарбонат
C3H5ClCO3 (цикл.)
70
Триизобутил фосфат
(C4H9O)3PO
70
Нитрометан
CH3NO2
70
JMeтилдихлорсилан
силан
Vl
Нитробензол
C6H5NO2
70
Адипонитрил
(NCCH2CH2)2
70
Трифторпропилдиметилдисилоксан
[C3H4F3(CH3)2Sil2O
70
Сульфолан
CH2(CH2)2CH2SO2
I I
70
Цимол
CH3C6H4C3H7
70
Декалин
CioHib
70
1,1,3-Трихлорпропац
Ci2CHCH2CH2CI
70
1,4-Дихлорбутан
(ClCH2CH2)2
70
1,4-Дибромбутан
(BrCH2CH2)2
70
1,1,1,5-Т етрахлорпентан
Cl3C(CH2)3CH2Cl
70
1,5-Дибромпентан
(BrCH2CH2)2CH2
70
Бромистый изоамил
C5HiiBr
70
1,9-Дихлорнонан
ClCH2(CH2)7CH2Q
70
Хлорбензол
C6H5Cl
70
Хлористый бензил
C6H5CH2Cl
70
Перфтормасло
—
70
Ацетофенон
CH3COC6H5
70
Хлористый бензоил
CeH5COCl
70
β,β'-Дихлордиэтиловый эфир
(ClCH2CH2)2O
70
Диметилдиоксан
(CH3)2C4H6O2
70
Анизол
CH3OC6H5
70
Дибензиловый эфир
(C6H5CH2)2O
70
Этилмонохлорацетат
CICh2COOC2H5
70
Метиловый эфир трихлоруксусной
CI3CCOOCh3
70
кислоты
Диэтиловый эфир перфторглутаро-
CF2(CF2COOC2H5)I
70
BOй кислоты
Изоамил бензоат
C6H5COOC5Hii
70
Диметилфталат
C6H4(COOCH3)2
70
Диизобутилфталат
C6H4(COOC4H9)2
70
Хлорпропиленкарбонат
C3H5ClCO3 (цикл.)
70
T р иизобу тил фосфат
(изо-С4Н90)3РО
70
Нитрометан
CH3NO2
70
Нитробензол
C6H5NO2
70
Адипонитрил
(NCCH2CH2)2
70
Трифторпропилдиметилдисилоксан
[C3H4F3(CH3)2SiJ2O
70
Продолжение
Разделяемая система
Разделяющий агент
формула
Литера¬
тура
Диметилдихлорсилан — триметил-
хлорсилан
Сульфолан
Цимол
Декалин
1,1,3-Трихлорпропан
1.4-Дихлорбутан
1.4-Дибромбутан
1.1.1.5-Тетрахлорпентан
1.5-Дибромпентан
Бромистый изоамил
1,9-Дихлорнонан
Хлорбензол
Хлористый бензил
Перфтормасло
Ацетофенон
Хлористый бензоил
β,β'-Дихлордиэтиловый эфир
Диметилдиоксан
Анизол
Дибензиловый эфир
Этил монохлор ацетат
Метиловый эфир трихлоруксусной
кислоты
Диэтиловый эфир перфторглутаро-
вой кислоты
Изоамилбензоат
Диметилфталат
Диизобутил фталат
Хлорпропиленкарбонат
Триизобутилфосфат
Нитрометан
CH2(CH2)2CH2SO2
CH3C6H4C3H7
CioHi3
CI2CHCH2CH2Ci
(ClCH2CH2)2
(BrCH2CH2)2
Cl3C(CH2)3CH2Cl
(BrCH2CH2) 2СН2
C5HiiBr
CICH2(CH2)7CH2Ci
C6H5Cl
C6H5CH2Cl
CH3COC6H5
C6H5COCl
(ClCH2CH2)2O
(CH3)2C4H6O2
CH3OC6H5
(C6H5CH2)2O
CICh2COOC2H5
Ci3CCOOCH3
CF2(CF2COOC2H5)2
C6H5COOC5H1I
C6H4(COOCH3)2
C6H4(COOC4H9)2
C3H5ClCO3 (цикл.)
(IiSO-C4H9O)3PO
CH3NO2
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
70
Алкилтрихлорсиланы — диалкилди-
хлорсиланы
Диалкилдихлорсиланы — триалкил·
хлорсиланы
Гетероциклические соединения
Тетрагидрофуран — вода
Бензофуран — мезнтилен (псевдоку-
мол, бензциклопентан)
Алкилдибензофураны Ci3-17 нефтя¬
ная фракция (*КИп = 275—305° С)
Фурфурол — олефины
2-Пирролидон — вода
Карбазол — углеводороды
Алифатические углеводороды
С-алкилимидазолы (алкилы находят¬
ся у атомов углерода; — реакцион¬
ная смесь (этилендиамин 4- карбо¬
новая кислота)
Нитробензол
C6H5NO2
70
Адипонитрил
(NCCH2CH2)2
70
Трифторпропилдиметилдисилоксан
[C3H4F3(CH3)2Sil2O
70
Сульфолан
CH2(CH2)2CH2SO2
I I
70
Дицианобутан
(NCCH2)2
285
Адипонитрил
(NCCH2CH2)2
285
β,β'-Оксидипропионитрил
(NCCH2CH2)2O
285
Динитрилы
NC(CR)aZ(CR2)6CN 28)
285
Дицианобутан
(NCCH2)2
285
Адипонитрил
(NCCH2CH2)2
285
β,β'-Оксидипропионитрил
(NCCH2CH2)2O
285
Динитрилы
NC(CR2)aZ(CR2)6CN28)
285
Этиленгликоль + гидроокись натрия
(CH2OH)2 + NaOH
78
Пропиленгликоль 4- гидроокись на¬
СНзОНСНОНСНз 4- NaOH
78
трия
1,2-Бутиленгликоль + гидроокись на¬
СН2ОНСНОНСН2СН3 + NaOH
78
трия
2,3-Бутиленгликоль -f гидроокись на¬
трия
Изобутиленгликоль 4- гидроокись на-
(CH3CHOH)2 4- NaOH
78
(Ch3)2COHCH2OH + NaOH
78
1,2-Пропиленгликоль
СНаОНСНОНСНз
202
Полиэтиленгликоли
Н[ОСН2СН2]„ОН
453
Вода
H2O
243
Ксилол
C6H4(CH3)2
327
Нафтены
CnH2n
214
а-Метилнафталин
Ci0H7CH3
214
335
β-Метили афта лин
C10H7CH3
335
П родолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Пиридин-3 — бромпиридин
Вода
H2O
76
Пиридин-3,5 — дибромпиридии
Вода
H2O
76
Пиридин — вода
Бензол
C6H6
431
З-Пиколин — 4-пиколин
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлористая сурьма
SbCl3
334
Трехбромистая сурьма
SbBr3
334
Смесь 3-пиколина, 4-пиколина, 2,6-
Органические кислоты (уксусная,
—
202
лутидина
пропионовая и др.)
3,4-Лутидин—2,5-лутидин
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлористая сурьма
SbCl3
334
Трехбромистая сурьма
SbBr3
334
:2,4-Лутидин — 3,4-лутидин
Хлористый алюминий
AlCl3
334
Бромистый алюминий
AlBr3
334
Пятифтористый мышьяк
AsF5
334
Треххлористый мышьяк
AsCl3
334
Трехбромистый мышьяк
AsBr3
334
Треххлористая сурьма
SbCl3
334
2-Метил-6-этилпиридин—лутидиновая
фракция каменноугольной смолы
Смесь алкиленпиридинов
3-Бромпиридин — 3,5-Дибромпиридин
Пиридиновые основания — вода
Пиперидин — вода
Морфолин — вода
Ν-Алкилморфолин — вода
Пиразины — низшие алканоламины
Пиперазины — низшие алканолами¬
ны
2-Метилтиофен — 3-метилтиофен
Трехбромистая сурьма
Пропионовая кислота
Полиолы
Этаноламины*
Вода
Бензол
Бензол
Ксилол
2-Этилгексанол
Алканол C6-Io
4-Метил-2-пентилацетат
Ксилол
2-Этилгексанол
Алканол C6-Io
4-Метил-2-пентилацетат
Парафины
Алкилбензолы
Хлорбензол
Парафины
Алкилбензолы
Хлорбензол
Хлооисгый алюминий
Бромистый алюминий
Пятифтористый мышьяк
Треххлористый мышьяк
Трехбромистый мышьяк
Треххлористая сурьма
Трехбромистая сурьма
SbBr3
C2H5COOH
H2O
C6H6
C6H6
C6H4(CH3)2
C8Hi7OH
CnH2W+ιΟΗ
CH3COOC6Hi3
C6H4(CH3)2
C8Hi7OH
CnH2w+iOH
CH3COOC6Hi3
CnH2W +2
CnH2W-S
C6H5Cl
СпИ2п+2
CwH2W —6
C6H5Cl
AlCl3
AlBr3
AsF5
AsCl3
AsBr3
SbCi3
SbBr3
334
202, 248
375
375
76
237
68
428
428
428
428
428
428
428
428
334
334
334
334
334
334
334
420
Продолжение
Разделяемая система
Разделяющий агент
Литера¬
тура
название
формула
Г етероциклическое соединение — ка¬
Полиалкиленгликоль
H[0 (CR2)AOH'7)
333
менноугольное масло
Полиалкиленоксид
[(CR2)nO(CR2)m]., 17>
333
Полиэфир алкиленгликоля с двух¬
HOt(CR2)nOCO (CR2)mCOOlxH 17>
333
основной кислотой
Полиамид
[ (CR2) n NHCO (CR2) mb
333
*) R — водород, углеводородный, галогенуглеводород¬
ный остаток
Rr-водород, углеводородный, галогенуглеводород-
ный, цианоуглеводородный остаток
2) R — алкил Cj_IO
R'-алкил или алкоксирадикал Cj_6) арил или
арилоксирадикал Сб_1о. алкилзамещенный
арилоксирадикал
3) Rh R'-алкилы Cj^g
R"'-алкил или циклоалкил
4) m — Ι-ί-3
п — 4 -·- т
R, R', Rr'- алкилы C1 _4
5) R — водород или углеводородный остаток
х — степень полимеризации
6) R — арил
Rr и Rrr — водород или углеводородные остатки
7) R — алкилы C1 _5
Rr и Rrr-алкил Cj_4
8) R- углеводородыЙ остаток
Rr и Rrr — водород или углеводородный остаток
9) R — углеводородный остаток
Ю) Rh Rr — углеводородные остатки
11) Rh Rr-радикалы С3_?
X — функциональные группы О, S или NH
12) R— остаток гетероцикла С3_ 1о
13) R и Rr-водород или алкил Cj^4
Rrr-алкил C1 _4
14) R — углеводородный остаток
М —цинк или кадмий
15) R — углеводородный остаток
M — цинк, кадмий или ртуть
16) R —водород или алкил Cj__g
17) R —водород или алкил
JC-степень полимеризации
18) R — алкил
19) R — углеводородный остаток
Rr-Boaopoa, или углеводородный остаток
20) R — алкилен или оксаалкилен
21) X — фтор, хлор или бром
22) R и Rr-г алкилы С2_12
23) R, R', и Rrr — алифатические радикалы
24) R — алифатический или ароматический радикал
R — ароматический радикал
25) R — алкил
Rr и Rrr — водород или алкил
26) R и Rr-Boaopoa или алкил Cj _3, содержащий груп¬
пы — ОН или — NH2
27) R— углеводородный остаток C1 _3
28) R — водород или алкил
а и b = 0 -1-3
Z — группы — CR2—; -CR2-NH—CR2—;
-CR2-S-CR2; CR2-O-CR2; -С-=
29) Существенно не меняют коэффициент относи¬
тельной летучести компонентов разделяемой
системы.
30) Орто-, мета- и пара-изомеры.
Литература к приложению
1. Б е д н о в В. М., Привалов В. E., H о в и к о в В. H., Б о р к о в a JI. В.,
Силин А. В., сб. «Химические продукты коксования углей востока СССР»,
вып. 3, Свердловск, 1965, стр. 154.
2. Бл юмберг Э. А., Г е л ь п е р и н Н. И., Ч и ж о в Е. Б., Авт. свид. 149772,
1962; Бюлл. изобрет., № 17 (1962).
3. Б о г д а н о в М. И., А р о н о в и ч X. П., Авт. свид. 113555, 1958, Бюлл. изо¬
брет., № 6 (1958).
4. Богданов М. И., А р о н о в и ч X. А., Авт. свид. 131349, 1960; Бюлл. изо¬
брет., № 17 (1960).
5. Брукс Б. Т., Бур д С. E., К у р т ц С. В., Шмеринг Л., Химия угле¬
водородов нефти, т. I, Гостоптехиздат, 1958.
6. Вяхирев Д. А., Решетникова Л. E., Газовая хроматография, Дзер¬
жинск, 1966, стр. 286.
7. Г а л а т а Л. А., Г у б с к а я 3. П., К и н я и и н а В. А., К о ф м а н Л. С.,
Труды по химии и химической технологии (Горький), № 2, 1962, стр. 256.
8. Г а л а т а Л. А., Г у б с к а я 3. П., К и н я п и н а В. А., К о ф м а н Л. С.,
Матвеева Т. H., сб. «Разделение и анализ углеводородных газов», Изд.
АН СССР, 1963, стр. 32.
9. Г а л а т а Л. А., К о ф м а н Л. С., M а т в е е в а Т. H., Труды по химии и
химической технологии (Горький), JMb 2, 1962, стр. 245.
10. Гарбер Ю. H., Бовкун Р. А., Кокс и химия, JMb 6, 45 (1965).
11. Гарбер Ю. H., Бовкун Р. А., ЖПХ, 37, JMb 4, 831 (1964).
12. Г а р б е р Ю. H., 3 е л е н о в с к а я С. И., P а б у х и н а Г. Г., Там же, 33,
№ 3, 694 (1960).
13. Генкин A. H., Лестева Т. М., Огородников С. К., Нем¬
цов М. С., Там же, 39, JMb 9, 2058 (1966).
14. Генкин, A. H., Огородников С. К., Коган В. Б., Немцов М. С.,
П р е с м а н Б. И., Там же, 34, 142 (1963).
15. Гоголева Т. Я., Носалевич И. М., Сборник научных трудов Укр. н.-и.
углехим. ин-та, вып. 18 (40), 1966, стр. 136.
16. Григорьева И. Г., К упри к Н. E., Юрманская И. П., Хим. пром.
JMb 10, 66 (1965).
17. Грищенко Η. Ф., Покорений В. H., Шапиро Л. П., Авт. свид.
176920, 1965; Бюлл. изобрет., JMb 24 (1965).
18. Девятых Г. Г., Дудоров В. Я., Зорин А. Д., ЖПХ, 40, JMb 9, 1951
(1967).
19. Девятых Г. Г., Зорин А. Д., Дудоров В. Я., Ежелева A. E.,
Смолян Л. С., Там же, 35, 1597 (1962).
20. Дейзенрот И. В., Коган В. Б., Фридман В. М., Хим. пром., JMb 3,
178 (1965).
21. Зельвенский Я. Д., Ф а й т е к Я., Ш а л ы г и н В. А., ЖФХ, 35,2802 (1961).
22. Зорин А. Д., Девятых Г. Г., Дудоров В. Я., Кар аба но в Н. Т.,
Ежелева A. E., Авт. свид., 144472, 1962, Бюлл. изобрет., JMb 3 (1962).
23. Кагаку кодзё, Chem. Factory, 5, JMb 3, 82 (1961); РЖХим., 1961, 18 и 73.
24. К аф аров В. В., Г о р д и е в с к и й Л. А., ЖПХ, 29, 176, 535, 713 (1956).
25. Коган В. Б., Хим. пром., JMb 6, 356 (1957).
26. Коган В. Б., Огородников С. К., Там же, JMb 9, 660 (1962).
27. Коган В. Б., Фридман В. М., Дейзенрот И. В., Авт. свид. 106651,
1957; Бюлл. изобрет., JMb 5 (1957).
28. Козлов В. H., Крылов С. Ф., Труды Института химии и металлургии
Уральск, филиала АН СССР, JMb 2, 1955, стр. 26.
29. Комаров В. М., Кричевцов Б. К., Завел ьский Д. 3., Кар¬
лина М. X., Авт. свид. 180607, 1966; Бюлл. изобрет., JMb 8 (1966).
30. Кононов Η. Ф., Макаровой ий Я. И., Розенгарт М. И., Ко¬
ган В. Б., ЖПХ, 38, JMb 11, 2522 (1965).
31. Кононов Η. Ф., Розенгарт М. И., Коган В. Б., Макаров-
ск ий Я. И., Якубов Т. С., Вайнберг М. М., Авт. свид. 177863, 1966,
Бюлл. изобрет., JMb 2 (1966).
421
32. Kop а блин а Т. П., M о л о к а н о в Ю. К., Б а р и н о в а М. В., Пласт¬
массы, № 11, 22 (1966).
33. К о р н е е в Ю. К., Скобло А. И., Изв. вузов, Нефть и газ, № 7, 57
(1958).
34. К о ф м а н Jl. С., M а т в е е в а Т. H., сб. «Синтез мономеров для производ¬
ства синтетического каучука», Госхимиздат, 1960, стр. 28.
35. К о ф м а н JI. С., Матвеева Т. H., Митрофанова В. Б., К а ч-
кина Л. М., Концепольский JI. И., Авт. свид. 175499, 1965, Бюлл.
изобрет. № 20 (1965).
36. Крох и н Н. Г., ЖФХ, 40, № 2, 500 (1966).
37. JI а п и д у с И. И., Там же, 40, Ns 3, 637 (1966).
38. Лапидус И. И., H и с е л ь с о н Л. А., К а р а т е е в а А. А., ЖОХ, 36,
№ 5, 773 (1966).
39. Л е й т м а н Я. И., П е в з н е р М, С., сб. «Производство бензола», Госхим¬
издат, 1962, стр. 202.
40. Л е с т е в а Т. М., Клименко В. Л., Огородников С. К., Авт. свид.
195435, 1967, Бюлл. изобрет., № 10 (1967).
41. Лестева Т. М., Огородников С. К., Авт. свид. СССР 180588, 1966;
Бюлл. изобрет., № 8 (1966); РЖХим., 1960, 5870.
42. Линь Чжэнь-сянь, Цзянь-Юнь-яо, Мэн Чжи-гуан, Chem.
Ind. a. Eng., № I, 24 (1959).
43. Львов С. Б., Ф а л ь к о в с к и й В. Б., Старков А. В., Труды МИТХТ,
вып. 8, 1958, стр. 77.
44. M а к а р о в с к и й Я. И., Коган В. Б., Кононов Η. Ф., В а й н-
берг А. М., Якубов Т. С., Авт. свид. 189815, 1967; Бюлл. изобрет., № I
(1967).
45. Малафеев Н. A., M а л ю с о в В. А., Жаворонков Н. М., Хим. пром.
№ 6, 492 (1960).
46. M ал едкий В. Я., К о г а н В. Б., Авт. свид. 185867, 1966; Бюлл. изобрет.,
№ 18 (1966).
47. M е т ю ш е в Б. Д., К н о г о т к о в а Е. И., сб. «Пищевая промышленность»,
№ з, 1966, стр. 155.
48. Мехтиев С. Д., П и ш н а м а з з а д е Б. Ф., Кошелева Л. М., и др.,
Изв. АН Азерб. ССР. Сер. физ. техн. и хим. н., № 5, 53 (1958).
49. Мехтиев С. Д., Пишнамаззаде Б. Ф., Кошелева Л. М., Э й-
б а т о в а LU. Э., Азерб. хим. ж., № 6, 3 (1959).
50. H е м ц о в М. С., К о г а н В. Б., Б у р о в а Г. В., О г о р о д н и к о в С. К.,
Авт. свид. 150498, 1962; Бюлл. изобрет., № 19 (1962).
51. Нисельсон Л. А., Лапидус И. И., ЖФХ, 39, № I, 161 (1965).
52. Нисельсон Л. А., Лапидус И. И., Там же, 39, № 7, 1756 (1965).
53. Нисельсон Л. А., Лапидус И. И., Получение и анализ веществ осо¬
бой чистоты. Материалы Всесоюзной конференции, Горький, 1966, стр. 50.
54. О г а н е с я н Ш. С., Г о г и н я н Э. А., Хим. и технол. топлив и масел, № 3,
22 (1967).
55. Огородников С. К., Коган В. Б., ЖПХ, 35, № 2, 461 (1962).
56. О г о р о д н и к о в С. К., Коган В. Б., Хим. пром., № 4, 30 (1963).
57. Огородников С. К., Коган В. Б., Немцов М. С., ЖПХ, 34, № 3,
581 (1961).
58. О г о р о д н и к о в С. К., К о г а н В. Б., H е м ц о в М. С., Там же, 34, № 4,
841 (1961).
59. О г о р о д н и к о в С. К., К о г а н В. Б., H е м ц о в М. С., Там же, 34, № 11,
2441 (1961).
60. О г о р о д н и к о в С. К., Коган В. Б., H е м ц о в М. С., Авт. свид.
159832, 1964; Бюлл. изобрет., № 2 (1964).
61. О г о р о д н и к о в С. К., Коган В. Б., Немцов М. С., Бурова Г. В.,
ЖПХ, 34, № 5, 1096 (1961).
62. О г о р о д н и к о в С. К., Немцов М. С., Коган В. Б., Морозо¬
ва А. И., Авт. свид. 141148, 1961; Бюлл. изобрет., № 18 (1961).
63. Огородников С. К., Немцов М. С., Морозова А. И., Г1 е т р о-
в а Т. Г., Авт. свид. 173199, 1965; Бюлл. изобрет., № 15 (1965).
422
64. О г о р о д н и к о в С. К., P а б о в с к а я Р. В., Король Н. Г., Ко¬
ган В. Б., Авт. свид., 168637, 1965; Бюлл. изобрет., № 5 (1965).
65. Павлов С. Ю., Павлова С. П., Пром. синт. каучука, № 18 (1966).
66. Павлов С. Ю., Павлова С. П., С е р а ф и м о в JI. А., К о ф м а н JI. С.,
Пром. синтетич. каучука, № 3, 14 (1967).
67. Петухов Е. Ф., Химия и технология горючих сланцев и продуктов их
переработки, вып. 8, Гостоптехиздат, 1960, стр. 186.
68. С а ф а е в А. С., А б и д о в а С. А., С у л т а н о в А. С., Узб. хим. ж., № 3,
64 (1964).
69. С е р а ф и м о в Л. А., П о т а п о в а Г. E., Л ь в о в С. В., Хим. и технол.
топлив и масел, № 12, 10 (1960).
70. С и в ц о в а Э. В., К о г а н В. Б., О г о р о д н и к о в С. К., ЖПХ, 38, № 11,
2609 (1965).
71. С и в ц о в а Э. В., К о г а н В. Б., О г о р о д н и к о в С. К., Там же, 39, № 9,
2038 (1966).
72. Скляр С. Я., Докл. Нефтехимия, секции. Башк. респ. правл. Всес. хим.
общ-ва им. Д. И. Менделеева, вып. 2, Уфа, 1966, стр. 91.
73. С у м а р о к о в В. П. и др., Деревообрабатывающ. и лесохим. пром., 3, № 8,
15 (1954).
74. Христов Д. К., пат. НРБ 10030, 1962.
75. Ч и р и к о в а 3. П., А н и с и м о в а Е. Г., Г а л а т а Л. А., К о ф м а н Л. С.,
Пром. синтетич. каучука, № 3, 6 (1966).
76. Ч у м а к о в Ю. И., Довгань Н. A., M у р з и н о в а 3. H., Авт. свид.
156953, 1963; Бюлл. изобрет., № 17 (1963).
77. Ш а р ф В. 3., Г е р м а н Е. H., Ф р е й д л и н Л. X., О п а р и н а Г. К.,
Хейфец В. И., Журн. ВХО, 9, № 6, 698 (1964).
78. Ш н итк о В. А., Коган В. Б., Авт. свид. 174636, 1965; Бюлл. изобрет.,
Nb 18 (1965).
79. Ahrens G. L., пат. США 2459403, 1949.
80. Akahosi Ts., Urakami К·, О k u m а Км япон. пат. 7914, 1959.
81. Amir Е. М., Edwards W. R., пат. США 3105017, 1963.
82. A m i г Е. М., E d w а г d s W-Rm пат. США 3220933, 1965.
83. Anderson LR., пат. США 2581344, 1952.
84. A n d е г s о n R., D е а I С. H., пат. США 3050573, 1962.
85. Anglo-Iranian Oil Co., англ. пат. 613867, 1948.
86. А г η о I d G. В., G г о s s Н. H., пат. США 3132092, 1964.
87. A s с h е г I А., В и 11 η е г F., нем. пат. 956576, 1957.
88. A t s и m i Т., T а к a h a s h i М., Tsunazima К., япон. пат. 4064, 1964.
89. Baccaredda М., Nencetti G. F., Tartarelli R., Chim. е ind
(Ital.), 48, No 8, 811 (1966).
90. Backlund P. S., пат. США 3132078, 1964.
91. Bains М. S., J a i η С. L., Indian J. Technol., 2, № 3, 109 (1964).
92. Bailey W. А., пат. США 3116224, 1963.
93. В a m f о г d W. R., англ. пат. 1007689, 1965.
94. В а г а η а и с к a s С. F., С а г г R. L. K-, H о d a n J. J., пат. США 3184496,
1965.
95. В а и m g а г t е n P. K-, Gerster LA., Ind. Eng. Chem., 16, 2396 (1954).
96. Berg С. Н. О., пат. США 2423861, 1947.
97. Berg L., Buckland S. V., R о b i n s о η Т.-Κ., Petrin J. W., Hydro¬
carbon Process, 45, № 12, 103 (1966).
98. Berg L., H a r r i s ο n J. М., пат. США 2442229, 1948.
99. Bergeron С. R., W i к m а η А. О., пат. США 3113079, 1963.
100. Binning R. S., пат. США 3007851, 1961.
101. Binning R. С., пат. США 3007985, 1961.
102. Birch S. F., H a b е s h a w J., Collis С. В., англ. пат. 606797, 1948.
103. Birch S. F., Habeshaw J., Collis С. В., англ. пат. 606799, 1948.
104. Black С., пат. США 2961383, 1960.
105. Black С., пат. США 2981661, 2981662, 2981663, 1961.
106. Bloomer W. J., пат. США 2380019, 1945.
107. Bondor F. S., L е b е I s Е. H., пат. США 2776936, 1957.
423
108. Borders А. М., Wolfe W. D.. O s t e r h о f H. J., Walton C. W., пат.
США 2386735, 1945.
109. Boyd J. H., пат. США 2609333, 1952.
110. B r e m n e r J. G. М., Coats R. R., англ. пат. 614056, 1948.
111. Britton Е. С., Horsley L. H., Kellom D. В., пат. США 3033864,
1962.
112. В г о u g h t о n D. В., пат. США 2911452, 1959.
113. В г о u g h t о η D. В., пат. США 2925452, 1960.
114. Brown С. J., англ. пат. 1017522, 1966.
115. BuelI С. К.. Boatringht R. С., Ind. Eng. Chem., 39, 695 (1947).
116. Burch J. S., пат. США 3087866, 1963.
117. С a b b a g е J. Т., пат. США 3257292, 1966.
118. Cahn R. Р., пат. США 3059037, 1962.
119. С а г I s о η С. S., пат. США 2620294, 1952.
120. Carlson С. S., Morrell С. E., Smith P. V., пат. США 2551584, 1951.
121. С а г I s о η С. S., S m i t h Р. V., пат. США 2570205 1951.
122. Carlson С. S., S m a t h Р. V., пат. США 2575243, 2575244, 2575245, 1951.
'123. Carlson С. S., S m i t h Р. V., пат. США 2575285, 1951.
124. Carlson С. S., S m i t h Р. V., пат. США 2583412, 1952.
125. Carlson С. S., Smith Р. V.. Morrell С. E.. Ind. Eng. Chem., 46, 350
(1954).
126. Carpenter S., Taylor W. E., McNair W. Т., Talbert F. Т., пат.
США 3228985, 1966.
127. Carver H. G., L a к e G. R., пат. США 2773006, 1956.
128. Catterall W. E., пат. США 2591671, 1952.
129. Catterall W. E., пат. США 2591672, 1952.
130. Catteral! W. Е„ пат. США 2669541, 1954.
131. Celanese Corp. of America, англ. пат. 686278, 1953.
132. С h a m b е г s J. М., пат. США 2695867, 1954.
133. Chambers J. М., пат. США 3075890, 1963.
134. Chambers J. М., Chem. Eng. Progr., 47, 555 (1951).
135. Chambers J. М., Proc. 3rd World Petrol. Congr., Haague 1951, Sect. Ill,
p. 90.
136. Chandramouli V. V., L a d d h a G. S., J. Sci. a Industr. Res., 21, № 8,
269 (1962).
137. Chandramouli V. V., L a d d h a G. S., Indian J. Technol., 2, № 9, 285
(1964).
138. Chang Y. С., C h a n H. T., Jan Liao Hsiich Pao1 2, 63 (1957).
139. C h 111 ο n C. H., Chem. Eng., 64, № 2, 146 (1957).
140. Chu J. С., K h a r b a u d о O. P., Brooks R. F., W a n g S. L., Ind. Eng.
Chem., 46, 754 (1954).
141. Cier H. E„ W a d d e l I М. Т., пат. США 2891894, 1959.
142. Clnes M. R., пат. США 2692227. 1954.
143. Cines М. R., пат. США 2699422, 1955.
144. CinesM. R., пат. США 2789087, 1957.
145. Cines М. R., Ruehlen F. N., пат. США 2794773, 1957.
146. Clay Н. А., пат. США 3235471, 1966.
147. Cobb J. E., пат. США 3179655, 1965.
148. Colborne R. S., англ. пат. 573111, 1945.
149. Colburn А. P., Schoenborn Е. М., Trans. Am. Inst. Chem Eng, 41,
421 (1945).
150. Coogler W. W„ Canad. Petrol., 8, № II, 48 (1967).
151. Coogler W. W., Chem. Eng., 74, № 16, 70 (1967).
152. Cornell D., пат. США 3018228, 1962.
153. Cornell D., пат. США 3158555, 1964.
154. Cornell D., Birum G-. H., пат. США 3155597, 1964.
155. С о г n е 11 D., В i г u m G. H., пат. США 3155598, 1964.
156. Cornell D., В i г и m G. H., F a i г J. R., пат. США 3206377, 1965.
157. Cornell D.. F a i г J. R., пат. США 3210259, 1965.
158. Coulson Е. A., Holt Е. С., J. Soc. Chem. Ind., 63, № 11, 329 (1944).
424
159. Coulson E. A., H о 11 Е. С., Sleven A., J. Soc. Chem. Ind., 63, № 11,
333 (1944).
160. Cubicciotti R., пат. США 2483625, 1949.
161. D а к s h i n a m u г t у P., Rao G. J., Acharya М. V. R., Venkata
Rao С., Chem. Eng. Sci., 9, № I, 69 (1958).
162. D а V i d s о η М. W, пат. США 2506858, 1950.
163. Deal С. H., Derr Е. L., Industr. a. Eng. Chem. Process, Design and De-
velopm., 3, N? 4, 394 (1964).
164. Dean F., англ. пат. 981943, 1965.
165. D e a n e s I у R. М., пат. США 2360655, 1944.
166. Deprez А. С., Colton J. W., пат. США 3031515, 1962.
167. DettloffR., Nafta (Polska), 21, № 7, 198 (1965).
168. Dicks R. S., Carlson С. S., Trans. Am. Inst. Chem. Eng., 41, 789 (1945).
169. Dijck W. J. D., Kooijman P. L., пат. США 2820001, 1958.
170. Dippel W. А., пат. США 3196085, 1965.
171. Distillers Co., англ. пат. 609871, 1948.
172. Dolezalik V., F ο n i о к А., чехосл. пат. 99988, 1961.
173. Donald М. В., Ridgway К.» J. Appl. Chem., 8, № 7, 408 (1958).
174. Doring С., Z. Chem., I, № 11, 347 (1961).
175. Doumas А. С., пат. США 3212998, 1965.
176. Drickamer Н. G., Brown G. G., White R. R., Trans. Am. Inst. Chem.
Eng., 41, 555 (1945).
177. Drickamer Н. G., H u m m e I H. H., ibid., 41, 607 (1945).
178. Drout W. М., пат. США 2610141, 1952.
179. Dunn С. L., Millar R. W., Pierotti G. I., Shiras R. N., Soun¬
ders М., Trans. Am. Inst. Chem. Eng., 41, 631 (1945).
180. D u^ г u m Е. L., пат. США 2407820, 1946.
181. DusIova L., Grubner О., Hames V., KossIer I., Matyska R.,
Chem. priimysl., 13, № 10, 513 (1963).
182. Enk E., К η 6 г г F., S р е s H., пат. ФРГ 1127339, 1962.
183. Enk E., К η б г г F., S р е s H., пат. ФРГ 1172677, 1964.
184. Erdoelchemie G. m.-b. H., франц пат. 1385145, 1965.
185. Evans Т. W., пат. США 2379696, 1945.
186. Evans Т. W., M о г г i s R. С., пат. США 2360859, 1944.
187. E V a n s Т. W., M о г г i s R. С., пат. США 2549586, 1951.
188. Evans Т. W., Morris R. С., Shokal Е. С., пат. США 2426821, 1947.
189. Evans Н. D., S а г η о D. H., 7 Congr. mund. petrol., Mexico, 1967, p. 57.
190. E w a n eh у n а I. E., Ambridge С., Canad. J. Chem. Eng., 36, 19
(1958).
191. Fainberg A. H., P е 11 е г m a n D. S., H a u р t s с h е i η М., пат. США
3152051, 1964.
192. Fannin L. W., пат. США 3272723, 1966.
193. Fannin L. W., Middlebrooks С. H., пат. США 3219546, 1965.
194. Farbenindustrie A. G., бельг. пат. 444255, 1942.
195. F е I d m a n J., О г с h i η М., пат. США 2581398, 1952.
196. Feldman J., Orchin М., Ind. Eng. Chem., 44, 2909 (1952).
197. Fenske М. R., Carlson С. S., Quiggle D., 39, 1322 (1947).
198. Fenske М, R„ M с С о г m i с к R. IT., пат. США 2909576, 1959.
199. Field E., пат. США 2302608, 1943.
200. Fisher W. E., пат. США 2341433, 1944.
201. Fleck R. N, пат. США 2842484, 1958.
202. Franck IT. G., Brennstoff. Chem., 32, № 13/14, 199 (1951).
203. Freure В. Т., пат. США 3105018, 1963.
204. Fried V., С а р к о v a A., Coll. Czech. Chem. Comm.. 28, Λβ 12. 3171 (1963*.
205. Garwin L., H a d d a d P. D., Ind. Eng. Chem., 45, 1S58 (19S3l
206. Geiser E. М., пат. США 2957811, I960.
207. Gerster J. A., Gorton J. A., E к I и n d R В . J Chem. Erg Data 5,
№ 4, 423 (1960).
208. Gerster J. A., M e г t e s T. S.. С о I b и r n A. P., Ind Eng Cbem, 39. TSfT
(1947).
HS
209. Oerster J. A., Mizushina Т., Mark T. N., Catartach A. W., Am.
Inst. Chem. Eng. J., I, 536 (1955).
210. Gesting P. P., Heinz W. E., пат. США 3174913, 1965.
211. G i 11 i I a n d E. R., M о г г e 11 С. E., С а г I s о п С. S., R о b е г t s о п N. С.,
пат. США 2551593, 1951.
212. Glazier Е. М., H а г г i s о n J. М., пат. США 2848387, 1958.
213. Goldup A., S w a n t о n W. Т., англ. пат. 903793, 1962.
214. Gorzyunka J., польск. пат. 46704, 1963.
215. Gotthard F., Pop A., Minea I., Serban С., Barbul М., Rev.
Chim. (RPR), 11, Nb 6, 313 (1960).
216. G г е е n b u г g R. В., пат. США 2352534, 1944.
217. Greene В., пат. США 2480919, 1949.
218. Grice R., Millidge A. F., N е w m a n F, С., англ. пат. 970629, 1964,
219. GriswoldJ., пат. США 2537459, 1951.
220. Griswold J., A n d г е s D., v a n Berg С. F., Kasch J. E., Ind. Eng.
Chem., 38, 65 170 (1946).
221. Griswold J., M о г г i s J. W., ibid., 41, 331 (1949).
222. Gundermann E., Erdol u. Kohle, 13, Nb 8, 556 (1960).
223. Gyoerkoes Т., пат. США 3048527, 1962.
224. Haarer E., Plass R., SchoIz H., Siissenguth H., пат. ФРГ
1204683, 1966.
225. Hachmuth К. H., пат. США 2434796, 1948.
226. Hacker J., L и с a s К·, G е b b i n D., Chem. Techn., 16, Nb 2, 75 (1964).
227. Hamilton С. E., Chem. Eng. Progr., 62, Nb 2, 92 (1966).
228. Hanson D. О., Winkle М., J. Chem. a. Eng. Data, 12, Nb 3, 319 (1967).
229. HappeI J., Cornell P. W., Eastman D. B., Fowle M. J., Por¬
ter C. A., Schiitte A. H., Trans. Am. Inst. Chem. Eng., 42, 189, 1001
(1946).
230. H a r n e у W. S., S с h n e i d e r S., пат. США 2511847, 1950.
231. Hartley F. R., Petrol Ref., 24, 519 (1945).
232. Haskell D. М., пат. США 3248308, 1966.
233. Hess Η. V., Naragon E. A., Coghlan C. A., Chem. Eng. Progr.,
Symp. Ser., 48, Nb 2, 72 (1952).
234. Hill А., пат. США 3230157, 1966.
235. Hirata М., Preprints of 25-th Anniversary Congr., 1961. S. I. Soc. Chem.
Eng. Japan, s. a. 80.
236. Hirata M., Hirose Y., Mitsushima K., Ogasawara S., Chem. Eng.
(Japan), 26, Nb 12, 1246 (1962).
237. Hisamura M., Okazaki T., Matsuyama A., Coal. Tar., 2, 132
(1950).
238. Hoffmann H., W a I d m a η n H. J., S i m ο n W., пат. ФРГ 1129160, 1962.
239. Hollenshead R. N., v a n Winkle М., J. Chem. a. Eng. Data, 11, Nb 3,
420 (1966).
240. Hopkins W. C., Fritsch J. J., Chem. Eng. Progr., 51, 361 (1955).
241. Hunsmann W., Simmrock K. H., Chem. Ing. Techn., 38, Nb 10, 1053,
AI555 (1966).
242. Hutchings L. R. E., пат. США 2936283, 1960.
243. Hutto J. F., пат. США 3026254, 1962.
244. Hutson T, пат. США 2908726, 1959.
245. Hutton D. G., пат. США 3284348, 1966.
246. Ilisei М., Ciocoiu P., Rusu R., Georgescu М., Rev. chim., 13,
Nb 4, 198 (1962).
247. Issoire J., Pfertzel R., Genie Chim., 86, Nb 4, 101 (1961).
248. Jones J. I., J. Soc. Chem. Ind., 69, 99 (1950).
249. Jordan D., Gerster J. A., Colburn А. P., Wohl К., Chem. Eng.
Progr., 46, 601 (1950).
250. Jost W., Z. Naturforsch., I, 576 (1946).
251. Kaemmerlen С. J., Oualline С. М., Williams A. G., пат. США
3152968, 1964.
252. Karr А., пат. США 2463629, 1949.
426
253. Katzen R., пат. США 3230156, 1966.
254. Kelley R. Т., V г i е s A. D., J а ш е s J. D., W а I к е г J. E., пат. США
3012947, 1961.
255. King R. W., Mondria H., англ. пат. 983783, 1965.
256. К i г s he n b а и ш I., Jonach F. L., Etherington L. D., пат. США
2901404 1959.
257. Kobayashi Т., Thsuyusaki К., япон. пат. 12915, 1964.
258. Koble R. А., пат. США 2908731, 1959.
259. Koh Kim-Hoк, Industr. Eng. Chem. Process Design a. Developm., 4, № I,
26 (1965).
260. Kortum G., Chem. Ztg., 74, 151, 165 (1950).
261. Kortflm G., Buttel A., Chem. Ing. Tech., 28, 282 (1956).
262. Kortflm G., Faltusz Е„ ibid., 33, 599 (1961).
263. Kramis С. J., пат. США 2999053, 1961.
264. Kuble J. A., Gracham A. R., Long D. С. О., англ. пат. 865577, 1961.
265. Kflmmerle К., пат. ФРГ 1070165, 1959.
266. Kflmmerle К., пат. ФРГ 1083823, 1960.
267. Kflmmerle К., пат. ФРГ 1089744, 1960.
268. Kflmmerle К., пат. ФРГ 1142354, 1963.
269. Kyle В. G., Tetlow N. J., J. Chem. Eng. Data, 5, 275 (1960).
270. Kyle В. G., T е 11 о w N. J., С о и г Т. H., С h е η Т. С., M о к G. I., Kan¬
sas State Univ., Eng. Exptl. Sta, Spec. Rept., № 18 (1962).
271. Lab. Riuniti Studi e Ricerch S. p. А., франц. пат. 1327424, 1963.
272. Lake G. R., Trans. Am. Inst. Chem. Eng., 41, 327 (1945).
273. Lake G. R., пат. США 2406695, 1947.
274. Lake G. R., пат. США 2432771, 1947.
275. Lake G. R., McDonell J. М., пат. США 2456561, 1948.
276. Lake G. R., S t г i b I е у J. М., пат. США 2477303, 1949.
277. Lake G. R., S t г i Ы е у J. М., пат. США 2528761, 1950.
278. Lang К- F., Schildwachter H., пат. ФРГ 976125, 1954.
279. Lang К- F., Schildwachter H., пат. ФРГ 1159467, 1964.
280. Lathum J. W., С о η η о г s J. S., пат. США 2434322, 1948.
281. L а V е n d е г Н. М., пат. США 2775627, 1956.
282. Lehmann P., Schwerdt R., Chem. Techn., 17, № 12, 738 (1965).
283. Leseman С. J. G., пат. США 2785112, 1957.
284. L i η d s а у К- L., В у г d J. D., пат. США 3147198, 1964.
285. Linville R. G., McEntee Н. R., пат. США 3007956, 1961.
286. Long J. D., пат. США 2406695, 1946.
287. Long J. D., пат. США 2449610, 1948.
288. Mahrwald R., H fi 11 i g E., Chem. Techn., 12, № 8, 467 (1960).
289. Mair В. J., К г о u s к о р N. С., Rossini F. D., J. Chem. a. Eng. Data,
5, № 2, 186 (1960).
290. Maisel D. S., пат. США 2746911, 1956.
291. Makin Е. С., пат. США 2979545, 1961.
292. Makin Е. С., пат. США 3033763, 1962.
293. Makin Е. С., пат. США 3034969, 1962.
294. Matsumoto Y., Sasaki Т., Yamauti Y., ,Kogyo Kagaku Zasshi, J. Chem.
Soc. Japan, Industr. Chem. Soc., 70, № 4, 411 А29 (1967); РЖХим., 1968,
24П170.
295. Mayland В. J., W h i t е Е. E., пат. США 2527951, 1950.
296. Mayor Y., Ind. petrole, 35, № 375, 93 (1967).
297. McCants J. F., пат. США 2476205-6, 247606, 1949.
298. McCloskey A. L., T а у I о г D. S., S р е i n b е г g H., пат. США 3044943,
1962.
299. McCullins J. Т., англ. пат. 833627, 1960.
300. McCinn С. J., J. Phys. Chem., 65, № Ю, 1898 (1961).
301. M с К i η n i S А. С., пат. США 2844527, 1958.
302. McKinnis А. С., пат. США 3043890, 1962.
303. McKinnis А. С., Flint D. L., пат. США 3114679, 1963.
304. McKinnis А. С., Flint D. L., пат. США 3114680, 1963.
427
305. Megantz S. О., H о р к i n s G. М., пат. США 3114678, 1963.
306. Metallgesellschaft. Aktiengesellschaft, франц. пат. 1021887, 1950.
307. Miller S. Р., канад. пат. 451985, 1948.
308. Millikan A. F., пат. США 3031383, 1963.
309. Millikan A. F., пат. США 3089829, 1963.
310. Morrell CE., пат. США 2591714, 1952.
311. Morrell С. E., Carlson С. S., S m i t h Р. V., пат. США 2551626, 1951.
312. Morrell С. E., С а г I s о η С. S., Smith P. V., пат. США 2591713, 1952.
313. Morrell С. E., Robertson N. С., пат. США 2591712, 1952.
314. Morrell С. E., Robey R. F., Robertson N. С., пат. США 2575284,
. 1951.
315. Morrell С. E., S t е w а г t J., С а г I s о η С. S., пат. США 2706707, 1955.
316. Morris R. С., E V a n s Т. W., пат. США 2371908, 1945.
317. Morris R. С., E V a n s Т. W., пат. 2437230, 1948.
318. Muller Н. J., пат. ФРГ 1188075, 1965.
319. Munk Р., пат. США 2856442, 1958.
320. Nagata I., J. Chem. a. Eng. Data, 7, JSIb 4, 461 (1962).
321. Nelson W. Т., пат. США 2786804, 1957.
322. Nelson W. Т., пат. США 2809925, 1957.
323. Nelson W. Т., пат. США 2922753, 1960.
324. Nelson W. Т., T u г k S. D., пат. США 3070518, 1962.
325. Newman М., H а у w о г t h С. В., Treybal R. E., Ind. Eng. Chem., 41,
2039 (1949).
326. Newton R. H., пат. США 3293154, 1966.
327. NeyW. О., англ. пат. 1007838, 1965.
328. Niemann G., К и t е р о w N. V., нем. пат. 729289, 1942.
329. Nixon А. С., D е а I С. H., англ. пат. 649982, 1951.
330. Nixon А. С., D е а I С. H., англ. пат. 649983, 1951.
331. Nixon А. С., D е а I С. H., англ, пат. 650319, 1951.
332. Nixon А. С., Deal С. H., Evans R. J., пат. США 2532031, 1950.
333. Novak J., H г i ν η а с М., чехосл. пат. 108020, 1963.
334. N. V. Bataafsche Petroleum Maatschappij, англ. пат. 666167, 1952.
335. Oakes M D., пат. США 3170849, 1965.
336. Okuma К·, Uragami К., Akaboshi М., англ. пат. 877360, 1959
337. Olin J. F., пат. США 2388217, 1945.
338. Othmer D. F., Chem. Eng. Progr., 54, № 7, 48 (1958).
339. Othmer D. F., ibid., 59, № 6, 67 (1963).
340. Othmer D. F., С о n t i J. J., пат. США 3024170, 1962.
341. Palm J. W., Oil a. Gas J., 61, № 25, 117 (1963).
342. Patterson J. А., пат. США 2407997, 1946.
343. Patterson J. А., пат. США 2461346, 1946.
344. Patterson J. A., S с h е е I i η е Н. W., пат. США 2426705, 1947.
345. Paulech J., Dykyi J., Kratky S., чехосл. пат. 106617, 1963.
346. Pennsalt Chemicals Corp., франц. пат. 1365315, 1964.
347. Perrus R., Bull. Assoc, franc, techn. petrole, № 133, 85 (1959).
348. Petrol. Ref., 32, № 11, 164 (1953).
349. Pierotti G. J., пат. США 2375035, 1945.
350. Pierotti G. J., D и n n С. L., англ. пат. 563164, 1944.
351. Pierotti G. J., D и η η С. L., пат. США 2341812, 1944.
352. Pierotti G. J., D и η η С. L., пат. США 2375036, 1945.
353. Piha Paivco, Suomen Ket., 32, № 5—6, BlOO (1959).
354. Podder С., Ζ. phys. 'Chem. (BRD), 39, № 1—2, 79 (1963).
355. Poffenberger N., Horsley L. H., Nutting Н. S., Britton С.,
Trans. Am. Inst. Chem. Eng., 42, 815 (1946).
356. Prabhu P. S., van Winkle M., J. Chem. a. Eng. Data, 8, № I, 14
(1963).
357. Prabhu P. S., v a n Winkle M., ibid., 8, № 2, 210 (1963).
358. Prinz R., G a η n J., R a m e у J., пат. США 3039940, 1962.
359. Privott W. J., Paul D. R., Jolis К. R·, Schoenborn E. М., 4.
Chem. a. Eng. Data, 11, № 3, 331 (1966).
m
360. Puchowicz A., Korciepinski Rm Wiadom. Chem., 19, № 3, 199
(1965).
361 -Qozati А., V a n Winkle М., J. Chem. a. Eng. Data, 5, № 3, 269 (1960).
362. Raji В. Nm R а о М. N., Indian Chem. Eng., 8, № 4, 108 (1966).
363. Raff S. J., D u m m e n t G. А., пат. США 2450381, 1948.
364. Ramanujam М., L a d d a G. S., Chem. Eng. Sci., 12, JSib I, 65 (1960).
365. Read C. Lm пат. США 2391104, 1945.
366. Rhone-Poulenc Soc. An., франц. пат. 1399555, 1965.
367. Richter Hm A n d e r s Wm пат. ГДР 32788, 1965.
368. Robinson С. S., Gilliland Е. F., Elements of Fractional Distillation,
New York, 1950, p. 285.
369. Robu V., Soare S., Bull. Inst, petrol, gaze si geol., 6, 261 (1960).
370. Rock H., Chem. Ing. Techn., 28, 489 (1956).
371. Sagenkahn M. L., Lake Placid Am. Inst. Chem. Eng. Muting, September,
1961.
372. Samddar S. P., N a n d i S. Km Trans. Indian Inst. Chem. Eng., 2, 29
(1948—1949).
373. Sandberg C. R., W r e n G. В., пат. США 2428815, 1947.
374. Sarno D. H., пат. США 2993841, 1959.
375. Saruwatori Κ., Matsushima М., япон. пат. 13078, 1963.
376. Sato К, Kawamura H., Yamashita H., Hattory М., япон. пат.
7487, 1965.
377. Sauer R. О., R е е d С. E., пат. США 2388575, 1945.
378. Scarth V., пат. США 2404253, 1946.
379. ScarthV., пат. США 2419039, 1947.
380. Scarth V., пат. США 2442474, 1948.
381. Schaeffer W. D., StiIes V. E., пат. США 3244759, 1966.
382. Schipioni A., Ferrero G., Atti Inst. Veneto sci. Iettere ed arti cl. sci.
mat. е. natur., 120, 93 (1961—1962).
383. Schley H., Teichmann W., F й г s t H., пат. ГДР 28594, 1964.
384. Schmalenbach A., Kessel К, Schulze М., пат. ФРГ 1206414, 1966.
385. SchmaIenbach A., Schulze М., Kessel К., пат. США 3227632, 1966.
386. Schmid В. Km пат. США 3071632, 1963.
387. Schmidt J., Adams E., Budde А., пат. ФРГ 1199749, 1966.
388. Schneider Gm Z. phys. Chem. (BRD), 27, № 3—4, 171 (1961).
389. Schwoegler Е. J., Putscher R. E., пат. США 2996438, 1961.
390. Sennewald Km Erpenbach H., V о g t W., пат. ФРГ 224293, 1967.
391. Serwinjski М., Michalowski S., Lesz. nauk. Politechn. todzk., № 74,
45, 57, (1965).
392. Sheets М. R., Marchello J. М., Hydrocarbon Process a. Petrol. Ref.,
42, № 2, 99 (1963).
393. S h i г a s R. N., J о h n s о n L. J., пат. США 2357028, 1944.
394. Skalak P., H г и δ i г i к F., S t о с е s J., чехосл. пат. 107841, 1963.
395. Smith Р. V., Cartson С. S., пат. США 2559519, 2559520, 1951.
396. SNAM-S. p. Am франц. пат. 1367345, 1964.
397. SNAM-S. р. А., франц. пат. 1367388, 1964.
398. Soc. D’Electro-chimie, D’EIectro-Metallurgie et des Acieries Electriques D’Ugu-
пе, англ. пат. 984725, 1965.
399. Soc. d’Electrochim., d’Electromet. et des Aci6ries Electriques d’Ugine, франц.
пат. 1359885, 1964.
400. Soc. d’Electrochim., d’Electromet. et des Acieries Electriques d’Ugine, франц.
пат. 1427860, 1966.
401. Sosnkowska-Kehiaian Km Przem. Chem., 41, № 12, 712 (1962).
402. Spall В. С., англ. пат. 983131, 1965.
403. Spencer Dm англ. пат. 804221, 1958.
404. Spencer D., англ. пат. 963451, 1964.
405. Staaterman Н. Gm M о г г i s R. С., Stager R. М., P i е г о 11 i G. J.,
Chem. Eng. Progr., 43, № 4, 148 (1947).
406. Standart Alcohol Co., англ. пат. 560712, 1944.
407. Staridart Oil Development Co., англ. пат. 593463, 1947.
429
408. Stephenson R. W., van Winkle M., J. Chem. a. Eng. Data, 7, Ks 4,
5—10 (1962).
409. Subbarao В. V., RaoC. V., ibid., 11, № 2, 158 (1966).
410. Suryanarayana Y. S., van Winkle M., ibid., 11, Ns 11, 7 (1966).
411. Swanson R. W., Gerster J. A., ibid., 7, 132 (1962).
412. Sweeney W. J, пат. США 2378808, 1945.
413. Szczepanik R., Chem. stosow., 2, Ns I, 51 (1958).
414. S z у n a ge I P, пат. ПНР 51837, 1966.
415. Takao S., Hydrocarbon Process, 45, № 11, 151 (1966).
416. Talbert F. Т., пат. США 3281336, 1966.
417. T a у I о r W. H., N е w t о η С. А., пат. США 3288877, 1966.
418. Teramoto Т., Yamatoto I., япон. пат. 11617, 1964.
419. Teshima Т., Hioyshi S., M a t s u d a H., Monta S., Iwaba S., J.
Chem. Soc. Japan. Ind. Chem. Sect., 55, 801 (1952).
420. Teter J. W., пат. США 2388506, 1945.
421. Teter J. W., M е г w i n W. J., пат. США 2388507, 1945.
422. Thizy А., пат. США 3125496, 1964.
423. Tindall J. В., пат. США 3211630, 1965.
424. Tooke J. W., L a n g Е. Z., пат. США 2465047, 1949.
425. Tschopp L. D., пат. США 3000794, 1958.
426. Ueki С., Tsuji Т., япон. пат. 4064, 1958.
427. Uitti К. D., пат. США 2894047, 1959.
428. Union Carbide Corp., франц. пат. 1407305, 1965.
429. Updike О. L., L а и g h t о n W. М., К е у е s D. В., Trans. Am. Inst. Chem.
Eng., 41, Ns 6, 717 (1945).
430. Valentine R. S., пат. США 2900309, 1959.
431. Vigh A., P а р р О., Szasz G., Acta pharmac. hung., 35, Ns 2, 53 (1965).
432. Vilim Otakar, чехосл. пат. 106714, 1963.
433. Wagner CR., пат. США 2415921, 1947.
434. Warren G. W., Warren R. R., Yarborough V. A., Industr. a. Eng.
Chem., 51, № 12, 1475 (1959).
435. W е i t z Н. М., L о г е n z L., пат. ФРГ 1142164, 1963.
436. Weller R., Schuberth H., L е i b n i z E., J. pract. Chem., 21, Nq 5—6,
234 (1963).
437. Welling С. E., пат. США 2386375, 1945.
438. Welty F., Gerster J. A., Colburn А. P., Ind. Eng. Chem., 43, 162
(1951).
439. Wentworth Т. О., пат. США 2358193, 1944.
440. Wichterle J., Chem. Listy, 58, Ns 2, 142 (1964).
441. Wichterle J., Coll. Czech. Chem. Comm., 30, Ns 10, 3388 (1965).
442. Wiist Н. А., пат. США 3101304, 1963.
443. Wiist Н. А., пат. США 3282801, 1966.
444. Wirth J., Herbert W., пат. ФРГ 1103316, 1961.
445. Wisznowski К·, Koks, smola, gas, 3, № 5, 189 (1958).
446. Woerner R. С., пат. США 3026253, 1962.
447. Wynkoop R., Alien J. G., англ. пат. 990006, 1965.
448. Wynkoop R., А 11 е n J. G., англ. пат. 1049971, 1966.
449. Wynkoop R., А 11 е n J. G., пат. США 3171794, 1965.
450. Wynkoop R., Allen J. G., пат. США 3171863, 1965.
451. Yamamoto Y., Maruyama Т., Hori К·, Chem. Eng. (Japan), 16, 166
(1952).
452. Yamamoto Y., Maruyama Т., Kogaku kogaku, Chem. Eng. (Japan),
23, No 10, 635 (1959); РЖХим., 1960, 85058.
453. Yew Foch Fu H s i s, M a i г В. J., Anal. Chem., 38, Ns 2, 231 (1966).
454. Yoshimura Т., Chem. Eng., 73, Ns 10, 134, I А (1966).
455. Young S, J. Chem. Soc., 81, 742, 761 (1902).
456. Zieborak К·, Wyrzykowska-Stankiewicz D., Bull. Acad, polon.
Sci., Ser. sci. chim., geol. et geogr., 7, Ns 4, 247 (1959).
457. Zimmer W. F., В о w m a n R. A., S h е р а г d A. F., пат. США 3214444*
1965.
430
ОГЛАВЛЕНИЕ
Предисловие
Основные обозначения
Введение
Глава I
Термодинамические основы учения о фазовом равновесии
жидкость — пар. Основные термодинамические закономерности
Уравнения равновесия
Изобарный и химические потенциалы идеальных и реальных фаз. Летучесть, актив¬
ность и коэффициент активности
Частные случаи равновесия
Идеальные и реальные системы. Характер изменения коэффициентов активности и отно¬
сительной летучести в бинарных системах
Законы Коновалова и Вревского
Г л а в а II
Физико-химические основы методов
азеотропной и экстрактивной ректификации
Основное уравнение теории азеотропной и экстрактивной ректификации
Механизм действия разделяющих агентов и критерии их выбора
Выбор разделяющих агентов
Методы выбора разделяющих агентов по данным о свойствах растворов
Выбор разделяющих агентов по данным о равновесии между жидкостью и паром . .
Выбор разделяющих агентов по данным о температурах кипения смесей
Выбор разделяющих агентов по данным о растворимости
Выбор разделяющих агентов по данным о свойствах аэеотропных смесей.
Применение метода газо-жидкостной хроматографии для выбора разделяющих агентов
Выбор разделяющих агентов по данным о свойствах компонентов растворов
Методы выбора разделяющих агентов, основанные на оценке отдельных составляю¬
щих межмолекулярного взаимодействия
Корреляция селективности с помощью уравнений Гаммета — Тафта .
Применение минеральных веществ в качестве разделяющих агентов при экстрактивной
ректификации . . . .
Связь между растворимостью и эффективностью разделяющих агентов. Выбор комби¬
нированных разделяющих агентов для процессов экстрактивной ректификации ....
Сравнительная оценка методов выбора разделяющих агентов и некоторые практиче¬
ские указания
3
5
6
14
19
24
28
32
35
38
43
44
44
46
50
53
55
64
73
81
93
96
99
Азеотропные смеси ................ . ..... HO
Условия образования и характеристика азеотропных смесей IOl
Бинарные системы 102
Трехкомпонентные системы, образованные полностью смешивающимися веществами . 103
Трехкомпонентные системы, образованные ограниченно растворимыми веществами . Ю5
Предсказание азеотропии 106
Свойства азеотропных смесей, образованных компонентами с ограниченной взаимной
растворимостью . 135
Экспериментальное определение свойств азеотропных смесей 143
Влияние давления на состав и температуру кипения азеотропных смесей 146
Дистилляция трехкомпонентных смесей 155
Правило азеотропии 162
Ректификация трехкомпонентных смесей 174
Ректификация системы с двумя положительными бинарными азеотропами (система
дихлорметан — ацетон — метиловый спирт) . . . . 176
Ректификация систем с одним отрицательным бинарным азеотропом (системы дихлор¬
метан — ацетон — хлороформ и ацетон — хлороформ — бензол) 177
Ректификация систем с положительными и отрицательными бинарными азеотропами . 181
Разделяющие линии ректификации 186
Применение принципов ректификационного анализа к азеотропной ректификации ... 188
Определение равновесия между жидкостью и паром 194
Экспериментальные методы 195
Очистка исходных веществ 195
Приборы для изучения равновесия между жидкостью и паром 197
Исследование равновесия между жидкостью и паром в системах, образованных ком¬
понентами с ограниченной взаимной растворимостью 202
Исследование равновесия между жидкостью и паром с помощью газо*жидкостной
хроматографии 203
Методы проверки и исправления экспериментальных данных о равновесии между
жидкостью и паром 204
Бинарные системы 205
Трехкомпонентные системы 209
Методы расчета равновесия между жидкостью и паром· 211
Бинарные системы . . 211
Расчет равновесия по данным о давлении паров смесей 216
Расчет равновесия по данным о температурах кипения смесей 219
Расчет равновесия по данным о свойствах азеотропной смеси 220
Расчет равновесия по данным о взаимной растворимости 221
Расчет равновесия по данным о критической точке растворимости 222
Расчет равновесия по кривой открытого испарения 223
Сравнительная оценка методов расчета равновесия в бинарных системах и некоторые
практические рекомендации 224
Методы расчета равновесия между жидкостью и паром в многокомпонентных системах 226
Аналитические методы 226
Графо-аналитические методы 232
Г л а в а III
Технологическое оформление процессов
азеотропной и экстрактивной ректификации
Технологические схемы процессов азеотропной и экстрактивной ректификации ..... 238
Лабораторные установки для азеотропной ректификации 238
Лабораторные установки для экстрактивной ректификации , 240
Промышленные установки для азеотропной ректификации 244
Промышленные установки для экстрактивной ректификации 246
Материальный иттепловой баланс процесса азеотропной ректификации 248
Периодический процесс 248
Непрерывный процесс 251
Особенности расчета процесса азеотропной ректификации с расслаиванием конденсата 254
Материальный баланс процессов экстрактивной ректификации ............. 259
Тепловой баланс процесса экстрактивной ректификации 268
Влияние агрегатного состояния разделяемой смеси в процессе экстрактивной ректи¬
фикации 273
Расчет процессов азеотропной ректификации 278
Расчет процессов экстрактивной ректификации 293
Регенерация разделяющего агента 305
Массообмен в процессах азеотропной и экстрактивной ректификации . 306
Сопоставление азеотропной и экстрактивной ректификации 314
Применение методов азеотропной и экстрактивной ректификации 317
Примеры применения методов азеотропной и экстрактивной ректификации 319
Литература . 333
Приложение . . 341
Литература к приложению 421