Автор: Бойчук Л.М.
Теги: регулирование и управление машинами, процессами теория автоматического управления
Год: 1971
Текст
БИБЛИОТЕКА ПО АВТОМАТИКЕ
Выпуск 442
Л. М. БОЙЧУК
МЕТОД СТРУКТУРНОГО СИНТЕЗА
НЕЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
«ЭНЕРГИЯ»
МОСКВА 1971
6П2.12
УДК 62-501.14
Б 72
РЕДАКЦИОННАЯ КОЛЛЕГИЯ:
И. В. Антик, Г. Т. Артамонов, А, И. Бертинов, А. А. Воронов,
Л. М. Закс, В. С. Малов, В. Э. Низе, О. В. Слежановский,
Б. С. Сотсков, Ф. Е. Темников, М. Г. Чиликин, А. С. Шаталов
Бойчук Л. М.
Б 72 Метод структурного синтеза нелинейных систем
автоматического управления. М., «Энергия», 1971.
112 с. с ил. (Б-ка по автоматике. Вып. 442).
Книга посвящена новому методу структурного синтеза по задан-
ным переходным процессам нелинейных систем автоматического управ-
ления. Рассмотрен синтез одномерных и многомерных систем для слу-
чаев, когда задание есть функция времени (системы стабилизации,
следящие и программные) и когда задание есть определенная функ-
циональная зависимость между выходными величинами объекта управ-
ления. Приведены примеры использования метода для нахождения
структуры различных нелинейных автоматических систем (системы
управления компрессором, ядерным реактором, движущимся телом,
электродвигателем, генераторы синусоидальных колебаний, дифферен-
циальные анализаторы, аналоговые схемы для решения уравнений
и нахождения экстремума, логико-динамические системы и т. д.).
Книга рассчитана на инженеров и научных работников, занимаю-
щихся разработкой и проектированием систем автоматического управ-
ления.
Метод структурного синтеза нелинейных систем автоматического
управления
3-3-13
236-70
6П2.12
Бойчук Леонид Михайлович
Редактор Е. П. Маслов
Технический редактор О. П. Преснякова
Корректор В. С. Антипова
Сдано в набор 22/XII 1970 г. Подписано к печати 11/V 197J г.
Формат 84Х1087з2 Бумага типе
Усл. печ. л. 5,88 У
Тираж 9 ООО экз. Цена 38 коп.
ll/V 197J г. Т-05267
Бумага типографская № 2
Уч.-изд. л. 7,63
Зак. 10
Издательство .Энергия*. Москва, М-114, Шлюзовая наб., 10.
Московская типография № 10 Главполиграфпрома
Комитета frn П*Ч*™^ТР?_£™УШ! ¥ицИРТ?п Г^Р
ПРЕДИСЛОВИЕ
Во многих отраслях народного хозяйства {разрабатываются
автоматические системы, в которых объект управления описывает-
ся нелинейными дифференциальными уравнениями или в которых
требуется регулировать определенные соотношения между выход-
ными величинами объекта управления. Эти соотношения, как пра-
вило, также являются нелинейными (системы для регулирования
соотношений называют системами функционального регулирова-
ния). Основные трудности при проектировании указанных систем
часто возникают именно на первом этапе — этапе структурного
синтеза (выборе закона управления) — и определяются нелиней-
ным характером задачи.
При проектировании указанных выше нелинейных систем авто-
матического управления разработчик, по существу, весьма огра-
ничен в выборе инженерных методов синтеза. Известные методы
структурного синтеза линейных автоматических систем либо не-
применимы из-за недопустимости линеаризации, либо сводятся
к сложной проблеме синтеза управления объектом с переменными
во времени параметрами. Существующие вариационные методы
позволяют, по крайней мере в настоящее время, осуществить до
конца синтез структуры нелинейных систем только для некоторых
относительно простых случаев.
(Предлагаемая читателю книга посвящена обоснованию и при-
менению разработанного автором метода структурного синтеза не-
линейных автоматических' систем по заданным переходным процес-
сам регулируемых величин. Этот метод применим для объектов
любого порядка и дает возможность решать сравнительно широ-
кий круг задач. Метод позволяет найти такую структуру управле-
ния, которая обеспечивает изменение во времени регулируемой вели-
чины согласно задаваемому дифференциальному уравнению. Тем
самым при синтезе учитывается качество (регулирования. Главная
особенность метода заключается в том, что его процедура явля-
ется относительно простой и сводится прежде всего к алгебраи-
ческим операциям. Это обстоятельство делает метод удобным для
применения в инженерной практике.
Разумеется, ни один метод синтеза не может охватить все
•многообразие задач управления. Применительно к одним задачам
данный метод может оказаться более эффективным по сравнению
с известными, применительно к другим — менее эффективным.
К настоящему времени использование метода позволило решить
ряд интересных задач и получить новые структуры управления,
в частности, при синтезе систем функционального (регулирования
и нелинейных следящих систем.
3
В книге автор в первую очередь рассматривал определение
закона улравления объектом с точки зрения качества регулирова-
ния и устойчивости, пытался подчеркнуть общность и основные
принципы приложения метода при синтезе различных нелиней-
ных автоматических систем. В соответствии с этим назначением
книги и ее опраниченным объемом пришлось опустить описание
конструкций и (расчет элементов систем управления. Приводятся
только структурные схемы систем.
Книга, вероятно, не лишена недостатков, указания на кото-
рые автор с благодарностью примет от читателей.
Автор выражает признательность член-корр. АН УССР
А. Г. Ивахненко, труды и внимание которого содействовали появ-
лению данной книги.
Автор благодарит рецензента доктора техн. наук, проф.
А. В. Нетушила, чьи советы и замечания были весьма полезными
при подготовке рукописи к печати.
Работа выполнена в Институте кибернетики АН УССР.
Пожелания и замечания просьба посылать по адресу: Москва,
М-114, Шлюзовая набережная, 10, издательство «Энергия».
Автор
ВВЕДЕНИЕ
Структурный синтез автоматических систем состоит в опреде-
лении схемы (структуры) регулятора, необходимого для отработ-
,'ки объектом некоторого задания. При этом надо соблюдать оп-
ределенные требования к качеству такой отработки. Проектируя
.любую автоматическую систему, следует прежде всего выбрать
«ее структуру, т. е. вид связей по регулируемой величине, заданию
;и действующему на объект возмущению. С ростом требований
к качеству работы автоматических систем значение этой стадии
проектирования все более увеличивается.
Разработка методов структурного синтеза автоматических си-
стем становится особенно актуальной в связи с расширением кру-
га нелинейных задач регулирования. iK их числу относятся:
слежение или программное управление объектом, описываемым
нелинейным дифференциальным уравнением;
регулирование некоторых соотношений (в общем случае не-
линейных) между выходными величинами объекта, который может
описываться - как линейным, так и нелинейным дифференциальным
уравнением;
определение связи по возмущению при управлении нелинейны-
ми объектами и т. д.
Существуют два пути решения задачи структурного синтеза
нелинейных систем. Можно рассматривать какой-либо конкретный
нелинейный объект и искать для него рациональную схему управ-
ления. К сожалению, найденное при этом решение будет слишком
узким, неприменимым к управлению другими нелинейными объек-
тами. Можно, напротив, сосредоточить внимание на общих мето-
дах, относящихся к сравнительно широкому классу нелинейных
объектов (или нелинейных задач), хотя для частной задачи общий
подход может иногда оказаться более сложным, чем метод, пред-
назначенный специально для ее решения. В данной работе исполь-
зуется второй путь.
Общие методы структурного синтеза, применяемые в настоя-
щее время, наиболее полно разработаны для линейных или линеа-
ризуемых систем, в то время как динамика реальных объектов
гораздо точнее описывается нелинейными дифференциальными
уравнениями. В практике синтеза нелинейных систем обычно за-
дают структуру управления и затем производят проверку на
устойчивость известными методами анализа (т. е. по существу
применяют метод проб и ошибок) либо линеаризуют уравнение
объекта, что во многих случаях приводит к довольно сложной за-
даче синтеза управления объектом, описываемым линейным диффе-
ренциальным уравнением с переменными параметрами (коэффи-
б
циентами линеаризации) [Л. 1]. Известные аналитические методы
структурного синтеза нелинейных автоматческих систем не охва-
тывают многих црактически важных случаев и приводят к отно-
сительно сложной -процедуре синтеза управления.
Управляемое движение отличается от неуправляемого прежде
всего своей целенаправленностью, т. е., управляя, мы навязываем
объекту некоторое желаемое движение. Это движение, очевидно,
должно быть задано. Формы задания такого движения различны.
Можно, например, потребовать, чтобы регулируемая величина не
выходила за определенные пределы, или задать уравнения, по
которым она должна изменяться во времени. Эти уравнения мо-
гут быть либо конечными, например x=x(t), либо дифференциаль-
ными, причем такими, что их решения при любых начальных ус-
ловиях дают желаемую зависимость регулируемой величины от
времени.
Задание требуемого движения объекта в виде конечного урав-
нения используется в некоторых случаях при синтезе корректи-
рующих нелинейных элементов следящих систем [Л. 2]. Однако
получаемые при этом результаты справедливы только для кон-
кретных начальных условий движения, т. е. область применения
такого метода ограничена. В отличие от конечных дифференциаль-
ные уравнения охватывают не одно, а целый класс движений, об-
ладающих общими свойствами. Такая форма задания требуемого
движения объекта, называемая иногда «дифференциальной про-
граммой» [Л. 3], используется в настоящее время почти исключи-
тельно для синтеза линейных систем. На ее. основе построены из-
вестные методы синтеза автоматических систем .по требуемым пе-
редаточным функциям [Л. 4].
Аналогичный подход возможен и при синтезе нелинейных си-
стем. Поставим задачу синтеза такой структуры управления, кото-
рая обеспечивает движение регулируемой величины нелинейного
объекта согласно определенному дифференциальному (в общем
случае нелинейному) уравнению. Это уравнение должно быть, оче-
видно, таковым, чтобы любое его решение удовлетворяло необхо-
димым показателям качества регулирования.. Указанное уравнение
может быть получено из различных условий, например, из условия
достижения определенного характера переходного процесса при
отклонении регулируемой величины от задания; поддержания тре-
буемого соотношения между регулируемой величиной и ее произ-
водными; соблюдения заданной зависимости между выходными
величинами объекта и т. д.
Для синтеза таких систем управления автором был разра-
ботан единый метод, который впервые было изложен в 1964 г.
в связи с решением одной задачи динамического программирова-
ния (Л. б]. Идея этого метода сводится к определению требуемой
структуры управления путем исключения высшей производной ре-
гулируемой величины из требуемого дифференциального уравнения
движения системы, полученного при минимизации некоторого ин-
тегрального функционала, и дифференциального уравнения объек-
та. Впоследствии удалось показать, что этот подход применим не
только для синтеза управления, обеспечивающего оптимальное
в некотором смысле движение системы, но и, что очень важно,
для синтеза управления, обеспечивающего любое требуемое дви-
жение, которое можно представить как решение, соответствующего
дифференциального уравнения. Такая постановка задачи являет-
6
ся более широкой и практически более ценной, ибо нахождение
требуемого дифференциального уравнения движения системы с по-
мощью методов теории оптимального управления во многих слу-
чаях весьма 'затруднительно. В то же время это 'уравнение часто
можно определить исходя из обычных инженерных соображений
(качество регулирования, устойчивость и т. д.) или путем исполь-
зования уравнений эксплуатируемых систем. Следует, кроме того,
подчеркнуть, что существуют задачи синтеза, которые нецелесооб-
разно по тем или иным причинам формулировать с позиций теории
оптимального управления (например, задача синтеза структуры ге-
нератора синусоидальных колебаний, решаемая в гл. 3, когда не-
обходимо выдержать вполне определенное соотношение между вы-
ходной величиной объекта и скоростью ее изменения).
•Необходимо отметить, что в данной книге движение выход-
ной величины синтезируемой системы исследуется главным обра-
зом вблизи такого задания, которое объект по своим мощност-
ным данным может реализовать, причем при небольших отклоне-
ниях от этого задания управляющее воздействие не выходит на
максимум. К таким задачам относятся многие прикладные задачи,
связанные с синтезом устойчивых нелинейных систем, обладаю-
щих требуемым качеством переходного процесса.
Итак, данная книга посвящена первому этапу" проектирования
автоматической системы, а именно — структурному синтезу, когда
основная трудность при проектировании состоит в учете нелиней-
ной природы объекта или задания. Что касается анализа, то он во
многом упрощается благодаря самому предлагаемому методу син-
теза, который основан на задании дифференциального уравнения
движения замкнутой системы. Выбором коэффициентов этого урав-
нения можно достичь требуемого качества и устойчивости про-
цесса регулирования, что, конечно, не отрицает в каждом кон-
кретном случае необходимости дополнительного анализа системы,
в частности, оценки чувствительности к изменению параметров
объекта, влияния неидеальности дифференциаторов, статистически
заданных помех и т. д. Для решения этих вопросов, которые вы-
ходят за рамки данной работы, могут быть использованы извест-
ные методы анализа систем заданной структуры, обычно приме-
няемые в теории автоматического регулирования.
Основная цель книги—изложить метод синтеза, который по-
зволяет аналитически решать указанные выше нелинейные задачи,
исследовать особенности метода, определить область его примене-
ния и довести до решения практически важных задач синтеза си-
стем управления. Главные результаты разработки метода изло-
жены в (Л. 6—33].
Книга состоит из шести глав.
В первой главе приведена общая постановка задачи исследо-
вания и обзор существующих методов ее решения, изложена сущ-
ность предлагаемого метода синтеза, а также определены основ-
ные свойства синтезируемых систем и область применения метода.
Вторая глава посвящена использованию метода для структур-
ного синтеза одномерных и многомерных нелинейных автомати-
ческих систем, задающие воздействия которых суть функции вре-
мени. Приведен пример синтеза структуры следящей системы для
регулирования скорости компрессора.
'В третьей главе излагается приложение метода к структур-
ному синтезу односвязных систем функционального регулирования,
7
требуемое движение которых задается в виде некоторого соотно-
шения .между выходными величинами объекта управления; рас-
смотрен синтез структуры генератора синусоидальных колебаний,
а также системы автоматического управления спуском тела в ат-
мосфере.
Четвертая глава поовящена использованию метода для струк-
турного синтеза многосвязных систем функционального регулиро-
вания, требуемый режим работы которых задается более чем од-
ним соотношением между выходными величинами объекта управ-
ления. Рассмотрена задача структурного синтеза системы автома-
тического управления положением и скоростью тела, а также
совпадением двух тел.
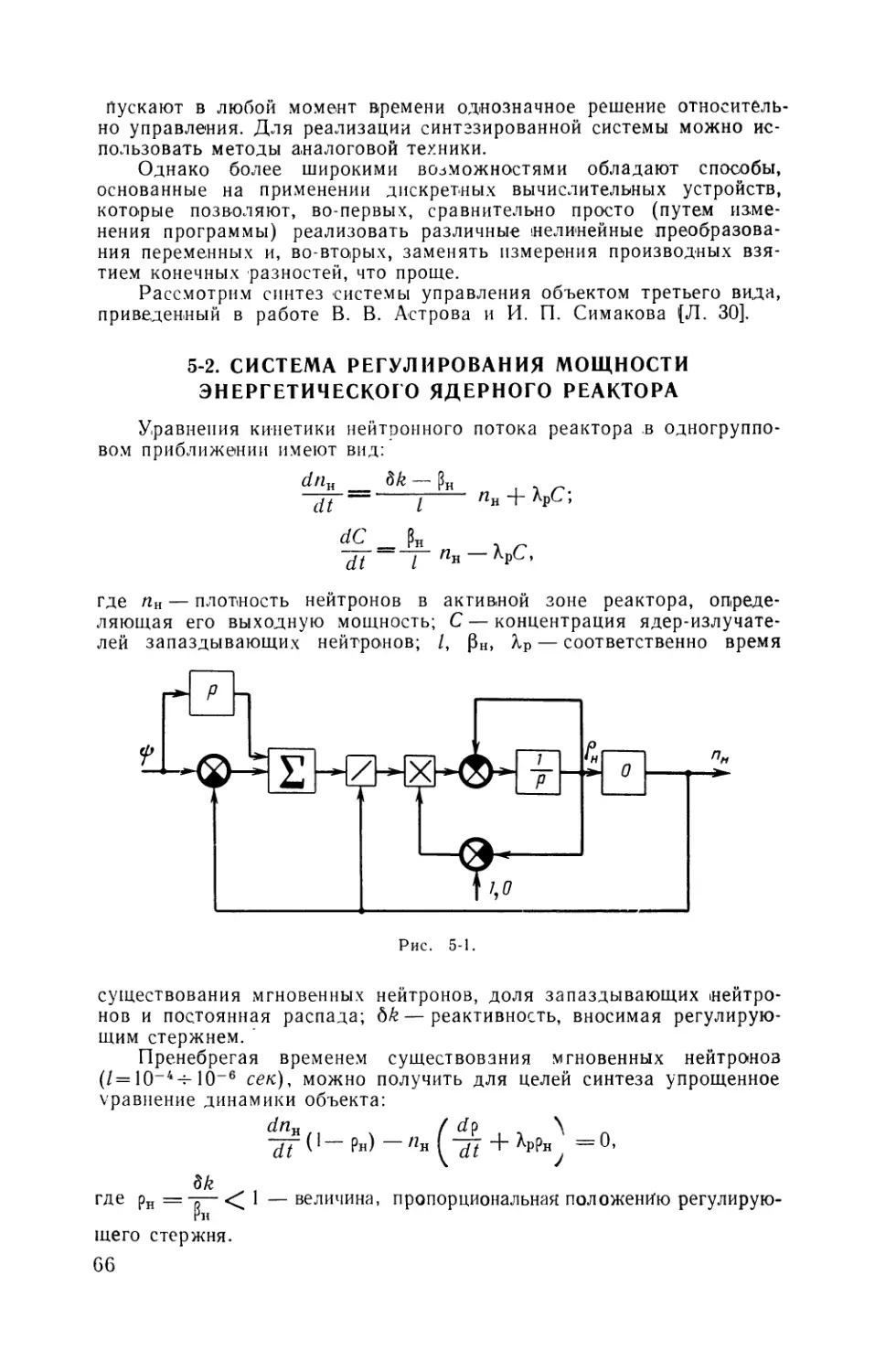
В пятой главе приведены обобщения метода синтеза:
использование функционального преобразования независимой
переменной для целей синтеза (в качестве примера синтезируется
структура электропривода, работающего в гармоническом ре-
жиме);
применение метода для случая, когда дифференциальные урав-
нения объектов неразрешимы явно относительно управляющих воз-
действий или содержат их производные (в качестве примера рас-
смотрен синтез структуры системы управления мощностью энерге-
тического ядерного реактора);
применение метода для случая когда дифференциальные урав-
нения объекта известны не полностью.
В шестой главе изложено применение основной формы мето-
да и его обобщения для решения специальных задач функцио-
нального регулирования, iK ним относятся задачи синтеза диффе-
ренциальных анализаторов для систем программного управления
станками, аналоговых вычислительных систем для решения урав-
нений и поиска экстремума функции многих переменных, а также
задача синтеза логико-динамических систем автоматического
управления (логико-динамическими называют системы, у которых
объекты управления описываются дифференциальными уравнения-
ми, а задания сформулированы в виде логических соотношений).
Глава первая
ОСНОВЫ СТРУКТУРНОГО СИНТЕЗА
НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
ПО ЗАДАННЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ
1-1. ЗАДАЧА СТРУКТУРНОГО СИНТЕЗА
а) Постановка задачи
Выбор структуры системы автоматического регулирования —
это наиболее важный этап ее проектирования. Вполне- очевидно,
что многие варианты схем регуляторов могут давать удовлетво-
рительные результаты. Выбор того или иного варианта определя-
ется не только требованиями к точности и качеству регулирова-
ния, но также такими дополнительными соображениями, как на-
дежность, простота схемы и конструкции, экономичность и т. д.
Первоначальное нахождение структуры системы (помимо
включения таких функционально необходимых элементов, как уси-
лители или исполнительные двигатели) обычно основано на опре-
делении корректирующих устройств, при включении которых пе-
редаточная функция системы (или дифференциальное уравнение
движения) соответствует желаемой. Поэтому, решая задачу син-
теза, можно задаться дифференциальным уравнением системы,
а затем так подобрать управление, чтобы обеспечить ее движение
согласно этому уравнению. При этом исходят из того, что свойства
решения таких уравнений определяют по ряду показателей свойств
соответствующих автоматических систем.
•Изложим вначале постановку задачи для одного достаточно
общего вида уравнений объекта и системы. В последующих гла-
вах эта постановка будет расширена.
Пусть задана некоторая неизменяемая часть системы, назы-
ваемая' в дальнейшем объектом управления. В эту часть системы
могут входить также исполнительные устройства. Объект предпо-
лагается одномерным, т. е. с одним управляющим воздействием и
и с одной регулируемой величиной х. На объект действуют неко-
торые возмущения А,. Далее в изложении используются следующие
формы записи дифференциальных уравнений объекта управления:
нелинейное дифференциальное уравнение п-го порядка
м*<*>. Kj))=u> £'=°' 2' •••>п> 5==1>2' ••• 'S;
' /«О, 1, 2, ...,£в; (1-1)
9
частный случай уравнения (1-1)—линейное дифференциальное
уравнение п-го порядка
п
2 яя_<х(*) =*= и;
система п нелинейных дифференциальных уравнений первого
порядка
Xi=fi(xt, U, и); / = 1, 2,
Требуемое дифференциальное уравнение . замкнутой системы
должно связывать регулируемую величину и задающее воздейст-
вие г|)=г|)(/) и может быть в общем случае нелинейным:
Ф (*<*>, Ф(0, Ct) =0;
1=0, 1, 2, ... ,л,; г = 0, 1, 2, ... , Я,
(1-2)
где С» — параметры настройки.
'В качестве требуемых используются также линейные диффе-
ренциальные уравнения.
Следует указать также на возможность задания этого урав-
нения в форме, при которой сохраняется зависимость регулируе-
мой величины от возмущений:
Ф(х<<>, Ф(0, Си Х<л)=0.
Выбор формы данного уравнения позволяет получить закон
управления, не содержащий сигналов по возмущениям. 1При таком
управлении в ряде случаев
можно уменьшить вероятность
появления больших управляю-
т г щих сигналов, превышающих
<Р | ^ | ^ | л допустимые величины.
Уравнение (1-2), определя-
ющее цель синтеза, выбирается
исходя из требуемых динами-
ческих и статических свойств
замкнутой системы. В после-
дующих главах приводятся
примеры составления требуе-
мых дифференциальных уравнений движения замкнутой автомати-
ческой системы для различных типов решаемых задач. Условия, на-
кладываемые на эти уравнения и уравнения объекта, связаны с воз-
можностью реализации структуры управления и будут ниже рассмо-
трены.
Задачу структурного синтеза системы управления можно сфор-
мулировать следующим образом. Для объекта, описываемого диф-
ференциальным уравнением (1-1), необходимо найти управление
(1-3)
как функцию регулируемой величины, задания и возмущения,
обеспечивающее движение замкнутой системы в соответствии
с требуемым дифференциальным уравнением (1-2). Таким образом,
10
Рис. 1-1.
и = и (*(<>> 'Ф<г>> ЧП> Id)
необходимо синтезировать регулятор, на вход которого посту-
пают данные о/регулируемой величине, задании и действующем на
объект возмущении. Общая схема соответствующей системы
управления представлена на рис. 1-1, где О — объект управления,
У — регулятор (блок управления).
б) Краткий обзор (методов синтеза
Линейные системы. Синтез систем по требуемым дифферен-
циальным уравнениям движения (или по их требуемым переда-
точным функциям) используется для линейных систем уже срав-
нительно давно. Он заключается в выборе требуемой передаточной
функции, удовлетворяющей поставленным техническим требова-
ниям, и в последующем определении параметров элементов, входя-
щих в систему, из условия равенства требуемой и фактической пе-
редаточных функций этой системы.
Расчету параметров автоматических систем по их требуемым
передаточным функциям посвящены работы многих ученых [Л. 4,
34, 35, 43 и др.]. При использовании указанных, методов струк-
турная схема системы регулирования обязательно должна быть
задана. В данной же работе задача синтеза ставится прежде все-
го как задача структурного синтеза. С этой точки зрения следует
отметить работы по синтезу линейных автоматических систем,
в которых определяются требуемые передаточные функции систе-
мы в замкнутом и разомкнутом состояниях, а затем находятся
последовательные и параллельные корректирующие устройства.
Наиболее распространенным является логарифмический метод син-
теза линейных систем автоматического регулирования, который со-
стоит из двух основных этапов:
определения требуемой логарифмической характеристики замк-
нутой системы;
определения передаточных функций корректирующих
устройств.
Задача решается графо-аналитическим способом. Сравнительно
просто определяются передаточные функции последовательных
корректирующих устройств. Для параллельных корректирующих
устройств используются специально разработанные номограммы.
В монографии (Л. 34] задача структурного синтеза делится
на следующие три этапа:
определение требуемой передаточной функции, удовлетворяю-
щей условиям качества регулирования;
энергетический расчет элементов;
определение структурной схемы и параметров проектируемой
системы по требуемой передаточной функции.
На первом этапе из функционально необходимых элементов
составляется структурная схема нескорректированной системы ре-
гулирования и определяется требуемая передаточная функция из
условия удовлетворения необходимому порядку астатизма, мини-
муму среднеквадратичной ошибки, допустимому перерегулирова-
нию, длительности переходного процесса, динамической ошибке и
т. д. Энергетический расчет системы сводится к нахождению тре-
буемой зависимости между скоростью и ускорением управляюще-
го воздействия, исходя из желаемой передаточной функции си-
стемы при заданном входном воздействии. Далее эта зависимость
сравнивается с .аналогичной известной зависимостью применяемо-
го исполнительного устройства (например, двигателя). Задаваясь
11
схемой включения корректирующих устройств (последовательных й
параллельных), находят передаточную функцию скорректирован-
ной системы, а затем, приравнивая желаемую и скорректирован-
ную передаточные функции, определяют вид и параметры пере-
даточных функций корректирующих устройств с учетом их физи-
ческой реализуемости.
Необходимо отметить, что в (Л. 34] подробно рассмотрен во-
прос о выборе требуемых передаточных функций систем с учетом
предъявляемых требований по качеству переходного процесса. Эти
результаты могут быть использованы для составления требуемого
дифференциального уравнения движения замкнутой автоматиче-
ской системы.
Отличительная особенность указанных выше методов струк-
турного синтеза заключается в том, что при их использовании
структурная схема системы, т. е. количество и место включения
корректирующих устройств, вид связей по регулируемым величи-
нам или возмущениям и т. д., предварительно задаются. Опре-
делению подлежат только передаточные функции корректирующих
устройств.
Нелинейные системы. Можно выделить следующие методы
структурного синтеза нелинейных автоматических систем, исполь-
зующих в той или иной форме задание требуемого уравнения дви-
жения и обеспечивающих желаемый переходный процесс при про-
извольных начальных условиях.
iB 1961 г. М. 3. Литвин-Седым и А. Б. Саввиным {Л. 36] был
предложен метод синтеза, который состоит в задании некоторого
конечного уравнения, связывающего фазовые координаты объекта
второго порядка таким образом, чтобы переходный процесс в систе-
ме обладал нужными свойствами. Далее, используя уравнения
динамики объекта, выбирают закон управления, обеспечивающий
требуемое изменение выходной величины объекта.
Данный метод обладает той особенностью, что требуемое
уравнение движения для систем выше второго порядка трудно
найти аналитически. Кроме того, необходима проверка устойчи-
вости движения системы относительно заданного уравнения фазо-
вой траектории, что для нелинейных систем управления представ-
ляет самостоятельную и в большинстве случаев сложную про-
блему.
Следует подчеркнуть, что для синтеза управления необходимо
измерять все фазовые координаты объекта, а закон регулирова-
ния получается зависящим от произвольной в некотором классе
функции. Конкретный вид ее выбирается исходя из определенных
требований к переходному процессу, причем таких функций, во-
обще говоря, существует бесчисленное множество. Произвол в за-
даний этой функции можно использовать для получения наиболее
простых в конструктивном отношении характеристик управляюще-
го устройства.
Американский ученый Г. Ван-Трис (Л. 37] предложил ориги-
нальный метод структурного синтеза систем автоматического
управления нелинейными объектами. Целью синтеза является опре-
деление уравнений корректирующих устройств, соединенных либо
последовательно с объектом управления, либо в цепи отрицатель-
ной обратной связи и выбранных таким образом, чтобы замкнутая
система управления представляла собой оптимальный нелинейный
фильтр задающего сигнала. При использовании этого метода
12
объект описывается обыкновенными нелинейными дифференциаль-
ными уравнениями. Однако корректирующие устройства и желаемое
поведение (движение) замкнутой системы управления описыва-
ются интегральными соотношениями в виде функциональных сте-
пенных рядов (типа Вольтерра). Метод сводится к подстановке
указанных интегральных соотношений в уравнение динамики
объекта. Из полученного выражения определяются ядра инте-
гральных соотношений, характеризующих корректирующее устрой-
ство как функцию ядер интегральных соотношений, которые долж-
ны характеризовать замкнутую систему. Это позволяет найти
уравнения корректирующих устройств. Однако область применения
этого метода ограничена, а для решения задачи используются до-
вольно трудоемкие алгоритмы расчета.
В некоторых случаях для управления нелинейным объектом
можно использовать так называемое обращение объекта. Под об-
ращением объекта управления понимают следующее. Пусть зави-
симость между выходной и входной величинами объекта задана
в виде некоторого дифференциального уравнения, или, в общем
случае, в виде оператора, который в каждый момент времени ста-
вит в соответствие входной величине объекта выходную величину.
Обратным оператором объекта называется устройство, подключе-
ние которого к данному объекту дает коэффициент передачи всей
системы, равный единице. Идея обращения объекта для синтеза
системы управления по заданной передаточной функции системы
также была предложена Г. Ван-Трисом (Л. 37]. По схеме Г. Ван-
Триса обратный оператор объекта включают последовательно
с объектом, а в цепи обратной связи включают обратный оператор
требуемой передаточной функции системы.
Для синтеза многомерных систем управления оригинальный
метод использования обратных операторов объекта предложен
впервые в работах Г. Е. Пухова и К. Д. Жука [Л. 38, 76, 77]. Не-
обходимо подчеркнуть, что этот метод применим, когда объект
имеет устойчивое обращение и не содержит разрывных нелиней-
ностей. Кроме того, точное обращение объекта практически не-
возможно, что связано в первую очередь с трудностью получения
«чистых» производных до п-то порядка включительно. Следова-
тельно, описанная выше схема реализует требуемый оператор си-
стемы только с определенной степенью точности и для определен-
ного класса входных воздействий.
Сравним кратко изложенные выше методы.
С точки зрения исходной информации общей для всех мето-
дов является необходимость знания дифференциального уравнения
объекта. Кроме того, во всех методах задается уравнение, опре-
деляющее требуемое движение автоматической системы. Минималь-
ное число измеряемых производных регулируемой величины рав-
но единице, а при использовании обращения объекта управления
равно п.
1-2. ОБОСНОВАНИЕ МЕТОДА СИНТЕЗА
Пусть в каждый момент времени необходимо знать состояние
объекта п-то порядка с одним управляющим воздействием и од-
ной выходной величиной. Для этого должно быть известно п ве-
личин, однозначно определяющих состояние объекта в любой мо-
мент времени, — его фазовые координаты, которые представляют
13
собой значения выходной (регулируемой) величины объекта и ее
(л—(1) производных:
x№(t)=xM; *=0, 1, 2 л— 1.
Знание фазовых координат объекта еще не позволяет, од-
нако, предсказать движение объекта, т. е. состояние его в после-
дующий момент времени (через бесконечно малый интервал вре-
мени dt). Для знания движения объекта необходимо в общем слу-
чае знать не только фазовые координаты объекта, но и скорости
их изменения. Например, для объекта второго порядка состояние
ь любой момент времени однозначно определяется двумя величи-
нами: выходной величиной объекта и скоростью ее изменения.
Если же надо определить движение объекта, т. е. его состояние
в любой ближайший момент времени, то помимо этих величин
следует знать также скорости их изменения в тот же момент вре-
мени. Таким образом, необходимо дополнительно знать вторую
производную выходной величины объекта.
Отметим существенную особенность скоростей изменения фа-
зовых координат. Дело в том, что из всех этих величин только
скорость изменения фазовой координаты х*71-1), равная — выс-
шей производной регулируемой величины объекта, в любой мо-
мент времени (при любых фиксированных значениях фазовых ко-
ординат и внешних возмущений) зависит явно от управляющего
воздействия, т. е. может быть изменена в нужном направлении,
а скорости изменения остальных фазовых координат i=0, 1,
2, ..., п—il не могут в тот же момент времени зависеть от управ-
ляющего воздействия. Действительно, из уравнения объекта (1-1)
следует:
%\ = X = Xg»
%2 == X === Х%\
Xj == X = #4»
£я = *(»)=*/,(*(<), *У>, и),
где функцию fi получаем, разрешив уравнение (1-1) относитель-
но высшей производной регулируемой величины.
Пусть необходимо задать движение объекта, т. е. задать изме-
нение его выходной величины во времени, что представляет основ-
ную цель управления. IB этом случае, очевидно, надо задавать
в каждый момент времени для определенных значений фазовых
координат скорости их изменения. Но задавать в каждый момент
времени можно только высшую производную регулируемой вели-
чины, ибо только она в данный момент времени явно Зависит от
управления. Задаваемое же значение высшей производной долж-
но при этом обязательно соответствовать требуемому движению,
т. е. требуемой зависимости высшей производной от фазовых ко-
ординат, объекта. Эта зависимость определяется из требуемого
дифференциального уравнения (1-2).
На указанное свойство высшей цроизводной регулируемой ве-
личины объекта было обращено внимание еще Н. Винером [Л. 39].
Первые известные нам применения этого свойства для синтеза не-
линейных систем приведены в работе-Р. Хэддеда [Л. 40] — регуля-
14
тор угла тангажа самолета — и в работе Г. С. Поспелова [Л. 41],
причем в последней рассмотрен общий случай объектов п-го по-
рядка. Поспелов предложил строить замкнутую систему регулиро-
вания по отклонению высшей производной от требуемого значения,
что делает необходимым измерение п производных регулируемой
величины. В этой системе, которая обладает свойствами самона-,
страивающейся, надо обеспечить устойчивость при бесконечно боль-
шом коэффициенте усиления, что не всегда возможно.
Ниже рассмотри другой подход к синтезу, также учитываю-
щий отмеченное свойство высшей производной регулируемой ве-
личины, названное нами свойством управляемости.
Таким образом, для требуемого движения системы в каждый
момент времени должно соблюдаться условие
(О» О-4)
где — требуемое значение высшей производной. Это значение
высшей производной необходимо определять из требуемого урав-
нения движения (1-2), рассматривая его относительно *(п> как ко-
нечное:
4Я> =«&,(*(<>, ФС), Ct). (1-5)
Из условия (1-4) вовсе не следует, что должно выполняться
равенство x(t) =Xd(t). Задание сформулировано не как функция
времени Xd=Xd[t), а как соотношение между регулируемой вели-
чиной и ее производными, т. е. в форме уравнения (1-2).
Чтобы движение системы соответствовало заданному, требуе-
мый закон управления должен иметь, например, вид уравнения
объекта (1-1), в которое вместо высшей производной регулируе-
мой величины подставлено ее требуемое значение
ud=f(x(dn\ *(<), Х</>); /=0, 1, 2, ...,л—1 (1-6)
(при таком законе управления все входящие в него величины
предполагаются измеряемыми). Тогда уравнение замкнутой систе-
мы принимает вид:
К*<«>, xyW(*§°, *<'),
Если все измеряемые переменные рассматривать как пара-
метры, то
/(*<•>) (1-7)
Равенство функций определяет равенство аргументов только
тогда, когда функция, обратная заданной, является однозначной.
В этом случае заданное условие (1-4) выполняется.
Рассмотрим основные условия, накладываемые на левые части
дифференциальных уравнений объекта (1-1) и на требуемое урав-
нение системы (1-2). Из уравнения (1-7) следует, что левая часть
дифференциального уравнения объекта (функция /) должна быть
такой, чтобы высшая производная регулируемой величины была
однозначной функцией управления (в реальных объектах это ус-
ловие обычно соблюдено, так как при определенных начальных
15
условиях, возмущении и управлении, движение одного и того же
объекта вполне определейно и, следовательно, ,при этих условиях
существует только одно значение высшей производной регулируе-
мой величины). Кроме того, с точки зрения реализации управле-
ния (1-6) функция / должна существовать и быть конечной при
всех возможных значениях своих аргументов, в том числе и пос-
ле подстановки требуемого значения высшей производной. (В част-
ности, если уравнение объекта учитывает на входе звено с насы-
щением, то требуемое управление будет содержать обратную
функцию, которая существует не при всех значениях сигнала на
входе этого звена).
Левая часть требуемого дифференциального уравнения систе-
мы (функция Ф) должна быть такой, чтобы решение этого урав-
нения x(t) удовлетворяло необходимым показателям качества ре-
гулирования. Кроме того, функция <Di — решение требуемого урав-
нения относительно высшей производной регулируемой величины
должна существовать и быть конечной при всех возможных зна-
чениях своих аргументов. Это связано с возможностью реализации
управлений (1-6). "Порядок требуемого дифференциального урав-
нения синтезируемой системы должен быть равен порядку объек-
та, т. е. п\—п.
Правило синтеза требуемого управления объектом заключает-
ся в следующем. Для того чтобы найти управление объектом, не-
обходимое для реализации требуемого движения системы, в урав^-
нение объекта следует подставить вместо высшей производной
регулируемой величины ее значение, которое определяется из тре-
буемого дифференциального уравнения системы.
Это правило подразумевает всего две алгебраические опера-
ции, а именно: нахождение требуемого значения высшей произ-
водной регулируемой величины и подстановку его в уравнение
объекта. Относительная несложность этих операций определяет
простоту предлагаемого метода синтеза и, следовательно, возмож-
ность его использования.в инженерной практике.
Управление (1-6) найдено как функция текущих значений фа-
зовых координат объекта, задания и возмущения, т. е. в струк-
турной форме. Величина управления в каждый момент времени
такова, что поддерживает необходимое соотношение между выс-
шей производной выходной величины и координатами объекта и
тем самым реализует определенное дифференциальное уравнение
движения синтезируемой системы управления. Отметим, что уп-
равление (1-6) в любой момент времени определяется через зна-
чения регулируемой величины, задающего воздействия, возмуще-
ния и их производных в тот же момент времени.
Для иллюстрации метода рассмотрим пример синтеза системы
управления.
Пример 1-1. Пусть объект управления, на который действует
возмущение, описывается дифференциальным уравнением второго
порядка
а0х -^-а1х\ = и.
Необходимо синтезировать следящую систему, отрабатываю-
щую некоторое задание я|?(0 устойчиво и с удовлетворительным
качеством регулирования. Решение этой задачи осложняется нали-
чием возмущения, которое входит в уравнение объекта мультипли-
кативно.
16
Потреоуем, чтобы реакция системы на задающее воздействие
была такой же, как в линейной системе второго торядка, диффе-
ренциальное уравнение движения которой имеет вид:'
а2х + агх + (я4 + С) х = Сф.
Свойства такой системы хорошо изучены, в частности вопро-
сы устойчивости и качества регулирования. Из этого уравнения
зс
6У
зп
Рис. 1-2.
находим требуемое значение второй производной выходной вели-
чины объекта
хл ==— [СФ — (д4 + С)х — агх]
и, подставляя его в уравнение объекта, получаем требуемое управ-
ление в виде
а0
ud == — [С (Ф — х) — а^х — а% х] + агх\.
Соответствующая структурная схема системы управления
представлена на рис. 1-2. На этом и последующих рисунках ис-
пользованы обозначения: О — объект управления, р — дифферен-
циатор, 2—сумматор, БУ — блок умножения, ЭС — элемент срав-
нения двух величин, ЭП — элемент суммирования двух величин.
Рис. 1-3.
В синтезированной системе управления требуется измерять
возмущение, действующее на объект, и регулируемую величину,
а также использовать дифференциатор регулируемой величины и
блок умножения. Осциллограммы изменения регулируемой вели-
чины представлены на рис 1-3, где а соответствует апериодичес-
кий 17
кому, а 6 — слабо колебательному процессам. Начальный * участок
осциллограмм 1 соответствует свободному (в данном случае не-
устойчивому) движению объекта. Точка излома кривой соответст-
вует моменту включения блока управления, а последующий учас-
ток 2 — работе замкнутой системы управления.
1-3. ОСНОВНЫЕ СВОЙСТВА СИНТЕЗИРОВАННЫХ СИСТЕМ
И ОБЛАСТЬ ПРИМЕНЕНИЯ МЕТОДА
Так как при использовании предложенного метода синтеза
обеспечивается движение системы согласно задаваемому диффе-
ренциальному уравнению, то путем выбора его вида, в частности
коэффициентов этого уравнения, можно достичь указанных
свойств. Это имеет место, если управляющие воздействия и коор-
динаты объекта не превосходят в процессе регулирования макси-
мально допустимых значений, что проверяется анализом системы
и выбором затем соответствующих значений коэффициентов на-
строек С{.
Применение этого метода обеспечивает инвариантность изме-
нения выходной величины относительно контролируемого возму-
щения. Действительно, если требуемое управление. реализуемо, то
движение системы описывается уравнением (1-2). Так как в это
уравнение рассматриваемое возмущение не входит, то вынужден-
ная составляющая движения от него не зависит [Л. 42].
Использование данного метода целесообразно при сравнитель-
но небольших отклонениях регулируемой величины от уставки, ко-
торая является функцией времени и которую объект отрабаты-
вает без выхода управляющего воздействия на максимум. В этих
случаях часто бывает важно обеспечить качество и устойчивость
регулирования с учетом нелинейной природы объекта управления.
В одном из таких примеров, рассмотренном в гл. 2 (синтез убав-
ления компрессором), показывается, что в случае нелинейного
объекта и переменного во времени задания ' устойчивость и тре-
буемое качество регулирования при использовании данного метода
синтеза достигаются конструктивно более простыми средствами,
чем в применяемых схемах. Данный метод особенно предпочтите-
лен при синтезе систем функционального регулирования, задание
для работы которых есть соотношение между фазовыми координа-
тами объекта
ф (*(«)) =0; /=0; 1, 2, ...,л0; л0<п (1-8)
или в более общем случае — соотношение между выходными вели-
чинами многомерного объекта управления, которое можно запи-
сать в виде
Ф(х*);=0; / = 1, 2,... , т.
Методы структурного синтеза таких систем в теории автома-
тического регулирования разработаны менее всего. Поэтому соз-
дание простого инженерного аппарата синтеза систем функ-
ционального регулироваия, устойчивых и обладающих требуемым
качеством переходного процесса, представляется актуальным.
В гл. 6 показано, что к такого рода системам можно отнести ав-
томатические системы для решения алгебраических и трансцен-
дентных уравнений, системы для поиска экстремума, дифферен-
циальные анализаторы для систем программного управления и др.
18
Отметим, что если требуемое дифференциальное уравнение за-
дано в форме (1-8), то структура управления, естественно, не со-
держит обратной связи по ошибке (регулирования как разности
некоторого задающего воздействия и выходной величины объек-
та. Это связано с тем, что такое задание в уравнении i(l-8) отсут-
ствует. Системы этого типа рассмотрены в гл. 3 и 4.
(Предложенный метод с точки зрения основной идеи синтеза
(задание требуемого уравнения движения системы, уравнения
объекта и определение, исходя из этого, требуемого управления)
примыкает к известным методам синтеза линейных систем,
в- которых используются соответственно понятия передаточных
функций или логарифмических частотных характеристик, и
в частности к обратным методам [Л. 43], а также к рассмотрен-
ным выше методам синтеза нелинейных систем [Л. 37 и 38].
С точки зрения вида получаемой структуры этот метод наи-
более близок к методам, в которых используется обращение
объекта управления. Действительно, если объект управления опи-
сывается, например, уравнением
/ (*(*)) =и\ * =0, 1, 2, ... ,п,
где и — входная величина, a — выходные величины, то в на-
шем случае структура управления определяется с помощью урав-
нения, .аналогичного по форме уравнению объекта, т. е. путем
реализации обратных функциональных зависимостей вида
ud = f (4Л\ *(<));/=0, 1, 2,.
так как здесь иа рассматривается уже как выходная величина,
а —как входные величины. Однако не все выходные вели-
чины объекта, под которыми в данном случае подразумеваются
регулируемая величина и ее дроизводные, являются входными
величинами блока управления. Вместо высшей производной ре-
гулируемой величины формируется сигнал, равный ее требуемо-
му значению. Он и подается в блок управления. Более подроб-
но этот вопрос рассмотрен в гл. 2. Такое обращение дифферен-
циального уравнения объекта назовем неполным обращением
в отличие от полного обращения, присущего методам, рассмот-
ренным в [Л. 37 и 38]. При полном обращении последовательное
соединение объекта и его обратного оператора дает результиру-
ющую передаточную функцию, равную единице (это следует из
определения обратного оператора). При неполном обращении
соединение объекта и блока управления дает результирующую
передаточную функцию, не равную единице. Система в целом
описывается при этом требуемым дифференциальным уравнени-
ем п-то порядка.
Неполное обращение объекта связано также с той особенно-
стью метода, которая состоит в необходимости измерения п—1
производных регулируемой величины, в то время как в методе
обратных операторов требуется измерение п производных. Кро-
ме того, предложенный метод отличается относительной просто-
той использования и возможностью задания широкого класса тре-
буемых дифференциальных уравнений движения системы.
Предложенный метод структурного синтеза нелинейных авто-
матических систем обладает, однако, и определенными ограниче-
ниями, которые следуют из существа метода.
2* 19
Ёо-первых, можно задавать регулируемую величину объекта
управления только в переходном процессе (путем .выбора формы
требуемого дифференциального уравнения). Что касается вели-
чин других переменных процесса, например управляющего воз-
действия, то задание их процедурой синтеза не предусматривает-
ся. Для контроля этих величин необходим анализ синтезирован-
ной системы, в частности" с использованием известных методов
качественного или численного анализа дифференциальных уравне-
ний. Указанное обстоятельство важно в тех случаях, когда для
повышения качества регулирования, особенно для достижения
инвариантности, изменяют коэффициенты требуемого дифферен-
циального уравнения. Это может привести к появлению в систе-
ме недопустимо больших сигналов управления или промежуточ-
ных переменных.
Во-вторых, принятые нелинейные характеристики объекта
управления могут отличаться от действительных, что вызывает
отклонение формы переходного процесса в системе от задавае-
мой. В общем случае при этом может потребоваться анализ по-
лученной нелинейной системы, например, на устойчивость. Для
такого анализа на практике используются главным образом ме-
тоды, основанные на применении функции Ляпунова.
В-третьих, в дифференциальных уравнениях системы могут
быть не учтены малые динамические параметры. Эти параметры,
повышая порядок системы, иногда приводят к неустойчивости.
В таких случаях используют методы анализа нелинейных диффе-
ренциальных уравнений с малыми параметрами при старших
производных.
В-четвертых, для требуемого управления объектом необходи-
мо измерение производных регулируемой величины. В ряде слу-
чаев эти производные соответствуют непосредственно измеряе-
мым физическим параметрам объекта (например, скорости или
ускорению управляемого тела). Однако во многих случаях нуж-
ны специальные дифференцирующие звенья. Точная реализация
их невозможна. Практически включение таких звеньев приводит
к появлению малых динамических параметров, о которых гово-
рилось выше. Таким образом, указанные ограничения могут привести
к дополнительному использованию при проектировании известных
методов анализа.
Глава вторая
СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ДЛЯ ОТРАБОТКИ ЗАДАНИИ, ЯВЛЯЮЩИХСЯ
ФУНКЦИЯМИ ВРЕМЕНИ
2-1. ВЫБОР ТРЕБУЕМОГО ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ СИСТЕМЫ
Основные условия, которым должны удовлетворять требуемые
дифференциальные уравнения системы, сводятся к следующему.
1. Порядок уравнения системы должен быть не меньше поряд-
ка уравнения объекта. Далее рассматривается случай, когда поря-
док системы равен порядку объекта. Как показано в [Л. 34], такое
20
Допущение правомерно, если в схему управления включены так
называемые активные дифференциаторы (Л. 44]. (Активные диффе-
ренциаторы, построенные, например, на операционных усилителях
постоянного тока, имеют передаточную функцию, весьма близкую
в определенном диапазоне частот к передаточной функции идеаль-
ного дифференциатора).
2. Решение должно быть устойчивым. Судить об устойчивости
по виду уравнения наиболее просто для линейных дифференциаль-
ных уравнений, что во многих случаях определяет их использование
в ^качестве требуемых.
3. Инвариантность решения относительно основных возмуще-
ний, действующих на объект. Для этого достаточно, чтобы возму-
щения не входили в рассматриваемое дифференциальное уравнение
[Л. 42}. Тогда вынужденная составляющая решения не зависит от
возмущений.
4. Решение уравнения должно быть таким, чтобы обеспечива-
лось нужное качество регулирования, например, минимум инте-
гральной квадратичной ошибки, заданное перерегулирование и т.д.
Сформулированные условия не исчерпывают всех возможных
требований, предъявляемых к автоматическим системам. Первые
два условия необходимо соблюдать для всех синтезируемых систем.
Соблюдение остальных условий определяется рассматриваемой за-
дачей. Выбор требуемого дифференциального уравнения движения
замкнутой системы, удовлетворяющего сформулированным выше
условиям, можно производить как в классе линейных, так и нели-
нейных дифференциальных уравнений заданного порядка.
Линейные дифференциальные уравнения наиболее изучены,
хотя, конечно, их использование при синтезе не всегда дает наи-
лучшую структуру управления. Для объекта п-то порядка требуе-
мое линейное дифференциальное уравнение движения замкнутой
системы запишем, исходя прежде всего из условий 1 и 2. В общем
случае такое уравнение имеет вид:
п m
Ед.-,х<0=г]2бж-,ф<*>; т<п. (2-1)
/=0 1=0
'Выбором численных значений коэффициентов этого уравнения
можно всегда одновременно удовлетворить и всем остальные выше
условиям, накладываемым на требуемое уравнение движения. Дей-
ствительно, устойчивость системы достигается при удовлетворении
коэффициентов левой части уравнения (2-il) условию Раута-Гурви-
ца; при соответствующем подборе коэффициентов левой и правой
частей этого уравнения получим, как показано в ряде работ по
линейной теории автоматического регулирования, требуемое качест-
во регулирования, а также нужную степень астатизма. Определе-
ние требуемой передаточной функции системы (или линейного
дифференциального уравнения) исследовано в (Л. 34]. Результаты,
полученные в этой работе, можно использовать при выборе требуе-
мого дифференциального уравнения системы.
Рассмотрим один важный частный случай- уравнения (2-1),
когда порядки правой и левой частей уравнения равны и, кроме
того, равны все коэффициенты уравнения при членах одинакового
порядка. Тогда это уравнение можно записать в виде
21
п
Цсл-*<р(*)=0, (2-2)
где Cn_! = an-.t = 6m_<; ?(*) = ф(*) — xi{) — ошибка регулирования
и ее производные,
Системы управления, описываемые этим уравнением, обладают
следующими важными свойствами.
Во-первых, как показано в [Л. 7], решение этого уравнения*
есть экстремаль, т. е. функция, доставляющая минимум определен-
ному критерию качества работы системы. Таким критерием явля-
ется обобщенный интегральный критерий качества
00 п
где Ai — весовые коэффициенты. Обобщенный интегральный кри-
терий примечателен тем, что, минимизируя его, мы запрещаем дли-
тельное существование не только самой ошибки, но и всех ее
производных. При этом характер переходного процесса определя-
ется выбранными значениями весовых коэффициентов.
Во-вторых, из устойчивости решения уравнения (2-2) следует,
что
(оо)=0; /=0, 1, 2, ... , л—1,
т. е. синтезируемая система обладает астатизмом п-то порядка.
В-третьих, так как задающее -воздействие ф(/) не входит явно
в уравнение движения системы (2-2), то рассматриваемые системы
являются инвариантными относительно формы задания. Ивариант-
ность относительно формы задания означает, что переходный про-
цесс не зависит от вида функции а определяется только на-
чальными условиями <p((i,(0), если, конечно, соблюдены общие
условия применимости метода/указанные в гл. 1.
В классе линейных дифференциальных уравнений можно вы-
брать также такие уравнения, решения которых удовлетворяют
заданным ограничениям на фазовые координаты объекта управле-
ния. Этому вопросу посвящены исследования И. А. Опрышко
[Л. 45}.
Нелинейные дифференциальные уравнения описывают дина-
мику систем, обладающих в ряде случаев более высоким качеством
регулирования, чем линейные системы того же порядка. Это отно-
сится, в частности, к системам оптимальным или близким к опти-
мальным по быстродействию. В частности, для повышения быстро-
действия при больших ошибках демпфирование системы следует
уменьшать, а при малых — увеличивать. Одной из первых и отно-
сительно простых автоматических систем с переменным демпфиро-
ванием является система второго порядка, предложенная Дж. Льюи-
сом [Л. 46J. В этой системе сигнал по производной регулируемой
величины уменьшается с увеличением абсолютного значения ошибки
регулирования. Уравнение системы имеет вид:
*Ч(С,-|Ф-*|)х + С,*»Ф(/).
Такая система дает улучшение переходного процесса по срав-
нению с обычной линейной системой, описываемой уравнением
22
того же порядка с постоянными коэффициентами. Однако при
очень больших ошибках коэффициент при первой производной мо-
жет стать отрицательным, поэтому его необходимо ограничивать.
Тем не менее, уравнение этого типа можно применять в качестве
требуемого дифференциального уравнения систем второго порядка.
В общем случае выбор требуемых нелинейных дифференциаль-
ных уравнений представляет сложную задачу. Целесообразно ис-
пользовать для этой цели дифференциальные уравнения разрабо-
танных нелинейных систем соответствующего порядка.
2-2. ОДНОМЕРНЫЕ СИСТЕМЫ
а) Особенности реализации требуемого закона управления
Рассмотрим вначале случай, когда объект управления описы-
вается одним дифференциальным уравнением л-го порядка. Из
формулы (11-6) следует, что необходимо, во-первых, измерять
производные задания регулируемой величины и возмущения и,
во-вторых, осуществить определенные нелинейные преобразования,
определяемые уравнением объекта и требуемым дифференциальным
уравнением.
Для реализации управления (1-6) объектом /1-го порядка
необходимо измерять R^n производных задания, я—1 производ-
ную регулируемой величины и ks^n производных контролируемого
возмущения. Измерение производных выше первого-второго поряд-
ков весьма затруднительно. Строго говоря, точная реализация про-
изводной любого порядка, в том числе и первого, невозможна.
Существуют специально разработанные схемы дифференцирования,
отличающиеся высоким качеством (Л. 34, 44 и др.]. Подчеркнем,
что проблема дифференцирования регулируемых величин является
известной технической проблемой, которая в данной книге не рас-
сматривается. При использовании в каждом конкретном случае
реальных дифференциаторов надо проверять влияние на устойчи-
вость системы малых параметров, которые появляются из-за инер-
ционности устройств дифференцирования [Л. 47]. Интересный
пример в этом отношении приведен в работе Р. Т. Янушевского
[Л. 48], показавшего, что изменение схемы дифференциатора вто-
рого порядка позволяет существенно увеличить область устойчи-
вости системы. Можно, однако, указать примеры управления объек-
тами высокого порядка, когда, например, измерение производных
задания не вызывает затруднений.
Системы стабилизации. \В этом случае вообще не требуется
измерение производных задания, так как оно постоянно.
Программные системы. В этом случае задание всегда известно,
т. е. известны и все его производные как функции времени. На
вход объекта можно подавать новую программу, определяемую
выражением для требуемого значения высшей производной регули-
руемой величины. Если, например, ty(t) входит в это выражение
аддитивно
x(dn) = Ф'2 (*(')) + Ф"г (<ИГ>).
то для программных систем~можно записать:
4я>=ф',(х<«)).+фн(о.
23
гДе Фн (0 = Ф"г (<ИГ)) — новая (измененная) программа. Требуемый
закон управления при этом имеет вид:
«* = f№'i (*<*>) +МО. *<*>. Ч7)Ь
В частности, для линейного требуемого уравнения движения
(2-2) необходимое значение высшей производной в случае про-
граммных систем
An)
Cn-iX(«),
(2-3)
где
i=0
п-\
i=0
*ф<*)
— новая программа. Такой прием используется в линейных систе-
мах программного управления [Л. 49}.
Следящие системы, если известен характер изменения задаю-
щего воздействия. Пусть, например, задание изменяется во времени
линейно
причем величина <х неизвестна. Очевидно, что достаточно ограни-
читься измерением задания и максимумом только его первой произ-
водной, так как производные более высоких порядков равны нулю.
—I Lr—I
о1
От
1
х1 ~*
Рис. 2-1.
Иногда единственно возможным способом измерения производ-
ных регулируемой величины и возмущения является косвенный
(дифференциальный) метод измерения, основанный на сравнении
входных и выходных величин какого-либо звена объекта или
объекта в целом [Л. 7, 50, 51]. Пусть объект управления имеет вид
последовательно соединенных звеньев 04—От («цепочная» струк-
тура), у которых измеряются все входные и выходные величины
(рис. 2-1). Каждое звено объекта описывается в общем случае
нелинейным дифференциальным уравнением порядка v&:
*fc) = *fc-,; *=0, l,...,vft, (2-4)
где Xh и Xk-i — выходная и входная величины звена; А* — возму-
щение, действующее на входе звена.
Из уравнения (2-4) можно выразить Vft-ю производную выход-
ной величины каждого звена
24
Таким образом, измеряя входные величины, выходную величину
и ее (vA — 1) производных, а также возмущение, определяем произ-
(у )
водную xkh . При этом максимальный порядок измеряемой произвол.
ной не выше наибольшего из порядков звеньев минус единица.
В *гом случае, когда требуется косвенное измерение возмущения,
необходимо измерение Vk производных выходной величины звена.
Действительно, из уравнения '(2-4) получаем:
Следовательно, измеряя входную и выходную величины звеньев
объекта и их производные, можно определить все требуемые зна-
чения производных регулируемой величины, а также возмущения,
и затем преобразовать их в соответствии с законом управле-
ния (1-6). Это приводит к построению многоконтурной системы
управления, причем контуры образованы соответствующими свя-
зями по входным и выходным величинам звеньев.
Пример 2-1. Пусть объект управления состоит из двух после-
довательно соединенных звеньев. Пусть динамика этих звеньев
описывается следующей системой дифференциальных уравнений:
: (2-5)
а0х + ахх + а2х = хг
или одним дифференциальным уравнением третьего порядка
(а^х +агх + а2х )1/3 =и.
Требуемое уравнение движения системы представим в виде
С0х*+ dx + С2 х + Сгх = Ф (t),
где ty(t)—задающее воздействие. Из последнего уравнения опре-
делим требуемое значение высшей производной 'регулируемой
величины
"xd = J- (Ф — С ii — С2 х — Сгх).
Тогда требуемое управление можно представить в виде
/ а0 , .. . \1/з
ud = [ -^г-ф + тхх + т2х — т3х\ »
где
а0Сг a0Ci а0С3
ml==al — -jT- ; т2 = я2 — —jft- ; тг = -77- •
Для формирования такого закона управления необходимо из-
мерение первых двух производных регулируемой величины. Однако
в данном случае достаточно измерения только первой производной,
ибо вторая производная, как следует из выражения (2-5), равна:
^ = T-(*i — ахх— а2х),
и0
25
f. е. Может быть определена путем измерения величины х и ее
первой производной, а также измерения величины х\. Тогда тре-
буемое управление можно представить в виде
ud = ( -gr- Ф + — Хг + т\ х — т'гх
где
т\ = m2 — m1-^L, т'г = т1+ т1
"о ао
Соответствующая структура управления представлена на
рис. 2-2.
Нелинейные преобразования, необходимые для реализации
требуемого закона управления, зависят в общем случае от вида
как уравнения объекта, так и требуемого уравнения системы.
?
г
- о,
- Р
Рис. 2-2.
Рассмотрим в первую очередь нелинейности, связанные с урав-
нением объекта. Запишем это уравнение таким образом, чтобы
выделить явно функциональную зависимость между управляющим
воздействием и высшей производной регулируемой величины:
ft (*<">) fi (*<«>. ЧП) + h (*<*>> ЦП) = «. (2-6)
Хотя такая "запись и не исчерпывает всех возможных форм
нелинейного уравнения объекта (1-1), но она является достаточно
общей. Структура объекта О, соответствующая приведенному урав-
нению, представлена на рис. 2-3 и содержит: в прямой цепи — де-
лительное устройство, нелинейный преобразователь, реализующий
функцию, обратную той, под знаком которой находится в уравнении
объекта высшая производная регулируемой величины; в цепях
обратной связи — нелинейные преобразователи, реализующие функ-
ции f2 и .соответственно, устройство сравнения и интеграторы.
Управление этим объектом согласно выражению (1-6) имеет
вид:
«*=h (4п)) и (*<*>> Кп)+и (*<*•>> Чп). (2-7)
На рис. 2-3 представлена также структура регулятора, соответ-
ствующая этому уравнению. В блоке управления необходимы:
нелинейные преобразователи НПх и НП2, реализующие функции,
26
обратные тем, которые находятся в прямой цепи объекта; нелиней-
ные преобразователи ЯЯ4 и НП5, реализующие функции, анало-
гичные тем, которые содержатся в цепи обратной связи объекта;
^ мп. мп, мп, Г"
? ,—i ,—I
мп^
мл*
"Л
Рис. 2-3.
нелинейный преобразователь НП3, реализующий функцию, опреде-
ляемую видом выражения для требуемого значения высшей про-
изводной, которое зависит только от типа поставленной задачи;
сумматор (соответственно элементу сравнения в прямой цепи
объекта).
б) Управление объектами, описываемыми системой
дифференциальных уравнений первого порядка
Широкий класс объектов управления удобно описывать систе-
мой дифференциальных уравнений первого порядка (форма Коши)
где Xj — выходная координата объекта, Xj — возмущение, щ —
управляющее воздействие, которое входит в общем случае не
в одно, а в несколько уравнений. Для любой из координат может
быть указано задание tyj(t). Необходимо найти структуру управле-
ния, которое позволяет отработать задание при соблюдении опре-
деленных условий ^устойчивость, качество и т. д.). Поскольку
принципиально методика синтеза остается прежней, то дальнейшее
изложение удобно провести на примере.
Пример 2-2. Пусть объект управления описывается следующей
системой дифференциальных уравнений:
= х| + х, + X; }
х, = м. ]
Необходимо, чтобы выходная координата Xi следовала неко-
торому заданию tpi(/).
27
Составим дифференциальное уравнение интересующей нас си-
стемы (вход — управление, выход — координата Xi). Для этого
продифференцируем первое из уравнений системы (2-8):
Xi = 2х2х2 -Ь Хз + А^
С учетом выражений для х2 и хг получаем:
xl = 2xlx2 + u + \l- (2-9)
В это уравнение входят регулируемая величина *i (до второго
порядка включительно), другие выходные координаты, возмущение,
а также управляющее воздействие объекта. Требуемое дифферен-
циальное уравнение движения системы должно быть уравнением
второго порядка, например
а0Хг + аххх + я2*1 = M»i-
Отсюда находится требуемое значение высшей производной:
Требуемое управление найдем путем подстановки этого выра-
жения в уравнение (2-9):
ud = -^~ (62Ф1 — axix — а2хх) — 2ххх2 — X,.
Схема управления для данного примера представлена
на рис. 2-4.
в) Нелинейные инвариантные системы
Приведенная на рис. 2-3 схема управления позволяет опреде-
лить также необходимые связи по возмущениям для инвариант-
ности регулируемой величины. Как уже отмечалось, в этом случае
достаточно, чтобы требуемое уравнение системы не содержало
возмущений. Из уравнений (2-6) и (2-7) следует, что если возму-
X
Рис. 2-4.
щение входит в уравнение объекта нелинейно и мультипликативно,
то в схеме управления должны быть соответствующие блоки
умножения и нелинейные преобразователи. Если же возмущение
входит в уравнение объекта нелинейно и аддитивно, то в структуре
управления должны быть осуществлены соответствующие нелиней-
ные преобразования со знаком минус.
28
Известные методы синтеза связи по возмущению сводятся
в основном либо к созданию в контуре этой связи оператора,
обратного оператору объекта до места входа возмущения [Л. 52],
либо, если возмущение действует на объект через некоторый не-
линейный оператор, — к нелинейному оператору такого же вида
![Л. 53]. Предлагаемый метод позволяет получить не только такие
же структуры связи по возмущению, но и принципиально другие —
для широкого класса задач управления, определяемых видом тре-
буемого уравнения движения, и для довольно общей формы записи
уравнений объектов.
2-3. СИСТЕМА УПРАВЛЕНИЯ СКОРОСТЬЮ ВРАЩЕНИЯ
КОМПРЕССОРА
Рассмотрим синтез системы управления скоростью вращения
компрессора, установленного на корабле и предназначенного для
подачи воздуха в топку. Объект управления описывается нелиней-
ным дифференциальным уравнением. Хотя порядок этого уравне-
ния невысок (первый), тем не менее из-за его нелинейности полу-
чить удовлетворительное качество переходного процесса технически
достаточно сложно.
Известная схема решения этой задачи [Л. 54] сводится к синте-
зу самонастраивающейся системы управления. iB зависимости от
режима горения для изменения расхода воздуха скорость нужно
изменять. Б общем случае программа изменения скорости враще-
ния компрессора может быть любой. Таким образом, речь идет
о системе с переменным во времени заданием, и, следовательно,
линеаризация нелинейного уравнения объекта приводит к расчет-
ной системе с переменными параметрами ((коэффициентами линеа-
ризации).
Для получения устойчивой системы с нужным качеством регу-
лирования Бенхем и Смит [Л. 54] предложили следующий закон
управления объектом со связями по ошибке регулирования и ее
интегралу, коэффициенты которых переменны (зависят от величины
ошибки) :
t t
u^ktf + h^ ffdt + кг (у) ? + £4 (<р) ^ ffdt.
6 6
Зависимости коэффициентов от ошибки подбираются экспери-
ментально и эффективны только для одного конкретного вида
задания, например линейного изменения скорости.
Ту же задачу регулирования решим с использованием предло-
женного метода синтеза.
Дифференциальное уравнение объекта получаем из, условия
равновесия моментов на валу компрессора
J^=M-Me, (2-10)
где / — момент инерции вращающихся масс;
со — скорость;
ЛГ— вращающий момент паровой турбины, сочлененной с ком-
прессором;
Мс — момент сопротивления (аэродинамический).
29
Вращающий момент турбины
Q
М:
^(AW-m.-^} (2-Н)
где Q — расход пара, Qmekc, ©макс — максимальные значения рас-
хода пара и скорости ©ращения соответственно. Относительное
значение расхода пара равно:
5^--F(e). (2-12)
^макс
Здесь и — перемещение управляющего органа (клапана), ха-
рактеристика которого F задается.
Момент сопротивления компрессора
м*-9* (-£—)** <2-13>
\ адмакс /
где рс — коэффициент аэродинамического сопротивления системы,
который будем считать постоянным.
При совместном решении уравнений (2-10) —(2-13) получаем
нелинейное дифференциальное уравнение объекта первого порядка:
dco / со \ / со \2
^=H«)(^.c-4—)• (2-14)
Необходимо найти такой закон управления, т. е. зависимость
и от регулируемой величины со и задания со3(0. чтобы процесс
Рис. 2-5.
регулирования был устойчивым и с приемлемым качеством. Пусть
величина со изменяется в соответствии с линейным дифференциаль-
ным уравнением первого порядка:
где
9 + =0,
<р =С08 — со.
(2-15)
Решение этого уравнения при С>0 устойчиво и имеет одина-
ковый вид для различных законов изменения задающего воздей-
ствия. Для определения требуемого управляющего воздействия най-
30
дем из уравнения (2-15) значение высшей производной регулируе-
мой величины:
<Dd = С03 + С ((0, — СО).
Подставив его в уравнение объекта (2-14), получаем:
/ [С0з + С (СО, - »)K+" ) 2
AfMtKC — m0
"'макс
Соответствующая структура системы управления представлена
на рис. 2-5. Она содержит три нелинейных элемента (квадратор,
блок деления и функциональный преобразователь с характеристи-
кой, обратной характеристике исполнительного органа), два эле-
мента сравнения, сумматор, масштабный блок (например, потен-
Риг. 2-6.
циометр П) и дифференциатор задающего воздействия. Эта струк-
тура не изменяется в процессе .работы и позволяет получить оди-
наковое качество регулирования для различных форм задающего
воздействия. В этом ее принципиальное отличие от схемы Бенхе-
ма и Смита.
Синтезированная система была экспериментально проверена на
электронной моделирующей установке МНБ-.1. Эта установка опи-
сана, например, в [Л. 78]. На осциллолраммах (рис. 2-6) приведе-
но изменение в процессе управления задающего воздействия /,
регулируемой величины 2 и ошибки регулирования 5. Осцилло-
граммы на рис. Й-6,а соответствуют случаю треугольного задания,
а на рис. 2-6,6 — синусоидального. В обоих случаях изменение
ошибки регулирования одинаково.
2-4. МНОГОМЕРНЫЕ СИСТЕМЫ
IB практике автоматизации технологических процессов .встреча-
ются сложные объекты управления, режим работы которых опре-
деляется не одной, а несколькими взаимосвязанными величинами
Такие объекты и соответственно системы управления ими принято
называть многомерными. Каждая из регулируемых величин долж-
31
на в этом случае поддерживаться (или следовать заданию) с вы-
сокой точностью. Автоматизация подобных процессов представляет
значительные трудности и может быть успешной лишь при усло-
вии применения схем связанного регулирования, где регуляторы
отдельных величин взаимодействуют между собой .вне технологи-
ческого процесса. Следовательно, на первый план ib многомерных
системах выдвигается задача структурного синтеза, т. е. опреде-
ление связей по регулируемым величинам, заданиям и возмуще-
ниям, действующим на объект [Л. 38 и 5'5].
Решим задачу структурного синтеза многомерных нелинейных
систем предложенным методом.
(Пусть имеется объект управления с nti регулируемыми вели-
чинами Xj и mi управляющими воздействиями «j, причем на объ-
ект действуют возмущения Xs. Каждая регулируемая величина Xj
в общем случае может изменяться под действием не только соот-
ветствующего управления Uj и возмущений Я«, но и других управ-
лений щ и регулируемых величин Хь Воздействия типа Xs на-
зовем собственными, а воздействия типа щ, xi — взаимными. Раз-
деление воздействий на собственные и взаимные в достаточной
мере условно и в каждом конкретном случае определяется осо-
бенностями .'рассматриваемого технологического процесса. Под соб-
ственным управляющим воздействием понимается, по крайней мере,
одно из тех управляющих воздействий, фигурирующих в диффе-
ренциальном уравнении движения данной регулируемой величины,
порядок которых не выше нулевого.
Рассмотрим случай, когда число управляющих воздействий
равно числу регулируемых величин (mi=i/n2=m). Пусть для каж-
дой регулируемой величины задано дифференциальное уравнение
порядка я,-, связывающее эту регулируемую величину и все соб-
ственные и взаимные воздействия:
) = 1, 2, ... , т\ I = 1, 2, ... , т\ i = 0, 1, 2, ... , щ\ I (2-16)
и = 0, 1, 2, ... , У,; 5 = 1, 2, ... ,m; р = 0, 1, 2, ... , Pt\ |
<7=0, 1, 2,... ,т. )
Пусть, кроме того, для каждой регулируемой величины зада-
но ее желаемое изменение во времени:
Цель исследования — найти такое управление Uj как функцию
регулируемых величин, всех взаимных воздействий, влияющих на
эту величину, возмущения и соответствующего задания, которое
обеспечивает нужный характер переходного процесса. Потребуем,
чтобы* изменение каждой регулируемой величины во времени опи-
сывалось нелинейным дифференциальным уравнением порядка tij
ФИ*}°. Ф}г). С«)=0; г = 0, 1, 2, (2-17)
где Сц — коэффициенты настройки.
'Использование этого уравнения при синтезе приводит к тому,
что во-первых, качество регулирования зависит только от коэф-
фициентов настройки; во-вторых, изменение любой регулируемой
32
величины во времени не зависит от всех взаимных воздействий й
возмущений. Следовательно, синтезируемая многомерная автома-
тическая система инвариантна относительно возмущений и авто-
номна как по регулируемым величинам, так и по управлению.
Такая постановка задачи является наиболее общей, ибо в этом
случае полностью развязываются все регулируемые величины.
Основная идея метода структурного синтеза многомерных авто-
матических систем такова же, как и для одномерных систем.
'Пусть для многомерного объекта управления, у которого ди-
намика каждой регулируемой величины описывается уравнением
(2-.16), в любой момент времени известны, т. е. измеряемы, регу-
лируемая величина Xj и ее (п$—1) производные, возмущения и их
производные, а также взаимные воздействия и их производные.
Из уравнения (2-17) находим требуемое значение rtj-й производ-
ной регулируемой величины:
ffl-Ourfh Ф}'>).
Подставляя это выражение вместо высшей производной в урав-
нение (2-16), найдем требуемый закон управления:
• *}"• «}Р). АЧ)). (2-18)
Система управления является комбинированной, т. е. со свя-
зями как по регулируемым величинам, так и по заданиям и воз-
мущениям. Если в уравнение (2-16) входит высшая производная
взаимной регулируемой величины хи 1Ф\\, то ее надо рассматри-
вать как возмущение, которое также следует измерять. Процедура
синтеза при этом принципиально не меняется.
Что касается реализации закона управления (2-18), то, как и
в случае одномерных систем, основные проблемы сводятся к изме-
рению производных и взаимных воздействий и к реализации тре-
буемых нелинейных преобразований. Основные свойства синтези-
рованной системы управления с точки зрения динамики каждой
регулируемой величины такие же, как и для одномерных систем,
ибо достигается их автономность.
Для иллюстрации метода рассмотрим синтез структуры управ-
ления движением тела в плоскости.
2-5. СИСТЕМА УПРАВЛЕНИЯ ДВИЖЕНИЕМ ТЕЛА
Дифференциальные уравнения движения центра масс тела
в плоскости:
m* + dxx + fx=ux; (2-19)
my + dvy + fy^uyt (2-20)
где xt # — геометрические координаты тела; /п —масса; dXi dv —
коэффициенты составляющих силы, зависящей от скорости движе-
ния тела (например, силы сопротивления); /ж, fv — составляющие
3—10
33
внешних (в частности, нёупраЁляемых) сил, действующих на тело
и зависящих от его координат или времени (например, силы при-
тяжения планет, возмущающие силы и т. д.); их, иу — управляю-
щие силы. В общем случае коэффициенты сопротивления и состав-
ляющие внешних сил являются нелинейными функциями координат
тела и скоростей их изменения. Масса тела в общем случае также
является переменной величиной (например, при движении ib воз-
духе — в связи с расходом топлива, а при движении в воде —
в силу эффекта присоединения массы). Указанные зависимости
в ряде случаев известны или могут быть определены в процессе
управления.
Задающие воздействия суть известные функции времени:
У=Ув (t),
что соответствует регулированию скорости и координаты тела, на-
пример высоты.
Ошибки выполнения этих заданий:
ф1 = у3—v\ (2-21)
4>2 = у3-у. (2-22)
Рассмотрим выбор требуемых дифференциальных уравнений
для изменения ошибок во времени. Порядок этих уравнений дол-
жен быть равен порядку той производной ошибки, которая в лю-
бой момент времени явно зависит от управляющих воздействий.
Порядок уравнения (2-21) относительно ошибки равен единице,
так как ее первая производная явно зависит от управляющих
воздействий:
У
V у /
= Ft(ux, у, х, иуу х, у, t). (2-23)
Аналогично относительно ошибки (2-20) порядок требуемого
дифференциального уравнения должен быть равен двум, ибо ее
вторая производная равна:
Ъ = Уз— !/'= Ft ("у> х, У, х, у, t). (2-24)
Вид требуемых дифференциальных уравнений выберем линейным:
fi + Cf!=r0; (2-25)
Ъ+СгЪ+С2ъ=0, (2-26)
34
где Си С2, С — коэффициенты настройки. Решения этих уравне-
ний устойчивы относительно заданий, а качество переходного про-
цесса определяется коэффициентами настройки при любой форме
заданий.
Требуемые значения высших производных регулируемых вели*
чин определяем из уравнений (2-23)—- (2-26):
Ул^Уь + Сх <р2 +С2<р2.
'Подставив эти выражения в уравнения динамики объекта
(2-19) и (2-20), получаем систему двух алгебраических уравнений
для расчета требуемых значений управляющих воздействий как
функций фазовых координат объекта и программ:
axd = mxd + dxi + fx; (2-27)
uyd = myd + dy'y + fy. (2-28)
Реализация этого управления приводит к необходимости из-
мерения всех фазовых координат объекта, знания нелинейных за-
висимостей коэффициентов уравнения динамики, а также измере-
ния первой производной задания по скорости, первой и второй
производных задания по координате тела.
Измерение производных задания обусловлено выбранной фор-
мой требуемых дифференциальных уравнений. Однако если взять
их, например, в виде
v + Cv=*bxv9 (0;
У + Сху + С2у = b2y3 (О,
то измерения этих производных не потребуется, но качество пере-
ходных -процессов регулируемых величин будет зависеть от формы
заданий.
Закон управления в этом случае также имеет вид выражений
(2-27) и (2-28), однако требуемые значения высших производных
принимают вид:
v (Ms (t) — Cv)—y'yd.
*d= -х .
Уй = Ь2Ув (0 — С, у — С2у.
Соответствующая структурная схема системы управления пред-
ставлена на рис. 2-7, где обозначено: О — объект управления; dx,
dy, fx, fy — нелинейные преобразователи.
Основное достоинство синтезированной структуры управления
заключается в том, что она позволяет достичь требуемого каче-
3* 35
ства регулирования по каждой регулируемой величине для широ-
кого класса нелинейных функций, входящих в уравнение объекта,
не прибегая к их линеаризации.
Рис. 2-7.
Отметим, что синтез предложенным методом системы управ-
ления движением тела (летательного аппарата) для более общего
случая (движение в пространстве) проведен А. А. Тимченко
[Л. 31 и 32].
Глава третья
ОДНОСВЯЗНЫЕ СИСТЕМЫ
ФУНКЦИОНАЛЬНОГО РЕГУЛИРОВАНИЯ
3-1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Во многих задачах управления необходимо отрабатывать за-
дания, представленные не в функции времени, а в виде уравнений,
связывающих выходные величины объекта, например: управление
электроприводом шахтного подъема, когда необходимо соблюдать
определенное соотношение между положением груза и скоростью
его перемещения; поддержание функционального соотношения меж-
ду скоростями секционных моторов в многодвигательном приводе
[Л. 56]; управление мощностью в системе первичный двигатель —
генератор — электрический двигатель по соотношению величин тока
и напряжения (Л. 38]; управление движением тела по траектории
[Л. 3]; программное управление станками [Л. 57] и т. д.
При решении подобных задач соотношения между перемен-
ными обычно преобразуют в соответствующие программы как
функции времени (например, с помощью дифференциальных ана-
лизаторов), а затем синтезируют следящие системы для отработ-
36
ки этих программ. Однако этот метод синтеза имеет существенные
недостатки (Л. 58]. В данной работе синтез структур управления
такими системами производится без преобразования заданий в про-
граммные зависимости.
Классификация рассматриваемых систем проведена, исходя из
количества поддерживаемых соотношений между выходными ве-
личинами объекта (уравнений связи) и их структурного вида.
С точки зрения количества уравнений связи разделим эти системы
на два основных класса:
системы управления для отработки только одного соотноше-
ния между выходными величинами объекта (односвяэные систе-
мы) ;
системы управления для отработки более одного соотношения
между выходными величинами одного или нескольких объектов
(многосвязные системы).
Так как число поддерживаемых соотношений должно быть не
меньше числа управляющих воздействий, то, очевидно, в послед-
нем случае речь идет об объектах с несколькими управляющими
воздействиями.
Указанные системы можно также классифицировать с точки
зрения вида регулируемых соотношений. Если в уравнение связи
входит высшая, п-я производная выходной величины, то такие
системы назовем системами с полным заданием; если же в урав-
нение связи она не* входит, то такие системы назовем системами
с неполным заданием. Это деление является существенным, ибо
оно, как будет показано ниже, определяет способ синтеза струк-
туры управления.
Определение систем с полным и неполным заданием произве-
дено в предположении, что объект управления описывается одним
дифференциальным уравнением. В ряде приложений, однако, пред-
почтительным является описание объекта системой дифференци-
альных уравнений первого порядка. Применительно к этому слу-
чаю системами с полным заданием назовем такие системы, в урав-
нения связи которых не входит производная координаты, явно
зависящей от управления.
3-2. СИСТЕМЫ С ПОЛНЫМ ЗАДАНИЕМ
Объект управления описывается нелинейным дифференциаль-
ным уравнением л-го порядка, например, вида (1-1). Необходимо
выдержать следующее соотношение между фазовыми координа-
тами объекта
ф(х(<))=0; /=0, 1, 2, (3-1)
которое представляет полное задание, ибо оно включает высшую
производную регулируемой величины. В этом случае выражение
(3-1) рассматриваем как требуемое дифференциальное уравнение
замкнутой системы, порядок которого равен порядку объекта.
Принцип синтеза управления остается прежним, а именно — из
уравнения (3-1) находим требуемое значение высшей производной
регулируемой величины, подставляем его в уравнение объекта
(1-.1) и получаем требуемое управление.
Рассмотрим теперь объект управления, описываемый системой
дифференциальных уравнений первого порядка, причем потребуем,
37
чтобы управляющее воздействие явно рходилд только б ОДНО из
дифференциальных уравнений объекта:
fii**Ui*v М. /■*•!• 2' ...,я—1; (3*2)
Необходимо выдержать следующее соотношение между фазо-
выми координатами объекта:
ф(х,, i,)«0; (3-4)
/ = 1, 2, ... ,я,
которое также представляет полное задание.
При любых фиксированных значениях фазовых координат дви-
жение объекта определяется значениями их производных (3-2) и
(3-3). Из них только производная координаты, явно зависящая
от управления, может быть в любой момент времени изменена
с помощью управления в нужную сторону. Если выдержать усло-
вие
*« (0 =*пЛ0>
где xnd находится из заданного соотношения (3-4) и равно:
*nd = ®i (*j> (3"5)
то движение системы соответствует требуемому. Для этого управ-
ление находят подстановкой выражения (3-5) в уравнение (3-3).
С учетом этого получаем уравнение
fn{*1> К* а) =$i(**>
из которого находим:
ud = ud (х^ Xj, ln); j = 1, 2, ... , n — 1,
или, используя уравнения (3-2),
ud = ud(Xj, Xj, Xn)\ j = 1, 2, ... , n— 1.
Итак, управление, требуемое для поддержания соотношения
(3-4), есть функция всех координат объекта и действующих на
него возмущений. Вид этой функции определяется уравнениями
объекта и заданным уравнением связи.
Рассмотрим конкретный пример синтеза односвязной системы
с полным заданием.
3-3. СИНТЕЗ СТРУКТУРЫ ГЕНЕРАТОРА СИНУСОИДАЛЬНЫХ
КОЛЕБАНИИ
Генератор синусоидальных колебаний можно представить как
автоматическую систему, поддерживающую заданный автоколеба-
тельный режим, т. е. заданное соотношение между выходной ве-
личиной й скоростью ее изменения.
38
Пусть необходимо генерировать синусоидальные колебания
с частотой со и амплитудой А:
х—А sin со/.
Уравнение связи, выражающее зависимость между величиной х
и скоростью ее изменения,
х2
Ф (х, х) = х2 + — — Л2 = 0. (3-6)
Объектом управления является интегратор
а1х = и, (3-7)
где ui — коэффициент пропорциональности.
Для того чтобы синтезировать управление, реализующее дви-
жение объекта соответственно уравнению связи (3-6), найдем из
(3-6) требуемое значение высшей производной и подставим в урав-
нение объекта (3-7):
ud = ах<й / А2 — х2 sign х.
По модулю такое управление изменяется в пределах от нуля
(при х—А) до своего максимального значения а^А (при х=0).
После прохождения через нуль величины х знак управления дол-
жен измениться на противоположный. Однако состояние рассма-
триваемой системы первого порядка при х=0 является устойчи-
вым и, таким образом, выходная величина интегратора остается
в дальнейшем неизменной. Во избежание «застревания» системы
переключение знака управления надо производить при приближе-
нии х к нулевому значению. Этого можно достичь, если пере-
ключать знак с помощью сигнум-реле, на вход которого подана
разность х—а0х, где ао — величина, намного меньшая единицы.
Тогда требуемое управление принимает вид:
ad = я,<0 VA2 — х2 sign ( х — а0х). (3-8)
При таком управлении выходная величина интегратора изме-
няется не точно по синусоидальному закону. Но чем меньше время
срабатывания сигнум-реле и, следовательно, чем меньше величина
ао, тем ближе кривая выходной величины интегратора к требуе-
мой. С увеличением длительности периода колебаний величина ко-
эффициента а0 и время переключения сигнум-реле все меньше ска-
зываются на их форме. Это обстоятельство определяет наиболее
предпочтительную область применения рассматриваемого типа ге-
нератора, а именно — низкие и инфранизкие частоты.
Структурная схема генератора приведена на рис. 3-1. С выхода
интегратора сигнал подается на вход нелинейного преобразователя,
реализующего зависимость ^ А2— х2. Его выходная величина изме-
няется с помощью блока Пи имеющего переменный передаточный
коэффициент (например, потенциометр). Знак сигнала, снимаемого
с этого блока, переключает сигнум-реле. Последнее можно собрать
в виде схемы, состоящей из поляризованного реле Р и инвертора.
Контакты этого реле Pi и Р2 подают выходной сигнал блока Fli
либо непосредственно на вход интегратора, если входной сигнал
39
реле положителен, либо через инвертор, если входной сигнал .реле
отрицателен. На вход реле — через блок Я2, имеющий передаточ-
ный коэффициент -do (например, потенциометр), подают разность
входной величины интегратора и его выходной величины.
Блок Пх является задатчиком частоты колебаний, а блок Я2
служит для настройки формы колебаний.
7 «i
Рис. 3-1.
Схема генератора проверялась экспериментально. На осцилло-
грамме (рис. 3-2) приведена кривая У выходного напряжения ге-
нератора, соответствующая частоте 0,15 гц. Для контроля пра-
вильности формы полученной синусоиды на этой же осциллограм-
ме приведена кривая 2 входного сигнала интегратора, представ-
ляющая ее производную. Эта кривая имеет излом вблизи . нуле-
Рис. 3-2.
вого значения, но в остальной части достаточно близка к косину-
соиде. Указанный излом кривой входного сигнала и уплощение
кривой выходного сигнала в тот же момент времени определяется
переключением реле.
Указанный способ генерирования синусоидальных колебаний
обладает определенными преимуществами но сравнению с извест-
ными, оонованными на использовании автоколебательных систем
не ниже второго порядка. Одной из наиболее распространенных
и типичных схем генератора синусоидальных колебаний инфраниз-
кой частоты является схема на двух интеграторах, охватываемых
внешней отрицательной и внутренней нелинейной положительной
обратными связями {Л. 59]. Такая схема обладает, однако, сле-
дующими недостатками.
40
Во-первых, для возникновения автоколебаний коэффициент
усиления разомкнутой системы должен быть достаточно большим
на всех частотах. Этим ограничивается нижний предел изменения
частоты, так как для уменьшения частоты надо уменьшать коэф-
фициент усиления.
iBo-вторых, требуется не менее двух инерционных элементов
(интеграторов).
В-третьих, на очень низких частотах при изменении частоты
процесс установления амплитуды колебаний длится долго.
'Принципиальные особенности синтезированного генератора за-
ключаются в следующем:
возникновение колебаний не зависит от величины передаточ.-
ного коэффициента at разомкнутой системы, так как он не входит
в уравнение (3-6) замкнутой системы;
для генерирования колебаний достаточно иметь только один
инерционный«элемент (интегратор), ибо синтезируемая система —
система первого порядка, а дополнительный фазовый сдвиг на 90°
создается нелинейным преобразователем;
изменение частоты колебаний производится с помощью только
одного настроечного элемента (потенциометра), причем без пере-
ходного процесса, если не считать времени перемещения движка по-
тенциометра. Последнее обстоятельство связано с тем, что при
изменении напряжения на выходе этого потенциометра в схеме
сразу же устанавливается такое соотношение между выходным
сигналом и скоростью его изменения, которое соответствует соот-
ношению (3-6);
нижний предел генерируемой частоты может быть сведен до
нуля, так как система поддерживает соотношение (3-6) для любой
задаваемой частоты. С уменьшением задаваемой частоты форма
колебаний улучшается,. ибо меньше сказывается влияние времени
срабатывания сигнум-реле;
верхний предел, генерируемой частоты определяется, в частно-
сти, временем срабатывания сигнум-реле, которое должно быть на
порядок меньше периода задаваемых колебаний, в противном слу-
чае их форма ухудшается.
Пусть требуется определить структуру управления объектом,
описываемым одним дифференциальным уравнением, необходимую
для поддержания следующего соотношения между выходной ве-
личиной объекта и ее производными:
Это уравнение представляет неполное задание, ибо оно не
включает высшую производную регулируемой величины.
Основной принцип синтеза заключается в том, что вместо не-
полного задания рассматривается другое, полное задание, связан-
ное с первым аналитически. Этот принцип назван нами принципом
дополнения. Зная уравнения объекта и полное задание, затем на-
ходим требуемую структуру управления.
Новое задание целесообразно связать с исходным (3-9), рас-
сматривая ошибку его поддержания
3-4. СИСТЕМЫ С НЕПОЛНЫМ ЗАДАНИЕМ
ф (*(*)) =0; / = 0, 1, 2, ... , /г0; п0 < п.
(3-9)
ср=Ф(х<*)).
(3-10)
41
Требуется так синтезировать управление, чтобы уменьшить эту
ошибку до нуля. Изменение ошибки должно, очевидно, подчинять-
ся некоторому дифференциальному уравнению.
Определим порядок этого дифференциального уравнения. Пред-
варительно отметим, что порядок динамической системы относи-
тельно некоторой выходной величины равен порядку той произ-
водной, которая явно зависит от управляющего воздействия. Ма-
тематически явная зависимость означает, что управляющее воз-
действие в каждый момент времени связано с высшей производ-
ной конечным уравнением. С физической точки зрения явная за-
висимость означает, что в каждый момент времени управляющее
воздействие оказывает непосредственное влияние лишь на выс-
шую производную рассматриваемой выходной величины объекта.
В данном случае нас интересует порядок объекта относитель-
но ошибки регулирования (3-.10). Если выражение (3-10) продиф-
ференцировать по времени п—л0 раз, где. п — порядок объекта,
а по — порядок уравнения связи, то производная (п—/г0)-го по-
рядка будет явной функцией /г-й производной выходной величины
объекта х. Учитывая уравнение объекта управления i(l-'l), можно
считать, что производная (л—/г0)-го порядка ошибки регулирова-
ния (3-10) является явной функцией управляющего воздействия.
Таким образом, синтезируемую систему управления необходимо
рассматривать относительно ошибки (3-10) как систему порядка
п—по. При этом функция (3-9) и ее частные производные всех
аргументов до порядка п—п0 включительно должны быть одно-
значными, а их величины конечными.
Из приведенной схемы оценки порядка системы относительно
ошибки регулирования следует, что для нахождения начальных
условий системы по ошибке следует знать все начальные условия
объекта по его выходной величине, т. е. информация, характери-
зующая состояние объекта в любой момент времени, не теряется.
Это связано с тем, что производная ошибки порядка п—п0 зави-
сит от производной регулируемой величины порядка п.
Обратим внимание также на то обстоятельство, что порядок
синтезированной системы управления меньше порядка объекта.
Это связано с тем, что в обоих случаях порядки относятся к раз-
личным величинам: в первом случае — к некоторому функционалу
от координат объекта, а во втором — к выходной величине объ-
екта.
Составим требуемое дифференциальное уравнение системы,
например, в виде
П—По
Sct ?(') = 0. (3-11)
/=о
Выбором коэффициентов настройки d можно добиться устой-
чивости и нужного качества переходного процесса ошибки регули-
рования. Из уравнения (3-11) находим требуемое значение высшей
производной выходной величины объекта. Подставляя его в урав-
нение объекта, определяем требуемое управление.
Пусть объект управления описывается системой дифференци-
альных уравнений первого порядка (3-2) и (3-3). Задание пред-
ставим в виде
42
Ф (xj) = 0; / = 1, 2, ... , я,; л,<л.
введём ошибку выполнения задания y—<t>(xj).
Порядок синтезируемой системы относительно этой ошибки
равен порядку той ее производной, которая с учетом уравнений
объекта явно зависит от управляющего воздействия. Затем, как и
в предыдущем случае, составляем требуемое уравнение движения
системы и находим из него требуемое значение производной явно
управляемой координаты. Подставляя это значение в соответствую-
щее уравнение объекта, получаем выражение для закона управле-
ния.
Изложенный способ проиллюстрируем на примере синтеза
структуры следящей системы управления движением тела вдоль
заданной траектории.
3-5. СИСТЕМА УПРАВЛЕНИЯ СПУСКОМ ТЕЛА В АТМОСФЕРЕ
Одной из важных задач управления является обеспечение
движения тела (летательного аппарата) вдоль заданной траекто-
рии в поле притяжения планеты. При входе в атмосферу планет
единственным управляющим воздействием часто является только
аэродинамическое качество. Движение тела в этом случае описы-
вается системой существенно нелинейных дифференциальных урав-
нений (Л. 4, 60—62]. Известны, по крайней мере, два следующих
подхода к решению такой задачи (Л. 60].
Во-первых, применяют линеаризацию уравнений динамики тела,
в результате чего получают расчетную систему с переменными
параметрами (коэффициентами линеаризации). В этом случае ис-
пользуют систему управления с настройкой коэффициентов регу-
лятора в функции параметров траектории (самонастраивающаяся
система).
Во-вторых, применяют системы управления с переменной
структурой, что позволяет улучшить качество регулирования по
сравнению с первой схемой. Система с переменной структурой,
применяемая для рассматриваемой задачи, отличается все же
определенной сложностью в. силу необходимости установки запо-
минающих устройств и логических элементов.
Указанная выше задача решена с использованием предложен-
ного метода синтеза, что позволило найти систему управления
с постоянной структурой, которая обеспечивает требуемый пере-
ходный процесс при отклонении от заданной траектории.
Примем следующие допущения:
планета имеет идеальную сферическую форму, а ее поле тяго-
тения является центральным;
экваториальная скорость вращения планеты и окружающей
ее атмосферы мала по сравнению со скоростью движения тела;
высота полета гораздо меньше радиуса планеты;
температура атмосферы постоянная, так что зависимость плот-
ности от высоты имеет экспоненциальный характер;
рассматривается движение только центра масс тела в про-
дольной плоскости, а переходные процессы при движении вокруг
центра масс предполагаются гораздо более быстро протекающи-
ми, чем при движении самого центра масс;
продольное и боковое движения считаются взаимно независи-
мыми.
43
Дифференциальные уравнения движе-
ния центра масс тела (рис. 3-3) имеют сле-
дующий вид:
dv
— = __d_£Sin9;
db 1 Г fv2 \ 1
-di=-v[y + [—-e) cosej;
dH
dt
— v sin I
dL
•^j- == vcos 0,
(3-12)
где d = D/m — удельная сила сопротивле-
ния; g — ускорение притяжения к центру
планеты; 0 — угол между вектором скоро-
сти и местной горизонталью; y—Y/m—
удельная, подъемная сила; т — масса тела;
v — скорость; г — расстояние тела от центра массы планеты;
И — высота над поверхностью планеты; L — дальность полета, от-
считываемая по поверхности планеты.
Состояние тела в каждый момент времени однозначно опреде-
ляется четырьмя фазовыми координатами: у, 6, Я, L; из них коор-
динатой, явно зависящей от управляющего воздействия, является
угол между (вектором скорости и местной горизонталью.
К системе уравнений (3-fi2) необходимо добавить уравнения
для удельной подъемной силы и удельной силы сопротивления:
d-
: 2т '
(3-14)
где р — плотность воздуха;
су, cD — аэродинамические коэффициенты для подъемной силы и
силы сопротивления;
S — характерная площадь тела.
Согласно [Л. 4, 61, 62] примем:
Р = Р.«~РЯ. Ро
2т
р(0);
const; р = const;
■ = а = const.
(3-15)
Отношение аэродинамических коэффициентов (аэродинамиче-
ское качество) обозначим через
(3-16)
44
Ъта величина рассматривается как управляющее воздействие.
Для решения .поставленной задачи целесообразно несколько
видоизменить форму записи уравнений движения (3-12). С этой
целью введем относительные единицы, причем за базовые величи-
ны примем:
v6 = vxV; #б = Я0; £б = #; Рб = Ро* (3"17)
где икр — —круговая (первая космическая) скорость; Н0 — на-
чальная высота полета.
Произведем далее замену аргумента в дифференциальных
уравнениях (3-12). iB качестве нового аргумента примем дальность.
Действительно, в данной задаче (движение тела в атмосфере без
силы тяги) дальность изменяется во времени монотонно, так как
ее производная при |8|<л/2 всегда положительна. Такая замена
позволяет упростить структуру управления.
Таким образом, с учетом выражений (3-15) —(3-17) уравнения
движения примут вид:
dv
dB
flp^2 + sin6
1
~dL WcosV К*2 - 0 cos 0 + a9v*u];
dn
dL
= Atg9
(3-18)
или для малых углов |9|<10,1:
dv
_=_арг)__
(3-19)
где
L_
Если известна требуемая (программная) зависимость высоты
полета от дальности #=/(L), то ошибка выполнения этой про-
граммы
f =/(Е)-Д. (3-20)
^ Требуемое дифференциальное уравнение имеет второй порядок.
Действительно, производные ошибки (3-20) по дальности равны:
с/? _ df
dU
dL dL dL dL
df
(3-21)
rf2y _ d*f
dL2
dB
dL2 ~~ dL
(3-22)
45
Вторая производная ошибки явно зависит от производной угла
Э или, с учетом уравнения (3-18), от управляющего воздействия.
Форму требуемого дифференциального уравнения выберем линей-
ной:
d2<? dy
(3-23)
где Ci, С2 — коэффициенты настройки на желаемый переходный
процесс.
Задача синтеза заключается в том, чтобы найти структуру
управления, при котором движение системы описывалось бы тре-
Рис. 3-4.
буемым дифференциальным уравнением (3-23). Следуя принятой
методике синтеза, найдем сначала из этого уравнения требуемое
значение высшей производной ошибки:
Cl dZ ~~С^'
Используя уравнение i(3-22), найдем требуемое значение про-
изводной переменной, явно зависящей от управления:
[dL )- h \dL* +Cl dl +СгЧ)
С учетом уравнения (3-18) требуемое управление равно:
1 Г d2f „ ( df \
+ с2(НГ)-й)-а(1-^-)]-
46
Схема управления изображена на рис. 3-4. Как следует из
полученного выражения, для реализации закона управления объ-
ектом О необходимо:
измерять все фазовые координаты тела и плотность среды;
иметь^нелинейные блоки, вычисляющие непрерывно величины f
df/dL., d2f/dZ2 как функции дальности, а также блок, выдающий ве-
личину 1—-^2", блок деления и сумматор.
Отметим, что величина скорости тела определяется путем ин-
тегрирования ускорения летательного аппарата. Дифференциаторы
в этой схеме управления не требуются.
Основные свойства синтезированной системы совпадают с об-
щими свойствами систем, синтезируемых данным методам и изло-
женными в гл. 2. При u = ud ошибка системы при любом началь-
ном отклонении в области управляемости стремится к нулю. Ха-
рактерной особенностью синтезированной системы является то, что
при изменении опорной (заданной) траектории спуска структура
системы управления не изменяется и обеспечивает устойчивое дви-
жение относительно этой траектории.
Глава четвертая
МНОГОСВЯЗНЫЕ СИСТЕМЫ
ФУНКЦИОНАЛЬНОГО РЕГУЛИРОВАНИЯ
4-1. ПРОЦЕДУРА СИНТЕЗА
'Многосвязными системами функционального регулирования
называют системы, задание для работы которых представляет бо-
лее чем одно соотношение между выходными величинами объекта.
Существующие методы синтеза таких систем основаны либо на
предварительном задании структуры управления (по ошибкам под-
держания уравнений связи), либо на преобразовании уравнений
связи в соответствующие задания как функции времени. В обоих
случаях необходим дополнительный анализ систем. Отметим также,
что в литературе пока отсутствуют достаточно общие методы син-
теза структур указанных систем.
Ниже синтез структуры управления проведен таким образом,
что достигаются как требуемое качество поддержания заданных
уравнений связи, так и инвариантность относительно контролируе-
мых возмущений. При решении этой задачи мы исходим из того,
что число независимых заданий — уравнений связи — не может
быть больше числа управляющих воздействий. Далее рассматри-
вается случай, когда число уравнений связи равно числу управляю-
щих воздействий.
Очевидно, применительно к данной задаче объект управления
должен быть многомерным. Общая структура объекта, обозначе-
ния и дифференциальные уравнения такие же, что и в разделе,
относящемся к синтезу многомерных систем автоматического регу-
лирования (гл. 2).
47
Задание для работы системы управления в случае объектов,
описываемых уравнениями (2-16), представляется в виде:
Ф*.(*}°)=0; ; = о, 1, 2, noi;
rioj^rij; k = \y 2, К,
(4-1)
где К — число регулируемых соотношений. Задания (4-1) могут
быть полными или неполными при тех же условиях, что и для
односвязных систем.
Известные практические примеры многосвязных систем функ-
ционального регулирования, в том числе приведенные ниже, по-
зволяют сделать вывод о том, что наиболее важными являются
системы с неполным заданием. К таким мы относим системы, для
которых все задания (4-1) являются неполными (n0j<nj). Далее
рассматриваются именно эти системы.
Основная идея нх синтеза состоит, как и для односвязных
систем, в использовании способа дополнения задания, т. е. в та-
ком преобразовании уравнений связи, чтобы получить новые за-
дания, зависящие от высших производных выходных величин объ-
екта, выполнение которых влечет за собой выполнение также ис-
ходных (неполных) заданий.
Введем в рассмотрение ошибки выполнения заданий (4-1)
Необходимо так синтезировать управление, чтобы свести с те-
чением времени эти ошибки к нулю. Следуя принятому методу
синтеза, составим требуемые дифференциальные уравнения для их
изменения во времени. 'Порядок каждого .уравнения определяется
порядком той производной ошибки, которая явно зависит от выс-
шей производной, по крайней мере, одной из выходных величин
объекта, т. е. от соответствующего управления.
Требуемые дифференциальные уравнения, составленные отно-
сительно ошибок выполнения заданий (44), можно записать, на-
пример, в линейной форме. Из этих уравнений можно получить
систему конечных уравнений (относительно требуемых значений
высших производных), коэффициенты которых являются функция-
ми выходных величин объекта. Если эта система конечных урав-
нений разрешима, то можно найти аналитические выражения для
высших производных. Подставив их в соответствующие дифферен-
циальные уравнения объекта, определим требуемый закон управле-
ния. Более подробное рассмотрение метода синтеза целесообразно
провести на примерах.
Пример 4-1. Пусть объект с двумя управляющими воздейст-
виями и тремя выходными величинами описывается следующей
системой дифференциальных уравнений:
Чь=*ь (*}°).
(4-2)
#2 ~Ь #1 #8»
(4-3)
*1 =>?•
(4-4)
48
Требуется выдержать следующие соотношения • между выход-
ными величинами объекта:
Xi—x2\
Х2 = Хз.
Ошибки выполнения этих заданий:
q>i = *i—*2; (4-5)
<Р2=х2—х3. (4-6)
Относительно ошибки (4-5) систему управления надо рассма-
тривать как систему первого порядка. Действительно, состояние
системы в любой момент времени можно определить величиной
ошибки, однозначно связанной с выходными величинами хх и х2.
Первая производная ошибки зависит от высшей производной вы-
ходной величины *ь т. е. с учетом уравнения объекта (4-2)—от
управляющего воздействия. Потребуем, чтобы изменение ошибки
(4-5) во времени удовлетворяло линейному дифференциальному
уравнению первого порядка:
fi+Cft=0, (4-7)
где С — коэффициент настройки.
Относительно ошибки !(4-6) систему управления необходимо
рассматривать как систему второго порядка. Действительно, ее
состояние в любой момент времени можно определить величиной
ошибки и ее производной
»•
<р2 = Х2 — х»,
которые однозначно связаны с выходными величинами объекта и
их производными. Вторая производная этой ошибки
?2 = Х2 — х\
зависит от высшей производной выходной величины х3, т. е. от
управляющего воздействия. Потребуем, чтобы изменение ошибки
(4-6) во времени удовлетворяло линейному дифференциальному
уравнению второго порядка
?2 + С^2+С2<р2-0, (4-8)
где С\у С2 —коэффициенты настройки.
Для синтеза структуры управления необходимо прежде всего,
исходя из дифференциальных уравнений движения (4-7) и (4-8),
найти требуемые значения высших производных выходных вели-
чин объекта, явно зависящие от управляющих воздействий:
iid = *2 — С?,; *з = *2 + Ct(p2 + C2TV
Подставляя эти выражения вместо соответствующих высших
производных в уравнения объекта (4-2) — (4-4), получаем требуе-
мые законы управления:
«id = *2 — С?! + х3;
«га = CiS>2 + С2<р2 —
4-Ю 49
Результаты моделирования синтезированной системы управле-
ния (рис. 4-1) представлены в виде осциллограмм (рис. 4-2), на
которых приведены законы изменения выходных величин объекта
*i—х3 (соответственно кривые /—3) и ошибок регулирования ф»
Рис. 4-1
и ф2 (соответственно кривые 4 и 5). Из осциллограмм видно, что
ошибки регулирования стремятся к нулю, а значит, требуемые соот-
ношения между выходными величинами объекта выполняются,
хотя сами эти величины во времени
4ВЬь!'ijdHfet!.'^ёШЬк^ и изменяются.
^И^^НР^^Йг ' ^ЧЯр Пример 4-2. Пусть необходимо
.'■^f воспроизвести на плоскости кривую,
уравнение которой таково:
Отработку проведем с помощью
двух исполнительных устройств, опи-
сываемых дифференциальными урав-
нениями
Рис. 4-2.
с2 = и2, )
(4-Ю)
которые справедливы, например, для электродвигателей с постоян-
ным моментом. Кроме того, необходимо, чтобы скорость отработки
была постоянной, т. е.
v2 = х\+ х\--
-.А0 == const.
Следовательно, задано также второе соотношение между ко-
ординатами объекта
Ф2(^1> х2)= ^ + ^2—^о = °. (4-11)
Ошибки выполнения соотношений (4-9) и (4-11), а также их
производные таковы:
50
<Pj = xx — 2bx2x2\
= x1 — 2b (x\ + x2x2);
• О -o
?2 = X\ + *2
исполнительных
(4-12)
y2=2(xlx1 + x2x2).
Учитывая дифференциальные уравнения
устройств (4-10), можно написать:
<р, = их — 2Ь (х\ + х2и2)\
у2 = 2 (ххих-\- х2и2).
Следовательно, относительно ошибки объект следует рас-
сматривать как систему второго порядка, а относительно ошибки
фг — как систему .первого порядка. Требуемые дифференциальные
уравнения для изменения каждой из ошибок во времени запишем
в виде линейных уравнений:
?i+C1(Pl + C2f1 = 0;
^2 + <Р2 = 0.
откуда с учетом выражений (4-12) получаем систему уравнений
для расчета требуемых значений управляющих воздействий:
где
их— 2bx2u2 = dx; |
ххих + х2и2 = d2, \
С С
dx = — -^-<Р1 — "ТГ?! + 2^2;
(4-13)
d2 = -
2х
т
-СЕЗОНУ/
-А
ЧИт*
Рис. 4-3.
51
Для единственности решений системы 'уравнений (4-13) необ*
ходимо, чтобы выполнялось неравенство
х2 ф — 2ох2х1.
Определение требуемых управляющих воздействий проведем,
решая систему линейных уравнений (4-13) с использованием, на-
пример, аналоговых устройств.
Структурная схема синтезированной системы приведена на
рис. 4-3, где ВРУ — вычислительный блок для решения системы
линейных уравнений (4-13) с переменными коэффициентами.
Постановка задачи, рассмотренная в приведенном примере,
характерна для систем программного управления станками, а так-
же для систем управления движением тел в плоскости.
4-2. СИСТЕМА УПРАВЛЕНИЯ ПОЛОЖЕНИЕМ
И СКОРОСТЬЮ ДВИЖУЩЕГОСЯ ТЕЛА
Одним из важных частных случаев многосвязных систем функ-
ционального регулирования являются автоматические системы управ-
ления движением тел (например, летательных аппаратов).
Известны следующие две задачи управления движением тел:
задача движения тела по определенной траектории;
задача совпадения управляемого тела с другим телом.
Далее рассматривается только движе-
ние центров масс тел в плоскости. Наибо-
лее сложным для синтеза является случай,
когда динамика тела описывается нелиней-,
ными дифференциальными уравнениями.
Обычно эти уравнения линеаризуют, что,
однако, приводит всегда к довольно слож-
ной задаче синтеза управления объектом,
имеющим переменные во времени параме-
тры (коэффициенты линеаризации). В дан-
ном параграфе поставленные задачи реша-
ются предложенным методом. Отличитель-
ная особенность этого подхода состоит
в том, что он не связан с линеаризацией
уравнений динамики и, следовательно, по-
зволяет более полно учесть реальные свой-
ства объекта управления.
Движение твердого тела состоит из двух движений: движения
центра масс и движения тела вокруг центра масс. Будем считать,
что переходные процессы движения вокруг центра масс протекают
гораздо быстрее, чем при движении самого центра масс, а продоль-
ное и боковое движение являются взаимно независимыми (Л. 4].
Рассмотрим продольное движение тела в безвоздушном прост-
ранстве в поле притяжения, например, Земли. Полагаем, что Земля
(или другая рассматриваемая планета) представляет невращающую-
ся сферу, а ее гравитационное поле имеет сферическую симметрию.
Дифференциальные уравнения движения тела в полярной системе
лоординат, связанной с центром Земли (рис. 4-4) [Л. 4]:
(dv v\ \
ЧГ-ТГ+R) = -rng + Psin(a + в); (4-14)
52
/ dv& Ьарг \
m{-dt+7T+r)=Pcos(a + b)- {А-Щ
где m — масса тела, в общем случае переменная; vr и — радиальная
и трансверсальная составляющие скорости; Я— высота; R — радиус
Земли; Р — сила тяги; а — угол атаки.
Уравнения кинематики для данного случая имеют вид:
H + R dL .
i>p = v cos 9 = —£ jj-; (4-16)
dH
vr = vsin 9 = -~[f* (4-17)
где о — скорость тела; L — дальность полета, отсчитываемая по по-
верхности Земли.
Уравнения (4-14) — (4-17) полностью характеризуют движение
центра масс тела. Их можно привести к следующей системе четы-
рех дифференциальных уравнений первого порядка:
y = pcosa — gsin8; (4-18)
^[ ij" ~~g)cos 9 + р sin a]; (4"19)
Z,'^ у cos 9; (4-20)
tf = asin9, (4-21)
где р=Р/т — удельная тяга; г=«/? + Я; r/\R&\ (при #<<#).
Таким образом, состояние управляемого тела с точки зрения
движения его центра масс в каждый момент |Времени однозначно
определяется четырьмя переменными: и, 0, Я, L, а управляющими
воздействиями являются сила тяги и угол атаки.
Определение требуемых значений силы тяги и угла атаки явля-
ются целью настоящего исследования. Целесообразно, однако, на-
ходить вначале не эти величины, а требуемые значения производ-
ных переменных состояния тела, явно зависящих от них: v, 0. За-
тем, исходя из формул (4-18) и (4-19), находим требуемые законы
управления. Зная удельную тягу и массу тела, можно определить
требуемую полную силу тяги в каждой точке траектории.
'При управлении движением тела необходимо соблюдать задан-
ные соотношения между его переменными (фазовыми координата-
ми), называемые программами движения. Так как число программ
не может быть больше числа управляющих .воздействий, то, следо-
вательно, в нашем случае число программ движения не может быть
больше двух.
«Разделим программы движения тела на основные и вспомога-
тельные. К основным программам отнесем те, которые определяют
пространственное положение тела:
/4(Я, L)=0. (4-i22)
К вспомогательным отнесем программы, которые определяют
взаимосвязь между всеми фазовыми координатами:
/2(о, 0, Я, L)=0
(4-23)
53
Например, тело должно двигаться rto некоторой траекторий,
т. е. требуется выдержать соотношение между высотой и дально-
стью полета, а его скорость определенным образом должна зави-
сеть от дальности. Тогда основная программа имеет вид (4-22),
а вспомогательная /2(0, L)=0.
©ведем в рассмотрение ошибки выполнения указанных выше
программ:
*1 = М". £); (4-24)
<p2 = f2(y, 9, Я, L). (4-25)
Необходимо, во-первых, привести эти ошибки с течением вре-
мени к нулю и, во-вторых, обеспечить нужное качество переходного
процесса. Это достигается соответствующим выбором вида требуе-
мых дифференциальных уравнений. Выбор этих уравнений необходи-
мо начать с определения их порядка. Для ошибки вида (4-25) по-
рядок должен быть равен единице. Действительно, фазовые коорди-
наты тела однозначно определяют ее значение, а скорость ее изме-
нения, равная
df* . df2 • df2 . df2 .
= f'2vv + f'2Bb + f'2HH + f'2LL
есть функция не только переменных состояния тела, но и управляю-
щих воздействий, ибо производные г; и 0 согласно уравнениям
(4-18) и (4-19) зависят от них. Зададимся следующим дифферен-
циальным уравнением изменения ошибки (4-25) во времени:
?2 + С<р2 = 0, (4-26)
где С — коэффициент настройки. Задание такого уравнения обеспе-
чивает (при С>0) устойчивость системы и нулевую установившуюся
ошибку.
Аналогично, можно показать, что для ошибки вида (4-'24) тре-
буемое дифференциальное уравнение движения системы должно
иметь второй порядок. Действительно, выражения для этой ошибки
и ее первой производной
зависят от фазовых координат тела и программы. Вторая произ-
водная ошибки
f 1 = Г'\нй2 + 2V'XHLHL + f"lLL> + f'lHH + f'IL L, (4-27)
где
trr Li-* iff fff — .
' 1Я — dtf2 у I il — dL*' I \hl — dHdL
Можно показать, что выражение (4-27) в каждый момент вре-
мени явно зависит от управляющих воздействий.
54
Для определения ошибок (4-24) и (4-25) и их производных на
задания (4-22) и (4-23) должны быть наложены следующие усло-
вия: как -сами функции, так и их частные производные по всем пе-
ременным до требуемого порядка включительно должны быть одно-
значно определенными и не иметь разрывов непрерывности второ-
го рода в области возможных значений аргументов.
Зададимся требуемым дифференциальным уравнением для из-
менения во времени ошибки (4-24):
?i + С^г + С2<?г = 0,
(4-28)
где Ci и С2 — коэффициенты настройки.
Необходимо найти такую структуру управления телом, чтобы
изменение ошибок выполнения программ во времени удовлетворяло
требуемым дифференциальным уравнениям (4-26) и (4-'28).
Процедура структурного синтеза системы управления состоит
из двух этапов. На первом этапе из уравнений (4-26) и (4-(28) на-
ходят требуемые значения высших производных ошибок. На втором
этапе, используя полученные выражения и уравнения динамики тела,
определяют требуемые законы управления.
Из уравнений (4-26) и (4-28) получаем следующие выражения
для требуемых значений высших производных ошибок:
Ъй = ~ CtV>
Требуемые значения высших производных ошибок в каждый мо-
мент времени явно зависят от значений производных v и 0. Решая
совместно уравнения (4-18) — (4-28), находим:
где
#21Г\* + #220d = ^2>
Лц = я sin в + f'1L cos в;
#12 = v (f'j^cos 0 — f'lL sin 0);
dt =-(f"1Hh2 + 21"\hl"L + f"4Lt +c'b + C,f,);
(4-29)
(4-30)
Таким образом, получена система линейных уравнений, решение
которой единственно, если
D =
ф0.
au #12
#21 ^22
Требуемые значения высших производных равны:
55
где
#12
t
D2 =
#11
d2
#22
#21
d2
Из уравнений динамики (4-18) и (4-19) находим:
(р cos a)d = vd + g sin 8 = /?,; (4-31)
(p sin a)d = vbd + (g - cos 0 = p2. (4-32)
Определение требуемых управляющих воздействий как функции
переменных состояния тела и программы можно производить с по-
мощью выражений:
+ Р2 .
ad = arctg—,
= \/ р] + р\.
Требуемое значение полной силы тяги равно:
Pd = Pdm(t),
где m(t) —текущее значение массы тела, определяемое автономной
измерительной системой.
Нахождение управления можно в ряде случаев упростить, если
рассматривать процесс не как функцию времени, а как функцию
какой-либо другой, монотонно изменяющейся переменной. Например,
если основная программа движения (4-22) такова, что высота есть
однозначная функция дальности, то, следовательно, не предполагает-
ся программного движения .«назад» и |0|^л;/2. Допустим, кроме
того, что подобное движение не возникает также под влиянием тех
или иных возмущений. При указанных допущениях монотонно из-
меняющейся координатой является дальность, так как скорость ее
изменения знакопостоянна. В этом случае уравнения динамики тела
можно представить в виде:
dv __р cos ос — g sin 8 9
dL v cos 8 '
( v2 \
^ — — gJ cos 0 + p sin a
dB
dL v2 cos 0
dH
Число дифференциальных уравнений, описывающих динамику
объекта управления, уменьшилось при этом с четырех до трех.
56
Ошибки Выполнения программ и требуемые дифференциальные урав-
нения рассмотрим как функции нового аргумента:
^2 . г п
где
dL —Рш dL +P\l>
dL* —*'\H\dL J + 2'\HL dL +P'\L + Pw dL*'9
dL — l 2* dL "+*' 29 d£ + / 2Я + / 2L
Используя приведенную выше методику синтеза, определим тре-
буемые значения производных переменных состояния, явно завися-
щих от управления:
/ dH \2 dH
KdLl _i_f,
cos2 8' «и
(4-33)
, / \ / £(9 \ dH
f'*v [ЧГ)л + Г» ("5Г Jd " - C<?* - ^" IT - f2L' (4-34)
Учитывая уравнения объекта, находим следующие выражения
для требуемых управляющих воздействий:
{ dv \
(р cos a)d = v cos 8 + g sin 0; (4-35)
(p sin а)л = cos 0 |t,2 J ("ЗГ)Л + T~] + 4' (4"36)
Рассмотрим основные свойства синтезированной системы
управления:
система является устойчивой, если коэффициенты требуемых
дифференциальных уравнений положительны;
установившиеся значения ошибок выполнения программ движе-
ния равны нулю, ибо указанные уравнения являются однородными;
имеется .возможность изменять характер переходного процесса
при отработке ошибок изменением величин коэффициентов на-
стройки.
Структура системы управления зависит от способа представле-
ния требуемых дифференциальных уравнений движения, т. е. от
того, какая переменная принята в качестве аргумента. Если в каче-
57
ётвё аргумента принято время, то схема должна иметь следующие
основные блоки:
блок основной программы, на вход» которого подаются текущие
значения высоты и дальности, а «а выходе получаются значения
частных производных первого и второго порядков функции (4-22),
а также ошибка (4-24);
блок вспомогательной программы, на вход которого подаются
текущие значения переменных состояния тела, а на выходе получа-
ются значения частных производных первого порядка функции
(4-23), а также ошибка (4-25);
блок расчета коэффициентов по формулам (4-30), в который
обязательно входят перемножающие устройства;
блок решения системы двух линейных уравнений (4-29), на вы-
ходе которого получаются требуемые значения производных va
и 6d;
блок решения системы двух нелинейных уравнений (4-31) и
(4-32), на выходе которого получаются требуемые значения управ-
ляющих воздействий.
Если в качестве аргумента принята дальность, то структура си-
стемы управления упрощается, так как не требуется блок расчета
коэффициентов. Требуемые значения производных переменных, явно
зависящих от управления, можно непосредственно определить по
формулам (4-33) и (4-34), а управление — по формулам (4-35) и
(4-36). При реализации систем управления в обоих способах пред-
ставления требуемых дифференциальных, уравнений следует изме-
рять все фазовые координаты тела. Для получения значения произ-
водной ошибки (4-24) необходим только один дифференциатор. Од-
нако эту производную также можно вычислить.
Для конкретных задач общая структура управления может быть
более простой.
Пример 4-3. Пусть необходимо синтезировать управление телом,
которое должно двигаться в безвоздушном пространстве по пара-
болической траектории Н=Ho + kL2 с постоянной скоростью у=Ло =
=const.
В этом случае программы движения таковы:
L) = Я — Я0 — kL2 = 0;
h (v) = v-A0=0.
Ошибки выполнения программ и их производные:
<p2=t> — А0.
Производные программ по переменным состояниям равны:
/'.* = *;
flt = _2*I;
Гш = °; f"lL = -2k> /",„1=0;
58
По формулам (4*33) и (4-34) находим требуемые значения произ»
родных, явно зависящих от управления;
(ж)4 cos* е^^ + с^-г*);
Требуемые значения управляющих воздействий находим из уравне-
ний (4.35) и (4-36):
(р cos a)d = — (v cos 9) C<p2 + g sin 9;
Рис. 4-5.
Для малых значений угла между вектором скорости тела и ме-
стной горизонталью (|8|^0,1) структура управления может быть
упрощена. В этом случае требуемые значения управляющих воздей-
ствий равны:
(р cos a)d = —£>Сф2+£б;
(р sin a)d = - V* [Сt (9 - 2Щ + С2<рх - 2k - + g.
Соответствующая схема управления представлена на рис. 4-5.
4-3. СИСТЕМА УПРАВЛЕНИЯ СОВПАДЕНИЕМ
ДВУХ ДВИЖУЩИХСЯ ТЕЛ
Пусть даны два тела в пространстве: управляемое тело (объ-
ект), имеющее координаты гх и Pi, и цель с координатами г2 и рг
(рис. 4-6). Возможны два вида задачи совпадения:
найти управление, которое сводит к нулю рассогласование как
по положению тел, так и по их скорости (задача мягкой стыковки);
найти управление, которое сводит к нулю только рассогласова-
59
ние по положению тел, в то время как скорость управляемого тела
может быть любой (задача попадания в цель).
(Как и в предыдущем параграфе, (рассматриваем только движе-.
ние тел, описываемое уравнениями (4-14) —(4-17).
а) Задача мягкой стыковки
Рассогласования по положению тел запишем в виде:
ф1«Г1—г2; (4-37)
Ф2=р1—р2. (4-38)
Скорости их изменения с учетом уравнений (4-20) и (4-21) и соот-
ношения $ = L/R равны:
у, = vx sin 0! — v2 sin 92; (4-39)
Ъ = ~jf (vi cos 0, — v2 cos 02). (4-40)
Вторые производные ошибок равны:
'^j == vt sin 0! + vlB1 cos 0! — t>2 sln ^2 — ^282 cos V> (4*41)
<p2 = -j^z (y, cos 0, — tf,0, sin 0, — v2 cos 02 — y202 sin $i) • (4-42)
Если принять во внимание уравнения динамики тела (4-18) и
(4-19), то систему управления можно рассматривать относительно
введенных ошибок как систему BTOiporo порядка, ибо вторые произ-
водные ошибок явно зависят от управляющих воздействий.
Следуя принятой методике синтеза, со-
ставим требуемые дифференциальные урав-
нения для изменения каждой из ошибок:
fi + C'^ + Cf^O; (4-43)
ft + C"1f, + C''1j, = 0. (4.44)
При положительных коэффициентах
этих уравнений переходные процессы, опи-
сываемые ими, являются устойчивыми и,
следовательно, как ошибки, так и скорости
их изменения стремятся к нулю. Характер
переходного процесса определяется значе-
я" ниями коэффициентов уравнений.
Уравнения (4-43) и (4-44) целесообраз-
Рис. 4-6. но применять при малых по абсолютной
величине значениях ошибок. Для компенса-
ции больших ошибок надо задать такие
требуемые уравнения, решения которых дают процесс, близкий
к оптимальному по быстродействию с использованием максимальных
по модулю управляющих воздействий. При таком подходе можно
получить систему с переменной структурой управления, зависящей
от модуля ошибок/
60
Решая совместно уравнения (4 41) — (4-44), составим систему
для расчета требуемых значений производных переменных, явно
зависящих от управлений;
+ | (4.45)
ЬцЬ1Л + Ь2%В1Л = е2* '
где,
Ьи з sin 0J-, bl2 = t/j cos 64;
&8l == cos 8j; b22 = — Vi sin 0,;
£, = — C'xf! — C72f! + 02 sin 0 2 + (*>2 cos 82) 62*.
*2 = R (—C"^ — C"2<P2 + v2 cos 92 — y202 sin 82).
Исходя из формул (4-31) и (4-32), определяем требуемый закон
управления:
«d = arctg —,
где
Pd = Pd™ "= т Yр\ +
/>i = 0id + gsin0;
/?2 = у9н+ (^""Т") cos9'
6И
.?.1Итаг>п
>Н
Рис. 4-7.
Из полученного закона управления следует, что для синтеза си-
стемы необходимо измерять все фазовые координаты объекта и цели,
а также производные по времени скорости и угла наклона к мест-
ной горизонтали (для цели).
61
Структурная схема синтезированной системы управления приве-
дена (для случая постоянной массы тела) на рис. 4-7, где БИ—
блок измерения параметров цели: О —объект управления. Схема
подачи входных сигналов на блок БРУ составлена в соответствии
с уравнениями (4-37), (4-40) и (4-45); схема получения управляю-
щих воздействий — в соответствии с полученным выше законом
управления. На вход объекта эти воздей-
ствия подаются через усилители мощности.
Синтезированная система позволяет осуще-
ствить мягкую стыковку объекта с целью
при заранее не известном характере движе-
ния цели. Если же известно, что цель дви-
жется с постоянной скоростью и, кроме то-
го, направление движения цели также по-
стоянно, то тогда структурная схема систе-
мы существенно упростится.
б) Задача попадания в цель
Известны различные методы наведе-
ния на цель: прямое наведение, наведение
с упреждением, параллельное сближение,
Рис. 4-8. пропорциональное сближение, наведение
по лучу (Л. 3 и 4]. Отличительная особен-
ность указанных методов заключается в том,
что соответствующие кинематические соотношения представляют со-
бой неполные задания, т. е. по ним нельзя непосредственно опреде-
лить требуемые управляющие воздействия.
Рассмотрим синтез системы управления телом при прямом на-
ведении с учетом дополнительного условия:
V\ =Ао=> const,
.(4-46)
т. е. потребуем, чтобы скорость тела была постоянной, например
максимальной.
Основную программу выведем из условия, чтобы вектор скоро-
сти объекта в каждый момент времени был направлен точно в цель.
Применяя теорему синусов" для треугольника От\т2 (рис. 4-8), по-
лучаем:
sin 04
sin а2
(4-46a)
где
: л — (а2 + Ар); а2
Ошибки выполнения программ (4-46) и (4-46а):
sin а, г, cos (0, + Ар)
т-1 =
sin а2
cos 0,
62
<р2 — А0.
Производные этих ошибок равны!
sin Др
cos2
sin (9t + Aft) др
(4-47)
?i=»i. (4-48)
где Др = р1 —р'а.
Если принять во внимание уравнения динамики тела (4-18) и
(4-19), то систему управления надо рассматривать относительно вве-
денных ошибок как систему первого порядка, ибо первые произ-
водные ошибок явно зависят от управляющих воздействий.
Составляем требуемые дифференциальные уравнения для изме-
нения ошибок:
+ Ъ = о>
(4-49)
(4-50)
где ti, t2 — постоянные времени требуемых переходных процессов.
Требуемые значения производных фазовых координат объекта,
явно зависящих от управления, находим из уравнений (4-47) — (4-50)
Ml
i I y I Г
rrcty
>
Рис. 4-9.
с учетом уравнений (4-20) и (4-21), а также с учетом соотношений
P = L//? и ri/r2«l. (Последнее соотношение связано с тем, что
cos2 Gj
'1<J~~ sin Ар
sin (9! + Aft)
<pi sin 9j — v2 sin 92
+
[(9, + Др) 1
/^cos0i— (»i cos 9j — y2 cos 92) ; (4-51)
(4-52)
63
По формулам (4-31) и (4-32) определяем затем, как и 6 Пре-
дыдущем случае, требуемые законы управления. Соответствующая
структурная схема системы представлена на рис. 4-9, где О — объ-
ект, БИ — блок измерения фазовых координат цели. Отметим, что,
в отличие от системы управления для мягкой стыковки, в случае
управления телом для попадания* в цель требуется меньший объем
измерений, а именно: для управляемого тела можно не измерять
величину г2, а для цели — производные по времени скорости и угла
наклона к местной горизонтали.
Схема на рис. 4-9 составлена для заранее не известного закона
движения цели. Если же задаться некоторой гипотезой о движении
цели, например принять движение цели прямолинейным и с постоян-
ной скоростью, то структурная схема синтезированной системы
управления упростится.
Глава пятая
ОБОБЩЕНИЯ МЕТОДА СИНТЕЗА
5-1. СИСТЕМЫ УПРАВЛЕНИЯ, СОДЕРЖАЩИЕ
ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
Структура управляющего устройства тесно связана с видом
дифференциального уравнения объекта. В рассмотренных ранее слу-
чаях уравнения объекта были таковы, что управляющее воздействие
могло быть вынесено в одну часть уравнения, а все остальные пере-
менные (выходная величина, возмущения) — в другую. Такая фор-
ма записи дифференциального уравнения объекта приводит к тому,
что регулятор реализуется в виде безынерционного усилителя и не-
линейного преобразователя, на вход которого подаются составляю-
щие требуемого закона управления. Однако часто в уравнениях
объектов управляющее воздействие трудно либо нецелесообразно
выделять в одну из частей уравнения. Кроме того, в уравнении объ-
екта- могут содержаться производные управляющего воздействия.
Предложенный метод синтеза можно обобщить и на эти случаи.
Для более четкого разграничения структур управления, получае-
мых при таком подходе, классифицируем объекты с точки зрения
вида их дифференциальных уравнений :
объекты управления первого вида, уравнения которых разреши-
мы явно относительно управляющего воздействия и не содержат
его производных;
объекты управления второго вида, уравнения которых неразре-
шимы явно относительно управляющего воздействия и не содержат
его производных;
объекты управления третьего вида, уравнения которых содержат
производные управляющего воздействия.
Синтез систем управления объектами первого вида рассмотрен
в предыдущих главах. Обобщение этого метода для синтеза управ-
ления объектами второго и третьего видов предложено И. П. Сима-
ковым и В. В. Астровым (Л. 30].
Дальнейшее исследование ограничим рассмотрением одномерных
систем. Однако приводимые выводы могут быть распространены на
случай многомерных систем с заданиями как в виде функций вре-
мени, так и соотношений между выходными величинами объекта.
64
Синтез систем управления объектами второго и третьего видов
приводит, как лравило, к системам с вычислительными устройства-
ми. Эти устройства предназначены для решения в зависимости от
вида объекта либо конечных, либо дифференциальных уравнений.
а) Системы управления с вычислительными устройствами
для решения конечных уравнений
Задан объект управления второго вида, описываемый следую-
щим дифференциальным уравнением /i-го порядка относительно ре-
гулируемой величины:
^SVK и) =0; / = 0, i, 2, .... п\ v = 0, 1, 2,
s= 1, 2, S. (5-1)
Поставим задачу выбора такой структуры управления, которая
обеспечивает движение этого объекта соответственно некоторому
требуемому дифференциальному уравнению п-то порядка типа (1-2).
Ьсли выразить из требуемого уравнения значение высшей произ-
водной регулируемой величины и подставить его в уравнение
объекта, то получаем:
/(*<л\ *(<), \{sv), tf)=0; i = 0, 1, 2,..., /1—1. (5-2)
Это уравнение составлено относительно управления как конеч-
ное, ибо все входящие в него величины, кроме управления, непре-
рывно измеряются и в любой момент времени считаются известными.
Решение уравнения (5-2) относительно управления дает значение
управляющего воздействия, требуемое для движения системы со-
гласно уравнению (1-2).
Это решение должно быть, конечно, единственным (для опреде-
ленности движения). Управляющее устройство выполняется в виде
блока, нецрерывно решающего конечное уравнение (5-2).
б) Системы управления с вычислительными устройствами
для решения дифференциальных уравнений
Задан объект управления третьего вида, описываемый диффе-
ренциальным уравнением:
/(*('), ^у>, и(Ю) = 0; * = 0, 1, 2, п; о = 0, 1,2, ...
e = l,2, ...,5; р = 0, 1, 2, ..., Р. (5-3)
Для движения объекта соответственно требуемому уравнению
(1-2) управляющее устройство должно быть выполнено в виде бло-
ка, непрерывно решающего следующее дифференциальное (относи-
тельно управления) уравнение:
/ (л#>, Ж'), иЩ =0; / = 0, 1, 2, п — 1, (5-4)
которое получено путем подстановки в уравнение объекта вместо
высшей производной регулируемой величины ее требуемого значе-
ния.
В рассмотренных случаях определение управляющего воздейст-
вия возможно .только в том случае, когда уравнения объектов до-
5 —10 65
пускают в любой момент времени однозначное решение относитель-
но управления. Для реализации синтэзированной системы можно ис-
пользовать методы аналоговой техники.
Однако более широкими возможностями обладают способы,
основанные на применении дискретных вычислительных устройств,
которые позволяют, во-первых, сравнительно просто (путем изме-
нения программы) реализовать различные нелинейные преобразова-
ния переменных и, во-вторых, заменять измерения производных взя-
тием конечных разностей, что проще.
Рассмотрим синтез системы управления объектом третьего вида,
приведенный в работе В. В. Астрова и И. П. Симакова (Л. 30].
5-2. СИСТЕМА РЕГУЛИРОВАНИЯ МОЩНОСТИ
ЭНЕРГЕТИЧЕСКОГО ЯДЕРНОГО РЕАКТОРА
Уравнения кинетики нейтронного потока реактора в одногруппо-
вом приближении имеют вид:
dt
I
dC_
dt
где nH — плотность нейтронов в активной зоне реактора, опреде-
ляющая его выходную мощность; С — концентрация ядер-излучате-
лей запаздывающих нейтронов; /, рн, ЯР — соответственно время
гЧ Р h
Рис. 5-1.
существования мгновенных нейтронов, доля запаздывающих нейтро-
нов и постоянная распада; 6k— реактивность, вносимая регулирую-
щим стержнем. '
Пренебрегая временем существования мгновенных нейтронов
(/= Ю-4-^ 10_6 сек), можно получить для целей синтеза упрощенное
уравнение динамики объекта:
dn» п \ ( d? . 7 ^ п
-5Г(1-Рн)-/Ц-27 + *рЬ, =0'
bk
где рн =-«— <С 1 — величина, пропорциональная положению регулирую-
Рн
щего стержня.
66
Требуемое дифференциальное уравнение ззпишем в виде
где ср = \|)—пн — ошибка регулирования; г|) = г|>(/) — задание по мощ-
ности реактора.
Используя изложенную методику, получаем дифференциальное
уравнение регулятора:
1 — Рн Пн
Структурная схема синтезированной системы управления приве-
дена на рис. 5-1. Данная система была исследована на аналоговой
моделирующей установке. На рис. 5-2,а приведены осциллограммы
Рис. 5-2.
переходного процесса для случая линейно изменяющегося во време-
ни задания (серия треугольных импульсов), а на рис. 5-2,6 — для
случая синусоидального задания, где / — задание; 2 — регулируемая
величина; 3—управляющее воздействие; 4 — ошибка регулирования.
Как следует из осциллограмм, качество переходного процесса по
ошибке практически не зависит от формы задания. -
5-3. ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА СОСТОЯНИЙ
а) Вводные замечания
Переходный процесс, являющийся решением требуемого диффе-
ренциального уравнения движения, можно рассматривать не только
как функцию времени /, но и как функцию любой другой перемен-
ной s, которая во времени растет. Между этими двумя переменными
должно быть такое соотношение:
|f=p,>0, (5-5)
где fis = $s(x, х) —некоторая неотрицательная функция координат
объекта, в общем случае нелинейная, называемая коэффициентом
преобразования.
5*
67
Частный случай такого преобразования был использован в гл.З
и 4, где под 5 подразумевались дальность, а под (5« — скорость дви-
жения тела, т. е. конкретные физические величины.
(Пусть задан некоторый переходный процесс в функции пере-
менной s:
<р=ф(5),
причем эта функция однозначна, непрерывна и существует при всех
5^0 (рис. 5-3). Пусть задано также соотношение для перехода от
переменной s к переменной /, которое, учитывая выражение (5-5),
следует записать в виде
s
(5-6)
(такое преобразование известно в математике как преобразование
Лиувилля (Л. <63]). Для того чтобы получаемый переходный процесс
во времени <p=<q>(0 также представлял собой однозначную и не-
прерывную функцию, существующую при всех t^O, преобразование
(5-6) должно быть взаимно однозначным.
t
Рис. 5-3.
Отметим, что при указанном преобразовании независимой пере-
менной сама величина функции «р не изменяется, т. е. при задании
процесса в координатах «р, s характерные особенности этой функ-
ции по оси ординат, например устойчивость, остаются без изменения
и в координатах <р, t.
б) Синтез нелинейной автоколебательной системы
(электронного генератора)
Рассмотрим построение автоколебательной системы как струк-
туры управления, необходимой для автоматического регулирования
соотношения между фазовыми координатами объекта второго по-
рядка, описываемого дифференциальным уравнением
ал = а. (5-7)
68
'Потребуем, чтобы величина х менялась по синусоидальному за-
кону
х=А sin (!>г\
где А — амплитуда колебаний, о) — круговая частота.
Соотношение между х и х можно записать в виде
Ф (*.*)-Л»-*»-^р-0. (5-8)
Ошибка поддержания соотношения (5-8)
? = Л*-хг-5-- (5-9)
CD
Производная этой величины по времени
f, 2х(х + ^г) 2* (х+^г)-
(5-10)
Так как эта производная явно зависит от управляющего воздей-
ствия, то, следовательно, синтезируемую систему необходимо рас-
сматривать относительно ошибки (5-9) как систему первого порядка.
Требуемое дифференциальное уравнение для ошибки запишем в виде
где х — постоянная времени желаемого переходного процесса. От-
сюда с учетом выражения (5-10) требуемое управление
(^-*)- (5"П)
Таким образом, для синтеза полученного управления необходи-
мы два квадратора и одно делительное устройство. Последнее вы-
зывает наибольшие трудности при реализации, особенно когда надо
делить на величину, близкую или равную нулю при ср#0. Это при-
водит к застреванию системы ттри скорости, близкой к нулю, т. е.
к неустойчивому процессу (относительно заданного). Следовательно,
структуру управления (5-11) нельзя признать удовлетворительной.
Для улучшения структуры используем особенность разработанного
метода синтеза, заключающуюся в том, что в задании формы тре-
буемого дифференциального уравнения существует известная свобо-
да выбора (кроме выбора порядка уравнения).
Требуемое дифференциальное уравнение системы запишем
в виде
где Т—постоянная времени. Отсюда о учетом выражений (5-5) и
(5-10) получаем требуемое управление:
Если принять ps = xf, то
= я0со2 (^f- — *)' (5-12)
Таким образом, управление содержит не делительное устройство
а устройство умножения. г
В работе В. В. Павлова и О. С. Яковлева [Л. 63] исследована
устойчивость этой системы относительно траектории (5-8) причем
показано, что устойчивость не нарушается даже при ps = 0
<
"Л
.6
Рис. 5-4.
Для удобства аппаратурного синтеза выражение (5-12) преоб-
разуем с учетом выражения (5-9):
Г (Л2 — х2) со2 — х2 . 1
ud=aQ I тур х— со2х|' (5-13)
Полученная схема (рис 5-4) отличается прежде всего раздель-
ным и независимым регулированием частоты и амплитуды колеба-
ний: частоты — с помощью сдвоенного потенциометра П\, а ампли-
туды— с помошью потенциометра Я2. При уменьшении задаваемой
Рис. 5-5.
частоты ни амплитуда, ни форма колебаний не изменяются. Нижний
предел частоты практически неограничен (вплоть до нуля). Верхний
предел частоты определяется максимально возможным коэффициен-
том усиления усилителей.
70
Хотя ни частота, ни амплитуда колебаний, в отличие от извест-
ных схем регулируемых генераторов, непосредственно не измеряют-
ся, однако схема позволяет получить лучшее качество регулирова-
ния, так как устраняется задержка, связанная с измерением ча-
стоты.
Экспериментальная проверка полученной системы на электрон-
ной моделирующей установке МНБ-1 дала следующие результаты:
1. Устойчивое генерирование сигнала синусоидальной формы
с независимой настройкой частоты и амплитуды возможно.
Рис. 5-6.
2. Время регулирования может быть доведено до относительно
малой величины путем увеличения коэффициента усиления дайной
системы, равного 1/7, с помощью потенциометра 77i. В частности,
если переключение задаваемой частоты колебаний производить при
х=(х)А, х=0, то длительность перехода на новый режим равна нулю.
3. Изменение параметров квадраторов и множительного устрой-
ства на 10—20% не сказывается на стабильности колебаний, и бо-
лее или менее значительно — на их форме.
Осциллограмма выходного напряжения генератора синусоидаль-
ных колебаний при частоте 0,2 гц для случая нулевых начальных
условий — х(0) =i(0) =0 приведена на рис. 5-5,а и для случая *(0),
£(0)=соЛ — на рис. 5-5,6. На рис. 5-6 приведены осциллограммы
ошибки регулирования для различных значений коэффициента 1/Г:
для 1/7=0,5 '(рис. 5-6,а), 1/7=2 (рис. 5-6,6} и 1/7=10 (рис. 5-6,в).
5-4. ЭЛЕКТРОПРИВОД ПОСТОЯННОГО ТОКА,
РАБОТАЮЩИЙ В ГАРМОНИЧЕСКОМ РЕЖИМЕ
Примененный выше принцип может быть использован для син-
теза такого управления электродвигателем постоянного тока, при
котором угол поворота его вала у изменяется во времени по сину-
соидальному закону (гармонический режим). Получение стабильных
71
колебаний двигателя, особенно -регулируемой амплитуды и частоты,
важно во многих практических приложениях [Л. 65—^67]. Рассмот-
рим синтез схемы и некоторые важные особенности такого электро-
привода.
Дифференциальное уравнение двигателя выведем исходя из из-
вестных соотношений:
da>
С е — г„ »
^ном — J пуская»
где / — приведенный момент инерции привода; М — движущий мо-
мент; Мс — приведенный момент сопротивления; со — скорость дви-
гателя; (/м, с'е — конструктивные постоянные двигателя; U — на-
пряжение якоря, (управление); / — ток двигателя; #я — полное со-
противление якорной цепи; «о — скорость идеального холостого хо-
да; Л!пуск, /пуск — пусковой момент и ток двигателя при номиналь-
ном напряжении. Решив совместно эти уравнения, получим:
_/ dz4^ U 1_ dy_ Mz_
-^пуск dt2 Г/ном g>0 dt Afnyc
(5-14)
Запишем уравнение (5-14) в относительных единицах, причем
за базовые величины примем:
Мб"=МпуСк;
^=791
где Гэм — электромеханическая постоянная времени двигателя;
сооГэм — угол поворота вала двигателя при вращении со скоростью
идеального холостого хода за время, равное Гэм. Тогда
d4 dV
-Лг+-5Ь + д7с=Г, (5-15)
где
V t ~ т „ М.
Рассмотрим синтез системы управления. Требуется, чтобы дви-
жение вала двигателя соответствовало уравнению
где
Рис. 5-7.
Задачу рассмотрим .в предположении, что двигатель работает
в режиме холостого хода (Мс=0). Тогда, используя приведенную
выше методику, получаем структуру управления в виде
(Л2-у2)со2-т2 т- - _ г-
U = 2Т ТГ — ®\ТГ + ТГ-
(5-16)
Соответствующая структурная схема системы управления пред-
ставлена на рис. 5-7. В этой схеме -настройка частоты производится
с помощью блока П\ (напри-
мер, строенного потенциомет-
ра), а амплитуды — с помощью
блока Я2, также имеющего пе-
ременный передаточный коэф-
фициент. Максимально воз-
можные частота и амплитуда
колебаний в такой системе за-
висят от максимальных коэф-
фициентов усиления усилите-
лей и предельных энергетиче-
ских возможностей двигателя:
допустимых значений управ-
ляющего воздействия и мощ-
ности. Эти величины опреде-
ляют область управляемости
системы.
73
/,0s
ъ
и
-1,0
0 Хп]а- N.
Ряс. $-&
Область управляемости найдем из условия касания так назы-
ваемого «эллипса нагрузки» и механической характеристики двига-
теля {Л. 66]. Эллипс нагрузки (рис. 5-8) представляет зависимость
между скоростью и ускорением двигателя в гармоническом режиме:
аг "Г b2 — I.
где
х —
df .
1л'
У-
d2f.
di2'
С учетом этих обозначений при U=UHom имеем следующее
уравнение механической характеристики двигателя:
х+у=\.
Из условия касания этой характеристики и эллипса нагрузки
получаем
_ 1
^пред =
(о Y\ + ;
Это и есть уравнение предельной амплитудно-частотной харак-
теристики электропривода постоянного тока при учете ограничения
по напряжению (рис. 5-9,а). Оно определяет максимально возмож-
ч
1дА
i
-;
- /
0
1
-1
Ч
ч
1
-1
-1
ч;
Iqw
1
0,5
-ч
0,1
б)
Рис. 5-9.
ную амплитуду колебаний, которую может развить привод при лю-
бой заданной частоте. Значение управляющего воздействия не пре-
восходит при этом номинальной величины.
Определим теперь максимальную мощность, необходимую для
поддержания колебаний заданной амплитуды и частоты. Мгновенное
значение мощности равно произведению скорости двигателя на мо-
мент, пропорциональный ускорению:
р 1Г х2.
— =Р = ху= xby \—^> Р6 = со0Мпуск.
Исследование этой функции на экстремум показывает, что он име-
ет место при x = a/Vr 2 , 'у =b/Y 2 и равен Рмакс = я&/2.
74
Однако нагрев двигателя определяется не максимальной, а сред-
ней за lU периода мощностью нагрузки. Последняя в гармониче-
ском режиме в я/2 раза меньше амплитуды мощности, т. е.
_ аЬ
Для того чтобы привод мог длительно работать без перегрева
во всем диапазоне частот, номинальная мощность двигателя долж-
на удовлетворять соотношению
Предельную амплитудно-частотную характеристику привода при
учете ограничения по мощности получаем из условия
Л2а>8 _
^ср — п — Р ном
ИЛИ
Эта зависимость представлена на рис. 5-9,6 для двух значений
номинальной .мощности двигателя — 0,5 и 0,1.
Таким образом, с увеличением частоты колебаний их допусти-
мая амплитуда уменьшается как с точки зрения ограничения по
напряжению якоря двигателя, так и его мощности. Эти допустимые
области в общем случае не совпадают, т. е. при заданной частоте
некоторая амплитуда колебаний может быть допустима по ограни-
чению напряжения якоря и недопустима по ограничению мощности
двигателя, и наоборот. При нагрузке эти области уменьшаются.
В пределах области управляемости синтезированный электропривод
обладает важными преимуществами по сравнению с существующи-
ми системами привода такого же назначения, которые обычно со-
стоят из отдельного задающего генератора синусоидальных колеба-
ний и следящей системы для их отработки. В нашем случае необхо-
димость в отдельном задающем генераторе отпадает, ибо двигатель
является элементом автоколебательной системы.
5-5. УПРАВЛЕНИЕ ОБЪЕКТАМИ С НЕПОЛНОЙ
ИНФОРМАЦИЕЙ
В рассмотренных примерах синтеза дифференциальное уравне-
ние объекта предполагалось известным и все фазовые координаты
объекта и основные возмущения измеряемыми. Однако на практике
параметры объекта ^(коэффициенты соответствующего дифференци-
ального уравнения) даны только с определенной точностью. То же
относится к измерению фазовых координат и возмущения. Если их
отклонения от действительных значений относительно невелики, то
это мало скажется на характере переходного процесса. Если же
в процессе работы системы управления происходят существенные
изменения структуры объекта или его параметров, то обычная от-
рицательная обратн-ая связь может компенсировать такие влияния
на объект только при очень большом значении коэффициента уси-
ления, что, в свою очередь, часто связано с потерей устойчивости.
75
Известны следующие основные направления решения такой задачи:
системы с переменной структурой управления;
адаптивные (самонастраивающиеся) системы;
системы, устойчивые при сколь угодно большом коэффициенте
усиления [Д. 47];
комбинированные системы с косвенным измерением возмущений
[Л. 50, 51].
(Покажем, что предложенный метод позволяет получить струк-
туры управления, близкие по своим свойствам к последним двум, но
в отличие от них приемлемые для широкого класса нелинейных и
нестационарных объектов.
Основная цель синтеза во всех рассмотренных примерах заклю-
чается в том, чтобы свести к нулю разность между требуемым и
текущим значениями высшей производной регулируемой величины.
При этом движение системы (переходный процесс) соответствует
требуемому дифференциальному уравнению. 'Главное отличие поста-
новки задачи в данном разделе от изложенной в гл. 1 заключает-
ся в том, что информация об объекте неполная, т. е. не известен
точно вид дифференциального уравнения объекта и неизмеряемы
возмущения. Предполагается достоверно известным только порядок
дифференциального уравнения объекта относительно регулируемой
величины п.
Представим объект управления в виде некоторой модели, опи-
сываемой дифференциальным уравнением того же порядка, что и
объект, например линейным, но с переменными во времени коэффи-
циентами. Коэффициенты этой модели будем постоянно корректи-
ровать таким образом, чтобы в любой момент времени дифферен-
циальное уравнение модели обращалось в тождество при подста-
новке в него значений регулируемой величины, ее п производных
и управляющего воздействия.
Пусть уравнение модели объекта имеет вид:
Коэффициентами этого уравнения служат пока не определенные
функции времени. Подчеркнем, что, например, коэффициент a\(t)
может учитывать влияние производных регулируемой величины бо-
лее низкого порядка. Вообще выбор вида уравнения модели являет-
ся в достаточной степени произвольным. Основное условие — равен-
ство порядка этого уравнения заданному.
Если подставить в уравнение (5-17) действительные значения
u(t) и *<*)(/), то получим некоторую невязку:
Однако при произвольных значениях коэффициентов условие
равенства высших производных (1-4) также не выполняется. Сле-
довательно, получаем вторую невязку:
а0 (0 *<»> (0 + ах (t) = и.
(5-17)
А, (t) = u(f)-a0 (0 *<*>(0-Я1 (О-
(5-18)
А2 (О^х^О-"*<*>«.
(5-19)
В соответствии с используемым в данной работе методом син-
теза при принятых произвольных значениях коэффициентов уравнв-
76
нйя модели требуемое управление объектом следует записать
в виде
МО = М0 4Л)М+МО. (5-20)
Зависимость между невязками (5-18) и (5-19) имеет вид:
А, (0 = \(а - а0 (0 х$> (0 - ах (*)) + А2 (0 а0 (t).
Если управляющее воздействие выбрано в форме (5-20), то вы-
ражение в скобках равно нулю, т. е.
Если закон управления объектом выбран в форме, адекват-
ной принятой модели объекта, и является функцией требуемого зна-
чения высшей производной (ao(t) =#=0), то для того, чтобы динамика
синтезируемой системы управления описывалась требуемым диффе-
ренциальным уравнением (Лг=0), необходимо и достаточно, чтобы
выполнялось условие Ai=0. Последнее означает, что коэффициенты
а0 и а4 должны всегда удовлетворять уравнению модели объекта
при подстановке в него действительных значений и и х<п>. Но урав-
нение модели объекта для любых известных значений и и *(п)
является уравнением с двумя неизвестными. Поэтому один из них
можно задавать произвольно, а второй определять из уравнения
модели (5-17) как функцию величин и и х^пК Из сказанного сле-
дует, что одно и то же движение системы можно обеспечить при
большом числе законов управления вида (5-20), и при возможно-
сти точного измерения управления и высшей производной знание
действительного дифференциального уравнения объекта принци-
пиально не является необходимым.
Рассмотрим основные виды синтезируемых законов управления:
1. Пусть ао(0 = 1. Тогда из уравнения модели (5-17) получаем
ai(t)=u(t)—xL»){t)9
т. е., согласно (5-20), управление
mo=4w)(o-*<"> (о + «(о.
Соответствующая структурная схема (рис. 5-10,а) управления
объектом О является линейной и содержит внутреннюю положитель-
ную обратную связь по управляющему воздействию, внешнюю отри-
цательную обратную связь по высшей производной регулируемой
величины, сумматор, устройство сравнения и блок формирования
высшей производной ВВП.
Отрицательная обратная связь обеспечивает устойчивость си-
стемы, несмотря на наличие в схеме эквивалентного звена с бес-
конечно большим коэффициентом усиления (усилитель, охваченный
положительной •обратной связью).
2. Пусть ai(/)=0. Тогда из уравнения модели (5-17) следует:
_ u(t)
МО =Х(п) (,)'
Соответственно выражению (5-20) имеем закон управления:
xf (0
77
шп
а)
6ВП
И7
Структурная схема для этого случая (рис. 5-10,6) является
нелинейной, так как содержит ."устройства деления (для сравнения
требуемого и текущего значений высшей производной) и устройство
умножения.
Эти две структуры являются основными. Получение одной из
них зависит от того, задаемся ли мы коэффициентом при высшей
производной уравнения модели или определяем его.
Рассмотренная выше линейная структура управления соответ-
ствует дифференциальной схеме измерения возмущений [Л. 50 и 51]
и схеме самонастраивающейся
системы Г. С. Поспелова
U | 1 [Л. 41]. Как и в дифференци-
альных схемах, изменяя коэф-
фициенты положительной и от-
рицательной обратной связи,
можно получить перекомпенса-
цию и недокомпенсацию дина-
мической ошибки, вызванной
возмущением, и, следователь-
но, абсолютную инвариантность
регулируемой величины.
Однако из-за того, что по-
лучение производных регули-
► руемой величины часто связа-
но с применением инерцион-
ных измерителей, обе получен-
ные схемы управления обяза-
тельно следует проверять на
устойчивость как системы с ма-
лыми параметрами при выс-
6) ших производных [Л. 47].
5.10 При рассмотренном под-
ходе к синтезу основной
упор делается не на изу-
чение объекта (определение его действительного дифференциаль-
ного уравнения), а на измерительную часть (измерение регу-
лируемой величины и ее производных до п-го порядка включи-
тельно и управляющего воздействия). Такой объем измерений впол-
не достаточен для того, чтобы обеспечить в системе требуемый пе-
реходный процесс. Основное затруднение при реализации заклю-
чается в измерении высшей производной регулируемой величины.
Существуют объекты управления, для которых измерение высших
производных вполне возможно. К таким объектам относятся дви-
жущиеся тела, высшая производная регулируемой величины кото-
рых физически представляет ускорение, измеряемое непосредствен-
но с помощью акселерометров.
Необходимо отметить, что если требуемое движение системы
и динамику объекта можно представить в конечно-разностной форме,
то тогда структура управления объектом с неполной информацией
не содержит измерителей производных (Л. 41, 80, 81].
Рис.
73
Глава шестая
СПЕЦИАЛЬНЫЕ СИСТЕМЫ
ФУНКЦИОНАЛЬНОГО РЕГУЛИРОВАНИЯ
6-1. СИСТЕМЫ ДЛЯ ПАРАМЕТРИЧЕСКОГО ЗАДАНИЯ
ФУНКЦИЙ
а) Дифференциальные анализаторы
Метод синтеза, принятый в этой книге, и его обобщения поз-
воляют синтезировать специальные схемы, важные во многих прак-
тических приложениях. К таким схемам относятся дифференциаль-
ные анализаторы — устройства для преобразования некоторых функ-
циональных зависимостей, отображающих линии на плоскости или
поверхности (линии) в пространстве, в функции времени соответст-
венно каждой геометрической координате. Дифференциальные ана-
лизаторы являются одним из основных элементов систем програм-
много управления станками, вырабатывая задания для следящих си-
стем приводов подач.
Задание линии на плоскости
'Пусть некоторой линии на плоскости соответствует уравнение
F(xu *2)=0, (6-1)
где F есть функция, имеющая частные производные первого поряд-
ка по всем своим аргументам.
Это уравнение полагаем функциональным заданием для двух
объектов управления (интеграторов), описываемых дифференциаль-
ными уравнениями:
Х!=и,; (6-2)
х2=и2, (6-3)
где хи х2 — выходные величины; ии и2 — управляющие воздействия.
Необходимо найти структуру управления объектами (6-2) и
(6-3), отрабатывающую задание (6-1) устойчиво и с заданным ка-
чеством переходного процесса. Ошибка отработки задания (6-1)
q> = F(xit xz). (6-4)
Примем, что требуемое дифференциальное уравнение должно
иметь вид:
rS + *=°- (6-5>
Переходный процесс задаем относительно переменной s, связан-
ной со временем соотношением
ds
~di = Ь- (6-6)
79
йодстабиб в уравнение (6-5) выражения (6-4) и (6-6), получаем"
Р.
где Fx ^dF/дХг, F2=*dF/dx2, или с учетом уравнения объектов
(6-2) и (6-3),
F^+FzU^-^r- F. (6-7)
Для нахождения двух управляющих воздействий имеем одно
уравнение, что делает задачу неопределенной. Следуя работе
М. Б. Игнатьева [Л. 57], представим управляющие воздействия как
линейные функции частных производных Fi и F2:
«i ==c11F1 + cx2F2\ (6-8)
u2 = u2lFx + c22F2. (6-9)
Коэффициенты в этих уравнениях найдем из условия обраще-
ния уравнения (6-7) в тождество и дополнительных условий, если
таковые заданы. Подставив выражения '(6-8) и (6-9) в уравнение
(6-7), имеем:
CnF\ + (^12 + Сгх) FiF* + c22Fl + -j- F = 0.
Это уравнение обращается в тождество, если принять, например,
_ М.. п
Сц о » С22— "» С\2 С21
Для упрощения коэффициента схх принимаем % == . Тогда
_ F
с1Х j •
Таким образом, искомая структура управления:
«1 = — ~jr FFX -f- cF2; (6-10)
U2=-cFu (6-11)
где сф 0 — произвольная постоянная. При найденном управлении
изображающая точка (точка, координаты которой равны теку-
щим значениям выходных величин) стремится попасть из любого на-
чального положения на заданную линию и остаться на ней, так
как переходный процесс по ошибке (6-4) устойчив. Скорость пере-
мещения по заданной линии определяется свободным коэффициен-
том с.
Свойства этого коэффициента:
его значение может быть произвольным, но ни в коем случае
не равным нулю;
его знак определяет направление, а величина — скорость пере-
мещения изображающей точки.
80
Зададим скорость перемещения изображающей точки вдоль ли-
нии (6-1) при F=0:
(6-12)
и из этого условия найдем значение коэффициента с. Из уравнений
(6-2), (6-3), (6-10) — (6-12) следует, что при ^=0
с = r 1° о (6-13)
Таким образом, получена структура управления, необходимая
для устойчивого движения изображающей точки вдоль заданной
линии и с заданной скоростью:
«i= — ~f~ FFX ±
v0F2
Vf\ + f\
Щ?1
(6-14)
(6-15)
«Главная особенность полученной структуры дифференциального
анализатора состоит в том, что она обеспечивает устойчивое дви-
жение изображающей точки вдоль заданной линии. iB этом ее
принципиальное отличие от схем дифференциальных анализаторов,
F
X-
>
7
Р
F,
► п ■
Fl
п
>
1
Р
Рис. 6-1.
рассматриваемых в (Л. '57] и построенных по принципу разомкнутой
системы управления, т. е. без связи по ошибке (6-4).
Структурная схема дифференциального анализатора для закона
управления (6-14) и (6-15) представлена на рис. 6-1. Для получе-
ния функции (6-1) помимо таких функционально необходимых эле-
ментов, как интеграторы, усилители и нелинейный преобразователь,
схема содержит нелинейные преобразователи, соответствующие
функциям
Fx F2
Vf\ + fI * Vf\+fI
6—10 81
и частным производным функции (6-1), а также блок умножения
и блоки П с переменным передаточным коэффициентом (например,
потенциометры) для задания скорости движения вдоль контура.
Следует отметить, что если требуемое дифференциальное урав-
нение системы, составленное относительно ошибки регулирования
(6-4), взять .нелинейным
7-^ + sign? = 0,
то структуру управления можно упростить. В этом случае имеем
закон управления.
1 ^0^2
£*,= — — Fls\gnF±-r/
т 1 1 sign i ;т_ , — — ,
1 YF\ + F2
u2 = + —y==.
При малых значениях T качество переходных процессов не-
сколько хуже, чем при законе управления (6-14) и (6-15), однако
при этом достигается упрощение схемы управления за счет замены
множительного устройства релейным, реализующим сигнум-функцию.
Пример 6-1. Необходимо синтезировать структуру дифферен-
циального анализатора для воспроизведения с заданной скоростью
параболы
F (*!, х2) = хх — ах\— Ьх2 — с = 0.
Частные производные этой функции равны:
^i = l; F2~ — 2ях2 — Ь.
Из уравнений (6-14) и (6-15) получаем структуру дифферен-
циального анализатора:
v0 (2ах2 + Ь)
Ux— — -у- (Xj — (IXi>— ЬХ2— С) ±
|/1 4- ь2+ 4abx2+ 4a2xl '
и2 = +
[Л+&2+ *abx2 + Aa2xl
Пример 6-2. Необходимо синтезировать структуру дифферен-
циального анализатора для воспроизведения с заданной скоростью
ломаной линии — квадрата (рис. 6-'2,а), описываемого уравнением
F{xl,xt) = \xl\ + \xt\-l=0.
Частные производные [Л. 68 и 69]:
F1 = signx1; F2 = signx2.
82
Из уравнений (6-14) и (6-15) получаем:
* 1 Vo
«i = — у (I *i I + | *21 — О sign хх ± ^— sign х2;
Соответствующая структурная схема дифференциального анали-
затора (рис. 6-2,6), помимо таких функционально необходимых эле-
ментов, как интеграторы, содержит два реле, сумматоры и инвер-
Рис. 6-2.
торы. Как видно из схемы, реле и инверторы необходимы для реа-
лизации абсолютных значений и сигнум-функций. Эта схема прове-
рялась экспериментально. Результаты приведены на осциллограмме
(рис. 6-3), на которой изображена траектория переходного процесса
в системе. Заданный контур воспроизводится устойчиво.
Пример 6-3. Рассмотрим синтез дифференциального анализатора
для воспроизведения с достоянной скоростью линии, составленной
из отрезков прямых и полуокружности (рис. 6-4). Эта линия описы-
вается уравнением (см. приложение):
F (ххх2) = 2 — *i — I *21 — *? — А — I *i + I *21 — Xj — *2 I = °-
Частные производные этой функции равны:
Fx = - 1 - 2х, - (1 - 2хл) sign (хх + | х21 - х\ - х\);
F2 = — sign х2 — 2х2 — (sign х2 — 2х2) sign (х, + | х21 — х] — х\).
Структуру дифференциального анализатора определяем ло фор-
мулам (6-14) и (6-/15).
6* 83
б) Генератор двух синусоидальных колебаний
Требуется определить структуру генератора двух синусоидаль-
ных колебаний:
хх = A cos (о/;
х2 = A cos (wt + z)
с регулируемыми частотой, амплитудой и сдвигом фаз. Эту зада-
чу можно рассматривать как задачу автоматического поддержания
такой функциональной зависимости между переменными, при кото-
X,
\
-ко/
0
V
Рис. 6-3. Рис. 6-4.
(6-16)
рой они изменяются согласно уравнениям (6-16). Требуемую зависи-
мость получаем из уравнения, соответствующего фигуре Лиссажу:
F (х19 х2) = х\ + х\ — 2xxx2zo$>z— A2 sin2 2 = 0. (6-17)
В качестве силовых элементов, на выходе которых необходимо
получить колебания, возьмем интеграторы. Тогда поставленная зада-
ча сведется к синтезу структуры дифференциального анализатора,
воспроизводящего зависимость (6-17).
Следуя изложенному выше методу синтеза, находим сначала
частные производные функции (6-17), а затем по формулам (6-14)
и (6-15) находим требуемый закон управления:
2
их = — -у (х\ + х\ — 2x^2 cos z — A2 sin2 z) (х, — х2 cos z) +
+ 2С (x2 — Xi cos 2);
u2 = — 2C (Xj — x2 cos z).
Можно показать, что в установившемся режиме (F=0) коэффи-
циент С связан с частотой зависимостью
84
Так как требуемый переходный процесс в системе соблюдается
при любом СФ*0, то закон управления можно записать в форме
2
Hi = — у (*? + *| — 2*Л cos ^ — Л2 sin2 z) (Xj —
—x2cosz) + sing (x8 —x^osz);
«2 = — sin'z " (Xl ~ *a cos^'
(6-18)
Если необходимо генерировать синусоидальные колебания со
сдвигом фаз в 90°, «например для частотного регулирования скоро-
сти двухфазных асинхронных двигателей, то тогда структура управ-
ления существено упрощается:
2
tix =s — -у- (*i!+'*2 ~~ ^ Xl + И2 ^ ""^i*
Полученную структуру управления, как, впрочем, и структуру
(6-18), можно еще более упростить заменой операции умножения
на функцию (6-17) операцией умножения на ее знак (этот прием
уже рассматривался ib предыдущем разделе). Тогда
2х "\
«1 =* — -у1-sign*1— Л2) + I (б-19)
Н2= —* ©Xi. J
Рис. 6-5.
Общая структура синтезированного генератора, соответствую-
щая закону управления (6-18), представлена на рис. 6-5, где #i —
блоки переменных коэффициентов, пропорциональных отношению
<o/sinz; #2 — блоки переменных коэффициентов, пропорциональных
COS Z;
85
Главная особенность синтезированного генератора заключается
в том, что в нем возможно независимое регулирование частоты и
амплитуды колебаний, а такжз сдвига фаз между ними. Это озна-
чает, что при перестройке задатчика частоты III амплитуда колеба-
ний не изменится, а лри перестройке задатчика амплитуды (вход-
ное напряжение на сумматор) не
изменятся частота и сдвиг фаз и т. д.
Нижний предел генерируемой часто-
ты практически неограничен (вплоть
до нуля), а верхний предел частоты
|| определяется максимально возмож-
ными коэффициентами усиления вы-
ходных усилителей схемы управле-
ния. Верхний предел регулируемого
сдвига фаз равен ±90°, а нижний
отличен от нуля и также зависит от
максимально возможных коэффи-
циентов усиления выходных усили-
телей.
Отметим также, что в извест-
ных схемах для получения двух
колебаний переменной "частоты с ре-
гулируемым сдвигом фаз между
ними используются два конструк-
тивно различных элемента: генера-
торы и фазосдвигающее устрой-
ство 1(ФСУ). Для поддержания по-
стоянного сдвига фаз при измене*
|нии частоты требуется специаль-
ная перестройка ФСУ, что представ-
IlilllllllllllllMlrJ!} л*ет достаточно сложную техни-
ческую задачу fЛ. 70]. В синтезиро-
ванной схеме регулирование всех
трех параметров (частоты, амплиту-
ды и сдвига фаз) выполняется с по-
мощью одной автоматической си-
стемы, решающей задачу функцио-
нального регулирования этих пара-
метров.
Схема генератора была прове-
рена экспериментально на аналоговой
моделирующей установке МНБ-1. На
осциллограмме рис. 6-6,а показана
кривая переходного процесса при
изменении задаваемой амплитуды
колебаний для частоты 0,15 гц и
сдвига фаз, равного 30°. При изме-
нении сдвига фаз до величины, рав-
ной 60°, амплитуда и частота оста-
ются неизменными (рис. 6-6,6). При изменении задаваемой частоты
до величины, равной 0,06 гц, амплитуда и сдвиг фаз также остаются
неизменными (рис. 6-6,в).
Метки времени на этих осциллограммах представляют верти-
кальные линии с интервалом 1 сек.
Рис. 6-6.
6-2. АНАЛОГОВЫЕ СИСТЕМЫ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ
а) Определение корня, ближайшего к начальному значению
переменной
Требуется определить вещественные корни конечных уравнений
(алгебраических и трансцендентных) с помощью аналоговых
устройств: электронных усилителей, интеграторов и нелинейных пре-
образователей. Если искомое значение корня уравнения
F(x)=0 (6-20)
фиксировать на выходе интегратора
* = и. (6-21)
то тогда эту задачу можно рассматривать как задачу синтеза си-
стемы управления объектом (6-21) для автоматического поддержа-
ния функционального соотношения (6-20).
Соответствующая ошибка
4>=F(x). '(6-22)
Требуемое дифференциальное уравнение запишем в следующем
виде:
так как объект управления — звено первого порядка.
Из уравнений (6-6), (6-20)—i (6-23) получаем требуемое управ-
ление
№ (х)
где
Если коэффициент преобразования % = 1, то
Т F'x(x)
(6-25)
Этот закон управления является непрерывным аналогом алго-
ритма Ньютона.
Если ps=(f'x)2, то
ud=-y F'xF(x). (6-26)
Этот закон управления соответствует поиску .корня по методу
градиента [Л. 71].
(Варьируя форму требуемого дифференциального уравнения и
коэффициента преобразования, можно получить другие, более удоб-
ные для реализации законы управления. Если, например, Ps=|^'*|,
87
то при требуемом дифференциальном уравнении вида (6-23) закой
управления имеет вид:
ud = --Y ^р* ^ fx =— -jr-F (х) sign/7'*.
Такой закон управления примечателен тем, что вместо измере-
ния частной производной F'x достаточно измерять только ее знак.
Если требуемое дифференциальное уравнение является нели-
нейным,
r~||- + sign? = 0, (6-27)
то тогда для коэффициентов преобразования, равных 1, {F'x)2 и
l^'xl, получаем законы управления, соответственно в виде:
1 sign F (х) .
Ud = — ~f рг » (Ь~2Ъ)
tfd = — 4" f/* si2n F W; <6"29)
ud = — -jr sign F'x sign F (x) = — -jr sign (FXF). (6-30)
Последний закон управления является наименее чувствитель-
ным к отклонению параметров нелинейных преобразователей, так
как используется только знак функций.
Р
Рис. 6-7.
Схема решения уравнений для случая закона управления (6-30)
представлена на рис. 6-7. Она содержит интегратор, нелинейные
преобразователи для получения функций F(x) и F'x(x), реле, блок
умножения.
Особенность законов управления при $8ф\ заключается в том,
что устойчивость достигается не только при F(x)—0y но и при
F'x(x)=0. Поэтому результат на выходе интегратора можно счи-
тывать только тогда, когда сигнал ошибки (6-22) равен нулю. Если
уравнение (6-20) имеет несколько вещественных корней, то в за-
висимости от начального значения переменной устойчивость систе-
мы соответствует значению корня, ближайшего к начальному эна-
88
чению. Для получения других корней надо изменить начальные
условия. Однако порядок этой смены трудно наметить без аналити-
ческого исследования заданного уравнения.
Пример 6-4. (Пусть дано трансцендентное уравнение
F(x) =ех—х2=0.
Производная этой функции по переменной х
F'x=e*—2x.
Закон управления интегратором, требуемый для определения
корня по уравнению (6-26), имеет вид:
1
ud = — -jr(e* — 2х) (е* — х2).
б) Определение корня в заданной области изменения переменной
Ставится задача поиска корня уравнения (6-20) в определен-
ной области изменения переменной, характеризуемой неравенствами:
И*; } <6"31>
X<:Mg
где Mg, tng — соответственно верхняя и нижняя границы области.
Указанные неравенства можно представить в виде единого аналити-
ческого выражения — равенства (см. приложение)
So (*) = I х — mg I + I x — Mg\ —Mg + mg=0. (6-32)
Это уравнение определяет все точки допустимой области из-
менения переменной. Если границы области есть заданные функции
времени mg=\mg,(t) и Mg=Mg(t), то тогда для поиска всех корней
уравнения (6-20) можно производить сканирование по независи-
мой переменной х.
Зависимость (6-20) с учетом ограничения (6-32) можно запи-
сать в виде (см. приложение)
<bo(x) = \F(x)\+go(x) = 0 (6-33)
или
Фо (*) = F (*)]« +(*)=0. (6-34)
Ошибка регулирования для этого случая такова:
f = | F(x) I + I x-mg I + \х-Мй I _Afg + mg.
Закон управления интегратором для определения корня уравне-
ния (6-33) согласно уравнению (6-30) имеет вид:
ud = —— sign Ф'ох sign [\F(x)\ + \ x — trig \ + \ x — Me | —
— Mg + mg],
где Ф'рх = F'x sign F (x) + sign (x — mg) + sign (x — Mg).
89
Соответствующая структурная схема системы представлена на
рис. 6-8. Схема содержит два нелинейных преобразователя для по-
лучения функции (6-20) и ее производной, пять реле, которые с по-
мощью рассмотренных выше схем с инверторами |реализуют сиг-
Рис. 6-8.
нум-функции и абсолютные значения функции, а также сумматоры
и интепратор. Особенностью схемы является то, что она не содер-
жит множительного устройства.
Пример 6-5. Дано уравнение
F(x)=x2—3x+\2=0.
Требуется определить его корень в диапазоне изменения пере-
менной 1,5—2,5, С учетом ограничения составляем по уравнению
(6-33) выражение
ф0 (х) = | х2 — Зх + 2 | + | х — 2,5 | + | х — 1,5 | — 1 =0.
Производная этой функции равна:
ф'ох. (X) = (2х - 3) sign (х2 _ Зх + 2) + sign (х - 2,5) +
+ sign (х— 1,5).
Закон управления определяем по уравнению (6-26):
ud = —-^r [(2х — 3) sign (х2 — Зх + 2) + sign (х — 2,5) + sign (х —
— 1,5)] [|х2— Зх + 2 | + | х —2,5 | + | х— 1,5 | — 1].
90
бтметим, в частности, что если начальное значение х0=1, т. е.
соответствует одному из корней уравнения, не находящемуся в за-
данной области, то система в этой точке неустойчива. Однако лри
х=2 (второй корень уравнения) система устойчива.
•Изложенный метод может быть также использован для реше-
ния систем уравнений и определения комплексных .корней.
6-3. СИСТЕМА С ПЕРЕМЕННОЙ СТРУКТУРОЙ ДЛЯ ПОИСКА
ЭКСТРЕМУМА ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
а) Поиск в открытой области
Задана функция многих переменных, которую необходимо опти-
мизировать (целевая функция):
*n = fo i = 1.2, п— 1.
Эту функцию представим как дополнительную переменную и да-
лее рассмотрим оптимизацию одной из переменных уравнения
F (xt) =0; / = 1,2, (6-35)
(такая постановка задачи характерна в первую очередь для опти-
мизации функций, заданных в неявном виде).
Процесс поиска экстремума одной из переменных уравнения
(6-35) составим из двух этапов:
попадание на многообразие в п-мерном пространстве, опреде-
ляемое уравнением (6-35);
движение по этому многообразию в сторону уменьшения (или
увеличения) оптимизируемой координаты.
Структуру системы управления движением изображающей точки
к заданнному многообразию (6-35) (первый этап) находим, следуя
методу, изложенному в предыдущих параграфах этой главы. Вводим
ошибку регулирования
кр-Щх{). (6-36)
Зададим дифференциальное уравнение для изменения этой
ошибки во времени:
r-S-+*=o- <б-з7>
где
п
dy _ dF dXj
ds ~~ 2j dxt ds
i=\
Искомое значение каждой переменной определяем на выходах ин-
теграторов. Тогда из уравнений (6-36) и (6-37) получаем:
п
][]/чи< + -у^=0, (6-38)
где
г дР о ds
91
Зададим каждое управляющее воздействие на первом этапе
в виде линейной комбинации частных производных функций (6-35):
п
= £ CaFr, /=«1,2, .... я (6-3§)
1=1
(индекс I обозначает номер этапа работы системы).
Для определения значений коэффициентов d i подставим выра-
жение (6-39) в уравнение (6-38) и исследуем полученное уравнение:
п п
J] '« Р] + J] ('« + en) FtFi + If- - 0. (6-40)
/= 1 U=l
Чтобы это уравнение обратилось в тождество при любых функ-
циях F и Fx, достаточно, например, принять значения коэффициен-
тов равными:
F
с и = — j \
сц=0; 1ф1\ / = 1,2,
i=\
Полученная при этом структура управления
FF
Т
-И- (6-41)
не содержит перекрестных связей и соответствует известному ме-
тоду градиента. Однако если накладываются дополнительные усло-
вия на характер движения к многообразию (6-35), то тогда выбо-
ром коэффициентов перекрестных связей (сц\ 1Ф1 можно добиться
соблюдения этих условий.
Отметим, что если выбрать требуемое дифференциальное урав-
нение в форме (6-27), то тогда структура управления на этом этапе
упростится, ибо вместо блоков умножения структура содержит ре-
лейный элемент для реализации сигнум-функций:
и\= — -—-signF. (6-42)
Когда ошибка регулирования (6-96) станет равной нулю (этап II),
закон управления i(6-39) необходимо видоизменить таким образом,
чтобы обеспечить движение оптимизируемой координаты к экстре-
муму по многообразию (6-35). В этом случае уравнение 1(6-40) при-
мет вид:
л п
£ citF2t + £ (cu + CtJFtFt^O.
92
Для того чтобы это уравнение обратйДось в тождество, доста-
точно, например, принять*значения коэффициентов равными:
с„ = 0,
сц = — си; / = 1,2,...,/!.
Потребуем, чтобы оптимизируемая координата хп уменьшалась
(или увеличивалась) во времени при движении изображающей точ-
ки. Для этого коэффициенты закона управления по этой координате
необходимо принять равными [Л. 57]
Cni=±Fi.
Тогда
п
^=^ = ±2 F\. (6*43)
1=1
Знак плюс соответствуег увеличению координаты (движение
к максимуму), а знак минус — уменьшению координаты (движение
к минимуму).
Остальные управляющие воздействия при этом равны:
п
и}1 =%ctlFt; 1 = 1,2, .... (6-44)
f=l
причем cni = — с1п =5 ± /V, Сц = — си = const; I ф I.
Пример 6-6, Рассмотрим целевую функцию вида
Х2 — #1 ~Ь 2Xj.
Представим ее в виде уравнения
F (xltx2) = х2 — х\ — 2хх = О,
одну из переменных которого (х2) необходимо минимизировать.
Частные производные функции F:
Fi—2(*i+l);
F2=\.
Тогда по уравнению (6-39) получаем структуру управления на
первом этапе в следующем виде:
— 2с„(х, + 1) +с12;
и\= — 2с21(х1+\) + с22.
Коэффициенты этого закона управления принимаем равными:
с и = с22 = —- j (х2 х*^ — 2xi);
Cj2 =^ (?2 j = О»
93
Тогда закон управления на Первом этапе Примет следующий вид:
2
и\ = —(х2 — x2 — 2xl) (*i + 1);
i_ _L 2
и~2 — — j (х2 — Xj — 2Xj).
Когда значения переменных на выходах интеграторов станут таки-
ми, что будет выполнено условие х2 — X2—2х2 = 0, структуру
управления нужно будет переключить для движения по заданной
кривой в сторону экстремума. Закон управления на втором этапе,
согласно уравнениям (6-43) и 6-44):
«}1=-2(х,+ 1);
Эти уравнения обеспечивают уменьшение минимизируемой коор-
динаты до тех лор, пока составляющие скорости изображающей
точки не станут равными нулю. Это соответствует устойчивой точке,
которая является искомой точкой минимума.
б) Поиск при наличии ограничений
Пусть допустимая область изменения переменных функции
(6-35) определяется системой неравенств
gj(Xi)>0; 12, m, >(6-45)
которую представим в виде одного уравнения (см. приложение):
т т
go (*<) = 11 I gi[*t) I - S 81 (*«) 0. (6-46)
Возможны два. способа решения поставленной задачи.
Первый из них предусматривает три этапа управления: пере-
вод изображающей точки в область ограничений и затем управле-
ние, аналогичное управлению в открытой области, которое, как по-
казано выше, состоит из двух этапов.
Второй способ предусматривает два этапа управления: перевод
изображающей точки на ту часть многомерной поверхности (6-35),
которая находится в области ограничений, а затем движение изо-
бражающей точки по этой поверхности в сторону уменьшения (или
увеличения) оптимизируемой координаты.
При втором способе функцию (6-35), все точки которой удов-
летворяют ограничениям (6-45), представим в виде (см. прило-
жение)
Фо (**) - ! Р (xt) | + g0 (*t) = 0 (6-47)
или
Ф0 (*,) = [F (Хг)] 2 + go (xt) = 0. (6-48)
Особенность функции Фо(Хг) заключается в том, что при значе-
ния хи не удовлетворяющих ограничениям (6-45), она положи-
тельна.
94
Законы управления интеграторами аналогичны законам (6-39),
(6-43) и (6-44), с той разницей, что вместо функции (6-35) исполь-
зуются (в зависимости от этапа поиска) функции (6-46) или (6-47)
и (6-48). Как й .в предыдущем случае, система позволяет находить
только локальный экстремум.
В частности, законы управления видов (6-39) и (6-41) исполь-
зуются на первом этапе управления (второй способ) и на первом и
втором этапах (первый способ), а законы управления (6-43) и
(6-44) используются на втором этапе (второй способ) и «а третьем
этапе (первый способ).
Таким образом, синтезируемая система управления обладает пе-
ременной структурой (соответствено числу вводимых этапов). Такое
построение системы позволяет, с одной стороны, разделить во вре-
мени решение двух сложных задач, возникающих при оптимизации:
учет ограничений и движение к экстремуму. Однако, с другой сто-
роны, изменение структуры системы приводит к возможности воз-
никновения в ней скользящих режимов.
|По сравнению с известными методами оптимизации при нали-
чии ограничений, например методом «штрафных» функций (Л. 71],
предложенный метод обладает следующими преимуществами:
однократность решения задачи нахождения экстремума (нет
варьируемых весовых коэффициентов);
решение является методически точным;
учет ограничений прост;
аппаратурная реализация системы относительно проста, а имен-
но — не требует усилителей с большими коэффициентами усиления
и множительных устройств;
возможен учет ограничений, накладываемых не только на аргу-
менты оптимизируемой функции, но и на саму функцию;
оптимизируемая функция может быть связана с аргументами
неявной зависимостью.
Подробно этот метод оптимизации описан в (Л. 27, 82].
Для иллюстрации метода синтеза рассмотрим пример.
Пример 6-7. Пусть дана целевая функция того же вида, что и
в примере 6-6. Требуется минимизировать переменную х2 с учетом
ограничения
Xi>0,5.
Это неравенство сведем к равенству:
go(xi) = 0,5 +0,5=0.
Частные производные этой функции равны:
goi = sign.(*i+0,5)—1;
g02 = 0.
Первую структуру управления определим по уравнению (6-42),
при этом
с12 = с21 = 0;
g 1
Си =с22 == — — = f( \ х1 — 0,5\—х1 + 0,5);
P. = fioi +вог = 2[1 — sign (xt — 0.5)] >0.
95
Тогда закон управления примет вид:
и\ = у- №п (л.—0,5) —1J;
а| = 0.
Управления на втором и третьем этапах соответствуют управле-
ниям на первом и втором этапах примера 6-6, так как на этих эта-
пах ограничение уже не учитывается, следовательно,
и]1 = у- (х, -х* - 2*,) (х, + 1);
и*1 = — -i- (х2 — х^ — 2х,);
и\и = -2(х1+1);
«4" 4(^ + 1)».
Рассмотрим управление по второму способу (две структуры
управления).
Преобразованную целевую функцию запишем в виде
ф0 (Х!,х2) = | х2 — х\ — 2Xt I + 4" ( I x* — 0,5 I + 0>5) =0.
Частные производные этой функции:
Фо1 = - 2 (х, + 1) sign (х2 - х] - 2х,) + 4" fslSn (*i - °-5) - Ц »
O02 = sign (х2 — х? — 2xt).
Управление на первом этапе выберем согласно уравнению
(6-42):
«! = — -р-Ф01;
i 1 *
«2 == — — Ф02-
Управление на втором этапе соответствует управлению «а вто-
ром этапе в примере 6-6:
и]1=-2(х1+1);
а'1 = -4(х,+ 1И.
Структурная схема системы управления, соответствующая вто-
рому способу управления, приведена на рис. 6-9, где П\ — блок
с передаточным коэффициентом, равным 0,5; Я2 и /73 — блоки с пе-
редаточными коэффициентами, равными 1/Г.
По описанному выше методу поиска экстремума функции мно-
гих переменных необходимо отметить следующее. Выбор структу-
ры управления в целом, «а также на каждом из этапов является
до некоторой степени произвольным, хотя, конечно, дает возмож-
ность достижения экстремума. По-видимому, если исходные струк-
96
туры (6-39), (6-41)—(6-44) .выбрать в другой форме, то можно будет
упростить схему управления.
Например, на заключительном этапе поиска экстремума (движе-
ние по многомерной поверхности в сторону увеличения или умень-
Рис. 6-9.
шения оптимизируемой переменной) структура управления по этой
переменной была принята в форме (6-43), т. е. как сумма квадра-
тов частных производных. (Выберем структуру управления в виде
суммы абсолютных значений частных производных:
п—\
<#=i»=± 2 \Fil
l=\
что соответствует выбору части коэффициентов закона управления
в форме Cni=[±slgn Ft.
Такой закон управления также удовлетворяет условию увеличе-
ния (или уменьшения) оптимизируемой переменной во времени.
Однако в данном случае схема управления упрощается с конструк-
тивной точки зрения. Действительно, вместо нелинейных преобразо-
вателей (квадраторов) можно использовать простые элементы, на-
пример реле |(для получения абсолютных значений функций).
'Кроме того, расширяются функциональные возможности систе-
мы (при тех же конструктивных элементах). Дело в том, что когда
оптимизируемая переменная является неявной функцией, соответст-
вующая частная производная есть в общем случае некоторая функ-
ция
Fn = Fn(xt)£Ui = \X ...,'л.
Тогда при законе управления (6-43) и условиях Cni—dtFi,
Fn¥=l необходимо в каждом канале управления иметь блок умно-
7-Ю 97
жения. При рассматриваемом подходе структуру управления на
этом этапе можно записать в виде
п п—1
и}1 = £ cufi = £ cii?i TFnilgnFu / = 1,2, лг— 1,
/=1 1=2
учитывая, что cnl = — cln = + sign Ft, или при замене индекса cni =
= — Cin=± sign Ft.
Таким образом, вместо операции умножения (FxFn) ib каждом
канале управления достаточно реализовать операцию умножения. на
знак функции {Fn sign Fi), что конструктивно гораздо проще, так
как может быть произведено с помощью реле.
6-4. ЛОГИКО-ДИНАМИЧЕСКИЕ СИСТЕМЫ
Логико-динамическими назовем такие системы автоматического
управления, задания для работы которых включают логические со-
отношения, а динамика объекта управления описывается дифферен-
циальными уравнениями.
Имеется \х инерционных объектов с выходными величинами Xj
и управляющими воздействиями Uj, причем каждый из них описы-
вается некоторым дифференциальным уравнением порядка tij. Во
всех рассмотренных выше системах функционального регулирования
задание для работы формировалось в виде конечного соотношения,
связывающего выходные величины Xj. В данном случае задание
представляет логическую функцию от выходных величин объектов
управления
lfc(jc,)=0; Л = 1,2, (6-49)
где переменные связаны знаками основных логических операций, на-
пример конъюнкции, дизъюнкции и отрицания.
Задача структурного синтеза этих систем заключается в опре-
делении такой структуры управления каждый инерционным объектом
Uj = Uj (xf)y /=0,1,2, ...,п,— 1; / = 1,2, (6-50)
чтобы в установившемся режиме соблюдались заданные логические
соотношения (6-49).
(Помимо логических соотношений, могут быть заданы одновре-
менно конечные соотношения типа (4-1) или задания в функции
времени, причем общее число всех заданий не должно превосходить
числа управляющих воздействий.
Рассмотрим случай, когда все объекты управления описываются
дифференциальными уравнениями первого порядка («j='l), а вы-
ходные величины объектов Xi измеряются непрерывно. Последнее
означает, что логические задания вида '(6-49) относятся к катего-
риям непрерывной логики.
В непрерывной логике [Л.72] значения истинности величин образу-
ют ограниченное множество действительных чисел, содержащее свою
верхнюю грань В и нижнюю грань А. Пусть это множество симметрич-
но относительно точки С = -g- (А + В), которую назовем центром мно-
жества. При этом В есть значение истинности полностью истин-
98
нбго высказывания, а Л — полностью ложного высказывания. Если
х — это значение истинности -некоторого высказывания р, то р тем
более истинно, чем ближе х к В, и тем более ложно, чем ближе х
к Л. Если высказывание р в равной мере истинно и ложно, то его
значение истинности равно С. Основными логическими операциями в
этой системе являются обобщенные дизъюнкция, конъюнкция и от-
рицание. Значение истинности обобщенной дизъюнкции означает вы-
бор наибольшей величины из значений истинности двух каких-либо
высказываний хи х2 и определяется как
х, V*2 =max (ХрХ2).
Значение истинности обобщенной конъюнкции означает выбор
наименьшей величины из значений истинности двух каких-либо выс-
казываний Xi и Х2 и определяется как
хх/\х2 =min (Xj,x2).
Значение истинности обобщенного отрицания определяется сле-
дующим образом:
х = Л + В — х = 2С —X. (6-51)
Если указанные логические операции выразить через операции
обычной алгебры, то можно свести логические задания типа (6-49) •
к конечным соотношениям между выходными величинами объектов
управления. Тогда для решения задачи структурного синтеза можно
использовать разработанный метод синтеза систем функционального
регулирования. Дизъюнкция и конъюнкция при этом могут быть
выражены следующим образом {Л. 72]:
х, V*2 =-тг(*1 + *2 + I *i —*i | ); (6-52)
*i Л *2 = "У" <Xl + ^2 — I ^1 — ^2 I )• (6-53)
Логическая операция отрицания определена через понятия обыч-
ной алгебры (6-51). iB частности, если центр множества значений
истинности какой-либо величины совпадает с нулем (С=0), то опе-
рация отрицания сводится к инверсии знака:
х=-х. (6-54)
.Полученные выражения (6-52) — (6-54) относительно просты и
потому удобны для синтеза. Но они дифференцируемы только один
раз, т. е. применимы лишь в случае объектов первого порядка. Бо-
лее общим алгебраическим представлением логических операций
дизъюнкции и конъюнкции являются выражения вида (Л. 73 и 74]:
*i V *2 = -if ^ *i + *2 + — 2ах,х2 ^ ; (6-55)
XiA^ = y^i + ^- А + А — 2aXjX2 ^ ; (6-56)
-1<а<+1.
7* 99
Частным случаем (при а=1) являются формулы (6-52)—(6-54).
Необходимо подчеркнуть, что выражения (6-55) — (6-56) имеют про-
изводные по х .выше первого порядка.
Метод синтеза структуры управления дифференциально-логи-
ческими системами состоит из следующих основных этапов.
Во-первых, логические задания надо представить в такой фор-
ме, чтобы над ©ходящими в них переменными производились только
операции обобщенной конъюнкции, дизъюнкции и логического отри-
цания. Такое преобразование всегда возможно, так как эти опера-
ции обладают функциональной полнотой.
■Во-вторых, необходимо выразить операции непрерывной логики
через операции обычной алгебры по формулам (6-52) — (6-54). Тогда
задания для работы системы образуют конечные соотношения меж-
ду выходными величинами объектов:
I *<—I) =°; 1Фп
/,/= 1,2, .... р.. (6-57)
Далее используем процедуру синтеза, разработанную в преды-
дущих разделах.
Пример 6-8. Даны три объекта, описываемые дифференциальны-
ми уравнениями первого порядка с постоянными коэффициентами:
#20*2 "Г* #21#2 == #2»
a3Qxs + a3Xx3 = u3.
Требуемые соотношения между выходными величинами:
*i + *2 — 1 — 0;
«2 + *а — 1 = 0;
ХХ^Х3 + Х2ЦХ3.
Третье соотношение является логическим и означает, что ве-
личина Xi должна быть равна алгебраической сумме величины х3 и
наибольшей из величин х2 и х3. Используя выражение (6-52), это
соотношение приводим к ©иду
*i — *% — 4" (*2 + *г + 1 Х2 — Хг | ) —0.
Ошибки регулирования заданных соотношений равны:
?i = *i + *i — 1;
у8 = х2 + х,— 1;
Ъ — Хх — Хг — -д" (Х2 + Хг + \ Хг — Хь | ).
100
ЗаДадим требуемые дифференциальные уравнения в виде:
Mi + <Pi = °;
+ Ъ = 0;
*if з + Уз = 0.
Подставив в эти уравнения выражения для ошибок, находим:
Xj + х2 = — ~г~ '
м
• , • ?2 .
Х2 + Х3= — ,
— 0,5 (1 + sign (х2 — х3)) х2 — 0,5 (3 — sign (х2 — х3)) х3 = — ^ •
Таким образом, получены три уравнения с тремя неизвестными,
которые входят в них линейно и представляют требуемые значения
высших производных выходных величин объектов.
Из этих уравнений определяем:
• Ai . •. _ __^2_. • Аз_
Х\& — Д » #2* — Д » *3d — Д
где
Поэтому
А = sign (х2 — х3) ф 0.
iid = Ai sign (х2 — х3);
x2d = A2 sign (х2 — х3);
x3d = А3 sign (х2 — х8).
причем
Ai = (1 - sign (х2 - *,)) - (3 - sign (х2 - х3)) - ^ ,
А2 = (з-sign (х2-х3) ) - + ^ ;
Дз = -^" + -^7--^(3+ sign (х2 -*.))•
Структуру управления найдем, подставив эти выражения в диф-
ференциальные уравнения объектов вместо первых производных,
т. е.
U\& = #io#id + #nXi;
ui& = #2o#2<i + ^21x2;
M3d — #30*3* + Л31Хз.
101
Пример 6-9. На вход системы поступает некоторый сигнал y(t).
Необходимо найти такую структуру этой системы, чтобы на ее вы-
ходе выделилось и запомнилось максимальное значение сигнала
y(t) (независимо от времени появления этого максимума).
Такую систему можно (рассматривать как логико-динамическую.
Действительно, сформулированное условие запишем в виде
X =zx\J у,
где х — выходная величина системы. Тогда, используя уравнение
(6-52), получаем:
х = -^(х + у+ | х — у | )
или
У — х+ I У — * I =0,
что представляет требуемое соотношение между входной и выход-
ной величинами синтезируемой системы. Поскольку необходимо за-
поминание выходного сигнала, то в качестве исполнительного эле-
мента системы (объекта управления) возьмем интегратор >(х = и).
Ошибка регулирования заданного соотношения равна:
Ф=(е+'|е|,
где г—у—х. Особенность этой ошибки заключается в том, что она
неотрицательна. Требуемое дифференциальное уравнение запишем
в виде
Из этого уравнения с учетом выражения для ошибки получаем
требуемое значение высшей производной выходной величины объек-
та:
*й — У + Г (I + signs) *
Можно принять коэффициент преобразования равным 1 +sign е.
Действительно, когда 8^0, т. е. при х^у, коэффициент равен нулю.
Но тогда ошибка регулирования также равна нулю. Если же е>0,
то ошибка регулирования и этот коэффициент больше нуля. Тогда
закон управления принимает вид:
u^y + Y" (6-58)
Ори достаточно больших значениях коэффициента усиления
1/Г и относительно небольшой скорости изменения входного сигнала
у закон управления можно упростить:
ил^у- (6-59)
102
Эго следует из условия устойчивости системы
полученного для закона управления (6-59) и функции Ляпунова ви-
да 1/=«р2.
Структурная схема системы соответствующая закону управле-
ния (6-59), представлена на рис. 6-10. Помимо интегратора и эле-
мента сравнения, схема содержит усилитель с нелинейной характе-
ристикой, который усиливает только положительные входные сиг-
налы.
Аналогично можно синтезировать систему для выделения и за-
поминания минимального значения сигнала y(t).
Рис. 6-10.
ЗАКЛЮЧЕНИЕ
Рассмотрена задача структурного синтеза систем автоматическо-
го управления объектами п-го порядка. Изменение во -времени вы-
ходной величины объекта должно соответствовать дифференциаль-
ному уравнению, составленному относительно этой величины и зада-
ния. Нужного качества регулирования и устойчивости системы дос-
тигают путем выбора коэффициентов дифференциального уравнения
и его формы (линейной или нелинейной). IK такой постановке можно
свести синтез многих систем для отработки заданий, представлен-
ных как в виде функций времени, так и в виде нелинейных соот-
ношений между выходными величинами объекта.
Для синтеза этих систем предложен метод, основанный на со-
блюдении в каждый момент времени равенства .высшей производ-
ной выходной величины объекта ее значению, определенному из тре-
буемого дифференциального уравнения системы. Управление, необхо-
димое для соблюдения этого равенства, находится путем подстанов-
ки требуемого значения высшей производной .в уравнение объекта.
Определены основные условия выполнения этого равенства.
Метод распространен на объекты управления, описываемые си-
стемой дифференциальных уравнений первого порядка. При этом
в основу синтеза положено соблюдение равенства действительного
значения производной координаты, явно зависящей от управления,
ее требуемому значению.
1При использовании данного метода решение задачи структурно-
го синтеза (для определенного объекта управления) в первую оче-
редь зависит от вида требуемого дифференциального уравнения
движения системы. Каждому виду такого уравнения соответствует
своя структура управления. В этом смысле рассмотренное решение
задачи синтеза является неоднозначным.
Предварительное задание дифференциального уравнения систе-
мы, с одной стороны, обусловливает сравнительно широкую область
применения метода и относительную простоту пользования им, а
с другой стороны, диктует необходимость измерения п—1 произ-
водной выходной величины и максимум п производных задающего
воздействия и возмущения, а также знания дифференциального
уравнения объекта. Кроме того, такой подход требует реализации
некоторых нелинейных зависимостей, определяемых в общем случае
видом дифференциального уравнения объекта и задаваемого диффе-
ренциального уравнения.
Метод позволяет синтезировать системы управления как с вре-
менным заданием (одномерные и многомерные), так и с заданием,
которое является функцией выходных величин объекта (системы
Ю4
функционального .регулирования). Последние в зависимости of чйс\ла
задаваемых уравнений связи классифицированы на одноовязные и
многосвязные, на системы с полным и неполным заданиями (в за-
висимости от наличия в уравнениях связи высшей производной ве-
личины объекта). Решение задачи синтеза систем функционального
регулирования актуально, особенно в связи с тем, что к настоящему
времени отсутствуют регулярные инженерные методы их синтеза.
Для синтеза систем функционального регулирования с неполным
заданием предложен принцип, названный принципом дополнения.
Он заключается в формировании таких новых уравнений связи, ко-
торые следует рассматривать как требуемые дифференциальные
уравнения системы, причем их решения суть исходные уравнения
связи.
Автоматические системы, синтезированные предложенным мето-
дом, обладают важными свойствами.
Во-первых, обеспечивается требуемое движение системы управ-
ления нелинейным объектом с точки зрения устойчивости и качест-
ва регулирования.
во-вторых, если в требуемое уравнение системы не входит воз-
мущение действующее на объект, то полученные системы управления
являются инвариантными.
В-третьих, при синтезе многомерных автоматических систем
можно достичь не только инвариантности каждой регулируемой ве-
личины, но и -автономности их изменения во времени.
Предложенный метод синтеза обобщен на случай объектов
управления, описываемых дифференциальными уравнениями, которые
неразрешимы в алгебраической форме относительно управляющего
воздействия или содержат его производные. Это приводит к нали-
чию в структуре управления вычислительных устройств, решающих
уравнения конечные или дифференциальные.
(Метод может быть применен и в том случае, когда требуемое
уравнение движения системы имеет в качестве аргумента не время,
а некоторую функционально связанную с ним величину. Путем вы-
бора этой зависимости можно добиться упрощения структуры систе-
мы. Приведено также обобщение метода на случай объектов, вид
дифференциальных уравнений которых известен с точностью до по-
рядка. В этих системах требуется измерение п производных регу-
лируемой величины.
Экспериментальная проверка отдельных синтезированных не-
линейных систем показала, что они не являются критичными к изме-
нению параметров объекта и параметров нелинейных элементов бло-
ка управления.
Следует отметить, что разработанный метод нашел применение
для синтеза специальных систем функционального регулирования:
аналоговых вычислительных систем для решения уравнений и по-
иска экстремума, системы для воспроизведения линий и поверхно-
стей в пространстве и логико-динамических систем.
Решение таких различных по своему характеру задач синтеза
является, в частности, свидетельством общности метода.
Таким образом, основные особенности предложенного метода
синтеза заключаются в следующем.
Во-первых, метод позволяет синтезировать структуру широкого
класса нелинейных автоматических систем, т. е. определять связи
105
как по выходным величинам объекта, так и по контролируемым воз-
мущениям.
Во-вторых, метод дает возможность определить такую структу-
ру управления, которая обеспечивает требуемые динамические свой-
ства системы, например устойчивость. Тем самым метод дает струк-
турные условия устойчивости нелинейных систем. Задаваясь раз-
личной формой требуемых уравнений движения, в том числе раз-
личными независимыми переменными процесса, можно получить
множество различных структур управления для решения одной и
той же нелинейной задачи.
В-третьих, процедура синтеза относительно проста, ибо она сво-
дится прежде всего к алгебраическим операциям.
Возможность получения множества структур управления для
решения одной и той же нелинейной задачи, что важно при после-
дующей конструктивной разработке систем, простота процедуры
синтеза — все это делает метод инженерным в принятом смысле
этого слова.
ПРИЛОЖЕНИЕ
Ори синтезе, например, дифференциальных анализаторов для
воспроизведения ломаных линий и систем для поиска экстремума
с учетом ограничений первостепенное значение имеет запись систе-
мы неравенств в виде единого аналитичского выражения. Простой
и чрезвычайно эффективный способ такой записи был предложен
в 11930 г. М. Ф. Зиминым 1[Л. 75]. .К настоящему времени нам изве-
стно пока единственное применение этого способа, а именно — для
расчета вентильных электрических схем. Оно изложено в работах
Л. Л. -Иванова, опубликованных в 1959—1960 гг. |[Л. 68 и 69].
В (Л. 75] рассматриваются системы неравенств, определяющих
некоторую область в геометрическом пространстве двух и трех пе-
ременных. Можно распространить основные положения его работы
на пространство п переменных.
Пусть задана система неравенств:
i=l, 2, п; /=1, 2, т. (П-1)
Эти неравенства можно заменить равносильными им равенства-
ми:
1*И*<) I-= 0. (П-2)
Складывая их почленно, получаем уравнение:
т п
2 IftW (П-З)
Это уравнение определяет в я-мерном пространстве соответ-
ствующий объем.
106
Заметим, что решение обратной задачи — определение уравне-
ния известной ограниченной поверхности или объема с помощью
уравнений (П-3). — не всегда возможно. В этом случае следует при-
менять более общие, но в то же время несколько более сложные ме-
тоды, разработаннные В. Л. Рвачевым и Е. Л. Ющенко [Л. 73 и 74].
Уравнение части поверхности
F(Xi)=0; /= 1,2,..., л, (П-4)
ограниченной областью (П-1), имеет вид:
т т
I F (xt) | + £ \gj (х*) I - £ gj (xt) = 0. (П-5)
Если область в n-мерном пространстве задана системой нера-
венств (П-1), то задача об определении границы области сводится
к замене неравенств одним равносильным, а затем—к замене
в нем знака неравенства на знак равенства.
Пусть дана система двух неравенств:
gi(Xi)>0\
£2|(*г)>0.
Эта система заменяется одним равносильным неравенством:
gi М + g2 (xt) - ! (xt) - g2 (xt) I > 0. (П-6)
Если заданы дополнительные неравенства, то, комбинируя одно
из них с неравенством (П-6), получаем новое неравенство, которое
комбинируем с одним из оставшихся неравенств, и т. д.
ЛИТЕРАТУРА
1. Сол од ов А. В., Линейные системы автоматического управ-
ления с переменными параметрами, Физматгиз, 1962.
2. Б а ш а р и н А. В., Расчет динамики и синтез нелинейных си-
стем управления. Госэнергоиздат, 1960.
3. К о р е н е в Г. В., Введение в механику управляемого тела,
изд-во «Наука», 1964.
4. Б о д н е р В. А., Теория автоматического управления полетом,
изд-во «Наука», 1964.
5. Бойчук Л. М., Расчет оптимальных автоматических систем
методом динамического программирования, сб. «Теория автоматиче-
ского управления», ДНТП, Киев, 1964.
6. Б о й ч у к Л. М., Синтез оптимальних автоматичних систем
методом динам!чного програмування, «Автоматика», 1965, '№ 1.
7. (Б о й ч у к Л. М., Оптимальные системы автоматического ре-
гулирования, изд-во «Наукова думка», 1965.
8. Бойчук Л. М., Структурный синтез оптимального управле-
ния нелинейным объектом с помощью вариационного исчисления,
сб. «Сложные системы управления», вып. 1, изд-во «Наукова дум-
ка», 1965.
9. Бойчук Л. IM., Обернений метод структурного синтезу не-
Л1ншних систем автоматичного керування, «Автоматика», 1966, № 6.
10. Бойчук Л. М., Синтез нелинейных инвариантных автома-
тических систем обратным методом, сб. «Сложные системы управле-
ния», вып. 3, изд-во «Наукова думка», 1967.
И. Бойчук Л. М., Структурный синтез нелинейных автомати-
ческих систем обратным методом, сб. «Теория автоматического
управления», изд-во «Наукова думка», 1967, № 1.
12. Бойчук Л. М., Структурный синтез систем автоматическо-
го управления движением тел, сб. «Теория автоматического управле-
ния», изд-во «Наукова думка», 1967, № 2.
13. Бойчук Л. М., Использование функционального преобра-
зования независимой переменной процесса для структурного синтеза
нелинейной автоколебательной системы второго порядка, сб. «Теория
автоматического управления», изд-во «Наукова думка», 1967, № 3.
14. Бойчук Л. М., Студеновськ1 П., Синтез структури
генератора синусе дальних коливань, «Автоматика», 1967, № 4.
15. Бойчук Л. <М., Генератор, Авторское свидетельство
№ 203733, «.Бюллетень изобретений», 1967, № 21.
16. Бойчук Л. М., Синтез оптимальных многоконтурных си-
стем автоматического регулирования методом динамического про-
граммирования, сб. «Теория многосвязного регулирования», изд-во
«Наука», 1967.
108
17. Бойчук Л. М., Вол обоев Б. В., Тимченко А. А.,
Розвиток метчшв структурного синтезу нелшшних автоматичных си-
стем, «Автоматика», 1967, № 5.
18. Б о й ч у к Л. М., Метод структурного синтезу систем авто-
матичного кёрування об'ектами з неповною шформащею, «Автома-
тика», 1968, (No 3.
19. Бойчук Л. М., Использование функционального преобра-
зования независимой переменной процесса для структурного синтеза
нелинейной автоколебательной системы, сб. «Сложные системы
управления», вып. 4, изд-во «Наукова думка», 1968.
20. В о i с h u k L. М., Method of Structure Synthesis of Nonli-
near Multivariable Control Systems on Given Transients, IFAC Sympo-
sium on Multivariable Control Systems, Preprints, vol. 1, Dusseldorf,
1968.
21. Бойчук Л. M., Синтез систем автоматического управления
объектами с неполной информацией, сб. «Кибернетика и вычисли-
тельная техника», вып. 1, изд-во «Наукова думка», 1969.
22. Бойчук Л. М., Структурный синтез систем автоматического
управления движением тел вдоль заданной траектории», сб. «Кибер-
нетика и вычислительная техника», вып. 1, изд-во «Наукова думка»,
1969.
23. Б о й ч у к Л. М., Структурный синтез нелинейных инвариант-
ных автоматических систем обратным методом, сб. «Теория инва-
риантности автоматических систем», изд-во «Наука», 1970.
24. Бойчук Л. М., Структурный синтез инвариантных систем
автоматического управления движением тела по заданной траекто-
рии, сб. «Применение инвариантных систем автоматического управ-
ления», изд-во «Наука», 1970.
25. Бойчук Л. М., Про необхщи i достатш умови абсолютно?
1нвар1антност1 автоматичних систем з посередшм вимгрюванням
збурень, «Автоматика», 1969, № 4.
26. Бойчук Л. М., Метод структурного синтезу систем функ-
цюнального регулюаання одного класу, «Автоматика», 1969, № 6.
27. Бойчук Л. М., К о с т е н к о Ю. В., Автоматична аналогова
обчислювальна система для пошуку екстремуму при наявност1 обме-
жень, «Автоматика», 1970, № 1.
28. Б о й ч у к Л. М., Метод структурного синтеза нелинейных
многомерных систем автоматического управления, сб. «Кибернетика
и вычислительная техника». Вып. 5, изд-во «Наукова думка», 1970.
29. 'Б о й ч у к Л. М., Метод синтеза структур специальных си-
стем функционального регулирования (дифференциальных анализа-
торов, систем для решения уравнений и поиска экстремума, логико-
динамических систем), сб. «Кибернетика и вычислительная техника»,
вып. 5, изд-во «Наукова думка», 1970.
30. А с т р о в В. В., С i м а к о в I. П., Структурний синтез ком-
бшованих систем автоматичного кёрування нелшшними об'ектами,
«Автоматика», 1966, № 6.
31. Т и м ч е н к о А. А., Структурний синтез автоматичного кёру-
вання рухом тша в npocTopi, «Автоматика», 1967, 1№ 6.
32. Тимченко А. А., Структурный синтез нелинейных систем
автоматического управления движением тел одного класса, сб. «Тео-
оия автоматического управления», изд-во «Наукова думка», 1967,
109
33. Т и м ч е н к о А. А., Структурный синтез швар1антних нел1-
ншних систем з посередшм в!м1рюванням збурень, «Автоматика»,
1968, № 1.
34. Соколов Н. И., Аналитический метод синтеза линеаризо-
ванных систем автоматического регулирования, изд-во «Машино-
строение», 1968.
35. О р у р к И. А., Новые методы синтеза линейных и некото-
рых нелинейных динамических систем, изд-во «Наука», 1965.
36. Литвин-Седой М. 3., Саввин А. Б., О синтезе систем
автоматического регулирования второго (порядка с ограниченными
переходными процессами, Вестник Московского университета, 1961,
№ 5.
37. В а н - Т р и с Г., Синтез оптимальных нелинейных систем
управления, изд-во «Мир», 1964.
38. Пухов Г. Е., Жук К. Синтез многосвязных систем
управления по методу обратных операторов, изд-во «Наукова дум-
ка», 1966.
39. Винер Н., Кибернетика, изд-во «Советское радио», 1968.
40. X э д д е д Р. А., Некоторые необычные, но не приспосабли-
вающиеся системы, сб. «Приспосабливающиеся автоматические си-
стемы», Изд-во иностр. лит., 1963.
41. Поспелов Г. С, О принципах построения некоторых ви-
дов самонастраивающихся систем автоматического управления, «Са-
монастраивающиеся автоматические системы», Труды- международ-
ного симпозиума ИФАК, изд-во «Наука», 1964.
42. Павлов В. В., Достатш умови iHBapiaHTHOcri у нелшшних
системах, «Автоматика», 1963, № 4.
43. И в а х н е н к о А. Г., Электроавтоматика, Гостехиздат УССР,
1957.
44. Ильницкий Л. Я., Нагорный Л. Я., Дифференцирую-
щий усилитель с емкостной обратной связью, «Автоматика и телеме-
ханика», 1962, № 1.
45. О п р ы ш к о И. А., Определение желаемых передаточных
функций при. синтезе линейных систем автоматического регулирова-
ния для случая, когда ограничивается первая производная регули-
руемой величины, сб. «Теория автоматического управления», изд-во
«Наукова думка», 1969, № 2.
46. Льюис Дж., Применение нелинейной обратной связи для
улучшения переходного процесса в системах автоматического регу-
лирования, «Вопросы ракетной техники», 1954, № 4.
47. М е е р о в М. В., Синтез структур систем автоматического
регулирования высокой точности, изд-во «Наука», 1967.
48. Я н у ш е в с к и й Р. Т., О грубости решения задачи аналити-
ческого конструирования регуляторов, «Автоматика и телемехани-
ка», 1966, No 3.
49. К р е м е н т..у л о- Ю. В., Нова форма умов неабсолютно!
1нвар1антност1 для систем програмного керування, «Автоматика»,
1961, № 4.
50. К о с т ю к О. М., Корекщя по температур!, петм пстерезку
та нелшшносп в системах автоматичного керування за допомогою
звичайних зворотних зв'язюв, «Автоматика», I960, № 3.
-51. 1 в а х н ен к о О. Г., Комаров Б. О., Недокомпенсащя,
абсолютна швар1антн!сть i перекомпенсащя в системах автоматично-
го регулювання, «Автоматика», 1964, № 2.
110
52. Д о г а н о в с к и й С. А., Компенсация возмущений в нели-
нейных системах, «Автоматика и телемеханика», 1962, № 6.
53. Менский Б. М., Павличук К. И., Применение принци-
па инвариантности при нелинейном воздействии возмущений, «Авто-
матика и телемеханика», 1961, № 12.
54. В a n h a m J. W., S m i t h W. L., A Practical Approach to
Adaptive Control, Control Engineering, 1966, № 5.
55. Ч и н a e в П. И., Многомерные автоматические системы, Гос-
техиздат УССР, 1963.
56. Зайцева Е. В., До питания стшкоЫ багатозв'язних авто-
матичних систем з особливим функцюнальним зв'язком, нападе-
нием на регульоваш координати, «Автоматика», 1965, № 2.
57. И г н а т ь е в М. Б., Голономные автоматические системы,
Изд-во АН СССР, 1963.
58. К о з и о р о в А. М., Коробков М. Н., Метод стабилиза-
ции функциональной зависимости двух взаимосвязанных переменных
с помощью одного управляющего органа, Известия АН СССР, се-
рия «Энергетика и автоматика», 1961, № 4.
59. Вавилов А. А., Солодовников А. И., Электронный
генератор инфранизких частот с релейным управляющим элементом,
Известия вузов, серия «Приборостроение», 1962, № 4.
60. У к о л о в И. С, М и т р о ш и н Э. И., Кузьмин С. П.,
Ш е л е н к о в В. М., Некоторые вопросы синтеза системы управле-
ния движением летательного аппарата относительно номинальной
траектории, сб. «Автоматическое управление и вычислительная тех-
ника», вып. 9, изд-во «Машиностроение», 1968.
61. L о v е J. А., N е u s t a d t L. W., A Simple Re-entry Guidance
System, AIAA Journal, vol. 1, 1963, № 8.
62. Konig H., Uber Probleme bei Mehrfachflugregelsystemen
von Hyperschal-flugzeugen, IFAC Symposium uber Mehrgrossen-Re-
gelsysteme, Vorabdrucke, Bd 2, Dusseldorf, 1968.
63. Б e л л м а н P., Теория устойчивости решений дифферен-
циальных уравнений, Изд-во иностр. лит. 1954.
64. П а в л о в В. В., Яковлев О. С, Исследование устой-
чивости инвариантных множеств, сб. «Теория автоматического
управления», изд-во «Наукова думка», 1967, № 4.
65. П е т р о в ОБ. И., О воспроизведении синусоидальных коле-
баний следящими приводами, исполнительные элементы которых
имеют ограничения по моменту и скорости, Труды МАИ, вып. 146,
Оборонгиз, 1962.
66. Булгаков А. А., Энергетические процессы следящего
электропривода в гармоническом режиме, Изд-во АН СССР, 1960.
67. Чиликин М. Г., Петров И. И., Воронецкий Б. Б.,
Новые направления развития автоматизированного электропривода,
сб. «Автоматизированный электропривод производственных механиз-
мов», изд-во «Энергия», 1965.
68. Иванов Л. Л., К решению задач с функциями, имеющими
разрывные производные или разрывы непрерывности, Труды МВТУ
им. Баумана, вып. 87, Госэнергоиздат, 1958.
69. И в а н о в Л. Л., Начала аналитической теории разрывных
функций и расчет нелинейных электрических цепей, «Электриче-
ство», 1960, № 9.
70. А л ь м у х а м е т о в А. Г., Стабилизация коэффициента пе-
редачи фазовращателя на операционных усилителях, «Автоматика и
телемеханика», 1968, № 3.
111
71. Рыбашов М. В., Градиентный метод решений задач вы-
пуклого программирования на электронной модели, «Автоматика и
телемеханика», 1965, №11.
72. Г и н з б у р г С А., (Математическая непрерывная логика и
изображение функций, изд-во «Энергия», 1968. , ^\
73. Р в а ч е в В. Л., Ю щ е н к о Е. Л., Некоторые вопросы
аналитического описания геометрических объектов сложной логиче-
ской структуры, сб. «Вопросы программированного обучения и обу-
чающихся машин», ДНТП, Киев, 1965.
74. Р в а ч е в В. Л„ Геометрические приложения алгебры ло-
гики, изд-во «Технжа», Киев, 1967.
75. 3 и м и н М. Ф., Об уравнениях, определяющих площади,
объемы и их границы, «Математическое образование», 1930, № 1.
76. Пух о в Г. Е., Избранные вопросы теории математических
машин, «Наукова думка», 1964.
77. Жук К. Д., Про властивосп деяких структур багатозв'яз-
них систем з керуючими моделями, «Автоматика», 1964, № 4.
78. Грубое В. И., Кир дан В. С, Электронные вычисли-
тельные машины и моделирующие устройства-, «Наукова думка»,
1969.
79. Ф е л ь д б а у м А. А., Электрические системы автоматиче-
ского регулирования, Оборонгиз, 1957.
80. Б о й ч у к Л. М., Одержання пол1ном1альних опиав нелшй-
них динам1чних об'екпв першого порядку за методом «диферен-
щально!' вилки», «Автоматика», 1970, № 4.
81. Б о йч у к Л. М., Д у б р о в и н О. Ф., Метод полшом1аль-
ного (кшцево-р1зницевого) опису об'екпв керування з неповною
шформащею та його застосування, «Автоматика», 1970, № 6.
82. Б о й ч у к Л. М., К о с т е н к о Ю. В.., Автоматическая вы-
числительная система для нахождения экстремума функции многих
переменных, сб. «Механизация и автоматизация управления», Гос-
план УССР, Киев, 1970.
83. К о с т е н к о Ю. В., Б о й ч у к Л. М., Алгоритм розв'язання
задач1 лшшного програмуванйя як задач1 функцюнального регу-
лювання, «Автоматика», 1970, № 5.
ОГЛАВЛЕНИЕ
Предисловие 3
Введение ! ! ! ! ! 5
Глава первая. Основы структурного синтеза нелинейных
автоматических систем по заданным дифференциальным
уравнениям 9
1-1. Задача структурного синтеза 9
1-2. Обоснование метода синтеза 13
1-3. Основные свойства синтезированных систем и область
применения метода 18
Глава вторая. Системы автоматического управления для
отработки заданий, являющихся функциями времени . . 20
2-1. Выбор требуемого дифференциального уравнения си-
стемы 20
2-2. Одномерные системы 23
2-3. Система управления скоростью вращения компрессора 29
2-4. Многомерные системы 31
2-5. Система управления движением тела 33
Глава третья. Односвязные системы функционального
регулирования 36
3-1. Вводные замечания 36
3-2. Системы с полным заданием 37
3-3. Синтез структуры генератора синусоидальных коле-
баний 38
3-4. Система с неполным заданием . 41
3-5. Система управления спуском тела в атмосфере . . 43
Глава четвертая. Многосвязные системы функциональ-
ного регулирования 47
4-1. Процедура синтеза 47
4-2. Система управления положением и скоростью движу-
щегося тела 52
4-3. Система управления совпадением двух движущихся
тел 59
Глава пятая. Обобщения метода синтеза 64
5-1. Системы управления, содержащие вычислительные
устройства 64
5-2. Система регулирования мощности энергетического
ядерного реактора 66
5-3. Преобразование пространства состояний . . . . 67
5-4. Электропривод постоянного тока, работающий в гар-
моническом режиме 71
5-5. Управление объектами с неполной информацией . . 75
Глава шестая. Специальные системы функционального
регулирования 79
6-1. Системы для параметрического задания функций . . 79
6-2. Аналоговые системы для решения уравнений . . 87
6-3. Системы с переменной структурой для поиска экстре-
мума функции многих переменных 91
6-4. Логико-динамические системы 98
Заключение 104
Приложение 106
Литература ... ... . 108