ІЙЙЧЕНКО □.№. ІЙЙЧЕНКП Ю.П.
ДОСЛІДЖЕННЯ
^ОПЕРАЦІЙ
ЗиБ І РНИК ЗАДАЧ


Міністерство освіти і науки України
Зайченко О.Ю., Зайченко Ю.П.
ДОСЛІДЖЕННЯ ОПЕРАЦІЙ
Збірник задач
Рекомендовано Міністерством освіти і науки України
як навчальний посібник для студентів вищих
навчальних закладів, що навчаються за напрямами
«Комп’ютерні науки» та «Прикладна математика»
Київ 2007
УДК 519.8(076.1)
ББК 22.18я73
З 17
Рекомендовано Міністерством освіти і науки України
як навчальний посібник для студентів вищих навчальних закладів,
що навчаються за напрямами «Комп’ютерні науки»
та «Прикладна математика»
(Лист №1.4/18-Г-924 від 14.06.2007 р.)
Рецензенти:
О.А.Волков - доктор технічних наук, професор;
О.Ф.Волошин - доктор фізико-математичних наук, професор.
317 Зайченко О.Ю., Зайченко Ю.П. Дослідження операцій. Збірник
задач. -К.: Видавничий Дім «С9лово», 2007. - 472 с.
І8ВМ 966-8407-65-2
В посібнику в систематизованому вигляді представлено задачі і вправи по
всіх основних розділах курсу Дослідження операцій, включаючи лінійне, не-
лінійне, динамічне програмування, стохастичне програмування.
Нове видання суттєво розширене та доповнено новими розділами, що відоб-
ражають сучасні напрями цієї дисципліни, серед яких: прийняття рішень в
умовах невизначеності, задачі і методи нечіткого програмування, методи де-
композиції в задачах оптимізації, задачі і методи прийняття рішень у конфлік-
тних ситуаціях, що включають методи теорії антагоністичних та кооператив-
них ігор двох осіб, а також багатокритеріальні задачі прийняття рішень як у
чітких, так і в нечітких умовах.
Всі розділи посібника мають однакову структуру: спочатку викладається
необхідний теоретичний матеріал, далі йдуть приклади застосування викладе-
них методів та алгоритмів на конкретних задачах з детальними поясненнями
процесу вирішення, а потім наведені численні вправи та задачі для самостійного
розв’язання.
Теоретичний апарат, що викладається в посібнику, базується на підручнику
Ю.П. Зайченко ♦ Дослідження операцій », 7-ме вид., Київ., 2006, - 816 с.
Підручник орієнтовано передусім на студентів бакалавратів «Прикладна ма-
тематика», «Комп’ютерні науки», а також студентів економічних спеціальнос-
тей. Він буде корисний всім фахівцям, яким необхідно освоїти і використовува-
ти математичний апарат оптимізації. Підручник може служити довідником з
сучасних методів оптимізації.
І8ВМ 966-8407-65-2
©ЗайченкоО.Ю., Зайченко Ю.П., 2007
© Видавничий Дім «Слово», 2007
Дослідження операцій. Збірник задач
ПЕРЕДМОВА
Даний збірник задач є другою книгою комплексу навчальної лі-
тератури з курсу «Дослідження операцій» для бакалавратів напрямів
«Комп’ютерні науки» та «Прикладна математика», в який також вхо-
дить і підручник «Дослідження операцій».
Теоретичний апарат, що викладається в посібнику базується на
підручнику Ю.П. Зайченко «Дослідження операцій», 7-е вид., К., Ви-
давничий Дім “Слово”, 2006. — 816 с.
В збірнику підібрані та систематизовані задачі та вправи по всім
основним розділам курсу, а саме лінійному, дискретному нелінійно-
му та стохастичному програмуванню та ін.
З моменту видання попереднього збірника задач Дослідження
операцій (1990 р.) минуло понад 15 років і тому нове видання суттє-
во розширене та доповнено новими розділами, що відображають су-
часні напрямки цієї дисципліни, серед яких: Прийняття рішень в
умовах невизначеності, задачі і методи нечіткого програмування ,
методи декомпозиції в задачах оптимізації, задачі і методи прийняття
рішень в конфліктних ситуаціях, що включають методи теорії анта-
гоністичних та кооперативних ігор двох осіб., а також багатокритері-
альні задачі прийняття рішень як в чітких, так і в нечітких умовах.
Всі розділи посібника мають однакову структуру: спочатку ви-
кладаються необхідний теоретичний матеріал, далі йдуть приклади
застосування викладених методів та алгоритмів на конкретних зада-
чах з детальними пояснення процесу вирішення, а потім наведені
численні вправи та задачі для самостійного розв’язання.
Весь представлений матеріал, включаючи задачі та вправи,
пройшов багаторічну перевірку в при викладанні авторами курсу До-
слідження операцій в Інституті прикладного системного аналізу
НТУУ «Київський політехнічний інститут».для студентів бакалавра-
ту «Комп’ютерні науки» та магістрів різних спеціальностей.
Даний посібник орієнтовано насамперед на студентів та виклада-
чів бакалавратів «Комп’ютерні науки» та «Прикладна математика»,
З
Зайченко О.Ю., Зайченко Ю.П.
крім того він буде корисний студентам багатьох інженерних та еко-
номічних спеціальностей , які вивчають курси «Математичні методи
оптимізаціі» та «Математичне програмування».
Завдяки викладенню теоретичного матеріалу та численним при-
кладам практичного застосування методів з поясненнями хода
розв’язання, посібник можна використовувати також для самостійно-
го вивчення курсу.
Автори висловлюють щиру подяку студентам ННК «Інститут
прикладного системного аналізу», насамперед Кузнецовій Н., Майс-
трюк О., Скибі О. та Романовій С., за суттєву допомогу в підготовці
рукопису до видання.
О.Ю Зайченко
Ю.П. Зайченко
НТУУ«КП1», ННК «1ПСА»
4
ДоспОзкення операцій. Збірник задач
ЗМІСТ
Передмова.................................................З
РОЗДІЛ 1. Лінійне програмування...........................8
1.1.	Постановки задач ЛП і дослідження їх структури.......8
Приклади на складання математичних моделей задач.........11
1.2.	Симплекс-метод......................................19
Розв’язати геометрично наступні задачі ЛП................23
1.3.	Метод штучних змінних...............................28
Задачі і вправи на застосування симплекс-методу..........31
1.4.	Двоїста задача лінійного програмування..............38
Задачі і вправи на теорію двоїстості.....................44
1.5.	Двоїстий симплекс-метод.............................52
Задачі і вправи..........................................57
1.6.	Дослідження задач ЛП на чутливість..................65
Задачі і вправи на дослідження чутливості................70
1.7.	Метод оберненої матриці..........................'..76
Задачі і вправи..........................................88
1.8.	Багатокритеріальні задачі ЛП........................97
Задачі і вправи.........................................112
РОЗДІЛ 2. Транспортна задача лінійного програмування.....117
2.1.	Постановка та властивості транспортної задачі......117
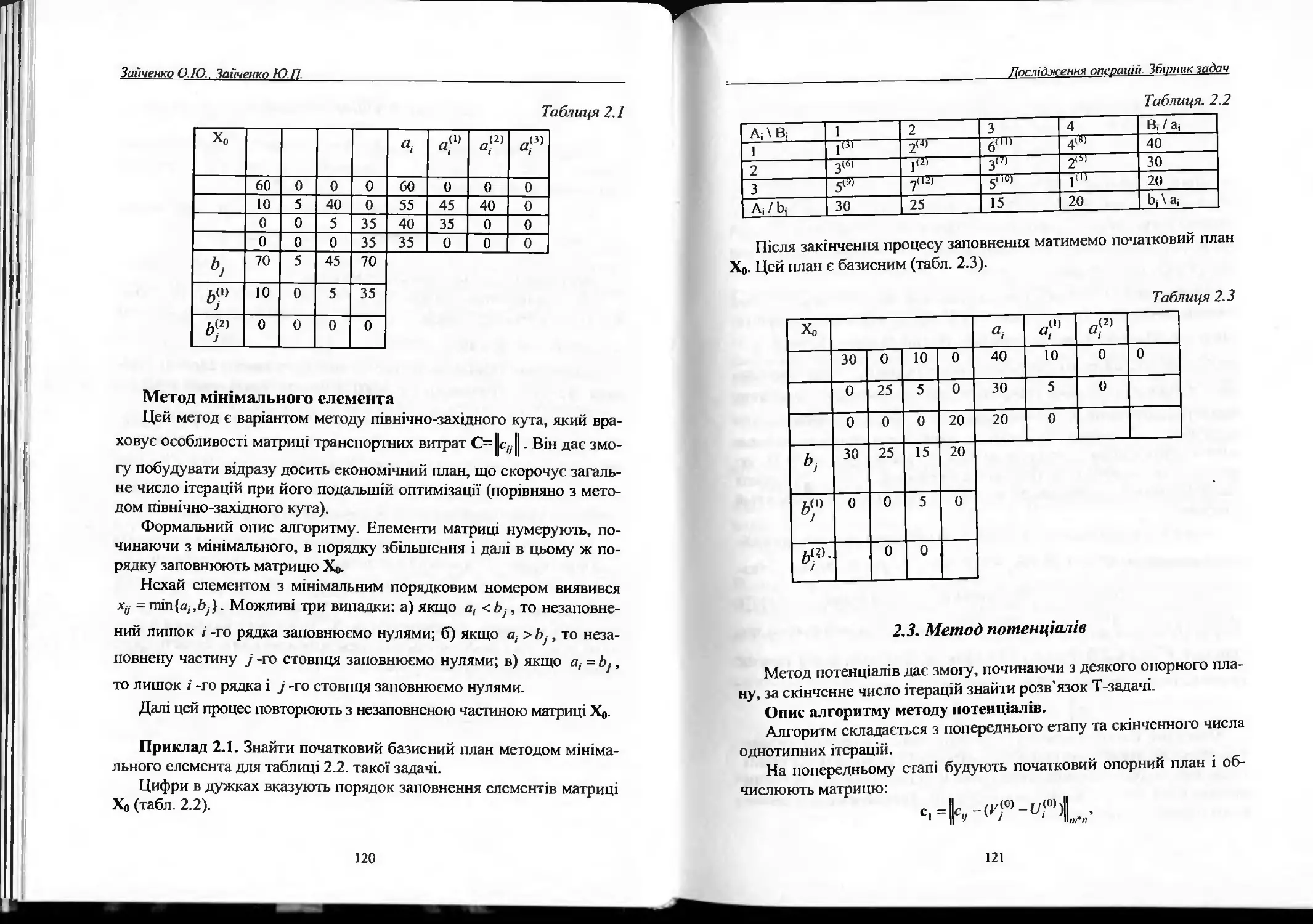
2.2.	Опорні плани транспортної задачі...................119
2.3.	Метод потенціалів..................................121
Задачі на метод потенціалів.........................1 ЗО
2.4.	Угорський метод....................................135
Задачі і вправи на угорський метод для транспортної задачі ....149
РОЗДІЛ 3. Дискретне програмування.......................151
3.1.	Метод відсікаючих площин ..........................152
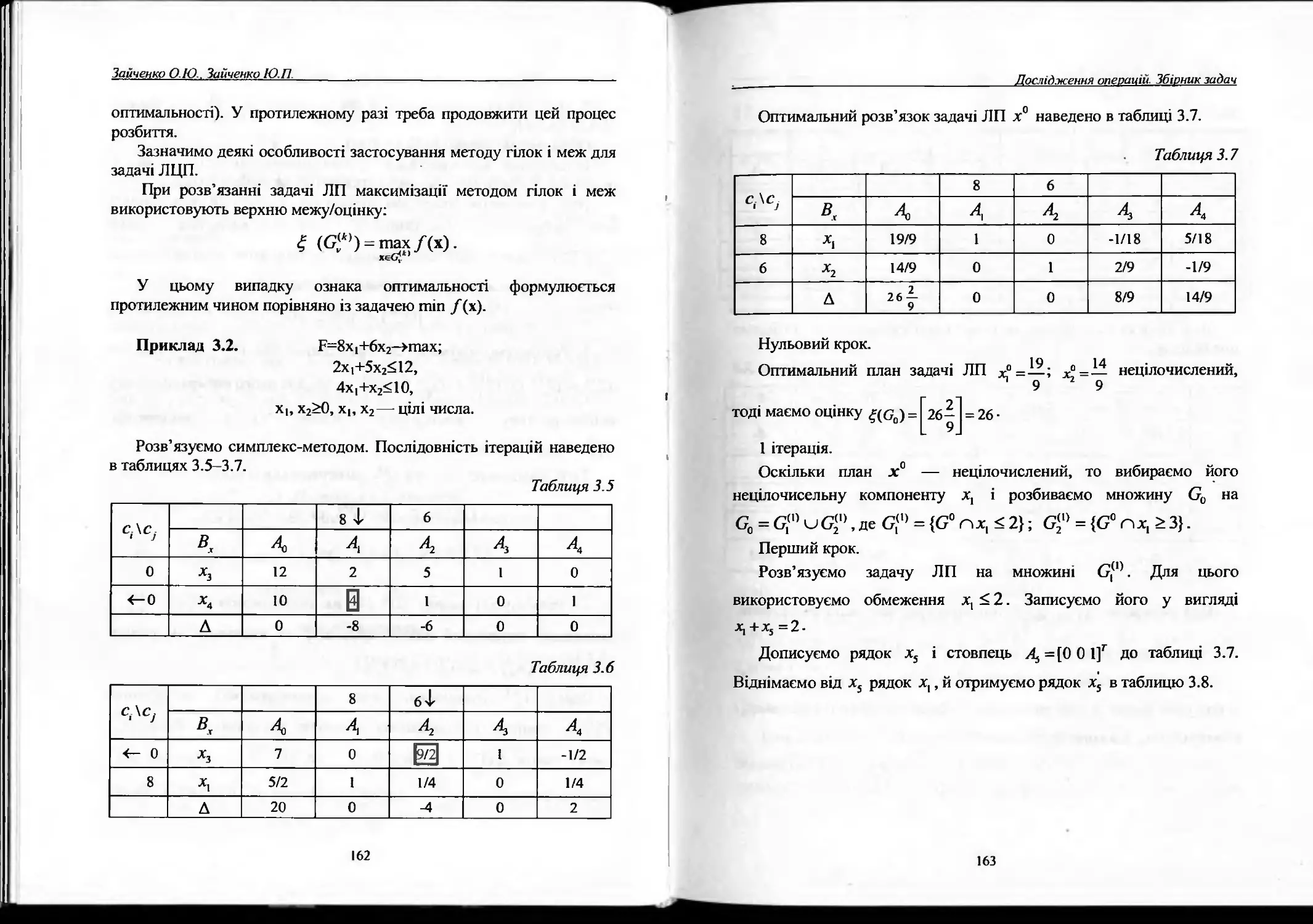
3.2.	Метод гілок та меж.................................158
3.3.	Метод гілок та меж для задач ЛЦП.........;.........160
5
Зайченко О.Ю., Зайченко Ю.П.
Задачі і вправи на рішення задач ЛЦП методами Гоморі
і гілок та меж...........................................168
3.4.	Метод гілок та меж для задачі комівояжера...........169
Вправи на рішення задачі комівояжера.......................178
3.5.	Послідовні алгоритми дискретної оптимізації.
Метод ПАВ для задачі ЛЦП...................................180
Задачі і вправи на метод ПАВ...............................185
РОЗДІЛ 4. Нелінійне програмування .......................195
4.1.	Класичний метод відшукання екстремуму...............195
4.2.	Метод множників Лагранжа............................197
4.3.	Задача нелінійного програмування при обмежених
нерівностях..............................................198
4.4.	Квадратичне програмування.............................200
Задачі і вправи на квадратичне програмування.............208
4.5.	Геометричне програмування...........................216
4.5.1.	Пряма та двоїста задачі геометричного програмування.216
4.5.2.	Опис алгоритму....................................220
Задачі і вправи............................................226
РОЗДІЛ 5. Динамічне програмування........................231
5.1.	Загальна схема обчислювального методу динамічного
програмування............................................231
5.2.	Процеси послідовного прийняття рішень. Задача про
трудові ресурси..........................................237
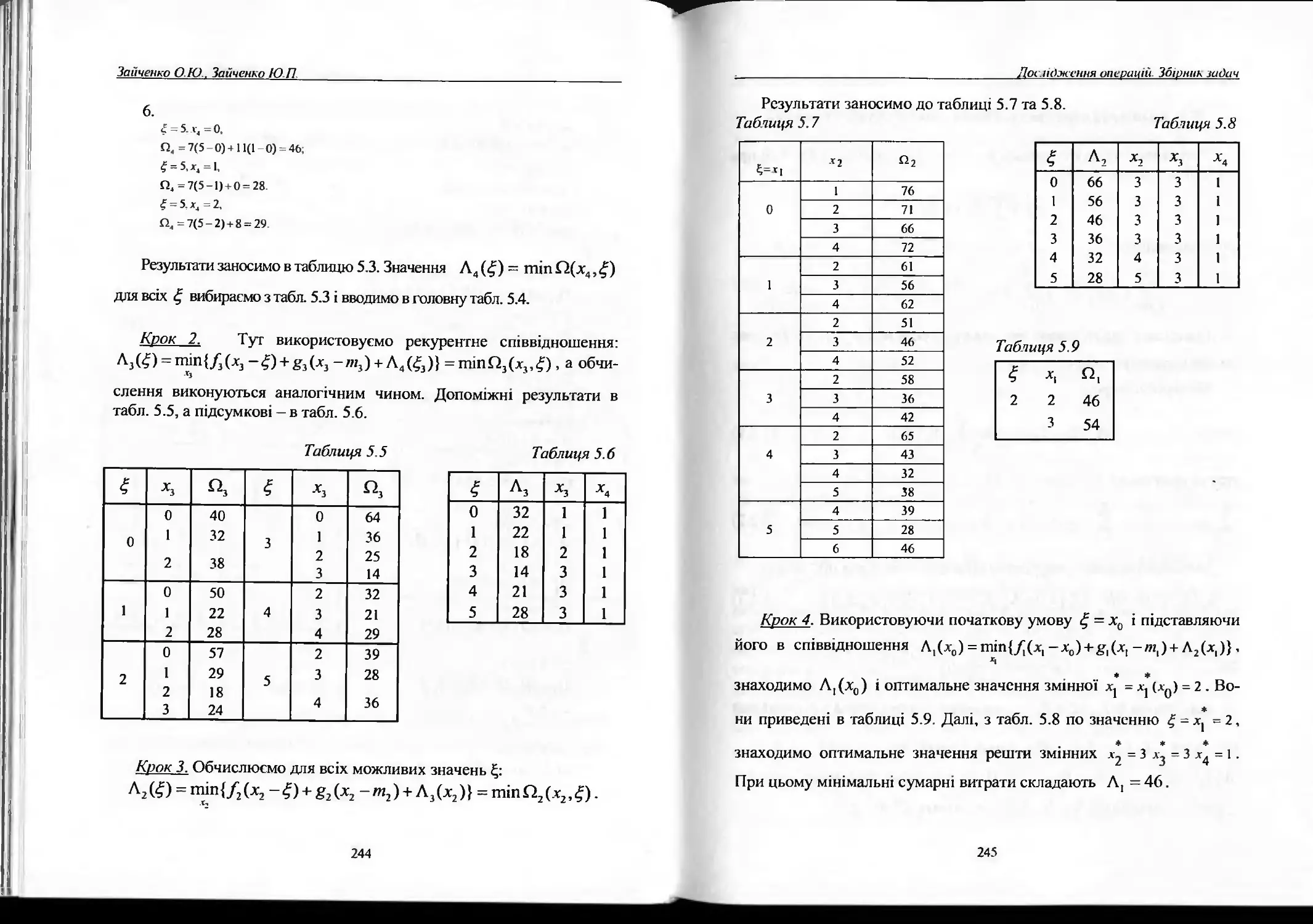
5.3.	Багатовимірні задачі динамічного програмування......246
5.4.	Динамічні задачі управління запасами................249
5.5.	Нескінченно шагові процеси динамічного програмування..256
5.6.	Задачі динамічного програмування на мережах.........259
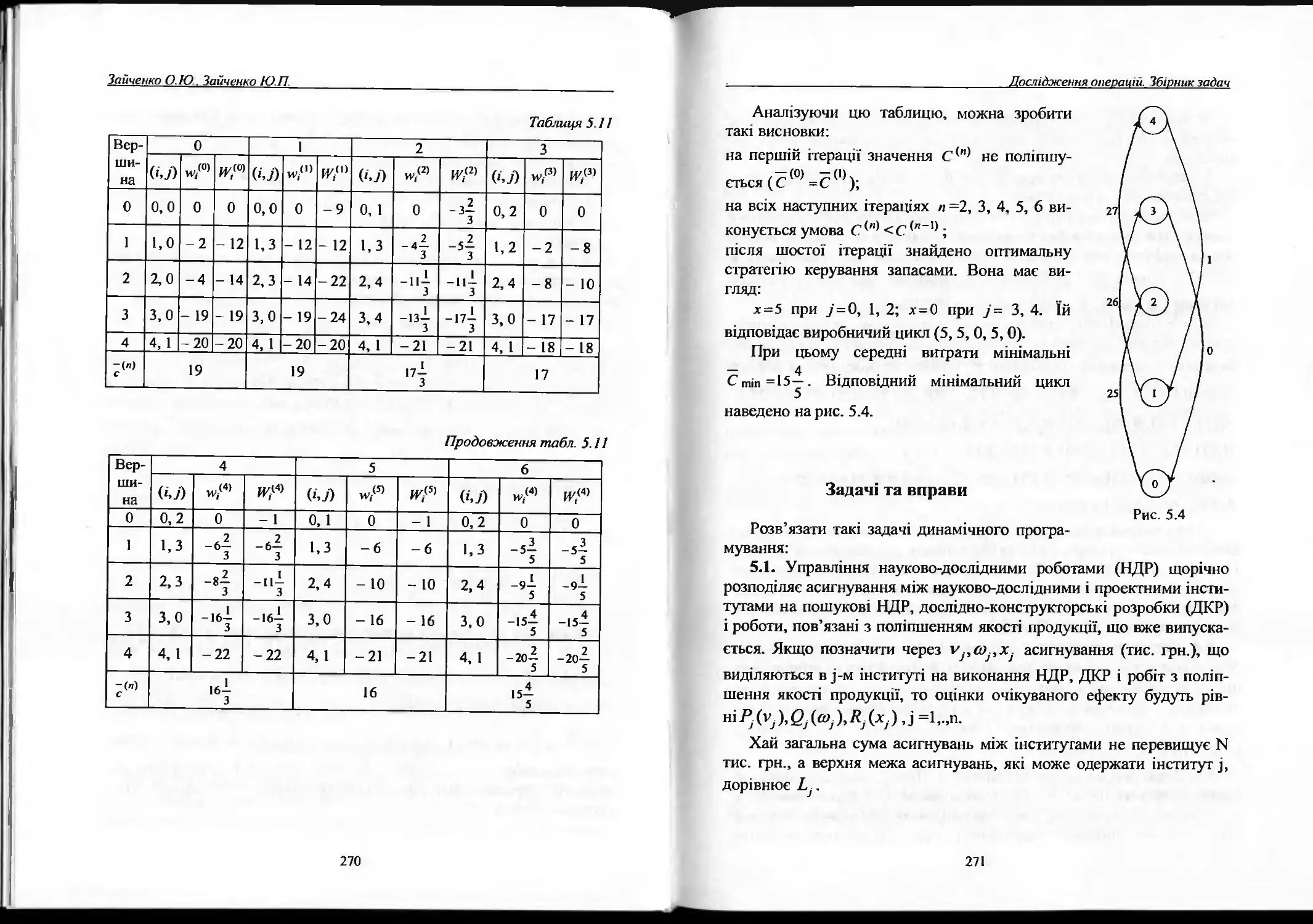
Динамічна задача управління запасами при нескінченному
плановому періоді........................................267
Задачі і вправи..........................................271
РОЗІДЛ 6. Стохастичне програмування .....................281
6.1. Загальна характеристика задач стохастичного
програмування............................................281
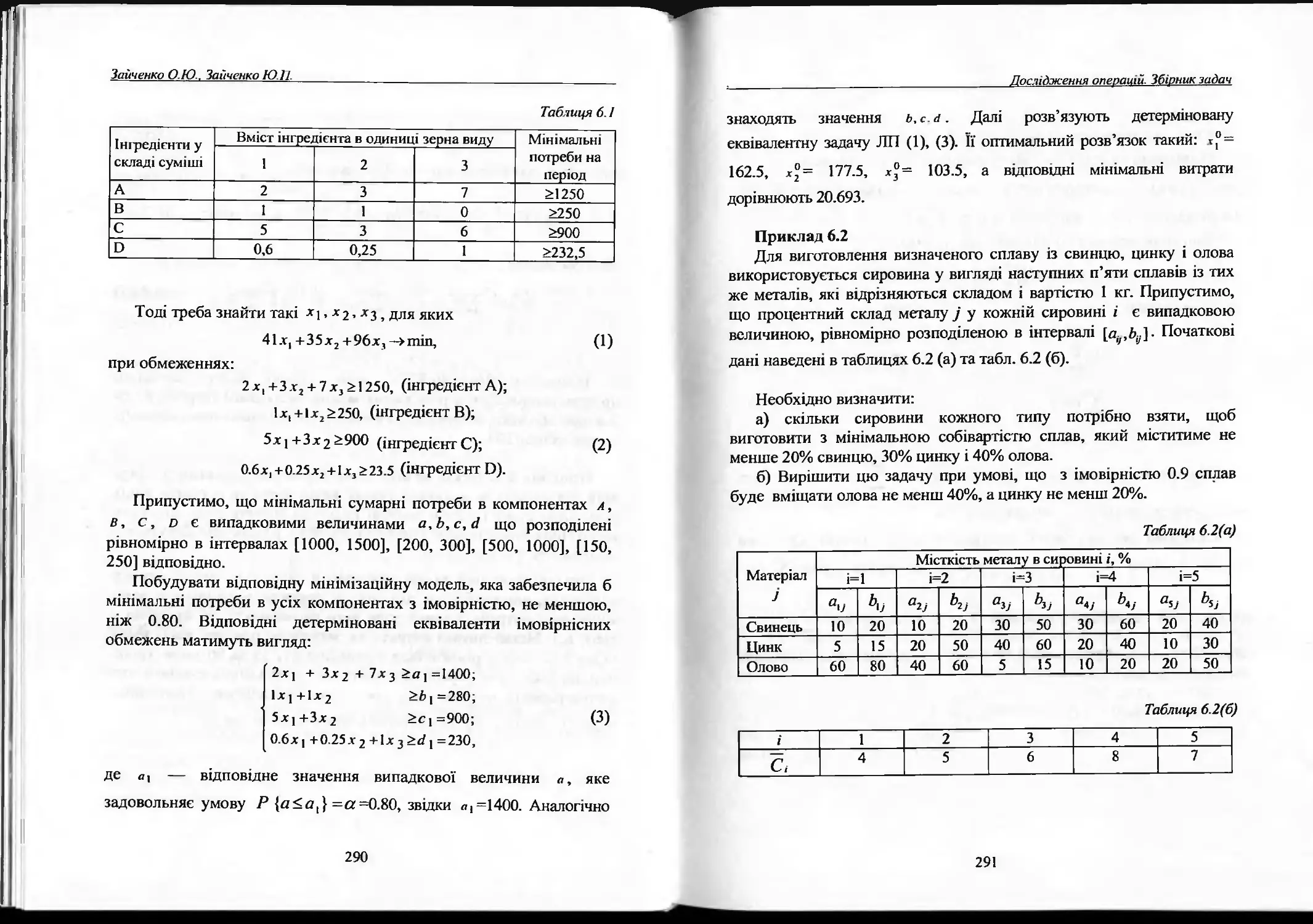
6.2. Одно етапні задачі стохастичного програмування......283
Задачі і вправи..........................................293
6
Дос лідження операцій Збірник задач
РО31ДЛ 7. Прийняття рішень в нечітких умовах..............309
7.1.	Нечіткі множини. Операції над ними...................310
7.2.	Нечіткі відношення. Операції над ними................313
7.3.	Задача досягнення нечітко визначеної мети............316
7.4.	Прийняггя рішень при нечіткому відношенню переваги ..318
Задачі і вправи...........................................333
7.5.	Загальна задача нечіткого математичного програмування і мето-
ди її розв’язання.........................................339
Задачі і вправи на розв’язання задач НМП..................351
7.6.	Багатокритеріальні задачі ЛП з нечіткими параметрами.360
Задачі і вправи...........................................368
РОЗДІЛ 8. Методи декомпозицїї в задачах великої
вимірності................................................374
8.1. Метод декомпозиції Данцига-Вульфа....................374
Задачі і вправи...........................................392
8.2. Метод декомпозиції Корнаї-Ліптака....................395
Задачі і вправи...........................................404
РОЗДІЛ 9. Прийняття рішень у конфліктних ситуаціях........406
9.1.	Основні поняття і визначення в області теорії ігор.
Позиційні ігри............................................406
9.2.	Стратегії гри. Нормальна форма гри...................408
9.3.	Змішані стратегії. Теорема про мінімакс
Джон Фон Неймана..........................................413
9.4.	Ігри із ненульовою сумою. Біматричні ігри............424
9.5.	Кооперативна гра двох осіб. Теорема Неша.............428
Задачі і вправи...........................................439
Відповіді.................................................442
Література................................................463
7
Зайченко О.Ю., Зайченко Ю.П.
1. ЛІШЙНЕ ПРОГРАМУВАННЯ
1.1. Постановка задач лінійного програмування
і дослідження їх структури
Більшість задач, що розв’язуються методами дослідження опера-
цій, можна сформулювати так:
максимізувати/(хьх2, •••,-»:„),	(1.1.1)
при обмеженнях:
Яі(хьх2, ...,хп) <Аь	(1-1-2)
£т(*і,х2, ...,хп)<Ьт',
де/(хь х2, ..., хп) — цільова функція, або критерій ефективності (на-
приклад, прибуток від виробництва якихось видів продукції, вартість
перевезень тощо); х = {хь.„, х„} — змінні параметри; #ї(х),...,
^„(х) — функції, що визначають обмеження на наявні ресурси.
Форма запису задачі ЛП. Задачу лінійного програмування мож-
на записати так:
максимізувати £с,х,,	(1.1.3)
і=і
при обмеженнях:
<ЗцХі + а|2х2 + - +
П/яіХі ат2х2 ... 4" а„:пх„ <Ьт,	(1.1.4)
хі>0, х2>0, .... хп>0.	(1.1.5)
Обмеження (1.1.5) називають умовами невід’ємності змінних.
Якщо всі обмеження задачі ЛП мають вигляд строгих рівностей
ацХі + щ2х2 + ... + а,^я = І1;
ат1хі + а„2х2 + ... + атпх„ = Ь,„. (1.1.6)
то форму запису називають канонічною.
У матричній формі задача ЛП записується так:
максимізу вати стх,	(1-1-7)
і)
Дослідження операцій Збірник задач
при обмеженнях:
Ах < Ь;
х >0,	(1.1.8)
де А — матриця обмежень розміром (пі х я);	— вектор-стовпець
довільних членів; х<”ХІ? — вектор змінних; ст=[сь с2,..., с„] — вектор
(рядок) коефіцієнтів ц. ф.
Допустимою множиною розв’язків задачі (1.1.3)-(1.1.5) зветься
множина К (х) усіх векторів х, що задовольняють умови (1.1.4)
і (1.1.5).
Множина К (х) являє собою опуклу многогранну множину або
опуклий многогранник.
Розв’язок х0 є оптимальним, якщо він задовольняє умові стх0 >
стх, для всіх хєТ? (х).
Оскільки пошук тіпДх) еквівалентний пошуку тах[-/(х)], то за-
дачу ЛП завжди можна звести до еквівалентної задачі максимізації.
Розширена форма задачі ЛП. Для розв’язання задачі ЛП треба
переходити від обмежень — нерівностей до обмежень у формі
рівнянь. Для цього у кожну нерівність вводять по одній вільній
змінній хп+і>0, х„+2>0,...лп+т^0, щоб перетворити її в рівність. У та-
кому вигляді задачу ЛП називають розширеною і записують так:'
максимізуватиДхі, х2,..., х„) = С1Х1+С2Х2+.. .+с,дп+0х,,+/+.. .+0х„+т, (1.1.9)
при обмеженнях:
ДцХі + а12х2 +	+ 1*п+і + 0х„+2 +	+0х„+пі= Ьх......(1.1.10)
єїтіХ) + ат2х2 + ... + а„,„хп + 0хя+і + 0хя+2 +... 4/хи+т ЬІ}1.
У матричній формі ця задача має такий вигляд:
максимізувати стх	(1.1.11)
при обмеженнях:
Ат"'’Х1 + ЕтхтХ2=Ь;	(1.1.12)
(1
0
1
0
де
- ої	ҐХ^Л
- 0 хг = хп+2
17	КАл+т,
9
Зайченко О.Ю., Зайченко Ю.П.
Допустимі базисні розв’язки
Нехай обмеження задачі ЛП задано у формі рівностей (рівнянь)
^ІХ(„хі)=Ь(,пхі>	(1.113)
Припустимо, що т<п і ранг матриці А дорівнює т. Виберемо з
матриці А = [АЬ...,А„] т лінійно незалежних стовпців, які позначимо
через Вг",лт>. Матриця В утворює базис системи. Сукупність стовпців
матриці А, що лишилися, позначимо через В. Тоді А = [В, В|
Сукупність змінних, пов’язаних з матрицею В, позначимо через
х*, а пов’язаних з матрицею В — через х0. Тоді
Ах = Вх,, + Вхо	(1.1.14)
Оскільки В — невироджена квадратна матриця, то існує обернена
до неї В ’. Множачи обидві частини (1.1.14) на В ’, дістанемо
В1Вх/1+В1Вхо = В1Ь.
Звідси
хй=В’Ь — В'Вхд	(1 1.15)
Змінні хл — базисні, а хо — небазисні.
Співвідношення (1.1.15) визначають повну множину розв’язків
системи лінійних рівнянь (1.1.13). У розгорнутому вигляді ці спів-
відношення можна записати так:
-гі=а,о- £аох7,/є/6;
X} Пр у Є Іцеб ,	(1.1.16)
де Іб —- множина індексів базисних векторів; Іиеа— множина індексів
небазисних векторів; а,0— і-та компонента вектора В *Ь; ач (]є
— рядок матриці В ‘В. Якщо покласти для всіх небазисних змінних
нульові значення, то одержимо базисний розв’язок Хі=аі0, і є Ц.
Якщо базисний розв’язок задовольняє умові невід'ємності, то він
зветься допустимим (ДБР).
Якщо серед компонент X/, і є Іб немає нульових, то базисний
розв’язок зветься невиродженим.
Справедлива така основна теорема лінійного програмування, що
встановлює місце розташування оптимальних розв’язків.
ТЕОРЕМА 1.1. Якщо цільова функція набуває максимального
значення в деякій точці допустимої множини К/, то вона набуває
цього значення в крайній точці Я/. Якщо цільова функція набуває ма-
ксимального значення більш, ніж в одній крайній точці, то вона на-
буває цього ж самого значення в будь-якій і’г опуклій комбінації.
10
Дослідження операцій. Збірник задач
Змістовні постановки задач ЛП.
Приклади на складання математичних моделей задач
Записати математичні моделі наступних задач
Задача №1
Механічний цех може виготовляти за зміну 600 деталей №1 або
1200 деталей №2. Виробнича потужність термічного цеху, куди ці
деталі поступають на термообробку у той же день, дозволяє оброби-
ти за зміну 1200 деталей №1 або 800 деталей №2. Ціни на деталі од-
накові. Потрібно визначити щоденну виробничу програму випуску
деталей, яка максимізує товарну продукцію підприємства, при таких
додаткових умовах:
а)	обидва цехи працюють одну зміну;
б)	механічний цех працює три зміни, а термічний — дві зміни;
в)	підприємство працює у дві зміни, при цьому деталей №1 повинно
бути виготовлено не більше 800 шт., та деталей №2 — не більше 1000 шт.
Задача №2
Із пункту А в пункт В щоденно відправляються пасажирські та
швидкі потяги. В табл. 1.1 наведено кількість вагонів різних типів, із
яких щоденно можна комплектувати потяги, і кількість пасажирів, на
яких розраховані вагони. Визначити оптимальне число швидких
і пасажирських потягів, при якому кількість пасажирів, що перево-
зяться, буде максимальна.
Таблиця 1.1
Вагон	Парк вагонів	Потяг		Число пасажирів
		ШВИДКИЙ	пасажирський	
Багажний	12	1	1	—
Поштовий	18	1	—	-
Жорсткий	89	5	8	58
Купейний	79	6	4	40
М’який	35	4	2	32
11
Зайченко О.Ю., Зайченко Ю.П.
Задача №3
Розв’язати задачу 2 при умові, що пропускна спроможність доро-
ги обмежує число пасажирів потягу до шести в день.
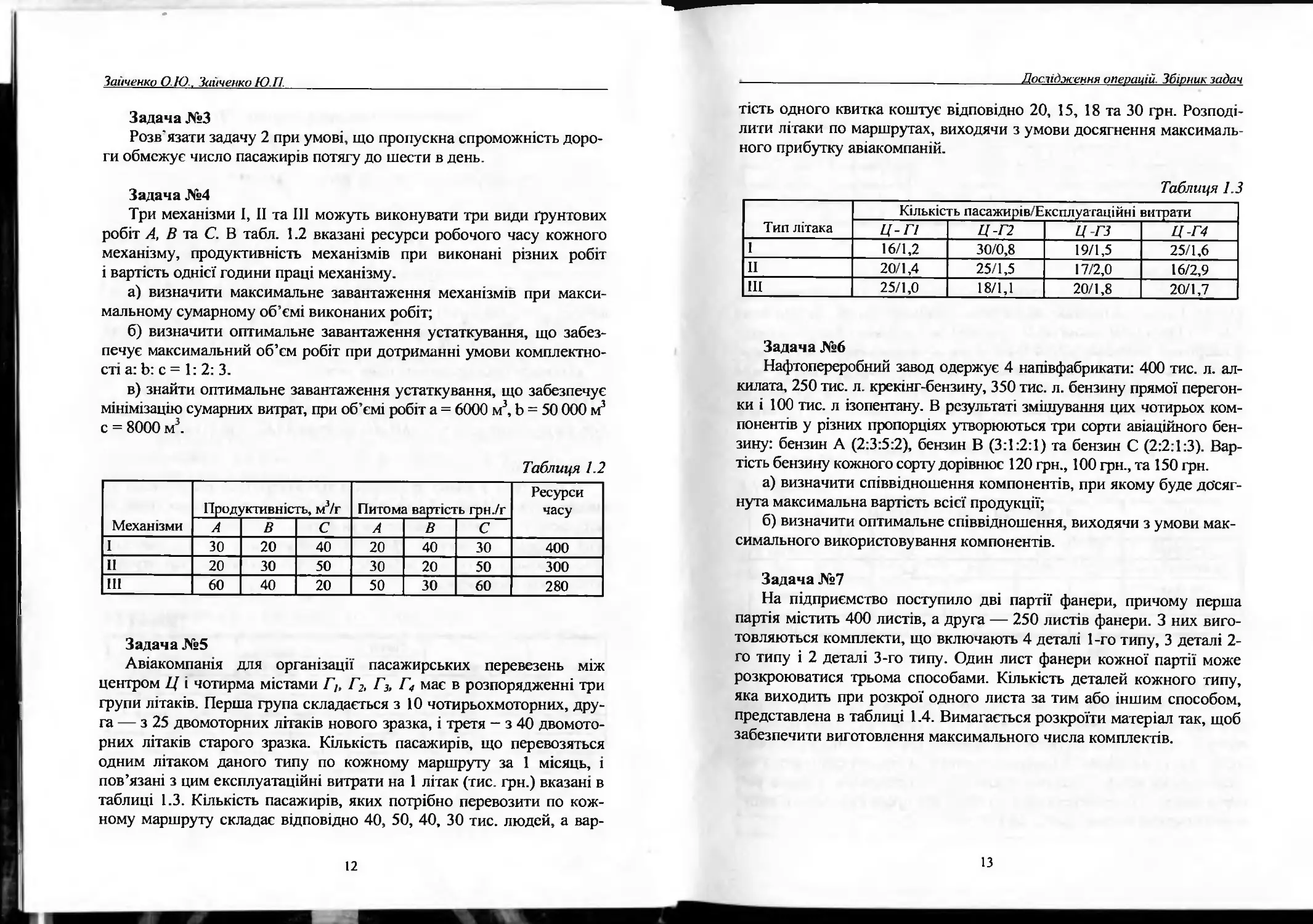
Задача №4
Три механізми І, II та 111 можуть виконувати три види ґрунтових
робіт А, В та С. В табл. 1.2 вказані ресурси робочого часу кожного
механізму, продуктивність механізмів при виконані різних робіт
і вартість однієї години праці механізму.
а)	визначити максимальне завантаження механізмів при макси-
мальному сумарному об’ємі виконаних робіт;
б)	визначити оптимальне завантаження устаткування, що забез-
печує максимальний об’єм робіт при дотриманні умови комплектно-
сті а: Ь: с = 1: 2: 3.
в)	знайти оптимальне завантаження устаткування, що забезпечує
мінімізацію сумарних витрат, при об’ємі робіт а = 6000 м3, Ь - 50 000 м3
с = 8000 м3.
Таблиця 1.2
Механізми	Продуктивність, м3/г			Питома вартість грн./г			Ресурси часу
	А	В	С	А	В	С	
І	зо	20	40	20	40	ЗО	400
11	20	зо	50	ЗО	20	50	300
111	60	40	20	50	зо	60	280
Задача №5
Авіакомпанія для організації пасажирських перевезень між
центром Ц і чотирма містами Г/, Г2, Г3, Г, має в розпорядженні три
групи літаків. Перша група складається з 10 чотирьохмоторних, дру-
га — з 25 двомоторних літаків нового зразка, і третя - з 40 двомото-
рних літаків старого зразка. Кількість пасажирів, що перевозяться
одним літаком даного типу по кожному маршруту за 1 місяць, і
пов’язані з цим експлуатаційні витрати на 1 літак (тис. грн.) вказані в
таблиці 1.3. Кількість пасажирів, яких потрібно перевозити по кож-
ному маршруту складає відповідно 40, 50, 40, 30 тис. людей, а вар-
12
Дослідження операцій. Збірник задач
тість одного квитка коштує відповідно 20, 15, 18 та ЗО грн. Розподі-
лити літаки по маршрутах, виходячи з умови досягнення максималь-
ного прибутку авіакомпаній.
Таблиця 1.3
Тип літака	Кількість пасажирів/Експлуатаційні витрати			
	Ц-Г1	Ц-Г2	Ц ҐЗ	Ц-Г4
І	16/1,2	30/0,8	19/1,5	25/1,6
II	20/1,4	25/1,5	17/2,0	16/2,9
III	25/1,0	18/1,1	20/1,8	20/1,7
Задача №6
Нафтопереробний завод одержує 4 напівфабрикати: 400 тис. л. ал-
килата, 250 тис. л. крекінг-бензину, 350 тис. л. бензину прямої перегон-
ки і 100 тис. л ізопентану. В результаті змішування цих чотирьох ком-
понентів у різних пропорціях утворюються три сорти авіаційного бен-
зину: бензин А (2:3:5:2), бензин В (3:1:2:1) та бензин С (2:2:1:3). Вар-
тість бензину кожного сорту дорівнює 120 грн., 100 грн., та 150 грн.
а)	визначити співвідношення компонентів, при якому буде досяг-
нута максимальна вартість всієї продукції;
б)	визначити оптимальне співвідношення, виходячи з умови мак-
симального використовування компонентів.
Задача №7
На підприємство поступило дві партії фанери, причому перша
партія містить 400 листів, а друга — 250 листів фанери. З них виго-
товляються комплекти, що включають 4 деталі 1-го типу, 3 деталі 2-
го типу і 2 деталі 3-го типу. Один лист фанери кожної партії може
розкроюватися трьома способами. Кількість деталей кожного типу,
яка виходить при розкрої одного листа за тим або іншим способом,
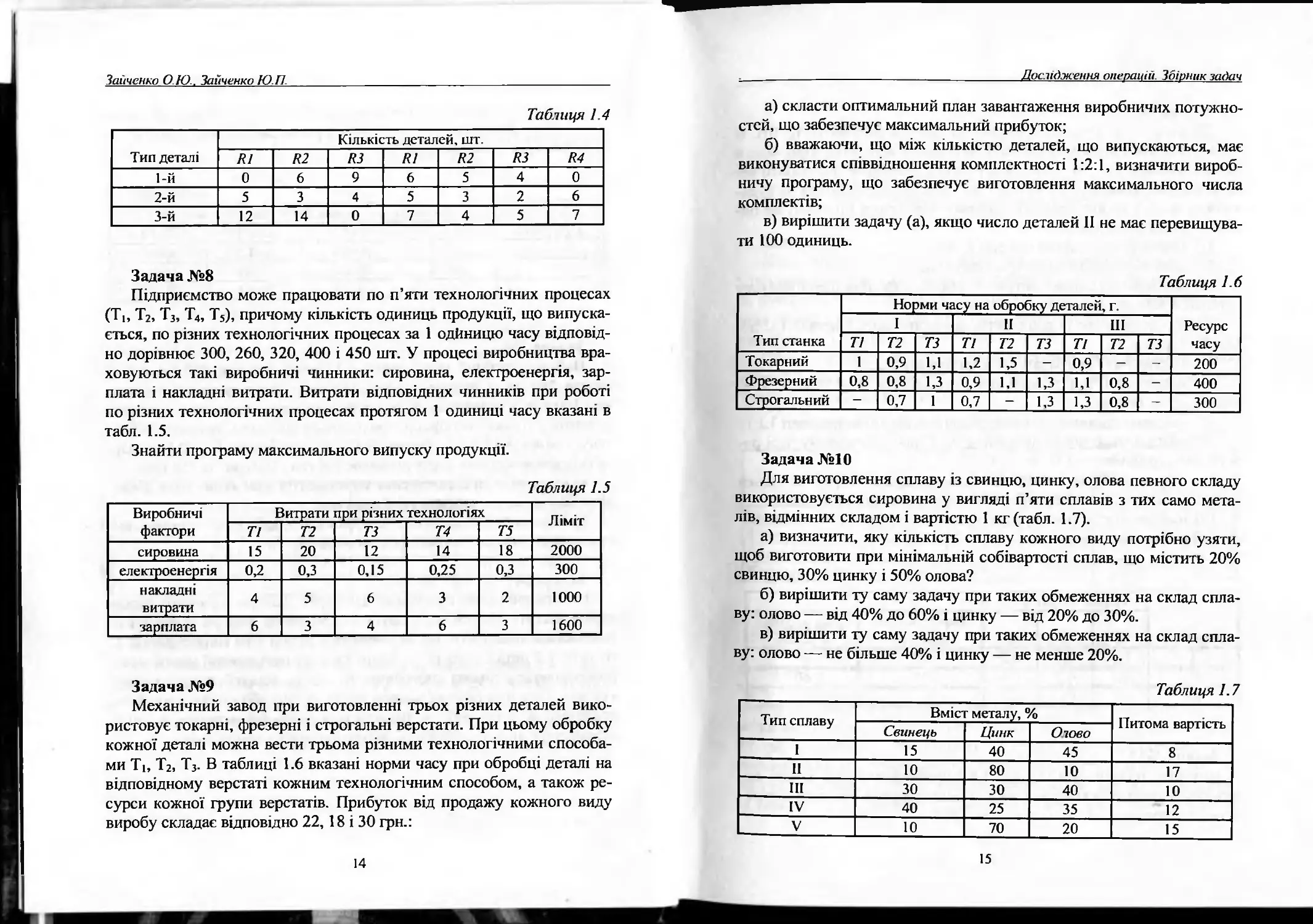
представлена в таблиці 1.4. Вимагається розкроїти матеріал так, щоб
забезпечити виготовлення максимального числа комплектів.
13
Зайченко О Ю.. Зайченко Ю.П.
Таблиця 1.4
Тип деталі	Кількість деталей, шт.						
	НІ	Р.2	КЗ	НІ	Я2	КЗ	М
1-й	0	6	9	6	5	4	0
2-й	5	3	4	5	3	2	6
3-й	12	14	0	7	4	5	7
Задача №8
Підприємство може працювати по п’яти технологічних процесах
(Т|, Т2, Т3, Т4, Т5), причому кількість одиниць продукції, що випуска-
ється, по різних технологічних процесах за 1 одйницю часу відповід-
но дорівнює 300, 260, 320, 400 і 450 шт. У процесі виробництва вра-
ховуються такі виробничі чинники: сировина, електроенергія, зар-
плата і накладні витрати. Витрати відповідних чинників при роботі
по різних технологічних процесах протягом 1 одиниці часу вказані в
табл. 1.5.
Знайти програму максимального випуску продукції.
Таблиця 1.5
Виробничі фактори	Витрати при різних технологіях					Ліміт
	ТІ	Т2	тз	Т4	Т5	
сировина	15	20	12	14	18	2000
електроенергія	0,2	0,3	0,15	0,25	0,3	300
накладні витрати	4	5	6	3	2	1000
зарплата	6	3	4	6	3	1600
Задача №9
Механічний завод при виготовленні трьох різних деталей вико-
ристовує токарні, фрезерні і строгальні верстати. При цьому обробку
кожної деталі можна вести трьома різними технологічними способа-
ми Ті, Т2, Т3. В таблиці 1.6 вказані норми часу при обробці деталі на
відповідному верстаті кожним технологічним способом, а також ре-
сурси кожної групи верстатів. Прибуток від продажу кожного виду
виробу складає відповідно 22, 18 і 30 грн.:
14
Дослідження операцій. Збірник задач
а)	скласти оптимальний план завантаження виробничих потужно-
стей, що забезпечує максимальний прибуток;
б)	вважаючи, що між кількістю деталей, що випускаються, має
виконуватися співвідношення комплектності 1:2:1, визначити вироб-
ничу програму, що забезпечує виготовлення максимального числа
комплектів;
в)	вирішити задачу (а), якщо число деталей II не мас перевищува-
ти 100 одиниць.
Таблиця 1.6
Тип станка	Норми часу на обробку деталей, г.									Ресурс часу
	І			11			III			
	ТІ	Т2	ТЗ	Ті	Т2	ТЗ	ТІ	Т2	ТЗ	
Токарний	1	0,9	1,1	1,2	1,5	—	0,9	—	—	200
Фрезерний	0,8	0,8	1,3	0,9	1,1	1,3	1,1	0,8	—	400
Строгальний	—	0,7	1	0,7	—	1,3	1,3	0,8	-	300
Задача №10
Для виготовлення сплаву із свинцю, цинку, олова певного складу
використовується сировина у вигляді п’яти сплавів з тих само мета-
лів, відмінних складом і вартістю 1 кг (табл. 1.7).
а)	визначити, яку кількість сплаву кожного виду потрібно узяти,
щоб виготовити при мінімальній собівартості сплав, що містить 20%
свинцю, 30% цинку і 50% олова?
б)	вирішити ту саму задачу при таких обмеженнях на склад спла-
ву: олово — від 40% до 60% і цинку — від 20% до 30%.
в)	вирішити ту саму задачу при таких обмеженнях на склад спла-
ву: олово — не більше 40% і цинку — не менше 20%.
Таблиця 1.7
Тип сплаву	Вміст металу, %			Питома вартість
	Свинець	Цинк	Олово	
І	15	40	45	8
11	10	80	10	17
III	ЗО	зо	40	10
IV	40	25	35	12
V	10	70	20	15
15
Зайченко ОЮ„ Зайченко ЮП_______________________________________
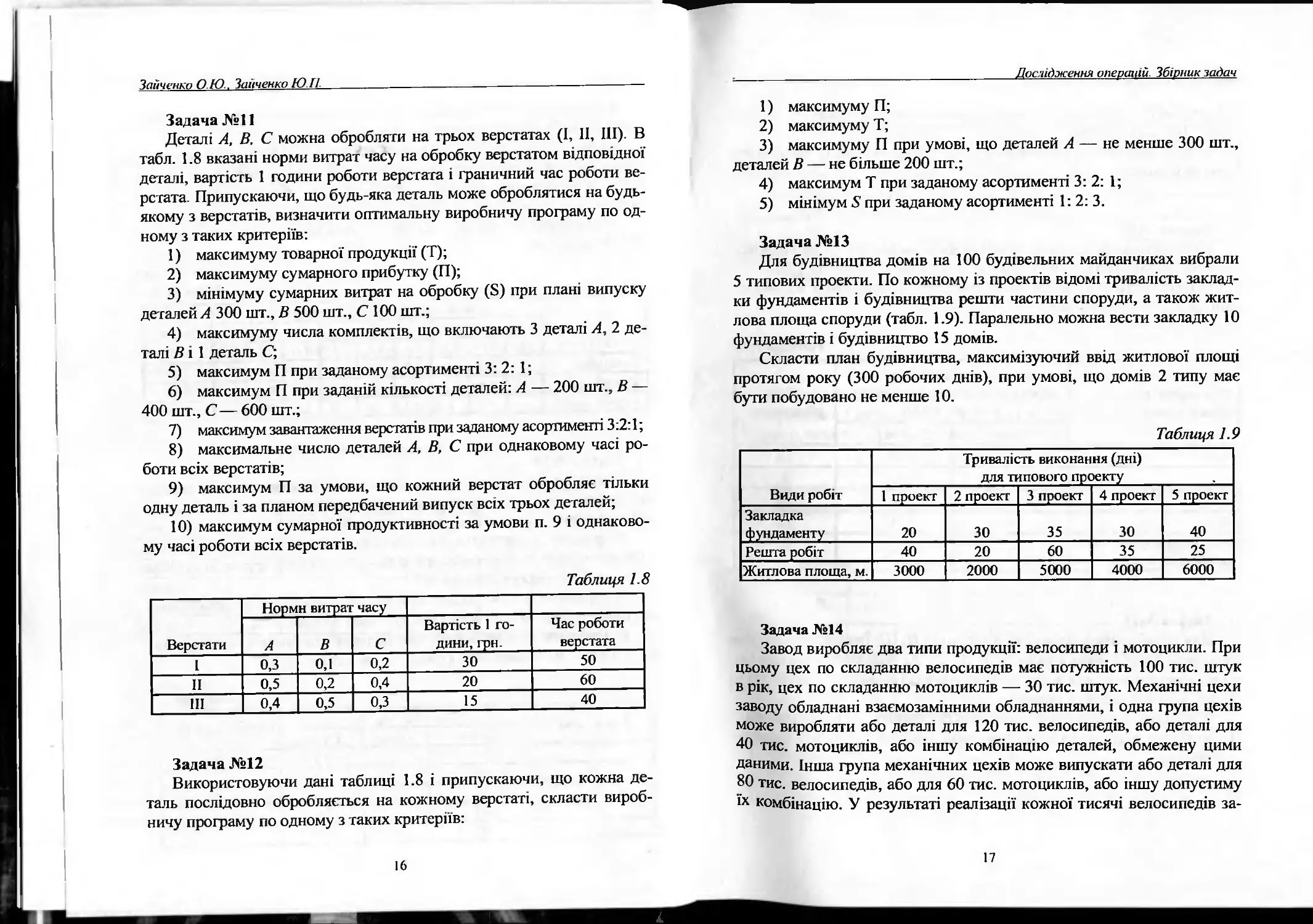
Задача №11
Деталі А, В. С можна обробляти на трьох верстатах (І, II, III). В
табл. 1.8 вказані норми витрат часу на обробку верстатом відповідної
деталі, вартість 1 години роботи верстата і граничний час роботи ве-
рстата. Припускаючи, що будь-яка деталь може оброблятися на будь-
якому з верстатів, визначити оптимальну виробничу програму по од-
ному з таких критеріїв:
1)	максимуму товарної продукції (Т);
2)	максимуму сумарного прибутку (П);
3)	мінімуму сумарних витрат на обробку (8) при плані випуску
деталей А 300 шт., В 500 шт., С 100 шт.;
4)	максимуму числа комплектів, що включають 3 деталі А, 2 де-
талі В і 1 деталь С;
5)	максимум П при заданому асортименті 3:2: 1;
6)	максимум П при заданій кількості деталей: А — 200 шт., В —
400 шт., С — 600 шт.;
7)	максимум завантаження верстатів при заданому асортименті 3:2:1;
8)	максимальне число деталей А, В, С при однаковому часі ро-
боти всіх верстатів;
9)	максимум П за умови, що кожний верстат обробляє тільки
одну деталь і за планом передбачений випуск всіх трьох деталей;
10)	максимум сумарної продуктивності за умови п. 9 і однаково-
му часі роботи всіх верстатів.
Таблиця 1.8
Верстати	Норми витрат часу				
	А	В	С	Вартість 1 го- дини, грн.	Час роботи верстата
1	0,3	0,1	0,2	зо	50
II	0,5	0,2	0,4	20	60
III	0,4	0,5	0,3	15	40
Задача №12
Використовуючи дані таблиці 1.8 і припускаючи, що кожна де-
таль послідовно обробляється на кожному верстаті, скласти вироб-
ничу програму по одному з таких критеріїв:
16
Дослідження операцій. Збірник задач
1)	максимуму П;
2)	максимуму Т;
3)	максимуму П при умові, що деталей А — не менше 300 шт.,
деталей В — не більше 200 шт.;
4)	максимум Т при заданому асортименті 3:2: 1;
5)	мінімум 5 при заданому асортименті 1:2:3.
Задача №13
Для будівництва домів на 100 будівельних майданчиках вибрали
5 типових проекти. По кожному із проектів відомі тривалість заклад-
ки фундаментів і будівництва решти частини споруди, а також жит-
лова площа споруди (табл. 1.9). Паралельно можна вести закладку 10
фундаментів і будівництво 15 домів.
Скласти план будівництва, максимізуючий ввід житлової площі
протягом року (300 робочих днів), при умові, що домів 2 типу має
бути побудовано не менше 10.
Таблиця 1.9
Види робіт	Тривалість виконання (дні) для типового проекту				
	1 проект	2 проект	3 проект	4 проект	5 проект
Закладка фундаменту	20	зо	35	зо	40
Решта робіт	40	20	60	35	25
Житлова площа, м.	3000	2000	5000	4000	6000
Задача №14
Завод виробляє два типи продукції: велосипеди і мотоцикли. При
цьому цех по складанню велосипедів має потужність 100 тис. штук
в рік, цех по складанню мотоциклів — 30 тис. штук. Механічні цехи
заводу обладнані взаємозамінними обладнаннями, і одна група цехів
може виробляти або деталі для 120 тис. велосипедів, або деталі для
40 тис. мотоциклів, або іншу комбінацію деталей, обмежену цими
даними. Інша група механічних цехів може випускати або деталі для
80 тис. велосипедів, або для 60 тис. мотоциклів, або іншу допустиму
їх комбінацію. У результаті реалізації кожної тисячі велосипедів за-
17
Зайченко О.Ю., Зайченко Ю.П.
вод отримує прибуток у 20 тисяч гривень, а кожної тисячі мотоцик-
лів — ЗО тисяч гривень.
Знайти таке поєднання випуску продукції, яке дасть найбільшу
суму прибутку.
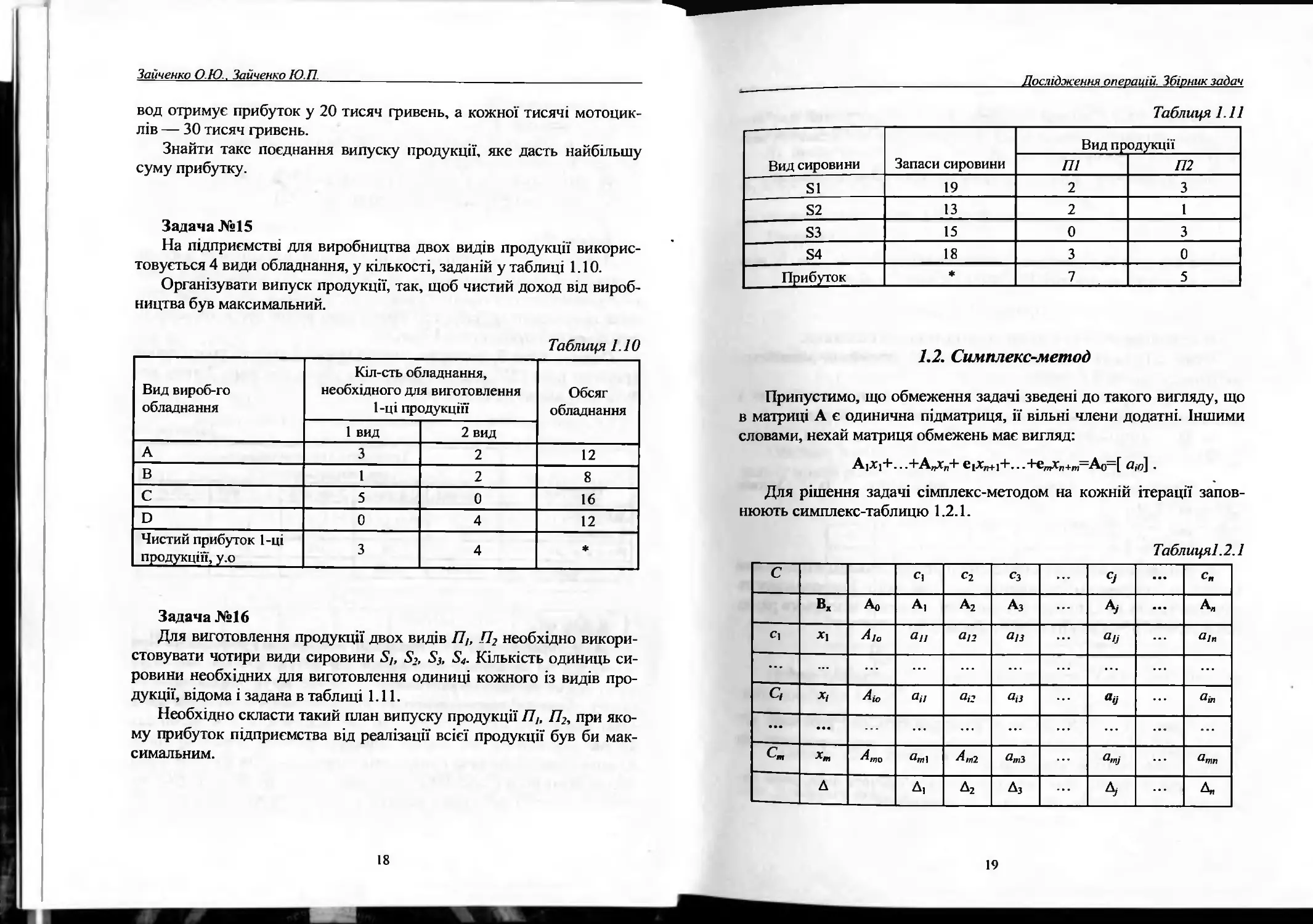
Задача №15
На підприємстві для виробництва двох видів продукції викорис-
товується 4 види обладнання, у кількості, заданій у таблиці 1.10.
Організувати випуск продукції, так, щоб чистий доход від вироб-
ництва був максимальний.
Таблиця 110
Вид вироб-го обладнання	Кіл-сть обладнання, необхідного для виготовлення 1-ці продукції!		Обсяг обладнання
	1 вид	2 вид	
А	3	2	12
В	1	2	8
С	5	0	16
О	0	4	12
Чистий прибуток 1-ці продукції!, у.О	3	4	♦
Задача №16
Для виготовлення продукції двох видів 77/, П2 необхідно викори-
стовувати чотири види сировини 5/,	$з. $4- Кількість одиниць си-
ровини необхідних для виготовлення одиниці кожного із видів про-
дукції, відома і задана в таблиці 1.11.
Необхідно скласти такий план випуску продукції П,, П2, при яко-
му прибуток підприємства від реалізації всієї продукції був би мак-
симальним.
18
Дослідження операцій. Збірник задач
Таблиця 111
Вид сировини	Запаси сировини	Вид продукції	
		ПІ	П2
51	19	2	3
52	13	2	1
53	15	0	3
54	18	3	0
Прибуток	♦	7	5
1.2. Симп.іекс-метод
Припустимо, що обмеження задачі зведені до такого вигляду, що
в матриці А є одинична підматриця, її вільні члени додатні. Іншими
словами, нехай матриця обмежень має вигляд:
АіХі4-...4-А^п+еІхп+14-...4-етхп+т=А0=[ а,0].
Для рішення задачі сімплекс-методом на кожній ітерації запов-
нюють симплекс-таблицю 1.2.1.
Таблицяі.2.1
С				С2	Сз		9	...	
	Вх	Ао	А,	а2	А3		А	...	А,
С|			ви	аіз	0/3	...	в/,	...	О/Я
...			...		...			...	...
С,	X,	^іо	0,7		0,3		в«		Ои
•••	...		...		...			...	...
С„		А	1		о,„з		о,„7		
	Д		А!	д2	Дз		А	...	А,
19
Зайченко О.Ю., Зайченко Ю.П
Останній рядок таблиці — індексний — він потрібний для зна-
ходження направляючого стовпця. Зрозуміло, для всіх базисних век-
торів {А,}/=1,...,7и оцінки (\=аГ)=0.
Значення цільової функції а№, визначається з співвідношення:
/і \
1=1
У стовпчику Вх записуємо базисні змінні {х,} і= 1,..., т. їх зна-
чення визнаються стовпчиком вільних членів а,о, тобто
Хї=ац), і=1, 2,. ..т.
Напрямні рядок \ і стовпець А, позначаються стрілками.
Отже, алгоритм розв’язання задачі ЛП табличним симплекс-
методом складається з етапів.
1.	Розраховують і заповнюють початкову симплекс-таблицю з
допустимим одиничним базисом, включаючи індексний рядок.
2.	За напрямний стовпець беруть Ау, для якого
д, = % =пйп{ам|пм <0}
3.	Напрямний рядок А вибирають із умови
„(*)
>0}.
4.	Виконують один крок (інтерацію) методу повного виключення
Гаусса із напрямним елементом ач, для чого використовують
співвідношення (1.2.16)-(1.2.18). Зокрема, елементи індексного рядка
нової таблиці обчислюють згідно з формулою
5.	Якщо всі Д/А+/)>0, 1=1п, то новий базисний розв’язок х,=
вю* ієІ6(кч>- оптимальний. У протилежному разі переходять до
етапу 2 й виконують чергову ітерацію.
6.	Другий, третій та четвертий етапи повторюють доти, доки од-
на з ітерацій не закінчиться одним з двох випадків:
20
Досаджений операцій Збірник задач
а)	всі аОі >0. Це ознака (критерій) оптимальності базисного
розв’язку останньої симнлекс-таблиці,
б)	знайдеться такий ао?=Д/<0, що всі елементи цього стовпця
л < 0, г = 1,...,л. Це ознака необмеженості цільової функції г ='^сіх,
на множині допустимих розв’язків задачі.
Приклад 1.2.1:
максимізувати х,+х2,
при обмеженнях:
2х, +х2< 18;
х, + 2х2< 16;
х,,х2 > 0.
Розширена форма задачі має такий вигляд:
максимізувати х,+х2>
при обмеженнях:
2х, + 1х2 + Іхз + Охд =18;
їх, + 2хг + 0х3 + 1х4 =16.
Оскільки Ао>О, а вектори А3, А4, утворюють одиничний базис, то
задачу можна розв’язувати методом симплекс-таблиць.
Таблиця 1.2.2
Сі			1	1	0	0
	В,	До	А,	а2	Аз	А4
0	х3	18	2	1	1	0
0	х4	16	1	2	0	1
	Д	0	-1	-1	0	0
Перша ітерація. Складаємо й заповнюємо початкову симплекс -
таблицю (табл. 1.2.2).
Напрямний стовпець — перший (Д2=Д,<0).
Склавши відношення вигляду - —
визначаємо напрямний ря-
док. Для цього знаходимо:
тіп ( 18/2; 16/1} =9.
21
Зайченко О.Ю., Зайченко Ю.П.
Отже, напрямний рядок перший напрямний елемент аИ =2.
Виконавши першу ітерацію симплекс-методу, одержимо табл. 1.2.3.
Таблиця 1.2.3
С/			1	1	0	0
	в.	0,0	Аі	а2	А3	А4
1	*|	9	1	0.5	0.5	0
0	хЛ	7	0	1.5	-0.5	1
	д	9	0	-0.5	0.5	0
Друга ітерація. Як бачимо з табл. 1.2.3, напрямний стовпець —
другий (Д2<0), а напрямний рядок — другий, оскільки
шіп { 9/0.5; 7/1.5} = 14/3.
Виконавши чергову ітерацію симплекс-методу, отримаємо симп-
лекс-таблицю 1.2.4.
Таблиця 1.2.4
Сі			1	1	0	0
	вх	0,0	А>	А2	Аз	А4
1	Х1	20/3	1	0	2/3	-1/3
1	хг	14/3	.0	1	-1/3	2/3
	Д	34/3	0	0	1/3	1/3
Оскільки в індексному рядку табл. 1.2.4 всі оцінки невід’ємні, то
знайдемо оптимальний розв’язок: хІот=20/3, х2оят=14/3.
Відповідне значення ц. ф. дорівнює шах (хі+х2)=34/3.
22
Дослідження операцій. Збірник задач
Розв’язати геометрично (або упевнитись у нерозв’язності)
наступні задачі ЛП:
1.1
Е = 7х, + 6х, —> шах
2х,+5х2 >10
5х,+2х,>10
х, <6
х2<5
ХрХг^О.
1.2
Е = 3х\ -2хг —>тах
2х, + х2 < 11
-Зх, + 2х2 < 10
Зх,+4х2>20
х,,х2 >0.
1.3
Е = 5х, - Зх2 —> тій
Зх, +2х2 >6
2х, — Зх2 > —6
х,-х2<4
4х, + 7х2 < 28
х},х2 >0.
1.4
Р = х, + 2х2 -> тах
ІХі +х2 <14
-Зх, +2х2 <9
ЗхІ + 4х2 > 27
*і,х2>0.
23
Зайченко О ІО , Зайченко Ю П.
1.5
Р = 7х, - 2х, —> тах
5х, -2х, < З
х, +х2 > 1
-Зх, +х2 <3
2х, +х2 <4
х„х2 >0.
1.6
Р = 2х, + х2 —> тах
-2х2 >4
5Х] + 2х2 > 10
4Х] -Зх2 <12
7Х] +4х, <28
х|5х2 >0.
1.7
Р = 2х, + 2х, —> тах
Зх, -2х2 > -6
х, + х, > З
х,<3
х2 <5
х,,х2 >0.
1.8
/7 = 2х| -4х2 —>тах
8х,-5х2 <16
х, + Зх2 < 2
2х, + 7х, > 9
х,,х2 >0.
24
Дослідження операцій. Збірник задач
1.9
Е = х, + 2х, -> тах
5х,—2х2 <4
х, -2х2 >-4
х, + х2 > 4
хгх2>0.
1.10
Г = 3х1+3х2 —>тах
х1 -4х2 <4
Зх, +2х2 <6
-х,+х2<1
х, + 2х2 > 2
Х],х2>0.
1.11
Г = 2х, -х2 ->тах
х, —х2 >-3
бХ] + 7х2 < 42
2х,-3х2 <6
х, + х2 > 4
Х],х2 >0.
25
Зайченко О.Ю.. Зайченко Ю П
1.12
Г = 5х, + х2 —> тах
х,+7х, >7
-2х, + х2 <6
2х, +5х2 >10
5х,+2х2>10
7х, +х2 >7
х, <6
х„х2 >0.
1.13
~ х\ ~ х2 ~тах
-X] + х2 > 8
8х, +5х2 <80
х(-2х2 <2
х,+4х, >4
хрх2 >0.
1.14
^” = 7х, +х2 —> тах
х,+х2 <14
ЗХ)-5х2 <15
5х,+Зх2>21
х„х2 >0.
26
Дослідження операцій. Збірник задач
1.15
Г = 7х,-х2 —>тіп
х, + х2 > З
5х, +х2 > 5
X] + 5х2 > 5
О < х, < 4
О < х2 < 4.
1.16
Г=х, + х2 —>тіп
ЗХ| + х2 > 8
х, + 2х2 > 6
х,-х2 <3
х,,х2>0.
1.17
Г = Х]+Зх2—>тах
-х,+х2<3
4х1 + Зх2 < 20
х„х2>0.
1.18
/7 = 2хі+х2 —>тах
х1-х2 >4
X! +х2 >10
4х, -х2 < 12
7х, + х2 < 7
Х|,х2 >0.
27
Зайченко О.Ю., Зайченко Ю.П.
1.19
Р = 2х, + 2х, —> шах
Зх, — 2х, > -6
х, + х2 > З
х,<3
х2 < 5
х,,х2 >0.
1.20
Р = 2х, - 4х2 —> тах
8х, — 5х, < 16
х1 + Зх2 > 2
2х, + 7х2 < 9
х,,х2 > 0.
7.3. Метод штучних змінних
У загальному випадку, коли деякі обмеження мають знак > ®, на-
приклад:
а,іхі 4- аах2 + ...+ аіпх„ > Ь,_
де і = 1, 2,..., т, то для зведення цих обмежень до стандартного ви-
гляду рівнянь вільні змінні треба віднімати. Тоді розширена форма
задачі матиме такий вигляд:
Пнх, + а12х2 4-...+ п1лхл-1хл+14-0хл+2 +...+0х„+т = Ьх;	(1-3.1)
4- @т2Х2 4"... 4" ОтлХл 4- 0хл+І 4- 0хп+2 4"... 1Х„+т — Ьт.
Вільні змінні {хл+і,...,х„^т} у цьому разі вже неможливо викорис-
тати як початковий базис, оскільки хп+і<0,..., х„,,„<0. Тому в рівняння
(1.3.1) додатково вводять штучні змінні хл+т+і,...рсл+2лі. Ці змінні не
мають нічого спільного з реальною задачею, і тому їх треба вивести з
базису якнайшвидше. Для цього після початку ітерацій штучним
28
Дослідження операцій. Збірник заоач
змінним у цільовій функції приписують для задач максимізації дуже
великі за модулем від’ємні коефіцієнти (-М), де М»Сі (і = 1, 2,..., т).
В разі розв’язання задач мінімізації штучні змінні вводять у ці-
льову функцію з великими додатніми коефіцієнтами +М.
Знаки штучних змінних х„+т+1,...дсл+2и, мають збігатися із знаками
відповідних членів. Штучні змінні створюють початковий базисний
розв’язок. Застосувавши симплекс-метод, треба вивести із базису усі
штучні змінні. Якщо вдається довести (чи показати), що штучні
змінні повністю вивести із базису неможливо, то це означає, що за-
дача не має розв’язків, тобто ії обмеження суперечні.
Якщо на поточній ітерації із базису виводиться штучна змінна, то
в наступній симплекс-таблиці відповідний їй стовпець можна вида-
лити, в подальших ітераціях він не братиме участі.
Приклад 1.3.1:
міні мізувати /(х)=2х1+3х2,
при обмеженнях:
2хі + х2 > 16;
хі + 2х2 > 16;
Х|, х2 > 0.
Застосувавши вільні змінні х3, х<, х5 приходимо до розширеної
форми задачі:
2хі + х2 —х3 =16;
х, + 2х2—х4 = 16.
Як бачимо, змінні х3, ха утворюють недопустимий базисний
розв’язок:
х3 = -16<0; х4 = -16<0.
Тому вводимо в обмеження і в цільову функцію штучні змінні ХА
хб і приходимо до такої задачі:
мінімізувати {2хі + Зх2 + Мх5 + Мх6 },
при обмеженнях:
2х| + х2 -х3 + х5 = 16;
Х| + 2х2 -^4 + х6 = 16.
29
Зайченко О.Ю., Зайченко Ю.П.
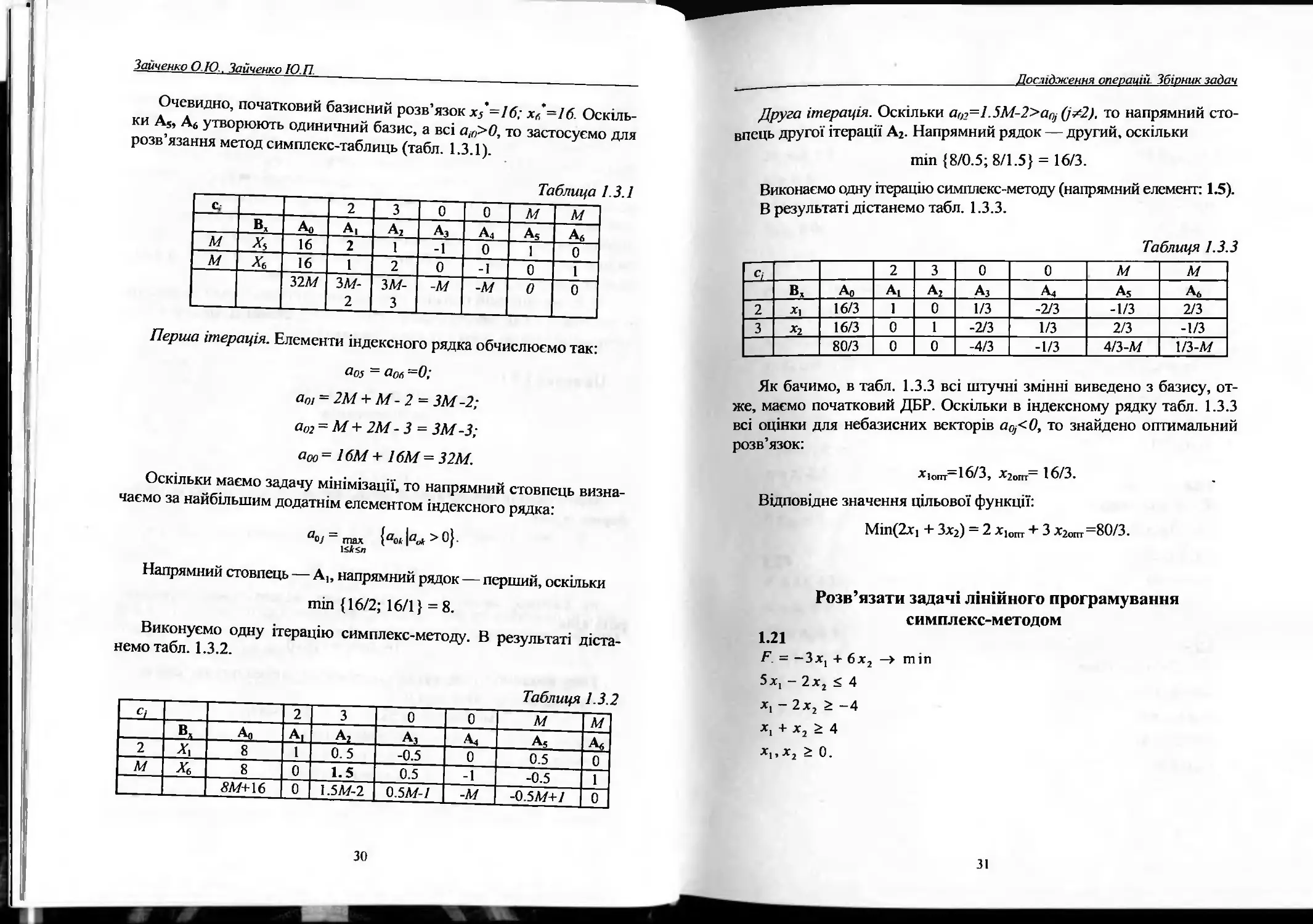
Очевидно, початковий базисний розв’язок х5*-16: хл=16. Оскіль-
ки А5, А6 утворюють одиничний базис, а всі а,г^>0, то застосуємо для
розв’язання метод симплекс-таблиць (табл. 1.3.1).
Таблица 1.3.1
9			2	3	0	0	м	м
	В,	Ао	А1	А1	А3	А4	А5	Аб
М	х,	16	2	1	-1	0	1	0
м	Х6	16	1	2	0	-І	0	1
		32Л/	ЗМ- 2	ЗМ- 3	-м	-М	0	0
Перша ітерація. Елементи індексного рядка обчислюємо так:
Ооз ~ аол =0;
апІ = 2М + М-2 = ЗМ-2;
а02 = М+ 2М-3 = ЗМ-З;
ам= 16М+ 16М=32М.
Оскільки маємо задачу мінімізації, то напрямний стовпець визна-
чаємо за найбільшим додатнім елементом індексного рядка:
°оу = птах {ао* |°<д > 0}.
її* їй
Напрямний стовпець — Аь напрямний рядок — перший, оскільки
тіл {16/2; 16/1} = 8.
Виконуємо одну ітерацію симплекс-методу. В результаті діста-
немо табл. 1.3.2.
Таблиця 1.3.2
Сі			2	3	0	0	м	М
		А«	А|	А2	. А,	А»	А5	Хб
2	х,	8	1	0.5	-0.5	0	0.5	0
М	х6	8	0	1.5	0.5	-1	-0.5	1
		ЯЛ/+16	0	І.5ЛЇ-2	0.5М-1	-м	-0.5ЛЇ+/	0
ЗО
Дослідження операцій. Збірник задач
Друга ітерація. Оскільки аГ)2=1.5М-2>а(^ 0^2). то напрямний сто-
впець другої ітерації А2. Напрямний рядок — другий, оскільки
тіп {8/0.5; 8/1.5} = 16/3.
Виконаємо одну ітерацію симплекс-методу (напрямний елемент: 1.5).
В результаті дістанемо табл. 1.3.3.
Таблиця 1.3.3
сі			2	3	0	0	М	М
	в.	Ао	А!	А2	Аз	А4	а5	Аь
2	хІ	16/3	1	0	1/3	-2/3	-1/3	2/3
З	х2	16/3	0	1	-2/3	1/3	2/3	-1/3
		80/3	0	0	-4/3	-1/3	4/3-Л/	1/3-Л/
Як бачимо, в табл. 1.3.3 всі штучні змінні виведено з базису, от-
же, маємо початковий ДБР. Оскільки в індексному рядку табл. 1.3.3
всі оцінки для небазисних векторів аоІ<0, то знайдено оптимальний
розв’язок:
Х|опт~1б/3, Хзопт 16/3.
Відповідне значення цільової функції:
Міп(2хі + Зх2) = 2 х1опт + 3 х2оітт=80/3.
Розв’язати задачі лінійного програмування
симплекс-методом
1.21
Р = — ЗХ] + 6х2 —> тіп
5х, - 2х2 < 4
X] - 2х2 > -4
X, + х2 > 4
хих2 > 0.
31
Зайченко ОЮ.. Зайченко Ю.П.
1.22
Р = Зх, + Зх2 —> тах
х, + хг < 8
Зх1 + 7х2 >21
х, + 2х2 > 6
0<х, <1
0<х2 <1.
1.23
Р = х, + х2 —> тах
х, + х2 > 1
-5х, + х2 < О
-X! +5х2 >0
х, + х2 < 6
х,,х2 > 0.
1.24
Р = х1 + х2 —> тах
5х, -2х2 < 7
-х1 + х2 < 5
х, +х2 < 6
х„х2 >0.
1.25
Р = -2х, + х2 -> тіп
2х, +х2 <8
X] +3х2 >6
ЗХ] +х2 >3
х,,х2 >0.
32
Дослідження операцій Збірник задач
1.26
р = —2х, + х2 -> тіп
2х,+х2<8
х,+х2 <6
-Зх, + 2х2 > З
х„х2 >0.
1.27
Р = 2х, -Зх2 ->тіп
х, +2х2 >10
Зх,+х2>15
х,,х2 >0.
1.28
Р = 2х, + 2х2 —> тах
Зхі - 2х2 > -6
х, + х2 > З
0<х, <3
0<х2<5.
1.29
Р = Зх, +3х2 -> тах
х, +х2 <:4
Зх, + х2 > 4
х, +5х2 >4
0<х, <3
0<х2 <3.
33
Зайченко О.Ю., Зайченко Ю.П.
1.30
Р = х, + 2хг —> тах
5л- - 2х, < 4
х, - 2х, > -4
х, + х2 > 4
х,,х2 > 0.
1.31
Р = 2.x, - х2 -> тах
х, -х2 >-3
6х1 + 7х2 < 42
2х1 — Зх2 < 6
х,,х2 >0.
1.32
Р = 2х, -4х2 ->тіп
8х1 -5х2 < 16
х, +3х2 >2
2х1 + 7х, < 9
х,,х2 >0.
1.33
/7 = 8хІ -5х, -> тах
2х1 -х2 -х3 < 4
4х, + Зх2 < 2
-Зх, + 2х, + х3 < З
х,,х2,х3 >0.
34
Дослідження операцій. Збірник задач
1.34
Г = 5х} -2х, -> тах
5х, + 2х, > 10
2х, + 5х, >10
-2х, + х, <4
0<х,<6
0<х2 <6.
1.35
Е = 7х1 + 5х2 -> тах
7х,+5х2>7
7х1 -5х2 >35
х1 —х2 <0
х,,х2>0.
1.36
/7 = 3х1 -2х2 ->тіп
2х,+х2 <14
—3х1 + 2х2 < 9
3х1 +4х2 < 27
х15х2 >0.
1.37
Р =-хх +2х2 +4х3-5х4 ->тіп
х, +4х2 + 2х3 - 2х4 = 40
х, +2х2 + х3 + 2х4 <80
Зх2+Зх3 — 1,5х4 >36
^1 ’ ^2 ’ ^3 » ^4 “ 0.
35
Зайченко О. Ю., Зайченко Ю.П.
1.38
Р - 8х1 + х, + 2х, —> тах
5Х] -х2 +х, <2
х, + 2х2 + 2х3 <4
х„х2,х, >0
1.39
Р = 2^ -Зх2 -> тах
5х, +2х2 >10
х, +3х2 <12
х„х2 >0.
1.40
Р = X] + х2 -> тах
2х, +11х2 < 38
х,+х,<7
4х,-5х,<5
х15х2 > 0.
1.41
Р = -2х, + х2 > тіп
X, + Х2 < 6
-Зх, + 2х2 > З
хрх2 >0.
1.42
Р = 6х, + 4х2 -> тіп
2Х] + х2 > З
х,-х2 <1
х,,х, >0.
36
Дослідження операцій. Збірник задач
1.43
Е = 4х, + 15х, + 12х3 + 2х4 —> тіп
2х2 + Зл'з + х4 > 1
х, + 3х2 +х3— х4 >1
х1>х2,х3,х4 >0.
1.44
Г = 3л1 + 2х2 —>тах
4х1 + 2х2 > 12
х,+2х2<10
2х, + 2х2 = 6
х„х2>0.
1.45
Е = 2Х| + 6х2 -> тах
8х,-5х2<40
2х, +5х2 > 10
-6х( + 5х2 < 60
2х,+х2<14
Х],х2 >0.
1.46
/? = 3х1 +х2 —>тах
X] +2х2 > 5
2х,+4х2<16
3х1 + х2 > 6
+ Зх2 < 9
х„х2 >0.
37
Зайченко О.Ю., Зайченко Ю.П.
1.47
Р = х, + 2х2 + Зх3 -х4 —> шах
+ 2х2 + Зх3 = 15
2х, + х2 + 5х3 = 20
х, +2х2 +х4 = 10
х,,х,,х,,х. >0.
1.4. Двоїста задача лінійного програмування
1.4.1. Структура та властивості двоїстої задачі
Запишемо пряму і двоїсту задачі в загальному вигляді.
Пряма задача:
п
	максимізувати	, і—І	(14.1)
при обмеженнях:		
	п У а..х. < Ь., ї=1,2,...,т, 7=1	(1.4.2)
Двоїста задача:	X) > 0,у=1,2,...,л.	(1-4.3)
	т мінімізувати У б.у,, і—1	(1-4-4)
при обмеженнях:	І—1	
	т /=1	(1.4.5)
	у, >0,1=1,2,..., т.	(1.4.6)
У матричному вигляді пара двоїстих задач записується так:
Пряма задача:
максимізувати стх,	(1-4.7)
при обмеженнях:
38
Дослідження операцій Збірник задач
Двоїста задача:
при обмеженнях:
Ах < Ь\ х>0;	(1.4.8) (1.4.9)
мінімізувати Ьту,	(1.4.10)
Ату > с;	(1.4.11)
у>о.	(1.4.12)
Порівнюючи форми запису прямої та двоїстої задач, можна вста-
новити між ними такі взаємозв’язки.
1.	Якщо пряма задача є задачею максимізації, пю двоїста буде
задачею мінімізації, і навпаки.
2.	Коефіцієнти цільової функції прямої задачі С/, ...,с„ стають
вільними членами обмежень двоїстої задачі.
3.	Вільні члени обмежень прямої задачі Ь\, ...,Ьт стають коефі-
цієнтами цільової функції двоїстої задачі.
4.	Матриця обмежень двоїстої задачі утворюється шляхом
транспонування матриці обмежень прямої задачі.
5.	Знаки нерівностей в обмеженнях змінюються на протилежні.
6.	Число обмежень прямої задачі дорівнює числу змінних двоїс-
тої задачі і навпаки.
Зв’язки між оптимальними розв’язками прямої та двоїстої задач
встановлюються в таких теоремах теорії двоїстості [15].
ТЕОРЕМА 1.4.1. Якщо х та у допустимі розв’язки прямої та
двоїстої задач, тобто Ах<Ь, та Ату>с, то стх<Ьту.
ТЕОРЕМ А1.4.2 (основна теорема двоїстості). Якщо Хр та у о
допустимі розв'язки прямої і двоїстої задач і, крім того, якщо
с Х0=Ь у о, то Крта у о—оптимальні розв’язки пари двоїстих задач.
Між оптимальними розв’язками прямої і двоїстої задач та елеме-
нтами індексних рядків симплекс-таблиць, що відповідають цим
розв’язкам, існує такий взаємозв’язок:
А,1+,пр=у,опт; -А,„+Удв=х,от	(1.4.13)
і= 1, 2,..., /и, у= 1, 2,..., п,
де и число змінних прямої задачі; т — число її обмежень;
39
Зайченко О.Ю., Зайченко Ю.П.
А„+,ГІр, Дт+/дв — відповідні елементи індексного рядка прямої і двоїс-
тої задач відповідно.
ТЕОРЕМА 1.4.3. Якщо в оптимальному розв'язку прямої задачі
(1.4.1)-(1.4.3) і-те обмеження виконується як строга нерівність, то
оптимальне значення відповідної двоїстої змінної дорівнює нулю,
тобто'.
якщо У'а.х. = А'х <Ь,тоу,впт =0,	(1.4.16)
у опт	опт і*	✓ / опт ’
ЛІ
де А'— ї-й рядок матриці А.
Зміст теореми 1.4.3 полягає в такому. Якщо деякий ресурс 6, є в
надлишку, й і-те обмеження в оптимальному розв’язку виконується
як строга нерівність, то це обмеження стає несуттєвим і оптимальна
ціна відповідного ресурсу дорівнює нулю.
Теорему 1.4.3. доповнює теорема 1.4.4, що встановлює взаємо-
зв’язок між оптимальним розв’язком прямої задачі й обмеженнями
двоїстої.
ТЕОРЕМА 1.4.4. Якщо в оптимальному розв’язку двоїстої задачі
обмеження у виконується як строга нерівність, то оптимальне значен-
ня відповідної змінної прямої задачі має дорівнювати нулю, тобто:
якщо Атууопт-су>0, тох)т„ =0.	(1.4.17)
Дамо економічну інтерпретацією теореми 1.4.4.
Оскільки величини у,, (/=1, 2,...,т) являють собою ціни відповід-
• т л
них ресурсів, то А7у=£аіуу, — це витрати на 7-й технологічний
і=і
процес, а величина с, — прибуток від реалізації одиниці відповідного
продукту. Тому з економічної точки зору теорема 1.4.4 означає таке:
якщо у-й технологічний процес є сірого невигідним щодо оптималь-
них цін ресурсів уогт, то в оптимальному розв’язку прямої задачі ін-
тенсивність використання даного технологічного процесу має дорів-
нювати нулю, і відповідний вид продукції не випускається як нерен-
табельний.
Таким чином, теорема 1.4.4 виражає принцип рентабельності для
оптимально організованого виробництва.
Доведення теорем двоїстості наведено в [15, 16].
40
Дослідження операцій. Збірник задач
Приклад 1.4.1.
Розглянемо задачу ЛП:
максимізуватиУ(хІГХ2)=сІХ|+с2Х2=4хі+Зх2,
при обмеженнях:
їх, + 0%2 < 4000;
Охі + 1x2 6000;
2
X] + — х2< 6000;
хьх2 >0.
Двоїста задача записується так:
мінімізувати § (уі,У2,Уз)=4000уІ+6000у2+6000уз,
при обмеженнях:
ІУі+Огг+Іуз Сі =4;
2
0уі+1у2+-уз >с2 =3.
Для розв’язання двоїстої задачі симплекс-методом введемо вільні
и4, и5, запишемо обмеження в такому вигляді:
Іуі+Оуз+Іуз -Р4 =4;
2
Оу,+ 1у2+уУз-Л5=3.
Таблиця 1.4.1
Сз			4000	6000	6000	0	0
	В«	Ао	А,	А2	Аз	А4	А5
4000	У1	4	1	0	1	-1	0
6000	Уг	3	0	1	2 3	0	-1
	А	34000	0	0	2000	-4000	-6000
За напрямний стовпець вибираємо А3, бо А3=2000>0.
Виконавши першу ітерацію симплекс-методу з напрямним еле-
ментом й|з=1, дістаємо таблицю 1.4.2.
41
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 1.4.2
с			4000	6000	6000	0	0
	В„	Ао	А,	а.	Аз	А4	А5
4000	Уз	4	І	0	1	-1	0
6000	Уі	1 3	2 3	1	0	2 3	-1
		26000	-2000	0	0	-2000	-6000
Оскільки в індексному рядку цієї таблиці всі оцінки недодатні, то
поточний базисний розв’язок — оптимальний.
Отже, ми знайшли розв’язок уіопт=0,у2опт=1/3,узопт=4. Очевидно,
х.опт = -ДІ’=2000;
х2опст =-А? =6000;
тіл (4000уІ+6000у2+6000уз)=26000;
тіп £(у)= тах/(х)= 26 000, тобто теорема 1.4.2 виконується.
Загальний випадок двоїстості
Вище встановлено основні співвідношення для пари двоїстих за-
дач ЛП при обмеженнях у формі нерівностей. Узагальнимо ці ре-
зультати на випадок довільних обмежень.
Нехай пряма задача ЛП задана у вигляді:
п
максимізувати ,	(1.4.18)
У=і
при обмеженнях;
£ аі^x^ <Ь( ,/ = 1,2,...,»!] <т;	(1.4.19)
7=1
£ аІ]хі = Ь, ,і = пц +!,«] + 2,...,т;	(1.4.20)
/=і
Хі>0,і= 1, 2, ..., п!<п.	(1.4.21)
42
Дослідження операцій Збірник задач
Тоді двоїста задача стосовно задачі (1.4.18)-( 1.4.21) записується
так:
т
мінімізувати ,	(1.4.22)
і=і
при обмеженнях:
=	< п;	(1.4.23)
1=1
=су,у = иІ + 1.И, +2,...,и;	(1.4.24)
1=1
у, > 0; і= 1, 2,	ті <пі.	(1.4.25)
Приклад 1.4.2.
Записати двоїсту задачу до наступної і розв’язати її:
максимізувати (х/+х?)>
при обмеженнях:
2 Х| - х2 = 6;
-X] + х2<2;
хі + х2 < 10;
X) > 0.
Двоїста задача записується так:
мінімізувати буї + 2у2 + 10у3,
при обмеженнях:
2уі-у2+у3> 1;
-уі+т2+тз= і;
Т2>Тз^0.
43
Зайченко О.Ю.. Зайченко Ю.П.
Задачі та вправи
Записати задачу, двоїсту до даної, вирішити одну з пари задач та
відшукати оптимальний розв’язок другої з них.
1.48
Р = х, + хг -> шах
-Зх, + 2х2 < 1
X] +2х2 <14
2х, +х2 < 13
Зх, -х2 <12
х? >0,7 =1,2.
1.49
Р = Зх, + х2 —> тіп
Зх, + 5х2 >15
5х, + Зх2 > 15
х,>1
х2 >1
ху>0,у = 1,2.
1.50
Р +3х^ ->тіп
х, +4х2 >4
4Х| + х2 > 4
ху >0,7 = 1,2.
1.51
Р = бх, - 5х, —> тах
2х, +5х2 < 10
5х, +2х2 <10
ху>0,7=1,2.
44
Дослідження операцій- Збірник задач
1.52
Р = 8х, + 2хг —> тах
-4х2 <4
-4х, + х2 < 4
х|+х2 <6
х.>0,у = 1,2.
1.53
Р = х, + 2х, —> тах
5х, - 2х2 < З
х, + х2 > 1
-Зх, + х2 < З
Зх, +3х2 <9
ху. >0,7= 1,2.
1.54
Р = 14х, + 10х2 + 14х3 + 14х4 —> тах
4х, + 2х2 + 2х3 +х4 < 35
X] + х2 + 2х3 + Зх4 < ЗО
Зх, +х2 +2х3 +х4 <40
ху >0,; = 1,2,3,4-
1.55
Р = 2хІ + Зх2 —> тіп
х, +5х2 > 10
Зх! +2х2 > 12
2х} +4х2 > 10
х,>1
ху >0,7 = 1,2.
45
Зайченко О.Ю-, Зайченко Ю.П.
1.56
Е - 5-ї, + 4х2 + 6х3 —> тах
X, 4- х2 4- х3 < 6
2х] 4-х2 4-х, >9
Зх, 4- х, 4- 2х3 >11
ху> 0,у =1,2,3.
1.57
Е = -7.Х] 4- 2х2 —> тіп
X] 4-Х2 >1
5х, 4-х2 >3
-Зх, 4-Х2 <3
2х,4-х2<4
ху >0,7 =1,2.
1.58
Е = 15Х] 4-ЗЗх2 —> тіп
ЗХ] 4- 2х2 > 6
6Х] 4- х2 > 6
х2 >1
Х],х2 >0.
1.59
Е = —х, -2х2	тіп
5^ -2х2 <4
4- 2х2 < 4
4-Х, >4
ху >0,7 =1,2.
46
Дослідження операцій. Збірник задач
1.60
Е = Зх, + Зх2 —> тах
X] + х, < 4
Зх, + х, > 4
0<х, <3
0<х2 <3.
1.61
Е = -2х, -х2 -> тіп
-х, +2х2 <14
5Х] +2х, > 10
4Х] -Зх2 <12
7^ + 4х2 < 28
хі >0,у = 1,2.
1.62
Е = їх, — 2х2 —> тах
х, + х2 < 5
2х, - Зх2 < 6
ЗХ] + х2 > З
X] + х2 > 2
-х2 > - З
ху >0,7 = 1,2.
47
Зайченко О.Ю., Зайченко Ю П.
1.63
Е = Зх, + хг + 2х3 —> тах
2х, + 2х2 + х3 > 2
Зх, - Зх2 - 2х3 < 6
Зх, -Зх2 + 2х3 < 10
х, - х2 < 2
ху >0,7 = 1,2,3.
1.64
Е = 6х1 -х2 ->тіп
4х, -х2 > -4
Зх, + 2х2 < 24
0 < х2 < 6
ху > 0,у = 1,2.
1.65
Е = —Зх, - 2х, —> тах
х, — 2х2 <—З
2х, +х2 <10
Зх, -х2 >-5
—х, + х2 > З
ху >0,7 = 1,2.
1.66
Е = 2х, + х2 -Зх, тах
х, +3х2 -2х3 <4
-5х, +х3 >—12
-2х, +х2 -Зх3 >- 4
ху> 0,7 =1,2,3.
48
Дослідження операцій. Збірник задач
1.67
Р - х, - 2хг -> тах
5х, + х2 > 1
-Зх, + х, < З
Зх, + Зх, < 2
ху >0,у = 1,2.
Визначити, чи являється пропонована пара векторів оптимальним
розв’язком прямої і двоїстої до неї задачі
1.68
Гплп = 3^, + 4^2 + 5у3 + 6 у,
2у1+У2-У3+5у4>5
3>'|+3>’2+5'з+4у4>4
Х>0.
1.69
21.41 У
5 ’5]’
17.9
5 ’5
;0;0
Р ттп = 5у, + 6у2 - 2у3 + Зу4
У!-2у2-Зуз-у4>7
Уу-'іУг-Уз+УЛ-2
У, 0.
49
Зайченко О.Ю. Зайченко Ю.П.
1.70
^ = {3;1}, У = {3,0;0;0;0}.
Гтт = 4Уі - 4у2 - 4у, + 3 у, + 3^5
У|-Зу2-у3+.у4 >3
Уі-У2-5у3 + У5 ^3
Уі ^0-
1.71
Ґ 2
Х = {0;5}, У = <!-;0;0
Л™ = х1+2х2
2х, +3х2 <15
X] + 2х2 > 6
х, + х2 < 8
ху > 0.
1.72
Т^тіп — Х| + 2X2
5Х( - 2х2 < З
х, +х2 >1
-Зх, +х2 <3
ЗХ] +3х2 <9
ху > 0.
50
Дослідження операцій. Збірник задач
1.73
І 4 2
У = |о;—;0>.
І 4 4 І
Р пгіп — Зу, + 42у2+6у,-4у4
-у,+6у2+2у3-2у4 >2
У1+7у2-Зу3-у4>1
у. °-
1.74
Х = {6;О;О},	=
Лпах =3-*1 -2х2 +х3
2х1 — х2 +Зх3 <12
%! +2х2 -х2 <16
ху >0.
1.75
%={6;О}, У = {0;0;0;5,0}.
Лпах ~	— 2х2
5х, +2х2 > 10
2х1+5х2>10
-2х1 +х2 <4
х, < 6
х2 <6
ху>0.
51
Зайченко О.Ю., Зайченко Ю.П.
1.76
А' = {8;0}, У = {0;0;0;5;0}.
Р — 5х — 'Хх
1 тах	^л2
5х, +3х2 > 10
2х, + 6х2 > 12
-2Х] + х2 < 4
х, <8
х2 < 6
х} >0.
1.77
% = {1;3}, У = {0;0;3;0}.
^пих — ЗХі + Зх2
х, + х2 < 4
ЗХ] + х2 > 4
1.5. Двоїстий симплекс-метод
Задача ЛП в канонічній формі має вигляд:
п
максимізувати £(х) = '£с^x^
7=1
при обмеженнях:
(А = 1.2,...»г)
7=1
або =Ь;
/=і
ху >0, у = 1,2,...,я.
(1.5.1.)
(1.5.2)
52
Дослідження операцій. Збірник задач
Припустимо, що п > т і ранг матриці А дорівнює т.
Двоїста задача до задачі (1.5.1), (1.5.2) записується так:
__ т
мінімізувати Ь(у) =	(1.5.3)
Ц=1
при обмеженнях:
т
А-¥>Су, ХаніУр ~С3 =	(15-4)
р=І
Назвемо спряженим базисом або базисом двоїстої задачі таку
систему з т лінійно-незалежних векторів матриці обмежень прямої
задачі {А( },є/в, для якої базисний розв’язок у відповідної системи
лінійних рівнянь вигляду
аГу = с,-,іє/й	(1.5.5)
задовольнятиме всім обмеженням (1.5.4).
Розкладемо вектор Ь за спряженим базисом:
ІАЛ=Ь = А.	(1-5.6)
ІСІ6
Розв’язавши систему (1.5.6), знайдемо деякий її базисний
розв’язок { хі0 } ісІ&, який зветься псевдопланом прямої задачі, оскі-
льки для нього може не виконуватися умова невід’ємності змінних
хі0-
Опис алгоритму. Задача ЛП має бути задана в канонічній формі
(1.5.1), (1.5.2) або зведена до неї. Відшукують спряжений базис дво-
їстої задачі й позначають його {А,}, ієІб. Розкладемо Ао за векторами
базису А,і,... , А/т й знайдемо псевдоплан {хі0 }, / є Іб прямої задачі.
Дослідимо знаки {х,0}. Якщо має місце випадок хі0>0, V іє/б, то
початковий псевдоплан є оптимальним планом прямої задачі. При
наявності від’ємних компонент {х,0} обчислюємо коефіцієнти роз-
кладання векторів Ау за векторами спряженого базису {х,у}.
Якщо для деякого г такого, що хгО<0, всі хгу>0, то задача не
розв’язна, і на цьому процес обчисленнь закінчується.
Якщо має місце випадок — для кожного г такого, що хг0<0, хоча б
одна компонента ха<0, переходимо до другого етапу. З цією метою
складають таблицю к-і ітерації (аналогічну симплекс-таблиці), яка
містить (т + 2) рядків і (п + 1) стовпців (табл. 1.5.1).
53
Зайченко О.Ю.. Зайченко Ю.П.
Стовпець Вх таблиці, як і звичайно, містить вектори {А,} базису
псевдоплану хк, а стовпець Ао — базисні компоненти псевдоплану
{х,,/^ }- Рядок (т + /)-індексний, його заповнюють параметрами
Д<*’, що є оцінками векторів А/
= ао, = Ес.Лу -с/ •
величина До — значення цільової функції при псевдоплані
д =усх (П
^0	/ < сілі0
Ітерація к закінчиться заповненням головної частини таблиці (від
першого до (т + 1)-го рядків).
Таблиця 1.5.1
С,			Сі	С2		С/		С„
	Вл	Ао	А|	Аг		А,		А„
Сі	Х|	хю	Х|1	ХІ2		Х1,		Х1„
сг	Х2	*20	*2І	*22		Х2|		Х2л
...	.. .	...						. .
с,	X,-	ХіО	Х,1	Хі2		Хц		%іп
...	...	...	...	...				...
Ст				•^-т2		%ті		^тп
	д	До	А.	Аг				Л„
	е		є.	02				
На першому етапі (к + 1)-ї ітерації з’ясовують, чи має місце пер-
ший, другий або третій випадок.
У третьому випадку переходимо до другого етапу. Спочатку ви-
значають вектор Аг, який треба вивести з базису. Його індекс г ви-
значають із умови:
хЛ= шіп{х,01 х10 < 0},	(1.5.7)
І
тобто за максимальною за модулем від’ємною компонентою ба-
зисного розв’язку.
Далі заповнюють елементи {0(уК)} (т + 2)-го рядка, які обчис-
люють за формулою:
54
Дослідження операцій Збірник задач
е(Л={_£і|	<0}.	(1.5.8)
Х4
У рядку 0 заповнюють лише ті позиції, для яких хгу<0. Вектор А„
який треба ввести до базису, знаходять із умови:
Д.
0, =тіп{0 } = тіп{—<0).
І	І хг.
Після визначення напрямного рядка г і стовпця І обчислюють
елементи головної частини таблиці (к+1)-і ітерації за рекурентними
співвідношеннями:
(1.5.9)
де хгІ — напрямний елемент перетворення.
Приклад 1.5.1. Розв’язати задачу лінійного програмування двоїс-
тим симплекс-методом.
Максимізувати (хі+4х2),
при обмеженнях:
2 Х| - х2<6,
-Хі + х2 < 2,
Хі + х2 < 10,
хь х2 > 0,
або в розширеній формі:
2 Хі - х2 + х3 + 0 Хд + 0 х5 = 6,
- Х| + х2 + 0 х3 + Хд + 0 х5 = 2,
хІ + х2+0х3 + 0х4+х5= 10,
X), ..., х5 >0.
Двоїста задача записується так:
мінімізувати 6у, + 2у2 + 10у3,
при обмеженнях:
2уі-у2+Уз^ 1 {А,}
-Уі+У2+Уз^4	{А2}
Уі ,Уг ,Уз 0	{А3} {Ад} {А5}
55
Зайченко О.Ю., Зайченко Ю.П.
Виберемо за спряжений базис вектори {А2, А3, А4}.
Тоді розв’язком системи лінійних рівнянь є:
Уі=0;
У2=0;
Уз =4.
Підставивши цей розв’язок в обмеження {А>} і {А5}, бачимо, що
вони також виконуються, а тому {А2, А3, А4} — спряжений базис
двоїстої задачі.
Знайдемо псевдоплан Хо прямої задачі. Для цього розв’яжемо
систему рівнянь Ао = А2х20 + А3х30 + А4х40. Звідси х2о = 10; х30 = 16;
х4о = -8.
Обчислюємо коефіцієнт розкладання { х0 }:
А|= А2х2і + А3х3| + А4Х41
і знаходимо
Х21 = 1; Х3| = 3; х4| = -2.
Аналогічно маємо:
А§= А2х25 + А3Х35 + АрСіз-
Розв’язок цієї системи рівнянь: х25 = 1; х35 = 1; х45 = -1.
Таблиця 1.5.2
Сі			1	4	0	0	0
	В,	Ао	А,	а2	Аз	а4	А5
4	х2	10	1	1	0	0	1
0	Х3	16	3	0	1	0	1
0	Хд	-8	-2	0	0	1	-1
	д	40	3	0	0	0	4
	є		3/2				4
Перша ітерація.
Визначимо напрямний рядок. Це рядок Х4, оскільки Х40 = -8 < 0.
Знаходимо напрямний стовпець, для цього заповнимо рядок ®у. На-
прямний стовпець Аі, тому що
Є ,=3/2 < 0 5=4.
Отже, напрямний елемент Х41 = -2. Виконавши першу ітерацію
симплекс-методу, одержимо таблицю 1.5.3.
56
Дослідження операцій. Збірник задач
Таблиця 1 5.3
Сі			1	4	0	0	0
	вх	Ао	А,	Аг	Аз	Ад	Аз
4	х2	6	0	1	0	1/2	1/2
0	X,	4	0	0	1	3/2	-1/2
1	X,	4	1	0	0	-1/2	1/2
	д	28	0	0	0	3/2	5/2
Оскільки всі елементи стовпця Ао хі0 > 0, V/ є Іб, то знайдено
оптимальний план, причому
х1опт“4 -Т2опт
Цільова функція Ілпах = 28.
Розв’язати задачі лінійного програмування
двоїстим симплекс-методом
1.78
Лпах = ХІ + 2л2
2х, + Зх2 < 8
2х, + х2 < 6
х, +х2 > 1
х,,х2 >0.
1.79
Лпіп=-2*і+*2
2х] + х2 < 8
х, + Зх2 > 6
Зх, +х2 >3
х,,х2 >0.
57
Зайченко О.Ю., Зайченко Ю.П.
1.80
Лпіп =6^ +4х2
2х, + хг > З
ХУ~Х2
—х] + 2х2 > 1
х,,х2 >0.
1.81
Лпах =4Х, +ЗХ2
5х, + 2х2 > 20
х, +3х2 <15
х,,х2 >0.
1.82
Лпах =^,+ЗХ2
+х2 >3
6х^ +х2 <42
2Х) - Зх2 > 6
х„х2>0.
1.83
^тах — Х1 ~ 2-^2
5х( - 2х2 < З
х,+х2>1
—Зх, + х2 < З
х,,х2 >0.
58
Дослідження операцій. Збірник задач
1.84
= 8х1+2х2
-4х2 <4
-4х, + х2 < 4
+ х2 < 6
х,,х2 >0.
1.85
Л„ах=5х,+4х2
2х, +3х2 <3
+3х2 <4
-X! + х2 < 5
5х, + 4х2 < 6
хрх2 >0.
1.86
/7ті„ =2х.+3х,
х,+5х2 >16
ЗХ| + 2хг > 12
2Х| +4х2 >16
х,>1
Хг>0.
1.87
= ЗХ! + ЗХ2
х, +х2 <4
Зхг +х2 >4
X! +5х2 >4
0<л, <3
0<х2 <3.
59
Зайченко О.Ю., Зайченко Ю.П.
1.88
— ~2х, — Х2
-х, + 2х2 <14
5л, + 2х2 >10
4х,—Зх2<12
7х, + 4х2 < 28
х,,х2 >0.
1.89
^тах —	~ 2х2
2х, —Зх2 <6
Зх, + х2 > 2
х, -х2 >-3
х^,х2 >0.
1.90
Лпах =5*1 +4х2 +6Х3
X, + х2 + х3 < 6
2х, + х2 + х3 > 9
Зх, +х2 +2х3 > 11
х,,х2,х3 >0.
1.91
Лшп =-7^і +2х2
х,+х2>1
5х, + х2 > З
-Зх, + х2 < З
2х, + х2 < 4
х,,х2 >0.
60
Дослідження операцій. Збірник задач
1.92
Лпах = 2х,+х2-Зх3
х, + Зх2 - 2х3 < 4
-5х, + х3 > -12
2х, +х2 -Зх3 >—4
хрх2,х3 >0.
1.93
У-’ = 2х. —х,
птах	1	2
Зх, +х2 >16
X! +2х2 <12
х,,х2 > 0.
1.94
Лпіп = 6Х1 + 4х2
2х1 +х2 >3
X! — 2х2 < 2
Зх, + 2х2 > 1
хрх2 >0.
1.95
Лпіп =-^-2х2
5х} - 2х2 < 4
-х( + 2х2 < 4
х( + х2 > 4
х,,х2 >0.
61
Зайченко О.Ю, Зайченко Ю.П.
1.96
Лпіп ~ •*! 2х2
5Х) - 2х2 < 20
х,-2х2 >-20
х, +х2 >16
хрх2 >0.
1.97
^тал ~ X] + Х2
2х, +х2 <18
х, + 2х2 < 16
хрх2 >0.
1.98
^*тал ~ \
2х} +х2 <8
X! + 2х2 > 4
х1 +4х2 <10
ХрХ2 >0.
1.99
^пші ^^4 Зх2
5х,+2х2 >10
х, +3х2 <12
ХрХ2 >0.
62
Дослідження операцій. Збірник задач
1.100
Лпзх =хі+2х2
2х, + х2 <18
х, +2х2 >14
х, -2хг <—10
х,,х2 >0.
1.101
Лпіп ~ ХІ + Х1
2х, + х2 > 8
х, + Зх2 > 6
х,,х2 > 0.
1.102
^ПИХ ~ Зх\ + 2х2
Зх, +х2 < 21
2х, +3х2 <30
2х, <16
х,,х2 >0.
1.103
^тіп =7Х,+Х2
х, + х2 > З
5х, + х2 > 5
х, +5х2 >5
х,,х2 >0.
63
Зайченко О Ю, Зайченко Ю П.
1.104
Лпах =Х,+2Х2
6х, + 2х2 > 6
Зх, — 2х2 < 6
Зх, — х2 >-3
2х, +2х2 < 10
х,,х2 > 0.
1.105
Лшп =15х,+33х2
Зх, + 2х2 > 6
6х, + х2 > 6
х2 >1
хрх2 > 0.
1.106
Лип = ^Х1 ~ Х2
5Х) +9х2 <45
6х, + Зх2 <18
-х( + 2х2 > 2
ХрХ2 >0.
1.107
Лпах =Х,+4Х2
2х, -х2 < 6
х, -х2 > -2
х, +х2 < 10
хрх2 >0.
64
Дослідження операцій Збірник задач
1.6.	Дослідження моделей задач
лінійного програмування на чутливість
Теорія двоїстості дає змогу аналізувати моделі ЛП на чутливість.
Розглянемо звичайну задачу ЛП у вигляді:
п
максимізувати = тах£(х),	(1-6.1)
7=1
п
при обмеженнях: аух) = 1,2,..., ти;	(1.6.2)
>=і
х7>0.	(1.6.3)
Нагадаємо її економічну інтерпретацію. Цільова функція £(х) —
це дохід від реалізації плану виробництва х; а,у — інтенсивність ви-
користання і-го ресурсу при ,/-му способі виробництва; 6, — наявний
рівень і-го ресурсу.
1.	Варіювання обмежених ресурсів. Припустимо, що значення ре-
сурсів Ь = Ц Ь, Ц варіюються. Тоді виникають питання: при яких варі-
аціях правих частин обмежень знайдений оптимальний план Хо не
змінюється; як ці варіації впливають на функцію максимального-до-
ходу £„их? Відповідь на ці питання дає аналіз відповідної задачі ЛП
на чутливість.
Нехай обмеження Ь( одержують деякі варіації ДД, що приводять
до варіації плану Хо, Хо= х0(Ь+ДЬ) і функції (хо(Ьо+ДЬ)).
Позначимо через Ах матрицю оптимального базису задачі ЛП при
векторі ресурсів Ь. Очевидно відповідний оптимальний розв’язок
хопт= А ‘х Ь.	(1.6.4)
хн = АІхЬн = А*х(Ь+ДЬ).	(1.6.5)
Якщо всі компоненти х,н >0, то цей розв’язок хн =[ х,н] оптималь-
ний (тобто оптимальний базис не змінився). У противному разі треба
реалізувати пошук нового розв’язку, для цього можна застосувати
двоїстий симплекс-метод, починаючи з поточного базисного
розв’язку хн.
2.	Варіювання цільової функції. Тепер розглянемо випадок, коли
варіюються коефіцієнти {с,},у = 1.2..п. Спробуємо визначити умо-
65
Зайченко О.Ю., Зайченко Ю.П.
ви, за яких знайдений раніше оптимальний план лишається оптима-
льним при таких варіаціях.
Нехай варіація 8Сг стосується коефіцієнта сг :с" =сг +8С . По-
значимо через /б, /не6 множину індексів базисних та небазисних век-
торів в оптимальному плані Хо відповідно.
Знайдемо значення оцінок Д(“1 після варіації сг для двох випадків:
1) ге/не6, тоді Д("’ = Дудля усіх
4Н) = £ <лаіг - (сг + &Сг) ДЛЯ}=Г,	(1.6.6)
ієУб
2)ге Уб,
ДгВ) = ХС!НЧ “С/ =ЕСіаі/ +8ег%	(1.6.7)
/е/б	іе3б
Очевидно, для збереження оптимальності попереднього плану
при варіаціях коефіцієнта сг необхідно і достатньо, щоб не змінилися
знаки оцінок Д(7н) для всіх небазисних змінних.
3.	Варіювання елементів матриці обмежень А. Розглянемо лише
випадок варіації компонентів небазисних векторів А, = [а,у],
і = 1.2 ... т, оскільки дослідження варіацій компонент базисних век-
торів А, досить складне, легше заново розв’язати задачу з новими
умовами.
Отже, припустимо, що небазисний вектор А, = [ат}] змінився.
Треба з’ясувати, чи залишиться оптимальним поточний базис. Для
цього корисно застосувати теорію двоїстості. Нехай оптимальний
базис прямої задачі Ах, а відповідні оптимальні значення двоїстих
змінних у,0. Як відомо, умова оптимальності Ду >0, V /е 7|іеб. Водно-
час, Ду =	• Отже, якщо Д(]0 = 'Еауу® -су >0, то попере-
дній базис лишається оптимальним.
4.	Додавання ще одного способу виробництва. Припустимо, що
додається ще один (н+1)-й спосіб виробництва, якому відповідає век-
тор технологічних витрат А„+1=[а,„+1] і коефіцієнт ц.ф. сл+і
66
Дослідження операцій. Збірник задач
Треба визначити, чи зміниться при цьому попередній оптималь-
ний розв’язок і при якому значенні коефіцієнта с„+і випуск (п+1)-го
продукту буде рентабельним (тобто хя+1 > 0).
Для того, щоб оптимальний розв’язок після введення вектора Ал+(
не змінився, необхідно, щоб вектор Ая+1 і змінна хя+І лишалися неба-
зисними, тобто, щоб Д„+і>0. На основі теорії двоїстості одержимо
А	V*	0
Дп+1 — £^аіп+\Уі сл+1 
1єУ6
Якщо Х'З/л+іУі0~сл+і -то попередній оптимальний план не
іє.3
зміниться після включення випуску (и+1)-го виду продукції.
Якщо ж Еа,п+|>>,0-С„+І <0, то випуск (п+1)-го виду продукції
іє/
стає рентабельним, і попередній оптимальний план змінюється.
Приклад 1.6.1.
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів складає відповідно С, = 2, С2 = 1, а обсяг ресурсів
дорівнюють: Ьх = 40, Ьг = 56 відповідно. Норми витрат ресурсів на
одиницю випуску задаються матрицею:
і}
1)	Потрібно знайти оптимальний план випуску, який максимізує
сумарний прибуток і дослідити чутливість цільової функції до варіа-
ції обмежених ресурсів, тобто як зміниться сумарний прибуток при
збільшенні на одиницю будь-якого з видів ресурсів.
2)	Нехай перший ресурс Ь{ зменшився до 36, а другий збільшився
до 60. Як зміниться при цьому оптимальне рішення, чи залишиться
оптимальний колишній базис?
3)	Нехай вводиться додаткове обмеження на випуск першого
продукту х, > 9. Визначити новий оптимальний план.
67
Зайченко О.Ю., Зайченко Ю.П
4)	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3 = 2, а норми витрат ресурсів складають
а13 = 3, а23 = 2. Знайти оптимальний план з урахуванням цієї умови
і визначити, при якому значенні с3 виробництво третього виду виро-
бів буде рентабельним.
Розв’язок:
Математична модель задачі має такий вигляд:
1)
тах(2х( +х,);
4х, +х2 <40;
2х, + 5х2 < 56;
х,,х2>0.
Знаходимо розв’язок даної задачі симплекс-методом. Оптимальне
рішення наводиться в наступній таблиці:___________
Оптимальний розв’язок:
а) прямої задачі:
х°=8, х°=8.
	Ао	4		4	А
	8	1	0	5/18	-1/18
Х2	8	0	1	-1/9	2/9
	24	0	0	4/9	1/9
б) двоїстої задачі
о 4	0	1
У' =9’ * =9-
Обернена матриця має такий вигляд:
г5_
18
» 9
18
2
9 ,
2)	Нехай введено додаткове обмеження х, > 9. Приведемо його до
стандартного виду:
х,-х6=9 -> -х,+х6=-9.
68
Дослідження операцій. Збірник задач
Допишемо його до симплекс-таблиці. Складемо рядок х6 зхі і
отримаємо рядок х^.
	в.		4	4	4	4	4
2	Хх	8	і	0	5/18	-1/18	0
1	Х2	8	0	1	-1/9	2/9	0
	ХЬ	-9	-і	0	0	0	1
<—	Х6	-1	0	0	5/18	-1/18	1
т
Виконавши 1-у ітерацію двоїстого симплекс-метода приходимо
Х2 = 4. Для нього тах/(х,,х2) = 22.
3)	Нехай перший ресурс Ьх зменшився до 36, а другий збільшився
до 60. Знайдемо нове базисне рішення для нового вектора х(н):
Так як нові значення невід’ємні, то оптимальний базис не змнить-
20	28
ся. Оптимальний розв’язок буде таким: Л<") = — хї"’ = —
1	3	2 З
4)	Рентабельність.
Перевіримо умову рентабельності:
69
Зайченко О.Ю., Зайченко Ю.П.
4+1	^°«л+1 'Уі 4+Р
Дз=«1з-Л°+«п-^-С’,=2.1 + 4-1-2=<0.
Так як оцінка д3 <0, то випуск третього виду продукції рентабельний.
Знайдемо .
А
Розв’язуємо симплекс-методом і знаходимо:
	вх	4	4	Л2	4	4	4
2	А	4	1	-1/2	1/3	1/18	0
2	х3	12	0	3/2	-і/б	-1/3	1
	Д	32	0	1	1/3	1/1	0
Так як всі Д^ > 0, то дане рішення являється оптимальним:
х,° = 4, х® = 0, х3° = 12.
Ми бачимо, що оптимальне значення цільової функції збільши-
лось від 24 до 32.
Задачі та вправи
Провести аналіз чутливості таких задач ЛП.
Задача 1.108
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно С|=3 та сг=2, обсяги ресурсів до-
рівнюють />і=40, Ь2=36 відповідно. Норми витрат ресурсів на одини-
Т З
цю випуску задаються такою матрицею: д - |о II =
70
Дослідження операцій. Збірник задач
1.	Треба знайти оптимальний план випуску, що максимізує сумар-
ний доход та дослідити чутливість цільової функції до варіації
обмежених ресурсів, тобто як зміниться сумарний доход при збі-
льшенні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс зменшився до 36, а другий збільшився
до 45. Як зміниться при цьому оптимальний розв’язок, чи зали-
шиться оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого про-
дукту Хі> 9. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид продукції,
для якого с3=3, а норми витрат ресурсів дорівнюють ав=2; <223=4-
Знайти оптимальний план за цієї умови і визначити, при якому зна-
ченні с3 виробництво третього ваду виробів буде рентабельним.
Задача 1.109
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно £^=4 та с2=2, обсяги ресурсів до-
рівнюють 6|=48, 62=36 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс збільшився до 60, а другий зменшився
до ЗО. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту х^ІО. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=3, а норми витрат ресурсів дорівнюють Оіз=2;
а23=4. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
71
Зайченко О.Ю., Зайченко Ю.П.
Задача 1.110
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно Сі=4 та с2=2, обсяги ресурсів до-
рівнюють ^=40, 62=3б відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
1 З
М“(|=
2 1
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс зменшився до ЗО, а другий збільшився
до 50. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту Хі> 12. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=4, а норми витрат ресурсів дорівнюють а13=2;
а2з=3. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с} виробництво третього виду виробів буде рентабельним.
Задача 1.111
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно с(=1 та сг=2, обсяги ресурсів до-
рівнюють іі=36, />2=24 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
А = кІ =
З 2
1 4
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
72
._________________________________Дослідження операцій Збірник задач
2.	Нехай перший ресурс Ьі збільшився до 40, а другий зменшився
до ЗО. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту х2> 9. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=4, а норми витрат ресурсів дорівнюють а13=3;
<22з=4. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
Задача 1.112
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно с(=3 та с2=2, обсяги ресурсів до-
рівнюють 6і=64, Ь2=56 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс 6( зменшився до 48, а другий збільшився
до 60. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту Х|> 10. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=3, а норми витрат ресурсів дорівнюють п|3=2;
«23=4. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
Задача 1.113
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно С]=4 та с2=2, обсяги ресурсів до-
73
Зайченко О.Ю., Зайченко Ю.П.
рівнюють Ьі—12, 62=48 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
А’ЬІ=[' ’}
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс 6( збільшився до 80, а другий зменшився
до 40. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту х2> 9. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=3, а норми витрат ресурсів дорівнюють а13=2;
п2з=2. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
Задача 1.114
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно с(=3 та с2=2, обсяги ресурсів до-
рівнюють 6і=50, 62=40 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс зменшився до 40, а другий збільшився
до 48. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту Х|> 12. Визначити новий оптимальний план.
74
Дослідження операцій. Збірник задач
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=4, а норми витрат ресурсів дорівнюють а,3=2;
а23=4. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
Задача 1.115
Підприємство випускає вироби двох видів, для виготовлення
яких використовуються ресурси двох типів. Нехай прибуток від про-
дажу виробів становить відповідно с{=3 та с2=2, обсяги ресурсів до-
рівнюють 2>(=72, /?г=54 відповідно. Норми витрат ресурсів на одини-
цю випуску задаються такою матрицею:
1.	Треба знайти оптимальний план випуску, що максимізує сума-
рний доход та дослідити чутливість цільової функції до варіації об-
межених ресурсів, тобто як зміниться сумарний доход при збільшен-
ні на одиницю кожного з видів ресурсів.
2.	Нехай перший ресурс зменшився до 54, а другий зменшився
до 45. Як зміниться при цьому оптимальний розв’язок, чи залишить-
ся оптимальним попередній базис?
3.	Нехай вводиться додаткове обмеження на випуск першого
продукту х2> 12. Визначити новий оптимальний план.
4.	Нехай підприємство може додатково випускати третій вид
продукції, для якого с3=3, а норми витрат ресурсів дорівнюють П|3=2;
а23=4. Знайти оптимальний план за цієї умови і визначити, при якому
значенні с3 виробництво третього виду виробів буде рентабельним.
75
Зайченко О.Ю, Зайченко Ю.П.
1.7.	Метод оберненої матриці
Критерії оптимальності та розв’язувальні множники
Нехай задано задачу ЛП загального вигляду із змішаними обме-
женнями:
п
максимізувати £ (х) =2>Л»	(1.7.1)
7-і
при обмеженнях:
Хаі)Х)<Ь,, і=ї,2,...,ті<т;	(1.7.2)
=бі, і=т{+ 1, т1+ 2,...,т;	(1.7.3)
7=1
^0;/=1,2,...,Л| <и.	(1-7.4)
Змінні Хі,..., називають розв’язувальними множниками, якщо:
а)	у=1, 2,...,щ	(1.7.5)
/=1
б)	ї=су,7=и1+1,Л| + 2,...,п;	(1.7.6)
/=і
в)Х,>0;і=1,2......ті	(1.7.7)
г) для деякого плану х=(х1,...д:л) задачі виконуються умови:
= су, якщо ху>0, (1</ <Пі);	(1.7.8)
і=і
Х,=0, якщо Х°(ух7 < Ьі, (1^ і <ті).	(1-7.9)
І
Вектор А = (Х|,..., Хт) називають розв’язувальним вектором задачі.
76
Дослідження операцій. Збірник задач
Покажемо, що відшукання розв’язувального вектора еквівалентне
розв’язанню задачі, двоїстої до задачі (1.7.1)-(1.7.3). Для цього роз-
глянемо таку теорему.
ТЕОРЕМА 2.10. Сукупність розв’язувальних векторів задачі
(1.7.1) (1.7.4) збігається з множиною оптимальних розв ’язків задачі,
двоїстої до неї.
Використовуючи поняття розв’язувальних множників, можна
сформулювати таку ознаку оптимальності розв’язку задачі ЛП.
ТЕОРЕМА 2.1 і. Для оптимальностірозв ’язку х=(хі,... л„) задачі
(1.7.1)-(1.7.4) необхідно і достатньо, щоб існував розв’язувальний
вектор Л = (Х|,..., Хт) — пов'язаний з цим розв’язком умовами
(1.7.8), (1.7.9).
Доведення цих теорем наведено в роботах [15, 16].
Встановлений критерій дає змогу перевірити, чи буде даний план
оптимальним розв’язком задачі ЛП. З цією метою складають систему з
рівнянь (1.7.6), (1.7.8), (1.7.9), з якої знаходять відповідний вектор
А = (7-і,..., Хт), після чого підстановкою перевіряють, чи задовольняє
цей вектор умови 1.7.5), (1.7.7), чи ні. Якщо так, то вектор х— оптима-
льний план, у протилежному разі — неоптимальний план
Зауважимо, що відшукання розв’язувальних множників еквівале-
нтне розв’язанню двоїстої задачі, що в загальному випадку аж ніяк
не легше відшукання розв’язку прямої задачі.
Головна роль розв’язувальних множників полягає в тому, що їх
використання дає змогу сформулювати нову ознаку критерію опти-
мальності й сконструювати новий метод лінійного програмування.
2. Розглянемо задачу ЛП в канонічній формі (1.7.14)-(1.7.16), яка
є окремим випадком задачі (1.7.1)—(1.7.4) при тх = 0, щ = п:
п
максимізувати У'сіхі,
7=«
при обмеженнях:
п
= Ьіг ї=1, 2,...,/п;
7=1
ху >0; у=1, 2,...,и.
(1.7.14)
(1.7.15)
(1.7.16)
77
Зайченко ОЮ, Зайченко Ю.П.
Для задачі (1.7.14)-(1.7.16) вектор Л = (Хь..., Х„) зветься
розв’язувальним вектором, якщо:
а)	Еа,?Х, >е?,7=1,2,...,л;	(1.7.17)
і=і
б)	для деякого плану х (розв’язку) задачі (1.7.14)-(1.7.16) викону-
ється умова:
У. в,у X, = су, якщо ху>0.	(1.7.18)
і=і
Критерій оптимальності в цьому випадку формулюється так. Для
оптимальності плану х необхідно і достатньо, щоб існував
розв’язу вальний вектор Л=(кі,..., ІД), пов’язаний з хумовою (1.7.17).
Отже, припустимо, що задачу ЛП задано в канонічній формі і ве-
ктори {Аіі,...,А5га}={Аі,} утворюють базис для деякого опорного
плану х. Позначимо через Іх множину індексів базисних векторів.
Визначимо вектор А* =(Х*І,..., Х*т) із системи рівнянь:
ЬуХ'.=Су,	(1-7.19)
1=1
Тоді план х - оптимальний, якщо:
7 = 1,2,...,л.	(1.7.20)
МІ
У процесі розгляду симплекс-методу ми отримали достатню
ознаку оптимальності у вигляді:
Ау=Ее^-Су^0.	(1.7.21)
Покажемо тепер еквівалентність форм (1.7.20), (1.7.21) для усіх
І= 1,2, ..., п.
Справедливий такий ланцюжок рівностей:
ь -Е<л ="’-“Тліла,=‘”ІлА- <І7-22>
/є/,	Іє/Т /7=1	/7=1 /е/я	/7=1
Рівність (1) випливає із (1.7.19), рівність (2) одержано зміною по-
рядку підсумовування, а рівність (3) випливає з розкладання небази-
сного вектора А,, через базисні:
78
Дослідження операцій. Збірник задач
А,=ЕАЛ '
<€/,
Таким чином, із (1.7.22) випливає, що умова
И=1
для всіх7=1, 2,...,л еквівалентна умові Д7> 0,7= 1, 2,...,л.
Метод оберненої матриці (Л-метод)
Використання ознаки оптимальності у формі (1.7.20) дає змогу
зконструювати інший алгоритм симплекс-методу — метод оберненої
матриці (в іноземній літературі цей метод зветься модифікованим
симплекс-методом). Цей метод розробив Л.В.Канторович для
розв’язання однієї із спеціальних задач ЛП ще 1939 р., а пізніше
(1951) й для загальної задачі ЛП [15, 16].
Нехай задачу ЛП задано в канонічній формі, х — її допустимий
базисний розв’язок для базису {А,} ієІх , де Іх множина індексів ба-
зисних векторів. Складаємо із векторів базису квадратну матрицю.
Очевидно, визначник матриці Ах не дорівнює нулю й існує обернена
матриця Ах
Покажемо, як, використовуючи Ах можна побудувати компактну
схему для обчислення параметрів, необхідних для реалізації симп-
лекс-методу.
Справді, базисні компоненти поточного ДБР х визначаються із умови:
х= Ах“‘ Ь або
т
хіО = Ха~'Л-
/1=1
Оцінки векторів А визначаються за формулами:
А> = 2і-С/ =	=	(1.7.23)
де параметри X, задовольняють рівняння:
Е^Х/=Су, 7’є/х.	(1-7.24)
79
Зайченко О.Ю., Зайченко Ю.П.
або у векторній формі ЛТАХ=СТХ, де Стх — вектор-рядок коефіцієнтів
ц.ф., що відповідають базисним змінним.
Отже,
АТ=СТКАХ'.	(1.7.25)
Формули (1.7.23)-(1.7.25) дають змогу обчислити оцінки Л7 век-
торів, якщо відомі елементи оберненої матриці Ах 1 та умови задачі.
Коефіцієнти х,* розкладання небазисного вектора А* по векторах по-
точного базису визначаються як елементи добутку (Ах '* А*) матриці
Ах’’ на вектор А*. Коефіцієнти х« разом із базисними складовими
ДБР визначають вектор, що підлягає виводу із базису.
Отже, для реалізації методу треба обчислювати на кожному кроці
матрицю Ах Елементи стовпців матриці Ах'' зручно розглядати як
коефіцієнти розкладання е,7 одиничних векторів е, (і=\,...,т) за век-
торами базису, де
При цьому переобчислення елементів {е,7} матриці Ах -І при вве-
денні до базису нового вектора А* виконується за такими рекурент-
ними формулами методу виключення Жордана-Гаусса:
е,7 —*г;і=1,т+1',} = 0,1,..., т;
Хгк
Хгк
(1.7.26)
де
а)	— напрямний елемент перетворення;
б)	е,о=х,о базисні компоненти ДБР Х0=||х,0|| /=!,...,/и;
в)	ет+І,0 = — розв’язувальні множникиу=1,...,7я;
г)	ет+і 0=Б(Хо) — значення ц.ф. при базисному розв’язку х0; А* —
вектор, що вводиться до базису; А,— вектор, що виводиться з базису.
Для реалізації методу оберненої матриці на кожній ітерації вико-
ристовується основна і допоміжна таблиці.
80
Дослідження операцій. Збірник задач
Основна таблиця складається з (іп + 3) стовпців та (т + 1)-го ряд-
ка (табл. 1.18).
Основна таблиця 1.18
N	ск	Вх	ео	?І	Є}	..		е,„	Ак	0
1	С,	А,	еІ0в>	еП	Є,"'			Є."	Хи	о,
2	с2	а2	ехт	е21	ег2°>				Х2к	02
...	•..			...		..		...	...	...
к	сг	А,	ег0(І)		вД»			е ф кпп	Х,к	0г
...	...		...	...	...	• •		...		
т	Ст	Ащ	етВ("		е ,0> ст2			е сішп	Хтк	От
т+1			Ь	Х|	х2	• •			Ак	
Допоміжна таблиця 1.19
N	Ь=Ао	А|	а2		Ак	...	Ап.і	А„
1								
2								
...	...	...	...		...		...	...
т								
т+1		Сі	С2		Ск		£п-і	С„
0	дО)	Д/0’	Д2(0)		Ак«»		Ап.,®	Ап(0»
1	Д(,)	д.(І)	а2(і>		Дк0’		Ап-,0’	А.®
2	Д<2>	Аі(2)	а2<2»		Ак®		Ап_,®	Д (2)
...			...				...	...
/	д(/>	А.М	а2«	...	Ак(/)	...	Ап_,(/)	д(/)
У стовпці е0 записуються базисні компоненти поточного
розв’язку, стовпці Єї, е2 ет — це стовпці оберненої матриці Ах 1
поточного базису; у стовпці А* записуються коефіцієнти хік розкла-
дення небазисного вектора А* за векторами базису; стовпець 0 —-
81
Зайченко О.Ю, Зайченко Ю.П.
ДОПОМІЖНИЙ, ВІН МІСТИТЬ величини 0 = Є,о /Хік, Х,*>0. Стовпці ео, Є|
е,„ — головна частина таблиці, в (»і+1)-му рядку основної таблиці
записують величини {X,} ієІх.
Допоміжна таблиця (табл. 1.19) містить вектори {АІ,...,АП},
1=1,...,п вихідної задачі, а також вектор с. У рядку 0 записують зна-
чення оцінок А,, що відповідають початковому ДБР.
У результаті кожної чергової ітерації (/) у допоміжну таблицю
дописують черговий рядок (/+1), що містить величини А,.
Опишемо (/+1) ітерацію алгоритму оберненої матриці. Нехай вже
проведено І ітерацій алгоритму, внаслідок чого обчислено матрицю
Ах 1(Г) й оцінки А,, але ще не знайдено оптимальний розв’язок.
1.	Визначаємо вектор А.к, що вводиться в базис згідно з умовою:
А(;)=тіп(Д(;)|А(') <0).	(1.7.27)
2.	Із допоміжної таблиці вибираємо компоненти небазисного век-
тора А*. Обчислюємо його коефіцієнти розкладання хік через базисні
вектори, використовуючи обернену матрицю Ах":
о-7-28)
У
Записуємо величини хік в стовпець А*. У позицію стовпця (щ+1)
записуємо оцінку А, цього вектора.
Переглянемо стовпець Ак. Якщо всі хік<0, то задача не розв’язна.
Припустимо, що є хоча б один х,р>0, то переходимо на п.З.
3.	Обчислюємо відношення віО/хікй визначаємо напрямний рядок
г із умови
0Г = пйп{—|хй > 0} •
%ік
4.	Виконуємо одну ітерацію симплекс-методу з напрямним еле-
ментом хгк.
5.	Одержимо нову обернену матрицю Ах ’, а також нові оцінки А,.
Заповнюємо елементами Ах-1 головну частину таблиці (/+1) ітерації,
при цьому замінимо індекс г вектора, що його виведено з базису, на к
у стовпці Вх. Одночасно замінюємо сг на ск у стовпці сх. Зауважимо,
82
Дослідження операцій. Збірник задач
що для контролю значення Л.,(/+1) можна обчислити також і за фор-
мулами:
М/+І> =ЕС^У+І)-	(1.7.29)
(Є/,
6.	Для всіх небазисних векторів обчислюємо оцінки згідно з спів-
відношеннями:
Д(/+І) = У а V" -с -з=\Гп.	(1.7.3°)
/	£—4 У <	У’*7	’
/є/.
Перевіряємо умову Д,(МІ) > 0 для всіх7=1,2,.. .,п.
Якщо вона виконується, то кінець роботи, у протилежному разі
переходимо до (/+2) ітерації. Усі таблиці алгоритму заповнюються за
тими самими правилами. Деякі особливості виникають лише при за-
повненні початкової основної таблиці. Тут у стовпець Єо записують
базисні компоненти вихідного ДБР. Перші ш позицій стовпців е0,
Єї е„ знаходять шляхом обернення матриці базису початкового
допустимого базисного розв’язку. Останній рядок головної частини
таблиці 0 заповнюється добутками стовпця сх й стовпців цієї таб-
лиці, тобто:
Ч0)=	7=0,1,(1.7.31)
/е/.
Для контролю обчислень можна скористатися двома можливос-
тями визначення цих величин.
На будь-якій ітерації ці параметри можна обчислити як за реку-
рентними формулами (1.7.26), так і безпосередньо за формулою
(1.7.29).
Мультиплікативна форма методу оберненої матриці
У розглянутій вище обчислювальній схемі методу треба за-
пам’ятовувати всю обернену матрицю Ах’*= ||еу ||, у мультиплікатив-
ній формі алгоритму запам’ятовування потребує значно менший об-
сяг даних.
Розглянемо її ідею. Нехай х та х ’ — два послідовних ДБР задачі
ЛП. Позначимо відповідні матриці векторів базису через Ах та Ах-:
83
Зайченко 010, Зайченко Ю.П.
ах=[а5|, А,г, ... А,, ... А, ];
Ах.=[А5|, А„, ...,А,4 А,,, ... А,.].
Можна перевірити, що обернені матриці А та А '*х- пов’язані
співвідношенням:
А;! = ЕГА,’,	(1.7.32)
0	0	...
о	0	... уті
0
0
0
І
№ = -^-, /=1,2.......т,і*г;
*гк
Угк =-----
Хгк
Співвідношення (1.7.32) еквівалентне застосуванню рекурентних
формул (1.7.26) при і = 1, 2,..,пі та у = 1,2,..., т.
Звичайно розв’язання задачі ЛП починається з одиничного бази-
су. Йому відповідає одинична матриця Е. Тому після першої ітерації,
коли замість вектора {А„} до базису вводиться А*, обернену матри-
цю базису для допустимого базисного розв’язку х ’ можна обчислити
за формулою:
а;1 = еге,
а після І —і ітерації:
а;1 =ЕГЕГ/ ,..£гЕ.	(1.7.33)
Матриця Ег визначається (/л+1)-м числом (г, у1к, у2ц •••>№*)• От-
же, при 1<т запис матриці Ах 1 у формі (1.7.32) потребує меншого
обсягу пам’яті, ніж звичайна форма запису, де на кожній ітерації
треба запам’ятовувати т2 чисел
Опишемо схему обчислень в окремій ітерації мультиплікативної
форми алгоритму оберненої матриці. Нехай вже проведено І ітерацій
у результаті яких встановлено, що х(/) — неоптимальний план (ДБР).
84
Дослідження операцій. Збірник задач
Знаходження вектора, що підлягає введенню до базису й виведенню з
нього, виконується за загальними правилами симплекс-методу, а
компоненти чергового базисного розв’язку обчислюються за рекуре-
нтними формулами (1.7.32). Вектор відносних оцінок умов задачі
(розв’язувальний вектор) А на у-й ітерації обчислюється за співвід-
ношенням:
А,г+І=сХЕг ...е е,
Г ГІ Гі І гї
вектор оцінок Л звичайним способом:
Д = ААх-сг.
Нарешті, коефіцієнти х,л розкладання вектора А*, що підлягає
включенню до базису за векторами базису визначаються із співвід-
ношення:
АГ’-Е,Е^..Ж,А,.	(1.7.34)
Отже, мультиплікативна форма алгоритму дає змогу не тільки за-
ощаджувати пам’ять ЕОМ, а й скорочує обсяг обчислень на початко-
вих ітераціях алгоритму оберненої матриці.
Приклад 1.7.1. Розв’язати методом оберненої матриці таку за-
дачу ЛП:
максимізувати 4х,+2 х2,	(1)
при обмеженнях:
-X] + 2х2 - 6;
хі + х2<9;
Зхі -х2 < 15;
хі, х2 > 0.	(2)
Зводимо її до розширеної форми. Маємо:
максимізувати 4х]+2х2,
при обмеженнях:
-X] + 2х2 + Іхз = 6;
X] + х2 + 1х4 = 9;
Зхі -х2 + Іхз = 15;
виберемо за початковий одиничний базис:
85
Зайченко О.Ю., Зайченко Ю.П.
А = [А,, А4, А,] =
1 О О
О 1 О
О О І
Заповнимо допоміжну таблицю 1.20 (початкову частину) та ос-
новну таблицю першої ітерації (табл. 1.21).
Перша ітерація. Заповнивши головну частину табл. 1.21 обчис-
люємо ЇЇ ІВДеКСНИЙ рЯДОК ЗГІДНО ІЗ СПІВВІДНОШеННЯМ А,° = ТРів/.
Оскільки Сі=0 при ї=3,4,5, то X/0-А.2(О)=Хз(О)=О. Переглянувши рядок
А0, табл. 1.20, вибираємо вектор Аь оскільки:
Д(,0) = тіпр7|Ду < о}= -4.
Таблиця 1.20
N	В	А,	а2	А3	Ад	а5
1	6	-1	2	1	0	0
2	9	1	1	0	1	0
3	15	3	-1	0	0	1
Ітера- ція	9	4	2	0	0	0
0	Д/°>	-4	-2	0	0 л	0
1	А,"	0	-10/3	0		4/3
2	д/^	0	0	0	2— 2	1/2
Таблиця 1.21
N	Сх	Вх	е0	Єї	е2	ез	Ак
1 2 3	0 0 0	Аз Ад а5	6 9 15	1 0 0	0 1 0	0 0 1	-1 1 3
		А	0	0	0	0	-4
Записуємо вектор А! у стовпець Ак праворуч від головної час-
тини табл. 1.21 і його оцінку в індексний рядок.
86
Дослідження операцій. Збірник задач
Стовпець Ак — напрямний. Знаходимо напрямний елемент згід-
но із загальними правилами симплекс-методу. Виконавши ітерацію,
заповнюємо головну частину табл. 1.22.
Таблиця 1.22
N	Сх	вх	е0	«І	Є2	е3	Ак
1	0	Аз	11	1	0	2 3	5 3
2	0	А4	4	0	1	і 3	1- 3
3	4	Аі	5	0	0	і 3	1 3
		Л	20	0	0	4 3	10 3
Отже, знайдено вектор розв’язувальних множників А(І)=[0, 0,
4/3]. Визначимо оцінки Д(|)7для всіх небазисних векторів, використо-
вуючи співвідношення (1.7.30):
а результати записуємо в рядок А/” табл. 2.22. Наприклад:
Д2 = 21(і)і+ 1Х(,)2 - 1Х(1)3 -с2= -1.1 - 2 = - 2°.
з	з
Друга ітерація. З індексного рядка Д/ вибираємо вектор А2
з найбільшою від’ємною оцінкою Д2‘<-10/3 <0.
Помноживши матрицю {Єї, е2, е3} табл. 1.20 на А2 дістанемо А2'
і запишемо його у стовпець А* табл. 1.22.
Визначивши напрямний елемент у стовпці А* і виконавши чер-
гову ітерацію симплекс-методу, приходимо до табл. 1.23. Обчислю-
ємо вектор оцінки за формулою (1.7.30), заносимо їх до табл. 1.20.
Останній базисний розв’язок у табл. 1.23 оптимальний, оскільки всі
Д/2)>0.
87
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 1.23
N	Сх	Вх	е0	Єї	е2	Єз
1	0	Аз	3	1	-5/4	3/4
2	2	А,	3	0	2 4	1 4
3	4	А,	6	0	2 4	1 4
		А	ЗО	0	1 2- 2	1 2
Розв’язати методом оберненої матриці
модифікованим симплекс-методом
1.116
Р = -Зх1 + 6х2 —» тіп
5х, - 2х2 < 4
х( - 2х2 > -4
х, + х2 > 4
х1гх2 >0
1.117
Р = Зх, + Зх2 —> тах
х, + х2 < 8
Зх} + 7х2 >21
х, + 2х2 > 6
0 < х, < 1
0 < х2 < 1
88
Дослідження операцій. Збірник задач
1.118
Е = х, + х2 -> тах
х|+х2>1
-5Х] + х, < О
-х, + 5х, > О
х, + х2 < 6
х„х2 >0
1.119
Е = х, + х2 —> тах
5х, - 2х2 < 7
-X] + х2 < 5
X, + X, < 6
х,,х2 >0
1.120
Е = -2х1 + х2 -> тіп
2х, + х2 < 8
X! + Зх2 > 6
Зх, + х2 > З
х(, х2 > О
1.121
Е = -2х, + х2 —> тіп
2х, + х2 < 8
х, + х2 < 6
-Зх, + 2х2 > З
х„х2 >0
89
Зайченко О.Ю, Зайченко Ю.П.
1.122
Е = 2х1- Зх, —> тіп
+2х2 > 10
3х1 +х2 >15
х,, х2 >0
1.123
Е = 2х1 + 2хг -> тах
3%! - 2хг > -6
х, + х2 > З
0<х,<3
0 < х2 < 5
1.124
Е = Зх, + Зх2 —> тах
X] + х2 < 4
Зх, + х2 > 4
х, + 5х2 > 4
0 < х, < З
0<х2 <3
1.125
Е = X! + 2х2 —> тах
5х( — 2х2 < 4
х, - 2х2 > -4
X] + х2 > 4
хрх2 >0
90
____________________________Дослідження операцій. Збірник задач
1.126
Лпах=*1+2*2
2х( + Зх2 < 8
2х, + х2 < 6
х} + х2 > 1
х„х2 >0
1.127
Лпіп =-2х,+х2
2х, + х2 < 8
х, + Зх2 >6
Зх, + х2 > З
х„х2 >0
1.128
Г. = 6х. + 4х2
2х{ + х2 > З
х( - х2 < 1
-х1 + 2х2 > 1
хрх2 >0
1.129
Лпах =4Х,+ЗХ2
5х, + 2х2 > 20
X] +3х2 < 15
хрх2 >0
91
Зайченко ОІО., Зайченко Ю.П
1.130
^тах =*І +ЗХ2
х, + х, > З
6^ + х2 < 42
2х, -Зх, >6
х,,х, >0
1.131
^*тах -^І ~~ 2х2
5х( - 2х2 < З
+ Х2 > І
- Зх, + х2 < З
х,,х2 >0
1.132
тах	2х2
— 4х2 < 4
-4х( + х2 < 4
Х| + х2 < 6
хрх2 >0
1.133
Лпах =5*І +4х2
2хг + Зх2 < З
х, + Зх2 < 4
-X, + Х2 < 5
5х, + 4х2 < 6
х,, х, >0
92
Дослідження операцій. Збірник задач
1.134
Літі = 2х, + Зх2
х, + 5х2 > 16
Зх, + 2х2 >12
2х, + 4х2 > 16
х,>1
х2 >0
1.135
Лпах =ЗХ,+ЗХ2
х, +х2 < 4
Зх, + х2 >4
х, + 5х, > 4
0<х, <3
0<х2 <3
1.136
Л™ =-2х,-х2
-х, +2х2 <14
5х, + 2х2 > 10
4х, -Зх2 < 12
7х, + 4х2 < 28
х(,х, > 0
93
Зайченко О Ю , Зайченко Ю.П.
1.137
^пих — "^Х, ~~
х,+х2<5
2х, - Зх2 <6
Зх, + х2 > 2
х, -х, >-3
хрх2 >0
1.138
Лпах =5хі +4Х2 +6Х3
X, + х2 + х3 < 6
2х, + х2 +х3 >9
Зх{ + х2 + 2х3 > 11
х,,х2,х3 >0
1.139
^пип — ~ "7-^1 + 2Х2
+ X, > 1
5Х] + х2 > З
-Зхг + х2 < З
2Х' + х2 < 4
хрх2 > 0
94
Дослідження операцій Збірник задач
1.140
= 2х,+х2-Зх3
х, + Зх2 - 2х3 < 4
-5х( + х3 >—12
2хІ + х2 - Зх3 > -4
х„х2,х3 >0
1.141
Лпах =2ХГ-Х2
Зх( +х2 > 16
х, +2х2 <12
хрх2 > 0
1.142
Л>ип =6Х,+4Х2
2х( + х2 > З
— 2х2 < 2
Зх, + 2х2 > 1
х,,х2 > 0
1.143
^тіп = ~ХІ ~ ^Х2
5х( - 2х2 < 4
—х, + 2х2 < 4
х, + х2 > 4
хрх2 >0
95
Зайченко О.Ю., ЗайченкоЮП.
1.144
Л,™	+2х2
5х, - 2х, < 20
х, - 2х, > -20
х, +х2 > 16
х,,х2 >0
1.145
Лпах = *.+*2
2х, + х2 < 18
х, +2х2 < 16
х,, х2 >0
1.146
Л™х =*1+*2
2х( + х2 < 8
х( + 2х2 > 4
+4х2 <10
х(, х2 >0
96
Дослідження операцій. Збірник задач
1.8.	Багатокритеріальні задачі лінійного програмування
Постановка багатокритеріальної задачі прийняття рішень і її
властивості. Розглянемо ситуацію прийняття рішень на заданій
множині допустимих альтернатив при потребі врахування сукупності
властивостей, що описуються множиною, цільових функцій:
у = {/}(«)}, де У (а) — відповідає 1-Й властивості, за якою оці-
нюються альтернативи а є А .
Вважатимемо, що перші т цільових функцій максимізуються, а
інші М-т — мінімізуються. Позначимо через /, ={1,2,...,от} і
12 = {от+1, т+2,...,М} множини індексів відповідно для функцій, що
максимізуються та мінімізуються. Щоб сформулювати задачу прий-
няття складних рішень у термінах багатокритеріальної оптимізації,
спинимося на питанні порівняння альтернатив на множині цільових
функцій.
Введемо такі відношення на множині альтернатив при наявності
множини цільових функцій (критеріїв):
а)	слабкої переваги (не гірше) >: казатимемо, що х( >х2 > коли
(Г8 1)
б)	строгої переваги (краще): х, >- х2. тоді 1 тільки тоді, коли сис-
тема нерівностей (1.8.1) виконується і хоча б одна з них — строго;
в)	сильної переваги: х1 >->-х2,якщо всі нерівності (1.8.1)— строгі;
г)	еквівалентності: Х| ~х2 тоді і тільки тоді, коли
Слід наголосити, що відношення > , яке описується співвідно-
шеннями (1.8.1), не є лінійним, або сильним упорядкуванням. Це
означає, що не будь-яка пара альтернатив може бути порівняна на
множині цільових функцій //, тобто не для всяких пар альтернатив
X], х2 є А має місце або х, х2, або х2> х,, або те й інше разом
Дамо означення ефективної альтернативи в термінах цільових
функцій.
97
Зайченко О.Ю., Зайченко Ю.П.
Альтернатива х0 зветься ефективною, якщо на множині допу-
стимих альтернатив А не існує такої альтернативи х, дія якої б
виконувалися нерівності'
ЧієІх,	(1.8.2)
/(і)</(х0), \/ієІ2,	(1.8.3)
і хоча б одна з них була строгою. Це означає, що жодна інша альтер-
натива не може поліпшити значення деякої цільової функції порівня-
но з ефективною альтернативою, не погіршуючи при цьому хоча б
одну з інших цільових функцій.
Тому іноді ефективну альтернативу називають не поліпшуваною
на множині і/, ф. або оптимальною за Парето [39].
Із означення ефективної альтернативи випливає така теорема [33].
ТЕОРЕМА 1.8.1. Дві ефективні альтернативи або еквівалентні,
або не порівняні поміж собою на множині цільових функцій.
Із теореми випливає, що якщо існує тільки одна ефективна альте-
рнатива, то вона надає оптимального значення кожному з критеріїв
/,(х), хєА. Справді, оскільки	то очевидно
/(х0)>/.(х); Ух,У/є/, і /(х0)</(х); Ух,Уіє/2.
Як і у випадку прийняття рішень за одним критерієм, у задачах
прийняття рішень із множиною ц. ф. можуть існувати декілька мно-
жин ц. ф., яким відповідатимуть ті самі відношення строгої переваги
та еквівалентності. На підтримку сказаного введемо таке означення.
Множини ц. ф. /(,)(х) = {/}(,\х)}. і є/] і /(2)(х)={/(2)(х)},іє/2 >
визначені на тій самій множині допустимих альтернатив А, називати-
мемо еквівалентними, якщо вони визначають на ній одне й те саме
відношення слабкої переваги, тобто для будь-яких двох альтернатив
/0)	/(2)	/(2)
Х|, хг із х, > х2 випливає, що х, > х2, і навпаки, із х, > х2 виїзди-
ло
ває, що х, > х2.
Еквівалентні множини ц. ф. визначають на множині допустимих
альтернатив однакові відношення еквівалентності та строгої переваги.
ТЕОРЕМА 1.8.2. Якщо існує множина монотонних перетворень
И/ = {и;(г)} /є/ таких, що і-те перетворення переводить область
значень функції /Р\х) в область значень функції	і
98
Дослідження операцій Збірник задач
/^\х) = м</;(2)(х)) для всієї множини допустимих альтернатив А, то
множини цільових функцій /т = {//''(х)} і /т -	еквіва-
лентні.
Оскільки цільові функції /фх) мають різну фізичну розмірність,
бо характеризують різні властивості вибраного рішення, то часто до-
цільно розглядати не саму множину ц. ф., а еквівалентну їй множину
функцій И' = {и,(/,(х))}, де IV,(/,(%)) —монотонні перетворення, які
приводять ц. ф. до безрозмірного вигляду і дають змогу порівнювати
їх між собою.
Позначимо через И7 с Км множину значень функцій к= {и,(х)},
на якій кожній альтернативі х відповідає певний вектор уу є й7, де
IV = {и,(х)}, і навпаки. Тоді відношення слабкої переваги, еквівален-
тності і строгої переваги, введені для альтернатив, виявляються при-
датними і для множини А¥. Нехай і*',є IV, тоді:
и'.' > IV,’, V/ є /.
IV; < IV,', V/ Є 12
V/' ~ уД <-> IV,- = IV*, V/ є І
>у' > УУ" <->
IV' > V/ є /,
V/ є І2
(1.8.4)
і хоча б одна з нерівностей (1.8.4) буде строгою.
Вектор и>0 є IV , який відповідає ефективній альтернативі, назива-
тимемо ефективним.
ТЕОРЕМА 1.8.3. Нехай х0 — ефективна альтернатива множи-
ни цільових функцій IV = {и>,(х)}, IV, (х) > 0, Уіе 1. Тоді існує вектор
С = {с,}, і є 1Х з компонентами с,- > 0 і ^сі=1 такий, що критерій
ІЄІ
Г(х) = птах с,іу, (х)
ІЄІ
(1.8.5)
досягає мінімуму на множині допустимих альтернатив А.
99
Зайченко О.Ю., Зайченко Ю П.
Як компоненти Сі можна взяти числа —, де Д =----; Л= У Л..
А	’Ф)	/є/
Цю теорему довів Ю.Б. Гермеєр [7].
Ці теореми дають змогу будувати різні способи відшукання ефек-
тивних альтернатив.
1.8.1.	Прийняття рішень
в задачі багатокритеріальної оптимізації
Розглянемо, як знайти найбільш раціональне рішення в задачі ба-
гатокритеріальної оптимізації. Таке рішення може виявитися не оп-
тимальним для усіх цільових функцій, але разом з тим, воно буде
найкращим компромісним рішенням з урахуванням усіх ц. ф. (крите-
ріїв) одночасно. Очевидно, найкращим рішенням слід вважати таку
альтернативу х, при якій відхилення від оптимальних значень для
кожної цільової функції /, (х):
Д/(х) =

досягає свого мінімального значення. Тут через позначено опти-
мальне значення ї-ї ц. ф. / на множині допустимих альтернатив.
Однак оскільки найменші значення величин Д ^(х^ієї, не дося-
гаються одночасно на жодній альтернативі, то виникає необхідність
порівнювати ці величини між собою, що пов’язано з потребою залу-
чення додаткової неформалізованої інформації від експертів.
Оскільки ц. ф. мають різну розмірність, то потрібно ввести деяке
перетворення	, що приведе /(х) до безрозмірного вигляду.
Це перетворення мас задовольняти, принаймні, такі вимоги [15,16].
а)	врахувати необхідність мінімізації відхилень від оптимальних
значень для кожної цільової функції;
б)	мати спільний початок і один порядок змінювання значень на
множині допустимих альтернатив;
в)	зберігати відношення переваги на множині альтернатив, що
порівнюються для сукупності цільових функцій і завдяки цьому
не змінювати множини ефективних альтернатив.
100
Дослідження операцій Збірник задач
Остання вимога, як було показано раніше (в теоремі 1.8.2), озна-
чає, що перетворення и'Д/Д.г)) має бути монотонним. За таке пере-
творення можна вибрати монотонну функцію вигляду:
(/(х)) =
і - С
У і	У і тіп
С	- і
У і тах У і
(1.8.6)
де /< тіп >/ тах — відповідно найменші значення функцій, які мак-
симізуються і найбільші значення функцій, що мінімізуються, на
множині допустимих альтернатив. Зазначимо, що в перетвореннях
(1.8.6) величини м'(Д(х)) завжди знаходяться в межах інтервалу
[0,1]. Вибрані перетворення и'Дх), і є І одночасно визначають розта-
шування множини допустимих альтернатив, яка описується одним із
співвідношень (1.8.6) у просторі И'с/^ значень функцій .
Тепер визначимо, яку альтернативу будемо вважати рішенням за-
дачі багатокритеріальної оптимізації, якщо вибрано множину функ-
цій IV = {іг,(х)}, і є / , кожна з яких мінімізується, 0 < и’Дх) < 1, і задано
відношення переваги на множині цільових функцій.
Справедливе таке твердження.
ТЕОРЕМА 1.8.4. Для кожної допустимої альтернативи хєА
такої, що 0< и' (х) < 1, V/ є 1 у просторі IV, існують вектор р, який
задовольняє співвідношення:
Р - {Р,І = {Рі  Р,>®> V' є І, ^р, = 1}.	(1.8.7)
/е/
і число к0, такі, що альтернатива х задовольняє одночасно М рів-
ностей вигляду:
Р,и',(х) = к0, V/ є І •	(1.8.8)
Доведення цієї теореми наведено в [16]. Довільний вектор ваго-
вих коефіцієнтів р = {р,} > 0, який задовольняє співвідношення
101
Зайченко О.Ю., Зайченко Ю.П.
(1.8.8), розглядатимемо як переваги одних цільових функцій множи-
ни / над іншими, що виражені в кількісній шкалі оцінок.
Тому під розв’язком задачі векторної оптимізації будемо розумі-
ти таку компромісну альтернативу, яка належить множині ефектив-
них альтернатив і лежить на заданому напрямку, що визначається
вектором р= {р(} в просторі И7. Якщо для деякої альтернативи х та
заданого вектора р>0 виконується співвідношення р,(и',(х)) = Л0,то
будемо казати, що альтернатива х лежить на напрямку, що визнача-
ється вектором р. Знайдемо, яке значення параметра к0 відповідає
ефективній альтернативі, що лежить на напрямку, визначеному век-
тором р. Відповідь на це питання дає така теорема.
ТЕОРЕМА 1.8.5. Якщо х0 — ефективна для даного векто-
ра р>0, то їй відповідає найменше значення параметра к0, при
якому система нестрогих рівностей (1.8.8) виконується одночасно
для всіх і є І.
Отже, під розв’язком задачі векторної оптимізації для заданого
вектора переваги р (р > 0) розуміють таку компромісну альтернативу
х0, що забезпечує однакові мінімальні зважені відносні втрати
>Ч(*о) = Рїи'/(ло) за всіма критеріями одночасно.
Метод обмежень для пошуку компромісних рішень
у задачах векторної оптимізації
Розглянемо підхід до пошуку компромісного рішення (альтернати-
ви) в задачі векторної оптимізації. Він грунтується на такій теоремі.
ТЕОРЕМА 1.8.6. Для того, щоб альтернатива х є А така, що
уу,(х )> 0, V/ є І, була ефективною при заданому векторі перевагр>0,
достатньо, щоб х був єдиним розв ’язком системи нерівностей:
ррч^х) < Ао, Х/ієІ,	(1.8.9)
для мінімального значення параметра к(,, при якому ця система сумісна.
102
Дослідження операцій Збірник задач
Доведення. Припустимо супротивне, що єдиний розв’язок
системи (1.8.9) х при значенні параметра А0=Ар неефективний.
Тоді існує альтернатива х' є А така, що иДх') < щ(х ),\/і є /, причому
хоча б одна нерівність буде строгою. Помноживши ці нерівності на
Рі > 0, V/ є І дістанемо, що р.ил(х') < /7,и',(х*) < і хоча б одна не-
рівність строга. Отже, маємо суперечність: альтернатива х задово-
льняє систему (1.8.9) із значенням параметра Ао, яке не перевищує
к0. Таким чином, теорему 1.8.6.доведено.
Із цієї теореми випливає, що визначене вище компромісне рішення
можна знайти як єдиний розв’язок системи нерівностей вигляду (1.8.9)
для мінімального значення параметра к0 при якому ця система ще сумі-
сна. Для знаходження компромісної альтернативи будується ітераційний
процес з параметром к0 є (0; —) на кожному кроці якого перевіряється
М
сумісність системи нерівностей (1.8.9) для хє А і заданого вектора р .
Параметр к$ є (0; —) обмежує відносні втрати (х), ХНєД. При
М
к0 -> 0 відносні втрати наближаються до нуля, тобто цільові функції
наближуються до своїх оптимальних значень Д(х) -» /(х0) = /,°, а при
к0 нерівності (1.8.9) виконуються на всій множині допустимих
М
альтернатив А
Зменшуючи параметр к0 і тим самим зменшуючи зважені втрати
для всіх ц. ф., наближаємося до альтернативи, що забезпечує мініма-
льні втрати по всіх ц. ф., тобто до компромісної альтернативи. Ітера-
ційний процес припиняється, коли найменше значення к0(п) (де
п — номер ітерації), при якому система нерівностей на множині
допустимих альтернатив ще сумісна, відрізняється від свого найбли-
жчого значення А0(и + 1), при якому вона стає вже не сумісною, не
більш як на £ (г > 0), де є — досить мала величина, яка задається із
міркувань припустимого часу розв’язання задачі. При цьому, якщо
розв’язок системи нерівностей єдиний, то це і буде шукана компро-
місна альтернатива Якщо ж цей розв’язок не єдиний, то для знайде-
103
Зайченко О.Ю., ЗайченкоЮ.П.
них альтернатив відносні втрати будуть еквівалентні із точністю до
є. Єдину компромісну альтернативу тоді можна одержати, оптимі-
зуючи на цій множині еквівалентних альтернатив деякий додатковий
узагальнений критерій. За такий критерій можна взяти, наприклад,
критерій вигляду:
Г(х) = £ Рі^і, (х),	(1.8.10)
іє/
і мінімізувати його на множині альтернатив:
А' = {х: р.^х) < кОтт, Уі є І, х є А}.	(1.8.11)
Як показано вище, такий узагальнений критерій завжди дас ефек-
тивні рішення.
Розглянемо деякі відомі методи відшукання компромісних рі-
шень у задачах векторної оптимізації.
Одним з таких методів є метод, запропонований Ю.Б.Гермеєром
[7]. Він грунтується на мінімізації узагальненого критерію вигляду:
Е(х) = тах р^мДх) —> тіп ,	(1.8.12)
ієі	хєА
де иДх) —задається перетвореннями (1.8.6).
Цей метод мінімаксу дає змогу відшукати таку альтернативу
хе А, для якої або виконується система рівностей р(иДх) = /:0 для
усіх іеік і мінімального значення параметра к0, або для деяких і
рівності не виконуються і ди’Дх) < £Отоіп. Якщо при цьому така аль-
тернатива єлина, то це і є шукане компромісне рішення. Тому роз-
глянутий далі метод обмежень, оснований на пошуку допустимих
альтернатив системи нерівностей (1.8.9) при мінімальному значенні
параметра к0, можна розглядати як метод розв’язання мінімаксної
задачі вигляду:
мінімізувати /г(х) = тіп тахр^иДх).	(1.8.13)
хєА ієі
Якщо розв’язок (1.8.13) не єдиний, то для вибору компромісної аль-
тернативи треба застосувати додатковий критерій вигляду (1.8.10).
Таким чином, якщо за монотонні перетворення ц. ф. вибрати
співвідношення (1.8.6), то задачу знаходження єдиної компромісної
альтернативи можна сформулювати так.
104
,	________________________________Дослідження операцій Збірник задач
Знайти розв’язок такої задачі параметричного програмування
стосовно параметра Ао при заданому векторі переваг р :
мінімізувати ко,	(1.8.14)
за умов:
/•(*) >	-^(/,° - / тіп), V/ є /,,	(1.8.15)
Рі
/іИ< /	(1 -8-16)
Рі
Розв’язок задачі (1.8.14)—(1-8.16) при мінімально можливому значенні
параметра к0 є (0; —) визначить шукану компромісну альтернативу.
1.8.2.	Багатокритеріальиі задачі лінійного програмування
У багатьох практичних задачах дослідження операцій, що опи-
суються моделями ЛП (наприклад, із сфери економіки) вибір рішен-
ня за одним показником якості може бути неадекватним до змісту
розв’язуваної задачі, бо треба враховувати одночасно декілька таких
показників — критеріїв [6; 15; 16].
Це призводить до потреби розв’язування багатокритеріальних за-
дач ЛП.
Нехай задано деяку множину цільових функцій /і (X), де
/і(Х) = с^х = ]Гсі:/ху-,і = 1,М >	(1.8.17)
2=і
причому перші т цільові функції треба максимізувати, а інші (М-
т)— мінімізувати. На вектор керуючих змінних X = {ху},у = 1,лна-
кладемо лінійні обмеження виду:
АХ<В(ІГІ),	(1.8.18)
хі >0,у = 1,л.	(1.8.19)
105

Зайченко О.Ю., Зайченко Ю.П.
Для розв’язування цієї задачі застосовується метод обмежень,
описаний у розд. 1.8.1. Перетворення, що приводять критерії до без-
розмірного вигляду, у розглядуваному випадку матимуть такий ви-
гляд:
а)	для цільових функцій, що максимізуються:
СГХ° -С7Х
^(/(Х))= 7? Г .VI €/,={!,...,/»}; (1.8.20)
с,гх«-сгх,.ті„
б)	для цільових функцій, що мінімізуються:
СГХ —Г’гХ°
^(/(х)) = 7?;	. V/ є І2 = и +1,/л + 2,..,М};	(1-821)
де Х° — розв’язок, що задовольняє умови (1.8.18), (1.8.19) і оптимі-
зує і цільову функцію;
Х;гпт(Х1Іпах) — розв’язок, що мінімізує (максимізує) відповідну
ц.ф. на допустимій множині розв’язків.
Компромісним розв’язком даної багатокритеріальної задачі буде
такий ефективний розв’язок X, для якого зважені відносні “витрати”
однакові і мінімальні, тобто:
р,^(Х) = р2^2(Х) =... = ртГт(Х) = *Отіп.
Згідно з методом обмежень, шуканий компромісний розв’язок
можна знайти, розв’язавши систему лінійних нерівностей:
С7Х > С7 Х,° - (С7 Х,° - С7 X, ^), V/ є Д;	(1.8.22)
Р,
С7X < С7Х“ +(С7Х/пш -С7Х,°), V/ є /2;
Р,
АХ<В,
х] > 0,7 = 1, п.
для мінімального значення параметра Ло, при якому ця система сумісна.
Розв’язок системи (1.8.22) еквівалентний розв’язку такої задачі ЛП [33]:
мінімізувати Л0=хп+і,	(1.8.23)
при обмеженнях:
106
Дослідження операцій. Збірник задач
Е^Х;+^1и+Іхи+|+<^0’
7=1
^^х?+^1п+|Хп+|+< >0;
7='
^мзх)+і1м^\х^+(1м ^°-
7=1
£^-^<0
7=1
• >
ІХ*,-** <0
7=1
хі >0,) = \,п,
де</..=
У
-Рісіі,) = Іп;ієІ1,
*А.п+1
7=1
і/"1
-аІс„40)>у'є7і;
7=1
р.Ес№’у'є/2-
І 7=1
Розглянемо приклад.
Приклад 1.8.1.
Максимізувати /і(х) = х{ + 4х2
мінімізувати/Xх) ~ ^хі —х2
при обмеженнях:
(1.8.24)
(1.8.25)
(1.8.26)
(1.8.27)
(1.8.28)
(1.8.29)
(1)
(2)
107
Зайченко О.Ю., Зайченко Ю.П.
х, + 2х2 > 4;
Зг Зх, + х2 > 7;
<5, :-Зх,+5х, <17;	(3)
З, : 5х, -х, < 23;
<55 :3х,-4х2 <7;
х„х2>0.
Допустиму множину розв’язків задачі К(х) зображено на рис.
1.8.1 у вигляді многокутника АВСВЕ.
Неважко отримати графічно оптимальний розв’язок цієї задачі
за критерієм/(х). Він знаходиться в точці С(х, = 6; х2 = 7).
Йому відповідає Д =/(х1 = 6; х2 = 7) = 34.
Мінімальне значення буде в точці Е(хі = 3; х2 = 0,5),/|тіп = 5.
За другим критерієм Д(х) оптимальний розв’язок буде в точці В(1,4),
йому відповідає /2°=/2(і,4)=-і , а найгірше значення критерія/>(х) — у
точці 0(5,2):/2таіі = із. Відрізок ВС являє собою ефективний план.
Розглянемо випадок, коли критерії рівноцінні, тобто Р| = р2 бу-
демо шукати компромісний розв’язок, що забезпечує мінімальні
однакові відносні витрати. Функції відносних витрат дорівнюють:
108
Дослідження операцій. Збірник задач
И'1, = р,И',(х) =
1 /і0-/і(^)
2/і0-/,™
1 34—х, -4-у,
2	29
И',2= р2И/2(х) =
1 /2М-/2 __ 1 Зх,-х2 4-1
2/2^-/2	2	14
Запишемо еквівалентну задачу ЛП згідно з (1.8.22)-(1.8.23):
мінімізувати х3= к0,
при обмеженнях:	/і° /і(Л) _ 1 34-х, —4х2 < .	/дх 2	29	3’ _ /2<х)-/2° _ 1 ЗХ, -Х2 +1	/ех р2 г - Г0	2	14	’’	і	; 32ПОХ 32	1 х, + 2х2 > 4 Зх, 4- х2 > 7 -Зх, 4-5х2 < 17 •	(6) 5х, — х2 < 23 Зх, - 4х2 < 7 х, > 0,х2 >0,х3 >0
Після елементарних перетворень зводимо цю задачу до вигляду
мінімізувати х3
(7)
при обмеженнях:
X, + 4х2 + 58х3 > 34;
- Зх] 4- х2 4- 28х3 > 1;
X] 4- 2х2 > 4;
Зх, 4-х2 > 7;
Зх| — 5х2 > —17;
- 5х, 4- х2 > -23;
-Зх, +4х2 > —7;
X] >0,х2 >0,х3 >0 .
(8)
(9)
109
Зайченко О.Ю., Зайченко Ю.П.
Ця задача має п = 3 змінних та т = 7 обмежень. Оскільки т > п,
для спрощення пошуку оптимального розв’язку перейдемо до дво-
їстої задачі, спряженної з (7)-(9). Вона має такий вигляд:
максимізувати ( 34у1 + у2 + 4у3 + 7у4 - 17у5 - 23у6 - 7у7)	(10)
при обмеженнях:
ІЛ ~ Зу2 + І-Уз + З У4 + Зу5 - 5у6 - Зу7 < 0;
4ц + 1у2 + 2Уз + 1У4 - 5 Уз + 1Уб + 4Уі
58у, + 28у2 ^1;
Уі >0,у2 >0,у3 >0.
Розв’язуватимемо її симплек-методом. Для цього введемо вільні
змінні і заповнимо початкову симплес-таблицю (табл. 1.24).
Результати послідовних ітерацій наведено в таблиці 1.24-1.27.
Таблиця 1.24
				і									
	Сі			34	1	4	7	-17	-23	-7	0	0	0
		Вх	Ао	А(	а2	Аз	Ад	а5	А,,	а7	а8	а9	Аю
<—	0	у8	0	1	-3	1	3	3	-5	-3	1		
	0	¥,	0	4	1	2	1	-5	1	4		1	
	0	¥і 0	1	58	28	0	0	0	0	0			1
		А	0	-34	-1	-4	-7	17	23	7	0	0	0
Таблиця 1.25
					і								
	Сі			34	1	4	7	-17	-23	-7	0	0	0
		Вх	Ао	А,	А2	А3	Ад	а5	А6	а7	А8	а9	Аю
	34	¥,	0	1	-3	1	3	3	-5	-3	1		
<—	0	¥9	0	0	5	-10	-11	-17	21	16	-4	1	
	0	¥,0	1	0	86	-174	-174	-174	290	174	-58		1
		А	0	0	-33	98	95	119	-147	-95	34	0	0
ПО
Дослідження операцій. Збірник задач
Таблиця 1.26
								і					
	Сі			341		4	7	-17	-23	-7	0	0	0
		вх	Ао	А,	а2	Аз	а4	а5	Аб	А?	Ав	А»	Аю
	34	¥,	0	1	0	1	4 5	2 5	_ 4 5	£ 5	2 5	_1_ 5	0
	1	У2	0	0	1	-2	_Н 5	17 5	21 5	16 5	1 0-1 1	2 5	0
<—	0	¥ю	1	0	0	-2	15— 5	118- 5	-71 — 5	-101,2	10,8	-17,2	1
		Д	0	0	0	22	18	-13	7	28	5	9	0
Таблиця 1.27
Сі			34	1	4	7	-17	-23	-7	0	0	0
	Вх	Ао	А,	А2	Аз	Ад	а5	Аб	а7	Аз	А»	Аю
34	У.	0,068	1	0	0,932	0,851	0	-1,04	-1,144	0,236	0,141	0,068
1	¥2	0,058	0	1	-2,06	-2,63	0	2,15	0,284	-0,49	-0,295	0,058
17	¥5	0,0168	0	0	0,017	0,128	1	-0,6	-0,855	0,091	-0,145	0,016
	Д	0,175	0	0	26,27	15,02	0	0,8	16,9	3,03	5,22	0,175
Оскільки в таблиці 2.35 всі оцінки ду>0, то знайдено оптималь-
ний розв’язок двоїстої задачі. Скориставшись співвідношенням
Л° = Д<Х;> відшукаємо оптимальний розв’язок багатокритеріальної
прямої задачі.
Маємо:
=|Д(7Й'’НДГ 1=3,03;
х° 1=5,22;
х3°=|Д%” |=Л0 =0,175.
111
Зайченко О.Ю.. Зайченко Ю.П.
Цьому розв’язку відповідає точка Р на відрізку ВС (рис. 2.5).
Йому відповідають мінімальні відносні втрати і відхилення від оп-
тимального значення для обох критеріїв:
(/. (Х1°, х2° )) = У'0;71^'’^0-2 0,175 = к0,
^(/2(х,°,х“))= 1	= 0,175=V
7 2 тах 7 2
Розглянемо тепер графо-аналітичний метод знаходження комп-
ромісного рішення. Для цього використовуємо дві умови:
у шуканій точці відносні зважені відхилення повинні бути рівні:
РІИ'|(*) = Р2И'2(Х);
ця точка повинна розташовуватись на відрізку ВС, що визнача-
ється обмеженням б3
Отже, складемо систему рівнянь:
34-х, -4х2 _ Зх, -х2 + 1
	29	"	14	’
-Зх, +5х2 = 17.
Вирішуємо цю систему й одержуємо 117,2х, = 355, звідки знахо-
димо шукане рішення: х° = 3,03;х2 =5,22. Воно збігається з рішен-
ням, знайденим раніше симплекс-методом.
Розв’язати наступні багатокритеріальні задачі ЛП
Задача 1.147
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
Рх (х) = Зх, + 2х2 -> тах;
Р2 (х) = х, - х2 -> тах,
112
Дослідження операцій Збірник задач
при умовах:
х, — 6х2 <3;
х, + х2 >10;
-2х( + х2 < 1;
х2<11;
2Х| + х2 < 32;
х,,х2 > 0;
А = А=°Л
Задача 1.148
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
Г, (х) = х, + 4х2 -> тах;
Е2(х) = 2х, — 2х2 —> тах,
при умовах:
х, + х2 > 7;
—2х( + х2 < 4;
х, <10;
х,+2х2<24;
х,,х2 >0;
д=р2=0,5.
Задача 1.149
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
(х) = Х( + х2 -> тах;
(х) = 2х, - х2 -> тіп,
113
Зайченко О.Ю., Зайченко Ю.П.
при умовах:
х,+2х2 >32;
-2х, + х2 > 16;
х, + 2х2 < 64;
-х, +4х2 <40;
х, < 24;
х(,х2 > 0;
р, = р2 =0,5.
Задача 1.150
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
Рх (х) = 2х, + 2х2 —> тах;
Р2{х) = Зх, +х2 —> тах,
при умовах:
2х, + Зх2 > 28;
-5х( +3х2 < 14;
х, +4х2 <57;
2х, +х2 <30;
х,,х2 >0;
р, =р2 =0,5.
Задача 1.151
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
Р} (х) = 4х, + 2х2 тах;
Р2 (х) = х1 - х2 —> тах,
114
Дослідження операцій Збірник задач
при умовах:
х{ — 6х2 < 3;
х, + х2 > 10;
—2х, + х2 < 2;
х2<12;
2х, + х2 < 32;
хрх2 >0;
Р, = р2=0,5.
Задача 1.152
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
р(х) = Зх, + 2х2 —> тах;
Г2 (х) = х, - Зх2 —> тіп,
при умовах:
2Х]+х2<3;
х, + 2х2 > 8;
Х| + 2х2 < 20;
-хІ +4х2 > 12;
х, <6;
х},х2> 0;
р, =р2=0,5.
Задача 1.153
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
/^(х) = х, + 4х2 —> тах;
Г2 (х) = ЗХ] - х2 -> тіп,
115
Зайченко О Ю, Зайченко Ю П
при умовах:
х, + 2х2 > 4;
Зх, + х2 > 7;
-Зх, +5х2 < 17;
5х, - х2 < 23;
Зх, -4х2 <7;
х,,х2 > 0;
Рі =Р2 =°>5
Задача 1.154
Знайти найкращий компромісний розв’язок наступної задачі ба-
гатокритеріальної оптимізації:
Е\ (х) = Зх, + 2х2 -> тах;
Г2 (х) = Х| - Зх2 —> тах,
при умовах
х, - 6х2 < 6;
х, + х2 > 20;
—2х, + х2 < 2;
х2 < 22;
2х, + х2 < 64;
х,, х2 > 0;
Р\ =Рг =0,5.
116
Дос цдження операцій. Збірник задач
РОЗДІЛ 2. ТРАНСПОРТНА ЗАДАЧА
ЛІНІЙНОГО ПРОГРАМУВАННЯ
2.1.	Постановка і основні властивості транспортної задачі
Постановка Т-задачі. Нехай у пунктах А(,...., А1П випускають де-
який однорідний продукт, причому обсяг виробництва в пункті А,
становить аі одиниць, і = І.т. Припустимо, що цей продукт спожи-
вають у пунктах В|, ... , Вл , а обсяг споживання в пункті В, стано-
вить Ь> одиниць) = 1,п. Припустимо, що з кожного пункту виробниц-
тва можливе перевезення продукту в будь-який пункт споживання.
Транспортні витрати на перевезення одиниці продукту з пункту А, в
пункт В дорівнюють Су (і = 1, т і = 1, п). Задача полягає у визна-
ченні такого плану перевезень, при якому попит всіх споживачів В,
повністю задовольняється, увесь продукт з пунктів виробництва ви-
везений і сумарні транспортні витрати мінімальні.
Треба визначити множину змінних х^ >0, і = І, пі, у = 1, п, що
задовольняють умови:
Ух;, =аі>/ = 1.щ	(2.1)
7=1
£х,=*,,7=І7	(2.2)
і=|
і таких, що цільова функція
т п
=	(2.3)
і=17=1
досягає мінімального значення.
Умова (2.1) гарантує повний вивіз продукту з усіх пунктів вироб-
ництва, а (2.2) означає повне задоволення попиту в усіх пунктах
споживання.
Таким чином, Т-задача являє собою задачу ЛП з ти числом
змінних, та (т + її) обмеженнями рівностями.
117
Зайченко О.Ю., Зайченко Ю.П.
Змінні хі} зручно задавати у вигляді матриці:
(2-4)
Матрицю X, що задовольняє умови Т-задачі (2.1) і (2.2), назива-
ють планом перевезень, а змінні ху. — перевезеннями. План х0, при
якому цільова функція мінімальна, зветься оптимальним, а матриця
С= |С,|| —матрицею транспортних витрат.
Властивості транспортної задачі
1.	Для розв’язання Т-задачі необхідно і достатньо, щоб задоволь-
нялась умова балансу:
=	(2-5)
<=і	/=і
тобто, щоб сумарний обсяг виробництва дорівнював обсягу спожи-
вання.
2.	Ранг системи обмежень (2.1), (2.2) дорівнює г = т + п -1.
Двоїста транспортна задача (Т -задача). Для Т-задачі, як і для
довільної задачі ЛП, існує двоїста задача до неї Т -задача.
Змінні Т -задачі позначимо Уь У2,..., Уп, -Пі, -П2, ...,-Пт.
ТЕОРЕМА. Для оптимальності плану Хо Т-задачі необхідне і до-
статнє існування таких чисел У1г У2, —, Ут -Пі, -<7* —,-Т!т, що
У2-Ц <С9,і=\^п;і=ї~п.	(2.6)
При цьому, якщо
40)>0, тоУі-П^Сц
118
Дослідження операцій. Збірник задач
2.2.	Опорні плани Т-задачі
Опорним (базисним) планом Т-задачі зветься будь-який її допус-
тимий, базисний розв’язок. Сформулюємо критерій перевірки
довільного плану на опорність.
План X =||*у|| Т-задачі є опорним (базисним), якщо з його основ-
них комунікацій не можна скласти замкнений маршрут.
Знаходження початкових опорних планів
Метод північно-західного кута. Основну ідею методу розгляне-
мо на конкретному прикладі: а{ = 60; а2 = 55; о, = 40; а4 = 35, та
1\ = 70; Ь2 =5; іу =45; ЬЛ =70
Заповнення таблиці починають з лівого верхнього елемента таб-
лиці Х0-хп.. Порівнявши а, =60 з =70 і вибравши менше з
них, одержимо х(І=60. Записуємо це значення в матрицю Хо.
Оскільки перший вибір було зроблено за рядком, то всі інші позиції
першого рядка заповнимо нулями. У допоміжному рядку а}0 запи-
шемо залишки невивезеного продукту, а,1’ =а|-Хц = 0, а в стовпці
— незадоволений попит після першого кроку заповнення.
Переходимо до другого рядка й починаємо заповнення з елемента
х2І (новий північно-західний кут незаповненої частини таблиці 2.1).
Порівнюючи а2 = 55,	= 10 вибираємо менше з них, і тому х2І =10.
Далі заповнюємо таблицю аналогічно. Після закінчення процесу за-
повнення матимемо початковий план Хо. Цей план є базисним (опор-
ним), оскільки з його ненульових елементів неможливо скласти цикл.
Крім того, він задовольняє умови задачі, оскільки:
ХЧ = а,;і = 1,4;£х.. = Ь/, у = 1,4.
/=і	і=і
119
Зайченко ОЮ, Зайченко Ю.П.
Таблиця 2.1
Метод мінімального елемента
Цей метод є варіантом методу північно-західного кута, який вра-
ховує особливості матриці транспортних витрат С=||с,7||. Він дає змо-
гу побудувати відразу досить економічний план, що скорочує загаль-
не число ітерацій при його подальшій оптимізації (порівняно з мето-
дом північно-західного кута).
Формальний опис алгоритму. Елементи матриці нумерують, по-
чинаючи з мінімального, в порядку збільшення і далі в цьому ж по-
рядку заповнюють матрицю Хо.
Нехай елементом з мінімальним порядковим номером виявився
Ху =тіп{д,,&7). Можливі три випадки: а) якщо а, <Ь],, то незаповне-
ний лишок і -го рядка заповнюємо нулями; б) якщо а, > Ь], то неза-
повнену частину у -го стовпця заповнюємо нулями; в) якщо аі = Ьі ,
то лишок і -го рядка і у -го стовпця заповнюємо нулями.
Далі цей процес повторюють з незаповненою частиною матриці Хо.
Приклад 2.1. Знайти початковий базисний план методом мініма-
льного елемента для таблиці 2.2. такої задачі.
Цифри в дужках вказують порядок заповнення елементів матриці
Хо (табл. 2.2).
120
Дослідження операцій. Збірник задач
Таблиця. 2.2
ЛАВ;	1	2	3	4	В,/а;
1	-рт-			4<»>	40
2	3<А)		3(7)	2 -	ЗО
3	5^>	7<І2)	-уліг-	-рп-	20
Аі/Ь,	ЗО	25	15	20	Б, \ а.
Після закінчення процесу заповнення матимемо початковий план
Хо. Цей план є базисним (табл. 2.3).
Таблиця 2.3
2.3.	Метод потенціалів
Метод потенціалів дає змогу, починаючи з деякого опорного пла-
ну, за скінченне число ітерацій знайти розв’язок Т-задачі.
Опис алгоритму методу потенціалів.
Алгоритм складається з попереднього етапу та скінченного числа
однотипних ітерацій.
На попередньому етапі будують початковий опорний план і об-
числюють матрицю:

с
121
Зайченко О.Ю., Зайченко Ю.П
ДЄ Г<0’,Ц(0) - попередні потенціали пунктів;
Д(ї=йо,в,(7=й).
Попередній етап.
Користуючись одним з відомих методів (наприклад, північно-
західного кута або мінімального елемента) відшукують початковий
опорний план Хо і обчислюють попередні потенціали
Попередні потенціали обчислюються так. За знайденим опорним
планом Хо будують схему перевезень Т-задачі із основних комуніка-
цій плану. Нагадаємо, що основні комунікації Ру плану Хо = |х*0)|| —
це ті, яким відповідають базисні компоненти плану, тобто комуніка-
ції для яких х<°> > 0. Далі створюють такі множини: Л — множину
індексів всіх пунктів Вр які пов’язані з пунктом Аі основними кому-
нікаціями; І! — множину індексів тих пунктів А,, що пов’язані осно-
вними комунікаціями з множиною Л; Л — множину пунктів Вр які
пов’язані основними комунікаціями з множиною 1, і т.д. Утворення
таких множин Ік виконуємо доти, доки не приходимо до порожньої
множини.
Беремо для визначеності Ц<0) = 0 і обчислюємо систему потенці-
алів стосовно Ар Тоді У^'} =	+[/І(0) = су1, де у є .І,. Відтак за зна-
ченнями	обчислюємо потенціали пунктів
Д (г є/(): (/*0) = Иу0) — с/у(7 є є/,). Аналогічно визначаємо по-
тенціали Р,<0)(_/ є Л): = Ц, + Ц ’ є Л •) • т.д. Після того як
потенціали всіх пунктів знайдено, будуємо матрицю:
Сі = ||сі/ “	0> “ 17<-0) )||-' = 1,т;у = 1,п.
Очевидно, позиції матриці Сь що відповідають базисним елемен-
там плану Хо, зайняті нулями. Якщо матриця С| не містить від’ємних
елементів, то Хо — оптимальний план. В іншому випадку Хо — не
оптимальний план, який можна поліпшити. Тоді переходимо до ви-
конання однотипних ітерацій.
122
Дослідження операцій. Збірник задач
(Л+/)-а ітерація. Припустимо, що вже проведено к ітерацій
(к=1,2,...), внаслідок яких отримано план Хк і допоміжну матрицю Ск.
Перший етап.
Обчислюють матрицю Ск+). Перетворення матриці Ск в матрицю
Ск+і полягас ось у чому. Знаходять найбільший за модулем від’ємний
елемент Ск. Нехай це елемент = ДА(ДА < 0). Тоді викреслюють
(чи виділяють) рядок X, де він розташований. Переглядають цей ря-
док і відшукують множину суттєвих його елементів. Хк-суттєвими
елементами називають ті елементи Ск , які відповідають базисним
елементам плану Хк, тобто для яких х^А) > 0. Викреслюють стовці,
які містять ці елементи. Далі переглядають викреслені стовці і шу-
кають в них нові суттєві елементи, що лежать у рядках відмінних від
уже викреслених раніше. Якщо такі елементи є, то викреслюють ряд-
ки, в яких вони містяться. Далі описаний процес продовжують, поки
чергова множина нових суттєвих елементів не буде порожньою. Далі
величину |А, | додають до усіх елементів виділених рядків і відніма-
ють від елементів усіх виділених стовців матриці Ск.
Якщо всі елементи таблиці Ск+і невід’ємні, то Хк — оптимальний
план і на цьому процес закінчується. У протилежному випадку пере-
ходять до другого етапу.
Другий етап.
Мета цього етапу — побудувати більш економічний план Хк+І.
Відшукують найбільший за модулем від’ємний елемент матриці Ск+).
Нехай ним буде = ДА+1 < 0 . Будують ланцюжок із додатніх еле-
ментів плану, який замикається на . Після того, як ланцюжок по-
будовано, у ньому знаходять мінімальний непарний за порядком
слідування злемент:
0І+1 = тіп .
Додають 0^ до всіх парних елементів (за порядком слідування)
ланцюжка і віднімають 0А+І від усіх непарних елементів. Всі інші
елементи Хк залишають без зміни.
123
Зайченко ОЮ, ЗайченкоЮ.П.
Новий план Хк+1 побудовано. Він є базисним, оскільки число його
нснульових елементів не змінилося.
Нехай Ьк — транспортні витрати, що відповідають плану Хк. Тоді
нове значення цільової функції, яке відповідає плану Хк+і, обчислю-
ють за співвідношенням:
~ Ц + ©Л+ІДА+1 •	(2-2.1)
Оскільки 0;+1 > 0 і ДА+) < 0, то £А+, < . Тому Хк+і — поліпше-
ний опорний план.
Далі переходять до (к+2)-ї ітерації.
Приклад 2.2. Розв’язати методом потенціалів Т-задачу, умову
якої наведено в таблиці 2.4.
Таблиця 2.4
.А, \ В,	1	2	3	4	В, / а,-
1	7	8	5	3	11
2	2	4	5	9	11
3	6	3	1	2	8
Аі/Ьі	5	9	9	7	Ь, \а;
Перевіримо умову балансу:
з
=11 + 11 + 8 = 30;=30 = £а,- ,
і=і	/=і	/=і
отже, задача розв’язана.
В процесі розв’язання цієї задачі скористаємося такими позна-
ченнями: Хк — суттєві елементи матриці Ск відмічатимемо рискою
зверху; при обчисленні матриці Ск+і будемо ставити (- ДА. ) праворуч
від виділених рядків матриці Ск, а ДА.(ДА <0) — під виділеними сто-
впцями; мінімальний елемент матриці Ск ДА обводимо рамкою;
елементи ланцюжка в плані Хк відмічатимемо знаком *.
Попередній етап. За допомогою методу північно-західного кута
знаходимо початковий опорний план Хо:
5 6 0
Хо= 0
0
о
7
З
0
0
124
Дослідження операцій. Збірник задач
Таблиця 2.5
					аі	аН)	ч<2’		
Хо	5	6	0	0	11	6	0	0	0
	0	3	8	0	11	11	8	0	0
	0	0	1	7	8	8	8	8	7
Ьі	5	9	9	7					
	0	9	9	7					
	0	3	9	7					
		0	1	7					
ь?			0	7					
V?				0					
3 4
Значення цільової функції Ь = ^£^сііхі} = 150.
<=і>і
Знаходимо попередні потенціали задачі. Для цього будуємо схе-
му перевезень вздовж основних комунікацій плану Хо (рис. 2.1).
Рис. 2.1.
125
Зайченко О.Ю., Зайченко ЮП
Наносимо на основні комунікації відповідні значення транспорт-
них витрат.
Попередні потенціали обчислюємо в такому порядку. Нехай
Ц(0) = 0. Розглянувши комунікацію А(Ві, знаходимо
У/0’ = С„ + Ц<0) = СП =7. Далі за комунікацією А(В2 визначаємо
К2<0) =С12+0О) =8 + 0 = 8.
Аналогічно:	= Г2(0) - С22 = 8 - 4 = 4;
И3(0)=Си+С/<°> =5 + 4 = 9;
<73(0, = И3(0)-С33 =9-1 = 8;
К4(0,=С34+Ц(<” =2+8 = 10.
Відтак обчислюємо елементи матриці Сі=|с?-(к)0)-Ц<0,)|, на-
приклад, = С21 -(Р|<0) -Н<0))= 2-(7-4) = -1, і так далі.
Зауважимо, що суттєві елементи С| (тобто ті, які відповідають
елементам х<°> > 0 ) дорівнюють нулю, тому їх можна заповнити без
обчислень:
'-Е'
0 -4 -7
0 0	3
3 0	0
Перша ітерація. Тут перший етап відсутній, бо матрицю С\ вже
визначено.
На другому етапі в матриці С( знаходимо найбільший за модулем
від’ємний елемент: С(4 = -7 = Д]. Переходимо до плану Хо і будуємо
ланцюжок із його базисних елементів, що замикається на х|4.
Елементи ланцюжка відмічатимемо знаком *. Непарні за поряд-
ком слідування (чергування) елементи ланцюжка х*і2 = 6, х‘2з = 8,
х 34=1. Визначивши мінімальний серед них елемент
®і = тіп{6,8,7} = 6, додаємо 0| до всіх парних елементів (за порядком
слідування) ланцюжка, а також до хІ4 і віднімаємо від усіх непарних
елементів ланцюжка.
126
Дослідження операцій. Збірник задач
Таким чином одержуємо план Хь який також є базисним, оскіль-
ки число ненульових елементів у ньому не змінилося, і, крім того, з
них неможливо побудувати цикл. Маємо:
Х,=
5	0	0	6
0	9	2	0
0	0	7	1
Цільова функція Ь, = Ьо + Д,®, = 150 -7*6 = 108.
Друга ітерація. Перший етап. Він полягає в побудові матриці С2
по С|. У матриці Сі рискою зверху відмічаємо Х( — суттєві елементи
(нулі). Викреслюємо в С| перший рядок, що містить найбільший за
модулем від’ємний елемент С|4 = Д, = —7 . Переглядаємо цей рядок й
відшукуємо в ньому суттєвий нуль (тобто 0), що належить першому
стовпцю. Тому викреслюємо далі перший стовпець й переглядаємо
його елементи, щоб визначити чи є серед них нові суттєві нулі. Оскі-
льки таких немає, то процес викреслення закінчується. 1 з викрис-
ленного рядка віднімаємо Д, = -7 (тобто додаємо 7), а до викресле-
ного стовпця додаємо Д, = -7 (тобто віднімаємо 7).
Отже, маємо матрицю С2. Оскільки С2 містить від’ємні елементи,
то план Х2 треба поліпшити.
С,
-п—0	1 —V
-1о о З
7 3оо
-7
+7
С2 =
0 7 3 0
т 0 0 3
0 3 0 0
На другому етапі знаходимо в матриці С2 найбільший за модулем
від’ємний елемент С2( = Д2 = -8, відшукуємо в плані Х( відповідний
йому елемент х21 і будуємо ланцюжок з базисних елементів цього
плану, що замикається на х2|. Його непарні елементи за порядком
слідування: х23 =2;х34 =1;х1‘ =5. Знаходимо ®2 = тіп {2,1,5} =1, дода-
ємо ®2 до усіх парних елементів ланцюжка, а також до х21 і відніма-
ємо 02 від усіх непарних елементів ланцюжка.
127
ЗайченкоО.Ю., Зайченко Ю.П.
Одержимо новий поліпшений план:
X,
15" 0 0	6+
Іо+ ^,2 0
0 0 17і г
02 = 1
--------* Х,=
4	0 0	7
19 10
0	0 8	0
Цільова функція £2 = 7, +02Д2= Ю8 - 8 =100.
Наступні ітерації виконуємо аналогічно.
Третя ітерація. Перший етап.
С2
+8--------►
+8
о -і т 0
0 0 0 11
8 3 0 8
Другий етап.
Х2
І 4" 0 І0+ 7
ТІ* 1 ІГ о
0	0	8	0
0, = 1
----------* Хз =
3	0	17
2	9	0 0
0	0	8 0
®з =тіп{4;1} = 1;£3 =95
Четверта ітерація. Перший етап.
С3
—її т іг
і—V—9-НЬ
8 о і!
-5 -5	-5
+5
+5-------
С4 =
0-100
0 0 5 11
з т 0 З
128
Дослідження операцій. Збірник задач
Другий етап.
З' О і'п
X 9’ О
О |О+ 8~
£4 =95-3*2 = 89
---------- Х4 =
04 = 3
П’ята ітерація. Перший етап.
С4
Ч—г—:г-
о о 5 11
з РП л—і.
-2 -2
+2
+2
С5 =
2	10	0
0	0 3	9
5	0 0	3
7
О
О
0	0	4	7
5	6	0	0
0	3	5	0
Всі елементи матриці С5 С^р > 0. Отже, Х4 — оптимальний план
перевезень. Йому відповідає значення Ь4= 89.
129
Зайченко О.Ю., Зайченко Ю.П.
Розв'язати такі Т-задачі
методом потенціалів
	1 8	2	3	ЗО
2.1 С =	4 7	5	1	
				50
	5 3	4	4	
				20
Ь, 15	15	40	ЗО	
2.6
13 3 4
5 2 7 5
6 4 8 2
7 15 7
а,
50
20
30
20
2.2
2 6
С= 1 5
З 4
З
6
1
4
9
6
8
7
10
аі
40
ЗО
35
Ь}- 20 34 16 10 25
2 4
2.3
С= 2 З
З 4
5
9
2
1
4
5
аі
60
70
20
Ь} 40 30 30 50
2.4
2 4 13
5 6 5 4
3 7 9 5
12 2 7
аі
30
20
40
50
2.5
40 ЗО 35 15
2.7 С =
,2
2
;з
4
з
4
5
9
2
1
5
а,
60
70
20
Ь{ 40 30 ЗО 50
12 6 4
2-8 С=ІЗ 1 3 2
1,5 7 5 1!
Ь, ЗО 25 18 20
2 4 3
2.9
С=3 1 2
5 4 1
Ь) 35 20 55 30
4	5	5	7
'8	7	5	4
9	6	4	5
3	2	9	3
аі
100
120
150
130
Ь> 140 130 90 140
а,
40
ЗО
2
З
5
о,
60
65
70
Ь{ 40 60 70 25
2.10 С =
10
7
6
5
4
14
7
9
8
4
10
7
а,
40
25
35
Ь> 15 40 ЗО 15
130
Дослідження операцій. Збірник задач
З
2
4
1
2.11 с =
2
З
1
5
аі
50
|2
З
.13
2
4
40
2.16 С =
ІЗ
4
9
6
7
1
20
ЗО 25
35
8
12
2.12
7
9
5
5
4
З
Ь, ЗО 80
2.13
2
8
7
2
З
1
4
8

ПО
50
2.14
С =
18
ЗО
6
Ь, 2
2.15
З
6
24
Ь, 70 5
4
20
20
5
4
1
5
Ь, 16 18
2
8
12
2
1
15
16
14
11
4
15
6
2
9
З
12
10і
6
6
7
4
а,
60
40
100
50
2.17
З
7
6
З
7
5
4
1
1
8
8
7
5
6
З
4
4
З
2
2
аі
зо
5
45
65 35
40
70
Ь, 10 35
15
25
35
6
2
4
5
8
З
1
1
2
5
4
З
6
8
ЗО 80
100
а,
130
90
100
140
90
2.18
4
10
4
5
З
10
6
2
5
8
З
1
10
15
16
130
90
40
90
2
9
4
4
З
2
40
4
З
45
1
8
З
9
15
8
З
70
Ь. 110 ЗО 50
80
7
55
аі
68
1
З
З
З
16
7
5
З
1
55
40
а,
60
55
40
35
2.19 С =
2.20
8
6
2
|7
7
З
6
8
аі
20
20
Ь,
|5
2
4
5
40
45
25 ЗО
С =
2
5
6
З
4
Ь, 20 60
40
15
З
2
З
55
41
5
8
а,
45
35
70
45
131
Зайченко О.Ю., Зайченко Ю ГІ
1
2.21
7
8
З
2
4
5
5 '
1 40
" ЗО
З
50
2.26
З
4
7
12
5
5
4
6
10
З
6
2
9
4
8
12
10
5
З
4
7
9
4
9
2
8
5
8
6
7
105
ЗО
80
20
2.22
2.23
2.24
2.25
Ь) 20 18 44 75
20
Ь
80 43 10
17
50
ЗО
2
С= 9
5
7
4
7
З
5
6
6
7
2
а,
ЗО
70
50
2.27
4
З
5
8
4
4
о.
10 40 20 60
19 7	5
3 15	5
6 8 3 4
2 3 13
II
35 80 25 70
13 3 8
8	6	2	6
І4	7	’3,
|5	2	4	5|
Ьі 25 ЗО 40 15
5
С = 10
12
5
8
7
9
5
Ь, ЗО 20
9
2
З
8
100
4
6
6
80
7
5
7
60
6
2
8
10
11
2
40
70
80
45
75
ЗО
а,
ЗО
40
70
60
а,
10
20
35
45
1	5	2	2	1	6
3	6	2	4	3	3
8	10	4	5	6	8
7	3	7	9	1	2
о,
100
15
90
55
2.28
2.29
Ь/ 30 40 55 80 45 10
4
З
с=
8
5
6
2 9 5
З 5 7
4 6 9
6 5 7
2 8 7
11 8 4
8 4 2
4 2 3
З 5 0
4 4 5
а,
80
ЗО
50
50
40
і, 40 80 35 15 10 60 10
5	2	10	10	6	5	4
6	4	3	9	2	2	3
С= 8 9 7 8478
6	2	5	4	5	4	5
|0	0	0	0	0	0	0
6, 40 ЗО ЗО 15 65 20 80
2.30
а,
80
80
40
ЗО
50
4	9	7	16	9	2	11
З	8	3	15	8	6	10
с 15	8	10	14	12	2	5
~ 2 7 5 49 11 4
10	5	3	5	8	3	6
11	12	12	10	5	8	7
Ь) 60 ЗО 15 40 20 35 75
а,
40
25
70
70
20
80
132
Дослідження операцій. Збірник задач
	7 6 14 2 6	а,
		10
	5 3 6 2 7 9	
		15
2.31	2 7 5 4 7 6	
С =		5
	2 6 5 4 8 3	
		20
	6 2 4 2 8 3	
		36
	7 3 6 9 4 6	
		14
Ь} 16	14 28 12 20	10
	6	5	10	3	1	3	2	
2.35	2	6	10	8	3	6	8	80 75
с =	4	7	10	7	6	4	7	
	9	8	10	4	5	2	3	15
Ь 40	5	3 20	1 ЗО	2 50	4 10	4	3 ЗО	ЗО 60
	9 4		1 8	8 1	2 8		аі 100 150
	4	5			5	6	
2.32	4	3	3	9	9	3	50
С =	9	5	2	5	7	4	
							
							200
	6	2	3	3	9	3	360
	8	4	3	6	4	7	140
Ь{ 160		140	280		120		200 100
2.36
2.37
2.33
і8
110
І 5
З
2
7	6	3	4	2
10	80	10	І	10
3	6	4	7	9
4	5	7	9	8
6	3	8	2	4
а,
25
25
20
20
70
Ь) 40 20 35 10	25	ЗО	
5 2 7 2 1	7	3	Ч 60
2.34	4 4 5 5 1	5	8	40
С=|ю	3	4	6	1 9	2	3	7	1 8	5	8	6	1	8 4 3	4 10 1	ЗО 50 50
Ь] ЗО 20 70 ЗО 40 15 25
2.38
	6 4	5 2	6 3	9 4	1 10	9 7	3 4	а, зо зо
С =	3	4	5	4	10	3	3	
	8	7	2	2	10	8	4	□V
	5	4	5	1	15	5	6	□V
								ЗО
Ь) 15 15 15 45 10 20 ЗО
5 5
6 6
7 7
8 4
Ь] 40 40
4	6	2	4
5	5	1	5|.
2	7	5	6
4	8	4	3
а,
ЗО
50
50
50
20 20 ЗО ЗО
4	8	5	1	1	4
2	3	6	4	2	3
5	4	2	3	3	2
12	18	6	5
а,
60
40
40
50
Ь, ЗО ЗО 40 20 20 50
133
ЗайченкоОЮ., Зайченко Ю.П
4
8
9
6
З
2-39 С =
З
З
10
8
6
7
8
а>
200
2.43
4
5
7
5
4
1
З
100
5
6
7
8
2
З
З
4
З
5
6
170

з
8
6
7
9
2
Я
90
4
6
7
8
9
4
100
130
4
6
З
8
5
4
10
160
Ь,
100
200
100
70
ЗО
100
З
2
4
6
7
1
200
80
2.40
Ь,
80 120
100
200 60
40
ЗО
4
10
5
6
З
4
15
5
5
4
8
7
6
15
аі
200
4
10
4
8
9
7
8
7
4
8
5
З
10
120
,4
5
4
6
7
8
1
130
2.44
5
6
10
10
6
6
З
5
5
6
4
7
50
З
6
7
8
5
З
Ь. 40 70
100
60
130
50
50
5
З
4
5
6
2.41
Ь, 200
100
80 100
100
а,
100
400
60
60
60
100
4
11
9
10
7
6
а,
С =
5
9
8
4
12
4
400
6
8
15
12
5
2
160
7
15
6
7
2
1
400
60
Ь, 400
200
100
80
100
60
2.42
4
З
4
7
6
6
15
8
З
7
10
6
8
8
12
З
5
9
4
4
4
10
5
9
Ь, 100
100
300 150
150
а,
200
250
250
200
100
134
Дослідження операцій Збірник задач
2.4.	Угорський метод
Угорський метод є одним з найцікавіших і найпоширеніших
методів розв’язання транспортних задач.
Розглянемо спочатку головні ідеї угорського методу на прикладі
розв’язання задачі вибору (задачі про призначення), яка є окремим
випадком Т-задачі, а потім узагальнимо цей метод для довільної Т-
задачі.
Угорський метод для задачі про призначення
Постановка задачі. Припустимо, що є п різних робіт А1,А2,...,А„
і п механізмів ВІ,В2,...,В„, кожний з яких може виконати будь-яку
роботу, але з неоднаковою ефективністю. Продуктивність механізму
Ві при використанні роботи Л, позначимо через Су, і = 1у =
Треба так розподілити механізми по роботах, щоб сумарний
ефект від їх виконання був максимальним. Ця задача зветься задачею
вибору або задачею про призначення.
Формально вона записується так. Треба вибрати таку
послідовність елементів {С17і,С2/і,...,С^} із матриці
Сп С12 ... С„
^-21	^22	•••	^2л
.С>1 ^>2 — Си.
щоб сума була максимальною і при цьому із кожного рядка
*=і
і стовпця С було вибрано рівно один елемент.
Введемо такі поняття.
Нульові елементи 21,22,...,2к матриці С звуться незалежними
нулями, якщо для будь-якого і 1<і<к рядок і стовпець, на перетині
яких розташований елемент 21, не містять інших таких елементів 2к.
Дві прямокутні матриці С і В звуться еквівалентними (С ~ О),
якщо су =	+ а,- + р7 для всіх і,у. Задачі про призначення з
135
Зайченко О.Ю, Зайченко ЮП
еквівалентними матрицями є еквівалентними (тобто оптимальні
розв’язки однієї з них будуть оптимальними і для другої, і навпаки).
Опис алгоритму угорського методу
Алгоритм складається з попереднього етапу і не більше, ніж (и-2)
послідовно виконуваних ітерацій. Кожна ітерація пов’язана з
еквівалентними перетворюваннями матриці, отриманої внаслідок
проведення попередньої ітерації, а також з вибором у ній
максимального числа незалежних нулів. Кінцевим результатом ітерації
є збільшення числа незалежних нулів на одиницю. Як тільки число
незалежних нулів досягне п, то проблему вибору вирішено, а
оптимальний варіант призначення визначається позиціями незалежних
нулів в останній матриці.
Попередній етап. Відшукують максимальний елемент в у-му
стовпці та всі елементи цього стовпця послідовно віднімають від
максимального. Вказану процедуру виконують над всіма стовпцями
матриці С. В результаті отримують матрицю з невід’ємними
елементами, у кожному стовпці якої є хоча б один нуль.
Далі розглядають і-й рядок одержаної матриці, відшукують її
мінімальний елемент а, і від кожного елемента даного рядка
віднімають мінімальний. Цю процедуру повторюють з усіма
рядками. В результаті отримаємо матрицю Со (Со ~ С), в кожному
рядку і стовпці якої є хоча б один нуль. Описаний процес
перетворення С в Со зветься зведенням матриці.
Знаходимо довільний нуль у першому стовці й відмічаємо його
зірочкою. Далі переглядаємо другий стовпець, і якщо в ньому
знайдеться нуль, що розташований у рядку, де немає ще нуля із
зірочкою, то відмічаємо його зірочкою. Аналогічно переглядаємо
один за одним всі стовпці матриці Со й відмічаємо, якщо можливо,
наступні нулі знаком «*». Очевидно, що нулі матриці Со, відмічені
зірочкою, є незалежними. На цьому попередній етап закінчується.
(А+1)-а ітерація. Припустимо, що к-ту ітерацію вже
проведено внаслідок чого одержано матрицю С*. Якщо в ній вже є
рівно п нулів із зірочкою, то процес розв’язання закінчується. В
іншому випадку переходимо до (£+1)-ї ітерації.
Кожна ітерація починається першим, а закінчується другим
етапом. Між ними може декілька разів проводитися пара етапів:
136
Дослідження операцій Збірник задач
трстій-перший. Перед початком ітерації знаком “+” виділяють
стовпці матриці Ск, які містять нулі з зірочками.
Перший етап. Переглядають нсвиділені стовпці Ск. Якщо в них
немає нульових елементів, то переходять до третього етапу. В іншому
випадку, якщо нсвиділений нуль матриці С*. знайдено, то можливий
один з двох випадків; 1) рядок, що містить нсвиділений нуль, містить
також і нуль із зірочкою; 2) цей рядок не містить нуля із зірочкою.
У другому випадку переходимо одразу до другого етапу,
відмітивши цей нуль штрихом.
У першому випадку цей невиділений нуль відмічають штрихом й
виділяють рядок, в якому він розташований (знаком «+» праворуч від
рядка). Переглядають цей рядок, знаходять нуль із зірочкою й
скасовують знак «+» виділення стовпця, в якому лежить даний нуль.
Відтак проглядають цей стовпець (який вже став невиділеним)
і відшукують у ньому нсвиділений нуль (або нулі). Цей нуль відмічають
штрихом і виділяють рядок, де він розташований. Далі розглядають цей
рядок і шукають у ньому нуль із зірочкою.
Цей процес за скінченне число кроків закінчується одним з двох
результатів:
1) всі нулі матриці Ск виявилися виділеними, тобто розташовуються
у виділених рядках або стовпцях. Тоді переходять до третього етапу;
2) знайдеться такий невиділений нуль у рядку, в якому немає
нуля із зірочкою. Тоді переходять до другого етапу, відмітивши цей
нуль штрихом.
Другий етап. На цьому етапі будують такий ланцюжок із нулів
матриці Ск: вихідний зі штрихом, нуль із зірочкою, що розташований
в одному стовпці з першим нулем, потім нуль із штрихом,
розташований в одному рядку з попереднім нулем із зірочкою і т.д.
Таким чином, ланцюжок утворюють рухаючись від 0 до 0 вздовж
стовпця, від 0* до 0 — вздовж рядка і т.д.
Можна довести, що описаний процес побудови ланцюжка
однозначний і скінчений, при цьому ланцюжок завжди починається і
закінчується нулем зі штрихом.
Далі над елементами ланцюжка, що розташований на непарних
місцях (О'1 - ставимо зірочки, знищуючи їх над елементами на парних
позиціях (тобто 0*). Відтак знищуємо всі позначки типу штрих над
елементами Ск і знаки виділення «+». Кількість незалежних нулів
збільшується на одиницю. На цьому (£+1 )-ша ітерація закінчується.
137
Зайченко О.Ю., Зайченко Ю.П.
Третій етап. До цього етапу переходять після першого, якщо всі
нулі матриці С* виділені. У цьому випадку серед невиділених
елементів С* знаходять мінімальний й позначають його через Л (Л>0).
Віднімають Л від усіх елементів матриці С*, розташованих у
невиділених рядках і додають до всіх елементів виділених стовпців.
В результаті отримують нову матрицю Секвівалентну до С*.
Зауважимо, що при такому перетворенні, всі нулі з зірочкою матриці
С* залишаються нулями і в С*, крім того, в ній з’являються нові
невиділені нулі. Тому переходять знову до першого етапу. Виконавши
перший етап, залежно від його результату або переходять до другого
етапу, або знову повертаються на третій етап.
Після скінченного числа повторів пара етапів третій-перший
обов’язково закінчиться переходом на другий етап. Після його
виконання кількість незалежних нулів збільшиться на одиницю
і (Лн-І)-а ітерація закінчиться.
Приклад 2.3. Розв’язати задачу про призначення з матрицею
3 4 2 2 1
4 5 3 13
С =
4 3 111
3 12 2 2
13 12 1
У процесі розв’язання використовуємо такі позначення:
Знак виділення «+», який потребує скасування, обводимо
кільцем; ланцюжок, як і раніше, показуємо стрілками.
Попередній етап. Відшукуємо максимальний елемент першого
стовпця — 4. Віднімаємо від нього всі елементи цього стовпця.
Аналогічно для отримання другого, третього, четвертого і п’ятого
стовпців нової матриці віднімаємо всі елементи цих стовпців від їх
максимальних елементів (5, 3, 2, 3). Дістаємо матрицю С(С~С).
Оскільки в кожному рядку та стовпці С' є хоча б один нуль, то С =
Со і процес зведеня матриці закінчується. Далі шукаємо й
відмічаємо знаком «*» незалежні нулі в Со, починаючи з першого
рядка.
Перша ітерація. Перший етап. Виділяємо знаком «+» перший,
другий, та четвертий стовпці матриці Со, які містять 0*.
138
Дослідження операцій. Збірник задач
Переглядаємо невиділений третій стовпець, знаходимо в ньому
невиділений нуль С23 = 0, помічаємо його штрихом й виділяємо
знаком «+» другий рядок. Переглядаємо цей рядок, знаходимо в
ньому елемент С22 = 0* й скасовуємо знак виділення другого стовпця,
в якому лежить 0*. Відтак переглядаємо другий стовпець — у ньому
немає невиділених елементів. Переходимо до останнього
невиділеного стовпця (п’ятого), шукаємо в ньому неввділені нулі.
Оскільки невиділених нулів немає, то переходимо до третього етапу.
Третій етап. Знаходимо мінімальний елемент у невиділеній
частині матриці Со (тобто елементи, що лежать у стовпцях та
рядках, не відмічених знаком «+»). Він дорівнює А = 1.
Віднімемо А = 1 від усіх елементів невиділених рядків (тобто
усіх, крім другого) й додамо до всіх елементів виділених стовпців
(першого та четвертого). Отримаємо матрицю С1 і перейдемо до
першого етапу.
Перший етап. Перед його початком знову виділяємо знаком «+»
перший, другий та четвертий стовпці. Переглядаємо невиділений третій
стовпець, знаходимо в ньому невиділений нуль С2з = 0, відмічаємо його
знаком штрих. Оскільки в другому рядку є 0* (елемент С^), то
виділяємо знаком «+» другий рядок, далі скасовуємо знак виділення
другого стовпця, де лежить 0*. Потім переглянемо другий стовпець,
знаходимо в ньому невиділений нуль С12 - 0, відмічаємо його знаком
штрих. Оскільки в першому рядку є нуль із зірочкою С14 = 0 , то
виділяємо його знаком «+», й скасовуємо знак виділення четвертого
стовпця, де розташовувався цей знак 0 . Відтак переглядаємо четвертий
СТОВПеЦЬ Й ЗНаХОДИМО В НЬОМУ НеВИДІлеНИЙ НУЛЬ С54 = 0. Скільки в
рядку, де він лежить, немає нуля із зірочкою, то відмітивши цей 0
знаком штрих, переходимо до другого етапу.
Другий етап. Починаючи з елемента с54 = 0, будуємо ланцюжок,
рухаючись від нього по стовпцю. Знаходимо нуль із зірочкою с14 =
0*, далі від нього рухаємося вздовж першого рядка й знаходимо
0 (сіг), від цього елемента рухаємося вздовж першого стовпця до с22 =
0*, нарешті, рухаючись від с22 = 0* вздовж другого рядка приходимо
до вихідного с23 = 0 . Таким чином, ланцюжок побудовано: 054 —
0*І4 — 012 — 0*22 — 023. Замінюємо знак штрих на зірочку й
скасовуємо знак зірочки над парними елементами ланцюжка, а
також всі позначки виділення стовпців та рядків. На цьому перша
ітерація закінчується. В результаті число незалежних нулів
139
Зайченко О.Ю., Зайченко Ю.П
збільшилося на одиницю. Оскільки наступні ітерації виконуються
аналогічно, то наведемо результати їх виконання без додаткових
пояснень. Після другої ітерації кількість незалежних нулів (0 )
стала дорівнювати 5 (розмірності матриці С) і тому алгоритм
закінчує роботу. Шукані елементи призначення відповідають
позиціям незалежних нулів матриці С3 (тобто 0 ).
Відповідне значення цільової функції:
^шах — СІ2 + С23 + СЗІ + С45	С54 = 15 .
Перша ітерація. Перший етап
		е		
	1	1	1	0*
	1	0’	0	1
Со =	0*	2	2	1
	1	4	1	0
	3	2	2	0
Третій етап
		+ е	♦	
2		1	1	1 0' 2	-1
0	+	1 0* 0’ 1 0	+
2	С,=	0* 2 2 1 2	-1
1		14 10 1	-1
2		3	110 2	-1
		+ 1 +1	
Л=1
Перша ітерація.
Перший етап.
Другий етап.
1
1
С2= 0*
1
2
0*	0	0
0	0*	2
1	1	1
3	0	0
1	1	о’
І
о
1
о
1
Друга ітерація.
Перший етап
	+		+	ж	
	1	0*	0	0	1
	1	0	0*	2	0
с2 =	0'	1	1	1	1
	1	3	0	0	0'
	3	1	1	0’	1
С3
Другий етап
1	0*	0	0	1
1	0	0*	2	0
0*	1	1	1	1
1	3	0	0	о’
31	1 0* 1
140
Дослідження операцій Збірник задач
Угорський метод для транспортної задачі
Розглянута вище задача про призначення являє собою окремий
випадок Т-задачі, коли = І,і = 1,п;Ьу = 1,у = 1,я. Тому угорський метод,
що був спочатку розроблений для розв’язання транспортної задачі
спеціального вигляду, можна поширити на загальний випадок Т-
задачі [15; 16].
Нехай треба розв’язати Т-задачу такого вигляду:
т п
мінімізувати £	>
>=О=і
при обмеженнях:
Хху -аі,і = \,тп\
/=1
ху>0.
Алгоритм розв’язання Т-задачі на основі угорського методу складається
із попереднього етапу та скінченного числа однотипних ітерацій.
В результаті попереднього етапу обчислюють матрицю
Хо = |х|0)|,і = 1,я»,у = 1,я, елементи якої задовольняють такі обмеження:
Іх^<а,.,ї = ї^,	(2.3.1)
7=1
^х‘0,<Лу.,у = 1,я-	(2.3.2)
1=1
Якщо в умовах (3.3.1), (3.3.2) строгі рівності, то матриця Хо
є розв’язком Т-задачі.
Матрицю, побудовану в результаті к-і ітерації, позначимо
X* =||х,^)|. Позначимо також
+	(2.3.3)
<=1	7=1	>=О=1
141
Зайченко О.Ю., Зайченко Ю.П.
Величина ДА. зветься сумарною нев’язкою для матриці Хк . Вона
характеризує близькість Хк до шуканого плану Т-задачі. Ітерації
виконують доти, доки величина ДЛ не буде дорівнювати нулю.
Опис алгоритму угорського методу
Попередній етап. У кожному із стовпців матриці транспортних
витрат С = ||с1?| відшукують мінімальний елемент, який віднімають
від усіх елементів даного стовпця. Отримують матрицю С. Далі в
кожному рядку матриці С вибирають мінімальний елемент і
віднімають його від усіх елементів даного рядка. Одержують
матрицю Со (Со ~ С), всі елементи якої невід’ємні і, крім того, в
кожному рядку і стовпці Со є хоча б один нуль. Будують матрицю Хо
так, щоб її ненульові елементи були розташовані в позиціях нулів
матриці Со-
Нехай і,у— номер рядка, в якому розташований к-й нуль у-го
стовпця матриці Со- Тоді елементи першого стовпця матриці Хо
визначають за рекурентною формулою:
0, якщо і * ік.,к = 1,2,...,г,(С'Гі' > 0);	..
л«п _	м	(2-3-4)
11 іліпіа,.,^-^*^), якщоі = /и;(СІ01=0).
д.І
Тобто всі елементи першого стовпця Хо, яким відповідають
ненульові елементи в матриці Со, заповнюють нулями, а всі інші
елементи цього стовпця заповнюють згідно з методом північно-
західного кута.
Припустимо, що вже заповнено стовпці Хо від першого до (/-1)-го
включно. Тоді елементи )-іо стовпця визначають згідно з формулою:
0, якщо і *	= 1,гу;	т
х(1”=	і-і >-	І •
* тіп{а, --ХЧ/’Ь якшо'= V
д-1
Далі обчислюють сумарну нев’язку:
т	п	т п
і=1	/=І	і=1 У=1
Якщо До = 0, то Хо — оптимальний план Т-задачі. Якщо д0 > 0,
то переходимо до першої ітерації.
142
Дослідження операцій. Збірник задач
( к + 1) - а ітерація. Кожна ітерація складається з двох або
трьох етапів. Ітерація починається з першого етапу, а закінчується
другим, а між першим та другим етапами в загальному випадку
декілька разів можуть виконуватися третій та перший етапи.
Припустимо, шо вже виконано к ітерацій, причому АЛ > 0. У
цьому разі необхідно, використовуючи матриці Ск та Хд-, провести
наступну (А+1)-у ітерацію. Перед початком ітерації виділяють знаком
«+» ті стовці матриці СЛ, для яких нев’язки по стовпцях
дорівнюватимуть:
/=1
Перший етап. Якщо всі ненульові елементи матриці С*
розташовані у виділених стовпцях, то одразу ж переходять до
третього етапу. У протилежному разі, нехай деякий невиділений
нуль розташовується в і -му рядку і в у -му стовпці. Тоді
обчислюють значення нев’язки і -го рядка:
Я=І
Можливий один з двох випадків: 1) б-*’ = 0,2)б,(А:) > 0. У першому
випадку і -й рядок С* відмічають знаком «+» праворуч від нього, а сам
невиділений нуль відмічають штрихом. Далі переглядають елементи
ї-го рядка, що лежать у виділених стовпцях і шукають серед них
суттєві нулі (нагадаємо, що суттєвим нулем С* зветься такий елемент
с^к} = 0 , для якого х^р > 0 ). Якщо таким суттєвим нулем виявився
елемент с^к = 0, а сам стовпець ц — виділений, то знак виділення
«+» над стовпцем д скасовують, а сам цей нуль відмічають зірочкою.
Відтак переглядають р-й стовпець і підшукують у ньому нуль
(нулі), що лежать у рядках, відмінних від і-го. Якщо такий нуль є, то
відмічають його штрихом і аналізують нев’язку його рядка.
Потім процес пошуку нулів та відмічання їх (штрихами або
зірочками) продовжується аналогічно, і через декілька кроків він
закінчується одним з двох результатів:
1) знайдемо черговий невиділений нуль матриці С*, для якого
нев’язка в рядку 5, > 0. Тоді відмітивши його штрихом, переходимо
до другого етапу;
143
Зайченко О.Ю., Зайченко Ю.П.
2) усі нулі матриці Сд. виявилися виділеними, причому для
кожного з нулів, що відмічалися штрихом, нев’язка = 0. Тоді
переходимо до третього етапу.
У другому випадку, відмітивши цей нуль штрихом, одразу
переходимо до другого етапу.
Другий етап. Його зміст полягає в побудові ланцюжка в матриці
С* із нулів, відмічених штрихами і зірочками, та в переході до нової
матриці Х*+1.
Нехай для деякого нуля із штрихом матриці С*, розташованого,
наприклад, в позиції (Я,,//,), нев’язка рядка 8? > 0. Починаючи з цього
елемента Дд^о', побудуємо ланцюжок із відмічених нулів матриці С*:
рухаючись по стовпцю д, вибирають нуль із зірочкою 0*л2д,, далі
рухаючись від нього вздовж рядка Л,, знаходять нуль із штрихом 0л2Я2 -
Потім рухаються від нього вздовж стовпця /л2 до наступного нуля із
зірочкою і т.д. Такий послідовний перехід від 0 до 0 по стовпцю та від 0
до 0 по рядку продовжують доти, доки це можливо.
Можна довести, що процес побудови ланцюжка однозначний
і скінчений, ланцюжок не має циклів, починається і закінчується
нулем із штрихом.
Після того як ланцюжок вигляду
побудований, здійснюють перехід до матриці ХЛ+1 від матриці X* за
формулами:
.(*+!) _
V
х^}, якщо С(Р не належить до ланцюжка-,
х-*} +	, якщо Су - непарний за порядком слідування (2.3.7)
елемент ланцюжка < тобто Сук) =0 >;
х?*’ - ® к, якщо - парний за порядком слідування
елемент ланцюжка < тобто = 0* >;
144
Дослідження операцій. Збірник задач
Є, = ™п{х“
да«'=\-їл..	(238>
1=1
^А)=а. -Ух‘*’
А А і—і \з
7=1
Таким чином, &к — мінімальний елемент серед сукупності
парних елементів ланцюжка, нев’язок рядка, де починається
ланцюжок, та стовпця, де він закінчується.
Обчислюємо нев’язку для х<+1: Д*+І = Д* - 20* .
На цьому (й+1)-а ітерація закінчується.
Третій етап. Отже, припустимо, що всі нулі виділені. Третій етап
полягає в переході від матриці С* до еквівалентної матриці С'*, в якій
з’явиться новий невиділений нуль (або нулі). Нехай Л = тіп{с^*)}, де
мінімум береться серед усіх невиділених елементів матриці Ск. Тоді
від усіх елементів невиділених рядків матриці Ск віднімають Л, а до
всіх елементів виділених стовпців додають й. В результаті
отримують матрицю С'*(С* ~ С*), в якій всі суттєві нулі матриці С*
залишаються нулями, і, крім того, з’являються нові невиділені нулі.
Далі переходять до першого етапу, і в залежності від його
результату або переходять до другого етапу, або знову вертаються на
третій етап. За скінченне число повторів пари етапів третій-перший
обов’язково перейдемо до другого етапу.
Якщо після виконання другого етапу Д*+1=0, то Х*+і —
оптимальний план. В іншому випадку переходимо до (к+2) ітерації.
Зазначимо деякі важливі особливості угорського методу.
Оскільки цей метод, на відміну від методу потенціалів, не використовує
опорних планів, то явище виродженості плану для нього відсутнє Це
виключає можливість зациклювання, пов’язаного з виродженністю планів Т-
задачі, що полегшує програмування методу і його реалізацію на ЕОМ.
Метод дає змогу на кожній ітерації за значенням нев’язки
д* оцінювати близкість X* до оптимального плану, і, крім того,
верхню межу необхідного числа ітерацій, що лишилися N^1
(2.3.9)
145
Зайченко О.Ю., Зайченко Ю.П.
Приклад 2.4. Знайти розв'язок транспортної задачі з такими умо-
вами:
7 8 5 3
С= 2 4 5 9
6 3 12
а, = 11,а2 = 11;а3 = 8,
/>, =5,Ь2 = 9;Ь, = 9;Ьа =7.
З	4
Перевіряємо умову балансу Уа, = У',ЬІ =30
/=І	у=1
Попередній етап. Віднімемо від елементів першого стовця 2,
другого - 3, третього -1, від четвертого -2. Приходимо до матриці Сі-
Далі, віднімаючи мінімальний елемент від елементів кожного рядка,
одержуємо матрицю Со:
5
5
С,=
З 0
4 7
0 0
0
4
1
0
4 7
0 0
4
Побудуємо початкову матрицю перевезень
аі
0
о
8
0
0
0 7 114
0 0 116
0 0 8 0
Ь; 5 9 9 7
0 19 0
Нев’язки для стовпців = 0, 1, 9, 0, для рядків 5, = 4; 6; 0.
Сумарна нев'язка
До =	=£5,- +	= 20
І 3 і і
Перша ітерація. Перший етап. Відмічаємо знаком “+” зверху
перший і четвертий стовпці, яким відповідають нульові нев'язки, а
знаком “х” ліворуч перший і другий рядки, яким відповідають
ненульові нев'язки, рискою зверху - суттєві нулі.
146
Дослідження операцій. Збірник задач
+
4 4
О 1
4 О'
+
З О
4 7
0 О
Переглядаємо невиділений другий стовпець матриці Со,
знаходимо в ньому невиділений нуль Сзз = 0 і відмічаємо його
штрихом. Оскільки 53 = 0, то виділяємо третій рядок знаком “+”.
Переглядаємо третій рядок щодо виділених стовпців. Там суттєвих
нулів немає. Оскільки в Со більше не лишилося невиділених нулів
(всі нулі містяться у виділених рядках або стовпцях), то переходимо
до третього етапу.
Третій етап. Серед елементів
матриці Со знаходимо мінімальний
всіх елементів виділених стовпців
невиділених рядків і стовпців
елемент Ь = 1, додаємо його до
і віднімаємо від усіх елементів
невиділених рядків. Отримаємо матрицю Сь
II X х	+ + 4 4 3 0 0 14 7 4 0' 0 0	А = 1	_ х » С[ - X
З
0'
0
2
З
0
0
7
1
Переходимо до першого етапу.
Перший етап. Серед невиділених стовпців знаходимо нульовий
елемент С22 у рядку з ненульовою нев'язкою, а тому переходимо до
другого етапу.
Другий етап. Ланцюжок складається з одного елемента С22 = 0.
Знаходимо ©і =тіп(1-6> = 1 і додаємо 0, = 1 до елемента хь Одержуємо
матрицю Хр
$
0
0
0 0 7
1 0 0
8 0 0
4
5
0
0 0 9 0
Друга ітерація. Перший етап. В матриці С! відмічаємо знаком “+”
перший, другий і четвертий стовпці, яким відповідають нульові
нев‘язки. Знаходимо в третьому стовпці нуль Сзз = 0 і відмічаємо
його штрихом Оскільки нев'язка третього рядка дорівнює нулю, то
147
Зайченко О.Ю., Зайченко Ю.П.
Дослідження операцій. Збірник задач
виділяємо її знаком “+”. Переглядаємо цей рядок, знаходимо в ньому
суттєвий нуль С32 у виділеному стовпці. Позначаємо його зірочкою й
скасовуємо знак виділення другого стовпця.
Далі переглядаємо другий стовпець й відшукуємо в ньому
невиділений нуль С22. Оскільки відповідає нев'язка в другому 52 > 0,
то відмітивши цей нуль штрихом, переходимо до другого етапу.
Другий етап. Будуємо ланцюжок в матриці Сі вигляду
°32 °зз, а потім аналогічно ланцюжок з матриці Хь
В результаті дістаємо матрицю Х2: 62 = тіп {5, 8, 9} = 5
0
5
0
0
0 0 7 4
6 0 0 5
3 5 0 0
0 9 0
На цьому процес виділення нулів закінчуємо. Оскільки більше
виділених нулів не має, то переходимо до третього етапу.
Третій етап. Знаходимо мінімальний невиділений елемент в
матриці С2 Ь = 2, віднімаємоЬ від усіх елементів невиділених рядків
(першого) й додаємо до всіх елементів виділених стовпців (тобто
четвертого). В результаті отримаємо матрицю С3, в якій з'явився
НОВИЙ невиділений нуль (Сіз). Переходимо до першого етапу.
Перший етап. В матриці С3 знаходимо невиділений нуль С13.
Оскільки 5) > 0, то переходимо до другого етапу.
Другий етап. Увесь ланцюжок складається лише з одного
(2)	/2)
елемента . Тому 03 = тіп {5і = 4, 52 = 4} = 4. Додаємо 03 до 13 ,
одержимо матрицю Х3.
Третя ітерація. Перший етап. У матриці С2 відмічаємо знаком “+”
перший, другий і четвертий стовпці, яким відповідають нульові
нев'язки. Знаходимо нульовий елемент Сзз у третьому стовпці.
Оскільки цьому відповідає нульова нев‘язка в третьому рядку, то
відмічаємо цей нуль штрихом. Далі, переглядаємо третій рядок,
відшукуємо в ньому суттєвий нуль С32 = 0, що знаходиться у
виділеному другому стовпці, відмічаємо зірочкою цей нуль та
скасовуємо знак виділення над другим стовпцем. Переглядаємо
другий стовпець, знаходимо в ньому нульовий елемент С22 = 0 і
відмічаємо його штрихом, а другий рядок, де він лежить, знаком “+”
(бо 52 = 0).
Далі переглянувши другий рядок, знаходимо в ньому суттєвий
нуль С2) = 0 у виділенному першому стовпці. Тому позначаємо цей
нуль зірочкою й скасовуємо знак “+” над першим стовпцем.
З 2
0’ З
0 0'
0
7
1
И = 2
5
+
1
о
о
0і о
З 9
0 З
0 0’
6 0
З 5
0 4
7 4
0 0
0 0
0
0	0	4	7	0
5	6	0	0	0
0	3	5	0	0
0	0	0	0
Оскільки Д3 = 0, то Х3 - оптимальний план. Відповідне значення
цільової функції Ьорт =ХХсух^) = 89 (порівняйте з результатами
* У
розв'язання цієї ж задачі методом потенціалів, див. приклад 2.2).
Вирішити угорським методом такі транспортні задачі
2.45		2.46		
		Ді		а\
	4	5	5	7	100	13	3	4	50
	8	7	5	4	120	5 2	7	5	20
С =	9	6	4	5	С = 150	6 4	8	2	зо
	3	2	9	3	130	7 15	7	20
*>,	140 130 90 140	Ьз	40 30 35 15	
148
149
Зайченко О.Ю., Зайченко Ю.П.
2.47.
2.48.
2
С= 2
З
4	5
З 9
4	2
аі
1 60
4 70
5 20
а,
Ьі 40 ЗО ЗО 50
2.49.
10
С= 7
6
5
4
14
7
9
8
4
10
7
аі
40
25
35
Ь, 15 40 ЗО 15
2.51.
8	12	4	9	10
с	7	5	15	3	6
" 9	4	6	12	7
5	3	2	6	4
Ь) ЗО	80	65	35	40
°і
60
40
100
50
2
С = З
5
Ь. 40
2.50.
С =
з
2
З
Ь, ЗО
2.52
С =
Ь,
1
З
6
24
70
4
І
4
З
2
1
2
З
5
60
65
70
60
70
25
2
З
2
25
2
40
4
З
5
4
1
7
1
5
4
а,
50
40
20
35
20
9
15
8
З
45
7
5
З
1
70
аі
60
55
40
35
150
Дослідження операцій. Збірник задач
Розділ 3. ДИСКРЕТНЕ ПРОГРАМУВАННЯ
Математичні моделі задач дискретного програмування
Багато задач такі як, розподіл ресурсів, сітьового планування і
керування, календарного планування, описуються математичними
моделями дискретного програмування.
Розглянемо загальну задачу максимізації:
максимізувати /(хх,х2,-,х„),	(3.1)
при обмеженнях:
^1(х1,х2,..,х„)<0;
.............................. (3.2)
^га(хі,х2,..,х„)<0;
Х=[х1,х2,..,хя]єО,	(3.3)
тут Л — деяка множина.
Якщо множина £> скінченна або зліченна, то умова (3..3) —•. це
умова дискретності і задача (3..1)-(3..3) є задачею дискретного
програмування.
Найчастіше умова дискретності розподілена по окремих змінних так:
х^ &О -\,п.
Якщо ВВОДИТЬСЯ обмеженння Ху — ціле ЧИСЛО, І = \,п, то
приходимо до задачі цілочисельного програмування (ЦП), а якщо
вводиться обмеження ху - {0,1}, то до задачі булевого
програмування.
У задачах дискретного програмування область допустимих
розв’язків є неопуклою і незв’язною.
151
Зайченко О.Ю.. Зайченко Ю.П
3.1. Метод відсікаючих площин
Метод відсікаючих площин вперше розробив Р.Гоморі в 1957—
1958 рр. для задач лінійного цілочисельного програмування (ЛЦП) [15; 16].
Для групи методів відсікаючих площин використовується ідея
«регуляризації» задачі. Вона полягає в зануренні вихідної незв’язаної
області допустимих розв’язків (дискретних точок) у відповідну
неперервну опуклу область, тобто в тимчасовому відкиданні умов
дискретності. Далі до одержаної регулярної задачі застосовують
стандартні методи оптимізації.
Якщо отриманий у результаті розв’язок задовольняє відкинуту
умову дискретності, то задачу розв’язано. У протилежному разі треба
продовжити процес розв’язання.
Для задачі ЛЦП відповідну ідею «регуляризації» запропонував
Г.Данціг, її було покладено в основу методу відсікаючих площин.
Отже, припустимо, що треба розв’язати задачу ЛЦП:
п
мінімізувати >	(3-1.1)
7=1
при обмеженнях:
£ауХ^=Ьі, і=1,т,	3.1.2)
7=1
ху>0, у = й,	(3.1.3)
х7 — цілі числа, у = 1,л .	(3.2.4)
Відкинувши на певний час умови цілочисельності (4.2.4),
знайдемо оптимальний розв’язок. Якщо виявиться, що він
задовольняє також умові цілочисельності, то цей розв’язок і є
шуканим. У протилежному разі треба сформувати додаткове
обмеження, яке задовольняє будь-який цілочисельний план, але не
задовольняє знайдений оптимальний нецілочисельний план. Таке
обмеження називають «правильним відсіченням». З точки зору
геометрії, правильне відсічення являє собою гіперплощину, яка
відсікає від опуклого многогранника відповідної задачі ЛП деякий
многогранник, який містить всі цілочисельні розв’язки вихідної
задачі.
152
Дослідж ення операцій. Збірник задач
Далі до вихідної системи обмежень задачі додають правильне
відсічення й описаний процес розв’язання продовжують аналогічно.
Якщо правильне відсічення сформоване задовільно, то можна
сподіватися, що за скінченне число ітерацій буде знайдено розв’язок
задачі ЛЦП або зафіксовано несумісність її умов.
Розглянемо задачу ЛП (4.2.1)-(4.2.3) і припустимо, що всі {аІ}},
{Ьі}, {сД — цілі числа і т < п.
Нехай {Аі5 А2,	А„} — лінійно незалежні вектори обмежень,
що утворюють базис системи {Аь А2,	А„}. Очевидно, матриця
Ах= { Аь А2,..., А„} — невироджена й існує обернена до неї А,1.
п
Помноживши обмеження задачі	= Ь на А/, отримаємо:
І=і
Ха;‘АЛ=А-,Ь = х0.	(3.1.5)
7=1
Це співвідношення в розгорнутій формі запису має вигляд:
/=т+1
Звідси:
п
хі = хі0 - Х^Хр І = \,т,	(3.1.6)
у=т+1
де х,- — базисна змінна; хі0 — її значення.
Співвідношення (3.1.6) справедливе для будь-якого розв’язку, у
тому числі й оптимального.
Розв’яжемо задачу ЛП (3.1.1)—(3.1.3) симплекс-методом або
двоїстим симплекс-методом. Припустимо, що оптимальним виявився
базис (Аь А2, ..., А„}. Елементи останньої симплекс-таблиці
позначимо через ху, причому Ду = хОу , а стовпець вільних членів —
через [ хі0 ], і = \,т.
Виберемо один з них, наприклад х,0, і починаючи з і-го рядка,
виведемо співвідношення для додаткового обмеження (правильного
відсічення).
Позначимо через [ху] цілу частину, а через уіі =	- [ху] —
дробову частину числа ху, причому ху > [ху]. Очевидно, 0 < уи< 1.
153
Зайченко О.Ю., ЗайченкоЮ.П
Нехай х = [х,] і= Цт — деякий оптимальний план задачі (3.1.1)—
(3.1.3). Його компоненти зв’язані рівнянням (3.1.6). Підставимо
ху = [*»] + в (3.1.6) і після нескладних перетворень одержимо:
Хі-Ко]+ ХІХі/ІХу = Гіо - ^ГуХу- (3.1.7)
У=т+|	у'=т+1
Співвідношення (3.1.7) справедливе для будь-якого плану
розв’язуваної задачі. Припустимо, що х — цілочисельний план. Тоді,
враховуючи цілочисельність лівої частини (3.1.7), дістанемо:
Гю~
У=Я1+1
де 2,— ціле число, а 0< /,0< 1, 0 < %< 1.
Тепер можливі два випадки:
а)£>1;б)£<0.
У першому випадку, якщо припустити, що Е, > 1, то
п	п
УіО = <5 + ИГуху 2 1 +	1 > звідки ут > 1, що суперечить умові
У=т+1	і=т+\
0 < /(0 < 1. Тому лишається прийняти Е, < 0, тобто справедлива нерівність:
(3.1-8)
У=т+І
Нецілочисельний план х не задовольняє нерівності (3.1.8),
оскільки /,0> 0, а ліва частина нерівності (3.1.8.) дорівнює нулю, бо
ху = 0, для всіх небазисних компонент] = т +1, т +2, Водночас
будь-який цілочисельний план задовольняє (3.1.8) як строгій
рівності, тому що /,0 = 0 для всіх і.
Отже, обмеження (3.1.8) є правильним відсіченням. Його
записують в еквівалентній формі:
*л+1=->70+	^п+і^0,	(3.1.9)
У=т+І
або
-/<0= Ц-ГуХу+хп+і,	(3.1.10)
у=т+1
154
Дослідження операцій. Збірник задач
і додають до початкової системи лінійних обмежень задачі.
Змінні нової задачі такі: {хьх2, ...,х„+1}. Її обмеження вже
розв’язані стосовно базисних змінних плану х = {хьх2, ...,х„,} і нової
змінноїхя+і, отже, маємо псевдоплан з базисними компонентами:
х, х,о, і — 1,т 9
Симплекс-таблиця цього псевдоплану утворюється шляхом
дописування до таблиці знайденого оптимального плану х рядка з
елементами
~ 77о> при у=0;
-уу, ПРИ І^Іцеб* Іцеб - множина індексів
небазисних векторів;
0, в інших випадках.
Одночасно до таблиці дописують одиничний вектор А„+1 такий,
и+1
що А„+| = [0,0,..., 0,1].
л
Для цього плану застосовують двоїстий симплекс-метод. На
першій же ітерації із базису обов’язково буде виведено вектор, що
відповідає змінній хи+1, оскільки в стовпці аі0 таблиці є один
від’ємний елемент Х„+1 = -/,0 < 0.
Називатимемо великою ітерацією методу відсікаючих площин
сукупність ітерацій алгоритму двоїстого симплекс-методу, що
приводять від псевдоплану з дробовими компонентами до
наступного оптимального плану (не обов’язково цілочисельного).
Залежно від результату великої ітерації розрізнятимемо три випадки:
1)	у стовпці а,0 всі х,0— цілі числа, причому хю>0. Ця умова
визначає оптимальність знайденого плану;
2)	отримано новий план, де всі х,0 > 0, але не всі хі0 — цілі числа.
Тоді треба сформувати нове правильне відсічення і перейти до
чергової великої ітерації;
3)	отримано деякий проміжний псевдоплан, де є елемент х10 < 0
такий, що Ху> 0 для всіх у = 1,2,..., п. Це ознака нерозв’язності задачі.
155
Зайченко О.Ю., Зайченко Ю.П.
Змінні х„+/, шо вводяться в задачу на початку кожної нової
ітерації, звуться додатковими, а змінні х7, у = 1,л — основними. Якщо
додаткова змінна є небазисною для деякого проміжного
псевдоплану, то рівняння х„+/=0 входить до сукупності
співвідношень, що визначають цей псевдоплан. Тільки-но змінна
знову стає базисною (тобто вводиться до базису), її значення стає
байдужим до основних змінних. Тому рядок і стовпець, що
відповідають змінній хи+/, у відповідній симплекс-таблиці (та в усіх
наступних) викреслюють.
З геометричної точки зору це правило можна пояснити так. Якщо
псевдоплан опиниться всередині півпростору х„+г> 0, то додаткове
обмеження, що визначається гіперплощиною х„+/ = 0, стає
несуттєвим, тому його можна випустити.
Зробимо деякі зауваження стосовно методу Гоморі.
1.	В основі методу відсікаючих площин Гоморі лежить двоїстий
симплекс-метод, бо він дає змогу легко врахувати нові обмеження
(правильні відсічення) в процесі розв’язання задачі й переходити від
поточного псевдоплану до нового оптимального плану.
2.	При деяких умовах можна гарантувати скінченнісіь алгоритму Гоморі.
Достатні умови скінченності алгоритму встановлюються в такій
теоремі [17].
п
ТЕОРЕМА 3.1. Якщо цільова функція задачі Ь - "^/ух^ обмежена
7=1
зверху’ і знизу на множині розв ’язків, причому множина оптимальних
розв’язків являє собою опуклий многогранник, правильне відсічення
формується за рядком таблиці з нецілочисельною компонентою хі0,
що має мінімальний номер, а індекс вектора, що вводиться до базису,

визначають за величиною
= тіп-
ху < 0 , то алгоритм Гоморі
буде скінченним, тобто за скінченне число ітерацій приведе до випадку
\)абоЗ>).
3.	Правильне відсічення можна формувати й за індексним
рядком. Нехай на к-іл ітерації елементи індексного рядка такі:
Ао*’, А{*’, ..., А^’, причому А^ = ^(Хц)—не ціле число.
156
Дослідження операцій. Збірник задач
Позначимо через у0? дробову частину елемента Ау: /Оу=А;-
[ Ау ]. У цьому випадку правильне відсічення записується так:
-Гоо=- 2>оУЛ/+х«+і-	(3.1.12)
4.	На відміну від звичайної задачі ЛП, ця задача цілочисельного
програмування потребує великого обсягу обчислень навіть при
малих т та п. Кількість ітерацій суттєво залежить від того, наскільки
вдало сформовано правильні відсічення.
Приклад 3.1.
Розв ’язати методом Гоморі наступну задачу.
0110(2*! +3х2)
2х, + х2 >16
+ 2хг >16
х,,х2 >0
ХрХз —2.
Записуємо задачу в розширеному вигляді і вирішуємо відповідну
задачу ЛП (її рішення наведено в розділі «Лінійне програмування»;
приклад 1.3).
Оптимальний розв’язок задачі ЛП наведено в такій таблиці:
2

16
2	1	1
з]”з’ Х,3-з’
Записуємо рядок з правильним відсіченням у таблицю 3.2.
157
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 3.2
г \<?7			2	3	0	0	0
	Вх	4	4	4	4	4	4
2	X,	16/3	і	0	1/3	-2/3	0
3	х2	16/3	0	1	-2/3	1/3	0
0	х5	-1/3	0	0	-1/3	-1/3	1
Т
Розв’язуємо двоїстим симплекс-методом і одержуємо таблицю
одержано оптимальний розв’язок х® = 6, х° = 5, тіп / = 27 -
3.2. Метод гілок та меж
Метод гілок (віток) та меж належить до групи комбінаторних
методів дискретного програмування і є одним з найпоширеніших
методів цієї групи.
Розглянемо задачу дискретного програмування в загальній формі:
мінімізувати г=/(х),	(3.2.1)
при обмеженнях:
158
Дослідження операцій Збірник задач
х є С.
де С — скінченна множина.
Обчислення нижньої межі (оцінки) тіп г. Часто можна, не
розв’язуючи задачу (3.2.1), знайти нижню межу (оцінку) цільової
функції на множині розв’язків С (або на деякій її підмножині) Е, (С)
таку, що для всіх хєХ:
/(х)>^(С).
Розбиття на підмножини. Реалізація методу пов’язана з
постійним розбиттям множини планів С на дерево підмножин. Це
розбиття проводиться за такою схемою.
Нульовий крок. Задано вихідну множину С = С(0). Певним чином
вона розбивається на скінченне число підмножин О'1’, б^1’, ...,
к-а ітерація (к > 1). Нехай множини	,..., Сг^ ще не
підлягали розбиттю. Згідно з правилом, наведеним нижче, серед них
вибирають множину й розбивають її на скінченне число
підмножин С,(*+0,С<*+,),..., С<*+1).
(к+1)-й крок
159
Зайченко О.Ю., Зайченко Ю.П.
Перерахування оцінок. Якщо СІ с С2, то тіп /(х)>тіп /(х).
хєС]	хеС2
Тому, розбиваючи в процесі розв’язання множину на підмножини
СІ,(72,...,(7ж(С0=ис,), завжди вважають, що оцінка для будь-
«=
якої з них не менша за оцінку для вихідної множини Со, тобто для
всіх множин С,:
^(Сі)>^(СО).
Відшукання розв’язків. Для конкретних задач можуть бути різні
способи відшукання розв’язків у послідовних розбиваних
підмножинах. Кожен такий спосіб опирається на специфіку задачі.
Ознака оптимальності. Нехай С = і деякий план хО є Су .
«=і
Якщо при цьому Е (хО) = £, (Су) < £, (Сі) для всіх і, то хО —
оптимальний план.
3.3. Метод гілок та меж
для задач цілочисельного програмування
Розглянемо частково-цілочисельну задачу ЛП:
п
мінімізувати г=/(х)= Xе(3.3.1)
/=•
при обмеженнях:
> Ь{, і = 1,т;	(3.3.2)
7=1
0<ху<4, з = 1,п;	(3.3.3)
— ціле, і = \,п (П] < п).	(3-3.4)
Опис алгоритму
Нульова ітерація. 1. Визначення множини Со. Множина
визначається умовами (3.3..3), (3.3.4)
160
Дослідження операцій. Збірник задач
2. Знаходимо оптимальний план х0 задачі (3.3.1) при умовах
(3.3.2), (3.3.4).
Обчислюємо оцінку £ (Со) =/(Хо).
Якщо план Хо задовольняє умови цілочисельності, то він є
шуканим. У протилежному разі переходимо до першої ітерації.
(А+1)-а ітерація. Нехай вже проведено к ітерацій, у результаті
яких побудовано підмножини С-к\ і = \,гк, визначено оцінки
£ (6-к)), і ще не знайдено оптимальний розв’язок. Тоді вибираємо
найбільш перспективну підмножину таку, що
£ (О®) = тіп£ (С'4’).
1
1. Розбиваємо множину на підмножини	так, що
І) і Сг<к) П = 0- Для цього вибираємо деяку
нецілочисельну компоненту плану	, наприклад,
Тоді підмножини та визначаються із умов:
С^={х:хєС^ та х5<[х50]};
= { х : х є та х, > [хі0]+1}.
2. Розв’язуємо задачу ЛП (4) на підмножинах 6$, і
знаходимо оптимальні плани х^, х^ та відповідні їм оцінки
^(С&))=Ях^);
Якщо х^А? задовольняє умову цілочисельності, то вершина
— кінцева, і подальшому розбиттю не підлягає. Якщо при
цьому також Е, () = тіп £, (6*), де { С^к) } — множина всіх
’ і
висячих вершин, то х$ — шуканий цілочисельний план (це ознака
161
Зайченко О.Ю.. Зайченко Ю.П.
оптимальності). У протилежному разі треба продовжити цей процес
розбиття.
Зазначимо деякі особливості застосування методу гілок і меж для
задачі ЛЦП.
При розв’язанні задачі ЛП максимізащї методом гілок і меж
використовують верхню межу/оцінку:
£ (С^) = шах/(х).
хєо;.1
У цьому випадку ознака оптимальності формулюється
протилежним чином порівняно із задачею тіп /(х).
Приклад 3.2.
Г=8х1+6х2->тах;
2хі+5х2<12,
4х!+х2<10,
хь х2>0, хь х2— цілі числа.
Розв’язуємо симплекс-методом. Послідовність ітерацій наведено
в таблицях 3.5-3.7.
Таблиця 3.5
			8	6		
	в X	4	4	4	4	4
0	хз	12	2	5	і	0
<-0	Х4	10		1	0	1
	А	0	-8	-6	0	0
Таблиця 3.6
			8	6		
	в.	4	4	4	4	4
<- 0	хз	7	0	|9/2|	і	-1/2
8	X,	5/2	1	1/4	0	1/4
	А	20	0	-4	0	2
162
Дослідження операцій. Збірник задач
Оптимальний розв’язок задачі ЛП х° наведено в таблиці 3.7.
Таблиця 3.7
			8	6		
	Вх	л	4	4	4	4
8	X,	19/9	1	0	-1/18	5/18
6	х2	14/9	0	1	2/9	-1/9
	Д	26 — 9	0	0	8/9	14/9
Нульовий крок.
Оптимальний план задачі ЛП х°=—; х°=— нецілочислений,
9	2 9
2
тоді маємо оцінку = 261 = 26 -
1 ітерація.
Оскільки план х° — нецілочислений, то вибираємо його
нецілочисельну компоненту х, і розбиваємо множину Со на
Со = б?0 и б'0, де С™ = {С° пх, < 2};	= {С° пх, > 3}.
Перший крок.
Розв’язуємо задачу ЛП на множині . Для цього
використовуємо обмеження х{ <2. Записуємо його у вигляді
х1 +х5 =2-
Дописуємо рядок х5 і стовпець Л, =[0 01]г до таблиці 3.7.
Віднімаємо від х5 рядок х,, й отримуємо рядок х5 в таблицю 3.8.
163
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 3.8
С,.\С7			8	6		Ф			
	в,	4	4	4	4	4			4
8	х,	19/9	1	0	-1/18	5/18			0
6	х2	14/9	0	1	8/9	-1/9			0
	х5	2	1	0	0	0			1
	4	-1/9	0	0	1/18		-5/18		1
Далі розв’язуємо задачу двоїстим симплекс-методом. Знайдемо
новий план.
Таблиця 3.9
с.\ сі			8	6	0	0	0
	4	4	4	4	4	4	4
8	х(	2	1	0	0	0	1
6	х2	8/5	0	і	13/15	0	-2/5
		2/5	0	0	-1/5	1	-18/5
	Д	25 — 5	0	0	26/5	0	48/5
Цей розв’язок %<” =
2;*
5
оптимальний, але нецілочисельний.
Тепер знаходимо розв’язок на множині = {Со ґ^х, > 3}.
Записуємо це обмеження у вигляді - х6 — 3, або —х, + х6 = —3.
Дописуємо рядок х6 до таблиці 3.9 і складемо його з рядком х6,
отримуємо х6. Складаємо таблицю 3.10.
164
Дослідження операцій. Збірник задач
Таблиця 3.10
Єі ХС/			8	6	о4<	0	0
	в.	4	4	Аг	4	4	4
8		19/9	1	0	-1/18	5/18	0
6	х2	14/9	0	1	2/9	-1/9	0
	хе	-3	-1	0	0	0	1
<—	хе	-8/9	0	0	|-1/18|	5/18	1
Таблиця 3.11
с,.\су			8	6	0	0	0
	вх	4	4	4	4	4	4
8		3	1	0	0	0	-1
6	х2	-2	0	1	0	1	4
0	хь	16	0	0	1	-5	-18
	д		0	0	0		
В таблиці 3.11 х20=-2<0, а всі інші компоненти рядка х2
невід’ємні, тому ця задача нерозв’язна. Отже, С2 = 0, а £((72) — —°о.
Друга ітерація. Переходимо до подальшого розбиття множини
. Для цього використовуємо змінну х2 =8/5. Використовуємо
2 обмеження:
= 1 та
= 2,-
8
5
Отже:	= С|2) и С22), де с,т = С‘” п(х2 < 1); С'2’ = п(х2 > 2) -
Вирішуємо задачу ЛП на множині О<2). Для цього використовуємо
обмеження х2 < 1 або х2 +х6 = 1 і дописуємо цей рядок у таблицю 3.9 і
отримуємо таблицю 3.12. Вирішуємо цю задачу двоїстим симплекс-методом.
165
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 3.12
схс^			8	6	оі	0		0
	Вх	4	4	4	4	4	4	4
8	*1	і	1	0	0	0	1	0
6	Х2	8/5	0	1	13/15	0	-2/5	0
0		2/5	0	0	-1/5	1	-18/5	0
	хе	1	0	1	0	0	0	1
<—	ХЄ	-3/5	0	0	1-13/15|	0	2/5	1
Виконавши одну ітерацію двоїстим симплекс-методом
приходимо до таблиці 3.13.
Таблиця 3.13
СІ\С]			8	6	0	0		0
	4	4	4		4	4	4	4
8	4	2	і	0	0	0	1	0
6	4	1	0	1	0	0	0	1
0	х4	27/13	0	0	0	1	48/13	-3/13
	хз	9/13	0	0	1	0	-6/13	-5/13
	Д	22	0	0	0	0	8	6
Оскільки всі компоненти плану х, = [2; І] — цілочисельні, то
знайдено цілочисельне рішення і вершина — кінцева.
Вирішуємо задачу ЛП на множині С^2). Для цього використовуємо
обмеження у вигляді -х2+х7=-2. Записуємо це обмеження в
радок х7 до таблиці 3.9, склавши цей рядок з рядком х2 приходимо до
таблиці 3.14. Далі вирішуємо задачу ЛП двоїстим симплекс-методом.
166
Дослідження операцій. Збірник задач
Таблиця 3.14
СІ\С)			8	6	0	0	г	0
	вх	4	4	4	4	4	4	4
8		2	1	0	0	0	і	0
6	Х2	8/5	0	1	13/15	0	-2/5	0
0	4	2/5	0	0	-1/5	1	18/5	0
	х7	-2	0	-1	0	0	0	1
<—	4	-2/5	0	0	13/15	0	2/	1
Виконавши чергову ітерацію приходимо до таблиці 3.15
Таблиця 3.15
с,.\ 4			8	6	0	0		0
	вх	4	4	4	4	4	4	4
8		1	і	0	13/6	0	0	5/2
6	Х2	2	0	1	0	0	1	-1
0	4	-16/5	0	0	38/5	1	0	9
	х5	1	0	0	1	0	1	-5/2
Знаходимо оцінку •
Оскільки х4=-^<0, а всі елементи рядкахА невід’ємні, то
С‘2’=0 і £(6*2)) = -оо.
Таким чином, оскільки = тіп^(С*2)) для всіх висячих
вершин дерева, то Х,2> = [2; 1] — оптимальний розв’язок.
Значення цільової функції /тх = 22.
Дерево розв’язків наведено на рис. 3.1.
167
Зайченко О.Ю., Зайченко Ю.П.
Рис. 3.1.
Розв’язати задачі ЛЦП методом Гоморі та гілок та меж
3.1.1
Р=Х|+4х2->тах;
2х|+4х2<17,
10хі+Зх2<15,
хн х2>0,
хь х2 - цілі числа.
3.1.3
Р=Х|+2х2—>тах;
2х(+2х2<7,
4хг5х2<9,
Х|, х2>0,
Х|, х2 — цілі числа.
3.1.5
Р=8Х|+6х2—>тах;
2х|+5х2<12,
4х,+х2<10,
Х|, х2>0,
Х|, х2- цілі числа.
3.1.2
Р=2х,+х2->тах;
Х|+2х2<16,
Х|+2х2^2,
2хі+х2<16,
хь х2>0,
Хь х2 - цілі числа.
3.1.4
Р=8Х|+6х2—>тах;
Зхі+5х2<11,
4х!+х2<8,
Хь х2>0,
Х|, х2 - цілі числа.
3.1.6
Р=х|+4х2-»тах;
2хі+4х2<7,
10х|+Зх2<14,
Х|, х2>0,
Хь х2 —цілі числа.
168
Дослідження операцій. Збірник задач
3.1.7
Р=Х|+2х2-»тах;
5хі+7х2<21,
-Х|+Зх2^8,
Х|, х2>0,
хь х2 - Нілі числа.
3.1.9
Р=Х|+х2-»тах;
6Х|+5х2<20,
2хі+Зх2<10,
Х|, х2>0,
Х|, х2 - цілі числа.
3.1.11
Р=8хі+6х2—>тах;
2х|+5х2<11,
4хі+х2<10,
Хь х2>0,
Хь х2 - цілі числа.
3.1.8
Р=5х । +6х2+6х3—>тіп;
2хі+4х2>10,
2х!+2х2+2хз>8,
хь х2, х3>0,
Хь х2, х3 - цілі числа.
3.1. іо
Р=Х|+2х2->тіп;
2х!+9х2<36,
Х|+х2<7,
Хь х2>0,
Х|, х2 - цілі числа.
3.1.І2
Р=хі+х2-»тах;
2хі+х2<18,
Х|+2х2<16,
хь х2>0,
Хь х2- цілі числа.
3.4. Метод гілок та меж для задачі комівояжера
Постановка задачі. Нехай є п міст Аь А2, ... , А„, зв’язаних
транспортною мережею. Задано матрицю відстаней С = |с(у|,
причому в загальному випадку су * Су,.
Комівояжер починає рухатись, наприклад, із міста Аь повинен
побувати в кожному місті тільки один раз і повернутися у вихідне
місто Аь Треба відшукати такий замкнений маршрут, або цикл
Оь І2, ... , і„), що проходить через кожне місто один раз, при якому
мінімізується сумарна (загальна) довжина шляху:
Ції, і2, ...,іП)= сі[І2 + сІ2Із + + сІЛ .	(3.4.1)
Опис алгоритму. 1. Визначення множини С(о), яка складається з
усіх циклів (замкнених маршрутів).
2. Визначення підмножин = \,2,...,гк ; А = 1,2,...), кожна з
яких складається з усіх циклів, підпорядкованих одній із таких
додаткових умов:
169
Зайченко О.Ю., Зайченко Ю.П.
а)	із пункта і належить безпосередньо перейти в пункт у для усіх
пар (і,у), які входять у деяку множину .
б)	із пункта і забороняється безпосередньо перейти в пункт у для
усіх пар (і,у), які входять у деяку множину «заборон» .
3.	Обчислення оцінки для С(0). Розглянемо деякий цикл ц, і2,... ,
і„. Відповідна йому відстань дорівнює:
701, і2, ...,іг) = сІІІ2 + сІ2,-3 + + СІПІІ.	(3.4.2)
Нехай тіпс^ = й. Тоді с'у = с~ >0.
Далі, нехай тіп с' =	. Тоді є" = с'2 -Н' = су - /? -Н} > 0,
п п
...,і„)= ЕЛі + Е/77+(с',2 +с,;(1 +... + с?;і). (3.4.3)
/=1	1=1
Вище описану процедуру перетворення матриці, що дає змогу з
вихідної невід’ємної матриці С отримати матрицю С", називають
зведенням, а величину
(3-4.4)
і=1	і=1
сумою констант зведення.
4.	Розбиття. Кожній вершині множини дерева рішень
відповідатиме своя оцінка Е/С^) і своя зведена матриця .
Множину розбивають на дві підмножини. Для цього певним
чином (див. нижче) вибирають пару пунктів (г, ги), що не входить до
множин та Після цього виконують розбиття на
підмножини , (7^ так, що
170
Дослідження операцій Збірник задач
Тут 6^ утворюється із введенням додаткової умови: із пункта г
здійснити безпосередній перехід у пункт т, а — із умови: із
пункту г заборонено безпосередній перехід у пункт т.
Таким чином:
Р$ = РУ’Щг.тУ.Р™ = Р<к\ Р$ = Р^',Р^ = Ру(к) ІДг,»») .
Вибір пари (г , т) базується на таких вимогах. Підмножину
вибирають так, щоб вона з найбільшою ймовірністю містила
оптимальний цикл, а — навпаки, не містила.
Щоб виконати першу вимогу, пару (г, т) треба вибрати так, щоб
задовольнилась умова:
4*>(г,т) = 0,	(3.4.5)
де с(к\г,т) — (г , /и)-й елемент зведеної матриці С$А). Щоб
виконати другу вимогу, пару (г , т) необхідно вибрати так, щоб
циклам, які входять до множини відповідали якнайдовші
шляхи. Згідно з визначенням множини , для будь-якого циклу
шлях із пункту г в пункт т має містити такі переходи: із г в деякий
проміжний пункт у (/ * т) та із деякого пункта і (і г) в пункт іп.
Довжина цього шляху буде не менша, ніж:
0 (г,пі) = тіп + тіп с^\і,т) = аг + Рт .	(3.4.6)
і*г
Отже, лишається вибрати пару (г, ?и) так, щоб 0 (г, пі) було
максимальним, тобто:
0 (г, пі) = тах 0 (р,д) = тах {а + В },	(3.4.7)
(р-ч)	р
де а = тіп с[к\р,/);	= тіп с(к\і,д).
При цьому, звичайно, необхідне виконання умови:
171
Зайченко О.Ю., Зайченко Ю.П
с(к\р,д) = О.
(3.4.8)
5.	Обчислення оцінок. Розглянемо розбиття С(к>> = СІ .
Спочатку розглянемо підмножину і вкажемо правило переходу
від матриці С(/> до .
Матриця містить ті самі рядки і стовпці, що й матриця .
Побудуємо деяку проміжну матрицю згідно з правилом:
г<*)(і>у) = .	якщо ('-А * (г,т);
оо , якщо (/,_/) = (г,т).
Застосувавши до процедуру зведення, отримують С(к\. При
цьому сума констант зведення дорівнює 0 (г, /л). Таким чином:
Е. (	) = $ (	) + 0 (г, лі).	(3.4.9)
Тепер розглянемо множину с[ку і визначимо правило переходу
від матриці С(к) до .
Оскільки, за визначенням, підмножина	містить
безпосередній перехід із пункта г до пункта т, то при переході від
до треба викреслити рядок г і стовпець т.
В результаті дістають 0^.
Далі необхідно перевірити, чи не містить рівно один цикл.
Якщо це так, то до матриці застосовують процедуру зведення.
Одержавши суму констант зведення Лг = £Л, + £н , перераховують
«=	7=1
оцінку:
^(0<*,)= ^(С<А’) + ЛЕ.	(3.4.10)
172
Дослідження операцій. Збірник задач
При цьому значення Е, () дорівнюватиме довжині цього
єдиного циклу.
Якщо підмножина <7^ містить більше одного циклу, то треба
заборонити можливість утворення підциклів (тобто часткових
циклів), які проходять через меншу, ніж п, кількість пунктів. Для
цього необхідно знайти всі маршрути, що містять перехід (г, пі).
Процес заборони утворення підциклів виконують так.
Насамперед можливий підцикл (г, пі. г). Його виключають
шляхом заборони переходу (т, г). Для цього приймають
г^*)(»’,г) = оо.
Якщо з елементів Р/А) можна скласти маршрут (іь і2, ... , ір, г), то
можливі підцикли вигляду (ї9, і9+і, ... , ір, г, т, іч), де І < <7 < р.
Забороняють ці підцикли, прийнявши г^*Ч»и,«9) = оо. Аналогічним
чином, якщо з елементів множини можна скласти маршрут
(т, її, і2, ... , ір), то можливі підцикли вигляду (г, т, іь ... , ір, г). Щоб
їх виключити, забороняють переходи (і9, г). Для цього вважають
= оо, 1 < д <р. Всі інші елементи матриці С(к{ лишають без
змін. Далі до матриці застосовують процедуру зведення і
знаходять матрицю . Позначимо через /і£ (С^ ।) відповідну суму
констант зведення. Тоді оцінки Е, (	) обчислюють за формулою:
) =	(С<*>).	(3.4.11)
Приклад 3.3. Розв’язати задачу комівояжера, що визначається
матрицею С.
173
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 3.16
	і/І	0	1	2	3	4	5
	0	X	5	8	2	7	3
	1	2	X	9	7	1	5
с=	2	5	3	X	2	6	7
	3	7	8	8	X	2	10
	4	9	3	7	9	X	2
	5	10	1	5	2	7	X
Нульовий крок. Застосувавши процедуру зведення, отримаємо
матрицю Со (таблиця 3.17).
Таблиця 3.17
		0	1	2	3	4	5	Ьі	а.
	0	X	3	2	0	5	І	2	1
	1	0	X	4	6	0	4	І	0
	2	2	1	X	0	4	5	2	1
Со=	3	4	6	2	X	0	8	2	2
	4	6	1	1	7	X	0	2	1
	5	8	0	0	1	6	X	1	0
	Ц	1	0	4	0	0	0		
	Рі	2	1	1	0	0	1		
Знаходимо оцінку £(6( ,) = £Л/+£я,.=15.
Оскільки, тах{(9м} = тах{(9оз,6'34,6’іо,(9|4,<923,<945,(95,,6’я} = 034=2, то
вибираємо для першого розбиття пару (3;4) (со(3;4)=О).
Перший крок. Проводимо розбиття с(0} =о|(,)ис£),
де О,0’ = Со П (3,4), С<" = Со ГІ(3,4)
Обчислюємо оцінку: ^((7)'’) = £(С0)+#34 = 17.
174
Дослідження операцій. Збірник задач
Для обчислення	треба побудувати матрицю сі". Для
цього в матриці с0 викреслюємо 3-й рядок і 4-й стовпець і. беручи
елемент С34= 00, здійснюємо процедуру зведення. В результаті
одержуємо матрицю с{” (табл. 3.18).
Таблиця 3.18
		0	1	2	3	5	Ні	А,
	0	X	3	2	0	1	0	1
	і	0	X	4	6	4	0	4
	2	2	І	X	0	5	0	1
с,(1)=	4	6	1	1	X	0	0	1
	5	8	0	0	1	X	0	0
	Ні	0	0	0	0	0		
	Рі	2	1	1	0	1		
Визначимо оцінку для множини с}п: ^(О^) = £(С0) + /4? =15. ’
^’=Ел,+Е^=о-
* і
Другий крок.
0ІО = тах0(р,<7) = 6 •
(р.«)
Проводимо розбиття = 0[2} ЦІ , де
О?2’ ={(3,4),(1,0)};
С}2»={(3,4),(Ц6)}-
Знаходимо оцінку: ^(О*2,) = ^(6|<|)) + 0(1,О) = 21.
Побудуємо матрицю С,2)(табл. 3.19)
175
Зайченко О.Ю.. Зайченко Ю.П.
Таблиця 3.19
	і/І	1	2	3	5	й.	«1
	0	X	2	0	1	0	1
с<2»=	2	1	X	0	5	0	1
	4	1	1	X	0	0	1
	5	0	0	1	X	0	0
	Ц	0	0	0	0		
	Рі	1	1	0	1		
обчислимо оцінку
Оскільки Е, (о’1’) < Е, (б*1’), т0 на наступному кроці розбиттю
підлягає підмножина о}1’.
Третій крок.
Оскільки ,0(4,5) = тах0(р,<7) = 2, то вибираємо для розбиття
пару (4;5). Проводимо розбиття:
с<2>=с<з>ііс<3>
де,	б-<3) =С<2)ГІ(4,5);
с<”=с<2)П(43).
Обчислюємо оцінку:
<(С‘3)) = £(О<2))+0(4,5) = 17.
Побудуємо матрицю С,3). Викреслимо 4-й рядок і 5-й стовпець,
покладемо = оо (таблиця 3.20).
176
Дослідження операц Збірник задач
Оскільки ^(С(3)) <	, то на наступному кроці розбиттю
підлягає підмножина С^}.
Четвертий крок.
Оскільки 0 (0;3) =2 = тах 0 (р, д), то вибираємо для розбиття пару
(03).
Знаходимо оцінку: ^(С’4)) = ^(С,3*)+0(0,3) = 17.
Побудуємо матрицю С(<4), викреслимо 0-й рядок і 3-й стовпець,
покладемо С51 = °о. Виконаємо процедуру зведення (таблиця 3.21).
Таблиця 3.21
*</	і	2	Ьі
2	0	X	1
С<4) =	5	X	0	0
	Нь_	0	0	
177
Зайченко О Ю., Зайченко Ю.П.
^‘=1
Знаходимо оцінку:	) = £(О,3)) + /4? =16.
Із матриці с{6) вибираємо дві останні пари (2;1) і (5;2). В
результаті отримаємо цикл, що відповідає підмножині с[е> =
{(2; 1); (3;4); (1;0); (0;3); (4;5);(5.2)}. Довжина цього циклу дорівнює
оцінці для множини с{8): / =	) = 16.
У цьому можна переконатися безпосередньою перевіркою.
Оцінка £(с<8») є найменшою серед оцінок для всіх висячих вершин
дерева розв’язків (рис. 3.2), отже, знайдено оптимальний цикл.
Процес побудови дерева розв’язків наведено на рис. 3.2, а знайдений
мінімальний цикл — на рис. 3.3.
Розв’язати задачі комівояжера
3.4.1 X 7	3 X	8 4	4 3	3.4.2					
				2 4	X 4	2 X	9 3	4 2	4 3
с = з	4	X	2	3	С = 2	1	X	7	3
5	7	2	X	4	6	4	2	X	4
6	5	2	3	X	5	7	8	9	X
3.4.3 X	1	4	9	4	3.4.4 X	3	7	6	2
8	X	1	3	7	9	X	9	3	8
С=3	2	X	8	1	с = і	8	X	3	2
2	9	4	X	5	3	4	5	X	1
9	8	7	6	X	1	2	5	6	X
3.4.5 X	7	3	6	4	3.4.6 X	3	6	6	5
7	X	1	3	2	2	X	9	2	3
С = 5	4	X	2	9	С=1	8	X	1	4
6	4	3	X	4	4	9	3	X	2
3	2	2	6	X	5	7	8	2	X
178
Дослідження операцій. Збірник задач
Є=15
(ЗЛ)
£=15
(1.0)
£ = 15
(4.5)
£=16 (с;
£=15
Пі)
?=21
6
£=17
сад
(0,3)
£=17
(2.1)
=17
(4.5)
(5.2)
£=16 (О>
£=16 (с;
Рис. 3.2.
Рис.. 3.3.
179
Заиченко О.Ю., Зайченко Ю.П.
3.5.	Послідовні алгоритми дискретної оптимізації
Загальна характеристика
Методика послідовного розвитку, аналізу та відсіву варіантів
полягає в такому способі розвитку варіантів і побудові операторів їх
аналізу, які дають змогу відкидати безперспективні початкові
частини варіантів до їх повної побудови. Оскільки при відсіві
безперспективних початкових частин варіантів відсівається і вся
множина їх продовжень, то досягається значна економія
обчислювальних витрат.
Метод послідовного аналізу варіантів (ПАВ) базується на відсіві
безперспективних елементів як за обмеженнями, так і за цільовою
функцією.
Основою метода ПАВ для задачі є процедура ГГ послідовного
відсіву значень змінних. Ця процедура складається з двох процедур IV\
та И^. Процедура в свою чергу, складається з <2 елементарних
процедур И\р, р = 1,0, кожна з яких полягає у відсіві за р-м
обмеженням елементів; процедура полягає у відсіві за цільовою
функцією.
Алгоритм розв’язання задачі
лінійного цілочисельного програмування
Як приклад окремого випадку задачі дискретного програмування
розглянемо задачу ЛЦП:
п
максимізувати /(х)= ХсуХу,	(3.5.1)
>=і
при обмеженнях-
і = 1,0;	(3.5.2)
7=1
0<^м<ху <^2< у = ї^,	(3.5.3)
де
ху,^-\д(р — цілі числа, і = 1,л.	(3.5.4)
180
Дослідження операцпі. Збірник іадич
Замінимо умови (3.5.3), (3.5.4) такими:
*у є Ху = {</<'’ ,</<*’+1,.... г/‘2)}, у = 1, п .
л
Неважко помітити, що к-та компонента вектора х = аг^тіп Хвул'у
7=1
дорівнюватиме іИ1’, якщо аік > 0, або г/р’ — в протилежному разі.
Тоді правило відсіву для обмежень формулюємо таким чином:
якщо ху (х^ є Ху) задовольняє нерівність
(3-5.5)
«<л>0	"і*<0
хоча б для одного і = 1, то /-та компонента розв’язку задачі
(3.5.1)-(3.5.4) не може набувати значення, що дорівнює ху є Ху.
Таким чином, у процесі роботи алгоритму будуть відсіяні такі
значенння ху : ху- < Ху <є^2\ якщо а,у>0 або </(1) <ху- <ху, якщо
а,У < 0. В результаті множина Х(/) для даної задачі матиме вигляд:
Х</)={а(/),а</)+1,...,Р</)},
>=і
деа^^руЧ^2’.
Правило відсіву за цільовою функцією для задачі Л*(£>(Х(/)))
має такий вигляд:
СуХу<єГ- МІ0 -	,	(3.5.6)
А*/	А*/
сд->0	сд<0
де
е* = | (тіп /(х) + тах /(х)) = -
_ X + X ск^ +
А:сд<0	А:сд>0
+ х^р(/’ 4 хм^’+рМ
к:ск<0 /	^\.А=1	7
то /-та компонента допустимого розв’язку задачі Л1 не може
набувати значень x^ = х^ . Тобто, якщо с? > 0, то значення Ху такі, що
181
Зайченко О.Ю., Зайченко Ю.П.
а у < х^ < х^ відсіюються за обмеженням на цільову функцію, а в
протилежному випадку відсіюються значення Ху з інтервалу
У процесі роботи алгоритму для задачі Л(ї), 5 = 2,3, ... величини
с* обчислюються за такими формулами:
а) с*= '( тіп /(х)+с*_г)= * Е	(3.5.7)
лєХ5 1	А:г*<0	)
якщо треба розширити множину ;
б)с;=|( шах/(х)+с;_1)=-Ч і с*р^,)+ 1^4'’|)+с,*-і І (3-5-8)
хєХ* 1	Азд<0	)
для звуження множини Х(/і-,);
з • Ь •
В) с5 = ^(СІ-І +сі-2) ДЛЯ звуження множини

після
попереднього розширення, і навпаки, де с*„2>с*-і — значення,
отримані на попередніх ітераціях.
Для застосування алгоритму необхідно задати обмеження
вигляду (3.5.3). На практиці ці межі (</(1),</(2^) можна в багатьох
випадках визначити із фізичного змісту задачі. Якщо ж межі
змінювання кожної змінної заздалегідь не визначено, то їх завжди
можна знайти, розв’язавши 2т задач ЛП вигляду:
х у —> шах	ху -> тіп
п	___ п
Т.ауху =	£аух  < />,, і = 1,0;
7=1	7=1
Ху ^0,3 = 1, л;	Ху > 0, у = 1, п .
У деяких випадках визначення </^2) особливо просте:
1)	якщо для всіх і = 1,0 та у = 1,и ау > 0, то
де знак [х] означає цілу частину х;
<Л2) = тіп '
*	і п -
182
Дослідження операцій Збірник задач
2)	якщо серед обмежень (3.5.3) знайдеться хоча б одне,
наприклад А-те, для якого ац > 0 для усіх у = 1, п , то
Приклад 3.4. Для ілюстрації роботи методу ПАВ розглянемо
таку задачу:
максимізувати (8х, + 6х2),
при обмеженнях:
2х} +5х2< 12,
4х! + х2< 12,
х,,х2>0;
х,, х2 — цілі числа.
Попередній етап. Знайдемо початкові множини -Х-( (0), -Х-2 (0).
х1тах=[ 12/4] = 3;х2_=[12/5]=2.
Таким чином, ’ХДО) = {0, 1, 2, 3};-Х-2(0) = {0, 1, 2}.
Перша ітерація.
Процедура ІУ/.
Відсів за першим обмеженням:
2х|>12-тіп{5х2} = 12,х,>6—нема відсіву;
5х2> іг-тіп^х, }=12, х2> 12/5—нема відсіву.
Друге обмеження:
4Л| >12-тіп{ х2 }= 12, > 3 — нема відсіву;
х2>12-тіп{4х| }= 12, х2>12—нема відсіву.
Тому переходимо ДО процедури 1?2-
Процедура Иу-
/Г = ’ (/т,п(*) +/ти(’<) ) = 2 (° + 36) =18-
Правило відсіву таке:/(х) < у’ =18.
Отже, 8х, < у* - тах{6 х2 }=6 ; х, < 6/8 — відсівається х, = 0;
183
Зайченко О Ю. Зайченко Ю.П.
6л,<	-тах{8х,}—6 ; х2<-1 —нема відсіву.
Процедура
Відсів за першим обмеженням:
2 х, > 12-тіп{5 х2} = 12, х, > 6— нема відсіву;
5х2 > 12-тіп {2 х,} = 10, х2>2—- нема відсіву.
За другим обмеженням:
4 хі > 12-тіп { х2} = 12, Х|> 3 — нема відсіву;
х2 > 12-тіп{4х|} = 8, х2> 8— нема відсіву.
Друга ітерація. Оскільки відсів за процедурою не відбувся, то
перейдемо знову до процедури ІУ2, та звужуємо множину варіантів:
Л'=|«+./тіп)=27.
8х, < /2’ - тах{6х2 }=15; х,< 15/8-—відсівається х,= 1;
6х,< /2 -тах{8х|}=3; х2<3/6— відсівається х2=0;.
*.(!) = {2, 3};*2(1) = {1,2}.
Процедура IVу.
2 X] >12-тіп {5 х2} = 7, х, > 7/2 — нема відсіву;
4х, > 12-тіп{ х,} = 11, X!>11/4— відсівається х, = 3; х, °р‘=2 ;
5 х2 > 12-тіп {2 х,} = 8, х2> 8/5 — відсівається х2 = 2; х2 ор| =1.
Далі знову переходимо до
Перевіряємо умови відсіву:
8х,< /2’ -тах {6 х2} =27-6=21 ; Х| < 21
8
— відсівається х, = 2.
Таким чином ми отримали -Х’1(2) = 0. Тому переходимо на
процедуру И2 і розширюємо множину варіантів.
Третя ітерація. Для цього вибираємо новий поріг відсіву:
/з’ = |(Л’+£) = | (18 +27) = 45=22-1.
2	2	2	2
І відновлюємо попередні множини варіантів:
*,(0)= {1,2, 3};*2(0)= {0, 1, 2}.
Проводимо відсів за процедурою \¥2:
8Х| < /2*-тах{6х2}= 22--12 = 10-; х, < — = і. Відсівається
2	2 1	16
16
х, =1,
184
Дослідження операцій. Збірник задач
6х, < /,* - иіах{8х, }=22^-24 < 0—нема відсіву.
Далі переходимо до процедури IVр
2 г, > 12-пііп{5 х,} = 12, х, > 1 — нема відсіву;
4 х, > 12-тіп {х2} = 11, х, >3 — нема відсіву;
5х2 > 12-тіп{2 х,} = 14 - 4 = 8, х2 > 8/5 — відсівається х2= 2;
х2 > 12-тіп 14.»,} = 12 - 8 = 4 — нема відсіву.
Отже, ми отримали дві множини варіантів:
*,(3)={2,3};*2(3)={0,1}.
З них допустимими є Х(1) = [2,1] та Х(2) = [3,0], а оптимальним
буде Х^=хор,, оскільки /(Х(2)) = 24>/(ХО)) = 22, отже
/оР<=24.
Задачі та вправи
Знайти рішення наступних задач лінійного цілочисельного
програмування методом послідовного аналізу та відсіву варіантів
3.5.1.	Р — х, + 4х2 —> тах;
2х1 +4х, < 17,
10х, +3х2 <15;
х( > 0, х2 > 0,
х,, х2 - цілі.
3.5.2.	Р = 2х, + х, —> тах;
+2х2 < 16,
х, + 2х2 > 2,
2х, +х2 < 16;
х, > 0, х2 > 0,
х,, х2 - цілі.
185
Зайченко О Ю, Зайченко Ю.П.
3.5.3.	Р = х, + 2х2 —> тах;
2Х] + 2х2 < 7,
4х, - 5х2 < 9;
х, > 0, х2 > О,
х,,х2 — цілі.
3.5.4.	Р = 8х, + 6х2 —> тах;
Зх, + 5х2 < 11,
4х, + х2 < 8;
х, > 0, х2 > О,
х,,х2 — цілі.
3.5.5.	Р = 8х, + 6х2 —> тах;;
2х, +5х2 < 12,
4х,+х2 <10;
х, >0, х2 >0,
Х|,Х2 - цілі.
3.5.6.	Р = х, + 4х2 тах;
2х, + 4х2 < 7,
ІОх, +3х2 ^15;
х, > 0, х2 > 0, х,,х2 - цілі.
3.5.7.	Р - х, + 2х2 —> тах;
5х, +7х2 <21,
-їх, +3х2 < 8;
х, > 0, х2 > О,
х,, х2 — цілі.
186
Дослідження операцій. Збірник задач
3.5.8.	Р = 5х1 + 6х2 + 6х3 —> тіп;
2х, +4х2 >10,
Зх, +2х2 + 2х3 >10,
х, > 0, х2 > 0, х3 > 0,
х,,х2,х3 - цілі.
3.5.9.	Р - х, + х2 —> тах;
6х, + 5х2 < 20,
2х, +3х2 < 10;
х1 > 0, х2 > 0,
х,, х2 — цілі.
3.5.10.	Р = х, + 2х2 -> тах;
2х, + 9х2 < 36,
х, +х2 < 7;
х, >0, х2 >0,
х,,х2 - ЦІЛІ.
3.5.11.	Р = 8х, +6х2 —> тах;
2х, +5х2 <11,
4х, +1х2 <10;
х, > 0, х2 > 0,
х,,х2 - цілі.
3.5.12.	Р - х, + х2 -> тах;
2х1 + 1х2 < 18,
їх, +2х2 <16;
х, >0, х2 >0,
187
ЗайченкоО.Ю.. ЗайченкоЮ.П.
- ЦІЛІ.
3.5.13.	Е = А', + х, —> шах;
х, 4-2х2 <10,
2Х] +х2 < 10,
+ 2х2 > 2;
х, > 0, х2 > 0,
х,,х2 — цілі.
3.5.14.	Е =2х}+ х2 —>птах;
2х, +3х2 < 12,
4^ +х, <10;
х, > 0, х2 > 0,
Х|,Х2 - цілі.
3.5.15.	Е = х} 4- х2 —> тах;
4-4х2 <14,
2х, 4-Зх2 < 12;
х, > 0, х2 > 0,
х,, х2 — цілі.
3.5.16.	Е = X] 4- х1 —> тах;
Зх( 4- 2х2 < 5,
х2 <2;
х, >0, х2 > 0, х,, х2 - цілі.
183
Дослідження операцій. Збірник задач
3.5.17.	Р = х, + х2 —> тах;
20х, + ІОх, <75,
12х, + 7х2 < 55;
х, > 0, х2 > О,
х,, х2 — цілі.
3.5.18.	Р = 5х, + 3х, —> тах;
Зх, +5х2 < 15,
5х, +2х2 <10;
х, >0, х2 >0,
х,, х2 - цілі.
3.5.19.	Р = 5х, - Зх2 —> тіп;
Зх, + 2х, > 6,
2х, - Зх2 > -6,
х, + х2 < 4;
х, > 0, х2 > О,
х,, х2 — цілі.
3.5.20.	Р = 6х, + 4х2 —> тіп;
2х, + 1х2 > З,
їх, -х2 > 1;
х, > 0, х2 > О,
х,, х2 — цілі.
3.5.21.	Р = 2х, +х, —> тах;;
2х, + Зх2 < 11,
4х, +х2 <10;
х, > 0, х2 > 0, х,, х2 - цілі.
189
Зайченко О.Ю., Зайченко Ю.П.
3.5.22.	Р = х, + хг —> тах;
2х1 +11х2 < 38,
х, + х2 < 7;
4х, - 5х2 < 5;
х, > 0, х, > О,
Х|, х2 - цілі.
3.5.23.	Р - 4х, + 4х2 —> тах;
2хІ + х2 < 5,
2х, + х2 < 9;
х, > 0, х2 > О,
х,,х2 - цілі.
3.5.24.	р = 2х, - х2 —> тах;
2х, + х2 <8,
X] + Зх2 > 6,
Зх, + х2 > 3;
х, >0, х2 >0,
х,,х2 — цілі.
3.5.25.	Р = х, + х2 -> тах;
6х, + 5х2 < 20,
2х, +3х2 <10;
х, >0, х2 >0,
хх,х2 — цілі.
190
Дослідження операцій. Збірник задач
3.5.26.	р = 7х, - 2хг -> тах;
х,+х2 <5,
3х1 + х2 > 2,
2х1 - Зх2 < 6,
х( -х2 >-3;
х, > 0, х2 > О,
х,,х2 - цілі.
3.5.27.	У7 = х, - Зх2 + Зх3 —> тах;
2х1 + х2 + х3 < 4,
4х1 -Зх2 < 4,
—Зх1 + 2х2 < З,
х, > 0, х2 > 0, х3 > О,
хрх2,х3 — цілі.
3.5.28.	Р = 6х, + 4х2 —> тіп;
х,-х2<1>
2х, + х2 >3;
х, > 0, х2 > О,
х,, х2 — цілі.
3.5.29.	Р = 2х, + х2 —> тах;
7Х| +4х2 < 28,
5х, +2х2 >10,
-х, +2х2 <14,
4х, -Зх2 <12;
х, > 0, х2 > О,
х,, х2 - цілі.
191
Зайченко О.Ю., Зайченко ІО П
3.5.30.	Е = 8х, + 2х, —> тах;
-4х2 <4,
-4х, 4- х, < 4,
+х2 < 6;
х, > 0, х2 > 0,
х,, х2 — цілі.
3.5.31.	Е = 2х, + Зх2 —> тіп;
х, +2х2 > 16,
2х, +х2 >18;
х, > 0, х2 > 0,
х,, х2 — цілі.
3.5.32.	Е - 2х, +х2 -Зх3 —> тах;
х, + 2х2 - 2х3 < 4,
5х, —х3 < 12,
2х, 4-х, -Зх3 > -4;
х, > 0, х2 > 0, х3 > 0,
х,,х2,х3 — цілі.
3.5.33.	Е = 6х, 4- 4х2 —> тіп;
2х, 4- х2 > З,
Зх, 4- 2х2 > 1,
х, -2х2 < 2,
х, > 0. х2 > 0,
х,, х2 — цілі.
192
Дослідження операцій. Збірник задач
3.5.34.	Е — х, + 2х2 —> шах;
+Х2 > 1,
2х, + х2 < 6,
2^ + Зх2 < 8;
х, > 0, х2 > О,
хрх2 - цілі.
3.5.35.	Е = х, -х2 —> тах;
2х, + Зх2 < 9,
2x,4-х, <6;
х, > 0, х2 > О,
Х|, х2 — цілі.
3.5.36.	Е = 2х, - х2 —> тах;
-х, + х2 < З,
6х, + 7х2 < 42,
2х, -Зх2 < 6;
х, > 0, х2 > О,
ХрХ2 - цілі.
3.5.37.	Е = х, + х2 —> тах;
х, + х2 < 6,
5х! -2х2 < 7,
-х,+х2<5;
х, > 0, х2 > О,
х,,х2 - цілі.
193
Зайченко О.Ю.. Зайченко Ю.П.
3.5.38.	Е = х, + 2х, —> тах;
2х, + 9х2 < 36,
х, +х2 <7;
х, >0, х2 >0,
х,,х2 - цілі.
3.5.39.	Е = х, + Зх, + х3 —> тах;
х( + 2х2 + 4х3 < 4,
5х, +3х2 <3;
х, > 0, х2 > 0, х3 > 0,
х,,х2,х3 - цілі.
194
Дослідження операцій. Збірник задач
Розділ 4. НЕЛІНІЙНЕ ПРОГРАМУВАННЯ
4.1.	Класичний метод видшукання екстремуму
Задача нелінійного програмування (задача НП) в загальному ви-
гляді формулюється так:
максимізувати /(х,, х2,..., хл ),
при обмеженнях:
,х„)>0;
г2(л,,л2, , л„)>0;
де функції /(ху,х2,...,хп), Єі(хі,хг,...,хп)> 0, і = 1,т нелінійні.
У задачах НП опуклість допустимої множини і скінченність чи-
сла її крайніх точок зовсім необов’язкові.
ОЗНАЧЕННЯ 4.1. Множина точок 8}(х1,х1,...,хл) функції
Дхр х2,..., хл) зветься множиною стаціонарних точок, якщо вони
задовольняють умові
^=0, у‘=їГл.	(4.1.1)
дх2
ОЗНАЧЕННЯ 4.2. Нехай Я— опукла множина точок «-вимір-
ного простору. Функція / , визначена на Я , зветься опуклою догори
(угнутою), якщо для будь-якої пари точок х,,х2єЯ і довільного
0 < к < 1 виконується нерівність (рис. 4.1)
ЛЧ + (1 - к)х2 ] > /Дх,)+(1 - к)/(х2).	(4.1.2)
Якщо
ДАх, + (1 - А)х2 ] < 4С(х,)+(1 - А)/(х2 ),	(4.1.3)
то функція зветься опуклою (рис. 4.2).
Якщо (4.1.2) або (4.1.3) виконуються як строгі нерівності, то функ-
ція зветься строго вгнутою або строго опуклою відповідно.
Ознаки опуклості та вгнутості функції п змінних можна сфор-
мулювати у вигляді такої теореми.
195
Зайченко О.Ю., Зайченко Ю.П.
Рис. 4.2
ТЕОРЕМА 4.1. Диференційовна функція Дх) строго вгнута в
деякому окопі точки х°=	якщо виконуються такі
умови:
>0;
(4-1.4)
196
Дослідження операцій. Збірник задач
1 так далі, тобто якщо знаки визначників чергуються починаючи з
<0, де
Л(хо)=
дхі8хі
Функція /(х)строго опукла в околі точки х0, якщо всі визначники
(записані вище) додатні.
Приклад 4.1.
Максимізувати Дх}, х2) = тах(32.Г| +1 20л2 - 4х? -15)
Оскільки /„ = д = -8 < 0,
/и /12 = "8	0 >о
/21 /22	0 -30	’
то /(-ч.х,) угнута.
4.2.	Метод множників Лагранжа
Метод множників Лагранжа дає змогу відшукувати максимум
(або мінімум) функції при обмеженнях-рівностях.
Мінімізувати /(х,, х,,..., хп ),	(4.2.1)
при обмеженнях:
Л,(х1,х2,...,хя)=0,
й2(х„х2,...,хл)=0,
йт (х,,х2,...,хл) = 0.
Припустимо, що усі функції /,йІ,й2,...,йЛІ- диференційовні.
Введемо набір змінних 2Р 22, ...,2,л (число яких дорівнює числу об-
межень). які мають назву множників Лагранжа, і складемо функцію
Лагранжа такого вигляду:
і(х, ,х2,...,хл ,2] ,22,...,2т ) =
Л	З V 2 ,(	1	(4-2’3>
= Дх1,х2,...,хл)+і,АйДхі,х2,...,хл)
197
Зайченко О.Ю., Зайченко Ю.П.
Справедливо таке твердження: для того щоб вектор
х° = {х°,х°,...,х°} був розв’язком задачі (4.2.1) при обмеженнях
(4.2.2), необхідно, щоб існував такий вектор А° = {Я,0,що
пара векторів (Х°,Л°) задовольняла б системі рівнянь:
^^1 = 0. У = і^;	(4-2.4)
дх>
, =	(4.2.5)
ді
4.3.	Задача нелінійного програмування
при обмежених нерівностях
Теорема Куна-Таккера.
Розглянемо випадок задачі із обмеженнями-нерівностями вигляду:
мінімізуватиДх),	(4.3.1)
при обмеженнях: ^(х)<0,і = 1,те.	(4.3.2)
У точці мінімуму х* нерівності &,(х) можуть виконуватись як рі-
вності або строгі нерівності.
Умови оптимальності розв’язків задач НП формулюються в такій
теоремі, яка відіграє винятково важливу роль у теорії нелінійного
програмування.
ТЕОРЕМА 4.2. (Куна-Таккера). Нехай функції ^і(х),і = \,т,
мають неперервні частинні похідні на деякій відкритій множині Я",
яка містить точку х'. Якщо х’ є точкою мінімуму функції /(х) при
обмеженнях #,.(х)<0,/ = 1,іи, що задовольняють умові регулярності
у вигляді лінійної незалежності векторів У#,(х’), то існують такі
невід’ємні множники Лагранжа 2|,Л2,...,Лга, що
У/(х’)+І№(х’) = 0;	(4.3.3)
і=і
2Л1г,(х*) = 0,Лі >0,г = Гт.	(4.3.4)
198
Дослідження операцій. Збірник задач
Сідлова точка і задача нелінійного програмування
Розглянемо функцію Лагранжа £(х,А) = /(х)+£Л,#,(х).
/=і
ВИЗНАЧЕННЯ: 4.3.1. Пара векторів х", А* зветься сідловою точ-
кою функції Лагранжа £(х,Л), якщо при всіх Л > 0, х є Л("’ вико-
нується умова:
£(х*,Л)< £(х*,Л*)< £(х,Л*).	(4.3.5)
Нерівність (4.3.5) називають нерівністю для сідпової точки. Оче-
видно, що в сідловій точці виконується умова:
£(х* ,Л") = тах тіп £(х,Л) = тіп тах £(х,Л). (4.3.6)
лго хеЯ"	хєЯ” Аго
Застосування теореми Куна-Таккера
для задачі опуклого програмування
Нехай задача НП має вигляд:
мінімізувати	Лх),	(4.3.7)
при обмеженнях
^і(х)< 0,ї = 1,ти.	(4.3.8)
х>0.	(4.3.9)
ТЕОРЕМА 4.3. Нехай задачу НП задано у вигляді (3.3.7)-(3.3.9),
а функції /(х) та £|(х),£2(х),...,£п(х) диференційовані та опуклі
(по х). Вектор х° >0 є оптимальним розв’язком задачі НП тоді і
тільки тоді, коли існує такий вектор Л° >0, що пара (х°,Л°) є сід-
ловою точкою функціїЛагранжа, тобто виконуються такі умови:
=	(4.3.10)
(4.3.11)
дхі
а£(хо,Ло)=&(х0)^0. = —.	(4312)
^(х0,А0) ло=г (хо)Ло=о,і = І^;	(4.3.13)
199
Зайченко О.Ю., Зайченко Ю.П.
Задача (4.3.7)-(4.3.9) за умов, що всі /(х), £,(х) опуклі функції,
є задачею опуклого програмування. Розглянемо задачу вгнутого про-
грамування.
Максимізувати	Лх),	(4.3.14)
при обмеженнях:	о’ о ЛІ	(4.3.15)
	Єм(х)^0, х>0,	(4.3.16)
де /(х) і всі функції #,(х) вгнуті по х .
ТЕОРЕМА 4.4. Нехай задачу НП задано у вигляді (4.3.14)-
(4.3.16), а функції /(х), Яі(х), і = \,т, — диференційовні.Для того щоб
вектор х° був оптимальним розв’язком цієї задачі, необхідно, щоб
існував такий вектор Л° > 0, для якого виконувалися б такі умови:
а)а£(х°,Ло)^0 = —;	(4.3.17)
8хз
б) а£(х°,Л°)	= 0, . = — _	(4.3.18)
в) ^(х°,Д°)= (хо)>о .	(4.3.19)
дЛі
0 ацх л) ло = (%0 0 = 0 .=—
оЯ,
Якщо функції /(х), &,(х) вгнуті, то умови (4.3.17)-(4.3.20) є вод-
ночас й достатніми.
4.4. Квадратичне програмування
До задач квадратичного програмування належить спеціальний
клас задач НП, в яких цільова функція /(х) квадратична та вгнута
(або опукла), а всі обмеження лінійні.
200
Дослідження операцій. Збірник задач
Застосувавши до цієї задачі теорему Куна-Таккера, одержимо
умови для оптимального розв’язку у вигляді системи лінійних рів-
нянь, розв’язати які можна симплекс-методом.
У матричному вигляді ця задача записується так:
максимізувати
/(х) = Ьтх +1 хтСх = X 1
1	7=і
при обмеженнях:
Ах$ Ао ,
(4.4-1)
(4-4-2)
де С- симетрична від’ємно визначена матриця,
(»лхл)
і = 1, п, і = 1, п ;
ЙІО
а2О
о
_атО
Зазначимо, що коли С- від’ємно визначена матриця, то квадра-
тична форма хтСх вгнута (опукла догори). Отже, задача (4.4.1),
(4.4.2) є задачею вгнутого програмування.
ТЕОРЕМА 4.5. Вектор х0 >0 є оптимальним розв’язком задачі
квадратичного програмування тоді і тільки тоді, коли існують такі
т -вимірні вектори А > 0, XV > 0 і п -вимірний вектор V > 0, що ви-
конуються такі умови:
1)	Ь+Сх-АТЛ + V = 0;
2)	Ао-Ах-ХХ' = 0;
3)	Утх = 0;
4)	ХУТЛ = О.
Зазначимо, що умови 1), 2) утворюють стосовно змінних
х,Л, V, XV систему (п + т) рівнянь з 2(л + л0 невідомими.
Із умов 3), 4) випливає, що принаймні л змінних із X, V та т
змінних серед А, XV дорівнюють нулю.
Отже, якщо існує оптимальний розв’язок задачі (4.4.1), то він має
бути одним з базисних розв’язків 1), 2). Оскільки для знаходження
201
Зайченко О.Ю., Зайченко Ю.П
допустимого базисного розв’язку можна застосувати симплекс-метод
Данціга, то цей метод (як і інші методи ЛП) придатний для
розв’язання задач квадратичного програмування.
Запишемо 1), 2) увигляді:
Сх-АТА +V =—Ь,
Ах +ХУ = Ао.
Для відшукання початкового базису системи (4.4.3) застосуємо
метод штучних змінних. Введемо штучні змінні і. Матимемо таку
систему:
(4.4.3)
(4.4.4)
Сх-АТЛ + У + Х = -Ь,
Ах + \¥ + У = Ао.
При цьому знаки перед компонентами векторів 2,, У вибираємо
однаковими із знаками відповідних компонентів вільних членів - Ь
та Ао.
Побудувавши псевдоцільову функцію виводимо з базису штучні
змінні і вводимо X, А, V, XV . При цьому слід враховувати умови до-
повняльної нежорсткості X т V = 0;	А т XV = 0
Якщо вдається вивести з базису всі штучні змінні і при цьому за-
довольняються умови 3), 4) теореми 4.5, то знайдений базисний
розв’язок є оптимальним.
Приклад 4.2. Розв’язати таку задачу:
максимізувати /(х,, х2) = тах(х, + 2х2 - х2 - х2)
при обмеженнях:
х,+2х2<16,	16-х,-2х2>0,
х(+х2=8,	•	->	8-х,-х2=0, 
х, > 0, х, > 0,	X! > 0, х2 > 0.
(О
(2)
Оскільки [ -.	- -2 < о
" дх;
/,,=-2 0 =4>(),
Лі /22	0-2
то /<Л|.х,) угнута, і ця задача є задачею квадратичного програмування.
Побудуємо функцію Лагранжа:
А(Х],х2, Я,, Я2) — (Х| + 2х2 — Х| — х2) + (16 — Х| — 2х2) + Я, (8 — х( — х2).
202
Дослідження операцій. Збірник задач
(3)
Застосувавши теорему Куна-Таккера, одержимо такі умови для
оптимального розв’язку:
яг
— = 1-2х,-Я,-Л2<0:
дх,
— = 2-2х2-2Х,-Л2 <0,
йх2
— = 16-х,-2х2 >0;
ВЛ, 1
= 8 - х, - х2 = 0.
ал2
Та умови доповняльної нежорсткості:
о£	дЬ _ дЬ
---х, = 0;	---х, =0;	— А = о-
ах, 1	дхг 1	ад 1
Увівши в систему (3) вільні змінні дістанемо таку систему:
1 - 2х2 -Лі~Л2+у1=0
2 - 2х2 - 2Д - Д + V, = 0
16-х, -2х2 -зг, =0
8 - х1 - х2 = 0
Та умови доповняльної нежорсткості:
х, • V, = 0; х2  у2 = 0; Л,  зг, = 0.
(4)
(5)
(7)
(6)
Друге обмеження в умовах (2) виконується як строга рівність,
тому немає обмеження на знак змінної л2. Проте оскільки симплекс-
метод дає змогу знаходити лише невід’ємні базисні розв’язки, то
зробимо заміну змінних:	л3го-, /4 >о. Запишемо систему
(5) в еквівалентному вигляді:
1	— 2Х| — Д + Д — Д + V, =0,
2	— 2х, — 2Д + Д — Д + V, =0.
16-х, -2х, — зг, =0,
х, +х2 -8 = 0.
Треба знайти ДБР системи (7), що задовольняє всі умови (6). Для
цього застосуємо метод штучних змінних. Введемо штучні змінні
в перше, друге та четверте обмеження. В результаті отрима-
ємо таку задачу ЛП:
203
Зайченко О.Ю., Зайченко Ю.П.
мінімізувати М(у{ +у2 +_у3),	(8)
при обмеженнях:
2х, + 2, - 2, + 24 - я, + у, = 1,
2х2 + 22, -23 + 24 -у2 4-у, = 2
х, + 2х, + IV, = 16,
х, + х, + у3 = 8.
Розв’язуємо задачу (8), (9) симплекс-методом при додатковому
обмеженні (6) на вибір базису.
Результати послідовних ітерацій наведено в табл. 4.1-4.4.
Одержимо оптимальний розв’язок, що задовольняє умовам доповня-
льної нежорсткості:
х° = 15/4; х°=17/4; 2? =2,°-2° =-13/2.
Таблиця 4.1
с} сі		0	0	0	0	0	0	0	0	0	м	м	м
	Вх	ло	*1	Х2	А	Л	Л	Ч	у2	И/,	У,	У2	Уз
0	”ї	16	1	2	0	0	0	0	0	1	0	0	0
м	У,	1	2	0	1	-1	1	-1	0	0	1	0	0
м	У2	2	0	2	2	-1	1	0	-1	0	0	1	0
м	Уз	8	1	1	0	0	0	0	0	0	0	0	1
	л	1 ЇМ	зм	ЗМ	ЗМ	2М	-2М	-М	-м	0	0	0	0
204
Дослідження операцій. Збірник задач
Таблиця 4.2
сі		0	0	0	0	0	0	0	0	0	м	м
	Вх	Л		Х2	Л		А		V,		Уз	Уз
0		31/2	0	2	-1/2	-1/2	1/2	1/2	0	1	0	0
0		1/2	1	0	1/2	1/2	-1/2	-1/2	0	0	0	0
м	Уз	2	0	2	2	1	-1	0	-1	0	1	0
м	Уз	15/2	0	1	-1/2	-1/2	1/2	1/2	0	0	0	1
	А	19/2 М	0	ЗМ	3/2М	1/2М	-1/2М	1/2М	-м	0	0	0
Таблиця 4.3
с. У с,		0	0	0	0	0	0	0	0	0	м
	Вх	А,		Х2	л		4.	V!	V,		Уз
0		27/2	0	0	-5/2	-3/2	3/2	1/2	1	1	0
0		1/2	1	0	1/2	1/2	-1/2	-1/2	0	0	0
0	Х2	1	0	1	1	1/2	-1/2	0	-1/2	0	0
м	Уз	13/2	0	0	-3/2	-1	1	1/2	1/2	0	1
	А	13/2М	0	0	-3/2М	-М	М	1/2М	1/2М	0	0
205
Зайченко О.Ю, Зайченко Ю.П.
сі сІ		
	Вх	Ао
0		15/4
0		15/4
0	Х2	17/4
0	л	13/2
	д	
Таблиця 4.4
Розв’яжемо тепер цю задачу методом перебору. Отже, маємо та-
ку вихідну систему нерівностей та рівнянь:
дхх
^ = 2-2х1-2А,-Л2<0,
дх2
= 16 — х, — 2х, > 0,
дЛ, ‘	2
-^- = 8-хІ-х2 =0.
аі
—х, =0,
1
8Ь п
V2 ’’
—Л=о,
5А
(10)
(11)
Х| > 0, х2 > 0, Я, > 0 .
206
Дослідження операцій. Збірник задач
Припустимо що X] * о, х2 * 0, 2, * 0,
тоді отримаємо:
1 -2х, -2, -2, = 0,
2-2х2—22,	=0,
1-х, -2х2 = 0,
8 —х, -х2 = 0.
(12)
Із останніх двох рівнянь отримуємо: 8 - х2 = 0; т2 = 8 -
х, =0, тоді 1-Л-А=О.	1
-14-22,-^=0.]
В результаті отримуємо: 2, = -15 < 0, 22 = 16.
Оскільки 2, < 0 не задовольняє умові невід’ємності, то вибира-
ємо другий варіант: х, * 0, х, * 0, 2, = 0.
Тоді отримуємо:
1 - 2х, -2, = 0
2 - 2х2 - 2, = 0 ;
8 — х, — х2 = 0
х, > 0; х2 > 0
1-2х,=2 —2х2	-2х,+2х2=1
х, + х2 = 8	х, + х, = 8
'	4
, , _	13
Л, = 1 —2х =-.
2
Оскільки на 2^ немає обмежень у знаку; а х, > 0, х2 > 0, то
знайдений розв’язок - оптимальний: як бачимо він співпадає з
роз’вязком, знайденим симплекс-методом.
207
Зайченко О.Ю, Зайченко Ю.П
Задачі і вправи
Розв’язати такі задачі квадратичпго програмування.
4.1.	2~ -х, - 2х, + х2 —> тіп;
Зх, +2х, < 6,
х,+2х, <4;
х, > 0, х, > 0.
4.2.	2 = х2 + х2 - 8х, -10х2 —> тіп;
З.г,+2х2 + х3 = 6,
Х| >0, х2 >0, х3 >0.
4.3.	2 = —х2 -Зх2 + 2х, -Зх2 —> тах;
Зх(+х2 +х3 + х4 = 16,
—х,+3х2 —х3 -х4 = 4;
х, >0, х2 >0, х3 >0, х4>0.
4.4.	2 = 2х}х2 - х2 - х2 —> тах;
2Х]—х7 < 6,
Х]+2х, < 10;
х, >0, х2 >0.
4.5.	В п’ятикутнику з вершинами О (0,0), А (0,6), В (5,8),
0(0,4) іЕ (8,0) знайти екстремуми наступних функцій:
1)	2 = х2 + х2 - бХ] - 4х2 —> тіп;
2)	2 = -Зх2 - 5х2 — X) х7 +18х, +16х2 —> тіп;
3)г = -х2 - х2 + 20Х] +16х2 -> тах;
208
Дослідження операцій. Збірник задач
4)	г = х,х2 —> тах;
5)	2 = 2х2 + Зх2 -40х, - 48х2 -> тіп;
6)	г = 2х,2 4-х2 -2х,х, —> тіп.
4.6.	2 = х2 4- х2 4- х3 - 2х, 4- х, —> тіп;
Х]4-2х2 4-Зх, < 12,
2x,4-х, 4-х3 < 6.
4.7.	2 = х, 4- 2х,х, - х2 -> тах;
х,4-х2 = 8,
х24-х3 = 4.
4.8.	2 = (х, 4- х2 4-х3)’ —> тіп;
х, < 2, х, < 4, х3 < 6.
4.9.	2 = -х2 - х2 4- х, 4- 2х2 -> тах;
х,4-2х2 -х3 = 6,
х, > 0, х, > 0, х3 > 0.
410.	2 = х2 4- 2х2 - 2х,х2 4- 5х, - 6х2 —> тіп;
2х,4-х2 <8,
х,4-Зх2 < 15;
х, > 0, х, > 0.
4.11. 2 = х2 4- 2х2 — 2х,х2 4- 5х, — 6х2 —> тіп;
х,4-Зх2 < 12,
х, 4-х2 > 6;
х, > 0, х2 > 0.
209
Зайченко О.Ю, Зайченко Ю.П.
4.12.	2 = 2х2 + 2х2	+ 5х, - 6х, -> тіп;
х,-х2 >6,
2хх+х2 > 15;
х, > 0, х2 > 0.
4.13.	2 - х2 + 2х2 - 2х,х, + 5х, —> тіп;
2х,+Зх2 <15,
х,+2х2 < 10;
х, > 0, х2 > 0.
4.14.	2 = -х2 - х2 + Зх, + 4х2 -> тах;
х,+2х2 < 20,
х,+х2 >8;
х, > 0, х2 > 0.
4.15.	2 = -х2 -х2 + х, + 2х2 -> тах;
х,+2х2 <16,
х,+х2 > 8;
х, > 0, х2 > 0.
4.16.	2 = -4х2 - Зх2 + 32х, + 120х2 —> тах;
2х,+5х2 < 20,
2х,-х2 =8;
х, > 0, х2 > 0.
210
Дослідження операцій Збірник задач
4.17.	2 = -х2 - х2 + х,х2 + 5х, + 2х2 -> тах;
2х,+3х2 <15,
х^х? = 8;
х, > 0, х2 > 0.
4.18.	2 = х2 + 2х2 - 2х, — 4х2 —> тіп;
х,+х2 > 8,
х,+2х, < 20;
х, > 0, х2 > 0.
4.19.	2 = -2х2 - Зх2 + х1 + Зх2 -» тах;
х,+х2 > 6,
х,+3х2 < 12;
х(>0, х2>0.
4.20.	2 = 2х2 + 2х2 - Зх,х2 + 5х, + 6х2 —> тіп;
х,— х2 = 6,
2х,+х2 = 15;
х, > 0, х2 > 0.
4.21.	2 = -х2 - 2х2 + Зх, + 8х2 тах;
2х,+х2 >8,
2х,+Зх2 < 20;
х, > 0, х2 > 0.
4.22.	2 = —х2 - 2х32 + 8х, + 2х> + 4х3 —» тах;
2х,+х2 -х3 < 16,
Зх2+4х3 < 20;
х, > 0, х2 > 0, х3 > 0.
211
Зайченко О.Ю., Зайченко Ю.П
4.23.	2 - -х2 + 8Х] + х, —> тах;
2х,+х, < 16,
х(+5х, = 20;
х, > 0, х2 > 0.
4.24.	г = -2х2 -5х2 +3х( + 10х2 —> тах;
4Х(-х2 < 8,
х,+х, < 12;
х( > 0, х2 > 0.
4.25.	2 = -х2 - Зх2 + х,х, +15х, + 8х2 —> тах;
Зх, +х, <15,
х,+2х2 < 10;
х,>0, х2>0.
4.26.	2 = х2 + 2х2 - 2х(х, + Зх( + 4х, —> тіп;
х(+х2 > 6,
2х (+3х2 <18;
х, > 0, х2 > 0.
4.27.	2 = х2 + 2х2 + Зх2 -> тіп;
2х1+х2 +х3 = 10,
ЗХ]-2х2 -х3 > 6;
х, > 0, х2 > 0, х3 > 0.
212
Дослідження операцій. Збірник задач
4.28.	2 - х* + х2 + х; - хгх2 - 5х( + 6х2 -> тіп;
х^х, + х3 < 20,
Х(+.г2 <15,
х2 + х3 < 10;
х, >0, х2 >0, л3>0.
4.29.	тах /(х,,х,) = тах(32х, +120х, - 4х(2 -15х2);
2х, + 5х2 < 20,
2х, - х, =8,
х,,х2 > 0.
4.30.	тіп /(х,,х,) = тіп(х2 + 2х2 - 2х,х2 + 5х, - 6х2);
2х,+х, <8,
х, +3х2 <15,
х„х2>0.
4.31.	тіп/(х,,х2) = тпХх,2+2х2-2х,х2+5^-6х2);
х, + Зх, < 12,
х, +х2 >6,
х,,х, >0.
4.32.	тах/х|5х,() = тах(3х, +4х, -х2 -х2);
+ 2х2 < 20,
X] + х, > 8,
хрх2 >0.
213
Зайченко О.Ю. Зайченко Ю.П.
4.34.	тіп /(х,, х2) = тіпСх2 + 2х2 - 2х, - 4х2);
х]+2х2< 20,
х, + х7 > 8,
хі,х2 > 0.
4.35.	тах /(х,, х2) = тах^ + Зх2 - 2х\ - Зх2);
+3х2 <12,
X) + х2 > 6,
хрх2>0.
4.36.	тах /(х,, х2) = тах(3х, +10х2 - 2х* - 5х2);
4Х) -х2 <8,
х, +х2 <12,
х,,х, >0.
437.	тіп /(х,, х2) = тіп(2х2 - Зх,х2 + 2х2 + 5х, + 6х2);
х, -х2 =6,
2х, +х, = 15,
х,,х2>0.
4.38.	тах/(х},х2)= тах(ЗХ] +8х2 -х* -2х2)
2х1 + х2 > 8
2х( + Зх2 < 20
Л],х2 >0
4.39.	тах /(х,, х2) = тах(8х1 + х2 - х(2);
2х( +х2 < 16,
X] + 5х2 = 20,
х„х2 >0.
214
Дослідження операцій. Збірник задач
4.40.	тах /(х}, х2, х3) = тах(8х, + 2х, + 4х3 - х2 - 2х3);
2х, + х2 -х3 <16,
Зх2 + 4х3 < 20,
х,,х2,х3 >0.
4.41.	тах /(хр х2) = тах(5х, + 2х2 - х, + х,х2 - х2);
2х( + 3х2 < 15,
х, + 2х, = 8,
хрх2 > 0.
4.42.	тіп /(х, ,х2) = тіп(-х, - 2х, + х2);
Зх, + 2х, < 16,
х, + 2х2 < 4,
х,,х2>0.
4.43.	тах/(х|,х2) = тах(-х,2 -2х2 +2х}х2 -5Х]);
х, — х2 > 6,
2х, +х2 >15,
х,,х2 >0.
215
Зайченко О.Ю., Зайченко Ю.П.
4.5. Геометричне програмування
4.5.1. Пряма і двоїста задачі геометричного програмування та
їхні взаємозв’язки
Досить широкий клас задач НП становлять задачі геометричного
програмування, в яких цільова функція та обмеження — це так звані
функції-позиноми вигляду:
Ц(0 = С,<''72я'-’.де 1. >0, у = 1...т.
Пряма задача А. Знайти мінімальне значення функції [15, 16]:
Мої
при обмеженнях:
/, >0, і2 >0,...,/„ >0,	(4.5.2)
^2(0<1;...;^(/)<1;
(4.5.3)
де
8к (0 = Е ССІ?...іп- , к = 0,1,..., р;	(4.5.4)
ієУ[А]
7[0] = {1...л0]	(4.5.5)
У[Л] = {тк,тк +1,...,лА}, Л = 0,1,...,р;
т0 =1; т, =п0 +1; тк = пк+1;...; пр~п. (4.4.6)
Всі С, > 0 , і = 1,л, а показники степеня - дійсні числа. От-
же, всі функції §к(і) — позиноми. Функція, що мінімізується, До(/)
зветься прямою функцією, обмеження (4.5.2) — умовами не-
від’ємності, а обмеження (4.5.3) — вимушеними умовами. Матриця
Л = ||ау || — матриця експонент.
216
Дослідження операцій. Збірник іадач
ДЄ
при
Двоїста задача В. Двоїста задача В, відповідно до прямої задачі
А, формулюється так.
Знайти максимальне значення функцїї-добутку:
		*(<?)=п /1	ч		Пл,(г.Т«. А=І	(4.5.7)
обмеженнях:		Л.и= У<5,.*=1.Р, <5, >0, <У2 >0,>0, /єДо] = °> г=1			(4.5.8) (4-5.9) (4.5.10) (4.5.11)
Функція	№	зветься двоїстою функцією.			а змінні <\,
-А-	двоїстими змінними. Умова (4.4.10) —				умова нормалі-
зації, співвідношення (4.5.11) —умови ортогональності.
Зіставляючи форми запису прямої (4.5.1)-(4.5.6) і двоїстої (4.5.7)-
(4.5.11) задач, можна встановити такі співвідношення між ними.
Кожному члену позиномів прямої задачі вигляду
и. = С/""/"'2 .. .Iа* відповідає одна двоїста змінна 8І, і навпаки.
Кожен множник АД(£)Л‘1<>) функції визначається обмежен-
нями &(/)<! 
Зауважимо, що цільова функція не приводить до появи такого
множника, бо згідно з умовою нормалізації Л0(Л) = 1.
Умова нормалізації (4.510) - це єдина умова, за якою відрізняють-
ся цільова функція 80(ї) і позиноми-обмеження
217
ЗайченкоО.Ю., Зайченко Ю.П.
ТЕОРЕМА 4.6. Нехай пряма задача А сумісна і існує розв'язок
і'такий, що £*(/')<!, к = \,р, а також оптимальний розв'язок.
Тоді справедливі такі твердження.
1.	Відповідна двоїста задача сумісна і існує точка, що задоволь-
няє її обмеження, в якій досягається умовний максимум двоїстої
функції у(<5).
2.	Максимальне значення ц.ф. двоїстої задачі дорівнює мінімаль-
ному значенню ц.ф. прямої задачі:
тіп £0(/) = тах г(5).
3.	Якщо і —мінімізуюча точка прямої задачі А, то існують не-
від 'ємні множники Лагранжа рк, к =\,р, такі, що пара векторів
(і ,р ) є сідловою точкою функції Лагранжа прямої задачі, тобто'.
< !(/’, А) * Ц‘,Я)	(4-5-12)
для всіх довільних > 0, рк > 0,
де
і(ґ,//) = £0(/) + £А[£а(/)-1].	(4.5.13)
*=і
Крім того, існує максимізуючий вектор 3 двоїстої задачі з ком-
5,
понентами, що визначаються з умов:
•' 2	/є 7(0],
и СҐ'і" '- Iа'"	—
 ' 2	, іеДк], к = \,р.
£0(')
(4.5.14)
де
і = і’ =[*’], У = 1,/м та р = р .
218
Дослідження операцій. Збірник задач
Далі
(4.5.15)
4.	Якщо 8’ - максимізуюча точка двоїстої задачі В, то мінімізу-
юча точка І прямої задачі задовольняє систему рівнянь:
і є /[0],
/є 7[Н
л*(г>)
(4.5.16)
/12	т
де к перебігає усі додатні цілочислені значення, для яких
ТЕОРЕМА 4.7. Якщо 8 задовольняє обмеження двоїстої задачі
В і усі компоненти 8 додатні, то 8 буде максимізуючою точкою
двоїстої задачі, тоді і тільки тоді, коли:
кз = П^'’П. І = 1,<*.	(4.5.17)
І=1	*=І
Де
кз=Х[С^ , ] = \Д.	(4-5.18)
1=1
При цьому, якщо 8 задовольняє співвідношення (4.1.17), то
П	(01	(0)
г(г) = ^П^(ИЧ ҐІА(НА‘ .	(4.5.19)
і=і	*=і
Рівняння (4.4.17) звуться максимізуючими. Вони утворюють сис-
тему, яка складається з сі нелінійних рівнянь стосовно т/ базисних
змінних гу(у = 1,<7). Розв’язавши цю систему, можна визначити мак-
219
Зайченко 0.10., Зайченко Ю.П.
симізуючу точку двоїстої задачі В. Формула (4.4.18) задає максима-
льне значення двоїстої цільової функції для такої максимізуючої точ-
ки. Зауважимо, що оскільки базисні константи к], та двоїсті змінні
^,(г) входять у різні частини максимізуючих рівнянь, то таке розді-
лення змінних і сталих (констант) полегшує дослідження залежності
оптимальних точок двоїстої задачі В та прямої задачі А від коефіціє-
нтів С,.
4.5.2.	Опис алгоритму
На основі викладених вище результатів наведемо опис алгоритму
геометричного програмування.
Нехай задано пряму задачу ГП у вигляді (4.5.1)-(4.5.6).
1.	Складемо задачу, двоїсту до початкової, (4.5.7)-(4.5.11).
2.	Знаходимо розв’язки обмежень ортогональності та нормаліза-
ції (4.5.10), (4.5.11) — 8 . Якщо ступінь складності задачі
сі = п - т — 1 = 0, то цей розв’язок єдиний, і переходимо до кроку З,
в протилежному випадку (коли сі > 0 ), до кроку 4.
3.	Використовуючи значення 8' = {<5. }, складемо систему рів-
нянь (4.5.16), яку розв’язуємо стосовно невідомих /* = {6} . При цьо-
му для оптимальних розв’язків у(<5*) = §0(і ) .
4.	Якщо ступінь складності 8 > 0, то знаходимо загальний
розв’язок системи рівнянь (4.510), (4.5.11) у вигляді:
<і	___
8І(г) = Ь'0) + ^г$п>(), і = 1,п,	(4.5.20)
/=і
де г — вектор довільних параметрів.
220
Дослідження операцій Збірник іадач
5.	Використовуючи умови оптимальності теореми 4.7 складаємо
та розв’язуємо систему нелінійних рівнянь (4.5.17) стосовно невідо-
мих г , у = 1,</. Знайшовши її розв’язок і підставивши його в
(4.5.19), визначимо оптимальні значення двоїстої цільової функції
г(£*) = тахг.
6.	Переходимо до прямої задачі і, використовуючи співвідно-
шення (4.5.16), розв’язуємо систему рівнянь стосовно оптимальних
значень прямої задачі	на основі відомого розв’язку дво-
їстої задачі 8" = {8*} , і = 1, п.
Приклад 4.3.
5/, ґ, ґ3 + 20г, 122І2 —> тіп,
при обмеженнях:
1
1Л +-Л2 /,5 < 1;
з з
/р/2,/з>0
сі = 0 — ступінь складності.
Відповідна двоїста задача має такий вигляд:
5Ї 1Ґ20^ 2( 1 ’ґ 2 V
Т Т ЧТ ТГ (<5з + ^)	4 —> тах;
\	)	\ ^^3 7	\ ^4 )
О. 8. + 82 — 8. — 28 = 0;
112	3	4	’
8. +—82— 58. = 0;
2 ’
£>, 8{ - 282 +^3=0;
(1)
(2)
(3)
(4)
8, +82 =1.
221
Зайченко О.Ю., Зайченко Ю.П.
Розв’язуємо систему (4), знаходимо оптимальні значення двоїс-
тих змінних
з;=~, 8;=-, г;=-,5;=-.
7	2 7	7	7
Тоді максимум двоїстої функції дорівнюватиме: 0(3*) = 13,82
З	4	5	16
1) =
= 13,82.
Ц = 5//2/3 = 8{у(8 ) = 5,92
Складаємо рівняння стосовно невідомих прямої задачі:
5,92
/ =—-—і / 
*1	‘з ’
20/;1/2/;3 = 7,89;
и2 = гО/./^/з’2 = 82г(8') = 7,89
3 3 1 3 <53+<54 6
гт 2 _2 _5 8Л 1
^4=^.4
83 + 8. 6
/, =0,528; /2
Приклад 4.4.
= 1,7; і3 =1,32.
ґ
тіп 20^ І/2І/2
,! ^ ь
/з,+40/1/з+10/,/2/з
(1)
при обмеженнях:
-2г2+-іі/2г
1 12	з‘2 13
>0
(1 = п — пі —1 = 5 — 3 —1 = 1 — ступінь складності.
(2)
4
З
222
______________________________________Дослідження операцій Збірник задач
Відповідна двоїста задача мас такий вигляд:
(3)
Л| + 3 2 + £3 — 1
-8х+8г+8у-28, =0
'	1 х з,	1	„	(4)
2<54 + 85 — 0
- 8{ + 82 + 82 - 85 = 0
8{ >0, 82 > 0, 8, >0, 85 > 0.
Таблиця 4.5
	А		А		4
1	1	1	0	0	і
-1	1	1	-2	0	0
- V /2	0	1	-2	1/ /2	0
-1	1	1	0	-і	0
Таблиця 4 б
3	5.				А
1	і	1	0	0	і
0	2	2	-2	0	і
0	1/ /2	з/ /2	-2	1/ /2	і/ /2
0	2	2	0	-і	1
Таблиця 4.7
		А			Ао
1	0	0	1	0	1/ /2
0	1	1	-1	0	1/ /2
0	0	1	_3/ /2	1/ /2	X
0	0	0	2	-1	0
Таблиця 4.8
	8.				А
1	0	0	1	0	і/ /2
0	1	0	1/ /2	- V /2	1/ /4
0	0	1	-3/ /2	1/ /2	1/ /4
0	0	0	2	-1	0
223
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 4.9
3	#2				4
1	0	0	1	0	Уг
0	1	0	-1/ /2	0	У
0	0	1	- 1/ /2	0	1/ /4
0	0	0	-2	1	0
Розв’язуємо систему (4) методом Гаусса. Результати послідовних
операцій наведені в таблицях 4.5-4.9, звідси одержуємо такий базис-
ний розв’язок:
8*	8' =-; 8Ї 8* =0; 8'5 =0.
1	2	2 4	3	4	4	5
Повний розв’язок системи рівнянь при 84 = г має вигляд: (5)
$=-
2
с	1	1
8-, — —і—
2	4	2
(5)
. 1 1
>, =- + —
3 4 2
85 = 2г.
224
Дослідження операцій. Збірник задач
Записуючи повний розв’язок системи (4), визначаємо, що:
/>("	(6)
І 2 2	)
К =ПС/’-,) = 20‘‘-4(А1(/	;
7 У	ШШ 27
Л, (г) = + <5, = г + 2г = Зг;
Л,(1) = Е ^ММ0 =1 + 2 = 3,
і>єУ[А]
де 8\г) визначається з (5),	— з (6):
Підставляючи г* = — в (5), знаходимо оптимальні значення двоїстих
6
змінних:
X- 1	1	1 X- *	1 1	1 • X* — 1  X* — 1 • х*-2-1
о, =---= —; о, = —І---— —, о, — —, о4 — —, о3 — — —
'	2 6 3	2 4 2 6 З 3	6	6 З
225
Зайченко О.Ю., Зайченко ІО П.
Тоді максимум двоїстої функції дорівнюватиме:
л,(л=<5;+<?;=Т
Складаємо рівняння стосовно невідомих прямої задачі:
20гДч V = 1-60 = 20,
40лл=- 60 = 20,
3 З
З ' 2
І/2'2/;1
з2 3
10//2/3 = 1-60 = 20,
1/1 = 1,
6 2 3
1/1=1
3 2 3
_ 2 *	—	— і
Задачі і вправи
При розв’язку наступних прямих задач геометричного проірамування
скласти двоїсту задачу, знайти її оптимальний розв’язок, визначити
вклад кожного позиному и,(/) в значення цільової функції £0(/).
226
Дослідження операцій. Збірник задач
4.5.1.	Знайти тіп(20/,/2 + 40/,/3 + ЗО/2/3), при обмеженнях:
+	20.
4.5.2.	Знайти тіп(5/1/2+10/2/3), при обмеженнях:
5 0Ґ +	+ /0 Фз $ Ь * 0 
4.5.3.	Знайти тіп^О/,1'2/^1 + 5і''21~‘ + 10і22і~'), при обмеженнях:
4.5.4.	Знайти тіп(20/,/2 4- ЗОт~1Г3 + 50/3/2), при обмеженнях:
4.5.5.	Знайти тіп(5/, 121~2 + 10/2/3/2 + 20/,2/2/3І), при обмеженнях:
<15,	>0-
4.5.6.	Знайти тіп(20г|-|/2ґ3"5 + 40/2'ґ3), при обмеженнях:
4.5.7.	Знайти тт(ЗО/1',/2Г3’1 +10г2'ґ3), при обмеженнях:
^чЛ^'з4^1’
4.5.8.	Знайти тіпф,^ + 10л,г3), при обмеженнях:
4.5.9.	Знайти 01111(20/, іг13 +ЗО/2/3), при обмеженнях:
’/.^-' + ^/./А'^І./п/г^з^О.
227
Зайченко О.Ю, Зайченко Ю П.
4.5.10.	Знайти 1010(5/' ’ґ2/3 -ь-10/2 2/3 2 4-20/, 'ґ2/31), при обмеженнях:
/,/*/3^ < 1, /,,/2ї/з >0.
4.5.11.	Знайти тіп(ЗО/,Г2ґ3 +20/2'/3”1), при обмеженнях:
4.5.12.	Знайти тіо(10/,/2/з + 20/'1/,2 +30/, '/2’2/3'3), при обмеженнях:
Іб/^/з <1, /,,/2,/з >0.
4.5.13.	Знайти тіп(5/, ґ2Л3 -+-10/~‘/32 + 20/2/3), при обмеженнях:
4.5.14.	Знайти тіп(10/І/2/3+20/'І/3"2), при обмеженнях:
^'з+|*г2';’+
4.5.15.	Знайти тіп(20/І"1/, ,/2/3' + 40/,/3 + 10/,/2/3), при обмеженнях:
|/Г2/2-2+|/Г2/3-<ьЛ^2^з^о
4.5.16.	Знайти тіп(4/,/2/з+8/1“і/2’/з',/3), при обмеженнях:
’/2/3 +|/2/з'/2<1, І.М >0.
4.5.17.	Знайти тіп(20/, /2/3‘ + 10/2/3), при обмеженнях:
З СФз + з	1	0 •
4.5.18.	Знайти шіп(5/І/3 +10/1‘І/2/3), при обмеженнях:
|/ЛГ,2+’/, 724Г-' <1, /р/,,/3^0.
228
Дослідження операцій. Збірник задач
4.5.19.	Знайти тіп(5/,/2/3 + 10/,/2/4 +15/2,'/3 '/41), при обмеженнях:
‘/-7;73^/Г7Л/^Ь/і,/2,/3,/4>0.
4.5.20.	Знайти тіп(5/, 'г2,2і} 4 10//, + 20/,/33), при обмеженнях
’ /, /2/;4 + 2 /'73/“ < і, /, ,і2, і і > 0.
4.5.21.	Знайти тіп(5/,/2/,+ 20//2 7;2), при обмеженнях:
’/, '/3 ч-2/,2/,5 <1, ^,/2,ґ3 >0
З З
4.5.22.	Знайти тіп(20/, 12і3 +1О//;1), при обмеженнях:
З І, І22^ + ’ Ії 2і2 '6і'2 < 1, , /2 Л 0 
4.5.23.	Знайти тіп(10/,/2/3 + 5/“722), при обмеженнях:
1 ф;‘V + 41,%* + 2і,<і,/„12,і3>0.
5	5	5
4.5.24.	0101(20/,/2 + 40/, /3 +30/2/|), при обмеженнях:
/,>0.
4.5.25.	тіп(5/,/, +10/2/3), при обмеженнях:
Г1/,72, + 2/,7;'+-ґ273,>|<1.
\5	2	5 ' 3	10 2 3 )
/,,/2,/3>0.
4.5.26.	тіпОО/^л,1 +5/,^/3' +10/^/3 '), при обмеженнях:
>о.
229
Зайченко О.Ю. Зайченко Ю.П.
4.5.27	171111(20/, (2 + ЗО/2'ґ3 +50/,/*), при обмеженнях:
/,,/2,/3>0.
4.5.28	тіп(5г^ґ2ґ3+10ґ2/^+20ґ,І/2ґ3'), при обмеженнях:
ґ,Г'/3>15.
г,Л,/3>0.
4.5.29.	тіп(20/,Л/33+40г2'/3), при обмеженнях:
Ґ1 2 Л ,
[з'.'з+у'Л'з 1^1-
'іЛ.'з^О.
4.5.30.	тіпСЗОґ’1^/,1 +10/2'/3), при обмеженнях:
/і»г2,/3 >о.
4.5.31.	тіп(5/,/2г3 + 10/2/3), при обмеженнях:
(-і^22 + -Ґ(^ |<1.
І5 2	5	3 /
>0.
4.5.32.	тіп(20г, іг(3 +30/2/3), при обмеженнях:
(1 -У . 2	,
15	1 5 2 ’ )
^Г2,Г3>0.
4.5.33.	тіп(5/^/2/3 +1О/“2/3^+20/І“'г2г3'), при обмеженнях:
і ҐС4 <1
Ч‘2‘3 — *•
/,и2,/3 >о.
230
Досіїдження операцій Збірник задач
Розділ 5. ДИНАМІЧНЕ ПРОГРАМУВАННЯ
5.1. Загальна схема обчислювального методу
динамічного програмування
Динамічне програмування - це обчислювальній! метод для
розв’язування задач оптимізації спеціальної структури з адитивними
або мультиплікативними цільовими функціями.
Динамічне програмування виникло і сформувалося в 1950-1953 рр.
завдяки роботам Р.Беллмана та його співробітників. Перші задачі, що
привели до появи обчислювального методу, були динамічними зада-
чами керування запасами.
Ідею обчислювального методу динамічного програмування (ДП)
розглянемо на такому прикладі:
п
максимізувати 2 = ^7/^, (х,),	(5.1.1)
/=і
п
при обмеженнях:	а^>0; ху >0; Ь>0.	(5.1.2)
7=1
Як бачимо, цільова функція задачі та обмеження є сумою функ-
цій від однієї змінної кожна. Така функція, як відомо, називається
адитивною. Якщо всі /у (х • ), 7 = 1,и опуклі, то для розв’язання за-
дачі можна застосувати метод множників Лагранжа.
Коли існує багато локальних мінімумів, то цей метод дає лише
один з них. Якщо треба знайти глобальний максимум, метод множ-
ників Лагранжа застосувати неможливо.
Тому розглянемо інший метод, який забезпечує відшукання гло-
бально-оптимального розв’язку. Припустимо, що всі а} , Ь - цілі
числа. Припустимо також, що в розглядуваній задачі всі змінні мо-
жуть набувати лише цілочисельних значень.
231
Зайченко О.Ю., Зайченко Ю.П.
Через г позначимо абсолютний (глобальний) максимум г за
п
умови л-у <Ь . Виберемо деяке значення хл і, зафіксувавши йо-
7 = 1
ГО, максимізуємо 2 ПО ВСІХ ІНШИХ ЗМІННИХ Х1т Х2,-, А„_|. Припус-
тимо, що така максимізація проведена для всіх можливих значень
хп. Тоді г буде найбільшим з усіх можливих значень г. Формаль-
но цей процес (ця процедура) записується так:
(5-1.3)
причому
/1 — 1
І	(5.1.4)
7=1
п-І
Оскільки тах £ /у (ху) дая невід’ємних цілих чисел, що задо-
вольняють умові (5.1.4), залежить від Ь-а п хл , то позначимо
тах £	)=А„_1(Ь-алхл).	(5.1.5)
Ли-І у = І
Припустимо, ЩО МИ обчислили Л (Ь-а п х„ ) для всіх допус-
тимих цілих значень хл - <0,1,...,
ь
ап
ап
означає цілу

ь
частину —.
Очевидно, що
г'=тах{/п(хя) + Ля_1(Л-опхп)}.
(5.1.6)
232
Дослідження операцій. Збірник задач
Для знаходження (5.1.6) визначимо /(л„ ) та Л„ । (Ь-аП х„ )
для всіх допустимих значень х „ і виберемо максимальне г . Одно-
часно знайдемо оптимальний розв’язок л „. Таким чином, якби була
відома функція А (Ь-а„ х, то вся задача звелася б до задачі
з однією змінною.
Покажемо, як обчислити Л	(Ь - а „ х „ ).
Позначимо
Лв-і«)= тах Е-М*/)’
*• 1 у=І
за умови
п — 1
Е ауЛ-у<^.
7=1
Повторивши вищенаведені викладки, одержимо
А „_!<£)=тах	( хл ч )+А л_2	-ал_, хл_,)},	(5.1.7)
-Тя-1
де
п — 2
Ап-2(^-аП-ІЛП-і) = рах|2	(51'8>
причому максимум у (7.1.7) відшукується за умови
п—2
Е а 3Хі-^~ап-Іхп-і-
7=1
Аналогічним чином обчислюємо Лл_2(^)> Лл_3(^)і т.д. Наре-
шті на к -му кроці ми використовуємо «основне рекурентне співвід-
ношення (ОРС) динамічного програмування»:
А* (£)=тах{Д (хк ) + Л4_, (£-ак хк)},	(5.1.9)
за умови, що
А
У а .х ,<£, к=п, 2.
7=1
233
Зайченко О Ю., Зайченко Ю.П.
Використовуючи ОРС (7.1.9), організуємо процес обчислень, як ба-
гатокроковий процес таким чином. На першому кроці, зафіксувавши
початок інтервалу 0 і змінюючи його правий кінець Е,, обчислюємо
Л,(^)= тах /|(Л|)	(5.1.10)
для всіх можливих значень £=0, 1, ... , Ь. Оптимальний розв’язок
першого кроку позначимо через х® (£). Складаємо таблицю динамі-
чного програмування першого кроку (табл. 7.1) і заповнюємо її ре-
зультатами обчислень.
На другому кроці (к = 2) знаходимо Л 2 (Е,) згідно зі співвідношенням:
Л2(£)= тах {/2(х2) + Л1(^-д2х2)}, (5.1.11)
причому значення \і(^-а2х2) вибираємо із табл. 5.1.
Обчислюємо послідовно Л2(%) для всіх значень £, = 0, 1, ..., Ь,
використовуючи результати табл. 5.1. Одночасно знаходимо х2 (£)
і X®(х^(£)). Результати обчислень заносимо в таблицю другого
кроку (табл. 5.2).
Таблиця 5.1
5	Лі(О	*!0(О
0		
1		
ь		
Таблиця 5.2
	А 2 ($)	Іч» ’о	
0			
1			
ь			
Далі, користуючись співвідношенням (5.1.8), послідовно обчис-
люємо Л3(^), Л4(^), .... Лл. (^), ...,ЛП_] (£) для всіх значень
Е, = 0, 1,2,..., Ь.
Нарешті, на останньому кроці при к = п знаходимо:
234
Дос лідження операцій Збірник задач
і =Кп^=Ь)= тах {/„ (х„) + Л„_1 (Ь-ап х„)} ,	(5.1.12)
Ч^]
а також відповідне оптимальне значення для останньої змінної
л„=л-*(/>). Для відшукання значень всіх інших змінних
А'„-і»хл-2.А’і 1Ре^а скористатися таблицею (и-1),(л-2) і т.д.
кроків. Прийнявши =/>,із таблиці попереднього кроку
знаходимо (без обчислень):
х„0_( =х„-і (Ь-ап х°), х°_2 =х„-2 (£,), х° =х, (£,).
Отже, динамічне програмування - це напрямлений послідовний
перебір варіантів, який обов’язково приводить до глобального мак-
симуму. Для застосування методу треба табулювати функції
А, (£), А 2 (£) , ... , Ал_( (£)для всіх можливих значень £.
Оцінимо число операцій, потрібне для розв’язання цієї задачі ме-
тодом динамічного програмування.
Для обчислення А к (£) при фіксованому потрібно виконати
(£+1) обчислень функції /4(хл)+Аа_1 (^-хА) при х0<хА<^. От-
же, щоб заповнити одну таблицю (при і, =0, 1, ... , Ь) потрібно
(£+1) _(^+1)^+2) 0ПЄрацій.
4=о	2!
Таким чином, щоб обчислити всі функції А, (£), Л2 (£),... ,
А „_,(£) потрібні (и-1)^+1^+2)
операцій.
З урахуванням обчислень функції А и (Ь) загальна кількість опе-
рацій становить:
(и-1)(6 + 1)(д+2)	(/, + !)[ (и-1)(Ь + 2)+2]
ДП	ОІ	2
2!
235
Зайченко О Ю, ЗайченкоЮ.П.
Це значно менше, ніж С*+61, тобто маємо суттєве скорочення
обсягу обчислень порівняно з простим перебором.
Підведемо деякі підсумки. Розглянуту вище задачу (5.1.1), (5.1.2)
з економічної точки зору можна трактувати як задачу розподілу од-
ного обмеженого ресурсу Ь між п різними способами виробництва,
де ху — обсяг виробництва за у-м способом; / (ат) — прибуток
від досягнення обсягу х у; а у х у — витрати ресурсу на виробництво
за у -м способом (при обмеженні на загальний обсяг використаного
ресурсу £ а}Х]<Ь).
/=і
Тому А* (і;) можна трактувати як максимальний прибуток від
перших к способів виробництва, коли загальний обсяг ресурсу (си-
ровини) дорівнює £ одиниць.
Розглядувану задачу можна інтерпретувати як п -кроковий про-
цес прийняття рішень, в якому на у -му кроці приймається рішення
про те, яку кількість ресурсу із загального обсягу £, треба виділити
на переробку за у -м способом виробництва. Як бачимо, структура
цієї задачі не змінюється від числа кроків, тобто задача інваріантна
щодо п.
Розв’язок для к -крокової задачі одержується із розв’язку (Л-1)-
крокової задачі шляхом додавання к -го кроку та використанням ре-
зультатів попереднього (к -1 )-го кроку.
Отже, суть динамічного програмування полягає в заміні
розв’язання даної «-крокової задачі послідовністю однокрокових
задач.
Підсумовуючи, назвемо головні ознаки (властивості) задач, до
яких можна застосувати метод динамічного програмування:
Задача має допускати інтерпретацію як п -кроковий процес прий-
няття рішень.
Задача має бути визначена для довільного числа кроків і мати
структуру, яка не залежить від їх числа.
Для ^-крокової задачі має бути заданою деяка множина парамет-
рів, яка описує стан системи і від якої залежать оптимальні значення
236
Дослідження операцій. Збірник задач
змінних. Ця множина не повинна змінюватися при збільшенні числа
кроків. (У розглядуваному вище прикладі таким параметром була
загальна кількість ресурсу.)
Вибір розв’язку (стратегії керування) на к -му кроці не повинен
впливати на попередні рішення, крім необхідного перерахунку змінних.
Нехай Е, - вектор параметрів, що описують стан процесу (вектор
стану). Тоді оптимальне значення цільової функції для к -крокового
процесу Л к (£) називатимемо функцією стану.
Нехай X* - вектор змінних керування (стратегія), який треба ви-
значити на к -му кроці. Тоді для задач, до яких можна застосувати
метод динамічного програмування, має використовуватися таке ос-
новне рекурентне співвідношення:
ЛД^)=таХ{/А(Х4,^)+Л4_,(7’(^, Х4))},
ч
де Т(^, Хк) - вектор стану попереднього (Л-1 )-го кроку за умов Е,
та хк. У розглядуваній задачі Т (£, хк)=£-акхк.
Сформулюємо принцип оптимальності Беллмана, який обгрун-
товує це співвідношення [4; 16].
Оптимальна стратегія має таку властивість: Для довільних по-
чаткового стану та початкової стратегії х ।, стратегія на к -му
кроці має бути оптимальною тільки стосовно поточного стану си-
стеми і не залежати від попередніх станів.
Таким чином, принцип оптимальності Беллмана стверджує, що
оптимальне керування системою на кожному кроці не залежить від
передісторії процесу, тобто від того, яким чином система досягла
поточного стану, і визначається лише самим станом. Системи (про-
цеси), що мають таку властивість, називаються марковськими.
5.2.	Процеси послідовного прийняття рішень.
Задача про трудові ресурси
Структура розглянутої задачі розподілу ресурсів була такою, що
змінні х -, у=1, 2, ..., и в ході побудови процесу можна було визна-
чати в довільному порядку (тобто їх можна було міняти місцями).
237
Зайченко 0.10., Зайченко Ю.П
Однак існує багато задач, в яких рішення мають прийматися в стро-
гій часовій послідовності, і тому змінні х,, гу не можна міняти міс-
цями. Такі задачі називають задачами послідовного прийняття рі-
шень. Для цих задач існує вибір між двома різними схемами
розв’язання [18; 49]:
-	розв’язання в прямому напрямку, коли перший крок схеми ди-
намічного програмування відповідає першому за часом рішенню, що
приймається;
-	розв’язання задачі в протилежному напрямку, коли останній
крок схеми динамічного програмування відповідає першому фактич-
но прийнятому рішенню.
Для пояснення цих двох схем звернемося до такої задачі.
Задача про використання трудових ресурсів
Підприємцю треба визначити оптимальну кількість робітників на
кожний з и місяців. Виробничі завдання для кожного місяця відомі,
що дає змогу визначити оптимальну кількість робітників на цей мі-
сяць. Припустимо, що в у -й місяць ідеальне число робітників дорів-
нює т ,. Якби підприємець міг звільняти та набирати нових робітни-
ків без додаткових витрат, то він в у -й місяць нттчяв би рівно т у
робітників (у=1, 2,..., л).
Нехай х — фактичне число робітників в у -й місяць. Витрати
на зміну кількості робітників при переході з (у -1) -го до у -го місяця
задаються функцією /у(ху-хуч). Залежно від знака різниці
Ху-х^ функція /у(ху-х () визначає витрати по найму (якщо
ху >ху_|) або по звільненню. Очевидно, /. (0)=0 
Відхилення чисельності від ідеальної величини ту призводять
до додаткових виробничих витрат, які задаються функцією
^у(ху-ліу), причому £у(0)=0, у=Гл- Припустимо, що в початковий
момент чисельність робітників становила т 0. Цільова функція зада-
чі г - сумарні витрати на виробництво та набір робітників визнача-
ються співвідношенням:
238
Дослідження операцій. Збірник задач
г = Х їїх> ~хі-0 +%з (х> ~т^'
7 = 1
де х0 = лг0. Треба знайти таку чисельність робітників в кожний мі-
сяць Ху, при якій сумарні витрати мінімальні.
Розв’яжемо цю задачу методом динамічного програмування.
Оскільки задано початковий стан системи х0, то використаємо схе-
му розв’язання в зворотному напрямку. Позначимо
Лл(£)=тіп{/„ (хл-^) + ^л(хл-тл)},
де £=*л-| •
Тоді основне рекурентне співвідношення матиме вигляд:
А* (£)=тіп{ [/к (хк(хк -тк )] + А*+І (хк)},	(5.1.13)
т*
де Аа(£) - мінімальні сумарні витрати за місяці з А-го по и-й
включно, якщо число робітників в (к—1) -й місяць дорівнювало Е, .-
Використовуючи (5.1.13), послідовно обчислюємо Ал(£),
Д„-і(^)’ •••• Д2 (£) Для всіх можливих значень Е,.
Нарешті, на останньому кроці при А=1 знаходимо оптимальну
чисельність робітників Х| в перший місяць при початковій умові
Х0 = 7П0.
Для цього знаходимо:
А|(^ = 7л0)=тіп{/1(х1-»іи) + й1(х1-7л1) + Л2(х1)} • (5.1.14)
Х1
Визначивши із (5.1.14) х1 і поклавши Е,] = х], із таблиці попе-
реднього кроку знаходимо х*(х‘), далі х3’=х3(х*) і т.д.
У розглянутому випадку розв’язання в зворотному напрямку
доцільне, бо невідоме число робітників наприкінці робіт, тобто на
(и + 1 )-й місяць.
239
Зайченко О.Ю., Зайченко Ю.П.
Розглянемо випадок, коли крім т0 задано також потрібну кіль-
кість робітників після закінчення робіт »і„+|. Шукатимемо цілі чис-
ла, для яких досягає мінімуму вираз:
2=І ІЛ	(х7	+	-*„)]	(5.1.15)
>=•
Тут можна записати:
2=тіп {/п+1(тл+|-х„)+
+ тіп ^[/,(ху-х ,)+^(ху.-/иу)]}.
•'і.
Оскільки тепер задано кінцевий стан системи, то
розв’язуватимемо задачу в прямому напрямку.
Визначимо послідовність функцій стану:
А* (£)= тіп {/*+1(£-ха) +#*+1(£-/иа+1) +
*|.-Ч
і	___
+ X Л (*7 -х7-і)+^>(тз *=1’п-
3=1
Тоді:
А1(^)=тш{/2(^-х1)+^2(«2-^)+/1(хІ-х0)+5|(?иІ-х1)}.
Основне рекурентне співвідношення ДП для цього випадку ма-
тиме вигляд:
Л*«)=тіп{/1+1(^-х4)+я*+1(^-«*+1) + Л4_1(х2)}, £=х,+|. (5.1.16)
Функція Лл(£) - не мінімальні витрати за перші (Л+1) місяців
при умові, що чисельність робітників у ( к +1 )-й місяць дорівнює Е,.
Використовуючи ОРС (5.1.16), послідовно обчислюємо Л( (£),
Л2 (£),..., Ал_( (£) для всіх можливих значень Е,-
240
Дослідження операцій. Збірник іадач
Нарешті, на останньому кроці при к = п, поклавши ^ = »і„+і, оде-
ржимо співвідношення:
Л,И=т„1)=п™!/,1і («„я-^Л+Ли-іОО}-	(5.1.17)
Визначивши із (5.1.17) оптимальне значення хп за таблицею по-
переднього (п-1 )-го кроку і, поклавши £= хп, знайдемо оптимальні
значення всіх інших змінних хп_1, хп_2,	. Підведемо деякі
підсумки вищерозглянутої задачі.
Нехай маємо задачу послідовного прийняття рішень на п пері-
одів. Якщо задано початковий стан системи, то задача розв’язується
методом динамічного програмування в зворотному напрямку; якщо
ж задано кінцевий стан системи, то - в прямому напрямку. Нарешті,
коли задані як початковий, так і кінцевий стани системи, то задачу
можна розв’язувати як в прямому, так і в зворотному напрямках. Ре-
зультати за обома схемами збігаються.
Приклад 5.1
Застосуємо метод динамічного програмування для розв'язку’за-
дачі про набір робітників із такими початковими даними: число мі-
сяців п = 4, потрібне число робітників піі = 2, т2 = 5, т3 = 3, ггц = 4;
число робіьників на початок роботи піо = 2. Нехай функції витрат
приймають вигляд:
_ 1 ЦХу -	), ЯКЩОХ} > х„, У(Х) Ху-1	^-Х^якщох.-х^,	//0);
'8(х/-т^х)>т/ ЯД/п: —х,) = 7 7	*	1 \(т. — ху),х7< ш;	«,(0) = 0.
Оскільки початкова умова фіксована, то задачу будемо
розв'язувати у зворотному напрямі.
241
Зайченко О.Ю., ЗайченкоЮ.П
Запишемо основне рекурентне відношення:
Л*(^) = тіп{/ДхА-^) + ^(хА-/иА) + Л4+І(х*)}, де £ = хі+І.
Крок 1 (к= 4):
Л4 (£) = тіп{/4 (х4 - £) + £4 (х4 - м4 )} = тіп П(х4, £).
*4	-Ч
Для пошуку Л4(£) складаємо допоміжну таблицю значень
£2(х4,£) (табл. 5.3). Оскільки всі функцій /1{х},-х^) та §)(т}-х/)
опуклі по змінних х , тоді і функція О(х4, £) опукла по х4 для всіх Е,.
Таблиця 5.3
	Х4	Ч		х4	ч
	0	11		0	32
	1	10		1	14
0	2	20	3	2	15
	0	18		0	39
	1	0		1	21
1			4	2	22
	0	25		0	46
	1	7		1	28
2	2	8	5	2	29
Таблиця 5.4
	л4(£)	х4
		
0	10	1
1	0	1
2	7	1
3	14	1
4	21	1
5	28	1
Тому для знаходження Л4(£) досить визначити перший віднос-
ний мінімум О4(х4,£) пох4, який і буде глобальним. Відповідно до
цього, значення функції £1(х4,£) обчислюємо лише для області зна-
чень х4, шо містить цей мінімум (табл. 5.3).
Обчислення виконуємо таким чином.
242
Дослідження операцій. Збірник задач
£ = 0,х4=0,
Я4 =0+11(1-0) = 11;
£ = 0,х4 = 1,
Я4 = 10(1 - 0 + 0 = 10;
£ = 0,х4=2,
Я4 = 10(2-0) + 8(2-1) = 28.
^ = 1,л4=0,
О4 = 7(1-0)+11(1-0) = 7+Н = 18;
£ = 1,х4=1.
П4=0+0 = 0.
£ = 2,х4=0,
П4=7(2-0)+11(1-0) = 25;
£ = 2,х4=1,
П4 = 7(2-1)+0=7.
£ = 2,х4 = 2,
П,=70+8(2-0) = 8.
£=3,х4 = 0,
Я4 = 7(3-0) +11(1-0) = 32;
£ = 3,х4 = 1,
О4=7(3-1)+0=14.
^ = 3,х4 = 2,
О4=7(3-2) + 8(2-1) = 15.
^ = 4,х4=0,
Я4=7(4-0)+11(1-0) = 39;
£ = 4,х4 = 1,
Я4 = 7(4-1)+0 = 21.
< = 4,х4 = 2,
Я4 = 7(4-2) + 8(2-1) = 32.
243
Зайченко О.Ю. Зайченко Ю.П
6.
£ = 5.л4=0.
П4 =7(5-О)+ 11(1-О) = 46;
£ = 5,х4=1,
Я4 = 7(5-1)+О=28.
£-5.х4=2,
Я4 = 7(5-2) + 8 = 29.
Результати заносимо в таблицю 5.3. Значення Л4 (£) = тіп П(х4, £)
для всіх	вибираємо з табл. 5.3 і вводимо в головну табл. 5.4.
Крок 2. Тут використовуємо рекурентне співвідношення:
Л3(£) = тіп{/3(х3-£) + #3(х3-ш3) + Л4(£)} = тіп£23(х3,£), а обчи-
гз
слення виконуються аналогічним чином. Допоміжні результати в
табл. 5.5, а підсумкові - в табл. 5.6.
Таблиця 5.5	Таблиця 5.6
£	х3	п3	£	*з	
	0	40		0	64
0	1	32	3	1	36
	2	38		2 3	25 14
	0	50		2	32
1	1	22	4	3	21
	2	28		4	29
	0	57		2	39
2	1	29	5	3	28
	2	18			
	3	24		4	36
£	Аз	хз
0	32	1
1	22	1
2	18	2
3	14	3
4	21	3
5	28	3
Крок 3. Обчислюємо для всіх можливих значень
л2 (£) = иііп{/2 (х2 - £) + £2 (х2 - т2) + А3(х2)} = тіп П2 (х2, <).
244
Дослідження операцій Збірник задач
Результати заносимо до таблиці 5.7 та 5.8.
Таблиця 5.7
5=4	•т2	
0	1	76
	2	71
	3	66
	4	72
1	2	61
	3	56
	4	62
2	2	51
	3	46
	4	52
3	2	58
	3	36
	4	42
4	2	65
	3	43
	4	32
	5	38
5	4	39
	5	28
	6	46
Таблиця 5.8
£	А,	х.		л-4
0	66	3	3	1
1	56	3	3	1
2	46	3	3	1
3	36	3	3	1
4	32	4	3	1
5	28	5	3	1
Таблиця 5.9
		О,
2	2	46
	3	54
Крок 4. Використовуючи початкову умову £ = х0 і підставляючи
його в співвідношення Л1(х0) = тіп{/(х1-х0) + ^І(хІ-ш,)+Л2(х,)},
• * *
знаходимо	і оптимальне значення змінної (л0) = 2 . Во-
ни приведені в таблиці 5.9. Далі, з табл. 5.8 по значенню £, = х1 = 2,
знаходимо оптимальне значення решти змінних х2 = 3 х3 = 3 х4 = 1.
При цьому мінімальні сумарні витрати складають Л! = 46.
245
Зайченко О.Ю., Зайченко Ю.П.
5.3.	Багатовимірні задачі динамічного програмування
Розглянемо задачу оптимального розподілу ресурсів, але вже при
двох обмеженнях [6; 18]:
тах£ Л
/=і
при обмеженнях:
п	п
’Е.а^х^Ьі; £ а2? х, <62 ; Ху >0 , ху - ціле.
>='	7=1
Оскільки в задачі маємо два види ресурсів Ь1 і Ь2, то треба ввес-
ти два параметри стану: Е, ।, Е, 2 -
Позначимо через
к
Л*«І,<2)=гпахХЛ(^)І	(5-2.1)
*	* 7=1
при обмеженнях:
*	к	__
X	; х «27 <7 ^2 ;	. 7=1. -ціле. (5.2.2)
7=1	з=і
Запишемо основне рекурентне співвідношення для цієї задачі:
Л*(£ц£г)={/*(**)'*’І\_І(£1— аікхк, ^2~а?кхк)}’	(5.2.3)
де
8 к =тіп-
аік
^2
«2*
Одночасно з ЛА(^, £2) знаходимо і відповідний оптимальний
розв’язок -**(£,, £2). Послідовно знаходимо Л1(^,,^2), ...»
Л*(£і,£г)’ •••’ Л„-і (£і > ^г)- На "-му кроці, поклавши £,= Ьу,
£ 2 = ^2. знаходимо ЛП (Ь}, Ь,), і водночас х° (Ь1, Ь2).
246
Досчідження операцій. Збірник задач
Оптимальні значення всіх інших змінних х°_, , х° 2.х® мо-
жна одержати із таблиць попередніх кроків за допомогою співвідно-
шень:
=х„-і (6, -а,„ х°; 62-а2п х°);
х°л-2 =х"-2	-«.„-і х°„-, і Ь2 -а2л х° -а2л_, х°_,)
І Т.Д.
Як бачимо, функції ЛА (£,, £2), хл , £2) є функціями двох
змінних (параметрів). Якщо кожна із змінних ^1,^2 може мати 10 2
значень, то функцію Л к (£,, £2) треба табулювати в 10 4 точках.
Коли маємо три обмеження вигляду
X а^х^Ьі , і=1,2, 3,	(5.2.4)
7=1
то для розв’язання задачі (5.2.1), (5.2.4) методом динамічного про-
грамування треба ввести три параметри стану £,,, Е, 2, з 1 функцію
А	). Коли кожен з параме грів Е,!, Е, 2> £ з набуватиме
10 2 значень, то функцію Л^^,,^,^) доведеться табулювати
вже в 10 6 точках. Як бачимо, обсяг обчислень за схемою ДП зростає
експоненціально залежно від розміру задачі (тобто від числа параметрів
стану т). Без спеціальних способів задачу, що містить більш як три
параметри стану, неможливо розв’язати на сучасних ЕОМ через над-
то великий обсяг обчислень, який зростає експоненціально залежно
від розміру задачі. Це плата за пошук глобального оптимального
розв’язку. Цей феномен Р.Беллман свого часу охарактеризував як
«прокляття багатовимірності» динамічного програмування [4; 16].
247
Зайченко О.Ю., Зайченко Ю.П.
Задача з двома змінними управління (керування)
Розглянемо попередню задачу в дещо зміненій постановці, коли є
дві змінні управління ху, у у і два типи ресурсів (Ь], Ь2), а дохід
І і (* /> У— 4е функція кількості обох типів ресурсів, розподіле-
них на даному кроці.
Отже, нехай треба
п
максимізувати	(Лу > Уу),
7=1
при обмеженнях:
X ачХ)<Ьі ; X а2іу :<Ь2 ;
7=1	;=1
%у>0; уу>0; а1у>0; а2у>0; Л1,Ь2>0.
Щоб описати стан системи на к -му кроці, знову треба ввести два
параметри Е,1, Е, 2. Визначимо функцію стану:
Л* (£і > £2)= ™ах £ /у (х., у/),
-•
при обмеженнях:
*	*
І	; X а2уу7<^2.
7 = 1	7=1
ОРС для цієї задачі має вигляд:
Л* ^2)=тах {Д (хк, ук)+^к_і (£,-аік хк; <2-а2к у4)},
причому максимум у (7.2.3) по х к, у к знаходять перебором усіх
можливих комбінацій. Наприклад, якщо х к, у к можуть набувати по
102 значень, то для знаходження ЛА(^,,^2) при фіксованих
Е,2 треба перебрати 10 4 значень функції
(Л* ’ Ук ' ’ £2) —{/* (Хк > Ук)+^к-\(^1 ~а\к Хк ’ ^2 ~а2кУк)}-
248
Дослідження операцій. Збірник задач
Отже, обсяг обчислень ще більше зростає порівняно з попере-
дньою задачею, і ми знову стикаємося з «прокляттям багатовимірно-
сті» Беллмана.
5.4. Динамічні задачі керування запасами
Якщо розглядається функціонування системи за п періодів, при-
чому попит нестаціонарний, то маємо динамічні моделі задач керу-
вання запасами. Такі задачі, як правило, не допускають аналітичного
розв’язання, проте оптимальну стратегію керування можна знайти,
застосувавши метод динамічного програмування.
1. Нехай розглядається задача керування запасами на п періодів,
коли попит в і -й період детермінований і визначається величиною
4 і , /=1, п.
Введемо такі позначення: у к - залишок запасу від (к -1 )-го пе-
ріоду; <1 к — попит в к -му періоді (к: = 1, п ); х к — запас, що створю-
ється в к -му періоді (або замовлення на поставку).
Припустимо, що замовлення на поставку виконується миттєво,
причому витрати на виконання замовлення (виробничі витрати) по-
значимо через Ск(хк,ук). Нехай 5к (хк +ук -сік) — витрати на
зберігання залишкового запасу в к -му періоді, причому дефіцит у
системі недопустимий.
Тоді сумарні витрати системи на виробництво та зберігання над-
лишкових запасів за п періодів становлять
Ьпт = ^к (хк ’Ук) + $к (Хк + Ук	(5.3.1)
*=1
при обмеженнях:
+Ук -4к=Ук+і> к = У п.
Треба знайти такі {х*}, {ук}, для яких (7.3.1) буде мінімальним.
Щоб мінімізувати Ь„т, скористаємося методом динамічного про-
грамування. Послідовно мінімізуватимемо витрати за 1,2...к пе-
249
Зайченко О.Ю., Зайченко Ю.П.
ріодів при умові, що на початку ( к +1 )-го періоду є залишковий запас
. Визначимо послідовність функцій стану:
А* (£)=шіп£ С?(ху ,у/) + 8} (х; +у}-<Т) =
7=1	(5.3..2)
І ’>’А
при обмеженні:
Хк+Ук~^к=^-	(5.3.3)
Тоді основне рекурентне співвідношення ДП запишеться так:
А* (£)=тіп{/, (хд ,У*)+АДІ(уЛ)}=
ж*	(5.3.4)
=тіп{/, (х, ,£-хк +О + ЛІЧ(^-х4 +ак),
лк
де
Хк+Ук~(ік=^-
На першому кроці (при Л=1) одержимо:
А, (<?)=тіп{/, (х, ,у,)} =тіп {С,(х, ,у,) +5, (Х( + у, -//,)},
при обмеженні:
Обчисливши послідовно ЛД^), Л2(£), ..., ЛД£), на остан-
ньому кроці, прийнявши £=у„+1, знайдемо Л„(у„+І) та х*(уп+|).
Оптимальні значення хк знаходимо далі послідовно за формулою
*»*=**| Ля + Е	-х]) ] •	(5.3.5)
V >=*♦!	)
2. Розглянемо окремий випадок, який значно спрощує обчислю-
вальну схему ДП. Припустимо, що:
усі функції С? (ху) вгнуті по змінних ху ;
250
Дослідження операцій. Збірник задач
функції витрат на зберігання запасів лінійні, тобто:
8з	+У> ~с1^ = 8з (У^=83	•
Тоді загальний вираз для функції витрат матиме вигляд:
£»г = | тіпД С,(ху)+$,ум,=тп _£ /,(*,,уЛ1),	С5-3 6)
при обмеженні:
х )+У і~У 3+і=(1 р 7=ПЛ-	(5.3.7)
Припустимо, що у і, у„+і задано, замовлення на поставки запа-
сів виконуються на початку періодів, часом на виконання замовлення
нехтуємо (поставки миттєві), а попит кожного періоду Н к має бути за-
доволений повністю (дефіцит не допускається). Треба відшукати такі
послідовності {ху}, {уу}, які мінімізують функцію загальних витрат
Т„7- в (5.3.6).
Розглянемо процедуру розв’язання. Оскільки треба знайти міні-
мум суми вгнутих функцій (хі ,_Уу+І) на опуклій множині, то оп-
тимальним розв’язком буде одна з крайніх точок допустимої множи-
ни розв’язків, яка визначається обмеженням (5.3.7).
Оскільки кількість обмежень дорівнює п, а загальне число змін-
них {ху} та {У;} дорівнює 2и, то оптимальний розв’язок містить
не більш як п ненульових значень змінних. З урахуванням того, що
ху , уу не можуть дорівнювати нулю одночасно (у протилежному
разі не виконуватиметься (5.3.7)), оптимальний розв’язок {х°,у°},
має властивість:
У°=0, 7 = 17^.
Умова (5.3.8) еквівалентна такій парі умов:
якщо ув=О, то ху>0,
якщо уу>0, то ху=0.
(5.3.8)
(5.3.9)
251
Зайченко О.Ю., Зайченко Ю.П.
Дослідження операцій Збірник задач
Пояснимо зміст умов (7.3.8), (7.3.9). Замовлення на виготовлення
(поставку) нової партії х у не робиться, якщо на початку періоду у
був ненульовий запас (у° >0), і навпаки, якщо на початку періоду у
запас у7=0, то робиться замовлення на поставку ху >0. Звідси ви-
пливає, що — 0, або х° = г/у, або х® = д у т<7у+1 і т.д., тобто
оптимальний розмір замовлення дорівнює попиту на ціле число пе-
ріодів.
Припустимо, що у„+1 =0. Тоді розв’язуємо задачу (5.3.6) в пря-
мому напрямку. Нехай ЛА (£) — мінімальні витрати за к періодів,
якщо запас на початок ( к +1 )-го періоду дорівнює Е,. Основне реку-
рентне співвідношення ДП для цієї задачі має вигляд:
А* (£) = гпіп{/а (хк ,£)+АА_, (£-х4 +</,)},	(5.3.10)
ч
при обмеженні:
^=>Л + 1 = *к +Ук~ак- *=1, и.
де (/) — витрати за к періодів за умови, що останнє замовлення
робилось на початку періоду і.
3. Розглянемо окремий випадок функції виробничих витрат на
виконання замовлення С} (х;)- Нехай
0 , якщо х • = 0;
А,+Сх/ , якщо ху >0,
де А у — фіксовані витрати на замовлення;
і0 , якщо х,=0;
<5,(х,) = { ,	л
7 7 II, якщо х) >0.
(5.3.15)
(5.3.16)
У розглядуваному випадку, оскільки х° у °к =0, мінімум у (5.3.10)
внаслідок вгнутості функції {Д (хА ,£)+А Д£-х4досягається
в одній з крайніх точок хк =0 або хк = Е,+йк.
У цьому випадку задача спрощується і зводиться до задачі ЛП:
мінімізувати
Тому
^(Лугу.(ху) + 57уА1),	(5.3.17)
7=1
ЛД£)=тіп
/Д£+Д;£)+Л, ,(0);
' /ДОіЯ+Л,., (£+<).
(5.3.11)
при обмеженнях:
хз+уз ~Уз+і і ’ ЛуТу=О.	(5.3.18)
Аналогічно:
л*-і (£ +Д)=пгіп
-/*- +	+ )+Л( 2(0);	12)
Л-,(о^+<)+л4 ,(£+Д+Д ,)
Виписавши вирази, аналогічні (5.3.12), для Л*_2(о), Л.к_і
А । і підставивши їх у (5.3.12) та (5.3.11), одержимо в результаті:
Використовуючи вирази (5.3.15)-(5.3.17) і підставляючи їх у
(5.3.14), одержуємо, з урахуванням, що ^=0, співвідношення:
2,(0 = Л ,_,(0)+ Аі + X 5 з І	(5319)
І = І	« = І + 1
Л4(0)=тіП£4(«).	(5.3.20)
А Д£) = тіл £,(,)
(5.3.13)
252
253
Зайченко О.Ю., Зайченко Ю.П.
Подальше спрощення в обчислювальній схемі можна отримати,
якщо врахувати таку обставину. Якщо при обчисленні Л ь 1 (0) ви-
явилося, що замовлення, за допомогою якого задовольнявся попит
(А-І)-го періоду, робилося на початку періоду V. то і замовлення,
яке задовольняє попит к -го періоду в оптимальному рішенні, має
виконуватися також не раніше періоду V. Отже, при обчисленні
ЛА (0) достатньо розглядати
А* (0)=тш £,(/).
(5.3.21)

Приклад 5.2.
Підприємство планує свою роботу на 7 місяців вперед. Для вико-
нання плану йому необхідно виробляти деякі деталі, що входять до
складу готових виробів. Хай місячна потреба (попит) у деталях дорі-
внює 61=20; 62=10; 63=25; 64=20, 65=10, 66=12, 67=16.
Витрати на виробництво х деталей в сі-місяці рівні:
Я<5(ху), якщо ху>0,
0, в протилежному випадку,
де А = 100 грн. — витрати на переналадку устаткування, яка прово-
диться тільки в ті місяці, коли випускаються деталі, а часом випуску
нехтуємо.
При виготовленні деталей на декілька місяців вперед з’являються
додаткові витрати на зберігання надмірного запасу. Питомі витрати
зі зберігання надмірного запасу складають 5 = 3 грн./місяць.
Визначити періоди виробництва деталей, а також обсяги вироб-
ництва х® при яких мінімізуються сумарні витрати по виробництву
продукції і зберіганню надмірного запасу за 7 місяців.
Іншими словами, необхідно знайти такі х°, для яких
£ = 100£	) + 3£у>+1 -> тіп.
>=•	7=1
при умові х +у. — <7. =уі+х,і = 1,...,7. Задачу потрібно розв’язати
за умови, що кінцевий запас у8 = 0.
254
Дослідження операцій. Збірник задач
Для розв’язку задачі скористуємося співвідношенням:
&(0 = 4-і(0) + 4+&
і=і
1.	Знаходимо д, (0) = л, = 100,
2.	Визначаємо
/4(0) = тіп
4+хс/2 = 100 + 310 = 130
4(0)+ А, =100 + 100 = 200
= 130.
3.	Розраховуємо
4+х(с/2+с73+с73) = 1ОО + 3-(1О + 25) + 3-25 = 28О
А3 (0) = тіп М, (0) + Л, +	= 100 +100 + 3 • 25 = 275
Л2(0) + Л3 = 130 + 100 = 230’
Л3(0) = 230, і=3.
Решту кроків виконуємо аналогічно, а результати заносимо в
табл. 5.10
Таблиця 5.10
Період к	1	2	3	4	5	6	7
Попит сік	20	10	25	20	10	12	16
і=1	100*	130(*)	280				
І=2		200	275				
&(0і=3			230(*)	290(*)	350(*)	466	
і=4				380	405	432	
і=5					390	425(*)	522
1=6						450	498(*)
І=7							526
ЛД0)	100	130	230	290	350	425	498
	1	1	1	1	1	1	1
			3	3	3	3	3
Період						5	6
255
Зайченко О.Ю., ЗайченкоЮ.П
У кожному стовпчику цієї таблиці зірочкою відмічений міні-
мум (/), який рівний ЛА (0). У останньому стовпчику таблиці вка-
зані номери періодів, в які випускаються деталі, /—1,3,6.
Звідси: х® = //,+<, =30, х3 =//3+Л4+//5 =55, х" = <+//7 = 28,
х° = 0, х° = х° = 0, х° = 0.
Цьому плану відповідає мінімум витрат Л7(0) — 498 .
5.5. Нескінченно шагові процеси
динамічного програмування
Способи оцінки нескінченних послідовностей ефектів (витрат)
Розглянуті вище моделі задач планування та керування (напри-
клад, трудовими ресурсами або запасами) охоплювали деякий інтер-
вал часу, який складався із скінченого числа періодів (відрізків). Як-
що функціонування системи на цьому не закінчується, то раніше
прийняті рішення безумовно впливають на її поведінку в майбутньо-
му. З такої точки зору ці моделі можна розглянути як елементи не-
скінченного планового періоду. При цьому сам нескінченний плано-
вий період можна трактувати як межу скінченого планового періоду
при И->оо .
Для того, щоб у моделях з нескінченним плановим періодом
отримати певні рішення, вводиться обмежуюче припущення про ста-
ціонарність, яке означає, що всі функції витрат або ефектів (економі-
чних) та зовнішні умови для кожного з періодів стаціонарні або змі-
нюються циклічно. Якщо ж розглядається імовірнісна система, то її
імовірнісні характеристики також вважаються стаціонарними.
Перш ніж розглянути методи прийняття рішень при нескін-
ченному плановому періоді, викладемо основні способи оцінки та
порівняння нескінченних послідовностей ефектів (або витрат).
Існує три основних способи оцінки таких послідовностей [5, 16]:
1) середній ефект за інтервал часу - СЕ; 2) інтегральний дисконтова-
ний ефект - ІДЕ; 3) еквівалентний середній ефект - ЕСЕ. Розглянемо
256
Дослідження операцій. Збірник задач
ці оцінки. Припустимо, що деякій стратегії керування системою від-
повідає така послідовність ефектів (витрат):
. Я „.тоді СЕ = 1іт-£
п-+<к П & =]
Головний недолік критерію СЕ полягає в тому, що він однаково
оцінює як прибуток, одержаний у даний момент, так і майбутній до-
ход. Водночас цінність того самого прибутку зараз і в майбутньому
через Л часових інтервалів (наприклад кроків), зовсім неоднакова,
через дію інфляції. Щоб урахувати цю нерівноцінність, вводиться
коефіцієнт дисконтування а (0<а<1), за допомогою якого всі по-
слідовності майбутніх ефектів (прибутків або витрат) зводяться до
теперішнього часу.
В результаті приходимо до інтегрального дисконтованого ефекту.
ІДЕ	. +	/?„+...= У Кь •	(5.4.1)
*=1
Величину а можна обчислити, наприклад, як
річна процентна ставка (тобто річні проценти, що одержує вкладник
за гроші, вкладені в банк).
Зв’язок між критеріями СЕ та ІДЕ здійснюється через еквівалент-
ний середній ефект (ЕСЕ).
Під ЕСЕ розуміють таку величину ефекту, сталу для всіх інтерва-
лів часу, А=1, оо, що ІДЕ для послідовності із значень ЕСЕ і для ви-
хідної послідовності збігаються.
Припустимо, ЩО ДЛЯ ПОСЛІДОВНОСТІ , Л2 »—•
ІДЕ= ^ак~' Пк=Р(а).	(5.4.2)
*=1
Позначимо ЕСЕ через х(«) . Маємо послідовність
х(а) + ах(а)+а2 х(а)+...+а* х(а)=(1 + а+а2 +...).г(ог)=Л — •
1-а
257
Зайченко О.Ю, ЗайченкоЮ.П
Оскільки за значенням обох послідовностей величини ІДЕ збіга-
. х(а)
ються, то Р(а) =— -, звідки:
1-а
ЕСЕ = х(а)=(1-а)Р(а)=(1-а) ІДЕ. (5.4.3)
Приклад 5.3. Модель експлуатації лісового господарства. Для
ілюстрації використання введених оцінок розглянемо таку задачу.
Ліспромгосп планує засадити лісом нову земельну ділянку. Припу-
стимо, що дерево, зрубане в *-й відрізок часу (наприклад, в *-й
рік), з моменту його посадки принесе прибуток кк (грн.). Припус-
тимо також, що витратами на посадку та догляд за лісом можна
знехтувати і що всі дерева на ділянці мають бути зрубані одночас-
но. Треба визначити оптимальний момент (рік) * рубання лісу, при
якому досягається максимальний прибуток при коефіцієнті дискон-
тування а. 0<а<1 .
1. Розглянемо спочатку випадок, коли після вирубання лісу не
робитимуться нові насадження (одноразове прийняття рішень).
Треба знайти таке значення * , що
[ДЕ(*)=	>тах
к
Шукане значення к визначається таким співвідношенням:
Кк-\	Кк
	<а<	
Кк--------л4+1
2. Тепер розглянемо нескінченний плановий період. Припусти-
мо, що кожного разу після вирубання лісу на * -му інтервалі часу,
на (л+і)-му здійснюються нові насадження лісу, причому цей про-
цес повторюється нескінченну кількість разів. Якщо кожного разу
рубання лісу здійснюється через * відрізків після посадки, то ІДЕ
послідовності прибутків для нескінченного планового періоду дорі-
внюватиме:
Е (к)=ЩЕ [ £]( 1 + ак + агк +...).
258
Дослідження операцій. Збірник задач
Звідси
/7(Л)=Я*1.	(5.4.4)
Оптимальною для нескінченного планового періоду є така стра-
тегія к, для якої максимізується величина Р (к):
Р* = шах Р (к) = тах	-	(5.4.5)
к	к=\л,- 1-а
Шукане значення к 0, при якому Р (к) досягає максимуму, ви-
значається за умови:
/Д£[1]</ДД2]	<ЩЕ[к0]>ЩЕ[к°+\]>	(546)
1-а	1-а2 " 1-а*"	1-а*4'
Звідси приходимо до співвідношення
При цьому оптимальне значення *° задовольняє нерівності
к0	, де к - оптимальне значення при одноразовому прийнятті
рішень.
5.6.3адачі динамічного програмування
на мережах
Багато динамічних задач оптимального планування та керування
(наприклад, керування запасами, розподілення ресурсів та ін.) можна
подати у вигляді мережі (або графа), в якій кожному стану системи
відповідає деяка вершина мережі і задача оптимального керування
зводиться до задачі відшукання найкоротшого маршруту в мережі
(на графі).
259
Зайченко 0.10. Зайченко Ю П
Розглянемо, наприклад, деяку мережу, що містить Р вершин, і м-
ножину орієнтованих дуг, які з’єднують деякі вершини (рис. 5.1).
Поставимо у відповідність кожній допустимій стратегії в стані і ду-
ГУ 0, У)- Переміщенню по кожній дузі (/, у) відповідають певні
витрати (ефект) С,7. Припустимо, що час переміщення із вершини і
у вершину у дорівнює одному часовому відрізку, а коефіцієнт дис-
контування (дисконт-фактор) позначимо через а.
Нехай маршрут починається з деякої довільної вершини і. При-
пустимо, що із вершини у переходимо до вершини к, при цьому ви-
никають дисконтовані витрати С^к. Якщо процес триває протягом не-
обмеженого часу, то маршрут є нескінченним.
Позначимо через у, інтегральні дисконтовані витрати (ІДВ) для
оптимального нескінченного маршруту, який починається з вершини
і. Якщо вибрана стратегія є стаціонарною, кожного разу, повернув-
шись до вершини і, знову виберемо ту саму стратегію (і, к) (тобто
дугу), що і в попередньому разі знаходження в цій вершині.
Нехай існує стаціонарна стратегія, яка є оптимальною, тоді відпові-
дні величини ІДВ задовольнятимуть таку систему функціональних
рівнянь:
у =тіп(ау +с. ) для всіх вершин і; 0<а<1.	(5.5.1)
’ І і. Л 1	'>
Виникають питання:
Чи завжди можна для всіх значень у,- відшукати однозначний
і скінчений розв’язок?
Якщо відповідь на перше питання - «так», то чи буде відповідна
стаціонарна стратегія справді оптимальною?
Відповіді на обидва запитання ствердні. Вони випливають із тео-
реми про стаціонарну стратегію [5;
16].
Завжди існують однозначно ви-
значені скінченні у і, ї=1, Р, і відпо-
відна стаціонарна стратегія є оп-
тимальною.
260
Дослідження операцій Збірник задач
Розглянемо методи розв’язання системи функціональних рівнянь
(7.6.1) і відшукання оптимальних стратегій.
Метод ітерацій за критерієм
Розглянемо систему функціональних рівнянь вигляду:
у =гпіп(«у,+С.) для всіх /=1, Р.
(/.» ‘ '
Її розв’язання методом ітерацій за критерієм складається з таких
кроків.
1.	Задаємося початковими значеннями у? (наприклад, у,-0)=0) та
и=0.
2.	Обчислюємо у.л+,) =тіп(а у(п) + С, ) для всіх і.
(».у)	'	•'
3.	Якщо у-"+1) =Уі для всіх і, то скінчити обчислення, у про-
тилежному разі - переходимо до другого кроку чергової ітерації, взя-
вши п = п + 1 .
Якщо всі у <°> =0 і всі С,7- >0 , то значення у7-п> зростають моно-
тонно і кожне з у <п) збігається до своєї межі, однак збіжність не га-
рантується за скінченне число ітерацій.
Метод ітерацій за стратегіями (в просторі стратегій)
Розглянемо метод ітерацій по стратегіях для розв’язання системи
функціональних рівнянь (5.5.1).
Перший крок. Виберемо довільну початкову стратегію і покла-
демо у^о,=О, 1=1,/’. Зауважимо, що вибір стратегії означає вибір
деякої дуги С у для кожної вершини.
Другий крок. Для заданої пробної стратегії обчислимо значення
у}п) згідно з системою рівнянь (розрахунку «вартості» вершин):
у(">=ау<.")+С/7 або у}п)-ау<л)=С,7,	(5.5.3)
261

Зайченко О.Ю.. Зайченко Ю.П.
де дуга (/, у) відображає вибрану пробну сгратегію для стану (вер-
шини) і.
Третій крок. Перевіримо можливість дальшого поліпшення стра-
тегій, для чого обчислимо:
тіп(ау‘я) + С. )=К.<И) для всіх і.	(5.5.4)
(<•>) 1 1
Четвертий крок. Якщо = для всіх і, то скінчити обчис-
лення. Поточна стратегія буде оптимальною. У протилежному випа-
дку змінити поточну стратегію для кожної вершини к такої, що
Для цього за нову стратегію виберемо дугу, яка дає змогу
досягти значення в (5.5.4). Перейдемо на другий крок (и + 1)-ої
ітерації з новою пробною стратегією.
Метод ітерацій за стратегіями має такі властивості:
для будь-якої вершини і у-п+І)£у;П) і, якщо	’ то
ИЯ+,)<ИП);
у к у к ’
алгоритм є скінченним;
стратегія, що дає змогу по закінченні обчислень досягти у,, і=1,Р, є
оптимальною.
Мінімізація середніх витрат
Розглянемо випадок, коли критерій оптимізації мережі являє со-
бою середні витрати (ефект) за інтервал часу.
Припустимо, що середні витрати для даної моделі існують і по-
значимо їх мінімальне значення через С. Крім того, припустимо, що
в розглядуваній мережі існує орієнтований маршрут від будь-якої
вершини і хоча б до однієї з вершин, що входять у відповідний мі-
німальний цикл.
Побудуємо функціональні рівняння для визначення С.
262
Дослідження операцій. Збірник задач
Нехай у і — ІД В для системи (мережі), якщо її поточний стан у
даний момент є і. Тоді еквівалентні середні витрати (ЕСВ) для сис-
теми в початковому стані і дорівнюватимуть (1 — а)уі.
ЕСВ для кожної вершини і зручно зв’язати з С таким співвід-
ношенням [16]:
+С, 0<«<1 ,	(5-5.5)
де и ,- — «вага» і -ої вершини.
Тоді
Уі = ^і+-^~ •	0<а<1.	(5.5.6)
1-а
Підставивши у,- з (5.5.6) в (5.5.1), після нескладних перетворень
одержимо функціональне рівняння у вигляді:
гг =шіп(«и', +С -С),	(5.5.7)
' Щі.Л у 7
або в такому еквівалентному вигляді:
+С = тіп(аи’ +С, ) Для всіх вершин і.
‘	*(і.7)	7	‘7
Якщо а=1, одержимо шукані функціональні рівняння:
и' +С = тіп(и'. +С ) для всіх вершин і. (5.5.8)
' 7 '7
Для розв’язання функціональних рівнянь (5.5.8) доцільно скорис-
татися методом ітерацій за стратегіями. Зауважимо, що коли обчис-
лено значення м',-, які задовольняють функціональні рівняння (5.5.8),
то і значення и,/ =»г,- +а для всіх і, де а - деяка довільна констан-
та, також є розв’язками цієї системи. Таким чином, розв’язки іг,- не є
єдиними і для зручності доцільно взяти одне з них таким, що дорів-
нює нулю (наприклад, =0).
Припустимо, що на кожній ітерації пробна стратегія, що переві-
ряється, утворює рівно один цикл.
263
Зайченко О.Ю., Зайченко Ю.П.
Алгоритм методу ітерацій за стратегіями складається з таких процедур.
Перший крок. Виберемо довільну пробну стратегію, тобто для
КОЖНОЇ вершини І деяку дугу (/, у), І покладемо И’| =0.
Другий крок. Для вибраної пробної стратегії обчислимо значення
м:п), і=І, Р та С(л) розв’язавши таку систему рівнянь:
+ с ~си для вс’х ' ’	(5-5.9)
де дуга (і, )) відображає поточну пробну стратегію в стані і.
Третій крок. Перевіримо можливість подальшого поліпшення,
обчисливши:
тіп (	+С.-.- -С^ )=щ/л> для всіх і.	(5.5.10)
Четвертий крок. Якщо Я'/”* для всіх т=1,Р, то зупинитися.
Поточна стратегія оптимальна. У протилежному разі замінити поточ-
ну стратегію для кожної вершини к такої, що И^л) , вибравши
відповідну дугу, яка дає змогу досягти значення И'А(л) в (5.5.10). Пере-
йти до другого кроку ( п +1 )-ої ітерації при новій пробній стратегії.
Отже, на кожній ітерації треба розв’язувати систему функціона-
льних рівнянь (5.5.9). Якщо пробна стратегія, що перевіряється,
утворює лише один цикл, то рівняння (5.5.9) завжди матимуть єди-
ний розв’язок [5].
Зауважимо, що якщо скласти рівняння (5.5.9) для всіх вершин, які
входять у цикл, то всі ваги м'(л) зникнуть, отже, одержимо:
с(л,=- X си,
де А - сукупність дуг, які утворюють цикл, а ти - кількість дуг у цьому
циклі.
Даний алгоритм має такі властивості [5, 16]:
на кожній ітерації с(")>С<"+,);
264
Дослідження операцій. Збірник задач
У обчислення закінчується після скінченого чис-
ла ітерацій;
, оптимальною є та стратегія, яка дає можли-
вість досягти значень IV-,, при цьому
С(л)=С=тіп.
рис 5 2	Приклад 5.3. Розглянемо мережу, що зо-
бражена на рис. 5.2. На її дугах проставлено
відповідні значення с,7 . Для того, щоб засто-
сувати метод ітерацій за стратегіями, треба вибрати початкову про-
бну стратегію, в якій для кожної вершини і є одна дуга, що вихо-
дить з неї. Нехай такою пробною стратегією є така:
для вершини 1 - дуга (1,4);
для вершини 2 - дуга (2,1);
для вершини 3 - дуга (3,2);
для вершини 4 - дуга (4,1).
Таким чином, ця стратегія включає єдиний цикл (1,4)-(4.1).
Складемо систему функціональних рівнянь для вибраної пробної
стратегії:
у<0’=«Х0)+с21,
 у™=ау™+Сіг,
у1*=ау™+Сп.
Її можна записати в такому еквівалентному вигляді:
' у™-ау™=3,
у™-ау{°'=4,
' уГ-«Н0,=і.
у^-ау[п=1.
Розв’язок цієї системи такий:
(0) 3 + 1а	(0) 4 + За-За2	(0) 1+4а+2а2-За3	(0) _ 1 + За
1 =----5"’ у2 ~------з--’ -У3----------т > і 2
1	1-а2	1-а2	1-а2	1-а
265
Зайченко О Ю, Зайченко ІО П
Як видно з рис. 5.2, зміна розв’язків можлива лише для вершин
1 і 2, де мається більше однієї дуги, що виходить з них.
При о<а <і, згідно з формулами (1) для вершини 1, одержимо:
- .	(0)	<о>	, І 4+4а-а2-Зо’ 3+а
тш(а^‘ * + СІ2 ; а у' ’+См)=тіп^-------; ----
\-а	1-а
: 3 + « =у(0>
1-а2	1
ДЛЯ дуги (1,4) прио<а <1 .
Аналогічно для вершини 2:
тіп (а	+С2І; а >5” + Сп )=тіп
4+За-За2 4+а +2а3-За4
1-а2	’ Г^а2
(2)
4+За-За2
1-а2
= Г2"”,
для дуги (2,3) при у 5а <1 .
Таким ЧИНОМ, ЯКЩО у 5а<1, ТО для кожної вершини і викону-
ється умова у2(0) =у<0), і початкова стратегія є оптимальною. Якщо
“<-|, то мінімум досягається на дузі (2,3), і цей розв’язок повинен
на наступній ітерації замінити стратегію (2,1).
Приклад 5.4. Розглянемо знов ту саму мережу (рис. 5.2) при
а=і і покладемо с2з=з. Нехай треба знайти оптимальну стратегію,
яка мінімізує середні витрати за інтервал часу.
За початкову пробну стратегію виберемо ту саму, що і в при-
кладі 5.3, і, застосувавши формули (5.5.9), запишемо таку систему
функціональних рівнянь:
<>-иД0,=С14-С(0’;
^°’-^0)=С21-С<<”;
<)-и40,=С32-С‘0) ;
^0,-^0’=с41-с(0).
266
Дослідження операцій. Збірник задач
Ця система мас розв’язок:
С(0,=2; и’}0,=0; и’‘0) = 2; и'<0) = 1. и><0,=-І.
Розрахунок показників можливого поліпшення
за формулами (5.5.10) дає такі нові значення для ва-
гових коефіцієнтів и-,:
для вершини 1:
тіп(<> + С12-Г'0>, ^0,+С14-С<0’) =
=тіп(2+4-2, -1+3-2)=0=Я,1 (для дуги (1,4));
для вершини 2:
тіп^и’1(0)+С2і-С(()), м^0)+С23-С(О) ^=2=^2
(для дуги (2,1)). Оскільки IV х =н1(0) ,	= Ц0) , то знай-
дено оптимальну стратегію, для якої с=с(0)=2.
Динамічна задача керування запасами
з нескінченним плановим періодом
Розглянемо важливу з практичного погляду дина-
мічну задачу керування запасами з нескінченним
плановим періодом, яка являє собою узагальнення
динамічної задачі зі скінченним плановим періодом.
Нехай маємо систему постачання, яка виробляє
продукцію, накопичує її в запас і постачає замовнику
відповідно до попиту. Вихідні дані системи (задачі)
такі: обсяг випуску продукції х<5 од., попит на інтер-
валі часу сталий і дорівнює ії=3 од., при цьому рівень
запасів на кінець інтервалу часу має задовольняти
умову у < 4. Витрати на виробництво С (х) обсягу
випуску продукції х задаються співвідношенням
С(х)=
0, якщо х=0,
13 + 2х, якщо х>0,1<х<5.
Рис. 5.3
267
Зайченко О.Ю., Зайченко Ю.П
Витрати на зберігання запасу рівня у дорівнюють Л7, де Л=1.
Припустимо, що система функціонує безмежно довго. Треба визна-
чити таку оптимальну стратегію керування запасами (тобто знайти
обсяг випуску х у кожному інтервалі (відрізку часу)), при якій міні-
мізуються середні витрати за відрізок.
Виберемо рівень запасів на початку відрізка і (де і = 0, 1, 2, 3, 4)
за змінну стану системи. Стаціонарна стратегія являтиме собою пра-
вило визначення оптимального обсягу випуску продукції для кожно-
го значення і.
Для розв’язання цієї задачі треба передусім подати її у вигляді
мережі (сітьової моделі). Кожному можливому стану поставимо у
відповідність одну вершину мережі; при заданому і кожному допус-
тимому обсягу випуску відповідає деяка дуга {і, /). Так, якщо рі-
вень запасів на початку відрізка дорівнює і, обсяг випуску становить
х одиниць, а попит </ = З одиниці, то запас у на початку наступного
відрізка дорівнюватиме у=ї+х-3. Отже, дуга (/,/) відповідає об-
сягу виробництва х=у-/ + 3.
Таким чином, витрати при виборі стратегії (дуги) (і, /) задають-
ся виразом:
С,-у=С(у-ї+3)+А,.	(5.5.11)
У зв’язку з існуванням обмежень на обсяг випуску х та рівнянь
запасів, деякі сполучення і та у недопустимі. Наприклад, при і = 0
має бути у < 2, оскільки х < 5.
Мережу, яка відповідає умовам задачі, наведено на рис. 5.3. При
цьому величини С/у обчислені згідно з(5.5.11).
Припустимо, що за критерій оптимальності взято мінімум серед-
ніх витрат (СВ) за інтервал часу. Тому функціональне рівняння, що
його треба розв’язати, має вигляд:
и'(=тіп(и'у+С(у-С) для всіх і.
За пробну стратегію виберемо таку: випускати недостатню для
повного задоволення попиту кількість продукції при і < 3, так щоб
рівень запасів на кінець інтервалу часу дорівнював у=0; і взагалі
268
Дослідження операцій. Збірник задач
нічого не випускати, якщо на даному інтервалі і = 4 . На мережі цю
стратегію представляють так (див. рис. 5.3):
вершина 0 - дуга (0,0), х = 3;
вершина 1 - дуга (1,0), х = 2;
вершина 2 - дуга (2,0), х = 1;
вершина 3 - дуга (3,0), х = 0;
вершина 4 - дуга (4,1), х = 0.
Розв’язання. Перша ітерація. Використовуючи алгоритм ме-
тоду ітерацій за стратегіями, складемо систему функціональних рів-
нянь, які відповідають пробній стратегії:
 <>-.и,<0)+С(0’=С00=19;
„<0’-ї,<0,+С<0,=С10=17;
^<0,-и-<0)+С(0,=С20=15;
и-'о,-и-<о,+С(О,=Сзо=О;
<-^0, + С(0,=С„=1;
<>=0.
Її розв’язок такий:
С(°>=19; ^0)=0, и><°)=-2; ^0)=-4; ^°>=-19; и,<°>=-20.
Для всіх і обчислюємо:
И7/"’ =тіп(и'^") +С,, -С(я)), і отримуємо:
И/0(0) = 0 для дуги (0,0);	= -12 для дуги (1,3); И'2(0^ = -14 для
дуги (2,3); И/3(0) =-19 для дуги (3,0); И/4(0) = -20 для дуги (4,1).
На цьому перша ітерація закінчується. Оскільки
і IV <м'*°\ то треба перейти до другої ітерації, а за нову пробну
стратегію вибрати таку: (0,0), (1,3), (2,3), (3,0), (4,1). Результати об-
числень, одержані в ході виконання ряду послідовних ітерацій наве-
дено в табл. 5.11.
269
Зайченко О.Ю., Зайченко Ю.П
Таблиця 5.11
Вер- ши- на	0			1			2			3		
	О.Т)	щ<0)	И'/°>	0,7)	уу/”	и<(,)	0.7)	у,/2’	И?2’	0,7)	щ<3)	И'<3>
0	0,0	0	0	0,0	0	-9	0, 1	0	гм | гл 1	0,2	0	0
1	1,0	-2	- 12	1,3	- 12	- 12	1,3	7 -4— 3	А,	1,2	-2	-8
2	2,0	-4	- 14	2,3	- 14	-22	2,4	-ці 3	-111 3	2,4	-8	- 10
3	3,0	- 19	- 19	3,0	- 19	-24	3,4	-13— 3	-17— 3	3,0	- 17	- 17
4	4, 1	-20	-20	4, 1	-20	-20	4, 1	-21	-21	4, 1	- 18	- 18
	19			19			17— 3			17		
Продовження табл. 5.11
Вер- ши- на	4			5			6		
	0,7)	уу/4’	И?4)	0,7)	у^ст		0,7)	(4)	И'/4’
0	0,2	0	- 1	0, 1	0	- 1	0,2	0	0
1	1,3	<м|м 1	еч | гл о 1	1,3	-6	-6	1,3	СЛ 1 «л «л 1	•л 1
2	2,3	1 00 Ш 1 ю	-ЦІ 3	2,4	- 10	- 10	2,4	-9± 5	-9І 5
3	3,0	-1б1 3	-16— 3	3,0	-16	- 16	3,0	-15-1 5	-15-1 5
4	4, 1	-22	-22	4, 1	-21	-21	4, 1	-20— 5	-20— 5
-(я) с	16— 3			16			15— 5		
270
Дослідження операцій. Збірник задач
Аналізуючи цю таблицю, можна зробити
такі висновки:
на першій ітерації значення С(л) не поліпшу-
ється (С(0) -С(,) V
на всіх наступних ітераціях п =2, 3, 4, 5, 6 ви-
конується умова С(л) <С(п-1);
після шостої ітерації знайдено оптимальну
стратегію керування запасами. Вона має ви-
гляд:
х=5 при У=0, 1, 2; х=0 при у= 3, 4. їй
відповідає виробничий цикл (5, 5, 0, 5,0).
При цьому середні витрати мінімальні
—	4
Стіп =15—. Відповідний мінімальний цикл
наведено на рис. 5.4.
26
Рис. 5.4
Задачі та вправи
Розв’язати такі задачі динамічного програ-
мування:
5.1.	Управління науково-дослідними роботами (НДР) щорічно
розподіляє асигнування між науково-дослідними і проектними інсти-
тутами на пошукові НДР, дослідно-конструкторські розробки (ДКР)
і роботи, пов’язані з поліпшенням якості продукції, що вже випуска-
ється. Якщо позначити через грсорх. асигнування (тис. грн.), що
виділяються в ]-м інституті на виконання НДР, ДКР і робіт з поліп-
шення якості продукції, то оцінки очікуваного ефекту будуть рів-
ні (уі ),	), Я, (*,), ) =1 ,.,п.
Хай загальна сума асигнувань між інститутами не перевищує N
тис. грн., а верхня межа асигнувань, які може одержати інститут ),
дорівнює
271
Зайченко О.Ю., Зайченко Ю.П.
Розподілити асигнування між інститутами так, щоб забезпечити
максимум загального економічного ефекту галузі при введених об-
меженнях.
Скласти математичну модель задачі і записати ОРС динамічного
програмування для її розв’язку.
5.2.	Дослідити завдання 5.1 за додаткової умови, що асигнування
виділяються також на фундаментальні дослідження, і оцінка еконо-
мічного ефекту, яку одержить галузь при виділенні асигнувань в
об’ємі у, рівна (У;) . Показати, як необхідно змінити постановку
завдання і які зміни потрібно внести в ОРС Беллмана.
5.3.	У підшефний радгосп з міського підприємства були направ-
лені 10 чоловік для прибирання помідорів на одному із трьох полів.
За оцінкою директора, виділивши у чоловік на поле, можна зібрати
урожай Я,(у,), де Я1(1) = 50,ЯІ(2) = 100,Я1(3) = 150,Я1(4) = 250,
Я, (5) = 350, Я, (6) = 500, К2 (1) = ЗО, К2 (2) = 60,
К2 (3) = 120, Я2 (4) = 180,/^ (5) = 300,
Я2(6) = 55О,Я3(1) = 200, Я3 (2) = 350Я3(3) = 450Я3(4) = 550,
Я3 (5) = 600, Я3 (6) = 650.
Якщо направити на кожне поле більше 6 чоловік, то це не збіль-
шить зібраного урожаю. Скільки працівників слід направити на кож-
не поле, щоб зібрати найбільший урожай? Побудувати відповідну
модель завдання динамічного програмування і знайти її оптимальне
рішення. Показати, як зміниться рішення, якщо для збору помідорів
будуть направлені 12 або 14 чоловік.
5.4.	Дослідити завдання 5.3 за умови браку міських працівників.
Мінімізувати число міських працівників, направлених на прибирання
овочів за умови, що з трьох полів потрібно зібрати не менше Я кг
помідорів. Сформулювати завдання в термінах динамічного програ-
мування і знайти оптимальне рішення за умов; а) /? = 800 кг;
б)	Я2 = 1000; в) Я3 = 1100 кг
5.5.	Досліджуємо ще раз завдання 5.3. Припустимо, що директор
прагне витратити не більше М людино-дня на прибирання овочів на
трьох полях. Йому відомо, що якщо направити на будь-яке поле від
одного до трьох чоловік, то для збору помідорів буде потрібно З лю-
272
Дослідження операцій. Збірник задач
дино-дні. Якщо ж направити на одне поле більше трьох чоловік, то
вони витратять 1 людино-день. Як потрібно розподілити 10 чоловік
для роботи на трьох полях за умов: а) М = З, б) М = 4.
5.6.	Календарне планування трудових ресурсів. Підприємство пла-
нує свою роботу на N періодів (місяців). Обсяг робіт у різні періоди не
залишається постійним. Позначимо через тк оптимальне число праців-
ників у к-й період, що дозволяє виконати заданий обсяг робіт з най-
меншими витратами. При числі працівників хк(хк X тк) підприємство
несе додаткові виробничі витрати %к (хк -тк), причому (0) = 0 -
Підприємство може варіювати число працівників. Позначимо че-
рез /(хк - хА_]) витрати з найму-скороченню працівників при пере-
ході к-1 -го періоду в к-й. Приймемо /(0) = 0.
Визначити таке число працівників у кожному періоді хк, до =
1.,М при якому мінімізується сума виробничих витрат і витрат по
найму-скороченню за весь час роботи підприємства. Прийняти, що
перед початком роботи х0 = 0.
Скласти математичну модель завдання і розв’язати її методом
динамічного програмування.
1.	^ = 5,т| =5,т2 =10,/и3 =14, т, = 20,т5 =10;
Гб(х4 -тк),хк >тк
[10(^ -хДх*<тк,
,, ч ^(хк-хкч),хк >хк_},
/(**-**-,) =
4(^-і ~хк),хк<хм.
2.	N = 5, ти, =5,ти2 = 10, т3 = 14,лн4 = 20,тп5 =10;
&(хк-тк) =

\0(хк-тк),хк>тк
6(тк -хк),хк<тк,
\5(хк-хк_і),хк >хкА,
— х*)»Л*<хк.г
Розв’язати задачу при додатковій умові, що після закінчення ро-
боти число робітників має дорівнювати 0.
273
Зайченко О Ю, Зайченко Ю.П.
3.	N = 5,пі, =5,т2 =15, пі, = 12, т, = 10,лі5 =5;
^(х4-т11) = 2(х4-т4)2;
, _	, р(х*-х1ч),х4 >х4_„
/и* **-,) |10(Х1і_хдХ4<Хкі.
5.7.	Динамічна задача управління запасами. Підприємство має
розробити календарну програму випуску деталей на плановий пері-
од, що складається з N відрізків часу. Попит на продукцію іїп, п = 1,
А, що випускається в кожен відрізок часу, відомий. Часом виготов-
лення деталей нехтуємо. Вартість випуску партії деталей С(хп) за-
лежить від її обсягу хп.
Підприємству може виявитися вигідним виготовляти протягом
деякого відрізку часу продукцію в обсязі, що перевищує попит, і збе-
рігати надлишки, щоб використовувати їх у подальші відрізки часу.
Зберігання запасів пов’язано з певними витратами, які позначи-
мо 5(уп+1), де уп+І — надмірний запас, що зберігається на відрізку
часу п. Скласти таку програму випуску хп, в кожному з відрізків ча-
су, при якій мінімізується загальна сума витрат на виробництво і збе-
рігання запасів, за умови повного задоволення попиту на продукцію.
1.	А = 6,/(хи,уи+І) = С(х„)+%+1,
СО,х =0,
С(хя) = {
"	|30 + 10хл,х„>0.
Попит по відрізках часу:
а, = ю,< = і5,а3 =8,а4 = 25,а, = і2.< = зо,5=2.
2.	У = 8,
С(х„) =
0,х„=0,
16 + 4хя,хл>0.
= 2у„.
Попит по відрізках часу:
а, = 20, < = і о, а, = 15, < = їі,а5=&,а6 = і о, а, = 20,</, = 25.
З’ясувати при якому співвідношенні між витратами на перенала-
дку устаткування (А) і питомими витратами на зберігання 5 оптима-
274
.Дослідження операцій. Збірник задач
льний обсяг випуску на кожному відрізку часу співпадатиме з попи-
том, тобто Л|° =	= <7„.
3.	N = 7,
Г100+8х„,х >0,
С(х„) = {
[0, в протилежному випадку,
4, =20,42 =10,^=15,г74 = 20,<75 =10,<76 =12,<77 =16.
Знайти оптимальні обсяги партій деталей і порівняти їх при 5 =
1,2,3,4.
5.8.	Дослідити модель відновлення з нескінченним плановим пе-
ріодом, прийнявши К = 5, Я, = 5, Я2 =8,Я, =10,/?4 =12, А, =18.
а)	Визначити оптимальну стратегію при будь-якому значенні
а,0<а <1.
б)	Нехай а = 0,9. Застосувати до розв’язку задачі підхід, при
якому нескінченний період розглядається як межа кінцевого плано-
вого періоду зростаючої тривалості. Завершити обчислювальний
процес за умови, що одна і та сама стратегія вибирається на п’яти
ітераціях підряд.
в)	Нехай а = 0,9. Застосувати алгоритм ітерацій по критерію,
прийнявши спочатку = 0, а потім	= ——. Позначити через
1-а
п першу ітерацію, на якій к є оптимальним для нескінченного пла-
нового періоду, завершити обчислювальний процес на ітерації
п+2.
г)	Нехай а = 0,9. Застосувати алгоритм ітерації по стратегіях,
прийнявши в якості початкового к = 1.
5.9.	Дослідити задачу управління запасами.
1.	Розв’язати її методом ітерації по стратегіях при таких значен-
нях коефіцієнта дисконтування: а) а = 0,9 ; б) а = —; у) а = 0.
2.	З’ясувати вплив а на вибір оптимальної стратегії.
3.	Знайти найменше значення», при якому стратегія х = 5 при
/ = 0,1,2 і х - 0 при і — 3,4 залишається оптимальною.
275
Зайченко О.Ю., Зайченко Ю.П.
5.10.	Застосувати алгоритм ітерацій по критерію в розв’язанні за-
дачі управління запасами при нескінченному плановому періоді.
Прийняти на початку уі<0)=0. Нехай- а) а = 0,9; б) а = ^’
в) а = 0 . Позначивши п як першу ітерацію, на якій загальна страте-
гія узгоджується з оптимальною поточною стратегією, обчисленою в
задачі 5.9, припинити розрахунок на ітерації п + 3.
5.11.	У задачу управління запасами внести зміни згідно з варіан-
тами:
а)	попит на кожному відрізку часу = 2,
б)	попит на кожному відрізку часу — 4,
в)	обсяг випуску на одному відрізку часу не може перевищувати 4,
г) дозволені тільки обсяги випуску х = 0, 2, 4
д)	обсяг випуску на кожному відрізку часу повинен бути не мен-
ше одиниці,
е)	умовно-постійні витрати на переналадку устаткування склада-
ють 10 одиниць,
ж)	питома вартість зберігання /г — 5.
Визначити оптимальну стратегію за допомогою алгоритму ітера-
цій по стратегіях при а = 1.
5.12.	Нехай у задачі управління запасами при нескінченному пла-
новому періоді дозволяється затримувати задоволення попиту на те-
рмін не більше одного відрізка часу і штраф за таку затримку задово-
лення одиничного попиту рівний 10. Побудувати мережу, відповідну
даній моделі, і визначити величини с,-.
5.13.	Нехай у задачі управління запасами, приведеній у розділі
4.5, витрати на виробництво і зберігання запасів описуються функці-
єю С(х) + Лу, А = 1;
Ґ5х,х = 0,1,2,3,
С(х) = <
[12 + х,х>4.
а)	Знайти оптимальну стратегію« = 1, застосувавши алгоритм
ітерацій по стратегіях.
276
Дослідження операцій. Збірник задач
б)	Знайти оптимальну стратегію, застосувавши алгоритм ітерацій
по стратегіях, при а = 0,9 , а = 0,5 і а = 0 . В якості початкової
стратегії використати оптимальне рішення варіанта а). Охарактери-
зувати вплив вибору а на оптимальну стратегію.
в)	Прийняти <7 = 0,9 . Знайти оптимальну стратеїію, застосував-
ши алгоритм ітерацій по критерію і почавши з у-0> — 0.
Якщо п позначити як номер першої ітерації, на якій загальна
стратегія узгоджується з оптимальною поточною стратегією, то при-
пинити розрахунки на ітерації п + 3.
г)	Повторити розрахунки по варіантах а), б), в) при Л = 2.
5.14.	Розв’язати завдання 5.13, прийнявши, що функція витрат на
виробництво має вигляд:
С(х) =
0,х = 0,
3 + 2х,х>0.
5.15.	Дослідити мережу, зображену на рисунку 5.5.
Рис. 5.6
Рис. 5.5
а)	Скласти і розв’язати відповідні функціональні рівняння мето-
дом ітерацій по стратегіях при а = 1.
б)	Знайти уі і відповідні стратегії при а = 0,9 , а = -, а - 0, за-
стосувавши метод ітерацій по стратегіях. Використовувати як почат-
кову стратегію оптимальне рішення варіанта а).
277



Зайченко О.Ю., Зайченко Ю.П.
в)	Нехай а = 0,9 . Знайти оптимальну стратегію, застосувавши ал-
горитм ітерацій по критерію і почавши з у<0) = 0. Якщо п — номер
першої ітерації, на якій загальна стратегія узгоджується з поточною оп-
тимальною стратегією, то припинити розрахунки на ітерації п + 3.
5.16.	Дослідити мережу, приведену на рис. 5.6. Виконати завдан-
ня, сформульовані в завданні 5.15.
5.17.	Виробниче об’єднання, що випускає портативні телевізори,
розробляє модель, яка повинна бути максимально надійною. Тому в
конструкції телевізора, що складається з N блоків, вводяться надли-
шкові елементи. Позначимо через хл число надлишкових елементів
у п-м блоці, через Рл(х) — імовірність того, що и-й блок справно
працюватиме протягом першого року при заданому рівні надмірності
х, а через Сл(х) — вартість виготовлення вказаного блоку.
а)	Побудувати оптимізаційну модель, що максимізує надійність
роботи телевізора протягом одного року за умови, що сумарні витра-
ти на його виготовлення не можуть перевищувати С.
б)	Показати, як знайти рішення для побудованої Вами моделі за
допомогою методу динамічного програмування.
в)	Знайти оптимальне рішення:
^ = 3 Сл(х)=слхл С = 15 Рл(х) = 1-р;.р1 =0,1 рг =0,1 А = 0,3
с, =2,с2 = 3,с3 =1-
г)	Побудувати оптимізаційну модель, що мінімізує витрати на
виготовлення телевізора за умови, що надійність роботи телевізора
протягом першого року не менше К. Показати, як знайти рішення
для цієї моделі методом динамічного програмування.
5.18.	Екіпаж космічного корабля планує політ на одну з віддале-
них планет. Він повинен узяти з собою N різних типів електронних
приладів. Оскільки вони можуть виходити з ладу, необхідно брати
запасні прилади. Прилад типу і (і = 1..п) важить <Уу кг, сумарна вага
обмежена і не повинна перевищувати И" кг. Позначимо через
Рі(і) розподіл імовірності числа інтервалів часу і, протягом яких
прилад і нормально функціонує. Нехай хі — число запасних прила-
278
Дослідження операцій. Збірник задач
дів і, що знаходяться на борту космічного корабля. Як тільки запас
х. якого-небудь типу приладу стане рівним нулю, космічний кора-
бель повинен повернутися на Землю.
а)	Розробити алгоритм динамічного програмування, що дозволяє
визначити такі значеннях, , при яких максимізується математичне
очікування часу перебування космічного корабля на планеті. В про-
цесі виконання програми досліджень працюють усі N типів приладів.
б)	Розробити алгоритм динамічного програмування, що дозволяє
визначити такі значеннях, , при яких максимізується імовірність то-
го, що космічні дослідження на планеті проводитимуться принаймні
протягом Т інтервалів.
в)	Показати, як змінюються алгоритми, побудовані в пунктах а)
і б), якщо один прилад коштує с,, а сумарні витрати обмежені і не
можуть перевищувати С.
5.19.	Підприємство має в своєму розпорядженні парк малогаба-
ритних вантажних автомобілів, які здійснюють рейси в ряд населе-
них пунктів і доставляють І види продуктів. Припустимо, що одини-
ця маси продукту і(і = 1,...,/) займає у вантажівці об’єм .с,.
Корисний об’єм вантажівки рівний С. Попит ді на продукт і опи-
сує неперервним рівномірним розподілом зі щільністю:
—,0<а<Л.,
А(9,) = М
0,в інших випадках.
Позначимо через хі число одиниць продукту і, завантаженого у
вантажівку.
Визначити такі значення хі, при яких мінімізується математичне
очікування попиту, не задоволеного за рейс.
а)	Побудувати математичну модель даної задачі і показати, як її
можна буде вирішити методом динамічного програмування.
б)	Розв’язати вказану задачу запропонованим Вами алгоритмом
при таких початкових даних:
/ = 4,с, =1,с2 = |,с3=3,с4 =10, С = 15, Ь, =20, 62 =24, 6, =25, />4=27-
279
Зайченко О.Ю., Зайченко Ю.П.
5.20.	Потрібно вибрати набір каналів для передачі інформації між
двома вузлами комунікаційної мережі. Типи каналів по пропускній
спроможності складають 9600, 19200, 28800, 38400, 56000 біт/с.
Питома вартість складає відповідно 300, 500, 700, 1200, 1500 грн. Лі-
нія зв’язку повинна забезпечити передачу даних з швидкістю не ни-
жче 120 Кбіт/с.
Вибрати такий склад каналів, який забезпечить задану швидкість
передачі з найменшою вартістю.
5.21.	Підприємство, що випускає радіоприймачі, виробляє також
і конденсатори. Фіксовані витрати на випуск партії конденсаторів
рівні 250 доларів. Крім того, витрати на випуск одного конденсатора
складають 8,5 доларів. Зберігання одного конденсатора протягом мі-
сяця обходиться в 2 долари. Графік випуску радіоприймачів у насту-
паючому році вимагає таких кількостей конденсаторів у кожен мі-
сяць: 15000, 25000, 20000, 15000, 11000, 6000, 5000, 11000, 13000,
24000, 30000, 8000. Знайти найкращий час для випуску партій кон-
денсаторів і розмір цих партій, якщо зараз вже є 1000 конденсаторів,
а до кінця року бажано мати їх 5000.
280
Дослідження операцій Збірник задач
Розділ 6. ЗАДАЧІ СТОХАСТИЧНОГО
ПРОГРАМУВАННЯ
6.1. Загальна характеристика задач
стохастичного програмування
В стохастичному програмуванні розглядаються проблеми
прийняття рішень в умовах дії випадкових факторів, які треба
враховувати у відповідних математичних моделях.
Розглянемо типову задачу нелінійного програмування:
знайти такий вектор X, для якого
/(Х)->тіп,	(6.1)
при обмеженнях:
£,(Х)<0, і=\7т,	(6-2)
Хє*.
(6-3)
Задачі стохастичного програмування виникають у випадках, коли
функції /(х),	(х) залежать також і від випадкових параметрів со.
При цьому припускається, що со є елементом простору станів
природи (або простору випадкових параметрів) Г2. Тоді задачу
стохастичного програмування можна сформулювати так [14; 16]:
мінімізувати	/ (X, су),	(6.4)
при обмеженнях:
£,(Х,й))<0, і=ї?т,	(6.5)
Хє*.
Постановки задач стохастичного програмування суттєво залежать
від того, чи є можливість при виборі рішень уточнити деякими
спостереженнями станів природи со, чи її немає. Залежно від цього
розрізняють задачі оперативного і перспективного стохастичного
програмування [15].
281
Зайченко О.Ю.. Зайченко Ю.П.
У задачах оперативного стохастичного програмування рішення
приймають після деякого експерименту над станом природи <о, воно
залежить від результатів експерименту і є випадковим вектором
Х(й>). Подібні задачі виникають, наприклад, в оперативному
плануванні, медичній діагностиці. У задачах перспективного
стохастичного програмування рішення х приймається до проведення
деяких спостережень за станом природи і тому є детермінованим.
Такі задачі виникають у перспективному техніко-економічному
плануванні, у задачах проектування, якщо параметри системи мають
бути обрані конкретними детермінованими величинами,
розрахованими на визначений діапазон можливих збурень.
Задачі стохастичного програмування зазвичай задаються в одній
із таких форм:
мінімізувати	Л/и{/(Х, гу)} =Е(Х),	(6.6)
при обмеженнях:
Л/й){г,(Х,й>)}=С,(Х)<0, /=ЇГ^,Хє^,	(6.7)
де М ш — операція математичного сподівання;
мінімізувати
при обмеженнях:
Р{/(Х,й>)>о),	(6.8)
Р{£,.(Х, й>) <0} >Рі , і=Д~^,	(6.9)
де а, Рі —деякі числа; Р —імовірність.
Можливі і певні комбінації задач (6.6), (6.7) та (6.8), (6.9).
Наприклад, знайти мінімум (6.6) при обмеженнях (6.9) або
мінімум (6.8) при обмеженнях (6.7). Незважаючи на, здавалося б,
відмінність у постановках задач (6.6), (6.7) та (6.8), (6.9), їх можна
звести до деякої загальної форми, наприклад, вигляду (6.6), (6.7). Для
цього треба ввести характеристичні функції:
, /	\ [ 1, якщо
ЛО(Х,«)=	д	(6.10)
[ 0, у противному випадку-*
Л,- (Х,<а )=
1, якщо 8 і ( X, со )< 0;
0, у противному випадку,
(6-11)
для яких:
Мш {Л0(Х, гу)}=Р{/(Х, со)>а}, Ма {А,(Х, ®)}=Р{^(Х, й>)<0}.
282
Дослідження операцій Збірник задач
Задача (6.8), (6.9) тоді набирає вигляду:
мінімізувати	Ма {Ао (X, а>)},	(6-12)
при обмеженні:
(X, <«)}>/’ , і=1, іп.
Існують два основних підходи до розв’язування задач
стохастичного програмування:
1) непрямі методи, які полягають у визначенні функцій /7(Х),
Сі (X) і розв’язанні еквівалентної задачі НП вигляду (6.6), (6.7);
2) прямі методи стохастичного програмування, основані на
інформації про значення функцій /(X, <у),	(X, со), яку одер-
жують у результаті проведення експериментів.
6.2. Одностайні задачі стохастичного програмування
До одностайних задач стохастичного програмування належать
задачі, в яких рішення приймаються на підставі відомих
стохастичних характеристик розподілу випадкових параметрів умов
задачі, до спостережень за їхніми реалізаціями. При цьому має
прийматися найкраще в середньостатистичному розумінні рішення.
Постановки задач стохастичного програмування розрізняються за
такими ознаками: 1) характером рішень; 2) вибором показника якості
рішення (критерію); 3) способом декомпозиції обмежень задачі.
Обмеження на вид функції. У задачі стохастичного програ-
мування звичайно обирають такі функціонали, як математичне
сподівання або дисперсія цільової функції, або ймовірність пе-
ревищення цільовою функцією деякого порога.
Задачі з цільовою функцією вигляду М {сг х} називають М-
моделями, задачі в яких треба мінімізувати дисперсію
Л/{(сгх — х)2} називають У-моделями, а стохастичні задачі, в
яких максимізується імовірність Р{сгх>сгх=Л:0}, називають Р-
моделями [15; 16].
283
Зайченко О.Ю., Зайченко Ю.П.
До останньої групи моделей належать і задачі, де треба
мінімізувати поріг к, який не може бути перевищений із заданою
імовірністю а, наприклад:
	мінімізувати к,
при обмеженні:	Р{сТ х < к}~а .
Обмеження можуть мати одну з таких форм:
аі)х]<Ьі}>аі , і=\,2,...,т ;0<а,.<1;
б) Р{ Ах<В }>а , 0<«<1;
в) Р Розгі	п £	,ікєІ		•>аА , 0<аА <1; А = 1, К. і моделей одноетапних		задач
	іянемо деякі	варіанті			
стохастичного програмування. 1. Нехай задано задачу лінійного				стохастичного програмування	
з імовірнісними обмеженнями типу а): максимізувати	М {ст				х}	(6.2.1)
при обмеженнях: Р		X а І} х ;		• > а і , і = 1, т ;	(6.2.2)
При	детермінованії	У=1 >о, у=і7 і матриці	п . А=І	|| і випадковому	(6.2.3) векторі
ь=&]	задача (6.2.1)-(6.2.3;		зводиться до еквівалентної		
детермінованої задачі ЛП таким чином.
Нехай Р(Ь1,Ьг,...,Ьт) — сумісна щільність розподілу складових
Ь, випадкового вектора Ь. Знайдемо щільність розподілу Ь,:
Лї>()= | р(Ьі,Ь2,...Ь,п)сІЬі сіЬ2...сіЬІ
Обчислимо 6, із рівняння:
284
Дослідження операцій. Збірник задач
| Р(ЬІ)сІЬі=аі , і-1,т-	(6.2.4)
л,
Якщо розв’язок рівняння (6.2.4) не єдиний, то за Ь, виберемо
найбільший корінь.
Очевидно, що умови (6.2.2) при цьому еквівалентні нерівностям
X “цх^Ьі,
7=1
де 6, — задовольняє співвідношення (6.2.4). Звідси випливає, що
задачі стохастичного програмування (6.2.1)-(6.2..3) буде еквівалент-
на така детермінована задача ЛП:
с/х—>гпах,	(6.2.5)
при обмеженнях:
£ х<Ьі , і = 1, т,	(6.2.6)
7=1
>0,	(6.2.7)
де с=Л/{с}; Ь,- — корінь рівняння Г(6і)=1-аІ, або ‘(1-а,),
У7. (^») — функція розподілу випадкової величини 6, .
2. Розглянемо тепер більш загальний випадок, коли А —
випадкова матриця. Нехай елементи матриці А та складові вектора
Ь —- незалежні між собою нормально розподілені випадкові
величини: ао.є#(аі7,<т,2у) , 6,.є.М(6.,#2), тобто —випадкова
нормально розподілена величина з математичним сподіванням о,у-
та дисперсією о . Нехай, крім того, припустимо, що в умовах
(6.2.2)	> 0,5, і = 1,тп.
Покажемо, що при таких припущеннях стохастична задача
(6.2.1)-(6.2.3) зводиться до детермінованої задачі опуклого
програмування з лінійною цільовою функцією та квадратичними
обмеженнями.
285
Зайченко О.Ю., Зайченко Ю.П.
Справді, при згаданих припущеннях нев’язка і -ї умови —
випадкова величина £ (х)=£о Х .-Ь. —є нормально розподіленою
/=і
величиною з математичним сподіванням
^(х)=£аі7х,.-^
/•-І
та дисперсією
^2(х)=£<х2+^>
/=і
тобто:
(х) є N (Л( (х), <т. (х)) •
Тоді умови Р
п
1/='
>а,- еквівалентні нерівностям:
Р{8І (х)<0}>а, , і=1, т,
(6.2.15)
або (що те саме)
| ехр -
(<?-<Мх))2
2<т2(х)
1 <
Позначивши г і е 2 останню нерівність (6.2.16)
-«
зведемо до вигляду:
, /=1, т-
(6.2.16)
Ф
Л,(х)
сг,.(х)
звідки:
8 і (х)+Ф 1 (а,-) сг(. (х) < 0.
Враховуючи вирази для 8) (х) , сг. (х), одержимо остаточно:
2
( п	) 2   п	___
Ф'*(«,) ^о’,2 х2+^2	< Ьі-^аі.х) , і = 1, т- (6.2.17)
І /=і	)	>=>
286
Дослідження операцій. Збірник задач
Згідно з припущенням а,->0.5. Тому Ф_|(а.)>0, і можна
переконатися, що область, яка визначається умовами (6.2.17), опукла.
Для обмеження вигляду	детермінований
І і=|	]
еквівалент має такий вигляд:
£ аіуХ;-Ф~‘(а^ £ сг2 х2+02	>ЬІ , і=1, т. (6.2.18)
/=і	V /-і	>
Аналогічний результат здобудемо, коли випадкові елементи
рядка і -го обмеження {а, -} корельовані між собою.
Введемо такі позначення:
=М {(Ь,-Ьі)(аи-аи)} ; уиІ[ =М {(а,.у -а,7)(а/А -а,*)}.
Тоді розмірковуючи, як вище, дістанемо:
£
Ф',(«.)|<ЕЕ1'.7*Х>Х*-2Е1'.7Х>+^>|	(6-2’19)
І у *	і	)	У=1
Якщо матриця V, =||	|| , і,к — \,п додатно визначена, та
а і >0.5, і=\,т, то допустима множина розв’язків, що задається
(6.2.19), буде опуклою.
Отже, за прийнятих вище припущень лінійна стохастична задача
(6.2.1)-(6.2.3) з імовірнісними обмеженнями зводиться до
детермінованої задачі опуклого програмування вигляду:
п
Е Су Хунтах,
7=1
при обмеженні:
І
(	\І _ п	----
ф~‘(«з Е Е х>хі~2Е ”0х/+ві - ьі-Е х) 'і=х’т-
\ і *	/	У	/=>
287
Зайченко О.Ю., Зайченко Ю.П.
3. Розглянемо Р-моделлю: мінімізувати при обмеженні:	задачу стохастичного програмування, задану		
	к,		(6.2.20)
	Р	£ С}Х]<к .7=1	=а0.	(6.2.21)
Вважатимемо, що випадкові коефіцієнти с , і=\, п , розподілені
нормально із математичним сподіванням су та кореляційною
матрицею С=||с/у ||, де сІ}=М {(с, ~сІ')(с} -с?)} - За таких
припущень лінійна форма сгх=^с х розподілена з
;=і 7 7
__ " "
математичним сподіванням с х та дисперсією X Е счхіх}-
/=17=1
Тому співвідношення (6.2.21) можна записати у вигляді:
	г'	 ।		
ф	7=1		= а л.	(6.2.22)
	1 п п . Е І	СІ •	
Звідси випливає, що мінімізація к за умови (6.2.21) еквівалентна
мінімізації:
к(х)=х^х)+ф~'(ао).асих>х) •
у=1	V »=•
При «>0,5 к(х) являє собою опуклу вниз функцію по змінних
х }. Таким чином, за зроблених припущень, задачі стохастичного
програмування вигляду:
мінімізувати	к,	(6.2.23)
при обмеженнях:
Р {сгх < к}=а0,	(6.2.24)
288
Дослідження операцій. Збірник задач
п
>а і, і=\, т ,
(6.2.25)
відповідає такий детермінований еквівалент:
(6.2.26)
Л(х)=^сух7+Ф''(а0)
7=1
при обмеженні:
2
(«.)[ Е X ч» х-х, -2Е х,+в* ] - °ч х> ’ <6-2-27)
V і >	і	)	/=|
і = 1, т .
Задача (6.1.26), (6.1.27) являє собою задачу опуклого
програмування. Для її розв’язання можна застосувати теорему Куна-
Таккера, або використати один з варіантів методу можливих напрямків
та інші методи НП.
Приклад 6.1. Нехай велика свиноферма має можливість купу-
вати від одного до чотирьох різних видів зерна та готувати з них
різні види сумішів. Різні зернові культури містять різну кількість
необхідних компонентів. Припустимо, що в розрахунок беруться 4
компоненти ( А, в, с, о).
Вихідні дані цієї задачі наведено в табл. 6.1. Нехай фермер
встановив, що комбікорм для свиней повинен задовольняти деякі
мінімальні потреби з точки зору його споживності. їх наведено в
табл. 6.1. Нехай питомі витрати на закупівлю одиниці маси зерна
видів 1, 2 та 3 дорівнюються відповідно 41, 35 та 96 умов. грош.
одн. на 1 кг зерна. Треба визначити, яка з можливих сумішей, що
задовольняють потреби на споживність, найдешевша. Позначимо
через х і, х 2» х 3 шукану кількість зерна кожного виду.
289
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 6.1
Інгредієнти у складі суміші	Вміст інгредієнта в одиниці зерна виду			Мінімальні потреби на період
	1	2	3	
А	2	3	7	>1250
В	1	1	0	>250
С	5	3	6	>900
О	0,6	0,25	1	>232,5
Тоді треба знайти такі *і, *2•х3, для яких
41х1+35х2+96х,—>шіп,	(1)
при обмеженнях:
2х(+3х2 + 7х3 >1250, (інгредієнт А);
1х,+1х2>250, (інгредієнт В);
5х]+3x2 ^900 (інгредієнтС);	(2)
О.бх, + 0.25 хг +1 х3 > 23.5 (інгредієнт О).
Припустимо, що мінімальні сумарні потреби в компонентах а,
в, с, й є випадковими величинами а,Ь,с,<І що розподілені
рівномірно в інтервалах [1000, 1500], [200, 300], [500, 1000], [150,
250] відповідно.
Побудувати відповідну мінімізаційну модель, яка забезпечила б
мінімальні потреби в усіх компонентах з імовірністю, не меншою,
ніж 0.80. Відповідні детерміновані еквіваленти імовірнісних
обмежень матимуть вигляд:
2х] + 3x2 + 7х3 >Я] =1400,
ІХ|+ІХ2	>6|=280;
5х]+Зх2	>С|=900;
0 6х| +0.25x2 +1* з і =230,
(3)
де а। — відповідне значення випадкової величини а, яке
задовольняє умову Р {а<а= а =0.80, звідки Л|=1400. Аналогічно
290
Дослідження операцій. Збірник задач
знаходять значення ь, с а. Далі розв’язують детерміновану
еквівалентну задачу ЛП (1), (3). Її оптимальний розв’язок такий: .г°=
162.5, х°= 177.5, х°= 103.5, а відповідні мінімальні витрати
дорівнюють 20.693.
Приклад 6.2
Для виготовлення визначеного сплаву із свинцю, цинку і олова
використовується сировина у вигляді наступних п’яти сплавів із тих
же металів, які відрізняються складом і вартістю 1 кг. Припустимо,
що процентний склад металу у у кожній сировині і є випадковою
величиною, рівномірно розподіленою в інтервалі Початкові
дані наведені в таблицях 6.2 (а) та табл. 6.2 (б).
Необхідно визначити:
а)	скільки сировини кожного типу потрібно взяти, щоб
виготовити з мінімальною собівартістю сплав, який міститиме не
менше 20% свинцю, 30% цинку і 40% олова.
б)	Вирішити цю задачу при умові, що з імовірністю 0.9 сплав
буде вміщати олова не менш 40%, а цинку не менш 20%.
Таблиця б.2(а)
Матеріал У	Місткість металу в сировині і, %									
	і=1		і=2		і=3		і =4		і=5	
	аи		а1/		аз7		«4У			
Свинець	10	20	10	20	зо	50	зо	60	20	40
Цинк	5	15	20	50	40	60	20	40	10	зо
Олово	60	80	40	60	5	15	10	20	20	50
Таблиця 6.2(6)
І	1	2	3	4	5
с,	4	5	6	8	7
291
Зайченко О.Ю, Зайченко Ю.П.
Розв’язок
Складемо математичну модель даної задачі.
Позначимо через х, — масу сировини ї-го типу, через ау —
вміст металу у в сировині і (в %), а через — бажаний вміст металу
у в сплаві (в %), сі — вартість 1 кг сировини і.
Запишемо математичну модель даної задачі
тіпЛ/^С.хД,	(0
»-і
при обмеженнях:
Р{І^х.>Ь.}>0,35, 7 = 1.3	(2)
1=1
(з)
Г=1
Х->О,	(4)
5
Обмеження (3) необхідно ввести, тому що У^а;.х, — це маса
і=і
металу і в сплаві (кг), а /, виміряється в %.
Складемо детермінований еквівалент задачі (1)-(4). Оскільки
5
число доданків а-х,- в (2) дорівнює п = 5, то сума У'ауХ,
/-і
5	5
розподілена нормально з середнім //2йх,. 1 дисперсією ^сг’ух/ .
і=і	і=і
Використовуючи формули (6.2.17-6.2.18) запишемо детермінований
еквівалент задачі:
5
шіпЛ/^Срс,},
і-і
292
Дослідження операцій Збірник задач
при обмеженнях:
Ха,Л-Ф '(0,75)(Х «) >Ьу /=1.3;
1=1	1=1
£х,=1, х, 2:0, / = 1.5;
(6)
(7)
(8)
Підставляючи дані з таблиці 1 і 2 отримаємо модель даної задачі
тіп(4х, + 5х2 + 6х, + 8х4 + 7х5 ),
за умов:
І5х, +15х, + 40х, + 45х, + ЗОх, - Ф '(0,75)(ул; + ух; + ^ух; + 75х; + ^ух2)' 2 >20;
10л, + 35х, + 50х, + 30х, + 20х, ~Ф 1 (0,75)(—л:,2 + 75х; + —^х2 + ~у-х" + ~у-х5:)' 2 >30;
70л, + 50х, + 10л, + І5х, + 35х, - Ф '(0.75)(іух; +-^х; + у х= +ух; + 75х;)' 2 > 40;
х, + х, + х, + х, + х5 = 1;
х, >0, / = І..5.
Задачі та вправи
Розв’язати наступні задачі стохастичного програмування:
6.1.	Підприємство з обробки картоплі випускає 3 різних продукти
(1, 2 та 3). Картоплю можна купувати у двох постачальників. Об’єми
продуктів 1, 2 і 3, які можна одержати з однієї тонни картоплі
першого постачальника, відрізняються від об’ємів продуктів, що
одержуються з картоплі другого постачальника. Кількість продукту,
що одержується з 1 т картоплі різних постачальників, є величина
випадкова (див. табл. 6.3).
293
Зайченко О.Ю., ЗайченкоЮП
Таблиця 6.3
Продукт	Кількість продукту, із 1 т					Обмеження на обсяг випуску продукту
	Постачальник 1			Постачальник 2		
	р"=1/3	р,2=1/3	р,3=1/3	р21=2/3	р22=1/3	
1	0,1	0,25	0,3	0,3	0,35	8
2	0,2	0,25	0,1	0,1	0,1	6
3	0,3	0,35	0,3	0,3	0,25	12
Відносний прибуток при закупівлі картоплі у постачальника 1 рівна
5, а у постачальника 2 — 6. При ухваленні рішення про закупівлю
картоплі необхідно враховувати виробничі можливості випуску
продукції кожного виду, а також максимальні обсяги продукції, які
можуть бути продані. Нехай попит сІІ на і-й продукт, і=1,2,3
випадковий з відомою функцією розподілу р^). Припустимо, що
продукти 1, 2, 3, що опинилися в надлишку по відношенню до
фактичного рівня попиту!), можна продати оптовому покупцю і
одержати відносні питомі прибутки Е,Н,Ь відповідно.
Побудувати двоетапну лінійну модель, що дозволяє вибрати
обсяг закупівель картоплі у постачальників 1 і 2, так, щоб очікуваний
прибуток був максимальний.
Розв’язати це завдання при таких початкових даних:
Р,С) = 3,£>1(2) = 4,£>|<3) =5,рн = р12 = рі3 =1/3;
£>2'’ = 1,/^2) = 3,Р‘3) =5,р21 =1/6,р22 = 1/2,р23 =1/3;
=4,Р<2) = 6,Л1 =р(П‘‘>) = 1/3,Л2 =р(П3(2>) = 2/3;
£ = 2,Я=1,£ = 3.
6.2.	Нехай деяке підприємство після виконання основної
виробничої програми має в своєму розпорядженні запаси
заощадженої сировини трьох видів	в кількостях Ь{,Ь2,Ь3.3
цієї сировини може бути виготовлене 2 види виробів С} і С2. Відомі
величини аіу — кількість у-го виробу, і с.. — дохід, що одержується
від реалізації одного виробу.
294
Дослідження операцій. Збірник задач
Припустимо, що норми витрат ау є випадковими величинами з
рівномірним законом розподілу в інтервалі	^розподілені
нормально з середнім с. і дисперсією сН.
Відповідні числові дані приведені табл. 6.4а і 6.46
Таблиця 6.4а
Вид сировини	Запас сировини	Кіл-ть сировини, яка йде на виготовлення 1 виробу			
		першйи вид		другий вид	
		га		Гі2	
81 82 83	20 16 12	2 1 0	4 2 0	1 1 2	5 4 6
Таблиця 6.46		
Характеристики	Питомий прибуток від продажу виробу	
	і=1	1=2
Середнє Су	3	2
Дисперсія Су	4	1
Скласти такий план випуску продукції, при якому очікуваний
прибуток підприємства максимальний за умови, що з ймовірністю не
менше 0,90 план буде таким, що реалізується, тобто кількість всіх
видів сировини виявиться достатньою для його виконання.
6.3.	Для виробництва двох видів виробів (/ = 1,2) може бути
використане устаткування двох груп (/ = 1,2). Витрати часу ау цими
групами устаткування на виготовлення виробів різні і є випадковими
величинами. Вартість одного виробу Ь,.(/ = 1,2; у = 1,2) буде також
випадкова.
295
Зайченко О.Ю., Зайченко Ю.П.
Припустимо, шо щільність розподілу величин а- і Ьу відома,
розподілена згідно із законом N ),, а — рівномірно в інтервалі
Позначимо через Nx і ?У2 план випуску виробів першого
і другого виду. Нехай =100 шт., і /У2 = 200 шт.
Визначити оптимальний план роботи груп устаткування, при
якому мінімізуються очікувані сумарні виробничі витрати на випуск
виробів, якщо вірогідність перевищення фонду часу Т на виконання
всього планового завдання складає не більше 0,10, а імовірність
виконання плану випуску виробів не менше 0,95.
Скласти математичну модель завдання і знайти рішення для
початкових даних, приведених у табл. 6.5.
Таблиця б 5
Група устаткування і	Питомі витрати часу годЛ шт.				Питома вартість виробу				Фонд часу і-го устаткування
	7=1		7=2		7=1		7=2		
	ач		ач						
1	0,2	0,2	0,3	0,3	2	4	1	2	50
2	0,1	0,2	о,1	0,2	3	6	2	8	65
6.4.	Перевезення народногосподарських вантажів по регулярних
лініях виконують п різних типів суден. Виходячи з даних про
собівартість тонно-кілометра і комерційного завантаження кожного
типу судна на кожній лінії встановлюються: місячні експлуатаційні
витрати на судно у-го типу на і-й лінії ,і = 1, ш; у =1,..., п, місячний
обсяг вантажообігу (обсяг перевезень суднау-го типу на і-й лінії) .
Нехай величини Су і ау випадкові, де су мають рівномірний
розподіл з параметрами (у^,^), а — нормальний розподіл
Л7(пу.,сг(>);	—незалежні випадкові величини.
Мінімальний план перевезень по і-й лінії рівний =	.
Припустимо, що число судену-го типу дорівнює N^ .
296
Дослідження операцій Збірник задач
Потрібно скласти такий план розподілу суден по регулярних
лініях, який забезпечує мінімум очікуваних сумарних витрат при
виконанні плану перевезень з імовірністю не менше 0,80.
Скласти математичну модель задачі в одностайній постановці.
Знайти оптимальне рішення цієї задачі при різних варіантах
початкових даних, приведених у таблицях 6.6а, 6.66, 6.6в, 6.6г.
Таблиця 6.6 а
№ лінії і	Місячний вантажообіг а ! (У У У		
	/=1	,/=2	
1	15 5	зо 10	25 15
2	10 5	25 10	50 25
3	зо 15	10 5	зо 10
4	50 20	20 10	25 зо
Число суден	50	40	зо
300
200
1000
500
Таблиця 6.6 6
№ лінії і	Місячні експлуатаційні витрати г! 8..		
	і=\	/=2	У=з
1	5 20	40 100	20 60
2	10 ЗО	20 36	40 80
3	20 зо	12 18	25 45
4	зо 40	10 90	зо 100
297
Зайченко ОЮ, Зайченко Ю.П.
Таблиця 6.6 в	Таблиця 6.6 г
№ ЛІНІЇ і	аУІ(ТУ			
		/=2	/=з	7=4
1	25 15	20 10	50 10	50 20
2	20 10	12 6		45 15
3	15 15	10 15		40 10
4	10 5	40 20	18 4	25 25
Число суден	50	95	зо	45
№ лінії і	Г-.І8.. У У			
	/=1	,Г2	,Г3	,Г4
1	15 20	10 зо	4 10	12 18
2	20 40	20 40			10 16
3	20 зо	8 12			зо 40
4	10 50	5 10	15 25	20 70
6.5.	У колгоспі три поля у (/—1,2,3) площею £,=10000 га,
£, =15000 га, £,=5000 га засівають пшеницею. Для прибирання
полів можуть бути використані комбайни різних типів і (г-1.,п)
продуктивністю га/день. Нехай добові експлуатаційні виграти з
утримання комбайна типу і складають с. грн./день. Загальна
кількість комбайнів типу і рівно Величини — випадкові,
розподілені експоненціально з середнім ту = 1 / Лу, а сі —
рівномірно розподілені в інтервалі	Початкові дані завдання
приведені в табл. 6.7.
Визначити, яка кількість комбайнів кожного типу необхідно
направити на кожне поле, щоб з імовірністю р = 0,9. прибрати всі
поля не більше ніж за Т днів, при мінімальних очікуваних сумарних
витратах. Завдання розв’язати при Т = 4, 5 і 6 днів.
298
Дослідження операцій. Збірник задач
Таблиця б. 7
Тип комбайну і	Середня продуктивінсть комбайна на полі /			Число комбайнів	Експлуатаційни витрати	
	у=]	І =2	/=з		ч	Ь,
1	40	55	80	10	10	зо
2	80	120	150	10	20	40
3	120	175	200	8	26	45
4	100	160	180	16	зо	40
6.6.	В умовах завдання 6.5 визначити, яку кількість комбайнів
кожного типу необхідно направити на кожне з полів, щоб очікуваний
час прибирання був мінімальним, а сумарні виробничі витрати з
імовірністю /і) =0,9 не перевищили величину Сзагаз . Скласти модель
завдання стохастичного програмування і вирішити її при
Смга, = 7000 грн., 7500 грн., 9000 грн.
6.7.	Підприємство має в своєму розпорядженні ресурси сировини,
робочу силу і устаткування, необхідні для виробництва чотирьох
видів виробів. Нехай питомі витрати ресурсів типу у є випадковими
величинами, розподіленими в інтервалі [а,, 6,], а прибуток за
одиницю виробу виду і складає с, одиниць. Початкові дані
наводяться в таблиці 6.8а, 6.86.
Таблиця 6.8 б
Таблиця 6.8 а
Вид ресурсу	Норми витрат ресурсів при виготовлені виробу і				Об’єм ресурсів
	Г=1	/=2	і=3	і=4	
Сировина, кг	2-4	3-6	1-2	2-5	60
Робоча сила, нор-година	15-25	10-15	15-20	30-50	400
Обладнання, станко-год.	6-12	10-18	6-10	12-20	128
Вид виробу	1	2	3	4
Прибуток, грн.	зо	25	56	48
Визначити оптимальний асортимент виробів, що забезпечує:
299
Зайченко О.Ю, Зайченко Ю.П.
а)	максимум очікуваного прибутку за умови реалізації плану з
вірогідністю 0,95;
б)	максимум очікуваного прибутку при асортименті 3 : 2 : 1 : 2;
в)	максимум числа комплектів, шо включають один виріб типу 1,
два — типу 2, гри вироби типу 3 і одне — типу 4.
6.8.	При складанні добового раціону годування худоби можна
використовувати свіже сіно (не більше 50 кг) і силос (не більше 85
кг). Суміш повинна містити живильні речовини: білок (не менше 1
кг), кальцій (не менше 100 г) і фосфор (не менше 80 г). Кількість
кожного компоненту в 1 кг сіна і силосу є нормально розподіленою
випадковою величиною з середнім і дисперсією сг*, а
собівартість продукту с, — рівномірно розподілена в інтервалі
[<$;,/.]. Початкові дані наводяться в табл. 6.9.
Таблиця 6.9
Продукти і	Вміст компонентів у продукті						Питома собівартість грн./кг	
	Білок		Кальцій		Фосфор			
	Мі		А2,	°2,	Аз,	стз,	3	У,
Сіно Силос	40 10	20 5	1,25 2,5	1 1,5	2 1	1 0,8	1 0,6	1,5 1
Визначити оптимальний раціон виходячи з умови мінімуму
собівартості за умови, що з імовірністю р = 0,80 виконується вимога
заданої поживності.
6.9.	Підприємство може випускати продукцію, використовуючи
три технологічні процеси (ї = 1,2,3). Продуктивність аі ї-й технології
є нормально розподіленою випадковою величиною з середнім ц
і дисперсією <т2.
Нехай витрата у-го ресурсу за 1 годину робіт (табл. б.ІО.а) є
випадковою величиною, рівномірно розподіленою інтервалі [/,-,,<5^] -
Обсяг кожного ресурсу на підприємстві приведений у табл. 6.10.6.
300
Дослідження операцій. Збірник задач
Таблиця 6.10а
Спосіб виробництва і	Витратиу-го ресурсу										Продуктивність	
	>71	4і	Гі2	*І2	Л-3		Гі4	6-4	Гі5		А	7
1	1	3	2	4	4	10	1	3	0,5	1,5	20	10
2	1	2	3	5	2	4	0,5	1,5	0	0	25	15
3	2	4	1,5	2,5	3	5	2	2	0,8	1,2	зо	зо
Таблиця 6.106
Тип ресурсу	Сировина	Верстати	Робоча сила	Енергія	Транспорт
Обсяг ресурсу	60	80	70	50	40
Визначити оптимальний обсяг продукції, що виготовляється по
кожному технологічному процесу, при якому максимізується
сумарний обсяг продукції за умови реалізації плану з імовірністю не
менше 0,90.
6.10.	Підприємство планує роботу на шість місяців (і = 1,2., п)
так, щоб забезпечити споживача виробами, попит на які в 1-ому
місяці є випадковою величиною г/ розподіленою по показовому
закону з середнім г.
2_. Якщо попит г/. перевищить наявний обсяг
А
виробів хі, то підприємство зазнає втрат через дефіцит (питомий
штраф г. =30 грн./шт.). Якщо ж попит ^<хР то залишок продукції
зберігатиметься на складі, питомі витрати на зберігання складають
гри.
51 = 5 = 5---------_
иіт.місяць
а)	Визначити такий план виробництва виробів х,. по місяцях,
який мінімізує сумарні за 6 місяців виграти на зберігання і штрафи
через дефіцит за умови, що з імовірністю р = 0,80 попит
задовольнятиметься. Початкові дані приведені табл. 6.11.
б)	Розв’язати завдання за умови, що на складі можна зберігати не
більше 100 виробів.
301
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 6.11
Місяць і	1	2	3	4	5	6
Середній попит 1 / А	50	ЗО	40	20	60	10
Задача 6.11
Нехай деталі А, В, С можуть виготовлятися на трьох верстатах 1,
2, 3. Витрати часу на виготовлення деталі і на верстаті у є
випадковими величинами, рівномірно розподіленими в інтервалі
’ приводяться в таблиці 6.12, де також зазначена середня
продажна ціна одиниці деталі с, та собівартість однієї години
роботи кожного верстата. Нехай сумарний плановий фонд часу
роботи верстата — рівномірно розподілена випадкова величина в
інтервалі [^.тіп,^.тах].
Потрібно знайти оптимальну виробничу програму випуску
деталей, яка б була реалізована з імовірністю не менше 0.90 та
забезпечувала б екстремум одного з таких критеріїв витрат.
А) максимум товарної продукції Т;
Б) максимум сумарного прибутку П;
Таблиця 6.12
Станки	Деталі						Вартість ОДНІЄЇ години	Час роботи верстата	
	Норми часу								
	А		В		С				
	-Ч	іч	-21	(21		ІЧ		/ тіп	^утах
1	0.2	0.3	0.1	0.2	0.05	0.1	зо	20	60
2	0.5	1	0.2	0.4	0.2	0.4	10	60	90
3	0.1	0.2	0.15	0.3	0.3	0.5	20	20	40
Ціна деталі	10		16		12		—	—	—
302
Дослідження операцій. Збірник задач
Задача 6.12
Завод при виготовленні грьох типів деталей використовує
токарні, фрезерні і стругальні верстати. При цьому виготовлення
кожної деталі можна проводити трьома різними технологічними
способами (1, 2, 3). У табл. 6.13 зазначені наявні ресурси по кожній
/-тій групі верстатів (у верстато-год) ф:, /=1,3, норми витрати часу
при обробці деталей у (/=1, 2, 3) на верстаті / є нормально
розподіленими випадковими величинами з параметрами і су-.
Нехай прибуток від випуску одиниці деталі кожного виду складає
відповідно 18, ЗО і 20 грн./шт.
Скласти оптимальний план навантаження виробничих
потужностей, що забезпечує максимальний очікуваний прибуток, за
умови фізичної реалізованості плану з ймовірністю 0.90.
Таблиця 6.13
			Норми витрати часу						
Верстати	Деталь 1		Деталь 2			Деталь 3			Ресурс часу
		Технологічні способи ви				робництва			
	1	2	1	2	3	1	2		
	<6у	А,	Лу ач	А А	Ау	Ау <т,у	А, ач		Фі '
Токарний	0.4 0.2	0.5 0.2	0.4 0.2	0.3 0.2	0.8 0.5	0.7 0.3	—		300
Фрезерний	0.3 0.15	—	0.5 0.4	0.2 0.1	0.3 0.2	0.4 0.2	1.0 0.5		200
Стругальний	0.5 03	0.9 0 45	0.6 0.3	0.4 0.5	0.5 0.3	—	1.5 0.8		400
Прибуток	18			зо			20		
Задача 6.13
Три сорти взаємозамінної сировини (/=1, 2, 3) в кількості 200, 100
та 300 кг використовується для виробництва чотирьох виробів (/=1,
2, 3, 4). Норми витрат аі} сировини і на виробництво виробу у є
нормально розподіленими випадковими величинами з середнім
та дисперсію сг^ , а виробничі витрати рівномірно розподілені
303
Зайченко О.Ю.. Зайченко Ю.П.
випадкові величини на інтервалі [/у,	. Вихідні дані наведені в
таблицях 6.14(а) і 6.14(6).
Скласти такий план виробництва виробів, щоб з ймовірністю 0,9
випустити 25 одиниць першого виробу, 45 одиниць другого виробу,
ЗО одиниць третього та 70 одиниць четвертого при мінімальних
очікуваних сумарних виробничих витратах.
Таблиця 6.14(а)
Сорт сировини і	Норми витрат на виріб у							
	/				3		4	
	Аі	О’.і	Аг		Аз	°7з	Ад	о-.;
1	2	3	0/5	1	3	2	1	2
2	1	3	2	3	2	3	2	4
3	2	5	1	2	2	4	2	3
Таблиця 6.14(6)
Сорт сировини і	Виробничі витрати на одиницю продукції Су							
	1		2		3		4	
	Ги	її	Уі2	3І2	/із	^3	/і4	<^4
1	20	60	15	45	10	20	20	50
2	15	45	20	зо	40	50	зо	50
3	10	зо	зо	60	10	зо	25	45
Задача 6.14
В кормову суміш входять гри продукти: сіно, силос і
концентрати, які містять поживні речовини: білок, кальцій і вітаміни.
Кількість поживних речовин (таблиця 6.15) представляє собою
нормально розподілені випадкові величини із середній і
дисперсією . Мінімально необхідні норми споживання білка —
2000 г., кальцію — 120 г, вітамінів — 40 г.
А) Визначити оптимальний раціон харчування мінімальної
вартості, який забезпечує з ймовірністю не менше 0.8 добові норми
споживання всіх поживних речовин, якщо ціна 1 кг сіна дорівнює 30
коп„ силосу — 20 коп., концентратів — 50 коп.
304
Дослідження операцій. Збірник задач
Б) Розв’язати цю саму задачу за умови, що відомі граничні норми
споживання добової видачі: сіна — не більше 12 кг., силосу — не
більше 20 кг., концентратів — 16 кг.
Таблиця 6 15
Продукт	Склад поживних речовин / СГ7		
	1	2	3
Сіно	30/20	4/8	3/2
Силос	20/10	6/4	Уг
Концентрати	150/100	4/2	2/3
Задача 6.15
На трьох ділянках колгоспного поля (£= 1, 2, 3) можна вирощу-
вати три культури: жито, пшеницю і ячмінь (і = 1, 2, 3). Урожайність
Лік цих культур нормально розподілена із середнім /тй. і дисперсією
ст^. (табл. 6.16).
Нехай планове завдання із зібрання урожаю кожної культури
складає відповідно 500 ц., 600 ц. і 400 ц., а площі ділянок
дорівнюють відповідно 30 га., 50 га., 20 га.
А) Визначити оптимальну структуру посівів, яка мінімізує
сумарні очікувані витрати за умови виконання плану з ймовірністю
не менше 0.90.
Б) Визначити оптимальну структуру посівів, яка забезпечує
максимальну ймовірність перевиконання плану при збереженні
планового асортименту 5:2:4.
Таблиця 6.16
Ділянка к	Урожайність /-тої культури						Середні витрати		
	Ик\		Р-кІ	СТ*2		°кЗ	С*і	Ск2	СкЗ
1	10	15	12	6	8	4	2	3	4
2	12	8	14	10	18	12	3	6	8
3	20	10	16	8	24	8	4	7	10
305
Зайченко ОЮ, Зайченко Ю.П._______________________________________
Задача 6.16
Нехай три підприємства (/=1, 2, 3) використовують для випускуу-
ї продукції (/= А, В, С) два види ресурсів (1, 2) обсяги яких
складають для першого підприємства 250 і 150 одиниць, для другого
— 100 і 200 і для третього — 240 і 300. Нехай норми витрат кожної ©
ресурсу на ї-му підприємстві для виробництва у-ї одиниці продукції
— рівномірно розподілені випадкові величини в інтервалі
а собівартість виробництва одиниці у-ї продукції на ї-му
підприємстві су — випадкова величина із середнім Су.
Початкові дані наводяться в таблицях 6.17(а) і 6.17(6).
Нехай виробничий план випуску продукції складає відповідно
300, 170 і 250 одиниць.
Необхідно визначити оптимальну спеціалізацію виробництва,
при якій мінімізується сумарна очікувана собівартість випуску за
умови, що ймовірність виконання плану складає не менше 0.90.
Таблиця 6.17а
Підприємство і	Норми витрат сировини виду 1 і 2 на одиницю продукції											
	А				В				С			
	1		2		І		2		1		2	
1	1	3	2	6	0.5	1.5	2	3	2	3	2	4
2	1	2	3	7	1	3	1.5	3	2	2.5	1	4
3	1	3.5	2	4	1	1.5	1	2	1	4	3	5
Таблиця 6.176
Підприємство	Собівартість випуску одиниці продукції		
	А	В	С
1	2	8	5
2	3	6	6
3	3	9	5
306
Дослідження операцій. Збірник задач
Задача 6.17
Підприємство володіє ресурсами сировини, робочої сили і
обладнання, які необхідні для виробництва чотирьох видів виробів.
Нехай питомі витрати ресурсів типу у є випадковими величинами,
рівномірно розподіленими у інтервалі [аі}, Ь:/ ], а прибуток на
одиницю виробу і складає СІ одиниць. Початкові дані наведені в
таблицях 6.18(а) і 6.18(6). Визначити оптимальний асортимент
виробів, який забезпечує:
А)	максимум очікуваного прибутку, за умови реалізованості
плану із ймовірністю 0.95;
Б) максимум очікуваного прибутку при асортименті 3:2:1:2;
В)	максимум числа компонентів, яке включає один виріб типу 1,
два вироби типу 2, три вироби типу 3 і один виріб типу 4.
Таблиця б. 18а
Вид ресурсу/	Норми витрат ресурсу у				Об’єм ресурсів
	І=1	і=2	і=3	і=4	
Сировина	2-4	3-6	1-2	2-5	160
Робоча сила	15-20	10-15	15-20	30-50	400
Обладнай ня	6-12	10-18	6-10	12-20	200
Матеріал	8-16	10-20	4-8	12-16	300
Таблиця 6.186
Вид виробу і	1	2	3	4
Прибуток С,	зо	25	56	48
Задача 6.18
Меблева фабрика випускає столи, крісла, бюро і книжкові шафи,
використовуючи два типи дощок. Фабрика має 1000 дощок типу 1 и
500 дощок типу 2. Трудові ресурси фабрики складають 800 чоловік
на тиждень. Витрати кожного виду ресурсів на виготовлення одного
виробу є рівномірно розподіленими випадковими величинами в
інтервалі [а,у,6,7] (табл. 6.19). Прибуток від реалізації одного
307
Зайченко О.Ю., Зайченко Ю.П.
стола— 12 гр., одного крісла — 5 гр., одного бюро — 15 гр., одної
книжкової шафи — 20 гр.
Визначити оптимальний асортимент випуску, який забезпечує за
умови реалізованості плану з ймовірністю не менше 0.9:
А)	максимум очікуваного прибутку;
Б) максимум очікуваного прибутку за умови комплектності
(кількість столів відноситься до кількості крісел як 1:6);
В)	максимум очікуваного прибутку при додаткових умовах:
столів не менше 400 шт., бюро не менше 130 шт., книжкових шаф не
більше 10 шт.;
Г) максимум очікуваної вартості товарної продукції за умови
комплектності і таких цінах на продукцію: стіл — 40 гр., крісло —
15 гр., бюро — 30 гр., шафа — 80 гр.
Таблиця 6.19
Вид ресурсу і	Стіл		Бюро		Крісло		Книжкова шафа	
	ан	Ьп		ЬІ2	°,з	*,з		*,4
Дошки типу 1,м	4	6	8	12	1	2	9	15
Дошки типу 2, м	1	3	4	6	2	4	10	16
Трудові ресурси	2	5	5	8	1	3	8	12
308
Дослідження операцій. Збірник задач
Розділ 7. ПРИЙНЯТТЯ РІШЕНЬ
В НЕЧІТКИХ УМОВАХ
У задачах організаційного керування часто-густо трапляються
ситуації, в яких вихідні умови задачі нечітко визначені. Такі ситуації
відображають недостатню інформованість особи, що приймає
рішення (ОПР).
Використовувана інформація може бути суб’єктивною, а її
відображення в мові людей, як правило, містить багато невиз-
наченостей на кшталт «багато», «мало», «приблизно», які не мають
аналогів у мові математики. Тому опис цієї інформації засобами
традиційної математики сильно загрубляє математичну модель.
Таким чином, для подальшого застосування математичних методів
аналізу та дослідження дедалі складніших систем, з’явилася погреба
у створенні нового математичного апарату, який дав би змогу
формально описувати нечіткі поняття, якими користується людина,
описуючи свої бажання, цілі та уявлення про систему.
Таким апаратом стала теорія нечітких множин, створена Л.Заде,
перша фундаментальна праця якого була опублікована ще в 1965 р.
Протягом останніх сорока років цей напрямок інтенсивно
розвивався, з’явилися сотні праць, присвячених теоретичним та
прикладним аспектам теорії нечітких множин. Одним з
найактуальніших напрямків нової теорії є проблема прийняття
рішень при нечітких умовах та критеріях, що привела до появи
нового напрямку в математичному програмуванні — нечіткого
математичного програмування (НМП). У цьому розділі викладено
основні ідеї, задачі і методи нечіткого математичного
програмування.
309
Зайченко О.Ю., Зайченко Ю.П.
7.1. Нечіткі множини та операції над ними
Основні поняття та означення
Означення 7.1. Нечіткою множиною А, що задана на універсальній
множині X називається сукупність пар (х,рА(х)), де х є. X ,а рА —
функція х—>[0;1], яка має назву функції належності множини А.
Значення рА{х) для конкретного х називається ступенем належності
цього елемента до нечіткої множини А (рис. 7.1. а)
Звичайні множини утворюють підклас нечітких множин. Справді,
функцією належності звичайної множини В с X є її характеристична
функція рв(х) (рис. 7.1.6):

якщо хєВ;
якщо х і В.
Означення 7.2. Нечітка множина 0, визначена на X,
називається порожньою, якщо її функція належності дорівнює 0 на
всій множині X, тобто рв(х) = 0, Х/х є X .
Означення 7.3. Універсальна множина X описується функцією
належності вигляду ц (х) = 1 Х/хєХ-
Означення 7.4. Носієм нечіткої множини А з функцією
належностіназивається множина вигляду
впрр А = {х: рА(х) > 0,х є X}.
Нечітка множина А називається нормальною, якщо виконується
умова 8иріц/)(х)=1, у противному разі вона називається
субнормальною.
310
Дослідження операцій- Збірник задач
Нехай А та В — нечіткі множини на X, р 4(х) та рв(х) — їхні
функції належності відповідно.
Кажуть, що А включає в себе В (тобто В с А ), якщо для будь-
якого х є X виконується нерівність рі (х) <	(Г) (рис. 7.2).
Якщо В с А , то яирр В с яирр а .
Множини А, В еквівалентні (А ~ В), якщо ц (Л) =	(х), \/х є X .
Приклад 7.1. Розглянемо нечіткі множини:
А = {л : величина х близька до 1}
В = {г: величина х дуже близька до 1}.
Тоді Всл і функції належності цих множин мають
задовольняти умову:
Операції над нечіткими множинами
Означення 7.5. Об’єднанням нечітких множин А та В в X
називається нечітка множина С = Л ЦІ В з функцією належндсті
вигляду (рис. 7.3):
Ас(*)=піах{^(*);Ав(х)}’	(711)
Означення 7.6. Сильніш об’єднанням нечітких множин А та В в
X називається нечітка множина С = АО В з функцією належності:
(р .4 (*)+Нв (4 якщо На М + В в (*) <1 >
|1, ЯКЩО /4 л ( V) + н в (х) ’г 1
Означення 7.7. Перетином нечітких
множин А та В в X називається
нечітка множина С = АПВ з функцією
належності вигляду (рис. 7.4):
/7 с(*) = А яр в М=тіп । V / ; (4 •
(7-1.2)
311
Зайченко О.Ю., Зайченко Ю.П
Якщо {Л„} — скінченна або нескінченна сім’я нечітких множин
з функціями належності (х,у),де у є У —параметр сім’ї, то перетин
С = р Ау є нечіткою множиною з функцією належності вигляду:
у
//_(-*) = ц.^у)'хєХ-
• *	У^* *	-"у
Означення 7.8 Сильний перетин нечітких множин А та В в X
визначається як нечітка множина С = А(~]В з функцією належності
вигляду:
Дс(х) = Iі ' -Д (X) *нМ, хєХ .	(7.1.3)
ГС лрв ГЛ Г в
Означення 7.9. Різницею нечітких множин А та В в X нази-
вається нечітка множина А\В з функцією належності вигляду:
Вахв(х)
Па (*) ~ А в (Д якиі° Ра 00 В в (х) 0 »
0,е протилежному разі.
(7-1.4)
Означення 7.10. Декартовим добутком А1хА2х...хАп нечітких
множин А, в Х',і = \,п називається нечітка множина в
декартовому добутку Х{ х Х2 х... х Хп з функцією належності
вигляду.
рА(х) = тіп{^(хІ),/іЛ(х2),...,рЛ(л„)}.	(7.1.5)
312
Дослідження операцій. Збірник задач
Множини рівня та декомпозиції нечітких множин
Означення 7.11. Множиною рівня а нечіткої множини А на X
називається множина, складена з елементів х є X таких, ступінь
належності яких до множини А не менш а, тобто, якщо Ао —
множина рівня а нечіткої множини А, то
Аа = {х:рА{х)>а}.	(7.1.6)
Справедливі такі співвідношення [15; 34]:
(4Ж = 4и/?й;(ЛПВ)а=4П5о .	(7.1.7)
Якщо для операції об’єднання та перетину використовуються
відповідні сильні операції, то
(4Х 2 Аа ива ; (ЛР|Б)О ^АОПВО. (7.1.8)
В деяких випадках доцільно користуватися розкладанням
нечіткої множини А за її множинами рівня, а саме представленням
нечіткої множини у вигляді.
Л = йл>	СЧ-9)
а=0
де об’єднання нечітких множин береться згідно до означення (7.1.9)
по всіх а від 0 до 1.
7.2. Нечіткі відношення. Операції над ними
Перш ніж ввести поняття нечіткого відношення, розглянемо
звичайні відношення та їх властивості.
Відношенням В на множині X називається деяка підмножина
декартового добутку X х X.
Згідно з цим означенням, задати відношення /? на множині
X означає вказати всі пари (х,у), які зв’язані відношенням В . Для
позначання того, що елементи х є X зв’язані відношенням, будемо
користуватися такими двома еквівалентними формами запису: хВу
або (х,у)єЛ. Якшо множина X, на якій задане відношення В,
скінченна, то відношення задається в двох формах:
313
Зайченко О.Ю., Зайченко Ю.П.
1) у матричній:
л = 1к| і = 1'т > =
Г1, якщо (л;,х ) є Я
г« Іл
(О, у протилежному разі,
2) у графовій.
Нечіткі відношення
Введемо поняття нечіткого відношення і розглянемо його
властивості [16].
Означення 7.12. Нечітким відношенням Я на множині X
називається нечітка підмножина декартового добутку X *Х, яка
характеризується такою функцією належності рк(х,у), що
Х-кХ —^—>[0,1]. Причому рк(х,у) розглядається як суб’єктивна міра
виконання відношення хКу.
Носієм нечіткого відношення Я на множині X називається
підмножина декартового добутку X х X , яка визначається так:
зирр Я = {(х, у): рк (х, у) > 0, х є X, у є У].
Операції над нечіткими відношеннями
Нехай на множині X х X задано два нечітких відношення А та
В з функціями належності рА(х,у),рв(х,у). Тоді множина С = АIIВ є
об’єднанням нечітких відношень А та В на множині X, якщо її
функція належності визначається виразом:
Нс(х,У) = тах{Ал(х,у)„дв(х,у)} •
Аналогічно множина О = А П В є перетином нечітких множин А
та В, якщо
Ро(х,у) = тіп{рА(х,у),рв(х,у)} 
Можна ввести також операції сильного об’єднання та сильного
перегину, аналогічні операціям над нечіткими множинами.
314
Дослідження операцій. Збірник задач
Нечітке відношення В включає в себе нечітке відношення А
(Ас В), якщо для них виконується співвідношення ДА(х,у)<
<ДВ(х,у)Ух,уєХ.
Якщо В -нечітке відношення з функцією належності рк(х,у), то
відношення Я , що характеризується функцією належності р-^(х,у) =
= 1 -	(х, у), Ух, у є X, називається доповненням Я на множині X.
Обернене до Я відношення на X визначається так:
хВ~1у<--->уВх, при цьому функції належності зв’язані між собою
рівністю (х,у) = рк(у,х).
Властивості нечітких відношень
1.	Рефлексивність. Нечітке відношення називається рефлек-
сивним на X, якщо виконується умова /ул(х,л) = 1,Х/хє X (приклад
рефлексивних відношень: приблизно рівні, близькі).
2.	Антирефлексивність. Нечітке відношення Я на X антиреф-
лексивне, якщо для усіх х&Х рк(х,х) = й (Наприклад Я —набагато
більше).
3.	Симетричність. Нечітке відношення Я на X симетричне,
якщо для всіх х,уєХ Рц(х,у) = рк(у,х). Відношення Я
антисиметричне, якщо з того, що рк(х,у) > 0 випливає рк(у,х) = 0.
Важливе значення в теорії нечітких множин має композиція (або
добуток) нечітких відношень. На відміну від звичайних (чітких)
відношень, композицію (добуток) нечітких відношень можна
визначити різними способами.
Означення 7.14. Максимінна композиція (добуток) нечітких
відношень А та В на X характеризується функцією належності
вигляду:
Алв(*»-Г) = 5Ц’тіп{Ал(х,г),/^(г,у)} -	(7.2.1)
гєА'
Означення 7.15. Мінімаксна композиція нечітких відношень А та
В на X (вона позначається АВ) визначається функцією
належності вигляду:
В а в(-^У) = т*1) тах{/ул(х,г),Ав(2,у)}.	(7.2.2)
315
Зайченко О.Ю, Зайченко Ю.П.
Означення 7.16. Максимультиплікативна композиція нечітких
відношень А та В на X — нечітке відношення С = А*В
визначається функцією належності вигляду:
= 5ир{Ал(*,г)  цв(г,у)}.	(7.2.3)
хєЛ’
Приклад 7.2. Нехай задано два нечітких відношення а та В на
множині х , яка складається з двох елементів ,г = (х„х,), де матриці
нечітких відношень такі:
>і Уг
х, Г0.2
х, 0.5
0.6
0.8
-іГО-5
/'в(2.У)-^ 03
0.7
1
Тоді композиція (добуток) нечітких відношень визначається так:
а) максимінна п; = ав :
х 0.3 0.6
- 0 5 0 8
б) мінімаксна Л; = а »в:
0.5 0.7
Нлв{х,у)- о5 о7
в) максимультиплікативна к; = а*в :
Го.18 0.6
у) =
4	"	0.25 0.8
Нечітке відношення Я на множині X називається транзитивним,
якщо Я • Я с Я. З цього означення випливає, що властивість
транзитивності нечіткого відношення залежить від способу завдання
композиції нечітких відношень.
7.3. Задача досягнення нечітко визначеної мети
(підхід Белмана-Заде)
Задача досягнення нечітко визначеної мети, сформульована
Р.Белманом-Л.Заде, базується на припущенні, що мета прийняття
рішень та множина альтернатив розглядаються як рівноправні
нечіткі підмножини деякої універсальної множини альтернатив. Це
припущення дає змогу знайти розв’язок задачі досить просто [16].
316
Дослідження операцій. Збірник задач
Нехай х — універсальна множина альтернатив, тобто універ-
сальна сукупність можливих виборів ОПР.
Нечіткою метою в х є нечітка підмножина х , яку позначимо С.
Нечітка мета описується функцією належності рс : х--»[0.і].
Визначимо тепер, що розуміють під розв’язком задачі
досягнення нечіткої мети. Розв’язати цю задачу означає досягнути
мети та задовольнити обмеження, причому в даній постановці треба
говорити не просто про досягнення мети, а про її досягнення з
певним ступенем, з врахуванням ступеня виконання обмежень.
У підході Белмана-Заде ці фактори враховуються так.
Нехай деяка альтернатива х забезпечує досягнення мети із
ступенем //с(х) та задовольняє обмеження С із ступенем
/лс(х) .Тоді вважають, що ступінь належності згаданої альтернативи
розв’язку задачі дорівнює мінімуму серед цих величин. Таким
чином, нечітким розв’язком задачі досягнення нечіткої мети є
перетин нечітких множин мети та обмежень, тобто функція
належності рішень дв(х) дорівнює:
Ао(х) = тіп{до(х);Ас(х)}.	(7-3.1)
За наявності декількох цілей та обмежень нечітке рішення
описується функцією належності:
Ад(*) = тіп{//Сі(х),^с,(х),...,Ас (х),АС1(х),Ас,(х).-.Аст(х)} 
Якщо різні цілі та обмеження розрізняються за ступенем
вагомості і задано відповідні коефіцієнти відносної вагомості
цілей А, (х) та обмежень V,, то рп(х) задається виразом:
Ао(х) = тш{А1дг;](х),...,Апдс(х),г1рС| (х),...,итрс (х)}. (7.3.2)
Приклад 7.3. Нехай задано універсальну множину х = (і,2,....Ю}
на якій задано нечітку мету о(х близьке до 5), нечітке обмеження
с,(х близьке до 4) та с, (х близьке до 6). Нехай їхні функції
належності задано в табл. 7.1.
317
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 7.1
X	1	2	3	4	5	6	7	8	9	10
Дс(’)	0	0.1	0.4	0.8	1.0	0.7	0.4	0.2	0.1	0
й,(»)	0.3	0.6	0.7	1	0.9	0.8	0.5	0.3	0.2	0
Ис.М	0.2	0.4	0.6	0.7	0.9	1	0.8	0.6	0.4	0.2
Тоді ДЛЯ рішення О одержимо функцію належності рп(х) , а рішення
о інтерпретується як: л має бути близьким до 5 (для табл. 7.2).
Таблиця 7.2
X	1	2	3	4	5	6	7	8	9	10
ніМ	0	0.1	0.4	0.7	0.9	0.7	0.4	0.2	0.1	0
Це рішення можна інтерпретувати як нечітко сформульовану
інструкцію. При такому представленні лишається невизначеність,
яку ж альтернативу слід вибрати, тобто треба вирішити цю
невизначеність. Існують різні способи вирішення цієї
невизначеності. Найпоширеніший з них, запропонований Л.3аде,
полягає у виборі альтернативи, що має максимальний ступінь
належності до нечіткого рішення, тобто альтернатива визначається із
умови:
тах/^о(х) = тахтіп{х/с(х),х/с(х)}.
-Г
Такі альтернативи називають максимізуючими.
7.4. Прийняття рішень при нечіткому відношенні переваги
на множині альтернатив
Процес прийняття рішень як вибір найкращої (найбільш
раціональної") альтернативи із деякої універсальної множини
альтернатив X, може відбуватися при різному ступені
інформованості ОПР.
318
_____________________________________Дослідження операцій. Збірник задач
Якщо інформацію про реальну ситуацію, на основі якої
порівнюються різні альтернативи, можна задати у формі функцій
корисності, то маємо задачу НМП. Такі варіанти задачі розглянуто в
п. 7.3. Однак подібний спосіб опису інформації можливий не завжди.
Універсальнішим є опис інформації у формі відношення переваги на
множині альтернатив [34].
Розглянемо це відношення і його властивості. Припустимо, що на
основі інформації, отриманої від ОПР, на множині допустимих
альтернатив X введено чітке відношення нестрогої переваги Д . Це
означає, що для будь-якої пари альтернатив (х,у) можна висловити
одне з таких тверджень:
х не гірше за у, що записується так х>у або (х, у) є Д;
у не гірше за х, тобто у > х або (у,х) є Д;
х та у не порівняні між собою, тобто (у,х) є К, (х,у) і К.
Така інформація дає змогу звузити клас раціональних виборів,
включивши в нього лише ті альтернативи, що не домінуються
жодною альтернативою з множини X.
Для того, щоб визначити недоміновані альтернативи, введемо
відношення строгої переваги , відповідне відношенню нестрогої
переваги Д , а також відношення байдужості .
Казатимемо, що альтернатива х строго краща за альтернативу у,
коли одночасно, х > у , а У&х, тобто (х,у) є Д, (у,х) і Д. Сукупність
усіх таких пар(х,у) і називається відношенням строгої переваги Д$
на множині X.
Відношення строгої переваги Д5 згідно з його означенням
записується так:
Д8 = Д\Д~1.	(7.4.1)
Якщо (х,у)єЯ5, то казатимемо, що альтернатива х домінує
альтернативу у (записується х>у)- Альтернативу х є X назвемо
недомінованою на множині X із заданим відношенням Д5,
якщо (у, х) ? для будь-якої альтернативи у є А'. Іншими словами,
якщо х — недомінована альтернатива, то на множині X немає жодної
319
Зайченко О.Ю., Зайченко Ю.П.
альтернативи у, яка б домінувала х. Отже вибір недомінованих
альтернатив можна вважати раціональним у задачі прийняття рішень.
Таким чином, інформація у формі відношення переваги Я дає
можливість звузити клас раціональних виборів А' до підмножини
недомінованих альтернатив Хнд вигляду:
Хнд - {* '•х є А\(у,х) і Н\ Н~\\/у є X}.
Якщо наявна в ОПР інформація у формі відношення переваги
недостатня щоб зробити вибір між альтернативами х та у, то між
цими альтернативами існує відношення «байдужості» Я7
(індиферентність). Більш строго, між альтернативами х та у є
відношення байдужості (х,у) є Я7 тоді і тільки тоді, коли відношення
переваги х>у та переваги у>х одночасно виконуються або одночасно
не виконуються. Із цього означення випливає, що Я7 можна
записати у вигляді:
Я7 ={ЛхЛ'}\{яи/г'}ІІ{ЯП/Г1}.	(7.4.2)
Нечітке відношення переваги
При моделюванні реальних систем можуть бути такі ситуації, коли
в ОПР немає чіткого уявлення (інформації) про відношення переваги
між усіма або деякими альтернативами, а можна лише оцінити ступінь
виконання певної переваги між парами альтернатив у вигляді числа на
відрізку [0;1]. У такому разі за допомогою ОПР (або експерта) можна
ввести нечітке відношення переваги.
Означення 7.17. Нечітким відношення нестрогої переваги на
множині альтернатив X називатимемо будь-яке задане на цій
множині нечітке рефлексивне відношення К [34].
Отже, нечітке відношення переваги Я на X описуватимемо
функцією належності дй(х,у), що має властивість рефлексивності,
тобто х/я(х,х) = 1 для всіх хє.Х. Якщо Я — нечітке відношення
переваги на множині X, то для довільної пари альтернатив (х,у)єЯ
значення /лк{х,у) слід розуміти як ступінь виконання переваги х>у.
320
Дослідження операцій. Збірник задач
На основі заданого на X нечіткого відношення нестрогої
переваги К можна однозначно визначити три відповідних йому
нечітких відношення: 1) байдужості ; 2) еквівалентності Не; 3)
строгої переваги ЛЛ-, які використовуються для визначення і аналізу
властивостей множини недомінованих альтернатив у задачах
прийняття рішень [16; 34]. За аналогією із звичайними (тобто чіткими)
відношеннями переваги вони визначаються так;
Я, = {*x^¥}\{Я^/ГI}^{Япя,}; Я, =К\П
яе = яПл_|-
Тобто відношення еквівалентності Ке визначається так:
альтернатива х еквівалентна у (у ~ х), якщо одночасно виконуються
відношення х>у та у>х. Використовуючи раніш введені означення
операцій 1),П,\ неважко отримати вирази для функцій належності цих
відношень :
1)	нечітке відношення байдужості:
Ля (х, у) = тах[1 - тах {рк (х, у); (у, х)}; тіп {(х, у); рк (у, х)} ] = (7.4.3)
= тах [тіп {1 -	(х, у); 1 - ря (у, х)}; тіп {ря (х, у); р„ (у, х)} ];
2)	нечітке відношення еквівалентності:
Дек(х’У) = тіп{дя(х,у);//я(у,х)};	(7-4.4)
3)	нечітке відношення строгої переваги:
Дк(х,у)-рк(у,х), якщо р„(х,у)>рк(у,х),	(7.4.5)
0, у протилежному разі.
Розглянемо деякі властивості введених нечітких відношень.
1.	Нечіткі відношення , Ке рефлексивні і симетричні. Справді,
їхня рефлексивність випливає із того, що ря(х,х) = 1,Х/хє X,
оскільки вихідне відношення Н рефлексивне.
Тому	рЕ(х,х)=рЕ(х,х) = \.
Симетричність обох відношень випливає із їх означень.
Дк{х,у) =
321
Зайченко О.Ю., Зайченко Ю.П.
2.	Нечітке відношення строгої переваги антирефлексивне та
антисиметричне. Справді:
а)	х4(.г,х) = 0, оскільки вихідне відношення Я рефлексивне і для
нього рк{х,х) = 1 для ВСІХ X Є X',
б)	нехай у) > 0, тобто рк(х,у)>рк(у,х)> 0. Тоді ^(у,х) = О,
що означає антисиметричність цього відношення.
Можна показати, що коли вихідне нечітке відношення переваги Я
на X транзитивне, то транзитивні також і відповідні відношення
еквівалентності Не та строгої переваги Я5 [34].
Нечітка пддмножина недомінованих альтернатив
Використаємо введені вище відношення строгої переваги Я5 для
визначення підмножини недомінованих альтернатив. Згідно з
означенням нечіткого відношення переваги Я5 для будь-яких
альтернатив х,уєХ величина р^(х,у) є ступенем з яким альтер-
натива у домінується альтернативою х. Тому при фіксованому
уєХ функцію р£(у,х) можна розглядати як функцію належності
нечіткої множини альтернатив хє X, які строго домінуються
альтернативою у. Звідси випливає, що множина всіх альтернатив х,
які не домінуються альтернативою у, є доповненням введеного
відношення Я5. Згідно з означенням доповнення одержимо, що ця
нова нечітка множина описується функцією належності вигляду:
1-/4(у,х),хєХ.	(7.4.6)
Якщо, наприклад, аІ(у,х) = 0.3, то із ступенем 0.7 альтернатива
х не домінується альтернативою у. Звідси випливає, що для
виділення в X підмножини усіх альтернатив, кожна з яких не
домінується жодною альтернативою із X, треба взяти перетин
нечітких підмножин (7.4.6.) по всіх у е X. Такий перетин і назвемо
нечіткою підмножиною недомінованих альтернатив і позначимо його
Хна. Згідно з означенням операції перетину нечітких множин,
322
Дослідження операцій. Збірник задач
одержимо такий вираз для функції належності множини
недомінованих альтернатив:
р'к М = іпГ[1 -Ая(У.х)},хєХ.
уєХ
Або:
Аяй(х) = 1-8ирАк(у,л),хє X.	ФАТ)
У&Х
Згідно з (7.4.7) ц'п(х) - ступінь з яким альтернатива х не
домінується жодною з альтернатив множини X. Нехай /л'^{х) = а
для деякої альтернативи х0. Тоді х0 домінується будь-якими іншими
альтернативами із ступенем, який не перевищує (1-а) -
Користуючись означенням нечіткого відношення /л$(х,у) можна
показати, що
5иРАя(У.-«) = 8ир[Ай(У>л;)-Ая(^>')1>^єЛ' •	(7.4.8)
уєХ	уєХ
Вираз (7.4.8) дає змогу описати підмножину недомінованих
альтернатив функцією належності вигляду, дєад — вихідне нечітке
відношення нестрогої переваги. Оскільки величина а^(х) є ступінь
недомінованості альтернативи х, то раціональним слід, звичайно,
вважати вибір альтернатив, що мають найбільший ступінь
належності, нечіткій множині Хнд, тобто таких, що
/^(*°) = 5иРРкМ = 1 -іп£8ир{Ал(у,х) -		(7-4-9)
хеХ	Х*х уєХ
Множину всіх альтернатив хнд, які задовольняють умову (7.4.9),
назвемо максимальними недомінованими альтернативами на
множині X. Очевидно:
X™ = {* =	є X}.
хєХ
Приклад 7.4. Нехай у скінченій множині х =	задано
нечітке відношення нестрогої переваги (табл. 7.3).
323
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 7.3
/0г (*/,*/) =	•м	X]	х2	X,	ха
	«1	1	0.2	0.3	0.1
	X,	0.5	1	0.2	0.6
	X,	0.1	0.6	1	0.3
			0.6	0.1	0.5	1
Використовуючи введені вище означення, знайдемо відношення
строгої переваги /?, (табл. 7.4).
Таблиця 7.4
	’М	X]	Х2	х3	
	*1	0	0	0.2	0
	Х2	0.3	0	0	0.5
	X)	0	0.4	0	0
	х4	0.5	0	0.2	0
Звідси одержимо шукану функцію належності нечіткої множини
недомінованих альтернатив (табл. 7.5).
Таблиця 7.5
^(х)-			Хз	х4
	0.5	0.6	0.8	0.5
Як бачимо, найбільшу ступінь недомінованості має альтернатива
хз^їх)=0.8), тому її вибір слід вважати найкращим рішенням.
Чітко недоміновані альтернативи та їхні властивості
Розглянемо задачі раціонального вибору альтернатив, в яких
множина недомінованих альтернатив являє собою нормальну нечітку
підмножину множини X, тобто функція належності цієї підмножини
має властивіст:
8чрАкд(х) = 1 -
гєХ
(7.4.10)
324
Дослідження операцій. Збірник задач
У цьому разі для будь-якої альтернативи х із множини Х"й
максимальних недомінованих альтернатив виконується умова
р'£(х) = 1. Це означає, що для будь-якої альтернативи х є Xий та
довільної альтернативи у є X при цьому виконується рівність
Ря(У>Л) = 0’ тобто жодна з альтернатив не домінує з ненульовим
ступенем дану альтернативу х.
Такі альтернативи, для яких д'р(х) = 1 називатимемо чітко
недомінованими (скорочено ч.нд.), відповідну множину — множиною
чітко недомінованих альтернатив, і позначатимемо її Х""д. Тоді:
Х4"6 = {х:хєХ та р^(х) = \}.
Множина ч.нд. альтернатив відіграє визначну роль у задачах
раціонального вибору, оскільки її можна розглядати як чітке рішення
нечітко сформульованої задачі.
Розглянемо деякі властивості ч. нд. альтернатив. Передусім
розглянемо питання про еквівалентність ч. нд. альтернатив.
Покажемо, що ч. нд. альтернативи, якщо їх можна порівнювати,
обов’язково еквівалентні.
Як випливає із визначення Хч"д, Ддй(х), для довільної ч. нд.
альтернативи х є А"""’ виконується рівність:
5иРх4(У.*) = 0-	(7.4.11)
ієХ
Звідси можна зробити висновок, що для будь-яких
х(,х2 є Хч"д виконується рівність:
Дя(*і,*2) == °-	(7.4.12)
Тоді з означення д|(х„х2) випливає, що //я(х,,х2) = рк(х2,х1).
Згідно з означенням нечіткого відношення еквівалентності
Дя(х,,х2) одержимо:
Дк (*і ’х2) = тіп ІАя (*1>Х2).	)} = Дк (Х1 >х2 ) ’
для всіх	х,,х2 є X4"6.	(7.4.13)
325
Зайченко О.Ю., Зайченко Ю.П
Розглянемо два типи лінійності нечіткого відношення переваги:
1)	Я : Л — лінійне н.в.п. Якщо Я є Л - лінійним, тобто:
тах{ая(х,,х2 ),рк(х2,х,)} > Л,
то з (7.4.18) випливає:
^(х„х2)>Л.	(7.4.14)
Отже, дві довільні ч. нд. альтернативи еквівалентні із ступенем,
більш за Л.
2)	Я сильно лінійне н.в.п. Якщо Я сильно лінійне, тобто:
тах{Ай(хі,х2),АЛ(х2,Хі)} = 1,а х„х2 є Хчнд,
то із означення сильної лінійності та нестрогої рівності (7.4.14)
випливає:
д^х„х2) = 1.	(7.4.15).
Багатокритеріальний вибір альтернатив
на основі нечіткого відношення переваги
Розглянемо застосування нечіткого відношення переваги та
множини недомінованих альтернатив у проблемі раціонального
вибору за наявності декількох критеріїв. Нагадаємо, що цю проблему
докладно розглянуто у розд.1.
Нехай маємо ситуацію, коли кожний з критеріїв у заданий у
формі чітких функцій корисності : Х -> Я(1). Значення /}(х)
можна трактувати як числову оцінку альтернативи х є X за ознакою
у . Альтернатива х з більшою оцінкою / (х) вважається кращою за
критерієм (ознакою) у. Таким чином, кожна з функцій /7(х)
описує(задає) звичайне(чітке) відношення переваги Яу на множині
альтернатив X вигляду:
Яу = {(х,у): /7(х) > /у(у),х,у є X}.
Завдання полягає в тому, щоб вибрати альтернативу х0, яка мала
б найбільші оцінки за всіма критеріями (ознаками). Отже,
326
Дос йдження операцій Збірник задач
раціональним у розглядуваному випадку слід вважати вибір
альтернативи хоеХ, яка має властивість;
/, (*о ) /у (Я. V/і = 1, т, Х/у є X .
Такі альтернативи називають ефективними (або Парето-
оптимальними), і розв’язком цієї задачі вибору є множина всіх
ефективних альтернатив.
Для розв’язання сформульованої задачі багатокритеріального
вибору треба вибрати належний спосіб згортки багатьох критеріїв
(векторного критерію) в скалярний.
1.	Одним з найпоширеніших способів згортки критеріїв є
використання перетину. Нехай = Р|Я, • Тоді множина ефективних
1=1
альтернатив у множині X з відношенням переваги (У, збігається з
множиною ефективних альтернатив для набору функцій /}(х).
Таким чином, для відшукання множини ефективних альтернатив
можна замість набору відношень = 1,т використали їх перетин
(2 і знайти множину недомінованих альтернатив за н.в.п <2.
Позначимо через д2(х,у) функцію належності н.в.п. 7?у..
Очевидно:
'\, якщо ^(х)>/}(у), або (х,у)єЯ/,
0,у противному разі, (х,у)йЯу-
Тоді їх перетину — нечіткому відношенню переваги -
відповідає функція належності:
АЄ1 (*. У) = тш {д, (х, у), р2	УХ- (*> у)} •	(7-4.16)
Така згортка критеріїв аналогічна згортці вигляду:
Г(х) = гтпа>і/2(х),	(7.4.17)
що застосовується у багатокритеріальних задачах прийняття рішень.
Числа <иу у (7.4.17) — це коефіцієнти відносної ваги відповідних
критеріїв. У згортці (7.4.16) очевидно ліу = 1, V/ = 1,т. Якщо ж * 1, то
ау(*>у)=
327
Зайченко О.Ю., Зайченко Ю.П.
Нс^х,у)=тт{(охцх(х,у),согр1(х,у),..,(і)прп(х,у)}, (7.4.18)
тобто відношення 21 вже не є рефлексивним.
2.	Введемо згортку вихідних відношень {/?у} у вигляді суми:
Сг = 22	(*) > Де 2^®/= 1> — 0 ’
їй відповідає функція належності вигляду:
До,и.у)= 2>;А/(*..у) •
>1
Зазначимо, що результуюче н.в.п. рефлексивне, оскільки усі
вихідні н.в.п. Лу рефлексивні.
Побудуємо нечітку підмножину недомінованих альтернатив (2'2 ,
користуючись раніше введеними означеннями:
чпд
Позначимо через Х] підмножину чітко недомінованих
чнд
альтернатив множини {Х^}, а через А'2 відповідно підмножину
чітко недомінованих альтернатив множини {Х,()2}  Можна показати,
що Х^аХ?"*.
Далі доцільно шукати перетин множин в"д,^2^, ’ знайти
С„а=СҐЛСг"* та відповідну функцію належності Инд(х) =
= тіп{д^ (х),^ (х)}. На множині ^нд треба відшукати альтернативи
з максимальним ступенем недомінованості. Це і буде найкращим
вибором.
Дамо опис алгоритму вибору альтернатив за наявності багатьох
критеріїв оптимальності (нечітких відношень переваги) [16].
1.	Нехай на універсальній множині альтернатив X задано
відношення переваги КХ,К2,...,Кт (чіткі або нечіткі) з функціями
належності р^(х,у), а також щу, у = 1,щ — вагові коефіцієнти
відповідних відношень.
328
Дослідження операцій. Збірник задач
Будуємо згортку відношень Л,, Н2К,„ у вигляді перетину
т
= р|/?7 , з функцією належності:
7=1
Аа (х,у) = тіп{//1(х,у),х/2(х,у),..,х/Дх,у)} -	(7.4.20)
2.	Визначимо множину недомінованих альтернатив у
множині (Х^):
Аа (^) = 1-8ир{Аа(У^)-Аа(^^)}	(7.4.21)
>-еЛ'
3.	Використовуючи згортку критеріїв у вигляді суми, будуємо
нечітке відношення переваги (32:
Аа,(х,у) = Х^АуСх.у) ~	~	(7-4-22)
7=1	7=1
4.	Знаходимо нечітку підмножину недомінованих альтернатив по
відношенню ^2:
(х) = 1 - 8ир] £	(У, х) - Дв, (х, у)
>єХ [/=1
(7.4.23)
5.	Знаходимо перетин множин	, і спільну множину
недомінованих альтернатив <2нд = £?ГгіП ()2д з функцією належності:
А,„>(х) = тіп (х),	(*)} 	(7.4.24)
Раціональним вважаємо вибір альтернатив із множини:
Хчнд = {**  А»а(х*) = 8ирАи<)(х).х є X}.	(7.4.26)
X
Приклад 7.5. Нехай громадянин N планує здійснити туристичну
поїздку за кордон. При цьому він розглядає такі можливі варіанти:
Х| — туристична поїздка в Париж на 7 днів;
х2 — туристична поїздка в Італію на 14 днів, з них 7 днів—відпочинок
на узбережжі моря, а 7 днів—турпбіздка по країні (Рим, Неаполь);
329
Зайченко О.Ю., Зайченко Ю.П.
хз -туристична поїздка в Єгипет на 7 днів, з відвідуванням
древньоєгипетських пірамід;
х4 -туристична поїздка в Болгарію, 7 днів — відпочинок на
золотих пісках в м. Варна, а 7 днів — екскурсія по Болгарії.
Громадянин оцінює альтернативи за такими критеріями: я, -— вартість
туристичної подорожі; я2 — наявність екскурсій, Можливість ознайомлення
з історичними місцями, відвідування музеїв, виставок тощо; к, —
можливість відпочити на морі; я4 — рівень обслуговування та сервісу.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
Я,:х4 >-х3,х3 >- х,,х, > х2;
Я2:х, ~ х2,х, >- х3,х3 > х4.
К3'х2 »х4,х2 >х3,х3 >-х,;
я/х, >х2,х2 ®х3,х3 >х4.
Нехай ваги критеріїв такі: =0.4,<у2 =0.2,а>3 =03,а>л =0.1.
Побудувати згортку критеріїв	1	* знайти
/ >
найкращу альтернативу за обома згортками.
Розв’язок. 1. Побудуємо матрицю відношення я,. Скориста-
ємося співвідношеннями:
\,якщох.>-х. або х ~х.
М^)=„
О'ЯКЩОХ; -<ХГ
Одержимо матрицю відношення я, (табл. 7.6):
Таблиця 7.6
АЛ|(х,,ху) =	X, \хі		*2	*3	Х4
	*|	1	1	0	0
		0	1	0	0
	х3	1	1	1	0
	X.	1	1	1	1
= 0 4
330
Дослідження операцій. Збірник задач
2. Аналогічно будуємо матрицю відношення я2 (табл. 7.7)
Таблиця 7.7
	ХІ ^х)	ч	Х2	х.	Х«
	Х1	1	1	1	1
	Х2	1	1	1	1
	х3	0	0	1	1
	Х4	0	0	0	1
ш2 = 0.2
3. Аналогічно будуємо матрицю відношення в, (табл. 7.8)
4. Аналогічно будуємо матрицю відношення (табл. 7.9)
5. Будуємо згортку відношень = Л,Р|Л2ГілзГіЛ4 (табл- 7.10)
331
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 7.10
Мв](хі,хІ) =	Хі Х/	-Г|	Л2		Л4
	•ч	1	0	0	0
	Х2	0	1	0	0
	Ху	0	0	1	0
	*4	0	0	0	1
6.	Будуємо відношення строгої переваги = 2, \ £>,1 і знаходимо
множину недомінованих альтернатив (Зд :
Таблиця 7.11
/А?,(*„ху) =	X, \ х;	•ТІ	Хг	х3	X,
		0	0	0	0
	Х2	0	0	0	0
	Ху	0	0	0	0
	*4	0	0	0	0
		1	1	1	1
Як бачимо по першій згортці всі альтернативи
х|, х2, х}, х4 чітко не доміновані.
7.	Будуємо н.в.п. (адитивну згортку відношень лу), (X, = £а>Л(х)
4
і знаходимо її функцію належності (х(, х]) -	Нр.Xхі * х}) й
*=і
будуємо матрицю відношення ^г.
Таблиця 7.12
нв2(хі<х^ =	хі ^Хі	Х|	*2		*4
	*|	1	0.7	0.3	0.3
		0.5	1	0.6	0.6
	хз	0.7	0.5	1	0.3
	ХЛ	0.7	0.7	0.7	1
332
Дослідження операцій Збірник задач
8.	Будуємо матрицю відношення і знаходимо множину
недомінованих альтернатив по відношенню :
Таблиця 7.13
її* п (х X )	X, \х/	ч	*г	х3	
	X,	0	0.2	0	0
Л* 1/2	/ 7	<2	0	0	0.1	0
	ь	0.4	0	0	0
	х4	0.4	0.1	0.4	0
	нд	0.6	0.8	0.6	1
9.	Знаходимо перетин множин еГа, в? 1 обчислюємо функцію
належності результуючоїпідмножини =СГ’П в?-
Таблиця 714
хі		Ч	*з	Л4
	1	1	1	1
	0.6	0.8	0.6	1
	0.6	0.8	0.6	1
Таким чином, найкращою альтернативою виявляється х4 для
якої ц (х4) = 1. Це — поїздка до Болгарії.
Задачі і вправи
Задача 7.4.1
Нехай громадянин N планує якнайкращим чином витратити
наявні у нього кошти. При цьому він розглядає такі можливі
варіанти:
333
Зайченко О.Ю., Зайченко Ю.П.
X, — купити автомобіль;
х2 — поїхати в круїз;
х3 — вкласти гроші в акції компанії;
х4 — вкласти гроші у нерухомість.
Громадянин оцінює альтернативи за такими критеріями:	—
величина витрат; /?2 — можливий прибуток; К3 — рівень
задоволення естетичних потреб.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
: X] -< х3; X] ~ х2; х3 ~ х4;
К2:х1 >- х2,хі -<х3,х4 >х3;
7?3:X] -<х2,х, >х3,х3 » х4;
Нехай ваги критеріїв такі: гр, = 0.3, и>2 = 0.25, уу3 = 0.45.
Побудувати згортки критеріїв бі = П К, * <21 =	* знайти
і	}
найкращу альтернативу за обома згортками.
Задача 7.4.2
Нехай громадянин N хоче придбати автомобіль. При цьому він
розглядає такі можливі варіанти:
х1 - купити автомобіль марки «Жигулі»;
х2— купити автомобіль марки «Москвич»;
х3 - купити автомобіль марки «Запорожець» (новий).
Громадянин оцінює альтернативи за такими критеріями; К1-
ціна; К2 — дизайн; К3 — економічність (витрати і ціна палива); /?4
— динаміка автомобіля; К5 — зносостійкість.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
7?, :х, -<х2,х2 ~ х3;
К2 :х, » х2,х| >- х3;
334
Дослідження операцій. Збірник задач
К3:х3 > х1,х1 > х2;
К4 :х1 > х3, х3 > х2;
К5:х1 > х3,х3 >- х2.
Нехай ваги критеріїв такі:
и»! = 0.4, н>2 = 0.05, и'з = 0.2, ^=0.15, и», = 0.2 
Побудувати згортки критеріїв =П«, і й = 'У'уу.В,
у	І
і знайти найкращу альтернативу за обома згортками.
Задача 7.4.3
Нехай перед громадянином N стоїть задача вибору роботи. При
цьому він розглядає такі можливі варіанти:
х, — робота у вітчизняній фірмі;
х2 — робота на державному підприємстві;
х3 — робота в науковій організації;
х4 — робота на сучасному підприємстві (наприклад, Німецькому
або США).
Громадянин оцінює альтернативи за такими критеріями: Вх —
розмір і стабільність заробітної плати; В2 — наявність творчої та
цікавої роботи; В3 — перспективність роботи (можливість
професійного рівня).
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
Я,:%! « х2, х2 » х3, х4 >- х,;
В2 :х, > х,, х, -< х., х, я х,, х. > х.;
Л	X X	І	Л Л	І*
•* «-З •	’ Л4	7	*"4" ^2 "
Нехай ваги критеріїв такі: и>, = 0.4, и>2 = 0.25, ил, = 0.35.
Побудувати згортки критеріїв = ГК ’ ^2-XVV^К^
І	У
і знайти найкращу альтернативу за обома згортками.
335
Зайченко О.Ю, Зайченко Ю П
Задача 7.4.4
Нехай громадянин N володіє певного сумою для покупки
квартири. При цьому він розглядає такі можливі варіанти:
X] — купити квартиру в центрі Києва;
х2 — купити квартиру на окраїні Києва;
х3 — купити квартиру в пригороді недалеко від Києва.
Громадянин оцінює альтернативи за такими критеріями: 7?1 —
вартість квартири; К2 — витрати на проїзд; 7?3 — загазованість
навколишнього середовища; Л4 — відпочинок після роботи.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
К1 :х, -< х2, х2 -< х3;
К2 :х3 -< х2,х2 >- х1,х1 ~ х3;
К3 .х2 ® х3,х2 >х(;
К4:х{ >~х2,х2 ~х3.
Нехай ваги критеріїв такі: гц = 0.4, и>2 = 0.25, и>3 = 0.2,	= 0.15.
Побудувати згортки критеріїв ()і =	і ()2
7	І
і знайти найкращу альтернативу за обома згортками.
Задача 7.4.5
Нехай деякий молодий чоловік планує вступити у вищий
навчальний заклад після закінчення школи. При цьому він розглядає
такі можливі варіанти:
х, — Київський державний університет ім. Т.Г.Шевченка;
х2 — НТУУ «КПІ»;
х3 — один із недавно відкритих платних університетів;
х4 — національний економічний університет.
Громадянин оцінює альтернативи за такими критеріями; —
престижність ВНЗу; К2 — гарантоване працевлаштування після
336
Дослідження операцій Збірник задач
закінчення; 7?3 — безплатне навчання; /?4 — наявність у ВНЗі сучасної
" ^4,
~ х4, х3 ~ х2;
матеріально-технічної бази навчання; /?5 — якість навчання.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
К1:хі »х2,хі >х3,х3
К2 :х2 > х,, х, < х3, х,
К3: х1 ж х2, X] > х4, х4
КА: х3 ж х2, х2 > х,, х.
'З »
4 ’
4 *
*/'’2 ’	’ *"^3
Нехай ваги критеріїв такі: = 0.3, уу2 =0.15, и>3 = 0.2,
^=0.15, и^5 = 0.2.
Побудувати згортки критеріїв = П«, І
З	7
і знайти найкращу альтернативу за обома згортками.
Задача 7.4.6
Нехай громадянин N хоче якнайкращим чином вкласти свій
майновий сертифікат. При цьому він розглядає такі можливі варіанти:
х, — вкласти в приватизацію житла;
х2 — використати для купівлі акцій автомобільної компанії
ЛОГОВАЗ;
х3 — вкласти в акції будівельної компанії;
х4 — продати свій сертифікат.
Громадянин оцінює альтернативи за такими критеріями:	—
очікуваний дохід; К2 — можливий ризик пов’язаний із банкрутс-
твом; К3 — час отримуваного прибутку.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
Кі:х1 > х4, х2 ж х3, х2 > х1;
К2:х} >- х2,х{ ж х4, х3 > х2, х, > х3;
337
Зайченко О.Ю., Зайченко Ю.П.
л3: х, ~ х4, х4 > х2, х2 ~ х,.
Нехай ваги критеріїв такі: = 0.4, и>2 = 0.3, щ = 0.3.
Побудувати згортки критеріїв	і 0? = Х.уу,/?,
/	і
і знайти найкращу альтернативу за обома згортками.
Задача 7.4.7
Нехай громадянин N планує проведення своєї відпустки. При
цьому він розглядає такі можливі варіанти:
хІ — поїхати в Крим;
х2 — поїхати на закордонний курорт на березі Чорного моря;
х3 — відпочити на дачі на березі Дніпра;
х4 — поїхати в санаторій під Києвом.
Громадянин оцінює альтернативи за такими критеріями: /?, —
вартість відпочинку із врахуванням дороги; К2 — якість відпочинку,
рівень сервісу і обслуговування; К3 — можливість отримання
лікування; Т?4 — можливість розширення свого кругозору, наявність
екскурсій.
Нехай за оцінками експерта згадані критерії встановлюють такі
відношення переваги на множині альтернатив:
:х, «х2,х3 >-хрх3 >-х4,х, >-х4;
/?2 :х2 >- х,,х, > х4,х4 >- х3;
/?3:х, »х4,х, >-х2,х2 »х3;
/?4:х, » х2,хІ > х3,х3 » х4.
Нехай ваги критеріїв такі: уу, = 0.4, уу2 = 0.3, уу3 = 0.2, уу4 =0.1.
Побудувати згортки критеріїв	і
2	)
і знайти найкращу альтернативу за обома згортками.
338
Дослідження операцій Збірник задач
7.5.	Загальна задача нечіткого математичного програмування
і методи її розв’язання
Нехай деяка виробнича фірма планує випуск різних виробів
хІ на поточний період (квартал або рік). Позначимо через
^очікуваний прибуток на одиницю реалізованої продукції типу
у.у = 1,л . Для виробництва кожного з виробів використовуються
ресурси 6,,	— виробничі потужності фірми, причому питомі
витрати ї-го ресурсу при виробництві одиниці продукції типу у
становлять ау одиниць. Треба знайти такий раціональний план
випуску виробів кожного типу, який забезпечує максимальний
прибуток фірми. Математична модель цієї задачі така:
п
максимізувати	’	<7-5Л)
при обмеженнях:	(7.5..2)
у
х>0; хєК".
Цю задачу, якщо значення параметрів су, аі} є випадковими
величинами з відомими функціями розподілу Г(с}), Р(ад), можна
розв’язати методами стохастичного програмування, (див. гл. 6).
Однак на практиці буває, що ці параметри невідомі і для параметрів
Су, Оу можна лише вказати інтервал можливих значень. Задачу
такого типу можна назвати задачею з багатозначними коефіцієнтами.
У рамках цієї задачі немає сенсу говорити про максимізацію ц.ф.,
оскільки значення цієї функції — не числа, а множини чисел. Тут
треба з’ясувати, яке відношення переваги на множині альтернатив
породжує ця функція, а далі визначити, які рішення слід вважати
раціональними стосовно цього відношення переваги.
339
Зайченко О.Ю., Зайченко Ю.П.
Наступним етапом на шляху деталізації та уточнення розглянутої
тут моделі є опис параметрів задачі у вигляді нечітких множин.
У модель вводиться додаткова інформація у вигляді функції
належності цих нечітких множин. Ці функції можна розглядати як
спосіб наближеного відображення експертом наявного у нього
неформалізованого уявлення про реальне значення даного параметра.
Значення функцій належності — це вагові коефіцієнти, які експерти
приписують різним можливим значенням цього параметра.
Отже, після уточнення маємо таку постановку задачі НМП.
Задано лінійну форму вигляду:
/ (х, с) = сух7--------> тах,	(7-5.3)
/=і
в якій значення коефіцієнтів {с}} описано нечітко в формі нечітких
підмножин відповідних універсальних множин, тобто задано функції
належності //у(с),у = 1, п. Крім того, задано обмеження:
аііхі < Ь( і = \,т,х] > 0, у~ 1, п,
і
(7.5.4)
причому значення коефіцієнтів 0^,6, описано також у формі
нечітких множин з функціями належності V,, («у), 7, (6,). Треба
здійснити раціональний вибір вектора х є /?", який у певному
розумінні максимізує задану нечітку лінійну форму.
Формулювання задачі, її приведення до загальної задачі НМП
Нехай X — універсальна множина альтернатив. Підмножина
допустимих альтернатив описується нерівностями, що випливають з
(7.5.4):
& (*> ан ’ аі2	а.„	=	(7.5.5)
340
Дослідження операцій. Збірник задач
де — задані функції, Лхй"--------------->/?*; а^, і = 1,т, у = 1,л, —
числові параметри, значення яких описано у формі нечітких множин
числової осі.
Нехай !<(«,,) -— задані функції належності цих нечітких
множин.
Вважатимемо, що вихідне відношення переваги — це нестрогий
порядок > на /?’. Побудуємо математичну модель задачі у формі
загальної задачі НМП.
Для цього розглянемо спочатку нечітке відношення (7.5.4)
і побудуємо відповідну йому нечітку підмножину допустимих
альтернатив, функцію належності якої позначимо /лс(х).
Нехай {а } = 1,/и, у = 1,л — деякі конкретні числові значення
відповідних параметрів в обмеженнях (7.5.4), ступені їх належності
заданим нечітким множинам дорівнюють відповідно:
^(^),і = 1,т, У = 1,л.
Позначимо через д0 мінімальне з цих чисел, тобто
А° = тіпиДа®) • Якщо деяка альтернатива х&Х задовольняє
нерівності ^.(х.а’рй,”,...,^®,) < 0,ї = 1,т , то природно вважати, що
ця альтернатива належить множині допустимих альтернатив із
ступенем, не меншим, ніж у/°, тобто вважати, що /уг (х) > /у®. Цією
нерівністю і задається множина допустимих альтернатив. Для
зручності запису її функції належності введемо такі позначення:
и(Л) = тіп и (а..), А = ||а І, і = 1, т, і = 1, л;
о.д з_ 11 11	(7.5.6)
Р(х) = {А = ||а,|^ ;е,(а,„а12,...,а,л,х) < 0;ї = 1, т}.
У цих позначеннях одержимо рс(х) = зир и(Л).	(7-5.7)
А=Р(л)
341
Зайченко О.Ю., Зайченко Ю.П.________________________________________
Кожній альтернативі х функція рс(х) ставить у відповідність
ступінь її допустимості з урахуванням нечіткої інформації.
Розглянемо нечітко задану функцію /(х,с1,с2,...,сп) і
запишемо її у вигляді нечіткої ц.ф. аналогічно тому, як це було
зроблено для обмежень.
Нехай с°,у = 1,л — деякі конкретні числові значення
параметрів функції (7.5.3), ступені її належності заданим нечітким
множинам дорівнюють відповідно Х2(С/)*І =	•
Нехай ср° — мінімальне з них: <р = тіп х,(сЛ. Нехай, нарешті,
ХЄ.Х — деяка альтернатива і число г0 =/(х,с1°,с°,...,с®) є
відповідне альтернативі х та значенням параметрів {с®},у = 1,л
значення функції (7.5.3). Природно вважати, що це значення
о	.	~ .
г належить нечіткій оцінці альтернативи х із ступенем, не меншим
ніж <р° . Звідси шукана нечітка ц.ф. <р(х, г) має вигляд:
(о(х,г)= «ир ^(с),	(7.5.8),
СЄ0(л.г)
ДЄ
Х(с) = пил X) (с), с = [с, ,с2 с„ ]г; £>(х, г) = {с: с є К" ,/(х,с) = г}. (7.5.9)
Отже, вихідна задача з нечітко описаними параметрами форму-
люється у вигляді такої загальної задачі НМП.
максимізувати нечітко задану цільову функцію
(?(х,г)= 8ир х(с)	(7.5.10)
«=2(х,г)
на нечіткій множині допустимих альтернатив
/лс{х)= 8ир |/(Л),	(7.5.11)
АєР(х)
де <2(х, г) та Р(х) задаються відповідно (7.5.9) та (7.5.6).
342
Дослідження операцій. Збірник задач
Недоміновані альтернативи в загальній задачі нечіткого
математичного програмування
Розглянемо загальну задачу НМП, в якій нечітко задані
параметри су функції /(х) і параметри аіг обмежень (7.5.6). Перш
за все зазначимо, що в розглядуваній задачі вибір альтернатив має
здійснюватися з урахуванням двох відношень: нечіткого,
індукованого функцією <р(х,г) (7.5.8), і чіткого, індукованого
функцією /лс(х) та звичайним порядком на К'. Функція <р(х,г)
і звичайний порядок (>) на числовій осі генерують на множині
альтернатив X узагальнене н.в.п. вигляду 77:
^(х„х2) = 8ир тіп{р(х|,х),<г>(х2,у)} = 8ир тіп{ 8ир /(с), 8ир /(с)}.(7.5.11)
Х.уеЯ	-.ує/?	СЄ0(Л|.Г)	СЄ0(Х,.г)
:*У	Лу
Нехай Г]"° (х) — відповідна множина недомінованих альтернатив у
множині X з н.в.п. 7. Виберемо деяке число а з інтервалу
0 < а < 1 і розглянемо задачу відшукання альтернативи, ступінь
недомінованості якої не менший за а, тобто 7]"д (х) > х > а .
Вважатимемо, що всі вихідні нечіткі множини ху(су) такі, що
вир ху (су ) > а, / = 1, и.
і
В роботах [15, 16] доведено, що якщо всі задані нечіткі множини
сутакі, що 5ир^;(су)>а, то для знаходження альтернатив, ступінь
с!
недомінованості яких не нижчий ніж а, досить розв’язати таку
задачу:
максимізувати	г,	(7.5.12)
при обмеженнях:
г) >а;
(х, аі},..., аІП) < 0, і = 1, т, г є П'.
Припустимо, що множина X компактна, у] (сі), у = 1, м
неперервні на функція /(х,с|5с2,...,ся) також неперервна на
(7.5.13)
343
Зайченко О.Ю, Зайченко Ю П.
добутку ХхК" . В роботах [15, 34] показано, що при цих умовах
задача (7.5.12), (7.5.13) еквівалентна такій задачі:
максимізувати	/(х,с,,с2,...,сл),	(7.5.14)
при обмеженнях:	г (с )>«; 		(7.5.15) ^(х,о,І,...,а,п)<0,і = 1,щ.
Як було показано вище, функція <р(х,г) і звичайний порядок
(>) на К1 індукують на X нечітке відношення переваги вигляду:
?7І(хІ,х2) = вир тіп{^(х,,у),(г>(х2,г)}.	(7.5.16)
Друге відношення на X визначається тим, що переважатимуть
альтернативи, які мають більший ступінь допустимості, тобто ті,
яким відповідають більші значення функції.
Таким чином, ^2(х,,х2) = -
\,при рс(х,)>//с(х2);
0,при рс(х,) < рс(х2).
Отже, ми маємо задачу з двома нечіткими критеріями —
відношеннями г/і та ї]г.
Задачі такого типу розглянуто в розд. 7.4, де запропоновано
процедуру побудови підмножини недомінованих альтернатив за
наявності декількох критеріїв (відношень переваги). Відповідно до
неї треба побудувати дві згортки з вихідних н.в.п. 77, та т]2 — їх
перетин та зважену суму.
Перетин відношень , ?72 має вигляд:
хп) = тіп{ту, (х,,..., х„), г]2 (х,х„ )}.	(7.5.17)
Зважена сума (критеріїв) за умови рівності вагових коефіцієнтів
відношень ?7|, 72:
(х,, х2) = ^ [т/, (х,, х2) + т?2 (х,, х2)].	(7.5.18.)
344
Дослідження операцій. Збірник задач
Нехай	0^(х) — нечіткі підмножини недомінованих
альтернатив множин (х, £?,), (х, 02 ) відповідно. Тоді результуюча
підмножина недомінованих альтернатив має вигляд:
Є"й(х) = тіп{0*(х);0Г(х)}.	(7.5.19)
Функція належності (^"\х) і служить основою для вибору
конкретних альтернатив у загальній задачі НМП.
У цій задачі, як і раніше, практичний інтерес становить питання про
відшукання альтернатив х є X, для яких £2 "*(*) > а, де а є [0;1].
Однак для спрощення спочатку розглянемо задачу відшукання ч. нд.
альтернатив (тобто таких, для яких 0"д(х) = 1, а = 1).
Отже, розглянемо задачу знаходження ч. нд. альтернативи, для
якої С"д(х) = 1.
Із (7.5.19) отримаємо, що для цього необхідним і достатнім є
виконання умов: £2/Й(х) = 1 ,£?2яд(х) = 1.
З’ясуємо спочатку умови, за яких х є ч. нд. альтернатива на
множині (х, ), тобто коли (х) = 1.
В роботах [15, 34] показано, що для того щоб х° була ч. н. д.
альтернативою стосовно (2Х необхідно і достатньо, щоб вона була
ч. н. д. альтернативою одночасно по двох н.в.п. г)х та г]2.
Таким чином, щоб знайти ч. нд. альтернативу в множині X з н. в. п.
()х достатньо знайти ч. нд. альтернативу в множині Х2"а з н.в.п .
Нехай вихідні нечіткі множини и (<7іу. ), і = 1, т, у = 1, п такі, що
існують {а°}, для яких ^(а%) = 1. При цьому множину Х2"д
складають альтернативи, які задовольняють умовам г)х (х) = 1.
Задача відшукання ч. н. д. альтернативи аналогічна задачі
(7.5.14), (7.5.15), розглянутій в п. 1 цього розділу.
Якщо виконуються введені в ній припущення (компактність
множини X, неперервність функції /), то маємо таку задачу
знаходження ч. н. д. альтернативи в множині X:
345
Зайченко О.Ю, Зайченко Ю.П.
максимізувати
при обмеженнях:
У(х,с1,с2,...,ся),
(7.5.21)
&(*.«л, а,2,) < 0,є Л*;
^(о>) = 1,у = 1,и;
Уу(аіі) = \,і = \,т,і =\,п.
(7.5.22)
Будь-який розв’язок х° є X задачі (7.5.21), (7.5.22) є ч. нд. альтернатива
в множині (Х,(^), водночас він є ч.нд. альтернативою в множинах
(X ,г^) та (%, т]г) . Можна легко показати, що будь-який розв’язок цієї
задачі є ч. н д. альтернатива також і в множині (х, ^2) [15,16].
Таким чином, будь-який розв’язок задачі (7.5.21), (7.5.22)
задовольняє умов: С^Сх0) = 1,02д(х°) = 1, тобто х° — ч.нд.
альтернатива для вихідної загальної задачі НМП.
Наявність в одержаній задачі НМП (7.5.21), (7.5.22) обмежень
вигляду X)(С)) = 1»і(ау) = 1 означає, що для відшукання ч.нд.
альтернатив у вихідній задачі достатньо враховувати лише ті зі
значень параметрів, які напевно, тобто із ступенем 1, належать
відповідним нечітким множинам. Тобто, якщо шукати лише ч. нд.
альтернатива, то при формулюванні вихідної задачі можна не
вимагати повного опису нечітких множин значень параметрів, а
обмежитися лише значеннями інтервалів їх значень, які із ступенем 1
належать до цих множин.
Аналогічні міркування приводять до висновку, що для
знаходження альтернативи, яка має ступінь недомінованості не
нижче за а (тобто 77ий (х°) > а), достатньо розв’язати таку задачу
математичного програмування:
346
Дослідження операцій. Збірник задач
максимізувати	/{х,с1,с2,..., сп),	(7.5.26)
при обмеженнях:
^,(х,а,і,а,2,-,Чя) °>ау є Я*;	(7.5.27)
_	(7.5.28)
^(^)>а,/ = 1,/п,у=1,н.
Розв’язання задачі типу (7.5.26)-(7.5.28) дає змогу визначити
лише деякі з недомінованих альтернатив із відповідним ступенем а
для вихідної загальної задачі НМП.
Можна показати, що ще один спосіб знаходження недомінованих
альтернатив із ступенем а полягає в розв’язанні такої задачі:
знайти
тах тіп /(х,с,,...,с„),	(7.5.29)
при обмеженнях (7.5.27), (7.5.28).
Отримане в цій задачі значення функції /(х,с) — це найбільш
обережна («гарантована») оцінка альтернатив, недомінованих із
ступенем, не меншим, ніж а, а відповідне значення / в задачі
(7.5.26) — найменш обережна («оптимістична») оцінка. Інтервал між
цими оцінками дає змогу судити про можливі значення функції
/(х) при виборі альтернатив, недомінованих із ступенем а.
Приклад 7.6. Нехай треба
максимізувати
7=1
при обмеженнях:
^аі)х) <Ь,,і = 1,т ;	(2)
;=і
347
Зайченко О.Ю, Зайченко Ю.П
ху>0,у = 1,п.	(3)
причому змінні С] — нечіткі параметри з функціями належності:
Треба розв’язати відповідну задачу НМП, користуючись
співвідношеннями (7.5.28):
п
максимізувати /(л,с) = У с^х,.,	(4)
у=і
при обмеженнях: (2) та
А(С,) = 1~Л 1 ~Ч2 - °'8’ > =
1 + (с,-с7)2
Обмеження (5) записують у такому еквівалентному вигляді:
(с; -с?)2 < 0.25 або сі - 0.5 < су < су + 0.5.	(6)
Отже, задача зводиться до задачі параметричного програмування
і може бути розв’язана відомими методами.
Приклад 7.7. Для випуску продукції у=1, 2, 3 три підприємства
'=1, 2, 3 використовують два види ресурсів Л=1,2, відповідно у
обсягах ь; =250, Ь2 =150, Ь\ =100. Ь2г = 200,5’ =240, Ь2 =300.
Нехай норми витрат кожного ресурсу на ї-му підприємстві для
виготовлення у-ї продукції— нечітка множина в інтервалі [у* із
функцією приналежності (див. табл. 7.17):
Д,(«,у) = ехр-
ц-ау}
2
348
Дослідження операцій Збірник задач
Собівартість виготовлення у-ї продукції на ї-му підприємстві
також нечітка із функцією приналежності (див. табл. 7.18):
/ДС,) =
2
2 + (С^Сч)2'
Таблиця 7.17
Підприємство			7=2			7=3	
	—І аІХ	—1 а,\	—2 аі\	—2 аІХ	—з ац	—3 ац
1	2	4	1	2	3	4
2	1.5	5	2	2.5	2	3
3	3	2	2	3	3	4
Таблиця 7.18
Підприємство	Ц,7=1	С»’>2	
1	4	8	5
2	4	6	7
3	3	7	5
Нехай виробничий випуск виробів 17^ 360 од., П2=110од.,
П, = 250 од.
Скласти математичну модель. Знайти оптимальну спеціалізацію
виробництва, при якому мінімізується сумарна собівартість
виробництва виробів при заданому плані. Знайти підмножину не
домінованих альтернатив зі степенем а = 0.75.
Розв ’язання:
Нехай Ху — обсяг випуску продукції і на ї-му підприємстві.
Тоді математична модель матиме вигляд:
тіп £ £ СуХу , і = 1,3; к = 1,2,
і=І у=І
при обмеженнях:
349
Зайченко О.Ю., Зайченко Ю П.
Хх^піг у = 1,3,
ї=|
х„>0-
А(«Р>0.75,
/(Ц,)>0.75
(^) = ехр-
2
>0.75,
(а, -ау)2 < -2ІП0.75 = 21п—— = 21п-,
0.75 З
а у - ^21п — < а < а у +
2
>0.75,
0.5>0.75(С#-С#)2,
35С
Дослідження операцій. Збірник задач
Задача песиміста:
тіп
^>Пу, у = 1,3.
тіп
х#>0.
Задача оптиміста:
£^>Пу, 7 = 1,3.
х^>0.
Задачі і вправи
Задачі нечіткого математичного програмування
Задача 7.5.1
Меблева фабрика випускає столи, крісла, бюро і книжкові шафи,
використовуючи два типи дощок. Фабрика має 1000 дощок типу 1 і 500
дощок типу 2. Трудові ресурси фабрики складають 800 чоловік на
тиждень. Витрати кожного виду ресурсів на виготовлення одного
виробу є нечіткими параметрами із функцією приналежності^^) і
наведені в таблиці 7.19. Прибуток від реалізації виробів С; є нечіткою
величиною із функцією приналежності /у(С7) (табл. 7.20), де
7 2 ~ .2’
2 + Ц,-««)

351
Зайченко О.Ю., Зайченко Ю.П.
Визначити оптимальний асортимент випуску виробів, який
забезпечує за умови реалізованості плану максимум очікуваного
прибутку. Знайти множину недомінованих альтернатив зі степенем
а = 0.75.
Таблиця 7.19
	Стіл	Крісло	Бюро	Шафа
Дошки типу 1	4	2	8	12
Дошки типу 2	2	4	6	10
Трудові ресурси	5	3	6	12
Таблиця 7.20
	Стіл	Крісло	Бюро	Шафа
Су	12	5	15	20
Задача 7.5.2
Підприємство володіє ресурсами сировини, робочої сили і
обладнання, які необхідні для виробництва чотирьох видів виробів.
Нехай питомі витрати ресурсів типу у при виробництві виробів типу і
а у є нечіткими змінними на інтервалі	з ф.п. Д,у(я,у), а
прибуток одиниці виробу С,. — нечітка величина з ф.п. /,(Су) , де
^(^)=ехр-
(«,7-«>)*
2
МС,) =
1
1 + (Су-С,)2’
Початкові дані наводяться у табл. 7.20.а і табл. 7.20.6. Визначити
оптимальний асортимент випуску виробів, який забезпечує
максимум очікуваного прибутку за умови реалізованості плану.
Знайти підмножину не домінованих альтернатив зі степенем
а = 0.8.
352
Дослідження операцій. Збірник задач
Табчиця 7.20а
Вид ресурсу	Норми витрат ресурсу /				Обсяг ресурсів
	1=1	і=2	і=3	і=4	
Сировина	4	6	2	5	80
Робоча сила	20	12	20	40	400
Обладнання	10	15	10	16	150
Таблиця 7.206
Вид виробу	1	2	3	4
Прибуток	ЗО	25	56	48
Задача 7.5.3
В кормову суміш входять три продукти: сіно, силос і
концентрати, які містять поживні речовини: білок, кальцій і вітаміни.
Кількість поживних речовин (таблиця 1) є нечіткими величинами у
інтервалі [<5^,сг..] з ф.п. /^.(п^). Мінімально необхідні норми
споживання білка — 2000 г., кальцію — 120 г., вітамінів — 40 г.
Визначити оптимальний раціон харчування мінімальної вартості,
який забезпечує добову норму споживання всіх поживних речовин,
якщо ціна І кг і-го продукту нечітка величина з ф.п. (С.). Знайти
підмножину недомінованих альтернатив зі степенем а = 0.75.
/ ч	(ач ~а''
Мй») = ехР1----------
2
’Ху(С>) 2 + (Су-С>)2’
Початкові дані наведені у таблиці 7.21.
Таблиця 721
Продукт і	Вартість Сі (коп. за кг.)	Склад поживних речовин а у (г.)		
		Білок	Кальцій	Вітаміни
Сіно	зо	300	4	3
Силос	20	20	6	1
Концентрати	50	150	4	2
353
Зайченко О.Ю., Зайченко Ю.П.
Задача 7.5.4
На трьох ділянках колгоспного поля можна вирощувати три
культури: жито, пшеницю і ячмінь. Урожайність цих культур нечітка
величина з ф.п.	Очікувані затрати — нечітка величина з ф.п.
Нехай планове завдання із зібрання урожаю кожної культури
складає відповідно 500 ц, 600 ц і 400 ц, а площі ділянок дорівнюють
відповідно ЗО га, 50 га, 20 га.
Визначити оптимальну структуру посівів, яка мінімізує сумарні
очікувані витрати за умови виконання плану. Знайти підмножину не
домінованих альтернатив зі степенем а = 0.8.
=	V’ = ехр
(д-с,)2’
4
Початкові дані наведені в таблиці 7.22.
Таблиця 7.22
Ділянка	Урожайністьу-тої культури (цзга)			Середні витрати		
	«V		а У	С,І	С,2	С,з
1	10	12	8	2	3	4
2	12	14	18	3	6	8
3	20	16	24	4	7	10
Задача 7.5.5
Для виготовлення визначеного сплаву із свинцю, цинку і олова
використовується сировина у вигляді наступних п’яти сплавів із тих
же металів, які відрізняються складом і вартістю 1 кг. Допустимо, що
процентний склад металу у у кожній сировині і є нечіткою
величиною в інтервалі	з ф.п. ^.(д .), а вартість сплаву
С, — нечітка величина з ф.п. уДС) , де
354
Дослідження операцій. Збірник задач
Початкові дані наведені в таблицях 7.15 і 7.16.
Необхідно визначити скільки сировини кожного типу потрібно
взяти, щоб виготовити з мінімальною собівартістю сплаву, який
міститиме не менше 20% свинцю, 30% цинку і 40% олова. Знайти
підмножину недомінованих альтернатив зі степенем а — 0.7.
Таблиця 7 15
Матеріал у	Місткість металу в сировині і, %				
	і=1	і=2	і=3	і=4	і=5
	«0	а ч	ау	а у	а у
Свинець	10	10	зо	ЗО	20
Цинк	5	20	40	20	10
Олово	60	40	50	10	20
Таблиця 7.16
і	1	2	3	4	5
Сі	4	5	6	8	7
Задача 7.5.6,
На виробництво тканини трьох артикулів витрачаються ресурси
двох типів: вовна і барвник. Витрати вовни і фарби (кг на 1 000 м) —
нечіткі величини розподілені в інтервалі з ф.п. А(/(ау)-
Ціна 1 м тканини — нечітка величина з ф.п. /,(С^) .
Визначити оптимальний асортимент, який максимізує прибуток
за умови реалізованості плану, якщо середня собівартість 1 м
тканини дорівнює відповідно 8, 5 і 15 гр. Знайти підмножину
недомінованих альтернатив зі степенем а = 0.6.
З	1
З + Ц,-^)	1 + (Су-С7)
355
Зайченко О.Ю., Зайченко Ю.П.
Початкові дані наведені в таблицях 7.17 і 7.18.
Таблиця 7.17
Вид ресурсу 7	Обсяг ресурсу (тис. кг.)	Норми витрат на тканину (кг на 1 000 м)		
		і=1	і=2	і=3
		ач	ач	ач
Вовна	ЗО	100	160	180
Барвник	10	5	3	6
Таблиця 7.18
Тип тканини	/=1	/=2	/=3
Ціна (гр.)	16	18	20
Задача 7.5.7
Три сорти взаємозамінної сировини (і=1, 2, 3) у кількості 200, 100
і 300 кг використовується при виробництві чотирьох продуктів (/=1,
2, З, 4). Норми витрат ау сировини і на виробництво продукту у
нечіткі величини з фп. р0(ау). а виробничі витрати нечіткі
величини в інтервалі [/у,<5у.] з ф.п
Скласти план виробництва виробів, який мінімізує очікувані
сумарні витрати за умови реалізованості плану. Знайти підмножину
недомінованих альтернатив зі степенем а = 0.85.
Л,(«,у) = ехр-
1
1 + (Су-С,)2‘

Початкові дані наведені в таблицях 7.19 і 7.20.
356
Доспдження операцій Збірник задач
Таблиця 7 19
Сорт сировини і	Норми витрат на продукт у			
	1=1	1=2	1=3	1=4
	«</	«V	ац	а у
1	2	05	3	1
2	1	2	2	2
3	2	1	2	2
Таблиця 7.20
Сорт сировини і	Виробничі витрати на одиницю продукції Су			
	1=1	1=2	і=з	1=4
1	20	15	10	20
2	15	20	40	зо
3	10	зо	10	25
Задача 7.5.8
Меблева фабрика випускає столи, крісла, бюро і книжкові шафи,
використовуючи два типи дощок. Фабрика має 1000 дощок типу 1 і 500
дощок типу 2. Трудові ресурси фабрики складають 800 чоловік на
тиждень. Витрати кожного виду ресурсів на виготовлення одного
виробу є нечіткими параметрами із функцією приналежності //. (бт ) і
наведені в таблиці 7.21 (а). Прибуток від реалізації виробів Су є
нечіткою величиною із функцією приналежності у (С ) (табл. 7.21 (б)),
Де

2
2 + (а# — а і} )
/7(Су) = ехр<
(С7-СУ)2'
2
Визначити оптимальний асортимент випуску виробів, який
забезпечується за умови реалізованості плану максимум очікуваного
прибутку. Знайти множину недомінованих альтернатив зі степенем
а = 0.75.
357
Зайченко О Ю, Зайченко Ю П
Таблиця 7.21а
	Стіл	Крісло	Бюро	Шафа
Дошки типу 1	4	2	8	12
Дошки типу 2	2	4	6	10
Трудові ресурси	5	3	6	12
Таблиця 7.216
	Стіл	Крісло	Бюро	Шафа
	12	5	15	20
Задача 7.5.9
Підприємство володіє ресурсами сировини, робочої сили і
обладнання, які необхідні для виробництва чотирьох видів виробів.
Нехай питомі витрати ресурсів типу у при виробництві виробів типу і
є нечіткими змінними на інтервалі [%,<%,] з ф.п. ду(аіу), а
прибуток одиниці виробу С, — нечітка величина з ф.п. /у(Су),де
(а^-а^)2
^(^) = ехР1---—----
’Ху(Су) 1+(Су-Су)2'
Початкові дані наводяться у табл. 7.22а и табл. 7.226. Визначити
оптимальний асортимент випуску виробів, який забезпечує
максимум очікуваного прибутку за умови реалізованості плану.
Знайти підмножину недомінованих альтернатив зі степенем а = 0.8.
Таблиця 7.22а
Вид ресурсу	Норми витрат ресурсу у				Обсяг ресурсів
	і=1	і=2	/=3	і=4	
Сировина	4	6	2	5	80
Робоча сила	20	12	20	40	400
Обладнання	10	15	10	16	150
358
Дослідження операцій Збірник задач
Таблиця 7.22 б
Вид виробу	1	2	3	4
Прибуток	зо	25	56	48
Задача 7.5.10
Три сорти взаємозамінної сировини (і=1, 2, 3) у кількості 200, 100
і 300 кг використовується при виробництві чотирьох продуктів (/=1,
2, 3, 4). Норми витрат аіу сировини і на виробництво продукту у
нечіткі величини з ф.п. Ду(йу), а виробничі витрати нечіткі
величини в інтервалі	з ф.п /^(Су).
Скласти план виробництва виробів, який мінімізує очікувані
сумарні витрати за умови реалізованості плану. Знайти підмножину
недомінованих альтернатив зі степенем а = 0.85.
, х	(а -ау)2
/Ш> = ехР———
і+сс.-с,)2’
Початкові дані наведені в таблицях 7.23а і 7.236.
Таблиця 7.23а
Сорт сировини І	Норми витрат на продукт у			
	1=1	1=2	1=3	1=4
	«У	ац	«у	
1	2	0.5	3	1
2	1	2	2	2
3	2	1	2	2
Таблиця 7.236
Сорт сировини і	Виробничі витрати на одиницю продукції Су			
	1=1	1=2	і=з	1=4
1	20	15	10	20
2	15	20	40	зо
3	10	зо	10	25
359
Зайченко О.Ю., Зайченко ЮП
7.6.	Багатокритеріальні задачі ЛП
з нечіткими параметрами
Однокритеріальні задачі ПР з
інтервально-заданими нечіткими параметрами
цільових функцій
Нехай задача прийняття рішень з декількома критеріями
зводиться до багатокритеріальної задачі лінійного програмування
(МК ЛП-задача) такого вигляду:
тахг, =^суху =с,тх, і = 1,К,	(7.6.1)
7=1
за умов	Ах < В;	(7.6.2)
(7.6.3)
де всі коефіцієнти цільових функцій С,7 є нечіткими числами,
заданими на інтервалі сі? є [сі}1 сі]и ].
Розглянемо спочатку випадок, коли ЛПР невідома функція
приналежності (ФП) нечіткого параметра МУ(СУ), а відомі лише кінці
інтервалу, нижній — Су/ і верхній Суи Для такого ступеня
інформованості ЛПР пропонується такий метод рішення [15].
Складаємо і розв’язуємо так звану задачу «песиміста» вигляду:
л
	тах 2, =	= с]х,	(7.6.4)
	7=1	
за умов:	Ах<В;	(7.6.5)
	х>0.	(7.6.6)
360
Дослідження операцій Збірник задач
Знайдене її рішення позначимо через X/ , а оптимальне значення
Ц-Ф-	2тах/	=
Одночасно розв’язуємо відповідну задачу мінімізації:
тіп 2, (х) = 2,,	(7.6.7)
за умов (7.6.5), (7.6.6).
Потім розв’язуємо так звану задачу «оптиміста» (для найкращих
умов зовнішнього середовища):
тах ги (х) = £ су, ху = сит х,	(7.6.8)
У=і
*
за умов (7.6.5),(9.6.6) і знайдемо оптимальне її рішення Хи , а також
г’ = тахги(х)-
Далі визначаємо нижню границю критерію оптиміста:
ги = тіп 2и (х),	(7.6.9)
за умов (7.6.5), (7.6.6).
Тоді задачу знаходження оптимального рішення в умовах з
інтервально-заданими параметрами цільової функції можна звести до
задачі знаходження компромісного рішення такої багатокрите-
ріальної задачі:
тах
^і(х)=с]х
(7.6.10)
за умов (7.6.2), (7.6.3).
Для знаходження її рішення застосуємо такий підхід. Перейдемо
від критерію 2/(х) до нечіткого критерію (р,(х) з функцією
приналежності, що задається так:
361
Зайченко О Ю.. Зайченко Ю.П
О, ЯКПЮ 2у(л)<2,
2/(х)~г1	. .
—;—=,якщз 2, <г,(х)<г,
2і
1, якщо г,(х)>х*
(7.6.11)
Аналогічним чином для критерію оптимальності ги(х)
перейдемо до нечіткої ц.ф. з ФП /и (х), яка визначається так:
ГАХ) =
0, ЯКЩО 2Ц (х) < 2и	
2АХ)~2и	<ги(х)<х*
2 —2		 и	и 1,якщохи(х)>г’.	
(7.6.12)

Далі застосовуємо підхід Белмана-Заде і шукаємо таке компро-
місне рішення х°, для якого:
тіп{/(х),/и(х)}-»тах,	(7.6.13)
за умов (9.7.2), (9.7.3).
Дану мінімаксну задачу можна записати в такому еквівалентному
вигляді:	тах	(7.6.14)
за умов:	2(х/ -2,)- г,(х)< -2^	(7.6.15)
Величина	Ах<В; Х>0. Я°(Л є [0,1])	характеризує	(7.6.16) (7.6.17) досягнутий ступінь
задоволення кожного з нечітких критеріїв (/, и /и )-
362
Дослідження операцій. Збірник задач
Задача ЛП з нечіткими параметрами критеріїв
з відомими функціями приналежності
Розглянемо тепер випадок більшої інформованості ЛПР про
нечіткі параметри. Нехай ЛПР відома функція приналежності
/^(с/у) нечітких параметрів С^. Тоді він може задатися деяким
рівнем а(д є (0,1)) і визначити підмножину рівня а С& нечіткого
числа Су : с“ = [с“, с“ ].
Тоді можна сформувати два критерія-песиміста г“ (х) для лівого
кінця інтервалу і оптимиста — г" (х) для правого кінця інтервалу, і
перейти до розв’язання двокритеріальних задач вигляду:
2,“(х)=<х
/Г(х)=<х
тах
Для знаходження найкращого компромісного рішення цієї задачі
необхідно перейти до лінійної задачі вигляду:
тах * •
(7.6.18)
за умов:
Я«-£)-2/“(х)<-£;
Я(2/-2>>“)-2Дх)<^“
(7.6.19)
(7.6.20)
х>0
(7.6.21)
Вона є звичайною ЛП-задачею і розв’язується стандартними
методами ЛП (симплекс-методом, методом зворотньої матриці і т.д.).
363
ЗайченкоОЮ„ Зайченко Ю.П.
За необхідності більш повного обліку інформації про вигляд ФП
Д7(Су) ЛПР може задатися декількома рівнями а.ах,а2 і
тоді обмеження мінімаксної задачі (9.7.18) запишуться у вигляді:

г=1,К.
(7.6.22)
Тобто отримаємо 2К обмежень (зазвичай К = 3-4).
Багатокритеріальна задача ЛП з нечіткими параметрами в
цільовій функції
Розглянемо тепер загальний випадок МК ЛП-задачі з нечіткими
ц.ф. Вона запишеться у вигляді:
	тах сдх/ = с]х, і = 1 ,к ,	(7.6.23) 7=1
за умов:	(7.6.24) х>0,
де су - нечіткі числа з відомими ФП /7 (сІ} ).
Задамося декількома рівнями а:ах,а2 і знайдемо відповідні
інтервали невизначеності [с°[,	].
Далі, використовуючи вищеописаний підхід, приводимо задачу
(7.6.23), (7.6.24) до такої багатокритеріальної задачі:
за умов (7.6.24).
364
Дослідження операцій. Збірник задач
Вона зводиться до такої однокритеріальної задачі:
т ах А ,
(7.6.25)
за умов:
Ах<Д
х>0.
і=1,к, г=1,К;
(7.6.26)
(7.6.27)
Відмітимо, що число додаваємих обмежень вигляду (7.6.26)
складає 2К*К, тому число рівнів О. нечітких чисел слідує
обмежувати.
Приклад 7.8
В якості ілюстрації розглянемо таку багатокритеріальну ЛП-
задачу з нечіткими цільовими функціями:
тах Рх(х) = с11х1 + с|2х2;	(1)
тах Р2(х) = с2|х, + с22х2,	(2)
за умов:
х2>|х,;
о
хх+х 2> 1;
—2х,+х2<4;‘
х2 < 10;
х, + 2х2 < 24;
(4)
де сі] — нечіткі множини з функціями приналежності:
1
А(су) =
Си =1; Сі2 =4; Сгі =3; Сп = -2.
365
Зайченко О.Ю., Зайченко Ю.П.
Знайти найкращий компромісний розв’язок для рівня О. ~ 0,8.
Розв’язуємо задачу графоаналітично.
Побудуємо область допустимих рішень, яка визначається за умов
(3) і (4). Вона приведена на рис. 7.10.
Знаходимо крайні точки ОДР та їх координати:
А (1;6); В (3;10); С(4;10); О (18;3); Е (6; 1).
Розв’язуємо нерівності і знаходимо інтервали приналежності
рівня а = 0,8 ДЛЯ нечітких коефіцієнтів Су.
1 -	аО.8^(^-с8)^^-О,25; |е,-е,|<0,5;
1 + (с -Су)	0,8
Сі,- - 0,5 < Су < Су + 0,5.
Таким чином, знаходимо інтервали для Су.
0,5<с„<1,5;	3,5<си<4,5;
2,5 < с21 < 3,5;	- 2,5 < са < -1,5.
366
_____________________________________Дослідження операцій. Збірник задач
Виписуємо критерії песиміста і оптиміста:
21£ =0,5х, + 3,5х2;
2Ш = 1,5х,+4,5х2;
2а =2,5х, -2,5х2;
2Ш = 3,5х, -1,5х2.
Розв’язуємо графічно ці задачі:
тах2|£(х) = 2І£(С) = 2 + 35 = 37;
тах	(х) = 2|£, (С) = 51;
тах 22£(х) = 2|£(23) = 37,5;
тах 2^ (х) = 22£/ (£)) = 5 8,5;
тіп 21£(х) = 21£(£) = 6,5;
тіп 2ш(х) = 2Ш(Е) = 10,5;
тіп 22£(х) = 22Ь(В) = - ] 7,5;
тіп Х2и (х) = г2и (В) = -4,5.
Тепер запишемо задачу знаходження компромісного рішення:
тахЛ,
за умов	(37 - 6,5)Я - (0,5х, + 3,5х2) < -6,5; (51-10,5)Я-(1,5х,+4.5х2)<-10,5; (37,5 +17,5)Л - (2,5х, - 2,5х2) < 17,5; (58,5 + 4,5)Л - (3,5х, -1,5х2) < 4,5,
і умовах (3) і (4);
або:
ЗО, 5 А - (0,5х, + 3, 5х2 ) < -6,5;
40,5Я-(1,5х,+4,5х2)<-10,5;
55Л-(2,5хі-2,5х2)<]7,5;
63Л-(3,5х,-1,5х2)<4,5.
Розв’язуємо дану задачу симплекс-методом і знаходимо
найкраще компромісне рішення, яке максимізує X.
367
Зайченко О.Ю., Зайченко Ю.П,
Помітимо, що оскільки максимальні значення критеріїв
досягаються в точках С і І), то компромісне рішення належить
відрізку СП, тобто лежить на прямій хі+2х2=24. І шукану точку Р
можна в цьому випадку знайти графоаналітично. Виключивши одну
змінну (х/) приходимо до системи нерівностей з двома змінними: X
і х2 і, побудувавши область допустимих рішень, знайдемо значення
Лтах=о.юб і шукане компромісне рішення х“=12;х2=6. Відповідна
йому точка Р вказана на рис. 7.10.
Задачі та вправи
Задача 7.6.1
1. Вважаючи, що величини су є нечіткими числами з функцією
приналежності п(с..) =----—, де сц=3,, сп - 2, с2і=1,
’	1 + (С.-Су)2
С22 —— 1,, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
/\(х) = с, (х( + с12х2 —> тах;
Г2(х) = с21х} + с22х2 —> тах,
при умовах:
х, - 6х2 < 3;
х, + х2 > 10;
-2х, + х2 < 1;
х2 < 11;
2х( +х2 <32;
х,,х2 >0;
р,=р2=0.5.
368
Дослідження операцій. Збірник задач
Задача 7.6.2
1. Вважаючи, що величини су є нечіткими числами з функцією
2	-	-	-
приналежності д(су)-----------=	, де Сц=1, Сіг=4, сзі-2,
2 + (с,у —со)
с22 = —2, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
Р{ (х) = с, ,х1 + с|2х2 —> тах;
Р2(х) = с2Іх, +с22х2 тах,
при умовах:
1
О
х, + х2 >7;
—2хІ +х2 <4;
х, < Ю;
х, + 2х2 < 24;
хрх2 > 0;
д = р2 = 0.5.
Задача 7.6.3
1. Вважаючи, що величини су є нечіткими числами з функцією
2	_	_	_
приналежності	--------=—, де Сц=1, Сі2=4, Сгі=2,
у	2 + (сІу-Су)2
Сп = -2, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
Р{ (х) = с,,%, + с12х2 —> тах;
Р2(х) = с2іх{ + с22х2 —> тіп,
369
Зайченко О.Ю.. Зайченко Ю.П.
при умовах:
х, + 2х2 > 32;
—2х + х2 > 16;
х, + 2х2 < 64;
-х, + 4х2 < 40;
< 24;
х,,х2>0;
р,=р2=0.5.
Задача 7.6.4
1. Вважаючи, що величини с є нечіткими числами з функцією
2
приналежності р(с. ) =-----=—. знайти найкращий компроміс-
2 + ^-су)2
ний розв’язок наступної задачі багатокритеріальної оптимізації рівня
а = 0.8.
Р\ (х) = с, (х, + с|2х2 тах;
/^(х) - с21х, + с22х2 тах,
при умовах:
2х, + 3х2 >28;
-5х, + 3х2 < 14;
+ 4х2 < 57;
2х, +х2 <30;
х,,х2 >0;
= Рг = 0 5.
370
Дослідження операцій. Збірник задач
Задача 7.6.5
1.	Вважаючи, що величини су є нечіткими числами з функцією
приналежності р(е) =-------, де Сп=4, Сі2=2, с21=1,
*	1 + (С^-С,у)2
с22 =—І, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
/^(х)=сІ|ХІ + с12х2 ->шах;
Е2(х) = с2іхі ~с22х2 ~> тах>
при умовах:
-6х2 <3;
х, +х2 > 10;
-2х, +х2 <2;
х2 < 12;
2х, + х2 < 32;
х„х2>0;
р|=А=0.5.
Задача 7.6.6
1. Вважаючи, що величини с/у є нечіткими числами з функцією
приналежності /Яс.) =------—-—, де Сц=3, Сі2=2, с2і = 1,
"	1 + (^-с,)2
С22 = —3, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
Р\ (х) = с,+ с]2х2 —> тах;
Г2(х) = е2Іх, +с22х2 -> тах,
при умовах:
371
Зайченко О Ю., Зайченко Ю.П
2х, +х2 <3;
х, + 2х2 > 8;
х, + 2х2 < 20;
-х, + 4х, >12;
<6;
х,,х2 >0;
Рі = Р2 =°-5-
Задача 7.6.7
1. Вважаючи, що величини су є нечіткими числами з функцією
приналежності ц(с.) =-----, де Сн =1, Сі2 =4, с2і=3,
’	1 + (Є,-Єу)2’
С22=-1, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
(х) = снх,+с|2х2 —>тах;
/^(х) = с2Іх, +с22х2 -> тіп,
при умовах:
X] + 2х2 > 4;
Зх1+х2>7;
-Зх, +5х2 <17;
5х, -х2 <23;
Зх, -4х2 < 7;
х,,х2 >0;
р,=р2=0.5.
Задача 7.6.8
1. Вважаючи, що величини с(> є нечіткими числами з функцією
приналежності ц(с) =------!-=— , де Сц=3, Сіг=2, с2і=1,
372
Дослідження операцій. Збірник задач
С22 = -3, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
РІ(х)=сІІхІ +с12х2 -> тах;
Г,(х) = с21х, +с22х2 тах,
при умовах:
х, -6х2 <6;
х, + х2 > 20;
—2х, + х2 < 2;
хг<22;
2х, + х2 < 64;
х,,х2>0;
р,=р2=0.5.
Задача 7.6.9
1. Вважаючи, що величини сі? с нечіткими числами з функцією
приналежності р(с ) =------—=—, • Де Оі = 2, Сіз=4, Сгі =3,
"	1+(с#-с?)2
аг — —2, знайти найкращий компромісний розв’язок даної задачі,
оптимальний по Парето, рівня а = 0.8.
Рх (х) = є,,*, + с|2х2 —> тах;
/?2(х) = с2|х| +с22х2 —>тах,
при умовах:
1 .
~х, ^Х2>
о
х, +х2 >7;
-2х, + х2 < 4;
х2<10;
х, +2х2 < 24;
х,,х2 >0;
р, =р2=0.5.
373
Зайченко О.Ю., Зайченко Ю.П.
Розділ 8. МЕТОД ДЕКОМПОЗИЦІЇ
В ЗАД А ЧАХ ВЕЛИКОЇ ВИМІРНОСТІ
8.1. Метод декомпозиціїДанцига-Вульфа
У 1960 р. Данциг та Вульф розробили метод декомпозициї для
розв’язування задач високої вимірності зі спеціальною структурою
матриці обмежень.
Цей метод виявився найбільш ефективним для розв’язування
задач, матриця обмежень яких має блочно-діагональний вигляд з
невеликою кількістю змінних. Але як показали подальші
дослідження, метод можна застосовувати також і для задач Л.П. з
матрицею загального вигляду. Характерною особливістгю методу
декомпозиції є використання координуючої задачі, яка має у
порівнянні з початковою невелику кількість рядків і велике число
стовпців. Суттєвим є те, що для розв’язання координуючої задачі не
потрібно задавати усі стовпці в явному вигляді. Вони генеруються в
процесі використання симплекс-методу. Такий підхід називають
методом генерації стовпців. Його суть полягає в такому. Нехай
задача ЛП має такий вигляд:
максимізувати:
а'
<8Л)
при обмеженнях:
N
^АЛ=Ь-,	(8.2)
/=і
Ау та Ь — ш-вимірні вектори-стовпці (т<гі).
374
Дослідження операцій. Збірник задач
Припустимо, що відомий деякий допустимий базисний розв’язок
(Д.Б.Р.) Хв та відповідна йому матриця з базисних векторів Ах.
Припустимо також, що Хв було знайдено методом оберненої
матриці. Тоді одночасно було знайдено і вектор відносних оцінок
Л=[ЯУ] = СЛ ', де Сх — вектор коефіцієнтів цільової функції для
поточного базису.
Щоб визначити можливість покращення Д.Б.Р. Хв для кожного
небазисного вектора А] обчислюємо значення оцінки:
Д, = ЛЛу - с, = £ с,ач ~ с, 	<8-3)
Якщо тіп Ду = Д5 < 0 то початковий розв’язок може бути
поліпшений шляхом введення у, базис змінної Х5. Однак, коли маємо
велику кількість небазисних стовпців (п>103), то знаходження Д5
шляхом обчислення Д, для усіх небазисних векторів у = 1, п; і
наступного їх порівняння практично неможливо. І як виявляється, це
і не потрібно.
Вважатимемо, що усі стовпці вибираються із деякої опуклої
множини 5, що визначається системою нерівностей та рівностей.
Тоді вектор-стовпець, який необхідно ввести у базис, можна
визначити у результаті розв’язання допоміжної задачі вигляду:
мінімізувати
{ЛЛу.-С(4)},	(8.4)
де С(Лу) = сі — деяка задана функція вектора А^
Залежно від структури множини 5 та виду функції С(А})
обирається найбільш ефективний метод розв’язування вказаної
задачі. Такий спосіб називають методом генерації стовпців, оскільки
при розв’язуванні задачі (8.4) фактично використовується лише
невелика кількість стовпців, які генеруються поступово з потреби.
При цьому значно знижується необхідний об’єм пам’яті для
зберігання поточних результатів, що є суттєвою перевагою при
розв’язуванні задач великої вимірності
375
Зайченко О.Ю., Зайченко Ю П.
Принцип декомпозиції
Розглянемо задачу ЛП, матриця обмежень якої має блочно-
діагональну структуру вигляду:
	4	А	- а;	
	Д	0	... 0	
А =	0	А	... 0	(85)
	0	0	ВР.	
Рядок [Д,Ар] називається зв’язуючим, бо він зв’язує
разом усі змінні задачі у деякому обмеженні чи їх групі. Відповідна
задача ЛП записується у вигляді:
максимізувати
(8-6)
1=1
при обмеженнях:
(8.7)
/=1
і = \,р, хІ >0.	(8.8)
Зазначимо, що до вигляду (8.5) можна звести матрицю довільної
задачі ЛП при р = 1 в результаті відповідного розбиття обмежень на
дві підмножини. Дійсно, довільну задачу ЛП можна записати у
вигляді:
максимізувати
/ = СХ,	(8.9)
при обмеженнях:
А{х - Л,, (т, обмежень),	(8.10)
А2х = Ь2, (т2 обмеженнь),	(8.11)
*>0.	(8.12)
376
Дослідження операцій. Збірник задач
Припустимо, що опукла многогранна множина 52, що
визначається умовою (8.11), є обмеженою, тобто являє собою
многогранник (ця умова не дуже обмежуюча). Нехай
К - {х : Ах - Ь,х > 0} — непорожня замкнена обмежена множина,
ЛСІ(7 = 1,Л') — її крайні точки. Тоді довільну точку х є К можна
подати у вигляді опуклої комбінації крайніх точок множини К., тобто
х=5і -°’ 1=ЇХ= * (8ЛЗ)
і=|	1=1
Відповідно до леми, будь-який елемент 52 може бути записаний
у вигляді:
л
де 3} > 0, ^^3 = 1, х^_ крайні точки многогранника 52.
у=1
Початкову задачу (8.9)-(8.12) можна сформулювати таким чином. Із
усіх розв’язків (8.11)-(8.12) необхідно вибрати такий, який задовольняє
(8.10) та доставляє функції (8.9) максимум. Підставляючи (8.14) у (8.9),
отримаємо новий вираз для цільової функції:
/ = Х(сх})3},	(8.15)
7
а підставивши (8.14) у (8.10), одержимо
<8-16)
7
Позначимо:
А,Х7. = Р}, СХ;	(8.17)
377
Зайченко О. Ю., Зайченко Ю.П.
З урахуванням (8.15)-(8.17) приходимо до такої задачі:
максимізувати		(8.18)
при обмеженнях:	І	(8.19)
	у	(8.20)
	8: >0.	(8-21)
Ця задача, яка еквівалентна початковій (8.9)-(8.12), називається
координуючою задачею. Вона має тільки (тпх +1) рядків обмежень
порівняно з (лн, +пі2) рядками початкової задачі і дуже велику
кількість стовпців, яка дорівнює числу крайніх точок множини 5,.
Щоб не зберігати всі ці стовпці в пам’яті ЕОМ, будемо отримувати їх
з потреби, користуючись методом генерації стовпців. З цією метою
для кожного небазисного вектора обчислимо значення Ду:
Подамо вектор А у вигляді Л = [Л1,Я0], де вектор Л] відповідає
обмеженням (8.19), а Ло — єдиному обмеженню (8.20).
Використовуючи формули (8.16), (8.17) для визначення Р. та ,,
одержимо:
Д у = ЛіР7 + - 2о; = (Лі4 - сУхі + Л-	(8-23)
Відповідно до звичайних правил симплекс-методу для
визначення змінної 85, що вводиться у базис, необхідно мінімізувати
Д.^АД-с)^	(8.24)
378
Дослідження операцій. Збірник задач
Оскільки оптимальний розв’язок задачі ЛП (за умови, що
допустима множина 82 — обмежена) досягається у крайній точці
цієї множини, то виконання операції (8.24) еквівалентне розв’язанню
підзадачі вигляду:
мінімізувати
(\А}-с)х,	(8.25)
при обмеженнях:
А2х =Ь2,
х>0.
(8.26)
Знайшовши її розв’язок х^,
перевіримо умову
=(А,Д-С)х5+Л0 <0 і якщо вона виконується, то вектор
вигідно ввести в базис. Далі визначимо компоненти вектора Р5, який
слід ввести у базис координуючої задачі:
(8.27)
а також відповідний коефіцієнт у цільовій функції:
/ =сх .
(8.28)
Такий підхід виявляється особливо ефективним, якщо р < 1,
тобто початкова задача записується у вигляді:
максимізувати
/ = с1хі+с2х2+... + срхр,	(8.29)
при обмеженнях
А{х, + А2х2 + ...+ Архр = Ьо,	(8.30)
В2х2	= Ь2,	(8.31)
В х= Ь ,
р р р*
хі >0, і = 1,р.	(8.32)
379
Зайченко О.Ю., Зайченко Ю.П.
Для такої задачі підзадача (8.25)-(8.26) (блочна задача) матиме
вигляд:
мінімізувати
^(Л.Д-с,)*,,	(8.33)
>=і
при обмеженнях:
В,х,=Л;	(8.34)
х>0, і = \,р.	(8.35)
Внаслідок аддитивності цільової функції (8.29) та незалежності
обмежень (8.34) задача (8.33) розбивається на р незалежних задач
вигляду:
тіп(Л,Аі - сі )х.,	(8.36)
при обмеженнях:
В,Х= А, Х>0.	(8.37)
Позначимо розв’язок задачі (8.36) через х°, а {Л,^4,	= /°.
Якщо ^/,°+А0<0, то вектор х0 = {х,в(Д,)}, і = \,р можна
/=|
р
ввести у базис координуючої задачі. Якщо ж +ло ^0,то
(=і
поточний розв’язок оптимальний.
Опис алгоритму декомпозицїї
Дамо формальний опис алгоритму декомпозиції Данцига-Вульфа
для розв’язання задачі (8.29)- (8.32). Нехай вже маємо початковий
допустимий базисний розв’язок задачі (8.18)-(8.21), якому відповідає
вектор розв’язувальних множників А = [А1,Л0]. Кожна ітерація
алгоритму складається із двох етапів.
Перший етап. 1. Використовуючи вектор оцінок А, попередньої
ітерації, сформуємо і розв’яжемо підзадачі (8.36)-(8.37) та знайдемо
оптимальне значення цільової функції, а також відповідні розв’язки
<(л,),
380
Дослідження операцій. Збірник задач
2. Обчислимо мінімальну оцінку:
тіпЛ, =£/°+Д,.	(8.38)
Ї=1
р
3. Якщо +Л0 >0, то обчислення закінчується і визначаємо
/=і
оптимальний розв’язок задачі (8.29)-(8.32):
<8-39)
і
де {£,} — попередній базисний розв’язок координуючої задачі, а
Х; —крайня точка 82, що відповідає базисній змінній 8Г
р
Якщо У + Ло <0, то переходимо до другого етапу.
і=і
Другий етап. Формуємо стовпець Ро, який необхідно ввести у
базис задачі (8.18)-(8.21):
^ = Х4<(Л,).	(8-40)
і=і
Введемо вектор Ро у базис, виконуємо крок методу оберненої
матриці, після чого знаходимо новий допустимий базисний розв’язок
а ТаКОЖ НОВИЙ ВЄКТОр ОЦІНОК
Л(н) = {Л™,/^}.
На цьому ітерація закінчується і переходимо до першого етапу
наступної ітерації.
Як бачимо з описання, алгоритм декомпозиції Данцига-Вульфа
являє собою двохрівневий алгоритм, у якому на першому рівні
розв’язуються підзадачі (8.36), (8.37), а на другому рівні —
координуюча задача (8.18)-(8.21). Якщо координуюча задача є
невиродженою, то на кожній ітерації значення цільової функції
зростає і, оскільки число базисів її скінченне і жоден з них не
використовується двічі, оптимальний розв’язок знаходиться за
скінченне число кроків.
381
Зайченко О.Ю, Зайченко Ю.П.
Обмежена координуюча задача
Як випливає з наведеного вище описання алгоритму
декомпозиції, оптимізаційна задача в ньому розв’язується лише на
першому рівні, тоді як на другому фактично виконується лише одна
ітерація симплекс-методу. Однак можлива модифікація цього
методу, що полягає у розв’язанні оптимізаційних задач на двох
рівнях. У цьому випадку розв’язується так звана обмежена
координуюча задача, яку отримуємо з координуючої задачі (8.18)-
(8.21) в результаті відкидання усіх стовпців за винятком базисних та
тих, що претендують на включення у базис на поточній ітерації.
Таку обмежену координуючу задачу можна представити в такому
вигляді:
максимізувати
+	(8.41)
;=і
при обмеженнях:
+ ^2^2 + — +	+ ^0^0 = ^0»
^<5,+<50=1;	<5. >0, і = 1,т,	<50 > 0, (8-42)
і=І
де <5/1 = 1,т) — змінні поточного базису: 50 — змінна, що
вводиться в базис (для неї Д0<0). Якщо поточний бозис є
невиродженим, то з нього буде виведена змінна, для якої Д; > 0, і
отриманий розв’язок буде оптимальним.
Зауважимо, що можливі випадки, коли використання обмеженої
координуючої задачі порівняно із звичайною координуючою задачею
дає ефект.
Варіанти декомпозиції прямої задачі
Існує багато різних способів декомпозиції прямої задачі, кожний
з яких приводить до своєї форми координуючої та обмеженої
координуючої задачі.
382
Цоспідлсення операцій. Збірник задач
Розглянемо, наприклад, варіант декомпозиції для матриці
блочно-діагонального виду. Позначимо розв’язок системи Віхі = Ьг.
X, =^4/х‘7’>0,	(8.43)
7
де х/ - крайні точки многогранника 5,:
5,. = {х: Вхі = Л, х, > 0},	<5у > 0.
Тоді координуюча задача матиме такий вигляд:
максимізувати
ХІА2,’	<8’44)
при обмеженнях:
<8-45)
• і
(8-46)
І
ДЄ2і7=С,Х,.,	/^=Л.х/.
Координуюча задача (8.44)-(8.46) відрізняється від координуючої
задачі (8.18)-(8.21). По-перше, вона має не одне, а р обмежень типу
(8.46), по-друге, розв’язок для кожної підсистеми Дх(. = Л)5 X, >0
самостійно виражається через змінні 5у, тоді як у задачі (8.13)-
(8.21) ці розв’язки розглядались разом. Застосуємо метод оберненої
матриці з використанням процедури генерації стовпців для
розв’язання задачі (8.44)-(8.46).
Нехай В — базисна матриця вимірності (/П| + р) х (т, + р), а
А = {А,, Ао,^Я)2,...Я0/;} — вектор відносних оцінок для цього розв’язку
(Л( — оцінка обмежень (5.45), а Л01 — оцінка для і-го обмеження
(8.46)).
Обчислимо тепер оцінки ДІу для векторів, які відповідають
змінним 8у:
Д,>=(А1Д-с,.)х/+4.	(8.47)
383
Зайченко О Ю. Зайченко ЮП
Для визначення тіп Ду при фіксованому і розв’яжемо підзадачу
вигляду:
мінімізувати
(ЛД,-^)*,,	(8.48)
при обмеженнях:
В х =Ь', х >0.	(8.49)
Якщо т іпт і и(А, Д - с()х/ + Я. = т і п(/° + А ) > 0,
' І	і
то поточний розв’язок — оптимальний, а у протилежному випадку в
базис задачі (8.44)-(8.46) вводиться змінна, для якої
тіп(Л°+Л,)<0-	(8-50)
Якщо цей мінімум досягається при і = 5, а хз (А,) — розв’язок
підзадачі з індексом 8, то у базис координуючої задачі вводиться
стовпець
9
І
де и5 - р -вимірний вектор, усі компоненти якого дорівнюють 0, за
ВИНЯТКОМ 5 = і компоненти, що дорівнює 1.
Приклад 8.1
Розв'язати таку задачу методом декомпозиції Данцига-Вульфа:
Р = (2х, +х2 + Зх, + 2х4) —> тах;
2Х] + Зх2 +х, + Зх4 < 24;
Зх. + х, < 161
2 >£•
х, +2х2 <12| ’’
5х, - 2х4 < 41
-х3 + 2х4<4]
хі >0,у = 1...4.
384
Дослідження операцій Збірник задач
Дана задача мас одне зв'язуюче обмеження та два незалежних
блоки 5] і 82. Області допустимих рішень для обох підсистем
представлені на рис. 8.1 та 8.2:
Введемо позначення:
— допустимі розв'язки
блоків 5, і 82 відповідно. Тоді справедливі співвідношення:
У = ТАУг
І
де х. і у — крайні точки множини 5, і 82.
385
Зайченко О.Ю . Зайченко Ю П.
Запишемо цільову функцію у векторному вигляді: г = схх + сгх .
А зв'язуючі обмеження мають такий вигляд: ахх + а.,у = 24,
де < =[2,1], 4 =[3,2], а\ =[2,3], а\ =[1,3].
Запишемо тепер координуючу задачу:
тахг = £(с,х)а
X (О,х.)«, +£ («,>; )/?,+$ = 24,
і«.-к
/
а.>0,Д >0.
Виберемо в якості початкового допустимого базисного рішення:
4 =[0,0],/=[0,0]; а,=1, Д=1.
Будемо розв’язувати дану задачу методом оберненої матриці.
Початкова симплекс-таблиця буде мати такий вигляд:
сі	Вх	ео			ез
0	5	24	1	0	0
0	ах	1	0	1	0
0		1	0	0	1
		0	0	0	0
			Л,	Лл	Д)2
Таблиця 8.1
1-а ітерація І етап
Побудуємо і розв’яжемо підоадачі, які відповідають початковому ДБР.
1) тіп {(дУа, - с,г )х} = -2хі - х2.
Оптимальний розв’язок даної задачі знаходимо графо-
аналітично:
х2 =[4,4];
Г=-12.
386
Дослідження операцій. Збірник задач
Знайдемо мінімальну оцінку вектора-стовпця:
дО2=Г+4=-і2<0.
2) Складемо цільову функцію другої блочної задачі:
пип((ЛХ -«[)>} = -Зх, —х4.
Оптимальний розв’язок даної задачі знаходимо графо-
аналітично:
Л=[2,3];
/2о=-12.
Знайдемо мінімальну оцінку вектора-стовпця:
ДА=/°+Аа = -12<0.
Ми обчислюємо компоненти цільової функції та нових стовпців
координуючої задачі:
с>2 = 12; а'х2 = 20;	сіл = 12; а2У2 =И-
1-а ітерація II етап
Запишемо нову координуючу задачу:
тах(12а2 + 12Д);
20а, +1 ІД + х = 24;
«,+о2=1;
А+А=і;
а(>О,Д >0.
Розв’язуємо задачу методом оберненої матриці, для цього
обчислюємо стовпець Р? , вводимо його в таблицю 8.2 (яка
повторює табл. 8.1).
’1 0 01 Г111 Г11'
Рр. = 0 1 0-0 = 0
0 0 11	1
387
Зайченко О.Ю., Зайченко Ю.П.
Таблиця 82
с,	Л	ео	е.	Є2	ез	
0	5	24	1	0	0	11
0	а,	1	0	1	0	0
0-Є-	А	1	0	0	1	1
т
Виконавши одну ітерацію, ми отримаємо таблицю 8.3.
Таблиця 8.3
с.		«0	ех	Є2	ез	р а2
0<-	5	13	1	0	-11	20
0		1	0	1	0	1
0	А	1	0	0	1	0

Обчислюємо стовпець Ра і дописуємо його в табл. 8.3.
Виконавши одну ітерацію методу оберненої матриці отримуємо
таблицю 8.4:
Таблиця 8.4
Сі	вх	ео	Є.	Є2	ез
12	аг	13/20	1/20	0	-11/20
		7/20	-1/20	1	11/20
12	А	1	0	0	1
	Л		3/5	0	27/5
			А.	Ді	Л)2
388
Дослідження операцій Збірник задач
2-а ітерація І етап
Із останнього рядка таблиці 8.4 отримуємо такі значення для
вектора розрішаючих множників:
З 27
л=[АЛ,;Л»]= -Л— 
Використовуючи ці дані побудуємо дві нові підзадачі:
Г 3	1	4	4
1) тіпКА^а, -с[)х} = тіп-і (— -[2,3]—[2,1])лу =-—х, +—х2.
р  . , кТ 7x1 -ІхЗ
-------
Оптимальний розв’язок даної задачі знаходимо графо-
аналітично:
х3=[16/5;О];
=-64/15.
Знайдемо мінімальну оцінку вектора-стовпця х3:
д„ =/°+А>і=-—+0=	<0-
•/1	4)1	15	15
Оскільки ця оцінка менша нуля, то відповідний вектор необхідно
ввести в базис координуючої задачі. Ми обчислюємо компоненти
нового стовпця координуючої задачі:
т 32 т 32
с.х,=—; а. х. =—.
13 З	З
2) тіп{(Л^а2 -с2г )^} = тіп І(| • [1,3] - [3,2]) Л = -
12	1
--	Х4-
5-5 4
Оптимальний розв’язок даної задачі знаходимо графо-аналітично:
^=[2,3];
/2°=-27/5.
Знайдемо мінімальну оцінку вектора-стовпця:
27 27
у+у =0.
Оскільки оцінка = 0, цей вектор не вводимо в базис.
Так як < 0, переходимо на II етап.
389
Зайченко О.Ю.. Зайченко Ю.П
2-а ітерація II етап
Запишемо нову координуючу задачу:
32
тах(12а2 + 12Д +—а3);
32
20а2 +1 ІД +—а3 + 5 = 24;
а} +а2 +а3 = 1;
Д=і;
а;>0,Д>0.
Розв’язуємо задачу методом оберненої матриці, для цього
обчислюємо і вводимо в таблицю 8.4 стовпець Р. : Отримуємо
а3
табл. 8.5.
—1/20
-1/20
0
Р
0 -11/20] Г32/3
1 11/20 - 1
0	1 ] І 0
8/15
7/15
0
Таблиця 8.5
с	В*		«і	Є2		Р. “з
12	«2	13/20	1/20	0	-11/20	8/15
<—	«і	7/20	-1/20	1	11/20	7/15
12	А	1	0	0	1	0
т
Провівши одну ітерацію методу оберненої матриці, отримуємо
таблицю 8.6:
Таблиця 8.6
сі	А	ео		Є2	«3
12	«2	1/4	3/28	-8/7	-33/28
32/3	«3	3/4	-3/28	15/7	33/28
12	А	1	0	0	1
	Л	23	1/7	64/7	73/7
390
Дослідження операцій. Збірник задач
3-я ітерація І етап
Із останнього рядка таблиці 8.6 отримуємо такі значення:
А — А>г]
1.64.73
7’7’7
Використовуючи ці дані, побудуємо дві нові підзадачі:
1) тіпКА^л, -с|г)х] = тіп1(у[2,3]-[2,1])х
12	4
Оптимальний розв’язок даної задачі знаходимо графо-аналітично:
х4=[16/3;0],
у;0=-64/7.
Знайдемо мінімальну оцінку вектора-стовпця:
2) тіп«л:яІ-с1г)>-} = пііп|фіІ.31-р.2])й=—
Оптимальний розв’язок даної задачі знаходимо графо-аналітично:
у4 = [2,з];
/2о=-73/7.
Знайдемо мінімальну оцінку вектора-стовпця:
„0 ,	73 73 „
Дд — Уї + Л,2— з + з
Так як оцінки невід’ємні, то отриманий на другій ітерації
розв’язок являється оптимальним. Записуємо його:
1	3 16
А" =а,хг +а,х, =—[4,4]+— —,0
опт 2 2	5 5 Д І ’ І	*
=[5;Ч;
К„я=Ал=[2;3].
Отже ми отримали такий розв’язок:
х® = 5, х® = 1, х® =2, х® = 3; /° = 23.
391
Зайченко О.Ю., Зайченко Ю.П.
ПЕРЕВІРКА:
Підставимо отримані значення у зв’язуюче обмеження:
2*5 + 3*1+2 + 3*3 = 24.
Воно виконується строго, отже знайдений розв’язок є оптимальним.
Задачі та вправи
Розв’язати методом декомпозиції Данцига-Вульфа такі задачі;
Задача 8.1
Р = (2х, -х2 +Зх3) —> тах;
х, + 2х, + х3 -х4 <2,
2х, -х, < 1,
х,+2х, <3,
-х, + 2х4 < 2,
-2х, +х4 <1,
ху>0, у = 1?4.
Задача 8.2
Р = (х, +х2 + 2х3 +х4) —> тах;
х, + 2х2 + 2х3 + х4 < 40,
X] + Зх2 < ЗО,
2х, + х2 < 20,
х3 < 10,
х4 <10,
х3+х4 <15,
ху >0, у = 1,4.
Задача 8.3
Р = (Зх, + 2х2 + 4х3 + 8х4 + 6х3 +12х6 ) —> тах;
Зх, + х2 + 2х3 - х4 + 2х5 + х6 < 24,
х, + 2х2 + 6х3 + х4 < 18,
х5 +2х6 < 10,
Зх5 +х6 < 12,
ху > 0, у = 1,6.
392
Дослідження операцій. Збірник задач
Задача 8.4
р = (Зх, + 2х2 - 4х3 - х4 + 5х5 ) —> тіп;
Зх, + х2 + 2х3 + 4х„ + Зх5 < ЗО,
Зх, <10,
х5 + 2х6 < 10,
х, +- 4х3 < 20,
2х4 + х3 < 15,
х,>0, / = 1Ї5.
Задача 8.5
Г = (2х, + Зх2 + х3 + 2х4 ) -> тіп,
х,+2х2+2х3+Зх4 <20,.
2х, + х2 <18,
х, +2х2 < 12,
Зх3 - х4 <8,
х3 + х4 < 7,
ху >- 0,	1,4.
Задача 8.6
Р = (х, + х2 + 2х3 + х4) -> тах;
х, + 2х2 +х3-х4 < 10,
2х, + х2 <4,
х, + 2х2 < 6,
х3+х4 <5,
- 2х3 + Зх4 < 6,
ху >0, у = 1,4.
Задача 8.7
р = (2х, +х2 +Зх3 +2х4) -> тах,
2х, + Зх2 + х3 + Зх4 < 24,
Зх, +х2 <16,
х, + 2х2 < 12,
5х3 - 2х4 < 4,
-х3 + 2х4 <4,
ху >0, у = 1, 4.
393
Зайченко О.Ю, Зайченко Ю.П.
Задача 8.8
Р = (8х1 + 4х2 + 5х3 + 4х4 ) —> тах;
2х, + х2 + Зх3 + 2х4 < 16,
х, -4х2 <4,
х, + 2х2 < 6,
2х3 + Зх4 < 12,
4х3 +2х4 <16,
ху >0, у = 1~4.
Задача 8.9
Р = (X) + 2х2 + х3 + Зх4) -> тах;
х, + х2 + 2х3 + Зх4 < 20,
2х, + х2 <18,
X) + 2х2 < 12,
2х3 - х4 < 6,
х3 + х4 < 10,
ху >0, у = 1, 4.
Задача 8.10
Р = (2х, + 2х2 + х3 + х4) -» тах;
X! +2х22х3Зх4 < 24,
2х2 4-х2 —18,
х, +2х2 <12,
2х3+х4<12,
х3+х4 <12,
ху>0, У = 1Л
394
Дослідження операцій. Збірник задач
8.2. Метод декомпозиції Корнаї-Ліптака
Нехай маємо задачу ЛП вигляду:
максимізувати
сТх
при обмеженнях:
Л0х<й0,
х>0,
(8.2.1)
(8.2.2)
(8.2.3)
де
ст=[сі,сьхт=[хі,х2,...,хг]; Ьт0=[Ьі,Ь2,
4)=||й,ї||;' = 1."г;У = 1»л-
Розглянемо підхід до її розв’язання, що використовує метод
декомпозиції Корнаї-Ліптака.
Розіб’ємо матрицю Ао на підматриці ,...,А°, де при
кожному у є [1,7] матриця А° має вимірність т х пг Тоді розіб’ємо
відповідно вектор с на підвектори сІ,с2,...,сі,...,с2 та х — на
підвектори хьхл...,х>я, де С],х2 — вектори, які мають вимірність
лу, V иу = и, тоді задача (6.1)-(6.3) зводиться до вигляду:
7=1
максимізувати	(8.2.4) у=|
при обмеженнях:	<8.2.5) 7=1 >О,у=ЇД-	(8-2-6)
Введемо ти-вимірні вектори-стовпці у і, що задовольняють умови:
(8.2.7)
395
Зайченко О.Ю., Зайченко Ю.П
Сформулюємо]-у задачу ЛП:
максимізувати
(8.2.8)
при обмеженнях:
(8.2.9)
х >0,у =Г7.	(8.2.10)
Розглянемо вектор	Позначимо через А/>, множину
усіх векторів у таких, що виконується умова (8.2.7) і задачі (8.2.8)-
(8.2.10) мають розв’язки. Оптимальні значення функціоналів задач
(8.2.8)-(8.2.10) залежать від у, як від параметрів. Вказану залежність
запишемо у вигляді Позначимо	(у ) Тоді задача
7-І
(8.2.8)-(8.2.10) зводиться до такої координуючої задачі:
максимізувати
Г(У)	(8.2.11)
при обмеженнях
£у^Ь0.	(8.2.12)
7=1
Якщо розкладання матриці Ао інтерпретується як розбиття
системи на 3 підсистем, а вектор Ьо розглядається як спільний ресурс
системи, то задача (8.2.11)—(8.2.12) полягає у знаходженні
оптимального розподілу спільного ресурсу. Зауважимо, що тут не
вводиться обмеження на знак величини у,. с
Розглянемо задачу (8.2.11), (8.2.12). Її аналіз ускладнюється,
оскільки функція Е(у) аналітично не відома, а задана лише
алгоритмічно. Для її обчислення необхідно розв’язати задачу ЛП
(8.2.8)-(8.2.10).
Застосування певної системи максимізації функції Г(у) породжує
відповідний метод розкладання на основі принципу Корнаї-Ліптака.
Так, у роботі Корнаї-Ліптака пропонувалося зведення цієї задачі до
мінімаксної, яка далі розв’язується методами теорії гри. Розглянемо
цей підхід.
396
Дослідження операцій. Збірник задач
Запишемо двоїсті задачі до задачі (8.2.8)-(8.2.10):
мінімізувати
Л>,.,	(8.2.13)
при обмеженнях:
>су;У = Г7;	(8.2.14)
Яу>0,	(8.2.15)
де вектор-стовпець А (Д = 1,7) має т компонент {Я?,Л*	.
Нехай через позначені опуклі многогранники у просторі Л™,
що задаються умовами (8.2.14), (8.2.15). Введемо вектор А з
і
компонентами	Я,, Я^,..., Я,у та	множину Ол=Г]Пл. у
відповідності з основною теоремою двоїстості:
Таким чином:
//>,) = тіпЯ]>у;Яу єй',	(8.217)
і остаточно задача (8.2.11), (8.2.12) зводиться до відшукання сідлової
точки:
знайти
ДГУ = тах Г(У),	(8.2.18)
уєЛ/..
де А} —фіксовані, у = 1,7 та ДГУ = Х'.Я.у, •
і
Задачу (8.2.18) можна розв’язати методом матричних ігор для
фіктивної гри Брауна [16]. Зазначений метод являє собою
ітеративний процес, де кожна ітерація у термінах теорії ігор являє
собою певну партію гри і відповідає вибору деяких стратегій двох
гравців. Ці стратегії у даній задачі є векторами Д та ¥. Стратегії
кожного гравця вибираються найбільш вигідними з урахуванням
відповіді його противника.
397
Зайченко О.Ю., Зайченко Ю.П.
Оптимальні стратегії для задачі (8.2.18) визначаються у вигляді:
а)	для гравця 1: Л*г (.у) • У = тіп ЛгУ;	(8.219)
ЛєПл
б)	для гравця 2: А У* =ПВхД У.	(8.2.20)
уєМу
Ітеративний процес згідно з методом Брауна складається з таких
кроків.
Початкова ітерація /к=1/.
1.	Обирається довільна стратегія у1 єЛ/^;
2.	Покладемо У*[1] = у,;
3.	Визначимо Я, = Л (у [1]) згідно з (8.2.19);
4.	Покладемо Л,[1] = Я,.
Нехай вже проведено (к-7) ітерацію, в результаті якої визначені
У’[Л-1] та Л’(Л-І).
к-а ітерація.
1.	Знаходимо у(к) = у*(Л’(А-1)) згідно з (8.2.20);
2.	Обчислюємо У*(Л) =------У (к — 1)ч—у(к\,
к	к
3.	Знаходимо Л(к) = Л*(У*(£)) згідно з (8.2.19);
,	А-1 .	1
4.	Обчислюємо Л (к) =------Л (к —1)4—Л(к) .
к	к
Згідно з теоремою Робінсона про збіжність методу Брауна,
послідовність {У*(&),Л (&)} при А—>оо збігається до сідлової точки
задачі (8.2.18).
Метод розкладання Корнаї-Ліптака виявляється найбільш
ефективним у випадку, коли частина обмежень має блочно-
діагональну структуру. В окремих випадках, коли вдається знайти
аналітичні вирази для функцій //уі), можна запропонувати значно
більш ефективний метод розв’язання задачі методом декомпозиції
Корнаї-Ліптака (див. наступний приклад).
398
Дослідження операцій Збірник задач
Приклад 8.2
Розв ’язати таку задачу методом декомпозиції Корнаї-Ліптака:
Г = (2х1 + х,+ 3х, +х4) —> тах;
2х, + Зх, + х, + 2х4 < 20;
Зх,+х, <15;
х,+2х, <10,
5х,-2х, <4,
-х,+2х4 <6;
ху 50,7 = 1...4.
Розв’язок:
1)	Запишемо 1-у блочну задачу:
тах(2х1+х,)=/(у|);
2х, + 3х, <у,;
 Зх, + х, <15;
х,+2х, <10;
х, 5 0,х, > 0, .у, > 0.
Розв’язуємо її графоаналітично. Область рішення приводиться на
рис. 8.3.
Рис. 8.3
399
Зайченко О.Ю., Зайченко Ю.П.
Нехай у, = 6, тоді х° - 21;
1	1 о
х° = о. Тобто максимум спочатку
досягається на вісі абсцис х, до точки х, =5; у1 = 2х, —10. При
Цьому 7і(т1) = Т|-
Далі, при збільшенні у, > 10 точка максимуму знаходиться на
перехресті прямих 2х, + Зх2 = у, та Зх, + х2 = 15 -
Розв’язуємо систему:
ГЗх, +Х2 = 15;
[2х,+3х2=у1.
45-у. Зк-ЗО
Звідси одержуємо х, = —-— та х2 =----------.
/Ду,) = 2х, і х2 - + Це буде справедливо на всьому відрізку
до точки 4(4;3). їй відповідає у, = 17. В цій точці /(у,) = 11.
Таким чином ми отримуємо:

у,; 0<у,<10;
^|+6°; 10< у, <17;
7	1
11.
Неважко перевірити, що в граничних точках значення /(_У|)
співпадають для сусідніх інтервалів.
2) Запишемо 2-у блочну задачу:
тах(Зх3+х4) = /2(у2);
х3 + 2х4 <у2;
 5х3 — 2х4 < 4;
—х3 + 2х4 < 6;
х3 >0,х4 >0, у2 >0.	й
400
Дослідження операцій. Збірник задач
Розв’язуємо її графоаналітично^ Область рішення приводиться на
рис. 8.4.
Переглядаємо інтервали функції /2 (у2 ):
а)0<у2<^.
Тут х°3 = у2, х° = 0. /2(у2) = Зу2.
б) Уі^-
Точки максимуму знаходяться на прямій 5х3 - 2x4=4. Знайдемо
4
координати даної точки, для якої у2 > —. Наприклад в т. В. Для цього
розв’язуємо систему рівнянь:
х3 +2х4 =у2,
5х3 — 2х4 = 4.
Звідси одержуємо х = — +4 та х
3	6
5у2~4
12

11у2+20
12
401
Зайченко О.Ю, Зайченко Ю П
Граничною точкою, загальною для прямої х3 + 2х4=у2 та
відрізка АВ буде т.	В даній точці у, =11, а значення
І2’ 4 )
Л(л) = -г'
4
Таким чином ми отримуємо:
Зу2; о<у2<у;
Л(у2)=
11у2+20
12	’
4
у<у2<11;
47.
4 ’
Складаємо і розв’язуємо координуючу задачу:
шахГ(у) = Т;(у1) + /2(у2);
О^Уі+Уг -20.
Обчислюємо похідні:
Крок 1
^- = 1,	0<у,<10;
&-	.3,	0^-
Оскільки	то спочатку віддаємо ресурси першій
<ІУ2
підсистемі у =-.
1 5
Крок 2
^• = 1,	0<у,<10;
^2	12’ 5 У1
Віддаємо ресурс першій підсистемі у, =10.
402
Дослідження операцій Збірник задач
Крок З
_#=1
7’
#_=И
12’
4
5
= зз; д.о = з>і зо=^. ао = 2;
Віддаємо ресурс другій підсистемі у2 = 8.
Тоді, увесь залишок ресурсу отримує перша підсистема:
у, =20-8 = 12.
Обчислюємо:
Л.о ,45-у, 45-12
1	7	7	7	2	7	7' 1	'	'	'
Перевіряємо правильність обчислень за зв’язуючим обмеженням:
2х, + 3х2 +х3 +2х4 = 2 —-+^ + 2 + 3-2 = 20.
Тобто, дане обмеження виконується строго. Таким чином,
знайдене рішення є оптимальним.
Для нього:
тах / = 2—+-+3-2+3 = 19—.
7 7	7
403
Зайченко ОЮ., Зайченко Ю.П.
Задачі та вправи
Розв’язати методом декомпозиції Корнаї-Ліптака наступні задачі:
Задача 8.11
Р ~ (х, -2х2-Зх, + х4) -> тіп;
X) + Зх2 + х3 + 4х4 < 6,
х, + х2 <3,
х, + 2х2 < 5,
2х3 + х4 <6,
х3 - х4 <, 9,
х, £ 0, / = 1~4.
Задача 8.12
Р - (2х, + х2 + Зх, + х4) -> тах;
2х, + Зх2 + х, + 2х4 < 20,
Зх, + х2 < 15,
х, + 2х2 < 10,
5х3—2х4 <4,
— х3+2х4 <4,
х, >0, і = 1~4.
Задача 8.13
Р = (2х, + х2 + Зх3 + х4) -» тах;
2х, + Зх2 + х3 + 2х4 < 20,
Зх, +х2 < 15,
х, + 2х2 < 10,
5х3 -2х4 < 4,
- х3 + 2х4 < 6,
ху >0, ] = 1?4.
Задача 8.14
Р = (8х, + 4х2 + 5х3 + 4х4 ) -> тах;
404
Дослідження операцій. Збірник задач
2хІ + х2 + Зх, + 2х4 <16,
х1 - 4х3 < 4,
х, + 2х2 5 6,
2х3 + Зх4 < 6,
4х3 + 2х4 < 8,
х, > О, у = 1~4.
Задача 8.15
Р = (2х, + Зх2 + х, + 2х4 ) -> тах;
х, + 2х2 + 2х3 + Зх4 < 20,
2х, + 2х2 і 18,
х, + 2х2 < 12,
2х3 — х4 <8,
х3 + х4 < 7,
ху > 0, у = 1, 4.
Задача 8.16
Р = (2х, + х2+Зх3 + 2х4 ) —> тах;
2х, + Зх2 + х3 + Зх4 < 24;
Зх, + х2 516,
х, +2х2 512,
5х3 -2х4 <4,
-хз+х4<4,_
ху >0, у = 1,4.
Задача 8.17
Р = (2х, +х2 +Зх3 + х4) —> тах;
2х, +3х2 + х3 + 2х4 < 20,
Зх, + х2 <15,
х, +2х2 <10,
5х3 - 2х4 < 4,
- х3 + 2х4 < 4,
х2 >0, у = 1,4.
405
Зайченко О.Ю., Зайченко Ю.П.
Розділ 9. ПРИЙНЯТТЯ РІШЕНЬ
В КОНФЛІКТНИХ СИТУАЦІЯХ
9.1.	Основні поняття і визначення в області теорії ігор.
Позиційні ігри.
З іграми людство стикається протягом всієї своєї багатовікової
історії. Існують різні види ігор: салонні ігри, спортивні ігри і т.п.
Якщо розглядати салонні ігри, то гра починається з деякої похідної
позиції і складається з послідовності ходів, які гравці роблять по чер-
зі. Деякі ходи можуть бути випадковими (наприклад, кидання кістки,
тасування колоди карт). В деяких іграх, наприклад, шахи і шашки,
немає випадкових ходів. Крім того, ігри бувають з повною інформа-
цією, коли попередній хід супротивника відомий, і з неповною інфо-
рмацією, коли він невідомий і гравець повинен робити наступний
хід, не знаючи точної позиції гри.
Позиційні ігри
В наше загальне уявлення про гру входять такі 3 елементи:
1)	множина ходів, які можуть бути як особистими так і випадко-
вими; ходи гравців чергуються;
2)	наявність інформації про гру, яка може бути повною або не-
повною;
3)	функція виграшу.
Визначимо перш за все топологічне дерево, або дерево гри, як
скінченну сукупність вузлів (названих вершинами), які сполучені лі-
ніями {ребрами), так, що утворюється зв’язний граф, що не містить
простих (замкнутих) циклів.
В результаті ми приходимо до такого визначення.
406
Дослідження операцій. Збірник задач
ОЗНАЧЕННЯ 1: Нехай Г-топологічне дерево з виділеною початко-
вою вершиною А. Будемо говорити, що вершина С слідує за вершиною В,
якщо послідовність ребер, що сполучають А і С проходить через В.
Говоритимемо, що С слідує за В безпосередньо, якщо існує ребро,
що сполучає В із С.
Вершина х називається кінцевою, якщо за х не слідує жодної
вершини.
ОЗНАЧЕННЯ 2: Позиційною грою п-осіб ми називатимемо гру, в
якій задані такі елементи:
1)	топологічне дерево Г з виділеною вершиною А, яка назива-
ється початковою позицією гри',
2)	функція виграшу, яка ставить у відповідність кожній остато-
чній позиції дерева деякий л-мірний вектор (л - число гравців);
3)	розбиття множини всіх неостаточних позицій (тобто неоста-
точних вершин) дерева Г на (л+1) множин:£0,5\,...,5п називаються
множинами черговості, де 50 — позиція з випадковим ходом;
4)	імовірнісні розподіли для кожної позиції із 50на множині
безпосередньо наступних за нею позицій;
5)	розбиття множини 5. для кожного гравця (ї = 1,2,...,л) на
підмножини 8. , що називаються інформаційними множинами. При
цьому позиції з однієї і тієї ж інформаційної множини мають однако-
ве число безпосередньо наступних за ними позицій, тобто - альтер-
натив, і жодна позиція не може слідувати за іншою позицією з тієї ж
самої інформаційної множини;
6)	для кожної інформаційної множини 5/ задані множини інде-
ксів разом із взаємно однозначними відображеннями множини І/ на
множині альтернатив кожної позиції з 5/ .
Позначатимемо гру через Г.
Тут перераховані всі елементи гри. Зміст перелічених умов такий:
1.	Встановлює, що є початкова позиція;
2.	Задає функцію виграшу;
407
Зайченко ОЮ., Зайченко Ю.П
3.	Розділяє множину неостаточних позицій на позиції з ходом
випадку (50) і особисті позиції, відповідні кожному з гравців
(ад,-Л)-
ОЗНАЧЕННЯ 3: Гра Г називається грою з поєною інформацією
для гравця і, якщо кожна його інформаційна множина 8, склада-
ється з одного елемента. Інакше говорять, що Г є гра з повною інфо-
рмацією, якщо в Г кожний гравець має повну інформацію.
Наприклад, шахи і шашки - це ігри з повною інформацією, а
бридж і покер - ні.
9.2. Стратегії гри. Нормальна форма гри
Важливим елементом гри є стратегія, під якою розуміється план
розгортання гри.
ОЗНАЧЕННЯ 4: Стратегія гравця є деяка функція, яка ставить у
відповідність кожній інформаційній множині 8- цього гравця деяку
альтернативу з множини альтернатив, що описується відповідним
індексом з множини С (множини індексів всіх альтернатив).
Множину всіх стратегій гравця і позначатимемо X. Насправді, нас
(також як і учасників гри) цікавить, які із стратегій є найкращими з погляду
максимізацїї частки кожного гравця у виграші (очевидно, кожний гравець
і прагне максимізувати і -у компоненту функції виграшу).
Оскільки результати випадкових ходів відомі тільки в імовірніс-
ному значенні, то природно розглядати математичне очікування фу-
нкції виграшу, визначеної у випадку, коли гравці використовують
заданий набір стратегій.
Тому, для математичного очікування функції виграшу за умови,
що гравець і приймає стратегію сг, є Е, можна використовувати та-
кий вираз:
/7(ст1,сг2,...,сгя)=[Л1(<т1,ст2,...,сг„),/7г(ст1,сг2,...,стл),...,/7я(сг|,ст2,...,стя)].
408
Дослідження операцій. Збірник задач
Тобто, його можна записати у вигляді п-мірної таблиці п векторів
розмірності п.
У випадку п = 2, її можна представити у вигляді деякої матриці
А = ||а, Ц. Така матриця називається нормальною формою гри.
ОЗНАЧЕННЯ 5: Гра називається скінченною, якщо її дерево міс-
тить скінченне число вершин (наприклад, шашки, шахи).
Відмітимо, що в скінченій грі кожний гравець має лише скінчен-
не число стратегій.
Ситуація рівноваги
ВИЗНАЧЕННЯ 6: Нехай дана гра Г. Говорять, що ситуація (тоб-
то набір стратегій ,<?2,...,сгп) рівноважна або, що вона є ситуаці-
єю рівноваги, якщо для будь-якого / = 1,2,...,л і для будь-якого
сг, є Е має місце нерівність;
77.(сг,*,сг2’,...,, ст,, ст’+„..., сгя*) < Пі(сг,*,а2,...,	,сг*, ам,а").
Іншими словами, ситуація рівноважна, якщо жоден гравець не
має жодних розумних підстав для зміни своєї стратегії, за умови, що
вся решта гравців збирається дотримуватися своїх стратегій. У цьому
випадку, якщо кожний гравець знає, як гратимуть інші, то він має
підстави дотримуватися тієї стратегії, яка відповідає цій ситуації рів-
новаги, тобто, гра стає стійкою.
Приклад 9.1
Нехай для деякої гри Л, в нормальній формі задано таку матри-
цю виграшів:
	А	А
«і	(2;1)	(0;0)
«2	(0;0)	(і;2)
409
Зайченко О.Ю., Зайченко Ю.П.
Як (а,, Д ) так і («2, Д ) є стратегіями рівноваги. Не кожна гра
має ситуації рівноваги (наприклад, гра в орла).
Взагалі, якщо гра не має ситуацій рівноваги, то звичайно деякі
гравці намагаються відгадати стратегії решти учасників, зберігаючи
свої власні в таємниці.
Можна довести, що в іграх за повною інформацією ситуації рів-
новаги завжди існують.
Антагоністичні ігри
ОЗНАЧЕННЯ 7: Гра Г називається грою з нульовою сумою, якщо
в кожній остаточній позиції функція виграшу (//,,/72,...,/7п) задо-
вольняє умові:
£/7,=0.	(9.1)
«=і
Тобто, сумарний виграш рівний сумарному програшу.
ОЗНАЧЕННЯ 8: Гра 2-х осіб з нульовою сумою називається ан-
тагоністичною або строго конкурентною.
У випадку антагоністичної гри можна просто задавати першу
компоненту вектора виграшів. Друга компонента обов’язково рівна
першій з протилежним знаком.
В цьому випадку назвемо першу компоненту просто виграшем.
Далі покажемо, що антагоністична гра відрізняється від решти
ігор тим, що в ній немає підстав для будь-яких переговорів між грав-
цями: оскільки, якщо один виграє, то інший програє.
Значення цієї властивості випливає з наступної теореми.
ТЕОРЕМА 9.1. Нехай (сг,,сг2) і (т^^) - дві ситуації рівноваги
антагоністичної гри. Тоді, і (сг,,т2), і (т,,сг2) також є ситуаціями
рівноваги. При цьому:
П(а{, а 2) = ПІТ', т2) = //(сг,, г2) = /7(т,, сг2).	(9.2)
410
Дослідження операцій Збірник задач
ДОВЕДЕННЯ.
Ситуація (сг,, сг2) - рівноважна, отже П{<7,, сг2) > //(г,, а2).
Але з другого боку, (г,,г2) теж ситуація рівноважна. Тому
/7(т„сг2)>77(г1,г2).
Звідси випдиває, що
//(сг,, <т2) > /7(г,, бт2) > П(г,, г2).	(9.3)
Але за аналогією:
П(тх, т2) >	,т2) > П(а,,ст2).	(9.4)
1 ці дві системи нерівностей доводять рівність (9.2).
Далі для будь-якого сп:
77(сг і, сг2) < //(сг,, сг2) = //(т,, сг2).	(9.5)
І для будь-якого <72:
//(г,,сг2)> //(г,,г2) = //(г,,сг2).	(9.6)
Отже, (г, ,сг2) є ситуацією рівноваги. Аналогічно і ситуація
(сг,,т2) є ситуацією рівноваги.
Нормальна форма гри
ОЗНАЧЕННЯ 9. Гра задана в нормальній формі, якщо визначена
деяка матриця Я = |а,7|| і = 1,т - стратегія гравця 1; у = 1,п - стра-
тегія гравця 2, де:
ау - виграш гравця 1 (програш гравця 2), якщо гравець 1 вибирає
стратегію і, а 2-й гравець - стратегію у .
Як буде показано далі, пара стратегій (/,у) буде рівноважною
тоді і тільки тоді, коли відповідний елемент буде найбільшим по
стовпцю і одночасно найменшим по рядку.
Такий елемент називається сідловою точкою матриці А.
411
Зайченко О.Ю., Зайченко Ю.П.
Приклад 9.2
Нехай матриця гри Ао має такий вигляд:
5
Ао= З
-З
1 2
Е 4
О 1
Неважко помітити, що дана матриця має сідлову точку а22 = 2.
Якщо гравець 1 відмовиться від вибору стратегії і — 2 і вибере
стратегію і = 1, то гравець 2 також вибере стратегію ] — 2, і виграш
гравця 1 складе а12 — 1 < а22 = 2.
Аналогічною буде ситуація у випадку і = З
Якщо ж гравець 2 відмовиться від своєї стратегії у = 2 і вибере
стратегію у = 1 або у = 3, то його програш збільшиться.
Таким чином, стратегії і — 2 ,у = 2 є рівноважними і їм відпові-
дає сідлова точка а22 — 2 матриці А.
Назвемо величину Ух = тах тіп а - нижньою ціною гри (це га-
7	1	1
рангований виграш першого гравця, при будь-якій стратегії гравця
2), а величину У2 = тіп тах а. - верхньою ціною гри (гарантований
7 і 1
програш гравця 2 при будь-якій стратегії гравця 1). У загальному ви-
падку:
У}<У2.	(9.7)
Проте, якщо матриця А має сідлову точку аі0 у0, то
тах тіп а. = тіп тах а. = а 0 0.	(9.8)
Таким чином, у разі наявності в матриці А сідлової точки аі0 0,
оптимальні стратегії обох гравців (іо,у’о) і при цьому У} = У2 = V, де
V —ціна гри.
412
Дослідження операцій Збірник задач
9.3. Змішані стратегії.
Теорема про мінімаксДж. фон Неймана
Розглянемо антагоністичну гру двох осіб з платіжною матрицею
А в загальному випадку, коли А не має сідлової точки.
Введемо поняття змішаної стратегії.
ОЗНАЧЕННЯ 10: Змішаною стратегією гравця 1 в антагоністи-
чній грі двох осіб ми називатимемо вектор X = [х.] і = 1,/и, такий
що, 0 < х,. < 1 і X ^, = 1 	(9-9)
(=і
Аналогічно, змішаною стратегією гравця 2 в антагоністичній грі
двох осіб ми називатимемо вектор ¥ = і — 1, п, такий, що:
у.>0і£у.=1.	(9.10).
і=і
Величину х. можна трактувати як імовірність вибору гравцем
стратегії і, а у] — відповідно імовірність вибору ним стратегії у .
ОЗНАЧЕННЯ 11: Якщо х( = 1, відповідно . = 1, то така страте-
гія називається чистою.
Нехай гравець 1 використовує свою змішану стратегію X, а гра-
вець 2 свою змішану стратегію К
Тоді математичне очікування виграшу першого гравця (програшу
другого) дорівнює:
У(Х,¥) = ХТА¥.
При цьому гравець 1 прагне максимізувати свій виграш за будь-
якої відповіді гравця 2.
ОЗНАЧЕННЯ 12: Нижньою ціною гри ми називатимемо гаранто-
ваний виграш гравця 1 за будь-якої відповіді гравця 2:
шахтіпХгА¥ = V..	(9.11)
х г
413
Зайченко О.Ю.. Зайченко Ю.П.
ОЗНАЧЕННЯ 13: Верхньою ціною гри ми називатимемо гарантова-
ний мінімальний програш гравця 2 при довільній стратегії гравця 1:
тіптахЛ'гЛУ = К.	(9-12)
УХ
Справедлива така основна теорема матричних ігор двох осіб,
сформульована Дж. фон Нейманом (теорема про мінімакс).
ТЕОРЕМА ПРО МІНІМАКС:
Кожна антагоністична гра двох осіб має рішення в чистих або
змішаних стратегіях, і при цьому нижня ціна гри дорівнює верхній
ціні гри і дорівнює ціні гри, тобто:
тах тіп ХТ А ¥ = тіп тах Хт А¥ = ХІА ¥0 = У (9.13)
хго гас	гго хго
де (Х0,У0) —оптимальні змішані стратегії гравців 1 і 2 відповідно.
Ця теорема має фундаментальне значення для всієї теорії ігор
двох осіб.
ДОВЕДЕННЯ.
Для доведення використовуємо теорію двоїстості ЛП. Нехай дру-
гий гравець вибирає свою чисту стратегію у (тобто стовпець Ау).
Тоді нижня ціна гри:
V. =тахтіпХГАі.	(9.14)
ХєХ- у	7
Таким чином, задачу першого гравця можна записати як таку за-
дачу ЛП:
тах І7,	(9.15)
за умов:
Хглу>р;, у=ї^;	(11.16)
£х,=1;	(11.17)
х, >0.	(11.18)
414
Дослідження операцій. Збірник задач
У свою чергу, нехай гравець 1 вибирає чисту стратегію і (тобто ря-
док АІ). Тоді гравець 2 прагне мінімізувати свій програш, і ми маємо:
У2 - тіп тах Д.К	(919)
Тоді задачу гравця 2 можна записати так:
тіпГ2.	(9.20)
за умов:	А:У <У2, і = 1,/и;	(9.21)
л
=	(9.22)
7=1
у.>0.	(9.23)
Запишемо ці дві задачі в розгорненому вигляді:
Задача гравця 1
тах^,	(9.24)
за умов:	Ух - £аі}хі <0, у = 1, п;	(9.25)
І=І
(9.26)
х( >0, і = \,т.	(9.27)
Задача гравця 2
тіпИ2,	(9.28)
за умов:	+уг > °, і=Цй;	(9.29)
7=1
415
Зайченко ОЮ., Зайченко Ю.П.
2>у=і;	(9-зо)
7=1
^>0, У = ї^.	(9.31)
Неважко побачити, що задачі 1 і 2 є парою двоїстих задач ЛП.
Якщо в якості двоїстих змінних у задачі гравця 1 вибрати
у., і = 1,л та у2, то отримаємо задачу гравця 2 (9.28)-(9.31).
Тоді на підставі основної теореми двоїстості про оптимальні рі-
шення, цільові функції обох задач повинні бути рівні для оптималь-
них розв’язків, тобто:
тах У} = тіп У2 = V,
що і треба було довести.
З приведеного доведення виходить, що для знаходження оптима-
льних стратегій гравців у матричній грі двох осіб з нульовою сумою
можна застосувати апарат ЛП, записавши відповідну задачу гравця 1
(або гравця 2).
Тоді знайшовши розв’язок прямої задачі і оптимальну стратегію
одного гравця, можна одночасно знайти і стратегію іншого гравця як
рішення двоїстої задач.
Приклад 9.3
Розв ’язати матричну гру з матрицею методом ЛП (лінійного
програмування).
3 6 14
5 2 4 2
14 3 5
Розв’язок:
Запишемо задачу максимізації виграшу 1-го гравця.
416
Дослідження операцій Збірник задач
тах К
Зх, + 5х2 + х2 > V
6х, + 2х2 + 4х3 V
х, + 4х2 + Зх3 > V
4х, + 2х2 + 5х3 > V
х, + х2 + х3 = 1
ХрХ2,х3 > О
тах Г
-Зх,-5х2-х3+у£О и,
-6х,-2х2-4х3 + V <0 и2
—» -х, —4х2 -Зх3 + V £ 0 и3
-4х, —2х2-5х3+г< 0 и4
х, + х2 + х3 = 1
х,,х2,х3 > О
Вводимо вільні змінні и,, и2, и3, и4 та штучну змінну у в ці-
льову функцію.
Тепер функція має такий вигляд: тах(И — Му\).
Будуємо таблицю 9.1 та розв’язуємо задачу ЛП звичайним симп-
лекс методом (див. табл.9.1-9.4).
Таблиця 9.1
			*1	Х2	хз	V	иІ	и2	из	и4	Уі
с2\су			0	0	0	1	0	0	0	0	-м
		4>	4	4	4	4	4	4	4	л	4
0	ч.	0	-3	-5	-і	і	і	0	0	0	0
0	и2	0	-6	-2	-4	і	0	1	0	0	0
0	из	0	-1	-4	-3	і	0	0	1	0	0
0		0	-4	-2	-5	і	0	0	0	1	0
м	У,	1	1	1	1	0	0	0	0	0	1
д		-м	-м	-М	-М	-1	0	0	0	0	0

417
Зайченко О.Ю, Зайченко Ю.П.
Таблиця 9.2
			X,	X,	*з	V	“і	и,	из	и4
С1\с)			0	0	0	1	0	0	0	0
		4	4	4	4	4	4	4	4	4
0	“і	3	0	-2	2	і	і	0	0	0
0	и2	6	0	4	2	і	0	1	0	0
<-0	из	1	0	-3	-2	і	0	0	1	0
0	и4	4	0	2	-1	і	0	0	0	1
0		1	1	1	1	0	0	0	0	0
А		0	0	0	0	-і	0	0	0	0
т
Таблиця 9.3
			X]	х2	х3	V	и1	и2	из	и4
С1\с/			0	0	0	1	0	0	0	0
	в.	4	4	4	4	4	4	4	4	4
0	и!	2	0	1	4	0	і	0	-1	0
0	и2	5	0	7	4	0	0	1	-1	0
1	V	1	0	-3	-2	1	0	0	1	0
<—0	и4	3	0	5	1	0	0	0	-1	1
0		1	1	і	1	0	0	0	0	0
А		1	0	-3	-2	0	0	0	1	0
т
І через 2 ітерації остаточно отримуємо табл. 9.4.
418
Дослідження операцій. Збірник задач
Таблиця 9.4
			X,	X,	хз	V	«1		«3	“4 .
САС/			0	0	0	1	0	0	0	0
		4	4	4	4	4	4	4	4	4
0		1/8	1	0	0	0	1/8	1/8	-1/4	0
0	х2	1/2	0	1	0	0	1/6	-1/6	0	0
0		1/8	0	0	0	0	-13/24	19/24	3/4	1
0	хз	3/8	0	0	1	0	-7/24	1/24	1/4	0
1	V	13/4	0	0	0	1	1/12	5/12	1/2	0
А		13/4	0	0	0	0	1/12	5/12	1/2	0
Згідно останньої таблиці ми одержали:
З індексного рядка цієї таблиці вибираємо оптимальні значення
двоїстих змінних — оптимальну змішану стратегію гравця 2:
у°=-; уо=А. уо=1 о=0.
1 12	2 12	2
її
Ціна гри V0 = —
Розв’язання ігор з матрицею [2 х /г] і матрицею [т х 2]
Задача [2х«]
Нехай матриця А має вид:
. аН а!2 " аіі	аі„
А =
_^21 а21	^2і	@2п_
419
Зайченко О.Ю.. Зайченко Ю.П 
Запишемо задачу першого гравця:
тах г,.
аух, +а2]х2 > V,, У = 1,и.
Дану задачу представимо у виді:
тахтіп^*! + а2}х2),	(932)
х, + х2 = 1;
х,=1-х2.	(9.33)
Підставимо (9.33) в (9.32) і отримаємо:
тах тіп(а1у + (о2у - а1у )х2).
На інтервалі [0; 1] будуємо функцію /7(х2) = а1у+(а2>-аіу)х2.
Дана пряма проходить через точки ау/ при х2 = 0 та а2у при х2 = 1.
Шукаємо нижню огинаючу /(х2) = тіп{а1,+(а2,-а1,)х2}- Знайде-
мо її максимум.
Нехай максимум досягається на перетині прямих /\(х2) та
№)•
Тоді записуємо таку систему рівнянь, де у. —нижня ціна гри.
+«27*2 = *Р
а\кХ\ + а2кх2 = Г2>
х, + х2 = 1;
х,,х2 > 0.
Розв’язуємо задачу графоаналітичним методом:
420
Дослідження операцій. Збірник задач
Рис. 9.2
Розв’язуємо дану систему:
аі7+(°1, аі})Х2 ~ а\к +(аі*	а\к)Х1-
г	0 _	0	1	0
Та знаходимо х2 та х, - 1 - х2.
Приклад 9.4. Розв’язати таку задачу і знайти стратегії обох грав-
ців,
'2 3 15'
А =
4 16 0
Розв’язання:
Розв’язуємо дану задачу графоаналітичним методом:
Рис. 9.3
421
Зайченко О.Ю., Зайченко Ю.П
Стратегія першого гравця визначається таким чином:
Зх, + х2 = V,;
+ 6х2 = V,;
+ х2 = 1.
Звідси отримуємо, ЩО л = — , X = — ,«= — •
1 7	2 7	1	7
Стратегія другого гравця визначається таким чином:
у2+6уз=г2;
У2+Уз=1-
Звідси отримуємо, що у _2, у -1, у =2І,	=0, у = 0.
7	7 1 7
Задача [тх2]
Нехай матриця А має вид:
Ч
«12
«22
«.2
а
«ті «т2
Задача другого гравця при обранні першої і-тої стратегії матиме вид:
г2 = тіп тах + аі2у2),
Уі+>'2=1;
тіптахЦ, +(а,2 -аа)^2),
0<Ь <1-
422
Дослідження операцій Збірник задач
В даному випадку знаходимо верхню огибаючу /,{уг) і знахо-
димо її мінімум, який однозначно визначає суттєві стратегії гравця 1:
і, та і2.
Приклад 9.5. Розв’язати таку задачу:
2 4
З 1
А~ 1 6
5 0
Розв’язання:
Розв’язуємо графоаналітичним методом:
Рис. 9.4
у^+бу^г,;
Ь\ = ^2;
У2+Уз=^
6	4
Звідси у, + 6у2 = 5у,, 6у2 = 4у,. Тоді л , у2 = —,	= 3.
423
Зайченко О.Ю., Зайченко Ю.П.
9.4. Ігри із ненульовою сумою.
Біматричні ігри
На практиці зустрічаються задачі, які є іграми із ненульовими
сумами.
Біматрична гра — це гра, в якій задана матриця виграшу першого
гравця А і матриця виграшу другого гравця В при виборі відповідних
стратегій:
Л = 1к11’ 1 = =
Л = |1М’ і = ^'П,) = \,п.
1. Можлива некооперативна гра (коли гравці діють окремо на
ринку).
2. Кооперативна гра, або коли вони вступають у коаліцію.
Позначимо змішані стратегії обох гравців:
_	_	___ ГП
першого: X -1 х) І, і = 1, т, хі = 1;
і=і
другого: У = [уг ], у = 1, п, £ = 1.
/=•
Тоді випливає таке: для першого гравця оптимальна стратегія ви-
значається з умови:
тах тіп ХТ А ¥, для другого гравця — з умови: гаах тіп Хт В¥ •
хіО уіО	уіО х>0
Означення 9.13. Стратегія (X , ¥ ) називається стратегією рі-
вноваги. якщо для УХ їХ і У¥ У виконуєтьсятаканерівність:
ХТА¥' <Х‘ТА¥';
Х'ТВ¥ <Х'ТВ¥'
Теорема 9.2. Кожна біматрична гра має хоча б одну стратегію рі-
вноваги.
Розглянемо матричну гру двох осіб.
Перший гравець намагається максимізувати свій виграш:
тах тіп Хт А ¥ = и'.	(9.34)
424
Дослідження операцій Збірник задач
Також цього прагне і другий гравець:
тахшіпХ^ВУ = V*.	(9.35)
V ,Г
Нехай Хта У довільні змішані стратегії обох гравців. Нехай пер-
ший гравець вибирає і-ту стратегію — рядок А>. Тоді його виграш
4У.
Введемо величину
с, = тах{0; АУ - ХТ А ¥}.	(9.36)
Нехай другий гравець вибирає свою стратегію В}. Тоді введемо
величину
Л, = тах{0;ХгВ,-ХТВ¥}.	(9.37)
Введемо таке перетворення стратегій: Г(Х,У) = {X , У ), де
хі + сі
(9.38)
• У.+СІ]
Уз=-----п--->
3=1
л=КІІ’ і=^т^=^п-
Покажемо, що отримані стратегії, які також є змішаними:
(9.39)
425
Зайченко О.Ю., Зайченко Ю.П.
„	^Уі+а,^ Х +
також =—---------------=---------= 1, де 0 < х\ < 1, 0 < у\ < 1.
> + Е< І + Е'';
у=1	7=І
Змішана стратегія — це рандомінізована стратегія, коли із де-
якою ймовірністю вибирається одна із чистих стратегій (рядків мат-
риці А).
Справедливе таке твердження.
ТЕОРЕМА 93. (А”, У) = (X, У) тоді і тільки тоді, коли (X, У) —
стратегія рівноваги.
Доведення. Якщо (X, У) — стратегія рівноваги, то якщо перший
гравець відмовиться від неї і обере чисту стратегію і, то виграш зме-
ншиться, тобто АІ¥<ХТА¥, Х/і = 1,т.
З іншого боку аналогічно і для другого гравця, якщо він обере
чисту стратегію у, тоді:
ХТВу<ХгВ¥, Х//=їрі.
Звідси сі = 0 для довільного і та = 0 для довільного у.
Тоді із виразу (938) та (9.39) отримаємо: хі = х., Vі та
У І =УіУї-
Припустимо, що (Х,У) не є стратегією рівноваги. Тоді існує та-
ке X, для якого виграш буде більший, а саме:ХГА¥ > ХТА¥. Так як
Х = [хі] — це змішана стратегія, то існує таке і{, що
лу > Хт А¥ (тобто знайдеться така чиста стратегія ї,, при якій
виграш буде більший). Звідси с, * 0 і х, = —Ґ-ІІ *х .
‘І	Ч	ГИ
Аналогічно для У. Якщо У не є стратегією рівноваги, то існує таке
У, що ХтВ¥ > ХтВ¥. Так як У — це суміш чистих стратегій, то
426
Дослідження операцій. Збірник задач
існує таке у,, що ХТВ > ХтВУ. Звідси випливає, що
і уі * У Отже теорему доведено повністю. Розглянем відобра-
ження Т:(Х,У)->(Х’,У).
Це відображення Т відображає відрізок [0; 1] у той же самий від-
різок [0; 1] (див. рис. 9.5).
Рис. 9.5
Це означає, що існує така точка, яка відображається сама в себе,
оскільки відображення Т є неперервним і замкнутим і за теоремою
Брауера 3(Х, У): Т(Х, У) = (X, У) = (X, У).
А це і є стратегія рівноваги.
На відміну від ігор із нульовою сумою, якщо у нас (X , У ) —
одна стратегія рівноваги, а (X , У ) — друга стратегія рівноваги, то
стратегії (X , У ) і (X , У ) не є стратегіями рівноваги.
Приклад 9.6. Нехай задано біматричну гру з матрицею:
А, В =
(4;1) (0;0)
(0;0) (1;4)
Як бачимо,
(X =[1;0], У = [1;0])—перша стратегія рівноваги.
(Х’=[0;1], У’=[0;1]) — друга стратегія рівноваги.
Але в той же час (X , У ) і (X , У ) не є стратегіями рівноваги.
427
Зайченко О.Ю., Зайченко Ю.П.
9.5. Кооперативна гра двох осіб. Теорема Неша
Розглянемо тепер випадок біматричної гри двох осіб, в якій грав-
ці можуть вступати в коаліцію та можливий сумісний вибір змішаних
стратегій, а корисність (доля виграшу) може передаватись від одного
гравця до іншого. Необхідно визначити умови кооперації.
Умови можливості укладення угоди:
Нехай для обох гравців задані пара функцій корисності та розгля-
дається множина результатів такої кооперації:
5(н, г) — допустима множина результатів кооперації,
де и — корисність першого гравця;
V — корисність другого гравця.
Властивості функції 8 (її, г):
1. Обмеженість — виграші обмежені;
2. Замкнутість — ми включаємо крайні точки цієї області.
Якщо допустити можливість створення лотерей, а функція кори-
сності лінійна, то 5(щг) випукла.
Кооперація буде виникати у тому випадку, коли виграші гравців
будуть більшими, ніж у випадку відсутності кооперації.
Нехай (А, В) — біматрична гра. Позначимо:
и = тах тіп ХТ А У,
х>0 уїО
Xх-=1’
•	і
V = тах тіп Хт ВУ.
ГЙО
Виграш при коаліції повинен задовольняти умову:
(н,у): ц>ц*; г>г*.
Нехай 5 — допустима множина результатів кооперації і відомі
и та V , необхідно знайти таку вирішуючу функцію <р, яка забезпе-
чить найбільший виграш кожного гравця в коаліції:
ер'. ір(8,и , г ) = (н,г) —арбітражний розв’язок гри.
428
Дос лідження операцій Збірник задач
Дослідженням даної задачі і пошуком її рішення займався амери-
канський математик Непі, який сформулював такі аксіоми [33].
Аксіоми Неша:
АІ. Аксіома розумності: (м, у) > (и , у) .
А2. Аксіома допустимості: (и, у) є 8(и, у).
АЗ. Оптимальність по Парето. Якщо існує така пара (и , у ), що
(и , V ) > (її, у) та (и , у ) є 8(и, у), то (и , у ) = (и, у).
А4. Незалежність від сторонніх альтернатив. Якщо арбітражше
рішення (м,у)є7’с5, і (р(8,и ,у*) = (и,у), то розв’язок
гри на меньшій підмножині задовольняє умові:
(р(Т,и ,у) = (и,у).
А5. Лінійність. Якщо перетворення Т: (и , у ) отримано із 8 за
ДОПОМОГОЮ ЛІНІЙНОГО перетворення, де П = «,« + Д ,
у = л2у + Д та ^(5, і/, у) = (и,у), то <р(8,и",у ) = (м ,у ),
і відповідні розв’язки також зв’язують лінійні перетворення:
и = ахи + Рр, у = а2у + Д.
А6. Симетрія. Якщо (и, у) є 5 тоді і тільки тоді, коли (у,и)є8
і при цьому їх гарантовані виграші співпадають, тобто
и = у , то також співпадають їх арбітражні виграші и = у .
Справедлива наступна теорема.
ТЕОРЕМА 9.4 (Неша). Існує єдина функція ір визначена для за-
дачі про угоди, яка задовольняє аксіомам 1-6.
Доведення грунтується на двох лемах.
Лема 1. Якщо існує таке и > и і у > у — допустимі результати
і (и,у) є 5, то функція Неша:
^(и,у) = (и-и)(у-у),
досягає свого максимального значення тільки в одній точці (и, у) .
ДОВЕДЕННЯ: наведено в роботі [33].
429
Зайченко О.Ю., Зайченко Ю.П_________________________________
Лема 2. Нехай 8, и, V мають той самий зміст, шо в лемі 1 і нехай
функція А(м,у) = (у-у’)п + (п-п’)у. Тоді якщо (и,у)є5, то для
всіх (м, г) є 5 справедливе таке:
Л(п, V) < Л(и, у).	(9.40)
ДОВЕДЕННЯ:
Припустимо, що це не так, нехай існує (н,у), таке, що
Іі(и, и) > к(и, V). Візьмемо деяке £є[0;1] і візьмемо точку (ц,у),
яка є випуклою комбінацією ((м,у) і (ц,у)):
и-и + е(и-и) у = у + й(у-у).	(9.41)
Обчислимо:
%(и, у) = %(и, г) + єк(и - м; у - у) + £2(и- п)(у - у). (9.42)
Спрямовуємо £ —> 0 і отримуємо:
&(и, г) = %(и, V) + єк(и - и; V - у) + Є2 (и - и)(V - у) > §(и, у). (9.43)
Ми отримали противоріччя з лемою 1, так як точка (и,у) — точ-
ка максимуму, то нерівність (9.43) неможлива.
Отже, дана пряма И(иу) являється дотичною до допустимої обла-
сті рішень у точці (и, у), зауважимо, що кутовий коефіцієнт нахилу
дотичної дорівнює:
. V —V*
к =	---7.	(9.44)
и —и
ДОВЕДЕННЯ ТЕОРЕМИ НЕША:
Припустимо, виконані умови леми 1. Тоді існує тільки одна точка
(и,у)максимізуюча функцію Неша 8(и,у) . Дана точка задовольняє
аксіоми АІ і А2 по побудові. Вона задовольняє також і АЗ, так як
якщо (м,у)>(м,у) і (и, у)Х(^,у), то §(и, у) > %(и, у). Воназадово-
430
Дослідження операцій. Збірник задач
льняє і аксіому 4, так як, якщо вона максимізує £(м,г) на 5 , то тим
більше вона максимізує дану функцію і на меншій множині Г. Ана-
логічно, вона задовольняє і аксіому А5, так як, якщо и — о^и + Д
і V = а^ + Д2, то:
£(»>') = {[« -(«,«’ + Рі )Л>' -<аги + Д2)]} = а,а2^(и,у).
1 звідси випливає, якщо (и, у) максимізує функцію §(и, у) , то
і %(и ,г)=тах.
Внаслідок симетрії функції #(ц,и)вона задовольняє і аксіому 6.
Отже, ми показали, що точка (н, г) задовольняє шести аксіомам Неша.
Тепер потрібно показати, що ця точка є єдиною, яка задовольняє
усім аксіомам.
Розглянемо множину: і/ = {(н,у): Л(и,у)<Л(и,г)}, згідно леми 2
Введемо деяке лінійне перетворення:
Т = (и,у): м =(м—м’)/(м-м*); V =•=—
V — V
Тоді в перетворених координатах и = 1 та V = 1.
Запишемо рівняння (9.40) в перетворених координатах:
7’ = {(м',р): м+у<2},	(9-45)
и > 0, V > 0 і крім цього и = V = 0.
Тобто, маємо дві додаткові одиниці корисності, які розділені між
гравцями.
В силу симетрії и = V ми маємо єдиний розв’язок рівняння (9.45):
и = V = 1.	(9.46)
Згідно лемі 2, якщо межа множини 5 гладка (тобто вона має до-
тичну в точці (и, г)), то пряма, на якій функція й(м, г) — постійна, є
431
Зайченко О.Ю., Зайченко ЮП.
дотичною до 8 у цій точці. Але нахил межі множини 5 у довільній
точці є відношенням, в якому корисність може передаватися від од-
ного гравця до іншого. Інакше кажучи, схема Неша стверджує, що
додаткова корисність повинна ділитися між гравцями в такому ж
відношенні, в якому вона повинна передаватися. А оскільки не пе-
редбачається, що корисність лінійно трансферабельна, то природно
може існувати лише одна точка, в якій корисність передається в да-
ному співвідношенні (див. рис. 9.6).
Рис. 9.6
У випадку лінійної трансферабельної корисності (тоді границя
області 8(и,у) — пряма ) задача відшукання точки (п, г) ставиться
простіше. Дійсно, ми можемо припустити (змінивши за необхідності
шкали корисності), що відношення в якому додаткова корисність
може передаватися від одного гравця до іншого, рівна 1:1. Таким чи-
ном, 8 містить всі точки, які лежать на деякій прямій границі
и + V = К або нижче за неї, де К— максимально можлива корис-
ність, яку ці два гравці можуть одержати спільно і разом з тим, вище
і правіше за точку (и ,у*) (див. рис. 9.7).
432
Дослідження операцій Збірник задач
Рис. 9.7
Розв’язком задачі Неша буде така точка (и, г):
- _ (и-»)+К - = (у-и) + П
2	2
Додаткові одиниці корисності діляться пополам між обома учас-
никами:
-	. К-(и + г‘)	- . Л-(м* + г*)
Ли = и-и ----------- Дг - - V-V =------; (9.47)
2	2
-	. - . К-(и +г)
Ар-и-и = г-г =------------.
Стратегія погроз
Основним недоліком розглянутого підходу являється те, що стра-
тегія Неша не враховує стратегію погроз. Можливі ситуації, коли в
силу різних обставин один із гравців може опинитися у більш вигід-
ному становищі і шантажувати іншого гравця з метою отримання
більшого виграшу.
Приклад 9.7
Розглянемо задачу «продавець проти покупця»:
Продавець має такі стратегії:
а = 1 — продати товар за високою ціною с, = 103 грн.;
433
Зайченко О.Ю., Зайченко Ю.П.
а = 2 — продати товар за низькою ціною с2 = 500 грн.;
а = 3 -— не продавати товар.
Покупець має такі стратегії:
6 = 1 — заключити договір;
6 = 2 — відмовитися від угоди. При цьому він повинен заплати-
ти штраф.
У випадку а = 3 збиток продавця становить — 200 грн., а у ви-
падку 6 = 2 збиток покупця становить — 20 ірн.
Платіжна матриця (А,В) матиме вид:
аІ		Ь2
ах	(800; 100)	<-200;-20)
а2	(400;500)	(-200;-20)
	(0;0)	—
Ми бачимо, що можливе шантажування з боку другого гравця,
оскільки при другій чистій стратегії 62 він несе маленький збиток,
а у першого гравця великий збиток.
З метою урахування стратегії погроз Неш запропонував таку
трьохкрокову схему:
1.	Перший гравець пропонує свою стратегію погроз Ху.
2.	Другий гравець пропонує свою стратегію погроз ¥у.
3.	Вони торгуються між собою і намагаються знайти компромі-
сний розв’язок — заключити угоду. Якщо це вдається, то вони всту-
пають у договір. В іншому випадку гравці повинні реалізувати свої
стратегії погроз.
Пошук рішень:
У випадку дії механізму погрози, якщо гравці не домовились, то
виграші обох гравців складають відповідно:
17у = Х^А¥г Уу=Х;.В¥у-
434
Дослідження операцій Збірник задач
мета першого гравця: І/ = і/ -> тах;
другого гравця: V = Уу тах.
За наявності погроз функція Неша має такий вигляд:
V) = (17-С/ДЕ - Уу) -> тах.
Мають місце такі теореми.
ТЕОРЕМА 9.5. Кожна біматрична гра має хоча б одну точку
рівноваги у стратегії погроз.
Доводиться аналогічно теоремі про звичайну біматричну гру.
ТЕОРЕМА 9.6. Якщо (X ,У ) і (X ,У ) — дві ситуації рівно-
ваги в стратегіях погроз, то і (X ,У ), і (X ,У ) також ситуації
рівноваги. При цьому виграші гравців співпадають.
Доведення даної теореми аналогічне доведенню теореми для гри
з нульовою сумою.
Виникає питання знаходження оптимальних стратегій за наявності
погроз. Відповідне рішення досить складне і залежить від виду межі
5(ц,у). Але ця задача суттєво спрощується, якщо припустимо, Що
корисність лінійно трансферабельна між двома гравцями. У такому
разі можемо вибрати такі шкали корисності, за яких корисності між
гравцями передаватимуться в співвідношенні 1:1. Тоді застосування
даної теорії дає таке рішення (значення для точки Неша):
Якщо К — загальне число одиниць корисності, то
-	ХТУ(А-В)¥У + К
иу=-^----------------	(9.47)
-	-ХТ(А-В)У+П
*	у =	-	2---.	(9.48)
Розглянемо вирази в формулах (9.47) та (9.48).
Неважко помітити, що Ху (А - В)¥у — виграш першого гравця
із матрицею (А-В), а ХУ(В-А)¥ — виграш другого гравця із
матрицею (В-А).
435
Зайченко О.Ю, ЗайченкоЮ.П.
Отже, для знаходження стратегії погроз потрібно знайти рішення
гри із нульовою сумою з матрицею {А —В).
Тоді рішення задачі за наявності погроз визначається так:
1.	Знаходимо (X ,¥„) із задачі тахтіпХ(Л-.В)У.
* У
2.	Знаходимо величину К .
3.	Обчислюємо виграш гравців у випадку дії погроз иу та V за
формулами.
Приклад 9.8
Розглянемо біматричну гру (А,В), яка задається матрицею:
(9.47) та (9.47).
С ( 4
(1;4)
/-3;1)	(4;1) ,
Якщо припустити, що трансферабельного товару не існує, то
множина 5 буде опуклою оболонкою чотирьох точок	що
зображена на рис. 9.8.
Розв’язуємо незалежні задачі для першого і другого гравця:
436
Дослідження операцій. Збірник задач
-	задача першого гравця: тах тіп ХТА ¥ - 0 = и ,
х у
-	задача другого гравця: тах тіп ХтВ¥ — 0 = V .
у *
Оптимальні стратегії гравців: X =
2’2
Таким чином, 8 майже симетрична і значення и та V по першій
схемі Неша дорівнюють відповідно:
55
2’2
Проте ця схема не враховує можливостей загрози з боку 2-го гра-
вця. Дійсно, якщо гравець 2 застосує свою чисту першу стратегію, то
гравець 1 мало що може їй протиставити. Таким чином, необхідно
розглянути можливість погроз. Ми бачимо, що на оптимальній за
Парето межі 8(80) корисність лінійно трансферабельна в співвід-
ношенні 1:1.
Отже, ми можемо розглянути гру з матрицею С = А — В :
-З 8/1
з
-2 З
С=А-В=
Оскільки тах тіп с = -2 = тіп тах с = -2, то матриця С має
і І 1	І і *
сідлову точку на елементі с21 — — 2.
Так як максимальна загальна корисність двох гравців рівна
к = 5 , то ми отримуємо арбітражне рішення з урахуванням погроз:
-2 + 5 3	2+5 7
и=-------= —; у =-----= —.
2	2	2	2
Таке рішення можливе в тому випадку, коли масштаби кориснос-
ті гравців такі, що границя 8{и,у) розташовуватиметься під кутом
45° до осі абсцис.
В іншому випадку необхідно зробити перетворення маштабу ко-
рисностей, так щоб ця границя мала нахил 45°.
437
Зайченко О.Ю., Зайченко Ю П.
Приклад 9.9
Розглянемо задачу з матрицею (А, В) виду:
(6,2) ;
Розглянемо таке перетворення: и =и та у =2у, так щоб при
цьому суми виграшів В були рівні в обох випадках:
1 + 4а = 6 + 2а;
2а-5 = 0, а=-
2
Тоді матриця (А,В) матиме вигляд:
(Л,В) =
(1;10)
(6; 5)
К=1+10=6+5=11
Далі розв’язуємо задачу першого та другого гравця:
Задача першого гравця:
и = тах тіп Хт А ¥ = 0.
X у
Задача другого гравця:
г* = тах тіп Xі В¥ = 0.
У У
Для першого гравця ситуація не змінилася (тобто масштаб зали-
шився незмінним):
його виграш:	и = ——=— а для другого гравця:
2	2 ’
— и’-и'+Л 11
V =---------=—.
2	2
438
Дослідження операцій. Збірник задач
Знайдемо виграш другого гравця в вихідній системі координат:
- V 11 2 11
у =— =---= —.
а 2 5 5
Задачі і вправи
Задача 9.1
Знайти розв’язок біматричної гри (А, В) для таких випадків:
1.1.	При відсутності коаліції знайти найкращі стратегії обох грав-
ців і відповідні виграші.
1.2.	У кооперативній грі двох осіб вияснити доцільність створен-
ня коаліції і знайти точку Неша.
1.3.	Перевірити вплив дії погроз, визначити арбітражний
розв’язок у випадку дії погроз і порівняти із точкою Неша.
(Л5) =
(3;9)
(2;-2)
(12;3)
Для антагоністичної гри двох осіб із матрицею А записати відпо-
відні ЛП-задачі для визначення оптимальних стратегій гравців і
знайти їх.
5 2
8 З
А= 1 4
З 6
2 5.
Задача 9.2
Знайти розв’язок біматричної гри (А, В) для таких випадків:
1.1.	При відсутності коаліції знайти найкращі стратегії обох грав-
ців і відповідні виграші.
1.2.	У кооперативній грі двох осіб вияснити доцільність створен-
ня коаліції і знайти точку Неша.
439
Зайченко О.Ю., Зайченко Ю.П. 
1.3.	Перевірити вплив дії погроз, визначити арбітражний
розв’язок у випадку дії погроз і порівняти із точкою Неша.
(АВ) =
(4;6) (1;4)
,(-3;1) (8; 4)
Для антагоністичної гри двох осіб із матрицею А записати відпо-
відні ЛП-задачі для визначення оптимальних стратегій гравців і знай-
ти їх:
А =
2 3 16
5 4 3 2
Задача 9.3
Знайти розв’язок біматричної гри (А, В) для таких випадків:
1.1.	При відсутності коаліції знайти найкращі стратегії обох грав-
ців і відповідні виграші.
1.2.	У кооперативній грі двох осіб вияснити доцільність створен-
ня коаліції і знайти точку Неша.
1.3.	Перевірити вплив дії погроз, визначити арбітражний
розв’язок у випадку дії погроз і порівняти із точкою Неша.
{А,В) =
(6;10) (-1;-4)
,(-3;-1)	(8;4) .
Для антагоністичної гри двох осіб із матрицею А записати відпо-
відні ЛП-задачі для визначення оптимальних стратегій гравців і знай-
ти їх:
5 6 3 2 1
1 2 4 5 7
А =
Задача 9.4
Знайти розв’язок біматричної гри (А, В) для наступних випадків:
1.1.	При відсутності коаліції знайти найкращі стратегії обох грав-
ців і відповідні виграші.
440
Дослідження операцій. Збірник задач
1.2.	У кооперативній грі двох осіб вияснити доцільність створен-
ня коаліції і знайти точку Неша.
1.3.	Перевірити вплив дії погроз, визначити арбітражний
розв’язок у випадку дії погроз і порівняти із точкою Неша.
(А,В)=
(8,4)
(3;-1)
(4; 10)
Для антагоністичної гри двох осіб із матрицею А записати відпо-
відні ЛП-задачі для визначення оптимальних стратегій гравців і знай-
ти їх:
5 8 3 2
2 3 6 5
441
Зайченко О. Ю . Зайченко Ю П
Дослідження операцій Збірник задач
5 ^2
7 7
З 1
1.15./’ =-2-; ЛГ = ^-
5	[5
1.16.7^ = 4; Х = {2;2}.
„ ..2 .. Г
”7'
1.18.	Невирішувана.
1.19.	/’= 16; % = {3;5}.
1.20.	Невирішувана.
4	5
1Л.Г = 8-; Х = П-;2-к
7	7 7]
1.22.	Невирішувана.
1.23.	/' = 6; % = {5;1}.
1.24.	/’ = 6; Х = ]-;5Д.
12 2^
Г.З 41
5’5/'
Лп
—;4— .
5 5]
2	14 41
1.17./’ = 15—; У = П-;4-к
7	1 7 7І
2
1.25.	/’ =-6-; Х = \3~;
5 С
1.26.	/’=-
5
1.27.	/’= -45; Х = {0;15}.
1.28.	/’= 16; 2Г = {3;5}.
1.29.	/’=12; Х = {1;3}.
1.30.	/- = 8; Х = {2;3}.
1.31.	Г=9; 2Ґ = І5-;1Д.
І 4 2]
2
1.32.	/’ = -5—; 2Г=]о;1;|1.
7 І 7І
7
443
Зайченко О.Ю., Зайченко Ю.П.
1.33.	Р = 4; Х = Ц;О;ОІ.
[2	]
1.34.	Р = ЗО; X = {6,0}.
1.35.	Невирішувана.
1.36.	7 =-9;
1.37.	Р = -48; ^ = {0; 18; 4; 20}.
1.38.	Р = 7—; Х = ї—;1—;0І.
11 [11 11 /
1.39. У7 = 24; Х = {12;0}.
ґ	4	5І
1.40.У7 = 7; X = { 4—;2—}.
І	9	9
З	4	її
1.41.Г = -; Х = {1-;4-}.
5 І 5 5]
ґ 2 1 1
1.43. У7 = 6; А, = {0;-;-;0к
І 7 7 )
1.44.	Р = 9; % = {3;0}.
З	Ґ5	31
1.45.	Г = 77-; Х = ^-;12;-к
4	[8	4]
1.46.	Р = 24; ^Г = {8;0}.
ґ 4 7 21
1.47.	Р = 15; ^ = М-;2-;1-к
[ 9 9 3.
1.48.	Г = 9; Х = {4;5}; Г = |о;-;-;О
[ 3 3 /
1.49.	У7 = 6—; А" =/1;3;—|; У = /о;-;-;О-
З І 3]	[ 3 3 .
444
Дослідження операцій. Збірник задач
1.50. У7 = 4—; Х =
5
4 4
5’5
З 31
5*5 Г"
1.51. У7 = 12; Х = {2;0}; ¥ =
З
1.52.У7 = 45-; Х = <5-;
5
3 2
5’5
1.53. У7 = 6; Х = {0;3}; У = ^0;0;
У = (-;0;6;-|.
[5	5]
1 7 1
4’12] ’
1.54.^ = 225; X = ^0;5;12-;0к У = {3;4;0}.
' ’ 2'
4	1	5
1.55.У7 = 10—; Х = ІЗ—;1— к У = <
13	ІЗ 13]	І
У = {7;1;0}.
7
2
4
13
1.56. У7 = 33; Х = {3;0;3};
1.57. У7 = -14; Х = {2;0};
У = <{0;0;0;
13 13
1.58.У7 = 53; ^ = 0-;!^;
І З
У = {5;0;23}.
1.59.У7 = -8; ^ = {2;3}; У = •	•
1.60. У7 = 12; Х = {1;3}; У = {3;0;0;0;0}.
_21 28
37’37
1 -і
5’5
33
1.61. У7 =-7—; Х = <3—;
37	2"
4	І
1.62.	У7 = 27-; Х = <4—;
5	5
1.63.	Невирішувана.
1.64.	У7 =-4; ЛГ = {0;4};
1.65.	У7 =-6; ^ = {0;3};
; Г= 0-.0ДМ
37 37]
2 4
; У = ]3-;1-;0;0;(Н.
5 5
У = {0;1;0;0}.
У = {0;0;0;2}.
445
Зайченко О.Ю., Зайченко Ю.П.
1	Г 2 4 1
1.66.	Р = 5—; Х = і2-;-;0\;
7	І 7 7 ]
2	[2 1
1.67.	/’ =—; ЛГ = М;ОІ;
з	[з ]
1.68.	Так.
1.69.	Ні.
1.70.	Так.
1.71.	Так.
1.72.	Так.
1.73.	Так.
1.74.	Так.
1.75.	Так.
1.76.	Так.
1.77.	Так.
1.78.	Р =—\ Х = [о;— -.
3	І3.
2	Г З	41
1.79.	Р = -6—; Х = П-;-к
5	15	5.
1.80.	У7 = 10; X = {!;!}.
1.81.	У7 = 60; ЛҐ = {15;0}.
1.82.	Р = 13,8; X = {6,6;2,4}.
1.83. Р = -; Х =
7
5 2
- -ч-
І7 7]
З
1.84.	Р = 45—; X
5
53-Л
5 5
1.85.	Р = 6; 2Г = |—;0 -
І5 ]
1.86.	Г = 13; Х = {2;3}.
1.87.	Р = 12; Аг = {1;3}.
446
Дослідження операцій. Збірник задач
1.88. Р = -7—; 2Г = П—;
37	27
4	Г 1 4І
1.89. £ = 27—; Х = <4-~
5	І 5 5І
1.92. Р = 5—;
З
_21 28
37’37
1 4
5’5,4
1.90.	£ = 33; Х = {3;0;3}.
1.91.	£ = -14; Х = {2;0}.
2*;Д.
5 15]
1.93. Р = 24; Х = {12;0}.
1.94.	Р = 9; X = | 1-;0
І	2
1.95.	£ =-8; Лґ = {2;3}.
4	[34
1.96.	£ = 24-; 2Г = р-;8-к
7	І 7 7
2	2
і-;4-к
З З]
1 .51
7' 7
1.99. £ = -10—; Х = |—;3—
13 [із із]
1.97.	£ = 11-;
З
1.98.	£ = 4-; Х = П-;1-і..
7	” ”
_____	.„8
"ІЗ
1.100.	£ = 36; ЛГ = {0;18}.
кЗ 4"
5’5. '
Ґ.5 ,6
7'7
2	3 4
1.101.£ = 4-; % = р-;-к
2	[ 5 5]
1.102.Г = 27-; _У = І4-;6-[.
7 І 7 7]
1.103. £ = 5; % = {0;5}.
1.104.£ = 9-; 2Г = |-;4-..
2 І2 2
1 . 1
2’ 2
447
Зайченко О.Ю., Зайченко Ю.П.
1.105.	Г = 53; % = Н-;1к
І 3 '
1.106.	Е = -5; X = {0,5}.
1.107.	Р = 28; % = {4;6}.
4	5
1.116.	Г = 8-;% = П-;2
7	7
1.117.	Невирішувана.
1.118.	Г = 6,2Ґ = {5;1}.
5.21
7’ 7Г
1.119. Г = 6;^ = ^-;5-к
|2 2]
2	Г -
1.120. Р = -6--,Х = \3-;-
5	1 '
_____ _ З
5
З 4
і---- •
5 5.
-	4 1]
1.121. Г = -;У = П-;4-к
5 І 5 5
1.122.	/7 = -45,Х = {0;15}.
1.123.	77 = 16,Л' = {3;5}.
1.124.	Е = 12,Х = {і;3}.
1.125.	У7 = 8, X = {2;3}.
о;-1-
’з/
5 5]
1.126. Е = —;;
З
2
1.127. Р = -6-
5
1.128.	У7 = 10,>Г = {1;1}.
1.129.	У7 = 60,Х = {15;0}.
1.130.	У7 = 13,8,Х = {б;6;2;4}.
5 2
7’7 ‘
1.131. Е = -
7
448
Дослідження операцій. Збірник задач
З	( з 2І
1.132.	Г = 45-;Х = ^5-;-к
5	І 5 5]
1.133.	Р = 6,Х = 1-;0 
І5 }
1.134.	Р = 13,Х = {2,3}.
1.135.	Р = 12,Х={і;3}.
33
1.136.	Г = -7—;Х =
37
. 321.28 ,
\ 37*37
4	Г 1 4
1.137.	Р = 21-;Х = <4--,-\.
5	І 5 5]
1.138. Р = 33, Х = {3-0-3}
1.139.	Г = -14,ЛҐ = {2;0}.
і	ґ о о
1.140.	Р = 5-‘,Х = \2-- — к
З	[ 5 15]
1.141.	Г = 24, % = {12;0}
1.142.	Р = 9,Х = <1—;0 >.
І 2
1.143.	Р = -8,Х = {2-3}.
4	3 4]
1.144.	Р = 24--,Х = ]7-;8— к
7 І 7 7]
1	2 21
1.145. Г = 11-;Х = <6-;4— к
З І З З]
1.146. Г = 4-;Х = |з-;1-к
7	7 1}
449
Зайченко О.Ю., Зайченко Ю.П.
Розділ 2
	15 0 15 0	
2Лф £ = 240.% =	0 0 20 ЗО	
	0 15 5	0	
	20 10 0 10	0
2*2, £ = 432,% =	0 5 0 0	25
	0 19 16 0	0
	0 0 10 50	
2‘3' £ = 310,% =	40 ЗО 0 0	
	0	0 20 0	
	0 0 ЗО 0	
2.4.	0	0	0 20	
£=345,% =		
	ЗО 0 0 10	
	5 20 25 0	
	100	0	0	0
2.5.	0	70	0	50
£ = 2200,% =	0	60	90	0
	40	0	0	90
	40	0	10	0
2.6.	0	20	0	0
° £ = 320,% =				
	0	0	15	15
	0	10	10	0
	0	0	10	50
2-7, £=310,% =	40	зо	0	0
	0	0	20	0
450
Дослідження операцій. Збірник задач
	ЗО	10	0	0
2-8- £ = 142,% =	0	15	15	0
	0	0	3	17
2-9- £ = 265,% =	35	0	0	25
	5	60	0	0
	0	0	70	0
2Л0- £ = 555,% =	II0	15	10	15
	0	25	0	0
	|15	0	20	о
2Л1- £ = 190,% =		25 5		0 20 35 0 0 0			
		5 0	0 20				
		0	0	60 0		0	
2.12.		ЗО	0		0 10	0	
£ = 1180,%	—						
		! о	80		0 0	20	
		0	0		5 25	20	
		50	0	0	0	80	0
2.13.		0	50	ЗО	0	0	10
£ = 1190,%							
		0	0	0	80	20	0
		60	0	0	0	0	80
	0	3	0	0			
2Л4‘ £ = 69,% =	0	0	3	0			
	2	0	0	16			
451
Зайченко О.Ю., Зайченко Ю.П.
		55	5	0	0	
2.15.	£ = 585,% =	15	0	0	40	
		0	0	10	ЗО	
		|о	0	35	о	
		16	4	0	0	
2.16.	£ = 133,% =	0	12	0	4	
		0	2	12	0	
		0	0	0	11	
	1	10	0	15	0	0|
2.17.	£ = 225,%=|	0	0	0	0	0
		0	0	0	25	20
		0	35	0	0	15
2.18.	1	10	20	0	0 0	
	£ = 800,% =	0	10	50	ЗО	
		0	0	0	40 0	
		20	0	0	0	
2.19.	£ = 290,% =	0	0	20	0	
		5	0	20	0	
		о	ЗО	0	и	
2.20.		20	10	0	1‘	
	£ = 410,% =	0	35	0	0	
		0	15	55	0	
2.21.		20	0	20	0	
	£ = 240,% =	0	0	0	зо	
		0	18	0	32	
452
Дослідження операцій Збірник задач
	10	0	20	0
2-22- £ = 410,% =	0	40	0	10
	0	0	0	50
	ЗО	0	0	0
2 23	0	40	0	0
• £ = 695,% =				
	5	40	25	0
	0	0	0	60
	5	0	5	0
2 24	0	0	20	0
£ = 305 х =				
	20	0	0	15
	0	ЗО	15	0
	ЗО	0	40	ЗО	0	0
2.25.	0	0	15	0	0	0
£ = 715,% =						
	0	40	0	50	0	0
	0	0	0	0	45	10
	80	25	0	0	0	0
2.26.	0	0	10	0	0	20
£ = 860,% =	0	0	0	7	48	0
	0	0	0	10	0	10
	0	18	0	0	2	0
	10	20	зо	0	0	4Ц
2.27.	20	0	0	60	0	0|
£ = 980,% =	0	0	45	0	0	0
	0	0	5	0	40	0
	0	0	0	0	0	зо]
453
Зайченко ОЮ., Зайченко Ю.П.
	15	50	0	15	0	0	0
2.28.	25	0	5	0	0	0	0
£ = 715,% =	0	0	0	0	0	50	0
	0	0	ЗО	0	10	0	10
	0	ЗО	0	0	0	10	0
	0	15	0	0	0	0	65
2.29.	0	0	ЗО	0	25	20	5
£ = 735,% =	0	0	0	0	40	0	0
	0	15	0	15	0	0	0
	40	0	0	0	0	0	10
		40	0	0	0	0	0	0
		20	0	5	0	0	0	0
2.30.	£ = 1300,% =	0	20	0	0	0	35	15
		0	0	0	40	0	0	0
		0	10	10	0	0	0	0
		о	0	0	0	20	0	60
		0	0	4	0	6	0	
		0	3	0	12	0	0	
2.31.	£ = 285,% =	5	0	0	0	0	0	
							п	
	1 1	11	0	0	0	0	9,'	
							1	
		0	11	24	0	0	г II	
		0	0	0	0	14	о!	
		0	0		40	0	60	0
		110	0		0	40	0	0
2.32.	£ = 2740,% =	50	0		0	0	0	0
		0	0	200		0	0	0
		0	140		40	80	0	100
		0	0		0	0	140	0
454
Дослідження операцій. Збірник задач
	0	0	0	0	0	25
	0	0	0	0	25	0
2.33.						
£=400,% =	0	10	0	10	0	0
	10	10	0	0	0	0
	зо	0	35	0	0	5
	0	20	0	ЗО	10	0	0
2.34.	ЗО	0	0	0	10	0	0
£ = 560,% =	0	0	20	0	10	0	0
	0	0	50	0	0	0	0
	0	0	0	0	10	15	25
		0	0	0	0	0	0	40
2.35.		40	20	0	10	10	0	0
	£=900,% =	0	0	0	40	0	зо	5
		0	0	0	0	0	0	15
		0	0	зо	0	0	0	0
		0	0	0	0	10	0	2(Ч
2.36.		15	15	0	0	0	0	0
	£=340,% =	0	0	0	0	0	20	10
		0	0	15	15	0	0	0
		0	0	0	ЗО	0	0	0
		10	20	0	0	0	0	
2.37.	£ = 700,% =	0	0	0	20	зо	0	
		зо	0	20	0	0	0	
		0	20	0	0	0	зо	
		0	0	0	20	20	20	
2.38.	£ = 360,% =	10	ЗО	0	0	0	0	
		0	0	10	0	0	зо	
		20	0	ЗО	0	0	0	
455
Зайченко О.Ю., Зайченко Ю.П.
	100	0	0	70 ЗО		0	
2.39.	0	100 0		0	0	0	
£ = 2280,% =							
	0	0	70	0	0	00	
	0	100 ЗО		0	0	0	
	10	0	0	60 130 0			0
2’40, £ = 1890,% =	зо	70	20	0	0	0		0
	0	0	80	0	0 50		0
	0	0	0	0	0	0	50	
	400	0	0	0	0	0	
2.41. ,	0	0	80 80		0	0	
£ = 5180,% =							
	0	200 0		0	60	60	
	0	0	20 0		40	0	
	0	0	200	0	0		0
2.42. £=3700,% =	100	100	50	0	0		0
	0	0	0	0	150	100	
	0	0	50	150 0			з
	0	0	0	50	0 40		01
2.43.	0	70	0	0	0	0	зо	
							
£ = 2430,% =	80	50	0	ЗО	0	0		0!
	0	0	100	40	60 0		°І
	0	0	0	80	0	0		0
	80	0	20	0	0	0	
2.44.	120	0	0	100	100	80і	
£ = 3080,% =	0	0	60	0	0	0	
	0	40	0	0	0	20	
	0	60	0	0	0	0|	
456
Дослідження операцій. Збірник задач
Розділ З
3.1.1.	Е = 16, X = {0,4}.
3.1.2.	Е = 16, ЛГ = {6,4}, {8,0}.
3.1.3.	Г = 6,% = {0,3}.
3.1.4.	Р = 16,2Ґ = {2,0}.
3.1.5.	Е = 22,Х = {2,1}.
3.1.6.	Е = 5,Х = {1,1}.
3.1.7.	Е = 5,Х = {1,2}.
3.1.8.	У7 = 21,% = {3,1,0}.
3.1.9.	Е = З, X = {З,О}, {2,1}, {1,2}, {0,3}.
3.1.10.	/" = 10, X = {4,3}.
3.1.11.	Е = 22,Х = {2,1].
3.1.12.	У7 = 11,% = {7,4}, {б,5}.
3.5.1.	Е = 16, X = {0,4}.
3.5.2.	Е = 16, X = {б,4}, {8,0}.
3.5.3.	У7 = 6,% = {0,3}.
3.5.4.	У7 = 16,% = {2,0}.
3.5.5.	Е = 22, X = {2,1}.
3.5.6.	У7 = 5,% = {1,1}.
3.5.7.	У7 = 5,% = {1,2}.
3.5.8.	Е = 21, % = {3,1,0}.
3.5.9.	Е = З, X = {З,О}, {2,1}, {1,2}, {0,3}.
3.5.10.	У7 = І0,% = {4,3}.
3.5.11.	Е = 22, X = {2,1}.
3.5.12.	Г = 11,^ = {7,4}, {6,5}.
3.5.13.	Е = 6, X = {4,2}, {3,3}, {2,4}.
3.5.14.	У7 = 6,% = {2,2}.
457
Зайченко О.Ю., Зайченко Ю.П
3.5.15.	Е = \2,Х = {6,0}.
3.5.16.	Е = 2, А" = {1,1}, {0,2}.
3.5.17.	Г = 7,А = {0,7}.
3.5.18.	У7 = 11, А = {1,2}.
3.5.19.	Г = -1,А = {1,2}.
3.5.20.	Е = 12, X = {2,0}.
3.5.21.	Е = 6,X = {2,2}.
3.5.22.	Е = 5,Х = {3,2},{2,3}.
3.5.23.	Е = 20,Х = {0,5}.
3.5.24.	Г = 5,А = {3,1}.
3.5.25.	Е = З, X = {З,О}, {2,1}, {1,2}, {0,3}.
3.5.26.	У7 = 26,X = {4,1}.
3.5.27.	Е = 1, X = {1,0,2}.
3.5.28.	Е = 10, X = {1,1}.
3.5.29.	Е = 7, X = {3,1}, {2,3}, {1,5}, {0,7}.
3.5.30.	Г = 42, А = {5,1}.
3.5.31.	У7 = 28, X = {8,4}.
3.5.32.	Г = 5,А = {2,1,0}.
3.5.33.	Е = 10, X = {1,1}.
3.5.34.	Е = 5,Х = {1,2}.
3.5.35.	Г = 3,А = {3,0}.
3.5.36.	Е = 1, X = {4,1}.
3.5.37.	Е = 6, X = {2,4}, {1,5}.
3.5.38.	Г = 10,% = {4,3}.
3.5.39.	^ = 3,А = {0,1,0}
458
Дослідження операцій. Збірник задач
Розділ 4
1. Квадратичне програмування
0	14	о	2	.	-4
4.1.х?=	,х2 = ,тіпг = -2
9	3	9
4 2 х° = —	х° = —
1	13	2	13
4.3.	х° = 4.4, х2° = 2.8, х° = х° = 0.
4.4.	х° = х° = 0,х° = х° = {1,2,3}.
4.5.	1)%° = 3,х° = 2; 2)х° = 2.78, х° = 1.32; 3)х° = 6,х® = 6;
.4 0	4-0 О О О 40 о 46
4)х, = 5,х2 = 8 ;5)х, =	,х2 =	.
4.6.	х° = 1,х°=0,х° = 0.
4.7.	х° = 5.5,х° = 2.5,х° = 1.5 тах д = 26.75.
4.8.	х° = х2 = х° = 0,тіп 2 = 0.
4.9.х1о=0,х2о=-,х3°=-.
1	2	4 3 2
4.10.	х® =0, х2° = 1.5.
4.11.	х° =3,х° =3.
4.12.	х° =7,х° = 1.
4.13.	х° = х2 = 0.
4.14.
15 о 17
,х, = —.
4 2	4
4.15,
^х° =
4’^
17
4 '
0
459
Зайченко О.Ю., Зайченко Ю.П.
4.18.	х,° = 5, х2 = 3, тіп 2 = 21.
4.19.	х° = 3.4,х2° = 2.6.
4.20.	х,° = 7,х2 =1.
о 19 о 58
4.21.	х. = х, =
12 2 12
4.22.	х° =4,х,° =62-,х° =-.
2	9 3 З
4.23.	х° =3.9,х° =3.22,тах 2 = 19.21.
4.24.	х°=-,х°=1.
4.25.
4.26.
4.27.
о 138 0 51
х. =---,х2 = —.
31	31
х,° =3.7,х2 =2.3.
о 120 о ЗО 0 20
х. =---,х, =—,х. = —
29	29	29
4.28.	х? = |,х°=Хз =0.
4.29.	х°=5,х = 2.
4.30.	х°=0,х2 =1.5.
4.31.	х,°=3,х2 =3.
4.32. х,° = -,х2°
4 2
17
4 ’
2. Геометричне програмування
4.5.1.
£о0) = Ч<5) = 88.668, 8Х = 0.284, 8, = 0.432, 8У = 0.284,
^4 = 1.4,^5 =1.284, /,=1 071, /2 =1.175,/3 =0.894.
460
Дослідження операцій. Збірник задач
4.5.2.	#0(/) = г(£) = 4.786, £, = 0 57,8, = 0.43, 8. = 0.425,
8.	=0.144, 8, =0.575,/, =2.903, /2 = 0.188,/3 = 1.095.
4.5.3.	£0(/) = у(£) = 8.2,	£,=5/8,	£2=1/8,	£3=1/4,
8, =3/16, £5 =3/8, /, =0.52, /, = 1.45,/3 =3.62.
4.5.4.	Яо(/) = р(£) = 6О £, = 1/4, £2=1/2, £3=1/4, £4 = 1/4,
£5 =1/2, /, =15/16, /2 =0.8, /3 =0.8.
4.5.5.	£0(/) = г(£) = 1.6, £,=5/21, £,=2/21, £3=2/3,
£4 =23/21, /,=1.25, /2 =0.144, /3 =1.368.
4.5.6.	£0(/) = у(£) = 58.834, £,=1/3, £2=2/3, £3=1/6,
£4 =1/6, /, =2.08, /2 =0.721, /3 =0.707.
4.5.7.	£0(/) = у(£) = 22.905, £,=1/4, £2=3/4, £3=3/8,
£4 =1/8, /, =3.05, /2 =0.369, /3 =0.634.
4.5.8.	£0(/) = у(£) = 5.981, £,=3/4, £2=1/4, £3=1/2,
£,=1/4,/, =6,/2 = 0.224,/3= 0.669.
4.5.9.	Яо(О = у(£) = 5.291, £,=1/2, £2=1/2, £3=2, £4=1,
/, =1.5, /2 =0.221, /3 =0.398.
4.5.10.	£0(/) = р(£) = 28.284, £,=1/4, £2=1/2, £3=1/4,
£4 =1/8, /, =2.297, /2 =0.851, /3 =1.047.
4.5.11.	#0(/) = г(£) = 41.315, £,=7/8, £2 = 1/8, £3=1/4,
£4 =3/8, /, =0.311, /2 =2.049, /3 = 1.89.
4.5.12.	5о(/) = у(£) = 134.442, £,=1/3, £2=1/3, £3=1/3,
£4 =1/3, /, =7.378, /2 =2.47, /3 =0.246.
4.5.13.	^0(/) = р(£) = 29.9, £,=0.32, £2=0.52, £3 =0.16,
£4 =0.16, £5 =0.52, /, =8, /2 =0.603, /3 =0.317.
4.5.14.	£0(/) = у(£) = 103.293, £,=0.08, £2=0.92, £3=0.52,
£4 =0.2, £5 =1.24, /, =1.04, /2 = 1 745, /3 = 0.456
461
Зайченко О.Ю., Зайченко Ю.П.
4.5.15.	£о(О = у(<5) = 6О, £,=1/3, ^2 = 1/3, £3=1/3,
= 1/6, £5=1/3,1, =1/2, /2 =4, /3 = 1.
4.5.16.	£0(/) = г(£) = 10.998, £,=1/2, £2=1/2, £3 = 1/9,
£4 =8/9, /, =2.474, /2 =0.882, /3 =0.63.
4.5.17.	£0(/) = у(£) = 25.14, <5, =3/8, £2=5/8, £,=1/4,
£4 =1/2, /, =0.74, 12 =1, /3 =1.57.
4.5.18.	£„(/) = *(£) = 6.973, £,=4/5, £2=1/5, £3=2/5,
£4 = 1/2, 1, = 2.422, /2 = 0.856, /3 = 0.461.
4.5.19.	#0(/) = г(£) = 23.7, £,=1/8, £2=3/8, £3=1/2,
£4 = 1/4, £5 =1/8, /, =0.276, /2 =5.477, /3 =0.393, 14 =0.589.
4.5.20.	#0(/) = у(£) = 23.1, £,=0.34, £2=0.42, <53 =0.24,
£4 = 0.14, £5 = 0.04, /, = 0.046, і2 = 2.38, /3 = 0.406.
4.5.21.	&0(/) = у(£) = 13.847, ^,=3/7. <У2=4/7, <53=5/7,
54 = 1/7, /, =0.528, /2 =1.704, /3 =1.32.
4.5.22.	£о(О = у(<5) = 29.5, <5, =3/4, <52=1/4, <53=1/4,
34 =1/2, /, =0.303, /2 =1.642, /3 =2.226.
4.5.23.	^0(ґ) = у(5) = 17.7, <5, =0.6, <52=0.4, <53=0.4,
<54 = 0.7 , <5, = 0.1, /, = 1.373, і2 = 1.06, /3 = 1.
462