УДК 539.3
ББК 22.251
Б81
Бондарь В. С. Неупругость. Варианты теории. — М.:
ФИЗМАТЛИТ, 2004. - 144 с. - ISBN 5-9221-0521-3.
Изложены простейшие прикладные варианты теории неупругости, кото-
которые могут быть использованы для исследования закономерностей дефор-
деформирования и разрушения материала при сложном неизотермическом на-
гружении, а также для расчетов кинетики напряженно-деформированного
состояния и прогнозирования ресурса конструкций высоких параметров.
Для специалистов конструкторских и проектных организаций, научно-
исследовательских институтов, а также для аспирантов и студентов, зани-
занимающихся расчетами и исследованиями высоконагруженных конструкций
современной техники.
Рецензенты:
кафедра Теории упругости Механико-математического факультета
МГУ им. М.В. Ломоносова;
доктор физико-математических наук, профессор Ю.И. Кадашевич
Научное издание
БОНДАРЬ Валентин Степанович
НЕУПРУГОСТЬ. ВАРИАНТЫ ТЕОРИИ
Редактор М.Б. Козинцова
Оригинал-макет: В.В. Худяков
ЛР №071930 от 06.07.99. Подписано в печать 15.07.04. Формат 60x90/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 9. Уч.-изд. л. 10. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Московская типография № 6»
115088, Москва, Ж-88, ул. Южнопортовая, 24
9 785922п105217
ISBN 5-9221-0521-3
ISBN 5-9221-0521-3
© ФИЗМАТЛИТ, 2004
© B.C. Бондарь, 2004

ОГЛАВЛЕНИЕ
Введение
1. Упругость
Глава 1. Теория напряжений и деформаций		10
§ 1. Тензор напряжений и его инварианты		10
§2. Девиатор напряжений и его инварианты		11
§ 3. Тензор деформаций и его инварианты		13
§4. Девиатор деформаций и его инварианты		14
Глава 2. Векторное представление напряжений и деформаций . . .	16
§ 1. Вектор напряжений		16
§ 2. Вектор деформаций		17
§ 3. Векторные и скалярные свойства		18
Глава 3. Термоупругость		20
§ 1. Зависимости между напряжениями и деформациями		20
§ 2. Матричное представление зависимостей между напряжениями и
деформациями		21
§ 3. Зависимости между скоростями напряжений и деформаций		25
§ 4. Матричное представление зависимостей между скоростями напря-
напряжений и деформаций		26
2. Пластичность
Глава 1. Теория пластического деформирования		32
§ 1. Основные положения и уравнения теории		32
§ 2. Материальные функции		35
§ 3. Связь теории пластического деформирования с общими теориями
пластичности 		37
§ 4. Матричное представление уравнений теории		39

Оглавление
§ 5. Уравнения теории в случае обобщённого плоского состояния ....	41
§ 6. Уравнения теории в случае одноосного напряжённого состояния . .	44
§ 7. Критерии малоцикловой усталости при одноосном напряжённом
состоянии		44
§ 8. Расчётно-экспериментальный метод определения материальных
функций		47
§ 9. Материальные функции некоторых конструкционных сталей и
сплавов		52
Глава 2. Теория пластического деформирования материалов, чув-
чувствительных к виду напряжённого состояния		54
§ 1. Основные положения и уравнения теории		54
§ 2. Материальные функции и метод их определения		57
§ 3. Матричное представление уравнений теории		60
§4. Уравнения теории в случае обобщённого плоского состояния ....	61
Глава 3. Теория пластического деформирования материалов, об-
обладающих эффектом дополнительного упрочнения		63
§ 1. Основные положения и уравнения теории		63
§ 2. Расчётно-экспериментальный метод определения материальных
функций		67
§ 3. Матричное представление уравнений теории		70
Глава 4. Теории пластического деформирования в условиях
неизотермического нагружения и ионизирующего излучения . .	72
§ 1. Уравнения вариантов теорий		72
§ 2. Материальные функции и метод их определения		75
§ 3. Материальные функции некоторых конструкционных сталей и
сплавов		11
§ 4. Матричное представление уравнений вариантов теорий		79
§ 5. Уравнения теорий в случае обобщённого плоского состояния ....	83
3. Неупругость
Глава 1. Теория неупругого деформирования		88
§ 1. Основные положения и уравнения		88
§ 2. Материальные функции		92
§ 3. Связь теории неупругого деформирования с общими теориями ...	94
§ 4. Матричное представление уравнений теории		97
§ 5. Уравнения теории в случае обобщённого плоского состояния ....	99
§ 6. Уравнения теории в случае одноосного напряжённого состояния . .	101

Оглавление
§ 7. Критерии длительной прочности при одноосном напряжённом со-
состоянии 		102
§ 8. Расчётно-экспериментальный метод определения материальных
функций		109
Глава 2. Теория неупругого деформирования материалов, чув-
чувствительных к виду напряжённого состояния		118
§ 1. Основные положения и уравнения		118
§ 2. Материальные функции и метод их определения		122
Глава 3. Теории неупругого деформирования в условиях неизо-
неизотермического нагружения и ионизирующего излучения		124
§ 1. Уравнения вариантов теорий		124
§ 2. Материальные функции и метод их определения		127
§ 3. Материальные функции некоторых конструкционных сталей и
сплавов		129
§4. Матричное представление уравнений вариантов теорий		130
§ 5. Уравнения теории неупругого деформирования в случае обобщён-
обобщённого плоского состояния		133
Список литературы		142

Выдающимся механикам современности
Алексею Антоновичу Ильюшину и
Валентину Валентиновичу Новожилову
посвящается
Введение
Проблемы надёжного функционирования и снижения материалоём-
материалоёмкости конструкций современной техники, работающих в условиях вы-
высокого уровня силовых и температурных нагрузок, а также ионизиру-
ионизирующего излучения, делают весьма актуальной задачу математического
моделирования неупругого поведения и разрушения конструкций. Уве-
Увеличение рабочих параметров современных машин и аппаратов приводит
к возрастанию как общей, так и местной напряжённости конструкций.
Реальные процессы нагружения таких конструкций приводят к тому,
что в материале конструкций возникают неупругие (вязкопластиче-
ские) деформации. При этом нагружение является сложным неизотер-
неизотермическим, и характер его изменения может быть самым произвольным
в условиях повторности и длительности воздействия температурно-
силовых нагрузок и ионизирующего излучения.
Используемые в настоящее время для практических расчётов тео-
теории пластичности, ползучести и неупругости, обобщённые на неизо-
неизотермическое нагружение, могут привести к достоверным результатам
только в узко ограниченных условиях — при нагружениях близких
к простым и стационарным. Раздельное рассмотрение процессов пла-
пластичности, ползучести и накопления повреждений без учёта их взаим-
взаимного влияния свойственно практически всем применяемым в расчётах
теориям. Практически не рассматриваются такие важные аспекты, вли-
влияющие на накопление повреждений, как охрупчивание и залечивание.
Всё это существенно ограничивает области применимости использу-
используемых в расчётах теорий пластичности, ползучести и кинетических
уравнений накопления повреждений (критериев разрушения).
В настоящее время разработана теория неупругости [1-3], которая
является обобщением и развитием идей, содержащихся в различных
вариантах теорий пластичности, ползучести и неупругости, базиру-
базирующихся на концепции микронапряжений, выдвинутой В. В. Новожи-
Новожиловым и его школой [4-6]. Теория неупругости относится к классу
одноповерхностных теорий течения при комбинированном упрочнении.
Обоснование достоверности разработанной теории неупругости про-
проведено [7-10, 3] на широком спектре конструкционных материалов
(сталей и сплавов) и разнообразных программ эекспериментальных
исследований. Сравнения расчётов по различным теориям пластично-
пластичности, ползучести и неупругости показали, что результаты, полученные

Введение
с помощью разработанной теории неупругости, лучше всего соответ-
соответствуют экспериментальным данным. На основании этих исследований
сделан вывод, что разработанная теория неупругости может приме-
применяться для практических расчётов неупругого поведения и накопле-
накопления повреждений материала конструкций при произвольном процессе
сложного неизотермического нагружения и на основании этой теории
может проводиться достоверное прогнозирование ресурса материала
конструкций высоких параметров при повторном и длительном воздей-
воздействии температурно-силовых нагрузок и ионизирующего излучения.
Область применимости теории неупругости ограничивается малы-
малыми деформациями однородных и начально изотропных металлов при
температурах, когда нет фазовых превращений, и при скоростях дефор-
деформаций, когда динамическими эффектами можно пренебречь.
Следует отметить некоторые особенности разработанной теории
неупругости:
—	деформация имеет упругую и неупругую составляющие (услов-
(условного разделения неупругой деформации на деформации пластичности
и ползучести нет);
—	поверхность нагружения может смещаться, расширяться или
сужаться и изменять форму;
—	трёхчленная структура уравнений для смещения поверхности на-
нагружения обуславливает снятие ограничений на траектории сложного
нагружения;
—	кинетические уравнения накопления повреждений построены на
энергетическом принципе с учётом процессов охрупчивания и залечи-
залечивания;
—	уравнения неупругого поведения и накопления повреждений вза-
взаимосвязаны, т. е. повреждение влияет на поведение, а история нагру-
нагружения на процесс повреждения;
—	неупругое поведение и разрушение может зависеть от вида на-
напряжённого состояния;
—	при сложном (непропорциональном) циклическом нагружении
возможно дополнительное изотропное упрочнение;
—	аналитическое интегрирование уравнений теории неупругости
для простейших стационарных режимов нагружения приводит к из-
известным критериям малоцикловой и длительной прочности;
—	основу расчётно-экспериментального метода определения мате-
материальных функций теории неупругости составляет обработка экспери-
экспериментальных кривых, не связанная с определением пределов текучести
и других величин с какими-либо допусками;
—	базовыми экспериментами, на которых построен расчётно-экс-
периментальный метод, являются стандартные испытания материала
на малоцикловую и длительную прочность, а также деформирование
в условиях пластичности и ползучести.
В настоящей книге излагаются простейшие прикладные варианты
теории неупругости, которые могут быть использованы для иссле-

Введение
дования закономерностей деформирования и разрушения материала
при сложном неизотермическом нагружении, а также для расчётов
кинетики напряжённо-деформированного состояния и прогнозирования
ресурса конструкций высоких параметров.
Автор выражает благодарность профессорам Р. А. Васину,
Ю.И. Кадашевичу и И. А. Кийко за ценные советы и замечания
в процессе работы над монографией, инженерам Е.В. Карначевой
и И. А. Титареву за помощь в подготовке рукописи к печати, а также
В. А. Берстневу, А. П. Титареву и В. И. Яковенко за материальную
поддержку при издании монографии.
Автор будет благодарен всем приславшим свои пожелания и за-
замечания по адресу: 107 023 Москва, ул. Б. Семеновская, 38, МГТУ
«МАМИ», кафедра теоретической механики.
E-mail: tm@mami.ru

Часть 1
УПРУГОСТЬ

Глава 1
ТЕОРИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
§ 1. Тензор напряжений и его инварианты
Напряжённое состояние в точке тела определяется [11, 12] тензо-
тензором напряжений
= < 021 ^22 ^23 > =<7ij (i,j= 1,2,3).
A.1)
Согласно закону парности касательных напряжений
а- = cfji (i,j = 1, 2, 3; г ф j).
A.2)
Для изображения напряжённого состояния в точке тела в окрестности
этой точки выделяется элемент тела в виде прямоугольного паралле-
параллелепипеда, три ребра которого совпа-
совпадают с осями координат (рис. 1.1).
Таким образом, напряжённого
состояние в точке тела определяет-
определяется симметричным тензором второго
ранга.
Тензор напряжений имеет следу-
следующие инварианты:
-	1\(Та)=ап,	A.3)
2
к{Т„) = \сгз<Уц-\{<Укк?\ A.4)
Рис. 1.1. Модель напряжённого со-
состояния
g (crkkf. A.5)
Здесь и в дальнейшем наличие в одночлене повторяющихся индексов
указывает на суммирование по всем значениям этих индексов.

Глава 1. Теория напряжений и деформаций	11
На основе формул A.3)-A.5) можно получить следующие выраже-
выражения для инвариантов тензора напряжений:
1\(Та) = аи +о~22 + ^33,	A.6)
h(Ta) = -СГЦСГ22 -^22^33 -О-33О-П +О~\2 + Сг|3 +^31'	О-7)
|3
= СГЦСГ22СГ3З — ^11^23 "~ ^22^31 "~ ^33^12 + 2СГ12СГ2301-	A.8)
В качестве примера рассматриваются три различных случая нагру-
жения тонкостенного трубчатого образца: осевой силой (Р-опыты);
крутящим моментом (М-опыты); осевой силой, крутящим моментом
и внутренним давлением (Р, М, q -опыты). В первых двух случаях
реализуются одноосные растяжение (сжатие) и кручение, а в третьем
случае — обобщённое плоское состояние. Для всех трёх случаев тензор
напряжений и его инварианты имеют следующий вид (ось 1 направлена
вдоль оси образца):
1) одноосное растяжение (сжатие)
3 0 1
A.9)
= 0;	A.10)
A.11)
Ii(T<r)=0, I2(Ta) = a2l2, h(T<r)=0;	A.12)
3) обобщённое плоское состояние
{(Л	v
О~\\ Gi2 U	1
*21 ^22 0	\,	A.13)
0 0 <ТЗЗ
2) кручение
Т —
( О\\
о
1 о
h{Ta
{ °
1
о'
0
0
0
) =
О~\2
0
0
0
0
0
о,
0
0
0
= аи +о~22 + ^зз,
= -СГЦСГ22 -^22^33 -^33^11 + СГ?2>	A-14)
= СГЦСГ22СГ3З —
§ 2. Девиатор напряжений и его инварианты
Тензор напряжений разлагается [11, 12] на шаровой тензор и деви-
девиатор
а0 О О Л ( 5ц 5i2 5i3 )
> + < 521 522 523 > = <7Ouj + Stf-	A-15)
[531 532 533 J

12
Часть 1. Упругость
Здесь 5ij — символ Кронекера Eij = 1 при г = j; 5ij = 0 при г ф j);
сг0 = ац/3 — среднее напряжение; Sij — девиатор напряжений. Таким
образом, компоненты девиатора напряжений определяются по формуле
Девиатор напряжений Da имеет следующие инварианты:
h(D(T)=l-sljslj,
h{Da)=l-Sljsjkskl.
A.16)
A.17)
A.18)
A.19)
Или, раскрывая формулы A.18) и A.19), можно получить следующие
выражения для второго и третьего инвариантов девиатора напряжений:
1/9, 9 , 9 \ , 9 , 9 , 9	/1 oq\
A.21)
" S23
В теории напряжений вводится важное понятие интенсивности напря-
напряжений, характеризующей уровень напряжённого состояния,
2-	A-22)
Рассматривается также параметр, характеризующий вид напряжённого
состояния,
При одноосных сжатии, кручении и растяжении параметр вида напря-
напряжённого состояния, соответственно, равен: — 1, 0 и +1.
Рассматривая также три случая нагружения тонкостенного трубча-
трубчатого образца, можно получить:
1) одноосное растяжение (сжатие)
A.24)
A.25)
A.26)
A.27)
2) кручение
L
Z
0
0
= |<7ц
Ч
-
1>
' 0
0
0
1
0
1Л = +1
а 12 0
0 0
0 0
0
0
1
Г11 J
(-1);
О"?/ =
= 0;

Глава 1. Теория напряжений и деформаций
13
3) обобщённое плоское
' 2Gi 1 СГ22 + СЗЗ
3
G21
П
/9 9
М- 1 Г-3 '
(о
-.K L
3
her2 -
7 1 G
состояние
2G22 01 Н~ С
3 3
0
з 9
CS|
-о
-о
о
^ 0
2G33 СП
3
1 + СГ22
3 J
33^11
>, A
A
2 Ч1
A
.28)
.29)
.30)
§ 3. Тензор деформаций и его инварианты
Деформированное состояние в точке тела определяется [11, 12]
тензором деформаций
!?ц ?12 ?13 1
?21 ?22 ?23 \ =€ijt (i,j= 1,2,3).
?31 ?32 ?33 J
Тензор деформаций является [1,2] симметричным тензором,
с-- — с--	(о о — 1 9 Я- о -/- о\
bi<i — & 11	V^'J — 1 > ^> '-'j / J) '
Тензор деформаций имеет следующие инварианты:
/i(T?)=^,
1
1
1
1
A.31)
A.32)
A.33)
A.34)
A.35)
На основе формул A.33)—A.35) можно получить следующие выраже-
выражения для инвариантов тензора деформаций:
1\{Те) =ги
2 +?33»	A.36)
^2(^е) = —?ц?22 — ?22?зз — ?зз?п + ?12 + ?23 + ?31'	A-37)
l^yl?j = ?ц?22?зз — ?ц?23 — ?22?з1 — ?33?i2 ~l~ ^?i2?23?3i* (l.oo)
Рассматривая также три случая нагружения тонкостенного трубчатого
образца, можно получить:
1) одноосное растяжение (сжатие)
(?П 0 0 ^1
Т? = \ 0 ?22 0 \ (?3з =?22),	A.39)
0 0 ?зз

14	Часть 1. Упругость
A-40)
/3(Т?) = ?ц ?22^33 J
2) кручение
Г 0 е12 О 1
Ь	A.41)
?) = е\2, /3(Г?)=0;	A.42)
3) обобщённое плоское состояние
(?\\ ?\2 0 ^
T? = <U21 ?22 0 ,	A.43)
I 0 0 ?3з J
7l(Te) =?ц +?22+ ^33,
^12»	A.44)
§ 4. Девиатор деформаций и его инварианты
Тензор деформаций разлагается [11, 12] на шаровой тензор и деви-
девиатор
(г0 О О Л (еи ei2 ei3 1
Т? = <^ 0 е0 О I + <^ е21 е22 е23 ^ = ?0% + е^-.	A.45)
[О 0 е0 ) [е31 е32 е33 J
Здесь ?о = ?ц/3 — средняя деформация; ец — девиатор деформаций.
Таким образом компоненты девиатора деформаций определяются по
формуле
eij =?ij -?o$ij-	A-46)
Девиатор деформаций D? имеет следующие инварианты:
Ix{D?) = eu = 0,	A.47)
I2(Ds) = ±eijeij,	A.48)
k(Ds)=l-eijejkekl.	A.49)
Или, раскрывая формулы A.48) и A.49), можно получить выражения
для второго и третьего инвариантов девиатора деформаций:
h{De) = i (e?, + 4z + 4) + е?2 + 4 + eL	A-50)
= е11е22езз -епе|3 - егге^ - e33ef2+2е12е2зез1. A.51)

Глава 1. Теория напряжений и деформаций
15
В теории деформаций вводится важное понятие интенсивности дефор-
деформаций, характеризующей уровень деформированного состояния,
|1/! " ^.	A.52,
Рассматривая также три случая нагружения тонкостенного трубчатого
образца, можно получить:
1) одноосное растяжение (сжатие)
О
1
0 --
0
= <
2еи
0
'lieu
1
4е» J
-?22)
0
0
=
1 ,
0
?ц -
0
?22
о
о
— ?22)
= |ец| = з
2) кручение
3) обобщённое плоское состояние
2еи ?22 + ?зз
О
О
2?зз
3
= о (?11 + ?22
A.53)
A.54)
A.55)
A.56)
A.57)
A-58)

Глава 2
ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ НАПРЯЖЕНИЙ
И ДЕФОРМАЦИЙ
§ 1. Вектор напряжений
Для более наглядного представления и изучения процессов нагру-
жения рассматриваются вектора напряжений и деформаций, соответ-
соответствующие векторному представлению Ильюшина. Компоненты вектора
напряжений 5 связаны с компонентами тензора напряжений формула-
формулами [13, 14]
Si
S =
So
is5j
у/2
8i2
A-59)
Модуль вектора напряжений равен
1/2
5=151 =
.«)¦" = ,/|»..
A.60)
Вектор скоростей напряжений, а также длина дуги траектории напря-
напряжений, определяются выражениями:
^ г	it	f ^	г	/9
СУ	СУ СУ СУ СУ СУ	S~^	СУ Л 4-	I ( ' ' \ *¦ / ^ Л 4-	/1 С. 1 \
о = О1 О2 *Ьз О4 О5 , Ь = \ \о \ at = \ [SijSij) at.	11 .о 1)
L	J	J	J
Здесь и в дальнейшем E) = — E), t — время.
Для указанных ранее трёх случаев нагружения тонкостенного труб-
трубчатого образца компоненты вектора напряжений будут иметь следую-
следующий вид:
1) одноосное растяжение (сжатие)
S =
0 0 0 0
2) кручение
#=[0 0 л/2^12 0 0 Г;
A.62)
A.63)

Глава 2. Векторное представление напряжений и деформаций
3) обобщённое плоское состояние
17
S =
- 2 (a22 +
V2 0-12
О
О
A.64)
§ 2. Вектор деформаций
Компоненты вектора деформаций Э связаны с компонентами тензо-
тензора деформаций формулами [13, 14]
Э =
Эх
Э2
л/3/2ец
У2(е22+е„/2)
\/2ei2
A.65)
Модуль вектора деформаций равен
5
3 — |5| —
Э{
A.66)
Вектор скоростей деформаций, а также длина дуги траектории дефор-
деформаций, определяются выражениями
	ПТ
Э = 13, Э2 Э3 Э4 Э51 , s=| |3| dt = I (ёуёу)
I/2
A.67)
Для трёх случаев нагружения тонкостенного трубчатого образца ком-
компоненты вектора деформаций будут иметь следующий вид:
1) одноосное растяжение (сжатие)
2) кручение
Э= | А/|(?11-?22) О О О О | ;
Э= [0 0 а/2 ?12 0 0]Т;
A.68)
A.69)

18
Часть 1. Упругость
3) обобщённое плоское состояние
э =
A.70)
§ 3. Векторные и скалярные свойства
Векторные и скалярные свойства материалов являются [14, 15]
основными характеристиками, изучаемыми при экспериментально-тео-
экспериментально-теоретических исследованиях деформирования материалов как при про-
простом, так и при сложном нагружениях. В качестве векторных свойств
изучается ориентация вектора напряжений по отношению к траектории
деформаций. В качестве характеристик ориентации рассматриваются
отклонения вектора напряжений от касательной к траектории дефор-
деформаций и выход вектора напряжений из соприкасающейся плоскости
траектории деформаций (рис. 1.2). Рассматривается также выход век-
вектора скоростей напряжений (приращений напряжений) из плоскости
образованной векторами напряжений и скоростей деформаций (прира-
(приращений деформаций) (рис. 1.3).
Соприкасающаяся
плоскость
Траектория
деформаций
Pi d3
Рис. 1.2. Ориентация вектора напряжений
Характеристики ориентации определяются углами: сближения
компланарности 7 и соприкасания ф:
ft = arccos (a • р\),
7Г
7 = -^ - arccos
2
\Э X
L
sin ft
A.71)
A.72)

Глава 2. Векторное представление напряжений и деформаций	19
Траектория
деформаций
Рис. 1.3. Ориентация вектора приращений напряжений
ф = -? ~ arccos (a • [pi x р2])
A.73)
S_
S'
dS
ds'
Здесь а — единичный вектор напряжений; р\, р2, q\ — компоненты
реперов Френе траекторий деформаций и напряжений соответственно;
Xi — кривизна траектории деформаций. В качестве скалярных свойств
изучается изменение модуля вектора напряжений по траектории дефор-
деформаций и отличие этих значений от значений при простом нагружении
(от единой кривой деформирования [12]).
Характеристики ориентации A.71)—A.73) можно определить также
следующим образом:	_
S • Э
A^4)
V = arccos ¦ _ __ ,
\S\ \Щ
тг	S-\S хЭ]
7 = тг — arccos ^ _—=-,
2	|S||[Sx3)|
, тг	5-[3xl]
^ = - — arccos L^.—тг-.
2	|^||[ЗхЗ]|
A.75)
A.76)

Глава 3
ТЕРМОУПРУГОСТЬ
§ 1. Зависимости между напряжениями
и деформациями
В теории неупругости принимается, что тензор деформации пред-
представляется в виде суммы тензоров упругой деформации, не зависящей
от истории нагружения, и неупругой деформации, зависящей от про-
процесса нагружения,
е^ = 4 + 4-	A77)
В данной главе неупругая деформация пока рассматриваться не будет.
Упругие деформации [16, 17] при изменении напряжений следу-
следуют обобщённому закону Гука, при изменении температуры — закону
температурного расширения, а при изменении флюенса (интегрального
потока ионизирующего излучения) — закону распухания:
Sij=2Geeijf	A.78)
ао = К(еео-ет -еф),	A.79)
11	771	771
— _	е — _ е С —	К —
Здесь G, К, Е, v — соответственно, модули сдвига, объёмного сжатия,
Юнга и коэффициент Пуассона, являющиеся функциями температу-
температуры Т и флюенса Ф. Температурная деформация и деформация радиа-
радиационного распухания гт и гф определяются следующим образом:
\aTfdt (Т<->Ф),	A.80)
где ат и а<$> коэффициенты температурного расширения и радиаци-
радиационного распухания, являющиеся также функциями температруры Т
и флюенса Ф.
Из уравнений A.78) и A.79) можно получить два вида связи
между напряжениями и деформациями. В первом случае выражения
для деформаций через напряжения (случай так называемого мягкого
напряжения) имеют вид
ет =
A.81)

Глава 3. Термоупругость
21
Во втором случае выражения для напряжений через деформации (слу-
(случай так называемого жёсткого нагружения) имеют вид
ij = 2Geetj + (К -
Е р
% - К (еТ + гф) % =
Е
г- Е /
§ 2. Матричное представление зависимостей между
напряжениями и деформациями
В расчётных методах уравнения связи между напряжениями и де-
деформациями удобнее представлять в матричном виде
Здесь
[Щ] =
J E
[aj]
[
[
" l
—v
—v
0
0
0
E
A
r(i-
i
i
С
с
с
i
)
)
)
(\pT~
\ Vе j .
—v
1
—v
0
0
0
\/
V
(i-
z/
0
0
0
^22
11 ^
—v
—v
1
0
0
0
A
г
CSI
e
e
И \
' J /
33
T
Ф
«n
0
0
0
2A +
V
V
. —
0
0
0
0
0
2e
]
T
ф
+
1
1
12 '
СГ12
0
0
[*f]
2A
0
0
0
-2v
2
0
0
^23
0
0
0
0
0
0
+
0
o]
o]
?г]
у)
0
0
0
0
с
о
0
24i]T
73.]т,
т
т
_|_ [?^
0
0
0
0
0
2A4
Ъ
1
]).
-г/)
0
0
0
0
0
-2v
A.83)
A.84)
A.85)
A.86)
A.87)
A.88)
A.89)
A.90)
A.91)
A.92)

22	Часть 1. Упругость
Выражения A.83) и A.84) представляют, соответственно, случаи мяг-
мягкого и жёсткого нагружений. Но представляют интерес и случаи
смешанного нагружения, когда часть напряжений и часть деформа-
деформаций выражаются через остальные напряжения и деформации. Далее
рассматривается алгоритм получения таких уравнений. Пусть задано
уравнение
[yi] = [Cij][xj] + [bi]t	A.93)
и необходимо поменять местами у^ и хь, т.е. провести смену fc-ro
неизвестного. В этом случае компоненты матрицы [Cij] и вектора \bj\
преобразуются по следующему алгоритму:
-й Ч- A95>
В формулах A.94) и A.95) повторяющийся в одночленах индекс к не
означает суммирование. Верхний индекс (к) относится к преобразо-
преобразованным матрице [Cij]^ и вектору [bi]^ и указывает на номер неиз-
неизвестного, который подлежит смене. Последовательно применяя этот
алгоритм преобразования, можно получить уравнения связи между
произвольным набором задаваемых и определяемых величин.
В качестве примера рассматриваются, как и ранее, три случая
нагружения тонкостенного трубчатого образца:
1) одноосное растяжение (сжатие)
а)	мягкое нагружение
[xj] = [<tj] = [ап О О О О	О ]т, A.96)
[yi] = [el] = [геп е\2 ге33 0	0 0]т, A.97)
Ы = [Cij][xj] + [tf]	A.98)
или
Е	Е	' A.99)
е	v	. Т . Ф
б)	смешанное нагружение
[xj] = [en 0 0 0 0 0]т,	A.100)
[у i] = [an е\2 ^зз ^ ^ ^]Т'	A.101)
] + Ш{Х\	A.102)

Глава 3. Термоупругость
23
Е
—	V
—	V
О
О
О
Е
1/A+1/)
Е
О
О
О
E
0
0
0
0
0
0
2(l+i/)
0
0
0
0
0
0
2A + 1/)
0
0 0 0]T
о
о
о
о
о
2A + 1/)
или
аи=Е(е\1-еТ-еф),
2) кручение
а) мягкое нагружение
N = N = [0 0 0 ап О О]Т,
М = [??] = [О 0 0 2г^2 0 0]т,
Ы = [ctj] Ы + Щ]
ИЛИ
б) жёсткое нагружение
[Xj] = [e$ = [0 0 0 2г^2 О О]Т,
[уг] = [аг] = [0 0 0 G12 О О]Т,
или
Е
3) обобщённое плоское состояние
а) мягкое нагружение
Е
A.103)
A.104)
A.105)
A.106)
A.107)
A.108)
A.109)
A.110)
A.111)
A.112)
A.113)
CT12
2ei2
be]
0
0
o]T,
o]T,
A
A
A
.114)
.115)
.116)
ИЛИ

24	Часть 1. Упругость
42 = 4 [^22 - */(<7ц +а33)] +^Т +?Ф,	A.117)
2
hi
^12 =
б) смешанное нагружение
О 0]т,	A.118)
О 0]т,	A.119)
(Ы20)
?22
Матрица [^j]^3^ и вектор [dl]^ получаются из матрицы
:
вектора [df\ при смене третьего неизвестного, т.е. <тзз на ?33
0	0	0
1
1
Е
^2
Ev
— v
V
1
1
Ev
— v
E
2
— V
V
1 — v
Т^Т	0	0	0
\-v \-v	E(\-v)
0	0	0	^Д-
000
0 0	0
2(l+i/) J
A.121)
0 0 ol	A.122)
или
- eT - еф) + v (e|2 - eT - ефI + —^— a33;
AЛ23)
Е
в) смешанное нагружение
[&>] =
[rff],	A.124)

Глава 3. Термоупругость
25
<г\2 О О]Т,
A.125)
A-126)
^ ^]
^ ]
Матрица [JJ^ ;\^J и вектор [йгк ;\K^J получаются из матриц
и вектора [с^-]^ при смене второго неизвестного, т.е. <т22 на г^'-
v	О	О	О
V
— V
Е
—у	^~
0 О
О
о
1-^2 1/A + 1/) 0
о
о
Е
О
О
О
о
Е
2A + 1/)
О
О
О
О
О
Е
2A + 1/)
О
О
о
о
о
К
-eC)iB) _
\-Е
(l+i/) 0 0 0]т
2A+1/)
A.127)
A.128)
или
= Я (ef! - ?т - еф) + z/(cr22 + сг33),
22 = —V [?ц — s — г ) +
l-i/
е	/ е	Т	Ф\ ^A + v)
1—1/
сг33
f^, A.129)
§ 3. Зависимости между скоростями напряжений
и деформаций
Дифференцируя уравнения A.78) и A.79) по времени t, можно
получить следующие уравнения связи между скоростями напряжений
и деформаций:
stj =
stj =
AЛ30)
К
К
= Кгеп-К(атТ
1 дК
а1 =ат-^^а0Т (Т ~ Ф),
A.132)
A.133)

26	Часть 1. Упругость
1 dG^. 1 dG Л	sij , тф, фЛ n 1олЛ
^г—— 1 -\	о-^т- Ф Sij = —J- + <xwi + <х„Ф, A.1о4)
^ ЭТ 2G ^Ф J J 2G tJ	tJ
ie-—a -(— — T+— — Ф^1 сг +а Т + а Ф-
• | Тf~n i Фяч /1 i ос\
^— Go+Q^ i -j- (У, Ф. A. loOj
Из уравнений A.134), A.135) можно получить связь между скоро-
скоростями напряжений и деформаций для случая мягкого нагружения:
а?/Ф, A.136)
1	$i?
E	и!
-^(SaoSij-dij)^; (Т<->Ф). A.137)
Из уравнений A.130), A.132) следует связь между скоростями
напряжений и деформаций для случая жёсткого нагружения:
SnOa — К [а дц + —— а^- i —
U гз	\	Ч ту 13 /
г, ( ф? , 2G ф\ i	S .е ,
-К«/Т + </Ф), A.138)
^] i (т ^ ф)'
A.139)
§ 4. Матричное представление зависимостей между
скоростями напряжений и деформаций
Уравнения A.136), A.138) связи между скоростями напряжений и
деформаций в матричном представлении имеют вид
К] = [^][^]+И],	A.140)
[а1] = Щ]\е^ + Щ.	A.141)
Здесь	т
Где] 	 г-е -е -е 9<^е 9<^е 9<^е I1	(
[?i\ - [?U е22 ?33 Ze\2 1е2Ъ 1еЪ\\ '	\

Глава 3. Термоупругость
27
[0~i\ = [аи
*33
= [af]f
2af
fJ
(Т23 Ы,	A-143)
Ф]Ф,	A.144)
2a3f]T (Т~Ф), A.145)
[<*?] = -J
A - i/)(afft + aff Ф) + i/(afJT + af*Ф + af T + а|3фФ)
A - 1/)(а^Г + ag Ф) + i/(aff t + aff Ф + afjT + aff Ф)
A - v){agt + aff Ф) + i/(aff t + aff Ф + agf + а||Ф)
aff T + aff Ф
afjt
Ча|*Ф
3vE
-2./)
a
0
0
0
A.146)
а?
- и?Т
= Hi
Т сгТ сгТ сгТ (тТ~\Т (гтл яч\	/1 1 лг7\
r> Q33 С^12 ^23 ^31 J \^ ^^ ^/ • V^-^'/
Матрицы [Cfj] и [D^.] имеют такой же вид A.91) и A.92) как и для
связей A.83) и A.84) между напряжениями и деформациями.
Далее рассматриваются, как и ранее, три случая нагружения тон-
тонкостенного трубчатого образца:
1) одноосное растяжение (сжатие)
а) мягкое нагружение
= ?1 = ?Т
?22
о о о о о]т,
з 0 0 0]т,
:ы = [сы N
или
ffT
^11 — ^—г- аи 1
-^33
Е
б) смешанное нагружение
[xj] = [ёеи 0 0 0 0 0]т,
A.148)
A.149)
A.150)
A.151)
A.152)

28
Часть 1. Упругость
О 0 0]т,
Матрица [Cfj]O равна A.103), а вектор
основе преобразования A.95) и равен
A.153)
A.154)
определяется на
-?«Т + <Ф)
agf + ag Ф + i/(aff T + aff Ф)
или
42 = -ч1 - affT - aff Ф) + "ft + a|f Ф,
ё|з = -Кё?, - aff Г - aff Ф) + af Г + off Ф;
2) кручение
а) мягкое нагружение
о о G,2 о о]т,
о о 2^2 о о]т,
Ш =
или
Е
6) жёсткое нагружение
[xj] = Щ] =[000 2ё\2 0 0]т,
[Уг] = [&{] = [0 0 0 ai2 0 0]т,
ИЛИ
^12 =
f 2
Е
1 + v
3) обобщённое плоское состояние
а) мягкое нагружение
^22
+
A.155)
A.156)
A.157)
A.158)
A.159)
A.160)
A.161)
A.162)
A.163)
A.164)
A.165)
A.166)
A.167)

Глава 3. Термоупругость
29
или
[^
T + aff Ф,
^22 = -Б [^22 - К^П + ^33)] + «22^ + alf *»
[
33 = ^ [«3 -v{0\\+ 0-22)] + aff Г +
A.168)
б) смешанное нагружение
2ё\2 О О]Т,
*12 0 0]\
A.169)
A.170)
Матрица [Df-]^ определяется по формуле A.121), а вектор
[df\ — с помощью преобразования A.95) из вектора [df] A.146)
и матрицы [D\A A.91) и равен
или
d? -
т
1 — v
E(\-v)
d%
Е
а
2^11
:ff t + aff Ф
1 -v
\-v
Е
(aff f + aff Ф + aifT + а|*Ф) + a
+ i/(affT + aff^)]
22
Я
, A.172)
-^Ф + ^D2-а12тТ-а2?2фФ)]

30
Часть 1. Упругость
G22 =
Е
2
— 0L\\ 1 —
12ФФ)] +
¦ ^ЗЗ*
A.173)
в) смешанное нагружение
[xj] = [^11 ^2 о-зз 2^2 О	0]т,	A-174)
[^] = [6-ц ё|2 ё|3 ^12 °	°]Т'	A.175)
[^j = [?) > yj^z^ [xjJ + [a^v ;J .	A.176)
Матрица [D^ ^]^ определяется выражением A.127), а вектор
[d^ ^] получается на основе преобразования A.95) из матрицы
[Dlj]^ A.121) и вектора [df\ A.172) при смене второго неизвестно-
неизвестного <722 на if,9.
rAeC)iB)
Тогда вектор [^ ] будет равен
agf +
^33 J
/(aff Т + aff Ф)
Е
A.177)
или
V (СГ22
Е
¦ СГ22 —
Е
Е
A.178)

Часть 2
ПЛАСТИЧНОСТЬ

Глава 1
ТЕОРИЯ ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ
§ 1. Основные положения и уравнения теории
Материал однороден и начально изотропен. В процессе упругопла-
стического деформирования в нём может возникать только деформа-
деформационная анизотропия. Тензор скоростей деформаций представляется
в виде суммы тензоров скоростей упругой и пластической деформаций:
Упругие деформации при изменении напряжений следует обобщённому
закону Гука:
ёЬ = ё ^&ij ~ v C&o5ij ~ &i^'	B-2)
где Е, v — соответственно, модуль Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и упругопластического состояний. Поверхность нагружения изотропно
расширяется или сужается и смещается в процессе нагружения. Урав-
Уравнение поверхности нагружения принимается в следующем виде:
/К) = \ {Sij - atj)(stj - atj) - [Ср (?L)]2 = 0.	B.3)
Здесь s*j = s^ — dij — девиатор активных [4] напряжений; s^ —
девиатор напряжений; би* — длина дуги пластической деформации
(накопленная пластическая деформация, параметр Одквиста). Тензор
смещения (добавочных напряжений, остаточных микронапряжений [4])
ац характеризует смещение поверхности нагружения в девиаторном
пространстве напряжений и является функционалом процесса нагруже-
нагружения. Функция Ср (ви*) характеризует изотропное упрочнение, и в слу-
случае возрастания этой функции материал является циклически упроч-
упрочняющимся, убывания — циклически разупрочняющимся, а в случае
постоянного значения этой функции — циклически стабильным.
Смещение поверхности нагружения определяется уравнением

Глава 1. Теория пластического деформирования	33
(-ёр-ёр
Здесь ёи* — интенсивность скоростей пластической деформации (ско-
(скорость накопленной пластической деформации); g, g? ga — функции,
подлежащие экспериментальному определению. Уравнение B.4) описы-
описывает процессы образования и снятия добавочных напряжений при пла-
пластическом деформировании. Уравнение B.4) в данном виде впервые бы-
было рассмотрено в работе [18]. Трёхчленная структура уравнения B.4)
следует также из тензорно-линейного уравнения [19]. Предлагаемое
уравнение B.4) конкретизирует и существенно расширяет возможности
идей, изложенных в [19].
Пластические деформации зависят от истории нагружения и явля-
являются функционалами процесса. Считается, что поле скоростей пласти-
пластической деформации в пространстве напряжений имеет потенциал. То-
Тогда, принимая в качестве потенциала функцию B.3), тензор скоростей
пластической деформации будет определяться уравнением (ассоцииро-
(ассоциированный с B.3) закон течения, градиентальный закон течения)
аР _ д/ ; _ 3 Sij р	_ -v
М2
Здесь <т* — интенсивность активных напряжений.
Для получения уравнения для скорости накопленной пластической
деформации необходимо продифференцировать по времени интенсив-
интенсивность активных напряжений а^ и функцию Ср(е^) и приравнять эти
выражения, т.к. из B.3) следует, что
< = СР (eg,) ¦	B-6)
Итак
da*u _ 3 Sjj (sjj - ciij) _ 3 SjjSjj _ Sjj^j _
dt ~ 2	at	~ 2 at g a*u
— I rr Sii?i3 i rr ^ Sijaij \ -p _ 3 SijCJij _ 3 SjjSjj p _
\ёе а1 ^ёа2 а* j и* 2 a*	^2(^J «*
_ .p	,~
~ Qeu*'	l
dt ~ ds*
Приравнивая выражения B.7) и B.8) и разрешая относительно ёи*,
можно получить уравнение связи скорости накопленной пластической
2 В. С. Бондарь

34	Часть 2. Пластичность
деформации и скоростей напряжений
АР	_	1	3 Sjj&jj
-С/* Z CTU
Для получения уравнения связи скорости накопленной пластической
деформации и скоростей деформаций в уравнение B.9) подставляется
выражение, следующее из закона Гука и ассоциированного закона
течения B.5):
е--j
\	u J
B.10)
Следует отметить, что
Подставляя B.10) в B.9) с учётом B.11) и разрешая относительно г^,
можно получить уравнение связи скорости накопленной пластической
деформации и скоростей деформаций
ар _
Уравнение B.9) соответствует мягкому нагружению, а уравнение
B.12) — жёсткому нагружению.
Условия упругого и упругопластического состояний следуют из
того, что для упругопластического состояния необходимо, чтобы изоб-
изображающая точка процесса находилась на поверхности нагружения,
и определяемая скорость накопленной пластической деформации была
положительна, а упругое состояние следует при нарушении любого из
двух упомянутых выше условий. Тогда условия упругого и упругопла-
упругопластического состояний будут иметь вид
< < Ср (е?*) U ё?# < 0 - упругость,
аи = Ср (г^) П г^ > 0— упругопластичность.
Здесь под ?и* подразумевается выражение, задаваемое уравнени-
уравнением B.9) или B.12) или любым другим уравнением, связывающим ско-
скорость накопленной пластической деформации и любой набор скоростей
напряжений и деформаций (смешанное нагружение).
Для описания процесса накопления повреждений используется
энергетический подход. В качестве энергии, расходуемой на создание
повреждений в материале, принимается энергия, равная работе доба-
добавочных напряжений (остаточных микронапряжений) на поле пласти-

Глава 1. Теория пластического деформирования	35
ческих деформаций. Кинетическое уравнение накопления повреждений
принимается в следующем виде:
а = ^.	B.14)
Здесь и — мера повреждения, Wo — энергия разрушения. Критерием
разрушения материала будет достижение повреждением предельного
значения, обычно принимаемого равным единице.
Ответственность остаточных микронапряжений за процесс накоп-
накопления повреждений впервые была отмечена в работе [20], где и была
сформулирована гипотеза пропорциональности скорости накопления
повреждений и интенсивности остаточных микронапряжений. Экспери-
Экспериментальное обоснование ответственности остаточных микронапряже-
микронапряжений за разрушение в опытах на одноосную малоцикловую усталость
содержится в работе [21]. Кинетическое уравнение B.14) на основе
работы остаточных микронапряжений на поле пластических деформа-
деформаций (критерий работы микронапряжений) впервые было рассмотрено
в работах [22, 23, 24] при теоретических исследованиях малоцикловой
усталости конических оболочек при теплосменах. Сопоставление в этих
работах теоретических и экспериментальных результатов показало до-
достаточную работоспособность критерия работы микронапряжений по
сравнению с другими критериями. К тому же следует отметить, что на-
гружение материала оболочки в месте разрушения происходит в усло-
условиях двухосного напряжённого состояния и носит весьма сложный
неизотермический характер. То есть в этих работах критерий работы
микронапряжений впервые был апробирован при сложном (непропор-
(непропорциональном) неизотермическом нагружении.
§ 2. Материальные функции
Теорию пластического деформирования замыкают следующие опре-
определяющие параметры и функции, подлежащие экспериментальному
определению:
Е, v, g, ge, ga, Cp, Wo.	B.15)
Первые два и последние два среди перечисленных B.15) параметров
имеют вполне понятный механический смысл. Что касается параметров
g, g?, ga, то для определения механического смысла этих параметров
рассматривается процесс образования остаточных микронапряжений
или смещение центра поверхности нагружения при одноосном рас-
растяжении. При одноосном растяжении смещение центра поверхности
нагружения происходит только по оси растяжения, и тогда
аи --а, а22 - ^ а, а33 - ^ а,	^ ^
11	' 22	о ' 33	о '

36	Часть 2. Пластичность
где а и гр — смещение центра поверхности нагружения и пластическая
деформация вдоль оси растяжения. В этом случае на основании B.16)
уравнение B.4) примет вид
a = gep + (geep + ga)ip.	B.17)
Анализ [16] экспериментальных данных показал, что при пластическом
деформировании в условиях одноосного растяжения кривая образова-
образования остаточных микронапряжений хорошо апроксимируется зависимо-
зависимостью
а = ЕаеР + аа[1-ехр(-/ЗеР)}.	BЛ8)
В этом случае параметры Еа, аа и /3 имеют вполне определённый
смысл на кривой образования микронапряжений: Еа — тангенс угла
наклона асимптоты, или модуль образования микронапряжений линей-
линейного типа; аа — значение на оси остаточных микронапряжений в точке
пересечения оси и асимптоты или предельное значение микронапря-
микронапряжений нелинейного типа; /3 — показатель экспоненты, или показатель
интенсивности (скорости) образования микронапряжений нелинейного
типа.
Далее дифференцируя B.18) по времени, можно получить следую-
следующее уравнение:
а = (Еа + /Заа)ёр + (/ЗЕаер - /За)ёр.	B.19)
Сравнивая B.17) и B.19), можно сделать вывод, что
g = Еа + /Заа, gs = /3Ea, ga = -p.	B.20)
Итак, теорию пластического деформирования замыкают следующие ма-
материальные функции, подлежащие экспериментальному определению:
Е, v — упругие параметры;
Cp(su*) — функция изотропного упрочнения;
Еа, era, P — параметры анизотропного упрочнения;
Wo — энергия разрушения.
Следует отметить, что параметры g, ge, ga уравнения B.4), стро-
строго говоря, должны определяться из опытов на многоосное сложное
нагружение. Здесь же принимается, что параметры g, ge, ga есть неко-
некоторые константы материала, что и позволило связать эти параметры
с параметрами Еа, аа, C и определить их в дальнейшем из опытов на
одноосное растяжение-сжатие или знакопеременное кручение, которые
являются сложным нагружением по двузвенной траектории с изломом
на 180 градусов.

Глава 1. Теория пластического деформирования	37
§ 3. Связь теории пластического деформирования
с общими теориями пластичности
В качестве общих теорий рассматриваются теория Кадашевича [19],
в которой пластическое деформирование описывается общим тензорно-
линейным дифференциальным уравнением второго порядка, и общая
математическая теория пластичности Ильюшина [13, 14].
Тензорно-линейное уравнение Кадашевича имеет вид
Необходимо выяснить, относится ли теория пластического деформиро-
деформирования к классу общей тензорно-линейной теории Кадашевича.
Из уравнений B.5) и B.6) следует, что
9	(\pv
я • • — п ¦ ¦ — - С (рр ) lj	(9 99^
Дифференцируя B.22) по накопленной пластической деформации е^
и используя B.4), можно получить
или
dsi 2 г, 2
dst = 3 ge?V + 3
Из сравнения B.21) и B.23) следует, что
B.24)
Таким образом следует вывод, что теория пластического деформирова-
деформирования принадлежит к классу общей тензорно-линейной теории второго
порядка и является вполне конкретным вариантом этой общей теории.

38	Часть 2. Пластичность
В векторном представлении Ильюшина уравнения теории пластиче-
пластического деформирования будут иметь вид
, 3е = J^,	B.25)
2Gr
§ (%?)-*>•	B-26)
dl = gdBP + (g?3P + gal) dsP.	B.27)
Дифференцируя B.26) по длине дуги деформации	s и используя
B.25)-B.27), можно получить следующее уравнение:
где
2—o"H"-tVl~;—\-Woo = Dqc}-\-JJ\——\-JJ2—т,	(z.zo)
" ds	as	ds	ds
_Мз
Gj\ds I	2G \ds2 J\ds
Mx=g-gaCp{Sv) + ^f±, M2=ga, M3 = Cp{sP), M4 = ge.
При развитых пластических деформациях можно принять
^«1, ^^0.	B.30)
ds	ds2
И тогда коэффициенты уравнения B.28) будут иметь вид
D, = М, = ff- gaCp(sP) + ^ff-L, D2 = M3 = Cp(sP).
Согласно общей математической теории пластичности Ильюшина век-
,	о о	о о	dS d2S
тор деформации 3, вектор напряжении о и его производные — и —s-

Глава 1. Теория пластического деформирования	39
можно представить в репере Френе {pi} пятимерного девиаторного
пространства деформаций в виде
3 DiPi, Б РфЬ ^ PPi, ^ PPi
as	ds
или в пятимерном неортогональном репере {г^} = —j (i = 1, ..,5):
ds1
(ГЭ Я
ds*'
-o
ds% '
dS _
ds
ds{ '
dfS _
ds
g«^5
ds1
_Получая_ из последних трёх уравнений B.32) выражения для
d3B d4B db3
—Т' —4' —к и подставляя в первое уравнение, можно получить урав-
ds ds ds
нение полностью совпадающее по структуре с уравнением B.28) и ко-
коэффициентами, являющимися функционалами процесса. В случае тео-
теории пластического деформирования эти коэффициенты имеют конкрет-
конкретные выражения B.29) или B.31).
Таким образом, теория пластического деформирования является
конкретным вариантом общей математической теории пластичности
Ильюшина при полном сохранении всей структуры уравнений этой
теории.
§ 4. Матричное представление уравнений теории
Уравнения связи между скоростями напряжений и деформаций в
матричном представлении для случая мягкого нагружения имеют вид
[ёг] = [Сц\ Щ ,	B.33)
[hi] = [Gij] [&j].	B.34)
Здесь
[ii] = [in ?22 езз 2е12 2е23 2e3i]\	B.35)
[dj] = [аи Ьы азз ^12 ^23 ^3i]T,	B.36)
[^г] = [?и* ?п ?22 ^33 ^2 4з?31 «И «22 «33 «12 «23 «31 ^]Т, B.37)
[Cij] = [Ctj] + Щ]	B.38)
Ш = [??] + [??], №} = Щ][&А, [??] = Щ] [aj]).

40
Часть 2. Пластичность
Матрица [С^] определяется как A.90), а матрица [Cfj] определяется
на основе B.1), B.5), B.9) и равна
\С?.] = — -—L
*22*
*23*ll
22 22
n* n*
*33*22
On* n*
z*12*22
On* n*
z*23*22
*22*33
*33*33
22 12
522*31
512
523
4<S23531
^*31*31 J
B.39)
Для определения вектора внутренних переменных [/г^] формулируется
следующая система уравнений для кратности записанная в тензорном
виде
?u* j? о *
з 4 .p
B.40)
Матрица [С^-] и система уравнений для внутренних переменных имеют
рассмотренный выше вид, если выполняются условия упругопластиче-
ского состояния B.13). В случае, когда состояние упругое, матрица
[Cfj] и скорость накопленной пластической деформации ^* принима-
принимаются равными нулю.
Уравнения связи между скоростями деформаций и напряжений в
случае жёсткого нагружения имеют вид
[аг] = [А,-] [^], [А,-] = [^]-[ДУВД	B.41)
Матрица [D^-] определяется как и A.91), а матрица [D^-] определяется
на основе B.1), B.5), B.12) и равна
3G 3 1
ЗС2
511*22
п* п*
22 22
57,5:
11*33
57,5
11*12
*11*23
П* п*
*22*23
*11*31
П* п*
*22*31
533511
On* п*
z*12*ll
On* n*
z*31*ll
533522
25t2522
25* 5*
25* 5*
533533
2snsh
25* 5*
25* 5*
533512
25*25*2
On* n*
z*23*12
25* 5*
533523
On* n*
z*12*23
On* n*
z*23*23
On* n*
z*31*23
533531
On* n*
z*12*31
On* n*
z*23*31
On* n*
z*31*31 -
B.42)

Глава 1. Теория пластического деформирования
41
Матрица
]¦] определяется на основе A.91) и B.42) и равна
3G 3 1
511Л22
511Л12
<Soo<Soo (Sooooo <Soo<Sio Onnono
S33523
q or
*23
°11
511
?12'
SooS
512°33
33^12
* Q*
12*12
Si OUi
12*23
^11*31
Ь22*31
Soo 5oi
b12531
Q	Q	Q	С	С	С	С	С	С	С
*23*22 *23*33 *23*12 *23*23 *23*31
531522
B.43)
Для определения вектора внутренних переменных [hi] система уравне-
уравнений имеет вид B.41), но только для скорости накопленной пластиче-
пластической деформации будет иметь место уравнение
""*¦.	B.44)
и* E* + 3G at '
Аналогично, как и в случае мягкого нагружения, эти уравнения имеют
место при упругопластическом состоянии. При упругом состоянии [D^]
и ёи* принимаются равными нулю.
Следует отметить, что матрицы [Cfj] и [D?j] являются функциями
внутренних переменных [hi].
§ 5. Уравнения теории в случае обобщённого
плоского состояния
Рассматриваются три вида нагружения:
а) мягкое нагружение
1 3 1
«11 = 3
?22 ^33
^j2 ^11 ^22
«22)
¦42)
B.45)
B.46)
B.47)
B.48)

42	Часть 2. Пластичность
^22 = ^ [^22 - К^П + ^33)] +
B.49)
б) смешанное нагружение
[*j] = [eii ^22 ^3 2г12]т,	B.50)
[^г] = [<hl О2 ^33 О-12]Т,	B.51)
[^г] = [^S* ^П ^22 iP\2 ^И ^22 «12	&] , B-52)
	 X
2A - l/)s*2?i2 , 1 ~ 2l/ 3 ?з
2A - v)
2A -^)KJ
3?n_ .p	/,	п\	др _ 3 5?2др
z, си	z, uu
* A^2),	B.53)
9	/9
3	\3
¦А- П fKi • '7') /	\ / fKi • '7^ \ /~\ • '7^ 
CJ = — [an^ij + ^22^22 + (аП	+ а22) (^п + ^227 ^ ^аП^\2\ >
• _ Е Г/. _ .р ч	/. .р 41 I/ .
. _ Я Г/. .р\	/. -р 41 V .
hj /.	.г) \

Глава 1. Теория пластического деформирования	43
в) смешанное нагружение
[ij] = [in д-22 азз 2г12]т,	B.55)
[Уг] = [о-П ?22 ^33 0-12}Т ,	B.56)
[hi] = [^* ери ё%2 ер{2 ап а22 аХ2 о;] ,	B.57)
1
, 3 (S22 + ^g*i) ^22
h 7Г
W
&n = E(in -?n) + v(o-22 + ^33),
/. .v , \ — v2 . 1/A +1/)
22 = -^ (^11 - q) +	^22
Следует отметить, что выражения для скорости накопленной пластиче-
пластической деформации в случаях смешанного нагружения можно получить,
подставляя в выражение B.9) для мягкого нагружения или в выра-
выражение B.12) для жёсткого нагружения соответствующие зависимости
для скоростей напряжений или деформаций через задаваемые скоро-
скорости напряжений и деформаций. В рассмотренных выше случаях это
зависимости для скоростей напряжений B.54) и B.59), которые под-
подставляются в выражение B.48) для мягкого нагружения. Получение
этих зависимостей для скоростей напряжений описано в § 4 главы
3 части 1. Далее, подставляя в полученное выражение связь B.5)
между скоростями пластической деформации и скоростью накопленной
пластической деформации и разрешая относительно ?^*, можно полу-
получить необходимое выражение для скорости накопленной пластической
деформации.

44	Часть 2. Пластичность
§ 6. Уравнения теории в случае одноосного
напряжённого состояния
В условиях одноосного напряжённого состояния все компоненты
тензора напряжений равны нулю, кроме напряжения а\\. Это напря-
напряжённое состояние соответствует Р-опытам, и здесь возможны две
программы нагружения:
а) мягкое нагружение
[ij] = [&U 0]Т (G22=0),	B.60)
[Уг] = [гп Ы1 (?22=?зз),	B.61)
ё
= f-g-o-ц sign (sf,), если а* = Ср П eg* > 0,
\	0, если < < Ср U е?* < 0;
??,=?*„ sign (*п).	B-63)
B.64)
б) смешанное нагружение
[Хз] = [ёц 0]Т (G22=0),	B.65)
г] = [о-Ц ?22]Т (^22 = гзз) ,	B.66)
gn signal), если сг* =СрПг^ > 0,
2 *^(l*jx
B.67)
ё?« > 0,
0, если сг* < Cp U eS* < 0;
B.68)
тр( х	дР \ х	nfx*	xP \	хР /О ?Q\
— xi/^?l 1 — ?\\), <^22 — — ч^П — 11/ — г» 11 * V'^-O^'/
§ 7. Критерии малоцикловой усталости при одноосном
напряжённом состоянии
При одноосном растяжении-сжатии смещение центра поверхности
нагружения происходит только по оси растяжения-сжатия, и тогда

Глава 1. Теория пластического деформирования
45
1
= за'
_ р
— ? >
а22
р
р
1
~ ~2
-а
ер
— а^ъ — &ъ\ — 0>
.р 	 р 	 р 	 г\
19 — ^9^ — ?^1 — ^9
B.70)
'12
=-23
^31
где а и ?р — смещение центра поверхности нагружения и пластическая
деформация вдоль оси растяжения-сжатия.
В этом случае уравнение B.4) примет вид
da = (Еа + aap)dep - /3(а - Еаер) sign (dep)dep
(depu* = \dep\ = sign (dep)dep).
B.71)
Рассматривается циклическое одноосное нагружение, когда пластиче-
пластическая деформация на п-м полуцикле г^ меняется от грп до еркп, а сме-
смещение поверхности нагружения (добавочное напряжение) ап меняются
от аоп ДО акп (рис. 2.1).
Интегрирование уравнения B.71), при начальных условиях
ап = аоп при ер1=грп,
даёт формулу для определения добавочного напряжения на n-м полу-
полуцикле:
ап = Еае» + (аОп - ЕаерОп) exp [-/3sign (<fe
- e
g,,)
. B.72)
В случае циклического деформирования с постоянным размахом пла-
пластической деформации Аер формула B.72) примет вид
ап =
(аОп - ЕаерОп
aa sign(dep) [1 -
B.73)
Рис. 2.1. Изменение добавочного напряжения при циклическом одноосном
нагружении

46	Часть 2. Пластичность
Из формулы B.73) можно получить связь между добавочными
напряжениями нелинейного типа в конце n-го и (п— 1)-го полуциклов:
а* = а*_! ехр (-/ЗА^) + аа sign (de*>) [I - ехр (-/ЗА^)], B.74)
\п	n-\ = a/cn-l ~
Или вместо B.74) можно записать эту связь в виде смешанной про-
прогрессии
\<\ = 4\<-\\+d,	B.75)
q = - ехр (-/ЗДер), d = аа[\ - ехр (-/?Д?Р)].
Из формулы B.75) следует, что
2d + + qn~2d = |а, \qn~[ + d(l ~f~l\
d + qd + q2d + ... + qn~2d = |а, \q
1-я
B.76)
Но так как \q\ < 1, то
lim \a*n\ = j^-.	B.77)
Таким образом, через несколько циклов циклического деформирования
с постоянным размахом пластической деформации, процесс образова-
образования и снятия добавочного напряжения практически стабилизируется.
Стабилизированное значение добавочного напряжения в конце полу-
полуциклов растяжения и сжатия, соответственно, будут равны
а+ =
а~ -Е (ер - Аер) - a l exP(^Ag)	B 79)
Для добавочных напряжений нелинейного типа стабилизированное
значение равно
1
где плюс соответствует растяжению, а минус — сжатию.
Далее, рассматривая работу добавочных напряжений (остаточных
микронапряжений) на полуциклах растяжения и сжатия и учитывая
состояние стабилизации, можно получить
?Огг	?0гг+1
B.81)
Основываясь на B.81), критерий малоцикловой усталости будет
иметь вид
~

Глава 1. Теория пластического деформирования	47
Ш1=± \^Ea{sl2f + аа\е%2\ - G-j [1 - ехр (-/ЗЩ
Здесь Np — число циклов до разрушения; uj\ — повреждение на первом
полуцикле; г^2 — пластическая деформация на первом полуцикле. По-
Повреждение на первом полуцикле отражает влияние асимметрии цикла
на число циклов до разрушения.
При размахе пластической деформации, Агр <С 1//3, уравнение
B.82) приводится к виду
.	B.83)
А при размахе Агр ^> 1/C уравнение B.82) будет иметь вид
Де"ЛГр = A-(л)^..	B.84)
Следует отметить, что диапазон экспериментальных значений показа-
показателя степени в уравнении Мэнсона-Коффина [25] принадлежит интер-
интервалу предельных значений показателя степени [0.33; 1.0], следующих
из уравнений B.83) и B.84), структура которых совпадает с уравнени-
уравнением Мэнсона-Коффина.
§ 8. Расчётно-экспериментальный метод определения
материальных функций
Для определения материальных функций теории упругопластиче-
ского деформирования достаточно следующего минимального набора
экспериментальных данных:
—	упругие параметры Е и z/, которые определяются традиционными
методами;
—	диаграмма деформирования при одноосном растяжении &\(е) до
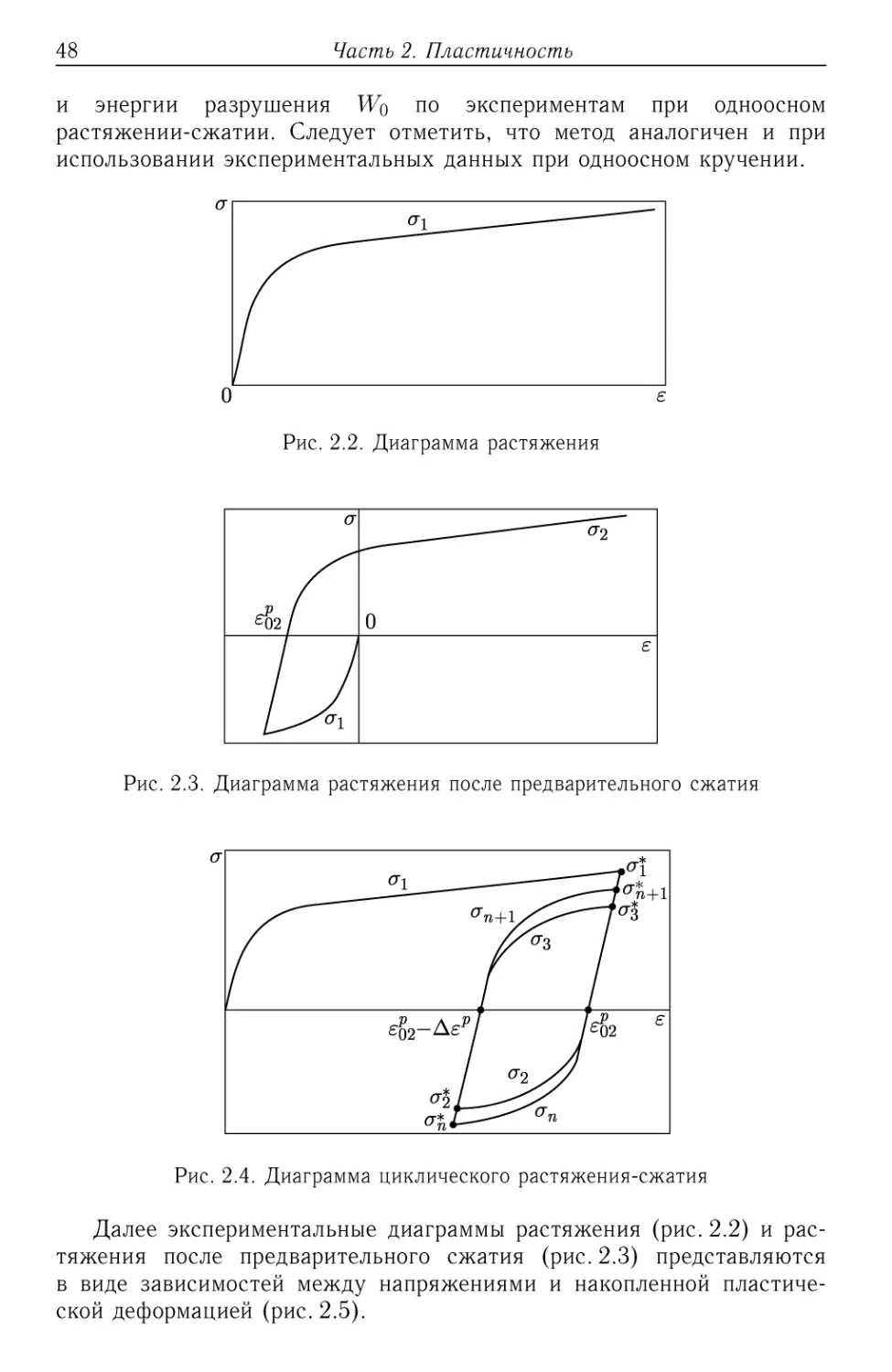
деформации 0.05^-0.1 (рис. 2.2);
—	диаграмма деформирования при одноосном растяжении o~2{s) по-
после предварительного сжатия до деформации 0.01 -!-0.02 (рис. 2.3);
—	данные по циклическому одноосному растяжению-сжатию при
постоянном размахе пластической деформации: число циклов до раз-
разрушения (появления макротрещин) и зависимость максимальных по
модулю значений напряжений а^ на полуцикле от числа полуциклов
нагружения п (рис. 2.4).
Следует отметить, что расчётно-экспериментальный метод строится
на обработке экспериментальных кривых и не связан с определением
пределов текучести и других величин с какими-либо допусками на
деформацию, что обычно вносит неоднозначность в получаемые резуль-
результаты при различных допусках на деформацию.
Рассматривается метод определения параметров анизотропного
упрочнения Еа,аа,C; функции изотропного упрочнения Cp{ePi^)

48
Часть 2. Пластичность
и энергии разрушения Wo по экспериментам при одноосном
растяжении-сжатии. Следует отметить, что метод аналогичен и при
использовании экспериментальных данных при одноосном кручении.
О	е
Рис. 2.2. Диаграмма растяжения
0
€
Рис. 2.3. Диаграмма растяжения после предварительного сжатия
Рис. 2.4. Диаграмма циклического растяжения-сжатия
Далее экспериментальные диаграммы растяжения (рис. 2.2) и рас-
растяжения после предварительного сжатия (рис. 2.3) представляются
в виде зависимостей между напряжениями и накопленной пластиче-
пластической деформацией (рис. 2.5).

Глава 1. Теория пластического деформирования
49
___*!	——
Рис. 2.5. Диаграммы растяжения и растяжения после предварительного сжатия
При одноосном растяжении-сжатии уравнения B.3) и B.4) при-
примут вид
а-а\ = Ср(ер*),	B.85)
da = (Еа + aa)dep - /3(а - Еаер) sign (dep)dep.	B.86)
Интегрирование уравнения B.86) даёт формулу B.72) для определения
добавочного напряжения на п-м полуцикле:
ап = Еаерп + (аОп - ЕаерОп) ехр [-/Jsign (de*)(e* - spOn)} +
+ Gasign((feP){l -exp [-/3 sign (dep)№-4n)]} • B-87)
Учитывая, что на первом полуцикле растяжения
гр{ = 0, aoi = 0, ?^* = ?р sign (^p) = +1,
на основании уравнений B.85) и B.87) можно получить зависи-
зависимость о\ (el*):
= Ср
ехр
= Ср
+
* + °а ~ (Ja ехр [-/3 (е^ - \ер021)] ехр (-/3|eg2|).
B.88)
Далее учитывая, что на втором полуцикле растяжения после предва-
предварительного сжатия
— _\с-Р
, «02 = - {Еа
02\
exp
Fp -
Fp - fp
ьи* — Ь2
?02
, sign(d?p) = +l,
на основании уравнений B.85) и B.87) можно получить зависи-
зависимость сг2 (Д*):
= Ср
аа- 2Еа\ер
2
ехр
(-/3 (е?* -
B.89)

50
Часть 2. Пластичность
Рассматривая разность величин напряжений растяжения а\ и растя-
растяжения после предварительного сжатия о^, при одинаковых значениях
накопленной пластической деформации, можно получить зависимость
О\ — G2
тг j_ a fi
= Ьа + р^-т [1 —
l?02l
ехр [-/3 (е?, -
Зависимость B.90) представляет собой в координатах
У= Чпгг>
B.90)
B.91)
У
экспоненту с горизонтальной асимптотой у = Еа, что позволяет графи-
графически определить значение параметра Еа. На рис.2.6 показана экспе-
экспериментальная кривая в координатах B.91).
На рис. 2.6 чётко прослеживается выход кривой (экспоненты) на
горизонтальную асимптоту.
Следует отметить, что в случае
использования экспериментальной диа-
диаграммы сжатия после предварительного
растяжения в формулах B.90) и B.91)
разность напряжений (а\ — G%) заменя-
заменяется алгебраической суммой (а\ + а^).
Можно также диаграмму сжатия после
предварительного растяжения перестро-
перестроить в диаграмму растяжения после пред-
предварительного сжатия и ничего в форму-
формулах B.90) и B.91) не менять, т.к. пред-
предполагается, что материал имеет одинаковые свойства при растяжении
и сжатии.
Для получения параметров C и аа зависимость B.90) перестраива-
перестраивается в полулогарифмических координатах
Рис. 2.6. Экспериментальная
кривая в координатах у и х
У -Eg
Еа
Полученная линейная зависимость,
х = еЬ-\е*\.	B.92)
^ — ^q /эх,
позволяет по углу наклона ср и ординате ;
аа по формулам
/3 = tg (
аа =
1-ехр Н
B.93)
определить параметры /3 и
B.94)
На рис. 2.7 показаны обработанные экспериментальные данные в ко-
координатах B.89) и аппроксимация этих данных прямой по методу
наименьших квадратов.

Глава 1. Теория пластического деформирования
51
Рис. 2.7. Экспериментальная кривая в координатах z и х
Получив параметры анизотропного упрочнения Еа,/3,аа, можно те-
теперь определить функцию изотропного упрочнения Ср (г?*) > используя
экспериментальную диаграмму растяжения, по формуле
С/ р \	 / р \
Р \?u*J — °1\?u*J
B.95)
Для остальных значений накопленной пластической деформации функ-
функция изотропного упрочнения определяется по результатам циклических
испытаний (рис. 2.4) при постоянном размахе пластической деформа-
деформации по формуле
сС lei
-Еа
^02 I ~
-Р I
'021
-Агр(п- 1).
1 - ехр (-EАер)
' 1 + ехр (—EАер)'
B.96)
Или, используя значение напряжений а^ только на полуциклах растя-
растяжения а~х = а^, при п нечётных и равных BN + 1), можно получить
формулу для функции изотропного упрочнения:
_ ^+ F v
- ^лг ^^02
- ехр (-(
B.97)
"и*	02
Здесь N — номер цикла, т. е. первый цикл включает в себя второй
и третий полуциклы, второй — четвёртый и пятый полуциклы и так
далее. Первый же полуцикл растяжения обычно называется отнулевым
циклом.
Следует отметить, что в формулах B.96) и B.97) используется ста-
стабилизированные значения B.80) остаточных микронапряжений нели-
нелинейного типа, т. е. формулы B.96) и B.97) должны применяться при
условии стабилизации процесса образования и снятия микронапряже-
микронапряжений, и практически это наступает при п > 7 или N > 3.
Энергия разрушения Wo определяется из испытаний на малоцик-
малоцикловую усталость (рис. 2.4), при постоянном размахе пластической де-

52
Часть 2. Пластичность
формации, используя критерий малоцикловой усталости B.82). Тогда
энергия разрушения будет определяться по формуле
B.98)
Здесь Np — число циклов до разрушения; W\ — работа микронапря-
микронапряжений на отнулевом цикле (первом полуцикле).
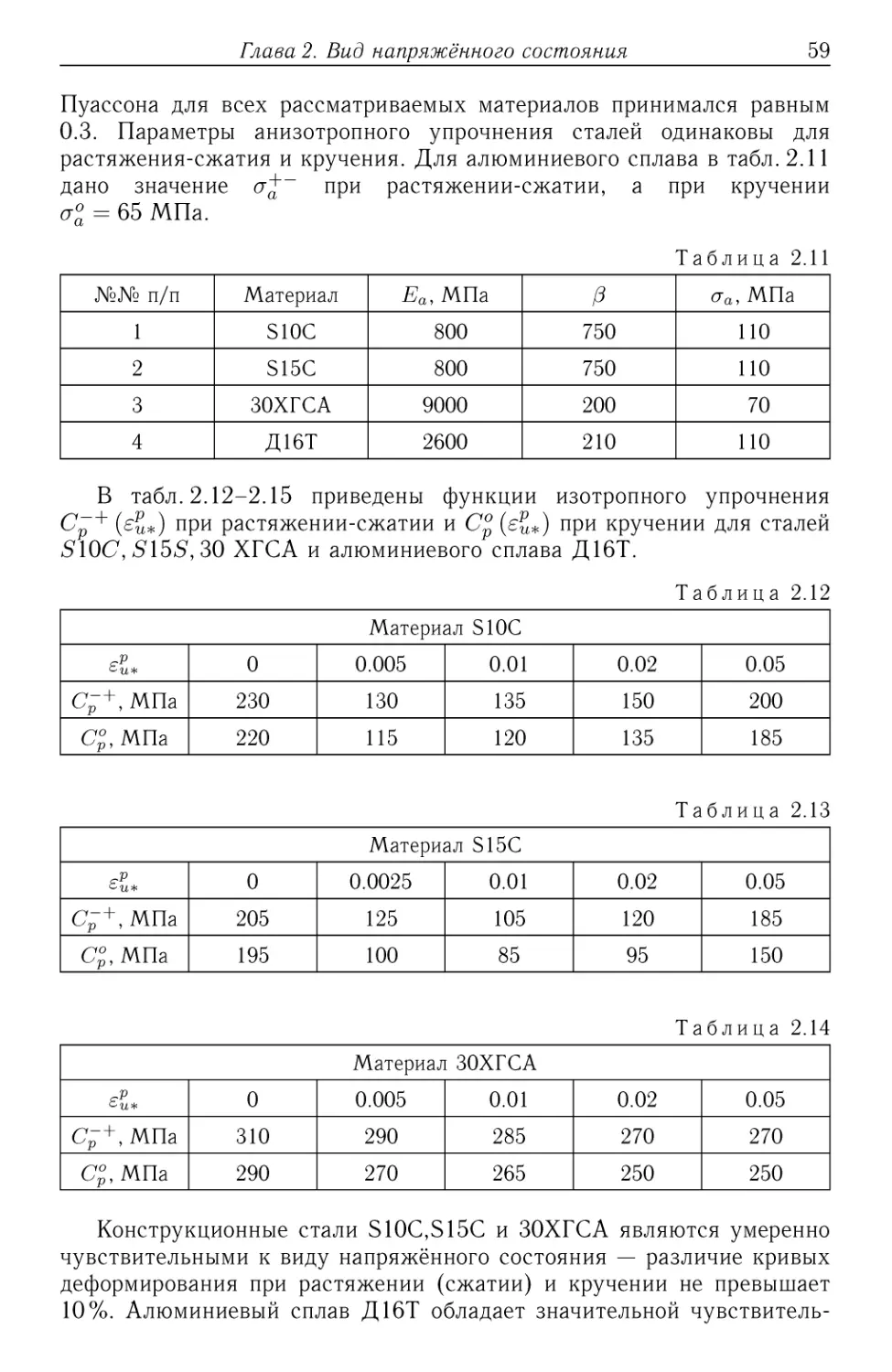
§ 9. Материальные функции некоторых
конструкционных сталей и сплавов
Ниже в таблицах приводятся модуль Юнга Е; параметры ани-
анизотропного упрочнения Еа,C,аа и функция изотропного упрочнения
Ср (ей*) для некоторых конструкционных сталей и сплавов. В том слу-
случае, когда для материала была известна только диаграмма растяжения,
для получения диаграммы растяжения после предварительного сжатия
использовался принцип Мазинга, и эта диаграмма получалась на ос-
основе уравнения а1 = 2/ (ег /2), где а = f(e) — диаграмма растяжения.
Коэффициент Пуассона для всех материалов принимался равным 0.3.
Таблица 2.1
№ п/п
1
2
3
4
5
6
7
8
9
Материал
30 ХГСА [26]
Ст. 10 [27]
BsBM 2 [28]
Ст.45 [29]
12X18 Н10Т [3]
AISI 304 [30]
Ст. 45 [31]
Ст.40Х16Н9Г2С [31]
Ст.9Х2 [31]
Е, МПа
2- 105
2- 105
1 • 105
2.1 • 105
2.2 • 105
1.8- 105
2.1 • 105
2- 105
2.3 • 105
Еа, МПа
1100
470
750
6770
2500
7400
6770
3550
6770
&
370
650
300
265
250
1050
265
445
265
сга,МПа
160
55
80
140
170
145
160
140
160
ср
el,
, МПа
0
295
Материал
0.005
300
ЗОХГСА [26]
0.01
305
0.02
315
Таблица
0.05
345
2.2

Глава 1. Теория пластического деформирования
53
а
Ср,
?*
МПа
0
135
Материал
0.005
ПО
Ст.
10 [27]
0.01
105
0.02
115
Таблица
0.05
155
2.3
ер*
Ср, МПа
0
100
Материал
0.005
85
BsBM 2 [28]
0.01
85
0.02
90
Таблица
0.05
ПО
2.4
а
Ср,
МПа
0
320
Материал Ст.
0.005
270
0.01
260
45
[29]
0.02
270
0.05
285
Таблица
0.21
305
2
.5
Таблица 2.6
Ср
?Ри*
, МПа
0
160
Материал
0.005
250
12X18 Н10Т
0.01
255
[3]
0.02
260
0.05
270
Ср
?Ри*
, МПа
0
130
Материал
0.005
130
AISI
304 [30]
0.01
130
0.02
130
Таблица
0.05
130
2
.7
Таблица 2.1
ер*
Ср, МПа
0
340
Материал Ст. 45
0.005
290
0.01
280
>[31]
0.02
285
0.05
305
0.21
325
гри*
Ср, МПа
Материал
0
165
0.006
120
Ст.40ХН9Г2
0.008
130
[31
]
0.024
184
Таблица
0.086
274
2.9
Ср
гри*
МПа
0
240
Материал Ст. 9X2
0.005
180
0.0084
175
[31]
0.027
250
Табли
0.047
275
ца 2.10
0.21
320

Глава 2
ТЕОРИЯ ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ
МАТЕРИАЛОВ, ЧУВСТВИТЕЛЬНЫХ К ВИДУ
НАПРЯЖЁННОГО СОСТОЯНИЯ
§ 1. Основные положения и уравнения теории
Материал однороден и начально изотропен. В процессе упруго-
пластического деформирования в нём может возникать только дефор-
деформационная анизотропия. Материал может быть чувствителен к виду
напряжённого состояния, т. е. иметь различные характеристики пласти-
пластического поведения и разрушения, например, при растяжении, сжатии,
сдвиге. В процессе деформирования возможно как упругое, так и пла-
пластическое изменение объёма материала.
Тензор скоростей деформаций представляется в виде суммы тензо-
тензоров скоростей упругой и пластической деформаций,
?у = 4-+??-	B-99)
Упругие деформации при изменении напряжений следуют обобщённо-
обобщённому закону Гука:
е% = | [дц - v (Ъдфц - atj)\,	B.100)
где Е, v — соответственно модуль Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и упругопластического состояний. Поверхность нагружения изотропно
расширяется или сужается, смещается и изменяет форму в процессе
нагружения. Начальная поверхность нагружения может иметь форму,
отличную от поверхности Мизеса. Уравнение поверхности нагружения
принимается в следующем виде:
/КО = \ (sij ~ aij^Sij - aij) - [Ср (агг,^,е^)}2 = 0. B.101)
Здесь s*j = s^ — dij — девиатор активных напряжений; s^ — деви-
атор напряжений; ац = 1\(Та) — первый инвариант тензора напряже-
напряжений; /i* — параметр вида активного напряжённого состояния; ?^* — на-
накопленная пластическая деформация. Тензор добавочных напряжений
(остаточных микронапряжений) ац характеризует смещение поверхно-
поверхности нагружения в девиаторном пространстве напряжений и является
функционалом процесса нагружения. Функция Ср (<r^,/i*,?S*) задаёт
форму поверхности нагружения в зависимости от параметров, которые

Глава 2. Вид напряжённого состояния	55
определяются следующим образом:
e =
р. ,«2,
1/2
Здесь e^j = ?^- — е^5^ — девиатор пластической деформации. Параметр
вида активного напряжённого состояния /i* Е [—1, 1] при сжатии
равен — 1, при сдвиге равен 0, а при растяжении равен +1.
В свою очередь, при определении добавочных напряжений ац,
учитывается, что процесс образования или снятия добавочных на-
напряжений зависит от вида добавочного напряжённого состояния, т. е.
от параметра \±а вида добавочного напряжённого состояния, который
определяется следующим образом:
27	h{Bа)
V =
2 [3/2(L>a)]3/2'
B.103)
Таким образом, поверхность нагружения B.101) зависит от первого ин-
инварианта тензора напряжений, вторых и третьих инвариантов активных
напряжений и добавочных напряжений. Зависимость поверхности на-
нагружения от первого инварианта тензора напряжений и следующее из
этого пластическое изменение объёма (разрыхление) материала впер-
впервые рассмотрено в работах [32, 33]. Учёт же зависимости поверхности
нагружения от параметров вида активного и добавочного напряжённых
состояний содержится в работах [2, 3].
Смещение поверхности нагружения определяется уравнением
?*•	B104)
Здесь g"(/xa), g"e(/xa), ga(lJ>a) — функции, зависящие от параметра /ia
вида добавочного напряжённого состояния.
Пластические деформации определяются на основе ассоциирован-
ассоциированного с B.101) закона течения, и тогда тензор скоростей пластической
деформации будет задаваться уравнением
: _ 3 rtjj p
Л - 2 < ^*
= 4 - з
1/2
/O 1
BЛ09)

56	Часть 2. Пластичность
Повторяющийся индекс к в формуле B.107) означает суммирование.
Тензоры riij и n*j являются симметричными девиаторами, в чём нетруд-
нетрудно убедиться, получая на основе формул B.106) и B.107), что пц = 0,
nii = °' ПЧ = n3i> nij = n)i'
Пластическое изменение объёма (разрыхление), следуя уравне-
уравнению B.108), определяется величиной накопленной пластической де-
деформации и имеет место только в случае зависимости поверхности
нагружения от первого инварианта тензора напряжений.
Для получения уравнения для скорости накопленной пластической
деформации необходимо продифференцировать по времени интенсив-
интенсивность активных напряжений и функцию Ср (<r^,/i*,?S*) и приравнять
эти выражения, т.к. из B.101) следует, что
а: = Ср(агг,^,е^).	B.110)
Итак
d°u _ 3 Sjj (sjj — djj) _ 3 Sjj&jj _ sijejj _ I sijeij .
dt 2	al	2 au g al ^ а*и ^
~ 2 a* g2 a*n* u* \gs a* ga2 a*
dCp dCp . , dCp . , dCp .„	. , 3n«,s*3
4- n.d-P = n гт-- -U
L+^S*- B.112)
Приравнивая выражения B.111) и B.112) и разрешая относительно
^2*, можно получить уравнение связи скорости накопленной пластиче-
пластической деформации и скоростей напряжений:
•р _ 1 \3nijaij р<7- .	/о 1 1 q\
p* _ nijeij	* _ 3
U	* '	W	2
2
В случае независимости поверхности нагружения от первого инвариан-
инварианта тензора напряжений пластическое изменение объёма будет равно ну-
нулю, и уравнения для скорости накопленной пластической деформации
соответственно для мягкого и жёсткого нагружений будут иметь вид

Глава 2. Вид напряжённого состояния	57
^*"E## + 3G < *	BЛ15)
Условия упругого и, соответственно, упругопластического состо-
состояний, полученные из принадлежности изображающей точки поверх-
поверхности нагружения B.101) и положительности скорости накопленной
пластической деформации, имеют следующий вид:
аи < Ср (°м, А**, ??*) U ^S* < 0 — упругость;
аи = Ср (аи, {1*,би*) П ёи* > 0 — упругопластичность.
Здесь под ^2* подразумеваются выражения, задаваемые уравнения-
уравнениями B.113), B.114),B.115) или аналогичными им.
Для описания процесса накопления повреждений используется
энергетический подход, и кинетическое уравнение накопления повре-
повреждений аналогично B.14) будет иметь вид
u=wafli v	B.117)
27 h{Da)
2
1\(Та) = аи, h(Da) = - dijdij, h(Da) = -
Здесь uj — мера повреждения, Wo — энергия разрушения, являющаяся
функцией первого инварианта тензора напряжений и параметра вида
добавочного напряжённого состояния, который при одноосном сжатии
равен — 1, при сдвиге равен 0, а при одноосном растяжении равен
+ 1. Критерием разрушения материала будет достижение повреждением
предельного значения, обычно принимаемого равным единице.
Учёт влияния инвариантов тензора и девиатора напряжений на
процесс накопления повреждений содержится в работах [34, 35]. Учёт
же влияния параметра вида добавочного напряжённого состояния на
процесс накопления повреждений рассматривается в работах [2, 3].
§ 2. Материальные функции и метод их определения
Теорию пластического деформирования материалов, чувствитель-
чувствительных к виду напряжённого состояния, замыкают следующие определя-
определяющие параметры и функции, подлежащие экспериментальному опреде-
определению:
E,v,g,ge,ga,Cp,W0.	B.119)
Функции g,g?,ga выражаются через параметры анизотропного
упрочнения аналогично B.20) и имеют вид
g=Ea+l3-aa, g? = f3Ea, ga = -f3.	B.120)
Итак, теорию пластического деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, замыкают следующие мате-
материальные функции, подлежащие экспериментальному определению:

58	Часть 2. Пластичность
Е, v — упругие параметры;
Ср(ац,11*,еи*) — функция изотропного упрочнения;
-^a(/ia)>(Ja(/ia)>/3(/ia) ~~ параметры анизотропного упрочнения;
Wo((Tii, iia) — энергия разрушения.
Для описания зависимости функции изотропного упрочнения от
вида активного напряжённого состояния предлагается следующая ап-
аппроксимация:
СР = С°р (e?J + [С-+ (e?J - С% (e?J] \^\п ,	B.121)
где Ср~+ (??*), С° (ви*) — функции изотропного упрочнения, соответ-
соответственно, при одноосных сжатии-растяжении и кручении; п — показа-
показатель степени. Для ряда конструкционных сталей п = 3, а для цветных
сплавов п = 5. Эти значения получены при обработке эксперименталь-
экспериментальных данных работы [28]. Для параметров Еа,аа, C,Wo принимается
такая же как и B.121) аппроксимация:
+	B.122)
B.123)
B.124)
Wo = Wo° + (W~+ - Wo°)|/xa|m.	B.125)
Здесь Е-+, сг-+, /3-+, W~+ и ^,<,/3°,W0° - параметры анизо-
анизотропного упрочнения и энергия разрушения, соответственно, при одно-
одноосных сжатии-растяжении и кручении. В уравнениях B.121) и B.125)
пренебрегается зависимостью поверхности нагружения и энергии раз-
разрушения от первого инварианта тензора напряжений. В противном
случае все перечисленные выше параметры соответствующие сжатию-
растяжению и кручению будут функциями первого инварианта тензора
напряжений.
Для определения материальных функций проводятся такие же ба-
базовые испытания как и для теории пластического деформирования,
но отдельно в условиях одноосного растяжения-сжатия и одноосного
кручения. Далее на основе изложенного ранее расчётно-эксперимен-
тального метода определяются функция изотропного упрочнения, пара-
параметры анизотропного упрочнения и энергия разрушения при растяже-
растяжении-сжатии (/i* = ±l,/ia = ±1) и при кручении (/i* = 0, /ia = 0). Для
определения показателей степеней п и m в уравнениях B.121)-B.125)
необходимы такие же базовые испытания, но по лучевым траекториям
напряжений в условиях двухосного напряжённого состояния при /i* =
= /ia т^ 0 и /i* = /ia т^ ±1. Если данных таких испытаний нет, то в пер-
первом приближении можно принять п = m = 3 для конструкционных
сталей и п = m = 5 для цветных сплавов.
Ниже в табл. 2.11-2.15 приводятся параметры анизотропного
упрочнения Еа,/3,аа для сталей S10C [28], S15C [28], ЗОХГСА [36]
и алюминиевого сплава Д16Т [37]. Модуль Юнга для сталей равен
2 • 105 МПа, а для алюминиевого сплава 0.7 • 105 МПа. Коэффициент

Глава 2. Вид напряжённого состояния
59
Пуассона для всех рассматриваемых материалов принимался равным
0.3. Параметры анизотропного упрочнения сталей одинаковы для
растяжения-сжатия и кручения. Для алюминиевого сплава в табл. 2.11
дано значение <т+~ при растяжении-сжатии, а при кручении
< = 65 МПа.
Таблица 2.11
№№ п/п
1
2
3
4
Материал
S10C
S15C
ЗОХГСА
Д16Т
Еа, МПа
800
800
9000
2600
&
750
750
200
210
аа, МПа
ПО
по
70
ПО
В табл. 2.12-2.15 приведены функции изотропного упрочнения
С~+ (б^*) при растяжении-сжатии и С° (^*) при кручении для сталей
, S155, 30 ХГСА и алюминиевого сплава Д16Т.
Таблица 2.12
С+ (б
510G,
Материал S10C
el,
С-+, МПа
С?, МПа
0
230
220
0.005
130
115
0.01
135
120
0.02
150
135
0.05
200
185
Таблица 2.13
Материал S15C
el,
С~+, МПа
С?, МПа
0
205
195
0.0025
125
100
0.01
105
85
0.02
120
95
0.05
185
150
Таблица 2.14
Материал ЗОХГСА
el,
<7"+, МПа
С?, МПа
0
310
290
0.005
290
270
0.01
285
265
0.02
270
250
0.05
270
250
Конструкционные стали S10C,S15C и ЗОХГСА являются умеренно
чувствительными к виду напряжённого состояния — различие кривых
деформирования при растяжении (сжатии) и кручении не превышает
10%. Алюминиевый сплав Д16Т обладает значительной чувствитель-

60
Часть 2. Пластичность
Таблица 2.15
Материал Д16Т
Ср+, МПа
С°, МПа
0
350
250
0.005
335
235
0.01
320
220
0.02
310
210
0.05
310
210
ностью к виду напряжённого состояния — различие кривых растяже-
растяжения (сжатия) и кручения достигает 40%.
§ 3. Матричное представление уравнений теории
Уравнения связи между скоростями напряжений и деформаций в
матричном представлении для случая мягкого нагружения имеют вид
[ii] = [Cij][&j],	B.126)
\hi] = [Gij][&j].	B.127)
Здесь
Ы =
-22
Z\2
?зз 2?12 2?23 2i3ly ,	B.128)
! ^33 ^12 ^23 0^31J ,	yZAZu)
.p .p	. . . . . . -i T
B.130)
[Qj] = Щ] + [Cfj] .	B.131)
Матрица [Cf-] определяется на основе A.90), а матрица [Cfj\ — на
основе B.99), B.105), B.113) и в случае пренебрежения пластическим
изменением объёма будет иметь вид
1 Q 1
П11П11
П22П11
пЦпч
23 11
П11П22
/ l/QO ' t'OO
nlln33
22 33
7'12П22 2п12П33
7'23П22 2п23П33
^31n22 ^n31n33
Znlln12
z n 22^12
lln23
I'OO ' too
ЪЪ1Ъ
4n*2n*3
4-Г7* T7*
t: / ^00 / tno
^77/oo 77/01
2n33n31
4n12n31
4n23n31
4n31n31
. B.132)
Для определения вектора внутренних переменных [/ц] формулиру-
формулируется следующая система уравнений в тензорном виде:
1 ^ П* /Т- •	^ П*
B.133)
гр

Глава 2. Вид напряжённого состояния	61
Матрица [CfA и система уравнений для внутренних переменных
имеют рассмотренный выше вид, если выполняются условия упруго-
пластического состояния B.116). В случае, когда состояние упругое,
матрица [С^-] и скорость накопленной пластической деформации ?^*
принимаются равными нулю.
§ 4. Уравнения теории в случае обобщённого плоского
состояния
Рассматриваются три вида нагружения:
а) мягкое нагружение
[Xj] = [&U ^22 ^33 <Т12]Т,	B.134)
[т] = [ёп ?22 езз 2е12]т,	B.135)
[/ц] = [ё*^ ёрп ер22 ё\2 аи а22 al2 w] , B.136)
spUif = J-| Дг (п*п&и + п*22а22 + п*гг&33 + 2п\2дх2),
.р _ 3 Пп .р	.р _ 3 П22 -р	.р _ Зпх2.р	/
a22 = з ^22 + C g"s?22 + ga«22) ??*-
3 &^2 + §"aa
1
^22 = ~В [^2 — У (^11 + 0з)] + ^22'
1	B.138)
?зз — -р [^зз — v{p\\ + <3"зз)] — (^п + ^22)'
1 + v • , .»
б) смешанное нагружение
[xj] = [in e22 a33 2s12]T,	B.139)
[Уг] = [0-П 6-22 ?33 ^12]T,	B.140)
[^г] = [^S* ^1 42 ^2 dH d22 U12	&] , B.141)

62	Часть 2. Пластичность
?** + за*
n22)iu + (щ2 + ущх)г<12 +2A - и)щ2?\2 1 - 2v 3 щ3а
[	ОК	^7 2 ^Tj'
B.142)
3 [(«.ГО2 + (nhf + 2vnnnh + 2A - v) (пЩ
2A-v) «J	'
Уравнения для остальных внутренних переменных такие же как
и в системе уравнений B.137). Далее
B.143)
в) смешанное нагружение
[xj} = [sn CT22 <J33 2el2}T,	B.144)
[Уг] = [^1 ^22 ^33 О2]Т,	B.145)
[hi] = [?u* ??i 42 ^2 йп d22 ai2	^]T, B.146)
АР _	1
12?i2 3 (гг22 + г/пц) а22 + (гг33 + wtl аз
2	nu
B.147)
Уравнения для остальных внутренних переменных такие же как и в
системе уравнений B.137). Далее
а\\ =Е{ё\\ -гри) + 1У (&22 + озз) •
е22 = -у (еи - ерп) + Х-=^~ о22 - ^^зз + ер22,	B.148)
?33 = -v (in -?[,)- ^^ <т22 + -^ а33 - (^ + е\2) ,

Глава 3
ТЕОРИЯ ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ
МАТЕРИАЛОВ, ОБЛАДАЮЩИХ ЭФФЕКТОМ
ДОПОЛНИТЕЛЬНОГО УПРОЧНЕНИЯ
§ 1. Основные положения и уравнения теории
Материал однороден и начально изотропен. В процессе упругопла-
стического деформирования в нём может возникать только деформа-
деформационная анизотропия. Материал может обладать эффектом дополни-
дополнительного изотропного упрочнения при непропорциональном (сложном)
циклическом нагружении.
Тензор скоростей деформаций представляется в виде суммы тензо-
тензоров скоростей упругой и пластической деформаций,
ёу = 4-+е?"	B.149)
Упругие деформации при изменении напряжений следуют обобщён-
обобщённому закону Гука:
ё% = ±1&ч-1уC&о6у-&ч)},	B.150)
где Е,и — соответственно модель Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и упругопластического состояний. Поверхность нагружения изотропно
расширяется или сужается и смещается в процессе нагружения. Урав-
Уравнение поверхности нагружения принимается в следующем виде:
/К) = | (sv - ау)(ву " ау) - С2 = 0.	B.151)
Здесь s*j = Sij — dij — девиатор активных напряжений; sij — девиа-
тор напряжений. Тензор (девиатор) а^- характеризует смещение поверх-
поверхности нагружения в девиаторном пространстве напряжений, а скаляр С
отвечает размеру (радиусу) поверхности нагружения. Тензор смещения
(добавочных напряжений, остаточных микронапряжений) а^ и ради-
радиус С являются функционалами процесса нагружения.
Для радиуса поверхности нагружения принимается следующее
уравнение:
C = q?iPu,.	B.152)

64	Часть 2. Пластичность
Здесь 8и* — длина дуги траектории пластической деформации (на-
(накопленная пластическая деформация); ?^* — интенсивность скоростей
пластической деформации (скорость накопленной пластической дефор-
деформации); q? — функция подлежащая экспериментальному определению.
Для функции q? — принимается следующее выражение:
Яе = ^+ЯеА,	B-153)
где Ср(г^) — радиус поверхности нагружения при пропорциональном
(простом нагружении); qeA — описывает дополнительное изотропное
упрочнение при непропорциональном (сложном) нагружении. Для q?A
принимается следующее выражение:
fAtfi,	B.154)
CA = (l-A)C0 + ACl.
Здесь $a(A) — характеризует интенсивность (скорость) дополни-
дополнительного упрочнения или разупрочнения, a Ca(A,?u*) — величину
дополнительного упрочнения или разупрочнения; А — параметр (ме-
(мера) непропорциональности нагружения. Параметр Со при упрочнении
и разупрочнении принимает различные значения, т. е.
6СЛИ Q">On (fe. = 0^e = ^V B.155)
если q?* < О у	ds^ J
Значение параметра Со при разупрочнении, т.е. Ср*, зависит
[27-29] от максимальной величины радиуса Стах, достигнутой при
упрочнении. Поэтому для Ср* принимается следующее выражение:
Ср» = Ср + d0 (Cmax - Ср).	B.156)
Для параметра С\, характеризующего дополнительное упрочнение,
можно также принять зависимость в долях от Ср, т. е.
Итак, для описания изотропного упрочнения на основе уравнений
B.152)—B.157) необходимо экспериментально определить:
Ср (?и*) — функцию изотропного упрочнения при пропорцио-
пропорциональном (простом нагружении);
do,®\,do,d\ — модули дополнительного изотропного упрочнения и
разупрочнения при непропорциональном (сложном) нагружении.
Основной проблемой в описании эффектов дополнительного упроч-
упрочнения при непропорциональном нагружении является выбор параметра
непропорциональности. В качестве параметров непропорциональности
может быть рассмотрено множество углов (всего 28) между вектора-
векторами деформаций, напряжений, пластических деформаций, добавочных

Глава 3. Эффект дополнительного упрочнения	65
напряжений и их скоростей. В качестве критериев отбора параметров
принимаются следующие эффекты непропорционального нагружения,
полученные при экспериментальных исследованиях [38-40]:
—	при циклическом непропорциональном деформировании по тра-
траекториям деформаций в виде окружностей, эффект дополнительного
упрочнения усиливается с увеличением радиуса окружности, т. е. пара-
параметр непропорциональности должен возрастать с увеличением радиуса
окружности траектории деформаций;
—	при циклическом пропорциональном деформировании, после
предварительного непропорционального деформирования, происходит
снятие дополнительного упрочнения (разупрочнение), т.е. при
разупрочнении параметр непропорциональности должен уменьшиться;
—	при изменении направления пропорционального циклического
нагружения происходит упрочнение, а затем разупрочнение (эффект
поперечного упрочнения [39]), т.е. для описания эффекта поперечно-
поперечного упрочнения параметр непропорциональности должен увеличиться,
а затем уменьшиться.
Проведённые численные исследования на основе уравнений вариан-
варианта теории пластического деформирования без учёта дополнительного
упрочнения показали, что только два параметра непропорциональности
в полной мере удовлетворяют приведённым выше критериям.
Первый параметр соответствует углу между векторами скоростей
деформаций и скоростей напряжений:
9
А= 1 - f-^Ф-) ,	B.158)
1/2 . _ /3 . . \1/2
' аи* — [ с, sijsij )
Данный параметр непропорциональности был предложен в работе [41]
и использовался в эндохронной теории пластичности при исследовании
процессов непропорционального нагружения.
Второй параметр соответствует углу между векторами скоростей
деформаций и скоростей добавочных напряжений:
А= 1- (^И-\	B.159)
2 . . у/2 . /з . . у/2
(	)
Данный параметр был предложен в работе [42] и использовался в тео-
теории пластического деформирования материалов, обладающих эффек-
эффектом дополнительного упрочнения, при исследовании различных про-
процессов пропорциональных и непропорциональных циклических нагру-
жений.
3 В. С. Бондарь

66	Часть 2. Пластичность
Смещение поверхности нагружения определяется уравнением
\ g%j + (| gД- + ga^ij) ?u*-	B.160)
Здесь g, g?, ga — параметры, связанные с параметрами анизотроп-
анизотропного упрочнения формулами аналогичными B.20):
g=Ea+Paa, g? = CEa, ga = -C.
Согласно ассоциированному (градиентальному) закону течения тензор
скоростей пластической деформации будет определяться уравнением
_ df д _
?
Здесь <т* — интенсивность активных напряжений; / = 0 — поверх-
поверхность нагружения B.151).
Аналогично, как и ранее для других вариантов теорий пласти-
пластического деформирования, можно получить уравнения для скорости
накопленной пластической деформации, соответственно, для случаев
мягкого и жёсткого нагружений:
^	B.162)
ар —
3G S
Е -а
ь —
°и	^ ии
Условия упругого и упругопластического состояний, найденные из при-
принадлежности изображающей точки поверхности нагружения и положи-
положительности скорости накопленной пластической деформации, имеют вид
<т* < С U ё?* < 0 - упругость,
а^ = С П ^2* > 0 — упругопластичность;
Здесь под ёи* подразумеваются выражения, задаваемые уравнения-
уравнениями B.162) и B.163) или аналогичными им.
Для описания процесса накопления повреждений используется ки-
кинетическое уравнение B.14)
Критерием разрушения материала будет достижение повреждением
предельного значения, равного единице.

Глава 3. Эффект дополнительного упрочнения	67
§ 2. Расчётно-экспериментальный метод определения
материальных функций
Теорию пластического деформирования материалов, обладающих
эффектом дополнительного упрочнения, замыкают следующие матери-
материальные функции, подлежащие экспериментальному определению:
Е,и — упругие параметры;
Еа,C,сга — параметры анизотропного упрочнения;
Ср (?и*) — функция изотропного упрочнения;
Wo — энергия разрушения;
i!)o,i!}\,do,d\ — модули дополнительного изотропного упрочнения и
разупрочнения.
Первые семь материальных функций определяются при испытаниях
в условиях пропорционального одноосного напряжённого состояния, и
метод определения этих материальных функций изложен в § 8 главы 1
части 2 и здесь рассматриваться не будет.
Модули дополнительного упрочнения определяются на основании
зависимостей (диаграмм) максимальной интенсивности напряжений
на цикле нагружения от накопленной пластической деформации при
пропорциональных и непропорциональных циклических нагружениях.
Первая диаграмма ар = о~р(е^) получается при испытании на одно-
одноосное пропорциональное циклическое растяжение-сжатие при постоян-
постоянной амплитуде пластической деформации порядка 0.005. Вторая диа-
диаграмма получается при испытании, состоящем из трёх этапов: первый
этап — одноосное пропорциональное циклическое растяжение-сжатие
при той же, что и при первом испытании, постоянной амплитуде пла-
пластической деформации; второй этап — двухосное непропорциональное
циклическое нагружение по круговой траектории деформаций с ра-
радиусом, при котором интенсивность пластической деформации равна
амплитуде пластической деформации на первом этапе; третий этап —
одноосное пропорциональное циклическое растяжение-сжатие как и на
первом этапе.
На рис. 2.8 показаны диаграммы получаемые при первом и втором
испытаниях. На первом этапе получается диаграмма ар = ap(sZ^) при
??* € [0»^S*i]; на втором этапе — о~а = а а (eg*) при eg* e К^р^*2]'
на третьем этапе — ар* = ар* (eg*) при е^ е К*2'^*з1 • Следует
отметить, что диаграмма на первом этапе является частью диаграммы,
получаемой при первом испытании ар = ap(sZ^) при е^* е [0, е^3] •
Следует также отметить, что окончание этапов соответствует стабили-
стабилизации процессов циклических нагружений.
На втором этапе нагружения по круговой траектории деформаций
изотропное упрочнение на основе уравнений B.152)—B.156) описыва-
описывается дифференциальным уравнением
^С).	B.165)

68
Часть 2. Пластичность
Рис. 2.8. Диаграммы испытаний при пропорциональных и непропорциональных
циклических нагружениях
При получении уравнения B.165) принималось, что на втором этапе
нагружения
dCp
dCp „ dC
7 V <^- 7 V
(IP	(IP
ИЛИ
: 0, и Ср « const.
B.166)
Интегрируя уравнение B.165) с учётом постоянства на втором эта-
этапе параметра непропорциональности А и, соответственно, Фа и Са,
а также используя начальное условие
С = СР, при
=4*1-
можно получить следующее выражение для изотропного упрочнения:
СА - Ср _
In
С а-С
Zu* ~?u*\
B.167)
На третьем этапе нагружения изотропное разупрочнение описы-
описывается также уравнением B.165) в предположении B.166). Интегри-
Интегрируя B.165) с учётом того, что на третьем этапе А = 0 и, соответствен-
соответственно, Ьа = ^о и С а = Со = Ср* = const, а также используя начальное
условие
С = Gд, при ?^# = ?и^2>
можно получить следующее выражение для изотропного разупроч-
разупрочнения:	~ ~
ь ^А ",;р* = 1?0 (^2* - ^L2) •	B.168)
В выражения B.167) и B.168) входят различные значения радиуса
поверхности нагружения, которые в первом и втором испытаниях на
этапах нагружения не определяются. Поэтому принимая, что разности

Глава 3. Эффект дополнительного упрочнения	69
радиусов приближённо равны разностям соответствующих интенсивно-
стей напряжений, можно получить следующие выражения:
<УА \?и*2) ~ °А \?и*)
I °А (g^2) - сгР* (g^3) _ о ( р _ v \	/
гг (fp ) гг (pv \ ~ ° { и* и*2> '	(
&Р* У?и*) — &р* (?и*з)
Для определения параметров дополнительного изотропного упроч-
упрочнения #i и разупрочнения #о строятся кривые в полулогарифмических
координатах:
af\aAfi
Т _ FV _ FV (Fp G \FP FV \\
X - ?u* ?u*l \?u* ^ \_?u*V?u*2)) '
(p \	( p \
ry — ,.,	?ц*2/ ~ аР* \?и*з)
2 — 111	T~P~\	T~P—V'
{l)	(<)
Vp* {el*) - CTp* (<*3)
T _ FP _ FP	(FP rz \FP	FP \ \
x — bu* bu*2 \bu* ^ lbu*2>bu*3j) '
Полученные линейные зависимости,
B.173)
B.174)
позволяют по углам их наклона определить значения #о и д\. Значение
параметра непропорциональности А определяется на основе расчёта по
уравнениям теории пластического деформирования без учёта дополни-
дополнительного упрочнения.
Параметры дополнительного изотропного упрочнения do и d\ опре-
определяются из уравнений B.154)—B.157) на основе следующих выра-
выражений:	п _г
do = ^ _" ,	B.175)
Ьтах ^р
di = \ + CA~°P-	B.176)
/Ю
Заменяя также разности значений радиуса поверхности нагружения
на разности соответствующих интенсивностей напряжений, можно по-
получить следующие формулы:
«О =
?и*з)
di = 1 + аА(<*?-°*(<**\	B.178)
Здесь Ср (s^2) — значение функции изотропного упрочнения (ма-
(материальной функции) при би* = ?^*2*
Значения параметров дополнительного изотропного упрочнения
и разупрочнения, полученные на основе уравнений B.171)—B.174)

70	Часть 2. Пластичность
и формул B.177)—B.178), являются их первым приближением. Для
уточнения их значений проводятся расчёты на основе уравнений теории
пластичности с учётом дополнительного упрочнения, и параметры кор-
корректируются до необходимого совпадения результатов расчёта с экспе-
экспериментальными результатами на этапах второго испытания. На втором
этапе корректируются #i и d\, а на третьем этапе -^и do.
На основе результатов экспериментальных исследований [38-40]
для стали 316 в первом приближении получено: #о = 3.3; #i = 5;
do = 0.30; d\ = 2.9. После корректировки параметры г?о и do остались
прежними, а параметры #i и d\ приняли значения: #i = 12; di = 3.3.
Для этой же стали на основе одноосных испытаний [38] получе-
получены параметры анизотропного упрочнения Еа = 9200МПа, C = 760,
аа = ПО МПа и стабилизированное значение функции изотропного
упрочнения Ср = 180 МПа.
§ 3. Матричное представление уравнений теории
Уравнения связи между скоростями напряжений и деформаций в
матричном представлении для случая мягкого нагружения имеют вид
[Ы] = [Gij] [&j].
Здесь
[?i] = [en ?22 ?зз 2е12 2е23 2е31]т,
]
[hi] = \iPt ёри ёР2 ёР3 ёр2 ё\ъ е\х аи а22 а33 а12
B.
B.
B.
B.
"I
й>\
BJ
B.
179)
180)
181)
182)
т
,
183)
184)
Матрица [С|^] определяется так же как и A.90), а матрица ^
как B.39). Для определения вектора внутренних перемещений [hi]
формулируется следующая система уравнений в тензорном виде:
АР _ 1 3 Sjj&jj	р _ 3 Sjj р
U*	771 О л-* '	ij	О л-* It*'
Ь* Z <7U	J Z gu
hi, = \gi% + (§&4 + &««) С	B.185)
Матрица [С^-] и система уравнений для внутренних переменных имеют
рассмотренный выше вид, если выполняется условие упругопластиче-

Глава 3. Эффект дополнительного упрочнения	71
ского состояния B.164). В случае, когда состояние упругое, то матрица
[CfA и скорость накопленной пластической деформации ?^* принима-
принимаются равными нулю.
Уравнения теории для обобщённого плоского напряжённого со-
состояния имеют такой же вид, как и в случае теории пластического
деформирования без учёта дополнительного упрочнения (см. § 5 гла-
главы 1 части 2). Только в системе для внутренних переменных будет
дополнительное уравнение для радиуса поверхности нагружения
и, соответственно, q? будет определяться на основе B.153). А также
условия упругого и упругопластического состояний имеют вид B.164).

Глава 4
ТЕОРИИ ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ
В УСЛОВИЯХ НЕИЗОТЕРМИЧЕСКОГО
НАГРУЖЕНИЯ И ИОНИЗИРУЮЩЕГО
ИЗЛУЧЕНИЯ
§ 1. Уравнения вариантов теорий
Для всех вариантов теорий пластического деформирования тензор
скоростей деформаций представляется в виде суммы тензоров скоро-
скоростей упругой и пластической деформаций:
ёу = 4-+е?-	B-186)
Упругие деформации при изменении напряжений следуют обобщён-
обобщённому закону Гука, при изменении температуры — закону температур-
температурного расширения, а при изменении флюенса (интегрального потока
ионизирующего излучения) — закону распухания:
' B-187)
(Т <г* Ф),
где Е,и, ат,&Ф — соответственно модуль Юнга, коэффициент Пуассо-
Пуассона, коэффициент температурного расширения и коэффициент радиаци-
радиационного распухания, являющиеся функциями температуры Т и флюен-
флюенса Ф.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и упругопластического состояний,
/КО = I (sij - агэ)(згэ - atj) - С2 = 0.	B.188)
Радиус поверхности нагружения в случае теории пластического
деформирования определяется выражением
С = Ср(Т,Ф,еР,),	B-189)

Глава 4. Неизотермическое нагружение	73
а в случае теории пластического деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, — выражением
С = Ср(Т,Ф,<т«,^,еР*);	B-190)
в случае теории пластического деформирования материалов, обладаю-
обладающих эффектом дополнительного упрочнения, — выражением
C = gee?u*+gTt + g^.	B.191)
Смещение поверхности нагружения определяется следующим урав-
уравнением:
«У = \ g%j
Следует заметить, что в уравнении B.192) ерг- = ?^-, кроме теории
пластического деформирования материалов, чувствительных к виду
напряжённого состояния, и то только тогда, когда радиус поверхности
нагружения зависит от первого инварианта тензора напряжений, т. е.
когда учитывается пластическое изменение объёма.
Пластические деформации определяются на основе ассоциирован-
ассоциированного с B.188) закона течения, и тогда тензор скоростей пластической
деформации для материалов, чувствительных к виду напряжённого
состояния будет задаваться уравнением
Еч дстгэ 2 п*и?и* ?° гу
Здесь n*j,6Q определяются на основе выражений B.106)—B.109).
Для остальных вариантов теорий пластического деформирования
уравнение B.193) будет иметь вид
?Р. = J^-A = \Ч^.	B.194)
При получении уравнений для скорости накопленной пластиче-
пластической деформации, соответствующих вариантам теорий, необходимо
продифференцировать по времени интенсивности активных напряже-
напряжений и функции B.189), B.190) и приравнять эти выражения. Для
материалов, обладающих дополнительным упрочнением, используется
выражение B.191). Разрешая полученные уравнения относительно ?^*,
можно получить следующие выражения для скорости накопленной
пластической деформации:
а) для материалов, чувствительных к виду напряжённого состо-
состояния,
B.195)

74	Часть 2. Пластичность
p* 	 nijeij	* 	 3 TlijCLij _
б) для материалов, обладающих и не обладающих дополнительным
упрочнением,
1
B.196)
Условия упругого и упругопластического состояний для всех вариантов
теорий имеют вид
сг* < С U г?* < 0 - упругость;
сг* = С П ?^* > 0 — упругопластичность.
Здесь радиус поверхности нагружения С определяется в соответ-
соответствии с вариантами теорий согласно B.189)—B.191), а скорость накоп-
накопленной пластической деформации ё^ задаётся выражениями B.195)
и B.196) или аналогичными им.
Кинетическое уравнение накопления повреждений для всех вариан-
вариантов теорий имеет вид
(Ь = 2щЬ-	BЛ98)
Для материалов, чувствительных к виду напряжённого состояния,
энергия разрушения является функцией температуры Т, флюенса Ф,
первого инварианта тензора напряжений ац = 1\(Та) и параметра вида
добавочного напряжённого состояния /ia:
W0 = W0(T^,au,fia).	B.199)
А для остальных вариантов теорий энергия разрушения есть функ-
функция только температуры и флюенса:
Wo = Wo (T, Ф).	B.200)
Критерием разрушения материала, как и ранее, будет достижение
повреждением значения, равного единице.

Глава 4. Неизотермическое нагружение	75
§ 2. Материальные функции и метод их определения
Теорию пластического деформирования материалов замыкают сле-
следующие материальные функции:
Е(Т,Ф), v{T, Ф), ат{Т, Ф), аф(Т, Ф) — упругие параметры;
Еа(Т,Ф), аа(Т,Ф), /3(Т, Ф) — модули анизотропного упрочнения;
СР(Т, Ф,??*) — функция изотропного упрочнения;
Wo(T,<&) — энергия разрушения.
Определяющие функции выражаются через материальные следую-
следующим образом:
ЯП	ЯП
g=Ea+ Caa, g? = CEa, ga = -C,	B.201)
т = дЕ^_Кда^ (Т^ф) о-т = ±^ (Т^Ф)
^?	дТ	(Та дТ К	} ' ^а	(Та дТ К	}
Теорию пластического деформирования материалов, чувствительных
к виду напряжённого состояния, замыкают следующие материальные
функции:
Е(Т, Ф), и(Т, Ф), ат(Т, Ф), аФ(Т, Ф) — упругие параметры;
Еа(Т,Ф,/ia), аа(Т,Ф,/ia), /3(Т,Ф,/1а) — модули анизотропного
упрочнения;
СР(Т, Ф,ац, [1*,8и*) — функция изотропного упрочнения;
Wo(T, Ф, аи, /ia) — энергия разрушения.
Определяющие функции выражаются через материальные также
как и B.201) кроме дополнительных функций, которые имеют вид
Теорию пластического деформирования материалов, обладающих
дополнительным изотропным упрочнением, замыкают следующие ма-
материальные функции:
Е(Т, Ф), и(Т,Ф), ат{Т,Ф), аФ(Т,Ф) — упругие параметры;
Еа(Т,Ф), аа(Т,Ф), C(Т,Ф) — модули изотропного упрочнения;
СР(Т, Ф,??*) — функция изотропного упрочнения;
$о(Т,Ф), $\(Т,Ф), do(T, Ф), d\(T, Ф) — модули дополнительного
изотропного упрочнения и разупрочнения;
\?о(Т,Ф) — энергия разрушения.
Определяющие функции выражаются через материальные также
как и B.201) кроме следующих функций [42, 43]:
qeA = [A - А)$о + А^][(\ - А)С0 + АСХ - С],

76	Часть 2. Пластичность
Ср,	если qeA > 0 / _ ^ _ ^С^
Ср + d0 (Cmax - Ср), если q?A<0 \sA	? де**
Сх = dxCp, А = 1 - (j^y-) ,	B.203)
s, если С > Стах;
О, если С < Стах U q?A < О,
При получении связи между определяющими и материальными
функциями при изменении температуры и флюенса в выражени-
выражениях B.201)-B.203) принимаются [3, 16] неизменными относительные
положения величин радиуса, максимального радиуса и остаточных
микронапряжений нелинейного типа между их предельными значени-
значениями. Следующие из данного положения уравнения имеют вид:
B-2о4)
д
дТ \ Ср
Следует отметить, что при независимости параметра анизотропного
упрочнения C от температуры, что в действительности и имеет место
при обработке [3] экспериментальных данных для ряда конструкци-
конструкционных сталей и сплавов, уравнение B.206) и гипотеза существова-
существования термомеханической поверхности (единая обобщённая поверхность
неизотермического пластического деформирования [16]) при простом
неизотермическом нагружении приводят к одинаковым выражениям
для определяющих функций.
При простом неизотермическом нагружении из уравнений B.188),
B.192) следует, что
сг = С + а = q?ev + qTf + ge*> + (gee* + gaa)i* + {ge* + gf )T.
B.207)
Гипотеза существования термомеханической поверхности при про-
простом неизотермическом нагружении соответствует следующему урав-
уравнению:
а(Т,еР) = Cp(T,eP) + Ea(T)eP + aa(T)[l-eW(-peP)]. B.208)
Дифференцируя по времени B.208), с учётом независимости /3 от
температуры, можно получить

Глава 4. Неизотермическое нагружение
77
dCv
dCv
Сравнение уравнений B.207) и B.209) приводит к выражени-
выражениям B.201), связывающим определяющие и материальные функции.
Существование термомеханической поверхности имеет место неза-
независимо от ограничений на /3 и в состоянии, когда добавочные напря-
напряжения нелинейного типа достигают насыщения, что происходит при
развитых пластических деформациях (гр > 0.005 ч- 0.01).
Определение материальных функций строится на основе изложен-
изложенных в главах 1, 2, 3 части 2 расчётно-экспериментальных методах
и экспериментальных данных при различных уровнях температуры
и флюенса полученных в условиях изотермического нагружения и по-
постоянного уровня флюенса.
§ 3. Материальные функции некоторых
конструкционных сталей и сплавов
Ниже в таблицах для некоторых конструкционных сталей и сплавов
приводятся: модуль Юнга Е\ коэффициент Пуассона v\ коэффициент
температурного расширения ат) параметры анизотропного упрочнения
Еа, /3, о~а, функция изотропного упрочнения Ср и энергия разрушения
Wo ПРИ различных уровнях температуры Т. Коэффициент Пуассона
для всех уровней температуры и для всех материалов кроме стали
12X18 Н9 принимался равным 0.3.
Таблица 2.16
№ и/и
1.
2.
Материал
Сталь 304 [44] (Г = 650 °С)
30 ХГСА [26] (Г = 550 °С)
Е, МПа
1.5- 105
1.2- 105
Еа, МПа
2000
1200
&
1050
370
аа, Мпа
40
90
ср
?р
МПа
Материал
0
90
i Сталь 304
0.001
по
(Г =
= 650 °С)
0.01
125
Таблица
0.05
195
2.17
г
ср,
V
и*
Мпа
Материал
0
100
ЗОХГСА
0.01
107.5
(Г =
:550
°С)
0.01
112.5
Таблица
0.05
127.5
2.18

78
Часть 2. Пластичность
Таблица 2.19
Материал АЛ-25 [45]
Г, °С
20
150
250
350
400
Е, МПа
0.8- 105
0.75 • 105
0.71 • 105
0.45 • 105
0.31 • 105
аТ, 1/град
19.7- 10~6
25.6- Ю-6
25.6- 10~6
25.6- 10~6
26.5 • 10~6
Еа, МПа
14000
13000
5000
5000
5000
100
100
100
100
100
аа, МПа
38
35
27.5
13
6
Wo, Дж/см3
0.65
0.65
1.0
11.3
30.0
Таблица 2.20
Материал АЛ-25 [45]
"\Т, °С
??*^\
20
150
250
350
400
0
120
ПО
60
20
10
0.001
140
130
75
25
12.5
0.003
150
140
85
30
15
0.005
150
140
85
30
15
0.01
135
125
75
25
12.5
0.025
115
105
65
20
9
0.05
105
95
55
17.5
7
0.15
97.5
87.5
47.5
16
6
0.3
95
85
45
15
5
1.0
95
85
45
15
5
Таблица 2.21
т,°с
20
150
300
500
650
Е, МПа
2.05 • 105
1.95- 105
1.8- 105
1.65- 105
1.55- 105
0.3
0.31
0.32
0.33
0.33
Материал
ат, 1/град
16.9- 10~6
17.7- 10~6
18.7- 10
20.0 Ю-6
20.9- 10~6
12X18 Н9
Еа, МПа
700
500
500
500
500
[3]
260
260
260
260
260
аа, МПа
150
124
117
96
60
Wo, Дж/см3
270
270
150
130
135

Глава 4. Неизотермическое нагружение
79
Таблица 2.22
Материал 12X18 Н9 [3]
20
150
300
500
650
0
20
15
10
10
10
0.0005
190
150
130
100
80
0.002
218
179
165
124
107
0.005
228
189
180
133
116
0.01
232
192
184
136
125
0.02
234
200
194
146
134
0.04
254
220
214
166
148
0.1
300
266
260
212
180
0.4
310
276
270
222
188
10
320
286
280
232
194
Таблица 2.23
Г, °С
-200
20
300
500
800
900
Е, МПа
1.8- 105
1.8- 105
1.75- 105
1.67- 107
1.5- 105
1.3- 105
Материал ВЖ-100 [3
аТ, 1/град
10.4- Ю-6
12.4- 10~6
15- 10~6
16.8- 10~6
19.6- Ю-6
20.5 • 10~6
сР,
МПа
330
330
240
220
180
150
Еа,
МПа
1800
1800
1550
1400
500
200
&
300
300
300
300
300
300
(Та, МПа
250
250
180
160
120
ПО
Wo, —^
см5
90
90
65
60
35
25
§ 4. Матричное представление уравнений
вариантов теорий
Уравнения связи между скоростями напряжений и деформаций
в матричном представлении для вариантов теорий в случае мягкого
нагружения имеют вид
гд л _ \п. .1 гл. .1 I \1.]	Г2 210"»
[Лг] = [Gij] [^-] + [ft] •	B-211)
Здесь
= [in
^31J
СТ\2
Для теории пластического деформирования и теории пластического
деформирования материалов, чувствительных к виду напряжённого
состояния, в случае пренебрежения пластическим изменением объёма
вектор внутренних переменных имеет вид
0>П ^22 «33 «12 «23 «31 ^\ •
B.212)
= \гр
-33
С23

80
Часть 2. Пластичность
А для теории пластического деформирования материалов, облада-
обладающих дополнительным изотропным упрочнением, вектор внутренних
переменных имеет вид
[hi] = [^* гр
12 е\ъ
Матрица [CV/] и вектор
составляющих, т. е.
Р	Г^ Г^	1
<Ьо1 Cl\\ u-22 ^33 ^12 ^23 ^31 ^ Umax 6<y
B.213)
bi\ состоят из упругой и пластической
= [С^] + [С?.],	B.214)
= №1 + [^1.	B-215)
где упругие составляющие [Cfj] и [d|] определяются выражения-
выражениями A.91) и A.144), а пластические составляющие [Cfj] и [6f] для
теории пластического деформирования определяются на основе B.39)
и следующего выражения:
Sc
22
zsl2
2sh
2s
31 J
B.216)
Для теории пластического деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, в случае пренебрежения
пластическим изменением объёма матрица [CfA определяется на осно-
основе B.132), а вектор [Ь^] имеет вид
^22
nh
zn12
9Г7*
zn23
B.217)
Для определения внутренних переменных B.212) и B.213) форму-
формулируются системы уравнений на основе B.191)—B.198), B.203).
Уравнения связи между скоростями деформаций и напряжений
в матричном представлении для вариантов теорий в случае жёсткого
нагружения имеют вид
[hi] = [Qij] [ij] + fe] •
B.218)
B.219)

Глава 4. Неизотермическое нагружение
81
Матрица [Dij] и вектор [d^] состоят из упругой и пластической
составляющих, т. е.
[Dij] = [D\j] - [DlkWDlj],	B.220)
[di] = [df] - Щ]Щ\]	B.221)
где [D\j] и [d|] определяется выражениями A.91) и A.146), а пласти-
пластические составляющие [D^] и [d?] для теории пластического деформи-
деформирования определяются на основе B.42) и следующего выражения:
Матрица
равен
<Si 1 <Si
^22"
S336
= -2G-
511522
22 22
Son S
<Si o<S
<Si o<S
12°22
1
+ 3G 2
с4"
22
533
Zs
3\ J
B.222)
определяется как B.43), а вектор
3G 3 1
SmS
11*12
523
S3\
OOOUOO Cnncin Onnono «_>OO«_
<Sqq 5'
33^22 О33°33 О33°12 О33°23 °33
«5qq on
533
<Si o<S
а31г
12 12
531512
S23 523531
S23 531531
a
Jt + <
g
2(agf ¦
О|*Ф)
-2G
1 3 1
E* + 3G2~Z
" S
S
S
S
S
_ S
11
*
22
*
33
*
12
*
23
*
31 J
B.223)
Для теории пластического деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, в случае пренебрежения
пластическим изменением объёма матрица [D|fc][D?.] и вектор [Z)|-] \dpA

82
Часть 2. Пластичность
равны
3G
?** + 3G 2
n31n
П11П22 П11П33 П11П12
/t/QQ/t/i 1	I Ьс\С\ I Ьс\С\
n33nll n33n22
n12nll n12n22
П23П11 П23П22
n31n22
/t/QQ/t/QQ	(Ьс\С\(ЬлС\
n33n33	П33П12
n12n33	n12n12
П23П33	П23П12
П11П23	П11П31
I V С\ С\ I V С\ О	/ С/Q Q / С/О 1
n33n23	n33n31
n12n23	n12n31
П23П23	П23П31
31nll
n31n33 n31n12 n31n23 n31n31
B.224)
nllnll	nlln22	nlln33
/i/oo/i/i i	/i/oo/7/oo	/i/oo/7/oo
n33nll	n33n22	n33n33
77/1о77/11	77/io77/oo	TT/ioTT/oo
П23П11	П23П22	n23n33
n31nll	П31П22	П31П33
-2G-
nlln12 nlln23 П11П31
n22n12 n22n23 n22n31
П23П12 П23П23 П23П31
П31П12 П31П23 П31П31
as
2«T +
1
3 1
+ 3G 2 <
22
^23
. B.225)
Для определения внутренних переменных B.212) и B.213) фор-
формулируется такая же, как и ранее для мягкого нагружения система
уравнений, кроме уравнений для скорости накопленной пластической
деформации, которые имеют следующий вид:
1
^ =
?* + 3G
3G
3G-
B.226)
B.227)
Уравнение B.227) относится к теории пластического деформиро-
деформирования материалов, чувствительных к виду напряжённого состояния,
в случае пренебрежения пластическим изменением объёма.

Глава 4. Неизотермическое нагружение	83
§ 5. Уравнения теорий в случае обобщённого
плоского состояния
Рассматривается, как и ранее, три вида нагружения:
а) мягкое нагружение
[xj] = [&u <J22 <J33 ЫТ,	B.228)
Ш = [ёп ^22 ^зз 2г12]т.	B.229)
Для теории пластического деформирования
[Ы} = [ёр, ери ер2 ер2 ап а22 аХ2 ou]T,	B.230)
•Р
и* =
Ж
2	иТф г>Флч
1 -В Ф
^11 о * гг*' 22 о * гг*' 12 о * и*'	\
Z GU	Z (Ju	Z Gи
Для теории пластического деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, в случае пренебрежения
пластическим изменением объёма,
\hj\ — [^S* ^П ^22 ^12 ^11 ^22 ^12 ^] >	B.233)
L ""*"" ^ 2п*12&12 - Bjt - В?ф] , B.234)
.р _ 3 ^п_ -р	-р _ 3 П22 .р	.р _ 3 77^2 -р	/
fcll — 9 n w*' 22 "" 9 n* w*' 12 "" 9 п* и*'	\
Li I ill*-	^ '"U	U
Для теории пластического деформирования материалов, обладаю-
обладающих дополнительным упрочнением,
, ерп ёр2 ё\2 аи а22 аХ2 С Стах Со^. B.236)
Уравнения для скорости накопленной пластической деформации и
скоростей пластической деформации такие же как и B.231) и B.232).
А для радиусов С и Стах имеют место уравнения
B.237)
тахФ-	B.238)
Остальные уравнения для всех вариантов теорий одинаковы и име-
имеют следующий вид:

Часть 2. Пластичность
О	\	/О
) ё
«22 = о g^22 + ( о &?22 + ?аа22 ) ёи* + о
о	\ о	/	\ о
+(§.
3
?*а22) Ф, B.239)
I; = — [ац^ + a22ef2 + (an + 022) (e^ + ?22) +
ё\\ = — \&\\ — v (&22 + 0"ззI + ?л\ + OiffT + aff Ф,
Г *	( ' i * М i 'V I вТ т1 I еФяч	/о о л с\\
^22 ^ 15 [^22 ~~ ^ (,^11 ~г <^3/J ~г ^22 ~^ ^22 ^ "¦" ^22 ^»	(Z.Z4UJ
?12 = —^ СГ12 + ??о + аиТ + 4f Ф;
б) смешанное нагружение
N = [?n ?22 a33 2?12]T,	B.241)
[ili] = [<тц ^22 ?зз ст12]Т.	B.242)
Для вариантов теорий пластического деформирования материалов,
обладающих и не обладающих дополнительным упрочнением, скорость
накопленной пластической деформации определяется выражением
* + 3G*
A-г/)аи
?l?<b) + 1 - 2i/ 3 ?33^33
- а|2фФ) ,
A - 1/)<т*	1 - v 2 a*	J'
B.243)
С3 (gnJ + (s*nf
Для теории пластического деформирования материалов, чувствитель-
чувствительных к виду напряжённого состояния, в случае пренебрежения пласти-
пластическим изменением объёма, выражение для скорости накопленной пла-
пластической деформации аналогично B.243). Только в этом выражении
Е*, Вт, ?>ф,сг* и компоненты девиатора s*j заменяются, соответствен-
соответственно, на Е**, Bj, Bf, n* и n*j.

Глава 4. Неизотермическое нагружение	85
Остальные внутренние переменные для всех вариантов теорий опре-
определяются так же, как и в случае мягкого нагружения на основе
уравнений B.232), B.235), B.237)-B.239).
Для всех вариантов теорий компоненты вектора [уг] определяются
следующими уравнениями:
(e22 - гр2 - agf -
&22 = —^Ц [(ё22 - ё\2 - agf -
(ёп ~ ipu - ofit - aff Ф)]
+ (е22 - ip22 - agt - aff Ф)] -
- (^ + ep22) + agf + аЦФ + ° + ffl^ ^зз, B.244)
в) смешанное нагружение
[xj] = [iu ?22 <тзз 2?12]т,	B.245)
г * 1 г*	*	*	* 11	/оол/2\
[Уг\ = [^1 ^22 ^33 О~\2\ •	yZ.ZW)
Для всех вариантов теорий с соответствующей заменой выражений
для случая материалов, чувствительных к виду напряжённого состо-
состояния, уравнение для скорости накопленной пластической деформации
имеет вид
1
Я. + 3G*
A + У)8'п (in - afft - aff Ф) + 2s\2
, 3 (S22 + ^S*l) 0-22
2	а
, B.247)

Часть 2. Пластичность
Остальные внутренние переменные определяют, как и ранее, на основе
уравнений B.232), B.235), B.237)-B.239).
Компоненты вектора [iji] для всех вариантов теорий определяются
следующими уравнениями:
<тц = Е(ёп - ери - aff Г - aff Ф) + и(а22 + а33);
(•	-V	sTrh	еФяч\ , 1 — ^2 •	1/A+1/) . . .р .
822 = -v(eu ~ qi - aff T - aff Ф) + —^^22	v ^ У сгзз + q>2 +
+ а|^Т + а|^Ф, B.248)
взз = -v(in - ери - aff Т - aff Ф) - ^^U22 + ^ а33 -

Часть 3
НЕУПРУГОСТЬ

Глава 1
ТЕОРИЯ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ
§ 1. Основные положения и уравнения
Материал однороден и начально изотропен. В процессе неупругого
деформирования в нём может возникать только деформационная ани-
анизотропия. Тензор скоростей деформаций представляется в виде суммы
тензоров скоростей упругой и неупругой деформаций:
Следует отметить, что здесь нет условного разделения неупругой де-
деформации на деформации пластичности и ползучести.
Упругие деформации при изменении напряжений следуют обобщён-
обобщённому закону Гука:
ё$, = ±[&ц-иC&о5ц-&ц)],	C.2)
где Е,и — соответственно модуль Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и неупругого состояний. Поверхность нагружения изотропно расши-
расширяется или сужается и смещается в процессе нагружения. Начальная
поверхность нагружения может быть стянута в точку. Текущая поверх-
поверхность нагружения определяется процессом нагружения. Воздействие
фактора времени тоже есть процесс нагружения. Уравнение поверхно-
поверхности нагружения принимается в следующем виде:
/К) = | (Sij - atj)(stj - atj) -C2=0.	C.3)
Здесь s*j = Sij — dij — девиатор активных [4] напряжений; sij —
девиатор напряжений. Тензор ац (добавочных напряжений, остаточных
микронапряжений) характеризует смещение поверхности нагружения
в девиаторном пространстве напряжений, т. е. направленное (анизо-
(анизотропное) упрочнение. Скаляр С отвечает размеру (радиусу) поверхно-
поверхности нагружения и характеризует изотропное упрочнение. Тензор сме-
смещения dij и радиус С являются функционалами процесса нагружения.

Глава 1. Теория неупругого деформирования
Для радиуса поверхности нагружения принимается следующее
уравнение:
С = q?el, - qR.	C.4)
Здесь е^* — длина дуги неупругой деформации (накопленная неупру-
неупругая деформация); г^ — интенсивность скоростей неупругой деформа-
деформации (скорость накопленной неупругой деформации); q?,qR — функции,
подлежащие экспериментальному определению.
Дифференциальная форма соотношения C.4) развивает идеи, вы-
выдвинутые в работе [46]. Первое слагаемое в уравнении C.4) отвечает
механическому упрочнению. По знаку q? определяются циклически
упрочняющиеся (q? > 0), стабильные (q? = 0) и разупрочняющиеся
(q? < 0) материалы. Параметр qn обеспечивает возврат механических
средств при отдыхе, отжиге.
Смещение поверхности нагружения определяется уравнением
Здесь g,g?,ga,g^,g^ — функции, подлежащие экспериментальному
определению.
Первые три слагаемых в уравнении C.5) описывают процессы об-
образования и снятия добавочных напряжений при неупругом деформи-
деформировании, а два последних слагаемых обеспечивают снятие добавочных
напряжений при отдыхе, отжиге. Параметры qR,g^,g^ в уравнени-
уравнениях C.4) и C.5) являются функциями повреждения, что позволяет
описать разупрочнение материала при ползучести, т.е. третью стадию
ползучести. Зависимость параметров от повреждения в уравнении для
добавочных напряжений ранее рассматривалась в работе [47].
Неупругие деформации зависят от истории нагружения и являются
функционалами процесса. Считается, что поле скоростей неупругой де-
деформации в пространстве напряжений имеет потенциал. Тогда, прини-
принимая в качестве потенциала функцию C.3), тензор скоростей неупругой
деформации будет определяться уравнением (ассоциированный с C.3)
закон течения, градиентальный закон течения)
?nij = —А = - Щ-е^.	C.6)
Здесь а^ — интенсивность активных напряжений.
Для получения уравнения для скорости накопленной неупругой
деформации необходимо продифференцировать по времени интенсив-
интенсивность активных напряжений <т* и функцию С и приравнять эти выра-
выражения, т.к. из C.3) следует, что
< = С.	C.7)

90	Часть 3. Неупругость
Итак
d(ju 	 3 Sij [Sij — dij) 	 3 SijSij sij?ij
dt	2	O*u	2 O*u	O*u
3 SjjCLij
. H
uu J	\	uu	* °u
	 _ ^ij^ij _ о &ijJ>ij_'H _ ( н* |	*\ -н _|_
*	Ьп / *\2 и* \Ssbu "r&aS/fcu* "г
-L СГ^/7*^ =	^ ^ — (сг -\- СГ РН* -U ХГ /7* ^ ГН -\-
s bu * Sa au
^ = <А - дд.	C.9)
Приравнивая выражения C.8) и C.9) и разрешая относительно
?^, можно получить уравнение, связывающее скорость накопленной
неупругой деформации и скорости напряжений,
1 ,и «„.„ , „«,	(ЗЛО)
^* = ^s + g + geC + ga<, BR = qR + gfe1^ + g^a;,
* н	о * . .
Для получения уравнения, связывающего скорость накопленной
неупругой деформации и скорости деформаций, в уравнение C.10)
подставляется выражение, следующее из закона Гука и ассоциирован-
ассоциированного закона течения C.6),
ён = 2Ge% = 2G (ё„ - ё",) = 2G (ёц - ё?Л = 2G (-¦ ¦ - 3 8« -н
(З.П)
Дополнительно следует отметить, что
Подставляя C.11) в C.10) с учётом C.12) и разрешая относительно
?^, можно получить уравнение, связывающее скорость накопленной
неупругой деформации и скорости деформаций,
1
* + 3G
C.13)
Уравнение C.10) соответствует мягкому нагружению, а уравнение
C.13) — жёсткому нагружению.

Глава 1. Теория неупругого деформирования	91
Условия упругого и неупругого состояний следуют из того, что
для неупругого состояния необходимо, чтобы изображающая точка
процесса нагружения находилась на поверхности нагружения и опре-
определяемая скорость накопленной неупругой деформации была положи-
положительна, а упругое состояние следует при нарушении любого из двух
упомянутых условий. Тогда условия упругого и неупругого состояний
будут иметь следующий вид:
а* < С U ёни* < 0 - упругость,
(о. 14)
<т* = С П ?^ > 0 — неупругость.
Здесь под ё^* подразумевается выражение, задаваемое уравнени-
уравнением C.10) либо C.13) или любым другим уравнением, связывающим
скорость накопленной неупругой деформации и любой набор скоростей
напряжений и деформаций (смешанное нагружение).
Из уравнения C.10) следует, что нагружение, соответствующее
движению по поверхности нагружения, не всегда является нейтраль-
нейтральным (упругим). При скоростях деформирования, когда пренебрежимо
малы временные эффекты, догружение по касательной к поверхности
нагружения, т.е. движение по поверхности, является нейтральным.
При меньших скоростях деформирования движение по поверхности
нагружения может не являться нейтральным. Причём на одной части
поверхности состояние может быть упругим, а на другой — неупругим.
Для описания процесса накопления повреждений используется
энергетический подход. В качестве энергии, расходуемой на созда-
создание повреждений в материале, принимается энергия, равная работе
добавочных напряжений на поле неупругих деформаций. В процессе
нагружения имеют место: накопление повреждений за счёт работы
добавочных напряжений, залечивание повреждений и охрупчивание
материала. Следует отметить, что залечивание повреждений и охруп-
охрупчивание связаны с длительностью процесса нагружения. Кинетические
уравнения накопления повреждений, залечивания и охрупчивания при-
принимаются в следующем виде:
W = -gwW.	C.16)
Здесь и — мера повреждения (и ? [0, 1]); W — энергия разрушения;
gu,gw — функции, подлежащие экспериментальному определению.
Первое слагаемое в уравнении C.15) описывает процесс накоп-
накопления повреждений за счёт работы добавочных напряжений на поле
неупругих деформаций. Второе слагаемое в уравнении C.15) описывает
процесс залечивания повреждений, интенсивность которого зависит
от уровня повреждения, а также характера напряжённого состояния.
Уравнение C.16) описывает изменение энергии разрушения (начальная
энергия разрушения равна Wq и определяется при пластическом дефор-

92	Часть 3. Неупругость
мировании) за счёт процесса охрупчивания материала, интенсивность
которого зависит от уровня энергии разрушения и уровня напряжённо-
напряжённого состояния.
Критерием разрушения материала будет достижение повреждением
предельного значения, обычно принимаемого равным (или близким)
к единице.
§ 2. Материальные функции
Теорию неупругого деформирования замыкают следующие опреде-
определяющие параметры и функции, подлежащие экспериментальному опре-
определению:
Е, v, qe, QR, g, ge, ga, gf, g?, gu, gw, Cp0, Wo.	C.17)
Здесь Cpo и Wo — начальные значения радиуса поверхности нагруже-
ния и энергии разрушения. Используя закономерности деформирования
и разрушения материала в условиях пластичности и ползучести, число
функций, подлежащих экспериментальному исследованию, может быть
сокращено, и они приобретут понятный механический смысл.
При скоростях деформирования, когда пренебрежимо малы эффек-
эффекты связанные с длительностью процесса, т.е. при пластическом де-
деформировании, радиус поверхности нагружения, энергия разрушения,
а также образование добавочных напряжений в условиях одноосного
растяжения определяются [3, 16] следующими зависимостями:
С = Ср(е^),	C.18)
W = W0,	C.19)
а = Еаен + аа [1 - ехр (-(Зен)} (ени* = е^,ен = ер). C.20)
На основании уравнений C.18) и C.20) в § 1,2 главы 1 части 2
получено, что
Че = ^Ч	C.21)
g=Ea + /3aa, g? = f3Ea, ga = -f3.	C.22)
Здесь Ср(г^), Еа, аа и (З уже имеют вполне понятный механический
смысл.
В условиях установившейся ползучести, когда уравновешиваются
два противоположных процесса — механического упрочнения и тер-
термического разупрочнения, скорость установившейся неупругой дефор-
деформации (деформации ползучести) определяется [48] уровнем напряже-
напряжения. Установлено [47], что при деформировании материала в условиях
установившейся ползучести не происходит изменения добавочных на-
напряжений. Таким образом, можно сделать вывод, что скорость устано-

Глава 1. Теория неупругого деформирования	93
вившейся ползучести enst связана с радиусом поверхности нагружения
и интенсивностью добавочных напряжений конечными зависимостями
?н = Р (С) ?н = Р (а )	C 23)
При одноосной ползучести смещение центра поверхности нагружения
происходит только по оси растяжения, и тогда
аи = -а а22 = --а а33 = --а ен = ен
з ^	з > ^	з '	' {32А)
где а и ?н — смещение центра поверхности нагружения (добавочное
напряжение) и неупругая деформация вдоль оси растяжения. В этом
случае на основании C.24) уравнения C.4) и C.5) примут вид
С = q?eH - qR,	C.25)
a = geH + (g?eH + gaa) iH - (g?eH + g^a) .	C.26)
В условиях установившейся ползучести, как ранее было сказано, имеют
место соотношения
С = 0, а = 0, гн = eHst.	C.27)
Далее на основании C.25)-C.27) можно получить следующие урав-
уравнения:
qeiH8t -qR = 0,	C.28)
Здесь следует отметить, что уравнение C.29) должно выполняться при
изменяющейся деформации ползучести гн, а добавочное напряжение
остаётся постоянным. На основании этого следует, что множитель при
tp в уравнении C.29) должен быть равен нулю. Тогда на основании
выше сказанного из уравнений C.28), C.29) и C.23), C.24) можно
получить следующие зависимости:
Для описания разупрочнения при ползучести (третья стадия ползуче-
ползучести) принимается зависимость функций Рс и Ра от повреждения и, т. е.
Pc = Pc{C,w), Ра=Ра(аи,ш).	C.31)
Залечивание материала зависит от характера напряжённого состояния.
При одноосных сдвиге или растяжении залечивания нет, а при сжа-
сжатии есть, и чем больше сжатие, тем более интенсивно залечивание
материала. Поэтому принимается, что параметр gu зависит от первого
инварианта тензора напряжений, т. е.
ёш = K°ii)	C-32)

94	Часть 3. Неупругость
A\(Та) = аи = ап+ а22
Охрупчивание материала принимается зависящим от уровня напряже-
напряжений, т. е. от второго инварианта девиатора напряжений или интенсив-
интенсивности напряжений,
gw = рЫ-	(з.зз)
Таким образом, теорию неупругого деформирования замыкают следу-
следующие материальные функции, подлежащие экспериментальному опре-
определению:
Е,и — упругие параметры;
Ср(г^) — функция изотропного упрочнения;
Еа,сга,Р — параметры анизотропного упрочнения;
Wo ~~ начальная энергия разрушения;
Pc(C,uj), Pa(cLu,Lj) — функции изотропной и анизотропной ползу-
ползучести;
Х(ац), р(аи) — модули залечивания и охрупчивания.
Функции изотропной и анизотропной ползучести предлагается ап-
аппроксимировать следующими выражениями:
Рс(С,и;)=ехр(Ъс)\С-Ср0\ПсA-и;)-т",	C.34)
Ра{аи,ш) =ехр(Ъа)(аи)п«(\ - и)~т".	C.35)
Здесь Ьс,Ьа,пс,па,тш — параметры изотропной и анизотропной ползу-
ползучести; Сро — предел длительной прочности.
Модули залечивания и охрупчивания предлагается аппроксимиро-
аппроксимировать следующими выражениями:
О,	если аи ^ 0;
>(Ь\)\ац\Пх, если аи < 0;
р{^и) — ехР {Ьр)(аи)пр.	C.37)
Здесь Ь\,Ьр,п\,пр — параметры залечивания и охрупчивания.
§ 3. Связь теории неупругого деформирования
с общими теориями
В качестве общих теорий, как и в части 2, рассматриваются теория
Кадашевича [19], в которой неупругое деформирование описывает-
описывается общим тензорно-линейным дифференциальным уравнением второ-
второго порядка и общая математическая теория пластичности Ильюши-
Ильюшина [13, 14].
Тензорно-линейное уравнение Кадашевича имеет вид

Глава 1. Теория неупругого деформирования	95
Необходимо выяснить, относится ли теория неупругого деформирова-
деформирования к классу общей тензорно-линейной теории Кадашевича.
Из C.6) и C.7) следует
s^-axj = Z-C^.	C.39)
Дифференцируя C.39) по накопленной неупругой деформации е^* и
используя C.4) и C.5), можно получить
3 g^i ga [S" 3 ° del. \ ^ e«ut ?v +
2
1 _ 2
?» ~ 3
ИЛИ
-ёа + 8?^) %¦ + P- = I U ~ g-f) 4 +
ь J	иь	° \	bu* J
-qR^)^ + 2-C-^. C.40)
?u* J d?u* 6 d(?u*)
Из сравнения C.38) и C.40) следует, что:
= \\g~ ga
Коэффициенты тензорно-линейного уравнения в данном случае будут
зависеть от параметров г^*, e^,au,C,uj, которые являются функцио-
функционалами процесса нагружения.
Итак, можно сделать вывод, что теория неупругого деформирова-
деформирования принадлежит к классу общей тензорно-линейной теории второго
порядка и является вполне конкретным вариантом этой общей теории,
но с более сложной структурой коэффициентов общего тензорно-ли-
тензорно-линейного уравнения.
В векторном представлении Ильюшина уравнения теории неупруго-
неупругого деформирования будут иметь вид
_ _ _ _ с
9 — 9е -I- 9Н 9е —	И 49^

96	Часть 3. Неупругость
§ = ±(S-A),	C.43)
dC = qedsH - qRdt,	C.44)
dl = gd3" + (g?3H + gaA) ds" - (gf3" + gf A) dt.	C.45)
Дифференцируя C.43) по длине дуги деформации s и используя C.42),
C.45), можно получить следующее уравнение:
где
|+iV1^+iVo5 JDo3 + D1^+D2^|)	C.46)
ds	as	ds	ds
M4	/ Мл/de-V1 М3
= — -М2, ЛГ1 = ^1 + — j^j
2G{ds) '	C47)
= M4,
D, = М, ^ - M3 P4r )[=-) , D2 = M3(^-
ds I	\ d.t I yds J	\ ds
gf(Aco)C-qR(s\C,c
При развитых неупругих деформациях можно принять
7 н	,2 н
as ~ 1 а g ~ о лн ^ •	/о дй^
ds	ds
И тогда коэффициенты уравнения C.46) будут иметь вид
No= 2G
C.49)
Уравнение C.46) полностью совпадает по структуре с уравнением сле-
следующим из общей математической теории пластичности Ильюшина.
Таким образом, теория неупругого деформирования является конкрет-
конкретным вариантом общей математической теории пластичности Ильюшина
при полном сохранении всей структуры уравнений этой теории.

Глава 1. Теория неупругого деформирования
97
§ 4. Матричное представление уравнений теории
Уравнения связи между скоростями напряжений и деформаций в
матричном представлении для случая мягкого нагружения имеют вид
Здесь
«] — [ё\\ ?22
2е12 2е
23
C.50)
C.51)
а22
d23
С W Со
3.52)
«] = [С«] + Ш •	C.53)
[bi] = [ВД	C.54)
^][а,-], [6е] = 0, [ё?] = [С^.] [а,-] + [6
Матрицы [Cfj] и [Cfj] определяются соответственно как A.91)
и B.39). Вектор [Ь"] имеет следующий вид:
Ь33
'*12
Э31 J
C.55)
Следует отметить, что здесь в выражениях B.39) и C.55) Е* и BR
вычисляются на основе формул C.10).
Для определения вектора внутренних переменных [hi] формулиру-
формулируется следующая система уравнений для кратности записанная в тен-
тензорном виде:
J_ [3 stj&
Е* 2 ol
dR
я	/
Р		 I —
ьи* [ q
C.56)
W =-gwW,
Матрица [Cfj], вектор [Щ] и система уравнений для внутренних пере-
переменных имеют рассмотренный выше вид, если выполняются условия
неупругого состояния C.14). В случае, когда состояние упругое, то
4 В. С. Бондарь

Часть 3. Неупругость
матрица [Cfj], вектор[Щ] и скорость накопленной неупругой деформа-
деформации ё^* принимаются равными нулю. Следует отметить, что в упругом
состоянии добавочные напряжения а^-, радиус поверхности нагруже-
ния С, энергия разрушения W и повреждение ио могут изменяться.
Уравнения связи между скоростями деформаций и напряжений в
случае жёсткого нагружения имеют следующий вид:
Ы = Ш [ij] + Ы ,
=0,
C.57)
C.58)
в =
Матрицы [Dfj] и [Dfj] определяются, соответственно, как
и B.42), а матрица [D\k][D\-\ — как B.43). Вектора [df\ и [di]
ветственно, равны
A.92)
соот-
соот1
Е* + 3G 2 с*и
22
S33
C.59)
= -2G
1
E* + 3G 2
s
s
s
s
4<
11
*
22
33
*
12
523
S
*
31 J
C.60)
Для определения вектора внутренних переменных [hi] система уравне-
уравнений имеет вид C.56), но только для скорости накопленной неупругой
деформации будет иметь место уравнение
C.61)
Аналогично, как и в случае мягкого нагружения, эти уравнения имеют
место при неупругом состоянии. При упругом состоянии [Dfj], [<Щ\ и
ё^* принимаются равными нулю.
Следует отметить, что матрицы [Cfj], [Щ^] и вектора [Щ], [<Щ] явля-
являются функциями внутренних переменных [hi].

Глава 1. Теория неупругого деформирования
99
§ 5. Уравнения теории в случае обобщённого
плоского состояния
Рассматриваются три вида нагружения:
а) мягкое нагружение
[Xj] = [&п 62 <33 СГ\2] »
IJiA = ?" ?" ?" s^2 an d22 ai9 С W to
L J I
1 | 3 S*i<7n + S22<32 + S22<3-33 + 2g*2Q"l2 , UR
3 S*2 -и
аи = |
C.62)
C.63)
C.64)
C.65)
A-2),
to = —
^11 = ^ [^1 -^(^22 +СГЗЗ)] +^ll,
^22 = ~B [^22 - У (<J\\ + ^33)] + ^22'
^33 = ^ [0-33 - ^ (<hi + ^22)] - (en + ^22)'
1 + 1/ . .H
?\2 =
б) смешанное нагружение
hi
e22	азз
0^22	^33
an	a22
C.66)
;2 + 2A - ^)st2?l2
C.67)
C.68)
C.69)
+
1-21/3 ^
-^2 a.

100	Часть 3. Неупругость
f + (hf
3 (sn) + (shT + 2iysnsh + 2A - v) (s*.
G« = G-±	5	 ,
2A-is) (a*J
•h _ 3 ?n_ .H /i ^^ o) pH — - —pH	C 7
2 cr*	'	2 cr*
ац W 1 <-> zj,
a12 = - gs:^ + ' " "H
a; = — [an^! + a22^2 + (an + a22) Омл + ^22) + 2«i2^2] - ёши>
^ii =	2 K^11 ~^ii) + ^(^22 -^22)] + угт^^зз,
fe - ^22) + ^ (en - e?i)] + т^- ^зз,	C.71)
—^ [(?22 ?22) + v (?n ?n)] + -r-^ азз,
\—V	Y — V
' е22Л ~ lell ~re22J
E ,.
в) смешанное нагружение
N = [?n	а22	стзз	2е12]т,	C.72)
Ш = [о-ц	?22	?зз	^12]Т,	C.73)
« ?fi ?2*2 ?^2	an	a22	a12 С	W w\T, C.74)
3 (S2*2 + ^g*l) 0-22 + (S33
2	<
9	/9	\	/9
= о ^?11 + ( о gsE\\ + &аП ) ?^* - 1 о ее ?U + i
о	\ о	/	\ о
2	-и /^2 н	А -и /^2 _я
a12 — Б" §"?12 + о" &?12 + §"aa12 ?u* ~ \ 4 &e 8
3	\3	У	\3

Глава 1. Теория неупругого деформирования	101
[аП?п
аи = Е(ёп -ёп) + v{byi + сгзз);
.Н Ч	1 — I/	.	1/A + I/) .	.Н	/О -^ч
1 -^ii) + —^СГ22	^ СГ33+?22>	C-76)
Со = — [аП?п + «22^22
.н ч	1/A + I/) .	1 — I/ .
?и)	а22 + -^-а
Е
^; (^12 -^12)-
§ 6. Уравнения теории в случае одноосного
напряжённого состояния
В условиях одноосного напряжённого состояния все компоненты
тензора напряжений равны нулю, кроме напряжения <тц. Это напря-
напряжённое состояние соответствует Р-опытам, и здесь возможны две
программы нагружения:
а) мягкое нагружение
[Xj] = [&n 0]T (G22=0),	C.77)
[j/i] = [en ?22]T (?22=?зз),	C.78)
[h] = \i"u* iHu dn С W
C.79)
, если <т* = С П ?^ > 0;
\ ^*	0,	если a*<CUelu^ 0;
??! =^s|esign(s]e1),	C.80)
2	.H /2 н	\ -и /2 в н п
3	\3?	аугг*\^з?	a
C.81)
¦ cm , -н ¦ ^^П А -н
?ll=-g-+?ll' ?22 =	^	2?ll>
б) смешанное нагружение
N = [?n 0]т (<722=0),	C.82)
fe] = [*ii ?22]Т (?22=?зз),	C.83)
[Л] = [е^ ёУ, о„ С WlJ\T
C-84)
=?

102	Часть 3. Неупругость
если < = С П ё?, >0;
0,	если а*и<Сиё»и^О;
C.85)
\ gfe"i + g?«
О
C.86)
Gц =Е(ёп-ени), ?22 = -z/(?n -ени) - -ёни.
§ 7. Критерии длительной прочности при одноосном
напряжённом состоянии
Для ползучести при постоянном напряжении растяжения компонен-
компоненты напряжений и внутренних переменных равны:
<7i 1 = а, G22 = 0, <7зз = 0, а \2 = СГ23 — 01 = 0,
2	11
аП = 3 а' а22 = ~за' «33 = -за' «12 = «23 = «31 = 0,
Sn = -(сг - а), 522 = -^(а ~ «)> 533 = -^(а ~ «)' S*\2 = sh = 4\ = ®'>
{	{	C.87)
аи = а, аи = а, а^ = а - а, г^ = гн, е1^ = гн; а* = а.
Тогда, используя C.87), уравнения C.65) примут следующий вид:
лн = QePcjC) + (g+g??H + gaa) Ра(а) ({ _ л-т^	/о
q+g + geH + ga	[	}	К '
(a)(l-u;)-m"},	C.89)
\u;)-m"],	C.90)
W = -p(a)W, ^ = ^r-	C.91)
В условиях установившейся ползучести имеет место соотношение
Pc(Cst) = Pa(ast) = eHst.	C.92)
Тогда, подставляя C.92) в уравнения C.88)-C.91), можно получить
следующие уравнения для второй и третьей стадий ползучести:
iH = iHst{\ -со)-т",	C.93)
а = (g+geeH + gaast) [e»t - Pa(ast)} A - a;)"» = 0,	C.94)
C = q? [ib - Pc{Cst)\ A - u)~m« = 0,	C.95)

Глава 1. Теория неупругого деформирования	103
W = -p(a)W,	C.96)
ш = a^"t(lw")~m\	C.97)
Здесь следует отметить, что добавочные напряжения и радиус по-
поверхности нагружения на третьей стадии ползучести не изменяются
и остаются такими же как и на второй стадии. Разупрочнение на тре-
третьей стадии ползучести обусловлено только повреждением материала.
Аналогичное утверждение содержится и в работе [47].
Интегрируя уравнение C.96) при начальных условиях
W = W0, при ? = 0,	C.98)
можно получить следующую зависимость, характеризующую измене-
изменение энергии разрушения в процессе охрупчивания материала:
W = Woexp(-pt).	C.99)
Подставляя C.99) в C.97), можно получить следующее уравнение для
повреждения:
,= af',expW .	C.100)
Wo A — и) °"
Следует отметить, что это уравнение описывает процесс накопления
повреждения на второй и третьей стадиях ползучести вплоть до разру-
разрушения.
Интегрируя уравнение C.100) при начальных условиях
и = ии при ? = 0,	C.101)
можно получить следующую зависимость, связывающую повреждение
и время:
—1— A - и)т"+х = —1-— A - их)т"+х + ^ф- [1 - exp (pb)].
C.102)
Здесь ио\ — повреждение полученное материалом до начала ползу-
ползучести и на первой стадии ползучести.
Условием разрушения является достижение повреждением предель-
предельного значения, т. е.
и = 1 при t = tp.	C.103)
Подставляя условие C.103) в уравнение C.102) и разрешая относи-
относительно времени разрушения tp, можно получить следующий критерий
длительной прочности:
tv = I iJi + ^iT "'Г»;11.	C.104)
у Р [	astest(mu + 1) J
Следует отметить, что в критерии C.104) время отсчитывается
с начала второй стадии ползучести и длительность первой стадии
ползучести не учитывается.

104	Часть З. Неупругость
Если принять в уравнении C.104) степенные аппроксимации функ-
функций от напряжений, т. е.
{(ju)ns'na	C.105)
(/90 = ехр (bp), Po = ехр (Ъ?), Ра0 = ехр (Ъа)),
то критерий длительной прочности будет иметь вид
f _ Мп И,.Г,,п/л чп-m/, ,.^ + И	(ЗЛ06)
6р — /i^CT^J Ш [1 ~h ±5уGи)	yY — U0\) ш J,
где
В случае отсутствия или малости охрупчивания материала уравнение
C.100) принимает следующий вид:
Со= аф± ^_wpWi	C.107)
Интегрируя C.107) с учётом начальных условий C.101), подставляя
в полученную зависимость условие C.103) и разрешая относительно
времени разрушения tp, можно получить критерий длительной прочно-
прочности материала в случае отсутствия охрупчивания:
tp = —^
Принимая степенные зависимости C.105), критерий длительной
прочности C.108) примет вид
tp = D(au)-m(l-u;i)m»+l,	C.109)
ГД6	Ш &/Па
Здесь необходимо отметить, что критерии C.108) и C.109) следуют
соответственно из критериев C.104) и C.106) при малости вторых
слагаемых в выражениях под логарифмом.
Для получения связи между деформацией и временем до разруше-
разрушения используется уравнение C.93)
ён = e?8t(l - ш)-т».	C.110)
Из критерия длительной прочности C.104) следует, что
astsast _	A-о.,Г-+1
pW0	(тш + 1)[1 - ехр (ptp)}'
C.111)

Глава 1. Теория неупругого деформирования	105
Подставляя C.111) в C.102) и разрешая относительно A-й;),
можно получить следующую зависимость:
1- А -^у	(ЗП2)
l-exp(ptp)J
Тогда на основании C.110) и C.112) деформация и время до разру-
разрушения будут связаны зависимостью
1- / ехр.(^.	dt.	3.113
l-exp(ptp)|
0 "
В случае отсутствия охрупчивания, интегрируя уравнение C.107) с
учётом начальных условий C.101), можно получить зависимость
C.114)
(\ио)	(lu;i)	ФЬ.
Из критерия длительной прочности C.108) следует, что
Подставляя C.115) в C.114) и разрешая относительно A-й;),
можно получить зависимость
C.116)
Тогда на основании C.110) и C.116) деформация и время до разру-
разрушения будут связаны зависимостью
о
Вычисляя интеграл в зависимости C.117), можно получить следу-
следующую связь между скоростью установившейся ползучести, временем
и деформацией до разрушения:
iHst(l -ujx)-m-tv= ?p .	C.118)
F	TTiuj + 1
Или учитывая, что минимальная скорость равна в данном случае
начальной, зависимость C.118) приводится к виду
$и*Р = ^.	C-119)
где ет[п -е0 - est(l -ш\) ш.
Следует отметить, что зависимость C.117) и соответственно крите-
критерии C.118) и C.119) получаются из C.113) при pt <C I (t e [0;tp]).

106	Часть 3. Неупругость
При большом охрупчивании, когда
ptp > 1, exp(ptp) > 1,
/-exp/f\«l,	C.120)
из уравнения C.113) можно получить следующую связь между скоро-
скоростью установившейся ползучести, временем и деформацией до разру-
разрушения:
iHst(l -un)-m"tp = ?Hp.	C.121)
Или пренебрегая повреждением и)\, зависимость C.121) приводится
к виду
ря t — ря	И 122^
При весьма высоких напряжениях и малых временах разрушения,
т. е. при кратковременной ползучести, на кривых ползучести отсутству-
отсутствуют [16, 48] первый и практически второй участки ползучести, и имеет
место только третья стадия ползучести. Учитывая также, что в этих
условиях отсутствует и охрупчивание материала, на основании C.110)
и C.116) уравнение для скорости ползучести будет иметь вид
/ 1 ~ rrioj + l
-	.	C.123)
Ъ\
Интегрируя C.123) с учётом начальных условий,
гн = 0, при ? = 0,	C.124)
можно получить следующее уравнение кривой кратковременной ползу-
ползучести:	т,„
1 х "	C.125)
н =
(iГ- [х ^ tp
Из уравнений C.123) и C.125) следует, что процесс ползучести
происходит с возрастающей скоростью, т. е. имеет место только третья
стадия ползучести, что соответствует экспериментальным результа-
результатам [12, 16, 48].
При очень малых напряжениях и больших временах разрушения на
кривых ползучести практически отсутствуют [16, 48] первый и третий
участки ползучести, и имеет место только вторая стадия ползучести.
В этом случае на основании C.110), C.112), условий C.120) и малости
uj\ уравнение для скорости ползучести будет иметь вид
eH = eHst.	C.126)
Интегрируя C.126) с учётом начальных условий C.124), можно
получить следующее уравнение очень длительной ползучести:
eH = eHstt.	C.127)

Глава 1. Теория неупругого деформирования	107
Из уравнений C.126) и C.127) следует, что процесс ползучести
происходит при постоянной скорости вплоть до разрушения, что прак-
практически и имеет место в экспериментах [12, 16, 48].
На основании экспериментов также утверждается [16, 48, 49], что
произведение минимальной скорости ползучести на время до разруше-
разрушения является величиной примерно постоянной для данного материала,
т. е.
?miA = const.	C.128)
В случае весьма высоких напряжений, т. е. при кратковременной
ползучести, в уравнении C.128) минимальная скорость ползучести
равна начальной скорости ползучести, а при остальных напряжениях
минимальная скорость ползучести равна скорости установившейся пол-
ползучести.
Уравнения C.119) и C.122) соответствуют этому утверждению,
но только при очень высоких и очень низких уровнях напряжений.
Причём величина константы в C.128) может быть различной: при
высоких напряжениях это ?ркр/(гпш + 1)' а ПРИ низких напряжениях
это SpM. Здесь следует отметить, что деформация разрушения ?^дл
при низких напряжениях обычно значительно меньше деформации
разрушения ?^кр при высоких напряжениях, что обусловлено процессом
охрупчивания материала. При близости по величине этих констант
можно говорить о справедливости критерия C.128) во всём диапазоне
напряжений.
Что касается кривой длительной прочности, соответствующей урав-
уравнению C.106), то при умеренных уровнях напряжений и малости
начального повреждения и охрупчивания материала в логарифмиче-
логарифмических координатах согласно следующему из C.109) уравнению имеет
место прямая линия, что полностью соответствует экспериментальным
данным по длительной прочности. По мере уменьшения уровня напря-
напряжений, увеличению времени разрушения и проявлению охрупчивания
материала происходит отклонение кривой длительной прочности, опи-
описываемой уравнением C.106), от прямой линии в логарифмических
координатах, что соответствует экспериментальным данным [16, 48]
по длительной прочности. При весьма высоких уровнях напряжений
может быть существенно влияние повреждения uj\, и кривая длитель-
длительной прочности, описываемая здесь уравнением C.109), может также
отклоняться от прямой линии в логарифмических координатах, что
и наблюдается в экспериментах [16, 48].
Таким образом на кривой длительной прочности могут иметь место
три участка, схематично изображённые на рис. 3.1 соответствующими
цифрами I, II, III.
На первом участке мало охрупчивание, но есть влияние поврежде-
повреждения и)\, и этот участок описывается уравнением
tp = D(au)-m{l-u>i)m" + l.	C.129)

108
Часть 3. Неупругость
Рис. 3.1. Кривая длительной прочности
На втором участке мало охрупчивание, и мало влияние поврежде-
повреждения ио\. В этом случае кривая описывается уравнением
tn = D (а,,
C.130)
и представляет собой в логарифмических координатах прямую линию.
На третьем участке мало влияние повреждения uj\, но велико вли-
влияние охрупчивания, и этот участок описывается уравнением
tP = A(au)-n In [1 + В(аи)п-т].	C.131)
А полностью кривая длительной прочности, имеющая все три
участка, описывается уравнением C.106).
Таким образом критерий длительной прочности C.106) работо-
работоспособен на всём реальном временном интервале от малых времён
разрушения при кратковременной ползучести до достаточно больших
времён разрушения при весьма длительной ползучести. Причём вхо-
входящие в критерий длительной прочности C.106) параметры легко
определить на основе изложенного ниже расчётно-экспериментального
метода, используя данные стандартных экспериментов.
Далее рассматривается ползучесть при одноосном сжатии. Урав-
Уравнение накопления повреждений, соответствующее второму участку
кривой длительной ползучести, будет иметь вид аналогичный уравне-
уравнению C.107), но учитывающее в данном случае залечивание, т.е.
UJ =
w0
— \ио.
C.132)
Анализируя процесс накопления повреждения при ползучести, мож-
можно сделать вывод, что скорость накопления повреждений практически
постоянна до некоторого значения повреждения uj* <C 1, а затем проис-
происходит лавинообразное накопление повреждений и разрушение. Причём

Глава 1. Теория неупругого деформирования	109
время достижения повреждением значения и* и время разрушения
весьма близки.
Таким образом, уравнения C.107) и C.132), с учётом вышеизло-
вышеизложенного, записываются соответственно в следующем виде:
^?	C.133)
Wq
^-Xu;-,	C.134)
Wo
где Со+ относится к растяжению, a Cu~ — к сжатию.
Интегрируя C.133) и C.134), с учётом начальных условий и усло-
условия разрушения,
оо = 0, при t = 0, и oj = oj*, при t = tp,	C.135)
можно получить следующие критерии длительной прочности:
<} = Д-м„	C.136)
dst?st
V = т In [l + .и w x 1 •	C.137)
р А [ CLstSst/ Wo - Лес;* J
Сравнивая критерии C.136) и C.137), можно получить следующую
связь между временем до разрушения при растяжении и при сжатии:
C138)
В случае, когда второе слагаемое под логарифмом мало, т. е.
<С 1, критерий C.138) преобразуется к виду
-L-4=A,	C.139)
tp tp
где Л — модуль залечивания, определяемый согласно формуле C.46)
и равный нулю, когда аи > 0, и отличный от нуля, когда аи < 0.
И чем больше \ац\, тем больше модуль залечивания и тем больше,
соответственно, отличия времени до разрушения ?+, при ац > 0, от вре-
времени до разрушения t~, при а и < 0, но происходящие при одинаковых
значениях интенсивности напряжений аи.
§ 8. Расчётно-экспериментальный метод определения
материальных функций
Функция изотропного упрочнения Ср (е^*) > параметры анизотроп-
анизотропного упрочнения Еа,аа,C и начальная энергия разрушения Wo опре-
определяются на основе расчётно-экспериментального метода изложенного
в § 8 главы 1 части 2, с использованием данных при пластическом
деформировании.

ПО	Часть 3. Неупругость
Для определения функций изотропной и анизотропной ползучести
используются данные при испытаниях на ползучесть при постоянном
напряжении растяжения и релаксацию напряжения при постоянной
деформации растяжения.
В опытах на релаксацию напряжения начальная пластическая де-
деформация должна быть порядка 0.03-0.05, чтобы в материале возникло
развитое добавочное напряжение. В этом случае процесс снятия анизо-
анизотропного упрочнения будет значительно превалировать над процессом
снятия изотропного упрочнения. Поэтому радиус поверхности нагру-
жения на начальной стадии релаксации можно считать неизменным
и равным радиусу в конце пластического деформирования. Численные
исследования процесса релаксации для ряда конструкционных сталей
и сплавов показали справедливость этого утверждения. Таким обра-
образом, изменение добавочного напряжения при релаксации напряжения
определяется выражением
a(t)=a(t)-Cp(ep),	C.140)
где гр — начальная пластическая деформация.
При релаксации напряжения растяжения уравнения теории неупру-
неупругого деформирования имеют вид
|+?н = 0,	C.141)
а = ge* + (geH + gaa) |sH| - (g + g?e« + gaa) Pa.	C.142)
Из уравнений C.140)—C.142), с учётом того, что в данном случае
гн\ = гн, следует формула для определения функции анизотропной
ползучести:
Следует отметить, что при релаксации напряжения неупругая
деформация изменяется незначительно, поэтому в формуле C.143)
неупругая деформация гн принимается неизменной и равной начальной
пластической деформации гр.
Уравнения C.143) и C.140) позволяют установить зависимость
функции анизотропной ползучести от интенсивности добавочных на-
напряжений аи = а. Далее полученная зависимость строится в лога-
логарифмических координатах и в соответствии с аппроксимацией C.35),
пренебрегая незначительным здесь повреждением, можно получить
линейную зависимость
In (Ра) =ba + na In К),	C.144)
на основании которой определяются параметры Ъа и па.

Глава 1. Теория неупругого деформирования	111
Функцию анизотропной ползучести можно определить также и на
основе критерия длительной прочности C.109) и аппроксимации ско-
скорости установившейся ползучести степенной функцией C.105). Таким
образом, используя экспериментальные данные второго участка кривой
длительной прочности и данные по скорости установившейся ползу-
ползучести можно определить параметры га, D, Ро,п? и по их значениям
вычислить па и Ъа по формулам
т — п?
Ъа = 1п
C.145)
(ЗЛ46)
где rriu определяется из опытов при кратковременной ползучести
(см. ниже), a Wq — начальная энергия разрушения, определяемая при
циклическом пластическом деформировании.
В состоянии установившейся ползучести процессы упрочнения и
разупрочнения уравновешиваются. В этом состоянии справедливы со-
соотношения
Рао(а)Па = ё%, Рсо\С - Сро|Пс = ё%,	C.147)
С = а-а	C.148)
(Ра0 = ехр (Ъа), Рс0 = ехр (Ьс)).
Из первого уравнения C.147) по известной функции анизотропной
ползучести и скорости установившейся ползучести определяется соот-
соответствующее этой скорости добавочное напряжение по формуле
¦	(ЗЛ49)
Затем по формуле C.148) определяется соответствующий этой ско-
скорости радиус поверхности нагружения, и устанавливается зависимость
между функцией изотропной ползучести РС(С) = e^t и радиусом С. Да-
Далее полученная зависимость строится в логарифмических координатах
и в соответствии с аппроксимацией C.34), пренебрегая незначитель-
незначительным здесь повреждением, можно получить линейную зависимость
ln(Pc) = bc + ncln|C-Cpo|,	C.150)
на основании которой определяются параметры Ьс и пс.
В случае отсутствия данных по релаксации напряжения или дан-
данных по длительной прочности, а также пренебрегая первым участком
ползучести, можно получить функции анизотропной и изотропной пол-
ползучести, используя зависимость скорости установившейся ползучести
от напряжения. Для этого на основе пластической диаграммы а\ (г^*)
по заданному значению напряжения а определяется пластическая

112	Часть 3. Неупругость
деформация гр. Далее по значению этой деформации вычисляется
соответствующее добавочное напряжение а по формуле B.18), а также
по формуле C.148) — радиус С. Таким образом, на основании C.147)
устанавливаются зависимости между функциями анизотропной и изо-
изотропной ползучести и соответственно интенсивностью добавочных на-
напряжений аи = а и радиусом С. Далее применяются указанные выше
процедуры логарифмирования и аппроксимации, на основании кото-
которых определяются параметры ba,bc,na,nc. Конечно, такое определение
функций изотропной и анизотропной ползучести справедливо, если на
кривых ползучести нет первого участка. В противном случае такой
метод определения функций изотропной и анизотропной ползучести
будет приближённым.
Для определения показателя тш степенной зависимости функций
изотропной и анизотропной ползучести от повреждения используется
формула C.119) и результаты опытов на кратковременную ползучесть
до разрушения. Тогда показатель тш определяется следующим об-
образом:
тш = -&--\,	C.151)
где Sp = In	 — гр — часть деформации разрушения за счёт только
ползучести; ф — поперечное сужение при разрушении; гр — начальная
пластическая деформация; ё$ = ?%(! — и\)~тиз — начальная скорость
кратковременной ползучести.
Показатель тш можно определить, используя данные первого и вто-
второго участков кривой длительной прочности. Логарифмируя левую
и правую части уравнения C.129) для первого участка кривой дли-
длительной прочности, можно получить линейное уравнение в логарифми-
логарифмических координатах:
g	a;i)f	(з.152)
где
Wl = Wo {ъЕ*(?РУ + а*?Р ~ J [1
Далее на основании линейной зависимости C.152) определяется
показатель тш.
Для определения модуля охрупчивания используются результаты
испытаний, относящиеся к третьему участку кривой длительной проч-
прочности. Значение модуля охрупчивания определяется для каждого уров-
уровня напряжения на основе критериев C.104) или C.106) из следующих

уравнении:
р = — In
Глава 1. Теория неупругого деформирования	113
или Р=г
C.153)
Здесь в уравнениях C.153) пренебрегается повреждением до вы-
выдержки, а добавочное напряжение ast определяется на основе фор-
формулы C.149). Решение нелинейных уравнений C.153) может быть
осуществлено любым итерационным методом. В качестве начального
приближения можно принять
1 п	Wo	1	/О 1СЛ\
р= — т	й- или р=—.	C.154)
tp	CLst^p	tp
Далее полученная зависимость между р и аи строится в логариф-
логарифмических координатах, и в соответствии с аппроксимцией C.37) можно
получить линейную зависимость
1п(р) = Ьр + пр In (au),	C.155)
на основании которой определяются параметры Ьр и пр.
Для определения модуля залечивания проводятся испытания на
малоцикловую усталость при постоянном размахе пластической дефор-
деформации порядка 0.01. После накопления повреждения порядка 0.5-1-0.7
осуществляется выдержка при постоянном сжимающем напряжении.
Далее образец доводится до разрушения при том же размахе пласти-
пластической деформации. Испытания проводятся при различных уровнях
сжимающего напряжения на режиме выдержки. В этом случае на
режиме выдержки на основе C.15),C.32),C.36) уравнение залечивания
повреждения будет иметь вид
и = -\и.	C.156)
Интегрируя C.156) и используя следующие условия в начале и кон-
конце выдержки длительностью Д?сж,
UJ = UJ\, ПрИ t = to,	И	U0 = 6^2, ПрИ t = to + Д?сж,
можно получить формулу для модуля залечивания,
A = -bln^.	C.157)
Далее учитывая, что при пластическом циклическом деформиро-
деформировании с постоянным размахом пластической деформации довольно
быстро наступает стабилизация процессов образования и снятия до-
добавочных напряжений, и пренебрегая временными эффектами ввиду
их малости при пластическом деформировании, можно принять, что
накопление повреждений пропорционально числу циклов нагружения.

114	Часть 3. Неупругость
Откуда следует, что повреждения и\ и ш% в начале и конце выдержки
при сжатии определяются на основе формул
W1 = v W2 = 1"v	(ЗЛ58)
Здесь Np — число циклов до разрушения без выдержки; N\ —
число циклов до выдержки (N\ = 0.5 -ir0.7Np); N2 — число циклов до
разрушения после выдержки.
Получив зависимость модуля залечивания от величины напряже-
напряжения сжатия, т. е. от первого инварианта тензора напряжения, далее
можно построить эту зависимость в логарифмических координатах,
и в соответствии с аппроксимацией C.36) можно получить линейную
зависимость
1п(А) = Ьл+пл1п|<7*|,	C.159)
на основании которой определяются параметры Ь\ и п\.
Модуль залечивания можно получить и на основании уравнения
C.138), используя данные по длительной прочности при растяжении
и сжатии. В этом случае имеет место нелинейное уравнение
Л= — 1п[1 + -^У '	C.160)
решение которого может быть осуществлено любым итерационным
методом. В качестве начального приближения можно принять
tp tp
C.161)
Получив модуль залечивания для различных уровней напряжений
растяжения и сжатия, можно построить линейную зависимость в ло-
логарифмических координатах между А и аи, на основании которой
определяются параметры Ь\ и п\.
Основной проблемой при построении кривой длительной прочно-
прочности является получение третьего участка, на котором происходит су-
существенное охрупчивание материала. Экстраполяция данных начала
третьего участка прямой в логарифмических координатах некорректна,
т.к. третий участок нелинеен, и такая экстраполяция приведёт к суще-
существенному завышению долговечности.
В первом приближении для построения третьего участка и кор-
коррекции всей кривой длительной прочности можно использовать крите-
критерий C.128) постоянства произведения минимальной скорости ползуче-
ползучести на время разрушения, так как минимальную скорость ползучести
можно получить на всём рассматриваемом интервале напряжений.
Для более достоверного прогнозирования значений времени раз-
разрушения при весьма длительной ползучести (например, более года)
на основе данных кратковременных испытаний (например, до года)

Глава 1. Теория неупругого деформирования	115
необходимо получить значения параметров пр и Ър или п и А(п = пр,
А= 1/ехр(Ьр)), характеризующих процесс охрупчивания материала.
Изменение энергии разрушения материала вследствии охрупчива-
охрупчивания описывается уравнением C.99), на основе которого
Исследуя материал на малоцикловую прочности при постоянном
размахе пластической деформации (порядка 0.01) после ползучести при
постоянном напряжении растяжения а в течение времени t, можно
получить число циклов до разрушения и изменённое значение энергии
разрушения на основе формулы
::"sh (злбз)
Если испытания на малоцикловую усталость до ползучести и после
ползучести проводились при одинаковом размахе пластической дефор-
деформации, то тогда модуль охрупчивания р будет равен
? = тыщ>	(ЗЛ64)
где Np — число циклов до разрушения без ползучести, N* — число
циклов до разрушения после ползучести.
Проведя такие испытания при различных уровнях напряжения пол-
ползучести, можно получить зависимость модуля охрупчивания от напря-
напряжения. Далее эта зависимость строится в логарифмических координа-
координатах и определяются значения параметров пр и Ър.
Таким образом для определения материальных функций теории
неупругого деформирования достаточно следующего основного (базо-
(базового) набора экспериментальных данных:
—	упругие параметры Е и z/, которые определяются традиционными
методами;
—	диаграмма пластического деформирования при одноосном растя-
растяжении а\(е) до деформации 0.05-0.1;
—	диаграмма пластического деформирования при одноосном растя-
растяжении <72(в) после предварительного сжатия до деформации 0.01-0.02;
—	данные по циклическому одноосному растяжению-сжатию при
постоянном размахе пластической деформации: число циклов до раз-
разрушения (появления макротрещин) Np и зависимость максимальных
значений напряжений а^ на цикле (в конце цикла) от числа циклов
нагружения N (размах пластической деформации порядка 0.01);
—	данные по ползучести при постоянном напряжении растяжения:
зависимость минимальной скорости ползучести от напряжения во всём
диапазоне изменения напряжений от кратковременной до весьма дли-
длительной ползучести;

116
Часть 3. Неупругость
—	данные по длительной прочности: кривая длительной прочности
при растяжении, включающая все три участка, и кривая длительной
прочности при сжатии, соответствующая только второму участку.
В качестве неосновных (дополнительных) экспериментальных дан-
данных могут быть:
—	данные по релаксации напряжения при постоянной деформации
растяжения порядка 0.03 ч- 0.05;
—	данные по длительной прочности: зависимость деформации раз-
разрушения от времени разрушения;
—	данные по малоцикловой усталости при постоянном размахе
пластической деформации с выдержкой при постоянном напряжении
сжатия.
И особо следует выделить испытания, заключающиеся в определе-
определении малоцикловой прочности материала после предварительной ползу-
ползучести, на которых может быть построено прогнозирование разрушения
при весьма длительной ползучести.
Пластичность
G
кор2|/
и
е
и
/
~У ?
Np
E,v,Ea,/3,aa,W0
Произвольные процессы
сложного нагружения
Рис. 3.2

Глава 1. Теория неупругого деформирования
117
Неупругость
lgcr
Произвольные процессы
сложного нагружения.
Три стадии ползучести.
Три участка кривой длительной
прочности. Знакопеременные
и нестационарные процессы
ползучести. Взаимное влияние
ползучести, пластичности и
повреждения и т.д.
Рис. 3.3
Далее схематично изображены базовые эксперименты, набор мате-
материальных параметров и функций, а также изложены некоторые воз-
возможности теории неупругого деформирования по описанию неупругого
поведения и разрушения материала.

Глава 2
ТЕОРИЯ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ
МАТЕРИАЛОВ, ЧУВСТВИТЕЛЬНЫХ К ВИДУ
НАПРЯЖЁННОГО СОСТОЯНИЯ
§ 1. Основные положения и уравнения
Материал однороден и начально изотропен. В процессе неупругого
деформирования в нём может возникать только деформационная ани-
анизотропия. Материал может быть чувствителен к виду напряжённого
состояния, т. е. иметь различные характеристики неупругого поведения
и разрушения, например, при растяжении, сжатии, сдвиге. В процессе
деформирования возможно как упругое, так и неупругое изменение
объёма материала.
Тензор скоростей деформаций представляется в виде суммы тензо-
тензоров скоростей упругой и неупругой деформаций:
?У = 4-+4-	C.165)
Упругие деформации при изменении напряжений следуют обобщён-
обобщённому закону Гука:
z\j = ? [eij - v C&o5ij - &ij)],	C.166)
где E,iy — соответственно модуль Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и неупругого состояний. Поверхность нагружения изотропно расши-
расширяется или сужается, смещается и изменяет форму в процессе нагру-
нагружения. Воздействие фактора времени также есть процесс нагружения.
Начальная поверхность нагружения может иметь форму отличную от
поверхности Мизеса. Уравнение поверхности нагружения принимается
в следующем виде:
/К) = | (sij - ау)(«У " ац) - С2 = 0.	C.167)
Здесь s*j = s^ — ctij — девиатор активных [4] напряжений; s^ — де-
виатор напряжений. Тензор а^- характеризует смещение смещение по-
поверхности нагружения в девиаторном пространстве напряжений, а ска-
скаляр С отвечает размеру (радиусу) поверхности нагружения. Тензор
смещения (добавочных напряжений, остаточных микронапряжений) а^

Глава 2. Вид напряжённого состояния	119
и радиус С являются функционалами процесса нагружения. Здесь сме-
смещение и радиус поверхности нагружения зависят от первого инвариан-
инварианта тензора напряжений, второго и третьего инвариантов девиаторов до-
добавочных напряжений и активных напряжений, что позволяет описать
зависимость неупругого поведения и разрушения от вида напряжённого
состояния.
Для радиуса поверхности нагружения принимается следующее
уравнение:
С = q??l* + qGdii + q^fi* - qR,	C.168)
1	/ 9
- ^T SijSjkSki> ?u* - J [-о eijeij
07 ч* ч*	о я*.	/о	Nl/2
z/ ^^fc^fcj о ^ 5г^ ОГ	^н	/ z
_
u
Здесь бих — длина дуги неупругой деформации (накопленная неупру-
неупругая деформация; аи = 1\(Та) — первый инвариант тензора напряже-
напряжений; /i* — параметр вида активного напряжённого состояния /i* G
G [—1, 1]; при сжатии /i* = — 1, при сдвиге /i* = 0, при растяжении /i* =
= +1; а^ — интенсивность активных напряжений; ^(Dp) и I^(D^) —
соответственно второй и третий инварианты девиатора активных на-
напряжений; q?,qa,q^,qR — функции подлежащие экспериментальному
определению.
Первое и последнее слагаемые в уравнении C.168) отвечают за ме-
механическое упрочнение и термическое разупрочнение, остальные обес-
обеспечивают изменение радиуса поверхности при изменении вида напря-
напряжённого состояния. Смещение поверхности нагружения определяется
уравнением
С " (| g?4 + gffly) .	C.169)
Здесь e^j — компонент девиатора неупругих деформаций;
§1§?1§а'?^'?а ~ Функ11ИИ подлежащие экспериментальному опре-
определению и зависящие от параметра вида добавочного напряжённого
состояния (jjLa Е [—1, 1]; при сжатии /ia = — 1, при сдвиге /ia = 0, при
растяжении /ia = +1), который определяется следующим образом:
27 h(D )
/^а = у———зд,	C.170)
= -zaijuij, h(Da) = -
Z	О

120	Часть 3. Неупругость
Неупругие деформации определяются на основе ассоциированного с
C.167) закона течения следующим образом:
дн = 1L д _
V г)гг
34 -
= 3 D - | ?мпу) А -
Откуда
Подставляя выражение для Л в выражение для скоростей неупругой
деформации ё\^ и скорости средней неупругой деформации гяс можно
получить следующие уравнения:
дн _
'	C.172)
ё8 = -4<Л.	C.173)
Неупругое изменение объёма (разрыхление), следуя уравнению
C.173), определяется величиной накопленной неупругой деформации
и имеет место только в случае зависимости поверхности нагружения
от первого инварианта тензора напряжений, т. е. в случае, когда qG ф 0.
Для получения уравнения для скорости накопленной неупругой
деформации необходимо продифференцировать по времени интенсив-
интенсивность активных напряжений и приравнять это выражение и выраже-
выражение C.168). Итак
d<Ju _ 3 Sjj{Sij — CLjj) __ 3 SjjGij ^ sijeij _ I Sijeij ,	3 SijUjj \ .H
dt ~ 2	at	~ 2 a*u g a*u \f? a*u ga 2 a*u ) u*
fee * т&ао *
Sij&ij \ о SijGij о
J J \ — 	 J J 	 re

Глава 2. Вид напряжённого состояния
121
dC
III
* - qR =
n--s*
<- О Ь? *
THj OiA -H
— п —СГ-
13Ь **
i
+
2
a*u )?u*
C.175)
Приравнивая C.174) и C.175) и разрешая относительно ё^*, можно
получить уравнение связи скорости накопленной неупругой деформа-
деформации и скоростей напряжений:
__
- В"аи + Bi
C.176)
BR - ^l
a* - -
В случае независимости поверхности нагружения от первого инвари-
инварианта тензора напряжений неупругое изменение объёма будет равно
нулю, и уравнение для скорости накопленной неупругой деформации
соответственно для мягкого и жёсткого нагружений будут иметь вид
3G
C.177)
C.178)
Условия упругого и неупругого состояний, полученные из при-
принадлежности изображающей точки поверхности нагружения C.167)
и положительности скорости накопленной неупругой деформации, име-
имеют вид
< < с и *1* < 0 - упругость
сг* = С П ?^0 — неупругость.
Здесь под el подразумевается выражение, задаваемое уравнени-
уравнением C.176) или C.177) или C.178) или любым другим, связывающим
скорость накопленной неупругой деформации с любым набором скоро-
скоростей напряжений и деформаций (смешанное нагружение).

122	Часть 3. Неупругость
Для описания процесса накопления повреждений используется
энергетический подход, и кинетические уравнения аналогичные C.15)
и C.16) будут иметь следующий вид:
g^,	C.180)
-gwW,	C.181)
A аи = - a^j , m^- = — ——f - 3/ia- -^ -
27 /3(Ai)	r /x. ч	1	r /x. ч	1
MM) = aijaij h(D) = а^
Z [3I2(Da)]2	Z	6
Здесь uj — мера повреждения и G [0, 1]; W — энергия разру-
разрушения; jia — параметр вида добавочного напряжённого состояния
(/ia G [—1, 1]; при сжатии \±а = — 1; при сдвиге \±а = 0; при растяжении
/ia = +1); I2(Da), h(Da) — второй и третий инварианты девиатора
добавочных напряжений; g^, g^, g^, g*^ — функции подлежащие
экспериментальному определению.
Критерием разрушения материала будет достижение повреждением
предельного значения, обычно принимаемого равным (или близким)
к единице.
§ 2. Материальные функции и метод их определения
Теорию неупругого деформирования материалов, чувствительных к
виду напряжённого состояния, замыкают семнадцать определяющих
функций, подлежащих экспериментальному определению:
Е, z/, q?, qa, q^ qR, g, g?, ga, gf, gj, gw, g^, g^, g-^, Cp0, Wo.
C.182)
Здесь Cpo и Wo — начальные значения радиуса поверхности нагру-
жения С и энергии разрушения W. Определяющие функции C.182)
выражаются через материальные функции, такие как и в § 2 гла-
главы 1 части 3, кроме функций qcr,q^, g^, g^. Для получения связи
между этими определяющими функциями, при изменении параметров
ац, /i*, /ia, принимаются [3] неизменными относительные положения
величин радиуса поверхности нагружения и энергии разрушения меж-
между их предельными значениями. Следующие из этого положения урав-
уравнения имеют вид
(зл84)

Глава 2. Вид напряжённого состояния	123
Тогда связь между определяющими и материальными	функциями
будет иметь вид
О Сив О CUjo	/o 1Ог\
ч° = с;ъй> q» = c-Poi>	(ЗЛ85)
~	W 8Wo	a	W
Таким образом, теорию неупругого деформирования материалов,
чувствительных к виду напряжённого состояния, замыкают следую-
следующие материальные функции, подлежащие экспериментальному опреде-
определению:
Е,и — упругие параметры;
Ср(сгц,/i*,?^*) — функция изотропного упрочнения;
EafauVa), Va(°iuli>a)> &{р%иНа) — параметры анизотропного
упрочнения;
Wq(ац, \iа) — начальная энергия разрушения;
Рс(ац,{1*,С,сл); Ра(ац, fia,au,cj) — функции изотропной и анизо-
анизотропной ползучести;
Х(о~ц), р{о~и) — модули залечивания и охрупчивания.
Для описания зависимости материальных функций от параметров
/i* и \ia можно использовать такие же степенные аппроксимации, как
и в § 2 главы 2 части 2, и материальные функции, полученные при
одноосных сжатии-растяжении и кручении. Метод определения мате-
материальных функций аналогичен описанному в § 8 главы 1 части 3, но
проводится это определение отдельно в условиях одноосного растяже-
растяжения-сжатия (/i* = fia = ±1), одноосного кручения (/i* = fia = 0) и, ес-
если возможно, по лучевым траекториям при ц* = ца ф 0 и ц* = ца ф 1.

Глава 3
ТЕОРИИ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ
В УСЛОВИЯХ НЕИЗОТЕРМИЧЕСКОГО
НАГРУЖЕНИЯ И ИОНИЗИРУЮЩЕГО
ИЗЛУЧЕНИЯ
§ 1. Уравнения вариантов теорий
Для всех вариантов теорий неупругого деформирования тензор ско-
скоростей деформаций представляется в виде суммы тензоров скоростей
упругой и неупругой деформаций:
Упругие деформации при изменении напряжений следуют обобщён-
обобщённому закону Гука, при изменении температуры — закону температур-
температурного расширения, а при изменении флюенса — закону распухания:
г% = 1 [ац - v (Зао<% - ац)\ + affT + а$Ф,	C.188)
(Т ^ Ф),
где Е, и, ат, суф — соответственно модуль Юнга, коэффициенты
Пуассона, коэффициент температурного расширения и коэффициент
радиационного распухания, являющиеся функциями температуры Т и
флюенса Ф.
Полагается, что в пространстве составляющих тензора напряжений
существует поверхность нагружения, разделяющая области упругого
и неупругого состояний,
/КО = I (si:i - aijKsij - atj) -C2=0.	C.189)
Для радиуса поверхности нагружения в случае материалов, об-
обладающих и не обладающих эффектом дополнительного изотропного
упрочнения, принимается следующее уравнение:
С = qs?Hu* + ЧтТ + дФФ - qR.	C.190)

Глава 3. Неизотермическое нагружение	125
В случае теории неупругого деформирования материалов, чувстви-
чувствительных к виду напряжённого состояния, радиус поверхности нагру-
жения определяется уравнением
С = q?sl* + Ч(Тдп + q^fi* + qTf + qфФ - qR.	C.191)
Смещение поверхности нагружения определяется следующим урав-
уравнением:
gaaij)	(| ^	)
X) (| f Л) C.192)
Следует заметить, что в уравнении C.192) е^- = ?"•, кроме теории
неупругого деформирования материалов, чувствительных к виду на-
напряжённого состояния, и то только тогда, когда радиус поверхности
нагружения зависит от первого инварианта тензора напряжений, т. е.
когда учитывается неупругое изменение объёма.
Неупругие деформации определяются на основе ассоциированного
с C.189) закона течения, и тогда тензор скоростей неупругой дефор-
деформации материалов, чувствительных к виду напряжённого состояния,
будет задаваться уравнением
Здесь n*j и Sq определяются на основе выражений C.172) и C.173).
Для остальных вариантов теории неупругого деформирования урав-
уравнение C.193) будет иметь вид
При получении уравнений для скорости накопленной неупругой
деформации, соответствующих вариантам теорий, необходимо продиф-
продифференцировать по времени интенсивность активных напряжений и ра-
радиус поверхности нагружения, приравнять эти выражения и разрешить
относительно ё^*. Для материалов обладающих и не обладающих эф-
эффектом дополнительного упрочнения используется выражение C.190),
и тогда уравнение для скорости накопленной неупругой деформации
примет вид
н =
и*
3 4ф _ втf _ вФф + br\ t	C195)
Вт = дт + ?е%+?а* (Т ~ Ф),
Я — an 4- рмрн* 4- Р^а* ^н* — %3 %3 а* — —
D — 4R \ &е ьи * Saa ' ьи ~~ ^* ' аи ~~ -
О SijClij

126	Часть 3. Неупругость
Для материалов, чувствительных к виду напряжённого состояния, ско-
скорость накопленной неупругой деформации определяется уравнением
1
Пи
C.196)
, н* ,
Уравнения C.195) и C.196) соответствуют мягкому нагружению.
В случае жёсткого нагружения, пренебрегая неупругими изменениями
объёма, уравнения для соответствующих вариантов теорий будут иметь
следующий вид:
-BTf -
C.197)
- - В.. + 3G
Условия упругого и неупругого состояний для всех вариантов тео-
теорий имеют вид
< < С U ё?* < 0 - упругость	199
сг* = С П ?^0 — неупругость.
Здесь радиус поверхности нагружения С определяется в соответ-
соответствии с вариантом теорий, согласно C.190) и C.191), а скорость накоп-
накопленной неупругой деформации задаётся выражениями C.196)—C.198)
или аналогичными им.
Кинетические уравнения накопления повреждений, залечивания
и охрупчивания в случае материалов, обладающих и не обладающих
эффектом дополнительного упрочнения, имеют вид
ш = ^ф--ёшш,	C.200)
W = g&t + g%r& - gwW.	C.201)
В случае материалов, чувствительных к виду напряжённого состо-
состояния, кинетические уравнения будут иметь следующий вид:
u> = ^-gwu,,	C.202)
W = ifwaH + g$v(ia+gl/f + g%i>-gwW.	C.203)
Критерием разрушения материала, как и ранее, будет достижение по-
повреждением предельного значения, равного (или близкого) к единице.

Глава 3. Неизотермическое нагружение	127
§ 2. Материальные функции и метод их определения
Теорию неупругого деформирования материалов замыкают следую-
следующие материальные функции:
Е (Т, Ф), v (Т, Ф), аТ (Т, Ф), аФ (Т, Ф) — упругие параметры;
Еа (Т, Ф), аа (Т, Ф), /3 (Т, Ф) — модули анизотропного упрочнения;
Ср(Т,Ф,бих) — функция изотропного упрочнения;
Wq (T, Ф) — начальная энергия разрушения;
Рс (Т, Ф, С, ш), Ра(Т,Ф,аи,ии) — функции изотропной и анизо-
анизотропной ползучести;
\(Т,Ф,ац), р(Т,Ф,аи) — модули залечивания и охрупчивания.
Функции изотропной и анизотропной ползучести, а также моду-
модули залечивания и охрупчивания аппроксимируются, соответственно,
выражениями C.34)-C.37). Тогда вместо этих функций и модулей
в качестве материальных функций будут:
Ъс (Т, Ф), Ъа (Т, Ф), пс (Т, Ф), па (Т, Ф), mu (T, Ф) - параметры изо-
изотропной и анизотропной ползучести;
Ъ\ (Т, Ф), Ър (Т, Ф), п\ (Т, Ф), пр (Т, Ф) — параметры залечивания и
охрупчивания.
Определяющие функции выражаются через материальные следую-
следующим образом:
C.204)
Т _ дЕа_ _ Еа, дОа_ (J1 ф)	т _ J_ дОа_
ge ~ ОТ аа ОТ [1 Ф;' ёа ~ аа ОТ
Теорию неупругого деформирования материалов, обладающих допол-
дополнительным изотропным упрочнением, замыкают такие же как и приве-
приведённые выше для материалов не обладающих дополнительным упроч-
упрочнением функции, но и к ним добавляются:
1!)о(Т,Ф); #i (T, Ф); с?о(Т, Ф); d\ (Т, Ф) — модули дополнительного
изотропного упрочнения и разупрочнения.
В этом случае определяющие функции выражаются через матери-
материальные, также как и для материалов, не обладающих дополнительным
упрочнением, по формулам C.204), кроме функций
q? = ^+qsA,	C.205)
geA = [A - A)j}0 + Atii][(l -A)Co + Ad -C],

128	Часть 3. Неупругость
Ср,	если qeA > 0;
Ср + d0 (^тах - Ср) , еСЛИ geA < 0,
9
,	C.206)
Стах = (Zemax^u* + ^Ттах^ + <?Фта
е, если С > Стах,
Qs max — л r\	гч ^ гч 11	^ r\
1 0, если С < Cmax U q?A < 0,
Здесь следует отметить, что в случае теории неупругого деформиро-
деформирования материалов, обладающих дополнительным изотропным упрочне-
упрочнением, добавляется ещё одно внутреннее перемещение Стах, которое
определяется уравнением приведённым в C.206).
Теорию неупругого деформирования материалов, чувствительных
к виду напряжённого состояния, замыкают следующие материальные
функции:
Е (Т, Ф), v (Т, Ф), ат (Т, Ф), аф (Т, Ф) — упругие параметры;
Еа(Т,Ф, fia), аа (Т, Ф, /ia), /3 (Т, Ф,/1а) — модули анизотропного
упрочнения;
Ср (Т, Ф, аи, /i*, 6^*) — функция изотропного упрочнения;
Wo (T, Ф, аи, 1^а) — начальная энергия разрушения;
Рс (Т, Ф, аи, /i*, С, ио), Ра(Т,Ф,ац, ца,аи,оо) — функции изотроп-
изотропной и анизотропной ползучести;
Х(Т,Ф,ац), р(Т,Ф,аи) — модули залечивания и охрупчивания.
Определяющие функции выражаются через материальные, также
как и для материалов, не чувствительных к виду напряжённого состо-
состояния, по формулам C.204), кроме функций
= С^дС,	=С^дС,
4G Срд*ц' Ч/л Cvd^
- W dW0 a W dW0	(
При получении связи между определяющими и материальными
функциями, при изменении параметров вида напряжённого состояния,
температуры и флюенса, в выражениях C.204)-C.207) принимают-
принимаются [3, 16] неизменными относительные положения величин радиуса,
максимального радиуса, добавочных напряжений нелинейного типа
и энергии разрушения между их предельными значениями. Следующие
из этого положения уравнения имеют вид
.*-(?-) =о -?-(?-) =о
дан CJ ' 9/ \CJ

Глава 3. Неизотермическое нагружение
129
О1
C.208)
(
дай \W
д (W
д (W
Определение материальных функций строится на основе изложенных
в главах 1, 2, 3 части 2 и главах 1, 2 части 3 расчётно-эксперименталь-
ных методах и экспериментальных данных, при различных уровнях
температуры и флюенса, полученных в условиях изотермического на-
гружения и постоянного уровня флюенса.
§ 3. Материальные функции некоторых
конструкционных сталей и сплавов
Ранее в § 3 главы 4 части 2 были приведены материальные функ-
функции, относящиеся к упругопластическим свойствам, для ряда конструк-
конструкционных сталей и сплавов. Ниже в таблицах для этих конструкцион-
конструкционных сталей и сплавов приводятся материальные функции, связанные
с временными процессами.
№ п/п
1
2
Материал
Сталь 304 [44] (Т = 650 °С)
ЗОХГСА [46] (Т = 550 °С)
Ьс
-13.1
-6.97
пс
2.5
1.59
Табл р
Ьа
-18.9
-10.64
ща 3.1
Па
2.5
1.59
Для стали 304 размерность Рс и Ра [1/час], т.е. время измеряется
в часах, а для стали ЗОХГСА — [1/мин] и время — в минутах.
Таблица 3.2
Материал АЛ-25 [45]
Г, °С
20
150
250
350
400
Ьс
-100
-100
-100
-100
-100
пс
0
0
0
0
0
Ьа
-15
-12.5
-11
-9.5
-6.5
Па
5.3
5.3
5.3
5.3
5.3
Для алюминиевого сплава АЛ-25 размерность Рс и Ра [1/с], т.е.
время измеряется в секундах. Здесь принимается, что функция изо-
изотропной ползучести Рс практически равна нулю.
Для нержавеющей стали 12X18 Н9 размерность Рс, Ра, р и
Л [1/мин], т.е. время измеряется в минутах.
5 В. С. Бондарь

130
Часть 3. Неупругость
Таблица 3.3
Материал 12X18 Н9 [3]
Г, °С
20
150
300
500
650
Ьс
-23
-22.3
-21.6
-20.7
-15.75
Пс
1.7
1.68
1.64
1.6
1.2
-46
-45.3
-44.4
-42.6
-18.4
8
7.8
7.56
7.2
2.4
тш
3
3
3
3
3
Таблица 3.4
Материал 12X18 Н9 [3]
Г, °С
20
150
300
500
650
ьР
-41.4
-41.4
-41.4
-41.4
-41.4
пр
5.75
5.75
5.75
6.05
6.64
Ьх
-125
-125
-125
-85
-80
17.7
17.7
17.7
17.7
17.7
§ 4. Матричное представление уравнений вариантов
теорий
Уравнения связи между скоростями напряжений и деформацией
в матричном представлении для вариантов теорий в случае мягкого
нагружения имеют следующий вид:
[ёг] = [Cij][&j]+ [hi],	C.209)
[hi] = [Gij] [<jj] + [g-.],	C.210)
ei2 2^33	2e3i]T, C.211)
^2 ^"зз	<^3i] • C.212)
Zi\ = [e\\ ?22 ^33
Vх j\ — [^1 ^2 CT[
Для теорий неупругого деформирования материалов нечувствитель-
нечувствительных и чувствительных к виду напряжённого состояния (в случае
пренебрежения неупругим изменения объёма) вектор внутренних пере-
переменных имеет вид
[hi] = [el* ени
е\ъ
е\ъ
а22
аХ2 а23 аз1 С W и]Т.
C.213)
А для теории неупругого деформирования материалов, обладающих
дополнительными изотропным упрочнением, вектор внутренних пере-

Глава 3. Неизотермическое нагружение
131
менных имеет вид
[hi] = К* ??
Матрица
ляющих т. е.
?33 ?]i2 ?23 ?31 аП а22 &33 ^12 &23 ^31 Cmax С W to] .
C.214)
и вектор [bi] состоят из упругой и неупругой состав-
состав[Су] = [Су] + [Су] ,
C.215)
C.216)
= [С
ё?] = [Су]
Упругие составляющие [Cf^-] и [d|] определяются выражениями A.91)
и A.144), а неупругие составляющие [С^-] и [Ь"] для материалов,
обладающих и не обладающих дополнительным упрочнением, опреде-
определяются на основе B.39) и следующего выражения:
533
2s
2s!
23
31 J
C.217)
Для теории неупругого деформирования материалов, чувствитель-
чувствительных к виду напряжённого состояния, в случае пренебрежения неупру-
неупругим изменением объёма матрица [С^-] определяется на основе B.132),
а вектор [Ь"] имеет вид
— - —
^33
2п*2
2п23
C.218)
Следует отметить, что здесь в выражениях для мягкого нагружения
и далее для жёсткого нагружения Е*, Вт, Вф, BR, E**, Bj, Bfu, BR
вычисляются на основе формул C.195) и C.196).
Для определения внутренних переменных C.213) и C.214)
формулируются системы уравнений на основе C.190)—C.196),
C.200)-C.203) и C.206), учитывая условия упругого и неупругого
состояний C.199).
Уравнения связи между скоростями деформаций и напряжений в
случае жёсткого нагружения имеют вид
[&{] = [AjH^-R Ш,	C.219)

132
Часть 3. Неупругость
Матрица [Dij] и вектор
ляющих, т. е.
= [Qij] Ш + Ш ¦	C-220)
di\ состоят из упругой и неупругой состав-
lDij}-[D!k}[Dkj]>	С3-221)
= [^-Щ][<1»}	C.222)
Упругие составляющие [Z)| • ] и [df] определяются выражениями A.92)
и A.146), а неупругие составляющие [D^] и d" для материалов,
обладающих и необладающих дополнительным упрочнением, опреде-
определяются на основе B.42) и следующего выражения:
Ш
1
: + 3G 2 ^
s;f
22
53
Матрица
равен
] [?)?•] определяются как B.43), а вектор
33
523
3C.223)
[]
3G 3 1
Sms;
11*33 *11*12
S22522 522533
512533
*1
^22*23 b22b?>\
О Q	Q Q	Q Q	Q Q	Q Q
b3\bU *31*22 *31*33 *31*12 *31*23
1 3 1
- 3G 2 at
хъъ
2(а||"Г + off Ф)
5
5
5
5
_ 5
*
11
*
22
*
33
*
12
*
23
*
31 J
. C.224)

Глава 3. Неизотермическое нагружение
133
Для теории неупругого деформирования материалов, чувствитель-
чувствительных к виду напряжённого состояния, в случае пренебрежения неупру-
неупругим изменением объёма матрица [D\k} [D%j\ определяется как B.224),
а вектор [Dfj] \<Щ равен
[Щ] Щ] = -
3G
3 1
n33nll	n33n22
77/1о77/11	77/io77/oo
П23П11	П23П22
n31nll	n31n22
JU+3G2(n.J
ППП33 nlln12
^22^33 ^22^12
nlln23 nlln31
П22П23 П22П31
n33n33 n33n12 n33n23 n33n31
/ioTT/oo
/io/T/io
T/io/T/oo
T/io/T/oi
П23П33 П23П12
П23П23 П23П31
n31n23 n31n31
3
- 3C 2 n*
+ aff Ф
afjf + a
fj
|3
T + aff Ф)
^33
^23
C.225)
Для определения вектора внутренних переменных C.213) и C.214)
формулируется такая же, как и ранее, для мягкого нагружения, систе-
система уравнений, кроме уравнений для скорости накопленной неупругой
деформации, которая определяется в данном случае уравнением C.197)
или C.198) в соответствии с вариантами теорий.
§ 5. Уравнения теории неупругого деформирования
в случае обобщённого плоского состояния
На примере теории неупругого деформирования рассматриваются
все возможные виды нагружения (всего 16 случаев) в условиях обоб-
обобщённого плоского состояния.
Для кратности ниже приводятся уравнения для скорости накоп-
накопленной неупругой деформации и для скоростей компонент тензоров
напряжений и деформации, при неизотермическом нагружении, без
учёта воздействия ионизирующего излучения.
Уравнения для остальных компонент вектора скоростей внутренних
переменных одинаковы для всех случаев нагружения и очевидны.

134
Часть 3. Неупругость
•н
6-22 ^зз ^12], Ш = [ёп
3 S*iGll + S22CT22 + «ЗЗ^ЗЗ + 2s*2Gi2
1 г-
В 1 + В
?зз = -^ [сгз;
2- [%j] = [ё\\ ^2 &с
1
+
(
SG
+
СТ\\ — Е I ?\\ — &п — «ц ) ~1~ ^ (^2 ~Ь ^3/ 9
/. .н sTrfi\ \—V. 1/A+1/) .
?22 = -^ (^11 - ?ц - «11 1 J Н	^— ^22	д	СГ33 +
^33 — —V \ё\\ — ?\\ — а\\ Т)	—	(J22 Н	р— ^33 +
- &\2 + ^?2 + а\2 Т•
¦ «2^,
a3f T,
3. [Xj] = [an ?22 ^33 СГ12] , fe] = [^11 ^22 ^33
^* = Е* + ЗС* [3G	<	+
3 (s*i + Z/S22) <7ц + (S33 + ^^22) СГЗЗ + 2s*2<3"i2
z	cr9/
= "I/ (^22 - ^2 -
2 ю
	^— ^1
^33 + ^1 +

Глава 3. Неизотермическое нагружение
135
Е
Т,
?12 =
4. [xj] = [&u &22 г33 о~12}т, [yi] = [in e22
1
я* + зс*
2	сг*
,
= —v
?22 =
-v [ e33 - e33
^"зз = i
E
-—g—an
ёзз-^3-а^т)+;
" ^22 + in + «ff 3
+ ^22),
5. \хЛ =
3G*
i] = [in ?22
1 3 Sn&u + 522^22 + ^33^33
2	cr*
,
= I [*n - v (a22 + a33)] + iHn + aff T
1 г.
^22 = ~^ [°
1 Г.
?33 = ^ [0
^2
— ^(ац + a22J
42

136	Часть 3. Неупругость
?и* = Е +3G 3G^—US22 —ап _ ^—VSn ——	h
, 3 A - 2^M33^33 + 2A - 1/)S*2&12 _ gTf 1 qr\
2	A-i/K
&u =
E X (	t ' \	(	т1 * N1	is
®Tl — 	9 K22 — ^22 "~ a22 ^ + ^ ( ^11 ~ ?\\ ~ аП Т I + -j	'
1 — 1/ L \	/ V	/ J 1 — 1/
•н eT^\ 1/A+1/) . . 1 — V . , -и ,
2 — ^22 ~~ a22 1	В	G\ 1 H	Ъ— аЗЗ + ^33 + a
• iT r. 1 r.	•	•	О• 1T
^33 ^12] > [2/iJ — [^11 ^22 ^33 ^^12j >
3 A - 2t/)s|2O-22 + 2A - 1/)8^^12
2	A-^K
G22,
?22 = -^ [(?11 - ??, - aff T
-2»/)

Глава 3. Неизотермическое нагружение
137
8.
СТ22
3G*
2sj2(ei2 ~ aiJ
3 (S22
2
CT22
&п=Е(ёп- ?нп ~ аи?) + v F-22
= -v (in - in - off
a22
= [en
cgt,
Тф
^3 + agT
(833 + V822) (g33 ~
3 A - 2l/)su&u + 2A - 1/)S*2&12 тэТф
2	AW
_ ^3 E22) + (^ЗЗJ + 2^522^33
E
E
+ (e33 - ^з -
^33 - ^33 - аЗЗ 1 ) + v I ?22
1+1/ .
?12 = т^ СГ]
h
&u,

138
Часть 3. Неупругость
* + 3G*
зс
?2
(и
= [in
?33
b
e22
2	(a*J
agf) + 1-^ an
G22 — E ( ?2 ~~ <^22 ~~ ^2$
= -v
agf) -
au
^12 - ^12
11. [Xj] = [(Гц
= [i\\
1 3 (g*i + ^533)^11 + (g22 + ^^Зз)о~22 _ лТф i
9	*
= -1/
= -1/
(^зз - ^зз - '
(^зз - ^з - '
+
an -
¦ ^22 + in + aU T,
i -и i eTrji
" <^22 ~r ?99 ~r СУ99 1 ,
12. [ij] = [en ^22 ^33 ^12]T,
з*п(ёп - ant) +
cr22),
^22 ^33
3C*
3G-
g22 - agf)

Глава 3. Неизотермическое нагружение	139
r _^3 (s*nf + (st2f + (shf
- ёп - aff t + ?33 - ?33 "
Т + ?22 " ?22 ~
?.2 = ^<т12 + ?f2 + af JT.
13. [ij] = [iu ?22 0-33 2?12]Т, [in] = [<тц ст22 ?зз
1 ГоГ(ап + vsy) (ёп - а|Гг) + (§22 + t/afi) (?22 -
[	AK
3A-2фзУзз
G = G-
2	(i-^ЖJ
Е
v
j [(e22 - ^2 " О$
" ё?, - afft) + (е22 - е\2 - agf)]

140
Часть 3. Неупругость
14. [xj] = [гп СТ22
i] = [аи
3G*
зз) (gn ~ <*nT)
,
tiJ + (аззJ + 2^si,s3*3 + 2A - v) (s,2J
an =
^22 —
E
1 -i
Е
1 -V
eT rh\\
-3G
; — <^зз -L)
(g^f + (^ЗЗJ + 2^522^33 + 2A-1/) (s*2f
1 -V
-2»/)
b\k
^зз — ?33 ~
O\2 =
ё22 - ё»22 - agf)]

Глава 3. Неизотермическое нагружение	141
16. [Xj] = [iu ?22 ^33 2?i2]T, [yi] = [&U ^22 ^33 °\2? ,
*п(^1 ~ cttff) + a2*2(g22 - agf) + a;3(g33 ~ alJ
r
G* =G,
егг - ?22 " ^ + ^зз - езз " "зз
?33
- ?п - aff T
~ п~ Х
Уравнения для материалов, обладающих дополнительным упрочнени-
упрочнением, аналогичны, но только в этом случае добавляется уравнение для
Стах- Для материалов, чувствительных к виду напряжённого состоя-
состояния, в случае пренебрежения неупругим изменением объёма, уравне-
уравнения такие же, но только в них Е*, Вт, Вф, BR, <т* и s*- заменяются
соответственно на Е**, Bj", Bf, BR, n* и п\у

Список литературы
1.	Бондарь B.C. Математическая модель неупругого поведения и накопления
повреждений материала // Прикладные проблемы прочности и пластично-
пластичности. Методы решения: Всесоюз. межвуз. сб. / Горьк. ун-т. 1987. С. 24-28.
2.	Бондарь В. С. Математическое моделирование процессов неупругого пове-
поведения и накопления повреждений при сложном неизотермическом нагру-
жении в условиях ионизирующего излучения // Расчёты на прочность. —
М.: Машиностроение, 1988. Вып. 29. С. 23-29.
3.	Бондарь В. С. Неупругое поведение и разрушение материалов и конструк-
конструкций при сложном неизотермическом нагружении // Автореферат дис-
серт. ... д.ф-м.н. — Москва: МАМИ, 1990. — 40с.
4.	Кадашевич Ю.И., Новожилов В. В. Теория пластичности, учитывающая
остаточные микронапряжения // ПММ. 1958. Т. 22, вып. 1. С. 78-89.
5.	Новожилов В. В. О сложном нагружении и перспективах феноменологи-
феноменологического подхода к исследованию микронапряжений // ПММ. 1964. Т. 28,
вып. 3. С. 393-400.
6.	Кадашевич Ю.И., Новожилов В. В. Об учёте миронапряжений в теории
пластичности // Инж. ж. МТТ. 1968. № 3. С. 83-91.
7.	Бондарь В. С. Теории пластичности, ползучести и неупругости в условиях
сложного нагружения // Прикладные проблемы прочности и пластичности.
Алгоритмизация и автоматизация исследований: Всесоюз. межвуз. сб. /
Горьк. ун-т. 1987. С. 75-86.
8.	Расчёты машиностроительных конструкций методом конечных элементов:
Справочник / Под. общ. ред. В. И. Мяченкова. — М.: Машиностроение,
1989. - 520 с.
9.	Бондарь B.C., Фролов Л.Н. Математическое моделирование процесов
неупругого поведения и накопления повреждений материала при сложном
нагружении // Из. АН СССР. МТТ. 1990. №6. С. 99-107.
10.	By До Лонг. Вариант теории и некоторые закономерности упругопластиче-
ского деформирования материалов при сложном нагружении // Авторефе-
Автореферат диссерт. ... к-ф-м.н. — Москва: МАМИ, 1999. — 21 с.
11.	Феодосьев В.Н. Сопротивление материалов. — М.: Наука, 1974. — 559 с.
12.	Малинин Н.Н. Прикладная теория пластичности и ползучести. — М.:
Машиностроение, 1975. — 400 с.
13.	Ильюшин А. А. Пластичность. Основы общей математической теории.— М:
Изд. АН СССР, 1963. - 271 с.
14.	Ильюшин А. А. Механика сплошной среды. — М.: Изд-во МГУ, 1990. —
310 с.
15.	Зубчанинов В. Г. Основы теории упругости и пластичности. — М: Высшая
школа, 1990. - 368 с.
16.	Термопрочность деталей машин: Справочник / Под ред. И. А. Биргера,
Б.Ф. Шорра. — М.: Машиностроение, 1975. — 455 с.

Список литературы	143
17.	Лихачёв Ю.И., Пупко В. А. Прочность тепловыделяющих элементов ядер-
ядерных реакторов. — М.: Атомиздат, 1975. — 280 с.
18.	Бондарь B.C. Решение нелинейных задач сложного нагружения оболочек
вращения // Расчёты на прочность и жёсткость: Межвуз. сб. / М.: Мос-
станкин, 1982.Вып. 4. С. 85-95.
19.	Кадашевич Ю.И. О различных тензорно-линейных соотношениях в теории
пластичности // Исследования по упругости и пластичности / Л.: Изд-во
ЛГУ, 1967. Вып. 6. С. 39-45.
20.	Новожилов В.В., Рыбакина О.Г. О перспективах построения критерия
прочности при сложном нагружении // Прочность при малом числе циклов
нагружения / М.: Наука, 1969. С. 71-80.
21.	Романов А.Н. Энергетические критерии разрушения при малоцикловом
нагружении // Проблемы прочности. 1974. № 1. С. 3-10.
22.	Бондарь B.C., Санников В.М. Малоцикловая усталость тонкостенных кон-
конструкций при повышенных температурах // Конструкционная прочность
лопаток турбин ГТД: Тезисы докладов IV научно-техн. конф / Куйбышев.
1976. С. 75-76.
23.	Бондарь B.C., Горохов В.Б., Санников В.М. Исследование малоцикловой
прочности оболочек вращения при сложном теплосиловом нагружении //
Прикладные проблемы прочности и пластичности. Механика деформируе-
деформируемых систем: Всесоюз. межвуз. сб. / Горьк. ун-т. 1979. Вып. 12. С. 120-126.
24.	Бондарь B.C., Санников В.М. Усталость и устойчивость оболочек враще-
вращения при цклическом теплосиловом нагружении // Прикладная механика.
1981.	Т. 17, №2. С. 118-121.
25.	Мэнсон СМ. Температурные напряжения и малоцикловая усталость. —
М.: Машиностроение, 1975. — 344 с.
26.	Дягтярев В. П. Пластичность и ползучесть машиностроительных кон-
конструкций. — М.: Машиностроение, 1967. — 131 с.
27.	Шишмарев О. А., Щербо А.Г. Исследование некоторых сложных процессов
нагружения стали с разгрузкой // Прикладная механика. 1982. Т. 18, №3.
С. 65-70.
28.	Ohashi Y. Effect of Complicated deformation history on inelastic deformation
behaviour of metals // Memoris of Faculty of Engineering Nagoya University.
1982.	V. 34, №1. P. 1-76.
29.	Вавакин А. С, Викторов В.В., Сливовский М., Степанов Л. П. Экспери-
Экспериментальное исследование упругопластического поведения стали при про-
простом и сложном циклическом деформировании. — М., 1986. — 175 с. Деп.
ВИНИТИ № 2607-В. 86.
30.	Соси. Модели разрушения при многоосной усталости // Теоретические
основы инженерных расчётов. 1988. №3. С. 9-21.
31.	Охлопков Н.Л. Закономерности процессов упругопластического деформи-
деформирования металлов при сложном напряжённом состоянии и нагружении //
Автореферат диссерт. ... д.т.н. — Тверь: ТГТУ, 1997. — 35 с.
32.	Новожилов В. В. О пластическом разрыхлении // ПММ. 1965. Т. 29,
вып. 4. С. 681-689.
33.	Кадашевич Ю.И. Теория пластичности, учитывающая эффект Баушин-
гера и влияние среднего нормального напряжения на границу текуче-
текучести // Тр. Ленингр. технол. ин-та целлюлозно-бум. пром-ти. 1965. Вып. 18.
С.234-235.

144	Часть 3. Список литературы
34.	Коротких Ю.Г. Описание процессов накопления повреждений материала
при неизотермическом вязкопластическом деформировании // Проблемы
прочности. 1985. № 1. С. 18-23.
35.	Мовчан А. А. Феноменологическое описание дислокационного механизма
образования дефектов при пластическом деформировании // Проблемы
прочности. 1987. № 1. С. 147-155.
36.	Вавакин А. С, Мохель А.Н., Степанов Л. П. Исследование характера пла-
пластического деформирования стали ЗОХГСА в точках резкого излома тра-
траектории нагружения. (Р-М опыты) // М., 1983. — 102 с. Деп. ВИНИТИ
№ 2895-83.
37.	Коровин И.М. Экспериментальное определение зависимости напряжение-
деформация при сложном нагружении по траекториям с одной точкой
излома // Инж. ж. МТТ. 1964. № 3. С. 592-600.
38.	Tanaka Е., Murakami S., Ooka М. Effects of plastic strain amplitudes on
nonproportional cyclic plasticity // Acta Mechanica / V. 57. 1985. P. 167-182.
39.	Беналлал, Марки. Определяющие уравнения упруговязкопластичности для
непропорционального циклического нагружения // Теоретические основы
инженерных расчётов. 1988. №3. С. 68-84.
40.	Benallal A., Calloch S., Laborderie С, Marquis D. Hardening of metals
under cyclic nonproportional loadings in tension-torsion and triaxial tension //
International seminar on Multiaxial plasticity. 1-4 September 1992. Cachan
France. P. 1-7.
41.	Кадашевич Ю.И., Мосолов А. Б. О соотношениях эндохронной теории пла-
пластичности с «новой» мерой внутреннего времени при сложном циклическом
нагружении // Технология лёгких сплавов. 1990. №3. С. 32-36.
42.	Бондарь B.C., Титарев И.А. Вариант теории пластичности для пропорци-
пропорциональных и непропорциональных циклических нагружении // Проблемы
прочности и пластичности: Межвуз. сборник. Вып. 63. Нижний Новогород:
Изд-во Нижегородского госуниверситета, 2001. С. 5-17.
A3. Бондарь B.C., Титарев И.А. Вариант теории неупругого деформирова-
деформирования и разрушения материалов при повторном и длительном воздействии
температурно-силовых нагрузок и ионизирующего излучения // Вестник
Нижегородского университета им. Н. И. Лобачевского. Серия механика.
Вып. 1D). Н. Новгород: Изд-во ННГУ, 2002. С. 39-49.
44.	Охаси Й., Оно, Каваи. Оценка определяющих уравнений ползучести для
нержавеющей стали 304 при повторяющемся многоосном нагружении //
Теоретические основы инженерных расчётов. 1982. Т. 104, №3. С. 1-8.
45.	Аверченков Б. А., Донченко А. С, Егоров В.И. О поведении материала
поршня при термосиловом нагружении // Повышение топливоной эконо-
экономичности и долговечности автомобильных двигателей. — М.: МАМИ,
1983. Вып. 5. С. 59-68.
46.	Коротких Ю.Г. О базовом эксперименте для модели термовязкопластично-
сти // Прикладные проблемы прочности и пластичности: Всесоюз. межвуз.
сб. / Горьк. ун-т. 1977. Вып. 6. С. 3-20.
47.	Хажинский Г.М. О теории ползучести и длительной прочности металлов //
Изв. АН СССР. МТТ. 1971. №6. С. 29-36.
48.	Работное Ю.Н. Ползучесть элементов конструкций. — М.: Физматгиз,
1966. - 752 с.
49.	Бойл Дж., Спенс Дж. Анализ напряжений в конструкциях при ползучести:
Пер. с англ. - М.: Мир, 1986. - 360 с.

!
I
писано
d
ё
A.12
A.12
° о
° о
(N Ь
b <?
11
II J^
4—y ч—^
H
О
о
	' en
^^
?—
II
, •*?
cn^
A.13
ъ
b°
E-h
ro
и
E^
cn^
СП
4—y
X
*E^
\
о
:>
E-h
ГО
1
II
Еч
A.13
A.13
A.14
ro
:S> ^ 1
<N Г0
td '—
r
:&> |
II \
c*
J
H
°iq <n ¦—¦
I T^
+
Е~ч E-h
II II
(>• O\ О
СП СП ^t
E^
ro
=1 II
о ^ en
Ь ^ +
1
4
II
E
с
1
b°
S ^ i
i ч
1 4
bq ^ -к
I
I
4?
b°
4? ^ ^
Е-н E^
IT
и
+
Q Q |
II II
A.14
^,
•E-h
II
1.14
4—y
«.»
q i
+
Е-,
II
A.16
. '^.
II
1.16
4—y
+
, IT
II
00
m
i
ев
Тогд
f
Тогда вею
О о сп
°
О
(N
pq
[й имеет
1
kiayp
..систем
ет вид (
ий име
ма уравнен
d
^ о о
°
ица 2.4
МПа
| о"
s ^
ю ^
d о
Н
ев
О

st читать
Сле
о
1
СП
¦TJ-
CN
+
1
1
и
1
Г
V
1
¦Л
СП
СП
¦TJ-
(N
1 . '
Н
i
•Е-н
1
* <N
-
V
1
+
+
00
(N
(N
СП
1
+
1
)<
„—^
1 1
•to1
^^
(N
(N
СП
1
_
1
1
Е-н
: +
II 3^
'Я 1
00
(о
СП
4—у
о
э
• 1
" 1
1
I
-&.
1 1
(DO м
a i
: о
Со"
uQ
Есспери?
СП
CD
^ 1
bo CD
i\
& .
1 2
Л 5
3 ч
Ьо р.
i §
On
СП
4—^
3
ьо
to
ьо
ьо
to
СП
ьо
3
ьо
й-;
ьо
ьо
to
bq4
On
СП
нении... (
PQ
д
to
C.29)
ИИ.
1
1
СО
а
'¦*
СП О СП
On Рч <N
сп"
СП
СП
4—у
II
ьо
сп"
СП
СП
II
ьо
00
СП
3.81
|>
СП
о1
СП
СП
СП
1
1
II
00
СП
^
00
СП
1О
СП
о"
СП
СП
C.56
1
II
97,
99-10
СП
1
СП
II
115
о
1
схем<
CD
pq
о
й
1
о
CD
<D
а
00
СП
1
ьо
+
•ьк
II
00
СП
ьо
1
•=?
ьо
+
•ь5
ьо
II
122
оо"
00
т~1
СП
•о
•Е-н
•ь^
t
•ь
1
. 'b,
1
40^
оо"
00
T~l
СП
Е-н
•ь^
1
1
,-ь^
II
чо^
124