Автор: Хакен Х.
Теги: физика квантовая теория квантовая физика физика твердого тела твердое тело
Год: 1980
Текст
Х.Хакен
КВАНТОВОПОЛЕВАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА
М.: Наука. Главная редакция физико-математической литературы, 1980.
В книге последовательно развиваются основы квантовой теории поля
применительно к рассмотрению элементарных возбуждений в твердом теле
(электронов, фононов, экситонов, плазмонов, магнонов и др.) и взаимодействий
между ними.
По мере изложения автор знакомит читателя с современными методами
квантовополевой теории твердого тела. Построение формального аппарата
проводится на примерах конкретных проблем, при этом постоянно уделяется
внимание физической стороне дела.
Приведенные в книге задачи с указаниями к их решению позволяют читателю
активно овладеть изложенным материалом.
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие автора 8
Указания к чтению книги 10
Глава I. Вступление 11
§ 1. Введение и обзор 11
§ 2. Некоторые основные понятия классической механики 17
Глава II. Гармонические осцилляторы 21
§ 3. Квантовомехапический осциллятор: операторы рождения и 21
уничтожения
§ 4. Вычисление средних значений 30
§ 5. Об обращении с богнмшераторами: мы учимся некоторым приемам 37
§ 6. Смещенный гармонический осциллятор: прообраз элементарных 47
возбуждении в твердом теле
Глава III. Квантование поля 55
§ 7. Линейная цепочка, атомов: классическое рассмотрение 55
§ 8. Линейная атомная цепочка: квантовотеоретическое рассмотрение. 62
Фононы
§ 9. Переход к континууму: классическое рассмотрение 67
§ 10. Переход к континууму: квантовотеоретическое рассмотрение. 77
Фононы
§ 11. Трехмерные проблемы: квантование скалярного волнового 83
уравнения и электромагнитного поля. Фотоны
§ 12. Квантование шредингеровских волновых полей, подчиняющихся 94
статистике Бозе (вторичное квантование). Бозоны
§ 13. Квантование шредингеровских волновых полей, подчиняющихся 104
статистике Ферми — Дирака: Фермионы
§ 14. Об обращении с ферми - операторами 113
§ 15. Взаимодействие между полями: электроны, «танцующие на канате» 123
§ 16. Методические приемы: представление взаимодействия и 130
представление Гейзенберга
Глава IV. Электроны в «замороженной» решетке 140
§ 17. Электроны в кристаллической решетке: краткое изложение теории 140
Блоха
§ 18. Метод эффективной массы 145
§ 19. Функции Ваннье: волновые пакеты из функции Блоха 149
$ 20. Электроны в кристаллической решетке: формулировка проблемы 150
многих тел. Приближение Хартри — Фока
§ 21. Электронные дырки 160
§ 22. Взаимодействие между электронами и дырками 166
§ 23. Экситоны с большим радиусом (экситоны Ваннье) 176
§ 24. Экситоны Френкеля 182
§ 25. Волны электронной поляризации 191
§ 26. Экситонная материя 198
§ 27. Плазмоны 200
§ 28. Спиновые волны: Магноны 207
Глава V. Взаимодействие электронов с колебаниями решетки 219
§ 29. Гамильтониан Фрёлиха для взаимодействия между электронами и 219
фононами
§ 30. Нестационарная теория возмущений (первый порядок). Спонтанное 226
и индуцированное испускание и поглощение фононов.
Представление с помощью диаграмм Фейнмана
§ 31. Электрическое сопротивление 235
§ 32. Нестационарная теория возмущений (второй порядок): собственная 244
энергия, перенормировка массы
§ 33. Теория возмущений высших порядков 251
§ 34. Теорема о точной форме решения 255
§ 35. Полярон Фрёлиха. Собственная энергия и перенормированная масса 258
§ 36. Эффективное взаимодействие между поляронами 262
Глава VI. Функции Грина 268
§ 37. Теория возмущений в координатном пространстве. Возникновение 268
функций Грина
§ 38. Функция распространения, пропагатор, функция Грина — все одно и 275
тоже
§ 39. Примеры уравнений для функций Грина и. их решение 280
Глава VII. Сверхпроводимость 294
§ 40. Основные экспериментальные факты, касающиеся 294
сверхпроводимости
§ 41. Теория сверхпроводимости: введение фрёлиховского взаимодействия 299
между электронами
§ 42. Основное состояние сверхпроводника по теории Бардина — Купера 305
— Шриффера (БКШ)
§ 43. Возбужденные состояния сверхпроводника 314
Глава VIII. Взаимодействие электронов с квантованным 319
электромагнитным полем
§ 44. Взаимодействие между излучением и веществом: оператор
§ 45. Поляритоны
Литература для дальнейшего чтения
Список обозначений
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
319
324
332
336
Амплитуда вероятности 108
Антинормально упорядоченная
функция 40
Антисимметричная волновая
функция 111
Атомная цепочка линейная 55
Елоховская волна 142
Бозе-операторы 37
— частицы 51
Бозоны 94, 100 Бра
33
Вакуумное состояние 99
Валентная зона 143
Вариационная производная 72
Векторный потенциал 85
Вероятность перехода полная 108
Вершина 229
Взаимодействие полей 123
— точечных зарядов 196
— электронов с квантованным полем
излучения 319
колебаний решетки
219
Внутреннее поле 207
Волновое уравнение, квантование 83
одномерное 68
трехмерное 83
Время жизни полярона 292
— соударения 240
Гармонический осциллятор 21
под внешним воздействием 47
Глубина проникновения 296
Граничные условия циклические 68
Групповая скорость 143
Двухатомная линейная цепочка 62
Двухуровневый атом во внешнем
электрическом поле 123
8-функция Дирака 71
, представления 76
, производные 76
Диаграммы 229
— связанные 255
Длина когерентности 298
— свободного пробега средняя 242
Закон дисперсии волны в атомной
цепочке 57
для двухатомной линейной
цепочки 62
одномерного континуума 09
скалярного волнового
уравнения 85
— Ома 241
Запрещенная зона 143
Звуковые волны 11
Зоны энергетические 142
Измеримые величины 31
Изолятор 144
Испускание виртуальное 230
— индуцированное фононов 226, 232
— фонона спонтанное 228
Калибровочное преобразование 86
Канонически сопряженный импульс
в континууме 73
Л-правило отбора 144
Квазичастица 280
Квантование волнового уравнения 87
— шредингеровского волнового поля
98
, подчиняющегося
статистике Ферми — Дирака
104
, , вторичное 94
— электромагнитного поля 86 Кет
33
Когерентные состояния 50, 66, 81
Колебания ионов в F-центре (центр
окраски) 48
Конденсация Бозе — Эйнштейна 198
Кронекера символ 27
Кулоновская калибровка 86
— обменная энергия 102
Кулоновский оператор 103
Кулоновское обменное
взаимодействие 158, 172
Куперовская пара 306
Магнетон Бора 207
Магнон 14, 207
Матричный элемент гармонического
осциллятора 36
Метод Ли — Лоу — Пайнса 259
— Эренрейха — Коэна 201
Модель Гайтлера — Лондона 207
Молекула водорода 207
Молекулярный кристалл 182
Наложение волновых функций 38
Нормально упорядоченная функция
39
Нормировочный множитель
осцилляторной функции 34
Нулевая энергия 27, 29
электромагнитного поля 92
Обменный интеграл 209
— оператор Гамильтона 210
Оператор Гамильтона
взаимодействия электронов с
квантованным полем излучения
319
колебаний атомной цепочки в
континуальном пределе 79
непрерывного
распределения электронов 128
решетки и электронов в
металлах 226
несвязанных осцилляторов 26
смещенных гармонических
осцилляторов 53
сверхпроводимости 306
электронной дырки 163
электронов и дырок 167
поляризационных колебаний
и электронов 222
— координаты 101
— Лапласа 83
— отклонения 65
— плотности числа частиц 100
— рождения 21
— трансляции 140
— уничтожения 21
— числа частиц 80
Операторная функция 39
экспоненциальная 39
Основное состояние гармонического
осциллятора 26
сверхпроводника, энергия 313
Перенормированная масса полярона
261
Перенормировка массы 244, 250
Перестановочные плюс-соотношения
105
— соотношения в континуальном
пределе 78
для бозе-операторов 24, 28
гармонического осциллятора
22
Перестановочные соотношения для
операторов линейной цепочки
64
— — — скалярного волнового
уравнения 84
ферми-частпц 105
— — — шредингеровского
волнового поля 98
электромагнитного поля 89,
91
между у и \|/+, фермионные 106
Периодические граничные условия
55
Плазменная частота 201
Плазменные колебания 200
Плазмой 16, 200
Плотность гамильтониана 85
— тока 297
Поглощение 226
Поглощения зона 144
— кривая 144
Поле 67
—, квантование 55
Полюс функции Грина 279
Поляризационные волны 12
электронные 191
— колебания 12
, квантование 219
Поляризация, облако 250
Поляритон 13, 324
Полярный кристалл 219
Полярон 16, 250, 258
— электронный 251
Поляроны, взаимодействие между
ними 262
Потенциал 17
—, вид для смещенного
гармонического осциллятора 48
Потенциальная энергия во внешнем
поле, оператор 102
Правило вычисления волновых
векторов 144
Представление взаимодействия 130,
226
— Гейзенберга 130
Преобразование Боголюбова 117, 316
— Холыптейна — Примакова 217
— ферми-операторов линейное 116
Приближение Бома — Пайнса 204
— случайных фаз 205
Примесный атом 54
Принцип Кондона 54
— Паули 100,207
— суперпозиции 57
Проводимость 241
Проводник 144
Производная в континууме 72
Пропагатор 275
Разложение по собственным
функциям 97, 127
Сверхпроводимость 294
Сверхпроводник, возбужденное
состояние 314
— жесткий 298
— мягкий 298
—, основное состояние по теории
Бардина—Купера—Шриффера
305
—, энергетическая щель 318
Смещенный гармонический
осциллятор 47
Собственная функция
гармонического осциллятора 26
— энергия 26
, диаграмма 274
полярона 292
частицы 195
Собственное состояние несвязанных
осцилляторов 29
Собственные состояния уравнения
Шредингера электромагнитного
поля 92
Состояние 24
Спин 207
— 1/2 в магнитном поле 122
Спиновые волны 14, 207, 214
— операторы 209
Среднее значение для фермионов 111
амплитуды когерентного
состояния 82
, вычисление 31
Ступенчатая функция 281
, производная 282
Суперпозиция волновых функций 38
Сфера Ферми 14
Т-оператор 280 Т-
произведение 281
Температура перехода Тс 294
Теорема Блоха 142
Теория Блоха 140
— возмущений в координатном
пространстве 268
нестационарная, второй
порядок 244
, высшие порядки 251
,первый порядок 226
Унитарное преобразование 44
Упругая постоянная 21
Уравнение Больцмана 239
Уравнение вынужденных колебаний
струны 125
— движения Ньютона 17
атомной цепочки 55
— колебаний свободной струны 124
— Пуассона 87
— струны 68
— Шредингера атомной цепочки 65
временное 130
гармонического осциллятора
30
Двух частиц 111
— — квантованного
шредингеровского волнового
поля 99, 106
п частиц 111
проблемы многих электронов
в твердом теле 151
Уравнения Гамильтона 17
— — в непрерывном пределе
(струна) 74
для линейной цепочки 58
— Лагранжа 17
в континуальном пределе 73
— Лондонов 295
— Максвелла в вакууме 85
Условие Лоренца 86
Фейнмановские диаграммы 226
Ферми-операторы 113
осциллятор смещенный 115,
122
Фермионный оператор уничтожения
в представлении Гензенберга
138
, уравнение 137
Фермионы, квантование 104
Ферромагнетизм, модель Гейзенберга
210
Фононы 12, 62
— в континууме 77
Фотоны 83
Фрёлиховский гамильтониан
взаимодействия между
электронами и фононами 219
Фрёлиховское взаимодействие 299
Функция Ваннье 149
— Гамильтона 17
вынужденного гармонического
осциллятора, классическая 138
линейной цепочки 58
в непрерывном пределе
(струна) 74
— — система электроны +
непрерывное поле 126
— — скалярного волнового
уравнения 84
шредингеровского волнового
поля 95
Функция Гамильтона
электромагнитного поля 88
— Грина 268, 275, 280
многоэлектронной проблемы
280
, определение 276
полярона 286
свободной частицы 277
— Лагранжа 17
континуума 70
системы электроны +
колебания континуума 125
скалярного волнового
уравнения 83
шредингеровского волнового
поля 96
электромагнитного поля 87
— распространения 275
— состояния избыточного электрона
159
невзаимодействующих
фермионов 106
Фурье-интеграл 76
—образ функции Грина 279
— преобразование 61
ряд непрерывной функции 75
Хартри приближение 285
Хартри — Фока метод 150
приближение 286
Числа заполнения 106
при тепловом равновесии для
бозе-частиц 238
Экситон Ваннье 176
— Френкеля 182
—, операторы рождения и
уничтожения 187
—, энергетическая схема 181
Экситонная молекула 198
Экситонное вещество 198
Экситонные капли 199
Электрическая индукция 221
Электрическое сопротивление 235
Электронная дырка 160
Электрон-электронное
взаимодействие в
сверхпроводнике 304
Элементарный магнит 207
Эрмитово-сопряженный оператор 34
Эффективная масса 143
, метод 145
Эффект Мейсснера — Оксенфельда
284
— Холла аномальный 166
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Одной из центральных концепций современной теоретической
физики твердого тела является концепция элементарного возбуж-
дения или квазичастицы. Элементарные возбуждения не являют-
ся привилегией лишь твердого тела. Они могут возникать в дру-
гих многочастичных системах: ядрах, плазме и т. д. Твердое
тело представляет собой один из примеров системы многих ча-
стиц, специфика которой состоит в том, что между частицами
действуют силы электрического происхождения и что довольно
часто можно провести достаточно четкое разделение всей систе-
мы на подсистемы, каждая из которых обладает характерными
особенностями и которые могут взаимодействовать друг с другом.
Поэтому твердое тело как объект исследования особенно инте-
ресно разнообразием существующих в нем элементарных возбуж-
дений. Понятие квазичастицы весьма успешно используется для
объяснения всей совокупности тепловых, электрических, магнит-
ных, оптических и других свойств кристаллов (и не только кри-
сталлов), а такие фундаментальные явления, как, например,
электросопротивление и сверхпроводимость, удалось описать как
результат взаимодействия элементарных возбуждений различной
природы.
Концепция элементарного возбуждения в теоретической фи-
зике твердого тела возникла с внедрением в нее методов кванто-
вой теории поля, которые сами при этом претерпели определен-
ные изменения. Изложение тех или иных вопросов приложения
квантовополевых методов в теоретической физике твердого тела
можно найти в целом ряде монографий и учебных пособий, на-
писанных советскими и зарубежными авторами. Среди них кни-
га западногерманского профессора X. Хакена «Квантовополевая
теория твердого тела», перевод которой предлагается читателю,
занимает особое место. Профессор Хакен предпринял попытку
и, скажем сразу, удачную попытку изложить лишь наиболее
общие и фундаментальные, важные в идейном отношении раз-
делы квантовополе(вой теории твердого тела, причем не просто
изложить, а просчитать от начала до конца, с тем чтобы начи-
нающий читатель уловил не только идейную основу подхода, но
и разобрался в методах, используемых в квантовополевой теории
твердого тела.
6 ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Чтобы выполнить эту задачу, автору, как он сам говорит об
этом в предисловии, пришлось провести строгий отбор материа-
ла и освободиться от всего того, что не является принципиально
важным для понимания существа дела. Совершенно очевидно,
что отбор проводился по двум направлениям: выбор материала
и стиль его подачи. Выбор материала, естественно, несет явный
отпечаток склонностей самого автора, который известен своими
работами по теории электронов и фотонов в твердом теле. Здесь
нет смысла пересказывать содержание книги. Следует лишь от-
метить несколько моментов. Очень полезный для общей ориента-
ции материал изложен в шестой главе о функциях Грина. Здесь
устанавливается связь между теорией возмущений, функциями
Грпна и функциями распространения.
Последняя, восьмая глава, посвященная взаимодействию
электронов с квантованным нолем электромагнитного излучения,
написана менее удачно. Она довольно схематична и при ее чте-
нии возникает впечатление, что она добавлена лишь для «пол-
ноты».
Лптор излагает материал в свободной разговорной манере,
довольно конспективно, что, впрочем, не следует считать недо-
статком изложения, том более, что во всех важных для понима-
ния моментах вычислений или при пояснении физики проблемы
автор не жалеет места.
С методической точки зрения следует признать особенно
удачным постоянное стремление автора построить гамильтониан
задачи, исходя из функций Лагранжа, так как именно этот мо-
мент обычно опускается другими авторами и поэтому особенно
труден для начинающего читателя. При этом очень четко фор-
мулируется исходная модель, которая выбирается для рассмотре-
ния. Развитие аппарата идет на примерах решения конкретных
проблем и постоянно сопровождается углублением в физику во-
проса. По понятным причинам все эти моменты изложения в мо-
нографиях и тем более в оригинальной литературе опускаются,
что создает дополнительные трудности для неискушенного чи-
тателя.
В результате профессору Хакену удалось написать книгу, ко-
торую в состоянии освоить читатель, имеющий знания по выс-
шей математике в объеме технического вуза и знакомый с осно-
вами квантовой механики. Стиль книги позволяет думать, что
полученные читателем знания будут достаточно основательными
и активными, чему способствуют приведенные в конце парагра-
фов задачи с указаниями к их решению. Внимательное прочте-
ние этой книги подготовит читателя к работе над более фунда-
ментальными руководствами и монографиями (см. описок лите-
ратуры для дальнейшего чтения в конце книги) и позволит чи-
тать оригинальную литературу. При дальнейшем чтении читатель
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА ¦ 7
сможет познакомиться и с обобщенным откликом системы на
внешнее воздействие и его выражением через функции Грина
и корреляционные функции и с основами теории необратимых
явлений, одним словом, со всеми теми вопросами, которые явля-
ются неотъемлемой частью современной теории твердого тела,
но которые остались за рамками этой книги.
При подготовке русского издания :ггой книги проф. Хакен
любезно прочитал корректуру и внес в текст книги некоторые
уточнения.
13 целом книга профессора X. Хакспа «Ь'вантошшолеиая тео-
рия твердого тела» будет полезла широкому кругу читателей,
приступающих к изучению твердого тела: студентам, аспирантам
л специалистам, работающим в других областях физики.
/'. Жданов
ПРЕДИСЛОВИЕ АВТОРА
Физика твердого тела является одним из обширных основных
разделов сегодняшней физики. Твердое тело, с его сложными
электрическими, оптическими, тепловыми и магнитными свойст-
вами, представляет собой чрезвычайно привлекательный объект
современных фундаментальных исследований. Действительно,
здесь удается объяснить и проследить во всех подробностях
очень сложные явления. Связанное с этим глубокое понимание
физических процессов в твердом теле приводит, кроме того,
к в высшей степени важным применениям, как, например, в об-
ласти вычислительной техники и техники связи.
Студент, который хотел бы овладеть этим разделом физики,
очень быстро, конечно, установит, что в нем в большом объеме
используются представления и методы квантовой теории поля.
Эти методы позволяют не только элегантным образом описать
физические процессы в твердом теле, но и приводят к принци-
пиально новым познаниям. В качестве замечательного примера
упомянем здесь объяснение сверхпроводимости.
С другой стороны, в курсе лекций, например по квантовой
механике, студенту вряд ли предоставляется возможность по-
знакомиться с квантовой теорией поля. Задача этой книги состо-
ит в том, чтобы устранить этот пробел и простым путем подвести
читателя к ее основным понятиям и методам. Читатель, знако-
мый с математикой в объеме трех первых семестров и основны-
ми понятиями квантовой механики, с помощью этой книги в со-
стоянии освоить квантовополевую теорию твердого тела.
При построении понятий, с которыми мы будем иметь дело,
речь пойдет преимущественно о так называемых элементарных
возбуждениях, таких как фононы, экситоны, магноны, поляроны,
поляритоны, электронные дырки. На протяжении всей книги мы
будем систематически развивать эти понятия и разрабатывать
лежащие в их основе физические представления.
Далее, квантовая теория ноля характеризуется применением
известных математических методов, таких как так называемая
диаграммная техника, методы функций Грина, а также опреде-
ленные методы решения уравнения Шредингера. Поскольку на
протяжения последних лет возникли целые направления или,
точнее сказать, школы, которые отдают предпочтение тому или
иному методу, то читателю следует предоставить возможность
в равной степени познакомиться с этими методами. Мы надеем-
ся, что по прочтении этой книги читатель сможет читать как
, ПРЕДИСЛОВИЕ АВТОРА Q
специальные монографии (см. описок литературы для дальней-
шего чтения в конце книги), так и оригинальные работы.
Вообще же квантовая теория поля применима не только в фи-
зике твердого тела. Столь же широко она применяется в ядерной
физике, физике элементарных частиц и квантовой оптике.
Читатель, знакомый с основами физики элементарных частиц,
с удовольствием обнаружит ряд аналогий между элементарными
возбуждениями в твердом теле и представлениями физики эле-
ментарных частиц. Также и физик-ядерщик припомнит, что, ска-
жем, энергетические щели, имеющиеся у некоторых атомных
ядер, были впервые обнаружены в сверхпроводимости.
При изложении мы постоянно старались обнажить сущест-
венные черты и избавиться от всего ненужного балласта. Так,
например, квантование колебаний решетки обстоятельно мы рас-
сматриваем только в одном измерении, поскольку уже здесь мож-
но обнаружить все основные черты этого метода. В начальных
параграфах специально приложен целый ряд заданий. Если чи-
татель выполнит то или иное задание, то освоение соответствую-
щего раздела, без сомнения, будет облегчено.
При составлении этой книги, и в особенности заданий к ней,
я опирался на мою более чем десятилетнюю лекционную дея-
тельность в университете Штуттгарта. Мне доставляет удоволь-
ствие, пользуясь этим удобным случаем, поблагодарить моих
штуттгартских коллег, в особенности гг. Вагнера и Вайдлиха из
отдела теоретической физики, за чрезвычайно приятную и дру-
жественную рабочую атмосферу. На заключительном этапе пред-
лагаемой книги мне, при написании ряда глав, в особенности об
экситонах, пригодились мои лекции, прочитанные по приглаше-
нию в университете Страсбурга. Я сердечно благодарю профессо-
ра С. Никитина (S. Nikitine) за чрезвычайно увлекательные дис-
куссии.
Я очень обязан научному сотруднику А. Шенцле за содейст-
вие. Он не только тщательно и критически проверил все реше-
ния, но и, сверх того, сделал ряд ценных предложений по их
улучшению. Особенно я благодарен моей секретарше фрау Функе,
которая не только отлично подготовила рукопись и рисунки, но
и своим неутомимым участием постоянно побуждала меня к до-
ведению работы над этой книгой до конца.
Штуттгарт, весна 1972 г.
X. Хакен
УКАЗАНИЯ К ЧТЕНИЮ КНИГИ
Для облегчения чтенпя этой книги мы приводим некоторые
указания.
1. Формулы, которые представляют собой важные промежу-
точные или конечные результаты, отмечены чертой.
2. Самый простой и, безусловно, эффективный способ изучить
эту книгу — систематически следовать изложению.
Для читателей, которые хотят получить только общее впечат-
ление пли которых интересует какая-либо специальная пробле-
ма, мы даем краткий обзор внутренней связи отдельных глав.
Основы, которые должен усвоить каждый читатель, изложены
в §§ 3, 4, 7—13 и 17—19. Те, кто интересуется только много-
электронной проблемой (метод Хартри — Фока, электронные дыр-
ки, экситоны, электронные волны поляризации, плазмоны, маг-
поны), могут сразу перейти к чтению §§ 20—28, причем для
чтения § 27 следует познакомиться еще с § 16. Напротив, те
читатели, которых интересует взаимодействие между электрона-
ми и колебапиями решетки (электрическое сопротивление, поля-
роны п сверхпроводимость), могут полностью опустить главу
о проблеме многих электронов, однако им следует изучить до-
полнительно §§ 5, 6 и 15, 16. Глава о сверхпроводимости пред-
полагает чтение главы V о колебаниях решетки. Изучению § 43
должно предшествовать чтение § 14. При чтении главы VI, целе-
сообразно прочитать все предшествующие главы, в то время как
при чтении главы VIII можно обойтись основными сведениями
с добавлением §§ 15, 16 и 24, 25.
Основы: §§ 3-4, 7-13, 17—19.
Многоэлектронная проблема: §§ 20—26, 28. Предпосылка:
Осповы.
§ 27: предпосылка: Основы и § 16.
Взаимодействие между электронами и колебаниями решетки:
§§ 29—36. Предпосылка: Основы и §§ 5, 6 и 15, 16.
Функции Грина (§§ 37—39): предпосылка: все предыдущие
параграфы.
Сверхпроводимость: §§ 40—42. Предпосылка: взаимодействие
с колебаниями решетки и § 4.
§ 43: дополнительная предпосылка: § 14.
Взаимодействие электронов с квантованным излучением:
предпосылка: Основы и §§ 15, 16 и 24, 25.
Глава I. ВСТУПЛЕНИЕ
§ 1. Введение и обзор
При теоретическом обсуждении физических свойств твердых
тел возможны в принципе два различных подхода: микроскопи-
ческая теория или макроскопические феноменологические моде-
ли. Как мы знаем, твердое тело, под которым мы в последую-
щем изложении постоянно будем понимать кристалл, образова-
но регулярным расположением очень большого числа (около 1033
на см~3) одинаковых атомов. Если бы мы захотели рассмотреть
соответствующую проблему многих тел для электронов и атом-
ных ядер, мы должны были бы решить уравнение Шредингора
примерно для 1024 или более частиц. Очевидно, что это было бы
абсолютно безнадежной затеей. Поэтому лучше опереться на
имеющиеся экспериментальные зависимости и развитые для них
модельные представления.
Задача теоретического кваитовонолевого рассмотрения состо-
ит, таким образом, в том, чтобы перебросить мост между атоми-
стическим представлением п модельными представлениями, со-
гласно которым кристалл рас-
сматривается как более или ме-
нее непрерывное тело. При этом
оказывается, что наряду с ос-
новным состоянием пристал- а)
ла существуют возбуждеиные
состояния, которые допускают
довольно простое описание. |/Л /Д Г\ /~\ /Л
Рассмотрим в качестве при- \у \J \J \_/ \_, ¦'
мера звуковые волны, которые jj
в континуальной теории рас- , „
смйтпивяются гяк прттолгтче- Гпс- L 3вУковые волны в среде:
сматриваются как периодиче а) областп повышенной плотности
ские в пространстве и времени заштрихованы; б) зависимость Др
изменения плотности Др(а;, t). от координаты х в фиксированный
Ради простоты рассмотрим стоя- момент времени.
чую волну, для которой Ар
можно представить в виде произведения Ар(а;)= A sin (of sin/о;
(рис. 1). Уже/в этой модели содержатся исходные предпосылки
для квантования. Поскольку временной множитель чисто гармо-
нический, можно полагать, что соответствующая амплитуда коле-
бания q{t)— A sin tat удовлетворяет уравнению гармонического ос-
циллятора, квантование которого хорошо ^известно. Тогда для каж-
ВСТУПЛЕНИЕ [ГЛ. I
дой отдельной волны к мы получаем термы энергии En
Ы = 0, 1, 2, ...), которые являются целыми кратными На. Эти
термы энергии следует трактовать в том смысле, что звуковой
волне соответствует квант энергии % со, т. е. фонол. Несколько
слов об образовании подобных слов. Слог «фон» греческого про-
исхождения и означает «звук», второй слог «он» означает «ча-
стица»*). Следовательно, речь идет о квантах звука. Перед нами
типичный пример квантования поля. При квантовании волне
приписывается характер частицы, свойства которой определяют-
ся нижеследующими основными соотношениями:
энергия Е = ft to t,
импульс р = ft к.
Связь между частотой мь и волновым вектором к определяется
с помощью вводимого уже в классической физике соотношения,
называемого законом дисперсии, например такого: со = vk, где
v — скорость звука. При рассмотрении в рамках квантовой тео-
рии поля решающим является корпускулярно-волвовой дуализм,
знакомый нам из квантовой
ОООООООООООО механики: колебательный
00©0га0©Э®Э©0 процесс следует рассматри-
0 ©0©|0]©О © О© © © вать в одном случае как
ОООООООООООО волну, в другом — как про-
а) цесс, происходящий с учас-
© тием частиц.
Наряду с колебаниями
© плотности в изоляторе встре-
| „ - "" ' чаются еще и другие колеба-
G Направление распространения — „ "f'
S) ния. Если кристалл состоит
Рис. 2. Волны поляризации решетки в из положительных и отри-
полярном кристалле: а) кристалл в от- цательных ионов, то пары
сутствие колебаний (положительно и положительных и отрица-
отрицательно заряженные ионы распо- тельных ионов при опреде-
ложены регулярно; в рамке находится ленных обстоятельствах мо-
некоторыи выделенный диполь); б) по- - -.
перечная волна поляризации. ГУТ быть объединены в ди-
поли. Если центры тяжести
отдельных атомов испытывают периодические смещения вблизи
положения равновесия, то возникают и колебания диполей, ко-
торые макроскопически проявляются как поляризационные коле-
бания. Если диполи связаны друг с другом, то поляризацион-
ные колебания распространяются в кристалле в виде продоль-
ных или поперечных волн (рис. 2). При этом поперечные поляри-
*) Неточно. Название элементарных возбуждений (как и большин-
ства элементарных частиц) образовано по аналогии с термином «электрон»
(от греч. electroa —янтарь), введенным Дж. Стони. (Прим. персе.)
ЁВЕДЁНЙЁ Я ОЁЗОР
13
зационные колебания можно возбудить с помощью света. Эти по-
ляризационные колебания также могут быть проквантованы
согласно закону A.1),
Поляризация кристалла может быть вызвана не только поля-
ризацией ионов, но также смещением электронных оболочек
атомов относительно положительного заряда ядра. Если не об-
ращаться к модели упруго связанных электронов, то на первый
взгляд кажется непонятным, почему электронные оболочки так-
же испытывают гармонические колебания, которые служат при-
чиной появления продольных или поперечных поляризационных
волн. Именно это мы покажем в последующем изложении.
Наряду с этими последними поляризационными колебаниями,
для которых дипольный момент может быть порядка величины
произведения заряда электрона на диаметр атома, в кристалле
возникают также гигантские дипольные моменты, при которых
электрон может быть удален
от положительно заряжен-
ного ядра очень далеко. Тогда
оооооооооо
ооосюоро о о
О О ?Ю О СИ§Ю О О
о.доооооЪоо
офоо©оо<роо
OQOOOOOPOO
0
ОООсЮООООО
'ОООООООООО
Рис. 3. Экситон в крис-
талле из нейтральных
атомов. Из одного атома
удален электрон, кото-
рый затем начинает об-
ращаться вокруг поло-
жительно заряженного
атома по водородоподоб-
ной орбите. «Дырка», во-
обще говоря, тоже мо-
жет перемещаться по
кристаллу.
Све./паяые ko/ihoi
<8о/?ны поляризации
Расщепление
Рис. 4. Поляритон. Тонкие линии относятся к
случаю отсутствия взаимодействия и пред-
ставляют дисперсионные кривые для волн из-
лучения и волн поляризации (с — скорость
света). Жирные линии описывают закон дис-
персии в присутствии взаимодействия. В ре-
зонансной точке, определяемой условиями
Лев = кП0Л = ко; (осв = Юпол = Wo, часто-
та (й0 расщепляется на две новые частоты coi
и юг. Это расщепление продолжается и в об-
ласти больших и малых значений к.
следует считать, что электронный заряд обращается вокруг по-
ложительно заряженной «дырки» по водородоподобной орбите
очень большого радиуса (рис. 3). Возникающее в этом случае
возбуждение называется жеитоном.
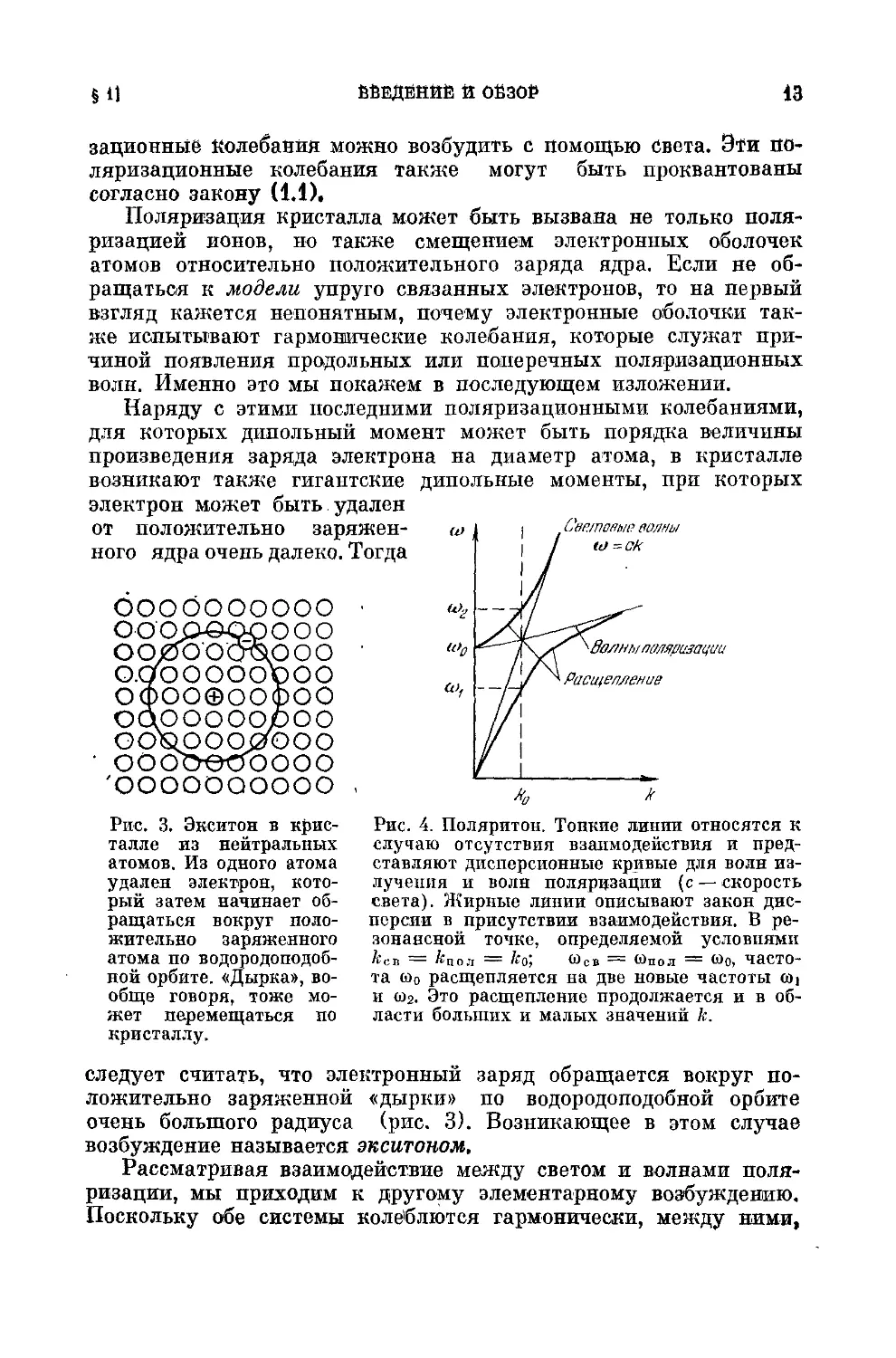
Рассматривая взаимодействие между светом и волнами поля-
ризации, мы приходим к другому элементарному возбуждению.
Поскольку обе системы колеблются гармонически, между ними,
14 ВСТУПЛЕНИЕ 1ГЛ. I
как между двумя связанными маятниками, можно ввести взаимо-
действие. Тогда, точно так же как и в случае связанных маят-
ников, возникает новый вид колебания (в нагаек случае совмест-
ное, распространение света и электронных поляризационных
волн), причем появляется и новый закон дисперсии (рис. 4). Ес-
ли проквантовать эти новые колебания, то мы получим так на-
зываемые поляритоны.
Другой пример элементарных возбуждений мы получим, если
примем во внимание спины электронов, отчетливо проявляющие-
ся в ферромагнетике благодаря создаваемому ими магнитному
полю. При абсолютной температу-
ре Т — О все спины в ферромаг-
нетике направлены параллельно.
Выстроенные таким образом спи-
ны могут быть отклонены, на-
пример, с помощью электромаг-
нитного поля. Эти отклонения за-
тем распространяются по крис-
таллу в виде спиновой волны
(рис. 5). Квантуя эту волну, мы
получаем так называемые маг-
Рас. 5. Спвновая волна в ферро-
До сих пор молчаливо предпо-
лагалось, что электроны в крис-
талле не слишком подвижны. Металлическую проводимость,; на-
против, можно понять, только допустив, что электроны ведут
себя практически как свободные частицы. Простейшее представ-
ление состоит в предположении, что электроны образуют газ
невзаимодействующих частиц. Согласно квантовой теории части-
це, но обладающей силовым полем, соответствует плоская волна
с волновым вектором к и импульсом р = Ш. Поскольку значе-
ния к в конечном кристалле лежат очень плотно, но тем не ме-
нее дискретно (граничные условия для электронных волн вы-
полняются только для определенных длин волн Я. = 2п/к), то
электроны заполняют отдельные состояния с определенными
значениями к. При этом следует учитывать принцип Паули, со-
гласно которому каждое такое k-состояние может быть занято
только двумя электронами с противоположно направленными
спинами. Если занятые состояния изобразить в к-пространстве,
то получится так 'называемая сфера Ферми, поверхность которой
при абсолютном нуле температур Т = 0 называется уровнем Фер-
ми (рис. 6). Внутренность сферы Ферми иногда называют ферми-
морем. Задача теоретического сквантовополевого рассмотрения ср-
стоит в том, чтобы объяснить, почему электроны и при. взаимо-
действии друг с другом и с неподвижно закрепленными в узлах
решетки ионами ведут себя практически как свободные частйць?:»
¦¦'•' ' ' /
ВВЕДЕНИЕ И ОБЗОР
15
Л а примере конечной электрической .проводимости мы осозна-
ем, с другой стороны, что введение одних «элементарных возбуж-
дений» не достаточно, чтобы понять физические свойства твер-
дых тел. Ведь обладающие свободной подвижностью электроны
вызывали бы бесконечную проводимость. В действительности,
однако, движение электронов благодаря постоянным колебаниям
решетки нарушается, причем электроны выбиваются со своих
траекторий, отчего и возникает конечное электрическое сопротив-
ление (рис. 7). Этот пример ясно указывает на то, что важной
задачей полевого рассмотрения является именно исследование
взаимодействий элементарных возбуждений друг с другом. Суще-
ствование подобных взаимодействий ведет к рассеянию из на-
чального состояния и тем самым к конечному времени жпзшт
начального состояния. Аналогичным образом, из-за взаимодей-
ствия звуковых волн друг с другом возникает тепловое сопро-
тивление.
Наряду с ятпм довольно очевидным следствием взаимодейст-
вия существует другое, менее очевидное, но весьма типичное для
кв.антовополевого рассмотрения. А именно, возникают не только
те процессы, при которых частицы рассеиваются друг на друге
Hi/Dap.
Рис. 6. Ферми-сфера. Каждая точка
в «/с-пространстве» обозначает состо-
яние, которое может быть занято не
более чем двумя электронами с про-
тивоположными спинами^ В состоя-
нии с наипизшей полной энергией
запятые k-состоянпя образуют сфе-
ру Ферми.
Рис. 7. Электрическое сопротивление
в решетке без дефектов возникает
благодаря «соударениям» электронов
(прямые линии) с квантами звука
(волнистая линия). На этом рисунке
показан процесс поглощения кванта
звука.
или рождаются и уничтожаются кванты, но также и такие, при
которых начальное и конечное состояния полностью идентичны.
Тем не менее взаимодействие, например между электроном и по-
лем звуковой волны, приводит к совершенно новым явлениям.
Оказывается, что масса электрона благодаря взаимодействию
с полем звуковой волны изменяется (возникает полярон; рис. 8)
и, itpoiwe того,; взаимодействие между электроном и нолем зву-
ВСТУПЛЕНИЕ
{гл. t
О
ковой волны приводит к возникновению силы притяжения между
электронами.
Этот эффект, который в физике твердого тела был установлен
вначале для экситонов, позднее оказался решающим для теории
сверхпроводимости. При определенных условиях это взаимодей-
ствие может привести к образованию электронной пары. Благо-
даря этому между основным состоянием и возбужденными со-
стояниями возникает щель, в результате чего
электронное состояние сверхпроводника в
целом получает определенную устойчи-
вость по отношению к внешним возмущени-
ям. Это и приводит к объяснению бесконеч-
но высокой проводимости и диамагнетиз-
ма сверхпроводников. Возмущения, связан-
ные с флуктуациями колебаний решетки,
оказываются, так сказать, выключенными.
В заключение обсудим еще одно элемен-
тарное возбуждение. Предположим, что су-
ществует местное нарушение плотности сво-
бодно движущихся электронов относительно
«фона» положительных ионов, так что ло-
кальное распределение зарядов в кристал-
ле более не является электронейтральным.
При этом возникают возвращающие поля,
которые стремятся вернуть электроны в их
первоначальное положение (рис. 9). Посколь-
ку электроны обладают инертной массой, они проскакивают свои
положения равновесия и создают новое неоднородное рас-,
пределение зарядов, а вместе с ним и возвращающие поля.
Интуитивно ясно, что плотность электронного заряда будет со-
вершать колебание, так называемое
плазменное колебание. Квантование 4°.
этого колебания ведет к плазмонам.
При квантовополевом рассмотре-
нии, как можно заключить из ска-
занного, необходимо иметь по воз-
можности ясное физическое представ-
ление об отдельных возможных эле-
ментарных возбуждениях. Задача
квантовополевой теории состоит в том,
чтобы на основе фундаментального
уравнения Шредингера теоретически
сконструировать эти элементарные возбуждения и изучить их
взаимодействия. Мы уверены в том, что здесь имеется широкое
поле для будущих исследований элементарных возбуждений но-
вого типа, например, при переходе от рассмотрения простых
Рис. 8, Полярон.
Электрон (штриховой
кружок в центре)
смещает ионы поляр-
ного кристалла из по-
ложений равновесия.
В результате этого из-
меняется эффектив-
ная масса электрона.
возвращающие ПОЛЯ
Рис. 9. Плазмоны — это кван-
ты колебаний плазмы. Эта ко-
лебания возникают благодаря
возвращающей силе электри-
ческих полей.
& 2] ОСНОВНЫЕ ПОНЯТИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ 17
кристаллов к сложным молекулярным кристаллам. Вообще же
применение методов квантовой теории поля не ограничивается
только кристаллами, они могут быть также использованы для
изучения свойств аморфных тел.
§ 2. Некоторые основные понятия классической механики
Квантование полей никоим образом не распространяется толь-
ко лишь на механические системы, скажем колебания решетки,
оно охватывает и совершенно другие системы, например электро-
магнитное поле. Тем не менее при квантовании поля обычно
исходят из формализма классической механики. При этом речь
идет об уравнениях Лагранжа и Гамильтона1).
Вначале мы поясним, как это делается, на примере одной ча-
стицы, которая движется в одном измерении. Соответствующую
координату мы обозначим через q. Уравнение движения Ньютона
гласит: масса X ускорение = силе:
m'q = K(q). B.1)
В данной книге почти всегда считается, что сила обладает потен-
циалом V(q), т. е. может быть представлена в виде
КЬ) = -¦%- B'2)
Кинетическую энергию мы обозначим буквой Т:
T = ^-q\ B.3)
Используя эти обозначения, введем функцию Лагранжа, кото-
рая равна разности кинетической и потенциальной энергии:
q) = T-V. B.4)
С помощью функции Лагранжа B.4) уравнение движения B.1)
формально можно переписать в совершенно ином виде, что вна-
чале может показаться усложнением, однако позже, при кванто-
вании поля, даст заметные преимущества. Это уравнение Лагран-
жа гласит:
в
Если выполнить дифференцирование L по q и q, то при учете
B.3) и B.2) получаем
4 W-#(?) = О, B.6)
') Читатель, знакомый с этим формализмом, может пропустить этот па-
раграф и начать читать следующий.
2 X. Хакен
18 ВСТУПЛЕНИЕ [ГЛ. I
что после выполнения ддфференцирования по времени дает пер-
воначальное уравнение B.1).
Наряду с функцией Лагранжа важную роль играет функция
Гамильтона, Эта функция равна сумме кинетической и потенци-
альной эпергин:
| B.7)
В действительности функцию Н рассматривают не как функцию
q и q, а вместо q в качестве навой переменной вводят импульс р.
В рассматриваемом здесь одномерном случае эта зависимость да-
ется выражением
p = mq. B.8)
При этом кинетическая энергия принимает вид
Т = ±Р*. B.9)
По причинам, которые станут более ясными позднее, связь
B.8) удобно переписать в другом, несколько более формальном
виде. Л именно, непосредственно видно, что B.8) можно полу-
чить также из
( у B10)
dq \ dq dq dq j
Это позволяет, далее, ввести связь между Н и L, которую в дан-
ном случае можно сразу проверить прямой подстановкой соотно-
шений B.8) и B.4):
| H = pq-L. B.11)
Исходное уравнение движения B.1) можно представить с по-
мощью функции Гамильтона в виде так называемых уравнений
Гамильтона. Для этого мы запишем два уравнения, а именно,
•
одно для q, согласно B.8), и второе для временного изменения
импульса р под действием силы K(q), которую заменим ее выра-
жением через потенциал B.2). Тогда вместо B.1) мы выпишем
два уравнения:
*¦«¦¦?¦• <2-12>,-
av
B.13)
I
Правые части этих уравнений с помощью производных функции
Гамильтона по р и q можно представить в весьма симметричном
§ 2] ОСНОВНЫЕ ПОНЯТИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ 19
виде
• _ дИ_ I JT_ , 8V_ = дТ \
9 ~ др \~ др "Г dp dp )'
• __дН_ ( _JT__JV_ _ _JV_\ '
Р ~ dq \= dq ~ dq ~ dq )'
Читателю должно быть, естественно, совершенно ясно, что
эти новые формулировки физически полностью эквивалентны
первоначальной формулировке с помощью уравнения движения
Ньютона B.1). Хотя эти формулировки тому или иному читателю
могут показаться непривычными и на первый взгляд даже слож-
ными, они являются, как мы вскоре увидим, исходным пунктом
для квантования полей. В действительности при этом необходимо
рассмотреть не одну частицу, а целый набор частиц. Ради просто-
ты мы рассмотрим далее .вновь одномерное движение, однако все
рассмотрение можно перенести и на случай трехмерного движе-
ния. Уравнения движения Ньютона для частиц, которые мы
будем различать индексом /, принимают вид
тдг = Kjiqi, ..., qN). B.15)
В последующем изложении для набора координат мы будем ис-
пользовать сокращенное обозначение
(?ь .-., ?*) = {?> = <fc>, B.16)
так что B.15) перепишется в виде
/ - B.17)
Далее, предположим вновь, что существует потенциал, из кото-
рого все силы получаются просто дифференцированием:
Определим, как обычно, кинетическую энергию в виде
так что функция Лагранжа имеет вид
| L = Т - V B.20)
и соответствующие уравнения Лагранжа
Подставляя B.20) в B.21) совместно с определениями B.18) и
2»
20 ВСТУПЛЕНИЕ {ГЛ. Г
B.19), тотчас же убеждаемся, что из B.21) можно непосредствен-
но вновь прийти к B.15). Импульсы
Pi = mjQj B.22)
B.23)
формально можно вновь получить из
P
Связь между функциями Гамильтона и Лаграижа сразу получа-
ется как обобщение B.11):
Н = ^рт-Ь. B.24)
3
Если сюда подставить B.22) и определение B.20), то выражение
для Н принимает вид
который мы будем в дальнейшем чаще всего использовать в каче-
стве исходного пункта теории. Аналогично и уравнения Гамиль-
тона сразу можно обобщить на случай многих частиц. Для этого
выразим формально уравнения
n.-Il
т.
B.26)
р, = - ¦— B-27)
1 J dq . v '
следующим образом через функцию Гамильтона:
а = п = — B 28^
4j др.' 1 i ~~ Qq.' \ • )
Если исключить из уравнений B.26) и B.27) р}, продифференци-
ровать первое уравнение по времени, а во втором уравнении вы-
разить р через q, то мы вновь возвращаемся к уравнению B.15),
причем сила определяется выражением B.18).
Задан и як § 2
= 0,
dq
4 rr W л W
1. Почему— = 0, —г =
V3
2. Для упругой силы K(q) — — fq (/ — константа упругой свя-
зи). Каков явный вид функций Гамильтона и Лагранжа B.4),
B.7) и уравнений движения B.14)?
Глава II. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
§ 3. Квантовомеханический осциллятор: операторы
рождения и уничтожения
Теперь мы займемся исследованием движения частицы с мас-
сой т, упруго связанной относительно положения равновесия.
В качестве координаты q частицы выбираем отклонение из поло-
жения равновесия (рис. 10, 11), а соответствующий импульс
Положение рав/ювеоия
a) h}
Riic. 10. Гармонический осциллятор: а) пример из механики; б) потенциаль-
ная энергия как функция отклонения.
u/p-j Пирабо/н/чести'
1
Рис. 11. Пример применения гармонического осциллятора. В покоящейся
атомной решетке отсутствует оддн тяжелый атом, который заменен легким
(черный кружок), а) Расположение атомов, б) Реальный потенциал при-
ближенно описывается параболой. Низколежащие колебательные состояния
практически «не замечают» отклонений от точного хода кривой потенциаль-
ной энергии; q — координата легкого атома.
обозначим р. Константу упругой связи / мы исключаем при по-
мощи известного из классической физики соотношения / = пко2,
где со — частота осциллятора. В этих обозначениях кинетическая
22 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
энергия имеет вид Т — pi/Bm), а потенциальная энергия равна
F(/2)y
Классическая функция Гамильтона, следовательно, дается
выражением
л — •* -r v — ^ "г ~Y M a • VJ-l;
Переход к квантовой механике осуществляется с помощью заме-
ны импульса р на оператор согласпо правилу
p~t-w-- C-2)
Операторы р п q удовлетворяют перестановочному соотношению
РЧ — ЯР==~Г~' C.3)
Это соотношение следует понимать в том смысле, что мы считаем
обе части C.3) действующими на некоторую волновую функцию
ф, используя явное представление C.2) оператора р:
h d ,.* л ( ^ ^ Л й . /о /\
Если продифференцировать первый член в C.4) по правилу диф-
ференцирования произведения, мы получим
Выделяя в этом выражении второй член, который взаимно
уничтожается со вторым членом в C.4), мы получаем, естествен-
но, сразу правую сторону C.4). Поскольку C.4) справедливо для
любой дифференцируемой функции, мы можем считать C.3)
тождеством.
Хотя обоснование C.3) может показаться тривиальным, пере-
становочные соотношения такого рода имеют основополагающее
значение для всей квантовой теории поля. Мы действительно
увидим, что многие проблемы физики твердого тела и квантовой
оптики (а также и других областей) могут быть сформулированы
с помощью квантовой теории поля и решены при умелом приме-
нении перестановочных соотношений. Однако вернемся вначале
пазад к гармоническому осциллятору. Если подставить C.2) в
C.1), мы получим оператор Гамильтона гармонического осцил-
лятора. Тогда уравнение Шгредингера принимает вид
= Яф (Я). C-5)
Для дальнейшего обсуждения C.5) введем безразмерную коорди-
нату | с помощью соотношения
» f ГО01
§ 31 ОПЕРАТОРЫ РОЖДЕНИЯ II УНИЧТОЖЕНИЯ 23
после чего уравнение Шредингера C.5) принимает вид
-5р + 5'}+ Ш = ?+№)¦ C.7)
Если бы с операторами | и dfd% можно было обращаться как с
обычными числами, было бы очевидно, что стоящий слева в C.7)
оператор
можно рассматривать как выражение
2) C.9)
и соответственно этому провести разложение вида
(-а + р)(я + р). C.10)
Попытаемся вместо левой части C.7) подставить выражение
Если мы перемножим скобки (при этом следует учесть точный
порядок следования операторов |, dfd\), то мы получим
/о лл\ ^w I d
C-11) = — (-^
Первое выражение, как мы и хотели, совпадает с левой стороной
C,7). Второе с учетом перестановочного соотношения
переходит в выражение
Ц = -^г|>. C.13)
(Перестановочное соотношение C.12) сразу получается из приве-
денного выше соотношения C.3), в котором мы заменяем q на \
согласно C.6).)
24 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ (ГЛ. II
Стоящие в C.11) выражения в скобках также представляют
собой некоторые операторы, которые мы вначале чисто формаль-
но обозначим кратко следующим образом:
*¦ (ЗЛ5)
Поскольку C.11) и левая часть C.7) отличаются лишь дополни-
тельным членом C.13), мы введем смещенную энергию
Е' = Е-~. C.16)
Тогда уравнение Шредингера C.7) окончательно принимает сле-
дующий вид:
| П&Ъ+ЪЦ = Е'ц. C.17)
Для того чтобы вывести перестановочные соотношения для
операторов Ь и Ь+, составим выражение ЬЪ+ — Ь+Ъ и заменим в
нем операторы согласно C.14) и C.15). Применяя затем C.12),
мы непосредственно получаем основополагающее перестановочное
соотношение
j bb+ - b+b = 1. C.18)
Операторы, удовлетворяющие соотношению C.18), мы назовем,
по соображениям, (которые будут ясны позже, бозе-операторами.
Покажем теперь, как с помощью операторов й+ и b и переста-
новочного соотношения C.18) простым образом можно сконстру-
ировать собственные состояния гармонического осциллятора. Для
этого будем исходить из того, что энергия квантовомеханического
осциллятора всегда положительна (см. задание 1) и всегда, следо-
вательно, ограничена снизу. Обозначим соответствующее наи-
низшему значению энергии Ео состояние через *фо.
Умножим уравнение
' C.19)
слева на оператор Ъ, что дает
% = Е'0Ь%. C.20)
Применяя перестановочное соотношение C.18), перенесем в ле-
вой части C.20) первый оператор Ъ направо, тогда получим
= Е'ф%, C.21)
Ь+ читается «б-крест».
3] ОПЕРАТОРЫ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ 25
Перенесем, наконец, ЙюЬфо в правую часть, после чего находим
ЫЬ+Ь (Но) = (#о - *и) Но- C.22)
Это уравнение, однако, означает, что Ьг|>о является новой собст-
венной функцией с собственным значением Ео — Тш, в противо-
положность нашему предположению, что т|H — наинизшее состоя-
ние. Это противоречие разрешается, если положить
Но = 0. C.23)
Именно это уравнение и служит в последующем изложении
определением основного состояния яро- Чтобы увидеть это по воз-
можности отчетливо и установить связь с известными волновыми
функциями осциллятора, вернемся на момент к операторам § и
dld\ согласно C.14) и C.15). Тогда C.23) переходит в дифферен-
циальное уравнение первого порядка
) = 0, * C.24)
которое, очевидно, имеет решение вида
th (I) = Се-М. C.25)
Это решение, естественно, есть волновая функция основного со-
стояния осциллятора. Теперь мы хотим провести решение урав-
нения C.17), для чего нам дифференциальные уравнения
больше не понадобятся. Мы найдем волновые функции и
значения энергии чисто алгебраически. Для этого умножим урав-
нение C.17) слева на Ь+:
?'й+г|). C.26)
С помощью перестановочного соотношения C.18) и проведенного
ранее преобразования мы затем получаем
= (Е' +%ы)Ь+^. C,27)
Отсюда очевидно, что если я|з — собственная функция, то й+гр
также является собственной функцией, соответствующей больше-
му на %& собственному значению. Действуя п раз оператором
Ь+, получаем собственную функцию га-го возбужденного состояния
ф» = (&+)"^ C.28)
Поскольку уравнение C.17) однородно относительно i|), то собст-
венная функция, как обычно, определяется с точностью до неоп-
ределенного постоянного множителя. Мы выберем этот множи-
тель таким образом, чтобы -фге была нормирована. Здесь и в по-
следующем изложении мы выбираем нормировку в безразмерной
26
ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
[ГЛ. II
координате | следующим образом:
f ¦,*
Нормировочный множитель, как мы покажем нпже (см. D.20),
можно определить чисто алгебраически. Здесь мы заранее ис-
пользуем этот результат и запишем нормированную собственную
волновую функцию в виде
^ &+)» ф0. C.29)
Каков явный вид соответствующих собственных значений?
Чтобы получить те собственные значения, которые соответствуют
п = 0, умножим C.23) на Ь+ и сравним результат с основным
уравнением C.17).
Очевидно, что Е'о — 0.
Поскольку при последовательном 72-кратном действии опера-
тора Ь+ на г|>о энергия Ео увеличивается каждый раз на #-<», то
\ Л
У
Ф
ТР
собствеппоо значение C.29) есть
Е' = п%®,
или, в первоначальной эпергетической
уравнения C.5),
Е
¦(-+4-)
йсо.
C.30)
шкале
C.31)
\Ь
Следовательно, C.30) можно интерпретировать
как наличие в и-м состоянии п квантов энергии,
каждый из которых равен й<в. Поскольку при
действии оператора 6+ на 1])„ число квантов уве-
личивается на один, т. е. рождается один доба-
вочный квант, то оператор Ь+ называется опера-
тором рождения. Поскольку при действии опера-
тора Ъ на ф (см. C.20—3.22)) один квант уничто-
жается, то оператор 6 называют оператором
уничтожения (рис 12).
Большое число несвязанных осцилляторов. Те-
перь мы перенесем результаты, полученные для
одного осциллятора, на случай большого числа
осцилляторов. Для этого предположим, что от-
дельные осцилляторы, координаты q которых мы будем различать
индексом к, колеблются независимо друг от друга. Массы и ча-
стоты осцилляторов могут быть разными и будут соответственно
также обозначаться индексом к. Классическая функция Гамиль-
тона этой системы равна просто сумме по всем функциям Га-
Рис. 12. Опера-
торы рождения
и уничтожения
вызывают
подъем или
спуск по лест-
нице состоя-
ний.
§ 3] ОПЕРАТОРЫ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ 27
мильтона отдельных осцилляторов:
Я=2ЯЙ, C.32)
h
где
Я1 1 , mk 2 2 /о лох
k = 2^Г ^ + ~Т U)A?ft" ^3-33^
Для перехода к квантованию, следует воспользоваться правилом
замены
Выполняя для каждого отдельного осциллятора все проведен-
ные выше преобразования, получим оператор Гамильтона для
несвязанных осцилляторов следующего вида:
#=2йо>л(&а6* + 1/2). C.35)
k
Сумму 2(^2)Й(иА мы назовем нулевой энергией. Поскольку она
h
является константой, то в последующем мы будем считать, что
нуль энергетической шкалы сдвинут, так что нулевая энергия
2A/2)й<вй в C,35) может быть опущена. Уравнение Шродош-
к
гера тогда имеет вид
2ъ?Ьг + ¦ •. + %(dNb%bN] Ф - ЕФ. C.36)
Здесь вновь имеют важное значение перестановочные соотноше-
ния. Естественно, мы имеем
btbh = \. C.37)
Наряду с этим перестановочным соотношением мы должны еще
указать, каким перестановочным соотношениям удовлетворяют
операторы bh и т. д. с различными индексами к и к'. Поскольку
операторы Ьк и bt состоят из gh и djdqh (см. C.14) и C.15)) и
d/dqh коммутирует соответственно с qk. {кфк'), мы сразу по-
лучаем »
bkbt>-bt-bk = O для кфк'. C.38)
С помощью символа Кронекера
\ A ДЛЯ
0 для кФк
28 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ (ГЛ. II
C.37) и C.38) можно объединить:
-&&>* = 6*Л'. C.40)
Таким же простым образом можно получить следующие переста-
новочные соотношения:
bhbh' - bh.bk = 0, C.41)
b?b?.-bt-b? = O. C.42)
Это и есть перестановочные соотношения для бозе-операторов.
В последующем изложении мы используем для комбинации двух
операторов А и В (здесь, например, А = bk, В — Ъ^) сокращенное
обозначение
АВ — ВА^Ы, В),
которое называется «коммутатором операторов А и ?».
Теперь мы покажем, как с помощью перестановочных соотно-
шений C.40—3.42) можно сконструировать собственные состоя-
ния и найти собственные значения энергии. При этом будем счи-
тать, что Фо является наинизшим состоянием. Соответствующую
наинизшую энергию обозначим Ео- Умножая теперь C.36) на bt
и используя перестановочные соотношения C.40) и C.41), полу-
чаем
2btbnbl 4-.. . + ftffli (bf
C.43)
Перенося /й»г&гФ0 в правую часть уравнения, получаем
{ТшАЧ + • • • + Umbtbt +...} &А = (Ео - ft©,) 6гФ0. C.44)
Отсюда следует, что й(фо является новой собственной функцией
с еще меньшей собственной энергией, что находится в противо-
речии с предположением, что Ео уже является наинизшей энер-
гией. Следовательно, вновь должно быть
ЬгФо = 0. C.45)
Так как индекс I может быть любым, то C.45) должно быть
справедливым для всех 1 — 1, ¦ ¦., N. Одновременно отсюда следу-
ет, что #о == 0.
Мы можем теперь последовательным применением операторов
bf точно так же, как для отдельного гармонического осциллято-
ра, образовать общее собственное состояние оператора Гамиль-
тона C.35), которое принимает вид
даз{bt)" ¦ ¦ ¦ (ъ+"Гф" C'4в)
¦3]
ОПЕРАТОРЫ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ
29
где радикал отвечает за нормировку. Показатели щ являются
целыми числами 5= 0, причем по определению
0! = 1, (&+)° = 1.
Энергия, соответствующая состоянию C.46), равна
| Е =%®1Щ +%(й2Щ + ... +haNnN (+ нулевая энергия),
причем
Нулевая энергия = (УгШо»! + ... + &ц).
Выражение C.46) можно переписать в краткой форме
C.47)
C.48)
C.49)
Эта запись имеет то преимущество, что мы можем использовать
ее и тогда, когда к — не целые числа 1, 2, ..., а, например, век-
торы.
и соответственно C.47) принимает вид
Е =
Числа заполнения п
, т,
1
1 2 3 4 5 S 7 к
/Индекс состояния
а)
Ш Ш
т
Занятые осцилляторы
Рис. 13. Два различных способа описания состояний (см. текст).
Формально в представлении C.46) или C.48) для функции
состояния присутствуют все nh, даже если они равны нулю. На
рис. 13, а приведен соответствующий пример. Здесь совокупность
{га} имеет следующий вид:
Ы) = @, 1, 0, 3, 0, 0, 2, 0).
Следовательно, возможно и другое представление, в котором сле-
дует учитывать только nh > 0. В этом случае индексы осциллято-
ров связаны неравенствами ki < кч < ... < км. В нашем примере
30 ГАШОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
ft, = 2, Й2 = 4, кг,— 7 (рис. 13, б). В общем случае мы пишем
Ф<*>- /д * , , №"* • ¦ • W МФ«- C-50)
где все пК . > 0.
Задания к § 3
1. Показать, что энергия гармонического осциллятора
всегда > 0.
Указание. Умножить обе стороны C.7) на г|з* и проинте-
грировать но |. Член
J
можно преобразовать с помощью интегрирования по частям.
2. На примере собственной функции наинизшего состояния
Ц>п=-Ц(Ь+)|>в (и = 0,1,2,3) (А 3.1)
у п\
показать, что функции, определенные выражением (А 3.1), будучи
представлены как функции аргумента |, принимают обычный
вид волновых функций осциллятора:
*«(&) = епв-6§/«Яп(?),
где с„ — константа нормировки, Ня{%) — полином Эрмита п-го
порядка.
Указание. Выразить i|50 согласно C.25) и Ъ+ согласно
C.14) через %.
3. На гармонический осциллятор действует дополнительно
внешняя зависящая от времени сила KU). Какой вид имеет зави-
сящее от времени уравнение Шредингера в представлении опера-
торов уничтожения и рождения Ъ и Ь+?
4. Показать, что общее решение зависящего от времени урав-
нения Шредингера Й(вЬ+Ьч|з = ?йл|) имеет вид
оде с„ — произвольные независящие от времени коэффициенты.
§ 4. Вычисление средних значений
В классической механике движение частиц описывается с по-
мощью измеряемых величин, таких как координата, импульс,
кинетическая энергия и т. д. Этим измеряемым величинам в кван-
§41
ВЫЧИСЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ
товой механике сопоставляются операторы. Образуя средние зна-
чения, мы можем затем сделать предсказания относительно изме-
ряемых величин. Для одномерного движения это делается по
приведенной в табл. 1 схеме. При вычислении средних значений
в основу следует положить условие нормировки
Пределы интегрирования от — °° до + °°.
Координата
Импульс
Кинетиче-
ская энер-
гия
Потенциаль-
ная энергия
Полная
энергия
Механические
величины
Р2
2т
т
А
2т
q @
Pit)
со2?2
771 о 9
+ — «V
Операторы
п
i
-il
2m
т
~2~
h2
2т'
q
d
dq
l_
шУ
Цг 2
f
I
X
\
\
+
Табли
Средние значения
*• (9. t) ?г|, (?f «) d?
П d
ill* (<7 (^ -r -г- 1b (a. t)
i|) (g1, i) dq
¦ф* (9i 0 "o" »?1! (9
i\i* (q, t) 1 — —;¦
— (U2j2) tj) (g1, f) if?
ца 1
dq
x
+
Вычисление средних значений с помощью Ъ и Ь+. В предыду-
щих параграфах мы определили собственные функции и собст-
венные значения только с помощью перестановочных соотношений
C.18), не пользуясь тем, что о|з является функцией q (или |).
С другой стороны, средние значения, согласно приведенной выше
табл. 1, определяются как интегралы по q. Следовательно, схема
решения с помощью операторов Ъ и Ь+ будет полной, если мы
найдем чисто алгебраический метод вычисления средних значе-
ний. Ради простоты мы сразу проведем вычисления в безразмер-
ной координате |. Предположим, что основное состояние уже
нормировано:
= 1.
D.1)
Приведенные в табл. 1 средние значения строятся с помощью
операторов, имеющих следующую структуру:
32 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
они содержат либо
а) координату q или теперь уже безразмерную координату g
и ее степени, либо
б) производные первого и более высоких порядков по |.
Вообще, можно представить себе оператор, который построен
как из степеней |, так и из производных по |. Как координату
1, так и производные d/d'§ мы можем, согласно формулам C.14)
и C.15), выразить через операторы Ъ и Ъ+ и наоборот. Если мы
подставим операторы Ъ и Ъ+ в выражения вида
то получим линейные комбинации выражений вида
Ъ, Ъ+, Ь2, Ь+а, ..., Ь+Ъ, ..., (Ь+)т. D.3)
Вместо того чтобы вычислять средние значения с помощью
выражений D.2), теперь нам нужно вычислить средние значения
с помощью операторов вида D.3). Для этого мы воспользуемся
некоторыми приемами.
Рассмотрим две исчезающие на бесконечности функции ср(|)
и %(|). Образуем с их помощью интеграл от — °° до + °°
1 D.4)
который согласно определению оператора Ь C.15) тождественно
равен интегралу
M D-5)
Мы хотим перенести действие оператора \ + (d/d%) в интеграле
D.5) с функции ф* на функцию %. Поскольку | является лишь
множителем, мы можем сразу расположить функции <р*, | и % в
указанном порядке. Операцию дифференцирования функции ер*
по § перенесем на функцию % с помощью интегрирования по
частям, т. е. воспользуемся тождеством
J (ig
=0
откуда получим
При этом мы использовали условие исчезновения функций
Ф и х на бесконечности, которое справедливо для всех функций
§ 4] ВЫЧИСЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ 33
гармонического осциллятора. Оператор
согласно определению C.14) является оператором Ь+, так что в
результате для D.4) мы получаем
, D.8)
Если объединить все промежуточные шаги, то конечный резуль-
тат принимает вид
Таким же образом можно показать, что
?i D.10)
и, применяя этот прием п раз, получаем соотношение
I ((Ь+)"ф*) 5С dl = J ср* (Ь»х) d\. D.11)
Соотношения D.9) и D.10) позволяют нам найти конечное
выражение для средних значений чисто алгебраическим путем.
Введем, далее, еще одно весьма четкое и часто используемое в
литературе краткое обозначение. Вместо интеграла введем угло-
вые скобки и соответственно этому напишем ')
Если между функциями % и Ф* стоит оператор Ъ, то мы пишем
D.13)
Если между указанными функциями стоит, наконец, какое-либо
операторное выражение совершенно общего вида Q(b+, b), то мы
пишем в этом случае
+, b)%dl = (Ф\п(Ъ+, Ь)|х>. D.14)
') В литературе вместо обозначения D.12) часто применяется еще и
другое, согласно которому в скобках стоят не функции, а соответствующие
квантовые числа. То есть делается замена <ФП| Фт>->-<и|т>. Волновые
функции, стоящие в скобках справа, записывают в видеФт-> | т>, волно-
вые функции Ф^ слева в скобках заменяют следующим образом: Ф*-><л|.
Согласно Дираку <ге| называют «бра», а |т>—«кет». Произведение <л(
и |т>, имеющее вид <.п\т>, дает, следовательно, «бракет». Эти обозна-
чения основаны на игре слов, поскольку по английски «bracket» — «скобка».
Названия «бра» и «кет» теперь уже стали специальными терминами.
3 х. Хакен
34 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
(Об операторных функциях такого рода мы обстоятельно погово-
рим в следующих параграфах.) Вторая вертикальная черта в вы-
ражениях D.13) и D.14), в общем, излишняя, и в последующем
изложении иногда мы будем опускать ее.
Правые части выражений (-1.12), D.13) и D.14) представляют
собой не более как сокращения. Однако, как мы сейчас увпдлм,
явные выражения интегралов нам более не нужны. Используем
теперь зти новые краткие обозначения, чтобы переписать соотно-
шения D.9) и D.10). Для этого мы положим
Ф = by D.15)
п вместо D.9) получаем
| <ЬФ1х> = <ф|6+1х>. U. 10)
Положив
Ф = Ь+Ф, D.17)
вместо D.10) получаем
I <Ь+ср1х> = <фШх> D.18)
л, обобщая эти соотношения, находим
Нначок + у Q означает, как и везде в этой книге, эрмитово сопря-
жение: каждый стоящий в О+ оператор нужно снабдить крести-
ком, причем следует полагать, что Ь++ = Ъ. Кроме того, во всех
произведениях следует поменять порядок следования операторов.
Наконец, все числа следует заменить комплексно сопряженными.
Покажем на примере операторного выражения Q = а{Ь+)"Ь'". как
следует применять это правило:
Q+ = а*((&IЯ)+((Ь+)п)+ = а*(&+)"'(Ь++)" = а*(Ь+)тЬ".
Для того чтобы поближе познакомиться с применением ново-
го формализма, рассмотрим
Пример. Определение нормировочной константы функции ос-
циллятора. В § 3 мы определили собственные функции гармони-
ческого осциллятора в виде
0, A.20)
причем нормировочная константа Nn осталась неопределенной.
Мы утверждаем, что эта нормировочная константа имеет вид
поскольку -фо уже нормирована, что постоянно предполагается
в дальнейшем. Доказательство поведем методом полной индукции.
§ 4] ВЫЧИСЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ 35
1. Наше утверждение справедливо, учитывая предположение
относительно я|зо, для п = 0.
2. Это утверждение уже доказано для п = щ, т. е. i|?ti0 нор-
мирована.
3. Покажем, что топда оно справедливо также для п = гео+1.
Для этого положим
il)no+1-Cnc+1&+a|3no, D.22)
причем Сщ+1 — постоянная, которую мы должны сейчас оп-
ределить, а г|зПо, согласно индукционной посылке, считается
нормированной.
Подставим D.22) в условие нормировки
<*K+il44+i> = l- D.23)
Тогда для левой части D.23) получаем
\Сщ+1\2(Ь+грщ\Ь+^ПоУ, D.24)
или, применяя соотношение D.18),
|С„0+1|2<^1^+^п0>. D.25)
Далее мы используем перестановочное соотношение C.18),
после чего D.25) принимает вид
1)Цп0}. D.26)
Учитывая, наконец, что tpn, является собственной функцией
оператора Гамильтона k(ob+b, находим, что D.26) принимает
вид
Согласно индукционной посылке, мы можем принять, что
<4Ч> I Чч) нормирована на 1. С другой стороны, выражение
D.27), согласно D.23), должно быть также равно 1, откуда мы
получаем
Если считать коэффициент Спо+\ действительным числом, то из
предыдущего равенства находим
1
Если теперь подставить это выражение, а также D.20) и D.21)
при п = щ в D.22), то мы получим '
36 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
т. е. именно выражение вида D.20) с учетом D.21), однако для
п = по+ 1.
Аналогичным образом можно доказать следующие формулы
(задание 1 в конце этого параграфа):
> = у/Т+Л, D.28)
<1'т Кп> = Km- D.30)
Стоящие здесь волновые функции я|зт зависят от безразмерной
координаты | и могут быть собственными функциями гармони-
ческого осциллятора.
Обобщение на набор осцилляторов. Развитый только что фор-
мализм можно сразу же распространить на большое число осцил-
ляторов. Для этого следует в соотношениях D.16—4.19) припи-
сать операторам Ь+, Ъ индекс к. Операторное выражение Q в
D.19) может также содержать операторы Ь, Ъ+ с различными
индексами к.
Если Ф{п) — функции (о.46), то справедливо, в частности*),
или, в краткой форме,
В данном случае индекс к в произведении JJ пробегает значения
целых чисел от 1 до N. В рассмотренных ниже случаях он мо-
жет иметь также другой смысл, например, он может быть волно-
вым числом. Далее, справедливы соотношения
I bf | Ф{т}> --= Д. Ч™Л;.™;+1 /п^ТТ. D.33)
Произведения распространяются на все к, исключая к = /.
Задания к § 4
1. Вывести-соотношения D.28), D.29), D.30).
Указание.
а) D.28): сделать ?+я|}„ нормированной функцией.
б) D.29): применить D.18) и сделать b+tyn-i нормированной
функцией.
*) Условие ортогональности. (Прим. перее.)
§ 5] ОБ ОБРАЩЕНИИ С БОЗЕ-ОПЕРАТОРАВШ 37
в) D.30): рассмотреть отдельно ва) т = п и вб) тФп.
ва) Доказан выше (нормировка).
вб) С помощью D.18)... перевести D.30) в выражение <o|5m_ila|5n_i>
и т. д., пока п или т не станет равным нулю. Тогда воспользо-
ваться тем, что &я|3о = 0.
2. Вычислить для собственных функций гармонического ос-
циллятора выражения
3. Считая, что D.16) и D.18) заданы наперед, доказать D.19)
для Q = (b+)nbm.
Указание. Последовательно использовать сначала D.18),
затем D.16).
4. С помощью интегрального представления D.14) доказать,
что
а также <ф|Ь+1х>* = <%\Ь\ц>>, <q\b\%>* = <%|&+|ср> и, наконец,
<|F+)mbBl>* <l(b+)nbml>
px xq
5. Вычислить ожидаемые значения /ф*A)й(|)ф(|)с/| для
П(|)= %; %2; d/dl; d2/d^2, используя формализм операторов
b, b+ и «скобок» <...!...>.
6. Пусть нормированные собственные функции двух несвя-
занных осцилляторов обозначены Фщ,п2 (см. C.46)). Показать,
что
(Фп,,п, | Фт!,т,} — ОП1>т1О„2]т2,
it вычислить следующие матричные элементы:
7. Обобщая задание 4, исследовать набор N несвязанных
осцилляторов с нормированными собственными функциями C.46).
Доказать выражения D.32), D.33), D.34).
§ 5. Об обращении с бозе-операторами: мы учимся
некоторым приемам
В квантовой теории поля нам приходится в еще большем, чем
в квантовой механике, объеме общаться с операторами. По опы-
ту известно, что это общение причиняет студентам трудности. Одни
из них слишком неосторожны и обращаются с операторами как
с обычными числами, при этом они быстро допускают ошибки в
решении, а другим, слишком боязливым, операторы представля-
ются ядовитыми змеями, с которыми по возможности лучше не
иметь дела. Мы покажем здесь, что, немного поразмыслив, можно
38 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
научиться правильному обращению с операторами и они станут
совершенно безобидными.
В этом параграфе мы рассмотрим только два основных опе-
ратора, а именно, оператор рождения Ь+ и оператор уничтожения
Ъ. Эти операторы удовлетворяют перестановочному соотношению
bb+-b+b = l. E.1)
Перестановочное соотношение E.1) является для последующего
изложения основным. Теперь мы хотим последовательно пораз-
мыслить о том, что можно делать с операторами и чего делать
нельзя. Как мы знаем, следует постоянно представлять себе, что
операторы действуют в конце концов на некоторую волновую
функцию. В качестве простого примера этого рассмотрим линей-
ную комбинацию двух волновых функций, а именно, волновой
функции основного состояния гармонического осциллятора и вол-
новой функции первого возбужденного состояния. Эту комбинацию
можно представить в виде
ф = рфо + ф, = рфо + &+ф0. E.2)
В цравой части волновую функцию основного состояния можно
формально вынести за скобку и представить Ф в виде
ф = (р + Ь+)ф0. E.3)
На основное состояние Фо действует новый оператор, который
мы кратко обозначим Ь+. Из выражения
6+ + р = 6+ E.4)
видно, что, добавляя к оператору Ь+ обычное число, мы получаем
новый оператор. Аналогично мы можем прибавить число *к опе-
ратору уничтожения и получим тогда новый оператор Ъ;
Ь + $* = ъ. E.5)
Если в перестановочное соотношение E.1) вместо операторов Ъ
и Ъ+ подставить операторы b и Ь+, то можно (фазу удостовериться
в том, что новые операторы b и Ь+ также удовлетворяют переста-
новочному соотношению E.1). Позже мы увидим, что это очень
важное свойство бозе-операторов.
Проследим,* однако, сначала в общих чертах, что получается
из суперпозиции волновых функций. Как нам известно из кван-
товой механики, любую функцию Ф можно представить в общем
случае в виде бесконечного ряда по собственным функциям rjv
Ф=2м>п- E.6)
п
Здесь, мы имеем в виду собственную функцию гармонического
§ 5] ОБ ОБРАЩЕНИИ С БОЗЕ-ОПЕРАТОРАМИ 39
осциллятора, Которая, как мы уже много раз видели, может быть
представлена в виде
ф,, = (б+)-Ф0> E.7)
причем нормировочную константу мы опустили. Если подставить
E.7) в E.6), мы получим сразу
ф --=]?. с„(Ь+)"Ф„. E.8)
Теперь кажется, что Фо можно вновь формально вынести за
скобку, тогда правая часть E.8) принимает влд
/(Ь+)Фо, ¦ E.9)
причем f{h+) определяется выражением
/С'+) --S сп (Ь+)п. E.10)
и
Мы подошли здесь вплотную к определению операторной функ-
ции. Эта функция строится следующим образом. Берем некото-
рую заданную функцию классической переменной /'«,'). затем
разлагаем ее в ряд Тейлора и заменяем везде переменную у и ее
степени оператором Ъ+ и его степенями. Таким образом, мы по-
лучаем операторную функцию f(b+). Если специально выбрать
коэффициенты разложения в виде
~
то в качестве примера мы получаем операторную экспоненци-
альную функцию
Как мы позже увидим, эта операторная экспоненциальная функ-
ция играет в теории гармонического осциллятора и тем самым
в квантовой теории поля и в ее приложениях к физике твердого
тела и квантовой оптике чрезвычайно важную роль.
Функция E.10) зависит только от оператора рождения Ь+.
Можно, конечно, из операторов Ъ+ и b образовать любые степени
н произведения, при этом, однако, следует обратить внимание на
точный, порядок следования операторов Ь+ и Ь. На основании
перестановочного соотношения E.1) операторы Ъ и Ъ+ могут
быть расставлены в желаемом порядке, так что, например, bb+
можно выразить через 1 + b+b. При этом особенно важными яв-
ляются два основных вида расположения операторов.
1. Так называемая нормально упорядоченная функция. Эта
функция состоит из сумм степеней вида (b+)mbn, причем в каж-
дом члене суммы справа стоит оператор уничтожения, а слева
40 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ ГГЛ. II
стоит оператор рождения. Такая операторная функция имеет
следующий общий вид:
2cmn(&+)m&". E.13)
тп
2. Наряду с такой функцией имеются антинормально упорядо-
ченные функции, которые состоят из слагаемых вида
bm(b+)n, E.14)
причем операторы рождения стоят справа, а операторы уничто-
жения стоят слева. Функции антшюрмально упорядоченных
операторов имеют следующий общий вид:
2 dmnbm (&+)". E.15)
mn
Как отчетливо видно из этих примеров, с операторами можно
обращаться как с обычными числами, за двумя исключениями.
1. Должен соблюдаться точно порядок следования операторов.
Этот порядок может изменяться только при применении переста-
новочного соотношения E.1).
2. Здесь мы должны указать на одно свойство, о котором еще
явно не упоминалось, а именно, что нельзя делить на оператор
Ь1). Тем не менее можно, например, образовать обратный опера-
тор вида
та- E-16)
Этот оператор должен вычисляться следующим образом: выраже-
ние E.16) рассматривается как функция Ь и разлагается в ряд
по степеням оператора Ь.
Нам нужно научиться некоторым очень полезным приемам,
которые позволяют простым образом вычислять операторные вы-
') Это видно из следующих рассуждений: будем исходить из, без сом-
нения, верного равенства
Ф = ЪФ0. (*)
Умножим обе части его на Ь:
&-*ф = Фо. (**)
Если в качестве волновой функции Фо выбрать основное состояние осцил-
лятора, то согласно (*) должно быть Ф = 0 и, следовательно, также
Ь~гФ = 0, в противоречие с (**), где Ф„ ф 0.
§ 5] ОБ ОБРАЩЕНИИ С БОЗЕ-ОПЕРАТОРАМИ 41
ряжения. Мы утверждаем, что справедливы следующие соотно-
шения:
b(b+)n - (Ь+)" Ь = п (b+)"-i = 'д ib+JU , E.17)
Ь+ (Ь)п - (b)nb+ = - re6"-i = - ^р. E.18)
Соотношение E.17) можно, прочитав его слева направо, интер-
претировать следующим образом: перестановка га-й степени опе-
ратора *Ъ+ с оператором b равнозначна простому дифференциро-
ванию функции F+)" по Ь+. Доказательство соотношения E.17)
мы проведем с помощью метода полной индукции. Для га = 1 это
соотношение действительно справедливо, поскольку оно согласу-
ется с исходным перестановочным соотношением E.1).
1. га=1:
2. Примем, что соотношение E.17) уже доказано для п = п0.
п = п0:
Ъ(Ъ+У> _ F+)».6 = щ (Ь+У°-\ E.18а)
3. Покажем, что оно справедливо для п = п0 + 1.
Выпишем соответствующую левую сторону E.17) для п =
п = п0:
п = п0:
и преобразуем ее следующим образом:
b(b+)n°b+-(b+)n°+1b. E.19)
Здесь мы явно пользуемся тем, что для этих операто-
ров справедлив ассоциативный закон. Первый член b (b+)n° в
E.19) мы выразим через другие присутствующие в E.17) члены.
Тогда E.19) принимает вид
(b+)n'bb+ + п0 (б+)"° - (b+)n°+1b. E.20)
Если теперь применить к стоящему в первом члене в E.20)
произведению ЪЪ+ перестановочное соотношение E.1), то мы по-
лучаем
(Ь+)"° (ЪЧ + 1) + п0 (Ь+)п° - (Ъ+)п'+1Ь, E.21)
что можно в кратком виде записать как
п: E.22)
42 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. It
Мы доказали соотношение E.17) также для п0 + 1 ц тем самым
для общего случая. Соответственно, конечно, доказывается соот-
ношение E.18). Обобщим теперь выражения E.17) и E.18) на
случай любой функции Ь+ или Ъ. Если разложить "функцию j(b+)
в ряд по степеням E.10), то для каждой отдельной степени вы-
полняется соотношение E.17) или E.18). Если просуммировать
все степени с соответствующими коэффициентами, то непосред-
ственно получаем
Ь/И-/(Ь+)Ь-в C.23)
ИЛИ
b+f(b)-f(b)b+^-^. (Г..2*)
Если применить E.23) и.ми E.24) к специальному случаю
икешшеицнальной функции, то непосредственно получается .
ЬеаЬ+ -еа»+Ъ^-аеаЬ+ E.25)
п
Ь+с«ь - Л+ .-_- - aeab. E.2G)
Для экспоненциальной функции мы можем, естественно, всегда
найти обратную фуикцию, для чего нужно лишь поменять знак
показателя экспоненты. Умножив теперь E.25) слева на е~а и
преобразовав равенства, получим
| c-ab+beab+ = b + a. E.27)
Поступая соответствующим образом с E.26), получаем i
| c-«Veab-= Ь+- а. E.28)
Соотношения E.27) и E.28), как мы увидим позже, являются
очень важными.
Попытаемся теперь аналогичным образом упростить следую-
щее выражение:
Для того чтобы решить эту задачу, мы займемся прежде общей
проблемой, которая часто встречается в квантовой теории доля.
А именно, речь идет о том, чтобы вычислить выражение вида
. V~lewV. E.30)
При этом V и W могут быть произвольными операторными функ-
циями. В данном случае V и W имеют вид
E.31)
§ 5] ОБ ОБРАЩЕНИИ С БОЗЕ-ОПЕРЛТОРАМИ 43
W = $b. E.32)
Мы утверждаем, что в самом общем случае, независимо от кон-
кретного вида V и W, выражение E.30) можно представить
в виде
E.33)
Для этого мы разложим экспоненциальную функцию в E.30) в
степенной ряд и получим
E.30) -= V'1 U ¦!- W + ...—¦ Wn + ...] V. @..V1)
Рассмотрим каждый член степенного ряда, причем вставим меж-
ду каждым множителем W единицу:
V-lWaV=V-lW-l-W-i -W...WV. E.35)
Представим теперь единицу несколько более сложным образом,,
а именно, в виде
1 = V ¦ У-1. E.36)
Тогда правую сторону E.35) можно переписать следующим об-
разом:
{V~lWV)(V-xWV).. AV-WV), .E.37)
что приводит, естественно, к выражению следующего вида:
(F-WF)". E.38)
Подставляя теперь результат E.38) с учетом E.35) в E.34) н
снова суммируя экспоненциальный ряд, мы получаем соотно-
шение
| V-lewV = eiv~lwv). E.39)
Данный пример показывает, что наше доказательство никоим
образом не ограничивается экспоненциальными функциями, а мо-
жет- быть применено к любой разложимой в степенной ряд
функции f(W):
f E.40)
Результат E.39) позволяет нам решить нашу задачу
Теперь мы можем сразу написать ответ
44 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
причем Ъ определяется выражением
Ь = е~аЬ+ЬеаЪ+. E.42)
Выражение E.42) мы уже вычислили в явном виде. Используя
E.27), получаем
b = b + a. E.43)
Отсюда находим окончательный результат
Эти промежуточные вычисления позволяют нам решить весьма
важную задачу, а именно, превратить преобразование с V — еа
в так называемое унитарное преобразование. Унитарное преобра-
зование определяется тем, что для осуществляющего ото преобра-
зование оператора U справедливо следующее соотношение:
U+ = U-\ E.45)
т. е. эрмитово сопряженный оператор тождествен обратному опе-
ратору. Вопрос, следовательно, состоит в том, каким образом мож-
но свести еа к унитарному оператору. Для этого построим
вначале оператор
А = еаь+е-"'ь E.46)
п посмотрим, как выглядит эрмитово сопряженный оператору А
оператор /1+. Согласно правилу, изложенному на стр. 34, опера-
тор А+ получается следующим образом: оператор b заменяем
на оператор Ь+, крестик у оператора Ь+ снимаем, заменяем а
на а* и ос* на -а, т. е. на комплексно сопряженные величины,
и, наконец, обращаем порядок следования операторов. Тогда по-
лучаем выражение
А+ = e-«bV*6. E.47)
Умножая теперь А+ на А:
А+А = e-abV*V*Va*6, E.48)
мы видим, что три первых множителя в правой части E.48)
имеют тот же вид, что и левая часть выражения E.41). Поэтому
мы можем прямо вычислить произведение операторов и по-
лучаем
А+А = еа* Vе" Va*bt E.49)
§ 5] ОБ ОБРАЩЕНИИ С БОЗЕ-ОПЕРЛТОРЛМИ 45
что Можно упростить далее:
А+А = е*а1\ E.50)
поскольку все величины здесь можно лереставлять.
Если бы А был унитарным оператором, то в правой части
E.50) стояла бы 1, а не е . Следовательно, мы должны попы-
таться подправить этот результат, введя такой новый оператор,
чтобы обе части E.50) можно было сократить на число, стоящее
в правой части E.50). Этого можно достичь следующим выбором
оператора U:
U = е-14.№е*ъ+е-**ъш E51)
В силу своей конструкции U является унитарным оператором
и удовлетворяет соотношению E.45). Как можно показать, опе-
ратор U можно представить в существенно более «красивой»
форме
U = еаЪ+-а*\ E.51а)
откуда сразу видно, что U действительно является унитарным
оператором. В последующем изложении, однако, мы будем посто-
янно использовать выражение E.51). С помощью этого унитарно-
го оператора U мы можем теперь вновь преобразовать опера-
торы Ъ и Ь+ и, применяя E.27) или E.28), получим
E.52)
E.53)
Унитарный оператор U играет, как мы сейчас увидим, важную
роль в теории смещенного гармонического осциллятора.
Наряду с только что рассмотренным оператором, в котором
показатель экспоненты линеен по Ъ или Ь+, имеется другой
важный оператор, в котором b и Ь+ присутствуют одновременно.
Спрашивается, каким образом следует вычислять выражение
/(а) = еаЬ+ьЬе-"ь+ь? E.54)
Как было уже указано, будем считать это выражение функцией
параметра а. Выведем для /(ос) дифференциальное уравнение,
в котором E.54) дифференцируется по а. Учитывая точный по-
рядок следования операторов, получаем тогда
/' (а) = еаъ+ь (b+bb - ЪЪ+Ъ) е~аЬ+ь. E.55)
Из выражения, стоящего в скобках, вынесем за скобки направо
оператор Ь, тогда получим
E>56)
4е ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. И
Новое выражение в скобках представляет собой с точностью до
знака левую часть перестановочного соотношения E.1), так что
E.56) переходит в выражение
-f(a). E.57)
Сравнение E.55) с E.57) приводит к дифференциальному урав-
нению для /:
/'(«)=-/(о) E.58)
с решением
/(а)=«-«-С, E.59)
причем постоянная интегрирования С определяется с помощью
«начального условия» при а = 0. Согласно E.54) должно быть
/@) = Ь,
где Ъ — оператор уничтожения. Сравнивая это выражение с
E.59), мы видим, что постоянная интегрирования С равна' опе-
ратору Ъ. На первый взгляд это кажется странным, однако ниче-
го странного здесь нет, поскольку ведь /(а) согласно E.54) яв-
ляется операторной функцией. Отсюда в качестве конечного ре-
зультата находим соотношение
Аналогичным образом доказывается следующее соотношение:
| eab+bb+e-ab+b = e%+. E.61)
Итак, для чисто мнимого о оператор еаь+ь является унитарным.
Задания к § 5
1. Положить в E.51а) а = ~ A/У2)|0, где а — действитель-
ное число. Используя C.14) и C.15), убедиться, что Z7<p(g) яв-
ляется не чем иным, как разложением по степеням ср(|+ ?<>)•
2. Показать, что если фо нормирована, то нормирована и
функция ij> = ?Лро, причем оператор V задан выражением E.51).
Указание? Применить D.19) и E.45).
3. Пусть iJTo — волновая функция осповного состояния осцил-
лятора, U—преобразование E.51) и i|> = Е/г|?о. Показать, что
a) <4>lb|i|>>=-a, б) <ф|6+|^> = а*.
Указание, а) Поскольку Ьфо = 0, то можно написать
&brif>o = (bU — С/Ь)ч{5о. Затем применить E.23) и задание 2.
б) Применить D.16), читая его справа налево.
§ 6] СМЕЩЕННЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 47
4. В задании 4 к § 3 положить сп = е '2 у" гТ7=гЪ убедить-
ся в том, что при этом для волповой функции г|з получается сле-
дующее выражение:
причем ц' нормирована.
5. Почему еАевФеА+в, если [А, В] ^ О?
§ 6. Смещенный гармонический осциллятор: прообраз
элементарных возбуждений в твердом теле
Продолжим исследование квантовомехаштческого гармониче-
ского осциллятора, который описывается с помощью безразмерной
координаты \. Предположим теперь, что этот гармонический ос-
циллятор подвержен действию еще одной, независящей от вре-
мени силы 12"^Тиа. (В упражнении 4 мы распространим эти ре-
зультаты на зависящую от времени силу.) Уравнение Шрединге-
[)а идгеег вид
- ]' 2yE \|- (t) ----- еф (?), F.1 ">
i
причем безразмерная энергия определяется выражением
б ,г: А. F.2)
Л (О v '
Уравнение @.1) можно интерпретировать и совершенно иным
образом: это уравнение описывает осциллятор, положение равно-
весия которого находится в \а = ^2 (рис. 14, 15). Решение и
отоп последней формулировке тривиально: вместо старой коорди-
наты \ вводят новую смещенную координату, так что в новой
системе координат положение равновесия находится в начале ко-
ординат. Однако мы хотим решить эту проблему другим спосо-
бом, с помощью операторов Ь и Ь+, поскольку отсюда можно за-
имствовать важный метод исследования тех проблем твердого
тела, с которыми мы встретимся позже. Множитель при | мы
написали в несколько искусственном виде У2у, чтобы позже по-
лучить некоторое упрощение. Если снова ввести вместо коорди-
наты % операторы рождения и уничтожения, согласно обратным
C.14) и C.15) соотношениям
ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
[ГЛ. II
то F.1) переходит непосредственно в уравнение
| {Ь+Ъ - у {Ь+ + Ъ)]тр = е'-ф,.
причем для краткости мы положили
8' =8— -j.
F.5;
F.6)
Будем искать решение проблемы смещенного гармонического
осциллятора двумя различными способами.
0 0
0 0©
а)ШЯ
Рис. 14. Вид кривой по-
тенциальной энергии
смещенного гармониче-
ского осциллятора. Вер-
шина параболы нахо-
дится в точке с коор-
динатами (V2 К, —Йсо^2) •
Штриховой линией пред-
ставлен потенциал не-
смещенного осциллято-
.ра.
Рис. 15. Прямой пример применения смещенного
гармонического осциллятора (схематически). Ко-
лебания ионов в ^-центре (центре окраски).
В полярном кристалле (например, в NaCl) от-
сутствует отрицательный ион. Его место занято
электроном. В зависимости от состояния возбуж-
дения электрон имеет различные распределения
заряда (заштриховано). Это в свою очередь ве-
дет к изменению поля ионов, о) Положение с на-
инизшей потенциальной энергией для иона, от-
меченного более жирным кружком, находится в
точке (+) (распределение заряда электрона до
перехода). Ъ) Положение с наинизшей потенци-
альной энергией теперь смещено вправо (зарядо-
вое распределение электрона концентрируется
правее) и находится где-то возле точки (X)
(распределение заряда электрона после пере-
хода).
1. Первый путь решения. Рассмотрим левую сторону уравне-
ния F.5). Если бы Ъ+ и Ь были не операторами, а обычными
числами, то члены, линейные по Ь+ и Ь, которые присутствуют
в F.5), можно было бы устранить, использовав линейное преоб-
разование вида
Ь = Ъ + у, b+ = b+ + у. F.7)
Как мы уже отметили ранее, новые операторы Ъ и Ь+ также удо-
§ 6] СМЕЩЕННЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 49
влетворяют перестановочному соотношению для бозе-частиц:
¦бЬ+-Ь+Ь = 1. F.8)
Поэтому действительно кажется естественным применить пре-
образование F.7). Если мы одновременно вместо старой функции
if>, связанной с операторами Ь+ и Ъ, введем новую функцию ц>,
которая связана теперь с операторами Ь+:
ф(Ь+) = <р(Ь+), F.9)
то уравнение F.5) примет вид
r- F.10)
Если, наконец, с помощью соотношения
s' = s-f F.11)
ввести новую энергию ,ъ, то F.10) можно окончательно предста-
вить в виде_
Ь+Ьф = еф. F.12)
Но это уравнение в точности совпадает с уравнением гармони-
ческого осциллятора. Поскольку операторы Ь и Ь+ удовлетворяют
обычным перестановочным соотношениям F.8), мы можем не-
посредственно построить собственные функции и собственные
значения уравнения F.12). Тогда с помощью процедуры, которая
нам известна из § 3, в качестве собственной волновой функции
уравнения F.12) мы получим функцию
^(Ь+Гфо8 F.13)
причем основное состояние определяется следующим свойством:
Ьфо = 0. F.14)
Собственные значения уравнения F.12) имеют вид
ё„ = га (п = 0, 1, 2, ...). F.15)
Следовательно, собственные значения уравнения F.5) даются вы-
ражением
| в' = п-т». F.16)
Собственные значения смещенного осциллятора мы получим
согласно F.2), умножив F.16) на Й-ш и приняв во внимание
F.6):
Е = %<л (п — у2 + х/2).
Здесь также явно учтена нулевая энергия Г-я
50 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
В F.14) мы определили основное состояние с помощью сме-
щенных операторов. Какой вид имеет основное состояние отно-
сительно первоначального оператора 6+? Подставляя F.7) и F.9)
в F.14), получим уравнение для смещенного основного со-
стояния:
5фО = F-^)г|з.F+)=О. F.17)
Функции ty(b+), которые удовлетворяют идентичному F.17)
уравнению
называются когерентными состояниями. Они играют в квантовой
оптике фундаментальную роль.
Смещенное состояние, естественно, должно быть представимо
через несмещенные собственные функции гармонического осцил-
лятора. Чтобы показать, как это делается, проведем одно фор-
мальное преобразование. Мы видели в § 5 (см. E.6—5.10)), что
любую функцию можно представить в виде
F.18)
причем функция / подлежит еще определению. Функция -ф0 яв-
ляется функцией основного состояния, которое, как обычно, оп-
ределяется свойством
= 0. F.19)
Подставим F.18) в F.17):
F.20)
Второй член в левой части выражения F.20) в силу F.19) равен
нулю; мы добавили его по соображениям, которые тотчас станут
очевидными. Коммутатор Ъ и f(b+) в левой части уравнения F.20)
можно упростить, использовав соотношение E.23), тогда вместо
F.20) мы получаем следующее уравнение:
Hr F.21)
Это уравнепие всегда разрешимо, если функцию f(b+) можно
определить так, чтобы она удовлетворяла уравнению
. F-22)
Уравнение F.22) имеет следующее решение:
/(&+) = с^ь+. F.23)
Если подставить явный вид решения F.23) в F.18), то мы дей-
§ 6] СМЕЩЕННЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 51
«ствительно получим представление основного состояния смещен-
ного .осциллятора через волновую функцию основного состояния
несмещенного осциллятора:
( г|)й(Ь+)=с0^ь'1>0, F.24)
где со— мпожитель, подлежащий еще определению с помощью
условия нормировки. Как мы увидим ниже, он равен
с0 = e~if/M\ F.25)
До сих пор мы конструировали только основное состояние.
Теперь, однако, с помощью исходных операторов Ь+ и Ъ мы мо-
жем сразу найти также и возбужденные состояния. Для этого
следует лишь выразить Ь+ и op0 в F.13) через F.7) и F.24).
Тогда оказывается, что решение для возбужденных состояний
имеет следующий вид:
(в.М)
Итак, нам удалось решить уравнение Шредингера F.5) в явном
виде. *
Прежде чем мы обсудим второй путь решения, рассмотрим
наши результаты F.13) или F.26) с точки зрения последующих
приложений к проблемам твердого тела. Как следует из вида
основного состояния для смещепного осциллятора, это основное
состояние имеет мало общего с основным состоянием несмещен-
ного гармонического осциллятора. Тем не менее, исходя из сме-
щенного основного состояпия, можно снова создать возбужденные
состояния, которые имеют «бозевский» характер1), для чего сле-
дует подействовать новым оператором рождения Ь+ на смещенное
основное состояние. Мы столкнемся с совершенно аналогичной
проблемой, например, при изучении плазменных колебаний в
твердом теле. Хотя основное состояние такой системы не имеет
практически ничего общего с основным состоянием невзаимодей-
ствующей системы, однако мы можем создать возбужденные со-
стояния с помощью многократного применения бозе-операторов.
Аналогичная ситуация встретится нам и в теории сверхпроводи-
мости.
Теперь мы сделаем еще один очень важный шаг, который
прямо приведет к важным приложениям в теории сверхпроводи-
мости. А именно, мы покажем, что можно найти все возбужден-
ные состояния гармонического осциллятора, если только удается
') Как будет еще раз пояснено в § 12, частицы, операторы рождения и
уничтожения которых удовлетворяют перестановочным соотношениям F.8),
называются бозе-частицами.
52 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II
найти такое унитарное преобразование, которое ведет от основ-
ного состояния несмещенной системы к основному состоянию
смещенной системы. Как мы сейчас увидим, для гармонического
осциллятора нам удастся сконструировать это преобразование в
явном виде. В этом нам помогут приемы, с которыми мы позна-
комились в § 5. Итак, мы переходим ко
второму пути решения'). Будем исходить из волновой функ-
ции основпого состояния смещенного осциллятора
, ' F.27)
причем Со— нормировочная постоянная, которую мы сейчас най-
дем. Выражение F.27) дает нам, если угодно, преобразование
старого основного состояния тфо в новое состояние tyg посредством
оператора
А=с?уь+. F.28)
Этот оператор, однако, имеет вид экспоненциального оператора,
которых! мы обстоятельно исследовали еще в § 5. Мы видели, что
преобразование, в котором участвует оператор А, можно превра-
тить в унитарное преобразование, доба^рв множители е~"тЬ и
е . Добавка множителя е~т'' фактически ничего не меняет,
поскольку Ъ или любая степень Ъ, действующая на ipo, всегда дает
нуль и от всей экспоненциальной функции остается только еди-
ница. Том самым мы находим искомое преобразование
Поскольку преобразование U, согласно § 5, унитарно, функция
\ps автоматически оказывается нормированной на единицу, если
предполагается, как обычно, что г|)о нормирована (см. задание 2
из § 5). Сравнение F.27) и F.29) дает затем
с, --=-- e-(V*)lv *. F.29а)
Введем теперь в совершенно общем виде новое преобразование
между искомым решением if> уравнения Шредингера F.5) и но-
вой функцией %
yp = U%, F.30)
где U дается в F.29). После подстановки F.30) в F.5) получаем
&'U%; F.31)
') Этот раздел при первом чтении также можно пропустить.
§ 6] СМЕЩЕННЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 53
умножив это уравнение слева на U~l, находим
U~4b+b-t(b+ + b)}U% = e'%. F.32)
Нам уже известно, как действует преобразование U на операто-
ры Ь+ и Ъ. Например, справедливо равенство
U~lb+U = b+ + 4, F.33)
а также U~lb+bU-» U~lb+U ¦ V~xbV = (b+ + у)F + у). Мы видим,
таким образом, что преобразование U действует как сдвиг опе-
раторов b и Ь+. Следовательно, уравнение F.32) можно привести
к виду
z'x. F.34)
Собственные функции определяются сразу. Они имеют вид
Х^-ЫЬ+У'Х,,, F-35)
У я!
причем можно установить тождественность %о с г|з0, определяемой
уравнением F.27):
Хо = Фо, Ио = 0. F.36)
С помощью преобразования F.30) можно вновь перейти от F.35)
к искомым волновым функциям \jx При этом мы получим
^U(b+)nU-1U^e. F.37)
Множитель U~XU равен, естественно, единице и введен только
для того, чтобы сделать возможным преобразование выражения
@.37) в выражение
и-1)пЪй. F.38)
При этом мы использовали соотношение E.40). Учитывая еще,
наконец, соотношение
4, F.39)
мы непосредственно обнаруживаем, что F.38) тождественно сов-
падает с F.26). Большое преимущество этого рассмотрения со-
стоит в том, что благодаря применению унитарного преобразова-
ния F.29) наша проблема может быть сведена к существенно
более простой проблеме F.34).
Заданияк § 6
1. Для комплексного ^ уравнение Шредингера имеет вид
Используя методы § 6, найти -ф и Е.
1 • <
54 ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ [ГЛ. II!
2. Оператор Гамильтона набора несвязанных, но смещенных
гармонических осцилляторов имеет вид
Н = 2fccofe {btbh - VA - ylbt).
к
Показать, что волновая функция основпого состояния дается вы-
ражением (ЪкФй = 0)
Ф = Д ехр{- 4 I Vfe I2} exp [ylb?] ехр (- yhbh] Фо.
Соответствующая энергия равна
Е = — 2 7шк | 7л |". (Доказательство?)
к
3. Пусть упруго связанный примесный атом находится в поло-
жении равновесия в основном состоянии. Благодаря электронно-
му переходу условия связи изменяются, так что потенциал, со-
гласно рис. 14, оказывается смещенным. Электронный переход
при этом происходит настолько быстро, что ядро (координата q,
одномерная модель) остается в прежнем положении (принцип
Кондона). Сколько в среднем фонопов (квантов колебания) со-
держит колебательное состояние около нового положения рав-
новесия?
Указание. Вычислить <\|)Ib+ b\ч?>>, где г|з — волновая функ-
ция смещенного осциллятора.
4. В уравнении Шредингера
1Щ (А 6.1)
величины if,'if* зависят от времени. Решить (А 6.1), используя
подстановку
Ч>(*) = Л*(ОЬ"ЧО (при б*. = 0)<
и определить f(t) и g(t) как интегралы от t(t), t*(t). Вычис-
лить средние значения
(см. задание 3 к § 5) и показать, что они удовлетворяют уравне-
ниям
(d/dt)F= fab*- iay(t), (d/dt)b"= - iab + i©^*(t).
Глава III. КВАНТОВАНИЕ ПОЛЯ
§ 7. Линейная цепочка атомов: классическое рассмотрение
Рассмотрим линейную атомную цепочку, все атомы которой
имеют равные массы М и их положения равновесия находятся
на равных расстояниях а. Атомы мы перенумеруем индексом /,
а отклонение /-го атома из положения равновесия обозначим че-
рез qi (рис. 16). Буква I должна, таким образом, указывать место
расположения атома (т. е.
координату равновесного по-
ложения центра тяжести ато-
ма). Для простоты мы огра-
ничимся продольными откло-
нениями. Связь между ато- l^-j
мами описывается гармони-
ческой силой с константой рис. ю. Линейная атомная цепочка,
упругости К (рис. 17). Тогда
ньютоновское уравнение дви-
жения Z-ro атома имеет сле-
дующий вид:
ком виде
-K(q,(t)-q,-i(t)).
а л)
Рис. 17. Энергия взаимодействия меж-
Приведя подобные члены в ду атомами 1 и 2. Атом 1 закреплен в
правой части уравнения G.1), точке ?i=0. Положение равнове-
запишем его в более крат- сия находится в точке а. При малых
г отклонениях д2 атома 2 из положения
равновесия фактический потенциал
.-f-л _, — 2G ) ^ ) с хорошей точностью можно
аппроксимировать параболой Vq) =
= const q\. Тем самым оправдывается
((.?) цаше предположение относительно уп-
' ругих сил.
Будем считать, что цепочка циклически замкнута, так что для
координат выполняется периодическое граничное условие
Ov = ffv+w, G.3)
5б КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
где iV — число атомов в цепочке. Для решения уравнения G.2)
мы предположим заранее, что колебательные состояния цепочки
можно описать плоскими волнами. Введем следующую зависи-
мость отклонения qAt) от координаты I:
G.4)
где w — действительное волновое число1), которое в силу G.3)
имеет следующий вид:
*>=7fi» G-4а)
п — целое число, удовлетворяющее условию — N/2 ^п< N12.
Множитель 1/У N отвечает за нормировку в следующем
смысле;
Далее, функции 1/(У N)eiwla взаимно ортогональны:
l{we""T{we""b° ди *+« ' <7-4в)
(см. задание 1 в конце этого параграфа). В обоих случаях сум-
мирование распространяется на все атомы цепочки. Коэффициент
Bw в предполагаемом виде решения G.4) имеет смысл амплитуды,
зависящей от волнового числа w и времени t. Для того чтобы
определить зависимость амплитуды Ва от времени, подставим ре-
шение G.4) в уравнение G.2), откуда непосредственно получаем
уравнение
В Jit) = g(e{»a + e-iaa - 2)ВМ), G.5)
где введено следующее краткое обозначение:
* = ?• . <7-6>
Уравнение G.5) представляет собой простое уравнение колебания
для зависящей от времени функции Bw. Для его решения сделаем
обычную экспоненциальную подстановку
Bw(t) = e~ie>wtAw. G.7)
') В литературе вместо этой буквы часто применяются буквы к и q,
причем последнее обозначение часто является поводом к недоразумению,
несколько буквой з одновременно обозначают и отклонение.
§7]
КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ ЦЕПОЧКА АТОМОВ
57
После подстановки G.7) в G.5) получаем связь между частотой ш
и волновым числом w.
- <*l = g (eiwa + e~iwa -2) = 2g (cos wa - 1),
или, после элементарных преобразований,
со-= 2Ki[sin(u7a/2)|.
G.8)
G.9)
Это выражение представляет собой закон дисперсии для распро-
странения волны по линейной цепоч-
ке.
Зависимость со от w, т. е. закон
дисперсии, представлена на рис. 18.
Поскольку в случае уравнения G.2)
речь идет о линейном уравнении,
можно использовать принцип су-
перпозиции, согласно которому сум-
ма решений G.4) с амплитудами
G.7) также является решением. За-
пишем это решение в виде
'а
О
Рис. 18. Закон дисперсии для
линейной атомной цепочки.
iwla -i
e е
1 л
A
GЛ0)
При этом мы учли, что комплексно сопряженная решению G.4)
функция также является решением уравнения G.2), а амплитуда
qi(t) должна быть действительной величиной.
Суммирование проводится по всем разрешенным условием
G.4а) значениям и>. Коэффициенты Ат и Aw определяются на-
чальными условиями, т. е. начальными положениями дг@) и на-
чальными скоростями дДО) отдельных атомов. Теперь мы займем-
ся более подробно формальным рассмотрением этой проблемы и
сформулируем ее еще ,раз с помощью функции Лагранжа и урав-
нений Гамильтона. Как известно, функция Лагранжа определяет-
ся выражением L = Т — V, где Т — кинетическая, а V — потен-
циальная энергии. В нашем случае кинетическая энергия равна
сумме вкладов отдельных атомов
а потенциальная
уравнения
Ki = -grade,F
энергия может быть определена с помощью
G.12)
58 КВАНТОВАНИЕ ПОЛЯ (ГЛ. III
и приводится элементарным образом к следующему виду:
N . ¦
Qi-gi+if- G.13)
1=1
N
В последующем изложении для краткости мы обозначим 2j
через 2- Уравнения Лагранжа, как обычно, имеют вид
i
-^^--^==0. G.14)
После подстановки G.11) п G.13) в G.14) мы вновь получаем
уравнение движения G.2). Для последующего изложения запи-
шем еще выражение для канонически сопряженного импульса,
который, как известно, равен производной L по qr.
Pi ^-'-4- -- Mqi- G! 15)
Посмотрим, далее, как выглядит функция Гамильтона, определя-
емая выражением II — Т + V. Как известно, она следующим обра-
зом связана с функцией Лагранжа:
Функция Гамильтона с учетом G.11), G.13) и G.15) принимает
вид
2
Соответствующие уравнения Гамильтона, как обычно, выглядят
следующим образом:
дН ' дН /п л ел
qi = w, Pl = -Wi . G.18)
и с учетом G.17) принимают следующий явный вид:
P ' P K(g + g2g) G.19)
Зададимся теперь вопросом, как будет выглядеть функция
Гамильтона, если мы перейдем от отклонений qt отдельных ато-
мов к новым «координатам», а именно, к амплитудам Aw, Aw.
При этом наряду с выражением G.10) мы должны также рассмот-
реть выражение для канонически сопряженного импульса. Диф-
§ 7] КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ ЦЕПОЧКА АТОМОВ 59
ференцируя правую часть G.10) по времени и умножая резуль-
тат на М, получим, согласно G.15), следующее выражение для
канонически сопряженного импульса рМ)
Hi*) = 2 (- m^"v^
G.20)
Теперь выразим функцию Гамильтона через амплитуды Аю,п-Аю,
что обеспечит нам позже непосредственный переход к квантова-
нию. Вычисляя выражение для кинетической энергии, вначале
получаем
4- комнл. сопряж.Г. G.21)
В G.21) присутствуют выражения вида
2 2 <~ ™*Щ(- ™*М) Bw (t) /?,, (t) ±- V еша^уь^ {122)
W ш' (
б№,-ги'
Последняя сумма, ввиду ортогональности дискретных волновых
амплитуд еШа, является символом Кропскера. Другие квадратич-
ные и билинейные по В выражения также упрощаются, так что
после кратких промежуточных вычислений вместо G.21) паходим
2Л? 2 Р* ^ Т 2 (— ®w®-wBw (f) B-w (*) ~
- www-wB* (t) Blw (t) + ulBw (t) B*w (t) +
G.23)
Рассмотрим выра)кенне для потенциальной энергии
v=4 2 (<?<
более обстоятельно, для чего разложим его на три различные
части:
к 2 ?! - 4 2 ?i-rfi -42 yi+i?" G-25)
2 ^ *<-i*< 2
У, F» V.
Используя ортогональность волновых амплитуд еш'° (см. G.22)),
после элементарных преобразований получаем следующие
60 • КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
выражения для Fi, F2, Vz'
+ Bw(t)Bl{t)+B*(t)Bw(t)), G.26)
4 2 ^ (t] B-« w e~iwa+к- °- +
w
+ Bw(t)Bl{t)e-iwa + Bl(t)Bw{t)eiwa), G.27)
Bw{t)B-w{t)eiwa+K-c- +
+ Bw (t) Bl (t) eiwa + Bt (t) Bw (t) e~iwa). G.28)
Рассмотрим выражение для полной энергии Т + V и сгруппи-
руем отдельные члены. При этом учтем, что согласно G.8) №» =
= (i>-w Далее оказывается, что множители выражений BuitJB-wit)
принимают вид
_ Е- &1 + к - К cos wa = 0 G.29)
и согласно закону дисперсии G.8) исчезают. Равным образом ис-
чезают множители выражений Bw(t)Blw(t). Множители членов
Bw(t)Bw(t) объединяются в-выражения следующего вида:
¦^¦(йЪ+К — К cos wa = Mai G.30)
и также в силу закона дисперсии не исчезают.
Таким образом, для Я мы получаем следующее выражение:
Я = ^Ма>1\в1{1)Вю (t) + Bw(t)B*w(t)}. G.31)
W
Имея в виду последующее квантовотеоретическое рассмотре-
ние, мы (не указывая до сих пор на это определенно) на всех
этапах получения Я очень тщательно следили за порядком следо-
вания амплитуд В* и В. Этот порядок отражен также в G.31).
Поскольку В имеет размерность длины, введем новые безраз-
мерные величины, причем, принимая во внимание последующее
квантовое рассмотрение, выберем соответствующий новый норми-
ровочный множитель. Итак, положим
5«*(') = Vmz-K- G-32)
§ 71 КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ ЦЕПОЧКА АТОМОВ 61
Тогда функция Гамильтона, выраженная через новые амплитуды,
принимает следующий вид:
Н = J^Hoiw ~Y {blbw + bwbt). G.33)
Заданияк § 7
1. Показать, что в силу G.3) волновое число w должно иметь
вид G.4а). Доказать G.46) и G.4в).
Указание. Наряду с G.4а) использовать формулу Z^ dl —
2. Пусть заданы начальные положения атомов #Д0) п началь-
ные скорости дДО). Какой вид имеет решение q№) для последую-
щих моментов времени? Более подробно обсудить следующие
частные случаи:
а) дДО) =А sin (wola), дДО)=О;
Указание. Коэффициенты при { = 0 в G.10) определяются с
помощью фурье-преобразования. Для читателя, незнакомого с
преобразованием Фурье: умножить обе части G.10) и G.20) на
e-iwoia (ц;о^о) и просуммировать по I. В силу G.4в), суммы по
w в правых частях G.10) и G.20) выпадают, так что AWa, Aw<t
выражаются прямо через суммы по qt и р,.
3. На каждый атом I исследованной в предыдущих параграфах
атомной цепочки дополнительно воздействует зависящая от вре-
мени внешняя сила Kiit), которая может меняться от атома к
атому. Какой вид имеют:
а) уравпения движения (вместо G.2)),
б) потенциальная энергия (вместо G.13)),
в) функция Лапранжа L — T — V,
г) функция Гамильтона Н (вместо G.17))
как функции Кi(t) и qtit)?
Как выглядят имеющиеся в случаях б), в), г) дополнительные
члены, если их разложить по функциям G.4)?
4. Вычислить qM) в специальном случае, когда указанная в
задании 3 сила имеет вид Кх (t) = K0&ij0 sin wot. Начальные
условия суть дДО) = дДО) = 0.
5. В линейной атомной цепочке с «упругим» взаимодействием
между ближайшими соседями массы атомов попеременно раз-
ИВАН?ОВАНЙЕ ПОЛЯ
[ГЛ. Ш
личны: М для I четных и т для I нечетных (рис. 19). Вывести
уравнение движения и решить его подстановкой
АеШае~ш для I четного,
веШае~ш для I нечетного.
ае
91 ^ = \веШае~ш
Рис. 19. Двухатомная линейпая це-
почка (к заданию 5).
Рис. 20. Закон дисперсии для
двухатомной линейной цепоч-
ки. / — упругая постоянная.
Убедиться, в том, что закон дисперсии имеет вид, показанный на
рис. 20.
§ 8. Линейная атомная цепочка: квантовотеоретическое
рассмотрение. Фононы
В рамках механики точки нам хорошо известно, каким обра-
зом мы могли бы перейти от классического описания к кваптово-
теоретическому рассмотрению. Если у нас есть система точечных
масс, которые описываются координатами от q\ до qN и соответ-
ствующими каноническими импульсами от р\ до pN, то, потребо-
вав выполнения для этих координат и импульсов перестановочно-
го соотношения
— QiPn = —б/„,
(8.1)
мы перейдем к квантованию. Причем координаты, а также им-
пульсы различных точек между собой коммутируют:
qign — qnqi = O, (8.2)
PnPi-рфп^О. ' (8.3)
Этот' рецепт квантования можно применить к атомной цепочке,
которую мы рассматривали в предыдущих параграфах, поскольку
составляющие ее отдельные точечные массы могут быть охарак-
теризованы своими координатами и импульсами. Однако мы ви-
дели, что вместо координат qt и pi целесообразнее использовать
новые координаты В„ и 5*,, которые имеют наглядный смысл
§ 8] КВАНТОВАННАЯ ЛИНЕЙНАЯ АТОМНАЯ ЦЕПОЧКА. ФоНОНЫ 63
амплитуд. Поскольку эти вторые координаты связаны с коорди-
натами q, и pi посредством линейного преобразования G.10) или
G.20), то из перестановочных соотношений (8.1—8.3) следуют,
естественно, новые перестановочные соотношения для Bw, В^-
Из эквивалентного G.10) выражения для qt{t) (см. G.7)):
^^Ша[Вю + В\} . (8.4)
следует после применения преобразования Фурье (см. указание
к заданию 2 § 7), что
N
2 е-ШаЯ1 --- Вш + В\ ^ aw, (8.5)
причем последнее равенство представляет собой повое сокращен-
ное обозначение. Аналогичным образом, с помощью преобразова-
ния Фурье находим импульсы
N
' -4= "S е~г11""р1 — — id)wMBw -f- m_wBlwM = Ра,Л/Юа,. (8.6)
В уравнениях (8.4), (8.5), (8.6) аргумент t у всех «переменных»
qi, pi, Bw, B-w опущен. Основанием для этого служит то обстоя-
тельство, что при квантовании, которое ведет к уравнению Шре-
дингера, зависящие от времени измеримые величины (как, напри-
мер, координаты q{l)) становятся независящими от времени
операторами.
Из двух последних уравнений (8.5) и (8.0), решая их относи-
тельно By, и B*_Vh получаем соотношения
&w — ~~2~ \aw ~Г Фи>) (о-')
S-u, -= ^- (аш — /р„). (8.8)
Исследуем теперь, какой вид имеют перестановочные соотно-
шения между операторами Bw и Bw , относящимися к одному и
тому же моменту времени. Для этого образуем коммутатор
Перемножим стоящие в правой части (8.9) скобки, соблюдая при
этом порядок сомножителей, и соберем вместе выражения,
64 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ш
представляющие собой коммутаторы [А, В] —АВ — В А:
(8.9)=-|-{[oIO> «_„.] + №». p-e'l + ifP». a-w<]-i[aw, p\_w-]}.
(8.10)
Выразим каждый коммутатор через коммутаторы для qi и ph ис-
пользуя при этом (8.5) и (8.6). Поскольку аю состоит только из
qt (см. (8.5)), а все операторы qi коммутируют друг с другом,
отсюда немедленно следует, что [аю, a-w] = 0. Аналогично, ока-
зывается, что [Рю, P_W'] = 0. В оставшееся в (8.10) выражение
подставим явные выражения (8.5) и (8.6), после чего получим
{ N N \
Согласно перестановочному соотношению (8.1), выражение (8.12)
переходит в
N
так что мы получаем перестановочные соотношения следующего
вида:
BWBW' — BW'BW = Tjjj—8WtW>. (8.14)
w
Введем теперь вместо амплитуд Вш и Bw со^гласно G.32) новые
безразмерные амплитуды Ью и bt>- Тогда получим окончательно
следующие перестановочные соотношения:
I b№bt. - bUw = Ьа,а.. (8.15)
Если мы будем исходить из перестановочных соотношений (8.2)
и (8.3), то с помощью совершенно аналогичных преобразований
получим следующие перестановочные соотношения:
bwbW'-bW'bw = O, . (8.16)
blbt. - b+'bt = 0. (8.17)
Наряду с перестановочными соотношениями нас интересует,
конечно, явный вид оператора Гамильтона в новых операторах bw
и Ьщ. Мы можем получить его, однако, непосредственно из
уравнения G.33) § 7. Там были сделаны аналогичные только что
§ 8] КВАНТОВАННАЯ ЛИНЕЙНАЯ АТОМНАЯ ЦЕПОЧКА. ФОНОЛЫ 65
проведенным преобразования от первоначальных координат qt и
импульсов pi к новым величинам bw, bj, поэтому формально для
оператора Гамильтона будет справедлив тот же самый результат,
только при всех преобразованиях мы должны строго следить за
порядком следования операторов, что, однако, делалось уже тогда.
Итак, перенесем сюда результат G.33) и, преобразуя второй член
в сумме по w с помощью перестановочного соотношения (8.15),
получим
Вторая сумма представляет собой энергию нулевых колебаний и
может, при соответствующем выборе начала отсчета энергии, быть
опущена. Итак, уравнение Шредингера для атомной цепочки
принимает окончательно следующий вид:
= ЕФ. (8.19)
Функции, являющиеся решением этого уравнения, и собственные
значения энергии мы ввели в § 3, так что мы сразу же можем
использовать здесь полученные там результаты.
Для ясности и удобства использования в приложениях приве-
дем явный вид зависимости между оператором отклонения qt и
операторами bw, bj (см. (8.4) и G.32)):
(8.20)
©_„). (8.21)
Принимая во внимание разложение (8.20), решение (8.19)
можно интерпретировать следующим образом: в стационарном
состоянии волны решетки с волновым числом w заняты nw части-
цами, так называемыми фонолами.
Такое представление в литературе иногда подчеркивается
слишком сильно; в действительности при процессах в решетке
5 X. Хакен
66 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
возникает наложение состояний с различными фононными числа-
ми. Мы будем постоянно встречаться с такого рода случаями.
В заключение мы укажем на еще одно существенное различие
между классическим и квантовомеханическим рассмотрением, ко-
торое часто доставляет неприятности не только начинающим. Оно
состоит в том, что начальные условия в этих случаях устанавли-
ваются совершенно различно: в классическом случае они задают-
ся просто с помощью д,@) и q,@). Теперь, однако, qt и />, явля-
ются операторами! Полное начальное состояние в квантовомеха-
ннческом подходе устанавливается заданием волновой функции Ф
(см. нижеследующие задания).
Задания к § 8
1. Вычислить для рассмотренной в § 8 линейной цепочки
и <Ф|р,|Ф>:
а) для Ф = Фо и Ф = Ц jj__ (^.)"№(tia, т. е. для энергетиче-
ских состояний (8.19);
б) для когерентного состояния
ф = е-°/2IР12еРь№„фо5 причем р =•-= уе~г<°'г°.
Убедиться, что Ф является решением зависящего от времени
уравнения Шредингера (8.19) (см. задания к § 3 и § 5).
Указание. Использовать (8.20), D.28—4.30), а также зада-
ние 3 к § 5.
2. Вычислить <Ф | q\ \ Ф> : а) для Ф =Ф0; б) для Ф ¦-= bt<\\.
3. Является ли волновая функция Ф однозначно определенной
(для всех I), если заданы средние значения координат и ям-
пульсов
qi = <Ф|д,|Ф> и pi =
4. В квантованной атомной цепочке в положении /о находится
дополнительный заряд, который действует с независящей от вре-
мени силой Ki-i0 на точечные массы I Ф Iq. Используя задание 3
к § 7, показать, что уравнение Шредингера в этом случае имеет
вид
+ gj? + gtbw) Ф = ?Ф.
Как зависят gw,gw от
§ 9] КЛАССИЧЕСКИЙ ПЕРЕХОД К КОНТИНУУМУ 67
Определить Ф для наинизшего энергетического состояния Ео
и найти зависимость последнего от ga,gw, а затем ж от #j-i0.
Энергия Eq называется собственной энергией дополнительного
заряда. Какова величина <Ф|дг|Ф>?
§ 9. Переход к континууму: классическое рассмотрение
Когда мы говорим о поле ев обычном смысле этого слова, мы
представляем себе, что в каждой его точке задано отклонение
или возбуждение, как, например, в случае колеблющейся стру-
ны — поперечное отклонение и или для электрического поля —
напряженность электрического поля Е. Непосредственная задача
квантовой теории поля состоит поэтому в том, чтобы прокванто-
вать эти и подобные им величины, которые в классической интер-
претации являются функциями непрерывной переменной. Для
проведения этого квантования было бы естественно, исходя из
уже известного квантования дискретной системы точек, просле-
дить, как происходит переход к континууму*). Для этого нам
послужит пример нашей линейной атомной цепочки. Выполним
вначале предельный переход к континууму для цепочки в рамках
классической физики. Будем считать что длина цепочки атомов L
фиксирована, но мы размещаем в цепочке все большее число ато-
мов N со все меньшим расстоянием а между ними. Рассмотрим
следующий предельный переход:
а ->¦ О, N -+ °°, L — aN — конечна. • (9.1)
Введем теперь вместо дискретных переменных I переменную
1а = х; (9.2)
цри этом будем помнить, что х позднее станет непрерывно изме-
няющейся координатой. Одновременно введем новую амплитуду,
которая зависит теперь не от дискретной переменной I, а от не-
прерывной переменной х. Используем, далее, соотношения
AZ = 1. (9.3)
Запишем теперь выведенное ранее уравнение
Мф) = K(ql+l + j,_! - 2?,) (9.4)
в непрерывных переменных. Поскольку мы полагаем «1» малой
по сравнению с I, a q рассматриваем как непрерывно изменяю-
щуюся переменную аргумента I, мы можем разложить правую
*) Мы сохраняем при переводе термин «континуум», под которым в
книге понимается и непрерывная среда, и непрерывный случай, и т. д., по-
скольку в каждом конкретном случае точный смысл этого термина легко
устанавливается из контекста. (Прим. перев.)
68 КВАНТОВАНИЕ ПОЛЯ • [ГЛ. Ill
часть (9.4) в ряд Тейлора. Если испольбовать затем (9.2) и (9.3),
а также ?
М = ре, (9.5)
то уравнение (9.4) принимает вид
дЩ^ (9.6)
дх
Из механики известно, что величина константы упругости удваи-
вается, если длина пружины уменьшается вдвое. Отсюда кажется
естественным также и в нашем предельном переходе а -*¦ 0 произ-
ведение Ка считать постоянным и ввести константу связи g со-
гласно выражению
Ка = g — конечна! (9.7)
Тоща чисто формальным образом мы получаем уравнение
^А (9.8)
дх
которое, естественно, напоминает обычное уравнение струны,
хотя следует помнить, что в случае струны q означает поперечное
смещение, здесь же оно является продольным смещением. Мы не
будем углубляться в это различие, а будем основываться на фор-
мальной аналогии с дискретной цепочкой, которая поможет нам
квантовать это уравнение. Прежде всего мы исследуем решения
(9.8). Для этого представим q в виде
q(x,t)=J=. eiwxBw(t). (9.9)
Подставляя (9.9) в (9.8), получаем уравнение
pBJt) = - w*gBw(t). - (9.10)
Поскольку смещение q(x, t), так же как и qAt) в дискретном
случае, должно удовлетворять циклическим граничным условиям
qix+L, t) = q(x, t),
то величина w в (9.9) должна иметь вид
w = ^ (в = 0,!± 1, ±2, ...), (9.11а)
причем п изменяется в бесконечных пределах. Множитель 1/VL
§ 9] КЛАССИЧЕСКИЙ ПЕРЕХОД К КОНТИНУУМУ 69
в (9.9) отвечает за нормировку в следующем смысле:
L
(T7l)W> (9Л1б)
Для различных w, и/ экспоненциальные функции взаимно орто-
гональны:
L
y^^ w^w'- (9Л1в)
С помощью подстановки
Bw(t)^Alce-ia^ (9.12)
мы можем сразу решить уравнение (9.10), причем зависимость
между со и w дает закон дисперсии
«I, - -f w\ (9.13)
Общее решение уравнения (9.8) мы получим в виде суперпози-
ции решений (9.9). Поскольку смещение q(x, t) должно быть
чисто действительным, представим общее решение в виде
9 (*> ') -= 2 (Ч77 е**ХА*е-Ши:* + к.с.\ (9.14)
Напомним еще раз вкратце, в чем состоит наша цель. Она
состоит в том, чтобы проквантовать волновое уравнение (9.8), ис-
пользуя аналогию с обычной механикой. В обычной механике при
квантовании уравнения движения Ньютона вначале находят со-
ответствующую функцию Лагранжа, откуда затем функцию Га-
мильтона с ее канонически сопряженными импульсами и коорди-
натами. Эта функция Гамильтона является исходным пунктом
для квантования. Для того чтобы выполнить эту программу, мы
должны определить соответствующую (9.8) функцию Лагранжа
и затем функцию Гамильтона. Для случая дискретной линейной
цепочки все это уже было проделано. Теперь речь идет о том,
чтобы перенести полученные в § 7 результаты на случай конти-
нуума. Для этого будем исходить из функции Лагранжа
L = T—V (9.15)
и рассмотрим сначала выражение для кинетической энергии
Т =<±Ум'д1 . (9.16)
Введя плотность массы (масса на единицу длины) р, перепишем,
70 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
согласно уравнению (9.5), выражение для кинетической энергии
в виде
^ (9.17)
Если «постоянную решетки» а интерпретировать как dx, чем мы
уже пользовались ранее, то (9.17) можно непосредственно пред-
ставить в виде интеграла
L
() (9.18)
о
Аналогичным образом поступим с потенциальной энергией
T
Умножая и деля правую часть (9.19) на а2, перепишем это выра-
жение в виде
Снова введем краткое обозначение (9.7) и учтем, что g при пре-
дельном переходе а -*¦ 0 остается конечным. Далее, в континуаль-
ном пределе мы можем заменить разность на отношение диффе-
ренциалов. Тогда получаем следующее выражение для потенци-
альной энергии:
СФ)' (9'20)
Объединяя (9.18) и (9.20), получаем функцию Лагранжа в кон-
тинуальном пределе
L
±U^lJx. (9.21)
Каким образом можно было бы теперь получить уравнения
Лагранжа и Гамильтона в континуальной формулировке? Для
этого кратко напомним случай дискретных точечных масс, в ко-
тором справедливы уравнения Лагранжа
§ 9] КЛАССИЧЕСКИЙ ПЕРЕХОД К КОНТИНУУМУ 71
Рассмотрим более подробно производную
где проведем следующие очевидные преобразования:
д(т~У) а ^(ФА
(9.23)
#г _У^(ФА -У^,^. (9.24)
2 ' ^ 2 дЬ д'ч « dqn
Для дальнейшего вычисления суммы применим очевидное в диск-
ретном случае соотношение
9f=Kn; (9-25)
где б;, „ — встречавшийся уже нам ранее символ Кронекера:
„ _|1 для I = п,
\о для IФ п.
Отсюда окончательно получаем
,.„ = Mqn. (9-26)
Аналогично (9.25), имеет место также соотношение
Щ-п = б;,п. (9.27)
Только что примененные нами правила (9.25) и (9.27) имеют
очевидный аналог в случае континуума, если вместо символа
Крон'екера ввести 8-функцию Дирака 8(х — х). Эта функция
определяется только под интегралом и обладает для каждой не-
прерывной функции fix) следующим свойством:
ъ
§(x)8(x-x')dx = f(x') (a<x'<b). (9.28)
Так же как 6i, R в сумме по I выделяет члены с 1 — п, функция
8(х — х') выделяет под интегралом значение подынтегральной
функции при х = х. Эта б-функция имеет в квантовой теории
поля важное значение. Не знакомому с ее свойствами читателю
мы рекомендуем прорешать задания 3 — 5 в конце этого параг-
рафа.
72
КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
Определим производные переменных в случае континуума
следующим образом:
Щ (х-х'). (9.29)
6? (ж ) bq (x)
Далее для этих новых производных справедливо правило диф-
ференцирования сложной функции
б/ (q (x)) = a/ (g (ж)) Ъд(х)
ж ) "г W 8q(x )
Наконец, следует подумать о том, что означает выражение
-ТЪ^' (9-31)
eq(x') dx V /
в котором производную dq(x)/dx мы будем рассматривать как
отношение дифференциалов. Используя (9.29), получаем затем
следующие очевидные преобразования (при dx -*¦ 0):
8 q (x -f- dx) ~~ д (х) 1 .« , . , ,.
Я /г г'^ — S (г r'\ /Q Ч?^
Теперь рассмотрим производную L no 8q в континууме. По
определению L получаем непосредственно
8q(x) b'q(x')
Поскольку V не зависит от q, при последующих преобразованиях
этот член можно опустить. По аналогии с преобразованиями
(9.24) можно предположить, что операции дифференцирования
по q и интегрирования можно поменять местами. Используя
правило (9.30), после преобразований выражения (9.33) полу-
чаем выражение')
I дш(-х' t (9.34)
bq (*')
которое после использования (9.29) приводит, наконец, к следу-
ющему результату:
(9.34)= \ р dx q\x)b\x — х') = pq\x ). ' (9.35)
') Читатель, знакомый с вариащюнпым исчислением, сразу установит,
что символ 6 означает не что иное, как вариационную производную, кото-
рая появляется, например, при формулировке принципа наименьшего дей-
ствия Гамильтона. В этой связи очень важно по возможности отчетливо
выявить аналогию с механикой дискретных точечных масс.
§ 9] КЛАССИЧЕСКИЙ ПЕРЕХОД К КОНТИНУУМУ 73
Полученные выше результаты позволяют ввести в контину-
уме канонически сопряженный импульс, для чего мы заменим
известное из механики точки правило (см. § 2)
Pi = ^- (9.36)
на следующее:
б? (*')
которое и определяет канонически сопряженный q(x') импульс
л(х'). Если теперь рассмотреть вариационную производную L
по координате, то сразу получим, используя правило (9.30) и
правило дифференцирования (9.31), соотношения
(дд
[dX
Ox )- 2 )dX idg\ bg(x')'
(9 38)
После проведения интегрирования по частям и использования
(9.32) последнее выражение следующим образом преобразуется к
конечному результату:
да (х) д с , /. С j д q (x) s , ,.
^ (9.з9)
дх
Полученные только что результаты позволяют перенести, урав-
нение Лагранжа (9.22) на случай континуума, если в качестве
исходного выбрать уравнение
d_e±__jL_==0 (940)
dt &q(x) bq(x)
Используя результаты (9.39) и (9.35), мы вновь получаем
уравнение движения для континуума:
p'q(^t)-gd-^rJ1 = o. (9.41)
ох
Сравнение (9.41) с уравнением движения (9.8) показывает, что
(9.41) и (9.8) тождественно совпадают. Это является очевидным
доказательством того, что проведенная выше процедура действи-
тельно позволяет перенести концепцию функции Лагранжа и
соответствующих уравнений движения Лагранжа на случай кон-
тинуума.
74 КВАНТОВАНИЕ ПОЛЯ (ГЛ. Ill
Обратимся теперь к соответствующему переходу для функции
Гамильтопа и уравнений Гамильтона. В случае дискретных то-
чечных масс нам известны соотношения (9.36) и
H = J^piqi — L. (9.42)
i
Они позволяют получить из функции Лагранжа канонически
сопряженный импульс и функцию Гамильтона. Применяя опре-
деления (9.37) и явный результат (9.35), получаем
^ -= рд (х), (9.43)
8q (x)
ИЛИ
q (Ж) ^ ?Eif}. (9.44)
Таким же образом, используя предельный переход к континууму,
получаем в (9.42) общую связь между функциями Гамильтона и
Лагранжа:
(9.45)
Если теперь ввести в выражение (9.45) для функции Гамильто-
на канонически сопряженный координате q импульс согласно
(9.44), а для L выражение (9.21), то почти непосредственно по-
лучим функцию Гамильтона для континуума {колеблющаяся
струна):
L L
(9.46)
Убедимся теперь в том, что с помощью выражения (9.46) мож-
но сформулировать уравнения Гамильтона для континуума, ко-
торые вновь ведут к (9.41). Для этого, по аналогии с механикой
точки, построим уравнения Гамильтона континуума
и
Дифференцирование по п(х) выполняется с использованием при-
веденных выше правил. Используя явное выражение (9.46), сразу
получаем результат , ¦ •
Я(х) — ~тп{х)- ' (9.49)
§ 9] КЛАССИЧЕСКИЙ ПЕРЕХОД К КОНТИНУУМУ 75
Таким же образом получаем второе уравнение Гамильтона
g^P-n. (9.50)
Если исключить из уравнений (9.49) и (9.50) канонически соп-
ряженный импульс я, то получим уже хорошо известные нам
уравнения движения (9.41) или (9.8). Это является, естествен-
но, еще одним подтверждением непротиворечивости применен-
ного здесь формализма. Результаты этих параграфов кратко
можно сформулировать следующим образом: в континууме, так
же как и в механике дискретных точечных масс, можно приме-
нить формализм Лагранжа и Гамильтона, причем следует лишь
заменить правила дифференцирования (9.25) и (9.27) на прави-
ла (9.29). Этой аналогии, как мы увидим в последующих параг-
рафах, оказывается достаточно, чтобы провести квантование.
Задания к§9
1. Доказать (9.116) и (9.11в).
2. Ряд Фурье непрерывной функции. Ввести определенную в
интервале O^x^L (и кусочно гладкую) функцию fix):
и определить с„.
Указание. Умножить обе стороны предыдущего уравнения
на 1/}'L ¦ e~iu"x, проинтегрировать по х от 0 до L и воспользо-
ваться соотношениями (9.116) и (9.11в).
Ответ:
L
e-wf{x)dx. (A 9.2)
3. Представления Ь-функции. Убедиться в том, что 6-функция
может быть определена с помощью следующих предельных пе-
реходов:
а) 6(ar) = -lim—, (A 9.3)
б) 6W = lim-i-e-s'/u'. (A 9.4)
U->-oo у Пи
Указание. Подставить (А9.3) или (А9.4) в интеграл
J f(z)b(x)dz и рассмотреть его значение для очень большого, но
конечного ц. Из-за очень быстрого спадания функции для хФО
(рис. 21) функцию fix) в точке х — 0 можно вынести за знак
76
КВАНТОВАНИЕ ПОЛЯ
[ГЛ. Ш
интеграла. Воспользоваться, наконец, следующими результата-
ми («#0):
С sin ил; j Г -х2/и2т„ -,/—,,
I dx = я, \ е dx = у к и.
4. Производные Ъ-функции. Показать:
-(-оо
Г f(T>
dx
и вообще для ге-й производной б(п> по х:
(А 9.5)
(А 9.6)
(А 9.7)
У Хч а з а н и е. Вычислить интегралы по частям.
sin их
-и
Рис. 21. Различные представления б-функции.
5. Интеграл Фурье. Если /(.г) определена во всем интервале
— оо < х < + оо, то от ряда Фурье (см. задание 2) следует перей-
ти к интегралу Фурье. Положим
(A9.8)
Определить см.
Указание. Умножить (А 9.8) на 1/(К2я) е"гж'жи проинтегри-
ровать в интервале — L < х < L, считая, что ? велико, но ко-
нечно. Поменять порядок следования интегралов в правой части
(А 9.8) и учесть, что
ь
5'>Л-г — * sin ? (u> — ц/) (А 9.9)
_1_ Г
2л J
для
дает б-функцию 8(w — w').
§ 10] КВАНТОВАНИЕ КОНТИНУУМА. ФОНОНЫ 77
Ответ:
cw, = -!= j / (x) e~iw'xdx. (A 9.10)
§ 10. Переход к континууму: квантовотеоретическое
рассмотрение. Фононы
Результаты предыдущих параграфов позволяют непосредст-
венно провести квантование континуума. В механике отдельных
точек у нас было следующее правило квантования: координаты
qi и соответствующие канонически сопряженные импульсы pi
заменяются согласно схеме
qL -*¦ оператор qt
п а МО 1)
о,—>-оператор —-:— viU-x/
' ( * * i дд.
на операторы, которые удовлетворяют перестановочным соотно-
шениям
[Pu4i>\ = уб'Л'. [pi,Pi'\=O, [?i,?c] =0. A0.2)
В случае континуума координатам qi теперь соответствуют не-
прерывно распределенные координаты q(x), а канонически сопря-
женным импульсам pi соответствуют непрерывно распределен-
ные импульсы п(х). При этом эти новые величины зависят от
непрерывной переменной — координаты х, в то время как до это-
го они зависели от дискретного индекса I. Как мы видели в пре-
дыдущих параграфах, при этом обычное правило дифференци-
рования d/dqi заменяется на вариационную производную 8/8q{x).
Отсюда сразу получаем соответствие
qi-+q(x) оператор q(x), A0.3)
Р1^л(х) оператор ~j--.
С помощью этого соответствия можно вывести перестановочные
соотношения для континуума. Для этого образуем выражение
¦к(х)д(х')-д{х')л(х) A0.4)
и воспользуемся, согласно A0.3), явным видом оператора импуль-
са л(х):
78 КВАНТОЁАНЙЕ ПОЛЯ - [ГЛ. III
Если теперь учесть хорошо известное из квантовой механики
правило, согласно которому при применении перестановочных
соотношений постоянно следует помнить, что операторы дейст-
вуют на стоящую за ними волновую функцию, а затем восполь-
зоваться соотношением (9.29) и обычным правилом дифферен-
цирования произведения, то вместо A0.5) получаем выражение
A0-6)
Отсюда автоматически выводится основное перестановочное со-
отношение для континуума:
Л (х) q (х1) - q (xf) л (х) = Д б (х - х'). A0.7)
Аналогично и так же тривиально получаются следующие пере-
становочные соотношения:
| q(x)q(x')-q(x')q(x)=0 A0.8)
и
I Tt \ T) Tt \ "V I ТТ f Т" ) ТТ I T" } —гг О I J О Q )
Чтобы показать, каким образом в случае континуума можно
ввести операторы рождения и уничтожения, вновь обратимся к
конкретному примеру линейной цепочки. Для этого будем исхо-
дить из разложения (9.14) пока еще классической величины
q(x, t):
vi / <iwxBw(t)-\-K.
Дифференцируя это выражение по времени и умножая его на
р, получаем
л (х, t) = р^ = 2 (-4- Р (- iah,) eiwxBw (t) + к. c.V A0.11)
Пусть теперь q(x, t), а также л(х, t) и тем самым неизбежно
Bw, Bw будут операторами. По аналогии с дискретной атомной
цепочкой введем новые операторы bw и bw согласно соотноше-
ниям
Тогда равенства A0.10) и A0.11) переходят в выражения
— l^ bin -r ? bw) (lU.loj
10] КВАНТОВАНИЕ КОНТИНУУМА. ФОНОНЫ 79
Теперь используем все проведенные нами в § 7 преобразова-
ния, чтобы перейти в функции Гамильтона от qt н р{ к bw, Ъ^,.
Единственное отличие по сравнению с предыдущими вычисления-
ми состоит в том, что вместо суммы по I мы имеем интеграл по х
от 0 до L и что вместо соотношения ортогональности
1 V еШа-Ш'1а ^ Kwi /где w^^ п_ целое Чпсло]
1 l V '
A0.15)
появляется соотношение ортогональности следующего вида:
— \ eiwx 1W dx = 6WW' (где w — -j—, n — целое число).
Li \ L I
A0.16)
Поскольку больше ничего не изменяется, мы сразу приводим
оператор Гамильтона для. колеблющейся атомной цепочки в пре-
дельном случае континуума к виду
II --- 2 Ucow {btbw + Ч2) A0.17)
и предоставляем проверку этого результата сомневающемуся
питателю. «Амплитуды» bw вновь, естественно, операторы. Пере-
становочные соотношения между операторами bt>, bw также полу-
чаются совершенно аналогично § 8. Для этого мы с помощью
преобразования Фурье разрешаем A0.13) и A0.14) относительно
l>w, bw, образуем, например, выражение bwbt,> — bw>bw и подстав-
ляем сюда перестановочные соотношения A0.7—10.9). Деталь-
ный расчет мы предоставляем читателю в качестве задания и
сразу выпишем результат
[bw, К'} '-= 8,OiW/, [bw, К,,\ ---.; [bt0, bt,'] ~ 0. A0.18)
Если разложения A0.13) и A0.14) проводятся не в конечном
«объеме», а во всем пространстве, то в A0.13) и A0.14) вместо
рядов Фурье появляются интегралы Фурье. При атом символ
Кронекера в перестановочном соотношении A0.18) следует за-
менить на б-функцию b(w-w'). На этом процесс квантования
полностью заканчивается. Поскольку операторы bw, bw зависят
gO КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ill
от дискретного индекса, дальнейшее рассмотрение проводится
аналогично случаю дискретных точечных масс:
решение уравнения Шрёдингера
НФ=ЕФ A0.19)
записывается в известном виде (ср. C.48))
ПЦ(^)П№Фо- A0.20)
Оператор числа частиц
nw = b+bw A0.21)
коммутирует с Н. Он показывает, сколько квантов имеется в
состоянии w. В случае упругой среды говорят о числе фононов,
занимающих моду w.
Теперь обсудим задачу построения средних значений, напри-
мер средних значений для qix) и я(х), которые по аналогии
с дискретным случаем определяются выражениями
A0.22)
яЫ*=<Ф1яЫ1Ф>. A0.23)
Рассмотрим несколько более подробно вычисление A0.22) и в ка-
честве нримера функции Ф выберем собственное состояние
A0.20) оператора Гамильтона A0.17).
Мы утверждаем, что соответствующее среднее значение исче-
зает:
)> = 0. A0.24)
Чтобы показать это, введем в A0.24) разложение A0.13) для
qix):
'" Г Ф{„)\ A0.25)
Поскольку суммирование не связано с вычислением среднего
значения, эт,и операции можно поменять местами и представить
A0.25) в виде
Заметим, что eiwx также не связано с вычислением среднего зна-
§ 10] КВАНТОВАНИЕ КОНТИНУУМА. ФОНОНЫ 81
чения! Таким образом, х всего лишь индекс. Вспомним § 3, где
Показано, что действие оператора рождения b? означает увели-
чение числа квантов на один, так что из Ф{п} возникает состоя-
ние, при котором в моде оказывается одним квантом больше.
Ввиду ортогональности волновых функций с разными числами
заполнения справедливы соотношения
| bt | Ф{п>> = О, <Ф{„} | bw\ Ф{п>> = 0. A0.27)
Из обращения этих средних значений в нуль сразу следует спра-
ведливость соотношения A0.24). Совершенно аналогичным обра-
зом доказывается, что среднее значение канонически сопряжен-
ного импульса я(х) также обращается в нуль. На первый взгляд
этот результат кажется удивительным, поскольку и в случае
колебаний континуума можно ожидать конечных амплитуд сме-
щения. Этот результат, однако, сразу становится понятным, если
вспомнить, что в квантовой механике мы имеем дело со средни-
ми значениями. В рассматриваемой ситуации любое положитель-
ное смещение qix) так же вероятно, как и отрицательное, так
что в среднем они взаимно уничтожаются. Для того чтобы по-
лучить порядок величины смещения, следует рассмотреть средне-
квадратичное значение амплитуды. Проведение соответствующих
вычислений довольно просто, и в результате получаем
Г 55F
Этот результат тем более замечателен, что даже при га„ = 0
A0.28) имеет отличное от нуля значение. Он означает, что ос-
цилляторы даже в самом глубоком состоянии с конечной вероят-
ностью имеют конечную амплитуду смещения. Аналогичный ре-
зультат получается также для <л2), что означает, что импульсы
также имеют конечные значения. Эти результаты являются не
чем иным, как математическим выражением того обстоятельства,
что квантовомеханические осцилляторы испытывают нулевые ко-
лебания. Теперь мы займемся интересным вопросом, нельзя ли
с помощью подходящего выбора волновой функции достичь того,
чтобы средняя амплитуда qix) также и в смысле, квантовомеха-
нического среднего была отлична от нуля. Этот вопрос приобре-
тает важное значение в связи с квантовой оптикой. В качестве
примера состояния, в котором среднее значение qix) не исчеза-
ет, рассмотрим когерентное состояние вида
ф = е-<1^"*'Лф01 ' A0.29)
где E должно быть равно
ye~i(aw'\ ' A0.30)
6 х. хакев
82
КВАНТОВАНИЕ ПОЛЯ . [ГЛ. ill
Согласно упражнениям 4'к §§ 3 и 5, выражение A0.29) при
р\ определяемом A0.30), является решением зависящего от вре-
мени уравнения Шредингера с оператором Гамильтона A0.17)
(однако без постоянной нулевой энергии 2'/2Йсвш). Подставляя
(однако без постоянной н
A0.13) в A0.22), получаем
2/
W J
(eiwx <Ф | bw | Ф> + e~iwx <Ф | bt ГФ>), A0.31)
причем мы вновь переставили порядок суммирования и образо-
вания среднего значения. Для вычисления выражения
<Ф|Ь.|Ф> A0.32)
вначале рассмотрим (ср. A0.29))
ьУЪу"Ф0. A0.33)
При w Ф wo мы можем подействовать оператором bw прямо на
Фо, тогда A0.33) обратится в нуль. При w = wo пишем
A0.33) = [bWl>e w' - е w°bW(l) Фо. A0.34)
^_
Перестановка е ' ' с bWl> дает, однако (ср. основное правило
E.25)),
A0.33) = РеРЬю°Ф0. A0.35)
Если подставить эти результаты в A0.32), то получим, поскольку
Ф нормирована,
<ф | bw ] Ф> = $Sw,Wa = ye~™Wl>tbw,Wo A0.36)
и соответственно
<ф | bt | Ф> = Р*8Ш110о = Y*etf°1'">'8u,),(V A0.37)
С -помощью выражений A0.36) и A0.37) для среднего значения
амплитуды смещения qix) получаем
<Ф | q (х) | Ф> =
При р =A0.30) и действительном f, таким образом, для когерент-
ного состояния в результате получается бегущая волна:
-С*), ¦ A0.39)
§ ill ТРЕХМЕРНЫЕ ПРОБЛЕМЫ. ФОТОНЫ 83
где
Аналогичным образом получается выражение для среднего
значения канонически сопряженного импульса:
<Ф | л (х) | Ф> = AptiWo sin (wQx — a>Wat), A0.40)
которое можно получить прямо из A0.39) с помощью дифферен-
цирования по времени. Этот пример отчетливо показывает, что,
применяя соответствующие волновые пакеты, можно проследить
распространение волн и на средних значениях. Приведенное
выше рассмотрение было применено Шредингером при обсужде-
нии проблемы гармонического осциллятора.
Задания к § 1Q
1. С помощью A0.13), A0.14) выразить Ът bw через
q(x), л(х).
2. Вывести A0.18) из A0.7—10.9).
3. Чем следует заменить A0.39), если ^ в A0.30) комплексна?
Указание. Положить у =<= г0егф.
4. Вычислить <Ф\д(х)\ф> для
Ф = {П ехр ( 11 yw |2)expG№e-iw^+) j Фо.
§ 11. Трехмерные проблемы: квантование скалярного
волнового уравнения и электромагнитного поля. Фотоны
Для квантования трехмерного волнового уравнения
мы применим рецепты квантования, полученные в § 10. В A1.1)
х — радиус-вектор с компонентами х, у, z, A — оператор Лапласа:
Обобщая рассуждения § 10, сразу находим функцию Лагранжа,
уравнения Лагранжа для которой в случае континуума согласу-
ются с A1.1). Запишем функцию Лагранжа в виде ийтеграла
A1.2)
6* . "
84 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
от плотности лагранжиана 2', которая в настоящем случае да-
ется выражением
2>(x)=-?-;p2_!_(grad<pJ, A1.3)
или, в явном виде,
=-^'-да+(?)'+(*
Соответствующие уравнения Лагранжа, совершенно аналогично
одномерному случаю, имеют вид
° A15)
Если в левую часть A1.5) подставить выражение A1.2), где
2Чх) задается A1.3), то после проведения дифференцирования
с учетом правила (9.29) получается волновое уравнение A1.1).
Канонический импульс вновь получаем в виде
Ф(х). (Ц.6)
^ РФ()
бф(х)
Перенесение перестановочных соотношений для одномерного слу-
чая на настоящий случай можно провести без каких-либо труд-
ностей, если заменить одномерную б-функцию на трехмерную.
Трехмерная б-функция >б(х — х') определяется с помощью
свойства
/(x'), (Ц.7)
где функция /(х) должна быть непрерывной. Здесь и в дальней-
шем изложении ] • • • ^х обозначает трехмерный интеграл
| ( \ i.. dxdy dz. Перестановочные соотношения приобретают вид
я (х) ф (х') — ф (х') я (х) = ~ S (х — х'),
ф(х)ф(х')-*<р(х')ф(х) = 0, A1.8)
я (х) я (х') — я (х') я (х) = 0.
Полноты ради приведем еще функцию Гамильтона, • которую
также можно записать в виде интеграла от плотности гамильто-
ниана:
#= Ж(х)<Рх. A1.9)
§ ill ТРЕХМЕРНЫЕ ПРОБЛЕМЫ. ФОТОНЫ 85
Плотность гамильтониана задается выражением
ж (х) = ~kя2+"f(grad ^2- (н-10)
Если аналогично одномерному случаю разложить ор и л по плос-
ким волнам с законом дисперсии
-, A1.11)
т. е. представить эти величины в виде
A1.12)
то оператор Гамильтона преобразуется к уже хорошо известному
нам виду
Из вида гамильтониана следует, что квантование трехмерного
волнового уравнения происходит совершенно аналогично случаю
одного измерения. Единственное отличие состоит в том, что сум-
мирование по w происходит теперь в трехмерном w-пространстве.
После этих подготовительных замечаний мы в состоянии предпри-
нять квантование электромагнитного поля.
Исходным пунктом для нас являются уравнения Максвелла
в вакууме, которые в системе СГС имеют следующий вид (при
Н = В и E = D):
rotE + -i-H = 0, A1.14)
rotH Le==—] A1.15)
divH = 0, A1.16)
A1.17)
Поскольку, согласно A1.16), дивергенция Н равна нулю, то
вектор Н можно рассматривать как ротор некоторого векторного
потенциала А:
H = rotA. A1.18)
Если подставить A1.18) в A1.14), то оказывается, что Е можно
86 ¦" • • КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
представить в виде
Е = - — A-grad 7, A1.19)
с
где V представляет скалярный электрический потенциал. Заме-
няя в уравнении A1.15) Н через A1.18) и Е через A1.19), по-
лучаем
А.. А - ДА + grad fdiv A + -J- v\ .= ^- j. A1.20)
с2 V
С другой стороны, после подстановки A1.19) в A1.17) получа-
ется уравнение
- AF - ~ div A = 4яр. A1.21)
Потенциалы А и V определены неоднозначно и могут быть пере-
калиброваны с помощью калибровочного преобразования
А = A'-grad х, V^V'+~'i. A1.22)
Эти калибровочные преобразования могут быть использованы для
дальнейшего упрощения уравнений A1.20) и A1.21). Известным
условием является условие Лоренца
divA + — F = 0, A1.22a)
С
с помощью которого уравнения A1.20) и A1.21) принимают сле-
дующий простой вид:
? A = -^j, A1.23)
? V = —4яр, A1.24)
где оператор ? определен следующим образом:
В последующем изложении, однако, мы будем использовать не
эту калибровку, а кулоновскую калибровку, которая определя-
ется следующим образом:
| divA = 0. A1.26)
Согласно кулоновской калибровке векторный потенциал содержит
только поперечные волны. Разложим в общем случае А* по плос-
ким волнам:
wx-f-K.c, , , A1.27)
§ 11] ТРЕХМЕРНЫЕ ПРОБЛЕМЫ. ФОТОНЫ 87
тогда" в силу линейной независимости экспоненциальных функ-
ций и условия div A =*= 0 отсюда следует соотношение
Aww = 0, A1.28)
которое и означает поперечность векторного потенциала. В ку-
лоновской калибровке A1.26) исходные уравнения A1.20) и
A1.21) принимают вид
= -4лр A1.29)
, ? A--i^i + ^-gradF. . A1.30)
Уравнение A1.29) представляет собой хорошо известное уравне-
ние Пуассона, в котором можно также считать, что плотность
заряда зависит от времени. В этом параграфе мы исследуем ва-
куум без зарядов и токов, т. е. рассматриваем квантование волно-
вого уравнения') .
I ПА = 0. A1.31)
Уравнение A1.31), очевидно, представляет собой совокупность
трех волновых уравнений вида A1.1) для отдельных компонент
векторного потенциала. На этом основании мы можем тотчас
построить функцию Лаграижа, являющуюся обобщением функ-
ции Лагранжа A1.4), и записать ее в виде
L = const \[~- l(grad Ax)* - 4r(grad Ayf- i-(grad Az)Ad3x.
A1.32)
Кроме того, мы должны учесть дополнительные условия A1.26),
благодаря чему при квантовании возникнут определенные отли-
чия от одномерного случая. Константа в A1.32) остается пока
еще неопределенной, поскольку при построении волнового урав-
нения из уравнений Лагранжа она выпадает. Однако мы можем
ее найти, для чего построим функцию Гамильтона и потребуем,
чтобы, функция Гамильтона соответствовала классическому выра-
жению энергии электромагнитного поля. Как известно, это клас-
сическое выражение имеет следующий вид:
* + RV3*- (И-33)
') В последующем изложении будем считать, что V не является дина-
мической переменной, а является классической функцией, определяемой
через плотность заряда р. В нашем случае следует считать' эту функцию
равной нулю. .
88 КВАНТОВАНИЕ ПОЛЯ [ГЛ. IH
Выражая здесь Е и Н с помощью соотношений A1.18) и A1.19)
через векторный потенциал, непосредственно получаем
(и-34)
Переписывая выражение (rot АJ в компонентах и учитывая, что
divA = 0, получаем с помощью интегрирования по частям сле-
дующее выражение для U, которое одновременно идентично вы-
ражению для функции Гамильтона (соответствующие промежу-
точные вычисления можно найти в конце этого параграфа):
-L ((grad AXY + (grad Ay? + (grad Azf) dsx.\ A1.35)
Переходя теперь к канонически сопряженным импульсам, следу-
ет учесть, что теперь у нас есть три компоненты вектора А и
соответственно этому три набора канонически сопряженных им-
пульсов, которые с учетом правила A1.6) и функции Лагранжа
A1.32) даются следующими выражениями:
Совершенно аналогично предыдущему рассмотрению, можно
вновь разложить А по плоским волнам, вводя одновременно на-
ши уже хорошо известные безразмерные амплитуды Ь и Ь+. По-
скольку А является вектором, при разложении по плоским вол-
нам наряду с волновым вектором w следует ввести еще один
индекс / для вектора поляризации е, который может принимать
значения 1 или 2. Вектор поляризации мы обозначим eWlj. Учи-
тывая, что плотность массы теперь формально должна быть за-
менена на 1/Dяс2), получаем разложение следующего вида:
I А>( х, t) =
A1.37)
Поскольку мы находимся еще в «классической области», bw>i и
bwj являются еще обычными классическими, зависящими от
времени функциями. Однако, имея* в виду последующее кванто-
вание, у комплексно сопряженной с Ъ величины мы поставили
& 111 ТРЕХМЕРНЫЕ ПРОБЛЕМЫ. ФОТОНЫ 89
значок (+) вместо (*). Ввиду поперечности А справедливо со-
отношение
I ew,,w = 0, /==l, 2. A1.38)
Далее можно принять, что направления поляризации взаимно
перпендикулярны, т. е. имеет место соотношение
e,v,iew,2 = 0. A1.39)
Для канонически сопряженных импульсов, совершенно анало-
гично скалярному полю, получаем разложение
A1.40)
После этой подготовки можно обратиться к квантованию по-
ля. Для отдельных компонент вектора, по аналогии со скаляр-
ным полем, можно принять, что коммутаторы между полями и
канонически сопряженными импульсами исчезают:
[4,(х),^(х')] = 0, A1.41)
[П,(х),П,(х')] = 0, A1.42)
i = х, у, 2, / = х, у, г.
Единственное обобщение теперь состоит в том, что мы требуем
выполнения этих соотношений также для отдельных i- и /-ком-
понент. Обратимся теперь к вопросу о том, как выглядят пере-
становочные соотношения между компонентой I канонически со-
пряженного импульса П н компонентой j амплитуды поля А.
Для этого введем, и это следует настоятельно подчеркнуть,
в виде пробы следующее перестановочное соотношение:
[П, (x),4j (*')] = 4-бцб(х-х'). ' (Ц.43)
Проверим теперь, увязывается ли перестановочное соотношение
A1.43) с равенством «дивергенции поля нулю», т. е. с условием
A1.26). Для этого дифференцируем левую часть уравнения
A1.43) по xj, суммируем по / и сразу находим в силу A1.26), что
divx- [Щ (х), А(х')]= [П,(х), divx,A(x')l = 0. A1.44)
90 ' КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
Применяя операцию дивергенции к правой части уравнения
A1.43), получаем
з
2 -р бцб (х - х') = * б (х - х') ф 0, A1.45)
5=1 °хз дх1
г. е. отличное от нуля выражение, что противоречит A1.44).
Поэтому мы вынуждены изменить перестановочные соотношения
A1.43). Для этого рассмотрим дивергенцию выражения
6tj6(x-x') = -±z f dW*~'>6,; (И.46)
более обстоятельно, для чего образуем выражение
з
2 -р 6;i6 (х - х') = -J- f d^i-uv:) e^*-*'\ A1.47)
Теперь спрашивается, как следует изменить б-функцию, чтобы
достичь равенства нулю дивергенции от правой части A1.43).
Поскольку наряду с б;;- имеется лишь единственный другой тен-
зор второго ранга itiiWj, то б(;б(х —х') можно изменить следую-
щим образом:
Fl} (х - х') = -1^- Г d*weix**-x>) (бц - wuvjf (w)). A1.48)
\
Для отыскания стоящей здесь еще неопределенной функции /, ко-
торая зависит только от переменной w, построим дивергенцию
Fij(x — x'). Эта дивергенция приводит пас к соотношению
{ d«weiMx-xr) ( - iwt + iivt(wl + wl + wl) f(w)). A1.49)
Для того чтобы правая часть исчезла, достаточно, очевидно, вы-
брать /(w) в виде
/И =4- ' - (И-50)
W
Это приводит нас к заключению, что изменение правой части
перестановочного соотношения A1.43) должно состоять в замене
6;j6(x — x') на так называемую поперечную 8-функцшр
^ j"
Щ. - A1.51)
§11] ТРЕХМЕРНЫЕ ПРОБЛЕМЫ, ФОТОНЫ 91
Интеграл A1.51) легко вычисляется, если выразить wt и ws че-
рез производные экспоненциальной функции по х} и Хи Тогда
A1.51) можно представить в виде
8п (X — X') — б,;б (X — X') + Б— 3—
A1.52)
Стоящий в скобках интеграл вычисляется просто и равен
1 1
4л j х — х' |'
A1.53)
Вводя, наконец, полученное выражение A1.52) с учетом A1.53)
в правую часть A1.43), получаем перестановочное соотношение
менаду канонически сопряженным импульсом П и полем А в
окончательном виде
= 4-(8W6 (х - х') +-4-т4-i—i—n\. (И.54)
Однако при установлении перестановочных соотношений подоб-
ного рода (если уж указывать, какие принципы лежат в их ос-
нове) нужно иметь полную ясность относительно того, что вве-
дению их сопутствует некоторый эвристический элемент. Явля-
ются ли перестановочные соотношения верными или нет, можно
установить в конце концов только при экспериментальной про-
верке выведенных на их основе положений. Мы сейчас увидим,
что перестановочные соотношения действительно прямо приво-
дят к описанию электромагнитного поля с помощью обычных
операторов рождения и уничтожения квантов света. Чтобы по-
казать это, вновь подставим, точно так же как и в случае ска-
лярного поля, разложения A1.37) и A1.40) в левую часть A1.54)
и после выполнения преобразования Фурье получим перестано-
вочные соотношения для операторов рождения и уничтожения
frw.i» bwj. Вычисления проводятся в принципе так же, как и в
дискретном случае § 8, так что мы эти несколько скучные вы-
числения, которые не ведут ни к каким новым физическим ре-
зультатам, не будем воспроизводить. Конечный результат пока-
зывает, что перестановочные соотношения полностью аналогичны
случаю дискретной решетки или случаю континуума со скаляр-
ным полем, т. е. имеют вид
[К,Ъ К1 A =Sjj'8WW', A1.55)
W] = 0, - (Н-56)
.J-]~O. , A1.57)
92" КВАНТОВАНИЕ ПОЛЯ .[ГЛ. III
С помощью только что использованных разложений A1.37) и
A1.40) можно вычислить также оператор Гамильтона, для чего
следует подставить эти разложения в выражение A1.35) и про-
вести интегрирование. Оператор Гамильтона тогда принимает
хорошо известный нам вид
Я = 2 ftcow (bwjbw.i + V2). A1.58)
Сумма 2 (Va) ^ww представляет пулевую энергию. Поскольку
частоты с ростом w растут и сумма распространяется на беско-
нечное число значений w, это выражение расходится. Однако,
поскольку нулевая энергия вакуума ненаблюдаема, мы можем
спокойно опустить это выражение. Число фотонов моды w, j опи-
сывается оператором
«w,j = b+jbWiJ. A1.59)
Собственные состояния уравнения Шредингера с оператором Га-
мильтона A1.58) имеют тот же самый вид, что и в предыдущих
параграфах:
Ф =n-7=i=fe)nw'4, (И.60)
W J.J означает произведение по всем значениям волнового век-
тора w и индексам поляризации /. Оператор числа фотонов nw< j
может принимать только какие-либо целые значения 0, 1, 2, ...
На практике большинство ?zw 3- = 0 и только некоторые немногие
?=0. Положим теперь по определению (Ь+)° = 1. Вакуумное со-
стояние Фо, как обычно, определяется свойством
bw ,Ф0 = 0 для всех w, /.
Поскольку операторы Ь+ между собой коммутируют, порядок сте-
пеней в A1.60) произволен.
Суммируем теперь кратко наши результаты! Мы видели, что
векторный потенциал при квантовании электромагнитного поля
становится оператором. Экспериментально наблюдаемыми вели-
чинами или, по принятой в квантовой механике терминологии,
наблюдаемыми являются, собственно говоря, электрическое поле
Е и магнитное поле Н, которые в выбранной нами кулоновской
калибровке связаны с А равенствами
Е = -4-А, A1.61)
H = rotA. ф A1.62) '
Поскольку А является оператором, полевые величины Е и Н
§ 11] ТРЕХМЕРНЫЕ ПРОБЛЕМЫ. ФОТОНЫ 93
в квантовой электродинамике также становятся операторами.
Элементарное рассмотрение показывает, что Н и Е не коммути-
руют с оператором Гамильтона1).
То обстоятельство, что Н и Е не коммутируют с Н, означает,
что напряженности полей и число фотонов одновременно точно
неизмеримы. Далее, следствием перестановочных соотношений
между напряженностями полей и канонически сопряженными им-
пульсами является невозможность одновременного измерения всех
компонент напряженностей Е и Н. Тем не менее можно устано-
вить, что divE коммутирует с Н и Н. К взаимодействию кван-
тованного электромагнитного поля с веществом мы еще вернемся
позднее в §§ 44 и 45.
Приведем теперь дополнительно для интересующихся читате-
лей доказательство тождественности выражений
I = j (rot AJ cPx A1.63)
П=| ((grad АхJ + (grad Avf + (grad Azf) ds.x. A1.64)
и
При атом следует предположить, что А исчезает на границе об-
ласти интегрирования, a divA = 0. Составим разность выражений
A1.63) и A1.64). Применяя краткое обозначение
дА
получаем затем
AXUI - Av\xf + (AvXz - АЛУ)* + (АЛх - AxVy -
lv + Al\x + AIVJ +
\x + A% + A%)) dH. A1.66)
Al
Возведение подынтегральных членов в квадрат и приведение по-
добных членов приводят к выражению
I - II = - j {2AAyAv\x + 2А„\гАг1у + 2AZ[XAX{Z +
+ Al\* + Alty + А*1гУ#х. A1.67)
') К доказательству этого можно подойти следующим образом. Для Н
используется выражение A1.58), а вместо А в соотношения A1.61) и A1.62)
подставляют разложение A1.37). Тогда проблема коммутации Е и Н или
Н и Н сводится к анализу перестановочных соотношений A1.55 —11.57).
94 КВАНТОВАНИЕ ПОЛЯ [ГЛ. TII
После двукратного интегрирования по частям это выражение пе-
реходит в следующее:
I - II = - J BЛЯ|ХЛМН + 2AlAllAA: + 2Az\zAxlx +
+ Alix + A%{u-'rA%)d*jr. A1.08)
Последнее выражение можно переписать в виде
-j(divAJd*x^0. A1.09)
-)то выражение, очевидно, в силу предположения A1.20) тожде-
ственно равно нулю.
3 а д а н п е к § 11
Определить функции Лагранжа п Гамильтона для урав-
d2q> (x, t) ...
нения р—l-Lr, #ф — 0 и провести его квантование.
dt
§ 12. Квантование шредингеровских волновых полей,
подчиняющихся статистике Бозе (вторичное квантование).
Бозоны
В предыдущих параграфах было показано, каким образом
можно проквантовать волновое уравнение для скалярного пли
векторного поля. При этом важнейший результат состоял в том,
что волновое поле приобретает свойства, характерные для час-
тиц, поскольку в нем имеются в наличии только определенные
кванты энергии /kow.
Если вспомнить обычную квантовую механику точечной ча-
стицы, обладающей массой, то там, напротив, дри квантовании
проявляется прямо противоположный эффект: мы исходим из ча-
стицы, движение которой описывается уравнениями Гамильтона.
Если затем перейти от функции Гамильтона к оператору Га-
мильтона и соответствующему уравнению Шредингера, то поведе-
ние частицы будет описываться с помощью непрерывной в прост-
ранстве функции, т. е. с помощью поля. Это поле, так называ-
емое шредингеровское волновое поле, вначале можно попытаться
считать классическим, а затем проквантовать его с помощью ре-
цептов, с которыми мы только что познакомились. По аналогии
с проведенным выше рассмотрением, следует ожидать, что кван-
тование вновь внесет в описание корпускулярный характер, что
позволит лучше описать процессы рождения частиц. Поскольку
при этом система вновь некоторым образом квантуется, то эта
процедура называется вторичным квантованием, хотя на самом
деле, если исходить с самого начала из нолевого представления,
§ 121
БОЗОНЫ
05
речь идет, естественно, о первичном квантовании. Как при пер-
вичном, так и при вторичном квантовании понятие частицы ни-
коим образом не заменяется полностью понятием поля и понятие
поля никоим образом не заменяется понятием частицы. Более
того, появляется новое двойственное представление: в зависимости
от экспериментальных условий проявляется либо корпускуляр-
ный, либо волновой характер поля.
Область
Исходная концеп-
ция
Результат перлит-
ного квантования
Квантовая механика
частица
также волновое поле
Квантованные
поля
волновое поле
также части-
ца
Вторичное кванто-
вание
Мохаттка: частпца '
I ,
Первичное кванто- поло
паште: 1
г
Вторичное кнапто- частица
иптшр:
¦ дуализм
дуализм
частица —
волна
Мы проведем программу вторичного квантования в два эта-
па. Вначале займемся рассмотрением классического поля, а затем
квантованием его.
а) Классическое волновое поле. В качестве классического
«волнового» уравнения нам будет служить уравнение ТПредин-
гера
а также комплексно сопряженное уравнение Шродпнгера
-— Aih* 4- V (х) ф* = — /Й\Ь*.
2т
A2.1)
A2.2)
Поскольку tJ) и ф* являются комплексными функциями координаты
х и времени t, мы можем рассматривать, как независимые друг
от друга, либо их действительные и мнимые части, либо с таким
дб КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
же успехом, сами if и if*. В последующем изложении мы будем
использовать последнее предположение. Теперь для нас A2.1) и
A2.2) являются уравнениями классического поля. Легко указать
функцию Лагранжа, уравнения Лагранжа для которой ведут
к уравнениям A2.1) и A2.2). Функция Лагранжа подобного ро-
да имеет вид
A2.3)
С помощью уравнения Лагранжа сразу же находим
т. е. просто уравнение поля A2.1). Функция Лагранжа A2.3)
ввиду ее несимметричности относительно "ф и яр* является не-
эрмитовой. Можно, конечно, с помощью искусственных приемов
сделать ее эрмитовой, однако при этом возникают трудности при
формулировке перестановочных соотношений. На этом основании
мы сохраним несколько упрощенное выражение A2.3), поскольку
все дальнейшие результаты, полученные с его помощью, будут
верными. Канонически сопряженный яр импульс мы введем обыч-
ным образом как производную функции Лагранжа
п = -^ = -Лф*. A2.5)
6i|> l
Функцию Гамильтона получим из функции Лаграпжа с помо-
щью следующего соотношения:
= f (i
— if* J^-Ai|> + т|)*1Л|)|сгзж. A2.6)
Причем в правой части этого выражения использован явный вид
функции Лагранжа A2.3). Поскольку два первых члена взаимно
уничтожаются, окончательно находим функцию Гамильтона
Н = J Г W {- ? А + V (х)} г|, (х) d*x. A2.7)
Выражение A2.7) имеет тот же вид, что и среднее значение
энергии в шредингеровской волновой механике.
Несмотря на эту аналогию или, вернее, именно благодаря
ей, здесь следует указать на одну понятийную трудность, кото-
рая доставляет много хлопот, в особенности начинающим. Поня-
тия функции Гамильтона и оператор^ Гамильтона возникают те-
перь совершенно другим образом:
§ 12] БОЗОНЫ 97
а) в исходном уравнении Шредингера оператор Гамильтона
выступает в виде — %2/Bт) А + F(x);
б) уравнение A2.7) определяет функцию Гамильтона (которая
позже становится оператором).
Следовательно, после квантования A2.7) речь идет о совершен-
но другом операторе, который следует четко отличать от выше-
упомянутого оператора Гамильтона.
Напомним читателю, что наше рассмотрение находится до
некоторой степени в классических рамках. Волновые функции if
и ty* теперь, как и ранее являются классическими полями. По
аналогии с рассмотрением колебаний атомной цепочки, разложим
амплитуду поля по собственным функциям волнового уравнения.
Поскольку теперь место волнового уравнения занимает уравне-
ние Шредпнгера, имеет смысл попробовать использовать решения
уравнения
в качестве функций, по которым производится разложение. Эти
функции мы запишем в виде
^ = e"\(x). A2.9)
Причем считается, что потенциал V не зависит от времени. Раз-
ложим теперь волновую функцию i|)(x) по этим собственным
функциям >qv. Введем временной множитель из A2.9) сразу в
коэффициенты разложения
МО = МО) e~TV, A2.10)
тогда разложения волновых функций г|> и ф* принимают следую-
щий вид:
I, A2.11)
Ч>* 00 = 2^00. A2.12)
Здесь проявляется существенное различие по сравнению с вол-
новым уравнением, которое содержит вторую производную по
времени. Присутствие второй производной по времени ведет к
тому, что наряду с решением еыг имеется решение е~ш, чем мы
воспользовались для конструирования действительной ампли-
туды. В данном случае мы, имеем дело с дифференциальным
уравнением, содержащим лишь первую производную по времени,
так что мы не можем больше представить if как действительную
функцию, суммируя комплексно сопряженные решения. Поэтому
7 X. Хакеы
g8 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ill
следует написать разложения A2.11) и A2.12) для комплексно
сопряженных величин. То обстоятельство, что if и if* являются
независимыми переменными, имеет, с другой стороны, важное
значение для последующей формулировки перестановочного со-
отношение A2.15), так как если, например, if и if* совпадают,
то соотношение A2.15) становится противоречивым. Поэтому мы
будем в дальнейшем считать, что if n х\'* являются независимы-
ми друг от друга переменными.
Вновь воспользуемся свойствами нормированное™ и взаим-
ной ортогональности собственных функций сг„. Если подставить
теперь разложения A2.11) и A2.12) в функцию Гамильтона
A2.7), то непосредственно получим выражение
Исходя из практических соображении, а также для того, чтобы
особенно ясно представить аналогию с полученными выше ре-
зультатами, в последующем изложении мы будем часто полагать
| , Е1,=%гт A2.13а)
причем ем имеет размерность частоты.
До сих пор мы рассматривали теорию, основываясь на том
соображении, что i|* представляет классическое поле. Теперь же
для того, чтобы выполнить нашу программу до конца, мы долж-
ны проквантовать это волновое поле if.
б) Квантование. Для квантования введем еще, согласно опре-
делению A2.5), канонически сопряженный импульс л, причем
правая часть возникает в результате применения явного вида
выражения A2.3). Потребуем выполнения между л и if обычного
перестановочного соотношения
\п(х),^(х')] = ±8(х-х'). A2.14)
Используя явный вид л, представим A2.14) в окончательном
виде
| tif(x'), if+(x)] =6(x-x'). ' A2.15)
Равным образом примем, что волновые функции между собой и
канонически сопряженные импульсы между собой коммутируют,
что мы сформулируем с помощью нижеследующих перестановоч-
ных соотношений:
I [if(x),\f(x')]=O A2.16)
4
)]=0. • A2.17)
§ 12] БОЗОНЫ 99
Теперь можно. непосредственно перейти вновь от перестано-
вочных соотношений A2.15), A2.16) и A2.17) к перестановоч-
ным соотношениям для амплитуд Ьц и Ьц . Для этого подставим в
A2.15), A2.16) и A2.17) разложения A2.11) и A2.12) и разрешим
полученные выражения относительно операторов Ъ. Поскольку все
это происходит совершенно аналогично изложенному в § 8, мы
отсылаем читателя к упражнению 1 в конце этого параграфа и
приводим сразу окончательный результат. Мы находим, что пе-
рестановочные соотношения для операторов Ъ и Ь+ имеют сле-
дующий вид:
[Ьц, bv] = «uv. A2.18)
[fe,x,bv] = O, A2.19)
[b+, Ь+]=0. A2.20)
Поскольку мы подчинили амплитуды Ь+ и b перестановочным со-
отношениям A2.18—12.20), то классическая функция Гамильтона
A2.13) становится оператором Гамильтона и соответственно, вви-
ду выполнения A2.15—12.17), оператором Гамильтона становит-
ся также и A2.7).
Если рассмотреть этот оператор одновременно с перестано-
вочными соотношениями A2.18—12.20), мы обнаружим полную
аналогию рассматриваемой здесь проблемы с проблемой, возник-
шей при квантовании обычного волнового уравнения, например,
в § 10. Поэтому можно воспользоваться всеми полученными нами
ранее результатами. Мы находим, что уравнению Шредингера ')
НФ=ЕФ,
соответствуют состояния вида
и У V
Вакуумное состояние Фо вновь определяется следующим образом:
I йAФо = 0 для всех ц. A2.23)
>) Так же я здесь следует указать, что выражение «уравнение Шредий-
гера» употребляется в совершенно различных смыслах:
а) в смысле первичного квантования (см. A2.1)); в этом случае соот-
ветствующий оператор Гамильтона действует на функцию координат ф(я);
б) в смысле вторичного квантования (см. выше); в этом случае соот-
ветствующий оператор Гамильтона действует на функцию состояния абст-
рактным образом через операторы рождения и уничтожения,
7*
ЮО КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ш
Соответствующие состояниям A2.22) энергии имеют вид
(^ = 0, 1,2,...). A2.24)
Результат, представляемый соотношениями A2.22) и A2.24), мож-
но интерпретировать следующим образом: из исходного уравне-
ния Шредингера A2.8) устанавливается последовательность энер-
гетических уровней ?„. Эти отдельные энергетические уровни ц
могут, как ясно из A2.24), быть заняты определенным числом
щ квантов, или, иными словами, частиц. Отсюда становится ясно,
что квантование поля также и в случае шредингеровского волново-
го уравнепия обеспечивает корпускулярный характер. Таким обра-
зом, очевидно, что состояния с энергией ?м можно занять щ час-
тицами, причем Иц может быть любым целым числом. Следова-
тельно, только что проведенное квантование относится к случаю
статистики Бозе. Соответственно этому, частицы, операторы рож-
дения и уничтожения которых удовлетворяют перестановочным
соотношениям A2.15—12.17) или A2.18—12.20), называются бо-
зонами. Примерами бозонов являются фотоны и ядра Не4. С дру-
гой стороны, электроны, протоны и ряд других частиц подчиня-
ются статистике Ферми — Дирака. Действующий в этом случае
принцип Паули утверждает, что нельзя привести две частицы
в одинаковое состояние. Очевидно, что для того, чтобы при кванто-
вании поля охватить также и эти частицы, следует изменить со-
ответствующим образом и перестановочные соотношения. Прежде
чем мы займемся этим в последующих параграфах, обсудим бо-
лее подробно вычисления средних значений в рамках нового
формализма. Мы будем исходить из классических величин, при-
чем под словом «классический» следует понимать «первично кван-
тованный». Этим классическим величинам поставим в соответ-
ствие оператор, с помощью которого образуем средние значения.
Применим теперь этот формализм к некоторым примерам.
Пример 1. Оператор плотности числа частиц. В теории Шре-
дингера плотность числа частиц имеет вид
, t). A2.25)
После вторичного квантования плотность числа частиц стано-
вится оператором
| p(x)==^+(x)f(x). A2.26)
Соответствующее среднее значение для плотности числа частиц
определяется согласно следующему правилу:
A2.27)
Для пояснения правила A2.27) рассмотрим пример одной части-
цы, которая находится в некотором состоянии х. Функция
§ 12] БОЗОНЫ 101
состояния Ф имеет тогда следующий вид:
Ф = Ь+Фо. A2.28)
Если теперь подставить разложения A2.11) и A2.12), а также
выражение A2.28) в A2.27), то мы получим
). A2.29)
Применяя перестановочное соотношение A2.18) и используя тот
факт, что оператор уничтожения, действующий на вакуумное
состояние, дает нуль, во второй сумме по v непосредственно по-
лучаем
(ф,
Далее применим D.18). Если теперь еще раз поменять местами
операторы Ьк и Ь^ , то получится следующий хзезультат:
Поскольку ср(х) является обычной числовой функцией, которая
не имеет никакого отношения к построению среднего значения,
то эту функцию можно вынести из угловых скобок и поставить
перед средним значением, что дает
Ф;(х)фи(х)<Фв|Ф0>- A2.32)
Поскольку, наконец, волновые функции вакуумного состояния
нормированы, то в качестве конечного результата получаем вы-
ражение
рОО = Фх(*)фх(х). A2-33)
Но это выражение является не чем иным, как обычной плотно-
стью числа частиц в состоянии и в теории Шредингера.
Пример 2. Оператор координаты. В качестве следующего при-
мера рассмотрим теперь в рамках вторичного квантования пост-
роение среднего значения для координаты. В теории Шредингера
среднее значение координаты вдоль оси х дается выражением
*(x, t)x$(x, t)d3x. A2.34)
Этому среднему значению мы ставим в соответствие оператор
жОп=| Ъ+к)х$Ы)сРх. A2.35)
Среднее значение этого оператора представляется далее с
102 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ш
помощью следующего выражения:
<Ф|жоп|ф> = <Ф||^+(х)^(х)й3а;|ф>. A2.36)
Для того чтобы проиллюстрировать этот случай несколько более
обстоятельно, вновь воспользуемся волновыми функциями
A2.28). Тогда после преобразований совершенно аналогичных тем,
которые были проведены в A2.29—12.33), в качестве окончатель-
ного результата получаем выражение
A2.37)
Весьма поучительный случай двух частиц рассматривается в
упражнениях.
Пример 3. Оператор потенциальной энергии во внешнем поле.
В качестве следующего примера рассмотрим потенциальную
энергию, которая в теории Шредингера описывается выражением
A2.38)
Ей соответствует оператор
00 Ф (х) d3x A2.39)
и среднее значение
V = (ф | J q+(x)V(x)q(x)d3x | ф)>. A2.40)
При Ф = fciO0 среднее значение равно
Пример 4. Оператор энергии кулоновского взаимодействия.
Несколько менее тривиальный случай возникает при исследова-
нии энергии взаимодействия двух частиц, например энергии ку-
лоновского отталкивания. Если вспомнить, что е-ф+-ф дает плот-
ность заряда частицы, то согласно электростатике для энергии
взаимодействия плотностей зарядов получается следующее выра-
жение:
V A2.41)
p(x',t)
При переводе этого выражения в квантовую форму возникает
характерная трудность! В классической теории волновые функ-
§ 12] БОЗОНЫ 103
цпи коммутируют, т. е. точный порядок следования этих функций
безразличен. В квантовой теории, однако, волновые функции,
напротив, не коммутируют, а удовлетворяют перестановочным
соотношениям A2.15). Поэтому в зависимости от того, в каком
порядке расположить операторы ф и \р+, получаются разные ре-
зультаты. При выборе порядка расположения операторов выра-
жения A2.41) в квантовой теории мы будем руководствоваться
тем, что если имеется только одна частица, то кулоновское вза-
имодействие равно нулю. Отсюда следует, что мы должны писать
оператор уничтожения if- справа, а оператор рождения -ф+ слева.
Кроме того, аргументы х и х' следует писать в том порядке,
в котором они стоят в выражении (.12.42), с тем чтобы при образо-
вании среднего значения мы могли вернуться назад к обычной
энергии взаимодействия в уравнении Шредпнгера. Ввиду весьма
близкого к предыдущим рассуждениям изложения этой, задачи,
мы отсылаем читателя к упражнениям.
Учитывая эти ограничения, энергии кулоновспого взаимодей-
ствия A2.4J) следует поставить в соответствие следующий опе-
ратор:
4 J Ъ+ Ф V" (х') ПГГГ1 * (х'} * W ®х d4- <12-42)
Среднее значение тогда определяется выражением
Ф). A2.43)
Задан и як§ 12
1. Разрешить A2.11) и A2.12) относительно Ь» и Ьц\
Указание к A2.11). Умножить обе части A2.11) на qv (x)
и проинтегрировать но пространству. Ввиду ортогональности .вол-
новых функций j фц' (х) ф^ (х) <Рх ¦— 8№' сразу же получается
выражение для Ь^.
2. Еще одно новое представление б-функции: б (х — х') =
= 2ф?(х')фц(х).
и-
Положить б (х — х') = 2 сцфц (х), причем суммирование ведется
по полному набору собственных функций, и показать, что Сц —
= Фд (х').
Указание. Как к заданию 1.
3. Вычислить среднее значение оператора координаты A2.35)
для двухчастичного состояния Ф = Ь^Ь^Фд.
104 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
4. Вычислить среднее значение кулоновского взаимодействия
A2.43) для Ф = Ь^,Ф0 и Ф = Ь^Ь^2Ф0.
Указание. Подставить разложения A2.11) и A2.12) в
A2.43), учитывая, что Ь„ и fej теперь операторы.
§ 13. Квантование шредингеровских волновых полей,
подчиняющихся статистике Ферми — Дирака. Фермионы
Как мы видели в предыдущих параграфах, шродингеровское
волновое поле может быть квантовано совершенно аналогично
волновому полю, описывающему, например, колебания решетки,
причем вновь проявляется корпускулярный характер поля. Прав-
да, мы обнаружили, что каждое состояние может быть занято
многими частицами. Чтобы исключить эту возможность в стати-
стике Ферми — Дирака, нам следует изменить перестановочные
соотношения. Для этого вновь будем исходить из разложения
волновых функций а|}(х) и г|з+(х) в виде A2.11) и A2.12). Эти
разложения представим в виде
D3.1)
A3.1а)
Здесь <р„(х) и фц(х) должны быть собственными волновыми
функциями уравнения Щредингера в представлении первичного
квантования:
A3.16)
При этом коэффициенты разложения («амплитуды») мы обозна-
чили не через Ъ, как раньше, а через а, чтобы подчеркнуть, что
последние как операторы удовлетворяют перестановочным соот-
ношениям нового типа, обсуждением которых мы теперь займем-
ся. Для этого предположим, что имеется вакуумной состояние Фо,
а (Хц, вновь имеет смысл оператора рождения. Тогда формально
можно создать две частицы в одном и том же состоянии и., для
чего образуем выражение а»а?Ф0. Поскольку, однако, в при-
роде такое состояние не может быть реализовано, потребуем,
чтобы
<44Фо = 0. A3.2)
Это требование должно выполняться не только для вакуумного
состояния Фо, но и для любого состояниеФ. Но если соотноше-
ние вида A3.2) выполняется для всех Ф, то отсюда следует, что
5 13] ФЕРМИОНЫ 105
6 квантовой теории
44 = 0. A3.3)
Теперь сформулируем перестановочное соотношение между 4
н 4, которое содержит условие A3.3) в качестве частного случая.
Перестановочное соотношение такого рода можно представить
следующим образом:
44 + 44 = о. A3.4)
Решающим моментом в этих перестановочных соотношениях по
сравнению с бозевскими перестановочными соотношениями явля-
ется замена знака «минус» на знак «плюс». Теперь кажется
естественным везде заменить знак минус на плюс, т. е. ввести
в качестве перестановочных соотношений для ферми-частиц сле-
дующие перестановочные соотношения:
44 = °' A3.4)
«v4 = 6мл» A3.5)
avav -- 0. A3.6)
Эти «плюс»-перестановочные соотношения в последующем изло-
жении мы кратко обозначим следующим образом:
1А, В\+ = ЛВ + ВЛ. A3.7)
Хотя на основании высказанных выше соображений одновремен-
ное введение знака плюс везде, где до этого стоял минус, кажется
удовлетворительным, это не является, однако, достаточным
обоснованием для квантования поля. Мы увидим, что эти новые
перестановочные соотношения ведут к антисимметричным волно-
вым функциям в координатном пространстве. Эти антисиммет-
ричные волновые функции являются, как известно из шрединге-
ровской теории многих частиц, типичными для статистики
Ферми — Дирака. Мы никоим образом не предполагаем, что чи-
татель знаком с упомянутой выше теорией многих частиц, а
ставим во главу угла (в известной степени аксиоматически) со-
отношения A3.4—13.6) и вводим затем подходящие свойства мно-
гочастичных волновых функций. Поскольку полевые операторы
ф(х) и -ф+(х) связаны с операторами а„ и а ? через разложения
A3.1) и A3.1а), то перестановочные соотношения A3.4—13.6)
имеют своим следствием, естественно, перестановочные соот-
ношения для т|) и г|з+ и наоборот. Поскольку все вычисления
аналогичны приведенным выше, мы опустим их точное воспроиз-
ведение, а интересующегося читателя отсылаем к заданию 1.
106
КВАНТОВАНИЕ ПОЛЯ
[ГЛ. III
Обсуждаемые сейчас перестановочные соотношения между if и "ф+
имеют, следующий вид:
+ г|)(х')ф+(х) = б(х - х'),
х') + \|)+(х')г|;+(х)=О, A3.8)
ф(х')ф(х) = 0.
Частицы, операторы рождения и уничтожения которых удов-
летворяют перестановочным соотношениям A3.4—13.6) или
A3.8), называются ферми-частицами (фермионами). Сравнение
этих перестановочных соотношений с перестановочными соотно-
шениями для ооновского поля показывает, что всюду, где
раньше стоял знак минус, теперь стоит знак плюс. Кроме этого
обстоятельства, весь формализм предыдущих параграфов полно-
стью остается в силе. Оператор Гамильтона вновь дается выра-
жением A2.21) и принимает следующий вид:
я-
A3.9)
Соответствующее уравнение Шредингера для квантованного со-
стояния имеет вид
НФ=ЕФ. A3.9а)
Собственные функции (состояния) и собственные энергии для
A3.9) находят точно так же, как в бозевском случае в § 12.
Мы постулируем существование
основного состояния Фо, обла-
дающего следующим свойством:
| йцФо = О для всех ц, A3.10)
/
1-2 3
ff 7 /&< а в качестве функции состояния
получаем
Фо.>-ПDГ1ф0.
A3.11)
Рис. 22. Пример функции состоя-
ния Ф{„) при {п} = {1, 0, 0, 1, 1,
О, 1, 0, 0, ...}.
Здесь мы формально полагаем (я^H = 1 и учитываем ввиду
(aJJ=O, что показатели п могут принимать значения только О
или 1. На рис. 22 представлен пример для in). Здесь
{п> = A, 0, 0, 1, 1, 0, 1, 0, 0, ...>.
Энергия Е дается следующим выражением:
A3.12)
§ 13) ФЕРМИОНЫ 107
где «„ = О или 1. Полное число частиц .равно
# = 2»д. A3.12а)
В нашем примере, следовательно, имеются четыре частицы.
Если полное заданное число частиц равно N, то, следователь-
но, только N чисел заполнения /^,= 1. Поэтому наряду с A3.11)
применяется еще одно очевидное представление, в котором с са-
мого начала учитывают только п^== 1:
Ф{п) = a^fit, ¦ ¦ ¦ </1'о. A3.11а)
При этом мы условимся, что jx 1 < (.is <...<-" \\к.
В приведенном на рис. 22 примере имеем \х\ = 1, ц2 = 4, и3 ==
= 5, U4 = 7. Познакомимся теперь с этим формализмом несколько
обстоятельнее. Для этого рассмотрим наиболее общее одночастич-
ное состояние. Такое состояние задается суперпозицией одыоча-
стичных состояний ЯдФ0:
ф Sc^v A3.13)
причем постоянные коэффициенты с,„ с точностью до условия
нормировки 2|cmI2 — 1i являются еще совершенно произволь-
ными. Мы сможем перейти к другому представлению состояния
Ф, если введем вместо операторов рождения а^ операторы г|з+(х).
Для этого умножим A3.1а) на ср^- (х) и проинтегрируем по объе-
му. Тогда получим, учитывая ортогональность и нормировку
функций ф((, по которым ведется разложение, представление опе-
раторов а%, через \|;+(х):
4 = J
(х) i|>+(х) d3*. A3.14)
Если подставить A3.14) в A3.13), то получим
Ф =-12здЛх)г|)+(х)^Ф0. A3.15)
Сумма по ц представляет собой, как показано фигурной скобкой,
некоторую функцию /(х), так что мы можем переписать Ф в виде
Ф = |/(х)г1)+(х)#жФ0. A3.16)
Как мы покажем сейчас, функция fix) удовлетворяет обычному
одночастичному уравнению Щредингера. Выражение A3.16)
можно интерпретировать следующим образом. Ниже мы увидим,
что оператор tf>+(x) создает в точке х одну частицу. Следователь-
jO8 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
но, Ф представляет наложение одночастичных состояний, которые
можно представлять себе возникающими в различных точках
пространства, каждое со своей «амплитудой вероятности» /(х).
Теперь покажем* что "ф+(х') действительно создает одну частицу
в точке х', т. е. что
ф+(х')Ф0 . A3.17)
представляет частицу в точке х'. Для доказательства подейству-
ем на A3.17) оператором плотности числа частиц р(х) = \|)+(x)i(>(x).
Тогда с учетом применения перестановочных соотношений A3.8)
и того обстоятельства, что действие г|; па вакуумное состояние дает
нуль, мы получим следующие соотношения:
г|)+(х')Фо = 1]}+(хM(х — х')Фо =
A3.18)
= «(х —х')ф+(х')Ф0.
Эти соотношения утверждают, что функции A3.17) являются
собственными функциями оператора, плотности числа частиц,
причем собственное значение = 0, если координата х' не совпа-
дает с координатой х, и собственное значение = 1 при интегриро-
вании в окрестности точки х = х'.
Подставим теперь общие одночастичные функции A3.16) во
вторично квантованное уравнение Шредингера A3.9а), причем
выберем Н в пригодном для фермионов виде A2.7). Тогда "ф+ и
я)? являются, естественно, операторами, которые подчиняются
плюс-перестановочным соотношениям.
Составим в левой части уравнения Шредингера A3.9а) выра-
жение
#Ф = j Ф+ (х) (- ? Ах + V (х)) ф (х) d*x j/ (х') Ф+ (х')
A3.19)
Это выражение при использовании перестановочного соотноше-
ния A3.8) переходит в
ЯФ = JJ / (х') {ф+ (х) (- hl Дх + V (х))б (х - х') d*x dV<D0}.
A3.20)
Учитывая равенство Лхб(х — х') = Лх'б(х — х') и свойства
б-функции, вместо A3.20) получаем
Я Ф = J Ф+ (х) Фо (- ? Д + V (х)) / (х) <Рх. A3.21)
Поскольку согласно уравнению Шредингера должно иметь (место
§ 13] ФЕРМИОШЛ 109
равенство #Ф =ЕФ, то мы приходим к утверждению, что A3.21)
должно совпадать с выражением
Е J/(х) Ф+(х) Фо d»ar. A3.22)
Но так как это соотношение должно выполняться для всех точек
х, а функции г|з+(х)Ф0 линейно независимы (см. задание 2), то
соотношение A3.21) = A3.22) может выполняться только тогда,
когда оно уже выполняется для отдельных множителей при
г|)+(х)Ф0, т. е., следовательно, если fix) удовлетворяет обычному
уравнению Шр'едингера
• A3.23)
Соответствующее доказательство можно провести также и для
зависящего от времени уравнения Шредингера. Этот пример по-
казывает, что в случае одной частицы формулировки обычной тео-
рии Шредингера и теории вторичного квантования идентичны.
Теперь мы покажем на примере двух частиц, что и в случае многих
частиц существует эквивалентность между формулировкой в
рамках вторичного квантования и обычной многочастичной тео-
рией Шредингера. Следует, однако, совершенно определенно ука-
зать на то, что формулировка в рамках вторичного квантования
обладает рядом существенных преимуществ и прежде всего по-
тому, что она является адекватной для рассмотрения многих про-
цессов. Рассмотрим теперь наиболее общее состояние двух частиц,
которое строится как наложение всех состояний, в которых одна
частица находится в состоянии pii, другая — в состоянии иг:
Ф = 2 с^на+ха+гФ0. A3.24)
Заменяя в этом выражении операторы aj на г|)+, согласно A3.14),
получаем вместо A3.24):
f f (
(х') с^Л ф+ (х) г|>+ (х') Фо d*x dV.
«x,x)
A3.25)
Сумма по Hi и |Х2 представляет обычную функцию координат х
и х', которую мы кратко обозначили fix, x'), так что Ф можно
представить в виде
Ф = J J / (х, х') t|;+ (х) 1|,+ (х') Фо dax d3x'. A3.26)
Мы покажем, что функция fix, x') антисимметрична относитель-
110 КВАНТОВАНИЕ ПОЛЯ (ГЛ. Ill
но координат х и х'. Для этого изменим в A3.26) обозначения
крординат, поменяв х и х' местами, тогда A3.26) переходит в вы-
ражение
J J / (x'f x) ф+ (х') t|;+ (x) Фо сРх d3x'. A3.27)
Сравнение этого выражения с A3.26) показывает, что порядок
следования операторов "ф+ теперь изменился. Чтобы получить тот
же порядок следования операторов, что и в A3.26), мы переста-
вим оба оператора i|)+, причем ввиду перестановочного соотно-
шения A3.8) поменяется знак, так что A3.27) принимает следу-
ющий вид:
V. A3.28)
После всех этих преобразований выражение A3.26), естественно,
не изменилось, так что мы получаем общее соотношение: выра-
жение A3.26) равно выражению A3.28). Однако под интегралами
в этих выражениях стоят функции 1ф+(х)"ф+(х')Фо, которые ли-
нейно независимы друг от друга. Поэтому соотношение A3.26) =
= A3.28) может быть выполнено только в том случае, если вы-
полняется условие
/(х, х'). = -/(х', х). A3.29)
Это условие и показывает, что волновые функции / антисиммет-
ричны. С помощью волновых функций A3.26) можно вновь прий-
ти к уравнению Шредингера в представлении вторичного кванто-
вания. Для дальнейшего обсуждения нашего примера двух частиц
мы выберем оператор Гамильтона уравнения Шредингера в сле-
дующем виде:
Я = JV (х) (- ? Дж + F (х)) г|, (х) д*х
В первом интеграле мы сразу узнаем обычное оредпее значение
шредингеровской теории для кинетической энергии и энергии в
некотором заданном потенциальном поле. Двойной интеграл
представляет, очевидно, энергию кулоновского взаимодействия.
Мы не будем проводить подробно решение, получающееся
после подстановки A3.26) во вторично квантованное уравнение
Шредингера, а отошлем интересующегося читателя к соответст-
вующему упражнению. Здесь мы ограничимся тем, что приведем
окончательный результат. Этот результат утверждает, что функ-
§ 13] ФЕРМИОНЫ HI
цпя /(xi, хг) удовлетворяет следующему уравнению Шредингера
для двух частиц:
= Ef(xl,x.1). A3.31)
Обобщение этого результата па случай п частиц легко угадать,
однако его можно также провести строго в рамках формализма
вторпчного квантования. Для случая п частиц получается урав-
нение Шредингера следующего вида:
A3.32)
причем / антисимметрична относительно всех координат.
Приведенные выше соображения позволяют нам сформулиро-
вать- с помощью вторичного квантования много'электронную про-
блему твердого тела (см. § 20).
Этот параграф мы закончим правилами
Вычисления средних значений. Ввиду тесной аналогии между
базе- и ферми-операторами кажется возможным определить
средние значения, которые вычисляются с помощью операторов
а н а+ точно так же, как это было сделано для бозе-операторов.
Тоща оказывается (см. задание 6), что вычисление средних 'зна-
чений дает тот же результат, что и в теории шредингеровской
' волновой механики, которая экспериментально лучше всего под-
тверждена в нерелятивистской области.
Руководствуясь § 4, мы введем аксиоматически следующие
правила:
Квантовомеханическое среднее значение оператора Q по со-
стояниям Ф строится следующим образом:
| Й = <Ф|О|Ф>. A3.33)
При этом постоянно предполагается, что Ф нормирована:
<Ф|Ф> = 1 A3.34).
Скобки (бра и кет) должны обладать следующими свойствами:
A3.35)
A3.36)
Здесь мы опустили индекс и. у операторов уничтожения а и рож-
дения а+. Используя перестановочные соотношения A3.4—13.6)
и свойство основного состояния, можно установить ортогональ-
^2 квантование поля [гл. ш
ность собственных состояний A3.11) (см. задание 4):
т. с. правая часть отлична от нуля только при щ = тп\, щ = Ш2, .. •
..., га,. = /гец, ...
Задания к § 13
1. Вывести соотношения A3.8), исходя из перестановочных
соотношений A3.4—13.6).
Указание. Подставить в левую часть A3.8)^ разложение
A3.1) и применить A3.4—13.6), а также представление 6-функ-
ции, приведенное в задании- 2 § 12.
2. Показать, что функции г|з+(х)Ф0 линейно независимы, т. е.
что нз
= J g (х) 1|з+ (х) Ф0A3х --= 0 следует g (х) = 0.
Указание. Построить выражение <1|з+(х')Фо1/>.
3. Показать, что если подставить A3.26) во вторично кванто-
ванное уравнение Шредингера НФ =
= ЕФ, причем // определено в
A3.30), то получится уравнение
1
1
I
4 5
I
I.
Шредингера для двух частиц в «кон-
фигурационном пространстве» A3.31).
4. Доказать A3.37).
Указание. Подставить A3.11)
в левую часть уравнения A3.37) и
последовательно применить A3.36),
/ 2 3 4 д 6 ^ что приводит к следующему резуль-
Рис. 23. Пример функции тату:
состояния Ф{«> (вверху) п п m
и функции состояния Ф{т} <Ш0 I .. .пр .. .а2 ах \а{) ^
(внизу).
(в качестве примера — рис. 23). Убедиться в следующем: если
для некоторого \i число заполнения т^ = 0, а п^ = 1, то оператор
а^ можно «протащить» направо к Фо, что дает а^Фо = 0. Если же
для некоторого ц число заполнения т^ = 1, а п^ = 0, то оператор
<zj можно «протащить» налево: <Ф0|яц •••>, а затем с помощью
A3.35) преобразовать к виду <ацФ0 | ••¦>, что дает в результате
=о
нуль. Почему справедлив результат <Ф{п>1Ф<п)> = 1?
§ 14] ОБ ОБРАЩЕНИИ С ФЕРМИ-ОПЕРАТОРАМИ ИЗ
5. Показать для Ф{П> = Фпг,пг nN, что
<Ф<И> | cfiav | Ф{„>> =0 для ц ф v,J ^A 13 ^
= 71ц ДЛЯ Ц = V.J
6. Вычислить среднее значение оператора потенциальной
энергии
j (A 13.2)
для
Ф = '41Ф0, Ф = «Ф0- (А 13.3)
Указание. Подставить (А 13.3), (А 13.2) и A3.1) в <Ф|У„П1Ф>
и применить результат предыдущего задания 5.
§ 14. Об обращении с ферми-операторами
а) Можно ли перенести сюда наши приемы § 5? Теперь вме-
сто рассмотренных в § 5 бозе-операторов Ъ и Ъ+ мы займемся
исследованием свойств ферми-операторов а и а+, удовлетворяю-
щих следующим соотношениям:
аа+ + а+а=1, A4.1)
(в+J = о, A4.2)
а2 = 0. A4.3)
Хотя перестановочное соотношение A4.1) отличается от соответ-
ствующего соотношения для бозе-операторов только лишь знаком,
это изменение знака приводит к существенным последствиям для
свойств операторов а. Легко убедиться, например, что операторы
а + а и а+ + а более не удовлетворяют перестановочным соотно-
шениям для ферми-операторов. Можно также сразу установить,
что все степени операторов а+ и а выше 1 исчезают
(о+)" = 0 для п>2, A4.4)
а" = 0 для п>2. A4.5)
Если мы рассмотрим комбинацию волновых функций вида
иа+)Фо, A4.6)
то обнаружим, что эта комбинация является уже полной. Тем не
менее формально можно определить функции операторов а+ и а.
В качестве примера мы можем, конечно, представить выражение
() A4.7)
8 х. Хакен
114 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ill
в виде экспоненциальной функции
A4.8)
Нужно лишь иметь в виду, что разложение этой экспоненты в
ряд по степеням оператора а+ должно обрываться на втором;
члене.
Теперь посмотрим, как можно было бы провести преобразова-
ния с применением экспоненциальной функции A4.8). Для этого
разложим в левой части выражения
е-сса+аеаа+ ^ ~ A4.9)
(которое мы кратко обозначили через а) обе экспоненциальные
функции, откуда сразу получим
а = A-аа+)аA+аа+). ¦-• ¦ ¦ • A4.10)
Если теперь перемножить учитывая точный порядок следования
множителей, скобки и применить еще перестановочные соотно-
шения A4.1), то сразу получим
а = а — а2а+ + aiaa+ — a+a). A4.11)
В последующем изложении последний члеп в A4.11) будет лам
еще часто встречаться. Поэтому мы введем особое сокращенное
обозначение
s=4r(aa+-a+a). A4.12)
Соответствующим образом можно вычислить и выражение
а+ = е-а"а+еаа. . A4.13)
Тогда, принимая во внимание сокращенное обозначение A4.12),
сразу получаем конечный результат
' а+ = а+ - а?а - 2as. A4.14)
Аналогия с бозе-операторами будет существенно более близ-
кой, если в показателе степени экспоненты стоит произведение
а+а. Если разложить экспоненциальную функцию
еаа+п ' • . ' ' ' ' A4.15)
в ряд по степеням а+а, то окажется, что ^операторы рождения и
уничтожения все время чередуются, так что правила A4.4) и
§ Щ ОБ ОБРАЩЕНИИ С ФЕРМИ-ОПЕРАТОРЛМИ 115
A4.5) более неприменимы. Рассмотрим теперь, что означает пре-
образование ')
е-аа+а. A4.16)
Для этого продифференцируем функцию /(а) по а, что дает
/' (а) = е+аа+а (а+аа - аа+а) е-аа+а. A4.17)
Первый член суммы в скобках ввиду A4.3) исчезает. Ко второму
члену применим перестановочное соотношение A4.1), в результа-
те чего выпадает еще одно произведение операторов
/'(а) = еаа+а (- а) <Гаа+а ^ - / (а). A4.18)
Отсюда получаем дифференциальное уравнение для /:
Па) = -/(а), A4.19)
решением которого является
A4.20)
причем мы приняли во внимание начальное условие /@) = а.
Отсюда окончательно получаем следующее соотношение:
| а =з еаа+аае~аа+а = е'аа. A4.21)
Совершенно аналогичным образом получаем
| ?3?«0+вЛ-да+" = «аа+. A4.22)
В последующем изложении соотношения A4.21) и A4.22) будут
нам часто необходимы.
б) Смещенный ферми-осциллятор. Рассмотрим уравнение
Шредингера так называемого смещенного ферми-осциллятора,
которое формально имеет тот же вид, что и уравнение смещенно-
го гармонического осциллятора:
0 -i-(а+а -г- аа+) + у*а+ + уа\ Ф = Ш>. A4.23)
Мы заменили лишь при этом выражение Еоа+а на Ео -^-(а+а — аа+),
что, как легко увидеть с помощью перестановочных соотношений
A4.1), сводится лишь к сдвигу нуля энергии на величину-j-iSj.
') В этом преобразовании оператор е ^ , вообще говоря, унитарный,
если а — чисто мнимое число. В этом4 случае (а) + =:-а+.
8*
116 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
Однако эта замена приводит к весьма симметричному рассмот-
рению проблемы. Для решения A4.23) возьмем волновую функ-
цию Ф в виде полной комбинации волновых функций основного
и возбужденного состояний:
\ ф = соФо + С10+Ф0. A4.24)
Если подставить A4.24) в A4.23), то мы получим с учетом соот-
ношений A4.1) и A4.3) и того обстоятельства, что Фо является
основным состоянием и обладает свойством аФо = 0, следующее
уравнение:
faa+Ф - с0Ф0) + У*соа+Фа + ^Ф,, = Е (с0Ф0 +
A4.25)
Поскольку волновые функции основного и возбужденного состоя-
ний ортогональны, т. е. справедливы соотношения
<а+Ф01Фо>=0, <Ф0|а+Ф0>==0, A4.26)
то уравнение A4.25) должно выполняться отдельно для коэффи-
циентов при Фо и а+Фо. Это условие приводит к двум однородным
уравнениям относительно со и с\\
-f Я. - EJcQ + ус, = 0, у*с0 + ^-Еа- Я) сх =0.
A4.27)
Условие разрешимости, т. е. условие обращения в нуль де-
терминанта этой системы, приводит непосредственно к соотно-
шению
+ \у\*. A4.28)
Отношение коэффициентов дается следующими выражениями:
С1 '
A4.29)
в) Много ферми-операторов.
1. Линейные преобразования. Рассмотрим набор ферми-опера-
торов, удовлетворяющих перестановочным соотношениям
aka++a+ah = 8kk., A4.30)
ahak> + ah'ak = °. A4.31)
•i4- + «k+=0. A4.32)
§ 14] 0Б1 ОБРАЩЕНИИ С ФЕРМИ-ОПЕРАТОРАМИ 117
Составим линейную комбинацию следующего вида:
k
причем считается, что матрица коэффициентов cjj, унитарна. Мы утверж-
даем, что тогда имеют место следующие соотношения:
AjA-, -!- AyAj = 0, A4.35)
А;А+, + АрАл = Ьи., A4.36)
а также сопряженное A4.35) соотношение. Если подставить в A4.35) выра-
жения A4.33), то мы непосредственно получим
H>cjkci>k'{akak' + ak'ak) = °- <14-37)
hh'
Выражения в скобках согласно A4.31) исчезают, что и доказывает справед-
ливость соотношения A4.35). Для доказательства A4.36) заменим вновь
операторы А и А+ согласно A4.33) и A4.34) на операторы ak и я^~. Ввиду
выполнения соотношения A4.30), левая часть сразу же принимает вид сум-
мы по произведениям коэффициентов с для одинаковых к. На основании
предполагаемой унитарности матрицы с (т. е. c*fe = {o~1)h-= (c+)/jj) не-
посредственно можно написать, что
2w*'* = e«" A4-38)
С помощью этого преобразования оператор Гамильтона
н = 2 *tMkk>ak» <14-39)
hh'
который, в общем, имеет недиагональный вид, можно сразу представить в
диагональном виде
Я = §»^, A4.40)
причем rrij являются действительными собственными значениями матрицы
Mkk,, которая по предположению эрмитова.
2. Преобразование Боголюбова. До сих пор нами
рассматривались только комбинации операторов рождения или
уничтожения. Преобразование Боголюбова исследует смешанное
преобразование. Рассмотрим две пары операторов аи а+ и а2,
а+. Преобразование Боголюбова определяется тогда соотноше-
ниями
lit = а\и — a2v, ах = ахи* — atv*, A4.41)
аа = atv -I- а2и, "а2 = aiv* + atu* A4.42)
118 ' КВАНТОВАНИЕ ШЛЯ ' [ГЛ. И1
с дополнительными условиями
| Ы2+М2=1, ш;*-уи* = 0. . A4.43)
Лент) установить, что новые операторы а± , а±, а2 ,\а2 вновь
удовлетворяют соотношениям A4.1—14.3). Например, для {аг у
мы получаем следующее соотношение:
(а?У = DY и* - uv Dа2 + а2а+) + a\v* = 0. A4.44)
То же самое можно установить и для (aiJ, (ягJ и (а2+J. Если в
выражение
а^аг + а2а^ A4.45)
подставить правые части A4.41) и A4.42), то симметричные про-
изведения оказываются равными нулю, поскольку оператор at
никогда не стоит за оператором щ.
Рассмотрим, наконец, еще выражение
af^ + aiai' A4.46)
в которое мы вновь подставим правые части A4.41) и A4.42).
Тогда получаем
[о+, ох]+ | и |2 - [а» аг]+ м*у - [а+, a+]+uv* + [а,, а+]+ \ v |2,
A4.47)
где квадратные скобки обозначают симметризованные произведе-
ния, т. е. определены следующим образом:
[А, В]+ = АВ + ВА. A4.48)
Первое и последнее симметризованные произведения дают, цри
определенных обстоятельствах, 1, в то время как остальные чле^
ны исчезают. Используя дополнительное условие A4.43), получа-
ем, наконец, соотношение
«i"ai + a^t == 1- A4.49)
Теперь покажем, что преобразование Боголюбова можно по-
строить с помощью некоторого унитарного преобразования. Эта
связь, как мы увидим позже, оказывается очень важной для уста-
новления полной эквивалентности поначалу формально различ-
ных теорий сверхпроводимости Бардина, Купера и Шриффера и
Боголюбова.
3. Представление преобразования Боголюб о-в а
с помощью унитарного преобразования1). Ана-
логия со смещенным гармоническим осциллято-
') Этот раздел требует несколько более глубокой подготовки, и при
первбм чтении может быть опущен. ¦ > ,
§ 14] ОБ ОБРАЩЕНИИ С ФЕРМИ-ОПЕРАТОРАМИ 119
р о м. Рассмотрим комбинацию вакуумного состояния Фо с функ-
цией, описывающей рождение двух частиц в состояниях A) и B):
A4.50)
Операторное выражение, стоящее перед Фо, формально можно
записать в виде экспоненциальной функции, поскольку все сте-
пени выше первого порядка по a^at исчезают:
са+а +
Ф = Ne l 2 Ф„. A4.51)
Велпчпны N и с определены здесь следующим образом:
| Лт = м, c = v/u. ' A4.52)
Введем для произведения пары операторов atat сокращение
a+at = A+ A4.53)
и зададимся теперь вопросом, нельзя ли таким же способом, как
и для бозе-онераторов (см. § 5), превратить оператор
NecA+ A4.54)
в унитарный оператор. Сделаем для этого в виде пробы подста-
новку
| Ф = МесА+Ф0 = есА+'сКАФ0, А+ = af at, A4.55)
где стоящее в правой части уравнения A4.55) экспоненциальное
выражение должно быть искомым унитарным оператором. Как
мы сейчас установим, этот оператор действительно обладает свой-
ством унитарности. Однако мы еще не знаем, выполняется ли
в действительности соотношение A4.55). Поэтому исследуем раз-
ложение экспоненты
A4.56)
п=0
широко используя перестановочные соотношения для ферми-опе-
раторов. С их помощью: сразу доказываются нижеследующие
результаты:
[А, Л+]_ .= 1 —atax - а%а„ A4.57)
0, A4.58)
+, _ . ..,.' . ..A459а)
. •_.. . -- "¦- :- J-":- ..-." A4.596)
J20 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ш
Исходя из A4.59а, б) и применяя метод математической индук-
ции, легко показать, что
A4.60а)
' A4.606)
Вычислим теперь степени (сА+— с*А)п, обращая особое внимание
на порядок следования А+ и А. Ввиду A4.58) остаются только
такие члены, в которых А и А+ попеременно следуют друг за
другом. При этом следует различать случаи п четного и п не-
четного:
а) п четное
(сА+ - с*А)п = (-1)F (А+АА+А...А+А | с \п+ АА+1.. АА+\с\п)',
п раз п раз
A4.61а)
б) п нечетное
(СЛ+ -с*А)п= (- 1) 2 (А+АА+... АА+\с\п~1 с-
п раз
-АА+А ¦¦¦Л+Л|с|я~1с«). A4.616)
п раз
Выражения A4.61а, б) при учете A4.59а, б) и A4.60а, 6) упро-
щаются:
п
(сА+ - с* Л)" = (- if | с |п {А+А + АА+) п четное, A4.62а)
П-1
(сА+ - с*А)п = (— 1) 2 | с р (сЛ+ - с*4) га нечетное.
A4.626)
Подставим A4.62а) и A4.626) в A4.56). Для различения четных
и нечетных п положим п = 2т или п = 2т + 1. Тогда получим
т=1
т=о
Операторные выражения не зависят от индекса суммирования,
поэтому их можно вынести за знаки сумм. Тогда оказывается,
§ 14] ОБ ОБРАЩЕНИИ С ФЕРМИ-ОПЕРАТОРАМИ 121
что эти суммы по существу представляют собой разложения си-
нуса и косинуса. Следовательно,
A4.63)
Вспомним теперь нашу исходную задачу. Мы хотели пока-
зать, что соотношение A4.55) действительно имеет место, при-
чем левая часть A4.55) тождественна левой части A4.50). По-
действуем теперь правой частью A4.63) на Фо и учтем, что ввиду
A4.57) A-(АА+ + А+А))Ф0 = 0 и что а,Ф0 = 0. Отсюда полу-
чаем
^Ф0 = (соз|с| + т^зт|с|Л+)ф0.
Сравнивая это выражение с левой частью A4.50):
(и + иА+)Ф0, A4.64)
сразу же получаем основополагающие соотношения
cos|c ] = и, A4.65)
« sin | с | = и. A4.66)
В последующем изложении будем считать, что постоянная с дей-
ствительна. Тогда A4.65) и A4.66) можно заменить на
cos с = и, A4.67)
sin с = v. A4.68)
Обратимся теперь снова к аналогии со смещенным гармони-
ческим осциллятором. В § 6 было показано, что свойства опера-
торов, действующих на возбужденные состояния, можно легко
найти, если известно, как эти операторы преобразуются при уни-
тарном преобразовании. При этом речь идет именно о тех уни-
тарных преобразованиях, которые связывают старое состояние
с новым основным состоянием. Вычислим выражение
h(c)=UatU+, A4.69)
где U имеет следующий вид:
и = есА+-сА.- A4.70)
Для этого продифференцируем A4.69) по с и получим
? (UatU+) = U {{А+ - A) at - at U+ - A)} U+ =
= - U [A, at] U*. A4.71)
122 ¦ КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
Исходя из перестановочных соотношений, легко проверить, что
справедливо равенство
= аг, . A4.72)
в результате чего A4.71) переходит в
- Ua2U+. A4.73)
Теперь мы должны, однако, вычислить еще A4.73). Соответст-
венно вышеизложенному получаем уравнение
JL {Ua.2U+) = U[A+, a,] U+ = Ua+U+. A4.74)
Если подставить A4.74) в A4.71) и учесть при этом A4.69), то
получится дифференциальное уравнение для /i следующего вида:
fl+h-=O. A4.75)
Учитывая начальные условия/х@) = а+, f\ @) = — а2, сразу полу-
чаем решение вида
Ua'iU'v = /i = af cos с — a2 sin с. A4.76)
Поскольку cose и sine связаны с и и v соотношениями A4.67)
и A4.68), мы получаем, наконец, окончательный результат
| а+ = UatU+ - afu - агьк A4.77)
Тем самым одновременно определен новый оператор af, который
получен преобразованием оператора а*- Аналогичным образом
получается результат
| а2 = Ua.2U+ = ua.t + vat. A4.78)
Этот результат показывает, что преобразование Боголюбова дей-
ствительно Может быть генерировано унитарным преобразова-
нием U (см. A4.70)). Как уже было отмечено, это обстоятельство
окажется чрезвычайно полезным в теории сверхпроводимости.
Заданияк§14
Приложения смещенного фермиевского осциллятора:
а) Спин 1/2: в магнитном поле. Доложить
а+ = а+, а = от, а2. = -|- (а+а ,- аа+) (AUA)
и показать, что справедливы следующие перестановочные соот-
§151 ' ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯМИ 123
ношения:
о+2 = о-2 - 0, а+а~ + а~а+ = 1,
(А14.2)
а+а~ — а~а+ = 2az, a±az — aza± — ^ а±.
Положим о* = ox±iay, а также Sj — TiOj, j — х, у, z. Тогда полу»
чаем оператор спина s = (sx, sv, sz) для спина 1/2. С помощью
(А 14.2) показать, что Компоненты s удовлетворяют перестано-
вочным соотношениям для момента количества движения:
szsx — sxsz =
Уравнение Шредингера для волновой функции ф спина 1/2 в
магнитном поле Н имеет вид
¦.'. ,:Д-(Н,8)
Показать, что левая часть (А 14.3) эквивалентна A4.23), и опре-
делить Ео, ч*, "f.
б) Двухуровневый атом во внешнем электрическом поле.
Пусть имеется атом только с двумя состояниями \i — 1, 2 и од-
ним электроном. Положить в уравнении A3.9) F(x) = Vq(.x) +
'+ Fs(x), где F0(x) — потенциальная энергия электрона, а энер-
гия Fs(x) вызвана внешним возмущением. Пусть фц(х) в
A3.1, 1а) —решение уравнения Шредингера A3.16) с F(x) =
= F0(x). Какой вид имеет оператор Гамильтона с учетом энергии
возмущения Fs(x), в представлении вторичного квантования
в операторах ajt> а^ Положить а+ах — а+, а+а2 = а и показать,
что при соответствующем выборе постоянных получившееся
таким образом уравнение Шредингера согласуется с уравнением
A4.23).
§ 15. Взаимодействие между полями: электроны,
«танцующие на канате»
В § 12 мы уже видели на примере кулоновского взаимодей-
ствия, что поле может взаимодействовать само с собой. Как в
физике твердого тела, так и, например, в ядерной физике часто
приходится иметь дело с взаимодействием между различными
полями. Например, электроны в твердом теле взаимодействуют
с колебаниями решетки или с квантованным полем излучения.
Для того чтобы показать, как можно было бы рассматривать
такого рода взаимодействия, мы займемся сейчас одним весьма
наглядным примером. Мы рассмотрим струну («канат»), вдоль
124
КВАНТОВАНИЕ ПОЛЯ
[ГЛ. III
которой могут перемещаться частицы (например, электроны),
причем на частицы действует поле силы тяжести. Воздействием
силы тяжести на струну мы пренебрежем. Таким образом, в на-
шей задаче речь идет в прямом смысле слова о «танцующих на
канате» электронах (рис. 24). Для про-
?fa>t)
Рис. 24. Взаимодействие то-
чечной массы со струной.
а) Отклонение q(x, t) стру-
ны как функция координа-
ты в заданный момент
времени, б) Потенциаль-
ная энергия V(x, t) элект-
рона (точечной массы) в
точке х струны.
ведения квантования связанной систе-
мы мы используем уже хорошо знако-
мый нам путь:
а) построение уравнений движения;
б) построение функции Лагранжа,
уравнения Лагранжа для которой вновь
приводят к уравнению движения;
в) переход к функции Гамильтона;
г) квантование;
д) разложение по собственным фун-
кциям.
а) Построение уравнений движения.
Уравнение колебаний неподверженной
действию внешней силы струны имеет
следующий вид:
р? (*,*)-«2^ = 0; A5.1)
здесь р — плотность массы, q — попе-
речное смещение в точке х в момент
времени t, s — натяжение струны.
Если на струну поместить частицу с массой т, струна будет
провисать под действием силы тяжести
К = - mg;
A5.2)
здесь т — масса частицы (электрона), a g — ускорение свободно-
го падения. Поскольку уравнение A5.1) в левой части содержит
плотность массы, то это — уравнение движения плотности массы.
Поэтому, если мы хотим ввести в A5.1) вынуждающую силу,
то A5.2) следует поделить на dx, а затем совершить предельный
переход и перейти к плотности силы. Если представить себе,
находясь полностью в рамках полевого представления, что элек-
трон «размазан» и соответственно этому его плотность массы за-
дается функцией рэд(х, t), то плотность силы будет определяться
выражением
, t)g.
A5.3)
Желая проквантовать уравнение Шредингера, мы предположим,
что электрон уже первично квантован и описывается волновой
§ 15] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯМИ 125
функцией. Тогда плотность массы электрона задается выраже-
нием
рэл(я, t) = т$+(хЦ(х). A5.4)
Если ввести в A5.1) плотность силы, определяемую выражения-
ми A5.3) и A5.4), то получится следующее уравнение вынужден-
ных колебаний струны:
pq(x, t) — s—q 2' ¦ = — mgty+ (x)ty(x). A5.5)
Теперь рассмотрим уравнение движения электрона или, точ-
нее сказать, волнового поля электрона, которое идентично обыч-
ному уравнению Шредингера для одной частицы. Изменение по-
тенциальной энергии частицы в поле силы тяжести прямо про-
порционально отклонению струны q, умноженному на вес ча-
стицы G. По определению
G = mg. A5.6)
Потенциал, который мы должны подставить в уравнение Шредин-
гера, таким образом, имеет вид
V(x, t) = mgqix, t). A5.7)
Тем самым по отклонению q(x, t) можно непосредственно судить
о величине потенциальной энергии электрона. Соответствующее
обычное уравнение Шредингера имеет вид
Установив уравнения A5.5) и A5.8), мы получили, таким обра-
зом, уравнения движения полей q(x, t) и ty{x, t).
б) Функция Лагранжа. Функция Лагранжа для свободно ко-
леблющейся струны уже встречалась нам в § 9, а функция Ла-
гранжа электронного поля с заданным потенциалом представлена
уравнением A2.3). Попытаемся представить функцию Лагранжа
нашей задачи в виде суммы отдельных вкладов, что приводит к
результату
L =
Jdqjx, t)\2\dx
Поначалу может показаться удивительным, что здесь через по-
тенциальное поле A5.7) учитывается воздействие струны на
электрон, а не наоборот — воздействие, вынуждающей силы, стояг
126 квантование поля (гл. ш
щей в A5.5), на струну. Но если теперь с помощью функции
Лагранжа A5.9) ввести обычные уравнения движения Лагранжа,
то мы придем не только к уравнению A5.8), но также и к пол-
ному уравнению A5.5). Ввиду этого функция Лагранжа A5.9)
дает правильное выражение для вынуждающей силы в A5.5).
в) Построение функции Гамильтона. Для того чтобы постро-
ить функцию Гамильтона, нам нужны канонически сопряжен-
ные импульсы, которые можно получить из функции Лагранжа
с помощью дифференцирования по q и if:
dL 6L
Яф = —Г, Яд = —~.
dty Oq
Решение проводится точно так же, как в §§ 9 и 12, так что
можно сразу воспользоваться полученными там выражениями.
Из общего выражения для Н:
' Я = f я.фг|) dx -\- (' nqq dx — L A5.10)
непосредственно получаем
A5.11)
Объединив первый и последний интегралы, можно увидеть, что
это есть не что иное, как среднее значение энергии электрона в
потенциальном поле — Gq(x), а второй интеграл представляет
просто энергию свободно колеблющейся струны. Отсюда мы по-
лучаем важное правило построения функции Гамильтона такого
рода систем с взаимодействием: нужно взять полную функцию
Гамильтона частицы и добавить к ней функцию Гамильтона сво-
бодно колеблющегося поля.
г) Квантование. Для того чтобы прийти к квантованию, сле-
дует подчинить функции я* = — (Й. /?i)ij3+ и if тем же, что и рань-
ше, перестановочным соотношениям, т. е. перестановочным со-
отношениям для ферми-частиц A3.8). Далее следует подчинить
яв и q перестановочным бозе-соотношениям, которые справедли-
вы для колебаний решетки или колебаний струны. Поскольку
ij;+, ij) и я„, q относятся к различным системам, далее следует
потребовать, чтобы пары операторов различных систем между
собой коммутировали:
[ф+.Ы, я,и')]=0, [ф(ж), я,(х')]=О, A5.12)
[¦ф+0г), </(#.')]= О, 1ф(ж), q(z')] *=0. .;
§ 15} ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯМИ 127
Это правило можно заимствовать из обычной теории Шредингера
для системы многих частиц или аксиоматически положить в ос-
нову рассмотрения проблемы взаимодействия.
д) Разложение по собственным функциям. Последний шаг
мы делаем, также основываясь на далеко идущей аналогии с
рассуждениями предыдущих параграфов. Там было проведено
разложение по собственным функциям как отклонений решетки
q(x), так и волновой функции электрона. Поскольку проблема
отыскания собственных функций оператора Гамильтона A5.11)
чрезвычайно сложна и на самом деле является важнейшей зада-
чей квантовой теории поля, не имеет смысла проводить разло-
жение Я по собственным функциям соответствующего классиче-
ского уравнения.
Лучше обратиться к разложениям по собственным функци-
ям несвязанных волновых уравнений. Итак, воспользуемся раз-
ложениями
A5.14)
Перестановочные соотношения между операторами ак и «ft*, а так-
же Ьш и btj те же самые, что и раньше (см. A3.4—13.6),
A0.18)). Из A5.12), напротив, сразу следует, что операторы обе-
их систем между собой коммутируют:
] К, М = [ah, bt] = [at, bw] = [at, b+] = 0. A5.15)
Теперь обозначим кратко в A5.11) отдельные интегралы в
порядке их следования через Но, зл, #0, р, Низ, после чего опе-
ратор Гамильтона примет следующий общий вид:
Н = Н0.о. + Но.р + Н„. A5.16)
Если теперь ввести разложения A5.13) и A5.14) в соответству-
ющие выражения в A5.11) и A5.16), то для первых двух членов
мы получим уже хорошо известные нам выражения
<15.17)
A5.18)
В последующем изложении мы будем очень часто применят*
12Й ИЁАНТОВАНЙЕ ПОЛЯ (ГЛ. Ill
следующее сокращенное обозначение:
Яо s Я0,эл + Я0,р see 2 Т55Г а* я* + 2 *«>»ЙЬ». A5.19;
ft U!
fe ~~ 2т '
Новым является для нас вычисление оператора Гамильтона взаи-
модействия Явз, который после подстановки разложений A5.13)
и A5.14) принимает следующий вид:
Для дальнейшего вычисления вынесем все выражения, по
которым не проводится интегрирование, за знак интеграла. Тог-
да перед интегралом получаем суммы по w, к, к', а также про-
изведения операторов bw -\- btw и afc, ah>. Далее, наконец, стоят
числовые множители и сам интеграл. Это последнее произведе-
ние обозначим кратко через fiGbh'w Тогда Явз принимает вид
Явз = 2 , (К + btw) atah.%Gkk.w. A5.21)
Явное выражение для GhWw имеет следующий вид:
ь
G^u, — ТГЪ1* \ pUw-k+h')Xf}r Dг. рр\
о
Поскольку интеграл по х является символом Кронекера, выра-
жение A5.22) принимает вид
у
A5-23)
Для этого выражения в свою очередь введем сокращенное обо-
значение
Ghh'w = gw&h,h'+w- A5.24)
После этих преобразований мы можем теперь выписать вы-
ражения для полного гамильтониана. Оно имеет вид
Н = Яо + Явз =
+ 2 (ahbwak+wgw + ah+wdhbwgwy\- A5.25)
h,w
§ 15] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯМИ 129
При этом мы сразу учли символ Кронекера A5.24). В последу-
ющем изложении будет использоваться сокращенное обозначе-
ние, указанное в выражении A5.25):
Как мы увидим позже, выражения, которые будут получены
для случая взаимодействия между электронами и колебаниями
решетки, а также для взаимодействия между электронами и све-
том, имеют очень похожую, если не тождественную структуру.
Выражение A5.25) является основой для многих исследований
взаимодействующих полей, и на протяжении книги мы познако-
мимся с целым рядом методов решения соответствующего гамиль-
тониану A5.25) уравнения Шредингера.
Примечание. Построение средних значений и матричных
элементов делается, как и раньше (§ 4 и § 13), с помощью при-
веденных там правил.
Задания к§ 15
1. Исключаем связь между полями и ищем решения уравне-
ния Шредингера
Н0Ф = 12 ЪЧ($Ч + Ц b(owbwbw\ Ф = ЕФ. ' (А 15.1)
w
J
Показать, что оно дается выражением
ФМ = П DРП тЦСйГ-ф., (А 15.2)
к w у mw\
причем щ = О, 1; щ = 0, 1, 2, ..., и
а&Фо = 6шФо = 0 для всех к, w. (A 15.3)
Соответствующие собственные энергии имеют вид
2 2 (A 15.4)
k
Если индексам к и w сопоставить целые числа 1, 2, 3, ..., то
выражение (А 15.2) принимает следующий явный вид:
• •'х
Указание. Подставить (А 15.2) в (А 15.1) и применить
перестановочные соотношения, а также (А 15.3).
9 X. Хакен
J30 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ill
2* Показать, что общее решение зависящего от времени урав-
нения Шредингера
(А 15.5)
имеет следующий вид:
Ф = 2 c{nh,mw)e ^V.".)- <А 15)
Сумма берется по всем возможным комбинациям
(щ, П2, ...; т\, mi, ...) с щ = 0, 1; т, = 0, 1, 2, ...
Коэффициенты — любые.
Указание. Подставить (А 15.6) в соответствующее завися-
щее от времени уравнение A5.1) и учесть, что решение (А 15.2)
является решением независящего от времени уравнения Шре-
дингера.
3. Доказать, что
= 8 /8 /...8 , ...8 /...8 , .../m4, (A 15.7)
nlnl n2n2 nfcnfc+l m1m1 mwmw-i
а также, что
,Л, r,k,...,m,,...,mm,...\akbi\^t> i t \ =
- 2. • ft» • l- > №• I « i nx,nv...,n]{,...,mxt...,ma},.../
= 8 /8 /...8 / ...6 '...8 / .. .V mw 4- 1.
(A 15.8)
В (А 15.7) и (А 15.8) nan' принимают значения лишь 0 или 1.
§ 16. Методические приемы: представление
взаимодействия и представление Гейзенберга "
а) Представление взаимодействия. В этом параграфе мы об-
судим некоторые „методические приемы, а именно, так называе-
мые представление взаимодействия и представление Гейзенбер-
га. Эти «представления» никоим образом не ограничены только
квантовой теорией поля. Они появляются уже в обычной кванто-
вой теории, однако мы не предполагаем здесь, что читатель зна-
ком с ними.
') Результаты этого параграфа будут использованы сначала в § 27, а
затем, начиная с главы V.
§ 16] ПРЕДСТАВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ГЕЙЗЕНБЕРГА 131
Во многих практически важных случаях оператор Гамильто-
на можно разбить на две части:
1) одну часть Но, которая описывает движение свободных
частиц, когда можно считать, что нам известны решения соот-
ветствующих уравнений Шредингера,
2) и другую часть, представляющую взаимодействие между
одинаковыми или разными частицами: Нвз.
В этих обозначениях, следовательно, уравнение Шредингера
имеет следующий вид:
| (#о + Я„)ФШ = ЙФ(«). A6.1)
В этом представлении, которое называется представлением Шре-
дингера, операторы не зависят от времени, а функция состояния
Ф, напротив, зависит от времени. Кажется удобным упростить
уравнение A6.1), используя то, что решение простого уравнения
Шредингера
#оФ°(*) = i№4t) A6.2)
уже известно. Для последующего достаточно даже, если это ре-
шение известно лишь формально. Запишем решение A6.2) в виде
Ф°(«) = иШФЧО), A6.3)
где оператор U'(t), действуя на начальное состояние Ф°@), дает
искомое решение Ф°Ш. Оператор U можно представить в виде
следующей экспоненциальной функции:
U = е Л . A6.4)
Доказательство того, что A6.3) вместе с A6.4) удовлетворяет
уравнению A6.2), проводится, как в случае обычного дифферен-
циального уравнения первого порядка, подстановкой экспонен-
циальной функции в уравнение и дифференцированием. Хотя Но
является оператором, этот метод применим и здесь, поскольку
Hq коммутирует сам с собой и, следовательно, с A6.4). Для ре-
шения A6.1) мы сделаем совершенно аналогичную A6.3) замену
в виде
| Ф = С/Ф, A6.5)
причем функция Ф еще неизвестна. Эта процедура является ана-
логом метода «вариации постоянной» в теории обычных диффе-
ренциальных уравнений. Если подставить A6.5) в A6.1), пере-
множить члены в левой части и выполнить дифференцирование
в правой части, то сразу получаем
H0UO + НвгиФ = ЯоС/Ф + i %иФ. A6.6)
J32 КВАНТОВАНИЕ ПОЛЯ [ГЛ. Ш
Члены с Но в уравнении A6.6), очевидно, выпадают, а остав-
шиеся члены уравнения мы умножим слева на U~l и введем
краткое обозначение
I U-*HS3U = HBS, A6.7)
после чего окончательно получим уравнение следующего вида:
1 ЯВЗФ=ШФ. A6.8)
Новый оператор взаимодействия Нт содержит Но теперь в экспо-
ненциальной функции (см. A6.4)), поэтому могло бы показаться,
что проблема стала только существенно сложнее, поскольку ведь
сначала нужно определить Йвз. На самом деле, однако, мы мо-
жем вычислить Явз очень просто. В качестве конкретного при-
мера рассмотрим Гамильтониан Нвз, который встретился нам в
предыдущем параграфе и который описывает взаимодействие
между электронами и колебаниями. Типичный член суммы Нвз
(см. A5.21)) имеет вид
. A6.9)
Преобразуем теперь A6.9) с помощью следующего приема: пред-
ставим единичный оператор в несколько необычном виде
1 = u-*U. A6.10)
Тогда выражение A6.9) преобразуется к виду
(С/" V-f/) (U'WU) (U^byyU). A0.11)
Рассмотрим теперь подробно первый член
еп а?.е п . A6.12)
Опираясь на рассмотренный в предыдущих параграфах пример,
представим Но в виде суммы двух членов: электронного вклада
и вклада от колебаний решетки
#„ = 2 Йека^ак + 2 ftoow&+6w. A6.13)
Поскольку электронные операторы коммутируют со всеми фо-
нонными операторами, то все фононные операторы, встречаю-
щиеся в Но в A6.12), выпадают. Равным образом можно принять,
что все операторы (&> коммутируют со всеми произведениями
ajj"ak для k=5^k', при этом сами операторы между собой антиком-
мутируют, но при двойной перестановке знак остается прежним.
§ 16] ПРЕДСТАВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ГЕЙЗЕНБЕРГА
Таким образом, наша задача состоит теперь в том, чтобы найти
выражения вида
e^4-%<<flk+,e-*W'^ A6Л4)
Эта задача, однако, уже была решена в § 14:
U^a^U = f(t) = еЕк''а?. A6.15)
Остальные присутствующие в A6.11) члены могут быть опреде-
лены совершенно аналогичным образом (см. §§ 14, 5). Таким
образом, мы получаем
U'WU = e'^W A6.16)
и
U'^U = e~iffl»V A6.17)
Ради полноты добавим еще одно соотношение
U^biU = eia^b+. - A6.18)
Из этого рассуждения становится очевидным, что все произ-
ведения операторов а, а+, Ъ н Ь+ можно, применив замены
A6.15—16.18), простым образом перевести в представление взаи-
модействия. Для нашего конкретного примера оператор Гамиль-
тона A5.25) переходит в следующий оператор Гамильтона в
представлении взаимодействия:
2
k,w
W ^1гк'а^). A6.19)
б) Представление Гейзенберга. В предыдущем разделе мы
воспользовались формальной возможностью решить уравнение
Шредингера с гамильтонианом Но. В представлении Гейзенберга
мы пойдем еще дальше, формально решив уравнение Шредин-
гера
| HO(t) = i%Q>(t), A6.20)
т. е. уравнение, относящееся- ко всей проблеме в целом, включая
взаимодействие, с помощью подстановки
-4-я*
ф(г) = е п ф@). A6.21)
Разумеется, мы ничего не выигрываем, применив это формальное
решение, поскольку явное вычисление оператора, представлен-
ного в виде экспоненциальной функции, в общем, сопряжено с
134 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
большими трудностями. Тем не менее подход A6.21) приводит
к новому способу решения. Как нам известно из совершенно
общих соображений, в квантовой теории в конечном счете имеет
значение лишь сравнение измеренных величин со средними ве-
личинами, которые можно представить в виде
<ФЫ1Ф>. A6.22)
Если в A6.22) подставить функцию A6.21), то, учитывая опре-
деление среднего значения A6.22), получим выражение
\
\Ф@)
еп Ае h
Ф@)/. A6.23)
При этом действие множителя e~(</W перенесено на А. Выраже-
ние A6.23) можно интерпретировать совершенно новым образом,
а именно, что теперь следует вычислить среднее значение ново-
го оператора
¦±-Ht —T-Ht л
eh Ае п =А, A6.24)
относящегося к начальной волновой функции Ф@). В представ-
лении Гейзенберга операторы зависят or времени, а функции
состояния, напротив, от времени не зависят.
Для дальнейшего учтем, что для А—И уравнение A6.24)
принимает вид
Не п = # = #.
Поскольку начальные волновые функции конкретной физической
-проблемы задаются заранее, то задача состоит в том, чтобы'
найти поведение во времени оператора A6.24). Продифференци-
ровав А по времени, можно очень легко найти уравнение, кото-
рому удовлетворяет оператор А. Тогда сразу получаем
Таким образом, уравнение A6.25) является уравнением движе-
ния операторов в представлении Гейзенберга. Ради простоты мы
предположили, что оператор А явно от времени не зависит. Для
вычисления коммутатора Ш, А] в явном виде нам нужны пере-
становочные соотношения. Теперь мы покажем, что при переходе
от представления Шредингера к представлению Гейзенберга пе-
рестановочные соотношения (для одного и того же момента вре-
мени) остаются да силе, если повсюду сделать замену А -*• А,
В-+В.
§ 16] ПРЕДСТАВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ГЕЙЗЕНББРГА 135
Для доказательства будем исходить из коммутатора
[А, В]-С A6.26)
(А, В, С — операторы). Умножим это выражение слева на
е<г/П)Ш, а справа — на e~{l/h)Hi. Тогда левая часть A6.26) примет
вид
4-Ht -4-Ht
еп (АВ-ВА)е п ==
¦i-m ~Ht -r-Ht —г-ж 4-я j -4-Ht ±-m -4-m
==eft Ае h eh Be h -eh Be h eh Ae h =в
ВА=в[А,В]. A6.27)
Правая часть непосредственно переходит в С, так что имеет ме-
сто равенство
[А, В] =С. A6.28)
Тот же результат справедлив, естественно, и для плюс-переста-
повочных соотношений.
Для пояснения уравнения A6.25) рассмотрим теперь конк-
ретный пример.
Пример. Взаимодействие между колебаниями и электронами
(см. § 15). В качестве величины А мы выберем оператор Ь+.
В представлении Гейзенберга этот оператор становится операто-
ром Ь+, который, согласно A6.25), удовлетворяет уравнению
Ь+ = 4-К#о + Явз), 6+J. A6.29)
Каким образом следует получить входящие в это уравнение Но
и #вз из Но и ЯВЗ) мы покажем на следующем примере: #0 =
%+
Согласно A6.24) справедливо равенство
~-т -4-я*
т 4я*
Яо = Imen b+be n ,
которое обычным образом, вставив «1» между операторами Ь+
и Ь, можно преобразовать к виду
4-Ht -4-ж 4-я< -4-я*
b+e h en be ,
1и-
т. е. к виду Но = %tob+b.
Этот пример позволяет вывести следующее правило: переход
от операторов Но, Нъз к операторам Но, Н„ осуществляется
136 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
с помощью следующих замен в операторах:
b —*¦ b, 6+ —*¦ b^, a —*¦ й, й+ —*¦ п+.
Часть выражения A6.29), которая относится к оператору Яо:
~[Й0,Щ A6.30)
можно легко вычислить, поскольку все операторы bw с различ-
ными w между собой коммутируют.
Таким образом, при образовании коммутатора A6.30) из все-
го оператора Но нам нужно учесть только член ^уммы с w. Ис-
ходя из перестановочных бозе-соотношений [frw, 6^'] = SW>W'> для
A6.30) сразу находим
i(ow&+. A6.31)
Аналогичным образом можно поступить со второй частью выра-
жения A6.29):
4rWm,btl A6-32)
Поскольку операторы b? между собой коммутируют, то с са-
мого начала в выражении A5.21) для Ньз все члены с Ъ^,
можно опустить. Поскольку, кроме того, все операторы bw' при
w^w' коммутируют с Ь-?, от суммы A5.21) остается один-един-
ственный член с w. На основании перестановочных бозе-соотно-
шений и предыдущего рассуждения A6.32) переходит в следую-
щее выражение:
A6.33)
Если теперь собрать вместе A6.31) и A6.33), то вместо уравне-
ния A6.29) мы получим в явном виде уравнение движения для
операторов Ь^ нашей задачи взаимодействия между электрона-
ми и колебаниями:
A6.34)
Совершенно^ аналогичным образом получаются уравнения для
операторов bw:
bw = — ia>w&w — г S Sw«k «k+w A6.35)
k
Эти уравнения чрезвычайно полезны потому, что они очень
сильно напоминают классические уравнения движения: если бы
§ 16] ПРЕДСТАВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ГЕЙЗЕНБЕРГА 137
операторы а+ и а были классическими величинами, то в рамках
теории колебаний решетки, которые возбуждаются классически-
ми силами (суммы по к в A6.34) и A6.35)), мы нашли бы точно
те же уравнения вида A6.34) и A6.35) для классических ампли-
туд b и Ъ+ (см. к этому задание 1). Эта тесная аналогия во мно-
гих случаях оказывается чрезвычайно полезной, поскольку она
позволяет решать уравнения вида A6.34) и A6.35) совершенно
аналогично уравнениям классической физики.
Задания к§ 16
1. Рассмотрим особый случай Ньа = 0. Используя для Но вы-
ражение A6.13), показать:
а) если решение уравнения
„ (А 16.1)
в шредпнгеровском представлении имеет вид
ф = в-«е1+1В1Ш1)»а+ --L (bt)mi Фо, (А 16.2)
причем Фо является вакуумным состоянием, то решение
1%Ф = 0 (А 16.3)
имеет в представлении взаимодействия следующий вид:
ф = в+_Ц(Ь+)'»'фв, (А 16.4)
и, в совершенно общем случае,
б) если решение (А 16.1) имеет вид
ф = S <ч«к,ж№)е
то соответственно решением (А 16.3) является
Ф=2^к,МФН,М. (А 16.6)
Указание. Применить преобразования A6.5), A6.4), правила
A6.15) и A6.18), а также равенство
_±н t
е п ° Фо = Фо. (А 16.7)
Последнее равенство доказывается с помощью разложения экспо-
ненциальной функции в ряд при учете того, что #оФо = 0.
138 КВАНТОВАНИЕ ПОЛЯ [ГЛ. III
2. а) Классическая функция Гамильтона гармонического ос-
циллятора, находящегося под воздействием вынуждающей силы,
имеет вид
(A 16.8)
Переписать уравнения Гамильтона для р и q в новых перемен-
TTT-TY
ных
и сравнить результат с (А 16.11) и (А 16.12).
б) Показать, что оператору Гамильтона
+hF(t)b+ (A 16.10)
отвечают следующие уравнения движения:
Ь+ = шЬ+ + iF*(t), (A 16.11)
Ь = - ивЬ - *F(t). (A 16.12)
При этом Fit) является классической «силой».
Решить (A16.ll) и (А 16.12) со следующими начальными
условиями (почему?):
6@) = 6, V@) = &+, (A 16.13)
причем операторы Ь+ и Ь заданы в шредингеровском представ-
лении. Убедиться с помощью решения, что bit), b+U) для всех
моментов времени удовлетворяют соотношению [Ь, Ь+] = 1. Вы-
числить <Фо1ЫФо> при ЬФо = О и сравнить результат с резуль-
татом задания 4 в § 6, причем положить F = — щ (^ — действи-
тельная величина).
i 3. Вывести уравнение для фермиевского оператора уничтоже-
ния ty(x, t) в представлении Гейзенберга, используя (см. A3.30))
§ 16) ПРЕДСТАВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ГЕЙЗЕНБЕРГА 139
заданный ниже гамильтониан
Н =
4~ f D+ (х) г|)+ (х'), " , ф (х') ф (х) d*xdsx'. (A 16.14)
J 0 | х — х |
Решение:
, t) r—^- г ф (x', t) $ (x, t) d3x'. (A 16.15)
| X — X I
4. С помощью оператора Гамильтона A5.25) вывести урав-
неиня движения для произведения операторов «к,«к-.,.
Г л а в а IV. ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ»
РЕШЕТКЕ
§ 17. Электроны в кристаллической решетке: краткое
изложение теории Блоха
Мы рассматриваем кристаллическую решетку, атомы которой
расположены в пространстве строго периодично и покоятся. Тем
самым мы временно не учитываем колебаний решетки. Каждый
электрон в кристаллической решетке движется в электрическом
поле атомных ядер и всех остальных электронов. Таким образом,
речь идет о чрезвычайно сложной проблеме многих частиц.
В блоховской теории электро-
нов в кристаллической решет-
ке проблема многих электронов
сводится к одноэлектронной
?-^ ' /^N. /***\—У^ч д?< сводится к одноэлектроннои
\/ \/ \/ \ ' проблеме следующим образом.
'' н w ' Представим себе, что действие
„ „ _, атомных ядер и всех остальных
Ряс. 2о. Общий вид изменения по-
тенциала решетки. электронов на выделенный
электрон можно описать в це-
лом, задав наперед поле потенциала F(x). Поскольку элементар-
ные ячейки решетки расположены строго периодично, то этот
потенциал тоже должен обладать периодичностью решетки
(рис. 25). Это свойство мы отобразим формулой
+ l)=F(x), A7.1)
где 1 — один из векторов решетки, т. е. вектор, проведенный из
одной точки решетки к следующей. Одночастичное уравнение
Шредингера, как известно из обычной квантовой механики, име-
ет вид
#<р а (- ?- Д + V (х)) Ф (х) = Яср (х). A7.2)
Теперь мы извлечем пользу из периодичности потенциала V.
Для этого определим «оператор трансляции» Т следующим свой-
ством: если оператор Т действует на некоторую функцию Fix),
то координата хъ F заменяется на х +1:
TF<x)=Fix + \).
§ 17] КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРИИ БЛОХА 141
Выберем в качестве функции Лх)=Я(х)ф(х) и примем во вни-
мание, что в силу A7.1) справедливо равенство
Шх)=#(х + 1)=Я(х).
Тогда получим Шх)ф(х)= Я(х)ф(х + 1)= Жх)Гф(х), или, после
небольшого преобразования, (ТН(х)— Жх)Г)ф(х)= 0. Поскольку
это равенство справедливо для любой функции ф(х), то отсюда
следует, что в квантовой теории
ТП-НТ = 0. A7.3)
Поскольку Т и Н коммутируют, волновую функцию ф(х) соглас-
но основным правилам квантовой механики можно выбрать так,
что она будет не только собственной функцией оператора Н со-
гласно уравнению A7.2), но и собственной функцией оператора
трансляции Т:
2\р(х)=Лф(х). A7.4)
Тогда га-кратное применение оператора трансляции к функции
ф(х) приводит к га-кратному умножению ср(х) на X:
Г"Ф=*Х"ф. A7.5)
Поскольку Г"ф(х) есть не что иное, как ф(х+га1), которая со-
гласно условию нормировки должна быть ограничена, то отсюда
следует, что и АЛр(х) также должна быть ограничена. Поскольку
ф(х) не может быть тождественно равна нулю, то X по величине
определенно не может быть больше единицы. С другой стороны,
X по величине не может быть и меньше единицы, так как в про-
тивном случае при движении в отрицательном направлении A за-
меняется на — 1) вновь придем к утверждению, что ф неограни-
чена. Поэтому должно иметь место равенство
1X1=1. A7.6)
Для того чтобы удовлетворить условию A7.6), представим X в
виде')
X = eikl. A7.7)
С помощью A7.7) соотношение A7.4) можно сформулировать
следующим образом:
ф(х + 1)=е'к1Ф(х). 017.8)
Для того чтобы удовлетворить функциональному соотношению
A7.8), представим ф в виде
| ф(х)= elk*Hk(x). A7.9)
') В согласии с большинством оригинальных работ мы обозначаем
волновой вектор электронной волны через к.
142
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
Подстановка A7.9) в A7.8) приводит к утверждению, что функ-
ция и периодична с периодом решетки:
| uk(x + l)=uk(x). A7.10)
Соотношения' A7.9) и A7.10) представляют собой георему Бло-
ха: собственные функции в бесконечно протяженной решетке
имеют вид плоских волн, модулированных е периодом решетки
(рис. 26). Проблема теперь, собствепно, состоит в том, чтобы
определить функции ц(х) при заданном потенциале V. Если под-
ставить A7.9) в уравнение Шредингера A7.2), то после элемен-
тарного вычисления получается следующее уравнение для и:
«к
= EkJuk (х).
A7.11)
и (со)
6)
Из этого уравнения вытекает, что и, а следовательно, и энергия
Е зависят и от волнового вектора к как от параметра. При фик-
сированном к уравнение A7.11)
допускает ряд собственных зна-
чений, которые поэтому следует
обозначить еще одним индексом
/. Следует ожидать поэтому, что
Е, с одной стороны, непрерыв-
ным образом зависит от к, ас
другой стороны, зависит от диск-
ретных индексов /. Для определе-
ния и и Е следует прибегнуть
либо к точно решаемым простым
моделям, либо к приближенным
методам, таким, например, как
теория возмущений или числен-
ные i методы решения. Определе-
ние зависимости энергии Ек, , от
к и / является важной задачей,
которую, однако, нам нет необхо-
димости здесь обсуждать, по-
"J скольку она ничего не дает для
Рис. 26. Елоховская волна пред- понимания квантовой теории поля.
ставляет собой плоскую волну Поэтому мы сразу приведем важ-
ртодоКГ?ешЯеткиДфЖВиейаи (б)" нейший результат, наглядно пред-
кривая (в) представляет деист- ставленный на рис. 27. Энер-
вительную часть результирую- гии как функции к расположе-
щей блоховскюй волны. ' ны полосами, т. е. так называе-
мые . разрешенные зоны переме-
жаются запрещенными зонами. В конечном кристалле в распоря-
жении электронов внутри этих полос имеются тесно расположен-
ные дискретные состояния {к =.2nn/L), Эти состояния, соглас-
§ 17]
КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРИЙ БЛОХА
143
но принципу Паули, могут заполняться снизу электронами с
двумя противоположно направленными спинами. Последнюю за-
полненную полосу обычно называют валентной зоной, а первую
пустую или частично заполненную зону — зоной проводимости.
Поведение электронов в кристалле, в особенности на краю
зон, в нашем случае при к. = 0, легко понять. Например, как
ясно из рис. 27, энергию Е на краю зоны можно разложить по
к и для достаточно малых значений к представить в виде
Zit i = tin ! -+- „ Г- A ( .1Z)
(B A7.12) мы ограничились простейшим случаем изотропной
зоны. В этом случае разложение начинается с члена, пропорцио-
нального квадрату величины к2.)
Зависимость A7.12) находится в
полном согласии со случаем свобод-
ных электронов, с той лишь разни-
цей, что теперь масса пг* совершен-
но отлична от массы свободного
электрона. Этот множитель пг*, на-
зываемый также эффективной или
кажущейся массой, может быть не
только существенно больше, но и су-
щественно меньше, нежели в случае
свободного электрона.
Эта аналогия между электроном
в кристалле и свободным электро-
ном, однако, простирается сущест-
венно дальше. Рассмотрим для это-
го волновой пакет, образованный
из волн вида A7.9) в окрестности
некоторого значения волнового чис-
ла к. Тогда легко показать, что
групповая скорость v этого волно-
вого пакета может быть представле-
на обычным образом в следующем
виде:
Рис. 27. Энергия валентной
зоны и зоны проводимости
как функция к. Вертикальные
черные участки на оси Ей
представляют собой проекции
разрешенных значений энер-
гии. При этом возникают зо-
ны, разделенные запрещенны-
ми областями. При поглоще-
нии и испускании электроны
совершают вертикальный пе-
реход между зонами (штри-
ховая стрелка).
Если теперь применить соотношение Е ¦
представить в виде
v~ П дк1
или, в трехмерном случае, в виде
I v = -^-gradkE.
%а, то A7.13) можно
A7.14)
A7.14а)
144 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Если воспользоваться для Е выражением A7.12), то получим
применяемое в случае свободных электронов соотношение между
импульсом ftk и скоростью v:
~. A7-15)
Таким образом, в присутствии внешних полей электрон ведет
себя совершенно как свободная частица с эффективной массой
№*, если только эти поля достаточно медленно изменяются в
пространстве и времени (см. § 18). Так, например, в присутст-
вии электрического поля F справедливо следующее уравнение
движения:
| m*'v^Tik=eF. A7.16)
Из сказанного следует, что зонная модель позволяет ввести
формулы для электрической проводимости, причем электроны
можно считать свободными частицами. Далее, эта модель пока-
зывает, что электрическая проводимость возникает при наличии
отдельных (или многих) электронов в зоне проводимости, а для
до конца заполненной зоны она равна нулю, что приводит
к естественному различию между изоляторами и проводни-
ками. Далее, зонная модель позволяет сделать предсказания
относительно оптического поглощения. Оказывается, что при
оптическом переходе имеет место так называемое правило отбора
по волновому вектору к, которое гласит, что электроны при оп-
тическом возбуждении переходят из валентной зоны в зону про-
водимости с сохранением их волновых
векторов к (см. рис. 27). На основе этих
представлений получается следующий ход
кривой поглощения. При малых энергиях
фотонов электроны не могут перейти
из валентной зоны в зону проводимости.
-U-—з—*?,. Если энергия возрастает до величины,
позлмцения равной ширине запрещенной зоны, то
переход становится возможным и тогда
Рис. 28. Коэффициент можно ожидать появления полосы погло-
цГТас^^с^а*5^ "W Ви«а- представленного на рис. 28.
межзонном переходе Несмотря на многочисленные успе-
(схематически), хи, зонная модель имеет, однако, су-
щественные недостатки, из которых
мы упомянем следующие:
1. Мы исходим из решеточного потенциала F(x), который
периодичен с периодом решетки, однако этот потенциал должен
быть определен, собственно говоря, через взаимодействие элект-
ронов между собой.
а
§ 18] МЕТОД ЭФФЕКТИВНОЙ МАССЫ 145
2. Если из валентной зоны удаляется электрон, то в ней
остается незанятое состояние (дырка), которая ведет себя, как
известно из эксперимента, как самостоятельная частица с поло-
жительным зарядом и определенной эффективной массой. Сле-
довательпо, нужно доказать, что система из N электронов в ва-
лентной зоне ведет себя в точности как отдельная частица, что
можно сделать удовлетворительным образом только в рамках
метода вторичного квантования. Уже эти примеры показывают,
что рассмотрение проблемы многих электронов (в особенности в
рамках метода вторичного квантования) представляет собой
первоочередную задачу теории твердого тела. На этих проблемах
мы остановимся в §§ 20, 21 и 22.
3. Кривая поглощения, представленная на рис. 28, обнаруже-
на не во всех объектах. Часто на подобную полосу поглощения
накладываются более или менее широкие дискретные линии,
которые происходят не от дефектов структуры, а являются свой-
ством системы электронов матрицы решетки. Поскольку эти ли-
нии не могут быть предсказаны в рамках зонной модели, сле-
дует включить в рассмотрение принципиально новые соображе-
ния в рамках теории многих частиц (§§ 23, 24).
§ 18. Метод эффективной массы
В этом параграфе будет доказано основополагающее для фи-
зики твердого тела
Предложение. Электроны, находящиеся в периодическом поле
кристалла вблизи нижнего края зоны проводимости, под воздейст-
вием дополнительного медленно меняющегося поля ведут себя как
электроны в свободном пространстве, но с эффективной массой ш*.
Это предложение утверждает, таким образом, что решеточный
потенциал можно полностью исключить, если заменить массу
электрона m на эффективную массу /га*.
Для доказательства этого предложения придадим ему преж-
де всего строгий математический вид. Для этого введем следую-
щие обозначения и предпосылки:
Пусть F(x)— периодический с периодом решетки потенциал.
Пусть W(x) — потенциал дополнительного поля. Это поле
должно меняться в кристалле столь медленно, что внутри одной
элементарной ячейки оно может считаться постоянным.
Решение уравнения Шредингера для V(x) (т. е. без W{x)):
x) A8.1)
согласно теореме Блоха A7.9), A7.10) имеет вид
^ A8.2)
146 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
В этом решении_в явном виде из и^{х) выделен нормировочный
множитель 1/TiV (N — число элементарных ячеек в кристалле),
так что Мк (х) нормирована в элементарной ячейке.
Пусть /?к в точке к = 0 можно представить в виде
Й2/с2
/?к — Ей -J- 5—*+(члены более высокого порядка, которыми
можно пренебречь). A8.3)
Точная математическая формулировка гласит:
Собственные значения энергии и волновые функции проблемы
в целом с учетом решеточного потенциала У(х) и дополнитель-
ного потенциала W(x):
&А + vw + w
могут быть определены с помощью собственных значений энер-
гии и волновых функций значительно более простой проблемы:
° ~ &* А + W (
в следующем смысле:
1. Собственные значения энергий совпадают:
2. Если разложить ф(х) по блоховскнм волнам A8.2), а ф
по плоским волнам, то коэффициенты разложения скфункций
ф(х) и ty(x) тождественны:
тождественны!
В A8.7) V обозначает объем кристалла.
Если в A8.7) и тем самым также в A8.6) существенны лишь
коэффициенты с малым к, то в Мк(х) можно положить к« 0.
Тогда в A8.6) ж A8.7) получим следующее приближенное ра-
венство:
Следовательно, решение A8.4), которое мы ищем, имеет вид
произведения быстро меняющегося решеточного множителя щЫ)
и медленно меняющегося «модулирующего» множителя т|>(х).
§ 18] МЕТОД ЭФФЕКТИВНОЙ МАССЫ 147
Перейдем к доказательству утверждений 1 и 21):
а) подставим разложение A8.6) в A8.4) и получим уравне-
ние для коэффициентов Ct;
б) исходя из наших предположений относительно W(\) и Ек,
упростим это уравнение;
в) покажем, что это новое уравнение тождественно A8.5),
если применить разложение A8.7).
а) Подставляем A8.6) в A8.4), умножаем слева на фк- и ин-
тегрируем по объему:
J q? (х) Фк (х) йЧ. A8.8)
Учтем в левой части этого уравнения, что фк(х) удовлетворяет
уравнению A8.1), и введем следующее сокращенное обозначение:
(x).w (x) «**«* (х)d3x- (!8-9)
Воспользуемся, наконец, в обеих частях A8.8) ортогональностью
блоховских волн. Тогда получаем
ск-Ек> + 2 ckWk'k = Я**'. A8.10)
к
б) Упростим уравнение A8.10). Для Ек> используем A8.3).
Интеграл Wk-k A8.9) разложим в сумму по отдельным элементар-
ным ячейкам с радиусом-вектором 1: *
. A8.11)
1 элементарная
ячейка 1
Согласно предположению следует считать' W(x) внутри элемен-
тарной ячейки постоянной, так что Wix)= W(\) можно вынести
за знак интеграла.
Примем теперь, что основную роль в A8.6) и A8.7) и тем
самым также в A8.11) играют только малые значения к. (Соглас-
но соотношению неопределенности Ак Ах я* 1 это означает, что
волновой пакет A8.7) имеет большую протяженность Ах.) От-
сюда следует:
') Читатель, более интересующийся полевыми методами, это доказа-
тельство может пропустить.
10*
148 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ (ГЛ. IV
ба) член e~ik'xelkx мало меняется внутри элементарной ячей-
ки, поэтому может быть вынесен за знак интеграла;
бб) в Uf (х) и Мк(х) можно положить к' = к = 0 (иными сло-
вами, и* л и разлагаются по к' и к, причем членами высшего
порядка малости можно пренебречь). Тогда получаем
± 2 w
элементарная
ячейка 1
A8.12)
Поскольку функции и периодичны с периодом решетки и нор-
мированы на 1 внутри элементарной ячейки, выражение A8.12)
переходит в
Wfk = jf^W A) e№-k-)i. A8.13)
l
Теперь сделаем один шаг назад: поскольку W(x) и экспонен-
циальные функции меняются медленно, сумму по 1 можно пре-
образовать в интеграл по кристаллу (причем справедливо со-
1 V 1 Г \
отношение -^- ? ->¦ -у \ ... d3x , тогда получим
Wkk = JJ=e-*'x'JF(x') ^=eft«'dV, A8.14)
причем множители в этом выражении расположены несколько
по-иному. Теперь подставим A8.3) и A8.14) в A8.10), поменяв
порядок следования J" и S:
у? e~ik'x'w ^ 2 ^
A8.15)
Умножим это уравнение на 1/у Feik'x, учитывая, что к'2егк'х =
= — Дегк'х, и просуммируем по к':
2 ^'^ ^ (х/) 2с* у?eikx'd%x> = E 2с"' ^7? eik'x •
A8.16)
§ 19] ФУНКЦИИ ВАННЬБ 149
Если теперь положить ? ск' тт=е'кх = Ф (х) и учесть, что
к' VV
1-у- ^ eik'(x-x')l — g (х — х'), то получим прямо уравнение A8.5).
Тем самым наше предложение доказано.
§ 19. Функции Ваннье: волновые пакеты
из функций Блоха
Волновые пакеты, в частности из плоских волн, хорошо из-
вестны в квантовой теории. С их помощью можно локализовать
волновые функции частиц в определенном объеме пространства,
отобразив тем самым локализацию частиц. Ввиду близкой ана-
логии между блоховскнми и плоскими волнами можно попытать-
ся построить волновые пакеты такого рода из блоховских волн.
Это делается следующим образом:
причем сумма распространяется на все значения к внутри дан-
ной энергетической зоны. N — число элементарных ячеек. Функ-
ции, определяемые с помощью ряда A9.1), называются функция-
ми Ваннье. Они обладают целым рядом важных для теории твер-
дого тела свойств, которые мы рассмотрим ниже.
1. Функции Ваннъе описывают локализацию электрона в ок-
рестности точки 1 на протяжении примерно одной постоянной
решетки. Чтобы увидеть это, рассмотрим особый случай, когда
функции Uk(x) не зависят от к:
ик(х) =*> щ(х). A9.2)
В этом случае суммирование в A9.1) выполняется сразу и для
кристалла, который имеет форму куба, дает (с точностью до
некоторого фазового множителя)
w (х - 1) =
i sin {(* - У -f } sin {(У ~ У -?-} sin f(z - lz) -7-]
= -4=»0(«)— Ц—L Ц— Ц. A9.3)
Vn { - У ^} -i { ) {^}
Здесь a — постоянная решетки, a L — линейный размер кристал-
ла. Как легко убедиться, синусы в знаменателе можно заменить
150 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. XV
их аргументами, так что A9.3) переходит в выражение
A9.4)
Как легко видеть из поведения функций A9.4), волновые функ-
ции w действительно локализованы в области пространства с ли-
нейным размером а.
Прежде чем мы двинемся дальше, обсудим еще некоторое
обобщение A9.1). Нам придется часто иметь дело с функциями
Ваннье, которые принадлежат различным зонам. В этом случае
следует различать модулирующие функции Uk с помощью еще
одного индекса ц. Тогда и функция Ваннье зависит от этого
индекса ц.
2. Функции Ваннье, локализованные в различных точках 1,
Г или принадлежащие различным зонам ц, ц/, взаимно ортого-
нальны. Для доказательства этого положения образуем следую-
щее выражение:
J Wp (х — 1) цу (х — Г) d3x =
= ~ 2 в*1"*'1' f «-**«kf,»(х) е*'*и*.ж (х) d*x. A9.5)
кк- i. . •
Skk'Snn'
Поскольку блоховские функции различных зон или различных
значений к взаимно ортогональны, интеграл преобразуется в
произведение символов Кронекера. Тогда A9.5) переходит в вы-
ражение
Суммирование по к выполняется сразу же (см., например, § 7)
и вновь дает символ Кронекера для различных точек локализа-
ции. Тогда получаем окончательно следующее соотношение:
l (x - 1) ay (x - Г) d3x = в№.в,г. A9.7)
§ 20. Электроны в кристаллической решетке: формулировка
проблемы многих тел. Приближение Хартри — Фока
В этом параграфе мы сформулируем проблему многих элект-
ронов в твердом теле с помощью вторичного квантования. Для
этогд положим в основу следующую модель; электроны должны
§ 2U] ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ 151
двигаться в строго периодической решетке, ионы которой счи-
таются бесконечно тяжелыми п поэтому покоятся. Далее примем,
что электроны внутренних атомных оболочек учитываются в це-
лом тем, что они вместе с положительными атомными ядрами
создают эффективный, периодический с периодом решетки по-
тенциал Vp. Поскольку энергия кулоновского взаимодействия
между электронами дает наибольший из всех взаимодействий
между электронами вклад, то в дальнейшем мы учтем явно толь-
ко эту энергию. Однако общий формализм можно распространить
и на другие взаимодействия, например магнитное взаимодейст-
вие. Оператор Гамильтона состоит из трех частей: кинетической
энергии электронов, потенциальной энергии в периодической
кристаллической решетке и, наконец, кулоновского взаимодейст-
вия между электронами. Как мы уже видели в § 13, соответст-
вующее уравнение Шредингера имеет вид
-^Л + VP (x)} г|) (х) dsx +
'1 ф = ЕФ.
B0.1)
При этом функции г|)+(х) и гр(х) являются еще операторами,
которые удовлетворяют ферми-перестановочным соотношениям
из § 13. Разложим эти операторы по собственным функциям
фь(х) и фй (х):
B0.2)
B0.3)
Примем вначале, что эти собственные функции фЛ и уи образуют
полный набор ортонормированных функций. Однако мы не пред-
полагаем, что эти волновые функции являются решением урав-
нения Шредингера, а наоборот, мы хотим найти уравнение Шре-
дингера, для которого эти фь являются «оптимальными» собст-
венными функциями. Под этим понимается следующее. Мы
намереваемся установить эти волновые функции в рамках мето-
да Хартри — Фока. Эта процедура проводится следующим обра-
зом. Считается, что волновые функции нулевого приближения
заданы, затем определяют ноле потенциала, вызванного распре-
делением зарядов для этих волновых функций; отсюда вновь
находят волновые функции, соответствующие полю атомных
остовов и упомянутого выше распределения зарядов, затем эти
новые волновые ^функции используются в качестве исходною
152
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
пункта для следующего приближения (см. таблицу). Мы не бу-
дем, однако, повторять этот метод обычным образом, а дадим его
обоснование прямо в рамках вторичного квантования. Для этого,
как уже говорилось, будем считать, что имеются волновые функ-
ции фь, заданные в указанном ниже смысле, и создадим теперь
1.
Волновая функция
2.
Потенциал
3.
Новая волновая функция
Сравнение с 1.
Если 3. = 1., то конец, в противном случае про-
цедура продолжается
Новая волновая функция
Потенциал
и т. д.
некоторое состояние Ф электронов кристалла. Для этого будем
размещать электроны один за другим по состояниям &ь &2, ..., kN.
То есть в основу рассмотрения кладется функция состояния
t%.. .а?„Ф0.
Ф =
B0.4)
Используя эту функцию состояния B0.4), образуем среднее зна-
чение оператора Гамильтона B0.1) с дополнительным условием,
что эта функция состояния нормирована. Нормировка Ф включа-
ет, очевидно, нормировку введенных выше функций <р, так что
это дополнительное условие в последующем изложении будет
считаться выполненным.
Функция B0.4), конечно, не является точной, поскольку она
не учитывает корреляции между электронами. Если же мы хотим
получить оптимальную, т. е. в вариационном смысле минималь-
ную, энергию, нам потребуются еще произвольные параметры.
§ 20] ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ 153
Поскольку амплитуды ak и а& являются строго заданными
операторами с перестановочными соотношениями A3.4), A3.5),
A3.6), то единственными величинами, которые можно варьиро-
вать, являются волновые функции <pft. Поэтому наша цель со-
стоит в следующем. Потребуем выполнения условия
| <Ф!Я|Ф> = Минимум! B0.5)
с дополнительным условном
| <Ф|Ф> = 1 B0.6)
и вычислим выражение в левой части уравнения B0.5) как
функцию или, точнее говоря, как «функционал» ф4. Затем опре-
делим ф,, с помощью варьирования. Для того чтобы выполнить
эту программу, подставим B0.2) и B0.3) в уравнение Шредин-
гера B0.1). Поскольку операторы а+ и а не зависят от интегри-
рования, а волновые функции ср коммутируют с операторами,
операторы можно вынести за знак интеграла, после чего получа-
ем следующее выражение для оператора Гамильтона 77:
Im
imVm'
X qw (x') Ф«' (x) d3^ dsx'. B0.7)
Теперь следует построить среднее значение этого гамильтониана
на функциях состояния B0.4). Для этого следует более обстоя-
тельно обсудить различные средние значения для отдельных опе-
раторов а+, а. Начнем с выражения
^| af am \ at[.. . а^Ф0}. B0.8)
Z.am'av ф( (х)фт(х ) ,-, а
Для того чтобы провести вычисление этого выражения, рассмот-
рим в качестве вспомогательного средства рис. 29. Точки на
оси к обозначают здесь отдельные квантовые состояния, в кото-
рые могут быть помещены электроны. Действительно, занятые
состояния &i, &2, к3 и т. д. обозначены вертикальными отрезками.
Согласно соотношению B0.8), под действием оператора уничто-
жения ат один электрон в состоянии т должен быть уничтожен.
Если в этом состоянии электронов нет, то оператором уничтоже-
ния можно подействовать нешосредственно на основное состоя-
ние Фо, в результате чего получим нуль. Отличный от нуля вклад
получится только тогда, когда т равно одному из к. В примере,
приведенном на рис. 29, т = кг. Для того чтобы уничтожить
электрон в состоянии kj, следует переставить ат со всеми опера-
торами рождения, стоящими слева от оператора с индексом kj.
_L
154 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Учитывая антиперестановочные соотношения A3.4—13.6), по-
лучим множитель (—1) в степени числа перестановок. Далее
следует учесть, что ата^ = 8mthj — atjum. Поскольку теперь в со-
стоянии т больше электрона нет, действие оператора уничтоже-
ния на стоящее в B0.8) электронное состояние дает нуль. Поэто-
му в конце концов остается вычислить лишь выражение следую-
щего вида:
переста-
\llk . . ¦ djijJiJQ I п\ uk . . .flfc ¦_1^fe-i . • • •аклМ'о) ' \ — 1) \iuV.y)
Теперь перепесем оставшийся оператор рождения at на освобо-
дившееся место с индексом к,; при этом придется провести ровно
столько же перестановок,
сколько и прежде, в резуль-
тате чего знак минус в B0.9)
а) ~к, % ' X~~J~~i"—к~1< выпадает. Согласно A3.37),
' функции состояния с раз-
личными электронными за-
селенностями взаимно орто-
гональны. Теперь в B0.9)
-± jl- _i j_ !__-а*. слева стоит функция состо-
яния, в которой состояния
к\, к2, ..., kN заняты, а спра-
Ift f ва стоит функция, в которой
| , I , , К Равным образом заняты все
в) к, кг к3 к,, к состояния, вплоть до к}. Со-
стояние kj = т, напротив,
Рис 29. К вычислению среднего зна- переставлено с состоянием I.
чения B0.8). Согласно условию ортого-
нальности, выражение B0.9)
отлично от нуля только тогда, когда kj = I. Поэтому получаем
следующий результат для среднего значения B0.8):
I Я; ttm | fflfe ¦ . . Яд:уФо/ =
бтЬ если *» = &!,..., kN,
0 в остальных случаях.
Тем самым мы вычислили те средние значения, которые служат
мерой одночастичных операторов в B0.7).
Теперь рассмотрим средние значения для энергии взаимодей-
ствия, которая задается выражением
<Ф | ajа^пт-пу \ Ф>. B0.11)
Для наглядности вычисления B0.11) снова приведем картинку
(рис. 30).
201
ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
155
Вертикальные отрезки на оси к вновь обозначают занятые
состояния. Рассмотрим вначале действие оператора уничтожения
<Zj'. Отличный от нуля результат действия этого оператора полу-
чается только тогда, когда состояние kj = V. занято. Тогда функ-
ция состояния Ф переходит в
/ а\число перест. (I'^hj)
+
к, к,
к,, к
B0.12)
причем всякий раз вновь, когда необходимы перестановки, что-
бы перенести оператор уничтожения at> слева через операторы
рождения й/;. до места kj, по-
является множитель (— 1).
Пусть теперь оператор
уничтожения ат> действует
соответствующим образом
на состояние B0.12). Вновь
не равный нулю вклад по- [тг=к.
лучится только в том слу-
чае, если т' совпадает с од-
ним из оставшихся состояний
к\, &2, • ¦., kN (исключая со-
стояние kj) и вновь появится
множитель (— 1) в степени
числа перестановок. Из со-
стояния B0.4), занятого N
электронами, возникает за-
нятое N ¦— 2 электронами
состояние
Ч- * Ч- ч/
к,, к
к, к.
*s
к, к
X .. . а^. _ xat.+l.
У / .\4HcnonepecT.(I'-»fe
X
к,
кг
к, к
B0.13)
В результате последующего
действия обоих стоящих в
к4 к
Рис. 30. К вычислению среднего эначе-
B0.11) операторов рождения Ния B0.11).
af и а^из состояния B0.13)
вновь образуется состояние с N электронами, которое либо сов-
падает с первоначальным состоянием B0.4), либо может отли-
чаться от него. Если это состояние отличается от первоначаль-
ного, то выражение B0.11) обращается в нуль, так как новое
состояние B0.13) ортогонально старому состоянию B0.4), кото-
рое также стоит слева в выражении B0.11). Поэтому необхо-
156 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
дпмо исследовать, каким образом, применив операторы рождения
а^пт, можно восстановить старое состояние. Это возможно толь-
ко в двух случаях:
либо т = т', 1 = 1', B0.14)
либо т = 1', 1 = т'. B0.15)
Для того чтобы посмотреть, не появляется ли какой-либо знак
плюс или минус, вновь проведем все шаги по отдельности.
В случае B0.14) старое состояние возникает благодаря тому,
что рождение происходит точно в порядке, обратном уничтоже-
нию. Это означает, что перестановок сделано столько, что знак
минус пропадает.
В случае B0.14) в качестве результата получаем для средне-
го значения B0.11) следующее выражение:
<Ф|а(+а+ат<аг.|Ф>^5(г.6тт. для 1фт,1'фт'\ I, m = ku ..., kN,
= 0 в остальных случаях. B0.16)
Теперь рассмотрим второй случай B0.15). Ввиду того, что
последовательность операторов рождения в B0.11) с индексами
I и т изменена, этот случай сводится к предыдущему случаю
B0.14), так что в результате получаем
<Ф | atatxum'uv | Ф> =
= — <Ф | atnatam>av | Ф> ^ — btm.bmv Для 1фт,У фт'; I, т =
— /гь . .., kN,
= 0 в остальных случаях.
B0.17)
Результаты B0.16) и B0.17) можно объединить и предста-
вить одной формулой
<Ф | аг+Ятйт'Яг'| Ф> ={6ц<6тт<— бгт-бтГ} для 1фт,1'фт';
1,т= къ. .., kN>
= 0 в остальных случаях.
B0.18)
Тем самым задача вычисления отдельных средних значений га-
мильтониана B0.7) решена. Используя результаты, полученные
выше для средних значений, а именно B0.10) и B0.18), полу-
§ 20] ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ 157
чаем окончательное выражение для полной энергии в виде
j ч w{- ?-
"Г 2 J f
~ -f 2 j j Ф*; (х) Фй{ (*') [7^F| fpfti (х'} Ф*1(х) d%xdV' B0Л9)
Суммы распространяются только на запятые состояния k\,..., kN.
Как уже отмечалось ранее, это выражение для полной энер-
гии является функционалом отдельных волновых функций фл.
Теперь определим эти волновые функции так, чтобы выражение
для энергии B0.19) имело экстремальное значение. В качестве
дополнительного условия следует предусмотреть нормировку
волновых функции, которая выражается условием
J <р^Фл daar =--= 1. B0.20)
Для этого применим обычным образом параметр Лагранжа, ко-
торый обозначим Е. Проведение варьирования б/бср^(х) выраже-
ния B0.19) с дополнительным условием B0.20) приводит непо-
средственно к уравнению1)
2 1 щ^, Г ... Л
X
j * ' I x x' I
Фа, (x ) d x Фл (х) "
X <ph (x') <Px' cpfej (x) == Eqh (x). B0.21)
Для интерпретации уравнения Шредингера B0.21) рассмотрим
входящие в него члены по отдельности. Оба члена в фигурных
скобках представляют знакомую нам потенциальную и кинети-
ческую энергии электрона в периодической решетке кристалла.
Следующее выражение представляет произведение искомой вол-
новой фуНКЦИИ фь И СуММЫ ПО kj'.
Ф»(х)У(х), B0.22)
') Читателю, незнакомому с вариационным исчислением, напомним, что
определение б/бф^(Х) (в другом обозначении 6/Sg(x)) детально обсужда-
лось в § 9.
158 Электроны в «замороженной» решетке [гл. iv
причем
V (х)
J | ^ (х')|2 |7^F1 dV- <20'22а>
Поскольку |ф|2е имеет смысл плотности заряда, то сумма по kj
имеет смысл электростатического потенциала, вызванного рас-
пределением зарядов электронов в состояниях kj. Последнее вы-
ражение в левой части B0.21) имеет вид
-St^WVW- B0-23)
где
Akj,k 00 = j Ф^ (х') p^rj Фй (х') d4. B0.23а)
Буква А указывает на то, что член B0.23) обусловлен «обменом»
(по-немецки «Austausch») электронов. Если сравнить это выра-
жение с B0.22), то можно увидеть, что в этом выражении вол-
новая функция фй, которая ранее стояла за интегралом, теперь
поменялась местами с волновой функцией q>kj под интегралом.
Здесь речь идет, следовательно, о так называемом обменном ку-
лоновском взаимодействии.
Суммы по kj распространяются, как мы уже видели при вве-
дении этого выражения, только на занятые состояния. С помо-
щью сокращенных обозначений B0.22) и B0.23) уравнение
B0.21) может быть переписано в очень ясной форме
B0.24)
Отсюда еще раз следует, что У(х) представляет собой дополни-
тельный потенциал. Система уравнений B0.24) нелинейна, по-
скольку все волновые функции фА стоят также под суммами
v. виде множителей к ц>к. Для численного решения системы урав-
нений B0.24) был развит целый ряд методов, однако в задачу
этой книги не входит подробное изложение этих методов, по-
скольку это не является предметом квантовой теории поля.
Обычный метод решения этой системы состоит в том, что, как уже было
сказано, волповые функции нулевого приближения считаются известными,
затем строится потенциал в том виде, в котором он входит в уравнение
B0.24), а затем из получившегося интегро-дифференциального уравнения
определяются новые волновые функции ф*. Эти новые волновые функции
затем служат исходным пунктом построения следующего приближения. Эта
процедура сходится, если после нескольких повторений вновь получаются
те же самые волновые функции, которые были заложены в предыдущем
шаге (метод «самосогласованного поля»).
§ 20] ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ |>ЕП1ЕТКЁ 159
Уравнение Шрединтера B0.24) можно переписать в кратком
впде
) = {- ?¦ А -f Vm (х)} Фл (х) ^ ЁФй (х), B0.25)
причем следует ясно представлять себе, что Уэфф не является
обычным потенциалом, а содержит еще и обменный член. В об-
щем случае можно лишь утверждать, что потенциал FD44 также
является функцией, периодической с периодом решетки. (По-
скольку блоховские функции применяются в ц> «самосогласован-
ным» образом.)
Уравнение B0.25) имеет в точности такой же вид, что и урав-
нение, положенное в основу теории Блоха в § 17. Поэтому все
сделанные там высказывания относительно волновых функций,
а также энергетическая схема остаются в силе и здесь, что по-
зволяет дать лучшее обоснование зонной модели. Правда, не
следует упускать из вида, что нами использована весьма специ-
альная функция состояния, а именно B0.4), так что целый ряд
эффектов нами не учтен. В последующем изложении на приме-
рах будет показано, как могут быть рассмотрены эффекты, свя-
занные с так называемой корреляцией между электронами.
В рамках рассматриваемого формализма до сих пор не уточ-
нялось, насколько заполнены получившиеся зоны. Наше рассмот-
рение справедливо, в частности, для случая, когда валентная
зона заполнена полностью и имеется еще один электрон в со-
седней зоне — зоне проводимости. Для более полной характери-
стики волновой функции B0.4) добавим к квантовому числу к
еще квантовые числа V и L для валентной зоны и зоны прово-
димости соответственно. Для избыточного электрона (т. е. ва-
лентная зона заполнена и имеется только один электрон в зоне
проводимости) волновая функция имеет следующий общий вид:
Ф = at.L (at,,v4,,v • ¦ <,уф.)• B0-26)
Поскольку находящееся в скобках выражение представляет
функцию, которая описывает электроны в валентной зоне, кратко
обозначим его через Фу и в последующем изложении будем пи-
сать функцию состояния избыточного электрона в виде
| ф = а^ьФу. B0.27)
Заданиек§20
Доказать следующие, справедливые для хартри-фоковской
функции состояния Ф B0,4) и чрезвычайно важные для
160 ЭЛЕКТРОНЫ Ё «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
приложений соотношения:
-<Ф|яИх,)г|)(хз)|Ф><Ф|яИх2)гИх4IФ>. (А 20.1)
Указание. Разложить г|з+, ф согласно B0.2), B0.3), применить
B0.4), а также B0Л8). Приведем еще один промежуточный ре-
зультат:
Если применять только числа заполнения щ = 1 для к= ки
А'2, ..., kN (см. B0.4)) и щ — О в остальных случаях, то левая
часть (А 20.1) принимает следующий вид:
2 ЩЧ>* Ы <Pi (xi)}{2 Щ'Ч>*' (ха) Ц>у (x3)j -
— B и;Ф* (xi) Ч>3 (хз)|( 2 пуц*у (х2) <ру (х4)] .
I з I iW . )
Но это выражение в силу равенства
2 п,-Ф* (х) cPj (x') = <Ф | Ф+ (х) гр (х') | Ф> (А 20.2)
з
совпадает с правой частью (А 20.1). Доказательство (А 20.2) про-
водится с помощью B0.10).
Примечание. В методе Хартри второе произведение в
правой части (А 20.1) опускают.
§ 21. Электронные дырки *)
Благодаря формализму вторичного квантования мы теперь
в состоянии особенно простым образом ввести понятие электрон-
ной дырки и осмыслить его математически.
При этом речь идет о следующей проблеме.
Будем исходить из заполненной валентной зоны, из которой
удален электрон в состоянии к. Как будет показано, это незапол-
ненное состояние ведет себя точно как одна частица, однако с по-
ложительным зарядом. Для математической формулировки будем
исходить из полностью заполненной валентной зоны с волновой
функцией Фу, в которой с помощью оператора уничтожения ahi v
уничтожаем электрон в этом состоянии
Фк = аК?Фу. B1.1)
*) В специальной литературе по физике полупроводников обычно упот-
ребляется термин «дырка». Однако мы будем придерживаться более близ-
кого к оригиналу термина «электронная дырка», поскольку мы не пред-
полагаем, что читатель знаком с физикой полупроводников. (Прим. перев.)
§ 21] ЭЛЕКТРОННЫЕ ДЫРКИ 161
Поскольку, как будет видно, благодаря этой операции рождается
электронная дырка, то вместо оператора уничтожения а^ v вве-
дем оператор рождения d и соответствующий оператор уничто-
жения с помощью соотношений
ak,v = d?, atv = dk. B1.2)
Поскольку валентная зона занята, для оператора уничтожения dh
справедливы следующие соотношения:
ййФу=а^Фу = 0. B1.3)
Отсюда видно, что состояние Фг для оператора dh представляет
вакуумное состояние. Из построения оператора Гамильтона B0.7)
нам известно, что операторы рождения в нем всегда стоят слева
от операторов уничтожения. Поэтому имеет смысл переписать
оператор Гамильтона через операторы электронных дырок таким
образом, чтобы опять операторы рождения электронных дырок
стояли слева от операторов уничтожения. Применяя перестано-
вочные соотношения A3.4), A3.5), A3.6), получаем затем для
пар операторов
dtdt, = 8lm - dUi. B1.4)
После повторного применения указанных перестановочных соот-
ношений для комбинации из четырех операторов получаем сле-
дующее выражение:
B1.5)
Поскольку все дальнейшие рассуждения в этом параграфе
относятся к занятым или свободным состояниям в валентной
зоне, мы отнесем оператор Гамильтона B0.7) к состояниям в ва-
лентной зоне, т. е. суммирование по I и т будет распространять-
ся теперь только на квантовые числа валентной зоны. Стоящие
здесь операторы можно заменить согласно B1.2) на операторы
электронных дырок. Затем мы поменяем согласно соотношениям
B1.4) и B1.5) порядок следования операторов. Как видно из
представления B1.4) и B1.5), у нас появляются члены, которые
более не зависят от операторов электронных дырок d, а именно,
символы Кронекера б(т. После подстановки B1.4) и B1.5) в опе-
ратор Гамильтона B0.7) получим поэтому для энергии некоторое
11 X. Хакен
162 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ (ГЛ. IV
постоянное выражение, которое имеет следующий вид:
Еу = 2 J ф* «{- ?
+ ~Т 2 f \ Ф' (Х)(Р™ {Х'] |х-х'| фт <Х'
lm
~~т2j 1ф*(х)ф™(х/
Если сравнить это выражение с выражением B0.19) и принять
во внимание при этом, что суммирование теперь распространено
на всю валентную зону, то становится непосредственно видно,
что выражение B1.6) представляет энергию электронов валент-
ной зоны в приближении Хартри — Фока. Это вполне разумный
результат. Если подействовать полным гамильтонианом B0.7)
после преобразований B1.4) и B1.5) на состояние заполненной
валентной зоны Фу, то должна сразу получиться энергия запол-
ненной валентной зоны. Теперь рассмотрим члены, содержащие
пары операторов dmd-i. После простой перестановки индексов по-
лучаем следующее выражение:
+ 2 Ф' (Х') |х-х'| Ф™' <Х') Л'*Фт (х) -
то' '
- j 2 4V (х') \х-х'\ фт (Х') dV< Ф-' (Х)} d'x'
Суммы по индексам I, т, т' распространяются на всю валент-
ную зону. Выражение в фигурных скобках нам уже встречалось
в предыдущих параграфах. Оно является не чем иным, как ле-
вой частью уравнения Шредингера B0.21), приспособленного для
электронов валентной зоны. Применяя обозначения B0.25), мож-
но придать B1.7) следующий вид:
— 2 dmdx J фг* (х) #Эфф фт (х) d3x. B1.8)
Поскольку, согласно соображениям предыдущих параграфов, вол-
новые функции <рт являются собственными функциями гамиль-
тониана Я,фф с собственным значением
Ет ¦ B1.9)
§ 21] ЭЛЕКТРОННЫЕ ДЫРКИ 163
то B1.8) переходит в выражение
- 2 d+diEm f фГ (х) Фт (х) <Рх. B1.10)
Ввиду ортогональности волновых функций, в сумме остаются
только диагональные члены, так что вместо B1.7) получаем сле-
дующее выражение:
'У ,7+ а /г, „ < о 1 \ \ \
к
Здесь введен индекс к вместо употреблявшегося ранее индекса тп,
так как собственные функции фт имеют вид блоховских функ-
ций, которые различаются волновыми векторами. Другой ин-
декс V должен подчеркнуть, что речь идет об энергии электрона
в валентной зоне. Выражение B1.11) имеет в точности вид опе-
ратора Гамильтона системы независимых отдельных частиц.
С гамильтонианом подобного вида мы уже познакомились для
случая свободных частиц в § 13. Напомним теперь кратко после-
довательность наших действий. С помощью правил B1.2) и пе-
рестановочных соотношений B1.4) и B1.5) электронные опера-
торы в гамильтониане B0.7) § 20 были заменены операторами
электронных дырок. До этого момента мы рассматривали только
те члены, которые не зависят от операторов электронных дырок
или содержат только пары таких операторов, что привело к вы-
ражениям B1.6) и B1.11). Как следует из B1.5), имеются еще
операторы, содержащие произведения четырех операторов элект-
ронных дырок, откуда возникает выражение, которое описывает
кулоновское взаимодействие между электронными дырками:
1 "^^ 4- 4-
#д-д == -о~ Jj dm'di'didmW(I, m\ m', I'), B1.12)
где
W (I, m | m', l')= \\ Ф*(х) qC (x') - e фт- (х') щ. (х) d3x d3x'.
B1.12a)
(Индекс д-д у Н указывает на взаимодействие между дырками.)
Объединяя B1.6), B1.11) и B1.12), получаем
Оператор Гамильтона электронных дырок. (Ниже обычные
квантовые числа I, тп, V', m заменены на волновые векторы к
блоховских волн.)
Я = Ev — 2 d?dkEklV +
1 ^S' + t-
Н—о~ ^L d^tdkldkldkiW (liski | kjk2). B1.13)
к„к,,к„к4
11*
164 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
В этом выражении Ev является энергией заполненной зоны,
а второй член представляет энергию электронных дырок без
учета их взаимодействия между собой. Последний член, наконец,
описывает кулоновское взаимодействие между электронными
дырками и представлен выражением B1.12).
В последующем изложении кулоновское взаимодействие меж-
ду электронными дырками мы опустим и обсудим выражение
B1.11). Сначала при поверхностном взгляде могло бы показать-
ся, что энергия электронной дырки отрицательна, так что ее
нельзя сравнивать со свободной частицей. Однако максимум
энергии типичной валентной зоны (см. рис. 27) находится точно
в точке к — О. Если теперь разложить энергию вблизи точки
к — О в ряд, то энергия примет вид
Ек v = Ео у — 4-^- mv>0. B1.14)
2mv
Опуская неинтересный постоянный член в B1.13), получим, на-
конец, следующее выражение для оператора Гамильтона элект-
ронных дырок:
B1.15)
Таким образом, становится очевидным, что электронные дырки
ведут себя как частицы с положительной эффективной массой тп^.
Отсюда, однако, еще не следует, что электронные дырки как
сами по себе, так и под действием внешнего поля ведут себя как
частицы с противоположным электрону, т. е. положительным,
зарядом. Для того чтобы показать это, рассмотрим оператор
плотности электронного заряда, который с помощью проведенных
в § 12 рассуждений можно сразу представить в виде
B1.16)
Если подставить сюда еще разложение оператора i|) по зонным
функциям, то получим
Р W = е 2 <р?(х) Фк' (х) 4аъ: B1.17)
Будем считать, что сумма в B1.17) распространяется на все
состояния валентной зоны. Чтобы перейти к электронным дыр-
кам, вновь воспользуемся соотношением B1.2) и поменяем, со-
гласно B1.4), порядок следования операторов так, чтобы опера-
торы уничтожения электронных дырок вновь оказались справа.
Тогда для оператора зарядовой плотности, который выражен
§ 21] ЭЛЕКТРОННЫЕ ДЫРКИ 165
теперь через операторы электронных дырок, получаем следующее
выражение:
р(х) = «2 I Фк (х) |2 - е2 qv (x) фк (х) <?&,. B1.18)
к кк'
Первая сумма в этом выражении представляет собой, очевидно,
плотность заряда всей заполненной электронами валентной зоны.
Поскольку кристалл в целом нейтрален, следует принять, что
эта зарядовая плотность компенсируется положительно заряжен-
ными ядрами. Итак, теперь остается лишь вторая сумма, в ко-
торой, впрочем, изменен порядок следования индексов. Эта сум-
ма имеет структуру, полностью аналогичную выражению B1.17),
которое относится к электронам, только знак заряда, очевидно,
изменен на противоположный. Проверим, действительно ли сред-
нее значение этого выражения представляет собой плотность
заряда, учитывая, естественно, что заряд электрона отрицателен.
Для этого вычислим среднее значение дырочной части выраже-
ния B1.18) для электронной дырки в состоянии к0:
к„ | (- в) 2 Фк- (х) фк(х) d?dv | ФкД B1.19)
\ кк' /
при
Фк„ = 4„Фу. B1.20)
Ход решения повторяет предыдущие вычисления этой главы и
непосредственно приводит к результату
к„|2. B1.21)
При этом, подчеркнем это еще раз, зарядовая плотность за-
полненной зоны, ввиду ее компенсации зарядами ядер, опущена.
В заключение покажем, что заряд электронной дырки в вы-
ражении, описывающем взаимодействие с внешним полем, меняет
свой знак на обратный. Для этого в качестве примера рассмот-
рим постоянное электрическое поле. Выражение оператора по-
тенциальной энергии тогда, согласно приведенным в § 12 рецеп-
там, имеет вид
= J
(х) (- еЕх) ф (х) d3x. B1.22)
Вновь подставим разложения B0.2), B0.3), после чего сразу
получим
Упоив = 2 Мкк'а?ак', B1.23)
k,k'
причем матричные элементы Afkk' даются выражением
.: B1,24)
166
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. ГУ
Теперь проведем преобразования B1.2) и B1.4), тогда сразу
получаем
^поле = 2 Мы, - 2 d& dk (JWk'k)*. B1.25)
к кк'
Первая сумма вновь представляет собой потенциальную энергию
заполненной зоны в электрическом поле. Здесь также можно
вновь предположить компенсацию заряда остовом решетки, так
что важным для нас остается второй член в выражении B1.25).
Также и здесь, очевидно, знак меняется на противоположный.
Это выглядит, следовательно, так, как будто поменялся знак
заряда.
В В
Рис. 31. а) В эффекте Холла носители заряда испытывают отклонение
при движении в скрещенных электрическом и магнитном полях. Благодаря
накоплению заряда возникает разность потенциалов Холла, б) Аномальный
эффект Холла можно понять, предположив, что заряды имеют положитель-
ный знак.
Как можно видеть из предыдущего изложения, обращение
знака электрического заряда электронной дырки является про-
стым следствием свойств перестановочных соотношений. С дру-
гой стороны, существование электронных дырок доказано многи-
ми экспериментами, в особенности аномальным эффектом Холла
(рис. 31), Все это дает прекрасный пример того, как на основе
простых закономерностей квантовотеоретического рассмотрения
можно прийти к далеко идущим физическим следствиям, кото-
рые оказываются чрезвычайно важными для приложений
(вспомним, например, транзисторы).
§ 22. Взаимодействие между электронами и дырками
Рассмотрим кристалл, обладающий полупроводниковыми свой-
ствами, т. е. примем, что в основном состоянии этого кри-
сталла валентная зона полностью занята электронами, а зона
проводимости, напротив, пустая. В этом параграфе будет иссле-
дован вопрос о том, какие эффективные взаимодействия воз-
никнут, если удалить некоторые электроны из валентной зоны,
т, е, создать я нее электронные дырки и одновременно перене-
§ 22] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ И ДЫРКАМИ 167
сти несколько электронов в зону проводимости. Физически это
может происходить, например, при облучении кристалла све-
том, в результате чего электроны из валентной зоны выбива-
ются в зону проводимости. Очевидно, что при этом число по-
явившихся в зоне проводимости электронов равно числу элек-
тронных дырок в валентной зоне. Можно, однако, впрыснуть
в кристалл носители заряда внешним током, так что в последу-
ющем изложении мы примем, что число электронов в зоне про-
водимости может отличаться от числа электронных дырок в ва-
лентной зоне. Исходным пунктом нашего рассмотрения, как
обычно, является уравнение Шредингера
НФ=ЕФ B2.1)
с оператором Гамильтона
Я = J ф+ (х) (- Ц- А + Fp (х)) г]) (х) d*x +
B2.2)
который уже встречался нам и поэтому не требует более пояс-
нений. Поскольку мы хотим рассмотреть состояния в валентной
зоне и зоне проводимости в явном виде, разложим операторы
поля по собственным функциям валентной зоны и зоны прово-
димости
ф+ (х) - 2 4.vti,v (х) + 2 d?,L<&.L (x), B2.3)
k k
^ (x) = 2 Як.гФк.у (х) + 2 «к.ьфк.ь (х). B2.4)
к к
При этом предположим, что эти волновые функции в валентной
зоне и зоне проводимости определены с помощью некоторого эф-
фективного гамильтониана
фффр, B2.5)
где
Ц . B2.5а)
Этот оператор Гамильтона встречался нам в предпоследнем па-
раграфе (§ 20) и мы полагаем, что нам удалось определить вол-
новые функции «рк.у и фк,ь, что, как уже было отмечено, не яв-
ляется задачей квантовополевой теории, а должно быть предо-
ставлено специалистам по вычислению зонной структуры.
J68 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Для дальнейшего предположим, что волновые функции ср
взаимно ортогональны;
J фк.г (X)
dsX = Sfck-Sij. B2.6)
Коэффициенты разложения а и а+ в B2.3), B2.4) вновь, естест-
венно, являются операторами, которые удовлетворяют переста-
новочным соотношениям
«k.iflk'J + ak',sak,i = °. ak>k\j + ак',зЯк,« = 0, B2.7)
ak,iCik'j + ak"',jak,i = Skk'Sij.
В соответствии с двумя слагаемыми в B2.2), разложим опера-
гор Гамильтона на часть, описывающую свободное движение
частиц, и на часть, которая описывает взаимодействие:
Я = ЯО + ЯВ3. B2.8)
Если подставить разложения B2.3) и B2.4) в соответствующие
выражения, то для Но получим следующее выражение:
2
k.k'.ij ii
tt j=l, V. B2.9)
Ввиду трансляционной симметрии задачи, двойное суммирова-
ние по к и к' переходит в однократное. Индексы i и / могут
принимать оба значения: L (зона проводимости) и V (валентная
зона). Второе стоящее в B2.8) слагаемое, которое связано
с взаимодействием, после подстановки разложений B2.3) и
B2.4) принимает вид
a^.5iak».S.ak»,5,ak,.3 X
i
JJ <№. J, W «№„5. (х') JT^FT фк»»"' (Х'} ^«^ (Х) ^ dV' B2Л0)
Последующая процедура в принципе очень проста. Вместо элек-
тронных операторов валентной зоны вводим операторы элект-
ронных дырок согласно соотношениям
ak,v=d,t, a?iV = db. B2.11)
Для упрощения обозначений опустим в дальнейшем у операто-
ров, относящихся к электронам проводимости, индекс L;<
§ 22] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ И ДЫРКАМИ 163
В последующем изложении будет сделано одно дополни-
тельное приближение. А именно, будем считать, что количест-
ва электронов в зоне проводимости и валентной зоне независи-
мы друг от друга. Это предположение на первый взгляд может
показаться само собой разумеющимся, поскольку мы не рас-
сматриваем реальные переходы между валентной зоной и зоной
проводимости, т. е. считается, что акты рождения электронов
и электронных дырок уже закончены. Мы рассматриваем только,
поведение уже созданных электронов и электронных дырок.
Следует, однако, подчеркнуть, что, несмотря на кажущуюся
очевидность этого предположения, здесь идет речь о существен-
ном приближении, согласно которому мы пренебрегаем так на-
зываемыми виртуальными переходами. Дело в том, что под вли-
янием взаимодействия устанавливаются поляризационные эф-
фекты, при которых, например, функции электронов в валентной
зоне накладываются на функции электронов в зоне проводимос-
ти, что, однако, не сопровождается реальным переходом. Эффек-
ты такого рода будут обстоятельно обсуждены позже в § 25, те-
перь же мы обратимся к расчету. Формализм этого расчета
состоит в том, что согласно B2.11) вводятся операторы электрон-
ных дырок, затем оператор Гамильтона преобразуется таким об-
разом, чтобы все операторы уничтожения стояли справа. Сог-
ласно нашим предположениям проведем в Но следующие упро-
щения и преобразования:
для i = 7 = L: а?,ьак,ь = акак, B2.12)
для i = j = V: a^tvak,v = 1 — d^d^. B2.13)
В Нт следует предусмотреть все возможные комбинации индек-
сов, а именно следующие:
1. Все индексы принадлежат зоне проводимости:
h = 72 = /з = 74 = L. B2.14)
2. Все индексы принадлежат валентной зоне:
71 =72 = /з = 74 = V. B2.15)
3. Два индекса принадлежат валентной зоне и два — зоне
проводимости. При этом, однако, речь идет не о таких комбина-
циях, когда одновременно рождаются две частицы в зоне прово-
димости и две в валентной зоне, а о таких комбинациях, когда
одна частица уничтожается и одна рождается в зоне проводи-
мости и одна частица уничтожается и одна рождается в ва-
лентной зоне. Это дает следующие комбинации индексов:
f/i = /4 = V h = U = L) B2.16)
которые, как будет доказано, дают .равные вклады, а также
170
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. ГУ
следующие комбинации индексов:
h = U = V h = U = L) B2.17)
которые равным образом дают одинаковые вклады. Для после-
дующего введем краткое обозначение матричного элемента, опи-
сывающего кулоновское взаимодействие:
g2
= w\
\h h h h\
B2.18)
Верхний ряд индексов в И7 относится к векторам к, а нижний
ряд — к индексам зоны проводимости или валентной зоны. Сог-
ласно комбинациям индексов B2.14) и B2.17) имеются разные
вклады в оператор взаимодействия, а именно: взаимодействия
в валентной зоне, взаимодействия в зоне проводимости и вза-
имодействия между зоной проводимости и валентной зоной:
+ HLV. B2.19)
В соответствии с B2.19) получаем следующие вклады:
1. Взаимодействие между электронами зоны проводимости:
B2.20)
V 1
к,...к.
2. Взаимодействие между электронными дырками:
- 1
— —
V V
B2.21)
Если в этом выражении перенести операторы уничтожения на-
право, то вновь получатся выражения, уже известные нам из
предыдущей главы об электронных дырках. Hvv можно далее
представить в следующем виде:
= -г" ^ {ok,k,fik1k4 —
8k k,d?4<
.1
v v
v v
)¦
B2.22)
Обсудим отдельные члены этого выражения от А до G, причем
для этого будет необходимо вычислить множитель
Член А вновь дает кулоновское взаимодействие в заполненной
р
).
§ 22] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ И ДЫРКАМИ 171
валентной зоне и, естественно, экспериментально необнаружим.
Член В представляет кулоновское обменное взаимодействие в за-
полненной валентной зоне, в то время как член С дает взаимо-
действие электронных дырок с валентными электронами, a D пред-
ставляет соответствующее кулоновское обменное взаимодействие.
Последующие члены совпадают с предыдущими: Е = D, F = С.
Наконец, последний член представляет кулоновское взаимодей-
ствие между двумя электронными дырками. Члены С и D уже
встречались нам в § 20 (и § 21). Как мы тогда видели, здесь
речь идет о вкладе эффективного потенциала, который привле-
кается для определения волновых функций зоны с помощью ме-
тода самосогласованного поля. Эти члены для нас теперь не
представляют интереса, за исключением одного только члена G.
3. Рассмотрим важнейший член, описывающий взаимодейст-
вие между электронами проводимости и электронными дырками.
Согласно табличкам B2.16) и B2.17), в нем присутствуют два
разнородных члена. Исследуем выражение
=42 ^ a+a
где на индексы /i ... /4 наложены ограничения B2.16) или
B2.17). Нам нужно, следовательно, рассмотреть вклады по сле-
дующей схеме:
LVV L + a?akA,4,} B2 24)
V L LV-+a?taktdklditty
] B2 25)
V LV L^~a?,aktdkid?\'
Покажем, что вклады в B2.23) от комбинаций B2.24) идентич-
ны и что то же самое справедливо для второй группы вкладов
от B2.25). Для этого изменим индексы в сумме B2.23) следую-
щим образом: к] заменим на кг, к2 на ki, k3 на к4 и к4 на к3.
Тем самым вторая строка в B2.24) переходит в первую строку.
Одновременно матричный элемент W в B2.23) переходит в но-
вый матричный элемент:
L V V L) w \V L \L V
причем в , явном выражении для матричного элемента следует
поменять координаты
х + х'. B2.27)
Самое ващное теперь состоит в том, что, как можно сразу же
172
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. ГУ
убедиться с помощью явного выражения B2.18), оба матричных
элемента в B2.26) равны друг другу. То же самое можно пока-
зать и для комбинаций B2.25). Таким образом, для последую-
щего достаточно, если мы ограничимся первыми комбинациями
B2.24) и B2.25), а оставшиеся комбинации учтем просто вве-
дением в сумме B2.23) множителя 2. Выражение для взаимо-
действия согласно первой строке B2.24) можно затем преобра-
зовать хорошо известным нам образом с помощью перестановоч-
ных соотношений для электронных дырок, в результате чего по-
лучим
¦ 2
k,...k4
3
) -
¦ s ¦
k,...k4
B2-28)
Первая сумма здесь описывает взаимодействие электрона в зоне
проводимости с заполненной валентной зоной. Это станет видно
особенно отчетливо, если несколько преобразовать это выраже-
ние, используя стоящие в нем символы Кронекера, Тогда для
первой части выражения B2.28) получаем
k]
L V
V L
B2.29)
Для того чтобы сделать это выражение полностью, очевидным,
воспользуемся явным видом W, представленным в B2.18), после
чего получим
• B2.30)
\ V\vl
<Pk,,L (x)
Это выражение показывает, как уже говорилось, что первая сум-
ма в B2.28) представляет собой энергию взаимодействия элек-
трона проводимости с заполненной валентной зоной. Второе вы-
ражение в B2.28) описывает уничтожение и последующее рож-
дение электронной дырки и одновременно тем самым уничтоже-
ние и последующее рождение электрона. Это выражение, таким
образом, описывает рассеяние электрона на электронной дырке,
которое обусловлено кулоновским взаимодействием. Это рассея-
ние в рамках нашего формализма заключено в выражении взаи-
модействия W. Аналогичным образом можно описать ту часть
§ 22] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ Й ДЫРКАМИ 1?3
оператора взаимодействия B2.23), которая обусловлена B2.25).
Отсюда сразу получаем
B2.31)
Первую сумму в этом выражении можно интерпретировать как
обменное взаимодействие электрона в зоне проводимости с за-
полненной валентной зоной, а вторая сумма является для нас
очень важной, поскольку она описывает кулоновское обменное
взаимодействие между электроном в зоне проводимости и элек-
тронной дыркой. То, что здесь действительно речь идет об об-
менном взаимодействии, станет ясно, если исследовать явное
представление B2.18) для W. При этом можно установить, что
для равных значений к в валентной зоне, т. е. для ki = к3, и для
равных значений к в зоне проводимости, т. е. для кг = к4, появ-
ляется смешанная зарядовая плотность. Проведенные нами выше
рассуждения были довольно элементарны, однако, естественно,
несколько длинноваты. Поэтому следует еще раз посмотреть,
чего же мы достигли в результате всех этих преобразований.
Задача состояла в том, чтобы вместо электронных операторов
в валентной зоне ввести соответствующие операторы электрон-»
ных дырок. При этом получились совершенно различные вклады,
которые следует теперь поставить в соответствие различным фи-
зическим процессам. Объединим полученные выше результаты
в общий оператор Гамильтона для электронов и электронных
дырок следующим образом:
II = Ш + Нвз = #эл + Яд + #эл-д + #эл-эл +ЯД_Д + W3unolIB.
B2.32)
Индексы эл (= электрон) и д (= дырка) указывают на то, какие
операторы появляются в отдельных членах Н. Рассмотрим те-
перь отдельные вклады, которые получим соответствующим при-
менением выведенных выше выражений:
Яэл = ^ «k"«k{] Фк.ь (- %^ А + V (х)J фк>ь d3x
(х)J фк>
Этот член описывает энергию электронов в зоне проводимости
(однако без учета взаимодействия электронов друг с другом или
с электронными дырками). Это выражение уже было найдено
нами в § 20 и там же обсуждено. Мы можем, учитывая трансля-i
ционную симметрию, положить к! = к4. Для электронных1 дырок
В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
мы получим совершенно аналогичное выражение (без учета вза-
имодействия дырок между собой или с электронами)
Ня = - 2
? А
(х))
к к'
V V
к' к
V V
к' к
F V
к' к
V V
B2.34)
И это выражение также встречалось нам уже ранее в § 21. Сле-
дующее выражение имеет основополагающее значение для рас-
смотрения свойств полупроводников. А именно, оно описывает
взаимодействие между электронами и электронными дырками
Я8Л-а=
+ 2
B2.35)
Здесь важен указанный в первой сумме в явном виде знак ми-
нус, который наглядно можно интерпретировать следующим об-
разом: в кулоновском взаимодействии, которое пропорционально
квадрату заряда е, один из знаков поменялся на противополож-
ный, что означает, как мы уже видели ранее, что заряд элек-
тронной дырки является положительным. Три последних члена в
B2.32) интерпретируются особенно просто. Эти члены суть сле-
дующие:
электрон-электронное взаимодействие в зоне проводимости:
B2.36)
4.Х...Ь.4
взаимодействие между электронными дырками в валентной
зоне:
н^=\ 2
V V
К К)
v v
B2.37)
и, наконец, постоянный член, не содержащий никаких опера-
торов;
= 2 J Фк-V [— 2^ А + У (x)J cpb.v d3x +
который описывает просто энергию заполненной валентной зоны.
22]
ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ И ДЫРКАМИ
175
В заключение рассмотрим еще стоящие в формулах для вкла-
дов в энергию B2.33) и B2.34) довольно длинные выражения
в фигурных скобках. Эти выражения, как можно установить
при ближайшем рассмотрении, уже встречались нам в §§ 20 и
21 и представляют средние значения энергий электронов и элек-
тронных дырок, Приведем эти выражения еще раз, чтобы чита-
телю не возвращаться назад,
J
~ \к А + V
W
к к'
L V
к' к
V L
B2.39)
и
~ ЬкА + F
к к'
к к'
f F
= Ek,v.
B2.40)
В большинстве важных в экспериментальном отношении слу-
чаев можно принять, что электроны и дырки находятся вблизи
края зоны. Поэтому энергию /?к,ь сразу же можно разложить
в ряд
2mL'
B2.39а)
Соответственно разложение энергии Е к,у принимает вид
B2.40а)
Если же минимумы вырождены и находятся в точках к Ф 0, то
и в этом случае можно, естественно, провести соответствующие
разложения. Мы не будем, однако, углубляться в такие тонко-
сти, так как все это не имеет отношения к фундаментальным
методам квантовополевой теории. Гамильтониан Н может слу-
жить исходным пунктом для рассмотрения целого ряда чрезвы-
чайно важных в физическом отношении проблем. В последующем
изложении мы особо выделим случай, когда в соответствующих
зонах находится один электрон и одна электронная дырка. Мы
увидим затем, что при этом сразу появляется совершенно новое
состояние, так называемый экситон.
Исследование свойств гамильтониана системы многих элек-
тронов и электронных дырок в последнее время также приобре-
176 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ {ГЛ. IV
ло актуальность, поскольку благодаря высокой интенсивности
лазеров оказалось возможным переводить большое число электро-
нов из валентной зоны в зону проводимости, К этому вопросу мы
еще вернемся в § 26 об «экситонной материи».
§ 23. Экситоны с большим радиусом (экситоны Ваннье)
В предыдущих параграфах мы ввели оператор Гамильтона
для следующей проблемы: в зоне проводимости находится опре-
деленное число электронов, а валентная зона занята другим коли-
чеством электронных дырок. Как мы уже видели, электроны и
электронные дырки можно описать как свободные частицы с оп-
ределенной эффективной массой. Между этими частицами, одна-
ко, действуют кулоновские силы. Оператор Гамильтона для такой
системы имел следующий вид:
i1...K.4
1 X' J+ .1+ .1 .7 TT7 / ~2 ~8 1 /no Л\
V V
V V
В этом выражении первый член представляет энергию пол-
ностью заполненной валентной зоны. Второй член представляет
кинетическую энергию электронов в зоне проводимости, третий
член — кинетическую энергию электронных дырок в валентной
зоне. Следующий член описывает взаимодействие между элект-
ронной дыркой и электроном. Стоящие в фигурных скобках мат-
ричные элементы W определены в выражении B2.18) и описыва-
ют кулоновское взаимодействие и кулоновское обменное взаимо-
действие. Предпоследний член описывает взаимодействие между
электронами в зоне проводимости; наконец, последний член пред-
ставляет взаимодействие между электронными дырками в валент-
ной зоне, Далее, наша задача состоит, естественно, в том, чтобы
решить соответствующее уравнение Шредингера
НобщФ=ЕФ. B3.2)
В следующем параграфе это решение будет проведено в явном
виде для случая одного электрона в зоне проводимости и одной
§ 23] ЭКСИТОНЫ ВАННЬВ 177
электронной дырки в валентной зоне. Волновые функции элект-
рона в состоянии ki и электронной дырки в состоянии кг можно
получить из состояния, описывающего полностью занятую ва-
лентную зону, последовательным действием операторов рожде-
ния йк"х и d?2 на функцию заполненной валентной зоны Фг;
«Фу B3.3)
Следует ожидать, что электрон и электронная дырка, проле-
тая друг относительно друга, испытывают взаимное рассеяние,
в результате чего попадают во все возможные различные конеч-
ные состояния к. Поэтому образуем сумму по всем состояниям к
электрона и электронной дырки. Поскольку, к тому же, отдель-
ные состояния могут быть заняты с различной вероятностью,
введем некоторые весовые коэффициенты Ck^ka, которые затем
подлежат определению. Согласно этим соображениям наш подход
к системе двух частиц, так называемому экситону, оказывается
основанным на волновой функции
Ф = 21 ck k2a? й^Фу. B3.4)
к1к2]
Исследуем теперь, какие возникнут упрощения, если подейство-
вать оператором Гамильтона B3.1) на функцию состояния B3.4).
В операторе Гамильтона B3.1) обе последние суммы описывают
взаимодействие только в валентной зоне или только в зоне про-
водимости и содержат, соответственно этому, два оператора унич-
тожения для электронов и электронных дырок. Поскольку, одна-
ко, наша функция состояния B3.4) содержит по одному электро-
ну и электронной дырке, то действие соответствующих операто-
ров взаимодействия дает нуль, так что обе последние суммы
в B3.1) можно опустить..
Укороченный таким образом оператор Гамильтона B3.1) раз-
ложим, как обычно, на две части: кинетическую энергию и вза-
имодействие между электроном и электронной дыркой (для того
чтобы опустить И^заполн, сдвинем соответствующим образом энер-
гию Е):
| -"общ -"кин ~г tl эл—д. \LtO.Oj
Учитывая явный вид #кия и волновой функции B3.4), получим
ЪЪ V a \2wL 2mV I 12^!
kjk2 \ /
const = EQ<L ~ EOtV, B3.6)
и, соответственно для части, которая описывает взаимодействие
12 х. Хакен
178 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
электрона и дырки,
V
[ГЛ. IV
kl-k4
Ckk'<flk4<42flk^Oy. B3.7)
X
Запишем правую часть уравнения B3.2) в явном виде
ЕФ = Е 2 c^^dt^v
B3.8)
Выражение B3.7) упростим известным образом, перетащив все
операторы уничтожения направо и учтя также, что действие на
Фг как электронных операторов уничтожения, так и дырочных
операторов уничтожения дает в результате нуль. Если еще поме-
нять индексы 3, 2, 4 местами, то мы, наконец, получим для B3.7)
W
V L
W
V L
V L
B3.9)
Взглянув на выражения B3.6), B3.8) и B3.9), можно увидеть,
что в этих выражениях появились линейные комбинации волно-
вых функций, которые в целом имеют вид B3.3). Но, как мы
знаем (см. 13.37)), функции вида B3.3) для различных векторов к
взаимно ортогональны. На этом основании уравнение B3.2), в ле-
вой части которого стоят выражения B3.6) и B3,9), а правая
часть представлена выражением B3.8), может быть удовлетво-
рено только тогда, когда равны между собой коэффициенты
функций B3.3). Сравнивая коэффициенты, сразу получаем си-
стему уравнений для коэффициентов Скхк2:
2
к„к4
V L
V L
V L
B3.10)
Ниже будет показано, что эта система уравнений полностью эк-
вивалентна обычному двухчастичному уравнению Шредингера,
причем между об*еими частицами существует кулоновское взаи-
модействие. Для этого упростим матричный элемент W, который
определяется выражением
J J
L V V
(
(x')
(х') Фк„х, (х)
, B3.11)
§ 23] ' ЭКСИТОНЫ ВАННЬЕ 179
использовав для волновых функций в зонах явный вид блохов-
ской волны
<pKS(x) = e**iibj(x). B3.12)
Затем разложим функции и, которые зависят как от х, так и от
к, в ряд Тейлора по к. Тем самым мы уже делаем предположе-
ние, что важны только те матричные элементы, для которых зна-
чения к малы. После этого получаем формулу
L V V
Se-ik4x' e—— eik2x'eik3x|| UQiL (x) |2| W() y (x') |2 _j_
|x — x I
+ ki(VkiMki,t (x))k1=o uo,t (x) I uo,r (x') P + • • •) d3x d3xr. B3.13)
В качестве следующего шага сделаем предположение, что иг-
рающие заметную роль значения к настолько малы, что из всего
ряда Тейлора нужно сохранить лишь самый первый член. Мы ос-
тавляем, таким образом, в фигурных скобках в B3.13) только
член \uOiL{x)\2\uo,r{x')\2. Эта функция периодична с периодом
решетки, однако внутри элементарной ячейки она может быстро
осциллировать. Поскольку мы приняли, что важны только малые
значения к (т. е, lk| <jt/Zo, где 1о — постоянная решетки), то экс-
поненциальные функции в B3.13) внутри каждой элементарной
ячейки можно считать практически постоянными. Поэтому выра-
жение B3.13) можно вычислить, усреднив его по отдельным эле-
ментарным ячейкам. Поскольку блоховские функции должны
быть нормированы в объеме V на 1, то при этом усреднении про-
является множитель 1/F2. После этого вместо B3.13) получаем
следующее выражение:
^ 1 Je*««* 1—^тт е«+D) dxdx. B3.14)
Пренебрежем, наконец, в уравнении B3.10) еще вторым членом
в фигурных скобках, который описывает кулоновское обменное
взаимодействие и который, как можно подробно показать, для
малых значений к, т. е. при достаточно больших расстояниях меж-
ду электроном и электронной дыркой, быстро стремится к ну-
лю. Мы утверждаем теперь, что система уравнений B3.10) с уп-
рощением B3.14) и при пренебрежении кулоновским обменным
взаимодействием совершенно эквивалентна следующему двухчас-
тичному уравнению Шредингераз
(const ~&L^ ~2^;^-|^7i)
B3.15)
180 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Для доказательства этого утверждения представим волновую
функцию i[)(xi, Х2) в виде
V (*1. х2) = 2 <*,*. -L <•«*.*.-*.». B3.16)
k,ka
и выведем из B3.10) (с указанным упрощением B3.10)) уравне-
ние B3.15) для \|), Для этого умножим B3.10) на
_l_eiklXl-ik2x2 B3.17)
и просуммируем по ki, кг. Рассмотрим вначале часть, относя-
щуюся к кинетической энергии:
- e*lXl-Jk2X2,kik2 1 + 2 + const 1
B3.18)
Поскольку k2eikx можно представить в виде
a2
— М- -I- -^- 4- —
то B3.18) переходит в следующее выражение:
- ^— A, —'¦?— A, + const Zi Аг е**-***^ . B3.19)
Согласно B3.16) это последнее выражение идентично выражению
- р— Ах — ^— А2 -)- const 1 г|з (хг, х2). B3.20)
Ь V I
Часть, описывающая взаимодействие, после умножения на B3.17)
и при использовании B3.14) принимает вид
к„к
С С
X
Яе-1к1Х+гк2Х' i t—j- eik.x-*4x' ^rfs^./^ B3.21)
|x~x I
Соберем вместе все экспоненциальные функции, которые содер-
жат ki и к2, и воспользуемся соотношением
-у- ^ е*к<х'-*'> = б (хх — х') (функция Дирака) B3.22)
к
к
при к =ki и к = к2.
§23]
ЭКСИТОНЫ ВАННЬЕ
181
Ввиду появления двух б-функций
оба интегрирования по d3x и d3xr про-
падают и B3.21) переходит (при х =
= xi и х' =х2) в выражение
V
B3.23)
Но это выражение тождественно сов-
падает с выражением
Т-4-гФОч.х,). B3.24)
//елрерывнШ
состояния
Экситонные
состояния.
Основное
состояние
кристалла
Если теперь собрать B3.20) и B3,24)
вместе, то получится левая часть урав-
нения B3.15). Поскольку правая часть
получается тривиальным образом, то
тем самым эквивалентность B3.15) уп-
рощенному уравнению B3.10) доказана.
Это рассмотрение показало, что
электрон и электронная дырка ведут
себя совершенно так же, как две час-
тицы с противоположными зарядами
и некоторыми эффективными массами
mL и ту. Поскольку между этими дву-
мя частицами существует кулоновское
притяжение, то получается связанное
состояние этих двух частиц, обладаю-
щее водородоподобным спектром. Спек-
тры подобного рода были обнаружены
и детально объяснены при поглощении
света кристаллами Никитиным и дру-
гими авторами. На рис. 32 представ-
лен один из подобных спектров.
Следует указать еще на одно важ-
ное обстоятельство. В нашем рассмот-
рении кулоновское взаимодействие по-
является без какого-либо дополнитель-
ного множителя. С другой стороны,
нам известно, что в поляризуемой сре-
де закон Кулона должен быть модифи-
цирован с учетом диэлектрической по-
стоянной, Следовательно, в уравнении
Рис. 32. Энергетическая
схема экситона с большим
радиусом. На графике
представлена полная энер-
гия Е всех электронов
кристалла как функция
полного волнового числа К.
В основном состоянии кри-
сталла экситонов нет, а
К = 0. Если рождается эк-
ситон, то его движение
раскладывается на движе-
ние центра тяжести (а)
и относительное движе-
ние (б).
(а) Движение центра
тяжести определяется пол-
ным волновым числом К.
Соответствующая энергия
ЕЦТ =h2K2/2mp, где тор =
= гоу + ijil — эффектив-
ная масса всего экситона.
(б) Относительное движе-
ние при больших ради-
усах, как в случае ато-
ма водорода, можно опи-
сать квантовыми числами
п, I, т. Соответствующая
энергия равна Еотнос =
=—тге*1BПЧ2п2) в = 1, 2,
3, ...). Здесь 1/гог=1/ту+
+l/mi, — приведенная мас-
са экситона. В реальном
случае в это выражение
следует ввести ряд уточне-
ний. Вертикальная штрихо-
вая стрелка представляет
оптический переход.
jg2 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
B3.15) нужно феноменологически заменить
-Г^Т-Т на - ,'* , B3.25)
То обстоятельство, что в нашем рассмотрении диэлектрическая
постоянная не появилась, связано со слишком сильным упроще-
нием оператора Гамильтона в § 22, где мы пренебрегли вирту-
альными переходами между зонами.
По существу же эффективная диэлектрическая постоянная
может быть последовательно выведена из микроскопической тео-
рии в рамках вторичного квантования, к чему мы подойдем не-
сколько ближе в § 25.
Задание к § 23
Как следует изменить B3,15), если учитывается обменное
взаимодействие между электроном и электронной дыркой?
§ 24. Экситоны Френкеля
В предыдущих параграфах было принято, что расстояние
между электроном и электронной дыркой относительно велико,
так что имело смысл разложение полевых операторов \|з+(х) и
¦ф(х) по блоховским волнам. В этом параграфе мы рассмотрим, об-
ратный предельный случай, который особенно важен для молеку-
лярных кристаллов, а именно, когда следует считать, что элект-
рон и электронная дырка находятся на одном и том же атоме.
При этом кажется разумным провести разложение не по блохов-
ским функциям, а по атомным волновым функциям или, еще
лучше, по функциям Ваннье, которые кратко обсуждались нами
в § 19. Соответственно двум имеющимся зонам — валентной и
проводимости — введем следующие функции Ваннье:
| Wi,r(.x) = wv(x — 1) (валентная зона V) B4.1)
и
| Wi,L(x) = wL(x — I) (зона проводимости L), B4.2)
где 1 — радиус-вектор точки локализации частицы. Разложение
полевых операторов гр(х) и ij)+(x) по этим функциям Ваннье запи-
шем в виде
,(-l), B4.3)
1 i
2 atvw*7 (x -1) + 2 at,Lwl (x -1). B4.4)
§24] "_'„•: .' ЭКСИТОНЫ ФРЕНКЕЛЯ 183
Оператор at,v рождает электрон в валентной зоне в точке 1,
а оператор а с теми же индексами уничтожает этот электрон.
Соответственно оператор fli,L создает один электрон в зоне
проводимости на атоме 1. Поскольку функции Ваннье образуют
ортогональную систему, то совершенно аналогично § 13 отсюда
следует, что а удовлетворяют перестановочным соотношениям
, л +"+ i + + п
Щ,$&1',У "г ',з'^1,5 = "» "'1,о"'1',У ~т~ Я\',у(*1,5 == "'
Индексы / и /' здесь имеют смысл У и L. Точно так же, как и в
§ 22, нам следует выразить оператор Гамильтона Я B2.2) через
операторы рождения и уничтожения а+, а. Разложим Я на два
слагаемых:
Я = Яо + Яв5, B4.6)
причем Но относится к кинетической энергии электронов в поле
заданного атома, а Явз представляет кулоновское взаимодействие
между этими электронами. После подстановки разложений B4.3)
и B4.4) в B2.2) получаем
= 2 af^aja^Hi^L 4- S ai>Om,r#i,m,v. B4.7)
l,m I,m
где использовано сокращенное обозначение
, j=L,V.
B4.7a)
Будем считать, что стоящий в фигурных скобках в B4.7) опера-
тор не приводит к переходам между различными зонами. Пре-
образуя соответствующим образом выражение
-
получим
Явз = -L J JV (X) ^+ (X') |7~7J * (X') $ (X) d?X d V,
учим ^
Явз =4 2 <h<Sflu.Sflu.Stw\yy\*lA B4.8)
5i,Ja,55>5« i
где W определяется следующим образом:
j84 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Верхние индексы в W относятся к точке локализации, а ниж-
ние — к зоне,
Для дальнейшего упрощения ограничимся случаем, когда
можно пренебречь перекрытием волновых функций. Отсюда сле-
дует, что 14 = li == 1, а также I3 = h = I'.
В последующем рассмотрим такие волновые функции, когда
создается только одна электронпо-дырочная пара. Это означает,
естественно, что электрон не может быть дважды уничтожен в ва-
лентной зоне и дважды рожден в зоне проводимости, что приво-
дит к условиям
h фП, Ь^Ъ- B4.10)
Если использовать эти условия в B4.8), то B4.8) примет вид
Явз = 2 atvat>,Lav,Lahv ? ?
+ 2 a?r*t:Lav,val,Lw(\r ? ? Л. B4.11)
Здесь мы уже воспользовались тем, что пары членов в B4.8) да-
ют одинаковые вклады, так что множитель 1/2 выпадает. По-
скольку предполагается, что валентная зона в отсутствие эксито-
на полностью заполнена и рассматривается только один экситон,
то имеет смысл вновь ввести операторы электронной дырки сог-
ласно рецепту
| altV = dt, a?v=<*i. B4.12)
Для упрощения обозначений, начиная с этого места, индекс
L у электронов проводимости будет опущен:
ahL = ai, at,L = at- B4.13)
Если ввести в B4.11) операторы электронной дырки B4.12), то
для операторов в первой строке B4.11) получим
at,v<iv,L<iv,La'i,v=d idvaydt, B4.14)
или, после перенесения оператора уничтожения dy направо,
B4.14) = — at'uvdfdi -f- a$av. B4.14a)
Первая строка Нвз в B4.11) принимает тогда следующий вид:
B4.15)
В этом выражении вторая сумма содержит только операторы
a^a-i и, следовательно, имеет ту же структуру, что и Но в B4.7).
§ 24] ЭКСИТОНЫ ФРЕНКЕЛЯ 185
Аналогичным образом поступим с операторами во второй стро-
ке B4.11):
afaid^di — afai8hV. B4.16)
Тогда вторая строка Нвз в B4.11) принимает следующий вид:
и$ - s, .,**,#(•„ •;;' у - $.t.# (>F > ¦
Также и здесь вторая сумма содержит только операторы ai «ь ко-
торые стоят в Но в B4.7).
Полный оператор Гамильтона // = #о + Явз = Но + Я„з +
+ Яш' получается суммированием B4.7), B4.15) и B4.17).
При этом имеет смысл все суммы в B4.7), B4.15) и B4.17),
относящиеся к зоне проводимости L, собрать в один эффектив-
ный гамильтониан Нь? (поменяв при этом в B4.15) 1 и 1'
местами);
= 2 atamHlim,L + 2 а+а, X
l,m 1
1'1 l r)-w(l 1 1 I)). B4.18)
V L L Vj \F L V Llj
В этом выражении AEL, как можно установить с помощью B4.9),
от 1 не зависит, так что AEL для электрона в точке 1 имеет
смысл дополнительной постоянной энергии, которая возникает
благодаря кулоновскому взаимодействию электрона с заполнен-
ной валентной зоной. Поэтому положим
Я?* = 2 at an (H1>m,L + 6,,mA?L) = 2 atamHl^,L. B4.19)
l,m l,m
Перепишем, наконец, электронно-дырочную часть Но в B4.7) хо-
рошо известным нам образом:
Яд = 2j а1,тйт,уЯ11ту = — ^j dmdiHitTa!y -\- 2jHit\ty =
l,m l,m 1
ДЕ
+ 4й. B4.20)
l,m
После этих элементарных преобразований полный оператор Га-
мильтона принимает следующий вид:
tam + 2 H3™,xdUm -
l,m
— 2 at-dvdtdxW (l l' l' J ) + 2 at-a^d{W f1 J' l' l) + AE.
B4.21)
186 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
Каждый член этого оператора Гамильтона имеет наглядный
смысл: в первой сумме с членом afam один электрон в точке m
уничтожается, а в точке 1 вновь рождается. Эта часть Я описывает,
следовательно, движение отдельного электрона. Совершенно так
же вторая сумма в B4.21) представляет движение отдельной
электронной дырки. Последняя сумма в B4.21) с операторами
описывает уничтожение электронно-дырочной пары в точке I и
последующее рождение в точке 1', т. е. описывает совместный
перенос электрона и электронной дырки. Третий член в B4.21)
не описывает никакого переноса: электронная дырка остается в
точке 1, а электрон — в точке Г. Как можно увидеть, взглянув
на определение W B4.9), W описывает кулоновское взаимодей-
ствие между электроном и электронной дыркой в соответствующих
точках кристалла.
Действительное движение электрона и электронной дырки осу-
ществляется, естественно, под влиянием всех членов в B4.21),
причем относительные величины этих членов определяют, какая
из «форм» движения в действительности реализуется.
В случае экситона Френкеля электрон и электронная дырка
должны оставаться постоянно в пределах атома или молекулы.
Какие члены в Н этому благоприятствуют, а какие препятствуют?
Оба первых члена в B4.21) служат причиной индивидуального
движения отдельных частиц и, следовательно, постоянно грозят
разорвать электронно-дырочную пару. Поэтому они являются
«вредными». Третий член приводит к притяжению между элект-
роном и электронной дыркой, и поэтому он является благопри-
ятным. Четвертый член, наконец, особенно важен, поскольку он
является причиной переноса пары частиц из одной точки кристал-
ла в другую. В предельном случае экситона Френкеля, поэтому,
члены в Нзфф, для которых 1Ф т, должны быть достаточно малы-
ми. Это требование выполняется довольно хорошо в случае мо-
лекулярных кристаллов, так как перекрывание между мо-
лекулярными функциями Wj(x — 1) незначительно, а именно ве-
личина этого перекрывания прямо определяет величину Яафф для
l^m (см. задание 1). Хотя в этой ситуации никакого индивиду-
ального движения не может быть, тем не менее электронно-ды-
рочная пара, как мы увидим, движется как целое.
Теперь целесообразно ввести явный вид функции состояния.
При этом будем исходить из полностью заполненной валентной
зоны, которая описывается функцией состояния <Dg. В точке 1
одновременно рождаются электрон и электронная дырка. Ввиду
трансляционной симметрии задачи следует провести суммирова-
ние по всем точкам локализации 1 с множителями e<kl • Волновая
§ 24J ЭКСИТОНЫ ФРЕНКЕЛЯ 187
функция, таким образом, имеет следующий вид:
B4.22)
Ш равно числу узлов решетки и отвечает за нормировку). Опе-
ратор
atdt^Bt B4.23a)
в B4.22) описывает рождение локализованного в точке 1 эксито-
на. Соответствующий B4.22) оператор уничтожения экситона име-
ет вид
= Bi. B4.236)
Наша цель состоит в том, чтобы выразить полный гамильтониан
B4.21) через операторы E>t и BY. Стоящие в последнем члене
B4.21) операторы могут быть следующим образом выражены че-
рез экситонный оператор Bt-
BtBlf B4.24)
так что
МФ »' l' M S tl1 l' !' >V B4.25)
V
2 4ММиФ M S BtB.wl
U' {V L V Lj ti' \V L V L
Это выражение описывает уничтожение экситона в точке 1 и
последующее рождение экситона в точке Г. Спрашивается теперь,
какой вклад дает третий член в B4.21)?
Рассмотрим действие стоящих в нем операторов на локализо-
ванное экситонное состояние. Тогда сразу получаем результат
B4.26)
при 1 = т, Г = т, т. е. 1 = 1'.
При использовании волновой функции B4.22) из третьего
члена B4.21) следует сохранить только те слагаемые, для кото-
рых индексы 1 и Г равны:
aTaidTdiWI = У, af di d,axW \ ) —
j Х ' \V L L V Т 2 \V L L V
Выражение B4.27) приводит лишь к изменению энергии лока-
лизованного экситонного состояния и не может привести к пере-
ходу между различными точками кристалла. Ради полноты рас-
смотрим два первых члена в B4.21). Действие типичного опера-
188 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
торного выражения из первой суммы в B4.21) на локализован-
ное состояние дает следующий результат:
+Pg = a^+O^'m- B4.28)
При 1 ?= m это означало бы, что возникает состояние совершенно
нового типа, а именно такое, в котором электрон удаляется от
электронной дырки. Для того чтобы не прийти к противоречию
с нашим основным предположением B4.22), мы вновь ограни-
чимся предельным случаем исчезающе малого перекрывания, так
что вкладом //эф* при I Ф m можно пренебречь. Начиная с этого
момента, мы рассматриваем только члены с 1 = m и полагаем
= EQlL. B4.29)
В действительности левая часть этого равенства больше не за-
висит от I, поскольку fl'f.m.i зависит только от разности 1 — ю.
Равным образом, для электронной дырки полагаем
#№„ = Е0,а. B4.30)
Выразим теперь произведение операторов afa\ (см. первую сум-
му в B4.21)) через произведение операторов BfBi- При этом
утверждается, что а+а1 можно заменить на произведение опера-
торов B\B\i по крайней мере при использовании функций со-
стояния B4.22):
atal-+BtB1. B4.31)
Утверждение. Соотношение
I atava+d+<I)e = 6ltma+a+&g B4.32)
может быть заменено соотношением
| BfBvB+&g = 8hmB+Og. B4.33)
Для доказательства нужно лишь подставить в равенство B4.33)
определения операторов/?*, Вг B4.23а) и B4.236) и воспользо-
ваться перестановочными соотношениями между операторами а:
afdUi^a+d+Og = б1>та+^+Фя. B4.34)
(Следует помнить, что di<&g = 0, aiQ)g = O.)
Используя соотношения B4.32) и B4.33), первую сумму в
B4.21) можно переписать следующим образом A = т):
2 H\%a<Ui = EOi L 2 BtBx. B4.35)
l i
Точно такое же соотношение справедливо и для второй суммы
в B4.21). После того как третья и четвертая суммы переписаны
§ 24] ЭКСИТОНЫ ФРЕНКЕЛЯ 189
с использованием операторов Бi~ и Bi (см. B4.25) и B4.27)), вы-
ражение B4.21) окончательно принимает следующий вид:
Я = 2 Я^Яо.общ + 2 BtiBiW A - Г), B4.36)
1 1,1'
причем мы положили
?о,оащ = Е0,ь + ЕОж - Wo, B4.37)
B4.38)
If l l vj
) = Wi1 V Y M, B4.39)
а постоянную энергию АЕ опустили. С помощью определения W
B4.9) легко убедиться, что B4.39) зависит только от 1 — 1', а
B4.38) совсем не зависит от 1.
Нельзя не признать аналогию между B4.36) и оператором
Гамильтона связанных гармонических осцилляторов. Правда, мы
не показали что В+, В являются бозе-операторами. Мы вернемся
к этому в § 26. Здесь же покажем в заключение, что функция
состояния B4.22) является решением соответствующего гамиль-
тониану B4.36) уравнения Шредингера, и определим собственные
значения энергии этого уравнения. Для этого подставим функцию
состояния B4.22), которая теперь выражена через операторы Вг '¦
B4.40)
в гамильтониан B4.36). Учитывая соотношение B4.33), получаем
ЯФ = ?0,общФ +-r=Y,Y,W(l-V) В$етФй. B4.41)
У N v\
Второй член преобразуем следующим образом:
W4k)
Очевидно, что выражение B4.42) можно трактовать как произ-
ведение исходной волновой функции B4.40) и энергии W(k). Тем
самым доказано, что при указанных выше упрощениях волновая
функция B422) или B4.40) является собственной функцией га-
мильтона B4.21), причем собственные значения энергии опреде-
ляются выражением
B4.43)
Если разложить Е по волновому вектору к, то, как обычно,
190
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
получаем
B4.44)
Сравнение этого результата с B4.43) дает явное выражение
для эффективной массы экситона. Из предыдущего изложения
следует, что подвижность экситона Френкеля обусловлена ис-
/II' 1' и
ключительно обменным членом W[y L у L] (Рис- 33). (Этот
процесс играет, вообще говоря, значительную роль при переносе
энергии органических молекул в растворах и известен как «про-
цесс Фёрстера».) Возбужденные состояния в твердом теле могут
Энергия' \ WL (х-1)
№6x-l'j
\
Рис. 33. Механизм распространения экситона Френкеля. Электрон, нахо-
дящийся на атоме I, переходит из возбужденного состояния в основное и че-
рез кулоновское взаимодействие передает свою энергию атому в точке Г,
который переходит в возбужденное состояние.
распространяться благодаря обменному взаимодействию, хотя эф-
фективная масса электрона и электронной дырки может быть бес-
конечно большой (это как раз тот случай, когда нет никакого пе-
рекрывания между соседними волновыми функциями).
На практике, конечно, могут одновременно присутствовать
оба механизма: обменное взаимодействие и перекрывание.
Заданияк § 24
1. Почему Hi,m,) B4.7а) при l^m в случае слабого перекры-
вания функций Ваннье значительно меньше, чем .ffi.i.j ?
2. Положить Bf = r4= У e~*lBi, Bi « ~=
VN <Г
вывести обратные' соотношения В? -
.25]
ВОЛНЫ ЭЛЕКТРОННОЙ ПОЛЯРИЗАЦИИ
191
= -r=2de ^i' Показать, что оператор Гамильтона B4.36)
1
при этом становится диагональным:Н =
§ 25. Волны электронной поляризации
На примере экситонов Френкеля объяснение того, каким об-
разом в рамках вторичного квантования можно было бы описать
поляризацию электронов кристалла и объяснить возникновение
поляризационных волн, оказывается особенно простым. Для того
чтобы по возможности наглядно представить наши рассуждения,
а)
Рис. 34. Схематическое, представление распределения заряда функции
Ваннье (или атомной функции): о)—в) р-функции зоны проводимости;
г) s-функция валентной зоны.
учтем, несколько обобщив результаты § 24, что функции Ваннье
Wy{x — 1) валентной зоны должны (подобно атомным s-функци-
ям) описывать сферически симметричное распределение электрон-
ного заряда (рис. 34). '
В зоне проводимости, напротив, в каждой точке 1, где распо-
ложен атом, имеются три волновые функции, распределение заря-
да которых имеет форму гантели, направленной вдоль одной из
осей х, у или z (р-функции) (см. рис. 34).
Будем помечать эти функции Ваннье индексом ц (=ж- или у-,
или z-ориентации) и запишем их в виде wLili(x — 1). Обозначим
индексы V и L, ц одним индексом /:
Разложим полевые операторы г|)+(х) и г|э(х) по функциям Ваннье:
* (х) = S auw}(х - 1), г|>+ (х) = 2 atjw! (* - 1). B5.1)
i.j hi
Эти волновые функции, естественно, теперь должны быть подстав-
лены в оператор Гамильтона B4.6). Следующие эатем преобразо-
вания проводятся практически так же, как и в предыдущих па-
192 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
/
раграфах, так что можно сразу написать конечный результат: га-
мильтониан B4.36) следует заменить гамильтонианом
Н = 2ЯиЛ,й#о,общ + 2 Bt^B^W^ A - 1'), B5.2)
1,Ц 1,1'
где
-Я1
(х - 1) ^ь,ц (х - 1) ** u?*i(i, (х'-Г
Смысл этого последнего выражения наглядно пояснен на рис. 33.
Однако значительно более важно, нежели повторное введение га-
мильтониана B5.2), для нашего понимания сходства экситонов
Френкеля с волнами поляризации, следующее: представим себе
ряд точечных зарядов et в точках h кристаллической решетки.
Выражение для энергии взаимодействия между некоторым до-
полнительным зарядом и квантованным полем кристаллических
электронов имеет следующий вид:
у+ (х) У гр (х) d3x. B5.3)
I i I
Если в это выражение вместо полевых операторов г|)+ и г|) под-
ставить разложения B5.1), то B5.3) переходит в
2 аЪ',1' [м?(х — 1) г—5V, wy (x - Г) d3x. B5.4)
1,1', },j' ' ' J 3 1Х г\
Как и в предыдущих параграфах, мы примем, что между вол-
новыми функциями нет никакого перекрывания, так что в сумме
B5.4) остаются только члены с Г=1. Далее, члены, в которых к
тому же / = /', для нас неинтересны, поскольку выражения вида
afjui,i \ • • • №х означают лишь постоянный сдвиг энергии, кото-
рый, таким образом, не связан с электронными переходами. Поэ-
тому далее будут рассмотрены только те вклады в B5.3), для ко-
торых/^/'. В интеграле B5.4), который распространен по всему
объему, исключим вначале элементарную ячейку с радиусом-век-
тором It и разложим 1/|х —lj| в ряд по степеням 1/11 — 1,1, причем
через 1 вновь обозначены фигурирующие в B5.1; 2) радиусы-век-
торы точек локализации функции Ваннье.
Введем сокращенные обозначения
х-1 = 1, . B5.5а)
1*-1 = Н, B5,56)
§ 25] ВОЛНЫ ЭЛЕКТРОННОЙ ПОЛЯРИЗАЦИИ 193
откуда следует
x-l, = |-R. B5.5в)
Для 1^1 < IRI =R справедливо разложение
+1? +¦¦¦}•
Если подставить это разложение в .интеграл B5.4), то получим
J I г IJ
Первый интеграл в правой части B5.7) исчезает ввиду ортого-
нальности функций Ваннье, принадлежащих разным зонам. Вто-
рой интеграл обозначим, как указано, через D,-,v.Можно показать
(что, однако, относится к атомной физике), что J)jj>=0, если оба
индекса / и /' относятся либо к s-функциям, либо к /^-функциям.
Для нас это означает следующее: Т)ц' ф 0 по меньшей мере тогда,
когда / является индексом валентной зоны, а /'— зоны проводи-
мости или наоборот. Вместо стоящих в B5.4) произведений опе-
раторов a+.aijr вновь введем с помощью операторов электронных
дырок d\ операторы рождения и уничтожения локализованных
экситонов, используя следующую схему:
для
atjaijr заменяется на af,y.d* = B~itll, B5.8a)
для
а+.а^у заменяется на diaittl = jE?iiM,- B5.86)
f = L, ц '3 '
Далее запишем дипольный матричный элемент D в несколько
упрощенном виде, а именно:
для
f = L, ц,
и для
7.,= Г' »Н' = К B5.9)
Ввиду s- и ^-симметрии функций Ваннье нашего примера можно
13 х. Хакен
194 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
показать (чего мы, однако, не будем делать), что при ц = х, у, z
Dx=(D,0,0)=Des,
DB = (О, D, 0) = D eу, вц—единичный вектор.
Dz = @, 0, #)=Дег,
Индексу {х, таким образом, соответствует дипольный момент D
в направлении jx (ц = х, у, z).
Если после всех этих рассуждений и преобразований подста-
вить B5.7) в B5.4), то сразу получим следующий результат:
выражение ег — (D^Sfц) с классической точки зрения
I * * I
B5-10>
il 1 |3 Jmd || 1 |3 v '
Правая часть B5.10) имеет весьма наглядный смысл. Например,
—
I *¦« ¦*¦ I
представляет энергию взаимодействия заряда е{ в точке 1< и дипо-
ля в точке 1 с дипольным моментом Р = ТУцВ^ц = De^B^. Ди-
польный момент Р, таким образом, равен произведению макси-
мально достижимого дипольного момента D, единичного вектора
в направлении \i и зависящей от точки 1 амплитуды В^. Ука-
занную величину Р следует трактовать как амплитуду поляри-
зационных колебаний электронов кристалла. Выражение B5.10)
нужно, естественно, прибавить к оператору Гамильтона B5.2).
Для того чтобы не перегружать наше рассмотрение излишними
подробностями, обратимся к обсуждению простого специального
случая, когда экситон Френкеля покоится, и опустим вторую сум-
му в B5.2). В этом случае уравнение Шредингера, описывающее
взаимодействие электронов кристалла с точечным зарядом е4, име-
ет с учетом B5.2) и B5.10) следующий вид (E0iO5m = Ео):
лГ
,n \ % I h~l\
ГГ-ТГз °м)) ф = ЕФ B5Л1>
и представляет не что иное, как квантованные поляризационные
колебания электронов кристалла, которые взаимодействуют с за-
крепленными зарядами.
§ 25] ВОЛНЫ ЭЛЕКТРОННОЙ ПОЛЯРИЗАЦИИ 195
Операторы В^ и jBiiM,, как будет показано в § 26, приближен-
но (только приближенно!) можно рассматривать как бозе-операто-
ры. В этом случае проблема B5.11) становится для нас совсем
привычной, поскольку в ней по существу речь идет о совокупно-
сти смещенных осцилляторов. Энергия основного состояния при
этом дается выражением (см. § 6)
где f — введенные в B5.11) сокращения.
Для того чтобы поближе познакомиться с физическим содер-
жанием результата B5.12), в него следует подставить явный вид
Y, при этом ради простоты мы ограничимся случаем двух точеч-
ных зарядов i = 1, 2. Тогда выражение для энергии принимает
следующий вид:
1 116
01,1»
и _ 1 |з 11 _ 1 |з г к- °.
I 1 I I 2 I
Оба выражения в первой строке B5.13) отрицательны и пропор-
циональны квадрату величины заряда е;; это означает, что вне-
сение в кристалл заряда приводит к уменьшению собственной
энергии частицы. Понятие собственной энергии играет в кванто-
во-полевой теории и в особенности в физике элементарных частиц
основополагающую роль. Эту энергию можно представить себе
совершенно наглядно. Введенный в кристалл заряд смещает бла-
годаря кулоновскому взаимодействию электроны кристалла из по-
ложений равновесия, т. е. поляризует их. Это смещение центров
тяжести в нашем примере можно представить в виде суперпози-
ции s- и ^-функций. В рамках вторичного квантования это оз-
начает, что электрон из основного состояния, в нашей модели из
s-состояния, частично удаляется и с определенной вероятностью
переводится в возбужденное, в нашей модели р-состояние
(рис. 35). Математически это выражается присутствием операто-
ров рождения и уничтожения В+ и В в B5.11). Поляризованные
таким образом электроны со своей стороны создают поле, кото-
рое действует обратно на введенный заряд, что и приводит к
изменению его собственной энергии.
13*
196
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
Вычислим теперь выражение во второй строке B5.13). Оно
пропорционально произведению е\ и е2 и представляет, следова-
тельно, дополнительное прямое взаимодействие между обоими
точечными зарядами. Положим для краткости
li-l2 = X B5.14)
и учтем, что в нашей модели D^ является вектором, три компо-
ненты которого вдоль направлений: х, у и z одинаковы по велп-
wl(x-l)i
X
а)
Рис. 35. Наглядное представление функций состояния «смещенного ос-
циллятора»
(+)Ф0 = аФ0 + Р5+сФ0, р = аТ.
а) Основному состоянию Фо отвечают занятые состояния в валентной зо-
не, которые представлены фунциями s-типа. б) Под действиемВ^ = afLal у
электрон в состоянии 1, V уничтожается и рождается в состоянии 1, L, ц=х.
в) Электрон находится в состоянии, которое описывается комбинацией V-
и L-функций. Его центр тяжести зарядового распределения смещен, т. е.
атом поляризован.
чине. Тогда для второй строки B5.13), которая представляет энер-
гию взаимодействия между зарядами и которую мы поэтому крат-
ко обозначим через Евз, получаем следующий результат:
B5.15)
При этом, используя B5.14), мы изменили индекс суммирования
1. Вычисление сумм в B5.15) зависит, естественно, от кристалли-
ческой структуры, которая определяет векторы положения 1, и до-
вольно утомительно. Поскольку нас интересует только принципи-
альная сторона дела, перейдем сразу к непрерывному распреде-
лению зарядов. Заменим сумму в B5.15) на интеграл (положив
1 ->• х). Вычисление, если вспомнить электростатику, оказывается
элементарным. Как показано там, имеет место результат
B5.16)
С учетом этого результата (дополнительная) энергия взаимодей-
ствия между двумя зарядами B5.15) принимает очень прос-
§ 25] ВОЛНЫ ЭЛЕКТРОННОЙ ПОЛЯРИЗАЦИИ 197
ТОЙ ВИД
Евз = — еге2 ¦ 1 _ 1 ¦ const, B5.17)
I I 1 21
где константа дается выражением
const =- —^ ' ; B5.18)
о
здесь v— объем элементарной ячейки. Дополнительная энергия
B5.17), которая добавляется к энергии взаимодействия согласно
закону Кулона в вакууме, может быть очень легко интерпрети-
рована с макроскопической точки зрения. Полная энергия взаи-
модействия складывается из энергии кулоновспого взаимодейст-
вия в вакууме e^/Ui —Ь1 и дополнительной энергии B5.17):
| \ 6\ const = ггг=ТТ B5Д9)
тт\т - |! \ , const = ггг=
В последнем равенстве этого выражения введена диэлектричес-
кая постоянная е = ?, которая постоянно встречается
8я^
в феноменологической теории. Из сравнения левой и правой час-
тей можно прямо определить е через атомные величины. Тем са-
мым мы получаем микроскопическую квантовую теорию поляри-
зации кристалла, а именно — электронов кристалла.
Настоящая формулировка с помощью вторичного квантова-
ния допускает ряд очевидных обобщений. Так, в § 24 мы видели,
что экситоны Френкеля, вообще говоря, движутся. Поэтому пер-
вую сумму в B5.11) в общем случае следует заменить операто-
ром Гамильтона B5.2), так что теперь возникает связь между
операторами Bt,\x, и #|'и' с различными индексами 1 и Г. Чтобы
устранить этот недостаток, нам следует вместо локализованных
экситонных операторов ввести такие, которые относятся к бе-
гущим волнам, как это было сделано в задании 2 к § 24. Затем,
внедренные заряды еи как правило, не являются бесконечно тя-
желыми. К проблеме подвижных внедренных зарядов, взаимо-
действующих с квантованным бозевским полем, мы вернемся об-
стоятельно в §§ 35, 36. Оба эти обобщения имеют своим след-
ствием изменение кулоновского закона B5.19) на малых рассто-
яниях. За подробностями мы отсылаем к специальной литературе.
Заданияк§25
1. По аналогии с § 24 вывести B5.2).
2. Показать, что при подстановке плоских продольных и по-
перечных поляризационных волн Н B5,2) (аналогично зада-
нию 2 к § 24) диагонализуется.
198 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
3. Перейти в Но6щ = B5.2) + B5.10) к бегущим поляризацион-
ным волнам экситонов Френкеля и преобразовать Н.
4. Обосновать интерпретацию рис. 35.
а) Почему справедлива указанная там формула?
б) Вычислить к этому <Ф|/ср+(х)е;гф(хЫ3;г|Ф>, использовав
для Ф а), б), в), а для я|з+(х)я|з(х) — B5.1).
§ 26. Экситонная материя
В этом параграфе мы хотим обратить внимание читателя на
совершенно новую область исследований в физике твердого тела.
При этом мы укажем лишь на некоторые важные моменты. Од-
нако изложенные в нашей книге математические методы вполне
достаточны, чтобы полностью рассмотреть упоминаемые ниже
задачи, так что читатель будет сразу в состоянии следить за
оригинальной литературой.
Благодаря высокой интенсивности лазерных источников ста-
ло возможным создать в кристалле высокую плотность экситонов.
Тем самым открывается чрезвычайно привлекательная возмож-
ность создания в некотором смысле искусственной материи. Каж-
дый экситон представляет собой своего рода водородоподобное
образование, причем благодаря различию кристаллов эффектив-
ные массы электрона, электронной дырки и величины диэлектри-
ческой постоянной в законе Кулона могут оказаться совершенно
различными. При высоких плотностях экситонной материи про-
являются такие явления, которые частично известны и для обыч-
ной материи. Прежде всего, экситоны, как впервые эксперимен-
тально убедительно показал Никитин с сотрудниками, могут об-
разовывать экситонные молекулы. Поскольку экситоны часто
можно считать бозе-частицами, было предположено, что при вы-
соких плотностях может иметь место бозе-эйнштейновская кон-
денсация, совершенно аналогично сверхтекучему гелию. Здесь все
же следует указать, что экситоны ни в коем случае не являются
в точном смысле этого слова бозе-частицами. Это можно увидеть
с помощью небольшого расчета, который мы проведем на приме-
ре экситонов Френкеля. Если исходить из операторов локализо-
ванного в узле Г (или 1) решетки экситона, то, как мы видели
в § 24, бегущие экситонные волны конструируются следующим
образом:
B6.1)
Бозевский характер экситона был бы установлен, если бы опе-
раторы рождения и уничтожения удовлетворяли обычным пере-
$ 26] ЭКСИТОННАЯ МАТЕРИЯ 199
становочным соотношениям. Для этого образуем коммутатор из
Вк и Вр, применив B6.1):
[вк, #?] = -^
Коммутатор под знаком суммы, содержащий электроны и элект-
ронные дырки, принимает вид
6U. A - at a, - <tfd,). B6.3)
Если подставить это выражение в B6.2) и использовать ортого-
нальность плоских волн, то получим
[К Щ = skk- - ±
Если бы в правой части B6.4) стоял только символ Кронекера,
то бозевские перестановочные соотношения были бы действитель-
но выполнены. Дополнительный член зависит, очевидно, от чис-
ла электронов и электронных дырок, поскольку он содержит
операторы числа частиц. Совершенно ясно, что этим членом мож-
но пренебрегать до тех пор, пока соответствующие функции со-
стояния содержат лишь незначительное число экситонов п, т. е.
когда n<LN. При рассмотрении более высоких плотностей экси-
тонов необходимо обращать внимание на это нарушение бозев-
ских перестановочных соотношений.
Согласно теории Келдыша и Козлова и Ханамуры при опре-
деленных обстоятельствах и в этом случае можно прийти к кон-
денсации Бозе — Эйнштейна. Мы не приводим вычислений этих
авторов, указывая лишь читателю, что математический метод со-
вершенно аналогичен методу теории сверхпроводимости, который
будет обсуждаться в § 42.
По предположению Келдыша возможно также, что экситоны
образуют своего рода металлические капельки. При этом плот-
ность становится настолько большой, что отдельные электроны
могут быть удалены от своих электронных дырок. Однако капель-
ки не распадаются, за что ответственно, как показал Андерсон
с сотрудниками, кулоновское обменное взаимодействие. Как мы
уже видели в рамках приближения Хартри — Фока, наряду с
обычным членом, описывающим кулоновское взаимодействие,
имеется еще только что упомянутЪш член обменного взаимодей-
ствия, знак которого противоположен знаку члена собственно
кулоновского взаимодействия, что может приводить к некоторо-
му притяжению между частицами с одинаковыми по знаку за-
рядами.
Кажется, что существование этих капелек на самом деле об-
наружено рядом авторов, в частности Бенуа а Ла Гийомом.
200 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ» [ГЛ. IV
§ 27. Плазмоны
а) Классическое рассмотрение. Под плазмонами мы понимаем
кванты плазменных колебаний. Прежде всего вспомним, что во-
обще значит плазма и ее колебания. Если очень сильно нагреть
газ, то атомы частично или полностью ионизуются. Тогда элект-
роны оказываются довольно подвижными относительно ионов и
ядер. Система такого рода, состоящая из противоположно за-
ряженных и подвижных частиц, называется плазмой.
Покажем вначале на примере классических частиц, что плаз-
ма такого рода может испытывать колебания. Ради простоты
будем рассматривать положительно заряженные тяжелые части-
цы как однородный и неподвижный фон и рассмотрим движение
«легких отрицательно заряженных частиц — электронов. Будем
считать, что зарядовая плотность р этих частиц является непре-
рывной функцией координат, и разложим ее по плоским волнам:
^ B7.1)
Одна из таких волн представлена на рис. 9. Разложения такого
рода уже встречались нам ранее, например, при рассмотрении
колебаний решетки. Уже там было ясно, что для колебаний яв-
ляется типичным наличие гармонической зависимости амплитуд
от времени:
pq(*) = ei?Vpq(O). B7.2)
С помощью простых соотношений классической электродинамики
можно получить уравнение для подобных колебаний плотности
и вычислить соответствующую плазменную частоту Q.
Для этого рассмотрим элемент объема AV, в котором нахо-
дятся AN электронов, различаемых индексом i. Пространственные
координаты электронов обозначим через хг(?), а их скорости —
через \t(t). Тогда каждый электрон под действием поля Е (в со-
ответствующей точке пространства х4) будет ускоряться соглас-
но уравнению
ду.
Усредним это уравнений по выделенному элементу объема:
/ <27-3>
С помощью следующего соотношения введем среднюю плотность
тока](х): j(x)= e—^v,-, а среднюю напряженность поля Е(х)с
§ 27] . ПЛАЗМОНЫ 201
помощью соотношения Е(х) = ^^Е(х?). Тогда уравнение
i
B7.3) примет вид
Применим к обеим частям этого уравнения операцию диверген-
ции и учтем, что согласно классической электродинамике справед-
ливы соотношения
j= — -0, divE
где р — плотность заряда. Тогда B7.4) переходит в ')
gt2 m AV г \ > / \ /
Но это уравнение есть в точности уравнение колебаний d2p/dt2-\-
? = 0 с плазменной частотой
B7.6)
где п = AN/A.V — средняя плотность частиц. Все волны имеют
одну и ту же плазменную частоту Qn.
б) Квантовомеханическое рассмотрение. Метод Эренрейха —
Коэна. Поскольку твердое тело представляет собой существенно
иной объект, нежели ионизированный газ, то поначалу может
показаться странным, что мы проводим параллель с плазмой.
Однако только что мы видели, что для плазмы необходимо лишь,
чтобы заряды одного типа легко смещались относительно зарядов
другого типа. Из теории Блоха нам известно (см. §§ 17, 20), что
электроны в твердом теле в действительности ведут себя практи-
чески как свободные частицы. Это и является предпосылкой для
возникновения плазмы твердого тела. Тем не менее в случае твер-
дого тела следует сделать некоторые существенные оговорки.
1. Электроны следует рассматривать в рамках квантовой
теории.
2. Электроны подчиняются статистике Ферми.
Таким образом, следует развить теорию, в которой отражены
оба эти момента. Для этого нам вновь лучше всего опереться
на формализм вторичного квантования и подумать, как можно
было бы перенести классический подход на случай квантовоме-
ханического рассмотрения. При этом в основу рассмотрения будет
') Мы не проводим различия между непрерывным и дискретным рас-
смотрением, поскольку здесь это не имеет значения.
202 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
положено представление Гейзенберга (ср. § 16). Объектом на-
шего исследования и здесь является электронная плотность, ко-
торая известным образом может быть сделана оператором:
р(х, f)=i|)+(x, t)y(x, t). B7.7)
Заряд электрона в B7.7) ради простоты опущен, поскольку при
определенных обстоятельствах колебания зарядовой плотности
можно идентифицировать с колебаниями плотности.
Теперь следует показать, что фурье-компоненты B7.7) дей-
ствительно зависят от времени так, как это указано в B7.2). Для
этого разложим зарядовую плотность B7.7) в ряд Фурье. Соот-
ветствующие компоненты Фурье даются выражением
р (t) = -L Г г|з+ (х, t) гЬ (х, t) e*» dsx. B7.8)
yV J
Это выражение можно преобразовать дальше, если разложить
операторы рождения и уничтожения г|з+(х), i]?(x) по плоским вол-
нам, которые нормированы в объеме V:
B7.9)
B7.10)
Если теперь подставить B7.9) и B7.10) в B7.8), то после крат-
ких промежуточных вычислений получим выражение
к(*), B7.11)
где pq(t) является, естественно, оператором, поскольку «к и а? —
операторы. Чтобы получить классические амплитуды, нам сле-
дует перейти, как обычно в квантовой теории, к средним значе-
ниям вида
=<Ф|р„|ф>. B7.12)
Теперь наша задача состоит в том, чтобы получить уравнение
движения для B7.11) и B7.12). Мы сделаем это, предварительно
введя уравнение движения для произведения операторов
ai+q(t)ak(t). B7.13)
Эти операторы, как можно видеть из выражений B7.7) и B7.11),
зависят от времени. Как уже было отмечено, рассмотрение про-
водится в представлении Гейзенберга (§ 16). Для того чтобы вве-
сти уравнение движения для оператора в представлении Гейзен-
берга, воспользуемся рецептами § 16. Уравнение движения неко-
§ 27] ПЛАЗМОНЫ 203
торого оператора Q в общем случае имеет вид
-.*.*а = [Я, Q], B7.14)
где Н — гамильтониан системы. Здесь мы рассматриваем опера-
тор Гамильтона, который описывает взаимодействие между элект-
ронами. Потенциал решетки учитывается нами с помощью метода
эффективной массы, так что в основу рассмотрения кладется
предположение о положительно заряженном непрерывном фоне.
Таким образом, оператор Гамильтона имеет впд
+ (х) {- -?р А} г|) (х) d*x +
+ \ J я|)+ (»') $+ (х) i х ^, | г|) (х) ф (х') д?х dV. B7.15)
Этот оператор Гамильтона построен с помощью операторов i]>+(x)
и г|з(х). Поскольку, однако, мы ищем уравнение движения для
B7.13), то подставим прежде всего известным нам образом
(см. § 20) выражения B7.9) и B7.10) в B7.15) и после неболь-
ших преобразований получим
| 2 W №; кзк4) ««ь.Як.. B7.16)
к кь-. ,ki
Здесь W дается выражением
W (к^; к3к4) =
= X Г Ге-гк,х--гкгх ^ e*^+Jk4x'^a;^V. B7.17)
Двойной интеграл Фурье B7.17) по кулоновскому взаимодейст-
вию может быть легко вычислен в явном виде, чего, однако, мы
не будем здесь делать, так как это не является задачей квантово-
полевой теории. В конце концов получается следующий резуль-
тат: B7.17) принимает вид
B7.18)
причем Vq определяется выражением
^q = ^, где q = ^-(k1 + k3-k2-k4). B7.19)
В выражении B7.16) значение q = 0 следует исключить, так как
предполагается, что отрицательный электронный заряд полностью
компенсируется положительным фоном. Применив соотношение
B7.14) и использовав для гамильтониана выражение B7.16), по-
лучим уравнение движения для оператора B7.13). Затем следует
вычислить коммутаторы между одной парой операторов и другой
204 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
нарой или четверкой операторов, т. е., например, выражения вида
Uk+qdb, a?av]. B7.20)
Эти коммутаторы вычисляются в упражнении 4 к § 16.
После небольших преобразований получаем уравнение дви-
жения
** () (?" ^) () +
+ S vq. {(fl^+qat+q.) {a?+q,ak>) — (a?'+<l-ak,) (a^+<l^ak)}. B7.21)
k'q'
Дальнейшему рассмотрению B7.21) существенно поможет об-
ращение к методу Эренрейха и Коэна. Поскольку мы все равно
ищем уравнения движения для средних значений вида B7.12),
то само собой напрашивается образовать средние значения в обе-
их частях B7.21) относительно функций состояния Ф. Тогда сра-
зу будет видно, что слева появляются средние значения, содер-
жащие два оператора, а справа, напротив,— четыре оператора.
Тем самым получается последовательность иерархически связан-
ных уравнений. Но эта последовательность, если обратиться к ос-
новам метода Хартри, может быть оборвана.
Как было отмечено в задании к § 20, в методе Хартри среднее
значение от четырех произвольных операторов можно разложить
на произведение двух средних значений, каждое из которых со-
держит по два оператора. С помощью очевидного видоизменения
этого правила полагаем
. B7.22)
Если сделать преобразование Фурье обеих частей B7.22), то не-
посредственно получается соотношение
<Ф | ata^ai3akt |Ф> = <Ф |а^а^|Ф><Ф|aj>kl|Ф>. B7.23)
Соотношение B7.23) дает нам возможность упростить правую
часть B7.21). Тогда получаем
i% -?¦ <Ф | ai+qaK\ Ф> = (Еъ - #k+q) <Ф | <?+,«* | Ф> +
2 17,' {<Ф|а?+чаъ+ч>|Ф><Ф|в^^'Оь' I ф> ~
k'q'
k'+q-вк' | Ф> <Ф| aini-q-ofc I Ф>К B7.24)
Уравнение B7.24) можно, используя идею Бома и Пайнса, уп-
ростить еще больше. Произведения средних значений в. правой
§ 27] Ш1АЗМ0НЫ 205
части содержат как волновой вектор q, так и волновой вектор
q'. Средние значения, вообще говоря, являются комплексными
величинами, т. е. имеют некоторые фазовые множители е**. Эти
фазовые множители зависят, естественно, от операторов а (или
их индексов). В частности, от индексов q и q'. Предположимте-"
перь, что фазовые множители при q^q' не связаны друг с дру-
гом. Если теперь провести суммирование в правой части B7.24)
по q', то все члены суммы, ввиду отсутствия корреляции между
фазами, выпадают и остается только один, когда фазы скоррели-
рованы, т. е. когда q = q'. В рамках этого «приближения случай-
ных фаз» выражение B7.24) переходит в выражение
ъ% -^ <Ф | а?+цак | Ф> = (Е* - Ek+q) <Ф | a$+qak | Ф> +
+ 2vq [пк+ч - пк) 2 <Ф I «k'+qflk' | Ф>, B7.25)
к'
где использовано сокращенное обозначение
йк. B7.26)
пк представляет, очевидно, среднее число заполнения состояния к.
Далее полагаем, что q в уравнениях B7.25) фиксировано, а к,
напротив, может принимать все значения. Поскольку в правой
части B7.25) стоит сумма по к', то мы по существу имеем дело
с системой связанных уравнений для средних значений
B7.27)
Эта система уравнений может быть решена сразу. Для этого
перенесем первое выражение, содержащее разность Ек —Ек+Ч, из
правой части B7.25) в левую часть и поделим на общий множи-
тель, вернее сказать оператор, при B7.27). Тогда получаем
<Ф | a?+qak | Ф> =
1
ih~+(E,,,.-E,,\ к
- nk] 2 <Ф I a^+qflk-1 Ф>. B7.28)
Поскольку мы уже научились обращаться с операторами, то де-
ление обеих частей B7.28) на выражение, содержащее оператор
d/dt, не должно шокировать читателя.
Наша конечная цель состояла в том, чтобы ввести уравнение
для фурье-компонент зарядовой плотности или, более точно, для
среднего значения B7.12). Для этой цели просуммируем обе ча-
сти B7.28) по к, после чего получим уравнение
Рч
= К 2 ***** "к 1 РЧ> B7-29)
206
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
[ГЛ. IV
т. е. уравнение для pq. Для решения уравнения B7.29) сделаем
подстановку
pq = ei?V-atpq(O). B7.30)
Дифференциальный оператор d/dt в знаменателе B7.29) при ис-
пользовании экспоненциальной подстановки B7.30) переходит
просто в выражение гйч— а. Поскольку обе части B7.29) сокра-
щаются на рь, то мы получаем важное соотношение
B7.31)
7\
Здесь частота Qq и фактор затухания а еще подлежат определе-
нию. Положение Qq(oc = 0) можно увидеть на рис. 35а. На этом
рисунке Q является абсциссой,
а правая часть B7.31)—орди-
натой. Проекции точек пересе-
чения графика функции /(Qlt)
с прямой, проходящей на вы-
соте, равной единице, на ось
абсцисс определяют возможные
значения Q. Из этой диаграм-
мы отчетливо видно, что имеют-
ся два типа собственных значе-
ний: собственные значения, ле-
жащие вблИЗИ (l/fo)(i?k+q—Ей),
и второй тип, лежащий за пре-
делами этой области и имею-
щий единственное собственное
значение. Численный расчет
.<?„
Рис. 35а. Графическое определение
энергий возбуждения электронного
газа согласно соотношению B7.31)
при а = 0. Для наглядности значе-
ния eqk при к = кь к2, к3, ... на
рисунке расположены далеко друг
от друга, что дает лишь качествен-
ное представление. В реальной си-
туации 8_к находятся очень близко
друг от друга. Проекции точек пе-
дру дру рц
ресечения /<О ) с единичной орди-
натои на ось О, дают искомые зна-
B7.31) для малых значений q
показывает, что это собствен-
ное значение действительно со-
ответствует плазменной частоте
Q = Qn (выражение B7.6)).
Тем самым доказано, что электроны в металле также могут
совершать плазменные колебания.
Займемся тепфь вопросом, что означают частоты, лежащие
в точках Еъ+ц—Еъ. Сделаем подстановку
\Ч> I flkkj4-q^kk- I 4*/f == \^ I ^kk +q^kk • | *^/о " > \^< .об}
в уравнение B7.25). Тогда можно увидеть, что с точностью до
§ 28] МАГНОНЫ 207
малых поправок члены
щ | Ф) {Еч - Еч+Ч) B7.33)
/
в обеих частях для определенного к,- выпадают. Оставшиеся в
B7.25) суммы должны быть, следовательно, исчезающе малыми.
Это согласуется с тем, что тем самым удовлетворяются и осталь-
ные уравнения для k=?kj и, следовательно, средние значения
(.27.32) для k^kj практически равны нулю. Из этих соображений
становится очевидно, что собственным значениям B7.32) соответ-
ствуют возбуждения, при которых только один электрон рожда-
ется в новом состоянии. Таким образом, это ни в коем случае не
коллективное возбуждение.
Коллективные плазменные возбуждения могут быть обнару-
жены экспериментально. Если, например, пропускать через тон-
кую фольгу электроны, то они могут дискретным образом пере-
давать свою энергию плазменным колебаниям.
§ 28. Спиновые волны: магноны
а) Причина возникновения ферромагнетизма. Магнитные
свойства ферромагнетика можно объяснить, вообще говоря, и в
рамках классической физики, если считать, что ферромагнетик
состоят из отдельных элементарных атомарных магнитов, кото-
рые выстраиваются под воздействием собственного, созданного
имя же «внутреннего поля». Однако два следующих центральных
вопроса в рамках классической физики остаются без ответа:
1. Какова природа элементарных магнитов?
2. Какова природа «внутреннего поля»?
Ввиду того, что напряженность «внутреннего поля» очень ве-
лика, его природу нельзя объяснить магнитным полем элемен-
тарных магнитов.
Квантовая теория дает следующий ответ:
К п. 1: каждый электрон независимо от его орбитального
движения обладает моментом импульса s, так называемым спи-
ном. Этот момент импульса квантован и принимает в выделенном
направлении (созданным, например, наложенным вдоль оси z
магнитным полем) значения sz = +U/2 или sz = — Ъ-11. В меха-
нической модели динамическое поведение спина можно описать,
используя аналогию с волчком. Со спином связан магнитный мо-
мент, имеющий величину магнетона Бора М = е%/Bтс); здесь
е — заряд, т — масса электрона, ас — скорость света. Элемен-
тарные магниты можно прямо идентифицировать с магнитным
диполем, который связан со спином.
К п. 2: спин электронов косвенным образом влияет на их ор-
битальное движение (даже если нет спин-орбитальной связи).
Это соображение вытекает из принципа Паули.
208
ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ
1ГЛ. ГУ
Согласно этому принципу невозможно привести в одно и то
же состояние два электрона с параллельными спинами. Как мы
уже видели в § 13, отсюда следует, что волновая функция
/(xi, хг) антисимметрична по обеим координатам. Но с другой
стороны, можно показать, что волновая функция двух электро-
нов с антипараллельными спинами симметрична относительно
координат. Следовательно, положение спина определяет симмет-
рию волновой функции.
Используя в качестве примера модель Гайтлера — Лондона
молекулы водорода, покажем, как зависит полная энергия от
Электрон /
у (г),
Ядро а
ЯдраЬ
Рис. 36. Молекула водорода.
Система координат.
Рис. 37. Вид ф(г) атома водо-
рода.
симметрии волновых функций. Рассмотрим случай, когда между
обоими закрепленными в пространстве протонами, обоими элек-
тронами и между электронами и протонами действует только
кулоновское взаимодействие. Расстояние между частицами обо-
значим через гаР B, 2 для электронов; а, Ъ для протонов}
(рис. 36).
Уравнение Шредингера A3.31) имеет вид
X ф (ХЬ Х2) = Е ф (xlf Х2). B8.1)
Для приближенного решения этого уравнения положим (с точ-
ностью до нормировочного множителя)
ФМ = Ф (го1>Ф (ГЬ2> — Ф (гад Ф (гы) параллельные спины,
B8.2)
Фн = Ф (roi) Ф (гы) + Ф (гог) Ф (гы) антипараллельаые спины.
Стрелки указывают относительные направления спинов электро-
нов. ф(г<хз) является действительной волновой функцией электро-
на ji—1, 2) в основном состоянии атома водорода а(=а, Ъ)
(рис. 37).
§ 28] МАГНОНЫ 209
С помощью B8.2) построим среднее значение стоящего в
B8.1) гамильтониана
#п (гаь) = j* J фп# Фтт d"*i Лъхг, Еп (гаЬ) =
= J J Фн#Фп d3xx cPx%. B8.3)
После простых вычислений приближенно находим
Ext = E, — A, Еп = Е0 + А. B8.4)
Таким образом, энергии в зависимости от направления спина
отличаются на 2А, причем обменный интеграл А имеет следу-
ющий вид:
д
Г '/11
= А (гаЬ) = ф (гв1) ф (гм) е2 — + 7
J Vab Г12
/ _J -f-VOcptaJd^d»^. B8.4a)
Очевидно, что А зависит от расстояния гЛ между ядрами. В то
время как в молекуле водорода А < 0, в ферромагнетиках А > 0
(поскольку там должны быть использованы другие волновые
функции ф(г)).
Хотя спин явно не присутствует в B8.4), знак этого интег-
рала А зависит от него. Поэтому мы обсудим теперь ¦ формализм,
в котором явно унитывается наличие спина, и начнем это об-
суждение с разъяснения свойств операторов спина.
б) Операторы спина. Поскольку по своей физической природе
спин близок к моменту количества движения, то операторы спи-
на удовлетворяют перестановочным соотношениям для момента
количества движения, которые мы запишем в виде
| SxSj, — sysx = isz, s^Sz — szsy = isx, szsx — s^z — isy. B8.5)
Множитель % у спиновых операторов опущен. Компоненты sx,
sy и sz можно, естественно, объединить в вектор
I s = (sx, Sy, st). B8.6)
В случае нескольких спинов каждому из них следует поставить
в соответствие вектор вида
Поскольку отдельные спины представляют совершенно различ-
ные не связанные друг с другом степени свободы, мы можем
принять, что операторы спина различных электронов коммути-
руют друг с другом:
| slmSj,m, — sj,m,sjm = O при тпФт'. B8.8)
Для наших последующих целей вместо первоначальных операторов
14 х. Хакен •
210 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГД, IV
sx и Sj, будет удобно ввести новые операторы вида
s+ = sx + isy, s~ = sx — isy. B8.9)
Определение B8.9) справедливо для любых по величине спинов.
Мы ограничимся спином 1/2. Собственные функции оператора st
обозначим <P(t) (спин направлен вверх) и ФЦ) (спин направлен
вниз). Тогда справедливы следующие уравнения:
*гФA)=1ГФ^' **ф(*) = —Гф№- B8.10)
Далее, как можно показать (см. задание 1), справедливы соот-
ношения
B8.11)
Таким образом, благодаря действию оператора s+ на состояние
со спином, направленным вниз, возникает состояние со спином,
направленным вверх.
Так как направленный вверх спин нельзя еще раз повернуть
вверх, то отсюда сразу следует выполнение соотношения
1 (s+J = 0. B8.12)
Аналогично, имеет место соотношение
| (s-J = 0. B8.13)
Далее, из перестановочных соотношений B8.5) следует
| s+s--ss+ = 2sz. B8.14)
И, наконец, для спина 1/2 следует соотношение
| s-s++ s+s-= 1, B8.15)
как можно сразу увидеть, если построить какую-либо функцию
из комбинации функций со спином вверх и вниз.
в) Обменный гамильтониан и гейзенберговская модель фер-
ромагнетизма. Мы продолжим рассмотрение проблемы из разде*
ла а) этого параграфа и выразим Ец, 2?tt B8.4) прямо че-
рез операторы спина Si и sa. Поскольку Ен, Е^^ зависят от
относительного направления спина, то имеет смысл ввести эф-
фективный гамильтониан следующего вида:
Н = const - /S1S2. B8.16)
Этот гамильтониан, как помазывает точное квантовомеханическое
вычисление с помощью операторов спина, дает правильные соб-
ственные значения анергии E\t, E^, если
/ •*= /r= 2A(г) (где г = гоЬ) B8.16а)
(см. задание 2).
§ 28] МАГНОНЫ 211
Обобщим теперь оператор B8.16) на систему многих элект-
ронов, находящихся в узлах кристаллической решетки. Вектор,
определяющий расстояние между узлами кристаллической решет-
ки I и т, обозначим I — т. Тогда обменный гамильтониан можно
сразу представить в виде
4" 2
mSiSm, B8.17)
причем постоянную энергию мы опустили и выбрали индексы
спинов соответственно индексам узлов решетки, в которых они
локализованы. Не ограничивая общности, можно принять, что
обменное взаимодействие симметрично относительно векторов 1
и т, т. е. справедливо соотношение
/l-m=/m-l. B8.17а)
Если бы интеграл / не был симметричным, то можно было бы
без труда (учитывая, что s i и sm можно переставлять) симметри-
зовать его. Множитель 1/2 учитывает, что пара электронов 1, m
в сумме B8.17) встречается дважды, а именно, в виде sism и
smsi- Оператор полного спина
S = 2»i. B8.18)
как можно показать (см. задание 3), коммутирует с обменным
гамильтонианом, т. е.
B8.19)
Для некоторых целей полезно выразить исходные операторы Si
sm через операторы sf, Sm. Как можно показать (см. задание 4),
обменный оператор Гамильтона B8.17) при этом принимает сле-
дующий вид:
Н« = - "Г 2 Ji-m №m + szlszm). B8.20)
Это, как и прежде, оператор, используемый в модели Гейзен-
берга. Наряду с этим оператором применяется, особенно в кван-
товой статистике, другой модельный оператор, а именно так на-
зываемый оператор «модели Изинга», в котором операторы s+,
s~ опущены:
На = 1- 2 /i-m*4**m. B8.21)
В нашем рассмотрении, однако, мы примем за основу оператор
B8.20).
В операторе B8.20) наряду с операторами s+, s~ стоят опе-
раторы sz. Эти операторы также можно простым образом выра-
14*
212 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГД, ГУ
зить через операторы s+ и s~. Из соотношении B8.14) и B8.15)
для спина 1/2 следует соотношение
sz = - ~ + s+s-. B8.22)
Если подставить B8.22) для различных узлов решетки 1 и m в
B8.20), то оператор Гамильтона примет вид
На = - 4" 2 Jl-m UUm + 4™ st^l + *1~«Г«?«т|. B8.23)
Соответственно количеству стоящих в B8.23) операторных вы-
ражений разложим На на три части:
B8.24)
где С — независящая от операторов константа:
1-т. B8.25)
Оператор На) билинеен по операторам s+ и s~:
ЯA) = - 4" 2 5i+sm/im. B8.26)
Здесь использовано сокращенное обозначение
/im = /l-m - 6lm S'0) ^I-m'. B8.27)
m'
Формальное различие между B8.23) и B8.26) связано с тем,
что все билинейные члены в B8.23) формально можно записать
в виде B8.26). Наконец, П2) содержит члены порядка выше
второго. Эти члены мы выпустим из рассмотрения, полагая, что
они дают лишь малый вклад. Более того, мы увидим, что в оп-
ределенных случаях эти члены точно пропадают. Штрих у знака
суммы в B8.27) и стоящий за ним индекс 1 указывает на то,
что член суммы с ш' = 1 опущен. Эту сумму кратко обозначим
в виде
m'
B8.28)
Поскольку стоящий в B8.28) в функции / вектор при сдвиге на
любой из векторов решетки не изменяется, то сумма действи-
тельно не зависит от индекса 1.
После этих подготовительных замечаний попытаемся решить
уравнение Шредингера с оператором Гамильтона B8.23)
НаФ = ЕФ. Поскольку На коммутирует, в частности, с Sz, то сле-
дует попытаться так определить волновые функции, чтобы они
§ 28] МАГНОНЫ 213
одновременно были еще и собственными функциями суммарной
компоненты оператора спина в направлении z:
i &Ф = Ж>. . B8.29)
Начнем с решения B8.29) и будем искать основное состоя-
ние системы, в котором все спины параллельны и направлены
вдоль направления z. Эта волновая функция имеет вид
I Ф8 = Ф (Щ ... |) = П Ф« (I), B8.30)
I m
причем произведение распространяется на все N узлов решетки.
Фт W является собственной волновой функцией оператора s2ja
со спином, направленным вниз. Собственное значение, соответ-
ствующее Фй, равно
М = — 4-- B8.31)
Если теперь подействовать на функцию B8.30) в каком-либо
узле решетки 1 оператором переворота спина s\ , то получит-
ся (см. B8.13) и приведенные там соображения)
sTOe(\...i) = 0. B8.32)
Подействуем теперь полным оператором Гамильтона B8.23) на
функцию B8.30). Ввиду свойства B8.32) после этого остается
только постоянный член B8.25). Энергия этого основного состоя-
нии: дается выражением
Ев = -± 2 /i-«, B8.33)
8
причем суммирование следует провести по всем отличающимся
друг от друга индексам 1 и т. Теперь попытаемся, исходя из
этого основного состояния, сконструировать первое возбужден-
ное состояние. Для этого вновь сначала ищем собственную функ-
цию оператора B8.29), однако для такого состояния, в котором
один спин перевернут. Соответствующее собственное значение,
дается выражением
М = - 4- +1. . B8.34)
Поскольку спин может быть перевернут в любом узле 1 решетки,
то имеется целый набор волновых функций1
--Ш-..|), B8-35)
ч
которым соответствует одно и то же собственное значение энер-
гии B8.34) в уравнении B8.29), Для того чтобы решить уравне-
gl4 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ 1ГЛ. IV
ние Шредингера с оператором Гамильтона B8.23), представим
функцию Ф как комбинацию состояний B8.35):
Ф = 2с1Фа..4П •••!). ¦ B8.36I
1 1
Так как кристалл трансляционно симметричен, то можно, как и
в случае блоховских функций, прийти к заключению, что коэф-
фициенты Cj должны иметь вид
Cl= Сйеш B8.37)
Далее воспользуемся приемом, который позволяет записать
функцию B8.35) в более элегантном виде. Относительно опера-
торов спина (см. B8.11)) нам известно, что оператор sf име-
ет свойство превращать спиновую функцию со спином вниз в
спиновую функцию со спином вверх. Поэтому можно воспользо-
ваться следующим соотношением:
ФA...Щ...1) = *&е, B8.38)
1
где Фе дается выражением B8.30). С учетом B8.37) и B8.38)
волновая функция B8.36) принимает вид
ф* = у= 2 еШ*1+ф?, B8.39)
где к — обычный волновой вектор. Совершенно очевидно, что
функция B8.39) представляет спиновую волну, распространя-
ющуюся по кристаллу и обладающую волновым вектором к. Здесь
обнаруживается явная формальная аналогия с оператором рож-
дения гармонического осциллятора. При рассмотрении гармони-
ческого осциллятора мы видели, что возбужденное состояние
может быть создано действием оператора рождения на основное
состояние. В данном случае из уравнения B8.39) также видно,
что спиновая волна, т. е. возбужденное состояние, может быть
создана действием оператора
на основное состояние. С помощью B8.40) состояние B8.39),
в котором присутствует спиновая волна, можно представить
в виде '
| Фк = $?Фв. B8.41)
Введем эрмитово сопряженный B8.40) оператор
который кажется естественным сопоставить оператору уничто-
§ 28] МАГНОНЫ 215
жения. Обратно, отдельные спиновые операторы можно полу-
чить обращением фурье-преобразования B8.40) и B8.42):
B8-44)
Согласно проводимой нами аналогии с гармоническим осцилля-
тором имеет смысл попробовать переформулировать теперь опе-
ратор Гамильтона B8.24) с помощью операторов B8.40) и
B8.42). Ограничимся стоящим в B8.24) оператором #A), который
дается выражением B8.26). Часть Н12) содержит более высокие
степени s, которые даже в случае гармонического осциллятора
невозможно рассмотреть точно. Мы проведем преобразова-
ние спиновых операторов, соответствующим отдельным узлам
решетки, в операторы спиновой волны B8.40) и B8.42). Для это-
го выразим в ЯA) (см. B8.26)) операторы sf и sf через опе-
раторы спиновой волны >Sk- Это дает сначала
2 ^2 B8.45)
^ k
или, после простого изменения порядка суммирования,
B8.46)
Так как
l = (l-m)+m, B8.47)
то сумму, стоящую в B8.46) в скобках, можно разложить сле-
дующим образом:
2 (m> B8.48)
Первая сумма в B8.48) очевидным образом представляет собой
символ Кронекера Stt'i а вторая сумма зависит от волнового
вектора к и не зависит, ввиду свойства трансляционной симмет-
рии, от индекса ш. Так как B8.48) имеет размерность энергии,
то мы запишем это выражение в виде — 2Жк). После этих про-
межуточных результатов получаем, наконец, для НП) выражение
I НA) = 2 SfSiE (к). B8.49)
I k
Теперь могло бы показаться, что согласно этому результату
проблема спиновых волн сводится к проблеме гармонического
216 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
осциллятора. Выражение B8.49) имеет точно ^тот же вид, что и
набор операторов Гамильтона отдельных осцилляторов, где опе-
раторы S?, Si соответствуют операторам b?, b^.
Юднако предлагаемый пример может елужить предостереже-
нием против поспешности в подобного рода операторных вычис-
лениях. Ведь мы еще не установили, каким перестановочным
соотношениям удовлетворяют операторы B8.40) и B8.42). Толь-
ко после этого можно было бы с уверенностью сказать, является
ли аналогия с гармоническим осциллятором гарантированной
или нет. Если образовать перестановочные соотношения, вновь
выразив B8.40) и B8.42) через операторы спина в узлах решет-
ки, то получим
i i А ^П i II
Правая часть B8.50) после использования перестановочных со-
отношений для операторов sf и s7 принимает вид
B8.51)
К сожалению, как следует из B8.50) и B8.51), получаются ни-
коим образом не осцилляторные перестановочные соотношения.
Этот результат станет чуть-чуть получше, если построить сред-
нее значение B8.51) на собственных функциях B8.29). Тогда
в общем случае можно положить
52.1- B8.52)
Если использовать в качестве Ф волновую функцию основного
состояния, то получим
В этом случае, как сразу видно, правая часть B8.50) становится
символом Кронекера 6kk' и мы получаем
SiS?> - S$Si = 6k)k'. B8.54)
Аналогичным образом можно было бы ожидать, что результат
B8.54) останется приближенно справедливым, если вместо основ-
ного состояния Ф8 теперь в B8.52) использовать волновые функ-
ции, в которых перевернуто лишь относительно небольшое чис-
ло спинов.
В любом случае следует констатировать, что перестановочные
соотношения между операторами S? и ?? не являются
точно бозевскими перестановочными соотношениями. Можно, ко-
нечно, задаться вопросом, нельзя ли так видоизменить опреде-
§ 281 МАГНОНЫ 217
ление операторов iS*, чтобы получились действительно точные
бозе-операторы. Это можно сделать с помощью преобразования
Холъштейна — Примакова. Для этого рассмотрим отдельный спин
и попытаемся выразить его операторы s+, s~ и sz через бозе-
операторы Ъ+ и Ъ. Для этого представим sz в виде
sz = 1- + Ь+&, B8.55)
где sz в основном состоянии соответствующего гармонического
осциллятора = —1/2, а в первом возбужденном состоянии, на-
против^ +1/2. Поскольку в перестановочных соотношениях
B8.50) в правой части стоит sz, то при преобразовании s+ и s"
в бозе-операторы кажется разумным ввести нормировочный мно-
житель, грубо говоря, вида Vsz. Этот подход еще не совсем точен,
однако он дает основополагающую идею. А именно, если сделать
следующие подстановки (преобразование Холъштейна — Прима-
кова):
B8.56)
s~ = 1/1-b+b Ъ, B8.57)
то оказывается, что, например, s+ и s~ удовлетворяют переста-
новочному соотношению
s+s- _ s-s+ = 2s2 B8.58)
(см. задание 6).
Аналогичным образом удовлетворяются перестановочные со-
отношения между s+ и sz, а также s~ и sz, если использовать для
s~ и sz правые части уравнений B8.55) и B8.57), а для Ъ при-
нять бозевские перестановочные соотношения. Очевидно, что пре-
образования B8.56) и B8.57) только тогда имеют смысл, когда со-
ответствующий гармонический осциллятор лишь слабо возбужден,
так что среднее значение Ь+Ъ меньше единицы. Преобразования
B8.55—28.57) можно провести для каждого спина в узле 1 и
тем самым: выразить оператор Гамильтона B8.20) через операто-
ры "i"&i. В этом случае Ь? и Ъ\ являются операторами ос-
циллятора, которые ставятся в соответствие локальному спину.
Теперь можно разложить радикалы по операторам b\bi и пе-
рейти от локальных бозевских операторов к таким, которые со-
ответствуют бегущим волнам, т. е., например, к операторам
B8-59>
Следует помнить, что при этом индекс 1 относится к локализо-
ванным осцилляторам, а индекс к, напротив, относится к осцил-
218 ЭЛЕКТРОНЫ В «ЗАМОРОЖЕННОЙ» РЕШЕТКЕ [ГЛ. IV
ляторам, соответствующим бегущим волнам. Операторы
эрмитово сопряженные им операторы Вк вновь удовлетворяют
бозе-перестановочным соотношениям.
Все члены нового оператора Гамильтона, вплоть до квадра-
тичных, теперь совпадают с членами прежнего выражения для
Н, если только заменить <Sk и SQ на операторы В^ и В^.
Преимущество преобразования Холыптейна — Примакова состоит
в том, что оно систематическим образом выявляет те отклонения
в членах высшего порядка, которые возникают яз-за того, что
S+ и S" не точно удовлетворяют бозевским соотношениям.
В литературе, вообще говоря, имеются другие методы, напри-
мер метод индефинитной метрики, однако мы не будем углуб-
ляться в них.
Задания к § 28
1. Доказать B8.11).
Указание. Умножить B8.10) слева на s~ или s+ и вос-
пользоваться B8.14).
2. Определить общую собственную функцию для (si + S2J и
«и + S2z и показать, что при подходящем выборе «const» и /
в B8.16) этот оператор Гамильтона дает правильные собствен-
ные значения энергии B8.4).
3. Показать, что B8.18) коммутирует с B8.17).
4. С помощью B8.9) преобразовать B8.17) в B8.20).
5. Сравнить экситоны Френкеля со спиновыми волнами. Для
этого воспользоваться аналогией s^ <^>- atdt, si*-*-di<ii.
6. Доказать, что для операторов B8.55—28.57) имеет место
перестановочное соотношение B8.58).
Г л а в а V. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ
С КОЛЕБАНИЯМИ РЕШЕТКИ
§ 29. Гамильтониан Фрёлиха для взаимодействия между
электронами и фононами
В этом параграфе будет введен оператор Гамильтона для взаи-
модействия между электронами и колебаниями решетки. Основ-
ная идея этой главы состоит в том, чтобы по возможности просто
представить как движение электронов, так и колебания решетки.
Для этого предположим, что электроны находятся вблизи ниж-
него края зоны, т. е. их функция Блоха имеет малый волновой
вектор к и тем самым соответствующие длины волн велики срав-
нительно с постоянной решетки. Равным образом примем, что
для взаимодействия с электронами важны только такие колеба-
ния решетки, длины волн которых много больше постоянной ре-
шетки. В обоих случаях кажется естественным отвлечься от де-
тальной структуры решетки и рассматривать движение электро-
нов и ионов в континуальной модели.
Вначале рассмотрим
а) Полярные кристаллы. Исследуем вначале поляризацион-
ные колебания. Эти поляризационные колебания будем рассмат-
ривать, руководствуясь классической электродинамикой. При-
помним кратко, как рассматривают поляризацию Р(х) среды в
классической электродинамике. Для этого вначале исходят из
отдельного диполя. Обозначим вектором q расстояние между за-
рядами диполя, колеблющуюся массу диполя — через т, а его
собственную частоту — через ю. Полная энергия тогда дается вы-
ражением
¦f-ti' + ttV)- <29Л>
От находящихся в узлах решетки дискретных диполей перейдем
к непрерывному распределению диполей. При этом будем счи-
тать, как это обычно предполагается в теории дисперсии, что
диполи не связаны друг с другом.
В остальном предельный переход к непрерывному распреде-
лению проводится совершенно аналогично § 9. При этом нужно
только еще учесть, что в итоге мы ищем не отклонение q, а вы-
водим уравнение для дипольного момента и затем переходим,
в смысле обычной электродинамики, от дипольного момента к
плотности диполей. Если эффективный заряд, входящий в ди-
220 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРбнОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
польный момент, обозначить е*, то следует, таким образом, сде-
лать замену
e*qn -- Р(х). B9.2)
Далее, как обычно, введем с помощью соотношения
та = р d3x B9.3)
плотность массы. Если воспользоваться сокращением
% B9.4)
то кинетическая Т и потенциальная U энергия свободных коле-
баний поля поляризации принимают вид
Т = j-|-Pa(x)d3x, U=§%fv*(x)&x. B9.5)
В то время как частоту <в можно отождествить с частотой опти-
ческих колебаний решетки (мы вскоре увидим, что нам следует
учитывать только продольные колебания), константа ч должна
быть еще определена из феноменологической теории.
Для этого рассмотрим энергию взаимодействия между элект-
ронами и поляризационными колебаниями. Согласно электроста-
тике, энергия взаимодействия электронного заряда е в точке х
с дипольным моментом Р в точке х' дается выражением
*|T5zpp- B9-6>
В случае непрерывно распределенной зарядовой плотности р(х)
и непрерывно распределенной плотности диполей Р(х') выраже-
ние B9.6) переходит в
^^ B9.7)
Интегрируя по х и х', получаем выражение для энергии взаимо-
действия Ею поля поляризации Р(х) с непрерывно распределен-
ной зарядовой плотностью р(х):
Еъь= [[9(x)S^^l3P(x')d3xd3x'. B9.8)
" " I X — X |
Предположим на время, что плотность заряда р(х) задана, и ис-
следуем уравнения движения для поляризационных колебаний
под влиянием зарядовой плотности р(х). Функция Лагранжа, как
известно, имеет вид
L = T-U-En. B9.9)
§ 29] ГАМИЛЬТОНИАН ФРЁЛИХА 221
Уравнение движения получаем из уравнений Лагранжа
4^-^=°' 1 = x,y,z. B9.10)
Проведение операции варьирования 6 уже обсуждалось подробно
в § 9. С помощью уравнения B9.10) и явных выражений B9.5)
и B9.8) сразу же находим уравнение движения
B9.11)
Правая часть этого уравнения согласно элементарным формулам
классической электростатики представляет собой электрическое
смещение D(x), которое создается зарядовой плотностью р(х).
Для отыскания не определенной до сих пор постоянной f рас-
смотрим уравнение B9.11) в статическом случае. Тогда получаем
. B9.12)
Напряженность поля и смещение, как известно, связаны друг с
другом соотношениями
D = Е + 4яР0ощ, B9.13)
или D = sE. B9.14)
Комбинируя B9.13) и B9.14), получаем непосредственно соотно-
шение
4яРобщ = (l - 4") D B9.15)
При этом через РОбЩ мы обозначили полную поляризацию, кото-
рая создается как поляризацией электронов ионных оболочек
так и смещениями ионов. Оба эти механизма поляризации откли-
каются на присутствие статического поля, так что под е следует
понимать статическую диэлектрическую проницаемость. Нас, од-
нако, интересует только та часть, которая связана с поляризаци-
ей собственно решетки. Чтобы выделить эту часть, представим
себе, что после того, как поле было медленно включено, оно очень
•быстро выключается. При быстром выключении за полем могут
следовать только электроны, так что в этом случае мы подучаем
связь между поляризацией и смещением D, которая формально
выглядит как B9.15), однако теперь левая часть относится только
к электронной поляризации 6Р, a s теперь следует заменить на
диэлектрическую проницаемость при очень высоких (порядка
222 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
оптических) частотах. Отсюда находим соотношение
4ябР = - ll - —-] D. B9.16)
Складывая B9.15) и B9.16) (при этом следует обратить внима-
ние на знак минус перед 6Р, который появляется из-за выключе-
ния поля), получаем для той части поляризации, которая созда-
ется только колебаниями решетки, следующее выражение:
4яР = 4я (Робщ + 6Р) = Ц L) D. B9.17)
Если сравнить теперь B9.12) с B9.17), то мы получим, наконец,
остававшуюся не определенной до сих пор константу у.
т=т-(т—4-Г- <29Л8>
0) \еоо Ё /
Чтобы получить полный оператор Гамильтона — поляризаци-
онные колебания плюс электроны — следует еще добавить часть,
описывающую энергию электронов. Для того, будем считать,
как уже предполагалось ранее, что электроны находятся на ниж-
нем крае зоны и во взаимодействие с колебаниями решетки дают
вклад только сравнительно большие длины волн. Это означает,
что можно уверенно воспользоваться методом эффективной мас-
сы, т. е. полностью отвлечься от периодичности потенциала элек-
трического поля и описывать электроны только с помощью их
эффективной массы т*. Если вновь операторы электронного вол-
нового поля обозначить через г|)+(х), я|з(х), то
(х) (- 2^г А) ф (х) сРх. B9.19)
При этом одновременно классическая плотность заряда р(х) пере-
ходит в оператор зарядовой плотности:
B9.20)
Если подставить B9.20) в B9.8) и провести интегрирование по
частям по координате х', то Нвз переходит в выражение
Явз = Г Г я|)+ (х) ф (х) , е—ТТ (- divx' P (х')) ^х д?х'. B9.21)
J J |х —х |
Тем самым мы получили все необходимые выражения, чтобы по-
строить полный гамильтониан. Для этого припомним еще заме-
чание из параграфа об «электронах, танцующих на канате», что
оператор Гамильтона взаимодействующей системы получается
следующим образом: вначале составляется; оператор Гамильтона
одной подсистемы с учетом влияния на нее другой подсистемы,.
а затем к ней прибавляется энергия (без учета взаимодействия)
§ 29] ГАМИЛЬТОНИАН ФРЁЛИХА 223
второй подсистемы. Здесь мы уже ввели выражение для энергии
подсистемы поляризационных колебаний. Теперь нам необходимо
лишь добавить энергию свободного электронного поля. Если в
выражение для энергии B9.5) вместо Р ввести канонически со-
пряженный Р импульс П и собрать вместе выражения B9.5),
B9.19) и B9.21), то получим, наконец, наш полный оператор Га-
мильтона
Н = | ф+ (х) (- ^ А) г|) (х) d*x+ J (± IF (x)+-J ©2P* (x)) d*x+
B9.22)
f Г
J J
7
|x —x
Если рассмотреть в B9.21) член divP, то с помощью разло-
жения по плоским волнам можно обнаружить, что в нем остаются
только продольные волны. Поэтому с самого начала в полном
операторе Гамильтона B9.22) можно ограничиться продольными
колебаниями решетки.
Выражение B9.22) вначале можно рассматривать как клас-
сическое выражение для энергии классического поля поляриза-
ции и шредингеровского волнового поля. В этом отношении
B9.22) представляет собой феноменологическое выражение для
энергии. Однако у нас есть все необходимые средства, чтобы про-
квантовать это выражение для энергии, что делается совершенно
аналогично правилам §§ 11, 13 и не нуждается в дальнейшем
обсуждении. Целесообразно, далее, провести разложение поля
поляризации Р и электронного волнового поля по плоским вол-
нам. Учитывая, что Р содержит только плоские волны, получаем
обобщение A0.13):
Р(*'> = T7f 2 /?-^х' (*w - btw). B9.23)
Если подставить это выражение в B9.22), то оператор Гамиль-
тона примет вид
Я = JV (х) {- ^ А} ф (х) d'x +
+ (х) ф (х)
B9.24)
где уже проведено интегрирование по х'. При этом интегриро-
вании следует применить некоторые хитрости, однако, поскольку
это не дает читателю никакой новой информации о квантовю-
полевой теории, мы не будем их обсуждать. Если еще разложить
224 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
электронные волновые функции в ряд
и использовать это разложение в B9.24), то исходный оператор
Гамильтона B9.22) принимает окончательный вид
2 fewM+w w>w) B9.26)
w,k
Константы связи gw имеют следующий явный вид:
„2* \1/2 л
Ш 4-« <29-27>
где f определена в B9.18). Чтобы перейти от B9.24) к B9.26),
было проведено интегрирование по х. Поскольку, однако, в этом
интегрировании согласно B9.24) и B9.25) участвуют только пло-
скпе волны, то оно проводится очень просто и может быть вы-
полнено самим читателем.
б) Металлы. И в этом случае наш замысел состоит в описа-
нии как электронов, так и колебаний решетки в рамках контину-
альной модели. Электронный оператор можно сразу позаимство-
вать из предыдущего изложения в виде B9.19).
Поляризационные колебания, однако, чтобы не было проти-
воречия с экспериментальными данными, следует рассматривать
несколько по-иному. В то время как в предыдущем изложении
нами использовалась модель, согласно которой частота поляри-
зационных колебаний не зависит от волнового вектора, что хо-
рошо согласуется с экспериментальными данными для полярных
кристаллов, в металлах прежде всего речь идет о взаимодействии
между электронами и акустическими колебаниями решетки, для
которых имеет место закон дисперсии m = vk, где v — скорость
звука. Этот закон уже был введен в § 11 для континуальной мо-
дели, причем потенциальная энергия была пропорциональна не
з
Р2, а 2 (gTa.dPjJ (см. A1.32), а также A1.35)). Представим
5=1
поэтому энергию колебаний решетки в виде
Ер = J {"Г ^2 (Х> +-" ((grad PxY + (grad Ру? + (grad P
B9.28)
где величины у и g еще подлежат определению и могут быть
§ 29] ГАМИЛЬТОНИАН ФРЁЛИХА 225
подогнаны под экспериментальные результаты. При введении
электрон-решеточного взаимодействия также следует быть осто-
рожным, поскольку электроны в металле смещаются свободно и,
следовательно, сильно экранируют поле, вызванное каким-либо
точечным зарядом. Можно показать, что из-за этой экранировки
вместо обычного кулоновского потенциала возникает другой закон
„-Мх-х'|
К (х- х') = Со р гг-, B9.29)
где % — так называемая постоянная экранировки. Поэтому в на-
шем предыдущем выражении для энергии взаимодействия B9.21)
кулоновский потенциал е/\х — х'| следует заменить на B9.29),
после чего получится следующее выражение для энергии взаи-
модействия:
Еъя = J J г|5+ (х) if (х) К(х — х')(— div P (х')) д?хd3x'. B9.30)
Если предположить, что экранировка очень сильная, то выраже-
ние B9.29) при х Ф х' дает практически нуль, а при х = х' —
бесконечно большой вклад. При подходящем предельном пере-
ходе для А, и Со выражение для К принимает вид б-функции. Так
как явное проведение такого предельного перехода ничего не да-
ет для понимания существа дела, то мы опустим его и в даль-
нейшем будем считать, что К имеет вид
К(х — х') -Сб(х-х'), где С = еЩ-. B9.31)
А
С помощью B9.31) выражение для взаимодействия B9.30) су-
щественно упрощается, так как теперь интегрирование по х' со-
вершенно выпадает. Если вновь вместо Р ввести канонически
сопряженный импульс П, то, как легко видеть, полный оператор
Гамильтона принимает вид
2
3=x,y,z
+ С j г|5+ (х) г|> (х) (- div P (x)) d3x. B9.32)
Также и здесь следует отметить, что поляризация опять-таки
обязана своим происхождением продольным колебаниям, поэто-
му для Р снова можно использовать подстановку
eiWXFw-^w), B9.33)
причем следует принять во внимание, что теперь частоты со за-
15 х. Хакен
226 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
висят от w. Подстановка B9.33) и B9.25) в B9.32) дает, после
проведения элементарных преобразований, совершенно аналогич-
ный B9.26) оператор Гамильтона, где лишь константы связи gw
имеют другое значение и в явном виде могут быть представлены
следующим образом:
%а - 4яе'
Для теории сверхпроводимости окажется очень важным то
обстоятельство, что константы связи gw, которые пропорциональ-
ны 1/1 'Y, тем самым также пропорциональны 1/УМ, где М — мас-
са иона решетки.
§ 30. Нестационарная теория возмущений (первый порядок).
Спонтанное и индуцированное испускание и поглощение
фононов. Представление с помощью диаграмм Фейнмана
В § 29 был введен оператор Гамильтона для взаимодействия
между электронами и колебаниями решетки. Хотя этот гамиль-
тониан выглядит еще довольно просто, выяснилось, что соответ-
ствующее ему уравнение Шредннгера не может быть решено
точно. Поэтому, чтобы получить представление о том, как про-
является взаимодействие между колебаниями решетки и электро-
нами, мы вынуждены обратиться к развитию соответствующих
приближенных методов. Вначале кажется естественным восполь-
зоваться теорией возмущений, в которой предполагается, что энер-
гия взаимодействия очень мала. Соответстненно этому предста-
вим оператор Гамильтона, как обычно, в виде суммы
Н = ИО + НЮ, C0.1)
где Но относится к невозмущенпой задаче, а //ля рассматривается
как малое возмущение. Решения уравнения Шредннгера с невоз-
мущеиным гамильтонианом
#0 = 2 tiska?ak + 2 %(owbtbw C0.2)
k w
могут быть легко найдены (см. упражнение 1 § 15). Различные
k-состояния электронов могут быть, смотря по обстоятельствам,
либо заняты электроном, либо свободны. Состояния колебаний
решетки с различными волновыми векторами w могут быть заня-
ты определенным числом фононов. Примерами таких состояний
могут быть
Ф@)=40Ф0; а?Ь+.Фв;...; а^^=(б+0)пФ0. C0.3)
Пусть теперь включено взаимодействие, так что функции
C0.3) более не являются решениями соответствующего гамильто-
§ 30] НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ 227
ниану C0.1) уравнения Шредингера. Теперь целесообразно пе-
рейти к представлению взаимодействия (см. § 16). Тогда соответ-
ствующее уравнение Шредингера принимает вид
I ih<b{t)=Ha»{.t)<S>(t), C0.4)
где //вз ниже будет выписан еще раз в явном виде. Положим,
что в начальный момент времени t = 0 существует состояние
вида C0.3), так что справедливо соотношение
Ф@) = Ф@), C0.5)
поскольку в начальный момент времени t = 0 представления Шре-
дингера и взаимодействия совпадают. Если C0.4) рассматривать
как дифференциальное уравнение по времени, то интегрирование
C0.4) сразу дает следующий результат:
Явз (т) Ф (т) йт + Ф@). C0.6)
о
Естественно, что пока мы еще ничего не выиграли, так как ис-
комая функция Ф вновь стоит под интегралом в правой части
C0.6).
Теперь воспользуемся тем, что возмущение должно быть ма-
лым. Тогда искомая функция состояния и после включения воз-
мущения, по меньшей мере в самом начале, изменится очень ма-
ло, так что левая часть C0.6) будет лишь незначительно отли-
чаться от Ф@). Тогда функцию Ф(т) под интегралом следует за-
менить на Ф@), что ведет к пренебрежению в C0.6) членами
второго и более высоких порядков относительно Нва. После этого
уравнение C0.6) переходит в
t
(зо-7)
о
В правой части этого уравнения как функция Ф@), так и опе-
ратор #„3 заданы в явном виде, так что можно вычислить иско-
мую функцию ФШ. В этом и состоит теперь наша задача. Для
этого зададим явно оператор Нъз в представлении взаимодействия.
Оператор Явз в представлении взаимодействия (см. B9.26)) точно
в тех же обозначениях уже был введен в § 16, однако ради пол-
ноты изложения выпишем его еще раз,
явз (т) = % 2 te
k,w
+ glaUb+vbte-^+^-^n C0.8)
Оператор C0.8) состоит из линейных комбинаций операторов
15*
228 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
вида
a^+wak6w C0.9)
и
atak+wb+, C0.10)
где C0.9) описывает уничтожение, а C0.10), напротив, ро;кдение
фонона, причем одновременно уничтожаются электроны в на-
чальном состоянии и рождаются в новом конечном состоянии.
Посмотрим теперь, как действуют эти операторы на начальное
состояние, и рассмотрим для этого некоторые типичные
Примеры. 1. Спонтанное испускание фонона. Пусть вначале
имеется электрон в состоянии ко, а фононов нет. Тогда начальное
состояние задается функцией
I ф @) = я?ф,. (зо.и)
Если подействовать оператором C0.9) на начальное состояние
C0.11), то соответствующее выражение исчезает, так как фонон
уничтожается, а в начальном состоянии, по предположению, фо-
нонов не было. Если, напротив, подействовать па C0.11) выра-
жением C0.10), затем воспользоваться перестановочными соот-
ношениями для ферми-операторов и тем обстоятельством, что
действие оператора уничтожения на Фо дает нуль, то мы получим
e?b>,A+w,k,. C0.12)
Чтобы получить ^взак„Ф<р следует перемножить C0.12) со сто-
ящими в C0.8) экспонентами и Й#„, а затем просуммировать по
к и w. Если затем подставить полученный таким образом резуль-
тат в C0.7), то без каких-либо дальнейших вычислений полу-
чаем
t
= 2 (- 0 Ak.-w j <Г'(Е* +w-ek-»w)' Л.а^+Ф0+як+Ф0. C0.13)
k,w 0
Ввиду присутствия в C0.13) символа Кронекера, это выражение
переходит в
t
= 2 (- 0 Sw J eiE*o-wVM«ViEk°T^.^o _*Ь+Ф„ + <Ф0. C0.14)
*' о
Результат C0.14) можно интерпретировать следующим образом.
Из начального состояния, в котором имеется электрон с волновым
§ 3°] НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ 229
вектором ко, под влиянием возмущения возникает новое состоя-
ние с фононом, волновой вектор которого равен w, и электроном,
который перешел из начального состояния к0 в новое состояние
ко — w. Этот процесс можно представить наглядно с помощью
диаграммы (ил графика).
Здесь и в последующем изложении мы постоянно будем чи-
тать эти диаграммы справа налево, что, возможно, потребует не-
которого изменения привычки, однако
окажется чрезвычайно полезным для
формулировки правил вычисления.
Приходящий электрон будем пред-
ставлять отрезком прямой линии сука-
зывающей влево стрелкой. Затем вза-
имодействие с колебаниями решетки
представим узлом диаграммы (или вер-
шиной от английского «vertex»). Ухо-
дящий после взаимодействия электрон Рис. 38. Спонтанное ис-
вновь представляется прямой линией пускание фопона.
со стрелкой, а уходящий фонон — вол-
нистой линией со стрелкой (рис. 38). С помощью этих и анало-
гичных диаграмм, с которыми мы познакомимся позже, можно
не только очеш) наглядно описать происходящие процессы, но —
и это как раз основное в применении диаграмм — с помощью
диаграммы можно установить точные правила вычисления, по-
зволяющие найти функцию конечного состояния. Для этого запи-
шем функцию конечного состояния в виде
Ф (t) - 2 ck>w (/) <?&+Ф„ + а?Ф0. C0.15)
k
Задача теории состоит в вычислении коэффициентов ct,w(f).
Рецепт вычисления этих коэффициентов следующий:
приходящая электронная волна е г к»т О"* ~—
уходящая электронная волна егЕкТ ч О
выходящая решеточная волна eiaw% <_~~~~Q
вершина — ig^ О
В вершине используется закон сохранения импульса %ко =
=ftk+ftw для приходящей и уходящих волн. Стоящие в схеме
справа функции следует перемножить и затем проинтегрировать
от начального момента времени to (мы постоянно будем полагать
to = 0) до конечного момента времени t. Этот рецепт позволяет
получить следующие выражения для коэффициентов:
t
о
Как показывает сравнение этого выражения с C0.13), это и есть
230 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
полученный нами ранее результат. Внимательный читатель уста-
новит, что вывести эти правила совсем нетрудно и его задача в
других случаях будет постоянно заключаться в том, чтобы само-
му получить аналогичные правила для каждого данного взаимо-
действия.
Интегрирование в C0.16) выполняется сразу и в результате
получаем
Ck,w (*) - *Жь*.*. ^Ь-1, C0.17)
где введено сокращенное обозначение
А = eko_w + cow - 8ko. C0.18)
Что же мы получили, вычислив коэффициенты с отдельных функ-
ций состояния? Согласно основному правилу квантовой механи-
ки, квадрат модуля
lck,wU)l2 ¦ C0.19)
определяет вероятность того, что система находится в соответ-
ствующем состоянии. В нашем случае, следовательно, в состоя-
нии с одним электроном с волновым вектором к и одним фопоном
с волновым вектором w. Дифференцируя C0.19) но времени, най-
дем вероятность перехода в единицу времени (в секунду), кото-
рая, таким образом, дает меру того, с какой скоростью электрон
из начального состояния рассеивается в конечное состояние с
испусканием фонона. Это выражение имеет вид
Функция д— в предельном случае большого t становится
б-функцией Дирака:
JL*k?? = fi(A). C0.21)
Условие, что она отлична от нуля, только когда ее аргумент
Д=0, представляет, как можно видеть с помощью C0.18), закон
сохранения энергии:
энергия приходящего электрона = энергия рассеянного
электрона плюс энергия испущенного фонона. C0.22)
Для приложений, как, например, в следующем параграфе, по-
священном электропроводности, важно вычислить, с какой вооб-
ще вероятностью электрон рассеивается из начального состояния
в какое-либо конечное состояние. Согласно основным правилам
статистики, вероятность протекания какого-либо процесса равна
сумме парциальных вероятностей каждого отдельного процесса.
§ 30] НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ 231
В данном случае мы получаем, таким образом, для полной ве-
роятности перехода следующее выражение:
C»,m-^k,.kr»- C0.23)
W
Если подставить сюда C0,20) и C0.21), то получим
И^олн == 2 | ?»¦ |3 2лб (ek,_w - eko + «О- C0.24)
w
б-функцпя, естественно, имеет смысл только под интегралом. На
этом основал и а сумму но w следует заменить интегралом. При
этом следует ввести еоотнетствующее правило вычисления вол-
новых векторов w. Как мы уже видели ранее на примере коле-
баний сплошной среды, волны решетки, так же как и электрон-
ные волны, должны удовлетворять условиям периодичности.
Следствием этих условии являются следующие явные выражения
для w:
2л 2л 2зт /,,п „гч
шх^ — пх, Wy^ — riy. wz---E-nz, (o0.25)
где пх, пя, пг — целые числа, которые ввиду конечности постоян-
ной решетки а кристалла изменяются вплоть до значений \rijl =.
= L/Bа) (L — линейный размер кристалла).
Сумму по w, как легко видеть, можно переписать формально
следующим образом:
2 = ^ -=^i...dnxdn,jdnz, где dni = \. C0.26)
Эта форма записи позволяет немедленно ввести интеграл, если
только выразить приращения dn согласно C0.25) через dw. Тогда
C0.26) переходит в
C0.27)
так что Тополи окончательно принимает следующий вид:
ТПолн = ЛГ75 f I ЬЧ I2 6(ek.-w - eko + cow) d»w. C0.28)
Вначале могло бы показаться, что вероятность перехода пропор-
циональна объему. Однако это не так, поскольку константы свя-
зи gw сами зависят от объема согласно соотношению
kw|2 = ^rCw, C0.29)
как это следует из формулы B9.27). Cw представляет собой за-
232 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
висящую от w функцию, различную для металлов и полярных
кристаллов (см., например, B9.27), B9.34)).
Окончательный результат вычисления C0.28) определяется,
естественно, функциональными зависимостями cow и Cw от w.
2. Индуцированное испускание и поглощение фононов. Рас-
смотрим начальное состояние системы Ф@), в котором наряду
с электроном с волновым вектором ко имеются еще и п фононов
с волновыми векторами wo:
ОпФ0. C0.30)
Чтобы вычислить с помощью формулы C0.7) новую функцию
состояния, следует вновь подействовать на начальное Состояние
Рис. 39. Спонтанное не- Рис. 40. Индуцирован-
пускание фонона w. ноо испускание фонона.
C0.30) оператором взаимодействия Нвз. При этом учтем, что этот
оператор содержит сумму по w. Здесь могут возникнуть два раз-
личных случая, в зависимости от того, совпадает ршдекс сумми-
рования w с wo или нет. Если эти волновые числа не равны друг
ДРУГУ) то можно полностью использовать предыдущие соображе-
ния, так что в качестве конечного состояния получаем комбина-
цию функций вида
4^ьг~(ь10)пФ0, C0.31)
поэтому для рассматриваемого процесса полная функция состоя-
ния после рассеяния имеет вид
ib+'XO». C0.32)
Весь процесс можно представить с помощью диаграммы рис. 39.
При этом коэффициенты Ck,w в явном виде задаются выражения-
ми C0.16) и C0.17). Теперь исследуем интересный случай, когда
§ 30] НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ 233
w совпадает с wo. Тогда мы придем, как будет видно из после-
дующего изложения, к процессам индуцированного испускания и
поглощения.
Выделим из Нвз (см. C0.8)) тот член, для которого w = wn и
рождается дополнительно еще один фонон. Подействуем этой
частью взаимодействия на начальное состояние C0.31), умножим
на l/(i%) п проинтегрируем. Тогда получим ту часть Ф(?) (см.
C0.7)), которая описывает рождение дополнительно еще одного
фонона и рассеяние электрона. Соответствующий член дается вы-
ражением
t
" L XФЛ. C0.33)
(I) (И)
Вычисление части II выражения C0.33) дает, если учесть еще
нормировку фононного состояния, следующий результат:
(Н) = 6k+Voik. /nTT^ 1| ,:(^.)'t+1 фо- C0.34)
Описываемый этим выражением процесс представим с помощью
диаграммы рис. 40 и введем далее рецепт вычисления коэффи-
циентов c(e'U) при соответствующих этому процессу волновых
функциях:
7,4w (') ak —/== \bw ) Фо- (oU.ob)
k ' V (re + 1)!
Индекс (е) указывает на то, что в этом процессе речь идет о
рождении, т. е. испускании фонона. Линиям и вершине диаграм-
мы рис. 40 поставим в соответствие следующие функции:
приходящая электронная волна e~ltk»x О*—^~
п приходящих фононов
уходящая электронная волна
(га+1) уходящих фононов е1
вершина (— ig'Wo) 6k,k0-Wtl Vn + 1 О
Эти функции следует перемножить друг с другом и проин-
тегрировать затем по времени т от 0 до t. Мы утверждаем, что
при этом получается правильное выражение коэффициента
cke,w0 =
t
" " >dx. C0.36)
Доказательство проводится легко, если просто использовать во
второй части C0.33) выражения C0.34) и сравнить коэффициен-
234 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
гы разложения C0.35) с C0.33). С помощью этих коэффициентов
сразу же определяется вероятность перехода, которая принимает
вид
I T<Ww. = I ?Wo I2 6k,k.-w. (» + 1) 2яб (eko_Wo - eko + coWu).
C0.37)
Вначале здесь возникает формальная трудность: так как началь-
ное и конечное состояния определены точно, то нет никакой сум-
мы, тем не менее появляется б-функция.
Как мы увидим позже, эта трудность
устраняется тем, что всегда приходится
усреднять по определенному распределе-
нию начальных состояний, так что вновь
появляется суммирование или интегриро-
вание по определенным к- или w-состоя-
Рис. 41. Поглощение фо- ниям. Наряду с членом в Нвз, который
пона- описывает испускание фопонов, появля-
ется еще один член, который описывает
поглощение фонона с волновым вектором wo. Эта часть получа-
ется совершенно аналогично полученной выше:
»VVo)T dx 4+WoakfeWo^ * (bt.)n Ф„, C0.38)
I И
где II с помощью перестановочных соотношений переходит в
II = Sk,ko Vn flkh+wo у=щ (bt-X'1 Фо- C0.39)
Этому процессу, когда поглощается один фонон, мы поставим в
соответствие диаграмму рис. 41. Соответствующая этому процес-
су функция состояния в общем виде дается выражением
Ф(п) (*) = 2 ^.w. («) *i у{п'_ 1)t (ь;.)" Ф.- C0-40)
Коэффициенты получаются совершенно так же, как и на стр. 233,
с той лишь разницей, что для этого процесса вершине следует
приписать множитель
-fcwA.k.+w'./»- C0.41)
После интегрирования по времени получаем для коэффициентов
следующее выражение:
„(«)
Ck0 =
li(eko+w.+(n-1)a'w-=ke-n«'wo)tdTi (зо.42)
§ 31] ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ 23^
согласно которому вероятность перехода имеет вид
I Wk"-*k0+wo = I S-wo I2 Sk.ko+wo^^ne (еко+„.о — eko — coWo). C0.43)
Здесь также отсутствует сумма, которая затем появляется, если
в качестве начального состояния выбрать некоторый волновой
пакет или распределение состояний (см. § 31).
Резюме. Подытожим кратко наши результаты. В началь-
ный момент времени t=0 начальное состояние имело вид
@) = п][0 —-j=. \bwj Фи- C0.44)
Это состояние представляется графически в виде падающего элек-
трона с волновым вектором к0 и п фононами с волновыми век-
торами wo. Под действием оператора возмущения //вз начальное
w
щ(п-1) ша(п)
Рпс. 42. Наглядное представление функции состояния C0.45).
состояние переходит во все возможные конечные состояния. Ко-
нечные состояния можно записать в виде суммы
C0.45)
и представить графически (рис. 42). Первое состояние с индек-
сом s описывает спонтанное испускание фононов с w^wo- При-
ходящие фонолы пе испытывают возмущения. Однако рождается
один новый фонон с волновым вектором w. Электрон после со-
ударения оказывается в состоянии k0 — w. Второй член описы-
вает испускание одного нового фонона с wo. Третий член, на-
конец, описывает поглощение фонона с wo. Явные выражения для
отдельных членов C0.45) даются формулами C0.32), C0.35) и
C0.40). Соответствующие коэффициенты представлены выраже-
ниями C0.17) с C0.18), C0.36) и C0.42). Равным образом при-
ведены соответствующие этим процессам вероятности переходов.
§ 31. Электрическое сопротивление
Теперь мы хотим показать, как с помощью результатов после-
дних параграфов можно явно вычислить электрическое сопротив-
ление полупроводника или металла. При этом нужно привлечь
236 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
на помощь соображения, которые, собственно говоря, находятся
за пределами квантовополевои теории. Чтобы лучше понять обыч-
ный образ действий, полезно представить себе для наглядности,
что электроны являются частицами, которые благодаря соударе-
ниям с квантами звука (точнее сказать — поглощению и испуска-
нию квантов звука) рассеиваются из начального состояния с им-
пульсом Йк в новое направление распространения с импульсом
Йк'. Так как эти соударения происходят статистически, то элек-
троны мы будем описывать с помощью функции распределения
/к. Эта функция указывает среднее число электронов, находя-
щихся в состоянии к. Ради простоты рассмотрим одно направле-
ние спина, что, вообще говоря, законно, если переходами между
различными направлениями спина пренебрегается. Поскольку
электроны подчиняются статистике Ферми, то число заполнения
одного состояния никогда не может быть больше 1, так что дол-
жно выполняться соотношение
0</к<1. C1.1)
Если полное число электронов N, то должно иметь место условие
tk = J\. (dl.2)
k
Мы исследуем временное изменение функции распределения, свя-
занное только с соударения-
ми, что пояснено с помощью
"I ¦ - рнс. 43. Если рассмотреть
интервал dk в окрестности к,
то число заполнения возра-
стает (штрихованный учас-
ток) благодаря соударениям,
которые переводят электрон
из других состояний в это
состояние к. Наоборот, чис-
ла заполнения уменьшаются
для всех тех соударений,
для которых электрон из
начального состояния к пе-
реводится в другие состояния. Таким образом, в совершенно
общем случае изменение / из-за соударений можно представить
в виде соотношения
/-л.
Л
к'
к" к.
Рис. 43. Изменение функции распреде-
ления /^ со временем (только с уче-
том соударений).
\ dt /соуд
скорость «в» — скорость «из».
C1.3)
Рассмотрим теперь эти скорости более подробно. Скорость пере-
хода из начального состояния к' в рассматриваемое конечное со-
стояние к представляет собой произведение чисел заполнения
§ 31] Электрическое сопротивление 237
начального состояния /к' на вероятность того, что конечное со-
стояние еще свободно (иначе нарушалась бы ферми-статистика).
Далее, результат следует умножить на удельную скорость пере-
хода из заполненного состояния в пустое WV-*k- Тогда C1.3)
принимает следующий явный вид:
Щоуд = 2 /*' (! - /О WV-k - 2 /к A - /к<) WW. C1.4)
Если же для чисел заполнения имеет место условие
/к<1, C1.5)
то можно воспользоваться приближением
A-/к)«1. C1.6)
Сделанные здесь предположения довольно часто выполняются в
случае полупроводников. Скорости перехода определяются соуда-
рениями с фононами или соударениями с дефектами кристалли-
ческой решетки. В качестве примера мы рассмотрим фононы.
Полная скорость перехода складывается из скоростей перехода
поглощения и испускания фононов:
WW = ИЧЦ, + WL-.v,f r | C1.7)
закон сохранения импульса: k'=k + w, k'=k — w', I
волновые векторы фононов: w = k' — k, w' = k — k', j
причем, как указано, закон сохранения импульса должен выпол-
няться в каждом отдельном процессе. В предыдущем параграфе
были вычислены вероятности переходов и показано, что они име-
ют вид
- Ek — ftu)w) C1.8)
и
W)Uk-w = 2n% | gw |2 (nw +1N (#k-w + ftcow — #k). C1.9)
Как теперь видно, 6-функции более не являются опасными для
решения, так как их следует подставить в правые части C1.4)
под знаки сумм, а суммы, естественно, сразу могут быть преоб-
разованы в интегралы. Для дальнейшего рассмотрения выраже-
ния C1.4) сделаем типичное приближение. В C1.8) и C1.9)
входят числа заполнения raw. Если говорить точно, то теперь
следовало бы получить уравнения, описывающие изменения чи-
сел заполнения фононов. Однако мы предположим, что фононы
образуют (в термодинамическом смысле) тепловой резервуар, ко-
торый поддерживается при определенной температуре Т. Как по-
казано в термодинамике (чего мы также не будем здесь выво-
дить), среднее число заполнения при тепловом равновесии для
У8 ЁЗАЙМОДЕЙСТВЙЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
бозе-частиц, каковыми являются фонолы, дается следующим вы-
ражением:
^ C1-ю)
Здесь кв — постоянная Больцмана. В последующем изложении
мы примем, что соотношение C1.10) остается справедливым и в
том случае, когда электроны выведены из равновесного состояния
внешним электрическим полем. Однако вначале исследуем слу-
чай теплового равновесия в отсутствие внешнего поля. Для име-
ющего теперь место равновесного распределения должно выпол-
няться соотношение
д4) =°- (з1л1>
ali)соуд
Это соотношение следует понимать так. В левую часть C1.11)
в качестве явного выражения следует подставить правую часть
C1.4), в результате чего получается уравнение для /к- Как мож-
но показать, соотношение C1.11) удовлетворяется функцией рас-
пределения
'-ew^sf(?k)' • C1Л2)
Здесь использовано сокращенное обозначение
5 — так называемый химический потенциал. Химический потен-
циал должен быть определен таким образом, чтобы удовлетворя-
лось соотношение C1.2). На рис. 44 показан ход кривой /к при
Г = 0и Г>0в случае металла. Очевидно, что /?" является функ-
цией только энергии Е. Теперь наложим внешнее электрическое
поле и исследуем вызванные этим изменения функции распре-
деления /к. Импульс электрона под действием внешнего поля F
изменяется согласно соотношению
Пкк = е?М. * ' C1.14)
Следствием этого является сдвиг всей функции распределения
как целого, как это показано на рис. 44а. Функция распределе-
ния в последующий момент времени t + At следующим образом
связана с функцией распределения в предыдущий момент вре-
мени:
• C1.15)
§31]
ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ
239
Если разложить обе стороны в C1.15) по At (и перейти к преде-
лу lim <^- ... |, то получится следующее уравнение:
—-1
.dt h
C1.16)
Если теперь предположить, что на электроны одновременно
действуют как фононы, так и внешнее поле, то полное измене-
Г>0
Рис. 44. Общий вид функ-
ции распределения /° для
металла.
/М)
лак
Рис. 44а. Изменение функции распре-
деления /к со временем только под
действием внешнего поля. Соотноше-
ние C1.15) непосредственно очевидно
из рисунка.
ние функции распределения складывается из обоих соответст-
вующих частей. В стационарном состоянии, таким образом, дол-
жно выполняться уравнение
(Jf\ = (М.) л- III) = 0. C1.17)
\ dt /поли V dt Jcoyn \ dt /поло
Это так называемое уравнение Больцмана. Решение этого урав-
нения чрезвычайно сложно, так что для обстоятельного рассмот-
рения следует обратиться к специальной литературе. Здесь же
для выявления важнейших моментов мы дадим только краткое
описание решения. Мы полагаем поле настолько малым, что
распределение возмущается лишь незначительно, так что /к мож-
но представить в виде
/к == /к ~~\ /к yol'Xoj
и предположить, что
C1.19)
При малых полях можно ограничиться линейным по полю чле-
ном, что немедленно приводит к возможности использования
240 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
приближения
-XT I ~ г- graQk /к- (Ol.ZUl
Так как функция равновесного распределения /к удовлетворяет
уравнению C1.11), то сразу после использования разложения
C1.18) получаем
ъи=ыи- C1-21)
Под правой частью C1.21) следует вновь подразумевать явное
выражение C1.4), которое, очевидно, чрезвычайно сложно. В ря-
де случаев C1.21) можно, однако, упростить с помощью введе-
ния так называемого времени соударения т. А именно, мы будем
считать, что под действием соударений возмущение /к равновес-
ной функции распределения через время т затухает, так что
справедливо соотношение
C1.22)
/ соуд
Приведем пример, в котором это предположение простым об-
разом оправдывается. С помощью
C1.18) и C1.19) и после кратких пре-
sj>N образований C1.21) принимает вид
//
\\
- C1-23>
Рис. 45. Функции распреде-
ления.
На рис. 45 представлена разность
возмущенной и невозмущенной функций распределения, т. е.
как раз/L причем мы имеем в виду случай полупроводника, так
что можно считать, что заполнение меняется очень медленно и
па величину, гораздо меньшую 1. Очевидно, что функция /к
практически в одинаковой мере принимает как положительные,
Так и отрицательные значения. Предположим, кроме того, что
вероятность перехода W меняется медленно, тогда первая сум-
ма в C1.23), как указано, обращается в нуль. Вторая часть это-
§ 31] ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ 241
го выражения уже имеет вид C1,22), причем время соударения
определяется следующим образом
4"=I]WW. C1.24)
к'
Время соударения принимает теперь весьма наглядный смысл:
обратная ему величина является просто суммой вероятностей то-
го, что электрон будет рассеян из начального состояния. Если
подставить C1.20) и C1.22) в C1.17), то получим
/k- = -T^gradk/?. C1.25)
Если учесть теперь, что /? зависит от к только через энергию,
то получим
/к1 = - eFvkx ||. C1.26)
Здесь было использовано соотношение
vk = -|-gradk?. C1.27)
Используя эти результаты, можно сразу же вычислить ток и тем
самым проводимость. Полный ток складывается из токов evk
отдельных электронов, причем состояния заняты согласно функ-
ции распределения /к- Так как в состоянии равновесия ток отсут-
ствует, то получаем соотношение
j = е j vk/k dak = е j vk/? d*k. C1.28)
Если сюда подставить /k согласно C1.25), то мы получим линей-
ное соотношение между током и электрическим полем следующе-
го вида:
__ X = х, у, z,
Л2Л ,,_г „ z C1-29)
ц [А — Я> У-, zi
где тензор проводимости Ощ определяется следующим образом:
^ vk^vkttx dsk. C1.30)
Если Е зависит только от абсолютной величины к, то выра-
жение C1.30) в силу C1.27) дает скалярную проводимость о,
т. е. имеет место закон Ома j = O"F.
Обсудим теперь качественно, какой вид имеет проводимость
о-в случае металла. При этом сначала мы не будем использовать
время соударения т. Поэтому заменим соотношение C1.26)
16 х. Хакен
242 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
общим соотношением
/i = -eF.Ak^,. C1.31)
где Лк является некоторой, еще неизвестной функцией к, кото-
рая, однако, в любом случае не зависит от поля, так как мы рас-
сматриваем только малые напряженности полей. Если теперь со-
поставить C1.31) с выражением C1.26), то мы получим соот-
ношение
C1.32)
откуда следует, что Лк представляет собой произведение скоро-
сти на время соударения и имеет, следовательно, смысл средней
длины пробега.
Теперь обсудим качественно зависимость проводимости от
температуры. Для этого следующим образом упростим C1.8) и
C1.9): будем полагать, что наибольший вклад в сопротивление
дают волны w, для которых выполняется условие |rew I ^э> 1, так
что можно положить (rew + 1) »rew. Далее, энергия кванта звука
%aw значительно меньше энергии электрона вблизи ферми-по-
верхности, где разыгрываются процессы рассеяния, так что
Ек — Е& ± %cow да Ек — Еь>.
Наконец положим, что константы связи Igwl2 изотропны, т. е.
равны просто IgJ2. Тогда получаем
WV-* да WW ~nw\gw\*8(Ек -Ek,), C1.33)
где имеет место и?=|к —k'l. C1.34)
Если подставить C1.31) и C1.33) в C1.17), учитывая при этом
C1.23), то получим
2 \gw |2 nw (Лк - Лк<) 8 (?к - Ек.) - vk. C1.35)
к'
Здесь мы уже поделили на все общие множители, что, вообще
говоря, требует некоторого размышления. Пусть теперь в C1.35)
к' заменено на к + w, а (Л k+w— At) разложена по степеням w.
Запишем это разложение в компонентах (^ = ж, у, z):
(Ak+w)Il - (Лк). = 2^^+12 ^ !№. C1.36)
Для дальнейшего обсуждения предположим, что система коорди-
нат к расположена так, что к направлен вдоль оси z. Поскольку
должен выполняться закон сохранения энергии, то соударения
происходят на ферми-поверхности, т. е. практически горизон-
тально. Наряду с проекцией + ш« в C1.34) также часто присут-
311
ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ
243
ствует и — wx (то же самое верно и для + wv, — wy), и поскольку
wz«0, то линейные по Юг. члены в C1.36) не дают никакого
вклада в C1.35), а последний член принимает вид
К
C1.37)
(рис. 46). Исходя из сравнения этого выражения с C1.32), сде-
лаем предположение, что At параллельно к: Ак=кУ(й:), где У
зависит только от абсолютной величины к. Это приближение
в случае изотропной задачи может быть строго обосновано. Эле-
ментарное дифференцирование приводит
к результату, что C1.37) ~kw2 ~AkW2,
откуда окончательно получаем
-Atw2. C1.38)
Заполненная афера Ферми
\\
Если подставить это приближение в
C1.35) <и преобразовать сумму в инте-
грал (с учетом б-функции), то получит-
ся следующий результат:
Ak J
|2 w2 nww dw ~vk,
C1.39)
Рис. 40. Рассеяние эле-
ктронов вблизи поверх-
ности Ферми.
Сравнивая C1.27), C1.28) и C1.30), мы обнаружим, что про-
водимость о прямо пропорциональна функции Ak- Поэтому мы
обсудим получающуюся согласно C1.39) температурную зависи-
мость Л к- Так как в конкретной ситуации скорость vk является
заданной величиной, то правая часть C1.39) не зависит от тем-
пературы, а левая, напротив, зависит от температуры через функ-
цию распределения nw:
»» = Лп * . C1.40)
е — 1
Для высоких температур имеет место соотношение
п-п ~ кцТ/Исвъ. C1.41)
Множитель квТ можно вынести за знак интеграла, который те-
перь больше не зависит от температуры, после чего непосредст-
венно получаем следующее справедливое при высоких темпера-
турах соотношение:
о ~ lAkt ~ Т~\ C1.42)
не зависящее от вида функциональной зависимости |g»l2 от ю.
16*
244 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
Если же, наоборот, Т мала, то мы должны учесть, что наиболь-
ший вклад дают фононы малых энергий (т. е. с малыми волно-
выми векторами). Тогда возможны только такие распределения,
для которых функциональная зависимость принимает вид
C1.43)
Далее, поскольку, как уже было отмечено, важны только фононы
с малыми волновыми числами, то верхний предел интеграла в
C1.39) можно устремить к бесконечности. Делая замену пере-
менной (w/T -*¦ w'), можно сразу же найти температурную зави-
симость интеграла
J (?)&*. C1.44)
о
Если, например, IgJ2 ~ w (металлы!; см. B9.34)), то мы полу-
чаем, что C1.44) ~ Т5. Подставляя это выражение в C1.35), на-
ходим температурную зависимость проводимости
(Т~|Лк|~:Г-5. C1.45)
Такая температурная зависимость действительно имеет место в
простых металлах.
§ 32. Нестационарная теория возмущений (второй порядок):
собственная энергия, перенормировка массы
Этот параграф является продолжением § 30, в котором была
рассмотрена нестационарная теория возмущений в первом поряд-
ке. Как мы видели, уравнение Шредингера можно формально
проинтегрировать, что приводит к уравнению
Здесь функция состояния Ф и гамильтониан взаимодействия взя-
ты в представлении взаимодействия. Так как интегральное урав-
нение C2.1) так же трудно решить, как и уравнение Шредин-
гера, мы попытались решить его приближенно, подставив в пра-
вую часть под интеграл вместо Ф(т) начальное состояние Ф@).
Эта подстановка привела к улучшенной функции состояния, ко-
торая определяется выражением
т.. , C2.2)
Эту процедуру можно продолжать, подставляя под интеграл в
§ 32] СОБСТВЕННАЯ ЭНЕРГИЯ, ПЕРЕНОРМИРОВКА МАССЫ 245
C2.1) на место^функции состояния Ф(т) теперь уже не началь-
ное состояние Ф@), а улучшенную функцию состояния ФA)(т).
В результате мы получили еще более точную функцию состоя-
ния ФB):
фB) (*) = ф @) + ± j Явз (т) ФA) (т) йт. C2.3)
о
Если в правую часть C2.3) подставить явный вид функции ФA),
то получим явное выражение для функции ФB):
t
ф<2> (*) = Ф @) + ±r j dxx Яю (ТХ) Ф @) +
о
J
+ (Jj-J J dx2 J dx, Явз (та) Явз Ы Ф @), C2.4)
о о
явное в том смысле, что в правой части следует подействовать
стоящими там операторами на начальное состояние, а затем вы-
числить получившиеся интегралы. Это вычисление мы проведем
на примерах, снова выбрав в качестве оператора Гамильтона Яв,
оператор взаимодействия между электронами и колебаниями ре-
шетки. Этот гамильтониан, как мы видели в предыдущей главе,
имеет следующий вид:
4-Яв8(т) = 2(—*
() 2 ( *w) +
Ij w поглощение фононов
+ 2 (- igV) aU^bte-^^-^-^)\ C2.5)
k,w испускание фононов
Тогда же мы обнаружили, что каждому члену можно поставить
в соответствие определенный процесс, как это указано в форму-
ле C2.5). Рассмотрим функцию состояния C2.4) более обстоя-
тельно. Первые два ее члена уже встречались нам в предыдущем
параграфе, так что теперь нужно исследовать лишь последний
член. В этом члене следует дважды последовательно подейство-
вать оператором Нва на начальное состояние. В качестве началь-
ного состояния выберем
1 Ф@) = а?Ф0. C2.6)
Если подействовать оператором Hs3(.xi) вначале на C2.6), то, как
нам известно из § 30, отличный от нуля вклад дает только члев
246 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ (ГЛ. V
вида
bta?-wak | о?Ф, = a?_wbiO.6k.k.. C2.7)
Следовательно, возникает процесс, представленный^на рис. 38.
Если теперь подействовать еще раз оператором Нвз в момент
времени тг, то мы получим два процесса, а именно: либо повтор-
ное испускание фонона, либо поглощение уже имеющегося фо-
нона с волновым вектором w (рис. 47). В качестве примера мы
обсудим процесс поглощения фонона. Для этого следует, учиты-
вая результат C2.7), вычислить выражение
bwat+wab\at^btOo, C2.8)
где в качестве конечного состояния принимается Як„Ф0, т. е. точ-
но начальное состояние. После-
J^ довательное включение операто-
/"^ т. ров взаимодействия в моменты
"~*к7 —f—h _w у- ¦—г— времени хх и т2 можно, очевид-
" ° но, представить с помощью диа-
Рис. 47. Собственно-энергетиче- граммы рис. 47.
екая часть диаграммы: виртуаль- Теперь мы рассмотрим об-
ное испускание фонона. стоятельно ту часть C2.4), кото-
рая вновь приводит (после толь-
ко что упомянутых процессов испускания и поглощения) к на-
чальному состоянию
| Ф (*) = ска (t) а?ф0 + а?,Ф0. C2.9)
Наша задача состоит в явном вычислении коэффициентов ск„(?).
Для этого в конечном итоге следует учесть, что вершины воз-
никают при действии операторов взаимодействия C2.5). Число-
вой множитель оператора, который представлен выражением
C2.7), имеет вид
'(%'-w+ew"8k')Tl^1, C2.10)
причем здесь учтено, что согласно C2.5) должно быть проведено
интегрирование по Ti от 0 до тг. Далее нужно учесть, что со-
гласно C2.5) следует еще провести суммирование по к и w.
В вершине 2 появляется множитель, который стоял в выражении
C2.8) (первое выражение) для оператора взаимодействия Нъз.
Учитывая C2.8), получим для вершины 2 выражение
t
2 (- tew) Sk',*0-w J dx2 e'(*ko-°>w-s*o-w)*.. C2.11)
K 0
Здесь w то же самое, что и в формуле C2.10). Нам следует еще,
§ 32] СОБСТВЕННАЯ ЭНЕРГИЯ, ПЕРЕНОРМИРОВКА МАССЫ 247
однако, провести суммирование по к'. Если собрать C2.10) и
C2.11) вместе, то мы получим следующее явное представление
коэффициентов ckt(t):
t
о
2 (- tew) f е-1^'+с^-^(^-и) (- igl) e"
w о
X 2 (- tew) f е-1^'+с^-^(^-и) (- igl) e""*." dTl. C2.12)
w о
Результат нашего расчета снова можно представить в виде ре-
цепта, соответствующего диаграмме рис. 47:
приходящий свободный электрон e~lEk°Xl
вершина 1—испускание фонона (— igw) 8k+W]ko
распространение электрона
и фонона от т, до т2 e--i(»w+Ek0-w) <**-*.)
вершина 2 — поглощение фонона (—ig-w) 6k-_W]k
УХОДЯЩИЙ Свободный ЭЛеКТрОН ег8кот»
Затем C2.12) слеудет проинтегрировать по временам Ti и Тг при
0 ^ п < Т2 < t и ввести суммы по w, k, к'. Ввиду присутствия в
вершинах символов Кронекера, которые представляют закон
сохранения импульса, суммы по к и к' можно опустить, как это
сделано в C2.12). Читатель обнаружит, что это просто последо-
вательное развитие приемов, которые уже встречались нам в
предыдущем параграфе, посвященном первому порядку неста-
ционарной теории возмущений. Теперь нетрудно представить
себе, как будут выглядеть эти приемы для еще более сложных
процессов. С примером такого процесса мы познакомимся в сле-
дующем параграфе.
Проведя интегрирование по Ti и перемножив между собой
экспоненциальные функции, получим
?w Iя ^т1 г dx2. C2.13)
*1 J l(eko-8ko_w-a)w) 2
Стоящая под интегралом единица после интеприроваиия приво-
дит к члену, пропорциональному t, а экспоненциальные функции
дают по существу осциллирующий член. Для достаточно боль-
ших времен член, пропорциональный t, становится превалирую-
щим, так что осциллирующим членом можно пренебречь. Тогда
это выражение принимает вид
, C2.14)
248 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
где введено сокращенное обозначение
w fck0 ko-w w
Используя этот результат, приводим искомую функцию состоя-
ния C2.9) к виду
ф (?) .= A _ гДеь/) яьФ0. C2.16)
Это в высшей степени примечательный результат. Он утвержда-
ет, что в исследуемом нами процессе испускания и последующе-
го поглощения фонона исходная функция состояния не изменя-
ется, коэффициент же при ней растет пропорционально времени.
К разумному результату мы придем только после того, как учтем
высшие порядки теории возмущений. Этим мы займемся в § 33,
а здесь воспользуемся полученным там результатом. Согласно
проведенному в § 33 анализу оказывается, что 1 — iAsi представ-
ляет собой первые два члена разложения экспоненты, так что
функцию состояния C2.16) можно записать в виде
ф (t) = <Г*Авк.'а?Ф0- C2.17)
Предположим заранее справедливость выражения C2.17) и по-
смотрим, что означает появление нового временного множителя
в C2.17).
Для этого вернемся от представления взаимодействия (функ-
ция состояния ФШ) к представлению Шредингера (функция со-
стояния ФШ). Согласно результатам § 16, ФШ и ФШ связаны
через невозмущенный оператор Гамильтона Ео:
г
ф(Ц = е п ° Ф(?). C2.18)
Подставим сюда для ФШ ее выражение C2.17) и сделаем пре-
образования:
г_ t _г_ г_ {
(г) = е е акое е Фи- (ол.19)
Y Yi
Согласно результатам § 16 получаем
т /7+«~*екп* ТТ гТ>
1 — «кое " 1 li — yjoi
так что
'-ieir.f _+rf> /on on\
§ 32] СОБСТВЕННАЯ ЭНЕРГИЯ, ПЕРЕНОРМИРОВКА МАССЫ 249
Сравнивая этот результат со стационарным решением полно-
го уравнения Шредингера с гамильтонианом Н= Но + Hs3:
O(t) = e~lTtO(Q), C2.21)
находим, что
| Е = %гко + Меко. C2.22)
Это соотношение и дает нам искомую интерпретацию: о
представляет собой сдвиг энергии электрона в состоянии к0.
В рамках второго порядка теории возмущений он определяется
выражением C2.15). Этот сдвиг энергии возникает благодаря
испусканию и последующему поглощению фонола. Поскольку
при испускании и последующем поглощении закон сохранения
энергии не выполняется, то говорят о «виртуальном» испуска-
нии или поглощении. Тем самым мы получаем чрезвычайно важ-
ный и для физики элементарных частиц результат, что энергия
электрона благодаря виртуальному испусканию и поглощению
квантов, в данном случае фононов, оказывается смещенной. Если
рассматривается покоящийся электрон, т. е. ко = 0, то говорят
о собственной энергии частицы.
Для не слишком больших значений к0 величины Е = Е^,
Еь0 = ЙБко, Д^к,, ==йЛвко можно разложить в ряд по к0:
Е = Е°+S'
AEkt = AEe — C-kl C2.25)
Здесь т* — эффективная масса электрона в отсутствие фонон-
ных колебаний решетки. Коэффициент разложения при к0 в
C2.24) выбран по аналогии с C2.23), так что пг** в этом разло-
жении имеет очевидный смысл эффективной массы электрона
в деформируемой решетке. С в C2.25) является коэффициентом
в разложении C2.15) и явно будет вычислен ниже (§ 35). Здесь
мы положим формально
С = Др. C2.26)
Если выражешия C2.23—32.26) внести в C2.22) и сравнить чле-
|ультат:
C2.27)
ны, пропорциональные к%, то получится следующий результат:
т** т* т*
250 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
или, если б < 1,
| то** = то*A + б)- C2.28)
В рамках физики твердого тела результаты, относящиеся как
к собственной энергии, так и к изменению массы, могут быть
легко поняты. Проходящий через решетку электрон взаимодейст-
вует с ионами, смещает их из положений равновесия и тем са-
мым создает для себя более глубокий потенциал. Следовательно,
ого энергия понижается, а его эффективная масса возрастает.
Этот электрон, сопровождаемый дефор-
мациями решетки («облаком поляриза-
ции»), называется поляроном (более под-
робно см. § 35). В противоположность
релятивистской квантовой теории, где
изменение массы бесконечно большое,
в данном случае оно конечно. В соответ-
'ко-ш-ш' ствии с состоянием движения электрона
в одном и том же кристалле могут на-
блюдаться различные массы: если элект-
Рис. 48. Спонтанное ис- рон движется медленно, то возникает
пускание двух фононов. рассмотренное здесь изменение массы
или, как говорят, «перенормировка мас-
сы»; если же электрон движется очень быстро, то ионы неусне-
вают следовать за ним и появляется масса «голого» электрона.
С помощью введенных выше правил мы можем рассмотреть
и другие процессы, которые ведут к действительному изменению
начального состояния. Речь идет о процессе с участием двух фо-
нонов. В качестве примера на рис. 48 приведена диаграмма,
представляющая спонтанное испускание двух фононов с волно-
выми векторами w и w'. Вычисление коэффициентов волновой
функции и соответствующих вероятностей перехода мы предо-
ставляем в качестве упражнения самому читателю.
Задания к § 32
1. Определить коэффициенты ?Wi»wa в разложении
Ф(')= 2 cWt>w,(*N+16+1o?^1_WlOe, (A32.1)
если в качестве начального состояшия выбрана функция
Ф@) = <Ф0 (А32.2)
и в основу рассмотрения положена представленная на рис. 48
диаграмма. Показать, что и в этом случае снова появляется
§ 33] ТЕОРИЯ ВОЗМУЩЕНИЙ ВЫСШИХ ПОРЯДКОВ 251
6-.функдия, выражающая закон сохранения энергии для двух-
фононного испускания.
2. Электронный полярон. Сопоставить электрон в зоне прово-
димости с экситоном Френкеля и найти его собственную энер-
гию. Указание. Применить метод эффективной массы и сде-
лать в B5,3) следующие замены:
Затем разложить полевой оператор i|Jz,(x') электрона в зоне про-
водимости по плоским волнам и воспользоваться заданием 3
из § 25.
§ 33. Теория возмущений высших порядков
В теории возмущений высших порядков мы поступаем в прин-
ципе так же, как и в первом и втором порядках теории возму-
щений. Нам следовало бы искать функцию состояния, которая
удовлетворяет точному уравнению
t
Ф(*)=Ф@) +-^-|явз(т)йтФ(т). C3.1)
о
Мы попытаемся найти искомую функцию состояния Ф(?), решая
t
Ф(п) @ = ф @) + -i- J Явз (т„) dxn ФСп"х) (т„) C3.2)
о
методом итераций, т. е. при n-м шаге в левой части этого урав-
нения получаем функцию Ф(п), если в правую часть C3.1) под-
ставлена найденная в предыдущей (п — 1)-й итерации функция
состояния Ф'"-". При этом условимся, что для нулевой итерации
справедливо соотношение
ф<о)(т) = ф(о). C3.3)
Как мы уже видели в § 32, во второй итерации получается сле-
дующая волновая функция:
ф<2> (t) = ф @) + ±. j явз (т,) dxt Ф @) +
Вз(тг)йт2|Явэ(т1)йт1Ф@), C3.4)
о о
которую можно представить в виде суммы ФA) и поправочного
члена, содержащего произведение двух операторов взаимодейст-
252 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
вия и, следовательно, имеющего второй порядок по величине
взаимодействия. Если теперь подставить это выражение C3.4)
в правую часть C3.2), то получим волновую функцию Ф<3>. Под-
становка двух первых членов C3.4) в C3.2) вновь прямо приво-
дит к выражению C3.4). А при подстановке последнего члена
в C3.4) в выражение C3.2) появляется еще один новый член,
так что в целом волновая функция третьего порядка принимает
вид
фC) (t) = ФB) +
+ -jL Йвз (т,) dr3 j Явз (т2) dx2 j HB3 (Tl) dx1 Ф @). C3.5)
{М) о о о
При каждой новой итерации, как легко видеть, к волновой функ-
ции добавляется новый член, представляющий собой просто п-
кратный интеграл по операторам взаимодействия. Отсюда следу-
ет, что функцию, полученную в п-м порядке приближения, мож-
но представить в виде следующего выражения:
" Д
ф(п) (t) = Ф @) + У -f- Явз (TV) dTv X
X j" #вз (Tv-i) rfTv_x ...]йт (xj) dxx Ф @). C3.6)
о о
Тем самым проблема отыскания Ф(п)(?) в принципе решена, если
известно, как действует оператор Нвз. При практическом реше-
нии, очевидно, необходимо последовательно действовать отдель-
ными операторами на Ф@) и определять коэффициенты. Выде-
лим из волновой функции C3.6) ту часть, которая вновь приво-
дит к присутствующему в этой функции начальному состоянию
Ф @) = вкоФ0. Эта часть представляется диаграммой вида рис. 49,
которая соответствует восьмому члену (v = 8) в формуле C3.6).
Наши рассуждения §§ 30 и 32 позволяют довольно просто вы-
числить стоящие при этом члене коэффициенты. В каждой вер-
шине, при этом, следует проследить за выполнением закона со-
хранения импульса.
Кроме того, нужно помнить, что каждому испусканию и по-
следующему поглощению соответствует множитель (—igw) (— 4?w)«
а по волновым векторам w виртуально испущенных фононов сле-
дует провести суммирование.
§ 33) ТЕОРИЯ ВОЗМУЩЕНИЙ ВЫСШИХ ПОРЯДКОВ 25Й
Наконец нам следует вычислить кратные интегралы, указан-
ные здесь для случая, представленного на рис. 49:
t Те т2
2 (-l)i\gwl\2...\gVl\2)dTg$dT7...]dx1e-. C3.7)
Wi...W4 0 0 0
Теперь нужно еще определить стоящие под интегралом ВреМеН-
U).
к„ ко~ш к„ kg-wj ка кв~шг ка к^ш, к0
Рис. 49. Диаграмма восьмого порядка (см. текст).
ные множители. Это делается с помощью следующих уже извест-
ных правил:
приходящий электрон е~гек«т,
УХОДЯЩИЙ ЭЛеКТрОН elSk,-Wtr^
уходящий фонон еи'1.
Таким образом, в вершине 1 появляется общий множитель
е^\ C3.8)
где введено сокращенное обозначение
Ai = sko-Wl + coWl — sko. C3.9)
В вершине 1 время т следует идентифицировать с и и проин-
тегрировать от 0 до %2'-
a, WTl = f!^zi. C3.10)
о
Вершина 2 описывает обратный процесс, которому соответствует
множитель
е-^лг. C3.11)
Теперь нам следует перемножить C3.10) и C3.11) и проинтегри-
ровать по %2. Это дает следующий результат:
? C3.12)
О
Осциллирующими членами здесь, как и ранее, пренебрегаем, по-
скольку для достаточно больших промежутков времени они несу-
щественны.
254 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ 1ГЛ. V
В следующей вершине получившийся результат следует ум-
ножить на множитель вида C3.8) цри т = тз и проинтеприро-
вать:
fе**йdx3%¦ = T* .' *' • C3.13)
J s гД. (Д.-гД™
о
Если умножить результат C3.13) вновь на соответствующий вер-
шине 4 множитель и снова проинтегрировать, то мы получим
J 4 гД -г'Д 2 5 г'Д гД '
О
Продолжение этой процедуры совершенно очевидно и после по-
следнего интегрирования приводит к результату
t
(*¦ з 1111 1 1111
J 8 8 3! гД, гД„ 1А„ 4! гД. (Д„ 'Дч* '^л*
о
Коэффициент волновой функции, соответствующий диаграмме
рис. 49 с четырьмя виртуальными процессами испускания, со-
гласно C3.7) и C3.15) имеет вид
-^^(-^(^e^-e^'-.J4- <ЗЗЛ6>
Полная волновая функция ФШ складывается из суммы членов
/7-раз
Рис. 50.
различного порядка. Различные вклады можно представить сум-
мой диаграмм типа той, что представлена на рис. 49. Таким об-
ращаем, существует взаимно однозначное соответствие между диа-
граммами и волновыми функциями (рис. 50).
Каждой из этих диаграмм соответствует одна и та же волно-
вая функция, однако со своим временным множителем, как это
показано на рис. 50. Очевидно, что суммирование в предельном
случае п -*¦ °° дает
Й C3.17,
§ 341 ТЕОРЕМА О ТОЧНОЙ ФОРМЕ РЕШЕНИЯ Й55
Тем самым мы действительно пришли к утверждению, что рас-
смотренные здесь процессы приводят только к смещению энер-'
гии, как это было указано в § 32.
Очень важно установить, что наряду с рассмотренными здесь
диаграммами возможны диаграммы совершенно другого типа.
а) б)
Рис. 51. Вклады четвертого порядка в собственную энергию.
Для этого следует лишь подумать о том, какие еще процессы
могут возникнуть при последовательном включении операторов
взаимодействия. И снова лучше всего это делать с помощью гра-
фического представления. При этом появляются диаграммы типа
представленных на рис. 51, которые, как можно показать, дают
коэффициенты, пропорциональные t, и, следовательно, так же
приводят к смещению энергии. Полное смещение энергии можно
получить, если просуммировать все подобные вклады, возникаю-
щие от так называемых «связанных диаграмм».
§ 34. Теорема о точной форме решения
В §§ 30, 32 и 33 мы рассмотрели решение уравнения Шре-
дингера для случая взаимодействия между электронами и коле-
баниями решетки с помощью нестационарной теории возмуще-
ний. В §§ 34—36 мы будем искать решения независящего от
времени уравнения Шредингера НФ = ЕФ.
Сначала в этом параграфе мы введем одну весьма общую
и полезную теорему о структуре решений этого уравнения. Для
этого следует более обстоятельно заняться видом оператора Га-
мильтона. Примеры гамильтонианов встречались нам в § 29,
например в B9.24), причем периодичный с периодом решетки
потенциал был опущен. Поскольку наша теорема так же легко
доказывается и в присутствии такого потенциала в //, то мы
будем исходить из общего оператора Гамильтона:
Я - J ф+ (х) {- Ц- А + V (х)} ф (х) d3x +
J
(х) (| (Ww (x) e*wx6w + Wl (x) e-iwx6+)) ф (х) d*x. C4.1)
Здесь предполагается, что потенциал периодичен с периодом
решетки:
.. . ' C4.2)
256 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
Равным образом примем, что функции, которые описывают вза-
имодействие между электронами и фононами,
Ww(x + l) = JFw(x), C4.3)
также периодичны с периодом решетки. Если теперь положить
V = 0, заменить т на эффективную массу т* и предположить,
что Ww постоянна в пространстве, то мы вернемся, естественно,^
от C4.1) к B9.24). Если же мы имеем дело лишь с малым чис-
лом частиц, то формализм вторичного квантования целесообразно
оставить и перейти к обычному представлению с помощью
уравнения Шредингера. Этот переход, как мы видели в
§ 13, осуществляется, если представить функцию состояния
в виде
Ф = J ...
X ... ф+ (xN) Ф0,эл cFx, ... dsxN. C4.4)
Здесь Фо, эл — вакуумное состояние системы электронов. Аргу-
мент {Ъ^\ в / следует понимать в том смысле, что / может за-
висеть от всех Ъ^. В следующем параграфе мы познакомимся с
соответствующим примером.
Обобщение по сравнению с § 13 состоит, таким образом, в том,
что волновая функция /, которая стоит в C4.4) как коэффициент
разложения, теперь может содержать еще операторы рождения
&w и, возможно, операторы уничтожения &w.
Как было показано на примере, приведенном в § 13, функция
/ удовлетворяет уравнению Шредингера в «конфигурационном
пространстве». Примененную там процедуру можно сразу пере-
нести на наш случай, после чего находим уравнение
(N
2 {- ?А'-+v (х4 + 2 ft«>wb?&w+
1 = 1 W
+ 2 2 Wv (x,) eiwx^w + Wl (Xj) e-™xJbt}) X
X / (xx, ..., xN; {&+}) - Ef (xlt ...,xN; {&+)). C4.5)
Это уравнение имеет в известной степени смешанный харак-
тер. Относительно пространственных переменных электронов
xi, ..., xw это обычное уравнение Шредингера, а относительно
колебаний решетки мы пользуемся, напротив, операторами Ь%
и &w Теперь введем теорему о виде волновой функции /, кото-
рая представляет собой существенное обобщение теоремыЕ Блоха
§ 17. При доказательстве теоремы Блоха мы исходили из того,
что оператор Гамильтона является периодичным с *йериодом! ре-
§ 341 ТЕОРЕМА О ТОЧНОВ ФОРМЕ РЕШЕНИЯ 257
шетки или, другими словами, что он инвариантен относительно
операции трансляции
Т^. Xi + Xi + 1. C4.6)
Поскольку теперь учитываются и колебания решетки, то Н бо-
лее не является трансляционно инвариантным. Между тем, сле-
дует позаботиться, чтобы при сдвиге координат электрона ко-
ординаты решетки преобразовывались таким образом, чтобы
электроны «видели» те же деформации решетки. Для этого рас-
смотрим в качестве примера разложение одномерных смещений
решетки A0.13), которые имеют вид
Я (х) = 2 const (eiwx&w + e-^bt). C4.7)
Если сдвинуться в решетке на вектор 1, то qix) переходит в
q{x + l). В правой части это означает замену
e^&w-^e^+'^w C4.8)
it
e-*xw fr+ _> e-i*-(x+i>b+. C4.9)
Если &w,&w рассматривать как «переменные», то исходное откло-
нение q(x) можно получить вновь, если одновременно с преоб-
разованием х -> х +1 предпринять следующее преобразование:
bw-»-bwe~iwl» &w->bw<?'wl. C4.10)
Объединяя C4.6) и C4.10), следующим образом определим опе-
ратор трансляции 2V
Тх\
C4.11)
Подстановкой C4.11) можно сразу же убедиться, что Н инвари-
антен относительно Ti или, другими словами, что оператор Т\
коммутирует с гамильтонианом Н:
I Г,Я-ЯТ,=0. C4.12)
Согласно известному правилу квантовой теории, / можно всегда
выбрать так, что эта функция будет собственной функцией не
только C4.5), ной fi, т. е.
Tif = Xf. C4.13)
По аналогии с доказательством теоремы Блоха § 17 следует
считать, что абсолютная величина X равна 1:
X-e*i. C4.14)
17 X. Хакен
258 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
В общем случае / можно представить в виде
| / = e*W(x1I...,xw;{6+))O0, . C4.15)
где U — операторная функция, действующая на основное состоя-
ние решетки Фо, X — координата центра тяжести электронов.
Если подставить C4.15) в C4.13), учитывая при этом C4.14), то
сразу получим важное соотношение
| U(x1 + l,...,xN + l;{bUiv'l}) = U(x1,...,xN;[b+}). C4.16)
Соотношения C4.15) и C4.16) утверждают, что электроны и в
колеблющейся решетке ведут себя как плоские модулированные
волны, причем коэффициент модуляции периодичен с периодом
решетки в предположении, что искажения решетки преобразу-
ются соответствующим образом. Особый случай C4.15), C4.16)
имеет место для непрерывной среды, т. е., например, для опера-
тора Гамильтона B9.24): вместо сдвига на вектор решетки (или
кратный ему вектор) в этом случае возможен сдвиг на любой
вектор, который, в частности, может быть и бесконечно малым
61. С важным приложением C4.15) и C4.16) мы познакомимся
в § 35.
§ 35. Полярон Фрёлиха. Собственная энергия
и перенормированная масса
Рассмотрим движение отдельного электрона, который дви-
жется в полярном кристалле, положив в основу рассмотрения,
как и в § 29, модель континуума, т. е. непрерывной среды.
В рамках этого приближения уравнение Шредингера C4.5) при-
нимает вид
- & Л + Йсо 2 fc>w + ft 2 fewelwxbw + g>~iwxbt)) f = Ef.
w w I
C5.1)
Ради простоты предположим, что частота и не зависит от w,
что приближенно выполняется для так называемых оптических
колебаний. Коэффициенты g даются выражением B9.27), одна-
ко их явный вид понадобится нам только в конце этого парагра-
фа. Согласно теореме C4.15—34.16) представим искомую волно-
вую функцию в виде
/=^=е**ц(х, {&+})Ф0. C5.2)
Для дальнейшего очень важно найти приемлемое выражение для
и(х, (&?}). Действие этой операторной функции и на основное
состояние должно описывать деформацию' решетки, которая воз-
§ ЗЬ) ПОЛЯРОН ФРВЛИХА 259
никает вокруг электрона, находящегося в точке х. В заданиях
к § 8 мы познакомились со случаем деформации решетки беско-
нечно тяжелым зарядом. Нам удалось показать, что волновые
функции деформированного состояния могут быть представлены
через волновые функции смещенного гармонического осциллято-
ра. Аналогично и в случае электрона конечной массы кажется
разумным описать деформацию решетки с помощью функции
C5.3)
где экспоненциальные функции снова представляют смещенные
гармонические осцилляторы.
Величина смещения fiw(x) будет, естественно, зависеть от х.
Кроме того, вовсе не следует ожидать, что отклонение будет не-
пременно таким, как в случае бесконечно тяжелой частицы. Глав-
ная задача состоит теперь в том, чтобы определить коэффици-
енты ?5w(x). Заметим еще, что нормировочныемножители в C5.3)
задаются выражением (см. F.25))
Л°„ = е 2l '. C5.4)
С помощью теоремы C4.16) можно сильно ограничить вид пока
еще совершенно произвольных функций ?5w(x). Согласно C4.16)
должно выполняться соотношение
и (х + 61, lfc+e'w61)) - и (х, (&+}), C5.5)
илторое должно быть справедливым и в случае бесконечно ма-
лых смещений 61. Если подставить сюда явный вид C5.3), то
сразу получим уравнение
b+eiW&lK (х + 61) = 6+pw (x). C5.6)
Это уравнение разрешается с помощью подстановки
pw(x) = e-iwxpw, C5.7)
где pw в правой части является независящей от х постоянной.
Тем самым мы нашли весьма специфическую форму волновой
функции (подход Ли, Лоу, Пайнса)
0 C5.8)
с нормировочным множителем
, C5.9)
В этом решении остались еще не определенными постоянные
коэффициенты pw. Для их определения подставим решение C5.8)
17*
260 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ 1ГЛ. V
в уравнение Шредингера C5.1). При действии оператора
—— Д следует просто продифференцировать экспоненциальную
2т*
функцию по х. Поскольку все операторы Ь^ между собой комму-
тируют, то нет необходимости следить за точным порядком сле-
дования дифференцируемых функций. Действие операторов Ь«
и bw оператора Гамильтона C5.1) на функцию C5.8) уже было
обстоятельно обсуждено в разделе о смещенном гармоническом
осцилляторе и не представляет никаких затруднений. Основываясь
на этих соображениях, практически без труда и длинных вычис-
лений получаем
2т* т* --»- "w w
2т*
w
2^ 2
C5.10)
Уравнение C5.10), совершенно аналогично случаю смещенного
гармонического осциллятора, мы «сократили» на функцию C5.8),
так что в C5.10) осталось только операторное выражение. Можно
подробно показать, что для не слишком сильной связи третьим
членом в левой части C5.10) можно пренебречь. Получившееся
после этого уравнение имеет следующую структуру: в уравнении
имеются величины, не зависящие от операторов 6^, и наряду
с ними величины, пропорциональные Ь^- Для того чтобы это
операторное уравнение удовлетворялось, коэффициенты при обо-
их типах выражений должны обратиться в нуль. Рассмотрим
вначале множитель, стоящий перед Ь^. Тогда непосредственно
получаем уравнения
—г- kw + о~г w2 + Йсо | + Tigl = 0, C5.11)
771 .4771* ) '
решая которые, получаем следующие выражения для коэффици-
ентов Bw:
Теперь рассмотрим в C5.10) коэффициенты при независящих от
Ъу, членах. Эти коэффициенты должны удовлетворять уравнению
§ 35] ПОЛЯРОН ФРЁЛИХА 261
Это уравнение частично содержит еще и pw. Если выразить fJw
в этом уравнении через C5.12), то все неизвестные устраняются
и мы получаем непосредственно собственные значения энергий
Сумма в C5.13) уже встречалась нам (с точностью до множите-
ля й ввиду связи tiE — Ъ Де) в C2.15). Она представляет собой
не что иное, как выражение для собственной энергии (при к = 0)
и перенормировки массы (см. § 32).
Для сравнения с экспериментом необходимо иметь явные вы-
ражения для собственной энергии и перенормированной массы.
Согласно B9.27) имеет место равенство
<35Л4)
Здесь V—объем кристалла, е — заряд электрона, еш — диэлект-
рическая проницаемость в оптической области частот, Ео — стати-
ческая диэлектрическая проницаемость. Если подставить это вы-
ражение в C5.13) и преобразовать сумму в интеграл, то C5.13)
легко вычисляется, причем результат удобнее всего выразить
через безразмерную постоянную а:
1/1 1 \ е и /or л с\
а — -^-( з—* C5.15)
где и имеет вид
) <35Л6)
В результате получаем следующее выражение для энергии по-
лярона:
^( ) , C5.17)
откуда заключаем, что собственная энергия и перенормирован-
ная масса равны соответственно
C5.18)
Постоянная а играет, вообще говоря, роль константы связи, в
зависимости от величины которой следует применять то или
иное приближение. Для a < б можно применять методы, исполь*
зованные в §§ 32 и 35, для а» 10 — другой метод, предложен-
ный Пекаром. Важный в практическом отношении промежуточ-
262 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ 1ГЛ. V
ный случай а« 10 стало возможным вычислять с помощью
«интеграла по траекториям» Фейнмана, что, к сожалению, не
может быть изложено здесь.
§ 36. Эффективное взаимодействие между поляронами
В предыдущем параграфе мы исследовали движение одного
электрона, взаимодействующего с колебаниями решетки. При
этом, если обратиться к наглядной интерпретации, физика этого
взаимодействия состоит в том, что электрон поляризует вокруг
себя решетку, т. е. смещает ионы.
В этом параграфе теперь следует показать, что поляризация
решетки ведет не только к изменению собственной энергии и к
неренормировке массы отдельных электронов, но и создает
взаимодействие между самими электронами. Для простоты здесь
будет рассмотрен случай двух электронов или поляронов. Однако
развитые соображения могут быть легко распространены на слу-
чай большего числа частиц. Исходным пунктом, как всегда, яв-
ляется гамильтониан, который в случае двух частиц, взаимодей-
ствующих с колебаниями решетки, имеет следующий вид:
1 Я=Яв„1 + ЯВЛ1 + Яр + Явз1 + Яв31 + Я1_а. C6.1)
Первые два оператора Гамильтона относятся к свободным ча-
стицам:
ЯВЛ. = --^Д„ 7=1,2, C6.2)
*m
причем следует допустить, что они могут иметь различные мас-
сы. Оператор Гамильтона Яр описывает колебания решетки:
w C6.3)
W
Следующие два оператора Гамильтона:
™1 bw + gle-^bt), 7 = 1,2, C6.4)
представляют взаимодействие 7"-й частицы с колебаниями ре-
шетки.
Выражения C6.2—36.4) уже встречались нам в предыдущих
параграфах и не нуждаются более в дальнейшем обсуждении.
Ради простоты в C6.4) предполагается, что константы связи
для различных частиц 1 и 2 имеют одинаковую величину. От-
метим все же, что для зарядов противоположных знаков знак
gwiSw B ^вз, также должен быть выбран противоположным знаку
- Гамильтониан В\-% описывает прямое кулоновское
§ 36] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯРОНАМИ 263
взаимодействие между поляронами. Следует также учесть, что
из-за поляризации атомных оболочек в это взаимодействие сле-
дует ввести диэлектрическую проницаемость е™:
#1-2 - е ,/_х |- C6.5)
Попытаемся решить соответствующее гамильтониану C6.1)
уравнение Шредингера и воспользуемся при этом следующим
наглядным представлением. Как мы видели в предыдущем параг-
рафе, смещение ионов решетки математически описывается дей-
ствием функции и(х, {&^})на состояние неискаженной решетки
(«вакуумное состояние»). Эта функция известна нам еще из
раздела о смещенном гармоническом осцилляторе. Если в решет-
ке имеются две частицы, то обе они будут поляризовать решет-
ку. Тогда, во всяком случае приближенно, можно ожидать, что
создаваемые частицами поляризации (возмущения решетки)
просто складываются. Поэтому имеет смысл попытаться ввести
волновую функцию, которая отражает это обстоятельство. Если
исходить из поляронов с волновыми векторами kj и кг и для
каждого из них воспользоваться волновой функцией вида C5.8),
то мы получим следующее выражение для волновой функции:
х2) =-i-е*
X
X exp ? Ъ1 (PU)e-lwXl + №е-™х*)\ Фо. C6.6)
\w t T
1 2 J
Цифры 1 и 2 указывают на парциальные вклады поляронов в
искажение решетки (см. также задание на стр. 267); явные вы-
ражения Pw* и р^ даны в C5.12), причем следует заменить т*
на nij и к на к3. В то время как множитель 1/V (V — объем
кристалла) обеспечивает нормировку плоских волн, решеточная
функция должна быть нормирована еще множителем Л3.
Согласно F.25) (смещенный осциллятор), Jf дастся выраже-
нием
П
W
где yw теперь имеет вид
Tw-P(wViwXl + P^V^. C6.8)
Подставляя C6.8) в C6.7), получаем явное выражение для JV:
f
264 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
где
jfc = ехр (-4-2 P^PwV*1*-*1' + A ** 2I. C6.10)
с
В первых двух множителях C6.9) мы узнаем нормировочные
множители отдельных поляронов C5.9). Новым является завися-
щий от расстояния нормировочный множитель Jfc. С помощью
подробного расчета, однако, можно показать, что этот множитель,
по крайней мере при больших расстояниях между частицами
1 и 2, можно считать постоянной величиной. Подействуем опе-
ратором Гамильтона C6.1) на C6.6). Дифференцирование при
действии операторов А] и Дг выполняется сразу, как и в C5.10).
При действии 6wHa C6.6) нужно учесть, что [}w из § 35 теперь
следует заменить на fw C6.8).
Простое, полностью аналогичное предыдущему параграфу
вычисление дает
2т* <~
W
W
+
t
Л 2jgw\l
W
"• + p<wVh
-2)
«,)
t
tlk,. C6.11)
При этом выражение, аналогичное третьему члену в C5.10), ко-
торым мы тогда пренебрегли, также опущено. Скобка в C6.11),
обозначенная через A-*-2), может быть получена из предыду-
щих слагаемых, для чего следует лишь всюду заменить индекс 1
на 2. Точно так же рассмотрим оставшуюся часть C6.11) и оты-
щем в ней прежде всего все члены, содержащие только индекс 1.
Эти члены в C6.11) подчеркнуты или выделены знаком f f.
Видно, что все эти члены совпадают с членами C5.10). Посколь-
ку мы здесь выбрали коэффициенты') pw> PwB том же виде,
как в C5.10), то сумму всех членов с индексом A) можно, со-
') Мы считаем, что в нулевом приближении Pw, pw определены из
однополяронной проблемы. Тогда pw можно заимствовать из C5.12).
§ 36] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯРОНАМИ 265
гласно C5.10), заменить па.Е$, где индекс A) вверху указы-
вает на частицу 1. Совершенно симметричным образом члены с
индексом B) приводят к Eg.
Самым главным для нас является член, стоящий в пятой стро-
ке C6.11), который зависит как от индекса A), так и от индек-
са B):
W = % 2 gw (P^eiw(x'-Xl) + p^V**-*'»). C6.12)
w
Заменим здесь E^ на его явное выражение C5.12) (при к ->- kj
и т* ->то*). Поскольку в последующем изложении мы будем рас-
сматривать только медленно движущиеся поляроны, положим в
C5.12), наконец, к\ =k2^k = 0. Тогда получаем
W (Х1 - х2) -= - 11 **„ Р {е— ha + HlV2< + A - 2)}.
C6.13)
Собирая вместе все стоящие в C6.11) члены, получаем
Я/к1к, - (Eg + Eg) /klki + (W^-xJ + H^) /klkl. C6.14)
Этот результат имеет для нас фундаментальное значение. Он по-
казывает, в частности, что (даже если #i_2 = 0) энергия двух
поляронов, взаимодействующих с колебаниями решетки, ни в
коем случае не равна сумме энергий отдельных поляронов, так
как в нее дает вклад дополнительная энергия взаимодействия W,
которая зависит от расстояния между частицами. Как будет вид-
но из C6.16), эта энергия отрицательна, т. е. благодаря взаимо-
действию с колебаниями решетки между частицами с одинаковы-
ми знаками зарядов появляется сила притяжения (при противо-
положных зарядах эта сила станет отталкивающей). Вывод, что
благодаря взаимодействию с некоторым полем между частицами
возникает прямое взаимодействие, является фундаментальным
для теории сверхпроводимости, которая будет обсуждаться в § 41.
Из-за этого прямого взаимодействия между частицами, которое
возникает благодаря полю, частицы, естественно, не могут оста-
ваться в исходных состояниях к], кг, а будут постоянно рассеи-
ваться друг нг друге. Поэтому, чтобы найти стационарное со-
стояние для волновой функции, следует сделать подстановку
/ ^Х15 Х2) = ?д CkjfcjjTtjfcj ^*и *a/' \OV. xo)
kikt
Мы не будем вдаваться в подробности вывода уравнения для оп-
ределения коэффициентов %%ь,1 поскольку аналогия этой ситуа-
266 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С КОЛЕБАНИЯМИ РЕШЕТКИ [ГЛ. V
ции с § 23 (об экситонах Ваннье) очевидна. Вместо этого обсу-
дим физический смысл взаимодействия W(xi — Х2) + Н\-2 =
BS WnOnB(xi — xz). В качестве определенного примера мы восполь-
зуемся константой связи gw C5.14) для полярного кристалла.
После вычисления C6.13), которое проводится заменой суммы
на интеграл, получаем (где Ixi — x2l = г)
C6.16)
C6.17)
(г) = - (-L - -L) l{l - 4- (е- - + е~ и.г)) +
Вначале рассмотрим предельный случай очень большого рас-
стояния г->°°. Тогда экспоненциальными функциями в C6.16)
можно пренебречь, в результате чего Waoilu принимает более про-
стой вид
И^полн = ?. C6.18)
В этом случае взаимодействие между поляронами принимает в
точности вид взаимодействия двух точечных зарядов в стати-
чески поляризованной решетке (ео = еСТатич). Обе частицы движут-
ся столь медленно, что успевает полностью установиться поля-
ризация решетки. Как следует из разложения C5.17),
+ !^, C6.19)
т. е. оба электрона имеют поляронные массы тп** и собственные
энергии — % ©aj. Если же,напротив, устремить г->0, то главные
вклады в И^полн дают члены
И^полн (г) = -%(т± - Йсоа2 + /-. C6.20)
Уравнения C6.18) и C6.19) дают правильные результаты для
больших расстояний г между частицами. При малых расстоя-
ниях поведение взаимодействия с достаточно хорошим прибли-
жением описывается C6.16), однако, приведенный выше метод
не учитывает, что при малых расстояниях может проявляться
масса «голой» частицы. (Как уже отмечалось, при малых рас-
стояниях обе частицы могут двигаться столь быстро, что ионы
не успевают следовать за ними.) Однако из-за недостатка места
§ 36] ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛИГОНАМИ 267
у нас нет возможности обсудить более точные методы, вроде уже
упоминавшегося в § 35 метода интегралов по траекториям
Фейнмана.
Приведенные выше аргументы легко можно распространить
на случай, когда обе частицы (поляроны) имеют противополож-
ные заряды, что действительно имеет место для экситонов.
В этом случае знак перед Т^полн следует изменить на противопо-
ложный, так что в результате получается — WnolSB. Следствием
этого является то обстоятельство, что при малых расстояниях г
собственно-энергетические члены в C6.19) компенсируются по-
стоянными членами, возникающими из-за взаимодействия (см.
C6.20), однако с противоположным знаком). При малых расстоя-
ниях между электроном и дыркой ионы не могут следовать за
ними достаточно быстро, так что возникают лишь малые поляри-
зационные эффекты.
Для некоторых экситонных спектров на эксперименте можно
достаточно отчетливо установить существование перехода от
кулоновского взаимодействия с е«, при малых радиусах эксито-
нов к взаимодействию с ео при больших радиусах экситонов.
Заданиек§36
С помощью волновой функции C6.6) вычислить ожидаемое
значение поляризации Р(х) B9.23).
Глава VI. ФУНКЦИИ ГРИНА
§ 37. Теория возмущений в координатном пространстве.
Возникновение функций Грина
В теории возмущений, которая была развита в §§30, 32 и
33, мы опирались на такое представление, в котором состояния
электронов и квантов звука описываются с помощью волновых
векторов к и w. Соответственно этому мы пользовались операто-
рами рождения и уничтожения вида
В этом параграфе будет показано, что теорию возмущений мож-
но сделать существенно более наглядной, если представлять себе
электроны и кванты звука определенным образом локализован-
ными. Для этого напомним читателю (см. § 13), что рождение
электрона в точке х можно представить с помощью действия опе-
ратора i|)+(x) на вакуумное состояние Фо. Поэтому в последую-
щем изложении для вычисления по возмущениям в качестве на-
чального состояния будем пользоваться функцией
ф@) = ф+(х)Фо. C7.1)
Кажется разумным попробовать развить теорию возмущений толь-
ко с помощью операторов
г(з+(х), ф(х).
Как мы сейчас увидим, «в принципе» это возможно, однако нам
все же следует сделать i|)+(x), г|з(х) операторами, зависящими от
времени; в предыдущих параграфах теория возмущений была
сформулирована с помощью представления взаимодействия
(§ 16).
При переходе4 от шредингеровского представления к пред-
ставлению взаимодействия все операторы, а следовательно и
i|)+(x), должны быть преобразованы с помощью невозмущенного
оператора Гамильтона Но (см. § 16):
4-я.* -4-я«*
г|>+(х, *) = eft aj)+(x)e n , C7.2)
откуда и появляется зависящий от времени оператор i|)J(x, t).
§ 371 ТЕОРИЯ ВОЗМУЩЕНИЙ В КООРДИНАТНОМ ПРОСТРАНСТВЕ 269
Индекс 0 у оператора tyt (x> *) указывает на то, что i|)+(x) пре-
образован с помощью оператора #о-
Если разложить г|з+(х) по плоским волнам, то для C7.2) по-
лучим
(V— объем нормировки). Стоящее в этом разложении преобра-
зование операторов вь уже было вычислено в § 16:
так что окончательно получается следующий результат:
к*. C7-4)
Эрмитово сопряженный C7.4) оператор имеет вид
^о (*. *) = 2 = e~ikxake"i8k'. C7.5)
Поскольку в начальный момент времени t — 0 оператор "ф<^ (х, f)
переходит в оператор \f>+(x), мы представим начальное состояние
C7.1) в виде
1 Ф@)=ф?(х„, 0)Ф0, C7.6)
где х заменено на Ха*), чтобы подчеркнуть, что х„ являются на-
чальными координатами частиц.
Функция C7.6) в последующем изложении при исследовании
взаимодействия между нолем электронов и полем колебаний ре-
шетки будет служить нам в теории возмущений в качестве на-
чального состояния. Для того чтобы не перегружать с самого
начала наше рассмотрение, будем рассматривать колебания ре-
шетки как классическое поле. Тогда гамильтониан взаимодейст-
вия принимает вид (см. B9.32))
& /if 1 V „+ „-ik"x+iet,,t I V* „ „ik'x-iek,t n . +ч
Нвэ =С \-?=¦ 2лаъ"е 47^2dai-'e "о(х> *)
J V v k» V У f
4fa
C7.7)
С помощью определений C7.4) и C7.5) суммы по к" и к' в
C7.7) можно выразить, как указано, через "ф"? и -фо- Оператор
*) Индексы шь й «е», встречающиеся в этом параграфе, дроисходят от
ецких слов «Anfang» — «начало» и «Ende» — «конец» соответственно.
) Индексы шь й «е», встречающ
немецких слов «Anfang» — «начало»
(Прим. перее.) '
2?о Функций гРйна [гл. vt
взаимодействия, таким образом, можно представить в более про-
стом виде
#вз = С J itf (х, *) ^0 (х, t) Qo (x, *) d3x, C7.8)
где под Qo следует понимать некоторую числовую функцию. Ес-
ли теперь перейти к теории возмущений, то оператором взаимо-
действия C7.8) следует подействовать на начальное состояние
C7.6). Если получившееся выражение прочитать справа налево,
то первым будет стоять выражение
%(x,t)y+(xa,0)<b0. C7.9)
Ниже эго выражение будет вычислено в общем случае, когда
оператор "фо" (ха, 0) заменен на oj)J(xa, ta). Если учесть, что Фо
является начальным состоянием, а \f>o состоит только из опера-
торов уничтожения а^, так что %)(х, ?)Фо = О, то C7.9) можно
представить в виде
Ы*. *L>0"(*a. *а) + <(»«. *«)Фо(*. *)}Фо- C7-10)
Как сейчас будет показано, выражение в фигурных скобках яв-
ляется числовой функцией, хотя ipo и aj>o~ являются операторами.
Поэтому мы полагаем
C7.10) = iG0(x, t; ха, *.)ф0. C7.11)
Чтобы получить явное выражение для GQ, подставим в C7.10)
разложения C7.4) и C7.5):
G0(x, t;xa, ta) =
= ~ ' 2 Т" е*'*~^е-**°+^а {аМ + а^}. C7.12)
k'k в?>
Тогда, учитывая также перестановочные соотношения для фер-
ми-частиц, получаем
G0{x, t; ха, ta) = _ «2-f eik(x-M-M*-M. C7.13)
При t — ta C7.13) переходит, как очевидно, в б-функцию;
к
При t < ta мы положим по определению
G0 = 0. -s C7.15)
Используя результат C7.11), получаем
~ #в8Ф @) = ~ j qt (х. t) Qo (x, t) ФОСО (х, *; xa, 0) d*x. C7.16)
§ 371 ТЕОРИЯ ВОЗМУЩЕНИЙ В КООРДИНАТНОМ ПРОСТРАНСТВЕ Й?1
Это выражение можно интерпретировать следующим образом.
В начальный момент времени электрон вылетает из точки х„ и
попадает в точку х к моменту времени t, где происходит взаи-
модействие (рис. 52).
Полученные выше результаты мы используем, чтобы в рам-
ках первого порядка теории возмущений более точно задать
функцию состояния. Согласно предыдущему
эта функция имеет вид (формула C0.7)) -*
t x,t xa,ta ¦
Ф (t) = Ф @) + f J- Я вз (х) Л Ф @).
0 ta) описывает рас-
C7.17) пространеняе сво-
бодного электро-
Это выражение с учетом только что получен- на из точки ха, ta
ного результата C7.16) и функции начально- в точку х, t.
го состояния C7.6) принимает вид
, т) т];+(х, т) Ф0СДх, т;ха, 0). C7.18)
Мы только что видели, что распространение электрона можно
очень наглядно представить с помощью функции Go, поэтому
представляется естественным выразить всю правую часть C7.18)
через Go, что может быть достигнуто умножением обеих частей
C7.18) на
<^К,дФ„|. C7.19)
Тогда сразу получаем
<Фо i % (хе, te) | Ф (*)> = iG0 (xe, te; xa, 0) +
0 (х„ te; х, х)% Qo (x, т) Go (x, т; хв, 0) tPx&%. C7.20)
Правая часть этого уравнения интерпретируется очень просто.
Первое слагаемое в правой части C7.20) описывает невозмущен-
ное распространение свободного электрона из х„, t« = fl в хе, te.
Второй член представляет распространение электрона из хв,
ta = 0 в х, т. В этой точке происходит взаимодействие с колеба-
ниями решетки. Затем частица распространяется из точки х, т
в точку хе, U (рис. 53).
На первый взгляд кажется совсем не просто узнать, какая
информация заключена во всем этом результате., Информацию,
272
ФУНКЦИИ ГРИНА
[ГЛ. VI
щая уравнению
C7.20) : рассеяние
ищим? ~а<?о(х
т) ( ). '
содержащуюся в функции Go, которую называют функцией Гри-
на, мы подробно рассмотрим в следующем параграфе. Здесь сто-
ит лишь упомянуть, что мы, естественно, сразу же вернемся
к привычному по предыдущим параграфам представлению (раз-
ложению по функциям аьФо)» если совер-
шить фурье-преобразование уравнения C7.20)
по координате хе и умножить его нае~г8кЧ
Тем самым видно, что из C7.20) можно
«вытянуть» всю ту информацию, которую мы
получили ранее в теории возмущений.
Мы еще раз поясним применение этого
Рис 53 Диаграм- нового способа описания на примере второго
ма, соответствую- порядка теории возмущений, приняв теперь,
что колебания решетки также квантованы.
Для того чтобы сразу же воспользоваться
только что полученными результатами, общее
основное состояние системы «электрон + ко-
лебания решетки» целесообразно разложить
на произведение отдельных состояний
Фо = Фо,элФо,р. C7.21)
Далее, в качестве начального состояния мы выберем состоя-
ние, в котором имеется электрон в точке ха и совсем нет квантов
колебаний решетки. Эту начальную функцию (см. C7.6)) можно,
учитывая C7.21), разложить в произведение
Ф @) = «(*«, 0) Ф0>Эл) Ф0.р, C7.22)
так что "фо относится только к Фо.эл- Подействуем теперь на
функцию C7.22) (во втором порядке теории возмущений) опе-
ратором
/ t t X, \
Ч) d-*! + (-ПТ-) Явз (та) 1 Явз (ti) dx± dx% .
¦> о oo /
I ' II Ш
C7.23)
Умножим результат по аналогии с C7.20) слева на функцию
и образуем среднее значение. Обсудим получившиеся члены по
отдельности:
I -* <Фо(*.IФ(О)> ш iG(xe, t.; x., 0), ; - C7.25)
1+ ± j #вз
ы-»-4-
C7.26)
§ 37] ТЕОРИЯ ВОЗМУЩЕНИЯ Б КООРДИНАТНОМ ПРОСТРАНСТВ!! 273
Как видно из C7.8), оператор НВЗШ содержит выражение
(?о(х, t), которое теперь является оператором.
Используя B9.32) и B9.33), разложим Qo следующим образом:
Qo (х, t) = Q+ (х, t) + Q; (x, *), C7.27)
где использованы сокращенные обозначения
C7.28)
C7.29)
To, что операторам уничтожения поставлен в соответствие опе-
ратор Q+, не является опечаткой, а связано с оиределением, при-
меняемым в квантовополевой теории, согласно которому через
Q+ должен обозначаться оператор, содержащий положительные
частоты. А поскольку во всех волновых функциях квантовой ме-
—Lei ~iffl'
ханики энергия присутствует в виде е п 5=е , то и C7.28)
действительно связано с положительной частотой.
Поскольку стоящие в C7.26) функции состояния представля-
ют вакуумное состояние решетки и, кроме того, (?о зависит от
6W, &w только линейно, то C7.26) исчезает:
II -*¦ C7.26) = 0. C7.30)
Таким образом, интересный для нас член в C7.23) — это III.
G помощью C7.8) перепишем этот член в виде
J j dr2dsx2Q0 (ха, т2) ... X
(- i СJ
X ... J J dT.d^Q, (xlt тх) ... Ф @)^, C7.31)
о
где точки обозначают пока еще отсутствующие операторы if>+, ij>.
При учете C7.22) и C7.24) выражение C7.31) распадается на
часть, относящуюся к решетке, и часть, относящуюся к электро-
нам. Рассмотрим в явном виде существенно новую для нас ре-
шеточную часть
<Фо.р1^о(х2, t2)<?o(xi, Ti)<D0>p>. C7.32)
Это выражение мы обозначим через
D(x2, т2; xt, ti). C7.33)
Если теперь для стоящих в @0 операторов &?, 6W воспользоваться
бозевекими перестановочными соотношениями, то вычисление
18 х. Хакен
274 ФУНКЦИИ ГРИНА [ГЛ. VI
C7.32) проводится аналогично C7.12) и в результате получаем
Ж*„ ',; «1, *i) = 2^у^-^^е-^и-и\ C7.34)
Это выражение мы будем интерпретировать как волновую функ-
цию, которая описывает распростране-
xe,t.. -*~~-~-~-w~~~- х f ние фонона из точки хь х\ в точку х2, тг.
7 Графически процесс распространения
этого фонона мы представляем с по-
Рис. 54. Функция Грина мощью волнистой линии (рис. 54).
D(x2, t2; xi, ti) описывает Теперь нам следует вычислить ту
распространение фонона из r J 1оп „..
точки х,, h в точку х2, ц. часть выражения в C7.31), которая
относится к электронам:
<Фо,эл | % (хе, te) ^ (х2, т2) х|з0 (х2, т2) г]з| (х17 тх) X
XiJ;0(x1, т^я^х,,, 0)Ф0,эЛ>- C7.35)
Так как вычисление проводится аналогично вычислениям на
стр. 269—271, то явное вычисление мы предоставляем читате-
лю и сразу ириводим результат
C7.35) = i3G0(xe, te; х2, та)С0(х2, т2; хх, tJGJxj, ti5 xe, 0).
C7.3G)
После этой подготовки мы в состоянии привести конечный
результат. Используя C7.36) и C7.32) = C7.33) в C7.31) и скла-
дывая затем I и III, мы получаем
<Ф0 I Фо (Хе' 1е) I ФB> (Ф = iGo (Хг> 1е\ ха' 0) +
t т2
I J— \ \ d%2(Pxfi0(xe, te; х2, т2) С I dTjd'^X
' й2 J J J J
о о
XD(x2;t2; x1? x1)G0{x2, т2; х1; тх) С Go (x1; хг; ха, 0). C7.37)
Второе слагаемое в C7.37) может быть интерпретировано сле-
дующим образом: электрон распро-
страняется ИЗ Х„, ta = 0 В X], Т[.
Там возникает взаимодействие с х ^
решеткой. Затем электрон и фонон ' *' * *"¦"'•'
летят из Xi.'ti в хо, Хо- Наконец, „ _, „
' ' ¦" „ Рис. 5о. Диаграмма, соответст-
имеет место еще одно взаимодеист- вующая уравнению C7.37):
вие, в результате которого фонон вклад в собственную энергию
уничтожается и электрон летит из электрона.
х2, т2 в хе, te (рис. 55). Поскольку
функции Go и D должны быть вычислены явно (см. задание),
то вычисление C7.37) сводится к ряду интегрирований по про-
странству и времени.
§ 38] ПРОПАГАТОР, ФУНКЦИЯ ГРИНА И ДР. 275
Приведенные выше соображения могут быть распространены,
естественно, на возмущения любого, сколь угодно высокого по-
рядка. Для этого, очевидно, следует выписать все соответствую-
щие вычислениям по теории возмущений диаграммы, каждой вер-
шине и каждой электронной и фононной линии которых отвеча-
ет определенное правило. С этими правилами мы только что поз-
накомились. Диаграммная техника образует фундамент мнбгих
современных теорий физики твердого тела.
Задание к§ 37
Переходя к пределу F-><» вычислить G0(x, t; х', 0).
§ 38. Функция распространения, пропагатор, функция
Грина — все одно и то же
Обратимся к результатам предыдущего параграфа. Мы ви-
дели там, что каждый шаг теории возмущений можно интерпре-
тировать совершенно наглядным образом, если представить се-
бе, что частицы распространяются в пространстве между неко-
торыми точками. Таким образом, мы представляли распростране-
ние свободного электрона из точки Xi в момент времени t\ в точ-
ку х2 к моменту времени t2 с помощью функции
G0(x2, t2] Xl, tx) = _;2^ik(x-Xl)-iEk(i2-4 C8.1)
k
которая является результатом суммирования по к.
При этом в рамках теории возмущений автоматически учиты-
валось, что t2 > t\. Для последующего будет также необходимо
определить эту функцию и для t2 < t\- Для этих моментов вре-
мени мы полагаем ее равной нулю:
G0(x2, h; хь *i) = 0 при t2<ti. C8.2)
Представляемая выражениями C8.1) и C8.2) функция описыва-
ет распространение свободного электрона и обычно называется
функцией распространения или пропагатором. Как мы уже виде-
ли, выражение C8.1) может быть также определено через опе-
раторы рождения и уничтожения: если умножить равенство
C7.9) = C7.11) или, в наших теперешних обозначениях,
Фо(х2, *2>4>o"(*i. *1)Фв = *Go(x2' V, «I. *iI>o C8.3)
слева на (Ф%\ то в качестве определения Gq мы получаем
G0(x2, t2; хи г,) = -г<Фо1фо(х2, t2)yfrt (xi, *1)Ф0>, t2>tu C8.4)
18*
276 ФУНКЦИИ ГРИНА [ГЛ, VI
Для ti > ?2 по аналогии с выражением C8.2) полагаем снова,
что G0{x2, h; xi, t\) = 0. Этот нуль мы представим, исходя из со-
ображений, которые тотчас будут очевидны, в несколько слож-
ном виде, а именно, сначала подействовав оператором уничтоже-
ния, а затем оператором рождения:
G0(x2, t2; Xj, tx) — 0 = <Фо|1|>о"(х1' ti)tyo(xv *г)Фо) ПРИ h<h'
C8.5)
В этом месте обратим внимание на одно важное свойство функ-
ции распространения, которое часто будет встречаться нам поз-
же. В левой части уравнения C8.1) xi и хг, так же как t\ и t%,
стоят отдельно друг от друга. В правой же части, напротив, ко-
ординаты и время всегда появляются в виде разностей Х2 —Xj
и 12 — t\. Это свойство является следствием пространственной
трансляционной инвариантности задачи — свободная частица
«видит» однородное пространство. Совершенно аналогично имеет
место и временная инвариантность, поскольку на частицу не
действуют никакие зависящие от времени силы.
Как мы только что видели, функцию распространения мож-
но представить с помощью среднего значения C8.4) и C8.5). Те-
перь мы обобщим эту концепцию еще на целый ряд направле-
ний. Прежде всего представим оба выражения C8.4) и C8.5) с
помощью одного выражения, введя так называемый хроноло-
гический оператор Дайсона Т, который имеет следующий про-
стой смысл. Если написать этот оператор перед произведением
зависящих от времени операторов, то операторы упорядочива-
ются справа налево в таком порядке, что операторы, относя-
щиеся к более ранним моментам времени, всегда стоят справа
от операторов, относящихся к более поздним моментам време-
ни, Тем самым в качестве определений оператора Т получаем
уравнения
7Ч|H (х2, ?2) i|)g (xj, tj) = o|H (x2, i2) i|)q (xj, У для ?2 > ^i C8.6)
и
Относительно знаков плюс и минус в правой части C8.7) дело об-
стоит следующим образом: знак минус ставится, если речь идет
о фермиоператорах, а плюс — если это бозевские операторы.
Если теперь в уравнениях C8.6) и C8.7) построить среднее
значение относительно вакуумного состояния, то непосредствен-
но получится соотношение
х2, *2H+(Xl, у|Ф0> =
- i <Фо 1% (Х2> h) Фо" (*i. *i) I фо> при *„ > «ц
I C8.8)
± i <Ф01 гро (хх, tt) г|}0 (х2, t2) | фо> при t% < tx.
§ 38] ПРОПАГАТОР, ФУНКЦИЯ ГРИНА И ДР. 277
Тем самым мы достигли своей цели — представить соотношения
C8.4) и C8.5) одним выражением. Функция C8.8) допускает
многие обобщения. Нам нет необходимости полагать, что свобод-
ная частица добавляется к вакууму. Мы можем, например, пред-
ставить себе, что в кристалле распространяется электрон, добав-
ленный к уже имеющимся, скажем, избыточной электрон в по-
лупроводнике. На этом основании функцию Фо, вообще говоря,
можно заменить вектором состояния Ф, описывающим новую.фи-
зическую ситуацию. Точно так же при распространении частицы
вовсе не необходимо, чтобы это была непременно частица без
взаимодействия. Более того, наиболее интересный случай возни-
кает именно тогда, когда частица находится во взаимодействии
с окружением, как, например, электрон с колебаниями решетки
(в особенности поляроны), или когда электрон взаимодействует
с другими электронами кристалла. При этом следует, естественно,
заменить оператор свободной частицы /То на полный оператор
Гамильтона с взаимодействием Н и, таким образом, в самом об-
щем случае определить зависящие от времени операторы унич-
тожения в представлении Гейзенберга:
¦ф (х, t) = е*Шу (х) е"Ш. C8.9)
Тогда получаем следующее определение функции Грина:
| G (х2, *а; хх, tj) = — i <Ф | Гг|5 (х2Т*2)':ф+ (х15 tt) Ф>. C8.10)
Эта и родственные ей функции приобрели в современной теории
твердого тела очень важное значение, и в последующем изложе-
нии на некоторых сравнительно простых примерах мы покажем,
почему функции Грина так важны я что можно описать с их
помощью.
Если задача обладает пространственной и временной инва-
риантностью, то функция C8.10) зависит не от отдельных аргу-
ментов X], х2, ti, t2, а, как уже было отмечено выше, от соответ-
ствующих разностей
х2 —xi=x, t2 — ti = t. C8.11)
При этих предположениях функция Грина становится функцией
только х и t:
G{x2, t2; xi, *i) = G(x, t). C8.12)
Далее, мы будем действовать следующим образом:
1. Сначала поясним, какая информация содержится в G или,
выражаясь проще, почему физики-теоретики вообще занимаются
функцией Грина G.
2. В следующем параграфе мы установим уравнение для G
и продемонстрируем полезность функции Грина G.
Информативность функции Грина G. Вновь начнем с при-
мера свободной частицы. Как мы уже видели, функция Грина" в
278 функции гринл [гл. vi
этом случае дается следующим явным выражением:
^„ • C8лз,
I 0 при t < 0.
Определение C8.13) представляет разложение G(x, t) по пло-
ским волнам, т. е. пространственное преобразование Фурье. Со-
ответствующие фурье-коэффициенты мы обозначим через G^it):
<38Л4>
При этом функция Gk(t) представляет собой совершенно иную
функцию, нежели G(x, t). Поэтому читателю следует обращать
особое внимание па аргументы х и к. Сравнение C8.14) с C8.13)
показывает, что G^(t) дается выражением
ie lEk ПРИ *>0' ПЯ1^
0 при*<0. (°8ЛО)
Естественно, здесь нет ничего нового для случая свободной ча-
стицы. Это выражение утверждает лишь, что вектору распростра-
нения к свободной частицы отвечает энергия ?"к=Й8к . Основ-
ная проблема возникает тогда, когда речь идет о частице, кото-
рая связана со своим окружением некоторым взаимодействием.
В этом случае следует ожидать, что энергия первоначально сво-
бодной частицы изменяется. Кроме того, как мы видели в § 30,
частица рассеивается из своего исходного состояния. Вероятность
обнаружить ее в исходном состоянии при этом уменьшается.
Как выразить теперь все это с помощью функции Грина?
Предположим вновь, что функция Грина G(x, t) разложена в
ряд Фурье. Тогда фурье-коэффициенты примут следующий вид:
Gk (t) = - ic^e'1^^'^ при * > 0, C8.16)
где Е B3,k=^ei,3,k—энергия частицы с учетом взаимодействия,
а 1 к— обратное время жизни частицы.
Возможно, что экстраполяция от частицы без взаимодейст-
вия, которая описывается выражением C8.15), к взаимодейству-
ющей частице, которая описывается выражением C8.16), тому
или иному читателю покажется несколько смелой. Однако на
примере конкретной модели мы покажем, что G действительно
имеет такую структуру.
До сих пор мы познакомились с функциями Грина двух ти-
пов, а именно, зависящих от координат и времени и зависящих
от волнового вектора к и времени. Можно сделать еще один шаг
§ 381
ПРОПАГАТОР, ФУНКЦИЯ ГРИНА II ДР.
279
и провестя преобразование Фурье по времени. Это преобразо-
вание определяется следующим образом:
+ ОО
бк(е)= J eiBtGk(t)dt. C8.17)
00
Мы вычислим этот фурье-образ для частного случая C8.16) п по-
сле проведения интегрирования получим
Ск(е) -=ск-
1
е —ек-г
C8.18)
Ime
Комплексная
г -плоскичти
Таким образом, C8.18) является пространственным и временным
фурье-образом исходной функции Грина G(x, t). Эта функция
Грина, рассматриваемая как функция кие (причем е имеет раз-
мерность частоты), довольно часто встреча-
ется в литературе и служит поводом к вве-
дению совершенно новой терминология.
Рассмотрим функцию C8.18) для фиксиро-
ванного к, т. е. для определенного вектора
распространения, по для переменного е! По-
скольку знаменатель C8.18) является комп-
лексной величиной, то функцию Gk(e) имеет
смысл рассматривать на комплексной е-пло-
скостп. Как функции аргумента е, C8.18)
имеет на комплексной плоскости один по-
люс. Действительная координата этого полю-
са равна бк, а мнимая — обратному времени
жизни-"Ч (рис. об). Тогда мы приходим
к фундаментальной интерпретации: полюс
или, возможно, полюсы функции Грина
Gfc(e) определяют энергию и время жизни ча-
стицы при ее взаимодействии с окружением. Поскольку при этом
взаимодействии может возникнуть совершенно новое возбужден-
ное состояние, которое имеет мало общего с исходным состоянием
свободной частицы, то говорят о рождении квазичастицы. На
самом деле это понятие следует трактовать еще шире. Возможны
случаи (например, нлазмоны; см. § 27), при которых вовсе
не требуется введения в систему дополнительной частицы, чтобы
создать возбужденное состояние, которое выглядит так, как
будто через систему движется своего рода частица. Простейший
пример — фонон, который распространяется в решетке как квант
возбуждения,— встречался нам уже в § 8.
Заметим также, что функцию G^it) можно определить прямо,
не пользуясь обходным путем через фурье-преобразование ис-
ходной функции Грина G(x, t). Мы утверждаем, что это делается
Res
Рис. 56. Полюсы фун-
кции Грипа ?к (е) на
комплексной е-плос-
кости (е — энергия).
280 ФУНКЦИИ ГРИНА [ГЛ. VI
следующим образом:
| C8.19)
Доказательство проводится легко, если разложить i|)+(x, t), ij)(x, t)
по плоским волнам, т. е., например,
Подробности вычисления мы предоставляем читателю в качест-
ве упражнения.
§ 39. Примеры уравнений для функций Грина и их решение
В этом параграфе мы приведем два примера, чтобы показать,
как выглядят уравнения для функций Грина и какие обычно де-
лаются приближения для их решения.
Первый пример связан с проблемой многих электронов в фи-
зике твердого тела, а второй — с взаимодействием электрона с
колебаниями решетки, т. е., в частности, с поляроном.
Пример 1. Уравнение для функции Грина проблемы многих
электронов. Наша задача состоит в том, чтобы вывести уравне-
ние для функции Грина, которая определена в координатном
представлении следующим образом:
GU, t; x', ?) = - *<Ф|2\|з(х, fty+(x'f ПФ>
(см. C8.10)). Самый простой путь — это установить связь с урав-
нением движения для оператора уничтожения if(x, t). Для опе-
ратора Гамильтона проблемы многих электронов (см. B0.1)) мы
уже ввели в § 16 уравнение движения для оператора уничтоже-
ния (см. (А 16.15)). Чтобы в последующем изложении не тащить
за собой слишком большое число членов и, кроме того, с самого
начала учесть трансляционную инвариантность проблемы, мы
опускаем решеточный потенциал V(x) и считаем, что это оправ-
дано введением эффективной массы (см. § 18).
Итак, в основу рассмотрения кладется следующее уравнение
движения:
X <J>(x", Ог|з(х, t)d?x". C9.1)
Умножим уравнение C9.1) справа на оператор ф+(х\ t'), подей-
ствуем слева хронологическим оператором Т и образуем среднее
значение относительно состояния Ф (которое пока нет нужды
§ 39] ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА
уточнять более подробно). Тогда получим
281
Ах <Ф'
° Ф>
Ф>
C9.2)
Чтобы получить уравнение движения для функции Грина, нам
следует, естественно, вынести производную по времени d/dt и
поставить ее перед средним значением. Однако здесь таится не-
кая сложность, о которую можно легко споткнуться. Чтобы не
стать жертвой этой сложности, мы запишем G(x, t; x', t') в та-
ком виде, что хронологический оператор Т окажется выражен-
ным с помощью «обычной» числовой функции. Для этого вос-
пользуемся ступенчатой функцией @(t — t'), которая, как извест-
но, определяется следующим образом:
t>t',
при
при t < t'.
C9.3)
Тогда Г-произведение можно сформулировать следующим обра-
зом:
=F q+W, ГЦЫ, tH(t' - t). C9.4)
При этом знак минус относится к ферми-операторам \|э, а знак
плюс следует использовать для бозе-операторов.
Как показывает сравнение с определением оператора Т (см.
C8.6, 7)), выражения C9.4) и C8.6, 7) действительно совпадают.
Чтобы от C9.4) перейти к правилу вычисления производной по
времени функции G, построим с обеих сторон C9.4) среднее зна-
чение относительно функции Ф, умножим на (— i) и продиффе-
ренцируем по времени t:
f. y/ fl
) ' 1 /ф
+, W
бф (х
dt
т \Х ' ' dt
*) i,+ / ' f'\
/
+ <Ф | ф (X, t) Tj)+ (X', t') | Ф> -| в (t - П =F
282 ФУНКЦИИ ГРИНА [ГЛ. VI
Используя Г-оператор, запишем два первых члена в C9.5) в
виде
ф\ C9.6)
Для преобразования обоих последних выражений в C9.5) мы вос-
пользуемся известным из математики фактом, что производная
ступенчатой функции дает б-функцпю:
После сложения два последних слагаемых в C9.5) принимают
следующий вид:
-КФКг|;(х, г)г|;+(х', t') ± ф+(х', Г)ф(х. t)) ШШ - П. C9.8)
Выражение в фигурных скобках с C9.8), однако, представляет
собой антикоммутатор (фермн-частицы) пли коммутатор (бозе-
частицы) между г|з и "ф+. Поскольку за ним стоит функция
8(t — t'), мы можем оба времени tut' положит!, ранными. Тогда
фигурная скобка превращается, согласно обычным перестано-
вочным соотношениям A3.8) и A2.15), в обычную б-функцию
8(х —х'). Поскольку оставшееся среднее значение <Ф|Ф) из-за
нормировки Ф равно единице, то C9.8) принимает простой вид
-18(х-х'Ш-П. C9.9)
Если сложить два первых члена C9.5), которые даются выра-
жением C9.6), с двумя последними членами C9.5), которые да-
ются выраженном C9.9), то окончательно получим
AG(X, t;x', t') =
'^Mf^x'.f) 0\-i8(x—x')8(t — t').
C9.10)
Возвратимся теперь к нашему исходному уравнению ^ C9.2).
Умножив обе его стороны на (— i) и подставив в левую часть
C9.10), получим окончательное уравнение
i% 4 G (х, *; х', V) = %Ь (f -t)8 (x' - х) -
_ i Г f .G(x", t; x", t - 0; x, *; x', Г) d*x". C9.11)
J Iх x I
§ 39] ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА 283
Здесь сразу введено сокращенное обозначение
"" (Х1' *1> Х2> *2> Х3' ^3> Х4' 4) =
= <Ф | ?V (хх, tt) г|; (ха, t2) г|з (х3, *3) i[)+ (х4, *4) ф>. C9.12)
Поскольку мы применили в C9.11) хронологический оператор,
а в уравнении C9.11), однако, должны пользоваться равными
временами 11 = ti = t, то, чтобы обеспечить правильный порядок
следования операторов ф+, гр, в аргументе мы написали t — 0.
В уравнении C9.11) кроется глубокое разочарование для теоре-
тика, который полагает решить эту задачу с помощью функции
Грина. Первоначально мы хотели ввести уравнение для функции
Грина G(x, t; x', t'). Однако это удалось нам лишь частично,
поскольку мы вынужденным образом пришли к введению еще
более сложной функции Грина C9.12). Для нее вновь следует
ввести уравнение, что в принципе возмолшо сделать. Но это но-
вое уравнение будет содержать функцию Грина, в которой по-
явятся шесть операторов. Эту процедуру можно продолжить,
в результате чего получится последовательность уравнений, ре-
шение которой определенно не проще, нежели решение исход-
ной задачи. Поэтому следует обратиться к приближениям. Преж-
де чем обсудить этот путь, мы рассмотрим точно решаемый
пример 1).
Свободные частицы без кулоновского взаимодействия. В этом
случае последний член в C9.11) выпадает, так что уравнение
принимает следующий вид:
ag(%i;i''°=i|> А,С(х, *; х'' П -i&V- *'N(x -х').
C9.13)
Поскольку неоднородный член этого уравнения зависит только
от разности координат ~ 6(? — t')8(x — x'), мы полагаем
G = G(x-x, t-t'). C9.14)
Для решения представим G в виде интеграла Фурье:
G(x~x',t- Г) = -±-т Г Г G (к, в) е'к<я-х'Ь«(*-*')^ ^
Bя) J J
C9.15)
Аналогично разложим функцию 8(t — t')8(x — x') в интеграл
Фурье:
8(t- V) 8 (х - х') = -Ц- Г Ге*(ж-х'Мв«- t')d3/c d^ C9Лв)
') Читатель, не достаточно глубоко знающий математику (преобразо-
вание Фурье, теорему о вычетах), этот пример может спокойно опустить
и читать дальше, начиная со стр. 285.
284 ФУНКЦИИ ГРИНА [ГЛ. VI
Оба выражения подставим в C9.13). Учтем, что имеют место ра-
венства
jL
C9.17)
Vkx
= - A,Vkx. C9.18)
Перенесем все члены в C9.13) в одну сторону, после чего по-
лучим
-, \d3kde^0 C9.19)
BяJ1 V ;
Поскольку экспоненциальные функции между собой линейно не-
зависимы, то левая часть C9.19) может равняться нулю только
тогда, когда обращается в нуль выражение в фигурных скобках.
Это приводит к результату
C9.20)
BяУ е-ек
где введено сокращенное обозначение
Я* = 0-. C9.21)
Подставляя C9.20) в C9.15), получаем
л /» /» -ik(x-3t')-ie({-t')
A I- Y'. f f'\ l I I _? JZh Ла ' /on O9\
BnLJJ 6~6k
Этот интеграл, очевидно, следует вычислять с помощью теоремы
о вычетах. При этом возникает типичная для функций Грина
трудность: подынтегральное выражение имеет полюс в точке
е = Ек, т. е. сингулярность на контуре интегрирования. Чтобы
избавиться от этой трудности, добавим в знаменателе бесконечно
малую мнимую величину ± if, у > 0, в результате чего знаме-
натель примет вид l/ie — eit+iy. По причинам, которые сейчас
станут понятными, мы выберем знак плюс перед iy. Итак, рас-
смотрим интеграл
I
е — e
ск
— 00
de (T = *_*'). C9.23)
Для того чтобы можно было воспользоваться теоремой о вычетах,
§ 39] ПРИМЕРЫ УРАВНЕНИЯ ДЛЯ ФУНКЦИЯ ГРИНА 285
контур интегрирования следует замкнуть на бесконечности, при-
чем интеграл вдоль этой части контура не должен давать вклада.
1. При т = t — t' > 0 замыкаем контур в нижней полуплоско-
сти, тогда Im е < 0, т. е. действительная часть показателя экспо-
ненты в C9.23) Re {— ?ет) < 0 (рис. 57). Полюс в точке г=гц— щ
находится внутри контура интегрирования. Теорема о вычетах
дает
V-vt ^ _ 2nie~i8kT, y->-0. C9.24)
е — ek + iy
2. При т = t — t' < О контур интегрирования следует замкнуть
в верхней полуплоскости. Тог-
да внутри контура нет ника- Ims
кого полюса, так что теорема о
вычетах дает § • • • =0. Тем
самым мы удовлетворили ус- /' Контур
ловию /
nput-f<0
G{x, t; x', i')=0 при t<t'
(см. 38.2)). C9.25) \ ~'7
ч
/
Нее
/
у
nput~t>0
Из процедуры интегрирования
(выбор знака щ) видно, что контуд
уравнение C9.13) не включает ' ¦
условие C9.25), так что его Рис. 57. К применению теоремы о
следует явно ввести. Применяя вычетах.
C9.24) и C9.25), получаем
™ 1 С OL A", t ^> t ,
BяУ J C9.20)
О, t<V. >
Сравним теперь результат C9.26) с C8.1) и C8.2). Совершенно
очевидно полное совпадение (если только учесть, что в § 38 ис-
пользовался ряд Фурье, а здесь, напротив, интеграл. Это по су-
ществу вопрос объема нормировки, и он не связан ни с физикой,
ни с формализмом). Несмотря на это совпадение, в нашей задаче
заключена еще одна ловушка (см. задание l).
Вернемся, однако, назад к нашему общему уравнению C9.11)
с кулоновсним взаимодействием.
Приближение Хартри. Для того чтобы мы могли решить урав-
нение C9.11), в теории функций Грина следует сделать типичное
приближение, которое полностью эквивалентно первоначальному
приближению Хартри (или несколько более общему приближе-
нию Хартри — Фока). Мы разложим функцию Грина, которая
зависит от четырех операторов, на произведение более простых
286 ФУНКЦИИ ГРИНА [ГЛ. VI
функций Грина, т. е. представим ее в виде (приближение
Хартри)
G(xx, ^; x2, t,; х3, t3; х4, i4) = ±G(x2, t.2; хх, ix)G(x3, *3; x4, *4),
C9.27)
или, в краткой записи,
| Gil, 2; 3, 4) = ±GB, 1) Ш, 4). C9.28)
Верхний знак относится к фермп-операторам ip+, if), а нижний —
к бозе-операторам. Подставим приближение C9.28) в уравнение
C9.11). Теперь учтем еще, что
G*(x, *-0; х, i) = ± КФ|г|з+(х, t)ty(x, *)|Ф> = ±*р(х, t) C9.29)
(р(х, t) — плотность числа частиц), после чего получим
.* OG (x, t; x', t')
= f_ «L
x '
|x — x | J
+ %6(t — t'N{x — x'). C9.30)
Стоящий в правой части уравнения C9.30) в фигурных скобках
оператор имеет вид:
кинетическая энергия + потенциальная энергия заряда е в
поле зарядовой плотности ер(х, t).
В качестве метода решения напрашивается решение с по-
мощью итераций (как в методе Хартри): задаем р(х, t), затем вы-
числяем с помощью уравнения C9.30) G, получаем отсюда со-
гласно уравнению C9.29) новую плотность и т. д.
Приближение Хартри — Фока. В этом случае используется
следующее приближение:
| G(l, 2; 3, 4) = ±GB, 1)GC, 4) - GC, 1)GB, 4). C9.31)
Мы предоставляем читателю самому по аналогии с методом
Хартри сделать подстановку приближения C9.31) в C9.11) и об-
судить получившееся уравнение.
Пример 2. Взаимодействие частицы с колебаниями решетки.
В предыдущем примере мы рассматривали функции Грина в ко-
ординатном пространстве. Теперь введем уравнения движения
для фурье-образов функций Грина. Мы ищем, таким образом,
уравнение для определенной в C8.19) функции Грина Gk'(t).
В принципе мы поступаем так же, как и в первом примере, исхо-
дя при этом из соответствующих уравнений движения опера-
торов в гейзенберговском представлении. Для случая взаимодей-
ствия электрона с колебаниями решетки уравнение движения
% 39) ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА 287
фоионных операторов было уже введено в § 16. Аналогичным
образом можно ввести и уравнение для электронных операторов.
Поскольку эти уравнения нам сейчас потребуются, приведем их
простоты ради, в явном виде
ак ^ — 'SkOk — i 2 gwflk-w&w — * 2 ?*-bw«k+w> C9.32)
w w
S- C9.33)
^ kowb+ -f / 2 SwOk+n-ffk- C9.34)
k
Уравнение C9.32) является исходным при выводе уравнения для
функции Грина. Далее, умножим обе стороны C9.32) справа
навк^'), а слева — на хронологический оператор Т и на (—?).
Образуем, наконец, среднее значение относительно состояния
Ф, причем в последующем в качестве Ф будем использовать ва-
куумное состояние. Тогда получим уравнение
^ - /ekGkk, - tfkt,6 (t - Г) -
Gk-w,w,k' — 2^w^w,k+w,k', C9.35)
w w
где введены следующие краткие обозначения:
C9.36)
= <ф I Ta^.v(t) 6W (*) a+, (*')Ф>, C9.37)
= <Ф I Tbl (t) flk+w (*) йк' (*') Ф>. C9.38)
Появление функции C9.36) и есть тот результат, который мы
хотели получить. Менее отрадно, что мы оказались вынужденны-
ми вновь ввести функции Грина нового типа, а именно C9.37) и
C9.38). Теперь можно было бы попытаться представить функции
C9.37) и C9.38) в виде произведения более простых функций
Грина. Например, так;
Gk-w,w,.c = <Ф | Tab-v (t) at- (П Ф> <Ф | bw (t) Ф>. C9.39)
Однако легко показать (см. упражнение 2), что C9.39) для ва-
куумного состояния Фо исчезает. Тогда получился бы результат,
согласно которому частицы в конечном счете движутся как сво-
бодные, поскольку дополнительные члены в C9.35), которые опи-
сывают связь между частицами и полем колебаний решетки, об-
ращаются в нуль. Этот пример, таким образом, отчетливо демон-
стрирует, что при применении функций Грина можно легко сде-
лать ошибку и использование этих функций требует тонкого
288 ФУНКЦИИ ГРИНА [ГЛ. VI
физического чутья. И действительно, в литературе имеются приме-
ры, где делаются совершенно неверные приближения и прежде
всего при заменах функций Грина их произведениями. Однако
мы вовсе не хотим слишком пугать читателя, напротив, мы хотим
показать, что с некоторой долей осторожности можно тем не
менее быстро прийти к хорошему результату. Для этого введем
еще уравнения для функций Грина C9.37) и C9.38). Дифферен-
цируя C9.37) по времени, получаем
"IT a*-w (*) К (t) at, (Г) ф\ +
+ <Ф | fak_w (t) fcw (t) a?, (*') Ф> + <Ф | Tat-w (*) к (*) <?. (*') Ф>.
C9.40)
Здесь выражение dT/dt имеет, вообще говоря, символическое зна-
чение. Оно должно лишь напоминать, что при дифференцирова-
нии следует обращать внимание на порядок следования времен
t и t'. В остальном оно приводит к появлению одного дополни-
тельного члена. Этот член выведен в упражнении 3. Он имеет вид
• C9.41)
Наряду с первым членом в C9.40), который мы только что при-
вели в явном виде. (см. C9.41)), в C9.40) имеются еще два дру-
гих члена. Для того чтобы вычислить эти члены, подставим вме-
сто а и Ь правые части C9.32) и C9.33). Тогда получим следую-
щее выражение:
4 Gk-w,w,k' = I + И + III, C9.42)
где отдельные члены даются следующими выражениями:
I = б (*-*') 8k,,k_w <Ф | bw (t)Ф>, C9.43.1)
П = /ф \Т\— fek_ wak_w — / 2 gw'flk-w-w'frw —
\ 1 w
C9.43.11)
111= /ФI rak.w (t) f - mwbw -1% gW'O^+w] «k+' (П Ф\.
C9.43.111)
Как будет показано в упражнении 2, член C9.43.1) исчезает.
Член C9.43.11) содержит в фигурных скобках выражения разных
§ 39] ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА 289
типов. Первое из них можно представить в виде
— Jek_wGu_WiWik/. C9.44)
Второе выражение в фигурных скобках содержит фононный опера-
тор уничтожения bw>, который после перемножения членов оказы-
вается рядом со вторым фононным оператором уничтожения. Это
означает, следовательно, что фононы уничтожаются дважды. Про-
цессу уничтожения каждый раз ставится в соответствие константа
связи gw. Если ограничиться наинизшим приближением ~grw> т0
это выражение, следовательно, можно опустить. Выражение, кото-
рое связано с последним слагаемым в фигурных скобках, также
исчезает, поскольку оператор &Х, действуя справа на Фо, дает
нуль (см. упражнение 2). Таким образом, все выражение
C9.43.11) принимает вид C9.44). Рассмотрим, наконец, выраже-
ние C9.43.III). Здесь также стоят фигурные скобки. Первое вы-
ражение в них с точностью до множителя —icow вновь приводит
к функция Грина C9.37). Теперь рассмотрим второе выражение в
C9.43.111), которое состоит из суммы операторных выражений
вида
flk-w (*) <*k" (*) flk"+wr@ 4, (Г). C9.45)
Используя обычные перестановочные соотношения для ферми-
частиц, можно обратить порядок следования двух первых опера-
торов, что дает
6k",k-wak"+w (t) а?> {t') — а^„ (t) ak_w (t) ak//+w (t) at- (*')• C9.46)
Теперь представим себе, что C9.45) и C9.46) действуют на ваку-
умное состояние. Рассмотрим действие второго стоящего в C9.46)
выражения на Фо. Сначала здесь рождается электрон. Затем,
однако, должны быть уничтожены два электрона, но поскольку
в наличии имеется только один, то действие соответствующего
оператора на Фо дает нуль. Тем самым, следовательно, выраже-
ние C9.45) оказывается тождественно равным первому слагаемо-
му выражения C9.46) и содержит поэтому только два электрон-
ных оператора, которые стоят в первоначальном определении
Gkk'. После этих несколько затянувшихся рассуждений мы обна-
руживаем, что C9.43.III) переходит в выражение
C9.43.111) = — JcowGk_WjW]k, -f gwGkk,. C9.47)
Теперь подытожим наши результаты. Мы ввели уравнение
для функции Gt-w.w.k'» которая была задана с помощью C9.42).
Вычисление отдельных выражений I, II, III приводит затем к
следующему конечному результату:
-fit ?k-w,w,k' = — i (ek-w + и?) Gk_w,Wjic' + #wGkk'. C9.48)
19 x. Хакея
290 ФУНКЦИИ ГРИНА [ГЛ. VI
Теперь могло бы показаться, что нам снова предстоит такая же
скучная задача вывода аналогичного уравнения для C9.38). Одна-
ко, как можно показать по аналогии с упражнением 2, C9.38)
обращается в нуль (по меньшей мере для состояния, в котором
пет фононов):
g' k, = 0. C9.49)
Тем самым наша задача — найти замкнутую систему уравнений
для функций Грина — решена. Используя результаты C9.48) и
C9.49), оба типа уравнений можно представить следующим
образом:
dG -«л
jt — ?¦ к кк' кк' (. )— и g\v k-w,w,t'i \" •• )
-fo Gk-w,w,k' = — i (ek_w -f- cow) Gk_WiVVk/ -+- KnfGkkr. C9.51)
При решении уравнений C9.50) и C9.51) кажется разумным по
аналогии с решением уравнения для частицы без взаимодействия
C9.13) вновь воспользоваться фурье-преобразованием. Поближе
мы займемся этим в задании 5, а сначала с помощью другого ме-
тода решения покажем, что взаимодействующий с колебаниями
решетки электрон может быть действительно описан с помощью
новой смещенной энергии и константы затухания. При этом огра-
ничимся случаем t>t' и k = k'. Тогда в уравнении C9.50) неод-
нородный член ~ 6(?—1')—0 и система C9.50) и C9.51) перехо-
дит в систему линейных однородных уравнений с постоянными
коэффициентами. Для решения подобных систем уравнений, как
известно, полагают, что неизвестные функции пропорциональны
экспоненциальным функциям:
Gk,k = Cke(~iE~v)f, C9.52)
Gk_w,w,k = Dk,we(~ie~y)t, C9.53)
где е, у, Ск, Z>k>w—постоянные, подлежащие определению. Подста-
новка C9.52) и C9.53) в C9.50) и C9.51) непосредственно
дает
(— is — v) Ck = — iEkCk — 2 gwAc.w C9.54)
w
И
(— ie — v) Z>k)W = — i (ek_w + cow) Z)kiW -f- gwCk. C9.55)
Из уравнения C9.55) можно найти D kw:
Dk w = —: b?±—__—. C9.5&)
§ 39) ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА 291
Если теперь подставить это выражение в C9.54), то Съ в обеих
частях сокращается и почти сразу получается уравнение
Z^+^7' ¦ C9l57)
Уравнение C9.57) представляет собой-уравнение на собственные
значения для (е — if). Поскольку (е — if) стоит под знаком сум>-
мы, то определение (е — if) может оказаться сложной задачей.
Если мы ограничимся малыми константами связи \gv I2, то имеет
смысл решать уравнение C9.57) методом итераций. В нулевом
приближении сумму в C9.57) мы опустим, после чего получим
е@) - ek, f"» - 0. C9.58)
В следующей итерации подставим под знак суммы е = еь. Ввиду
того, что в C9.58) f@) = 0, у нас могло бы возникнуть искушение
и в следующей итерации положить f = f@) = 0, что приводит,
однако, как показывает дальнейший анализ, к противоречию.
Поэтому сначала сохраним f, а затем рассмотрим с учетом C9.58)
предельный переход f<0) -*¦ 0:
е — iv = et — lira, УI ?w p ¦ т-г-.
Для дальнейшего вычисления суммы в C9.59) преобразуем ее в
интеграл. Как нам уже известно (см. B9.27)), константы связи
gw зависят от объема кристалла V следующим образом: gw ~
~ 1/У V. Поэтому положим
gw-=A=g%. C9.60)
Так как суммирование ведется по волновым векторам, то спра-
ведливо следующее соотношение (см. C0.27)):
Полученный таким образом интеграл
1 Г|„0 |2 ^ d3w ton (Ч\
5" I §w I 77Г\ (оУ.Ы)
вычислим при f@) -*¦ 0, используя соотношение
Ню -1 = Р j^-tt - Ш (I - %>), C9.62)
где Р означает главное значение. Если подставить C9.61) с уче-
19*
292 ФУНКЦИИ ГРИНА [ГЛ. VI
том C9.62) в C9.59) и отделить действительную и мнимую части,
то получим следующий конечный результат:
d3w, C9.63)
у = - n -±-3 Г | ?°. |2 S (- ek + ek+w + <ow) d'w. C9.64)
(<2Я) J
Результаты C9.63) и C9.64) уже встречались нам ранее в рам-
ках теории возмущений. А именно, в рамках первого порядка тео-
рии возмущений мы нашли, что электрон при взаимодействии с ко-
лебаниями решетки (более точно в данном случае — благодаря
испусканию фононов) рассеивается из начального состояния к с
вероятностью перехода в единицу времени, которая как раз да-
ется выражением C9.64). Следует учесть, что здесь рассматрива-
ется особый случай, когда нет термически возбужденных фоно-
пов. Выражение C9.63) также встречалось нам уже в § 35, где
вычислялась собственная энергия ноляронов. Настоящий пример
отчетливо демонстрирует большие преимущества применения
функций Грииа. Мы можем фактически, как мы уже видели в
предыдущем параграфе, одним махом найти как собственные
значения, так и время жизни возбужденного состояния. Читате-
лю, желающему глубже проникнуть в рассмотрение этой пробле-
мы, рекомендуются нижеследующие задания.
Задания к §39
1. Вычислить C8.10) для свободных частиц, т. е. при гр = г|50,
т|з+ = \\р0 , использовав, однако, в качестве Ф n-частичное состоя-
ние. Остается ли при этом верным равенство G(x2, t2, xi, fi) =
= 0 при t2< ti?
2. Показать, что by, ШФо — 0 (Фо — вакуумное состояние для
электронов и фопонов).
Указание. Положить bw (t) = el'/n'H(&w e-uihwt п разложить
экспоненциальные функции справа в степенной ряд.
Подсказка: Я"Ф0 = 0. Почему?
Показать также, что<Ф0 | &«• @ Фо> = 0.
3. Доказать C9.41).
Указание. Провести соответствующие преобразования, как
в C9.4) и последующих уравнениях.
4. Найти графически корни уравнения C9.59), определив
точки пересечения прямых /(е) = е с
/<«)=¦¦*-2
Для примера достаточно взять в сумме лишь несколько членов.
§ 39] ПРИМЕРЫ УРАВНЕНИЙ ДЛЯ ФУНКЦИЙ ГРИНА 293
5. Решить уравнения C9.50), C9.51) с помощью преобразова-
шш Фурье:
Gk,k (* - t') = -JL Г Ск (Я) e-toit-t') dQ, (A 39.1)
е-<°«-«') dQ. (A 39.2)
Указание. После подстановки (А39.1) и (А39.2) вместе с
представлением Фурье б-функции bit — t') в C9.50) и C9.51)
получаются уравнения
iCk (Q) (ek - Q) + 2 ?wDk.w (Q) = ^
(Q) = 0,
имеющие решение
1 1
Чтобы вычислить (А 39.1) и (А 39.2), следует воспользоваться тео-
ремой о вычетах и убедиться в том, что уравнение, определяю-
щее полюс QP: f(Qp) = 0, совпадает с уравнением C9.57).
Глава VII. СВЕРХПРОВОДИМОСТЬ
§ 40. Основные экспериментальные факты, касающиеся
сверхпроводимости
Прежде чем изложить микроскопическую теорию сверхпрово-
димости, зададимся вопросом, чего вообще следует ожидать от
теории такого рода. Для этого напомним кратко основные экспе-
риментальные факты.
1. При определенной критической температуре Тс некоторые
вещества переходят из нормального в сверхпроводящее состояние.
2. В сверхпроводящем состоянии электрическая проводимость
становится бесконечной.
3. Эффект Мейсснера — Оксенфелъда: независимо от преды-
стории, магнитная индукция в сверхпроводнике равна нулю (на-
пример, сначала можно включить магнитное поле, которое про-
никает в металл с обычной-прово-
димостью, а затем, при охлажде-
нии металла ниже температуры
перехода, вытесняется из него, или
сначала можно охладить, а затем
наложить магнитное поле, кото-
рое уже не может проникнуть в
металл (рис. 58)). Отсюда следу-
ет, что сверхпроводящее состоя-
ние в заданном внешнем ноле
является единственным стабиль-
ным состоянием, к которому при-
менимы законы термодинамики.
Согласно эффекту Мейсснера —
Рис. 58. Эффект Мейсснера — Ок- Оксенфельда, сверхпроводник ве-
~ дет себя как совершенный диа-
магнетик с равной нулю воспри-
Маеншлнал индукция Масниггмая индукция
Т>Т,:
сенфельда. Поведение поля в ци-
линдрическом сверхпроводнике
при Т <ТсжТ > Тс.
имчивостью').
Как для макроскопической, так и для микроскопической тео-
рии важно, что совершенный диамагнетизм и бесконечная про-
водимость являются независимыми свойствами сверхпроводника.
') Если говорить точно, то диамагнетизм не вполне совершенный, так
как магнитное поле проникает на глубину 10~е — Ю~5 см.
§ 40] ОСНОВНЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ 295
4. Переход «нормальный проводник — сверхпроводник» (не
говоря об одномерных сверхпроводниках) является фазовым пе-
реходом второго рода: удельная теплоемкость при Т = ТС испы-
тывает скачок.
5. Удельная теплоемкость электронов при низких температу-
рах меняется как ехр (— AEjkBT).
Теперь кратко обсудим уравнения, с помощью которых можно
огшсать бесконечную проводимость и совершенный диамагнетизм
сверхпроводника. Не вдаваясь в подробности, рассмотрим урав-
нения Максвелла без внешних зарядов. Плотность тока разложим
на части, одна из которых jn, вызывается нормальными электро-
нами, а другая j,, происходит от сверхпроводящих электронов.
Таким образом, мы полагаем
I j = b + j.. D0.1)
Далее пренебрежем временными изменениями электрического
тока смещения
Ь = 0 D0.2)
и положим
(х = 1. D0.3)
Пренебрегая }„ по сравнению с j,, запишем (при принятых выше
условиях) уравнения Максвелла в виде
divE = 0, D0.4)
divB = 0, D0.5)
rolE :¦= —-i-B, D0.G)
rotB-^j,. D0.7)
8th уравнения Максвелла братья Лондоны дополнили следующи-
ми материальными уравнениями:
1. Уравнение для ускорения:
Е. D0.8)
Это уравнение для ускорения описывает нарастание тока во вре-
мени при наложении поля, т. е. опдсывает бесконечную проводи-
мость. Если бы все электроны были подобны свободным части-
цам, для которых сопротивление отсутствует, то Л давалось бы
выражением
Л = -2L, D0.9)
пе
где m — масса электрона, аи — плотность электронов.
2. Второе уравнение Лондонов гласит:
js = — В/с. D0.10)
296 СВЕРХПРОВОДИМОСТЬ (ГЛ. VII
Как можно показать, постоянная Л в D0.10) должна совпа-
дать, чтобы не было противоречия, с постоянной в D0.8). Убе-
димся кратко в том, что уравнение D0.10) действительно пред-
ставляет диамагнитные свойства сверхпроводника.
Для этого рассмотрим сверхпроводник, имеющий неограниченную про-
тяженность. Координату, направленную вглубь сверхпроводника, обозна-
чим через z. Из уравнения D0.7) заключаем, как обычно в электродина-
мике, что Вг постоянна.
Исходя из специально выбранной конфигурации сверхпроводника, мож-
но принять, что В имеет только z-компоненту, которая может зависеть еще
и от z. Тем самым условие D0.5) оказывается выполненным. Исключая
из уравнений D0.7) и D0.10) плотность тока j, получаем
V В = — rot rot В =—5 В, D0.11)
или, если выписать только отличные от нуля компоненты,
~^ = Л?5ж' D0.12)
Решение DO.il2) имеет вид
-*1К D0.13)
Это решение показывает, что поле внутри сверхпроводника действительно
затухает экспоненциально, причем глубина проникновения К, как следует
из D0.12), дается следующим выражением:
Я= 1—1/2. D0.14)
Подставляя численное значение для Л, находим величину %:
Я = Ю-6 см. D0.15)
Таким образом, наше рассмотрение показало, что уравнение D0.10) дей-
ствительно описывает диамагнетизм сверхпроводника.
Следует заметить, что X зависит от температуры Т. При Т = Тс получа-
ем % = оо, а при Т = 0 получаем % = Xmin. Поскольку глубина проникнове-
ния К через Л зависит от концентрации сверхпроводящих электронов (см.
D0.9)), то это является прямым указанием на то, что число сверхпрово-
дящих электронов само является функцией температуры.
Покажем теперь одно следствие из уравнений Лондонов, ко-
торое может быть прямо использовано в микроскопической тео-
рии сверхпроводимости. Для этого рассмотрим поперечное поле,
введем, как обычно, векторный потенциал с помощью уравнений
В = rot A, D0.16)
E = --f§ D0.17)
и дополнительное условие поперечности векторного потенциала
divA = 0, D0.18)
§ 40] ч ОСНОВНЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ 297
Подставляя эти выражения в материальные уравнения D0.8) и
D0.10), получим
je = —-7-rot A D0.19)
Эти уравнения можно сразу проинтегрировать. Если принять, что
нормальная составляющая А на границе замкнутого сверхпровод-
ника исчезает, то интегрирование дает следующий результат:
Aj» = j-A. D0.21)
Обоснование этой связи между сверхпроводящим током js и век-
торным потенциалом А может, если не вдаваться в тонкости,
рассматриваться в качестве прямой цепи микроскопической тео-
рии. Для того чтобы установить смысл этого соотношения, рас-
смотрим выражение для плотности тока, которое, как известно
из квантовой механики, имеет следующий вид:
D0.22)
В квантовополевой формулировке г|э и г|з*, естественно, следует
заменить операторами поля. Среднее значение плотности тока в
формализме квантовой теории поля дается тогда выражением
j(x7=«D|j(x)|<D>. - D0.23)
Если нет магнитного поля и тем самым нет векторного потенци-
ала А, то в основном состоянии, естественно, плотность тока ис-
чезает, т. е. стоящее в фигурных скобках выражение дает тогда
нуль. Если бы и при включенном магнитном ноле это выражение,
как и прежде, было равно нулю, то плотность тока имела бы
требуемый выражением D0.21) вид. То есть тогда плотность тока
j была бы пропорциональна векторному потенциалу, умножен-
ному на плотность гр+гр электронов. Поэтому вначале могло бы
показаться, что каждый проводник мог бы стать сверхпроводни-
ком. Однако это ни в коем случае не так. Как показывает более
обстоятельное решение, при введении векторного потенциала
электронные волновые функции также испытывают его влияние.
При этом вклад от членов в фигурных скобках полностью ком-
пенсируется последним выражением в D0.22), которое пропор-
ционально А.
Как следовало бы сформулировать микроскопическую теорию,
которая гарантировала бы, что стоящее в фигурных скобках вы-
298 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
ражение, кратко обозначенное через ji, и в присутствии магнит-
ного поля остается равным нулю, так что лишь второе выраже-
ние в D0.22), кратко обозначенное через ]"г,
•ь = -&о А <ф 14>+ W ^ <х> I ф> = - Ш Аге' <40-24)
/дает ненулевой вклад? Это было бы возможно в том случае, если
бы волновые функции обладали своего рода жесткостью, остава-
ясь неизменными и при наложении магнитного поля. Как раз
такая ситуация имеет место в диамагнитном атоме. Жесткость
волновых функций была бы гарантирована, если бы возбужден-
ное состояние сверхпроводника было отделено от основного со-
стояния энергетической щелью. Эта идея, высказанная Лондона-
ми, оказалась чрезвычайно плодотворной, и основная цель разви-
тия микроскопической теории сверхпроводимости состояла в том,
чтобы показать существование такой энергетической щели. Такая
энергетическая щель, если бы она к тому же зависела от темпе-
ратуры, хорошо объясняла бы экспериментальное поведение
удельной теплоемкости. Прежде чем мы поближе подойдем к
Еопросу об энергетической щели, сделаем еще два замечания.
1. При слабых и медленно меняющихся полях предполагает-
ся, что основное состояние «адиабатически» меняется с полем.
Однако никаких заметных возбуждений над основным состояни-
ем нет.
2. Далее добавим, что наряду с глубиной проникновения Я в
теорию сверхпроводимости следует ввести (хотя бы феноменоло-
гически) еще вторую длину, а именно длину когерентности ?.
Как нам теперь известно, и мы увидим это в следующих пара-
графах, эта длина когерентности определяется пространственной
протяженностью парных волновых функций сверхпроводника.
Если
|>Ь, D0.25)
то говорят о мягком сверхпроводнике, а если
% > 1, D0.26)
то говорят о жестком сверхпроводнике. Здесь мы закончим наше
феноменологическое рассмотрение сверхпроводимости и перейдем
к вопросу о том, чего же следует требовать от микроскопической
теории. При этом важнейшая задача состоит в том, чтобы вскрыть,
какие взаимодействия между электронами являются решающими
для обоснования жесткости основного состояния и лежащей за
ним энергетической щели. Несмотря на большое число попыток,
прошло много времени, прежде чем Фрёлих нашел правильный
результат. Исходя из соображений, являющихся типичными для
представлений квантовополевой теории, Фрёлих установил, что
между электронами через посредство колебаний решетки может
§ 41] ФРЁЛИХОВСКОЕ ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ 299
возникнуть прямое взаимодействие. Это взаимодействие тем силь-
нее, чем сильнее взаимодействие электронов с колебаниями решет-
ки. С другой стороны, сила этого последнего взаимодействия опреде-
ляет величину электрического сопротивления. Чем более выраже-
но это взаимодействие, тем выше электрическое сопротивление
при прочих равных условиях. На основании этих рассуждений
следует ожидать «парадоксальный» результат, что вещества яв-
ляются тем лучшими сверхпроводниками, чем выше их сопротив-
ление в нормальном состоянии. Это одновременно гениальное и
смелое предположение нашло в проведенных сразу же экспери-
ментах по изотопическому эффекту блестящее подтверждение.
Амплитуда колебаний решетки и тем самым эффективное элек-
трон-решеточпое взаимодействие зависят от массы иона М, и чем
меньше масса, тем больше взаимодействие. Теория Фрёлиха
предсказала, что температура перехода Тс должна быть пропор-
циональна М~'и, как это действительно было обнаружено. Однако
абсолютная величина Гс оказалась слишком большой. Это было
связано с том, что Фрёлих вычислял собственную энергию элек-
тронов. Теперь мы знаем, что Те в значительной степени опреде-
ляется взаимодействием между электронами. Далее мы двинемся
вперед следующим образом. Из электрон-решеточного взаимодей-
ствия мы выведем эффективное фрёлиховское взаимодействие
между электронами и обсудим методы решения полученного та-
ким образом уравнения Шредингера.
§ 41. Теория сверхпроводимости: введение фрелиховского
взаимодействия между электронами
Исходным пунктом исследований в этом разделе является
оператор Гамильтона из § 29, который описывает взаимодействие
между электронами и колебаниями решетки. Как мы увидим
позже, для теории сверхпроводимости существенно наличие у
электрона спина. Поэтому к волновому числу к добавим еще
один индекс а, который указывает, находится ли электрон в од-
ном спиновом состоянии (спин вверх) или в другом спиновом со-
стоянии (спин вниз). Таким образом, это спиновое квантовое
число а может иметь два значения: «спин вверх» (стрелка вверх)
и «спин вниз» (стрелка вниз). Тогда отдельные слагаемые опера-
тора Гамильтона
D1.1)
можно представить следующим образом:
Но = S Uekak,aak,a + 21i(owb+bw,, D1.2)
к,a w
Нва = П S (?wMk+w,ffak,<j + gwbw«iMak+w,<7)- D1-3)
k.w.a
300 СВЕРХтЮВОДИВЮСТЬ [ГЛ. VII
При этом принимается, как обычно, что взаимодействие между
электронами и колебаниями решетки не оказывает влияния на
спин. Поэтому как у операторов рождения, так н у операторов
уничтожения электронов в D1.3) стоит один и тот же индекс а.
Вначале мы будем исследовать эту задачу в представлении
Гейзенберга, которое рассматривалось в § 16, и обратим особое
внимание на уравнения A6.34), A6.35). Как мы увидим, пред-
ставление Гейзенберга особенно наглядно и позволяет, по край-
ней мере интуитивно, лучше понять сделанные здесь приближе-
ния. Как можно увидеть, вернувшись назад к уравнениям
A6.34) и A6.35), в правых частях этих уравнений стоят также
частоты oow. Чтобы избавиться от них, предпримем преобразова-
ние фоноиных и электронных операторов рождения и уничтоже-
ния, предлагаемое представлением взаимодействия
bty - Ь+еи<"»\ D1-4)
bw = Ь>-"Ч D1.5)
ак,а = ак,ое-1^. D1.7)
Тогда уравнение для фононного оператора рождения принимает
вид
it- = * 2 ?w^8k+«'-Et-M^ a?+w,a вк,в. D1.8)
k,a
Если бы электронные операторы в D1.8) были классическими
величинами, то D1.8) означало бы, что фононная амплитуда 6W
изменяется во времени благодаря движению электронов. Это
лишь отражает то простое обстоятельство, что пролетающий сквозь
решетку электрон поляризует ее, смещая ноны решетки из их
положений равновесия. Со своей стороны, смещения ионов ока-
зывают обратное действие на электрон. Чтобы лучше понять это
обратное воздействие, рассмотрим временное изменение вначале
произвольного оператора А, построенного из электронных опера-
торов. Временные изменения мы получим, как обычно, применяя
уравнение
Q=-jU[#, Q]. D1.9)
Теперь примем во внимание, что мы пользуемся электронными
операторами в представлении взаимодействия, т. е. если приме-
нить преобразования D1.6—41.7), то для оператора А получим
§ 411 ФРЁЛЙХОВСКОЕ ВЗАИМОДЕЙСТВИЕ МЕЖДУ ЭЛЕКТРОНАМИ 301
следующее уравнение:
Я --= i 2 few [а?+*,<ГаКа, A] b^+Wk-w)' +
k,w,a
+ gl^ Raak+W,a, A] e-«<e*+w-«k-«w)'}. D1.10)
Поскольку by. и Ь^. коммутируют с электронными операторами
(в тот же момент времени), то порядок следования множителей
bw и Ьп в D1.10) безразличен. Имея в виду последующие при-
ближения, при которых эта перестановочность не гарантирована,
мы поставили все же в D1.10) оператор bw впереди, чтобы со-
хранить эрмитову форму выражения.
В то время как уравнение D1.8) описывает смещение ионов
под влиянием движения электронов, уравнение D1.10), повторим
это еще раз, описывает действие рюнов на электрон. Имеет смысл
попытаться исключить из этих двух уравнений координаты ко-
лебаний решетки, чтобы получить действие электрона на другие
электроны и на самого себя. Для проведения этой программы
проинтегрируем уравнение D1.8) по времени, в результате чего
сразу получим
J e*0V
_ X
k',a'
X (а?+*.о-вк'.а')т<*Т+Ь+(-оо). D1.11)
Это пока еще совершенно точное выражение. Индекс у выраже-
ния в скобках иод интегралом указывает на то, что стоящие здесь
операторы берутся в момент времени т. Последний член в D1.11)
относится только лишь к колебаниям решетки.
Для последующего будет полезно постоянно считать, что опе-
раторы представлены классическими числовыми функциями. На
первый взгляд это может показаться несколько странным, однако
с помощью методов, о которых мы не будем здесь говорить, во
многих случаях операторным уравнениям можно поставить в
соответствие классические уравнения. Во всяком случае, мы хо-
тим отметить, что это действительно возможно — обращаться с
операторами при исследовании их временного поведения как с
классическими величинами.
Теперь сделаем предположение, что взаимодействие между
электронами и колебаниями решетки не слишком сильное. Тогда
можно принять, что основная временная зависимость операторов
а* и а представляется стоящими в D1.6) и D1.7) экспоненциаль-
ными функциями, а операторы а и а+ меняются медленно. Это
означает, что операторное выражение в скобках под интегралом
в D1.11) берется в момент времени t и выносится из-под знака
интеграла. Тогда интеграл сразу вычисляется и мы, если, как
302 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
обычно, пренебречь нижней границей интегрирования (что можно
сделать с помощью «адиабатического множителя»), получаем
b?(t) fa 2i "«¦ Ka^'+w,o'ak',a')t, w_ek>4 ^ + ^w (— <*>)¦
(/il.l2)
Нам удалось выразить в явном виде амплитуды колебаний решет-
ки через электронные величины. Соответствующее выражение,
конечно, получается и для оператора bw {i). Если подставить
D1.12) и только что упомянутое выражение для bw{l) в D1.10),
то получим
(,i(ek+w-Ek-ek'+w+ek')i
*
о,о' ^ ^ ^
8k e ml«k-Mv,a«k,a)
X К"',в'ЯкЧж,„.,Л]. D1.13)
В правой части этого уравнения благодаря присутствию экспо-
ненциальных функций содержатся осциллирующие со временем
члены. Если провести усреднение по небольшому временному
интервалу, то заметный вклад будут давать толы;о такие члены,
и которых экспоненциальные функции близки к единице, т. е.
члены следующего вида:
ek+w — «k « ek/+w — ek/. D1.13а)
На этом же основании можно положить, что оба знаменателя в
D1.13) равны друг другу, вследствие чего общее выражение мож-
но вынести за скобки перед операторами. Небольшие промежу-
точные вычисления показывают, что для суммы оставшихся опе-
раторов имеет место соотношение
Lak+w,ciak,0' Щ ak',a' ak.'+w,a' + ak+w,aak,er Lak',a'ak'+w,a'> Al —
=¦-- [a?+Wtaak,aa?fi(,,ab,+W3a,,A]. D1.14)
Используя D1.14), можно упростить выражение D1.13):
I2
= i У.
r
a,a'
x[ak+w,a«k,cr«k',ei'ak'+w,eT'. 2]. D1.15)
При этом в вычислениях были опущены стоящие в начале выра-
§ 4i] фрёлйховское взаимодействие между электронами зоз
жения D1.13) члены, которые содержат фононные операторы
])ождения и уничтожения в момент времени t = — °°. Можно
действительно показать, что эти члены ведут к процессам рдссе-
яиия и не дают вклада в прямое взаимодействие между электро-
нами. Теперь наша цель заключается в том, чтобы привести вы-
ражение D1.15) к такому виду, в каком оно было первоначально
найдено Фрёлпхом для электрон-электронного взаимодействия.
Для этого сначала поменяем в коммутаторе D1.15) порядок сле-
дования электронных операторов так, чтобы слева стояли опера-
торы рождения, а справа — операторы уничтожения. Это приво-
дит, при использовании обычных перестановочных соотношений,
к выражению
2 l*wl'p. _"' R+w,^+w,a,3] D1.16)
k.k'.w
a,о'
k,er,w k+w k w
(поскольку электронные операторы теперь обозначаются не толь-
ко индексом к, но и, сверх того, индексом о, перестановочные
соотношения, которые у нас были ранее, следует обобщить так,
чтобы справа вместо бкк' теперь стояло произведение символов
Кронекера ЬкЪ'&вв'-
Видно, что вторая сумма в D1.16) содержит только два элек-
тронных оператора, а не четыре. Несколько ниже мы увидим
совершенно отчетливо, что эта вторая сумма описывает сдвиг
энергии отдельного электрона. Теперь преобразуем первую сум-
му, для чего рассмотрим выражение
Vfw.o аК',ог'
D1.17)
В первой сумме в D1.16) и в числителе D1.17) поменяем местами
к, о с к', а' (но только в числителе, а не в знаменателе, посколь-
ку соотношение D1.13а) считается справедливым). Тогда вместо
D1.17) получим выражение
V+w,tr' gk,a gk',a' ak+w,g D1.18)
8k'+w~8k' ~ ww
Теперь предпримем следующие замены:
k^-k — w
D1.19)
к' - w
— w
p' ak,g
304 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
с помощью которых выражение D1.18) переходит в выражение
D1.19). Поскольку эти замены относятся ко всей сумме в D1.16),
то значение этой суммы, естественно, остается неизменным. Да-
лее примем, что для колебаний решетки, как обычно, выполняет-
ся соотношение
co_w-cow, D1.20)
согласно которому частота зависит только от абсолютной величи-
ны фононного волнового вектора. Равным образом примем, что
то же самое справедливо и для констант взаимодействия
l?-wl2 = l?wl2. D1.21)
Тем самым выражение D1.19) после изменения порядка следова-
ния электронных операторов переходит в выражение
ak+w,aak',a'"k,aak'+Wla^_ D1 29^
Выражение D1.22), если выполнить в нем согласно D1.16) сум-
мирование, совпадает с соответствующей суммой членов D1.17).
Теперь приведем выражение для взаимодействия D1.17), как это
тотчас будет видно, к симметричному виду. Для этого возьмем
полусумму выражений D1.17), D1.22) и подставим ее затем в
D1.16). Это приводит к следующему результату:
B \g*\Чre
k,k',w (8k'+w~8k') ~ шуг
G.O'
X [ak+w,oak',o' ak'+\y,a'
В последней сумме D1.23) k + w заменено на к. Уравнение
D1.23) имеет фундаментальное значение. А именно, оно показы-
вает, что временная производная электронного оператора А по-
рождается перестановкой того же самого оператора с другим
оператором. В последующем изложении можно было бы исходить
из уравнения D1.23) и построить средние значения. Этот путь
приводит, как мы уже видели в §§ 38, 39, непосредственно к ме-
тоду функций Грина. Однако мы воспользуемся несколько более
общепринятым методом, а именно, будем держать курс на эффек-
тивное уравнение Шредингера. Для этого в качестве первого ша-
га откажемся от представления взаимодействия, т. е. согласно
формулам D1.6) и D1.7) перейдем от операторов а к операторам а.
§ 42] ОСНОВНОЕ СОСТОЯНИЕ СВЕРХПРОВОДНИКА 305
Тогда D1.23) можно представить в следующем общем виде:
i = i№^l + i№4 D1.24)
Сравнение D1.24) с D1.23) показывает, что эффективное взаимо-
действие дается оператором
ш
ггэфф _ f у , ,2 "V v
k.k'-w ('k' + w i;k'j ' w\v
'" I D1.25)
к,
'"'к
Вторая сумма в D1.25) имеет точно тот же вид, что п собствен-
ная энергия электронов в решетке. Следовательно, она ведет к сме-
щению энергии, которое можно сразу учесть с помощью метода
эффективной массы в еполн, к • В последующем, таким образом, бу-
дем считать, что этот эффект уже учтен в энергии электрона. Пер-
вая сумма в D1.25) содержит основной результат. В этой сумме
присутствуют четыре электронных оператора, которые описыва-
ют уничтожение двух электронов и последующее рождение двух
других электронов. Если кратко обозначить стоящий в этом вы-
ражении числовой множитель через — A/2) fk,k',w> то электрон-
электронное взаимодействие принимает окончательно следующий
вид:
Я"---.л-эл ~ — ~2 2d ^k,k'.w«k+w,a^,a'ak4Ty .j'tfk,<7> D1.26)
k,k',w
Co'
где v t k' w имеет следующий явный вид:
Тем самым мы выполнили пашу задачу. Нам удалось ввести
мгновенное взаимодействие между электронами, исходя из пх
индивидуального взаимодействия с колебаниями решетки.
§ 42. Основное состояние сверхпроводника по теории
Бардина — Купера — Шриффера (БКШ)
Взаимодействие электронов с колебаниями решетки приводит,
как было показано в §§ 36 и 41, к прямому взаимодействию меж-
ду электронами. Соответствующий оператор взаимодействия был
введен в явном виде в § 41. Если добавить теперь к нему опера-
20 х, Хакея
306 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
тор энергии свободных электронов, то получится полный оператор
Гамильтона
Н =
vk.k'.wak+w,oek',ff'ak'+w,a'ak,a- D2.1)
" k,k',w
a,o'
To, что взаимодействие между двумя электронами через посред-
ство решетки, вообще говоря, имеет характер притяжения, было
показано еще в § 36. Однако непосредственно из оператора Га-
мильтона D2.1) этого не видно. Как показал Купер, выражение
D2.1) приводит к притяжению между двумя электронами с анти-
параллелъными спинами в рамках следующей модели: все элек-
троны металла «искусственно» удерживают внутри сферы
Ферми и решают соответствующее D2.1) уравнение Шредингера
для двух лишних электронов, находящихся вне сферы Ферми.
В реальном случае, естественно, следует учесть то, что все элек-
троны из-за взаимодействия примут новую конфигурацию. Самое
очевидное предположение состоит в том, что электроны будут
образовывать пары. Согласно этому предположению кажется ра-
зумным следующий метод конструирования волновых функций
основного сверхпроводящего состояния: исходя из вакуумного
состояния, следует построить такие электронные состояния, в ко-
торых спарены электроны с антипараллельными спинами и про-
тивоположными импульсами. Если есть ./V электронов, то образу-
ются N/2 пар, так что соответствующая волновая функция Дается
выражением
2Ф0. D2.2)
Стоящие в нем коэффициенты разложения ct должны быть еще
определены, причем так, чтобы соответствующее D2.1) уравнение
Шредингера удовлетворялось «оптимально». Волновая функция
D2.2) соответствует фиксированному числу электронов, что пона-
чалу кажется совершенно само собой разумеющимся. Однако для
практических вычислений существенно более удобным оказалось
выражение с переменным числом электронов. Формально такую
волновую функцию можно получить, просуммировав выражения
типа D2.2) цо переменным показателям степени пг (вместо фик-
сированного N12):
Ф = 2 «т /2 <Wt «-k * ГФ„. D2.3)
\к 1
Коэффициенты ат пока что произвольны. Потребуем, чтобы эти
коэффициенты удовлетворяли следующим условиям:
§ 42] ОСНОВНОЕ СОСТОЯНИЕ СВЕРХПРОВОДНИКА 307
1. Они должны быть определены так, чтобы снова наиболь-
ший вклад в выражение D2.3) давали в конце концов только те
члены, у которых т весьма близко к среднему числу электронов
т = N12.
2. Кроме того, сумма по т в D2.3) по возможности должна
быть пред ставима в явном виде.
Оба требования можно выполнить с помощью подстановки
ат = 1/т\. Тогда D2.3) переходит в
Фо. D2.4)
7П=0
Получившаяся теперь сумма есть не что иное, как разложение
в ряд экспоненты, к чему мы уже привыкли. Члены разложения
являются операторами. Тогда D2.4) можно привести к виду
>о> D2.5)
где введен соответствующий нормировочный множитель -Л°.
В теории сверхпроводимости обычно применяется не выраже-
ние вида D2.5), а приведенные ниже эквивалентные ему выра-
жения. Поскольку операторы (йк~тя-к|) для различных к ком-
мутируют между собой, то экспоненциальную функцию в D2.5)
можно представить в виде произведения экспонент:
ф = jf Л /kQk ra-k i ф D2.6)
k
Многократное действие операторов рождения на одно и то же
состояние в ферми-статистике дает нуль. Поэтому разложение
экспоненциальной функции обрывается на втором члене, так что
D2.6) переходит в выражение
к
Чтобы не выходить за рамки общепринятых обозначений, разло-
жим нормировочный множитель в произведение парциальных
нормировочных множителей и внесем каждый из них под знак
произведения по к. Тогда окончательно получим
D2.8)
где ск = Х D2.9)
Разложение Ф в произведение по Ф* станет более ясным, если
разложить в произведение по Фо,к вакуумное состояние Фо:
20*
308 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
где ЯкгФо,к= а-к4Фо,к=О, и положить Фк = («к Jr vka?т а\± )Ф0,к-
Условие нормировки имеет вид (см. задание 2)
4 + 4 = 1, D2.10)
где ради простоты в последующем будет принято, что ик л v^
являются действительными константами. Как мы увидим, это
требование может быть выполнено всегда. Вероятность того, что
состояние с электроном со спином вверх и волновым вектором к
занято, дается выражением
^ D2.11)
(см. задание 1). Вероятность того, что электронные состояния к
si к' со спином вверх заняты одновременно, представляется вы-
ражением
Теперь нам следует кратко заняться воиросо.м, как можно бы-
ло бы обойти трудности, возникающие из-за того, что волновой
функции Ф не соответствует фиксированное число электронов.
Для этого введем оператор числа частиц
Л'оп = 2akaaker D2.13)
k,o '
и потребуем, чтобы среднее значение D2.13) относительно вол-
новой функции Ф совпадало с наперед заданным средним числом
электронов. Это дополнительное условие с помощью множителя
Лагранжа ц можно ввести в уравнение Шредингера, заменив
оператор Гамильтона // на оператор
H' = H-ixNoa. D2.14)
После того как установлена общая форма решения и известен
оператор Гамильтона, дальнейшая процедура в принципе ясна:
сначала следует образовать среднее значение оператора D2.14),
а затем таким образом определить коэффициенты ск и Ик и v^
в D2.5) и D2.8), чтобы это среднее значение было минимально.
При этом следует принять во внимание дополнительное условие,
что <ф|Ж0П|Ф> =iV, где N — наперед заданное число электронов.
Обсудим подробно вычисление подобных средних значений.
Для средних значений от 2 С#к — М<) «к^к „ с учетом D2.11)
к.ег
находим
D2.15)
к
где положено Е^ = Et — у,.
§ 42] ОСНОВНОЕ СОСТОЯНИЕ СВЕРХПРОВОДНИКА 309
Среднее значение энергии взаимодействия дается выражением
т'вк'+».о'вк,оФЧ. D2.16)
2
k.k'.w
При вычислении D2.16) следует исследовать различные случаи.
1. w = 0. Соответствующий член суммы D2.16) теперь равен
,оФ>- D2.17)
Члены такого рода уже встречались нам ранее в рамках метода
Хартри — Фока в § 20 и представляют собственную энергию.
2. Следующим рассмотрим член вида
а'Як,<,Ф>, D2.18)
который можно привести к виду
S^ D2.19)
Ниже увидим более подробно, как вычисляются выражения по-
добного типа, поэтому мы сразу привели конечный результат
D2.19). Этот член можно назвать собственной обменной энергией.
Действительно, видно, что электрон со спином о переходит из
состояния к в состояние к + w, в то время как другой электрон
со спином а' рассеивается из состояния k + w в состояние к.
Очевидно, в этом случае речь идет об электронном обмене.
И этот член также можно считать учтенным в рамках метода
самосогласованного поля.
3. Главный интерес для нас представляет член вида
D2.20)
Мы подробно покажем, как вычисляется это среднее значение.
Для этого разложим Ф в произведение по Фк" согласно D2.8) и
соберем вместе те члены к", которые не затрагиваются операто-
рами я+, а с индексами к, к'. Вынося соответствующее среднее
значение из D2.20) и разлагая его в произведение средних зна-
чений, получаем
П
к^к
(см. задание 2). Тем самым от выражения D2.20) остается ис-
следовать лишь следующее среднее:
<Ф | йк'|а_кч«-к1%|Ф> '¦=
) ) X
X at'fuX'i! а_к|йкт (цк + vka^at]s.i) X.
X (i%« + iv«kV-k'i) ФокФок«>- D2.22)
310 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
Вертикальные штриховые линии не имеют никакого математи-
ческого смысла; они стоят лишь для памяти, как разделитель-
ные линии при последующих вычислениях.
Вначале подробно вычислим выражение (при Фо = ФокФок')
я-к^кт («к + vka^atki) {ик, + *Vak'ta-k',i) фо- D2.23)
Тогда очевидным образом получаем соотношения
a_kiaktukuk'<&0 = 0, D2.24)
о = 0, к =7^= к', D2.25)
k>taIk4QH, D2.26)
D2.27)
Следует порекомендовать читателю самому еще раз проследить
отдельные этапы вычисления этих результатов, используя пере-
становочные соотношения и свойства вакуумного состояния Фо.
С учетом результатов D2.24—42.27) выражение D2.23) пере-
ходит в выражение
ик>икФ0 + fk^k'^k't^k'^o- D2.28)
Расчет, который сейчас был проведен слева направо по отноше-
нию к штриховой линии в D2.22), теперь можно соответству-
ющим образом провести справа налево (см. A3.35), A3.36)), по-
меняв местами к и к'. Тогда сразу найдем, что выражение
<Ф0 ] (ик, + vk>a_k4ak,t) ("к + vka-kiakr) a?ta-k'j. D2.29)
можно представить в виде
<Ф01 (Mkiv + Uk^va-kiflkt)- D2.30)
Если теперь подставить оба выражения D2.28) и D2.30) в вы-
ражение D2.22), то мы, наконец, получим
D2.20) = <Ф01 (мк + vka_klakt) vK-k-,k'-kvk>vk X
X (uk< + Ук'Яь'|а-кч) фо> = Ук,-к',к'-кИкУкИк'Ук'- D2.31)
Эти члены не появляются в приближении Хартри — Фока и яв-
ляются совершенно новыми. Они имеют, естественно, решающее
значение для всей теории сверхпроводимости.
Теперь вернемся к нашей первоначальной цели. Она состоит
в том, чтобы явно вычислить среднее значение полной энергии.
С помощью только что полученных результатов D2.15), D2.31)
находим
= 22Я*»1- 2 Fk,k,uki№zv, D2.32)
к к,к'
§ 42] ОСНОВНОЕ СОСТОЯНИЕ СВЕРХПРОВОДНИКА 311
где использовано сокращение
D2.33)
Теперь найдем минимум среднего значения. Для этого продиф-
ференцируем выражение D2.32) по Ук- При этом следует про-
следить, чтобы выполнялось дополнительное условие «к + ук ~
= 1, в результате которого, естественно, ггк становится функ-
цией tfik- При этом дополнительном условии дифференцирование
D2.32) по Vk выполняется немедленно и приводит к результату
2 Vwiirw (wk - г>1/щ)\ = 0. D2.34)
С установлением уравнения D2.32) или D2.34) программа кван-
товополевого рассмотрения оказывается завершенной. Интересно
лишь посмотреть, какие собственные значения энергии основно-
го состояния дает это решение и как выглядит распределение
электронов по состояниям к. Поэтому обратимся к решению сис-
темы уравнений D2.34). Для этого введем сокращенное обо-
значение
Ak =- zLj Vk k'Mk'iv, D2.35)
к'
с помощью которого D2.34) переходит в
v^k — ^k/ ^k ~т~ ^-^k^k^k == ^* D«iOb)
Уравнение D2.36) можно формально решить относительно u/v,
что дает
^k_ = gk ± (V + А1У \ D2.37)
vk Дк
Далее получаем соотношение
ukvk = ± А к/2Ек,; D2.38)
где введено сокращенное обозначение
Ек = (Ек + At)l/2. D2.39)
Можно показать (чего мы не будем здесь делать), что из выра-
жения для энергии следует условие и^и^>0, которое и решает
выбор до сих пор не определенного знака в выражении D2.38).
Отсюда получаем формулы
Л А
D2.40)
D2.41)
2Ек «к Ек + Ек
312 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
Теперь следует учесть, что А к также зависит от и, v. Поэтому,
если подставить результат D2.40) в D2.35), то и, v можно ис-
ключить и тогда получается уравнение для величин At:
1 у Fk,k'V
2
D2.42)
3
к' лк'
Это уравнение — относительно сложное, поскольку At входит так-
же и в Ек- Естественно, можно попытаться решить уравнение
D2.42) с помощью вычислительной машины. Однако определен-
ное представление о смысле этого уравнения можно получить,
приняв следующую модель для Vkx-:
kk (О в остальных случаях.
Эта подстановка следует из определения Fkk' (см. D2.33))
и ^k,k\w (см. D1.27); обратить внимание на знак знаменателя
в этом выражении). Положим, далее, в основу этой модели сво-
его рода среднюю частоту колебаний решетки со. Тогда в рам-
ках этой модели сразу получаем
Ак -" 0 при ( 7?к | > Й.0),
Ак = А при \Е'ъ\ < йсо.
При помощи подстановки D2.43) уравнение D2.42) принимает
вид
^оЕтТТРгЬ™- D2.44)
к
'2
Суммирование по к при этом, в силу условия D2.43), оказывает-
ся ограниченным. Как можно показать, в уравнении Е^ = Е^ — [о,
энергия [л — это энергия на поверхности Ферми, так что
суммирование в D2.44) следует распространить только на об-
ласть вблизи поверхности Ферми—Йсо <?' < Йсо. Как обычно,
сумму заменим интегралом. Поскольку к и Еъ связаны между
собой, то интеграл по d?h можно выразить через пнтеграл
по dE'x
d4 = D(E')dE',
где D{E') — плотность состояний.
Далее положим
Bnf
§ >*2] ОСНОВНОЕ СОСТОЯНИЕ СВЕРХПРОВОДНИКА 313
причем V — объем кристалла. Тогда D2.44) переходит в
йш
D (Ег) йЕ' 2
1
Так как 1ш значительно меньше энергии Ферми, то следует
сделать замену D(E') « /КО) и вынести это число за знак интег-
рала. После этого интеграл, естественно, сразу вычисляется.
Тогда вместо D2.45) получаем соотношение
А = s^W
Поскольку в практических случаях ЖО)Уо<1, то окончательно
вместо D2.46) получается следующее приближенное выражение:
I A = 2Йте-!/Г)(о)Уо D2 471
Подведем итог проведенным выше рассуждениям: наша цель
состояла в вычислении коэффициентов uk, i\. Поскольку в под-
становки для этих коэффициентов входит только параметр A, jo
задача свелась к определению этого параметра, что и было сде-
лано в D2.46) и D2.47).
Теперь вычислим энергию основного состояния сверхпровод-
ника, подставив в D2.32) «к и Vk- Из этой энергии вычтем энер-
гию электронов без учета взаимодействия, т. е. энергию ферми-
моря, тогда для добавки энергии за счет взаимодействия полу-
чаем следующее выражение:
К\ 1 т, V А2
D2.48)
_k\J
•Еферми-море
Чтобы понять выбранное выражение для ^ферми-море, вспомним,
что Ек = Ек — [х представляет собой разность энергий относи-
тельно уровня Ферми: Ек > 0 для электронов вне сферы Ферми
и Ек < 0 для электронов внутри сферы Ферми. Очевидно, что
/' Е'
Е'ь ( 1 — т-^г I =0 при Е'к>0,
D2.49)
я;|1-р^т)=2Д; при El<0.
21 д. X, Хакея
314 СВЕРХПРОВОДИМОСТЬ ' [ГЛ. VII
Отсюда получаем
^ферми-море = 2 2 -^к> D2.50)
кЕ
где множитель 2 учитывает оба направления спина.
Сложим в D2.48) первый и последний члены, упростим вто-
рую пропорциональную Fo сумму с помощью соотношения
D2.44) и преобразуем сумму в интеграл
Па
Г \\Е'\- Jl-^-т -S—^\dE'-
-1}, D2.51)
который при Д < ft en упрощается и приводится к виду
D2.52)
Таким образом, общая энергия с учетом электрон-электрон-
ного взаимодействия действительно ниже энергии состояния без
взаимодействия.
Заданияк § 42
1. Доказать D2.11).
Указание. Разложить Ф согласно D2.8) и разложить
<Ф | ak<tak<t<P> в произведение средних значений по отдельным
значениям к.
2. Показать, что
<фк ] фк,> =.- 6кк. при Фк = (мк + i\o^atki) Фо и
§ 43. Возбужденные состояния сверхпроводника
В этом параграфе мы сделаем нечто весьма замечательное.
А именно, мы покажем, как, аная волновые функции основного
состояния, можно сконструировать явные выражения для опе-
раторов, которые создают из основного состояния возбужден-
ные состояния. В качестве ведущей идеи мы будем руководст-
воваться идеей, развитой в § 6, где рассматривался пример сме-
щенного гармонического осциллятора. Ход мыслей при этом
будет следующий: как мы видели в предыдущем параграфе,
основное состояние сверхпроводника можно представить в виде
D3.1)
§ 43] ВОЗБУЖДЕННЫЕ СОСТОЯНИЯ СВЕРХПРОВОДНИКА 315
При этом действие экспоненциальной функции на вакуумное
состояние приводит к созданию определенного нового состоя-
ния. Теперь проведем аналогию между функцией D3.1) и функ-
цией смещенного гармонического осциллятора
0. D3.2)
В § 6 о гармоническом осцилляторе мы обнаружили следующее:
стоящие перед вакуумным состоянием Ф« экспоненциальные
функции можно представить в виде некоторого унитарного пре-
образования, в результате чего функция типа D3.2) приобрела
вид
еР(ь+-ь)Ф0. D3.3)
Затем было показано, что с помощью такого рода унитарного
преобразования можно получить новые операторы рождения и
уничтожения. Здесь мы воспользуемся тем же ходом рассуж-
дений.
Действительно, в § 14 мы видели, что для каждой отдель-
ной экспоненциальной функции ферми-операторов ах , а2:
NeCat4 D3.4)
можно найти унитарное преобразование
такое, что
NeC"x Ф„ = е °2 ~сО1Ф0. D3.6)
Предприняв теперь следующие обобщения:
ау^а*+ I'ZT' D3<7)
заменим волновую функцию D3.1) следующей волновой функ-
цией:
осн = Цб ®o- Dd.«)
k
Эту точную замену можно интерпретировать следующим обра-
зом. Основное состояние теории БКШ может быть создано из
вакуума с помощью унитарного преобразования U, т. е.
I Фоса = *7Ф0 D3.9)
21*
316 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
при
U = Д /*DW<Mu°kt) s д Uk D3Л0)
к к
д
к
Теперь мы хотим, как и в случае смещенного гармонического
осциллятора (см. §§ 6 и 14), перейти с помощью этого унитар-
ного преобразования к новому набору операторов и состояний,
так чтобы БКШ-основное состояние стало «вакуумным состоя-
нием» для наших новых операторов. Для этого построим опера-
торы
akr = Ukak]Ut. D3.11)
Как было показано в § 14, преобразование D3.11) можно про-
вести в явном виде, что приводит к результату
«kt = aktuk — a^klvk. D3.12)
Новый оператор akf тем самым оказывается представленным
в виде линейной комбинации операторов рождения и уничто-
жения. Соответствующим образом можно подействовать пре-
образованием U и на другие операторы akt и т. д. Эти преоб-
разования приводят к следующим результатам;
akf == aktwk — atklvk, D3.13)
aJti = atkiuk + aktvk, D3.14)
a_ki — a_kiuk + akri;k. D3.15)
Выражения D3.12—43.15) представляют собой известные пре-
образования Боголюбова — Валатина, Здесь отчетливо видна ос-
новная идея этих преобразований. Новые операторы, как было
уже показано ранее с помощью прямых расчетов, удовлетво-
ряют тем же перестановочным соотношениям, что и старые опе-
раторы. Следовательно, они снова представляют ферми-части-
цы. Однако теперь они описывают не рождение одного электро-
на, а представляют процесс рождения возбужденного состояния
или, другими словами, квазичастицы. Эти новые операторы от-
личаются тем, что они переводят основное состояние теории
БКШ в повое «вакуумное состояние»:
«ктФосн = 0 И а_к1ФОсн = 0.
Вакуумное состояние квазичастиц получается непосредственно
из соотношений D3.11) и D3.9):
Яктфосн =• иакГ1/иФ0 = иакГФ0 = 0
= 1 =0
(почему Uk в D3.11) можно заменить на С/?). Теперь, однако,
§ 43] ВОЗБУЖДЕННЫЕ СОСТОЯНИЯ СВЕРХПРОВОДНИКА 317
следует указать на существенное отличие этих результатов от
гармонического осциллятора. В случае гармонического осцилля-
тора основное состояние имело точно вид D3.2), и поэтому со-
стояния, полученные с помощью преобразованных операторов,
также были точными. Здесь же основное состояние представле-
но выражением D3.1) лишь приближенно. На этом основании
мы не можем быть наперед уверены, что с помощью нашего ме-
тода будут получены точные возбужденные состояния. В про-
тивном случае было бы возможно дать точное решение пробле-
мы многих частиц. На самом же деле получается следующая
ситуация. G помощью преобразований D3.12—43.15) одна часть
оператора Гамильтона дпагонализуется, т. е. становится точно
решаемой с помощью операторов числа частиц. Но при этом
остается еще и другая часть оператора Гамильтона.
Критерий качества всей процедуры состоит в следующем:
является ли эта недиагоналпзованная часть оператора Гамиль-
тона лишь малым возмущением или нет. Дополнительный член
такого рода ведет к тому, что квазичастицы взаимодействуют
друг с другом, т. е. рассеиваются из начальных состояний и,
следовательно, имеют конечное время жизни у. Вся процедура
имеет смысл лишь до тех пор, пока ушнрение энергетических
уровней за счет конечного времени жизни много меньше полной
энергии квазичастицы. То есть должно выполняться условие
k. D3,16)
В последующем изложении мы будем считать, что это условие
выполняется, и проведем упомянутую процедуру. Для этого раз-
решим D3.12—43.15) относительно операторов а, а+ и выразим
нх в виде линейных комбинаций операторов а, а+. Затем под-
ставим эти комбинации в .//' = Н — uJVon D2.14) и после элемен-
тарных преобразований получим
I Н' = 2 ^к ( Як т ак т -|- а-к | «-к i) + остаток. D3.17)
I k
Поскольку новые операторы а, а+ снова удовлетворяют переста-
новочным ферми-соотношениям, то теперь уже нахождение
возбужденных состояний и соответствующих им энергий явля-
ется тривиальным (если только не принимать во внимание
«остаток»).
Согласно § 42, энергия возбуждения Ек «квазичастицы» да-
ется выражением
I it = (X2 + д?I/3- D3-18)
Последующее простое рассмотрение показывает, что тем са-
мым мы показали существование энергетической щели-: без
318 СВЕРХПРОВОДИМОСТЬ [ГЛ. VII
взаимодействия между электронами Ак = 0. Энергия возбужде-
ния Ец = Еъ начинается от значения Еъ — j.i = 0 и непрерывно
нарастает.
При А Ф 0, напротив, самое глубокое возбужденное состоя-
ние к0 отделено от основного состояния энергией Ека —--Д, т.е.
энергетической щелью. Тем самым достигнута важнейшая цель
микроскопической теории сверхпроводимости. К этому можно
лишь добавить доказательство того, что в сверхпроводнике дол-
жен существовать эффект Мейсснора — Оксенфельда.
Мы не будем подробно проводить соответствующие расчеты,
хотя основная идея проста: к D2.1) добавляют еще один доба-
вочный член, который описывает взаимодействие электронов с
магнитным полем (см. также D4.2)), и учитывают его в наи-
низшем приближении теории возмущений. Если затем вычис-
лить среднее значение тока, то по существу получается соотно-
шение D0.24).
В заключение сделаем еще одно замечание относительно ус-
ловия возникновения сверхпроводимости. До сих пор в §§ 42, 43
мы исследовали лишь притягивающее взаимодействие между
электронами, которое возникает благодаря их взаимодействию
с колебаниями решетки, а кулоновское взаимодействие пол-
ностью опустили. Как можно показать, кулоновское (отталки-
вающее) взаимодействие между каждыми двумя электронами
сильно экранируется другими электронами. Так что в результа-
те имеется лишь остаточное отталкивающее взаимодействие.
Если теперь учесть оба (притягивающее и отталкивающее)
взаимодействия, то в соответствии с конкретными параметрами
данного твердого тела перевес имеет либо одно, либо другое
взаимодействие. Хотя имеются весьма полезные эмпирические
правила, которые позволяют установить характер взаимодейст-
вия, выполнить априорное вычисление вряд ли возможно.
Весьма интересный раздел представляет собой изучение фа-
зового перехода в точке перехода в сверхпроводящее состояние.
К сожалению, изложение этого явления, например, с помощью
температурных функций Грина или теории Ландау — Гинзбур-
га выходит далеко за рамки нашей книги.
Глава VIII. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ
С КВАНТОВАННЫМ ЭЛЕКТРОМАГНИТНЫМ ПОЛЕМ
§ 44. Взаимодействие между излучением п веществом:
оператор Гамильтона
В этом параграфе будет введен оператор Гамильтона взаи-
модействия электронов с квантованным полем излучения, при
этом будет использовано правило, с которым мы познакоми-
лись в § 15.
Построив оператор Гамильтона квантованного электронного
ноля, находящегося иод воздействием поля излучения, и добавив
к нему оператор Гамильтона свободного светового поля, мы по-
лучим полный оператор Гамильтона //.
а) Оператор Гамильтона электронного волнового поля. По-
скольку поле излучения описывается с помощью векторного по-
тенциала А, то сначала нам следует поближе познакомиться с
классической функцией Гамильтона, а затем и с оператором Га-
мильтона электрона, движущегося в поле векторного потенциа-
ла А. Мы подойдем к этой задаче в рамках метода первичного
и затем вторичного квантования, а начнем с функции Гамиль-
тона классической физики. Как можно показать (см. задание 1),
классическая функция Гамильтона для электрона, который дви-
жется в ноле векторного потенциала А(х) и скалярного потен-
циала F(x), имеет следующий вид:
я«л = -к (р ~ 1А <х)J+ v (x)- D4Л)
В рамках первичного квантования переход к оператору Га-
мильтона // шредингеровской волновой механики совершается
с помощью замены р на оператор (ft/i)V.
С помощью этого оператора Гамильтона Я во вторичном
квантовании мы строим §ty+(x)Hty(x)d3x и подчиняем ф+(х) и
г|)(х) перестановочным ферми-соотношениям A3.8). Добавив,
наконец, соответствующий оператор взаимодействия Нвз, мы
учтем и кулоновское взаимодействие между электронами. Вы-
ражение для Явз нам уже встречалось ранее, но мы приведем
его сейчас еще раз в явном виде. Таким образом, искомый опе-
ратор Гамильтона в представлении вторичного квантования
320 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ. VIII
имеет вид
Яэл = Г t+ (х) {-^ D V - ~ АJ + V (х)\ ф (х) d3x + Явз.
D4.2)
Выражение в D4,2), которое содержит векторный потенциал,
можно еще более упростить. А именно, если возвести выраже-
ние в круглых скобках в квадрат, то, учитывая точный порядок
следования операторов, получим
2т а 2mci
+ 42
Ввиду свойств оператора набла имеет место равенство
у(Аф) = г|эуА + Ауф, D4.4)
где первый член в правой части, ввиду равенства нулю дивер-
генции векторного потенциала (см.A1.26))
D4.5)
выпадает.
Тогда оператор Яэл можно представить в виде
\ TJ U l IT i ыЧнп' i it i r r a\
I Лэп = "о,эл т Яэия + лэл-св Т Два: D4.0)
где
Я0,эл = J ^ («) {- ^ А + V (х)} ф (х) d'x, D4.6a)
Яэл-св = Г V (х) (- ^rc A (a;) V) i|> (x) d3x, D4.66)
а также
^-4 А2) я|) (х) d»jf, D4.6в)
1 Г + + е2
Явз = Т |г (х) "Ф (х ) 1—_ г | г|э (х ) i() (х) сРхсРх . D4.6г)
Отдельные выражения D4.6а — 44.6г) имеют следующий смысл:
Яо, эл относится к движению электронов в потенциальном поле
F(x); Яэл-св описывает взаимодействие между электронами и све-
том, причем векторный потенциал входит сюда линейно. Яэл?св
описывает другое взаимодействие между электронами и светом,
причем сюда входит квадрат векторного потенциала А, следова-
тельно, это нелинейный член. В последующем изложении мы
пренебрежем этим членом, что оправдано для малого А. (Посколь-
ку А становится оператором, то это означает, что матричные
§ 44] ОПЕРАТОР ГАМИЛЬТОНА 321
элементы А для состояний поля, которые здесь будут рассмат-
риваться, достаточно малы.) Последний член, Явз, описывает
кулоновское взаимодействие между электронами.
б) Оператор Гамильтона свободного поля излучения. В этом
случае также целесообразно разложить векторный потенциал по
плоским волнам (см. § 11):
ф*Ц D4.7)
Здесь со t — частоты парциальных волн излучения, euj — вектор
поляризации волны к. Поскольку имеются два произвольных на-
правления поляризации, мы будем различать их индексом /.
V — объем нормировки, bkj и b^j —операторы рождения и
уничтожения, удовлетворяющие обычным бозевским перестано-
вочным соотношениям.
Согласно § 11, оператор Гамильтона в этом случае имеет вид
D4.8)
Оператор Гамильтона полной системы равен сумме //ол и Нсв:
I D4.9)
Для последующего представим сумму Яэл + /7СВ в D4.9) несколь-
ко иным образом:
Здесь оператор Но состоит из суммы операторов Гамильтона сво-
бодных нолей:
Яо = Яо. .„ + //„, D4.10а)
причем Яо, ол, Яол-св и #вз уже встречались нам в D4.6), а Яси
определен в D4.8). По ряду соображений оператор Гамильтона
полезно представить в другом виде. Как мы уже много раз виде-
ли ранее, полевые операторы г|т(х) и г|)+(х) имеет смысл разло-
жить по собственным фупкциям уравнения Шредингера
D4.11а)
. D4.116)
р.
В нашем случае в качестве функций фц(х) целесообразно выбрать
решения уравнения Шредингера
- Ж А + v <
322 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ. VIII
Прежде чем мы подставим разложения D4.11а) и D4.116) в
D4.9) и D4.6), поговорим немного о перестановочных соотноше-
ниях. Перестановочные соотношения только для операторов
ноля излучения и только для операторов электронного волнового
ноля нам уже довольно хорошо знакомы (см. A1.55—11.57),
A3.8)). Далее мы потребуем, чтобы перестановочные соотноше-
ния, связывающие нолевые операторы одного поля с нолевыми
операторами другого поля, обращались в нуль, т. е. чтобы имели
место ^равенства
[if>(x'), А(х)]=0, [т|;(х'), П(хI=0,
[ф+(х'), A(x)J=0, [ii>+(x'), Шх)]=0. D4.13)
Здесь Н(х) — канонически сопряженный А(х) импульс. Если
с помощью разложений D4.7) и D4.11а, б) ввести операторы поля
излучения b^j, bkj, а также электронные операторы рождения
и уничтожения а^, %,,, то согласно Di.l3) можно показать,
что
[аил &к ;] = 0, [яц. &t iI = О,
г + ' i г 4- 4.1 D4.14)
[4- Ьк,;] - 0, [а+, ЬЦ\ = 0.
Подставим разложения D4.11а) и D4.116), а также D4.7) в
D4.10). При этом члены в D4.10) примут новый вид, и мы при-
ведем их в явном виде. Оба стоящих в //о (см. D4.10а)) выра-
жения уже встречались нам ранее (см. §§ 13, 11), так что их
можно оттуда заимствовать:
2 ? А,5 (.15)
Новым для пас является член Ям.с„ поэтому мы выведем его
и явном виде. Сначала рассмотрим разложение векторного потен-
циала D4.7): совершенно очевидно, что А содержит две разно-
родные части: одна из них зависит только от Ь, а вторая содержит
только Ъ+. Соответственно этому запишем
D4.16)
и подставим это разложение в D4.66):
Яэл-св ~ f ф+ (х) Аь (х) уф (х) dzx + j i|)+ (х) Аь+ (х) уф (х) й'х.
D4.17)
Структуру гамильтониана Яэл-св, которую он принимает при под-
становке разложений D4.7), D4.16), D4.11а, б) в D4.17), мы об-
судим на примере первого интеграла, показав при этом, на что
§ 44] ОПЕРАТОР ГАМИЛЬТОНА 323
заменяется каждый член подынтегрального выражения:
|"г|)+(х) Аь(х) у г|з(х) сРх
i \ III | • D4.18)
О Ьь,/кх V av<pv(x) d3x
Поскольку операторы а^, /^k,.;- av не связаны с интегрирова-
нием, их можно вынести из-под знака интеграла:
k,j j ЧЫ (х) e'kxvcpv (x) Л. D i. 10)
Те же шаги можно предпринять п в отношении второго интегра-
ла в (.'54.17), причем для этого следует лишь в коночном резуль-
тате D4.19) заменить Ъ па Ъ+ и егкх на е —!кх. Чтобы получить
полное выражение для Нил-,,п, нам следует еще добавить посто-
янные множители, которые стоят в D4.7) н D4.66), а затем
провести суммирование по ц, v, k, /. Тогда получим
т -¦- h 2 («ii«v^k,./^ivk.; + «it«v^k.itVvkj). D4.20)
fivkj
Полный оператор Гамильтона, который мы положим в основу
нашего дальнейшего рассмотрения, дается выражением
// = Яо + Я.1Л.св+/Ув„ D4.21)
где Но, Ям-си и //„ заданы явно п D4.15), D4.20), D4.6г).
Константы снязп g даются следующим выражением:
D4.22)
=- const
Константы связи g' получаются из констант g простой заменой к
па —к:
.^(xvkj == tffiv, -k.r
Б приведенных выше вычислениях мы пренебрегли в D4.9)
квадратичным по А членом. Можно действительно показать, что
в целом ряде случаев это пренебрежение оправдано. Но посколь-
ку в некоторых случаях, особенно в нелинейной оптике, этот
член играет важную роль, то мы рекомендуем читателю в виде
упражнения найти его явный вид.
По своей структуре оператор Гамильтона D4.10) с D4.15)
и D4.20) полностью аналогичен встречавшемуся уже нам гамиль-
тониану, который описывает взаимодействие между электроном
и колебаниями решетки. Тогда операторы рождения и уничтоже-
ния относились к квантам колебаний решетки. В данном же слу-
324 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ. VIII
чае константы связи имеют совершенно иной смысл. Другое
различие состоит в том, что в проблеме взаимодействия между
электронами и колебаниями решетки речь шла об электронах,
которые движутся в периодичном с периодом решетки потен-
циале. В данном случае потенциал F(x) может быть любым.
Задания к § 44:
1. Получить соответствующие D4.1) уравнения Гамильтона
для р н х и вывести отсюда уравнения движения Ньютона, где
в качестве силы выступает сила Лоренца К = еЕ -| [v, В].
При этом учесть, что еЕ = — grad V — jA, а также В - rot A.
2. Выразить D4.6в) через операторы а+, а, Ь+, Ъ, применив
разложения D4.7), D4.11а), D4.116).
§ 45. Поляритоны
Под поляритопами понимают возбужденные состояния, возни-
кающие в решетке кристалла в результате взаимодействия меж-
ду светом и электронами. Как мы уже видели на примере экси-
тона Френкеля, в кристалле могут возникать поляризационные
колебания электронов, которые распространяются в кристалле
в виде продольных и поперечных воли. Если на кристалл надает
свет, то, как мы сейчас увидим, и в этом случае в кристалле
могут возбуждаться аналогичные поперечные поляризационные
колебания. Возникающие при этом процессы сильно напоминают
два связанных маятника, причем в нашем случае один маятник
представляет поляризационные колебания, а другой — колебания
ноля излучения. Как нам известно из механики, два связанных
маятника, которые в отсутствие связи имеют собственные часто-
ты «1 и 0J, совершают общее движение, причем новые собствен-
ные колебания происходят с новыми собственными частотами
ui и Q2.
Совершенно аналогичная ситуация возникает и в рассматри-
ваемом нами квантовомеханическом случае. Благодаря взаимо-
действию между светом и экситонами Френкеля возникают новые
стационарные состояния с новыми энергиями и новым законом
дисперсии. Чтобы не слишком перегружать формализм всевоз-
можными индексами, мы рассмотрим сравнительно простую кон-
фигурацию. Пусть атомы расположены в плоскостях перпенди-
кулярно оси х. Атомные волновые функции, из которых
образуется полоса проводимости, пусть будут ^-функциями, ори-
ентированными либо вдоль, либо поперек оси х. Пусть волна
излучения падает параллельно оси х и поляризована параллельно
оси у (рис. 59). Исходным пунктом нашего рассмотрения явля-
451
Поля^нтонЫ
325
ется оператор Гамильтона D4.9) (с D4.6), D4.8)), причем нели-
нейный член опущен нами еще в § 44. По аналогии с § 44 снова
введем для А разложение D4.7). Поскольку мы рассматриваем
только одно направление поляризации, индекс / теперь можно
опустить. В отличие от § 44, однако, мы разложим полевые опе-
раторы электронов i|) и 41+ по локализованным в узлах решетки 1
функциям:
«>,Дх-1). D5.1)
При этом речь может идти либо о функциях Ваннье (см. § 19),
либо, в простейшем случае, об атомных волновых функциях. Ин-
i/,
Электрическое поле
Рис. 59. Рассматриваемая в тексте конфигурация электрического поля, вол-
ны излучения и функций Ваннье зоны проводимости, е — направление век-
тора поляризации, к — волновой вектор.
деке и. показывает, о каком состоянии идет речь: об основном
или о возбужденном. Будем считать, что основное состояние
принадлежит валентной зоне и поэтому в данном случае индекс
[I соответствует индексу V. Соответствующие волновые функции
имеют s-симметрию. Индекс |i может обозначать также и воз-
бужденное состояние, которое принадлежит зоне проводимости.
Поскольку мы считаем, что функции возбужденного состояния
имеют вид /ьфункций, то нам следует ввести дополнительно ин-
дексы 1, 2 и 3 в соответствии с возможными пространственными
ориентировками /ьфункций. В этом случае ц принимает следую-
щие значения: u=L, 1 или >ц = L, 2, или [i = L, 3.
Если разложение
г|5(х) = 2 «i,n^n(x-l) D5.2)
1,И
и соответствующее ему разложение для эрмитово сопряженного
оператора подставить в оператор Гамильтона D4.9), то мы полу-
чим новый оператор Гамильтона
Я = ЯЭЛ + ЯСВ + ЯЭЛ.СВ. D5.3)
Здесь Яэл зависит от операторов а^ц и а^ц. Этот оператор
может также содержать выражения, описывающие кулоновское
326 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ. VIT1
взаимодействие между электронами. Явный вид этого оператора,
который здесь нам совершенно не нужен, можно найти, напри-
мер, в § 24. 7/св описывает энергию свободного поля излучения
и дается выражением D4.8). Третий оператор Гамильтона в D5.3)
описывает взаимодействие между электроном и излучением. Рас-
смотрим Яэл-св более подробно и разложим его на две части.
Первая часть содержит только операторы уничтожения кван-
тов поля излучения и поэтому представляет поглощение излуче-
ния
^эл-ев,погл "= Й- .Zj fll,n.a]',n.'bfc?n,n,]',n',lf D5.4)
l,l',H,M/,k
Вторая часть содержит только операторы рождения
//эл-св,исп = Й ^j Я|,цЯ1',д'Ьк?п,ц.1'.МЛЬ D5.5)
1''
и, тем самым, представляет процессы испускания квантов света.
Суммы в D5.4) и D5.5) распространяются на все точки локали-
зации электронов 1 и 1', а также на все возможные значения ин-
дексов и. и и/, которые отличают валентную зону от зоны прово-
димости. Наконец следует просуммировать по всем векторам к
поля излучения. При этом для простоты мы примем, что к па-
раллелен оси х и что имеется лишь одно направление поляриза-
ции. Матричные элементы G в D5.4) и D5.5) имеют вид
Gi,h.,i',h',ie = const I и>(х — 1) еке'кх 4- y«v (х ~ П d3x, D5.6)
причем константа в D5.6) совпадает с константой в D4.22). Мы
не вводим ее здесь, поскольку ее явный вид в последующем из-
ложении нам не понадобится. Посмотрим, как упрощается G
в нашей конкретной модели. Предположим, что между атомными
волновыми функциями в различных узлах нет перекрытия. Тогда
от пуля отличны только такие матричные элементы G, для кото-
рых 1' = 1. Далее, волновой вектор излучения к по величине зна-
чительно меньше постоянной решетки. Тогда е{кх внутри эле-
ментарной ячейки можно считать константой, что позволяет
в показателе экспоненты заменить х на 1 п вынести eikl за
знак интеграла:
G ~ e'klek Г wl (х - 1) A yuv (х - ]) ^х- D5-7)
Введем, наконец, следующее правило отбора для атомных
волновых функций: переходы могут происходить только между
основным и возбужденным состояниями, но не между одинаковы-
§ 451 ПОЛЯМГГОНЫ 32?
мп состояниями (см. также стр. 192—193):
D5.8)
Поэтому ниже нам следует учесть только матричные элементы
вида
G-e'tiekP,-,!, D5.9)
где рг1— матричный элемент оператора импульса между ос-
новным состоянием, имеющим s-характер, и возбужденным со-
стоянием, которое имеет ^-характер. Учитывая ориентацию
атомных волновых функций и поляризацию электрического поля,
находим, что от нуля отличен только такой множитель G, для
которого соответствующие волновые функции ориентированы
вдоль оси у:
eicPr, l = py. D5.10)
Следствием этого, как мы еще увидим, является то, что попереч-
ное поле излучения вступает во взаимодействие только с попе-
речными экситонамц Френкеля. Поэтому G можно записать в
следующем виде:
^eikl, D5.11)
причем мы учли, что от нуля отличны только совершенно опре-
деленные коэффициенты G. Величина N в множителе 1/1/N явля-
ется полным числом атомов в решетке; оно понадобится нам
сейчас.
С хорошей точностью можно принять, что константа D
в D5.11) практически не зависит от к. Совершенно аналогичным
образом найделг для G' следующее выражение:
G' = -4= De-*\ D5.12)
V N
Ради простоты здесь и ниже мы примем, что константа D дей-
ствительна. (Этого всегда можно добиться соответствующим вы-
бором атомных волновых функций.) После этих приготовлений
мы в состоянии представить оператор Гамильтона D5.4) и D5.5)
в существенно более простом виде. Например, вместо D5.4) ащ
328 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ.
получаем
—,==
#эл-св,погл = Й^6к ^a^L^ai.ve1*1—,==D
v«i,v,^ikl Т7= #• D5.13)
В D5.13) стоит сумма по 1, которая уже встречалась нам при
рассмотрении экситонов Френкеля. Вспомним теперь, что вместо
оператора уничтожения aity мы ввели оператор электронной
дырки di и тогда сумма по I совпадает, как указано, с опера-
тсфом рождения экситона Френкеля с волновым вектором к.
Соответственно во второй строке D5.13) получаем выражение
для оператора уничтожения экситона Френкеля. С помощью
этих выражений D5.13) принимает более простой вид
Яэл-ов.погл = * 2 bkB?D + % 2 Ъф-ф. D5.14)
к к
Совершенно аналогичным образом для D5.5) получаем следую-
щий оператор Гамильтона:
#эл-св,исп = Й S Ъ?Вф + % 2 btB\D. D5.15)
к к
Как мы только что видели, кажется естественным вместо опера-
торов рождения и уничтожения электронов ввести операторы
рождения и уничтожения экситонов Френкеля. Мы рассматрива-
ем ситуацию, когда экситоны Френкеля образуются в решетке
без взаимодействия с излучением. Тогда, согласно результатам
§ 24, мы знаем, что с помощью введения операторов для эксито-
нов Френкеля оператор //эл можно представить в виде
#эл = Й 2 ek?k~?k. D5.16)
к
Таким образом, нам удалось привести исходный оператор Га-
мильтона нашей системы «электроны — поле излучения» к весь-
ма простому виду
Н = B к?
( к
2 D (ЬкВ? + &kS_k + &t-Sk + &]№)}• D5.17)
к )
В принципе этот оператор Гамильтона содержит три части: энер-
гию экситонов Френкеля, которые ведут себя как бозе-частицы,
§ 45] ПОЛЯРИТОНЫ 329
энергию поля излучения и энергию взаимодействия между полем
излучения и операторами Бозе. Для каждого фиксированного
значения волнового вектора к существует связь между осциллято-
ром, который порождается полем электронов, и осциллятором
поля излучения. Уравнение Шредингера, соответствующее D5.17),
можно решить точно.
Ниже мы рассмотрим, чтобы не иметь дела со слишком слож-
ной ситуацией, приближенное решение. Как видно из оператора
взаимодействия D5.17), здесь возникают различные процессы
взаимодействия; среди них процесс, при котором одновременно
рождаются квант света и один экситон Френкеля или оба одно-
временно уничтожаются. Согласно закону сохранения энергии
такой процесс невозможен. В силу этого соответствующими чле-
нами мы пренебрежем, хотя в более высоких порядках приближе-
ния они, вообще говоря, дают вклады. Поэтому мы рассмотрим
несколько упрощенную модель, которая, однако, весьма хорошо
согласуется с действительностью. Итак, вместо D5.17) мы рас-
смотрим оператор Гамильтона
I # = 2#к, D5.18)
I k
где члены суммы по к имеют вид
| #к = % {вкВ?Вк + akb?bk + БЪкВ? + Db?By). D5.19)
Поскольку сумма D5.18) представляет собой сумму по отдельным
операторам Гамильтона, которые описывают независящие друг
от друга системы, то достаточно показать, как следует решить
уравнение Шредингера, соответствующее одному оператору
D5.19). При этом ради простоты в дальнейшем изложении мы
опустим индекс к. Этот пример показывает нам, как рассматри-
ваются проблемы, гамильтонианы которых содержат билинейные
комбинации бозе-операторов. (Здесь речь идет о квантовомехани-
ческом рассмотрении связанных маятников, так что упомянутая
в начале этого параграфа аналогия действительно очень тесная.)
Теперь введем новые операторы PL и Р2 так, чтобы оператор
Гамильтона принял вид
+ №tPtPv D5.20)
Для этого положим
B = »iiPi+-Bi2P2, Ъ = u2iPi + u22P2, D5.21)
или, в матричных обозначениях,
(Я-
D5.22)
22 X. Какен
330 ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ПОЛЕМ ИЗЛУЧЕНИЯ [ГЛ. VIII
где, естественно,
U =
Гамильтониан D5.19) также перепишем в матричном виде
D5.23)
где А — квадратная матрица. Если выполнить операции умноже-
ния в D5.23), то получим
.-= апВ+В + «12Я+Ь + а21Ь+В + ои
D5.24)
Сравнение D5.24) и D5.19) дает коэффициенты матрицы (А)
«11 == е, я22 = со, cii2 = а21= D. D5.25)
Еслп подставить D5.22) в D5.23), то вместо старых операторов В
и Ь появятся новые операторы Pi и Р%. Чтобы привести оператор
Гамильтона к виду D5.20), потребуем, чтобы матрица
U~lAU D5.26)
была диагональной, что, как известно, тождественно проблеме
отыскания собственных зпачений
AU---UA, Л= 1 . D5.27)
Если вместо А и U подставить матричные элементы, то уравне-
ния примут следующий явный вид:
(е — Qpwij + Du2j — 0,
Du\j+ (со — Qj)u2j' — 0, / = 1, 2. D5.28)
Нас интересуют в конечном счете собственные значения Qj. Они
имеют вид
Й1.2 = ^г1 =*= 4" /(со - еK + AD2. D5.29)
С помощью этих собственных значений оператор Гамильтона
можно представить в желаемом виде D5.20). Добавим всюду, где
это необходимо, индекс к. Тогда Н D5.18) окончательно прини-
мает следующий вид:
Н = ?iS(Qi,kPi-kPlk + QuPiP2k). D5.30)
k
Операторы Р^ и Р2к при этом соответствуют классическим нор-
§ 45] ПОЛЯРИТОНЫ 331
мальным координатам. Отсюда ясно видно, что два связанных
колебания порождают новую форму колебания.
Как можно показать, преобразование U можно выбрать так,
что оно будет унитарным. Тогда, пользуясь унитарностью преоб-
разования U, можно показать, что операторы Р удовлетворяют
обычным бозевским перестановочным соотношениям. (См. к это-
му § 16.)
Новые и старые собственные значения представлены на рис. 4.
Как можно видеть, дисперсионные кривые для экситонов и света
в точке пересечения расщепляются и возникают две новые дис-
персионные кривые. Элементарные возбуждения, которые опи-
сываются этими дисперсионными кривыми, называются поляри-
тонами. Существование поляритонов было доказано эксперимен-
тально. Согласно этим дисперсионным кривым, поляритоны
могут распространяться в кристалле с совершенно различными
по величине скоростями. Из-за тесной связи поляритонов с элек-
тромагнитным полем в кристалле возникают дисперсионные эф-
фекты нового типа.
Мы рассматривали в этом параграфе взаимодействие света
с экситонами Френкеля только ради простоты. Наше рассмотре-
ние без труда можно перенести, например, на случай экситонов
Ваннье.
22*
ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
К§ 2
Vote II. Einfiihrung in die Theoretische Mechanik, II. Lagrange-Hamiltonsche
Mechanik und Ansatzpunkte der Quantentheorie.— Frankfurt/M.: 1972.
*) Ландау Л. Д., Лифшиц Е. М. Механика.— М.: Физматгиз, 1965.
*) Лич Дж. У. Классическая механика.— М.: ИЛ, 1961.
К главе II
Блохинцев Д. И. Основы квантовой механики, 5-е изд.— М.: Высшая школа,
1976.
During W. Einfiihrung in die Quantenmechanik, 3. Aufl.— Gottingen: 1902.
Давыдов А. С. Квантовая механика.— M.: Наука, 1973.
Pick Е. Einfiihrung in die Grundlagen der Quantenmechanik.— Frankfurt/M.:
1968.
Franz W. Quantentheorie.— Berlin — Heidelberg — New York: 1971.
Mitter H. Quantentheorie.— Mannheim: 1969.
Sussmann G. Einfiihrung in die Quantenmechanik, I.— Mannheim: 1963.
К главе III
а) Распространение полн в периодических структурах, классическая
теория:
Brillouin L. Wave Propagation in Periodic Structures.— New York: 1948.
Русский перевод 2-го издания: Бриллюэн Л., Народи М., Распростране-
ние волн в периодических структурах.— М.: ИЛ, 1959.
Maradudin A. A., Montroll Е. W., Weiss G. H. Theory of Lattice Dynamics
in the Harmonic Approximation.— New York: 1963. Русский перевод:
Марадудин А., Монтролл Э., Вейсс Дж. Динамическая теория кристал-
лической решетки в гармоническом приближении.— М.: Мир, 1965.
б) Квантование поля:
Scliweber S. An Introduction to Relativistic Quantum Field Theory.—
Evanstonjll.: 1961. Русский перевод: Швебер С. Введение в релятиви-
стскую квантовую теорию ноля.— М.: ИЛ, 1963.
Wentzel G. Einfiihrung in die Quantentheorie der Wellenfelder,—Wien: 1942.
Русский перевод: Вентцелъ Г. Введение в квантовую теорию волновых
нолей.— М.: Гостехиздат, 1947.
Henley E., Thirrlng W. Elementary Quantum Field Theory.— New York:
1962. Русский перевод: Хенли д., Тирринг В. Элементарная квантовая
теория поля.— М.: ИЛ, 1963.
Mandel F. Introduction to Quantum Field Theory.— New York: 1965.
*) Добавлено при переводе. {Прим. перев.)
ЛИТЕРАТУРА
Общая литература к главам IV—VIII
333
а) Введения в физику твердого тела:
Azarofj L. V. Introduction to Solids.— New York — Toronto — London1
1960.
Brophy J. J. Electronic Processes in Materials.— New York — Toronto — Lon-
don: 1963.
Blakemore J. S. Solid State Physics. —Philadelphia — London — Toronto-
1969.
Hellwege К. Н. Einfiihrung in die Festkorperphysik, I, II.— Berlin — Heidel-
berg — New York: Springer, 1968, 1970. Ileidelberger Tusclienbticher
Bd. 33, 34.
Kitlel C. Introduction to Solid State Physics.— New York: 1966. Русский
перевод: Киттелъ Ч. Введение в физику твердого тела.— М.: Физмат-
гиз, 1963.
Kiitel С. Introduction to Solid State Physics, 4 Ed.— New York: 1971. Рус-
ский перевод: Киттелъ Ч. Введение в физику твердого тела.— М.: Физ-
матгиз, 1978.
Madelung О. Grundlagen der Halbleiterphysik.—• Berlin — Heidelberg — New
York: 1970.
Levy R. A. Principles of Solid State Physics.— New York — London: 1968.
Wert Ch. A., Thomson R. M. Physics of Solids.— New York — Toronto — Lon-
don: 1904. Русский перевод: Уэрт. Ч. А., Томсин Р. М. Физика твердого
тела.— М.: Мир, 1969.
б) Введения в теорию твердого тела:
Anderson P. W. Concepts in Solids.— New York: 1963.
Beam W. R. Electronics of Solids.— New York — Toronto — London: 1965.
Becker R., Sauter F. Theorie der Elektrizitat, Bd. 3: Elektrodynamik der Ma-
terie.— Stuttgart: 1969.
Brauer W. Einfiihrung in die Elektronentheorie der Metalle.— Braunschweig:
1966.
Callaway J. Energy Band Theory.— New York: 1964. Русский перевод: Кал-
лу ей Дж. Теория энергетической зонной структуры.— М.: Мир, 1969.
Clark H. Solid State Physics.— New York: 1968.
Frohlich H. Elektronentheorie der Metalle, Nachdruck.— Berlin — Heidel-
berg — New York: 1970.
Goldsmid H. J. Problems in Solid State Physics.— New York: 1968.
Harrison W. A. Solid State Theory.— New York — Toronto — London: 1969.
Русский перевод: Харрисон У. Теория твердого тела.— М.: Мир, 1972.
Harrison W. A. Pseudopotentials in the Theory of Metals.— New York: 1900.
Русский перевод: Харрисон У. Псевдопотенциалы в теории металлов.—
М.: Мир, 1968.
Haug A. Theoretische Festkorperphysik, Bd. I, II.— Wien: 1964, 1970.
Jones H. The Theory of Brillouin Zones and Electronic States in Crystals.—
Amsterdam — New York: 1960. Русский перевод: Джонс Г. Теория зон
Бриллюэна и электронные состояния в кристаллах.— М.: Мир, 1968.
Joshi S. К., Rajagopal А. К. Lattice Dynamics of Metals.— New York — To-
ronto — London: 1968, p. 159. Solid State Physics, Vol. 22.
Kittel C. Quantum Theor/of Solids.—New York: 1963. Русский перевод:
Киттелъ Ч. Квантовая теория твердых тел.— М.: Наука, 1967.
КиЪо R., Nagamiya Т. Solid State Physics.— New York — Toronto — Lon-
don: 1969.
Ludwig W. Einfuhrung in die Festkorperphysik I, II.— Frankfurt/M.: 1970.
Mott N., Jones W. The Theory of Properties of Metals and Alloys.— London:
1958.
Patterson J. D. Iatroduction to the Theory of Solid State Physics.— London:
1971.
334 ЛИТЕРАТУРА
Peierls R. E. Quantum Theory of Solids.— London: 1955. Русский перевод:
Пайерлс P. Квантовая теория твердых тел.— М.: ИЛ, 1056.
Pines D. Elementary Excitations in Solids.— New York: 1963. Русский пере-
вод: Пайне Д. Элементарные возбуждения в твердых телах.— М.: Мир.
1965.
Seitz F. The Modern Theory of Solids.— New York — Toronto — London:
1940. Русский перевод: Зейтц Ф. Современная теория твердого тела.—
М.: Гостехиздат, 1949.
Sachs M. Solid State Theory.— New York — Toronto — London: 1963.
Sham L. J., Ziman J. M. The Electron-Phonon Interaction.— New York:
1963, p. 221. Solid State Physics, Vol 15.
Slater J. C. Quantum Theory of Molecules and Solids, 3 Vol.— New York —
Toronto — London: 1965—1967.
Smith R. A. Wave Mechanics of Crystalline Solids, 2. Ed.— London:
1969.
Sommerfeld A., Bethe H. Elektronentheorie der Metalle.— Berlin— Heidel-
berg — New York: 1967; HeidelbergeT Taschenbuch Nr 19; Geiger-Scheel,
Handbuch der Physik, Bd. 24/2, 1933. Русский перевод: Бете Г., Зом-
мерфелъд А. Электронная теория металлов.— М.: Гостехиздат, 1938.
Raimes S. The Wave Mechanics of Electrons in Metals.— Amsterdam — New
York: 1961.
Taylor P. L. A Quantum Approach to the Solid State.— Englewood Cliffs.N. J.:
1970.
Wannier G. H. Elements of Solid State Theory.— Cambridge: 1959.
Weinreich G. Solids, Elementary Theory for Advanced Students.— New York:
1965.
Wilson A. H. The Theory of Metals.— Cambridge: 1958. Русский перевод:
Вильсон А. Квантовая теория металлов, пер. 1-го изд., М., 1941.
Ziman J. H. Electrons and Phonons.— London: 1960. Русский перевод: Зай-
мам Дж. Электроны и фононы. Теория явлений переноса в твердых те-
лах.— М.: ИЛ, 1962.
Ziman J. H. Principles of the Theory of Solids.— Cambridge: 1964. Русский
перевод: Займан Дж. Принципы теории твердого тела.— М.: Мир, 1974.
в) Теория многих частиц и ее приложения к твердому телу:
Абрикосов А. А., Горькое Л. П., Дзялошинский И. Е. Методы квантовой тео-
рии поля в статистической физике.— М.: Физматгиз, 1962.
Бокч-Бруееич В. Л., Тябликов С. В. Метод функций Грина в статистической
механике.— М.: Физматгиз, 1961.
Mattuck R. D. A Guide to Feynman Diagrams in the Many Body Problems.—
New York — Toronto — London: 1967. Русский перевод: Маштук Р.
Фейнмановские диаграммы в проблеме многих тел.— М.: Мир,
1969.
Nozieres Ph. Theory of Interacting Fermi Systems.— New York: 1964.
Pines D., Nozieres Ph. The Theory of Onantum Liquids, I,— New York: 1966.
Русский перевод: Пайнс Д., Нозьер Ф. Теория квантовых жидкостей.
Нормальные ферми-жидкости.— М.: Мир, 1967.
Thouless D. J. Quantenmechanik der Vielteilcnensysteme.— Mannheim: 1964;
BI Hochschultaschenbuch Nr. 52/52a. Русский перевод: Tat/лее Д. Кван-
товая механика систем многих частиц.— М.: ИЛ, 1963.
March N. Н„ Young W. H., Sampanthar S. The Many-Body-Problem in Quan-
tum Mechanics.— Cambridge: 1967. Русский перевод: Марч Л., Янг У., ,
Сампантхар С, Проблема многих тел в квантовой механике.— Мир,
1969.
SchulzT. D. Quantum Field Theory jind the Many-Bodyrproblem.— New York:
ЛИТЕРАТУРА 3_5
Специальная литература к отдельным параграфам глав IV—VIII
Экситоны:
Knox R. S. Theory of Excitons.— New York—London: 1963. Русский перевод:
Нокс Р. С. Теория экситонов.— М.: Мир, 1966.
Dexter D. L., Knox R. S. Excitons.— New York — London — Sydney: 1965.
Kuper C, Whitjield G. D. Polarons and Excitons.— Edinburgh — London-
1963.
Спиновые волны:
Matlis D. C. The Theory of Magnetism.— New York: 1965. P5'ccKiiii перевод.
Маттис Д. Теория магнетизма, М.: Мир, 1967.
Thompson E. D. Unified Model of Ferromagnetism, in: Advances in Physics,
Vol. CIV, 1965, p. 213.
Walker L. R. Magnetism/ed. by T. Rado; Suhl, H.— New York: 1963, p. 299.
Ахиезер А. И., Варъяхтар В. Г., Пелетмииский С. В. Спиновые волны.—
М.: Наука, 1967.
Поляроны:
Карег С. G., Whitjield G. D. Polarons and Excitons.— Edinburgh — London:
1963.
Сверхпроводимость:
de Gennes P. G. Superconductivity of Metals and Alloys (transl. by P. A. Pin-
cus).—¦ New York: 1966. Русский перевод: ДеЖен Л.Сверхпроводимость
металлов и сплавов.— М.: Мир, 1968.
Parks R. D. Superconductivity.— New York: 1969.
Rickayzen G. Theory of Superconductivity.— New York: 1965.
Schrieffer J. R. Theory of Superconductivity.— New York: 1964. Русский пе-
ревод: Шриффер Дж. Теория сверхпроводимости.— М.: Наука, 1970.
К главе VIII
Haken H. Laser Theory.— Berlin — Heidelberg — New York: 1970; Hand-
buch der Physik, Bd. XXV/2c.
Поляритоны:
Hopfield J. J. Theory of the Contribution of Excitons to the Complex Dielectric
Constant of Crystals.— Phys. Rev., 1956, 112E), p. 1555.
Пекар С. И.— ЖЭТФ, 1957, 33, с. 1022.
СПИСОК ОБОЗНАЧЕНИЙ
а — постоянпая решетки, оператор
уничтожения для ферми-частиц
а+ — оператор рождения ферми-час-
тиц
«*,l, dk,v— операторы уничтожения,
относящиеся к зоне проводимости
и валентной зоне соответственно*)
А — оператор, амплитуда
А — векторный потенциал
Ъ+, Ъ — операторы рождения и унич-
тожения бозе-частиц
В+, В — операторы рождения и
уничтожения электронно-дыроч-
ной пары
В — плотность магнитного потока
с — постоянная, скорость света
сп — коэффициент разложения
d+, d — операторы рождения и унич-
тожения дырок
Оj,y —ципольный матричный эле-
мент
D — плотность электрического сме-
щения
i5(e)—плотность состояний вблизи
уровня Ферми
$кк' —символ Кронекера
б (ж — х') — б-функция Дирака
5<™>(х — х') — ге-я производная
б-функция Дирака
Д — оператор Лапласа, параметр
энергетической щели
Ах — малое приращение координаты
е — элементарный электрический за-
ряд
е — вектор поляризации
е — диэлектрическая постоянная
Sk — частота к-то собственного со-
стояния
Е — энергия
Е — напряженность электрического
поля
/ — коэффициент упругой связи
fh, /? — функция распределения
электронов, функция распределе-
ния Ферми
f(x) — обычно обозначает какую-ли-
бо функцию
F — сила
Ф (х) — классическая и квантовоме-
ханическая волновая функция
ф„ — полный набор собственных
функций
Ф, U, % — волновые функции, функ-
ции состояния
Фо, Ф«, Фосн —основное состояние
Ф^ — функция состояния заполнен-
ной валентной зоны
Ф(|), Ф(|) — собственные функции
z-компонент оператора спина
g — ускорение свободного падения,
константа связи
G — вес
G (x, t; x', t') — двухвременная функ-
ция Грина
h = 2я h— планковский квант дей-
ствия (постоянная Планка)
Н — функция или оператор Гамиль-
тона
Ж (ж) — плотность гамильтониана
Н — оператор Гамильтона в пред-
ставлении взаимодействия
i — мнимая единица
/г m— обменное взаимодействие
lm — мнимая часть
j — плотность электрического тока
кв ¦— постоянная Больцмана
*) В этой книге, в отличие от обычно принятых в отечественной лите-
ратуре индексов валентной зоны и зоны проводимости v и I, используют-
ся индексы V и L. (Прим. перев.)
СПИСОК ОБОЗНАЧЕНИЙ
337
ективная масса
к — волновой вектор
К, К — сила, силовая константа
1 — индекс, обычно обозначающий
положение в решетке
L — функция Лагранжа (лагранжи-
ан), линейная протяженность об-
ласти квантования
2? (ж) — плотность функции Лагран-
жа, плотность лагранжиана
К — длина волны, глубина проник-
новения
т, М — масса частицы
m*' m^3** }—эффе
электронов или дырок
(.1 — магнитная восприимчивость
п — целое число, плотность частиц
rik — число заполнения
N — полное число частиц
JC — постоянная нормировки
ш — круговая частота
Q — круговая частота, какой-либо
оператор
р, р — импульс
Pi, Рг — поляритонные операторы
Р (х) — поляризация
П — произведение, канонически со-
пряженный импульс
q — амплитуда колебаний
Q(x, t)—поле колебапий решотки
Re — действительная часть
р (х) — плотность массы, заряда,
оператор плотности числа частиц
s — натяжение струны
s'+ Xg-Sy' Sz\— операторы спипа
*^к> "^к—операторы сшшовой волны
2 — сумма
<7+, а~, аг, ах, о у — матрицы Паули
о^ — тензор проводимости
t — временная переменная
Т — кинетическая энергия, темпера-
тура, оператор временного упоря-
дочения
Ti — оператор трансляции
Uk (x) — функция Блоха
U— энергия электромагнитного поля,
унитарное преобразование
v — скорость частиц, скорость звука,
постоянная связи
V — объем, потенциальная энергия
AF — элемент объема
w — волновой вектор фононов
W(x) — потенциал
(х _ 1\\ ~ Функции Ваниье зо-
,nL i i\ i ны проводимости и
ш '
ны
валентной зоны
W
вероятность перехода
единицу времени
АЛ, ' '
л
—матричный
элемент
hh
кулоновского взаимодействия в
зоппой модели
х, (х, у, z)— радиус-вектор в декарто-
вой системе координат
| — длина когерентности, коорди-
ната
Ф — волновая функция в представ-
лении взаимодействия
б
g ,х\—вариационная производная
{...} — обозначение совокупности
координат
И — кваптовомехашгаеское среднее
0(J—t')— ступенчатая функция
Хевисайда
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуда вероятности 108
Антинормально упорядоченная фун-
кция 40
Антисимметричная волновая функ-
ция 111
Атомная цепочка линейная 55
Блоховская волна 142
Бозе-операторы 37
— частицы 51
Бозоны 94, 100
Бра 33
Вакуумное состояние 99
Валентная зона 143
Вариационная производная 72
Векторный потенциал 85
Вероятность перехода полная 10S
Вершина 229
Взаимодействие полей 123
— точечных зарядов 196
¦— электронов с квантованным по-
лем излучения 319
— — — — — колебаний решетки
2,19
Внутреннее поле 207
Волновое уравнение, квантование S3
одномерное 68
— — трехмерное 83
Время жизни поляропа 292
— соударения 240
Гармонический осциллятор 21
под внешним воздействием 47
Глубина проникновения 296
Граничные условия циклические 68
Групповая скорость 143
Двухатомная линейная цепочка 62
Двухуровневый атом во внешнем
электрическом ноле 123
й-функция Дирака 71
— —, представления 76
, производные 76
Диаграммы 229
— связанные 255
Длина когерентности 298
— свободного пробега средняя 242
Закон дисперсии волны в атомной
цепочке 57
— — для двухатомной линейной це-
почки 62
одномерного континуума 09
— — скалярного волнового уравне-
ния 85
— Ома 241
Запрещенная зона 143
Звуковые волны 11
Зоны энергетические 142
Измеримые величины 31
Изолятор 144
Испускание виртуальное 230
— индуцированное фононов 226, 232
— фонона спонтанное 228
Калибровочное преобразование 86
Канонически сопряженный импульс
в континууме 73
k-правило отбора 144
Квазичастица 280
Квантование волнового уравнения
87
волнового
- шредингеровского
ля 98
по-
— — — —, подчиняющегося стати-
стике Фермп — Дирака 104
¦ , , вторичное 94
— электромагнитного поля 86
Кет 33
Когерентные состояния 50, 66, 81
Колебания ионов в F-центре (центр
окраски) 48
Конденсация Бозе — Эйнштейна 198
Кронекера символ 27
Кулоновская калибровка 86
— обменная энергия 102
Кулоновский оператор 103
Кулоновское обменное взаимодейст-
вие 158, 172
Куперовская пара 306
Магнетон Бора 207
Магнон 14, 207
Матричный элемент гармонического
осциллятора 36
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
339
Метод Ли — Лоу — Пайнса 259
— Эренрейха — Коэна 201
Модель Гайтлера — Лондона 207
Молекула водорода 207
Молекулярный кристалл 182
Наложение волновых функций 38
Нормально упорядоченная функция
39
Нормировочный множитель осцнл-
ляторной функции 34
Нулевая энергия 27, 29
электромагнитного поля 92
Обменный интеграл 209
— оператор Гамильтона 210
Оператор Гамильтона взаимодейст-
вия электронов с квантованным
полем излучения 319
— — колебаний атомной цепочки в
континуальном пределе 79
— — — непрерывного распределе-
ния электронов 128
— — —решетки и электронов в ме-
таллах 226
— — несвязанных осцилляторов 26
— смещенных гармонических
осцилляторов 53
— — сверхпроводимости 306
— — электронной дырки 163
— — электронов и дырок 167
— — — поляризационных колеба-
нпй и электронов 222
— координаты 101
— Лапласа 83
— отклонения 65
— плотности числа частиц 100
— рождения 21
— трансляции 140
— уничтожения 21
— числа частиц 80
Операторная функция 39
экспоненциальная 39
Основное состояние гармонического
осциллятора 26
сверхпроводника, энергия 313
Перенормированная масса поляро-
на 261
Перенормировка массы 244, 250
Перестановочные плюс-соотношения
105
— соотношения в континуальном
пределе 78
для бозе-операторов 24, 28
— — — гармонического осциллято-
ра 22
Перестановочные соотношения для
операторов линейной цепочки 64
— — — скалярного волнового урав-
нения 84
ферми-частиц 105
— — — шредингеровского волново-
го поля 98
— — — электромагнитного поля 89,
91
— — между г|) и t|7+, фермионные
106
Периодические граничные условия
55
Плазменная частота 201
Плазменные колебания 200
Плазмой 16, 200
Плотность гамильтониана 85
— тока 297
Поглощение 226
Поглощения зона 144
— кривая 144
Поло 67
—, квантование 55
Полюс функции Грина 279
Поляризационные волны 12
электронные 191 *
— колебания 12
— —, квантование 219
Поляризация, облако 250
Поляритон 13, 324
Полярный кристалл 219
Полкрон 16, 250, 258
— электронный 251
Поляроны, взаимодействие между
ними 262
Потенциал 17
—, вид для смещенного гармониче-
ского осциллятора 48
Потенциальная энергия во внешнем
поле, оператор 102
Правило вычисления волновых век-
торов 144
Представление взаимодействия 130,
226
— Гензенберга 130
Преобразование Боголюбова 117, 316
— Холынтейна — Примакова 217
— ферми-операторов линейное 116
Приближение Бома — Пайнса 204
— случайных фаз 205
Примесный атом 54
Принцип Кондона 54
— Паули 100, 207
— суперпозиции 57
Проводимость 241
Проводник 144
Производная в континууме 72
340
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Пропагатор 275
Разложение по собственным функ-
циям 97, 127
Сверхпроводимость 204
Сверхпроводник, возбужденное со-
стояние 314
— жесткий 298
— мягкий 298
—, основное состояние по теории
Бардина—Купера—Шриффера 305
—, энергетическая щель 318
Смещенный гармонический осцилля-
тор 47
Собственная функция гармоническо-
го осциллятора 26
— энергия 26
— —, диаграмма 274
— — полярона 292
— — частицы 195
Собственное состояние несвязанных
осцилляторов 29
Собственные состояния уравнения
Шредипгера электромагнитного
поля 92
Состояние 24
Спин 207
— 1/2 в магнитном поле 122
Спиновые волны 14, 207, 214
— операторы 209
Среднее значение для фермнопов
111
— — амплитуды когерентного со-
стояния 82
— —, вычисление 31
Ступенчатая функция 281
, производная 282
Суперпозиция волновых функций 38
Сфера Ферми 14
Г-оператор 280
Г-произведение 281
Температура перехода Тс 294
Теорема Блоха 142
Теория Блоха 140
— возмущений в координатном* про-
странстве 268
нестационарная, второй поря-
док 244
, высшие порядки 251
— — —,первый порядок 226
Унитарное преобразование 44
Уцругая постоянная 21
Уравнение Больцмана 239
Уравнение вынужденых колебаний
струны 125
— движения Ньютона 17
атомной цепочки 55
— колебаний свободной струны 124
— Пуассона 87
— струны 68
— Шредингера атомной цепочки 65
— — временное 130
— — — гармонического осциллято-
ра 30
двух частиц 111
— —¦ квантованного шредингеров-
ского волнового поля 99, 106
п частиц 111
— — проблемы многих электронов
в твердом теле 151
Уравнения Гамильтона 17
в непрерывном пределе (стру-
на) 74
— — для линейной цепочки 58
— Лагранжа 17
в континуальном пределе 73
— Лондонов 295
— Максвелла в вакууме 85
Условие Лоренца 86
Фешшановские диаграммы 226
Ферми-операторы 113
осциллятор смещенный 115,
122
Фермионный оператор уничтожения
в представлении Гензепберга 138
— —, уравнение 137
Фермионы, квантование 104
Ферромагнетизм, модель Гейзснбер-
га 210
Фононы 12, 62
— в континууме 77
Фотоны 83
Фрёлиховский гамильтониан взаи-
модействия между электронами
и фононами 219
Фрёииховское взаимодействие 299
Функция Ваннье 149
— Гамильтона 17
вынужденного гармонического
осциллятора, классическая 138
линейной цепочки 58
— — в непрерывном пределе
(струна) 74
система электроны + непре-
рывное поле 126
— — скалярного волнового уравне-
ния 84
шредингеровского волнового
поля 95 . .
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
341
Функция Гамильтона электромаг-
нитного поля 88
— Грина 268, 275, 280
— — многоэлектронной проблемы
280
, определение 276
— — полярона 286
свободной частицы 277
— Лагранжа 17
— — континуума 70
— — системы электроны + колеба-
ния континуума 125
— — скалярного волнового уравпе-
ния 83
— — шредингеровского волнового
поля 96
— — электромагнитного поля 87
— распространения 275
— состояния избыточного электро-
на 159
— — невзаимодействующих фермио-
нов 106
Фурье-интеграл 76
—образ функции Грина 279
— преобразование 61
ряд непрерывной функции 75
Хартрп приближение 285
Хартри — Фока метод 150
— — приближение 286
Числа заполнения 106
— — при тепловом равновесии для
бозе-частиц 238
Экситон Ваннье 176
— Френкеля 182
—, операторы рождения и уничто-
жения 187
—, энергетическая схема 181
Экситонная'молекула 198
Экситонное вещество 198
Экситонные капли 199
Электрическая индукция 221
Электрическое сопротивление 235
Электронная дырка 160
Электрон-электронное взаимодейст-
вие в сверхпроводнике 304
Элементарный магнит 207
Эрмитово-сопряженный оператор 34
Эффективная масса 143
— —, метод 145
Эффект Мейсснера — Оксенфельда
2S4
— Холла аномальный 166