Текст
ТЕОРИЯ КОДОВ,
ИСПРАВЛЯЮЩИХ
ОШИБКИ
ф, Дж. Мак-Вильямс Н. Дж. А. Слоэн
Перевод с английского
И. И. Грушко и В. А. Зиновьева под редакцией Л. А. Б а с с а л ы г о
МОСКВА «СВЯЗЬ» 1979
ТЕОРИЯ КОДОВ,
ИСПРАВЛЯЮЩИХ
ОШИБКИ
ф, Дж. Мак-Вильямс Н. Дж. А. Слоэн
Перевод с английского
И. И. Грушко и В. А. Зиновьева под редакцией Л. А. Б а с с а л ы г о
МОСКВА «СВЯЗЬ» 1979
THE THEORY OF ERROR-CORRECTING CODES
F.J. Mac Williams
N.J.A. Sloane
Parts I, II
Bell Laboratories Murray Hill NJ 07974 U.S.A.
north-holland publishing company amsterdam • hew york • oxford
ББК 32.81
М.15
УДК 621.391
Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А.
М15 Теория кодов, исправляющих ошибки: Пер. с англ. — М.: Связь, 1979. — 744 с., ил.
В пер.: 5 р. 50 к.
Авторы книги — американские ученые, крупнейшие специалисты по теории помехоустойчивого кодирования.
Две части оригинального издания выходят в русском переводе в одной книге.
Рассматривается алгебраическая теория кодирования. Освещаются традиционные вопросы и самые последние результаты кодирования. Большое внимание уделяется комбинаторным аспектам теории кодирования.
Предназначена для научных работников, занимающихся теорией кодирования.
30401—173 м—-—--------
045(01)—79
2—79
1502000000
ББК 32.81
6Ф0.1
Ф. Дж. Мак-Вильямс, Н. Дж. А. Слоэн
ТЕОРИЯ КОДОВ, ИСПРАВЛЯЮЩИХ ОШИБКИ
Изд. редакторы Г. В. Лихачева, В. К. Старикова Об л. художника Л. Н. Силья нова
Художественный редактор А. А. Данилин Технический редактор Г. И. Колосова Корректор В. С. Евдокимова
ИБ № 545
Сдано в набор 10,5.79 г. Подп. в печ. 20.9.79 г.
Формат 0ОХД>Лб т Бумага тип. № 1 Гарнитура литературная Печать высокая <Уел. печ. л. 46,5 Уч.-изд. л. 51,78 Тираж 5000 экз. Изд..№ 18341^ „Зак. -№ 96 Цена 5 р. 50 к.
Издательство .«Связь». Москва 101000, Чистопрудный бульвар, д. 2
Типография издательства «Связь» Госкомиздата СССР
Москва 101000, ул. Кирова, д. 40
© North-Holland Publishing Company, 1977
© Перевод на русский язык, предисловие, примечания. Издательство «Связь», 1979
ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
Издание русского перевода книги «Теория кодов, исправляющих ошибки» является для нас большой честью. Это вполне понятно, если учесть значительный вклад, сделанный советскими учеными в теорию кодирования. Чтобы убедиться в этом, достаточно обратиться к списку литературы и увидеть многочисленные ссылки на журнал «Проблемы передачи информации» и другие советские издания. Мы хотели бы поблагодарить переводчиков за тщательно выполненную работу. Мы пользуемся предоставившейся возможностью для исправления опечаток английского издания и признательны всем лицам, в том числе и переводчикам, приславшим нам свои замечания. Мы будем счастливы, если эта книга хотя бы в малой степени послужит дальнейшему развитию советской школы теории кодирования.
Ф. Дж. Мак-Вильямс
Н. Дж. А. Слоэн
ПРЕДИСЛОВИЕ РЕДАКТОРА
И ПЕРЕВОДЧИКОВ к РУССКОМУ ИЗДАНИЮ
На русском языке уже имеется несколько книг по теории кодирования. Самой замечательной из них является книга У. Питерсона «Коды, исправляющие ошибки», написанная в 1961 г. К тому времени теория кодов насчитывала немногим более десяти лет, и автор прекрасно- изложил практически все известные в тот момент результаты. Теперь теория кодов настолько разрослась, что охватить все достижения в одной монографии невозможно. Поэтому произошло естественное размежевание новых книг соответственно интересам и наклонностям их авторов — одни авторы стараются объявить как можно больше областей данной теории, не затрудняя себя утомительными подробностями, другие, наоборот, предпочитают подробнейшее изложение всех результатов в избранной области, создавая своего рода небольшие частные энциклопедии,
конечно, при наличии предметного указателя. Предлагаемая совет-скому читателю книга известных ученых Ф. Дж. Мак-Вильямс и Н. Дж. А. Слоэна принадлежит ко второй категории. Она посвящена наиболее разработанной и наиболее изящной области теории кодирования — алгебраической теории блоковых кодов, исправляющих независимые ошибки. Книга послужит превосходным новейшим справочником для специалистов и учебником для новичков, которые найдут в ней понятные и подробные доказательства и постепенный переход от простых и легко понимаемых фактов к более сложным и трудным.
Для удобства советских читателей вся отечественная библиография приведена в оригинале. Кроме того, указаны русские переводы иностранных книг. Эта библиография приводится отдельным списком, следующим за основным списком, причем сохранены номера, использованные для данной ссылки в основном списке. Кроме того, небольшая часть литературы была добавлена в процессе перевода; такие ссылки отмечены звездочкой. Если в имеющейся на русском языке ссылке указаны страницы, то они соответствуют русскому переводу.
Мы не останавливаемся на содержании книги и не даем рекомендаций по ее Чтению, так как это сделано авторами в их предисловии. Выход русского перевода отделен менее чем двумя годами от выхода оригинала. Это стало возможным лишь благодаря любезности авторов, предоставивших в наше распоряжение рукопись книги, за что мы их сердечно благодарим. Постоянный контакт с авторами позволил также исправить некоторые опечатки, вкравшиеся в оригинальное издание. Предисловие, гл. 4, 7—9, 12—16 и приложение В перевела И. И. Грушко, а гл. I—3, 5, 6, 10, 11, 17— 21 и приложение А — В. А. Зиновьев.
Л. А. Бассалыго
И. И. Грушко
В. А. Зиновьев
ПЕРЕЧЕНЬ НЕКОТОРЫХ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
ф — знак окончания доказательства
— эквивалент номера а | b — а делит b
/-вектор — вектор с г координатами г-подмножество — множество мощности г — тогда и только тогда
(тХпг)-матрица — матрица размерности (тХт)
]х[— наименьшее целое число, большее или равное х
[х1 — наибольшее целое число, не превосходящее х
wt (х) — вес вектора х
dim V — размерность пространства V
rank G — ранг матрицы G
trace G — след матрицы G
dist (х, у) —расстояние между векторами х и у
det А — определитель матрицы А
degPfxj—степень многочлена Р(х)
Aut (<g7) — группа автоморфизмов кода diag (ai, ак) —диагональная матрица с элементами at, ..., ап
(1° 0ь) — (1 1 ... 1 00 ... 0) а b
НОД — наибольший общий делитель
(а, Ь) — наибольший общий делитель чисел а, b
НОК — наименьшее общее кратное
МСТИ — Международный симпозиум по теории информации Т — знак транспонирования вектора нли матрицы 0 — пустое множество
А — равно по определению
== — приближенное равенство
|А| —мощность множества А
ВВЕДЕНИЕ
Теория кодирования возникла в конце 40-х годов с появлением работ Голея, Хэмминга и Шеннона. Истоками теории являются инженерные задачи, но ее развитие приводит к все более и более утонченным математическим методам. Наша задача — дать простое, доступное и одновременно раскрывающее все важные аспекты предмета изложение теории кодирования. В книге читатель найдет достаточно подробное описание как простейших семейств кодов (кодов Хэмминга, БЧХ, циклических и кодо:в Рида — Маллера) вместе с методами их кодирования и декодирования, так и современных вопросов теории, таких как квадратично-вычетные коды, коды Голея, Гоппы, альтернантные, Кердока, Препараты, само-дуальные коды и схемы отношений.
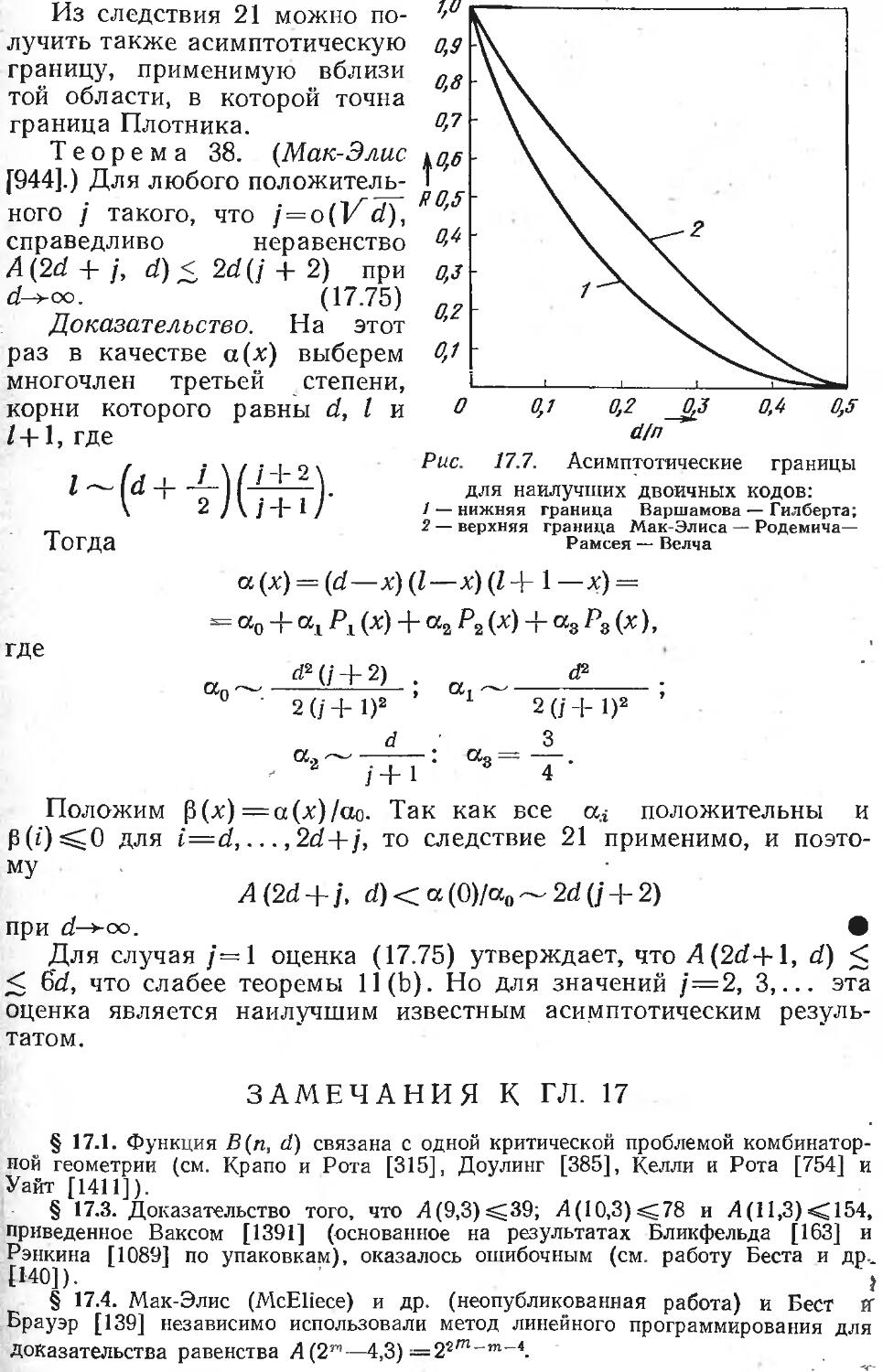
Тщательно освещается вопрос о границах объема кода. Обсуждаются простейшие результаты (границы сферической упаковки, границы Плоткина, Элайеса и Варшамова — Гилберта) и метод линейного программирования и асимптотически наилучший известный результат (граница Мак-Элиса, Родемича, Рамсея и Велча). В приложении приводятся таблицы границ и наилучшие известные на сегодняшний день коды длин вплоть до 512.
Соавторство помогло добиться простоты изложения: материал переделывался до тех пор, пока не становился полностью понятным обоим авторам. Поэтому эта книга может быть использована как новичком, так и специалистом, как инженером, так и математиком в качестве начального курса и в качестве справочника. Вследствие этого увеличился объем книги, поэтому мы рекомендуем следующий порядок пользования ею.
Начальный курс теории кодирования для математиков: гл. 1; гл. 2 (§ 2.6 до теоремы 2.22); гл. 3; § 4.1—4.5; гл. 5 (до упражнения 5); гл. 7 (за исключением § 7.7, 7.8); § 8.1—8.3; § 9.1—9.4; § 12.8; § 13.1—13.3; § 14.1—14.3.
Более полный курс для математиков: § 2.1—2.6, 2.8; § 4.6, 4.7 и часть § 4.8; гл. 5 (до упражнения 6 и§ 5.3—5.5, 5.7); § 6.1—6.3 (без доказательства теоремы 33); § 8.5, 8.6; § 9.2, 9.3, 9.5; § 10.1— 10.5, 13-4> 13.5, 13.9; § 16.1—16.6; § 17.7 (до теоремы 35);
Начальный курс теории кодирования для инженеров: гл. 1; _ 3‘ § 4 1—4.5; гл. 5 (до упражнения 5); гл. 7 (за исключением S 7 7Г § 9.1, 9.4, 9.6; § 10.1, 10.2, 10.5—10.7, 10.10; § 13.1—13.3, 13.6, 13-7; § 14.1, 14.2, 14.4.
Более полный курс для инженеров: § 2.1—2.6; § 8.1—8.3, 8.5, 8.6; § 9.2, 9.3, 9.5; § 10.11; § 12.1—12.3, 12.8, 12.9; § 16.1, 16.2, 16.4, 16,6, 16.9; § 17.7 (до теоремы 35).
’ В рассмотрение включены следующие важнейшие коды: альтернантные — гл. 12;
БЧХ — § 3.1, 3.3; § 7.6; <§ 8.5; гл. 9; § 21.8;
обобщения Ченя — Чоя кодов БЧХ — § 12.7;
каскадные —§ 10.11; § 18.5, 18.8;
конференс-матричные — § 2.4;
циклические — гл. 7; гл. 8;
Дельсарта — Геталса — § 15.5;
разностные циклические — § 13.8;
дважды-циркулянтные и квазициклические — § 16.6— 16.8; евклидово-геометрические и проективно-геометрические — § 13.8; обобщение Геталса кодов Препараты — § 15.7;
Голея (двоичный) —§ 2.6; § 16.2; гл. 20;
Голея (троичный) — § 16.2; гл. 20;
Гоппы — §12.3—12.5;
Адамара — § 2.3;
Хэмминга — § 1.7; § 7.3 и упражнение 8;
неприводимые или минимальные циклические — § 8.3, 8.4;
Юстесена —§ 10.11;
Кердока — § 2.8; § 15.5;
разделимые с максимальным расстоянием — гл. 11;
Нордстрома — Робинсона — § 2.8; '§ 15.5, 15.6;
симметричные, Плесе — § 16.8;
Препараты — § 2.8; § 15.6; § 18.7;
произведение — § 18.2 — 18.6;
квадратично-вычетные — гл. 16;
избыточные вычетные — § 10.9;
Рида — Маллера— § 1.9; гл. 13—15;
Рида — Соломона — гл. 10;
самодуальный — гл. 19;
нелинейные, исправляющие одну ошибку — § 2.7; § 18.7;
Сривэставы— § 12.6.
Методы кодирования описаны для:
линейных кодов — § 1.2;
Циклических кодов — § 7.8;
кодов Рида — СоЛомона — § 10.7;
кодов Рида — Маллера — § 13.6, 13.7; § 14.4.
Методы декодирования описаны для:
линейных кодов — § 1.3, 1.4;
кодов Хэмминга — § 1.7;
кодов БЧХ — § 3.3; § 9.6; § 12.9;
Кодов Рида — Соломона — § 10.10;
альтернантных (включая коды БЧХ, Гоппы, Сривэставы и обобще-ние Ченя — Чоя кодов БЧХ) —§ 12.9;
квадратично-вычетных кодов — § 16.9;
циклических кодов — § 16.9 (в замечаниях к гл. 16 упоминаются другие методы декодирования).
При чтении книги следуйте совету, который дается в любом предисловии: если материал вызывает у вас трудности, пропустите его, но продолжайте чтение! Не стесняйтесь пропускать доказательства теорем: мы часто делаем это. Материал, отмеченный звездочкой, является трудным или затянутым и может быть пропущен при первом (и даже при втором) чтении. В конце книги приводится обширный список литературы. Поскольку теория кодирования пересекается со многими другими областями (вычислительной техникой, дискретными системами, теорией групп, теорией чисел, планированием экспериментов и т. д.), то относящиеся к ней работы можно встретить в научной литературе практически всюду. Это, к сожалению, приводит к тому, что обычные реферативные журналы оказываются не всегда полезными. Именно поэтому мы чувствовали себя обязанными привести возможно более обширный список литературы. В конце каждой главы приводятся замечания, в которых указаны источники теорем, упражнений, таблиц, а также небольшой список литературы по некоторым вопросам (решенным или нерешенным), затрагиваемым в данной главе.
В книге рассматриваются только блоковые коды, предназначенные для исправления случайных ошибок; мы практически не касаемся кодов, исправляющих другие виды ошибок (пакетов или замещений), кодов с переменной длиной, сверточных кодов и кодирования источников (см. замечания к гл. 1). Более того, мы часто ограничиваемся только двоичными кодами, что существенно облегчает теорию. Многие авторы придерживаются другой точки зрения: анализируя двоичный случай, они формулируют результаты для произвольных полей.
Часть вопросов, включенных в первоначальный план книги, была с сожалением опущена, чтобы не увеличивать объем книги:
(i) . Коды Грея и коды для задачи «змея в ящике» — см. Адельсон и др. [5, 6], Бухнер [210], Кавио [253], Чин и др. [290], Кон [299], Данцер и Кли [328], Девайс [355], Дуглас [382, 383], Ивен 413], Флорес [432], Гарднер [468], Гилберт [481], Гюи [571], Харпер [605], Кли [764—767], Мекленберг и др. [951], Миллс [956], Препарата и Нивергемт [1083], Синглтон [1215], Тэнг и Лью [1307], Васильев [1440], Юен [1448, 1449].
(ii) . Коды без запятой — см. Болл и Каммингс [60, 61], Бау-мерт и Кантор [85], Крик и др. [316], Истмен [399], Голомб [523], Голомб и др. [528], Холл [587], Джиггс [692], Миякава и Морайя [967], Нихо [993], Рединбо и Уолкотт [1102]. О кодах для синхронизации см. также в замечаниях к гл. 1.
(iii) . Коды с неравной защитой символов — см. Гор и Килгас [549], Килгас и Гор [761], Мандельбаум [901].
fiv). Кодирование для каналов с о ратной связью — см. Ьер-лекэмп [124], Хорстейн [664], Шелквик и др. [1153—1155].
(v) . Коды для гауссовского канала — см. Бильери и др. [148— 1511 Блейк [155, 156, 158], Блейк и Муллин [162], Чедвик и др. Г956 257], Галлагер |[464], Ингемарссон ([683], Ландау [791], От-тосо’н [1017], Шеннон [1191], Слепян [1221—1223], Цеттерберг [1456].
(vi) . Сложность декодирования — см. Байога и Волбессер [59], Чейтин [257а—258а], Гельфанд и др. [471], Гросс [564], Юстесен [706], Колмогоров [774а], Маргино [916], Мартин — Леф [917а], Пинскер [1046а], Сервейт [1145], Сэведж [1149—1152а].
(vii) . Связь между теорией кодирования и задачей упаковки n-мерного евклидового пространства одинаковыми шарами — см. Лич [803—805], Лич и Слоэн [808—810], Слоэн [1226].
Нашей книге предшествовали следующие монографии и книги по теории информации: Берлекэмп [113, 116], Блейк и Муллин [162], Камерон и Ван Линт [234], Голомб [522], Лин [834], Ван Линт [848], Месси [922а], Питерсон [1036а], Питерсон и Уелдон [1040], Соломон [1251], Слоэн [1227а]; обширный список литературы имеется в работах: Берлекэмп [126], Блейк [157], Хартнетт [620], Манн [909], Слепян [1224], специальные выпуски— [377а, 678, 679]. См. также список литературы в [1022].
Мы обязаны нескольким друзьям, тщательно прочитавшим первый черновик, внесшим исправления и улучшения и спасшим нас от грубых ошибок. В частности, мы хотим выразить свою признательность И. Ф. Блейку, П. Дельсарту, Дж. М. Геталсу, Р. Л. Грехэму, Дж.-М. Ван Линту, Дж. Лонго, К. Л. Мэллоусу, Дж. Мак-Клею, В. Плесе, Г. О. Поллаку, Л. Д. Рудольфу, Д. У. Сервейту, а также многим другим коллегам по работе в лабораториях Белла, в частности А. М. Одлыжко, за их помощь. Однако мы следовали не всем их предложениям, поэтому авторы несут полную ответственность за оставшиеся ошибки. (Это замечание следует принимать всерьез.) Нам также приятно поблагодарить 1всех машинисток лабораторий Белла, помогавших нам на разных этапах подготовки рукописи, нашего секретаря Пегги ван Несс и особенно Мэрион Мессерсмис, печатавшую и перепечатывавшую большинство глав. Сэм Ломонако весьма любезно помог нам исправить опечатки в верстке.
Авторы
Часть I
Глава 1
Линейные коды
1.1. ЛИНЕЙНЫЕ КОДЫ
Рис. 1.1. Двоичный симметричный канал с вероятностью ошибки р (в общем случае Osgpsgd/2)
Коды были придуманы для того, чтобы исправлять ошибки в каналах связи с шумом. Предположим, что имеется телеграфная линия из Бостона в Нью-Йорк, по которой можно посылать 0 и 1. Обычно при посылке 0 принимается также 0, но иногда 0 может быть принят как 1 или 1 принята как 0. Будем считать, что в среднем один из каждых 100 символов будет ошибочным. Это означает, что для каждого символа имеется вероятность р= 1/100 того, что в канале произойдет ошибка. Описанная модель называется двоичным симметричным каналом (рис. 1.1).
По этой телеграфной линии передается много важных сообщений, и эти сообщения должны передаваться как можно быстрее и надежнее. Сообщения записаны в виде
последовательности из 0 и 1 (возможно, они порождаются вычислительной машиной).
Мы хотим закодировать эти сообщения, чтобы как-то защитить их от ошибок в канале. Блок из k символов-сообщения u = ui«2-.-...uk (щ = 0 или 1) будет кодироваться в кодовое слово х = =XiX2---xn (%i=0 или 1), где n~^k (рис. 1.2); эти кодовые слова образуют код.
шум
Рис. 1.2. Кодирование сообщения
Метод кодирования,' который мы сейчас собираемся описать, порождает код, называемый линейным кодом. Первая часть кодового слова состоит из символов самого сообщения: в
Xi = Ui, X2 = U2, . . ., Xh = Uk,
за которым следуют п—k проверочных символов ... ,хп. Про-
верочные символы выбраны так, чтобы кодовые слова удовлетворяли уравнению
Н
(1-1)
где ((и—k)X.n) —матрица Н, называемая проверочной матрицей кода, имеет вид
H = [A|I„_ft]. (1.2)
Здесь А — некоторая фиксированная ((л—k) Х&)-матрица из О и 1, а
/1 0\
— единичная матрица размера (п—k)\(n—k). Все операции в уравнении (1.1) выполняются по модулю 2, т. е. 0+1 = 1; 1 + 1 = 0;
—1 = + 1. Мы будем называть это двоичной арифметикой.
Пр и мер. Код 1. Проверочная матрица
011 100’
101 010
по 001
(1.3)
определяет код с k=3 и п=6. Для этого кода
"01Г
101 по
Сообщение UiU2Us кодируется в кодовое слово x=XiX2^3X4X5x6, которое начинается с самого сообщения:
~^2 — ^2’ ^3’
а последующих три проверочных символа х4х5Хб выбираются так, чтобы выполнялось уравнение Нхг=0, т. е.
х2 4~ хз + х4 — 0;
Xi+x2+x6 = 0..
(1-4)
Если сообщение u=011, то %i=0; х2=1; хз=1, и проверочные символы легко определяются;
х4=—1 —1 = 1 + 1 = 2 = 0;
х5=—1=1; х6=—1 = 1, так что кодовое слово х=011011.
Уравнения (1.4) называются уравнениями проверки на четность или проверками на четность для кода. Первое уравнение проверки на четность говорит, что 2, 3 и 4-й символы каждого кодового слова должны в сумме давать 0 по модулю 2, т. е. их сумма должна быть четной (откуда и название!).
Так как каждый из трех символов сообщения щщщ равен О или 1, то в этом коде имеется всего 23=8 кодовых слов. Эти слова:
000000 011011 110110
001110 100011 111000
10101 101101
В коде в общем случае имеется 2ft кодовых слов.
Как мы увидим, код #1 может исправлять одиночную ошибку в канале (в любом одном из шести символов), и применение этого кода уменьшает среднюю вероятность ошибки на символ от р = 0,01 до р=0,00215 (см. упражнение (24)). Это достигается ценой посылки шести символов, только три из которых являются символами самого сообщения.
Мы примем условие (1.1) как общее определение.
Определение. Пусть Н—любая двоичная матрица. Линейный код с проверочной матрицей Н состоит из всех векторов х таких, что Нхт=0 ( все операции производятся по модулю 2).
Удобно, но не очень существенно, если Н имеет вид, приведенный в (.1.2) и (1.3), когда первые k символов каждого кодового слова являются символами сообщения, или информационными символами, а последние п—k символов — проверочными.
Линейные коды наиболее важны для практических применений и просты для понимания. Нелинейные коды будут введены в гл. 2.
Пример. Код #2, код с повторением. Код с k = l, п—5 и с проверочной матрицей
1 1 1
1
1
1
1
Н =
(пустые места означают нули).
Каждое кодовое слово содержит только один символ сообщения и. Проверочные уравнения имеют вид
х1+х2=0; х1 + х3 = 0; х1 + х4=0; х1+х5 = 0,
т. е. х1=х2=хз=х4=х5=и. Таким образом, имеются всего два кодовых слова: 00000 и 111 1b. Передаваемый символ просто повторяется 5 раз; поэтому такой код называется кодом с повторением.
Пример. Код 41=5, код из всех слов четного веса. Код с /г=3, п=4 и с проверочной матрицей Н= (1111). Каждое кодовое слово содержит три информационных символа XiX2x3 и один прове-
ПОЧНЫЙ СИМВОЛ Х4 = Х1+Х2 + Х3. Кодовыми словами, число которых 23=8, являются последовательности 0000, ООП, 0101, 1001, ОНО, 1010,'1100, 1111, т. е. все возможные векторы длины 4 с четным числом единиц.
Упражнения. (1). Код ^4 имеет проверочную матрицу „ Г10101
I Н — .
1101
Выписать все кодовые слова. Проделать то же самое для мат
рицы
Н =
опг
1101
Как связаны эти коды?
(2). Код 41=5 имеет проверочную матрицу
7) 1 1
н= 1 0 1
110 0"
10 10
10 0 1
1 1 0
Выписать все кодовые слова.
(3). Показать, что при р>1/2 переименование на рис. 1.1 принятых символов преобразует этот канал в двоичный симметричный канал с р<1/2. Показать, что при р=Г/2 связь невозможна.
1.2. СВОЙСТВА ЛИНЕЙНОГО КОДА
(i) . Повторим еще раз определение: x—Xi... хп является кодовым словом, если и только если
Нхт = 0. (1.1)
(ii) . Обычно проверочная матрица Н — это ((и—k) Х«) -матрица вида
H=[AIU
и, как мы уже видели, имеется 2k кодовых слов, удовлетворяющих (1.1). (Это остается справедливым, даже если Н не имеет такого вида, при условии, что она состоит из п столбцов и п—k линейно независимых строк.) Если Н представлена в виде (1.2), то кодовые слова выглядят таким образом:
X = %! • -xh xfe+1 • • -хп.
Информационные Проверочные символы символы
(iii) . Порождающая матрица. Если известно сообщение и = =«1...ий, то как найти соответствующее кодовое слово x=%i... • •хп? Во-первых, х\ = ир, ...; Xk—Uk или
где Ц — единичная матрица.
Тогда из (1-1)' и (1.2) получаем, что
\хп/
/ Xk+1\ \
: I —Л| : =—А : , (1.6)
\ хп / \xh / /
где последнее равенство выполняется в силу (1.5). В двоичном случае —А=А, но в дальнейшем встретятся случаи, когда —А=#А. Объединяя теперь (1.5) и (1.6), имеем
(х. \ f Щ\
• 1 = [—]| ’ I
‘ / I — а]1 I
хп / \^k /
и, транспонируя, получаем равенство
x = uG, (1.7)
где
G = [Ife|— Ат]. (1.8)
Если Н представлена в каноническом виде, то G легко получается из Н (см. (1.2)). G называется порождающей матрицей кода, так как равенство (1.7) как раз означает, что кодовыми словами являются все возможные линейные комбинации строк матрицы G. (Мы могли бы использовать это в качестве определения линейного кода.) Из (1.1) и (1.7) следует, что матрицы G и Н связаны соотношением
GHT= 0 или HGr= 0. (1.9)
Пример. Код (продолжение). Выпишем порождающую матрицу
G = [l3 | — Ат] =
“100
010
001
011 ”| строка 1
101 строка 2
110 J строка 3
Согласно (1.7) каждое из восьми кодовых слов имеет вид: щ- (строка 1) +и2- (строка 2) + из- (строка 3)
(«ь и2, «з=0 или 1).
Вновь убеждаемся, что кодовое слово, соответствующее сообщению и=011, равно
x=uG =строка 2+строка 3=0101014-001110=011011, где, как обычно, сложение было выполнено по модулю 2.
(iv) . Параметры линейного кода. Говорят, что кодовое слово х=Х!...хп имеет длину п. Здесь имеется.в виду не длииа вектора в обычном математическом смысле, а число символов в этом векторе, т. е. его размерность. Число п называется также блоковой
длиной кода. Если’Н имеет п—k линейно независимых строк, то имеется 2k кодовых слов. Число k называется размерностью кода1. Мы назовем такой код [п, &]-кодом. Этот код использует п символов для передачи k символов сообщения, поэтому говорят, что код имеет скорость или эффективность R=kfn.
(v) . Другие порождающие и проверочные матрицы. Код может иметь несколько различных порождающих матриц. Например, мат-
рицы
Г11101 Г1011]
и 0101 0101
обе являются порождающими для кода #4. В действительности любое максимальное множество линейно независимых кодовых слов, выбранных из данного кода, может быть использовано в качестве строк порождающей матрицы для этого кода.
Проверочным соотношением для кода ‘g’ является любой вектор h, такой, что hxT=0 для всех кодовых слов хе?'. Аналогичным образом любое максимальное множество линейно независимых проверочных соотношений может быть использовано в качестве строк проверочной матрицы Н для кода ‘g’. Например, матрицы
ГЮ10] Г°111]
и 1101 1101
обе являются проверочными для кода 4М-
(vi) . Коды над другими полями. Вместо использования только символов 0 и 1 мы можем допустить, чтобы символы были из любого конечного поля (см. гл. 3 и 4). Например, троичный код имеет символы 0, 1 и 2 и все вычисления в проверочных соотношениях и т. п. выполняются по модулю 3 (1+2=0; —1=2; 2 + 2=1; 2-2=1 и т. д.). Если используются символы конечного поля из q элементов, то код по-прежнему определяется соотношениями (1.1) и (1.2) или, что эквивалентно, (1.7) и (1.8) и [п, &]-код содержат qk кодовых слов.
Пример. Код 4И- Троичный [4,2]-код задается проверочной матрицей
Н =
1110
1201
= [А | 12].
Тогда порождающая матрица имеет вид (см. (1.8)):
0-[1,| -АЧ = Г1022] crf,:"'a 1 [0121J строка 2 -
Код состоит из следующих девяти слов вида щ • (строка 1) + + и2-(строка 2) («ь «2=0, 1 или 2):
1 Обычно k называется числом информационных символов. (Прим, перев.)
Сообщение и Кодовое слово
00 0000
01 0121
02 0212
10 1022
11 1110
12 11201
20 2011
21 2102
22 2220
Этот код имеет скорость R—kln=}:i2.
(vii) . Линейность. Если х и у — кодовые слова данного кода, то х+у — также кодовые слова этого кода, так как Н(х+у)т=Нхт+ + Нут=0. Если с — любой элемент поля, то сх — также кодовое слово, так как Н(сх)т=сНхт=0. Например, в троичном коде, если х — кодовое слово, то 2х=—х также является кодовым словом. Поэтому эти коды и называются линейными кодами. Такой код является также аддитивной группой и векторным пространством над полем.
Упражнения. (4). Код #2 (продолжение). Выписать проверочную и порождающую матрицы для произвольного [п, 1]-кода с повторением. *
(5). Код 41= 3 (продолжение). Выписать проверочную и порождающую матрицы для произвольного [п, п—1]-кодй из всех слов четного веса.
(6). Что собой представляет код ’ё’, порождающая матрица которого является невырожденной?
1.3. НА ПРИЕМНОМ КОНЦЕ
(Снова возвращаемся к двоичным кодам.) Предположим, что сообщение и=ц1... Uk закодировано в кодовое слово x=xi... хп, которое потом передается по каналу. Так как канал с шумом, принятый вектор y=yi...yn может отличаться от х. Удобно ввести вектор ошибок
е = у—х=С! • .е„.
(1-W)
Тогда ег = О с вероятностью 1—р (в этом случае i-й символ правильный) и вг=1 с вероятностью р (i-й символ неправильный). В примере первого параграфа р было равно 1./100, но в общем случае р может быть любым числом в диапазоне 1/2. Итак, мы описываем действие канала, говоря, что он искажает кодовое слово х, прибавляя к нему вектор ошибок е.
Декодер (рис. 1.3) должен ца основании у решить, какое сообщение и или (что обычно проще) какое кодовое слово х было передано. Конечно, достаточно, если декодер найдет е, так как тбфда х=у—е. Но декодер никогда не может знать наверняка, какой был вектор ошибок е. Его стратегия, следовательно, будет заклю чаться в выборе наиболее вероятного для данного принятого у вектора ошибок е. При условиц, что все кодовые слова равновероят
ны эта стратегия оптимальна в том смысле, что она минимизирует вероятность ошибки декодера, и такая стратегия называется декодированием по максимуму правдоподобия.
Для того чтобы описать, как это делает декодер, нам нужны два важных определения.
Канал
Вектор ошибок
Рис. 1.3. Полная система связи
Определение. Расстояние (Хэмминга) между двумя векторами х=%1. .. хп и у—У1 Уп равно числу позиций, в которых они различаются; оно обозначается dist(х, у), например dist (10111, 00101) =2; dist (0122, 1220)—3 (то же самое определение справедливо и для недвоичных векторов).
Определение. Вес (Хэмминга) вектора x=xi...xn равен числу ненулевых хр, он обозначается wt (х), например wt( 101110) = =4; wt(01212110) =6.
Очевидно, что
dist(x, y) = wt(x—у), (1.11)
так как обе части выражают число позиций, в которых различаются векторы х и у.
Упражнение. (7). Определим пересечение двоичных векторов х и у как .вектор х * у— (XiZ/i,..., хпуп), имеющий единицы только в тех позициях, в которых их имеют оба вектора х и у, например 11001 *10111 = 10001. Показать, что
wt (х -Р у) = wt (х) + wt (у)—2wt (х*у). (1.12)
Теперь вернемся к декодированию. Ошибки происходят с вероятностью р, например
Prob {е = 00000} = (1 — р)5;
Prbb {е = 01000} = р (1 — р)4;
Prob{e= 10010} = р2(1—р)3.
В общем случае, если v — некоторый фиксированный вектор веса а, то
Prob{e = v} = pa(l—р)п~а- (1.13)
Так как p<Z 1/2, то 1—р>р и
(1— р)5>р(1 — р)4>р2(1 — р)3> . . .
Следовательно, фиксированный вектор ошибок веса 1 более вероятен, чем фиксированный вектор ошибок .веса 2, и т. д. Поэтому стратегия декодирования такова: у декодируется в ближайшее кодовое слово х (ближайшее в смысле расстояния Хэмминга), иначе говоря, выбирается вектор ошибок е с наименьшим весом. Это называется декодированием в ближайшее кодовое слово.
Декодирование полным перебором заключается просто в сравнении у со всеми 2k кодовыми словами и в выборе ближайшего слова. Это хорошо для небольших кодов. Но если k велико, это невозможно! Одной из целей теории кодирования и является отыскание кодов, которые могут быть декодированы более быстрым методом, чем этот.
Минимальное расстояние кода. Третьим важным параметром кода кроме длины и размерности, является минимальное расстояние Хемминга между его кодовыми словами:
d = min{dist(u, v)} = min{wt(u—v)}; и&'^; u=^v. (1.14)
Число d называется минимальным расстоянием или просто расстоянием кода. Любые два кодовых слова различаются по крайней мере в d позициях.
Линейный код длины и, размерности k и с минимальным расстоянием d далее будет называться [n, k, d]-кодом.
Для нахождения минимального расстояния линейного кода не обязательно сравнивать все возможные пары кодовых слов. Если и и v принадлежат линейному коду <ё>, то и—v=w также является кодовым словом, и, как следует из (1.14), d=min wt(w), где w^O и we??.
Другими словами, справедлива теорема.
Теорема 1. Минимальное расстояние линейного кода равно минимальному весу ненулевых кодовых слов.
Пример. Минимальные расстояния кодов ф=1, =)(=2, =Н=3> #6 равны 3, 5, 2, 3 соответственно.
Как много ошибок может исправлять код?
Теорема 2. Код с минимальным расстоянием d может исправлять l(d—1) /2] ошибок1. Если d четное, то код может одновременно исправлять (d—2)/2 ошибок и обнаруживать d/2 ошибок.
Доказательство. Предположим, что d=3 (рнс. 1.4). Шар радиуса г с центром в точке и.состоит из всех .векторов v такцх, что dist(u, v)^r. Если вокруг каждого кодового слова описать шар радиуса 1, то эти шары не пересекаются. Если передавалось кодовое слово и и произошла одна ошибка, то принятый вектор а находится внутри шара, проведенного вокруг и, и поэтому а ближе к и, чем к любому другому кодовому слову V. Таким образом, декодирование в ближайшее кодовое слово исправит эту ошибку. По-
1 [х] обозначает наибольшее целое число, меньшее или равное х. Например, [3, 5]=3, [—1, 5) =—2.
добным образом, если d=2?+l, то шары радиуса t, описанные-около каждого кодового слова, не пересекаются и код может исправлять t ошибок.
Рис. 1.4. Код с минимальным расстоянием d=3 ( 0 обозначает кодовое слово)
Рис. 1.5. Код с минимальным расстоянием d=4 ( ® обозначает кодовое слово)
Теперь предположим, что d четное (рис. 1.5, где d=4). Сферы' радиуса (d—2)/2, проведенные вокруг кодовых слов, не пересекаются, и поэтому код может исправлять (d—2)/2. ошибок. Но если произошло d/2 ошибок, то принятый вектор а может находиться посреди между двумя кодовыми словами (рис. 1.5). В этом случае-декодер может только обнаружить, что произошло d/2 (или больше) ошибок.
Таким образом, код #1, минимальное расстояние которого равно 3, является кодом, исправляющим одну ошибку.
С другой стороны, если произошло больше чем’d/2 ошибок, то: принятый вектор может быть (пли не быть) ближе к некоторому другому кодовому слову, а не к правильному. Если это произойдет, то декодер ошибется и выдаст неправильное кодовое слово. Это называется ошибкой декодирования. Конечно, с хорошим кодом это случается редко.
Пока что мы предположили, что декодер всегда будет пытаться найти ближайшее кодовое слово. Эта схема декодирования, называемая полным декодированием, хороша для сообщений, которые не могут быть переданы еще раз, таких как фотография с Марса или старая магнитная лента. В таком случае мы хотим извлечь из: принятого вектора как можно больше.
Но часто мы хотим быть более осторожными или просто не в состоянии воспользоваться самым дорогим методом декодирования. В таких случаях можно пользоваться следующей стратегией' неполного декодирования: если полагается, что произошло не более чем I ошибок, то они исправляются, в противном случае сообщение отвергается или переспрашивается.
Обнаружение ошибок представляет собой предельный вариант гакой стратегии, когда получатель не пытается исправлять ошибки, а только проверяет, является ли принятый вектор кодовым словом. Если это не так, то он обнаруживает, что произошла ошибка, и просит еще раз передать сообщение. Эта схема имеет, те преимущества, что алгоритм обнаружения ошибок очень прост (смотри следующий раздел) и что вероятность необнаруженной ошибки* эчень мала (см. § 1.5). Недостатком схемы является то, что в слу-
чае плохого канала слишком много времени будет затрачиваться .на повторную передачу, что является неэффективным использованием канала и ведет к нежелательным задержкам сообщений по
времени.
Недвоичные коды. Почти все, что мы сказали, в равной мере хорошо применимо к кодам над другими полями. Если поле F имеет q элементов, то сообщение и,
Рис. 1.6. Троичный симметричный канал (р — вероятность ошибки)
кодовое слово х, принятый вектор у и вектор ошибок е=у—x=eie2.-e?i— все имеют компоненты из F.
Предположим, что е, равно 0 с вероятностью 1—р>1/2 и равно любому из q—1 ненулевых элементов F с вероятностью pl{q—1). Другими словами, канал является /?-ич-ным симметричным каналом с q входами, q выходами, вероятностью 1— —р>1/2, что никакой ошибки не произошло, и вероятностью р<1/2, что произошла ошибка, причем все 1 возможных ошибок равновероятны.
Пример. Для случая q—З троичный симметричный канал
доказан на рис. 1.6.
Упражнения. (8). Показать, что для двоичных векторов:
(a).wt(x + y) > wt (х)—wt (у),
(1-15)
причем равенство выполняется, если и только если x<=l всегда, когда Уг=\\
(b). wt(х + z) + wt(у +z) + wt(х + у + z) > 2wt(х + у + х*у)—wt(z),
(1-16) шричем равенство выполняется, если и только если никогда не случится так, что х< и yi равны 0, a Zi равно 1.
(9) . Для векторов х и у над любым полем определим их произведение как вектор х *у= (JCiZ/i, -. -, xn«/n).
Для двоичных векторов это называется пересечением — см. упражнение (7). Показать, что для троичных векторов «
wt (х + у) = wt (х) + wt (у)—f (х*у), (1.17)
где if (и) ='Ь + 2с, если вектор и = щ .. ,ип содержит а нулей, й'еди-гниц и с двоек. Следовательно, -
'wt (х) + wt (у)—2 wt (х*у) < wt (х + у) < wt (х) Д- wt (у)—wt (х*у).
(1-18)
(10) . Показать, что в линейном двоичном коде либо все кодовые слова имеют четный вес, либо точно половина слов имеет четный вес и половина слов имеет нечетный вес.
(11) . Показать, что в линейном двоичном коде либо все кодовые слова начинаются с 0, либо точно половина слов начинается с 0 и половина слов начинается с 1. Обобщите!
Оба упражнения (10) и (11) следуют из упражнения (12)..
(12) . Предположим, что G — абелева группа, которая содержит' подмножество А, удовлетворяющее следующим трем свойствам:, (i) если Д1, а2^Л, то а\—(ii) если Ьг, Ь2^А, то bi—Ъ2^А\ (iii) если а^А, Ь^А, то а+Ь^А. Показать, что либо A = G, либо А — подгруппа G и существует элемент Ь^А такой, что
с=ли(ь+л),
где Ь+А —множество всех элементов вида b + а, а^А.
(13) . Показать, что расстояние Хэмминга удовлетворяет неравенству треугольника-, для любых векторов х=Х!... хп, y=yi... уп, Z = Zi... zn
dist(x, y) + dist(y, z)>dist(x, z). (1.19),
Показать, что равенство выполняется тогда и только тогда, когда для всех i либо Xt=yi, либо yi=Zi (либо и то и другое вместе).
(14) . Как следствие показать, что если минимальное расстояние кода равно d и при передаче кодового слова х произошло не более чем (d—1)/2 ошибок, то для всех кодовых слов z#=x выполняется неравенство dist(x, y)<dist(y, z), где у — принятый вектор (более формальное доказательство теоремы 2).
(15) . Показать, что код одновременно может исправлять ошибки кратности не более чем а и обнаруживать ошибки кратности. а+ 1,..., Ь, если и только если код имеет по крайней мере расстояние a + b+ 1.
(16) . Показать, что если х и у — двоичные векторы, то евклидово расстояние между точками х и у равно
^)2V/2 =( dist<x> у) У/2 •
\i=l / \ /
(17) . Комбинирование двух кодов (I). Пусть Gi, G2 — порождающие матрицы для [ni, k, di\ - и [п2, k, d2\ -кодов соответственно. Показать, что коды с порождающими матрицами
t Gj 0\ . „ .
L1 _ и (Gx | G2)
\ U ^2 /
представляют собой + п2, 2k, min{di, d2}]~ и [гц + п2, k, dj-коды: соответственно, причем d~^di + d2.
(18) . Биномиальные коэффициенты. Биномиальный коэффициент который читается «число сочетаний из х по т», определяется следующим образом:
, . х(х— 1) • - -(х—гп-\- 1)/т1, если т—натуральное число;
= 1, если т= 0;
п
(0 в других случаях,
гДе х — любое действительное число, a ml = 1 -2-3- ... • (tn—1)Х. Х/72, 01 = 1. Читатель должен знать следующие свойства:
(а) . Если х=п — натуральное число и то
/ п \ _ п\ \т ) т\ (п — т)! ’
что равно числу всех возможных неупорядоченных выборок по т элементов из множества п элементов.
(Ь) . Всего имеется двоичных векторов длины п и веса т. Число же всех векторов над полем из q элементов, имеющих длину п и 'вес т, равно (q—l)m^ J (так как каждая из т ненулевых координат вектора может быть занята любым ненулевым элементом поля).
(с) . Биномиальные ряду: п .
(а-[-Ь)п ="У ( ) ап~тЬт, если п — целое неотрицательное число;
т—0
со . .
=2 \ уm для । ^ । < 1и любого действительног° т=о''/И '
QO
----------= V \br для |Ь|<1 и любого действительного к.
(1-й)х+1 r )
[Помните о студенте, который на экзаменационный вопрос о разложении в ряд выражения (а+Ь)п ответил: (а + Ь)п, (а+Ь)п, '(a+ib)n, (a + b)n, (а+Ь)п, ... ?].
(d) . Простые тождества. (Здесь п и m — целые неотрицательные числа, х — любое действительное число.)
(19) . Предположим, .что и и v — двоичные векторы с расстоянием dist(u, v)=d.-Показать, что число векторов w таких, чтс dist(u, w)=r и dist(v, w)=s, равно где i==(d+r~
s)/2. Если d+r—s нечетно, то число таких векторов равно нулю, в-
. . / d \
то же время если r+s=d, то это число равно 1 I.
(20) . Пусть u, v, w и х — четыре вектора, любые два из которых находятся друг от друга на расстоянии d; при этом d четное число. Показать, что имеется точно один вектор, который находится на расстоянии d/2 от каждого из векторов u, v и w. Показать,, что имеется самое большее один вектор, находящийся на расстоянии d/2 от всех векторов u, v, w и х.
1.4. НЕМНОГО ПОДРОБНЕЕ О ДЕКОДИРОВАНИИ ЛИНЕЙНОГО КОДА
Определение смежного класса. Пусть Я? является [и, k] линейным кодом над полем из q элементов. Для любого вектора а множество
a + 'g’= {а-]-х : хе®7} называется смежным классом (или сдвигом) кода Любой вектор b находится в некотором смежном классе (например, в b-pg7). Два вектора а и b лежат в одном и том же смежном классе, тогда и только тогда, когда (а—Ь) Каждый смежный класс содер-
жит qk векторов.
Утверждение 3. Два смежных класса либо не пересекаются, либо совпадают (частичное перекрытие невозможно).
Доказательство. Если смежные классы a-j-'g7 и b+'g7 пересекаются, то возьмем ve(a+f) П(Ь + <®7). Тогда v=a + x=b+y, где х, ye'g7. Следовательно, Ь=а+х—у=а+х'(х/е'®7) и поэтому Ь + +&cza.+ff. Аналогичным образом получается, что a+'g’czb-f-'g7 и, значит, a-|-<g7=b + 'g’. *
Следовательно, множество Fn всех векторов может быть разбито на смежные классы <®7:
= U (ai + ^) U (а2 + ^) U • • - U (at + 4g), (1.21)
где t=qn-k—l.
Предположим теперь, что декодер принимает вектор у. Этот вектор должен принадлежать некоторому смежному классу в разложении (1.21), скажем, y=ai-|-x(xe<g7). Что собой представляют возможные векторы ошибок е, которые могли произойти? Если было передано кодовое слово х', то вектор ошибок — это вектор е==у—х'=а{-|-х—х'=а; + х"£а,:+$. Отсюда мы заключаем, что возможными векторами ошибок являются в точности все векторы из смежного класса, содержащего у.
Поэтому при данном у стратегия декодера заключается в выборе из смежного класса, содержащего у, вектора е с наимень
шим весом и в декодировании у как х=у—е. Вектор из смежного класса, имеющий минимальный вес, называется лидером смежного класса. (Если же имеется более одного вектора с минимальным весом, то выберем случайным образом любой из таких векторов и назовем его лидером смежного класса.)
Будем считать, что в разложении (1.21) векторы являются -лидерами смежных классов.
Стандартное расположение. Полезным способом описания работы декодера является таблица, названная стандартным расположением для кода. Первая строка ее состоит из самого кода с нулевым кодовым словом с левой стороны: х<!> = 0; х<2\ ..., x(s) (s=qk)', другими строками являются другие смежные классы ai-|-‘iF, расположенные в том же самом порядке и с лидерами этих классов с левой стороны:
аг + х(1), аг + х(2), • • •, af + x(s).
Пример. Код ^4 (продолжение). [4,2]-код с порождающей матрицей
Г- Г10111 [oioi
имеет стандартное расположение, показанное на рис. 1.7 (пока не обращайте внимания на последний столбец).
Сообщение: 00 10 01 11 Синдром S
Код: 0000 1011 0101 1110 л
Смежный класс: 1000 ООП 1101 оно
Смежный класс: 0100 1111 0001 1010 ?)
Смежный класс: 0010 лидеры смежных классов 1001 0111 1100
Рис. 1.7. Стандартное расположение
Заметим, что рис. 1.7 содержит все 16 векторов длины 4, которые разбиты на четыре смежных класса, образующих строки таблицы, и лидеры этих классов расположены в левом столбце.
Теперь о том, как декодер использует стандартное расположение. Когда принят у (например, 1111), определяется его положение в таблице. Затем декодер принимает решение, что вектор ошибок е — это лидер смежного класса, расположенный в первом столбце в той же строке, что и у, т. е. элемент (0100), и у декоди-л л
руется в кодовое слово х=у—е= 1011, которое находится в начале столбца, содержащего у. (Соответствующее сообщение равно 10.)
Декодирование, использующее стандартное расположение, является декодированием по максимуму правдоподобия.
Синдром. Имеется простой способ, как определить, в каком смежном классе находится у: надо вычислить вектор S=Hyr, который называется синдромом у.
Свойства синдрома. (1). S представляет собой вектор-столбец, длины п—k.
(2) . Синдром вектора у, S = Нуг, равен нулю, если и только если у — кодовое слово (по определению кода). Поэтому, если никаких ошибок не произошло, синдром вектора у равен нулю (но не обратное). В общем случае, если у=х + е, где то
S = Ну 7 = Нхт + Нет = Нет. (1,22>
(3) . Если для двоичного кода имеются ошибки на позициях с номерами а, Ь, с,..., так что е=0 ... 010 ... 1 ... 1 ... 0, то из (1.22)
а b с получаем, что
S = ^ezH^Ha + Hb + Hc+ . . .,
i
где Hj—i-й столбец Н.
Словами это можно сказать так:
Теорема 4. Для двоичного кода синдром равен сумме тех столбцов Н, где произошли ошибки. [Таким образом, S называется синдромом, так как он выделяет совокупность ошибок.]
(4) . Два вектора находятся в одном и том же смежном классе-кода ‘g7, если и только если они имеют один и тот же синдром. Действительно, и и v находятся в одном смежном классе, если и. только если (u—V) е^7, что эквивалентно Н (и—v)r=0 или Нит=: = Hvr. Следовательно, справедливо утверждение, приведенное ниже.
Теорема 5. Имеется взаимно однозначное соответствие между синдромами и смежными классами.
Например, смежные классы на рис. 1.7 занумерованы их синдромами.
Таким образом, синдром содержит всю информацию, которую, имеет приемник об ошибках.
По свойству (2) схема обнаружения ошибок, упомянутая в последнем разделе, как раз состоит в сравнении синдрома с нулем. Для этого мы еще раз вычисляем проверочные символы, используя принятые информационные символы, и смотрим, совпадают ли они с принятыми проверочными символами. Иначе говоря, мы перекодируем принятые информационные символы. Для этого требуется еще одно кодирующее устройство, которое обычно является весьма простым в сравнении с декодером (см. рис. 7.8).
Упражнения. (21). Построить стандартное расположение Для кода #1. Используя его, декодировать векторы 110100 и НИИ.
(22) . Показать, что, если ‘g7— двоичный линейный код и аеД'ё7,. то J также является линейным кодом.
1.5. ВЕРОЯСГЬ ШИБКИ1
Когда декодирование использует стандартное расположение, 'выбранный декодером вектор ошибок всегда представляет собой один из лидеров смежных классов. Декодирование является правильным, если и только если истинный вектор ошибок в действительности является лидером смежного класса. Если это не так, то декодер совершает ошибку и выдает неправильное кодовое слово. (Хотя при этом некоторые из информационных символов могут быть правильными.)
Определение. Вероятностью ошибки, или вероятностью ошибки на слово, Рош для данной схемы декодирования называется вероятность появления неправильного кодового слова на выходе декодера.
Если имеется М кодовых слов х(1),..., х(М), которые, как мы предполагаем, используются с равной вероятностью, то
м
выход декодера y=x(i) | х(г) было послано . (1.23)
Если мы декодируем, пользуясь стандартным расположением, то ошибка декодирования происходит тогда и только тогда, когда вектор ошибок е не является лидером смежного класса, так что Рош = Prob {е лидер смежного класса}.
Предположим, что имеется а.{ лидеров смежного класса веса I. Тогда, используя (1.13), получаем
Pon^i-JWU-p)"^. (1-24)
г=0
(Так как стандартное расположение обеспечивает декодирование по максимуму правдоподобия, то любая другая схема декодирования будет иметь вероятность ошибки Рош не меньше чем правая часть (1.24).)
Примеры. Для кода #4 (см. рис. 1.7) имеем а0=1; ai=3, так что
рош = 1—(!—Р)4—Зр(1—р)3 = 0,0103 - • ;
если р~ 1/100.
Для кода ф 1 имеем ао= 1си = 6; 02=1, так что
Рош=1- (1— Р)6— 6р(1— р)5 — ^(1— р)4 =0,00136 . . ;
если р = 1/100.
Если код имеет минимальное расстояние ^=2^ + 1 или 2/+2, то (по теореме 2) он может исправлять t ошибок. Поэтому каждый
* Здесь и далее имеется в виду вероятность ошибки декодирования. (Прим.
вектор ошибок веса не более t является лидером смежного класса. Другими словами,
(1.25) \ * /
Но для значений i>Z вычислить щ чрезвычайно трудно, и они известны только для очень немногих кодов.
Если вероятность ошибки в канале р очень мала, то 1—р = 1 и р’(1—p)n~i^> pi+1 {\—р)”-'-1. В этом случае в (1.24) можно пренебречь членами с большими i и формулы
Рош=1-(1-26) i=0 '
или t
?o,n = 1 - X ( • ) Р1 (1 -РУ1 - “ж pt+' (1 - Р^' (1 -27)
являются полезными аппроксимациями. В любом случае правые части формул (1.26) или (1.27) являются верхними границами для Р ОШ-
Совершенные коды. Конечно, если а; = 0 при i>t=[{d—1)/2], то формула (1.26) становится точной. Такой код называется совершенным.
Таким образом, совершенный код, исправляющий t ошибок, может исправлять все ошибки веса не более t и не может исправлять ни одной ошибки веса больше, чем t. Это эквивалентно тому, что шары радиуса t, проведенные вокруг всех кодовых слов, не пересекаются и вместе содержат все векторы длины п. В гл. 6 и 20 мы узнаем гораздо больше о совершенных кодах.
Квазисовершенные коды. Если же теперь «j = 0 при i>£+l, то становится точной формула (1.27). Такой код называется квазисо-вершенным.
Таким образом, квазисовершенный код, исправляющий t ошибок, может исправлять все ошибки веса не более t, некоторые ошибки веса t+1 и не может исправлять ни одной ошибки веса больше, чем Z+1. Шары радиуса Z+1, проведенные вокруг кодовых слов, могут пересекаться, и вместе они содержат все векторы длины п. Мы снова встретимся с квазисовершеиными кодами в гл. 6, 9 и 15.
Граница сферической упаковки, или граница Хэмминга. Предположим, что 'ё’ — двоичный код длины п, содержащий М кодовых слов, который может исправлять t ошибок. Шары радиуса t, проведенные вокруг всех кодовых слов, не пересекаются. Каждый из
/ п \ , , I п \ .
этих М шаров содержит 1 +' I у + • • + у I векторов (см. упражнение 18 (Ь)). Но число векторов во :всем пространстве равно 2”. Поэтому мы получаем следующую теорему.
Теорема 6. {Граница сферической упаковки, или граница Хэмминга). Если существует двоичный код длины п, исправляю-
щий t ошибок и содержащий М кодовых слов, то должно выполняться неравенство
ж(1+(1)+(г)+• •+(“))<2" (Ь28)
Аналогично для кода над полем из q элементов
лф + (<7-1)(")+ • • . + (9-1/(1.29)
Для больших п см. теорему 31 гл. 17. Так как при доказательстве этих двух границ не используется линейность кода, то они также справедливы и для нелинейных кодов (см. гл. 2).
По определению код совершенен тогда и только тогда, когда в (1.28) или (1.29) выполняется равенство.
Вероятность ошибки на символ. Так как некоторые из информационных символов могут быть правильными, даже если деко* дер выдает неправильное кодовое слово, то более полезной мерой качества декодирования является вероятность ошибки на символ, определяемая следующим образом.
Определение. Предположим, что код содержит М кодовых слов i=l,... ,М, и первые k символов x'i(i)...
... в каждом кодовом слове являются информационными сим-
Л Л А
волами. Пусть x=xi... хп— символы на выходе декодера. Тогда вероятность ошибки на символ РСимв определяется как средняя вероятность того, что после декодирования информационный символ является ошибочным:
k м
^симв^^ Prob {xjijAxj0 I х(г) было послано }. (1.30)
/=1 1^1
Упражнение. (23). Показать, что если при декодировании используется стандартное расположение и все сообщения равновероятны, то Рсимв не зависит от того, какое кодовое слово было послано. В самом деле, если послано кодовое слово x=Xi... хп и
ЛА Л
оно декодировано как x=xj.. .хп, то
1 Л, < (Л )
^симв = -у 2 Prob W ’ (1 -31)
/=1
^свмв у/(e)Prob{е}, (1.32)
е
где ./(е) обозначает число неправильных информационных символов после декодирования при условии, что е — вектор ошибок, и поэтому
1 k
гдс р. — вес первых k позиций кодового слова в начале i-го столб-ца стандартного расположения, а Р(с,) —суммарная вероятность появления всех двоичных векторов этого столбца1.
Пример. Вернемся к стандартному расположению на рис. 1.7. Здесь /(е)=0, если е находится в первом столбце таблицы (где расположены лидеры смежных классов), /(е) = 1, если е находится во 2-м или 3-м столбцах, и /(е)=2, если е находится в последнем столбце. Тогда из (1.32)
^симв = -^ (1 • (Р4 + Зр3<7 + 3pV + pg3) + 2 • (psq + 3p2g2)) =
= 0,00530 • • -, если p= 1/100; g=l—p.
Использование этого очень простого кода понизило среднюю вероятность ошибки на символ от 0,01 до 0,0053.
Упражнения. (24). Показать, что при декодировании кода 4г 1 с помощью стандартного расположения
Рсимв = (22pV + 3W + 24p4g2 + 12Р5<7 + 2р6)/3 = 0,00072, если р = 1/100.
Как видно из этих примеров, значение РСимв трудно .вычислять, и оно неизвестно для большинства кодов.
(25). Показать, что для [п, kJ -кода —- Рош рСимв РОш-
k
Неполное декодирование. Схему неполного декодирования, которая исправляет ошибки кратности не более чем I, следующим образом можно описать в терминах стандартного расположения. Расположим смежные классы в порядке увеличения веса (т. е. уменьшения вероятности) их лидеров (рис. 1.8).
Исправляемые ошибки (лидеры смежных классов веса не более Z)
Обнаруживаемые ошибки
(лидеры смежных классов веса более Z)
Рис. 1.8. Неполное декодирование, использующее стандартное расположение
Если принятый вектор у лежит в верхней части таблицы, то, как и прежде, у декодируется в кодовое слово, являющееся самым верхним в столбце, содержащим у. Если же у лежит в нижней половине, то декодер просто обнаруживает, что произошло больше чем ,/ ошибок.
Обнаружение ошибок. При обнаружении ошибок декодер ошибется и допустит кодовое слово, отличное от переданного, тогда и только тогда, когда вектор ошибок является ненулевым кодовым
1 Под вероятностью вектора-столбца здесь подразумевается вероятность
его как вектора ошибок. (Прим, ред.)
словом. Если код содержит А, кодовых слов веса i, то вероятность ошибки равна:
(1-33) i—1
Вероятность же того, что ошибка будет обнаружена и сообщение будет передано еще раз, равна
^переспроса = 1 ~(1 -р)"-РОш- (1 -34)
Пример. Для кода #1 Ло=1; А3=4; Л4 = 3 и РОш=4р3(1— —р)3 + 3р4(1—р)2 = 0,00000391 ..., если р= 1/100.
Это значение намного меньше, чем вероятность ошибки 0,00136, полученная при декодировании этого кода с помощью стандарт- ' ного расположения. Вероятность повторной передачи равна ^переспроса:= 0,0585 . . .
Задача (нерешенная). (1.1). Найти распределение {щ} лидеров смежных классов для любого из известных семейств кодов. Эта задача все еще не решена даже для кодов Рида — Мал-лера первого порядка (см. гл. 14, а также работы Берлекэмпа и Велча [133], Лейнера [797—799], Сарвейта [1144] и Слоэна и Дика [1233]).
1.6. ТЕОРЕМА ШЕННОНА О СУЩЕСТВОВАНИИ ХОРОШИХ КОДОВ
С(р)Ь
О 1/2 1 р
Рис. 1.9. Пропускная способность двоичного симметричного канала
В последнем разделе мы убедились, что очень простой код * 4 уменьшает среднюю вероятность ошибки на символ от 0,01 до 0,00530 (ценой передачи 4 символов вместо передачи 2 символов сообщения) и что код * 1, который также имеет скорость 1/2, уменьшает это значение до 0,00072 (теперь вместо 3 информационных символов необходимо передать 6 символов).
В общем случае для фиксированной скорости R = k[n хотелось бы знать, сколь малым мы можем сделать значение РСимв с помощью [п, й]-кода. Ответ дается замечательной теоремой Шеннона, которая утверждает, что Рош (а следовательно, и Рсимв в силу упражнения (25)) может быть сделана сколь угодно малой при условии, что скорость R меньше пропускной способности канала.
Определение. Пропускная способность двоичного симметричного канала с вероятностью ошибки р (см. рис. 1.1) равна (рис. 1.9):
С(р) = l + plog2p + (l— p)loga(l— р). (1.35)
Теорема 7. (Шеннон; доказательство опущено). Для любого е>0, если Д<С(р) и п достаточно велико, существует [и, /г] дво-
ичный код со скоростью kjn^R, вероятность ошибки которого Р ош< е.
(Подобный же результат справедлив и для недвоичных кодов, но с другим определением пропускной способности.)
К сожалению, эта теорема была доказана пока только вероятностными методами и ничего не говорит о том, как построить эти коды.
На практике (как мы уже видели) трудно вычислить Рош и РСимв, поэтому в качестве более удобного критерия, насколько хорош код, используется минимальное расстояние кода d. Ибо зная d, мы знаем, что код может исправлять [ (d—1)/2] ошибок (теорема 2), и формула (1.26) является хорошим приближением для Рош, особенно если р мало.
Таким образом, возможна такая формулировка основной проблемы теории кодирования: найти коды с большим R (для эффективности) и с большим d (чтобы исправлять много ошибок). Конечно, эти цели противоречивы. Верхнюю границу на мощность кода дает теорема 6; другие верхние границы будут даны в гл. 17 (см. рис. 17.7). С другой стороны, более слабой версией теоремы 7 является теорема 12 в конце этой главы, и она утверждает, что хорошие линейные коды существуют. В настоящее время, однако, мы не знаем, как найти такие коды1 *.
Конечно, для практических целей хочется также иметь код, который можно легко кодировать и декодировать.
1.7. КОДЫ ХЭММИНГА
Важным семейством кодов, которые легко кодировать и декодировать, являются коды Хэмминга, исправляющие одну ошибку. В этом параграфе мы обсудим только двоичные коды Хэмминга.
Согласно теореме 4 синдром принятого вектора равен сумме тех столбцов проверочной матрицы Н, где произошли ошибки. Следовательно, для того чтобы построить код, исправляющий одну ошибку, необходимо выбрать столбцы Н ненулевыми (в противном случае ошибка в этой позиции не будет влиять иа синдром, а значит, будет необнаруживаемой) и различными (ибо если два столбца Н равны, то ошибки в соответствующих двух позициях будут неразличимы).
Если Н должна иметь г строк (код имеет г проверочных символов), то существует только 2Г—1 допустимых столбцов, а именно’ 2’’—1 ненулевых двоичных векторов длины г. Например, если г=3, то имеются следующие 23—1=7 допустимых столбцов:
0001111
0110011 (I-36J)
1Q10101,
1 Строгую математическую постановку этой проблемы см. в [79*а, 79*6J,
(Прим, перев.)
являющихся двоичными представлениями чисел от 1 до 7. Для кода Хэмминга мы используем их все и получим код длины п = =2r—1.
Определение. Двоичный код Хэмминга Зёг длины п—2г—Г (г^2) имеет проверочную матрицу Н, столбцы которой состоят из всех ненулевых двоичных векторов длины г, причем каждый вектор встречается в матрице один раз. Код имеет параметры п—2Г—1; k=2r—1—г; d=3. »
Пример. Код 41=5 представляет собой [7, 4, 3]-код Хэмминга Зёъ с
[0001111 1
н= 0110011
(1.37)
1010101
Здесь, как и в (1.36), мы разместили столбцы Н в порядке возрастания чисел, двоичными представлениями которых они являются. Для того чтобы представить Н в стандартной форме (1-2), переставим столбцы1:
’0111100’ н'= юною 1101001
(1.38)
В общем случае
Н' = [А| 1Г],
где матрица А состоит из всех столбцов с двумя или более единицами.
Ясно, что перестановка столбцов Н не влияет на число ошибок, исправляемое кодом, или на вероятность ошибки этого кода.
Определение. Два кода называются эквивалентными, если они отличаются только перестановкой символов. Так, например, коды
0000 0000
ООП 0101 1100 1010
1111 1111
являются эквивалентными [4, 2, 2]-кодами. Поэтому матрицы Н и Н' задают эквивалентные коды.
Упражнения. (26). Показать, что матрицы '1 1 G= 1 1 1 1
порождают эквивалентные коды.
1 Чтобы представить проверочную матрицу кода 4 5 в стандартной форме, достаточно вспомнить, что код ф 5, по определению, задается именно матрицей Н'. Нетрудно проверить, что матрица Н также является проверочной матрицей кода ф 5, однако не потому, что она получена из Н' перестановкой столбцов. (Прим, ред.)
(27). Показать,
G=
что матрицы
41
11 , G' =
111111"
II 11
1 1
порождают эквивалентные коды.
(28). Показать, что код Хэмминга Д€г единствен в том смысле, что любой линейный код с параметрами [2'—1, 2Г—1—г, 3] эквивалентен Зёг.
По разным причинам (как инженерным, так и эстетическим) предпочтение может быть отдано одному из эквивалентных кодов. Например, третьей проверочной матрицей Н для кода =Н= 5 является матрица
Н"
4110100'
0111010
0011101
(1.40)
содержащая те же самые столбцы, но уже в другом порядке1. Эта1 матрица задает циклический код, т. е. циклический сдвиг любого кодового слова снова является кодовым словом. Далее мы увидим (гл. 7), что двоичные коды Хэмминга могут быть всегда сделаны циклическими.
Упражнение. (29). Код 41=7 представляет собой [15, 11, 3]-код Хэмминга Выписать для кода три формы матрицы Н, соответствующие выражениям (1.37), (1.38) и (1.40). Используя форму вида (1.38), закодировать сообщение u= 11111100000 и декодировать принятый вектор 111000111000111.
Декодирование. Предположим, что мы используем матрицу Н .вида (1.37), когда i-й столбец Н, равен двоичному представлению числа i. Если произошла ошибка в /-м символе, то из (1.22) следует, что синдром S = Нут= Нет = Нг, т. е. равен двоичному представлению числа I. Очень простое декодирование! (Никогда больше нам не встретится столь простое декодирование.)
Так как код может исправлять любую одиночную ошибку, то его минимальное расстояние d^3 (по теореме 2). На самом деле d равно 3, так как легко найти кодовые слова веса 3 (например, слово 11100... 0, если Н вида (1.37)) (см. также теорему 10).
Теорема 8. Коды Хэмминга являются совершенными кодами, исправляющими одиночные ошибки.
Доказательство. Так как код может исправлять одиночные ошибки, то шары радиуса 1 вокруг кодовых слов не пересекаются. В каждом таком шаре имеется п+1=2г векторов, а число всех шаров равно 2/!=22 г ' Ь что дает всего 22Г ~1=2’г векторов. Поэтому каждый вектор длины п находится в одном из этих шаров и, значит, код — совершенный. , (Ь
1 Матрица Н" является проверочной матрицей не кода * 5, а эквивалент-
ного ему кода. (Прим, ред.)
Сводка параметров и свойств кода Хэмминга Же t
длина п=2г—1 (г=2, 3, ...);
размерность k=2r—1—г;
число проверочных символов =г;
минимальное расстояние d=3.
Ж?,— совершенный код, исправляющий одиночные ошибки, и единственный с точностью до эквивалентности. Проверочная матрица Н кода представляет собой (гХ/г)-матрицу, столбцами которой являются все ненулевые двоичные векторы длины г.
Рис. 1.10. Свойства кода Хэмминга Ж?
Упражнения. (30). Выписать порождающую матрицу G для кода Жг и, используя ее, показать, что каждое ненулевое кодовое слово имеет вес не менее 3. [Указание. Предположить противное; тогда это кодовое слово должно быть суммой двух или менее строк G.]
(31). Показать, что для кода Хэмминга распределение лидеров смежных классов таково: ао=1; а\=п. Найти вероятность ошибки Р ОШ-
♦
1.8. ДУАЛЬНЫЙ КОД
Если u=Ui...«n; v=Di...un-—векторы (с компонентами из .поля F), то их скалярное произведение равно
U V = «IU1+ - --\-unvn (1.41)
(все вычисления производятся в F). Например, скалярное произведение двоичных векторов u= 1101 и v=llll равно uv—-1 + 1 + -j-0 +1 = 1.
Если u-v=0, то векторы и и v называются ортогональными.
Упражнение. (32). Для двоичных векторов u-v=0, если и только если wt(u* v) —четное число, и u-v=l, если и только если wt(u *v) —нечетное число. Поэтому u-u=0, если и только если wt(u) — четное число.
Как показывает это упражнение, свойства скалярных произведений векторов над конечным и действительным полями существенно отличаются.
Определение. Если У?— линейный [п, £]-код над F, то дуальный или ортогональный к нему код определяется как множество всех векторов, ортогональных всем кодовым словам кода
^х={и | u v=0 для всех ve>?}. (1.42)
Таким образом, из результатов § 1.2 вытекает, что <₽± —-это в 'точности множество всех проверок на четность для кода <ё>. Если 'F имеет порождающую матрицу G и проверочную матрицу Н, то +J- имеет порождающую матрицу Н и проверочную матрицу G. Таким образом, <g'± — это [п, п—£]-код. IF-L является подпро-
хтранством, ортогональным к'®’. (В гл. 5 мы обсудим минимальное расстояние кода g7-1-.)
Упр аж нения. (33). (а). Показать, что (g71-) -L=g7. (Ь). Пусть g7-|-S> = {u+v : uef, ve®}. Показать, что {<S'+3))A- = =g’-L П SD1-.
(34). Показать, что дуальным к двоичному [п, 1, и]-коду с повторением (код #2) является [п, п—1, 2]-код из всех слов четного веса (код #3).
Если fcf1, то назовем код слабо самодуальным, если же $’=<g'-L, то называется (строго) самодуальным.
Таким образом, код g7 слабо самодуален, если u-v=0 для каждой пары (не обязательно различных) кодовых слов в g7. Код g7 самодуален, если он слабо самодуален и имеет размерность k= =п!2 (поэтому п должно быть четным числом).
Например, двоичный код 2 с повторением слабо самодуален, если и только если п — четное. Когда п=2, код с повторением {00, 11} самодуален. Таким же является и троичный код =$=6.
Упражнения. (35). Построить двоичные самодуальные коды для длин п—4 и 8.
>(36). Для нечетного п пусть g7 будет слабо самодуальным двоичным кодом. Показать, что g7-L=g7(J {1+g7}, где 1—вектор из всех единиц.
(37) . Показать, что код с проверочной матрицей Н= [А| I] над любым полем строго самодуален тогда и только тргда, когда А — квадратная матрица такая, что ААТ=—I.
(38) . Показать, что в двоичном слабо самодуальном коде g7 каждое кодовое слово имеет четный вес. Более того, если каждая строка порождающей матрицы g7 имеет вес, кратный 4, то этому же свойству удовлетворяет каждое кодовое слово g7.
(39) . Показать, что в троичном слабо самодуальном коде g7 каждое кодовое слово имеет вес Хэмминга, кратный 3.
1.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (II)
(I). Добавление общей проверки на четность. Пусть g7 будет [и, k, d] двоичным кодом, в котором некоторые кодовые слова
л
имеют нечетный вес. Образуем новый код g7, добавляя 0 в конце каждого кодового слова g7 с четным весом и добавляя 1 в конце л
каждого слова с нечетным весом. Тогда g7 обладает тем свойством, что каждое кодовое слово имеет четный вес, т. е. этот код удовлетворяет новому уравнению проверки на четность Xi+x2+ + 4~хп=0, а именно уравнению общей проверки на четность.
Из (1.12) следует, что расстояние между каждой парой кодовых слов теперь четное число. Если минимальное расстояние кода было нечетным, то новое минимальное расстояние равно d-f-1 и
представляет собой [«4-1, k, б/+1]-код. Этот способ присоеди-
нения добавочных проверочных символов будем называть расширением кода.
л
Если имеет проверочную матрицу Н, то имеет проверочную матрицу
л
Н =
111 - -1
0
Н
6
Прим'ер. Код =4=8. Добавление общей проверки на четность к коду * 5 дает [8, 4, 4] расширенный код Хэмминга с проверочной матрицей
' 11111111 ~
Н= 00011110 (1лз>
01100110
_ 10101010
* позиции 12345670.
Так как расстояние этого кода равно d=4, то согласно теореме 2 он может исправлять любую одиночную ошибку и обнаруживать любую двойную ошибку. В самом деле, вспоминая, что
Л
синдром S равен сумме тех столбцов Н, где произошли ошибки, получаем следующую схему декодирования. Если ошибок нет, то S = 0. Если произошла одна ошибка на позиции с номером i, то
(1 \
Х Ь
У I
X / где вектор (х, у z)—двоичное представление числа i (см. (1.43)). Наконец, если произошли две ошибки, то
и декодер обнаруживает, что произошли две (или более) ошибок. Упражнения. (40). Показать код * 8 строго самодуален. (41) Показать, что расширенный код Хэмминга единствен (в том же самом смысле, что и в упражнении (28)).
Для недвоичных кодов подобный способ может как увеличивать, так и не увеличивать минимальное расстояние.
(42). Если добавить общую проверку на четность (т. е. сделать так, чтобы кодовые слова удовлетворяли уравнению
2;хг = 0 (mod 3)) к троичным кодам с порождающими матрицами
Г11000] Г12000 1 и ,
00111] [00122
то что случится с их минимальными расстояниями?
(II) . Выкалывание кодовых координат. Операция, обратная расширению кода называется выкалыванием и состоит в удалении одной или более координат из каждого кодового слова. Так, например, пусть у нас имеется [3, 2]-код 9:
000
код #9 0 И
101
ПО
Выкалывание последней координаты этого кода дает [2, 2, И-код
00
01
10
11
Выколотый код обычно обозначается через <&*. В общем случае каждый раз, когда удаляется одна координата, длина кода п уменьшается на 1, число кодовых слов не изменяется1 и (до тех пор, пока нам не везет) минимальное расстояние d уменьшается на 1.
(III) . Код с выбрасыванием. Простейший способ получения кода с выбрасыванием состоит в следующем. Предположим, что двоичный [п, k, б/]-код <8 содержит кодовые слова обоих весов, четного и нечетного. Тогда, как следует из упражнения (10), половина кодовых слов имеет четный вес и половина нечетный. Выбросим из кода все кодовые слова нечетного веса, и тогда получим [п, k—1, d'J-код. Часто d'>d (например, если d — нечетное).
ПР и мер. Из [7, 4, 3]-кода 4с 5 выбрасыванием всех слов нечетного веса получаем [7, 3, 4]-код.
(IV) . Пополнение кода путем добавления новых кодовых •слов. Простейший способ пополнения кода заключается в добавлении к нему вектора 1 из всех единиц при условии, что он не принадлежит коду. Это эквивалентно добавлению вектора 1 к порождающей матрице2. Если — [и, k, d] двоичный код, который не содержит вектора 1, то пополненный код равен
= U {1-Ш-
1 Это не всегда так — число кодовых слов может и уменьшиться в 2 раза, (например если в коде * 9 удалить две любые координаты. (Прим, ред.)
2 Так как полученный код должен быть линейным по определению. (Прим. <перев.)
Другими словами состоит из кодовых слов <8 и их допол-
нений и является [п, k + 1, -кодом, где d(o)=min{d, п—d'} и d' — наибольший вес кодовых слов кода <ё>.
Пример. Пополнение кода # 9 дает [3, 3, 1]-код, состоящий из всех векторов длины 3.
(V) . Удлинение кода путем добавления информационных символов. Обычный способ удлинения кода состоит из последовательного выполнения двух операций: пополнения кода путем добавления вектора 1 и расширения его с помощью общей проверки на четность. В результате этих операций число информационных символов увеличивается на единицу.
(VI) . Укорочение кода. Эта операция является обратной к только что описанной операции удлинения и заключается в выборе всех кодовых слов, первая координата .которых равна нулю, Xi=0, и в удалении этой координаты в выбранных словах. Описанная операция будет использоваться в дальнейших главах для укорочения нелинейных кодов.
Код, дуальный к коду Хэмминга. Для иллюстрации все эти шесть операций показаны на рис. 1.11 для кода Хэмминга и на рис. 1.13 для дуального к нему кода.
вектора (11...1))
Рис. 1.11. Применение конструкций к коду Хэмминга
Определение. Двоичным симплексным кодом Р/г называется код, дуальный к коду Хэмминга Ж- Из § 1.8 мы знаем, что Э^т представляет собой [2Г—1, г]-код с порождающей матрицей Gr, являющейся проверочной матрицей кода Ж- Так, например, для Ж матрица
и кодовые слова
ООО 011 101 НО
Для кода 5^3 имеем:
"ООО 1111" "000 1 111"
G3 = 011 ООН = g2 0 G2
Lioi 0101J 0
и кодовые слова
000 0 000 0
Oil 0 011 0 ^2-
101 0 101 0
110 0 110 0
cp„
000 1 111 1
Oil 1 100 1
101 1 010 1
no 1 001 1
По индукции мы видим, что код SPr состоит из вектора 0 и 2Г—1 кодовых слов веса 2Г~1. (Читатель может узнать в этом индуктивном процессе один из стандартных способов построения матриц Адамара — подробнее об этом будет сказано в следующей главе.)
Этот код называется симплексным, так как каждая пара кодовых слов находится друг от друга на одинаковом расстоянии. Поэтому, если на вершинах единичного куба размерности п отметить кодовые слова, то они образуют Например, когда г=3, код £?з, равный коду * 9, образует правильный тетраэдр (выделен двойными линиями на рис.
1.12).
Симплексный код д’? вновь появится в дальнейшем, но под другим именем: код максимальной длины, получаемый на регистре сдвига с обратной связью (см. § 3.4 и гл. 14).
Важным является также код, дуальный к расширенному коду Хэмминга, ибо
он представляет собой код Рида — Маллера первого порядка (см. гл. 13). Этот код получается удлинением 9\, как описано в (V). Например, такое удлинение кода SPr дает код, изображенный на, Рис. 1.14. - . . г'-.
правильный симплекс. 011
Рис. 1.12. Изображение кода # 9 в виде вершин тетраэдра
Рис. 1.13. Применение конструкций к симплекс-
ному коду
0 0 0 0 0 0 0 0
0 1 0 1 0 1 0 1
0 0 1 1 0 0 1 1
0 1 1 0 0 1 1 0
0 0 0 0 1 1 1 1
0 1 0 1 1 0 1 0
0 0 1 1 1 1 0 0
0 1 1 0 1 0 0 1
1 1 1 1 1 1 1 1
1 0 1 0 1 0 1 0
1 1 0 0 1 1 0 0
1 0 0 1 1 0 0 1
1 1 1 1 0 0 0 0
1 0 1 0 0 1 0 1
1 1 0 0 0 0 1 1
1 0 0 1 0 ' 1 1 0
Рис. 1.14. Код =$ 10, [8, 4, 4]-код Рида—Маллера первого порядка
Упражнение. (43). Назовем совокупность действительных векторов х= (%! ... хп) множеством сигналов. Определим скаляр-п
ное произведение х-у= XjZ/j (все вычисления производятся в
8=1
поле действительных чисел) и назовем число х-х энергией вектора х. Единичные векторы s(1), ..., s(n) (где s(i) имеет 1 в i-й компоненте и 0 во всех остальных) образуют множество ортогональ-
;ных сигналов, так как Рассмотрим теперь сдвиг
множества сигналов {t(;> = s^>—а}. Показать, что минимум полной энергии Snj=it(t)-t(<) достигается при
Множество сигналов называется симплексом (оно является непрерывным аналогом описанных выше двоичных симплексных кодов). Множество биортогональных сигналов {±s(;)} является непрерывным аналогом кодов Рида — Маллера первого порядка
1.10. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЛИНЕЙНОГО КОДА
В заключение этой главы приведем несколько важных свойств линейных кодов. Первые четыре из них справедливы для линейных кодов над любым полем.
Теорема 9. Если Н — проверочная матрица кода длины п, то код имеет размерность п—г тогда и только тогда, когда существуют г линейно независимых столбцов матрицы Н и любые г+1 столбцов Н линейно зависимы. (Таким образом, ранг матрицы Н равен г.)
Эта теорема не требует доказательства.
Теорема 10. Если Н—проверочная матрица кода длины п, то код имеет минимальное расстояние d тогда и только тогда, когда любые d—1 столбцов матрицы Н линейно независимы, но найдутся d линейно зависимых столбцов.
Доказательство. Вектор х веса w принадлежит коду тогда и только тогда, когда Нхт=0, что эквивалентно линейной зависимости некоторых w столбцов матрицы Н. •
Теорема 10 дает другое доказательство того, что расстояние кодов Хэмминга равно 3. В самом деле, все столбцы матрицы Н различны и, следовательно, любые два линейно независимы, в то время как имеются три линейно зависимых столбца.
Упражнение. (44). Пусть G — порождающая матрица '[п, k, г/]-ко.да Показать, что в качестве информационных символов могут быть взяты любые k символов, позиции которых соответствуют линейно независимым столбцам матрицы G, другими словами, существует порождающая матрица кода в которой эти k столбцов образуют единичную матрицу.
Теорема 11. (Граница Синглтона.) Если — [п, k, ефкод. to п~ k^d— 1.
Первое доказательство. Число г=п—k — это ранг матрицы Н, который равен максимальному числу линейно независимых столбцов.
Второе доказательство. Вес кодового слова, в котором только Один информационный символ не равен нулю, не превосходит п ^+1. Следовательно, d^n—&+1. •
Коды с r=d—1 называются разделимыми кодами с макси-малъным расстоянием (сокращенно кодами МДР), и они изучаются в гл. 11.
В теоремах 6 и 1Г приведены верхние границы мощности кода с заданным минимальным расстоянием. Наша последняя теорема является нижней границей, которая показывает, что хорошие линейные коды действительно существуют.
Теорема 12. (Граница Варшамова — Гилберта.) Если выполняется неравенство
то существует двоичный линейный код длины п с минимальным расстоянием по крайней мере d, имеющий не более чем г проверочных символов.
Доказательство. Построим (гХи)-матрицу Н такую, что любые ее d--1 столбцов линейно независимы. Тогда по теореме 10 мы получим требуемое утверждение Первый столбец матрицы Н может быть любым ненулевым r-вектором. Теперь предположим, что мы выбрали I столбцов матрицы Н так, что любые d—1 из них линейно независимы. Имеется не более
различных линейных комбинаций этих i столбцов, содержащих d.—2 или меньше столбцов. Если это число меньше, чем 2Г—1, то мы можем добавить еще один столбец, не равный ни одной из всех этих линейных комбинаций. При этом любые d—1 столбцов новой матрицы размера rX(i-H) линейно независимы. Мы будем продолжать эту процедуру до тех пор, пока выполняется неравенство
Для больших п см. теорему 30 и рис. 17.7.
. Упражнение. (45). Продолжение границы Варшамова — Гилберта. Доказать, что если
d—2
2о?-1)*Гу <<>
7=0 '
то над полем из q элементов существует линейный код длины п с минимальным расстоянием по крайней мере d, имеющий не' более чем г проверочных символов.
1.11. КРАТКОЕ СОДЕРЖАНИЕ ГЛ. 1
Двоичный’линейный [п, k, гДкод содержит 2А кодовых .слов х—X] ... хп, х{=0 или 1, и любые два кодовых слова отличаются друг от друга по крайней мере в d позициях. Код можно опреде
лить или как множество векторов, удовлетворяющих уравнению Нхт=0, где Н — проверочная матрица, или как все линейные комбинации строк порождающей матрицы G. Такой код может исправлять [(d—1)/2] ошибок. Декодирование по максимуму правдоподобия использует стандартное расположение. При скоростях передачи, меньших пропускной способности канала, вероятность ошибки (декодирования) может быть сделана произвольно малой при использовании достаточно длинных кодов.
Двоичный код Хэмминга представляет собой совершенный код, исправляющий одиночные ошибки, с параметрами [п=2г—1; k—2r—1—г; с?=3], г^2, и этот код задается проверочной матрицей Н, столбцами которой являются все различные ненулевые двоичные векторы длины г.
ЗАМЕЧАНИЯ К ГЛ. 1
§ 1.1. Более подробно использование кодов в системах связи рассматривается в книгах Абрамсона [3], Галлагера (464], Голомба [522] и Возенкраф-та и Джекобса [1433]. В следующих статьях идет речь о теории кодирования и применении кодов в реальных каналах связи: Эсеби и др. [31], Баумерт и Мак-Элис [88, 89], Блис и Эджкомб [167], Борель [171], Брауэр и др. [191— 194], Бухнер [209], Бартон [214], Бартон и Салливэн [217], Чейз [264, 265], Чень и др. 282, 287], Корр [309], Ковелл [311], Дорш [380], Эллиот [408], Фелконер 414], Форни [438], Фрэнецек [448], Франко и Сапорта [449], Фредриксен 450' , Фрейман и Робинсон [458], Фрей и Каванаух [460], Гудмэн и Форрел '535], Хеллман [639], Сю и Касами [671], специальные выпуски [678, 679], Джекобс [686], Касами и др. [735, 742], Клейн и Вулф [769], Лернер [818], Марси [977], Познер [1071], Поттон [1073], Ральфе [1088], Рочер и Пикхольц [1120], Роджерс [1121], Шмэнд [1156], Тонг [1333—1336], Таунсенд и Уатс [1337], Трондл [1340] и Райт [1434].
Имеются следующие обзорные статьи по теории кодирования: Ассмус и Мэттсон [47], Боуз [47-6], Добрушин [378], Гёталс [494], Джекобс [686], Касами [724], Каутц (749], Каутц и Левитт [753], Киязу [762], Мак-Вильямс [876], Слоэн [1225], Витерби [1374], Вулф [1429], Вайнер [1439] и Задэ [1450]1.
В этой главе мы описали канал как телеграфную линию связи, но столь же хорошо коды могут применяться и в других случаях, например при хранении данных в вычислительных машинах и их считывании. Различные применения кодов в вычислительных машинах рассматривались Брауном и Селлерсом [203], Ченем [278, 281, 284], Давыдовым [337], Давыдовым и Тененгольцем [338], Фи-члером [430], Хонгом и Пателем [662], Ксяо и др. [668—670], Касахарой и. др. [720], Лапиным [794], Мальхотрой и Фишером [890], Олдхэмом и др. [1011], Пателем и Хонгом [1029] и Слоэном [1230]2. _ ,
Обычно мы рассматриваем только двоичный симметричный канал без памяти и без выпадений и вставок символов. Большинство же реальных каналов отличается от такого канала тем, что в них случаются и пакеты ошибок и сбои синхронизации. (Например, один канал был описан «как очень хороший канал, ошибки в котором возникают в основном из-за коксовой установки око. ло приемника» [438].) Много работ посвящено использованию кодов для синхронизации— см., например, Боуз и Колдвелл >[182], Браун [202], Калаби и Хартнетт [226, 227], Истмен и Ивен [400], Фрейман [456], Фрейман и Вайнер [459], Гилберт [482], Голомб и др. [526, 527], Хатчер [627], Хеллман [640], Каутц [751], Левенштейн [820—822], Леви [829], Мандельбаум [900], Мак-Элис [943], Пирс [1045], Раднер [1129], Шольц и др. [11163—1166], Шимо и др. [1197], Шива и Сегуин [1203], Стенли и Уодер [1263], Стиффлер [1278—1280],
1 См.-также работу [1470* а]. (Прим, ред.)
2 См. также работу [789* а]. (Прим. перев.):
Танака и Касаи [1302], Таварес и Фукуда [1312, 1313], Тонг [1333], Уллман [1358], и Варшамов [1362—11365]. См. также статьи о кодах без запятой, упомянутые во введении. Коды, исправляющие пакеты ошибок, рассматриваются в гл. 10.
§ 1.2. Другие виды кодов. Рассматриваемые коды являются блоковыми-блоку информационных символов соответствует кодовое слово. С блоковыми кодами успешно соперничают не рассматриваемые здесь сверточные и древовидные коды, которые осуществляют кодирование информационных символов непрерывно, без деления их на блоки. Эти коды можно очень эффективно декодировать либо с помощью последовательного декодирования, либо алгоритмом Витерби (см. Форни [439, 441—444], Форни и Боуэр [445], Халлер и Джекобс [638], Джелинек1 [691], Витерби [1372, 1373] и By [1435, 1436]).
С другой стороны, криптографические коды имеют мало общего с рассматриваемыми кодами: их задача — скрывать информацию, в то время как наши коды имеют противоположную цель—см. Фейстел и др. [422, 423], Гейнс [463], Геффе [469, 470], Гилберт и др. [484], Хеллман и Диффай [640а], Кан [707] и Шеннон [1190].
Другой класс кодов — это коды, исправляющие -ошибки при арифметических операциях, — см., например, Питерсон и Уэлдон [1040] и Рао [1093].
§ 1.3. Слепян [1224] называет рис. 1.3 гербом специалиста по теории информации. Свойства биномиальных коэффициентов см. в книге Риордана [1114]. Упражнение (19) взято из работы Шива [1199].
§ 1.4. Линейные коды. Основополагающие статьи принадлежат Слепяну [1217—1219]. Иногда для обеспечения синхронизации вместо самого кода используется какой-либо его смежный класс — см. работу Познера [1071, рис. VII].
§ 1.5. Теорема 6 принадлежит Хэммингу [592]. Подробнее о вероятности ошибки для кодов можно узнать, например, из работ Батмэна и Мак-Элиса [80], Кейна и Симпсона [224], Кримминса и др. [317—319], Галлагера [464], Джелинека [690], Леонтьева [817], Познера [1070], Рединбо и Вулфа [1103], Слепяна [1220], Салливэна [1292]и Вайнера [1437, 1438]. Хоббс [656] приводит приближенное выражение для распределения лидеров смежных классов любого кода.
§ 1.6. Доказательство теоремы Шеннона [1188, 1189] см. в книге Галлагера [464, § 6.2.].
Замечание. Неполное декодирование (см. рис. 4.8), которое исправляет все конфигурации ошибок веса не более чем /= [(<4—1)/2], и ни одной большего веса, называется декодированием с ограниченным расстоянием. Из границы Элайеса или границы Мак-Э.^иса — Родемича — Рамсея — Велча (теоремы 34, 35, или 37 гл. 117) следует, что с помощью декодирования с ограниченным расстоянием нельзя достигнуть пропускной способности канала — детали см. в работах Вайнера [1437] или Форни [437]. С другой стороны, только небольшое усложнение схемы декодирования позволяет достигнуть пропускной способности (см., например, Абрамсон [3, с. 167]).
§ 1.7. Коды Хэмминга были открыты Голеем [506, 514а] и Хэммингом [592] (см. также упражнение (8) гл. 7).
§ 1.8. На языке векторных пространств вектор и называется изотропным, если u.u=0, и поэтому слабо само дуальный код называется полностью изотропным (см. например, Лэм [790]).
§ 1.9. Деза [373], Фабер [416], Холл [580], Холл и др. [581], Ландау и Слепян [792], Ван Линт [852] и Таннер [1308, 1309] изучали симплексные коды. Дополнительный материал к упражнению (43) см. в книге Возенкрафта и Джекобса [1433, с. 257].
§ 1.10. Хотя теорема 11 сейчас называется границей Синглтона (со ссылкой на работу Синглтона [1214]), Джоши [700] приписывает этот результат Ко-мамия [775]. Эта оценка применима также к нелинейным кодам (упражнение 3 гл. И и упражнение 17 гл. 17). По теореме 12 см. работы Гилберта [479], Варша-мова [1362] и Сакса [4140].
1 Эта работа фактически повторяет более раннюю работу Зигангирова [1469* а] (см. также его книгу [1469*6]). (Прим, ред.)
Нелинейные коды, матрицы Адамара, \ t -схемы и код Голея
2.1. НЕЛИНЕЙНЫЕ КОДЫ
«...хорошие коды как раз должны быть перемешаны ’»
ДЖ. л. МЭССИ
Одно из основных назначений кодов заключается в исправлении ошибок в каналах связи с шумами, и линейные коды, введенные в гл. 1, имеют много практических преимуществ с этой точки зрения. Но если мы хотим получить наибольшее возможное число кодовых слов с заданным минимальным расстоянием, то иногда необходимо использовать нелинейные коды.
Например, предположим, что нам нужен код длины 11, исправляющий две ошибки. Наибольший линейный код содержит 16 кодовых слов, в то время как имеется нелинейный код, показанный на рис. 2.1, содержащий 24 кодовых слова, что дает увеличение на 50%. (Это код Адамара, см. § 2.3.)
Определим нелинейные коды следующим образом.
Определение. Назовем (п, М, с?)-кодом множество из М векторов длины п (с компонентами из некоторого поля F), такое, что любые два вектора различаются между собой по крайней мере в d позициях и d является наибольшим числом с этим свойством.
В этой главе все коды будут двоичными. Еще раз напомним, что квадратные скобки обозначают линейный код, в то время как круглые скобки используются для кода, который может быть (или не быть) линейным. Двоичный линейный [п, k, с?]-код является (п, 2\ с?)-кодом.
Обычно мы предполагаем, что не существует координатной позиции, в которой каждое кодовое слово имеет нуль (в противном случае это был бы (п—-1, М, л?)-код). Кроме того, так как расстояния между кодовыми словами не изменяются, если ко всем кодовым словам прибавить фиксированный вектор, можно при желании предположить, что код содержит нулевой вектор.
Будем говорить, что два (п, М, d) двоичных кода f и ® эквивалентны, если один может быть получен из другого перестановкой п символов и добавлением фиксированного вектора, или более формально, если существуют подстановка л на множестве {1, 2, .... п} и вектор а такие, что S)= {л(u) -|-а : uef}. Если
1 Здесь игра слов: «...good codes just might be messy». Слово «messy» созвучно с фамилией Massey. (Прим, nepee.)
и 2b — линейные коды, то это определение сводится к определению эквивалентности, данному в § 1.7. Так, например, .коды
ООО 111 /
ОН и 100 /
и
101 010 /
НО 001
эквивалентны (если положить а=Н1).
0123456789 10
00000000000
11111 1
11 111 1
1 11 111
1 11 111
1 11 111
1 11 111
1 11111
11 1111
111 111
111 111
1 1111
1 1 111
1 1 111
11 1 11
111 1 1
1111 1
1111 1
1111 1
1111 1
1 1111
1 1111
11111111111
Рис. 2.1. Пример нелинейного (11,24, 5)-кода Ада-мара (первые 12 строк образуют (11, 12, 6)-код Ада-мара .Л 12’, все 24 строки образуют (11, 24, 5)-код Адамара 12
В общем случае эквивалентность недвоичных кодов определяется следующим образом. Пусть ? и ® будут кодами длины п над полем из q элементов. Тогда и 3) эквивалентны, если существуют п подстановок ш, ..., пп на множестве из q элементов <и подстановка, о на множестве {!, 2, ..., п} (позиций) такие, что
(^1, • - •, wn) (ЕЕ о (лг (Wj), • • •, лп (пп)) (ЕЕ «25.
; Другими словами, сначала в каждой позиции переставляются элемента поля, а затем сами координатные позиции. Если оба кода ? w ® являются линейными, то могут быть использованы только подстановки л,, порожденные скалярными множителями й автоморфизмами поля (см. § 4.6).
Определение. Обозначим через Д{ число кодовых слов веса i в (п, М, (2)-коде <ё>. Числа Ао, А, ..., Ап называются весо-вым спектром кода W. Ясно, что Ло+А + ... +Ап = М. Весовой спектр мы ужё. использовали при вычислении вероятностей ошибки ,в гл. 1.
Если вектор 0 является кодовым словом, то наблюдатель, находящийся в нулевом слове, увидел бы на расстоянии i от себя Аг кодовых слов. Для линейного кода картина была бы одной и той же в любой кодовой точке. (Почему?) Однако в нелинейном коде не обязательно так, как показывает пример кода {00, 01, 11}. (Если же это справедливо, то говорят, что код инвариантен относительно расстояния. Код Нордстрома — Робинсона (§ 2.8) инвариантен относительно расстояния; другие примеры будут даны в гл. 6.) Поэтому для нелинейного кода полезно рассматривать среднее число кодовых слов на расстоянии i от фиксированного кодового слова.
Определение. Спектр расстояний кода <6? состоит из чисел Во, В1г ..., Вп, где
1
М
число упорядоченных пар кодовых слов и, таких, что dist (u, v) = i
V
Заметим, что Во=1 и ... -\-Вп=М.
Для линейных кодов весовой спектр и спектр расстояний совпадают. Кроме того, код а-j-®7, полученный сдвигом, имеет такой
же спектр расстояний, что и код
Полезно геометрическое представление этих кодов. Двоичный вектор а\, .... ап длины п задает координаты вершины единичного куба размерности п. В таком случае (п, М, d) -код представляет собой некоторое
Рис. 2.2. Куб, иллюстрирующий (3, 2, 3)-код (а); четырехмерный куб, иллюстрирующий (4, 8, 2)-код (б)
подмножество этих вершин (рис. 2.2).
На этом геометрическом
языке проблема теории коди-
рования заключается в выборе как можно большего числа вер-
шин куба с заданным попарным расстоянием между ними.
Эта проблема представляет собой проблему упаковки, так как в коде с минимальным расстоянием d евклидово расстояние между кодовыми словами не менее чем d. Поэтому построение
(п, М, с?)-кода означает построение М непересекающихся шаров радиуса с//2 с центрами ,в вершинах куба.
Замечание. Задача (нерешенная). (2.1). Аналогичная проблема расположения М точек на поверхности единичной сферы размерности п также не решена. Другими словами, где должны построить дома на поверхности планеты М нелюдимов, чтобы максимизировать минимальное расстояние между любыми двумя домами? Эта проблема также важна в теории связи, так как представляет собой проблему нахождения наилучших сигналов при передаче по каналу с ограниченной полосой.
2.2. ГРАНИЦА ПЛОТКИНА
Теорема 1. (Граница Плоткина.) Для любого (п, М, d)-кода при n<.2d справедливо неравенство
М 2 \d/(2d—п)]. (2.1)
Доказательство. Вычислим сумму
dist (u, v) и е v е
двумя способами. Во-первых, так как при u#=v расстояние dist (u, v) ~^d, то сумма не меньше чем М (М—l)d. С другой стороны, пусть А обозначает (МХп)-матрицу, строками которой являются все кодовые слова. Предположим, что i-й столбец А содержит Xi нулей и М—Хг единиц. Тогда вклад этого столбца в нашу сумму равен 2Хг(АГ—х;), и поэтому эта сумма равна
2xf (Al—х^.
Z=1
Если число М — четное, то максимум этого выражения достигается при Хг=М/2 для всех i, и поэтому сумма не превышает пМ2!2. Таким образом, мы имеем:
М (М— 1) d < пМ*Г2, или
M^2d/(2d—n). ' (2.2)
Но число М — четное, и поэтому
M^2]d/(2d—п)1.
С другой стороны, если число М — нечетное, то сумма не превышает п(М2—1)/2, и вместо (2.2) получим
М С n/(2d—п) - - 2d/(2d—п) — 1.
Отсюда следует, что
M^)2d/(2d—n)l — 1 ^2Jd/(2d—п)1,
так как [2х] =^2[х] -}- 1. •
Пример. Векторы, изображенные в верхней половине рис. 2.1, образуют (11, 12, 6)-код (или код «$$12 в обозначении § 2.3), для которого в (2.1) имеет место равенство.
Упражнения. (1). Существует ли (16, 10, 9)-код?
(2). Построить (16, 32, 8)-код [Указание. Как следует из доказательства теоремы 1, каждый столбец должен содержать половину нулей и половину единиц.]
Обозначим через А(п, d) наибольшее число М кодовых слов в любом (п, М, г/)-коде. Следующая теорема показывает, что достаточно найти А (п, d) для четных значений d.
Т ео р е м а 2.
А(п, 2г—1)=Л(«+1, 2г).
Доказательство. Пусть будет (п, М, 2г—1)-кодом. Добавляя общую проверку на четность (§ 1.9), получаем (n+1, М, 2г)-код, откуда следует, что
Л(п, 2г—1)<Л(п + 1, 2г).
•В обратную сторону выкидывание одной координаты в заданном (п+1, М, 2г)-коде приводит к (п, М, d^2r—1)-коду, так что
А(п, 2г—1)>Л(п+1, 2г). •
Теорема 3.
Л(п, ф<2Л (п—1, d).
Доказательство. В заданном (п, М, с?)-коде разделим -все кодовые слова на два класса, отнеся в один класс те слова, которые начинаются с нуля, а в другой — те, которые начинаются с единицы. Один из этих классов содержит по крайней мере половину кодовых слов, что влечет
А(п—1, d)>A(n, d)/2. •
Следствие 4. (Граница Плоткина.) Если d — четное и 2с?>п, то
Д(п, d)^2\dl(2d—п)1; (2.3)
А (2d, d)^4d. (2.4)
Если d— нечетное и 2с?+1>п, то
А(п, d)^2I(d+l)/(2d+l— п)1; (2.5)
A(2d+1, d)^4d + 4. (2.6)
Доказательство. Из теоремы 3 и неравенства (2.1) следует,
что
А (4г, 2г) 2 А (4г— 1, 2г) < 8г,
что и доказывает (2.4). Если d — нечетное, то в силу теоремы 2 А(п, (/) = Л(п+1, d+l)<2[(rf+l)/(2t/+l—п)1.
Неравенство (2.6) получается таким же способом. 9
Если существуют матрицы Адамара всех возможных порядков (что, однако, до сих пор еще не доказано), то на самом деле в уравнениях (2.3) — (2.6) выполняются равенства. Таким образом, граница Плоткина является точной в том смысле, что существуют коды, достигающие этой границы. В этом и заключается теорема Левенштейна, которая доказывается в следующем параграфе.
2.3. МАТРИЦЫ АДАМАРА И КОДЫ АДАМАРА
Определение. Матрица Адамара Н порядка п представляет собой (7гХп)-матрицу из элементов +1 и —1, такую, что
ННт = п1. (2.7)
Другими словами, скалярное произведение любых двух различных строк Н в поле действительных чисел равно нулю, т. е. различные строки ортогональны между собой и скалярное произведение любой строки на саму себя равно п. Так как Н-1 = = (1/п)Нт, то мы получаем также, что НтН=н1, так что столбцы матрицы Н обладают теми же свойствами.
Легко видеть, что умножение любой строки или столбца на —1 переводит Н в другую матрицу Адамара. Это означает, что мы можем изменить все элементы первой строки и первого столбца матрицы Н на +1. Такая матрица Адамара называется нормализованной. На рис. 2.3 показаны нормализованные матрицы Адамара порядков 1, 2, 4, 8, где вместо элемента —1 изображен только символ —; это обозначение будем использовать во всей книге.
Рис. 2.3. Матрицы Адамара порядков 1, 2, 4 и 8 типа Сильвестра
Теорема 5. Если существует матрица Адамара Н порядка п, то п равно 1 или 2 или делится на 4. ,
Доказательство. Без ограничения общности будем считать,, что Н представлена в нормализованном виде. Предположим, что-п^З и первые строки имеют следующий вид:
1 1 . . .1 1 1 • • -1 11 ... 1 11 -.. 1
1 1 . . .1 1 1 . . .1-----------: . —------------ . —
1 1 • • 1---------- • — 1 1 ... 1---------------- • —
i j k I
Так как строки матрицы Н ортогональны, то мы имеем:
/ + /—k—1 = 0', i—j-\-k—1=0', i—j—k-\-l=0,
что влечет цепочку равенств i=j=k=l. Поэтому n=4i, т. е. ' п делится на 4
Предполагается, что существуют матрицы Адамара всех порядков п, кратных 4, хотя это до сих пор еще не было доказано. Известно -большое число методов построения, и наименьший порядок, для которого матрица Адамара еще не построена, равен 268 (на 1977 г.). Мы приведем два метода построения, которые важны для теории кодирования.
Метод построения I. Если Нп— матрица Адамара порядка п, то легко проверить, что
/Нп \НП
Нп\
представляет собой матрицу Адамара порядка 2п. Начав с Н1= (1), этим методом получаем матрицы Н2, Н4, Н8 (как показано на рис. 2.3) и т. д. и, следовательно, матрицы Адамара, порядки которых являются степенями двойки. Эти матрицы Адамара называются матрицами Сильвестра.
Для описания второго метода построения нам необходимы не-, которые сведения о квадратичных вычетах.
Квадратичные вычеты. Определение. Пусть р — простое-нечетное число. Ненулевые квадраты чисел, приведенные по модулю р, т. е. числа I2, 22, З2, ..., приведенные по этому модулю, называются квадратичными вычетами по модулю р или просто-вычетами по модулю р.
Для того чтобы найти все вычеты по модулю р, достаточно рассмотреть квадраты чисел от 1 до р —1. На самом деле, учитывая, что (р—а)2=(—o:)2=o:2(modp), достаточно рассмотреть квадраты I2, 22, ..., ((р—l)i/2)2(mod р).
Все эти вычеты различны, так как если i2=/2(modp) при: l=^i, Г<(р—1)/%, то р делит (а—/)(»+/), что возможно лишь при i=j.
Следовательно, имеются (р—1)/2 квадратичных вычетов' па-моду лю р. Оставшиеся (р—-1)/2 чисел по модулю' р называются невычетами. Нуль не является ни вычетом, ни невычетом.
Например, если /2=11, то квадратичные вычеты по модулю 11—это числа
12=1; 22=4; 32 = 9; 42 = 16 = 5(mod И) и 52 = 25 = 3 (mod 11),
т. е. числа 1, 3, 4, 5 и 9. Остальные числа 2, 6, 7, 8 и 10 являются невычетами. [Напомним читателю, что выражение
А = В (mod С), читаемое как «А сравнимо с В по модулю С», означает, что
С I (Л—В), где вертикальная черточка означает «делит» или, что эквивалентно, число А — В кратно С.
В этом случае числа А и В находятся в одном и том же классе .вычетов по модулю С.]
Рассмотрим теперь некоторые свойства квадратичных вычетов. *
(Q1). Произведение двух квадратичных вычетов или двух невычетов является квадратичным вычетом, а произ.ведение квадратичного вычета и невычета является невычетом. Доказательство оставляется читателю в качестве упражнения.
(Q 2). Если р имеет .вид 4& + 1, то число —1 является квадратичным вычетом по модулю р. Если же р имеет вид 4Л + 3, то —1 является невычетом по модулю р. Доказательство будет приведено .в гл. 4.
(Q3). Пусть р — простое нечетное число. Функция х1, называемая символом Лежандра, определяется на целых числах следующим образом:
х(0—0, если i кратно р;
Х(0 = 1> если остаток от деления i на р является квадратичным вычетом по модулю р;
х(0 =—1, если остаток от деления i на р является невычетом.
Теорема 6. Для любого с^О (mod р) р-i 2х(ь)х(^+с)= — 1-ь=о
Доказательство. Из свойства (Q 1) следует, что
Х(*У) = Х(*)х(Р) при О^х, уср— 1.
1 Символ Лежандра, конечно, зависит от выбора р и в теории чисел обозначается через | —1. (Прим, ред.)
\Р I
Вклад в сумму слагаемого при 6=0 равен нулю. Теперь пред-положим, что &¥=-0, и пусть число z= (b+ c)/b (mod р). Для каждого b имеется единственное целое число z, O'^z^p—1. Когда b пробегает все числа от 1 до р—1, число z принимает значения О, 2, р—1, но не 1. Итак, р—1 р—1 р—1
2x(b)x(fc+c) = £ X(6)%(M=2%(^)2%(z)== Ь=0 Ь=1 Ь=1
р—1
= 2 Х(2)=°—%(!)= -1- •’
г=0 г#=1
Замечание. Очень похожие свойства выполняются, когда р заменяется на степень рт любого нечетного простого числа р, числа 0, 1. ..., р—1 заменяются на элементы конечного поля GF(pm) (см. гл. 3), а квадратичные вычеты определяются как ненулевые квадраты в этом поле.
Метод построения И. (Метод Пейли.) Это построение-дает матрицы Адамара любого порядка п=р+1, кратного 4 (или порядка п=рт+1, кратного 4, если мы используем квадратичные вычеты в поле GF(pm)).
Сначала мы построим матрицу Джекобстола Q=6<7iJ. Она представляет собой (рХр) -матрицу, строки и столбцы которой перенумерованы числами 0, 1, ..., р—1, а элементы Уи~%а—I) (см. рис. 2.4 для случая р = 7):
0 1 2 3 4 5 6
0 1 2 Q= 3 4 5 6 0 1 1 — 1 — 0 1 1 — 1 — 0 1 1 — 1 1 0 1 1 — _ 1 о 1 1 1 — 1 0 1 1 1 — 1 0
Рис. 2.4. Матрица Джекобстола
Заметим, что qa=%(i—j) =х(—1)х(/—0 =—так как Р имеет вид 4k—1 (см. свойство (Q2)), и поэтому матрица Q является кососимметрической, т. е. QT=—Q.
Лемма 7. QQr=pI—J и QJ=JQ=O, где J —матрица из. всех единиц.
Доказательство. Пусть P=(PiJ = QQT. Тогда
р—1
Ра =2 С = Р-1;
р-о
р—1 р—1
Ра = 2QihQjh = i) (при z/)
k=o fe=O
p—1
= % (b) %(£ + €) (где b=k—i, c — i—j)
ъ=о
= — 1 (по свойству (Q3)).
Так же доказывается, что QJ=JQ=0, так как каждая строка и каждый столбец матрицы Q содержат (р—1)/2 элементов +1 и (р—1) /2 элементов —1. ®
Пусть теперь
Н= ( * 1 V (2.8)
Н Q—I /
Тогда
ннт / 1 1 W 1 1 0
\ 1Т Q—I/\1TQT—1/ 0T J +(Q—I)(QT—1) / '
Но из леммы 7 следует, что J+(Q—I) (QT—I)=J+pl—J—Q— —QT + I=(p+l)I, так что HHT=(p + l)lP+i. Таким образом, H -представляет собой нормализованную матрицу Адамара порядка р+1, которую называют матрицей типа Пейли.
Пр и мер. На рис. 2.5 изображены матрицы Адамара порядков 8 и 12, полученные описанным способом.
Н8=
1 — 1 1 — 1----------------------------------
1-------------1 1 _ 1 _
1-------------------1 1 — 1
1 1-----------------------1 1 —
1 — 1---------------------------1 1
1 1 _ 1-------------------------------1
1 1 1 — 1-----------------------------------
“111111111111“
1—1 — 1 1 1--1—
1-1 — 1 1 1--1
1 1-1-1 1 1-----
1 — 1-1 — 1 1 1-
1-- 1-1-1 1 1 —
1---1----1 — 1 1 1
1 1---1--1 — 1 1
1 1 1-1т--1 — 1
1 1 1 1--1 — 1—
1 — 111--1 — 1
11 — 11 1--1—
Рис. 2.5. Матрицы Адамара порядков 8 и 12
Методы построения I и I] дают вместе матрицы Адамара для всех порядков 1, 2, 4, 8, 12, ..., 32.
Назовем две матрицы Адамара эквивалентными, если одна сможет быть получена из другой перестановками строк и столб-
цов и умножением строк и столбцов на —1. Легко убедиться, что имеется только один класс эквивалентности матриц Адамара порядков 1, 2 и 4. В гл. 20 мы увидим, что имеется только один такой класс матриц порядка 8 (так что матрицы Адамара порядка 8, изображенные на рис. 2.3 и 2.5, эквивалентны) и один класс матриц порядка 12. Кроме того, известно, что имеется пять классов эквивалентности порядка 16 и три порядка 20. Число таких, классов порядка 24 неизвестно.
Упражнение. (3). Если п=2т, то пусть иь ..., и„ обозначают различные двоичные m-векторы. Показать, что матрица Н = (7^у), гДе ^ij=(—О 1 является матрицей Адамара порядка п, которая эквивалентна матрице, полученной методом построения I.
Коды Адамара. Пусть Н„ — нормализованная матрица Адамара порядка п. Если все элементы +1 заменить на 0, а элементы —1 заменить на 1, то Нп превратится в двоичную матрицу Адамара Так как строки Нп ортогональны,- то любые две строки матрицы Ап совпадают в п/2 позициях и различаются в-п/2 позициях, и поэтому расстояние Хэмминга между ними равно п/2.
Матрица Ап позволяет построить следующие три кода Адамара:
(i) . (п—1, п, п/2)-код s^n, состоящий из строк матрицы А„ с выкинутым первым столбцом1 (код показан на рис. 2.7, а код. 3^12 образован строками верхней половины рис. 2.1, если символы в строках взять в обратном порядке).
(ii) . (п—1, 2п, (п/2)—1)-код состоящий из векторов кода s£n и их дополнений 2 * (код ^12 изображен на рис. 2.1).
(iii) . (п, 2п, п/2) -код <8\г, состоящий из строк матрицы Ап и их дополнений.
Код является симплексным кодом, так как расстояние между любыми двумя кодовыми словами равно п/2 (см. § 1.9). В действительности эти три кода представляют собой нелинейные обобщения кодов, изображенных на рис. 1.13. Более того, если матрица Нп, где п=27", получена методом построения I, то все три кода и являются линейными и совпадают с ко-
дами, показанными на рис. 1.13.
С другой стороны, если Н„ построена методом 11, то все полученные коды нелинейны для всех п>8. Линейные коды получим, если возьмем линейные оболочки этих кодов; полученные коды называются квадратично-вычетными кодами, и они будут исследованы в гл. 16. Но если матрица Нп не строится ни методом I,. ни методом II, то мало что известно о двоичном ранге матрицы А„.
1 Этот столбец состоит из одних нулей. (Прим, перев.)
2. В терминологии гл. 1 код У/п является пополнением кода с по-
мощью 1= (11 ... 1). (Прим, перев.)
Упражнение. (4). Показать, что если п кратно 8, то AnATns »0(mod 2) и, следовательно, двоичный ранг Ап не превышает •п/2. [Указание. Использовать тот факт, что над любым полем rank (В)+rank (С) ^n + rank (ВС), где В и С — матрицы размера пХп (см. теорему 3.11 из работы Маркуса [914]).]
Теорема Левенштейна. В этом параграфе мы докажем теорему Левенштейна, которая утверждает, что существуют коды, достигающие границы Плоткина.
Вначале рассмотрим две простые конструкции.
(i). Кодовые слова кода s£n, которые начинаются с 0, после удаления этого нуля образуют (п—2, п,12, п/2)-код1 s£'n (код .^/'12 показан на рис. 2.7).
(й). Предположим, что
мы имеем (пь 7ИЬ </1)-код 'tFi и (п2, М2, йг)-код ^2- Склеим подряд а копий кода ЯД, а затем b копий кода ’Э’г (рис. 2.6). Теперь отбросим последние М2—Mi строк кода с&2 (если ЛКС-Мг) или последние М\—М2 строк кода ’g’l (если В результате для про-
извольных натуральных чисел а и b получим (п, М, й)-код с п=апч+Ьп2, где Л4=ш1п{Л41, Л42} и d^adi + bd2. Обозначим этот код через rz'g’iO&'SV
Теорема 8. (Левенштейн). Если существуют соответствующие матрицы
*
Рис. 2.6. Построение нового .кода «склеиванием» двух экземпляров кодов: 1 — отбрасываемая часть
.Адамара, то в границах Плоткина (2.3) — (2.6) выполняются равен-
ства. Таким образом, если d— четное, то
А(п, d)~2(d/(2d—п)\ при 2d>n > d", (2.9)
А (2d, d) = 4d; (2.10)
:и если d — нечетное, то
А(п, d)=2[(d+l)/(2d+l—п)1 при 2d+\>n>d\ (2-11)
A(2d+1, d)=4d + 4. (2.12)
Доказательство. Равенства (2.11), (2.12) следуют из (2.9), >(2.10), если воспользоваться теоремой 2, так что мы можем предположить, что d — четное.
Код Адамара ^2d, описанный выше, является (2d, 4d, d) -кодом, что доказывает (2.10).
Для того чтобы доказать (2.9), мы должны построить (п, М, £?)-код с M=2 \dl(2d—п)] для любого п и четного d, удовлетворяющих условию 2d>tiZ^d. Нам понадобится следующий простой результат, доказательство которого мы оставляем читателю. При 2d>n~^d положим k= \dl(2d—«)] и
a=d(2fe+!)—«(£+1); b—kn—d(2k— 1). (2.13)
Тогда а и b — неотрицательные целые числа и n=(2k—l)tz-}-+.(2fe+1)&; d=ka+(k+l)b.
1 Другими словами, — (укорочение кода по позиции Xi=0 (см.
1.9). (Прим, перев.)
ели п — четное, то а ио также четные (это следует из (2.13)). Если п — нечетное, a k— четное, то b — четное. Если п и k — нечетные, то а — четное.
Теперь рассмотрим код (в, где:
если п — четное, то 77=\h Ф ^'4^4-4;
если п — нечетное, k — четное, то
= a-^2k ® ^471+4’
п и k — нечетные, то ®’= — ф bs^2k+2.
если пик — нечетные, то 7У= — » 4й Ф bs&2u+2.
В каждом из этих случаев, как легко следует из конструкции (ii), описанной выше, код 77 имеет длину п, минимальное расстояние d и содержит 2k=2\dl(2d- -п) ] кодовых слов. Существование этого кода устанавливает справедливость (2.9). в
Заметим, что для доказательства (2.10) требуется матрица Адамара порядка 2d, а для доказательства (2.9) нам достаточно матриц Адамара порядка 2k (если k— четное), 2k + 2 (если k — нечетное), 4k, 4k 4-4.
Пр и м е р. Проиллюстрируем метод Левенштейна на примере построения (27, 6, 16)-кода. Обращаясь к доказательству теоремы, мы находим, что k=3, а=4, Ь — 1. В нашем случае п и k— нечетные, поэтому код получается склеиванием вместе двух копий кода s&'\2 и одной копии кода
Коды б78 и з£'\2, полученные из матриц Н8 и Н12 (см. рис. 2.4), изображены на рис. 2.7.
^8 = “0000000- 10 0 10 11 1 10 0 10 1 11 10 0 10 0 1110 0 1 10 1110 0 0 10 1110 0 0 10 111 с4'12 = ’0000000000“ 1 1 0 1 0 0 0 1 1 1 1110 110 10 0 0 1110 110 10 0 0 1110 110 1 1000111011
Рис. 2.7. (7, 8, 4)-код з$8 и (10, 6, 6)-код <&'12
Построенный (27, 6, 16)-код изображен на рис. 2.8.
Упражнение. (5). Построить (28, 8, 16)- и (32, 8, 18)-коды.
Другие применения матриц Адамара.
(1) . Максимальные определители. Если Н — матрица Адамара порядка п, то,' переходя в равенстве (2.7) к определителям, получаем, что det(HHT) =det H-det Нг = (det Н) 2=пп, так что определитель матрицы Н равен ±пп/2.
“0000000000
1 1 0 1 0 0 0 1 1 1 1110 110 10 0 0 1110 110 10 0 0 1110 110 1 1000111011
0000000000 1 1 0 1 0 0 0 1 1 1 1110 110 10 0 0 1110 110 10 0 0 1110 110 1
1 0 0 0 1 1 1 0 1 1
0000000“
10 0 10 11
110 0 10 1 1110 0 10
0 1110 0 1
10 1110 0
Рис. 2.8. (27, 6, 16)-код, иллюстрирующий метод построения Левенштейна
Теорема Адамара [572] утверждает, что если А= («ij) — любая (вещественная (яХп)-матрица с элементами —то J det А| ^пп/2.
Более того, равенство выполняется тогда и только тогда, когда существует матрица Адамара порядка п. Таким образом, п должно быть кратно 4 (см. книги Веллмана [100, с. 160], Харди и др. [601, с. 34], Райзера [1136, с. 109]. Если п не кратно 4, то мало что известно о наибольших возможных определителях (см. упражнение (8)).
(2) . Весовые планы. Взвешивая несколько объектов вместе, а не в отдельности, *иногда можно более точно определить их индивидуальные веса. Делается это с помощью так называемых весовых планов, и лучшие из таких планов основаны на матрицах Адамара.
Подобный метод применим к разнообразным задачам изменения не только веса, но и длины, напряжения, сопротивления, концентрации химических элементов, частотного спектра (см. работы Декера [341], Гиббса и Геббая [478], Голея [507, 508],Хар-:вита и др. [622], Филлипса и др. [1042], Слоэна и др. [1234— 1236]) и вообще к любому эксперименту, где мера множества объектов является суммой индивидуальных мер. Для простоты, однако, мы опишем сейчас задачу взвешивания.
Предположим, что надо взвесить четыре легких предмета на весах с двумя чашечками, которые допускают ошибку е при жаждом использовании. Пусть е —случайная величина со средним значением 0 и дисперсией о2, не зависящей от веса взвешенного предмета.
Сначала предположим, что предметы взвешиваются в отдельности. Если неизвестные веса обозначить через a, b, с, d, результаты взвешиваний — через ух, у2, у3, у4, а (неизвестные) ошибки, допущенные весами, через еь е2, е3, е4, то четыре взвешивания дают четыре уравнения:
а= b = y2-{-E%, с = у3-[-е3; d=yi-\-Ei.
При этом оценки неизвестных весов a, b, с, d получаются следующими:
л л
а=у1—а—Bjl b = y2=b —е2; • • .причем дисперсия каждой оценки равна о2.
С другой стороны, (предположим, что мы проделали следующие четыре взвешивания:
а + Ь+с+d— +
а—Ь-\-с—d= z/2-|-e2; a + b—с—d= У3 + е3; cl—b—c d= y4 -}- e4.
(2-14)
Это означает, что при первом взвешивании все четыре предмета положили на левую чашку весов, а при других взвешивани--ях два предмета положили на левую чашку и два предмета — на правую. Так как коэффициенты при неизвестных a, b, с, d в левой части (2.14) образуют матрицу Адамара, то эту систему легко решить относительно a, b, с, d. Так, оценка величины а равна:
л
а~ + + а—(8i + е2 + ез + еа)/4.
Дисперсия случайной величины се, где с — константа, в с2 раз •больше дисперсии е, а дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. Поэтому дисперсия ц равна 4-(о2/16) =о2/4, т. е. выигрыш в 4 раза. Аналогичный результат получается и для других неизвестных.
В общем случае, если п предметов надо взвесить за п взвешиваний и матрица Адамара порядка п существует, то описанный метод уменьшает дисперсию от о2 до о2/п. Известно, что это наименьшая дисперсия, которая может быть получена при любом выборе знаков в левой части выражений (2.14). Для доказательства этого факта и для более подробного знакомства с весовыми планами см. работы Банерджи [65, 66], Герамита и др. [473— 477], Хотеллина [665], Муда [972], Пейна [1032], Слоэна и Хэрвита [1236].
Теперь предположим, что весы имеют только одну чашку, так что можно использовать лишь коэффициенты 0 и 1. В этом случав дисперсия оценок также может быть уменьшена, хотя и не в столь большое число раз. Снова проиллюстрируем этот способ на примере. Если надо взвесить семь предметов а, Ь, с, g, то используем следующий весовой план:
а + с +е +g=y1 + e1> b-+-c +f+g'= Уг + Еа»
а-[-Ь H-c + Z =//з + ез>
d+e+f+g=yi + ^
a +c+d +f = Уъ + %’
b -|- с Т~ d Т~ с у $ Т~ £б>
cl b -|- d .
(2.15)
Коэффициенты определяются очевидным образом из матрицы Адамара Н8, изображенной на рис. 2.3. Тогда оценкой веса а является значение (см. упражнение (7))
л
а = (Z/i—У-г.+Уз — Уь+Уь~ У в + */7)/4 = а—(ег—е2 + е3—е4 +
+ е5--еб + е7)/4,
имеющее дисперсию 7сг2,/16, и то же самое получается для весов других предметов. В общем случае, если имеется п предметов и существует матрица Адамара порядка п-i-l, то этот способ уменьшает дисперсию до 4 nozJ(n +1)2, что в некотором смысле является наилучшим возможным выигрышем (см. работы М.уда [972], Рагхаварао [1085, гл. 17], Слоэна и Хэрвита [1236]).
Подобный метод можно описать иначе. Можно сказать, что использовался код Адамара, чтобы закодировать или преобразовать данные перед тем, как их измерить.
Другой тип задач взвешивания, также связанный с теорией кодирования, будет рассмотрен в гл. 6.
(3) . Преобразование Адамара. Пусть Н — матрица Адамара порядка п. Если Х= (хь ..., х„) — вещественный вектор, то его преобразованием *Лдамара (или Уолша, или дискретным преоб-л
разованием Фурье) называется вектор Х=ХН.
Пусть Fm обозначает множество всех двоичных векторов длины т. Матрица, строки и столбцы которой пронумерованы векторами u, v из Fm, образует матрицу Адамара порядка п=2т, если в ячейке (u, v) записано число (—l)uv (см. упражнение (3)). Если f — некоторое отображение, определенное на Fm„ то его преобразование Адамара f определяется как
f(u)= £ иеГ.
veF л
Мы воспользуемся f в важной лемме (лемма 2) в гл. 5 и при изучении кодов Рида — Маллера. Преобразования Адамара также широко используются в теории связи и в физике, и им посвящено большое число работ в широком диапазоне (см., например, работы Ахмеда и др. [12—15], Хармута [603—604, 680], Кеннета ([757], Пратта и др. [1079], Шенкса [1187], Вэдбрука и Вол-лонса [1375]). Анализ влияния ошибок на преобразование Адамара требует детального знания смежных классов кодов Рида— Маллера первого порядка (см. Берлекэмп [119]).
Упражнения. (6). Пусть
— нормализованная матрица Адамара порядка п. Показать, что SST=nI— J; SJ=JS=—J; S-1= (1,/n) (ST—J).
(7). Пусть Т= (1/2) ( —S) (так . что Т — матрица коэффици-ентов в соотношениях (2.15)). Показать, что Т‘=—(2/n) ST.
(8). Задачи о максимальных определителях. Предположим, чт0 A=faiJ —вещественная матрица порядка п. Пусть
f(n) =max | det (А) |, если а^=0 или 1;
§•(«)= max | det (А) [, если а1}= —1 или 1;
ft(n)=max | det (А) |, если ац^= —1,0 или 1;
E(n)=max| det(A)|, если 0<:аг;<:1;
G(n)=max | det (А) [, если —1<а4у<1.
Показать, что
(a)f(n) = E(«); (B)g-(n)=/i(n)=G(n); (c)g-(n) = — 1).
Таким образом, все пять задач эквивалентны! Адамар [572] доказал, что .[(и) ^2-n(n+1)(п+1)/2, причем равенство выполняется тогда и только тогда, когда существует матрица Адамара порядка п+1. Первые несколько значений функции f таковы:
«12345678 9 10 11 12 13
f(n) 1 1 2 3 5 9 32 56 144 320 1458 3645 9477
(См. по этому поводу, например, работы Бреннера и Каммингс [196], Кона [298], Элиха [403], Элиха и Зеллера [404] и Янга [1445].)
2.4. КОНФЕРЕНС-МАТРИЦЫ
Эти матрицы подобны матрицам Адамара, но определяются другим уравнением. Они также приводят к хорошим нелинейным кодам. Вкратце остановимся на этом вопросе.
Определение. Конференс-матрица С порядка п представляет собой («Х«)-матрицу с нулевой главной диагональю и с элементами +1 и —1 в других ячейках, которая удовлетворяет условию
ССт = (п —1)1. (2.16)
(Название для этих матриц возникло из-за их использования в сетях связи с одинаковым затуханием между каждой парой терминалов.) Иногда эти матрицы называются С-матрицами.
Свойства С-матриц. (1). Как и матрицы Адамара, матрицу С можно нормализовать умножением строк и столбцов на —1, так чтобы матрица С имела вид
с=(?г s)’ (2Л7)
где S — квадратная матрица порядка п—1, удовлетворяющая соотношениям
SST = (n—1)1—J; SJ=JS=O. (2.18)
Например, нормализованные конференс-матрицыпорядков Z 4 изображены на рис. 2.9.
с2=
0
1 °/
с4=
О 1 1 1 \
1 ° 1 — I 1 — 0 1 j 1 1 — о у
Рис. 2.9. Конференс-матрицы порядков 2 и 4
(2) . Если матрица С существует, то п должно быть четным. Если п=2 (mod 4), то матрица С может быть приведена к симметрическому виду умножением строк и столбцов на —1; если же n=0 (mod 4), то С может быть приведена к кососимметрическому виду.
(3) . Наоборот, если существует симметрическая конференс-матрица С, то (mod 4) и число п—1 представимо в виде суммы двух квадратов:
• п—1 =гг2 + Ь2,
где а и b — целые числа. Если же существует кососимметрическая матрица С, то п=2 или ri=0 (mod 4). (Для доказательства этих свойств см. работы Дельсарта и др. [366] и Белевича [97].) Известно несколько способов построения таких матриц. Наиболее полезным для наших целей является следующий способ. Метод построения С-м атриц. (Пейли.) Пусть п = рт+ + 1 = 2 (mod 4), где р — простое нечетное число. Как и в §2.3, определим (ртХрт)-матрицу Джекобстола Q=(<7+i)> гДе 0+/ = =%(/—л)- Так как /?m=l(mod 4), то матрица Q в силу свойства (Q2) симметрична. Поэтому матрица
является симметрической конференс-матрицей порядка п.
Пр и меры. (i). Пусть п=6; рт=5. Квадратичными вычетами по модулю 5 являются числа 1 и 4, и описанный выше метод построения дает первую матрицу, показанную на рис. 2.10.
(ii). Пусть п=10; /7’"=32. Пусть элементами поля Галуа GF(32), задаваемого многочленом а2+а-г2 —0, являются 0, 1, 2, a, а+1, а + 2, 2а, 2а+1, 2а-]-2 (см. гл. 4). Квадратичными вычетами в этом поле являются элементы 1, 2, а + 2, 2а+1. Тогда наш метод дает вторую матрицу, изображенную на рис. 2.10.
Описанный выше метод построения дает симметрические конференс-матрицы порядков 6, 10, 14, 18, 26, 30, 38, 42, 50, ... Матрицы порядков 22, 34, 58, ... не. существуют в силу свойства (3)’. Предложенный недавно Мотоном [1477] способ построения дает такие матрицы порядков 46, 442, .,..
Коды, полученные из конференс-матриц. усть Сп — симмет-рическая конференс-матрица порядка п (так что n=2(mod4)) и пусть матрица S определяется соотношением (2.17). Тогда строки двух матриц (S + I+J)/2 и (—S + I+J)/2, а также нулевой вектор и вектор из всех единиц образуют нелинейный мат-рично-конференсный код (п—1, 2п, (п—2)J2). Тот факт, что минимальное расстояние в этом коде равно (п—2) /2, следует из уравнения (2.18).
0 1 2 3 4 -
0 11111
О
3
4
1 0 1--------1
1 1 0 1---------
1 — 10 1 —
1-------1 0 1
1 1-------1 О
О 1 2 а а + 1 а -f- 2 2а 2а -|- 1 2а -|- 2
0| 1 1 1 | 1
Но —
0
1
2
а
а + 1
а-£2
2а
2а + 1
2а-£2
1 0 Illi 0 1 1 1110-
1 ---11
1 1-----1
£ 1 0 £
1
1 1 1
1 — 1
— 1—
1 — —
1 1 —
0 — 1
— 0 1
1 1 0
— 1 1
1
1 о
Рис .2.10. Симметрические конференс-матрицы порядков 6 и 10
Пример. Изображённая на рис. 2.10 конференс-матрица Сю задает (9, 20, 4)-код 'g’g, показанный на рис. 2.11. (Нулевое кодовое слово может быть заменено на вектор веса 1 без уменьшения минимального расстояния в этом коде. Следовательно, существуют по крайней мере два неэквивалентных кода с параметрами (9, 20, 4).)
Этот важный код впервые был построен Голеем [509] другим способом. В § 2.7 дадим два других способа построения кодов с параметрами (9, 20, 4). В § 2.8 (9, 20, 4)-код, изображенный на рис. 2.11, будет использован для построения бесконечного семейства нелинейных кодов, исправляющих одну ошибку.
Несколько первых нелинейных матрично-конференсных кодов имеют следующие параметры:
(5, 12, 2), (9, 20, 4), (13, 28,6), (17, 36, 8),
(25, 52, 12), (29, 60, 14), (37, 76, 18), (41, 84, 20).
Задача (нерешенная). (2.2). Так как п больше чем 2d, то граница Плоткина неприменима к этим кодам. Однако, как’ мы видим в гл. 17, (9, 20, 4)-код оптимален в том смысле, что' имеет наибольшее число кодовых слов для заданной длины и заданного расстояния. (Таким образом, А (9, 4) =20.) Мы предполагаем, что все эти коды, кроме первого и третьего, оптимальны в том же смысле.
(Существуют (5, 16, 2) линейный код1 и (13, 32, 6) нелинейный код — см. § 2.8.)
000 000 000
111 0 0 1 0 10
1 1 1 1 0 0 0 0 1
111 0 10 10 0
0 10 111 0 0 1
0 0 1 111 10 0
10 0 111 0 10
0 0 1 0 10 111
1 0 0 0 0 1 1 1 1
0 10 10 0 111
10 0 110 10 1
0 10 0 11 110
0 0 1 10 1 0 11
10 1 10 0 110
1 1 0 0 1 0 0 1 1
0 11 0 0 1 10 1
110 10 1 10 0
0 11 110 0 10
10 1 0 11 0 0 1
111 111 111
Рис. 2.11. Нелинейный матрично-конференсный (9,. 20, 4)-код *g?9
1 Это код с общей проверкой на четность. (Прим, перев.)
Определение. Пусть X будет ^-множеством (т. е. множеством состоящим из и элементов), элементы которого называются точками или иногда (исторически) независимыми переменными. Назовем t-схемой семейство различных1 k подмножеств (называемых блоками) множества X, удовлетворяющих следующему свойству: любое /-подмножество из X содержится точно в А блоках. Более образно, это—совокупность комиссий, выбранных из v человек, причем каждая комиссия состоит из k человек и любые / человек работают вместе точно в А комиссиях. Назовем такое семейство подмножеств /-(и, k, Л)-схемой2. Иногда /-схемы
называются также тактическими конфигурациями.
Пример. Семь точек и семь линий (одна из которых кривая) на рис. 2.12 образуют проективную плоскость порядка 2.
Если в качестве блоков мы выберем линии, то они образуют 2-(7, 3, 1)-схему, так как через любые две точки из семи проходит точно одна линия. Эти семь блоков таковы:
013, 124, 235, 346, 450, 561, 602.
2-схема называется также уравновешенной неполной блок-схемой, и терминология в этой области возникла вследствие первоначального применения таких схем в агротехнических и биологических экспериментах. Предположим, например, что надо сравнить между собой v различных видов удобрений по их влиянию на Ь различных культур. В идеальном случае каждую
Рис. 2.12. Проективная плоскость порядка 2
культуру надо испробовать с каждым из v видов удобрений, для чего требуется b земельных участков (по одному на каждую культуру), причем каждый участок (или блок) имеет размер v. Получается 2-(и, v, Ь)-схема, которая называется полной схемой. Такое
сравнение, однако, практически невозможно по экономическим соображениям, и мы ищем схему, в которой каждая культура испытывалась бы только с k различными удобрениями (так что каждый 'блок имеет теперь размер k) и любые два разных вида удобрений использовались бы вместе одно и то же число А раз. Таким образом, схема является уравновешенной, если речь идет о сравнении пар разных видов удобрений. Итак, эта схема представляет собой 2- (у, k, А)-схему с b блоками, и она является неполной, если k<v.
1 Это условие, вообще говоря, не обязательно в определении /-схем (см., например, работы Кармайкла [250], Холла [587] и Райзера [1136]). (Прим, перев.)
2 Некоторые авторы располагают буквы /, v, k, А в другом порядке.
Некоторые другие /-схемы также имеют свои собственные на-звания.
Определение. Системой Штейнера называется /-схема, в которой параметр А равен 1, и обычно t-(v, k, 1)-схема' обозначается через S(t, k, v). Таким образом, на рис. 2.12 был приведен пример системы 5(2, 3, 7).
Определение. Проективной плоскостью порядка п называется система 5(2, п+1, п2+п+1) с п^=2. Вот почему рис. 2.12 и изображает проективную плоскость порядка 2. (Подробнее см. в приложении В.)
Определение. Аффинной плоскостью порядка п называется система 5(2, п, п2) с nj>2.
Теорема 9. Пусть Рь ..., Pt обозначают любые / различных элементов заданной /-(и, k, А)-схемы и пусть А< равно числу-блоков, содержащих элементы Ри ..., Pi, l=OsC'/, а Ао=Ь равно общему числу блоков в данной схеме. Тогда число Аг не зависит от выбора элементов Ръ ..., Рг и в действительности определяется следующим равенством:
2 Шу — i \ / 7 k — i\ (v — i) (у — i — 1) . . .(у — / + 1)
1 ~ — — (k — i) (k — i— 1) . . .(A — /+ 1)
приО<г</. (2.19)
Отсюда следует, что /-(и, k, А)-схема является также i-(o, k, Аг)-схемой для любого >1=1, ..., /.
Доказательство. По определению /-схемы результат справедлив для i=t, так как любые / элементов содержатся точно -в А блоках. Воспользуемся теперь индукцией по i. Предположим, что мы уже показали, что число A<+i не зависит от выбора элементов Pi, Pi+i- Для каждого блока В, содержащего элементы Рь ..., Pi, и для каждого элемента Q, отличного от Pi, ..., Pi, положим %(Q, В) = 1, если Q^B, и %(Q, В) = 0, если 0.ЕДВ. Тогда получаем
В)=Аж(и-/)=2 В)=М*-0, (2.20)
QB BQ
что доказывает независимость числа А, от выбора элементов Pi, ..., Pi и устанавливает справедливость (2.19). •
Следствие 10. В /-(и, k, А)-схеме общее число блоков b равно
*=хС )/(*) (2-21)
и каждый элемент встречается точно в г блоках, где
bk—vr. (2.22)
Более того, в 2-схеме выполняется равенство
А (и— 1) = г(/г— 1). (2.23)
Доказательство. Так как fe=X0, то (2.21) .следует из (2.19) при i=0. Так как r='ki, то равенства (2.22) и (2.23) следуют из (2.20). ’ •
Если b = v и, следовательно, r=k, то схема называется симметричной.
Следствие 11. Необходимым условием существования t-(v k Z.)-схемы является целочисленность выражений
для всех'значений i=O, 1, ..., t.
В некоторых случаях, как, например, для систем Штейнера S(2, 3, и), 5(2, 4, п), 5(2, 5, и) и 5(3, 4, и), это условие является также и достаточным, но так бывает не всегда. Например, мы увидим в гл. 19 что система 5(2, 7, 43), или проективная плоскость порядка 6, не существует, хотя указанное выше условие выполнено.
Задача (нерешенная). (2.3). Имеется, предположение, что для любых заданных t, k и К, если выполняются условия следствия И и число v достаточно велико, существует t-(y, k, Z,)-схема. Но пока это предположение доказано только для t=2 (см. работы Вильсона [1420—1422]). В настоящее время не известно ни одной нетривиальной /-схемы с />5.
*Определение.' Пусть Р1г ..., Ph — элементы, принадлежащие одному из блоков заданной t-(v, k, X)-схемы. Рассмотрим блоки, которые содержат элементы Pi, ..., Pj, но не содержат ни одного из элементов Pj+i, .... Pi при (При /=0 рассмот-
рим блоки, которые не содержат Pi, .... Pi, а при j—i— блоки, которые содержат Pi, ..., Pj.} Если число таких блоков одно и то же независимо от выбора элементов Рг, ..., Рг, то обозначим его через Z,,j. -Параметры Z,<j называются индексами блоковых пересечений.
Теорема 12. Параметры Z,ij полностью определены для
В самом деле, Z-ii = Z,i при причем Z,h=A,, и все они находятся по теореме 9. Кроме того, если числа Х,, определены, то они удовлетворяют свойству Паскаля Z,i, = Z,i+i,j+Z,i+i,j+i.
Наконец, если схема является системой Штейнера (Z,= l), то Z,ff=.Z,f+i,f+i= ... =Z,fcfc=l и, следовательно, числа определены для всех значений
Доказательство. Свойство Паскаля выполняется, так как Кц равно числу блоков, которые содержат элементы Pi, ..., Pj, но не содержат элементов Pj+z, ..., Pi+i- Эти блоки могут быть разбиты на две группы: блоки, содержащие элемент Pj+i, — их число равно и блоки, не содержащие Pj+i, — их число равно
То что Z,i3- определены для всех является непосредственным следствием теоремы 9. Действительно, как общее число
* При первом чтении оставшаяся часть этого параграфа может быть пропущена.
блоков Хо=ХОо, так и число блоков 2v1 = A,11, содержащих элемент Pi, не зависит от выбора Следовательно, число блоков, не содержащих Pi, равно Хю=Хо—Xi и также постоянно, т. е. не зависит от выбора Pi, и т. д. Последнее утверждение теоремы очевидно. •
Таким образом, для любой t-(v, k, К) -схемы мы можем образовать «треугольник Паскаля» из ее индексов блоковых пересечений:
= ^2
Например, для системы Штейнера S(2, 3, 7), изображенной на рис. 2.12, получаем следующий треугольник:
7
4 3
2 2 1
0 2 0 1
Из данной t-(v, k, X)-схемы с индексами блоковых пересечений Кц можно получить несколько других схем. Пусть $ обозначает множество из b блоков первоначальной схемы.
Предположим, что мы исключили один из элементов, скажем, Р, из всех блоков 9а, и рассмотрим два множества получившихся блоков: первое, обозначим его S8i, состоит из Хю блоков (каждый блок из k элементов), не содержащих элемента Р в исходной схеме; второе, обозначим его состоит из Хп блоков, содержащих по k—1 элементов.
Теорема 13. Блоки множества 9ii образуют (t—1)-(и—1, k, X<,f-i)-схему, индексы блоковых пересечений которой X(1)i3-=Xi+i.j-Блоки множества 9>2 образуют (t—1)-(и—1, k—1, X)-схему с индексами блоковых пересечений X(2)i3=Xi+i,j+i. Эти схемы называются производными схемами.
Доказательство предоставляется читателю.
Следствие 14. Если существует система Штейнера S (/, k, о), то существует и система Штейнера S (t—1, k—1, v—1).
Если v—k^t, то, беря дополнения .всех блоков из За, получаем дополнительную схему, которая является t-(v, v—k, Хю)-схемой с индексами блоковых пересечений X(c)ij = Xi,i-j.
Матрица инцидентности. Пусть задана t-(v, k, X)-схема с v элементами Pi, ..., Pv и b блоками Bi, Вь. Матрица А= (агДразме-ра bXv с элементами
{1, если Pj^Bp,
0, если PjE^Bi называется матрицей инцидентности данной схемы.
Например, матрица’ инцидентности
рис. 2.12, имеет вид
/11010
0 110 1
0 0 110
0 0 0 1 1
схемы,
0 01
О 0\
1 0
О 1
изображенной на
(2.24)
1 0 0 0 1 1 0 0 1 0 0 0 1 1 '1 0 1 0 0 0 1/
(что это за матрица, читатель должен вспомнить по § 2.3).
Упражнение. (9). Показать, что при /^2 выполняются следующие соотношения:
(1) . ATA=.(r—MI+M-
(2) . det (АТА)' = (г—Л2) + г).
(3) . Если b> 1, то b^v (неравенство Фишера)1.
Коды и схемы. Каждому блоку системы Штейнера S(t, k, v) соответствует строка матрицы инцидентности А. Если мы рассмотрим эти строки как кодовые слова, то система Штейнера образует нелинейный (двоичный) код с параметрами
= щ M = b= Q
Так как любые два блока содержат не более чем t—1 общих элементов (иначе имелось бы t элементов, содержащихся в двух блоках, что приводит к противоречию), то, следовательно, расстояние Хэмминга между ними не меньше чем 2(k—/+1). Заметим также, что каждое кодовое слово имеет вес k; этот код является равновесным.
Можно также рассмотреть линейный код, порожденный блоками /-схемы, но, по-видимому, в общем случае немногое известно о таких кодах. (Как мы увидим в гл. 13, имеются некоторые результаты для /=2 относительно кодов, порожденных аффинными и проективными плоскостями.)
Наоборот, если задан (п, М, cTf-KOR, то иногда можно получить /-схему из кодовых слов фиксированного веса.
Теорема 15.Пусть^? т—[п—2т—1; k=2m—1—т\ </=3]-код
Хэмминга (см. § 1.7), и пусть код получен из кода добавлением общей проверки на четность. Тогда все кодовые слова веса 3 в коде образуют систему Штейнера 5(2, 3, 2т—1), а все ко-л
довые слова веса 4 в коде образуют 5(3, 4, 2т).
1 Неравенство Фишера обычно используется только для 2-схем. Для произвольных /-схем справедливо (см., например, [352]) обобщенное неравенство
Фишера ’ (Прим, перев.)
Определение. Двоичный вектор v покрывает двоичный вектор и, если позиции с единицами вектора и являются подмножеством позиций с единицамй вектора v; так, например, вектор 1001 покрывает .векторы 1001, 1000, 0001 и 0000. Эквивалентными формулировками являются следующие: u* v и*’;
wt (и 4- V) = wt (v)—wt (и).
Доказательство теоремы 15. Первое утверждение теоремы следует из второго, если воспользоваться следствием 14. Для доказа-л тельства второго утверждения обозначим координаты кода Жп буквами До, Р\, —, Рп, где Рп соответствует общей проверке на четность. Пусть и — произвольный вектор веса 3, единицы которого занимают позиции Ph, Pi, Pj, где h<i<j. Надо показать, что л
имеется единственное кодовое слово веса 4 из 3^т, которое по-л
крывает вектор и. Конечно, двух таких кодовых слов в коде 3^т быть не может, иначе они находились бы друг от друга на расстоянии 2, что невозможно. Рассмотрим случай (i), когда j<n. Так как 3^ёт — совершенный код, исправляющий одиночные ошибки, то он содержит кодовое слово с на расстоянии самое большее 1 от вектора и. Тогда либо с=и, и в этом случае расширенное кодо-л л
вое слово с= |с| 11 имеет вес 4, принадлежит коду Д5т и покры-л
вает и, либо с имеет вес 4, и тогда нам подходит слово с=|с[0|. Случай (и),' j=n. Вектор и' с единицами в координатах Ph, Pi покрывается единственным кодовым словом с из 3^т веса 3, и тог-л
да вектор с=|с|1| покрывает наш исходный вектор и. •
Следствие 16. Число кодовых слов веса 3 в коде Хэмминга равно
( 2т — 1 \ / (3\(2т —1)
\ 2 / / \2/~ 3
Л а число кодовых слов веса 4 в расширенном коде Хэмминга Ж» равно
/2й \ / /4 2m~2(2m — 1) ( 2m~* — 1)
\ з / / кз / з •
Как мы увидим в гл. 13, кодовые слова веса 3 в коде &вт могут быть отождествлены с линиями конечной проективной геометрии PG(m—1, 2).
Упражнение. (10). Найти все кодовые слова веса 3 в коде Хэмминга длины 7 и проверить следствие 16 для этого случая. Отождествить полученные кодовые слова с линиями на .рис. 2.12.
Точно так же, как теорема 15, доказывается следующая теорема. -
*’ См. упражнение (7) гл. 1. (Прим, перев.)
Теорема 17. Пусть Ч?— совершенный код длины п, исправ-л
ляющий е ошибок, где е — нечетное, и пусть код Ч? получен из кода Ч? добавлением общей проверки на четность. Тогда все кодовые слова веса 2е + 1 в коде Ч? образуют систему Штейнера л
S(e + 1, 2е+1; п), а кодовые слова веса 2е + 2 в коде Ч? образуют 5(е + 2, 2е+2, п + 1).
Обобщения сформулированного выше следствия, а также более обширные сведения о кодах и схемах будут приведены в гл. 6.
Упражнение. (11). Пусть Нп—-матрица Адамара порядка п^8, и пусть S — матрица, определенная в упражнении (6). Показать, что если элементы —1 заменить на элементы 0, то строки S образуют симметричную 2-^п—1, 1, —-схему, и наоборот.
2.6. ВВЕДЕНИЕ В ДВОИЧНЫЙ КОД ГОЛЕЯ
Код Голея, вероятно, является самым важным из всех кодов как с практической, так и с теоретической точки зрения. В этом параграфе мы дадим элементарное определение этого кода и установим ряд его свойств. Дальнейшие свойства будут приведены в гл. 16 и 20.
Определение. Расширенный код Голея S?24 имеет порождающую матрицу, показанную на рис. 2.13.
1 г >.
оо 0123456789 10 ОО 012345678 9-10 строка
1 1 11 111 1 0
1 1 11 111 1 1
1 1 1 11 111 2
1 1 1 11 111 3
1 1 1 11 111 4
1 1 1 11 111 5
1 1 1 11111 6
1 1 11 1111 7
1 1 111 1 11 8
1 1 111 1 11 9
1 1 1111 11 10
1 11111111111 11
Рис. 2.13. Порождающая матрица расширенного кода Голея g?24. Столбцы перенумерованы следующим образом: l/oo, lot lit •••, Йо» <Гоо, Го, ..., /*10-
Матрица размера 11X11 в правой части рисунка представляет собой матрицу Ап
Двоичная (ПХП)-матрица А1Ь находящаяся в правой части этой порождающей матрицы, получается из матрицы Адамара типа Пейли (см. рис. 2.1 и 2.5). Отсюда сразу следует, что сумма любых двух строк матрицы Ап имеет вес 6. Следовательно, сумма любых двух строк матрицы G имеет вес 8.
Лемма 18. Код ®24 является самодуальным; <§?a=<S1-<2a.
Доказательство. Если и и v — две (не обязательно различные) строки G, то wt(u *v)=0 (mod 2). Следовательно, каждая строка матрицы G ортогональна всем другим строкам, и поэтому S,24cnS’-L24. Но ранг матрицы G равен 12, поэтому код S'24 имеет размерность 12 и, следовательно, S,24=^±24- •
Лемма 19. (i). Каждое кодовое слово кода S24 имеет вес, кратный 4.
(ii). Код З24 содержит кодовое слово 1 = 11 ... 11.
Доказательство. Утверждение (1) совпадает с упражнением (38) из гл. 1. Для доказательства утверждения (ii) надо сложить все строки матрицы G. •
Л е м м а . 20. Код S24 инвариантен относительно перестановки координат 2"= (/ооГоо) (/о^о) (^1'^ю) (/2Гд)...(/юГ1), которая меняет местами две половины кодового слова. Более точно: если код S24 содержит кодовое слово |L|R| , где L=aooao«ia2 — «10; R= =|&оо&оЬ1&2 — Ь10, то он также содержит и кодовое слово |L/|R/|, где =ЬооЬД)\Д>^ ... R/=tZoo а^а^ад ... а^.
Доказательство. Перестановка Т переводит строку с номером 0 матрицы G в последовательность
0, 1, 0100011101, 1, 1, 0000000000, которая, как легко проверить, является суммой строк с номерами 0, 2, 6, 7, 8, 10, 11 и, следовательно принадлежит коду. Подобным образом поступим со строками матрицы G, имеющими номера от 1 до 10. Последнюю строку G перестановка Т переводит в последовательность 112012, которая представляет собой дополнение последней строки и поэтому по лемме 19 принадлежит коду. •
Замечание. Из этой леммы вытекает, что если код S24 содержит кодовое слово |L|R| с весами wt(L)=i и wt(R)=/, то он также содержит кодовое слово (L'lR7! с весами wt(Lz)=j; wt(R')=ii.
По лемме 19 возможными весами кодовых слов в коде S24 являются числа 0, 4, 8, 12, 16, 20, 24.
Если вектор и имеет вес 20, то вектор u +1 имеет вес 4. Мы по-, кажем сейчас, что кодовых слов веса 4 нет в коде и, следовательно, нет слов веса 20.
Лемма 21. Код S24 не содержит кодовых слов веса 4.
Доказательство. Для любого кодового слова | L|R| из S24 получаем, что wt(L) =wt(R) =0 (mod 2). По лемме 20 мы можем предположить, что кодовое слово веса 4 принадлежит одному из следующих двух типов:
(l)wt(L)=0, wt(R)=4; (2)wt(L) = 2, wt(R)=2.
Условие (1) невозможно, так как если wt(L)=0, то wt(R)=0 или 12. Условие (2) также невозможно, ибо если wt(L)=2, то вектор L равен сумме одной или двух строк G с прибавлением, возможно, последней строки. В каждом из этих случаев wt(R)=6 согласно абзацу, предшествующему лемме 18. •
Таким Образом, в коде S24 встречаются веса 0, 8, 12, 16, 24. Обозначим через Л, число кодовых слов веса i. Тогда Ло=Л24=1; Л8=Л16. Каждой левой части кодового слова L соответствуют две возможные правые части R и R*>. Если wt(L)=0, то wt(R)#=4 (в силу леммы 21) и wt(R)=?^8 (иначе wt(R)=4, что снова противоречит лемме 21), так что wt(R)=0 или 12. Если wt(L)=2, то подобными же рассуждениями получаем, что wt(R)=6. Продолжая таким образом, мы получим следующие возможности для весового распределения слов в коде ^24:
Число wt (L) wt (R) wt (R) Полный вес
1 0 0 12 0 12
"+(") 2 6 6 8 8
(ГЮ 4 4 8 8 12
а=? 6 2 10 8 16
₽=? 6 6 6 12 12
ст+й1) 8 4 8 12 16
(ПЛЩ 10 6 6 16 16
1 12 0 12 12 24
По лемме 20 число а равно числу кодовых векторов типа (2, 6), которое равно 2^11+
Следовательно, Л8 = 4^11+ =
и поэтому Л 12=2576. Таким образом, мы показали, что весовой спектр кода ^24 имеет вид
z:0 8 12 16 24
А{:1 759 2576 759 1
Теорема 22. Любой двоичный вектор веса 5 и длины 24 покрывается точно одним кодовым словом веса 8 из ^24-
Доказательство. Предположим, что вектор веса 5 покрывается Двумя кодовыми словами и и v веса 8; тогда dist (u, v)<:'6, что приводит к противоречию. Кроме того, каждое кодовое слово веса
> См. вид последней строки матрицы G. (Прим, перев.)
8 покрывает | r j векторов веса 5, которые все различны, и, значит,
Следствие 23. В расширенном коде Голея S?24 кодовые слова веса 8 образуют систему Штейнера S (5, 8, 24). Отсюда согласно следствию 14 получаем системы Штейнера S (4, 7, 23), S (3, 6, 22) и S (2, 5, 21).
Условимся кодовые слова .веса 8 и 12 в коде ^24 называть соответственно октадами и додекадами.
Теорема 24. Индексы блоковых пересечений Лц для системы Штейнера, образованной октадами, приведены на рис. 2.14.
i | О 1 2 3 4 5 6
7 8
759
506 253
330 176 77
210 120 56 21
130 80 40 16 5
78 52 28 12 4 1
46 32 20 8 4 0 1
30 16 16 4 4 0 0 1
30 0 16 0 4 0 0 0 1
Рис. 2.14. Индексы блоковых пересечений схемы, образованной октадами расширенного кода Голея 5? 24
Следствие 25. Кодовые слова веса 16 в коде S24 образуют 5-(24, 16, 78)-схему, и соответствующий треугольник Паскаля получается отражением рис. 2.14 относительно середины.
Доказательство. Данная схема является дополнительной к схеме, образованной октадами. •
Теорема 26. В коде S?24 додекады образуют 5-(24, 12, 48)-схему. Предположим, что элементы Ръ ... Ps образуют октаду. Временно злоупотребляя используемыми . обозначениями, положим Кц равным числу додекад, содержащих Рь ..., Pj и не содержащих элементов Р,+ъ ..., Pj для всех значений 0^'/^1^8. Тогда эти параметры изображены на рис. 2.15.
Доказательство. Покажем сначала, что Хбб=^7б=^8б=16. Действительно, имеется очевидное 1 -1-соответствие между додекадами, содержащими элементы Ръ ..., Р6 (которые не могут содержать Р? или Pg), и октадами, содержащими Ру и Pg, но не содержащими элементов Ръ ..., РЪ*Х Поэтому согласно рис. 2.14 параметр
*> Напомним, что g?24 —линейный. (Прим, перев.)
^66=16 Отсюда следует, что 3X16=48 до декад содержат элементы Pi, ...ДР5, так что %55=48. Поэтому додекады образуют 5-схему. Теперь оставшуюся часть таблицы можно заполнить с помощью теоремы 9] и свойства Паскаля. 9
О I 2576
1 \ 1288 1288
2 616 672 616
3 1 280 336 336 280
4 I 120 160 176 160 120
5 | 48 72 88 88 72 48
6 16 32 40 48 40 32 16
7 0 16 16 24 24 16 16 0
8 0 0 16 0 24 0 16 0 0
Рис. 2.15. Обобщенные индексы Кц блоковых пересечений схемы, образованной додекадами кода Голея 2г 21
В гл. 6 мы дадим достаточное условие того, что все кодовые слова фиксированного веса произвольного кода образуют Z-схему, которое включает эти результаты как частный случай.
Упражнения. (12). Показать, что код Голея приводит так-
же к следующим схемам:
V k b 7-2 Т-з Т,4
23 7 253 77 21 5 1
23 8 506 176 56 16 4
22 6 77 21 5 1
22 7 176 56 16 4
22 8 330 120 40 12
(13). Показать, что 4096 смежных классов кода S24 имеют еле-
дующие весовые спектры:
Число Вес 0 2 4 6 8 10 12 14 16 18 20 22 24
1 1 759 2576 759 1
276 1 77 352 946 1344 946 352 77 1
1771 6 64 360 960 1316 960 360 64 6
Число Вес 1 3 5 7 9 11 13 15 17 19 21 23
24 1 253 506 1288 1288 506 253 1
2024 1 21 168 640 1218 1218 640 168 21 1
Определение. Нерасширенный код Голея длины 23 З’зз получается выбрасыванием последней координаты из каждого ко
дового слова кода ^24- В гл. 16 мы увидим, что выбрасывание любой координаты из кода S?24 приводит к эквивалентному коду.
Теорема 27. Код Э’гз является [23, 12, 7]-кодом/с весовым спектром: I
г:0 7 8 11 12 15 16 23
At: 1 253 506 1288 1288 506 253 1
Доказательство. Доказательство следует непосредственно из рис. 2.14. Например, кодовые слова веса 7 в коде &2з) представляют собой октады кода S24, у которых последняя координата равна 1; число их равно &ц=253. | •
Теорема 28. Код Голея ^23 является совершенным кодом, исправляющим три ошибки.
Доказательство. Так как минимальное расстояние кода равно 7, то все смежные классы с лидерами веса не более 3 отличны друг от друга (по теореме 2 гл. 1). Число таких смежных классов равно
= 211 = 223~12
поэтому они составляют все смежные классы кода ^гз- Следовательно, код ^23 — совершенный. *
2.7. СИСТЕМА ШТЕЙНЕРА 5(5, 6, 12) И НЕЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОДНУ ОШИБКУ
Лемма 29. Нелинейный код, состоящий из строк матрицы Ап (см. рис. 2.13), попарных сумм этих строк и дополнений ко всем полученным векторам, является (11, 132, 3)-кодом.
Доказательство. Всего имеется 2^11 + = 132 кодовых сло-
ва. Типичное кодовое слово имеет вид а+b или a+b+1, где а и Ь — различные строки Ап; возможно Ь = 0. Для того чтобы показать, что расстояние между кодовыми словами по крайней мере равно 3, мы должны рассмотреть четыре случая:
(1). dist (a+b, а+с) =wt(b + c) =6 согласно абзацу, предшествующему лемме 18.
(п). Аналогично dist(a+b, а+с+1)=5.
(ill), dist (a+b, c+d) =wt(a+b + c+d) ^4. В противном случае соответствующее кодовое слово кода ^24 имело бы вес, меньший чем 8, что приводит к противоречию.
(iv). Аналогично dist (a+b, c+d+l)^3. •
Теорема 30. Кодовые слова расширенного (12, 132, 4)-кода образуют блоки системы Штейнера 5(5, 6, 12).
Доказательство. Любой вектор веса 5 может быть покрыт самое большее одним блоком, иначе нашлись бы два кодовых слова, расстояние между которыми было бы меньше 4, что невозможно. Поэтому 132 блока покрывают 132-6= (12 ) различных векторов
веса 5. Таким образом, каждый вектор веса покрыт точно од-ним блоком. •
Используя следствие 14, мы получаем системы Штейнера 5(4, 5, 11)\S(3, 4, 10) и 5(2, 3, 9).
Нелинейные коды, исправляющие одну ошибку. Удобно переставить координаты (12, 132, 4)-кода из теоремы 30 так, чтобы он содержал кодовое слово (или блок) 111 111 000 000. Обозначим координаты герез ..., Х12. Теперь мы можем включить в этот код 12 векторов, изображенных на рис. 2.16, не уменьшая минималь-
ного расстояния, и получить (12, 144, 4)-код, который мы обозначим через ‘g’l'a.
*1 *2 *з хе *7 *а *9 *10 *U *12
1 1 0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 [о 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1
0 0 1 1 1 1 1 1 1 1 1 1
1 1 0 0 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 0
Рис. 2.16. Двенадцать, добавочных кодовых слов
Лемма 31. В коде фц имеется кодовое слово (обозначим его с), находящееся на расстоянии 4 от 51 кодового слова.
Доказательство. Докажем, что в качестве слова с можно выбрать с=111 111 000 000. Для системы Штейнера 5(5, 6, 12) индексы блоковых пересечений имеют следующий вид:
132
66 66
30 36 30
12 18 18 12
4 8 10 8 4
1 3 5 5 3 1
1 0 3 2 3 0 1
Блоки, находящиеся от с на расстоянии 4, должны иметь с ним 4 общих элемента. Число таких блоков равно! ) •Аб4=15-3=45.
\ 4 J
Из кодовых слов, изображенных на^ рис. 2.16, шесть также находятся на расстоянии 4 от вектора с, чт'о 'и дает общее число 51. • (Из этого доказательства ясно, что для любого кодового слова число кодовых слов, находящихся от него на расстоянии 4, не превосходит 51.)
з кода 12 'Построим четыре Более коротких кода: /
(i) . Выбрав .в коде 4!?l2 кодовые слова, для которых д12=1, мы получим(11, 72, 4)-код &п. Те же рассуждения, что и р леммеЗ!, показывают, что в коде 'g’n имеется кодовое слово, находящееся на расстоянии 4 от 34 других слов. /
(ii) . Выбрав в коде кодовые слова, для которых Xi2=l, л'ю=0, мы получим (10, 38, 4)-код В коде &(а) J имеется кодовое слово, находящееся на расстоянии 4 от 22 других слов.
(iii) . Выбрав в ходе кодовые слова, для которых Х12=Хц= = 1, мы получим (10, 36, 4)-код который содержит нулевой вектор 0. В этом коде имеется слово, находящееся на расстоянии 4 от 30 других кодовых слов. \
(iv) . Выбрав в коде ^гкодовыеслова, для которыхх12=Хц=1, х10=0, мы получим (9, 20, 4)-код ^д, содержащий нулевой вектор 0. В коде имеется слово, находящееся на расстоянии 4 от 18 других слов. (Другой (9, 20, 4)-код был приведен в § 2.4.) Если в этом коде выбросить одну координату, то этот код станет (8, 20 3) -кодом.
00000000
1 1 0 1 0 0 0 0 01101000 0 0 1 10 10 0 00011010 00001101
1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 1 10100001
1110 0 10 0 0 1110 0 10 00111001 10 0 1110 0 0 10 0 1110 00100111 1 0 0 1 0 0 1 1 11001001
10 10 10 10 0 10 10 10 1
11111111
Рис. 2.17. Код (8, 20, 3)
Другой способ построения (о, , -кода показан на рис. . /.
Отметим, 'ято этот код является циклическим в том смысле, что циклический сдвиг любого кодового слова снова является кодовым словоц.
Так как ’кисло кодовых слов не равно степени 2, ни один из приведенных кодов не является линейным. Как уже указывалось в § 2.4, код №, 20, 4) оптимален.
Задачи! (неР ешенные) (2.4). Оптимальны ли коды с параметрами (10, 38, 4), (11, 72, 4), (12, 144, 4)? В настоящее время наилучшие известные оценки таковы: А (10,4) ^40; А (11,4) ^80; А (12,4) ^160| (см. гл. 17 и приложение А).
(2.5). Обобщить способ построения (12, 144, 4)-кода для нахождения других хороших нелинейных кодов с помощью матрицы Адамара, выбирая в качестве кодовых слов ее строки, суммы двух строк и т. д.
(2.6). Обобщить способ построения, изображенный на рис. 2.17, для нахождения других хороших нелинейных циклических (n, М, d)-кодов с длиной п больше чем 2d.
Заметим, что имеется несколько неэквивалентных конструкций кодов ^э, ..., ‘g’lg, так как 12 кодовых слов, изображенных на рис. 2.16, могут быть переставлены многими способами.
2.8. ВВЕДЕНИЕ В КОД НОРДСТРОМА—РОБИНСОНА
Расширенный код Голея S24 может быть использован для построения нескольких интересных нелинейных кодов, исправляющих две ошибки.
Построение. Удобно изменить порядок столбцов в коде SF24 так, чтобы он содержал кодовое слово 11111111 00 ... 0=18016. Пусть G — порождающая матрица для этого нового варианта кода ^24-
Первые семь столбцов матрицы G линейно независимы, иначе дуальный код ®’±24 содержал бы ненулевое кодовое слово веса 7 или меньше. Но ®’24=^±24, так что это невозможно. Таким образом, первые семь координат могут быть выбраны в качестве информационных символов, а восьмая координата равна сумме первых семи.
Разделим все кодовые слова в соответствии с их значениями на первых семи позициях; всего имеется 27 возможностей, и для каждой из них в коде найдется 212,/27=32 кодовых слова. Таким образом, в коде имеется 8X32 = 256 кодовых слов, которые начинаются либо с семи нулей (и тогда восьмая координата тоже нуль), либо с шести нулей и одной единицы1 (при этом восьмая координата равна единице).
Определение. Выбрасывая первые восемь координат в этих 256 кодовых словах, получаем код Нордстрома — Робинсона
1 Единица может занимать любую из семи позиций. (Прим, перев.)
Множество всех слов хода Голея
(см. рис. 2.18, на котором код ЛЛе заключен внутри двойных линий). I
Теорема 32. Код Нордстрома — Робинсона Л9^ представляет собой (16, 256, 6)-код. /
Доказательство. Пусть а, Ь — различные слова койа Л9^, полученные укорочением слов а', Ь' кода »24. Так как dist (а', Ь') ^8, то dist (а, b)>6. I •
„ , Заметим, что код ЛЛ6
Нордстрома- составлен из линейного Робинсона f 16, 5, 8]-кода, обозначим его через SB (образованного теми словами кода ^24, первые восемь координат которых равны нулю), и семи его смежных классов в коде ^24- В гл. 15 будет приведено несколько обобщений кода
Рис. 2.18. Построение кода Нордстрома— Нордстрома — Робинсо-Робинсона на, а именно коды Кер-
дока и коды Препарата, также имеющие структуру подобного вида.
У п р а ж не н и е. (14). Показать, что код Л9|6 нелинеен.
Так как код 5?24 содержит вектор из единиц I24, то его подкод .ВВ содержит вектор I16. Все другие слова кода S§ должны тогда иметь вес 8. Поэтому весовой спектр кода 9с> таков:
г:0 8 16
At:1 30 1
Рассмотрим один из смежных классов кода S3 в коде Л9^, скажем, 9h—Vi+SB. Ясно, что в смежном классе SBi могут встречаться лишь веса:
6 = 8—2; 10=12—2; 14 = 16—2.
Так как то наряду с вектором веса 14 смежный класс l^i должен был бы содержать вектор веса 2, что невозможно. |Аналогично Л6=Л1о. Следовательно, весовой спектр кода ВВ-; таков:
i: 6 10
Л-16 16
(В гл. 14 мы увидим, что SB является кодом Рида—Маллера первого порядка, а векторы кода представляют собой экстремально нелинейные функции *.) Объединяя все результаты вместе, мы находим, что весовой спектр кода Л9^ имеет вид, показанный на рис. 2.19.
1 В оригинале «bent functions». (Лрим. ред )
I : О 6 8 10 16
At : 1 112 30 112 1
Упражнения. (15). Показать, что для любого слова с кода yTi6 число кодовых слов, находящихся на растоянии i от него, такжц задается рис. 2.19. Таким образом, код Л’гв инвариантен относительно расстояния. [Указание. Рассмотреть весовой спектр (кода с + yTie, образованного сдвигой, и воспользоваться рис.
2.18.]
Таким образом, мы знаем, что в коде yTie спектр расстояний равен его весовому спёктру и задается рис. 2.19.
Укорочением кода yTie мы получаем коды (15, 128, 6), (14, 64, 6) и (13, 32, 6). Все четыре кода оптимальны (гл.
но, что коды (16, 256, 6), (15, 256, 5), (15, 128, 6), (14, 128, 5), (14, 64, 6), (13, 64, 5) и (13, 32, 6) единственны, но это неверно для укороченного (12, 32, 5)-кода.
Следующие упражнения дают другие способы построения (12, 32, 5)-кода и Л^е-
(16). (Ван Линт) Пусть
(1 0 0\ /1 ! 1\ /01 0\
о 1 о j; 1 1 1 b р=1 о о i); q=p2=pt=j—i— р.
0 0 1/ \1 1 1/ \1 о о/
Рис. 2.19. Весовой спектр кода Нордстрома — Робинсона yp’ie
17). Кроме того, извест-
Показать, что вектор 0 и строки матриц а, р, у, 6 образуют (12, 32, 5)-код, где
(J —I I I I \ /J Р I Q\
I J-I I I
I I J —I I I I 1 Q J P I
I I I J —I/ \P I Q J/
y = (J —I, J —I, J I, J—I);
(000 111 111 111\
111 000 111 111 |
111 111 000 111 I
111 111 111 000/
(17). (Семаков и Зиновьев). Пусть А, В, С, D — матрицы перестановок размера 4X4 такие, что A+B + C + D=J, и пусть K=A+D, L=A+C и М=А+В.
Показать, что строки матриц щ, ..., ав и их дополнения образуют (16, 256, 6)-код, где
~АААА’ ABCD ACDB
АААА BADC CABD
“1 = АААА ; а2 = CDAB ; а8 = DBAC »
АААА
DCBA
BDCA
«4- ADBC DACB BCAD CBDA ; a5= OKLM KO ML LMOK MLKO ; «6= OLMK i LOKM/ MKOL KMLO 9
a7 = OMKL MOLK ; a8 = PPPP PPPP p= 0 0 0 Jr 0 1 0 /1 1
KLOM LKMO_ PPPP _PPPP_ 0 0 11 0 1 1 0_
где черточка обозначает дополнение, а О — нулевую матрицу.
Задача (нерешенная). (2.7). Обобщить конструкции упражнений (16) и (17).
2.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (III)
Построение с помощью прямой суммы. Если заданы (ni, Mi, бЛ)-код и (п2, М2, d2)-KOR то их прямая сумма состоит из всех векторов1 | u | v |, где ue?i, Ясно, что множество
таких векторов образует (щ + п2, MiM2, d=min{di, ,с/2})-код. Этот способ прост, но не очень полезен. Более разумен следующий способ.
Конструкция |u|u + v|. Если заданы (п, Mi, <А)-код и (п, М2, ^2)-код *$2 одной и той же длины, то мы можем образовать новый код ‘g’s, состоящий из всех векторов вида | и | u+v|; U GE vGE ^2-
Теорема 33. Код ^з является (2п, MiM2, d = min {2di, d2})-КОДОМ.
Доказательство. Пусть a=|u|u + v|; b=|u/|u/+v/|—два различных слова кода ??з, где u, и'еТГ v, Если v=v', то
dist (a, b)=2dist (u, u/)^2di. Предположим, теперь, что v^v'. Тогда, учитывая упражнение 8 гл. 1, получаем
dist (a, b) = wt(u—u') + wt(u—u' + v—v') > wt(u—u') +
-j-wt(v—v')—wt(u—u')= wt(v—v') > d2- *
Этот способ построения очень быстро приводит к хорошим кодам.
Пр и меры. Выбрав в качестве <5’1 [4, 3, 2]-код из всех слов четного веса и в качестве ^2 [4, 1, 4]-код с повторением, получим в качестве 7?3 [8, 4, 4] - код Рида — Малдера первого порядка. Выбрав теперь .в качестве ®’1 полученный [8, 4, 4]-код и в качестве ¥?2 (8, 1, 8]-код, получим в качестве ‘Э’з [16, 5, 8]-код Рида—• Малдера первого порядка. На самом деле, как мы увидим в гл.
’Если u=ui ... um, v=vi ... vn, то |u|v| обозначает вектор щ ... um Vi ... —vn длины tn+n.
13, все кодк Рида — Маклера могут быть построены так.
Замечания, (а). Если коды *4 и имеют различные длины, то опиёанная конструкция применима, если мы добавим соответствующее число нулей в конце более короткого кода.
(Ь). Если коды 4 и Т?2 линейны, например klt di];
<5’2=[п2, ks, d2], то код 'ё’з представляет собой [2max{«i, п2}, ki+k2, с?=пйй {2d}, d2}] линейный код.
Бесконечное семейство нелинейных кодов, исправляющих одну ошибку. Беря в качестве исходных (8, 20, 3), ..., (11, 144, 3)-коды, приведенные в § 2.7, мы можем построить бесконечное семейство кодов:
(8, 128, 2), (8, 20, 3)->(16, (20/16)-211, 3);
(9, 256, 2), (9, 20, 4)-*(18, (20/16)• 212, 4)-^(17, (20/16)-21а, 3);
(12,2й, 2), (12,144, 4)->-(24, (18/16)-218, 4)-423, (18/16)-218, 3);
(16,215, 2), (16, (20/16)-2и, 3)-*(32, (20/16)-226, 3).
Продолжая таким путем, мы получаем следующий результат.
Теорема 34. Для любой длины п, удовлетворяющей условию 2m^n<3-2m-1, существует нелинейный (п, ^2n~m~I, 3)-код, где Х= (20/16), (19/16) или (18/16).
Замечания. Из границы сферической упаковки (теорема 6 гл. 1) следует, что наибольший линейный код той же самой длины, исправляющий одну ошибку, который представляет собой (п, п—m—1, 3) укороченный код Хэмминга, имеет только 2n-m-l КОДОВЫХ СЛОВ.
Нелинейные коды Васильева, исправляющие одну ошибку. Коды Хэмминга, которые были построены в' § 1.7, являются единственными, любой двоичный линейный код с параметрами \п = = 2т—1; k=n—т; d=3] эквивалентен коду Хэмминга. Это так, потому что проверочная матрица кода должна содержать все 2т—1 ненулевых двоичных m-векторов в некотором порядке.
Это не так, если отбросить предположение о линейности кода.
Упражнения. (18).Кобы Васильева. Пусть —совершенный двоичный (п=2т— 1, М=2п~т, 6=3)-код, исправляющий одну ошибку, не обязательно линейный. Пусть X — любое отображение слов кода в поле GF(2) (причем Х(0)=0), которое является строго нелинейным: найдутся векторы u, vei, для которых X(u+v) 4(и) +X(v). Положим л(и)=0 или 1 в зависимости от того, четно или нечетно число wt (и).
Показать, что код
W = { I и I u + v I n(u) + %(v) | :ueK, vG^} является совершенным (2m+1—1, 22n-7n, 3)-кодом, исправляющим одиночные ошибки, который неэквивалентен никакому линейному коду. Показать, что такие коды существуют для всех т^З.
(19). Пусть ‘g’j обозначают [п, ki\ линейные коды, i=l, 2. Показать что:
(i) если <®’={|u|u| : ue'g’J, то <g’-L = {|ala+v| : vg
(ii) если ®’={|u|u+v| iug^, vg?2},to <5’-L={|a+b|b| :ae e®’-L1, be?^};
(iii) если <5’={|a+x|b+x|a+b+x| : a, bf^Fi, xg^2}, to <&!-= {|u+w|v + w|u+v+w| : U, VG?1], WGii2}.
ЗАМЕЧАНИЯ К ГЛ. 2
§ 2.1. Эпиграф взят из работы [876]. Плоткин [1064] был первым, кто начал серьезно изучать нелинейные коды. Тот факт, что наибольший линейный код длины 11, исправляющий две ошибки, содержит 46 кодовых слов, следует из таблицы Хелгерта и Стинаффа [636]. О связи между кодами и проблемой шаровой упаковки см. работу Лича и Слоэна [810].
§ 2.2. Теорема 1 и следствие 4 принадлежат Плоткину [1064].
§ 2.3. Вопросы, связанные с матрицами Адамара, обсуждаются в работах Баумерта [81], Бассмейкера и Зейделя [221], Геталса и Зейделя [501], Голомба [522], Адамара [572], Холла [583, 586—588, 590], Ван Лиита [853], Пейли [1019], Райзера [1136], Сильвестра [1296], Сони и Голомба [1320], Тодда [1328], Турина* [1345—1347], Уоллиса и др. [1386] и Уайтмена [1413'.
Свойства квадратичных вычетов см. в работах Ле Векуа [825, I, гл. 5], Перрона [1035], Рибенбойма [ПШ] и Успенского и Хизлета [1359, гл. 10].
Плоткин [1064] и Боуз и Шрикхандэ [187] построили двоичные коды из матриц Адамара. Семаков и др. [1179—1182] обобщили эти построения на поля из q элементов. Теорема 8 взята из работы Левенштейна [819]. Наибольший возможный [n, ‘k, d] линейный код для значений n^2d определяется теоремой 27 из гл. 117.
§ 2.4. Конференс-матрицы были введены Белевичем [95—97]. Другие значительные работы — Дельсарт и др. [366], Геталс и Зейдель [500], Ван Линт [853], Ван Линт и Зейдель [856], Пейли [1019], Турин [1346] и Уоллис и др. [1386]. Коды Сп были предложены Слоэном и Зейделем [1238]. Кои-ференс-матрицы использовались также для построения матриц Адамара (Пейли [1019], Рагхаварао [1085, §17.4]), в теории цепей (Белевич [95—97]), для построения -весовых планов (Рагхаварао [1085, гл. 17]) и при 'изучении сильно регулярных графов (Зейдель [1175—1177]).
§ 2.5. По Асхемам см. работы Оллтопа (21—24], Боуза [173, 177], Кармайкла [250], Колленса [300], Дембовского [370], Дуайена и Роза [386], Холла [585, 587], Ханани [595—600], Хьюджса [673], Хьюджса и Пайпера [675], Ди-Паолы и др. [1020], Рагхаварао [1085], Роковской [1122], Райзера [1136], Стентона и Колленса [1266], Вайды [1360, 1361], Вильсона [1420— 1422] и Витта [1423, 1424].
§ 2.6. Код был открыт Голеем в 1949 г. [506] (см. в гл. 20 обширную литературу по этому коду).
§ 2.7. Приведенное построение системы Штейнера 5(5, 6, 12) принадлежит Личу [803]. Эта система является единственной (см. упражнение (19) гл. 20). Коды ‘g’s—^12 были построены Голеем [509] и Джулин [701]. Конструкции, приведенные здесь, взяты из работ Лича и Слоэна [810] и Слоэна и Уайтхеда [1239].
§ 2.8. Код был найден Нордстромом и Робинсоном [1002] (см. также [L119, 1253]) и независимо Семаковым и Зиновьевым, которые привели его в виде, указанном в упражнении ('1'7) '[1180]. Построение кода из кода Голея ^24 принадлежат Гёталсу [493] и Семакову и Зиновьеву [1181]. Коды (13, 64, 5) и (12, 32, 5) были найдены Стивенсом и Боурициусом [1277] в 1959 г. и переоткрыты Надлером [982] и Грином [556]. Коды (15, 256, 5), (14, 128, 5), (13, 64, 5) и (12, 32, 5) содержат в 2 раза больше кодовых слов, чем любой линейный код той же длины и с тем же минимальным рас
стоянием, так как Фонтейн и- Питербон [434], а также Калаби и Мирваанес [228] показали, что не существует [12, 5, 5] линейного кода. Конструкция в упражнении (16) найдена Ван Линтом [851]. Вопросы, связанные с единственностью этих кодов, см. в работах Геталса [497] и Сновера [1247].
§ 2.9. Способ построения |u|u+v| впервые, по-видимому, был приведен Плоткиным [1064] и переоткрыт Слоэном и Уайтхедом [1239]. См. также работу Лью и др. [858], где обобщение этого способа используется для построения кода Нордстрома — Робинсона. Теорема 34 взята из работы [1239], где можно найти также и другие применения этого метода построения. Упражнение (18) взято из работы Васильева [1366].
Глава 3
Введение в коды БЧХ и конечные поля
3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
Известно из гл. 1, что коды Хэмминга исправляют одиночные ошибки. В этой главе будут введены коды, которые в определенном смысле обобщают их на случай t ошибок и называются кодами Боуза—Чоудхури—Хоквингема (или, кратко, кодами БЧХ). в этой же главе мы введем одну из центральных тем теории кодирования, а именно теорию конечных полей.
Попытаемся вначале найти обобщение кодов Хэмминга, позволяющее исправлять две ошибки.
Двоичный код Хэмминга длины п=2т—1 должен иметь т проверочных символов, чтобы исправлять одну ошибку. Естественное предположение состоит в том, что для исправления двух ошибок необходимо 2т проверочных символов. Итак, попытаемся построить проверочную матрицу Н' кода, исправляющего две ошибки, добавляя еще т строк к проверочной матрице Н кода Хэмминга.
В качестве примера возьмем т=4; п=15. Тогда матрица Н имеет своими столбцами все возможные ненулевые 4-векторы:
Н =
го
о о
о о 1 1
О 1
о о
1 1 о о О 1
о о
1 1
1 1
О 1
[111111 0 0 0 0 1 1 1 0 0 1 1 0 0 1 0 10 10 10
1
1
1
1
о о
1
что мы сокращенно обозначим как
Н = [1, 2, 3, • • ; 14, 15],
(3.1)
где через число i обозначен соответствующий ему двоичный 4-вектор1. Мы собираемся добавить к Н еще 4 строки, например таким способом
Н' =
‘12 3 15 1
. f(l) f(2) f(3) • • 7(15)J ’
(3.2)
1 Этот 4-вектор является двоичным представлением числа i. (Прим, перев.)
где значением функции f(i) также является вектор длины 4 из нулей и единиц. Поэтому и'-й столбец матрицы Н'
(3.3)
представляет собой вектор-столбец длины 8.
Как выбрать функцию f(i)? Предположим, что две ошибки — на позициях i и /. Тогда (по теореме 4
произошли гл. 1) син-
дром равен
8 = Нг+Н> =
i + J \ f(0
Необходимо выбрать f(i) так, чтобы декодер по S мог найти I и j, т. е. чтобы он мог одновременно решить уравнения
i + ] (314)
f(i) + f(/) = z2l
относительно i и j при заданных Zi и z2. При этом все эти элементы i, j, f(i), f(j), Zj, z2 являются векторами длины 4.
Для того чтобы решить эти уравнения, нам хотелось бы уметь складывать, вычитать, умножать и делить эти 4 векторы. Другими словами, мы хотим, чтобы эти 4-векторы образовывали поле. Вначале опишем построение этого поля, а затем вернемся к проблеме построения кодов, исправляющих две ошибки.
Определение. Поле — это множество элементов, в котором определены операции сложения, вычитания, умножения и деления (за исключением деления на 0, которое не определено). Сложение и умножение должны удовлетворять коммутативному, ассоциативному и дистрибутивному законам: для любых элементов а, р, 7 в этом поле должны выполняться соотношения
а + Р = Р + а; «Р = Ра;
«+(₽+у) = («+₽)+?; а(₽т)=(«₽)?;
а(Р+у)=ар + ау;
кроме того, должны существовать элементы 0, 1 (и для любого а) —а, а 1 (а=И=0) такие, что
0-|-а=а; (—а) + а=0; 0а = 0;
1а=а и если а =^0, то (а г)а= 1.
Конечное поле содержит конечное число элементов, и это число называется порядком поля.
Конечные поля называются полями Галуа по имени их первого исследователя Эвариста Галуа.
3.2. ПОСТРОЕНИЕ ПОЛЯ <?Е(16)
Ясно, что последовательности длины 4 из элементов 0 и 1 можно складывать как векторы, а вычитание в нашем случае совпадает со сложением. Более того, а0П1020з + Оо^1«2Сз=0. Мы долж-
ны, однако, определить умножение Для этого сопоставим каждо-
му 4-вектору многочлен от а:
4-вектор Многочлен
0 0 0 0 0
10 0 0 1
0 10 0 a
110 0 1 +a
0 0 10 a2
10 10 1 +a2
0 0 0 1 a3
1’1 1 1 1 +a+a2+a3
Умножение двух, таких многочленов часто дает многочлен сте-пени, большей чем 3, т. е. нечто, не принадлежащее нашему множеству объектов.
Так, например, (1101) • (1001)-<—>(1 + а+а3) (1 -Та3) = 1 + а-*-
-Ьа4+а6.
Мы хотим свести ответ к многочлену степени- не более 3. Для этого условимся, что а удовлетворяет некоторому фиксированному уравнению степени 4; подходящее уравнение имеет вид л(а) = 1 + а+а4 = 0 или а4=1+а.
Тогда а5=а + а2; а6=а2+а3, так что
1 +а + а4 + а6— 1 -Та-j-l -|-а + а2+а3=а2-Та3.
Это эквивалентно делению на многочлен a4 + a4-l и нахождению остатка от деления:
ae + а4 -Т а -ф 1 |а4 + а 1
g+g,+a*
а4 ф а3 Т а2 Т я + 1
а4 + а -ф 1
а3 + а2 — остаток
Таким образ.о-м, произведение двух 4-векторов 1101 и 1001 равно
(1 -J-a+a3) (1 + a3) = 1 + a+a4 + a6= (1 + а2)л (a) + a24~a3=a2-i-a3 (так как л (а) =0) *—>0011.
Другой способ описания этого процесса заключается в приведении произведения многочленов по модулю л (а):
1 +а+а4 + а6= (1 + а2)л(а) + а2 + a3 s а2-Да3 (mod л(а)).
Аналогично а4=Ц-а (mod л (а)) и т. д.
Теперь, если введенное нами умножение должно быть обратимо (что необходимо для того, чтобы наша система элементов образовывала поле), то многочлен л (%) должен быть неприводим над полем GF(2).
Определение. Многочлен неприводим над полем, если он не является произведением двух многочленов меньшей степени над этим же полем. Грубо говоря, неприводимый многочлен подобен простому числу: он не имеет нетривиальных делителей.
Любой многочлен может быть представлен единственным образом с точностью до постоянного сомножителя в виде произведения неприводимых многочленов (точно так, как любое число может быть единственным образом представлено в виде произведения простых чисел). Очень легко можно убедиться, что многочлен х4+х+1 неприводим над G.F(2).
Теорема 1. Если л(х) неприводим, то каждый ненулевой многочлен В (а) степени не более 3 имеет единственный обратный многочлен В(а)1 такой, что В(а)-В(а)‘ч = 1 (modn(a)).
Доказательство. Рассмотрим произведения Л (а) В (а), где Л (а) пробегает все многочлены
1, а, а-|-1, а2, • • ’, а3 + а2 + «+1 (3-5)
степени не более 3. Все эти произведения должны быть различными по модулю л (а) потому, что если
А (а) В (а) = Лг(«)В (a) (mod л (а)), то л(а)|(Л1(а)—Л2(а))В(а) и (в силу неприводимости многочлена л(а)) либо л(а)|(А(а)—Л2(а)), либо л(а)|В(а). Так как степени многочленов А (а), Л2(а), В (а) меньше, чем степень л (а), то это может выполняться только в случае, когда А(а) = =Д2(а). Таким образом, все произведения А(а)В(а) различны, и поэтому с точностью до перестановки они должны совпадать с множеством (3.5). В частности, только для одного многочлена Л(а) должно выполняться равенство Л(а)В(а) = 1, и тогда Д (а) =В (а)-1. •
Пример, (i). Для того чтобы найти элемент, обратный к а, заметим, что l = a+a4=a(l +a3), так что a-1 = l + a3.
(ii). Для нахождения обратного элемента к a+a2 предположим, что он имеет вид По + П1а-|-а2а2-|-аза3. Тогда условие (а+ +а2) (по + П1а-|-а2а2-Таза3) = 1 влечет систему уравнений
а2 + а3 = 1;
а0 + а2= 0;
со + А + °з = 0;
А + с2=0,
решение которой: ао = П1=а2=1; а3=0. Следовательно, обратный элемент равен 1 + a + a2.
Так называемые таблицы логарифмов (например, рис. 3.1) значительно упрощают нахождение обратных элементов, как будет объяснено ниже.
Деление. Для того чтобы найти А,/В, вначале найдем обратный элемент В~1=1/В, а затем воспользуемся правилом А/В=А-В-1.
Проверим теперь, что многочлен л(х) неприводим. Его степень равна 4, и поэтому, если он не является неприводимым, то содержит делители степени 1 или 2. Единственными многочленами степени 1 являются х и х+1. Ясно, что хфл(х). Если (х-Ы) |л(х), то л(—1)=0. Но л(—1) = 1+ 1 +1 = 1, и поэтому
(х+1) ^п(х). Что теперь можно сказать о делителях степени 2? Сразу же исключим многочлены xz+x и х2+1 = (х-f-1)2. Остается единственный многочлен х2+х+1, который мы можем проверить с помощью деления, используя только одни коэффициенты:
10 0 11 1111
1111
1 1 1
1 =остаток
Следовательно, многочлен х4+х+1 неприводим.
Таким образом, мы превратили в поле 16 векторов длины 4 из элементов 0 и 1. Это поле называется полем Галуа порядка 16, сокращенно GF(24) или GF (16).
Как показано на рис. 3.1, элементы этого поля могут быть представлены несколькими различными способами.
В виде В виде В виде В виде
4-вектора многочлена степени логарифма
0 0 0 0 0 0 —ос
1 0 0 0 1 1 0
0 10 0 а а "1
0 0 10 а2 а2 2
0001 а3 а3 3
110.0 1 J- а а4 4
0 11'0 а а2 а® 5
0 0 11 а2 -j- а3 а6 6
110 1 1 + а + а3 а7 7
10 10 1 + а2 а8 8
0101 а -|- а3 а® 9
1110 1 + а+а2 а10 10
0 11.1 а -р а2 -{- а3 а11 11
1111 1 + а + а2 + а3 а12 12
10 11 Ц-а2+а3 а13 13
10 0 1 1 + а3 а14 14
Рис. 3.1. Поле 67 (24), порожденное элементом а, где й4+а+1=0
Заметим, что ненулевые элементы поля образуют циклическую группу порядка 15, которая порождается элементом а, где «15=1; это означает, что нам достаточно повезло в выборе неприводимого многочлена л(х), корнем которого оказался порождающий элемент этой группы (определение циклической группы дано на с. 102) _
Элемент а (или любой другой порождающий элемент этой циклической группы) называется примитивным элементом поля GF (24). Например, элементы а, а2, а4 являются примитивными, a элементы а3, а5 таковыми не являются. Многочлен, корнем которого является примитивный элемент, называется примитивным мно~
гочленом. Не все неприводимые многочлены примитивны; например, многочлен х4+х3+х2+х+1 неприводим и поэтому может быть использован для построения поля, но он не является примитивным многочленом.
Любой ненулевой элемент у поля GE(24) может быть единственным образом представлен .в виде степени а; пусть y=ai для 0^1^14. (Конечно, а° = а15=1.) Тогда число i называется логарифмом (или, иногда, индексом) элемента у. При этом удобно положить, что 0=а~°°.
Полезно сопоставить первое представление элементов поля (столбцы 1 и 2 на рис. 3.1) с представлением комплексного числа z в декартовых координатах: z=x-\-iy, а второе (столбцы 3 и 4) — с представлением этого числа z в полярных координатах: г=(гег0. Первое представление удобнее для сложения, в то время как второе — удобнее для умножения.
В самом деле, чтобы умножить два элемента поля, возьмем их логарифмы и сложим, помня, что а16=1. (Поэтому логарифмы рассматриваются по модулю 15.)
Пример. Умножение элементов 0111 и 1111:
Элемент log
0 111 .и
* 1 1 1 1 + 12
23
Но а15=1, поэтому ответ таков: (0111) • (1111) =.а23='а23~15= = а8=(1010).
Нахождение обратного элемента:
(1010)~1 = (а8)-1 = а~8 = а15—8 = а7 = (1101).
Нахождение квадратного корня:
(0110)1/2 =(а®)1/2 = (а20)1/2 =а10 = (1110).
В гл. 4 мы увидим, что любое конечное поле может быть построено точно таким же способом и что мультипликативная группа ненулевых элементов поля является циклической, причем порождающим элементом этой группы является примитивный элемент поля. Мы увидим также, что число элементов в конечном поле всегда .равно степени простого числа и что по существу имеется только одно поле с заданным числом элементов.
В частности, если в качестве л(х) выбрать примитивный неприводимый многочлен степени т над полем GF(2), то получим поле GF(2™) из всех 2т двоичных векторов длины т.
3.3. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (II)
Теперь тот факт, что в нашем новом поле GF(16) возможно выполнение арифметических операций с 4-векторами, позволяет нам вернуться к задаче построения кода БЧХ длины 15, исправляющего две ошибки. Как нам следует выбрать функцию if(i) в
системе уравнений (3.4), чтббы эта система имела решение (в по-ле GF(16))?
Примером плохого выбора является функция if(t)=ci, где с — постоянная. Ибо в этом случае система (3.4) выглядит так:
г+ / = %; c(z + /)=z2
и поэтому не может быть решена.
Другим примером плохого выбора является функция так как Е+/2= (z+/)2(mod 2) и система (3.4) приобретает вид
/+/=zx; (t + i)2=z2
и поэтому также не может быть решена.
К хорошему выбору приводит i/(z) = г3, так как тогда система (3.4) имеет вид
« + / = д=#0; i3+f = z2 (3.6)
и поэтому может быть решена. Имеем, что
г2 = Is + = (г + У) (г2 + ij + /2) = Д ( zf + ij), «откуда
O' = za/2i+z2 (3.7)
Из (3.6) и (3.7) следует, что элементы i и j являются корнями квадратного уравнения
x2 + z1x + (z2/z1 + z2) = 0 (%=#0). (3.8)
Заметим, что если ошибок нет, то zi=z2=0, но если произошла одиночная ошибка на позиции i, то z2=i3=z3i. Таким образом, имеет- место следующий результат.
Схема декодирования кодов БЧХ, исправляющих две ошибки.
По принятому вектору у вычисляем синдром S = HyT— ( /•
\г2/
Затем: (i). Если Zi = z2-=0, то решаем, что ошибок не произошло.
(ii) . Если z2=z3b то исправляем одиночную ошибку на позиции i=zP
(iii) . Если Zi^=0, то составляем квадратное уравнение
(3.8). Если это уравнение имеет два различных корня i и j, то исправляем ошибки на этих позициях.
(iv) . Если уравнение (3.8) не имеет корней или если Zi=0, Zz¥=0, то обнаруживаем, что произошло по крайней мере три ошибки.
Еще раз напомним, что все элементы i, j, Zi, z2 принадлежат полю GF (16) и что уравнение (3.8) должно быть решено в этом поле. (К сожалению, обычная формула для решения квадратных уравнений не работает в поле GF(24). Один из возможных способов нахождения корней состоит в проверке по очереди каждого элемента поля, а другой способ будет описан в § 9.7.)
Проверочная матрица. Преобразуем теперь матрицу Н так, чтобы элементы первой строки располагались в следующем порядке: 1, а, а2, а3,. .. ; в этом случае наша матрица имеет вид 1иа2С43а4а5С46а'С48С49С410С411С412И13С414 1а3а6а9а12 1 а3а6а9а121 а3а6а9а12
(3.9)
Н =
Как мы увидим в гл. 7, матрица такого вида обладает тем важным преимуществом, что код становится циклическим.
Заметим, что не все степени .а появляются во второй строке: это происходит потому, что а3 не является примитивным элементом (так как (а3)5=1).
Представляя эту матрицу в двоичной форме, получаем
Н =
“1000100110101 11“ 010011010111100 001001101011110 0001001 10101 111
10001 1000110001 ,000110001100011 001010010100101 011110111101111
(З.Ю)
Пример процедуры декодирования. Сначала предположим, что произошли две ошибки, скажем, на позициях 6 и 8 (т. е. в столбцах (а6, а3) и (а8, а9)).
Тогда Zi = 1001=a14, z2=0100=« и (z2/zi)+й21 = а2+а13== = 1001 = а14.
Таким образом, уравнение (3.8) для нахождения i и j имеет вид
х2 + а14 х + а14 = (х + а6) (х + а8),
и, действительно, корни этого уравнения указывают местоположения ошибок.
С другой стороны, предположим, что произошли три ошибки, скажем, на позициях 0, 1, 3. Тогда ^i = 1101 = a7; z2=1100=a4, и получаем уравнение (3.8) x2+a7x+a5=0.
Проверяя каждый элемент по очереди, декодер обнаруживает, что это уравнение не имеет корней в нашем поле, и поэтому он принимает решение, что произошли по крайней мере три ошибки.
Так как в нашем построении ничто не зависит от длины, которая равна 15, то можно использовать любое поле GF(2™) для построения кода БЧХ длины 2т—1, исправляющего двойные ошибки. Проверочная матрица этого кода имеет вид
9т_9
laa2 • • -a2
1зв з ( 2т—г)
la3a® • • -а
(З.П)
где каждый элемент должен быть заменен соответствующим двоичным т-вектором.
Приведенный выше алгоритм декодирования показывает, что этот код действительно исправляет двойные ошибки. В гл. 7 и 9 мы вернемся к этим кодам и построим коды БЧХ, исправляющие t ошибок.
Упражнения. (1). Найти позиции, в которых произошли ошибки, если синдром равен S= (1001 0110)г или (0101 1111)г.
(2). Если принятый вектор име’ет вид 11000 ... 0, то какое слово передавалось?
'3.4. ВЫЧИСЛЕНИЯ В КОНЕЧНОМ ПОЛЕ
Так как элементы GF(24) представляются в виде 4-векторов из нулей и единиц, то с ними легко оперировать, используя цифровые схемы или двоичные ЭВМ.
В этом параграфе будет дано краткое описание некоторых логических схем для выполнения операций в поле GF(24). (Подобное же описание может быть дано для любого поля GF(2™).) Подробную информацию по этому вопросу см. в работах Барти и Шнейдера [72], Питерсона и Уэлдона [1040, гл. 7] и Берлекэмпа [113, гл. 1—5]. Подробные сведения по регистрам сдвига см. в работах Гилла [485], Голомба [523] и Каутца [750].
Основными элементами при составлении схем являются следующие:
Ячейка памяти (или триггер), которая хранит 0 или 1.
Двоичный умножитель (выход равен 1, если и только если все входы равны 1). Он также называется схемой И.
Двоичный сумматор1 (выход равен 1, если и только если нечетное число входов равно 1). Он также называется схемой Исключающее ИЛИ.
Таким образом, любой элемент поля GF(24), порожденного корнем уравнения а4+а+1=0 (см. рис. 3.1), представляется четырьмя нулями и единицами, которые могут храниться в строке из четырех ячеек памяти (называемой регистром):
регистр | 0 | | 0 | | 1 0011^а2 + «3.
1 содержит элемент
1 Строго говоря, его следует называть полусумматором ввиду отсутствия пе-
реноса единицы в старшие разряды.
> Умножение на а. Устройство, показанное на рис. 3.2 и называе-мое регистром сдвига с линейной обратной связью, умножает содержимое регистра на элемент а в поле GE(24).
Ибо если в начальный момент времени регистр содержит элемент поля
Ы Ы Ы Щ~со + а1“ + й2а2 + й3а3.
то в следующий момент времени он будет содержать элемент поля
I_I |_| 1___| |_l^a(a0 + a1a + aza2 + a3a3) =
@8 «0 @3 ^2
= °3 + (а0 + аз) “ + Й1 а2 + а2 “3-
Если же в начальный момент времени этот регистр содержит 1000 «->1, то в последующие моменты времени он будет содержать 1, а, а2,..., а14, а15=1, а,... , так как а — примитивный элемент.
Рис. 3.2. Линейный регистр с обратной связью, выполняющий умножение на элемент а в поле
GF (24)
Рис. 3.3. Линейный регистр, на выходе которого образуются кодовые слова длины 15
Поэтому последовательность символов на выходе устройства, изображенного на рис. 3.3, является периодической с периодом 15. Это — максимально возможный период для четырех ячеек памяти
(так как имеется как раз 24—1 = 15 ненулевых состояний). Отрезки выходной последовательности длины 15 представляют собой кодовые слова кода максимальной длины, порожденного регистром сдвига с обратной связью. Этот код является также симплексным кодом (см. § 1.9 и гл. 14).
Умножение на фиксированный элемент поля. Рас-
Рис. 3.4. Схема умножения произволь- СМОТРИМ- например, умноже-ного элемента поля GF (24) на 1 + а2 ние произвольного элемента поля ао + ... + аза3 на элемент 1 + а2, которое выполняется с помощью устройства, показанного на рис. 3.4:
(tz0 + Oi« + «2 a2 +. a3 a3) (1 + сс2) = tz0 + a + (Oq + tz2) a2 +
+ (6ZX + <з3) a3 + a2 a4 + c3 as = (c0 + a2) + (a1 + «z2 + a3)a +
+ (Go 4- 6Z2 + cQ a2 + + a3)a3.
Аналогично для деления на фиксированный элемент поля надо умножить на элемент, обратный ему.
Умножение двух произвольных элементов поля. К сожалению (ибо умножение элементов поля существенно, например, при декодировании кодов БЧХ и кодов Гоппы; см. гл. 9 и 12), эта операция значительно сложнее.
Предположим, что необходимо найти произведение заданных элементов поля а и *Ь:
с = а-Ь-~- («0 + Ci a + я2 a2 + as а3) (Ьо -ф bt а + 62 а2 -|-63 а3).
Способы умножения. (1). Непосредственное вычисление.
Если с—с0+С1а+с2а2+сза3,
то с0 = а0Ь0 + а^з + о262 + а^;
сг = + d, (b0 + b3) + (b2 + bs) + g3 (&j + b2) и т.д.;
в этом случае требуется большая и сложная схема для вычисления всех элементов с,- по заданным a:i и Ь{.
(2) . Модель медленного умножения вручную. В этом случае мы записываем произведение в следующем виде:
с = Ьоа -ф Ьг (a а) -ф 62 (а2 а) -ф Ь3 (а3 а)
и используем схему, изображенную на рис. 3.5. На каждом шаге мы прибавляем к с элемент если и только если Z^=l, и затем умножаем a’a на а.
Лос и Рашфорс [796] описали недавно сотообразную схему, которая также умножает этим способом, но их схема представляет скорее итерацию в пространстве, чем во времени, и поэтому умножает существенно быстрее, чем вышеописанная схема.
(3) . Использование таблиц логарифмов и антилогарифмов. Для умножения двух элементов поля GF(24) возьмем их логарифмы по основанию а (см. § 3.2), где а—-примитивный" элемент поля, и сложим их, как целые числа по модулю 15, а затем возьмем антилогарифм ответа. Схематически это показано на рис. 3.6.
В отличие от логарифма действительного числа логарифм в ко-нечном поле является чрезвычайно нерегулярной функцией. Неизвестно никакого быстрого способа нахождения log a, ae=GF (24): либо его находят непосредственно, вычисляя подряд все последовательные степени элемента а до тех пор, пока не встретится элемент а (что очень медленно), либо (что несколько лучше) используется таблица логарифмов, как, например, на рис. 3.1 или 4.1, 4.2.
Рис. 3.6. Схема умножения с использованием таблиц логарифмов и антилогарифмов по основанию примитивного элемента поля
Этот метод прекрасен для поля GF(24), но он практически неприемлем для пблей»СЛ (2,п) при больших значениях т, особенно потому, что необходима также таблица антилогарифмов того же объема.
(4) . Логарифмы Зеча (Конвей [301]). В этой схеме умножения используется только полярное представление элементов поля (т. е. в виде степеней примитивного элемента а). Умножать теперь легко, но что можно сказать о сложении? Оно выполняется с помощью так называемых логарифмов Зеча. Логарифм Зеча от целого числа п определяется уравнением 1—ccz(n) (рис. 3.7). В таком случае сумма элементов а"1 и ап равна
ат + а" = ат (1 +а"-т) = a m+z (п~т),
и потребность в таблице антилогарифмов отпадает, например
а3-|-а5 = а3(1 +<z2) = a3az (2)=au.
п Z (п) п Z (п)
—оо 0 7 9
0 —оо 8 2
1 4 9 7
2 8 10 5
3 14 11 12
4 1 12 11
5 10 13 6
6 13 14 3
Рис. 3.7. Логарифм Зеча в поле GF (24) (1 + ап —az<п>)
ЗАМЕЧАНИЯ К ГЛ. 3
§ 3.2. Теорема о том, что любой многочлен над полем единственным образом представляется в виде произведения неприводимых многочленов, может быть найдена в любом учебнике по алгебре (см., например, Альберт [19, с. 49] или Ван дер Вард&н |[1376, т. 1, с. 79]).
§ 3.3. Схема декодирования. Заметим, что не все .квадратные уравнения имеют корни в поле GF(24) (см. Берлекэмп |[113, с. 252]). Поэтому предложенная схема декодирования является неполной, так как она не исправляет те тройные ошибки, которые код в состоянии исправить i(cm. гл. 9).
По вычислениям в полях Галуа см. также работы Берда [92], Левитта и Каутца [827] и Танаки и др. [1300]. См. также замечания к гл. 4.
Глава 4
Конечные поля
4.1. ВВЕДЕНИЕ
Конечные поля используются для построения большинства известных кодов и их декодирования. Они играют также важную роль во многих ветвях математики, например в теории блок-схем, в конечных геометриях (см. приложение Б) и др. В данной главе дается описание конечных полей.
В гл. 3 поле GF(24) было определено как множество многочленов степени не более 3 от переменной х с двоичными коэффициентами, операции в котором выполняются по модулю неприводимого многочлена л(х) =х4+х+1. В данной главе будет показано, что все конечные поля могут быть получены таким способом.
Поле GF (р), р — простое. Простейшими полями являются следующие поля. Пусть р — простое число. Тогда целые числа по модулю р образуют поле порядка р, обозначаемое через GF(p) или Zp. Элементами поля GF(p) являются {0, 1, 2,..., р—1}, а операции « + », «—», «X», «;» выполняются по модулю р.
Например, GF(2) —двоичное поле, {0, 1}. GF(3) —троичное поле, {0,1, 2}, в котором 1+2=3=0 (mod 3); 2-2=4 = 1 (mod3); 1—2=—1=2 (mod 3) и т. д.
Упражнения. (1). Проверить, что GF(p) есть поле.
^(2). Выписать таблицы сложения и умножения для GF(5) и
Мы говорим, что' поле Е .является” расширением поля F, если Е содержит F. Например, поле действительных чисел является расширением поля рациональных чисел. ;
Построение GF(pm). Та же Самая конструкция, которая была использована в гл. 3 для построения поля GF (24) из поля GF(2), может быть использована и в общем случае, если известен много-ЧЛен л (х), удовлетворяющий двум, условиям: (i). Коэффициенты Л(х) лежат в GF(p). ' - -
(ii) . л(-х)- неприводим над GF(р), т. е. пе может "быть представлен в виде произведения двух- многочленов меньшей степени с
коэффициентами из поля GF(p). (Такие многочлены кратко называются неприводимыми над GF (р). В следствии 16 доказывается, что такие многочлены всегда существуют.)
Например, многочлен х2+х+ 1= (хф-2)2 приводим над GF(3), а многочлены х2+х+2 и х2-Т1 — неприводимы.
Теорема 1. Предположим, что л(х)—неприводимый над GF(p) многочлен степени т. Тогда множество всех многочленов от х степени —1 с коэффициентами из поля GF(p), операции над
которыми выполняются по модулю многочлена л(х), образует поле порядка рт.
Ниже мы увидим (теорема 6), что существует только одно поле порядка рт. Оно называется полем Галуа (порядка рт) и обозначается через GF(pm).
Произвольный элемент поля GF(pm) может быть также записан в виде /7г-вектора с элементами из GF(p), как это было сделано в гл. 3.
Элементы поля GF (рт) могут также интерпретироваться как классы вычетов многочленов от х с коэффициентами из GF(p) по модулю л(х) (см. § 2.3). Пусть а обозначает класс вычетов, содержащих переменную х, т. е. элемент (010 ... 0) поля GF(рт). Тогда, ио построению поля GF(pm), л(а)=0. Таким образом, уравнение п(х)=0 имеет в поле GF(pm) корень а. Мы говорим, что GF(pm) получается из GF (р) присоединением к GF(p) корня многочлена л (х).
Таким образом, GF(pm) состоит из всех многочленов от а степени —1 с коэффициентами из GF(p). Элементом поля GF(pm) является
aoai- • • + «!« + • • •
где a^GF(р) и л(сс)=0.
Эта конструкция годится также и для бесконечных полей. Пусть, например, Q обозначает поле рациональных чисел. Если присоединить к Q корень многочлена х2-—2, то получим поле Q( К 2), состоящее из всех чисел вида 2, с обычными пра-
вилами сложения и умножения элементов. Конечные поля значительно проще бесконечных.
Пример. Используя неприводимый над GF (3) многочлен л (х) =х2ф-хф2, получаем представление поля GF(32), показанное на рис. 4.1.
00 = 0 = а— «о
Ю = 1 = а»
01 = а = а1 12= 1 ф-2а = а2 22 = 2 ф 2а = а3
20 = 2 = а4
02 = 2а = а5
21 — 2 ф а = а6
11 = 1 ф а = а7
Рис. 4.1. GF(32) с л(а) = а2+а+2=0
Упражнения.. '(3). Найти двоичные неприводимые много-члены степеней 2, 3 и 5. Выписать элементы поля GF(8) и провести в этом поле некоторые вычисления.
(4). Найти неприводимый над GF(3) многочлен степени 3.
Содержание главы. В § 4.2, 4.3 излагаются основы теории конечных полей. Любое конечное поле содержит рт элементов для некоторого простого р и некоторого целого m^l, и существует в точности одно такое поле, обозначаемое через GF(pm) (теорема 6). Более того, такое поле существует для каждых р и т (теорема 7). В теореме 4 доказывается, что каждое конечное поле содержит примитивный элемент, что позволяет ввести логарифмирование.
С каждым элементом поля связан неприводимый многочлен, называемый его минимальным многочленом. Эти многочлены играют важную роль для циклических кодов и изучаются в § 4.3. В § 4.4 дается правило построения неприводимых многочленов, основанное на важной формуле (4.8).
В § 4.5 содержатся таблицы полей небольшой мощности и примитивных многочленов. В § 4.6 показывается, что группа автоморфизмов поля GF(pm) является циклической группой порядка т (теорема 12). В § 4.7 приводится формула (теорема 15) для числа неприводимых многочленов. В последних двух параграфах обсуждаются различные свойства базисов поля GF(pm), рассматриваемого как векторное пространство над GF(p). В частности, в § 4.9 приводится доказательство важной (но трудной) теоремы о нормальном базисе (теорема 25).
4.2. КОНЕЧНЫЕ ПОЛЯ: ОСНОВЫ ТЕОРИИ
In Galois fields, Primitive elements
full of flowers, dance for hours.
S. B. Weinstein1
Характеристика поля. Пусть F — произвольное конечное поле порядка q. F содержит единичный элемент 1, и так как F конечно, то не могут быть различными все элементы 1 + 1=2; 1 + 1 + + 1 = 3; ... Следовательно, существует наименьшее число р такое, что р= 1 +1 + ... +1 (р раз) =0. Это р должно быть простым числом (так как если rs=0, то либо г=0, либо s=0) и называется характеристикой поля. Характеристика поля GF(24), построенного в гл. 3, равна 2. Если характеристика поля F равна р, то рр=О Для произвольного элемента реЕ.
Таким образом, F содержит р элементов: 0, 1, 1 + 1=2, 1 + 1 + + 1 = 3, ..., 1 + 1+ ... + 1 = р — 1. Сумма и произведение этих эле-
’В полях Галуа, полных цветов, Примитивные, элементы танцуют часами...
С. Б. Вайнстейн (Прим, перев.)
ментов имеют такой же вид, так что эти р элементов ооразуют подполе GF(p) поля F. Если q = p, то в F нет других элементов и F=GF(p).
Другие элементы в F. Предположим, что и выберем в F максимальное множество линейно независимых над GF(p) элементов, скажем, р0= 1, рь.. ., рт_ь Тогда F содержит все элементы вида tzopo + «iPi + ... +am_Jpm_i, ai^GF(p) и не содержит никаких других. Следовательно, F является векторным пространством размерности т над GF(p) и содержит q=pm элементов для некоторого простого р и некоторого целого т^1 (иначе, порядок F равен рт). Пусть F* обозначает множество всех q—1 ненулевых элементов поля F.
Важнейшим специфическим свойством конечных полей, отличающим их от бесконечных полей, является следующее.
Теорема 2. F* образует циклическую мультипликативную группу порядка рт—1. (Конечная мультипликативная циклическая группа определяется как множество элементов 1, a, а?,...,аг~х при условии аг=1. Элемент а называется образующей группы.)
Доказательство. То что F-* является мультипликативной группой, следует из определения поля. Пусть aef*. Так как мощность F* равна р™—1, то а’ может принимать не более рт—1 различных значений. Следовательно, найдутся целые числа <г и i такие, что —1 и аг+’=та® или ar=l. Наименьшее такое г
называется порядком элемента а.
Выберем теперь а так, чтобы его порядок г был максимально возможным. Покажем, что порядок I любого элемента p^F* делит число л. Пусть л — простое число такое, что г=лаг'-, 1=льГ, а г' и Г взаимно просты с л. Тогда элемент имеет порядок г', а элемент рг' имеет порядок ль, а порядок элемента аяСрг' равен льг' (см. упражнение (7)). Следовательно, Ь^.а, так как в противном случае г не является максимальным. Таким образом, если некоторая степень простого числа является делителем I, то она является также делителем г и, следовательно, I делит г. Отсюда следует, что каждый элемент р из F* удовлетворяет уравнению хг—1=0. Это означает, что многочлен хг—1 делится Ha[""|gef.s (х—р). Атак как F* содержит рт—1 элементов, то г^р™—1. Но г^рт—1, и, следовательно, г=р™—1. Поэтому Прет* (х—Р) —хрГп -1—1, и ненулевые элементы поля F образуют циклическую группу «, а2,..., ...,аРт~\ аРт-1 = 1. •
Следствие 3. (Теорема Ферма.) Каждый элемент р поля F порядка рт удовлетворяет тождеству ррт=р или, эквивалентно, является корнем уравнения xJ‘m=x.
Таким образом, ^т_х=Г1(х_р). (41)
Ре f
В поле F порядка рт элемент а называется примитивным, если его порядок равен рт—1 (см. § 3.2). Отсюда следует, что любой ненулевой элемент поля F является степенью элемента а. Вторым следствием из теоремы 2 является:
Теорема 4. Любое конечное поле F содержит примитивный элемент.
Доказательство. В качестве примитивного элемента выберем образующий элемент а циклической группы F*. *
Очень полезной оказывается следующая лемма.
Лемма 5. В любом поле характеристики р(х+у)р=хР-\-уР.
Доказательство. Согласно упражнению (18) гл. 1
р ( \
(х + #=£ Р jx^yb, ь=о V }
[р\ I р\ , где Г = = 1.
V / V /
При —1
Р V• + 0(modр),
\k I Ь2 ... k V
так как числитель содержит множитель р, а знаменатель — нет.
В частности, в поле характеристики 2 имеем:
(х + у)2=х2 + у2- (х + у^ = х^ + у\
(х-F у)8 = х8+у8 . . .
В заключение этого параграфа рассмотрим одно применение следствия 3. Воспользовавшись им в поле GF(p), получим следующий важный результат:
Ьр~1 = 1 (mod р)
для любого целого Ь, не делящегося на р. Это стандартная формулировка теоремы Ферма, из которой, например, следует, что
26 =1 (mod 7); 210: 1 (mod 11)
или, иначе, 7|26—1 = 63; 111210—1 = 1023.
Упражнения. (5). Производная многочлена над конечным полем. Если
f (х) = £ Щ х1; at е GF (pm), i=0
то определим производную равенством
^=Г(х)=У iaix dx
Показать, что:
(i)- (/ W + g (X))' -= /' (x) + g' (x).
(ii) . (f(x) g (x))' = f' (x) d(x) + f (x) g' (x).
(iii) . Если (x—a)h делит f(x), to (x—a)fe~’ делит f'(x).
(iv) . Если ни в каком расширении поля многочлен f(x) не имеет кратных корней, то f(x) и ?'(х) взаимно просты.
(v) . Если р—2, то f'.(x) состоит только из четных степеней и является полным квадратом, a f"(x)=O.
(6). Предположим, что F — конечное расширение поля GF(p), содержащее все корни многочлена хрт—х.
(i). Показать, что все корни многочлена хрГЛ—х в F различны. [Указание. Показать, что этот многочлен взаимно прост со своей производной.]
(ii). Доказать непосредственно, что эти корни образуют поле.
(7). Пусть G — коммутативная группа, содержащая элементы g и h соответственно порядков г и s.
(i) . Показать, что если gn=l, то г/п.
(ii) . Показать, что если г и s взаимно просты, то порядок элемента gh равен rs.»
(iii) . Показать, что если r=rxrz, то порядок элемента gr' равен г2-
(8). <р — функция Эйлера (или тотиент-функция), определяется для любого целого положительного числа т как число чисел, не превосходящих т и взаимно простых с т.
(i) . Показать, что
<р(т)=тП/ j— 1 р\т\ р
где р пробегает все простые делители числа т.
(ii) . Показать, что
Х<р (d)=m,
d\m
где суммирование ведется по всем делителям d числа т, включая 1 и т.
(iii) . Доказать теорему Ферма — Эйлера: если а и т взаимно просты, то a'P(m)=l (mod т).
(9). Пусть Ат обозначает число примитивных элементов поля GF(pm). Показать, что Ат=ср(рт—1), где <р — функция Эйлера, определенная в задаче 8. Отсюда вывести, что lim(Am/pTO) =0.
т->со
4.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ
Согласно теореме Ферма (следствие 3) каждый элемент р поля q—pm, удовлетворяет уравнению
х*—х = 0.
(4.3)
Все коэффициенты этого многочлена лежат в поле Сг7'(р), и он нормирован (старший коэффициент равен 1). Элемент р, однако, может быть и корнем многочлена более низкой степени.
Определение. Минимальным многочленом элемента р над полем GF(p) называется нормированный многочлен ц(х) с коэффициентами из GF(p) наименьшей возможной степени такой, что М(р)=0.
Пример. В поле CnF(24), где возможными коэффициентами для минимального многочлена являются 0 или 1, имеем:
Элемент Минимальный многочлен
О х
1 х+1
а х4+х+1
а-1 ’ х4+х3+1
а3 х4+х3+х2+х+1
а5 х2+х+1
В § 4.4 мы увидим, как находить минимальные многочлены.
Свойства минимальных многочленов. Предположим, что М (х) — минимальный многочлен элемента peGF(pm).
Свойство. (Ml)./И(х) неприводим.
Доказательство. Если М(х) =М1(х)Мг(х), причем степени Л41(х) и М2(х) строго положительны, то 7И(р) =MI (Р)М2(р) =0, так что либо М^р) =0, либо М2(р)=0, что противоречит тому, что Л'1(х) —многочлен наименьшей степени, для которого р является корнем. *
Свойство. (М2). Если f(x) —некоторый многочлен [с коэффициентами из GF(p)] такой, что f (р) =0, то М(х) |if(x).
Доказательство. Разделив if (х) на М(х), запишем: f(x) = —М(х)а(х) +г(х), где степень остатка г(х) меньше степени М(х). Положим х=р: О = О+г(р), так что р оказывается корнем многочлена степени меньшей, чем степень М (х). Это противоречит определению М(х), за исключением случая, когда г(х)=0, но тогда f (х) делится на М (х). •
Свойство. (М3). М(х) lx?"1—х.
Доказательство. Утверждение вытекает из (М2) и следствия 3. •
Свойство. (М4). degМ(х)
Доказательство. GF(pm) образует некоторое пространство размерности m над GF(p). Следовательно, любые тф-1 элементов, в частности 1, р,..., р™, являются линейно зависимыми, т. е. существуют все одновременно не равные нулю коэффициенты a^GF (р) m m
такие, что У ЦгР’ = 0. Таким образом, аг-хг является многочле-z=0 i=0
ном степени не более т, имеющим р своим корнем. Следовательно, degM(x)^m. •
Свойство. (М5). Степень минимального многочлена примитивного элемента поля GF(pm) равна т. Такой многочлен называется примитивным.
Доказательство. Пусть р— примитивный элемент поля GF(pm) и М(х)— его минимальный многочлен степени d. Как и в теореме 1, мы можем использовать М(х) для построения поля F порядка pd. Но F содержит р и, следовательно, все поле GF(pm), так что d^m. Согласно (М4) выполняется равенство d=m. •
Замечание. Если неприводимый многочлен л(х) используется для построения GF(pm) и элемент а поля GF(pm) является корнем л(х), то, очевидно, л(х) является минимальным многочленом элемента а.
Теперь мы можем доказать единственность поля GF(pm).
Теор ем а 6. Все конечные поля порядка р™ изоморфны. (Два поля F и G называются изоморфными, если существует взаимно однозначное отображение F на G, сохраняющее операции сложения и умножения.)
Доказательство. Пусть F и G — поля порядка рт и пусть а — примитивный элемент поля F с минимальным многочленом 7И(х). Из свойства (М3) вытекает, что М(х)\х?т—х. Следовательно, согласно следствию 3 в G найдется элемент р, минимальным многочленом которого является М(х). Теперь F можно рассматривать как множество многочленов от а степени не более т—1 (как множество классов вычетов по модулю М(х)), a G — как множество многочленов от р степени не более т—1. Тогда соответствие а <-»Р задает изоморфизм F*-> G. •
В качестве примера рассмотрим два способа задания поля GF(23), показанные на рис. 4.2 и определяемые соответственно многочленами л(x) =x3-j-x+ 1 и л (х) =х3 + х2+1.
Задание через х3+х+1 Задание через х3+х2+1
000=0 000 = 0
100=1 100=1
010=а 010=у
001 = а2 001= у2
110=а3 101=у3
011 = а4 111 =т4
111=а5 110=у5
101 =а6 011 =Y6
(а7=1) (У7=1)
Рис. 4.2. Два способа задания GF(23)
Минимальным многочленом обоих элементов а и Р=у3 является х3+х+1, и соответствие а «-’у3 устанавливает изоморфизм между двумя способами задания поля. Мы .выберем первый способ в. качестве стандартного (см. рис. 4.5).
Конечные поля можно также интерпретировать как неприводимые циклические коды (см. гл. 8).
Наоборот, конечное поле GF(pm) всегда существует:
Теорема 7. Для любого простого числа р и любого целого гпдЛ существует поле порядка рт, которое обозначается через
GF(pm). (Согласно предыдущей теореме это поле по существу единственно.)
Доказательство. Для т=1 поле GF (р) ==ZP было определено в § 4.1. Предположим, что т>1, и обозначим Fi — GF(p). Идея доказательства состоит в последовательном построении цепочки полей до тех пор, пока не будет построено поле, скажем, Fr, содержащее все корни многочлена хр m—х. Тогда согласно упражнению (6) все корни многочлена хр"1—х образуют необходимое поле порядка рт. Пусть (х) — неприводимый делитель степени не менее 2 многочлена хРт—х над FI (если таковой имеется); используя конструкцию теоремы 1 при л(х) =fi (х), построим новое поле F2. Пусть теперь Д(х) —неприводимый делитель степени не менее 2 многочлена хРт—х над F2 (если таковой имеется); используя конструкцию теоремы 1 при л (х) —f2 (х), построим новое поле Eg. После конечного числа шагов будет построено поле, содержащее все корни многочлена хРт—х. Это завершает доказательство теоремы.
Другое доказательство. Согласно доказываемому ниже следствию 16, над полем GF(p) всегда существует неприводимый многочлен степени т. Тогда утверждение теоремы вытекает непосредственно из конструкции теоремы 1. •
Упражнение. (10). Показать, что отображение у-+уР задает изоморфизм поля GF(pm) на себя.
Подполя в GF(pm). Мы можем проитерировать конструкцию теоремы 1 (так, как это было сделано при доказательстве теоремы 7). Сначала присоединим к GF(p) корень неприводимого над GF(p) многочлена л(х) степени т и построим GF(pm). Пусть теперь f(x)—неприводимый над GF(pm) многочлен степени п. Образуем новое поле, присоединив к нему корень многочлена f(x). Рассуждения, использованные в гл. 3, приводят нас к выводу, что это новое поле содержит ртп элементов. Согласно теореме 6 мы построили поле GF(pmn). Таким образом, итерация конструкции теоремы 1 не дает никаких новых полей. Однако такой двухшаговый переход от GF(p) к GF(pmn) позволяет доказать следующую полезную теорему.
• Теорема 8. (i). GF(pr) содержит подполе (изоморфное) GF(ps) тогда и только тогда, когда s делит г.
(ii). Элемент р из GF (рг) принадлежит полю GF(ps) тогда и только тогда, когда prs = р. В любом поле из равенства р2=р следует, что элемент р равен 0 или 1.
Для доказательства требуется следующая лемма.
Л ем м а 9. Если п, г, s — целые числа такие, что п^2; 1;
^1, то ns—1|пг—1 тогда и только тогда, когда з|г. (Напомним, что вертикальная черта означает «делит».)
Доказательство. Запишем r=Qs+R, где O^R^s. Тогда
ПГ —1 R rfiS— 1 nR 1 tls —1 ns — 1 tls — 1
Число nQs—1 всегда делится на ns—1. Последнее слагаемое меньше единицы и, следовательно, может быть целым тогда и только тогда, когда R=0.
Упражнение. (11). (i). Показать, что в произвольном поле Xs—1 |хг—1 тогда и только тогда, когда s|.г.
(ii). Показать, что НОД {хг—1, Xs—l}=xd—1, где d=HOfl {г, «}•
Доказательство теоремы 8. (i). Если s|г, то согласно упражнению (6) поле GF(pr) содержит подполе, изоморфное полю GF(ps). Наоборот, пусть р— примитивный элемент поля GF(ps). Тогда pps ppr -‘=1.
Таким образом, ps—11 рг—1 и согласно лемме s|r.
(ii). Первое утверждение вытекает непосредственно из следствия 3, а второе — очевидно. •
В качестве примера на рис. 4.3 показаны все подполя поля GF (212).
Сопряженные элементы и циклотомические классы. Свойство. (Мб). Минимальные многочлены элементов р и рг равны. В частности, в поле GF (2™) равны минимальные многочлены элементов р и р2.
Доказательство проведем на примере. Пусть х4+х3+1 — минимальный многочлен элемента р из GF(24). Тогда по лемме 5 (р2)4+(р2)3 + 1=(Р4 + р3+1)2 = 0.
Таким образом, в силу свойства (М2) минимальный многочлен элемента р2 должен делить х4+х3+ 1. Но (Р2)8 = р, так что это же рассуждение показывает, что минимальный многочлен элемента р должен делить минимальный многочлен элемента р2. Следовательно, эти многочлены равны. * Элементы поля, минимальные многочлены которых равны, называются сопряженными. (По этой же причине i и —I называ
ются комплексно-сопряженными числами: над полем действительных чисел многочлен х2+1 является минимальным для них обоих.)
Давайте посмотрим, что происходит в поле GF(24). Согласно (Мб) минимальным многочленом для элементов а, а2, (а2)2=а4, (а4)2=ю8 (а (а8)2=а опять) является один и тот же многочлен. Аналогично минимальным многочленом для а3, а6, а12, а24—а9 (и а18=а3 опять) является один и тот же многочлен и т. д. Мы видим, что степени элемента а распадаются на непересекающиеся множества, которые мы назовем циклотомическими классами. Когда / пробегает один циклотомический класс, то минимальным многочленом для всех а3’ является один и тот же многочлен.
Определение. Множество целых чисел по модулю рт—1 относительно операции умножения на р распадается на подмножества, которые называются циклотомическими классами по модулю рт—1.
GF(2,Z)
6F(2)
Рис. 4.3. Подполя поля GF(212)
Циклотомический класс, содержащий s, состоит из чисел { s, ps, p2s, p3s, . . , pms 's},
гдсЖ — наименьшее положительное целое число такое, что Xss^s (mod рт—1). Например, циклотомическими классами дулЮ^15 (для р=2) являются:
\ Со = {0};
Ci = {1,2,4,8};
Ill" p X
ПО MO-
Cs = {3,6,12,9};
C5={5,10}
C7 = {7,14,13,11}.
Наши обозначения выбраны так, что если s — наименьшее число в классе, то класс обозначается через Cs. Индексы {«} называются представителями классов по модулю р™—1.
У п р ажнения. (12). Проверить таблицы циклотомических классов, приведенные на рис. 4.4, для р=2.
mod 7
mod 31
mod 63
Со = с1 = . С’3 — - {0} (1.2,4} (3,6,5} Со = (0} Ci = (1,2,4,8,16} Cs = {3,6,12,24,17} С5 = {5.10,20,9,18} С7 = {7,14,28,25,19} Си = {11,22,13,26,21} С,5 = {15,30,29,27,23} Со = {0} Сх = {1,2,4,8,16,32} С3 = {3,6,12,24,48,33} С5 = {5,10,20,40,17,34} С7 = {7,14,28,56,49,35} С9 = {9,18,36} Си = {11,22,44,25,50,37} С13 = {13,26,52,41,19,38} С15 = {15,30,60,57,51,39} С21 = {21,42} С23 = {23,46,29,58,53,43} С27 = {27,54,45} С31 —{31,62,61,59,55,47}
mod 127 mod 127
Со = 1 С1 = . ^3 — 1 с5 = < с13= с15-С19—1 (0} ( 1 ( з ( 5 ( 7 ( 9 11 13 15 ;i9 2 6 10 14 18 22 26 30 38 4 12 20 28 36 44 52 60 76 8 16 24 48 40 80 56 112 72 17 88 49 104 81 120 113 25 50 32 64} 96 65} 33 66} 97 67} 31 68} 98 69} 35 70} 99 71} 100 73} С21 = {21 42 84 41 82 37 74} С23 = {23 46 92 57 114 101 75} С27 = {27 54 108 89 51 102 77} С29 = {29 58 116 105 83 39 78} С31 = {31 62 124 121 115 103 79} С43 = {43 86 45 90 53 106 85} С47={47 94 61 122 117 107 87} Си = {55 110 93 59 118 109 91} С63 = {63 126 125 123 119 111 95}
Рис. 4.4. Циклотомические классы ио модулям 7, 31, 63 и 127
(13). Найти циклотомические классы по модулям 8 и 26 (р—3).
Нахождение 7H({)(x). Пусть 7И({)(х) —минимальный многочлен элемента cdeGF(pm). В силу свойства (Мб)
M(₽0(x) + M(f)(x). (4.4)
Из предыдущих рассуждений следует, что если i лежит в цик-лотомическом классе Cs, то в поле GF(pm)
П (х—а') делит 714(г) (х). (4.5)
jgcs
(14). Показать, что-коэффициенты многочлена в левой части в (4.5), представляющие собой элементарные симметрические функции от a3, j<=Cs, лежат в поле GF(p). [Указание. Воспользоваться теоремой 8 (ii). Вывести отсюда, что левая и правая части в (4.5) равны.]
Свойство. (М7). Если i лежит в Cs, то
f 7И(г)(х)=["|(*—cG). (4.6)
jgcs
Более того, из уравнения (4.1) вытекает, что
хр m_1-1=П 2W(s’(x), (4.7)
где s пробегает все множество представителей классов по модулю рт— 1.
Упражнения. (15). Показать, что для р=2; п—2т—1 и выполняются условия: Gj^Cs; |С1| = |Сз|=т. Следовательно, degTI4(I)(x) = degTI4(3>(x) =т. Что можно сказать о С5?
(16) . Будем говорить, что неприводимый над GF(q) многочлен л(х) принадлежит показателю е, если порядок всех его корней равен е. Показать, что в этом случае л(х) |хе—1 и л(х) Ф хп—1 при п<е.
(17) . Пусть 714(х)—минимальный многочлен элемента ре eGF(<y). Показать, что degTI4(x)=d тогда и только тогда, когда d-—наименьшее положительное целое число такое, что р?“ = р.
m—1
(18) . Доказать, что если f(x)= |”| (х—asq ),
i=0
то f (х) = [714(S) (x)]d,
где d=\mlms-, ms— степень многочлена 7!4<s)(x).
Задание поля матрицами. Сопровождающая матрица многочлена а(х) =ай-]-а\Х+ ... +ar_iXr~l-]-xr определяется как матрица размерности г><г вида
“OlO-O
714 =
0 0 1 ... о
(4.8)
О О О • • 1
^0 ^1 • • ‘tZf—1
^Упражнения. (19). Показать, что характеристический мно-гочлен матрицы М, т. е. det(M—7Л), равен многочлену а(к). Вывести отсюда, что а(М)=0.
(20). Пусть М — сопровождающая матрица примитивного многочлена л(х) степени т над полем GF(q). Доказать, что Мг'=1, если |i=?m—1, и IWy=I, если 1г£Д<д™—1. Вывести отсюда, что степени матрицы М являются ненулевыми элементами поля GF(q™\.
Например, возьмем л(х)=х34-х+1 над GF(2). Тогда элементы GF (23) запишутся в виде
0 м М2 АР АР АР ар м1
000\ /0Ю\ /001\ /по\ /011Х /111\ /Ю1\ /100'
ООО 10011 1 1101 10111 1111 / 101 1 1100 1 010
ООО / 1 по/ 011 / 1111 / 1 101 / 1 100 / 1 010 / \ 001
Сложение и умножение в поле задается как сложение и умножение матриц.
Такой способ задания поля очень удобен в работе. Не составляет труда выписать первую строку каждой матрицы в виде коэффициентов многочлена от а, а именно: М«-»а, М2«-»«2, М3«-*1+а и т. д.; умножение следует выполнять по модулю ia3+«+l. Это, конечно, приводит к тому же заданию поля, которое дается теоремой 1.
4.4. КАК НАХОДИТЬ НЕПРИВОДИМЫЕ МНОГОЧЛЕНЫ
. Первые две теоремы содержат ключевые формулы.
Теорема 10. Многочлен хрт—х равен произведению всех нормированных неприводимых над GF(p) многочленов, степени которых делят т.
Доказательство, (i). Пусть л(х) —неприводимый над GF(p) многочлен степени d, где djm. Случай л(х)=х тривиален; поэтому предположим, что л(х)=£х. Если использовать л(х) для построения поля, то в этом поле найдется элемент, для которого л(х) является минимальным многочленом, и тогда по свойству (М3) л (х) | х*7 d-1—1. Согласно лемме 9 и упражнению (11) pd— —11pm—1 и хД1-1—1 ]хРт~1—1. Следовательно, л(х)[х?т—х.
(ii). Наоборот, пусть л(х)—неприводимый делитель х'рт—х степени d. Требуется показать, что d]m. Опять предположим, что л(х)у=х, так что л(х) |хгга-1—1. Как и в части (i), используем многочлен л(х) для построения поля F порядка pa. Пусть a^F — корень л(х) и пусть р— примитивный элемент поля F, так что
Р —йо + а1к+ • • +Ga_i а . (4.9)
Так как л(а)=0, то арт —а, и в силу леммы 5 из (4.9) вытекает, что рр/" = р. Следовательно, рр'”-1=1 и порядок элемента
P pd— 1 должен делить рт— 1. Тогда d\m согласно лемме 9./® Аналогичные рассуждения приводят к следующей теореме.
Теорема 11. Для любого поля GF(q), где q— степень простого числа, имеет место равенство: '
хчт—х=произведению всех нормированных неприводимых 0.10) над G-F(q) многочленов, степени которых делят т.
Используем уравнение (4.7) и теорему 10 для вычисления неприводимых многочленов и минимальных многочленов. Для примера выберем q=2 и будем действовать следующим образом.
т = 1: Согласно теореме 10
х2+х=х(х + 1).
Имеются два неприводимых многочлена степени 1, а именно х и х+1. Минимальными многочленами элементов 0 и 1 в поле GF(2) соответственно являются х и х+ 1:
т=2: х82 +х=х4 + х= х(х-\- 1)(х2 + х + 1).
Имеется один неприводимый многочлен степени 2, а именно х2+ 4-х-Ы. Минимальные многочлены элементов поля GF(22) имеют вид *
Элемент Минимальный многочлен
О х
1 М<°)(х)=х+1
а, а2 М<Ч(х) =ЛП2>(х) =х2+х+1
771 — 3: х23 +х=х8+х = х(х+ 1){х6 + х5 + х4 + х34-х2+х+1)= =х(х+1) х(х3 + х+1)(х3 + х2 +1). (4.11)
Имеются два неприводимых многочлена степени 3, а именно х3 + х+1 и х3+х2ф-1. Задавая поле GF (23) корнем а уравнения <х3+а+1=0, имеем:
Элемент Минимальный многочлен
О к
1 М<°)(х)=х+1
а, а2, а4 M<B(X)=M<2>(x)=M<4)(x)=x3+x+l
, а3, а6, а6 М<3> (х) =М<б>(х) =М(6) (х) = М<-‘> (х) =х3+х2+1
Разложение (4.11) согласуется с теоремой 10: делителями т= = 3 являются числа 1 и 3, и х23ф-х распадается в произведение двух неприводимых многочленов степени 1 и двух неприводимых многочленов степени 3.
Многочлены х3 + х+1 и х3 + х2ф-1 называются взаимными. В общем случае взаимный к anxn+«n-iXn~1+...+«ix+«o многочлен определяется обращением порядка следования коэффициентов: Д'оХ”-|-я1хп_1-|- ... +an-ix+an.
Иными словами, взаимный к f(x) многочлен определяется как многочлен хйе% Kx\f (х~1). Корни взаимного многочлена обратны к корням исходного многочлена. Многочлен, взаимный к неприводимому, сам неприводим.
\Таким образом, если ЛИ >(х) —минимальный многочлен эле-мента а, то минимальным многочленом элемента а-1 яв-
ляется взаимный к 7И(1>(х) многочлен.
/Д=4: Мы уже знаем следующие делители многочл'ена х24: х, х_|_1 \х2-|-х+1 (неприводимые многочлены степеней 1 и 2), х4-^ и взаимный к нему х4+х3+1 (неприводимые многочлены степени 4). Выполняя деление, находим оставшийся неприводимый многочлен степени 4: х4+х3 + х2+х+1, и, таким образом, х24 + х X х (х + 1) (х2 + х + 1) (х4 + х+1) (х4+х3 +1 )(х44-х3 4-х24-х +1).
Задавая поле GF(24) корнем уравнения а4-Ьа4-1=0, получаем:
Элемент
О j а, а2, а4, а8 а3, а6, а12, .а9 ю8, а10 а7, а14, а13, а11
Минимальный многочлен
х
М°)(х)=х+1
М<Ч=М<2) =М<4’=М(8)=х4+х+1 М<3)=М(8)=М(,2)=М(9)=х4+х3+х2+х+1 M<6)=M(I0>=x2+x+l
М<7)=М(14)=М(13)=М<11> =М(-4> =х44-х3-|-1
Согласно теореме 4 многочлен, задающий поле, всегда может быть выбран примитивным. (Достаточно выбрать минимальный многочлен л(х) примитивного элемента.) Как видно из рис. 3.1, каждый из способов задания поля — в виде многочленов от а степени не более т—1 или в виде степеней примитивного элемента, являющегося корнем л(х),— обладает своими преимуществами.
Однако задача определения, какой из неприводимых многочленов является примитивным, является весьма трудной (см. § 7.9 и ссылки, приведенные в замечаниях).
Упражнение. (21). Показать, что
л25 4-х = х(х-|- 1) (х54-х24- 1)(х54~х34~ 1) (х54-х44-х3-|-х24- 1)(х54-
4-х4 4-х3 4-х 4- 1) (х5 4-х4 4~ 4~ * 4- 1) (х5 4-х3 4-х2 4-х 4- 1)
и что в поле GF(2)5, задаваемом корнем уравнения а54-а24-1=0, имеет место:
Элемент-
0 j
а, а2, а4, а8, а18
а3, а6, а12, а24, а17
а5, а10, а20, а9, а18 а7, а14, а28, а25, а’9 а”, а22, а13, а28, а21 а15, а30=а~1, а29, а27, а23
Минимальный многочлен
х
М«»(х)=х+1 M<4(x) = Х5 + х2+1 ЛН3> (х) = Х6 + Х4 + Х3 + Х2 + 1 ЛН5> (х) =х5+х4+х2+х+1 Л4<7>(х) =х5+х3+х2+х+1 ЛЮ'Цх) = х5+х4+х3+х +1
М(15)(х) =х8+х3+1
4.5. ТАБЛИЦЫ МАЛЫХ ПОЛЕЙ
На рис. 4.5 приведены таблицы полей GF(2), GF(22), GF (23), GF(25), GF (2е), GF(3) и GF(33). В первом столбце дается запись элемента у в виде m-вектора, во втором — логарифм I, где у=с4. Таблицы полей GF(24) и GF(32) можно найти на рис. 3.1 и 4.1.
GF(22) GF (21)
GF(2) n(a)=a2+a+l=0 jt(a) =a3+a+l =0 /
Элемент log Элемент log Элемент log /
0 1 —oo 00 0 10 01 11 —oo 000 0 100 1 010 2 001 110 Oil 111 101 -j-OQ 2 3 4 5 6
GF(25) с л (а) =а5+«2+1=0
Элемент * log Элемент log
00000 —oo 11111 15
10000 0 11011 16
01000 1 11001 17
00100 2 11000 18
00010 3 01100 19
00001 4 00110 20
10100 5 00011 21
01010 6 10101 22
00101 7 11110 23
10110 8 01111 24
01011 9 10011 25
10001 10 11101 26
11100 11 11010 27
OHIO 12 01101 28
00111 13 10010 29
10111 14 01001 30
GF(26) с л(а) =a®+a+l=O
Элемент log Элемент log Элемент log
000000 —oo 110111 21 010111 42
100000 0 101011 22 111011 43
010000 1 100101 23 101101 44
001000 2 100010 24 100110 45
Puc. 4.5. Некоторые поля Галуа
0F(2e) с л(а) =а8+а+1=0
^лемент \ log Элемент log Элемент log
000100 3 010001 25 010011 46
000010 4 111000 26 111001 47
000001 5 011100 27 101100 48
110000 6 001110 28 010110 49
011000 7 000111 29 001011 50
001100 8 110011 30 110101 51
000110 9 - 101001 31 101010 52
000011 10 100100 32 010101 53
110001 11 010010 33 111010 54
101000 12 001001 34 011101 55
010100 13 110100 35 111110 56
001010 14 011010 36 011111 57
000101 15 001101 37 111111 58
110010 16 110110 38 101111 59
011001 17 011011 39 100111 60
111100 18 111101 40 100011 61
011110 19 101110 41 100001 62
001111 20
GF(3) GF (З3)
я (а) = а3 —f— 2ct —J— 1 — 0
Элемент
Элемент log Элемент log
о
1 2 0 1 000 —со
100 0 200 13
010 1 020 14
001 2 002 15
210 3 120 16
021 4 012 17
212 5 121 18
ш 6 222 19
221 7 112 20
202 8 101 21
НО 9 220 22
ОН 10 022 23
211 11 122 24
201 12 102 25
Рис. 4.5. (Продолжение)
Упражнение. (22). Ясно, что GF(26) содержит GF(23) согласно теореме 8. Пусть g— примитивный элемент поля GF(26). Показать, что GF(23) = {0, 1, g9, g18, .g27, ,g36, g45, g54}. Показать, что первый способ задания поля G77(23), приведенный на рис. 4.2, требует выбора g27, g45 или g54 в качестве примитивного элемента поля GF(23).
На рис. 4.6 приведен краткий список примитивных многочленов, выбранных так, что число ненулевых коэффициентов минимально. Для двоичных многочленов указаны только показатели степеней при ненулевых коэффициентах; так, например, пятая строка (5 2 0) означает, что многочлен хБ+х2+1 примитивен.
Над GF(2)
Над GF (3)
показатели степеней х+1
1 0 х2 + х+2
2 1 0 х3+2х+1
3 1 0 х4+х+2
4 1 0 х?+2х+1
5 2 0 хе+х+2
6 1 0
7» 1 0
8 6 5 4 0 Над GF,(5)
9 4 о
10 3 0 X-J-1
и 2 0 х2+х+2
12 7 4 3 0 х3+Зх+2
13 4 3 1 0 х‘,+х2+2х+2
14 12 11 1 0
15 1 0
16 5 3 2 0 Над GF (7)
17 3 0
18 19 20 7 6 3 0 5 0 1 0 х+1 х2+х+3 х3+Зх+2
Рис. 4.6. Некоторые примитивные многочлены над GF (р)
4.6. ГРУППА АВТОМОРФИЗМОВ ПОЛЯ GF(pm)
С полем GF(pm) связано множество отображений поля самого на себя, называемых автоморфизмами, оставляющих неподвижным каждый элемент подполя GF(p) и сохраняющих операций сложения и умножения.
Такое отображение будем обозначать через о : р—>~ра.
Определение. Автоморфизм поля GF(pm) над GF(p) определяется как отображение, которое оставляет неподвижный элементы поля GF(p) и удовлетворяет условиям:
(i). (а + р)а = аа + ра.
(ii). (сф)а = аХ
^Множество всех автоморфизмов поля GF(pm) образует группу относительно произведения ст и т, задаваемого формулой асх— = (аа)т. „
Эта группа называется группой автоморфизмов или группой Галуа поля GF(pm).
Пример. Рассмотрим поле GF(4) = {0, 1, а, сг) с о/=а+1; аз=1 Группа автоморфизмов этого поля состоит из тождествен* ного отображения 1 и отображения
Ясно, что о2=1.
Теорема 12. Группа автоморфизмов поля GF(pm) является циклической группой порядка пг и состоит из отображения ар : р—> и его степеней.
Доказательство. Используя лемму 5, легко показать, что и все его степени задают автоморфизмы поля GF (рт). Пусть а — примитивный элемент поля GF(pm), а о — автоморфизм поля. По определению автоморфизма элементы а и а? имеют один и тот же минимальный многочлен. Тогда согласно упражнению (14) а° является одним из элементов а, ар, ар2,..., арт~1. Но если аи= = apl , то о= (ор)г. •
Из этой теоремы вытекает, что в конечном поле характеристики р каждый элемент имеет единственный корень .степени р. Мы иногда будем пользоваться тем фактом, что каждый элемент поля GF(2m) имеет единственный квадратный корень У р=р2т~*.
Если рУ=2, то точно половина ненулевых элементов поля имеет квадратные корни. Эти элементы являются квадратичными вычетами, упоминавшимися в гл. 2. Если а - - примитивный элемент поля, то квадратичные вычеты задаются элементами а’ — четными степенями элемента а. Очевидно, что эти элементы образуют группу и что выполняется свойство (Q1) гл. 2, а именно:
вычет-вычет=вычет;
невычет- невычет=вычет;
вычет - невычет=невычет.
Мы можем доказать теперь свойство (Q2).
Теорема 13. Если pm=4k+l, то —1 — квадратичный вычет; если pm=4k—1, то —1 —квадратичный невычет.
1 т
(Р “О 1
Доказательство, а =—1. Если pm—4k+ 1, то — (pF1—1)=
=2k и —1 является четной степенью элемента а; в то же время если pm=4k—1, то-^- (рт—l)=2k—1 и —1 является нечетной степенью элемента а. •
Упражнения. (23). Доказать теорему Дедекинда: если Фь. -., <Рп — различные автоморфизмы поля F, то в поле F нельзя найти не все равные нулю элементы ..., а™ такие, что Gi рт + ...
+опрЧ1п-=0 для всех ре Г.
(24). Будем рассматривать ор как линейное преобразование, и пусть Т — матрица этого преобразования. Доказать, что f(x) = =хгл—1 — многочлен наименьшей степени такой, что f(T)=O.
4.7. ЧИСЛО НЕПРИВОДИМЫХ МНОГОЧЛЕНОВ
Обозначим через Iq(tri) число нормированных неприводимых над GF (q) многочленов степени т, где q — некоторая степень простого числа. Это число может быть выражено через функцию Мёбиуса, которая определяется следующим образом:
1, если п=1;
„ гп\ _ (—1)г, если п — произведение г различных простых чисел;
О в остальных случаях.
Основные свойства функции Мёбиуса описываются следующей теоремой.
Теорема 14.
SF1, если n= 1;
|0, если 1. djn
(ii) . Формула обращения Мёбиуса:
если f (n) = \' g(d) для всех положительных целых п, то g(n) = d\Ln
=2 vwfwd)-
d 1 n
(iii) . <p(n) = V dik(n/d) для n^sl*.
d I n
Упражнение. (25). Доказать эту теорему.
Теперь мы можем вывести следующую теорему.
Теорема 15.
d | т
Доказательство. Согласно теореме 11 </"=Vd/7(d),
v I m
и достаточно воспользоваться формулой обращения Мёбиуса. Например, для q=2 теорема 15 дает 72(1)=2; /2(2) = 1; Д (3) =2; /г(4)=3, что совпадает со значениями, вычисленными ранее. •
Следствие 16. Iq(tn) ^1 для всех q и пг.
Доказательство. Чтобы получить эту нижнюю границу, воспользуемся теоремой 15, заменив y,(rf) на —1 для d>l. Тогда нетрудно посчитать, что Iq(tn)>(qm—q™'-1—...—l)/m>0. •-
* q>(n) —функция Эйлера (см. упражнение (8)). (Прим, перев.)
Таким образом, для всех простых р и произвольного целого т существует неприводимый над GF(p) многочлен степени т, и это-дает второе доказательство теоремы 7.
4.8. БАЗИСЫ GF(p™) НАД GF (р)
GF(pm) является векторным пространством размерности т над GF(p). Любое множество из т линейно независимых элементов может быть выбрано в качестве базиса этого векторного пространства
При задании поля GF(pm) примитивным неприводимым многочленом л(х) в качестве базиса мы выбирали элементы 1, а, а2,..., ат-1, где а — корень многочлена л (х). Однако имеются и другие возможности.
След.
Определение. Сумма
. т—1 I
^(р)=р+₽р+рр + • -+рр
7=0
называется следом элемента peGF (рт). Так как
т—1
Трт(₽)=2 ₽
7=0
то согласно теореме 8 Тт(р) принимает одно из значений 0, 1, 2, ...,р—1 [т. е. является элементом поля GF(p)]. В частности, след элемента из GFfQF') равен 0 или 1.
Упражнение. (26). Показать, что след обладает следующими свойствами:
(i) . Тт (р + у) = Тт (Р) + Тт (у), р, ysGF(pm).
(ii) . Каждое из значений в GF(p) функция Тт(р) принимает одинаковое число раз, т. е. рт~г раз. [Указание. Согласно упражнению (23) Тт не может быть тождественным нулем.)
(iii) . T™(pp)=TPm(p)=Tm(p).
(iv) . Tm(l) =m(mod р).
(v) . Пусть Tm(x) —многочлен вида
т—1 ;
V/ .
/=о
Показать, что для любого s^GF(p)
Тт(х)—s=r|(x—р);
(₽)=s
хр —х = П (Тт(х)—s).
seGF (р)
(vi) . Показать, что если M(z) =zr+Mr-iZr~l+...— минимальный многочлен элемента peGF(pTO), то Тт(Р) =—mMr-ii'r.
Лемма 17. (Матрица Вандермонда.) Матрица / laxaf - -а"-1 \ | la^2 • - -а”—1 |, \ \апа2 .ап~-}/
где ai — элементы некоторого конечного поля, называется матрицей Вандермонда. Ее определитель равен
п—1 п
П П (ai—ai)
J=1 i=/+I
И всегда отличен от нуля, если — различны.
Доказательство. Легко показать, что этот определитель равен /(az—a1)(az—a1)a2(az—a1)a2 ’ ’ -(о2—ai) аг~2 \
det I (аз“°т)(аз—«1)03(03—«J of • ‘ -(«3—01) о?”2 j
\(оп —«1)(ап —ai)an(on —Oi)a2 • • • (ап—сц) an~2J *
Теперь результат сразу следует по индукции. •
* Дополнительные базисы. В остальной части этого параграфа мы ограничимся полями характеристики р=2.
Два базиса Pi, р2, . , Рт и Z2,... называются дополнительными, если
г„(₽л)=Рпри,'*!;
( 1 при I = J.
Иногда такие базисы называются двойственными.
Лемма 18. Пусть Pi, р2, ..., рто — базис. Матрица
обратима, и det В=1.
Доказательство. Выражая базис 1, а,..., am~l через базис рь Рг, ..., рт, получаем, что
* Материал, отмеченный звездочкой, можно при первом чтении опустить.
где с — некоторая двоичная матрица, огда
Эта матрица обратима согласно лемме 17, и, следовательно^ матрица В также обратима. Далее, матрица
Тт(Ш . . -ддр^)
ВВТ =| (Р1Рг) ^ГП (Рг) -^тФгРгп)
\7т(Р1РЛ(Р2рт) ‘ ‘ Тт$т) является двоичной, так что ее определитель равен 0 или 1. Таким образом, det BBr= (det В)2 = 1, откуда следует, что detB = l. •>
Упражнение. (27). Если Pi, Р2, • , ₽m — базис, то 7’m(pi) = = 1 по меньшей мере для одного Рг.
Теорема 19. Для каждого базиса существует дополнительный базис.
Доказательство. Напомним, что матрица, обратная к матрице получается путем замены ai:i на алгебраическое дополнение элемента a3i, деленное на det[tzi3]. Легко видеть, что В-1 имеет вид
А.3 Xg ® в s Х^ v ч ---ч
где Хц Хг, ..., Хт линейно независимы над GF(2).
Тогда из равенства ВВ-1 = 1 вытекает, что базисы Pi, Р2, ..., pm и Xi, Хг, ..., Xm являются дополнительными.
Упражнение. (28). Если yeGF(2m), то ? = (уХг)рг.
1=1
4.9. ЛИНЕАРИЗОВАННЫЕ МНОГОЧЛЕНЫ И НОРМАЛЬНЫЕ БАЗИСЫ
Пусть q=pa— степень простого числа.
Определение. Линеаризованным многочленом над GF(qs) h
называется многочлен вида L(z) = S liZ<ii, где li^GF(qs)\ lh=\^ 1=0
например z + z2H-24 — линеаризованный многочлен над GF(2S) для любого s.
Пусть корни L(z) лежат в расширенном поле GF(qm), tnZ^s.
Лемма 20. Рассмотрим GF(qm) как векторное пространство НаД GF(.q). Тогда корни L(z) образуют подпространство в GF(qm)..
Доказательство. Если |3i и р2— корни L(z), то согласно следствию 3 и лемме 5 при произвольных ki^GF(q) элементы Xi|3i+ +Х2Р2 также являются корнями L(z). •
Упражнение. (29). Показать, что если г делит т, то корни L(z), лежащие в GF(qr), образуют подпространство в GF(qr).
Так как L'(z)=lo, то все qh корней многочлена L(z) различны и образуют /z-мерное подпространство в GF(qm), если /оэ^О.
Лемма 21. Обратно, пусть U—й-мерное подпространство в GF(qm). Тогда L(z) = |~] (z—р) — линеаризованный многочлен над
Рео GF(qm), т. е.
L(z) = z? +Zft_ \Z4 + • -+Zoz. (4-13)
Доказательство. Пусть Ро, Pi,..., ^h-i^GF(qm)—базис U над GF(q). По лемме 18 матрица
~₽о • -рГ-1
₽1 ₽? -pf”'
• • рь* _
h h~~1 j
обратима. Следовательно, уравнения p? + VZ;P? = 0, i=0, 1, ...
. . . /=0
..., h—1 разрешимы .в поле GF(qm) относительно l0, h, , lh-i-Это означает, что элементы Ро, Pi, ..., p^-i являются корнями многочлена.
Л /
L(z) = z9 +'£ljz4 . i=o
Любая линейная комбинация элементов Рг, т. е. произвольный элемент из U, также является корнем многочлена L(z). Следовательно,
£(г) = П(г-р). •
Реи
Пример. Пусть U — подпространство в GF(23), состоящее из точек: ООО, 100, 010, ПО. Тогда (см. рис. 4.5)
П (2—P) = z(z— l)(z—a)(z—oc3) = z4 +a5z2 + a4z Peo
— линеаризованный многочлен над Gf(23).
Нормальные базисы. Определение. Нормальным базисом поля GF(pm) над GF(p) называется базис вида у, ур, ..., урП~1.
Например, а, а2, очевидно, является нормальным базисом поля GF(22) над FG(2). В будущих главах мы будем иногда пользо-
ваться нормальными азисами, и поэтому этот раздел посвящается доказательству того, что такой базис всегда существует.
Линеаризованный многочлен L(z) = У ltzp называется
i=0
р-многочленом, если все его коэффициенты Ц лежат в поле GF (р). Согласно леммам 20 и 21 корни р-многочлена образуют подпространство М поля GF(pm) (для некоторого т) над GF(p). Они обладают еще одним свойством: если ц, принадлежит М, то и рТ принадлежит М (так как 2>(у,) =L(p,₽)). Подпространство с таким свойством называется модулем. Если /о=т^0, то L(z) не имеет кратных корней, и в дальнейшем рассматривается только этот случай.
С другой стороны, если М — модуль, то согласно лемме 21 (z—р) —линеаризованный многочлен L(z). А так как модуль Рем
М представляет собой объединение множеств вида {р, р₽, рр2, то согласно упражнению (14) все коэффициенты многочлена L(z) лежат в GF(p). Таким образом, верна следующая лемма:
Лемма 22. Предположим, что L(z) —линеаризованный многочлен над GF(pm). Корни многочлена A(z) образуют модуль тогда, и только тогда, когда L(z) является р-многочленом.
Пример. Из таблицы поля GF(24), приведенной на рис. 3.1, легко видеть, что элементы 0, 1, а, а2, «4, а8, а®, а10 образуют мо-дуль. Соответствующий р-многочлен равен z8+z4+<z2 + z.
Обычное произведение двух р-многочленов не является р-многочленом. Определим символическое произведение двух р-многочленов F(z) и G(z) равенством F(z) ®G (z) =F (G (z)).
Упражнения. (30). Доказать коммутативность такого произведения, т. е. справедливость равенства F(G(z)) =G(.F(z)). По-h
ставим в соответствие р-многочлену F(z) = У обычный мнот
г=0 h
гочлен /(z) = ^ /iZ’:. (31). Показать, что обычный многочлен, со-i=0
ответствующий многочлену F(z) $G(z), равен f(z) -g'(z).
Лемма 23. Если р-многочлен 5£>(z) равен символическому произведению р-многочленов F(z) ® G(z), то делится в обычном смысле на F(z) и на G(z). Наоборот, если р-многочлен 3^(z) делится на р-многочлен G(z), то Зё(z) =F (z) (Xj G (z) для некоторого р-многочлена F(z).
Доказательство. Пусть сначала f(z) = (l/z)E(z). Тогда <^(z) = =f(G(z)) G(z), так что он делится на. G(z) и аналогично на F(z). Наоборот, предположим, что 3%>(z)=A(z)G(z). Тогда, выполняя символическое деление 3%>(z) на G(z), получаем
Ж (z) = F (г) ®G(z) + R (z) = f(G (z)) G (z) + R (z),
гДе deg R (z) <deg G (>z). Но так как 3^(z)=A(z)-G(z), то долж-но выполняться равенство 7?(z)=0.
Пример. Рассмотрим р-многочлен из предыдущего примера. Имеем
z8 + z4 + z2 + z = (z2 + z)(x) (z4+z)==(z4 + z + l)(z4 + z) =
= (z® + Z5 + Z4 + Z3 + 1) (z2 + z).
Если многочлен L(z) не может быть представлен в виде F(z)0 (х) G(z)1, то он называется символически неприводимым. Корень pi многочлена L(z) называется примитивным, если он не является корнем никакого р-многочлена более низкой степени.
Теорема 24. р-многочлен E(z), у которого /о=И=О, всегда имеет примитивный корень.
Доказательство. Пусть
L(z) = EJ*(z)0Fj»(z)0 • • -®F\T(z) (4.14)
— разложение L(z) на символически неприводимые делители, где все РДг) различны и рт‘—степень Д(г). Тогда степень L(z) равна рт, где т= X Цт.г. Так как /о^О, то все корни L(z) однократны.
Если р, — элемент поля GF(pm), то имеется единственный р-многочлен наименьшей степени, скажем, U(z), для которого р является корнем; иными словами, U(z) — многочлен, всеми корнями которого являются элементы р, рррр2,... и все их линейные комбинации. Более того, если р — корень L(z), то L(z) делится на U(z). Следовательно, корень многочлена L(z) является примитивным, если он не является корнем никакого его символического делителя. Используя принцип включения и исключения, получаем, что число примитивных корней многочлена L(z) равно
-------= р"( 1—^-)( 1—Д)- -X
i i, l
х . . .( 1---М>0. (4.15)
\ Р r /
Таким образом, L(z) всегда имеет примитивный корень. •
Пример. Многочлен z2+z является символически неприводимым делителем многочлена z8+zi+z2-\-z: z8+z4+z2-|-z= (z24-z) 0 .0 (z2+z) 0(z2+z).
Следовательно, число примитивных корней этого многочлена равно 23(1—1/2) =4. Действительно, элементы а, а2, а4 и а8 являются его примитивными корнями.
Пусть теперь
т—1
L(z)=2?m +lm^ zp + - - - + 1^ + 1^, li^GF(p)-, Zo=^0
— произвольный р-многочлен. Согласно теореме 24 iL(z) имеет примитивный корень ц, причем iL (z) — единственный р-многочлен
1 Степени F(z) и G(z), конечно, должны быть строго больше 1, так как -роль константы в символическом произведении играет р-многочлен г. (Прим, ред.).
степени рт, имеющий р своим корнем. Корнями многочлена L(z) являются рт элементов вида
2 т— 1
еор 4- Sipp + е2р₽ +-]- em—i рР
где E.i^GF(p), и согласно лемме 22 они образуют модуль. У этого модуля, естественно, имеется нормальный базис:
. т— 1
р р2 р
р, р , р , • -, р
Теперь мы можем доказать основную теорему этого раздела.
Теорема 25. (Теорема о нормальном базисе). В любом поле GF(pm) существует нормальный базис.
Доказательство. Выберем L(z) —z. Мы знаем, что корня-
ми L(z) являются все элементы поля GF(pm). Предыдущие рассуждения показывают, что в GF(pm) над GF(p) имеется нормальный базис. •
Упражнение. (32). Для полей характеристики 2 доказать, что базис, дополнительный к нормальному базису^ также является нормальным.
Предположим теперь, что р равно 2 и m — нечетно, так что многочлен хт+1 не имеет кратных корней. Пусть
/+1 = ПМХ); degff = mf i=l
— разложение xm+l на различные неприводимые множители. Согласно упражнению (31)
z2"14-z = F1(z)® • .®fr(z)*).
По формуле (4.15) число примитивных корней этого многочлена и, следовательно, число элементов р, порождающих нормальные базисы в GF(2m), равно:
М(2, т) = 2ХтгП( 1—^-) = П(2тг -1)
и поэтому нечетно. Число нормальных базисов равно М (2, т)/ти также нечетно.
Теорема 26. Если m нечетно, то в поле GF(2m) существует самодополнительный нормальный базис.
Пример. Имеем:
х® + 1 =(х+ 1)(х2 + х+1);
г23 + z = (z2 + z) ® (z22 + а2 + z).
*) р-многочлен Fi(iz), i=l, 2, ..., г, конечно, символически неприводим, так как неприводим обычный многочлен }i(x), который ему сопоставлен. (Прим. Ред.)
Следовательно, число элементов, порождающих нормальный базис поля G.F(23) над GF(2), равно 22—1=3. Используя, таблицу поля, приведенную на рис. 4.5, находим, что в данном случае такой нормальный базис составляют элементы <х3, а6, а5. Этот базис является самодополнительным.
Приведем без доказательств следующее усиление теоремы о нормальных базисах.
Теорема 27. (Давенпорт). Любое конечное поле GF(pm) содержит примитивный элемент у такой, что {у, ур,... ,урт *} — нормальный базис.
Следствие 28. Поле GF (2т) содержит примитивный элемент, след которого равен 1.
Задача (нерешенная). (4.1). Найти простое прямое доказательство следствия 28.
Упражнение. (33). Показать, что все символически неприводимые р-многочлены степени меньше 16 над GF(2) исчерпываются многочленами z, z2, z^-Fz, z4+z2+z, z8+z2-|-z и z8+z4+z.
* ЗАМЕЧАНИЯ К ГЛ. 4
§ 4.1. Хорошее изложение теории конечных полей см. в работах: Альберт [19], Артин [30], Берлекэмп [113], Биркгоф и Барти [153], Конвей [301], Джекобсон [687, т. 3], Питерсон и Уелдон [1040, гл. 6], Ван дер Варден [1376, т. 1] и Зарисский и Самюэль [1454, т. 1]. Кроме того, см. Берлекэмп и др. [131], Карлиц [242—246], Казаку и Симовичи [254], Давенпорт [329], Дэйкин [340], Рота [1126], Цирлер [1466, 1467] и Цирлер и Брилхарт [1469].
Эпиграф к § 4.2 взят из работы Вайнстейна [1395]. Мы сочли не требующими доказательства следующие две теоремы. Пусть f(x)— многочлен степени п с коэффициентами из поля F.
(1) . Если ДР)=О для P&F, то f(x)=(x—fi)g(x) для некоторого g(x) с коэффициентами из F (см., например, с. 40 в [19] или с. 31 в [1454]). (2). Следовательно, f(x) имеет в F самое большее п корней.
Что касается упражнения 8, см. Харди и Райт [602].
§ 4.4. Берлекэмп [113, с. 120] описал более тонкие методы нахождения минимальных многочленов.
§ 4.5. Более обширные таблицы полей малой мощности можно найти в работах: Аланен и Кнут [17], Басси [222, 223] и Конвей [301]. Обширные таблицы неприводимых многочленов содержатся в работах: Аланен и Кнут [17], Грин и Тейлор [554], Мэрш [917], Моссидж [973], Питерсон и Уэлдон [1040], Стенке [1260]. См. также Берд и Вест [93] и Голомб [524а]. Разложение многочленов над конечными полями обсуждаются в гл. 9.
§ 4.6. Что касается упражнения 23, см., например, [30, с. 25] или [687, т. 3; с. 25].
§ 4.7. Свойства функции Мёбиуса см. в работе Харди и Райта [602]. В работе Кнута [772, с. 36] приведено обращение матрицы Вандермонда. См. также Альтхауз и Лик [27].
§ 4.9. Обычное доказательство теоремы о нормальном базисе требует значительно большего вводного материала (см., например, Джекобсон [687, т. 3]). Приведенное в данной книге доказательство принадлежит Оре [1015]. Другое доказательство дают Бергер и Райнер [107]. Линеаризованные многочлены изучались Оре [1015, 1016], Пеле [1034] и БерлекэмпОм [113, гл. 11]. Теорема 27 принадлежит Давенпорту [330]. Лейпель [814] показал, что каждое поле GF(2”*) имеет самодополнительный базис. См. также Манн [910].
Глава 5
Дуальные коды и их весовые спектры
5.1. ВВЕДЕНИЕ
Основным результатом этой главы является неожиданная теорема 1, утверждающая, что весовая функция кода <ё>±, ортогонального к двоичному линейному коду <ё>, однозначно определяется весовой функцией исходного кода В действительности она задается линейным преобразованием весовой функции кода <ё>. Эта теорема доказывается в § 5.2. Если то же самое преобразование применить к спектру расстояний нелинейного кода, то мы получим множество неотрицательных чисел с очень полезными свойствами (§ 5.5). Для изучения нелинейных кодов нам необходимо развить некоторый алгебраический аппарат, а именно: многочлены Кравчука (конец § 5.2), групповые алгебры (§ 5.3) и характеры (§ 5.4). В § 5.6 мы вернемся к линейным кодам и рассмотрим несколько различных типов весовых функций недвоичных кодов. Для каждого из них справедлив результат, аналогичный теореме 1, а именно: весовой спектр дуального кода <ё>± задается линейным преобразованием весового спектра кода <ё>.
Весьма общий результат такого рода представляет собой теорема 14. Однако наиболее полезными следует считать результаты, относящиеся к полной весовой функции (теорема 10) и весовой функции Хэмминга (теорема 13). Е1оследний раздел (§ 5.7) посвящен дальнейшим свойствам многочленов Кравчука.
5.2. ВЕСОВОЙ СПЕКТР КОДА, ДУАЛЬНОГО К ДВОИЧНОМУ линейному коду
Напомним (из § 1.8), что если — линейный код над конечным полем, то дуальный (или ортогональный) код состоит из всех векторов и, скалярное произведение которых с каждым кодовым словом из равно нулю. Если "5F является [п, /г]-кодом, то 9>± представляет собой [и, п—&]-код.
Весовые спектры. Как и в гл. 2, пусть Аг обозначает число кодовых слов веса I в коде п
Назовем многочлен у, А{Хп^уг весовой функцией кода и i—0
обозначим его через W<@(x, у).
Заметим, что многочлен W<g(x, у) может быть записан двумя способами
п
Й = 2 = 2 <5J>
i=o ue<g
Здесь х и у — переменные, a W<g(x, у) — однородный многочлен степени п от х и у. Свойство однородности многочлена
(х, у) часто оказывается полезным. Но мы всегда можем избавиться от х, положив х=1 и по-прежнему имея вполне подходящую весовую функцию
^(1, y) = W^(y) = (5.2)
i=0
Подобным же образом обозначим через число кодовых слов веса i в коде <ё>±. Весовой спектр кода <ё,± тогда равен:
№ . (*> у) = У 4 х^ у1= У *n~wt (u) у”'(u)- (5-3)
«е®
Примеры, (i). Рассмотрим код из всех слов четного веса {ООО, 011, 101, ПО}, который мы обозначим через <&?,. Дуальным к нему является код с повторением ®?з± = {000, 111} (упражнение (34) гл. 1), и весовые функции обоих кодов равны соответственно:
У) = х3 + 3ху2; W (х, у)^хя + уч.
(ii). Код {00, И}, обозначим его через ^2, самодуален: ®?2± = =<ё,2 и
№<g2(x, У) = х2 + У2-
(iii). Рассмотрим [7, 4, 3]-код Хэмминга <9^3.
Как следует из § 1.9,
WMS(X’ У) = х7 + 7^ys + 7^yi + y1‘,
Wjx, y) = x'! + 7x3yi.
^з
Теорема Мак-Вильямс для двоичных линейных кодов. Основной результат этой главы состоит в том, что многочлен W^, х (х, у) задается линейным преобразованием многочлена W<%(x, у).
Рассмотрим сначала случай двоичных кодов (теорема 1).
Пусть, как и раньше, Fn обозначает, множество всех двоичных . векторов длины п. Оно представляет собой векторное пространство размерности п над двоичным полем F={0, 1}.
Теорема 1. (Теорема Мак-Вильямс для двоичных линейных кодов). Пусть g7 — двоичный линейный [и, k\ -код, a g’x — дуальный к нему [п, п—k] -код. Тогда
W , (х, у) == -A- (х + у, х—у), (5.4)
ТЕ? - | ТЕ? |
где |'g’| — 2h равно числу кодовых слов в коде g7.
Кроме ные (5.4):
того, справедливы' следующие тождества, эквивалент-
" A]xn-iAt(x + у)п~1 (x-у/ (5.5)
или
V xn-wt <u) r/wf <u) = -!_ £ (X + y)n~wt <u> (x-y)wt <u). (5.6)
—’j. I । ие<ё
ue<g
Уравнения (5.4) — (5.6) иногда также называются тождествами Мак-Вильямс.
Доказательство теоремы основывается на следующей важной лемме.
Пусть f — произвольное отображение, определенное на множестве Fn, и пусть на множестве значений f определены операции сложения и вычитания. Для данного отображения f введем его преобразование Адамара f (см. § 2.3) следующим образом:
f(u)= 2 (-1)u vf(v), иеГ. (5.7)
•veFn
Лемма 2. Если "5F является двоичным линейным [п, Л] -кодом (т. е. подпространством размерности k в Fn), то
Ef(u)=wEf(u)- (5-8)
UE^J- uEg
Доказательство леммы 2. Воспользовавшись определением /(и) и поменяв порядок суммирования, получаем соответственно
Sf(«)=S I (-i)u 7(v)= 2/(v) E(-duv.
ue<g ue<g vsFn veFn ue<g
Теперь, если ve^-L, то скалярное произведение u-v всегда равно нулю, и внутренняя сумма поэтому равна |^|. Но если то согласно упражнению (32) гл. 1 произведение u-v принимает значения 0 и 1 одинаковое число раз, и поэтому внутренняя сумма равна 0. Следовательно,
2 А“)=|^12 Hv). “6“^ ±
Доказательство теоремы 1. Применим лемму для отображения' /(U) = x"~wt (u) ywl (u).
Тогда мы имеем
/(U)= V(-l)u vx"-wf<v) ^wt<v)
(5-9)
Пусть u— (iii... tin), v— (Vi... vn). Тогда
A . n 1 1
f(")= S (-1)вд+- +"»’«п ?-• y-‘ -1 s vQFn i~ 1 y1=0'i’2=0
(5.10)
vn=° г=г
Теперь, так как1
^(РаРо Ч- ^ФаР1 Ч" Ч- Ч- й1^осо Ч~ ^jA/Т Ч- Ч- =
= (ао Ч- Gi) (А Ч- А) (с0 + Cj),
(5.10) равно выражению п 1
i=l w=0
Если Ui = 0, то внутренняя сумма равна х+у. Если W;—1, то она равна х—у. Таким образом,
*f(u) = (x+#-wt(и) (х-z/)wt (u). (5.11)
Воспользовавшись теперь уравнением (5.8), получаем:
£ xn-wt (u) ywt (u) = J (x + S/rWf (U) (X-S/)Wt (U)- •
(< uE^
Примеры. Применим теорему 1 к примерам в начале этого раздела.'
(i). W%3(x, y)=-^ + 3xy2;
-^-W^s(x + y, х—у) =-1- ((х + у)3 + 3 (хЧ-У) (х—у)2) = х3 + У3,
что и в'Самом.деле равно (%, у). Далее
-и / ®3
тэ:;! (х^-у- X—^/) = -1- ((х + ^)3 + (х—у)3)=х3 + Зху2 =
КМ./" 2 ч . 2
= ^3(х> У)>
фго иллюстрирует тот факт, что эта теорема симметрична относи-, тельно выбора ролей кодов и ®’-L.
(>•)• ^2(х, у)--=х2 + у2. Поэтому
vW2U + «/, x-y) = -^-((x + y)2 + (x—y)2)=x2 + y2 = W^ (x, у)’ что действительно верно, так как код является самодуальным.
1 Так как в данном случае сумма произведений равна произведению сумм. (Прим, перев.)
Упражнения. ( . Проверить, что
-^W^s(x.+ y' x~y) = x7+7xsyi = W х(х, у). 16
(2) . Показать, что теорема 1 симметрична относительно выбора ролей кодов и 'g’-L, т. е. что
№<ё(х, = + х—у).
[Указание. Положить и=х+у, v=x—у в уравнении (5.5) и воспользоваться однородностью многочлена IE.]
(3) . Показать, что весовая функция [п=2т—1, k=n—т, d= =3]-кода Хэмминга Ж-,,, имеет вид
(*> У> = ~ ((*+#)" + n (X + y)(n-I)/2 (х-^(п+1)/2).
(4) . (а). Показать, что для любого кода с минимальным расстоянием г/^3 имеется точно iAt векторов веса i—1, находящихся на расстоянии1 1 от кода <ё>, и (и—i)Ai векторов веса i+1 на расстоянии 1 от кода
(Ь). Учитывая (а), показать, что для кода Хэмминга п п п 1
У iAy/-1 + £ Ауф + £ (n-i) Atyi+i = (1 + у)п, i=l i=0 1=0
и, следовательно, весовой спектр удовлетворяет следующему рекуррентному соотношению
(i +1) А-+. + А + 1) А-! = (" ) ’
с начальными условиями Ло=1; /, = 0.
(5) . Как известно, расширенный код Голея (§ 2.6) является самодуальным кодом. Проверить это, раскрыв правую часть выражения (5.4) для этого кода.
Взаимосвязь коэффициентов А'г и Л<. Естествен вопрос: как связаны между собой весовые спектры {Л',} и {Л;}, раз они удовлетворяют формуле (5.5)? Если мы положим
(х + у)п~1 (х-у)* = У Ph^x^hy\ (5.12)
h=0
то из (5.5) вытекает, что
1 п
4=7^-24РИ<-). (5:13)
где Pk(i) называется многочленом Кравчука.
1 Расстояние disjt (х, <g?) вектора х из Fn от множества. ’gr'cz/7’1 определяется как min{dist (х, v)}. (Прим, перев.)
ve<jg .‘.I?
Дадим формальное определение этих многочленов.
Многочлены Кравчука. Определение. Для любого натурального числа п определим многочлен Кравчука Pk(x; n)=Pk(x) следующим образом:
k
Pk(x; n) = V(-iyH ;-х , (5.14)
k = 0, 1, 2, • •
где х является переменной, а биномиальные коэффициенты определены в упражнении (18) гл. 1. Таким образом, Рь(х', п) представляет собой многочлен от х степени k.
В тех случаях, когда нет опасений спутать, мы будем опускать параметр п.
Как следует из свойств биномиальных рядов (снова см. упражнение (18) из гл. 1), производящая функция многочленов Р/<(х', п) имеет вид
(1 + z)n~x (1 -2/ = у Рк (х) z\ (5.15)
Если же I и и —целые числа, причем то это выраже-
ние принимает вид
(1 +2)п~г(1- г)1 = jpPh(i)zh. (5.16)
Л=0
Выпишем несколько первых многочленов:
Ро (х)= * ’
Рк (х) = п— 2х;
Р2 (%) = Q j —2пх + 2х2;
Рз (х) = (з)~п+ Т •
Дальнейшие их свойства см. в § 5.7.
Числа A'i, задаваемые равенством (5.13), интересны также в тс?л случае, когда является нелинейным кодом (ср. теоремы 6 и 8). Но для исследования нелинейных кодов, нам необходим некоторый новый аппарат.
* Моменты весового спектра. Прежде чем приступить к изучению нелинейных кодов, мы приведем несколько других тождеств, связывающих весовой спектр {Л,} [п, &]-кода и весовой спектр {Л'г} дуального к нему кода.
Начнем с того, что напишем уравнение (5.5) для случая, когда х= 1,
V Л^ = -ЦУЛ;(1+^-г(1-^- (5.17)
пп—ft 4—л
i=0 Z i=0
Полагая zy=l, получаем''(так как Л'о=1) должное равенство
Дифференцируя по у выражение (5.17) и полагая у=\, получаем первый момент
V —= —(п—А'.) = —п, если А' = 0.
2ft 2 v l' 2 1
Итак, если Д'1=0, то средний вес слова в коде ’ё’ равен п/2. Продолжая таким же образом, получаем, что
для значений v = 0, 1, ..., п. Левая часть тождества (5.18) называется биномиальным моментом коэффициентов Лг-.
Предположим теперь, что дуальный код имеет минимальное расстояние d', так что A'i= ... =A'd-i = 0.
Если v<d', то правая часть соотношения (5.18) не зависит больше от кода. Таким образом,
(5.19)
Этим равенством мы воспользуемся в следующей главе. Оно показывает, что биномиальный момент порядка v для v= = 0, 1, ..., d'—1 не зависит от выбора кода и, в частности, равен моменту [п, п, 1]-кода, представляющему собой все пространство Fn.
Упражнения. (6). Доказать следующий вариант соотношения (5.18):
для v = 0, 1, ..., п.
(7) . Если вместо дифференцирования выражения (5.17) по у применим к нему v раз оператор y(d/dy) и затем положим у= 1, то получим степенные моменты коэффициентов Л,. Для чисел v<d' они особенно просты. Показать, что
V = — п(п+1), если 2<zd', (5.20)
АшЛ gh 4
1=0 2
и
i=0
Aj
2k
— jv ) , если 0 С v < d'. 2 /=о 1 z
(5.21)
Показать, что в общем случае для v = 0, 1, ...
n — j п — I
(5.22)
представляет собой число Стирлинга второго рода (использовать приведенные в гл. 1 соответствующие преобразования биномиальных коэффициентов). Равенства (5.22) часто называются тождествами Плесе.
(8) . Показать, что, если неизвестно только г коэффициентов Ait а коэффициенты A't, ..., A'r-i известны, то все At могут быть определены. [Указание. Коэффициенты при неизвестных в левой части (5.22) образуют матрицу Вандермонда (см. лемму 17 гл. 4).]
(9) . Моменты относительно среднего значения, (а). Показать, что (5.17) влечет следующее соотношение:
£ Д, £?("-2/) х = 2к У A’f ch"-/ х sh' х. /=0 j=0
(Ь). Отсюда вывести справедливость следующего для r=0, 1, ...:
(5.23)
тождества
(5.24)
где
(с). Показать, что FrW(ri)^0 и
(5.25)
Заметим, что правая часть неравенства (5.25) представляет собой r-й момент относительно среднего значения весового спектра для тривиального [п, п, 1]-кода Fn.
(е). Показать, что, если r^d'—1, то в (5.25) выполняется равенство.
Задача (нерешенная). (5.1). Пусть ^ — линейный код. Как и в § 1.5, пусть щ обозначает число лидеров смежных классов кода ’ё’ веса I и пусть a'i обозначает соответствующее число для дуального кода <ё'А-. Сколь однозначно числа {щ} определяют числа {a'J ?
5.3. ГРУППОВАЯ АЛГЕБРА
Нашей целью является описание двоичных векторов длины п посредством многочленов от переменных Zi, z2, ..., zn. Например, вектор 100... О будет представляться через zlt вектор 10100 ...0 — через ZiZ3 и т. д. В общем случае вектор v=vl'V2...vn представляется многочленом 2^2%... 2%^ который мы обозначим как zv. Ясно, что если мы знаем zv, то можем узнать и v. Таким образом, многочлен 2ve<g zV представляет собой весовую функцию кода '<F, выписанную в нескол ко необычной форме. (Мы снова воспользуемся этой формой в& вой функции в § 5.6 для кодов над GF(<7).) Условимся, что z2i=l для всех i. Это превращает множество всех многочленов zv в мультипликативную группу, обозначаемую через G. Таким образом, группы Fn и G изоморфны, причем операция сложения в Fn
v+w = (d1, • • •, + • • ->^n + ®n)
соответствует умножению в G
. . ,^n) = z^ . . .Z“n+-„ = zv+w
Определение. Групповая алгебра QG группы G над полем рациональных чисел Q состоит из всех формальных сумм вида
У a 2V, с £ О, 2VE G. veFn
Сложение и умножение элементов QG определяются естественным образом:
У o,zv + 2 6vzV= X (Gv + 6v)zV> vef” vef” vefn
r^avzv = ^rav2v, r£Q; vef” vefn
(£ Gvzj( £ vw)= 2 flvfc«zv+w-vef wef v, wg/'
Подмножества из Fn или коды могут быть представлены как элементы алгебры QG: коду ^czFn соответствует элемент
С = £2и ue<g
групповой алгебры QG. Например, коду {000, 011, 101, 110} соответствует элемент
С = 1 + 22Z3 4- ZjZ3 + zxz2.
В общем случае может оказаться полезным рассматривать элементы QG как «обобщенные коды» в следующем смысле: ко-
эффициент ау показывает, сколько раз вектор v встречается в «коде».
Упражнение. (10). Для п=3 показать, что
(zi + z2 + z3)2 = 3 + 2 (?jz2 + z2z3 + ZjZg).
Одним из достоинств, вытекающих из введения групповой алгебры, является возможность кратко формулировать некоторые свойства кодов. Пусть
Ъ = I wt (u)=i
представляет собой все векторы из Fn веса i. Например,
Го=1;
— Z1 + Z2 + ’ ' ’ + Zn’
F2 = Z1Z24-Z1ZS + ' ’ -+z„_izn-
Шар радиуса e, описанный вокруг точки v, представляется тогда элементом zv (Уо+ У1 + — + Уе)-
Если является совершенным (n, М, 2е+ 1)-кодом, то этот факт выражается тождеством
£•(^0 + ^+ • • .+Уе)=£ги, (5.26)
пек"
где С = У zv.
ve®
Пример. Для совершенного кода {ООО, 111}, исправляющего одну ошибку, С= l + ziz2z3; Уо +У[ = 1+Z]+z2+z3, и действительно,
С• (Уо -{- У1) = 1 + Zy 4~ z2 + zs 4- ZjZ2+z1z3 -{- z2z3 z^z^.
Упражнение. (11). На языке групповой алгебры описать следующие методы построения кодов: прямую сумму кодов и конструкцию типа |u|u+v| (§2.9).
5.4. ХАРАКТЕРЫ
Каждому вектору ueF" поставим в соответствие отображе-ние Хи группы G в поле рациональных чисел, задаваемое следующим образом:
Xu(zv) = (-l)uv. (5-27)
где u-v — скалярное произведение векторов u, v над полем Q-Отображение хц называется характером группы G. Оно линейно продолжается на групповую алгебру QG:
MS Gv?v)= X GvXu(zV)= V(-l)uvcv. (5.28)
vqF vqF vqF
Отметим, что < \ .
% zzv\_ ( 1» если векторы и и V ортогональны;
u ' ' I — 1 в противном случае.
Упражнения. (12). Доказать:
(i) . Xu(zv) = Xv(zm).
(»)• Xu(^)Xu(zw) = xu(zv+w).
(iii) . Если Ci, C2— произвольные элементы алгебры QG, то Xu (CJ xu (С2) = Xu (^1 ‘ Q.
(iv)- Xu ( zW) Xv ( zw) = xu_|_v ( zw).
(13). Если ^ — линейный код и C=2uegzu, то
v еСЛИ vG=^±;
I 0, если V qE'tf? .
(14). Показать, что если вектор ueF" имеет вес i, то
. £ (-l)U V=XuO = Pft(i).
Wt (v)=fe
(15). Дальнейшие сведения о характерах. Более точно характером х абелевой группы G является любой гомоморфизм Q в мультипликативную группу комплексных чисел с абсолютным значением 1. Для группы G, определенной в начале раздела 5.3, характеры принимают значения ±1. Показать, что характеры G образуют группу X, которая изоморфна группе G (и, следовательно, группе Fn). В этом случае равенство (5.27) как раз представляет собой один из примеров изоморфизма между Fn и X.
(16). (Формула обращения). Пусть
С= S.
vef”
и предположим, что нам известны числа
х.ю= х М-1Г
; vef”
для всех и из Fn. Показать, что тогда
uef"
и> таким образом, С полностью определяется числами х«(С)- ~
5.5. ТЕОРЕМА МАК-ВИЛЬЯМС ДЛЯ НЕЛИНЕЙНЫХ КОДОВ
Весовая функция элемента групповой алгебры
Пусть С= cvzV
уег"
— произвольный элемент групповой алгебры QG, такой, что
V cv=£0.
ver"
Назовем (и + 1)-вектор {Ао, Ап}, где
X cv
Wt (V)=t
весовым спектром элемента С. Это понятие является естественным обобщением понятия весового спектра кода. Конечно, ХАг-= =А1. Как и в § 5.2, для элемента С определим также его весовую функцию-.
п
Wc(x„y)= £ с^-^^у^^ = ^А^у\
VeFn i=0
Определение. Сопряженным к элементу С назовем элемент С' алгебры QG, задаваемый формулой
С’=[Д S х"(с)г“’ (5'29)
uer
где отображение у было определено в § 5.4.
Предположим, что
так что
<£ (-1Г с,, .ен (5.30) ver"
(Коэффициенты с и' пропорциональны преобразованию Адамара1 коэффициентов cv — см. § 2.3.) Тогда весовой спектр элемента С' задается вектором {А'о, —, А'п}, где
А<= S <=д Е х-(С)' <5ЗД wt (u)=i wt (u)=t
а весовая функция С'
wc- (х, у) = £А'г хп~г у1.
1 Ср. выражения (5.7), (5.28) и .(5.30). (Прим, перев.)
\ Как и в теореме 1, многочлен WC' задается линейным преоб-ра^рванием многочлена Wc-
Те орема 3.
\ Wc,(x, У) = -д Wc(x + y, х—у),
что эквивалентно с учетом (5.15) равенствам:
(5.32)
п
k = 0, 1, п. (5.33)
i=0
Эта теорема и теорема 5 могут быть интерпретированы как теоремы Мак-Вильямс для нелинейных кодов.
Доказательство. Соотношение (5.32) эквивалентно также равенству
У < xn~wt (v) у"* (V) = + (и) (х-уГ
vef” uefn
В силу (5.30) левая часть этого равенства равна
М S Cu S (_ 1)U V (V) <V) =^r S cu(*+^n-w‘(u) X
»eFn vef” ueFn
X(x-f/)wt (u)
согласно соотношениям (5.9) и (5.11) из § 5.2. •
Для любого (n+1)-вектора {Ло, ..., Лп}, такого, что
М = ргУ=0, i=0
назовем вектор {Л'о, Л'„} его преобразованием Мак-Вильямс.
По теореме 3 оно может быть получено либо по формуле (5.31), либо по формуле (5.33).
Упражнения. (17). Показать, что (С')'=С/с0 при Со=^О.
(18) . Показать, что А'о = 1.
. Показать, что Ап = — У А'..
"пП 1
2 1=0
(20). Пусть •g’— линейный [п, Л]-код, и предположим, что смежный класс v+ff содержит Е{ векторов веса i. Используя равенство (5.31), показать, что преобразование E't от чисел Ег равно ai—Где щ равно числу слов веса i в <g’-L, ортогональных вектору v, а р,- равно числу слов веса I в не ортогональных v. Следовательно, показать, что
S e^‘s‘=тД X -₽,) <x+s,r‘ •
i=0 i=O
Спектр расстояний в нелинейном коде. Пусть теперь — линейный или нелинейный (п, М, й)-код. Этому коду 'ё’ соответствует элемент
С= £ ?' (5.34)
ve<g
групповой алгебры QG.
Упражнение. (21). Показать, что, если код —линейный, то
c'“2zV-
ve®-*-
Таким образом, теорема 1 является частным случаем теоремы 3.
Пусть — линейный или нелинейный код. Пусть D= (l/M) С2. Если мы представим D как элемент QG,
то весовой спектр D равен {Во, •••, Вп}, где Bi= dw. wt(w)=i
Лемма 4. Вектор {Во, ..., Вп} представляет собой спектр расстояний кода гё".
Доказательство.
S? s ' i Е S 'S Д £ z"+,= ue<g ve<£ 1=0 u, vG<g
dist (u, v)=i
= S JwZW-wef” Следовательно,
B‘- S "--«V s *•
wt (w)=i u, VG^
dist (u, v)=z
Применяя теорему 3 к элементу D= (l/M) С2 групповой алгебры QG, получаем следующий результат.
Теорема 5. Преобразование Мак-Вильямс спектра расстояний кода равно п
B‘-k S ^(о>=^ЕВЛ(0; s=0’ "• <5 35)
wt (u)=s i=0
Доказательство. Утверждение вытекает из теоремы 3 и равенства
Е"-Ч,(ЕС-Г-"'-
wQF vgF
\ Свойства чисел t..
\т ео р е м а 6. В'^О; t = 0,’..., п.
Доказательство. Согласно определению и упражнению (12), получаем, что
S S S <’="(С),2>0- (5-32
) wt (u)=i wt (u)=i wt (u)=i •
Этот простой с виду результат оказался очень полезным (см. границу линейного программирования, § 17.4). Теорема 12 гл. 21 дает другое доказательство этого результата.
Теорема 7. (а). Если Ое®’, то (В; = 0) => (7U=0).
(b). (B'i = 0)=> (Xu(C’)=0 для всех и веса i)=>(A't=O).
(с). (B'i=/=0) =>(Хи (С)=/=0 для некоторого и веса Г).
Доказательство. Утверждение (а) очевидно, а утверждения (Ь) и (с) следуют из (5.36) и (5.31). •
Дуальное расстояние и ортогональные таблицы
Определение. Дуальным расстоянием d' кода называется число d' такое, что В\=0 для всех —1, а
Если код 7?— линейный, то d' — минимальное расстояние дуального кода <&А-.
Заметим, что при таком определении d' остаются справедливыми все соотношения (5.18) — (5.25) и упражнения (6) — (9) для спектра расстояний нелинейных кодов.
Пусть теперь [??] будет (М\п) -таблицей, строками которой являются все слова кода 7?. Ес пи код 7? линеен, то любые r^.d'—1 столбцов матрицы f®7] должны быть линейно независимы, в противном случае дуальный код <ё’А- содержал бы вектор веса r<_d'. (Это утверждение является двойственным к теореме 10 гл. 1.) Этот же результат справедлив также и для нелинейных кодов. Мы немного изменим его формулировку.
Теорема 8. Любые r^d'—1 столбцов матрицы [<g’] содержат каждый r-вектор точно М]2Г раз, и d' является наибольшим числом, удовлетворяющим этому свойству.
Замечание. Матрица с таким свойством называется ортогональной таблицей с п ограничениями, двумя уровнями, силой d'—1 и индексом Af/2rf'-1 (см. § 11.8).
Доказательство: Для доказательства первой половины вспомним, что из теоремы 7 следует равенство %ц (С)=0 для всех векторов и веса 1, 2, ..., d'—1. Условие хи(С)=0 для всех и веса 1 влечет, что каждый столбец матрицы [??] имеет М/2 нулей и М/2 единиц. Далее условие хи(С)=0 для всех и веса 2 влечет, что любые два столбца матрицы [<ё>] содержат каждую пару 00, 10, 01, 11 точно М/4 раз. Ясно, что подобные рассуждения можно продолжать вплоть до векторов и и веса d'—1. С другой стороны, так как В'=/=0, то имеется вектор u-веса d' такой, что %u (С) =т^0.
Примеры, (i). Рассмотрим (11, 12, 6)-код Адамара ^i2 (см. § 2.3). Так как это симплексный код, содержащий нулевое с/ю-во, то его спектр расстояний совпадает с весовым спектром:
„ t: ° 6 W (х, у) = хг1 + Их8/.
Лг = Вг: 111 ^12 ’
Преобразованный спектр получается из многочлена
W^lz (* + У> х—у) = ((* + + 11
1^ lz
II = £в:хп-г уг 1=0
и имеет следующий вид:
1:0 3 4 5 6 7 8 11
В' :1 18— 36— 29— 29— 36— 18— 1 1 3 3 3 3 3 3
2
Заметим, что 2В'г=170—=2“/12. Кроме того, Д'г^0 в соот-3
ветствии с теоремой 6. Эта таблица показывает, что d'=3.
Список всех кодовых слов [j^i2] находится в верхней половине рис. 2.1. Для иллюстрации теоремы 8 заметим, что в любых двух столбцах этой матрицы каждый из векторов 00, 01, 10, 11 встречается 3 раза.
(ii). На рис. 5.1 изображен (8, 16, 2)-код.
00000000
1 1 0 0 0 0 0 0
1 0 1 0 0 0 0 0
1 0 0 1 0 0 0 0
1 0 0 0 1 0 0 0
1 0 0 0 0 1 0 0
1 0 0 0 0 0 1 0
1 0 0 0 0 0 0 1
11111111
0 0 111111
0 10 11111
0 110 1111
0 1110 111
0 11110 11
0 111110 1
0 1111110
Рис. 5.1. Нелинейный (8, 16, 2)-код
(см. упражнение (22) гл. 15). В этом коде спектры весов и расстояний снова совпадают
i: 0 2 6 8
А = Д-:1 7 7 1
W (х у) = xs 4- 7х6/ + 7х2/ + уь.
Преобразованный (.1/16) W(x-\-y, х—у)
спектр получается из многочлена . Но после упрощения этот многочлен ока-
зевается равным W(х, у)\. Поэтому для этого кода В\ = В^ и, крРме того, d'=2. ,
Этот код имеет еще одно необычное свойство, заключающееся в том, что D'=D. Доказательство этого факта представляет собой хорошее упражнение по применению групповой алгебры.
Упражнения. (22). Показать, что если
то D'=f\
Заметим, что в общем случае, мы не можем найти С, если известно 'только D.
(iii). Рассмотрим нелинейный (16, 256, 6)-код Нордстрома— Робинсона (см. § 2.8). Еще раз получаем, что Аг=В{ (см. рис. 2.19). Этот код также обладает тем свойством, что В\=Вг, хотя и довольно трудно доказать это непосредственно. Это будет следовать из результатов гл. 15.
(23). Пусть ’ё’ — код и С определяется выражением (5.34). (i). Показать, что D = C, если и только если —линейный код.
(ii) . Показать, что С'=С, если и только если — линейный самодуальный код.
*5.6. ОБОБЩЕННЫЕ ТЕОРЕМЫ МАК-ВИЛЬЯМС ДЛЯ ЛИНЕЙНЫХ кодов
В этом разделе мы опишем несколько типов весовых функций для линейных кодов над произвольным полем F=GF(q) = = GF(pm), rjye. р — простое число. Обозначим через <во=0, (01, ..., <oQ—। элементы поля GF(q), выписанные в некотором фиксированном порядке.
Полная весовая функция. Рассм'отрим вначале весовую функцию, которая классифицирует кодовые слова и в пространстве Fn в соответствии с тем, сколько раз каждый элемент поля ац появляется в слове и.
Определение. Назовем композицией вектора и= (щ, ...,ип) и обозначим через comp (и) (/-вектор (s0, sb ..., sg-i), где хг= «—1
= £г(и) равно числу компонент щ, равных оц. Ясно, что Ss<=n.
z—О
Пусть &— линейный [п, &]-код над GF(q) и пусть A(t)— число кодовых слов иеФ, имеющих композицию согпр(и)=Д= = Go, ..., tg-\). Тогда полная весовая функция кода определяется как многочлен
• • •> ^_1) = ХЛ(/)4° ' ' • Vf'= Г zo° • Л-Г'- <5-37> t ue®
Например, пусть 'ё’л— троичный [4, 2, 3]-код#6 из гл. 1. pro полная весовая функция равна /
W(г0- Z1. z2) = го + М + z2 + Зг^г2 + zoz3 = z0 ( £3 4- (Z1 _|_ 4)3).
I (5.38)
Характеры поля GF(q). Для формулировки теоремы нам необходимо ввести понятие характеров поля GF(q). Вспомним из гл. 4, что любой элемент р поля GF(q) может быть представлен в виде P = Po+Pia + p2a2+ - + Pm-iam-1 или, что эквивалентно, в виде m-вектора р= (р0, Pi, ..., pm-i). где a — примитивный элемент GF(q), а рг- — целые числа, причем О^р,^р—1. /
Обозначим через g комплексное число e2ni/v, которо^ является примитивным корнем р-й степени из единицы, т. е. g? = e2lTi=l И в то же время gI=/= 1 для значений 0</<р.
Определение. Для любого элемента Р=(Ро, Pm-i)^ ^GF(q) определим Хр как комплексно-значное отображение эле-.ментов поля GF(q), задаваемое формулой
. Хр(у)= tPoVo+-+₽—1 , (5.39)
где у= (у0, ym-i)^GF(q).
Отображение Хр называется характером поля GF(q).
Упражнения. (24). Показать, что для всех р, y^GF(q') выполняется равенство х ₽ (у) = XV (Р) •
(25). Показать, что равенство
?-р (? + ?') = Хр (?) Хр (?) (5-40)
справедливо для всех р, у, yf^GF.(q). Таким образом, характер х р представляет собой гомоморфизм аддитивной группы поля GF(q) в мультипликативную группу комплексных чисел, модуль которых равен 1.
(26). Показать, что хp+p'Cv) =Хр(?)х₽-(у) Для всех р, р<, уе ^GF(q). Таким образом, множество всех q характеров Хр образует группу, которая изоморфна аддитивной группе..поля GF(q).
Пример. Пусть <? = р=3; GF(3) = {0, 1, 2} и g = co = e2jTi/3 = = cos 120°+isin 120°. У поля GF(3) имеется три характера:
Хо(0)= 1,
Хг(0)=-1,
Х2(0)= 1,
Хо(1)=1, Xi (1) = “> Х2(1) = со2,
Хо (2) = 1 (тривиальный характер) Xi (2) = со2;
Х2(2) = со.
• Лемма 9. Для любого ненулевого элемента $^GF(q) выполняется равенство
S Хр(?) = О-
тесл (<?)
Доказательство. Ясно, что
\ т—I / р—1 \
\ £ i₽oVo+" ’+₽m-1 Vm-1 = П 2 )
\ ?eGf (?) i=o ' Vj=O /
Так как 0=/=O, то хотя бы одно из Pi не равно нулю, например Ргт^Ол Тогда r-й множитель в выписанном произведении равен: j
\ =2|ft = JiT^“ = 0- •
\ Vr=0 71=0
Пример. В поле GF(3) при р=1 эта лемма утверждает, что
1 +<О|+<в2 = 0.
V—о
Для того чтобы сформулировать следующую теорему, мы должны выбрать какой-нибудь из характеров с р=/=0. Для определенности выберем р= 1, т. е. характер задающий отображение %1(Т) = ^ОДЛЯ ? = (То, • • •> Ym_i)eGF(9). (5.41)
В случае, когда q — простое число, q = p, это отображение выглядит совсем просто %i(y)=£v, y^GF(p), где c, = e'2ni/'JJ.
Теорема Мак-Вильямс для полных весовых функций. Теорема 10. Если — линейный [п, k] -код над GF(q) с полной весовой функцией то полная весовая функция дуального к нему кода <ё’А- определяется следующей формулой:
1
^<g-L (Z0> • > zr> • ’ > zn_i)= • • •
\s=0 fl—1 \
. . ., VX1(co,.4)zs, • • (5.42)
. s=0 /
Пример. Для кода над GF(3) эта теорема утверждает, что '^±(zo- zi> z2) = тД ^(zo + zi+z2. Zo + coz^^Za, e? ' | те I
zo + io2z1 + o>z2), (5.43)
гДе co = e2^i/3_
Другими словами, многочлен получается применением линейного преобразования
/1 ! ! \
11 со ю2 (5.44)
\ 1 (О2 СО /
к многочлену Ж<g и делением результата на число Тад, на-
пример, для кода ^4, приведенного выше, имеем:
(z0, zi> ^2)— (zo + zi 22) ((z0 + zx -Тz2)3 + (2z0 д 20 )/9-
Упражнение. (27). Показать, что 'ё’4 является самодуаль-ным кодом. Проверить это, доказав, что Ж^± =^<g4- (
Доказательство теоремы опирается на следующую лемму.
Лемма 11. Для векторов u, vgeF” пусть %и (v)=% (u-v). Так же как и в лемме 2, для отображения f, определенного на Fn, зададим его преобразование Адамара f 1
f(u) = 2 Xu(v)/(v)- I
veFn
Тогда, если ’ё’ представляет собой произвольный [п, Л]-код над GF(q), то
4гЕ^“>- (5Л5)
. в®1 к<е
Доказательство этой леммы в сущности ничем не отличается от доказательства леммы 2, но надо лишь воспользоваться леммой 9.
S (и)
Доказательство теоремы 10. Положим /(u)=z®»(u) -
Точно так же, как равенство (5.11) было выведено из (5.9), получим, что
Л е—1 /<?—1 \sr (и)
f(u)= 2 xu(v)^°(v) • • л-г1 (v)=n 2Х1(ад)Ч •
vg/1 r=0 \s=0
Применяя теперь к if (u) и f(u) лемму 11, получаем, что выражение (5.45) дает утверждение теоремы. •
Весовая функция Ли. Если в полной весовой функции положить некоторые переменные равными друг другу, то мы получим весовые функции Ли и Хэмминга, которые дают меньше информации о коде, но с ними проще работать.
Определение. Предположим теперь, что число q = 26+1 — степень простого нечетного числа и элементы поля GF(q) ®о=О, <01, ..., to , cog-i-j,..., co9-i обозначены так, что выполняется условие <Од-г = —o)i для 1 t6. Так, например, для q = 5 имеем GF(5) = = {сОо = 0, СО] = 1, <02 —2, <03 =-2 = 3, 404 = —1=4}.
Назовем композицией Ли вектора u^Fn и обозначим через Lee(u) вектор (/0, ..., /6), где /0=s0(u); /;=5г(и) +sg-i(u) для
1 Ct+Cd.
Например, для значения q = 5 композиция Ли классифицирует кодовые слова в зависимости от того, сколько компонент словй равно 0, сколько равно ±1 и сколько равно ±2.
Весовая функция Ли кода 7? определяется как многочлен
\ (z<” ' ’ zc) = 2-zo°zf‘ ‘ ' ’zc 6 •
\ «e<g.
Так, например, самодуальный код длины 2 над GF (5), со-стоящи15 из кодовых слов (0 0), (1 2), (2 —1), (—2 1), (—1 —2), имеет весовую функцию Ли
^(*0, Z2) = zo + 4z,2.2.
Теорема) Мак-Вильямс для весовых функций Ли. Т е о р е-м а 12. Весовая функция Ли дуального кода <g’-L получается из весовой функции Ли кода ’ё’ заменой каждой переменной zi на выражение \
' zo + ^{Xi(“M) + 7.i(—“i“s)}2s
S=1
и последующим делением результата на |®’|.
Доказательство. В теореме 10 положим zq~i = Zi для l^i^S.
•
Для кода из предыдущего примера получаем, что (o,cos) = = a’s, где a=e2jTi/s = cos 72°+it sin 72°, и преобразование теоремы 12 заключается в замене
/г0\ /12 2 \/z0\
I z, I на I 1 а + а4 а2 + а2 11 z, I (5.46)
\г2/ \1 а2 + а3 а-\-а4 / \г±/
Так как код самодуален, то теорема утверждает, что справедливо тождество
?2 + 4z,z2 = ((z0 + 2г, + 2г2)2 + 4 (20 + (а + а4) г, + (а2 + а3) г2) X
О
X (г0 + (а2 + а3) г, + (а + а4) г2)).
Упражнение. (28). Проверить это тождество непосредственно.
Весовая функция Хэмминга. Пусть теперь q — степень любого простого числа. Как и в § 1.3, весом Хэмминга (или просто весом) вектора u=(uI, ..., un)<=Fn назовем число ненулевых компонент Ui и обозначим это число через wt(u). Мы будем использовать обозначения § 5.2, пусть Л, — число кодовых слов веса I и многочлен
П'
YV7 , х я n—i , i V* 4 п~wt (u) . wt (и)
(х, у) = у, Aix У = 2 у г=0 ие®
является весовой функцией Хэмминга кода <ё.
Теорема Мак-Вильямс для весовых функций Хэмминга.
Теорема 13.
^l(x, £/)=~^(х + (9-1)£/, х-у). (8.47)
Доказательство. В теореме 10 положим Zo==х; г\=гг=г — = =zq-i — y и воспользуемся леммой 9. ' ®
Пример. Для кода из рассматриваемого нами Примера весовая функция Хэмминга W^(х, у)= х2 + 4у2 и теорема утверждает, что справедливо тождество
х2 + Ьу2 = 4- ((х + 4z/)2 + 4 (х—у)2).
5
Для случая q — 2 теорема 13 превращается в теорему 1.
Весовая функция, полностью описывающая код. Код можно описать полностью, если ввести достаточное количество переменных. Поясним это примером. Предположим, что ,F = GF(5). Вектор и= (2, 0, 4)е/"3 зададим с помощью многочлена Z\%zwZm. В общем случае переменная гц означает, что t-я координата вектора и равна /-му элементу и>/ поля F. Тогда вектор и= = (и>а1, (£>аг, .... соа„) задается многочленом
/(U)=ZlO,Z2Os • -(5-48)
Таким образом, вектор и однозначно определяется многочленом Ди). Для такого способа описания требуется nq переменных Zjj(l^t^/t, 0е|/^<7—1). (Это аналогично тому, что мы делали в § 5.3 для двоичных кодов.)
Назовем точной весовой функцией кода многочлен
«в®
Теорема Мак-Вильямс для точных весовых функций. Теоре-м а 14. Точная весовая функция <8 ± дуального кода <g’-L получается из функции <8заменой каждой переменной zir на выражение
«—1
2%i(<M>s)zis (5.49)
s=0
и последующим делением результата на |^|.
Доказательство. Достаточно применить лемму 11 к отображению f(u), определяемому (5.48). •
Теорема 14 представляет собой очень общую формулировку теоремы Мак-Вильямс, и, конечно, все предыдущие теоремы следуют из нее. В оставшейся части этого раздела мы приведем еще несколько следствий, дающих информацию о весовой структуре некоторых подмножеств позиций кодовых слов.
Совместные весовые функции. Совместная весовая функция двух кодов s& и сравнивает перекрытие нулевых позиций в типичном слове кода и типичном слове' кода !Д. Это обобщение весовой функции Хэмминга подобно обобщению плотности одномерного распределения на случай плотности совместного распределения. Для простоты мы рассмотрим только двоичный случай, когда F=GF(2).
: Для векторов u=(u,, цп); v= (щ, vn)^Fn введем следующие обозначения:
\ i(u, v)-—число г таких, что ur = 0, ur = 0;
\ j(u, v)—число г таких, что ur — 0, vr= 1;
\ k(u, v)—число г таких, что ur = 1,. ty = O;
) Z(u, v)—число г таких, что ur—l, vr = ’l.
Ясно, что
i (u, v) + j (u, v) + k (u, v) +1 (u, v) = n;
< |(u, v) + Z(u, v) —wt(v);
k(u, v) + Z(u, v) = wt(u).
Определим совместную весовую функцию кодов s& и S3 как многочлен
2А {а, Ь, с, d) = V У a1 <u- v) b’ (u’ v) ? (u’ v) dl (u’ v). (5.50)
то^ той
Совместная весовая функция кода с самим собой называется бивесовой функцией кода s&.
Упражнения. Установить следующие свойства совместных весовых функций.
(29>- Ъ, 1’ ’’ i)=MI-l®|;-
Ъу с’ с'
Весовые функции отдельных кодов задаются выражениями:
W^{X' ^)=7^7^,^(Х’ х’ у’
w^x’ = у’ х’ уУ'
°- у- °);
= У’ 0, 0).
Кроме Того, справедливо равенство
= xt, yz, yt).
(30) . Если s^={0, 1}—-код с повторением длины п, то
2А . Ла, Ь, с, d) = ап bn + сп dn.
Если з^={0}, а код произволен, то
Если код произволен, а код &=Fn состоит из всех векторов длины п, то
^(Ц, Ь, с, d) = W^a + b, c + d).
Если код произволен, а & представляет собой код из всех слов четного веса, то
ь- с- + c + d) + ^^(a-b. c-d).
(31) . (а, b, с, = ~Ла I-с, b + d, а—с, b—d);
Л , Ж 1*^ I ™
% , ^(а> Ь, с, 4) = -^—% &(а + ъ’ a~b’ c + d’ с—®-
(32) . ± ±(а, Ь, с, d) = —±—-K(a + b + c + d, a-b +
+ с—d, a + b—с—d, а—b—c + d). (5.51)
(33) . Показать, что для симплексного [п = 2т—1, т, 2™-1]-кода, являющегося дуальным к коду Хэмминга, при т^2 справедлива формула
+ Ла, Ь, с, d) = fln + na("-n/2(b(n+1,/2 + c("+,)/2 + d(n+1)/2) + «577 j 3&
а
(34) . Показать, что для [п = 2т—1, 2™—т—1, 3]-кода Хэмминга при т^2 справедлива формула
л (а> Ь’ с’ d>) = / 1п2 [ °" + П(П~Х) (<?4—2о22 + 8о1Ш) +
+ по1<«-1)/2 {(а_ ь _]_ c_d)("+i)/2 + (а + b—c—d)''n+Vl12 +
+ (а-b-с + d)(n+1’/2}] ,
где символ ст с нижними индексами обозначает различные симметрические функции от a, b, с, d:
О1=^а1 + Ь1 + с1 + dl;
Gij = ai(bj + ci+di) + bi(ai + cj + dj)+ Л+=] ;
Си = albl + а‘с‘ -)- aldl -|- blcl -|- bldl + cldl ;
сггш =а1Ь1с№.
(35) . Показать, что для [л=2т, тф-1, 2т-|]-кода Рида — Мал-лера первого порядка при т^2 справедливо равенство
&ЛЛ (a,b,c,d) = оп + 2 (n— 1)оп/2>„/2 + 4 (« — 1) (л— 2) .
(36) . Чтобы подчеркнуть, что бивесовая функция дает больше информации о коде, чем обычная весовая функция, показать, что
КОДЫ, порожденные словами. {110000, 001100, 000011} и {110000, 011000, 001111}, имеют одинаковые весовые, но различные бивесовые функции. Другую такую пару кодов составляют [32, 16, 8]-код Рида—Маллера второго порядка и квадратично-вычетный код с теми же параметрами (см. гл. 19).
Разделенная весовая функция. Во многих кодах векторы естественным образом разделены на левую и правую половину. К таким кодам относятся, например, коды, образованные конструкцией типа |u|u + v| (см. § 2.9), коды Рида—Маллера и коды, полученные из них (см. гл. 13 и 15). Для таких кодов полезно следить за -весами обеих половин раздельно.
Для вектора v=(ub ..., vm, <vm+i, ..., v2m) назовем величины wb = wt(r»i, ..., Vm) и a^wtffm+l, ..., V2m) ЛввЫЛ И ПравЫМ вв-сом v соответственно. Введем для [2 m, Л]-кода 'ё’ разделенную весовую функцию как многочлен
yg(x,S,X,V) = 2 V"-”1” х^ " у** ve<g
Упражнения. (37). Пусть и — коды длины п с весовыми функциями IFjfx, у), W2(x, у) и разделенными весовыми функциями P’tfx, у, X, Y), S?2(x, У, X, Y). Показать, что код, являющийся их прямой суммой,
' $©0 = {|u|v|:uGE$,v(=0}
имеет весовую функцию Wi(x, y)W2(x, у) и разделенную весовую функцию W\(x, y)W2(X, Y). С другой стороны, код ^||S>= = {|u'|v'|u"| v"|: u= v= | v'| v"|&£?>} (где каждый из
векторов и и v разбит на две равные половины) имеет ту же самую весовую функцию, но другую разделенную весовую функцию 9’\(х, у, X, Y)ff’2(x, у, X, Y). Заметим, что код WWS) может быть получен из кода ф S) перестановкой позиций кодовых слов. Так, например, возьмем коды %?=3)= {00, 11}, для которых
№г(х ,у)=х2 + у2,9\(х,у,Х, Y) = xX-\-yY.
Тогда разделенные весовые функции кодов
^Ф® = {0000, ООП, 1100, 1111};
II® ={0000, 0101, 1010, 1111}
равны соответственно IFjfx, y)Wi(X, Y) = (х2+у2) (Х2 + Y2) и &i(x, у, X, Y)2 = (xX+yY)2.
(38) . Доказать, что
5? L (x,y,X,Y)=~®<g(x+£/,x—y,X + Y,X— У). (5.52) 49 I <?l
(39) . Выписать разделенную весовую функцию для кодов Рида—Маллера первого порядка.
(40) . Пусть — линейный код длины 2m; предположим, что первые т символов каждого кодового слова посылаются по двоичному симметричному каналу с вероятностью ошибки р, а пос
ледние т символов — по такому же каналу с вероятностью Р. Пусть
4 = min {aj wL (u) + a2 wR (u)},
где минимум берется по всем ненулевым словам и из кода Ч? и си = log ((1— р) /р); а2=log ((1—Р) /Р).
Показать, что код 'tF может исправлять все ошибочные векторы е, удовлетворяющие условию
ai (е) + а2 (е) < di/2 •
(Если разделенная весовая функция кода 'tF известна, то число d\ может быть легко найдено.)
5.7. СВОЙСТВА МНОГОЧЛЕНОВ КРАВЧУКА
Результаты § 5.3—5.5, имеющие дело с весовыми функциями нелинейных' кодов, также могут быть обобщены на случай поля GF(q). Для этого требуются многочлены Кравчука несколько более общего вида; их мы и рассмотрим в этом разделе.
Определение. Для любой степени простого числа q и натурального числа п определим многочлен Кравчука
• • • ,«,(5.53)
где y=q—1, а биномиальные коэффициенты определены в упражнении (18) гл. 1. Производящая функция этих многочленов имеет вид
(l+Yz)"-*(l-zr = £Pft(x)zft-
fe=0
(5.54)
Если х—целое число, заключенное в пределах то
верхний предел суммирования в (5.54) может быть заменен на п.
Теорема 15. (Другие формулы для Pr(x))
Доказательство, (i). Ясно, что
(1 + у Z) п~х (1 -zK = (1 + yz)« (1 - rj- Y =
\ 1 i r /
= У(-q^(l+T^n-J:.(X\
Коэффициент при zk в этом выражении представляет собой многочлен Кравчука: . .
й
« 'Л—1] \ //
/=о и х *'
(ii). Доказательство аналогично; надо лишь воспользоваться следующим равенством:
/ QZ \п—х
(1+у2)"-"(1-2К = (1-2Г( 1 + 1У . •
Таким- образом, РДх) является многочленом степени k от х с коэффициентом при старшем члене (—q)k/k\ и свободным членом
/ п\
' (5.57)
Теорема 16. (Соотношения ортогональности.) Для неотрицательных целых чисел г, s верна формула
2 ( ? pr (i) Ps (/) = qnVr(nr) 6r.s, (5.28)
i=0 ' ' ' Г'
где 6r, s — символ Кронекера: 6r,s=l, если r=s, и 6r,s=0, если r=#s.
Доказательство. Левая часть (5.58) представляет собой коэффициент при yrzs в выражении
п
2 ( •) у1 (1 + ЧУ)П~1 (1 -У)1 (1 + Y (1 -г)г = ((1 + у У) (1 +
i=0 ' '
+ yz)+y(l — r/)(l— z))" = Q"(l +yyz)n. •
Теорема 17. Для неотрицательных целых чисел i, s справедливо равенство
?(”)ps(0 = / (”)Л(8). (5.59)
Доказательство. Утверждение теоремы сразу же следует из (5.53) преобразованием биномиальных коэффициентов. *
Следствие 18.
п
^РДПР^^Ь.!-
i=0
Доказательство. Это равенство непосредственно вытекает из теорем 16 и 17. *
Теорема 19. (Рекуррентное соотношение.) Многочлены Кравчука удовлетворяют следующему трехчленному рекуррентному соотношению:
(k + 1) Pk+l (х) = ((n — k) у + k—qx) Ph (х)—у (п—k + 1) Pk^ (х) (5.60)
Для k=\, 2, ... с начальными условиями Ро(х) = 1; Р1(х)=уи—qx.
Доказательство. Продифференцируем выражение (5.54) по z, умножим обе части на (l-f-уг) (1—z) и приравняем коэффициенты при zfe. •
Теорема 20. Если многочлен а(х) степени t разложен по многочленам Кравчука
а(х)= V akPk(x), (5.61)
ь=о
то коэффициенты этого разложения вычисляются по формуле
ak=q~n^a(i)Pi(k)-
f=0
Доказательство. Умножим обе части (5.61) на Pi(l), положим x~i, просуммируем по i от 0 до п, а затем воспользуемся следствием 18. •
Упражнения. (41). Показать, что
\П—1/ \ 1 /
k=o " ' '
(42) . Показать, что РДх\ п) + Р\(х\ п) + ...+ Ре(х; п) = = Ре(х—1; п—1).
В дальнейших упражнениях q = 2.
(43) . Показать, что Pk(i)= (—\)1Рп-н(1),
(44) . Показать, что Pn(k)={—l)fe; /4(1) = (1—(2^/n)) f ”'j .
\ k J
(45) . Показать, что
п
2^(А) = 2«бй,0;
i=0
^РДк)=2п~1 (пбЬ0-бЬ11); i=0
2 /2 Pt (k) = 2"—2 (/г (/г + 1) б/г ,0 - 2 /г д,; л + 2 6h,2). i—0
(46). Показать, что для неотрицательных целых чисел i и k выполняется рекуррентная формула
(n—k)Pi(k+l)=(n—2i)Pt(k)—kPt (k—1).
[Указание. Воспользоваться теоремами 17 и 19.]
(47). Так как многочлены Кравчука образуют семейство ортогональных многочленов (теорема 16), то многие из результатов
книги Сеге [1297] применимы к ним. Например, доказать формулу Кристоффеля—Дарбу (ср. с теоремой 3.2.2 работы [1297]):
^(х)^ («/)/(”} = -(f + 1)P<+1 Pt(x)Pt+i .
2 y—x
[Указание. Используя теорему 19 показать, что
(t + 1) (Pf+1 (х)Pt (У) ~Pt (x) Pt+l Ш (nt)=t (Pt (x) P^ (y)-
— Pt_i (x) pt (y))/ )—2 (x—y) Pt (x) Pt (y)l ( n^-
а затем просуммировать no t]
ЗАМЕЧАНИЯ К ГЛ. 5
§ 5.2. Теоремы 1, 10 и 13 принадлежат Мак-Вильмс [871, 872]. Лемма 2 взята из работы Ван Линта [848, с. 120]. Леммы 2 и 11 представляют собой варианты формулы суммирования Пуассона (см. Дум и Мак-Кин [396, с. 220]. Теорема 1 была также доказана методами комбинаторной геометрии (см. Грин [560]).
Многочлены Кравчука были введены Кравчуком [782]; см. также Данкл [393], Данкл и Рамирес [394], Иглесон [398], Кравчук [783], Вере—Джоунс [1370] и особенно Сеге [1297]. Дельсарт [350—352] первый явно применил эти многочлены в теории кодирования. В гл. 21 мы снова встретимся с этими многочленами как собственными значениями некоторых схем отношений.
Тождества для степенных моментов были приведены Плесе [1051]. См. также работы Стенли [1261] и Цирлера [1464]. Упражнение 8 также взято из работы Плесе [1051]. Дополнительный материал по числам Стирлинга см. в книге Риордана [1113, с. 43]. Берлекэмп [113, § 16.2] приводит более общее семейство моментов.
Назовем пакетной длиной вектора, расстояние между первой и последней единицами. Коржик [777] рассматривает распределение кодовых слов согласно их пакетным длинам. Упражнение (4) было предложено нашим коллегой Джоном И. Смитом (John. I. Smith).
§ 5.3, 5.4. Что касается групповых алгебр (иногда называемых также групповыми кольцами) и характеров, см. различные книги по алгебре, например книгу Манна [907, с. 73]. Все обобщается на случай кодов над GF(q) с сохранением всех результатов § 5.5.
§ 5.5. Теорема Мак-Вильямс для нелинейных кодов может быть найдена в работах Мак-Вильямс и др. [886] и Цирлера [1468]. Мак-Элис [942] получил эту теорему для случая, когда рассматриваемый алфавит не обязательно является полем.
Теоремы 6, 7 и 8 принадлежат Дельсарту [350]. Ортогональные таблицы были введены Боузом и Бушем [181]; см. также работы Буша [220], Холла [587] и Рагхаварао [1085]. Упражнение (20) взято из работы Ассмуса и Мэттсона [47].
§ 5.6. Что касается весовой функции Ли и кодов в метрике Ли, см. работы Ли [801], Берлекэмпа [115], Голомба и др. [524, 525, 529, 531, 532], Мазура [934], а также замечания к гл. 6. Теорема 12 взята из работы Мак-Вильямс и Др. [883]. Остальные весовые функции этого раздела были введены в [883] и в работе Мэллоуса и Слоэна [895]. Катаяма [747] доказал вариант теоремы Мак-Вильямс, который применим к наборам из г кодовых слов (что обобщает выражения (5.50) и (5.51), соответствующие случаю г=2), и применил эту теорему к коду Хэмминга и дуальному к нему коду.
§ 5.7. Хорошее изложение ’ ортогональных многочленов см. в книгах Сеге [1297] и Эрдели и др. [410, гл. 10].
1 лава 6
Коды, схемы и совершенные коды
6.1. ВВЕДЕНИЕ
В этой главе мы продолжим изучение теоретико-множественных свойств кодов, начатое в гл. 5.
В § 6.2 мы определим четыре фундаментальных параметра d, d', s, s', связанных с любым линейным или нелинейным кодом <ё>.
Параметр d представляет собой минимальное расстояние между словами Ч?, a s — число различных ненулевых значений расстояния между его кодовыми словами. Параметры d' и s', когда код Ч? — линейный, являются аналогичными величинами для дуального кода <ё>л-. Для нелинейного кода число d', по-прежнему называемое дуальным расстоянием, было определено в §' 5.5, а параметр s' обозначает число индексов i=#0 таких, что В'г#=0, где, как обычно,* В'; — преобразование Мак-Вильямс спектра расстояний кода Ч?. Параметр s' называется внешним расстоянием кода, так как любой вектор из Fn находится на расстоянии, не большем чем s', по крайней мере от Одного кодового слова из <ё>. (Теорема 21 из § 6.6. Однако число s' не обязательно является наименьшим числом с этим свойством, см. упражнение (11).)
Имеется довольно много интересных кодов, для которых либо s'^d. В таком случае минимальное расстояние кода Ч? (или дуальное расстояние) заведомо не меньше, чем число неизвестных в спектре расстояний, и уравнения Мак-Вильямс могут быть разрешены. Отсюда следует, что такие коды удовлетворяют следующим трем замечательным свойствам, которые мы установим в § 6.3, 6.4, 6.7:
(а) . Число кодовых слов, находящихся на расстоянии i от кодового слова v, не зависит от выбора v. Образно говоря, совокупность кодовых слов выглядит одинаково с точки зрения любого кодового слова (теорема и следствие 5 из § 6.3.) Такой код называется инвариантным относительно расстояния. Если код содержит нулевое кодовое слово, то спектры весов и расстояний совпадают. (Конечно, для линейных кодов свойство (а) выпол-. няется всегда.)
(Ь) . Если 0, ть ..., ts обозначают значения весов, встречающихся в коде, то число кодовых слов веса т< является явно выписываемой функцией от п, М и чисел т, (теоремы 2 и 4 из § 6.3 и теорема 7 из § 6.4).
(с) . Кодовые слова любого веса образуют f-схему, где t не меньше, чем d'—s или d—s'. (В действительности мы докажем более сильный результат, чем этот, — см. теорему 9 из § 6.4, следствие 14 из § 6.5 и теорему 24 из § 6.7.)
В § 6.5 мы покажем, что.если кодовые слова любого веса в линейном двоичном коде ‘g’ образуют /-схемы, то этому же свойству удовлетворяют кодовые слова любого веса в дуальном коде (теорема 13).
В § 6.6 изучается весовой спектр кода, являющегося сдвигом некоторого линейного или 'нелинейного кода.
В § 6.8 приводятся два результата, относящихся к совершенным кодам: доказывается, что код совершенен, если и только если s'—e (теорема 27), и выписывается необходимое условие совершенности кода, принадлежащее Ллойду (теорема 28).
Все перечисленные до сих пор результаты относились к двоичным кодам. Только в § 6.9 мы обсудим, как эти результаты могут быть обобщены для случая произвольного поля GF(q). Мы рассмотрим только построение /-схем из линейных кодов над GF(q) (теорема 29). В двоичном случае из теоремы 29 получается, по-видимому, более сильный результат, чем из следствия 14 (см. следствие 31).
Наконец, в § 6.10 будет доказана теорема Титвайнена—Ван Линта1 (теорема 33) о том, что единственными нетривиальными совершенными кодами над любым полем являются известные коды Хэмминга и Голея.
6.2. ЧЕТЫРЕ ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРА КОДА
Пусть ‘g’— двоичный (и, М, Д)-код, не обязательно линейный, содержащий нулевой вектор 0. Предположим, что {В<} является спектром расстояний кода ‘g’, т. е. равно числу упорядоченных пар кодовых слов, находящихся между собой на расстоянии i, деленному на М. Поэтому Во=1 (см. § 2.1).
Пусть 0, Ть Т2, ts обозначают те индексы I, для которых Bi=#0 и
0<Т1< ... <Ts^n.
Тогда d=T] представляет собой минимальное расстояние кода ‘g’, a s — число различных (ненулевых) значений расстояния между словами этого кода.
Пусть {5'i}—преобразование Мак-Вильямс спектра {В,}> °и-ределяемое условием (см. § 5.5)
!+ 2 BXiyXi =М-<Гп^В’^\+у)п-1(\-у)1 (6.1)
1=1 2=0
или, что эквивалентно, уравнениями (5.35) или (5.36). Предположим, что 0, ai, ..., oS' обозначают те индексы i, для которых B't=£O и
0<(Т1< ... <Os'-^n.
1 Теорема 33 была доказана одновременно Титвайненом [1322] и Зиновьевым и Леонтьевым [1472]. (Прим, ред.)
Назовем число s' внешним расстоянием кода 43, а число d'= = Oi— дуальным расстоянием. В теореме 8 гл. 5 мы убедились, что d' является наибольшим числом таким, что каждое (d'—1)-подмножество координат кода 4? содержит все возможные (d'—1)-векторы одинаковое число раз.
Обозначим через {Л,} весовой спектр кода <ё’, где Л, —число кодовых слов веса i, а через {А'г} — преобразование Мак-Вильямс спектра {А,}.
Лемма 1. Число ненулевых Аг не превосходит s, а число ненулевых А'г не превосходит s' и
Аг = 0 для 0<i<d;
А\ = 0 для
Доказательство. Утверждения относительно Аг следуют из определений параметров d и s. Утверждения относительно А'г следуют из теоремы 7 гл. 5. •
Предположим теперь, что' мы изменили начало отсчета, т. е. заменили код 47 на код 47* = 47+v, где v — кодовое слово. Новый код 47* по-прежнему является (п, М, d)-кодом со спектром расстояний {Bj} и,* возможно, с другим весовым спектром, скажем, {Л*{}. Однако лемма 1 остается справедливой и для {Л*,}.
Замечание. Если 47— линейный код, то Аг = Вг — весовой спектр кода 47, а А'г — весовой спектр дуального кода 4?у, ad' — минимальное расстояние кода 47-1-.
В этой главе прежде всего мы изучим интересные свойства кодов, для которых либо s^d', либо s'^d. Приведем несколько примеров таких кодов.
(Е.1). Код [п, п—1, 2], состоящий из всех слов четного веса, дуальным которому является [п, 1, д]-код с повторением. Здесь d = 2; s = n/2; d' = iv, s'=l.
(E.2). Симплексный [n=2m—1, tn, 2,п-1]-код дуален [2m—1, 2m—1—m, 3]-коду Хэмминга. Здесь d=2m~l; s=l; d' = 3; s'=n—4.
Упражнения. (1). Рассмотреть более общий случай — (п, п+1, («+1)/2)-код Адамара из § 2.3 (где n=3(mod4)) и показать, что d= (п+1) /2; s=l; dz = 3; s'=n—4.
(Е.З). Код Рида—Маллера первого порядка [n=2m, т+ 1, 2m l] (см. § 1.9), дуальным которому является расширенный [2’п, 2т—1—т, 4]-код Хэмминга. Здесь d=2m-1; s = 2; d'=+, s'— = n/2—2.
(2). Показать, что код Адамара 4?п имеет эти же параметры.
(Е.4). Для расширенного самодуального [24, 12, 8]-кода Голея (§ 2.6) имеем d = d'=8; s = .$' = 4.
(Е.5). Для (16, 256, 6)-кода Нордстрома—Робинсона (§ 2.8) имеем d=d'=6; s = s'=4 (см. конец § 5.5).
Другие примеры (включающие некоторые квадратично-вычет-ные коды, коды Рида—Маллера, Кердока и Препарата) можно будет найти в дальнейших главах.
(3). Показать, что у кода '{00000, 00011, 00101, 11011} для всех i выполняется равенство Ai=Bi, однако этот код неинвариантен относительно расстояния.
6.3. ЯВНАЯ ФОРМУЛА ДЛЯ СПЕКТРА ВЕСОВ И РАССТОЯНИИ
Теорема 2. Если sigjd', то явная формула для спектра расстояний {Вг}, выраженная через п, М и т<, имеет следующий вид:
1 Сг <s,
где N=2nfM. (Условимся, что произведение пустого множества сомножителей равно 1.)
Доказательство. Как и в § 5.2, продифференцируем / раз выражение (6.1), разделим результат на /! и положим у=\. Это дает s уравнений:
Для того чтобы их решить, положим/ Вх. —а%1 +Ьтг, где
Матрица коэффициентов (6.3) одна и та же и равна:
при неизвестных для обеих систем
1 1 • • • 1
/ Д, \ \ I \
_\S—1/ \S-1/ \S—l'_
Матрица, обратная Т, получается следующим образом. Пусть
4.«=П-^г-
1 . t /=1
Разложим ft.(x) по биномиальным коэффициентам, а именно:
где
= 1) • • (%—j+l)/j!
Ясно, что 2^Cfe) = ^(Tfc)==6zfe’ /=0 4 1 '
И поэтому Т-1 = [/г3].
Умножим теперь матрицу Т-1 на векторы-столбцы, стоящие в правой части каждой из систем уравнений (6.3). В результате получим, что
Так как
то
Теорема 3. Если s^d', то Ai = Bi для всех i.
Доказательство. Так как условие Лг-=#0 влечет Bi=j4=0, то единственными возможными ненулевыми числами Аг являются До> Лт , /4Ts. Из леммы 1 следует, что Л'!-=0 для l^i^d'—1.
Поэтому числа Ат. удовлетворяют системе уравнений (6.2), и к ним применимо доказательство теоремы 2. •
Упражнение. (4). Получить, используя теорему 2, спектр расстояний в коде Нордстрома — Робинсона Л9^, если известно, что расстояния в этом коде принимают значения 0, 6, 8, 10, 16, а d'=6.
Теорема 4. Предположим, что s'^d. Тогда А'г — В'г для всех i и
Доказательство повторяет' доказательства теорем 2 и 3. •
Следствие 5. Если s'^Jd, то Ai=Bi для всех I.
Доказательство. Спектры {Л,} и представляют собой преобразования Мак-Вильямс {/I'i} и {В'$.
Теорема 6. Если s=Cd' или s'^d, то код инвариантен относительно расстояния.
Доказательство. Теорема 3 и следствие 5 верны для сдвига ^+v кода где v—-любое кодовое слово. •
Замечание. Хотя условие s^d' или s'^Zd достаточно для выполнения условия Лг = Вг, оно не является необходимым, как показывает пример кода, изображенного на рис. 5.1 или в упражнении (3) этой главы.
6.4. ПОСТРОЕНИЕ СХЕМ ИЗ КОДОВ ПРИ s<d'
В этом разделе мы покажем, что если s<^d', то кодовые слова каждого веса образуют £-схему (см. определение в § 2.5). Вначале мы перепишем в несколько ином виде формулу для A
Из теоремы 3 следует, что если s^Zd', то Ап=Вп—0 или 1. Предположим теперь, что Ап известно (обычно это так), так что неизвестными являются коэффициенты ATi, ..., , где
— ( s , если А„ = 0;
8=1 п
| s—1, если Ап= 1.
Теорема 7. Если s^Zd', то для имеет место фор-
мула
Доказательство. Проводится аналогично доказательству теоремы 2, за исключением того, что уравнение (6.2) имеет теперь следующий вид: .
£(Г)Мт'-г^'4")С)- <6-5) •
Если Ап = 1, то Ts+i-i = n—т;. Поэтому первый и третий члены в выражении (6.4) могут быть объединены в один
f — 1 + 1)S ^Ап Г1 Г} .
I, п— T; J ’ Tj — Ti
Пусть 5(х)=П(т;—х). Тогда (6.4)-можно переписать такг /=1
s __
\ П (r,-r,)_ W-I + j
,=1 г \ n — Tt /
л6*
Кодовые слова веса т; образуют £-схему. Пусть и — фиксированный вектор пространства Fn веса t, где 0</<сГ. Для Xi~^t обозначим через Лт. (и) число слов веса тг- в коде •g’, которые покрывают вектор и.
Теорема 8. Числа (и) удовлетворяют следующим d'—t уравнениям:
(6.7)
1 Доказательство. Пользуясь теоремой 8 гл. 5, подсчитаем двумя способами число векторов веса t+j, которые покрывают вектор и и в свою очередь покрываются некоторым словом кода <ё>. . 1 •
Так как вектор 1 = (1, 1) покрывает все векторы, то выра-
жение (6.7) можно представить в виде
Если мы можем выбрать t так, что d'—t=s, то мы будем Иметь s линейно независимых уравнений относительно s неизвестных Хт, (и). Тогда числа ЪТ( не зависят от выбора вектора и. Поэтому все кодовые слова любого веса п образуют £-схему, где t=d'—s. Параметры т» этой схемы вычисляются следующим образом.
Уравнения (6.8) имеют такой же вид, что и уравнения (6.5), и поэтому их решение таково:
п—t
\eXr.t V (п~* )gx._t (r)-Ang (n—t),
5 • /V \ Г / i i
r=0
где
s
gXi-t w=ri(TJ—t—
Ясно, что g^-t (*—й, следовательно,
1 п / * ’ t \
(т‘> \=7Г X (" _,) Л.м - ЛЛ, <">
или
s
\. I I тг) =
/=1
/¥=г
AnS (п) n—ti
r=t
S(r)
Ъ — г
(6.9)
Таким образом, мы доказали следующую теорему.
Теорема 9. Если s<2d', то кодовые слова веса т, в коде ¥> при условии, что xd^d'—s, образуют ((сГ—s) — (п, Z.T.))-схему, причем параметр Z-г. задается равенством (6.9).
Примеры (продолжение). (Е.1). В предположении, что п— четное, код, состоящий из всех слов длины п четного веса, содержит вектор из всех единиц, так что s = s—1=/г/2—1. По теореме кодовые слова любого веса 2г^п/2 + 1 образуют (n/2+l)-схему. Но, так как рассматриваемый код содержит все векторы веса 2г, то в действительности эта схема является 2г-схемой. Таким образом, доказанная теорема не всегда дает наилучший возможный результат.
(Е.2). По теореме 9 кодовые слова веса (/г+1)/2 в коде Адамара J^n+i образуют 2-схему (что согласуется и с упражнением (11) гл. 2 и с примером (i) в конце § 5.5).
(Е.З). Подобным образом мы получаем 3-схемы из слов кода Рида—Маллрра первого порядка (и кода Адамара ’ё’п)-
Если же в качестве исходного кода взять расширенный код Хэмминга, то штрихи меняются местами, и мы получаем, что d'—s = 2m~I—(п/2—3) =3. Поэтому слова фиксированного веса расширенного кода Хэмминга образуют 3-схему, что согласуется с теоремой 15 из гл. 2.
(Е.4). Аналогично слова фиксированного веса расширенного кода Голея образуют 5-схему (см. следствия 23, 25 и теорему 26 гл. 2).
(Е.5). Аналогично слова кода Нордстрома—Робинсона дают 3- (16, 6, 4), 3- (16, 8, 3) и 3- (16, 10, 24)-схемы.
Упражнение. (5). Проверить (Е.5).
Тождества, которым удовлетворяют веса. Так как кодовые слова веса тг образуют (tf—s) -схему, то они, конечно, образуют p-схему для любого p<d'—s. Предположим, что это (р—(п, тг, ^ъ)))-схема.
Из выражения (6.9) для р= 1 получаем, что
S
ь( ч п (Tj-Tj = AnS{n±-+4 /=1 П — Xi N
Н*
S/n—1\ S(r) \r— 1/ т, — г
Так как тЛ тг = nX f Ti) и А^ задаются равенством (6.6), то имеет место следующее тождество, которому удовлетворяют значения весов в коде;
—£(0) + Д/ ( —1)г -s ----nS (п)- )4-
\ п — тг- п — тг /
+ Г)5(г) = 0.
К тому же если Ап = 1, то
S(n) = (-l)sn (n_T.) = e_-i)s S(0). (6.10)
4=1
Рассмотрим теперь два случая. Если Дп = 0, то выражение (6.10) принимает вид п
5(°) = 7гУ (6Л1)
N U\rJ
г=0
Аналогично если Ап=1, то (6.10) принимает вид п
эд (1+(-in1=4 У. И эд <6-12)
N U \r J
г=о
Упражнение. (6). Вывести формулу (6.12) непосредственно ' из выражений для Ат., задаваемых теоремой 2 и соотношением (6.6). Показать, что равенство (6.12) тривиально для нечетных s.
В общем случае, так как кодовые слова образуют p-схему для Й^р^бГ—s, мы имеем, что
(n-p + l)Ap)= (tt-p+l)^- (6.13)
Используя выражения для aJ и , из (6.9) получаем: < п
AnS(n) = 4 V (K-p+4s(r). (6.14)
N \ г ~ р + 1/
г=р—1
Таким образом, мы доказали следующую теорему.
Теорема 10. Предположим, что Тогда значения весов. кодовых слов удовлетворяют следующим условиям (здесь . . S \
s (%).== Г1 (т>— :
/=1 '
(i). Если Ап=0, то
s®4so:..°=y s r=0 • r=p—1
для 2^p^d'—s.
(ii). Если An=l, то S(0)(l + ( — l)s ) = J-VVnW);
N LU \r )
r=0
n
(_ipS(o)=s(n)=A. y; ^-p+Jjscr)
Л LU \r — p + 1/
r=p—1
для 2^'p^tK—s.
Упражнения. (7). Показать, что, если Ап = 0 и s = s=l (все ненулевые кодовые слова имеют один и тот же вес т), то кодовые слова могут образовывать самое большее 2-схему; при условии, что они образуют такую схему, показать, что т=(/г+1)/2; Л4=п+1 и AI делится на 4.
(8) . Показать, что если Ап=1 и s=l (т. е. т=п/2), то Л4=2н и кодовые слова образуют 3-схему.
6.5. ДУАЛЬНЫЙ КОД ТАКЖЕ ПОРОЖДАЕТ СХЕМЫ
В этом разделе будем считать, что является любым [п, k, d} двоичным линейным кодом, удовлетворяющим следующему свойству: для некоторого t<d все кодовые слова любого фиксированного веса w>0 образуют /-схему.
Обозначим через Т множество из t координатных позиций. Обозначим через ®7(т) код, полученный удалением этих t позиций из кода Таким образом, представляет ’ собой [п—t, k, d—/]-код. Пусть {А/т)} —весовой спектр кода
Лемма 11. Число не зависит от выбора множества Т.
Доказательство. Пусть V обозначает число слов кода ’g’ веса v, которые содержат точно i единиц на позициях из множества Т. Из § 2.5 следует, что Ki0 не зависит от выбора Т.
Тогда то же самое справедливо и для
Пусть ’ё’0 “т обозначает укороченный код, полученный удалением t позиций множества Т из слов кода имеющих нули во всех этих позициях. Таким образом, <g70oT представляет собой [п—t, k—t, d\-код. Кроме того, код (<g’-L)°“T дуален коду <g7(T) (см. рис. 1.11 и 1.13).
Следствие 12. Весовой спектр кода (<g’-L)OaT не зависит от выбора множества Т.
Доказательство Достаточно воспользоваться теоремой 1 гл. 5.
•
Теорема 13. Пусть ’g’—[n, k, d] двоичный линейный код с &>1 такой, что для каждого и?>0 кодовые слова веса w образуют • /-схему, где t<d. Тогда слова любого фиксированного веса кода 'g’J- также образуют /-схему.
Замечание. Если k=l, то, для того чтобы код •g’ порождал /-схемы, он должен быть кодом с повторением. Тогда код ‘ё’1-
состоит из всех векторов четного веса и образует тривиальные схемы (см. предыдущий пример (Е.1)).
Доказательство. Так как Д>1, то код ‘g’ содержит кодовые слова некоторого веса v, где 0<;о<;/г, и по условию теоремы эти кодовые слова образуют /-схему.
Выберем w так, что код <g’-L содержит кодовое слово, скажем, b веса w. Если w=n, то ничего не надо доказывать, поэтому мы можем предположить, что w<n.
Наша первая цель — показать, что w<n—t.
(а) . Предположим, что w = n—t. Если v—t нечетно, выберем в коде слово а веса о, которое имеет единицы на всех позициях, где вектор b имеет нули,
w ->
Ь=111 111
t 000000
а = 000 111 111111
V—t
Тогда а-Ь^г—/= 1 (mod 2), что противоречит ортогональности векторов а и b. С другой стороны, если v—t четно, то слово а выберем так, чтобы оно имело единицы на всех, кроме одной, позициях, где b имей? нули,
ч--w--> ч--t-->
b = 1 1 1 111 000000
а=000 111 111110
v—1+ 1
Это можно сделать, так как (см. § 2.5). Итак, а-Ь=
='V-—/+1 = 1 (mod 2), что снова приводит к противоречию. Поэтому w^=n—t.
(b) . Предположим теперь, что w = n—t+i—n—(t—Г), где i>0. Но это невозможно в силу (а), так как /-схема автоматически является (/—/)-схемой. Тем самым мы доказали, что w<n—/.
Покажем теперь, что если w<n—/, то множество кодовых слов веса w в ’g’1 образует /-схему. Пусть сь ..., cs — векторы, являющиеся дополнениями этих кодовых слов, где х=Д,го. Пусть Т обозначает любое множество из / позиций.
Число векторов с<, которые содержат единицы на позициях из Т, равно в точности числу слов веса w в коде (<ё’л-)ОаТ. Но по следствию 12 это число не зависит от выбора множества Т, и поэтому векторы Ci образуют /-схему. Следовательно, кодовые слова веса w образуют дополнительную к ней схему (§ 2.5). •
Пр и м е р. (Е.2) (продолжение). По теореме 9 кодовые слова симплексного кода образуют 2-схему. По теореме 13 кодовые слова каждого веса в коде Хэмминга также образуют 2-схему1.
1 Напомним, что код Хэмминга ортогонален (линейному) симплексному коду, или коду Адамара (Прим, перев.)
Объединяя теоремы и 13, мы получаем следующий резуль-тат.
Следствие 14. Пусть <8 — линейный код с параметрами d, s, d', s'. Параметр s определен выше (см. § 6.4), и пусть
s', если А' = 0; ’ п
s'— 1, если Л'п= 1.
Если s<2d' или s'<Zd, то кодовые слова веса w кода образуют /-схему, где / = max {d'— s, d— s'}, при условии, что t<zd.
Задача (нерешенная). (6.1)1. Во всех известных нам нетривиальных примерах число d'—s меньше, чем d, и в них последнее условие теоремы не является необходимым. Так ли это всегда?
6.6. ВЕСОВОЙ спектр КОДА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ СДВИГА
В этом разделе мы изучим весовой спектр кода, полученного в результате сдвига из любого (п, М, б/)-кода ¥>. Пусть f — произвольный вектор из Fn, a Ai(f)—число векторов веса i в коде ^+f. Конечно, если —-линейный код, то ’g’ + f представляет со-
бой смежный класс кода ’g’, содержащий f. Преобразование МакВильямс спектра {Ai(f)} согласно (5.31) имеет следующий вид: л;(')=д S *.<<}(-о-* •
wt (u)=i
где С = у zv представляет собой код, записанный как элемент ve<g
групповой алгебры (см. гл. 5).
Когда f=0, Ai(0)=A{ — весовой спектр кода и А'{(0) =А'{.
Заметим, что (см. упражнения (18) и (19) гл. 5)
1;
1=0
что равно нулю, когда f^’g’.
Теорема 15. Преобразования спектров A'i(t) ортогональны: (0 , если i#=j;
2nB'i, если i = j. !&•
1 Эта задача недавно решена в [392а*]. В ней доказано, что в линейном Ч-ичном коде max (4'—s, d—s') <min (d, d'), а в двоичном линейном коде max (Д'—s, d—s')<min(d, d'). Таким образом, последнее условие следствия 14 действительно излишне. (Прим, перев.)
Доказательство.
лр£л;(1)л;(П= S Мс) £ МО I (-i), ("+v|-fefn Wt (U)=i Wt (V)=/ f&Jl
Далее,
(— i)1'(u+v) = ( 0, если u + v =й 0;
JeFn ( 2", если u + v = 0.
Если i^=j, to u+v=/=0, что доказывает первую часть теоремы. Если i=J, то в силу соотношения (5.36)
7Иа £ Д: (f)2 = 2» ( £ х„ (С))2 = 2” M*Bi- (6-15) ieFn wt (u)=i
•
Следствие 16. Равенство В'г=0 выполняется тогда и только тогда, когда условие A'i=0 влечет условие A'i(f) = 0 для всех fsF”.
Доказательство. Утверждение вытекает из теоремы 7 гл. 5 и
уравнения (6.15)., •
Как и в § 5.3, пусть Уг — £ z. wt (v)=i
Лемма 17. Если вектор и из Fn имеет вес s, то
x.O=ij(-ir(““*)(’)-f<W. г=0 ' ' ' /
где Pi(x) — многочлен Кравчука.
Доказательство. По определению
7-„(П)= j (-о”, wt (v)=i
Имеется всего |п ® ) Is ) векторов v веса i, содержащих i—г \1 — Г J \ г j
единиц на п—s позициях, где вектор и имеет нули, и г единиц на s позициях, где и имеет единицы. Легко видеть, что вклад каждого из таких векторов v в рассматриваемую сумму равен (-!)’’• •
Введем аннулирующий многочлен кода (ё>
<6-16>
/=1
где 0, ел, О2> —, oS’ представляют собой те индексы i, для которых В'^О. Заметим, что для значений 0<1=Сп либо a(i)=0, либо B'i = 0. Поэтому по следствию 16 условие А'г (f) =/= 0 для не-, которого вектора f влечет a (i) =0.
Представление а(х) в виде > линейной комбинации многочленов Кравчука
= ^агр1(х) i=0
называется разложением а(х) по Кравчуку, а числа сц называются коэффициентами Кравчука. Последним членом этого разложения является Ps'(x), так как многочлен а(х) имеет степень s', и поэтому as-=#0. Кроме того (по теореме 20 гл. 5), имеем, что
аг = Ц-У a(^)Pfe(i).
2 h=0
Лемма 18.
s' c%a‘Y‘~ г=0 _П
UQF
Доказательство. Для того чтобы доказать равенство этих двух элементов групповой алгебры, достаточно (согласно упражнению (16) гл. 5) показать, что значения характеров yv на Этих Двух элементах совпадают для всех veFn. Согласно упражнению (12) гл. 5
х,( S /") = £(-l)"v=2"6,.„: uQFn UQFn
/ s' \ /s' \
Xv C£aiKf =XV(C)XV .
\ i=0 J \i=0 /
Если вектор v имеет вес ®>0, то по лемме 17
Xv (У ai= J at pt и = a И-\i=0 J i=0
Если w равно одному из о,, то по определению а(и?)=0, в .противном случае Xv(Q=0 п0 теореме 7 гл. 5. Таким образом, в любом случае, если v#=0, то
xv(c£aiy/j = O, V^O. (6.17)
\ i=0 /
Если теперь v=0, то
(S' \
С af Kf I — Хо (С) a (0) = М • 2П/М = 2". •
i=0 J
Свойство (6.17) послужило основанием для того, чтобы назвать а(х) аннулирующим многочленом кода <ё>.
Лемма 1 . Если сумма
±₽.^.
1=0
такова, что (t \
С^ргУг) = 0 для всех uG^Fn, u^O, 1=0 J
то аннулирующий многочлен а(х) кода 'ё’ делит многочлен
₽(*) = £ (W4
1=0
Упражнение. (9). Доказать лемму 19.
Теорема 20. Для каждого f^Fn числа АД!) однозначно определяются числами .......XS'_i(f).
Доказательство, (i). Вначале покажем, что следующим образом может быть выражено через /loft), ..., Aar-iff):
* as, Д., (f) = 1 — (6-18)
i=0
(Напомним, что aS'#=0.) Для доказательства этого вычислим
СГН5УО I г'-=1У-’'=Ултг‘
V6<g wt (w)=f ve<g Wt (w)=i vecg ieJ?n f eFn wt (f-J-v)=i
где f = v-f-w,
так как АД!) равно числу кодовых слов v, находящихся на расстоянии i от f. Тогда s' s'
^atAt (f)z = Cat Yt = zf (по лемме 18),
J€f" !‘=o i=0 teFn
и поэтому
2aMt(f)=l= (6-19)
i=0
что и доказывает требуемое равенство (6.18).
(ii). Если мы выпишем разложение s'+l
i=0
то из доказательства леммы 18 следует, что s'+l
С t=o
и, следовательно,
s'+l
£МЛП = о, 1=0
что дает выражение для AS'+i (f). Чтобы получить выражение для As'+2(V’ надо разложить по многочленам Кравчука функцию х2а(х) п т. д. •
Замечание. Чтобы получить разложение ха(х) из разложения а(х), оказывается полезной рекуррентная формула для многочленов Кравчука (теорема 19 гл. 5).
Пример. (1). Так как код Хэмминга Ж длины п с расстоянием d=3 является совершенным, то для такого кода имеется только два типа смежных классов, а именно: сам код и п смежных классов, лидеры которых имеют вес, равный 1. Если 1^Ж то At(t)=Ai. Если же f еДЖ то Ai+nAi(f) = ^n j , так что = = (1/п)((" )—Ai). Для п=1 см. рис. 6.1.
Число [смежных .классов Весовой спектр
Вес i 0 1 2 3 4 5 6 7
1 Ai 1 7 7 1
7 At(f) 1 3 4 4 3 1
Рис. 6.1. Весовые спектры смежных классов кода Хэмминга длины 7
Проиллюстрируем теперь теорему 20, проверив вторую строку этой таблицы.
Для рассматриваемого кода s'^=l и 01 = 4, поэтому а(х) = = 8(1—х/4)=8—2x=Pi (х) +Р0(х). Следовательно, a0=ai = l и A1(f) = l-A0(f).
Так как f & Ж, то До(f) =0 и ДДТ) = 1-
Рекуррентная формула из теоремы 19 гл. 5 дает:
xPh (X) = —^+ D^+1 W+т W-(4- v W’
т. е.
1 7
хР0(х) =—4 Л (*) + vPoW; Z Д
7 7
хР, (X) = -Р2 (X)+4- рх (X)—- Ро (X);
хр2 (х)=-4 р3 w+4 р2 ю-
Z
Далее ха(х)=хР1(х)+хР0(х)=—Р2(х)+ЗР1(х). Следовательно, —Л2(Г) = О, откуда A2(t)~3. Затем '
х2 а (х) = — хР2 (х) + ЗхРг (х) = — Р3 (х)—Р2 (х) + 2 А
откуда
Л3 (f) - -у 4 (f) + A, (f) - Ао (f) = О,
что дает 713(f)=4; тем самым проверка второй строки рис. 6.1 окончена.
Пример. (2). Код Нордстрома—Робинсона Л^е (см. § 2.8) имеет следующий спектр расстояний: So = Si6 = l; Дб = Дю = П2; Д8=30, причем преобразование Мак-Вильямс этого спектра совпадает с ним самим, т. е. B'i = Bi. Поэтому аннулирующий многочлен равен:
а(х) = 28/1— -^У1— —V1— — W1— —}=—Р4(х) +
v \ 6 J\ 8 Д 10)\ 16/ 20 '
+ 4 Д W + Р2 (х) + Д (х) 4- Ро (х)
и далее
ха(х) = -Ъ6 (х) + |Р3 (х) +4 Pi (Д
Продолжая таким образом, мы найдем весовые спектры всех кодов, полученных в результате сдвига кода Л3^, которые приведены на рис. 6.2.
Пример. (3). (Смежные классы кодов БЧХ, исправляющих две ошибки.) Пусть %?— код БЧХ, исправляющий две ошибки с параметрами [2т—1, 2™—1—2m, 5], где т — нечетное, т^З. В § 15.4 будет показано, что дуальный код <₽’± имеет только 3 ненулевых веса, а именно 2m-1 ± 2(т-1)/2 и 2т~х. Следовательно, аннулирующий многочлен (6.16) кода %? равен:
а ( V) ( 1_________X_______) ( I_____*______ \ у
(Д 2m-l _ 2(т-1)/2 I ( 1 2т—1 + г**"*»/2 )
3
X р-Ё’Е-чЗД ' 1 г=0
Для наших целей нам необходимо найти лишь величину а3.
22т
Коэффициент при х3 в а(х) равен---------------- ,
/ —2 —1 } 2т—1
Ч^сло смежных классов Весовой спектр
Вес 1 0 2 4 6 8 10
At 1 112 30 112 . ..
120 AM 1 14 63 100 63 . . .
7 20 48 120 48 . . .
Число смежных классов Весовой спектр
Вес i 1 3 5 7 9 . . .
16 AM 1 42 85 85 • . .
112 5 33 90 90
Рис. 6.2. Весовые спектры кодов, полученных сдвигами кода ^16
а коэффициент при № в многочлене Кравчука
Г> / \ — М /л — х\ , , \/х\ / х\
,w=( з )-( 2 )’+,"_4Нз)
4 г равен---— . Следовательно,
3 22т 3 4
а =---------------------=---------- .
4 ( <^т~2 2т—* ) 2т~1 2т~1 1
Таким образом, из соотношения (6.18) следует, что в смежном классе кода %? с минимальным весом 3 имеет место равенство
Л3(Г) = (2т-‘ —1)/3-
Поэтому все смежные классы с минимальным весом 3 имеют одинаковые весовые спектры. Уравнение (6.18) показывает также, что все смежные классы должны иметь минимальный вес О, 1, 2 или 3. Так как этот код исправляет две ошибки, то имеется один смежный класс, с весом 0, п классов с .весом 1 и ( 2 ) классов с весом 2. Минимальный вес в остальных смежных классах равен 3. Таким образом, код является квазисовершенным кодом (см. § 1.5).
Для четных значений т код БЧХ длины 2т—1, исправляющий Две ошибки, по-прежнему является квазисовершенным, как, мы
увидим в § 9.8, хотя дуальный код содержит в этом случае боль-ше чем 3 ненулевых веса. Следующая теорема объясняет, поче'му параметр s' называется внешним расстоянием кода. (
Теорема 21. Для любого вектора найдется кодовое слово, находящееся на расстоянии не более чем s' от f.
Доказательство. Из уравнения (6.18) следует, что не могут равняться нулю все числа Ai(f) при isgs'. •
Пример. Для кода Хэмминга s'= 1, и, в самом деле, так как код совершенный, то любой вектор из Fn находится на расстоянии не более чем 1 от некоторого кодового слова.
Замечание. Можно определить радиус покрытия для кода <ё’ как число
/ = шах min dist (u, f). fer" ие^
Таким образом, t представляет собой истинное внешнее расстояние кода, т. е. параметр t равен наибольшему из минимальных весов всех кодов, полученных в результате сдвига кода <ё. Теорема 21 говорит о том, что Как мы увидим в упражнении (11), параметр t может быть и меньше чем s'.
Определим дй'а других метрических параметра кода <ё!: диаметр
6 = шах dist (u, v) и. ve<g и радиус
p = min max dist (и, v). иегп
Параметр р может быть получен, если известны весовые спектры сдвигов кода так как р равно минимальному из наибольших весов всех сдвигов кода cff.
Упражнения. (10). Показать, что
6/2 <р <6. (6.20)
(11) . (i). Показать, что для симплексного [п=2т—1, k=m, г?=2т-1]-кода параметр /=2т-1—1. [Указание. Воспользоваться границей Плоткина.]
(ii). Показать, что для этого кода s,=n—4 и, таким образом, t<s'.
(iii ). Показать также, что р=6=2™-1.
(iV ). Вывести отсюда, что имеется бесконечно много кодов, для которых в правой части (6.20) выполняется равенство; показать то же самое для левой части (6.20).
Задача (нерешенная). (6.2). Для произвольного кода найти оценки его радиуса покрытия t и хороший метод его вычисления.
Теорема 22. Пусть 'ff — двоичный линейный [п, k, dj-код и пусть C=Sve<g zv. Для значений —1)/2] обозначим через Dt=CYt элемент групповой алгебры, представляющий все
векторы из Fn, находящиеся на расстоянии t от некоторого кодового слова из $?, т. е. объединение в’сех смежных классов кода
\ лидерами веса t. Пусть fs,t обозначает число векторов веса s в множестве Dt- Тогда
\ >4 t^n~sys+ (6.21)
\ Z-U oft—FL I
' s=0 Z /=0
Доказательство. Представим Dt в виде
\ Dj=:SvgFn dvzv.
Согласно упражнениям (16) и (14) гл. 5 получаем, что
С = S (-I>“V Х" {QP‘ S (-l)”VP,(Wt(u))
иеРП „ ue<?J'
(последнее равенство имеет место согласно упражнению (13) гл. 5). Следовательно, левая часть выражения (6.21) равна:
£ £ ^(-irp,(wt(u))x
veFn uerdJ' veFn
X xn~wt (v) ywt (v). (6.22)
С другой стороны, правая часть этого выражения равна:
„Ь £ Р,М(и»(х+г,)"-’,«(х-Й”,и’.
ие®-1-
что равно (6.22) в соответствии с равенствами (5.9) и (5.11). •
Упражнение. (12). Предположим, что код имеет минимальное расстояние d=2e + l, и рассмотрим для этого кода неполный алгоритм декодирования (§ 1.5), исправляющий любые t ошибок (но не более) для некоторого фиксированного Показать, что вероятность правильного декодирования равна1
£Л)р;(1-р)п-г,
г—0 ' а вероятность того, что декодер примет неправильное решение., равна
2 2 /...р’н-рГ’-
i~0 S=i-H
6.7. ПОСТРОЕНИЕ СХЕМ ИЗ НЕЛИНЕЙНЫХ КОДОВ ПРИ s'<d
Для нелинейного кода в случае s'<d мы не можем утверждать справедливость следствия 14. В этом случае мы можем доказать лишь более слабый результат.
’Здесь р— вероятность ошибки в канале [см. § 1. 1]. (Прим, перев.)
Теорема 23. Пусть задан (п, М, г/)-код <ё>. Если d—s'-^'< <d, то кодовые слова веса d в коде <ё> образуют схему
(d—s')~(n, d, (1— ad_s,)/as,). (6.23)
Доказательство. Пусть f — вектор веса d—s'. Если d—d'<s', то для кода 'tF’-l-f, полученного сдвигом, мы 'имеем:
ло(О= - - •=4_!,_1(1)=л^,+1(п= • • -=A'-iW=o.
4_S'(n = i.
и представляет собой число кодовых слов веса d, кото-
рые покрывают f. В силу (6.18)
A,(f)=(l-ad_s,)/as„
и это число не зависит от выбора f. Если s'=d—s' (т. е. s'=d/2), то
А(П = • - - = А'-1(П as,A'(f)=l-
В этом случае Л8/(1)—1 равно числу кодовых слов веса d, которые покрывают f, и поэтому
A.(f)-l=(l-as,)/as„
что также не зависит от выбора f. Итак, в любом случае число кодовых слов веса d, которые покрывают f, одно и то же для всех векторов f веса d—s' и поэтому все кодовые слова веса d образуют схему
(d—s')—(n, d, (1— Oj_s,)/as,). •
Теорема 24. Если s'<d, то все слова кода любого фиксированного веса w образуют (d—s')-схему.
Доказательство. Пусть вектор f имеет вес d—s'. По теореме 23 утверждение теоремы выполняется для кодовых слов веса d. Число кодовых слов веса d+1, которые покрывают вектор f, равно Л8,+1(Т). Так как по теореме 20 число As,.И(Т) не зависит от выбора f, то теорема верна для w=c?+l.
Число As,+2(f) можно представить в виде As,+2(f) = Ti + T2, где 7\ равно числу кодовых слов веса d + 2, которые покрывают f, а Т2 равно числу кодовых слов веса d, которые покрывают точно d—s'—1 единиц вектора f. Число Т2 определяется теоремой 23 и не зависит от выбора вектора f. Следовательно, Ti также не зависит от выбора f, и поэтому теорема справедлива для w = d+2. Ясно, что мы можем продолжать и далее таким способом. •
Теорема 24 слабее, чем следствие 14. Так, кодовые слова веса 8 в расширенном коде Голея образуют 5-схему (если воспользоваться следствием 14 или даже теоремой 9), но теорема 24 гарантирует только, что они образуют 4-схему.
Задача (нерешенная). (6.3). Усилить теорему 24 для нелинейных кодов1.
1 Эта задача недавно решена в работе [392а*]-В ней доказано, что для нелинейных двоичных кодов справедлив результат, аналогичный следствию 14: если в двоичном коде /г=грах (d'—s, d—$') и если код содержит нулевое елбвб, то векторы фиксированного веса w (гдеа®^0 образуют (-схему. (Прим пёрев.)
V 6.8. СОВЕРШЕННЫЕ КОДЫ
\в этом разделе мы докажем, что (/г, М, г/=2е+1)-код является совершенным, если и только если s'—e. Закончим этот раздел '.важным необходимым условием существования совершенного кода (теоремой Ллойда).
Теорема 25. Для любого кода выполняется неравенство s'>i(d—1)/2.
Доказательство. Допустим, что код содержит нулевое слово. Вначале предположим, что d — нечетное, и пусть v — вектор веса (d—1)/2. Если s'<Z (d—1)/2, то по теореме 21 найдется кодовое слово с, находящееся на расстоянии меньшем, чем (d—1)/2, от вектора v. Но тогда wt(c)<d, что приводит к противоречию. Те же самые рассуждения проходят и для случая четного d. •
Лемма 26. Если s'— (d—1) /2 (d — нечетное), то
а(х) = Р0(х) + Р1(х)4- • • -+P(d_1)/2(x).
Доказательство. Пусть f — вектор веса i<(d—1)/2. Для кода ^F+f, полученного сдвигом, получаем, что
Ло(О= • • =A_1(f) = O; A(f)=l;
А+1(П= - • =A,(f)=o.
Тогда в силу (6.18) Иг=1 для 1=0, 1, ..., s'—1. Если вектор f имеет вес s'=(d—1)/2, то
A(f) = • • •=4,_1(f) = 0; 4(f) = l,
и снова из (6.18) получаем, что as,=l.
Теорема 27. (и, М, 2е+1)-код 77 является совершенным, если и только если s'=e.
Доказательство. Предположим, что s'=e. Тогда по теореме 21 для любого вектора из Fn найдется кодовое слово, находящееся от него на расстоянии не более чем е. Это соответствует тому, что шары радиуса е с центрами в кодовых точках заполняют все множество’ F”, и поэтому код 7? является совершенным. Наоборот, предположим, что Ф — совершенный код, так что выполняется соотношение (5.26).
Применяя теперь лемму 19 к многочлену р(х)=.Р0(х) + + ... +Ре(х), получаем, что аннулирующий многочлен а(х) кода должен делить многочлен Л)(х)т ... +Ре(х). Следовательно, е = deg{Ро(х) + • • -+Ре(х)}> dega(x) = s'.
Но по теореме 25 s'^e. •
’ Таким образом, аннулирующий многочлен совершенного кода имеет вид
а(х) = Р0(х) + -+Ре(х).
[/ Этот многочлен называется многочленом Ллойда и обозначается через Le(x). Согласно упражнению 42 гл. 5 Le(x)= Ре-\(х— ~—1; 'П—1). Отсюда получаем, что верна следующая теорема.
Теорема 28. (Ллойд). Если существует двоичный совершей-ный (п, М, 2е + 1)-код, то многочлен Le(x) имеет е целых корней оь ое, удовлетворяющих условию
0<<л< • • -<ое</г. /
Пример. Для [7, 4, 3]-кода Хэмминга Le(x)=%>—2х.
6.9. КОДЫ НАД GF(q)
Большинство результатов этой главы может быть распространено на коды над GF(q). Сначала надо ввести, так же как это было сделано в § 6.2, параметры d, s, d', s' с той лишь разницей, что вес и расстояние заменяются соответственно на вес Хэмминга и расстояние Хэмминга.
Уравнение (6.1) теперь запишется в виде
S п
1 + У Вх.yxi = Mq~n VВ’ (1 + у yy-i (l-y)i, i J
J=1 /=0
где y=q—1, а теорема 2 формулируется следующим образом.
Теорема 2.* Если s^d', то
для всех где N=qnIM. Аналогично изменяется и теоре-
ма 4, в то время как лемма 1 и теоремы 3, 6, следствие 5 остаются неизменными.
Так как в рассматриваемом случае не существует больше единственного вектора веса п, то нельзя ввести параметр $, и поэтому не существует аналога теоремы 7.
Асхемы, получаемые из недвоичных кодов. Если — линейный код длины п над GF(q), то попытаемся образовать Асхему из кодовых слов веса w(w>0) следующим образом. Множество из w координат, в которых кодовое слово имеет ненулевые элементы, назовем опорным множеством кодового слова. Конечно (так как данный код — линейный), q—1 кодовых слов, пропорциональных данному слову, имеют одно и то же опорное множество. Каждое такое опорное множество (взятое, конечно, один раз,-а не q—1) и составляет блок Асхемы.
Полученная таким образом Асхема может все еще содержать одинаковые блоки. Однако этого не может быть для двоичных кодов, а также и для кодов над GF(q), если w равно минимальному весу d кода. Действительно, предположим, что с и с' — два кодовых слова веса d, не пропорциональных друг другу, опорные, множества которых совпадают. Тогда найдется кодовое слово, пропорциональное с, скажем, tc такое, что 0<dist(fc, c')<Zd, что приводит к противоречию.
\ Например, рассмотрим код #6'.из гл. 1. Кодовые слова 0121 и 021х2 имеет опорное множество 0111. Таким образом, восемь кодовых слов веса 3 дают следующие четыре блока 0111, 1011, 1101\ 1110, образующих тривиальную 3-(4, 3, 1)-схему.
Приведем теперь теорему, дающую достаточные условия того, что нар! метод построения приведет к /-схеме.
Теорема 29. (Ассмус и Мэттсон.) Пусть <ё>—[п, k, d] линейный код над GF(q). Предположим, что мы можем найти целое число /, где 0</<d такое, что имеется самое большое d—t чисел а, удовлетворяющих условию l^or^n—/. (Здесь, как и в § 6.2, числа Gi представляют собой значения весов, встречающихся в коде <₽’±.) Тогда опорные множества кодовых слов веса d в коде образуют /-схему.
Доказательство. Пусть Т — любое множество / координат и пусть (как и в § 6.5) код образован удалением этих / координат из св. Таким образом, — это [п—/, k, d—/]-код. Дуальным этому коду является код (^<т))±= (<ё’^)ОаТ. По предположению, код (<g’<I’))J- имеет не более d—t ненулевых весов, а дуальный ему код имеет минимальное расстояние d—t. Поэтому мы можем применить теорему 2* и найти весовой спектр кода ^’(Г))±, а следовательно, согласно теореме 13. гл. 5 мы можем найти также и весовой спектр кода В частности, это дает то, что число кодовых слов веса d—t в коде '(обозначим его через а) не зависит от выбора Т.
Каждое из этих а кодовых слов получено из некоторого кодового слова кода веса d, причем опорное множество любого такого слова в коде содержит множество позиций Т. Далее (как мы показали выше) все кодовые слова веса d, имеющие одинаковые опорные множества, пропорциональны друг другу. Следовательно, число блоков, которые содержат множество позиций Т, равно а/(q—1), и оно не зависит от выбора множества Т. •
Пример. Самодуальный код # 6 из гл. 1 содержит только кодовые слова веса 0 и 3. Таким образом, n=4; d=Gi=3. Следовательно, мы можем выбрать /=2 и заключить на основании теоремы 29, что опорные множества кодовых слов веса 3 образуют 2-схему. На самом деле, как мы видели выше, они образуют 3-схе-му, поэтому утверждение теоремы не всегда приводит к наилучшему возможному результату.
Следствие 30. Предположим, что мы находимся в условиях теоремы 29 и у>2. Тогда для каждого веса ту в интервале опорные множества кодовых слов веса т.; в коде образуют /-схему, где v0 — наибольшее целое число, удовлетворяющее условию
I <7— 1 I
Доказательство. Из определения числа Ио вытекает, что если опорные множества двух кодовых векторов веса совпадает, то эти вектора должны быть пропорциональны друг другу.
Далее доказательство аналогично доказательству теоремы 29. •
Например, троичный [12, 6, 6]-код Голея ^12 (см. гл. 20) является самодуальным кодом со значениями весов 0, 6, 9, 12. Тогда »о=Н, и поэтому опорные множества кодовых слов весов 6 и 9 образуют 5-схемы.
В двоичном случае мы никогда не можем получить одинаковых блоков, следовательно, справедлив следующий результат.
Следствие 31. Пусть ^ — двоичный линейный [n, k, dj-код. Если выполняются условия теоремы 29, то кодовые слова любого веса т, образуют /-схему.
Пример. Для расширенного [24, 12, 8]-кода Голея можно выбрать /=5, так как имеется d—t=3 числа щ в интервале 1 Щ 19, а именно 8, 12, 16. Таким образом, кодовые слова любого веса образуют 5-схему, в чем мы уже убедились ранее.
Нам не удалось обобщить теорему 13, и поэтому мы сформулируем следующие задачи.
Задачи (нерешенные). (6.4)*. Обобщить теорему 13 на случай GF(q).
Упражнение. (13) Показать, что следствие 31 влечет следствие 14. »
(6.5)1 2. Верно ли, что следствие 31 сильнее, чем следствие 14?
Весовые спектры сдвигов кода и совершенные коды. Все результаты § 6.6, 6.8 справедливы и для кодов над GF(q). В двоичном случае доказательства проводятся на языке групповой алгебры, введенной в гл. 5. Для кодов над GF(q) доказательства совершенно аналогичны, но требуют более разработанного аппарата групповой алгебры, который мы не намерены вводить.
Например, теорема Ллойда звучит следующим образом.
Теорема 32 (Ллойд). Если существует совершенный (п, М, 2е+1)-код над GF(q), то многочлен Ллойда
Ге(х) = Р0(х; п)+ - • -+Ре(х; и) = Ре(х—1; п—1) =
(6.24)
имеет е целых корней сть ..., сте, удовлетворяющих условию 0<oi<; ... <Ое</г. Здесь многочлен Рй(х, п) определяется выражением (5.53).
Упражнение. (14). Пусть — линейный [п, k, 2е+1]-код. над GF(q). Показать, что является совершенным кодом, если и только если кодовые слова веса 2е+1 образуют ((е+1) — (п,
1 Такое обобщение недавно предложено в [392а*], где доказано, что если векторы любого веса линейного <?-ичного кода образуют <?-ичную /-схему (в смысле Дельсарта [351]), то в дуальном, коде векторы любого фиксированного веса также образуют (/-схему. Исходя из этого в [392а*] показано, что векторы любого фиксированного веса <у-ичного линейного кода образуют /-схему с Z=max (d'—s, d—s'). (Прим, перев.)
2 Эта задача недавно решена в [392а*], где доказано, что следствие 31 эквивалентно следствию 14. (Прим, перев.)
2е + 1, (q— 1)е))-схему. Показать, что если — совершенный код,., то число кодовых слов веса 2е+1 в коде 7? равно:
ла+,=(?-1Г'(4,)/(-+]).
*6.10. НЕ СУЩЕСТВУЕТ НЕИЗВЕСТНЫХ СОВЕРШЕННЫХ КОДОВ
В конце 40-х годов были открыты три типа совершенных: кодов:
(i) . Линейные коды Хэмминга, исправляющие одиночные ошибки. С двоичным вариантом этих кодов мы встречались в § 1.7. В гл. 7 мы построим коды Хэмминга над GF(q). Эти коды имеют параметры
[n = (gm—1)/(^—1); k = n—m; d = 3],
(ii) . Двоичный [23, 12, 7]-код Голея Т?2з (§ 2.6 и гл. 20).
(iii) . Троичный [11, 6, 5]-код Голея ЭД (гл. 20).
Как мы увидим в гл. 20, параметры двух кодов Голея определяют их однозначно: любой код с такими параметрами эквивалентен одному из кодов Голея. Однако положение не таково для; совершенных кодов, исправляющих одиночные ошибки. В 1962 г. Васильев построил семейство нелинейных двоичных кодов, исправляющих одиночные ошибки и имеющих те же самые параметры,, что и коды Хэмминга (см. § 2.9). Позднее Шонхейм и Линд-стрем построили нелинейные коды с теми же самыми параметрами, что-и коды Хэмминга, над полями Галуа GF(q) для всех q. Этот вопрос все еще не решен до конца.
Задача (нерешенная). (6.6). Найти все совершенные нелинейные коды, исправляющие одиночные ошибки, над полями: Галуа GF(q).
Наконец, имеются еще тривиальные совершенные коды: (i)-код, содержащий только одно кодовое слово;
(ii) все пространство Г";
(iii) двоичный код с повторением нечетной длины.
Многие пытались найти другие совершенные коды или при неудаче доказать несуществование таковых. Ван Линт существенно^ продвинулся в исследовании этой проблемы, которая была полностью,решена Титвайненом 1 в 1973 г.
Теорема 33. (Титвайнен и Ван Линт). Нетривиальный совершенный код над любым полем Галуа GF(q) должен иметь те.-Же самые параметры п, М и d, что и один из кодов Хэмминга или. Голея.
Доказательство мы разобьем на пять частей, а именно на теоремы 37—41. Идея доказательства состоит в том, чтобы пока-
1 Одновременно этот же результат был получен Зиновьевым и Леонтьевым £1472, 1472а*]. (Прим, ред.)
зать, что только в случаях, приведенных выше, многочлен Ллойда имеет различные целые корни, лежащие на отрезке [1, п —1].
Пусть код на всем протяжении § 6.10 обозначает совершенный (n, М, 2е-Н)-код над GF(q), где q=pr, р— простое число, и :пусть <Т1<О2< <ое обозначают целые корни многочлена Le(x) (см. теорему 32).
Вначале приведем несколько лемм.
Лемма 34. (Условие сферической упаковки.) Число кодовых 'слов М является степенью q, и для некоторого целого числа I выполняется равенство
е / \
<6-25)
г=0 V >
Доказательство. Так как код — совершенный (см. теорему 45 гл. 1), то
е .
i=0'1 '
Следовательно, M=pi и
S____f\ ' S
Таким образом, q—\=рт—1 делит число pnr 'i—1. По лемме '9 гл. 4 г делит /, а значит, М является степенью q. •
Лемма 35. Le(0)=«7z, и если код SF нетривиален, то Le(l) и £е(2) не равны нулю.
Доказательство. Из выражения (6.23), используя равенство
=(—I)3’ (см. упражнение (18) гл. 1), получаем
= <7
;(по лемме 34).
Кроме того, из (6.23) следует:
что не равно нулю, так как е^п—1, и
£е (2) = (9~ 1)6-1 (П ~ 2 ) {q (п—е — 1) - п + 1}, (6.26)
е' 1 е \ е — 1/
что равно нулю, только если q=l-t-ej(fi—е—1). Но q^2, и поэтому это влечет неравенство п^2е + 1, которое означает, что код — тривиальный.
Л е м м а 36. Числа щ,..., ие удовлетворяют равенствам:
. _ра е(» —е)(4—0 । е(е+1) .
4 2
. .Ge = e\ql~e.
Доказательство. Из теоремы 15 гл. 5 вытекает, что Le(x) представляет собой многочлен от х степени е. Коэффициент при хе равен (—q)e!e]; а коэффициент при хе~х равен
( —<7)е (е(е+1)
el 1 2
е(п—е)
Теорема 37. Совершенный код над GF(q), исправляющий одиночные ошибки, имеет те же самые параметры п, М и d, что и код Хэмминга.
Доказательство. Условие сферической упаковки (лемма 34) означает, что 1 + (q—\)n=ql, а теорема Ллойда (теорема 32) говорит, что многочлен
£1 (х) = Ро (х) + Рг (х) = 1 4- {(q— 1) п—qx}
имеет целый корень х=о1. Таким образом, 1 + (</—1)п—<7сц = О. Следовательно, O\=ql~l и n=(ql—l)j(q—1). Теперь из границы •сферической упаковки1 получаем, что мощность этого кода равна qn~l- •
Более того, как и код Хэмминга, этот совершенный код имеет одинаковые спектры весов и расстояний. Это следует из теоремы 4, обобщенной на случай кодов над GF(q), так как d=3 и s'=e= 1.
Теорема 38. Не существует нетривиального двоичного совершенного кода, исправляющего двукратные ошибки.
Доказательство. Условие сферической упаковки означает, что
или
1+« + (^ = 2г
(2п4-1)2 = 2г+3 —7.
(6.27)
Многочлен Ллойда имеет вид L2(-^)=Z/2—•2(и-|-1)г/-|-2г+1, где У=2х. Следовательно, по лемме 35 этот многочлен должен иметь различные корни i/i=2oi и z/2=2g2, являющиеся четными числами, большими чем 4. Так как yiy2=2l+1, то yi=2“ и у2=2ь, где Тогда yi+y2=2aJr2b=2(ti+1), и поэтому условие (6.27) принимает вид
|2_______2 w____________у______________________________у
( 2а + 2ь
Это равенство невозможно, так как приведение обеих его частей по модулю 16 дает сравнение 1=—7(mod 16), т. е. противоречие. •
Теорема 39. Единственными возможными параметрами для нетривиального совершенного кода, исправляющего двукратные-ошибки, над полем GF(q), q=pr, являются параметры троичного кода Голея.
1 См. теорему 6 гл. 1. (Прим, перев.)
Доказательство. Условие сферической упаковки выглядит теперь таким образом:
1+(<7~1)п + (<7—l)aQ)=V. (6-28)
что влечет 2(q—l)n = q—3 + ]/~ q2—69+ 1 + 8<?г.
Из. леммы 36 следует, что
<да2 = 2дг~2;
01 + (Т2 = 2(н-2)(7-1)_+3.
q
.'Заменяя п, получаем, что
q (*i + <т2) = 1 + / <72-69+ 1 +8gl. (6.29)
Так как по лемме 35 oi, <т2>2, то можно положить 02=
—2р»-, где X, р,^1 и Х+р,=г(/—2). Подставляя это в (6.29), возводя в квадрат и деля обе части на q, получаем выражение
- 2 ( рК + 2рц) + q ( рк + 2рцУ = q—6 ф 8ql~x. (6.30)
Все члены этого выражения, кроме — 6, делятся на р. Следовательно, р=2 или р=3. Если р=2, то q—6 должно делиться на -4, и поэтому q—2, что невозможно в силу теоремы 38.
Теперь предположим, что р=3. Если q=3, то (6.30) принимает вид
—2(Зхф2-Зц)фЗ(Зхф2-Зц)2 =— Зф8-Зг-1.
'Если /^3, то это уравнение не имеет решения. Для значений ,1^.4 после деления на 3 получаем соотношение
За ф 4 • 3?+,х ф 4 • 32ц—2 • 3?'-1—4 • Зц~1 = — 1 ф 8 Зг~2.
Следовательно, ц=1, и поэтому Х=2. Это влечет 1=5 и (из (6.28)] п=11, т. е. мы получили параметры троичного кода Голея.
Наконец, предположим, что q=3r, где г>1. Сравним обе части уравнения (6.30) по модулю 9:
7 ( 3х ф 2 • Зц) е= 3—ql~' (mod 9),
что показывает, что />1, так что 7(Зх+2-Зц) =3(mod 9) или иначе (умножая обе части на 4) 3?-+2-3,xs3(mod 9).
Следовательно, Х=1 и р,>1. Из условия 1Фц=г(/—2) следу-
-ет, что 31+»х=9г“2. Тогда выражение (6.30) принимает вид
—2 (Зф2-Зц)фЗг(Зф2-Зц)а = 3Г—6ф8-Зг+ц+1 или .
—4 • 3й ф 8 • Зг = 4- 3r+fx+1 —4 • 32ц+г. .
Таким образом получили, что правая часть этого равенства .делится на более высокую степень 3, чем левая часть. -= л'< •
Замечание, поиск на вычислительной машине показал», что единственными решениями уравнения (6.25) в диапазоне nsglOOO; е^ЮОО; <7^'100 являются тривиальные решения, параметры кодов Голея и кодов Хэмминга и еще одно решение: п= =90; .fe=78; е=2; <7=2. Но теорема 38 показывает, что кода с-, такими параметрами не существует.
Задача (нерешенная). (6.7). Как близко мы можем подойти к этим параметрам: существует ли [90, 77, 5] двоичный; линейный код?
Теорема 40. Не существует нетривиальных совершенных: кодов над полями Галуа GF(q); q=pr, исправляющих е ошибок,., если q>2 и е>2.
Доказательство, (i). Вначале мы покажем, что 2oi’^oe. Если-s — целое число, s=pai, где (р, /) = 1, то положим ap(s)=t. Ясно, что np(sis2) =ap(si)ap(s2) и ap(s)^'s. По лемме 36 OiO2 — ... ве=е\ - ql~e, поэтому
йр(а1)й₽(а2) • • -Ор(сте) = ар(е!)<е!
Следовательно, либо два некоторых числа ap(oi) равны, скажем, пр(ог-) =пр(о3), либо для случая, когда р>е^3, числа;; пр(о1), ..., пР(ое) равны числам 1, 2, ..., е в некотором порядке.
В первом случае Gi=p“/; о3=р₽/, и если i<j, то 2oi^o3. Во-втором случае для некоторых i и j tzp(oj) = I; tzp(o3)=2; ог-=р“; Oi=2p|3, и (меняя местами i и /, если это необходимо) получаем, что 2аг^а3-. Следовательно, 2с>1^2о;^ст3^с>е.
(ii). Легко получить теперь, что
(6.31>.
Полагая x=oe/oi, сразу же получаем неравенство
2
х (1 -)-х)а для х > 2.
(iii). Далее имеем
(_1)еГе(0)
О1О2 • • -ое =--------L—1---------------
коэффициент при хе в Le (х)
= <7 с! Vfg-lW А> i=o
(6.32)-
(если из суммы взять только член с / = 0)
>9~e(g— l)en(n — 1) • • •(«—е+ l)>q~e(q— 1)епе(1— с (е~1} .
(6.33).
(iv). Теперь мы воспользуемся известным неравенством между взвешенным средним геометрическим и взвешенным средним арифметическим, которое утверждает, что
N N
5 (6.34),
i=l i=l
для любых действительных чисел х-^О и аг>0, удовлетворяю-N
щих условию аг = 1.
г=1
Поэтому е
П °* == (°1<) (<?2 ’ • -0^) <
г=1
,,[в силу (ii) и (6.34)]
8 / Oi-I-Ое \2/а2+ . . .-Не-! У-2
9 \ 2 / ( е — 2 ]
Денова согласно (6.34))
< 8 / °1 ~Ь • • + Ре у
" 9 \ е )'
Итак, мы применили к числам ог усиленный вариант неравенства между средним геометрическим и средним арифметическим. JB силу леммы 36 последнее выражение равно
8 / (« —е) (4—1) , (е+ О |е < /6 35)
, 9 | q 2 J " k ‘ ’
<у9_е(?-1)епе; (б.зб)
это неравенство получено путем элементарных преобразований при условии, что <?>2 и е>2. Объединение выражений (6.33) и (6.36) дает следующую верхнюю оценку для п:
! е(е— 1) 8
2и *^9
ИЛИ
Я<Ае(е_1). (6.37)
(v). Так как число
[”| (а. — 1) = A Le (1) = (9~-1)е -(п~е) (6.38)
i=i 9е 9е
должно быть целым, то получаем следующее условие:
рге\(п — 1)(л—2) • • -(л—е).
Предположим, что а является наибольшей степенью р, делящей одно из чисел п—1, ..., п—е. Что в таком случае мы можем сказать о числе, являющемся степенью р и делящем произведение (п—1) ... (л—е)? Это число равно самое большее
Л _ па+Ге/Р14-Ге/р»1+...
Р I
й при этом необходимо, чтобы А~^рге. Следовательно,
а > ге—
г
р — \
Таким образом, число р’Ге/21=<yje/2i делит п—для некоторого i, и поэтому
п>^. (6.39>
(vi). Из (6.37) и (6.39) следует, что
3Ге/21<Уе/21<п<-|-е(е-1),
откуда получаем, что е^П; 7^’8 и п<495. Но упоминавшийся выше машинный поиск показал, что в этом диапазоне нетривиальных совершенных кодов не существует. •
Теорема 41. Единственными возможными параметрами нетривиального двоичного совершенного кода, исправляющего е ошибок, е>2, являются параметры кода Голея.
Доказательство. Из (6.26) получаем, что
П (°f — 2) = е! Le(2)/2с =-(п—2)(и—3) • • -(п—е)(п—2е—1)/2е.
(6.40>
Так как число (сч—1)(пг—2)—четное, то из (6.38) и (6.40) следует, что число (п—1)(п—2)2 ... (п—е)2(п—2е—1) делится на
2
23е и, следовательно, п> — -2е/2. е
Оставшаяся часть доказательства проводится диалогично доказательству теоремы 40: используя соотношения (6.32) и (6.35), получают верхнюю границу для п, подобную оценке (6.37). •
Код, параметры .которого совпадают с параметрами двоичного [23, 12, 7]-кода Голея, имеет те же самые спектры весов и расстояний, что и код Голея. Это следует из теоремы 4, так как d=7 и s'=e = 3. Аналогичное утверждение справедливо и для троичного кода Голея.
ЗАМЕЧАНИЯ К ГЛ. 6
Пейдж [1018] и Боуз [174], вероятно, первыми стали строить схемы из кодов, в то время как Ассмус и Мэттсон [37, 41, 47] первыми получили результаты, подобные теоремам 9 и 23*. Наше изложение следует Дельсарту [350— 352]. Семаков и Зиновьев [1180, 1'181] изучили взаимосвязь между равновесными кодами и /-схемами.
§ 6.3. Теоремы 2 и 4 являются, по всей видимости, новыми.
§ 6.5. Этот параграф основан на работе Шаугнесси [1195].
§ 6.6. Большинство результатов этого раздела принадлежит Дельсарту [351], хотя некоторые доказательства отличаются от оригинальных. Другое доказательство теоремы 21 может быть найдено в работе Ассмуса и Мэттсона [41].
В Евклидовом пространстве размерности п неравенство (6.20) может-быть улучшено:
2 6й£'Р<6 Г 2 (п 4- 1)
См. также [33, 79]. (Прим, перев.)
<см, работу Джанга [702]). Упражнение (И) показывает, что в Хэмминговом «пространстве такое улучшение невозможно. Теорема 22 взята из работы МакВильямс >[872].
§ 6.8. Теоремы 25, 27 принадлежат Мак-Вильямс [871, 872]. Упражнение (13) можно найти у Ассмуса и Мэттсона [37]; см. также [47].
Теорема 28 доказана Ллойдом [859]. Что касается теоремы 32 и других «обобщений теоремы Ллойда см. работы Ассмуса и Мэттсона [41], Бассалыго [76а, 77], Биггса [144], Дельсарта [380], Ленстра [815] и Руза [1123].
Код называют равномерно упакованным, если 1 s'=e+l [505].
§ 6.9. Теорема 29 и следствие 30 принадлежат Ассмусу и Мэттсону [41, 47]. Другое обобщение теорем 9 и 24 на случай кодов над GF(q) проделано .Дельсартом [351].
§ 6.10. Ван Линт [855] сделал прекрасный обзор работ по совершенным .кодам и, в частности, включил ссылки на более ранние работы по этой теме (которые мы опустили). Работы Титвайнена по совершенным кодам могут быть здайдены в [1321—1324] и Ван Линта в [845—850, 854, 855]. См. также некоторые недавние работы советских авторов [1471, 1472].
Шонхейм [1159] (см. также [1160]) и Линдстрем [842] показали, что для любого <7^3 и т^2 имеется существенно нелинейный совершенный код над GF(q) длины n=(qm+1——1), исправляющий одиночные ошибки.
Доказательство теоремы 33 следует Ван Линту [848, 854] и Титвай-яену [1323] с добавлениями Ленстра и Смита (N. W. Lenstra and D. Н. Smith) (неопубликованная работа) при доказательстве теоремы 41. Поиск.на вычислительной машине, использованный при доказательстве теорем 40 и 41, был .'Выполнен Ван Линтом [845]; Ленстра и Одлыжко (N. W. Lenstra and А. М. Odlyzko) (неопубликованная работа) показали, что счет на машпне можно не использовать,*если уточнить неравенства. Неравенство между средним арифметическим и средним геометрическим см., например, в работе Беккенба-ха и Веллмана [94].
Обобщения совершенных кодов. По совершенным кодам в метрике Ли. над смешанными алфавитами или в графе см. работы Астолы [54], Бассалыго [77], Баумерта и др. [84] Биггса [144—147], Камерона и др. [236], Голомба и др. [524, 525, 529, 531, 532], Хэммонда [593, 594], Хедена [628—630], Герцога и Шонхейма [643], Джонсона [698], Линдстрема [843], Поста [1072], Рашмани [1084], Шонхейма [1159, 1160, 1162] и Тзэса [1319].
Глава?
Циклические коды
7.1. ВВЕДЕНИЕ
Наиболее изученными среди всех кодов являются циклические коды, так как они легко кодируются и содержат важное семейство кодов БЧХ. Кроме того, они используются для построения многих других кодов, как, например, кодов Кердока, Препараты и Юстесена (см. следующие главы).
Глава начинается с определения циклического кода как идеала в кольце многочлена по модулю многочлена х”—1 (§ 7.2). Циклический код длины п над GF(q) состоит из всех кратных порождающего многочлена g'(x), который является нормированным многочленом наименьшей степени в коде и делит многочлен хп~1 (§ 7.3). Многочлен h(x) = (xn—l)Jg(x) называется проверочным многочленом кода (§ 7.4).
1 Имеется несколько различных определений равномерно упакованных кодов s(cm., например [78, 79, 504, 505, 1183]). (Прим, перев.)
В § 7.5 изучается разложение многочлена хп—1. Всюду предполагается, что числа п и q взаимно просты. При этом условии все корни многочлена хп—1 лежат в поле GF{qm'), где т — наименьшее положительное целое число такое, что п делит qm—1.
В конце § 7.3 доказывается, что коды Хэмминга и коды БЧХ с исправлением двух ошибок являются циклическими. В § 7.6 дается общее определение кодов БЧХ над GF(qm) с исправлением t ошибок. ,В § 7.7 вводится общее определение .кода над GF(q), задаваемое матрицей над GF(qm). В последнем параграфе описывается техника кодирования циклических кодов.
Дальнейшие свойства циклических кодов раскрываются в последующих главах.
7.2. ОПРЕДЕЛЕНИЕ ЦИКЛИЧЕСКОГО КОДА
Код называется циклическим, если он линеен и любой циклический сдвигкодового слова также является кодовым словом, т. е. если (со ci, ..., Си-i) принадлежит то и (cn-i, c0, сп-2) при-
надлежит сё'. Например, код Хэмминга (1.40) является циклическим. Цикличен также код ^з = {ООО, 110, 101, 011}.
Для того чтобы дать алгебраическое описание, сопоставим каждому вектору с=(с0, сь ..., cn-i) из Fn (где F— некоторое конечное поле GF(p)) многочлен c(x)=c0+cix+ ... +сп-1хп~1. Например, коду 'ё’з соответствуют многочлены . 0,1-j-х, 1-{-х2, х + х2.
Будем использовать следующее обозначение; если F — поле, то F[х] — множество многочленов от х с коэффициентами из F. Множество Г [х] является кольцом.
Определение. Кольцо .7? (в широком смысле) определяется как множество, в котором возможны сложение, вычитание и умножение. Формально R — аддитивная абелева группа с умножением, удовлетворяющим условиям: ab=ba-, а(Ь4-с) = ab + ас и (ab)c=a(bc), которая содержит единичный элемент 1 такой, что \-а=а. (Такое кольцо иногда называется коммутативным кольцом с единицей.)
Кольцо Rn = F[x]/(xn—1). Для наших целей более важным Является не кольцо F[х], а кольцо 7?п=Е[х]/(х”—1), состоящее из классов 'вычетов кольца Е[х] по модулю многочлена хп—1. Все многочлены степени не больше п—1 попадают в различные классы вычетов. Мы выберем эти многочлены в качестве представителей этих классов. Таким образом, можно сказать, что с(х) принадлежит Rn. Кольцо Rn является n-мерным векторным пространством над F.
Умножение на х соответствует циклическому сдвигу. Умножая в Rn многочлен с(х) на х, получаем:
хс(х) = с0х + с1х2+ +cn__2xn~1+cn_ixn^cn_l+cox +
; . + • • -+с^2х^, .
так как в имеет место равенство хп=1. Но этому многочлену соответствует вектор (cn-i, с0, сп-2)- Таким образом, в ум-
ножение на х соответствует циклическому сдвигу!
Идеалы. Определение. Идеалом кольца Rn называется линейное подпространство такое, что: (i). Если с(х)^её>, то r(x)c(x)<=ctf для всех r(x)<^Rn. Условие (и), очевидно, может быть заменено на условие:
(ii). Если с(х)^(ё>, то хс(х)^<ё>.
Наше первое определение циклического кода теперь может быть переписано в следующем виде.
Определение. Циклическим кодом длины п называется идеал кольца Rn.
Пример. Ф3={0, 1+х, 1+х2, xs-i-x)—идеал в Rs>, так как это множество замкнуто относительно сложения (и, следовательно, линейно) и любое кратное многочлену с(х)<=(ё' опять лежит в (например, х2(1+х2) =xz+x4=x2+x, так как в R3 имеет место равенство х=х4).
Групповая алгебра FG. Часто полезно другое описание кольца Rn- Пусть G={1, х, х2, ...,хп~1}; хп=1— циклическая группа порядка п. Групповая алгебра FG группы G над полем F (см. § 3 гл. 5) состоит из всех формальных сумм вида
П—1
С(х)=£с,Хг, CffEiF. i=0
Сложение в FG выполняется покоординатно, а умножение — по модулю многочлена хп—1. Ясно, что FG совпадает с Rn-
Упражнения. (1). Каким идеалом описывается циклический код {0000, 0101, 1010, 1111}?
(2) . Описать наименьший циклический код, содержащий вектор 0011010.
(3) . Показать, что Rn не является полем. [Указание. Элемент х—1 не имеет мультипликативного обратного.]
(4) . Показать, что многочлен f (х) имеет мультипликативный обратный в Rn тогда и только тогда, когда f(x) взаимно прост с хп—1 в кольце Е[х].
(5) . Показать, что в циклическом (n, k) -коде любые k последовательных символов могут быть выбраны в качестве информационных.
7.3. ПОРОЖДАЮЩИЙ МНОГОЧЛЕН
Особенно простым видом идеалов являются главные идеалы, состоящие из всевозможных произведений элементов из Rn на некоторый фиксированный многочлен g(x). Они будут обозначаться через <g(x)>. Многочлен g(x) называется порождающим многочленом идеала.
Действительно, каждый идеал в Rn является главным идеалом, а каждый циклический код имеет порождающий многочлен.
Следующая теорема содержит доказательство этого факта и других основных свойств цикличёских кодов.
Теорема 1. Пусть Ф — ненулевой идеал кольца Rn, т. е. циклический код длины п.
(а) . В имеется единственный нормированный многочлен g(x) наименьшей степени.
(b) . <&=<g(x)>, т. е. g(x)—порождающий многочлен идеала <ё>.
(с) . g(x) делит хп—1.
(d) . Любой многочлен с(х)^<ё> в кольце F[x] однозначно записывается в виде c(x)=f (x)g(x), где степень f(х)меньше чем п—г, a r=degg (х). Размерность равна п—г. Таким образом, сообщение f(x) кодируется словом f(x)g(x).
(е) . .Если g(x)=go+gix-t- ... +grxr, то порождается (как подпространство в Fn) строками порождающей матрицы
G =
• • Дг О
gogl -gr-igr
_о go • • • gr_
g(x)
xg(x)
xn-r-l g(x)
(7.1)
(Здесь использованы очевидные обозначения.)
Доказательство (а). Предположим, что оба многочлена f(x), g(x)^^ нормированы и имеют минимальную степень г. Тогда многочлен f(x)—g(x)<^(F> имеет более низкую степень, что приводит к противоречию, за исключением случая f(x)=g(x).
(b). Пусть с(х) ^<ё>. Воспользуемся в Rn равенством a(x)=q(x)g(x) +г(х), где degr(xj<r. В силу линейности кода г(х)=с(х)—q(x)g(x)^eS>, так что г(х)=0. Следовательно, a(x)EE<g(x)>.
(с). Воспользуемся в Е[х] равенством хп—\^=h(x)g(x) + где degr (х)<г. В Rn это означает, что •—г(х) = =h(x)g(x)^cg>, что приводит к противоречию, за исключением случая г(х)=О.
(d), (е). Согласно (Ь), любой многочлен с(х)^<ё> в Rn равен многочлену q(x)g(x). Следовательно, в кольце Е[х]
С (х) =- q (х) g (X) + с (х) (х" — 1) = (q (х) + с (х) h (х)) g (х) = f (х) g (х), (7-2)
где degffxj^n—г—1.
Таким образом, в кольце Е[х] (но не в Rn) код состоит из произведений g(x) на многочлены степени не больше п—г—I. Всего имеется п—г линейно независимых произведений такого вида, а именно g(x), xg(x), ..., xn^~lg(x). Соответствующие векторы и являются строками матрицы G. Это означает также, что размерность кода равна п—г. •
Теперь дадим несколько примеров циклических кодов.
Двоичные коды Хэмминга. Напомним, что в § 1.7 проверочная матрица двоичного кода Хэмминга длины n=2m—1 определялась как матрица, столбцами которой являются все 2™—1 различных ненулевых яг-векторов. Если теперь а — примитивный элемент поля GF(2m) (см. § 3.2 и § 4.2), то все элементы 1, а, а2,..., а2”1-2 различны и могут быть представлены как различные ненулевые двоичные т-векторы.
Таким образом, проверочная матрица двоичного кода Хэмминга с параметрами [и=2™—1; k=n—rrr, d = 3] может быть представлена в виде
Н = (1, а, а2, • . •, а2"1-2), (7.3)
где каждый элемент должен быть заменен на соответствующий двоичный вектор-столбец длины т.
Например, для кода
/00101114
Н = (1, а, а2, а3, а4, а3, а6) = | 0101110 I» (7.4)
\1001011/ *
где a^GF(23) —корень уравнения а3+а+1=0.
Вектор с=(с0, С], ..., сп-1) принадлежит коду
;*Нсг = 0;
Л—1
2 V а' = 0;
1=0
с(а) — 0,
где c(x) = c0+cix+ ... +cn+1xn~i.
Согласно свойству (М2) гл. 4 вектор тогда и только
тогда, когда Л+’Цх) делит с(х). Таким образом, код 3@т состоит из всех кратных многочлена М(1)(х) или, иными словами, верна следующая теорема.
Теорема 2. Определенный ранее код Хэмминга Жт является циклическим кодом с порождающим многочленом g’fx) = =MU) (х).
Согласно теореме 1 порождающая матрица кода Эёт равна:
~М(1) (*)
хМ(1) (х)
х2М(1) (х)
х"'"1-1 М(1) (х)
(7.5)
Например, для Ж-s
110 1
1 16 1
110 1
110 1
(7.6)
Упражнение (6). Проверить, что строки матрицы (7.4) ортогональны строкам матрицы (7.6).
Коды БЧХ, исправляющие две ошибки. Код с&, исправляющий две ошибки, длины n=2m—1 был определен соотношением (3.11) как код с проверочной матрицей
„ / lota2 - а2"7—2 \
Н = , I , (7.7)
UaW - - -а3(2'"—2) /
каждый элемент которой опять должен быть заменен соответст вующим двоичным m-вектором. Теперь
Нст = 0;
п-1
2Сг а‘_ г=0
п— 1
0 и У ct a3i = 0;
г-0
2:c(a) = 0 и c(a3) = 0;
ZMw(x) | c(x) и M(3)(x) | c(x.)
по свойству (М2), где Л4(3)(х)— минимальный многочлен элемента а3, тогда и только тогда, когда НОК {ЛН'Дх), Л4<3)(х)} |с(х). Но ЛК'Дхри Л4<3>(х) согласно свойству (Ml) неприводимы, и согласно упражнению (15) гл. 4. различны. Поэтому окончательно имеем: се?1 тогда и только тогда, когда Л4<1)(х)Л4(3)(х) |с(Х)- Таким образом, может быть сформулирована следующая теорема.
Теорема 3. Код БЧХ, исправляющий две ошибки, имеет параметры [п = 2т—1; k=n—2т; d^5], т^З и является циклическим кодом с порождающим многочленом
£(х) = М(1> (х)М(3> (*)•
Доказательство. Равенство degg(x)=2m следует из упражнения (15) гл. 4. Минимальное расстояние было найдено в гл. 3. (Другое доказательство приведено ниже в теореме 8.) •
Упражнение. (7). Показать, что порождающий многочлен кода БЧХ длины 15 с исправлением двух ошибок, определенного в § 3 гл. 3, равен g(x) = (х4+х+ 1) (х4+х3 + х2 + х+ 1) (использовать § 4.4). Выписать порождающую матрицу кода.
Замечание. До сих пор ничего не было сказано о минимальном расстоянии d циклического кода. Это объясняется тем, что определить d в общем случае очень трудно. Граница БЧХ (доказываемая ниже теорема 8) дает нижнюю границу для случая, когда известны корни многочлена g(x). В гл. 8 мы увидим.
что в некоторых случаях минимальное расстояние может быть найдено с помощью многочлена Мэттсона — Соломона1.
Упражнения. (8). (Недвоичные коды Хэмминга.) (а). Код Хэмминга 3Sm(q) над полем GF(q) задается проверочной матрицей размерности rnX(Qm—!)/(<?—1), столбцами которой являются все ненулевые m-векторы над GF(q), первая ненулевая координата которых равна 1. Код,„6 из гл. 1 является кодом <3^2(3). Доказать, что код 3@m(q) является совершенным с параметрами [n=(qm—l)J(q—1); k=n—пц d=3].
(b). Доказать, что если tn и q—1 взаимно просты, то <Ffim(q) эквивалентен циклическому коду с нулями2 а, а9, «®2,..., где a^GF(qm) — примитивный корень n-й степени из единицы.
(9) . Укороченные циклические коды. Иногда, практические ограничения, накладываемые на кодовые длины, таковы, что для требуемых кодовых длин не существует хороших циклических кодов. В- этом случае можно использовать укороченный циклический код <ё’*, который получается из циклического кода путем выбора всех кодовых слов, начинающихся i последовательными нулями и отбрасыванием этих нулей. Результирующий код уже, конечно, не будет циклическим. Докажите, однако, что найдется такой многочлен* f(x), что является идеалом кольца многочленов по модулю многочлена f(x), и наоборот, что каждый идеал такого кольца является укороченным циклическим кодом.
7.4. ПРОВЕРОЧНЫЙ МНОГОЧЛЕН
Пусть W — циклический код с порождающим многочленом g(x). Согласно теореме 1 многочлен g(x) делит хп—1. Тогда k
h(x) = (xn— \)/g (х) = У hpc‘, hk^0
1=0
называется проверочным многочленом кода с&. Причина такого п— 1
названия кроется в следующем. Если с (х) = срс1 = f(x)g U)
1=0
— произвольное кодовое слово из <ё’, то
п— 1 k в Rm
с (х) h (х) = V ctxl V hjx1 = f(x) g (x) h (x) = 0.
_________ i=0 i=o
1 Важным в этом направлении является следующий результат С. Д. Бермана [135]. Пусть п=р“‘ ... ps s , где рь ..., ps — фиксированные простые числа, и пусть М= {V} —семейство циклических кодов длины п над конечным полем F характеристики p¥=Pi для всех i—1, s. Если для всех кодов VeM скорость удовлетворяет условию (й(V)/n)'^р>0, то существует такая константа С, что для каждого кода VeM минимальное расстояние d(V) не превышает С. Интересно' отметить, что если в определение циклических кодов вместо ограничения (q, n)=.l наложить условие (п, q)—p, то удается выписать точную формулу для минимального, расстояния циклического кода [136]. (Прим, перев.)
2 Нулями циклического кода называются корни его порождающего 'многочлена. (Прим, перев.) - •
Коэффициент .при xJ в этом произведении равен
= i = п—1,
г=0
(7-8)
где индексы берутся по модулю п. Уравнения (7.8) задают проверочные уравнения, которым должен удовлетворять код. Пусть
hk
Ilk
h{x) xh (x)
(7-9)
где использованы очевидные обозначения. Тогда (7.8) означает, что если се®1, то Нст=0. Так как &=degh(x)=n—degg(x) — размерность 7? и так как строки Н, очевидно; линейно независимы,- то условие Нсг = 0 является также достаточным для того, чтобы вектор с принадлежал коду. Таким образом, Н — проверочная матрица кода <ё>. »
Пример. Для кода Хэмминга <Э^з имеем: h(x) = (x7+l)/(x3+ +х+1) == (x-i-1) (х3+х2+1) =х4+х2+х+1. Таким образом,
Это совпадает с (7.4).
Упражнение. (10). Для кода из задачи 7 выписать h(x) и Н и проверить, что эта матрица определяет тот же код, что и соотношение (3.10).
Заметим, что уравнение (7.8) означает, что кодовое слово должно удовлетворять системе проверочных уравнений:
cn^hk + cn-khk-A =
Cn—k—2 + Сп—k—1 ^h—1 + ‘ + Сп_2 h0 = 0,
с(Ль + Ci^h—1 + • • + ckh0 = 0.
(7.Н)
Иными словами, с удовлетворяет линейному рекуррентному уравнению
сД+cf+1/2ft_1+ +ct+kho = O (7.12)
для —k—1. Таким образом, если выбрать cn-i,cn-k в
качестве информационных символов, то уравнение (7.12) последовательно определяет проверочные символы cn-k-i,..., с0 (так как hk=j£=O).
Дуальный код. Пусть 'g’ — циклический код с порождающим многочленом g(x) и проверочным многочленом h(x) = (xn— ~V/g(x).
Теорема 4. Дуальный код ^-L является циклическим кодом с порождающим многочленом
(x) = xdeehMh(x~i).
Доказательство. Утверждение вытекает из (7.9). ®
Согласно этой теореме код с порождающим многочленом h(x) эквивалентен коду На самом деле он состоит из кодовых слов кода ®,-L, записанных в обратном порядке.
Упражнение. (11). Показать, что [7, 4, 3] -код с порождающим многочленом g(x) =х3+х-{-1 и [7, 3, 4]-код с порождающим многочленом g(x) =x4-Fx3+x2+ 1 дуальны.
7.5. ДЕЛИТЕЛИ МНОГОЧЛЕНА хп— 1
Так как порождающий многочлен циклического кода длины п над GF(q) является делителем многочлена хп—1, то в данном параграфе мы изучаем эти делители и вводим поле разложения многочлена хп—1.
Мы всюду предполагаем, что п1 и q взаимно просты. (Таким образом, в двоичном случае п нечетно.) Согласно упражнению (8) гл. 4 существует такое наименьшее положительное целое число т, что п делит qm—1. Это число т называется мультипликативным порядком q по модулю п. В соответствии с упражнением (11) гл. 4 многочлен хп—1 делит х —1 и ие делит —1 ни для какого s, 0<s<m.
Таким образом, корни многочлена хп—1 (которые называются корнями степени п из единицы) лежат в расширении GF(qm) и не лежат ни в каком меньшем поле.
Производная многочлена хп—1 равна пхп-1 и взаимно проста с хп—1, так как п и q взаимно просты. Следовательно, многочлен хп—1 имеет п различных корней.
Разложение многочлена хп—1 в GF(qm). Таким образом, в поле GF(,qm) имеются п различных элементов «0, aj, ..., an-i (корни n-й степени из единицы) такие, что
/2—1
ХП— 1 =П (Х~аг)-1=0
Поле GF(qm) называется поэтому полем разложения многочлена хп—1.
Упражнения. (12). Показать, что корни многочлена хп—1 образуют циклическую подгруппу группы GF(qm)*, т. е. в GF(qm) существует элемент а (называемый примитивным корнем степени п из единицы) такой, что
п—1
х"—1 = п (*—“*)• (7-13)
1=0
Во всей этой главе а будет обозначать примитивный корень степени п из единицы.
(13). Доказать, что корни'многочлена хп—1 образуют мультипликативную группу поля тогда и только тогда, когда n=,qm—1.
Разложение многочлена хп— 1 над GF(q). Циклотомические классы по модулю рт—1 были определены в § 4.3. В более общем случае циклотомический класс по модулю п над GF(q) определяется как множество:
Cs={s, sq, sq2, • • , sqms~i}>
где sqms =s(modn). (Выбор в качестве s наименьшего целого числа в Cs удобен, но не существен.) При этом множество всех целых чисел по модулю п разбивается на циклотомические классы:
{О, 1, • • и-1} = и cs,
S
где s пробегает множество представителей классов по модулю п. Отметим, что m равно числу ть элементов в классе Сь
Например, для и=9 и <?=2 имеем:
Со = {0};
^ = {1, 2, 4, 8, 7, 5};
С3 = {3, 6}.
Таким образом, т=6 и многочлен х9—1 разлагается на линейные множители в GF(26).
Как и в гл. 4 (см., в частности, упражнение (14)), минимальный многочлен элемента а® равен:
M(s)(x) = П U—«г).
iecg
Он представляет собой нормированный многочлен наименьшей степени с коэффициентами из поля GF(q), для которого as является корнем.
Также
хп-1 = Г|Л1(’’(4 (7.14)
S
где s пробегает все множество представителей по модулю п. Это Дает разложение многочлена хп—1 на неприводимые многочлены над полем GF(q).
Например, для п=9 и q=2 имеем:
4-1 = Л4(0) (х) Л1(1) (х) Л4(3) (х), где
Л4(0) (х)=1+х;
Л4(1) (х)=1+х34-х8;
Л4(3) (х)= Ц-хф-х2.
Па рис. 7.1 приведено разложение многочлена хп—1 над GF(2) на неприводимые множители для иДбЗ и п=127. Так как x2m+ j = (хт-р 1)2 (лемма 5 гл. 4), то в таблицу включены только нечетные значения п. Далее в таблице отсутствуют значения
п Делители (восьмиричное представление, наименьшая степень слева)
7 6.54.64
9 15 6.7.444. 6.7.46.62.76.
17 6.471.727.
21 6.7.54 64.534.724
23 25 6.5343.6165. 6.76.4102041.
27 6.7.444.4004004.
31 6.45.51.57.67.73 75.
33 6.7.4522.6106.7776.
35 6.54.64.76.57134.72364.
39 6.7.57074.74364.77774.
11 6.5747175.6647133.
43 6.47771.52225.64213.
45 6.7.46.62.76.444.40044.44001.
47 6.43073357.75667061.
49 6.54.64.40001004.40200004.
51 6.7.433.471.637.661.727.763.
55 6.76.7776.5551347.7164555.
57 6.7.5604164.7565674.7777774.
63 6.7.54.64.414.444.534.554.604.634.664.714.724.
127 6.406.422.436.442.472.516.526.562.576.602 626.646.652.712. 736.742.756.772.
Рис. 7.1. Разложение многочлена х” + 1 над СЛ(2)
«=3, 5, 11, 13, 19, 29, 37, 53, 59, 61, так как для этих простых чисел имеются только два циклотомических класса Со и С) и, следовательно, х'ЛД-1 — (хД1) (хп-1Д ... хД 1). Делители выписаны в восьмиричном представлении, и слева расположены более низкие степени. Таким образом, первая строка таблицы означает:
1 Дх7 = (1 Дх)(1 Дх2Дх3)(1 ДхДх3).
Упражнения. (14). Доказать, что если s и п взаимно просты, то Cs содержит т элементов.
(15) . Пусть f(x) — [~j (x—cd)> где К—подмножество чисел ieK
в {0, В- Доказать, что коэффициенты $(х) лежат в
GF(q) тогда и только тогда, когда АеК =7^(modn)eK.
(16) . Доказать, что если к(х)=П(х—а,) делит хп—1 над
GF(q), то
*deg" w h( х~*) = П (x-аГ>). i
(17) . Доказать, что свойства (Ml) — (Мб), выведенные в гл. 4, имеют место и для данного выше общего определения минимальных многочленов над произвольным полем.
Нули кода. Пусть — циклический код с порождающим многочленом g(x). Так как g(x) делит хп—1 над GF(,q), то
£(Х) = П (*—“')> (7-15)
ieK
где, по упражнению (15), ieK=^ i?i(modn)eK.
Множество К равно объединению циклотомических классов. Корни п-й степени из единицы {cd : называются нулями
кода. (Остальные корни степени п из единицы, которые естественно назвать ненулями кода, образуют множество корней многочлена h(x)= (хп—l)/g(x).)
Ясно, что если c(x)^Rn, то с(х) принадлежит тогда и только тогда, когда c(cd)=0 для всех ieK. Это дает определение циклического кода в терминах корней многочлена с(х). Согласно упражнению (16) нули дуального кода обратны ненулям исходного кода. Иными словами, если {cd} — нули кода <&, где i пробегает классы CU1, CUs, .... то ненули кода Я71— это элементы cd, где / пробегает циклотомические классы С—, С-и2 ,
До сих пор в качестве порождающего многочлена g(x) кода выбирался нормированный многочлен наименьшей степени в коде. Однако возможны и другие порождающие многочлены.
Лемма 5. Если p(x)^Rn не вводит никаких новых нулей, т. е. если p(cd)#=O для всех то многочлены g(x) и
p(x)g(x) порождают один и тот же код. (В частности, g2(x) порождает тот же код, что q(x).)
Доказательство. Включение <g(x) >3<p(x)g(x) > очевидно. Согласно предположению многочлены р(х) и h(x) взаимно просты, так что по следствию 15 гл. 12 найдутся многочлены а(х) и Ь(х) такие, что 1 =а(х)р(х) +b(x)h(x) в Е[х].
Отсюда
в Л[х] в Rn
g(x) = а (х) р (х) g(x) + b (х) g (х) h(x) = a (х) р (х) g (х)
Следовательно, <g(x)>^<p(x)q(x)>.
Упражнение. (18). Пусть <S’ = <f(x)> и K={i, O^is^n— 1 ' f(cd) =0}. Доказать,, что &= <g(x)>, где
g(x) = НОК {M(i) (х) :,iGK}.
Лемма 6. Пусть £,^GF(qm)—произвольный корень многочлена хп—1. Тогда
yi 10, если 1;
Ао ' п> если В = 1 •
Доказательство. Если g=l, то сумма равна п. Предположим, что g=#l. Тогда
£ ё = (i-Г)/(1-Ю = о. •
1=0
Лемма 7. (Формула обращения). Вектор с=(с0, сь cn-i) можно найти по многочлену с(х) =Со+С1Х-Ь ••• +Cn-ixn~I по формуле
q = -’-2c(a')a“'/- (7-16)
" i=o
Доказательство.
V с(а‘) а~1’ = V У ck a'(fe-z) = V ch \ а' №—° = (по лемме 6) = /То /То /Ло ' й=о £о
= nct. •
Упражнения. (19). Обозначим через А следующую матрицу Вандермонда над GF(2m) (см. лемму 17 гл. 4):
I1 1 • - -1
а0 ai • -“п-1
А = “о «у а2 , п—I
к~ а”-1 а”-} / п— 1 /
где аг — корень степени п из единицы.
Доказать, что det(A) = l и
/1 а-1 • • -a-t"-1’
1 ар1 а~(п~ *>
А-1 =
1 «71, • .a-1-J-O
(20). Пусть с(х)=с0 + щх+ ... +cn-ixn~i^Rn-, /со С± • -Cn_j
М = | СП-1СО • 'сп~2
\С1 С2 • • • с0
Доказать, что A“IMA = diag [c(cto), c(cti), c(an-i)] (см. упражнение (7) гл. 16). Это .дает другое доказательство того, что dim^=n—degg(x).
(21). Показать, что вектор 1 принадлежит циклическому коду тогда и только тогда, когда g(l)#=0. Показать, что двоичный циклический код содержит вектор нечетного веса в том и только в том случае, когда он содержит вектор 1.
7.6. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ t ОШИБОК
Теорема 8. (Граница БЧХ.) Пусть Ч?— циклический код с таким порождающим многочленом' g(x), что для некоторых це
лых чисел Ь^О и 6^1 выполняется равенство
g(«b) = g(ab+i)= . • .=^(аЬ+е-2) = 0.
Иными словами, точно 6—-1 последовательных степеней а являются нулями кода. Тогда минимальное расстояние кода равно по меньшей мере 6.
Доказательство. Если с=(с0, Ci, —, c«-i)—кодовый вектор из то
с (аь) = с (ab+1) = • • . = с (аь+б~2) = О, так что выполняется равенство H'cT=Q, где
/1 аь а2Ъ • - .а("-1)Ь ' \
Н' —I 1 „ь-н 2 (Ь-f-i) (n-i) (b+i) I
11 --- I 1 са Uj • • • I .
\ / ’ь+б-2..........„(п-1) (Ь+6—2> ’ /
\ 1 1а • • СА /
(Заметим, что матрица Н' не обязательно должна быть полной проверочной матрицей кода '<?.)
Идея доказательства состоит в том, чтобы показать, что любые 6—1 или менее столбцов Нл являются линейно независимыми. Предположим, что вес w вектора с удовлетворяет условию
—1, т. е. что 0, если и только если а2, ..., aw}.
Тогда из равенства Я'сг—0 вытекает, что
Следовательно, определитель левой матрицы равен нулю. Но этот определитель равен произведению a(ai+-+aw)b на определитель
(1 . . .1
а1 -а™
a“i (и>-1) . . _aaw (to—1)
который является определителем Вандермонда и согласно лемме 17 гл. 4 отличен от нуля. Получаем противоречие. •
Примеры. Порождающим многочленом двоичного кода Хэмминга является TWO) (см. § 7.3). Так как по свойству (Мб) гл. 4 ЛК')(а) ^ЛК'^а2) =0, то код имеет пару последовательных нулей: а и а2. Следовательно, по теореме 8 минимальное расстояние кода не меньше 3.
Порождающий многочлен двоичного кода БЧХ с исправлением двух ошибок равен g(x)=M<r>(x)MW(x). Но М(1)(а) = =ЛР>(а2) =Л1(1)(а4) =0 и ЛК3>(а3)=0. Следовательно, код имеет четыре последовательных нуля: а, а2, а3, а4, так что t/^5, что совпадает с результатом гл. 3.
На самом деле минимальное расстояние кода ’ё’ может быть и больше чем 6, так как при замене элементов матрицы Н' соответствующими им m-векторами над GF(q) может оказаться, что больше чем 6—1 столбцов матрицы Н' линейно независимы.
Следствие 9. Минимальное расстояние циклического кода длины п с нулями аь, аь+г, аь+2г, ..., аь+(б-2)г, где числа г и п взаимно просты, равно по меньшей мере 6.
Доказательство,. Пусть р = аг. Так как г и п взаимно просты, то р также является примитивным корнем степени п из единицы. Следовательно, найдется такое t, что ctb = pf и код имеет 6—1 последовательных нулей: р(, pt+1, ..., р(+6-2. Дальнейшее доказательство совпадает с доказательством теоремы 8 с заменой а на р. •
Коды БЧХ. Опр еделение. Циклический код длины п над GF(q) называется кодом БЧХ с конструктивным расстоянием 6, если для некоторого целого числа его порождающий многочлен равен:
g(x) = HOK{M(b)(x)M№+1)(x), • . ., ТИ(Ь|й‘2)Ц)}. (7.17)
Иными словами, g(x) — нормированный многочлен над GF(q) наименьшей степени такой, что элементы аь, аь+1, ..., аь+б-2 являются его корнями. Следовательно, с — кодовый вектор тогда и только тогда, когда
с(аь) = с(аь+1)= - . =с(аь+6-2) = 0. (7.18)
Таким образом, точно 6—1 последовательных степеней элемента а представляют собой нули кода. Из теоремы 8 заключаем, что минимальное расстояние кода больше или равно конструктивному расстоянию б.
Равенство (7.17) означает, что проверочная матрица кода равна:
/1 аь а2Ь ...а'"-1»6 \
Н= 1 аЬ+' а2(Ь+1> • • (Ь+1) |, (7.19)
\ 1 Г7ь+б~2 „(«->) <Ь+6-2) /
где каждый элемент должен быть заменен на соответствующий столбец из m элементов над GF(q).
Строки полученной таким образом матрицы над GF(q) задают проверочные соотношения кода. Всего их имеется т(б—1), но не обязательно все они линейно независимы. Таким образом, размерность кода самое меньшее равна п—т(Ь—1). Второе доказательство можно получить из свойства (М4) гл. 4, согласно которому deg MW (х) ^т, так что degg(x)=n— размерность кода, что не больше чем т(б—1). Таким образом, мы доказали следующую теорему.
Теорема 10. Код БЧХ над GF длины п с конструктивным расстоянием б имеет минимальное расстояние с!^б, а его размерность не меньше чем п—.т(б—1). (Число т определено в § 7.5.)
Размерность больше этой нижней границы в том случае, когда строки матрицы Н, выписанной над GF(q), линейно зависимы, или (что эквивалентно) когда степень многочлена, стоящего в правой части равенства (7.17), меньше чем т(б—1). Примеры такой ситуации приводятся ниже.
Уравнения (7.1) и (7.9) задают соответственно порождающую матрицу и одну из форм проверочной матрицы кода.
Замечания. (1). Коды при Ь=1 иногда называют кодами БЧХ в узком смысле. При n=qm—1 коды называются примитивными, так как в этом случае а — примитивный элемент поля GF(cpn) (а не только примитивный корень степени п из единицы).
Если некоторый элемент а1 является нулем кода, то нулем является также а1 для произвольного I из циклотомического класса С{. Так как циклотомические классы минимальны при n = qm—1, то этот случай является наиболее важным.
(2). При фиксированном b коды БЧХ вложены друг в друга так, что код с конструктивным расстоянием содержит код с конструктивным расстоянием бг в том и только в том случае, когда б[ ^бг-
(3). В общем случае дуальный коду БЧХ кодом БЧХ не является.
Двоичные коды БЧХ. при q = 2 из свойства (Мб) гл. 4 вытекает равенство Л4(2г’> (х) =ЛТ<2>(х). Следовательно, степень g(x) мот жет быть снижена. Например, если 6 = 1, то можно всегда предполагать, что конструктивное расстояние нечетно, так как коды с конструктивным расстоянием 2/ и 2/ + 1 совпадают: для обоих порождающий многочлен равен:
g(x) = HOK{M(1) (х), ЛГ3)(х), . . •, М'^^х)}. (7.20)
Таким образом, deg g(x)^mt и размерность кода не менее п—mt. Проверочная матрица кода равна:
(1а а2 -а"-1 ' \
1 а3 а6 • .а3(п-1) | , (7.21)
1 „2t-i (2t—ц /
1 U ... у
где каждым элемент заменен соответствующим двоичным /тг-век-тором. Второй столбец матрицы Н, конечно, должен содержать только элементы а, cP1, а*2, ..., где 1, й, 1’2, ... принадлежат различным циклотомическим классам.
Приме ры. Начнем с перечисления на рис. 7.2 и 7.3 всех (в узком смысле примитивных) двоичных кодов БЧХ длины 15 и 31. К счастью, минимальные многочлены элементов полей GF(16) и GF(32) уже были выписаны в § 4.4.
Конструктивное расстояние 6 Порождающий многочлен g (х) Показатели корней для g (х) Размерность и—deg g (х) Истинное расстояние d
1 1 15 1
3 1, 2, 4, 8 11 3
5 1—4, 6, 8, 9, 12 7 5
7 Л4(1>(Х)Л1<3) ^(б) 1—6, 8—10, 12 5 7
9, 11, 13 М0)Л['(3) = 1—14 1 15
или 15 = (х1Б+1)/(х+1)
е Рис. 7.2. Коды БЧХ длины 15
Конструктивное расстояние ё Порождающий многочлен g (х) Размерность п—deg g (х) Истинное . расстояние d
1 1 31 1
3 AKD 26 3
5 МИ) Л4(3) 21 5
7 ЛК1) Л4(3) Л4(5) 16 7
9 или 11 ТИО) ТИО) Л4(5) Л4(7) 11 11
13 или 15 ЛК1) ТИ(3) 7И(5) Л1(7) ТИ(И) 6 15
17,19,...,31 ТИО) ЛТ(З) М(5) Л4(7) ЛК11) Л4(*3> 1 31
Рис. 7.3. Коды БЧХ длины 31
Заметим, что коды с конструктивным расстоянием 9 и 11 совпадают. Это происходит по следующей причине. Порождающий многочлен последнего кода равен:
g‘(x) = HOK{Al(I) (х), Л1(3)(х), Л1(5)(х), ТИ(7) (х), М(9)(х)}.
Но 9еС5, и поэтому элементы а9 и а5 имеют один и тот же минимальный многочлен 7И(9)(х) =Л1(5)(х). Следовательно,
£(х) = НОК{М(1)(х), М(2)(х), М(5)(х), М(7) (х)}, что совпадает с порождающим многочленом для кода с конструктивным расстоянием 9.
Этот\пример показывает, что код БЧХ с конструктивным рас-стоянием б может совпадать с кодом БЧХ с конструктивным рас стоянием б', где б'>б. Наибольшее возможное такое б7 называется расстоянием Боуза. Согласно границе БЧХ истинное мини мальное расстояние кода равно по меньшей мере б', но, как показывает следующий пример, может быть и больше.
На рис. 7.4. приведены двоичные (непрцмитивные) коды БЧ> длины n=t23. Циклотомические классы имеют вид:
Ро={0};
Vi = {l. 2, 4, 8, 16, 9, 18, 13, 3, '6, 12};
Са = {5, 10, 20, 17, 11, 22, 21, 19, 15, 7, 14}.
Так как | GJ =11, то мультипликативный порядок 23 по модулю 2 равен 11 (см. § 7.5). Таким образом, х23+1 распадается на линейные множители GF(211) и а — примитивный корень степени 23 из единицы в GF(211)-
Над GF(2H) многочлен х23+1 согласно таблице на рис. 7.1 имеет следующее разложение:
х23 + 1 = (х + 1) Л4(1) (х) М(5) (х),
где
Л4(1) (х) = х11 + х9 + х7 + х? + х5 4- х+ 1;
ТИ(5) (х) = х11 + х10 + х® + х5 + х4 + х2 -ф 1.
Порождающим многочленом кода БЧХ с конструктивным расстоянием 6=5 при Ь=1 является
g(х) = НОК {М(1) (х) М(3) (х)}.
Но ТИ^^х) =ЛБ3>(х). Следовательно, g'(x)=7l4<1>(x) и проверочная матрица кода Н=(1, а, а2, ..., а22), где каждый элемент представляется двоичным столбцом длины 11. Размерность кода равна 23—degg(x) =42.
Согласно рис. 7.4 расстояние Боуза этого кода также равно 5. Однако, как мы увидим в гл. 20, этот код БЧХ эквивалентен коду Голея ^23, и его минимальное расстояние равно 7. Таким образом, минимальное расстояние этого кода больше его конструктивного расстояния, и это иллюстрирует тот факт, что граница БЧХ не является точной.
Конструктивное расстояние б Порождающий многочлен S (х) Размерность и—deg g (х) Истинное расстояние d
1 1 23 1
3 или 5 Л4(1) (х) 12 7
7, 9, .... 23 М(О(х)М<5)(х) 1 23
Рис. 7.4. Коды БЧХ длины 23
Мы вернемся к кодам БЧХ в гл. 9.
Упражнения. (22). Используя таблицу циклото.уических классов для п=63, найти размерности кодов БЧХ для 6=гЗ, >5, 7, 9, 11. То же самое проделать для п=51. '
(23) . Используя границу БЧХ, показать, что минимальное расстояние симплексного [2™—1, т]-кода с проверочным многочленом h(x)=M^l'>(x) равно d=2m~1.
(24) . Обобщение Хартманна и Тзенга границы БЧХ. Предположим, что нулями циклического кода являются элементы вида аь+г,с,+г2с2 для некоторых фиксированных целых чисед й и <+, взаимно простых с п, и всех й=0, 1, ..., б—1 и i2=0, 1,1 ..., s. Доказать, что минимальное расстояние циклического кода равно по меньшей мере 6 + s. (Таким образом, код имеет s+1 цепочек из б—1 последовательных нулей. Граница БЧХ получается отсюда как частный случаи при s = 0.)
Реверсивные коды. Определение. Код 4F называется реверсивным, если из (с0, ci, ..., сп-2, Cn-Je'g’ следует, что (cn-i, сп. 2, .... сь с0)е^, например {ООО, ПО, 101, 011} — реверсивный код. Ре-версивен также двоичный [15, 6, 6]-код БЧХ с порождающим многочленом g(x) =7И<-1>(х)Л1(0)(х)Л1(1>(х).
Упражнения*. (25). Доказать, что код БЧХ с Ь=—t и конструктивным расстоянием б=2/+1 является реверсивным.
(26) . Доказать, что циклический код реверсивен тогда и только тогда, когда все элементы, обратные корням его порождающего многочлена, также являются корнями порождающего многочлена.
(27) . Доказать, что если —1 равна некоторой степени q по модулю п, • то каждый циклический код над GF(q) длины п реверсивен.
(28) . Коды Меласа, исправляющие две ошибки. Используя упражнение (24), показать, что если m нечетно, то минимальное расстояние двоичного реверсивного [п=2’к—1, k=n—2m]-кода .с порождающим многочленом g(x)=K[(~^(x)Xl(i)(x) не меньше 5.
(29) . Коды Цеттерберга, исправляющие две ошибки. Пусть n=22’ + l(i>l) и пусть aeGF(24i)—примитивный корень степени п из единицы. Используя опять упражнение (24), доказать, что многочлен g(x) = ЛГ1> (х) порождает реверсивный код с d^5.
(30) . (Коржик). Показать, что если h(x) делится на хт—1, то минимальное расстояние не может быть больше чем njT.
7.7. ИСПОЛЬЗОВАНИЕ МАТРИЦЫ НАД GF(qm) ДЛЯ ЗАДАНИЯ КОДА НАД GF(q)
В данном параграфе более подробно изучается вопрос о том, как матрица над большим полем GF(qm) может быть использована для задания кода над маленьким полем GF(q).
Предположим сначала, что код задан проверочной матрицей Н над GF(qm). Более точно, пусть Н =(//;;), где Н—(гХп) — матрица ранга г над GF(,qm). Здесь НF(qm) для ls^i«S+;
l^j^n\ Пусть далее wH— код над GF(q), состоящий из всех векторов\а= (щ, ..., ап); at^GF(q) таких, что Нат=0.
Другим способом получения является следующий. Выберем базио аь ат поля GF(^m) над QF(q) и запишем:
i т
Н^ = ^Н1па1, HiU&3F(q).
' ) 1=1
Определим Н как (rmХп)-матрицу, которая получается из Н путем замены каждого элемента Я,-,- соответствующим вектор-столбцом (Ягд, , над GF(q). Таким образом,
/^111 ^121 Н1п1
1 ^112 ^122 • Н1П2
н = j Н1п1П
11 rim нгпт I
Тогда
п
V Н^а3 = 0 для г=1, 2,
н
п
= 0 для i = 1, -, г; I — 1, • - •, т;
/=1
й „Т_п
Таким образом, для определения <Й’Н можно использовать и Н и Н. Ранг Н над GF(.q) не превосходит гт, так что в предположении, что гт^п, н является [n, k^n—rm]-кодом.
Мы можем также рассмотреть код 'Ян над GF(qm), состоящий из всех векторов Ь= (6Ь ..., bn), bi^GFiq") таких, что НЬТ=О. Тогда ё’н является [п, п—>г]-кодом над GF(q™). Так как GF(q) <^GF(qm), то каждое слово из (ё’н лежит и в коде Я* . Код н состоит точно из тех слов кода 'g7*, все компоненты которых лежат в поле GF(.q). Введем для этого следующее обозначение:
(7.22)
и будем называть код ограничением кода на подполе
(иногда 'й’д называют подкодом ё" # над подполем)1.
В общем случае, если —некоторый [п, &",/Я]-код над GK(^n), то его ограничение на подполе <ё# \GF(q) является [n, k, (ZJ-кодом, где п— пг(п—k#)^k^k*rn d^d1'.
1 Подчеркнем, что ^^\GF(q) является линейным пространством над GF(q) и не является таковым над GF(qm). (Прим, перев.)
Например, пусть 'g’*—{7, 6, 2]-код БЧХ над GF(23)lc порож-дающим многочленом х+а, где а — примитивный элемент поля GF(23). Пусть ‘g’— ограничение 'g’* |GF(2). Кодовое слово а(х) = = (х+а) (х+а2) (х+а4) = х3+х+1 лежит в ‘g’ * ив?. Следовательно, ‘g? содержит [7, 4, 3]-код <3^3. .На самом деле ’ё’—Звз, так как минимальное расстояние кода ‘g’ равно по меньшей мере 2.
Для определения кода, дуального ‘g’ * | GF(q), чер^з код, дуальный ‘g’ # , удобно воспользоваться следом Тт, отображающим поле GF(qm) в поле GF(q). След Тт определяется (равенством
Тт(х) = х + хч+ хч2 + -+хч , x^GF(qF)
(см. § 4.3). Пусть Тт(&#) —код над GF(q), состоящий из всех различных векторов .вида (
7’m(b) = (7’m(61), • • -, Tm(bn)), ЬеГ. (7.23)
Тогда T'mCg'*) является [п, k, с!]-кодом над GF(q), k# ^.k^. ^.mk# и d^d# и называется следом кода ‘g2".
Теорема 11. (Дельсарт.) Дуальным к ограничению кода на подполе является след от кода, дуального исходному коду, или
№ \GF(q)Y = Тт((Г)х). (7.24)
Доказательство, (i). Tm{ (‘g’* )->-) сд(^ * | GF(q))х. Для доказательства этого включения мы должны показать, что если а принадлежит левому подмножеству, то а-с=0 для всех ce'g’* | GF(q). Действительно, afTm^), ..., Tm(bn)) для всех Ье(^# )->-. Следовательно,
а-С = 2 Tm (&i) Ci = Тт (S М = Тт (0) = °-7=1 \1=1 /
(И). (Г |ОЕ(?))хсТ„ЖТ)
или, что эквивалентно,
СМОЛОЙ c<g*|GF(9). (7.25)
Для доказательства этого включения мы должны показать, что если а принадлежит его левой части, то ае®’*. По определению а-с=0 для всех c=(Tm(b1)), ..., Tm(bn), где Ье^*)1. Если be('g’'' )-L, то и %Ь принадлежит (‘g’ #)х три всех ~k^GF (qm). Следовательно, для всех %eGF(^m) имеет место
£ аДт (К bt) = T,Jb 2 “th ) = °-
7 = 1 \ 7=1 /
так что
ci^bf — 0 и i i
7=1
Напрймер, порождающий многочлен дуального упомянутому выше [7,\ 6, 2]-коду равен (х7+1)/(х-Р1)=х6 + а6х5-|-а5х4 + а4х3-|-+ a3x2+aU-!-a. След этого элемента равен х6-!-х3+х+1 и мы получаем таким, путем [7, 3, 4]-код
Упражнения. (31). Пусть С — обратимая (гХг)-матрица над GF(qm и пусть Ht = CH. Показать, что %? = ^н, т. е. что
матрица Ни СН задают один и тот же код.
(32) . Задача, обратная предыдущей: пусть ‘g’—[п, &]-код над GF(q). Доказать, что если riri^n—k, то существует (гХп)-матрица Н над полем GF(qm) такая, что <ё=(ё
(33) . (a)J. Пусть ‘g’ * —циклический код над GF(</in) с нулями а’, где ie/flii a^GF{qs}. Доказать, что Я? # \ GF(q) является циклическим кодом с нулями аг, а’е, а’®2, ..., , где 1^.К.
(Ь). Для иллюстрации пункта (а) выберем в качестве ^*[7, 5]-код над GF(23), с порождающим многочленом (х + a) (х-Ра2), где а — примитивный элемент поля GF(23). Показать, что ‘g? *|GF(2)=<^3.
7.8. КОДИРОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
В этом параграфе описываются два кодирующих устройства, которые пригодны для произвольного циклического кода. Схемы иллюстрируются двумя примерами.
Примеры. (Е1). [15, 11, 3]-код Хэмминга <9^4 — циклический код с порождающим многочленом g(x)=x4+x+l.
(Е2). [15, 7, 5]-код БЧХ, исправляющий две ошибки, — циклический код с порождающим многочленом
g (х) — (х4 + х + 1) (х4 + Xs + х2 + х + 1) = х8 + х7 4-х6--!-.х4+ 1.
Предположим, что сообщение кодируется кодом (Е1) и соответствующее кодовое слово равно:
С = Cq, • • •, С3 , СД
, Проверочные Информационные
символы символы
(см. рис. 7.5).
Проверки Сообщения
Сообщение
Рис. 7.5. Кодирование сообщения систематическим кодом
Кодер 1. В первой схеме кодера требуется degg(x) элементов задержки. Вектор с принадлежит коду тогда и только тогда, когда с(х) делится на g(x)=x4+x+l. Следовательно, мы
Должны выбрать проверочные символы с0,сз так, что^ы это ус-ловие удовлетворялось. Одним из способов такого выбора является деление I
с' (х) = сихи + х13х13 + • 4- с3х4 I
на х4 + х + 1 и нахождение остатка г(х) =г3х3+ ... -'-Го. Полагая затем Сг=г, (i=0, 3), получаем с(х) =с'(х) +г(х),1 делящийся
на х4+х+1. /
Для реализации способа необходимо устройство, выполняющее деление на х4 + х+1. Простой пример показывает, как сконструировать такое устройство. Предположим, что надо разделить х9-|-х8ч-х5+х4 на х4+х-|-1, используя лишь коэффициенты (т. е. вместо х4 + х-\-1 запишем 10011 и т. п.):
110110 = частное ’
1001111100110000 = делимое
10011 ”10101 » 10011
01100
00000
11000
10011
ЮНО
10011
01010
00000
1010 = остаток
Частное равно х5+х4+х2+х, и остаток равен г(х)=х3+х.
Ключевое замечание состоит в том, что каждый раз, когда в частном появляется 1, делимое меняет содержимое третьей и четвертой позиции на противоположное.
Устройство, выполняющее это вычисление, показано на рис 7.6.
Остаток (0101 =х+х3) равен тому, что оказывается записанным в регистре (слева направо), когда делимое полностью введено.
Рис. 7.6. Схема деления на х4+х+1
Итак, йаша первая попытка закодировать данные состоит в том, чтобы! ввести делимое (информационные символы, за которыми следуют нули) 0000 с4,' с5, ..., сц.
После в^ода всех 15 символов в регистре получаем остаток С0С1С2С3. Подран схема кодера, выполняющего эту операцию, показана на рйс. 7.7.
Рис. 7.7. Предварительный вариант кодера 4М
Каждый из ключей имеет три позиции: в положении А ключ находится 11 тактов, в течение которых сообщение вводится в канал и регистр; в положении В ключ находится четыре такта, в течение которых в регистр вводятся четыре нуля; в положении С ключ .находится четыре такта, в течение которых в канал подается остаток.
Недостатки этой схемы очевидны: канал простаивает, когда ключи находятся в положении В.
Для устранения этого недостатка будем подавать информацию в правый конец регистра сдвига. Это эквивалентно предварительному умножению на х4. Поэтому вместо схемы деления, приведенной на рис. 7.6, будем использовать схему, показанную на рис. 7.8. Остаток теперь формируется в регистре сдвига, как
Частное
с^-- • С к
Рис. 7.8. Схема деления с предварительным умножением на х4
только символ с4 введен в него. Окончательный вариант кодера представлен на рис. 7.9. Ключи находятся в положении А в течение 11 тактов работы и в положении В — в течение четырех тактов.
Ясно, что кодер такого типа годится для любого циклического кода, и необходимый регистр сдвига содержит degg(x) элементов задержки. На рис. 7.10 показан кодер для примера (Е2).
Кодер =|ф 2. Для второго кодера требуется deg/z(x) элементов задержки. Мы уже отмечали ранее, что проверочные символы определяются уравнениями (7.11).
Для примера (Е2)
/г(х) = (х15 + 1 )/g (х) = (х + 1)(х2 + х-|- 1) (х4 + х3 + 1) = х7 + х6-гх4 +1.
Таким образом, кодовое слово удовлетворяет уравнениям:
Рис. 7.10. Кодер # 1 Для кода БЧХ
Если 014, ..., с8 — информационные символы, то эти уравнения определяют проверочные символы с7, се, ..., Со. Соответствующее кодирующее устройство показано на рис. 7.11. Ключ находится в положении А в течение семи тактов работы и в положении В — в
Рис. 7.11. Кодер # 2 для кода БЧХ
течение восьми тактов. Устройство показано в момент, когда только что введен последний информационный символ с8 и вычисляется первый проверочный символ с7=с8+сю+с14.
Ясно, что кодер # 2 пригоден для произвольного циклическо-го кода и использует регистр с deg/z(x)=n—degg(x) элементами задержки. Часто выбор кодера определяется требованием минимальности числа элементов задержки.
Упражнения. (34). Построить кодер 4J3 2 для примера (Е1).
(35). (а). Показать, что кодер 1 соответствует порождающей матрице вида
аоо а01 0, г—1
G1 = аю «И - - -a. . 1, Г“1
(7.26)
а. . п а. . . • • -а. . . О
h—I, 0 h—I, 1 h—1, г—1
О”
1
1
в том смысле, что если на вход кодера 1 подается сообщение u=tzo«i — Uk-i=cn-kCn-k+i ... c-n-i, то на его выходе формируется кодовое слово c=uG!. Здесь многочлен — остаток aio + atlx + + ... + tZi,r-i%r-1 является остатком от деления х’’+г на g(x) при i=0, ..., k—1. Таким образом, (7.26) получается из (7.1) путем диагонализации последних k столбцов. Если записать (7.26) в виде 61=[А,|1], то соответствующая проверочная матрица будет иметь вид: Н1 = [1|АГ1].
(Ь). Аналогично показать, что кодер 2 соответствует проверочной матрице вида
= [I j В2]
(7.27)
и порождающей матрице вида G2=[Br2| I], где -i-bi:fl_2xk~2-l- ... +bio — остаток от деления на h(x) для t=0, ..., г—1. Таким образом, (7.27) получается из (7.9) путем диагонализации первых г столбцов.
Вычисление синдрома. Техника декодирования циклических кодов будет рассматриваться в § 9.6 (коды БЧХ), 12.9 (альтер-нантные коды), 13.7 (PM-коды) и 16.6 (циклические коды общего вида и, в частности, квадратично-вычетные коды). Во всех случаях первый шаг алгоритма декодирования состоит в вычислении синдрома, которое по существу представляет собой перекодирование полученного вектора (см. § 1.4). Если код используется только для обнаружения (не для исправления) ошибок, то этим работа приемного устройства и ограничивается.
Упражнения. (36). (а). Предположим, что полученный вектор у=г/о*/1 — Уп-i вводится в кодер # 1- Пусть SoSi — Sr-i — 'Содержимое регистра сдвига в момент, когда все п символов у уже введены. Показать, что S=i(so«i — Sr-i)r удовлетворяет условию S = Hiyr и, следовательно, является синдромом вектора У- [Указание. Записать у в виде у(х) = (уо+ — + yk-ixh~l) +
-\-(ykxh + ... +yn-^~l)=yb(x)+yt(x) И y(x)=q(x)g(x)+$(x), тогда s(x)=Ssixi=f(x) + f/b(x) и т. д.]_
(b). Показать, что после одного дополнительного такта работы регистр .сдвига содержит синдром, соответствующий вектору ху(х) — циклическому сдвигу вектора у.
(с). Если для вычисления синдрома использовать кодер # 2, то схема рис. 7.11 должна быть немного изменена так, как это показано на рис. 7.12. Показать, что схема рис. 7.12 действительно вычисляет синдром S=H2yr. В положении А ключи находятся четыре такта работы, >в течение которых в регистр сдвигов вводятся (возможно искаженные) информационные символы.
Рис. 7.12. Модифицированный кодер # 2, предназначенный для вычисления синдрома
Затем ключи перебрасываются в положение В, где они остаются в течение трех тактов работы устройства, и на выход подается синдром S.
ЗАМЕЧАНИЯ К ГЛ. 7
§ 7.2. По-видимому, впервые циклические коды изучались Пренджем [1074—1077] (см. также Абрамсон [2]).
§ 7.3. Дополнительные сведения о кодах Хэмминга и связанных с ними кодах можно найти в работах: Абрамсон [1], Азуми и Касами [55], Боуз и Бартон [180], Кок [296], Форрел и Эль-Бендер [419], Голей [512], Ксяо [667], Ван Линт [848, 855], Лайтл [867],'Марковиц [913], Питерсон и Уэлдон [1040], Санкар и Кришнамурти [1143], Стирзакер и Юен [1281].
Две комбинаторные задачи, связанные с совершенными кодами, в частности, с недвоичными кодами Хэмминга — задача о взвешивании монет и задача о футбольном тотализаторе, детально рассмотрены в работах: Беллман [101], Голей [510], Кампе и Ван Линт [712, 713], Катона [748], Ван Линт [855], Стентон [1265], Стентон и др. [1267], Заремба [1452, 1453] (см. также нерешенные задачи приложения А).
Укороченные циклические коды: Питерсон и Уэлдон [1040, § 8.10], Токура и Касами [1332]. Касами [728] показал, что эти коды лежат на границе Вар-шамова — Гилберта.
§ 7.5. Делители многочлена хп~' над полем действительных чисел называются циклотомическими многочленами (см. Берлекэмп [113], Куршан [788], Лехмер [811], а также [1200]). Упражнение (20) может быть сформулировано для циркулянтных матриц над произвольным полем (см. Мюир [974]). Лемма 7 является. частным случаем формулы обращения для характеров абелевой группы (см. Манн [907]).
§ 7.6. Двоичные коды БЧХ были открыты одновременно Боузом и Рой — Чоудхури [184, 185] и Хоквингемом [658]. Недвоичные коды предложены Го-ренстейном и Цирлером [552]. Левинсон [826] дал краткое описание кодов БЧХ (см. также Лум [863]). Упражнение (24) взято у Хартманна и Тзенга [615] (см. также Хартманн [608, 610]). Что касается реверсивных кодов, см.
Хартманн и Тзенг [615], Хонг й' Боссен [661], Месси [919], Мелас [953], Тзенг и Хартманн [1350] и Цеттерберг [1455]. Упражнение (30) взято из работы Коржика [778].
Коды БЧХ не всегда являются лучшими циклическими кодами. Например, Чень [266] нашел [63, 45, 8], [63, 24, 46] и [63, 28, 15] циклические коды, которые лучше кодов БЧХ (см. рис. 9.1) (см. также Берлекэмп и Юстесен [127] и приложение А).
§ 7.7. Теорема 11 взята из работы Дельсарта [359].
§ 7.8. В описании техники кодирования мы следовали Питерсону и Уэлдону [1040], давшим прекрасное изложение дискретных устройств.
Глава 8
Циклические коды (продолжение): идемпотенты и многочлены Мэттсона—Соломона
8.1. ВВЕДЕНИЕ
В этой главе продолжается исследование циклических кодов, начатое в гл. 7. В § 7.2 мы видели, что циклический код состоит из всех кратных порождающего многочлена g(x).
Другим полезным многочленом, принадлежащим всякому циклическому коду, является его идемпотент Е(х), определяемый равенством Е2(х) =Е (х) (§ 8.2). (Иногда оказывается легче найти идемпотент, чем порождающий многочлен.) Наименьшие циклические коды являются минимальными идеалами (§ 8.3). Они представляют интерес по нескольким причинам: (i). Любой циклический код представляет собой сумму минимальных идеалов (теорема 7). (ii). Минимальный идеал изоморфен полю (теорема 9). (iii). Минимальные идеалы содержат важное семейство симплексных кодов.
Группа автоморфизмов кода (т. е. множество всех перестановок координат, относительно которых код инвариантен) рассматривается в § 8.5. Эта группа играет важную роль при выяснении структуры кода и его декодировании.
, Полезным аппаратом для вычисления весового спектра кода является преобразование Мэттсона — Соломона (МС-многочлен) (§ 8.6). В последнем параграфе главы это преобразование используется для вычисления весов некоторых циклических кодов.
Во всей главе ‘g’ обозначает циклический код над GF(q) длины п, где п и q взаимно просты. Как и в § 7.5, т — мультипликативный порядок q по модулю п и u^GF (qm) —примитивный корень степени п из единицы. Также Rn—кольцо GF(q) [х]/(хп—1) всех многочленов с коэффициентами из GF(q), степень которых —1.
' 8.2. ИДЕМПОТЕНТЫ
В § 8.2—8.4 мы ограничимся случаем двоичных кодов длины и, где п — нечетное число.
Определение. Многочлен Е(х) кольца Rn называется идемпотентом, если Е (х) =£2(х) =Е (х2).
Например, х+х2+х4— идемпотент -в Д7, так как (х+х2+х4)2= = х+х2+х4. Многочлены 1 и х3+х6+х5 также являются идемпо-п—1
тентами. В общем случае Е (х) = е; хг
1=0
— идемпотент тогда и только тогда, когда ei = esi (индексы берутся по модулю п). Таким образом, множество показателей степени ненулевых членов представляет собой объединение циклотомических классов.
Ясно, что если Е(х)—идемпотент, то 1-|-£'(х)—также идемпотент.
Теорема 1. (i). Циклический код, или идеал <g’=<g(x)>, содержит единственный идемпотент Е(х) такой, что <СЕ(х) >. Кроме того, Е (х) = р (х) g (х) для некоторого многочлена р(х) и £'(ai)=0 тогда и только тогда, когда ^(сТ^—О.
(ii). c(x)e‘g’ тогда и только тогда, когда с(х)Е(х) =с(х).
может содержать несколько идемпотентов, но только один из них порождает Ф’.)
Доказательство. Пусть хп 4-1 = g (х) h (х), где g(x) и h(x) взаимно просты. Легко доказываемое следствие из алгоритма Евклида (следствие 15 гл. 12) состоит в том, что тогда существуют многочлены р (х) и q (х) такие, что в кольце 77[х]
p(x)g(x) + q(x)h(x)= 1. (8.1)
Положим E(x)=p(x)g(x). Тогда из (8.1) следует, что
Р W g (х) [р (х) g (х) + q (х) h (х)] = р (х) g (х),
т. е. в кольце Rn Е2(х)-|-0=Е'(х), так что Е(х) —идемпотент. Корень степени п из единицы является корнем только одного из многочленов g(x) или /г(х). Из (8.1) следует, что многочлены р(х) и h(x) взаимно просты. Поэтому если какой-то корень степени п из единицы является корнем многочлена р(х), то он также должен быть и корнем g(x). Так как р(х) не вводит новых нулей, то согласно лемме 5 гл. 7 многочлены £(х) и g(x) порождают один и тот же код.
Для доказательства п. (ii) заметим, что из равенства с(х) = = с(х)Е(х), очевидно, следует, что с(х)е<?’. Обратно, если с(х)е то с(х) =’Ь(х)Е(х) и c(x)£(x)=i&(x)E'2(x)=&(x)E'(x)=c(x).
Наконец, для доказательства того, что Е(х) — единственный идемпотент, порождающий ‘g’, предположим, что существует другой такой идемпотент К(х). Тогда согласно п. (ii) имеем: К(х)£(х)=К(х)=£(х). ®
Например, для [7, 4, 3]-кода Хэмминга имеем: g(x)=x3 + +х-(-1, й(х) = (х+1) (х3+х2+1) =х4+х2-|-х-|-1 и xg(x) 4~/i(xj = 1-
Таким образом, идемпотент этого кода равен E(x)=xg(x) = =х4 + х2+х.
Упражнение. (1). Убедитесь, что Е(х) действительно порождает этот код.
Лемма 2. Е (х) является -.идемпотентом тогда и только тогда, когда E'(iai)=0 или 1 для всех i.=r=0, —1.
Доказательство. Предположим, что Е (х) -- идемпотент. Тогда £2 (ц*) = Л (та7), Так что согласно теореме 8 гл. 4 эта величина равна 0 или 1. Для доказательства обратного утверждения предполо-п— 1
ЖИМ, ЧТО Е (х) = 2 е{Хг‘. i =0
Так как Л (а3) равна 0 или 1, то Л (та23) =Л2(та3’) =Е(<Д). Согласно формуле обращения из леммы 7 гл. 7
ег = J Л (а7) а~ч = V \ а~1', /=о s jecs
где s пробегает некоторое подмножество циклотомических классов. Следовательно, ei = esi и Л(х) — идемпотент. •
Следствие 3. Размерность ‘g’ равна числу элементов таг, для которых g(aY)=T^0, и равна числу элементов а7, для которых Л(а’) = 1.
Упражнение. (2). Доказать, что g(x) = (Е(х), хп+1), где (а, Ь) обозначает наибольший общий делитель чисел а и Ь.
По многочлену а(х) =ao+aix+ ... +an^txn '1 определим многочлен а* (х) =ao + an-ix+ ...+aiXn~l (так что постоянный член остается без изменений, а остальные члены выписываются в обратном порядке). Ясно, что a(a-1) = а* (а).
Лемма 4. Если Л(х) — идемпотент, то Л*(х) —также идемпотент.
Доказательство. Если Л (х) = V V х', s iecs то
£*(x) = V V х1. s /ec_s
Теорема 5. Пусть ‘g’ — код с идемпотентом Л(х). Тогда код <^’± имеет идемпотент (1+Л(х))*.
Доказательство. Пусть аь ... ,тап — корни степени п из единицы; предположим, что аь ..., at — нули кода ‘g’, т. е. что Л(та<) =0 для и Л(аг) = 1 для t+ 1Тогда элементы щ-ы,..., an являются корнями многочлена 1 + Л(х), а элементы a-1t+i, ... •-.,an“1— корнями многочлена (1+Л(х))*. Но согласно теореме 4 гл. 7 эти же элементы являются нулями кода <g’±. •
Упражнения. (3). Доказать, что 1+Л(х) является идемпотентом кода с порождающим многочленом /г(х).
(4). Найти порождающий многочлен и идемпотент для всех Циклических кодов длины 15 и установить, какие из них являются
8.3. МИНИМАЛЬНЫЕ ИДЕАЛЫ, НЕПРИВОДИМЫЕ КОДЫ И ПРИМИТИВНЫЕ ИДЕМПОТЕНТЫ
Минимальным называется идеал, который не содержит никакого меньшего ненулевого идеала. Соответствующий код называется минимальным или неприводимым кодом, а его идемпотент — примитивным. Мы увидим, что каждый идемпотент равен сумме примитивных идемпотентов и что каждый вектор из Rn однозначно записывается в виде суммы векторов из минимальных идеалов.
Множество ненулей минимального идеала должно быть множеством вида {а® : ieCs} для некоторого циклотомического класса Cs. Мы обозначим этот минимальный идеал через Ms, а соответствующий примитивный идемпотент через 6S, и часто будем пользоваться записью j^s—<zQs>- Таким образом,
6s (а7) = / 1 ’ еСЛИ 7 е Cs’ (8.2)
[ 0 в остальных случаях.
В частности, единственный ненуль многочлена 6о(х) равен х=1 и
й0(х) = (хп + 1)/(х+1) = У*/.
i=0
Точная формула для 6s(x) может быть получена с помощью формулы обращения из леммы 7 гл. 7.
Теорема 6.
п—1
(*) = V ег х1,
i=0
где ez= Va“'7 для i > 0.
/ecs
Доказательство. Согласно лемме 7 гл. 7 имеем:
ег = У 6S (а7) а~4 = V аГ1’. •
i=o fecs ‘
Например, для п=7 коэффициенты многочленов 91 и 6з равны:
i 1 —-i i 4z.
1 I 8j — CC —|— OS —CC f
e' z i " "-бi i * 5z 3 • 8j === (X —j— CC —|— CC
Так как 7=23—1, то а в данном случае является примитивным элементом поля GF(23).
Упражнения. (5). Используя таблицу поля GF(2S) на рис. 4.5, показать, что 60= 1 +х+ ... НН*6; 6i = 1 +x+x2+*4; 9з=1 + +*3+*6'+*6-
(6). Показать, что если, поле GF(2s). задать равенством а3+ +а2+1=0, то многочлены 61 и 63 меняются местами.
1аким ооразом, исиользов ние различных многочленов для задания поля приводит к переупбрядочиванию примитивных идемпотентов.
Теорема 7. Примитивные идемпотенты удовлетворяют условиям:
(i) . у ее = 1.
s
(ii) . е.б^О, если г#=/.
(iii) . Кольцо Rn равно прямой сумме минимальных идеалов, порождаемых идемпотентами 6S. Таким образом, любой вектор а(х) из Rn может быть однозначно записан в виде 2 as(x), где
S
as(x) лежит в идеале, порожденном многочленом 6S.
(iv) . Любой идемпотент Е(х) может быть записан в виде ущ0к для некоторых as^GF (2). Наоборот, всякий многочлен та-S
кого вида является идемпотентом.
Доказательство, (i). Согласно лемме 6 гл. 7 имеем: п—1 п— 1 п—1
у 0S = у / у г,) \ ? = у х(г) у а~г/ = 1.
s 1=0 \ /eCs / i=0 i=o
(ii). Пусть Жг и ЛД— минимальные идеалы с- идемпотентами 6г и 0,. Идеал Mi Г) является собственным подыдеалом в ЛД и поэтому равен нулю. Так как 0г6,<=Л7г f] Лд то 6i0j = 0.
(iii). Из п. (i) вытекает, что
а (х) 1 = а (х) V 6S = V as (х),
S S
где as(x) лежит в идеале, порожденном идемпотентом 6S.
(iv),. Множество элементов, не являющихся корнями многочлена Е(х), совпадает с объединением множеств ненулей соответствующих минимальных идемпотентов. Поэтому результат следует из леммы 2 и формулы (8.2). Обратное утверждение вытекает из п. (ii).
Многочлен 0*s (х) также является примитивным идемпотентом, и, следовательно, существует такое наименьшее целое число s', при котором 0*s(x) =0S (х). Таким образом, s'eC_s. Множество {аг: teC_s} равно -множеству элементов, не являющихся корнями многочлена 0*s(x).
Если n=2m—1, то 0г(х) порождает [2m—1, m, 2™"1] симплексный код 9!m=^ym и имеет вес, равный 2m~l. Все ненулевые кодовые слова исчерпываются 2™—1 циклическими сдвигами многочлена 01 (х). Если п=2т—1 и s взаимно просто с т, то as также является примитивным элементом и, следовательно, порождает код, эквивалентный коду S^m- Это дает другое доказательство того, что если й(х)—некоторый примитивный многочлен, то код с проверочным многочленом Л(х) эквивалентен коду Дт-
Упражнения. (7). Используя таблицу поля GF(24) на рис. 4.2, показать, что примитивные идемпотенты для п=15 равны:
ей = е;=х14+х13+ • . .+x2+x+i;
0х = 6* — х12 4- х9+х9 + %® + х4 + х9 + ха + х;
е7 = 6’ = х14 + X13 + X12 + X11 + х9 + х7 + х® + х3;
е3 = е; = (%14+х13+х12+х11)+(х9+х®+х7+х6) +
+ (х4 Ц- х3 + х2 + х);
е5 = е;=(х14+х13)+(х11+х10)+(х8+х7)+(х6+х4) +
+ (х2 + х).
(8) . Аналогично показать, что примитивные идемпотенты для п = 31 равны (выписаны только показатели степеней ненулевых членов многочлена):
оо = о;=(о, 1, 2, • -, зо);
ех = е75 = (О, 5, 7, 9, 10, И, 13, 14, 18, 19, 20, 21, 22, 25, 26, 28);
ез = о; = (О, 3, 6,*7, 12, 14, 15, 17, 19, 23, 24, 25, 27, 28, 29, 30);
е5 = е;1==(0, 1, 2, 4, 5, 8, 9, 10, 15, 16, 18, 20, 23, 27, 29, 30);
07 = е* = (0, 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 17, 19, 24, 25, 28);
е11.= 0* = (0, 1, 2, 4, 8, 11, 13, 15, 16, 21, 22, 23, 26, 27, 29, 30);
е15 = е; = (о з, 5, 6, 9, ю, п, 12, 13, 17, 18, 20, 21, 22, 24, 26).
Примитивные идемпотенты для п=63 приведены на рис. 8.1. Здесь идемпотенты выписаны в двоично-восьмиричной системе,
61 = 3 2 1 02625 1 03 = 012231 301 е5 = 044 1 60277 0, = 044 04 40 44 09 = 7235 1 6472 0п = 0 1 0305 172 013 = 375263355 016 = 3 2 3 1 1 2032 021 = 333333333 023 = 3 3 1 3 2 7 3 6 3
02? = 4 56 2 7 1 34 5
031 =3 7 5 3 4 3 1 6 6
170156307277 22313 0122313 124317353233 044044044044 351647235164 162267315277 1 16136243020 311203231120 333333333333 052375016044 627134562713 036225150213
Рис. 8.1. Примитивные идемпотенты для и=63
причем слева расположены элементы наименьших степеней, например 6i=x+x2+x4+x8+x13+...
(9) . Найти примитивные идемпотенты кольца для п—5, 7, 9, 11.
(10) . Если Ei — идемпотент идеала Ai и Е2 — идемпотент идеала А2, то: (а) Е\Е2 — идемпотент идеала Д1ПД2; (Ь) Ти+ЕгЧ-+EiE2 — идемпотент идеала Ar U Л2 (наименьшего идеала, содержащего и Л] и А2).
(11) . Если идемпотент кода ‘g’ равен 0.гЧ-6.7 + ... Ч-бь, то все не-нули кода ‘g’ исчерпываются элементами а® для i^Ci U Cj U ••• U [J Cfe. Если идемпотент кода ‘g’ равен 1 + 0,i + 0j+ ... Ч~6&, то все нули кода 7? исчерпываются элементами а4 для i^Ci (J Cj [J ... [J U ck.
(12) . Показать, что идемпотент кода Хэмминга равен 1+ 4-0i(x) и что идемпотент |[2™—1, 2m—1—2m, 5]-кода БЧХ, исправляющего две ошибки, равен 1 +0i(x) Ч-0з(х).
(13) . Исследовать [9, 6, 2] неприводимый код с идемпотентом 0i(x) =х3+х6. Найти все слова кода и показать, что его распределение весов имеет вид: Ло=1; Ла=9; Л4=Л6=27.
(14) . Два кода ‘g’l и длины п называются непересекающими-ся, если П Т?2=0. Пусть ‘g’l и — циклические коды соответственно с идемпотентами Е\ и Ег и порождающими многочленами ё\ и ёг-
(i) . Доказать, что ‘g’l и Т»2 не пересекаются тогда и только тогда, когда в записи Е\ и Ег в виде сумм примитивных идемпотентов 0.,- (см. теорему 7) не содержится общих идемпотентов.
(ii) . Доказать, что ‘g’l и с&2 не пересекаются в том и только в том случае, когда (хп +1) | ё\ё%-
(iii) . Доказать, что di-st(‘®’i, ТЧг) =rnin{dist(u, v) :
uy=0, vy=0} и равно минимальному расстоянию кода с порождающим многочленом НОД{£1, ё%} и идемпотентом Д + Е2 + Е\Е2.
(15) . (Лемпель.) (i). Пусть т]8(х) = х< Доказать, что iecs
T]s(я) (1+T]s(x)) =T]s<0)(x) (l+xn), где T]s(0)(x) —сумма по всем нечетным степеням переменной х, содержащимся в щ(х).
(ii). В условиях теоремы 6 доказать, что е7=бг-т],4(ю-1), где б< = =0, если m/\Ci\ четно, и б7=1, если т/|С7| нечетно. (Напомним, что т= | С] |.)
(16) . Доказать, что всего имеется q>(n)/m минимальных идеалов, эквивалентных коду (и такое же число циклических кодов, эквивалентных коду 3>ёт), где ср(п) —функция Эйлера, определенная в упражнении (8) гл. 4.
(17) . Пусть Е(х)—некоторый делитель многочлена хп+1. Пусть Е (х) — идемпотент идеала с порождающим многочленом g(x) = (х" + 1)/Е(х). Доказать, что
Е(х)Нх"+1)Ру7 + б),
\ h(x) /
где h'(x) —производная от h(x) и 6=0, если h(x) —многочлен четной степени, и 1, если степень h(x) нечетна. Иными словами, доказать, что
Е (х) = xdes h U)~’ g (x) r' (1/x),
где r(x) =xdegh(x)/i(l/x). [Указание. Показать, что degE'(x)^
—1. Затем доказать, что £'(ai) = l, если ft(cti)=O, и E(a.i)=0, если h(ai) #=0.]
Вырожденные циклические коды. Циклический код, состоящий из нескольких повторений кода с меньшей блоковой длиной, называется вырожденным. Например, код с повторением <0о> = {О, 1} вырожден, так как он состоит из нескольких повторений кода {0- 1)-
Упражнение. (18). Проверить, что при п=15 многочлены 0з
и 05 являются идемпотентами вырожденных идеалов. Найти размерности этих идеалов.
Лемма 8. Код <?g(x)> вырожден тогда и только тогда, когда его проверочный многочлен h(x) делит xr+1 для некоторого r<Zn.
Доказательство. Если код <Zg(x)> вырожден, то каждое его слово, включая*и g(x), представимо в виде s(x) (I +xr+x2r+ ... для некоторого г. Следовательно, г делит п (упражнение (11) гл. 4) и g(x) =s(x) (хп+ 1)/(хг+ 1); h(x) = (xr+l)/s(x).
Наоборот, пусть r<ji — наименьшее целое число такое, что h(x) делит хг+1. Тогда г делит п, так как в противном случае h(x) делит хг' + 1, где г'=(г, п). Следовательно,
+ I h(x)
g W
ХП -|- 1 Xr -|- 1 , , / , . г . , п—г\
------ ——-—— s(x)(l+x + • • -4-х ). хг + ] h (х)
Тогда каждое кодовое слово имеет вид a(x)s(x) (1+хг+х2г+ ...
...+хп-г), где по теореме 1 гл. 7 (iega(x)s(x) <2. г. •
Упражнение. (19). Показать, что для п= 15 и s= 1,5 или 7 код <0S> состоит из 0 и всех циклических сдвигов многочлена 0S. С другой стороны, код <03> состоит из векторов вида | и | и | и |, где и — кодовое слово [5, 4, 2]-кода с общей проверкой на четность. Алгебраически код <0з> состоит из всех элементов вида а(х) (x+x2-f-x3+x4) (1 +х5+х10), где dega(x)^3.
Замечание. Теперь у нас есть метод, позволяющий сказать, примитивен ли неприводимый многочлен h(x) степени m (см. § 3.2, 4.4). Построим идемпотент Е(х) = (xn + 1) (xh'(x)/h(x) +6), где n=2m—1 (упражнение (17)). Если все циклические сдвиги этого идемпотента различны, то многочлен h(x) примитивен; в противном случае код, порожденный многочленом Е(х), вырожден.
Упражнения. (20). Проделать эти операции для многочлена h(x) =х4+х3+х2+х+1.
(21) . Доказать, что:
(а) . Если (s, п) — 1, то |Cs|=m, deg А1(ч) (x) =m, размерность идеала <0«> равна m и он невырожден.
(b) . Если (s, n) >1, to идеал <0S> вырожден, его размерность делит т и может быть равной“т..
(с) . Если s взаимно просто с н=2те—1, то идеал <0S> состоит из кодовых слов 0 x;0s для i=0, 1,..., 2™—2.
. (22). Пусть Ч?— линейный код, в котором ни одна из координат не равна постоянно нулю и в котором имеется только один ненулевой вес. Доказать, что существует минимальный идеал Jt\ такой, что эквивалентен коду {|u|u| ... |u| ruejj-
Изоморфизм минимального идеала и поля. Теорема 9. Минимальный идеал размерности ms изоморфен полю
GF(2ms).
Доказательство. Для доказательства теоремы достаточно показать, что если йДх) и аДх) —элементы из Jfts и ai (х)аДх) =0, то либо пДх), либо аДх) равен нулю.
Предположим, что at (х) =?^0. Пусть Л’= (х) : Ь (х) а\ (х) =
= 0}.
Множество Д’ является идеалом. Так как Jts минимален и Л’аЖв-, то либо либо 7T=0. Согласно теореме 1 имеем:
0stzi (х) =а\ (х) и, следовательно, Таким образом, д2(х) =
=0. •
Например, идеал <0о> является сильно избыточным представлением основного поля GF(2).
Лемма 10. Изоморфизм <р между и GF(2 s). задается формулой а(х)‘₽=й(р), где а(х)е^#к и peGE(2 s)—примитивный корень степени п из единицы и является ненулем кода (Конечно, различные выборы р задают различные отображения).
Например, рассмотрим [7, 3, 4]-код и с идемпотентом 0i(x) =
= 1+х+х2+х4. Используя рис. 4.5, можно выбрать р = а, а2 или а4. Соответствующие отображения кода на поле GE(23) показаны на рис. 8.2.
Кодовое слово Элементы поля б/?(23)
0 1 2 3 4 5 6 а (а) а (а2) а (а4)
0 0 0 0 0 0 0 0 0 0
1110 10 0 1 1 1
0 1110 10 а а2 а4
0 0 1 110 1 а2 а4 а
10 0 1 110 а8 а6 а5
0 10 0 111 а4 а а2
10 10 0 11 а6 а8 а6
110 10 0 1 а6 а6 а3
—
Рис. 8.2. Три отображения кода на поле GF(2~}
Доказательство. Предположим для простоты, что p=as. Пусть g — примитивный элемент поля GF(2 ®), и рассмотрим отображение ф поля GF(2m) в Jts, задаваемое равенством
(8-3)
i=o
Покажем, что -ф обратно отображению <р. Обозначим правую часть равенства (8.3) через а(^(х). Покажем сначала, что с(г)(х)е
п—1 п—1 it I \
(с?) = V Tms ( Г a~'s) aik = J V Г a{k~s2 ) =
/=0 Z=0 /=0
I2l I
_ £ а, если k=s2 для некоторого Г,
0 в остальных случаях.
Таким образом, c(’)(aft)=0, за исключением случая, когда k<=Cf; следовательно, Отсюда сразу же вытекает, что
a<i>(x)<₽=c(i)(.p) =a=g’_
Согласно теореме 9 ср должно быть преобразованием, обратным ф, и оба они задают взаимно однозначное соответствие и являются отображением «на». Очевидно, <р также сохраняет сложение и умножение и, следовательно, является изоморфизмом. •
Идемпотент идеала Ms отображается в единицу поля GF(2 s). Если ci, c-^Jll, и Ci (х)с2(х) = 0s(x), то элементы с{ и с2 являются в взаимно обратными. (В кольце Rn, естественно, элементы ci и с2 обратных не имеют.) Заметим также, что (хй(х))ф=рй(р).
Идемпотенты циклических кодов над GF(q). Пусть — циклический код длины п над GF(q), где q и п взаимно просты. Элемент Е(х) кольца Rn (кольца GF(q) [х]/(хп—1)) называется идемпотентом, если Е(х)=Е2(х).
Упражнения. (23). Доказать, что в имеется единственный многочлен, который является одновременно идемпотентом и порождающим многочленом.
(24) . Доказать, что если Е(х) — идемпотент в 'iF, то (1— —Е (х)) * — идемпотент в 'g?±.
(25) . Доказать, что существует множество примитивных идемпотентов 0о, 01,..., 0г таких, что
t
0? = 0Z; 0г0,- = 0, если i=£j', V0;=I.
г=0
Показать также, что Rn распадается в прямую сумму минимальных идеалов, порожденных идемпотентами 0г-.
(26) . Доказать, что минимальный идеал размерности ms, порожденный многочленом 0S, изоморфен полю GF(q s).
8.4. ВЕСОВОЙ СПЕКТР МИНИМАЛЬНЫХ КОДОВ
Пусть — невырожденный минимальный циклический [п, Л]-код с ненулями р, р2,..., р2 . Кроме того, пусть ns=2k—1 и k — наименьшее целое число, для которого выполняется это равенство. (Таким образом, k=m.) Предположим, что s>l.
Пусть g— примитивный элемент поля GF(2h) и p = gs. Пусть Z (х)е'К— такое кодовое слово, что л(х)ч,=^. Тогда (хХ(х))ч>= = gs+1; п циклических сдвигов слова Х(х) соответствуют элементам g, £s+1, g2s+1, ••-, g<K~1)s+1. Таким образом, кодовые слова в К1, соответствующие элементам 1, g, g2, . ..,g®-1, образуют полное множество циклических представителей для и определяют весовой спектр кода
Способ нахождения циклических представителей. Рассмотрим [2/!—1, k] симплексный код 9^ с ненулями g, g2,..., g2fc~'. Кодовые слова из ff’h будем записывать в виде многочленов от у, где у&~i = i. Идемпотент кода ff’h равен:
2ft— 2
£(*/) = £ еуД i=0
Коэффициенты многочлена Е(у) могут быть упорядочены в ви-
де (sX^)-таблицы:
е0 . . .Р * c(n-l) s’
es+l • . t C(n-1) s+1’ (8.4)
es-l C2s+1 ’ ' 'ens~r
Пусть
п—1
Cj w = v ei+is хг для 0 < j < s— 1.
г=0
Теорема 11.
с} (х) е $ и с} (х)ч =
Таким образом, сДх) образуют множество циклических представителей кода
Доказательство.
с°(х)=2Z*(rSi} xi = х1'
i=0 1=0
что является идемпотентом кода Далее
мх)=2д(гуггЦг
и, следовательно, ®
Ясно, что произвольный циклический сдвиг идемпотента также даст множество циклических представителей кода. Циклический сдвиг идемпотента из 9^ легко может быть сформирован на выходе соответствующего регистра сдвигов (см. рис. 14.2, 14.3).
Например, [15, 4, 8] -код 54 порождается идемпотентом ООО 100 ПО 101 111 (см. уравнение (14.1) или упражнение (7) гл. 8).
В этом случае при s=3 и п—5 (8.4) приобретает вид:
0 1111
0 0 10 1 0 0 0 1 1, что сразу дает множество циклических представителей для [5, 4, 2] -кода.
Упражнение. (27). Показать, что [21, 6]-код имеет следующий весовой спектр:
i:0 8 12
Лг:1 21 42
Частный слуцай. Предположим, что циклические представители задаются многочленами 0(х), 71 (х),..., 7s_i (х), где 0(х)<₽—1 и
Ясно, что 7,2(х) = 72i (х) =Xi (х2), так что вес многочлена 7,2 (х) равен весу многочлена АЦх). Простым частным случаем является случай, когда все многочлены 7<(х) имеют вес, равный весу многочлена 7Цх). Например, если п=51=(28—1)/5, то 7,(х)'₽=£; i7(x2)<₽=g2; 7(x4)‘₽=g4; 7(x8)<₽=g8=l£3+s. Таким образом, 7(х8) равно циклическому сдвигу слова, соответствующего элементу |3. Следовательно, рассматриваемый код имеет только два ненулевых веса, а именно: wt(0(x)) и wt(A,(x)).
В общем случае, если s — любое простое число, для которого 2 является примитивным корнем (т. е. по модулю s имеется только два циклотомических класса — Со и С)), то код имеет не более двух ненулевых весов, скажем ту и т2- состоит из п слов веса ть являющихся циклическими сдвигами многочлена 0Ь и n{s—1) слов веса 12-
Весовой спектр в случае, когда имеется только два ненулевых веса. Предположим, что ./6 имеет только два ненулевых веса — ti и 12, где ii — вес идемпотента 0ь Минимальное расстояние дуального кода в соответствии с границей БЧХ равно 3. (И никогда не больше — почему?)
Согласно теореме 1 гл. 5
1+/г^ + /г(5_1)^==2т-'1{(1+< + Лз(1+<-3(1-г/)3+ .
Дифференцируя дважды это выражение и полагая у=1, получаем:
Ti + (s—1)та = 2т~’;
Ч (Ч-1) + (s-1) т2 (т2—1) = (и—1) 2т~2.
Решая эту систему относитезшно т2, находим, что _ ( Чт1г ± 1 \
Т2— 2 S /•
Таким образом, т должно быть четным, п
т
2'П/2 + 1_1 ), если s делит 2 2 + I;
S /
т
2ml2~ i (———4-1), если s делит 2 2 —1.
1 \ s J
На рис. 8.3 приведены некоторые примеры кодов с двумя весами.
п т S т2
21 6 3 8 12
51 8 5 32 24
85 8 3 48 40
93 10 11 32 48
315 12 13 128 160
341 10 3 160 176
819 12 5 384 416
1365 12 3 704 672
13797 18 19 26-2» 27-2»
Рис. 8.3. Некоторые примеры кодов с двумя весами
Замечание. Кроме случая, когда 2 является примитивным корнем по модулю s, имеется еще много других случаев, когда код имеет только два ненулевых веса (см. упражнение (5) гл. 15).
8.5. ГРУППЫ АВТОМОРФИЗМОВ КОДА
Пусть — двоичный код длины п. Любая перестановка п координат переводит в эквивалентный код, многие свойства которого совпадают со свойствами исходного кода (те же минимальный вес, весовой спектр и т. п.).
Определение. Множество перестановок координат, отображающих код «на себя» (переводящих кодовое слово в кодовое слово, возможно, отличное от исходного), называется группой автоморфизмов кода и обозначается через Aut(^).
Упражнение. (28). Показать, что Aut(^) действительно группа.
Подстановка л символов {1, 2,...,п} переводит i в зт(г) (или, в более удобном обозначении, в in). Вектор с= (ci,..., сп) переходит в вектор1 сл= (с пт, , Сл(п)). Если р — некоторая другая под
1 В равной степени хорошим, хотя и отличным от этого, является обозначение сл=(Сл1 {1),...,С
становка, то произведение др означает: сначала применим л, а затем р. Таким образом, с(лр) = (сл)р. Например, если л=(123) и р— (14), то1
(Г1> ^2> ^3’ £4) = (^2> ^3> Н> ^4)’
(с1> С2, Cs, С4) Яр = (С2, С3, С4, Cj).
Таким образом, AutCiF) является подгруппой симметрической группы 5%, состоящей из п\ перестановок п символов.
Примеры. (1).И для кода с проверкой на четность, и для кода е повторением группой автоморфизмов является вся группа ff’n-(2). Группа автоморфизмов кода
12 3 4
0 0 0 0
0 0 11
110 0
1111
состоит из следующих восьми подстановок:
(1), (12), (34Г), (12) (34), (13)>(24), (14) (23), (1324), (1423).
Упражнения. (29). Если код 'S' линеен, то Aut(<ё’) = ^AutC??1).
(30). Если код Яо линеен и 'g'l получается из fF: (а) путем добавления проверочной позиции или (Ь) путем добавления вектора из всех единиц, то Aut(??i)2DAut('??). В случае (Ь), если блоковая длина ЧП нечетна, а все кодовые векторы имеют четный вес, то Aut(®’1)=Aut(®’).
(31). Показать, что из включения не следует включение
AutCg’JoAutfg’z).
(32). Пусть — [12, 6, 3]-код, порождающая матрица которо-
го показана на рис. 8.4. Таким образом, первая строка содержит 1
в координатах {1236}, вторая строка-—в координатах {345} и т.д.
Рис. 8.4. [12, 6,
3]-код с тривиальной группой автоморфизмов
Показать, что группа Aut (^) состоит только из тождественной подстановки.
В общем случае трудно найти полную группу автоморфизмов линейного кода, даже сложнее, чем для нелинейного кода. В гл. 16 мы увидим, как группа автоморфизмов кода может быть использована для декодирования.
Пусть ‘g’— линейный [и, &]-код с порождающей матрицей М; М содержит k линейно независимых строк.
Лемма 12. Подстановка координат, задаваемая некоторой (яХп)-матрицей А, принадлежит группе Aut CF) тогда и только тог
1 Здесь автор пользуется общепринятой записью подстановки в виде циклов, согласно которой л=(123) обозначает: л(1) =2; л(2)=3, л(3) = 1, л(4)=4, а р=('14) обозначает: р(1) =4; р(2)=2; р(3)=3; р(4) = 1. (Прим, перев).
да, когда КМ=МА для некоторой обратимой (kytk)-матрицы К.
Доказательство. Матрица'МА является порождающей для кода 'g? тогда и только тогда, когда соответствующая подстановка лежит в группе AutC^). МА может быть получена из М путем линейного преобразования с матрицей К. •
Пример. [7, 3, 4] симплексный код ff’z задается порождающей матрицей
0 1 2 3 4 5 6
/1 1 1 0 1 0 Ч)^
М= о 1 1 1 0 1 0 ] •
\0 0 1 1 1 0 1/
Подстановка о2 = (0) (124) (365; ) переводит
кодовые слова. В самом деле,
кодовые слова в
0 1 2 3 4 5 6
/1 1 1 0 1 0 0\ /1 0 0\
мо2=(о looii 1)=(о 1 11м-\0 1 1 1 0 0 1/ \0 1 о/
Определение. Множество всех обратимых (&Х&)-матриц над полем F называется полной линейной группой и обозначается через GL(k, F). Если F — конечное поле GF(q), то этот факт записывается в виде GL(k, q).
Теорема 13. Порядок полной линейной группы GL(k, q) равен
(^_1)(^_<?)(^_(?2) . .
Доказательство. Пусть К — матрица из GL(k, q). Первым столбцом К может быть произвольный ненулевой вектор над GF(q), который может быть выбран соответственно qh—1 способом. Второй столбец не должен быть кратным первому и, следовательно, может быть выбран qk—q способами, и т. д. •
Согласно лемме 12 группа автоморфизмов двоичного линейного кода размерности k изоморфна подгруппе группы GL<(k, 2).
Упражнения. (33). (а). Предположим, что никакая из координат кода 7? не равна постоянно нулю. Тогда при любой K^GL(k, 2) матрица КМ является порождающей матрицей того же самого кода <&. Показать, что К задает элемент л из группы Aut(^) (т. е. что существует (п'Дп)-матрица А, соответствующая л и удовлетворяющая условию КМ = МА) в том и только в том случае, когда К сохраняет вес каждого кодового слова. (Ь). Вывести отсюда, что группа автоморфизмов симплексного кода Д’™ изоморфна группе GL(m, 2).
(34). Другие группы, связанные с кодом. Предположим, что —1п, /г]-код над GF(q), и пусть
^-1 = {AgGA(m1(7):uA = u для всех uEt};
^2 = {Ае6£(ад);иАЕ^ для всех иЕ^}.
Доказать, что
(" ) h n—k
1=1 Z=1
Приведем теперь одно полезное свойство, описывающее весовой
спектр.
Теорема 14. Предположим, что — код длины N, все веса в котором четны и который обладает следующим свойством: какую бы из координат мы ни удалили, получающийся при этом выколотый код (см. § 1.9) имеет один и тот же весовой спектр. Если {Л,} — весовой спектр кода а {аД — весовой спектр любого из
таких выколотых кодов, то
а N — 2j .
Более того, минимальное расстояние этих выколотых кодов нечетно.
Доказательство. Рассмотрим таблицу 9?, строками которой являются А2- кодовых слова кода веса 2/. Эта таблица содержит 2/Л2,- единиц. Согласно предположению число единиц в каждом столбце таблицы 9? одно и то же и равно a2j-ь Таким образом,
a2/-i = 2/^2j/Ar- (8.5)
Отсюда следует и вторая формула, так как A2j=a2j+a2j-i. •
Группа G подстановок символов {!,...,п} называется транзитивной, если для любой пары символов i и j найдется подстановка леб такая, что in.=j. Более общо G называется t-кратно транзитивной, если для t различных символов ц, i2, ..., it и t различных символов /1, j2,...,jt найдется подстановка tgG такая, что iin=/i; iofo- -/2» * • • i
Следствие 15. Предположим, что код SF инвариантен относительно транзитивной группы подстановок. Тогда: (i). Удаление любой из координат приводит к эквивалентным кодам (ё>*. (ii). Если все веса кода четны, то минимальный вес в коде <ё>* нечетен.
Позже мы увидим, что многие расширенные циклические коды обладают транзитивными группами подстановок. Но будьте осторожны! Как видно из упражнения (35), теорема 14 применима не ко всем циклическим кодам.
Упражнения. (35). Пусть — невырожденный [9, 3, 3] циклический код с порождающим многочленом х®-|-л:3+1. Показать, что расширенный код не удовлетворяет условиям теоремы 14.
(36) . Доказать, что если код длины N фиксируется транзитивной группой подстановок, то У|ь4.г-, где’ Аг— число кодовых слов веса I.
(37) . Пусть код длины.У инвариантен относительно транзитивной группы подстановок и “содержит слова только четного веса; пусть W(x, у) —его весовая функция. Пусть далее — код, получаемый из 7? путем выкалывания одной любой его координаты, а ^2 — подкод кода ‘S’i, образуемый словами только четного веса; W\ (х, у) и W2(x, у) —соответственно весовые функции кодов и ^2. Доказать, что
W2(x, y) = -L2-W(x, у)-,
N \дх ду J
(38) . (Камьон.) Предположим, что Яо — [п, k, J] циклический код над GF(q) с /-кратно транзитивной группой Aut('S'). Доказать, что (п—:t+ 1)1 (d—1+ 1).
Группа автоморфизмов циклического кода. Согласно определению группа автоморфизмов циклического кода содержит все циклические подстановки на множестве 0, 1, 2, ...,n— 1 и все их степени.
Так как п предполагается нечетным, то отображение о2 : х-^-х2 является подстановкой на кольце Rn (так как .о2 переставляет базис 1, х, х2,..., х’1-1). Далее слово а(х)с2==а(х2) =а2(х) принадлежит тому же коду, что и слово а(х). Следовательно, группа автоморфизмов циклического кода содержит наряду’с циклическими подстановками подстановку стг- Порядок подстановки г>2 равен т, где т = |С,|.
Упражнения. (39). Найти группу автоморфизмов кода, представленного на рис. 5.1.
(40) . Показать, что с>2 и 7'=0, 1, 2, ...,п—1 порождают группу порядка тп, состоящую из подстановок вида <Р2Тэ для 0^t<m и
Пример. На рис. 8.5 показано действие подстановки о2 на слова симплексного кода ff’s,-
1 X X2 X3 X» X5 Xs
1 1 1 0 1 0 0 Е (х) =1? (х)
0 1 1 1 0 1 0 а (х) = с? (х)
0 0 1 1 1 0 1 а2 (х)
0 1 0 0 1 1 1 а4 (х)
1 0 0 1 1 1 0 Ь (х) = 6» (Х)
1 1 0 1 0 0 1 Ь2 (х)
1 0 1 0 0 1 1 64 (х)
Рис. 8.5. Действие автоморфизма <т2 на слова симплексного кода
Эквивалентность циклических кодов. Будем сейчас рассматривать Рп не как кольцо многочленов, а как групповую алгебру Циклической группы G порядка п. Отображения о : х^х^, где
(i — число, взаимно простое с п, образуют группу & автоморфизмов группы G. (Автоморфизмом группы G называется такое отображение >о группы «на себя», которое сохраняет умножение в группе; о(а6)=о(с)-о(.6)). Таким образом, элементы из S переставляют координаты кольца Rn и переводят циклический код в циклический код.
Например, если п=7 и ц=3, то о3=(1) (х> х?,>- х^> x<i> х*> %5)-Таким образом, о3 переводит идемпотенты 01=4 +х+х2+х4 и 03= = 1+х3+х6+х5 друг в друга и, следовательно, переводит друг в друга циклические коды, порождаемые этими идемпотентами.
S является мультипликативной абелевой группой, изоморфной мультипликативной группе целых чисел, меньших п и взаимно простых с п, и имеет порядок tp(n) .(см. упражнение (8) гл. 4).
Отображение i—где ц взаимно просто с п, задает перестав новку на циклотомических классах. Например, если и=31, то действие отображения i->-3i описывается следующим образом:
Со—»-С0, Сх—>С3—>СБ->С1Б—>С7-
(см. рис. 4.4).
С другой стороны, если ц равно степени 2, то отображение Оц i-Ир фиксирует (оставляет на месте) циклотомические классы. Соответственно такое отображение фиксирует циклический код. Следовательно, чтобы выделить отображения, действительно изменяющие циклические коды, надо взять фактор-группу группы S по подгруппе {сц : teCi}. Эта фактор-группа состоит из подстановок оц, взятых по одной из каждого циклотомического класса, содержащего числа, взаимно простые с п, и поэтому имеет порядок, равный <$(ri)lm.
Например, для п=63 циклотомические классы, содержащие числа, взаимно простые с п, имеют вид:
Cj={ 1 2 4 8 16 32};
СБ = { 5 10 20 40 17 34};
С1Х = {11 22 44 25 50 37};
С31=={31 62 61 59 55 47};
С23 = {23 46 29 58 53 43};
С13=--{13 26 52 41 19 38}.
Выделенные жирным шрифтом числа задают степени 5 по модулю 63; следовательно, в данном случае фактор-группа является циклической порядка 6.
Действие Og на примитивных идемпотентах (или па циклотомических классах) описывается следующим образом:
01 —> ОБ-^О11^-О31->021->013-»-01;
021~>021;
Оз->01Б—>03;
07->0,.;
09—>027—>09.
Мы видим, что подстановка о5 разбивает примитивные идемпо-тенты на классы. Идемпотенты первого класса порождают невырожденные циклические коды длины 63. Идемпотенты второго класса задают повторения циклических кодов длины 3, из третьего класса — повторения циклических кодов длины 21, из четвертого — длины 9 и из пятого — длины 7. Нетрудно сообразить, что порядок вещей всегда таков: любой невырожденный идемпотент длины п может быть получен из 01 применением подстановки
Таким образом, невырожденные минимальные идеалы одной и той. же блоковой длины эквивалентов!.
Используя подстановку 05, можно установить, конечно, эквивалентность и многих других кодов. Например, коды длины 63 с идемпотентами
61+®5> 6б + 0Ц> 611+031, 031 + 023, 023 + 013, 613 + 01 эквивалентны.
Упражнение. (41). (а). Показать, что при п=7 подстановка /->31 отображает С1->Сз->Сь
(Ъ). Для п = 15 подстановка t->7i отображает Ci->Ct~>Ci, С3-> —*-Сз, С5—>Сб.
(с). При 72= 127 подстановка £—>3/ отображает
Группа автоморфизмов кода БЧХ. Пусть ‘g’ — код длины п= =2™—1. Сопоставим координатам ненулевые элементы поля GF{2m), т. е. элементы 1, а, а2,..., а2™-2. Добавим общую проверку на четность, присвоив ей номер оо и сопоставив нуль поля GF(2™):
Координата: 0 1 2 ... п—1 оо.
Соответствующий
элемент поля GK(2m): 1 а а2... а71-1 0.
Определение. Аффинная группа. Пусть Ри, v — подстановка элементов поля GF(2m) вида
Ри v: а’^-и а' Д v, 0->t’, где и, v^GF(2m)\ и=£0.
Величина Pak 0 задает циклический сдвиг на k позиций, оставляющий на месте 0, т. е. оставляющий на месте координату оо.
Например, при длине п—7 действие подстановки Ра, а в поле GF(23), задаваемом таблицей на рис. 4.5, описывается следующей Цепочкой переходов:
1 —>0->а->а4->а6->а3->а2-> 1, а5->а5.
Таким образом, 1 а а2 а3 а1 а5 а6 0
Кодовое слово: с0 с2 cs с4 с5 с6
Кодовое слово после подстановки: с4 с0 с2 с6 с5 с3 сГ
Множество всех подстановок PUtV образует группу, называемую аффинной группой поля GF(2m). Эта группа дважды транзитивна и имеет порядок, равный 2™(2т—1). (В гл. 13 будет рассматриваться ^-мерное обобщение этой группы.)
Упражнение. (42). Доказать, что эта группа дважды транзитивна: если ii=#i2 и /i=#/2, то уравнения wa’, + n=|aJ'1 и ua^+v— = aiz или уравнения wai, + n=iaji и паг’2+.у = оо разрешимы относительно и и v в поле GF(2m).
Теорема 16. Пусть 7?— примитивный код БЧХ длины п= л
= 2ТО—1 с конструктивным расстоянием 6, и пусть SF— его расши-л
рение. Тогда группа автоморфизмов кода ё содержит аффинную группу поля GF(2m).
Доказательство. Пусть Ри v — некоторая любая подстановка из л
аффинной группы. Пусть с= (с0, Ci,..., cn-i, сто) <=ё — кодовое слово веса и.', у которого 1 стоит на позициях, соответствующих элементам Xi....Xw из поля GE(2m). Таким образом, Хг-=,а 1, ес-
ли Cat = 1, И Хго=0, если Стс= 1.
Пусть Sk= V Xki, k—G, 1, 2,...,где 0°=1. Тогда So= г=1
w Л
— 1 = 20 = 0, так как ce'g’. Также 5ь=с(аЛ)=0 для k=], 2, ...
г=1
..., 6—1, так как ё — код БЧХ.
Пусть X'i=uXi+v — локаторы единиц в кодовом слове, полученном после подстановки. Тогда
k . , .
‘ y»>-‘2x‘=
i i 1=0 ' 7 i
h
= £( ) = 0 Для 1.
z=o'1 '
Следовательно, слово, полученное в результате подстановки, л
также лежит в ё. 9
л
Следствие 17. Пусть ё— циклический код в ё— его рас-л
ширение. Если группа Aut(^) транзитивна, то минимальное расстояние d кода ё нечетно и код ё содержит также слова (четного) веса d+1. В частности, это имеет место для двоичного примитивного кода БЧХ.
Доказательство. Согласно теореме 14 если а, — число слов веса i в коде ё, то (TV—2j)«2j-i=2/a2j.
Упражнение. (43). Видоизмените доказательство теоремы 16 так, чтобы получить следующее ее обобщение, принадлежащее Касами, Лину и Питерсону. Пусть i — положительное целое число
и J (i) обозначает множество положительных целых чисел, двоичное представление которых ^«покрывается» двоичным представлением числа 1. Таким образом,-если i= S б,-2г, где б, =0 или 1, то
7(0 = {й/ = £Бг 2Г; вг = 0 или 1, ег бг} •
Пусть SF — циклический код длины 2т—1, для которого элемент л
1 служит ненулем, и пусть ‘g’ — расширение этого кода. Тогда код л
‘ё’ инвариантен относительно аффинной группы, если и только если cP является нулем кода SF для всех /e7(i) всякий раз, когда а’ — нуль кода
Теорема 18. Если двоичный циклический код ‘g’ инвариантен относительно /-кратно транзитивной группы G, то кодовые слова любого фиксированного веса i образуют t-(n, i, X) схему, где
Доказательство. Пусть (Рь ..., Pt) — множество кодовых слов веса i, которые в координатах Pt,...,Pt содержат единицу. Так как G—t кратно транзитивна, то |S.i(Pi,..., Pt) | не зависит от частного выбора координат Ръ..., Pt. Следовательно, кодовые слова веса i образуют t-(n, i, X) схему. Согласно теореме 9 гл. 2 имеет место равенство A.t — 7^ ” •
Следствие 19. Кодовые слова каждого веса в расширенном двоичном примитивном коде БЧХ образуют 2-схему (ср. с теоремой 15 гл. 2).
Упражнения. (44). Доказать, что при т^4 минимальное расстояние кода БЧХ длины 2,п—1, исправляющего две ошибки, равно точно 5.
(45). Пусть а+'ё’ — смежный класс кода ‘ё’ и jteAut('g’). Доказать, что п(а+<ё') —также’смежный класс кода <ё'.
(46). (Камьон.) Каждой r-и матрице (аг-,), r=l, 2,...,п= = \GL(\m, q) | из группы GL(m, q) сопоставим вектор-столбец x,= ((Zii, 012,..., атт)Т длины т2. Показать, что параметры кода над GF(q) с порождающей (т2Х«) -матрицей G=(xb х2, ...,хп) равны:
—?')> k==m2-, d — n(qm—q—1) х г=0
Группа автоморфизмов недвоичного кода. Определение. Мономиальной называется матрица, у которой в каждом столбце и в каждой строке имеется точно один ненулевой элемент. Таким образом, над GF(2) мономиальная матрица является матрицей подстановки, а над произвольным полем — произведением матрицы подстановки на некоторую обратимую диагональную матрицу.
Пусть —код над GF(q) длины п. Предположим сначала, что q=p — простое число.
Определение. Группой автоморфизмов линейного кода называется группа Aut('g’), состоящая из всех мономиальных (иХ Х«) -матриц А над GF(p) таких, что cAe'g’ для всех ce'g’.
Например, порядок группы автоморфизмов |[3, 1, 3]-кода '?’= = {000, 111, 222} над GF(3) равен 2-3! = 12, так как этот код инвариантен относительно любой перестановки координат и умножения всех кодовых слов на 2, что соответствует мономиальной матрице
200\
020
002/
Таким образом, группа Aut('g’) состоит из мономиальных матриц
тоох /100\ /ООП /010\ /010\ /00 Г
010 11 001 I I 010 1 1 100 1 ( 001 | | 100
.001/ \010/ \юо) \001/ \Ю0/ <010,
'200\ /200\ /002Х /020\ /020\ <002'
020 j 1 ’ 002 11 ' 020 II200I 1 002 1 200
002/ (020/ <200 J <002/ \200/ ’ <020.
Упражнение. (47). Показать, что порядок группы автоморфизмов кода 41= 6 из гл. 1 равен 48.
Если q — степень простого числа, то группа автоморфизмов кода <£? также содержит любой автоморфизм поля GF(q), сохраняющий код '/?. Пример будет приведен в гл. 16.
8.6. МНОГОЧЛЕН МЭТТСОНА—СОЛОМОНА
В гл. 7 каждому вектору а= (<20, ..., (zn_j) был сопоставлен многочлен а(х) =a0+aix + ... +ап-1хп^1. Сейчас будет введен другой многочлен, связанный с вектором а, а именно многочлен Мэттсона— Соломона A(z). Пусть F=iGF(q)-, g~=GF(qm) и — примитивный корень степени п из единицы.
Определение. Многочленом Мэттсона — Соломона (МС-многочленом), соответствующим вектору а = (по, аь...,an-i), а-;^ называется следующий многочлен из кольца £Р~[г]:
A(z) = £ AjZn~’, (8.6)
/=i где
п—I
4 = «(а') = £аг-аг7, / = 0±1, + 2, . . . (8.7)
г—О
(,N.B. A(z) не берется по модулю zn—1.) Другой формой записи многочлена A (z) является:.
п— 1 * п—1 п—1
Л(2) = 2Л-/ (8.8)
/=0 1=0 j=0
Например, МС-многочлены, соответствующие кодовым словам 1+х+х2 + х4 и х(1+х-+-х2+х4) симплексного |[7, 3, 4]-кода З’з, равны соответственно z3+z5+z6 и a4^3+«2z5+az6, где oteGF(23) (использовано задание поля, приведенное на рис. 4.5).
Замечания. (1). Коэффициенты А, определяются равенствами:
Поэтому многочлен A(z) иногда называют дискретным преобразованием Фурье вектора а; мы, однако, всегда будем называть его многочленом Мэттсона — Соломона1.
(2). Заметим, что (Aj)v=AjQ для всех / (индексы берутся по> модулю п).
(3). Код БЧХ в узком смысле с конструктивным расстоянием 6 может быть теперь определен как множество всех таких векторов, для которых Л1=Л2= ... =А 6-1 = 0.
i(4). Мы просим прощения за использование символа Л., для обозначения числа кодовых слов веса i и для коэффициентов МС-многочлена, надеемся, что смысл будет ясен из контекста.
Теорема 20. {Формула обращения.) Вектор а восстанавливается по многочлену A(z) в соответствии с формулами:
at = — Л(аг)> 1 = 0, 1, • • •, п—1; | и
а = — (Л (1), Л (а), - - -, ЛСа"-1});
и (8.9)
п—1
а (х) = — А (аг) х\
i=0
Доказательство. Воспользоваться формулами (7.16) и (8.5). •
1 В переводе на русский язык удобно (и мы будем этим иногда пользоваться) называть A(г) МС-преобразованием многочлена а(х). (Прим перев.).
Определение. Покомпонентное произведение двух многочле-
нов
п— 1 п—1
f (у)=2 и 8 2gtyl
i=0 i=0
определим равенством
f )*g(y) = £ftgiyl-i=0
Обозначим через ]эт остаток от деления произвольного многочлена ?(у) на уп—1.
Лемма 21. Если а — двоичный вектор, то его МС-многочлен A(z) является идемпотентом кольца многочленов над GF(2m) по модулю многочлена zn—1, т. е.
[A?(z)]n = A(z).
Доказательство. Согласно теореме 20 А (а’) равно 0 или 1. Тогда утверждение следует из леммы 2. 9
Теорема 22. (Другие свойства.)
(i) . Если с (х) = а (х) + b (х), то С (z) = A (z) + В (г).
(ii) . с(х) = [а(х)6(х)]п
тогда и только тогда, когда
С (z) = A (z)*B (z)
(iii) . Аналогично с(х) — а(х) *Ь (х) тогда и только тогда, когда
C(z) = —[A(z)B(z)]n. п
(iv) . МС-многочлен циклического сдвига вектора a (ai, щ, аг,. an~i, «о) равен A (az).
(v) . МС-многочлен векторов 0 и 1 равен соответственно 0 и п.
(vi) . Общая проверка на четность на векторе а задается равенством
V аг = Л (0) = Ао. г=0
(8.10)
Доказательство, (ii). Если с(х) = [а(х)&(х)]эт, то С3= = c(ai) =а(а'з)Ь(а^) =AjBj и, следовательно, C(z) =А (z) * B(z). Наоборот, предположим, что Cj—AjBj для всех /. Тогда нам надо показать, что
п—I
" п—1 п—1
У ape bjX1 t=o i=o Jn
(8.H)
Согласно. (7.16) правая часть в (8.11) равна многочлену
приведенному по модулю хп—1. Коэффициент при xk в этом произведении равен:
Согласно лемме 6 гл. 7 внутренняя сумма равна нулю, за исключением случая так что выражение становится равным н—1 п— I п~ I
J] а (a1) b ( a') a~'k = J] AjBi a~'h = J] G a~'k> 1=0 j=0 j=0
что согласно теореме 20 равно коэффициенту ck при xk в левой части равенства (8.11).
Доказательство остальной части теоремы состоит в непосредственной проверке и поэтому опускается. ' *
Проанализируем теперь более тщательно соответствие а(х) и его многочлена Мэттсона — Соломона A (z) (см. рис. 8.6).
Пусть Т(х) обозначает множество всех многочленов от х с коэффициентами из GF(qm), степень которых менее п. Множество Т(х) может быть превращено в кольцо (см. § 7.2) двумя способами. В обоих кольцах сложение определяется обычным образом. Умножение двух многочленов в кольце Т (х) о осуществляется по модулю хп—1, т. е. a(x)b (х) =|[c(x)fe(x)]n. В кольце Т’(х)* произведение многочленов а(х) и Ь(х) —есть определенное выше покомпонентное произведение а(х) *Ь(х).
Тогда отображение, которое ставит в соответствие многочлену <з(х) его МС-многочлен A(z), является согласно теореме 22 изоморфизмом колец Т(х)в и Т(х)„. Обратное отображение определяется равенством (8.9). (Отображение ф кольца А в кольцо В, сохраняющее операции сложения и умножения: ф= (сц + а2) — ='Ф («1) -Нф (а2) и ф («Шг) =|ф («О'Ф («г), — называется гомоморфизмом этих колец. Если ф взаимно однозначно и является отображением «на», то ф называется изоморфизмом колец А и В.)
О двоичном случае можно сказать еще следующее. Пусть qm= и пусть S(x) —подмножество в 7(х), состоящее только из тех многочленов, коэффициенты которых лежат в GE(2). Кольца в(х)@ и S(x)* определим, как и раньше. Каждый двоичный многочлен fi(x)GS(x)„ является идемпотентом, т. е. удовлетворяет условию а(х) *а(х) =а(х). Согласно лемме 21 а(х) отображается
в идемпотент A(z) из T(z)0. Заметим, что идемпотенты кольца T(z) 0 сами образуют кольцо £(z)®, так как в поле характеристики 2 сумма двух идемпотентов опять является идемпотентом. На самом деле кольцо E(z)q является образом кольца S(x)* при МС-отображении, так как согласно лемме 2 и теореме 20 прообраз идемпотента из T(z)® лежит в S(x)„. Таким образом, отображе-мс
ние S(x)*—>E(z)& является кольцевым изоморфизмом.
Т(х) —многочлены от х с коэффициентами из GF(q™) степени <п. Т(х)ж = (Т(х), + , *) 1^7’(z)0 = (7’(z), + , •) „ мс
т (х)0 = (Т (х). + , .) р Т (г)в = (Т (г), + , *)
Если 9=2 и S(x) — подмножество в Т(х') (с коэффициентами из GE(2)), то
МС
S (х)* j—Е (2)0 — идемпотенты CZ Т (z)Q МС
s (х)0 р Е (Z)*cz т (г).
Рис. 8.6. Отображение Мэттсона—Соломона
Пусть Е (z) * — кольцо, состоящее из всех многочленов кольца E(z)q, но с покомпонентным умножением. (Отметим, что относительно покомпонентного умножения элементы кольца E(z)r идем-мс
потентами не являются.) Тогда отображение S0^-E* также является кольцевым изоморфизмом (см. рис. 8.6).
Двоичные линейные коды являются линейными подпространствами в S(x)0 (или в S(x)*) и, следовательно, в E(z)* (или в Е(г)&). Как мы видели в теореме 1, идеал в 5(х)0 состоит из всех кратных некоторого фиксированного многочлена. Идеалы в Е (z)» также имеют простую структуру.
Лемма 23. Идеал в Е (z) * состоит из множества всех многочленов A(z)='ZA_izi таких, что = ...=Ai[=0 для некоторого фиксированного подмножества индексов {ii,
Доказательство. Пусть ‘g’— образ рассматриваемого идеала в S(x)q. Так как — также идеал, то в поле GF(2m) у него имеется определенное множество нулей, а б, а li— а именно корни порождающего многочлена, так что
<2 (х) 6Е'й? <-а (а‘‘) = • . =с(ач) = 0;
а(х)^(ё<- А^ = - • • = Д?г —0. •
Например, код БЧХ в узком смысле с конструктивным расстоянием 6 является идеалом в Е(г)«, с Д1=Д2= ••• =Дс—i =0.
В гл. 12 показано, что коды Гоппы могут быть описаны как кратные некоторого фиксированного многочлена в E(z)&. Однако идеалы в E(z)q не представляют специального интереса (см. упражнение (50)).
Упражнения. (48). Показать, что при п=3 кольцо E(z)& состоит из многочленов: 0, 1, z+z2, l+z+z2, az+a2z2, ot2z+az2, l+«z+ot2z2, l+a2z+az2.
(49). Пусть ^ — «циклический код» в E(z)&, т. е. такое подпространство в E(z)e , что A[zA(z)] ^.^4-. Показать, что ^={0} или ^={0, l+z+z2 + ... +zn-1}.
(50). Пусть st-— идеал в E(z)@. Показать, что соответствующий ему в S(x)* код состоит из всех векторов, у которых в некоторых фиксированных координатах стоят нули. Таким образом, такие коды неинтересны. [Указание. Работать в кольце £(+)*.]
Многочлен локаторов. Предположим, что ненулевыми координатами вектора а— (a0, ai,...,an-2, an-i), aieF являются (Zjp dit,..., только они (здесь ro = wt(a)). Сопоставим вектору а элементы поля вида Xi = c+, ..., Xw=aw, называемые локаторами вектора а, и элементы поля F вида Yi=atlt ..., Yw=at , задающие значения ненулевых координат. Таким образом, вектор а полностью определяется набором (Xi Fi), ..., (Xw, Yw). В случае двоичного вектора а все У,, естественно, равны 1.
Заметим, что
а(а') = Л,-= У УД/.
Определение. Многочлен локаторов вектора а равен
o(z) = П С1—xiz)=Оо=1-
(Корни многочлена o(z) являются величинами, обратными локаторам.) Таким образом, коэффициенты сц представляют собой элементарные симметрические функции от Хр
01=—(-К1+ • • + хю); о2 = ХД2 + ХД3 + • •
ota = (-l)“’X1 - - -Xw.
Обобщенные тождества Ньютона. Величины {Дг} и {ог} связаны системой однородных линейных уравнений.
Теорема 24. Для всех / величины {/!<} удовлетворяют рекуррентному соотношению
А/+а1 +ОхД/+ш_1 + - • •+о-и,Д; —0.
(8.12)
В частности, выбирая /=1, 2, w, получаем:
Доказательство. В уравнении
П(1—X£z)=l+o1Z+ • •
г=1
(8.13)
положим z= l/Xj и умножим его на YiXp+w'.
УгХ>+™ + ох FfX/+® + . . . + YгХ< = 0.
Суммируя по i= 1, ..., w, получаем (8.12). •
Упражнения. (51). Пусть а — вектор веса w. Показать, что матрица
av 4-, • • А\
Аж Av ’ ’^2 I
^2v A2v_I • • ‘Av J невырождена при v=-w и вырождена, если v>w.
(52) . Обычная форма тождеств Ньютона. Пусть Хц ..., Xw — переменные и
<Ф) = П(1— ^z) = 2 <hz,
i=l i=0
где tJi — элементарные симметрические функции от Хг, причем оо= 1 и (Уг = О для всех i>w. Для всех i определим степенные суммы Pi равенством
W
Pi = V X'.
Г=1
СО
(а) . Показать, что если Р (z) — Р tZ*, то
i=l
о (г) Р (z) + z о' (z) = 0.
(b) . Приравнивая коэффициенты при одинаковых степенях переменной, показать, что
Pi + Oi = 0;
Pw + CjP^i + • • •+стЕИ_1 P1+w<TK, = 0 И ДЛЯ
Pi + °1 Pj-i + • ‘ •+°u>Pi_a„ = 0-
(8-14)
(8.15)
Заметим, что в случае, когда все Уг равны 1 (т. е. в случае, когда вектор а двоичный), формула (8.15) совпадает с (8.12).
(53) . Предположим, что Ж принимают значения в поле характеристики р. Показать, что если' при фиксированном s имеет место равенство 07=О для всех I в диапазоне 1^/^s, не делящихся на р, то Pt=O для Is^/sCs.
(54) . Показать, что в двоичном случае из уравнений (8.14) и (8.15) вытекает равенство
1 0 0 оо . -0 \
1 оо . • -0 \ °2
4 4 дд • -0
д д А \г>
2к>—2 2да—3 ' ’ ' ‘ I \uw
(8.16)
(55) . (Чень.) Используя уравнение (8.12), дать другое доказательство границы БЧХ.
(56) . (Чень и Чой). Показать, что в двоичном случае (<? = 2) МС-многочлен для а(х) может быть получен из многочлена локаторов о(х) для а(х) по формуле
Д(2) =
Z ( zn+ l)o^(z)
+ (z"+ 1) w,
где eR(z) = zw(j(l/z) и ю = а(1) =wt(a).
Следовательно, <jR(z)A(z) = 0mod(zn + 1).
Применение к декодированию кодов БЧХ. Как мы увидим в следующей главе, уравнения (8.12) — (8.16) играют важную роль при декодировании кода БЧХ с конструктивным расстоянием 6. В этом приложении роль а играет вектор ошибок, по которому декодер легко находит Дь ..., Де—ь Затем на основании уравнений (8.12) — (8.16) определяется многочлен o(z). Для определения значений {У,} введем многочлен значений для а(х)
W W
(О (z) = о (z) + ^zXiYi П (1 -Х7г). (8.17)
i==l j=l
j=/=i
Если многочлен co(z) известен, то Уг определяются равенствами
=«> (ХГ1) / П (1 - W) = - (V)- (8-18)
Теорема 25.
<b(z) = (1 4-S(z))a(z), (8.19)
где
5(г) = ^Д^. (8.20)
г—1
Заметим, что так как deg со (z) ^dego(z) = w, то для опреде-ления многочлена co(z) по формуле (8.19) необходимо только знание величин At, ..., Aw.
Доказател ьство.
W W СО
3=1+5^-=1+Ёг‘Ё(Л,)'=1+5и- •
г=1 i=l /=1
Вес вектора. Теорема 26. Вес вектора а равен п—г, где г —число корней степени п из единицы, являющихся корнями его многочлена Мэттсона—Соломона A(z).
Доказательство. Вытекает из (8.9). •
Следствие 27. Если А (г) — МС-многочлен вектора а, то wt(a) ~^п—deg Л (г).
Воспользуемся теоремой 26 для того, чтобы дать другое доказательство границы БЧХ.
Теорема 28. (Граница БЧХ.) Пусть ‘ё’ — циклический код с порождающим многочленом g(x) = nie к(х—cd), где множество К содержит отрезок последовательных целых чисел b, & + 1, ... ..., b+d—2 для некоторого Ь. Тогда минимальный вес любого ненулевого кодового слова а из Ч? равен по меньшей мере d.
Доказательство. Так как а(х) кратен многочлену g(x), то согласно предположению для всех —2 выполняется ра-
венство cz(cd)=O. Следовательно,
А (г) = a (a) zn~'+ • • - + й(аы)/-ь+Ча(аЖ-1 )zn~b~d+l + + • • • +а (а")-
Пусть
A (z) = zb~1 A (z) + (a (a) z~2 + • • •-J-a(ab—*)) X
x(z"-l) = a(ab+*-1)z"-d+ • - •+й(ап)гь-1 +
+ a(a)z^2+ ••• • + a(ab~‘).
Ясно, что число корней степени п из единицы, являющихся корнями многочлена A(z), равно числу корней степени п из еди-л
ницы, являющихся корнями многочлена A(z). Это число не пре-л
восходит degA(z)^n—d. Таким образом, согласно теореме 26 вес вектора а не меньше d. •
Многочлены Мэттсона — Соломона для минимальных идеалов. В остальной части параграфа мы ограничимся рассмотрением только двоичных кодов.
МС-многочлены элементов 6S, 6*s и хг0*6 соответственно равны:
iecs iecs iecs
Из этих формул видно, что легче работать с идемпотентами 6%, чем с идемпотентами 6S. При условии достаточной внимательно-
стиможно упроститьооозначения,используяункциюследа. Пусть
7г(г) + г + г2 + г22 + • • •+^~1,
причем показатели, большие чем п, немедленно приводятся по-модулю п. Например, если и=15, то 74(z3) = z3+z6+z12+z9 и не равно z3+z6+z12+z24. Игнорирование этого соглашения’ приведет к ошибке.
Упражнение. (57). Для и=31 показать, что если со — примитивный кубический корень из единицы, то T5(z3)'=co2 при z=co.
Таким образом, МС-многочленами элементов 6*s, хг0*6 и x’Ss. соответственно являются: 7’ms(zs), Тms (a~iszs) и Tm& (a~iszn~s).
Нам придется встречаться также с минимальными идеалами, которые не являются циклическими сдвигами идемпотентов. Пусть-^<s=<6*s> — произвольный минимальный идеал. Согласно теореме 9 элементы a(a~s), а{х)^Л.$ образуют подполе £7"s поля-GF(2m), изоморфное полю GF(2 s). Следовательно, МС-преобра-зование многочлена а(х) равно
А (z) = V a (o'1) z1 = T„,s (a (a~s) zs) = Tms (p zs), iecs
где p = a(a~s)—элемент из £7"s. В последнем выражении показа-тель р должен быть редуцирован по модулю 2 —1, а показатель z — по модулю п.
Многочлены Мэттсона — Соломона для кодовых слов. Согласно пункту (iii) теоремы 7 каждый многочлен a(x)^Rn может быть записан в виде
a(x) = y)as(x)eir(x). (8.21)
s>0
Его МС-преобразование равно:
А (г) = 2 Tms (Р8 2s), ps е fs, (8.22)
s»0
где s пробегает полное множество представителей по модулю п;. as(x) может равняться нулю, и в этом случае элемент ps также равен нулю.
Заметим, что равенство (8.21) может быть переписано в виде
G(x) = y/s еМ (8.23)*
где S — множество представителей с возможными повторениями. Тогда МС-преобразование многочлена а(х) равно:
Л(г)=2 2(а Jsz)/-se-s iecs
(8.24)'
Пусть ‘ё’ — циклический код, ненули которого лежат в цикло-томических классах С__и\, C_ui. Кодовое слово а(х) из ‘ё’ тогда .записывается в виде
i
а(х) = ^аи. (х)0*.(х),
г=1
.а его МС-многочлен
Л(2) = £тпг(|3^),
г=1
ггдеПг=]С_иг | и Рг^^~п. , Кодовое слово из <ё’± имеет вид
&(*) = £ Ьи(х)ви(х),
u^ui
•а его МС-многочлен
^Т\си\&гП-У
Пример. Коды длины 15. (см. упражнение (7)). [15, 4, 8] симплексный код <0*г> = <67> состоит из векторов, МС-много-'член которых
Д(г) = Т4(рг), peGF(24).
В общем случае [п=2т—1, т, 2™-1] симплексный код &т за-.дается условием:
А (г) = Тт (pz), р е GF ( 2т). (8.25)
[15, 2, 10] симплексный код <05> = <0*5> состоит из векторов 0, 05, х05, х205. Их МС-многочлены равны:
T2(pz5); ре{0, 1, a5, а10} s GA (22), т. е.
0, z5 -J- 2, а5 z5 -]- а10 210, а10 z5 -f- а5 z10.
[15, 4, 6]-код <0з> = <0*з> имеет МС-многочлены ^(pz3), :peGK(24).
[15, 11, 3]-код Хэмминга состоит из векторов вида
Ц» 60 W + aL^1 ei (*) + fs W 63 И + с^х1' 05 (х),
:где а0, а\, a^GF{2}-, ii, г5е{0, 1,..., 14}; degf3(x) ^3.
Соответствующие МС-многочлены:
S=£-1
Аналогичные формулы имеют место для любого кода Хэмминга.
Упражнение. (58). Показать, что [23, 12, 7]-код Голея состоит из векторов, МС-многочлен которых имеет вид:
«+Л1(Р25); aeG>(2); ре GE (II).
Другая формула для веса вектора. Теорема 31 дает формулу, которая иногда позволяет найти точное распределение весов кода. Доказательство этой формулы основано на одном тождестве (теорема 29) для МС-многочлена.
Пусть A'(z)—производная от многочлена A(z). Заметим, что в поле характеристики 2 многочлен zA'(z) состоит только из тех членов jzi многочлена А (г), в которых / нечетно.
Теорема 29. МС-многочлен произвольного вектора a^Rn удовлетворяет равенству
,, , , Л (г) (Л (г) +1)
г" + 1
Доказательство. Согласно (8.24) утверждение теоремы достаточно доказать для A(z)= (рг)3, где рп=1. Пусть [г]s озна-
/ecs
чает остаток от делении г на $. Тогда
ms~1 г •
Л(2)= 2(pZ)[s2']";
?=0 ms— 1
Л2(г)= 2 (P2)2kl]n.
i=0
Отметим, что степени переменной z в многочлене A2(z) могут' быть больше чем п. Если [х2г]п четно, то
[s2z]n =2[s2i~1]n,
и в выражении A2(z) +A(z) члены со степенями [$2’]п, входящие в многочлен A(z), аннулируются членами со степенями 2[s2i-1]n, входящими в многочлен A2(z). Если [s2‘]n нечетно, то [s2f]n = 2 [s2f-’]n-ti.
Объединяя члены со степенями 2[$2{]п—п многочлена A(z) и члены со степенями 2[$2’]п многочлена A2(z), получаем:
(pz)[s2‘ ln(l+zn)
(напомним, что рп=1). Таким образом, окончательно получаем произведение многочлена (х”+1) на нечетные степени многочлена A(z), т. е. zA'(z) (zn + l). •’
Упражнение. (59). Проверить теорему для п=9 и (Д = = {1, 2, 4, 8, 7, 5}.
Следствие 30. Если g— корень многочлена A'(z) или многочлена zn+1+z, то 71(g) равно нулю или единице.
Определим:
A(s) = G4(z), 2"+1);
/а (z) = (Л (z), zA'(z)), тде (a(z), b(z)) обозначает нормированный наибольший общий делитель многочленов a(z) и b(z). Так как многочлены A(z) и A(z) + 1 взаимно просты, то из теоремы 29 следует, что для некоторого ненулевого элемента p&GF(2m)
^(2) = РЛ(2)/2(2).
Теорема 31. Вес вектора с МС-многочленом A(z) равен:
п—deg fL (z) = n — deg A (z) + deg f2 (z).
Упражнение (60). Пусть двоичное представление веса да .вектора а= (а0. «ь —, an-i) имеет вид
да = Г1(а) + 2Г2(а) + 4Г4(с)+ • • -,
дде 1\(а) равно нулю или единице.
Доказать, что:
(i) rz(a) = \^ mod 2.
[Указание. Воспользоваться теоремой Лукаса-—теоремой :28 гл. 13.]
(ii) - = J] ataj-
Ki
(iii) . Таким образом, если вес w четен, то
(п-1)/2
^2(G)= 2 t-
i=l
8.7. НЕКОТОРЫЕ ВЕСОВЫЕ СПЕКТРЫ
Теорема 31 полезна в тех случаях, когда легко определяется степень многочлена f2(z).
Примеры. (1). Симплексный код с длиной п = 2т—1. Сог--ласно (8.19) МС-многочлен любого кодового слова записывается в виде
т—1
/l(z) = V(pz)<
i=0
Следовательно, zA'(z) = $z и f2fz) = HOA (A(z), zA'(z)) = z. ‘Степень f2 равна 1, и вес кодового слова равен с)т । о™—1 । । 1
(2) . Вырожденный симплексный код <6*s> длины п—2т—1, :где т — 2и^4— четно и s = 2u+l.
Циклотомический класс Cs содержит следующие и чисел:
S = 2“+1, 2“+* + 2, • • у,2т~Х + 2“~1.
(Проверить для п=15; $ = 5 и /г=63; s=9.)
Размерность идеала с идемпотентом 6% равна и, и все ненулевые кодовые слова исчерпываются многочленами x’6*s для1 0^/^2“—2. МС-многочлен типичного кодового слова имеет вид
Л(р, г)= £(И.
k+s
а его степень равна 2m~1—2й-.1. Таким образом, zA'(fte) = pszs; f2(z)=zs и степень fs(z) равна 2“ + 1, что дает для каждого кодового слова вес, равный
g2«-l 2«-1.
(3) . Код, порожденный идемпотентом 6*i+6*2, с теми же параметрами, что и в примере 2. Размерность этого кода равна Зи, а типичное кодовое слово имеет вид
ах161 -J- bx16s,
где a, b^GF(2) и 0^i^22u—2, 0^j^2u-—2.
Если а= 1 и Ь — 0, то вес кодового слова равен 2й-1.
Если а=0 и &=1, то вес равен 22u~i + 2u~1.
Если а=Ь=\, то получаем циклическую перестановку слова X’6*i+6*s. МС-многочлен этого слова равен
Л (р. г)= J (pz)7 + 2 Z /ее, ieca
и Л'(р, z)=fi+zr, где г = 2и. Нам надо найти f2(z). Так как Л'(р, z) =0 для p=zr или для
то
Д(р, |3') = 7Up'+‘)+ Р"’-
iecs
Далее согласно теореме 8 гл. 4 pr+1 лежит в GF(2U). Следовательно,
Тт (p'+I) = 2Ти (рл+1) = 0;
У [Г7 = pr+1 + p2r+2 -L ЛИ»
J6^s
• • -+rs/2 = T;( Рас-
последнее выражение равно 0 или 1 в зависимости от р. Если Л (р, Рг)=0, то степень ,f2(z) равна г+1 и вес кодового слова равен 22“~I+2'u l. Если А (р, рг) = 1, то степень многочлена /2(2) равна 1 и вес кодового слова равен 22“-1—2“-1. Таким образом,, верна следующая теорема.
Теорема 32. При m=2tz^4; s=2“+l код, порожденный идемпотентом 0*1+10%, имеет три ненулевых веса, а именно: 2й”1; т2 = 22“-1; т3 = 22«-1 +2“-'.
Теорема 33. Весовой спектр этого кода имеет вид:
Вес Число кодовых слов
0 1
ND N3 К £ ND ( 22“ — 1)
—1 г2"-!
22И_1+2Й_1 2^ I 2^"
Доказательство. Так как этот код содержит код Ж», то его дуальный содержится в коде Зёт. Следовательно, d'^3 и можно воспользоваться теоремой 2 гл. 6. •
Упражнения. (61). Показать, что минимальное расстояние дуального кода равно 3.
(62). Пусть ‘ё’ — код, порожденный идемпотентом 0o+0*i + 0*s, т. е. сформированный из предыдущего кода путем добавления кодового слова 1. Доказать, что размерность равна Зд+1 и что минимальное расстояние дуального кода 'ё’± равно 4. Пусть л
,(ё— код, получаемый из путем добавления общей проверки на л
четность. Показать, что весовой спектр кода <ё’ имеет вид:
Вес Число кодовых слов
О 1
__ —*1 2^—1 ^4 • 2^w
т2 = 22'^ Л2 = 2(22и-1)
^ = 2^ +2й-1 ЛТз = 23“-22“
4и 1
Некоторые примеры. [16, 7, 6]-код, полученный расширением циклического кода, порожденного идемпотентом 0О + + 0*1+0%:
г:0 6 8 10 16
А:1 48 30 48 1
[64, 10, 28]-код, полученный расширением циклического кода, порожденного идемпотентом 0о+ 0*1 + 0%:
i: 0 28 32 36 64
At: 1 448 62 448 I
Пример. (4). Код длины п=2>п—1, где т—2и-\А нечетно, порождается идемпотентом *01+0;*, где /=2“+1. В этом случае I и п взаимно просты и циклотомический класс Ci состоит из т чисел:
ci = { 2“+1,2“+1+2, • • ., 22“ + 2", 2"+1 + 1, • • •, 22“ + 2и-1}.
(Проверить для и=31, 1=5 и и=127, 1=9.)
Код имеет размерность 2m и состоит из слов вида ах161 + Ьх‘6/.
Если один из коэффициентов а идя b равен нулю, то вес кодового слова равен 22и. При а=Ь—\ кодовое слово является.' циклической перестановкой слова вида хг‘6*1 + 6*г.
Степень МС-многочлена этого слова равна 22и+2и, и он задается формулой
Л(₽, Z) = 2(p2y + £Z peGF(2,n).
1 fee I
Пусть г = 2“; тогда А'(|3, z) = p+zr+z2,’= (p2T+z+z2)r. Многочлены т(р, z) =|32r+z+z2 и A(z) могут иметь два общих корня,, или один, или ни одного; соответственно степень многочлена fz(z) равна 2г+1, г+1 или 1. Таким образом, единственно возможными значениями весов являются числа:
. Om 1 / О2“ I С>“ 1 \ _ о2и о"-
2т—1—( 22“ + 2“—I—2"+1) = 22“ + 2“.
Приведенные рассуждения не доказывают того, что в коде действительно имеются оба крайних экстремальных веса. Однако так как минимальное расстояние дуального кода не мерее 3, то можно воспользоваться теоремой 2 гл. 6 и вычислить число слов каждого веса.
Теорема 34. [п=2т—1, 2m, 22“—2й] циклический код с zn = 2w+l, порожденный идемпотентом 0*1 + 0*/, /=2“+1, имеет следующий весовой спектр;
Вес Число кодовых слов
О 1
Т1 = 22U_2„ а, = «( 22“~‘ + 2й-1),
т2 = 22“ ЛТг = п(22“+1),
т3 = 22и + 2и ЛТз = п(22и-1-2и-1).
Некоторые примеры, иллюстрирующие теорему 34, приведены на рис. 8.7.
[ 31, 10, 12] 1:0 А:1 12 10.31 16 17.31 20 6.31
[127, 14, 56] 1:0 56 64 72
А:1 28.127 65.127 36.127
[511. 18, 240] 1:0 240 256 272
Я>.Т 136.511 257.511 120.511
Рис. 8.7. Примеры к теореме 27
Упражнение. (63). Для п=35 и т=5 доказать следующие утверждения:
(1) . Если Г5(а)=0, то для некоторого Л из GF(25) имеет место равенство a=&+Z2= (Z-f-1) + (Z+1)2. Следовательно, многочлен т(р, z) при a=p2r имеет в GF(25) два корня.
(2) . В этом случае точно один из них является корнем А (р, z).
(3) . Если Г5(р) = 1, то т(р, z) неприводим в кольце Е[х] над полем GE(25).
Следствие 35. Минимальное расстояние кода <d?-L равно 5. Таким образом, кодовые слова каждого фиксированного веса образуют 2-схему с параметром
7 Д Ч (ТХ 1) д2и—2 / g2« gU 1 \.
a д Та (т2 1) __g2u—-1 Z g2u , j \.
ч - \ (2™_1)(2™_2)--2 12 +1 ь
Ч-Лт,(2т_1)(2т_2) ~2 *2 2 + '•
Л
Упражнение (64). Построить [2т, 2т + 1]-код 'd? путем добавления общей проверки на четность к коду с идемпотентом 6o+'6*i + 6*;. Показать, что векторы каждого веса образуют 3-схему и найти ее параметры.
ЗАМЕЧАНИЯ К ГД. 8
§ 8.2. Некоторые результаты § 8.2, 8.3 являются прямым следствием общей теории колец (см. Барроу [212], Кэртис и Райнер [321]). Так как порядок п группы G = {1, х, х"-1} |(см. § 7.2) взаимно прост с q, то любое представление группы G над GF(q) вполне приводимо (теорема Машке). Следовательно, групповая алгебра FG (и также кольцо /?„) полупроста. Согласно первой теореме Веддерберна —прямая сумма минимальных идеалов, и каждый минимальный идеал порождается единственным идемпотентом. Свойства идемпотентов см. в работах: Коэн и др. [297], Гоппа [540] и Мак-Вильямс [874, 882].
§ 8.3. Мы не рекомендуем использовать теорему 6 для вычисления примитивных идемпотентов на ЭВМ. Более пригодным для этого является алгоритм Прэнджа [1077] (см. также Мак-Вильямс [874]). Упражнения (14), (15), (17) и (22) взяты из работ: Гудман [534], Лемпель [813], Гоппа [540] и Вейс [1397].
§ 8.4. Весовой спектр циклических и связанных с ними кодов рассматривался в следующих работах: Баумерт [83], Баумерт и Мак-Элис [86], Берлекэмп [113, 114, 118], Бухнер [208], Дельсарт и Геталс [362] (коды с двумя весами), Геталс [488], Хартманн и др. [613], Касами [727, 729], Кердок и др. [759], Мак-Вильямс [874], Мак-Элис [940, 941, 945], Мак-Элис и Рамсей [949], Оганесян и др. [1003—1006], Робийярд [1117], Сегуин [1174], Соломон [1249], Стейн [1275] и Виллетт [1418].
§ 8.5. Упражнение <(33), теорема, 14, теорема 16 и упражнения (38), (43), (46) взяты из работ: Мак-Вильямс [870, 871], Прэндж [1074—1077], Питерсов [1038], Касами и др. [738] (см. также Дельсарт [344] и Камьон [239]). Лин [832] доказал теорему 18 для случая /=2.
§ 8.6. МС-многочлены были введены Мэттсоном и Соломоном [928]; см. также: Чень и Чой [286], Кердок и др. [759], Дум и Мак-Кин [396, гл. 4] (дискретное преобразование Фурье). Тождества Ньютона и другие свойства симметрических функций см.; Дэвид и Бартон [331, гл. 17], Дэвид, Кэндалл и
Бартон [332], Фулке [447],- Кэндалл и Стюарт [756, гл. 3], Тоибулл [1342, § 32] и Ван дер Варден [1376, т. 1]:‘Упражнение . (55) взято из [283] (см. также [346]), упражнение (56) — из [286], а теорема 25 принадлежит Форни [435].
Упражнение (60) взято из [1256]. Другие свойства величин Гг(а) можно найти в [939, 940]. Эти свойства оказываются очень полезными при нахождении весовых спектров.
§ 8.7. Для нечетного т весовые спектры всех кодов с длиной 2т—1, порожденных идемпотентами вида 0*i+6*s, s = 2£ + l, даны в [759]. Берлекэмп [118] и Дасами [729] доказали очень общие результаты о весовых спектрах подкодов кодов Рида—Маллера второго порядка—кодов, порожденных идемпотентами вида 2^7’ где I пробегает множество целых чисел вида 2£+1 (см. гл. 15).
/
Глава 9
Коды БЧХ
9.1. ВВЕДЕНИЕ
Коды БЧХ представляют большой практический интерес с точки зрения исправления ошибок, особенно когда ожидаемое число ошибок мало по сравнению с блоковой длиной. Впервые мы встретились с этими кода в гл. 3, где коды БЧХ, исправляющие две ошибки, были построены как обобщение кодов Хэмминга. Лучше, однако, рассматривать коды БЧХ как циклические коды, что и было сделано в § 7.6 при общем определении кода БЧХ, исправляющего t ошибок. Естественно, что основная часть теории циклических кодов, развитой в гл. 7 и 8, приложима к кодам БЧХ.
Например, коды БЧХ легко кодируются любым из методов, описанных в § 7.8. Декодирование будет рассматриваться ниже в § 9.6.
Напомним, что в гл. 7 код БЧХ над полем GF(q') длины п и конструктивным расстоянием 6 был определен как наибольший максимально возможный циклический код, нулями которого являются аь, аь+1, ..., аь+е“2, где a^GF(qm}—примитивный корень степени п из единицы; b — неотрицательное целое число, ат — мультипликативный порядок q по модулю п (см. § 7.5).
Важнейшие частные случаи задаются условиями: Ь = \ (соответствующие коды называются кодами БЧХ в узком смысле} и n=qm—1 (так называемые примитивные коды БЧХ). В тех случаях, когда не оговорено противное, под кодами БЧХ понимаются примитивные коды БЧХ в узком смысле. Другим важным подклассом кодов БЧХ являются коды с n = q—1 (т. е. с т=1; cceGF(,^)). Этот подкласс известен как коды Рида — Соломона, и следующая глава посвящена описанию специфических свойств этих кодов.
В § 7.7 получены границы для размерности k и минимального расстояния d произвольного кода БЧХ.
Теорема 1. (а). Код БЧХ над GF(q) длины п с конструктивным расстоянием 6 имеет размерность k^n—m(f>—1) и минимальное расстояние
(b). Двоичный код БЧХ блоковой длины п и конструктивным расстоянием 6=2/+1 имеет размерность k^n—mt и минимальное расстояние d^6. —
Возникает естественный вопрос, сколь близки эти границы к истинным значениям k и d; этот вопрос рассматривается в § 9.2 и 9.3. Ответ, грубо говоря, означает, что они достаточно близки. Однако в общем случае точная формула для d не найдена до сих пор.
§ 9.4 содержит таблицу двоичных кодов БЧХ длин не более 255. В этом диапазоне (а на самом деле для длин, достигающих нескольких тысяч) коды БЧХ принадлежат к лучшим известным кодам (см. приложение А). Однако, как показано в § 9.5, если зафиксировать скорость R — kln и устремить длину п к бесконечности, то их характеристики ухудшаются.
Декодированию кодов БЧХ посвящена обширная литература, предложены весьма эффективные алгоритмы их декодирования. § 9.6 содержит простое введение в описание алгоритма декодирования и его этапов.
Последний шаг алгоритма состоит в определении корней многочлена локаторов ошибок. Как мы увидим в § 9.7, в случае, когда этот многочлен является квадратным над полем характеристики 2, его корни находятся просто. Результаты § 9.7 используются также в § 9.8 для доказательства квазисовершенности двоичных кодов БЧХ, исправляющих две ошибки.
Использование глубоких результатов теории чисел позволяет показать в § 9.9, что если конструктивное расстояние кода БЧХ 7? не превосходит примерно м1/2, то все значения весов кода <ё>л-расположены около ’/гп. Можно заметить, что весовой спектр для многих кодов хорошо аппроксимируется функцией плотности нормального закона распределения. В § 9.10 дается частичное объяснение этого феномена.
В последнем параграфе главы описывается интересное семейство кодов не-БЧХ, исправляющих три ошибки.
Обозначения. Обычно в этой главе 4F обозначает [п, k, d] (примитивный в узком смысле) код БЧХ над GF(q) с конструктивным расстоянием 6. Как и выше a^GF(qm)—примитивный корень степени п из единицы, где т — мультипликативный порядок q по модулю п (см. § 7.5).
Пусть а= (а0, ..., an-i) —вектор над GF(q') веса w и
п—1 a(Aj = VQ;/.
г=0
Если ait, ..., aiw— ненулевые координаты вектора а, то назовем величины Хг=аг, г=1, ..., w локаторами вектора а, а многочлен
о(и)=П(1-лл=2^гГ (9-i)
r=l r=0
— многочленом локаторов. Пусть далее Yr=air, г=1, w, и определим степенные суммы вида
А{ = а(а1) = 2 YrXlr, 1 = 0, 1, • • - (9.2)
r=l
(см. также § 8.6). В частности, если вектор а принадлежит коду 'g', то Л;=0 для всех 1=S7/=S76—1.
9.2. ИСТИННОЕ МИНИМАЛЬНОЕ РАССТОЯНИЕ КОДА БЧХ
Первые три теоремы устанавливают, что при известных условиях истинное минимальное расстояние кода БЧХ равно его конструктивному расстоянию. Последняя теорема. описывает верхнюю границу истинного минимального расстояния для произвольного кода БЧХ. Первые два результата являются очень простыми.
Теорема 2. (Фарр.) Минимальное расстояние двоичного кода БЧХ длины п=2т—1 с конструктивным расстоянием 6=2/+1 равно 2/+1, если (а)
__ 1 \
2 >2га* (9.3)
г=0 \ I J или (Ь)
т > log2 (t + 1)! + 1 — t log2 (t/n).
Доказательство, (а). По следствию 17 гл. 8 минимальное расстояние d нечетно. Предположим, что d^2/+3. Размерность кода больше или равна п—mt, так что согласно границе сферической упаковки
Ж . .
/П \ <_ _
\i / г=0 ' '
Но это противоречит (9.3). Условие (Ь) выводится из (а) путем непосредственных вычислений, которые мы опускаем. • Пример. Пусть лг=5; /=1, 2, 3. Тогда' легко проверить, что
Ж
2/31\ 25*
( i J
i=o4 1
Таким образом, коды длины 31 и 6 = 3, 5, 7 действитёльно имеют минимальное расстояние d = 3, 5, 7, как показано на рис. 9.1.
Теорема 3. (Питерсон.) Если п=аЬ, то минимальное расстояние двоичного (не обязательно примитивного) кода БЧХ Длины п и конструктивным расстоянием а равно точно а.
п k d п k d п k d п k d
• 7 4 3 127 29 43* 127 120 3 99 47
22 47 113 5 91 51
15 11 3 15 55 106 87 53*
7 5 8 63 99 9 79 54
5 7 92 11 71 59*
255 247 3 85 13 63 61*
31 26 3 239 5 78 15 55 63
21 5 231 7 47 85
16 7 223 9 71 19 45 87*
11 11 215 11 64 21 37 91*
6 15 207 13 57 23 29 95
199 15 50 27 21 111
63 57 3 191 17 43 31* 13 119
51 5 187 19 36 31 9 127
45 7 179 21*
39 9 171 23
36 11 163 25*
30 13 155 27
24 15 147 29*
18 21 139 31
16 23 131 37*
10 27 123 39*
7 31 115 43*
107 45*
Рис. 9.1. Таблица кодов БЧХ: 4М='6 + 2; * — нижняя граница для d
Доказательство. Пусть а — примитивный корень степени п из единицы, так что aib=^=l для i<a. Так как хп—1=(хь—1)(1 + + хь + х2ь+ ... +х(а~1)Ь), то элементы а, а2, ..., аа-1, не являющиеся корнями многочлена хь—1, являются корнями многочлена 1 +хь+ ... +х(а“1)Ь. Последний многочлен и является словом веса а в коде (ё>.
Пример. Минимальное расстояние кода блоковой длины 255 и конструктивным расстоянием 51 равно в точности 51.
Следующая лемма дает характеристику многочленов локаторов векторов (над произвольным конечным полем), состоящих только из нулей и единиц.
Лемма 4. Пусть о (г) — сц zl г=0
— некоторый многочлен над GF(qm~). Многочлен o(z) является многочленом локаторов некоторого слова а, состоящего из нулей и единиц и принадлежащего коду БЧХ над GF(q') с конструктивным расстоянием б, в том и только в том случае, когда выполняются условия (i) и (ii):
(i) . Корни многочлена o(z) являются различными корнями степени п из единицы.
(ii) . Если q — степень простого числа р, то коэффициенты Qi равны нулю для всех I, лежащих в интервале l^i^m и не делящихся на р.
Доказательство. Если cr(z)—многочлен локаторов вектора а. удовлетворяющего условиям леммы, то Д;.= 0 для 1^/^б—1. Тогда результат вытекает из упражнения (53) гл. 8. С другой стороны, предположим, что выполнены условия (i) H .(ii), и пусть Xi, ..., Xw — элементы, обратные корням многочлена o(z). Тогда вектор а, содержащий единицы на позициях с этими локаторами, удовлетворяет равенствам А = 0 для всех 1^/^б—1 (опять согласно упражнению (53)) и, следовательно, принадлежит коду БЧХ. •
Мы используем эту лемму для доказательства теоремы.
Теорема 5. Минимальное расстояние кода БЧХ длины п= — q-m—[ и конструктивным расстоянием б=9Л—1 над полем GF(q') равно qil— 1.
Доказательство. Мы укажем кодовое слово веса б. Пусть U — Л-мерное подпространство поля GF(qm). По лемме 21 гл. 4
Ч*) = П(2-Р) = ^ + /Л_У~1+ • • -+4Z (9-4)
Реи
— линеаризованный многочлен над GF(qm). Рассмотрим вектор а, локаторами которого являются все ненулевые элементы |3 из U, причем координаты на позициях с этими локаторами равны 1. Многочлен локаторов такого вектора а равен:
н. 4h —i
°(z)=-TlU—Pz) = z’ ^(г-1)= V Gtz1,
P#=o г=0
Pea
где Oi = 0, если i не равно qh—qi для /=0, 1, ..., h. Согласно лемме 9.4 вектор а принадлежит коду БЧХ с конструктивным расстоянием qh—1, и его минимальный вес равен qb—1. 9
Пример. Пусть 9 = 2; щ = 3; Л = 2, т. е. рассмотрим код БЧХ с длиной 7 и конструктивным расстоянием 3. Этот код является [7, 4, 3]-кодом Хэмминга. Как видно из доказательства теоремы, этот код содержит векторы инцидентности всех линий проективной плоскости над GF(2) (см. рис. 2.12 и уравнение (24) гл. 2), и, следовательно, его истинное минимальное расстояние равно 3.
Теорема 6. Истинное минимальное расстояние d кода БЧХ над GF(q) с конструктивным расстоянием б не превосходит 96—1.
Доказательство. Определим d0 условием qh~*^.&<d0= qh—1. Так как коды БЧХ вложены друг в друга, то 'd? содержит код с конструктивным расстоянием d0, и согласно предыдущей теореме истинное минимальное расстояние этого кода равно d0. Следовательно,
d < с/0 < 9 б — 1- •
Хотя известно большое число результатов типа теорем 2, 3, 5 данной главы (см. замечания в конце главы), однако следующая задача остается нерешенной до сих пор.
Задача (нерешенная). (9.1). Найти необходимые и достаточные условия, которым должны удовлетворять п и конструктивное расстояние б для того, чтобы минимальное расстояние кода было равно б.
Задача нахождения точного значения для d в случае, когда d>6, представляется еще более тяжелой.
9.3. ЧИСЛО ИНФОРМАЦИОННЫХ СИМВОЛОВ КОДОВ БЧХ
Предположим, что — код БЧХ над GF(q') длины п—с^—1 с конструктивным расстоянием б. Мы видели, что согласно теореме 1 число информационных символов, которое мы обозначим через 1 (п, б), равно по меньшей мере п—тб. Но точное значение этого числа зависит от степени порождающего многочлена g(x), так как 1(п, б) = п—dcgg(x).
Степень многочлена g(x). По определению g(x)—многочлен наименьшей степени, имеющий своими корнями а, а2, ..., а6-'1, где а — примитивный элемент поля GF(qm). Если cd—-корень многочлена g(x), то корнями являются также и все его сопряженные, т. е. элементы a’9, aiq\ ... Число различных элементов, сопряженных с cd, равно наименьшему целому числу такому, что iq ' = i(mod<y'm—1). В обозначениях § 4.3 равно мощности циклотомического класса, содержащего i.
Имеется легкий способ определения числа rrti. Выпишем раз-, ложение числа i по основанию q:
i = 5n-i fl"1-1 + • • + irq + i0,
где 0^.iv^q—1.
Тогда qi^im_2qm~l+-+iiq2 + ioq+im-i(^odqm—l), т. e. умножение на q приводит к сдвигу т-последовательности Gm—ь io)-
Например, предположим, что q~2; т=4-, «у™—1 = 15. Тогда для 1=1 получаем 4-последовательность (0001), период которой равен 4; таким образом, имеются циклические сдвиги (0001), (0010), (0100), (1000), (0001), ..., и, следовательно, mi = 4. Мощность никлотомического класса Cj={1, 2, 4, 8} равна 4. С другой стороны, 1=5= (ОЮЦимеет период 2: (0101), (1010), (0101), ...; следовательно, т2 = 2. Соответственно С5= {5, 10}.
Если 1 достаточно мало по сравнению с п, то =
Теорема 7. Если q=2 и п = 2т—1, то циклотомические классы Ci, Сз, С5, ..., Сг различны и содержат каждый по т элементов при условии, что
г-<21т/2Г + 1
(9.5)
(где обозначает наименьшее целое число, большее чем х). Таким образом, если 1 удовлетворяет условию (9.5), то тг=т.
Доказательство, (i). Докажем прежде всего, что эти циклотомические классы различны. Рассмотрим класс С<. Двоичное раз
ложение числа i, записанное в виде /^-последовательности, имеет
О 0 • -О XX XI, (9.6)
где Xi равно 0 или 1. Может ли существовать циклический сдвиг последовательности (9.6), который также начинается ]т/2[ нулями и кончается единицей? Очевидно, нет. Следовательно, не может существовать нечетного /<2!’"/2, + 1 такого, что
(ii). Число элементов в циклотомическом классе G равно числу различных циклических сдвигов ^-последовательности, задаваемой двоичным разложением числа I. Легко видеть, что если г<21т/2Г-|-1, то все т циклических сдвигов различны. ®
Пример. n=63; т = 6. Несколько первых циклотомических классов имеют вид:
Двоичная
6-последовательность
С,={1, 2, 4, 8, 16, 32}, 060001
С3 = {3, 6, 12, 24, 48, 33}, 000011
С5 = {5, 10, 20, 40, 17, 34}, 000101
С7 = {7, 14, 28, 56, 49, 35}, 000111
Св = {9, 18, 36}. 001001
Как и было предсказано теоремой, все классы’ С\, ..., С7 различны, и мощность их равна 6. Эта теорема имеет непосредственное следствие.
Следствие 8. Пусть — двоичный код БЧХ длины п—2^—1 с конструктивным расстоянием 6=2£-|-1, где 2t—1<21’п/2,-|-1- Тогда dim‘§’ = 2™—1—mt.
Это следствие применимо к кодам с маленьким конструктивным расстоянием б. Для произвольного б верна следующая теорема.
Теорема 9. Степень многочлена g(x) равна числу целых чисел i, лежащих в диапазоне —1, и таких, что некото-
рый циклический сдвиг последовательности, задаваемой /у-разло-жением числа I, приводит к числу, не превосходящему б—1;
Доказательство. Это условие просто означает, что cd является корнем многочлена g(x') тогда и только тогда, когда у него имеется сопряженный элемент aiqr, где 1^[/<7'|и^б—1. •
Например, рассмотрим двоичный код БЧХ длины 15 и конструктивным расстоянием 5. Корнями g(x) являются а, а2, а4, а3 И а3, а6, а12, а9. Разложения показателей по основанию 2 имеют вид:
000.1, 0010, 0100, 1000, ООН, ОНО, 1100, 1001, и степень многочлена g(x) равна 8, что подтверждает лемму. Число информационных символов равно: / (15,5) = 15—8 = 7.
Но если 6 = 7, то g(x) имеет дополнительные корни а5 и а10 соответственно с /=(0101), (1010) и deg g(x) = 10; Z (15,7) = = 15—10 = 5.
Упражнения. (1). Чему равно число информационных символов двоичных кодов БЧХ длины 63 с 6=5, 7, 11, 21 и 27?
(2) .Решить ту же задачу для кодов БЧХ над GF(3) длины 80 с 6 = 4, 7 и И.
Конструктивное расстояние 8=q\ В остальной части этого параграфа находится верхняя граница Цп, 6) для частного случая, когда /г=1</'т—1 и 6 = </Л. Заметим, что при 7->оо
6
— = —---------Я
П
где г=т—7.
Наибольший отрезок последовательных нулей в т-последова-тельности назовем серией. Будем различать линейные и круговые серии. Например, последовательность 0100100 имеет две линейные серии длины 2 и одну длины 1, а также по одной круговой серии длин 3 и 2.
Из теоремы 9 теперь вытекает следующее утверждение.
Лемма 10. Степень многочлена g(x) равна числу целых чисел i, лежащих в диапазоне l^i^<7™—1 и таких, что т-после-довательность, задаваемая «/-разложением /, содержит круговую серию длины не меньше чем г.
Доказательство. Число i = im_i^TO_1+ ... -pir^+io не превосходит q'K—1 тогда и только тогда, когда й—4+i=... =0, т. е. тогда и только тогда, когда ..., й, i0) начинается с серии, длина которой равна по меньшей мере m—Х—г. •
Зафиксируем теперь г. Пусть s(m) обозначает число т-после-довательностей с элементами из множества {0, 1, .... q—1}, содержащих линейные серии, длина которых равна по меньшей мере г; пусть с(т) обозначает число ^-последовательностей, содержащих круговые серии, длина которых равна по меньшей мере г, и не содержащих ни одной такой линейной серии. Тогда согласно лемме 10
deg g (х) = s (m) -f-с (т)—1 (9.7)
(последний член обусловлен исключением из рассмотрения случая i=0) и
7(qm—1, qK) = qm—s(m) —c(tn). (9.8)
Таким образом, задача сводится к чисто комбинаторной задаче определения s(m) и с(т), причем с(т) можно опустить:
I(qm-1, qK)^qm-s(rn) (9.9)
(см. упражнение (3) в конце этого параграфа). Не составляет труда вывести рекуррентное уравнение для s(m).
. Лемма II.
s(k) = O для 0<&<r; s(r)=l; (9.10)
s (m) — qs(m—l) + (<7~ 1) (qm~r~1 — s(m—r— 1)}, m>r. (9.11)
Доказательство. Равенства (9.10) очевидны. Для доказательства уравнения (9.11) заметим, что m-последовательность, входящая в оцениваемое множество мощности s(m), содержит серию длины г в последних m—1 позициях (соответствующих младшим членам разложения), либо имеет вид
0> • ' ^пг— г—Р ^т—г—2’ ' * > г'о>
где гт_г-1У=0 и последние т—<г—1 позиций не содержат серии длины г. •
Если мы положим <p(rn)'=.(7m—s(m), то
/(^-1,Л<Ф(т), (9.12)
и по лемме 11
q)(k) = qh для 0<A<r; <p(r) = qr—1; (9.13)
<p(m) = <7<p(m—1) — (q— l)<p(m—г — 1), m>r. (9.14)
Общее решение рекуррентного соотношения (9.14) дается формулой
Ф(™) = £йгР?. (9-15)
i=0
где а, ..., аг определяются начальными условиями (9.13), а ро, ..., рг — действительные или комплексные корни уравнения
рг+1-<7рг-(<7-1). (9.16)
Далее все корни уравнения (9.16) удовлетворяют условию |рг|<<7. Для действительных корней это очевидно. Для комплексных корней р='Ьеге; 6=^=0; при Ь<1 это также очевидно. Предположим теперь, что Ь^1. Используя неравенство треугольника, из (9.16) получаем:
br+i+q— l>qbr. (9.17)
С другой стороны, из (9.16) также вытекает: рг=(9-1)(рг~1+ • • - + 1); &г<(9-1)(ьл-1+ • • +1); br+1<qb’-(q-l),
что противоречит неравенству (9.17).
Итак, мы доказали следующую теорему.
Теорема 12. (Манн.) Число информационных символов кода БЧХ (в узком смысле) над полем GF(q) длины —1 с конструктивным расстоянием qK удовлетворяет неравенству
1,
2=0
где г=т—К, величины а0, .... аг, ро, —, Рг зависят от г (и не зависят от т) и выполняется условие |р<| <q.
Этот результат будет использован в § 9.5.
Упражнение. (3). (Манн.) Показать, что точное значение I(qm—1, может быть найдено следующим образом:
(i) . Если т^2г, то
г—2
c(m) = (q—l)" у (г—k— I) { qm-r~k-z—s(m—r—k—2) }.
k=0
(ii) . Следовательно, для m^2r неравенство (9.12) можно заменить равенством
I(qm—I, </")г=ф(т)—(q—I)2 V (г—k—\)ц>(т—г—k—2). ь=о
(iii) . Корни (9.16) удовлетворяют условию р0= 1; pi является действительным числом, лежащим в интервале qr](r+1) <Cpi<<7 и |ipi| < 1 для 2<ЧгСг.
(iv) . Коэффициенты а; в равенстве (9.15) задаются формулами
Рг ( Рг — 1) =-------—-— .
рГ+> —1)г
(v) . Наконец, после некоторых преобразований для больших т получаем, что
Г
I (qm — 1, q7') = у (F1 = ближайшему к р'?: целому числу, г—0
9.4. ТАБЛИЦА КОДОВ БЧХ
Хотя, как мы увидим в § 9.5, при фиксированной скорости передачи характеристики кодов БЧХ с ростом п ухудшаются, для умеренных длин, вплоть до нескольких тысяч символов, они попадают в число наилучших известных кодов. На рис. 9.1 приведена таблица примитивных двоичных кодов БЧХ, блоковая длина которых не превосходит 255. Для каждого кода указаны длина п, размерность k и минимальное расстояние d.
Среди приведенных на рис. 9.1 кодов только для одного [127, 43, 31]-кода конструктивное расстояние 6 = 29 и известно,
что d>&. Однако (см. замечания к гл. 9) для больших значений т имеется бесконечное множество кодов такого сорта. Как мы видели в гл. 7, примеры непримитивных кодов БЧХ, для которых d>&, строятся просто.
Интересные непримитивные коды БЧХ. Иногда непримитивные коды БЧХ (при укорочении) содержат больше информационных символов, чем примитивные коды БЧХ с тем же числом проверочных символов.
Например, пусть п = 33. Первые два циклотомических класса имеют вид:
Ст = {1, 2, 4, 8, 16, —1, — 2, —4, —8, —16};
С3 = {3, 6, 12, 24, 15, —3, —6, —12, —24, —15}.
В общем случае если п=2т+1, то |С]|=2т, так что корни многочлена хп+1 лежат GF(22m). Если (3—-корень минимального многочлена, то р1 также является его корнем. Следовательно, любой циклический код длины 2^+1 реверсивен (§ 7.6).
Пусть — код БЧХ (в широком смысле непримитивный!) с порождающим многочленом Л4° (х)Л4(1)(х) ... (х). Тогда эле-
менты а1 при i—0, ±1, ..., ±(u-|-l) являются корнями g(x), и, следовательно, согласно границе БЧХ минимальное расстояние не меньше чем 2и+4.
При и=1 код ‘g’ является [2™ + 1, 2т—т, 6]-кодом и при том же числе проверочных символов имеет на один информационный символ больше, чем расширенный [2™, 2™—1—2m, 6] примитивный код БЧХ (см. § 18.7.3).
Упражнение. (4). Пусть п нечетно, а Т и R соответственно подстановки: Т=(0, 1, ..., п—1) и Д=(0, п—1) (1, п—2)... ...((п—3)/2, («+1)/2)((п—1)/2). Подстановка Т порождает циклическую группу Gi={P : 0^i<n}.
(i) . Показать, что Т и R порождают группу С2={1\ RT1: O^z<n} порядка 2п. Эта группа называется группой диэдра и представляет собой группу вращений и осевых симметрий правильного п-угольника. Доказать, что
Tn = № = (TR)2 = I. (9.18)
(ii) Пусть G — группа, содержащая элементы Т и R такие, что имеют место условия (9.18); 7’=#/ для всех 1 R=/=I и
TR=£l. Доказать, что подгруппа группы G, порожденная элементами Т и R, изоморфна группе диэдра порядка 2п.
(iii) . Реверсивный циклический код длины п инвариантен относительно группы G3, порожденной подстановками Т, R и о2: i—>2z(mod п). Показать, что: (а) если т, мультипликативный порядок 2 по модулю п, четен и n|2m/2 +1, то R = 62rnJ2T~1, порядок группы G3 равен \тп и она совпадает с группой, рассмотренной в упражнении (40) гл. 8; (б) в остальных случаях G3— {ог2Тг,-<№Тз : 0</<н} и порядок G3 равен 2тп.
9.5. ДЛИННЫЕ КОДЫ БЧХ
Границы Варшамова—Гилберта (теорема 12 гл. 1, теорема 30 гл. 17) устанавливают, что при фиксированном 7?, су-
ществуют двоичные [п, k, d]-коды с kjn^R и dlri^H2~l (1— R), где 7/2—1 (-^)—функция, обратная энтропии (см. § 10.11). Однако, за исключением случаев R = 0 и Д = 1, до сих пор неизвестны коды, достигающие этой границы.
Определение. При фиксированном q семейство кодов над GF(q) называется хорошим, если оно содержит бесконечную последовательность кодов ^i, (где —[щ-, ki, di\-код) та-
кую, что и скорость Ri = kilni и отношение dijni стремятся к ненулевому пределу при i->oo.
К сожалению, как мы сейчас увидим, примитивные коды БЧХ этим свойством не обладают — асимптотически они плохи!
Теорема 13. Не существует бесконечной последовательности примитивных кодов БЧХ над GF(q) таких, что оба отношения din и kin отделены от нуля.
Доказательство. Предположим, что ®Т, ®’2> — — последовательность таких кодов: —[ni = q'n‘—1, ki, с?г]-код, причем = Z?i>0 и dilni = B2>0. Пусть ^'г — код БЧХ длины иг с конструктивным расстоянием 6i= [ (di+ 1)//?]. Согласно теореме 6 истинное минимальное расстояние кода не превосходит di, и, следовательно,
Я-+1 яг
Выберем ki так, чтобы выполнялись условия q >0i~^q , и пусть — код БЧХ длины и конструктивным расстоянием q Ясно, что Wi, так что
7(<Л -1,
(9.19)
Далее
П; Чп1
d; В.2
~^~=В3>0. ср
Пусть Гг=1т<—ki. Так как ————&q~'1, то г, не мо-
«г qml —1
жет расти бесконечно; пусть, скажем, Согласно теореме 12
7(^-1, V й<г’(р<*))т; •
Так как — целое число, заключенное между 0 и Аг, то различных коэффициентов существует лишь конечное число.
Пусть Л2=тах|а/г)| и ?l3 = max|pi(i)| <q. Тогда
7(^-1, <(4+ 1)Л2Л3т* •
Следовательно, при i—>оо-------------1 ->0.
qmi — 1
Но из (9.19) имеем:
I ( gmi — 1, g'-i ) kj
qmi — 1 гц
что приводит к противоречию. 9
Итак, длинные коды БЧХ являются плохими; что можно сказать о других циклических кодах? Ответ на этот важный вопрос остается открытым *.
Задача (нерешенная). (9.2). Имеются ли хорошие циклические коды над GF(q) при фиксированном <у?
9.6. ДЕКОДИРОВАНИЕ КОДОВ БЧХ
Вопросу декодирования кодов БЧХ посвящено большое количество работ, и к настоящему времени найдены- эффективные алгоритмы их декодирования. В данном параграфе содержится простое описание основных этапов, на которых основаны эти алгоритмы. Дополнительные сведения можно получить в литературе, обширный список которой приведен в конце главы.
Пусть для начала — двоичный [п, k, с?]-код БЧХ с нечетным конструктивным расстоянием б. Предположим, что передавалось кодовое слово с= (с0, ci, ..., cn-i) и получено искаженное слово у = с + е, где е= (е0 еь ..., en-i)—вектор ошибок (рис. 9.2).
Кодовое слово
с - с@ • • с о -/
Принятое слово
!------------У
y=c+e=y0---yh_f
e = e0---e„_j Вектор ошибок
Рис. 9.2. Общий вид системы связи
Декодирование можно разбить на три этапа. (I). Вычисление синдрома. (II). Нахождение многочлена локаторов ошибок о(г). (III). Нахождение корней многочлена o(z). Опишем по очереди каждый из этапов.
- Этап (I). Вычисление синдрома. Проверочную матрицу можно положить равной
О П---1 \
1 а а2 • -а \
в г-i ® 9 I
1 а3 ст • • I .
1г76-2п2(б-2) а(6-2) ("-1) /
1 ОС (Л » • /
1 См. примечание на с. 194. (Прим, перев.)
Как обычно, пусть с(х) ='£cixi-t е(х) = 2е.,лг’; у(х) =^угХ1. Синдром вектора у равен (§ 1.4):
(1 а а2 . . -ап~1 \ /у0
1 а3 ае • • -а3 (п-1) Г1 У1
1„С-2 П Г7(6-П) ("~1) / \ U 1
, 1 сс а . - -сс / \ уп—1
(9.20)
где Ai=y{al). (Заметим, что Л21.= г/(а2’’) =г/2(о:’’) =42г.) Декодер может легко вычислить значения Ai по многочлену у(х) следующим образом. Разделим многочлен у(х) на минимальный многочлен 7И(0 (х) элемента а1:
У (х) = Q (х) А4(1) (х) + 7? (х); deg 7? (х) < deg 7И(г) (х).
Тогда At=y(al) равно значению многочлена R(x) в точке х=а1. Схема, выполняющая эти вычисления, приведена в § 3.4 и 7.8.
Например, рассмотрим [15, 7, 3]-код БЧХ с 6 = 5 из гл. 3. Предположим, что получен многочлен у(х) — У0+У1Х+ ... -J-z/ux14. Для вычисления А] разделим у(х) на 7И(1) (х) =х4+х-|-1 (см. §4.4) и вычислим значение остатка в точке х=а: 711=7? (а) =«0 + ща+ + u2ct2 + u3a3. Схема, выполняющая эти вычисления, показана в верхней половине рис. 9.3. Для вычисления А3 многочлен у(х) надо разделить на 7И<3)(х) =х'1-|-х3+х2+х +1 и найти остаток R(x) =7?0+7?!%+... +7?3х3. Тогда A3—R (a3) =i7?0+J?ia3+7?2a6 + +7?3а9 = 7?0+7?1а3+7?2(а2 + а3)+i7?3(ci+a3) = 7?0 + 7?3а + Т?2а2+ + (7?1+7?2 + /?3)а3'=Уо + Ща+о2с12 + У3а3.
Схема, выполняющая эти вычисления, показана в нижней половине рис. 9.3.
Таким образом, к концу первого этапа в декодере вычислены 41, 43...,4с-2. При необходимости также легко могут быть найдены величины 42=42i; Д4=Д22, ..., 46_, =Д26_1)/2.
Этап (II). Определение многочлена локаторов ошибок а(г). Предположим, что вес вектора ошибок е равен w и ненулевыми его компонентами являются ег\ > ..., £i, так что вектор у содержит ошибки в координатах ц, ..., iw. Как и в конце § 1, определим локаторы Xr=alr, г= I, ..., w, и многочлен локаторов ошибок
W W
o(2)==ri(i-^)=S <9-21>
z=l i=0
Рис. 9.3. Этап (I) декодера — вычисление синдрома
Для 1 sC 1 6—1 имеем:
Аг = У (а) = с (az) 4- е (а1) = е (а1), так как с(а1)=0 согласно определению кода БЧХ с конструктивным расстоянием б. Следовательно,
W
1=1
На этапе (I) алгоритма декодер вычислил степенные суммы А[, А2, Аб-ь Задача этапа (II), являющегося наиболее сложной частью алгоритма, состоит в определении многочлена о (г) по уже вычисленным Аь А2, Ae-i Коэффициенты а многочлена g(z) и величины Ai связаны тождествами Ньютона (которые могут быть записаны двумя способами: равенствами (8.12) или (8 14) — (8.16) из упражнений (52) и (54) гл. 8). Однако, как мы видели в § 1.3, синдром, т. е. величины А;, определяет вектор е или многочлен о (г) неоднозначно. Декодер должен определить вектор е наименьшего веса w или, что эквивалентно, многочлен o(z) наименьшей степени, удовлетворяющий тождествам Ньютона. (Именно эта неопределенность относительно w делает столь трудным второй этап алгоритма.)
Известно несколько методов нахождения о (г).
Начнем с простого, уже рассматривавшегося в § 3.3 примера кода БЧХ, исправляющего две ошибки. Описанный там алгоритм декодирования может быть интерпретирован теперь следующим образом.
Этапы. (I). Вычислить синдром
W
(II).
(i) . Если Д1=Л3=0, то положить o(z) =0.
(ii) . Если Д1=7^=0 и Д3=Д31, то положить o(z) = 1 +AjZ.
(iii) . Если 4=т^0 и /43=7^=/43i, то положить
о (z) = I 4- А& 4-
(>+4)А
(9.22)
(iv) . Если Aj — 0 и Л3=4=0, то можно заключить, что произошло по меньшей мере три ошибки.
Если многочлен o(z) будет найден [в случаях (i), (ii), (iii)], то декодер переводит к этапу (III) алгоритма, на котором вычисляются величины обратные корням многочлена o(z) и указывающие место локализации ошибок.
В случае произвольного кода БЧХ, исправляющего t ошибок, возможны два способа нахождения многочлена o(z), соответствующих двум формам тождеств Ньютона.
Метод (1). Использование тождеств Ньютона в виде уравнений (8.14), (8.16). Мы начнем с этого метода, так как он проще, хотя, за исключением случая малых t, и менее практичен. Согласно упражнению (54) гл. 8 если произошло w ошибок, то величины {щ} и {А,} связаны между собой уравнениями:
1 О О О О--- О
а2 4 1 о о-.-о а4 а3 а2 Al 1.. - о
А А л
^2®—4 2ж—5 ж—3
АД А
2 2®—3 ' 1
1 Q Q Q w to м 1 — - 4 “ /з 4 . (9.23)
1 А ™2w—3
А _ 2w— 1 _
Например, для кода, исправляющего две ошибки, эти уравнения (если w = 2) записываются в виде
1 01 Гщ
Al <з2
’4’ Л.
Решения этих уравнений даются формулами
^ = 4; а2=^+4=^+4-
/11 /11
и, следовательно, многочлен локаторов ошибок равен:
o"(z) = 1 + о, z + <т2 22 = 1 + AjZ + z2,
что совпадает д, (9.22).
В общем случае' уравнения (9.23) могут быть решены методом итераций, основанным на следующей теореме.
Теорема 14. {Питерсон.) Пусть
\ W
(vXv)-матрица
“1 0 0 0 0 -0 "
Л2 4 1 0 0 • • -0
Х2 Аг 1 - -0
д А А
_ 2V—2 2v—з ' ’ v—1 —
невырождена, если w = v или w = v—1, и вырождена, если w<_v—1. Доказательство (i). Предположим, что w<v—1. Тогда из (9.23) следует, что
~ 0 -
Mv
и, следовательно, матрица Mv вырождена.
(ii). Предположим, что w = v. Тогда
det Mv= П (Хг- + Х;)-
Действительно, если положить Xi = Xj, то согласно п. (i) detMv = = 0. Следовательно, det = const Пг</ (Xj + X,), и нетрудно показать, что эта константа должна равняться 1.
(iii). Наконец, если w = v—1, то невырожденность матрицы М следует из п. (ii). •
Используя эту теорему и предполагая, что произошло ошибок, для кода БЧХ с конструктивным расстоянием б = 2г+1 имеем следующий итеративный алгоритм для определения o(z).
Предположим, что произошло t ошибок, и попытаемся решить уравнения (9.23), полагая в них w=t. Если действительно произошло t или t—1 ошибок, то по теореме 14 решение существует и можно перейти к этапу (III). Если же произошло меньше чем t—1 ошибок, то уравнения не будут иметь решения. В этом случае
пбложим w = t—2 и снова попытаемся решить уравнения (9.23 j, заменив теперь w на t—2. И так до тех пор, пока решение не будет найдено.
Трудность этого метода состоит в том, что он требует многократных вычислений большого определителя над G7'(2”‘). Поэтому, если t велико (например, больше чем 3 или 4), то более предпочтителен следующий метод.
Метод (2). Использование обобщенных торкдеств Ньютона— алгоритм Берлекэмпа. Если произошло t ошибок, то величины {Л/} и {о,-} связаны между собой уравнениями (8.12) и (8.13). Уравнение (8.12) можно интерпретировать так, как показано на рис. 9.4: величины Лг являются выходом линейного регистра сдвигов с обратной связью, состоящего из w ячеек, находящихся в
Рис. 9.4. Вычисление величин А; на регистре сдвигов
начальных состояниях Дь А2, ..., Aw. Регистр показан в момент, когда в ячейках содержатся Дь А2, ..., Aw, а на выходе формируется
= ] Ао РшЛ|.
Задача декодера. По данной последовательности Ai, Л2, ..., Л6—1 найти линейный регистр сдвига с обратной связью наименьшей длины, генерирующий на своем выходе последовательность Ль Л2, Лб-1из начального состояния Ль ..., Aw.
Берлекэмп предложил эффективный алгоритм построения такого регистра сдвига (и, следовательно, многочлена локаторов ошибок o(z)). В гл. 12 мы опишем один из вариантов этого ал-ropirr?via, пригодный для широкого класса кодов, включая коды Гоппы и другие обобщения кодов БЧХ.
Какой бы из методов не использовался, в конце этапа (II) декодер знает многочлен локаторов ошибок о (г).
Этап (III). Нахождение корней многочлена o(z). Так как o(z)=IIf=1(l—XjZ), то величины Xi=«'s Xw=a’w являются обратными корням многочлена o(z) и ошибки содержатся в координатах ii, ..., iw.
Если степень многочлена o(z) равна I или 2, то его корни находятся непосредственно (см. § 7). Но в общем случае проще всего подставить каждую степень элемента а и проверить, является ли она корнем многочлена o(z). Эту часть алгоритма деко
дирования часто называют процедурой Ченя. Ошибка в координате i содержится тогда и только тогда, когда о(а~*)=0.
На рис. 9.5 показаны все три этапа работы декодера. Для иллюстрации 'работы схемы декодера на этапе (III) рассмотрим опять
код. Соответствующая часть схемы показана на
Ув\"У>зУ«
Р
У
Канал
Задержка
С Роль зоба-7* тем
_ Формирование /?/
А,
_______
Вычисле,-г-р.—т—7“I A S 5- -*\ние 6(a) ФормУроба- _£.§•§ б,1------
ние г
^0.
Нет
Этап! ЗтапП ЭтапШ
Рис. 9.5. Полный декодер
рис. 9.6. Первым символом, приходящим в точку Р, является уы, и ошибка в этом символе содержится в том и только в том случае, когда оба 14) =о(а) = 14-Gia+o2a2=0. Следующим приходит символ z/i3, и он ошибочен тогда и только тогда, когда о(а-13) = = о(а2) = 1 + oi«2 + Ога4 = 0, и т. д.
Умножение на <х записанного в регистре элемента
ii
Умножение на аг записанного 6регистре элемента бг
Рис. 9.6. Этап (III)
I
е
Схема, приведенная на рис. 9.6, в точности- выполняет эти требования. В начальный момент в три рассматриваемых регистра введены соответственно 1, сц и 02, вычисленные на этапе (II). Обратная связь во втором регистре осуществляет умножение на а, а обратная связь в третьем регистре — умножение на а2. После одного цикла работы регистры содержат соответственно I, ад, <Уга2, и выход элемента ИЛИ (внизу рисунка) равен 0 тогда и
только тогда, когда 1 + uia + u2a2 = u(a) =0. В противном случае этот выход равен 1. Элемент НЕТ заменяет этот выход на противоположный, так что в точку Q поступает 1 тогда и только тогда, когда символ уы ошибочен. Сумматор Р затем исправляет ошибку в «/и. /
Спустя один цикл, 1 приходит в точку Q тогда и только тогда, когда ошибочен символ z/13, и т. д. /
Таким образом, на этапе (III) определяются корни многочлена g(z) и исправляются ошибки, произошедшие в у.
Декодирование недвоичных кодов БЧХ. э/ап (I) совпадает с этапом (I) для двоичных кодов—декодер вычисляет ..., Ае_!. На этапе (II) вместо тождеств Ньютона (8.16) надо использовать уравнения (8.13). После нахождения u(z) можно использовать уравнение (8.19) для вычисления многочлена значений ошибок <o(z). Можно поступить и иначе, используя алгоритм Берлекэмпа для одновременного вычисления многочленов u(z) и co(z). На этапе (III) после нахождения корней многочлена u(z), указывающих место ошибок, для вычисления значений ошибок надо использовать уравнение (8.18).
Исправление более чем t ошибок. Описанные выше алгоритмы декодирования позволяют исправлять только t или меньшее число ошибок для кодов БЧХ с конструктивным расстоянием 2^+1. Для всех кодов БЧХ, исправляющих две ошибки, и для некоторых кодов, исправляющих три ошибки, известны (см. замечания к гл.) полные алгоритмы декодирования (см. § 1.5); однако следующая задача остается нерешенной.
Задача (нерешенная). (9.3). Найти полный алгоритм декодирования для всех кодов БЧХ.
Упражнение. (5). Для кода БЧХ, исправляющего три ошибки, найти выражение многочлена u(z), аналогичное (9.22), в случае, когда произошли ровно три ошибки.
9.7. КВАДРАТНЫЕ УРАВНЕНИЯ НАД GF(2’«)
Последний этап при декодировании кодов БЧХ состоит в вычислении корней многочлена локаторов ошибок u(z). Как мы увидим в этом параграфе, над полем GF(2m) квадратные уравнения решаются почти так же просто, как и линейные. Полученные здесь результаты будут использованы в § 12.5 при изучении кодов Гоппы, исправляющих две ошибки.
В § 4.6—4.9 было показано, что в поле GF (2т) имеется базис вида у, у2, у4, ..., у2”1-1, ’называемый нормальным. Любой элемент Р поля GF(2m) записывается в виде
т—1
₽ = &оТ + М2 + М4+ • • •+^m_IY2 > (9-24)
где bi равны 0 или 1 и след элемента р
7Д(Р) = />0 + 61+ • +&„_, (9.25)
(так как Tm(y2) = Тт(у) = 1).
Теорема 15. Квадратное уравнение x2+x + p = 0, ре GF (2™) имеет два корня в GF(2in), если T?n(p)=Q, и не имеет корней в GF(2m), есл1^Тт(р) = 1. Таким образом,
x\rhx + P = (x + T])(x + £), »]> £ СЕ GF (2'”),
если Tm(P)=O, \ многочлен х2 + х+р неприводим в поле GF(2m), если Tm(P) = 1. \
Доказательство. Выпишем разложение х и х2 по нормальному базису: \
\ о —1
х = + • • +xm_1Y2 ;
*2 = *т_1'т + *оТ2 + • •
Если х — решение уравнения х2+х+р = 0, то, приравнивая коэффициенты при у2', получаем:
*o + *m-i = bo'> х.+хо^Ьу, • • хт_] +х^_2 = Vi-
Сложение этих равенств согласно (9.25) дает:
m—1
i=0
Следовательно, равенство Тт(р)=О является необходимым условием для того, чтобы уравнение х2+х+р = 0 имело решение. Это условие также достаточно, так как если Тт(Р)=О, то имеются два решения этого уравнения, задаваемые соответственно равенствами х0=5; Xi = 6-|-6i; x2=6+6i+62, —,xm-i = 6+fei + ...
... где 6 = 0 или 1. Ф
Примеры. В поле GF(2) многочлен х2 + %+1 неприводим, так как 7'1(1) = 1. В поле GF(2) многочлен х2 + х+а неприводим, так как Т2(а)=1.
Теорема 16. Пусть р — некоторый фиксированный элемент поля GF(2m), след которого равен 1. Тогда любой неприводимый квадратный многочлен над GF(2) с помощью подходящей замены переменной может быть приведен к виду |(х2 + х+Р) для некоторого ceGF(2m).
Доказательство. Предположим, что многочлен ах2 + Ьх+с неприводим, причем п=7^0 и с=7^0. Более того, 6=7^0, так как в противном случае мы имеем полный квадрат. Заменяя х на bxfa, приводим многочлен к виду
— (х2 + х+ — } = Цх2 + х + сГ), d-ac/b?. а \ /
Согласно теореме 15 Tm(d) = l. Следовательно, 7’TO(P + d) = = Tm(p) +Tm(d) =0. Применяя опять теорему 15, заключаем, что в поле GF(2m) найдется такой элемент е, что е2 + е+ (P+d) =0. Заменяя х на х+е, приводим квадратное уравнение к виду ?(х2 + х+р). Ф
Упражнение. (6). Пусть р— некоторый фиксированный элемент поля GF(2m), след которого равен 0. Показать, что любой приводимый квадратный многочлен над GF(2m) с различными корнями может быть путем подходящей замены переменной приведен к виду £(х2 + х+Р) для некоторого ^GF(2m).
9.8. КВАЗИСОВЕРШЕННОСТЬ КОДОВ БЧХ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
Теорема 17. (Горенстейн, Питерсон и Цирлер.) Пусть 'g? — двоичный код БЧХ длины п = 2т—1, исправляющий две ошибки. Тогда — квазисовершенный код (см. § 5 гл. 1), т. е. любой смежный класс кода 'g? содержит вектор, вес которого не превосходит 3.
Доказательство. Для нечетных m этот результат был доказан в § 6.6.
Предположим, что m четно. (В этом случае <К± имеет пять весов (см. рис. 15.4), так что аргументация, использованная в гл. 6, не годится.) Выпишем проверочную матрицу кода
Н =
1а а2 •а'1 1
1а3 а6 - - -а301-1’
Если и — некоторый вектор длины п с локаторами Xj, ..., Xt, Z = wt(u), то синдром вектора и равен:
Ниг = <ЛУ А
[1= УХр, А3 = УХЗ. «। ни
Согласно теореме 5 гл. 1 между синдромами и смежными классами имеется взаимно однозначное соответствие. Поэтому достаточно показать, что для любого синдрома (Лц А3) найдется соответствующий вектор, вес которого не превосходит 3. Иными словами, для любой пары Ai, AS^GF(2m) мы должны указать три элемента Х2, Х3 в поле GE(2m) такие, что
Х1 + ХЩ-Х3 = Л1; 1
1 “ ' 3 1 I (9.26)
Х* + Х1 + Х1 = А3. |
Положим y-i=Xi+Ai, i=l, 2, 3. Тогда Х2, Х3 удовлетворяют условиям (9.26) в том и только в том случае, если уь у2, уз удовлетворяют системе
У1 + Уъ + Уз — 0;
где s=A3i+A3.
Подставляя у3—у\+у2 во второе уравнение, получаем
УуУАУг + У^^^.
Будем искать решение при у 2=^0. Полагая У=УаУъ, имеем \ У2 + у+^=0. (9.27)
\ У?
Согласно тео'реме 15 мы должны найти такое у?, чтобы выполнялось равенство Tm(s/ys2) =0. Если s = 0, то решениями уравнения (9.27) являются у=0 и у=1. Предположим, что s = a3k+v, где v=0, 1 или 2. Если v=0, то положим y2=ak, тогда T’m(s/j/23) = = Тт(1) = 0, как и требуется. Случаю v=0 соответствует и/3 элементов. Так как п/3<п/2, то в поле GF(2m) найдется элемент 0 такой, что Тт(0)=0, и не является кубом, скажем, 0 = азг+1 (случай 0 = a3z+2 аналогичен). Тогда след элемента 02 = a3z+2 также равен нулю. Таким образом, если, например, s = aSh+1, то выбор y2=ah~l приводит к требуемому результату: Tm(s/y32) = Tm(Q) =0.
©
Упражнение. (7). (Горенстейн, Питерсон и Цирлер.) (i). Пусть — код БЧХ над GF(q) с расстоянием Боуза, равным di = 2/+1 (см. § 7.6). Предположим, что (ё>2— код БЧХ с конструктивным расстоянием 2/1+2 и расстоянием Боуза </2. Показать, что ^2 имеет смежный класс, вес которого не меньше чем dt.
(ii). Вывести отсюда, что двоичный примитивный код БЧХ, длина которого больше или равна 7 и который исправляет три ошибки, имеет смежный класс, вес которого не меньше 5, и, следовательно, не является квазисовершенным.
Задача (нерешенная). (9.4). Доказать, что, кроме указанных, не существует квазисовершенных кодов БЧХ.
9.9. ГРАНИЦА КАРЛИЦА—УШИЯМЫ
Теорема 18. Предположим, что SF— двоичный код БЧХ длины п = 2т—1 с конструктивным расстоянием 6 = 2/+1, где
2/ —1 < 21m/2r + 1. (9.28)
Тогда вес w любого ненулевого слова кода <ё>± заключен в границах
2т—1 —(/—1) 2ml2 ^w^2m~l +(/—l)2m/2. (9.29)
Заметим, что вес w должен быть четным.
Доказательство. Идея доказательства состоит в следующем. Разность между числом нулей кодового слова а= (п0, ..., an_i)e‘₽’-L и числом его единиц равна S(—1)а\ Используя многочлен Мэттсона—Соломона, эту величину можно записать в виде показательной функции от следа [с. (9.30)]. Затем, опираясь на глубокий результат Карлица и Ушиямы, мы показываем, что эта сумма мала. Следовательно, число нулей кодового слова примерно равно числу его единиц, а вес, грубо говоря, равен ~п-
Нули кода liF лежат в циклотомических классах Сь С3, ..., СД-ь Из условия (9.28) и следствия 8 вытекает, что все эти
классы различны и мощность их равна т. Согласно § 7.5 классы С-i, С_3> C-2t+i образуют ненули кода ®’±. Поэтому согласно § 8.6 МС-многочлен вектора ае?1 равен:
2t—I / 2t—l \
A (z) = V Тт (pf г1) = Тт V рг zl = Тт (f (г)), ₽г GE GF ( 2т),
. i=l ' i=l J
i—неч i—неч
где степень многочлена f(z) равна 2t—1 и ^(0)=0.
Далее, используя теорему 20 гл. 8, запишем разность между числом нулей и числом единиц кодового слова а в виде
V (—1)“* =п—2wt (а) = У(—1)л(а‘ —l)T™(f » • (9.30)
1^0 S) i=0
Воспользуемся теперь без доказательства следующим результатом.
Теорема 19. (Карлиц и Ушияма.) Если f(z) — многочлен над GF(2m) степени г такой, что \f(z)^g2(z)-\-g(z)-\-b ни для одного многочлена g(z) над GF(2m) и ни для одной постоянной константы ЬеСД(2т), то
2 (-1)
feCf ( 2™)
Tm(f (₽))
<(r— l)2m/2.
Рассматриваемый многочлен f(z) удовлетворяет условиям этой теоремы, так как его степень нечетна. Следовательно,
(_i)rm<f <°)) +2*(—i)Tm(f (“г)) i=0
<(2М-2)2т/2 ;
| 1 + п — 2 wt (а) | С (2^—2) 2т/2, откуда вытекает (9.29). •
Следствие 20. Пусть ‘g’ — двоичный код БЧХ длины /г= = 2™—1 с конструктивным расстоянием 6 = 2t+l. Тогда минимальное расстояние кода <g’-L равно по меньшей мере
2"1-1 — (/—1)2т/2. (9.31)
Доказательство. Если 2t—1 <2[m/2l+1, то результат следует из теоремы 18. А если 2t—1^2[m/2, + l, то выражение (9.31) становится отрицательным. ®
Примеры. При t= 1 является симплексным кодом, все ненулевые веса которого равны 2т-1; это совпадает с (9.29), так как при t=\ следует, что w = 2m~1. При t=2 из (9.29) имеем: 2’”-1—2m/2^ny^2m-1 + 2m/2, что согласуется с рис. 15.3 и 15.4.
В качестве заключительного примера рассмотрим код БЧХ длины 127 с конструктивным расстоянием 11. Как видно из рис. 4.4, код имеет 15 последовательных нулей а113, ..., а126, 1, и, следовательно, согласно границе БЧХ (теорема 8 гл. 7) его минимальное расстояние не меньше 16, d~^ 16. Однако согласно теореме 18 с/^19, и так как d должно быть четным, то d^20.
На самом деле, некоторые данные говорят о том, что должен иметь место более сильный результат.
Задача (нерешенная). (9.5). Можно ли усилить утверждение теоремы 18, записав границы. В' виде
2m~‘ 2lm/2{^w^2m~1 + (t—l)2]m/2f?
Более простая граница для минимального расстояния кода, дуального коду БЧХ, дается следующей теоремой.
Теорема 21. (Сидельников.) Пусть — двоичный код БЧХ длины 2т—1 и конструктивным расстоянием 2/+1. Тогда минимальное расстояние d' кода удовлетворяет условию
дг C)tn—1—riog2 (21—1)1
Доказательство. МС-многочлен вектора ае??1 записывается в виде
4(г) = Ур/ ₽r-eGF(2m),
« ЮС;
где i пробегает все различные представители смежных классов Ci, Cz, ..., С2г-1. Двоичное разложение любого такого i имеет вид
(О, • - ; 0 Zr_p I, 10),
где li равны 0 или 1 и 1 -1- [log2(2.t—1)]. Такая последовательность содержит серию нулей длины по меньшей мере тп—1— — [log2(2Z—1)]. Двоичная последовательность, соответствующая разложению числа j^Ci, представляет собой некоторый циклический сдвиг последовательности, задаваемой двоичным разложением числа i, и, следовательно,
Так как 0 — корень многочлена A(z), то по теореме 26 гл. 8 имеем:
wt (а) > 2m — 1 — (deg A (z) — 1) > 2m-1-riog2 (2'-1 ’1. ®
9.10. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ НЕКОТОРЫХ ВЕСОВЫХ СПЕКТРОВ
Пусть — двоичный [и, k, Д|-код со спектром весов Ао, А1, ...
—, Ап, где Ai — число кодовых слов веса i. Тогда а = (а0, ch, •• ап), (9-32)
где aj=Aj/2k представляет собой вектор, у которого a0=2~fe; аЛ = ==а2= ... = щ;.1 = 0; а<^0; 2аг=1.
Пример. Пусть —[31, 21, 5]-код БЧХ, исправляющий две ошибки. Тогда согласно рис. 15.3 код имеет следующий весовой спектр:
i:0 12 16 20
д:: 1 310 527 186
Согласно теореме 1 гл. 5 весовая функция кода Ч? равна
^ [(* + yf- + 310 (х + уГ (х—у)12 + 527 (х + z/)15 (х-у)16 +
+ 186(% + 4/)И(х-J/)20]-
Следовательно, весовой спектр кода ‘ё’ равен:
z: 0 5 6 7 8 9 10 11
Л/31: 1/31 6 26 85 255 610 1342 2760
i: 12 13 14 15 16 17 - • •
Л/31 :4600 6300 8100 9741 9741 8100 • • •
На рис. 9.7 приведен график чисел aD, ..., Пзь Читателя сразу должна осенить мысль о гладкости и правильности полученной фигуры. Этот феномен наблюдается для многих кодов. Как правило, для многих кодов величины cij хорошо аппроксимируются биномиальным распределением, т. е.
1 In \
2" Ч /
для j > d.
(9.33)
Заметим, что в случае, когда 'К является [п, п, 1]-кодом К", в (9.33) имеет место строгое равенство. Нетрудно также показать, что равенство (9.33) выполняется
при случайном выборе кода (см. упражнение (8)).
В теореме 23 этого параграфа мы дадим некоторое обоснование формулы (9.33) для случая, когда минимальное расстояние дуального кода <К± велико. Мы предполагаем некоторое знакомство с теорией вероятностей.
До сих пор мы ничего не говорили о том, как понимается знаков формуле (9.33). Для того чтобы дать точную формулировку, определим функцию распределения A (z), ассоциированную с кодом.
Пусть а = (а0, ..., ап) — некоторый вектор над полем действительных чисел, для которого выполняются условия а^Ои = 1. Среднее и дисперсию вектора а определим равенствами
В = р, (а) = у ja}; о2 = о2 (а) = у (ц—/)2 Од 1=о j=0
Центральный момент порядка г равен
Ма)^= у\ г = °> !> • • • i=o' ° '
Таким образом, р0(а)=1, pi(a) =0; р2(а) = 1. Ниже естественно, особую роль будет играть биномиальный вектор Ь= (Ьо, ...,Ьп), где fcj=2"n( п ). Для него
Лемма 22. Пусть — код и вектор а задается формулой (9.32). Если минимальное расстояние кода <iFJ- равно d', то р, (а) =р, (Ь) для г = 0, 1, ..., d'—1.
Доказательство. Утверждение вытекает из упражнения (9)е гл. 5. Ф
Определение. Для произвольного действительного числа z функция распределения A(z) вектора а определяется равенством
п
Согласно классической центральной предельной теореме функция распределения B(z) вектора b при п->оо сходится к нормальному (или гауссовскому) распределению
2 Ф(г) = -Ь f e~t2/2dt. /2л
В данном параграфе рассматривается следующий частный случай этой общей теоремы.
Теорема 23. (Сидельников.) Пусть ’g’— двоичный код, и пусть минимальное расстояние d'- дуального кода <g’-L не меньше чем 3. Тогда
20 |Л(г)-Ф(г)|<^.
Доказательство. (Некоторые детали опускаются.) .Пусть а — некоторое слово кода <&. Согласно (5.20) о2 (а) = п4/4. Определим характеристическую функцию a(t) вектора а
r=0 г—О j=0
a(O = V ajeit(tl~i}/a. i=o
(9.35)
(9.36)
Уравнение (9.35) представляет собой разложение функции a(t) в ряд Тейлора, и нам нужна оценка остатка этого ряда. Прежде всего (индукцией по г) показывается, что для г=1, 2, ... и t>0
|е“_!—|<_С
I 1 1! (г~1)! I Н ’
Отсюда, используя равенство (9.36), получаем, что для всех четных г и произвольного t имеет место неравенство
t /О'—1)' ,
ocd + O-a©--^'©- • • •(5) =С
1! (г — 1) I
/ ч Н |г < р-r (а) .
и, следовательно, полагая £=0, имеем
а (О —V Ps(a)-^-1 S!
S=0
<P-r(a)-^~-г!
(9.37)
Положим теперь г равным наибольшему четному числу, не превосходящему d', r=2[(d'—1)/2]. Тогда согласно лемме 22 неравенство (9.37) можно заменить неравенством
“(О—У P-s(a)
s=0
(9.38)
В качестве отправной точки для доказательства используем следующую классическую формулу теории вероятностей (см., например, [427], уравнения (3.13) на с. 616 и (5.3) на с. 621)
|Д(г)—Ф(г)|<— [|-(0 c_t/2_|^4 л J I г I
—т
—, (9.39) Т п /2л
справедливую для всех Т>0. Используя неравенство (9.38), интеграл в (9.39) можно оценить сверху так:
4 J Л + [|1'<Ь)1£7ГЛ- (9•40,
—Т I s=0 — т
Первый из этих двух интегралов равен:
_LCJ_I I 2 (‘ e~f2/2
я J [ / [ | cos'2 Z/г 2 — e~*2/2 | dt~ nJ t
—t о
n J— (t/(/7T))S+lOg cos (t/(/n )) e I 2
At.
_ i
2 1
Пусть %—tn . Оценим величину —т2 + log cost с помощью разложения в ряд по степеням 1—cost функции log(l—(1—cost)). При ]т| <1 с учетом неравенств
. т
1-------< cos т <
2!
получаем, что
I I
------j- log cos т <
I 2 I
COST—l+-^-l+ — (.1—COST)fe
‘ fe=2
t4 . t4 __7т4
41' 4 ~ 24
Таким образом, подынтегральное выражение не превосходит
e-t2/2
т
7/3 7/4/24и—12/2’
24п 6
и, используя при лг^О оценку ех—1 ^.хех, а также предполагая, что 7’<и1/2, получаем, что оцениваемая величина не превосходит
7 е-542/24
24 п
Таким образом, первый интеграл в (9.40) не превосходит
12л п J 25л п
0
Второй интеграл в (9.40) равен — .
Согласно упражнению (9) эта величина не превосходит
4Г' р Г/2 д/г i/б лг-И \ е ) ‘
Собирая вместе все полученные результаты, для 7’<п1/2 получаем
|Л(3)-Ф(2)|<
168
25 л и
4ТГ е1/6 / г \г/2 л г! У г \ е /
24
Т л |/2л
1
/ г \ 9 / 6 \
Выбор 7’ = ^—) (77г) тату.
приводит к желаемому резуль-
9
В отличие от границы Карлица—Ушиямы и теоремы 21 эта теорема применима к кодам БЧХ с небольшим конструктивным расстоянием. Другие применения этого результата даны в замечаниях к главе, а также в главе, посвященной квадратично-вы-четным кодам.
Следствие 24. (Вариант классической центральной предельной теоремы.) Функция распределения B(z) биномиального вектора b удовлетворяет условию |В (z)—Ф(г) | .
Доказательство. Пусть ‘g’—[п, п, 7]-код Fn. Тогда d'=n. 9
Константа 20, участвующая в формулировке теоремы 23, конечно, не очень хороша, так как теорема приобретает смысл лишь при d', превосходящих 400. С другой стороны, рис. 9.7 может служить подтверждением того, что Ф (z) является хорошей аппроксимацией функции A (z) даже для коротких кодов.
Задача (нерешенная). (9.16). Усилить теорему 23.
Упражнения. (8). (см. также упражнение (31) гл. 17). Рассмотрим двоичный [п, &]-код 77 с порождающей матрицей G = = [11 А], где А — матрица размерности kx(n—k), состоящая из нулей и единиц (см. уравнение (1.8)). Предположим, что каждый элемент матрицы А выбирается равным 0 или 1 случайным образом с вероятностью ‘/а, а затем случайным образом выбирается слово и из кода <S>. Доказать, что Prob{wt(u) =0} =2~ft;
Prob {wt (u) = /} = 2~n [(n )—(n ~ k V , j > 0.
l\ i ) \ i
Таким образом, можно утверждать, что для случайно выбранного [п, &]-кода выполняется равенство (9.33).
(9). Доказать, что величины цг(Ь), определяемый условиями (9.34), для всех четных г^2 удовлетворяют неравенствам
[Указание. Ввести в рассмотрение независимые случайные величины Xi, ..., Хп, каждая из которых принимает значение +1 или —1 с вероятностью 7г- Величина Х{ аппроксимируется нормально распределенной случайной величиной ¥-; со средним, равным 0, и дисперсией, равной 1. Если г четно, то EXir= 1^ЕУ/.
п
Тогда
Ег (Ь) = —
„г/2
— Е V К, Iii
9.11. КОДЫ HE-БЧХ, ИСПРАВЛЯЮЩИЕ ТРИ ОШИБКИ
В этом заключительном параграфе описываются двоичные коды не-БЧХ, исправляющие три ошибки 7 Эти коды аналогичны кодам БЧХ и имеют те же самые параметры, но техника опреде-
1 См. задачу (нерешенную) (9.7).
ления их минимального расстояния d отлична от рассмотренной для кодов БЧХ и представляет самостоятельный интерес. Эти коды будут использованы в § 15.7 для построения нелинейных кодов Геталса.
Блоковая длина равна n=2m—1, где m = 2t+t, t^2, а — примитивный элемент поля GF(2m) и (х) — минимальный многочлен элемента
Порождающий многочлен двоичного кода БЧХ, исправляющего три ошибки, равен g(x) = (х)Л1<3) (х)Л1<5> (х). Порождающий многочлен нового кода равен g(x) = (х) (х) (х),
где г=1Н-2<-1; s= l-f-2*. Согласно упражнению (14) гл. 7 степень обоих многочленов Л1(7)(х) и Л1<8>(х) равна т. Первыми кодами в новом семействе являются:
т—5. [31, 16, 7]-код с порождающим многочленом g(x) = =Л1(1)(х)Л1(3)(х)Л1(5)(х)—обычный код БЧХ с исправлением трех ошибок.
т = 7. [127, 106, 7]-код с порождающим многочленом g(x) = =М™(х)М™(х)М™(х).
Сначала рассмотрим [и, п.—2и]-код & с порождающим многочленом g(x) =Л1(г)(x)M(s)(х). Этот код исправляет две ошибки. Для доказательства этого факта воспользуемся линеаризованными многочленами.
Пусть а(х)=х**+... -|-х*ю представляет собой многочленную запись двоичного вектора длины п, весом w и локаторами X={at,) ..., a<w}. Заметим, что
а ( с?) = V |У' = Aj. (9-41)
еех
Элементы множества X могут быть представлены как двоичные m-последовательности. Обозначим через V Е подпространство в GF(2m), порожденное этими т-последовательностями.
Обозначим через га и назовем рангом вектора а размерность этого подпространства. Очевидно, что ra^w, причем равенство достигается тогда и только тогда, когда все элементы из X линейно независимы над GF(2).
Каждый вектор подпространства Va представляет собой некоторый элемент |3 из GF(2m). Положим L(z) =Прега (z—13). Так как ХсдУа, то для
Гф) = 0. (9.42)
Из результатов § 4.9 следует, что L(z)—линеаризованный многочлен, т. е.
Г
= liEEGF(2m). (9.43)
г=0
Лемма 25. Если а(х) — слово кода ранга ra^~4, то й(а *+2' ) = 0 для всех 1^0.
Доказательство. Для рассматриваемого а(х) имеем: L (?) = Zoz + Z4z2 ++ Z3z8 + Z4zle, где Zo^O.
Для всех реХ согласно (9.42) выполняется равенство L(P)=0, и, следовательно, по (9.41) 4 4
2₽’+!,+" =S )
Ре* ;=о рех 1=о
Выделяя первое слагаемое, имеем:
Далее согласно определению кода &
ц(а1+2<~*) = 4«+2<) = 0;
4а^<+1) = ^+1(^%0; \(аЧ-2<+2) = ^+2(а1+2<“%0; I_____2
следовательно, а (а1+2 ) =0. Более того, для 1 Z^Z—2 VpL2t-2-z(p) = 0i Рех
и, таким образом, мы можем последовательно доказать, что а(а1+2< 3) = а(а1+2< *) = • • = й(а2) = 0. О
Следствие 26. Если а(х)—слово кода ранга га^4, то wt(a(x)) ^7.
Доказательство. Из леммы 25 вытекает, что а(а2)=а(а3) = = ц(а5)-=0. Тогда согласно границе БЧХ wt(a(x))^7. •
Теорема 27. Минимальное расстояние кода $ равно по меньшей мере 5.
Доказательство. Если ае,^, то wt(a) <j4=>ra<4=>- wt(a) ^7 (по следствию 26), что приводит к противоречию. •
Упражнения. (10). Показать, что если а(х)^^, то wt(a(x)) =5=>г а=5, т. е.
а (х) = х 1 -Т • - • -Т х Б, где .а*1,..., ats линейно независимы над GF(2).
(И). Пусть а(х)—-слово четного веса кода Хэмминга с порождающим многочленомЛРДх). ПустьХ= {pi, Рг, Бгг}; Х= {Р1+Ри, P2 + P2Z, ..., P2Z-1 + P2Z} и й(х) —вектор, задаваемый множеством X. Показать, что а(х) также принадлежит коду Хэмминга.
Наконец, найдем минимальное расстояние рассматриваемого кода, исправляющего три ошибки.
Теорема 28. Пусть W — [п, п—Зт} -код с порождающим мно-гочленом Л1(1) (я) Л1(г) (х)Л4<«> (х). Тогда минимальное расстояние кода равно 7.
Доказательство. Пусть st— код Хэмминга с порождающим многочленом 7И(1>(х). Тогда &=st и, следовательно, минимальное расстояние кода ‘g’ не меньше 5.
Предположим, что вес вектора a(x)^& равен 5. Тогда согласно упражнению (10), а(а)=Н=0. Следовательно, a(x').^st, что приводит к противоречию.
Предположим теперь, что wt(«(x))=6 и X={|3i, ..., |3б}- Так 6
как то |3; = 0. Пусть X— {|31-}-|Зб, Р2 +|3е+Ps + pe},
г=1
и пусть а (х) — вектор, задаваемый множеством X. Мы покажем, что и это даст нам противоречие, так как wt(a(x))=5.
Согласно упражнению (11) a(x)^st. Кроме того, так как Х|Зг = О, то
«(а’+2%(Р1 + рв)(р1+рв)2< + • + (р5 + рв) (р5 + рв)2< =
^(P1 + Pe)(pf + Pf)+ • + (₽5 + Рв)(Р52<+рб =
= Р’+2<+ • . w2 =Ф+2<)==0.
Аналогично п(а’+2 ) = а(а1+2 ) = 0. О
Задача (нерешенная). (9:7). Имеет ли код 'g’ такой же весовой спектр, как и код БЧХ, исправляющий три ошибки? Если да, то не являются ли эти коды эквивалентными? (Мы предполагаем, что нет.)
ЗАМЕЧАНИЯ К ГЛ. 9
§ 9.1. Ссылка на оригинальные работы Боуза, Рой-Чоудхури и Хоквингема дана в гл. 7. Весовые спектры различных кодов БЧХ можно найти в работах: Берлекэмп [113, табл. 16.1], Голдман и др. [518], Касами [727], Мирваанес [981]. Чень и Фрезер [289] применили коды БЧХ к задаче нахождения документации (см. также Боуз и др [179]).
§ 9.2 и 9.4. Истинное минимальное расстояние кодов БЧХ. По этому вопросу известно большое число результатов помимо приведенных выше. Например, Касами и Лин [734] показали, что если п=2т—1 и 6 = 2m-s-1—2”1-8-1-1— —1 для 1 <.««1—s—2 и —2t, то d=6.
Питерсон [1039] также доказал, что если минимальное расстояние d кода БЧХ длины п=2™—1 равно его конструктивному расстоянию 6, d=6, то минимальное расстояние кода с конструктивным расстоянием 6'=(6+1) 2m~h—1, где А^б, также равно 6'.
Для того чтобы определить минимальное расстояние кодов, приведенных на рис. 9.1, мы использовали следующие источники: Берлекэмп [113, табл. 16, 116], Чин [266], Касами, Лин и Питерсон [737], Питерсон [1038, 1039], а также теоремы 2, 3 и 5. Другие результаты, связанные с точным вычислением минимального расстояния, можно найти в работах: Чин и Лии [274], Хартманн и др. [612], Кни и Голдман [770], Лин и Велдон [839], Вулф [1428]. Теорема 2 принадлежит Фарру [417], а теоремы 3 и 4 — Питерсону [1038, 1039] (см. также [932]).
Мы будем признательны каждому, кто сможет убрать любую из звездочек на рис. 9.1. Коды, помеченные значком 4k были найдены Касами и Токурой [744], построившими бесконечное семейство примитивных кодов БЧХ, для которых 6<d. Сервейра [25], а также Лум и Чень [864] построили непримитив-ные коды БЧХ, для которых d>6.
Стенбит [1276] выписал порождающие многочлены для всех кодов, приведенных на рис. 9.1.
§ 9.3. В этом параграфе мы следовали Манну [906]. (В резюме к работе [906] имеется досадная опечатка: в третьей строке вместо 1=1, ..., v надо читать 1=1, .... v—1). Берлекэмп [112; 113, гл. '12] дал общее решение задачи вычисления I (п, 6) (см. также Питерсон [1036]).
§ 9.4. Что касается упражнения (4), см. Коксетер и Мозер [314].
§ 9.5. Теорема 13 была впервые доказана Лином и Велдоном [838] и Камь-оном [237]. Берлекэмп [122] доказал следующий результат:
Теорема 29. При и->-оо для любой последовательности примитивных двоичных кодов БЧХ со скоростью передачи R
d — 2и
loge log2n
где d может быть интерпретировано как конструктивное расстояние, расстояние Боуза или истинное минимальное расстояние.
К сожалению, доказательство этого результата слишком , длинно, чтобы приводить его здесь.
Касами [728] дал следующее обобщение теоремы 13. Любое семейство циклических кодов Является плохим, если оно обладает тем свойством, что соответствующие расширенные коды инвариантны относительно аффинной группы преобразований. Согласно теореме 16 гл. 8 это относится и к кодам БЧХ. С другой стороны, Мак-Элис [938] показал, что существуют (возможно, нелинейные) коды, которые инвариантны относительно больших групп преобразований и лежат на границе Варшамова — Гилберта (см. также теорему 31 гл. 17).
§9.6. Декодирование. Основным источником является Берлекэмп [113]. Замечательное описание дано 'также Питерсоном и Уэлдоном [1040] и Галла-гером [464]. Работа Ченя [282] содержит хороший обзор.
Частные алгоритмы декодирования для некоторых кодов БЧХ были описаны Бенерджи [67], Барти и Шнайдером [71], Блохом [164], Коулесом и Давида [312], Давида [333], Касами [725], Матвеевой [929, 930] и Полкин-хорном [1065].
Теорема 14 взята из [1036]. Алгоритм Берлекэмпа см. в его оригинальной работе [113, гл. 7], а также в работах: Месси [922, 922а], Галлагер [464], Питерсон и Уэлдон [1040, гл 9], а также гл. 12 настоящей книги. Улучшения алгоритма были предложены Бартоном [216], Онгом [1014], Салливэном [1293], Тзенгом и др. [1352]. Вопрос о сложности алгоритма рассматривали Байога и Волбессер [59].
Процедура Ченя описана Ченем [279]. Гор [543, 547] и Мандельбаум [896, 899] предложили методы, позволяющие ускорить процедуру Ченя, а иногда избежать ее совсем. Можно не использовать в алгоритме процедуру Ченя, если имеется непосредственный способ определения корней многочлена о(г). В этой связи приведем следующие ссылки на литературу, освещающую вопрос о разложении многочленов над конечными полями: Берлекэмп [111, 113, 117, 121], Берлекэмп и др. [131], Чень и др. [288], Голомб [523], Мак-Элис [937], Миллс и Цирлер [961]. Дополнительная литература по декодированию кодов БЧХ: Берлекэмп [НО], Чень и Тзенг [293], Давида [334], Форни [435] Лоус [795], Месси [920], Михельсон [954], Несенбергс [985], Сцвайя [1298], Танака и др. [1301, 1304], Уллман [1357], Вулф [1426].
Исправление более чем t о ш и б о к. Полное декодирование кодов БЧХ, исправляющих две ошибки, описано Берлекэмпом [113, § 16] и Хартманном [607]. Полное декодирование некоторых (возможно, всех) кодов БЧХ, исправляющих три ошибки, предложено Ван деп Хорстом и Бергером [663]. Их алгоритм будет пригоден для всех кодов БЧХ, исправляющих три ошибки, если будет доказано следующее утверждение.
Задача нерешенная (9.8). Доказать, что максимальный вес лидера смежного класса для любого смежного класса кода БЧХ, исправляющего три ошибки, равен 5. (Известно, что это действительно так, за исключением, быть может, случаев, когда m=2(mod 4) и т^12.)
Бергер и Ван дер Хорст [106] применили алгоритм декодирования кодов БЧХ, исправляющих три ошибки, к кодированию источников.
Хартманн [609], Хартманн и Тзенг [619], Редди [1096], Тзеиг и Хартманн [1351] предложили алгоритмы декодирования, которые в некоторых случаях позволяют исправлять несколько большее число ошибок, чем дает граница БЧХ.
§ 9.8. Результаты этого параграфа заимствованы из работ: Горенстейн, Питерсон и Цирлер [550] (см. также Берлекэмп [113, § 16] и [663]). Частичное решение задачи (нерешенной) 9.4. дал Леонтьев [816]: двоичные коды БЧХ длины п=2т—.1 и конструктивным расстоянием 6=21/4-1 не являются квазисовершенными, если т^7 и 2<.t<Zn'h log п.
§ 9.9. Теорема 19 взята из работы Карлица и Ушиямы [249] и опирается на глубокий результат Вейля [1394] (см. также Вильямс [1419]). К теории кодирования теорему 19 первым применил Андерсон [28]; однако наш результат является более сильным.
Задача (нерешенная) (9.9). Можно ли какие-либо другие границы нз теории чисел, например границы Ленга и Вейля [793], использовать для получения границ для минимального расстояния кодов?
Теорема 21 принадлежит Сидельникову [1208].
§ 9.10. Теорема 23 также принадлежит Сидельникову [1208] (с той разницей, что у него стоит константа 9 там, где у нас 20). Этот результат обобщен Дельсартом [360]. Его доказательство аналогично доказательству центральной предельной теоремы Берри — Эссена, данному Феллером [427, гл. 16.5]. Сидельников также доказал, что для многих кодов БЧХ
= ”)(1 + в), где |е|Сп 10,
2 \ / /
но доказательство этого факта слишком сложно, чтобы быть здесь приведенным.
На основании теорем 21, 23 и 29 заключаем, что при фиксированной скорости весовые спектры примитивных кодов БЧХ асимптотически нормальны.
Глава 10
Коды Рида—Соломона и коды Юстесена
10.1. ВВЕДЕНИЕ
В первой части этой главы изучаются коды Рида—Соломона, представляющие собой такие коды БЧХ над GF(q), длина которых п равна q—1. Они не только являются хорошей иллюстрацией кодов БЧХ, но, как мы увидим дальше, и сами представляют значительный практический и теоретический интерес. На их основе удобно строить другие коды, либо используя только сами коды Рида—Соломона, например отображая их в двоичные коды (§ 10.5), либо комбинируя их с другими кодами, как в каскадных кодах (§ 10.11).
Таким способом могут быть получены коды Юстесена (§ 10.11), представляющие собой семейство каскадных кодов. Эти коды замечательны тем, что являются первым семейством из рассматри
ваемых кодов, обладающих следующим свойством: при увеличе-нии длины п оба параметра кода — и скорость, и отношение рас-стояние/длина остаются положительными. Таким образом, в отличие от кодов БЧХ (см. § 9.5) коды Юстесена являются асимптотически хорошими кодами.
10.2. КОДЫ РИДА—СОЛОМОНА
Определение. Код Рида—Соломона (или PC) над GF(q) — это код БЧХ длины N=q—1. Конечно, q никогда не равно двум. Таким образом, длина кода равна числу ненулевых элементов в основном поле. Для обозначения длины кода, размерности и минимального расстояния мы будем использовать буквы N, К. и D (мы используем большие буквы, чтобы отличить эти параметры от параметров двоичных кодов, которые будут построены ниже). На рис. 10.6 представлена краткая сводка свойств этих кодов.
Так как х«-1—1 = ПребГ(<;г (х—13), то минимальный многочлен элемента а» просто равен М^(х)=х—ai. Следовательно, порождающий многочлен кода PC длины q—1 с конструктивным расстоянием 6 равей:
g(x) = (x— аь)(х— ab+1) (х—а’+6“2). (10.1)
Обычно, но не всегда полагают Ь = 1.
П римеры. (1). Рассмотрим, как обычно, поле GF(4) = = {0, 1, а, р=а2}, где а2+а+1 = 0. Для кода PC над GF(4) длины N=3 с конструктивным расстоянием 2 g(x)=x—а. Множество из 42 кодовых слов изображено на рис. 10.1.
ООО 0 1 а О а Р 0 р 1
1 а 0 а Р О
Р 1 0
) а; 0 1
Р 0 а 1 0 р 1 Р а а 1 Р
Р а I
1 1 1
а а а
Р Р р
Рис. 10.1. [3, 2, 2]-код PC над GF(4)
(2) . Построим PC код над GF(5) длины N—4 с конструктивным расстоянием 3. В качестве примитивного элемента поля GF(5) возьмем а=2, так что
g (х) = (х—а) (х—а2) = (х—2) (х — 4) = хя + 4х + 3.
Выпишем некоторые из 25 кодовых слов: 3410, 2140, 1320, 0341, НИ, ...
Размерность кода PC равна A = /V—degg(x) = N—6 + 1. Согласно границе БЧХ (теорема 8 гл. 7) минимальное расстояние D равно по крайней мере 6 = М—/<+1. По теореме И гл. 1 мини-
мальное расстояние не может превышать'этого значения. Следовательно, D—N—К+1 и коды PC являются разделимыми кодами с максимальным расстоянием, или МДР кодами (см. § 1.10 и следующую главу). Отсюда следует, что весовой спектр Хэмминга любого кода PC определяется теоремой 6 гл. 11.
PC коды важны по нескольким причинам:
(i). Их естественно использовать, когда требуется код, длина которого меньше чем размер поля, так как, являясь МДР кодами, они имеют наибольшее возможное минимальное расстояние-
(ii). Как мы увидим в дальнейшем, они удобны для построения других кодов. Например, они могут быть отображены в двоичные коды с удивительно большим минимальным' расстоянием. (§ 10.5). Они также используются при построении каскадных кодов и кодов Юстесена (§ 10.11).
(iii ). Они полезны для исправления пакетов ошибок (§ 10.6)-Кодирование и декодирование этих кодов обсуждаются в § 10.7' и 10.10.
Упражнение. (1). Показать, что код, дуальный коду РСХ, является кодом PC.
10.3. РАСШИРЕННЫЕ КОДЫ PC
Как показывает упражнение (42) гл. 1, добавление к коду общей проверки на четность не всегда увеличивает его минимальное расстояние. Однако для кодов PC это всегда так.
Теорема 1. Пусть является [N=qm—1, К, £)]-кодом PC с порождающим многочленом
g(x) = (x— а)(х— а2) • (х—aD~} ). (10.2^
Тогда расширение каждого слова с=с0С]... cN-i кода ‘g’ путем, добавления общей проверки на четность
N— 1
с№ 2С‘
i=0
приводит к [7V+ 1, К, £> + 1]-коду.
Доказательство. Предположим, что слово с имеет вес. D. Miis-нимальный вес с увеличивается до 0+1 при условии, что
N— 1
cU)=— cn= 2Ci °-
i=0
Но с(х) = a(x)g(x) для некоторого а(х), так что” с(1) — =fl(l)g'(l). Конечно, g(l)¥=0. Кроме того, а(1)У=0, иначе с(х)> делилось бы на (х—l)g'(x) и согласно границе БЧХ имело бы вес не менее чем 0+1.
Пример. Расширение описанного выше кода приводит'к. [4, 2, 3]-коду, изображенному на рис. 10.2. Действительно,, всегда: возможно дальнейшее расширение (см. § 11.5).
0 0 0 0 1 а 0 0 0 0 а 1 0 а 1 0
0 1 а 0 а 0 0 1 10 0а 1111
0 а 0 1 0 10а 1 0 а 0 а а а а
0 0 1а а 0 1 0 а 1 0 0 0 0 0 0
Рис. 10.2. Расширенный [4, 2, 3]-код PC
10.4. ИДЕМПОТЕНТЫ КОДОВ PC
В этом параграфе мы предположим, что ^=2т. Минимальные коды PC имеют размерность 1 (и, следовательно, D=N), и их легко описать. Проверочный многочлен равен h(x)=x+a{ для некоторого i=0, 1, ..., N—1 и g(x)= (xN-pl)/h(x). Имеется всего q—1 ненулевых кодовых слов, каждое веса N, и все они пропорциональны одному кодовому слову.
N—1
Предположим, что Д(х) = 2рг-х‘ представляет собой соответ-i=0
ствующий примитивный идемпотент с 0О=1. Так как код циклический, то многочлен
N— 2
Pi хЕ (х) = 0,0^, + 0, х + £ 0Д х1+1
i=l
также принадлежит коду и должен быть равен Е(х) (в противном случае кодое слово Е(х)—$ixE(x) имело бы вес, меньший чем N).
1- Следовательно, 02=02ь Повторение таких же рассуждений показывает, что
F(x)=l+0x + (0x)a + (0x)3+ • • • + (0х)"~1 (10.3)
для некоторого 0.
Например, для значения N=7 примитивные идемпотенты вместе с соответствующими проверочными многочленами приведены на рис. 10.3 (полагаем 0=1, а, .... а6).
Е (х) й(х)
0О = 1 4~ X +х2 +х3 + X4 +х5 + Xе х+1
Oi = 1 + ах -f- а2 х2 -|- а* х3 + а4 х4 + ав х5 + а6 х6 х-ра®
g2 = 1 + а2 х + а4 х2 + а6 xs + а х4 + а3 хБ -|- аБ хс х-ра5
63 = 1 -р а8 х -|- а6 х2 + а2 х® -|- аБ х4 -р а х6 -|- а4 х® х4- а4
04 = 1 4- а4 х 4- а х2 4- аБ х3 -J- а2 х4 -}- а6 *Б + Х-|- а3
06 = 14- аБ х 4- а8 х2 4- а х3 4- а6 х4 4- а4 хБ 4- а2 х8 х-р а2
бе = 1 + а3 х 4- аБ х2 4- «4 х3 4- а* х4 + ц2 хБ + сх х8 х-р «
Рис. 10 3. Идемпотенты минимальных [7, 1, 7]-кодов PC над GF(8)
к
Идемпотент [2™—1, К, 2™—К]-к<^да PC (/>=1) равен 2 6»-г=1 (Иногда проще найти идемпотент, чем порождающий многочлен кода, хотя оба требуют знания таблицы поля GF(2m).)
Упражнение. (2). Показать, что идемпотент [7, 2, 6]-кода PC (Ь = 1) имеет вид
Е (х) — а4 х + а х2 + а4 х® + сс2 х4 4- а2 х5 -р а х®.
Показать, что все ненулевые кодовые слова состоят из циклических перестановок следующих девяти кодовых слов: 0Ь 02, срЕ(х), 0^i^6.
10.5. ОТОБРАЖЕНИЕ КОДОВ НАД 0^(2™) В ДВОИЧНЫЕ КОДЫ
Как мы знаем из гл. 4, элементы поля GF(q), где q=pm, могут быть представлены щ-векторами с элементами из GF(p). Следовательно, [N, К, Д]-код PC над GF(q) становится [n=mN, k—mK, d^D] -кодом над GF(p). Если q=2m, то, как мы сейчас увидим, двоичные коды, получаемые таким путем (и другие коды, полученные из них), часто имеют большое минимальное расстояние.
Пусть gi, — базис элементов поля GF(2™j над G77(2). tn
Тогда, если |3= —любой элемент GF(2m), где bt^GF(2),
г=1
то отобразим |3 в m-вектор bt, bi, ..., bm. Это отображение переводит линейные коды в линейные (но циклические коды не обязательно переходят в циклические).
Примеры. (1). Используя базис 1, а для элементов GF (4) над GF(2), получаем отображение: 0->00, 1->-10, а->01, Тогда [3, 2, 2]-код PC над GF(4), изображенный на рис. 10.1, становится двоичным [6, 4, 2]-кодом, который приведен на рис. 10.4. .....
0 0 0 0 0 0 100100 110 0 0 1 1 1 0 1 1 0
0 0 10 0 1 0 1110 0 1.0 0 0 1 1 1 0 1 0 .1 0
0 0 0 111 1 1 10 0 0 10 11 0 1 0 1 0 1 0 1
0 0 1110 0 10 0 10 0 110 1 1 111- 1 1 1
Рис. 10.4. Двоичный [6, 4, 2]-код, полученный из [3, 2, 2]-кода PC, изображенного на рис. 10.1
(2) . Пусть вектор с= (с0, щ, ..., cK-.ij принадлежит \N,K,D\-коду PC над GF(2m). Заменим каждый элемент d соответствующим двоичным m-вектором и к каждому такому m-вектору ^добавим общую проверку на.., четность. Получившийся двоичный код будет иметь параметры
n = (m4-l)(2m-l); k = mK:, d^2D = 2 (2т-Е),: (ВД
где К — любое, К=1, 2, 2т—2. То же самое построение, при-
мененное к расширенному коду PC, приводит к
[(rn+l)2m, m/C, d>2(2m—/С+1)] (1С.5)
двоичным кодам, где /С=1, ..., 2т—1.
Например, из [15, 10, 6]- и [16, 10, 7]-кодов над GF(24) мы получаем [75, 40, 12] и [80, 40, 14] двоичные коды. Хотя существуют несколько лучшие коды — в гл. 12 мы построим [80, 40, 16] квадратично-вычетный код, простота этого построения производит глубокое впечатление (см. также § 18.8.1).
(3) . Если в качестве базиса для элементов GF(23) над GF(2) выбрать 1, а, а6, то получим отображение:
0-^0 0 0, 1-> 1 0 0, а->0 1 0,
а2-^1 0 1, а3->1 1 0, а4—>1 1 1,
а5->0 1 1, ае->0 0 1.
Рассмотрим [7, 5, 3]-код PC над GF(23) с порождающим многочленом gi (х) = (х+а5) (х+а6) =ia4 + cix+x2.
Удивительно, что при данном отображении этот код переходит в [21, 15, 3] Двоичный код БЧХ с порождающим многочленом ,g<Ay) =М<М(у) = 1 +У+У2+У^ + уъ. Действительно, сам многочлен ,Д;'(х) отображается в вектор 1 1 1, 0 10, 1 0 0, 0 0 0, 0 0 0, 00 0, Ю0 0, представляющий многочлен §2(у)- Кроме того, agi (х) отображается в ygz(y), a2gi(x) — в y2gz(y), xgi(x) — в y3g2(y) и т. д. Это единственный известный нетривиальный пример циклического кода, переходящего при таком отображении в циклический код!
Упражнение. (3). Пусть ф— линейное отображение из CGF(2m) на (GF(2))m и пусть ф—-отображение векторов длины 2™—1 над GF(2m) на двоичные векторы длины m(2m—1), индуцированное отображением ф. Предположим, что — циклический код над GF(2m) с порождающим многочленом g] (х), а ^2— двоичный циклический код с порождающим многочленом (у) Покапать, что ф отображает код 'S’i на код ‘ё’г тогда и только тогда, :когда для всех i, i=0, 1, ..., т—1, кодовое слово y'gA.y) является .образом при отображении ф некоторого кодового слова, пропорционального gi(x).
Задача (нерешенная). (10.1). Найти другие примеры циклических кодов, отображаемых на циклические коды.
Выбор базиса. Замена базиса может изменить весовой «пектр и даже минимальный вес кода. Например, рассмотрим [7, 2, 6]-код МДР с идемпотентом 0i + 06 и проверочным многочленом (х+а) (х+а6). (Этот код не является кодом PC.) Кодовые слова (над GF(23)) представляют собой циклические переустановки девяти векторов, изображенных на рис. 10.5.
Выбирая базис 1, а, а2, мы получим двоичные веса, приведенные в восьмом столбце. Выбирая же базис а3, а6, а5, получим .{Отображение
о -> о о о,.. 1->1 1 1, а->0 1 1,
а2—> 1 О 1, а3-> 1 О 0,' а4^1 1 О,
а5->0 О 1,
fz(i-^O 1 О,
которое дает двоичные веса, приведенные в девятом столбце. Заметим, что минимальный вес, полученный при первом отображении, равен 8, в то время как при втором — только 6.
1 Кодовое слово Базис # 1 Вес Базис # 2 Вес
X X2 X3 X4 X8 X6
1 а а2 а3 а4 а8 а6 12 12
1 а6 а8 а4 а3 а2 а 12 12
0 а8 а3 а6 а6 а3 а8 14 6
0 а6 а4 1 1 а4 а6 10 12
L0 1 а8 а а а8 1 10 12
0 а а6 а2 а2 а6 а 8 10
0 а2 1 а3 а3 1 а2 8 12
0 а3 а а4 а4 а а3 10 10
0 а4 а2 а8 а8 а2 а4 12 10
Рис. 10.5. Циклический код и веса двух двоичных кодов, полученных из него
Упражнение. (4). Показать, что первый двоичный код имеет следующий весовой спектр: Ао=1; -/18=14; Ai0=Ai2=21; Ai4=7. Спектр второго кода таков: Ло=1; А6=7; А10 = 21; Ai2=35.
Задача (нерешенная). (10.2). Для заданного кода ‘g’ над GF(2™) указать базис элементов поля GF(2m) над GF(2), который отображает код ‘g’ в двоичный код 'g'* с наибольшим минимальным расстоянием. Как сильно сказывается выбор базиса на минимальном расстоянии кода &*? Помогает ли использование нелинейных отображений?
Коды PC содержат коды БЧХ. Коды в примере 2 столь хороши, что заслуживают исследования их параметров при больших значениях т. Они ухудшаются, так как верна следующая теорема.
Теорема 2. [7V=2m— 1, К, 7)]-код PC с корнями порождающего многочлена а, а2, ..., аТ>1 содержит примитивный двоичный код БЧХ длины N и с конструктивным расстоянием D. Аналогично расширенный код PC содержит расширенный код БЧХ.
Доказательство. Если вектор с принадлежит коду БЧХ, то с — двоичный вектор такой, что с(а) = ... =е(ас-1) =0, и поэтому он также принадлежит коду PC. •
Следовательно, минимальное расстояние кода PC равно самое большее минимальному расстоянию кода БЧХ. Отсюда можно
вывести, что раз длинные коды БЧХ являются плохими (§ 9.5), то таковы же и длинные двоичные коды, полученные из кодов PC.
Теорема 3. Двоичные коды, полученные из кодов PC и имеющие параметры, заданные выражениями (10.4) и (10.5), являются асимптотически плохими, т. е. они не содержат бесконечного семейства кодов, у" которых и скорость, и отношение расстоя-ние/длина были бы отделены одновременно от нуля.
Доказательство. Пусть —1, К, D = N—Д+1]-код
PC. В силу теоремы. 2 код содержит двоичный БЧХ код ‘g’j длины N с конструктивным расстоянием D. Определим d2 следующим образом:
2f-1<P<dg = 21'—1, так что код содержит код БЧХ ^2 с конструктивным расстоянием rf2. По теореме 5 гл. 9 расстояние d2 представляет собой истинное минимальное расстояние кода ^2.
Пусть теперь 'ё’з — двоичный [(т-Ы)М m!\, <Д]-код с параметрами (10.4), полученный из кода (Доказательство для кодов с параметрами (10.5) аналогично.) Тогда
d3 С 2Д2 < 4D.
Следовательно, если скорость кода ^з, равную m/C/(im+l)A«* ~K)N, зафиксировать, то отношение
Расстояние rf3 4D 4 (Д'— К-|-1)
____Длина - (ш+ \)N
стремится к нулю, когда т->оо. *
Однако если использовать лишь немного более сложное построение, то из кодов PC можно получить асимптотически хорошие двоичные коды (см. § 10.11).
10.6. ИСПРАВЛЕНИЕ ПАКЕТОВ ОШИБОК
Во многих каналах ошибки не случайны, а имеют тенденцию скапливаться группами или пакетами.
Определение. Пакетом длины b называется вектор, все ненулевые элементы которого расположены среди b подряд идущих компонент, из которых первая и последняя являются ненулевыми.
Особенно подходят для исправления нескольких пакетов двоичные коды, полученные из кодов PC. Ясно, что двоичный пакет длины b может повлиять самое большее на г соседних символов из GF(2m), где г определяется условиями (г—2)т-р2^Ь^(г—1)Х Х^г+ 1.
Поэтому если D намного больше г, то могут быть исправлены многие пакеты ошибок.
10.7. КОДИРОВАНИЕ КОДОВ РИДА—СОЛОМОНА
Так как коды PC являются циклическими, к ним применим любой из методов кодирования, описанных в § 7.8. Однако некоторые практические преимущества имеет следующий простой метод ко
дирования (фактически представляющий собой метод, описанный в оригинальной работе Рида и Соломона).
Пусть и= («о, Щ, Uk-i), Ui^GF(q)—информационные символы, которые должны быть закодированы, и пусть
Д-1 и (z) = V utzl.
1=0
В качестве кодового слова, соответствующего и, выбирается вектор с, многочлен Мэттсона—Соломона которого равен Nu(z), N=q—1. Таким образом,
c = (w(l), и(а), • • u(aN~1}). (10.6)
[Или ы(0), ы(1), ы(а), ..., u(aN~x)) для расширенного кода, т. е. кода, к которому добавлена общая проверка на четность]. Чтобы показать, что вектор с принадлежит коду Рида—Соломона, убедимся в том, что элементы a, a2, ...,aD~l являются- корнями многочлена
N— 1 с(х)= ^CiX\ i=0
Действительно, согласно равенству (8.8) многочлен Nu(z), являющийся МС-многочленом вектора с, равен
N-1
S А~,zi>
i=o
где Д = с(а
Отсюда, приравнивая коэффициенты и пользуясь равенством N=— 1, справедливым в поле GF(q), получаем, что
с(1)=—ы0; с(а-1)=—Hj, • • •, с(а~л+’)=—(10.7) и с(ц5')=0 для IjgC/^Af—K—D—1. Таким образом, вектор с принадлежит коду PC и описанная процедура является процедурой кодирования для этого кода. Заметим, однако, что это кодирование не является систематическим.
Определение. Предположим, что ‘g’ — линейный или нелинейный (п, M = qk, й)-код над полем GF(q)\ кодер кода отображает сообщение w0, Чь-i в кодовое слово с0, cn-i- Кодер называется систематическим, если имеются координаты io, ..., ik-i такие, что u0=cto, ..., uk-i=Cth , т. е. если сообщение входит в кодовое слово без изменений.
Например, такой кодер:
Сообщение Кодовое слово
00 000
01 010
10 101
11 111
является систематическим (причем 1’о'=О; й = 1), в то время как
тот же самый код может иметь несистематический кодер:
Сообщение Кодовое слово
00 000
01 111
10 101
11 010
Несистематический код перемешивает сообщение. Даже после того как найдены вектор ошибок и кодовое слово, в несистематическом коде необходимо еще выполнить соответствующие вычисления, чтобы извлечь само сообщение. В рассмотренном выше примере выражение (10.7) как раз говорит, как восстановить сообщение по кодовому слову.
Упражнение. (5). Показать, что любой линейный код имеет систематический кодер. А что можно сказать о нелинейных кодах {000, ПО,'011, 111} и {000, 100, 010, 001}?
Рассмотрим, например [4, 2, 3]-код PC над GF(5), описанный в примере 2 (§ 10.2). Кодер* 1 из § 7.8 отображает сообщение (и0, щ) в кодовое слово (2«о+2«1, по+Зщ, и0, щ). С другой стороны, только что описанный кодер отображает (и0, U\) в кодовое СЛОВО С= (Ufl + iZi, Wq + 2Wi, Wo + 4wb w0+3wi).
Упражнение. (6). Проверить два последних утверждения.
Код PC длины -N=q—1 над GF(q) представляет собой циклический код с порождающим многочленом g(x) = (x—аь) (х—аь+1)...(х— —аь+б-2у где а — примитивный элемент поля GF(q). Размерность кода равна К — F— 6+1, а минимальное расстояние 6. (Часто 6 = 1.) Этот код является и кодом БЧХ, и кодом МДР (гл. 11). Он может быть расширен до [</+!, К, q—К+2]-кода и (если q = 2m) до [2т+2, 3, 2т]- и [2"Ч-2, 2й1—1, 4]-кодов (§ 11.5).
В § 10.4 описано как найти его порождающий идемпотент. Коды PC важны для каскадных кодов (§ 10.11) и при исправлении пакетов ошибок (§ 10.6).
Рис. 10.6. Свойства кодов Рида — Соломона
*10.8. ОБОБЩЕННЫЕ КОДЫ РИДА—СОЛОМОНА
Несколько более общий класс кодов, чем коды PC, получается, если выражение (10.6) заменить на следующую формулу:
€ = (^^(1), п2п(а), • •, vNu (aN~1)), (10.8)
где Vi-—ненулевые элементы GF(q).
Выражение (10.6) соответствует случаю, когда п<=1 для всех i. Это подсказывает дальнейшее обобщение.
Определение. Пусть а= (а1( ..., соД, где а< — различные элементы GF(qm), и пусть v= (щ,..., щД, где — ненулевые (но не обязательно различные) элементы GF(qm). Тогда обобщенный
код PC, обозначаемый через ОРСК (a, v), состоит из всех векторов вида
»2*F(“2), • • •. vNF(aN)), (10.9)
где F(z) пробегает все многочлены степени меньше Д с коэффициентами из поля GF(qm).
Этот код представляет собой [К, /С]-код над GF(qm). Так как многочлен F имеет самое большее К—1 корней, то минимальное расстояние кода равно по крайней мере N—К+1 и, следовательно, в точности равно N—К+1. Это код МДР.
Теорема 4. Код, дуальный ОРСк(а, у)-коду, является OPCjv-K(a, v')-кодом для некоторого вектора v'.
Доказательство. Предположим сначала, что K=N—1, и пусть код Ф дуален коду OPCjv_i(a, v). Тогда Ф имеет размерность 1 и состоит из всех векторов, пропорциональных некоторому фиксированному вектору v'= (v'i, ..., v'w). Мы должны показать, что все г/г=И=О. Вектор v' удовлетворяет следующим4 равенствам:
^' + . . ,+Vjv^ = o;
«1^;+ • .+-«^^=0;
или
(10.10)
Если произвольное </< = 0, то (10.10) дает систему уравнений относительно других Vtv'i, матрица коэффициентов которой представляет собой матрицу Вандермонда. Следовательно, по лемме 17 гл. 4 получаем, что для всех i Vtv'i = O и, значит, все сД=О, что невозможно.
Но тогда ОРСк(а, v) дуален коду OPCjv-K(a, v') для всех К<К—1, так как в силу (10.10)
N М
X (“! («I = 2 al+t ViVi=0
для ssCK—1; /=СК
Из теоремы 4 ОРСК (a, v) равна которая имеет вид
вытекает, что порождающей
проверочная матрице
матрица кода кода OPCAr_K(a, v'),
(10.11)
В § 12.2 мы снова встретимся с этими кодами.
Упражнение. (7). (а). Показать, что если Pi=cai + d(i= = 1, /V), где с=^=0 и с, d^GF(qm), то OPCK(a, v) = ОРСк(₽, v).
(b). В каких случаях коды ОРСк(а, v) и OPCK(a, w) эквивалентны?
(с). Показать, что ОРСк(а, v)=OPCK(a, w) тогда и только тогда, когда v=Xw, где Х^=0 и 7.<=GF(qm).
10.9. ИЗБЫТОЧНЫЕ ВЫЧЕТНЫЕ КОДЫ
Равенство (10.6) подсказывает также другую точку зрения .на коды PC. Заметим, что u(ai) представляет собой остаток от деления многочлена и(х) степени меньше Л, соответствующего сообщению, на двучлен М^(х)=х—щ. Поэтому мы можем так интерпретировать равенство (10.6): сообщение и(х) кодируется в вектор *
(ГО, Д, • ; (10.12)
где Гг — вычет и(х) по модулю ЛЕ«)(х).
Многочлен и(х) может быть восстановлен по своим вычетам с помощью следующей теоремы.
Теорема 5. (Китайская теорема об остатках для многочленов.) Пусть т0(х), ..., mK-i(x)—попарно взаимно простые мно-члены над GF(q), и пусть М(х) = т0(х)т1(х) ...тк.Л(х). Если Го(х), rK_i(x)—произвольные многочлены над GF(q), то существует единственный многочлен и(х) степени degw(X)<degM(х) такой, что ’ к
и (х) == гг (х) (mod m-i(х)) (10.13)
для всех i=0, ..., К—1. Действительно, пусть многочлен йг(х) таков, что
-М а, (х) = 1 (mod т, (х)), г = 0, 1, • • •, К—1-mt (х)
(По следствию 15 гл. 12 такой многочлен at(x)' существует.) Тогда решением системы сравнений (10.13) является многочлен
(10.14)
приведенный по модулю М(х).
Упражнение. (8). Сформулировать соответствующую теорему для. целых чисел.
Теорема 5 показывает, что знания вычетов г0, ..., rK-i в выражении (10.12) достаточно для восстановления и(х) в отсутствие
шума. Таким образом, гк(х), ..., rN-i(x) являются избыточными вычетами, которые включаются в кодовое слово для защиты от ошибок. Любой код такого типа называется избыточным вычет-ным кодом. Мы показали, что коды PC представляют собой избыточные вычетные коды, а в гл. 12 мы увидим, что таковыми являются также некоторые коды Гоппы. Другие примеры будут упомянуты в замечаниях к этой главе.
10.10. ДЕКОДИРОВАНИЕ КОДОВ PC
Так как коды PC являются частным случаем кодов БЧХ, они могут быть декодированы методами, рассмотренными в § 9.6. Стоит напомнить также мажоритарный метод декодирования, первоначально предложенный Ридом и Соломоном, ввиду его значительного теоретического интереса, хотя он и не очень практичен.
Предположим, что было передано кодовое слово (10.6), имел место вектор ошибок е= (во, ..., е^-i) и был принят вектор у= = (у0, ..., yn-t)- Таким образом, декодер знает следующие суммы: ^о = ео+ыо + ы1 +Ы2_Ь • • • +
i/1 = e1 + w04-aw1 + a2w2 + • + а*-1 ик_^ ;
Vn-i = eN-i + “о + aN~' ui + а2 {N~1} и2 + • • • + .
(10.15)
Если ошибок не произошло, то е=0, и для определения сообщения и= (ио, ..., «к-i) могут быть решены любые К из этих уравнений, так как матрица коэффициентов является матрицей Ван-дермоида (см. лемму 17 гл. 4). Таким образом, всего имеется
\л/ различных возможностей, или голосов, для определения истинного вектора и.
Если имеются ошибки, то некоторые множества из К уравнений будут давать неправильные значения и. Но ни один неправильный вектор и не может получить слишком много голосов.
Теорема 6. Если произошло w ошибок, то любой неправиль-
„ /w + К - 1\ тт
ныи вектор и получит самое большее I | голосов. Истин-
„ „ „ /N — w\
ныи вектор и получит по крайней мере I ) голосов.
Доказательство. Так как уравнения в системе (10.15) независимы, то любые К из них имеют точно одно решение и. Для того чтобы получить больше чем один голос, вектор и должен быть решением больше чем К уравнений. Любой неправильный вектор и может быть решением самое большее w + —1 уравнений, состоящих из w ошибочных уравнений и К—1 правильных (так как если и — решение К правильных уравнений, то и — правильный вектор). Таким образом, любой неправильный вектор и мо-
жет быть решением самое
множеств из К
И ГТ / IV - W \
уравнении. Ясно, что всего имеется ( ) i
ных уравнений, дающих правильный вектор и.
Таким образом, сообщение и будет восстановлено правильно,
еСЛИ , , , , X. X, , X, х ... ~ х. х, ,
I К I \ К I
+ 1>2ж Поэтому векторы ошибок, вес которых меньше половины минимального расстояния (и, возможно, некоторые другие), х tz /ЛР
могут быть исправлены. Конечно, если число ( метод практически неприменим.
множеств правиль-
w+K— 1 К
j , т. е. если N—w>w + K—1 или D = N—К+
велико, то
этот
10.11. КОДЫ ЮСТЕСЕНА И КАСКАДНЫЕ КОДЫ
В § 9.5 мы увидели, что длинные коды БЧХ плохи, а в § 10.5 настоящей главы убедились, что также плохи и длинные двоичные коды, полученные из кодов PC. Однако из кодов PC можно получить с помощью очень простой конструкции бесконечное семейство хороших двоичных кодов (называемых кодами Юстесе-на), что мы сейчас и покажем.
Рассмотрим в качестве исходного кода код PC над полем GF(2m) с параметрами \N=2m—1, К, D = N—К+1]. Пусть а— примитивный элемент GF(2m). Пусть а= (а0, ..., Civ-i), ^GF(2m), представляет собой типичное кодовое слово из 5?. Введем следующий вектор Ь:
Ь = (а0, а0- а1г ааг; а2, а?а2, ;
Заменяя каждую компоненту вектора b соответствующим двоичным .m-вектором, мы получим двоичный вектор с длины 2mN.
Определение. Для любых N и К, где 0<К<А, код Юсте-сена ^n,k состоит из всех таких векторов с, которые получаются из [N, К]-кода Рида — Соломона 91.
Ясно, что ^xv, к — двоичный линейный код длины n = 2mN и размерности k = mK.. Скорость этого кода равна й/п=/</2А<’/2-Ниже будет описан более широкий класс кодов Юстесена, которые включают коды со скоростью, большей или равной ’/г-
Коды Юстесена представляют собой, пример каскадных кодов, которые мы сейчас опишем.
Каскадные коды. Рассмотрим устройство, изображенное на рис. 10.7. Предположим, что внутренний кодер и декодер исполь-
'’иперканал
Рис. 10.7. Каскадный код
з^ют код (называемый внутренним кодом),который является1 двоичным [п, k, d] -кодом. Комбинацию внутреннего кодера, канала и внутреннего декодера можно представить себе как новый' канал (называемый суперканалом), который передает двоичные-jfe-векторы. Если эти ^-векторы рассматривать как элементы поля GF(2h), то мы можем попытаться исправлять ошибки суперканала выбором внешнего кода, представляющего собой [7V, Л, Z)]-код над GF{2k). В качестве внешнего кода часто используется какой-нибудь код Рида—Соломона. Описанная комбинация кодов; (как и любая подобная схема) называется каскадным кодом. Результирующий код (или суперкод) является двоичным кодом: длины nN, размерности kN со скоростью (k/n) (K/N).
Кодирование осуществляется следующим образом. Все kK двоичных информационных символов делятся на К ^-векторов, которые рассматриваются как элементы поля GF(2h). Эти К элементов GF(2N) кодируются внешним кодером в кодовое слово* а0Д1 а^-и Затем каждый элемент кодируется внутренним кодером в двоичный n-вектор Ьг-. Вектор bobj... bjv—1 является кодовым словом суперкода и передается по каналу.
Упражнение. (9). (а). Показать, что минимальное расстояние каскадного кода равно по крайней мере dD.
(b). Получить, например, двоичный каскадный [96, 24, 28]-код, используя в качестве внутреннего кода двоичный [8, 4, 4]-код, а в качестве внешнего кода [12, 6, 7]-коД PC над полем; GF(24). Таким же путем можно получить [104, 24, 32]-код.
Коды Юстесена можно рассматривать как каскадные коды, в которых внутренний кодер использует N различных кодов. Обозначим через двоичный [2m, т]-код, состоящий из двоичных: представлений элементов (и, aHi), u^GF(2m). Тогда i-й символ; Gt внешнего кода кодируется кодом ‘ё’г.
Минимальное расстояние кодов Юстесена. Основная идея заключается в том, что каждый двоичный вектор (u, v) длины 2m,’. для которого u=#0, v=/=0, принадлежит точно одному из кодов Следовательно, типичное кодовое слово с кода содержит по крайней мере D различных двоичных 2т-векторов.
Так как не может быть много различных 2т-ве_кторов маленького веса, то полный вес кодового слова с должен быть большим.-Таким образом, если I — наибольшее число, удовлетворяющее ус-
ловию то, когда D велико, I также велико, а зна-
2=1
чит, и вес
, , , . V» , /2т \ Wt (С) > 2j Ч . ) 2=1
также велик.
Оценки биномиальных коэффициентов. Перед тем как доказать первую теорему, нам необходимы некоторые оценки бино
миальных коэффициентов. Эти оценки включают в себя функцию энтропии НДх), определяемую равенством
Я2 (*) = —х 1°ёг х~ (1 — х) 1°ёг (1 —х)-
где (рис. 10.8). Фано [415] привел полезную таблицу
значений Н2(х). Эта функция используется в теории информации как мера «неопределенности», но для нас она представляет интерес в силу той роли, которую она играет в леммах 7 и 8.
Нг(х)
Рис. 10.8. Функция энтропии Н2(х)
Рис. 10.9. Обратная функция Я2-1(х)
Нам также понадобится обратная функция Н2~'(у) (рис. 10.9), определяемая таким образом:
х = Н~' (у)^у = Н2 (х) Для значений 0^х^1/2.
Л е м м а 7. (Оценка биномиального коэффициента.)
Предположим, что 7.п— целое число, где 0<Х<1. Тогда _________1____________ \ ______1____9пНг (10 16) / 8n X (1 - X)___________________________\Кп J " ]/2лпХ(1 —X) " ’ 1 >
Доказательство. Доказательство основано на формуле Стирлинга для п\
УТлпп+1/2 е-п+^п-!Ж <nl<y^nn+l/2 e~n+i/l2n. (10.17)
Следовательно, полагая р=1—X, имеем: / П \ n! 1 1 е~ 1/12м?.— 1/12пц _
\Хп/ (Хп)1 (рп)! У&ппкц
__ 1 рпН2 W р—Ч^пкц У 2л п Хр.
Левая часть неравенства (10.16) следует отсюда после элементарных алгебраических преобразований. Доказательство правой части (10.16) проводится аналогично и предоставляется читателю (упражнение (10)). •
Замечание. В большинстве случаев вполне пригодны более простые варианты формулы Стирлинга
К2лп"+1/2 ё~п <п!<К2л«"+1/2 е“п+1/12п (10.18)
или
п\ ~ У 2Л n"+1/2 g—п ПрИ п > оо .
(Лемма 8. Предположим,
(Оценка суммы биномиальных коэффициентов.) что '/.п—целое число, где Тогда
(?v) У Н < 2пНг w
Г8«М1-Ь) " ^nk>
(10.19)
Доказательство. Вначале мы докажем правое неравенство. Для любого положительного числа г имеем:
п
k~Kn
Таким образом,
2rh
п . .
V п U(2-rX + 2r(1-X))"
k=7.n '
Выберем r = Iog2(Z/(l—L)). Тогда эта сумма не превосходит
2»h2 (М
(1 —^ + ^)n = 2n/f2 w
Левая часть неравенства (10.19) следует из неравенства
и предыдущей леммы. •
Следствие 9. Для любого р,, 0<ц<’/2 справедливо неравенство
2пн2 (ц)
у 8лр(1 — и)
пН2 (ц)
(10.20)
k=0
Анализ кодов Юстесена.
Лемма 10. Если у нас имеется М различных двоичных ненулевых L-векторов, где
Л4 = у(26Д—1), 0<у< 1, 0<6< 1, то сумма весов всех этих L-векторов равна самое меньшее
Lv(26L-l)(//r1(6)-o(l)).
(Напомним, что условие f(L)=o(l) означает, что f(L)-*~O при L—>оо.)
Доказательство. Для любого Z, (КХ-С’/г число рассматриваемых L-векторов, имеющих вес не более LL, не превосходит
м. <
\ < 2lh* (?v)
t=i
согласно следствию 9.
Поэтому суммарный вес всех L-векторов не менее чем
L L (АГ—2LHi (1)) = L LM (1 — 2Lfi* {К)/М).
Выберем Z=#2-1(6—l/log2L) =#2-1 (6)—о(!)» где ХС’/г- Тогда суммарный вес равен по крайней мере
£Т(26Д—1)(1-о(1))(НТ1 (б)-o(l))==Ly(26L- ОС#?1 (б)-о(1)).
Теорема 11. (Юстесен.) Пусть R фиксировано, 0<Т?<*/2-Для каждого m выберем
Г/?-2ЛЛ = f/?2 ( 2^—1)]- (10.21)
Тогда код Юстесена fN,K представляет собой двоичный код длины n=2tnN со скоростью Rm= (R/2N)^R и минимальным расстоянием dm, удовлетворяющим неравенству
> (1 — 2R) (Н^1 (0,5)—о (1))« 0,110 (1 — 27?).
Нижняя граница для dm/n является линейной функцией от R, :и эта граница изображена на рис. 10.10.
Доказательство. Пусть с — любое ненулевое кодовое слово. Дак мы видели ранее, с содержит по крайней мере N—К+1 различных ненулевых двоичных (2m)-векторов. В силу (10.21)
• 7?+ — >Rm = — >R;
2N 2N
N —K+l=/v(l — >7V(1 — 2R).
Применяя теперь лемму 10 при L = 2m; 6=1/2; у=1—27?, получаем, что
wt(c)> 2m (1— 27?) (2m— l)(HTl(0,5) —о(1)); > (1-2К)(ЯГ'(0,5)-о(1)).
Теорема 11 дает только коды, скорости которых меньше чем ‘/г-Более широкий класс кодов может быть получен следующим выкалыванием координат кода f n.k- Каждая компонента вектора
Рис. 10.10. Сравнение кодов Юстесена с границей Варшамова — Гилберта:
1 — граница Варшамова — Гилберта;
2 — граница Зяблова; 3 — теорема 11;
4— теорема 12
а2а2, • ayv_] > a/v 1 Gyv—i)»
жак и раньше, представляется в виде двоичного m-вектора, а за»
тем отбрасываются последние s двоичных символов в каждой из чередующихся компонент
а0, аак, а? а2, aN~1 aN__x.
Множество всех таких выколотых векторов образует код Юстесена Этот код представляет собой двоичный линейный код с параметрами п= (2т—s)N; k=\mK.
Выбором s мы займемся позднее. Итак, мы построили каскадный код, у которого внутренние коды имеют скорость rm= =m/(2m—s), внешний код PC имеет скорость JRrs=K/N, а скорость результирующего кода к
Rm —rm'RftS
тК
(2m — s)N
Как и прежде, вектор (а0, ..., aN-i) имеет вес
wt (п0,
Однако после выкалывания каждая ненулевая пара элементов может встретиться 2s раз. Наименьший вес достигается в случае, когда каждый ненулевой (2 m—s)-вектор встречается точно 2s раз. Число различных ненулевых (2m—s)-векторов равно тогда по крайней мере
ЦгЛф—( 2m-s —1)(1—V
2s k N J \ N J
Для заданного Д выберем
К = p^(2m~s)l ; (10.22)
I tn I
К — 1 , R (2m — s)
так что ----- 5.
ЛГ т
Следовательно, число различных ненулевых (2m—s)-векторов не менее чем
R (2т — s)
т
Применяя теперь лемму 10 при L = 2m—s; 6=(m—s)/L', у = = 1—R(2m—s)]m, получаем, что вес кодового слова равен по крайней мере
2s (2m—s) (1-K(2m-s} .) ( 2m~s — 1)(H~X (б)—о (1)),
\ т )
(2m“s —1)(
где первый множитель 2s появился потому, что каждый (2m—s)-вектор встречается 2s раз, и это наихудший случай. Поэтому для этого кода
Расстояние Длина
2т-2
2т — 1
_ R(2m — s) \ М_! fm-s \ °
т /\ 2 \2т— $/
Выберем г таким, чтобы и положим
s = [—(2?-—1)1 , (10.23)
1 г I
т так что Гщ = —------> г.
2т — s
гр s 2г — 1 ,
Тогда если т->оо, то----->----< 1;
т г
и достигается следующая нижняя оценка для отношения расстоя-ние/длина
(1——г) при т-^оо. \ rJ
Итак, мы должны выбрать г так, чтобы максимизировать это выражение. Дифференцируя его по г и приравнивая производную нулю, получаем, что г надо выбрать равным решению г0 уравнения
г2
» R =-------------------- (10.24)
1 + log2 (1 - Я-1 (1 - г))
при условии, что г0^1/2. Если же г0<’/2, что соответствует случаю 7?<0,30, то надо выбрать г—х12. Таким образом, мы доказали следующую теорему.
Теорема 12. (Юстесен.) Пусть R фиксировано, 0<7?<1. В выколотом коде к с параметром г, равным максимуму из ’/г и решения уравнения (10.24), и с параметрами s и К, определяемыми (10.23) и (10.22), отношение расстояние/длина не меньшем чем
(1—— УНтЧ!-----г) при т->оо. \ г )
Для сравнения асимптотическая форма границы Варшамова— Гилберта (теорема 12 гл. 1, теорема 30 гл. 17) утверждает, что существуют коды, для которых отношение расстояние/длина достигает величины Н2~1(1—R), когда длина кода неограниченно возрастает (см. рис. 10.10). Рассмотрим точку с координатами (г, Н2~1(1—г)) на этой кривой. Прямая линия, соединяющая проекции этой точки на оси координат, т. е. точки (г, 0) и (0, Я2^(1—г)), имеет уравнение у=(1—^/г)Н2~1(1—г). Граница Юстесена из теоремы 12 представляет собой максимум выражения (1—R/r)H2~l (1—г) для'1, и поэтому эта граница является огибающей всех этих линий. Эта граница также приведена на рис. 10.10.
Когда Д = 0,30, границы, соответствующие теоремам 11 и 12, дают одинаковые результаты.
Наконец, следующее простое соображение показывает, что «существуют каскадные коды, которые для всех значений- г,
1> лежат не ниже огибающей этих линий. Рассмотрим коды, получаемые каскадированием внутреннего [п, k, d] двоичного кода и внешнего [АГ, К, £>]-кода над GF(2h). Для того чтобы избежать тривиальных случаев, потребуем, чтобы оба числа и и N неограниченно возрастали. Результирующая скорость </? = =kKJnN.
Теорема 13. (Зяблое.) При и->оо и /V->oo существуют каскадные коды, в которых внешние коды являются разделимыми кодами с максимальным расстоянием и которые удовлетворяют неравенству
Расстояние (f. R\u т
---------> max 1-------| (1 —г) .
Длина o<r<l (А г J )
Доказательство. Так как внешний код — код МДР, то D = .. r, . D . К . 1
=/v—д + 1, и поэтому —— 1---—+ — ’
В качестве внутреннего кода возьмем код, удовлетворяющий границе Варшамова—Гилберта, для которого d/п >Hz~l (1—г), где r=kln. Тогда для результирующего кода при n->oo, /V->oo получаем
Расстояние
Длина
На рис. 10.10 эта граница показана прерывистой линией. Для значений J?>0,30 коды Юстесена удовлетворяют этой границе.
Задача (нерешенная). (10.3). Построить в явном 1 виде каскадные коды, которые достигают этой границы и для значений 7? <0,30.
Замечание. Блох и Зяблов показали [165], что класс всех каскадных кодов (для которых п->оо и М->оо) содержит коды, удовлетворяющие границе Варшамова—Гилберта. Как обычно, это доказательство неконструктивно.
Упражнение. (10). Доказать правую часть неравенства (10.16).
>— >(1 ——^Я7*(1— И-nN V г / 2
ЗАМЕЧАНИЯ К ГЛ. 10
§ 10.2. Впервые коды PC появились как коды в работе Рида и Соломона [1106]. Однако на языке ортогональных таблиц они были .построены Бушем [220] еще в 1952 г. Коды PC были подробно исследованы Форни [436]. Гор Г547] показал, что во многих случаях двоичные коды, получаемые из кодов PC, имеют меньшую вероятность ошибки, чем двоичные коды БЧХ с теми же самыми параметрами.
Соломон [1254] использует кодовые слова максимального веса в коде PC для кодирования сообщений над алфавитами, мощность которых не позволяет задать на них структуру поля, т. е. не является степенью простого числа, как, например, английский алфавит.
'Коды, предложенные Зябловым [1475], построены в явном виде, если попытаться придать этим словам какой-нибудь «явный» смысл. Лучше эту задачу сформулировать так: построить такие коды способом, похожим на способ Юстесена. (Прим, ред.)
Соломон [1250] и Рид и др. [1105 1107] описали синхронизируемые коды, построенные из кодов PC (см. также Эберт и Тонг [402] и Волвертон [1432]).
§ 10.3. Что касается расширения кодов PC, см. Буш [220], Гросс [563], Танака и Нишида[1303] и Вулф [1427].
§ 10.5. Пример 3 был построен Соломоном [1252] (см. также Мак-Вильямс [879]).
§ 10.6. Коды, исправляющие пакеты ошибок. Этот вопрос превосходно освещен в книге Питерсона и Уэлдона [1040]. Некоторые наиболее важные статьи; Бал и Чень [57], Брайдвелл и Вулф [197], Бартон [215], Бартон и др. [218], Чень и др. [280, 285, 292], Эллиот [407], Форни [440], Фудзияра и др. [462], Ха-гельбергер [573], Ивадаре [684, 685], Касами [723], Касами и Матора [743], Мандельбаум [897], Пелерт [1033], Познер [1069], Шива и Шенг [1204], Танака и Нишида [1305], Тауглих [1310], Таварес и Шива [1314], Тонг [1334— 1336], Вайнберг и Вулф [1382, 1384].
§ 10.7. Другие методы кодирования кодов PC описаны Стоуном [1282].
§ 10.8. Дельсарт [359] исследовал обобщенные коды PC.
§ 10.9. Что касается китайской теоремы об остатках, см. работы Нивена и Цукермана [995, с. 33] или Успенского и Хизлета [1359, с. 189—191]. Боссен [188], Боссен и Яу [189], Мандельбаум [896, 898, 899] и Стоун [1282] описали другие избыточные вычетные коды, которые также являются кодами МДР над GF(qm). Однако, коды Рида — Соломона оказались наиболее важными кодами в этом классе.
§ 10.10. Декодирование кодов PC исследовалось в работах: Бартон [215], Гор [543, 547], Мандельбаум [896, 898, 899] и Яу и Лью [1446].
§ 10.11. Оригинальная статья Юстесена [704] появилась в 1972 г. (см. также работу [705]). Сугияма и др. [1285, 1287] и Уэлдон [1405] (см. также работу [1406]) несколько улучшили конструкцию Юстесена для очень малых скоростей. Каскадные коды были введены Форни [436]. См. также: Блох и Зяблов [165, 166], Сэведж [1151], Зяблов [1475, 1476] и § 18.5 и 18.8.2. Упражнение (9Ь) принадлежит Сугияма и Касахара [1286].
Лемма 7 представляет собой частный случай границы Чернова (см. Эш [32] или Джелинек [690, с. 117]). Парк [1021] приводит индуктивное дока-зательство правой части выражения (10.16). Месси [923] привел другой вариант леммы 9. Теорема 13 принадлежит Зяблову [1475]1 (см. также работы [165, 166 и 1476]).
Глава 11
Коды МДР
11.1. ВВЕДЕНИЕ
Мы подошли теперь к одному из самых удивительных разделов во всей теории кодирования: кодам МДР. В теореме 11 гл. 1 было показано, что для линейного кода над любым полем выполняется неравенство d^n—k + 1. Коды с d — n—Л+1 называются разделимыми кодами. с максимальным расстоянием или кратко кодами МДР. Это название объясняется тем фактом, что такой код имеет максимально возможное расстояние между кодовыми словами и что кодовые слова могут быть разделены на информационные символы и 'проверочные символы (т. е. в терми
1 Работу Зяблова [1475] хотелось бы выделить из этого списка, ибо в ней впервые были предложены асимптотически хорошие коды со степенной сложностью построения. (Прим, ред.)
нологии § 10.7 код имеет систематический кодер). В действительности, как показывает следствие 3, любые k символов этого кода могут быть взяты в качестве информационных. Иногда МДР коды также называются оптимальными, но мы предпочитаем более определенное название.
В настоящей главе рассмотрены различные свойства кодов МДР. Мы увидим также, что проблема построения кода МДР максимально возможной длины при заданной размерности кода эквивалентна ряду интереснейших комбинаторных задач, ни одна из которых полностью не решена —см. нерешенные задачи (11.1а) — (11.If). На рис. 11.2 и в нерешенной задаче 11.4 мы выскажем предположения о решениях некоторых из этих проблем.
В § 10.2 было показано, что для всех k=\, п существует [n = q—1, k, d=n—£+1]-код Рида—Соломона (или код PC) над полем GF(q) и что эти коды являются кодами МДР. Более того, в § 10.3 было указано, что добавление общей проверки на четность превращает этот код в [«+1, k, п — k + 2] расширенный код PC, также являющийся кодом МДР. Естественно задать вопрос, можно ли добавить еще несколько проверочных символов,, не нарушая свойства кода быть кодом МДР. Представляется, что: ответ таков (см. ниже § 10.5, 10.7): можно добавить еще один или два проверочных символа, но не более. В общем случае первый вариант нашей задачи формулируется следующим образом.
Задача (нерешенная). (11.1а). Для заданных k и q найти наибольшее значение п, для которого существует [п, k, п— &+1]-код МДР над полем GF(q). Обозначим это наибольшее значение п через m(k, q).
Оказалось, что во всех известных случаях, когда существует [п, k, cQ-код МДР, существует также и [п, k, с?]-код PC или расширенный код PC с теми же параметрами. Таким образом,, насколько известно в настоящее время, коды PC и расширенные коды PC являются наиболее важными классами кодов МДР. Поэтому мы не рассматриваем отдельно декодирование кодов МДР, а отсылаем читателя к § 10.10.
Упражнение. (1). Показать, что над любым полем существуют МДР коды с параметрами [п, 1, п], [п, п—1, 2] и [п, п, 1]. Эти коды называются тривиальными кодами МДР. Для нетривиального кода выполняется неравенство 2^^^п—2.
11.2. ПОРОЖДАЮЩАЯ И ПРОВЕРОЧНАЯ МАТРИЦЫ
Пусть —[п, k, с!]-код над GF(q) с проверочной матрицей Н и порождающей матрицей G.
Теорема. 1. Код представляет собой код МДР тогда и только тогда, когда любые п — k столбцов матрицы Н линейно, независимы.
Доказательство. Код .содержит кодовое слово веса w тогда и только тогда, когда w столбцов матрицы Н линейно зависимы
'(теорема 10 гл. 1). Следовательно, в коде расстояние d=n— —£+1 тогда и только тогда, когда никакие п—k или меньше столбцов матрицы Н не являются линейно зависимыми.
Теорема 2. Если — код МДР, то дуальный ему код также является кодом МДР. •
Доказательство. Проверочная матрица Н кода является порождающей матрицей кода (S>i-. Согласно теореме 1 любые п—k столбцов матрицы И линейно независимы, поэтому единственным 'кодовым словом, имеющим нули в п—Л координатах, является нулевой вектор. Следовательно, минимальное расстояние кода ®’-1-кравно по крайней мере k+l, т. е. код имеет параметры [п, п—k, й+lj. •
П ример. Матрица
1 0 1 1\ 0 1 а 0/
является порождающей для [4, 2, 3]-кода МДР над полем бД(4) = {0, 1, а, Р=а2}. Дуальный ему код <ё>± имеет порождающую матрицу е
/1 сс 1 0 \
\1 р 0 1 )
и также представляет собой [4, 2, 3] -код МДР.
Следствие 3. Пусть —[п, k, Д|-код над GF(q). Следующие утверждения эквивалентны:
(i) . — код МДР.
(ii) . Любые k столбцов порождающей матрицы G линейно независимы (т. е. любые k символов в кодовых словах могут быть выбраны в качестве информационных символов).
(iii) . Любые п—k столбцов проверочной матрицы Н линейно независимы.
Доказательство. Вытекает из теорем 1 и 2.
Открытая проблема может быть теперь сформулирована следующим образом.
Задача (нерешенная). (11.1b). Для заданных k и q найти наибольшее п, для которого существует (kXn)-матрица над полем GF(q), любые k столбцов которой линейно независимы.
Или, что эквивалентно, в терминологии векторных пространств:
Задача (нерешенная). (11.1с). Для заданного £-мер-ного векторного пространства над полем GF(q) найти наиболь-•шее число векторов, любые k из которых образуют базис этого пространства.
Упражнения. (2). Показать, что единственными двоичными кодами МДР являются тривиальные коды.
(3). Граница Синглтона для нелинейных кодов. Показать, что «если —[п, М, d] -код над GF(q), то всегда d^n—loggAf-|-l.
11.3. ВЕСОВОЙ СПЕКТР КОДА МДР
Интересно, что весовой спектр Хэмминга кода МДР полностью известен.
Теорема 4. Пусть —[и, k, с?]-код над GF(q). Тогда SF’ представляет собой МДР код, если и только если в коде найдется слово минимального веса, ненулевые элементы которого занимают любые d позиций.
Доказательство. (Необходимость.) Пусть заданы любые-п—& + 1 координат. Выберем в качестве информационных символов k—1 дополнительных координат и одну из заданных (это можно сделать согласно следствию 3). Полагая, что эта единственная координата равна 1, а остальные k—1 координат равны О, получаем кодовое слово веса п—£-4-1. Доказательство достаточности 'предоставляется читателю. *
Следствие 5. Число кодовых слов веса п—£+1 в коде 2? равно (q—1)( ", ) .
\ М — k -J- 1 /
Код МДР имеет не более k различных ненулевых весов, а-именно п — &+1, ..., п, а минимальное расстояние дуального кода равно d'=k+i. Следовательно, по теореме 29 гл. 6 кодовые слова веса d образуют /-схему, которая, впрочем, по теореме 4 этой главы тривиальна.
Теорема 4 гл. 6 также определяет весовой спектр, но в этом-случае легче воспользоваться уравнениями Мак-Вильямс в форме, приведенной в упражнении (6) гл. 5, а именно:
/=о, !,•••, п.
г=0 ' 1 '
Так как Аг = 0 для —k и А'г — 0 для 1 то это»
выражение переписывается в следующем виде:
2 W-'-o. /=о, 1,. -k-i.
i=n-k+l ' 1 ' 1 '
Полагая j=k—1 и j=k—2, получаем, что
^+.=(7,)&-»;
(‘z;)a-»+,+4-»«-c2)w-i)'
- (Д + 2> (1-'»•
Нетрудно догадаться (а затем проверить), что общее решение; таково:
Лм+г =(д д|'(-1)'(’-‘+') <<г<-1).
Итак, мы доказали следующую теорему.
Теорема 6. Число кодовых слов веса w в [п, k, d=n—& + 1]-коде МДР над полем GF(q) равно:
-Заметим, что Лп_й+2 = / п \(q—V)(q—n + k—1).
Это число должно быть неотрицательным, и поэтому справедлив следующий результат.
Следствие 7. Пусть 7?—[п, k, п—& + 1]-код МДР. Если ^^2, то q^n.—k+\. Если же k^n—2, то q^J?+l.
Доказательство. Второе утверждение следует из рассмотрения весового спектра дуального кода ®
Упражнения. (4). Доказать достаточное условие в теореме 4.
(5). Действительный код состоит из всех линейных комбинаций с действительными коэффициентами строк порождающей матрицы G=(qij), где q^— действительные числа. Объяснить тот факт, что большинство подобных кодов являются кодами МДР.
Задача (нерешенная). (И.2). Что можно сказать о полной весовой функции (см. § 5.6) кода МДР или даже кода PC?1
11-4. МАТРИЦЫ, У КОТОРЫХ ВСЕ КВАДРАТНЫЕ ПОДМАТРИЦЫ НЕВЫРОЖДЕНЫ
Теорема 8. [п, k, cQ-код с порождающей матрицей 'G = [I | А], где А — матрица размера kX(n—k), является кодом МДР тогда и только тогда, когда каждая квадратная подматрица (образованная любыми i строками и i столбцами для любого i=l, 2, ..., min {fe, п—fe}) матрицы А невырождена.
1 1 1 1 1 1
1111 1 3 6 4 2 5
п ч 1 2 3 4 7 <7=5 q = l 1 6 4 2 5
1 3 4 1 4 2 5
1 4 1 2 5
1 5
Рис. 11.1. Конфигурации для q=5 и q=7
1 Для эквидистантного |[?+1, 2, д]-кода (а значит, и для [?+1, q—1, 3]-кода) он легко выписывается. (Прим, перев.)
Доказательство. (Необходимость.) Предположим, что — код МДР. В силу следствия 3 каждые k столбцов G линейно независимы. Идея доказательства очень проста, и мы лишь проиллюстрируем его, доказав, что левая верхняя (ЗхЗ)-подматрицд А' матрицы А невырождена. Рассмотрим матрицу В, состоящую из последних k—3 столбцов матрицы I и первых 3 столбцов матрицы А:
Тогда det B = det А'=^=0. Общий случай доказывается таким же образом. (Достаточность.) Очевидно. ©
Примеры. (1). Изображенный на рис. 10.2 [4, 2, 3]-код над GF(4) имеет матрицу
Р а а р
и, действительно, любая квадратная подматрица матрицы А (порядка 1 или 2) невырождена.
(2). Расширенный [5, 2, 3]-код PC над GF(5) имеет матрицу
3 4 2
3 2 4
С учетом теоремы 8 наша открытая проблема может быть, сформулирована в таком виде.
Задача (нерешенная). (11.Id). Для заданных k и q найти наибольшее число г такое, что существует (k X г) -матрица с элементами из поля GF(q), каждая квадратная подматрица которой невырождена.
Упражнение. (6). (Синглтон.) Показать, что любая прямоугольная подматрица А конфигураций, изображенных на рис. 11.1, обладает тем свойством, что любая (feXfe)-подматрица матрицы А невырождена под полем GF(q).
Задача (нерешенная). (Н.З.). Обобщить рис. 11.1 для больших q.
Упражнение. (7). (а). Показать, что любая квадратная подматрица матрицы Вандермонда, элементами которой являются действительные положительные числа, невырождена. Показать, что это несправедливо для матриц Вандермонда над конечными полями.
(b). При заданных xt, хп, у\, уп матрица С=(с^), где £гз= 1/(Xi+уj), называется матрицей Коши. Показать, что
П (xi Xi) У^ det(C)=. Ki</<n.
П (Xi+yj)
Ki,j<n
Следовательно, если все Xt различны, все у г различны и хг- + +i0¥=0 для всех i, j, то любая квадратная подматрица матрицы Коши невырождена над любым полем.
11.5. КОДЫ МДР, ПОЛУЧЕННЫЕ ИЗ КОДОВ PC
Пусть щ, ..., ctg-i—ненулевые элементы поля GF(q). Расширенный [q, k, d=q—fe + lj-код PC,описанный в § 10.3, имеет следующую проверочную матрицу:
II X 4г <-> О О ‘О - ' 7 I х : и - 8 Ъ . • I Г 8 8 Л-!
К этому коду всегда можно добавить еще один проверочный символ и получить [q-M, k, q—й-|-2]-код МДР с проверочной матрицей вида
" 1 «1 1 10 • • 0 0
н2 2 ai (U.1)
«1 • • • aq—l О 1
Чтобы показать это, мы должны проверить, что любые q—fe-H столбцов матрицы Н2 линейно независимы, т. е. образуют невырожденную матрицу. В самом деле, любые q—&+1 из первых q—1 столбцов образуют матрицу Вандермонда (лемма .17 гл. 4) и поэтому линейно независимы.
Аналогично, если q—&+1 столбцов включают один или оба последних столбца матрицы Н2, то, разлагая определитель полученной матрицы по этим столбцам, мы вновь придем к определителю матрицы Вандермонда.
В действительности существуют циклические коды с такими
же параметрами.
Теорема +Для любого k,1 /г=£+<у + 1, существует [<7+1, к, q—k+2] циклический код МДР над полем GF(q).
Доказательство. Мы рассмотрим только случай <7=2т; для нечетных q доказательство аналогично. Чтобы исключить тривиальные случаи, предположим, что —1. Рассмотрим мно-
гочлен х2'"+1 + 1 над полем GF(2m). Циклотомические смежные-классы, образующиеся при умножении на 2т и приведении по модулю 2т+1, равны:
{0};
{1,2т} = {1,— 1};
{2,2т— 1}=={2,— 2};
[2т-1,2т—1 4-1} = {2т~1> — 2т—1}.
то мы имеем следующие цик-
Так, например, если 2т+1=33, лотомические смежные классы:
{0};
{1,32}; { 9,24};
{2,31}; {10,23};
{3,30}; {11,22};
{4,29}; {12,21};
{5,28}, {13,20};
{6,27}; {14,19};
{7,26}; {15,18};
{8,25}; {16,17}.
Таким образом, все делители многочлена х2/71+1 + 1, за исклю-чением х + 1, являются квадратными трехчленами над полем, GF(2m) и имеют вид
х2 + (а1 + аГг) х + 1 = (х + а') (х + а~1), где а — примитивный корень' (2т+1)-й степени из единицы. Здесь a^GF(22m); действительно, если § — примитивный элемент GF(22m), то можно положить a=g2m'“1.
Упражнение. (8). Показать, что при этом значении а элемент а® + а_< принадлежит полю GF(2m).
Рассмотрим теперь [2m+l, 2m+l— 2t—1] циклический код с порождающим многочленом
(х+1)П(^2 + («/ + а-г)х+1).
г=1
Этот многочлен имеет 2/+1 последовательных нулей а-1, art+1, ..., а-1, 1, а, ..., а*-1, а*; и, следовательно, согласно границе-
БЧХ минимальное расстояние кода равно по крайней мере 2t-\- 2. Так как n=2m+l; fe = 2mH-l—2/—1; п—.k+l = 2t-\-2, то построенный нами код — код МДР. Этим способом строятся требуемые коды для всех четных значений k.
Аналогично код с порождающим многочленом
|”| (х2 + (а1 + а~1 )х + 1), z=2m-l-t+l
который имеет 2/ последовательных корней
„т~ 1 т— 1 m—1+1 „т—I
а2 — *+' , . . а2 ,а2 + а2
представляет собой [2mTl, 2т+1—2t, 2/+1]-код МДР. Этим способом строятся требуемые коды для всех нечетных значений k. •
Пример. Коды длины н=9 над GF(23). Пусть £— примитивный элемент поля Gf(26), p=g9— примитивный элемент поля <GT(23) и а = £7 — примитивный корень девятой степени из единицы. Тогда, как следует из рис. 4.5, р3=р2+1 и
♦ а + «—1 = В7 + £56 = Р6;
a2 + a-2=gM_|_g49=p3.
a3 + a-3==g21 + ^2=1;
а4 + а~4 = £28 + £35 = ре.
Следовательно,
Д’ + 1 = (х+ 1) (х2 + х + 1) (х2+ р3х + 1) (х2 + р5х + 1) (х2 + Р6 %+ 1).
Код над полем GF(8) с проверочным многочленом х2 + х + 1 •вырожден (так как х2+х+1 делит х3+1, см. лемму 8 гл. 8). Это—[9, 2, 6]-код1 с порождающим идемпотентом х+хЧхЧ -]-х5 + х1+Xs или 011011011 в обычных обозначениях.
Три других кода размерности 2 являются [9, 2, 8]-кодами. Их порождающие идемпотенты легко находятся и имеют следующий вид:
Порождающий идемпотент Проверочный многочлен
1 X X2 X3 X4 Xs X6 X7 X8
0 Р3Р® 1 Р5 р6 1 р6 рз х2 + р3х+1
0 р6р3 1 р6 р® 1 рз р5 х2 + Р5х+ 1
о р6р5 1 р3 р3 1 'р5 р® х24-р®х+ 1
Коды, имеющие эти идемпотенты, являются минимальными кодами (§ 8.3) и состоят из девяти циклических сдвигов своих идемпотентов и пропорциональных им векторов. Код с порожда-
1 Представляет собой трехкратное повторение [3, 2, 2] -кода МДР. (Прим, перев.)
ющпм многочленом х2 + рих,+1, имеющим нули а4 и а“4, представ-ляет собой [9, 7, 3]-код. Многочлен (х +1) (х2 + р5х+1) имеет корни а-1, 1, а и поэтому порождает [9, 6, 4]-код; многочлен (х*-!-х+1) (х2-|-р6х +1) имеет корни а3, а4, а5, а6 и порождает £9, 5, 5]-код и т. д. -
Упражнение. (9). Найти порождающие идемпотенты и весовые спектры этих кодов.
Случай fe=3 и q — четное число. Известны только два случая, когда можно добавить еще один проверочный символ, а именно когда q=c2m и /г = 3 или k=q—1.
Теорема 10. Существуют [2™+2, 3, 2т] и [2т+2, 2™—1, 4] (трижды) расширенные коды PC (а следовательно, МДР).
Доказательство. Воспользуемся матрицей
1 .. 110 0
Ki • aQ_I 0 10
а? • • 0 0 1
(Н-2)
в качестве порождающей матрицы либо проверочной. Любые три столбца ее линейно независимы, так как все элементы а2г различны. ®
11.6. « МНОЖЕСТВА
Между кодами МДР и конечными геометриями имеется глубокая связь. Из следствия 3 мы видим, что задачу построения [п, k, п—k -1-1]-кода МДР можно рассматривать как геометрическую задачу нахождения множества S из п точек конечной проективной геометрии PG(k—1, q) (см. приложение В), любые k точек которого линейно независимы, т. е. множества S, никакие k точек которого не лежат в одной гиперплоскости. Координаты этих точек представляют собой столбцы порождающей матрицы G.
Например, столбцы матрицы (11.2) состоят из 2т+2 точек проективной плоскости PG(2, 2m), никакие три из которых не лежат на одной прямой.
Определение. Множество п точек проективной геометрии PG(k—1, q) называется п-множеством, если никакие k точек этого множества не лежат в одной гиперплоскости PG(k—2, q), где n^k^3. Например, матрица (11.2) определяет (2т+2)-мно-жество в PG(2, 2m).
Таким, образом, другой вариант нашей открытой проблемы выглядит так.
Задача (нерешенная), (ll.le). Для заданных k и q найти наибольшее значение п, для .которого существует «-множество в проективной геометрии PG(k—1, q).
Этой геометрической задаче посвящено много работ, но мы ограничимся только одной теоремой.
Теорема И. Если — нетривиальный [п, k^3, п—k + + 1]-код МДР над полем GF(q), q — нечетное, то n^q+k—2. Или, что эквивалентно, для любого «-множества проективной геометрии PG(k—1, q), q—нечетное, справедливо неравенство, ti q -pife—2.
Доказательство. Пусть G=(ga)— порождающая (^Хн)-мат-рица кода Обозначим через гь ..., г?£ строки матрицы G и через С—множество точек в PG(k—1, q), координатами которых являются столбцы матрицы G. Пусть (хь ..., xk) — произвольная точка PG(k—1, q).
Ясно, что гиперплоскость, определяемая условиями Xi=0, пересекается с множеством С в тех точках, для которых gn = 0-Следовательно, вес первой строки и матрицы G равен разности между п и числом точек, в которых гиперплоскость %1=0 пересекается с С. Аналогично вес кодового слова 2+^+гП кода равен разности между п и числом точек, в которых гиперплоскость, определяемая условием Sfti=iXiXi = 0, пересекается с С.
Из следствия 7 мы знаем, что n-^q+k—1. Предположим теперь, что n=q+k—1; тогда An-k+2=0 и множество С пересекается с гиперплоскостями геометрии PG(k—1, q) в k—1, k—3» k—4, ..., 1 или 0*точек (но не в k—2 точках, так как нет кодовых слов веса п—fe-p2).
Рассмотрим гиперплоскость, которая содержит k—3 точек из С, например, точки Рь ..., Рй-з. Пусть 2 — подпространство PG(k—3, q), лежащее в этой гиперплоскости и содержащее точки Р[, ..., Pk-з- Любая гиперплоскость, проходящая через 2, должна пересекаться с С в 2 или 0 других точек. Обозначим через г число гиперплоскостей, пересекающихся с С в двух других точках. Объединение всех гиперплоскостей, проходящих через 2, представляет собой PG(k—1, q), и поэтому оно, конечно, содержит все точки С. Следовательно, 2r+k—3 = <7 + fe—1, или 2 г= = <7+2, что противоречит нечетности q. Г •
11.7. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
Для k — З и нечетного q теорема 11 утверждает, что «^<7 +1, и поэтому коды из теоремы 9 имеют максимально возможную длину п. Таким образом, один случай из нерешенной задачи (11.1а) известен: если q— нечетное, то m(3, q,) =<7+!.
С другой стороны, для k=3 и четного q в силу следствия 7 должно выполняться неравенство fi+j<?+2, и коды из теоремы 10 показывают, что m(3, q)=q+2, если q — четное.
Наилучшие известные результаты для произвольного q представлены графически. На рис. 11.2 приведены значения k и г, для которых известно существование [n=^k+r, k, г+1]-кода МДР над полем GF(q) (таким образом, г равно числу проверочных символов).
В силу теоремы 2 рисунок симметричен относительно /?-и г. За исключением кодов из теоремы 10, неизвестно ни одного кода,.
который лежал бы выше пунктирной линии п = k + г = = + 1 (г^2; £^2)-
Согласно следствию 7 не существует кодов, лежащих выше сплошной линии.
Имеются очень веские основания предположить, что пунктирная линия является истинной верхней границей, и мы сформулируем это в виде следующей задачи.
Задача (нерешенная). (11.4). Доказать (или опровергнуть) , что все коды МДР, за исключением кодов, указанных в теореме 10, лежат ниже прямой n = k + r = q+ 1, изображенной на рис. 11.2.
Известно, что это предположение справедливо для кодов с =С5, или <7^11, или 9>(4й—9)2, чаях.
В терминах функции m(k, q) следующим образом:
m(k,q) =
U+1
Рис. 11.2. Наилучшие известные МДР-коды [n=k+r, k, г+1]. Символ 9 означает, что код существует для всех q\ символ * означает, что код существует, если и только если q=2m
I также в некоторых других слу-наше предположение выглядит
для (П З)
для q<k,
за исключением случая
т (3, q) — т (q— 1, q) — q + 2, если q = 2m. (11 -4)
11.8. ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
Определение. Матрица А размера М'/.п с элементами из множества мощности q называется ортогональной таблицей размера М с п ограничениями, q уровнями, силы k и индекса "К, если любое множество из k столбцов матрицы А содержит все qk возможные векторы-строки точно Z раз. Такая таблица обозначается через (М, п, q, k). Ясно, что M=‘hq11. Случай 9=2 был рассмотрен в теореме 8 гл. 5.
Пр име.р. Код з^12, изображенный на рис. 2.1, представляет собой таблицу (12, И, 2, 2) (см. теорему 8 гл. 5). На рис. 11.3 показана таблица (4, 3, 2, 2), а кодовые слова, приведенные на рис. 10.1, образуют таблицу (16, 3, 4, 2) с элементами из поля GE(4).
Теорема 12. Строки (qh, п, q, k) ортогональной таблицы А индекса один с элементами из поля GF(q) представляют собой кодовые слова [п, /г]-кода МДР над GF(q), и наоборот.
Доказательство. Любая (^Xfe)-подматрица матрицы А содержит каждый fe-вектор точно один раз соответствующие k координат могут быть выбраны в качестве информационных символов код является кодом МДР, согласно следствию 3. •
Рис. 11.3. Ортогональная таблица (4, 3, 2, 2)
Упражнение. (10). Показать, что если Н4Л—нормализованная матрица» Адамара порядка 47. (§ 2.3), то последние 47,—1 столбцов матрицы Н4Л образуют (4Z, 47,—1, 2, 2) ортогональную таблицу индекса 7,. Рисунок 11.3 соответствует случаю 7=1.
Таким образом, последний вариант нашей открытой проблемы выглядит так.
Задача (нерешенная), (ll.lf). Найти наибольшее возможное п, для которого существует (qh, п, q, k) ортогональная таблица индекса один.
ЗАМЕЧАНИЯ К ГЛ. 11
§ 11.1. Синглтон [1214], по-видимому, первый стал изучать в явном виде коды МДР. Однако на языке ортогональных таблиц (§ 11.8) Буш [220] уже в 1952 г. построил коды Рида—Соломона и их расширения, описываемые теоремами 9 и 10.
Помимо кодов PC некоторые другие избыточные вычетные коды также являются кодами МДР (см. § 10.9).
Ассмус и Мэттсон [41] показали, что коды МДР, длина которых п равна простому числу л, очень распространены, а именно они показали, что всякий циклический код длины л над полем СГ(р') является кодом МДР для всех значений i и для всех, кроме конечного числа, простых чисел р.
Не вдаваясь в подробности, мы укажем только, что код МДР с fe = 2 эквивалентен также множеству п—й попарно ортогональных латинских квадратов порядка q (Денеш и Кидвелл [371, с. 351], Познер [1068], Синглтон [1214]). Таким образом, более общая задача построения всех кодов МДР над алфавитом порядка s (не обязательно являющимся полем) включает очень трудную задачу нахождения всех проективных плоскостей! (см. приложение В).
§ 11.3. Весовой спектр кодов МДР был найден независимо Ассмусом, Глисоном, Мэттсоном и Туриным [50], Форни и Кохленбергом [436] и Касами, Лином и Питерсоном [736]. Мы следуем Геталсу [491] (см. также [933]).
Следствие 7 принадлежит Бушу. Оно также имеется в [1214] и у Бородина [172]. Наше доказательство следует Робийярду [1118].
§ 11.4. Что касается упражнения 7, см. Кнут [772, с. 36] и Пойа — Сеге [1067, т. 2, с. 45].
§ 11.5. См. замечания к § 10.3.
§ 11.6. Сегре [1170—1173] и позднее Тзэс [1316, 1317], Кассе [252], Хиршфельд [655] и многие другие авторы исследовали n-множества и связанные с ними проблемы в конечных геометриях. Два недавних обзора принадлежат Барлотти [69, 70]. См. также работы Даулинга [385], Гулати и др. [565—569].
Используя методы алгебраической геометрии, Сегре [1170; 1173, с. 312] и Кассе [252] улучшили теорему II1.
Теорема 13. Предположим, что 1.
(1). Если k=3, 4 или 5, то имеют место равенства (11.3) и (11.4).
(ii). Если то m(tk, q)^q+k—4.
Тзэс [1316] получил следующий результат.
Теорема 14. Если q— нечетное и q>(4k—9)2, то m(k, q) = q+l.
Мэнери и Сильверман [904, 905] и Джурик [703] доказали следующую теорему.
Теорема 15. Для 11 имеют место равенства (11.3) и (11.4).
Тзэс [1318] .нашел некоторые другие условия, при которых выполняются (11.3) и (11.4).
Из геометрической теории также следует, что если q — нечетное число, то во многих случаях '(предположительно во всех) существует единственный [n=q+l, k, q—ife+2] код МДР. Но если q — четное число, то известно, что это не так.
Множество С из /г+1 точек проективной плоскости порядка h, никакие три из которых не лежат на одной прямой, называется овалом. Сегре [1171; 1173, с. 270] показал, что в дезарговой плоскости нечетного порядка (т. е. h=q — степень простого нечетного числа) такое множество точек образует коническое сечение. Например, если в качестве точек множества С мы выберем столбцы порождающей матрицы (11.2) (за исключением предпоследнего столбца) [?+1, 3, q—1]-кода МДР, то увидим, что они удовлетворяют уравнению X22 = X]XS.
Однако если q=2m, то все прямые, пересекающие овал С в одной точке, имеют общую точку; эта точка называется центром или узлом С. Точки овала С вместе с центром образуют множество 2™>+2 точек, никакие три из которых не лежат на одной прямой, а значит, и [2т+2, 3, 2™]-код МДР имеет те же параметры, что и код из теоремы 10.
Глава 12
Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ
*12.1. ВВЕДЕНИЕ
Альтернантные коды представляют собой большое и мощное семейство кодов, получающееся путем незначительной модификации .проверочной матрицы кодов БЧХ. Напомним, что в гл. 7 коды БЧХ над GF(q) блоковой длины п и конструктивным расстоянием 6 определялись как коды с проверочной матрицей Н=ЯЪ-, где 1; 1) и a* *(=GF(q™) —
’Теорема 11 принадлежит Бушу [220]. (Прим, перев.)
* Мы приносим извинения за использование символа а в двух разных смыслах.
примитивный корень степени п из единицы. Заменив Hij на эле-мент вида а/-149, где а=(аь ап) —вектор с различными компонентами из поля GF(qm) и у=(у, ..., Уп) —вектор с ненулевыми компонентами из GFfcfn), получим альтернантный код st-{а, у). Свойства этого кода резюмированы на рис. 12.2.
Большая свобода выбора в определении альтернантных кодов служит гарантией того, что некоторые длинные альтернант-ные коды попадают на границу Варшамова—Гилберта (теорема 3) в противоположность ситуации, имеющей место для кодов БЧХ (теорема 13 гл. 9).
Альтернантные коды, как оказалось, действительно образуют большой класс, и многие вопросы для них пока еще остаются открытыми. Например, какие альтернантные коды лежат на границе Варшамова — Гилберта? Как находить их размерность и минимальное расстояние?
Коды БЧХ, естественно, являются частным случаем альтернантных кодов. В § 12.3—12.7 определяются различные другие подклассы альтернантных кодов, а именно коды Гоппы (§ 12.3— 12.5, рис. 12.3), коды Сривэставы (§ 12.6, рис. 12.4) и обобщения Ченя — Чоя кодов БЧХ (§ 7, рис. 12.5)- Сложные взаимоотношения между этими кодами показаны на рис. 12.1 (без выдерживания масштаба).
Рис. 12.1. Взаимосвязь между различными классами альтернантных кодов:
1 — альтернантные коды; 2 — коды Гоппы; 3 — коды БЧХ. примитивные в узком смысле; 4 — коды БЧХ; 5 — обобщение Ченя — Чоя кодов БЧХ;
6 — коды Сривэставы; 7 — обобщенные коды Сривэставы
Кодирование и декодирование альтернантных кодов аналогично кодированию и декодированию кодов БЧХ и обсуждается в § 12.9. Ключевым этапом в декодировании является использование алгоритма Евклида для перехода от вектора-синдрома к многочлену локаторов ошибок и многочлену значений ошибок. Этот метод, естественно, применим также и к кодам БЧХ, и мы сможем восполнить пробел в декодировании кодов БЧХ, оставленный в § 9.6.
Алгоритм Евклида для вычисления наибольшего общего делителя двух целых чисел или многочленов описывается в § 12.8. Как следствие из алгоритма мы сможем, наконец, доказать результат (следствие 15), несколько раз уже использованный нами в предыдущих главах: если fug — взаимно простые многочлены (или целые числа), то существуют многочлены (или целые числа) U и V такие, что l7f+gV=l.
12.2. АЛЬТЕРНАНТНЫЕ КОДЫ
Альтернантные коды тесно связаны с рассмотренными в § 10.8 обобщенными кодами Рида — Соломона — ОРСьо(а, v). Для удобства напомним их определение. Пусть a=(ai, ..., а«), где щ — различные элементы поля GF(qm), и ¥=(0! ..., vn), где Vi— ненулевые (но не обязательно различные) элементы из GF(qm). Тогда код OPCfeo (a, v) состоит из всех векторов вида
(^F (а2), • • ,vnF (ап)), (12.1)
где F(z)—любой многочлен с коэффициентами из GF(qm), степень которого не превосходит kQ. Код OPCft (a, v) является [п, kQ, л+1]-кодом МДР над GF(qm) для г=п—ko, и его-проверочная матрица равна:
У1 Уъ . . . Уп
ai У1 аъУъ ... ссп уп
2 2 9
Щ.У1 ОъУъ ... апуп
<А~ХУ1 • • а~Хуп
1
«2
С&2
=XY,
(12.2)
«Г1 аГ1
где вектор у=(г/ь ..., г/п) таков, что y^GF yt^G и OPC-Lbo («, v) =OPC„_fto (а, у).
Определение. Альтернантный код s£(a, у) состоит из всех слов кода ОРСхй„ (a, v) таких, что их компоненты лежат в поле ^(?); иными словами, st-{а, у) равен ограничению кода OPCft„ (a, v) на подполе GF(q). Таким образом, д£(а, у) состоит из всех векторов а над GF(q), удовлетворяющих равенству Наг = О для матрицы Н, задаваемой условием (12.2).
Проверочная матрица Н, элементы которой лежат в поле GF(y)> может быть получена заменой каждого элемента матрицы Н соответствующим вектором длины m над GF(q) точно так Же, как это было сделано для кодов БЧХ. Так как ^(а, у) является ограничением кода ОРС/4о (a, v) на подполе, то из § 7.7 следует, что s£(a, у) •—[n, k, dj-код над GF(q), параметры которого удовлетворяют условиям
п—mr<k^n—г, d>r^i.
(Свойства кода з^(а, у) собраны на рис. 12.2). Приведенную оценку для d можно получить непосредственно из проверочной матрицы.
Теорема 1. Минимальное расстояние кода з$(а, у) не меньше чем г+1.
Доказательство. Предположим, что а — ненулевое слово кода ^(а, у), вес которого не превосходит г. Тогда Har = XYaT = 0. Положим br=Yar. Тогда wt(b)=wt(a), так как матрица Y является диагональной и, следовательно, обратима. Таким образом, ХЬГ=О, что невозможно, так как X — матрица Вандермонда (см, лемму 17 гл. 4). •
Код (а, у) определяется проверочной матрицей (12.2) или (12.3), где аь ..., ап — различные элементы поля GF(qm) и yi... уп— не-
нулевые элементы из GF(qm). .+ (а, у) —линейный код над GF(q) с параметрами:
длина и, размерность k~^n — mr, минимальное расстояние d^r+1.
<+(а, у) представляет ограничение кода ОРСьо (a, v) на подполе GF(q), где kQ = n—г. Дуальный код: г+Г(а, у) = Tm(OPCn-k0 (а, у)) (теорема 2). Существуют длинные альтернантные коды, лежащие на границе Варшамова — Гилберта (теорема 3). Важнейшими подклассами альтернантных кодов являются коды БЧХ, коды Гоппы (§ 12.3—12.5), коды Сривэставы (§ 12.6), обобщения Ченя — Чоя кодов БЧХ (§ 12.7). Декодирование описано в § 12.9.
Рис. 12.2. Свойства альтернантных кодов .+ (а, у)
. Пусть С=(с^), Cij^GF(‘qm),—произвольная обратимая матрица. Тогда в равной степени хорошим заданием проверочной матрицы кода з$(а, у) является матрица (см. упражнение (31) гл. 7)
С11 С12 • С1Г 1 I ... 1
Уп
ййЫ Упё1(ап)
У1ёЖч) УгёДаъ) УпёЛап)
(12.3)
_У1ёД^1) УгёДаг) . УпёгМ
гДе gi(x)=cil + ci2x + ci3x2+ . . .+cirxr~1, Z = l, . . „г (12.4) — многочлен над GF(iqm), степень которого строго меньше чем г.
Заметим, что из равенств (12.2) и (12.3) видно, что коорди-ты кодового слова естественно занумеровать элементами
ai, ...» «п- Это оказывается очень полезным при кодировании и де-кодировании.
Примеры (1). Выберем сначала а=(1, а, а2, а6) и у=(1,
1, 1), где а — примитивный элемент поля GF(23). Тогда про-
верочная матрица в форме (12.2) для альтернантного кода st (а, у) равна:
HY Г 11111 111
11 А
1 a a2 as а4 а5 a6J
Заменяя каждый элемент матрицы соответствующим двоичным вектором длины 3, получаем:
Н =
1111111
0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 0 10 11 0 10 1110 0 0 10 111
Таким образом, s^(a, у) является [7, 3, 4]-кодом. С другой стороны, если у=(1, а, а2, а3, а4, а5, а6), то 1а а2 а3 а4 а5 а6 1 а2 а4 а6 а а3 а5
Н =
Вторая строка матрицы избыточна, так как если п "У = а, г=1
где h^GF (‘2'"') и ai равны нулю или единице, то
Таким образом, можно положить
Н =
10 0 10 11
0 10 1110
0 0 10 111
И в этом 'случае sF(u, у) представляет собой [7, 4, 3]-код Хэмминга. (В данном случае роль вектора у сводится к уменьшению Минимального расстояния и увеличению числа информационных символов.)
(2). Другим примером альтернантных кодов являются коды БЧХ. Действительно, проверочная матрица кода БЧХ в общем виде задается равенством (см. уравнение (7.19))
la6 a26 a("-D 6
la6 „2(6+d „(n-i) (6+1) LA LA
1 ab+6~2 • • a(6+6-2) (n-,)
11 1 ... 1
la a2 . . _an~’ la2 a4 . . ,a2(n-,)
1
ab a26
1 ae~2 .... a(6~2) (n-1)
a(n-l)6
и, следовательно, код является альтернантным.
Код, дуальный альтернантному.
Теорема 2. Дуальным альтернантному коду ^(а, у) является код
TmXOPCn_k(a, у)) = Тт (ОРС4 (a, V). (12.5)
Напомним, что согласно определению, данному в § 7.7, след T-mffi™) произвольного кода 7?^ над GF(qm) является кодом над GF(q), состоящим из всех векторов вида
(ТМ,Тт(сг), - -,Tm(cn)),
где (ci, ...,
Доказательство. Утверждение вытекает из теоремы 11 гл. 7 и теоремы 4 гл. 10. •
Примеры применения этой теоремы можно найти по аналогии с теоремой 11 гл. 7.
Длинные альтернантные коды являются хорошими.
Теорема 3. (а). Пусть числа п, h и 6 заданы, и пусть m — некоторое число, делящее п—h. Тогда существует альтернантным код у) над GF(q) с параметрами [п, k~^h, d^6], удовлетворяющий условию
6-1
V (q— 1)га Г ) < (qm— (12.6)
\w/ w=l
(b). Следовательно, существуют длинные альтернантные коды, лежащие на границе Варшамова — Гилберта.
Доказательство, (i) Пусть а — произвольный ненулевой вектор над GF(q). При фиксированных ko и а и переменном v число кодов OPCfto (a, v), содержащих этот вектор а, равно самое большее (qm—1)4 Чтобы доказать это, заметим, что согласно (12.1) вектор а принадлежит коду OPCfe(1 (a, v) тогда и только тогда, когда для всех 1=1, 2, ..., п ailvi=F(ui) для некоторого
(12.7)
многочлена F(z), степень которого меньше, чем ko. Так как F(z) полностью определяется своими значениями в deg/7 точках, то для определения F(z) достаточно -задать самое большее kQ величин Для каждой Vi имеется (qm—1) способов такого задания.
(ii). Рассмотрим семейство SF альтернантных кодов s£(a, у), являющихся ограничениями некоторых кодов ОРС^о (a, v) на подполе GF(,q), где k0=n—(п—h),/m. Тогда размерность k каждого .9/(а, у) не меньше чем п—т(п—Л0)=Л. Согласно п. (i) число различных кодов .9/(а, у)е£Г, содержащих заданный вектор а, равно самое большее (qm—Следовательно, число кодов s£(q, у)е£Г, минимальное расстояние которых строго меньше чем 6, равно самое большее
6-1 .
Г£)=1
(iii). Мощность множества 2Г равна (q™—1)'л, т. е. числу различных выборов вектора v. Таким образом, если это число превосходит значение (12.7), то найдется код л^(а, у) размерность которого не меньше h и минимальное расстояние которого не меньше 6. Это доказывает утверждение (а). Асимптотически, когда п велико, а отношение h/n фиксировано, условие (12.6) совпадает с границей Варшамова — Гилберта (теорема 12 гл. 1, теорема 30 гл. 17). 9
Ясно, что теорема 3 не отвечает на вопрос, какой альтернант-кый код является наилучшим, а только гарантирует существование хорошего кода в этом классе. Так как класс альтернантных кодов очень велик, то полезно выделить в нем некоторые подклассы. В следующих параграфах мы описываем такие подклассы, известные как коды Гоппы, коды Сривэставы и обобщения Ченя — Чоя кодов БЧХ. Эти подклассы получаются путем наложения некоторых ограничений на вектор а, или вектор v, или сразу на оба вектора.
Упражнение. (1). Рассмотреть двоичный альтернантный код длины 6, у которого аг=а’+1, г=1, ..., 6, где а — примитивный элемент поля GF(23), все равны 1, gi(x) = l-}-x и gz(x)=x. Показать, что он является [6, 2, 4]-кодом.
12.3. коды ГОППЫ
Коды Гоппы являются наиболее интересным подклассом альтернантных кодов. Так же как циклические коды определяются в 'терминах порождающих многочленов (теорема 1 гл. 7), так и Коды Гоппы определяются в терминах многочленов Гоппы G(z). Ь противоположность циклическим кодам, для которых трудно п° порождающему многочлену определить их минимальное расстояние, коды Гоппы обладают тем свойством, что dz^deg G(z) + + 1. Мы дадим сначала определение этих кодов в терминах мно
гочленов Гоппы, а затем покажем, что они являются альтернант-ными.
Определение кода Гоппы длины п с символами из поля GFff?) опирается на два объекта: многочлен с коэффициентами из поля GF(qm) для некоторого фиксированного т, называемого многочленом Гоппы, и подмножество L = {си, ..., «?<.} элементов из GF(qm) таких, что G(a,)#=0 для всех Обычно в качестве L выбирается подмножество всех элементов поля GF(qm), которые не являются корнями многочлена G(z).
С каждым вектором а=(аь ..., ап) над GF(q) свяжем рациональную функцию
Определение. Код Гоппы r(LG) (или Г) состоит из всех векторов а таких, что
7?а (г) == 0 mod G(z), (12.9)
или, что эквивалентно, таких, что iRa(X)=O в кольце многочленов GF(qm) [z]/G(z).
Если G(z) неприводим, то Г называется неприводимым кодом Гоппы.
На рис. 12.3 приведены основные свойства этих кодов. Примеры приведены после теоремы 6.
Г (L, G) — линейный код над GF(q), определяемый уравнением (12.9).
длина п— |£|,
размерность k^n—mr, r=deg G(z), минимальное расстояние d^r+1-
F(L, G)—альтернантный код (а, у), где ^i = G-1(cti). Г(ъ, G)ъ = Гт(ОРСг(а, у)). В двоичном случае, если у многочлена Gfz) нет кратных корней, то d^2r+l. Существуют длинные коды Гоппы, лежащие на границе Варшамова — Гилберта. Расширенные двоичные коды Гоппы, исправляющие две ошибки, являются циклическими.
Рис. 12.3. Свойства кодов Гоппы Г (Г, G)
Проверочная матрица Г. Очевидно, что Г — линейный код. Его проверочная матрица может быть найдена из (12.9). Многочлен z—щ в кольце многочленов по модулю G(z) имеет обратный многочлен (так как он не делит G(z)). Этот обратный многочлен равен:
G (г) — G (аг) (г-аг)-1= - О-1(аг);
действительно,
G (z) — G (аг)
— (г—аг) - — G-1 (аг) = 1 modG(г).
z —аг
Следовательно, вектор а лежит в коде T(L, G) тогда и только тогда, когда
уа.^г)-о'(и0С-1( аг) = 0 (12.10)
z — at
как многочлен (а не по модулю G(z)).'
Г
Если G(z) = ^giZ*, где gi<=GF(qm) и £,#=0, то i—o
G(z)—G(at) г —at
= gr(zr~t+zr~2ai + • - •+«/-’) 4-^(zr-2 +
+ • • •+«/ 2)+ • • + £2(2 + ai) + gi-
Приравнивая согласно (12.10) нулю коэффициенты при z’-1, z’-2, ..., 1, видим, что а принадлежит коду Г(Ь, G) тогда и только тогда, когда Наг=0, где
grG 4ai)
(g'r_i+ai£r)G-1 (ах)
(£i + ai£a +
- - (grG-1^)
(£r_) + an £r) G-1 (ап)
g^G-^ay) • gr 0 gr-! gr
. . .0
ёг-2 ё,
gr
. - -0
. . .0
• (gl + angi + • • + ап
“1
~lgr)G~4an)_ -"G-^aJ
G-4a2)
gi
gi gs • • -g_r o~
а?
«2п
=CXY (12-11)
0
0
1
1
«2
«2
0
а„
_aj c&2
— проверочная матрица кода T(L, G).
Так как матрица G обратима, то согласно упражнению (31) гл. 7 'проверочная матрица может быть записана в иной форме:
H XY .
G-Чах) . - - G~4an)
OjG-1(a1) . . . anG_2(an)
(12.12)
ar’G^(Oi) • • G-^an)
Эта форма обычно проще.
Проверочная матрица с элементами из GF(q) получается из Н (или Н') заменой каждого элемента матрицы соответствующим вектором-столбцом длины т над GF(\q).
Сравнивая (12.11) с (12.13), видим, чтоГ(£, G) является аль-тернантным кодом з^(а, у) с а= (сц ..., «п) и y=(G“’(ai), ..., G-1(an)). Следовательно, размерность k кода T(L, G) не меньше чем п—гт, а минимальное расстояние d не меньше чем г+1.
На самом деле легко указать обобщенный код Рида — Соломона, который задает код T(L, G).
Теорема 4. Г(£, G) представляет собой ограничение на подполе GF(q) кода OPCn-r(a, v), где v= (щ, ..., vn),
G («О ,. .
Vi=—--------- i = l, . . п.
П <«{ —а/)
Доказательство (i). Выберем ueOPCn-r(a, v)\GF(q). Тогда
F (a,) G (af) Цг = игР(аг) г=Г---
I |(«г —«/)
где F(z) — многочлен, степень которого меньше чем п—г.
Таким образом, п , « , ,
- П
г=1
Пусть
N (?) :=^F (af) G П (Z ——“/)•
i=l j^i
Тогда N(a;) = F(ai) G (ai) для всех i=l, ..., n. Кроме того, deg N(z)^n—1 и degF(z)G(zj—1. Так как многочлен
—F(z)G(z) определяется своими значениями в п точках, то N(z) =F(z)G(z). Таким образом,
2" Ui — F(z)G (z) z — af «
П (z —af)
S=1
и, следовательно, ugP(L, G).
Итак,
P(L,G)oOPC„_r(«,v)|GF(9).
(ii). Обратное включение доказывается аналогичным образом, и мы оставляем это доказательство читателю. •
Из теоремы 2 получаем следующую теорему.
Теорема b. Код, дуальный коду Гоппы, равен:
Г (Л, G)L ==Tm(OPCr(a,y)), (12.13)
где
Упражнение. (2). Доказать непосредственно, что коды ОРСДа, у) при yi=G~1(ai) и ОРСп_г(а, у') при
П (а/ — «О дуальны.
Двоичные коды Гоппы. Как и для двоичных кодов БЧХ, в двоичном случае для кодов Гоппы исследования продвинуты несколько дальше (ср. § 7.6). Предположим, что Г=Г(Д G) — двоичный код Гоппы (9 = 2). Пусть a=(ai, ..., ап)—слово кода Г веса w, причем = ...=a, =1; положим
4(2)= П(г-«/3- (12-14)
Тогда /а (2) = J? ["I (г—<Чг)
i=l /Vi
и согласно (12.8)
R (г) = V----!---= - (12.15)
^г~ач М?) V
По определению кода Г все az различны, так что многочлены (?) и f (z) не имеют общих делителей и дробь (12.15) несократима. Так как С(аг)=^0, то многочлены fa (?) и G(z) взаимно просты, и, следовательно, из (12.15) вытекает, что
7?a(z)^0(modG(z))-G(z)|4(z).
Так как все операции выполняются по модулю 2, то f'а (z) содержит ^только четные степени и является полным квадратом. Пусть G(z)—полный квадрат наименьшей степени, делящийся на G(z). Тогда
G (Z) 7а (z)^G(z) 14 (z).
Отсюда заключаем, что
a е Г £Ra (z) = 0 (modG (z)) G (z) | fa (z). (12.16)
В частности, если a 5^=0, то deg f'a (z) deg G(z). Следовательно, для минимального расстояния d кода Г выполняется неравенство
d>deg G(z)-{-1 .
(12.17)
Важнейшим частным случаем является следующий.
Теорема 6. Предположим, что многочлен G(z) не имеет кратных корней, так что G(z) = G2(z). Тогда минимальное расстояние d кода Г удовлетворяет условию
d>2degG(z)+l. (12.18)
Если многочлен G(z) не имеет кратных корней, то код Г называется сепарабельным кодом Гоппы.
Примеры двоичных кодов Гоппы. (1). Выберем G(z) =z2+z+ + 1; jL=GF(23) = {О, 1, а, ..., а6}, где а — примитивный элемент поля, .^=2 и qm=8. Для всех [3eGF(23) выполняется условие ^(₽)=#0, так как корни многочлена z2+z+l лежат в полях GF(22), GF(24), GiF(26), ... и не лежат в поле GF (23) (см. теорему 8 гл. 4). Получаем неприводимый код Гоппы для h=|lL|=8, размерности Л^8—2-3=2 с минимальным расстоянием d^5. Согласно (12.12) проверочная матрица этого кода равна:
~_J 1 1 1 G(0) G(l) G (a) G (a6)
»н = 0 1 a a6
G(l)
G (а6) _
<?(«)
LG(0)
Из рис. 4.5 находим:
1 1а2 а4 а2 а
О 1 а3 а6 а5 а5
а
а6
а4
а3
Кодовыми словами являются
О О
О
1 1
1 о о
1
1
а О
1 О
1
.в
0 1 a a2 a: a4 a5 a'
1 1 0 0 0 0 0 0
0 0 0 1 0 1 1 1
0 0 1 1 1 0 0 1
0 1 1 1 1 1 1 1
0 0 1 0 1 1 6 1
° 0 0 1 1 1 1 0
a2 a 3 c c4 a5 a6
о о о
1
о
1 1 о
о
1 о
1
о
1 1 о
о
1 1 о
н =
они образуют [8, 2, 5]-код Гоппы. Добавляя общую проверку на четность и переупорядочивая столбцы, получаем следующий [9, 2, 6]-код:
1 а4 а6 оо
0 0 0 0
0 110
10 11
110 1
а2 а5 0 а а3 0 0 000'
110 11
0 110 1
10 110
(12.19)
Этот код оказывается циклическим. Объяснение этого явления дано в § 12.5.
Этот пример может быть также использован для иллюстрации теоремы 4. Здесь п—г=8—2=6 и z/i=G(aj) =а2’-|-а’-г 1, так как П,„ы(а,-—а<) = 1 для всех i. Таким образом, теорема 4 утверждает, что [В, 2, 5]-код Готтпы является ограничением на подполе GF(2) кода GF (23) с порождающей матрицей
1 : 1 a5 a3 a5 a6 a6 a3
0 1 I a6 a5 a a3 a4 a2
о : 1 1 1 a4 1 a2 a
0 j 1 a a2 1 a4 1 1
0 1 I a2 a4 a3 a a5 a6
0 1 I a3 a6 a6 a5 a3 a®
Легко проверить, что:
строка 1 + строка 2 -|- строка 6=1 1 1 10100;
строка 1 + строка 5 + строка 6=1 100101 1;
строка 2 -г строка 5 = 00111111.
(2) Выберем G(z)=z3+z+l и L=GF(25). Опять G((3)=#0 для всех (на основании теоремы 8 гл. 4). Тогда Г(£, G) является [32, 17, 7] неприводимым кодом Толпы, проверочная матрица которого согласно (12.12) имеет вид (здесь а — примитивный элемент поля GF(25))
1 1 I 1
G(0) G(l) G(a) G (a30)
0 1 a a30
G(0) G(l) G(a) G (a30)
02 I2 a2 a60
G(0) <3(1) G(a) G (a30)_
1 a4 a8 a14 . . a28
0 a5 a10 a17 . a25 —
0 a8 a12 a20 . . a24
110 11
0 0 0 0 0
0 0 0 1 1
0 0 0 11
0 0 10 1
0 1111
0 0 0 0 1
0 0 10 0
0 0 0 0 0
0 0 0 1 1
0 10 0 0
0 0 110
0 0 0 1 1
0 0 111
0 0 0 0 0
1 1
1 о
1
1 о о
1 1
о
1
1
1
1
Здесь мы воспользовались таблицей поля GF(25), приведенной на рис. 4.5. Весовой спектр кода Г(Д G), найденный на ЭВМ,
имеет вид:
i: 0 7 8 9 10 11 12 13
А= 1 128 400 800 1903 4072 6876 10360
г: 14 15 16 17 18 19 20 21
А: 14420 17448 18381 17336 14330 10360 6860 4136
t: 22 23 24 25 26
Ар. 2068 760 250 136 47
(3) . Конечно, совсем не обязательно ограничивать возможные значения коэффициентов многочлена G(z) нулем и единицей. Например, можно выбрать G(z) =z2+z-l-a3, где а — примитивный элемент поля GF(24). По теореме 19 гл. 9 этот многочлен G(z) неприводим в поле GF(24), так как Т4(а3) =а3та6та12та9= 1. Следовательно, в качестве L можно выбрать все поле GF(24). Это приводит к неприводимому [16, 8, 5]-коду Гоппы.
Упражнение. (3). Найти проверочную матрицу этого кода.
(4) . Неприводимые коды Гоппы. Рассмотрим неприводимый в GF(2) многочлен G(z)—z3+z-t-l. Корни этого многочлена лежат в поле GF(23) и, .следовательно, по теореме 8 гл. 4 в полях GF(26), GF (29), ... Предполагая т не делящимся на 3 и выбирая L = GF(2m), получаем неприводимый код Гоппы с параметрами [n = 2m,Jfe> 2m—3m,d> 7](ЗГт). (12.20)
Как мы видели в примере (2), при т=5 границы для k и d являются точными.
С другой стороны, выбирая в качестве G(z) неприводимый многочлен третьей степени над GF(2m), получаем код с параметрами (12.20) для произвольного т.
В общем случае, выбирая в качестве G(z) произвольный неприводимый многочлен над GF(2m) степени г, получаем неприводимый код Гоппы .с параметрами
[n=2m,k>2:n—rm,d^2r+\] (12.21)
для произвольных целых чисел г и т. Сопоставимые примитивные коды БЧХ имеют параметры
[n = 2m— l,k^2'n— 1— rm,d^2r+ 1], (12.22)
т. е. при одинаковых k и d они имеют на один информационный символ меньше.
Упражнения (4). Пусть G(z) многочлен степени г с коэффициентами из поля GF(2S), и пусть GF(2f)—наименьшее поле, содержащее все корни многочлена G(z). Доказать, что для построения кода Гоппы с параметрами (12.21) можно выбирать L=GF(2m) для любого т такого, что s|m и (/, т) = 1.
(5) . Коды БЧХ. Примитивные коды БЧХ в узком смысле являются частным случаем кодов Гоппы. Выберем G(z)=zr и L—
= {1, а, ап где n—qm—1, а а — примитивный элемент поля GF(qm). Тогда из (12.12) получаем:
” 1 а~г а~2г - • - г ~
Н= 1 сс—(г~1> сс~2(г-” • • • er'"-1’ (г~1) ,
1 а-1 а-2 • оС(п-1)
что дает проверочную матрицу кода БЧХ (7.19), если заменить а-1 на (3.
Для построения двоичных кодов БЧХ, исправляющих t ошибок, надо .выбрать G(z)=z2t и L=G.F*('2m).
В примерах (1) и (2) получилось, что значения k и d совпадают с граничными значениями, приведенными на рис. 12.3. Однако, как показывает пример кодов БЧХ, это не всегда так.
Задача (нерешенная). (12.1). Найти истинную размерность и минимальное расстояние кодов Гоппы.
Упражнение. (5). Другая форма проверочной матрицы. Предположим, что G(z) не имеет кратных корней, скажем, G(z) = (z—Zj) (z—z2) ... (z—zr), zb z2, ..., z,. — различные
элементы поля GF (2s). Показать, что aeF(L, G), если и только если Наг=0 для матрицы Н=(Д^), где Нц=Л1(гг—а;) для 1=5Д^г; 1
Замечание. Заметим, что в этом упражнении матрица Н является матрицей Коши (см. упражнение (7) гл. 11). Если Н—• проверочная матрица кода, иоправляющего t ошибок, то .согласно теореме 10 гл. 1 любые 2/ столбцов матрицы Н должны быть линейно независимыми. В классической теории матриц известны два вида комплексных матриц, обладающих тем свойством, что любая их квадратная подматрица является невырожденной: матрицы Вандермонда и матрицы Коши—(см. лемму 17 гл. 4 и упражнение (7) гл. 11). Матрицы Вандермонда лежат в основе определения кодов БЧХ (i§ 7.6), и, как мы только что увидели, матрицы Коши лежат в основе сепарабельных кодов Гоппы.
Упражнения. (6). Коды Гоппы с G(z) = (z—р)г для некоторых (3 называются комулятивными. Доказать, что между кодом r(GF(2m)—{р}, (z—(3)г) и кодом БЧХ V(GF* (2™)> zr) существует взаимно однозначное соответствие, сохраняющее вес.
Пример (1) подсказывает следующее упражнение.
(7). (Кордаро и Вагнер.) Пусть ^„—двоичный [п, 2, Д-код с наибольшим возможным d, исправляющий большинство ошибок веса [(1/2) (d—1)] + 1. Положим г= [1,/3(/г+1)]. Доказать, что d~2r, если п сравнимо с 0 или 1 по модулю 3, и d=2r—1, если fiEs2 (mod 3); показать также, что порождающая матрица кода может быть выбрана в виде матрицы, содержащей (г—1) столбцов, равных f ° , г столбцов, равных ), и осталь
ных столбцов, равных
12.4. ДАЛЬНЕЙШИЕ СВОЙСТВА КОДОВ ГОППЫ
Добавление общей проверки на четность. Пусть Г ( A, G) — код Гоппы над GF(q) длины n=qm\ L=GF(qm) = {О, 1, а, ..., а”-1} и многочленом G(z) степени г, ни один из корней которого не лежит в поле GF(qrn). Согласно (12.12) вектор а=(с(0), а(1), ..., а (а”-1)) принадлежит коду Г (A, G) тогда и только тогда, когда для .всех t= 0, 1, г—1
SP* а (Р) =0 G(P)
РеСГ (д'”)
(12.23)
Код Г (A, G) можно расширить, добавив общую проверку на четность а (оо), задаваемую равенством
а(оо) = — J] «(₽)
Р eGF (gm) ИЛИ
J а(₽) = 0. 12.24)
PeGF(g'”) U{oo}
Условившись, что 1/оо=0, область суммирования в равенстве (12.23) можно изменить на область GF(qm) {оо}. Наконец, л объединяя (12.23) и (12.24), получаем, что вектор а= (а (0), а (1), ..., «(а”-1), й(оо)) принадлежит расширенному коду Гоппы тогда и только тогда, когда
S 4S=0-i=M............' (12-25)
РбСГЦд'”) U{°°}
Л
Расширенный код будем обозначать через Г (A, G).
Упражнение. (8) (а). Пусть л — подстановка на множестве GF(qm) (J {оо}, задаваемая формулой
л:у
ау + b су + d
(12.26)
где а, Ь, с, d<=GF (qm) удовлетворяют условию ad — Ьс=£О и yf^GF(qm) g {оо}. Проверить сначала, что это действительно подстановка на множестве GF(qm) (J {оо}. Затем доказать, что л л
переводит расширенный код Гоппы Г(А, G) в эквивалентный код Г (A, GJ, где
G^^cz + dYGf^y \cz+d J
(Ь). Предположим, что многочлен G(z) таков, что для некоторого eeG/’*(<7m) выполняется условие
G(z)=e(Cz+drGf^
\cz + а
л
Показать, что код Г(£, G) инвариантен относительно подстановки л.
Коды Гоппы и многочлены Мэттсона — Соломона. В частном случае, когда L состоит из всех корней степени п из единицы, коды Гоппы хорошо описываются в терминах многочленов Мэттсона— Соломона (см. следствие 8). Мы рассмотрим только двоичный случай.
Напомним, что в § 8.6 многочлен Мэттсода — Соломона A (z) для многочлена a(x)=Y'}~^aiXi, «1=0,1 был определен равенством
Д(г) = £Д_{г\ (12.27)
. i=0
где Аг~а(а{) и aeG/’(2r")— примитивный корень степени п из единицы.
Обратная операция задается равенством
п—1
а(х) = 2 (12.28)
i=0
Если L={1, a, a2, ..., а71-1}, то между рациональной функцией
задаваемой равенством (12.8), и многочленом A(z) существует взаимосвязь. Эта взаимосвязь описывается следующей теоремой. Мы будем использовать запись [f(#)]n для обозначения остатка от деления многочлена f(y) на уп—1.
Теорема 7.
Д(2)= [г(г« + 1)Яа(г)]п; (12.29)
(12.30) а Х-: z + а1 i=0
Доказательство. Запишем (2) = F(z)/(z7l+l),
где F (г) = 2 П (г+ “')•
i=0 jy=i
Тогда (z" + 1) Ra (2) = zF (z) = £ atz [”] (2 + a7).
j=0
n—l n— 1
Кроме того, A (z) = at У; a“'7 z>.
t=o j=o
Следовательно, для доказательства (12.29) достаточно показать, что
2 П (? + «>) =
- /#=! П 1=0
т. е. что
п—1 z П (z + «') + 2я + 1 = У а~° zA
/=о
Для того чтобы убедиться в справедливости этого равенства, достаточно умножить обе его части на z+a\ Наконец, равенство (12.30) вытекает непосредственно из (12.28). •
Следствие 8. Пусть Г(£, G)—двоичный код Гоппы с £={1, а, ..., а71-1}, где a^GF(2m)—примитивный корень степени п из единицы. Тогда
Г(£, G)={c(x): [z^M(z)]n = 0(modG(z))}. (12.31)
Доказательство. Как и в доказательстве теоремы, запишем Да (Х)=Д(Х)/(2” +1) • Так как многочлены zn + \ и G(z) взаимно просты, а(х)^Г(Ь, G) тогда и только тогда, когда F(z) = =0 (mod G(z)). Согласно (12.29) A(z)=zF(z) и, следовательно, [z^A(z)]n=F(z). •
Заметим, что если вес wt(a(x)) четен, то Ло=О и [znlA (z)]n=A (z)/z. Таким образом, в этом случае многочлен zG(z) делит А (г).
Пример. Рассмотрим двоичный код Гоппы Г(£, G)c G(z) = =z34-z+l и L=?={1, а, ..., а14}, где а — примитивный элемент поля GF(24). Проверочная матрица (12.12) равна:
Н =
11000111 00110111 0 10 1110 1 00010010 10010110 01000000 00001011 0 11110 10 11001010 0 110 1111 01111100 00000001
1100110 10 110 11 0 1110 11 0100100 1110 0 11 110 110 1 1000110 1 10 0 10 0 0011100 1111000 10 11110 0001011
Тогда код T(L, G) ждающей матрицей
представляет собой [15, 3, 7]-код с поро-
Uj Г1 I 1 0 1 1 0 0 1 0 1 0 0 0 О' и2 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 и3 011111111111111
Этот код является плохим, но служит хорошей иллюстрацией к следствию. Многочлены Мэттсона — Соломона для кодовых слов пь иг и и3 соответственно равны:
l+z + z2+z4 + z8;
z+z2 + z3+ . . , + г14;
1 + w2z + wz2 + wz3 + ш2г4 + wz5 + w2ze 4- ш2г7 -f- wz8 -f- ю2г9 + ai>2zle + + wz11 + шг12 + ш2г13 + шг14,
где через w обозначен элемент а5.
Применяя следствие к первому из этих многочленов, получаем многочлен
[z14 A (z)]15 = 1 + z + z3, + z7 + z14, кратный многочлену G|z| =z3+z+1. Читателю предлагается проверить утверждение следствия для остальных двух многочленов.
Следствие 9. Пусть SF— двоичный код Гоппы Г(£, G) с £={1, а, ..., а”-1}, где а — примитивный корень степени п из единицы. Если код цикличен, то он является кодом БЧХ и G(z)—zr для некоторого целого г.
Доказательство. Предположим, что G(z)^=yzl ни для какого целого числа I и yeGf(2mj. Тогда многочлен G(z) имеет некоторый корень Р=И=О, лежащий в некотором поле GF(2S). Пусть с(х) — ненулевое слово кода четного веса. Согласно следствию 8 многочлен (z)]n=A (z)/z кратен многочлену G(iz) и, следовательно, Д((3)=0. Так как — циклический код, то по п. (iv) теоремы 22 гл. 8 равенство Л(агР)=0 выполняется для всех t = 0, 1 ..., п—1. Таким образом, многочлен A(z) имеет по меньшей мере п различных корней и, следовательно, degA(z)^ ^п, что невозможно. •
Длинные коды Гоппы являются хорошими. В § 12.2 было доказано, что альтернантные коды лежат на границе Варшамова— Гилберта. На самом деле, как показывает следующее упражнение, это утверждение справедливо для значительно более узкого класса кодов.
Упражнение. (9). (а). Доказать, что если G(z) —неприводимый многочлен степени г над GF(<?m) и L = G/’(7m), то существует код Гоппы над GF(q) с параметрами [н=9т, k~^n—rm, ^], удовлетворяющий условию
(12.32)
[Указание. Опираясь на теорему 15 гл. 4, показать, что
всего имеется I m(r)^ — (qrm— (г— l)qrmJ2) неприводимых
9 г
Многочленов степени г над полем GF(qm).]
(b). Вывести отсюда существование длинных неприводимых
Кодов Гоппы, лежащих на границе Варшамова — Гилберта.
Но это не дает способа отыскания наилучшего многочле-на G(z).
Задача (нерешенная). (12.2). Какой из многочленов Гоппы G(z) обеспечивает наибольшее минимальное расстояние (или наименьшую избыточность)?
*12.5. цикличность УДЛИНЕННЫХ кодов гоппы, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
В данном параграфе доказывается, что некоторые расширенные двоичные коды Гоппы, исправляющие две ошибки, являются циклическими (обобщение примера 1 из § 12.3). Для этого находится группа подстановок, относительно которой код инвариантен, а затем показывается, что одна из этих подстановок состоит из единственного цикла.
Для рассматриваемых кодов многочлен Гоппы G(z) является квадратным многочленом с различными корнями, а множество L состоит из всех элементов поля GF(2m), не являющихся корнями G(z). Следовательно, Г(Ь, G)—код, исправляющий две ошибки. Возможны два случая, зависящих от того, приводим или неприводим многочлен G(z). В соответствии с теоремой 16 и упражнением 6 гл. 9 многочлен G(z) может быть записан в виде z2+z+₽, где (3—элемент поля GF(2m) со следом, равным 1,еслиб(г) неприводим, и со следом, равным 0, если G(z) приводим. Пусть Г(£, G) —расширенный код, получаемый из Г(£, G) добавлением общей проверки на четность, а его координаты перенумерованы элементами множества L (J {°°}- Таким образом, блоковая дли-А
на кода Г(Ь, G) равна 2’’г-Ы, если G(z) неприводим, и 2т—1, если G(z) приводим.
Сначала рассмотрим неприводимый случай, л
Теорема 10. Пусть Г(Ь, G)—определенный выше расширенный [2™+1, 2т—2т, 6]-код Гоппы, исправляющий две ошибки, где G(z) — неприводимый многочлен над GF(2m). Тогда код Г (L, G) инвариантен относительно следующей группы Gr, состоящей из 2т(2”Ч-1) подстановок:
Gr={Cf,CzB(»]),CzO,Cf£)B(T1),t = 0, . . .,m-l,i]EG/’(2m)}, (12.33)
где
nv+Р+n. т + n
в h):v -*
С:у-> у2 + р ;
(12.34)
D:y-> у-J- 1
для всех yeGF(2m) (J {оо}. (Дополнительно о группе Gr см. следующую теорему.)
Доказательство, (i). Докажем прежде всего, что код Г(Г, G) инвариантен относительно подстановок В(т\), С и D. (Заметим,
что согласно упражнению (8а) преобразование 2?(ц) является подстановкой, так как Тт(т]2+т]) =0, Гто((3) = 1 и, следовательно, ц2+т1 + Р=И='О.) Подстановки В(т]) и D сохраняют код согласно упражнению (8Ь). Чтобы показать, что С -сохраняет код Г, предположим, что а = (п(0), п(1), ..., tz(oo)) — слово кода Г, и обозначим через Са=(а' (0), а' (1), ..., п'(оо)), где с/(у)=б!(у2+ + Р). .В соответствии с (12.25) СаеГ тогда и только тогда, когда для i=0, 1, 2
V ......=°- <12-35*
Li у2 + у + Р
V eGF (2т) U {оо}
Положим а=у2+р или 7=]/ а+(3 (напомним, что согласно § 4.6 каждый элемент поля GF(2m) имеет в нем единственный квадратный корень). Тогда (12.35) можно записать в виде
S(a + Р);/2 a (a) a + ]/a+P aeGF(2m) U {co}
Возводя в квадрат, получаем выражение
a e
GF (2m) и {“}
(a + PT a (a) a2 + a + P
s
которое равно нулю для i=0, 1, 2 в соответствии с определением л
кода Г, даваемым (12.25).
(ii). iBo-вторых, покажем, что группа, порожденная подстановками С, D п В (ц) для всех ц, задается формулой (12.33). Любая подстановка вида1
? ay + Ь , a,b,c,dеGF(2т), су-рс ad—Ъс=£О
может быть представлёна обратимой матрицей £(т]) и D представляются соответственно матрицами
(12.36)
[а . Например, \с d)
4 P+4V/1 1\ И [
1 4/ \° 1/
Матрицы (а и е (а при любом ее GF(2m)*, естест-
\с b) \с dj
венно, задают одну и ту же подстановку. Если подстановки и л2 представляются матрицами Mj и М2, то подстановка (которая означает, что сначала применяется подстановка зтц а
* Группа всех таких подстановок называется полной проективной линей-группой и обозначается через PG.Z.2(2m) (см. § 16.5). [В литературе на ком языке ее часто называют дробно-линейной группой (Прим. перев.)\
затем л2) представляется матрицей M2Mi. Например, ДВ(ч) пред-ставляется матрицей
Ч Р + ч\ /1 /ч Р \
1 чДо 1/ \1 1 + 4/ '
(12.37)
Заметим, что
В2(г])=£)2 = /; (12.38)
С'":т-т + Тго(Р)=т+1, (12.38)
так что Cm=D и С2т=1.
Пусть Н — группа, порождаемая подстановками D и В(ч) для .всех т]. Из равенств (12.38) и
в (Л) в (6) = db (
В(ч)П = ПВ(1+г1)
следует, что
Н = {I,B (n), D,DB (ri)- r^GF (2m)}
л что порядок группы H равен 2(2m-Fl). Остается доказать, что группа, порожденная группой Н и подстановкой С, задается (12.33). Это следует из равенства
В(т])С = СВ(л2 + р);ОС = СО. •
Упражнение. (10). Доказать, что СВ('ч)С_1==В(('П~ЬР)2т-1).
л
Докажем теперь, что код Г(Д G) эквивалентен циклическому -коду.
Теорема 11. (Берлекэмп и Морено). Пусть, как и в теореме л
10, Г(Д G)—расширенный неприводимый двоичный код Гоппы, исправляющий две ошибки. Группа Gr, задаваемая (12.33), содержит подстановку ZZB(i]o), которая представляет собой один цикл, содержащий все элементы .множества GF(2m) (J {оо}.- Следовательно, координаты можно переупорядочить так, чтобы код £(GF) стал циклическим.
Доказательство. Элементы множества GF(2m) (J {00} можно представить ненулевыми векторами { r | , где г, s^GF (2™) и вектор ( г ) соответствует элементу r/s, если s#=0, а вектор ( )
\ s / \ 0 /
соответствует элементу оо. Кроме того, векторы ( ) и е ( )
\ s / \ «у
представляют один и тот же элемент для всех e^GF* (2m). Действие подстановки DB{x\), задаваемой (12.37), записывается в виде
ОО ->т]->Ч2 + ₽
, ч3 + Рч + Р Ч2-НН-1+Р
или, что эквивалентно, в векторной записи
\о/ \11+чДо/ U/ к 11+1)Л1/ к 1 /
/п3+Рп+Р
кп2 + п+1+Р/
Мы хотим найти такой элемент т]о, чтобы подстановка DB (т]о) состояла из одного цикла, т. е. хотим найти такое наименьшее число п, для которого при некотором feeGF(2m) число
k I 1-Н1/ ко/ к 0 /
равнялось бы 2т+ 1. Собственные значения матрицы )
равны X и 1 + X, где
2v(1+?v) = t]2+t] + ₽.
Собственные векторы задаются равенствами:
/П Р ХД+п\:« + 1) Д+пХ . к 1 1 + пЛ 1 / к 1 / ’
/ц р X Д+4+Д _Д+т]-|-1 X к« i + vk 1 ) 'к 1 /.
Запишем разложение вектора ( по собственным векторам:
/ 1 X _ Д + цХ । Д + 41+ 1\ к 0/ к 1 / ’ к 1 J ‘
Тяда(? ,+„)”( Др-+1)Д t ”)+>.« (1+;+*).
Пусть теперь п — такое наименьшее целое число, что G'.U"Q-Q
Для некоторого k^GF(2m). Тогда
(Л+ 1)«(2v + t]) + 2v«(X + t]+ 1) = /г; (12.40)
(Х+1)'г + 2^ = 0. (12.41}
Подставляя (12.41) в (12.40), получаем:
k = №. (12.42}
Пусть geGF(22-) и GF(2™). Тогда (|2m + g)2m=g-Fg2m;
так что по теореме 8 гл. 4 g2™ +g=aeGF(2m).
Предположим теперь, что g — примитивный корень степени (2,п+1) из единицы. Тогда g2m = g-1, так что g-1 + g+a=O или. В2+а|+1=О.
Выберем т]о так, чтобы выполнялось условие Х=|/а; разом,
таким об-
пНЧо + ₽ = ^(1+?0 = (В2 + а£)/а2 = ^.
Теперь Z=^/ct является корнем многочлена х2-1-х-+
(12.43)
1
— и, сле-а2
довательно, Тт(1/а2) =1 по теореме 15 гл. 9. Тогда Tm(p-F 1/а2) = =0 и в силу (12.43) и теоремы 15 гл. 9 т]о лежит в поле GF(2m).
Согласно (12.42) должно выполняться условие Zn=
Согласно (12.42) = (g/a) "ее GF(2™), т. е.
(J-j =(^-l)n=L
Но числа 2т—1 и 2т+1 взаимно просты, так что g2”-1 является также примитивным корнем степени 2™+1 из единицы. Следовательно, п = 2™4-1 является наименьшим целым числом, для которого выполняется равенство (12.44), и, таким образом, подстановка ОВ(т]о) состоит из единственного цикла. (Заметим, что равенство (12.41) справедливо при n = 2m+l). •
Согласно § 9.4 любой циклический код длины 2т+1 является реверсивным. [Код (12.19) именно таков.] Поэтому, так как мы л
знаем из теоремы 11, что T(L, G) —циклический код, отсюда вы-А
текает, что группа автоморфизмов кода Г(Ь, G) содержит подстановку-реверсию (переводящую i в 2i) при соответствующей нумерации координат и подстановку о2 (см. § 9.4). Порядок
А
группы автоморфизмов кода Г(С, G) согласно упражнению 4 :гл. 9 равен по меньшей мере 2rn(2m-[-l). На самом деле (см. упражнение (11)) подстановки R и о2 принадлежат группе Gr, и поэтому Gr в точности совпадает с группой, порожденной подстановками DB(t\0) и о2.
А
Конечно, группа автоморфизмов кода T(L, G) может быть .и больше группы Gr, что мы и увидим из приводимых ниже примеров.
Упражнение. (11). (i). Показать, что подстановка
Г->---2--- (12.45)
у2+Р+1
принадлежит группе Gr, фиксирует точку
(12.44)
1 \
1 1 и переводит
1 1
1 1
новка является подстановкой о2.
[Указание. Использовать разложение
(£>В(р0))*
и (£>В(т]0))2г
. Таким образом, эта подста-
+Х+т] + 1)
(ii). Доказать, что подстановка /?=о”г2(£)В(г]0) )_1=ОВ(т]о) Д’ является реверсией.
Пример. Для иллюстрации теорем 10 и 11 рассмотрим [9, 2, 6']-код Г(£, G), задаваемый (12.19) из § 12.3. Этот код, в частности, инвариантен относительно подстановок:
С :у->у2+1, которая равна (оо)(01) (аа6а4а3а2а5);
О : у->у+1, которая равна (оо) (01) (аа3) (а2а6) (а4а5) и
DB (n0) = DB (а2): у -> а 1 , которая равна (1 а4 а6 оо а2 а5 0 аа3) -
у + а6
Как было показано в § 12.3, следующее переупорядочивание координат: 1, а4, а6, оо, а2, а5, 0, а, а2 превращает этот код в циклический. Согласно (12.45) подстановка о2 для этого кода равна о2: у->1,/у2 и через циклы записывается в виде (1) (а4а6а2а3аа5) (ооО).
Согласно теореме 11 этот код инвариантен относительно группы подстановок G , порядок которой равен 54. На самом деле этот код инвариантен относительно гораздо большего множества подстановок.
Упражнение. (12). Доказать, что порядок группы автоморфизмов^, 2, 6]-кода (12.19) равен 1296.
Применяя теорему 11 к примеру 3 из § 12.3, получаем [17„ 8, 6] циклический код, который на самом деле является квадра-тичпо-вычетным кодом (см. гл. 16) с группой автоморфизмов порядка 2448.
В качестве третьего примера выберем G(z)=z2-t-z+1 и £= = GF (2s). Тогда f(L, G) — [33, 22, 6] циклический код с порождающим многочленом g(x) = 14-х2+х5+х6+х9+а:11.
Случай, когда G(z) приводим. Аналогичный результат имеет место для приводимого многочлена над GF(2™), скажем, для G(z)=z2 + z+^(z+K) (г+Х+1), где р, Хе GF (2™) и ТТО(Р)=О. Выберем теперь L = GF(2m) —{X, Х-Н1}; 2™—1 координат кода Г(£, G) занумеруем элементами множества L U {оо}. Предполагая т]#=Х и г] X +1, снова определим подстановки 23(т)), С и D равенствами (12.34). Это действительно подстановки на множестве L (J {оо}, так как В(ц) и D меняют местами X и Х+1, а С просто фиксирует оба этих элемента.
Теорема 12. Если многочлен G(z) приводим, то [2™—1, 2т— л
—2т—2,6] расширенный код Гоппы Г(£, G) инвариантен относительно группы G'r, состоящей из 2т(2т—1) подстановок вида {Cl,ClB^,ClD,ClDB^)-,i = Q, . . „т— 1; т] eGF (2m) —{W- +
+ 1}}, (12.46)?
действующих на множестве L (J {оо}. Эта группа содержит подстановку DB(i]o), представляющую собой один цикл, содержащий все элементы множества L [} {оо}. Следовательно, код. л
Г(£, G) эквивалентен циклическому коду..
Доказател ьство. П е рвоеутверждение доказывается точно так же, как и в теореме 10. Заметим, что теперь Cm=I. Для доказательства второго утверждения надо показать, что в поле GF(2m) найдется элемент, скажем, Х=Хо, для которого ни при каком rf<2m—1 не выполняется равенство
Xd + (X+l)d = O. (12.47)
Затем выберем г]0еОД(2™) так, чтобы имело место равенство 'П2о+'По4"Р==^о(Ао + 1).
Это всегда можно сделать, так как T’m(P) = ?"т(>-2о+М =0. Тогда п=2т—1 будет наименьшим целым числом, для которого будут .выполняться равенства (12.41) и (12.42), что и завершит
доказательство.
Итак, остается показать, что существует ZeGF(2'n), для которого равенство (12.47) не выполняется ни при каком d<2m—1. Минимальное d, для которого' имеет место (12.47), должно быть делителем 2т—1. Действительно, так как XeGF(2m), то А2'"~1= = (VH)2m-i, и, следовательно, <в силу (12.47) должно выполняться равенство Хе=(%-!-1)6, где б=НОД(Д 2’п—1). Но так как d минимально, то d=6 и d|2m—1.
Обозначим через F& число корней многочлена Xd+(Z+l)d, лежащих в поле GF(2m) при d|2™—1. Так как многочлен Z,d + + (F+l)d делит многочлен + (Х+1)2"1-х , а последний мно-
гочлен имеет в поле GF(2™) точно (2т—2) корней (а именно все элементы GF(2m), за исключением 0 и 1), то и все корни многочлена Zd + (Х-гl)d также лежат в поле GF(2m), так что Fd—d—1.
Число корней многочлена Х2"*-1 + (Х+I)2"1-1, которые не являются корнями (12.47) ни при каком d, d<2m—1, равно
£ F^^Ll), (12.48)
а/2^-1
где у, — функция Мебиуса, определенная в гл. 4.
Действительно, если £ — такой корень, то он будет учтен только в члене, соответствующем d=2m—1, т. е. только один раз. С другой стороны, если g— корень многочлена Zd-r(A+l)d при d<2m—1,то он также является корнем многочлена XD+(Х+1)D для произвольного D такого, что d\D, т. е. число раз его учета в сумме равно:
VI /2т — 1 \ WT /2т — 1 \
у н--------1=Ун ——)=о
\ £> ) Li \ dd' J
d | D | 2m—I d' I (2m—1 )/d
D=dd' по теореме 14 гл. 4.
Наконец, опять по теореме 14 гл. 4 величина (12.48) равна:
d|2m—.1 d|2m-l d|2m-l
= Ф(2т— 1) — 0>0, что и требовалось доказать. *
Упражнение. (13). Доказать, что этот код также реверси-вен и что в качестве подстанорки, осуществляющей реверсию,, можна взять В (i]0).
л
Следовательно, в рассматриваемом случае код Г(£, G) инвариантен относительно группы порядка 2m (2™—1), порожденной, циклической подстановкой £Ш(г]0), подстановкой о2 (12.45) и‘ подстановкой-реверсией В(т]0) (см. упражнение (4) гл. ‘9).
Задача (нерешенная). (12.3). Какие другие расширенные коды Гоппы являются циклическими?
*12.6. ОБОБЩЕННЫЕ КОДЫ СРИВЭСТАВЫ
Другим интересным классом альтернантных кодов являются, обобщенные коды Сривэставы (рис. 12.4).
Код определяется проверочной матрицей (12.51), где си, .... ап, Wi, ws—n+s различных элементов поля GF(qm) и Zi, ..., гп — ненулевые элементы из GF(qm). Код является альтёрнантным кодом над GF(q) с параметрами [п, k^n—mst, d^.sZ+1], Исходный код Сривэставы получается при /=1 и Zi=a,M- для некоторого |.i.
Рис. 12.4. Свойства обобщенных кодов Сривэставы
Определение. Положим в проверочной Матрице (12.3) альтернантного кода r=st. Пусть сц, ..., ап, ..., ws—n+s различных элементов поля GF(qm) и ..., zn — ненулевые элементы из GF(qm). Положим также
["](* —
gn п,хь = —-------------^=1. • • -,s-,k=l, . . .,t, (12.49)'
&(Z-l)t+fe V ' (x_Wl)k
(заметим, что это многочлен от х), и
У1 = ----z-i-- ,i=l, . . .,п, (12.50)
П(аг—сё/Д /=1
так чТО S, г(М) 1+l (а,) =
Результирующий код называется обобщенным кодом Сривэставы. Таким образом, проверочная матрица для обобщенного кода Сривэставы равна:
(12.51}
где
Z1 z2 zrt
Щ — Wl Oz — Wl On — W[
Z1 z2 Zn
(ax—wz)2 (a2—w)2 (a„—u>i)z
(12.52)
^2 Zn
(ax—ayz/ (a2—ayz/ (un—wtf
для /=1, ..., s.
Исходные коды Сривэставы получаются из обобщенных как частный случай при t=l и Zi = aiv‘ для некоторого ц, так что их проверочная матрица имеет вид:
(12.53)
Так как число различных Wi равно s, то максимально возможное число различных at равно qm—s, так что блоковая длина обобщенных кодов Сривэставы не превосходит qm—s.
Если в качестве си, ..., ап выбираются все элементы поля GF(qm), за исключением {wj, то n = qm—s и коды называются примитивными (по аналогии с кодами БЧХ).
Так как обобщенные коды Сривэставы образуют подкласс альтернантных кодов, то для них выполняются неравенства k^n—mst и d^zst+l.
Пример. Рассмотрим обобщенный двоичный код Сривэставы с m=6; n = 8; г=2; s=l; t=2 и множеством щ, ..., as, равным множеству тех элементов поля GF(23), которые попадают в поле GF (26), т. е.
{«j, . . ., а8} = {0,1, а9, а18, а27, а36, а4В, а54},
где а — примитивный элемент поля GE(26). wi = a и z,= l для i=l, ..., 8.
Таким образом,
1 1 1 1 О — a 1 — a a9 — a a18 — a
(0—a)2 (I—a)2 (a9—a)2 (a18—a)2
Кроме того, выберем
1
as4 — a
1
. (12.54)
(as4—a)2_
Вторая строка равна квадрату первой и поэтому избыточна. Разлагая элементы первой строки по степеням а согласно рис. 4.4, находим
н =
1 0 0 0 0 0 0 1
0 10 0 111 1
0 110 10 0 0
0 10 11100 0 110 0 10 0
10 0 110 1 1
(12.55)
Кодовыми словами являются
00000000 11110001 0 10 11110 10 10 1111
Этот [8, 2, 5]-код на самом деле эквивалентен коду Гоппы, рассмотренному в примере 1 из § 12.3.
Упражнения. (14). Показать, что код Сривэставы (при Г=1) является кодом Гоппы, и, следовательно, для двоичных кодов Сривэставы d:>2s+l.
(15) . Показать, что двоичный код Сривэставы (12.53) при m=4; s=2; п=14; 0^ = 0; w2=l; {аь ..., а14} ='GF(24) —{0,1} и р=0 является [14, 6, 5]-кодом и что минимальное расстояние дуального ему кода равно 4.
(16) . Показать, что двоичный код Сривэставы с m=4; s=2; «=13; Wi = a-1; w2=a-3; {ab ..., ai3} = GF(24)—{0, a”1, ®~3} и p= 1 является [13, 5, 5]-кодом и что минимальное расстояние дуального ему.кода равно 5.
(17) . Доказать, что при т=1 обобщенные коды Сривэставы являются кодами МДР. Эти коды иногда называются кодами Га-бидулина.
(18) . Пусть SF— двоичный примитивный обобщенный код Сривэставы с Zi = 1 для всех i и п = 2™—s.
(i). Доказать, что при s=l код определяется однозначно и равен примитивному коду БЧХ в узком смысле.
(ii). Доказать, что при s=2 код SF также определяется одно
значно и что его расширение 7? инвариантно относительно транзитивной группы подстановок.
(19). Доказать следующие свойства для двоичных непримитивных обобщенных кодов Сривэставы с параметрами: m=mim2, тг>1, m2>l; s=m2; a>i=a2(1~1)mi, i=l, ..., m2, a — примитивный элемент поля GF(2m); сц, ..., an — различные элементы поля G/7<2m>)(=G,f'(2™); n^2™', Zi, ..., zn — ненулевые элементы поля GF(2m').
(i) . Строки подматриц H2.... Н8 в (12.51) являются избыточ-
ными. Следовательно, матрица Н может быть выбрана в виде правой части равенства (12.52) с заменой Wt на а.
(ii) . Код с проверочной матрицей (12.54) является кодом этого типа.
(iii) . k^n—mt и dz>m2£+l.
(iv) . Если все Zj= 1, то k^n—mt/2.
(v) . Если все Zi=l и m2=.2, то расширенный код инвариантен относительно транзитивной группы подстановок.
*12.7. ОБОБЩЕНИЕ ЧЕНЯ—ЧОЯ КОДОВ БЧХ
Эти коды представляют собой другой частный класс альтер-нантных кодов и определяются в терминах двух многочленов P(z) и G(z) (рис. 12.5). Пусть п и q взаимно просты, и пусть GF(</m)—наименьшее расширение поля GF(q), содержащее все корни степени п из единицы.
ОБЧХ (Р, GJ-код состоит из всех многочленов а(х), для которых выполняется сравнение (12.56), и является [п, k^n—rm, d^r+l]-кодом над GF(q). P(z) и G(z) — многочлены над G7(g™) со степенями deg-Psgn—1 и r=deg G^n—1, взаимно простые с многочленом zn—1. Проверочная матрица кода задается (12.57). Эти коды образуют частный подкласс в классе альтер-нантных кодов.
Рис. 12.5. Свойства обобщения Ченя — Чоя кодов БЧХ — ОБЧХ (Р, G) ♦
Определение. Обобщение Ченя—Чоя кода БЧХ длины п над полем GF(q), ассоциированное с многочленами P(z) и G(z), — ОБЧХ(Р, G)—определяется следующим образом. Пусть P(z) и G(z) — многочлены с коэффициентами из поля GF(qm), степени которых соответственно удовлетворяют условиям degP(z)^n—1 и г = deg G(z)^n—1 и которые взаимно просты с zn—-1. Тогда ОБЧХ(Р, G)-koa состоит из всех многочленов а(х) с коэффициентами из GF(q) таких, что степень их не превосходит п—1 и их МС-многочлены A(z) удовлетворяют сравнению
[A (z) P(z)]n = 0 mod G (z). (12.56)
Например, двоичный код OB4X(zn-1, G) совпадает с кодом Гоппы Г(£, G), у которого множество L состоит из всех корней степени п из единицы (см. следствие 8).
Проверочная матрица кода ОБЧХ(Р, G) находится следующим образом:
а(х)<=ОБЧХ(Р, G)
^’A.u(z) такой, что [A(z)P(z)]n= U(z)G(z) и degt/z^n—1—г;
(из теоремы 22 гл. 8) Я и(х) с коэффициентами из GF(qm) такой, что а(х) * р(х) = и(х) * g(x) и U= ... = (7г=0, где и(х), р(х) и g(x) получаются из U(z), P(z) и G(z) путем обращения преобразования (8.9).
, un-i^GF(qm) такие,, что aiPi=Uigi (i=0, ..., п—1) и Ui= ... = Ur=0. (Заметим, что, по предположению, £<=#0, £<=#0.)
i=0
для всех / = 1, г.
Другими словами, а= (а6> •••, an-i) еОБЧХ(Р, G) тогда и только тогда, когда Нат = 0, где
Ро/^о ру ^/ё1 P^/gb
Н = Po/go Pi&lgi Pz&lgz
Po/go Pi^/gt P^'lgz
. . . Pn-i a'1-1/gn_±
• • • Pn-l«2("-1)/gn-l
. . . Pn—! _
1 ar—1 a2^-1) , . . a(r-i»(»-i)
Po/go 0
P^/gx
0 pn_! a'^Vgn-i
(12.57)
Таким образом, H — проверочная матрица рассматриваемого кода. Отсюда видно, что ОБЧХ(Д б)-код является альтернант-ным кодом, у которого в качестве множества щ, ..., an выбраны все корни степени п из единицы и tji = Pi-iap-'gi-i. Следовательно, код ОБЧХ(Р, G) имеет параметры [n, k~^n—rm, d^r+l], где r=deg G(z).
Если P(z) = zb+b~2 и G(z)=zb~l, то код ОБЧХ(Д G) является кодом БЧХ, так как в этом случае его проверочная матрица, как нетрудно увидеть, равна
1 аь а2Ь . . . a(n—ь
1 a*+1 a2^+2 . схР1 (®+*)
1 afc+e-2 a2 (*+б-2) _ . _ а<й-1) (6+c-2)
т. е. равна проверочной матрице кода БЧХ (7.19).
Если P(z) =z6lhi 2+z6+h2*2 и G(z)=z6-1, то код ОБЧХ(Д G) содержит пересечение соответствующих кодов БЧХ и может сов-
падать с этим пересечением.
Например, пусть п=15; P(z)=z и G(z)=z2. Тогда провероч-
ная матрица равна
1111111111111111’
1 а а2 а3 а4 ав а® а7 а8 а9 а10 а11 а12 а13 а14 а15
и определяет [15, 10, 4]-код БЧХ с идемпотентом 63 + 65 + 67 (см.
Упражнение (7) гл. 8). Если P(z)=zs и G(z)=z2, то провероч-
ная матрица равна
1 а4 а8 а12 а ав а9 а13 а2 а6 а10 а14 а3 а7 а11
1 а5 а10 1 а5 а10 1 а5 а101 а5 а10 1 а5 а10 ,
Это определяет [15, 9]-код БЧХ, порожденный идемпотентом 60 + 63 + 67.
Код ОБЧХ (z+z5, z2) имеет проверочную матрицу
Ча а2 а11 а4 а10 а7 а6 а8 а13 а® а3 а14 а9 а12'
1 а2 а4 а14 а8 1 а13 а13 а а7 1 а14 а11 а7 а11
Если записать эту матрицу в двоичном виде, то видно, что одну строку можно выкинуть; следовательно, матрица определяет код размерности 8, который на самом деле представляет собой циклический код с нулями 1, а, а2, а4, а8, а5, а10, порожденный идемпотентом 6з+67.
Так как рассмотренный код является примером циклического кода, не являющегося кодом БЧХ, то из следствия 9 получаем, что в классе альтернантных кодов содержатся циклические коды, отличные от кодов Гоппы. Дальнейшие свойства кодов ОБЧХ(Р, G) и дополнительные примеры дадим в виде упражнений (см. также [286]).
Упражнения. (20). Доказать, что а(х)^ОБЧХ(Р, G) тогда и только тогда, когда deg|[A (z)P(z)/G(z)]„^n—1—г.
(21) . Доказать, что ОБЧХ(Р, G)=OB4X(P*, zr), где P*(z) = =[zrP(z)/G(z)]^ и r=deg G(z). Таким образом, этот код может быть определен в терминах многочлена P*(z) без введения многочлена G(z). Однако определение кода через два различных многочлена упрощает его анализ.
12.8. АЛГОРИТМ ЕВКЛИДА
На основном этапе декодирования альтернантных кодов используется алгоритм Евклида. Он является наиболее простым и прямым способом для вычисления наибольшего обшего делителя (НОД) двух целых чисел или двух многочленов или для представления действительного числа в виде цепной дроби.
Мы опишем этот алгоритм применительно к многочленам, так как этот случай представляет для нас наибольший интерес. Для применения алгоритма к целым числам требуются тривиальные изменения. В этом параграфе коэффициенты многочленов могут лежать в произвольном поле. Наибольшим общим делителем двух многочленов f(z) и g(z) (НОД(/, g)) называется многочлен наивысшей степени, который делит одновременно и f(z), и g(z). Умножение такого многочлена, на произвольную константу также дает НОД f(z) и g(z).
Теорема 13. (Алгоритм Евклида для многочленов.) Для заданных многочленов r-i(z) и r0(z) таких, что degro^Cdegr^i, выполним следующий ряд делений, выписанный в виде последовательности уравнений:
r_! (z) = gr (z) г0 (г) + ту (z), deg zy < deg r0;
ro (z) = g-2 (z) ri (z) + r-2 (z), deg r2 < deg zy;
r}_2 (z) = qj (z) г,--! (z) + rj (z), deg zy < deg r^f, rj-1(z) = qj+1(z)rj\z).
Полученный- в процессе деления последний ненулевой остаток rj(z) равен НОД многочленов f-i(z) и r0(z).
Доказательство. Очевидно, что гДг) делит r^i(z), следовательно, делит rj-2(z), следовательно, делит оба многочлена r0(z) и ri(z). Наоборот, если h(z) делит и rA(z), и r0(z), то h(z) делит гДг), ..., rj(z). Следовательно, гДг) равен НОД многочленов ,r-i(z) и r0(z). •
Пример. Найдем НОД многочленов r_t(z) =z^+ z3+z2+ 1 и r0(z) = z3 + 1 над полем GF (2):
z4 + z3 + z2+1 =(z+l)(z3+1) + (г2 + г);
z3 -h 1 = (z + 1) (z2 4-z) 4- (z+ 1);
z2 + z = z(z+ 1).
Следовательно, r2(z) =z+l равен НОД многочленов r0(z) и r-i(z).
В качестве побочного результата алгоритма Евклида получаем следующую полезную теорему.'
Теорема 14. Пусть r-i(z) и r0(z) такие многочлены, что deg ro^Cdeg г_|, и пусть h(z) —их НОД. Тогда существуют многочлены U(z) и V(z) такие, что
И (z) г_х (z) 4- V (z) r0 (z) = h (z), (12.58)
причем степени U(z) и V(z) меньше степени многочлена r_i(z).
Доказательство. Определим многочлены Ui(z) и V,(z) начальными условиями
и_^=ь,ио{г}^-,
V_1(z)=l, Vo(z) = 0
и рекуррентными соотношениями
Ui (z) = Qi (z) (z) + Ue_2 (z);
(z) = qt (z) (z) + Vi_2 (z).
Тогда
(12.60)
Также
I— 1 (2) _ 1 (2)
Vi-x^J^LVi-jz)
1 о 1 Гft (z) 1 ' .0 1J i о
t/i-2(z) 1 Г ft(z) 1
Vi_2(z)J[ 1 0
’ft(z) 1 1
’ . 1 oj.
(12.61)
>i-2(z)'
7»-i(z).
Fft (z) 11 Г G-1 (Z)
L 1 о] |_гг (z)
rt-3 (z)
rt-2 (Z)
ft-i(z)
1
11 Г <7i-2 (z)
0] [ 1
O' 0
rt-i (z)j , G (z) J ’
Vz (z)
r-i (z)
Jo (?)
I <71 (Л 1
L 1 0
<7i-i(z) 1
1 0
Qi (z) 11 ГП-х (z)
1 0 J U (z)
._ (2) ^i— 1(Z)1 ri— 1 (2) (12 62)
_vz(z) Vi-x (z) | (z) .
Определитель правой части в (12.61) равен (—1){. Следовательно, из (12.61) и (12.62) имеем:
П-i СО
rt (z)
= (-1)г
V{_1(Z) —^-1(2)1 [Г_х(г)
—!z,(z) Ui(z) J [ r0(z)
(12.68)
В частности,
rj (z) = (— 1 у [—Vj (z) r-x (г) + Ui (z) r0 (z)], (12-64)
что дает (12.58) Кроме того,
degt/i = y deg<7fe;
ь=1
degri_x = degr_x—У deg<?ft;
k=i
deg Ut = degг_г — deg< deg r_lt
и аналогично для Vj. •
Следствие 15. Если r-i(z) и r0(z) взаимно просты, то существуют такие многочлены U (z) и V (z), что
Lf(z)r_x(z) + V(z)r0(z)= 1.
Аналогичный результат, естественно, имеет место и для целых чисел.
Пример. Продолжая предыдущий пример, находим:
(7_х==0; С70= 1; 77x = z+l; U2 = z2;
К-х=1; lzo = 0; lzx=l; V2 = z + 1
и согласно уравнению (12.58)
(z 4-1) = (z + 1) (z4 + z3 + z2 + 1) + z2 (z3 4- 1).
Упражнение. (22). Доказать, что Ui(z) и Vi(z) взаимно просты.
12.9. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
В данном параграфе мы опишем эффективный алгоритм декодирования альтернантных кодов, основанный на описанном в предыдущем параграфе алгоритме Евклида. Как и для кодов БЧХ, алгоритм состоит из трех этапов: этап (I) — вычисление синдрома; этап (II)—нахождение многочлена локаторов ошибок и многочлена значений ошибок с помощью алгоритма Евклида; этап (Ш) — вычисление локаторов и ошибок и исправление ошибок.
Так как этот метод декодирования в равной мере пригоден и для кодов БЧХ, то это восполняет пробел, оставленный в описании декодирования кодов БЧХ, данном в § 9.6.
Пусть — альтернантный код л$(сс, у) над GF(q) с проверочной матрицей H = XY, задаваемой (12.2), и с минимальным расстоянием d^r+\, где г четно. Предположим, что произошло ^г/2 ошибок с локаторами
*! = %, . . .,Xt = ait
и со значениями
^1 = ^, ^Yt = att •
как и в § 9.6.
Этап (I) алгоритма декодирования состоит в вычислении синдрома. Синдром определяется равенством
где = 2
= (например)
(12.65)
для ц=0, 1,..., г—1.
Этап (II) состоит в нахождении по вычисленному синдрому многочлена локаторов ошибок
t t
о(г) = П(1— xiz)=yi°i гг,о0= 1, z=l г=0
(12.66)
и многочлена значений ошибок
<o(z) = Vrv^vn (1-V)' <L2’6^
V=1 Ц=1
[Заметим, что это определение незначительно отличается от определения, даваемого равенством (8.17).] Эти многочлены связаны условием
5^-=S(z)modzr, (12.68)
o(z)
где S(z) = V S^.
ц=0
(Доказательство условия (12.68) совпадает' с доказательством^
Данным в теореме 25 гл. 8.)
Итак, задача этапа (II) состоит в определении по заданному •S(z) многочленов o(z) и и(z) таких, чтобы выполнялось соотношение (12.68) и степень многочлена o(z) была наименьшей Сравнение (12.68) заведомо имеет решение, .так как мы предположили, что произошло не более чем г/2 ошибок. Уравнение (12.68) называется ключевым уравнением процесса декодирования.
Для решения ключевого уравнения можно использовать алгоритм Евклида из предыдущего параграфа. Действительно, из уравнения (12.63) вытекает, что
ri (?) = (— IУ Ut (z) Го (z) (mod r_! (z)). (12.69)
Следовательно, на этапе (II) можно воспользоваться следующим алгоритмом.
-Алгоритм. Положим
r_1(z) = zr;r0(z) = S(z),
и будем действовать согласно алгоритму Евклида до тех пор, пока не достигнем такого г^(г), что
*g Д-i (г) > у г и deg (z)< г— 1. (12.70)
Тогда многочлен локаторов ошибок и многочлен значений ошибок задаются соответственно равенствами
o(z) = 6Hft(z); (12.71)
W(z) = (-l)^rfe(z), (12.72)
где константа б выбирается так, чтобы удовлетворялось условие <т(0) = 1 и имели место соотношения:
со (z) = о (z) S (z) mod zr; (12.73)
deg о (z) С-’г; (12.74)
degco(z) —1. (12.75)
Доказательство. Равенство (12.73) вытекает из (12.69). Неравенства deg(lj = degrfe=C-^-r—1 и deg o=deg C7ft = degr_i—degr^-i^ (l/2)r следуют из (12.70).
To, что алгоритм приводит к правильным решениям для o(z) и' to(z), вытекает из следующей теоремы.
Теорема 16. Многочлены o(z) и <в(г), задаваемые (12.71) и (12.72), являются единственным решением сравнения (12.73) при .<т(0) = 1, dego^-yr, deg со —1 и наименьшей возможной сте-
лени многочлена о(г).
Доказательство. !). покажем прежде всего, что если имеются два решения уравнения (12.73), скажем, (о, со) и (o', со'), причем dego^yr; degco^yг—1; deg о'^уГ; deg co'^—г—1, то для некоторого многочлена р о=ро' и со = рсо'.
Действительно, co=crS mod z’’; co'=o'S mods’’; coo'=co'omods’’.
Но степень многочленов в каждой из сторон этого сравнения меньше чем г. Следовательно, соо' = со'о и со/.со'=о/'о'^ р.
(2). Если в решении (о, со), задаваемом (12.71) и (12.72), степень многочлена о (г) не является наименьшей, то из п. (1) следует, что о=ро' и со=рсо', где (o', со') —также решение сравнения (12.73),.а р — некоторый многочлен. Тогда из (12.63) и (12.72) имеем:
co(z) = (—l)6orft(z)= —oVft(z)zr + o(z)S(2); (12.76)
р (z) со' (z) = — 61Д (z) zr + p (z) o' (z) S (z).
-Кроме того, из (12.73) для некоторого ф(z)
со' (z) = о' (z) S (z) + ф (z) zr.
(12.77)
Из (12.76) и (12.77) следует, что p(z)|Vfe(z). Но p(z) также делит и o(z) =SUk(z). Так как t4(z) и КДг) взаимно просты (см. упражнение (22)), то р(г) равно константе. в
Этап (Ш) алгоритма совпадает с этапом (Ш) алгоритма декодирования кодов БЧХ: локаторы ошибок находятся как величины, обратные корням многочлена o(z), а затем по формуле
У* Па-Мй1) определяются значения ошибок.
(12.78)
ЗАМЕЧАНИЯ К ГЛ. 12
§ 12.2. Альтернантные коды были предложены и изучены Хельгертом [631—635]. Многие важные результаты были получены Дельсартом [359]. В основу названия альтернантных кодов положен тот факт, что матрица или определитель вида
fo Со) fi (Ао) • - • fn-1 (л°)
называются альтернантными (см. например, [974]).
Другие обобщения кодов Гоппы были предложены Мандельбаумом [903], а также Тзенгом и Зиммерманом [1356].
§ 12.3. Гоппа предложил свой класс кодов в [536] и [537]. Краткий обзор его результатов дал Берлекэмп в [125]. § 12.3, 12.4 частично основаны на
этих трех работах. Дальнейшие свойства были описаны Гоппой в [538— 539] и Сугияма в [1291]; в этих работах предложены некоторые хорошие коды, при построении которых коды Гоппы используются в качестве составных частей. Ссылку на коды Габидулина можно найти в работе Гоппы [537].
§ 12.5. Теорема 11 принадлежит Берлекэмпу и Морено [130], а теорема 12 — Тзенгу и Зиммерману [1355]. Другие классы расширенных кодов Гоппы, которые являются циклическими, были описаны в [1355], а также Тзенгом и Ю [1353]. Однако задача 12.3 остается пока нерешенной. Свойства группы PGL2 (</) и связанных с ней групп можно найти, например, у Хыоп-перта [676].
§ 12.6. Первая публикация по кодам Сривэставы содержится в книге Бер-лекэмпа [113, § 15.1]. Эти коды и их обобщение были описаны Хельгертом [631—635], и этот параграф основан на его работе. Истинные размерность и минимальное расстояние для многих кодов Сривэставы приведены в [631] и [632]. Модифицируя коды Сривэставы, Сугияма и др. [1291] нашли несколько хороших кодов.
§ 12.7. Обобщенные коды БЧХ описаны Ченем и Чоем в [286]; в той же работе получены многие свойства этих кодов.
§ 12.8. Алгоритм Евклида можно найти, например, в работах: Нивен и Цукерман [995], Старк [1272] и Успенский и Хизлет [1359].
§ 12.9. Идея сведения основного этапа алгоритма декодирования к построению кратчайшей рекурсии, порождающей данную последовательность, принадлежит Берлекэмпу [113, гл. 7] и Месси [992]. Хельгерт [635] выписал ключевое уравнение для альтернантных кодов. Декодирование кодов Гоппы см. также у Реттер [1109, 1110]. Использование алгоритма Евклида для решения ключевого уравнения, по-видимому, принадлежит Сугияме и др. [1288] (см. также [1290]), и наше изложение следует этой работе. Миллс [960] отметил связь алгоритма декодирования с алгоритмом представления действительного числа в виде цепной дроби1. Отличный от описанного алгоритм декодирования, также основанный на алгоритме Евклида, был дан Мандельбау-мом [903] (см. также [902]). Еще один отличный от остальных алгоритм был предложен Паттерсоном [1030] (см. также Сейн [1141]).
Какой же из алгоритмов декодирования является лучшим? Ахо, Хопкрофт и Уллман [16, § 8.9] описали алгоритм вычисления НОД двух многочленов степени п, содержащий О (и log2 * п) шагов. Используя этот алгоритм вместо алгоритма Евклида, Сервейт [1145] показал, что декодирование кода Гоппы длины п, исправляющего t ошибок, при фиксированном отношении tin может быть проведено за О (и log2 и) арифметических операций. (Аналогичный результат для кодов Рида — Соломона получил Юстесен 2 [706].)
Аналогично, используя теорему 29 гл. 9, можно показать, что примитивные коды БЧХ длины п со скоростью R можно декодировать вплоть до их конструктивного расстояния за O(nlogn) арифметических операций. Этот результат лучше, чем тот, который получается при использовании алгоритма Евклида, но, к сожалению, только при достаточно больших п. Практически, по-видимому, наиболее быстрый результат дает первоначальный вариант Берлекэм-па [113, гл. 7], хотя это зависит от возможностей машинного декодирования. В любом случае декодирование с помощью алгоритма Евклида является наиболее простым для понимания, и по быстродействию оно, по меньшей мере, сравнимо с другими методами при п<106; именно поэтому мы предпочли этот метод декодирования.
1 Эта связь была отмечена также Гоппой [540а]. (Прим, перев.)
2 Независимо и одновременно этот результат был получен В. Б. Афанась-
евым [6а*]. (Прим, перев.)
Глава 13
Коды Рида—Маллера
13.1. ВВЕДЕНИЕ
Коды Рида — Маллера (РМ коды) являются одним из наиболее старых и хорошо изученных семейств кодов. Минимальное расстояние РМ кодов меньше, чем минимальное расстояние кодов БЧХ, за исключением кодов первого порядка и кодов с умеренными длинами. Однако большим достоинством РМ кодов является то, что они достаточно просто декодируются при помощи мажоритарно-логических устройств (см. § 13.6 и 13.7).
РМ коды являются простейшим примером класса геометрических кодов. Этот класс содержит также евклидово-геометрические и проективно-геометрические коды. 'Все коды этого класса допускают мажоритарное декодирование. Краткое описание геометрических кодов дано в § 13.8. К сожалению, объем книги не позволяет дать более детального анализа этих кодов, и в качестве компенсации мы приводим довольно подробную библиографию.
В § 13.2—13.4 описываются основные свойства РМ кодов, которые сведены воедино на рис. 13.3 и 13.4. В § 13.9—13.11 изучаются группы автоморфизмов и МС-многочлены этих кодов.
В следующей главе рассматриваются РМ коды первого порядка и их применения, а в гл. 15 изучаются РМ коды второго порядка, а также общая задача вычисления весовых функций для РМ кодов.
13.2. БУЛЕВЫ ФУНКЦИИ
'Очень простое определение кодов Рида—Маллера может быть дано в терминах булевых функций. Мы собираемся определить коды длины n=2m, и, чтобы его сделать, нам понадобится w переменных щ, ..., vm, принимающих значения 0 или 1. Другими словами, пусть v= (vt, ..., vm) пробегает множество Vm всех двоичных m-последовательностей. (В предыдущих главах это множество мы обозначали через Fm, но в гл. 13 и 14 нам Удобнее пользоваться обозначением Vm.) Любая функция f(v) = ..., vm), принимающая значение 0 или 1, называется булевой функцией. Такая функция может быть задана таблицей ис-
тинности, определяющей 'значение f на всех возможных 2т аргументах. Например, таблица
v3 = 0 0 0 0 1 1 1 1.
v2 = 0 0 1 1 О О 1 1
vx = 0 1 0 1 0 1 0 1
Г==О 0 0 1 1 0 0 0
является таблицей истинности для булевой функции f при т=3. Последняя строка таблицы, обозначенная вектором f, содержит значения, принимаемые функцией f, и представляет собой вектор длины п=2т. Вектор f будет принадлежать коду, если функция f будет принадлежать заданному классу.
Предположим временно, что столбцы таблицы истинности естественно упорядочены, как в приведенном выше примере. Так как последняя строка таблицы может быть задана произвольным образом, то всего имеется 22"1 различных булевых функций от т переменных.
Обычно для булевых функций определяются следующие логические операции:
f Исключающие ИЛИ g = f+g', f и g=fg;
f или g = f + g + fg~, НЕ f = f=l+f.
(13.1)
Правая сторона этих равенств определяет операции в терминах двоичных функций.
По таблице истинности булева функция выписывается сразу же; например, в предыдущем случае f=ViVzv3 ИЛИ vivzv3, поскольку правая часть равна 1 как раз в тех случаях, когда равна 1 функция f. Это представление называется дизъюнктивной нормальной формой для f (см. упражнение (1)).
Используя правила (13.1), последнее равенство можно переписать в упрощенном виде (проверить!) f=V3-rViV2 + viv3-{-V2V3.
Заметим, что v2i=Vj. Ясно, что любую булеву функцию можно аналогичным образом записать в виде суммы 2т функций
1, V., v2, vm, V1v2, vtv3, - - -,
(lo.Z) v±v2 -vm
с коэффициентами, равными 0 или 1. Всего имеется 22™ булевых функций, поэтому .все такие суммы различны.
Иными словами, 2т векторов, соответствующих функциям (13.2), являются линейно независимыми.
Упражнение. (I). (Разложение булевых функций.) Доказать следующие свойства булевой функции f:
(a) . f(vlt , • • • , vm_x, 1) ИЛИ vm X
xf^, • • vm_x, 0).
(b) . f(vlf • ; Vm) = vmg(vly . • vm_x)+h(vx, - vm_x), где g и h — булевы функции.
с). Дизъюнктивная нормальная форма:
1 1
f(vlt vm) = £ • - J f(ilf • • • • .uPm,
г i=0 г„=0
1 m
где Wr = vr; w°r = vr.
Теорема 1. Любая булева функция f может быть записана в виде разложения в ряд по степеням переменных vp.
f(vr, • • , vm)= V g(a)u“i - • .uam , (13.3)
aev
причем коэффициенты разложения задаются равенствами g(a)= 2 f(blt • • bm), (13.4)
bcza
и bczza означает, что единичные координаты вектора b образуют подмножество в множестве единичных координат вектора а.
Доказательство. При т=1 дизъюнктивная нормальная форма для f равна:
f О' i) = HO) (1 + У1) +. f( 1) Ui = ЦО) 1 + (HO) + H 1)) Vi,
что совпадает с (13.3) и (13.4). Аналогично при т=2 имеем: H*’i> v2)=f(0, OHH-^Hi+oj + no, l)(l+u1)u2 + + П1, 0)v1(l+v8) + Hbrl)v1fa = f(0, 0)1+{Н0, 0) + +7(1, 0)}^+{H0, 0)+f(0,1)}02+{HO, 0)+7(i, 0) + +П0, D+H1, 1)}%
что доказывает (13.3) и (13.4) для m=2. Ясно, что этот процесс можно продолжить и дальше. •
Упражнение. (2). (Лемма о рандомизации.) Пусть f(vlt ...г Vm—i)—п-роизвольная булева функция. Доказать, что функция ..., vm-i) принимает значения 0 и 1 одинаково
часто.
13.3. КОДЫ РИДА—МАЛЛЕРА
Как и в предыдущем параграфе v= (щ, ..., vm) — вектор, пробегающий пространство Vm, a f — вектор длины 2!П, соответствующий булевой функции f(vly ..., vm).
Определение. Для произвольного г, двоичный
код Рида — Маллера Stir, т) порядка г и длины 2™ определяется как множество всех векторов f, задаваемых булевыми f(vi, ...
vm) функциями, равными всем многочленам, степень которых не превосходит г. Например, PM-код первого порядка длины 8 состоит из 16 слов вида а01 + щУ1 + «2У2+«зУз, где равны 0 или 1, и представлен на рис. 13.1.
0 0 0 0 0 0 0 0 0
v3 0 0 0 0 1 1 1 1
v2 0 0 1 1 0 0 1 1
vi 0 1 0 1 0 1 0 1
V2 + v3 0 0 1 1 1 1 0 0
Vl + V3 0 1 0 1 1 0 1 0
V1 + V2 0 1 1 0 0 1 1 0
V1 + V2 + V3 0 1 1 0 1 0 0 1
1 1 1 1 1 1 1 1 1
1 +v3 1 1 1 1 0 0 0 0
1 + v2 1 1 0 0 1 1 0 0
* -pv3 1 0 1 0 1 0 1 0
* + v2 + V3 1 1 0 0 0 0 1 1
1 + V1 + v3 1 0 1 0 0 1 0 1
l+Vi+v, 1 0 0 1 1 0 0 1
* + Vi + V2 + v3 1 0 0 1 0 1 1 0
Рис. 13.1. Код Рида — Маллера первого порядка длины 8
Этот код приведен также на рис. 1.14, и легко видеть, что код 1%(1, т) всегда дуален расширенному коду Хэмминга. Код ^?(1, т) совпадает также с кодом полученным в § 2.3 из матрицы Адамара типа Сильвестра.
Вес всех слов кода $?(1, т), за исключением векторов 0 и 1, равен 2'"'1. Действительно, согласно упражнению (2) любая булева функция степени 1 соответствует вектору веса 2™-1.
В общем случае PM-код порядка г состоит из всех линейных комбинаций векторов, соответствующих произведениям 1, щ, ..., vm, ^1^2,fit’s, ..., fm-ifjn, ... (вплоть до степени г), которые, таким образом, задают базис кода. Всего имеется
k =
таких базисных векторов (как мы видели в § 13.2, 'все они линейно независимы). Следовательно, размерность кода равна k.
На рис. 13.2 в качестве примера приведены все 16 возможных базисных векторов для РМ-кодов длины 16. (т=4) (проверить!).
Базисными являются: векторами для PM кода 91 (г, 4) порядка г длины 16
Порядок г 0 1 2 3 4 Строки (рис. 13.2) 1 1— 5 1—11 1 — 15 Все
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
v4 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
V3 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
v2 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
Vl 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
vs V4 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
V2 V4 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1
Vl V4 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1
V2 V3 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1
Vl V3 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1
Vl V2 0 0 0 1 0 0 0 1 0 0 0 .1 0 0 0 1
va V3 V4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
V1 V.3 V4 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1
V1 V2 V4 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1
V1 V2 V3 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1
Vl V2 V3 V4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Рис. 13.2. Базисные векторы РМ-кодов длины 16
РМ-коды длины 2™+1 очень просто могут быть получены из PM-кодов длины 2™ при помощи конструкции |u|u + v| из § 2.9.
Теорема 2.
Я(г+1, т+ 1) = {| u| u-j- v |: не J?(r + 1, т), уе^(г. т)}.
Например, именно таким способом в § 2.9 был построен код •S?(l, 4). Эквивалентное утверждение можно сформулировать для порождающих матриц. Пусть G(r, т)—порождающая матрица кода $?(г, т). Тогда теорема означает, что
О(г+1, И+1)=(0(г+1’т) \ 0 G(r, т)
(Ясно, что кодовое слово, порождаемое этой матрицей, имеет форму |u|u-rv|, где ue5?(ir+l, т) v^9t(r, т).)
Доказательство. Типичное слово f кода $?(г+1, лг+1) соот-ветствует многочлену f(vi, ..., vm+l), степень которого не превосходит г+1. Можно записать (так же как в упражнении (1)), что
> £’m+i) = <?(£’i. • • •> + . -, vm),
где deggCV+1 и deg/z<+. Пусть g и h — векторы (длины 2га), соответствующие функциям g(vb ..., vm) и h(v^, ..., vm). Очевидно, что ge^?(r+l, пг) и he^?(r, m). Рассмотрим теперь g(ui, ... ..., vm) и Vm+ih(vi, vm) как многочлен от Vi, ..., vm+r. Соответствующие им векторы (теперь уже длины 2m+1). равны |g|g| и |0|h| (см. упражнение (7)). Следовательно, f=|g|g| + |O|h|. • Отметим сходство между рекурсией для PM-кодов, описываемой теоремой 2, и рекуррентным соотношением для биноминальных коэффициентов:
(13.5)
(см. упражнение (4)).
Теорема 2 позволяет легко вычислить минимальное расстояние кодов Рида — Маллера.
Теорема 3. Минимальное расстояние кода 5?(г, т) равно 2»п-г
Доказательство. Индукцией по m используя теорему 33 гл. 2. *
На рис. 13.3 приведены размерности для нескольких- первых [п, k, d] РМ кодов (проверить!).
Длина п m 4 2 8 3 16 4 32 5 64 6 128 7 256 8 512 9
Расстоя- Размерность k
ние
1 4 8 16 32 64 128 256 512
1 3 7 15 31 63 127 255 511
4 1 4 11 26 57 120 247 502
8 1 5 16 42 99 219 466
16 1 6 22 ' 64 163 382
32 1 7 29 93 256
64 1 8 37 130
128 1 9 46
256 1 10
512 1
Рис. 13.3. Коды Рида — Маллера
. Заметим, что код 3?( т, т) состоит из всех векторов длины 2пг, код 9Дт—4, т)— из всех векторов четного веса, а код ^2(0, т) — только из векторов 0 и 1 (упражнение (5)).
Теорема 4. Для всех г, —1 код 91(т—г—1, т) ду-
ален коду 5? (г, т).
Доказательство. Пусть аей(т—г—1, т)Ъ^91(<г, т). Тогда степень многочлена a(yi, vm) не превосходит т—г—1, а степень многочлена &('Щ, vm) не превосходит г, так что степень произведения ab не превосходит т—1. Следовательно, —1, т) и
вес вектора ab четен. Таким образом, скалярное произведение ab=O (модулю 2). Следовательно, $?(т—if—1, m)<^^?L(r, m), но
dimj?(m—г—1, m) + dim J? (r, m)=l-H )4- • • •+
откуда вытекает, что 5?(m—г—1, m)=5?-L(r, m).
Свойства кодов Рида — Маллера подытожены на рис. 13.4.
Для произвольного т и произвольного г, О^г^т, существует двоичный РМ код порядка г со следующими свойствами:
длина n=2m;
размерность fe=l + ( )+...+( );
минимальное расстояние d=2m~T.
Код (г, т) состоит из (векторов, соответствующих) всех многочленов от двоичных переменных щ, ..., vm, степень которых не превосходит г. Дуальным к коду 3t (г, т) является код 3t (т—г—1, т) (теорема 4). Код 31. (г, т) является расширенным циклическим кодом (теорема 11) и допускает простое кодирование и декодирование (основанное на мажоритарной логике, § 13.6, 13.7). Декодирование является особенно простым для РМ кодов первого порядка (см. гл. 14). Aut (3l(', m)) — GA(т) (теорема 24). Практически хорошие коды, они служат также основой построения многих других кодов (гл. 15).
Рис. 13.4. Свойства кодов Рида — Маллера
Выколотые коды Рида — Маллера. Определение. Для любого г, —1 выколотым РМ кодом 91* (г, т) называется код,
который получается из кода 5?(г,- т) выкалыванием (или вычеркиванием) из всех кодовых слов координаты, соответствующей нулевой т-последовательности щ = ... = пт=0.
(В следующем параграфе мы увидим, что на самом деле не существенно, какую из координат выколоть, — во всех случаях получаются эквивалентные коды.)
Очевидно, что код ^2*(ir, tn) имеет длину 2т—1, минимальное (т\, ,[т\
। -ь ... 4 I 1.
Упражнения. (3). Доказать, что ^?(г, т) является подкодом кода 91 (г+1, т). Показать точнее, что Я{г+1, т) = {а+Ь : ае
m), b — многочлен от v\, ..., vm, степень которого равна точно 1}.
(4) . Используя теорему 2 в качестве рекуррентного определения РМ кодов, вычислить на основании уравнения (13.5) размерность РМ кода. Проверить рис. 13.3, используя треугольник Паскаля для биноминальных коэффициентов. ,
(5) . Доказать, что коды 91 (0, пт) и 91* (О, т) являются кодами с повторением, что код 91(т—1, т) содержит в-Се векторы четного веса и что коды $?(т, т) и 91* (т—1, tn) содержат все векторы соответствующей длины.
(6) . Пусть |S| Г| = {|s|:s&S, t<=T}. Доказать, что 5?(r+l, m-rl) = U |S|S|, где S—‘пробегает те смежные классы по коду 91 (г, т), которые содержатся в коде 91 (г+1, т).
((7). Пусть f (щ, ..., vm) —'булева функция от т переменных, и пусть f —соответствующий двоичный вектор длины 2т. Доказать, что векторы, длины 2m+1, соответствующие многочленам g(vi, ... :..., Um+i) =if(fi, ..., vm) nh(vi, vm+i)=vm+if(vi, ..., vm), равны |f|f| я |0|f|.
13.4. PM КОДЫ И ГЕОМЕТРИИ
Многие свойства РМ кодов лучше всего устанавливаются на языке конечных геометрий. Евклидова геометрия EG(m, 2) размерности т над полем GF(2) определяется как множество из 2т точек, координатами которых являются все двоичные векторы v= = (щ, ..., vm) длины т. Если из этого множества удалить нулевую точку, то получим проективную геометрию PG (пт—1, 2). (Для более подробного знакомства см. приложение В.)
С любым подмножеством S точек из EG(m, 2) ассоциирован двоичный вектор инцидентности %(S) длины 2™, содержащий 1 во всех компонентах seS и 0 в остальных позициях1. Это дает нам другой способ трактовки слов кода 91(г, пт), а именно как подмножеств (векторов инцидентности) в EG (пт, 2).
Например, евклидова геометрия EG (3, 2) состоит из 8 точек Ро, Ei, , Рт, координаты ‘которых могут быть заданы следующими вектор-столбцами:
Ро Pl Р2 Р.з Р4 Р5 Ре Рт ^11110000 v21 10 0 1 10 0
vx 1 0 1 0 1 0 1 0
Вектор инцидентности подмножества S={P2, Рз, Pi, Ps} равен X(S)=l00111100. Ив рис. 13.1 видно, что этот вектор являет-. <ся словом кода ^2(1,3).
1 Предполагается некоторое упорядочение точек геометрии. (Прим, перев.)
Для произвольного целого т введем дополнения векторов vm, ..., V] следующим образом:
\ ут 1 1 • • О О О О
\ Ут_,1 1 • • -О О О О
\ v2 11-110 0
7, 1 0 -1 0 1 О
Выберем столбцы этой таблицы в качестве координат точек геометрии EG(m, 2). Это задает взаимно однозначное соответствие между точками EG(m, 2) и координатами двоичных векторов длины 2т. Любой вектор длины 2™, х задает в EG(m, 2) подмножество, состоящее из тех точек Р, для которых хР=1. Очевидно, что1 х — вектор инцидентности этого подмножества. Число точек в подмножестве равно весу вектора х.
Например, сами 'векторы Vj являются характеристическими векторами гиперплоскостей, проходящих через начало координат; векторы vfv3- описывают подпространства размерности т—2 и т. д. (Естественно, что в геометрии EG(m, 2) имеются помимо плоскостей V; и другие гиперплоскости, проходящие через начало координат. Например, ни одна из гиперплоскостей v< не проходит через точку 11 ... 1. Аналогично подпространства VjV3- не исчерпывают всех подпространств равномерности т—2 и т. д.)
Одним из преимуществ геометрического языка является возможность точного указания слов минимального веса, лежащих в РМ коде порядка г и длины 2™: эти слова являются векторами инцидентности (т—г)-мерных плоскостей -в EG(jn, 2). Этот факт доказывается в теоремах 5 и 7. В теореме 9 этот факт используется для определения числа кодовых слов минимального веса. Затем в § 13.5 мы показываем, что кодовые слова минимального веса порождают код 5? (г, т). По ходу дела мы доказываем, что выколотый код <%*(г, т) является циклическим. Доказательства, содержащиеся в § 13.4 и 13.5, могут быть при первом чтении опущены..
Пусть Н — некоторая гиперплоскость в EG (т, 2). По определению вектор инцидентности h=%(/7) задается точками V, удовлетворяющими некоторому линейному уравнению относительно щ, .... ..., vm. Другими словами, булева функция h представляет собой линейную функцию от »!, ..., vm, и, следовательно, задает слово веса 2m-! в коде 5?(г, т).
Заметим, что если /€Е^?(г, т)—вектор инцидентности множества S, то 1, т) и является вектором инцидентности
множества S Н. Теперь можно перейти к первой основной теореме.
Теорема 5. Пусть f — слово минимального веса кода Я(г, т)г скажем, f=^(S). Тогда S— (т—г)-мерная плоскость в EG \т, 2) '(которая не обязательно проходит через начало координат).
- Например, 14 слов веса 4 в [8, 4, 4] расширенном коде Хэмминга являются 14 плоскостями в £G(3, 2). /
Доказательство. Пусть И — некоторая гиперплоскость EG(m—1, 2) в EG(m, 2), и пусть Н' — -параллельна^ гиперплоскость, так что EG^m, 2)=Я J И'. Согласно сделанному выше замечанию множества S (] Н nS(]H' лежат в &(r+l\ m) и, следовательно, содержит 0 или не менее 2m~r~l тоМек. Так как |S|=2m-’-=|Sn^| + |SH Я'|, то |5 П Я|=0, 2т-г-¥или 2m~r. Следующая лемма завершает доказательство теоремы.
Лемма 6. (Ротшильд и Ван Линт.) Пусть .>— подмножество в EG(tn, 2) такое, что |S|=2m-r и |5 Q Я] =j0, 2m-r-1 или 2п‘г для всех гиперплоскостей Я в EG(m, 2). То?да 5 является (т—г)-мерной плоскостью в EG\m, 2).
Доказательство проводится индукцией по т. При т=2 ре-
зультат тривиален.
(i) . Предположим, что для некоторого Я выполняется равенство |5 П Н\=2т~т. Тогда ХсдЯ, т. е. SczEG(m—1, 2). Пусть X— некоторая гиперплоскость Я. В EG(m, 2) найдется другая гиперплоскость Я" такая, что Х=Яр Н", и S f] X=S f] Н", т. е. |S f] Х|=0, 2(’n~'1>-<r-1>_1 или 2(то"1)_(г_1). По предположению индукции X является ((т—1) — (г—1))-мерной плоскостью в EG(tn—1, 2 ) и, следовательно, в EG(m, 2).
(ii) . Если |Х Q Я|=0 для некоторого Я, то, заменяя Я параллельной гиперплоскостью, сводим этот случай к предыдущему.
(iii) . Остается рассмотреть случай, когда |Х ("] Я| =2m-r-1 для всех Я. Имеем:
у isn^p- £ (Zx.w)!-T2 2 х
Ht^EG {т, 2) H^EG (т, 2) a^S agS fceS H^FG (m, 2)
Xb(a)X„(b) = |Sl(2m-l) + |S|(|S|-l)(2m-1-l),
так как через одну точку в EG{m, 2) проходит 2т—1 гиперплоскостей, а через одну прямую 2™-1—1. Левая часть в этом равенстве равна 23’п-2г-2. Подстановка 1X1=2^-’ в правую часть приводит к противоречию. •
Обратным теореме 5 является следующее утверждение:
Теорема 7. Вектор инцидентности любой (т—г)-мерной плоскости в EG(m, 2) является словом кода 5?(>г, т).
Доказательство. Любая (т—г)-мерная плоскость в EG(tn, 2) состоит из всех точек, которые удовлетворяют системе г линейных уравнений над GE(2), скажем:
1=1, , г,
/=1
т
или, что эквивалентно, V ai}Vf 4- bt + 1 = 1, i== 1, •
/-1
Это можнохзаменить одним уравнением \ т / т \
\ П £ад + 6г + 1)=1> У i=i \/=i ' /
т. е. некоторым многочленом от переменных ..., vm, степень которого не превосходит г. Следовательно, вектор инцидентности этой плоскости попадает в Sl(r, т). *
Соединяя теоремы 5 и 7, 'получаем:
Теорема 8. Множество слов минимального веса в коде 5? (г, т) в точности совпадает с множеством векторов инцидентности (т—г)-мерных плоскостей в EG (tn, 2).
Слова минимального веса кода 5?* (г, т) получаются удалением координаты 0 из тех слов минимального веса кода Sl(r, т), которые имеют 1 в этой координате. Такие слова представляют собой векторы инцидентности подпространств PG(m—г—1, 2) в PG(m—1, 2). Напомним читателю, что в проективных конечных геометриях между плоскостями и подпространствами нет различий (см. приложение В).
Теорема 9. Число слов минимального веса:
(а) в коде SI* (г, т) равно
2т~г — 1
2ш-г-1 _ J
(Ь) в коде S£(r, tri) равно пт—i |
А = 2Г П —-___________~ 1
i=0 z 1
Доказательство. Теоремы 3 и 5 приложения В.
*13.5. ВЕКТОРЫ МИНИМАЛЬНОГО ВЕСА ПОРОЖДАЮТ КОД
Теорема 10. Векторы инцидентности проективных подпространств PG([i—1, 2) геометрии PG(m—1, 2) порождают код St* (г, т) при р,=т—г.
Доказательство. (Начинающий читатель может его пропустить). Пусть а—примитивный элемент поля GF(2m). Тогда в качестве точек геометрии PG(m—1, 2) могут быть выбраны 1, а, а2, •а3, ..., а2т~2. Пусть Z=2’1—2.
Как обычно, представим подмножество T={ad°, ..., ad«} этих точек в виде многочлена да(ж)т=хйо-{- ... +xd“.
Если T—{ad°, ..., adl} является подпространством PG(p— 1, 2), то точки множества Т представляют собой все ненулевые линейные комбинации над GF(2) некоторых р, линейно независимых точек из GE(2m), скажем, а0, ..., ац-ь Другими словами, все точ-ки 'Множества Т можно записать в следующем виде:
и-1
а; = оГг , i = 0, 1, • • •, I, i=o
где (ai0, ац, aiu -i) пробегает все ненулевые двоичные р-по-следовательности. Многочлен xwT(x) также представляет подпространство PG(p—1, 2), натянутое на аао, аац-ь Таким образом, каждый циклический Сдвиг вектора инцидентности подпространства PG([i—1, 2) также является вектором инцидентности некоторого другого подпространства PG(n—>1, 2).
Пусть — код, порождаемый всеми многочленами wT(x), где Т—некоторое подпространство PG(n—1, 2). Очевидно, ‘ё’ — циклический код, содержащийся в ^2* (г, т); теорема утверждает, что на самом деле {г, т). Мы докажем это, показав, что
dim^> 1 -+Н .
\1 / \г J
Размерность кода равна числу таких элементов as, что они не являются нулями кода <ё1, т. е. числу as таких элементов, что а>т(а®)=#0 для некоторого Т. Имеем:
I I \S
ш7-(°о=2аЧ==2( 2 йРа/) =V(&oao+ • • •+
i=o i=0 \/=0 ) Ь
где суммирование распространяется на все ненулевые ц-после-дователыюсти Ь= (Ьо, ..., йц-i). Обозначим последнее выражение через Fs(ao, .... ац -i). Тогда, полагая -p=&1ai + ... рхц имеем:
fs(a0. • • •> %_i)= 2 (6oao + y)s = S ( YS + (“о + тГ) =
=Е ai- "VV1- (13-6)
Это выражение является однородным многочленом степени s от а0, •••, Ощ.
Следовательно, размерность кода равна числу s таких, что многочлен Fs(a0, ..., ащ) не равен тождественно нулю при линейно независимых щ.
Итак, необходимо подсчитать число таких многочленов Fs= (ао, ..., ссц-i), которые содержат коэффициенты, не равные нулю по модулю 2. Заметим, что: (i) такой многочлен не может равняться тождественно нулю, и (ii) ао, —, «г -i должны быть ли-
нёйно зависимы (упражнение (8)). По теореме Лукаса полиномиальный коэффициент
s!
/о! • • -Vfl
несравним с нулем по модулю 2 тогда и только тогда, когда для всех i, —1,
(/о)г+(/1)г + • +( /м_))г <(s)h
где (x)i обозначает i-ю цифру в двоичном разложении числа х.
Таким образом, выражение (13.6) содержит ненулевой коэффициент тогда и только тогда, когда двоичное разложение числа s содержит не менее чем р, единиц. Например, если 5=2гс+2г‘-г 4-...-[-2гм—1, то многочлен (13.6) содержит ненулевой коэффици-
J1—1
ент, соответствующий /0=2“ ..., /м_1=2’
Число таких s в диапазоне [1, 2т— 1] равно
Упражнение. (8). Доказать, что если а0, ..., ащ линейно зависимы, то многочлен Д(ао, , ац-i) по модулю 2 равен тождественно нулю.
Важное замечание. Пусть w2(s) обозначает число единиц в двоичном разложении неотрицательного целого числа s. В процессе доказательства предыдущей теоремы мы показали, что элемент as является ненулем кода 5?* (г, т) тогда и только тогда, когда l^s^2m—1 и йУ2(5)^ц- Другими словами, справедлива следующая теорема.
Теорема И. Выколотый PM-код ^2* (г, т) является циклическим кодом, все нули которого исчерпываются элементами сц, удовлетворяющими условиям —г—1 и lsCs<:'2m—2.
Порождающий и проверочный многочлены выколотого РМ кода 01* (г, т) для —1 равны:
£(*) = П M(s)(x); (13.7)
Kt»2 (s)<m—г—1 Ks<2m—2
/1(х) = (х+1) П A4(s)(x), (13.8)
т—г<кг2 (s) <т—1
l<s<2m—2
гДе s пробегает множество представителей циклотомических классов, MSs> — минимальный многочлен элемента as. (Напомним, что произведение по пустому множеству равно 1.)
Другой вид порождающего и проверочного многочленов получается, если в качестве примитивного многочлена выбрать не а,
а а-1. Это приводит к замене s на 2m—1—s и w2(s) на т—w2(s). Соответственно получаем:
£(*) = П M<s,(x); (13.9)
г+Ки?2 (s)<m-l
l<s<2m—2
й(х) = (х+1) fl M<S,W- (13-Ю)
Kw2 (s) < г l<s<2m—2
Если порождающий многочлен кода 91* (г, т) задан формулой (13.7), то согласно теореме 4 гл. 7 формула (13.10) задает порождающий многочлен дуального кода.
Порождающий идемпотент кода 91* (г, т) равен
бо+ S es,
Kt», (s)<r
Ks<2—2
или, что эквивалентно (опять при замене а на а-1), е0+ V eSJ
♦ т—r<®2 (s)<m—1
l<s<2m—2
где s пробегает множество представителей циклотомических классов, а 0S определено так же, как в гл. 8.
Порождающий идемпотент кода, дуального 91* (г, т), согласно теореме 5 гл. 8 равен:
р+е0+ V esV= V е;.
I т—r<w2 (s)<m—I I Kw2 (t) <m—r— 1
\ 1 / l<t<2m— 2
Например, идемпотенты кодов 5?*(1, m) и 5?* (2, m) соответ-rn— i
ственно равны 0о -г-0* и 0o + 0*+ V 0*.,
i=(m+l)/2
где Zi= 1+21. В общем случае слово произвольного PM-кода длины 2т имеет следующий вид: первой частью слова является общая проверка на четность, а второй частью — слово циклического кода Я*:
J?(0, иг): | а\ я0о|;
J?(l, т): ]а] ав0 + 0*|;
т— 1
3? (2, иг): | а\авд + ^х^ 0*+ V
г=(т+1)/2
Я(т-2, т): |f(l)|f(x)(l + 0J|;
J?(m—1, т): | f (1) | f (х)
где а, аь а^вР(2), ih $if={0, 1, 2,..., 2т—2}, а f(x) —произвольный многочлен.
.Вложенные семейства. На рис. 13.5 показано, как вкладыва-ются друг в друга семейства кодов БЧХ и выколотых РМ кодов. Здесь через 91(d) обозначен код БЧХ с конструктивным расстоя-вием d, а двоичные числа в фигурных скобках задают показатели нулей кода (по одному из каждого циклотомического класса).
91* (т — 1) = ^(1) {0}
99 (т — 2)=й>(3){1} I
<®(5) {1, 11}
I
—3) {1,11,101,1001,.
(7) {1, 11, 101}
I
99 (т — 4) {ш;<3>
..} ^>(9) {1,11,101,111}
^(11) {1,11,101,111,1001}
^(13) {1,11,101,111,1001,1011}
^(15){1,11,101,111,1001,1011,1101}
^(17) {1....1111}
Рис. 13.5. Вложенные семейства кодов БЧХ и выколотых РМ-кодов
При движении вниз страницы объем кодов становится меньше. Мы видим, что
91* {г, m) cz код БЧХ с конструктивным расстояниём 2m-r—I;
5?(r, т) CZ расширенный код БЧХ с конструктивным расстоянием 2m“r—1.
Теорема 12. Векторы инцидентности (т—г)-мерных плоскостей в EG(m, 2) порождают код 91* (г, т).
Доказательство. Напомним, что 91 (г, т) представляет собой код 91* (г, т), дополненный общей проверкой на четность. По, теореме 10 векторы инцидентности (т—г)-мерных плоскостей, в нулевой координате которых стоит 1, порождают 91 (г, т). Поэтому, конечно, все (т—г)-мерные плоскости тем более порождают код 91 (г, т). •
Не приводя доказательства, упомянем следующее обобщение этого результата.
Теорема 13. (Мак-Вильямс и Манн.) Ранг над GF(p) матрицы инцидентности гиперплоскостей в m-мерной евклидовой или в проективной геометрии над GF(ps) равен
[т + р — 1 Xs . ( ) +₽-, \ т /
гДе е равно +1 для проективной и —1 для евклидовой геометрии.
Задача (нерешенная). (13.1). Существует ли кодовое слово а(х)^.91* (г, т), которое равно вектору инцидентности некоторого подпространства PG(m—г—1, 2) и порождает код Я*.(г, т)?
13.6. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (I)
Имеются два очевидных 'способа кодирования РМ кодов. Первый основан на записи порождающей 'матрицы в форме, показанной на рис. 13.2, что приводит к несистематическому кодеру. Второй, являющийся систематическим, основан на том факте (доказанном в теореме 11), что РМ коды являются расширенными циклическими кодами. В данном параграфе мы приведем алгоритм декодирования, пригодный именно для первого кодера, а затем в § 13.7 опишем более о'бщий алгоритм декодирования, применимый к любому кодеру.
Первый алгоритм опишем на конкретном примере [16, 11, 4] PM-кода второго порядка, Ж(2, 4). В качестве порождающей матрицы кода G выберем первые 11 строк на рис. 13.2. Тогда последовательность ИНформаЦИОННЫХ СИМВОЛОВ а = «оЯ4«за2«1«34Я24Х X «14«2з«1з«12 кодируется в кодовое слово
x = aG = o0 1+a4v4+ + OiV1+ • + а12 v4v2 = хох1 -*15.
(13.11)
Этот код исправляет одну ошибку, и мы покажем, как она может быть исправлена при помощи мажоритарной логики. (В отличие от приводимого в гл. 10 мажоритарного декодера для кодов PC данный декодер является практически работающей схемой.) Первый шаг декодирования состоит в определении шести символов «12, ..., «34- Из рис. 13.2 видим, что если ошибок не было, то
«J2 : *0 Ч” *1 4“ *2 Ч” *3
= х4 Ч- х5 Ч- *с Ч~ *7
= *8 Ч~ Х9 4“ *10 Ч- *11
= *12 Ч" *13 Ч" *14Ч~*15’
й13 = *0 Ч~ *1 4“ *4 + *5
= х2 Ч- *3 Ч- *6 Ч~ *7 = *8 + *9 Ч~*12 Ч~*13
=*ю ч- *11 ч- *14 ч- *i5;
(13.12)
(13.13)
^34 *0 Ч" *4 Ч~ *8 Ч~ *12
= *1 Ч- *5 Ч- *9 Ч- *13
= *2Ч-*6Ч-*юЧ-*14
= *3 4“ *7 Ч~ *Ц Ч- *15-
Уравнения (13.12) дают четыре независимые проверки для определения символа «12. Уравнения (13.13) дают четыре независимые проверки для определения символа «13 и т. д. Если произошло не более одной сшибки, то голосование по большинству
проверок приводит к правильному результату, так что каждое1 ац будет правильно определено.
Для определения символов ai п4 вычтем tZ34v3v4+ ... + + C12V1V2 из значения х, и результат обозначим через x'=x'ox'i ,.г ... х'15- Из рис. 13.2 опять видно, что
^ = .^4-%;
= Х2 + х3
^2 Xq "4” х2
Теперь легче: имеется восемь независимых проверочных уравнений для каждого символа cz,, и, следовательно, если произошла только одна ошибка, то голосование по большинству проверок дает правильное значение Имеем:
х" = х'— zz4v4— • • —= а0 1 + ошибка,
и а0 равно 0 или 1 в соответствии с числом единиц в векторе х". Эта схема называется алгоритмом декодирования Рида и,, очевидно, пригодна для любого РМ-кода.
Как были найдены координаты вектора х, включенные в про-верки (13.12), (13.13), ...? Чтобы ответить на этот .вопрос, дадим-геометрическое описание алгоритма Рида для декодирования кода 5?(г, пг). Прежде всего найдем ас для некоторого g=Oi ... о,-. Со
ответствующая строка порождающей матрицы va ... va равна
вектору инцидентности некоторого (т—г)-мерногоподпространства S геометрии EG(m, 2). Например, на рис. 13.6 двойной линией выделена плоскость S, соответствующая символу п12. Пусть Т обозначает «дополнительное» к S подпространство с вектором инцидентности vT, .., vT , где множество индексов {ть ...
т—г
..., Тт-Л является дополнением к множеству {oi, ..., ог} во всем
множестве {1, 2, ..., т}. Очевидно, пересекаются в одной точке — в начале координат.
Пусть U 2т-г— все парал-
лельные переносы подпространства Т в EG(m, 2), включая и само Т (на рис. 13.6 они заштрихованы). Каждое подмножество Ui пересекается с S точно в одной точке.
Рис. 13.6. Геометрия £6(4, 2); показаны пространство S (двойные линии) и Ut, ..., Ut (заштрихованы)
что подпространства Т и S
0001
Теорема 14. При условии отсутствия ошибок символ а •задается равенствами
= 2 хр> 2, • • ; 2т~г.
peut
Эти уравнения являются обобщениями уравнений (13.12), (13.13) и определяют 2т~Т проверок для символа ав.
Доказательство. В соответствии с видом порождающей матрицы кодовое слово может быть записано в виде
х= У a v • • -v , Р Рх PS
Р Р1• *Pg
где суммирование ведется по всем подмножествам {рь ..., ps} множества индексов {1, 2, ..., т}, объем которых не превосходит г. (Это обобщение равенства (13.11).) Следовательно,
S хр^% 2(vp.-- • vps)p=Sgp7V(^£’ ₽)i
p&Jt р РеД р
где N(Uj, р)—число точек в пересечении подмножества Ui и подпространства W с вектором инцидентности v ... v .
Pl Ps
Воспользуемся тем, что пересечение двух подпространств является подпространством, и тем, что все подпространства (за исключением одноточечных) содержат четное число точек. Подпространства Т и W пересекаются по подпространству
vt. • ' ’Ч, г vp. ‘V
Если s<r, то размерность этого подпространства равна по меньшей мере 1 и N(U-t, р) четно. С другой стороны, если s=r, но W^S, то одно из р< должно равняться одному из т,, скажем, pi = Ti. Тогда Г и IF пересекаются по подпространству
и размерность этого пересечения опять равна по меньшей мере 1, так что N(U-t, р ) четно. Наконец, если IF=S, то N (Ui, р) — 1. •
Из этой теоремы следует, что если произошло не более чем ошибок, то мажоритарное декодирование даег
,т-л_!
правильное значение символа ав, где о — любая цепочка из г символов. Остальные символы определяются так же, как и в рассмотренном примере. Таким образом, алгоритм Рида позволяет исправлять
! — ( 2m г — 1)1 ошибок.
L 2 ZJ
13.7. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (II)
Алгоритм Рида неприменим при систематическом кодировании РМ.-кода как расширенного циклического кода (такое кодирование описано в § 7.8). К счастью, в этом случае работает другая
схема мажоритарного декодирования, и ее описание приведет нас к более общему классу кодов — конечно-геометрическим кодам.
Если — некоторый [и, А]-код над GF(q) с проверочной матрицей Н, то слова этого кода должны удовлетворять системе проверочных уравнений, задаваемых строками матрицы Н:
п— 1
V/i.x£ = 0.
1=0
Ясно, что каждая линейная комбинация строк проверочной матрицы Н также задает .проверочное соотношение; таким образом, всего имеется qn~h проверок. Идея мажоритарного декодирования состоит в выборе наилучшего подмножества проверок.
Определение. Множество проверочных уравнений называется ортогональным относительно i-й координаты, если переменная Xi входит во все уравнения, а другие переменные х, входят не более чем в одно уравнение.
Пример. Рассмотрим [7, 3, 4] симплексный код с провероч-. ной матрицей
"1 1 0 1 0 0 0'
н= 0 1 1 0 1 о о 0 0 110 10
.0 0 0 1 1 0 1 _
На рис. 13.7 приведены 7 из 16 возможных проверок для этого, кода
“0123456-
110 10 0 0
0 110 10 0
0 0 110 10
0 0 0 1 1 0 1
1 0 0 0 1 1 0
0 1 0 0 0 1 1
1 0 1 0 0 0 1
Рис. .13.7. Проверки, для [7, 3, 4]-кода
Строкам ' 1, 5 и 7 на рис. 13.7 соответствуют проверочные, уравнения
, Хо+м+хз=
Х0 + Х4 + Х5 = 0;
Хо 4" Х2 4~ Хв = 0.
которые ортогональны относительно координаты и. на рис. Z.1Z .это, очевидно, соответствует линиям, проходящим через точку О Аналогично линии, проходящие через точку 1, задают три проверочных уравнения, ортогональных на координате 1, и т. д.
Предположим, теперь что вектор ошибок равен е, так что получен вектор у=х + е. Если имеется J проверок, ортогональных относительно координаты 0, то обозначим через Sb ..., Sj результаты применения этих проверок к вектору у. Для рассмотренного выше примера имеем:
— Уо + Vi + Уз = ео + ei + ез-^2 ~ У0 + У4 + Уъ ~ е0 + е4 + <?5’ S8 ~ Уо "Ь У% + Уб = Р0 + е2 + ее •
Теорема 15. Если число ошибок не превосходит то
правильное значение е0 равно величине, принимаемой большинством проверок {SJ; в случае альтернативы принимается решение ео=О.
Доказательство. Предположим, что произошло не более чем f—ошибок, (i). Если во=0, то не более чем Г— /1 проверок могут быть искажены. Следовательно, по меньшей мере jj .величин {£,-} будут равны 0.
(ii). Если Сот^'О, то заведомо меньше чем проверок бу-
дут искажены остальными ошибками. Следовательно, большинство из величин {Sj} будут равны е0. •
Следствие 16. Если для каждой координаты имеется / проверок, ортогональных относительно нее, то код может исправ-
Г 1 ,1 й
.лять I — J ошибок.
I 2 I
Замечания, (i). Если код циклический, то, найдя / -проверок, ортогональных относительно одной координаты, системы ортогональных проверок для остальных координат можно получить путем циклического сдвига первой системы J проверок.
(ii). Из хода доказательства теоремы 15 видно, что некоторые 'векторы ошибок, вес которых больше чем могУт ‘при-
нести к неправильному декодированию. Однако одно из замечательных свойств мажоритарных декодеров состоит в том, что (без удорожания устройства) они позволяют правильно декодировать многие векторы ошибок, вес которых больше чем
(iii). В случае альтернативы решение принимается в пользу '0, если 0 является одной из альтернатив; в противном случае мо
жет 'быть принята любая из альтернатив. Это эквивалентно принятию мажоритарного решения по множеству проверок {0, Sb. S2,
Рассмотренный метод декодирования называется мажоритарным декодированием в один шаг. Однако, как показывает следующая теорема, как правило, не существует достаточного числа ортогональных проверок для исправления мажоритарным декодированием в один шаг числа ошибок, равного половине минимального расстояния кода.
Теорема 17. Число ошибок, которые можно исправить мажо
ритарным декодированием в над GF(q) не превосходит
расстояние дуального кода.
Доказательство. Проверки, вой координаты, имеют вид
один шаг, для произвольного кода п — 1 ,,
------- , где а — минимальное 2 (d’~ 1)
ортогональные относительно пер-
>d'—1
1 X X X
10 0 0
0 0 0 0
X X X X ,
>d’ — l
так как каждая из них является словом дуального’ кода. Следовательно, Л^'(п——1). Согласно сделанному выше замечанию (ii) некоторые ошибки |"~(п—l)/(d'— l)j+l могут привести к неправильному декодированию.
Примеры. (1). Для [23, 12, 7]-кода Голея сГ=8, и, следовательно, мажоритарное декодирование в один шаг позволяет исправить самое большое [22/(2• 7) ] = 1 ошибку.
(2). Большинство кодов PC также не могут -быть декодированы мажоритарным образом в один шаг, так как для .них сГ=п+2—d.
Однако имеются коды, для которых возможно мажоритарное декодирование в один шаг. Таким кодом является [7, 3, 4]-код, приведенный на рис. 13.7, и более общий класс разностных циклических кодов, описываемых ниже.
Декодирование в L шагов. Некоторые коды, например РМ коды, могут быть декодированы за счет многократного использования мажоритарной процедуры.
Определение. Множество проверок называется ортогональным относительно координат а, Ъ, ..., с, если сумма ха+хъ-т-+ ... Тхс входит в каждую проверку S, этого множества, а все остальные х, входят не более чем в одну проверку этого множества.
Пример. Декодирование [7, 4, 3]-кода в два шага. Рассмотрим семь ненулевых проверок.
0 1 2 3 4 5 6
11 10 10 0
0 1110 10
0 0 1110 1
10 0 1110
0 10 0 111
10 10 0 11
110 10 0 1
Среди них имеются две проверки, ортогональные относительно координат 0 и 1, а именно:
= е0 + 61е2 + е4;
"^2=ео + е1 +63 -+еб>
и две, ортогональные относительно координат 0 и 2:
= ео е4’
$з= ео + е2 + еъ + ее
и т. д. Предположим, что произошла одна ошибка. Тогда мажоритарное правило дает правильное значение e0 + ei (из 'первой пары уравнений) и правильное значение е0 + в2 (из второй пары). Далее уравнения
\ = ео +
^5 = е0 + 62
являются ортогональными относительно во, так что мажоритарное правило дает правильное значение е0. Описанный алгоритм является алгоритмом мажоритарного декодирования символа е0 в два шага. Схема, реализующая это правило, показана на рис. 13.8.
Рис. 13.8. Двухшаговый мажоритарный декодер для [7, 4,
Поскольку рассматриваемый код являетсяциклическим,до-статочно построить устройство,, правильно декодирующее первую координату. Тогда остальные координаты Зудут автоматически декодироваться правильно.
Декодер с L уровнями мажоритарной логики называется L-шаговым декодером. Основная идея такого декодера, как было показано на примере, состоит в том, что число координат, относительно которых принимается решение, уменьшается от уровня к уровню так, что на конечном шаге решение принимается относительно одной координаты.
Лемма 18. Если каждый уровень мажоритарного декодера содержит J проверок, то могут быть исправлены | jj ошибок.
Доказательство. Аналогично доказательству теоремы 15. ®
Даже L-шаговое декодирование может оказаться недостаточным для того, чтобы исправлять все ошибки вплоть до половины минимального расстояния.
Теорема 19. Число ошибок, которые могут быть исправлены с помощью L-шагово'ГО мажоритарного декодирования, для произвольного кода над GF(q) не превосходит величины
п 1 d' 2 ’
где d'— минимальное расстояние дуального кода.
Доказательство. Предположим, что имеется J проверок, ортогональных относительно е координат. Надо показать что J^2njd'—1, и тогда согласно замечанию (ii) теорема будет доказана. Пусть i-я проверка содержит кроме указанных е координат еще at координат. Так как проверки соответствуют словам ортогонального кода, то
е + аг<>с!'; а^-аДД^’ (i =Д j). (13.14)
j
Пусть 5 = Тогда —I, и из (13.14) следует, что
1=1
Jl + S>Jd’-, (J—Y)S>\^d'.
Исключая е, получаем, что п—S~^\Jd'—S)/J, а исключая S, приходим к неравенству
(J — l)d' <2п—2d'. •
Пр им ер. Для [23, 12, 7]-кода Голея L-шаговое мажоритарное декодирование не позволяет исправлять больше чем две ошибки.
Контрастом к этому является следующее утверждение.
Теорема 20. Для РМ кода 91 (г, т) порядка г мажоритарное декодирование в г+1 шагов позволяет исправлять [у (d— l)| = [^-(2m-r— 1) j ошибок.
Доказательство. Дуальным к &t(r, т) является код &1('т—г— —1, т), и согласно теореме 8 слова минимального веса в &(т—г—1, т) являются векторами инцидентности (г+ ^-мерных плоскостей в EG(m, 2).
Пусть V — некоторая r-мерная плоскость. Найдем множество проверок, ортогональных относительно координат уР для P^V. Действительно, пусть U—(г+1)-мерная плоскость, содержащая V. Ясно, что каждая из 2т—2Г точек, не принадлежащих V, определяет некоторую плоскость U и что каждая плоскость U полностью задается 2’+1—2’’ такими точками. Следовательно, всего имеется (2™—2r)/(2r+1—2r)=2m-r—1 различных плоскостей U. Любые две такие плоскости U пересекаются только по V. Это дает нам оценку для суммы ур, причем оценка будет пра-
вей
вильной, если произойдет не более чем ^-~-(2т~г—1)^ ошибок. Такое решение может быть принято для каждой r-мерной плоскости V.
Далее, пусть W— некоторая (г—1)-мерная плоскость, и пусть V — любая r-мерная плоскость, содержащая W. Всего имеется 2m-r+i—1 таких плоскостей V, и для каждой из них после первого шага нам известны значения соответствующих сумм. Поэтому мы можем получить оценки для сумм V ур.
P£W
Продолжая таким образом, мы на (г+'1)-м. шаге получим оценку для уР для произвольной точки Р, которая будет давать правильное значение уР при условии, что произошло не более чем
(d—l)j = |^-у- ( 2т~r—1) ошибок. •
Улучшения алгоритма декодирования. Практически более удобным (по сравнению с описанной схемой) является использование циклического кода 5?* (г, т), так как в этом случае надо строить схему только для декодирования первой координаты. В этом случае ортогональный код т))^ содержит векторы
инцидентности всех (г+1)-мерных плоскостей в EG(m, 2), не проходящих через начало координат.
Иллюстрацией к этому является пример [7, 4, 3]-кода, для которого на рис. 13.8 приведена схема, реализующая декодирование в два шага. На самом деле этот код является кодом 1%*(1, 3).
Следующий метод, известный под названием последовательной редукции кода, позволяет существенно снизить число мажоритарных элементов за счет увеличения задержки декодирования. Опишем этот -метод применительно к декодеру на рис. 13.8. Идея очень проста. Пусть на рис. 13.8 S4, S'4, S"4 обозначают выходы первого мажоритарного элемента в последовательные моменты времени. Тогда S4 = е0 + ец S'4 = fii + es; ...
Заметим, что S4-|-S'4=S5!
Таким образом, если мы согласимся подождать один такт, то S5 может быть получено без введения дополнительного мажори тарного элемента. Соответствующая схема декодера показана на рис. 13.9.
Рис. 13.9. Декодер для [7, 4, 3] -кода, основанный на методе последовательной редукции кода
В общем случае этот метод (если он применим) позволяет уменьшить число мажоритарных элементов, сумматоров и т. п. с экспоненциальной функции от числа шагов до линейной функции ценой увеличения линейной задержки (рис. 13.10).
Рис. 13.10. Схема декодера, основанного на последовательной редукции кода (а), и схема £-шагового декодера (б)
Название «последовательная редукция кода» этот метод получил потому, что на каждом последовательном шаге декодирования вводятся дополнительные проверки, так что кодовое слово по существу рассматривается как слово меньшего кода. В рассмотренном примере после первого шага декодирования мы знаем в'се суммы 6i + ej, которые на самом деле являются проверками [7, 1, 7] -кода с повторением.
К сожалению, метод последовательностей редукции применим не ко всем кодам (и даже в тех случаях, когда он применим, задача выбора наилучшего декодера представляется очень трудной).
Ссылки на работы о различных модификациях и обобщениях основного алгоритма мажоритарного декодирования даны в замечаниях к главе.
Пороговое декодирование. Вернемся ненадолго опять к вопросу о декодировании произвольного двоичного линейного кода. Предположим, что передано слово х, а получено слово у. Декодер решает, что наиболее правдоподобным вектором ошибок яв-Л
ляется лидер е смежного класса, содержащего вектор у, и деко-л л л л
дирует у как у=х + е. В теореме 5 гл. 1 мы видели, что е является функцией синдрома S. Более точно е представляет собой двоичную векторную функцию от п—k компонент Sb S2, ..., Sn-h л
вектора S (рис. 13.11). Для небольших кодов вектор е может быть синтезирован 'посредством простой комбинаторно-логической схемы, использующей элементы И, ИДИ и др. и не использующей элементы 'задержки. В случае циклических кодов эта схема может быть упрощена еще больше, и тогда она называется декодером Меггитта. Устройство, приведенное на рис. 13.8, является простым примером декодера Меггитта (см. также упражнение (36) гл. 7). л
Однако синтез вектора е для больших кодов (например, для кодов БЧХ, суд. рис. 9.5) требует значительно более сложных
Рис. 13.11. Вычисление вектора ошибок
элементов. Например, в данной главе для декодирования РМ-ко-дов мы использовали мажоритарные элементы. Более общий подход состоит в использовании взвешенных мажоритарных элементов, или пороговых элементов, представляющих собой функции в(иь •-, Шп) от ..., vm с действительными весами alt ..., am и определяемых равенством
e(nx, • -, р,„) =
(13.15)
где все суммы вычисляются как действительные числа.
В противоположность, мажоритарному декодированию любой код допускает пороговое декодирование в один шаг. Легко показать, что такое декодирование всегда возможно, однако очень трудно найти эффективный способ реализации такого декодирования.
Теорема 21. (Рудольф.) Любой двоичный линейный код допускает пороговое декодирование в один шаг. л
Доказательство. Запишем e=(fb ..., fn), где каждая координата fi=fi(S) =fi(Si, ..., S„.fe) является функцией синдрома. Пусть Fj(Sj = l—2fi(S)—соответствующая действительная функция, принимающая значения ±1. Согласно уравнению (14.11) Fi(S) может быть записана в виде
АР) = -Дг V A(U)(-1)“'S.
uev
где Pi(u) — коэффициент Адамара для функции Fi(S), задаваемый равенством (14.8). Тогда
A(S) = ^fi----Ц V Л(и)(-1)и8 V
,,п—k uev
Если 0 — некоторая пороговая функция от 2п h входов 2j=i uEEVn~h с весами аи, то из определения функции 6 сразу вытекает, что
0(2^:usl/'1-ft)= y-^l-sgn au(~i)u-sy i trn~^^
uev
где sgn(x) = l, если x^O, и sgn(x) =—1, если x<?0. Следовательно,
М8) = е(£ыД.:иеГ-й) , (13.16)
i
если выбрать аи =Fi(u)/2n ,г. Так как это может быть проделано для каждого i, то теорема доказана. *
А
К сожалению, уравнение (13.16) определяет е как пороговую функцию от всех 2n~k проверок, так что рассмотренный алгоритм практически непригоден. Однако в отдельных случаях удается найти различные одношаговые пороговые алгоритмы вычисления л
е, использующие значительно меньшее число проверок (см. замечания к главе).
Задача (нерешенная). (13.2). Найти более эффективную одношаговую пороговую процедуру реализации заданной булевой функции.
13.8. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ КОДЫ
Разностные циклические коды. Пусть П—проективная плоскость PG (2, ps) порядка ps (см. приложения о конечных геометриях). Плоскость П содержит n=p2s+ps-rl точек, которые могут быть заданы тройками элементов p^eGF(ps) : (рь р2, р3).
Подчеркнем, что (ЭДИ, ^₽2, ^Рз), 'f.^GF* (ps) представляет собой ту же точку, что и (рь рг, р3). Каждую тройку можно рассматривать как элемент поля GF(p3s), т. е. она может быть представлена'как некоторая 'степень примитивного элемента а поля GF(p3s). Некоторое скалярное кратное каждой тройки равно а2 для O^i<n. Перенумеруем п точек плоскости этими степенями а.
Пусть а21, ..., а1*, l=ps+1 —прямая в плоскости П. Вектор инцидентности этой прямой содержит единицу точно в координатах й, ..., ii. Согласно доказательству теоремы 9 любой циклический сдвиг этого вектора равен вектору инцидентности другой прямой. Так как имеется всего п циклических сдвигов и п прямых, то каждая прямая плоскости П получается таким образом.
Пусть S) — код над GF(p), образуемый этими векторами инцидентности, и пусть <g’=S)-L. Ясно, что ££> —• циклический код с блоковой длиной п. По теореме 13 размерность кода Я) равна р+1У+1.
{ 2 J
Код допускает мажоритарное декодирование в один шаг, так как векторы инцидентности /=р®+1 прямых, проходящих через одну точку плоскости П, образуют множество ортогональных проверок относительно этой координаты. (Проверки ортогональны потому, что две прямые, проходящие через данную точку, не имеют других общих точек.) Согласно следствию 16 одношато-вое мажоритарное декодирование позволяет исправлять ps + 1) ошибок, и минимальное расстояние кода равно по меньшей мере ps+2.
Примеры. (1). Простейший пример получается при р=2 и s=l. Это опять приводит к показанному на рис. 13.7 двоичному [7, 3, 4] симплексному коду <ё>.
(2). Если p=s=2, то порождается прямыми проективной плоскости порядка 4 и является [21, 11, 6] двоичным кодом.
Эти коды тесно связаны с разностными множествами.
Определение. Плоскостным разностным множеством по модулю п=1(1—1) + 1 называется множество I чисел d\, ..., di таких, что разности di—dj , приведенные по модулю п, про-
бегают в некотором порядке в точности числа 1, 2, ..., п—1.
. Примеры. (1). При /=3 числа cG=O; сй=1 и d3=3 образуют плоскостное разностное множество по модулю 7. Действительно, разности по модулю 7 равны: 1—0=1; 3—0=3; 3—1 = 2; О—1=6; 0—3=4 и 1—3=5.
(2). {0, 1, 3, 9} является разностным множеством по модулю 13 и {0, 2, 7, 8, 11} — разностным множеством по модулю 21.
Все известные плоскостные разностные множества исчерпываются теми, которое получаются из проективных плоскостей порядка ps следующим Образом: пусть а21, ..., ай —точки некоторой прямой линии в плоскости П. Тогда числа {й, й} образуют
плоскостное разностное множество1 *. Действительно, предположим, что некоторые две разности равны, скажем, при
ir ts = it iu-
Тогда циклический сдвиг этой линии, переводящий точку а1 г в точку аЧ дает новую прямую линию, которая пересекается с исходной в двух точках, что приводит к противоречию. Таким образом, мы доказали следующий результат.
Теорема 22. (Зингер.) Если а1’1 .... аЧ , l=ps+\,— точки прямой линии в проективной плоскости PG(2, ps), то числа {izb ..., ii) образуют плоскостное разностное множество по модулю p2s+ps-}-1.
Задача (нерешенная). (13.3). Существуют ли другие плоскостные разностные множества?
Евклидово-геометрические и проективно-геометрические коды. Выберем в качестве 2D не код, порожденный векторами инцидентности прямых линий проективной плоскости, а код, образованный векторами инцидентности всех r-мерных плоскостей в евклидовой геометрии EG(m, ps) или в проективной геометрии PG(m, ps). Тогда <g’=S>± называется соответственно евклидово-геометрическим или проективно-геометрическим кодом. Для размерностей этих кодов не существует простых ‘формул. Декодирование может быть осуществлено с помощью r-шагового мажоритарного декодера, так же как и для РМ кодов. Более подробное описание свойств этих кодов и их обобщения можно найти в работах, указанных в замечаниях к главе. Все эти коды можно рассматривать как обобщения РМ кодов.
13.9. ГРУППЫ АВТОМОРФИЗМОВ РМ КОДОВ
Пусть К=(ац)-—двоичная обратимая (m Хт)-матрица, и пусть b — двоичная m-последовательность. Преобразование
/ \ / Ч \
Т:заменить| : ] на Al | + b (13.17)
\ Пт J \ Пт )
представляет собой подстановку на множестве 2т т-последова-тельностей, переводящую 0 в Ь.
Преобразование Т можно трактовать так же как перестановку на булевых функциях:
Т:.заменить f(vt, vm) на f (Sao'Hj+b, ... ^amjVj + bm). (13.18).
Множество в‘сех таких преобразований Т образует группу с композицией в качестве групповой операции. Порядок этой группы находится следующим образом. Первый столбец матрицы А может быть выбран произвольным ненулевым, т. е. 2™—1 способа
1 Раз,костные множества такого типа называются зингеровыми (см. М. Холл
[587]). (Прим, перев.)
ми, второй — 2т—2 способами, третий — 2т—4 способами ... Кроме того, имеется 2™ способов выбора вектора Ь. Таким образом, порядок этой группы, которая называется полной аффинной группой и обозначается GA(m), равен
|GA(rn)| = 2m(2m — 2)(2т—2а) • •' • ( 2т—2т~1 ). (13.19)
Полезным приближением этой величины для ‘больших т является | GA(m) | -0,29-2m2+m. (Мы уже встречались с этой группой в другой форме в § 8.5.) Из (13.18) видно, что если f — многочлен степени г, то Tf также является многочленом степени г. Следовательно, группа GA(m) переставляет слова РМ кода 1%(г, т) порядка г и
GA (m)cz Aut (5? (г, т)). (13.20)
Подгруппа группы GA(m), состоящая ив всех преобразований вида
/ <Т \ ( 1<1\
Т: заменить! | на Al | (13.21)
\ / ♦
,(т. е. преобразований, для которых Ь=0), называется полной линейной группой, обозначается через GL(m, 2) (см. § 8.5) и имеет порядок
\GL(m, 2)| = (2m—1)(2'п—2)(2m—22) • -(2т—2т~* )«
«0,29-2т2 (при больших т). (13.22)
Так как преобразование (13.21) фиксирует нулевую т-после-довательность, то группа LG(m, 2) переставляет слова выколотого РМ кода (г, т):
GL(m, 2) cz Aut («Я?* (г, т)). (13.23)
Заметим, что группа GL(m, 2) дважды транзитивна, а группа GA(m) трижды транзитивна (упражнение (9)).
Теорема 23. Для l^r^m—1;
(a) . Aut (5?* (г, tri)) cz Aut (3?* (г + 1, tri)).
(b) . Aut (5? (r, tri)) <zz Aut (5? (r, tri)).
~ Доказательство, (b). Пусть xb ..., xB— векторы минимального веса в коде 5?(r, т). Пусть nXi=Xi, для neAutl%(r, т). Да-Лее Хг—плоскость-;:р азмерности т—г. Если Y — произвольная (т—г—1)-мерная плоскость, то Y=Xi * х,- для некоторых i и /. Следовательно, множество.
Л Y = Л (X;* X;) = Л X; * Л Х; = X., * X., - _ . \ t V J I J
представляет собой пересечение двух (т—ir)-мерных плоскостей, и состоит ns- 2™“<-1 точек, так как л — подстановка. Таким образом, nY •—плоскость размерности т—г—1. Следовательно, л переставляет образующие векторы кода Й?(г+1, т), так что весь код Й?(г'+1, т) инвариантен относительно л. Пункт (а) доказывается аналогичным образом. •
Из упражнения 5 сразу вытекает, что
Aut(J?* (г, т)) = &> т для г = 0 и г = т—1;
2 —1
Aut(3? (г, т)) = GA для г = 0; т—1 и т.
: 2
В оставшейся части параграфа мы докажем, что в (13.20) и (13.23) имеет место равенство.
Теорема 24. Для l^r^im—2:
(a) . Aut(J?*(r, m))=GL(m, 2).
(b) . Aut (J? (г, m)) = GA(m).
Доказательство, (i). Имеем:
выкалыва-
ние коорди-добавле- наты с но-
ние 1 мером 0
симплексный код --------------->$?*(!, tri)—•—«--->^(1, tri).
Согласно упражнению (30) гл. 8 Aut(<94?-Lm) =Aut(.'%*(!, m)). Так как размерность кода равна т, то из (13.21) и замечания, следующего за теоремой 13 гл. 8, получаем, что Aut^^) =Aut(52* (1, m)) = GL(m, 2). Наконец согласно упражнению (29) гл. 8 Aut (5^m) = GL (т, 2).
(ii) . Пусть G1=Aut(j2*(l, m)); G2=Aut($?(l,. т)). Ясно, что Gi является подгруппой группы G2, фиксирующей координату 0. Так как GA (т) транзитивна, то группа G2 такжетранзитивна. Поскольку каждый смежный класс в группе G2 по подгруппе Gt переводит точку 0 в различные точки, то |G2|=2m|Gi|. Следовательно, ' из (13.20) и (13.21) вытекает равенство Gz=GA(m). Используя опять упражнение (28) гл. 8, получаем Aut($?(m—2, m)) = =Aut(i%(l, m)) = GA(m).
(iii) . Из теоремы 23 и пунктов (i) и (ii) следует:
GA (m) — Aut (5? (1, m))SAut (.Я (2, m))E • • •
. • Aut(5?(m—2, m)) = GA(m);
GL(m, 2) = Aut ($.*(1, m))c Aut(5?*(2, m)E • • 'E.
c Aut(J?*(/n—2, m)) = GL(m, 2). •
Упражнение. (9). Доказать, что группы GL(m, 2) и GA(m) на самом деле'являются группами указанных порядков и соответственно дважды и трижды транзитивны.
*13.10. МНОГОЧЛЕНЫ МЭТТСОНА—СОЛОМОНА для рм кодов
В этом параграфе мы докажем, что булева функция, задающая слово РМ кода, представляет собой в действительности ту же самую функцию, что и многочлен Мэттсона — Соломона (гл. 8) для этого кодового слова.
Пусть а — примитивный элемент поля GF(2™). Тогда элементы 1, а, ат~1 образуют базис поля GF(2m). Пусть Zo, ..., Zm-i — дополнительный базис (см. гл. 4). Нам сейчас удобно рассматривать РМ коды как таблицы истинности, столбцы которых выписаны в порядке 0, 1, а, ..., а2"1-2. Например, таблица истинности для т=3 имеет вид, изображенный на рис. 13.12.
0 1 а а2 а3 а4 а5 ав
V3 0 0 0 1 0 1 1 1
V2 0 0 1 0 1 1 1 0
Vi 0 1 0 0 1 0 1 1
Рис. 13.12. Таблица истинности для т=3
Лемма 25. МС-многочлен слова V,- кода Й?(1, т) равен Тгл(^з, z), где Тт — функция следа, определенная в § 4.8.
Доказательство* Пусть М —матрица, состоящая из всех строк vm, ..., Vi таблицы истинности, в которой выброшен первый, т. е. нулевой столбец. Матрица М является (тх2™—1)-матрицей с m— 1
элементами Мм, и ai=z S Mkiam~k~l, 0^л^2т—2. Нам надо ь=с
показать, что Тт^ср)
Действительно, согласно свойству дополнительного базиса имеем
т—1
k=0
Следствие. 26. Если а — некоторый двоичный вектор длины 2т, соответствующий булевой функции a(vi, ..., vm), то МС-многочлен вектора а равен:
A(z) = a(TmM, • •, W 2))- (13-24)
Замечания, (i). А(0) =22т-2г=04 (с?) =а(0, ..., 0) равно общей проверке на четность вектора а.
(ii). При вычислении правой части равенства (13.24) высокие степени переменной z приводятся по правилу 22™=1. Однако после того как многочлен A(z) уже вычислен, при использовании его свойств, доказанных в гл. 8. МС-многочлен надо рассматривать в кольце многочленов 3~[z] над полем ff~=GF(2m).
Обратно, если а — вектор с МС-многочленом A(z), то булева функция, соответствующая вектору а, равна А (щ + гга+ ... + Утат~1)-
Пр и мер. Предположим, что т=3, и рассмотрим кодовое слово 0*ь для которого МС-многочлен равен A(z) =z+z2+z4. Тогда соответствующая ему булева функция равна
Л (»! + V2 а 4- v3 с?) = vt + v2T3 (а) ф vsT3 (а) = vL ф + (у2 + уз) (а + а2 + а4) = vx, что согласуется с рис. 13.12.
Упражнение. (1'0)- Проделать все то же самое для кодового слова 0*з.
*13.11. ДЕЙСТВИЕ ПОЛНОЙ АФФИННОЙ ГРУППЫ НА МНОГОЧЛЕНАХ МЭТТСОНА—СОЛОМОНА
Опр ед ел ен ие. Аффинным многочленом называется сумма линеаризованного многочлена и константы (см. § 4.9), т. е. многочлен вида т~~1 i=0 где уг^СЕ(2т).
Упражнение. (11). Доказать, что корни аффинного многочлена, лежащие в GF(2m), образуют r-мерную плоскость в EG(tn, 2).
Основной результат данного параграфа состоит в следующем.
Теорема 27. Действие преобразования из полной аффинной группы GA(m) на МС-многочлен A(z) некоторого вектора длины 2т состоит в замене z на F(z), где F(z) — аффинный многочлен, имеющий в GF (2т) точно один корень. Обратно, любое такое преобразование МС-многочленов является результатом преобразования из группы GA(m).
Доказательство. Рассмотрим произвольное преобразование из группы GA(rn), скажем, vT—> AvT ф b,
где v= (щ,..., vm) = (7m(Zoz),..., Tm(km-iz)).
Переменная z MC-многочлена связана с вектором v следую-
щим равенством:
г = о1фоааф • • •+oTOam-1 =a-vr,
гдеа=(1, a.... а™-1). Следовательно, z преобразуется по пра-
вилу
z->aAvr + a-b. (13.25)
где Х2/ = (Хо\ • • Xm-i), а Т означает транспонирование.
Пусть «А—р—(Ро Pm i)—новый базис поля GE(2m). Тогда
z^a-b + (P-XT)z + (P-a2)T)22+ . . . + (р-(^т-1)Ъ2,”_1, (13.26)
где справа стоит аффинный многочлен.
Упражнение. (12). Доказать, что многочлен (13.26) имеете поле GF(2m) точно один корень.
Обратно, любое преобразование
z-+F(z) = u0 + f(Z), u0^GF(2m),
(13.27)
такое, что f(z)—линеаризованный многочлен и F(z) имеет в GF(2m) точно один корень, принадлежит группе GA(m).
Для доказательства этого разложим преобразование (13.27) на два: преобразование z-^-z+uo, которое, очевидно, принадлежит GA(m), и преобразование
2-^J(z) = y yj г21.
j=o
(13.28)
Упражнение. (13). Доказать, что преобразование (13.28) принадлежит группе GL (т, 2), т. е. в некотором базисе {ро, Рт-1} поля GF(2m) имеет вид
т— 1 z-y(₽.(x2')T)22/. 1=0
ЗАМЕЧАНИЯ К ГЛ. 13
§ 13.1. Коды Рида — Маллера получили свое название в связи с работами Рида [1104] и Маллера [975] (хотя Питерсон и Уелдон [1040] связывают открытие этих кодов с более ранней неопубликованной работой Митани [963]).
Недвоичные РМ коды были введены несколькими авторами: Дельсарт и др. [365], Касами, Лин и Питерсон [739—741], Месси и др. [924] и Велдон [1401] (см. также [99, 1396]1).
§ 13.2. Таблицы истинности широко используются в теории переключательных схем (см., например, Мак-Класки [935]) и в элементарной логике, где обычно пишется ЛОЖЬ вместо 0 и ИСТИНА вместо 1 (см., например, Кемени и др. [755]). В каком бы виде они не возникали, их роль в дискретной математике очень велика. Что касается дизъюнктивной нормальной формы, см.: Харрисон [606] или Мак-Класки [935].
§ 13,3. Упражнение (6) принадлежит С. М. Редди.
§ 13.4. Лемма 6 взята из работы Ротшильда и Ван Линта [1128].
§ 13.5. Доказательство теоремы 10 принадлежит Дельсарт-у [343].
В доказательстве теоремы 10 используется формула Лукаса для. полиномиальных коэффициентов. Эта формула является непосредственным обобщением обычной теоремы Лукаса для биномиальных коэффициентов, которая в двоичном случае формулируется следующим образом.
'А также [137]. (Прим, перев.)
Теорема 28. (Лукас.) Пусть
и=Хи^*; |/г=2А;2*; Z=XZj2‘—соответственно двоичные разложения чисел
п, k и 1=п—Л, где tii, ki и li равны 0 или 1. Тогда
1 (mod 2) ^5: для всех i,
О (mod 2) ^ki>nt для некоторого I.
Эквивалентно
1 (mod 2) ki+h^rii для всех I, О (mod 2) для некоторого Z.
Доказательство этой теоремы можно найти, например у Берлекэмпа [113.] Обобщение доказал Сингмастер [1216].
Тот факт, что РМ коды являются расширенными циклическими кодами (теорема 11), был замечен одновременно Касами, Лином, Питерсоном [739, 740] и Колесником и Мирончиковым ([774] и приведенные там ссылки) (см. также Камьон [237]).
Теорема 13 доказана Мак-Вильямс и Манном [884]. Ранги’ матриц инцидентности подпространств других размерностей были вычислены Геталсом и Дельсартом [499], Ямадой [591], а также Смитом [1243—1246].
§ 13.6. Алгоритм декодирования Рида был описан в [1104]; это был первый нетривиальный пример алгоритма мажоритарного декодирования. Дополнительные сведения об этом алгоритме содержатся в работах Гора [544], Грина и Сан-Суси [555]. Месси [918] (см. также [921]) и Колесник с Мирончиковым (см. также [378]) провели обширное исследование мажоритарных и пороговых методов декодирования. Рудольф [ИЗО, 1131] ввел взвешенное одношаговое мажоритарное декодирование. Его исследования были развиты следующими авторами: Чой [294], Дюк [387], Гор [544, 545], Нг [990], Рудольф и Роббинс [1134]. Способы более быстрого декодирования додов Рида — Маллера были описаны Велдоном [1040]. Декодирование кодов Рида — Маллера
и других кодов с использованием универсальных вычислительных машин исследовал Пэшбург [1025, 1026].
Дюк [388] указал условия, которым должен удовлетворять код, для чтобы исправлять при L-шаговом декодировании (d—l)'j ошибок (см.
того
так-
же Кугураков [786]).
Алгоритм декодирования Рида которых больше чем (d—1)^.
позволяет исправлять много ошибок, вес Число исправляемых ошибок подсчитал
Кричевский [784]. Теоремы 17 и 19 доказаны Лином [835—837].
Другие работы по мажоритарному декодированию: Берман и Юданина [137], Чень [271], Дельсарт [348], Дюк и Скэттебол [390], Дынькин и Те-ненгольц [397], Касами и Лин [732, 733], Кладов [763], Колесник [773], Лонгобарди и др. [860], Редиибо [1101], Шива и Таварес [1205], Смит [1245] и Уоррен [1390].
§ 13.7. Декодирование методом последовательной редукции кода было предложено Рудольфом и Хартманном [1132]. Некоторые применения этого Метода даны в [1112]. Декодеры Меггитта описаны в [952]. Теорема 21 принадлежит Рудольфу [1131]. Рудольф и Роббинс [1134] доказали, что те же результаты справедливы для случая, когда в (13.15) допускаются только положительные веса at Лонгобарди и др. [860], а также Роббинс [1115] построили для некоторых кодов эффективные процедуры порогового декодирования.
§ 13.8. Разностно-циклические коды были введены Велдоном [1400]. Размерность этих кодов была вычислена Грэхемом и Мак-Вильямс [553]. Теорема 22 взята из работы Зингера [1213].
Дополнительные сведения о разностных множествах содержатся в работах: Баумерт [82], Холл [589], Манн [908] и Рагхаварао [1085].
Евклидово-геометрические и проективно-геометрические коды исследованы Лрэнджем [1074, 1075], однако первое их публичное обсуждение принадлежит Рудольфу [ИЗО]. В настоящее время имеется обширная литература, по-
священная этим кодам и их обобщениям (см., например, Чень [267—270], Чень и др. [273, 275, 276], Купер и Гор [307], Дельсарт [343], Геталс [491, 494], Геталс и Дельсарт [499], Гор и Купер [548], Хартманн и др. [611], Касами и др. [732, 740, 741], Лин и др. [833, 835 — 837, 840], Рао [1092], Смит [1246] и Велдон [1402]).
§ 13.9. Класс кодов, инвариантных относительно полной линейной группы, изучался Касами, Лином и Питерсоном [738], а также Дельсартом [344].
§ 13.11. Упражнение (11) взято из книги Берлекэмпа [ИЗ, гл. 11].
Глава 14
Коды Рида—Маллера первого порядка
14.1. ВВЕДЕНИЕ
В данной главе мы продолжим начатое в предыдущей главе исследование кодов Рида — Маллера, концентрируя свое внимание на кодах первого порядка 5?(1, т). Слова кода 5?(1, т) или, точнее, симплексного кода Э’т под названием псевдошумовых или ПШ-последовательностей широко используются при решении задач радиолокации, 'Синхронизации модуляции и фильтрации. В § 14.2 дается описание этих последовательностей. В § 14.3 исследуется сложная (и по существу нерешенная) задача классификации смежных классов по коду 5?(1, т). В § 14.4 описывается кодирование и декодирование кодов 5?(1, т). Это семейство кодов является одним из немногих, к которым применимо декодирование по максимуму правдоподобия, использующее в декодере схему Грина. (Один из кодов этого семейства использовался при передаче изображений с Марса.) В последнем параграфе рассматриваются смежные классы с наибольшим минимальным весом. Это соответствует исследованию булевых функций, которые меньше всего похожи на линейные, так называемые максимально-нелинейные функции.
14.2. ПСЕВДОШУМОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
0 0 0 0 0 0 0 1110 10 0
0 1110 10 0 0 1110 1 10 0 1110 0 10 0 111 1 .0 1 0 0 1 1 110 10 0 1
Слова (за исключением векторов 0 и 1) циклического [2т—1, т, 2ml] симплексного кода Э’т или [2т, т+1, 2m-1] расширенного циклического кода Рида — Маллера первого порядка 5?(1, т) похожи на случайные последовательности из нулей и единиц (рис. 14.1). Мы увидим, что, действительно, если с — некоторое ненулевое -слово кода 9\ то оно обладает многими свойствами, характерными для последовательностй, которые получаются при случайном подбрасывании мо-.неты 2т—1 раз. Например, число единиц и нулей в с примерно равно друг другу,
Рис. 14.1. Слова циклического симплексного [7, 3» 4] -кода
как это и должно быть. .Да-лее назовем серией максимальный от-резок последовательных равных символов. Тогда половина серий в с будет иметь длину, равную 1, четверть — длину, равную 2, восьмая часть — длину, равную 3, и т. д. В каждом случае число серий нулей равно числу серий единиц. Пожалуй наиболее важное свойство вектора с состоит в том, что его автокорреляци-1 т
онная функция равна р(0)=1; р(т)=—————для 1<т<2 —2
(см. рис. 14.4).
Случайность, задаваемая кодовыми словами такого типа, оказывается очень полезной во многих приложениях, таких как радиолокация, синхронизация, модуляция, фильтрация и др.
Рассматриваемые кодовые слова, конечно, не являются действительно случайными, и одним из доказательств этого.служит тот факт, что перечисленные выше свойства имеют место для всех ненулевых кодовых слов, в то время как случайное подбрасывание монеты приводит к некоторому разбросу от 'последовательности к последовательности. (По этой причине эти кодовые слова непригодны для шифрования данных.).
Рассматриваемые кодовые слова можно генерировать при помощи регистров сдвигов, и сейчас мы перейдем к описанию того, как это делается, и приведем свойства этих последовательностей.
Пусть h(x)=Xm-t-hm_iX™-~l+ ... -Ь/iiX-j-1 — неприводимый примитивный многочлен над GF(2) степени m (см. гл. 4). Согласно § 8.3 h(x) является проверочным многочленом [2т—1, т, 2"1-1] симплексного кода ^т. Построим регистр сдвигов, линейные обратные связи которого описываются многочленом h(x) так, как это показано на рис. 14.2.
Рис. 14.2. Регистр сдвигов с обратной связью, задаваемой многочленом h(x)
Например, если h(x) =х4-{-х+1, то регистр имеет вид, показанный на рис. 14.3.
Предположим, что начальное содержимое (или состояние) регистра сдвигов равняется «1, а0 (рис. 14.2). Выход счи-
тывается с правого конца регистра и равен бесконечной двоичной последовательности а=а0, th, —
Определение. При любом ненулевом начальном состоянии1 выход а называется псевдошумовой (или ПШ) последовательно-
1И любом примитивном многочлене h(x). (Прим, перев.)
стью. (Эти последовательности называются также псевдослучайными, т-последовате.пьностями или регистровыми последовательностями максимальной длины.) Приведенный на рис. 1,4.3 пример такой последовательности представляет собой последовательные
Повторения
Рис. 14.3. Регистр сдвигов, соответствующий многочлену h(x)=xi+x+l, и соответствующая последовательность состояний
состояния регистра сдвигов с обратной связью при начальном состоянии, равном 0001. Выходная последовательность равна четвертому столбцу таблицы, т. е. равна
а = аоа1 . - . = 100 010 011 010 111, 100 •• • (14.1)
и имеет период, равный'15.
Свойства ПШ-последовательности. Свойство I. Для всех 1=т, т+1, .... ПШ-'Последовательность удовлетворяет рекуррентному соотношению
Hi = а. , h , -4- * - • -4- а, ., h, -4- а.
I I—1 т—1 1 1 I—m-j-1 1 1 I—т
Свойство II. При некотором начальном состоянии а0 ... am-i последовательность а является периодической с периодом п = 2?п—1, т. е. an+i = ai для всех i^0 и п представляет собой наименьшее целое число с таким свойством.
Доказательство. Заметим, что для произвольной последова-
тельности а из свойства I вытекает, что
а1—m-pi 1 -n 0 1 0 • 0 I [ at-m •' ' i
0 0 1 -0 I a\
l—m I—tn—1
— *
al—\ 0 0 O-l I ° 1-2
al / 1 h. h. -h . 1 * m—1 1 at-l -1
Обозначим эту (/иХт -матрицу через U. Тогда
Так как U— сопровождающая матрицы ’Многочлена h(x). (см. § 4.3), то согласно упражнению (20) гл. 4 n=2m—1 является наименьшим цель)м числом таким, что Un=I. Следовательно, найдется такой вектор Ь=(йо, Om-i), что UnbT = bT и UTbT#=bT для всех —1. Следовательно, если выбрать b в качестве
начального состояния, то последовательность а будет периодической с периодом 2т—1. *
Свойство III. При таком начальном состоянии регистр сдвигов принимает все 2т—1 возможных ненулевых состояний, прежде чем состояния начинают повторяться.
Доказательство. Очевидно, так 'как период равен 2т—1. •
Заметим, что, за исключением последовательности а, тождественно равной нулю, нулевое состояние регистра не наступает никогда и что 2т—1 является максимально возможным значением периода для линейного регистра сдвигов с m ячейками.
Свойство IV. Для любого ненулевого начального состояния регистра ’период выходной 'последовательности равен 2т—1, й действительно, выходная последовательность может - быть получена из последовательности а путем выбрасывания нескольких первых ее символов.
Доказательство. Вытекает из свойства III. «
Теперь рассмотрим свойства произвольного отрезка с длины и=2т—1 последовательности а, с=ц, ... ai+nx.
Свойство V. с является словом симплексного кода с проверочным многочленом h(x).
Доказательство. Так как вектор с удовлетворяет уравнению (7.12), то он, очевидно, принадлежит коду с проверочным многочленом h(x). Согласно § 8.3 этот код является симплексным, так как многочлен h(x) примитивен. . @
Свойство VI. (Свойство «сдвиг—сложение».) Сумма произвольного отрезка с длины 2т—1 последовательности а со своим циклическим сдвигом равна некоторому другому циклическому сдвигу с.
Доказательство. Вытекает непосредственно из свойства (V).
Упражнения. (1). (Свойство скользящего окна.) Показать, что если вдоль ПШ-последовательности скользит окно шириной в п символов, то в' течение одного периода каждая' 'ненулевай ^-последовательность из 2т—1 возможных встречается точно один раз.
(2) . Рассмотреть регистр сдвигов длины т, обратные связи которого описываются не обязательно примитивным многочленом h(x) (как на рис. 14.2). Показать, что при начальном состоянии «0=1; £?]= ... =п?п_1 = 0 период выходной последова'гельности а равен наименьшему положительному числу р такому, что h(x) делит х?—'1. /
(3) . Если h(x) неприводим, но не обязательно примитивен, то р делит 2т—1. t
(4) . Если а=поп1 ...—ТПП-последовательность', то для всякого /, взаимно простого с 2т—1, последовательность b=«0«j«2j — также является псевдошумовой.
(5.). Некоторый сдвиг последовательности а, скажем, Ь= =£Zsas+1as+2 ... =bobib2, обладает тем свойством, что bi=b2i для всех i (b состоит .в точности из повторений идемпотента симплексного кода, см. § 8.4).
Псевдослучайные свойства. Свойство VII. Произвольный отрезок с длины 2т—1 последовательности а содержит 2т-1 единиц и 2т~1—1 нулей.
Доказательство. Вытекает из свойства (V) •
Свойство VIII. В отрезке с половина серий имеет длину, равную 1, четверть — длину, равную 2, восьмая часть — длину, равную 3, и т. д. до тех пор, пока эти доли дают целое число серий. Во всех случаях число серий из нулей равно числу серий из единиц.
Упражнение. (6). Доказать это утверждение.
Автокорреляционная функция. Мы переходим к наиболее важному свойству — к автокорреляционной функции. Автокорреляционная функция р(т) бесконечной последовательности действительных или комплексных чисел sGsis2 ... с периодом п определяется для всех т=0, ±1, ±2, ... равенством
/=о
где черта обозначает комплексное сопряжение. Эта функция периодична: р(т)=р(т+«). Автокорреляционная функция двоичной последовательности «о«1 — периода п определяется как автокорреляционная функция последовательности действительных чисел (—1)“°, (—1)“', которая получается из исходной путем замены 1 на —1 и 0 на 1. Таким образом,
1 п~'1
р(т) = J-V (__1р+“л-т. (14.3)
п 4-1 i=o
Иначе, пусть А — число совпадений символов у «-последовательности а0 ... an-i и ее циклического сдвига ат«т+1 ... ««г?!-!, а D — число несовпадений (так что A+D=n). Тогда
Р(т) = — • (14.4)
п
Например, автокорреляцией-ная функци5\ПШ-последова-тельности (14.1), как показано на рик 14.4, равна: р(0) = 1 и р(т)= —1/15 для
Свойство IX. Автокорреляционная функция ПШ-последовательности периода /2 = 2™—1 равна: (
функция
Рис. 14.4. Автокорреляционная ПШ-последовательности
р(0)= 1; р(т) = —- для 1
п
Доказательство. Из (14.4) имеем
, . п — 2d
р ^т) =-----
п
(14.5)
(14.6)
где d = dist(a0 ... an-i', a-t, ..., a-c+n-i) = wt(ao... ao+n-i) для некоторого о (по свойству VI). Тогда результат сразу вытекает из свойств V и VII. •
Упражнения. (7). Показать, что функция (14.5) является наилучшей возможной среди всех автокорреляционных функций для всех двоичных последовательностей с периодом п=2™—1, если в качестве критерия выбрать минимум функции max p(i).
0<i<n
(8). (Тест для отличия ПШ-последовательности от последовательности случайных бросаний «на удачу».) Пусть со, .... C/v-i — последовательные двоичные символы (У<2™—1) из ПШ-после-довательности периода 2™—1. Для m<.b< (l/2)N построим матрицу
М= ci
С1 • 'ск—ь
С2 • ‘Cw—b-1-l
Cb—l СЬ • • 'CN~ 1
Доказать, что ранг матрицы М над GF(2) меньше чем Ь. [Указание. В коде имеется только m линейно независимых последовательностей.] С другой стороны, доказать, что если с0, ..., С/у_] —отрезок последовательности случайных бросаний, где каждый символ Cj принимает значения 0 и 1 с вероятностями ’/г, то’вероятность того, что 'rank (М) <£> не превосходит 22b“JV-1, что при b^Zl/2N дает очень малое значение.
Таким образом, вопрос «Имеет место равенство гапк(М)=й?» явля.ется тестом для различия малой выборки символов из ПШ-последовательности и выборки из действительно случайной последовательности. Например, если m=ll; 2m—1=2047 и b —15, то тест будет давать отрицательный ответ для любой выборки из
N=50 последовательных символов ПШ-последовательнбсти, в го время как вероятность отрицательного ответа для / последовательности случайных бросаний монеты не превышаем' 2-21.
14.3. СМЕЖНЫЕ КЛАССЫ ПО КОДУ РИДА—/^АДЛЕРА ПЕРВОГО ПОРЯДКА /
Задача вычисления весовых функций для смежных классов по коду Рида—-Маллера первого порядка возникает в различных практических ситуациях. В общем виде эта задача не решена до сих пор (см. задачу (1.1) из гл. 1), хотя для п^32 все веса описаны полностью. Однако некоторые интересные! факты мы уже можем изложить. Например, задача вычисления весового спектра смежного класса, содержащего вектор v, сводится к вычислению преобразования Адамара для вектора v. Кроме того задача вычисления весовых функций для смежных классов по коду 5?(1, т) оказывается эквивалентной задаче классификации булевых функций по модулю линейных функций. Описанные в этом параграфе свойства смежных классов оказываются также полезными при декодировании (см. § 14.4). В конце этого параграфа приводится таблица смежных’классов по коду 5?(1, 4). иОсо1бенный интерес представляют смежные классы с наибольшим минимальным весом, которые изучаются в последнем параграфе этой главы.
Замечание. Как и в § 13.2, v=(u, ..., vm) обозначает вектор из Vm (эти векторы считаются упорядоченными), и если /(oi, ..., vm) — некоторая булева функция, то f — соответствующий ей двоичный вектор длины 2т.
Код Рида — Маллера первого порядка 1%.(1, т) состоит из всех векторов
т
uo I+2£иг Vj, Щ=0 или 1, г—1
(14-7)
пи
—11
соответствующих линейным булевым функциям. Определим ортогональный код (Ут как [2т, т, 2т-|]-код, состоящий из векторов т
вида X WjVi, иге{0, I}. Таким г=1
образом, 5?(l,m) =6?m(J {1+б7щ}-Предположим, что во всех
словах кода $?(1, т) символ 1 заменен на символ —1, а символ О на символ 1. Получающееся при
Рис. 14.5. Четырехмерный обобщенный октаэдр, вершины которого соответствуют словам кода . - ^(.1. 2)
этом множество из 2т+’ действительных векторов представляет собой множество вершин правильной фигуры в 2т-мерном евклидовом пространстве, которая называется обобщенным октаэдром. Например, на\ рис. 14.5 для т=2 изображен четырехмерный октаэдр (он имеет 16 трехмерных -граней и поэтому называется также 16-гранником).
Множество всех таких действительных векторов называется также множеством биортогональных сигналов (см. упражнение (43) гл. 1). Еслц такое же преобразование применить к словам кода (Ущ, то мы (получим множество 2™ взаимно ортогональных действительных векторов.
f(u) обозначает значение функции f на произвольном векторе u=fHb ..., tim) из Vm или, что эквивалентно, координате вектора f в позиции, соответствующей и. Нам будет удобно ввести обозначение для действительного вектора, получающегося из двоичного вектора f путем замены 1 на —1 и 0 на 1. Обозначим его через F. Таким образом, координата вектора F,. стоящая в позиции, соответствующей и, равна:
Е(и) = (-1/(и).
Преобразование Адамара и смежные классы по коду 5?(1, т). Напомним, что преобразование Адамара действительного вектора
F было определено в гл. 2 равенством £(u)= JJ(-l)u-V(v)= J](- , ,т r,tn vev vgv l)u v+Hv), ue Vm. (14.8)
л F представляет собой действительный вектор длины А F=FH, где Н — симметричная матрица Адамара (2mX2m), равная 2m. Иначе, размерности
"-(V «... v, u, vEVm. (14.9)
Следовательно,
1 Л F = — FH 2т (14.10)
или
V(u). (14.П)
uev
л
Из (14.8) видно, что F(u) равно разности между числом нулей и числом единиц в двоичном векторе
m f + У и, vt.
Таким образом,
л ™
F(u) = 2m—2 dist f,
i=l
(14.12)
ИЛИ
dist
Аналогично
dist
(14.13)
(14.14)
Следовательно, весовой спектр смежного класса по коду 5?(1, т), содержащего вектор f, задается набором расстояний
вектора f, от всех слов кода <%(1, т). Таким образом, доказано
следующее утверждение.
Теорема 1. Весовой спектр смежного класса по коду 5?(1, т), содержащего f, равен
{ 2т ± F (u)}, u€El/m.
Таким образом, весовой спектр смежного класса, содержащего f, определяется преобразованием Адамара вектора f.
Упражнение. (9). Доказать, что если весовой спектр смежного класса по коду От, содержащего f, равен А'ДГ), 0i^i^2'n, то весовой спектр смежного класса по коду 5?(1, т), содержащего f, равен Аг (f) =A'i(f) +A'2«_f(f), Osgi^2m.
Уравнения (14.13) и (14.14) означают, что ближайшими к f словами кода ^?(1, пг) являются те слова 2iZiVi, для которых ве-;
л
личина |F(u) | имеет наибольшее значение.
Пример. Для пг=2 имеем:
v2 = 0 0 1 1;
vx = 0 1 0 1.
Предположим, что f= ООО 1 =ViV2. Тогда F=1 1 1 — (где «--» обозначает —1). Согласно (14.8) коэффициенты преобразования Адамара равны:
F (00) = F (00) + F (01)+F (10) + F (11) = 1 + 1 + 1 — 1 = 2;
F(01) = F(00)—F(01)+F(10)— F(ll) = 2;
F(10) = 2;
F(ll)=— 2.
Очевидно,
F = y{2 x (1111)4-2 x (1 — 1— )4-2 x (11--)—2 X
X (1-----1)}= 111 —,
что соответствует (14.11).
Код 5?(1, 2) состоит из векторов {0000, 0101, ООП, ОНО, 1111, 1010, 1100, 1001}. Согласно теореме 1 весовой спектр смежного класса этого кода, содержащего f=0001, равен:
4(f) = 4, 4(f) = 4,
что имеет местА. на самом деле.
Коэффициенты преобразования Адамара вектора F с координатами ±1 удовлетворяют следующим соотношениям ортогональности.
Лемма 2.
yW(u + v)U22m>ec™v = °>
I О, если v=^0. uev
Доказательство.
2^(u)F(u+v) = J] £(-1)u vA(w) V(-l)(,,+v) xF(x) =
o€V uev wev
= 2 (-l)vxA(w)A(x)V(-l)u(x+w). w, xgvm uev771
Внутренняя сумма равна 2m 6W . Следовательно,
2 F (u)F (u + v) = 2m (- l)v‘w(w) = 2m 2 (- l)v w = 2^4, 0, • ^..ТП
uev wev wev
так как F(w) = ±l.
Следствие 3. (Равенство Парсеваля.)
2^2(u) = 2a”. (14.15)
uevm
Отметим, что ив следствия 3 и равенства (14.12) вытекает, что весовой спектр 0<Ji^2m, смежного класса f+t?m удовлетворяет условию
2(2m—2i)24 (f)=22m. i=±0
Булевы функции и смежные классы по коду Й?(1, т). Слова кода Й?(1, т) представляют собой линейные функции (14.7) от vi... vm. Две булевы функции f(vi, ..., wm) и g(vi, ..., vm) назо-
вем эквивалентными, если разность
; vj—gfa, • • •, Vm)
лежит в 5?(1, т). Если это так, то f и g лежат в одном смежном классе по коду 5?(1, т). Относительно этого соотношения эквивалентности классы эквивалентности булевых функций находятся во взаимно однозначном соответствии со смежными классами во коду 5?(1, т).
Теорема 4. Предположим, что булевы функции f и g связаны равенством
g(v) = f(Av + B) (14.16)
для некоторой двоичной обратимой матрицы А и некоторой двоичной m-последовательности В. Будем говорить, что g получается из f аффинным преобразованием. В этом случае смежные классы, содержащие f и g, имеют один и тот же весовой спектр.
Доказательство. Согласно теореме 1 достаточно показать, что л л
множества {±С?(и) :ие1/и} и {±Д(и) :ие1/и} совпадают. Действительно,
G (и) = £ (- l)u v G (v) = J (~ l)“ v F (Av + в)-vevm
Положим v=A“1w+А-1В, тогда
G( u) - £(- l)u A“,w(_ I)U A-*B F(w) = ±2 (-1)“' *F(w)=±F (u')> wgv wev
гдеи' = иА_1. •
Таким образом, для того чтобы выделить смежные классы с одним и тем же весовым спектром, необходимо ввести более сильное соотношение эквивалентности, а именно, определим эквива-лентность f и g равенством
m
g (v) = f (Av + В)а0 1 (14.17)
i=Г
где А — некоторая двоичная обратимая матрица; В — двоичный вектор и Oj — константы (0 или 1). При таком определении все булевы функции из одного класса эквивалентности принадлежат к смежным классам по коду 5?(1, tn) с одним и тем же спектром весов. *
"Однако смежные классы, содержащие f и g, могут иметь один и тот же весовой спектр и в том случае, когда f и g не связаны соотношением (14.17). Впервые это происходит при «=32; для этого п, например, смежные классы, содержащие функции
7 = ^.2 + ^4
и „ .
. = • . -А
имеют один и тот же спектр весов:-
л;2(^=л;0(П ^ 16; л;6(/>=з2,
,В завершение --этого параграфа приведем таблицу весовых спектров смежных классов по коду 5?(1, 4) (рис. 14.6). Для каж--дого ресового спектра в таблице указаны наиболее простая соответствующая булева функция и число смежных классов с этим весовым спектром. Например, последняя строка таблицы означа-
Типичная .’ Спектр весов
Число булева q функция 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 163амечания
1 — 1 30 1 Сам код
16 1234 1 15 15 1
120 123 1 7 16 7 1
560 1234 -]- 12 1 3 12 12 3 1
840 123-|-14 2 8 12 8 2
35 12 4 24 4
448 1234+12+34 6 10 10 6
28 12 + 34 16 1 6 Максимально-нелинейная
функция
Рис. 14.6. Смежные классы по коду Рида—Маллера первого порядка длины 16
ет, что имеется 28 смежных классов со спектром весов A6(f) = =ДюШ='16, где f=-fiV2 + v3^4 или может быть получена ив этой функции при помощи преобразования вида (14.17). Эти 28 булевых функций называются максимально-нелинейными по причинам, которые станут ясными в последнем параграфе (см. также: упражнение (16).
14.4. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ КОДА 5?(1, т)
В гл. 13 были описаны общие методы кодирования и декодирования кодов Рида — Маллера. К кодам первого порядка, однако, применим особый метод, который будет описан в этом параграфе. 52(1, т) является [й™, т-j-l, 2™^] -кодом и, следовательно, имеет низкую скорость и позволяет исправлять много ошибок. Практически он чрезвычайно пригоден для очень зашумленных каналов. Например, код 5?(1, 5) успешно применялся на космическом корабле «Маринер-9» для передачи изображений с Марса,
одно из которых показано на рис. 14.7. (Каждая точка на рисунке соответствует одному из 64 уровней градаций яркости черного цвета и кодировалась двоичным словом длины 32.)
Рис. 14.7. Часть большого каньона на Марсе. Эта фотография была передана космическим кораблем «Маринер-9» 19 января 1972 г.; для передачи использовался код Рида—Маллера первого порядка 50(1, 5). Служба фотографии
NASA/JPL
Кодирование является особенно простым. Мы тод на примере кодера для [8, 4, 4]-кода 5?(1, 3).
Сообщение иощи^и^ кодируется словом
Г1 1 1 1 1 1
1 И
(Л^ • • -Х7) — (iZo^UgUg)
опишем этот ме-
(14.18)
О 1 1
1 О О
1 0 1
1 1
1 1
О 1
О О
О 1
1 О
О О О
'Такое кодирование реализуется схемой, показанной на рис. 14.8. Часы в этой схеме проходят через последовательные состояния Л^з=000, 001, 010, ОН, 100, ..., 111, 000, 001, ... (т. е. считают
ют0 до7). Схема формирует вектор По+^щ+^г-ИзМз, который согласно уравнению (14.18) равен кодовому слову - х7. Вряд
ли существует что-либо проще.
Сообщение
Часы
Рис. 14.8. Кодер для кода (1,3)
Декодирование. Как мы видели в § 1.3, декодирование по максимуму правдоподобия сводится к сравнению 'полученного вектора f с каждым словом (14.7) кода $?(1, пг) и выбору ближайшего из них в качестве результата декодирования. Согласно уравнениям (14.13) и (14.14) это равносильно нахождению наиболь-л
шего значения |/?('п)|, где F — преобразование Адамара вектора F, задаваемое формулой (14.8). Предположим, что это наиболь-л
.шее значение равно |А(пь ..., ит) |. Если ..., ит) ^0, то по (14.13) f декодируется в вектор
т
2UfVi’
г=1
если же ..., Um)<0, то f декодируется в т
\ г=1
- .. Непосредственное вычисление вектора A=FH2m путем умножения Fn H2m требует примерно 2mXQm=22m сложений и вычита-
ний. К счастью, имеется более быстрый способ вычисления векто-л
pa F, основанный на дискретном варианте так называемого быстрого преобразования Фурье. Этот способ применим благодаря возможности представления Н2т в виде произведения т матриц размерности 2™Х2т, каждая из которых содержит только два ненулевых элемента в каждом столбце. При таком вычислении, л
F= ГН2т требуется только m-2m сложений и вычитаний.
Чтобы объяснить это разложение матрицы Н2т, нужно ввести кронекеровское произведение матриц.
Кронекеровское произведение матриц. 'Определение. Если — некоторая (тХт)-матрица над любым полем и B = (bij) — некоторая (пХп)-матрица над тем же полем, то кро-некеровским произведением матриц А и В называется (тпХтп)-матрица, получающаяся при замене каждого элемента ац матрицы А на матрицу ацВ. Это произведение обозначается через-А0Ви символически записывается в виде
Например, если
то
A®B = (cf/B).
1 0" и Н2 = ’1 1
^2 0 1 1 —
Н2®12= ?
1 0 0“
— 00
0 1 1
о 1 — _
0 J о
1 0 1
0—0
1 о —
(14.19))
(14.20)1
Отсюда видно, что в общем случае А®В^В0А.
Упражнение. (10). Доказать следующие свойства кроне-керовского произведения:
(i) . Ассоциативный закон:
А®(В®С) = (А®В)®С.
(ii) . Дистрибутивный закон:
(А + В)®С = (А®С) + (В®С).
(iii) . (A®B)(C®D) = (AC)®(BD). (14.21>
. Матрицы Адамара. Определим матрицу Адамара Н2т порядка 2™ индуктивно равенством
для т 2.
Матрица H2m представляет собой матрицу Адамара типа Сильвестра из гл. 2 (см. рис. 2.3; она также является матрицей, задаваемой уравнением (14.9) при условии, что и и v принимают -значения из Vm в нужном порядке).
Теорема 5. (Теорема о быстром преобразовании Адамара.)
Н„-М»М« • • .М<«, (14.22)
эд In — единичная («Хп)'-матрица.
Доказательство. Воспользуемся индукцией по т. Для т= 1 результат очевиден. Предположим, что результат справедлив для т. Тогда для IsgT^wi
М<^+1 = 12т+1_г ® н2® = i2 ® ® н2 ® I2f_, = 12 ®
эд
М<1>М<2> = 1 ~
I 0 0
\0 0
Для «1=3:
Таким образом, учитывая (14.21) и предположение индукции, .получаем:
м*й+. • •м;а1>=(ч®м«).. .(1,0 мм);
(H,®I„)»H,0(MW . .
Пример. Для ш=2 имеем:
МР = 12®Н2; М<2> = Н2®12
*(см. (14.19) и (14.20), и, очевидно,
0 0\ /1 0 1 0\ /1 1 1 1\
0 0 | I 0 1 0 1111— 1 — | = Н4. .
1 1111 о — о I I 1 1--------I
1 — / \0 1 О — / \1-----1/
М<1) = 14®Н2;
М<2> = 12®Н2®12;
М<з> = Н2®14.
' Схема декодирования Грина. Опишем теперь схему .декодирования кода 5?(1, т), основанную на теореме 5. Эта схема была предложена Р. Р. Грином, поэтому она называется схемой Грина. Описание метода проведем на примере кода 5?(1, 3).
Предположим, что получен вектор t=fofi ...f?, и положим F=
=F0Fi... F7= ((—l)/o, (—1)K Нам надо найти F=*
=FH8, или, согласно (14.22),
F = FH8 = № • -F,) Mg1* Mg2> Mg3).
Так как
“1 1
1 —
1 1
M<*> = о
1. —
1 1
1 —
1 1
РМ<1> = (Г0 + Л, Fo—Fn ^+F3,
; Fe+F7, F6-FJ.
Схема, приведенная на рис. 14.9, вычисляет координаты вектора FMgt1) парами. Ключи управляются таким образом, что после считывания символов Fo, ..., F3 в двух двухъячеечных регистрах, изображенных справа, содержатся соответственно числа
Вход
F0-Ft FB+Ft
Fz~F3 Fz+Fs
Рис. 14.9. Первый этап схемы Грина
(Fo—Fi, Fd+Fi) и (F2—F3, F2+F3). Эти четыре величины используются (см. рис. 14.10) на втором этапе. Затем считываются символы F4, ..., F7 и в той же паре двухъячеечных регистров формируются величины (F4—F5, F4+F5) и (Fe—F7, Fe+F7).
На втором этапе вычисляется вектор
(Fo-I-Л, F0-Fp Fe—F7)M<2>,
(14.23)-
M<2> = о
Таким образом, произведение (14.23) равно (Fo+Fi+F2+F3, Fo—Fi + F2—F3, Ft—F5—F6+F7). Это произведение формируется схемой, изображенной на рис. 14.10. На третьем этапе вы-гчисляется вектор
(^о+Л+^ + ^з, • • ; F^F&-F0-F7)!A^, (14.24)
тде
1
1
1 1
1 1
Рис. 14.10. Второй этап схемы Грина
Таким образом, произведение (14.24) равно
(Л)+Л+ • • -+^7» F'o—F1 + F2—Fs + Fi—F5+Fe—
-F., • • -, Fo-F1-Fis+F3-Fi+F6+Fs-F7) =
и дает нам искомое преобразование Адамара. Схема, реализующая эти вычисления, показана на рис. 14.11.
Все схемы, приведенные на рис. 14.9—14.11, представляют собой схему декодирования Грина. Последний этап декодирования л
состоит в определении i, для которого значение | F, | максимально. После этого f декодируется в i-e слово кода <%(1, т), если А л
Fi^O, и в дополнение i-ro слова, если Fj<0.
Отметим, что схема Грина обладает тем полезным свойством :что схема декодирования для кода <Я(1, т + 1) получается из схе-.мы декодирования для кода 5?(1, т) добавлением еще одного этапа и одного дополнительного регистра на m-м этапе.
Упражнение. (11). Доказать, что "
(Это означает, что порядок этапов может быть изменен без изменения окончательного результата.)
Рис. 14.11. Третий этап схемы Грина
14.5. МАКСИМАЛЬНО-НЕЛИНЕЙНЫЕ ФУНКЦИИ
Особый интерес представляют смежные классы по коду Рида—Маллера первого порядка, минимальный вес которых имеет-наиболыпее возможное значение. Соответствующие булевы функции для четного т называются максимально-нелинейными функциями, так как в некотором смысле они наиболее удалены от линейных функций. В данном параграфе изучаются свойства этих: функций и даются некоторые их конструкции. Максимально-нелинейные функции будут использованы в следующей главе для: построения нелинейных кодов Кердока.
Определение. Булева функция f(vb vm~) называется максимально-нелинейной, если все коэффициенты ее преобразования Адамара, задаваемые уравнением (14.8), равны ±2т/2.
Примеры. (1). f(vt, v2)=vtv2 — максимально-нелинейная л
функция, так как F(u) = ±2 для всех и (см. пример, предшествующий лемме 2).
(2). f(vi, v2, v$, и4) =ViV2+03О4 — максимально-нелинейная функция, как следует из последней строки на рис. 14.6. Посколь-
А
ку F(u) — целое число (из уравнения (14.8)), т должно быть, четным, если f(vt, vm) — максимально-нелинейная функция. В дальнейшем т предполагается четным.
Теорема 6. Максимально-нелинейная функция f(vt, ..., vm) т
удалена от любой линейной функции aol+2ajVi дальше, чем лю-г=1
бая другая булева функция. Более точно, функция f(V\, ..., vm) максимально-нелинейна тогда и только тогда, когда соответствующий}
«ей вектор f отстоит на расстояние 2m~1±2m/2~1 от любого слова кода <%(1, т). Если f не является максимально-нелинейной, то в коде 5?(1, т) найдется слово такое, что его расстояние от f меньше чем 2т-1—2™/2"1.
Доказательство. Если f не является максимально-нелинейной, то не все коэффициенты F(u) равны ±2т/2. Так как в (14.15) имеется ровно 2™ слагаемых, то из следствия 3 вытекает, что некото-л
рые величины |F(u) | должны быть больше чем 2т/2. Следовательно, из уравнений (14.13) или (14.14) вытекает, что расстояние между f и некоторым словом кода 5?(1, tn) меньше чем ^т/2_2т/2-1 •
Теорема 7. Функция f(vlt ..., vm) является максимально-не-.линейной тогда и только тогда, когда (2тХ2т)—'Матрица Н, (j \т/2 _
— I F(u + v) представляет со-
‘бой матрицу Адамара.
Доказательство. Вытекает из леммы 2.
Заметим, что если f(ui, ..., vm) является максимально-нелинейной функцией, то можно записать:
= 1)Ни). (14.25)
2m/2 V ’
Это задает булеву функцию f(ui, ..., ц„г). Коэффициенты преобразования Адамара от функции f (для их вычисления надо положить в (14.8) f=f) равны 2’п/2(—1)Ди)= ±2™/2. Следовательно, I также является максимально-нелинейной функцией!
Таким образом, максимально-нелинейные функции образуют естественные пары: f f.
Упражнение. (12). Доказать, что функция f является максимально-нелинейной тогда и только тогда, когда матрица, (u, v)-fi элемент которой равен (—1) f <u+v> для u, vel/m, представляет собой матрицу Адамара.
Теорема 8. Если ,f(fi, ..., vm) —-максимально-нелинейная ^функция и т>2, то deg if т.
< Доказательство. Предположим, что f — максимально-нелинейная функция и т>2. Доказательство основано на разложении •функции f, даваемом теоремой 1 гл. 13, и на результате, который мы выделим в отдельную лемму.
Пусть F(u)==(—l)Au); К(и) — преобразование Адамара функции Ё(и), задаваемое формулой (14.8), и f(u) определяется уравнением (14.25).
Лемма 9. Если — произвольный [п, k] -код, то
1 , 1 '
— 1 — tn—k д
2. f(u) = 2m~K-1—2 2 +2 2‘ 2 Мц)> (1426)
тдё'все суммы вычисляются в поле действительных чисел.
Доказательство. Это .утверждение, является простой пёрефор-мулировкой леммы 2 гл. 5. Достаточно вспомнить, что
й положить, в этом равенстве F(u) = l—2f(u) и /?(и) = =2^/2(1—2f (и)). •
Возвращаясь теперь к доказательству теоремы, применим лемму при
«MbEVm:bca[;
g=[beVffl:bcaj,
а а — его дополнение. Тогда wt (а)— — т а
+ 2 2 2 НЬ). (14-27)
ьсГ
(а)ц“* • • -v°m,
(mod 2).
где а — некоторый вектор из Vm,
1 =2wi(a), и (14.26) дает:
- tn—1
Vf(b) = 2rt(aH-2 2 bcza
Далее согласно теореме 1 гл. 13
/Ч. • • Ч) =
где
£(а)= У f(t>) ЛЕВЕ) Ьса
Отсюда следует, что g(a) задается уравнением (14.27). Но если to/(a)>m/2 и т>2, то правая часть в (14.27) четна и g(a) равно нулю. Таким образом, степень многочлена f не может превосходить т/2.
Упражнение. (13). Доказать, что f максимально-нелинейна тогда и только тогда, когда для всех v^O, v^Vm, производная от f по направлению v, определяемая равенством fv(x) =f(x+v) + H-f(x), xel/m, принимает одинаково часто значения 0 и 1.
Перейдем теперь к построению некоторых семейств максимально-нелинейных функций.
Теорема 10.
• • •> um, • •, Цп) = /(и1. • • •, um)-\-g(vv, -, vn)
является максимально-нелинейной функцией (от т + п переменных) тогда и только тогда, когда обе функции f и g являются максимально-нелинейными функциями от своих аргументов.
Доказательство. Запишем w^Vm+n в виде w= (u, v), где ue у™ и veV". Из уравнения (14.8) для t= (г, s) имеем:
H(w) = £ (_1)<*+МЬ= £ 2(-irr+vs+Hr)+g(s) = tevm+n reviser"
— F(u)G(v). (14.28)
Если обе функции f и g максимально-нелинейны, то из (14.28) вы-Л
текает, что Н (w) = ± 2<т+и)/2, так что h также максимально-нелинейна.
Обратно, предположим, что h — максимально-нелинейная л
функция, a f — нет, так что |F(%)|>2m/2 для некоторого leV'”1. Тогда при w= (%, v) для всех veF" выполняется равенство
± 2(m+n)/2 = н (W) = F (X) G (v).
Следовательно, |d(v)|<2m/2 для всех veV’1, что невозможно в силу следствия 3. •
Теорема 10 позволяет обобщить примеры (1) и (2).
Следствие 11. Функция
1^2 + г>3и4 + • • (14.29)
максимально-нелинейна для любого четного т.
Нетрудно видеть, что если f(v) — максимально-нелинейна, то функция f(Av+B), полученная из f произвольным аффинным преобразованием, также максимально-нелинейна.
Упражнения. (14). Доказать, что если т четно, то функция ViV2 + viV3+vm-ivm является максимально-нелинейной.
(15) . Используя теорему Диксона (теорему 4 гл. 15), доказать, что любая квадратичная максимально-нелинейная функция получается из (14.29) аффинным преобразованием.
(16) . (а). Максимально-нелинейная функция v3v4 может быть представлена графом
7-------‘2
4 ‘
Показать, что 28 квадратичных максимально-нелинейных функций от v2, v3, v4 задаются графами
(3 типа) (12 типов) (12 типов) (1 тип)
(Ь). Пусть f=v 102 + ^3^4- Доказать, что векторы веса 6 в смежном классе [+5?(1, 4) образуют схему 2-(16, 6, 2). (Эта схема называется биплоскостью; см., например, Камерон [231]).
(17) . Доказать, что щц2 и uiu2+u3u4 являются по существу единственными максимально-нелинейными функциями от 2 и 4 переменных.
Булева функция f(v)=f(th, ..., vm) называется разложимой, если существует такая двоичная матрица А, что для некоторого I имеет место равенство /(Av) =,fi (щ, ..., иг) +/2(иг+1, —> ит). В противном случае она называется неразложимой.
Упражнение. (18). Доказать, что всякая максимально-нелинейная функция f(vb ..., vm) степени (1/2) т^З неразложима.
Теорема 12. Функция
f(«l. • • •> «И. • • --М = ^ад+^(О1. • • ’ vm) (14.30)
1=1
максимально-нелинейна при произвольной функции g(vb ..., vm).
Доказательство. Согласно уравнениям (14.8) и (14.13) функция f(ui, ..., um, vb ..., vm) является максимально-нелинейной тогда и только тогда, когда число векторов (u, v) = (ut, ..., um, иь .... Dm), являющихся корнями многочлена
h = f(ult um, ux, + + (14.31)
i=l i=I
равно 22m-1±2m~1 для всех k= (M, ..., ft,m) и p= (pi, .... p™). Подставляя (14.30) в (14.31), получаем:
fi=g(vlt . - »ra) + J(o<+M«j+ £ Hivi-i=l i=l
(i). При произвольном v#=Z. первая сумма не равна тождественно нулю и h является линейной функцией от иь ..., Um. Следовательно, имеется 2т-1 способов выбора щ, ..., и™, при которых h обращается в нуль. Общее число корней такого типа для многочлена h равно 2™-1(2т—1).
(ii). Теперь предположим, что v=Z.. Тогда h=g(vb ..., vm) + m
+^2 piUj, что дает 0 или 1 независимо от иь ..., ит. Если эта величина равна 1, то общее число корней многочлена h равно 22m~i—2m-1. Но если эта величина равна 0, то имеется 2т дополнительных корней (и — произвольно, v=Z,), что в общем дает 22m~1+2m_1 корней. 9
Упражнения. (19). Пусть
• • '• Ъп,
i=l
Доказать, что fb fi + uiu2u3, /1-|-м1м2м3М4, .... fi + u1u2... ит являются W—1 неэквивалентными максимально-нелинейными функциями степеней соответственно 2, 3, ..., т.
(20). Доказать, что если g-(v) — произвольная булева функция, а функция ср (и) = (<р! (и), ..., фт(и)) задает взаимно-однозначное отображение пространства V™ на себя, то функция
/(«1, • • • -,ит) = V <рг(М1, -, + •, vm)
i=l
является максимально-нелинейной.
Таким образом, мы построили несколько семейств максимально-нелинейных функций; много других семейств можно найти в литературе, указанной в замечаниях к главе. Однако нерешенной до сих пор остается следующая проблема.
Задача (нерешенная). (14.1). Дать классификацию всех максимально-нелинейных функций от т переменных.
ЗАМЕЧАНИЯ К ГЛ. 14
§ 14.2. Псевдошумовым последовательностям посвящено большое количество работ. См., например: Болл и др. [62], Бэлза и др. [63], Бриггс и Годфрей [198], Брусиловский [207], Картер [251], Ченг [262], Ченг и Хо [263],. Каммин [320], Дэвайс [336], Дюволл и Киблер [395], Филлмор и Маркс [429], Фредриксон [455], Годфрей [487], Голд [515—516], Гольдштейн и Цирлер [521], Харвей [621], Хард [677], Котов [780], Майо [931], Персли и Сер-вейт [1024], Робертс и Дэвис [1116] Сколфилд [1167], Сидельников [1207], Треттер [1339], Тсао [1341], Везерс и др. [1392], Венг [1407], Виллетт [1416—1417] и особенно Голомб [522, 523], Каутс [750], Селмер [1173] и Цирлер [1461, 1465].
Вопросы применения ПШ-последовательностей к задачам обнаружения---см.: Эванс и Хэгфорс [412], Голомб [552], Горнстейн и Вейс [551], Петтенн-гилл [1041]; к задачам синхронизации: Барроус [213], Голомб [522, гл. 8], Килгас [760] и Стиффлер [1280]; к задачам модуляции: Голомб [522]; к задачам фильтрации: Фейстел и др. [423], Хенриксон [641], Накамура и Ива-даре [984] и Сэведж [1148]. Указание на непригодность ПШ-последовательностей для криптографии имеется, например, у Геффе [469, 470].
Последовательности периода 2™ могут быть получены при помощи нелинейных регистров сдвигов легче, чем последовательности периода (2™—1); они получили название последовательностей де Брейна-, см., например, де Брейн [206], Фредриксон и др. [451—454] и Кнут [772].
Если So, ..., sn-i — последовательность длины п, то ее периодическая автокорреляционная функция определяется формулой (14.2). Ее апериодическая автокорреляционная функция определяется равенством
п—х—1
Ф (т) = У SjSj_|.T, О^т^л—1. (14.32)
i=0
Задача отыскания двоичной последовательности с наименьшей апериодической автокорреляционной функцией — значительно более трудная задача, см., например, Баркер [68], Бартон и Мэллоус [73], Каприо [241], Голей [511, 513, 514], Голомб и Шольц [530], Крускал [785], Линднер [841], Мак-Виль-ямс [875], Мохарир и др. [968—970], Шнейдер и Орр [1157], Симмонс [1212], Турин [1343, 1344], Турин и Сторер [1348], Тзенг и Лью [1349]. Упражнения (7) и (8) взяты из Голомба [522] и Гилберта [480],
§ 14.3. Геометрические свойства обобщенных октаэдров описаны у Коксе-тера [313]. Лехнер [797—799] показал, что число классов эквивалентности бу-' левых функций (относительно соотношения (14.17)) равно:
m : 1 2 3 4 5
число.: 1 2 3 8 48.
Задача (нерешенная).. (14.2). Найти число классов эквивалентности при т^б. Как быстро растет число эквивалентных классов с ростом т?
Классификация смежных классов по коду cfy (1,5) проделана Берлекэмпом и Велчем [133]. Рисунок 14.6 основан на результатах работы Слоэна и Дика [1233]; см. также Хоббс [656], Холмес [660], Куршан и Слоэн [789], Сер-вейт [1144], Берлекэмп [119] применил теорему 1 для исследования влияния ошибок в преобразованном векторе F на восстановленный вектор F. Эта задача возникает при использовании преобразования Адамара в передаче изображений. Что касается применения этих смежных классов в спектроскопии, см. в работе Тэй и др. [1298а].
Смежные классы некоторых [л2, 2л—1, л]-кодов возникают в задаче Бер-лекэмпа — Гейла о переключениях (Браун и Спенсер [204], Гордон и Витсенха-узен [542]).
§ 14.4. Кодирование и декодирование кода 5? (1, и его использование на космическом корабле «Маринер-9» хорошо изложено в работе Познера [1071]. Детальное описание кодера и декодера дано Дюффи [392] и Грином [557, 558]. Что касается теории быстрых преобразований Адамара и Фурье, см. Берглэнд [108], Бригхэм [199], Кэйрнс [225], Джентельмэн [472], Грин [557, 558], Никольсон [991], Рашфорс [1135], Шене [1187] и Велч [1398]. Кронекеровское произведение матриц — см. Беллман [100] или Маркус [914]..
Кларк и Дэвис [295] описали модификацию схемы Грина, пригодную для декодирования других кодов’.
Для синхронизации принимаемых кодовых слов в космическом корабле «Маринер» на самом деле использовался не сам код 5? (1.5), а смежный класс по этому коду (см. Познер [1071] или Баумерт и Рамсей [90, 91]).
§ 14.5. Термин «максимально-нелинейная функция» и большинство результатов § 5 принадлежат Ротхаузу [1127]. Диллон [376] (см. также [377]) дал замечательный обзор этих результатов и построил несколько семейств, максимально-нелинейных функций, отличных от описанных выше. Он доказал, что максимально-нелинейные функции эквивалентны элементарным адамаро-вым разностным множествам (см. также Мак-Ферленд [950]).
Глава 15
Коды Рида—Маллера первого порядка Кердока и Препараты
15.1. ВВЕДЕНИЕ
Ключевая идея данной главы состоит в том, что код РидаА Маллера второго порядка 5? (2, т) представляет собой объедине? ние смежных классов по коду первого порядка 5?(1, т) и что эти смежные классы находятся во взаимно-однозначном соответствий с симплектическими формами (теорема 1). Симплектическая форма определяется булевой функцией от 2т переменных ..., ит, Vi, vm вида 2 UiBtjVj, где В=(В<3) — двоичная симметриче-П
Ская матрица с нулевой диагональю. Ранг этой матрицы называется рангом симплектической формы и рангом смежного класса и однозначно определяет весовой спектр смежного класса (теорема 5). В § 15.2 дается перечисление симплектических форм по рангам и, следовательно, определяется весовой спектр кода 5? (2, т}
'См. также [1451 а*]. (Прим, ред.)
(теорема 8 . Несмотря на то что в общем случае задача описа-ния весового спектра произвольного PM-кода не решена, в § 15.3 мы приводим без доказательства два общих результата по этому вопросу. Первым из них является формула Касами и Токуры для числа слов в коде 5? (г, т), вес которых строго меньше чем 2™-r+1 (теорема 11). Второй результат дается теоремой Мак-Элиса о том, что вес произвольного слова кода 5? (г, т) кратен 2К’п-1>/'1 (следствие 13).
В § 15.4 выводятся формулы для весовых спектров некоторых интересных малых подкодов кода 5?(2, т), в частности для кода, дуального к коду БЧХ и исправляющего две ошибки (см. рис. 15.3 и 15.4).
В § 15.5 строится максимальное множество симплектических форм, обладающее тем свойством, что ранг суммы любых двух форм из этого множества не меньше чем 2d. Соответствующие подкоды кода 3?(2, т) имеют несколько интересных свойств. Эти подкоды линейны, если т нечетно; но при четных т они являются нелинейными обобщенными кодами Кердока ЗУЗ (т, d). При d—m/2 код <£>$ (т, т/2) равен коду Кердока Ж(т). Первый из кодов Кердока ^(4), эквивалентен (16, 256, 6)-коду Нордстрома—-Робинсона Л16, приведенному в гл. 2. Вскоре после открытия кода Ж1е Препарата успешно обобщил этот код и построил бесконечное семейство кодов (т) с параметрами (2m, 22 ~2т, 6) для всех четных т^4 (см. рис. 15.12). После этого в 1972 г. Кер-док открыл коды Ж(т'). Они имеют параметры (2m, 22"1-2, 2™-1— —2<т-2)/2) и являются дуальными к кодам ^(т) в том смысле, что весовой спектр (или спектр попарных расстояний) кода Ж(т) задается преобразованием Мак-Вильямс от весового спектра кода йДт) (см. рис. 15.6). Оказалось, что при той же длине и том же минимальном расстоянии коды ^(т) и Ж\т) содержат по меньшей мере вдвое больше слов, чем лучшие линейные коды.
Коды (т, d) были открыты Дельсартом и Геталсом. В последнем параграфе мы описываем коды /’(т), найденные Геталсом, которые в некотором смысле дуальны кодам (т’~7Г (т~2)) •
Конструкции кодов Ж(т), 0(т), ЗУЗ (т, d), ... существенно используют развитый в предыдущих главах алгебраический аппарат, например групповую алгебру и аннулирующий многочлен из гл. 5 и идемпотенты и многочлены Мэттсона—Соломона из гл. 8.
15.2. ВЕСОВОЙ СПЕКТР КОДА РИДА—МАЛЛЕРА ВТОРОГО ПОРЯДКА
Слова кода Рида—Маллера второго порядка 5? (2, tri) длинй 2т задаются булевыми функциями от v= (щ, ..., vm), степень которых не превосходит 2 (см. § 13.3). Таким образом, типичное кодовое слово задается булевой функцией
S(v) — У qiJuivi + У liVi+e.
Это можно записать в виде
S (v) = у Q vT + L vr + e— Q (v) + L (v) + e. (15.1)
где
Q(v) = vQvT; Z.(v) = Lvr; (15.2)
Q= (gVj) — верхняя треугольная двоичная матрица; L= (Zi, ... ..., Im) — двоичный вектор и е равно 0 или 1.
Q(v)=Q(ub ..., vm) называется квадратичной формой, а £(v) = L(vi, ..., vm) — линейной формой. (Формой называется однородный многочлен.)
Если Q(v) фиксирована, а линейная функция L(v)+e пробегает по коду Рида—Маллера первого порядка 5?(1, пг), то S(v) пробегает по смежному классу кода 5? (2, т) по коду 5?(1, т). Этот смежный класс полностью характеризуется формой Q. Другой характеристикой является симметрическая матрица B = Q+ + Q7'; элементы главной диагонали матрицы В равны нулю.
С матрицей В связана другая форма ^(u, v), определяемая равенством
• -Д(и. v) = uBvT (15.3)
или иначе
SB(u, v)==u(Q + Qr)vr=uQvT + vQu2’=
= Q(u + v) + Q(u) + Q(v)= (15.4)
= S(u + v) + S(u)+S(v) + e. (15.5)
(Последнее равенство следует из формулы (15.1). Форма $(и, v) называется билинейной и согласно (15.3) удовлетворяет условиям
53(u + v, w)=®(u, w)-|-S3(v, w);| (15 6)
SB (a, v + w)=53(u, v) + -®(u, w). f
Из уравнения (15.4) следует, что форма ^(u, v) является также альтернированной, т. е. удовлетворяет условиям
S3 (и, и) = 0 (15.7)
и
®(u, v) = 53(v, и). (15.8)
Двоичная билинейная и альтернированная форма называется симплектической. Аналогично двоичная симметрическая матрица с нулевой диагональю называется симплектической матрицей. Таким образом, В — симплектическая матрица. Например, матрица
является симплектической, и соответствующая ей симплектиче-ская форма равна
33(ult и2, vit o„)=(u1, ич) | Ц ( 1 | =w1t»24-u2u1.
Ц 0/ \о2/
В качестве конкретного примера рассмотрим PM-коды первого и второго порядков длины 16. 5?(1, 4) представляет собой [16, 5, 8] расширенный симплексный код и порождается первыми пятью строками на рис. 13.2. 5?(2, 4) представляет собой [16, 11, 4] расширенный код Хэмминга и порождается первыми одиннадцатью строками на этом рисунке. Код 5?(2, 4) состоит из 211-5=64 смежных классов по коду 5?(1, 4). Одним из смежных классов является сам код 5?(1, 4), а квадратичная и симплектическая формы, соответствующие этому смежному классу, равны нулю.
Другой смежный класс состоит из 16 векторов вида &1У2 + -гЦз^4+3?(1> 4), четыре из которых указаны на рис. 15.1.
000100010001 1 1 1 o=wlv2+v3v4 111011101110000 1 =VjV2~t~^3~i~^4~t~ 1
010 0* 01000100101 1 = г’1Г'2+г'3Ь4 +V] 101110111011010 0=vIv2 + r3r4+vI + l
Рис. 15.1. Четыре вектора из смежного класса 4)
Булевы функции S(v) (выражение (15.1)), соответствующие этим четырем векторам, имеют вид:
и^з + о^;
^2 + ^’4+
^Цз + из^ + Цр t’l«2 + U3U4 + yi+ 1-
Отметим, что в данном случае они являются максимально нелинейными функциями (см. § 14.5). Все они имеют одну и ту же квадратичную часть (15.2)
Q (v) = vx v2 + v3 v4= [ux v2 v3 u4]
Таким образом, ГО 0 о о
Q=
1
0
0
0
0
0
0
0
O’
0
1
0
И B = Q-|-Qr =
~0
1
0
0
1
0 0
0
0
0
0
1
0~
0
1
0
(15.9)
являются соответственно верхней треугольной и симплектическои матрицами, соответствующим-и этому смежному классу. Симплек-тическая форма, соответствующая данному смежному классу, равна (15.3)
S3 (u, v) = U В V7 = и2 + и2 Щ + «3 V4 + U4 V3-
Упражнение (1). Доказать, что если функция &(и, v) удовлетворяет уравнениям (15.6) и (15.7), то найдется квадратичная форма Q(u) такая, что <%(и, v) = Q(u + v) +ф(и) + Q(v).
Таким Образом, мы доказали, что:
Теорема 1. Между симплектическими формами и смежными классами кода 5? (2, т) по 5?(1, т) существует взаимно-однозначное соответствие. Нулевая форма соответствует самому коду 5?(1, т).
Будем использовать символ. одновременно для обозначения смежного класса и соответствующей ему симплектической формы. Ясно, что число различных симплектических форм (или матриц)
(")
равно 2; . Но нам необходимо также знать, сколько имеется
форм каждого ранга.
Теорема 2. Пусть N (т, г) обозначает число симплектических (тХт) -матриц ранга г над полем G.F(2). Тогда
N (т, 2/г+1)=0;
й 2. 2ft—1
N (tn, 2h)= П 2 ,~2- П (2т~г —1) = г=1 1 г=0
= (2m-l)(2m~1 -l)...(2m-2ft+1-l) 2h (h-i)
( 22/г — 1) ( 22ft-2 — 1)...(22 — 1)
Доказательство. Заметим, что Л7(1,0) = 1, ДД1, 1)=0 и N(2, 0) = 1, N(2, 1)=0, N (2, 2) = 1.
Мы теперь выведем рекуррентную формулу для N(m, г). Пусть А — фиксированная симплектическая (mXtri)-матрица ранга г, и пусть
В =
А уГ>|
У О/
— матрица размерности (m+1) X (т+ 1).
Лемма 3. Среди всех 2™ различных матриц В точно 2™—2Г имеют ранг г + 2 и ровно 2Г — ранг г.
Доказательство леммы. Если вектор у независим от строк матрицы А и может быть выбран 2т—2Г способами, то ранг матрицы равен г+1 и соответственно ранг В равен г + 2. С другой стороны, если у зависит от строк матрицы А, скажем у=хА, то мат-
рица I ) имеет ранг г. Чтобы доказать, что вектор ( у ) зависит \у / \ О )
л /А\
от столбцов матрицы ( , заметим, что
\У 1
А\ т ( УТ \ У / \ ухт /
Ут \ хАхт /
Из леммы 3 следует, что число <N(т, г) удовлетворяет следующему рекуррентному уравнению:
N(m+1, r) = 2rN(m, г)+ (2т—2r~2) N (т, г—2).
Начальное условие 1V(1, 1)=0 влечет за собой равенство 2h+ 1) =0 для всех h. При начальном условии N(т, 0) = 1 непосредственной проверкой убеждаемся, что решение этого уравнения задается формулами
... ох (2т — 1) (2гга—1 -1)
N(m, 2) = ------—---------—
' 22—1
( 2,т - 1) ( 2т—1 - 1) ( 2т~2 - 1) С^-3 - 1)
1 ’ >' (2«—1) (22—1) Z’
что и дает общее решение, указанное в теореме. •
Теперь мы докажем, что весовой спектр смежного класса £% зависит только от ранга матрицы В. Для этого нам понадобится фундаментальная теорема, доказанная Диксоном, которую мы сформулируем в следующем виде:
Теорема 4. (Теорема Диксона.) (1). Если В — симплекти-ческая (m Xга)-матрица ранга 2h, то существует такая обратимая двоичная матрица R, что у матрицы RBRT все элементы равны нулю, за исключением двух диагоналей, лежащих непосредственно над и под главной диагональю, и эти диагонали имеют вид 1010...100...0, где число единиц равно h.
Примерами матрицы RBRr для h=2 являются
(2). Любая булева функция, степень которой не превосходит 2, vQvr+L(v) +е, где Q — верхнетреугольная матрица, a L и е — произвольны, может быть приведена к виду Т(у) == h
— .2 y^i-xyu+Li (у) +е преобразованием переменных у = vR 4
где R — матрица, определяемая п. (1) теоремы при B=Q+QT. Более того, y2h линейно независимы.
(3). Если Lj (у) линейно зависит от уъ y2h, то существует аффинное преобразование, приводящее Т (у) к виду
л
x2i-i^2i + si. £1= 0 или 1, (15.10)
1=1 •
где Ль x2h линейно независимы и каждая из х< представляет собой линейную форму от ylt y2h, 1.
Доказательство. (1). Утверждение очевидно для т=1, 2. Предположим, что оно выполняется для всех m^t и h^[t/2]. Тогда (/+1) X (^+1) симплектическая матрица В может быть записана в виде
в= (А И 'у о/
где А имеет такой же вид. Например, 3X3 симплектическая матрица может быть записана в виде
/0 0 аД /0 1 сД
I 0 0 а2 или 1 о а2 I-
XOj с2 0 J \а± о2 0 J
Если ранг матрицы А меньше чем 2[t/2], то с помощью элементарных операций над строками и столбцами , матрица В может быть приведена к виду
/А у'т 0 . . . о\
/ У' 0 0 . • 0 1
1 ° 0 0 . . о
\о 0 0 . . . о/
где
/А У' Д
\У 0 )
— матрица, размерность которой не более чем txt. Согласно предположению индукции такая матрица может быть приведена к указанному виду. Таким образом, можно предполагать, что ранг матрицы А равен 2|7/2]. Если 2ft/2]=t, то ранг В равен t и
0 1 1 0 0 . . 0 . . . 0 . 0 0 о, 1
0 °2
в= 0 0 0 . 0 1 a*-i
0 0 1 0
й2 а3 • at—1 at 0
В этом случае /1 0 0 0 . 0 0. 0\
R '0 1 0 0 . . о 0 °
\а2 «1 «4 с3 • at -г 1/
Если 2[//2| =f—1, то
/ 0 1 ... О О О \
/ 1 О ... О О О е2 \
О О ... О 1 О at_2
I О О . . 1 О О
\ О О ... О О Os.
\Oi Gg . . . at—2 at—\ E 0
где ранг матрицы В равен t—1, если е=0, и Z+1, если е=1. В любом случае
/го о ... о о о 0\
R = | О 1 о ... о о о о
Хаг с4 . . . af_2 О 1/
(Проверить это для т=4,5.)
(2). Преобразование x=uR~1; y=vR-1 переводит билинейную форму uBvr в
h xRBRTy = y2i + x2i у21_г).
* i=i
Соответствующая квадратичная форма равна h
У । Ун— 1Ун-
(3). Пусть h
Т ~ ^2i—1 Ун + (у) + Е>
i=l 2й где Л (у) линейно зависит от yit скажем, L(y) = S/^. 1—1
Например, если /1 = 1; /2 = 0, так что Т (у) = yiyz+yi + ..., то подстановка yi=Xi; y2—Xi+x2 переводит эту форму в
h 2й
Т^^х^ъ + ^у^Ум + УЦу^ i=2 i=3
Если /i = Z2=l, то T(y)=yly2+yi+y2 + ... при подстановке У1—*1 + 1; */2=^2+1 переходит в h 2ft
т (У) = %! х2 + 2 Z/21-1 Ун + 2 li Уг + 1 • i=2 i=3
Ясно, что продолжая таким образом, придем к желаемому результату. •.
Замечания. (1). Так как код 5?(1, т) содержит булеву функцию 1, то смежный класс содержит одновременно х h h
x2i—j x2i и -^21—1 x2i Ч- 1 •
i=l i=l
(2). Многочлен Мэттсона—Соломона, соответствующий канонической форме
л
X2i—1 X2i>
согласно следствию 26 гл. 13, равен h
УТт(а12)Тт(^?);
(15.11)
где ai, ..., я/,; рь .... рл — линейно независимые элементы поля GF(2m).
Упражнение. (2). Доказать, что в п. (3) теоремы констан-k
та 61 равна 6i= S 12{_ iZ2i Тб. £=1
Доказать, таким образом, что число линейных форм L(y), для которых ei = l, равно 22h~1—2h~Y.
Задаваемое теоремой 4 каноническое представление квадратичной формы мы используем теперь для вычисления весового спектра соответствующего смежного класса (нижеследующая теорема). Этот результат будет использоваться в данной главе много раз.
Теорема 5. Если ранг матрицы В равен 2h, то спектр весов смежного класса & кода 91 (2, т)
Вес
—1_
2т~х 2^—1 । ^rri—h—1
по коду 5?(1, т) равен:
Число векторов
22Ь
22'1
Предпошлем доказательству две
Лемма 6. Число векторов (хь ся в нуль форма
леммы.
..., х2л), на которых обращает-
h
7 , X2i—1 X2b
равно 22h~l + 2h~i.
Доказательство. Если /?^= 1, то это число равно 3 (этими векторами являются 00, 10, 01), и лемма справедлива. Далее продолжим индукцией по h
Л+1 . h
X2i—1 X2i У x2i—1 X2i 4" X2fi+l X2h-4-2 4" ^2-
г=1 i=l
Имеются 3 (22h~1 + 2h~1) случая, при которых Fl = F2=0 и (2271-1—2'1^1) случаев, при которых Fl=F2=l. Общее число равно:
4.22Л-1 | 2 • г'1-1 = 22 (,1+1)-1 2(М4)_1 •
Таким образом, число векторов (хь х2ь, x2h+i, —> хт), на ко-ft
торых форма Sx2i-ix2i обращается в нуль, равно 2m-2ft (22Л-1 + + 2Л-1) = 2™ i-f-2m~h~1.
_ т
Лемма 7. Пусть L2/i+i= 2 а-Л, где не все а{ равны нулю.
1=211+1
Число различных векторов (хь ..., хт), для которых многочлен
S x2i~iX2i + LZh+i обращается в нуль, равно 2т~1. г—1
Доказательство. Использовать лемму о рандомизации из упражнения (2) гл. 13. •
Доказательство теоремы 5. Пусть ранг матрицы В равен 2h. Согласно теореме Диксона квадратичная часть булевой функции, принадлежащей смежному классу может быть приведена к
виду Q(x) = Z x2i_ix2i.
1=1
Предположим, что линейная часть L(x) этой булевой функции имеет вид (это возможно в 22h случаях)
♦ гл
L (х) = у at хг.
i=i
Используя п. (3) теоремы Диксона, приведем >Q(x)+L(x) к одному из видов
h h
или У а—1У%1Н- 1-
i=i 1=1
Согласно замечанию, сделанному после леммы 6, веса этих многочленов нравны соответственно 2,п-1—2’n-h-1 и 2m-l+2m^'г-,. С другой стороны, если линейная часть L(x) зависит не только от Xi, ..., x2h (что возможно в 2та+1—22h+1 случаях), то согласно лемме 7 вес кодового слова равен 2,п“1. •
Замечание. Из теоремы 5 следует, что чем больше h, тем больше минимальный вес в смежном классе. Значение /г=0 соот-. ветствует самому коду 5?(1, т). Наибольший возможный минимальный вес соответствует 2h—m (и, следовательно, т должно быть четным). Булева функция, соответствующая такому смежному классу, является квадратичной максимально нелинейной функцией (см. § 14.5, в частности упражнение (15)).
Для иллюстрации теоремы 5 вычислим весовой спектр смежного класса О1и2 + озо4+<й(1, 4). Матрица В задается равенством (15.9), и ее ранг равен 4. Следовательно, /1=2 и спектр весов смежного класса равен Л6=/4ю=16 (что соответствует последней строке на рис. 14.6).
Непосредственным следствием из теоремы 5 является следующая теорема.
Теорема 8. (Спектр весов кода Рида—Маллера второго порядка.) Пусть Ai — число слов веса i в коде 5?(2, т). Тогда Л,=
= 0, за исключением случаев •t=2m~1 или i=2m~I±2m~I~h для некоторого h, 0^/г^{(1/2)т]. Кроме того, А0—А2т — 1 и для IsgAsCf (1/2)т1
А . -
1 |-
= 2й (Л+1) ( 2W - 1) ( 2m~* - 1) ... ( 2^+» - 1) ( 22Л — 1) ( 22/i—2 — 1) ... (22 — 1)
(15.12)
Для числа Л2т—1 нет простой формулы, но, естественно,
Л"1-1
1+т+
= 2
Доказательство. Вытекает’ из теорем 2 и 5 *
Пример. Весовой спектр [32, 16, 8]-кода Рида—Маллера
<%(2, 5) равен:
Ai
0 или 32 1
8 или 24 620
12 или 20 13 888
16 36 518
Замечания. (1). Полагая в формуле (15.12) h=l, получаем, что число кодовых слов минимального веса равно А2т^2 = = (4/3) (2™—1) (2™“'—1), что согласуется с теоремой 9 (Ь) гл. 13.
(2). Формула (15.12) имеет громоздкий вид, который может быть упрощен, если использовать для записи гауссовские биномиальные коэффициенты.
Определение. Для произвольного действительного числа 6=#1 и всех неотрицательных целых чисел k гауссовский Ь-ичный биномиальный коэффициент определяется равенством
1
х j = (^-i)(^-1-i)...(^-ft+1-l), k = ! 2 /г] (^-i)(^-1 _!)... (6-1)
(15.13)
(Здесь х — действительное число, как правило, целое). Например,
Г 3 = &
. 2 J (ft2 — 1) (6—1)
Между гауссовскими биномиальными коэффициентами и обычными биномиальными коэффициентами, как показывает следующее упражнение (ср. с упражнением (18) гл. 1), имеется много аналогий.
Упражнение (3). Свойства гауссовских биномиальных коэффициентов:
ь-i |_ £ J \ « /
(Ь) [п 1=[ п 1.
[ k J \п—а]
(с) Определим [п] равенствами
[01 = 1;
[n] = (bn— l)(bn~l — 1)... (Ь— 1) для п=1, 2,... Тогда
(d) И1 =------И-------;
[ k J [A] [n — k]
(е)
L к j — 1 j L А J
(У + 1) (У + b) (у+ bz)...(y + h"->) = [ " ] b(n~h} ("-ft-1)/2yh.
k=0
(f) yn^ S I ](y+1)({/+ь)-(^+^-1)-
(g) У (— l)fe~* (k-i-D/2 Г k 1Г / 1 = s...
В терминах гауссовских биномиальных коэффициентов при Ь — 4 уравнение (15.12) переписывается в виде
лт-1±2т-1-^=2ft (л+п w [Т ] р ~1)/2]- (15-14>
Эти коэффициенты обладают еще одним полезным свойством.
Теорема 9. Число различных (хотя не обязательно неэквивалентных) [п, ft]-кодов над полем GF(q) равно д-ичному гаус-
\п I совскому биномиальному коэффициенту I .
Доказательство. Число способов выбора k линейно независимых векторов равно (qn—1)(<7П—q) ... (qn—qh~1)- Каждое такое множество задает базис [п, ft]-кода Число базисов в равно (qh—1) (qh—q) ... (qk—qh ^). Следовательно, число различных кодов равно
.(г-1)(г-?)-(г-г-‘) L*J'
Это очень легко запомнить: число [п, fe]-кодов равно
\Упражнения. (4). ' (Сервейт.) Пусть W(x, у) — весовая функция кода й?(2, т), и пусть w{z; m) = W(l, z). Доказать, что
\ w(z; m)=w(z2; т—l) + z2'n~1w(l; tn—1) +
+ 2т—1 ( 2т — 2) z2>n~2'w(z2; т—2).
[Указание. Эти три члена соответствуют словам кода 5?(1, т) весов 0, 2т-1 и 2т~2.]
(5). Используя развитые в этом параграфе методы, доказать следующую теорему. Пусть ns = 22rl—1, s> 1, />1 и s делит 2г+1. Пусть [п, 2rl] минимальный циклический код. Доказать, что состоит из нулевого вектора 0, п слов веса (22гг-—l + e(s— —\')2rl~x)ls и n(s—1) слов веса (22гг-1—E2rl~l)/s, где е=(—l)z. [Указание. Пусть peG.F(22ri) — не нуль кода 4g. Если (а0, — ..., то аг = 7’2ц(тРг) для некоторого y=GF(22rl) (см. теоре-
му 9 гл. 8). Выбрать сначала s = 2r+l и p=g2r +1, где § — примитивный элемент поля GF(22rl). Показать, что
Q© = ^(tS2''+1)
является квадратичной формой от g и что ранг соответствующей симплектической формы равен 2rl—2г, если у=т]-'’+1 для некоторого элемента г] из GF(22rl) и равен 2г/ во всех остальных случаях. А затем рассмотреть случай, когда s является собственным делителем числа 2г-|-1, разбить подгруппу, порожденную элементом на смежные классы по подгруппе, порожденной элементом Г+1.]
*15.3. СПЕКТР ВЕСОВ ПРОИЗВОЛЬНЫХ КОДОВ РИДА—МАЛЛЕРА
Спектр весов PM-кода первого порядка 5?(1, т) равен
^о=-^2т= 15 = — 2, (15.15)
а спектр весов PM-кода второго порядка описывается теоремой 8. Далее, так как код 5?(т—г—1, т) ортогонален коду 91 (г, т), то согласно теореме 4 гл. 5 спектры весов кодов 5?(т—2, т) (расширенного кода Хэмминга) и кода 5?(т—3, т) также известны. Однако ни для какого другого общего класса кодов Рида—Маллера такой формулы нет.
Задача (нерешенная). (15.1). Найти спектр весов кодов 5?(3, т) ...
Тем не менее имеется несколько общих результатов о весовых функциях кодов 3?(г, т), которые мы сейчас сформулируем без доказательств.
Как показано в теореме 8, минимальное расстояние кода ^?(2, т) равно d=2m~2, а все веса в диапазоне от d до 2d имеют вид w=2d—2Z для некоторого i. Это свойство характерно для всех PM-кодов; действительно, Касами и Токура нашли число
слов веса w в коде 5?(г, т) для всех w<z2d=2m~r+l (на самом деле для всех to<2,5d — см. ниже). Для этого они выписали канонические формы всех соответствующих булевых функций.
Теорема 10. Пусть f(vJt ..., vm) — булева функция, степень которой не превосходит г для г ^2, такая, что wt(/) <2ТО-Г+1. Тогда существует аффинное преобразование, приводящее f к одной из форм:
(О- / = о1...цЛ_|Х(цЛ_ц+1 ...ь-г+ил+1...цг+и),
где р удовлетворяет неравенствам З^р^г и р^т—г, или
(ii). f = t’i .• vr_з (vr_i t'r + t'r+1 ог.|_24- ... + t’r+an—з L'r+2U—a)>
где p удовлетворяет неравенствам 2=C2p<7m—r+2.
Используя этот результат и теорему 8, Касами и Токура [745] доказали следующую теорему.
Теорема 11. (Спектр весов кода 91(г, т) в диапазоне от d до 2d.) Пусть Aw — число слов веса w в коде й(г, т) для г^2, причем d=2m~r^.w<C2d.
Положим a=min(m—г, г) и [3= (т—г+2)/2. Тогда:
. . (i). Ля=0, за исключением w=w(p) =2m-r+1—2m-r+1“w для некоторого р в диапазоне 1^р^тах(а, (3). Случай р—1 соответствует весу w=d и описан теоремой 9(b) гл. 13.
(ii) . Если р=2 или тах(а, 2) <р=£5р, то
г+2ц—з
2r-HiE+u-2 р| (2т-г —1)
^(Ю = —------------. (15.16)
П(2-2--1)П(4г+1-1)
i=0 1=0
(iii) . Если шах(р, 2)<р=Са, то
r+u— 1 2r+u2+u— 1 [“| ( 2т—» — 1)
Aw =---------------. (15.17)
г—ц—1 ц—1
П ( - 1)П ( - I)2
г=0 1=0
(iv) . Если 3^p^min(ct, р), то Aw(g) равно сумме величин (15.16) и (15.17).
Теорема 11 была распространена Касами, Токурой и Азуми [746] на слова, веса которых не превосходят 2,5/7; однако используемая для этого алгебра усложняется настолько, что для дальнейшего продвижения в этом направлении представляется необходимым искать иной подход.
К настоящему времени известны весовые функции кодов Рида—Маллера для всех nsC256 (см. Касами и др. [746], Сервейт [1144], Сагино и др. [1248] и Ван Тилборг [1325]). Наименьшими PM-кодами, для которых весовые функции в настоящее время (в 1977 г.) неизвестны, являются 5?(3, 9), 5? (4, 9) и S?(5, 9).
^Второй общий результат, даваемый теоремой Мак-с)лиса, со-стоит в том, что вес каждого слова кода 91 (г, т) делится на of(m-V)/ri_ Этот результат вытекает из следующего утверждения.
Теорема 12. (Мак-Элис [939, 941].) Если 'g’ — двоичный циклический код, то вес каждого слова из ‘g’ делится на 2г-1, где I — наименьшее целое число такое,- что произведение I ненулей (разрешаются повторения) кода 'g? равно 1.
Доказательство этой теоремы является трудным и опускается.
Следствие 13. Вес каждого слова в коде 91 (г, т) кратен 2Г (т— 1)/г] _ 1
Доказательство. Согласно уравнению (13.10) элемент а’, l^s^2m—2, является ненулем выколотого циклического кода 91* (г, т) тогда и только тогда, когда двоичное разложение числа s содержит от 1 до г единиц. Далее произведение aS|a®2... as i равно единице aSlaS2... asi =1 тогда и только тогда, когда
+ sz = 2'” -1. (15.18)
Взяв двоичное разложение левой и правой частей этого равенства, видим, что каждый член слева содержит не более г единиц, в то время как справа имеется т единиц. Отсюда вытекает, что наименьшее I, для которого имеет место (15.18), равно [т/r]. Тогда утверждение следует сразу из теоремы 12.
Пример. Веса кода 91 (2, 5) делятся на 22, что мы и видели в примере, следующем за теоремой 8.
*15.4. ПОДКОДЫ РАЗМЕРНОСТИ 2m В КОДАХ 91 (2, т)* И 91 (2, т)
Мы начнем с доказательства одной простой теоремы, облегчающей задачу вычисления спектра весов многих малых подкодов в кодах 91* (2, т) и 91 (2, т) путем ее сведения к задаче вычисления ранга соответствующей симплектической формы.
Теорема 14. Пусть В — симплектическая матрица ранга 2/г. Тогда множество всех двоичных m-векторов v таких, что uBvr=0 для всех и^К”1, образует пространство размерности т—2h.
Доказательство. Пусть В — матрица, описанная в теореме 4, и положим u'=uR-1= (u'i, ..., u'mY, v/=vR~1 = (и'ь ..., v'm). Тогда uBvr=u'RBRrv'.
Так как матрица RBRr имеет вид
Ч-----2h------
t ~ ~
0 1 ... о о
0 0.01
О О 1 о
о |о
то
u' RBRT v' = u] v' 4- u' v' + u' v'4 +
+ U4 V3 4~ ... + ^h—l V2h “b U2h V2h—1 •
Эта величина равна тождественно нулю для всех и' тогда и только тогда, когда v'=(0..О, ь'2л+1, —, v'm).
Таким образом, векторы vz образуют пространство размерности m—2ft. •
Пусть теперь S(v) (уравнение (15.1)) будет булевой функцией, описывающей слово с кода j?(2, т). Координаты вектора с являются значениями S(v) на всех двоичных m-векторах (щ, ... ..., vm). Эти координаты можно также рассматривать как значения S(£) на всех элементах ^eGF(2m). Для произвольного £ из GF(2m) определим Q(£) равенством
где | представляет собой m-вектор, соответствующий элементу geGF(2m). Согласно уравнению (15.4) значения соответствующей симплектической формы задаются равенством
T]) = Q(g+T])+Q©+Q(n)- (15.19)
Мы увидим, что обычно ^(i, т]) может быть записана в виде л) = Tm(S,LB (т])), где £в (х) — линеаризованный многочлен. Тогда в силу теоремы 14
ранг В = т—размерность (ядра LB), (15.20)
где ядро LB определяется как подпространство таких элементов TjeGL’(2™), что Lb (т])=0.
Малые подкоды кода <%*(2, т). В этом разделе будет найден спектр весов [2т—1, 2m] циклического кода с порождающим идемпотентом 0*1 + 0*;., где /г= 1-1-2* для произвольного i. Он представляет собой подкод кода (2, т). В частности, код с порождающим идемпотентом 6*i + 6*3 является дуальным к коду БЧХ, исправляющему две ошибки.
Наш метод вычисления весового спектра состоит в следую-.’ щем. Сначала выписывается многочлен Мэттсона—Соломона для типичного кодового слова и, следовательно, булева функция S(£), описывающая это слово. Эта функция является квадратичной, так как код представляет собой подкод Й?*(2, т). Затем мы находим соответствующую симплектическую форму ^(^, т]), ее ранг (см. (15.20)) и, используя теорему 5, вычисляем возможные веса в коде. Наконец, применяя методы гл. 6, находим спектр весов.
Из уравнения (13.8) следует, что ненули кода $.* (2, т) должны выбираться в виде as, где w2(s)>m—3; иными словами, они представляют собой те степени а, показатели которых принадлежат циклотомическим классам Со, С_х и C-i. для ВСех Zr-= l-j-2z, lsCi=C[m/2].
Порождающий идемпотент кода. 5?* (2, т) равен 60+6*i +
Сл^чай (I). т — нечетно: m=2t-'-l. Этот случай легко анализируется с помощью результата, доказательство которого мы предоставляем читателю.
Упражнение. (6) (а). Показать, что если m=2t-rl и то числа 2т—1 и 2*-г1 взаимно просты.
(Ь). Доказать, что 2т-г1 и 2m-i + l являются единственными нечетными числами в циклотомическом классе Сг и что циклото-м'ический класс Сг содержит т элементов.
Найдем спектр весов [2т—1,2m] подкода 'g’j кода 5?* (2, т), порожденного идемпотентом 0*(-г0*/.. Ненулевые слова кода записываются в одной из форм: xJ0*i, xj6*n или x»0*i + xhQ*i. где / и k •— некоторые целые числа. Вес слов первых двух видов равен 2т~х, и они не представляют трудностей.
Слова третьего, типа являются циклическими сдвигами кодового слова а = x’_ft0*i + 0*г . МС-многочлен слова а определяется так (см. § 8.6):
л(г)= £(у2)г+ 2 ^=Tm(Y2)+rm(21+2i). leCi ieclt
Пусть 5 (I) — булева функция, описывающая вектор а. Тогда согласно теореме 20 гл. 8 для всех ^eGF*(2m)
S©=Tm(Yg) + Tm(g1+2i). (15.21)
Постоянный член (см. (15.1)) e=S(0)=0. Пусть а7 обозначает вектор, получаемый из а путем прибавления общей проверки на четность (равной нулю).
Воспользуемся уравнением (15.21) для вычисления симплектической формы, соответствующей тому смежному классу кода Й?(2, т) по 5?(1, т), который содержит вектор а. Эта формула согласно (15.21) равна:
(1. л)=тт (у (|+л))+тт ((|+л)1+2г) +
+Тт (у I)+Тт ( )+Тт (у л)+Тт ( т1«+2г ).
Поскольку Тт(х) = Тт(х2) и
(l+n)1+2f =l1+2i +l2i n+^)2i+л1+2\ форма ^(g, т]) переписывается в виде
Тт tj + g rf) = Тт (I (1]2'п~г + л2'))-
Теперь мы воспользуемся равенством (15.20) для вычисления ранга формы 9%. Форма ^(g, т]) равна нулю при всех значениях ^112т"г + ц2/ = 0
^=T)2m-2Z
^i]GCF ( 2m—2/) П GF (2m) = GF (2s),
где s= (m—2i, m) = (i, m) (по теореме 8 гл. 4). Таким образом, размерность пространства элементов т] таких, что ^(^, tj) =0 для всех £, равна s. Из равенства (15.20) получаем, что ранг матрицы В равен т—s. Из теоремы 5 заключаем, что вес кодовых слов вида x3'0*i + хЧ)*!.равен 2™-1 и 2’"-1 +-2(m+s~2)/2.
Наконец, так как дуальный код представляет собой подкод кода Хэмминга, то d'^3. Поэтому, используя теорему 2 гл. 6, находим спектр весов кода ‘g7,, который приведен на рис. 15.2. Рисунок 15.2 обобщает результаты теоремы 34 гл. 8.
i At
0 1
2т~1 2(m+s-’2P2 (2m—l)(2m~s-1 _p2(m“-s~2)/2)
2m-l (2m-l)(2m —2m~s +1)
2m~1 | (<yn s—1 s—2)/2)
Рис. 15.2. Спектр весов кода с порождающим идемпотентом 6Ч+Ю*(г> где li = 1+2‘; s=(i, т)\ т — нечетно
Отметим, что код 'g’s с порождающим идемпотентом 0*i + 6*3 представляет собой [2т—1,2т, 2т~1—2<т~1)/2]-код, ортогональный коду БЧХ, исправляющему две ошибки. В этом случае i= 1, s=l, и спектр весов кода приведен на рис. 15.3. (Это было использовано в § 9.8 для доказательства квазисовершенности кода БЧХ, исправляющего две ошибки).
i At
0 1
2»i—1 (pm l)(2m~—2 | 2^m~3^2)
2m~l (2'n— l)(2m“‘ + 1)
2m~1 O/2 (2m l)(2m~2 2^т~3^2
Рис. 15.3. Спектр весов кода, дуального коду БЧХ длины 2™—1, исправляющего две ошибки; т нечетно
Примеры. Для п=31 коды <g71 и являются [31, 10, 12]v кодами; для n=127 'g’l, и 7?з являются [127, 14, 56]-кодами; для и=511 'g’j, и ^4 являются [511, 18, 240]-кодами. Спектры весов этих кодов совпадают с теми, которые приведены на
рис. Для /2=511 код 'g’s является-[511, 18, 224]-кодом,и его спектр'имеет вид:
\ Вес Число слов
\ 0 1
224 36 511
256 449 511
288 48 511
Случай (II). т четно. Этот случай вызывает большие затруднения, так как число /,= 1+2* часто оказывается не взаимно простым с 2т—1.
Мы начнем рассмотрение этого случая с частного случая [2™—1, 2m, 2"1-1—2*п/2]-кода с порождающим идемпотентом 6*!+10*з, являющегося дуальным к коду БЧХ, исправляющему две ошибки.
В рассматриваемом случае 3 делит 2т—1, так как т четно и слово кода в общем случае записывается в виде czox*'0*i + + Ь(х)6*3. Его МС-многочлен равен (см. § 8.6)
£ (iw +2(М'-iecl /ecs
Соответствующая булева функция по теореме 20 гл. 8 для всех EeGF*(2m) принимает значения S(£) = Em(Pi£ + (Ps|)3)-
Симплектическая форма равна:
®(5. и)=Г„(Й(Е“п+5ч!)) =
Таким образом, задача сводится к определению размерности пространства нулей функции
₽32 Л2 + Л2"1-’ = (у2 П + yrfm~2 )2, (15.22)
где у2=р2Т *+1 иу4 = р32.
Далее т] является корнем для (15.22) тогда и только тогда, когда т] равно нулю или
^"*-2-1 (15.23)
Сколько имеется в GF*(2m) различных элементов у, удовлетворяющих этому уравнению?
Если со — примитивный элемент поля GF(22)t=GF(2’n), то т]2'”~2-1=.-((от])2т~2-1 = (со2п)2'п-2-1 для всех TjeGF(2m).
Обратно, если т]2”1 2~l=T]i2'n -1, то (tj/tji)eGE(2m-2) Q fl GF (2m) = GF (22).
Следовательно, в GF* (2™) имеется (1/3) (2m—1) элементов у, Удовлетворяющих уравнению (15.23).
Если элемент у имеет вид т]2 для некоторого Т]Е GF (2т), то (15.22) имеет в GF(2m) четыре корня и ранг матрицы В равен
т—2. Вес соответствующего кодового слова равен 2т-‘ или 2m->±2m/2. Если элемент у не имеет такого вида, то нулем функции (15.22) является только ц=0, а вес соответствующего кодового слова равен 2™-1 ±2<ТО~2У2.
Минимальное расстояние дуального кода равно 5, и, используя опять теорему 2 гл. 6, находим спектр весов кода сёг, указанный на рис. 15.4.
i At
0 1
2т~ 1 2>п/2 j 2>-m~2)/2—1 (2(m—+ 1) (2"£ — 1)
2^1—1 2т^—* ) 2(m+2)/2—1 (2m/2 -|- 1) (2™ — 1)
2т-1 (2m-2 + j) (2m _
qW—1 । ^п/2—I ♦ f2(m4-2)/2—1 (2m/2 q \ 3 /
1 i 2m/2 Г—1 2('n-2)/2-l (2(m-2-)/2 _ ц \ 3 J
Рис. 15.4. Спектр весов кода, дуального коду БЧХ, исправляющему две ошибки; т четно
Теперь рассмотрим общий случай кода 'ёг с порождающим идемпотентом Л=1 + 2\ где l<t<(l/2)m. (Случай
( = т/2 проанализирован в гл. 8.)
Слова кода записываются в одной из форм х’0*ь а(х)0*г. или х’0*1+«(х)0*г.. Вес слова первого вида всегда равен 2”г-1, для других получаем симплектическую форму
® Q, = Тт(I (₽+ р2"1-1' ))•
Следовательно, надо найти число элементов ц таких,, что
о = pn2i + р2т~1’ 1]2т-г = (у2« л + ут}2’^-2г) 2\ (15.24)
или, что эквивалентно, число ненулевых ц таких, что
Tj2m~2i-i = (15.25)
Число решений уравнения (15.25) дается ниже в упражнении (7). Из этого упражнения следует, что если (т, i) = (m, 2i)~ s, то (15.24) имеет в поле GF(2m) точно 2® решений при произвольном выборе у. Следовательно, в этом случае код ёг содержит слова только трех весов: 2т-1 и 2т-1 ±2<т+®_2^2 и спектр кода равен спектру кода для нечетного т, выписанному на рис. 15.2.
С другой стороны, если (m, 2i)=2(m, t)=2s., то (15.24) имеет либо 1, либо 22s решений в зависимости от выбора у, и в этом слу-
чае код имеет пять весов, .а именно: 2m-1, 2m~l±2(m+2s~2 * *)/2 и. 2?n-i+2т/2-1. Согласно упражнению (8) минимальное расстояние,-дуального кода 'ё’г1- не меньше чем 5, и, используя опять теорему 2 гл. 6, получаем спектр весов, приведенный на рис. 15.5.
i At
0 1
2m-‘ (2m — 1) {(2s — 1) 2m~Zs + 1}
1 । л (m-±-2s—2)/2 g(m—2s—2)/2 (gm (g(m—2s)/2 ^1)/(2S-|-1)
gm—1 _|_gm/2—1 g(m-f-2s—2)/2 (gm _ ц ^m/2+ 1)/(2s + 1)
Рис. 15.5. Спектр весов кода с порождающим идемпотентом 6Ч+Й*;г, где-/1=1+2\ Ki<-±- т, (т, 2i)=2(m, i)=2s
Упражнения. (7). Пусть т — четно, a g — произвольно. Доказать, что число целых чисел х, лежащих в диапазоне ^х^2т—2 и удовлетворяющих сравнению
(2т~2'—1)х = (2г—l)g- inod2m—1, равно:
(i) . 2s — 1, если (tn, 2i) = (т, i) = s.
(ii) . 22s—1, если (tn, 2i) = 2(tn, i) = 2s и (2s +l)|g-.
(iii) . О, если (tn, 2i) — 2(m, i) = 2s и (2s + iXg.
(8) . Используя обобщение Хартманна—Тзенга для границы. БЧХ (упражнение (24) гл. 7), доказать, что минимальное расстояние кода <g7 равно по меньшей мере 5.
(9) . Доказать, что числа 2™—1 и 2г+1 взаимно просты тогда и только тогда, когда (т, i) = (m, 2i). Если (tn, 2i)=2(m, i), то, числа 2г + 1 и 2т—1 имеют нетривиальный общий делитель.
(10) . Показать, что код, дуальный [2™, 2™—1—2т, 6] расширенному коду БЧХ, исправляющему две ошибки, имеет параметры: [2™, 2m+1, 2т~1—21т/21].
*15.5. КОД КЕРДОКА И ЕГО ОБОБЩЕНИЯ
В этом несколько длинном параграфе мы собираемся исследовать один частный случай подкодов РМ кода второго порядка $(2, т). Пусть & обозначает множество симплектических форм, ^('ё, л)> соответствующих словам этого подкода (см. уравнения (15.4) и (15.19) )1. Тогда ранг каждой ненулевой формы из не-Меньше, чем 2d и ранг суммы любых двух различных форм из 91'
1 Уместно напомнить, что одна снмплекстическая форма соответствует-
2™+г словам подкода, так как каждый подкод, по определению, состоит из.
сбъединения смежных классов и существует взаимно-однозначное соответствие-
Между формами и смежными классами. (Прим, ред.)
также равен по меньшей мере 2d, где d — некоторое фиксирован-яое число в диапазоне В гл. 21 мы увидим, что
максимально возможный объем такого множества ЗР равен
। 2(2t+i) (t-d+D, если m = 2f+lj (15.26)
| 2(2i+i) p-d+2)^ если m = 2/ + 2. (15.27)
Следовательно, максимально возможный объем соответствующего подкода в $?(2, т) равен 21+,п|5’|. В гл. 21 мы найдем также число симплектических форм каждого ранга в множестве максимальной мощности и, следовательно, спектр весов соответствующего кода.
Оказывается, что при нечетном т эти максимальные коды линейны; однако для четного т они оказываются нелинейными и содержат в качестве частных случаев коды Нордстрома—Робинсона и коды Кердока. Результаты, изложенные в этом параграфе, принадлежат Дельсарту и Геталсу.
Случай (I). т — нечетно; m=2t+l. Типичное слово кода ,Й?*(2, т) записывается в виде
♦ t
feв0 + а0До©; + J? Zj-==l +2''.
/=>
Многочлен Мэттсона—Соломона для такого слова равен t
S (To2)s + Z W
sec, /=1 sec^
так что соответствующая булева функция и симплектическая фор-’ма имеют вид
5© = 2^+1Ы2/+1) /=о
® (£, л) = X =
/•=>
= Л#+1 (I Тв (т])),
где
LB (n) = V (у,- Т|2' 4- (у, T])22t+1 ').
/=1
(15.28)
(15.29)
Полагая в (15.28) первые или последние d—1 элементов у, равными нулю, получаем симплектическую форму, ранг которой не меньше, чем 2d. Ясно, что сумма двух таких симплектических форм также имеет уг=0 для тех же значений индекса i. (Это и обусловливает линейность соответствующего кода.)
Теорема 15. Если у!=у2= =yd-i = O, то ранг симплекти-•ческой формы (15.28) не меньше чем 2d.
Доказательство. Если У1=У2= — Td-i=O, то t
lb h) = £ П)22<+1~') = (Ев (т])) 2d,
i=d
где степень L'n (ц) не превосходит 22(*-d>+1.
Следовательно, размерность пространства элементов rq, для которых Ев(т])=0, не превосходит 2(t—d)+l, так что rank В >2/-1-1— 2(t—d) —l=2d. •
Теорема 16. Если yt-d+2=yt-d+s= —yt—0, то ранг симплектической формы (15.28) не меньше чем 2d.
Доказательство. В этом случае показатели степеней, с которыми элемент ц входит в функцию Ев (ц), равны 2, 22, ..., 2/-й+1, 2i+d,. t-j-d
2i+d+1, ..., 22t. Пусть Р=т]2 • Тогда показателями степеней р в
Лв (л) будут 1, 2, ..., 2*-d, 2i-d+2, ..., 22(i-d>+2. Наивысшая степень Р не превосходит 2(t—d)+2, так что размерность пространства элементов [3, для которых Ев (т])=0, не превосходит 2{t—d) +2. Так как m нечетно, то и эта размерность должна быть нечетной (см. уравнение (15.20)), и, следовательно, она не превосходит 2(t—d) + l. Таким образом, ранг матрицы В не меньше чем 2^+1—2 (t—d) — 1=2сЕ •
Полагая yi = 0, мы удаляем из кода идемпотент 0*?.. Поэтому в качестве следствия из теорем 15 и 16 имеем.
Следствие 17. Пусть m—2t+\, и пусть d — любое число в диапазоне Тогда в коде Й?(2, т) существуют два подкода
с параметрами [2т, m(t—d+2) Т 1, 2™”1—2m-d-1]. Они получаются путем расширения циклических подкодов в 5?* (2, т), порожденных идемпотентами t
©0+©; + 2©|. (15.зо>
/=d
И
t—
®o + @i+ X (15.31)
Z=1 7
Эти коды содержат слова весов 2т~1 и 2™-1 ±2m-h~l для всех h в Диапазоне
Доказательство. Мы видели, что ранги всех ненулевых симп-лектических форм, соответствующих кодовым словам, не меньше-чем 2d. Тогда утверждение вытекает сразу из теоремы 5. •
Замечание. Согласно формуле (15.26) эти коды имеют максимально допустимую мощность. Спектр весов этих кодов может быть вычислен с помощью результатов, приведенных в § 2.1.
Случай (II). m = 2t-T-2. Мы опять начнем с поиска максимального по объему множества симплектических форм, ранг которых не меньше чем 2d, и такого, что ранг суммы любых двух Различных форм также не меньше чем 2d. Но в данном случае-Для четного m это множество уже оказывается нелинейным. Мм
•начнем со случая d— (1/2)т и построим коды Кердока. Прежде чем давать определение, дадим на рис. 15.6 краткое описание этого семейства кодов (при т—4—см. рис. 2.19).
Для четного т, т^4, код Ж (т) является нелинейным с параметрами:
длина и=2т;
мощность 22т кодовых слов;
минимальное расстояние 2,п~1—2<т~2>Р.
Первыми тремя кодами семейства являются (16, 256, 6), (64, 212, 28) и (256, 216, 120)-коды; первый из них эквивалентен коду Нордстрома—Робинсона Общий вид слова из кода Ж (т) задается уравнением (15.34). Ж (т) является систематическим кодом. Спектры весов и расстояний совпадают и приведены на рис. 15.7. Кроме того, АН (1, т) с с: Ж (т) с: 31 (2, т). Слова каждого фиксированного веса в коде Ж (т) образуют 3-схему.
Рис. 15.6. Свойства кода Кердока
i At
* 0 1
2m—1 2^т~21/2 2m (2m~1 - 1)
2т~1 2^4-1 2
2т~1 । 2^т~232 2m(2m-l _ j)
2т 1
Рис. 15.7. Спектр весов (или расстояний) кода Кердока Ж (т)
Определение кода Кердока JZ’(m). Код Ж(т) является объединением кода <%(1, т) и 2т-1—1 смежных классов кода Й?(2, т} но 5?(1, т). Смежные классы выбираются так, чтобы они имели максимальный ранг т и чтобы ранг суммы любых двух смежных классов также был равен т. Иными словами, булевы функций, соответствующие этим смежным классам, являются максимально нелинейными квадратичными функциями (см. § 14.5) такими, что сумма любых двух из них опять является максимально нелинейной. Так как имеется всего 2"1-1 таких смежных классов (или со--ответствующих симплектических форм), то согласно (15.27) мощ-•ность кода Ж(т) имеет максимально возможное значение.
Мы будем записывать слова кода Й?(1, т) в виде |u|u-rv|, •где ие^?(1, т—1) и vg$(0, т—1) (см. теорему 2 гл. 13). В этих 'обозначениях код 5?(1, т) состоит из слов
| а\ а@0-\-агх1> 0* | b | Ь0О + 0^x60*(15.32)
:где а, аъ b, bi^GF(2) и 0sCi^2’"-1—2.
Код Кердока Ж(т) определяется для m=2t+2^4 как код, ’состоящий из кода <%(1, т) и pt=22t+1—1 смежных классов кода
$,(2, т) по коду 5?(1, т), для которых в качестве представителей смежных классов выбираются
t / i \
о |х'£®;.|°! %'©;+ ^©;. (15.зз>
1=1 \ 1=1 /
для всех /= 1, р, где, как обычно, /г=1 + 2г. В качестве w& всегда выбирается нулевое слово.
Таким образом, типичное кодовое слово из Ж(т) записывает-
ся в виде
t
| а | а ©0 + в, + е х> V©* | b | b ©0 +
г=1
z t
+ at хг10* + ел:'1 ©* + ^©*
V 1=1
(15.34)5
где е=0 или 1 и 1^/^р.
Упражнения. (11). Пусть — код, состоящий из линейного кода Ж и I его смежных классов, в качестве представителей которых выбраны элементы w,:
= (w7-+5?).
/=1
Таким образом, |'g’| = (./+ 1) \Ж\. В групповой алгебре коды
Ж и представляются соответственно элементами (см. § 5.5)
i
Н = Jzv и = zwiH.
Nt&e /=1
Доказать, что спектр расстояний кода равен спектру весов множества элементов
Н+7ТГЁ г‘,//+7УтЕ S г^‘Н-г=1 г=1 /=Н-1
(12). Доказать, что линейный код, порождаемый кодом Ж(т), равен коду Й?(2, т).
МС-многочлены для левой и правой половин элемента wj, задаваемого выражением (15.33), соответственно равны:
M2) = v У(т2)5 i=l scCj. И
^(г) = У У(угГ+У (Yz)s, i=l secz. SEC,
где yeGT*(22i+1) зависит от j.
Пусть элементы поля GF(22t+l) выписаны в некотором фикси-рованном порядке {go=O, £д). Тогда
= | L (g0) | L (gj, L (^) | R (g0) | R (U R Ы где для всех
^(^)=2T«+i(v^+’:
t
R (gv) = 2 T2(+1 (y U2*+1 + ^t+i (Y U i=l
Если элементы поля GF (22t+2) записать в виде пар (g, е), где Z^GF(22f+1), а е равно 0 или 1, то координаты вектора w, (или любого другого вектора из Й?(2, т)) можно нумеровать этими парами, полагая в них е=0 для левой половины вектора w, и е= = 1 — для правой.
Например, если /=1 (так что длина вектора w, равна 16), то элементы поля GF(24) могут быть записаны в виде пар (g, е), где £eGF(23), а е равно 0 или 1, как это показано на рис. 15.8. Здесь у — примитивный элемент поля GE(24), причем у4-т-у+1 = 0, а а — примитивный элемент поля GF(23), причем а3+ат1=0.
У
4-последовательность
о
1
У У2 У3 У4 У3 У6 У2 У8 Vs У10 У11 У12 У13 У1*
О I О О О 1 О О 1
1 о 1 о 1 1
1
о о
1 о о
1 1 о
1 о
1 1
1
1 о о
о о о
1 о о
1 1 о
1 о
1
1
1
1 о
о о о о
1 о о
1 1 о
1 о
1
1 1
1
о, о 1, о а, О а2, О
О, 1 а3, О а4, О а2, 1 а3, 1 а6, О
а, 1 а5, О а4, 1 а5, 1 а6, 1
1, 1
О
Рис. 15.8. Запись элементов поля GF(24) в виде пар i(E, е), где £e=GF (23)
На рис. 15.9 приведен конкретный пример, в котором сначала (рис. 15.9(a)) представитель смежного класса w7 и некоторые, слова кода Й?(1, 4) записаны как слова циклического расширенного кода с общей проверкой на четность, помещенной в позиции с номером оо, а затем (рис. 15.9(b)) указана нумерация координат этих же слов с помощью пар (g, е), geGF(23), е=0 или 1. Для перехода от записи на рис. 15.9(a) к записи на рис. 15.9(b)
надо пользоваться рис. 15.8. Отметим, что выбранный для рис. 15.9 элемент w7 равен w7=x46*i + 6*3+6*5 и, следовательно, лежит в коде Й?(2, 4).
(а) Как слова расширенного циклического кода:
ОО 1 У yi У3 У11 Уъ У8 У4 У8 У9 У10 У11 У12 У13 Ум Наименование
0 1110011101 0 1 1 1 0 w7=x4+0*i+0*3+6*s
0 00010011 [0 1 0 1 1 1 1 a=0*i
0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 Ь={/46*1
1 11101100100 1 000 c=0o+iO'*i
(Здесь 0*i—идемпотент с блоковой длиной 15, см. упражнение (7) гл.
(Ь) .. Нумерация парами (g, е), geGF(23), е=0 или 1.
ОО 1,0 а,0 а2,0 а8,0 а4,0 а5,0 а6,0 0,1 1,1 а,1 а2, 1 а3,1 а4,1 а5,1 а6,1
0 1 1 1 0 1 0 0 0 0 1 1 1- 1 1 1
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 1 1 0 0 1 0 I 0 0 0 1 1 0 1
1 1 1 1 1 1 1 1 0 0 0 0 0 , 0 0 0
Наименование
w7 = J 0 | ©з ] 0 ] 6j -f- &з | а = | 0 | 0 | 1 | 60 | ь= । о I %2е] 11 । бо + ^е* I с = | 1 1 ©О I 0 1 О I
(Здесь 6*1 — идемпотент блоковой длины 7, см. упражнение (5). гл. 8.)
Рис. 15.9. w7 и некоторые слова кода <%(1,4)
Теперь будем искать булеву функцию (v) =f т(щ, ...» ^гг+г), задающую wy, т. e. функцию, для которой =wj (равенство векторов длины 22f+2). Будем полагать, что g равно элементу поля GF(22*+!), соответствующему вектору (щ, ..., ^2f+i), и что е= ~v2t+2. Тогда функция f задается равенством
fv (vlt..., v2t+2) = fv (g, e) = V 71i+i (y g) + e T2i+, (у g) r=l
и, конечно, fv (v)=wj.
Основной результат раздела дается следующей теоремой..
Теорема 18. /v(v) является максимально нелинейной функцией, и при у=#б функция f6(v)+fv (v) также максимально нелинейна.
Доказательство. Для доказательства достаточно показать, что ранги симплектических форм, соответствующих функциям fv(v) ъ fv(v)+f6 (v), равны 2/4-2. Согласно равенству (15.5) симплек-тическая форма, соответствующая функции /v(v), равна:
®?(& еД (т), e^ = £T2H.Jv2Mg2in + ^)) +
г=1
+ ^24+1 (т (61Т] + e2g)) — 7\t-H (у2 ? г1) +
+ Т21+1 (уЮ ^244-1 (у n) + T2t+i(y(ei п + е2?))- (15.35)
Для того чтобы определить ранг , надо найти размерность ^подпространства пар (т), е2) таких, что v((£, ei), (т], е2))=0 для всех (g, ei). Выбирая (g, ei) = (0, 1), приходим к выводу, что T2t+i (ул) =0 и, следовательно, ^v=724+i((yg) (уг]те2)). Таким образом, должно выполняться равенство уг] + е2=0, что приводит к следующей цепочке равенств:
ут]-ге2=0;
^Т24+1(У11 + е2) = 0;
T^-^+i (е)= 0’
= 0 (так как 2t -j- 1 — нечетно);
= 7’24+i (у2 ? *1)’
и, следовательно, элемент ц должен быть равен 0.
Таким образом, единственной парой, для которой ^т((^, ei), (т), 82))=0 при всех (g, ед), является (ц, е2) = (0, 0). Следовательно, ранг формы равен 2t-{-2.
Остается доказать, что ранг формы при у=И=б также
равен 2t + 2. Доказательство этого факта аналогично предыдущему и предоставляется читателю. •
Спектр весов кода Ж(т). Согласно теореме 5 смежный класс кода Й?(1, т) ранга т содержит 2т векторов веса 2’"-1—2™/2~1 и 2™ векторов веса 2m-'1-|-2m/2-1. Сам код Рида—Маллера первого порядка содержит 2т—2 слов веса 2m-1, слова 0 и 1. Это приводит к спектру весов, выписанному на рис. 15.7. Согласно упражнению (11) и теореме 18 спектр попарных расстояний также ра-. вен спектру на рис. 15.7. В частности, Ж(4) эквивалентен коду Ж16, так как Ж\Ъ единствен (§ 8 гл. 2).
В § 15.6 будет описан другой нелинейный код, код Препараты ^(т), который обладает тем удивительным свойством, что его спектр весов (или расстояний) равен преобразованию Мак-
Вильямс от спектра весов кода Л'(т). Иными словами, согласно (5.13)
22m = Рг (0) + 2m (2m—1 — 1) {Pt (2m~l — 2<m-2)/2) +
+ Рг(2т-' +2('и~2)/2)} + (2т+1—2)Pi(2m~1)—Рг(2т), (15.36)
где Pi(x) '— многочлен Кравчука (§ 5.2). Легко проверить, что минимальное расстояние кода ЗДт) равно d'=6. Тогда из теоремы 9 гл. 6 сразу вытекает, что слова каждого фиксированного веса в коде Ж(т) образуют 3-схему (так как $ = 3).
Случай (II). m=2t+2 (продолжение). Рассмотрим теперь общий случай, когда d — произвольное число в диапазоне 1^ (1/2) т. Нелинейные коды, к описанию которых мы переходим, были открыты Дельсартом и Геталсом и обозначаются через 3)3 (т, d). Вот их определение.
Положим для d=m/2 код ‘g’ равным <®’=Й?(1, 2/+1), а для l^d<Zm/2 выберем в качестве <g’ [22Ui, (27+1) (t—rf+2) + l, 22t—22(~гг]-код, задаваемый выражением (15.31) следствия 17. Пусть wo=O, wb ..., wg — векторы, определяемые условием (15.33), и пусть vo=O ... 01 ... 1.
Определение. При l=Cd^ (l/2)m=/-|-1 код 3)3 (т, d) определяется как множество векторов вида
|c(x)|c(x)| + w7 + ev0:
(15.37)
где Osgj^p, и е равно 0 или 1.
Теорема 19. При т=2/+2^4 код 3)3 (т, d) имеет длину 22*+2, минимальное расстояние 22*+’—22ul-d и содержит 2(2<+i)(i-d+2)+2t+3 слов. Если d=l, то 3)3 (т, 1)=‘%(2, т), а при 2^d^(l/2)m код 3)3 (т, d) является нелинейным подкодом кода 5? (2, т).
Доказательство. Всего имеется 2<2*+1)(г-Щ-2)+2г+3 слов вида (15.37). Тот факт, что все они различны и что действительно минимальное расстояние между ними равно 22(+1—22f+1-d, будет следовать из доказываемой ниже теоремы 20. 9
Заметим, что 3)3 (m, d) содержит код Кер дока У)(т) в качестве подкода. Это происходит потому, что множество векторов 1с(х)\с(х) | -Pevo содержит все слова кода Й?(1, 2Z + 2). Кроме того, код 3)3 (т, (1/2) т) равен коду Ж’(т). Таким образом, рассматриваемые коды являются обобщением кодов Кердока. Согласно упражнению (12) линейный код, порожденный кодом 3)3(т, d), совпадает со всем кодом Й?(2, т).
Несколько первых кодов семейства 3)3(т, d) приведены на рис. 15.10; здесь k равно двоичному логарифму числа кодовых слов и б равно минимальному расстоянию кода.
Код 3)3(tn, d) содержится в Й?(2, т) и является объединением некоторых смежных классов кода (2, т) .по коду Й?(1, т). Рассмотрим смежный класс, содержащий слово, задаваемое выра-
£0& (m, d) б Наименование
т d п k
4 I 16 И 4 Л(2, 4)
2 16 6 6 Ж (4) = Nlt
6 1 64 22 16 /%(2, 6)
2 64 17 24
3 64 12 28 Ж (6)
8 1 256 37 64 Я(2, 8)
2 256 30 96
3 256 23 112
4 256 16 120 <ЗГ(8)
Рис. 15.10. Параметры (п, 2ft, б — минимальное расстояние) первых кодов S)& (т, d)
жением (15.37). Симплектическая форма, соответствующая этому классу, равна:
И), (Т), е2)) = Т24+1|У +
\ г=1 /
+ ^гн-!(у2^1) + T2t+1 (уЮТи-н (уч) + 'г2(+1(У(81П-|-е2Ю)- (15.38)
Первый член в этом равенстве обусловлен частью |с(х) [с(х) | в соответствии с выражениями (15.28) и (15.29), а остальные — вектором Wj в соответствии с выражением (15.35). Элемент у соответствует вектору wj. Число различных симплектических форм такого типа равно (22*+’)/-d+2. Из (15.27) и следующей ниже теоремы вытекает, что это число является максимально возможным.
Основное свойство кодов рассматриваемого класса описывается следующим образом.
Теорема 20. Ранг любой симплектической формы вида (15.38), так же как и ранг суммы двух таких форм, не меньше чем 2d.
Доказательство. Перепишем (15.38) в виде
(& ei) (Л> 82)) = T2t+1 (g L (л)) + T2i+1 (g Ly (n)) +
+ T2i+i (у (пп + чЛ)).
t—d+i
где Т(г))= V (угт)2г + (угл)22<+1~');
1=1
Tv(i])-=y2r]-|-y T27+1(yr]). (15.39)
Достаточно показать, что ранг суммы ^v+^6, у=И=б, двух та-' ких форм не меньше чем 2d. Так как <g’ — линейный код, то T2ui(^(il))+r2i+i(?b/(il))=T2t+i(gL"(T])), где L" задается ра
венством (15.39) при соответствующем выборе {у{}. Следова-
£i)- Ob £2» + ®б((В, £i), (т £г)) =
= ^2f+l (? L (1])) + J^2f+1 (? ('*])) +
+ Tit+1 (£ L6 (Л)) + Т2(+1 ((у + б) (е, т] + е2 g)). (15.40)
Нам удобно определить функцию (1, Л)=^т((£, 0), (л>0)) + -Ь^6((£, 0), (т), 0)), которая представляет собой симплектиче-•скую форму от g, iqeGf (22*+1). Тогда
= (15.41)
где t
Ьв(п)= У (тг n2'+ (Ti il)22i+I~Z) + (т2 + 62) Т] + г—1
+ V Т 2(+1 (у Т]) + б Т 2t+1 (б Т]).
Пусть ранг формы (g, rj) равен 2/г. Покажем, что 2/i^2J—2. Рассмотрим разложение 21+1
Лв(т])== У AjT)2'.
г=0 Тогда
Л,г = уг+2*-|-§т+2г (15.42)
для t—d-\-2^i^d+d—1.
Будем предполагать, что рассматриваемая булева функция имеет канонический вид, задаваемый теоремой 4. Ее МС-многочлен определяется выражением (15.11). Нетрудно догадаться, что соответствующая симплектическая форма равна Т21+1(^в (т]))> где ,
£в (»]) = Т2t+1 + ₽•* Т24+1 15’43)
/=1
и аь ..., ak\ |3i, ..., |3п — линейно независимые элементы поля GF(22i+1).
Сравнивая (15.41) и (15.42), видим, что для t—d+2^i^t+ +d— 1 h
vl+2* + §1+2* = £ (a> 02* + a2*0y) _
h
=2 «;+2Z+₽;+2t+(a> + p,-)i+2£-/=1
Если положить
s. = vl+2* + §1+2* + V(aJ+2* + 01+2* + (a. + p .)1+2*)J
1=1 то станет ясно, что
Si = 0 (15.44)
Для t—d + 2^:i^t-Jrd—-I.
Определим U как множество элементов {-у, 6, |3i, cn + |3i, ....
ah, |3h, ct/i+|3Л), так что
s. = y ai+< (15.45)
aeu
Пусть V(U) — наименьшее подпространство в GF (22t+i), содержащее все множество U. Ясно, что dim V(U)^.2h-'-2. Пусть a(z) — линеаризованный многочлен, соответствующий множеству U (см. § 4.9); он задается равенством
2Л+2
°U)= П (z + A)= V^z2'-ЯбГ(П) г—О
Заметим, что ао#=О (так как в противном случае o(z) — полный квадрат). Тогда, используя (15.45), получаем:
О = £ а ааг (а) = а^г V а1+2' ф-аеи аеи
+ of 2 a1+2*+‘ + ... + а^+2 2 al+2f+2ft+2 = аеи аеи
2/г4-2
-о^<+ £<Л+,. <1МС’
/=1
Теперь предположим, что 2h + 2^.2d—2, и придем к противоречию. Это и будет служить доказательством того, что 2/z-j-2> >2d—2 или 2h^2d—2, как и утверждалось.
Полагая в (15.46) i=t—J+1 и используя (15.44), заключаем, что st-d+i=O. Полагая затем i=t—d, ..., приходим к заключению, что s£ = 0 для всех O^i'^+d—1. Но so=y2 + 62#=O, что и дает противоречие.
Таким образом, ранг ограниченной формы не меньше, чем 2d—2. Если ранг формы равен 2d или больше чем 2d, то этим же свойством обладает и ранг +й?в> и все доказано. Поэтому предположим, что ранг формы равен точно 2h=2d—2. Нам необходима следующая лемма.
Лемма 21. Пусть ^((g, 81), (т), 82)) — симплектическая форма вида
®((£, е1)> (П. 82)) = T2t+i(gL(T])+₽(82g + 81T])),
где L(f]) — линеаризованный многочлен над GF(22t+l) и |3е eGE(22'+'). Пусть <Г(£, n)=^((g. 0), (П. 0))=T2i+iUI(n))-Тогда, если уравнение L (т]) = |3 не имеет решений в поле GF(22i+1), то rank^=rank^/+2.
Доказательство леммы. Для того чтобы определить ранг формы S3, надо знать число пар (rj, 82) таких, что ^((g, 81), (т), 82)) — = 0 для всех (g, 81). Полагая (g, 8i) = (0, 1), видим, что Ти+\ (|3т]) =0. Таким образом, ^=7^+1 (£(Ь(г)) +|3е2)), и должно выполняться равенство Т(т]) +|38.2=0. Если уравнение L(i]) —13 не
имеет решений, то единственной возможностью является 62=0. Так что множество корней задается условием
{(П> 0):T(T]) = T2i+j(pi1) = 0}.
Из (15.20) далее имеем: rank ^'=2/-|-1—dim (ядро L(t])), и, следовательно, rank.®^2/ + 2—dim (ядро L(t])). Таким образом, ранг формы $ больше ранга формы дЦ', т. е. rank^= = rank ЗУ2 (так как он не может быть больше этой величины). Это завершает доказательство леммы. ®
Возвращаясь к доказательству теоремы, напомним, что формы gj и д' задаются равенствами (15.40) и (15.41) и что |3=у+б. Чтобы завершить доказательство, мы должны доказать, что если ранг формы равен 2d—2, то уравнение Lb (tj) =у-!-б не имеет решений в поле GF(22i+1). Предположим, что y + 6 = Lb (tj) для некоторого T)eGF(22f+l). Тогда из равенства (15.43) следует, что y-i-б линейно зависит от щ, ..., щ; |3i, ..., |3/г, т. е. для некоторых a:,, b,eGL(2) выполняется равенство
h ft
У + 6 = £ (ai a-i + &Л₽у) = 2+ b} + bj + а} /=1 /=1
Обозначим через U' множество элементов:
П' = {у4~б, <44-^1?, Pi 4- ai vai 4* Pi 4* (°г 4~ ^i) ?>•••»
ah 4" bfi у, Pft 4” ah У> ah 4- pft 4“ (ah 4- bh) y},
а через V(U') — наименьшее подпространство поля GF(22f+1), содержащее U'. Очевидно, что dim V(U') ^.2h—2d—2. Определив далее величину
<= 2 “1+аг-new
легко непосредственно проверить, что s'i=Sj. Тогда, повторяя те же самые рассуждения, что и выше, заключаем, что з,=0 для всех + d— 1. Но опять so¥=O, и получаем противоречие. Следовательно, наше предположение о том, что у-гб=Ав (г)), неверно, что и завершает доказательство теоремы. •
Из теоремы 5 вытекает, что возможными значениями расстоянии для кода (т, d) являются: 0, 2™-1, 2т и 2m~l±2m~h~l при d=^L^-;-l.
В § 2Е8 мы покажем, как вычисляется спектр расстояний этого кода. Спектры расстояний для частных случаев d—f+1 и d=t приведены на рис. 15.7 и 15.13.
Упражнение. (13). Доказать, что ЯУЗ(т, d+1) представляет собой объединение непересекающихся сдвигов кода ®^(m,. d).
*15.6. КОД ПРЕПАРАТЫ
Теперь мы опишем другой нелинейный код, код Препараты ^(т), который обладает тем свойством, что его спектр весов (или расстояний) равен преобразованию Мак-Вильямс от
спектра весов кода Кердока {т) и задается равенством (15.36). Код Препараты, конечно, не является дуальным к коду Кердока в юбычном смысле, так как оба эти кода нелинейны.
Аналогично кодам Кердока код Препараты Д(т) строится как х>бъединение некоторого линейного. кода П в —2, т) и
2т~’—1 смежных классов кода <Й(т—2, т) по П. Напомним, что код Й?(т—2, т) является расширенным кодом Хэмминга и дуален коду ^?(1, т).
Согласно теореме 2 гл. 13 код 5?(т—2, т) состоит из слов |u| u + v|: вес вектора и четен, ve5?(m—3, т—1),
т. е. из кодовых слов вида |Л(1) |/г(х) |/г(1)-Н&(1) |/г(х)+£(х) (1 + + 61) |, где h(x) и k(x) произвольны.
Определение. Код Препараты определяется для четного т, m=2t-'r2^4, как код, состоящий из линейного подкода П кола —2, т) и р.=2™-1—1 смежных классов кода —2, т)
по подкоду П. Подкод П состоит из слов |g(l) |g(x) (1 + 6i) |f (1) + +&(1) |g(x) (1 + 61) (l+01+бз) j, где f(x) и g(x) произволь-
ны, а смежные классы.задаются представителями
w,- = | 11X'10 |а+ех |, / = 1, 2,..., щ (15.48)
Таким образом, размерность кода П равна 2m~I—1—(т—1)4-4-2”i- 1—1—2(т.—1) =2™—3m+1. Код П является [16, 5, Sj-кодом, если т=4, и [2™, 2т—3m + 1, 6]-кодом, если 6.
Словами кода &(т) являются следующие 2h векторов, где Ji=2m—2т-.
l^(I) + «lg.(x)(l+61) + axq/(i) + g(l)|g(x)(l+ei) + + f(x)(l+.ei + e3) + ax'61|, (15.49)
где l^/^jx и а равно 0 или 1 (см. рис. 15.12).
Первый из кодов Препараты совпадает с первым кодом Кердо-ка (и, следовательно, эквивалентен коду Нордстрома—Робинсона Лдб).
Лемма 22. ^(4)=Ж(4), т. е. код Кердока и код Препараты .Длины 16 представляют собой один и тот же код.
Доказательство. Примитивные идемпотенты длины 7 равны ©о, 6] и 63, причем i0*i = 63; 6*з=6г, 60+61 + 6з=1. Таким образом, П состоит из кодовых слов
k(i)kW(6o+63)l/(i)+g(i)lgW(Po+63)+fWeel= =lg(i)|g(i)eo+4i^e;|f(i)+g(i)|f(i)0o+
+ g(l)60 + o1xil6i|.
Следовательно, 77=5?(1, 4).
Согласно уравнениям (15.33) и (15.48) представители смежных классов для кодов JSf (4) и £4(4) соответственно равны:
w^)=lo|x'-e3’|o|x'|0;+03‘;
w?.(^) = l 11 х/|о | х'ех|-
Их сумма равна
11 |^(е0+е;) |oix/e,|
и представляет собой слово из кода Й?(1, 4). Следовательно, w, (X) и являются представителями одного и того же смежного класса по коду Й?(1, 4). Таким образом, 5*(4) =.%’(4). *
Упражнение. (14). Доказать, что линейный код, порождаемый кодом &(т), равен [2т, 2т—2т + 1,4] -подкоду кода Sl(m—2, т), состоящему из слов вида |F(1) |F(x) |g-;-B(l) + G(1) |ебо + + Л'(х) + G(x) (1 I-61 + 63) |.
Лемма 23. Слова кода П' равны
| с | с б0 + с± х1' б’ + с3 х1* б* | d | d б0 -4- dL 6* + с xis б* |,
где с, Ci, с3, d, dt равны б или 1 и ih i3, /i&{6, ..., 2™-1—2].
Доказательство. Код П можно записать в виде n=s^i + s^2r где и состоят соответственно из векторов вида
|о.о7(1Ш(Х)(1+е1+б3)|,
.g'(i)Ig'(%)(1+et)|g(1) |g(%)(1-}- 6j|.
Тогда л^г1- и состоят соответственно из векторов
| с | hy (х) | d | d б0 dt х^ б* 4- с3 х1> б*|,-
I 1 (вл + е2) б0 + h (х) + q хС б* |е2| h (х) |.
Следовательно, (см. упражнение (33) гл. 1), в коде П1- — =л^1± n«s^2L должны содержаться векторы с=е\\ h1(x) = (e1-}r +е2)бэ-;-/г(х) + с1Хг'б*1 и т. д. Из этих уравнений следует, что код Л1 состоит из векторов, перечисленных в формулировке леммы. •
Отметим, что <%(1,
<=Й?(2, т) (см. рис. 15.11).
Теперь мы перейдем к основной теореме данного раздела.
Теорема 24. Спектр весов (или расстояний) {Вг} кода 5s (m) равен преобразованию
Мак-Вильямс от спектра весов кода ffl(m), и его производящая функция равна:
/п
22mV Вг-2г = (1+z)2'” + 2m(2m-1—1) {(1-bz)2"1 ’+2<m 2,/2>С Ео
X (1 -гг"-1-’+ (1 + 1 +
+(2»+i-2)(1- ТО -г)< (15.50»
Иначе говоря, Вг определяется равенством (15.36).
Доказательство. Спектр расстояний кода £Р(т) равен согласно упражнению (11) спектру весов элемента групповой алгебры вида
г"1-1 -1
+ £ *’,Н+-Дг S г"'+"'й-
i=1 где
H = YzV-
ven
Преобразование Мак-Вильямс этого спектра весов задается набором чисел
л;-^ЬгЕ Оа:,<2“
wt (u)=Z
где суммирование ведется по всем векторам и длины 2™ и веса / (по теореме 5 гл. 5).
Мы покажем,* что A'i=0, за исключением случаев, когда I равно одному из чисел О, 2та~1±2(та~2)/2, 2т-1 или 2™, т. е. за исключением I, равных одному из возможных значений веса в коде Х’(т); точнее, мы покажем, что множество чисел A'i равно спектру весов кода Ж(т').
Рассмотрим отдельно вклад, вносимый в A't элементами ue5?(l, tn), ug/I1—5?(1, tn) и и^/71.
Случай (I). ue5?(l, tn).
Лемма 25. Если не5?(1, т), то %u (-D) = \ &(т) |.
Доказательство. Так как ^(т)ей?-*-(1, tri), то (—1) uv=l для всех •
Следствие 26. Вклад слов кода 5?(1, т) равен 1 для числа А'о, 1 для числа А'2т и 2™+'—2 для числа
Случай (П).и^ЕП-1-.
Лемма 27. Если П±, то % (D) =0.
Доказательство. Так как %u(f/)=0, то
Х„(г’‘+">Я) = (-1)“<’>+’Лх„(Н) = 0. •
Случай (III). ug/71—$(1, т). Этот случай сложнее. Нам надо вычислить величину
XU(£) = XU(#) Н +
2т~'-1
-1— У
—2
1
от—2
кг</<2т“1
(_ l)u(wi+"7)\
Предположим, что скалярное произведение u-w; четно для а значений индекса i и нечетно для р его значений. Тогда, очевидно,
2m-'-l = a + p; £ ( — l)u wt =a—р.
1=1
Кроме того, произведение u-(wj+wj) четно для (2)^(2} пар (wi, wj и нечетно для ар пар. Таким образом,
— 1
Найдем теперь возможные значения для числа р.
Лемма 28. Пусть s+5?(l, т) — смежный класс кода Пг по коду 5?(1, т). Для любого вектора и из этого смежного класса вы-1 wiu 1 i\ w/ s
полняется равенство (—1) =(—1)
Доказательство. u=s + r для некоторого ге5?(1, т);
(— 1) w'r =1. •
Размерность кода П- равна 3m—1, а размерность кода 5?(1, tn) равна т+1, так что число рассматриваемых смежных классов равно 22т~2. Выберем в качестве представителей смежных классов векторы
s=। о | хг> 6,+с3 х*з е; 101 с3 х1> 0* |, где ci, c3eGF(2) и i3^2m~l—1.
Рассмотрим скалярное произведение векторов s и w,= = 11 |xJ‘|0|xT)i|. Произведение х’0ь хЧ)*3 всегда четно, так как код дуальный к коду, порожденному идемпотентом 0ь порождается идемпотентом l+0*i=SO*r и, следовательно, содержит под-код с порождающим идемпотентом 0*3. Скалярное произведение будет равно единице, если в многочлене С1Хг’’О*1 + с3х»з0*3 при xi стоит ненулевой коэффициент, и равно нулю в остальных случаях, так что lp=wt(cixii0*1-f-c3x4)*3). Вес таких векторов, как показано на рис. 15.3, может быть равен 0, 2™-2 или 2™~2±2<т-2)/2.
Если р=2’и~2, то а=2т~2 и из (15.51) следует, что Хи(£>)/|^(|т)|=0.
Если р=2™~2±2<т-2)/2, то a=2™-2+2(™-'2)/2—1 и Xu(£>)/|^fm)| = l/2™-2.
Если вес многочлена С1Хй0*1 + с3хгз0*3 равен 2т~2±2(m~2)/2, то вес представителя s смежного класса равен 2ТО-1 ± 2<т-2)/2, так как вес многочлена хМЭ*3 равен 2т~2. Таким образом, смежный класс по коду 5?(1, т) является смежным классом максимального Ранга кода 5?(2, т) по 5?(1, т) й содержит 2т векторов веса
27П-1 + 2(™“2)/2 и 2т векторов веса 2™-1—2<™_2>/2. Вклад этого смежного класса в числа.A'i равен 2™/2™~2=4 для всех /==2’п-1± +2(т~2)/2. Далее заметим, что согласно рис. 15.3 общее число представителей s веса .2™~'1 -у2(''”-2)/2 и веса 2”1-1—2(т-2)/2 равно 2»n-2(2m-i—j). Это завершает рассмотрение случая (III).
Вклады всех трех рассмотренных случаев в числа A'i описываются следующим образом:
Случай: I и ш
Л' 1 0 0
Л;га-1 2m+1 — 2 0 0
1 0 0
Л^т—l+2<m—1)/2 0 0 2m(2m“I —!)
Складывая эти числа, получаем спектр весов кода Кердока,
приведенный на рис: 15.7. Это доказывает, что спектр расстояний кода ^(т) задается преобразованием спектра весов кода Ж(т). Остается доказать, что спектры весов и спектр расстояний кода ZPfm) совпадают.
Используя (15.50), легко проверить, что минимальное расстояние кода &(т) равно 6. Так как для кода Ж(т)' имеем $=3, то согласно теореме 3 гл. 6 код &(т) инвариантен относительно расстояния. 9
Следствие 29. Минимальное расстояние кода &(т) равно 6.
Замечание. Минимальное расстояние и длина кода РР(т) равны минимальному расстоянию и длине расширенного [2'п, 2т—2m—1,6]-кода БЧХ, однако число слов вдвое больше. Мы увидим в гл. 17, что код ^(т) содержит максимально возможное число слов при такой длине и таком минимальном расстоянии.
На рис. 15.12 дается краткое резюме свойств кода ^(т).
Для четных т, т^4, код SP (т) представляет собой нелинейный код с параметрами:
длина и=2то;
объем кода 2п_2то слов; минимальное расстояние 6.
Общий вид кодового слова задается ’ выражением (15.49). Код 3° (т) является систематическим, квазисовершенным и содержит вдвое больше слов, чем расширенный код БЧХ той же длины, исправляющий две ошибки; число слов кода равно наибольшему возможному значению при таком минимальном расстоянии. Спектр весов совпадает со спектром расстояний и описывается равенством (15.36) или (15.50). SA (4) = <7Г(4) = (16, 256, 6)-коду Нордстрома— Робинсона. Кроме того, Ж (т—3, tn)c.£fi —2, m).
Слова каждого фиксированного веса кода &(т) образуют 3-схему (теорема 33).
Рис. 15.12. Свойства кода Препараты <р(т)
Укороченный код Препараты Пусть — код, по-
лучаемый из кода .^(т) путём вычеркивания одной координаты (безразлично какой). В этом разделе мы покажем:
(1) . Спектр весов и спектр расстояний кода &*(т) не зависит от того, какую из координат мы выбрасываем (теорема 32).
(2) . Слова каждого фиксированного веса в. коде 53* (т) образуют 2-схему (теорема 33).
J ст
(3) . Полное пространство F-1 -1 равно объединению непересе-кающихся сдвигов кода &*(т), задаваемых векторами 1, 2 и 3; иными словами, 0>*(т) — квазисовершенный код (теорема 34).
Пусть Ч? — произвольный код четной блоковой длины, содержащий нулевой вектор, такой, что все его слова имеют четный вес. Пусть ‘g’* — код, получаемый из Я? путем вычеркивания произвольной координаты, для определенности — последней. Пусть {Лг} и {а,} — соответственно спектры весов кодов и <g’*. Как обычно, штрих обозначает преобразованный спектр весов.
Теорема 30.
А'. = а. -4- а ..
I I ‘ п—I
Л
Доказательство. Пусть di— {ugF" : wt(u) =i}; <г;={пе
: wt(u) =i}. Согласно теореме 5 гл. 5 преобразования спектров весов кодов <ё* и <ё соответственно равны:
2 (-ir*A'
Л Л Л Л
we<yt «> v6®*
2 (-i)w(u+v,= wecr. u, ve'g
., Л. Л Л u , , АЛЛ
= у T (_______j^Cu+a) У у (__________l)w(u+v)+un+vn
Л Л ЛЛ Л Л ЛЛ
wgOj u.ve'g* u.ve^*
Л A
где использованы обозначения w=|w|w„|; u=|u|un| и т. д. при
i=l i=l
(что возможно, так как все веса кода четны). Следовательно.,
|^|М: = |^|2Щ+ у у (_ !}("+<) (и-Н) Л Л Л Л we<ri__1 «, ve'g*
Но последний член равен I’g’^a'n-i- •
Следствие 31. A'i=A'n_1; в частности А'0=А'п=1.
Замечание. Для линейных кодов утверждения теоремы 30 и следствия 31 тривиальны, так как {А'г} и {a'i} являются соответственно спектрами весов кодов <ё и (&*) К
Упражнение. (15). Доказать, что в случае линейных кодов код (<ё?*)± получается из кода (ё’А- путем вычеркивания фиксированной координаты и последующего удаления всех векторов, вес которых оказался нечетным.
Применим теперь теорему 30 к коду ^(т), а именно:
Л'т—1_|_2 (rn—2) /2 = A 'm—1_2 (т—2) /2 = 1ц_2 (т~2) /2 +
-|-a2m—1_2(т—2)/2; Д’т—1 = 2fl2m—1‘
Таким образом , преобразование спектра расстояний кода &*(т) помимо а,о=1 содержит s'—3 ненулевых члена. Так как минимальное расстояние кода ^*(т) равно по меньшей мере 5, то по теореме 2 гл. 6 можно найти числа a'2m—i±2(m-2)/2 и a'2m-i . Так как s'<Cd, то по теореме 6 гл. 6 эти числа совпадают также с преобразованием спектра весов. Этот результат мы сформулируем в виде следующей теоремы.
Теорема 32. Пусть 0*(т) — выколотый код Препараты длины п—1, где п=2™ и т^4 — четно.
(1) . Преобразование спектра весов (и расстояний) кода ^(т)1 равно:
ао=1= </2=«--1;
а(„-^)/2 =~(П-2)(п + Уп)-, а'п+/_)/2=(1/4)(п-2)(п-Гп).
(2) . Производящая функция для спектра весов (и расстояний) задается формулой
гг—1 П~^
-У]аг^ =(1+гГ-1 + (1/4)(/г + ^)(/г_
I У' (m)| Li г=0
— 2)(1 4-z)<1/2) <«+Tn)-1 (]_2)(i/2) (n-V5T)_|_
+ (l/4)(n —|/n)(n-2)(l +z)(I/2) z)<>/2) («+^) +
+ (n —'l)(l+z)n/2-1(l—z)"/2, где | &>(m) | = | .'33*(m) | =2n~2m~2.
(3) . Спектр весов (и расстояний) кода ,^'(т) не зависит от того, какая имецно из координат вычеркнута.
(4) . Минимальное расстояние кода &*(т) равно 5.
Теор ем а 33. Слова любого фиксированного веса в коде. ^*(т) образуют 2-схему. В частности,
а5 = (1/60) (2га— 1) (2т—2) (2т—4) (15.52)
слов веса 5 в коде &*(т) образуют схему
2-(2m—1, 5, (1/3) (2т —4)). (15.53)
Кодовые слова любого фиксированного веса в /?(т) образуют 3-схему. В частности,
Л6 = 1/360 2m(2m— l)(2m—2)(2m—4) (15.54)
кодовых слов веса 6 в коде ZPfm) образуют схему.
3-(2т, 6, (1/3) (2"г—4)) ' (15.55)
Доказательство. Так как для кода 5э*(т) d=5 и s'=3, то первое утверждение вытекает непосредственно' из теоремы 24 гл. 6. Аналогичная ситуация имеет место и для третьего утверждения. Для нахождения параметра X в (15.53) заметим, что аннулирующий многочлен для кода SP*(m) равен:
а (х) = 22т 1 ^1 2т—1 — 2(1/2) («’—2) ) (1 2т~1 2(1/2) 2) )
X (1 - = ро (X) + р. (X) + А (р2 (х) + рз (Х))) (15.56)
где г= (1/3) (2™—1). Из теоремы 23 гл. 6
X = 1 - С.1/''). = — (2т—4).
(Д/г) 3
Коэффициент а$ равен числу блоков в этой схеме и согласно формуле (2.21) задается равенством (15.52). Формула для Лб вытекает теперь из теоремы 14 гл. 8. *
Упражнение. '(16). Доказать, что в коде £Р*(т) имеется ае= (1/360) (2m—1) (2™-—2) (2те—4) (2т—6) слов веса 6.
Последние две теоремы этого раздела показывают, что как все пространство, так и код Хэмминга являются объединением непересекающихся сдвигов кода <р*(т).
Теорема 34. Все пространство Fn~l, п=2т, представляет собой объединение непересекающихся сдвигов кода зада-
ваемых всеми векторами веса 0, 1 и 2 и 2т~1—1 векторами gi, ..., g2 m-i _j веса 3.
Доказательство. Пусть {о; (f)} — спектр весов сдвига f+ Воспользуемся уравнением (6.19), где (согласно (15.56)) ao = ai = l; а2 = аз=1/г. Тогда из равенства wt(f) = l следует, что а0 (f) = 0; (f) = 1 и с2 (f) = а3 (f) = 0.
Из равенства wt(f)=2 следует также, что а0 (f) =oi (f) =0; a2(f) = l и a3(f)=ir—1=(1/3) (2m—4).
Очевидно, что 1 + (2m—l) + (2m2—1) сдвигов кода &>*(m), задаваемых векторами веса 0, 1 и 2, не пересекаются. В пространстве F"-1 остается еще \£Р*(т) | (2т—1) векторов. Все они должны принадлежать сдвигам, для которых a0(f) =о! (f) =zz2(f) =0 и аз (f) =>г.
Пусть Т — множество всех векторов веса 3 в Fn~l. Представим Т в виде Т=Т2 U Т3, где
T2 = {f^T: dist (f, u)=2 для некоторых ueF(m)};
Т3 = {fGET: dist (f, u) > 3 для всех ue^ (m)}.
Мы покажем, что остальные сдвиги кода й3* т равны g+ +£Р*(т) для тех g.^T3, которые имеют 1 в некоторой фиксированной, координате.
Упражнения (17). Доказать, что если g^T3, то сдвиг g+ + <7>*(т) не пересекается ни с каким сдвигом вида где
вес вектора f равен 0, 1 или 2.
(18). Доказать, что сдвиги gi+.T^/m) и g2+&*(m) не пересекаются, если пересечение gb g^T3 не пусто.
Согласно теореме 33 всего в коде ф*(т) имеется (1/3) (2™—4) кодовых слов веса 5, которые содержат 1 в двух различных любых фиксированных координатах. Для каждого из этих кодовых слов в множестве Т2 имеется 3 вектора, у которых символ 1 стоит в этих же двух фиксированных координатах. Всего в пространстве Fn-1 содержится 2™—3 векторов веса 3, у которых в двух рассматриваемых координатах стоят 1. Следовательно, в множество Т3 из них попадает (2т—3) — (2™—4) = 1 вектор.
Таким образом, векторы множества Т3 образуют 2-(2т—1, 3, 1)-схему, а следовательно, также 1-(2™—1, 3, Х)-схему при <к= =2™-*—1 (по теореме 9 гл. 2). Следовательно, в Т3 содержится 2m~I—1 векторов? gi, ..., g2"i—1_ь у которых в некоторой фиксированной координате стоит 1. Все сдвиги кода £Р*(т), задаваемые этими векторами, не пересекаются и в точности покрывают оставшиеся векторы из F”-1. •
Следствие. 35. ,^(т') является квазисовершенным кодом1.
Теорема 36. Объединение кода .^*(т) и его сдвигов gi + +&*(т), 1=1, ..., 2т~'—1, образует линейный [2™—1, 2™—1—т, 3]-код Хэмминга.
Доказательство. (1). Прежде всего покажем, что векторы
| х< | 1 | х’ | (15.57)
и
|х'63|0|0| (15.58)
для всех /=0, 1, ..., 2,п-1—2 принадлежат одному и тому же смежному классу. Действительно, их сумма равна |хД1 +03) | 1 |x’| и,, очевидно, лежит в ^*(пг); достаточно в уравнении (15.49) положить g(Y)=xj03; f(x)=xi и а=1.
(II). Теперь покажем, что минимальный вес смежного класса по коду £р*(т), представителем которого является вектор (15.58), равен 3; таким образом, векторы (15.57) на самом деле совпадают с векторами gb ..., gp из теоремы 34. Рассмотрим типичный вектор из такого смежного класса
| g(x)(l +е1)+ах'+х* 03|/(l)|g(x)(l +0J +
+fto(i+e1+e3)+«*'e1|- (15.59)
Если а=0, то правая половина вектора принадлежит коду Хэмминга, и поэтому либо ее вес не меньше чем 3, либо эта по
1 Впервые этот результат доказан в [1451]. (Прим, перев.)
ловина равна нулю. Если она равна нулю, то f(x)=g(x)—0 и вес левой части равен 2™-2. Если же а=1, то и левая, и правая половины вектора отличны от нуля. Учитывая проверку в середине вектора, получаем, что его вес не меньше чем 3.
(HI). Таким образом, сдвиг кода £Р*(т), задаваемый вектором (15.57) (или (15.58)), образует код с минимальным расстоянием 3, содержащий 22 векторов. Остается показать линейность этого кода; тогда согласно упражнению (28) гл. 1 он будет эквивалентен коду Хэмминга. Нам надо показать, что сумма двух векторов вида (15.59), т. е. вектор
I (Si (х) + §2 (-’'-)) (1 + 51) + aiх11 + а2 х'2 +
+(хч+xh) е3| А (1)+А (1) I (Я! w+gz (х)) (I + ej +
+ (fi (*) + fz (x)) (1 + 0i + 6з) + (<4 xh + хы)011, (15.60)
опять является вектором вида (15.59). Некоторые трудности вызывает только случай, когда а1 = а2=1- Так как слова веса 3 в коде Хэмминга образуют 2-схему (теорема 15 гл. 2), то найдутся gz(x) и /3 такие, что
Х11 + Xfl -L Xf, = gs (х) (1 + 6J, (15.61)
или, умножая на 0Ь получаем, что
(хб + хы) 0Х = х^'« 0Х. (15.62)
Заметим, что х’03 являются представителями смежных классов кода Хэмминга (длины 2™-*—1) по коду БЧХ, исправляющему две ошибки. Следовательно, при подходящем выборе /4 и р(х)' можно записать:
gs (х) (I+0J=хбб3+р (X) (I + ех+03). (15.63)
Кроме того, воспользуемся равенством
(1+ex)(i +01+о3)= i+e1+es. (15.64)
Из равенств (15.63) и (15.64) видно, что вектор (15.60) имеет вид (15.59) при g(x)==g1(x)+g2(x) +р(х) (l+Oi + Оз), а=1, }=/з; хг'0з= (х’'+х'2+х34)03 (это возможно потому, что 0з — идемпотент симплексного кода) и f(x)=fi(x)+f2(x) +fi(x) (l + 01 + бз)-
Упражнения. (19). Препарата определил код .^(т) как множество всех векторов вида
• |m(l) + g(l)|m(x)+g(x) |i |m(x)4-(m(l) + i)0o4-s(x) ±q(x) 611, где m(x) — слово кода Хэмминга с порождающим многочленом MCOjfx); s(x) — слово кода БЧХ с минимальным расстоянием 6 и порождающим многочленом М(0)(х)М^(х)М<3^(х); q(x)^{0, 1, х, ..., х2 ~2} и i равно 0 или 1. Показать, что это определение совпадает с определением кода, даваемым уравнениями (15.47) и (15.48).
(20) . (а). Доказать, что первые 2™—2т символов кода <р*(т) могут быть выбраны в качестве информационных, следовательно, <р*(т) является систематическим.
(Ь). Доказать, что остальные символы кода &*(т) задаются квадратичными функциями от информационных символов.
(21) . Показать, что код Нордстрома—Робинсона состоит из [16, 5, 8]-кода Рида—Маллера и семи смежных классов, которые в обозначениях упражнения (16) гл. 14 соответствуют максимально нелинейным функциям, задаваемым графами
1 I С 2 2 Я X К
(22) . Доказать, что нелинейный код, приведенный на рис. 5.1, состоит из векторов (хь ..., х8), координаты которых удовлетворяют пяти квадратным уравнениям.
*15.7. ОБОБЩЕНИЕ ГЕТАЛСА КОДОВ ПРЕПАРАТЫ
<
В § 15.5 мы видели, что коды ЯУЗ (т, d) обобщают коды Кердока, так как ЯУЗ (т, т/2) =Ж(т) (напомним, что т — четно). Коды Препараты, как мы только что видели, дуальны к кодам Кердока в том смысле, что спектр весов кода &(т) получается как преобразование Мак-Вильямс от спектра кода ^(т). В данном параграфе строится нелинейный код У(т), исправляющий три ошибки, который в этом же смысле дуален коду 03 (т, (1/2) (т—2)). Эта конструкция была предложена Геталсом в работах [495] и [496], и мы предлагаем читателю посмотреть в этих статьях доказательства следующих фактов.
Код У(т) определяется для произвольного т=2/ + 2^6 как нелинейный код с длиной 2т и минимальным расстоянием 8, содержащий 2h слов, где k=2m—3m + l. Первые несколько кодов из этого семейства кодов имеют параметры
(64,247,8), (256,2233,8), - •
Код У (т) содержит в 4 раза больше слов, чем расширенный код БЧХ той же длины, исправляющий три ошибки.
Как и ранее, код ^~(т) состоит из некоторого линейного кода л и 2т~1—1 смежных классов по л. Словами кода л являются векторы
1^(1)1яМ(1+е1)|7(1)+я(1)1яМ(1+е1)+/(х)(1ч-е1+ег+е5)|,
(15.65) где r= 1+2*-1 и s= 1+2'.
Следовательно, размерность кода л равна 2т—4m+ 2. Представители смежных классов задаются выражениями (15.48).
Спектр весов кода Z(т)1 совпадает с его спектром расстояний и равен преобразованию Мак-Вильямс от спектра весов кода 0$(т, (1/2) (т—2)), который .приведен на рис. 15.13 (хотя вычисление этого спектра откладывается до гл. 21).
1 At
0 или 22(+2 1
^2 i-{-1 2*+1 22t(22t+I _ (22t+2_1)/3
22(+*+2* 22t+2 (22t+l _ ц (22*+l+4)/3
224+’ 2 (22t+2 — 1) (24t+1 — 22t 1)
Рис. 15.13. Спектр весов и (расстояний) кода && (т, (1/2) (т—2))
Задачи (нерешенные). (15.2). Пусть £Р'(т) получается из &(т) путем замены в линейном подкоде идемпотента 63 идемпотентом 6S. Обладает ли код ^'(т) теми же свойствами, что и код £Р(т)?
(15.3) . Найти код, спектр весов которого равен преобразованию Мак-Вильямс от спектра весов кода (т, d) при произвольном d.
(15.4) . Доказать, что коды ^(т) и Ж (т) содержат по меньшей мере вдвое больше слов, чем любой линейный код той же длины и с тем же минимальным расстоянием. Что можно сказать о кодах Ф^(т, d) и (т)1?
ЗАМЕЧАНИЯ К ГЛ. 15
§ 15.2. Теорема 2 восходит к Альберту [18] (см. также Мак-Вильямс [878]). Теорема 4 принадлежит Диксону [374], а теорема 8 — Слоэну и Бер-лекэмпу [1232] (см. также Мак-Элис [936]). Свойства слов минимального веса в кодах 5? (2, т) были изучены Берманом и Юданиной [138].
Свойства гауссовских биномиальных коэффициентов — см. Берман и Фрайер [134]. Голдман и Рота [519], Полина и Александерсон [1066]. По поводу упражнения (4) см. Сервейт [1144]. Упражнение (5) принадлежит Дельсарту и Гаталсу [362], а также Вулфмэну {1431].
§ 15.3. Теорема 10 доказана Касами и Токурой [745] и обобщает результаты Берлекэмпа и Слоэна [132].
Теорема 12 обобщает более ранний результат Соломона и Мак-Элиса [1256]; доказательство приведено в [939] и [941]. Этот результат обобщен на случай произвольных групповых абелевых кодов (см. Дельсарт [349] и Дельсарт и Мак-Элис [369]). Ван Линт предложил непосредственное доказательство следствия 13 [848].
§ 15.4. Приведенные в этом параграфе спектры весов были вычислены Касами [727, 729].
§ 15.5. Для нечетных т описанный в этом параграфе линейный код был проанализирован Берлекэмпом [118], а также Дельсартом и Геталсом [364]. Спектры весов других подкодов кода 5?(2, т) можно найти в. [118, 729] (см. также Даулинга [384]).
Задача (нерешенная). (15.5). Код (4)=.<>гз(4) является единственным. Является ли единственным хотя бы один из кодов Ж(~т) или <F(m) при щ>4?
Мы приведем (без каких-либо ’ объяснений) следующий результат.
Теорема 38. (Берлекэмп [120], Геталс [493], Сновер [1247]). Группами автоморфизмов кодов Нордстрома — Робинсона у£* (4) и У£ (4) являются соответственно знакопеременная группа ^7 и расширение группы ^7 с помощью элементарной абелевой группы порядка 16. Последняя является трижды транзитной группой порядка 16X15X14X12.
Коды Кердока были открыты в 1972 г. (см. Кердок [758]). Приведенное в главе описание этого класса кодов следует работе Паттерсона (неопубликованной), а также Дельсарта и Геталса [364]. Обобщение на коды <ЗУЗ(пг, d) также дано в [364]. Другой подход к кодам Кердока был предложен Камероном и Зейделем |[235]. Возможные обобщения на случай поля GF(8) описаны Паттерсоном [1031].
§ 15.6. Коды Препараты были введены в работе [1081] (см. также [1080, 3082]). В этой работе Препарата показал, что эти коды являются систематическими, и дал алгебраические методы их кодирования и декодирования. Мик-кельтвейт [978] показал, что коды Кердока также являются систематическими. Спектр весов кода ^(т) был вычислен Семаковым и Зиновьевым [1181]*>. В гл. 18 коды Препараты будут использованы для построения многих других хороших нелинейных кодов, исправляющих две ошибки.
Коды Препараты являются одним из главных примеров класса так называемых почти совершенных кодов (определение дается в гл. 17). Более общим .классом кодов являются равномерно упакованные коды (см. Бассалыго и др. [78, 79], Геталс и Сновер [504], Геталс и Ван Тилборг [505], Линдстрем и др. '[844а, 844b], Семаков и др. [1183] и Ван Тилборг [1326, 1327]). В доказательстве теоремы 36 мы следовали работе Зайцева и др. [1451].
§ 15.7. Материал этого параграфа взят из работ Геталса [495] и [496]. Задачи (нерешенные) ([5.2) и (15.3) были решены Геталсом [498]**>.
Глава 16
Квадратично-вычетные коды
16.1. ВВЕДЕНИЕ
Квадратично-вычетные коды (KB-коды) S, S, JF, являются циклическими кодами над полем GF(l) с блоковой длиной р, где I и р — два различных простых числа таких, что I является квадратичным вычетом по модулю р. (Сколько-нибудь изученными являются только случаи 1=2 и 3). Коды S и являются эквивалентными и имеют параметры [р, (р+1)/2, р]; S’ и также являются эквивалентными кодами, но их параметры равны [р, (р—1)/2, d^]/~ р]. Кроме того, S^S и Все эти коды
определяются в § 16.2, а на рис. 16.1 дается краткая характеристика их свойств.
Примерами квадратично-вычетных кодов являются двоичный Т7, 4, 3]-код Хэмминга, а также двоичный [23, 12, 7] и троичный (11, 6, 5] совершенные коды Голея ^2з и (см. § 6.10 и гл. 20). Другие примеры приведены на рис. 16.2.
Таким образом, скорость KB-кодов близка к 1/2, а минимальное расстояние достаточно велико (по крайней мере при не слиш-
Там же доказана теорема 33. (Прим, перев.)
. **> Задача 15.2 (нерешенная) решена также в [392b]. (Прим, перев.).
ком больших р; впрочем, см..нерешенную задачу (16.1)). Некоторые методы декодирования KB-кодов и других циклических кодов-рассматриваются в § 16.9. Наиболее сильным среди них является перестановочное декодирование, основанное на том, что рассматриваемые коды обладают большой группой автоморфизмов.
В данной главе обсуждаются и другие вопросы, относящиеся к KB-кодам, как-то: порождающие идемпотенты кодов (§ 16.3), дуальные коды и расширенные коды длины р+1 (§ 16.4) и группы автоморфизмов (§ 16.5). Расширенные KB-коды при 1=2 инвариантны относительно группы PSL2(p), а при />2 — относительно группы, представляющей собой слабое обобщение группы PSL2(p) (теорема 12), и во многих случаях эта группа автоморфизмов является полной (теорема 13).
В § 16.6 продолжается описание свойств KB-кодов, в частности предлагаются методы нахождения истинного минимального расстояния. В § 16.6 также показывается, что порождающая матрица некоторых KB-кодов может быть записана в виде [I|А], где А — циркулянтная или окаймленная циркулянтная матрица. Такие коды названы дважды циркулярными кодами. В § 16.7, 16.8 исследуются дважды циркулянтные коды над GF(2) и GF(3) для одного частного случая выбора матрицы А. Свойства этих кодов аналогичны свойствам KB-кодов, хотя о них мало что известно. Для GF(3) эти коды являются симметричными кодами Плесе.
В этой главе доказательства проводятся, как' правило, только» для случая р=4/г—1; доказательства для случая p=4k+1 аналогичны и предоставляются читателю.
16.2. ОПРЕДЕЛЕНИЕ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
Мы переходим к определению квадратично-вычетных кодов (KB-кодов) длины р(р простое) над GF(l), где I — простое число», являющееся квадратичным вычетом по модулю р. В важном случае двоичных квадратично-вычетных кодов (1=2) это означает,, что р должно быть простым числом вида 8т±1 (согласно теореме 23, приведенной в замечаниях к главе).
Пусть Q обозначает множество квадратичных вычетов по модулю р, а N — множество квадратичных невычетов (см. § 2.3 и 4.6). Если р — примитивный элемент поля GF(p), то pceQ тогда и только тогда, когда е четно, и pe^N тогда и только тогда, когда е нечетно. Таким образом, Q — циклическая группа, порождаемая элементом р2. Так как l^Q, то множество Q замкнуто относительно умножения на I. Следовательно, Q представляет собой объединение непересекающихся циклотомических классов по модулю р. Таким образом, если а — примитивный корень степени р из единицы в некотором поле, содержащем поле GF(l), то коэффициенты многочленов
?(х)=П(х—а0 и (х— а") (16.1);
reQ neN
лежат в поле GF(l). При этом
хр—1 = (х—1)7(х)п(х). (16.2)
Обозначим через 7? кольцо GF(l) [х]/(х?—1).
Определение. Квадратично-вычетными кодами S, S, Л3, Л3 называются циклические коды (или идеалы) кольца R, порожденные соответственно многочленами
q(x), (х—1)д(х), п(х), (х—1)п(х). (16.3)
Иногда 2 и Л3 называются пополненными KB-кодами, a S’ и Л3 — KB-кодами с выбрасыванием.
Ясно, что 37^2 и В двоичном случае 2 представляет
собой подкод кода 2, состоящий из всех кодовых слов четного веса, а Л3 — подкод кода Л3, состоящий из всех кодовых слов четного веса.
Подстановка на множестве координат кольца R, индуцируемая отображением х->хп при некотором фиксированном невычете п, переводит коды S и Л3 (а также 2 и Л3) друг в друга, так что эти коды эквивалентны.. Размерность кодов S и Л3 равна (р+1)/2, а размерность кодов S и Л3 равна (р—1)/2 (см. рис. 16.1).
Пример. Если /=2 и р=7, то порождающий многочлен кода S равен (х+а) (х+а2) (х+а4) =х3+х+1, где aeGF(23), так что код S равен [7, 4, 3]-коду Хэмминга. S представляет собой [7, 3, 4]-подкод с порождающим многочленом (х+I) (х3+х+1). Код Л3 эквивалентен [7, 4, 3]-коду Хэмминга с порождающим многочленом (x+a3) (х+а5) (х+а6) =х3+х2+1. (Отметим, что различные выборы элемента а приводят к перестановке кодов S и Л3.)
KB-коды определяются порождающими многочленами (16.3) и являются кодами над полями GF(l) с параметрами:
длина р — простое число;
размерность: (р+1)/2—для S> Л3;
(р— 1) /2 — для S^^3;
минимальное расстояние d~^ ]7р, где I — простое число, являющееся квадратичным вычетом по модулю р. Если р=4 k—1, то d2—d+l^p (теорема 1). Порождающие идемпотенты кодов описываются теоремами 2 и 4. Порождающие матрицы задаются равенствами (16.22), (16.23), (16.28), (16.31), (16.39), (16.44), (16.45). Если p=4,k—1, toS±=S и Л/,±=Л/>; если р=4&+1, toS —JF и 2^ = — Л Л
— $6. Расширенные коды S? , 2 задаются добавлением общей проверки Л Л
на четность (16.27). Если р=4й—1, то коды 2'иЖ самодуальны; если Л Л Л
р=4&+1, то ^Н^Л3- Группа Aut(S) содержит группу PSLz(p) (теоремы 10 и 12). На рис. 16.2 приведены примеры таких кодов, а на рис. 16.3—их свойства.
Рис. 16.1. Свойства квадратично-вычетных кодов S> S> Л3> Л3
Коды Голея. Мы уже упоминали в § 2.6 и 6.10 о существовании двух совершенных кодов Голея, а именно [23, 12, 7] двоичного кода ^23 и [11, 6, 5] троичного кода ^ц. Одно из определений кода ^23 было дано в гл. 2. Мы дадим теперь другое его определение как KB-кода, одновременно определив также и код ^п.
Определение. Код Голея ^2з является KB-кодом S (или Л3) при /=2 и р=23. Код Голея является КВ-кодом S (или Л3) при Z=3 и р=11. Параметры этих кодов соответственно равны [23, 12, 7] и [11, 6, 5]. (В § 16.7 будет доказана эквивалентность двух данных определений кода З^з- Она вытекает также из следствия 16 гл. 20).
Над GF(2) (см. рис. 7.1) имеет место разложение
х23 4-1 = (х 4-1) (х114- -г10 + х6 4- х® 4-х4 4-х2 4- 1) (хц-|-х9 4-4-х7 4-х6 4-х5 4-х 4-1),
так что в качестве порождающего многочлена кода ^2з можно выбрать один из многочленов
х114- я10 4- Xе 4- х5 4- х4 4- х2 4- 1 или х114- х8 4- х7 4- х6 4- х5 4- х 4- 1.
(16.4)
Над GF(3) имеет место разложение
(х11—1) = (х— 1) (х54-х4—х34-х2— 1)(х5—х34-.х2—х— 1), гак что в качестве порождающего многочлена для 9ц можно выбрать один из многочленов
х®4-х4—х34-я2—1 или х5—х34-*2—х—1. (16.5)
Другие примеры приведены на рис. 16.2. (В некоторых случаях указаны верхние и нижние границы для d.)
Граница квадратного корня для минимального расстояния.
Теорема 1. Если d — минимальное расстояние кодов S или Л3, то d2^p. Если р=4/г—1, то эту границу можно усилить следующим образом:
d2—d-{-1 > р. (16.6)
Доказательство. Пусть а(х) — слово минимального ненулевого веса d в коде S. Если п — невычет, то а(х)—а(хп) — слово минимального веса в коде Л3. Следовательно, произведение а(х)а(х) должно лежать в пересечении S[\JT, т. е. быть кратным многочлену р—1 р—1
П (х—аг) П (*—“") = П (x — ai) = £ х>.
reQ neN i—1 i=°
Следовательно, вес произведения а(х)а(х) равен р. Поскольку нес многочлена а(х) равен d, максимальное число ненулевых коэффициентов в произведении а(х)а(х) равно d2, так что d2^p.
Если р—4/г—1, то согласно свойству (Q2) гл. 2 можно выбрать п~—1. Тогда в рассматриваемом произведении имеется d членов, равных 1 так, что максимальный вес равен d2—d+l. *
n k d n (а) Над полем GF (2) n k d
k d
8 4 4 74 37 14 138 69 14—22
18 9 6 80 40 16 152 76 20
24 12 8 90 45 18 168 84 16—24
32 16 8 98 49 16 192 96 16—28
42 21 10 104 52 20 194 97 16—28
48 24 12 114 57 12—16 200 100 16—32
72 36 12 128 64 20
(b) Над полем Gf(3)
n k d n k d n k d
12 6 6 48 24 15 74 37 ?
14 7 6 60 30 18 84 42
24 12 9 * 62 31 ? 98 49
38 19 ? 72 36 ?
Рис. 16.2. Таблица расширенных квадратично-вычетных кодов S
Пример. Минимальное расстояние [7, 4, d] квадратично-вы-четного кода над GF(l) удовлетворяет условию (и если 1=2, то d=3).
Примеры кодов, приведенные на рис. 16.2, показывают, что минимальное расстояние часто больше, чем граница, задаваемая теоремой 1.
Задачи (нерешенные). (16.1). Заполнить пробелы на рис. 16.2; расширить обе таблицы и вычислить аналогичные таблицы для других значений I.
(16.2). Как ведет себя минимальное расстояние KB-кодов при р—>-О0?
16.3. ИДЕМПОТЕНТЫ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
Сначала рассмотрим случай 1=2.
Теорема 2. Если 1=2 и р—41г—1, то а можно выбрать так, что порождающие идемпотенты кодов S, S, JF, JF будут соответственно равны:
reQ
n^N
Fq(x} = 1 + 2X">
Fn {x) = 1 + 2 xr-reQ
(16.))
Доказательство. Поскольку 2 — квадратичный вычет по мо-дулю р, то (Eq(x))2 = Eq(x)-, (En{x>jf Еп(х) и т. д. так что эти многочлены являются идемпотентами. Таким образом, согласно лемме 2 гл. 8 Eq (а’) равно 0 или 1. Для любого квадратичного вычета s имеют место равенства
Eq (as) = 2 K'S = 2 ar' = Eq (a).
reQ r’eQ
Аналогично E'g(a)i= 2 art= S a~r=Eq(a~1) для любого невы-reQ reQ
чета t. Так как E^(a)+Eg(a-1) = 1, то в зависимости от выбора a либо
£'?(as) = 0 для всех seQ и Eg(a*) = 1 для всех t^N, (16.8) либо
Eq(a) = 1 для всех s^Q и £’,7(at) = 0 для всех i<=N.
Выберем элемент а так, чтобы выполнялись условия (16.8). Тогда Ед(х) — порождающий .идемпотент кода S,
Далее для t^N
Еп («о=2ant=2 “г= 0 n^N reQ
и E'n(as) = l для seQ. Таким образом, многочлен Еп(х) является идемпотентом кода Л.
Наконец, Eg(as)=0 для всех seQ и Ед(1)=0, так что Fq(x) является порождающим идемпотентом кода S. Аналогично Fn(x) — идемпотент кода Л. •
Замечание. Если 1=2 и p=4k+1, то порождающие идемпотенты кодов S, S, Л и Ж могут быть выбраны соответственно в виде
1+Х%Г’ 1 + хг. (16.9)
reQ rieN xqn reQ
Пример. При 1=2 и р=23 множество вычетов Q—{1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18} и порождающие идемпотенты кодов S’ и Л соответственно равны
2 *г и
reQ reQ
Оба кода эквивалентны коду Голея ^2з-
Идемпотенты для случая />2. Для вывода формул идемпотентов в случае Z>2 оказывается полезным следующий теоретикочисловой результат. Напомним определение символа Лежандра, Данное в гл. 2:
(16.10)
х (0 =
0, если i делится на р,
1, если i — квадратичный вычет по модулю р, — 1, если i—невычет по модулю р.
Кроме того, х(0х(1)'~х(ч)- Определим сумму Гаусса равенством р—1
е = £х(/)аг. (16.11)
i=l
Так как 6г=6, то G^GF(l).
Теорема 3. Если р=4!г—1, то 62=— р- (Это утверждение справедливо для любого поля при условии, что а является примитивным корнем степени р из единицы.)
Доказательство.
р-i р—1
02=S 2x(o%(/)^+/-i=i /=i
В этой сумме у р—1 членов таких, что i+j—p, коэффициент равен —1, так как в этом случае если одно из чисел I или / является квадратичным вычетом по модулю р, то второе является невычетом (так как —1 является невычетом). Следовательно,
02 = _(р_ 1) + у 2 х (ОX (/)аг+/.
i+MP
Вклад членов с i=j равен:
р—1 р— 1 р—1
У Х2(г)а2г=2а2г=£аг== — !•
i=i 1=1 1=1
Таким образом,
р-i
62 = — р + V ф (k),
где
р—1
ф(^)= 2 х(Ц£—о)-г=1 i=£k, 2i^=k
Остается показать, что ф(7г)=0. Пусть Mh—{t:t=i(k—i) для некоторого i такого, что l^i^p—1, i=^=k, 2i=£k}. Тогда |Alfe| = = (р—3)/2. Мы покажем, что множество Мъ состоит из (р—3)/4 вычетов и (р—3)/4 невычетов по модулю р, что, конечно, равносильно равенству ф(^) = 0. Если t—i(k—i), то i2—ki+t=O и k2— —4t=((i2—t)/i)2. Так как i2#=Z, то k2—4t^Q. Следовательно, —4t=r—k2 для некоторого reQ, r=£k2 или {—4Л4Л = {г—k2-.rc= ^Q, r^k2}.
Согласно теореме Перрона (теорема 24 из замечаний к главе) это множество содержит равное число вычетов и невычетов.
3 а м еч а н и е. Если р=4/г + 1, то 02= +р. •
Пр и мер. Для р—7 и любого I имеем:
0 = а-|-а2—-а3-|-а4—а5—а6;
6
02= — 6 + Va*= — 7.
Теорема 4. Если Е>2 и р=4/г±1, то коды 2, 2, порождаются соответственно идемпотентами
reQ «е^
(16.12)
Fq(x}=-*- fl - —-Ч-+-) У!*г——f———) Vхп.
4 2\ р) 2\р 0 } Zj 2\р 0/Zj
reQ ieN
(16.13)
^<^iO4)+T(i+i)S-+T(-7-v)S«
reQ neN
(16.14)
Fn (x)=-41 - -4—L У! (-+-4 Уxn-
K ' 2 \ p / 2 \ p e ) ZJ 2 \ p e / ZJ reQ neN
(16.15)
Доказательство. Легко проверить, что если r^Q, то
Е9 (от) = Fq (or) = 0; Еп (от) = Fn (от) = 1,
а если n^N, то Fg(a”) =Fg(a") = 1; En(an) =Fn'(an) — 0.
Кроме того, Eg(l) =En(l) = 1 и Fg(l) =Fn(l) =0. Отсюда согласно лемме 2 гл. 8 следует, что Eq(x), Fq(x), Еп(х) и Fn(x) — порождающие идемпотенты указанных кодов. *
Пример. Если /—3 и р=11, то Q— {1, 3, 4, 5, 9}. Кроме того, aeGF(35) — примитивный корень степени 11 из единицы. Вместо вычисления 6 по (16.11) воспользуемся лучше теоремой 3: 62=—11 = 1 (mod 3), так что 6=±1. Выберем а так, чтобы выполнялось равенство 6=1. Тогда из (16.12) и (16.14) получаем, что порождающие идемпотенты кодов 2 и Л3 равны соответственно
— V хг и —’2х(16.16) reQ reQ
Оба эти кода эквивалентны коду Голея 9ц. Заметим, что если 1=3 и p=4k—1, то идемпотенты всегда имеют такой вид, так как в этом случае 62 — квадратичный вычет по модулю 3, и, следовательно, 02=1.
Представляется полезным указать, как были найдены эти идемпотенты. Наиболее правдоподобная гипотеза состояла в том, что они имеют вид
а-\-Ь^хг + сУ хп. (16.17)
> reQ «елг
При возведении выражений такого вида в квадрат полезно следующее утверждение.
Лемма 5. Предположим, что р=4/г—1. Тогда в кольце
(£ А"У “"Ь(₽ _ 3) Sх’+т{р+1 ’X*"
' reQ ' reQ n<sN
(Хл"Уг(р+1'Хг+т('’ \ new г reQ neN
. ' р—i
Sхг £хп=т {р~!)+-г (z?~3)Sxi-- reQ neN i=i
Доказательство. Вытекает из теоремы Перрона 24. •
Отсюда сразу следует, что выражение (16.17) является идем-
потентом тогда и только тогда, когда
а2 + (/?—\)Ьс = а',
2g&+4-(p-3)^+^-(p+1)C2+4-(p-3)6c=&; 4 4 2
2ас + 4 (Р+ 1) Ь2 + 4-(Р-3) с2 + V ^~3) Ьс = с-4 4 2
Решение этих уравнений и приводит к формулам, указанным в теореме 4.
16.4. РАСШИРЕННЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ Сначала мы найдем коды, дуальные к КВ-кодам.
Теорема 6.
= если р = 4/г—1; (16.18)
^T-L = ^ если р = 4/г+1. (16.19)
В обоих случаях
Ж порождается кодом Ж и вектором 1, (16.20)
ЛР порождается кодом и вектором 1. (16.21)
Доказательство. Предположим, что р=4А—1. Нулями кода S являются элементы «г для всех reQ. Следовательно, согласно теореме 4 гл. 7 нулями кода ZL являются элементы 1 и а-п для всех n^N. Но —neQ, так что ZL=Z. Согласно теоремам 2 и 4 р—1
Е9 (х) = Fq (х) +— У х1’,
Р 4J
г=0 откуда вытекает (16.20).
Аналогично доказываются и остальные утверждения. 9 Найдем теперь порождающие матрицы этих кодов. Пусть
р—1
F4(X) = Y fixi i=0
— идемпотент, порождающий код 2? и задаваемый теоремами 2 и 4. Тогда порождающая матрица кода 2 является рХр цирку-лянтной матрицей:
По
G = (^j) =
Р—1 /0 • • / р— 2
(16.22)
Ji f2 - - - /о J
где O^i; /^р—1; gij—fj-i и индексы вычисляются по модулю р. Порождающая матрица кода 2? равна
[ггЛтг]- (16.23)
Аналогичные равенства имеют место для Л3 и Л3. Ранг матрицы (16.22) равен, очевидно, (р—1)/2.
Примеры. Если 1=2 и р=7, то порождающая матрица [7, 4, 3]-кода Хэмминга 2? равна
0 1 2 3 4 5 6
1 111
11 11
111 1
111 1
1 111
1 111
1 111
1111111
(16-24)
Если /=3 и р=11, лея равна го порождающая матри 0123456789 1С ца [11, 6, 5]-кода Го- (16.25)
11 1111 11 1 111 11 1 111 1111 11 11111 1 111 11 1 11111 1 111 11 1 111 11 1 1 111 11 1 1110 11
11111111111
Расширенные KB-коды. KB-коды можно расширить путем добавления общей проверки на четность таким образом, что
(S?)-L==S?; (,+‘)-L = ./К", если p = 1, (16 26)
(Ж)± = Л/П, если р = 4&+1, где « Д » обозначает расширенный код.
Если а= («о, j Hp-i) — слово кода S (или Л9) и p=4k—1, то расширенный код получается путем дописывания позиции
р—1 ^со 21 " У ^г> г=0 где l+f/2p=0.
Так как (ур)2——р=&, то отсюда следует, что у=е$1р, где е=±1 (допустим любой выбор знака). Отметим, что у выбирает-А А
ся так, что слово (1, 1, ..., 1, —ур) кода S (или кода Л9) ортогонально самому себе. Если I равно 2 или 3, то у можно выбрать А А равным 1. Кодрт S и Л9 являются [р + 1, (р+ 1) /2] -кодами.
А
Теорема 7. Если p—4k—1, то расширенные KB-коды S и л
Л9 самодуальны.
А
Доказательство. Порождающая матрица кода S получается из матрицы (16.23) добавлением одного столбца и имеет вид
— 0 "
0
А G = G 0 (16.28)
_1 1 . . .1 ~УР_
Поскольку Scz(S)-, каждая строка матрицы G ортогональна самой себе и любой другой строке матрицы G. Следовательно, и каждая строка матрицы G ортогональна самой себе и любой дру-А ЛА
гой строке матрицы G так, что Scz^S)^. А так как ранг матрицы G равен (р +1)/2, то S=(S)J-.
Л Л
Таким образом, расширенные коды Голея ^24=^23 и ^12—^0 самодуальны.
Замечание. Если р=4&+1, то расширенный код можно оп-л л
ределить так, чтобы выполнялось равенство (2’)Л-==Л9.
Теорема 8. (i). Если 1=2 и p=4k—1, то вес каждого слова л
кода S кратен 4, а вес каждого слова кода S сравним с 0 или 3 по модулю 4.
. (ii). Если 1—3 (без всякого ограничения на р), вес каждого л
слова кода S кратен 3, а вес каждого слова кода S сравним с О или 2 по модулю 3.
Доказательство, (i). Если 2 — квадратичный вычет по модулю
р, то согласно теореме 23 p=8m±l. Таким образом, мы можем предположить, что р=8т—1. Число вычетов и невычетов в этом случае равно 4т—1, и, следовательно, вес каждой строки матрицы G кратен 4. Тогда утверждение теоремы вытекает непосредст-.
Л
венно из упражнения 38 гл. 1 (ii). Если ае^', то по теореме 7' a2o+a2i + ... +а2оо=0 (mod3). А так как а^— ± 1, то а2<= 1, и отсюда сразу вытекает утверждение теоремы.
Замечание. Если 1=2 и р=4&+1, то единственное, что мы л
можем сказать о весе слов кода S, это то, что он четен.
Применение. Из теорем 1 и 8 следует, что минимальное расстояние кодов ^2з и SBi равно соответственно 7 и 5. Поэтому код ^24 содержит слова только веса 0, 8, 12, 16 и 24 (как мы видели в гл. 2), а код ^12 — только слова веса 0, 6, 9 и 12 (см. гл. 19)..
Упражнение. (1). Доказать асимптотическую нормальность, спектра весов квадратично-вычетного кода. [Указание. Воспользоваться теоремой 23 гл. 9.]
16.5. ГРУППА АВТОМОРФИЗМОВ КВ-КОДОВ
В данном параграфе доказывается, что расширенный КВ-код. л
S инвариантен относительно мощной группы подстановок PSL2(p).
Определение группы PSL2(p). Пусть р — простое число вида 8т±1. Совокупность всех подстановок на множестве {О,. 1, 2, ..., р—1, оо} вида
ау + Ь су+(1’
(16.29).
где а, Ь, с, d^GF(p) и ad—bc=\, образует группу, которая называется проективной специальной линейной группой PSL2(p) (иногда она называется дробно-линейной группой).
Необходимые нам свойства группы PSL2(p) описываются следующей теоремой.
Теорема 9. (а). Группа PSL2(p) порождается тремя подстановками:
5: у —> 1;
V: у р2 у.
Т:у->~—(1/у), . где р — примитивный элемент поля GF(p).
(16.30),
(b) . Группа PSL2(P) состоит из р(р2—1)/2 подстановок вида: VlSi: уу+ j;
V1 S' TSh:y-+ k—(р2г у + /)-1.
где 0^i<(p—1)/2, 0^/; k<Z.p.
(с) . Если р=8т—1, то образующие подстановки S, V и Т связаны соотношениями: Sp= I/(V2)(p-1)= Т2= (VT)2= (ST')3=1 и V-iSV==Sp!.
(d) . Группа PSL2(p) дважды транзитивна.
Доказательство, (а), (Ь). Типичный элемент группы PSL2(p)
у -+ ау b-, ad — be = 1,
су+ d
может быть записан либо как y^>-ay2+ab, если с=0 (так как в
этом случае d=l/a), либо как у^~—--------------, если с#=0 (так
с с2 у + cd
, ad 1 \
как в этом случае b =-----------, и это дает соответственно
с с )
ViSab (где a=pi) и У18сЛТ8а1с (где с=рг). Случаи (с) и (d) мы оставляем читателю для непосредственной проверки. •
Основной результат для двоичного случая дается следующей теоремой.
Теорема 10. (Глизон и Прэндж.) Если /=2 и р=8т±1, то расширенный квадратично-вычетный код £ инвариантен относительно группы PSL2(p).
Доказательство. Так как порождающий идемпотент кода £ инвариантен относительно подстановки V, а подстановка S представляет собой циклический сдвиг, то код £ и, следовательно,
код £ инвариантны относительно S и V. Согласно п. (а) теоремы
9 остается доказать инвариантность £ относительно подстановки Т. Мы рассмотрим только случай р=8т—1 и покажем, что каждая строка порождающей матрицы (16.28), т. е. матрицы
(Г 0
0
1 1 . . .1 ] 1_
(16.31)
преобразуется под действием подстановки Т в другое слово ко-л
да £.
Л х
(i). Первая строка матрицы G, скажем, Ро, равна
1 + Хх"1°1-
Тогда
^(Яо)==|2хг|1| = Яо + 1е1
toQ
л •
(ii). Пусть seQ; ($ + 1)-я строка матрицы G равна:
^=:^s+2 *n+s i°i-ne^v
л
М.ы покажем, что T(Rs)=R-i/s+R0+l^S. Для этого в отдельно-сти для каждого члена равенства проанализируем координаты, содержащие символ 1. Вектор T(RS) содержит символ 1 в координатах —1/s и —l/(n+s) для n^N, что включает в себя сю (еслц п——s), 2m—1 вычетов и 2m невычетов (по теореме Перрона 24), Вектор
new
содержит символ 1 в координатах —1/s и п—l/s что вклю-.
чает в себя 2m вычетов и 2m невычетов. Следовательно, сумма T(Rs)+R-i/s содержит символ 1 в координате сю и символ 0 в координате —1/s (невычет). Если —l/(n+s) то —1/(n+s) = =п'—(1/s) для некоторого n'^N, и символы 1 в сумме взаимно, уничтожаются. Таким образом, координаты, соответствующие в сумме невычетам, всегда содержат символ 0. С другой стороны, если —1/(fi+s)eQ, то —l/(«+s) #=«'—(1/s) для всех n'^N, и координаты, соответствующие в сумме вычетам, содержат символ 0. Таким образом,
T(fle) + fl_Ve = |J>|l| = Z?0+l. I reQ
Аналогично, если то Т (Rt) = R-i/t + Ro- •-
Согласно теореме 18 гл. 8 слова каждого фиксированного веса л
кода S образуют 2-схему. В некоторых случаях имеет место более сильное утверждение (см. конец § 16.8).
л
Следствие 11. Все коды S, получаемые из S удалением одной координаты, эквивалентны между собой независимо от того, какая из координат вычеркивается.
Доказательство. Это вытекает из следствия .15 гл. 8, так как группа PSL2(p) транзитивна. •
Группа автоморфизмов недвоичных KB-кодов. Если />2, то л
(как было определено в § 8.5) группа Aut (S’) состоит из всех мо-л
номиальных матриц, относительно которых код S инвариантен.
В силу линейности код Z инвариантен относительно I—1 скалярных матриц
где ребЕ*(7). Этими матрицами удобно пренебречь и рассматри-л
вать в качестве группы автоморфизмов группу Aut+(S’) = л л
=Aut(S’)/{скалярные матрицы}. Очевидно, что |Aut(S’)| = = (Z-1) • |Aut+(<?) |.
Теорема 12. (Глизон и Прэндж.) Если Z>2, то группа л
Aut+(S’) содержит группу, изоморфную группе PSL2(p) и порождаемую элементами S, V и Т', где Т' представляет собой следующее мономиальное обобщение подстановки Т: элемент, стоящий первоначально й координате i, IsCis^p—1, умножается на %(i); элемент, стоящий первоначально в координате 0, умножается на е; элемент, первоначально стоящий в координате оо, умножается на ±е, где е было определено в предыдущем параграфе, и знак плюс берется для p=4k +1, а знак минус —• для p=4k—-1.
Доказательство. Аналогично доказательству теоремы 10. ®
Из теорем 10 и 12 следует только тот факт, что группа л
AuH(S’) содержит PSL2(p). Известны три1 случая, когда л
Aut+(S’) на самом деле больше группы PSL2(p), а именно при л
Z=2 и р=7 код S£ равен [8, 4, 4]-коду Хэмминга и согласно тео-л
реме 24 гл. 13 | Aut (S’) | = 1344. Два других случая получаются л
при Z=2; р—23 и Z=3; р=П; в этих случаях код S£ равен рас-л ширенному коду Голея, а его группа автоморфизмов Aut+(S’) равна группе Матье (см. гл. 20).
Но представляется очень вероятным, что для остальных значе-л
ний Z и р группа AuH(S’) равна группе PSL2(p). Это предположение выполняется во многих случаях; например, имеет место следующий результат.
Теорема 13. (Ассмус и Мэттсон.) Если (р—1)12. — простое число и 5<р^4079, то, за исключением указанных трех случаев, группа Aut+(S’) равна (изоморфна) группе PSL2(p).
Доказательство опускается.
1 Четыре, если учесть [6, 3, 4]-код над GF(4) (см. с. 503).
Упражнения. (2). Доказать, что коды S’ и S’ имеют одно и то же минимальное расстояние, а минимальное расстояние кода S’ на 1 меньше.
(3) . Доказать, что подстановка (16.29) принадлежит группе PSL2(p) тогда и только тогда, когда число ad—be является квадратичным вычетом по модулю р.
(4) . Доказать, что образующая V в (16.30) является избыточной: группа PSLz(p)1 порождается подстановками S и Т.
(5) . Доказать, что если р=8т—1, то соотношения, задаваемые п. (с) теоремы 9, определяют абстрактную группу порядка р(р2—1)/2 изоморфную, естественно, группе PSLz(p).
Задача (нерешенная). (16.3). Доказать, что утверждение теоремы 13 справедливо для всех р>23.
16.6. ДВОИЧНЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
На рис. 16.3 приведена краткая характеристика свойств двоичных КВ-кодов.
Блоковая длина кодов S3, SB,JP,JV‘ равна р=8т±\ (теорема 23), а порождающие многочлены соответственно равны:
ё(Ч = П(* + аГ) > (*+ В 9(4. »(х) = Г1(*+ а")> (*’+ 1) « (Ч.
reQ neN
(16.32) где а — примитивный корень степени р из единицы над полем 66(2). Размерность кодов SB и JP равна (р+1)/2, а размерность кодов SB и JP , состоящих из слов четного веса кодов SBuJP, равна (р—1)/2. Коды SB и JV' эквивалентны. Минимальное расстояние этих кодов описывается теоремой 1. Примеры приведены на рис. 16.2.
При р=8т—1 порождающие идемпотенты кодов равны:
2^. 1+2*п> 1 + 2Г- <16-33)
reQ neN neN reQ
При p=8m+l порождающие идемпотенты равны:
1+2Z’11У- (16‘34)
reQ neN neN reQ
Если р=8т—1, то добавление общей проверки на четность х Л Л
к кодам S и Л приводит к самодуальным кодам 33,.Л'" с пара-Л л
мётрами 1р+1, (1/2) (р+1)]. Все веса слов в S’ и уу3 кратны 4.
Л Л Л Л
Если р=8т+1, то (S’)-L==yE- В обоих случаях коды S’ и JP Л
инвариантны относительно группы PSL2(p). Код SB является квази-циклическим, порождающая матрица которого задается равенствами (16.31) и (16.44), а иногда равенствами (16.39) или (16.48).
Рис. 16.3. Свойства двоичных КВ-кодов
Примеры Двоичных квадратично-вычетных кодов 9?. (i). [7, 4, 3]-код Хэмминга (см. с. 464).
(ii) . [17, 9, 5]-код с порождающим многочленом х3+х5+х4+ +х3+1 и порождающим идемпотентом xI6+xls+xI3-r-x11+x3+x4+ д' | _
(iii) . [23, 12, 7]-код Голея Э’гз (см. с. 465).
(iv) . [31, 16, 7]-код с порождающим многочленом х13+х12-}-+ х7+х6+х2 + х+1. Множество квадратичных вычетов по модулю 31 равно Ci U С5 (J С7.
(v) . [47, 24, 11]-код с порождающим многочленом х23+х19+ + х13+х14+х13+х12 + х10+х9+х7+х6+Xs+х3+х2+х +1.
Первый и третий коды с р=8т—1 являются совершенными кодами. Если & — некоторый двоичный самоортогональный код, все веса которого кратны 4, то, как мы увидим в гл. 19, ^4[и/24]+4. Эта (верхняя) граница значительно больше, чем (нижняя) граница квадратного корня, задаваемая теоремой 1, и KB-коды длин 8, 24, 32, 48, 80, 104 (а также, возможно, и других длин) достигают этой границы. Этот феномен вызвал существенный поток работ по определению истинного минимального расстояния KB-кодов, некоторые из которых мы сейчас рассмотрим.
А
Другие формы порождающей матрицы кода 9?. Порождающая л л
матрица G кода Z, задаваемая равенством (16.31), представляет собой (р+ 1) X (р+ 1)-матрицу, ранг которой равен (р +1)/2. Иногда проще найти порождающую матрицу кода в виде [1|А], где 1 — единичная матрица, а А — либо циркулянтная матрица, либо окаймленная циркулянтная матрица.
Каноническая форма 1 — два циркулянта. Лемма 14. Для любого простого р>3 группа PSL2(p) содержит подстановку ль равную произведению двух циклов длины (/?-;-1)/2.
Доказательство. Как и в § 12.5, координаты {0, 1, ..., р—1, сю}, на которых действует группа PSL2(p), будем задавать ненулевыми векторами [ ], где х, y^GF(p). Таким образом, ( х ] задает \У) \ У )
координату х/у. Будем также задавать элемент i->~(ai + b)/(ci+'d) группы PSL2(p) матрицей - Нам надо найти подстановку
^i^PSL2(p) такую, что для каждого ненулевого вектора I) pax'// венство
= (16.35)
\ у / \ у /
выполняется при некотором k^.GF*(p) тогда и только тогда, когда ((р+1)/2) [г. Это и будет означать, что Л1 распадается в произведение двух циклов длины (р +1 )/2.
Пусть a^GF(p2) — примитивный корень степени (р2—1) из единицы. Тогда т] = а2р-2 — примитивный корень из единицы сте-
пени (р+1)/2. Положим Х=1/'(1+т]). Тогда ясно, что V=(l—h)r тогда и только тогда, когда (р-t-1)/2|г.
Определим теперь а=/.2—X. Тогда —а представляет собой квадратичный вычет по модулю р. Действительно, —n=a2p-2/(l + +т])2 = Ь2, где Ь = ар”1/(1 + 'П) и b^GF(p), так как
„ ар2-р а1-р
Ьр = —-------- = —-----= Ь.
1 + rf 1 + Ч — 1
Выберем теперь Л1 = подстановки Л1 равны:
векторы
1 Ц
,а 0 /
^PSL2(p). Собственные
так что
лг = В (
\ О
°
(1-Ь) )
Следовательно, равенство (16.35) выполняется тогда и только тогда, когда Хг=(1—k)r=k, что согласно определению X имеет место тогда и только тогда, когда (р+1)/2|г. 9
Например, если р=1, то Л1 равно подстановке i—»-(г4-l)/3t, распадающейся в произведение циклов (оо56 0) (1 3 2 4).
Пусть Hi— произвольная подстановка, равная произведению двух циклов:
• 1 \ • г 1
-у(Р+1) (р+1)
(16.36)
Возьмем произвольное кодовое слово се^ и упорядочим его координаты в соответствии с порядком, задаваемым (16.36): /iZ2.../1 и... г 1 . Тогда кодовые слова с, n,c, л21С,
- (р+1) - (р+1)
2 2
Л1(р-1)/2с образуют таблицу вида
[L|R], (16.37)
где L и R — циркулянтные (р+1) X — (р+1) -матрицы. Например, если с= (е0С1... с6Соо) = (01101001) — порождающий
л
идемпотент расширенного [8, 4, 4]-кода 2?, то матрица [L| R] равна:
оо 5 6 0 1 3 2 4
с:
лг с: л2 с: л® с:
1 10 11
1 110 1
1 1110
10 111
(16.38)
Конечно, матрица (16.37) всегда порождает подкод кода it. Но если нам удастся найти такое слово с, что ранг хотя бы одной из матриц L или R будет равен (р+1)/2, то мы можем обратить ее (см. упражнение (7)) и получить порождающую матрицу кода Л
Z в первой канонической форме
G = [I|A], (16.39)
где А — циркулянтная ((р+1)/2)Х ((р+1)/2)-матрица. Например, матрица (16.38) уже имеет такой вид.
Код с порождающей матрицей вида (16.39) называется дважды' циркулянтным кодом. Мы будем использовать это же название для кодов с порождающими матрицами вида (16.45), (16.46) и т. д., которые отличаются от матриц вида (16.39) только наличием окаймлений вокруг различных частей матрицы..В § 16.7 будет показано, что все эти коды представляют собой различные примеры квазициклических кодов. Ниже мы приведем дополнительные свойства таких кодов.
Пример. [24, 12, 8]-код Голея S?24- Если р=23, то подстановка щ: i->-(i+l)/5j распадается в произведение следующих двух циклов:
(21, 7, 16, 12, 19, 22, 0, оо, 14, 15, 18, 2)Х
Х(20, 17, 4, 6, 1, 5, 3, 11, 9, 13, 8, 10). (16.40)
В качестве с(х) возьмем сумму порождающего идемпотента
Е (х) = 2 хг reQ
кода ^23 и трех его циклических сдвигов (с добавлением общей проверки на четность):
оо 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Е(х)~ 1 1111111 11 1 1
хЕ(х)= 1 1111111 11 1 1
х2Е(х)=1 1111111 11 1 1
х3Е(х)=1 11111 11 11 1 1
с(х) = 11111 1 11
Переупорядочивая координаты вектора с(х) в соответствии с порядком (16.40), получаем порождающую матрицу кода ^24 в виде, показанном на рис. 16.4.
Задача (нерешенная). (16.4). Всегда ли можно найти такой вектор с, что хотя бы одна из матриц L или R окажется обратимой? Найти общий метод получения канонической формы (16.39) для порождающей матрицы расширенного КВ-кода.
Каноническая форма 2 — два окаймленных циркулянта. Вторая каноническая форма связана с другим элементом группьг
21 7 16 12 19 22 Ооо 14 15 18 2 20 17 4 6 1 5 3 11 9 13 8 10
Л G =
1 1111111
,1 1111111
1 1111111
1 1111111
1 1 111111
1 1 111111
1 11 11111
1 111 1111
1 1111 11 1
1 11111 11
1 11111 11
1.1 1111 1 1
Рис. 16.4. Дважды циркулянтная порождающая матрица кода Голея g?24
PSL2(p), а именно с подстановкой л2: где г=р2 — образую-
щая циклической группы квадратичных вычетов по модулю р. Разложение подстановки л2 на циклы равно
(оо)(щ пг, пг2, nr(p~~3'>/2) (1, г, г2,..., r(P"“3>/2) (0), (16.42)
где п — произвольный невычет. (При р=8т—-1 в качестве п мож-л л
но выбрать —1.) Обозначим через G2 матрицу, получаемую из G переупорядочиванием строк и столбцов в соответствии с (16.42).
Пример. Порождающая матрица [8, 4, 4]-кода преобразуется к виду (фактически к виду (16.24) с общей проверкой на четность)
В общем случае G2 записывается в виде
где
( 1, если р = 8т—1, е = J г
I 0, если р = 8т + 1.
Упражнение. (6). (а). Доказать, что А, В, С, D — цирку-лянтные матрицы.
(Ь). Доказать, что если р=8т—1, то C=CT=B + J и D— = AT=A+C+J, где J — матрица, все элементы которой равны 1. Показать также, что в этом случае вес всех строк матриц А, В и D равен 2т, а вес строк матриц С равен 2т—1.
(с). Доказать, что если р=8т + 1, то А=АТ; В = СТ; D = DT и вес всех строк матриц В, С и D равен 2т, а вес всех строк матрицы А равен 2т—1.
Таким образом, если р=8т—1, то матрица С может быть обратима (матрицы А, В, D заведомо необратимы, так как вес их «строк четен), а если р=8т+1, то матрица А может быть обратима. Если это так, то мы сразу приходим к следующей канонической форме порождающей матрицы:
матрица;
(16.45)
.где 1 — единичная
Т — циркулянтная
— 1)Х (2^—1^-матрица (здесь п=р+1) и а, b и с равны 0 или L Этот код называется (окаймленным) дважды циркулянтным ко
дом.
Примеры (1). Матрица С, задаваемая равенством (16.43) для р—1, равна единичной матрице, так что получаем:
"1 1 1 1 0 ~
л 1 1 1 1
G3 = 1 1 1 1 (16.46)
1 1 1 1
(2). Опять код Голея ^24. Первые две строки порождающей мат-л
рицы G, задаваемой равенством (16.39), равны:
оо 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
1 11 11 11 1 1111
11 11 11 111 1 1 1... (*>
Используя (16.42), переупорядочим столбцы следующим образом:
оо 14 5 10 20 17 11 22 21 19 15 7 1 2 4 8 16 9 18 13 3 6 12 0
1 11111111 111
Первые строки матриц С и D получаются из строки, отмеченной звездочкой, и показаны выше. Для того чтобы найти матрицу, обратную матрице С (см. упражнение (7)), запишем первую' строку матрицы С в виде многочлена а(х) =х3+х5+х6+х7+х9 и найдем обратный к нему по модулю хп + 1. Он равен 1+х+х2+ +х5-гх8+х9+х10.
Чтобы найти матрицу C ’D, вычислим
(1 +х + х2+х5+х8+х9 + х10) (1 + х3 + х4+х6+х9-;-х10) mod (х11-)- 1) =
= 1 + х2 + хе + х7 + х8 + х10 = 1 + 2 х”> neN
(16.47)1
где N — множество невычетов по модулю 11.
Таким образом, порождающая матрица кода ^24 может быть выбрана в виде
1 1 • • 1
Л-
1 1
(16.48)»
где Т=С 'D — циркулянтная матрица, первая строка которой задается многочленом (1Q.47):
О 1 2,3 4 5 6 7 8 9 10 ...
(10.49)
. : , 1 Q 1 0 0 0 1 1 1 0 1
Это эквивалентно определению кода §24, данному на рис. 2.13 (см. упражнение (9)). Таким образом, мы видим, что некоторые двоичные KB-коды эквивалентны (возможно, окаймленным) дважды циркулянтным кодам. (Та же самая процедура .может быть применена к недвоичным кодам.)
Задача (нер ешенная). (16.5). Иногда не удается обратить ни одну из матриц С или А (например, при р= 127, см. Карлин [715]). Возможно ли, однако, и в этих случаях записать порождающую матрицу в виде (16.45)?
Упражнения. (7). Циркулянтные матрицы, (i). Доказать, что алгебра циркулянтных (нХп)-матриц над полем F изоморфна алгебре F[x]/(xn—1) относительно отображения циркулянтной матрицы -
...
ап—1 °6 • ап—2
(16.50)
на многочлен
«1 а2 . . . а0
а(х) = а0 + а1х + ... + ап_1хп-1. (16.51)
(ii). Сумма и произведение двух циркулянтов есть циркулянт.
В частности, АВ = С, где с(х) =а{х)Ь{х) (mod (Xй—1)).
•= (iii).'Матрица А обратима тогда и только тогда, когда многочлен а(х) взаимно прост с хп—1. Обратная матрица, если она существует, равна В, где a (x)b (х) = 1 modxn—1.
' (iv). Матрица. Ат представляет собой циркулянт, соответствующий многочлену а0 + ап-1Х+ап-2Х2+ ... +а1хп-1.
(v). Пусть Т — циркулянт, у которого «1 = 1 и Oj=0 для всех : ‘ П=1
/=Й1. Доказать, что А= 2 а{Т*.
, г=о
(vij. Пусть .р — примитивный корень степени п из единицы, лежащий в некотором поле, содержащем поле F. Доказать, что собственные значения матрицы А равны о(1), о(Р), ..., о(.рп~1) (см..упражнение (20) гл. 7).
(8). Пусть (соответственно .^?) — двоичный [2m, т]-код с порождающей матрицей [11 А] (соответственно [1|В]). где А и В — циркулянты, первая строка, которых задается многочленами
т—1
а(х) = £ дгхг;
г=о
т—1
Ь(х)= bixi-г=0
(i). Доказать эквивалентность кодов и $ в следующих случаях: (а) если В = АТ; (Ь) если ai=bm-i-i для всех i (т. е. если
многочлен b(x) взаимен' многочлену а (х)); (с) если а(х)Ь(х)= ==l(mod(xn—1)); (d) если b(x)=a2(x) и т нечетно; (е) если Ь(х) = а(хи), где и и т — взаимно простые числа.
(ii) .-Доказать, что коды и л/ эквивалентны.
(iii). Доказать, что тогда и только тогда, когда ААТ=
i=I. - - - - - -------—---------
! (9). Доказать, что порождающие матрицы (16.48) и (16.49)
(кода §24 эквивалентны матрице, приведенной на рис. 2.13.
Г- (10). Пусть код 'й’ задается ’ порождающей“ ‘'матрйцёйП'вйда '(16.45) при д=с=1 и Ь—0. Доказать, что ‘g7-L=‘iF тогда и только тогда, когда TTT=I + J.
! Метод нахождения слов малого веса в коде S. (Карлин и ^Мак-Вильямс [718].) Порождающая матрица вида (16.45) облегчает задачу вычисления минимального расстояния йода 9? или i д
Многие из результатов, приведенных на рис. 16.2, были полуйены именно таким способом.
: В некоторых случаях, как мы сейчас покажем, слова малого веса „могут быть найдены непосредственно- —---------д . -,
Подстановка V: y-*-p2y, где р — примитивный элемент поля GF(p), является элементом группы Aut(5?). Порядок этой подстановки равен (р—1)/2. Если это число является составным, скажем, (р—l)/2=sf, то код S содержит слова, инвариантные относительно подстановки U: y->-p2sy. Пусть — подкод кода Z, состоящий из этих слов. Покажем, как при р==8т—1 можно найти подкод <2/. Пусть е=2$; р—l=ef, где s и f — нечетны. Разобьем множество чисел по модулю р на е классов:
7’г={р«Ж:/ = 0, 1,..., f— 1}, i = 0,..„ е— 1.
Например, если р=71, то р—1 =70= 14-5е= 14, р=7:
7’0 = {1,714, 728, 742, 756} = {1, 54, 5, 57, 25};
7\ = {7, 715, 729, 743, 757} = {7, 23, 35, 44, 33};
Определим многочлены Xi для i=0, 1, ..., е—1 равенством =2 х*. (16.52)
*егг
Упражнение (11). (i). Доказать, что многочлены Хг инвариантны относительно подстановки U и что произвольный многочлен, инвариантный относительно U, может быть представлен в виде линейной комбинации многочленов 1, Хо, ..., Хе-х.
(ii) . Доказать, что Eq(x)=X0+X2+ ... +Хе_2.
(iii) . Доказать, что для всех i=0, 1, ..., е—1 имеет место ра-е—1
венство XiEq(x) =t]i+ S ецХ, при некоторых тщ eh^GF(2). i=i
(iv) . Таким образом, подкод °U кода Z, инвариантный относительно подстановки U, состоит из линейных комбинаций многочленов Eq(x) и XiEq(x), i=0, 1, ..., е—1.
Коэффициенты г); и приведены на рис. 16.5. (Матрицы А и
В на этом рисунке отличны от матриц А и В в (16.44).)
1 Х0Х2 . . .хе_2 . -Xe_2_|_s
Eq (х) 0 1 1.1 0 0 0
Хо Eq (х) 0 А в
2 W 6
XsEq(x) 1 в +J А-г 1+J
Xe_q+s Eq (х) i —
Рис. 16.5. Коэффициенты 1], И 6г3
Тогда матрица
(16.53)'
является порождающей матрицей кода СИ*. Приведем без доказательства следующий результат. Матрица G представляет собой (2s+l) X (2s+l)-матрицу ранга s+1. Матрицы А и В являются циркулянтными, и их первые строки задаются следующей простой формулой. Пусть
[т] =
1, если т—квадратичный вычет по модулю, О, если т—квадратичный невычет или 0;
Р
тогда
*) Точнее, эта матрица однозначно определяет порождающую матрицу подкода (U^£- (Прим. ред.).
c. = [p2i7_l]; &;= — 1], i = 1, . S— 1;
a0 = (l/2)(s+l)mod2; bo = 0.
Таким образом, <U можно рассматривать как [2s +1, s+1]-код. В таком случае между словами минимального веса кода <Н и спектром весов кода £ имеется следующая связь: если r) + Ail + + ... +Xts — слово минимального веса кода <2/, то код £ содержит кодовые слова веса rj+ir/. Следовательно, минимальный ненулевой вес в <2/ задает верхнюю границу для минимального веса в коде £. На самом деле, во всех случаях, в которых известен минимальный вес в коде £, он был получен в коде
Пример. р=71; е=14; [=5; р—7.
Чтобы найти первые строки матриц А и В, воспользуемся работой Виноградова [1371] для вычислений вычетов и невычетов:
49® — 1 = 44e7V 49м—l = 36eQ 4915— 1=31еА 4920— 1 = 19EEQ 4925—1 = 17еА 4930—1 =29sQ
— 49s—1 =25е<2
—4910— 1 = ЗЗеА
—4915— 1=39geQ
—4920— 1 = 50GEQ
—4925— 1 = 52f=W — 4930— 1 = 40eQ
Следовательно, первые строки матриц А и В равны:
О 1
О О
2
1
3 4 5 6
0 10 1’
0 12 3
0 10 1
4 5 6
1 0 1
Отметим, что для выписывания матрицы G нам нужна лишь таблица степеней примитивного элемента р. В дальнейшем такие же матрицы будут появляться для многих различных простых чисел р.
Матрица А часто оказывается обратимой, и в этих случаях порождающая матрица кода <2/ может быть записана в виде
0 11... 1 0 0 . . . 0
0
- I R+J
0
11... 1 1 1 ... 1
(16.54)
где R — ортогональная циркулянтная матрица.
Пример. (Продолжение.) Обратным многочлену х2+х4+х6 по модулю х7+1 является многочлен х+х2 + х3+х4+х5. Таким образом, матрица G приводится к виду
О 1111111 ооооооо
0 1 1 1 г 0 1 1 1
0 1 1 1 1 1 0 1 1
0 1 1 1 1 1 1 0 1
0 1 1 1 1 1 1 1 0
0 1 0 1 1 1 1 1 1
0 1 1 0 1 1 1 1 1
1 1 1 0 1 1 1 1
11 1 1 1 1 1 1 1 I 1111111
Р Г раница
р = 8m — 1 : 631 83
727 67
751 99
991 91
р = 8m + 1 233 ' 25
241 41
257 33
761 75
1361 135
Рис. 16.6. Верхние границы для минимального расстояния кода 3
Сумма первой, второй и последней строк этой матрицы равна 1 + Ло+-Х\зл так что S представляет собой [71, 36]-код, содержащий слова веса 1+2-5=11.
Для р=8/п+1 процедура нахождения слов минимального веса аналогична описанной.
На рис. 16.6 приведены некоторые отрицательные результаты, полученные на этом пути.
Задача (нерешенная). (16.6). Пусть 3? содержит нетривиальные подкодр! <U\ всегда ли слово минимального веса в 3? попадает в один из подкодов
Другой способ использования группы автоморфизмов для нахождения весов кода 3. Мик-кельтвейт, Лэм и Мак-Элис [979] предложили другой мощный метод нахождения весового многочлена квадратично-вычетных и других кодов. В его основе лежит следующее утверждение.
Лемма 15. Пусть Н — неко-которая подгруппа группы автоморфизмов Aut С®7) кода Если Аг — число слов веса i в коде 'й7, а Аг(Н) — число слов веса i в ко-
де 1F, инвариантных относительно некоторого элемента из подгруппы Н, то
Аг==А (Я) mod| Н |.
Доказательство. Разобьем множество всех слов веса i кода IF на два класса: слова, инвариантные относительно некоторого элемента из подгруппы Н, и остальные слова. Если слово tze'g7 неинвариантно относительно ни одного слова из Н, то все слова ga ПРИ должны быть'различны (число таких слов равно |Я|). Следовательно, Аг равно сумме Аг(Н) и некоторого числа, кратного числу |Я|. •
Обозначим через Sq максимальную подгруппу в группе Aut(IF), порядок которой равен степени простого числа q, делящего:
|Aut(^)|. (Sq называется силовской подгруппой группы Aut(^); в случае Aut(^) = PSL2(p) эти подгруппы имеют очень простую структуру.) Заставляя Н пробегать по подгруппам Силова Sq, по лемме 15 можно определить все величины Afmod^a и, следовательно, по китайской теореме об остатках, все величины Atmod| Aut(^) | (упражнение (8) гл. 10). При больших значениях |Aut(‘₽’)| это часто позволяет точно найти величины (см., например, [979]).
Упражнение. (12). В обозначениях гл. 6 для некоторых значений р коды ЗД приведенные на рис. 16.2, удовлетворяют условию d'~>s. Найти эти значения р и исследовать образующиеся при этом схемы.
16.7. ДВАЖДЫ ЦИРКУЛЯНТНЫЕ И КВАЗИЦИКЛИЧЕСКИЕ КОДЫ
Дважды циркулянтные коды были определены в предыдущем параграфе как коды, порождающая матрица которых имеет вид
(16.55)
где А — циркулянтная матрица, первая строка которой задается многочленом a(x)=ac + a\x + azx2+ а числа а, b и с равны 0 или 1. То же самое название мы будем использовать для различных кодов, получающихся из кода с порождающей матрицей (16.55), например для кода, получающегося при выбрасывании первой строки или первого и последнего столбцов матрицы (16.55). В результате последнего преобразования из матрицы (16.55) получаем матрицу
[1|А], (16.56)
где I и А — (Ах-матрицы. Матрица (16.56) порождает [26, k\ дважды циркулянтный код, который мы в этом параграфе будем обозначать через 3)а. Некоторые из свойств кода 3)а указаны в упражнении (8).
Упражнение. (13). Показать, что код 3)а допускает чрезвычайно простое кодирование: сообщение и(х) переходит в кодовое слово ju(x)l и(х)а(х)|.
Квазициклические коды. Код называется квазициклическим, если для некоторого целого числа s каждый циклический сдвиг кодового слова на s позиций опять является кодовым словом. Очевидно, что циклический код является квазициклическим при s=l.
Выписывая столбцы матрицы (16.56) в порядке 1, &+1, Л+2, ..., видим, что дважды циркулянтный код 3)а является квази-
циклическим кодом с s=2. Например, матрица (16.46) перепишется в виде
'1 1 О О О Г
O111OO.
0 0 0 11 1.
что определяет квазициклический код с s=2. Из леммы 14 и равенства (16.44) также следует, что двоичный КВ-код £ с одной л вычеркнутой координатой или любой расширенный код £ эквивалентны квазициклическому коду с s=2.
Так как порождающая матрица многих кодов, изучаемых в этой главе, имеет вид (16.56), то мы знаем, что среди кодов такого типа имеются хорошие коды. В частности, некоторые длинные дважды циркулянтные (или квазициклические) коды £)а лежат на границе Варшамова—Гилберта. Следующая теорема представляет собой несколько более слабый результат.
Теорема 16. Если k — такое простое число, что 2 является примитивным элементом поля GF(k), и если для 2r<_k выполняется неравенств^
то существует [2/г, k\ дважды циркулянтный двоичный код £)а, минимальное расстояние которого равно по меньшей мере 2г.
Доказательство. Выберем а(х) так, чтобы его вес был нечетным числом, меньшим чем k. Число таких кодов £)а равно 2fe-1—1. В силу выбора числа k полное разложение многочлена xfe + l над fe-i
полем GF(2) равно (х+1)Ехг’. Следовательно, в кольце 1=0
GF(2) [x]/(xv+1) многочлен а(х)1 обратим.
Пусть 11(х) | г(х) | — типичное слово кода £>а, согласно упражнению (13) г(х) = 1(х)а(х). Следовательно, веса wt(/(x)) и wt(r(x)) имеют одну и ту же четность. Заметим также, что код £>а содержит слово 1 (сумма строк матрицы (16.56)).
Если вес многочлена 1(х) нечетен и меньше чем k, то при заданном г(х) слово г(х) | является кодовым точно для одного кода £)а, а именно того £)а, для которого а(х) = 1~1(х)г(х).
Если вес 1(х) четен, то слово [1(х)г(х)1 опять попадает точно в один код £)а, а именно в тот, для которого
a(x) = (l+Z(x))-1(l+''W).
Таким образом, каждое слово 11(х) | г(х) |, вес которого меньше чем k, принадлежит точно одному коду £)а. Остальная часть доказательства является стандартной (ср. с теоремой 31 гл. 17).
К сожалению, в настоящее время имеется только предположение о том, что существует бесконечно много простых чисел k, для которых 2 является примитивным элементом поля GF(k). Если бы
это было доказано, то, выбирая в теореме 16 достаточно большие k, мы могли бы утверждать, что некоторые достаточно длинные КОДЫ SDa лежат на границе Варшамова—Гилберта. Однако, и не имея такого результата, Касами использовал теорему 16 для доказательства существования кодов SDa, весьма близких к границе Варшамова—Гилберта —- (см. [730]*)-
Дважды циркулянтные коды Мы определим сейчас семейство двоичных дважды циркулянтных кодов длины 8/п, где q= =4т—1 — простое число вида 8k-r3 (но теперь мы не накладываем требования, чтобы 8m—1 было простым числом).
Определение. Пусть & — [8/п—2q+2, ^+1]-код, порождающая матрица которого задается матрицей вида
(16.57)
где А — циркулянтная матрица, в Гг-й позиции первой строки которой стоит символ 1 тогда и только тогда, когда i—О или i является квадратичным вычетом по модулю q, так что
а(х)= 1 +^Х-
reQ
Например, если q—8, то
1 СО ^0 ^2 Гоо го П Г2
1 1 0 0 0 1 1 0
м = 1 0 1 0 0 0 1 1 (16.58)
1 0 0 1 0 1 0 1 »
0 0 0 0 1 1 1 1
что, конечно, эквивалентно расширенному коду Хэмминга (16.46). При <7=11, как мы видели в упражнении (8), получаем [24, 12, 8]-код Голея.
Упражнение. (14). Доказать, что код S% самодуален и все его веса кратны 4.
При q= 19 код является [40, 20, 8]-кодом, а при <у=43 — [88, 44, 16]-кодом; в обоих случаях, как будет показано в гл. 19,
*> Этот результат Касами, доказанный только для скоростей 1/Z и (/—1)//, был обобщен Кабатянским на случай скоростей v/l, —1 (см. (706а].
. (Прим, перев.)
эти коды обладают максимально возможным минимальным расстоянием в классе самодуальных кодов, все веса которых кратны 4. Спектры весов этих кодов также будут приведены в той же главе.
Код $ можно рассматривать также как расширенный циклический код над GF(4). Пусть (oeGK(4) — примитивный кубический корень из единицы такой, что со2+® +1=0. Заменим Ц и гг- на Пг=/<(о+г<(й2, т. е. установим соответствие
h vt
0 0^0
1 0 и
0 1 ®2
1 12 1
Упражнение. (15). Доказать, что это отображение переводит 91 в расширенный циклический код S) над GF(4). Порождающий идемпотент кода S) равен
®2V + хП’ reQ neN
где Q и N — соответственно множество квадратичных вычетов и невычетов по модулю \q. Доказать, что 3) получается путем расширения циклического кода с порождающим многочленом П^р (х+аг), где а — примитивный корень степени q из единицы, лежащий в G77(4/). (Таким образом, можно сказать, что 3) представляет собой расширенный квадратично-вычетный код над GF(4).)
Пример. Рассмотрим код, первая строка порождающей матрицы которого равна
1 1000000000001 101 1 10001 0.
(Это код Голея.) Указанное отображение переводит эту строку в следующий вектор над полем GF(4):
со 1 а2 0 а2 ®2 й2 0 0 0 о2 0.
Прибавляя вектор 1 и умножая на е>, получаем порождающий, идемпотент расширенного кода
1 0 б)2 ® и2 ®2 и2 о и о а2 а.
Упражнения. (16). Доказать, что группа Auti(^) содержит (i) группу PSL2(q), действующую одновременно на обе половины матрицы (16.57), и (ii) перестановку
(1<х> ^со) GoG) (^iG—i) G2G—2) ••• (^<7—1ri)i (16.59)
пеняющую местами обе половины.
(17). Доказать, что 2D как код над GF(4) инвариантен относительно группы PSLz(q)' и обобщенной перестановки (Ооо) (по) X X (v2vq-2) ПРИ взаимной замене а» и а»2.
Задача (нерешенная). (16.7). Имеет ли место для минимального расстояния кода $ граница квадратного корня, аналогичная теореме 1?
В заключение этого параграфа приведем таблицу (рис. 16.7), дающую некоторые примеры хороших дважды циркулянтных кодов. Первая строка матрицы A, a(x)~ao+aix-j- ..., на этой таблице записана в восьмерично-двоичной системе: | а0а\а21 | ...,
например 426 обозначает многочлен 1 +х4+х6+х7.
п k d С )пределение а (*) п k d Определение а (х)
6 3 3 (16.56) 3 28 14 8 (16.56) 727
8* 4 4 (16.38) 7 30 15 8 (16.56) 2167
10 5 4 (16.56) 7 31 16 8 (16.57)# 23642
12 6 4 (16.56) 6 32 16 8 (16.56) 557
14 7 4 (16.56) 77 39 20 8 (16.57)* 236503
16 18 20 22 8 9 10 11 5 6 6 7 (16.56) (16.56) (16.56) (16.56) 426 362 75 355 40# 40 42 20 20 21 8 9 10 (16.57) (16.56) (16.56) 636503 5723 14537
24* 24* 12 12 8 8 (16.41) (16.48) 675 5072 или 6704 56# 64# 28 32. 12 12 (16.57) (16.57)
26 13 7 (16.56) 653 88# 44 16 (16.57) а (х)
28 14 8 (16.57) 26064 108 54 20 (16.57)
# Самодуальный код; все веса кратны 4.
* С выброшенным первым столбцом.
а(х) = 62473705602153.
Рис. 16.7. Хорошие дважды циркулянтные коды
16.8. КВАДРАТИЧНО-ВЫЧЕТНЫЕ И СИММЕТРИЧНЫЕ КОДЫ НАД GE(3)
Примеры расширенных KB-кодов над GF(3) приведены на рис. 16.2. Длина этих кодов равна 12m или 12m+ 2 (согласно нижеследующему упражнению (25)), а все веса кратны 3 (теорема 8). Первым из них является код Голея ^12 (см. с. 465). Минимальные расстояния кодов [24, 12, 9], ,'[48, 24, 15] и [60, 30, 18] были найдены на вычислительной машине. Как будет показано в гл. 19, эти расстояния являются максимально возможными для само-Дуальных кодов над GF(3).
Симметричные коды Плесе. Эти коды являются дважды цир-кулянтными над GE(3) (см. рис. 16.8).
Определение. Пусть р — простое число, сравнимое с —1 по модулю 6, и пусть S — следующая (р+1) X (р+1) -матрица
(строки и столбцы которой перенумерованы р-1):
числами оо, 0, 1, ...,
оо 0 1... р— 1
оо
О
S= 1
р—1
О 1 1 ... 1
е
е
(16.60)
где е= 1, если р=4й+1, и е=—1, если р=4й—1, а С — цирку-лянтная матрица, первая строка которой содержит 0 в нулевом столбце, 1 в столбце, номер которого является квадратичным вычетом по модулю р, и —1 в столбце, номер которого является квадратичным невычетом по модулю р. Тогда симметричный код Плесе S2P+2 определяется как [2р+2, р+1]-код над GF(3), порождающая матрица которого равна матрице [I|S] , где I — единичная (р+1) X (р+1)-матрица.
Пример. При р=5 порождающая матрица кода Sj2 равна оо 0 1 2 3 4
1 0 11111
1 1 0 1 1
1 1 10 1
1 1 — 10 1 —
1 1 10 1
1 1 1 1 0
(16.61)
Упражнения. (18). Доказать, что код 'S12 эквивалентен коду Голея ^12.
(19). (1). Доказать, что SST=—I (над GF(3)).
(ii). Доказать, что если p=4k + l, то S = ST = S1, а если р = =4k—l, то S=—ST=S~1.
Теорема 17. Код S2p+2 является самодуальным, и все веса кода кратны 3.
Доказательство. Вытекает из упражнения (19). •
Примеры. Параметры первых пяти симметричных кодов равны
[12, 6, 6], [24, 12, 9], [36, 18, 12], [48, 24, 25], [60, 30, 18].
(16.62)
Весовые функции кодов S24, S46 и S60 совпадают с весовыми функциями Хэмминга расширенных КВ-кодов с теми же параметрами (см. гл. 19), однако эти коды неэквивалентны (упражнение
(20)). Отметим, что для всех пяти кодов минимальное расстояние равно d=(l/4)n+3, что является максимально возможным в данном случае (см. гл. 19). К сожалению, для следующего [84, 42]-кода известно, что d^21.
Теорема 18. Группа автоморфизмов кода S2p+2 содержит следующие мономиальные преобразования: если |А|Л| — слово кода S2p+2, т0 кодовыми словами являются также
-|L|7?|, |7?| -в£|, |S(L)|S(tf)|,
|V(L)|’/(7?)|, | Г (L) | T' (R) |,
где S, V, T' — преобразования, определенные в теореме 9.
Следовательно, Aut(S2p+2) содержит подгруппу, изоморфную-группе PSL2(p).
При р=—1 (mod 6) код S2p+2 является дважды циркулянтным, самодуальным [2р+2, р+1]-кодом над GF(3), порождающая матрица которого равна где S задается формулой (16.60). Группа Aut(S2p+2) содержит PSL2(p), и если |£|/?| —кодовое слово, то |/?|—е£| также является кодовым словом. Примерами кодов являются коды (16.62).
Рис. 16.8. Свойства симметричных кодов Плесе
Упражнения. (20). Используя теоремы 12- и 13, доказать, л
что при 2р + 2=24, 48, 60 коды S и S2p+2 неэквивалентны. [Указание. PSL2(p)<£PSL2(2p + 1).]
(21). Доказать, что любой расширенный КВ- или симметричный код длины п=\2т над GF(3) содержит по меньшей мере 2п слов веса п. На самом деле, имеется эквивалентный код, содержащий строки матрицы Адамара порядка п и их отрицания.
(i) Из КВ-кодов
[п, k, Ф Поле Схема из слов минимального веса Эти веса также приводят к 5-схемам
[12, 6, 6 GF (3) 5-(12, 6, 1) 9
[24, 12, 8 GF (2) 5-(24, 8, 1) .12, 16, 24
[24, 12, 9 GF (3) 5 (24, 9, 6) 12, 15
[48, 24, 12 GF (2) 5-(48, 12, 8) 16,20,24,...36,48
[48, 24, 15 GF(3) 5-(48, 12, 364) 18, 21, 24, 27
[60, 30, 18] GF(3) 5-(60, 18, 1530) 21, 24, 27, 30, 33
(ii). Из симметричных кодов
[24, 12, 9] GF (3) 5-(24, 9, 6) 12, 15
[36, 18, 12] GF(3) 5-(36, 12 , 45) 15, 18, 21
[48, 24, 15] GF (3) 5-(48, 12 , 364) 18, 21, 24, 27
[60, 30, 18] GF (3) 5-(60, 18, 1530) 21, 24, 27, 30, 33
Рис. 16.9. 5-схемы, полученные из кодов
Задача (нерешенная). (16.8). Как растет с р минимальное расстояние d кода S2p+2?
5-схемы. Применение результатов гл. 6, в частности теоремы 9 и следствия 30, к кодам (16.62) и кодам, приведенным, на рис. 16.2, позволило построить несколько 5-схем. Параметры этих схем были вычислены с помощью весовых функций соответствующих кодов (найденных в гл. 19) и приведены на рис. 16.9. Например, вторая строка рисунка означает, что слова весов 8, 12, 16 и 24 в двоичном расширенном [24, 12,. 8]-коде Голея образует 5-схемы, первой из которых является схема 5-(24, 8, 1) (в соответствии с теоремами 24—26 гл. 2) (см. также приведенную ниже формулу (16.67)).
16.9. ДЕКОДИРОВАНИЕ ЦИКЛИЧЕСКИХ И НЕКОТОРЫХ ДРУГИХ КОДОВ
Кодирование циклических кодов было описано в § 7.8; специфические методы декодирования кодов БЧХ были рассмотрены в § 9.6, декодирование альтернантных кодов — в § 12.9, декодирование кодов Рида—Маллера — в § 13.6, 13.7. В данном параграфе описываются некоторые методы декодирования, пригодные для всех циклических и дважды циркулянтных кодов.
Пусть — двоичный [п, k, г/]-код. Предположим, что передавалось слово с= (с0, Сь ..., сп-1), что получено слово у=с+е= ~'(Уо, У\> , Уп-i), причем вес вектора ошибок е= (е0, ех, ..., еп-Х) равен t, где 2^+1 Для простоты предположим, что порождающая и проверочная матрицы кода равны соответственно G= = [А| I] и Н=[1|АТ]. Таким образом, Сд, ..., cr~i являются г— =п—k проверочными символами кодового слова, а ст, cn-i—k информационными символами. Например, мы могли бы использовать кодер # 1 из § 7.8.
Рассматриваемые ниже методы декодирования основываются на следующей теореме.
Теорема 19. Предположим, что вес вектора ошибок е== = (е0, еь ..., en-i) равен t, где 2^+1 Пусть 8=Нут — синдром принятого вектора у. Если wt(S)<;/, то принятые информа: ционные символы уг, уп_х правильны и вектор ошибки .равен S=(e0, > ег_х)т- Если wt(S) >/, то по крайней мере один из информационных символов уДг —1) неправилен.
Доказательство, (i). Предположим, что все информационные символы правильны, т. е. е^—О для всех 1. Тогда S =
=i[I|Ат]ет= (е0, ..., er-i)T и wt(S)^t (ii). Пусть е(1)= (е0, ..., er~i); е{2)= (ег, е„_1), и предположим, что е(2)=^0. Рассмотрим кодовое слово cz=e(2)G=ie(2)[А| IJ = |в(2)А| е(2> |. Так как с'=т^О, то, по предположению, wt(c') ^2/+1. Следовательно, wt(e(2)) + +wt'(e(2)A) ^2/+1. Далее
S = 4eT = e(r1)-p Аге[2) , так что wt(S) > wt(Aref2))—wt(efi))>->2^+1— wt(e(1))—wt(e(2)) > t+1. ф-
Метод декодирования I: перестановочное декодирование. Этот метод применим к кодам с достаточно большой группой автоморфизмов, например к циклическим кодам или, еще лучше, к квадра-тично-вычетным кодам.
Предположим, что мы хотим исправлять все векторы ошибок е, вес которых не превосходит t при некотором фиксированном ^[(d—1)/2]. Для выполнения декодирования надо найти такое множество подстановок P={jti = 1, лг, jis}, чтобы . код ‘ё был инвариантен относительно этого множества и чтобы для каждого вектора е, вес которого не превосходит t, нашлась бы подстановка л^Р, передвигающая все ошибки из информационных позиций в проверочные.
Пример. Пусть —[7, 4, 3]-код Хэмминга и /=1. Тогда, как показано на рис. 16.10, подходящим множеством подстановок является множество Р={1, S3, S6}, где S — циклический сдвиг. Например, если е=ООО 1000, то S6 выводит символ 1 из информационных позиций: S6e = 0010000.
Информационные ПОЗИЦИИ
1 • С — Cq с± с2 S3-c = с4с5с6 S6-c = с4 с2 с3 С3 Cq С0 С1 С2 С3 С4 ^5 ^6 С0
Рис. 16.10. Три перестановки для перестановочного декодирования (7, 4, 31-кода
Метод декодирования состоит в следующем. По полученному вектору у вычисляются векторы л,у и их синдромы S<2')= Н (ЛгУ)Т до тех пор, пока не будет найден индекс I, для которого wt(S<9)^ При этом согласно теореме 19 все ошибки сосредоточены в первых г позициях вектора Лгу и задаются равенством (е0, ..., er-i) = S<Y>T. Следовательно, полученный вектор декодируется как слово
с = лГ* ((лг у + (е0,..., er_!, 0,..., 0)). (16.63)
Если wt(S(i))>7 для всех i, то заключаем, что произошло более чем t ошибок.
Задаче нахождения минимальных множеств Р посвящено очень мало работ.
Метод вылавливания ошибок. (Рудольф и Митчел [11’33].) Этот метод декодирования является частным случаем перестановочного декодирования, при котором используется только циклическая подстановка S, так что Р={1, S, S2, ..., Sn-1}. Метод позволяет исправлять все векторы ошибок е, содержащие круговую серию нулей длины не менее k, т. е. содержащие цепочку нулей Длины по меньшей мере k при записи координат вектора е по кругу.
Упражнение. (22). Доказать, что при этом могут быть исправлены все ошибки, вес которых не превосходит t, где /= = [(«— l)/k].
Таким образом, этот метод декодирования оказывается пригодным только в тех случаях, когда символы 1 в векторе ошибок е разделены большими отрезками нулей; иначе говоря, в случаях малого числа случайных независимых ошибок или в случае пакетов ошибок. Например, применительно к [23, 12, 7]-коду Голея имеем: t= [22/12] = 1, так что некоторые ошибки веса 2 и 3 не могут быть исправлены.
Однако этот метод очень легко реализуем. Единственное, что требуется, это сдвигать вектор у до тех пор, пока не получится вектор Sy, вес которого не превосходит t, а затем использовать равенство (16.63). Заметим, что согласно упражнению (36 b) гл. 7 если для вычисления синдрома вектора у использовать схему деления кодера 4f 1, то синдромы всех циклических сдвигов вектора у вычисляются очень легко: они просто равны содержимому регистра сдвигов в соответствующие моменты времени.
Примеры. (1). Код БЧХ [31, 21, 5] с исправлением двух ошибок. В этом случае [30/21] = 1, так что использование метода вылавливания ошибок не позволит исправить некоторые двойные ошибки. Используем, однако, подстановку о2, переводящую вектор (у0, уъ узо) в вектор (z0, zb г30), где z2i=yi (индексы вычисляются по модулю 31). Как было показано в § 8.5, код инвариантен относительно о2. Кроме того, о52=1. Легко показать, что множество Р={5’о’2, 0^it^30, 0^/^4}, содержащее 155 подстановок, передвигает из информационных позиций любую ошибку веса 2 и, следовательно, пригодно для перестановочного декодирования.
(2). Код Голея [23, 12, 7]. Метод вылавливания ошибок опять позволяет исправлять только одиночные ошибки. Однако множество P={SiGi2, 0sCtsC22, /=0, 1, 2, 11}, содержащее 92 подстановки, позволяет передвинуть за пределы информационных позиций любую ошибку, вес которой не превосходит 3 (см. МакВильямс [873]), и может быть использовано для перестановочного декодирования.
Ни одно из указанных множеств не является минимальным.
Задача (нерешенная). (16.9). Найти минимальное множество Р для перестановочного декодирования (а) кодов Голея §зз и ^24, (Ь) [31, 21, 5]-к0да БЧХ, (с) [48, 24, 12]-кода Z и т. д.
Метод декодирования II: покрывающие многочлены. (Касами [725].) Этот метод представляет собой модификацию метода вылавливания ошибок, позволяющую исправлять большее число ошибок. Мы теперь будем пытаться исправить любую ошибку, вес которой не превосходит t, где 2^+1
С этой целью выберем множество покрывающих многочленов Qo(x) = O; СДх),..., Qa(x),
которые обладают следующим свойством: для произвольного вектора ошибки е(х), вес которого не превосходит I, найдется многочлен Qj(x) такой, что некоторый циклический сдвиг е(х) совпадает с Qj(x) в информационных позициях. Например, если е(х) содержит круговую серию из k нулей, то некоторый циклический сдвиг е(х) будет совпадать в информационных позициях с многочленом Q0(x)=Q.
Пример. Для [23, 12, 7]-кода Голея ^23 с t=3 покрывающими многочленами являются: Qo(x) = O-, Qi(x) =х1с; Q2(x)=x17. Действительно, легко проверить, что любой вектор е(х), вес которого не превосходит 3, изображенный на левой окружности на рис. 16.11, можно повернуть так, что его информационные позиции 11—22 будут совпадать с информационными позициями одной из остальных окружностей. Например, если е(х) =х8+х15 + х22, то х17е(х)> имеет точно один ненулевой информационный символ, а именно при х16, и совпадает с Qi(x) в позициях 11—22.
Вектор ошибок е(к)
Рис. 16.11. Покрывающие многочлены для кода Голея
Обозначим через qj=HQ/ синдром многочлена Qj(x), j=0, ..., а. Тогда доказательство теоремы 19 может быть перенесено на доказательство следующего результата.
Теорема 20. Пусть S = HyT. Информационные символы (т. е. последние k символов) вектора у(х) +Qj(x) являются правильными тогда и только тогда, когда wt(ST-!-q3) —wt(Q3(x)).
Если это условие выполняется, то ошибки, расположенные в первых г позициях вектора у(х) +Qj(x), задаются равенством (е0, ..., <?т-1) = ST+qj, и ошибки в самом векторе у(х) равны Q3+ST+qj.
Эта теорема является обоснованием следующего алгоритма декодирования. Будем сдвигать вектор у(х) до тех пор, пока не получим вектор х?у(х), для синдрома S(T) которого справедливо неравенство wt(SW-J-q3) —wtfQjfx)1) при некотором /=0, 1, ..., «. Тогда у(х) декодируем как
е (х) = хп~1 (хг у (х) + Qf + Sr + q>). (16.64)
Упражнение. (23). Доказать, что многочлены Qo(x)=0; Qi(x)=x22 и Q2(x)=x^ являются покрывающими для [31, 16, 7]-кода БЧХ с 7=3.
Очень простые алгоритмы декодирования были предложены Карлиным [716], Тзенгом и Зиммерманом [1354] и Берлекэмпом
[123]. Например, вместо того, чтобы сдвигать принятый вектор и прибавлять синдромы покрывающих многочленов, можно прибавлять все векторы, вес которых не превосходит Z/2, к информационным позициям принятого вектора или к проверочным позициям до-тех пор, пока не будет найден синдром, вес которого не превосходит t.
В качестве иллюстрации приведем метод Берлекэмпа декодирования [24, 12, 8]-кода Голея ^24. Он использует задание кода порождающей матрицей вида (16.48), которую мы перепишем в виде
где буквами обозначены столбцы матрицы G, причем и$ обозначает вектор с 1 в координате i. Так как код ^24 самодуален, т. е. если GGT=0, то 1Ч-ВВГ = 0 или В-1==ВТ. Положим также
где буквами обозначены строки матрицы В.
Предположим, что передавалось кодовое слово с= (сь ..., с24) и что вектор ошибок равен е= (еь ..., е24), так что получен вектор y=c-j-e. Синдром равен
S = HyT = He7’ = 2 + et (16.65)
i=l i=13
Кроме того,
12 24
BT S = Вг H ег = [Вт 11] ег = £ et Ьг + £ et щ-_12. (16.66)
{=1 1=13 '
Предположим, что wt(e)^3. Тогда должно выполняться по меньшей мере одно из следующих условий:
12
Случай I: wt (ей, ..., е24) =0; wt(S) гСЗ; S 6^=5.
1=1
24
Случай II: wt(e1(..., е12) =0; wt(BTS)sC3; S e.iU,-_i2=BTS. „ *=13
г Случай III: wt(ei3,..., е24) = 1, так что для некоторого /, 13=С =0^24, выполняются условия wt(S+b3)^2 и
12
2e«u*=s+b/--
г-=1
Случай IV: wt(eb ..., = 1, так что для некоторого /, 1=С
24
</< 12, wt(BTS+bj)==£2 и S е{11{_12=BTS-+b,-. i=13
Таким образом, для декодирования надо вычислить веса 26 векторов S, S+b3-(1 гС/гС 12), BTS, BTS-j-bj (1^/^ 12).
Пример. ST=111O...O, wt(S)=3, так что имеет место случай I: ST=Ui+112 + u3 и е=1110 ... 0.
Метод декодирования III: использование /-схем. (Ассмус и др. [33, 42, 43], Геталс [492, 493].) Если дуальный код содержит /-схемы, то часто оказывается возможным применение порогового декодирования (см. § 13.6 и 13.7). Идея состоит в следующем. Предположим, что для некоторого t слова дуального кода некоторого фиксированного веса w образуют /-схему. Пусть hi......
...,ha — блоки этой схемы ( -кодовые слова веса w в коде ®>1), в первой координате которых стоит символ 1. Сформируем а проверок y-h,, где у — полученный вектор, и обозначим через v число случаев, в которых y-h,$=l.
Рассматриваемый нами алгоритм состоит в следующем:
(i) . Если v=0, то ошибок не произошло.
(ii) . Если-т<61 или если v принадлежит некоторому специальному множеству ф1 значений, то первая координата является правильной.
(iii) . Если v^02 или если т&фг, то первая координата ошибочна.
(iv) . Для всех остальных значений v принимается решение, что произошла неисправимая ошибка.
Процедуру повторить для всех координат полученного вектора.
Этот метод мы проиллюстрируем описанием порогового, декодирования для кода Голея ^24 (см. [493]). Так как ^24 самодуа-лен, то любое кодовое слово может быть взято в качестве проверки. Рассмотрим, как происходит декодирование какой-нибудь одной координаты, скажем, первой. Выберем в качестве проверок 253 кодовых слова веса 8, содержащих 1 в первой координате (см. рис. 2.14). Если произошла точно одна ошибка, то число v невыполняемых проверок равно либо 253, либо 77 в зависимости от того, ошибочен или нет первый символ. Если произошло две ошибки, то v равно либо 176, либо 2-56=112 в зависимости от наличия или отсутствия ошибки в первой позиции. Наконец, если произошло три ошибки, то v равно либо 120 + 21 = 141, либо Зх Х40+5= 125 в зависимости от двух указанных возможностей. Подводя итог, получаем:
Число Значение v, если первая ошибок координата
ошибочна правильна
1 253 77
2 176 112
3 141 125
Таким образом, имеется простой пороговый тест: если из 253 проверок не выполняется более 133, то координата ошибочна, а если меньше чем 133, то координата правильна. Этот тест может быть успешно применен ко всем координатам (на основании транзитивности группы Aut (^24), теорем 9 и 10).
В работе [43] описан (более сложный) алгоритм декодирования [48, 24, 12] КВ-кода.
Задача построения общего порогового алгоритма декодирования такого типа представляется весьма трудной; не ясен даже вопрос, сколько ошибок можно исправлять таким алгоритмом. Рахман и Блейк [1086] дали нижнюю границу для этого числа в терминах параметров /-схемы.
Задача (нерешенная). (16.10). Сколько ошибок можно исправлять пороговым декодированием, если слова каждого веса в коде ®’-L образуют /-схему?
Конечно, если разрешается в качестве проверок выбирать слова произвольного веса, то теоретически, как мы знаем из теоремы 21 гл. 13, можно для любого кода исправлять [(1/2) (J—1)] ошибок (мы только не знаем, как надо это делать).
‘ЗАМЕЧАНИЯ К ГЛ. 16
§ 16.1 . Дальнейшие свойства квадратичных вычетов (ср. § 2.3). Общие сведения— см. Ле Векуа [825, т. 1] и Рибенбойм [1111]. Мы начнем с доказательства фундаментальной теоремы о том, что 2 является квадратичным вычетом по модулю р, если р = 8т=Е1, и квадратичным невычетом, если р = 8т+3. Доказательству предпошлем некоторые леммы.
Лемма 21. (Критерий Эйлера.) Если р нечетно, то для любого целого а имеет место сравнение %(iz) =iz(₽-1)/2(mod р).
Доказательство. Если а кратно р, то результат тривиален; поэтому предположим, что (mod р). Пусть р—примитивный элемент поля GF(p)\ тогда p(₽-i)/2=^l (mod р). Так как a=p’(mod р) для некоторого 1, то сКе-^Р^ (—l)’(modp). Согласно § 4.6 а — квадратичный вычет тогда и только тогда,-когда i — четно. ф.
Лемма 22. (Критерий Гаусса.) Пусть р — нечетное простое число, и пусть р.— число элементов в множестве {а, 2а, ... (1/2) (р—1)а}, абсолютные наименьшие вычеты по модулю р которых отрицательны. Тогда %(а) = (—1)р.
Пример. р = 7; а=2. Множество 2, 4, 6 приводится к множеству 2, —3, —1, так что [1 = 2.
Доказательство. Пусть гь г2,. .., —r'j, —г'2,... — система абсолютно наименьших вычетов чисел а, 2а,..., (1/2) (р—1)« по модулю р. Ясно, что г-;=Дг-;'. r'i¥=r'j, если /=/=/ и г,У=г'3-; действительно, если m1izsri (mod р) и т2а= = —//(modp), то из ri = r'j следует, что (mi+m2)a=0(mod р), т. е. что тД-т2 делится на р. Но это невозможно, так как mi+m2<p—1. Следовательно, все (р—1)/2 чисел г,, r'j различны и лежат между 1 и (р—1)/2, так что они являются числами 1, 2..., (р—1)/2, выписанными в некотором порядке. Таким образом,
«2я . . (р— 1) а = (— 0й (modp)
ИЛИ
g(p-1)/2= (-DHmodp.
Теперь результат сразу вытекает из леммы 21.
Теорема 23. 2 является квадратичным вычетом по модулю р, если р = =8/?И±1, и невычетом, если р=8т|±3.
Доказательство. Положим в лемме 22 а=2. Тогда р.— число целых вида 2m, 1<т<(р—1)/2, таких, что 2т>р/2, или m^pfi. Таким образом, р.= = (р—1)/2—[р/4].
Соответствующими четырьмя возможностями являются:
И
р
8m—3 4m—2—(2m—l)=2m—1
8m—1 4m—1—(2m—l)=2m
8m+l 4m—2m=2m
8m-j-3 4m+l—2m=2m+l
•
Теорема 24. (Перрон.) (i). Пусть p = 4k-~1, пусть гь ..., г2л—2k квадратичных вычетов по модулю р, учитывая и 0, и пусть а — число, взаимно простое с р. Тогда среди 2k чисел вида г—|-а имеется k вычетов (возможно, включая 0) и k невычетов.
(ii) . Пусть р=4/г—1, пусть ni, ..., и2&-1 представляют собой (2k—1) невычетов по модулю р, и пусть а взаимно просто с р. Тогда среди 2k—1 чисел вида п,-|-а имеется k вычетов (возможно, включая 0) и k—1 невычетов.
(iii) . Пусть р=4А+1. Среди 2&+.1 чисел вида п+а содержится fe+1 вычетов (включая 0) и k невычетов, если а само является вычетом, и k вычетов (не включая 0) и А-|-1 невычетов, если а само является невычетом.
(iv) . Пусть р = 4й-|-1. Среди 2k чисел вида п4+а содержится k вычетов (не включая 0) и k невычетов, если а само является вычетом, и й+1 вычетов (включая 0) и k—1 невычетов, если а само является невычетом.
Доказательство см. в работе Перрона [1035].
Упражнения. (24). Квадратичный закон взаимности Гаусса. Пусть
1, если а — квадратичный вычет по модулю р, —1, если а — квадратичный невычет по модулю р.
Доказать, что если р и q — различные нечетные простые числа, то
(р-D (<7-1)
(25). Доказать, что 3 является квадратичным вычетом по модулю р тогда и только тогда, когда p=zhl(mod 12).
§ 16.2. Квадратично-вычетные коды интенсивно изучались Ассмусом и Мэттсоном в серии статей и отчетов [34, 37—39, 41—47, 49—53, 927], и большая часть материала этого параграфа основана на результатах этих работ. Другое определение KB-кодов и их обобщение было недавно предложено Уордом [1387]. Его подход безусловно заслуживает дальнейшего изучения.
Равенство (16.3) можно использовать для определения KB-кодов над произвольным полем GF(q), где q уже не обязательно простое число; большинство свойств кодов, описанных в данной главе, переносится на этот случай. Кратко KB-коды над GF(4) были упомянуты в упражнении (15). Мы ограничили рассмотрение случаями, когда q и I — простые числа, так как случаи q=2 и q=3 представляются наиболее важными. Однако несколько интересных KB-кодов было построено над полем Gf(4) (см. Ассмус и Мэттсон [42, 44]). Первым из этих кодов является [6, 3, 4]-код над Gf(4), рассмотренный в примере (Е9) § 19.1. Группой автоморфизмов этого кода является трехкратное прямое произведение знакопеременной группы подстановок на 6 символах. При этом единственном ограничении теорема 13 переносится и на тот случай, когда I степень простого числа (см. также Стейн и Баргава [1274]). Другой пример кодов над GF(4), а именно [30, 15, 12]-код, описан в работе [41]. Найденный (гл. 19) спектр весов этого кода позволяет на основании следствия 30 гл. 6 присоединить к рис. 16.9 следующие 5-схемы:
5-(30, 12, 220); 5-(30, 14, 5390); 5-(30, 16, 123000). (16.67)
Дополнительные сведения о кодах над GF(4) можно найти в работе [1478].
Для составления таблицы на рис. 16.2 были использованы следующие источники: Ассмус и Мэттсон (указанные выше работы), Берлекэмп [ИЗ], Карлин [715, 717], Карлин и Мак-Вильямс [718], Миккельтвейт и др. [979], Розен-старк [1124] (см. также Плесе [1052] и Соломон [1248]).
Ван Тилборг [1325] доказал следующее усиление теоремы 1.
Теорема 25. Если 3?— двоичный KB-код длины р=8т—1 и d2—d+l = =р, то: (i) p=64i2+40i+7^2551 и d=8i+3 для некоторого г; (ii) существует проективная плоскость порядка d—1. Если cP—d+l>p, то d2—d—11^-р.
Из этой теоремы следует, что минимальное расстояние d [47, 24] КВ-кода удовлетворяет условию dj>ll. Неравенство d:> 13 невозможно из-за границы сферической упаковки (гл. 1). Следовательно, согласно теореме 8 d равно 11 или 12. Но в силу следствия 15 гл. 8 d должно быть нечетным, откуда заключаем, что d=ll.
Ассмус, Мэттсон и Сачар [49] получили следующее обобщение теоремы 1.
Теорема 26. Предположим, что <£?—[и, (n-|-l)/2, d] циклический код над GF(q) такой, что ’g’s’g’-L. Если опорные множества слов минимального веса образуют 2-схему, то d2—d-J-l^n.
§ 16.3. Теорему 3 см. у Рибенбойма [1111]. Теорема 4 доказана Паттерсоном (не опубликовано).
§ 16.5. Что касается свойств группы PSLz(p), см., например: Конвэй [306], Коксетер и Мозер [314] или Хупперт [676]. Теоремы 10, 12, 13 доказали Ассмус и Мэттсон [41, 47, *927] (см. также Шаугнесси [1193, 1194]). Не вдаваясь в подробности, упомянем следующий результат Ассмуса и Мэттсона [47, 53] и Шаугнесси [1193].
Л
Теорема 27. Предположим, что группа Aut(^)+ содержит PSLz(p) в качестве собственной подгруппы. Тогда: (i). Aut(.27)+ изоморфна неразрешимой транзитной группе подстановок на р символах.
Л
(ii). Если р=2т+1^23 и т — простое число, то группа Аи1(^)+ проста и изоморфна 5-кратно транзитивной группе.
Доказательство теоремы 13 основано на теореме 27 и результатах Паркера и Николаи [1023], полученных на ЭВМ для групп с определенными свойствами.
Задача (нерешенная)-. (6.11). Расширить результат Паркера и Николаи для больших значений р.
Некоторые дальнейшие результаты о группах подстановок, применимые к KB-кодам, получены Нейманом [988, 989]. Заслуживает упоминания работа Кантора [714], где он доказал, что PSLz(p) представляет собой полную группу автоморфизмов матриц Адамара размерности (р+1) X (р+1) типа Пейли для всех р>11 (см. также Ассмус и Мэттсон [39], Холл [588, 590]). Упражнение (2) взято из работы [47].
§ 16.6—116.7. Кажется, Лич [803] первым из исследователей выписал порождающую матрицу (16.48) для кода ^24. Карлин [715] изучил разложение КВ-кодов на двойные циркулянты. Что касается свойств и таблиц дважды цирку-лянтных и квазициклических кодов, см.: Баргава и др. [142], Чин и др. [275], Хоффнер и Редди [659], Карлин [715], Касами [730], Питерсон и Уелдон [1040, § 8.14], Стейн и Баргава [1273], Таварес и др. [1311], Таунсенд и Велдон [1338]. Другое доказательство леммы 14 дано Хупертом [676, теорема 8.4 (d), с. 192].
Методы нахождения кодовых слов малого веса основаны на работах: Карлин [715], Карлин и Мак-Вильямс [718], Миккельтвейт, Лэм и Мак-Элис [979]. Ассмус и Мэттсон [44] описали другой метод, использующий циклотомические классы.
Утверждение о том, что 2 является примитивным элементом бесконечного множества простых полей, известно как гипотеза Артина; по этому поводу см-Шенке [1186, с. 81].
Дважды циркулянтные коды $ описаны в работах Карлина {715, 717]. Данные для рис. 16.7 взяты из работ [275, 715, 717, 1273, 1311]. Весовые спектры для некоторых из этих кодов приведены в [1273] и [1311]. В этих же работах
приведены некоторые хорошие кратно-циркулянтные коды, порождающие матрицы которых имеют вид [1|А|В ... ] , где А, В - . — циркулянтные матрицы. Про коды такого типа известно еще меньше, чем про дважды циркулянтные (см. также Баргава и Стейн [14П). Что касается циркулянтных и других матриц над конечными полями, см.: Беллман [100], Берлекэмп [109], Карлин [247, 248], Дэйкин [339], Мак-Вильямс i[878, 881], Мюир [974].
§ :16.8. KB-коды над 07(3) описаны в работах Ассмуса и Мэттсона. Симметричные коды Плесе интенсивно узучались Плесе в работах: [1055—1057, 1060] (см. также Блейк [160, 161]). Рисунок 16.9 взят из работы [47] Ассмуса и Мэттсона.
§ :16.9. Перестановочное декодирование было введено Прэнджем [1078], но наше изложение следует Мак-Вильямс [873]. Общие свойства циклических кодов, к которым применимо перестановочное декодирование, изучали Шива и др. [1201, 1202] и Уайп и др. [1447].
Берлекэмп (не опубликовано) нашел множество из 40 перестановок, которое можно использовать для декодирования кода Голея g<23.
Касами [725] построил схему реализации метода декодирования II и выписал множества покрывающих многочленов для некоторых кодов.
Задача (нерешенная). (16.12). Дать систематический метод построения множества покрывающих многочленов.
Берлекэмп [123] рассмотрел также вопрос, какие векторы ошибок веса 4 могут быть исправлены. См. также следующие работы по декодированию циклических и других кодов: Ахмед [8—11], Чейз [264], Чень и Лум [291], Эрих и Я у [405], Хартманн и Рудольф [614], Каутц [749], Митчел [964], Миякава и Канеко [966], Нили [994], Омура [1012, 1013], Паирс [1046], Соломон [1255], Танака и Канеку [1299], Велдон [1404], Цирлер [1462, 1463], Злотников и Кайзер [1473].
Глава 17
Границы для объема кода
17.1. ВВЕДЕНИЕ
Вероятно, основной проблемой в теории кодирования является нахождение наибольшего кода заданной длины с заданным минимальным расстоянием. Пусть А (п, d) — максимальное число кодовых слов в произвольном двоичном коде (линейном или нелинейном) длины п с минимальным расстоянием d между кодовыми словами.
, В этой главе будут приведены верхние и нижние оценки величины А (п, d) как для небольших значений п (см. рис. ПА.1, ПА.2), так и для больших значений п (см. рис. 17.7). Для больших п наилучшей верхней границей является граница Мак-Элиса— Родемича — Рамсея — Велча (теоремы 35 и 36), которая получена посредством существенного использования линейного программирования (см. § 17.4). Эта граница значительно улучшает границу Элайеса, долгое время являвшуюся наилучшей (теорема 34). Наилучшей нижней оценкой для больших п является граница Варшамова — Гилберта (теорема 30), но между верхней и Вижней оценками имеется все еще значительное расхождение (см. задачу (нерешенную) (17.9)).
Один из возможных путей исследования величины А (п, d) состоит в изучений множеств кодовых слов,, имеющих один и тот же
вес. С этой целью определим Л (п, d, w) — максимальное число двоичных векторов длины п, веса w, находящихся друг от друга на расстоянии Хэмминга по крайней мере d.
На рис. ПА.З представлена таблица небольших значений величины А (п, d, w). Наилучшими верхними границами для А(п, d, w) являются границы Джонсона (§ 17.2), которые используются в § 17.3 для получения верхних оценок для А (п, d). Метод линейного программирования, применимый и для больших и для маленьких значений п, а также для оценки А (п, d) и А (п, d, w), описан в § 17.4.
Другой важной функцией является В(п, d) —наибольшее число кодовых слов в произвольном линейном двоичном коде длины п с минимальным расстоянием d.
Ясно, что В (п, d)^A(n, d). В § 17.5 приведена верхняя граница Грайсмера, применимая только для оценки величины В (п, d). В § 17.6 описан интересный способ построения линейных кодов, которые иногда достигают границы Грайсмера. Это построение использует антикоды, являющиеся кодами, у которых ограничено сверху расстояние между кодовыми словами (и поэтому антикод может содержать повторяющиеся кодовые слова). Замечательная таблица значений В(п, d) в диапазоне 127 была составлена Хелгертом и Стинаффом [636], и поэтому подобная таблица здесь не приводится. Для больших п наилучшие известные оценки для В(п, d) совпадают с оценками для А(п, d).
Вместо поисков наибольшего кода заданной длины с заданным минимальным расстоянием можно искать код наименьшей длины, имеющий М кодовых слов и минимальное расстояние d. Эту наименьшую длину обозначим через N(M, d).
Упражнение. (1). Показать, что решение любой из этих проблем дает решение другой. Более точно показать, что если известны значения А(п, d), то известны и значения N(M, d), и наоборот. Сформулировать подобный результат для линейных кодов.
Почти всю эту главу можно читать независимо от других глав. Следующие статьи, относящиеся к границам, не упоминаются где-нибудь в другом месте в этой главе и включены для полноты: Бомбах и др. [64], Бартоу [74, 75], Бассалыго [76], Бергер [105], Шакраварти [259], Фрейман [457], Хатчер [626], Джоши [700], Левенштейн [823, 824], Леви [830], Мак-Дональд [868], Мак-Элис и Рамсей [948], Мирваагнес [980], Питерсон [1037], Сакс [1140], Сидельников [1209, 1210], Стрейт [1283] и Велч и др. [1399].
17.2. ГРАНИЦЫ ДЛЯ А(п, d, w)
Начнем с исследования величины А (п, d, w) — максимального числа двоичных векторов длины п, веса w, находящихся на расстоянии друг от друга не менее d. Эта функция важна как сама по себе, так и с точки зрения получения оценок для А (п, d) с помощью теорем 13 и 32. В этом разделе мы рассмотрим границы
Джонсона (теоремы 2—5)- для А\п, d, w), а затем приведем ряд теорем, дающих точное значение этой величины в некоторых частных случаях. На рис. ПА.З приведена таблица небольших значений А (п, d, w). (В § 17.4 приведена другая оценка для А (п, d, w), полученная с помощью линейного программирования.)
Теорема 1.
(а) . А (п, 26—1, w) — A(n, 26, w).
(b) . А (п, 26, w)= А(п, 26, п—ш).
(с) . А(п, 26, и>) = 1, если w <6.
(d) . А (п, 26, 6) = [п/6].
Доказательство. Утверждение (а) следует из четности расстояния между векторами одинакового веса. Для получения (Ь) надо взять дополнения ко всем словам. Утверждение (с) очевидно, а (d) верно потому, что множества позиций, занятых единицами в различных кодовых словах, не пересекаются. *
Следующий результат обобщает оценку (d).
Теорема 2. (Джонсон [693]; см. также [694—697].)
Л(п. 26, - 1 (17.1)
I — wn -р on |
при условии, что знаменатель положителен.
Доказательство. Пусть —(/г, М, 26) равновесный код, который достигает границы А (п, 26, w); так что М=А (п, 26, w). Пусть Х= (х,:,) представляет собой (М\п)-матрицу из кодовых слов SF; каждая строка матрицы имеет вес w. Подсчитаем двумя способами сумму скалярных произведений строк:
М М п
У У XtvXiv‘
г—1 ,=1 V=1
Так как расстояние между любыми двумя строками равно по крайней мере 26, то их скалярное произведение равно самое большее w—6. Следовательно, сумма не превышает (w—8)М(М—1).
С другой стороны, эта сумма равна также
п м м
У У У xivxi V-
v=! i=l /=1
М*
Если kv—число единиц в v-м столбце матрицы X, то вклад этого столбца в сумму равен kv (kv—1). Следовательно, .
£ МД,—1) < (да—6)М(М—1). (17.2)
V=1
Но 2 kv—wM (общее число единиц в матрице X) и сумма V=I
2 k2v минимальна, если все k -^=wM/n, и в этом случае v=l v
V—I
Следовательно, из (17.2) имеем
———-wM < (ш—6)Л4(Л4-—1). п
Решая это неравенство "относительно М, получаем (17.1). • Так как числа kv. должны быть целыми, то полученную оценку можно немного усилить. .
Теорема 3. Предположим, что А (п, 26, и определим
целые числа k и / посредством равенства wM=nk + t, O^t<n. (Это равно общему числу единиц во-всех кодовых словах.) Тогда справедливо неравенство ;
[я£(£—l) + 2£/<(w—6)М(М—1). (17.3)
п
Доказательство. Минимум суммы &v ПРИ Условии> что
V=I п
kv=wM и что kv — целые положительные числа, достигается, V=1
когда
k\ = . . . — kfk—р 1, ; . . . — —'k.
Этот минимум равен 1)2н-(/г—t)k2, так что из (17.2) име-
ем .t(k +1)2 + (п-—t)k2—(nk + t) (w—8)М(М—1).
Примеры. По теореме 2
А (9, 6, 4) < Г - - 1 = 3 v ’ 116 — 36+ 271
и код {111100000, 100011100, 010010011} показывает, что Л (9,6, 4)=3.
Снова по теореме .2
Но если Л (8, 6, 4)=3, то, применяя .теорему 3, имеем 3-4= 1-8+ + 4, так что k = \, \t=A и неравенство (17-3) нарушается. Следовательно, Л (8, 6, 4)^2. Код {11110000, 10001110} показывает, что А (8, 6, 4) =2. Следующая рекуррентная оценка полезна в тех случаях, когда неприменима теорема 2 (и также в некоторых случаях, когда она применима).
Теорема 4.
Л(/г, 26, ш)< — Л(п— 1, 26, щ -1)
I оу
(17.4)
Доказательство. Рассмотрим все кодовые слова, у которых стоит 1 в i-й координате. Если эту координату отбросить, то получается код длины п—1 с расстоянием не менее 26, слова которого имеют вес w—1. Следовательно, число таких кодовых слов не более чем А(п—1, 26, w—1). Таким образом, общее число единиц в первоначальном коде удовлетворяет неравенству
wA(n, 26, w)^nA(n—1, 26, w—1). •
Следствие 5.
Л(и, 26, №)<Г-А . И-гс+б I . 1] {17.5)
I w |w — 1. I 5 I (I
Доказательство. Применим вначале несколько раз теорему 4 и затем воспользуемся теоремой 1 (d). •
На практике теорема 4 применяется до тех пор, пока не достигается известное значение А (п, d, да).
Пример.
Л (20,8,7) <|у- Л (19, 8, 6)| в силу (17.4)
< f-y-p^-Л(18, 8, 5)^ в силу (17.4).
Теперь применим теорему 2:
Л (18, 8,5) С Г--------1 = Г—1 = 10.
| 25 — 90 + 721 [ 7 |
Но равенство Л (18,8,5) = 10 невозможно в силу теоремы 3, так как 50=18-2+14, но 18-2 + 2-2-14> (5—4)-10-9. Следовательно, Л (18,8,5) ^9, и поэтому
Л (20, 8, 7) с |у- = рр| = 80.
На самом деле в обеих этих оценках выполняются равенства (см. рис. ПА. 3).
Упражнение. (2). Показать, что
Л (п. 26, да) < Г—-—Л (п—1, 26, да) In — W
(17.6)
[Указание. Воспользоваться теоремой 1 (Ь).]
Иногда (17.6) дает более хороший результат, чем (17.4).
Задача (нерешенная). (17.1). В каком порядке надо применять оценки (17.4), (17.6) и (17.1) при заданных значениях п, 26, да, чтобы получить наименьшую оценку для Л (п, 26, .да) ?
Упражнения. (3). Несколько простых примеров. Показать, что Л(10,6,3)=3; Л(10,6,4)=5; А(10,6,5) = 6; Л(11,6,4) =6; Л (11,6,5) = 11; Л (12,6,4) =9.
(4) . Предполагая, что (4r~X4r) -матрица Адамара существует, показать, что
А (4г— 2, 2г, 2г—1) = 2г; (17.7)
А (4г— 1, 2г, 2г—1) = 4г—1; (17.8)
А (4r, 2r, 2г) = 8г—2. (17.9)
[Указание. Использовать коды из гл. 2 на
с. 57].
(5) . Показать, что
A(n4rl, 26, w) с А(п, 26, w)A-A(n, 26, w—1).
(6) . Показать, что
А(п, 26, w) < и(п-1} • • •fr-'+A (17.10)
w(w — 1) . . .5
причем равенство достигается тогда и только тогда, когда существует система Штейнера S(w—6+1, w, п) (ср. § 2.5)*.
Таким образом, из известных фактов о системах Штейнера (см. Чин [277], Колленс [300], Дембовский [370], Деннпстон [372], Дуайен и Роза [386], Ханани [595—600], Ди Паола и др. [1020], Витт [1423, 1424]) вытекают соответствующие результаты о величине А (п, d, w). Так, например, системы Штейнера S(3, <7+1, </2+1) существуют для всех q, равных степени простого числа [370, гл. 6], и поэтому
Л(<72+1,2<7—2, g + l)=<7(g2+ 1), q—степень простого числа. (17.11)
Аналогично унитарные поляры проективных геометрий [370, с. 104] дают равенство
A (q3 + 1, 2q, qA-}) — q2(q2—</+1), Q—степень простого числа.
(17.12)
Упражнение (6) показывает также, что определение величины А (п, 26, w) является в общем случае очень трудной проблемой. Так, например, из (17.10) следует, что А (111,20,11) ^111, причем равенство достигается тогда и только тогда, когда существует проективная плоскость порядка 10.
Следующие результаты приводятся без доказательств.
Теорема 6. (Шонхейм [1158]; см. также Форт и Хедлунд [446], Шонхейм [1161], Спенсер [1259] и Свифт [1294].)
А(п, 4, 3) =
для п 5 (mod 6),
для п = 5 (mod 6).
*> Это предложение впервые отмечено в [1180]. В [1181] указано также, что из существования системы Штейнера S(w—5+1, w, п) следует равенство
п(п— 1). (п—к+6+1) п— к> + 6— 1
А (п—1, 26, ш) =-------------7~~— •--------ё------ • (Прим, ред.)
W (W — 1). • (6 + 1) о
Теорема 7. (Калбфлейш и Стэнтон [708], Брауэр [201а].
А(п, 4, 4) = п (п — 1) (п — 2) 4-3-2 п (п — 1) (и — 3)
4-3-2 п (и* 2 3 * — Зп — 6)
4-3-2
Задача (нерешенная), если /z=5(mod6).
Теорема 8. (Ханани [595-
А(п, 6, 4
если п = 2 или 4 (mod 6),
если п = 1 или 3 (mod 6),
если n = 0 (mod 6).
(17.2). Найти величину А (п, 4,4), 598].)*
_ п (п — 1)
— 4-3 ’
если и только если п=1 или 4 (mod 12);
А (п, 8, 5) = Я(Я~1) -, v 7 5-4
если и только если п= \ или 5 (mod 20).
Доказательства теорем 6—8 заключаются в явном построении кодов, достигающих этих границ.
Теорема 9. (Ердеш и Ханани [411], Вильсон [1420—1422].)
(а) . Для произвольного фиксированного 2-существует число /го(^) такое, что для всех /г>/го(&)
А (п, 2/г—2, fe) = -(”~1)-, k(k — 1)
если и только если п=1 или k (mod&(&—1). Кроме того,
lim В А(п, 2k—2, /г)=1.
П->со П (П — 1)
(Ь) . Если р — степень простого числа, то
jim (р+ Вр(р-В д 2р—2, р + 1) = 1.
п(п—1) (п — 2)
(см. также работы Оллтопа [21—24] и Роковской [1122]).
Но даже если ни одна из приведенных выше теорем не применима, имеется все же достаточно хороший метод получения нижних оценок А (п, 26, w): надо построить код длины п с минимальным расстоянием 26, а затем рассмотреть множество всех кодовых слов веса w. Например, в [24, 12, 8]-коде Голея 3^4 имеется 2576 кодовых слов веса 12, и поэтому получаем, что А (24, 8, 12)^2576. (На самом деле имеет место равенство.)
п(п—2)
*) Можно также добавить [1181], что Д(п, 6, 4) = '——, если п=0 или
п(п—2)
3 (mod 12), и А(п, 8, 5) = ———, если п=0 или 4 (mod 20). (Прим, перев.)
5-4
В общем случае можно воспользоваться векторами веса w в любом смежном классе кода длины п с расстоянием 26. Например, использование смежных классов кода Голея К24, приведенных в упражнении 13 гл. 2, показывает, что А (24,8,6) ^77; А (24,8,10) >960 и т. д.
Равновесные коды имеют ряд практических применений (см. Ковер [310], Фрейман [456], Гилберт [483], Ксяо [666], Кауц и Элспас [752], Маракл и Волвертон [911], Накамура и др. [983] Нейман [986, 987], Шварц [1169] и Танг и Лью [1307]). Но в. общем о них известно немного.
Задача (нер ешенная). (17.3). Найти хорошие методы кодирования и декодирования равновесных кодов (см. Ковер [ЗЮ]).
Упражнение. (7). Из оценок (17.4) и (17.1) следует, что
А(12, 6, 5) < [12А(11, 6, 4)/5] = 14.
Показать, что А (12,6,5) = 12.
[Указания, (i). Методом проб и ошибок построить соответствующую матрицу, показывающую, что А (12,6,5) 12.
(ii). В любой матрице, реализующей А (12,6,5), число единиц в столбце не более чем А (11,6,4) =6.
(iii). Любые два столбца такой матрицы содержат пару единиц не более чем в А (10,6,3) =3 позициях.
.(iv). Предположим, что столбцы 2 и 3 содержат 3 пары единиц. Без ограничения общности можно считать, что первые 3 строки выглядят следующим образом:
01111 1000000
011000111000
011000000111
Обозначим через b, с, d, е число строк, начинающихся с последовательностей ПО, 101, 100, 000 соответственно. Тогда i> + c+ +d+e^9; Ь^З; с^З; b-j-c-j-d^6 и, следовательно, е^З. Но е^А (9,6,5) =3, следовательно, е=3 и всего имеется не более 12 строк.
(v). Предположим, что никакие два столбца не содержат 3 пар единиц. Тогда число единиц в каждом, столбце не превышает 5 и, значит, число строк не превышает 12. Ибо, если 1-й столбец содержит 6 единиц или более, то, рассматривая строки с единицей в первой координате, нетрудно убедиться, что найдется столбец, скалярное произведение которого с первым столбцом не менее 3.]
Упражнение. (8). (Трудное.) Показать, что А(13,6,5) = 18.
Величина А (п, d w) изучалась также в работах Нивена [996] и Стэнтона и др. [1270].
*> Эта работа повторяет результаты работ [1180, 1181]. (Прим, ред.)
17.3. ГРАНИЦЫ ДЛЯ А (п, d)
Полученные в § 17.2 оценки для А (п, d, w) могут быть теперь использованы для оценивания A(n,d). Вначале мы вспомним некоторые результаты, установленные в § 2.2 и 2.3.
Для случая n^.2d точное значение A(n,d) дается теоремой 11.
Т е о р е м а 10.
(а) . А(п, 26) = А(п — 1, 26—1).
(b) . А(п, d)<2A(n—1, d).
Теорема 11. (Плоткин и Левенштейн.) В предположении, что существуют соответствующие матрицы Адамара, имеют место равенства:
(а) . А(п, 26) = 2 | 25 1, если 46>п > 26: 146 — и |
А (46, 26) ==86-
(Ь) . А(п, 26+1) = 2Г—^-±-2—1, если 46+3 >п> 26+1;
| 46 + 3 — и I
4(46 + 3,26+ 1) = 86 + 8.
В случае, когда d невелико, оказывается полезным следующий результат, доказанный в теореме 6 гл. 1.
Теорема 12. (Граница сферической упаковки или граница Хэмминга.)
А(п, 26+l)fl+( ” 1+ . . .+(”))< 2". (17.13)
Эта теорема введением функции A(n,d,w) может быть усилена.
Теорема 13. (Джонсон.)
А(п, 26+1)
!+(")+ . . • + (") +
\ 1 / \ о ]
( п )_/2б+Цд(п> 26 + 2, 26+ 1)
\6+ 1/ \ 6 / _________
Ш
16+11
(17.14)
Доказательство, (i). Пусть —(п,М, <Д-код с М=А(п, d) и d=26+l, содержащий нулевой вектор. Обозначим через S.i множество векторов, находящихся на расстоянии i от кода гё>, т. е. S.i={ueAn : dist(u, v) для всех ve? и distfu, v)=i для некоторого ve?}.
Таким образом, So—'ё. Тогда So U Si U ••• U Sd-i = Fn, так как если бы нашелся вектор, находящийся на расстоянии d или боль
ше от кода то мы могли бы добавить его к Ч? и получить код еще большей мощности. Поскольку множества .So, Si,..., So не пересекаются, то отсюда следует граница сферической упаковки (теорема 12). Для получения оценки (17.11) оценим мощность ^6+1.
(ii) . Выберем произвольное кодовое слово Р и соответствующим сдвигом кода переведем его в начало координат. Кодовые слова веса tZ=26+l образуют равновесный код с расстоянием не менее 26+2, и поэтому число кодовых слов веса d не превышает А(п, 26 + 2, 26+1).
(iii) . Обозначим через множество векторов Fn веса 6+1. Любой вектор из И7б+1 принадлежит либо So, либо S6+i. Каждому кодовому слову Q веса d соответствует ( ) векторов веса 6
6+ 1, находящихся от Q на расстоянии 6.
Все эти векторы различны и принадлежат множеству 1176+1 П f]:S6. Следовательно,
IF6+1 n s6+11=I r6+l I -1F6+1 n se । >
)д(п, 26 + 2, 26+ 1).
\б+ 1/ \ 6 /
(iv) . Вектор R из множества 117с-и П S6+i находится на расстоянии 6+1 самое большее от [п/(6+1)] кодовых слов. Действительно, перенесем начало координат в точку R и подсчитаем, сколько кодовых слов может находиться от R на расстоянии 6+1 и иметь между собой расстояние Хэмминга d (а на самом деле 6+1=26 + 2). Такие кодовые слова должны иметь непересекаю-щиеся множества позиций, занятых единицами, и поэтому число их не превышает |+/(6+ 1) ].
(v) . Пусть теперь Р пробегает по всем кодовым словам; подсчитав общее число точек в множестве So U ••• U Se+i, получим неравенство (17.14). •
Пример.
Л/шсч 212
— ЮЛ (12,6,5)|/ 4
Но согласно упражнению (7) А (12, 6,5) = 12. Следовательно, 4(12,5)^39. Отметим для сравнения, что граница сферической упаковки дает только 4(12,5)^51. В следующем разделе мы увидим, что на самом деле 4 (12,5) =32.
Следствие 14.
А(п, 2 6+1)
!+(")+ • • • + (")
\ 1 / \ б /
(17.15)
Доказательство. Согласно следствию 5
А (п,
2 6+2,
26+1)<
и (и — 1) .
(26 + 1)2 6
(к - 6 + 1) (6 + 2)
Г и — 61 е+ 1 г.
Подставляя это неравенство в (17.14), получаем (17.15). ®
Если в (17.13) имеет место равенство, то код называется совершенным (см. гл. 6). Если же равенство выполняется в (17.15), то код называется почти совершенным (см. Геталс и Сновер [504]).*»
Упражнения. (9). (а). Показать, что совершенный код яв
ляется почти совершенным.
(Ь) . Показать, что почти совершенный код является квазисо-вершенным.
(10) . Показать, что [2Г—2, 2Г—г—2, 3] укороченный код Хэмминга и выколотый код Препараты ^(т)* (с. 455) являются почти совершенными кодами. Следовательно, А (2Г—2, 3) =22Г~Г~2 и А(2т—1,5) =22т~2т для четных т^:4.
Это показывает, что код Препараты имеет наибольшее возможное число кодовых слов при заданных длине и расстоянии.
Как показал недавно Линдстрем [844], не существует никаких других почти совершенных двоичных кодов. Доказательство очень похоже на доказательство теоремы 33 гл. 6.
Упражнения. (11). Для четного п показать, что
А(п, 3) < 2п/(п + 2).
[Указание. Использовать теоремы 6 и 13. Немного больше можно сказать о значениях n=4(mod6).]
(12) . (Джонсон.) Доказать следующее усиление неравенства (17.14):
{[ п X f п \ Cr ,,
б/^Л(п, 26+2, 6+1)
।_________________________ 1 пП
""г" А (п, 26 + 2, 6+2) !
(17.16)
где
C6+, = f " 2б + 2’ 26+1);
\б+1/ \ 6 }
Св+2 = (я " 9)-А (п, 26 + 2, 26+ 1)-
\о + 2/ \ о — 1 /
_/2в +1\/« —26— IX А , 26+2, 2 6+1) — \ б Д. 1 /
-f2S + 2U(ft, -26 + 2, 2 6+2)—/2s+ 3) л (П,-26+2,.. 26 + 3).
\ 6 / \ 6 + 1 /
Коды, удовлетворяющие равенству в (17.15), ранее были рассмотрены в
Работе [1183]. (Прим, ред..) .
[Указание. Любой вектор, находящийся на расстоянии 6 + + 2 от кодового вектора, принадлежит одному из множеств S -i, S6, Se+i или S +2.]
(13) . Обобщить оценку (17.16).
(14) . В предположении, что существуют соответствующие матрицы Адамара, показать, что если n^2d, то А (п, d) либо равно 1, либо четному числу. [Указание. Воспользоваться теоремой 11.] Используя рис. ПА.1, показать, что если А(п, d) нечетно и больше 1, то Л («, d) 5s 37.
Задача (нерешенная). (17.4). Верно ли следующее предположение: если А(п, d)^>l, то A(n,d) —четное число для любых п и <ДЭлспас [409])?
Так же как граница для А(п, 26+1), задаваемая выражением (17.14), зависит от величины А(п, 26 + 2, 26+1), можно получить границы для А(п, d, w), зависящие от функции, обозначаемой через T(w\, п1г w2, п2, d). Эти оценки довольно сложны, и мы не будем их здесь приводить (см. [697]). Но функция Т представляет самостоятельный интерес.
Определение. Функция T(w\, пъ w2, п2, d) равна максимальному числу двоичных векторов длины n] + n2, находящихся.
друг от друга ifa расстоянии Хэмминга по крайней мере d и содержащих точно wt единиц в первых п} позициях и точно w2 единиц в последних п2 позициях.
Пример. 7(1, 3,2,4,6) =2, 1 0 0 0 1 0
как показывают векторы
110 0
0 0 11
(Позиции, занятые единицами, должны быть различными!)
Упражнение. (15). Доказать:
(a), 7(wb п\, w2, п2, 28)=T(tii—wlt п\, w2, п2, 26). (Ь). Если 2wi + 2w2=26, то
Т(щ1; ш, w2, «2, 26) = min([-^-l
U a'i I I O>2 IJ
(с) . T(щ,, /ij, w2, n2, 26) + —1, — 1, ®2> n2 2 6)1.
I I
(d) . T (wlt nlt w2, n2, 2 6)<Г—"*. — T (g)1, ^—1, w2, n2, 26)1.
I «1 — 1 •
(e) . T (wL, ny, w2, n2, 26) + Г —---— ----------
I aq
--- + --- +6 —W1 —
I nl n2
при условии, что знаменатель положителен.
(f) . 7(0, nlt w2, n2, 26) = A(h2, 26, w2)-
(g) . T(w1, nlt w2, n2,"28) + A(n2, 26—2wL, w2).
(h) . (Обобщение теоремы 3.) Предположим, что
7(&У!, п1г w2, п2, 26) = Л4;
для 1=1, 2 запишем Mwi=qini+ri, О^г^Пг.
Тогда
М2 (wj + и>2) > G (<Л + 1 )2 + («1—rt) qj +
+g (?2+1)2+(«2-^2) +6 м (M-1).
(i)
7(1, 9, 4, 9, 8) = 3;
7(1, 9, 5, 13, 10) = 3;
7(1, 8, 7, 15, 10) < 11;
Таблицы значений 7(&уь пь [ИО].
7(1, 9, 4, 9, 10) = 2;
7(1, 9, 6, 14, 10) = 7;
7(1, 9, 7, 15, 10) < 12.
W2, nz, d) приведены Бестом и др
17.4. ГРАНИЦЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Иногда для получения хороших оценок мощности кода с заданным спектром расстояний можно использовать линейное программирование. Мы начнем этот раздел с краткого описания линейного программирования. Затем будут даны приложения, сначала для произвольных двоичных кодов, а затем для равновесных кодов. Асимптотические результаты, справедливые для больших п, излагаются в § 17.7.
Линейное программирование (см., например, Симоньяр [1211] или Фикен [428]). Оно изучает методы нахождения максимума (или минимума) линейной формы, называемой целевой функцией, которая удовлетворяет некоторым линейным ограничениям. Типичная задача выглядит так.
Задача. (I). Прямая задача линейного программирования. Найти действительные числа x\,...,xs так, чтобы максимизировать целевую функцию
s
Vqx; (17.17)
/ 1 .
при условии, что эти числа удовлетворяют неравенствам
/=-1, .... s; (17.18)
^ai}x}> — bt, i=l,...,n. (17.19)
/=1
Имеется двойственная задача связанная с этой, в которой число переменных равно числу ограничений в прямой задаче, а число ограничений равно числу переменных в прямой задаче.
Задача. (II). Двойственная задача линейного программирования. Найти действительные числа щ,..., ип так, чтобы минимизировать
(17.20)
1=1
при условии, что эти числа удовлетворяют неравенствам
и, 0, i=l, ... , п; (17.21)
j=l..... s. (17.22)
г—1
Обе задачи удобно формулировать на матричном языке: (I)'. Максимизировать схг при условии, что
х 0; А хт > — Ьт.
(II)'. Минимизировать ubr при условии, что
и 0; и А < — с.
Вектор х называется допустимым решением задачи (I) или (I)', если он удовлетворяет соответствующим неравенствам, и оптимальным решением, если он также максимизирует схг. Аналогичные определения справедливы для задачи (II). Основные факты, которые нам понадобятся, приведены в следующих трех теоремах.
Теорема 1^. Если х и и — допустимые решения задач (I) и (II) соответственно, то cxr^ubr.
Доказательство. Условия
^аих-> — bt и пг>0
i=i
приводят к неравенству
s
пг у atjxj > —щ bt или u AxT -u br.
/=i
Аналогично из условий
О и Xy>0
1—1
вытекает, что пАх7<:—схг. Поэтому сх3"^—uAxr^ubr. •
Теорема 16. {Теорема двойственности.) Пусть х и и — допустимые решения задач (I) и (II) соответственно. Тогда оба решения х и и оптимальны, если и только если схг— ubr.
Доказательство. (Необходимость.) Предположим, что схг = = ubr, но х не оптимально. Тогда существует допустимое решение у задачи (I) такое, что cyr>cxr = ubr, что противоречит предыдущей теореме. Вторая половина доказательства опущена (см. [12И]). •
Теорема 17. (Теорема о дополнительной нежесткости.) Пусть хин являются допустимыми решениями задач (I) и (II) соот-
ветственно. Тогда оба решения х и и оптимальны, если и только если для каждого /= 1,..., $
ИЛИ Xj = 0, или
и для каждого 1= 1,..., п, или иг = О, или
Другими словами, если в ограничениях прямой задачи не выполняется равенство, то соответствующая переменная двойственной задачи должна равняться нулю, и наоборот.
Доказательство может быть предоставлено читателю.
Применения к кодам (Дельсарт [35'0—352]). Пусть Ч? — двоичный (п, М, <Д-код, в котором расстояния между кодовыми словами принимают значения to=O<ti<;t2<; . . . <ts. Пусть {В,} — спектр расстояний кода т. е. — среднее число кодовых слов, находящихся на расстоянии i от фиксированного кодового слова (см. § 2.1). Таким образом, Во=1; Bt/ ^0 (/=1,.. ., s) и Bj=O в остальных случаях. Кроме того,
/=1
Преобразованный спектр {В\} задается формулой (теорема 5 гл. 5)
П s
В‘=^ЕВ'Р‘Й = -ДЕВ'А(ТА * = °.............. “• <1723>
г=0 /=0
где Ph(x) — многочлен Кравчука (см. § 5.2).
Кроме того, Вд= 1 и Bk = 2п/М.
k=0
Теперь нам будет весьма полезна теорема 6 гл. 5 (или теорема 12 гл. 21), которая утверждает, что
B’k > 0 для всех & = 0, ..., п. (17.24)
Таким образом, если — произвольный код, расстояния между словами которого принимают значения {т3}, /=0, ...,8, то ^т,,...,Вт представляет собой допустимое решение следующей задачи линейного программирования.
Задача. (III). Найти числа Вт,,..., В хе, максимизирующие
при условии, что
BXj > О, j — 1, s; (17.25)
s
У.ВХ}Рк(ъ)>-(п\ n. (17.26)
4J \ k J
i=i
Следовательно, имеет место следующая теорема.
Теорема 18. (Первый вариант границы линейного программирования для кодов.) Если В* ,..., В) —оптимальное реше-
С1 Ts
S
ние задачи (Ш), то величина 1 4~ V В* является верхней грани-i=l ‘
цей для объема кода <ё’.
Заметим, что задача (III) всегда имеет, конечно, следующее допустимое решение: Вх. =0 для всех i.
Помимо (17.25) и (17.26) часто можно использовать другие ограничения на числа Вх. . Мы проиллюстрируем это на примере.
Пр и мер. (Оптимальность кода Надлера.) Найдем максимально возможный код длины 12, исправляющий две ошибки. Если к такому коду добавить общую проверку на четность, то мы получим код ?? длины 13 с минимальным расстоянием 6, расстояния между различными словами которого принимают только значения 6, 8, 10 и 12; предположим, что код содержит М кодовых слов.
Пусть А, (и) обозначает число слов кода 'А, находящихся на расстоянии i от слова и, ие?’. Выпишем спектр расстояний этого кода
в‘ = ТТ Е А‘<“>• г=0....13-
ue<g
Тогда Во=1 и все числа Вх равны нулю, кроме (возможно) Въ, В8, Bio и В12. Неравенства (17.26) принимают вид:
В6-ЗВ8 —7В10—11В12 > —13;
-6В6-2В8+ 18В1о + 54В12>-( “ 1 ;
(1Ч \ з):
15В6-5В8-25В10 + 275В12>-(13); {17’27)
15В6—25В8 + 63В10—297В12 > — ( 13 ) ;
\ 5 /
—20В6 + 20В8—36В10+132В12 >—(13) .
\ 6 J )
(Всего имеется только 6 различных неравенств — см. упражнение (43) гл. 5.)
Может быть найдено и другое неравенство. Ясно, что Ai2(u) + 1 (если мы выберем и = 0, то нетрудно видеть, что число векторов v, veg’, веса 12 равно самое большее одному). Кроме того, А10(и) < А (13, 6, 10) (по теореме 1(b));
= Д(13, 6, 3) (из рис. ПА.З);
= 4.
(Легко доказать это непосредственно). Наконец, если Л12(и)=1, то Д10(и) = 0.
Поэтому, конечно,
До (и) + 4Д12 (и) < 4 для всех ueg.
Суммирование по всем u eg’ дает новое неравенство
В10 + 4В12<4.
(17.28)
В действительности оказываются достаточными ограничение (17.28) и первые два ограничения (17.27), так что мы рассмотрим следующую задачу:
максимизировать Вб + В8 + Вю + Bi2 при условии, что
Л6>0; Bs > 0; В10>0; > 0
и
В6—ЗВ8—7В10—11В12 —13;
—6В6—2Bg + 18В10 + 54В12 > — 78;
—BJo—-4В1г >—4.
Двойственная задача такова: минимизировать 13н1+78и2-Ь4нз при условии, что + >0; н2 > 0; us > 0
и
(17.29)
— 6н2
— Зн*—2и., — 7иг + 18н2
1 1Wj -{— 54н2
< —1;
< —1;
—нз< —1;
—4н3< —1.
(17.30)
Допустимыми решениями обеих этих задач являются следующие решения:
В6 = 24; В8 = 3; В10 = 4; Л12 = 0; (17.31)
«з=т- <17-32)
5 о
На самом деле, так как соответствующие целевые функции Равны
24 + 3 + 4 + 0= 13-—+ 78- —+ 4- — = 31,
5 5 5
то согласно теореме 16 решения (17.31) и ( 7.32) оптимальны. (Эти решения легко получаются вручную, если воспользоваться симплекс-методом, см. [428] или [1211].)
Следующие рассуждения показывают, что (17.31) —единственное оптимальное решение. Пусть хв, хв, *ю, *12 обозначает другое оптимальное решение прямой задачи. Все числа задаваемые (17.32), положительны и удовлетворяют первым трем ограничениям (17.30) со знаком равенства, а четвертому — нет. Следовательно, по теореме 17 числа Xt должны удовлетворять ограничениям (17.29) прямой задачи со знаком равенства, и причем Xi2= = 0. Эти уравнения имеют единственное, решение:
х6 = 24; х8 = 3; xJ0 = 4.
Таким образом, (17.31)—единственное оптимальное решение. Решение (17.31) удовлетворяет также и другим ограничениям (17.27), и, следовательно, по теореме 18 код имеет самое большее, 32 кодовых слова. Таким образом, мы доказали, что любой . код длины 12, исправляющий двойные ошибки, имеет не более 32 кодовых слов. Эта граница достигается кодом Надлера из § 2.8.
Заметим, что- этот метод дал нам спектр расстояний .кода Кроме того, так как первые два условия (17.27) выполняются со знаком равенства, то в преобразованном спектре Bri = B'z=0 и d'=3. Но в коде '7? встречаются всего три ненулевых значения расстояния. Следовательно, согласно теореме 6 гл. 6 код '7? инвариантен относительно расстояния и Д1-(и)=В!- для всех векторов UGE'g’. (Эти замечания относятся только к расширенному коду ЯЗ, а не к исходному коду длины 12.)
Если получаемая методом линейного программирования граница оказывается нечетным числом, скажем, b — нечет-
ное, то эта оценка может быть иногда уменьшена с помощью следующего рассуждения (см. Бест и др. [140]). Если предположить, что [&1=Ь, то из выражения (5.36) получаем
i=o wt (и)=й yve'g /
Внутренняя сумма содержит нечетное число элементов ± 1 и поэтому не равна нулю. Следовательно, bBrk^ (1/&) ( П ), т. е, k мы можем заменить (17.26) более сильным условием
S
^В,;Р,(г;)>-(1 —(17.33) /=1
Следующий пример показывает, как это используется.
Пример. (/(8,3) =20). Пусть — максимальный код длины 8, исправляющий одиночные ошибки, и пусть 33 — расширенный
код длины 9 с расстоянием 4, имеющий спектр расстояний Во=1, Bt, В6, Bs. Условия.(17.26) таковы:
В4 — ЗВ6 —7Ве >—9;
— 4В4 +20В8>—36;
— 4В4 + 8В6 — 28ВЯ > — 84;
6В4—6Вв + 14В8 > — 126,
(17.34)
и, кроме того, мы можем добавить следующие ограничения:
1;
Вв + 4В8<12, (17.35)
которые доказываются так же, как и неравенства (17.28). С помощью линейного программирования мы находим, что наибольшее значение суммы чисел Bi + Be + Bs, удовлетворяющих условиям (17.34) и (17.35), равно 2073, так что \<ё’\^21.
Предположим, что |в’|=21. Тогда имеет место неравенство (17.33) и правая часть (17.34) может быть умножена на 20/21. Теперь линейное программирование дает следующий результат:
S4 + Be + S8 < 19,619 . . .,
так что ]'ё>\^20. Поскольку в гл. 2 приводился (8, 20, 3)-код, отсюда получаем, что /(8,3) =20. Таким способом были получены многие оценки, приведенные на рис. ПА.1.
Вернемся к общему случаю и рассмотрим задачу, двойственную задаче (III). Это позволит нам получить аналитические границы. Двойственная задача такова.
Задача (IV). Найти числа pi,..., р„, минимизирующие
при условии, что
р/; > 0, k = 1, . ., п;
i>^(7-)<-i. /=1.
k=i
(17.36)
(17.37)
(17.38)
Переход к двойственной задаче имеет то преимущество, что любое допустимое решение задачи (IV) согласно теореме 15 является верхней границей для объема кода. В то же время только оптимальное решение задачи (III) дает верхнюю оценку. Оказалось, что допустимое решение задачи (IV) проще всего выражать посредством многочлена, который мы обозначим через р(х).
Лемма 19. Пусть
Р(х)=1 +'£phPft(x).
А—1
Тогда pi,.... рп представляет собой допустимое решение задачи (IV), если и только если рй^0 для &=1.......п и р(т7)^О для
Доказательство.
0(T,)=l + £₽ftPft(TA •
ъ=\
Из предыдущего замечания мы сразу же получаем следующую теорему.
Теорема 20. (Второй вариант границы линейного программирования для кодов.) (Дельсарт [350].) Предположим, что мы можем найти многочлен р(х) степени не более п, удовлетворяющий следующим свойствам. Если разложение р(х) по многочленам Кравчука (с. 169) имеет вид
P(x) = VpftPft(x), (17.39)
k=0
то р (х) должен удовлетворять условиям
Ро=1; (17.40)
[V > 0 для /г=1, .... п; (17.41)
Р(т,-)<0 для /=1,..., s. (17.42)
Тогда, если 7? — произвольный код длины п, расстояния между различными словами которого принимают значения {tj}, j = 1, ..., s, то
< р(0) = 1 + у pft ( nY ь=1 4 )
Следствие 21*>. Если многочлен
PW=ypftPh (X)
k=0
удовлетворяет условиям (i) р0=1; pfe^0 для
k=l..... п и (ii) р (/) < 0 для j = d, 1, ..., п,
то
А (п, d) < р (0).
Из теоремы 17 вытекает, что любой код, для которого в имеет место равенство, должен удовлетворять следующим нительным свойствам.
(17.43)
(17.44)
(17.43)
допол-
*> Более естественный и общий метод, чем линейное программирование для получения границ, подобных теореме 20 и следствию 21, предложен в работах [462*а] и [706а*]. (Прим, ред.)
Теорема 22. Пусть Вх, и рь...,рп являются допус-
тимыми решениями задач (III) и (IV) соответственно. Они являются оптимальными решениями тогда и только тогда, когда -
(i) . B'k =0 для 1 < k < п
и
(ii). р(т7-)ВТ/ = 0 для
1 < / С s.
Примеры. (1). Мы начнем с очень простого примера и покажем, что код, дуальный к коду Хэмминга, оптимален. Для этого мы воспользуемся следствием 21, чтобы показать, что код 2? длины 2т—1 с минимальным расстоянием 2т-1 может иметь самое большее 2™ кодовых слов. (Конечно, это следует также из теоремы 11(a).) Выберем многочлен
Р (х) = 2 (2"1-1 -х) = Р0 (х) + Л (х),
так что Po = Pi = 1; Рл = О для 1.
Поскольку
Р(/)СО для j = 2m~l, 2m-1 + l, ..., 2т — 1, условия следствия 21 выполняются, и поэтому согласно оценке (17.44)
|^| <Р(0) = 2т.
Таким образом, код, дуальный к коду Хэмминга, оптимален.
Более того, согласно теореме 22 (ii) в коде Вг=0 для всех i>2m”1; поэтому в коде встречается только одно ненулевое расстояние, а именно 2т-1.
(2) . Код Адамара из гл. 2 с параметрами (4</и, 8m, 2т) оптимален: А (4т, 2т)=8т (другой частный случай теоремы Па). Чтобы показать это, воспользуемся следствием 21 с р(х) =
— —(2т—х) (4т—х) = P0(x)-j-Pi(x) + — Pz(x).
т 2т
(3) . Найдем теперь границу для объема кода с минимальным расстоянием d, используя линейный многочлен р(х), скажем, p(x) = l + p1Pi(x) = l-f-Pi(«—2х), где Pi>0. Нам нужно, чтобы выполнялись неравенства p(cQ, p(d-f-l),.. ., р(п)^0 и значение р(0) = l-|-!pIn было минимально возможным. Наилучший выбор — положить р(с0=О, т. е. Pi = l/(2d—п). Тогда неравенство (17.44) дает следующую оценку: |^?| ^р(О) =2d/(2d—п). Итак, мы получили более слабую версию границы Плоткина из теоремы 11.
Упражнение. (16). (Дельсарт.) Получить из следствия 21 границу сферической упаковки. [Указание. Пусть d=2e+l. Положим
0 < k с п,
где Le(x) —многочлен Ллойда (см. теорему 32 гл. 6). Воспользуемся следствием 18 гл. 5, чтобы показать, что
p(i) = 0 для 2e+l<i<n; 0(0) = 2" / V(
Пример. (4). (Граница Синглтона (Дельсарт).) Чтобы выполнялись условия следствия 21, можно положить ₽(/)=0 для /= —d, Таким образом, мы имеем
р (х) = 2"-d+I Г|( 1 — ~• \ / / /=<г
Коэффициенты определяются следующим образом (теорема 20 гл. 5):
₽* - тг s ₽ <> р< <‘> - рД S (»Д+,)(*> /(Д.)= i—0 z=0
. ЖЖ-Ж'
Для получения последнего равенства мы воспользовались упражнением (41) гл. 5. Заметим, что pfc—0 для п—d+2^k^n. Следовательно, верно утверждение:
если Ч? — произвольный двоичный (п, М, d)-KOR, то
М < P(0) = 2"-d+I. (17.45)
Полученное неравенство является обобщением границы Сингл--тона (гл. 1, теорема 11) для нелинейных кодов.
Упражнения. (17). Показать, что если %?— (п, М, d) -код над полем GF(q), то M^qn~d+l.
(18) . (Дельсарт.) Пусть •g’— двоичный (п, М, d)-Koji, удовлетворяющий следующему свойству: если то дополнительный вектор и также при,надлежит <ё’. (Пример: любой линейный код, содержащий вектор из всех единиц.) Доказать, что
М < ——(n—d) __ (j 7 46)
п — (п — 2d)2
при условии, что знаменатель положителен. Неравенство (17.46) известно как граница Грея — Рэнкина (см. работы Грея [561] и Рэнкина [1090, 1091]). [Указание. Образовать (п, М/2, с?)-код SF', выбирая по одному кодовому слову из каждой пары дополнительных векторов кода <ё. Тогда расстояния в коде принимают ненулевые значения в диапазоне [d, п—d]. Далее воспользоваться многочленом p(x)=a(d—х) (п—d—х), где а — соответствующим образом подобранная константа.]
Заметим, что для конференс-матричных (п—1, 2п, (п—2)/2)-кодов из § 2.4 в условии (17.46) имеет место равенство, однако коды не могут быть разбиты на пары дополнительных векторов (см. задачу (нерешенную) (2.2)).
(19) . Показать, что каждое допустимое решение задачи (III) удовлетворяет неравенству Вх. ( ).
(20) . (Мак-Элис [944]). Другой вариант следствия 21: если многочлен
п
s(*)=— (х)
2" Ш
Л=0
удовлетворяет условиям (1) 6(0) = 1; (6(/)^0
для 7=1,..., п и (ii)6fe < 0 для k = d, d+1,..., п, то
л(«, d)<60=2(n)6o> (17.47)
/=0 ' 1 '
[Указание. Положить Рь=6(&) и воспользоваться следствием 18 из гл. 5.]
(21) . ([944]). Для четного п выбрать в качестве 6(х) квадратный многочлен с 6(0) = 1; 6(п/2+1)=0 и вновь сделать упражнение (11).
(22) . ([944]). Для значений «=1 (mod 4) выбрать
6(х) = {(x-Д)2—1/2 — (1/2) Рп (х)}/(а2—- 1),
где а=(п-|-1)/2, и показать, что А(п, 3) =С2п/(/г+3). Показать, в частности, что А (2™—3,3) = 22т-т~3.
Задача (нерешенная). (17.5). Дать комбинаторное доказательство того, что А (2™—3,3) = 22m_™~s.
Граница линейного программирования для равновесных кодов. (Дельсарт [352].) Для равновесных кодов также справедлива граница линейного программирования. Пусть S) обозначает двоичный код длины п, веса w с расстоянием 26. Тогда \0 [ ^А (п, 26, w). Обозначим через {й2г}, i=0, l,...,w, спектр расстояний кода S). Как. следует из теории схем отношений (см. теорему 12 гл. 21), преобразованные величины Brih неотрицательны, где
W
B'2k=Sв*Qh (0, k=0........w- (17‘48)
г=0
и коэффициенты Qk(i) определяются равенствами
(и.»,
8 многочлен
Е. (х) = (-If"' (17.50)
/=о
представляет собой многочлен Эберлейна (см. § 21.6).
Таким образом, с помощью линейного программирования можно получить оценки величины А (п, 26, w): для этого нужно максимизировать Bo+B2-i- • • +B2w, где и В'щ^О для
всех i и k. Как и ранее, часто можно использовать дополнительные ограничения.
Пример. (Л (24, 10, 8)^69.) Когда п=24; 26=10 и &у=8, переменные Bw, В\2, Blit Bi6 должны удовлетворять дополнительному ограничению, а именно Вщ^А (16,10,8) =4 (см. приложение А) (так как Вх6 не превышает числа векторов веса 8, отличных от фиксированного вектора веса 8 и находящихся друг от друга по крайней мере на расстоянии 10). С помощью линейного программирования можно получить, что при заданных ограничениях максимум суммы Вю+В12 + равен 68 и достигает-
ся, когда
В*о = 56; BL2 = 0; В14 = 8; В1в = 4.
Таким образом, А (24,10,8) ^69.
Задача (нерешенная) (17.6)*. Существует ли код с таким спектром расстояний?
Именно таким путем были получены значения, приведенные на рис. ПА.З и помеченные там буквой L. Для оценки величины T(wi, ni, w2, п2, d) также можно использовать границу линейного программирования (см. Бест и др. [140]).
17.5. ГРАНИЦА ГРАЙСМЕРА
Для линейного [п, k, Д|-кода граница Синглтона (17.45) утверждает, что n^d + k—1. Граница Грайсмера, задаваемая выражением (17.52), увеличивает правую часть этого неравенства. Лучше всего привести эту границу, используя величину 7V(A d) — минимально возможную длину двоичного линейного кода размерности k с минимальным расстоянием d.
Теорема 23.
N (k, d)>d + N(k~ 1, ]d/2f). (17.51)
Доказательство. Пусть Я?—[A (k, d), k, сфкод с порождающей матрицей G. Без ограничения общности можно считать, что
-<-Аг (/г, d) — ----------d-
0000 ... 000 111 . . . 11
Gt
где матрица Gi имеет ранг k—1, в противном случае мы бы обратили в нуль первую строку матрицы Gi и минимальное расстояние кода было бы меньше чем d.
Ответ отрицательный. (Kibler R. Е., частное сообщение).
Пусть матрица Gi порождает [Лг(/г, d)—d, k—1, dj-код. Предположим, что вектор |и | v| e'g’, где wt(u) = di. Так как |u|v[е??, то
d± 4-wt (v) > d;
d± + d—wt(v) > d,
и, складывая эти неравенства, получаем, что 2dt^d или di+= ^]d/2f. Следовательно,
N(k— 1, ]d/2\) <N(k, d)—d. •
Теорема 24. (Граница Грайсмера [562]; см. также работу Соломона и Стиффлера [1257].)
а—1
]v-[- (17-52)
i—0
Доказательство. Многократно применяя теорему 23, находим, что
N(k, d)^d + N(k—\,
>d + P4 + W—2.
£ 2
k— 2
i=0
П римеры. (1). Найдем число N(5, 7), т. е. самый короткий код размерности 5, исправляющий три ошибки. Согласно теореме 24
= 74-4 + 2 + 1 + 1 = 15.
В действительности существует [15, 5, 7]-код БЧХ, и поэтому М(5,7) = 15.
(2). Если d=2k~l, то из теоремы 24 вытекает, что
N (k, 2ft~‘) > 2fe-1+2Й—2 +...+2 + 1 = 2й—1.
На самом деле симплексный [2й—1, k, 2й1]-код (см. гл. 1) показывает, что эта граница достигается.
17.6. ПОСТРОЕНИЕ ЛИНЕЙНЫХ КОДОВ; АНТИКОДЫ
Пусть Sb — порождающая матрица симплексного [2й—1, k, 2ft-1]-KOfla; таким образом, столбцами матрицы Sft являются все Различные ненулевые двоичные ^-векторы, расположенные в некотором порядке. Как показал предшествующий пример, этот код
достигает границы Грайсмера, так же как и код, порождающая матрица которого состоит из нескольких экземпляров матрицы St, выписанных друг за другом.
Замечательный способ построения хороших линейных кодов заключается в следующем: надо взять матрицу Sfe или несколько экземпляров Sa и вычеркнуть некоторые столбцы (см. рис. 17.1а и 17.1b).
Вычеркиваемые столбцы сами образуют порождающую матрицу так называемого антикода (согласно Фореллу и др. [418, 420, 421]; см. также [889], [1098]*). Антикод представляет собой код, у которого расстояния между кодовыми словами ограничены сверху. Допускается даже нулевое расстояние между кодовыми словами, и поэтому антикод может содержать одинаковые кодовые слова.
Определение. Если G—произвольная двоичная матрица размера k~Xm, то все 2й линейных комбинаций ее строк образуют кодовые слова антикода длины т. Максимальное расстояние б .антикода равно максимальному весу его кодовых слов. Если rank G = r, то каждое.кодовое слово встречается 2k~r раз.
Пр и мер. (1). Матрица
”0 1
G= 1 о
Г
1
1 1 о
порождает антикод
ООО 0 1 1 1 0 1 1 1 0 1 1 0 1 0 1 0 1 1 ООО
длины т=3 с 23 кодовыми словами и максимальным расстоянием 6=2. Каждое кодовое слово встречается дважды. Аналогично для любого k^:2 легко строится антикод длины 3 с 2й кодовыми словами и максимальным, расстоянием 2.
Использование антикода для построения новых кодов. Предположим сначала, что порождающая (k\m)-матрица антикода имеет различные столбцы. Тогда (см. рис. 17.1а) порождающая матрица нового кода' получается вычеркиванием из матрицы S;{ столбцов порождающей матрицы антикода. Ясно, что длина нового кода равна 2й-—1—т, размерность не более k и минимальное расстояние 2й-1—6.
’> См. также работу [1470]. (Прим, ред.)
2й - - I m 2k-~i—m
Порождающая ма- Порождающая матрица Порождающая матрица трица симплексно- антикода. Кодовые ело- нового кода длины го кода. Кодовые ва имеют максимальный 2к—1—т, размерности k слова имеют один вес б или меньше с минималь-
и тот же вес 2'1-1 ным весом 2s-1___б
Рис. 17.1а. Использование антикода для построения новых кодов
k
Sft
s(2ft- 1)
Sfe
s (2й - 1) --
— k
т
s экземпляров ма- Порождающая матрица Порождающая матрица трицы Sa. Каждое антикода с максималь- нового кода. Минималь-слово имеет вес ным весом б ный вес равен s-2fc-1—б
s-2k~l
Рис. 17.1Ь. Случай, когда антикод содержит повторяющиеся столбцы
Пример. (2). Если k~^3, то, вычеркивая из матрицы Sa столбцы антикода из примера (1), мы получим [2й—4, k, 2й'1—2]-код.
Предположим, что новый код имеет размерность г и что
—1. В этом случае порождающая матрица кода 7? содержит 2й—1—т различных ненулевых столбцов таких, что любые k из них линейно зависимы. Таким образом, должно выполняться неравенство 2й—1—т^2й-1—1, так что т^2,:Л.
Следовательно, если т<2й-1, то размерность кода 7? равна k.
В более общем случае предположим, что любой столбец порождающей матрицы антикода встречается не более s раз. Тогда новый код получается вычеркиванием столбцов этой матрицы из s экземпляров матриц Sa, выписанных друг за другом (рис. 17.1b). Код имеет длину s-(2fe—1)—т, размерность не более k и минимальное расстояние s-2fe_1—б.
Мы рассмотрим другие примеры, используя язык проективной геометрии (см. приложение В). Точками проективной геометрии PG(k—1, 2) являются все 2й—1 ненулевых двоичных ^-векторов, и поэтому они в точности совпадают со столбцами матрицы Sa-Подмножество этих столбцов, таким образом, является подмножеством точек этой проективной геометрии.
Примеры. (3). Вычеркнем прямую (состоящую из трех точек) из матрицы S3:
"0 0 0 1 1 1
0 110 0 1
10 10 10
11 ГО 1 г
1 — 10 1
1J [1 1 °
"0 0 1 г 0 10 1 10 0 1
Матрица S3
Порождающая матрица антикода (прямая PG в (2, 2))
Порождающая матрица нового кода с параметрами п = 4; k = 3;
4 = 2
(4). Образуем для k=5 антикод, столбцами которого являются 15 точек проективного подпространства размерности 3 и еще одна точка, не лежащая в этом подпространстве, как изображено на рис. 17.2.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
Рис. 17.2. Порождающая матрица антикода с параметрами т=16; й = 5; 5=9
Вычеркивание этих столбцов из матрицы S5 приводит к [15,5, 7]-коду, удовлетворяющему границе Грайсмера.
(5). Выберем в S6 проективное подпространство В$ размерности 4 (4-плоскость), содержащее 31 точку, и 3-плоскость Bt, содержащую 15 точек. Эти подпространства пересекаются по плоскости С3 (состоящей из 7 точек). Выберем плоскость В3, которая не пересекается с С3. (В3 и В5 пересекаются по прямой С2, а В3 и Вц пересекаются в точке Сь) Выберем прямую В2, которая не пересекается с Bt или jB3 (и пересекается с В$ в точке C'i). Наконец, выберем точку Вг, которая не принадлежит ни одному из выбранных Bi. В качестве столбцов порождающей матрицы антикода возьмем 31+15+7-4-3+1 = 57 точек конфигураций В5, Bt, В3, В2 и Bi. Столбцы С3, С2, Ci и C'i встречаются в этой матрице дважды. Максимальный вес равен 16+8 + 4+2+1 = 31 и k = 6. Вычеркнем столбцы этого антикода из двух экземпляров матрицы S6, Как показано на рисунке:
I s° I I s6 I
Вычеркнуть Вычеркнуть
В5, Ci, Bi Bt, Br-Ci, в2
Заметим, что точки конфигураций С3, С2, Ci и C'i вычеркиваются дважды, по одному разу из каждого экземпляра матрицы
Se- Результирующий код имеет параметры п=2-63—57=69; k= =6; d=2-32—31=33 и удовлетворяет границе Грайсмера.
Упражнения. (23). Используя прямую и 3-плоскость в; PG(5, 2), получить антикод с параметрами т=18; &=6; 6=10 иг следовательно, получить [45,6,22]-код.
(24). Построить [53, 6, 2б]-код.
Общий метод построения (Соломон и Стиффлер [1257], Белов; и др. [102]; см. также Оллтоп [25]). Следующий способ построения антикодов из подпространств обобщает предыдущие примеры и приводит к широкому классу кодов, достигающих границы Грайсмера.
Для заданных d и k положим
р
8 = и d = 2ft_1 -J}2"-1, (17-53}|
i=l
где ... >и-р^ 1.
Предположим, что мы можем найти такую совокупность р проективных подпространств Bt,... ,ВР в Sh (где Bi состоит из 2ut — — 1 точек), которая удовлетворяет следующему свойству:
Пересечение любых s +1 подпространств Bi пусто. (17.54)>
Это означает, что любая точка принадлежит .самое большее s подпространствам В{. Составим из столбцов jBi,...,Bp антикод; ни один из его столбцов не встречается более s раз. Новый код получается вычеркиванием этого антикода из s экземпляров матрицы Sft. Код имеет длину р
n = s(2h~ 1) — £(2“г— 1),
размерность k, минимальное расстояние, определяемое формулой (17.53), и достигает границы Грайсмера. На рис. ПА.2 эти коды обозначаются буквами ВК.
Теорема 25. (Белов и др. [102].) Описанное построение возможно тогда и только тогда, когда
min (s-|-I, р)
£ Щ < Sk.
Доказательство. (Необходимость.) Пусть [<(%) обозначает двоичный неприводимый многочлен степени k—щ, где 1=1,...,р, и пусть обозначает множество всех многочленов степени меньше k, которые делятся на fi(x). Тогда А{ представляет собой векторное пространство размерности щ, натянутое на /т(х), xfi(x), — ..., хи i -'fifx). Точки подпространства Bi могут быть очевидным) образом отождествлены с ненулевыми элементами этого пространства. Предположим, что
mi n (s-f-1, р)
У щ < sk.
Нам надо показать, что если I — любое (s +1) -подмножество 'множества {1, 2, ...,р} (когда s+l^p) или если 7= {1,..., р} {когда s+ Г>р), то f| ieIBi=0.
.Действительно,
ПВ( = 0^ пл = о
iei tei
iMegH.O.K.
ip.l
так как по условию теоремы Ui>u2> ...
(Достаточность). Предположим, что построение возможно, т. е. условие (17.54) выполняется. Если s+l>p, то ничего доказывать не надо. Предположим, что s+l^p. Тогда согласно (17.54) для .любого (s+1)-множества 1 выполняется условие р?е/ В!==0. Но ,в силу упражнения (27)
Следовательно, S u-i^sk. •
iei
Следствие 26. Если для заданных d и k выполняется неравенство
min (s+I. р)
где числа s, U\,...,uv определяются условиями (17.53), то существует [п, k, гД-код, достигающий границы Грайсмера.
Заметим, что [5, 4, 2]-код из всех слов четного веса достигает границы Грайсмера. В этом случае s=l; d=2=8—4—2; щ = 3;
2
U2=2; p=2 и S u0>sk. Поэтому условия, сформулированные в 1=1
'следствии, не являются необходимыми для того, чтобы код достигал границы Грайсмера. Как показали Баумерт и Мак-Элис [87], для заданного k граница Грайсмера достигается при всех достаточно больших d.
Задача (нер ешенная). (17.7). Найти необходимые и до-статочные условия, которым должны удовлетворять числа k и d,. чтобы граница Грайсмера (17.52) была точной.
Описанный метод построения может быть использован для нахождения линейных кодов наибольшей мощности в диапазоне .n^2d.
Теорема 27. (Вентурини [1369]; переоткрыто Пейтлом [1027]. Обобщение на GF(q) см. в работе Пейтла [1028].) Пусть для заданных nud
i-i
d = Xj2'— при / = 0, 1,..., (17.55);
i=0
где х} — целые положительные числа и (z,j=O или 1, и пусть
/-1
Ь = X Gii' (17.56);
i=D
Существует единственное значение /, скажем, j~k, для которого tk-i~^2d—п и tk<2d—п. Тогда линейный код наибольшей MOiiiHOi сти длины п с минимальным расстоянием d содержит В(п, d)=2h кодовых слов.
Доказательство опускается. Чтобы построить такой [п, k, d]-код, мы поступаем следующим образом. Положим t=2d—п. Тогда
k—2
hi — 1 = 1 У, ai, k—1 h
i=D
(17,57).
и из (17.55) следует, что
k—2
и = 2d - i = (Д_х - 0 + (2* - 1) - у а, (2г+] - 1). (17.58);
г=0
Теперь для каждого i такого, что ait ft_i = l, образуем' антикод, состоящий из проективного подпространства Д,-н (в котором 2i+1—1 точек). Вычеркнем этот антикод из Xk-i экземпляров матрицы Sfe, что возможно в силу (17.57). Наконец, добавим tk—i—t произвольных столбцов. Результирующий код имеет длину п (согласно (17.58)), размерность k, и минимальное расстояние (по й—2
крайней мере) xk_12h~i—У , ь_г2г = d согласно (17.55). i=0
Упражнение. (25). Показать, что А (100,50) =200, В(100,50) =32. Таким образом, В(п, d) может быть намного меньше чем А (п, d).
Теорема 28. Если d^.2k~i и [п, k, й]-код ‘g’ достигает гра- . ницы Грайсмера, то ‘g’ не имеет одинаковых столбцов.
Доказательство. Предположим, что код ‘g’ имеет одинаковые-столбцы. Тогда порождающая матрица может быть приведена, к следующему виду:
г 1 1 . . .
о о
. . . G, о о
Обозначим через [п—2, k—1, гГ]-код, порожденный матри-
цей Gp Тогда согласно оценке (17.52)
ь—2 h—2
i=0 i=C
h~~2 k— I
i=0 i=D
и поэтому код ‘g’ не достигает границы Грайсмера. •
Определение. Оптимальным называется антикод наибольшей длины m для заданных значений размерности k и максимального расстояния б.
Предположим, что мы вычеркиваем антикод из соответствующего числа экземпляров симплексного кода. Ясно, что если результирующий код достигает границы Грайсмера, то этот антикод юптимален. Таким образом, описанные выше способы построения дают много оптимальных антикодов, образованных из подпространств. В частности, антикоды, рассмотренные в примерах 3, 4, 5, оптимальны. форрел и Форрег [420, 421] привели таблицы оптимальных антикодов.
Теорема 29. Пусть — оптимальный антикод длины т, мощности 2к с максимальным расстоянием б такой, что каждый ^столбец в s/ встречается не более s раз. Предположим, кроме того, что код, полученный вычеркиванием антикода из s экземпляров матрицы Sfe, достигает границы Грайсмера. Тогда новый антикод , полученный двукратным повторением каждого кодового слова также оптимален.
Доказательство. По условию теоремы
(17.59)
Из (17.59) и равенства
’ s2ft —б 2*
•справедливого для любого i^k—1, вытекает, что
ж, следовательно, код sSfe+i—достигает границы Грайсмера. •
Эта теорема часто позволяет нам получать из оптимального антикода с параметрами пг, k, б оптимальный антикод с параметрами т, £+1, б.
Простое геометрическое описание имеют не все оптимальные .антикоды. Так, [Z+l, t, 2]-код ‘g’ из всех слов четного веса дости
гает границы Грайсмера. Таким образом, S(—•g’ представляет собой оптимальный антикод длины 2г—t—2 с 2‘ кодовыми словами и максимальным расстоянием 2*-’—2. Согласно теореме 29 для всех k^t мы получаем оптимальные антикоды, имеющие 2fc кодовых слов, и, следовательно, новые коды, достигающие границы Грайсмера.
Пример. (6).
/ = 3,т = 3,6 = 2|115’4’8]^[12’4’61 <^4)>
|[31, 5, 16]->[28, 5, 14] (6 = 5),
/ = 4, W=10, б = б|(31'5’ 161-Н21’5’ 101
1[63, 6, 32]->[53, 6, 26] (/г = 6),
= 5 щ = 25, б=14|[63’6’32^[38’6’ 181 =
[[127. 7, 64]->[102, 7, 50] (6 = 7).
0110
0111
1110
0011
1001
1100
0101
Рис. 17.3. Конфигурация Дезарга
1011
Первые два антикода состоят из трех точек одной прямой. Однако другие антикоды не имеют подобного геометрического описания. Например, антикод из второго примера и 10 прямых в PG(3, 2), причем каждая прямая состоит из трех точек и через каждую точку проходят три прямые, как изображено на рис.
17.3. На рисунке изображена конфигурация Дезарга; так она называется потому, что возникает при доказательстве теоремы Дезарга (см. книгу Гильберта и Кон-Фоссена (654, рис. 135, с. 123]).
Задача (нерешенная).
(17.8). Имеется ли естественное описание геометрических конфигураций, соответствующих другим оптимальным антикодам?
Упражнение. (26). ([420].)
Так как антикод может содержать одинаковые слова, то антпкоды можно «объединять», чтобы получать новые.
(а). Построить антикоды д/ и с параметрами m=10; 6=5;. 6=6 и т = 16; 6=5; 6 = 9 соответственно.
состоит из 10 точек;
1010
(Ь). Показать, что конструкции
0 Л Л 0 33 33
1 л Л И 1 33 33
(где 0 и 1 обозначают столбцы из нулей и единиц соответственно) образуют антикоды с параметрами m=21; k—6; 6=12 и т=33; 6=6; 6=18.
(с). Получить, следовательно, [42, 6, 20]- и [30, 6, 14]-коды.
В заключение на рис. 17.4 перечислены некоторые оптималь-
ные линейные коды с Л=6 (даюшие, таким образом, значения ЛЦ6, d)).
Намного более полную таблицу привели Хелгерт и Стинафф [636]..
Код
[63, 6, 32 [60, 6, 30 '56, 6, 28 53, 6, 26 48, 6, 24 '45, 6, 22' 42, 6, 20‘ 38, 6, 18 '32, 6, 16' '30, 6, 14' 26, 6, 12 '23, 6, 10 18. 6, 8] '15, 6, 6' 11, 6, 4 7, 6, 2]
Антикод
прямая
плоскость
плоскость + прямая, или рис. 17.3
3-плоскость
3-плоскость + прямая
см. упражнение (26)
см. пример (6)
4-плоскость
см. упражнение (25)
см. Баумерт и Мак-Элис [87[
см. Баумерт и Мак-Элис [87
см. Баумерт и Мак-Элис [87 код БЧХ
укороченный код Хэмминга код из всех слов четного веса
Рис. 17.4. Оптимальные коды с k=6
Упражнения. (27). ([102].) Пусть — двоичный линейный [п, kij-код для i=l.t. Показать, что
t
dim П > max
t
0, £ kt—(t— l)n j=i
[Указание. Использовать индукцию по A]
(28). Показать, что если ‘й’ — оптимальный антикод с четным 6 и т<2/г—1, то к порождающей матрице может быть добавлен еще один столбец, что приведет снова к оптимальному антикоду с параметрами m + 1, k, 6+1-
(29). ([889].) Пусть код имеет порождающую матрицу ГЬ|А] , где А — матрица размера &Х («—k), строки которой имеют вес не более единицы, а столбцы имеют четный вес более нуля. Отсюда' следует, что 3k^2n. Показать, что представляет собой [п, &]-код с максимальным весом k.
ПЛ. АСИМПТОТИЧЕСКИЕ ГРАНИЦЫ
В этом разделе рассматриваются асимптотические оценки, применимые, когда п велико. Оказывается, что в этом случае проще всего записывать результаты как функцию скорости кода наибольшей мощности
R = — log„ А (п, d) п
от отношения d,n. Наилучшие известные к настоящему' времени' оценки изображены на рис. 17.7. Все коды лежат не выше верхней1 границы Мак-Элиса — Родемича — Рамсея —, Велча (теоремы 35,, 37), в то время как наилучшие коды лежат не ниже нижней границы Варшамова — Гилберта. Последняя была приведена в гл. 1 (теорема 12) и асимптотически имеет следующий вид.
Теорема 30. (Нижняя граница Варшамова — Гилберта.) Предположим, что 0^'б<1/2. Тогда существует бесконечная последовательность двоичных линейных [п, k, d] -кодов с dln^S и скоростью В —kin, удовлетворяющей неравенству /?>1—Т/2 (—\ \ п / для всех п.
Обозначения. Неравенство f(n)<g(n), когда п->оо, означает, что f(n)^g(n) (1 + £(н)), где |е(п) |->0 при и->со. Кроме того, /72(х) =—xlog2x—(1—x)log2(l—х)—двоичная энтропия (см. § 10.11).
Доказательство. Следует из теоремы 12 гл. 1 и следствия 9 гл. 10.
Имеется целый ряд кодов, в том числе альтернантные коды (теорема 3 гл. 12), коды Гоппы (упражнение (9) гл. 12), дважды; циркулянтные или квазициклические коды (§ 16.7) и самодуаль-ные коды (§ 19.6)л которые достигают границы Варшамова — Гилберта (см. также задачу (нерешенную) (9.2)). Чтобы показать, что семейство кодов содержит коды, достигаклцие границы Варшамова — Гилберта, часто бывает достаточным следующее очень простое утверждение.
Теорема 31. Предположим, что существует бесконечное семейство двоичных кодов Фь Ф2,..., где Ф,4 — множество [ш, &<]-кодов таких, что: (1) kilnC>R и (ii) каждый ненулевой вектор’ длины п( принадлежит одинаковому числу кодов в Ф<. Тогда в этом семействе существуют коды, асимптотически достигающие: границы Варшамова — Гилберта, или, более точно, такие, что
Н>1 — Н„(—\, когда п->оо.
“ \ п j
Доказательство. Обозначим через No полное число кодов в Ф,, а через Ni — число кодов, содержащих фиксированный ненулевой вектор v. По условию теоремы число Ni не зависит от выбора v, следовательно,
г?
. (2 г--1)А\ = (2 г-1)Я-
Число векторов v веса меньше чем d равно-
d— 1
и, следовательно, число кодов в семействе Фг- с минимальным расстоянием меньше чем d равно самое большее
Если это число меньше чем No, т. е. если выполняется неравенство
d— I
/=1 4
то семейство Фг содержит код с минимальным расстоянием по крайней мере d. Утверждение теоремы следует теперь из следствия 9 гл. 10. » •
Упражнения. (30). Показать, что для любой заданной скорости R существуют линейные коды, удовлетворяющие границе Варшамова — Гилберта. [Указание. В качестве Фг надо выбрать множество всех линейных кодов длины i и размерности &>W]
(31). (Кошелев [779], Козлов [781], Пирс [1044]; см. также Галлагер [464, 465].) Пусть G представляет собой двоичную матрицу размера k)x(n, все элементы которой выбраны случайно, и пусть (G) обозначает код с порождающей матрицей G. Показать, что если kjn фиксировано и rw-oo, то с вероятностью, стремящейся к единице, код Г? (G) удовлетворяет границе Варшамова — Гилберта.
Если dM^l/2, то из границы Плоткина следует, что (l/n)log2/4(и, d)—>0 при л—>оо, и поэтому в дальнейшем мы бу-' дем считать, что 1/2.
Приведем ряд верхних оценок, последовательно усиливающих друг друга (доказательства, конечно, усложняются). Первой является граница сферической упаковки (теорема 12), асимптотически принимающая следующий вид.
Теорема 32. (Граница сферической упаковки или верхняя граница Хэмминга.) Для любого (п, М, d) -кода
R<1—H2(dl2n)' при п->оо.
Перейдем теперь к границе Элайеса, которая выводится с помощью следующего простого результата (функция А(п, d, w) была определена в § 17.1).
Т е о р ем а 33.*
л, 2" Л (я, 26, о>) п
А (п, 26) <---/ п \--- Для всех №=;0’-" п-
\ w J
* Эта и следующая теорема впервые доказаны в [76]. (Прим, перев.)
. Доказательство. Пусть ‘g’ обозначает (п, М, 26)-код с максимально возможным числом кодовых слов, т. е. М~А(п, 26).
Для любых векторов u, vgM положим
. . f 1. если и dist (u, у) = w,
Х(и, v) =
( 0 в противном случае.
Оценим двумя способами следующую сумму:
Е £ *<“ 26>-
u£Fn vf?Fn u6®
=S Sx(u’v)<
veFn ueFn
< A (n, 26, w) = 2" A (n, 26, w). •
veFn
Теорема 34. (Верхняя граница Элайеса [1192].) Для любого (п, М, с?)-кода
R< 1—(4----------г V 1—;Дг) ПРИ п~^со- (17.60)
Доказательство. В силу теоремы 2
А(п, 26, <х;)<6п/(ш2—wn-\-&ri).
Положим
Г п п 4(6—1)] № = №о = |__—У 1--------L__2|.
Тогда А(п, 26, tco) ДД, и согласно теореме 33
А(п— 1, 26— 1) = Л(и, 26)<2rt6 К п Y
I \w0J
Отсюда, учитывая лемму 7 из гл. 10, получаем оценку (17.60). •
Мы переходим, наконец, к 'наилучшей из известных в настоящее время верхних оценок. Она состоит из двух частей; начнем с более простой.
Деорема 35. (Первая верхняя граница Мак-Элиса — Роде-мича — Рамсея — Велча [947].) Для любого (п, М, с?)-кода
R<H2(-±-----V~ (1-------Й при /2 —>СО. (17.61)
I ’ п \ п / у
Доказательство. Оно будет следовать из второй границы линейного программирования (следствие 21) с помощью соответствующего выбора многочлена р(х). Положим
а (х) = —{Л+1 (*) Pt («)-pt М Pt+i (а)}2, (17.62)
а —х
где параметры а и t будут сейчас выбраны.
- По формуле Кристоффеля — Дарбу (см. упражнение (47) гл. 5) .. ..
Pt+i (х) Рt(a)—Pt(x) pt+i (tt) == t
__ 2 (a — x) / n \ (x) pi (a)
~ *+i \ t) L ( n \ ’ i=° G J
и поэтому
« (*) = ” ) {^t+1 (x> pt (a) —
- Pt (x) Pt+1 (a)} V . (17.63)
Ы (n\
Так как a(x) —многочлен от x степени 2/+1, то он может быть представлен как
a(x) = £ akPk (х). k=0
Выберем теперь
Р (х) = a (x)/a0.
Чтобы воспользоваться следствием 21, надо показать, что:
(i) . a(f)<0 для i = d, .... п.
(ii) . аг > 0 для i = 1, ..., п.
(iii) . a0>0 (так что р0= 1).
В силу (17.62) a(i)^0, если х>а, и поэтому при a<Zd условие (i) выполняется. Так как многочлены Кравчука образуют семейство ортогональных многочленов (см. теорему 16 гл. 5), то из теоремы 3.3.1 Сеге [1297] получаем, что:
(а) многочлен Pf(x) в интервале (0, п) имеет t различных действительных корней;
(Ь) если хр< ... <х[б —корни многочлена Pt(x) и если положить хр = 0; х^ = п, то многочлен Pt+i(x) имеет точно один Корень в каждом интервале ( х!4), хЦ^)', i=0,... ,t (см. рис. 17.5). Чтобы выполнялись условия (ii) и (iii), выберем число а в диапазоне- х^+б <; а<_ хр. Тогда для значений i,
Pt{a)Pt («)>0;
Pl+1(a)Pi(a)<.0-
Теперь согласно следствию 4 гл. 21 следует, что
Ph {Х} Р1.(Х} 1 ^klm Рщ (Х)’
т
. (17.64) при k+l<Zn (17.65)
что приводится (если воспользоваться (17.63)) к виду ао=
2 / п \ t + 1 \ t J
и доказывает условие (iii). Поэто-
му если выполняются условия a<Zd и то следствие
21 применимо и приводит к следующей оценке:
,п. —ii/, 1 h/1 pt+i(a) i
A (n, d) < P (0) =c^- = _E_1y_±12------------L =
«о 2 f n \
-7Тг(/Г*(а)РНй)
( ” ){„-/_(/+ 1) Q}2
~~ — 2a(Z-J-l)<2 ’ (17.66)
где
Q
pt+^ Pt (a)
<0.
Здесь нам необходим результат об асимптотическом поведении корня Xi(i) при п->оо и при фиксированном (приблизительно) отношении t/п.
Лемма 36. Если t— ГХп], где 0<Х< 1, то
— XjUnl<----^(1—X) при И—>оо.
п 2
(17.67)
Доказательство леммы. Предположим, что (17.67) не выполня-ется. Тогда существуют фиксированное е, 0<е< у Х(1—X), и бесконечная последовательность чисел п такие, что
xiA nl > п (г ф-2 е), где г — -—^)-
Для каждого п из этой последовательности положим t=t(n) = = [Хп]. Тогда
РДх) = (-2У(х-х<‘)) . . .(x-x^)/t\;
Положим i=i(n) = [п(г + е)], так что 1 - ~xh 1 | > en
Ш (1 ч ?— ) ~ -+o
in^ + ’U Pt(i) t fe=l 4-0( n /
Аналогично
1н-Р^-1).. = _ Pt (i) t -s fe=l ‘-4° +O( 4)- (17.68)
Следовательно,
Pt (i) -ln-p*(o = Pt (i-n
(17.69)
+ Pt(i) Л_, Pt (О Pt (i -1)1 '
Далее из упражнения (46) гл. 5 имеем, что
(n - i) Pt (i + 1) = (n - 2t) Pt (i) -iPt{i-\) или
(n—i) р<^+1)РД0--------------------H = 0. (17.70)
Pt(i) Pt(i-1) Pt(l~l)
Если мы положим p=Pt(i)i'Pt(i—1), то из соотношений (17.69) и (17.70) получаем, что
(п—г) р2—(п—2г)р + /+ р2-О(1) = 0.
Согласно (17.68) р^е1/е(1 + О(1/п)), и поэтому
(n—i)p2 —(п —20р-М+О(1) = 0. (17.71)
Так как р — действительное число, то должно выполняться неравенство
(п — 20а—4i (п—i) + O(ri) > 0, т. е. (1—2Х)2—4(г-Д-е)(1—г—е)-|-0
0.
Но (1—2X)2=4r(l—г), и поэтому
Е2_е(]_2г)-!-0(— \ п /
Но это неравенство не может выполняться для больших п, так как е<)/гХ(1—Л) = (1 -2г)/2,
что завершает доказательство леммы. •'
С помощью коитусного интегрирования можно показать, что
—X) при п—>оо, но для доказательства теоремы 35 нам хватит грубой нижней оценки. Предположим, что t<nl2. Так как Pt(0)= (”) >° и Л (1) = 1—(2//н) • ( " j>0, то из теоремы 3.41.2 Сеге [1297] вытекает, что Pt(x)>0 для значений 0<х<1. Следовательно,
хр > 1. (17.72)
Теперь мы можем выбрать параметры а и t для доказательства теоремы. Согласно рис. 17.5 существует значение а, скажем, а=а0 в диапазоне Xi(f+1)<a<x1(f)> для которого Q = Pt+i (a0)/Pt(a0) =—1. Положим а=а0. Согласно лемме если мы выберем t= [Хп], где Л такое, что
-----]/Х(1—Х)<—, 2----п
другими словами, если
то x^^d при больших п. Используя эти значения, из неравенства (17.66) получаем, что
(«+D2( " )
2 (Z + 1) х }i+1)
и поэтому
R = — ЮеаЛ(«. d)<ff2(—}< П \ п /
(если воспользоваться (17.72) и леммой 7 из гл. 10)
(в силу (17.73)). #
Подобные же рассуждения могут быть применены к границе: линейного программирования для А (п, d, w) (см. с. 527). СочетД--ние получающейся при этом оценки с теоремой 33 дает следующий результат.
Теорема 37. {Вторая верхняя граница Мак-Элиса — Родеми-ча — Рамсея — Велча [947].) Для любого (и, М, й)-кода имеет
место неравенство
Я<в(—) при П->ОО, \ п )
где
В (б) = min В {и, б), 0<«< 1—2 6, и
В{и, б)=1+й(и2)—/г (и2-ф 2 б и + 2 6),
(17.74)
Доказательство этой теоремы мы опускаем.
Заметим, что В (1—26, &)—Н2
; поэтому
и утверждение теоремы 37 всегда не слабее утверждения теоремы 35. В действительности оказывается, что при d/n^z0,273 функция В {d/n) на самом деле равна функции
и теоремы 35 и 37 совпадают в этом диапазоне. Для значений d/«<0,273 теорема 37 несколько сильнее, что показывает таблица на рис. 17.6. Наилучшие верхняя и нижняя границы изображены на рис. 17.7.
Задача (нерешенная). (17.9). Чему равна истинная верхняя граница величины (l/«)log2^ («, d) как функции от d/n при /г—э-оо?
(В настоящее время даже не известно, существует ли предел lim — log2 А {п d), П— со П
когда d/n фиксировано и заключено между 0 и 1/2).
d п Нижняя граница Варшамова—Гилберта Теорема 30 Верхняя граница сферической упаковки Теорема 32 Верхняя граница Элайеса Теорема 34 Верхние границы Мак-Элиса—Родемича—Рамсея—Велча Теорема 35 | Теорема 37
0 0,1 0,2 0,3 0,4 0,5 1 0,531 0,278 0,119 0,029 0 1 0,714 0,531 0,390 0,278 0,189 1 0,702 0,492 0,312 0,150 0 1 0,722 0,469 0,250 0,081 0 1 0,693 0,461 0,250 0,081 0
Рис. 17.6. Границы для скорости R наилучшего двоичного кода как функции, от d/n при больших значениях п
Из следствия 21 можно получить также асимптотическую границу, применимую вблизи той области, в которой точна граница Плотника.
Теорема 38. (Мак-Элис [944].) Для любого положительного j такого, что / = 0(1^6/), справедливо неравенство
А (2d + /, d) < 2d (j + 2) при d-^oo. (17.75)
Доказательство. На этот раз в качестве а(х) выберем многочлен третьей степени, корни которого равны d, I и Z+1, где
для наилучших двоичных кодов:
1 — нижняя граница Варшамова — Гилберта;
2 — верхняя граница Мак-Элиса — Родемича— Рамсея — Велча
Тогда
<z(x) = (d—х)(1—x)(l+ 1—х) —
где
Положим ₽(0 ^0 для му
== «0 + «1 р1 W + «2 Р2 (х) + «з рз (х),
dz(j + 2) .
2(j+l)2 ’
3 а, = —
3 4
P(x) — a(x)/ao. Так как все аЛ положительны и i=d,..., 2d+j, то следствие 21 применимо, и поэто-
А (2d + j, d)<z& (0)/ао — 2d (j + 2)
при d-^co. •
Для случая /=1 оценка (17.75) утверждает, что A(2d+1, d) < < 6d, что слабее теоремы 11(b). Но для значений /=2, 3,... эта оценка является наилучшим известным асимптотическим результатом.
ЗАМЕЧАНИЯ К ГЛ. 17
§ 17.1. Функция В(п, d) связана с одной критической проблемой комбинаторной геометрии (см. Крапо и Рота [315], Доулинг [385], Келли и Рота [754] и Уайт [1411]).
§ 17.3. Доказательство того, что Д(9,3)^39; Д(10,3)<:78 и А(11,3)< 154, приведенное Баксом [1391] (основанное на результатах Бликфельда [163] и Рэнкина [1089] по упаковкам), оказалось ошибочным (см. работу Беста и др.. [140]). j
§ 17.4. Мак-Элис (McEliece) и др. (неопубликованная работа) и Бест й" Брауэр [139] независимо использовали метод линейного программирования для Доказательства равенства А (2™—4,3) =22m_m_4.
Глава 18
Методы комбинирования кодов
18.1. ВВЕДЕНИЕ
В этой главе описываются методы комбинирования кодов с целью построения новых кодов. Один из простейших способов скомбинировать два кода -— это образовать их прямое произведение, и в первой части этой главы как раз исследуются произведение кодов и его обобщения. Мы используем неформальный термин «произведение кодов», как будто бы кодовые слова являются прямоугольными таблицами. После того как (в § 18.2) будет определено прямое произведение кодов, мы приведем необходимое и достаточное условие того, чтобы циклический код представлялся в виде прямого произведения двух циклических кодов (§ 18.3). Так жак это не всегда возможно, то в § 18.4—18.6 рассматриваются .«некоторые другие способы представления циклических кодов в виде произведения.»
Построение, описываемое в § 18.4, основано на прямом произведении кодов, взятых над большим полем, и переходе к двоичному коду с помощью функции следа. Мы уже видели в § 10.11, что каскадные коды могут быть очень хорошими. Конечно, каскадный код также является разновидностью произведения кодов.
В § 18.5 исследуется частный случай каскадных кодов, когда в качестве внутреннего кода используется неприводимый циклический код,-—это называется (*)-конструкцией. Наконец, в § 18.6 приводится другой метод представления кода в виде произведения, предложенный Касами и применимый к любому циклическому коду. Суть этого метода заключается в выражении многочленов Мэттсона — Соломона (МС) слов исходного кода через МС-многочлены более коротких кодов.
Во второй части главы рассмотрен ряд других мощных и остроумных способов комбинирования кодов; краткое описание этих способов может быть найдено в начале второй части (см. с. 561).
I. ПРОИЗВЕДЕНИЕ КОДОВ И ИХ ОБОБЩЕНИЕ
18.2. ПРЯМОЕ ПРОИЗВЕДЕНИЕ КОДОВ
Пусть st и обозначают соответственно [щ, ki, di]- и [пг, &2, ^-линейные коды над полем GF(q). Для простоты предположим, что первые ki символов кода st и первые kz символов кода являются информационными.
Определение. Прямое произведение st® 2% представляет «Собой'[«102, ^i^2, did2]-KOfl, кодовыми словами которого являются все («1Х«2) -матрицы, ' построенные следующим образом <(рис. 18.1). Верхняя левая подматрица содержит k\kz информа-
ционных символов. Первые fe столбцов матрицы выбраны так, чтобы они принадлежали коду S&, а затем строки заполняются так, чтобы они принадлежали коду ЗА.
П2
А
!| щ — t 1 информационные символы проверки по строкам
проверки по столбцам проверки проверок
Рис. 18.1. Кодовые слова кода , являющегося прямым произведением
Описанная конструкция называется также кронекеровским произведением кодов и и является простейшей разновидностью произведения кодов. Столбцы построенной матрицы — слова кода а строки — слова кода <%.
Пример. (1). Прямое произведение двоичного [3,2,2]-кода с самим собой является [9, 4, 4]-кодом, состоящим из 16 матриц, изображенных на рис. 18.2.
[3, 2, 2](х)[3, 2, 2] = [9, 4, 4]-код
ООО ООО ООО ООО 0 1 1 0 1 1 ООО 1 0 I 1 0 1 ООО 1 1 0 1 1 0
0 1 1 ООО 0 1 1 0 1 1 0 1 1 ООО 0 1 1 1 0 1 1 1 0 0 1 1 1 1 0 1 0 1
1 0 1 о е о 1 0 1 1 0 1 0 1 1 1 1 0 1 0 1 1 0 1 ООО 1 0 1 1 1 0 0 1 1
1 1 0 ООО 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 1 0 1 1 0 ООО
Рис. 18.2. Прямое произведение двоичного [3, 2, 2]-кода с самим собой
Упражнения. (1). Проверить, что $®$ представляет собой линейный код над GF(q) с параметрами [щ/Тг, k\k2, did2].
(2). Кодовые слова могут быть также образованы сначала заполнением верхних ki строк, а затем заполнением всех столбцов. Показать, что это дает тот же самый код.
В более общем случае пусть s& и & обозначают произвольные линейные [пь k\, dj- и [п2, k2, г/2]-коды без предположения о том, что начальные символы являются информационными. Тогда прямое произведение л^®^ определяется как [щ/гг, k\k2, didsj-код, кодовыми словами которого являются все («1X^2)-матрицы, в которых столбцы принадлежат коду .ГУ, а строки — коду Й?.
К сожалению, коды, получаемые прямым произведением, обычно имеют плохое минимальное расстояние (зато их легко декодировать). Прямоугольная форма кодовых слов иногда оказывается полезной в некоторых применениях (см. замечания к главе).
Упражнение. (3). Пусть Gi и G2 — порождающие матрицы кодов <5# и. 92 соответственно. Показать, что кронекеровское произведение этих матриц Gi®G2 (определенное в § 14.4) является порождающей матрицей кода
Предположим, что .$$ и 92 — циклические коды, как это было в примере (1). Тогда их прямое произведение 3^®^ инвариантно относительно циклической перестановки одновременно всех строк или одновременно всех столбцов. Представим типичное слово
йоо “01 • • ’“о, П2-1 “10 “11 ‘ ’ “1, п2_]
(18.1)
а -а
1_ —1,0 nt—1, п2—1 J
кода 92 в виде многочлена
* Ж #) = j (18.2)
z=0 /=0
Если мы предположим, что хП|=1 и уИ2=1, то xf(x, у) и yf(x, у) представляют собой циклические сдвиги строк и столбцов и также принадлежат коду Другими словами, код
является идеалом групповой алгебры (F абелевой группы, порожденной элементами х и у такими, что хП1=1/П2=1.
Предположим, что П\ и «2 взаимно просты. Тогда согласно китайской теореме об остатках (§ 10.9) для каждой пары й, 1'2, где 0=Сй<«ь 0^2<«2, существует единственное целое число /(й,й) в диапазоне 0^/(й, й)<ЩН2 такое, что
I (г\, i2) == iy (mod tij); I (ix, z2) = i2 (mod «2). (18.3)
Отсюда следует, что мы можем выразить f(x, у) посредством единственного переменного z=xy, заменяя каждое выражение хг'у^ на (В этом случае 29— групповая алгебра цикличе-
ской группы порядка п{П2, порожденной z.)
Например, если щ = 3; «2=5, то I (ii, 1’2) принимает следующие
Кодовое слово f (х, у) принимает вид
f (х, у) = а00 4- а01г6 + <W12 + <W3 + с04г9 + ^W10 + anz + a^z' +
+ ai3z13 + й14г4 + V5 + a21zn + а22г2 + a^z* + a^zu. (18.4)
Теорема 1. Если и & — циклические коды и («ь я2) = 1> то код <&=зФ® S3— также циклический.
Доказательство. Как было показано выше, кодовое слово f(x, y)^& может быть представлено как g(z), где z=xy. Кроме того, если f(x, у)^&, то yf(x, у)<^Я? и поэтому xyf(x, y’)=zg(z)<=&. Следовательно, код Ч? представляет собой идеал групповой алгебры циклической группы, порожденной z. в
Пример. (2). Пусть «5$ и 9% обозначают [3, 2, 2]- и [5, 4, 2]-коды, состоящие из всех слов четного веса. Так как (3, 5) = 1, то ^=^0 &— циклический [15, 8, 4]-код. Приведем несколько типичных слов кода ’S’:
'0 1010’ '0 0 0 0 0 '
и = 1 0 0 10 ; v 0 1111
.1 1 0 0 0 _ .0 1111.
w =
ООО’
1 о о
1 о о
п ]
О 1
1 о
В этих словах первые четыре столбца представляют собой произвольные слова из кода а последний столбец равен их сумме. Выражение (18.4) дает циклическое представление кода %?. Например, порождающий идемпотент кода 7? (см. упражнение (7) гл. 8) равен
= 2 + za + 24 + z7 + z8 + г11 + z13 + z14,
а порождающий многочлен равен 1 +z-i-z2-±-z5-}-z?-[-z7. Они представляют собой кодовые слова v и w соответственно.
Упражнения. (4). Предположим, что (щ, «2) = 1 и ЕДх), Е2 (у) —порождающие идемпотенты кодов з& и За. Показать, что порождающий идемпотент кода з4-®9а получается из Е] (х).Е2(у) заменой ху на z.
(5) . Предположим, что («1, я2) = 1. Показать, что если рь..., ••.,₽&, и Yi,...,Yh, —ненули1 кодов и 98 соответственно, то kikz ненулей кода з^®9а имеют вид PyYj» гДе 1=^
С/С&2-
(6) . Выбрать в качестве кодов зФ и 38 [3, 2, 2]- и [7, 3, 4]-коды соответственно. Найти параметры, весовой спектр, порождающий идемпотент и порождающий многочлен кода зЗ®9а.
(7) . При выборе z, отличном от z=xy, код з£® За может быть также превращен в циклический. В каких случаях разные выборы z приводят к разным циклическим кодам? [Указание. Показать, что для кода, рассмотренного в упражнении (6), z—xy и z=xr/3 приводят к разным результатам.]
Иногда знание того факта, что код является прямым произведением, позволяет найти его весовой спектр.
1 Напомним, что нуль кода — это корень порождающего многочлена этого кода. (Прим, перев.)
(8) . (Трудное.) Пусть и представляют собой
[2m‘—1, mY, 2т'~1] и [2m2 —1, т,, 2т‘~1] симплексные коды, где (тъ /д2) = 1 и mi>m2. Показать, что код ^0^ имеет т2 различных ненулевых весов, принимающих значения Wi=(2^2—2m2~i)2?n,_1 для z=l,...,т2. Показать, что число кодовых слов веса Wt равно
F(m2, • .(2m*-2m^).
где F(r, k), rz^k, определяется следующим рекуррентным соотношением:
F(r, 0)= 1; F(r, r)= 1;
F(r+1, k)—F(r, k—l) + 2kF(r, k).
*18.3. HE ВСЕ ЦИКЛИЧЕСКИЕ КОДЫ ЯВЛЯЮТСЯ ПРЯМЫМИ ПРОИЗВЕДЕНИЯМИ циклических кодов
Предположим, например, что ‘g’ — невырожденный неприводимый ДВОИЧНЫЙ ЦНКЛИЧеСКИЙ [п, &]-КОД, у КОТОРОГО П = П1/12, («ь п2) = 1 и Hi>l; /?2>1. Покажем сейчас, что только в определенных случаях код 'g’ можно представить как где «9/ и
— циклические коды длины пх и п2.
Пусть а, а2, а4,..., а2*-1 обозначают ненули кода ®?, где а — примитивный корень н-й степени из единицы в поле1 GF(2k). Так как (fii, п2)~1, то согласно § 12.8 существуют целые числа а, b такие, что ап^+Ьп?— 1. Положим р=аь”2 и у=ааП1, и пусть kx, k2 — наименьшие целые числа,' для которых peGF(2ft'), yeGF(2h2).
Теорема 2. Циклические коды si- и длины пх и п2 такие, что <5?=.$$0^?, существуют тогда и только тогда, когда (kx, fe2) = = 1. (Размерности кодов s4- и 9% равны в этом случае kx и k2.}
Доказательство. Применение подстановки z=xy переводит любое кодовое слово g(z)^<g’ в матрицу размера пх\п2, описываемую многочленом f(x, у). Заметим, что zo-nl=xan,yani—yanl = =ybn2yant=y и аналогично zbri2=x. Тогда zan'g(z)—yf(x, у)^& и аналогично х[(х, у)^&. Следовательно, столбцы образованной таким образом матрицы образуют циклический код, скажем, st-, а строки образуют циклический код S8.
Далее pni=y«2= ] и а=|3у. Поэтому ненули кода <g? суть элементы Ру, (ру)2,..., (Ру)2’5-1 .
Л е м м а 3. Ненулями кодов s4- и являются элементы р, р2, ... ..., Р2,ч~1 и у, у2,..., у2*2-1 соответственно.
Доказательство. Пусть y,eGF(2ft)—корень п2-й степени из единицы, не принадлежащий множеству {у, у2,..., у2*2-1 }, и пусть
‘Так как код неприводим. (Прим, перев.)
pteGF(2fc) — произвольный корень «i-й степени из единицы. Таким образом, ргу,- является нулем кода
Пусть f(x, y)=r0(y)+xrr(y) + .. .-]~xn'~lrni^1(y) обозначает ненулевое слово кода где гДу)—i-я строка. Тогда равенство
Ki—1
f(₽z. Vj)= £ гI (?,-) = О
г=0
выполняется для всех пх выборов элементов рг, что дает п} линейных однородных уравнений относительно пх неизвестных л(у3), 0^i^«i—1. Так как коэффициенты при неизвестных образуют матрицу Вандермонда (см. лемму 17 гл. 4) и, следовательно, невырожденную матрицу, то гг(у3)=0 для всех i. Поэтому элемент у3 является нулем кода SB, образованного строками. Следовательно, ненулями кода SB должны быть элементы, указанные в формулировке леммы. Доказательство для кода аналогично. •
Ясно, что k\ и /г2 делят k, и действительно, если s= (kx, kz),
то = = HOK{fej,
s
Отсюда теорема выводится просто. Если (kx, ^г) = 1, то k—k\kz и 7?=.57(х)М С другой стороны, если ^=^7® то k=k\kz и, следовательно, s=l. •
Примеры. (3). Пусть 7? обозначает [15, 4, 8] циклический код с порождающим идемпотентом z4-z24-z3+z4+z64-z84-z94-z12. Пусть «1 = 3; «2—5. Ненулями 7? являются элементы а, а2, а4, а8, где а15=1. Тогда а=2; Ь——1; |3 = а10; у=а6; р4=₽; у6=у и &i = 2; fe2=4. Так как числа 2 и 4 не взаимно просты, то =B=s£®SB.
Действительно, 4 представляют собой [3, 2, 2]- и [5, 4, 2]-коды соответственно, а их произведение .s7(x) 98 представляет собой [15, 8, 4]-код.
(4). Пусть 7?—[21, 6, 8]-код, рассмотренный в упражнении (6), ненулями которого являются элементы а, а2, а4, а8, а16, а11, где а21 = 1. Тогда «1 = 3; «2=7; (—2)-34-7=1; ₽=а7; у=а15; &i = 2; k3—3, и на самом деле код 7? представляется в виде прямого произведения
18.4. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ НЕПРИВОДИМЫХ циклических кодов В ВИДЕ ПРОИЗВЕДЕНИЯ КОДОВ
В обозначениях § 18.3, если (fei, kz) ==s>\, то 7?#=«9£(® SB. Од-
нако код 7? может быть представлен в виде произведения кодов
Другим способом.
Теорема 4. Всегда можно найти неприводимые циклические л л
коды и $ над полем GF(2S) такие, что
Л = Ы); ® = 7\(i) (18.5)
и
= (18-6)
Как и в гл. 10, если S) обозначает [п, k, с?]-код над GF(2S), то следом S5, TS(JZ>) является двоичный [п, k'^SZsk, сГ^с?]-код, состоящий из всех различных кодовых слов {ТДи\),...,ТДип)), где л л
Доказательство. Чтобы найти коды и поступим следующим образом. Ценулями кода являются элементы а, а2, ... ,..,а2*—*, соответствующие циклотомическому смежному классу Ci={l, 2, 22, ...,2h-1} по модулю п. Над GF(2S) этот класс Ci расщепляется на s циклотомических смежных классов:
Сх = 1, 2s, •• •, 2s№/s-1);
G =2 2s+1 • 2s —O-H .
C , = 2S-1, 22s—1, • - 2ft~'.
2S—J
Идемпотенты над GF (2s), соответствующие этим смежным классам, определяются условием
ЪЛ(а1) = 1. если /еСЛ
(0 в противном случае,
где i=0,... ,s—1.
Тогда согласно теореме 6 из гл. 8
e2i(z)= (18.7)
/=0 где
8г;= £ a~li. (18.8)
л
iec2i
Порождающий идемпотент самого кода равен:
п—1
0(2) = (18.9)
/=о
'Де
в; = £аЛ (18.10)
lec.
Тогда из приведенных выше определений вытекает, что S—-1 д п— 1
0(z) = 2 2 Ts^Ei^z’ для всех г==0> • • •’ S—1- (18.11)
i=0 /=0
А . А
Таким образом, (S>=Ts(<g>21), Oz^i^s—1. Далее представля-
ет собой [«1^2, £/х]-код над GF(2S) с ненулями а, а2> ,...,•ah~s. л
Применим к коду 'g’l технику предыдущего параграфа. Как и раньше, р=аЬп2; у=<аап‘, где fi^GF(qh,/s)\ \^GF(qh2ls) и q=2s. л
Тогда слово кода 'Fi может быть представлено как (щХ^г)-матрица, в которой каждый столбец принадлежит &]/х]-цикличе-A L _
скому коду с ненулями (3, |32s ,..., р2 1 , а каждая строка при-А
надлежит [п2, ^/«^циклическому коду <%h с ненулями у, у2 , ...
—s АЛ
...,у~‘ .Так как числа ki/s и fe2/s взаимно просты, то ^1 = ^1® л и.
Пример (3). (Продолжение.) Пусть является [15, 4, 8]-ко-дом с s=2, который был рассмотрен выше. Положим со=а5; со — л примитивный элемент GF(22). Порождающие идемпотенты 0i(z), л
02 (z) представлены на рис. 18.3.
0 1 2 3 4 5 6 7 8 9 10 11 12 12 14
Л 0! 0 й И2 й Й 0 Й2 1 со2 _со2 0 1 со 1 1
Л 02 0 И2 й й2 СО2 0 со 1 со со 0 1 со2 1 1
Сумма= =след 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0
Рис. 18.3. Порождающие идемпотенты [15, 4, 8]-кода
Идемпотент 01 расположим в виде матрицы размера 3X5
1 У У3 У3 У*
Таким образом, 0i(x, у) — (1 + со2хЧ-сох2) (й^+со^+со^+со^4) , что представляет собой произведение порождающих идемпотен
тов кодов и J?i. Эти коды являются [3, 1, 3]- и [5, 2, 4]-ко-л
дами над GF(22). Аналогично 02 представляется в виде матрицы
и 02 (х, у) = (1 + ых+(а2х2) (ау+ы2у2+ы2у3 + (ау4).
= T2(^i (X)^l) = T2(sl'2®^2) •
Упражнени^. (9). Показать, что оба кода
Ясно, что '?’==
7а(А® А) и Л (Л® А) равны другому [15, 4, 8]-коду1.
(10). Используя описанный выше метод, представить в виде произведений невырожденные неприводимые коды длины 63= =7-9. (Нужные Для этого порождающие идемпотенты приведены на рис. 8.1.)
18.5. КАСКАДНЫЕ КОДЫ: (* )-КОНСТРУКЦИЯ
Любой каскадный код (см. гл. 10) можно рассматривать как код, полученный произведением кодов. Если внутренний код неприводим и «1 и п2 взаимно просты, то мы увидим, что каскадный код является циклическим. Мы будем называть это (*)-конструкцией.
Нам нужны два кода: (i). Неприводимый двоичный циклический [пь ki, dij-код si-, ненулями которого являются элементы р, р2, р4,.... р2^1-1, где ре GA (2М) —примитивный корень степени п\ л
из единицы, (ii). Циклический [n2, &2, d2]-код $ над GF(2hl). Напомним, что согласно §8.3 код «9/ изоморфен полю GF(2hi). Существует изоморфизм <р, переводящий в поле GF(2fei)> задаваемый равенством
а (х)ф = с(р), причем существует и обратное отображение ф, переводящее элементы поля 6eGF(2hi) в двоичные векторы длины П\, (6)ф=(т?[1(б), ЛДбр-1), 7\(бр~2), • • 7\1(бр-<",-1)))еХ
(18.12)
(* )- конструкция. Новый код, который мы обозначим через л
получается, если мы в каждом слове (6о, - • •, 6n2-i) из кода
1 Приведенному в начале упражнения (3). (Прим, ред.)
$ заменим каждый элемент б.; двоичным вектором-столбцом, по-Л
лученным транспонированием (б.с)*. Таким образом, st* представляет собой [П1П2, &1&2]-Двоичный код, минимальное расстояние которого не менее чем did2, а кодовые слова являются матри-л
цами размера «1Х«2- Другими словами, код st* образован кас-л кадированием внутреннего кода st с внешним кодом
Пример (5). Пусть st обозначает [3, 2, 2]-код, изоморфный полю GF(22) при следующем отображении:
ф Л
GF(22)--------->
О ООО
1 0 11 (18.13)
£0 10 1
со2 110
Л
Пусть обозначает [5, 2, 4]-код над полем GF(22) с порождающим идемпотентом <o2#-Hco#2-t-coz/3+o)2#4.
л
Тогда код & состоит из кодовых слов 0 0 0 0 0 0 Сй2 й) й) СО2 Сй2 0 Сй2 Сй Сй Сй Сй2 0 Сй2 Сй
Сй Сй Сй2 0 Сй2 Сй2 Сй Сй Сй2 0
Л и слов, получающихся из них умножением на <о и со2. Код st* S3
получается следующим образом:
0 1 1 1 1
0 Сй2СйСЙСй2 -> 0 1 0 0 1
О 0 1 1 0.
’0 0 0 1 1
101 ю2сй2-> 1 0 1 1 1
.1 0 1 0 0_
и является нашим старым знакомым [15, 4, 8]-кодом.
Напомним, что порождающий идемпотент Е(х) кода st отображается в единичный элемент поля GF(2fcl). Если st — симплексный код, то типичное кодовое слово xiE(x) отображается в Р*. Но в общем случае нам необходимо знать (gp, где g— примитивный элемент поля GF(2fcl).
Упражнение. (11). Показать, что порождающий идемпо-л
тент кода отображается в порождающий идемпотент кода s&* зз.
л
Теорема 5. Если (щ, п2) = 1, то код 93 может быть превращен в циклический с помощью преобразования, использованного в теореме 1 (т. е. полагаем z—xy).
л
Доказательство. Пусть типичное кодовое слово получен-л
ное из (60,..., б„2 -1) имеет вид (18.1). Как и в теореме 1, мы л
получим, что код .9/* 93 является циклическим, если циклические
сдвиги
G0, «а—2
1,0
fl00 ‘ *
—1, п2—1
и
принадлежат коду «$$* 93. Но это и в самом деле так, ибо эти слова получены из кодовых слов (6Пя—1, бо,..., б„2-2) И (рбо, ... . -,рбп.-1) (согласно лемме 10 гл. 8). •
л
Пример. В качестве кода 93 выберем циклический МДР-код, например [9, 4, 6]-код над GF (23), нулями которого являются а-2, а-1, 1, а, а2, где а — примитивный элемент GF(26). Весовой спектр этого кода таков (см. гл. 11):
/ 0 6 7 8 9
Ai 1 588 504 1827 1176.
В качестве кода выберем симплексный [7, 3, 4]-код. Тогда л
93 представляет собой циклический [63, 12, 24]-код со следующим весовым спектром:
i 0 24 28 32 36
Ai 1 588 504 1827 1176.
Теорема 6 Предположим, что (щ, п2) = 1. Если ₽, р2, ...
* —1 Л
..., р2 1 и у1,...,у/,2 являются ненулями кодов и 93 соответ-л
ственно, то kik2 ненулей кода г/* 9 имеют вид
<z = p2/y2-, где j = 0, 1, • -, ^—1; Z= 1, • • -, k2>.
л
Доказательство. Типичное слово кода .$$* 93 имеет вид
г0 (У) + хг1(у)+ • • • + х"1-1 гП1_1 (У).
Далее
г0(у) + ^гДу)+ - - •+(р2/)"1_1г„1_1(У) = 6о/ + ^+ • • +
Л +<_!
где (бо, 61, ..., бП!-1)?=^.
Кроме того, вектор (б027 > • • •, 62п _j ) представляет собой слово л
циклического [«2,. ^2]-кода ненулями которого являются элементы Yi2^,... ,у242 Таким образом, элементы [32/удивляются л
ненулями кода .5/* •
Пр и мер (5). (Продолжение.) Пусть а — примитивный эле-л л мент GF(24), и пусть и = а5. Тогда ненулями кодов «s7, $ и SB являются элементы р=а,ь; р2=<ос10; yi=a3; у2=а12 и а5-а3=а8; а5-а12=’а2; а10-а6==а; а10-а9=а4.
Но элементы а, а2, а4, а8 и в самом деле представляют собой ненули [15, 4, 8]-кода.
Упражнение. (12). Показать, что любой неприводимый [«i«2, ^-двоичный код Ф7, у которого (tii, «г) = 1; «1>1; «2>1, л может быть представлен в виде произведения кодов л
[Указание. В качестве кода S5 выбрать неприводимый [«2, £/&1]-код над GF(2hi) с ненулями у2^1 , i=0, l,...,k/ki—1.]
*18.6. ОБЩИИ ПОДХОД К разложению циклических КОДОВ
Этот раздел описывает метод Касами [731], в котором многочлены Мэттсона — Соломона любого циклического кода составной длины выражаются через МС-многочлены более коротких кодов. (Методы, развитые в § 18.3—18.5, не всегда применимы к приводимым кодам.)
Пусть ‘g’— двоичный циклический [п=П1П2, k, </]-код, где («ь «2) = 1; П1>1; «2>1. (Тот же самый способ действует и для случая любого конечного поля.)
Обозначения. Как и прежде, ап\ + Ьп2=\-, а”=1; |3 = аЬп2; у_|аате Кроме того, числа I(i, j) определяются условиями (18.3).
Случай (I). Код неприводим, и ненулями его являются элементы i^C\, где — циклотомический смежный класс {1, 2, 22, 23,..., 2fe-1} (mod «1«2). Можно написать, что С1 = {/(ць Vi),...,Z(p,h, Vh)}. Тогда ць... ,ц/г состоят из нескольких повторений циклотомического смежного класса С/1={1, 2, 22,..., 2Г-1} (modn!). Множество {v:/(l, v)eCi} состоит из вычетов {1, 2Г, 22г,..., 2hr} (mod п2).
Например, если g7—[63, 6, 32]-код, то
п = 63, «1 = 7, п2 = 9, k = 6 и Сх = {1, 2, 4, 8, 16, 32} = {7(1,1), /(2,2), /(4,4), /(1,8), /(2,7), /(4,5)};
С] = {1, 2, 4}, r = 3, {v:/(l, 8}.
Пусть — неприводимый двоичный циклический [нь г]-код, ненулями которого являются элементы [3, р2,.. -, р2 , а — неприводимый циклический [п2, k—г+1]-код над полем GF(2r) с не-нулями у, у2 , . . • , у •
МС-многочлен слова кода имеет вид F(Y) = 7'Г(£У~1), где g — произвольный элемент поля GF(2r).
МС-многочлен слова кода & имеет вид O(Z)=cZ-1 + + (cZ~iyr+... + (cZ~l)ik~r, где с — произвольный элемент поля GF(2fe).
Теорема 7. (Касами.) МС-многочлен любого кодового слова 'S’ получается из F(Y), если элемент £ заменить на Ф(2) и положить X=YZ и Yn'—Zni=\.
Доказательство^. Обозначим через F(Y, Z) многочлен, полученный таким способом. После ряда алгебраических преобразований получаем, что
F(Y, Z) = 7r(O(Z) Y~l)=Tk (cX~Ill-l}) = Th(cX~l).
Но это и является МС-многочленом слова кода S’. •
Для предыдущего примера
F (У, Z) = Т3 (cY~l Z~l + с8К~‘ Z-8) = Т3 (сХ~! (1’1) 4-c8X“z (I ’8)) =
= 76(сА~*), cG GF (2е).
Случай (II). В общем случае обозначим через S любой циклический [п, &]-код, ненулями которого являются элементы а3, j(^{Ca. : i=l,...,sj.
Предположим, что |Са. Пусть для каждого' i— 1,..., s C'i= {p :/(ц, v)^Ca. для некоторого v}; bt обозначает-наименьшее число в множестве C'i, г;=\СД и Ki = {v ' I(bi, v) ^Ca. ). (Может так случиться, что C'i = C'j, в то время как K-t^Kj, или наоборот.) Пусть «9/— двоичный циклический код длины fii с ненулями рз, j^{C'i, i—l,...,s}, и пусть — неприводимый циклический код над GF(2>ri) длины п2 с ненулями у11, цеКь МС-многочлен слова кода имеет вид
F(Y)=^Trf агу-ьо f=i
для ^eGF(2G). Заметим, что если C'.i=C'j, то этот циклотомический смежный класс встретится дважды в сумме, один раз с элементом и один раз с элементом Ej. МС-многочлен слова кода имеет вид
Фдг) = с^ +(Ciz-~^ri+ - +
где цеМ; Ci^GF(2hi).
Теорема 8. (Касами.) МС-многочлен любого слова кода S получается из F(Y), если элемент заменить на O<(Z) и положить X=YZ; y"i=Zn»=l.
Пусть, например, 7?—[63, 18]-код с ненулями а3’, где /eCi (J (J С5 (J С15. Тогда «=63; «1=7; «2=9;
^ = {/(1,1), /(2,2), /(4,4), /(1,8), /(2,7), /(4,5)};
С6 = {/(5,5), /(3,1), /(6,2), /(5,4), /(3,8), /(6,7)};
С1б = {/(1,6), /(2,3), /(4,6), /(1,3), /(2,6), /(4,3)};
^' = ^ = {1, 2, 4}; &1==&3=1; rL=rs = 3’,
С' = {5, 3, 6}; 62 = 3; г2 = 3;
/<i = /<2 = {1,8}; К3 = {6,3}; ₽ = а36; у = а28.
Код «9/ имеет ненули рз, /=0,.. ..,6 и представляет собой [7, 6, 2]-код. из всех слов четного веса. Код ^i=^2 имеет ненули у, у8, и его проверочный многочлен равен (х+у) (х+у8) =х2+а54х+1, а код имеет ненули у3, у6, и его проверочный многочлен равен (х+у3) (х+у6) =х2+х+1. МС-многочлены кодовых слов из
равны соответственно
F (Y)=т3 & у-1)+Ts а2 у-3) + Ts у-1);
O1(Z) = c1Z-1 + cfZ~8;
O2(Z) = c2Z~1 + c2Z“8;
Ф3 (Z) = c3Z~3 + с8 Z~6.
Заменяя на многочлен Ф+Z), имеем
Т6 + Т6 (с2 X-5) + Тв (с3Х-15), что является МС-многочленом слова кода <ё>.
II. ДРУГИЕ МЕТОДЫ КОМБИНИРОВАНИЯ КОДОВ
Мы уже встречались раньше с несколькими способами комбинирования кодов для получения новых кодов:
(i) . Прямая сумма двух кодов (упражнение (17) гл. 1, § 2.9).
(ii) . Последовательное соединение двух кодов (упражнение (17) гл. 1, рис. 2.6).
(iii) . Конструкция типа |u|u-J-v| (§ 2.9).
(iv) . Каскадирование двух кодов (§ 10.11) и, конечно, различные типы произведения кодов, описанные в части I этой главы. Очень легко придумать другие способы комбинирования кодов, и, действительно, этому посвящена обширная литература (см. работы, указанные в замечаниях к этой главе). Приводимые ниже конструкции отличает то, что все они были использованы для построения чрезвычайно хороших кодов. Они как бы являются обладателями рекордов. Обычно мы говорим, что один код лучше другого, если он содержит больше кодовых слов (и имеет ту же самую длину и то же минимальное расстояние), или, что эквивалентно, если он имеет большую длину (при той же самой избыточности и том же минимальном расстоянии). При этом упускают
ся из виду все проблемы, связанные с кодированием и декодированием, но мы оправдываем это тем доводом, что, как только будут найдены хорошие с этой точки зрения коды, за ними последуют и алгоритмы их декодирования. Приложение А содержит таблицу, в которой приведены наилучшие известные к настоящему времени коды длины вплоть до 512; многие из них были найдены методами, описанными здесь.
Мы начнем (в § 18.7) с описания способа эффективного увеличения длины кода. Сначала приводятся конструкции X и Х4, заключающиеся в добавлении суффиксов. Далее идет небольшое отклонение от темы, содержащее краткую сводку известных результатов о наилучщих кодах, исправляющих одиночные и двойные ошибки; даже эти сравнительно простые задачи еще не решены. Конструкция типа |a+x|b+x|a+b-[-x|, описанная в § 18.7.4, важна потому, что является одним из простейших способов построения кода Голея. В § 18.7.5 приводится конструкция Пирета, заключающаяся в удвоении-длины неприводимого кода.
В § 18.8 описываются некоторые построения, связанные с каскадными кодами. В частности, в § 18.8.2 дается эффективное обобщение каскадных кодов, предложенное Зиновьевым1.
Наконец, в §* 18.9 приводятся некоторые остроумные методы укорочения кода.
18.7. МЕТОДЫ ПОСТРОЕНИЯ, КОТОРЫЕ УВЕЛИЧИВАЮТ ДЛИНУ
18.7.1. КОНСТРУКЦИЯ Х-. ДОБАВЛЕНИЕ СУФФИКСОВ К КОДОВЫМ СЛОВАМ
В этой конструкции комбинируются три кода, чтобы построить четвертый код. Предположим, что и ‘ё’? представляют собой («1, Mi, di)- и (Hi, M2=bMt, г/2)-коды, удовлетворяющие следующему свойству: код является объединением b различных сдвигов кода
^2 = (x1 + ’g1) U (х2 + ^г) U • -U (Xb + 'gJ, (18.14) где хь х2, ...,х6— некоторые подходящим образом выбранные векторы.
Пример. (6). Пусть —(4,2,4)-код с повторением {0000, 1111}, a — (4, 8, 2)-код из всех слов четного веса {0000, 1111, ООП, 1100, 0101, 1010, 1001, ОНО}. Тогда Ъ=4 и
U (0011+^) U (ОЮЦ-^) U (1001+^).
Пусть ®’з={у], уг, ...,Уб}—любой (пз, b, ds)-кол. В рассмотренном примере в качестве мы можем взять (3, 4, 2)-код {000, 011, 101, ПО}. Тогда новый код®’ определяется как код
lxi + ^i|yi|U |х2 -b^Jysl U • • • U |хь + ^11уь|. (18.15)
1 Более точно: предложенное Блохом и Зябловым [166, 166а*] для линейных кодов и несколько позже (независимо) Зиновьевым [1470] для произвольных кодов. (Прим, ред.)
Другими словами, св состоит из векторов вида |xi + u|vil. где ue^i, i=l,..., b.
Попросту говоря, код ^2 разбивается на смежные классы по коду 'g’l и к каждому смежному классу присоединяется свой суффикс (Уг) (рис. 18.4).
/ — смежные классы кода •gr’i; 2 — суффиксы
Теорема 9. Новый код имеет параметры
(П1 + «3, М2, min {^, d2 + ds}).
Доказательство. Пусть Х=|х|у| и X' =|х/|у/|—различные кодовые слова кода Я?. Если х и х' принадлежат одному и тому же смежному классу кода ®2 по коду то
dist (X, X') dist (х, х') > dr.
Если х и х' принадлежат разным смежным классам, то dist (х, х') > d2 и dist (у, у') > da. •
Пример. (6). (Продолжение.) Присоединяя суффиксы из ^з, мы находим, что представляет собой (7, 8, 4)-линейный код
{0 00000 0, 111100 0, 001101 1, 110001 1,
0 1 0 1 1 0 1, 1 0 1 0 1 0 1, 1 0 0 1 1 1 0, 0 1 1 0 1 1 0}.
Как показывает этот пример, если коды ‘SFi, ^2 и 'g’a линейные, то мы можем упорядочить векторы х, и yi так, чтобы код также был линейным.
Конструкция X может быть применима, когда имеются вложенные семейства кодов. Например, примитивный код БЧХ с конструктивным расстоянием d% является объединением смежных классов кода БЧХ с конструктивным расстоянием d\Z>d% (см. § 7.6). Поэтому эта конструкция применима к любой паре примитивных кодов БЧХ. Например, если с?j с?2+2 и Ь = 2\ то в качестве кода может быть выбран (&4-1, 2ft, 2)-код. Комбинируя в этом случае [пц fei, di^d2~h2]- и [nb с?г]-коды, мы полу
чаем [ni+fe+1, k-\-k\, d2+2] -код. (Это обобщает конструкцию Андрианова — Сасковца [113, с. 340].)
Приведем несколько примеров:
[31, 6, 15] [31, 11, 11] [37, 11, 13]
[63, 36, И] [63, 39, 9Г [67, 39, 11]
Коды, полученные при применении конструкции X к кодам БЧХ, на рис. ПА.2 обозначены буквами ХВ.
Другими вложенными семействами кодов, к которым может быть применима эта конструкция, являются циклические коды (обозначены буквами ХС); коды Препараты (ХР) (см. § 15.6) и коды Дельсарта — Геталса (DG) (см. рис. 15.10). Например, воспользовавшись теоремой 36 из гл. 15, мы можем в качестве кода 'g’l взять код £F(m)*, а в качестве — код Хэмминга и получить бесконечное семейство нелинейных
( 2m + m—l,22m-m-1, 5), m = 4, 6, 8, • • -, (18.16)
кодов. Для случая т=4 получаем (19, 2", 5)-код.
Упражнения. (13). (а). Применить конструкцию X к (т, с?)-кодам (см. § 15.5) для получения (74, 217, 28)- и (74, 212, 32)-кодов.
(Ь). Применить конструкцию X к кодам ®’i=5?(l,6) и ^2= =J5f(6) для получения (70, 212, 30)-кода.
(14). (а). Конструкция ХЗ. Пусть (nb M3=cM2—bcMi, г/3)-код является объединением с различных сдвигов (щ, M2=bMi, ^2)-кода например
^з — U (Ui + ^2)’ г=1
где код (&2 является объединением b различных сдвигов («ь Afi, г/1)-кода 'g’l, например
ь
^2= U (V; + %).
/=1
Каждое кодовое слово кода может быть единственным образом представлено в виде Ui + v3-|-a, .ae'g’i. Кроме того, пусть ®4={yi,... ,уь} и ®5= {zi,... ,zc} обозначают (пц, Ь, А)- и (п$, с, б)-коды. Показать, что код, состоящий из всех векторов вида |иг + У3-[-а|у3|гг|, имеет параметры (ni+n4-|-n5, Л!3, d=min{di,d2+ +A, г/з+6}).
(b) . Например, выбрать БЧХ коды ®’1=[255, 179, 21], <ff2= = [255, 187, 19], <&s= [255, 191, 17] и коды ^4= [9, 8, 2], ^5= = [8, 4, 4] и получить [272, 191, 21]-код.
(с) . Касахара и др. [721] успешно применили следующую конструкцию, заключающуюся в добавлении двойных суффиксов.
Пусть а — примитивный элемент 1'(2т).Определим три кода БЧХ:
Дод Корни Параметры
®х 1. а, а2, • • a2i [2т— 1, k, 21 + 2]. -
/ а-2, а-1, • • • , a2i \2т—1, k—m. 2i + 4]
533 1, а, а2, • - •, а2г+2 [ 2т—1, k — т', 2i + 4],
где т'—-степень минимального многочлена элемента <z2<+1. Здесь код является объединением 2т смежных классов кода ^2- Поэтому мы можем присоединить суффикс г(х) длины т к вектору и(х)^<$1 таким образом, чтобы векторы из одного смежного класса имели один и тот же суффикс, но векторы из разных смежных классов имели бы различные суффиксы. Далее код является объединением 2т' смежных классов кода <%13, и мы подобным же образом добавляем суффикс s(x) длины т'. Тогда новый код состоит из векторов | и (х) | г (х) | s (х) | s (1) |.
Показать, что код 'g’ имеет параметры
[2m + m + tn', k, 2i + 5]. (18.17)
(d) . Получить, используя описанное построение [22, 6, 9] (т=4) и [76, 50, 9] (т=6) коды.
Другие примеры и обобщения можно найти в работе [721]. Полученные таким способом коды на рис. ПА.2 обозначены буквами XQ.
18.7.2. КОНСТРУКЦИЯ Х4: КОМБИНИРОВАНИЕ ЧЕТЫРЕХ КОДОВ
Предположим, что у нас имеется четыре кода: (пь Mj, d\)-код g’l, (nb M2—bAIi, й2)-код g^, (п3, мз, Йз^б/1)-КОД g’3 и (Пз, Мц=ЬМз, <Д)-код g’4, удовлетворяющие следующим свойствам: (i). Код <ё,2 является объединением b различных смежных классов кода 'g’l,
U (х2 + ^х) U • • -U (Хь + ^х).
(ii) . Код g’4 является объединением b различных смежных классов кода g’3
^4= (Ух + ^з) U (у2 + ^з) U . * • U (Уь + ^з), где Xi, ..., х& и yi, ..., уь — некоторые подходящим образом выбранные векторы. Тогда новый код g7 состоит из всех векторов вида
|xf + u|yf -Т v |, 4=1, ••«,#, uE^x, vE^. (18.18)
Попросту говоря, векторы i-ro смежного класса кода по коду 'g’l всеми возможными способами присоединяются к векторам i-ro смежного класса кода g’4 по коду 'g’s (рис. 18.5).
Теорема 10. Новый код g7 имеет параметры
(Пх + «з> М2Л13, d>min{d1, d2 + d4}). (18.19)
Доказательство очевидно. Если все исходные коды <81, i=l, ... ..., 4 линейны, то код с8 также может быть превращен в линейный.
Пример. (7). Выберем в качестве кода (15, 256, 5)-код Нордстрома-—Робинсона (лемма 22 гл. 15), ^2 —(15, 1280, 3)-код, состоящий из *^1 из любых четырех (из восьми) смежных
Рис. 18.5. Конструкция Х4: комбинирование четырех кодов
классов [15, 11, 3]-кода Хэмминга по коду *SFi, — (5, 2, 5)-код {00000, 11111} й ^4—(5, 10, 2)-код {00000, 11111, 11000,
00111, 10100, 01011, 10010, 01101, 10001, OHIO}. Тогда код <8 представляет собой (20, 2560, 5)-код.
Дальнейшие примеры приводятся в § 18.7.3 и на рис. ПА.2 (обозначены Х4).
Сугияма и др. [1291] успешно применили конструкции X и Х4 и их модификации к кодам Гоппы. Большое число хороших кодов, найденных таким образом, обозначены на рис. ПА.2 буквами GP.
Упражнение. (15). Применить конструкцию Х4 для расширения кодов БЧХ длины щ = 2т—1, исправляющих е ошибок. Пусть т=ае—р, где О^р<е, и пусть коды <8i, ^2, *8з являются соответственно [щ, щ—ет, 2е-|-1]-, [щ, щ—(е—i)m, 2е—1]-, [2а, 2“—еа—1, 2е-|-2] -кодами БЧХ. Пусть код равен объедине-нию кода 'g’s и 2™—1 смежных классов [2“, 2“—1, 2]-кода, состоящего из всех слов четного веса, по коду ^з- Показать, что код является [2тЧ-2а—1, 2т-}-2а—ет—р—2, 2е+1]"к°Д°м- В наиболее благоприятном случае, когда т делится на е и р = 0, число информационных символов в коде увеличивается на' 2т/е—1~п1/е за счет добавления одного проверочного символа.
18.7.3. КОДЫ, ИСПРАВЛЯЮЩИЕ ОДИНОЧНЫЕ И ДВОЙНЫЕ ОШИБКИ
Коды, исправляющие одиночные ошибки. Наилучшие двоичные линейные коды, исправляющие одиночные ошибки, известны. Это коды Хэмминга с параметрами [п, п—т, 3], где 2’п-1^п^2’п—1.
Упражнение. (16). Доказать это утверждение!
По крайней мере для половины значений п существуют нелинейные коды, имеющие больше кодовых слов (см. теорему 34 гл. 2 и рис. ПА.2.).
Задачи (нерешенные). (18.1). Найти величину А(п, 3) для (см. рис. ПА.1 для значений nsc:8).
Коды, исправляющие двойные ошибки. О них известно еще меньше.
(18.2). Что представляет собой двоичный линейный код наибольшей длины, исправляющий двойные ошибки и имеющий фиксированную избыточность г, где г—4, 5,...? Обозначим эту длину через nL(r). Известны следующие значения этой величины (из работы Хелгерта и Стинаффа [636]):
г:4 5 6 7 8 9 10 . . .
nL(r):5 6 8 11 17 23—29 32—42 . . . (18.20)
Займемся теперь исследованием наилучших линейных или нелинейных кодов, исправляющих двойные ошибки. Следующие коды мы уже знаем.
(i) . Примитивные коды БЧХ с параметрами [2т—1, 2™—1 — —2m, 5]. Однако они всегда хуже следующего семейства кодов.
(ii) . Непримитивные коды БЧХ с параметрами [2™, 2т—2m, 5], получаемые укорочением кода длины 2m-j-l, порождающий многочлен которого имеет корни ой, i^C0 U Су
(iii) . Коды Препараты £F(m)* с параметрами( 2т—1, 22т_2т, 5) для четных значений т^4.
(iv) . Коды Препараты, расширенные с помощью конструкции X, с параметрами (18.16).
(v) . Код Адамара из § 2.3 с параметрами (11, 24, 5) и рассмотренный в примере 7 (20, 2.560, 5)-код.
Кроме того, известны следующие коды, исправляющие двойные ошибки:
(vi) . Приведенные ниже в упражнении (28)
[ 2т + 2Г (т+1)/21 — 1,2т + 2Г (т+1)/2] — 2т—2,5]
укороченные коды БЧХ.
(vii) . Укороченный альтернантный [74, 61, 5]-код (Хелгерт [633]) и укороченный обобщенный [278, 261, 5]-код БЧХ (Чень и Чой [286]).
(viii) . Квазисовершенный [23, 14, 5]-ход Вагнера ([1378]).
Задача (нерешенная). (18.3). Предложить простой способ построения последнего кода.
Обозначим через п*(г) длину двоичного кода, исправляющего двойные ошибки (линейного или нелинейного) наибольшей длины, имеющего заданную избыточность г. Конечно, ri* (r)^nL(r). Из (ii) и (iii) следует, что
п*(4а + 2)>22й+1 и п*(4а + 3) > 22с+2—1. (18.21)
Упражнение (17). Показать, что п* (4а+3) —22а+2—1.
[Указание. Воспользоваться следствием 14 гл. 17.]
Конструкция Х4 может быть использована для получения дальнейших нижних оценок величины и* (г). Положим в
качестве c&2 выберем код Хэмминга — код с расстоянием
6, имеющий избыточность т и наибольшую длину n*(m—1) + 1, ^4 — код из всех слов четного веса той же длины. Тогда новый код Я? имеет длину 2т-\-п*(т—1), избыточность 2m, и поэтому п* (2m) > п* (т— 1) + 2т для четных т > 4. (18.22)
Таким образом, к коду Препараты £F(m)* может быть добавлен "К п+1 информационных символов за счет добавления только одного проверочного символа.
Упражнения. (18). Показать, что для четных т^4 выполняется неравенство п* (2m+ 1) ^п* (т) +2т.
(19). Показать, что п* (12)^70; п* (16) ^271;
п*(20) > 1047 и п*(21) > 1056.
Известные нам наилучшие нижние оценки величины п*(г) изображены на рис. ПА.2 (и в таблице II работы [1237]). Единственными известными точными значениями являются
п*(6) = 8; п*(7)=15 и n*(4n + 3) = 22с+2— 1
(см. упражнение (17)). Кроме того, п*(8) = 19 или 20.
Задача (нерешенная). (18.4). Найти величину п*(г). Еще меньше известно о кодах, исправляющих тройные ошибки!
18.7.4. КОНСТРУКЦИЯ |a+xlb+x|a+b+x|
Пусть 'g’l и представляют собой (n, Mi, di)- и (п, М2, <Д)-двоичные .коды. Новый код Т? состоит из всех векторов
|a + x|b + x|a + b + x|, а, Ь^'й1; хе^2. (18.23)
Ясно, что ’ё’ — код длины Зп, содержащий М2[Мч кодовых слов, и что этот код линейный, если коды T?i и линейные. Неизвестно никакой простой формулы для минимального расстояния кода хотя его нижняя оценка дается следующей теоремой.
Теорема И. Для любых двоичных векторов а, Ь, х имеет место неравенство
wt|a + x|b + x|a + b + x| = 2wt (а \/b)*> —wt (х) + 4s >
>2wt(a\/b)—wt(x), (18.24)
где s — число позиций, в которых у векторов а и b стоит 0, а у вектора х стоит 1.
Упражнение. (20). Доказать теорему 11.
Теорема 12. (Турин.) Пусть обозначает [7, 4, 3]-код Хэмминга, ненулями которого являются элементы а\ ieCi, и пусть код образован кодовыми словами <%i, записанными в обратном порядке. Пусть далее коды ‘S’i и Т>2 обозначают [8, 4, 4]-коды, полученные из кодов 9&\ и $2 добавлением общей проверки на
• *> Здесь (avb)—вектор, являющийся поразрядной дизъюнкцией векторов а и Ь. (Прим, ред.)
четность. Тогда код, задаваемый формулой (18.23), является [24, 12, 8]-кодом Голея ®24-
Доказательство. Необходимо вычислить только минимальное расстояние. Тогда тот факт, что это код Голея, будет следовать из теоремы 14 гл. 20.
Пусть u= |a+x|b-|-x|a+b-|-x| — ненулевое кодовое слово <ё>. Каждый из векторов а, Ь, х имеет вес 0, 4 или 8.
(i) . Если самое большее один из векторов а, Ь, х имеет вес 4, то wt(u) ^8.
(ii) . Если два из векторов а, Ь, х имеют вес 4, то wt(u)^8. (Так как если wt(a) =4; wt(x) =4, то wt(a+x) ^2 и т. д.)
(iii) . Предположим, что wt(a) =wt(b) =wt(x) —4. Если a=#b, то wt(a\/b)^6, и из теоремы 11 вытекает, что wt(u)^8. Следовательно, во всех случаях wt(u)^8. •
Упражнение. (21). Обобщая теорему 12, выберем в качестве кодов ^]И ^2 [2™, т+1, 2,п-1]-коды Рида — Маллера первого порядка, в одном из которых слова записаны в обратном порядке (за исключением позиции, соответствующей общей проверке на четность). Показать, что код Я? имеет параметры [3-2™, Зт+З, 2т], т^З. [Указание. См. работу [1237].] При т=4 полу-' чаем [48, 15, 16]-код.
Задача (нерешенная). (18.5). Найти другие применения конструкции (18.23). Существуют ли другие конструкции, подобные (18.23), которые дают хорошие коды?
18.7.5. КОНСТРУКЦИЯ ПИРЕТА
Она представляет собой способ удвоения длины неприводимого кода. Пусть Я? — неприводимый циклический двоичный [п, k, с?]-код, порождающий идемпотент которого равен 0i(x) (см. гл.8). Здесь k равно наименьшему целому числу такому, что п делит 2ft—1. Положим N= (2fe—1) /п. Пусть £ является примитивным элементом поля GF(2ft), и пусть а=^. Таким образом, ап=1 и в качестве ненулей кода могут быть выбраны элементы а, а2, а22,..., а2к~г. Кроме того, отметим, что код & состоит из слов i(x)0j(x) (mod хп—1), где degi(x)<fe.
Напомним, что согласно гл. 8 код изоморфен полю GF(2ft), причем имеет место следующее взаимно однозначное соответствие:
Элемент ‘й’
61
х (0j (х)
Т (х) 61 (*) £
Элемент G F (2й)
1
а
(это условие определяет у(х)).
Тогда любое ненулевое слово кода может быть представлено как у (х) J-0i (х)+*^', где 0^/^2fe—2.
Пусть u>j=wt(y(x)3'6i(x)). Тогда (так как
у (х) j+JV0i (х) =рь^+^=а^=^ху (х) ^01 (х)).
Выберем теперь целое число а так, чтобы максимизировать d'= min (wt + г^л-J. (18.24а)
0<j<N— 1
Новый код Ф состоит из 0 и векторов
Uy = Iу (x)i 0Х (х) | у (х)’+а 0Х (х) j, (18.25)
где 0^/^2ft—2. Тогда Ф представляет собой [2п, k, сГ]-код, где d' определяется выражением (18.24а).
Часто можно увеличить объем кода Ф добавлением одной или двух порождающих строк (11... 100... 0) и (00 ... 011 ... 1) и добавлением одной или двух общих проверок на четность.
Например, пусть Т? обозначает [9, 6, 2]-код с порождающим идемпотентом 01 (х) =х3-|-х6. Здесь М=7; £ — примитивный элемент GF (26) (см. рис. 4.5); <х=£7; у(х) =х3+х4-|-х6+х8 и (ш0, и»!,..., Ws) = (2, 6, 6, 4, 6, 4, 4). Лучше всего выбрать а= 1*, и код Ф представляет собой [18, 6, 6]-код, который может быть увеличен до [20, 8, 6]-кода.
Полученные таким способом коды обозначены на рис. ПА.2 буквами РТ.
Упражнение (22). Пусть Т? обозначает [17, 8, 6]-код, где N—15. Получить [34, 8, 14]- и [35, 9, 14]-коды.
(23) . Пусть Т? обозначает [21, 6, 8]-код, где N=3. Получить [44, 8, 18]-код.
Задача (нерешенная) (18.6). Пусть g7— циклический код длины п. Как надо выбрать многочлен а(х), чтобы минимальное расстояние кода {|и(х) |а(х)и(х) (mod хп—1) | : и(х)eg} было максимально возможным?
18.8. КОНСТРУКЦИИ, СВЯЗАННЫЕ С КАСКАДНЫМИ КОДАМИ
18.8.1. МЕТОД УЛУЧШЕНИЯ КАСКАДНЫХ КОДОВ
Рис. 18.6. Типичное кодовое слово кода g:
L — столбец, соответствующий общей проверке на четность
Пусть обозначает [пг, kr, d' = п' — k' + 1] МДР-код над GF (2й) (см. гл. 11), кодовые слова которого записаны как векторы-столбцы. Если каждый символ кодового слова заменить на соответствующий двоичный fe-вектор (как в примере 2 § 10.5), то получается двоичная (n'y.k)-матрица. Добавление общей проверки на четность к каждой строке приводит к двоичному {п' (k + 1), kk', 2Д]-коду (рис. 18.6). Этот код является простейшим каскадным кодом. Минимальное расстояние кода g равно по крайней мере 2d', так как в любом ненулевом слове имеется не менее чем d' ненулевых строк, а вес каждой строки равен самое меньшее 2.
* Здесь подходит любой выбор а= 1, 2,.... 6. (Прим, перев.)
Касахара и др. [722] обнаружили, что размерность кода св часто можно увеличить на 1. Новый код ф состоит из слов кода и кодовых слов, полученных при замене последнего столбца на рис. 18.6 на его дополнение.
Теорема 13. Новый код Ф имеет параметры
[n'(fe+l), kk' + l, 2d'] (18.26)
при условии, что n~^2d'.
Упражнение. (24). Доказать эту теорему.
Например, пусть <ё"—[17, 11, 7]-код Рида — Соломона над GF(24). Тогда ф является [85, 45, 14]-кодом. Дальнейшие примеры и обобщения см. в работе [722]. Полученные таким способом коды на рис. ПА.2 обозначены буквами ZGS*).
Упражнение (25). Построить [156, 76, 24] и [168, 76, 28] коды.
18.8.2. ОБОБЩЕННЫЕ КАСКАДНЫЕ КОДЫ ЗИНОВЬЕВА * 1
Эта конструкция обобщает каскадные коды и приводит к целому ряду хороших кодов (помеченных буквами ZV на рис. ПА.2).
Для построения этих кодов требуются следующие исходные коды: (1). Семейство г кодов ... ,s£r, где является (п, Mi, б<)-кодом над полем GF(qi) и дл — степень числа 2. (2). Двоичный (т, q\qz...qr, гЛ)-код ^<0), который представляет собой объединение qx различных кодов (0<Л^1—1), где код ЗЗг^ имеет параметры (т, q2...qr, d2). Каждый код 33^ должен быть объединением q2 различных кодов i2 (O^i^
—1), где код имеет параметры (т, q3, ..qr, d3)
и т. д. Наконец, каждый код ir_2 должен быть
объединением qr-i различных кодов ^7,?.... (0^ir-i^
—1), которые имеют параметры (т, qT, dr)**. Таким образом,
-®(0) = ?,и г,..
г\=0 гг=0
причем d\<id2<_ ... <(dr. Типичное кодовое слово кода будем обозначать через bj,. ..г (O^t'i^^i—1, ..., 1), где
индексы выбраны так, чтобы слово Ьг„ г2.ir принадлежало коду
Ж 33% lt и т. д. и чтобы оно было кодовым словом кода 93^,..., i с номером ir.
построенные в работе [722], являются частными случаями
Все коды, обобщенных каскадных кодов (см. § 18.8.2). Поэтому многие из кодов, приведенных в [722], несколько ранее построены в работе [1470]. {Прим, ред.)
1 См. примечание на с. 562. (Прим, ред.)
**> Коды называют внешними, а коды — внутренними кодами. (Прим.
Построение кода сводится к следующему. Образуем («Х/')"мат' рицу
“ z/2> z>(r> —
О1 О] . . . О1
4° 42) . . . Й2Г) t (18.27)
42)
где первым столбцом является произвольное слово кода вторым — произвольное слово кода «s/2 и т. д. Теперь каждую стро-
ку этой матрицы а»<б, ....о/б заменяем на двоичный вектор
О<2)
а(Г) . (Чтобы сделать это, надо перенумеровать элемен-
ты каждого поля GF(^i) числами 0, 1 qi—1 некоторым произвольным, но фиксированным образом.) Полученные двоичные (пУ(уп) -матрицы (рассматриваемые как двоичные векторы длины пт) образуют новый код Z, называемый обобщенным каскадным кодом.
Теорема 14. (Зиновьев [1470].) является (пт, NiNz.. -'Nr, d^min{6iidi,..., Srdr}) -двоичным кодом. (Конечно, код SE, не обязательно линеен.)
П р и м ер. В качестве ^(0) выберем (4, 16, 1)-двоичный код. Код ^?<0) является объединением (4, 8, 2)-кода ^о(1), состоящего из всех слов четного веса, и (4, 8, 2)-кода состоящего из всех слов нечетного веса. Каждый из кодов W!) и является объединением 4 кодов, полученных сдвигами (4, 2, 4)-кода {0000, 1111}. Таким образом, г—3; z/i=2; ^2=4; ^3=2. Выберем также следующие
коды:
^1—(8, 2, 8)-код над GF(2);
•5^2== (8, 44, 4)-код над GF(4) (см. теорему 10 гл. 11*);
^з=(8, 27, 2)-код над GF(2).
Тогда SE, представляет собой (32, 216, 8)-код.
Доказательство теоремы. Не очевидна только оценка минимального расстояния. Предположим, что мы имеем две различные матрицы (а/б) и (с/б) вида (18.27), которые различаются в v-m столбце. Тогда они различаются в этом столбце по крайней мере в 6V позициях. По определению оба вектора b81, i2...fv_b а,„.
и bilr j2.г v_i, р,.._ («#=₽) принадлежат коду tv_-i
и поэтому различаются по крайней мере в dv позициях. Следовательно, соответствующие двоичные слова кода Z различаются не менее чем в dv позициях. •
* Не совсем правильно. Код не может быть получен из этой теоремы. Здесь можно использовать конструкцию |u|u+v| (см. § 2.9). Так, если взять РС-коды ^4= [4, 3, 2] и ^6= [4, 1, 4] над GF(4), то {|u|u+v| : us ve^sj. (Прим, перев.)
Упражнения. (26). Пусть г=2; ^1 = 8; ^2 = 2; ^<°)=[8, 4, 4] и 1, 8]—двоичные коды; ^=[7, 2, 6]-код над
GF(8) и ^2= [7, 4, 3]-код над GF(2). Получить двоичный [56, 10, 24]-код Z.
(27) . Пусть г=4; ^<°>=[16, 11, 4]; ^=(16, 28, 6); ^2)г,з = [16, 5, 8] и = [16, 1, 16] — двоичные коды; =
= [6, 1, 6]-код над GF(8); ^2= [6, 3, 4]-код над GE(8); ^3= = [6, 4, 3]-код над GE(16) и «s$4=[6, 5, 2] —двоичный код. Получить (96, 233, 24) -двоичный код
18.9. МЕТОДЫ УКОРОЧЕНИЯ КОДОВ
18.9.1. КОНСТРУКЦИИ Y1—Y4
Пусть обозначает {п, k, с?]-двоичный код с проверочной матрицей Н. Если i информационных символов' положить равными нулю, то получается [п—i, k—i, с!]-код. Мы можем улучшить эти параметры, если нам известно минимальное расстояние d' дуального кода ®’-L. В этом случае мы можем предположить, что первая строка матрицы Н имеет вес d'. Если мы вычеркнем те столбцы матрицы Н, у которых первая строка содержит единицы, то оставшаяся матрица Hs имеет строку из нулей и представляет собой проверочную матрицу кода ’ё’г длины п—d', размерности (п—d') — (п—k—1)=А—d'+l с минимальным расстоянием по крайней мере d (согласно теореме 10 гл. 1). Действительно, код состоит в точности из тех кодовых слов содержащих нули на всех позициях, где первая строка матрицы Н имеет единицы (причем эти позиции с нулями вычеркнуты). Короче говоря:
«[«, k, Д-код, дуальный к которому имеет расстояние d'»,
->[н—d', k—d' + 1, >Д-код. (18.28)
В § 1.8 был рассмотрен пример, где этот способ был использован для построения кода Нордстрома — Робинсона из кода Голея. Дальнейшие примеры приведены в работах Хашима [623], Хелгерта и Стинаффа [636, 637] и Слоэна и др. [1237]. На рис. ПА.2 коды, полученные таким способом, обозначаются буквой У1.
Упражнения. (28). (а). Выбрать в качестве Л? расширенный [2m+1, 2т+1—2т—3, 6]-код БЧХ. Согласно упражнению (10) гл. 15 дуальный код ®’-L имеет минимальное расстояние d'=2™— —2I(m+I)/2]. Получить отсюда код длины 2m+2,(m+1)/21—1, исправляющий две ошибки и с избыточностью 2m-j-l.
(b). Код, дуальный к [48, 15, 16]-коду из упражнения (21), имеет минимальное расстояние 4. Получить [44, 12, 16]-код.
(29). Конструкция Y2. Предположим, что первая строка матрицы Н веса d' имеет вид 11... 100... 0, и пусть подкод S состоит
из всех слов кода 9’, начинающихся c.d' нулей. Таким образом, код 7?i представляет собой код S с вычеркнутыми первыми d' координатами. Обозначим через Т объединение кода 5 и всех d'—1 смежных классов кода 7? по коду S, лидеры которых имеют вид ПО"-2, 1010й-3,..., 10d'-210"-d'. Показать, что если в множестве Т вычеркнуть первые d' координат, то в результате получится нелинейный
{п-d’, d'-2k~d’+l, >d—2)-код. (18.29)
В качестве примера, учитывая, что код, дуальный к [31, 10, 12]-коду БЧХ, имеет минимальное расстояние d'=5, получить (26, 320, 10)-код.
Конструкция Y3. Аналогично, используя все смежные классы с лидерами веса 2 в этих d' позициях, получаем нелинейный
*
(n—d', (1 ^2n-d'+1, >d—4)-код. (18.30)
(Приложения см. в работе [1237].)
Упражнение. (30). Конструкция Y4. Пусть d" равно минимальному весу вектора u \/v, где и, ve®'1; u#=v.
Показать, что* вычеркивание соответствующих столбцов дает
[п—d", k—d" + 2, > t/J-код.
Приложения приведены в работе [637]. t
18.9.2. КОНСТРУКЦИИ ХЕЛГЕРТА И СТИНАФФА
Предположим, что 7?— [n, k, <^]-код с порождающей (/гХ«)-матрицей G. Можно считать, что первая строка G имеет вид u=ld 0n-d, и поэтому
G = Г1 1 • • • 1 00 • • • 0'
G2
Тогда G2 — порождающая матрица [п—d, k—1, б12]-кода ^2, где d2^]J/2[. В самом деле, пусть v — любое ненулевое кодовое слово кода ^2 веса w, соответствующее кодовому слову te®’:
-<—%—> -<—d— <—w—>•
11=11 . . . 1 11 . . . 1 00 . . . 0 00 . . . . 0;
t= 11 . . . 1 00 . . . 0 11 . . . 1 00 . . . . 0;
u + t = OO . . . 0 11 . . . 1 11 . . . 1 00 . . . . 0.
Тогда h-Kw^d и d—K+w^d, откуда 2w^d и w^]d/'2[. Короче говоря, (Хелгерт и Стинафф [636]):
[п, k, d]->[n—d, k—1, ]d/2[]. (18.31)
Например,
( 4, 12,J-код Голея-* (.16, ' 1, ]-код Хэмминга,
. циклический (51, 8, 24]-код (см. [266])—>[27, 7, 12]-код.
На рис. ПА.2 коды, полученные таким способом, обозначены буквами HS.
ЗАМЕЧАНИЯ К ГЛ. 18
§ 18Л. Общие сведения о произведении кодов и их обобщениях см. в работах: Берлекэмп и Юстесен [127], Бартон и Велдон [219], Элайес [406], Форни [436], Геталс [490], Гор [546], Касами [726, 731], Ли и Ченг [802] и Венг [1407]. См. также Хартманн и др. [616—-618]. Что касается применения таких кодов, см.: Бал и Чень [58], Чень и Нгэ [292], Геталс [489], Курода [787], Тэнг и Чень [1306], Венг и Соллмэн [1408] и Вулф и Элспас [1430].
О декодировании произведения кодов см.: Абрамсон [4], Дюк [389], Дюк и Скэттбол [391], Касами и Лин [733], Лин и Велдон [839], Редди [1097, 1099], Редди и Робинсон [1100], Вайнберг [1381] и Велдон [1404].
В некоторых применениях используются кодовые слова, являющиеся прямоугольными таблицами (а не векторами), и в таком случае оказываются очень полезными произведения кодов и их обобщения. О теории двумерных кодов и кодов более высокой размерности см.: Калабро и Вулф [229], Гордон [541 , Икай и Койима [681], Мак-Вильямс и Слоэн [885], Намура и др. [998—100Г , Рид и Стьюарт [1106а] и Спэнн [1258]. Приложения см.: Калингэрт [230 , Имаи [682], Ноултон [771], Накамура и Ивадаре [984], Пейтл и Хонг [1029], Шредер [1168], Слоэн и др. [1230, 1234—1236] и особенно [885].
Голдберг [517] и Рао и Редди [1094] нашли несколько хороших кодов, объединяя коды, получаемые произведением, и некоторые их смежные классы. Этот многообещающий способ требует дальнейших исследовании.
Задача (нерешенная). (18.7). Обобщить конструкции, использованные в работах [517] и [1094] *.
§ 18.2. Что касается теории идеалов групповой алгебры см.: Икай и Койима [681] и Номура и др. [998—.1001].
§ 18.7. В следующих статьях рассматриваются некоторые другие методы построения кодов: Оллтоп [25], Ассмус и Мэттсон [40], Бамбах и др. [64], Белл [98], Блейк [159], Боброу и др. [168—170], Бредисон [195], Кампопиано [240], Даньино [326], Денеш и Кидвелл [371, гл. 10], Гоппа [538], Хакими и др. [575—577], Хашим и Константинидес [624], Ксяо и др. [668—670], Леку-ант [800], Левитт и Вулф [828], Марчуков [912], Мэсси и др. [924], Ольдерог-ге [1010], Сальцер [1142], Сауэр [1147], Шива [1198], Шрикханде [1206], Уоллис [1385] и Вулф [1425, 1428].
Другой класс кодов, абелевы групповые коды, хотя и кажется многообещающим, но все еще не привел пи к каким действительно хорошим кодам (см.: Берман [135, 136], Камьон [238], Дельсарт [345] и Мак-Вильямс [877, 880]).
Для отыскания хороших кодов был предпринят ряд интересных поисков на ЭВМ. Например, см.: Чин [266], Фонтейн и Питерсон [433, 434], Хашим и Константинидес [625], Токура и др. [1331] и Вагнер [1377—1380].
Конструкции X и Х4 были описаны Слоэном и др. [1237], которые рассмотрели также методы кодирования и декодирования таких кодов. См. также: Зайцев и др. [1451] 1 2 и Миякава и др. [965]. Теорема 12 взята из работы [53]. Кэртис [322] предложил другое и очень интересное доказательство этой теоремы. Упражнение (13) (Ь) принадлежит Охно и др. [1009]. Упражнения (14) (а), (Ь) и 28 (Ь) принадлежат Тезука и Наканншн [1315], а упражнения (14) (с), (d) — Касахара и др. [721].
'§ 18.7. О конструкции Пирета — см. [1047], а также [1048—1050].
1 Обобщенные каскадные коды можно считать обобщением этих конструкций. (Прим, ред.)
2 В этой работе (см. также [1183 а*]) описаны обе эти конструкции X и Х4 и, в частности, получены коды с параметрами (18.16) и (18.22). (Прим, ред.)
Глава 19
Самодуальные коды и теория инвариантов
19.1. ВВЕДЕНИЕ
Линейный код называется самодуальным, если (см.
§ 1.8). Мы уже убедились, что многие хорошие коды самодуаль-ны, среди них: расширенные коды Голея и некоторые квадратич-но-вычетные коды. Наиболее важное свойство самодуальных кодов описывается теоремой Глисона (теорема Зс), которая налагает сильные ограничения на весовую функцию. Эта теорема доказывается посредством мощной техники, развитой в XIX столетии и называемой теорией инвариантов (см. § 19.2, 19.3). Та же самая техника доказывает целый ряд подобных теорем, касающихся разного рода весовых функций (см. § 19.4). Одним из следствий теоремы Глисона является верхняя граница для минимального расстояния самодуального кода (теоремы 13, 17). Однако эта верхняя граница может быть достигнута только при небольших значениях п (следствие 16, теорема 17). Тем не менее существуют самодуальные коды, которые удовлетворяют границе Варшамова— Гилберта (теоремы 21, 24).
Большинство результатов этой главы одинаково хорошо применимо к широкому классу кодов, а именно к линейным или нелинейным кодам, удовлетворяющим тому условию, что преобразование спектра расстояний равно самому спектру расстояний (как, например, в коде Нордстрома — Робинсона). Такие коды называются формально самодуальными. Спектр расстояний формально самодуальных кодов, рассматриваемых в этой главе, совпадает с весовым спектром, и поэтому мы будем иметь дело с весовым спектром.
Напомним читателю, что самодуальные коды имеют четную длину п и размерность п/2.
Наиболее интересные самодуальные или формально самодуальные коды обладают тем свойством, что все значения расстояний кратны некоторому фиксированному постоянному числу />1. Имеется ровно четыре нетривиальных случая, когда это может произойти.
Теорема 1. (Глисон, Пирс и Турин [53].) Предположим, что — формально самодуальный код над GF(q), в котором расстояние между кодовыми словами всегда кратно числу />1. Тогда либо 7?— тривиальный [п, п/2, 2]-код с весовой функцией Хэмминга
((9-1)x2 + Z/T/2 (19.1)
для любого q, либо имеет место одно из следующих условий:
(j) q = 2, t = 2;
(ii) q = 2, t = 4;
(iii) q=3, t=3;
(iv) 9,— 4, t = 2.
Доказательство мы опускаем. Коды типа (ii) иногда называются четными самодуальными кодами.
Приведем несколько примеров самодуальных кодов.
Коды типа (i). (Е1). Двоичный код {00, 11} представляет собой простейший самодуальный код с весовой функцией
Wr(x, У) = х2 + У2- (19.2)
В общем случае код над GJ!(q) с порождающей матрицей [а, Ь], а, Ь=А0 является формально самодуальным с весовой функцией х2+(<?—1)у2. Прямая сумма п/2 таких кодов формально са-модуальна и имеет весовую функцию, задаваемую уравнением (19.1).
(Е2) . (16, 256, 6)-код Нордстрома — Робинсона (§ 2.8 и гл. 15).
(ЕЗ) . Расширенный [18, 9, 6] KB-код (см. § 16.6).
(Е4) . Формально самодуальный (8, 16, 2)-код, изображенный на рис. 5.1.
Коды типа (ii). (Е5). [8, 4, 4]-код Хэмминга с весовой функцией
Г2(х, #) = х8ф 14х4^ф^. (19.3)
(Е6) . [24,.12, 8]-код Голея ^24 с весовой функцией ;
W3 (х, у) = х24 + 759х16 у3 + 2576х12 г/12 ф 759х8у10 + y2i- (19.4)
В общем случае любой расширенный KB-код длины п—8т является кодом типа (ii) (теоремы 7, 8 гл. 16).
Напомним, что согласно гл. 5 код над GF(3) имеет две весовые функции: полную весовую функцию
’W' (х, у, г) = Ajk У’ Л
где Aijk равно числу кодовых слов, содержащих I нулей, / единиц и k двоек, и весовую функцию Хэмминга W(х, у) =Ж(х, у, у). •
Коды типа (iii). (Е7). Троичный [4, 2, 3]-код # 6 из гл. 1 е весовой функцией Хэмминга
Wi(x, у) = х4 ф 8ху3. (19.5)
(Е8). Троичный [12, 6, 6]-код Голея ^Та, задаваемый выражением (16.25), с весовыми функциями
>5(х, у, z)==x12 + y12 + z12 + 22(x6y6 + x6z6 + y6z6) +
+ 220 (х® у3 г3 ф х3 у3 z3 ф х3 у3 2°);
Wo (Хг у) = xi2 ф 264х« у6 ф 440х3 у3 ф 24 у™. (19.6)
В общем случае любой расширенный троичный KB-код или симметричный код Плесе представляет собой код типа (iii) (согласно условию (16.26) и теоремам 7, 8 и 17 гл. 16).
Коды типа (iv). (Е9). Формально самодуальный [6, 3, 4] КВ-код над GF(4) (см. с. 503). Он получается добавлением общей проверки на четность к циклическому коду с порождающим многочленом (х—р) (х—р4), где ре GF (16) —корень степени 5 из единицы. Порождающая матрица этого кода имеет вид
Г1 со2 1 0 0 со2
0 1 со2 1 0 со2 .
[о 0 1 со2 1 <о2_
где <jjeGF(4); ico2-4-gj-J-1=0.
Упражнения. (1). Пусть ^ — циклический [2п—1, д]-код. Найти необходимое и достаточное условие, которому должны удовлетворять корни порождающего многочлена 9’, чтобы расширенный код 7?* был самодуален. [Указание. Рассмотреть случаи л=8, 16]
(2). Пусть ^ — четное число. Показать, что существует РС-код "S’ над GF (q) такой, что код самодуален. Показать, что это неверно, если q — нечетное.
Замечание. Как следует из приводимой ниже теоремы Зс, [32, 16, 8]-код КВ и [32, 16, 8]-код РМ второго порядка имеют одинаковые весовое спектры. Однако они не эквивалентны по следующим причинам, (i). Они имеют разные группы автоморфизмов. Согласно теореме 13 гл. 16 группа автоморфизмов KB-кода включает проективную специальную линейную группу Р5£г(31) порядка-~31(312—1) = 14880. Однако так как 29 и 31-—простые числа-близнецы, то из теоремы Неймана [988, 989] следует, что группа автоморфизмов не больше, чем эта группа. С другой стороны, согласно теореме 24 гл. 13 группа автоморфизмов РМ-кода представляет собой полную аффинную группу GA (5) порядка 32-31-30-28-24-16=319979520. (ii). Смежные классы этих кодов имеют разные весовые спектры (Берлекэмп и Велч [133]). (iii). Они имеют разные бивесовые функции (см. упражнение (36) гл. 5).
Два неэквивалентных [14, 3, 5]-кода с одинаковым весовым спектром были приведены Фонтейном и Питерсоном [434].
19.2. ВВЕДЕНИЕ В ТЕОРИЮ ИНВАРИАНТОВ
Этот раздел представляет собой элементарное введение в теорию инвариантов, показывающее, как эта теория используется для изучения весовых функций.
Предположим, что — двоичный самодуальный код такой, что веса всех кодовых слов кратны 4, или, короче, четный самодуальный код, и пусть W(x, у) — его весовая функция. Так как код 'g’ самодуален, то из теоремы 1 гл. 5 вытекает, что
(19.7)
(ибо W(x, у)—однородный многочлен степени п). Так как веса всех кодовых слов делятся на 4, то W(x, у) содержит только степени у4. Следовательно,
№(х, y) = W(x, iy), (19.8)
где г= (—1). Задача, которую мы хотим решить, заключается в отыскании всех многочленов W(x, у), удовлетворяющих уравнениям (19.7) и (19.8).
Инварианты. Уравнение (19.7) говорит о том, что многочлен W(x, у) не изменяется, или инвариантен, при следующем линейном преобразовании:
т . заменить х на (х у)/К2, •* 1 • _
заменить у на (х—у)/У2
или в матричных обозначениях:
Т,: заменить на —L-П
\у) /2 U — 1)\у)
Аналогично уравнение (19.8) говорит о том, что W(x, у) инвариантен также относительно преобразования
, . заменить х на х,
2 •
заменить у на i у
или
Т2:заменить
х \
У )'
Конечно, как следствие многочлен W(x, у) должен быть инвариантным относительно любой комбинации T2i, TiT2, ...этих преобразований. Нетрудно показать (как мы увидим в § 19.3), что матрицы
-Ц1 1)и С °) /2 и — 1/ \0 ij
при умножении друг на друга всеми возможными способами порождают группу ^], состоящую из 192 матриц.
Поэтому наша задача звучит теперь так: найти все многочлены W(x, у), которые инвариантны относительно преобразований,, задаваемых всеми 192 матрицами группы
Сколько существует инвариантов? Первое, что мы хотим выяснить — это сколько существует инвариантов. Этот вопрос поставлен не совсем строго, так как, конечно, если f и g — инварианты, то инвариантами являются и любое их скалярное кратное cf, и также сумма f+g, разность /—g, и произведение fg. Кроме того, нам достаточно изучить только однородные инварианты (у которых все одночлены имеют одинаковую степень).
Поэтому правильно так поставить вопрос: сколько существует линейно независимых, однородных инвариантов заданной степени d? Обозначим это число через ад-
Чтобы было удобнее оперировать с числами Оо, ai а2,..., пред-ставим их в виде степенного ряда или производящей функции
Ф (X) = а0 + ar I + о2 X2 + ...
Обратно, если мы знаем функцию Ф(Х), то числа можно найти, разлагая Ф(^) в степенной ряд.
Сейчас мы приведем замечательную теорему Т. Молина, опубликованную в 1897 г. ([971], Бурбаки [190, с. 138], Бернсайд [211, с. 301], Миллер и др. [955, с. 259]).
Тео р е м а 2. Для любой конечной группы & комплексных (тХиг)-матриц Ф(^) определяется выражением
ф m = —— V -------!----- (19.9)
I SM Zj det (I — X А) ’
Ае^
где 1^1 —число матриц в группе S'; det обозначает определитель и I — единичная матрица. Другими словами, функция Ф(^) равна усредненному по всем матрицам Л из группы многочлену, обратному det (I—ZA).
Назовем Ф(Х) рядом Молина группы Доказательство этой теоремы приводится в § 19.3.
Для нашей группы состоящей из матриц, соответствующих преобразованиям 1, Т\, Т2, ..., получаем, что
Ф(Х)=_Ц—1—+—!—+------------------?-----+ ... | (19.10)
V 1921 (1—X)2 1-k2 (1-%) (1 — iX) I
Можно сократить выкладки, но вполне допустимо иметь дело непосредственно со всеми 192 членами этого ряда (многие из них совпадают) и складывать их. Результат удивителен: окончательное выражение имеет вид
фП) =--------1-----. (19.11)
(1 — X8) (1 -X24)
>: Интерпретация Ф(Х). Очень простой вид выражения (19.11) позволяет нам высказать некоторые предположения. Разлагая по степеням X, мы имеем:
Ф (X)= а0 аА X -р а2 X2 -]-... =
= (1 + Xs + Vе+ Х24 + -..)(1+Х24 + Х48+ ...). (19.12)
Одно следствие мы можем вывести сразу: ad равно нулю, если п не кратно 8, т. е. степень однородного Инварианта должна быть кратна 8. (Это уже доказывает тот факт, что длина четного само-дуального кода делится на 8.) Но мы можем сказать больше. Правую часть выражения (19.12) мы могли бы найти точно, если бы мы имели два «базисных» инварианта степени 8 и 24 таких, что все инварианты получались бы из них сложением и умножением.
Ути два инварианта, 0 степени в и степени 24, породили ы следующие инварианты:
Степень d Инварианты Число
0 1 1
8 0 1
16 02 1
24 03, <р 9
32 04, 0<р £ (19.13)
40 05, 02ф 2
48 0®, 03 <р, <р2 3
При условии, что все произведения fHcpj линейно независимы,
что эквивалентно алгебраической независимости 0 и <р, числа аа в формуле (19.13) точно равны коэффициентам ряда
1 + X8 + + 2724 + 2732 + 2Х40 + ЗХ48 +... =
^(l+^ + V° + ^4+...)(l+^4 + ^ + ...)= ,
(19.14)
что согласуется с (19.11). Поэтому если мы можем найти два алгебраически независимых инварианта степеней 8 и 24, то мы решим нашу задачу. Ответ будет таков: любой инвариант этой группы является многочленом от 0 и <р. Далее весовые функции W2(x, у) и 1Г3 (х, у) кодов Хэмминга и Голея имеют степени 8 и 24 и инвариантны относительно этой группы. Поэтому мы можем выбрать Q=W2(x, у) и <p=IF3(x, у). (Нетрудно проверить, что они алгебраически независимы.) На самом деле, удобнее работать с инвариантом
<р' = W'3 (х, у) = й?3 (%’ y)S~ W'3 (х’ = х*у* (х*—у^, (19.15)
чем с самим инвариантом W3(x, у). Таким образом, мы доказали следующую теорему, открытую Глисоном в 1970 г.
Теорема За. Любой инвариант группы является многочленом от W2(x, у) (выражение (19.3)) и W'3(x, у) (выражение (19.15)).
Это дает нам решение также и нашей первоначальной задачи.
Теорема ЗЬ. Любой многочлен, удовлетворяющий уравнениям (19.7) и (19.8), является многочленом от W2(x, у) и W'3(x, у).
И, наконец, мы охарактеризовали весовую функцию четного са-модуального кода.
Теорема Зс. (Глисон [486].) Весовая функция любого четного самодуального кода является многочленом от W2(x, у) и ^'г(х,У).
Другие доказательства этой теоремы даны Берлекэмпом и др. [129], Бруе и Энгехардом [201] и Фейтом [424] (см. также Асс-мус и Мэттсон [47]). Но приведенное здесь доказательство пред-
ставляется наиболее содержательным и наиболее легким для понимания и обобщения.
Заметим, что показатели 8 и 24 в знаменателе выражения (19.11) помогли нам угадать степени базисных инвариантов.
Такая ситуация типична, что побуждает использовать этот метод. Начинаем с группы матриц 'З, вычисляем сложную с виду сумму, представленную в выражении (19.9), и упрощаем результат. Все сложности чудесным образом пропадают, оставляя окончательное выражение, похожее на формулу (19.11) (хотя не всегда столь простое — точный вид окончательного выражения приводится в § 19.3). Это выражение подсказывает нам, как найти степени базисных инвариантов.
Упражнение. (3). (Глисон [486; 129, 883].) Используя описанный выше метод, показать, что весовая функция любого двоичного самодуального кода представляет собой многочлен от Wi(x, у)=х2+у2 и
W'2(x, y) = W1-{Х- У-4- $ = х2у2(х2—у2)2. (19.16)
[Указание. Согласно упражнению (38) гл. 1 веса всех кодовых слов должны делиться на 2. Группа, порожденная преобразованием 7\ и преобразованием, задаваемым матрицей
I1 °).
\0 — 1/
имеет порядок 16 и ряд Молина 1/(1— %2) (1—X4).]
Нахождение базисных инвариантов. В общем случае нахождение базисных инвариантов является более простой задачей, чем нахождение функции Ф(20. При этом можно либо использовать весовые функции кодов, обладающих подходящими свойствами, как в описанном выше примере, либо находить базисные инварианты усреднением, используя следующий простой результат (доказанный в § 19.3).
Теорема 4. Если f(x)=f(xi,...,xm)—произвольный многочлен от '.т переменных и ^ — конечная группа (т^т) -матриц, то многочлен
f"(x)=7^rS Aof(x)
является инвариантом, где А с f(x) обозначает многочлен, полученный применением преобразования А к переменным многочлена [.
Конечно, f(x) может равняться нулю. Ниже будет приведен пример использования этой теоремы.
Применение теоремы 3. Чтобы показать силу теоремы Зс, воспользуемся ею для нахождения весовой функции [48, 24]-кода КВ. Согласно теоремам 7, 8, 25 гл. 16 это четный самодуальный код с минимальным расстоянием 12. Следовательно, весовая
функция этого кода, представляющая собой однородный много-член степени 48, имеет вид:
W(x, у) = х48 + Л12х36^12 + ... . (19.17)
Коэффициенты при х41у, х46у2,... ,^у11 равны нулю. Здесь А12 — неизвестное нам число кодовых векторов веса 12. Замечательно, что раз мы знаем выражение (19.17), то весовая функция кода полностью определяется теоремой Зс, ибо теорема Зс утверждает, что W(x, у) должен быть многочленом от W2(x, у) и W'3(x, у). А так как W(x, у) —однородный многочлен степени 48, W2— однородный многочлен степени 8 и U7'3 — однородный многочлен степени 24, то этот многочлен должен быть линейной комбинацией многочленов W62, W32W'3 и (U7'3)2.
Таким образом, теорема Зс утверждает, что
W(x, y)^a0We2 + aiW3W’3 + a2(W'3)2 (19.18)
для некоторых действительных чисел я0, аг, а2. Раскрывая выражение (19.18), имеем
W (х, у) = а0 (х48 + 84х44 у4 ф- 2946х40 у8 ф-...) ф-
ф- а± (х44 у4 + 38х40 у8 +...) ф- а2 (х40 у8 —...), (19.19)
и, приравнивая коэффициенты в выражениях (19.17) и (19.19), получаем, что
а0=1; аг =—84: й2 = 246.
Следовательно, W (х, у) определяется единственным образом. Подставляя значения а0, аъ а2 в выражение (19.18), находим, что
W (х, у) = х48 ф-17 296х38 у42 + 535 095х32 у16 ф- 3 995 376х28у 20 ф-
ф- 7 681 680х24 у24 ф- 3 995 376х20 у28 ф- 535 095х16 у32 ф-
ф-17 296х12 у36 ф- у48. (19.20)
Поскольку минимальное расстояние этого кода равно наибольшему возможному значению, то полученное выражение называется экстремальной весовой функцией (с. § 19.5). Непосредственное вычисление этой весовой функции потребовало бы нахождения веса каждого из 224~ 1,7-107 кодовых слов, т. е. значительной работы даже для вычислительной машины.
Конечно, метод теории инвариантов также требует иногда значительных алгебраических вычислений, хотя предыдущий пример мы и смогли проделать вручную. Но читатель наверняка найдет этот метод полезным, когда мы приведем второй пример, в котором полностью продемонстрированы все преимущества алгебры.
Очень простой пример. Согласно теореме 13 гл. 5 весовая функция самодуального кода над GF(q) удовлетворяет уравнению
^. = Ц7(х, у). (19.21)
\ V q V q /
Задача: найти все многочлены, удовлетворяющие уравнению (19.21).
Для решения этой задачи поступаем, как и прежде. Уравнение (19.21) утверждает, что многочлен W(x, у) должен быть инвариантным относительно преобразования
Т3: заменить ( * ) на А х j, где
А = -^Р (19.22)
Уд \1 -1/
Далее А2=1, и поэтому W(x, у) должен быть инвариантным относительно группы ^2, состоящей из двух матриц I и А.
Чтобы узнать, сколько инвариантов существует, вычислим ряд Молина Ф(Х), воспользовавшись выражением (19.9). Находим, что
det (I — XI) = (1— X)2;
/1----к \
। я Vя I
det(I —XA) = det| 1-1—X2;
I х i . X I
. \ T7 TT J
ф (%) = —- ( - - + —2— =----------1, (19.23)
2 \ (1 — Z)2 1 — V/ (1 —X)(l—Z2)
что даже проще, чем формула (19.11). Формула (19.23) говорит о том, что могут существовать два базисных инварианта степеней 1 и 2 (показатели степеней знаменателя). Если мы сможем найти алгебраически независимые инварианты степеней 1 и 2, скажем, g и h, то из выражения (19.23) получим, что любой инвариант группы З'а является многочленом от g и h.
На этот раз для нахождения базисных инвариантов мы воспользуемся методом усреднения. Усредним многочлен х по.группе, т. е. применим теорему 4 к многочлену f(x, у) = х. Матрица 1 оставляет х, конечно, без изменения, а матрица А преобразует х в (1/)/q) (х-J- (q—1) £/). Следовательно, среднее
Их,
(х + (<7— 1) У)
; (Уд + 0 (*+(/? - Оу) 2/7
является инвариантом. Конечно, при умножении J(x, у) на любое число снова получается инвариант, и поэтому мы можем разделить Цх, у) на число (’|/—^,+ 1)/2 У q и выбрать
g = x + (Vq — 1)у
(19.24)
в качестве базисного инварианта степени 1. Чтобы определить инвариант степени 2, усредним по группе многочлен х2 и получим
2
х2 + — (x + (q— 1)< д
Чтобы упростить это выражение, вычтем из него многочлен ((g+l)/2?)g2 (который, конечно, Также является инвариантом) и разделим на соответствующую константу. Полученный таким образом многочлен h=y(x—у) и представляет собой желаемый базисный инвариант степени 2.
Наконец, надо показать, что g и h алгебраически независимы: для этого надо показать, что ни одна из сумм вида
(19.25)
i. i
не равна тождественно нулю (где Сц — комплексные числа, не равные одновременно нулю) при разложении g и h по степеням х и у. Это можно увидеть, рассматривая старшие члены. (Старшим членом многочлена является член, который выписывается
первым при использовании естественного упорядочения, иллюстрируемого выражениями (19.15), (19.20), (19.24).) Таким образом, старшим членом g является х, старшим членом h является ху, а старшим членом g^ii является x'+iyi. Так как различные слагаемые в сумме (19.25) имеют различные старшие члены, то эта сумма может равняться нулю, только если все коэффициенты а, равны нулю. Следовательно, g и h алгебраически независимы.
Итак, мы доказали следующую теорему.
Теорема 5. Любой инвариант группы Sz, или, что эквивалентно, любой многочлен, удовлетворяющий уравнению (19.21), или, что эквивалентно, весовая функция любого самодуального кода над GF(q) представляет собой многочлен от g=x+ (]/ q— —1)1/ и h= (х—у)у.
В этом месте читатель должен воскликнуть: «Стоп!» и указать, что самодуальный код всегда имеет четную длину и поэтому каждый член в весовой функции должен иметь четную степень. Но в теореме 5 g имеет степень 1.
Таким образом, мы использовали не все, что мы знаем о коде. Весовая функция W(x, у) должна также быть инвариантна относительно преобразования:
заменить ( ) на В( х
\ У J \ У
где
В = °'|=—I.
\ 0—1/
Это условие исключает члены с нечетными степенями. Поэтому функция W(x, у) инвариантна относительно группы .%, порожденной матрицами А и В и состоящей из матриц
I, А, —I, —А.
Читатель легко может доказать сам, что новый ряд Молина имеет вид
(%3 W ~ !ф.92 W + ф.% (—^)} =
= —(---------———4------------------! = — ----. (19.26)
2 I (1—X)(l—X2) , (1 + Х)(1—X2) J (1-Х2)2
Теперь имеются два базисных инварианта, оба второй степени (что соответствует показателям степеней в знаменателе выражения (19.26)), скажем, g2 и h или эквивалентная более простая пара g*=x2+(q—1)у2 и h=y(x—у). Итак, имеет место следующее утверждение.
Теорема 6. Весовая функция любого самодуального кода над GF(q) является многочленом от g* и h.
Общий план решения. Как показали рассмотренные нами примеры, решение поставленной задачи с помощью теории инвариантов распадается на два этапа.
Этап I. Превращение условий задачи (т. е. свойств кода) в алгебраические ограничения на многочлены (т. е. на весовые функции) .
Этап II. Использование теории инвариантов для нахождения всех возможных ’многочленов, удовлетворяющих этим ограничениям.
19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
Группы матриц. С помощью заданной совокупности Аь ...,АГ невырожденных (myjn)-матриц можно образовать группу умножая матрицы друг на друга всеми возможными способами. Таким образом, группа S содержит матрицы I, Аь А2,..., ..., А^г,..., A2Ai-1A2-1A3, ... Будем говорить, что группа S порождается матрицами Аь ...,АГ. Конечно, группа S может быть бесконечной, и в этом случае описанная здесь теория инвариантов прямо неприменима. (Однако см. Дьедонне и Керрол [375], Рэл-лис [1087] и Вейль [1410].)
Пр и м ер. Покажем, что группа Sb порожденная матрицами
с которой мы встречались в § 19.2, действительно имеет порядок 192. Существенный момент заключается в обнаружении того (при случайном умножении матриц друг на друга), что Si содержит матрицы
J2=f1 °V E = (MJ)3 = -!-±J-(1 °);
\0 — 1/ ' /2 \0 11
E2 = i/1 °); R = MJ2 М = (° ’Y \0 11 \1 0/
Поэтому Si содержит матрицы
“С ±?)’ “С о)’ “~{1' г’
образующие подгруппу <Ж порядка 16. Отсюда легко видеть, что группа Si является объединением 12 смежных классов по подгруппе Зёр.
^=и (19.27).
где матрицы аь ..., а6 соответственно равны
/1 0\ /1 0\ 1 /1 1\ 1 /1 1\
\0 1/’ \о i)’ /2\Г- — 1)’ /2 V — ij‘ 1 /1 i\ 1 /1 i\ .
/2 \1 —ij’ V2 \i 1/ ’
a7 = Tja1,a12 = rja6 и tj = (1 + 0/1^2. Таким образом, группа состоит из 192 матриц вида
iff1 °Y тр/° 'Л''-?—Г ₽ \ (19.28)
\0 aj 1 \а 0/ /2 \а — а р J
и ict, ре{1, i, —1, —i}.
Для проверки достаточно убедиться в том, что каждая матрица из семейства (19.28) может быть представлена как произведение степеней матриц М и J; что произведение двух матриц вида (19.28) имеет такой же вид и что матрица, обратная любой матрице из семейства (19.28), принадлежит этому же семейству. Следовательно, семейство матриц (19.28) является группой, которая порождается матрицами М и J. Таким образом, группа действительно совпадает с семейством (19.28).
Мы подробно разобрали этот пример, чтобы подчеркнуть, как важно начать с досконального изучения группы. (Другой возможный подход к изучению группы см. в [201; с. 160—161].)
Инварианты. Процитируем Германа Вейля [1409]: «Теория инвариантов возникла в середине XIX столетия 'отчасти подобно Минерве: взрослая дева, одетая в сияющие доспехи алгебры, она выпрыгнула из Юпитеровой головы Кэли». Теория инвариантов стала одним из ведущих направлений математики XIX столетия, но вышла из моды после работы Гилберта (см. Фишер [431] и Рейд [1108]). В последнее время, однако, интерес к ней возродился в связи с применениями в алгебраической геометрии (Дьедон-не и Керрол [375], Мамфорд [976]), физике (см., например, Агра-вала и Белинфант [7] и ссылки, приведенные там), комбинаторике (Дубиле и др. [381], Рота [1125]) и в теории кодирования ([883, 894, 895]).
Имеется несколько различных типов инвариантов, но здесь инвариант определяется следующим образом.
Пусть 'З представляет собой группу, состоящую из g комплексных (т'Х.т)-матриц Ai,...,Ag, где (i, k)-& элемент матрицы Аа равен Другими словами, 3 — группа линейных преобразований переменных ...,хт, состоящая из преобразований
Т(а):заменить xt на х[ге) = (19.29)
ь=1 где «=1, 2,... ,g.
Имеет смысл точно описать, как многочлен /(x)=|f(M.....*т)
преобразуется матрицей Аа из группы 3. Преобразованный многочлен имеет вид
А«о/:(х) = /:(х[“>,..., х^’),
где каждое хг(“> заменяется выражением 2mk=iawi,kXk.
Другой способ описания этого преобразования состоит в представлении х— (xi,..., хт)т в виде вектора-столбца. Тогда f(x) преобразуется в многочлен
Аяо/(х) = /(Аах), (19.30)
где Аа х — обычное произведение матрицы и вектора. Можно проверить, что
Во(Ао/: (х)) = (A B)of (х) = f (АВх). (19.31)
(1 2\
] преобразует x2i+x2 в (xi + + 2х2)2—х2.
Определение. Инвариантом группы ‘З называется многочлен /(х), который остается неизменным при действии любого линейного преобразования из группы 3. Другими словами, /(х) — инвариант 3, если Аао f(x) =/(Аах) =if(х) для всех a—l,...,g.
гт гт ет 1/Ю\ / — 1 0X1
Пример. Пусть ^4 = |( j )• { 0 j )| —группа по-
рядка g=2. Тогда х2, ху и у2 являются однородными инвариантами степени 2.
Даже если $(х) не является инвариантом, то, как указывалось в § 19.2, его среднее по группе является таковым.
Теорема 4. Пусть f(x) — произвольный многочлен. Тогда многочлен
g
f(x) = —Аао7(х) (19.32)
а=1
является инвариантом группы 3.
Доказательство. Любая матрица Ар ^3 преобразует правую часть выражения (19.32) в сумму
g
— (АаAp)of (х) (согласно (19.31)). (19.33)
Так как матрица Аа пробегает всю группу S’, то при фиксированной матрице Ар произведение Аа Ар также пробегает всю группу. Следовательно, выражение (19.33) равно
g у J] Avof(x), v=I
что совпадает с )(х). Таким образом, f(x) —инвариант. •
В более общем случае любая симметрическая функция от g многочленов А[С if(x),..., Agof(x) является инвариантом S.
Ясно, что если f(x) и h(x) — инварианты S, то f(x)+h(x), f(x)h(x) и cf(x) (с — комплексное число) также являются инвариантами. Это эквивалентно утверждению о том, что множество
инвариантов группы которое мы обозначим через У(^), образует кольцо (см. с. 189).
Одна из основных задач теории инвариантов заключается в описании кольца Так как преобразования группы 'З не изменяют степень многочлена, то достаточно описать однородные инварианты (ибо любой инвариант представляет собой сумму однородных инвариантов).
Базисные инварианты. Наша цель-—найти «базис» для инвариантов 3, т. е. найти множество базисных инвариантов таких, что любой инвариант может быть выражен через элементы этого множества. Существуют два различных типа базисов, которые можно было бы искать.
Определение. Многочлены fi (х),..., fr(x) называются алгебраически зависимыми, если существует многочлен р от г переменных с комплексными коэффициентами, не равными одновременно нулю, такой, что р(Цх),...,/г(х))^0. В противном случае fi (х),..., f, (x) называются алгебраически независимыми. Следующая теорема представляет собой фундаментальный алгебраический результат.
Теорема 7. (Джекобсон [687], т. 3, с. 154.) Любые т-|-1 многочленов от т переменных алгебраически зависимы.
Первый тип базиса, который мы могли бы искать, представляет собой множество т алгебраически независимых инвариантов fi (х),..., fm(x). Такое множество в самом деле является «базисом», так как по теореме 7 любой инвариант алгебраически зависит от и поэтому является корнем некоторого много-
члена от fi,..., fm. Существование такого базиса обеспечивает следующая теорема.
Теорема 8. (Бернсайд [211, с. 357].) Всегда существует т алгебраически независимых инвариантов группы 3.
Доказательство. Рассмотрим многочлен
g
П if ’AaOXj)
а=1
от переменных /, хь. ..,хт. Так как одна из матриц Аа —единичная, то значение t—является нулем этого многочлена. Если этот многочлен разложить по степеням t, то его коэффициенты являются инвариантами в силу замечания, следующего непосредственно после доказательства теоремы 4. Следовательно, Xi — алгебраическая функция от инвариантов. Аналогично каждая из переменных х2, ...,хт является алгебраической функцией от инвариантов. Далее, если число алгебраически независимых инвариантов равнялось бы то т независимых переменных хь
...,хт были бы алгебраическими функциями от т переменных, что приводит к противоречию. Следовательно, число алгебраически независимых инвариантов по крайней мере равно Рг. Согласно теореме 7 это число не может быть больше чем т. •
Пример. Для рассмотренной выше группы К4 в качестве алгебраически независимых инвариантов мы можем выбрать ft — = (х-^-у)2 и f2= (х—у)2. Тогда любой инвариант является корнем многочлена от и f2. Например,
Х2==Д_^+-1//-)2;
И т. д.
Однако намного удобнее описание инвариантов как множества инвариантов обладающих тем свойством, что любой
инвариант является многочленом от f1, В этом случае множество называется полиномиальным базисом (или це-
лостностным базисом) для инвариантов группы 'З. Конечно, если 1>т, то по теореме 7 будут иметь место полиномиальные уравнения, связывающие и называемые сизигиями.
Например, многочлены fi=x2; f2=xy\ fs=y2 образуют полиномиальный базис для инвариантов З4. Их связывает сизигия fifg— -f22=0.
Существование полиномиального базиса и метод его нахождения определяются следующей теоремой.
Теорема 9. (Нетер [997]; см. также Вейль [1410 с. 369].) Кольцо инвариантов конечной группы 3 комплексных (т'/т)-матриц имеет полиномиальный базис, состоящий не более чем из инвариантов степени, не превышающей g, где g— порядок группы 3. Более того, этот базис может быть получен усреднением по S’ всех одночленов вида хь^ х^^.х^1, , где полная-
степень "Lbi не превосходит g.
Доказательство. Пусть группа S? состоит из преобразований (19.29). Предположим, что многочлен
*m) = 2ce4* . . .
где се — комплексное число, является произвольным инвариантом группы 3. (Сумма берется по всем наборам е= (еь ..., ет), для которых в многочлене f(xi,...,xm) имеется ненулевой член Xie‘, ..., Xmem). Так как f(xi, ..., xm) — инвариант, то он не изменится, если мы усредним его по группе, и поэтому
Xm)=±{f(xV... x(i)) + ... + f(Xi4..„ X(g))! =
e e
Таким образом, каждый инвариант представляет собой линейную комбинацию специальных инвариантов (число которых бесконечно велико)
g
'•-SW
а=1
\ Далее 7е является (с точностью до мультипликативной константы) коэффициентом при и\е'... и^т в выражении
g
Л = £ +... +итх<ру, (19134)
а=1
где е=вг + ... +ет.
Другими словами, значения Ре представляют собой степенные суммы g величин
«1 х<1> +... + ит . «j +... + ит х$.
Любая степенная сумма Ре, е=1, 2, ..., может быть записана как многочлен с рациональными коэффициентами от первых g степенных сумм Pi, Pz,...,Pg (упражнение (3)). Следовательно, т
любой инвариант Je с индексом е = ^ e-P>g (являющийся ко-2=1
эффициентом в Ре) может быть записан как многочлен от специальных инвариантов Je таких, что ei + ...+em^g (являющихся коэффициентами в Pi,..., Pg). Следовательно, любой инвариант может быть записан как многочлен от Je таких, что Smi=iei^g. Число таких Je равно числу наборов (еь е2, ...,ет), где и ei-f-+ .. -\-em^g, а это число равно Након'ец, deg Je^g и 1е
получается усреднением xei1---xmm по гРУппе- •
Теорема Молина. Так как из теоремы 9 мы знаем, что полиномиальный базис всегда существует, то мы можем уверенно двигаться дальше и попытаться найти его, используя методы, описанные в § 19.2.
Для проверки того, что найден базис, мы используем теорему Молина (теорема 2). Она утверждает, что если аа — число линейно независимых однородных инвариантов группы ‘З степени d и Ф^(А)= ^adKd, d=0
ТО
g
Ф® П) = — V--------5-----. (19.35)
det(l-XAa) f
1
При доказательстве используется следующая теорема.
Теорема 10. (Миллер и др. [955, с. 258], Серр [1185, с. 29].)
Число линейно независимых инвариантов степени 1 равно
g
аг = — У] t race (Аа).
а=1
Доказательство. Пусть
Замена переменных Xi,...,xm, на которые действует группа S, на j/i, ..., ym, где (гц, ..., ym) = (xi, хт)Тт, переводит матрицу S в матрицу S'=TST-1. Мы можем выбрать Т так, чтобы S' была диагональной матрицей (см. Бернсайд [211], с. 252). Далее S2==S и (S')2=S', следовательно, диагональными элементами S' являются 0 или 1. Поэтому, изменив порядок переменных, мы можем считать, что
Обозначим через г число единиц на диагонали. Таким образом, So если l;g:.f:g:r, и S о y.i=0, если r+l^f^m.
Любой линейный инвариант группы S, конечно, остается неподвижным при действии матрицы S, и поэтому aI^r. С другой стороны, согласно теореме 4
g
8ог/г = —^А„ог/г
<х=1
является инвариантом S для любого i, и поэтому а-^г. •
Прежде чем доказывать теорему 2, введем некоторые обозначения. Соотношение (19.29) показывает, как преобразуются переменные хь...,хт при действии матрицы Ак . Индуцированная матрица кратности d, обозначаемая через АИЯ , показывает, как Аа преобразует все rf-кратные произведения переменных х,, а именно xdlt xd2,..., Xid~lxa,... (Литлвуд [857, с. 122]). Например, матрица
преобразует x2b XjX2 и х22 в многочлены а2х2 + 2 abxr х2 + Ь2 х2, асх2 4- (ad + be) хх х2 bdx2, с2 х2 + 2cdx1 х2 + d2 х2
соответственно. Таким образом, индуцированная матрица кратности 2 имеет вид ' - ,
’ At2 3= а
"а2
ас с2
2аЬ Ь2~
ad 4- be bd
2cd d2
Доказательство теоремы 2. Чтобы доказать формулу (19.35), заметим, что равно числу линейно независимых инвариантов степени 1 группы = {A[dla :a=l,...,g}. Согласно теореме 10
g
а-а = — t race AgO.
a=l
Следовательно, чтобы доказать теорему 2, достаточно показать, что след матрицы Aa[dl равен коэффициенту при № в выражении
„ 1 , Л , =-----------------------, (19.36)
det(/-XA„) (1- Xcoj . . . (1-Xcom)’
где coi,..., (ота — собственные значения матрицы Аа .
Соответствующей заменой переменных можно представить матрицы Аа и AK[dl в виде
(0j 0
0 -
(od 0
Ю2
АИ =
а (of-1 (02
0
и след Ак!с!1 равен сумме d-кратных произведений элементов иь
..., (От- Но это в точности равно коэффициенту при № в разложе-
нии выражения (19.36) по К. •
Стоит заметить, что ряд Молина не определяет однозначно группу. Например, существуют две группы (2X2)-матриц порядка 8, для которых
v (1-/.2)(1— л4)
(а именно группа диэдра* ДД и абелева группа ^2X^4). В действительности существуют абстрактные группы и чьи матричные представления могут быть сопоставлены попарно так, что каждое представление группы .$4 имеет тот же ряд Молина, что и соответствующее представление группы 3$ (Дейд [324]).
О Полная группа преобразований симметрии правильного «-угольника называется группой диэдра и обозначается символом (Прим, перев.)
Стандартный вид базисных инвариантов. Следующие обозначе-ния очень полезны для описания кольца (3?) инвариантов группы 3?. Обозначим множество комплексных чисел через С, и для заданных многочленов р(х), <?(х),... обозначим через С[р(х), <?(х),...] множество всех многочленов от р(х), q(x),... с комплексными коэффициентами. Например, теорема За как раз утверждает, что f (g’l) =C[i0, <р]. ч
Обозначим также через ф обычную прямую сумму. Например, утверждение вида ^(g) ф S означает, что каждый инвариант группы g может быть единственным образом представлен в виде суммы r+s, где r&R, s^S. (Примером является приводимая ниже теорема 12.)
Используя эти обозначения, мы можем теперь задать наиболее удобный вид полиномиального базиса для /"(g).
Определение. Хороший полиномиальный базис для (8?) состоит из однородных инвариантов (Г^т), где /ь...,
. ,fm алгебраически независимы и
Z(^) =C[f1,..., fm], если Z = m (19.37а)
или если 1>т,
= C[ft, .... Мф^С^,..., ^]Ф...ФЛС[Л,..„ fm]. (19.376)
Другими словами, это означает, что любой инвариант g может быть записан как многочлен от (если 1—т) или как та-
кой же многочлен плюс fm+i раз взятый другой такой многочлен, плюс... (если />т). Грубо говоря, это означает, что при описании произвольного инварианта играют роль «свободных»
инвариантов, которые могут использоваться столько раз, сколько необходимо, a играют роль «случайных» инвариантов,
каждый из которых может использоваться не более одного раза.
Для хорошего полиномиального базиса мы можем точ-
но сказать, сколько существует сизигий. Если 1—т, то сизигий нет. Если 1^>т, то имеется (•/—т)2 сизигий, выражающих произведения j>m) через fi,
Важно заметить, что ряд Молина может быть выписан только через степени. хорошего полиномиального базиса. Пусть di = = deg fb...,di= deg ft. Тогда
Ф<^(Х)=----------—, если l = m, (19.38а)
п“ ('->•)
i—1
или
т
ф^(Х)= ’т , П (1-/9 i=l
если Z>m.
(19.386)
(Это легко проверяется разложением выражений (19.38а) й (19.386) по степеням X и сравнением с выражениями (19.37а) и (19.376).) ,
Приведем для пояснения несколько примеров.
(1). Для группыиз § 19.2 многочлены Д = 1Р'2(х, у) и f2— ^W'3(x, у) образуют хороший полиномиальный базис со степенями di = 8; cf2=24. Действительно, согласно теореме За и формуле (19.11)
Z (&1) =С[Г2(х, у), W'3(x, у)]
и Фео (7) =----------------.
(1 — X8) (1 — X24)
(2). Для группы ^4, введенной выше, многочлены f1=x2; .f2= = t/2; f3=xy образуют хороший полиномиальный базис, причем di=d2—ds=2. Инварианты описываются следующим образом:
Z(^4) =С[х2, у2]фхуС[х2, у2]. (19.39)
Другими словами, любой инвариант группы может быть представлен единственным образом как многочлен от х2 и у2 плюс другой такой многочлен, взятый ху раз. Например,
(х+у)* = (х2)2 + 6х2 у2 + (у2)2 + ху (4х2 + 4г/2).
Ряд Молина имеет вид
Фу (Ч =±L L _ + _±_)__1+Щ, ,у<> 2 I (1—X)2 (1 + X)2! (1—X2)2
что согласуется с выражениями (19.386) и (19.39). Единственная сизигия имеет вид х2-у2— (ху)2. Заметим, что выбор ^—х2; f2= =ху, h=y2 уже не является хорошим полиномиальным базисом, так как инвариант у4 не принадлежит множеству
С[х2, ху] © у2 С [х2, ху].
К счастью, имеет место следующий результат.
Теорема 11. (Хочстер и Итон [657, утверждение 13]; независимо доказана также Дейдом [325].) Для инвариантов любой конечной группы комплексных (т^т)-матриц существует хороший полиномиальный базис.
(Доказательство слишком сложно, чтобы приводить его здесь.)
Таким образом, мы знаем, что для любой группы ряд Молина может быть выписан в стандартной форме, задаваемой выражениями (19.38а) и (19.386) (со знаменателем, состоящим из произведения т сомножителей вида (1—Xdi ), и числителем, состоящим из суммы степеней X с положительными коэффициентами), и что может быть найден хороший полиномиальный базис, удовлетворяющий выражениям (19.37а) и (19.376), степени которого соответствуют степеням X, встречающимся в ряде Молина.
С другой стороны, обратное утверждение несправедливо. Не всегда верно, что если ряд Молина выписан в виде (19.38а) или (19.386) (где сокращены общие сомножители и умножены числи
тель и знаменатель на новые сомножители), то может быть найден хороший полиномиальный базис для ^'(S’), степени которого соответствуют степеням X в Ф(Х). Это показывает следующий пример, приведенный Стенли [1262].
Пусть Э’б обозначает группу порядка 8, порожденную матрица
ми
/— 1 0 0\ /10 0\
I 0—1 0 I и I0 1 0 I -
\ 0 0—1/ \р 0 ij
Ряд Молина имеет вид
(2.) =-!--
’ (1 —X2)»
1 + X2
t. (1 — X2)2 (1 — X4)
(19.40)
(19.41)
Существует хороший полиномиальный базис, соответствующий формуле (19.41), а именно
Z (^в)=сНх2> У2> Ф **/сП'2, У2 , 24], но не существует такого базиса, соответствующего формуле (19.40).
Задача (нерешенная). (19.1). Какому виду Ф(7.) соответствует хороший полиномиальный базис и какому нет?
Один важный частный случай был решен. Шефард и Тодд [1196] охарактеризовали те группы, для которых имеют место соотношения (19.37а) и (19.38а), т. е. для которых существует хороший полиномиальный базис, состоящий только из алгебраически независимых инвариантов. Эти группы известны как унитарные группы, порожденные отражениями. Полный список 37 неприводимых групп такого типа приведен в работе [1196].
Упражнение. (4). Пусть
Ре=У Уе1. е = 0, 1, 2,..., г—1
где уь ..., уп — переменные. Показать, что Ре представляет собой многочлен от Рь ..., Рп с рациональными коэффициентами. [Указание. Воспользоваться упражнением (52) гл. 8; см. также [756].]
*19.4. ОБОБЩЕНИЯ ТЕОРЕМЫ ГЛИСОНА
Все обобщенные весовые функции самодуальных кодов могут быть охарактеризованы с помощью теории инвариантов. Мы подробно разберем один пример, чтобы пояснить описанный в § 19.2 общий план решения в случае, когда достаточно трудно найти хороший полиномиальный базис. Несколько других обобщений приведено в качестве упражнений.
Полная весовая функция троичного самодуального кода. Пусть обозначает троичный [п, nfo, d] самодуальный код, который со
держит некоторое кодовое слово веса п. Соответствующим умно-жением столбцов на —1 мы можем привести код к виду, когда он содержит кодовое слово 1 = 11 1....1.,
Цель этого раздела состоит в описании полной весовой функции кода посредством следующей теоремы.
Теорема 12. Если W(x, у, г) — полная весовая функция троичного самодуального кода, содержащего вектор 1, то
W(х, у, z)geC [а12, 636] ф ре у18 С [а12, 0|, 636]
(т. е. функция "tf(x, у, z) может быть единственным образом записана как многочлен от а12, р2в, б36 плюс другой такой многочлен, умноженный на р6у18, где
а12 = а (с? 4- 8р3); р6 = а2—12&;
Vis = о6—20 с3 р3—8р6; 636 = р3 (а3—р3)3 и
а = х3 + у3 4- z3; р==3ху2\
b = х3 у3 4- х3 г3 4- У8 Z3.
Заметим, что
Т?8^а?2-64636.
(Индекс многочлена обозначает его степень.)
Доказательство. Доказательство состоит из двух этапов, описанных в § 19.2. --
Этап I. Предположим, что типичное кодовое слово содержит а нулей, Ъ единиц и с двоек. Так как самодуальный код, содержащий вектор 1 = (1 ... 1), то
u-и= 0 (mod 3) -4 31 (Ь + с)
(вес Хэмминга делится на 3);
и-Г=0(тос1 3) ^3|(&—с)дДЗ|& и 31с;
1-1=0 (mod3) 31 (а 4- ЬДс) 31 а.
Следовательно, функция ТД(х, у, г) инвариантна относительно преобразований
/со 0 0\ /10 0\ /1 0 0\
(о 1 о); J3 = [og)Oj; Io 1 он ю=е2:п:г/3.
\0 0 1/ \0 0 1/ \0 0 со/
Кроме того, вектор — и содержит а нулей, с единиц, b двоек,
а вектор 14и содержит с нулей, а единиц, b двоек. Следовательно, 7Г(х, у, z)1 инвариантна относительно преобразований
/1 0 0\ /0 1 0\
I о о 114 о о 1 >
\0 1 О/ \1 о о/
т. е. относительно любой перестановки ее аргументов.
Наконец согласно равенству (5.43) у, z) инвариантна также относительно преобразования
/1 1 1\
М3 = —— | 1 со со2 I •
1/3 \1 со2 со/
Эти шесть матриц порождают группу порядка 2592, состоящую из 1944 матриц вида
/1 \ /1 \
И со" МЦ сос I. s = e
\ со6 J \ cod / и из 648 матриц вида /1 \ Sv га" Р. \ соь / где 11; b, с, d^2; г=1 или 3 и Р — любая (3X3)-матрица перестановок.
Таким образом, этап I завершен; из свойств кода вытекает, что его весовая функция у, г) инвариантна относительно Группы $7.
Этап II. Этот этап представляет собой доказательство того факта, что кольцо инвариантов группы равно
С [а12> Рб’ б3б]Ф₽6 Т18 С [а12> Рб’ ^зв]-
Вначале, так как у нас имеется список всех матриц группы S’?, необходимы непосредственные вычисления вручную для получения ряда Молина в виде (19.9). Как всегда, все сложности пропадают, и окончательное выражение имеет вид
(1 —Х12)2(1 —X36)’
Это выражение подсказывает нам степени многочленов хорошего полиномиального базиса, который мы должны искать.
Далее группа S’? порождается матрицами J3, М3 и всеми матрицами перестановок Р. Ясно, что инварианты должны быть симметрическими функциями от х, у, z, степень которых кратна 3. Поэтому рассмотрим алгебраически независимые симметрические функции а, р, b и определим, какие функции от них являются инвариантами относительно преобразований J3 и М3. Например, функция р6 инвариантна относительно J3, но преобразование М3 переводит ее в —р6. Запишем это следующим образом:
J3 М3
Рвч >Ре> Рвч > Ре-
Следовательно, р26 — инвариант. Далее
М3 1 J3 1 М3 i
« *-^-^-(а + 2р) —у^(аф 2сор)^->— («-|-2со2р),
поэтому другим инвариантом является многочлен
а12 = а {а + 2р) (а + 2 со р) (а + 2 со2 р) = а (а2 4- 8р3).
Затем
J3 Mg
TiS* > Т18» Т184 ’ Т18>
и поэтому p6yi8 инвариант. Наконец
AAq 1 Jo 1 iWq С
р <—*—~(а—р)<-->—27(0—СОр)(а—со2р) Уз ' уз Уз
приводит к инварианту
бзе = р3 (о—р)3 (о—со р)3 (а—со2 р)3 = р3 (а3—р3)3.
Сизигия у218=сх312—64б3б легко проверяется, и можно показать, что ai2, ₽2б, 6зб алгебраически независимы. Таким образом, многочлены ^1 = 012; f2=P2e; /з=бзб; /ч=1РбТ18 представляют собой хороший полиномиальный базис для кольца ^(Sy), и теорема доказана. •
Замечание. Без предположения о том, что код содержит вектор из всех единиц, теорема (принадлежащая Мак-Элису (R. J. Me Eliece)) становится значительно более сложной ([883, § 4.7], Мэллоус и др. [892]) (см. также упражнение (5)).
Применения теоремы 12. Для троичного кода Голея (выражение (19.6)) Ж=—(5«12+р2б). Для [24, 12, 9] симметричного ко-6
да Плесе из гл. 16
сиУ = — а2+— Oi2₽l + — + — Mis- ' 144 12 8 ‘1 6 432 6 27 1 6 Г18
С помощью теоремы 12 были также получены полные весовые функции для симметричных кодов Плесе длины 36, 48 и 60 (см. Мэллоус и др. [892]).
Другие обобщения. Следующие упражнения содержат дальнейшие теоремы подобного типа. Здесь не приводятся некоторые результаты для весовой функции Ли самодуального кода над GF(7) (Мак-Вильямс и др. [883, § 5.3.2], Мэллоус и Слоэн [894]), для различных разделенных весовых функций — (см. Мэллоус и Слоэн [895]), для бивесовой функции и совместной весовой функции (§ 5.6) двоичных самодуальных кодов [883, § 4.9, 5.4.1]. Значительно меньше известно о полной весовой функции и весовой функции Ли самодуального кода над GF(q) (см. [883, § 5.3.1, 5.3.2] и приведенную выше теорему 6.
Весовые функции Хэмминга кодов типов (i) и (ii) теоремы 1 описываются теоремой Зс и упражнением (3). Два других типа кодов описываются следующим образом.
Упражнения. (5). (Глисон [486], Берлекэмп и др. [129], Фейт [425], [883].) Весовая функция Хэмминга самодуального
кода над GF(3) представляет собой многочлен от W^(x, у) (выражение (19.5)) и
W’6(x, r/) = X(ttz4(Xi y)3-We(x, y)) = ys(x*-tfp. (19.42)
[Указание. Группа, порожденная матрицами
имеет порядок 48 и ряд Молина 1/(1—i?.4) (1—Я12)-]
(6) . ([883].) (а). Весовая функция Хэмминга самодуального кода над GF(4), веса всех слов которого делятся на 2, представляет собой многочлен от f—x2 + 3y2 и g—y2(x2—у2)2. [Указание. Соответствующая группа имеет порядок 12.] Весовая функция Хэмминга [6, 3, 4]-кода, рассмотренного в примере (Е9), равна f3—9g. Приведенный на с. 503 гл. 16 [30, 15, 12]-код имеет весовую функцию Хэмминга f15—45f12g+585/9g2—2205f6g3 + + 1485/3g4—3249g5.
(b). [2m, т]-код над GF (4), веса всех слов которого четны, формально самодуален. Если же он самодуален, то у него имеется двоичная порождающая матрица.
(7) . Весовая функция Ли для GF(5). Пусть — самодуальный код над GF(5) с весовой функцией Ли
Х(х, у, z)= <“> <“) z*, (“),
где /о (и) — число нулей в векторе и; /](и) — число элементов ±1, а /2 (и) — число элементов ±2 (см. с. 146 гл. 5). Тогда S? (х, у, z) является многочленом от Л, В и С, где
(19.43)
A = x2 + YZ;
В = 8х* YZ—2x2 Y2 Z2 + Y3 Z3—х (У5 + Z5);
С = 320 х6 Y2 Z2 — 160х4 Y3 Z3 + 20х2 У4 Z4 +
+ 6У5 Z5—4х (У5 4- Z5) (ЗЗх4—20 х2 YZ + 5У2 Z2) У10+Z10;
У = 2у, Z.- 2z.
[Указание. Группа имеет порядок 120, см. [883, § 5.3.2] и Клейн [768, с. 236—243].] Следующие примеры иллюстрируют этот результат:
Векторы, порождающие код
Весовая функция Ли
{12}
{1 0 0 1 3 3, 0 1 0 3 1 3,
0 0 1 3 3 1}
{1 12200000 0, 000010012 2, 000001021 3, 141414141 4, 242043010 0}
А
А3--— В
8
А5—-А2В + — С
8 256
(8) . (Фейт [424], Мэллоус и Слоэн [895].) Предположим, что п — нечетное число и что — двоичный [п, (п—1)/2]-код, который содержится в коде, дуальном ему; и веса всех слов которого делятся на 4. Примерами таких кодов являются уменьшенные [7, 3, 4]-код Хэмминга и ;[23, 11, 8]-код Голея с весовыми функциями
Ф7 = х1 + 7№ г/4; (19.44)
Та3 = х23 4- 506х15 у8 + 1288хи у12 + 253х7 у1в. (19.45)
Тогда п должно иметь вид 8т±1. Если п=8т—1, то весовая функция кода представляет собой элемент из
<р7 С [Г2 (х, у), (х, у)] ф у23 С [Г2 (х, у), W' (х, у)], (19.46)
в то время как при п=8т + 1 весовая функция кода 7? представляет собой элемент из •
xC[W2(x, у), W’3(x, г/)] ф ф17 С [W2 (х, у), IF' (х, f/)], (19.47)
где
ф17 = х17 + 17x13zy4+ 187x9zy8 + 51x5zy12 (19.48)
является весовой функцией [17, 8, 4] -кода 7(3>17, найденного Плесе [1058]. Вывести отсюда, что весовые функции [31, 15, 8] и [47, 23, 12] KB-кодов равны соответственно
—14 <р7 IF' (х, у) + у23 IF2 (х, у);
-у-{—253<p7IF2(x, у^х, t/) + T23(7IF2(x, r/)3-41 IF;(x, у))}.
Соответствующие теоремы для двоичных самодуальных кодов с весами, кратными 2, и для троичных самодуальных кодов см. в работах Мэллоуса и др. [892, 895].
(9) . Разделенные весовые функции. Предположим, что 7? — четный самодуальный [2m, т]-код, содержащий кодовые слова 0т1т и 1т0т и обладающий тем свойством, что число кодовых слов с (wb, wR) = (j, k) равно числу слов с (wL, wR)=t(k, j). (Здесь wL и wR обозначают веса левой и правой половин слова, см. с. 151 гл. 5.) Такой код «уравновешен» относительно своей середины, и деление его на две половины вполне естественно. Тогда разделенная весовая функция (х, у, X, У) кода 7? (см. с. 151 гл. 5) представляет собой многочлен от т)8, 016 и у24, где
т]8 = х4Х4 + х4Г4Ч-1/4Х4 + г/4Г4+12х2г/2Х2Г2; (19.49)
016 = (х2 X2—у2 Г2)2 (х2 Г2—у2 X2)2; (19.50)
y24 = x2i/2X2F2(x4—t/4)2(X4—К4)2. (19 51)
(10) . Примеры разделенных весовых функций. Будем использовать обозначение для определенных коэффициентов при записи ЗР, и вместо выражения
а (ха уь Xе + х“ Xd Yс + хь уа Xе Yd + хъ уа Xd Yc
будем писать следующую строку таблицы: с/о х у X Y # а а b с d 4 ,
в которой соответственно указаны коэффициент, показатели степеней и число членов такого типа. Сумма произведений первого и последнего столбцов равна полному числу кодовых слов. Используя предыдущее упражнение, получить разделенные весовые функции, приведенные на рис. 19.1 (взять из соотношений (16.57)
Код & с/о х у X Y
[8, 4, 4]-код Хэмминга Пв 1 12 4 0 4 0 2 2 2 2 4 1
6 is 1 —2 4 8 0 4 4 6 2 6 2 4 4 4 4 4 4 1
724 1 —2 4 10 2 10 2 10 2 6 6 6 6 6 6 4 4 1
[24, 12, 8]-код Голея 1 132 495 1584 12 0 12 0 10 2 6 6 8 4 8 4 6 6 6 6 4 4 4 1
[48, 24, 12] КВ-код 1 276 3864 13524 9016 125580 256335 950544 1835400 3480176 24 0 24 0 22 2 14 10 20 4 16 8 20 4 12 12 18 6 18 6 18 6 14 10 16 8 16 8 16 8 12 12 14 10 14 10 12 12 12 12 4 8 8 4 4 8 4 4 4 1
Рис. 19.1. Разделенные весовые функции четных самодуальных кодов
канонические формы порождающих матриц для этих кодов).
(11) . Предположим, что П — проективная плоскость порядка п, где n=2(mod4) (см. с. 68 гл. 2). Пусть А= (аг-3) обозначает (п2 + п-|-1) X (n2 + n+1) -матрицу инцидентности П, где 0^=1, если i-я прямая проходит через /-ю точку, и ац=О в противном случае. Пусть <g2 обозначает двоичный код, порожденный строками матрицы А, и пусть код 77* получен из "JF добавлением общей проверки на четность.
(i) . Показать, что если п=2, то —[7, 4, 3]-код Хэмминга.
(ii) . Показать, что в общем случае <&* представляет собой jn2 + n + 2, (п2 + п + 2), и+ 2^ четный самодуальный код.
(iii) . Отсюда вывести, что не существует проективной плоскости порядка 6. [У к а з а н и е. Следует из теоремы Зс, так как 8144]. Заметим, что результаты упражнения (8) применимы к весовой функции кода <ё>. Весовая функция гипотетической проективной плоскости порядка 10 обсуждалась Ассмусом и др. [43, 48], Мак-Вильямс и др. [888] и Мэллоусом и Слоэном [895].
Задача (нерешенная). (19.2). Пусть — двоичный код, веса всех слов которого делятся на 4 и параметры которого равны [п, п/2] для четного п и [п, (п—-1)/2] для нечетного п, причем ‘g’S'S’1. Охарактеризовать бивесовую функцию кода
19.5. НЕСУЩЕСТВОВАНИЕ НЕКОТОРЫХ ОЧЕНЬ ХОРОШИХ КОДОВ
В этом разделе теорема Зс используется для получения верхней границы (теорема 13) для минимального расстояния четных самодуальных кодов. Затем будет показано (следствие 16), что эта верхняя граница достижима лишь при небольших значениях п. Используемый при этом метод обобщает приведенное в § 19.2 вычисление весовой функции [48, 24, 12] KB-кода. Аналогичные результаты справедливы и для других типов самодуальных кодов, описываемых теоремой 1.
Пусть обозначает [п, п/2, d] четный самодуальный код, имеющий весовую функцию W(x, y)=xn+Adxn-dyd+ .... Согласно теореме Зс W(x, у) является многочленом от 1К2(х, у) и 1Е'3(х, у), который может быть записан как
м
W(x, у) = у arW2(x, yy-3rW^x, y)r, (19.52) r=0
где n=8/ = 24p+8v, v = 0, 1 или 2. Предположим, что р,+ 1 = = [и/24] + 1 коэффициентов а± в выражении (19.52) выбраны так, что
W (х, у) = х" + Л*ц+4 х"~4'х~4 у4и+4 + ... = A W (х, у)*, (19.53) т. е. щ выбраны так, что в многочлене W(x, у)< равно нулю максимально возможное число старших коэффициентов. Ниже будет показано, что это условие однозначно определяет Многочлен W(x, у)*, задаваемый формулой (19.53), представляет собой весовую функцию четного самодуального кода с наибольшим минимальным весом, которого мы надеемся достичь, и называется экстремальной весовой функцией.
Если существует код с весовой функцией W(x, у)*, то он имеет минимальное расстояние d*=4p + 4, пока коэффициент А*4 +4 в
(19.53) случайно не окажется нулем, в этом случае d*^4p+8. Но этого не происходит.
Теорема 13. (Мэллоус и Слоэн [893].) Число Д*4ц+4 кодовых слов минимального ненулевого веса в экстремальной весовой функции определяется следующими выражениями:
( 5 )(5ц~1)/(4И5+4)’ еслип==24н; (19.54)
— и(и — 1)(п—-2)(п—4)—если и = 24р + 8; (19.55)
4 [л! (4[л + 4)!
— п(п—2) (5|Х + 2)~'—, если и = 24 р+16, (19.56)
2 'р!(4ц + 4)1 ’ Г
и это число никогда не равно нулю. Следовательно, минимальное расстояние четного самодуального кода длины п равно самое большее 4 [и/24] +4.
Доказательство. Мы дадим здесь элементарное доказательство для случая п=24ц; другие случаи аналогичны. Ниже будет дано второе доказательство, которое применимо ко всем случаям одновременно. ,
Согласно теореме 9 гл. 6 кодовые слова веса 4ц+4 образуют 5-схему. Но нам проще вычислить параметр Р34)4и +4 соответствующей 4-схемы. Из равенства (6.9) получаем, что
М4|1+4 44ц~2(4 ц—2)! =--44ц~2(5ц —2)! +
24ц 1X1
,__1 <1/24р-4\ S(r)
• 212м г —4 / 4р, + 4 — г '
' г=4
ГДе 4 1
ЭД = П(4н + 4/—х).
/=>
Следующие тождества легко проверяются:
5 (г-4)-5 (г) S(r) 16ц —4 4ц + 4— г ’
24 ц
1 /24 ц — 4
212 К \ г — 4
г=4
Следовательно,
А&’-Н 4ш“2(4ц—2)! =
^S(r) = S(24p) (уравнение (6.14)).
44м“2(5ц —2)! _1_2-44ц~2(5ц—1)!
(4|л-1)ц!
ц!
-(4) _ (6ц—1) (5ц —2)!
*+' ц|(4ц —1)1
и поэтому
<1 (5) 4 g (4)
24g^4 4ц+4=“
5 g — 2 g — 1
Таким образом, число кодовых слов веса 4ц+ 4 определяется вы ражением (19.54). •
Известные коды, которые достигают границы, установленной в теореме 13, приведены на рис. 19.2. Что касается дважды цир-кулянтных кодов, имеющихся в этой таблице, см. рис. 16.7.
Экстремальные весовые функции для п^200 и «=256 (и, в частности, весовые функции всех кодов, представленных на рис. 19.2) приведены в работе [893]. Они были получены с помощью теоремы 15.
[п, k, d] Код
[8, 4, 4] 16, 8, 4] [24, 12, 8 [32, 16, 8] [40, 20, 8 [48, 24, 12] [56, 28, 12] [64, 32, 12] [80, 40, 16] [88, 44, 16] [104, 52, 20] Код Хэмминга Прямая сумма двух кодов Хэмминга Код Голея PM-код второго порядка или КВ-код Дважды циркулянтный код (рис. 16.7) КВ-код Дважды циркулянтный код Дважды циркулянтный код КВ-код Дважды циркулянтный код КВ-код
Рис. 19.2. Четные самодуальные коды с d=4[«/24]+4
Фейт [426] построил [96, 48, 16] четный самодуальный код, используя конструкцию типа | а+х | b + х | а + b + х|, описанную в гл. 18. Все четные самодуальные коды длины nsC24 приведены Плесе [1058] и Плесе и Слоэном [1062, 1063]. Первая невыясненная точка на рис. 19.2 соответствует значению п=72.
Задача (нерешенная). (19.3). ([1227].) Существует лн [72, 36, 16] четный самодуальный код?
Упражнение. (12). Предположим, что g’ — двоичный самодуальный код (типа (i)) длины п=8т с минимальным расстоянием 2т + 2. Показать, что число кодовых слов веса 2т + 2 равно
8m (8т — 1) (8m — 2) /Зт — 2 (2т.-р 2) (2т -|- 1) 2т \ т — 1 )
Но если п очень велико, то экстремальная весовая функция содержит отрицательный коэффициент, и граница, описываемая теоремой 13, не может быть достигнута. Как показывает следующее упражнение, это может быть доказано, методом, использованным Для доказательства теоремы 1.3.
Упражнение. (13). Предположим, что — четный самодуальный код длины п=24р, весовая функция которого совпадает с экстремальной весовой функцией W(x, у)*. Кодовые слова каждого веса образуют 5-схему (а). Показать, что параметр W4,4u+8 для 4-схемы, образованной кодовыми словами веса 4р,+8, равен
(4 р. — 1) (6 р, — 1) /5 р — 2 \ /5 [1 — 1 \_
р \р — 1/ \ р + 1 /
/5 р — 3\ 6р— 1 /5р — 2\ / 20 р — 4 \ / /4 р -|- 4 \
\р-1/Ф р \р-1Д 4 }/\ 4 J
(Ь). Вывести отсюда, что Д*4ц+в<0 для достаточно больших ц.
Другое, более мощное доказательство использует следующий результат.
Теорема 14. (Борман—Лагранж.) (См. Уиттекер и Ватсон [1414, с. 186], Голдстейн [520], Гуд [533], Сэк [1137—1139].) Пусть f(x) и Ф(х) — функции, аналитические в окрестности точки х=0, причем Ф (0) =й=0. При условии, что уравнение х=>еФ(х) определяет х однозначно в некоторой окрестности нуля, функция f(x) при достаточно малых е может быть следующим образом разложена в ряд по степеням е:
/(X) = /(0) + V [f (а)Ф(а)г]а=в. r!dar-'
(19.57)
(Штрих обозначает дифференцирование.)
Чтобы применить эту теорему к экстремальной весовой функции, заменим вначале в выражении (19.52) х на 1, а у4 на х. Тогда 1У2(х, у) превращается в f (х) = 1 + 14х+х2, а W'3(x, у) превращается в g'(’x)=x(l—х)4. Для простоты предположим, что п кратно 24 и поэтому v=0 и / = 3р.; два других случая доказываются аналогично. Приравнивая (19.52) 'и (19.53), получаем, что
Ц 6ц
IF*=VcJ(x)3M-3rg(x)r=l+ £ А\гхг. (19.58) г=0 л=Щ-1
Разделив на f(x)^, имеем
ц 6ц
£л;,у. (19.59)
r=0 r=M+l
где
g(x) = х(1 — х)4_____х
f (х)3 (1 + 14х-|-х2)3
для малых х.
Используя теорему 14, разл'ожим теперь f(x)~3^ по степеням s=g(x)/f(x)3 с
Ф/.л- * _ (1 + 14х+х2)з
J е (!— х)4
Получим, что
/(х)~3ц = 2 (19.60)
г=0 где ао= 1 и
1 d1-1 Г d /ii 1л . 21-зн (1 + 14х+х2)3г’
аг =--------- —(14-14х + х2) • —!‘—— =
г! dZ-1 (1— x)4r J^o
— Зр, dr~l Г (14 + 2x) (1 + 14x + x2)3'-3**-1 r'- dxT~l (1 — x)ir
(19.61)
для r=l, 2, ... Сравнивая (19.59) и (19.60), убеждаемся, что
ar = ar для r = 0, 1, . . . , ц, (19.62)
и поэтому
оо 6|_1
arf(x)3il-3rg(xy=- Y А*4гхг. (19.63)
r=U4-I r=u+l
Таким образом, мы доказали следующую теорему.
Теорема 15. ([893].) Экстремальная весовая функция четного самодуального кода длины п=24р определяется выражением (19.58), где коэффициенты аг задаются в явном виде равенствами (19.61) и (19.62). Кроме того, приравнивая коэффициенты при х^ ’- и х^+2 в (19.63), получаем, что
/44ц4-4= —аЩ-1 (19.64)
и
Ац-р = —аи+2 +(4р + 46) (19.65)
Теперь из (19.61) непосредственно следует, что ац+1<0 и Д!,,4ц+4>0, и это дает другое доказательство верхней границы теоремы 13. Но следующий коэффициент становится отрицательным.
Следствие 16. (Мэллоус и др. [891].) /4*4ц+8<0 для всех достаточно больших п—24ц.
Доказательство. Несколько утомительных алгебраических выкладок показывают, что из (19.61) вытекает ограниченность величины | ац+г/ац-и | для больших значений ц, и поэтому из равенства (19.65) следует, что Л*4щ.8<0. Подробности опущены. •
Приведенное доказательство показывает, что коэффициент впервые становится отрицательным, когда значение п
близко к 3720. Действительно, при п=3720 вычисления на ЭВМ показали, что
W (х, у)* = %3720 _|_ Д*24 д.3096 ^624 _|_ ^3092 ^28 ...,
где Л* = 1,163.... 10170; Л* =—5,848...-10170 uz-t Ozo
и Л! > 0 для значений 632 i < 3088.
Подобные же рассуждения могут быть использованы, чтобы показать, что следствие 16 справедливо также и для случаев и— =24р + 8 и л=24|х+16. Другой способ доказательства того, что отношение | сщ+сдя1 ограничено, приведен в работе [891]. Он использует метод перевала для разложения в ряд выражения внутри квадратных скобок в (19.61).
Итак, мы рассмотрели только коды типа (ii) из теоремы 1. Соответствующие результаты имеют место и для кодов других типов, причем доказательства аналогичны.
Теорема 17. Минимальное расстояние самодуального кода над GF(q), веса всех слов которого кратны t, равно самое большее d*, где
д t d*__
2 2 2[n/81 + 2 (19.66)
2 4 4[n/24] + 4 (19.67)
3 3 3 [и/12] + 3 (19.68)
4 2 2[n/61 + 2 (19.69)
Но для всех достаточно больших п не существует кодов, достигающих этих оценок.
Заметим, что при п-^оо из границы Мак-Элиса и др. (теорема 37 гл. 17) для двоичных кодов со скоростью 1/2 получаем, что rf/n <0,178, а из границы Элайеса (теорема 34 гл. 17) для кодов со скоростью 1/2 получаем, что d/n< 0,281 (для кодов над GK (3)) и d/п < 0,331 (для кодов над Gf(4)). Таким образом, выражения (19.67) и (19.68) являются более сильными оценками, в то время как (19.66) и (19.69) хуже указанных оценок.
Оценка (19.66) достигается самодуальными кодами длины 2, 4, 6, 8, 12, 14, 22, 24 и не достигается для других значений (см. доказательство в [893, 1058, 1062, 1063] и Уорда (Н. N. Ward) [1389]). Кроме того, для п=10, 16, 18, 28 и, возможно, для других значений «([893, 1389]) существуют формально самодуаль-ные коды, удовлетворяющие (19.66).
Граница (19.68) достигается для значений п=4, 8, 12 (код Голея), 24, 36, 48 и 60 (КВ и симметричные коды Плесе), 16 и 40 (код с порождающей матрицей [I | Н], где Н — матрица Адамара; частное сообщение Уорда) и, возможно, для других значений (см. [892]). Гораздо меньше известно о кодах, достигающих границы (19.69) (см. [1478]).
Задача (н е р е ш е н н а я).'(19.4). Чему равно наибольшее п, для которого существуют коды, достигающие границ, приведенных в теореме 17?
В работе [891] доказан также следующий более сильный результат. Для любого фиксированного числа Ь существует п0(Ь) такое, что все самодуальные коды длины, большей чем По(Ь)г имеют минимальное расстояние, меньшее чем d*—b, где d* определяется теоремой 17.
19.6. ХОРОШИЕ САМОДУАЛЬНЫЕ КОДЫ СУЩЕСТВУЮТ
В этом разделе различными способами подсчитывается число самодуальных кодов и показывается, что некоторые из них удовлетворяют границе Варшамова—Гилберта. Для простоты рассматривается только двоичный случай (общий случай см. в работах Мэллоуса и др. [892], Плесе [1053, 1054], Плесе и Пирса [1061] и также Зе-Хяна [1457]).
Если ‘g’cz'g’-1-, то назовем код слабо самодуальным.
Теорема 18. (Мак-Вильямс и др. [887].) Пусть n=2t, и предположим, что —(двоичный) слабо самодуальный [п, &]-код, причем /г^1. Тогда число самодуальных [п, Г]-кодов, содержащих код <ё!, равно i—k
П(2‘+1). (19-70)
i=i
Доказательство. Обозначим через on.m, k^m<Zt, число слабо самодуальных [п, т] -кодов, которые содержат код IF. Найдем рекуррентную формулу для on,m- Слабо самодуальный [и, т]-код SE), содержащий может быть пополнен до слабо самодуального [п, т+1]-кода, содержащего IF, присоединением любого вектора из кода 3)^, не принадлежащего 3). Представим 3)± как объединение 2n^m/2m смежных классов кода ЗУ.
S-L = S) U (hi + 25) U - U (К + 25),
где 1=2п~2т—1. Всего имеется I различных пополнений кода ЗЬ, а именно 3) U (hj+S>), где /=1, 2, ..., I. В каждом из этих пополнений имеется 2т+1Чг—1 |[ц, т]-подкодов ЗУ, содержащих %?, так как таково число ненулевых векторов в 3) U (hj+S>), ортогональных коду <ё‘. Таким образом, для значений k^m<Zt имеет место формула
пп—2т _, •
On, т+1 — °п, т---~ " • (19.71)
gzn-f-1—R_ |
Так как исходное значение опл=1, то получаем (19.70). •
Следствие 19. Полное число двоичных самодуальных ко-
дов длины п равно
п/2—1.
П(2г+1)-
(19.72)
Доказательство. В качестве кода в теореме 18 выберем код
{О ... О, 1 ... 1}. •
Следствие 20. Пусть v —: двоичный вектор четного веса, отличный от 0 ... 0 и 1 ... 1. Число самодуальных кодов, содержа-щих вектор v, равно
п/2—2
П(2г + 1). (19.73)
i=l
Теорема 21. ('[887].) Существуют длинные двоичные само-дуальные коды, достигающие границы Варшамова—Гилберта.
Доказательство. Получается стандартным способом из следствий 19, 20 (см. теорему 31 гл. 17). О
Соответствующее рассуждение показывает, что аналогичный результат имеет* место для самодуальных кодов над GF(q) (см. [1061]). Самым трудным оказался случай четных самодуальных кодов, и за доказательством следующего результата читатель отсылается к работе [887].
Теорема 22. Пусть п кратно 8. Предположим, что — двоичный слабо самодуальный [и, k] -код, веса всех слов которого делятся на 4. Число [п, п/2]-четных самодуальных кодов, содержащих код <ё>, равно
п/2—/г—1
2|"| (2f+l)- (19.74)
z=0
Следствие 23. Полное число четных .самодуальных кодов длины п равно
п/2—2
2 Г1 (2г+1)- (19.75)
г О
Число таких кодов, содержащих фиксированный вектор V, отличный от 0... 0 и 1... 1, веса wt(v)=0 (mod 4), равно
п/2—з
2 П (2f + 1). (19,76)
i=0
Теорема 24. (Томпсон [1320а]; см. также [887].) Существуют длинные четные самодуальные коды, достигающие границы Варшамова—Гилберта.
В следующих шести упражнениях через Фпл обозначен класс всех двоичных слабо самодуальных [п, k] -кодов, а через Ф'п,ь — подкласс в Фп,&, состоящий из кодов, содержащих вектор (1 ... 1), где 0<C//sCn/2 (см. [1063]).
Упражнения. (14). Пусть п — четное и $еФ\£. Показать, что число кодов из Ф'пл (k^s), содержащих равно
*Г-1 1 2n-2s-2/)
П 2У+1-1 '
/=0
(15) . Показать, что полное число кодов в Ф'л,й равно
если п — четное, и равно нулю, если п — нечетное.
(16) . Пусть ^£®ri,s—Ф'п.б- Показать, что число кодов з Фпл—Ф'тьй (k^s), содержащих' код равно
оп—2s—2/ 1
2 I I------------- если n—четное,
2'-l /=1
k__s
П2«—2s—2/4-1 _ J
---------------если n—нечетное.
2'-1 ’
(17) . Показать, что полное число кодов в Фп,&—®'n,k равно k
ъ Г“1 2”~2; — 1
2 I I----------, если п—четное,
2'~1
I—а 2п~ 2;'+’ — 1
I I---------——, если п — нечетное.
/=' 27-*
(18) . Пусть п — четное и ^еФп,8—Ф^. Показать, что число кодов в ФпЛ (k>s), содержащих код <ё>, равно
(2"~ft-s —!) р (2„_2s_2/_ р / р (2/_ р /=1 / /=1
(19) . Показать, что для четного п полное число кодов в Фп,ь. равно
(2n~k — 1)П (2n-2/—1) / П(2' — 1).
/=1 / /=1
(20). Показать, что сумма весовых функций ных кодов длины п (для четного и) равна
всех самодуаль-
(п/2)—2
П (2'41)
/=1
2(n/2)-l(A.„ + ^) + J1^n) 2 I i
х" 1 уг
Та же сумма для четных самодуальных кодов (если п делится на 8) равна
(п/2)—з
П (2/+1)
/=о
2("/2)-2(хп+ту<пЬ"^г
Ы \ I /
4 I i
(21) . ([1053, 1054].) Пусть ‘ё’ — слабо самодуальный [п, k]-код над GF(3), наибольший в том смысле, что не содержится ни в каком слабо самодуальном коде той же длины и большей мощности.
(а). Показать, что п/2, k= (п—1)/2, (п—2)/2, если п = 0 (mod 4), если п—нечетное, если п = 2 (mod 4).
(b). Показать, что число таких наибольших кодов равно (п-2)/2
2 П (Зг + 1), если /г = 0 (mod 4), i=l
(n-l)/2
П (Зг + 1), если п—нечетное,
г=1
п/2
П(Зг + 1). если п = 2 (mod 4).
1=2
(с). Показать, таким образом, что самодуальный код существует, если и только если п кратно 4.
(22) . ([1054].) Показать в общем случае, что самодуальный [п, п/2]-код над* GF(q) существует тогда и только тогда, когда выполняется одно из следующих условий: (i) оба числа q и п являются четными; i(ii) (mod 4) и п — четное число; (iii) q= s3 (mod 4) и n делится на 4.
(23) . ([1054].) Показать, что если выполнены условия предыдущего упражнения, то число [п, п/2] самодуальных кодов над GF(q) равно
(п/2)—1 ь П +
г=1
где 6 = 1, если q — четное, и 6=2, если q — нечетное.
Задача (нерешенная). (19.5). Сколько неизоморфных самодуальных кодов длины п существует? (Для небольших значений п см. [1058, 1059, 1062, 1063, 892] .)
ЗАМЕЧАНИЯ К ГЛ. 19
Имеется много параллелей между самодуальными кодами и некоторыми типами решетчатых укладок сферы. Большинству теорем этой главы соответствуют аналогичные теоремы и для решеток, см. Берлекэмп и др. [129], Бруэ [200], Бруэ и Енгехард [201], Конвей [302—306], Ганнинг [570] Лич [804, 805, 807—809], Лич и Слоэн [810], Мэллоус и др. [891], Милнор и Хьюзмоллер [962], Нимейер [992] и Серр [1184].
Система ALTRAN (Браун [205], Холл [579]) для вычислений с рациональными функциями очень облегчает действия с весовыми функциями на вычислительной машине.
Частично эта глава основана иа обзоре [1231]; см. также [1228]. Другой работой, в которой рассматриваются самодуальные коды, является статья [141]. Более подробно о самодуальных и формально самодуальных кодах над GE(4) см. в работе [1478] ‘.
1 См. также [392 6*], в которой построен самодуальный [12, 6, 6]-код над GF (4). (Прим, перев.)
Глава 20
Коды Голея
20.1. ВВЕДЕНИЕ
В этой главе мы завершим изучение кодов Голея, показав, что их группами автоморфизмов являются группы Матье и что эти коды единственны. Этих важных кодов всего четыре: [23, 12, 7] и [24, 12, 8] двоичные коды и [11, 6, 5] и [12, 6, 6] троичные коды, обозначенные через 2?2з, ®24, ^и, Э’ы соответственно.
Свойства двоичных кодов Голея. Мы начнем с кода (а не с кода ®2з), так как его группа автоморфизмов больше и, следовательно, он является более фундаментальным. Код [24, 12, 8] может быть определен либо с помощью любой из порождающих матриц, приведенных на рис. 2.13 и в выражениях (16.41), (16.48) или (20.6), либо с помощью конструкции |a+x|b+x|a+b+x| (теорема 12 гл. 18), либо добавлением общей проверки на четность к коду ^з1 *- Код ’g724 самодуален (лемма 18 гл. 2 или теорема 7 гл. 16), веса всех его кодовых слов делятся на 4 (лемма 19 гл. 2, теорема 8 гл. 16), и его весовой спектр равен:
I: 0 8 12 16 24
Лг: 1 759 2576 759 1
(20.1)
Слова веса 8 кода ’g724 образуют блоки системы Штейнера 3(5, 8, 24) (следствие 23 гл. 2; см. также следствие 25 и теорему 26 гл. 2). Эти кодовые слова называются октадами, и это же название используется также для множества номеров тех восьми координат, в которых кодовое слово отлично от нуля. Пусть С?~ = {%!, х2, ..., Хе} — октада; обозначим через число октад, содержащих- элементы xlt Xj, но не содержащих x,+i, > Xi (0^ ^/^i^8). Эти числа не зависят от выбора октады (У (теорема 10 гл. 2) и приведены в виде таблицы на рис. 2.14. Ниже мы покажем (теорема 9), что система Штейнера 3(5, 8, 24) единственна. Так как существует порождающая матрица кода ^24, все строки которой имеют вес 8, то отсюда следует, что октады системы 3(5, 8, 24) порождают код ®24- Этот факт используется в § 20.6 для доказательства того, что и сам код ®24 единствен (теорема 14). Кодовые слова веса 12 кода ®24 называются додекадами.
Группа автоморфизмов кода ®24 содержит группу PSL2(23) (теорема 10 гл. 16), но на самом деле равна гораздо большей группе Матье Л124 (теорема 1). Группа Матье представляет собой 5-транзитивную группу порядка 24-23-22-21-20-48=244823040, и она порождается группой PSL2(23) и дополнительной перестановкой W, задаваемой выражением ((20.8).
1 Либо переходом от самодуального [12, 6, 6] -кода над GF (4) к двоично-
му каскадному коду [3926*]. (Прим, ред.)
Совершенный [23, 12, 7]-код 5?2з может быть получен вычеркиванием одной координаты из кода S?24 (не имеет значения, какой согласно следствию 11 гл. 16) или как квадратично вычетный код, порождающий идемпотент которого равен любому из многочленов в выражении (16.10), а порождающий многочлен задается выражением (16.4). Весовой спектр этого кода имеет вид:
i: 0 7 8 11 12 15 16 23
Ai. 1 253 506 1288 1288 506 253 1
Слова веса 7 кода ^2з образуют блоки системы Штейнера 5(4, 7, 23), и эти слова порождают код ®2з- Как код так и система 5(4, 7, 23) единственны (следствие 16 и упражнение (14)).
Полная группа автоморфизмов кода 32ъ представляет собой группу Матье ЛР23 (следствие 8). Она является 4-транзитивной группой порядка 23-22-21-20-48= 10200960.
Алгоритмы декодирования для этих кодов описаны в § 16.9.
Свойства троичных кодов Голея. Код ^12 [12, 6, 6] может быть построен либо с помощью любой из порождающих матриц, приведенных в выражениях (16.25), (16.61) или (20.13), либо добавлением общей проверки на четность к коду 3?ц. Код ^12 самодуален (теорема 7 гл. 16), и поэтому веса всех слов этого кода делятся на 3. Минимальное расстояние кода равно 6 (по теореме 1 гл. 16), следовательно, весовая функция Хэмминга и полная весовая функция определяются соотношением (19.6). Опорные множества (ненулевые позиции) кодовых слов веса 6 образуют 132 блока системы Штейнера 5(5, 6, 12) (см. рис. 16.9). И код ^12, и система 5(5, 6, 12) единственны (теорема 20 и упражнение (18)).
Группа автоморфизмов этого кода Aut (^12)+ (с. 475 гл. 16) содержит группу, изоморфную P5L2(11) (теорема 12 гл. 16), но на самом деле она изоморфна гораздо большей группе Матье Afi2 (теорема 18). Эта группа является 5-транзитивной группой порядка 12-11 • 10-9-8=95040.
Совершенный [11, 6, 5]-код может быть получен либо вычеркиванием одной координаты из кода ^12 (снова не имеет значения, какой), либо как квадратично-вычетный код, порождающий идемпотент и порождающий многочлен которого задаются выражениями (16.5) и (16.16). Весовая функция Хэмминга и полная весовая функция кода приведены в работе Мэллоуса и др. [892]. Опорные множества кодовых слов веса 5 образуют блоки системы Штейнера 5(4, 5, 11). Код и система 5(4, 5, 11) единственны (следствие 21 и упражнение (18)).
20.2. ГРУППА МАТЬЕ Л1,4 ’ ’
В этом разделе определяется группа Матье М24 и показывается, что код ®24 инвариантен относительно этой группы.
Обозначения. Координаты кода ^2з будем нумеровать элементами множества {0, 1, ..., 22}, а координаты кода S?24 —
элементами множества £2= {0, 1, 22, оо}, где последняя коор-
дината соответствует общей проверке на четность. Пусть также множества
<2 = {1, 2, 3, 4, 6, 8, 9. 12, 13, 16, 18};
N = {5, 7, 10, И, 14, 15, 17, 19, 20, 21, 22}
обозначают квадратичные вычеты и невычеты по модулю 23.
Выберем конкретный способ задания ^з как циклического кода с порождающим идемпотентом
0(х) = £ х1 (20.4)
ieN
и порождающим многочленом
(1 + х + х20) 0 (х) = 1 + х2 + х4 + х5 + х6 + х10 + х11. (20.5)
Тогда код ^24 получается добавлением к коду 3?2з общей проверки на четность, и его порождающая матрица имеет вид
1
(20.6)
П
где П представляет собой (23х23)-циркулянтную матрицу, первая строка которой равна в(х). Строка матрицы (20.6) с номером г+1 равна |хЮ(х)|1|, где 0^л^22.
Согласно теореме 10 гл. 16 код ®24 инвариантен относительно группы P5L2(23), которая имеет порядок -у--23-(232—1)=6072 и порождается следующими перестановками элементов множества £2 (выражение (16.30)):
S: i —> i Т" 1 j
V: i 2г;
(20.7)
Другими словами,
S=(oo)(0 1 2 3 . . . 22);
iz=(oo)(0) (1 2 4 8 16 9 18 13 3 6 12)-
•(5 10 20 17 11 22 21 19 15 7 14);
Т = (со 0) (1 22) (2 11) (3 15) (4 17) (5 9) (6 19)-
•(7 13) (8 20) (10 16) (12 21) (14 18).
Определение. Группа Матье М24 является группой, порожденной перестановками S, И, Т и W, где
в
oo
W переводит
0, 0 в оо, (I \2 „
— г) если i^Q, 2 J
(2г)2, если lEEN,
(20.8)
i
i
в
в
или, что эквивалентно, № = (оо 0) (3
17 6 14 2 22 4 19 18 11)-
10 9 20 13 21 16).
15) (1
•(5 8 7 12
Теорема 1. Код 324 инвариантен относительно группы Л424-
Доказательство. Нам надо только проверить, что код 3^4 инвариантен относительно перестановки W. Легко видеть, что
к/(|0(х)|1|)=|е(х)|1| + 1е^24;
W (I X 0 (х) I 11) = I х2 е (х) 4- х110 (х) + X20 О (х) 11 |е$24;
W (I х22 0 (х) I 1 I) = 10 (х) + х 0 (х) + х20 0 (х) + X22 0 (х) I 01 е $24.
Теперь мы воспользуемся тождеством
Vr = W2 = (oo 0) (18 21) (1 22 16 20 6 10 13 15 12 17)-
(2 19 3 14 8 5 9 11 4 7). (20.9)
Так как К(|х'0(х)) 11) = )x2i0(x)111, то получаем, что
W (| х2г 0 (х) | 11) = (W) (| х10 (х) 111) = (W2) (| хг 0 (х) 111), и поэтому W переводит каждую строку (20.6) в кодовое слово 3^24- ®
20.3. ГРУППА М24 5-ТРАНЗИТИВНА
Теорема 2. Группа М24 5-транзитивна.
Доказательство. Группа М24 содержит перестановку U= IF-2:
t/ = (oo) (0) (3) (15) (1 18 4 2 6) (5 21 20 10 7)-
•(8 16 13 9 12) (11 19 22 14 17).
Поскольку W=TU2, группа Af24 порождается перестановками S, Т, U, V. Перемножая эти порождающие перестановки, мы находим перестановки со следующими длинами циклов: 1-23, I2- II2, 13-73, 14-54, 18-28, 212 и 46. (Например, таковыми являются перестановки S, V, US2, U, (SU)3, Т и (S13?!/2)3.)
Перестановки с длинами циклов 1-23 и 212 показывают, что группа М24 транзитивна. Используя действие сопряжения (и упражнение (1)), мы видим, что стабилизатор любой точки (т. е. подгруппа, оставляющая эту точку неподвижной) содержит перестановку типа 1-23, и поэтому он транзитивен на оставшихся
23 точках. Следовательно, группа М24 2-транзитивна. Вновь посредством действия сопряжения убеждаемся, что стабилизатор двух точек содержит перестановки типов I2-112 и 13-73, и поэтому он транзитивен на оставшихся 22 точках. Следовательно, группа Л124 3-транзитивна. Аналогично стабилизатор трех точек содержит перестановки типа 13-73 и 14-54, и поэтому он транзитивен на оставшихся 21 точках. Следовательно, группа М24 4-транзитивна. Подгруппа, оставляющая неподвижным множество из 4 точек как единое целое, содержит перестановки типов 14-54 и 46, и поэтому транзитивна на оставшихся 20 точках. Следовательно, группа М24 транзитивна на 5-элементных подмножествах множества Q. Подгруппа, оставляющая неподвижным любое 5-элементное подмножество как единое целое, содержит перестановки типов 14-54 и 18-23, которые индуцируют перестановки типов 5 и 13-2 на 5-элементных множествах (снова надо рассмотреть действие сопряжения и использовать упражнение (1)). Так как последние две перестановки порождают полную симметрическую группу на 5 элементах (упражнение (2)), то группа Л124 5-транзитивна. •
Упражнения. (1). Пусть л, о — перестановки, причем л выписана в виде произведения непересекающихся циклов. Показать, что перестановка, сопряженная с л посредством о, т. е. о-1ло, получается из л применением перестановки о к символам л. Например, если л = (12) (345); сг= (1524), то о-1лс>= (54) (312).
(2) . Показать, что любая перестановка на множестве {1, 2, ..., п} порождается перестановками (12... и) и (12).
(3) . Показать, что и 67—1 Vt7= V3.
(4) . Показать, что Т— IF5 и поэтому Л124 порождается перестановками S, К и W.
(5) . Показать, что U переводит х->х3/9, если х—0, оо или хе eQ, и х—>9х3, если хе;А.
(6) . Показать, что группа М24 транзитивна на октадах. [У к а-з а н и е. Воспользоваться теоремой 2.]
20.4. ПОРЯДОК ГРУППЫ М24 РАВЕН 24-23-22-21 -20-48
Вначале нам понадобится одна лемма. Пусть Г — группа перестановок на множестве S, и пусть Т — подмножество S. Перестановка у, уеГ, переводит Т в y(T) = {y(t) : feT}. Множество всех образов у(Т)< называется орбитой Т под действием Г и обозначается Тг. Пусть Гт обозначает подгруппу Г, относительно которой множество Т инвариантно (т. е. если feT и уеГт, то у(/)еГ).
Лемма 3. |Г| = | Гт| • | Гг|.
Наиболее важным является случай, когда Т состоит из одной точки.
Доказательство. Для перестановок у, бе Г получаем, что равенство у(Т)=8(Т) выполняется тогда и только тогда, когда
уб-’еГу. Таким образом, мощность орбиты |7Т| равна числу смежных классов группы Г по подгруппе Гг, что равно |Г|/.|Гг|.
Теорема 4. |Л124| =24-23-22-21-20-48=244823040.
Доказательство. Предположим, что {a, b, с, d, е, f, g, h} — октада. Обозначим через Г подгруппу Л124, относительно которой эта ©ктада инвариантна, а через Н — подгруппу Г, которая вдобавок оставляет неподвижной девятую точку i. Так как группа Л124 транзитивна на октадах (упражнение (6)), то согласйо лемме 3|Af24| =759-|Г|1. Вычисление |Г| проводится в четыре этапа.
(i) . Мы покажем, что Н — подгруппа группы Г индекса 16, т. е. ||Г| = 16|Н\.
(ii) . Рассматривая действие Н на оставшихся 15 точках, мы покажем, что Н изоморфна подгруппе GL(4, 2) и поэтому <|GL(4, 2) |=2б160.
(iii) . Рассматривая затем действие Н на октаде, мы получим, что Н содержит подгруппу, изоморфную знакопеременной группе <s$8. порядок которой равен 81/2=20160.
(iv). Следовательно, 7/a^GL(4, и поэтому |Я| =20160;
|Г[ = 16-20160 и |M24| =759-16-20160=244823040.
Этап (i). Если относительно перестановки л из группы Aut(®’24) инвариантно множество из 5 точек, то инвариантна и октада С, содержащая эти точки (в противном случае wt(<S?+ + л(С?))<8). Группа Л124 содержит перестановку типа 1-3-5-15, например I7S11. Октада, содержащая цикл длины 5 из этой перестановки, инвариантна относительно нее и поэтому должна быть объединением циклов длины 3 и 5. В таком случае, учитывая сопряженные с 67S11 перестановки и упражнение (1), мы можем предположить, что группа Г содержит перестановку Л= (abode) X ^(fgh) (i) (jkl... x). Группа M24 содержит также перестановку типа'12-2-4-82, например L/S5. Октада, содержащая одну из неподвижных точек и цикл длины 4, должна быть объединением циклов длины 4, 2 и 1. Следовательно, Г содержит перестановку, относительно которой множество точек октады {а, ..., h} инвариантно и которая на оставшихся 16 точках {i, j, k, х} представляется двумя циклами длины 8. Таким образом, группа Г транзитивна на точках {I, х}, и поэтому индекс подгруппы Н, оставляющей
неподвижной точку i, в группе Г равен 16 в силу леммы 3.
Этап (ii). Пусть 7? обозначает код длины 15, полученный из кодовых слов S724, имеющих нули в 9 координатах {а, Ь, i}. Так как код ^24 самодуален, мы точно знаем те проверочные соотношения в таком коде, которые связывают эти 9 координат — имеется ровно одно такое соотношение, соответствующее октаде {а, Ь, ... .... h}. Следовательно, код 7? имеет мощность 2I2./2S = 24. Кроме того, код 7? содержит только слова веса 8 и 12, причем вес 12 невозможен, ибо в противном случае код S724 содержал бы кодовое слово веса 20. Поэтому 7? представляет собой [15, 4, 8]-код, содержащий
1 Напомним, что число октад в коде g?24 равно 759. (Прим, ред.)
15 кодовых слов веса 8. Из упражнения (7) следует, что эквивалентен симплексному коду с порождающей матрицей
1 1 1 1 1 1 1 1 о о о о о о 0\
1 14 100001 1 1 1 0 0 0 |
1100110011001 101
10101010101010 1/
(20.11)
и имеет группу автоморфизмов GL(4, 2).
Каждая нетривиальная перестановка группы Н индуцирует нетривиальную перестановку на ЯЗ. (Так как если h, h'^H индуцируют одну и ту же перестановку на й7, то перестановка h~lh' оставляет неподвижными 16 точек, а согласно упражнению (8) только тождественная перестановка в группе Л124 может оставлять неподвижными 16 точек.) Таким образом, группа Н изоморфна подгруппе GL(4, 2).
Этап (iii). Пусть Н2 — группа перестановок на октаде {а, ... ..., h}, индуцированная группой И. Тогда 5-я степень перестановки %, которая была определена на этапе (i), влечет за собой (fgh)^H2, и, рассматривая сопряженные (fgh) перестановки, можно получить все циклы длины 3. Следовательно, Н2 содержит знакопеременную группу (которая согласно упражнению (9) порождается циклами длины 3). в
Эта теорема имеет ряд важных следствий.
Следствие 5. Группа Л124 представляет собой полную группу автоморфизмов кода $F24-
Доказательство. Пусть M=Aut (S?24). Мы знаем, что М^М24. Доказательство теоремы 4 не изменится, если Л124 заменить на М. Следовательно, |М| =244823040 и М=М24. •
Следствие 6. Порядок подгруппы М24, относительно которой инвариантна октада, равен 8-8!
Следствие 7. GL(4, 2)^^8.
(Следствия 6 и 7 непосредственно следуют из доказательства теоремы 4.)
Определение. Группа Матье М23 состоит из перестановок группы Л124, оставляющих неподвижной некоторую точку из Q. Таким образом, Л123 является 4-транзитивной группой порядка 23-22-21.20-48.
Следствие 8. Группа Л123 представляет собой полную группу автоморфизмов кода $23.
Упражнения. (7). Пусть g7 — произвольный двоичный [15, 4, 8]-код, содержащий 15 кодовых слов веса 8. Показать, что й7 эквивалентен симплексному коду с порождающей матрицей вида (20.11). Вывести отсюда, что группой автоморфизмов кода й7 является группа GL (4.2). [Указание. Воспользоваться теоремой 24 гл. 13.]
(8). Показать, что перестановка л из группы М24, которая оставляет неподвижными 16 точек (каждую в отдельности), и при этом другие 8 точек образуют октаду, должна оставлять непод
вижными все 24 точки. [Указание. Предположить, что л остав-ляет неподвижными точки 8, оо, и при этом множество t= {О, ..., 7} — октада. Тогда октада s такая, что |s П £| = 4 переводится перестановкой л в октаду s или £+s. Рассматривая все такие октады s, показать, что л — тождественная перестановка.]
(9). Показать, что знакопеременная группа s£n порождается всеми циклами (ijk) длины 3.
(10). Показать, что поточечный стабилизатор октады является элементарной абелевой группой порядка 16 и что он транзитивен на оставшихся 16 точках. Показать также, что поточечный стабилизатор любых 5 точек имеет порядок 48. [Указание. В первой части воспользоваться перестановкой (VS5)4, а во второй — перестановкой Л5.]
(11). Показать, что группа M2i транзитивна на додекадах. »
20.5. СИСТЕМА ШТЕЙНЕРА S (5, 8, 24) ЕДИНСТВЕННА
Цель этого раздела — доказать следующую теорему.
Теорема 9. Существует единственная система Штейнера S (5, 8, 24). Более точно, если имеются две системы Штейнера 5(5, 8, 24), обознгбшм их через и <%, то существует перестановка, действующая на 24 точках, которая переводит октады системы в октады системы ЗТ (В этом разделе октада означает блок системы Штейнера 5(5, 8, 24).)
Для доказательства удобно воспользоваться таблицей значений Хгд приведенной на рис. 2.14. В частности, из последней строки этой таблицы следует, что две октады пересекаются в 0, 2 или 4 точках. Мы начнем с нескольких лемм.
Лемма 10. (Лемма Тодда.) Если В и С — октады системы 5(5, 8, 24), пересекающиеся в 4 точках, то В + С также является октадой.
Доказательство. Пусть В= {abcdefgh}- С= {abcdijkl}, и предположим, что В + С не является октадой. Тогда октада D, содержащая точки {efghi}, должна содержать еще ровно одну точку из С и имеет, например, вид D= {efghijmn}. Аналогично октада,
держащая точки {efghk}, должна иметь вид Е= {efghklop}. Но теперь невозможно найти октаду, содержащую точки {efgik}
со-
И пересекающуюся с октадами В, С, D, Е в 0, 2 или 4 точках. Это приводит к противоречию, так как должна существовать октада, содержащая любые 5 точек. •
Лемма 11. Если известны 280 октад, пересекающих данную октаду О в четырех точках, то все 759 октад определены.
Доказательство. Согласно рис. 2.14 мы должны найти 30 октад, не пересекающихся с О и 448 октад, пересекающихся с О в двух точках, т. е. 16 октад, пересекающихся с О в двух заданных точках а и Ь.
Пусть C={xyzab...}. Помимо О имеется еще четыре октады, содержащие точки {xyza}, скажем, Аь А2, А3, А4, и 4 октады, содержащие точки {xyzb}, скажем, Вь В2, В3, В4. Согласно лемме
10 суммы Ai+Bj представляют собой октады, и легко видеть, что все они различны и являются 16 октадами, содержащими точки а и Ь. Шесть сумм Аг+А, являются октадами, не пересекающимися с О. Ясно, что они различны и что At+Aj^Bi+Bj. Так как точку а можно выбрать пятью способами, то это и дает 30 октад, не пересекающихся с О. ®
Определение секстета. Любые четыре точки abed определяют разбиение 24 точек на 6 множеств по 4 точки в каждом, называемых тетрадами и удовлетворяющих следующему свойству: объединение любых двух таких тетрад является октадой. Это множество из 6 тетрад называется секстетом (т. е. шесть тетрад). (Чтобы убедиться в этом, выберем пятую точку е. Существует единственная октада, содержащая точки {abede}, скажем, {abcdefgh}. Тогда {efgh} — вторая тетрада. Девятая точка i определяет октаду {abcdijkl} и тетраду {ijkl}. Согласно лемме Трдда {efghijkl} является октадой и т. д.)
Лемма 12. Пересечения любой октады с 6 тетрадами секстета имеют следующий вид: 3-15, или 42-04, или 24-02. (Первое из этих выражений 3-15 означает, что октада пересекает одну тетраду в трех точках, а другие пять — в одной точке.)
Доказательство. Две октады пересекаются в 0, 2 или 4 точках. ®
Лемма 13. Матрица пересечений тетрад из двух секстетов имеет один из следующих видов:
~4 0 0 0 0 0~ ~2 2 0 0 0 0~ “2 0 0 0 1 1“ “3 1 0 0 0 0~
0 4 0 0 0 0 2 2 0 0 0 0 0 2 0 0 1 1 1 3 0 0 0 0
0 0 4 0 0 0 0 0 2 2 0 0 0 0 2 0 1 1 0 0 1 1 1 1
0 0 0 4 0 0 5 0 0 2 2 0 0 0 0 0 2 1 1 0 0 1 1 1 1
0 0 0 0 4 0 0 0 0 0 2 2 1 1 1 1 0 0 0 0 1 1 1 1
_0 0 0 0 0 4 0 0 0 0 2 2_ 1 1 1 1 0 (J_ 0 0 1 1 1 1
Доказательство. Следует из леммы 12 и определения секстета.
•
Доказательство теоремы 9. Пусть (У — фиксированная октада системе Штейнера S(5, 8, 24). Идея доказательства, заключает-: в том, что однозначно определяются все октады, пересекающие в 4 точках; теорема тогда будет следовать из леммы 11. Чтобы найти эти октады, мы построим 7 секстетов ..., S7.
Пусть Xi, ..., х6 — шесть точек октады С, а х7 — точка, не принадлежащая С. Предположим, что S] — секстет, задаваемый че-
тырьмя точками {X]X2x3x4}, и пусть тетрады этого секстета являются столбцами следующей (4x6)-матрицы:
Х5 Х~ 2g Z12
Х2 Xq 2. 2g ZI3 %3 У1 ^2 2 6 ^10 4 4 ^"4 У2 *3 ^7 Дб _
Таким образом, октада С?'состоит из двух первых столбцов э4ой матрицы.
Согласно лемме 12 пересечение октады, содержащей точки {х2ХзХ4х5Х7}, с Si должно иметь вид 3-15, и поэтому, изменив соответствующим образом нумерацию точек Zi, мы можем выбрать эту октаду в виде {x2x3x4x5x7z4z8zl2}. Тетрада {х2х3х4х5} определяет секстет, который согласно лемме 13 может быть выбран в виде
S,=
2
1
1
1
3
4
5
6
3 3
1 3
4 4
5 5
2 4
2 5
2 6
6 6
Эта диаграмма означает, что тетрадами секстета S2 являются множества {х2х3х^х5}, {х1хеу1у2}, {x7z4z8z12}, {ziZsZgZia}, {z2Z6zwzl4}, {Z3Z7Z11Z15}. В этих обозначениях
Замечание. Мы описали сейчас 30 октад, не пересекающихся с октадой О. Эти октады представляют собой (i) суммы любых
двух строк матрицы
х7 z4
*8
Ч zs zs z13
Z-l Z6 z10 z14
_z3 z7 zn z15
(ii) суммы любых двух столбцов этой матрицы, (iii) суммы октад вида (i) и (ii)*>. Схематически это можно проиллюстрировать следующим образом:
Пересечение октады, содержащей точки {х1хзх4х5х7}, с обоими секстетами Si и S2 имеет вид 3-15, и поэтому эта октада может быть выбрана в виде множества {x1X3X4x5X7Z5z10Zi5}. Тетрада {xix3x4x5} определяет секстет, который можно выбрать в виде
1
1
Г 3
2 4
2 6
2 5
4 6
5'
6
4
3
3 5
5 3
6 4
Имеется по 6 октад вида (i)
и (ii) и 18 октад вида (iii). (Прим, ред.)
если воспользоваться леммой 13 и рассмотреть пересечения с 30 октадами, указанными в предшествующем замечании. Здесь мы отметим, что секстеты Sb S2 и S3 инвариантны относительно следующих перестановок точек множества {уь у2, zb z2, ..., Z15}:
П ~ (Z4 Z8 Zlz) (Z6 Z10 Zls) (Z1 Z2 'в) (Z9 ’14 Z?) (Z6 Z11 21з)>
О = (Z4 z8) (z7 zll) (Z1 22) (z13 Zl4) (26 210) (z6 Z9);
Ч> = (У1 y2)-
Октада, содержащая точки {x^x^x-j}, не может содержать ни одной из точек zb z2, zs, z4, z8, zI2, z5, zl0 или Zi5 в силу условий, накладываемых пересечениями с предыдущими октадами, и поэтому она должна иметь вид
ки о, то в качестве октады может быть выбрано множество {xlx2x3x5x7z7zgz14). Тетрада {х^гХзХь} определяет ‘ в таком случае секстет
Аналогичным способом получаем, что
1
1
2
1
13 4 5
2 6 5 4
2 4 3 6
2 5 6 3
6“
3
5
4
Далее пересечение октады, содержащей точки {х!х2х5хех7}, с S] имеет вид 24-02, и поэтому, используя перестановку л, можно предположить, что пересечение этой октады с первыми четырьмя столбцами секстета Si имеет вид 24. Поэтому в качестве этой октады мы можем выбрать множество {xiX2X5x6x7Zi2425}. Это приводит к секстету
4 4'
4 4
6 6
6 6
“113 3
113 3
2 2 5 5
2 2 5 5
Подобным образом, используя перестановку <р, в качестве октады, содержащей точки {xiX3X5x7z2}, можно взять множество {xIx3x5X7^Iz2Z4Z6}, что дает секстет
1
2
1 3
2 4
1 3
2 4
3 5 51
4 6 6
3 5 5
4 6 6
Остается показать, что все 280 октад, -пересекающих О в 4 точках, определяются секстетами Sb S7.
Если два секстета пересекаются равномерно (т. е. если матрица пересечений тетрад из этих секстетов совпадает с третьей матрицей, приведенной в лемме 13), то мы можем сложить в них соответствующие октады и получить новую октаду и новый секстет. Например, из S6 и S7 получаем
X X X X + X X X X
X X X X
X X X X
=35 секстетов, которые определяются четырьмя точками 0. Но эти секстеты дают все октады, пересекающие октаду 0 в 4 точках. в
Первоначальное доказательство Витта теоремы 9 заключается в последовательном доказательстве единственности систем Штей-’ нера 5(2, 5, 21), 5(3, 6, 22), 5(4, 7, 23) и, наконец, 5(5, 8, 24). Отправные точки этого доказательства даются в следующих упражнениях.
Упражнения. (12). Доказать единственность аффинных плоскостей 5(2, т, т2) для значений т—2, 3, 4, 5 (см. § 2.5 я теорему 11 приложения В). [Указание. Выбрать семейство из т непересекающихся блоков системы 5(2, т, т2) и назвать их «горизонтальными прямыми», а другое семейство из т непересекающихся блоков назвать «вертикальными прямыми». Точка пересечения вертикальной прямой х и горизонтальной прямой у определяется координатами (х, у). Каждый из т2—т оставшихся блоков состоит из точек вида (1, щ), (2, а2), ..., (т, а-m). Образовать ((rn2-—т) Хт) -матрицу А.(т), строками которой являются
векторы (ab а2, ат). Показать, что для значений 'т—2, 5
матрица А.(т) по существу единственна].
(13) . Доказать единственность проективных плоскостей 5(2, т+1, т2 + т+ I) для значений т==2, 5. [Указание. Так как
аффинные плоскости единственны, то их можно построить с помощью конечных полей (что приведено в § 2 приложения В). Существует единственный способ расширения такой плоскости до проективной плоскости.]
(14) . Доказать единственность систем Штейнера 5(3, 6,. 22) и 5(4, 7, 23). [Указание. Пусть Р — фиксированная точка 5(3, 6, 22). Идея состоит в доказательстве того, что блоки, содержащие точку Р, образуют систему 5(2, 5, 21), которая единственна в силу упражнения (13), а другие блоки образуют овалы (с. 321 гл. 11) в системе Штейнера 5(2, 5, 21) (см. Витт [1424] или Лун-берг [866]).]
(15) . (а). Показать, что матрица Адамара Н8 порядка 8 единственна с точностью до эквивалентности (ср. с.. 56 гл. 2). [Указание. Воспользоваться тем, что система 5(2, 3, 7) единственна.] (Ь). Показать, что матрица Адамара Hi2 единственна.
(16) . Показать, что система Штейнера 5(3, 4, 8) единственна, и, следовательно, расширенный [8, 4, 4]-код Хэмминга также единствен.
20.6. КОДЫ ГОЛЕЯ S’ss И ^24 ЕДИНСТВЕННЫ
Теорема 14. Пусть — произвольный двоичный код длины 24 с минимальным расстоянием 8. Тогда: (i) |'₽’| ^212.(ii). Если |'₽’| =212, то код эквивалентен коду Голея ^24-
Доказательство, (i). Это утверждение следует из границы линейного программирования (§ 17.4, см. также упражнение (16) гл. 17) или из границы сферической упаковки (теорема 6 гл. 1). (ii). Предположим, что |®?|=212. Тогда граница линейного программирования показывает, что спектр расстояний кода равен
Во = д24=1; В8 = В16 = 759; В12 = 2576, (20.12)
т. е. он такой же, что и у кода ^24- Преобразование Мак-Вильямс спектра (20.12), т. е. выражение (17.23), совпадает с (20.12). Следовательно, в предположении, что код содержит вектор О, весовой спектр кода согласно теореме 3 гл. 6 совпадает с его спектром расстояний.
Пусть а, b — слова кода Из формулы (см. равенство (1.16)) dist (a, b) = wt(a) + wt(b) — 2wt(a*b)
вытекает, что число wt(a*b) является четным (так как все другие члены этого равенства делятся на 4). Следовательно, каждое кодовое слово ортогонально самому себе и любому другому кодовому слову. Следующая простая лемма утверждает, что в таком случае — линейный код.
Лемма 15. Пусть А, В — взаимно ортогональные подмножества Fn, т. е.
п
'^aibi = 0 для всех (пг ... ап)€ЕЛ; (Ь^-.Ь^^В. i=l
Пусть далее |A|=2fe и |В| ^2n~h~l +1. Тогда А представляет собой линейный код.
Доказательство. Обозначим через А и В линейные оболочки множеств А и В. Ясно, что А и В взаимно ортогональны и, следовательно,
dim А + dim В^п.
Но по условию леммы dimA^fe и dimB^n—k. Таким образом, dimA = & и А—А. •
Согласно теореме 22 гл. 2 кодовые слова веса 8 в представляют собой октады системы Штейнера S(5, S, 24). По теореме 9 эта система единственна, и, как указывалось выше, она порождает код, эквивалентный S?24- Следовательно, 'S’ эквивалентен коду Голея ^24- •
Следствие* 16. Любой двоичный (23, 212, 7)-код эквивалентен коду Голея ^23-
Доказательство. Добавим общую проверку на четность и воспользуемся теоремой 14. •
20.7. ГРУППЫ АВТОМОРФИЗМОВ ТРОИЧНЫХ КОДОВ ГОЛЕЯ
В этом разделе мы покажем, что группа- автоморфизмов Aut (^12)+ изоморфна группе Матье М12. Напомним из гл. 16, что если — троичный код, то группа Antes’) состоит из всех мономиальных матриц А (матриц перестановок, ненулевые элементы которых равны ±1), которые оставляют код 'S’ неизменным, причем группа
Aut(^)+ = Aut(^)/{±I}
представляет собой фактор-группу, полученную отождествлением матриц А и —А. Таким образом, |Antes’) | =21Antes’) + |.
Обозначения. Координаты кода ^12 занумеруем символами множества Q={0, 1.. 9, X, оо}, и пусть Q={1, 3, 4, 5, 9};
N= {2, 6, 7, 8, X}. В качестве порождающей матрицы кода выберем матрицу
(20.13)
1 1 . . . 1
где П — циркулянтная (И X 11)-матрица, первая строка которой соответствует многочлену
—1—2*г+2
iP.Q iGN
т. е. является вектором (----1-------.111 — 1), где вместо
«—1» мы пишем «—». (Проверьте, что эта матрица порождает код ^12, см. с. 469.)
Из теоремы 12 гл. 16 следует, что S?i2 инвариантен относительно группы, изоморфной PSL2(11), которая порождается преобразованиями S, V и Т', где S и V — перестановки
S: i-> i + 1;
(20.14)
V: i -> 3 i,
a T' — мономиальное преобразование, которое переводит элемент, находящийся в позиции i, в позицию —• 1/i, умножив его на 1, если i=oo или ieQ, и на —1, если i=0 или isM
Кроме того, код &12 инвариантен относительно перестановки
Д = (оо) (0) (1) (2Х) (34) (59) (67) (8). (20.15)
Действительно, легко проверить, что если Wi(i=0, 1, ..., 10)' является (t+ 1)-й строкой матрицы (20.13), то
Д(ау4) = и/б(0,
Где
6 = (оо) (0) (3) (X) (19) (26) (45) (78). (20.16)
Мономиальную группу, порожденную перестановками S, V, Т' и Д, будем обозначать через М\2; мы показали, что
Аи1(^12)+ЕМ2.
Определение. Группа Матье Mi2 представляет собой группу перестановок на множестве £2, полученную из группы М'12, если не учитывать знаки элементов. Таким образом, М12 порождается S, V, Т и Д, где перестановка Т переводит элемент из позиции i в позицию —1/Y. Ясно, что группа ЛД2 изоморфна группе М'12.
Проводя доказательства, аналогичные доказательствам теорем 2 и 4, получаем теоремы 17 и 18.
Теорема 17. Группа М12 5-транзитивна и имеет порядок 12-11-10-9-8=95040.
Теорема 18. Группа M'i2 является полной группой автоморфизмов Аи1(^12)+.
Следствие 19. Группа Aut(S^n)+ изоморфна группе Матье ДЛь образованной перестановками группы М12, оставляющими неподвижной некоторую точку из Q. Группа Л4ц представляет собой 4-транзитивную группу порядка 11-10-9-8.
Упражнение. (17). Показать, что подгруппа группы М24, относительно которой инварианта некоторая додекада, изоморфна группе ЛД2.
20.8. КОДЫ ГОЛЕЯ И За ЕДИНСТВЕННЫ
Теорема 20. Любой троичный (12, З6, 6)-код эквивалентен коду g’is.
Схема доказательства. (1). С помощью границы линейного программирования находим, что максимальный код длины 12 и с расстоянием 6 содержит З6 кодовых слов и имеет такой же спектр расстояний, что и код ^12.
(2). Как и в предыдущем случае '(хотя и несколько сложнее), можно показать, что код ортогонален самому себе и, следовательно, должен быть линеен.
(3). Полное число троичных самодуальных кодов длины 12 равно No = 29-5-7-41 -61 (упражнение (21) гл. 19). Имеются два неэквивалентных [12, 6, 3]-кода, а именно код 'й’ь являющийся прямой суммой трех экземпляров [4, 2, 3]-кода =Н= 6 из гл. 1 и код 'g’s с порождающей матрицей
~ 1 1 1
1 1 1
1 1 1
♦ 1 1 1
1 — 1 — 1 —
— 1 1 — 1 —
(20.17)
Далее |AutC^i) | =23-3!(4!)3 и | Autfg^) | =2(3!)44! Согласно лемме 3 имеется N]=212-12!/23-3! (4!)3 = 29-3-52-7-11 кодов, эквгг-валентных коду '₽’ь и N2=212-12!/2(3!)4-4! = 214-52-7-11 кодов, эквивалентных коду 'gV Наконец, имеется N3=212- 12!/2|Mi2| = = 27-33-5-11 кодов, эквивалентных коду ^i2. Так как N0=Ni + + N2+N3, то мы перечислили все самодуальные коды длины 12, и поэтому код ^i2 единствен. •
Следствие 21. Любой троичный (11, З6, 5)-код эквивалентен коду S?n.
Упражнение. (18). Показать, что системы Штейнера 5(3, 4, 10), 5(4, 5, 11) и 5(5, 6, 12) единственны. [Указание. См. Витт [1424], Лунберг [866].]
ЗАМЕЧАНИЯ К ГЛ. 20
Коды Голея были открыты Голеем [506]. В этой главе были использованы следующие работы. Все, что относится к § 20.2 — 20.4 и 20.7 — см. Конвей [306]. Теорема 9 принадлежит Витту [1424], но приведенное здесь доказательство взято из работы Кэртиса [322]. Другое доказательство приведено йонссоном [699]. Лемма 10 взята из работы Тодда [1330]. В этой работе имеется список всех 759 октад. Упражнения (12), (13), (14), (16) принадлежат Витту (цит. работа), см. также Лунберг [865, 866]. Теорему 14 первым доказал Сновер [1247], но приведенное здесь доказательство принадлежит Дельсарту и Геталсу [363] и Плесе [1054]. Теорема 20 также взята из работ [363] и [1054]. Подробнее о перечислении самодуальных кодов над GF (3) см. в работе Мэллоуса и др. [892]. Для доказательства единственности кода также может быть использован метод перечисления всех кодов, хотя при этом пришлось бы рассмотреть гораздо большее количество кодов (см. Плесе и Слоэн [1063]).
Группы Матье были открыты Матье в 1861 г. ([925, 926]), и им посвящена обширная литература—см., например, Ассмус и Мэттсон [35, 36], Берлекэмп [120], Биггс [143], Конвей |[306], Кэртис [322, 323], Гарб и Менник [466], Гринберг [559], Холл [584, 590], Джеймс [689], йонссон [699], Лич [806], Лунберг [865, 866], Пейдж [1018], Расала [1095], Стентон [1264], Тодд [1329, 1330], Уорд [1388], Уайтло [1412] и Витт [1423, 1424]. Эти группы Матье являются простыми, т. е. они не содержат нормальных делителей (доказательство этого см., например, в работе Биггса [143]) и не принадлежат ни одному из известных бесконечных семейств простых 'Групп. Многие свойства группы М24 могут быть получены из кода g?24, например таким образом могут быть очень просто описаны максимальные подгруппы М24 (Конвей [306]; Кэртис [323]). Хорошим общим справочником по группам перестановок является книга Виеландта [1415].
Наконец, имеются три следующих весьма интересных вопроса, не рассмотренных в этой главе:
(i) Чудо-генератор октад Кэртиса, или MOG, [322], с помощью которого удивительным образом находится октада из системы Штейнера S (5, 8, 24), содержащая 5 заданных точек.
(11) . Диаграмма Конвея (рис. 1 в [306] или с. 41 в [322]), показывающая действие группы М24 на всех двоичных векторах длины 24.
(ill) . Решетка Лича (см. Лич [804], Конвей [302—306], Лич и Слоэн: [810]), представляющая собой очень плотную упаковку сферы в пространстве, размерности 24, построенную с помощью кода 4^24- Группа автоморфизмов этой, решетки, действительно, очень велика (см. Конвей [302, 303]).
Глава 21
Схемы отношений
21.1. ВВЕДЕНИЕ
В этой главе изложены основы теории схем отношений. Схема отношений представляет собой множество, на котором определены отношения, удовлетворяющие определенным свойствам (см, § 21.2). Целый ряд проблем в теории кодирования и в комбинаторике, таких как построение кода наибольшей мощности или построение наибольшего равновесного кода с заданным минимальным расстоянием, может быть естественным образом сформулирован в терминах построения подмножества наибольшей мощности, некоторой схемы отношений. Во многих случаях- это приводит к границе линейного программирования для подобных задач (если: воспользоваться теоремой 12).
Схемы отношений впервые были введены статистиками в связи с планированием экспериментов (Боуз и Меснер [183], Боуз и Шимамото [186], Джеймс [688], Огасавара [1007], Огава. [1008], Ямамото др. [1444], Рагхаварао [1085]), и они оказались, с тех пор очень полезными и для изучения групп подстановок (см. замечания к этой гл.) и графов (Биггс [144—147] и Деймрелл [327]). Изложенные в этой главе применения этих схем в теории, кодирования были разработаны Дельсартом [352—358, 361 и 364], В главе принят следующий порядок изложения. В § 21.2 вводятся схемы отношений и формулируются основы теории. Три наи-
•Солее важных с точки зрения теории кодирования примера, а .именно схемы Хэмминга, Джонсона и схемы, образуемые симплек-тическими формами, обсуждаются в § 21.3—21.6. Мы увидим, что код является подмножеством в схеме Хэмминга, а равновесный код является подмножеством в схеме Джонсона. Свойства подмножеств произвольной схемы отношений изучаются в § 21.7. Наконец, в § 21.8 и 21.9 рассматриваются подмножества симплекти-ческих форм и /-схемы.
21.2. СХЕМЫ ОТНОШЕНИЙ
В этом разделе излагаются Основы теории.
Определение. Схемой отношений с п классами (или отношениями) называется конечное множество X из v точек1, на котором заданы и+? отношений До, Дь ..., Rn, удовлетворяющих следующим условиям:
(i) . Каждое Д1 симметрично: (х, y)^Ri-+(y, x)^Ri.
(ii) . Для любых двух точек х, у^Х условие (х, y)^Ri выполняется точно для одного значения i.
(iii) . Ro={(x, х) :хеХ} представляет собой тождественное отношение.
(iv)’. Если (х, y)^Rh, то число точек геХ таких, что (х, г)еДь а (у, является константой с^, зависящей от чисел I, j, k,
:но не зависящей от выбора точек х и у.
Две точки х и у называются i-связанными, если (х, y')^Ri. .Другими словами, определение утверждает, что если точки х и у i-связаны, то также i-связаны точки у и х; каждая пара точек i-связана точно для одного значения i; каждая точка нуль-связана ‘С самой собой, в то же время различные точки никогда не могут быть нуль-связаны; и, наконец, если точки х и у fe-связаны, то чис--ло точек z, которые одновременно i-связаны с х и /-связаны с у, является константой с,-^.
Полезно иногда представлять схему отношений в виде полного графа, ребра которого занумерованы. Граф имеет v вершин, по одной для каждой точки из X, причем ребро, соединяющее вершины х и у, имеет номер i, если соответствующие точки х и у •i-связаны. Каждое ребро имеет точно один номер и число треугольников с фиксированным основанием с номером k, два других ребра которого имеют номера i и /, является константой djk, зависящей от i, j, k, но не зависящей от выбора основания. В частности, каждой вершине соответствует точно с-цо ребер, имеющих номера i; называется валентностью отношения Rt.
В каждой вершине этого графа имеется также петля с номером 0, соответствуюшая отношению До.
В следующих разделах будут приведены примеры схем отношений. Для теории кодирования наиболее важными являются схе-
11 Обычно называемых элементами. (Прим., перев.}
мы Хэмминга, Джонсона и схемы, образованные симплектически-ми формами.
Коэффициенты Ctjh удовлетворяют нескольким тождествам.
Теорема 1.
CUk — CHk’ С0 jh
Vh ciik ~ vi chJi>
/-о п п
Cijm ^тМ Clhl ^ihh-т=0 h=0
(21-2>
Доказательство. Последнее тождество следует из подсчета числа четырехугольников вида
, либо
I
I
Мы будем описывать отношения с помощью их' матриц смежности. Матрица смежности D, отношения (для t=0, ..., ri) представляет собой (о X о)-матрицу, строки и столбцы которой занумерованы точками множества X, определяемую следующим образом:
. ,п \ - _ [ h если (*> У)^ь
У — 1 л
I 0 в противном случае.
Определение схемы отношений эквивалентно утверждению, что-Df являются (vXv)-матрицами из элементов 0, 1, удовлетворяющими следующим свойствам:
' (i). D;—симметричная матрица.
п
(ii) . Рг = J—матрица из всех единиц. (21.3)-
i—О
(iii) . D0 = I. (21.4)-
п
(iv) . Dz D7 = ^c/JfeDfe = DJ Df, i, j = 0,..., n. (21.5> k=0
Действительно, элемент с координатами (х, у), стоящий в левой части равенства (21.5), равен числу путей вида х O_LO2_о у в графе. Кроме того, строки и столбцы матрицы Dj содержат единиц:
Рг J = J D; =vt J.
(21.6)*
Алгебра Боуза—Меснера. Рассмотрим векторное пространство состоящее из всех матриц вида 2+i=o<+Dj, сц — действительные числа. Согласно условию (i) эти матрицы симметричны. В силу (ii) матрицы Do, ..., Dn линейно независимы и размерность пространства равна /г+1. По условию (iv) замкнуто относительно умножения, причем умножение коммутативно. Кроме того, умножение ассоциативно (умножение матриц всегда ассоциативно; ассоциативность следует также из (21.2)). Эта ассоциативная коммутативная алгебра называется алгеброй Боуза— Меснера схемы отношений.
Так как матрицы алгебры симметричны и коммутируют друг с другом, то они могут быть одновременно диагонализированы (Маркус и Минк [915]), т. е. существует матрица S такая, что каждой матрице^ соответствует диагональная матрица ЛА> где
S- 1AS = Aa- (21.7)
Следовательно, алгебра полупроста и имеет однозначно определяемый базис из примитивных идемпотентов Jo, ..., Jn- Они представляют с^бой действительные (/гХн)-матрицы, удовлетворяющие условиям (см. Барроу [212], Огава [1008], Веддербарн 11393]):
J? = J., i.= 0, ..., п\ (21.8)
Jj — 0, (21.9)
2^ = 1. (21-Ю)
i0
Согласно условиям (21.3) и (21.6) матрица (l/o)J является примитивным идемпотентом, поэтому мы всегда можем выбрать
Je = —J.
V
Итак, мы имеем два базиса алгебры и поэтому выразим один базис через другой, положив
= k = 0,..., п, (21.11)
i=0
где pk(i) — однозначно определенные действительные числа.
Из соотношений (21.8), (21.9) и (21.11) получается, что
(21-12)
Следовательно, числа pk(i), i=0, ..., п являются собственными значениями матрицы D/,. Кроме того, линейная оболочка столбцов матрицы J, совпадает с i-м собственным подпространством всех матриц D/,. Обозначим через pi=rank(J,) размерность i-ro собственного подпространства, т. е. кратность собственного значения ph(i).
Обратно, чтобы выразить J; через матрицы D ь обозначим че-
рез Р действительную ((и+1)> < (и-Ы) ^матрицу
Ро(О) Pi(0) . - Pn(0)q
р = Ро ( 1) Pi(l) • • -PnU) » (21.13)i
_Ро («) Pi (и) . • Рп (п)_
и пусть *
~<7о(О) Pi (0) . - <7п(0 л
Q^p-’= МО <71(1) • - <7nU ) (21.14)
_<7о(«) <7i(«) • 9п(«)_
Будем называть Р и Q собственными матрицами схемы. Тогда
п
Jfe=^S%(z)D/’ /г=0.......п' (2115>
г-0
Теорема 2.
Po(i) = Qo(i)= И pfe(O) = t>ft; <7fe(0) = p.fe.
Доказательство. Нетривиально лишь последнее равенство. Так как J/t — идемпотент, то диагональными элементами матрицы, SJfeS (см. равенство (21.7)) являются элементы 0 и 1. Следовательно, trace(S-1JfeS) =trace Jfe=rank Jfe=p,fe.
Поскольку trace (D^ =i)6oj, из (21.15) получается, что pfe= = <?Н0). •-
Упражнение. (1). Показать, что \pk(i) |
Теорема 3. Собственные значения ph(i) и удовлетворяют следующим соотношениям ортогональности:
£ V-tPk(i)Pi(i) = vvk8kl; г=0 (21.16)<
2t’i9fe(0<7l(0 = I,Hfe 6fcl- i—0 (21.17).
Кроме того,
Pi Pi (i) = ^iQAi)> i, j = o, n. (21.18),
На матричном языке это означает, что
РтАцР = у AD; (21.19).
QT AtJ Q = v Ац, (21.20)
где A0 = diag{r>o, a,, -.., wn}; Au==diag{p0, ..., pn}.
Доказательство. Собственными значениями матрицы D/.DZ яв-ляются числа pb(i)p;(i), кратность которых равна ц,. В силу (21.5) п
V 8kl = trace (Dft Dz) = Jp-f pk (i) pt («),
i=0
что доказывает равенства (21.16) и (21.19). Согласно (21.19) Q = v Р-1 = Д~1 Ру V
что доказывает равенства (21.17), (21.18) и (21.20). *
Следствие 4. п
Pi (S) Pj (s) = £ ciJh pk(s), s = 0, ..., n.
k=0
Доказательств^. Приравняем собственные значения в выражении (21.5). •
Изоморфная алгебра ((п + 1)х(«+1))-матриц. Мы кратко отметим, что существует алгебра ((/г-|-1)Х(и-Н))-матриц, изоморфная алгебре с которой часто проще работать. Пусть
Ci 00 ci 10 • nO
ц = Ci 01 Ci 11 • • ci nl
On in • c. • binnJ
Тогда из равенства (21.2) получается, что
= (21.21)
k=0
Таким образом, матрицы Li перемножаются так же, как и матрицы D.i. Так как то отсюда следует, что Lo, ...,Ln ли-
нейно независимы. Следовательно, алгебра £8, состоящая из всех матриц вида Sni=oaiLi- (а, — действительные числа), представляет собой ассоциативную коммутативную алгебру, изоморфную алгебре при отображении Dr->Lj.
Согласно следствию 4
PLfep—1 = diag{pfe(0), .... pk (1)}, (21.22)
откуда вытекает, что Рь(0 (i=0, являются собственными значениями матрицы L/t. (Или, иначе, матрицы D/. и имеют одинаковые собственные значения, так как алгебры и 93 изоморфны). Поскольку Lfe много меньше чем D/., то числа pk(i) иногда легче найти таким способом.
Рассмотрим теперь несколько примеров.
21.3. СХЕМА ОТНОШЕНИЙ ХЭММИНГА
Наиболее важным для теории кодирования примером схем отношений является схема Хэмминга, или гиперкубическая схема. В этой схеме X=Fn, т. е. множество двоичных векторов длины п,
причем два вектора х, уеГ” i-связаны, если они находятся друг от друга на расстоянии Хэмминга i. Ясно, что условия (i), (ii) и (iii) определения схемы отношений выполнены. Упражнение (19) из гл. 1 показывает, что условие (iv) также выполнено, причем
cijk ~
О,
если / + /—k—четное, если i + j—k—нечетное.
Oil 111
ООО 100
Рис. 21.1. Граф для кубической схемы
Кроме того, v= |Х| = 2П и Матрицы алгебры Боуза—
Меснера представляют собой (2ПХ2")-матрицы, строки № столбцы которых перенумерованы векторами хеР-. В частности, (х, у)-й элемент матрицы Dfe равен 1, цели и только если dist (х, y)=k.
Пусть, например, п = 3 и строки, и столбцы матриц нумеруются векторами ООО, 001, 010, 100, 011, 101, ПО, 111. Граф, ребра которого имеют номера 1, представляет собой куб (рис. 21.1).'
Диагонали граней куба занумерованы цифрой 2, а четыре главные диагонали занумеро
ваны цифрой 3. .Матрицы смежностей имеют следующий вид: Do = - I;
“0 1 1 1 0 0 0 0“
1 0 0 0 1 1 0 0
10001010
Di = 1 0 0 0 0 1 1 0 01100001
01010001
0 0 1 1 0 0 0 1
00001110
“0 0 0 0 1 0 0 110 1 1 0~
0 0 0 0 1 0 1 0 1
0 1 0 1 0 1 1 0 0 0
Ог 1 0 0 0 0 1 1 0
1 0 0 0 1 0 1 0
1 0 0 0 1 1 0 0
_0 1 1 1 0 0 00
D3 =
"0 о о о о о о
1
0 0 0 0 0 0 1-
0 0 0 0 0 1 0
0 0 0 0 1 0 0
0001000
0010000
0 1 0 0 0 0 0 1000000
о о о о о о 0_
Заметим, что
D2 = 3I+2D2;
D, О2 2О,4 3О.(;
(21.23)?
Ч Соответствующие векторы имеют между собой расстояние Хэмминга, равное 1. (Прим, перев.)
£iio — — 3, £щ — о, £ц2 ' £цз О,
С220 = £-2 — SJ Cggg = V3 ~ 1 И Т. Д.
Теорема 5. Примитивный идемпотент J/t (k=Q,... ,п) схемы Хэмминга представляет собой матрицу, (х, у)-й элемент которой равен
_L (_1)<х+у>Л (21.24)
wt (z)=fe
Собственные значения схемы определяются равенствами
Pk(i) = <1k(i) = ptAi'’ п)> (21.25)
где Рн(х; п)—многочлен Кравчука, определяемый выражением (5.14).
Доказательство. Пусть A/t обозначает матрицу, элемент которой в позиции (х, у) задается равенством (21.24). Покажем, что п
n)Df (2L26) i—о
и поэтому Айел^. Затем мы докажем справедливость равенств (21.8) — (21.10), откуда будет следовать, что А& — примитивные идемпотенты. Далее из (21.26) вытекает, что qk(i) =РДг, и), и из (21.18) (и теоремы 17 гл. 5) следует, что
Чтобы доказать (21.26), вспомним, что согласно упражнению (14) гл. 5
(Afe)x,y = -^-^fe(wt(x + y); п)
и, следовательно,
A‘=vSPi₽;',)D-
i=0
Элемент в позиции (х, у) матрицы А/-А; равен
-f.E Е (^1)W,V Е
uer" wt (v)==fe wt <w)=z
что приводит к выражению
-г^Е (-о1*”’.
wt (v)--fe
представляющему собой (х, у)-й элемент матрицы 6ыА^, и доказывает соотношения (21.8) и (21.9). Соотношение (21.10) легко выводится. •
Соотношения (21.16) превращаются теперь в знакомые нам соотношения ортогональности для многочленов Кравчука (теоре-
ма 16 из гл. 5).
Например, когда
о I 1 I-n=3; Jo=—J 8
1 " 3 1 1 1 — 1 — 1 — 1 —3“
1 3 — 1 — 1 1 1 — 3 — 1
1 — 1 3 — 1 1 — 3 1 — 1
1 1 — 1 — 1 3 3 1 1 — 1
J1 — 8 — 1 1 1 — 3 3 — 1 — 1 1
— 1 . 1 — 3 1 — 1 3 — 1 1
— 1 —3 1 1 — 1 — 1 3 1
со — 1 — 1 — 1 1 1 1 3_
- 3 — 1 — 1 — 1 — 1 — 1 — 1 3"
— 1 3 — 1 — 1 — 1 — 1 3 — 1
— 1 — 1 3 — 1 — 1 3 — 1 — 1
J‘2 = 1 8 — 1 — 1 — 1 — 1 — 1 — 1 3 3 3 3 — 1 — 1 — 1 — 1 — 1 — 1
— 1 — 1 3 — 1 — 1 3 — 1 — 1
— 1 3 — 1 — 1 — 1 — 1 3 — 1
3 — 1 — 1 — 1 — 1 — 1 — 1 3_
- 1 — 1 — 1 — 1 1 1 1 — 1“
— 1 1 1 1 — 1 — 1 — 1 ' 1
— 1 1 1 1 — 1 — 1 — 1 1
•1.3 = —< | ОС — 1 1 1 — 1 1 — 1 1 — 1 — 1 1 — 1 1 — 1 1 1 — 1
1 — 1 — 1 — 1 1 1 1 — 1
1 — 1 — 1 — 1 1 1 1 — 1
— 1 1 1 ] — 1 — 1 — 1 1
тогда
I — Jo + Ji + Ja + J-?’
Dj — 3 Jo + Ji'— J2 — 3J3;
С '2 — 3J0- J±—J2 "b 3J3;
= Jo Ji+J2 J3’
"1 3 3 г
P = Q = 1 I — 1. —1 ; l0 = I;
а 1 —1 — 1 1
_i — 3 3 —1_
"0 10 0" "0010" 0 0 0 Г
3 0 2 0 l2= 0 2 0 3 ; J3 = 0 0 10
0 2 0 3 3 0 2 0 0 10 0
_0 0 1 0_ _o 1 0 0_ .1000.
Упражнения. (2). Проверить, что собственными значениями матрицы L; является (i-f-l) -й столбец матрицы Р.
(3) . Найти матрицу Р при п=4.
21.4. МЕТРИЧЕСКИЕ СХЕМЫ
Схема Хэмминга и другие схемы, приведенные ниже, являются примерами метрических схем, которые определяются графами.
Пусть Г обозначает связанный граф с v вершинами, не содержащий петель и кратных ребер, и пусть X обозначает множество вершин. Расстояние р(х, у) между вершинами х, у^Х равно числу ребер кратчайшего пути, соединяющего этщ.вершины. Максимальное расстояние (обозначим его через п) между любыми двумя вершинами называется диаметром графа Г.
Определение. Граф Г называется метрически регулярным (или совершенно регулярным, или регулярным по расстоянию), если для любых х, у^Х, для которых р(х, y)=k, число вершин z^X таких, что р(х, z)=i и р(у, z)=j, является константой Сцк, не зависящей от выбора х и у.
Ясно, что из гйетрически регулярного графа диаметра п мы получим схему отношений с п классами, если назовем i-связанными вершины х, у^Х, находящиеся на расстоянии р(х, y)=i. Схемы отношений, которые могут быть получены таким способом, называются метрическими схемами. Чтобы построить граф из схемы, вершины х и у назовем смежными, если и только если (х, например, схема Хэмминга является метрической, а соответствующий ей граф представляет собой остов единичного /г-мерного куба (см. рис. 21.1).
Метрически регулярные графы диаметра 2 называются сильно регулярными графами.
Упражнения. (4). Показать, что любая схема отношений с двумя классами является метрической (и может быть получена из сильно регулярного графа).
Но не все схемы отношений — метрические.
(5) . Показать, что схема отношений — метрическая, если и только если (i) Ci,i,<+i=z^=O и (ii) ciij=#O->i—l^/^t'+l. [Указание. (Необходимость.) Пусть Г обозначает граф, задаваемый отношением Ру, показать, что р(х, y)=i тогда и только тогда, когда (х, у) &Ri.]
Таким образом, если схема отношений является метрической, то для k= 1, 2,...
DiDfc = Ci, h, м-i Dfc+i + Cifcb Dfe + c(, k, ь-i (21.27)
и, следовательно, D& — многочлен относительно D! степени k. Тогда — алгебра многочленов от Db и если известны собственные значения матрицы Di (или L]), то легко находятся все собственные значения. В рассмотренном выше примере 2L2=L2i—31 (в силу (21.23)), поэтому если а — произвольное собственное значение
матрицы Li, то (а2—3)/2 является собственным значением матрицы L2. В общем случае согласно соотношению (21.27)
Pl (О Ph (0 = Cl, h, Н-1 Pk+1 (0 + С1 h h Ph (О + С1, h. h—1 Pk—1 (z)> (21 -28) где i—0,... ,п.
Упражнение, (6). Доказать, что если Dfe — многочлен относительно D, степени k, то схема — метрическая.
Наиболее интересным свойством метрической схемы является тот факт, что собственные значения pk{i) могут быть получены с помощью семейства ортогональных многочленов.
Определение. Схема отношений называется Р-полиноми-альной схемой, если существуют неотрицательные действительные числа zo=O, Z\,...,zn и действительные многочлены ф0(г), Ф1 (z),..., Фь (z), где deg Фа (z) —k, такие, что
риО = Фьиг), С k = 0, 1, .... п. (21.29)
Из теоремы 3 вытекает, что Ф/Дг) образуют семейство ортогональных многочленов
£ (21-30)
1=0
Аналогично определяется Q-полиномиальная схема.-
Например, схема Хэмминга одновременно является и Р-, и Q-полиномиальной схемой (с z<=i; Фа(z) = Ph(z; п)).
Теорема 6. (Дельсарт.) Схема отношений является метрической тогда и только тогда, когда она является Р-полиномиальной схемой.
Доказательство. Если схема — метрическая, то pft(i) —многочлен относительно рДД степени k. Положим Zi=vx—pi(i). Тогда существуют многочлены Фь(г) такие, что рь(1') =Ф^(гД и deg Фй(z) —J?. Кроме того, zo=O и согласно упражнению (1) ^0. Все числа гг- различны, так как из условия- Zi=Zj вытекает, что Pk(i) =Ph(j), k=0,... ,п, что невозможно, так как матрица Р невырождена. Следовательно, схема является Р-полиномиальной.
Обратно предположим, что схема является Р-полиномиальной, и пусть ФДг)=Ь—(l/a)z, где а>0. Тогда из условий рДг) = = ФДгг) и рД0)=пг- вытекает, что b = vi и Zi=a(v,i—pi(i)). Так как многочлены Фй(г) ортогональны, то они удовлетворяют некоторому трехчленному рекуррентному соотношению (см. Сегё [1297], с. 55) ®feTi®fe+i(z) = (₽*r—г)ФДг)— уьФь-Дг), где afe+i>0. (Коэффициенты этого соотношения должны удовлетворять различным условиям, что нас сейчас не интересует.) Подстановка в это соотношение значения IZ; дает:
—Zf ф« (zf) = afe+1 Ф^+1 (Zf)—Ра Фа (?;) + yk ф*-! (гг);
Р1 (0 Ph (г) = с1, k, fe+1 Pk+l (0 + Cikh Ph (0 + cl, h, h—l Pk-1 (0
Для соответствующим образом подобранных коэффициентов сць-
'Из упражнения (5) теперь следует, что схема является метрической. •
Задача (нерешенная). (21.1). Дать подобное описание для Q-полиномиальных схем.
*21.5. СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
В этом разделе мы построим схемы отношений симплектиче-ских форм, которые существенны при изучении подкодов кодов Рида — Маллера второго порядка (см. гл. 15).
Множество X состоит из всех двоичных симплектических форм от т переменных или, что эквивалентно, из всех (тУ^т) -симметричных двоичных матриц с нулевой диагональю (см. § 15.2). Таким образом, |Х| =ц = 2т(т-,)/2. По определению (х, y)^Rit если и только если ранг матрицы х+у равен 2ц. где i=0, 1,...; п= = fm/2], Число еимплектических форм ранга 2ц т. е. число v.i, дается теоремой 2 гл. 15. Пусть D; обозначает матрицу смежности отношения Rt.
Докажем, что мы ввели схему отношений, показав выполнение условий (21.3) — (21.5), и построим одновременно соответствующую алгебру Боуза — Меснера. Изложение аналогично изложению схемы Хэмминга, но использует гауссовские биномиальные коэффициенты при Ь=4 (см. упражнение (3) гл. 15).
Определим внутреннее произведение матриц x=(xi)) и у= = (yi})f=X т т
У У xii уц
<х, у> = (-1Г1/=г . (21.31)
Упражнение. (7). Показать, что
2<х* У> == v 6о у •
xgX
Теорема 7. Если ранг матрицы х равен 2ц то
rank у=2k j=0
где b—4 и с—2т (т — нечетное) или с=2'т1 (т — четное). Схема доказательства. Вначале мы покажем, что сумма
rank (y)=2ft
зависит только от ранга матрицы х. Если R — невырожденная (гаХ^г)-матрица, то отображение у—>RyRr действует как подстановка на множестве симплектических матриц, которая сохраняет ранг. Следовательно,
2 <Х, у>- 2 <х, RyR7>.
rank (y)=2fe rank (y)=2fe
Кроме того, <х, RyRT> = <RxRT, у>. По теореме 4 гл. 15 находится матрица R такая, что
“G
RxR7 =
AN;
(21.33)
где
и всего на диагонали имеется i=rank(x) таких матриц G. Тогда
V <Х, у>= £ <Nb у>Л/4т)(г),
rank (у) rank (y)=2k
что зависит только от t, /гит.
Следующий шаг состоит в доказательстве рекуррентного соотношения для ph(m) (i):
pW (i) = 1; p(-) (0) = -у (2m-1) (2m—1 - 1);
Plm) (0 = Pj^ V— 1) — p$=V (i— 1).
(21.34)
(21.35)
Соотношение (21.34) следует из теоремы 2 гл. 15, и затем индукцией по i получаем
(21.36)
Пусть x=Nj, и пусть Mi — матрица, полученная из N< заменой первой матрицы G на матрицу
Тогда
P^(i— l)_p(m)(t-)= 2 «МЬ У>-<Ni, У» =
rank (y)=2fc
= S <МЬ У>(1 — (- 1)М = 2 2 <Mi> у>
и 4/12=1
(здесь ум — соответствующий элемент матрицы у).
Далее <Mj, у> = <А, D>, где A, D — матрицы размера (m—2)X(°i—2) и
y =
Если
[G Z]
Zr D
Z1i... Zj, tn—2
Z2i... Zz, m—2
Zij==O или 1. (21.37)
, to LT у L =
G 0|
.0 FJ
Z =
L =
где F=D-|-ZrGZ представляет собой (т—2) X (т—2) симплекти-ческую матрицу ранга 2k—2. Таким образом,
p<m)(/-l)-p<m)(/) = 2 £ <А, F-|-ZTGZ>.
rank (F)=2fe—2 по всем Z
Далее либо матрица ZrGZ равна нулевой матрице, либо ее ранг равен 2. Согласно упражнению (8) число матриц Z таких, что ZTGZ=0, равно 3-2’" 2—2, а число матриц Z таких, что ZrGZ — фиксированная матрица ранга 2, равно 6. Таким образом, p^(i— 1)—(г) = (3-2т-1— 4) "£ <А, F> +
rank (F)=2fe—2
+ 12 2 <А, F> £ <А, Е> =
rank (F)=2fe—2 rank (Е)=2
® =(3-2—1-4)р« (Z-l)+ 12^-2(Z-l)p(—2> (i_1} (21.38)
Объединяя выражения (21.36) и (21.38), получаем рекуррентное соотношение (21.35). Наконец, выражение (21.32) представляет собой решение рекуррентных соотношений (21.34) и (21.35); детали мы опускаем. •
Обозначим правые части выражений (21.32) через ph(i), так как окажется, что они являются собственными значениями схемы.
Определим матрицы Jfe, k=0,..., п с помощью равенства
(Jfe)x,y = Y J] <х + у, z>. (21.39)
rank (z)=2fe
Рассуждения, аналогичные тем, которые мы использовали при доказательстве теоремы 5, показывают, что матрицы + удовлетворяют свойствам (21.8) — (21.10) и, следовательно, являются примитивными идемпотентными матрицами и что
п
(21-40)
i=0
где Pk(i) определяются выражением (21.32).
Лемма 8.
ViPbW^VbPitk).
Доказательство. Вычислим двумя способами сумму
2 £ <х> У>- •
rank (х)=2г rank (y)=2fe
Теорема 9. (Соотношение ортогональности.}
PiU) = vvh8kl.
; - i=o
Доказательство. Сначала вычислим двумя способами сумму
2 2 2 <х’ У><х’ z>’
х(~Х rank (у)=2к rank (z)=2!
а затем воспользуемся упражнением (7). 41
Согласно лемме 8 и теореме 9
YPk(i)Pi (l) = v8ki, f=0
следовательно, матрица Р, (i, k)-n элемент которой равен pfe(Y), удовлетворяет условию Р2=о1, откуда Р — &Р-1. Таким образом, из (21.40) вытекает, что
1=0
Пусть .+ — коммутативная алгебра, порожденная матрицами Jh. Из условия (21.10) следует, что ее размерность равна п+1, и из равенств (21.40) и (21.41) следует, что матрицы Dft также образуют базис. Поэтому соотношения (21.3) — (21.5) выполняются, и тем самым мы ввели схему отношений. Согласно (21.40), (21.41) собственные значения =#ь(г), определяемые выражениями (21.11), (21.15), действительно задаются выражением (21.32), как и утверждалось.
Упражнения. (8). Показать, что: (i) число матриц Z вида (21.37) таких, что ZrGZ=0, равно 3-2т-2—2; (ii) если гапк(В) = = 2, то имеется точно 6 матриц Z таких, что ZrGZ=B.
(9) . Показать, что pk(i)—многочлен степени k относительно переменной Ь~* и, следовательно, в силу теоремы 6 наша схема является метрической схемой отношений.
21.6. СХЕМА ДЖОНСОНА
Схема Джонсона, или треугольная схема отношений, является нашим третьим примером. В этом случае X — множество всех двоичных векторов длины I и веса п, поэтому v— |Х| = 1 j. Два вектора х, уеХ называются i-связанными, если distfx, у) = 21 для i=0, 1,.. ,,п.
Упражнение. (10). Показать, что это является схемой отношений с п классами, и найти числа с^. Показать, что
Теорема 10. Собственные значения задаются
Рк (i) = Ek (Ъ <lk (i) = — Ei(k),
Vi где
l~ 2i-p 1 { l\
‘ ’ I— i+ 1 \ij
равенствами
(21.42)
(21.43)
a Ek (x) — многочлен Эберлейна, определяемый следующим образом:
k
...- <*'«)
/=0
Доказательство см. в работах Ямамото и др. Г1444] и Дельсар-та [352].
Теорема 11. (Свойства многочленов Эберлейна.)
(i) . Ek(x) — многочлен от х степени 2k.
(ii) . Ek(x) —многочлен степени k относительно переменной z=x(L-(-l—х). Следовательно, данная схема является P-полиномиальной.
(iii) .
(iv) . Имеет место рекуррентное соотношение ^о(#)=Е EL(x) = n(l—п)—x(Z-|-l — х); (k+W Eh+i W = {^1W-k(I—2k)}Eh (x)--------------(n — k-\- 1)(Z—tl-l)£fe-i (x).
Доказательства см. в работах Дельсарта [352, 361].
Упражнение. (11). Пусть А, — матрица размера ( 1 X f 1 V \ п / \ i)
строки которой занумерованы двоичными векторами х веса п, а столбцы занумерованы двоичными векторами веса i, причем
1, если § с х,
О, в противном случае.
Пусть также Сг = АгАгг-. Показать, что
(Ai)xl
Следовательно, матрицы Со,..., Сп образуют базис алгебры
21.7. ПОДМНОЖЕСТВА СХЕМ ОТНОШЕНИЙ
Код является подмножеством схемы Хэмминга. В этом параграфе мы рассмотрим непустое подмножество У произвольной схемы отношений X с отношениями Ro, Rt, • •, Rn-
Предположим, что |.У|_М>0. Внутренним спектром У называется (п-|-1)-вектор (Во, В{,..., Вп) с рациональными компонентами, где Bt = | Rt f) У2| представляет собой среднее число
точек геУ, которые ё-связаны с точкой ре У. Для схемы Хэммин
га вектор (Во, ...,Вп) является спектром расстояний (см. § 2.1) кода Y.
Конечно, Во=1;
Вг>0, г=1, .... и, (21.45)
и
В0 + В1 + ... + Вп = М. (21.46)
Дельсарт заметил, что некоторые линейные комбинации чисел Bi также неотрицательны.
Теорема 12. (Дельсарт.)
п
(2Е47)
i=0
для k=Q,...,n, где qk(i)—собственные значения, определенные в § 21.2.
Доказательство. Пусть и обозначает вектор, указывающий, какие элементы X принадлежат У:
цж=1, если /БУ иж = 0, если х=ДУ.
Тогда
Вг=—uDzur; 1 м 1
(п \
J]^(ODf 1иг = ^.и^ит (в силу (21.15)). (21.48)
1=0 /
Так как — идемпотент, то его собственные значения равны О или 1 и, следовательно, — неотрицательно определенная матрица. Поэтому B'k^O. •
Например, применяя теорему 12 к кодам, мы получим другое доказательство теоремы 6 гл. 5. Применяя ее к схеме Джонсона, мы получим результаты по равновесным кодам, которыми мы пользовались на с. 527 гл. 17. В общем случае равенство (21.46) позволяет применить методы линейного программирования ко многим задачам, которые включают отыскание наибольшего подмножества схемы отношений, удовлетворяющего некоторым ограничениям на числа В, и В\. Такую задачу можно сформулировать следующим образом: максимизировать сумму B0-f-Bi-|- ... -J-Bn (=Ai), где Bi удовлетворяют условиям (21.45), (21.47) и любым дополнительным ограничениям. Примеры см. на с. 520 и 528 гл. 17.
*21.8. ПОДМНОЖЕСТВА СИМПЛЕКТИЧЕСКИХ ФОРМ
Пусть X — множество симплектических форм от m переменных (см. § 21.5), а У—подмножество X, обладающее тем свойством, что для у, y'^Y ранг формы у+у' равен по крайней мере 2d. Такое множество У называется (т, с?)-множеством. В этом разделе мы выведем верхнюю границу для объема (tn, d)-множества.
Пусть (Во, п=\т12}, обозначает внутренним
спектр У. Тогда Вх = ... = Bd-i = 0.
Теорема 13. (Дельсарт и Геталс.) Для любого (т, d)-множества У имеет место неравенство | У | cr,‘<!+1, где с было опреде-
лено в теореме 7.
Доказательство. Как было показано в § 21.5, для схемы отношений, образованной симплектическими формами, выполняется равенство
k Mr -.г -п
= 2 т' с/-
[и — я] L ] J
1=0
Используя пп. (b), (с), (g) упражнения (3) гл. 15, получаем, что
/=0’-’п- (21-49)
h=0
Далее
и В'^^ДДВ., i=0
11—1 11 П—
S Е
fe=0 i=0 fc=O
= УвЛ п~\ lcn-d+1. (21.50)
W (и —d-j-lj i=0
С учетом того что Вх = ... = Ba-i — 0 и
I " 1 1 = 0 для d [п~ d+lj
наше выражение принимает вид
n-d 1-1
п 1r'_l V \,l~k}R' = Г п lr"~d+1 rf-l| 0 L |d-l] h Irf-ll
k=i
Кроме того, согласно теореме 2
= f qo^Bi B( = \Y\.
i=0 i=0
Следовательно,
n—d 1-1
S [dZi]^==[Zi](c"_d+1_,rj)- (2L51)
k=i
По теореме 12 B7k^0, поэтому |У|^сп-<3+1. •
Эта теорема показывает, что множества симплектических форм, описанные в гл. 15, действительно являются максимальными множествами.
Теорема 14. Если (т, d)-множество Y таково, что |У| = _стг-й+1; то внутренний спектр Y задается равенствами
n~d (/-г)
Bn_t = J (- 1)(/-г> b ['][”](cn~a+1~f—1), (21.52)
i=i
где 7=0, 1,..., п—d.
Доказательство. Если Y достигает верхней границы, то каждый член в левой части выражения (21.51) равен нулю, т. е.
В'о = | У | = с'1~<г+1; B'k =0, k-= 1,..., п— d+ 1.
Далее для /=0,..., п справедливо равенство
При j^n—d все члены в левой части этого равенства, кроме первого, обращаются в нуль, и оно с учетом (21.49) превращается в следующее равенство:
: =о
Но Во= . - =В<г-1=0, и поэтому
и—d n—d
Утверждение теоремы следует из упражнения (3) (g) гл. 15. • Эта теорема позволяет вычислить спектры расстояний кодов, построенных из максимальных (m, d)-множеств в гл. 15.
Упражнение. (12). (Касами [727].) Используя теорему 14, показать, что, если т^5— нечетное число, то код, дуальный коду БЧХ, исправляющему тройные ошибки, имеет параметры [2m—1, 3m, 2m_1 — 2(m+1)/z]
и весовой спектр
L Af
0 1
2й—1 1 . 2<m^5>/2 ( 2(m—3)/2 qz 1) ( 2m 1)( 2m—1 1) 3
2»1-1 _|_ 2<m-l)/2 J_. 2M/2 ( T !) ( 2m — 1) (5 2m-’ + 4)
2пг~1 (2m— 1) (9 22,ra~4 + 3 2m-3 + 1).
Замечание. Для четных т этот метод непригоден. Однако для этого случая весовой спектр был найден Берлекэмпом ([ИЗ, табл. 16.5], [114] и [118]). Код, дуальный расширенному -коду БЧХ, исправляющему тройные ошибки, имеет параметры
[A = 2m, 3m-)-1, 2m~l — 2<m+2)/2], т> 6 —четное, и весовой спектр
i Ai
0,2m 1
/2 А (А— 1) (А —4)/960
2«г—1 2'га/г 7 А2 (А— 1)/48
2^-1 2<пг—2)/2 2 А (А— 1) (ЗА 4-8)/15
2^-1 (А — 1) (29 А2—4А + 64)/32.
Упражнение. (13). Применить конструкцию У1, описанную в § 18.9.1, к коду равному [2m+I, 2”l+1—3m—4,8] расширенному коду БЧХ, исправляющему тройные ошибки, и получить для всех т^З коды с расстоянием 7, избыточностью Зт-\-2 и длиной 2m-)-2(m+2)/2—1, если т — четное, или длиной 2”1-|-2(™+3)/2—1, если т — нечетное.
21.9. АСХЕМЫ И ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
Подмножество Y множества X называется Асхемой, если В\= = ... =B't=0. Следующая теорема оправдывает это определение.
Теорема 15. Подмножество Y в схеме Джонсона является Асхемой тогда и только тогда, когда векторы из Y образуют обычную t- (I, п, К) схему для некоторого X.
Доказательство. Заметим, что согласно (21.48) в любой схеме отношений подмножество Y является Асхемой, если и только если
uJftuT = 0 для k=l, t, (21.53)
где и — характеристический вектор множества Y, введенный при доказательстве теоремы 12.
Предположим, что векторы из Y образуют А(/, п, X) схему. Для значений 1=^Д^£ пусть Аг- и С/—матрицы, определенные в упражнении (11). Тогда АД иг представляет собой вектор-столбец, £-й элемент которого равен числу векторов из Y, содержащих вектор £ веса i. Так как векторы из Y образуют также i-(l, Кг) схему с параметром К5= | У| , Т(
/1 \ /1 аГиг=J 1 Цшап !
(')
Так как Ci=AiAI\, то
(21.54)
Матрицы Сг образуют базис алгебры и поэтому равенство
(21.54) выполняется для всех матриц из и, в частности, справедливо равенство
Но, как мы знаем,
Jfc ит = 0 для
1 <
следовательно,
иЛЛиг = 0 для
и согласно (21.53) Y является ^-схемой в схеме отношений.
Обратно, если Y—t-схема в схеме отношений, то uJfeur=0 и, следовательно, Jfetir=O, так как матрица неотрицательно определена. Проводя предыдущее доказательство в обратном порядке, получаем, что Y — обычная Лсхема. 41
Например, пусть У состоит из 14 слов [8, 4, 4]-кода Хэмминга веса 4. Внутренний спектр и его преобразование имеют вид
Ло=1; В2=12; В4=1;
в; = в;=в;=о, в;=5б,
и действительно, эти кодовые слова образуют 3-(8, 4, 1) схему.
Теорема 16. Подмножество У является ^-схемой в схеме Хэмминга, если и только если векторы из У образуют ортогональную таблицу размера | У| с п ограничениями, двумя уровнями, силы t и индекса |У|/2*.
Доказательство. См. теорему 8 гл. 5 и § 11.8. •
ЗАМЕЧАНИЯ К ГЛ. 21
§ 21.1. Схемы отношений были введены Боузом и Шимамото [186], а алгебра была введена Джеймсом [688] и Боузом и Меснером [183]. Дальнейшие свойства этих объектов см. в работах Янга [103, 104], Блеквельдера [154], Боуза [178], Ямамото и др. [1442—1444], Вана [1458] и Ваиа и Янга [1459].
Случай группы. Важный класс схем отношений возникает из групп подстановок. Пусть g? обозначает транзитивную группу подстановок на множестве X, содержащем v точек. Множество X называется однородным пространством группы g?. Пусть g?x обозначает подгруппу группы %, которая оставляет неподвижной точку хеА, и пусть S0={x}, Sb . ,.,S„ обозначают орбиты g?x в множестве X. Тогда говорят, что группа У? имеет ранг n-j-1.
Определим действие g? на. ХхХ равенством g(x, y) = (g(x), g(y)), где geg’; х, у<^Х. Тогда ХхХ под действием g? разбивается на орбиты 7?о = = {(х, х) :xs=X}, R.i, .. .,Rn, и имеется взаимно однозначное соответствие между Ri и S;. В терминологии Хигмана (X, Ro, ,Rn) представляет собой однородную конфигурацию, a \R, являются отношениями на X, которые, однако, необязательно должны быть симметричными. Если же эти отношения симметричны, то конфигурация называется когерентной и образует схему отношений с п классами. Алгебра может быть определена, даже если Ri несимметричны. Она представляет собой множество всех комплексных (vXо) -матриц, которые коммутируют со всеми матрицами перестановок, представляющими элементы группы g?, и эта алгебра называется централизатором группы g?. В этом случае алгебра коммутативна тогда и только тогда, когда отношения R, симметричны, и в этом случае совпадает с алгеброй Боуза — Меснера, определенной в § 21.2. Хигман [652] доказал следующую теорему.
Теорема 17. Алгебра коммутативна, если и<5.
Подробнее об этом см., например, в работах Камерона [232], Хестнеса [644], Хестнеса и Хигмана [645], Хигмана [646—653], Курнвиндера [776] и Виеландта [1415].
Например, схемы Хэмминга, Джонсона и симплектические схемы являются когерентными конфигурациями, которые соответствуют следующим группам: (i) группе всех преобразований «-мерного двоичного куба порядка 2"и!; (ii) симметрической группе (iii) группе всех (тХ от)-невырожденных матриц (см. теорему 4 из гл. 15).
Тесно связана со схемами отношений комбинаторная задача отыскания максимального числа прямых в «-мерном евклидовом пространстве, углы между которыми принимают заданные значения—(см. Камерон и др. [233], Дельсарт и др. [367], Хейл и Шульт [578], Лемменс и Зейдель [812] и Ван Линт и Зей-дель [856]).
§ 21.4. Что касается метрически регулярных графов, см. Биггс [144—147], Деймрелл [327], Дуб [379], Хигман [649] и Смит [1240—1242]. Сильно регулярные графы рассматривались в работах Берлекэмпа и др. [128], Боуза [175], Бассмейкера и Зейделя [221], Шакраварти и др. [260, 261], Дельсарта [349], Геталса и Зейделя [502, 503], Хигмана [646], Хьюбота [672] и Зейделя [1175— 1177].
§ 21.5, 21.8 основаны на работе Дельсарта [364], в которой изложена также теория симплектически'х форм над GF{q) (в’этом случае В — кососимметрическая матрица). Схема отношений билинейных форм над GF(q) описана Дель-сартом в работе [355].
§ 21.6. Многочлены Эберлейна определены в работе [401]. Они тесно связаны с двойственными многочленами Хана (см. Хан [574] и Карлин и МакГрегор [719]). Схема отношений, образованная подпространствами векторного пространства, тесно связана со схемой Джонсона—(см. Дельсарт [357, 361]).
Работа [1229] может рассматриваться как предварительный вариант этой главы.
ПРИЛОЖЕНИЕ А
ТАБЛИЦЫ НАИЛУЧШИХ ИЗВЕСТНЫХ КОДОВ
1. Введение
Это приложение содержит три таблицы наилучших известных нам кодов. На рис. ПА.1 приведена таблица верхней и нижней границ для величины А(«, d), т. е. числа кодовых слов в максимально возможном (линейном или нелинейном) двоичном коде длины п, с минимальным расстоянием d при п<23 и
d^9. На рис. ПА.2 приведена обширная таблица наилучших известных кодов, котррая покрывает диапазон n<512; d<29. Таким образом, рис. ПА.2 дает нижние границы для А(п, d). На рис. ПА.З приведена таблица значений А(п, d, w), т. е. числа кодовых слов в наибольшем возможном равновесном двоичном коде длины п, веса w с расстоянием d при и<24 и 10.
Эти таблицы служат как справочник очень хороших кодов, как эталон при оценке качества новых кодов и как примеры метр до в построения, описанных в книге. Мы были бы чрезвычайно признательны узнать о тех или иных улучшениях этих таблиц (предложения высылайте по адресу: N. J. A. Sloane, Math. Research Center, Bell Labs, Murray Hill, New Jersey, 07974, USA).
Многие из нижних оценок, приведенных на рис. ПА.З, чрезвычайно слабы (или они отсутствуют).
Общие замечания
(1) . С точки зрения теорем 1а и 10а гл» 17 достаточно построить таблицы только для нечетных значений d (или только для четных значений).
(2) . Код, приведенный без ссылки, часто получается добавлением нулей к более короткому коду. (Таким образом, A (n+1, d)^A(n, d) и A(n+1, ^А(п, d, w).)
(3) . Заслуживают упоминания некоторые другие таблицы: таблица Берле-кэмпа [113] избранных линейных кодов длины менее 100 и их весовые спектры; таблица Ченя [266] всех циклических кодов длины не более 65; таблица Дель-сарта и др. [368] верхних оценок для А(п, d, w); таблица Хелгерта и Стинаф-фа [636] верхних и нижних оценок для линейных кодов длины не более 127; таблицы Джонсона [695, 696] верхних оценок для А(п, d) и А(п, d, id) и таблица Мак-Элиса и др. [946] верхних оценок для величины А (п, d). Кроме того, ряд полезных таблиц содержит книга Питерсона и Уэлдона [1040].
Задача (нерешенная). (ПА.1). Весьма полезным был бы расширенный вариант таблицы Берлекэмпа, в которой были бы приведены весовые спектры ряда наилучших линейных и инвариантных относительно расстояния нелинейных кодов длины вплоть до 512.
2. Небольшая таблица значений А(п, d) (рис. ПА.1)
На рис. ПА.1 приведены верхняя и нижняя оценки величины А (и, dj. Теорема Плоткина — Левенштейна (теорема 11 гл. 17) дает все коды в этой таблице. лежащие не ниже прямой n=2d+l. Отсутствие ссылок при верхних границах ниже прямой п=|2/Ц-1 означает, что они получены с помощью линейного программирования (§ 17.4) или с помошью теоремы 10b) из гл. 17. Нижние границы продолжены на рис. ПА.2.
Задача (нерешенная). (ПА.2). Конечно, все неизвестные случаи в этих таблицах являются нерешенными задачами. В частности, возможно, существует один особенно интересный код с параметрами (20. 4096, 5), соответствующий значению А (20,5) =4096. Согласно границе линейного программирования (§ 17.4) весовой спектр расширенного (21, 4096, 6)-кода имел бы следующий вид: Во=1; Be=314; Bg=595; Вю=1596; Bi2=1015; Ви=
= 490; Bi6 = 84; В2о=1-
Объяснения к рис. ПА.1 *
а. См. с. 522 гл. 17.
Ь. Построен в § 2.9.
d. Код Хэмминга (§ 1.7).
е. См. с. 520 гл. 17.
/. Код Нордстрома — Робинсона (§ 2.8).
I. Получен из кода Адамара ^24 (§ 2.3).
g. См. § 18.7.3.
h. Конференс-матричиый код (§ 2.4).
i. Из работы Беста и др.- [140].
J, Код Голея gzi (§ 2.6).
k. Построен Оллтопом [26].
- * М..Р. Бест показал (Binary Uodes with Minimum Distance Four. —Report ZW 112/78, Math/ Centre, Amsterdam, 1978), что: A(10,4)-=40, 72<А(11А)< <79 и 144<A(li2,4)<158.
п d= 3 d = 7 d = 9 /
5 4 2
6 8d 2
7 16 2 2
8 20й 4 2
9 386—40 6 2 2
10 726—80 12 2 2
И 1446—160 24 4 2
12 256 32е 4 2
13 512 64 8 2
14 1024 J28 16 4
15 2048d 256/ 32 4
16 25606—3276 256—340 36ft—37г 6
17 51206—6552 512—680 64—74 10
18 97286—13104 1024—1288 128—144 20
19 194566—26208 2048^—2372 256—279 40
20 2560^—4096 512 40—55
21 4096—6942 1024 48z—90
22 8192—13774 2048 64—150
23 ♦ 16384^—24106 4096/ 128^—280
Рис. ПА.1. Значения А(п, d)
3. Расширенная таблица нанлучпшх известных кодов (рис. ПА.2)
Пусть М обозначает мощность наибольшего известного (линейного или нелинейного) двоичного кода длины ДГ<512 с минимальным расстоянием Д<29. На рнс. ПА.2 приведена таблица избыточности R=N—log2Al этого кода.
Так как код может быть нелинейным, число R не обязательно целое. Небольшая таблица после рис. ПА.2 облегчает нахождение М при заданном R. Если R—I-\-X, где I — целое число и 0<Х<1, то число кодовых слов равно
M = F-2N~l~5 , где F приводится в таблице. Например, рассмотрим строку А=8; 3,678; тип кода=£и7 Ссылка [509],
которая находится недалеко от начала таблицы. Здесь /=3; Х= 0,678; Е=20, и число кодовых слов равно
М = 20-2° = 20.
Это (8, 20, 3)-код типа SW (см. перечень всех типов кодов в конце рнс. ПА.2), который был построен Голеем [509] (см. §. 2.7).
Для экономии места несколько строк объединяются в одну. Например, для расстояния 0=11 строка таблицы
48—50 24—26
является объединением следующих строк:
48 24
49 25
50 26
Обозначение для укороченного кода совпадает с обозначением для исходного кода. Например, СУ обозначает циклический код или укороченный циклический код.
Рис. ПА.2. Наилучшие известные коды длины вплоть до 512 с минимальным
\ расстоянием вплоть до 29
\ Для каждой длины N и минимального расстояния D — в таблице приводится наименьшая избыточность Д = (длина) — log2 (число кодовых слов) лю-I бого известного двоичного кода *>.
Замечания. Последние поправки внесены 12 августа 1976 г. Коды не обязательно должны быть линейными. Более ранний вариант этой таблицы появился в работе [1225].
РАССТОЯНИЕ D = 3 (см. § 2.9 и 18.7.3)
N R Тип Ссыл-кода ка
4—7 3 HG [592]
8 3.678 S1K [509]
9 3.752 S-IT [509]
10—11 3.830 SIT [701]
12—15 4 HG [592]
16—17 4.678 SIT [1239]
18—19 4.752 SIT [1239]
20—23 4.830 SIT [1239]
24—31 5 HG [592]
32—35 5.678 SIT [1239]
36—39 5.752 SIT [1239]
40—47 5.830 SIT [1239]
48—63 6 HG [592]
64—71 6.678 SIT [1239]
72—79 6.752 SIT [1239]
80—95 6.830 SIT [1239]
96—127 7 HG [592]
128—143 7.678 SIT [1239]
144—159 7.752 SIT [1239]
160-191 7.830 SW 1239]
192—255 8 HG [592]
256—287 8.678 SIT[1239
288—319 8.752 SIT [1239
320—383 8.830 SIT[1239
384-511 9 WG[592]
512 9.678 SIT[1239]
РАССТОЯНИЕ D = 5
(см. § 18.7.3)
N R Тип Ссыл-
кода ка
7—8 6 £/[308]
9—11 6.415 //£>[819]
12-15 7 PR [1002]
16—19 8 XP[1237]*
20 8.678 X4[1237]
21—23 9 £/[1378]
24—32 10 B[518]
33—63 11 PR [1081]
64—7'0 12 X4[1237]**
71—74 13 AT [633]
75 -128 14 В [1237]
129—255 15 РЛТ1081]
256—271 16 X4[1237]**
272—278 17 GB [286]
279—512 18 В [1237]
РАССТОЯНИЕ 0 = 7
N R Тип Ссыл-кода ка
10—11 9 £/[308]
12—15 10 RM
16 . 10.830 СМ[ 1239]
17—23 11 GO [506]
24 12
25—27 13 £>С[715]
28—30 14 ОС[715]
31—35 36—63 15 16 £/[1094] £М[495]
64 17
65—67 18 АС[1237]
68—72 19 £/[625]
73—87 20 ZV[1470]
88—128 21 GP[536]
129—255 22 /Л1[495]
256—257 23—24
258—265 25 GP[1291]
266—311 26 SV[631]
312—512 27 GP [536]
РАССТОЯНИЕ 0 = 9
N R Тип Ссыл-кода ка
13—14 12 LI [308]
15 13
16 13.415 ДО [819]
17—19 13.678 HD [819]
20 14.678
21 15.415 //£>[819]
22—23 16 £/[26]
24—26 17 £/[625]
27—30 18 РТ[1047]
31—35 18.415 У2[1237]
36 19.415
37—41 20 0/?[ПЗ]
42—45 21 QR
46—47 22 £/[625]
48—49 22.193 У2[1237]
50-52 23 SV[631]
53—73 24 В[741]
74 25
75—76 26 %Q,[721]
77—91 27 А £[633]
92—128 129—135 28 29 В[1237] ХВП225]
136—142 30 %О[721]
143—167 31 А£[633]
168—256 32 В[1237]
257—265 33 GP[1291]
266—274 34 GP[1291]
275—311 35 S V[631]
312—512 36 В[1237]
РАССТОЯНИЕ Г - И
N R Тип Ссыл-кода ка
16—17 15 6/[308]
18 16
19 16.415 ЯП [819]
20 17 В[518]
21—23 17.415 Z7D[819]
24 18.300 СМ [1238]
25—26 19 HS [636]
27—31 20 « в
32 21
33—35 22 FH1237]
36—47 23 QR
48,—50 24—26
51—63 27 В
64—67 28 ХВП225]
- ;-.68 29 .
69—71 30 ZV[1470]
72 , 31.
73—77 . 32 GP 1291]***
78—89 33 CY 1083А]
90—96 34 GB 286]
97—128 35 GP 536]
129—135 36 ХВ 1225]
136—142 37 XQ 721]
143—149 38 GP 1291]
150—191 39 У/[637]
192—256 40 GP [536]
257—264 41 ХВ 1225]
265—272 42 XQ 721]
273—280 43 GP 1291]
281—311 44 SV 631]
31^515 45 GP Г536]
РАССТОЯНИЕ D = 13
R Тип Ссыл-кода ка
iHs'd 18 £/[308]
21—22 19—20
23 20.415 HD 819]
24 . 21 BV 102]
25—27 21.1193 HD 819]
22.093 СМ 1238]
"Д' 23 RM
30—-si ’с- 24 GP[625A]
32—34 25., РТ [1047]
35—37 26 ' ХВИ225]
' .38' ‘ 27
39 43 28 • GFfl 13]
44—45' ' 29—30
46-55 56 **• 31 ' 32' У2[1237]
67—63 зз В
Продолжение рис. Г1А.2
64—70 71—73 34 35 ХВ[ 12251 XQ[721]/
74 36
75—77 37 QB [715]
78—79 38 AS [722]
.80—90 91 39 40 СУ [1083А]
92—99 41 GB [286]
100—128 42 В[1237]
129—135 43 ЛВ| 1225]
136—142 44 XQ[721]
143—149 45 GB[1291]
150—156 46 GB[1291]
157—191 47 У1[637]
192—256 48 В[1237]
257—264 49 X В [1225]
265—272 50 XQ[721]
273—280 51 GB[1291]
281—288 52 GP[1291]
289—327 53 Fl [637]
328—512 54 В[1237]
РАССТОЯНИЕ D = 15
N R Тйп Ссыл-
кода ка
22—23 21 £/[308]
24—25 22—23
26 23.415 Я£>[819]
27 24 В FT 102]
28' 24.678 Я£>[819]
29—31 25 RM
32 26
33 26.830 //£>[819]
34- 27.752 СМ [1238]
35 28 ZH225I
36—39 29 GP[1291]***
40—41 30 ХС[1237]
42—44 31 £/[859А].
45—47 32 АХ [1237]
48—50 33 СУ 113
51—55 34 СУ [113
56—63 35 . СУ[744
64—72 36 CY Г1083А]
73—74 37—38
75—79 39 Q/?[715]
80—81 40—41
82—87 42 QAJ715]
88—90 43—45
91—92 ' 46 СУ [1083А]
9,3—95 46.678 KS 722 ***
96—99 47 ' QR [715
100—101 47.678 KS 722
102—104 ' 48' GB[286
105—128 ’ 49' GP .-5361
129—135‘ 50. ХВ[1225]'
136—142 51 XQT721]'
143—149 527 GP[1291
150—156 53 GP[1291
157—163 54 GP 1291
164—191. 55 Fl[637]
192—256 56 GP [536]
257—264 57 ХВ 1225]
265—272 58 XQ ‘721]
273—280 59 GP 1291'
2811—288 60 GP 1291
289А-296 61 GP 129 Г
297Д327 62 У1[637]
328—512 63 GB [536]
РАССТОЯНИЕ D =*17
N R Тип Ссыл-
кода ка
25 26 24 L1[308]
27—28 25—26
29 26.415 //£>[819]
30 27.415
3! 28 BV[102]
32 28.415 HD [819]
33—35 28 830 HD ‘819]
36 29.752 CM 1238]
37 30.678 HD 819]
38 31.608 CM 1238]
39 32.541 HD 819]
40—41 33 GP [26]
42 34
43—44 35 GB[1291]
45—46 36 XQ[721]
47—49 37 Г/Г717]
50 38
51—53 39 LI 715]
54—55 39.142 УЗ 1237]
56 40 У1 1237]
57—62 41 СУ [266]
63—66 42 XC[1237]
67—71 43 71 [1237]
72—89 44 QBR15]
90—93 45—48
94—101 49 QB [715]
102 50
103—105 51 DC[715]
106-107 52—53
108—125 54 В
126 55
127—128 129—135 56 57 Ж 237] [1225]
136—142 58 XQ 721]
143—149 59 GP 1291
150—156 60 GP 1291’
157—163 61 GP 1291
164—170 62 GP 1291
171—191 63 У1[637]
192—256 257—264 64 65 s 237] [1225]
265—272 66 XQ 721]
273—280 .67 GP 1291
281—288 68 GP 1291
289—296 j69 GP 1291
297—304 70 GP 1291
305—331 71 У1 [637]
332—512 72 В[1237]
Продолжение рис. ПА.2
РАССТОЯНИЕ D = J9
N В Тип Ссыл-
я кода ка
28—29 27 £/[308]
30—32 28—30
33 30.415 //£>[819]
34 31 СУ [266]
35 31.678 HD 819
36 32.415 HD [819]
37—39 32.678 HD Г 8191
40 33.608 СМ [1238]
41 34.541 HD 8191
42 35.541
43—44 ’36 АХ [26]
45 37
46—48 38 Я5[636]
49—51 39 £/[717]
52 40
53—55 56-59 41 42 1237] [364]
60—61 43 в
62—63 44 СУ[266]
64—72 45 СУ [1083А]
73—76 46—49
77—83 50 У1 [ 1237]
84—103 51 QB [715'
104 52
105—107 53 £>С[715]
108—109 54—55
110—127 56 В
128—129 57—58
130—131 59 GP [1291]
132—135 60 GP [1291]
136—139 61 ХС 11237]
140—141 62—63
142-143 64 NL [1291
144—147 65 HL 1291]
148—151 66 GP 112911
152—191 67 У1[637]
192—255 68 В
256—260 69 ХВН225]
261—263 70—72
264—271 73 GP [1291]
272—273 74 GP [1291
274—280 75 GP [1291]
281—288 76 GP 1291]
289—296 77 GP [1291
297—304 78 GP [129Г
305—312 79 GP [1291
313—339 80 У1[637]
340—512 81 GP [536]
РАССТОЯНИЕ D = 21
В Тип Ссыл-
кода ка
31—32 30 £/[308]
33—35 31—33
36 33.415 //£>[819]
37 34.415
cs cs cs cs cm cs
CS —' cs cs
4 0
cs cs cs
cs cs
□o oo oo
“cs
a
ЩО
<o
ox
sjxcqx
" w
<O — 1Я Ю sf
s
ITJ co о c
О
sf^u?u?iq«?<p<5
^QQQ
— co c~ о ocs
s n Q
м s
ж ас
cs cs cs cs cs cs cs
— CS —
“cs
QQ, ^<3
cs cs
а. СУ
oq oa. fflXXO
u о о <o <o о <o
^qqaq^Q
OLCIC
CKC S Ж-X C. CQ-' CS CS sr CSCMCSCSCSCSCSCSCSCOcOCOCOCO
><COOOOCC>,eQ
Й
cs cs co co co com
тою
\ 55 48 LI [25]***
56—61 62г-бЗ 64-V66 \б7 49 50—51 52 53 DG [758] L/[715]
68-171 72—73 74—75 76—78 54 55—56 57 58—60 DG Гл. 18 X [26]
79—81 82 83—86 87—91 61 62 63 64—68 РТ [1047] В[637]
92—93 94 69 70 LI Гл 10
95—99 71 GP[1291]
100—101 102 103—109 110—125 126—127 72 73 74 75 76—77 PS [722]*** У1[637] В
128—135 78 ХВ[1225]
136—142 79 XQ[721]
143—149 150—152 80 81—83 GP[1291]
153—156 157—161 162—167 168 173 174—179 180—185 186—191 192207 208—255 84 85 86 87 88 89 90 91 92 GP[1291] PS [722] KS [722 PS [722 PS [722 PS [722 PS [722 У1[637] В
256—264 93 ХВ 1225]
265—272 94 XQ 721]
273—280 95 GP 1291]
281—284 285—287 96 97—99 GP[ 1291]
288—295 100 GP[1291
296—297 101 GP 1291
298—304 102 GP[1291
305—312 103 GP[1291'
313—320 104 GP[1291
321—328 105 GP[1291
329—336 337—347 348—512 106 107 108 GP[1291 У1[637] В[1237]
РАССТОЯНИЕ D = 27
Н Л Тип Ссыл-
кода ка
40—41 39 LI [308]
42—45 40—43
46 43.415 HD [819]
47 44.415
48 45 СУ[266]
49 46
50 46.678 HD [819]
51 47.193 HD[819]
52 53—55 56 57 58—63 64—67 68—73 Продолжение рис. ПА.
47.830 48.193 49.193 50.093 51 52—55 56 HD [819] HD [819] HD[819] DG [758]
DG Гл. 18
74—77 57—60
78—79 61 Hi[1291]
80—81 62—63
82—84 64 СУ [1083A]
85—88 65 В [637]
89—93 66—70 -
94—95 71 LI Гл. 10
96—97 72—73
98—99 74 ZV[1470]
100—103 75 У4[637]
104—111 76 УН637]
112—127 77 В
128—129 78—79
130—131 80 GP [1291]
132—135 81 GP [1291
136—139 82 XC [1237]
140—141 83—84
142143 85 NL [1291]
144—147 86 NL [1291]
148—151 87 GP [1291]
152—156 88 GP [1291]
157—158 89—90
159—167 91 KS 722]
168—173 92 KS [722
174—179 93 KS [722]
180—185 94 KS 722]
186 -191 95 KS 722]
192—197 96 KS 722]
198—199 97—98
200—207 99 У1Г6371
208—255 100 в
256264 101 XB [1225]
265 272 102 XQ [721]
273—280 103 GP 1291
281—288 104 GP [1291]
289—292 105 GP [1291]
293—295 106—108
296—303 109 GP [1291]
304—305 НО GP [1291
306—312 111 GP [1291
313—320 112 GP [1291
321—328 ИЗ GP [1291]
329—336 114 GP [1291
337—344 115 GP [1291]
345—352 116 GP [1291]
353—512 117 GP 536]
РАССТОЯНИЕ D = 29
N R Тип Ссыл
кода ка
43—44 42 LI [308]
45—48 43—46
49 46.415 HD [819]
Окончание рис. ПА.2
50 51 47.415 48.415 128—135 136—138 85 86—88 XB [122^1
52 49 BV 102] 139—142 89 GP[12J01]
53 49.678 НВ 819 143—146 90 XQ[7^1]
54 50.415 HD 819' 147—148 91—92
55 51.193 HD 819' 149—150 93 KL[1!291
56 51.678 HD 819 151—154 94 K.L[1291
57—59 52.093 HD 819 155—158 95 GP[1291
60 53.046 СМ 1238] 159—163 96 GP[1291
61 54 RM 164—167 97 KS [722]
62 55 168—179 98 KS [722
63 55.913 7/1)18191 180—185 99 KS [722
64 56.913 186—191 100 KS [722'
65—69 57 X Гл. 18 192—197 101 KS [722'
70—74 58—62 198—202 102—106
75—77 62.752 ZV[1470] 203—207 107 Г1[637]
78 63.752 208—255 108 В
79 64 АЦ1291]*** 256—264 109 ХВЦ225]
80—81 65 GP[1291] 265—272 110 XQ[721]
82—83 66—67 273—280 111 GP[129r
84—86 68 GP[1291] 281—288 112 GP[1291
87 69 289—296 113 GP 1291
88—89 70 'ZV[1470] 297—300 114 GP[1291’
90 71 301—303 115—117
91—95 72 ZV[1470] 304—311 118 ОР[129Г
96—99 73—76 312—313 119 GP[1291
100—101 77 LI Гл. 10 314—320 120 GP 1291
102—104 78 Zl/[1470] 321—328 121 G/>[1291
105 79 329—336 122 GP[1291
106—111 80 ZV[1470] 337—344 123 G/>[1291'
112 81 345—352 124 GP[1291
113—125 82 В[744] 353—360 125 G/>[1291
126—127 83—84 361—512 126 В [1237]
Число кодовых слов на рис. ПА.2. Если избыточность /?=/Ц-Х, где / — целое число, а X заключено между 0 и 1, то число кодовых слов равно.
Е-2Л’-1 * *-6,
где F задается следующей таблицей:
X: 0 F: 32 0,046 31 0,093 30 0.142 29 0,193 28 0,245 27
X: 0,300 0,356 0,415 0,476 0,541 0,608
F: 26 25 24 23 22 21
X : 0,678 F : 20 0,752 19 0,830 18 0,913 17
1 Коды,. отмеченные *, **, *** в работах [1180], [1183а*] (см. также
[1451]), [1470] соответственно, построены ранее или одновременно с работами,
на которые ссылаются авторы книги. (Прим, ред.)
\Типы кодов, приведенные на рис. ПА.2
. AL — альтернантами код (линейный) (гл. 12, [633]);
АД—метод построения типа |А+Х| B+XI A-j-B+XI (линейный код)
\ (§ 18.7.4, [1237]);
В J— код БЧХ или укороченный код БЧХ (линейный) (гл. 3, 7, 9);
BV — линейный код Белова и др., достигающий границы Грайсмера (§ 17.6,
СМ—конференс матричный код (нелинейный) (§2.4, [1238]);
'CY — циклический или укороченный циклический линейный код;
DC — дважды циркулянтный код (линейный) (§ 16.7, [715]);
DG — Дельсарта—Геталс.а обобщенный код Кердока (нелинейный) (§ 15.5,
СВ—обобщенный код БЧХ (линейный) (§ 12.7, [286]);
СО —код Голея (линейный) (§ 2.6, [506]);
GP—код Гоппы или модифицированный код Гоппы (линейный) (§ 12.3, [536], [1291]);
Ни—код, построенный с помощью матрицы Адамара (нелинейный) (§ 2.3, [819]);
HG —код Хэмминга (линейный) (§ 1.7, [592]);
HS — метод построения Хелгерта и Стинаффа (§ 18.9.2, [636]);
Ш —нелинейный код Геталса I (М) (§ 15.7, [495]);
KS — модифицированные каскадные коды Касахары и др. (линейные или нелинейные) (§ 18.8.1, [722]);
LI — линейный, код;
NL—нелинейный код;
PJ?—код Препараты (нелинейный) (§ 15.6, [1081]);
РТ—метод построения Пирета (линейный код) (§ 18.7.5, [1047]);
QR —квадратично вычетный код (линейный) (гл. 16); ...
7?Л1 — код Рида — Малдера или укороченный код Рида — Маллера (линейный) (гл. 13);
XV—код Сривэставы (линейный) (§ 12.6) ;
51Г—нелинейный код, исправляющий одиночные ошибки (§2.9, [1239]);
X — метод построения X (линейный или нелинейный код) (§ 18.7 7, [1237]);
ХВ -— применение метода построения X к коду БЧХ (линейный код) (§ 18.7.1, [1237]);
ХС — применение метода постооения X к циклическому коду (линейный код) (§18.7.1, [1237]);
ХВ — применение метода построения X к коду Препараты., (нелинейный код) (§ 18.7.1, [1237|); .
XQ—расширенные коды БЧХ Касахары и др (линейные коды) (упражнение (14) гл. 18, [721]); . .. ,
ХЗ -- метод построения ХЗ (линейный или нелинейный код) .(упражнение (14) гл. 18);
Х4 — метод построения Х4 (линейный .. или , .нелинейный код) . (§ 18.7.2, [1237]),; .. •' -
XI — метод построения Y1 (линейный код) (§18.94); ..
У.2 — метод построения Y2 (нелинейный код) (упражнецие.(29). гл.. 18).;
УЗ —метод построений УЗ. .(нелинейный код) (упражнение (.29)-.гл.. 18); .
У4 — метод построения Y4 (линейный код) (упражнение, (30) гл. 18„ [637]) ;
X—метод построения типа |7/|7Л]-К| (линейный иди. нелинейный -.код) (§2.9, [1239]); . _ ... • _ _ ----- -
XV —метод построения Зиновьева (динедный или нелинейный код) (§ J.8-.8.2, [1470]). • .о - joft;* ги по;Я:
4. Таблица значений А(п, d, w) (рис. ПА.З)
Эта таблица важна, так как она ведет к оценкам величины A,(n, d) (.§ 17.3), сама по себе представляет i границы равновесных кодов (§1'7.2) и; наконец, дает решения задачи об упаковке1’. Ийогда задача об упаковке формулируется
1 Называемой также задачей о максимальном покрытии. (Прим, перев.)
следующим образом. Найти D(t, k, ri)—максимальное число ^-множеств из «-множества S, так чтобы каждое /-множество из S принадлежало самое большее одному fe-множеству (см., например, Гарднер [467], Калбфлейш и др. [708—711], Миллс [957—959], Стентон [1265], Стентон и др. [1267—1271] и Свифт [1295]. См. также задачу о футбольном тотализаторе, упоминавшуюся в гл. 7.). Так как D(t, k, п)=А(п, 2k—2^4-2, k), то рис. ПА.З дает также н таблицу значений D(t, k, ri).
Отсутствие ссылки при верхних границах на рис. 3 означает, что они получены из оценок Джонсона (теоремы 1—4 и упражнение (2) из гл. 17) или из упражнения (4) гл. 17. Неотмеченные нижние оценки также получены из теоремы 4 и упражнения (2) гл. 17 или могут быть найдены несложными построениями. Значения маленьких букв объяснено ниже. Буквы слева относятся к нижним оценкам, а буквы справа — к верхним. Возможно, существует несколько способов построения одного из указанных кодов, но отмечается только простейший из них. Немного более поздний вариант этой таблицы появится в работе Беста и др. [140]*
Упражнение. (1). Используя последнюю строку на рис. 5 гл. 14, показать, что А (16, 8, >6) = 16 и А (15, 8, 6) = 10.
Задача (нерешенная). (ПА.З). Известно, что 2-(17, 6, 15) схема существует |(Ханани [600]). Но имеется ли такая 2-(17, 6, 15) схема, что ее блоки образуют код, существование которого доказывает, что А (17, 6, 6) = = 136?
Задача (нерешенная). (ПА.4). Укажем еще параметры равновесных кодов н их спектры .расстояний (найденные с помощью линейного программирования), которые могут существовать:
А (21, 4, 5)JL 1197 (Во=1; В4=80; Вв=320; В8=540; В10 = 256);
А (16, 6, 8)JL 150 (Во=1; В6 = 64; В8=20; В10 = 64; В16=1).
Задача (нерешенная). (ПА.5). Верно ли, что если wi<w2^n/2, то А(п, d, W!)<^A(n, d, w2)?
Объяснения к рис. ПА.З
а. Теоремы 6, 7 гл. 17.
Ь. Шен Лин [831].
с. А. Р. Финней [1043].
d. А. Е. Брауэр [201а].
е. Из упражнения (6) гл. 17 и существования систем Штейнера S (5, 6, 12k (3, 5’ 1?)' (3, 6, 26), S (5, 8, 24), S (4, 7, 23) (Чин [277], Дениистон
[372], Дуайен и Роза [386]).
f. Из несуществования систем Штейнера S (4, 5, 15), S (4, 6, 18) ([386]).
g. Циклический код.
h. Из /-схемы* 1 3-(16, 6, 4) (полученной из кода Нордстрома — Робинсона).
i. Из сдвигов кода Нордстрома — Робнисона (см. рис. 6.2 и работу Г201а1)
/. Из [124. 12, 8]-кода Голея.
k. См. упражнение i(l).
L. Граница линейного программирования (§ 17.4).
т. Из конфереис-матрицы.
п. Квазициклический код.
q. Упражнения (7) и (8) нз гл. 17.
г. Вальян (W. G. Valiant), частное сообщение.
s. Стинсон (D. Stinson), частное сообщение.
t. См. [140].
Более поздний вариант таблиц для кодов А(п, d, w) опубликован в статье (Graham R. L., Sloane N. J. A. Lower Bounds for Constant Weight Codes. — IEEE Trans. Info. Theory, 1979, vol. 25, N 6.).
1 Такая /-схема, одновременно являющаяся максимальным равновесным кодом, впервые приведена в работе [1180]. (Прим, ред.)
Рис. ПА.З. Таблица A(n, d, w)
Расстояние 4: А (п, 4, w) n/w 2 3й 4й 5 6 7 8 9 10
4 5 6 7 8 9 10 И 12 2 2 3 3 4 4 5 5 6 1 2 1 1 3 7 —
1 1 3 8 18
4 7 8 12 13 17-го 1 1 4 12 30 66
1 1 4 13 35 73—84
14 18 30 '35 51 1 1 5 17 51
1 1 5 20
36 66 "73—84 1 1 6
1 1
432 1
13 6 26 65 "99—132 d 143—182 143—182 99—132 65 26 6 1
14 7 28 91 443—182 J210—308 d216—364 210—308 143—182 91 28 7
15 7 35 105 d213— —272f 321—455 d435—660 435—660 321—455 213—273 105 35
16 8 37 140 d305—336 513—725 —1040 ? —1320 ? —1040 513—725 305—336 140
17 — 8 44 154— —157 d424—476 792—952 ? —1760 —2210 ? —2210 ? —1760 792—952 424—476
Продолжение рис. ПА.З
Расстояние 4: А (п, 4, ш>)
—“-‘Г'- 18 9- 48 й198 480—565 41-88—1428 —2448 ? —3960 ? —4420 ? —3960 ? —2448 1188—1428
19 9 57 228 612—752 1428—1789 ? —3876 ? —5814 * ? —8360 ? —8360 —5814 ? —3876
20 10 60 285 816—912 4640—2506 ? —5111 ? —9690 ? —12920 ? — 16720 ? — 12920 ? —9690
21. 10 70 3,5 е 1071— —1197 е2856—3192 4 -. ? —7518 —13416 ? —22610 ? —27132 ? —27132 —22610
22 11 73 385 I 1386 3927—4389 ? — 10032 ? —20674 ? —32794 ? —49742 —54264 ? —49742
23 11 83 415— —419 1771 5313 ? — 14421 ? —28842 ? —52833 ? —75426 ? — 104006 — 104006
24 12 88 498 4859— —2011 4084 ? — 18216 ? —43263 —76912 ? — 126799 —164565 ? —208012
Продолжение рис. ПА.З
Расстояние 6: А (п, 6, w)
n/w 2 3 4 5 6 7 8 9 10 И 12
6 1 2 1 1 1
7 1 2 2 _ 1 1 1
8 1 2 2 2 1 1 1
9 1 3 3 3 3 1 1 1
10 1 3 5 6 5 3 1 1 1
11 1 3 6 11 11 6 3 1 1
12 1 4 9 *12“ 22 12 9 4 1 1 1
13 1 4 ^13 “18“ •«26 26 18 13 4 1 1
14 1 4 14 *28 *42 d42—51г 42 28 14 4 1
15 1 5 15 *42 *70 ‘60—88* 60—88 70 42 15 5
16 1 5 20 18 *112 ‘90—156 ‘120 -150* 90—156 112 48 20
17 1 5 20‘‘ ‘'68 112—136 112—244* 125—283 125—283 112—244 112—136 68
,8 1 6 *22 68—72 ‘‘144—203/ ‘ИО—349 ‘232—428* 249—425* 232—428 160—349 144—203
19 1 6 “25s ‘72—83 472—228 ‘228—520* ‘332—739 ‘‘472—789* 472—789 332—739 228—520
20 1 6 "30 ‘81—100 ‘'232—276 310—651 ‘492—1199* ‘‘672—1363* ‘‘944—1421* 672—1363 492—1199
Продолжение рис. ПА.З n/w 2 3 4 5 6 1 3 9 10 11 12
Расстояние 6 А (п, 6, то)
21 1 7 “31 rf102— —126 ‘253—350 465—828 d668—1708 d1068—2364L d1286—2702l 1286—2702 1068—2364
22 1 7 “37 d132— —136 294—462 675—1100 d708—22^7 d1288—3775L d1450—4416L d1574—50641 1450—4416
23 1 7 “~40 d~147— —170 399—521 969—1518 ? —3162 ? —5819 ? —7521b ? —7953l ? —7953 .
1 8 “42 “168— — 192 “532—680 “1368—1786 ? —4554 ? —8432 ? —12418l ? — 14682 ? —15906l
Расстояние 8: А(п, 8, го)
8 1 1 2 1 1 1 1
9 1 1 2 2 1 1 1 1
10 1 1 2 2 2 1 1 1 1
11 1 1 2 2 2 2 1 1 1 1
12 1 1 3 3 4 3 3 1 1 1 1
13 1 1 3 3 4 4 3 3 1 1 1
14 1 1 3 4 7 8 7 4 3 1 1
15 1 1 3 6 ft10 15 15 10 6 3 1
16 1 1 4 6 ft16 16—22 30 16—22 16 6 4
1 1 4 7 bl7 >21—31r “34—35 34—35 21—31 17 7
Продолжение рис,-ПА.З
18 1 1 4 >9 >20—21 >33—41» >46—63 >48—70 46—63 33—41 20—21
19 1 1 4 >12 >28 >52—57 >78—97 >88—122» 88—122 78—97 52—57
20 1 1 5 •46 >40 >80 >130—142 >160—215 >176-244» 160—215 130—142
21 1 1 5 >21 >56 >120 >210 >280—331 >336—399» 336—399 280—331
22 1 1 5 21* >77 >176 >330 280—497» >616—728 >672—798 616—728
23 1 1 5 ^23 77—80 >253 >506 >400- 816 616—1111» >1288—1417» 1288—1417
24 1 1 6 *24 77—92 253—274 >759 >640—1160» >960—1639» 1288—2305» >2576
Окончание рис. ПА.З Расстояние 10: (м, 10, w) 2 3 4 5 6 7 8 9 10 11 12
10 11 12 13 14 15 16 17 18 19 20 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 3 1 2 1 1 2 2 1 1 1 2 2 3 1 1 1 ’ 1 2 3 1 1 1 3 1 1 1 1 1 1 1 1 1
2 2 2 3
2 3
1 1 1 1 1 3 3 3 3 4 3 3 4 4 5 3 5 6 8 п10 4 6 9 ь12 *17—18 3 6 3 5 9 19 3 3 6 12 20—24 1 3 4 8 17—18
10 19 «20—24
38
21 1 1 1 4 7 13* «21—26 «21—41* 38—49* 38—49 21—41
22 1 1 1 4 7 15—19 «22—35 «22—57* ? —74г ? —82l —74
23 1 1 1 4 8 *16—23 «23—50* «23—87* ? — Ц7Г ? — 135L ? —135
24 1 1 1 4 9 «24—27 «24—69 > —119* ? — 171г ? —223r ? —247L
ПРИЛОЖЕНИЕ В
КОНЕЧНЫЕ ГЕОМЕТРИИ
1. Введение
Конечные геометрии представляют собой такой же важный комбинаторный-объект, как и коды, и поэтому нет ничего удивительного в том, что они возникают во многих главах этой книги (см., в частности, гл. 13). В данном приложении мы даем эскиз основ теории конечных геометрий, начиная (в § 2) с определения проективной и аффинной геометрий. Наиболее важными (для нас) примерами конечных геометрий являются проективная геометрия PG (т, q) и аффинная (или евклидова) геометрия EG (т, q) размерности т, конструкции которых основаны на конечном поле GF(q). Для этим исчерпываются все возможные конечные геометрии (теорема 1).
В § 3 этого приложения исследуются свойства геометрий PG (т, q) и EG (т, q), в частности их группы коллинеаций (теорема 7 и следствие 9), и выводится формула для числа подпространств данной фиксированной размерности (теоремы 4—6).
Дело обстоит несколько сложнее, если размерность т=2. Проективная плоскость эквивалентна системе Штейнера S(2, п+1, п2+п+1) для некоторого. п;>2, а аффинная плоскость — системе S (2, и, и2) для некоторого п^2 (теорема 10). Но в этом случае существуют и другие типы плоскостей, отличные от PG (2, q) и EG (2, q) (см. § 4).
2. Конечные геометрии PG(m, q) и EG(m, q)
геометрией называется
Определение 1. Конечной проективной геометрией называется конечное. множество й точек р, q,... и совокупность подмножеств М, L, . .. множества Й, называемых прямыми, удовлетворяющая аксиомам (i) — (iv). (Если peJL, то. будем говорить, что р лежит на L или что L проходит через р).
(i) . Через любые две различные точки р и q проходит только одна прямая (обозначаемая через (pq)).
(ii) . Каждая прямая содержит по меньшей мере три точки.
(iii) . Если различные прямые L и М имеют общую точку р и если точки q и I прямой L не равны точке р и точки s и t прямой 7' прямые (qt) и (rs) также имеют общую точку (см. рис. ПВ.1).
(iv) . Для любой точки р найдутся по меньшей мере две прямые, не содержащие р, и для любой прямой L найдутся по меньшей мере две точки, не принадлежащие L.
Подпространством проективной геометрии называется такое подмножество S в й, для которого выполняется условие:
(v) . Если р и q — различные точки из S, то все точки прямой (pq) принадлежат S.
Примерами подпространств в й являются точки и линии в Й, а также само й. Гиперплоскостью Н называется максимальное собственное подпространство, так что й представляет собой единственное подпространство, содержащее Н в качестве собственного подпространства.
Определение 2. Аффинной, или евклидовой,
проективная геометрия, у которой нз всех подпространств удалены точки некоторой фиксированной гиперплоскости Н (так называемой бесконечно удаленной гиперплоскости). Образующиеся в результате .множества называются подпространствами аффинной геометрии.
Л4ножество Т точек в - аффинной -или проективной геометрии называется. независимым, если для каждого точка х не принадлежит никакому мень-.
:шему подпространству, содержащему Т—{%}. Например, любые три точки, не лежащие на одной прямой, являются независимыми. Размерность подпространства S равна г—1, где г равно мощности максимального множества независимых точек в S. В частности, если S = Q, то это определяет размерность проективной геометрии.
Проективная геометрия PG(m, а). Наиболее важные примеры проективной .и аффинной геометрий получаются из конечных полей.
Пусть GF(q) —конечное поле (см. гл. 3, 4), и предположим, что т^2. Выберем в качестве точек множества О ненулевые (т+1) -последовательности
(а0> Сь - - - , ат), ai<=GF(q),
положив, что последовательности
(Со, • • •, Ст) И (Хсо, • • > ?-Ст)
.задают одну и ту же точку для любого ненулевого элемента А из GF(q). Это так называемые однородные координаты точки. Всего имеется qm'rl—1 ненулевых (т+1)-последовательностей, и каждой точке соответствует q—1 последовательностей, так что число точек в множестве О равно (qm+l—1)/(q—1).
Прямая, проходящая через две различные точки (с0, • , ат) и (+, • • -, bm), состоит из точек вида
(Хсо+р1?о, +/<Рт) , (1)
где X, \x<sGF(q) не равны одновременно нулю. Прямая состоит из </+1 точек, так как всего имеется <?2—1 возможностей выбора пары р) и каждая точка появляется при этом в (Bl) q—1 раз. Аксиомы (1) и (ii), очевидно, выполняются.
У пр ажнение.г (1). Проверить выполнение аксиом (iii) и (iv). Определенная так проективная геометрия обозначается через PG(m, q).
Упражнение. (2). Доказать, что размерность геометрии PG (т, q) рав-жа т.
Примеры. (1). Если m = q — 2, то проективная плоскость PG (2, 2) состоит, как показано на рис. ПВ.2, из семи точек (100), (001), (010), (011), (101), (ПО), (111) (ср. с рис. 2.12).
Рис. ПВ.2. Проективная плоскость /’6(2,2)
Рис. ПВ.З. 13 точек и 9 из 13 прямых проективной плоскости /6(2,3)
(2). Если т=2 и </=3, то получаем держащую 32+3+1 = 13 точек
проективную плоскость PG (2, 3), со-
(001) (010) (011) (012)
(100) (101) (102) (ПО)
(Ill) (112) (120) (121)
(1122)
и 13 прямых линий, 9 из которых показаны на рис. ПВ.З.
Удобно расширить определение геометрии PG(rn, q), включив значения jn——1, 0 и 1, хотя эти вырожденные геометрии не удовлетворяют аксиоме (iv). При этом PG{—1, q) — пустое множество, PG (0, q) — точка и PG (1, q) — прямая.
Гиперплоскость, или подпространство размерности m—1 в PG (m, q), определяется как множество точек (со, ...,ат), удовлетворяющих однородному лиией-.ному уравнению
Xoao+Xiai+ - - - ^'тПт==б, (q).
Такая гиперплоскость на самом деле представляет собой геометрию PG(m— —1, q) и будет в дальнейшем обозначаться через [?.о,. . . ,Ат]. Отметим, что [Хо,.. . ,.Хт] и [ц\о,_. •, р'Ат] при любом р#=0 соответствуют одной и той же гиперплоскости (т. е. гиперплоскости при т=2) и на рис. ПВ.12 и ПВ.З обозначены именно таким образом. Ясно, что точка (а0, , ат) принадлежит гиперплоскости т
[Хо, .... Хт], тогда и только тогда, когда 2 Х,аг = 0.
1=0
Упражнения. (3). Показать, что точки геометрии PG (т, q) допускают •однозначную нумерацию последовательностями, крайняя левая ненулевая координата которых равна 1 (как в примере 2).
(4) . Показать, что геометрия PG (т, q) может быть построена из векторного пространства V размерности (т-|-1) над полем GF(q) путем объявления точками геометрии PG(m, q) всех одномерных подпространств в V, а прямыми—двумерных подпространств в V.
(5) . Провести четыре пропущенные на рис. ПЗ.З прямые.
(6) . Построить PG (3, 2).
Аффинная, или евклидова геометрия EG(m, q). Она получается из геометрии PG(m, q) путем удаления точек гиперплоскости Н (безразлично какой именно в силу следствия 8). Например, удаление прямой линии [100] на рис. ПВ.2 приводит к EG (2, 2;):
В общем случае, если в качестве Н выбирается гиперплоскость [1,0.. .0], состоящая из всех точек, для которых а0=0, то остаются точки, допускающие нумерацию последовательностями (1, щ, ...ат). Таким образом, q™ точек геометрии EG(m, q) можно нумеровать просто m-последовательностями (ai...,am), де ^GF(9);
Мы опять примем, что EG(—1, q) — пустое множество, £G(0, q) —точка 0 и £G(1, q) ~ прямая.
Упражнение. (7). Доказать, что (определенная выше) размерность геометрии EG(m, q) равна т. Показать также, что EG(m, q) является векторным пространством размерности т над полем GF(q).
Замечание. Все ненулевые элементы поля GF(qm+l) соответствуют точкам геометрии PG(m, q), но каждой точке при этом соответствует q—1 различных элементов поля. Например, пусть G£(4) = {0, 1, о>, со2}. Тогда элементы 100, со 00 и со2 00 поля G£(43) представляют собой одну и ту же точку геометрии •PG(2,4). Прямая, проходящая через точки (100) и (0 10), содержит пять точек:
100 (или со 00 или со2 00)
010 (или ОсоО или 0со20)
ПО (или сосоО или со2со20)
1.со0 (или сосо2О или со2Ю)
1<о20 (или со 10 или со2со0)
Точками аффинной геометрии EG(m, q) являются все.элементы поля GF(q™).
Дезарговы геометрии. Все аффинные и проективные геометрии, размерность которых больше двух, строятся с помощью конечных полей. Но в двумерном случае дело обстоит несколько сложнее.
Теорема 1. Если т^З, то всякая конечная проективная геометрия размерности т является геометрией PG(m, q) для некоторого q и всякая аффинная геометрия размерности т является EG(m, q) для некоторого q.
Геометрия PG(m, q) называется дезарговой, так как в ней выполняется теорема Дезарга.
Доказательство теоремы 1 проводится в три шага. (i). Показывается, что в-, проективной геометрии, размерность которой больше двух, выполняется теорема Дезарга. (ii). Доказывается, что все точки дезарговой геометрии могут быть заданы координатами, принадлежащими, возможно, некоммутативному полю S. (iii). Если S — конечно, то оно коммутативно п, следовательно, S—GF(q) для некоторого q. Детальное доказательство можно найти в книгах: Артин [29, гл. 2],. Бэр [56, гл. 7], Дембовский [370, гл. 1], Херстейн [642], Веблен и Янг [1368. т. 1, гл. 2].
3. Свойства геометрий PG(m, q) и EG(m, q)
Подпространства геометрии PG(m, ^.Упражнение. (8). Доказать, что если S — подпространство в PG (т, q), то S является также подпространством в PG(r, q) для некоторого г, и что S может быть задано как множество
точек, удовлетворяющих системе т—г независимых однородных линейных уравнений.
Отсюда следует, что пересечение двух различных геометрий PG(m—1, q), лежащих в PG(m, q), равно геометрии PG(m—2, q) (так как точки пересечения удовлетворяют системе двух линейных уравнений). Пересечение PG(m—1, q) в PG(m—2, q) в PQ(m, q) равно либо PG(m—2, q), либо PG(m—3, q) и т. д. Пересечение PG(m—1, q) и прямой линии равно либо прямой, либо точке.
В общем случае при s~^r пересечение PG(r, q) (определяемой т—г уравнениями) и PG(s, q) (определяемой т—s уравнениями) имеет размерность г, или г—1,..., или г—m+s. При г—подпространства могут не пересекаться.
Принцип двойственности. Так как и точки, и гиперплоскости геометрии PG(m, q) задаются (m-J-1) -последовательностями, то между ними существует естественное взаимно-однозначное соответствие, согласно которому точке р соответствует двойственная гиперплоскость [р]. Аналогичное взаимно-однозначное соответствие существует между прямыми линиями и подпространствами PG(m—2, q), согласно которому прямая (pq) соответствует двойственному подпространству [р] П М- Это соответствие обладает тем свойством, что если точка р принадлежит прямой .(<//-), то двойственная гиперплоскость [р] содержит двойственное подпространство.
Аналогично существует взаимно-однозначное соответствие между подпространствами размерности г и подпространствами размерности т—г—1, сохраняющее отношение инцидентности (и называемое иногда корреляцией). Например, если две геометрии PG(m, q) пересекаются в одной точке, то линейная оболочка объединения двойственных геометрий PG(m—г—1, q) равна гиперплоскости.
Это соответствие удовлетворяет принципу двойственности, согласно которому любое утверждение относительно геометрии PG(m, q) остается справедливым, если заменить «точку» на «гиперплоскость», «.PG(r, q)» на «PG(m—г—1, q)», «пересечение» на «линейную оболочку объединения» и «содержит» на «содержится».
Важнейшим следствием этого принципа является следующий факт.
Теорема 2. Если з5=г, то число подпространств PG(s, q) в геометрии PG(m, q), содержащих данную геометрию PG(r, q), равно числу подпространств PG(m—s—1, q), содержащихся в данной геометрии PG(m—г—1, q).
Упражнение. (9). Доказать непосредственно следующий частный случай теоремы 2: число линий, проходящих через заданную точку, равно числу точек в гиперплоскости.
Число подпространств. Теорема 3. Число подпространств PG(r, q), содержащихся в геометрии PG(m, д), равно
(gm+l_1) (gm+l_g) . , .(q”+'-qr} = Г 1 (/+1-1) (/+*-?) • . •(‘Л1~<7Г) L r+1J’
где
Г/тг+1 ] L Ж J
— гауссовский биномиальный коэффициент, определенный в упражнении (3) гл. 15.
Доказательство. Число способов выбора г+1 независимых точек в геометрии PG(m, q), определяющих геометрию PG(r, q), равно числителю выражения (2). Однако многие из этих множеств точек задают одну и ту же геометрию PG(r, q), и поэтому мы должны поделить выражение (.2,) на знаменатель, который равен числу способов выбора г+1 независимых точек в геометрии PG(r, q).
Аналогичным образом доказывается следующее утверждение. О
Теорема 4. Пусть в геометрии PG(m, q) выполняется условие <R = PG(r, q)<=S = PG(s, q). Тогда число подпространств Т размерности t таких, что ccT’czS, равно
[s—г 1 t—r ] '
Упражнение. (10). Используя теорему 3, доказать, что число подпространств PGi(r, q), содержащихся в геометрии PG(m, g), равно числу подпространств PG(m—г—1, q), содержащихся в геометрии PG(m, q).
Подпространства и плоскости в геометрии EG(m, q). Подпространство S геометрии EG(m, д) называется плоскостью.
Упражнение. (11). Показать, что если плоскость проходит через начало координат, то она представляет собой линейное подпространство геометрии EG(m, q), являющееся обычным векторным пространством; если же плоскость не содержит начала координат, то она представляет собой смежный класс геометрии EG(m, q) по линейному подпространству.
Таким образом, плоскость размерности г в геометрии EG(m, д) равна смежному классу по некоторой геометрии EG (r, q), и мы будем называть се /--плоскостью или EG (г, q). Подпространство PG(r, q) геометрии PG(m, q) также называется г-плоскостью.
Теорема 5. Число r-плоскостей EG (г, q) в геометрии EG(m, q) равно
Доказательство. Пусть EG(m, q) получается из PG(rn, q) путем удаления гиперплоскости И. Геометрия PG(r, q) либо пересекается с Н по PG(r—1, q), либо содержится в Н. Таким образом, интересующее нас число равно разности между числом геометрий PG(r, q), содержащихся в PG(m, q), и числом геометрий PG(r, q)„ содержащихся в И. Согласно теореме 3 и упражнениям (ЗЬ) и (3d) имеем;
m-Mir ™ 1 г Г"Я в
. г+1 j Ir-Flj 1+.'
Теорема. 6. Пусть в геометрии EG(m, q) имеет место включение Д = —EG (г, q)aS=EG(s, q), где г^1. Число плоскостей Т размерности t, для которых RaTaS, равно
’ s—г 1
. г J ‘
Доказательство. Вытекает из теоремы 4. О
Заметим, что в проективной геометрии любые две гиперплоскости пересекают-ся по подпространству размерности т—2, в то время как в аффинной геометрии две гиперплоскости могут пересекаться по подпространству любой размерности или вообще не пересекаться. Непересекающиеся гиперплоскости называются параллельными.
Упражнение. (12). Доказать, что геометрию EG(m, q) можно разложить на q взаимно параллельных плоскостей.
Группа коллинеаций геометрии PG(m, q). Определение. Коллинеацией проективной или аффинной геометрии называется такая перестановка ее точек,, которая переводит прямые линии в прямые. Отсюда следует, что каждое подпространство отображается в подпространство той же размерности.
Например, перестановка (011), (010), (001), (ПО), (111), (100)) является коллинеацией геометрии _PG(2,2) (см. рис. ПВ.2).
Множество всех коллинеаций геометрии PG(m, q) образует ее группу коллинеаций. Предположим, что q=ps, где р простое. Напомним, что согласно теореме 12 гл. 4 группа автоморфизмов поля GF(ps) является циклической группой по* рядка s и порождается отображением ор : (ieGF(ps). Отображение ар,
очевидно, является коллинеацией геометрии PG(m, ps).
Пусть С — обратимая .(m+1) X (т+1)-матрица над GF(ps). Тогда перестановка точек геометрии PG(m, ps), задаваемая отображением (а0,... ат)-+-->(со, .. ., ат)С, также является коллинеацией. Ясно, что матрицы С и ХС, Л^О, задают одну и ту же коллинеацию.
Отображение ар и матрицы С порождают группу, состоящую из перестановок вида
(«0...ат) -^(«о....ат) С> 0<i<s ,
Всего имеется s H.mi=o(qm+l—ql) таких перестановок, но только
т
П tf^-qi) (4>
q—I
i=0
из них задают различные коллинеации. Эта группа коллинеаций обозначается че~ рез PPLm+t(q), q = ps.
Теорема 7. (Основная теорема проективной геометрии.) Группа PFLm+i(q) является полной группой коллинеаций геометрии PG(m, q).
Доказательство этой теоремы можно найти, например, у Артина [29], Бэра [56, гл. 3] или Кармайкла [250].
Так как группа PTLm+i(q) дважды транзитивна, то справедливы следующие утверждения.
Следствие 8. Имеется по существу только один способ построения геометрии EG{m, q) из геометрии PG(m, q).
Следствие 9. Полная группа коллинеаций геометрии EG(m, q) равна подгруппе группы PFLm + ]{q), относительно которой инвариантна бесконечно удаленная гиперплоскость, и имеет порядок
т—1
П (/”-<Й (5>
i=l
(см., например, Кармайкл [250]).
Упражнение. (13). Доказать, что для заданной геометрии EG(m, q) имеется по существу только один способ добавления гиперплоскости, приводящий к геометрии PG(m, q).
4. Проективные и аффинные плоскости
Проективная геометрия размерности 2 называется проективной плоскостью. В отличие от случаев большей размерности проективная плоскость не обязательно представляет собой геометрию PG(2, q) для некоторого q.
В § 5 гл. 2 мы определили проективную плоскость как систему Штейнера S (2, /г+1, п2+/г+1) для некоторого /г^|2 или, иными словами (определение 2), как совокупность п2+п+1 точек и н2+н+1 прямых, причем на каждой прямой лежат п+1 точки и через любые две точки проходит точно одна прямая. Однако иаилучшим определением проективной плоскости является следующее.
Определение 3. Проективной плоскостью называется совокупность точек и прямых, удовлетворяющая следующим условиям; (i) через любые две точки проходит точно одна прямая; (ii) любые две различные прямые пересекаются в одной точке и (iii) существуют четыре точки, из которых никакие три не лежат на одной прямой линии.
Теорема 10. Все три определения проективной плоскости эквивалентны.
Набросок доказательства. Определение 1 (§ 2) определение 3. Необходимо только доказать, что любые две прямые пересекаются. Это следует из того, что в противном случае две прямые будут содержать четыре независимые точки, так что размерность пространства не будет равна 2.
Определение 3 ^определение 2. Выберем две точки р и q и линию L, не содержащую этих точек. Тогда число прямых, проходящих через р (или через q), равно числу точек на прямой L. Обозначим это число через п+1. Тогда общее число точек (или прямых) равно n(n+l) + l=n2+n+l.
Определение 2 ^определение 1. Чтобы доказать (iii), покажем, что любые две прямые пересекаются. Для доказательства .этого факта используются два разных метода подсчета 2%(р, L, Л1), где функция %(р, L, М) равна 1, если p = L [)7И, и равна 0 в противном случае, а суммирование ведется по всем точкам р и парам различных прямых L и М. Размерность системы равна 2, так как если р, q, г и s — четыре независимые точки, то прямые (pq) и (rs) не пересекаются. •
Система Штейнера S (2, п+1, п2+п+1) называется проективной плоскостью порядка п. Таким образом, на рис. ПВ.2, ПВ.З показаны проективные плоскости порядков 2 и 3. В общем случае PG(2, q) является проективной плоскостью порядка q. Согласно теореме 7 гл. 4 это дает нам дезарговы проективные плоскости всех порядков, равных степени простого числа.
Однако не все проективные плоскости являются дезарговыми. Действительно, для всех п=ре>8, где р — простое число и е>1, известны недезарговы плоскости порядка п. Для п<8 имеет место следующий результат.
Теорема 11. Проективные плоскости порядков 2, 3, 4, 5, 7, 8 определены однозначно (и представляют собой дезарговы плоскости PG(2, п)).
Для доказательства теоремы см. упражнение (13) гл. 20 и результаты, приведенные Домбовским [370, с. 144].
Из упражнения (11) гл. 19 мы узнаем, что не существует ни одной проективной плоскости порядка 6. Это утверждение является частным случаем следующего результата.
Теорема 1й. <(Брук и Райзер.) Если пе= 1 или 2 (mod 4) и если п не является суммой двух квадратов, то не существует проективной плоскости порядка п.
Доказательство этой теоремы можно найти в книге Холла [587] или в работе Хьюза и Пайпера [674].
Таким образом, известны проективные плоскости порядков 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19,... Известно (теорема 12), что не существует плоскостей порядков 6, 14, 21,..., и вопрос остается открытым для порядков 10, 12, 15, 18, 20 ... Связь между кодами и плоскостями порядков п, где n=s2(mod4), дается в упражнении (11) гл. 19.
Аффинные, или евклидовы, плоскости. Аффинной плоскостью называется аффинная геометрия порядка 2; она получается из проективной плоскости удалением всех точек некоторой фиксированной линии. В § 5 гл. 2 было дано второе определение аффинной плоскости: аффинной плоскостью называется система Штейнера S (2, п, п?), п^2. Третье определение выглядит следующим образом. Аффинной плоскостью называется множество точек и прямых, удовлетворяющих следующим условиям: (i) через любые две точки проходит точно одна прямая; (ii) для любой заданной прямой L и любой точки pfy L существует прямая линия, проходящая через р и не пересекающаяся с L; (iii) существуют три
точки, не лежащие на одной прямой. Эти три определения опять эквивалентны, и мы будем обозначать через 5 (2, п, я2) аффинную плоскость порядка п. Тогда все приведенные выше результаты о возможных порядках проективных плоскостей переносятся на случай и для аффинных плоскостей.
Замечания к приложению В
Проективные геометрии изучали Артин [29], Бэр [56], Биге [143], Биркгофф [152, гл. 8], Кармайкл [В,50], Дембовский [370], Холл [583, гл. 12], Мак-Нейш [869], Сегре [1173], Веблен и Юнг [1368]. Что касается проективных плоскостей, см: Альберт и Сандлер [20], Холл [582, гл. 20 и 587, гл. 12], Сегре [1173] и в особенности Дембовский [370], Хьюджс и Пайпер [674]. Подсчет числа подпространств можно найти, например, у Кармайкла [250] или у Голдмана и Роты [519]. См. также серию работ Зе-Хяна, Бен-Фу, Зонг-Ду и Ху-Нинга [103, 104, 1441, 1457—1460, 1474].
СПИСОК ЛИТЕРАТУРЫ
Vi
В конце каждой ссылки в квадратных скобках стоит число, указывающее номер главы или приложения, к которым относится данная ссылка. Мы старались, где только возможно, давать ссылки иа публикации на английском языке; отметим, что работы из журналов «Проблемы передачи информации», «Доклады Академии наук СССР», «Электроника и связи в Японии», а также некоторые другие работы являются переводами с других языков1.
е
А
[1] N. М. Abramson, A class of systematic codes for non-independent errors, IEEE Trans. Info. Theory, 5 (1959) 150-157 [7].
[2] N. Abramson, Error correcting codes from linear sequential networks, in: C. Cherry, ed., Fourth London Symposium on Info. Theory, (Butterworths, London, 1961) [7].
[3] N. Abramson, Information Theory and Coding, (McGraw-Hill, New York, 1963) [1].
[4] N. Abramson, Encoding and decoding cyclic code groups, Problems of Information Transmission, 6 (2) (1970) 148-154 [18].
[5] L. E. Adelson, R. Alter and T. B. Curtz, Long snakes and a characterization of maximal snakes on the d-cube, Proc. 4th S-E Conf. Combinatorics, Graph Theory, & Computing, (Utilitas Math., Winnipeg, 1973) pp. 111-124 [Intro.].
[6] L. E. Adelson, R. Alter and T. B. Curtz, Computation of d-dimensional snakes, Proc. 4th S-E Conf. Combinatorics, Graph Theory, & Computing (Utilitas Math., Winnipeg, 1973) pp. 135-139 [Intro.].
[7] V. K. Agrawala and J. G. Belinfante, An algorithm for computing SU(n) invariants, BIT 11 (1971) 1-15 [19].
[8] S. V. Ahamed, The design and embodiment of magnetic domain encoders and single-error correcting decoders for cyclic block codes, Bell Syst. Tech. J., 51 (1972) 461-485 [16].
[9] S. V. Ahamed, Applications of multidimensional polynomial algebra to bubble circuits. Bell Syst. Tech. J., 51 (1972) 1559-1580 [16].
[10] S. V. Ahamed, Extension of multidimensional polynomial algebra to domain circuits with multiple propagation velocities, Bell Syst. Tech. J., 51 (1972) 1919-1922 [16].
[11] S. V. Ahamed, Serial coding of single error correcting BCH codes, to appear [16].
[12] N. Ahmed, R. M. Bates, and K. R. Rao, Multidimensional BIFORE Transform, Electronics Letters, 6 (1970) 237-238 [2].
1 Отечественные работы восстановлены в оригинале и даны дополнительным списком; сюда же включены ссылки на переведенные книги и статьи. (Прим, перев.).
[13] N. Ahmed and K. R. Rao, Discrete Fourier and Hadamard transforms, Electronics Letters, 6 (1970) 221-224 [2].
[14] N. Ahmed and K. R. Rao, Complex BIFORE transform. Electronics Letters, 6 (1970) 256-258 and 387 [2].
[15] N. Ahmed and K. R. Rao, Additional properties of complex BIFORE transform, IEEE Trans. Audio Electroacoustics, 19 (1971) 252-253 [2].
[16] A. V. Aho, J. E. Hopcroft and J. D. Ullman, The Design and Analysis of Computer Algorithms (Addison-Wesley, Reading, MA., 1974) [12].
[17] J. D. Alanen and D. E. Knuth, Tables of finite fields, Sankhya, Series A, 26 (1964) 305-328 [4].
[18] A. A. Albert, Symmetric and alternating matrices in an arbitrary field, Trans. Amer. Math. Soc., 43 (1938) 386-436 [15].
[19] A. A. Albert, Fundamental Concepts of Higher Algebra, (University of Chicago Press, Chicago, 1956) [3,4].
[20] A. A. Albert and R. Sandler. An Introduction to Finite Projective Planes (Holt, New York, 1968) [В].
[21] W. O. Alltop, An infinite class of 4-designs, J. Comb. Theory, 6 (1969) 320-322 [2, 17].
[22] W. O. Alltop, Some 3-designs and a4-design, J. Comb. Theory 11 A (1971) 190-195 [2, 17].
[23] W. O. Alltop, 5-designs in affine space, Pacific J. Math., 39 (1971) 547-551 [2, 17].
[24] W. O. Alltop, An infinite class of 5-designs, J. Comb. Theory, 12 A (1972) 390-395 [2, 17].
[25] W. O. Alltop, Binary codes with improved minimum weights, IEEE Trans. Info. Theory, 22 (1976) 241-243 [17, 18, А].
[26] W. O. Alltop, private communication [A],
[27] H. L. Althaus and R. J. Leake, Inverse of a finite-field Vandermonde matrix, IEEE Trans Info. Theory, 15 (1969) 173 [4].
[28] D. R. Anderson. A new class of cyclic codes, SIAM J. Appl. Math.. 16 (1968) 181-197 [9].
[29] E. Artin, Geometric Algebra (Wiley, New York, 1957) [В].
[30] E. Artin, Galois Theory (Notre Dame, IN, 2nd edition, 1959) [4].
[31] T. Asabe, H. Nakanishi and Y. Tezuka, On cyclic multilevel codes, Electron. Commun. Japan, 55-A (2) (1972) 8-15 [1].
[32] R. Ash, Information Theory (Wiley, New York, 1965) [10].
[33] E. F. Assmus, Jr., J.-M. Goethals, and H. F. Mattson, Jr., Generalized (-designs and majority logic decoding of linear codes. Info, and Control, 32 (1976) 43-60 [16].
[34] E. F. Assmus, Jr., and H. F. Mattson, Jr., Error-correcting codes: An axiomatic approach, Info, and Control, 6 (1963) 315-330 [16].
[35] E. F. Assmus, Jr., and H. F. Mattson, Jr., Disjoint Steiner systems associated with the Mathieu groups, Bull. Am. Math. Soc. 72 (1966) 843-845 [20].
[36] E. F. Assmus, Jr., and H. F. Mattson, Jr., Perfect codes and the Mathieu groups, Archie der Math., 17 (1966) 121-135 [20].
[37] E. F. Assmus, Jr., and H. F. Mattson, Jr., On tactical configurations and error-correcting codes, J. Comb. Theory, 2 (1967) 243-257 [6, 16].
[38] E. F._ Assmus, Jr., and H. F. Mattson, Jr., Research to Develop the Algebraic Theory of Codes, Report AFCRL-68-0478, Air Force Cambridge Res. L.abs., Bedford, Mass., September, 1968 [16].
[39] E. F. Assmus, Jr., and H. F. Mattson, Jr., On the automorphism groups of Paley-Hadamard matrices, in: R. C. Bose and T. A. Dowling, eds. Combinatorial Mathematics and Its Applications, (Univ. North Carolina Press, Chapel Hill, NC 1969) [16].
[40] E. F. Assmus Jr., and H. F. Mattson, Jr., Some (3p,p) codes, in: Information Processing 68, (North-Holland, Amsterdam, 1969) pp. 205-209 [18].
[41] E. F. Assmus, Jr., and H. F. Mattson, Jr., New 5-designs, J. Comb. Theory, 6 (1969) 122-151 [6, 11, 16].
[42] E. F. Assmus, Jr., and H. F. Mattson, Jr., Algebraic Theory of Codes II, Report AFCRL-69-0461, Air Force Cambridge Res. Labs., Bedford, Mass., 15 October, 1969 [16].
[43] E. F. Assmus, Jr., 'and H. F. Mattson, Jr., Algebraic Theory of Codes II, Report AFCRL-71-0013, Air Force Cambridge Res. Labs., Bedford, Mass., 15 October, 1970 [16,19].
[44] E. F. Assmus, Jr., and H. F, Mattson, Jr., On weights in quadratic-residue codes, Discrete Math., 3 (1972) 1-20 [16].
[45] E. F. Assmus, Jr., and H. F. Mattson, Jr., Contractions of self-orthogonal codes, Discrete Math., 3 (1972) 21-32 [16].
[46] E. F. Assmus, Jr., and H. F. Mattson, Jr., Error-Correcting Codes, Report AFCRL-72-0504, Air Force Cambridge Res. Labs., Bedford, Mass., August 31, 1972 [16].
[47] E. F. Assmus, Jr., and H. F. Mattson, Jr., Coding and combinatorics, SIAM Review, 16 (1974) 349-388 [5,6,16, 19].
[48] E. F. Assmus, Jr., H. F. Mattson, Jr., and M. Garcia, Self-orthogonal Steiner systems and projective planes, Math. Z.. 138 (1974) 89-96 [19].
[49] E. F. Assmus, Jr., H. F. Mattson, Jr., and H. E. Sachar, A new form of the square-root bound, SIAM J. Appl. Math.. 30 (1976) 352-354 [16].
[50] E. F. Assmus, Jr., H. F. Mattson, Jr., and R. J. Turyn, Cyclic Codes, Air Force Cambridge Research Labs., Report AFCRL-65-332, Bedford Mass., April 28, 1965 [11, 16].
[51] E. F. Assmus, Jr., H. F. Mattson, Jr., and R. J. Turyn, Cyclic Codes, Report AFCRL-66-348, Air Force Cambridge Res. Labs., Bedford, Mass., April 28, 1966 [16].
[52] E. F. Assmus, Jr., H. F. Mattson, Jr., and R. J. Turyn, Low Weights in Quadratic Residue Codes, Inst, of Stat. Mimeo Series 484.3, Dept, of Stat., Univ, of N. Carolina, Chapel Hill, N. C„ 1966 [16].
[53] E. F. Assmus, Jr., H. F. Mattson, Jr., and R. J. Turyn, Research to Develop the Algebraic Theory of Codes, Report AFCRL-67-0365, Air Force Cambridge Res. Labs., Bedford, Mass., June 1967 [16, 19].
[54] J. Astola, On the nonexistence of certain perfect Lee-error-correcting codes, Ann. Univ. Turku., Ser. A, (1975) 167 [6].
[55] S. Azumi and T. Kasami, On the optimal modified Hamming codes, Trans. Inst. Elect, and Commun. Engineers, (Japan) 58 (6) (1958) 325-330 [7].
t-
В
156] R. Baer. Linear Algebra and Projective Geometry, (Academic Press, New York, 1952) [В]. 5V] L. R. Bahl, and R. T. Chien, On Gilbert burst-error-correcting codes, IEEE Trans. Info. Theory 15 (1969) 431-433 [10].
[5&] L. R. Bahl and R. T. Chien, Single - and multiple - burst-correcting properties of a class of cyclic product codes, IEEE Trans. Info. Theory, 17, (1971) 594-600 [18].
[59] B. G. Bajoga and W. J. Walbesser, Decoder complexity for BCH codes, Proc. IEE 120 (1973) 429-432 [Intro., 9].
[60] A. H. Ball and L. J. Cummings, The comma-free codes with words of length two, Bull Austral. Math. Soc., 14 (1976) 249-258 [Intro.].
[61] A..H. Ball and L. J. Cummings, Extremal digraphs and comma-free codes, Ars Combinat., 1 (1976) 239-251 [Intro.].
[62] J. R. Ball, A. H. Spittle and H. T. Liu, High-speed m-sequence generation: a further note, Electronics Letters, 11 (1975) 107-108 [14].
[63] C. Balza, A. Fromageot, and M. Maniere, Four-level pseudo-random sequences, Electronics Letters, 3 (1967) 313-315 [14].
[64] R. P. Bambah, D. D. Joshi and I. S. Luthar, Some lower bounds on the number of code points in a minimum distance binary code, Information and Control, 4 (1961) 313-323 [17, 18].
[65] K. S. Banerjee, An introduction to the weighing problem, Chemica Scripta 6 (1974) 158-162 [2].
[66] K. S. Banerjee, Weighing Designs for Chemistry, Medicine, Economics, Operations Research, Statistics (Marcel Dekker, New York. 1975) [2].
[67] R. B. Banerji, A decoding procedure for double-error correcting Bose-Ray-Chaudhuri codes, Proc. IEEE, 49 (1961) 1585 [9].
[68] R. H. Barker, Group synchronizing of binary digital sequences, in: Communication Theory (Butterworth, London, 1953) pp. 273-287 [14].
[69] A. Barlotti, Some topics in finite geometrical structures. Institute of Statistics Mimeo Series No. 439, Univ, of N. Carolina, Chapel Hill, N. Carolina, August 1965 [11].
[70] A. Barlotti, Some classical and modern topics in finite geometrical structures, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory, (North-Holland, Amsterdam, 1973) [11].
[71] Т. С. Bartee and D. I. Schneider, An electronic decoder for Bose-Chaudhuri-Hocquenghem codes, IEEE Trans. Info. Theory, 8 (1962) 17-24 [9].
[72] T. C. Bartee and D. 1. Schneider, Computation with finite fields. Info. Control 6 (1963) 79-98 [3].
[73] D. E. Barton and C. L. Mallows, Some aspects of the random sequence, Annals Math. Stat. 36 (1965) 236-260 [14].
[74] J. E. Bartow, A reduced upper bound on the error correction ability of codes, IEEE-Trans. Info. Theory, 9 (1963) 46 [17].
[75] J. E. Bartow, An upper bound on the error correction ability of codes, IEEE Trans. Info. Theory, 9 (1963) 290 [17].
[76] L. A. Bassalygo, New upper bounds for error correcting codes, Problems of Information Transmission, 1 (4) (1965) 32-35 [17].
[76a] L. A. Bassalygo, A generalization of Lloyd’s Theorem to the case of any alphabet» Problems of Control and Information Theory, 2 (2) (1973) 25-28 [6].
[77] L A. Bassalygo, A necessary condition for the existence of perfect codes in the Lee metric, Math. Notes, 15 (1974) 178-181 [6].
[78] L. A. Bassalygo, G. V. Zaitsev and V. A. Zinov’ev, Uniformly packed codes, Problems of Info. Transmission, 10 (1) (1974) 6-9 [15].
[79] L. A. Bassalygo and V. A. Zinov’ev, Remarks on uniformly packed codes, Problemy Peredachi Informatsii, to appear [15].
[80] S. A. Batman and R. J. McEliece, The ultimate limits of binary coding for a wideband Gaussian channel, JPL Progress Report 42-22 (1975) 78-79 [I].
[81] L. D. Baumert, Cyclic Hadamard matrices, JPL Space Programs Summary, 37-43-IV (1967) 311-314 and 338 [2].
[82] L. D. Baumert, Cyclic Difference Sets, Lecture Notes in Math. No. 182 (Springer, Berlin, New York, 1971) [13].
[83] L. D. Baumert, Weight Distributions of Some Irreducible Cyclic Codes, JPL Technical Report, 32-1526 (1973) 128-131 [8].
[84] L. D. Baumert et al., A combinatorial packing problem, in: G. Birkhoff and M. Hail? Jr., eds., Computers in Algebra and Number Theory, Am. Math. Soc. Providence, R. I. (1971) pp. 97-108 [6].
[85] L. D. Baumert and D. Cantor, Evolution and coding: inverting the genetic code, JPL Space Programs Summary, 37-65-DU (Oct. 31, 1970) 41-44 [Intro.].
[86] L. D. Baumert and R. J. McEliece, Weights of irreducible cyclic codes, Inf. Control, 20 (1972) 158-175 [8].
[87] L. D. Baumert and R. J. McEliece, A note on the Griesmer bound, IEEE Trans. Info. Theory. 19 (1973) 134-135 [17].
[88] L. D. Baumert and R. J. McEliece, A Golay - Viterbi Concatenated Coding Scheme for MJS’77. JPL Technical Report, 32-1526 (1973) 76-83 [1].
[89] L. D. Baumert and R. J. McEliece, Golay - Viterbi Decoding: Results of The MVM’73 X-Band Telemetry Experiment, JPL Progress Report, 42-25 (1974) 108-110 [I].
[90] L. D. Baumert and H. C. Rumsey, Jr., The index of comma freedom for the Mariner Mars 1969 high data rate telemetry code, JPL Space Programs Summary, 37-46-IV (1967) 221-226 and 249-250 [14].
[91] L. D. Baumert and H. C. Rumsey, Jr., The maximum indices of comma freedom for the high-data-rate telemetry codes, JPL Space Programs Summary 37-51-Ш (June 1968), 215-217 [14].
[92] J. T. B. Beard, Jr., Computing in GF(q), Math. Comp., 28(1974) 1159-1168 [3].
[93] J. T. B. Beard. Jr., and К. I. West. Some primitive polynomials of the third kind, Math. Comp., 28(1974) 1166-1167 [4].
[94] E. F. Beckenbach and R. Bellman. Inequalities (Springer, Berlin, 1961) [6].
[95] V. Belevitch, Theory of 2n-terminal networks with applications to conference telephony, Electronics Comm., 27 (1950) 231-244 [2].
[96] V. Belevitch, Synthesis of four-wire conference networks and related problems, in: Proc. Symposium Modem Network Synthesis, Polytech. Inst. Brooklyn, (April 1956), pp. 175— 195 [2].
[97] V. Belevitch, Conference networks and Hadamard matrices, Ann. Soc. Scientifique -.Bruxelles, 82 (1) (1968) 13-32 [2],
1*0] и. А. вен, ass ot binary codes, Proc. IEE, 122 (1975) 47 [18].
[99] D. A. Bel and R. Laxton, Some BCH codes are optimum, Electronics Letters, 11 (1975) 296-297 [13].
[100] R. Bellman. Introduction to Matrix Analysis (McGraw-Hill, New York, 1960) [2, 14, 16].
[101] R. Bellman, On various versions of the defective coin problem. Info, and Control, 4 (1961) 118-131 [7].
£10 2] В. I. Belov, V. N. Logachev, and V. P. Sandimirov, Construction of a class of linear binary codes achieving the Varshamov-Griesmer bound, Problems of Info. Transmission, 10 (3) (1974) 211-217 [17, А].
[103] Y. Ben-Fu, Studies in finite geometries and the construction of incomplete block designs VII, Acta Math. Sinica, IS (1965) 812-825 [21, В].
[104] Y. Ben-Fu, Studies in finite geometries and the construction of incomplete block designs VIII, Acta Math. Sinica, 15 (1965) 826-841 [21, В].
[105] E. R. Berger, Some additional upper bounds for fixed-weight codes of specified minimum distance, IEEE Trans. Info. Theory, 13 (1967) 307-308 [17].
[106] T. Berger and J. A. van der Horst, see Ref. 663.
[107] T. R. Berger and 1. Reiner, A proof of the normal basis theorem, Amer. Math. Monthly, 82 (1975) 915-918 [4].
[108] G. D. Bergland, A guided tour of the fast Fourier transform, IEEE Spectrum. 6 (July, 1969), 41-52 [14].
[109] E. R. Berlekamp, Distribution of cyclic matrices in a finite field, Duke Math. J. 33 (1965) 45-48 [16].
[НО] E. R. Berlekamp, On decoding binary Bose-Chaudhuri-Hocquenghem codes, IEEE Trans. Info. Theory, 11 (1965) 577-579 [9].
[Ill] E. R. Berlekamp, Factoring polynomials over finite fields. Bell Syst. Tech. J., 46 (1967) 1853-1859 [9]. *
[112] E. R. Berlekamp, The enumeration of information symbols in BCH codes, Bell Syst. Tech. J., 46 (1967) 1861-1880 [9].
[113] E. R. Berlekamp, Algebraic coding theory (McGraw-Hill, New York, 1968) [many references].
[114] E. R. Berlekamp, Weight enumeration theorems, Proc. Sixth Allerton Conf. Circuit and Systems Theory, (Univ, of Illinois Press, Urbana, IL, 1968) pp. 161-170 [8,21].
[115] E. R. Berlekamp, Negacyclic codes for the Lee metric, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics, (Univ, of N. Carolina Press, 1969) pp. 298-316 [5].
[116] E. R. Berlekamp, A Survey of Algebraic Coding Theory, (International Centre for Mechanical Sciences, Udine, Italy, 1970) [1,9].
[117] E. R. Berlekamp, Factoring polynomials over large finite fields, Math. Comp., 24 (1970) 713-735 [9].
[118] E. R. Berlekamp, The weight enumerators for certain subcodes of the second order Reed-Muller codes, Info, and Control, 17 (1970) 485-500 [8, 15, 21].
[119] E. R. Berlekamp, Some mathematical properties of a scheme for reducing the bandwidth of motion pictures by Hadamard smearing, Bell Syst. Tech. J., 49 (1970) 969-986 [2, 14].
[120] E. R. Berlekamp, Coding theory and the Mathieu groups. Info. Control, 18 (1971) [2, 15,20].
[121] E. R. Berlekamp, Factoring polynomials, in: Proc. 3rd S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnipeg, 1972) pp. 1-7 [9].
[122] E. R. Berlekamp, Long primitive binary BCH codes have distance d ~2n In R 'llog n..., IEEE Trans. Info. Theory, 18 (1972) 415-426 [9].
[123] E. R. Berlekamp, Decoding the Golay code, JPL Technical Report 32-1526, Vol. IX, pp. 81-85, Jet Propulsion Laboratory, Pasadena, Calif., 1972 [16].
[124] E. R. Berlekamp, Block coding for the binary symmetric channel with noiseless, delayless feedback, pp. 61-85 in: H. B. Mann ed., Error Correcting Codes, (Wiley, New York, 1973) pp. 61-85 [Intro.].
[125] E. R. Berlekamp, Goppa codes, IEEE Trans. Info. Theory 19 (1973) 590-592 [12].
[126], E. R. Berlekamp, editor, Key Papers in the Development of Coding Theory (IEEE Press, New York, 1974) [Intro.].
[127] E. R. Berlekamp and J. Justesen, Some long cyclic linear binary codes are not so bad, IEEE Trans. Info. Theory, 20 (1974) 351-356 [7,18].
[128] E. R. Berlekamp, J. H. van Lint, and J. J. Seidel, A strongly regular graph derived front the perfect ternary Golay code, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory (North-Holland, Amsterdam, 1973) Ch. 3 [21].
[129] E. R. Berlekamp, F. J. MacWilliams, and N. J. A. Sloane, Gleason’s theorem on self-dual codes, IEEE Trans. Info. Theory, 18 (1972) 409-414 [19].
[130] E. R. Berlekamp and O. Moreno. Extended double-error-correcting binary Goppa codes are cyclic, IEEE Trans. Info. Theory, 19 (1973) 817-818 [12].
[131] E. R. Berlekamp, H. Rumsey, and G. Solomon, On the solutions of algebraic equations over finite fields. Inform. Control, 10 (1967) 553-564 [4,9].
[132] E. R. Berlekamp and N. J. A. Sloane, Restrictions on weight distribution of Reed-Muller codes. Info. Control, 14 (1969) 442-456 [15].
[133] E. R. Berlekamp and L. R. Welch, Weight distributions of the cosets of the (32,6) Reed-Muller code, IEEE Trans. Info. Theory, 18 (1972) 203-207 [1, 14. 19].
[134] G. Berman and K. D. Fryer, Introduction to Combinatorics (Academic Press, New York, 1972) [15].
[135] S. D. Berman, On the theory of group codes. Cybernetics 3 (1) (1967) 25-31 [18].
[136] S. D. Berman, Semisimple cyclic and abelian codes II, Cybernetics 3 (3) (1967) 17-23 [18].
[137] S. D. Berman and A. B. Yudanina, Codes with generalized majority decoding and convolutional codes. Problems Info. Trans., 6 (1) (1970) 1-12 [13].
[138] S. D. Berman and A. B. Yudanina, Irreducible configurations of minimum-weight elements r- in second order Reed-Muller codes, in: B. N. Petrov and F. Csaki, eds., 2nd Intemat. Symp. Info. Theory. (Tsahkadsor, 1971) (Akademiai Kiado, Budapest, 1973) pp. 151-168 [1-5].
[139] M. R. Best and A. E. Brouwer, The triply shortened binary Hamming code is optimal, preprint [17].
[140] M. R. Best, A. E. Brouwer, F. J. MacWilliams, A. M. Odlyzko and N. J. A. Sloane, Bounds for binary codes of length less than 25. IEEE Trans. Info. Theory. 23 (1977) to appear [П, A).
[141] V. K. Bhargava and J. M. Stein, (v, к, Л) configurations and self-dual codes. Info. Control, 28 (1975) 352-355 [16, 19].
[142] V. K. Bhargava, S. E. Tavares, and S. G. S. Shiva, Difference sets of the Hadamard type and quasi-cyclic codes, Info, and Control, 26 (1974) 341-350 [16].
[143] N. Biggs, Finite Groups of Automorphisms, London Math. Soc. Lecture Note Series, No. 6, (Cambridge Univ. Press, London 1971) [20, В].
[144] N. L. Biggs, Perfect codes in graphs, J. Comb. Theory. 15B (1973) 289-296 [6,21].
[145] N. L. Biggs. Algebraic Graph Theory (Cambridge Univ. Press. London, 1974) [6,21].
[146] N. L. Biggs. Perfect Codes and Distance-transitive Graphs, in: Combinatorics, T. P. McDonough and V. C. Mavron eds., London Math. Soc., Lecture Notes No. 13 (Cambridge Univ. Press, London 1974) pp. 1-8 [6,21].
[147] N. Biggs, Designs, factors and codes in graphs. Quart. J. Math. Oxford (2) 26 (1975) 113-119 [6,21].
[148] E. Biglieri and M. Elia, On the existence of group codes for the Gaussian channel, IEEE ' Trans, on Info. Theory, 18 (1972) 399-402 [Intro.].
[149] E. Biglieri and M. Elia, Cyclic-group codes for the Gaussian channel. IEEE Trans. Info. Theory. 22 (1976 ) 624-629 [Intro.].
[150] E. Biglieri and M. Elia, Optimum permutation modulation codes, and their asymptotic performance, IEEE. Trans. Info. Theory, 22 (1976) 750-753 [Intro.].
[151] E. Biglieri and M. Elia, Some results on symmetric-group codes for the Gaussian channel, preprint [Intro.].
[152] G. Birkhoff, Lattice Theory, 2nd Edition, Colloq. Publications vol. 25, (Amer. Math Soc., Providence, RI, 1961) [В].
[153] G. Birkoff and T. C. Bartee, Modem Applied Algebra, (McGraw-Hill, New York, 1970) [4].
[154] W. C. Blackwelder, On constructing balanced incomplete block designs from association matrices with special reference to association schemes of two and three classes, J. Combinat. Theory, 7 (1969) 15-36 [21].
[155] I. F. Blake, The. Leech lattice as a code for the Gaussian Channel, Info. Control, 19(1971) 66-74 [Intro.].
[156] I. F. Blake, Distance properties of group codes for the Gaussian channel, SIAM J. Appl. Math. 23 (1972) 312-324 [Intro.].
[157] I. F. Blake, editor, Algebraic Coding Theory: History and Development (Dowden, Stroudsburg, PA., 1973) [Intro.].
[158] I. F. Blake, Configuration matrices of group codes, IEEE Trans. Info. Theory, 20 (1974) 95-100 [Intro.].
[159] I. F. Blake, Permutation codes for discrete channels, IEEE Trans. Info. Theory, 20 (1974) 138-140 [18].
[1.60 ] I. F. Blake, Properties of generalized Pless codes, in: Proc. 12th Allerton Conference on Circuit and System Theory, Univ. Illinois, Urbana, III. (1974) pp. 787-789 [16].
[161] I. F. Blake, On a generalization of the Pless symmetry codes. Info, and Control, 27 (1975) 369-373 [16].
[162] I. F. Blake and R. C. Mullin, The Mathematical Theory of Coding, (Academic Press, New York 1975) [Intro.].
[163] H. F. Blichfeldt, The minimum value of quadratic forms, and the closest packing of spheres, Math. Ann., 101 (1929) 605-608 [17].
[164] E. L. Blokh, On a decoding method for 3-error-correcting Bose-Chaudhuri codes, Izv, Akad. Sci. USSR (Tekh. Kibem.), No. 3, Sect. IV, (1964) 30-37 (in Russian) [9].
[165] E. L. Blokh and V. V. Zyablov, Existence of linear concatenated binary codes with optimal error-correcting properties, Problems of Info. Trans., 9 (4) (1973) 271-276 [10].
[166] E. L. Blokh and V. V. Zyablov, Coding of generalized concatenated codes, Problems of Info. Trans, 10 (3) (1974) 218-222 [10].
1167] J. H. Blythe and K. Edgcombe, Net coding gain of error-correcting codes, Proc. IEE, 122 (1975) 609-614 [1].
[168] L. S. Borrow, Decoding augmented cutset codes, IEEE Trans. Info. Theory, 17 (1971) 218-220 [18].
[169] L. S. Bobrow and В. M. Franaszczuk, On cyclic codes generated by graphs, Info. Control 22 (1973) 296-301 [18].
[170] L. S. Bobrow aind S. L. Hakimi, Graph theoretic Q-ary codes. IEEE Trans. Info. Theory 17 (1971) 215-218 [18].
[171] D. Borel, Application of the theory of cyclic codes to data transmission (in French), Onde Elec., 48 (1968) 55-59 [1].
[172] L. F. Borodin, Some problems in the theory of group codes, Radio Engineering and Electronic Physics, 7 (8) (1962) 1199-1207 [11].
[173] R. C. Bose, On the construction of balanced incomplete block designs, Ann. Eugenics, 9 (1939) 353-399 [2].
[174] R. C. Bose, On some connections between the design of experiments and information theory, Bull. Intern. Stat. Inst., 38 (1961) 257-271 [6].
[175] R. C. Bose, Strongly regular graphs, partial geometries and partially balanced designs, Рас. J. Math., 13 (1963) 389-419 [21].
[176] R. C. Bose, Error correcting, error detecting and error locating codes, in: Essays in. Probability and Statistics, Univ, of North Carolina Press, Chapel Hill, N.C., (1970) pp. 147-178 [1].
fl 771 R. C. Bose, Graphs and designs, in: Finite Geometric Structures and their Applications (Edizioni Cremonese, Rome, 1973) Y>p. 1-104 [2].
[178] R. C. Bose, Characterization problems of combinatbrial graph theory, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory (North-Holland, Amsterdam, 1973) [21].
[П9] R. C. Bose, С. T. Abraham and S. P. Ghosh, File organization of records with multiplevalued attributes for multi-attribute queries, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applications, (U. of N. Carolina Press, 1969) pp-277-297 [9].
[180] R. C. Bose and R. C. Burton, A characterization of flat spaces in a finite geometry, and the uniqueness of the Hamming and MacDonald codes, J. Combinatorial Theory, 1 (1966) 96-104 [7].
[181] R. C. Bose and K. A. Bush, Orthogonal arrays of strength two and three, Ann. Math. Stat., 23 (1952) 508-524 [5]1
[182] R. C. Bose and J. G. Caldwell, Synchronizable error-correcting codes. Info. Control, 1® (1967) 616-630 [1].
[183] R. C. Bose and D. M. Mesner, On linear associative algebras corresponding to association schemes of partially balanced designs, Ann. Math. Stat., 30 (1959) 21-38 [21].
[184] R. C. Bose and D. K. Ray - Chaudhuri, On a class of error correcting binary group codes. Info, and Control, 3 (1960) 68-79 [7].
[185] R. C. Bose and D. K. Ray - Chaudhuri, Further results on error correcting binary group codes, Info, and Control, 3 (1960) 279-290 [7].
[186] R. C. Bose andT. Shimamoto, Classification and analysis of partially balanced incomplete block designs with two associate classes, J. Amer. Stat. Assoc., 47 (1952) 151-184 [21].
[187] R. C. Bose and S. S. Shrikhande, A note on a result in the theory of code ^construction, Info, and Control, 2 (1959) 183-194 [2].
[188] D. C. Bossen, b-adjacent error correction, IBM J. Res. Devel., 14 (1970) 402-408 [10].
[189] D. C. Bossen and S. S. Yau, Redundant residue polynomial codes, Info, and Control, 13 (1968) 597-618 [10].
[190] N. Bourbaki, Croups et Algebres de Lie, (Hermann, Paris, 1968) Ch. 4, 5 and 6,’[19].
[191] K. Brayer, Error control techniques using binary symbol burst codes, IEEE Trans. Commun., 16 (1968) 199-214 [1].
[192] K. Brayer, Improvement of digital HF communication through coding, IEEE Trans. Commun.', 16 (1968) 771-786 [1].
[193] K. Brayer, Error correction code performance on HF, troposcatter, and satellite channels, IEEE Trans. Commun., 19 (1971) 781-789 [1].
[194] K. Brayer and O. Cardinale, Evaluation of error correction block encoding for high-speed HF data, IEEE Trans. Commun., 15 (1967) 371-382 [1].
[195] J. G. Bredeson and S. L. Hakimi, Decoding of graph theoretic codes, IEEE Trans. Info. Theory, 13 (1967) 348-349 [18].
[196] J. Brenner and L. Cummings, The Hadamard maximum determinant problem, Amer. Math. Mnthly, 79 (1972) 626-630 [2].
[197] J. D. Bridewell and J. K. Wolf, Burst distance and multiple burst correction, Bell Syst. Tech. J., 49 (1970) 889-909 [10].
[198] P. A. N.' Briggs and K. R. Godfrey, Autocorrelation function of a 4-level m-sequence, Electronics Letters, 4 (1963) 232-233 [14].
[199] E. O. Brigham, The Fast Fourier Transform (Prentice-Hall, Englewood Cliffs, 1974) [14].
[200] M. Broue, Codes correcteurs d’erreurs auto-orthogonaux sur le corps a deux elements et formes quadratiques entieres definies positives a discriminant +1, in: Comptes Rendus des Journees Mathematiques de la Societe Math, de France (Univ. Sci. Tech. Languedoc, Montpellier 1974) pp. 71-108 [19].
[201] M. Brone and M Enguehard, Polynomes des poids de certains codes et fonctions theta de certains reseaux, Ann. Scient. Ec. Norm. Sup., 5 (1972) 157-181 [19].
[201a] A. E. Brouwer, personal communication [17, А].
[202] D. A. H. Brown, Some error-correcting codes for certain transposition and transcription errors in decimal integers, Computer Journal, 17 (1974) 9-12 [1].
[203] D. T. Brown and F. F. Sellers, Jr., Error correction for IBM 800-bit-per-inch magnetic tape. IBM J. Res. Dev., 14 (1970) 384-389 [1].
[204] T. A. Brown and J. H. Spencer, Minimization of ±1 matrices under line shifts, Colloq. Math., 23 (1971) 165-171 [14].
[205] W. S. Brown, ALTRAN User's Manual, 4th ed. (Bell Laboratories, N.J , 1977) [19].
[206] N. G. de Bruijn, A combinatorial problem, Nederl. Akad. Wetensch. Proc. Ser. A. 49 (1946) 758-764 (= Indag. Math. 8 (1946) 461-467) [14].
[207] K. A. Brusilovskij, Hardware simulation of pseudorandom binary sequences, Automation and Remote Control 36 (5) (1975) 836-845 [14].
[208] M. M. Buchner, Jr., Computing the spectrum of a binary group code, Bell Syst. Tech. J.. 45 (1966) 441-449 [8].
[209] M. M. Buchner, Jr., Coding for numerical data transmission, Bell Syst. Tech. J., 46 (1967) 1025-1041 [1].
[210] M. M. Buchner, Jr., The equivalence of certain Harper codes, Bell Syst. Tech. J., 48 (1969) 3113-3130 [Intro.].
[211] W. Burnside, Theory of Croups of Finite Order, 2nd ed. (Dover, New York, 1955) [19].
[212] M. Burrow, Representation Theory of Finite Croups (Academic Press, New York, 1965) [8,21].
[213] N. E. Burrowes, The' timing of remote events using periodic telemetry samples, Proc: I.R.E.E. Australia, 27 (1966) 244-253 [14].
[214] H. O. Burton, A survey of error correcting techniques for data on telephone facilities, in: Proc. Intern. Commun. Conf., San Francisco, Calif., 1970, pp. 16-25 to 16-32 [1].
[215] Н. О. Burton, Some asymptotically optimal burst-correcting codes and their relation to single-error-correcting Reed-Solomon codes, IEEE Trans. Info. Theory, 17 (1971) 92-95 [Ю].
[216] H. O. Burton, Inversionless decoding of binary BCH codes, IEEE Trans. Info. Theory, 17 (1971) 464-466 [9].
[217] H. O. Burton and D. D. Sullivan, Errors and error control, Proc. IEEE 60 (1970) 1293-1301 [1].
[218] H. O. Burton, D. D. Sullivan, and S. Y. Tong, Generalized burst-trapping codes, IEEE Trans. Info. Theory, 17 (1971) 736-742 [10].
[219] H. O. Burton and E. J. Weldon. Jr., Cyclic product codes, IEEE Trans. Info. Theory, 11 (1965) 433-439 [18].
[220] K. A. Bush, Orthogonal arrays of index unity, Ann. Math. Stat., 23 (1952) 426-434 [5, 10, 11].
[221] F. C. Bussemaker and J. J. Seidel, Symmetric Hadamard matrices of order 36. Ann. New York Acad. Sci., 175 (Article 1) (1970) 66-79 [2,21].
[222] W. H. Bussey, Galois field tables for p" s 169, Bull. Amer. Math. Soc., 12 (1905) 22-38 [4].
[223] W. H. Bussey, Tables of galois fields of order less than 1,000, Bull. Amer. Math. Soc., 16 (1910) 188-206 [4].
c
[224] J. B. Cain and R. Simpson, Average digit error probability in decoding linear block codes, Proc. IEEE 56 (1968) 1731-1732 [1].
[225] T. W. Cairns, On «the fast Fourier transform on finite abelian groups, IEEE Trans. Computers, 20 (1971) 569-571 [14].
[226] L. Calabi and W. E. Hartnett, A family of codes for the correction of substitution and synchronization errors, IEEE Trans. Info. Theory, IS (1969) 102-106 [1].
[227] L. Calabi and W. E. Hartnett, Some general results of coding theory with applications to the study of codes for the correction of synchronization errors, Info. Control, 15 (1969) 235-249 [1].
[228] L. Calabi and E. Myrvaagnes, On the minimal weight of binary group codes, IEEE Trans. Info. Theory, 10 (1964) 385-387 [2, А].
[229] D. Calabro and J. K. Wolf, On the synthesis of two-dimensional arrays with desirable correlation properties. Info, and Control, 11 (1968) 537-560 [18].
[230] P. Calingaert, Two-dimensional parity checking, J. ACM,.8 (1961) 186-200 [18].
[231] P. J. Cameron, Biplanes, Math. Zeit., 131 (1973) 85-101 [14[.
[232] P. J. Cameron, Suborbits in transitive permutation groups, in: M. Hall, Jr., and J. H. Van Lint, eds., Combinatorics, (Reidel, Dordrecht, 1975) pp. 419-450 [21].
[233] P. J. Cameron, J.-M. Goethals, J. J. Seidel, and E. E. Shult, Line graphs, root systems and elliptic geometry, J. Algebra, 43 (1976) 305-327 [21].
[234] P. J. Cameron and J. H. Van Lint, Graph Theory, Coding Theory and Block Designs, London Math. Soc. Lecture Note Series, No. 19 (Cambridge Univ. Press, London, 1975) [Intro.].
[235] P. J. Cameron and J. J. Seidel, Quadratic forms over GF(2), Koninkl. Nederl. Akad. Wetensch., Proc., Ser. A, 76 (1973) 1-8 [15].
[236] P. J. Cameron, J. A. Thas and S. E. Payne, Polarities of generalized hexagons and perfect codes, Geometriae Dedicata, to appear [6].
[237] P. Camion, A proof of some properties of Reed-Muller codes by means of the normal basis theorem, in; R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applicants, (Univ. North Carolina Press, Chapel Hill, N.C. 1969) Ch. 22 [9, 13].
[238] P. Camion, Abelian codes, Math. Res. Center, Univ, of Wisconsin, Rept. 1059 (1970) [18].
[239] P. Camion, Linear codes with given automorphism groups, Discrete Math., 3 (1972) 33-45 [8].
[240] C. N. Campopiano, Construction of relatively maximal, systematic codes of specified minimum distance from linear recurring sequences of maximal period, IEEE Trans. Info. Theory, 6 (1960) 523-528 [18].
[241] J. R. Caprio, Strictly complex impulse ^equivalent codes and subsets with very uniform amplitude distributions, IEEE Trans. Info. Theory, 15 (1969) 695-706 [14].
[242] L. Carlitz, Some problems involving primitive roots in a finite field. Proc. Nat. Ac. Sci., 38 (1952) 314-318 [4].
[243] L. Carlitz, Primitive roots in a finite field, Trans. Amer. Math. Soc., 73 (1952) 373-382 [4].
[244] L. Carlitz, Distribution of primitive roots in a finite field. Quart. J. Math. Oxford, (2) 4 <1953) 4-10 [4].
[245] L. Carlitz, The distribution of irreducible polynomials in several indeterminates. III. I Math., 7 (1963) 371-375 [4].
[246] L. Carlitz, The distribution of irreducible polynomials in several indeterminates II, Canad. J. Math., 17 (1965) 261-266 [4],
(247] L. Carlitz and J. H. Hodges, Distribution of matrices in a finite field, Pacific J. Math. 6 (1956) 225-230 [16].
[248] L. Carlitz and J. H. Hodges, Distribution of bordered symmetric, skew and hermitian matrices in a finite field, J. Reine Angew. Math. 195 (1956) 192-201 [16].
[249] L. Carlitz and S. Uchiyama, Bounds for exponential sums, Duke Math. J., 24(1957) 37-41 [9].
[250] R. Carmichael, Introduction to the Theory of Groups of Finite Order (Dover, New York, 1956) [2, В].
[251] D. E. Carter, On the generation of pseudo-noise codes, IEEE Trans. Aerospace and Electronic Systems, 10 (1974) 898-899 [14].
[252] L. R. A. Casse, A solution to Beniamino Segre’s “Problem f,„” for q even, Atti Accad. Naz. Lincei, Rend. Cl. Sc. Pis. Mat. Natur., 46 (1969) 13-20 [11].
[253] S. R. Cavior, An upper bound associated with errors in Gray code, IEEE Trans. Info. Theory, 21 (1975) 596-599 [Intro.].
[254] C. Cazacu and D. Simovici, A new approach to some problems concerning polynomials over finite fields. Info, and Control, 22 (1973) 503-511 [4].
[255] A. G. Cerveira, On a class of wide-sense binary BCH codes whose minimum distances exceed the BCH bound, IEEE Trans. Info. Theory, 14 (1968) 784-785 [9].
[256] H. D. Chadwick and L. Kurz, Rank permutation group codes based on Kendall’s correlation statistic, IEEE Trans. Info. Theory, IS (1969) 306-315 [Intro.].
[257] H. D. Chadwick and I. S. Reed, The equivalence of rank permutation codes to a new class of binary codes, IEEE Trans. Info. Theory, 16 (1970) 640-641 [Intro.].
[257a] G. J. Chaitin, On the length of programs for computing finite binary sequences: statistical considerations, J. ACM, 16 (1969) 145-159 [Intro.].
[258] G. J. Chaitin, On the difficulty of computations, IEEE Trans. Info. Theory, 16 (1970) 5-9 [Intro.].
[258a] G. J. Chaitin, Information-theoretic computational complexity, IEEE Trans. Info. Theory, 20 (1974) 10-15 [Intro.].
[259] I. M. Chakravarti, Bounds on error correcting codes (non-random), in: R. C. Bose, ed., Essays in Probability and Statistics, (Univ, of North Carolina, 1970) Ch. 9 [17].
[260] I. M. Chakravarti, Some properties and applications of Hermitian varieties in a finite projective space PG(N, q2) in the construction of strongly regular graphs (Two-class association schemes) and block designs, J. Combin. Theory. 11B (1971) 268-283 [21].
[261] I. M. Chakravarti and S. Ikeda, Construction of association schemes and designs from finite groups, J. Combin. Theory, 13A (1972) 207-219 [21].
[262] J. A. Chang, Generation of 5-level maximal-length sequences, Electronics Letters, 2 (1966) 258 [14].
[263] R. W. Chang and E. Y. Ho, On fast start-up data communication systems using pseudorandom training sequences, Bell Syst. Tech. J., 51 (1972) 2013-2027 [14].
[264] D. Chase, A class of algorithms for decoding block codes with channel measurement information, IEEE Trans. Info. Theory, 18 (1970) 170-182 [1, 16].
[265] D. Chase, A combined coding and modulation approach for communication over dispersive channels, IEEE Trans. Commun., 21 (1973) 159-174 [1].
[266] C.-L. Chen, Computer results on the minimum distance of some binary cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 359-360, and Appendix D of Peterson and Weldon, Ref. [1040]; [7,9, 18, А].
[267] C.-L. Chen, On decoding Euclidean geometry codes, Proc. 4th Hawaii Int. Conf. Systems Sciences, (1971) pp. 111-113 [13].
[268] C.-L. Chen, On majority-logic decoding of finite geometry codes, IEEE Trans. Info. Theory, 17 (1971) 332-336 [13].
1269] C.-L. Chen, Note on majority-logic decoding of finite geometry codes, IEEE Trans. Info. Theory, 18 (1972) 539-541 [13],
[270] C.-L. Chen, On shortened finite geometry codes, Info, and Control, 20 (1972) 216-221 [13].
[271] C.-L. Chen, Some efficient majority-logic decodable codes, NTC'73 Conference Record, 1973 [13].
[273] C.-L. Chen and R. T. Chien, Recent developments in majority-logic decoding, Proc. 26th Annual National Electronics Conf., (1970) pp. 458-461 [13].
[274] C.-L. Chen and S. Lin, Further results on polynomial codes. Info, and Control, 15 (1969) 38-60 [9, 13].
[275] C.-L. Chen, W. W. Peterson, and E. J. Weldon, Jr., Some results on quasi-cyclic codes, Info, and Control, 15 (1969) 407-423 [16].
[276] C.-L. Chen and W. T. Warren, A note on one-step majority-logic decodable codes, IEEE Trans. Info. Theory, 19 (1973) 135-137 [13].
[277] Y. Chen, The Steiner system S(3,6,26), J. of Geometry, 2 (1) (1972) 7-28 [17, А].
[278] R. T. Chien, Orthogonal matrices, error-correcting codes and load-sharing matrix switches, IEEE Trans. Computers, 8 (1959) 400 [1].
[279] R. T. Chien, Cyc[jc decoding procedure for the Bose-Chaudhuri-Hocquenghem codes, IEEE Trans. Info. Theory, 10 (1964) 357-363 [9].
[280] R. T. Chien, Burst-correcting codes with high-speed decoding, IEEE Trans. Info. Theory, 15 (1969) 109-113 [10].
[281] R. T. Chien, Coding for error control in a computer-manufacturers environment: A foreword, IBM J. Res. Devel., 14 (1970) 342 [I].
[282] R. T. Chien, Block-coding techniques for reliable data transmission, IEEE Trans. Comm., 19 (1971) 743-751 11,9].
[283] R. T. Chien, A new proof of the BCH bound, IEEE Trans. Info. Theory, 18 (1972) 541 [8]. [284] R. T. Chien, Memory error control: beyond parity. Spectrum, 10 (7) (1973) 18-23 [1]. [285] R. T. Chien, L. R. Bahl and D. T. Tang, Correction of two erasure bursts, IEEE Trans.
Info. Theory, 15 (1969) 186-187 [10].
[286] R. T. Chien and D. M. Choy, Algebraic generalization of BCH-Goppa-Helgert codes, IEEE Trans. Info. Theory, 21 (1975) 70-79 [8,12,18, А].
[287] R. T. Chien, V. E. Clayton, P. E. Boudreau and R. R. ^.ocke, Error correction in a radio-based data communications system, IEEE Trans. Commun., 23 (1975) 458-462 [1].
[288] R. T. Chien, B. D. Cunningham, and I. B. Oldham, Hybrid methods for finding roots of a polynomial - with application to BCH decoding, IEEE Trans. Info. Theory, 15 (1969) 329-335 [9].
[289] R. T. Chien and W. D. Frazer, An application of coding theory to document retrieval, IEEE Trans. Info. Theory, 12 (1966) 92-96 [9].
[290] R. T. Chien, С. V. Freiman and D. T. Tang, Error correction and circuits on the n-cube, Proc. 2nd Allerton Conf. Circuit Syst. Theory, Sept. 1964, Univ, of Ill., Monticello, Ill., pp. 899-912 [Intro.].
[291] R. T. Chien and V. Lum, On Golay’s perfect codes and step-by-step decoding, IEEE Trans. Info. Theory, 12 (1966) 403-404 [16].
[292] R. T. Chien and S. W. Ng, Dual product codes for correction of multiple low-density burst errors, IEEE Trans. Info. Theory, 19 (1973) 672-677 [10,18].
[293] R. T. Chien and К. K. Tzeng. Iterative decoding of BCH codes. Coordinated Science Lab, Univ, of Illinois, Urbana, Ill., Tech. Report, Feb. 1968 [9].
[294] D. K. Chow, On threshold decoding of cyclic codes, Info, and Control, 13, (1968) 471-483 [13].
[295] G. C. Clark, Jr., and R. C. Davis, A decoding algorithm for group codes and convolution . . codes based on the fast Fourier-Hadamard transform, unpublished paper presented at IEEE 1969 Inti. Symp. on Info. Theory, Ellenville, NY [14].
[296] J. Cocke, Lossless symbol coding with nonprimes, IEEE Trans. Info. Theory, 5 (1959) 33-34 [7].
[297] G. Cohen, P. Godlewski, and S. Perrine, Idempotents of cyclic codes, preprint [8].
[298] J. H. E. Cohn, On the value of determinants, Proc. Amer. Math. Soc., 14 (1963) 581-588 [2].
[299] M. Cohn, Affine m-ary Gray codes, Inlfo. and Control, 6 (1963) 70-78 [Intro.].
[300] R. J. Collens, A listing of balanced incomplete block designs, in: Proc. 4th S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnipeg, 1973) pp. 187-231 [2, 17].
[301] J. H. Conway, A tabulation of some information concerning finite fields, in: R. F. Churchhouse and J.-C. Herz eds., Computers in Mathematical Research, (North-Holland, Amsterdam, 1968) pp. 37-50 [3, 4].
[302] J. H. Conway, A perfect group of order 8,315,553,613,086,720,000 and the sporadic simple groups, Proc. Nat. Acad. Sci., 61 (1968) 398-400 [19,20].
[303] J. H. Conway, A group of order 8,315,553,613,086,720,000, Bull. London Math. Soc., 1 (1969) 79-88 [19,20].
[304] J. H. Conway, A characterization of Leech’s lattice, Invent. Math., 7 (1969) 137-142 [19,20].
[305] J. H Conway, Groups, lattices, and quadratic forms, in: Computers in Algebra and Number Theory, SIAM-AMS Proc. IV, (Am. Math. Soc., Providence, R.I. 1971) pp. 135-139 [19,20].
[306] J. H. Conway, Three lectures on exceptional groups, in: Finite Simple Groups, ed. M. B. Powell and G. Higman (Academic Press, New York, 1971) pp. 215-247 [16, 19,20].
[307] A. B. Cooper and W. C. Gore, A recent result concerning the dual of polynomial codes, IEEE Trans, on Info. Theory, 16 (1970) 638-640 [13].
[308] J. T. Cordaro and T. J. Wagner, Optimum (N, 2) codes for small values of channel error probability, IEEE Trans. Info. Theory, 13 (1967) 349-350 [А].
[309] F. P. Corr, Statistical evaluation of error detection cyclic codes for data transmission, IEEE Trans. Commun. Systems, 12 (1964) 211-216 [1].
[310] T. M. Cover, Enumerative source encoding, IEEE Trans. Info. Theory, 19 (1973) 73-77 [17].
[311] W. R. Cowell, The use of group codes in error detection and message retransmission, IEEE Trans. Info. Theory, 7 (1961) 168-171 [1].
[312] J. W. Cowles and G. I. Davida, Decoding of triple-error-correcting BCH codes, Electronics Letters, 8 (1972) 584 [9].
[313] H. S. M. Coxeter, Regular Polytopes, 2nd Edition. (MacMillan, New york, 1963) [14].
[314] H. S. M. Coxeter and W. O. J. Moser, Generators and Relations for Discrete Groups, 2nd Edition, (Springer, Berlin, 1965) [9, 16].
[315] H. H. Crapo and G.-C. Rota, On the Foundations of Combinatorial Theory : Combinatorial Geometries, (MIT Press, Cambridge, Mass., 1970) (Preliminary version) [17].
[316] H. C. Crick, J. S. Griffiths and L. E. Orgel, Codes without commas. Proc. Nat. Acad. Sci., 43 (1957) 416-421 [Intro.].
,[317 ] T. R. Crimmins, Minimization of mean-square error for data transmitted via group codes, IEEE Trans. Info. Theory, 15 (1969) 72-78 [1].
[318] T. R. Crimmins and H. M. Horwitz, Mean-square-error optimum coset leaders for group codes, IEEE Trans. Info. Theory, 16 (1970) 429-432 [1].
[319] T. R. Crimmins, H. M. Horwitz, C. J. Palermo and R. V. Palermo, Minimization of mean-square error for data transmission via group codes, IEEE Trans. Info. Theory, 13 (1967) 72-78 [1].
[320] I. G. Cumming, Autocorrelation function and spectrum of a filtered, pseudo-random binary sequence, Proc. IEE, 114 (1967) 1360-1362 [14].
[321] C. W. Curtis and I. Reiner, Representation Theory of Finite Groups and Associativi Algebras, (Wiley, New York, 1962) [8].
[322] R. T. Curtis, A new combinatorial approach to Мы, Math. Proc. Camb. Phil. Soc., 79 (1976) 25-41 [18,20].
[323] R. T. Curtis, The maximal subgroups of M2i, in preparation [20].
D
'[324] E. C. Dade, Answer to a question of R. Brauer, J. Algebra, 1 (1964) 1-4 [19].
[325] E. C. Dade, private communication [19].
[326] G. Dagnino, On a new class of binary group codes, Calcolo, S (1968) 277-294 [18]. .[327] R. M. Damerell, On Moore graphs, Proc. Comb. Phil. Soc., 74 (1973) 227-236 [21].
[328] L. Danzer and V. Klee, Length of snakes in boxes, J. Combin. Theory, 2 (1967) 258-265 [Intro.].
[329] H. Davenport. On primitive roots in finite fields, Quart. J. Math. Oxford, (1) 8 (1937) 308-312 [4].
[330] H. Davenport, Bases for finite fields, J. London Math. Soc., 43 (1968) 21-39 [4].
[331] F. N. David and D. E. Barton. Combinatorial Chance, (Hafner, New York, 1962) [8].
[332] F. N. David, M. G. Kendall and D. E. Barton, Symmetric Function and Allied Tables, ' (Cambridge Univ. Press, London, 1966) [8].
[333] G. I. Davida, Decoding of BCH codes, Electronics Letters, 7 (1971) 664 [9].
[334] G. I. Davida, A new error-locating polynomial for decoding of BCH codes, IEEE Trans. Info. Theory, 21 (1975) 235-236 [9].
[335] D. W. Davies, Longest “separated” paths and loops in an N-cube, IEEE Trans. Computers, 14 (1965) 261 [Intro.].
[336] W. D. T. Davies, Using the binary maximum length sequence for the identification of system dynamics, Proc. IEE, 114 (1967) 1582-1584 [14].
[337] A. A. Davydov, Higher data-storage reliability with the aid of programmable errorcorrecting codes. Automation and Remote Control, 34 (1) (1973) 137-143 [1].
[338] A. A. Davydov and G. M. Tenegol’ts, Codes correcting errors in the exchange of information between computers, Eng. Cyber., 9 (1971) 700-706 [1].
[339] D. E. Daykin, Distribution of bordered pcrsymmetric matrices in a finite field, J. Reine Angew. Math., 203 (1960) 47-54 [16]. i
[340] D. E. Daykin, Generation of irreducible polynomials over a finite field, Amer. Math. Mnthly, 72 (1965) 646-648 [4].
[341] J. A. Decker, Jr.» Hadamard-transform spectrometry: A new analytical technique, Analytical Chemistry, 44 (1972) 127A-134A [2].
[342] P. Deligne, La conjecture de Weil I, Institut des Hautes Etudes Scientifiques, Publ. Math. No. 43, pp. 273-307 [9].
[343] P. Delsarte, A geometrical approach to a class of cyclic codes, J. Combin. Theory, 6 (1969) 340-358 [13].
[344] P. Delsarte, On cyclic codes that are invariant under the general linear group, IEEE Trans. Info. Theory, 16 (1970) 760-769 [8, 13].
[345] P. Delsarte, Automorphisms of abelian codes. Philips Res. Rept., 25 (1970) 389-402 [18].
[346] P. Delsarte, BCH bounds for a class of cyclic codes, SIAM Jnl. Applied Math., 19 (1970) 420-429 [8].
[347] P. Delsarte, Weights of p-ary Abelian codes, Philips Res. Repts., 26 (1971) 145-153 [15].
[348] P. Delsarte, Majority-logic decodable codes derived from finite inversive planes, Info, and Control, 18 (1971) 319-325 [13].
[349] P. Delsarte, Weights of linear codes and strongly regular normed spaces, Discrete Math., 3 (1972) 47-64 [21].
[350] P. Delsarte, Bounds for unrestricted codes, by linear programming. Philips Res. Reports, 27 (1972) 272-289 [5,6, 17].
[351] P. Delsarte, Four fundamental parameters of a code and their combinatorial significance. Info, and Control, 23 (1973) 407-438 [5,6, 17].
[352] P. Delsarte, An algebraic approach to the association schemes of coding theory, Philips Research Reports Supplements, No. 10 (1973) [5,6, 17,21].
[353] P. Delsarte, Association schemes in certain lattices, Report R 241, MBLE Res. Lab., Brussels, 1974 [21].
[354] P. Delsarte, Association schemes and t-designs in regular semi-lattices, J. Combin. Theory, 20 A (1976) 230-243 [21].
[355] P. Delsarte, The association scheme of bilinear forms over GF(2), unpublished notes, 1974 [21].
[356] P. Delsarte, The association schemes of coding theory, in: M. Hall, Jr. and J. H. van Lint, Combinatorics, (Reidel, Dordrecht, 1975) pp. 143-161 [21].
[357] P. Delsarte, Hahn polynomials, discrete harmonics and t-designs, Report R295, MBLE Res. Lab., Brussels, 1975 [21].
[358] P. Delsarte, Regular schemes over an abelian group, Report R302, MBLE Res. Lab., Brussels, 1975 [21].
(359] P. Delsarte, On subfield subcodes of Reed-Solomon codes, IEEE Trans. Info. Theory, 21 (1975) 575-576 [7, 10, 12].
[360] P. Delsarte, Distance distribution of functions over Hamming spaces. Philips Res. Reports, 30 (1975) 1-8 [9].
(361] P. Delsarte, Properties and applications of the recurrence F(i + 1, к + 1, n + 1) = qk*'F(i. k + l,n) qkF(i.k,n), SIAM J. Appl. Math.. 31 (1976 ) 262-270 [21].
[362] P. Delsarte and J.-M. Goethals, Irreducible binary cyclic codes of even dimehsion, in: Combinatorial Mathematics and its Applications, Proc. Second Chapel Hill Conference, May 1970 (Univ, of N. Carolina, Chapel Hill, N.C., 1970) pp. 100-113 [8, 15].
[363] P. Delsarte and J.-M. Goethals, Unrestricted codes with the Golay parameters are unique, Discrete Math., 12 (1975) 211-224 [20].
[364] P. Delsarte and J.-M. Goethals, Alternating bilinear forms over GF(q), J. Combin. Theory, 19A (1975) 26-50 [15,21, A],
[365] P. Delsarte, J.-M. Goethals and F. J. MacWilliams, On generalized Reed-Muller codes and their relatives, Info, and Control, 16 (1974) 403-442 [13].
[366] P. Delsarte, J.-M. Goethals, and J. J. Seidel, Orthogonal matrices with zero diagonal II., Canad. J. Math., 23 (1971) 816-332 [2].
[367] P. Delsarte, J.-M. Goethals, and J. J. Seidel, Bounds for systems of lines and Jacobi polynomials. Philips Research Reports, 30 (1975 ) 91*-105* [21].
[368] P. Delsarte, W. Haemers and C. Weug, Unpublished tables, 1974 [A],
[369] P. Delsarte and R. J. McEliece, Zeroes of functions in finite abelian group algebras, Amer. J. Math., 98 (1976) 197-224 [15].
[370] P. Dembowski, Finite Geometries (Springer, Berlin, 1968) [2, 17, В].
[371] J. Denes and A. D. Keedwell, Latin Squares and their Applications, (Academic Press, New York, 1974) [11,18].
[372] R. H. F. Denniston, personal communication [17, А].
[373] M. Deza, Une propriete extremale des plans projectifs finis dans une classe de code equidistants, Discrete Math., 6 (1973) 343-352 [1].
[374] L. E. Dickson, Linear groups with an exposition of the Galois, field theory (Dover. New York, 1958) [15].
[375] J. Dieudonne and J.. B. Carrell, Invariant Theory, Old and New, (Academic Press, New York, 1971) [19].
[376] J. F. Dillon, Elementary Hadamard difference sets, Ph.D. Thesis, Univ, of Maryland, 1974 [14].
[377] J. F. Dillon, Elementary Hadamard difference sets, in: Proc. 6th S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnepeg, 1975) pp. 237-249 [14].
[377a] Discrete Mathematics, Special triple issue on coding theory, 3 (Numbers h 2,3, 1972) [Intro.].
[378] R. L. Dobrushin, Survey of Soviet research in information theory. IEEE Trans. Info. Theory, 18 (1972) 703-724 [1,13].
[379] M. Doob, On graph products and association schemes, Utilitas Math., 1 (1972) 291-302 [21].
[380] B. G. Dorsch, A decoding algorithm for binary block codes and j-ary output channels. IEEE Trans. Info. Theory, 20 (1974) 391-394 [Р].
[381] P. Doubilet, G.-C. Rota, .and J. Stein, On the foundations of combinatorial theory: IX Combinatorial methods in invariant theory. Studies in Appl. Math.. 53 (1974) 185-216 [19].
[382] R. J. Douglas, Some results on the maximum length of circuits of spread к in the d-cube, J. Combin. Theory, 6 (1969) 323-339 [Intro.].
[383] R. J. Douglas, Upper bounds on the length of circuits of even spread in the d-cube, J. Combin. Theory, 7 (1969) 206-214 [Intro.].
[384] T. A. Dowling, A class of tri-weight cyclic codes, Instit. Statistic Mimeo series No. 600.3, (Univ. North Carolina, Chapel Hill, N.C., Jan. 1969) [15].
[385] T. A. Dowling, Codes, packings and the critical problem, Atti Del Convegno Di Geometria Combinatoria e Sue Applicazioni, Universita Degli Studi di Perugia, Istituto di Matematica (1971) 209-224 [11, 17].
[386] J. Doyen and A. Rosa, A bibliography and survey of Steiner systems, Bollettino Unione Matemataa Jialiana, 7 (1973) 392-419 [2,17, А].
[387] N. Q. Due, Pseudostep orthogonalization: a new threshold decoding algorithm, IEEE Trans. Info. Theory, 17 (1971) 766-768 [13].
[388] N. Q. Due, On a necessary condition for L-step orthogonalization of linear codes and its applications. Info, and Control, 22 (1973) 123-131 [13].
[389] N. Q. Due, On the Lin-Weldon majority-logic decoding algorithm for product codes, IEEE Trans. Info. Theory, 19 (1973) 581-583 [18].
[390] N.' Q. Due and L. V. Skattebol, Algorithms for majority-logic check equations of maximal-length codes. Electron. Letters, 5 (1969) 577-579 [13].
[391] N. Q. Due and L. V. Skattebol, Further results on majority-logic decoding of product codes. IEEE Trans. Info. Theory, 18 (1972) 308-310 [18]. 1
[392] J. O. Duffy, Detailed design of a Reed-Muller (32,6) block encoder, JPL Space Programs Summary, Vol. 37^17-111, (1967) 263-267 [14].
[393] C. F. Dunkl, A Krawtchouk polynomial addition theorem and wreath products of symmetric groups, Indiana Univ. Math. J., 25 (1976) 335-358 [5].
[394] C. F. Dunkl and D. E. Ramirez, Krawchouk polynomials and the symmetrization of hypergroups, SIAM J. Math. Anal., 5 (1974) 351-366 [5].
[395] P. F. Duvall and R. E. Kibler, On the parity of the frequency of cycle lengths of shift register sequences, J. Combin. Theory, ISA (1975) 357-361 [14].
[396] H. Dym and H. P. McKean, Fourier Series and Integrals, (Academic Press, New York, 1972) [5,8].
[397] V. I. Dyn’kin and G. M. Tenengol’ts, A class of cyclic codes with a majority decoding scheme, Problems Info. Trans., 5 (No. 1, 1969) 1-11 [13].
E
[398] G. K. Eagleson, A characterization theorem for positive definite sequences on the Krawtchouk polynomials, Australian J. Stat., 11 (1969) 29-38 [5].
[399] W. L. Eastman, On the construction of comma-free codes, IEEE Trans. Info. Theory, 11 (1965) 263-267 [Intro,].
[400] W. L. Eastman and S. Even, On synchronizable and PSK-synchronizable block codes, IEEE Trans. Info. Theory, 10 (1964) 351-356 [1].
[401] P. J. Eberlein, A two parameter test matrix, Math. Comp., 18 (1964) 296-298 [21].
[402] P M. Ebert and S. Y. Tong, Convolutional Reed-Solomon codes, Bell Syst. Tech. J., 48 (1969) 729-742 [10].
[403] H. Ehlich, Determinantenabschatzung fur binare Matrizen mit n = 3 mod 4, Math. Zeit., 84 (1964) 438-447 [2].
[404] H. Ehlich and K. Zeller, Binare Matrizen, Zeit. Angew. Math. Meeh., 42 (1962) 20-21 [2].
[405] R. W. Ehrich and S. S. Yau, A class of high-speed decoders for linear cyclic binary codes, IEEE Trans. Info. Theory, 15 (1969) 113-117 [16].
[406] P. Elias, Error-free coding, IEEE Trans. Info. Theory, 4 (1954) 29-37 [18].
[407] E. O. Elliott, Estimates of error rates for codes on burst-noise channels, Bell Syst. Tech. J., 42 (1963) 1977-1997 [10].
[408] E. O. Elliott, On the use and performance of error-voiding and error-marking codes. Bell Syst. Tech. L. 45 (1966) 1273-1283 [1].
[409] B. Elspas, A conjecture on binary nongroup codes, IEEE Trans. Info. Theory, 11 (1965) 599-600 [17].
[410] A. Erdelyi et al., Higher Transcendental Functions, Vols. 1-3, (McGraw-Hill, New York. 1953) [5].
[411] P. Erdos and H. Hanani, On a limit theorem in combinatorical analysis, Publ. Math. Debrecen, 10 (1963) 10-13 [17].
[412] J. V. Evans and T. Hagfors, eds., Radar Astronomy, (McGraw-Hill, New York, 1968) [14].
[413] S. Even, Snake-in-the box codes, IEEE Trans. Computers, 12 (1963) 18 [Intro.].
F
[414] D. D. Falconer, A hybrid coding scheme for discrete memoryless channels, Bell Syst. Tech. I.. 48 (1969) 691-728 U],
[415] R. M. Fano, Transmission of Information, (MIT Press, Cambridge, MA, 1961) Appendix B-[10].
[416] S. Farber, On signal selection for the incoherent channel, Abstract 4.5, International Symposuim on Info. Theory, Program and Abstracts of Papers, (IEEE New York, 1969) [1].
[417] E. H. Farr, unpublished [9].
[418] P. G. Farrell, Linear binary anticodes, Electronics Letters, 6 (1970) 419-421 [17].
[419] P. G. Farrell and Z. Al-Bandar, Multilevel single-error-corrccting codes. Electronics Letters, 10 (1974) 347-348 [7].
[420] P. G. Farrell and A. A. M. Farrag, Further properties of linear binary anticodes, Electronics Letters, 10 (1974) 340-341 [17].
[421] P. G. Farrell and A. A. M. Farrag, New error-control codes derived from anti-codes, in preparation [17].
[422] H. Feistel, Cryptography and computer privacy, Scientific American, 228 (No. 5, 1973) 15-23 [1].
[423] H. Feistel, W. A. Notz and J. L. Smith, Some cryptographic techniques for machine-to-machine data communications, Proc. IEEE, 63 (1975) 1545-1554 [1, 14].
[424] W. Feit, Some remarks on weight functions of spaces over GF(2), unpublished (1972) [19].
[425] W. Feit, On weight functions of self orthogonal spaces over GF(3), unpublished (1972) [19].
[426] W. Feit, A self-dual even (96,48, 16) code, IEEE Trans. Info. Theory, 20 (1974) 136-138 [19].
[427] W. Feller, An Introduction to Probability Theory and its Applications, Vol. 2 (Wiley, New York, 1966) [9].
[428] F. A. Ficken, The Simplex Method of Linear Programming, (Holt, Rinehart and Winston, New York, 1961) [17].
[429] J. P. Fillmore and M. L. Marx, Linear recursive sequences, SIAM Review, 10 (1968) 342-353 [14].
[430] M. A. Fischler, Minimax combinational coding, IEEE Trans. Info. Theory, 14 (1968) 139-150 [1]. . >
[431] C. S. Fisher, The death of a mathematical theory: A study in the sociology of knowledge, Arch. Hist. Exact Sci., 3 (1967) 136-159 [19].
[432] I. Flores, Reflected number systems, IEEE Trans. Computers, 5 (1956) 79-82 [Intro.].
[433] A. B. Fontaine and W. W. Peterson, On coding for the binary symmetric channel, Trans. AIEE, 77 Part I (1958) 638-646 [18].
[434] A. B. Fontaine and W. W. Peterson, Group code equivalence and optimum codes, IEEE Trans. Info. Theory, 5 (Special Supplement) (1959) 60-70 [2,18, 19].
[435] G. D. Forney, Jr., On decoding BCH codes, IEEE Trans. Info. Theory, 11 (1965) 549-557 [8,9]. Э
[436] G. D. Forney, Jr., Concatenated Codes, (M.l.T. Press, Cambridge, MA., 1966) [10,11, 18].
[437] G. D. Forney, Jr., Generalized minimum distance decoding, IEEE Trans. Info. Theory, 12 (1966) 125-131 [1].
[438] G. D. Forney, Jr., Coding and its application in space communications, IEEE Spectrum, 7 (June 1970) 47-58 [I].
[439] G. D. Forney, Jr., Convolutional codes I: algebraic structure, IEEE Trans. Info. Theory, 16 (1970) 720-738 and 17 (1971) 360 [1].
[440] G. D. Forney, Jr., Burst-correcting codes for the classic bursty channel, IEEE Trans. Commun., 19 (1971) 772-781 [10].
[441] G. D. Forney, Jr., Maximum likelihood estimation of digital sequences in the presence of intersymbol interference, IEEE Trans. Info. Theory$il8 (1972) 363-378 [1].
[442] G. D. Forney, Jr., The Viterbi algorithm, Proc. IEEE, 61 (1973) 268-278 [1].
[443] G. D. Fqrney, Jr., Convolution codes, II: maximum likelihood decoding. Info, and Control, 25 (1974) 222-226 [1].
[444] G. D. Forney, Jr., Convolutional codes III: sequential decoding, Info, and Control, 25 (1974) 267-297 [1].
[445] G. D. Forney, Jr., and E. K. Bower; A high-speed sequential decoder: prototype design and test, IEEE Trans, on Commun., 19 (1971) 821-835 [1].
[446] M. K. Fort, Jr., and G. A. Hedlund, Minimal coverings of pairs by triples, Pacific J. Math., 8 (1958) 709-719 [17].
[447] Н. О. Foulkes, Theorems of Kakeya and Polya on power-sums, Math. Zeit., 65 (1956) 345-352 [8].
[448] P. A. Franaszek, Sequence-state -coding for digital transmission, Bell Syst. Tech. J., 47 (1968) 143-157 [1].
[449] A. G. Franco and L. J. Saporta, Performance of random error correcting codes on the switched telephone network, IEEE Trans. Commun., 15 (1967) 861-864 [1].
[450] H. Fredricksen, Error Correction for Deep Space Network Teletype Circuits, Report 32-1275, Jet Propulsion Lab., Pasadena, CA., June 1968 [1].
[451] H. Fredricksen, The lexicographically least de Bruijn cycle, J. Combin. Theory, 9 (1970) 1-5 [14].
[452] H. Fredricksen. Generation of the Ford sequence of length 2", n large, J. Combin. Theory, 12A (1972) 153-154 [14].
[453] H. Fredricksen, A class of nonlinear de Bruijn cycles, J. Combin. Theory, 19A (1975) 192-199 [14].
[454] H. Fredricksen and I. Kessler, Lexicographic compositions and de Bruijn sequences, in: Broc. 6th S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnipeg, 1975) pp. 315-339 [14].
[455] S. Fredricsson, Pseudo-randomness properties of binary shift register sequences, IEEE Trans. Info. Theory, 21 (1975) 115-120 [14].
[456] С. V. Freiman, Optimal error detection codes for completely asymmetric binary channels, Info, and Control, 5 (1962) 64-71 [1,17].
[457] С. V. Freiman, Upper bounds for fixed-weight codes of specified minimum distance, IEEE Trans. Info. Theory, 10 (1964) 246-248 [17].
[458] С. V. Freiman, and J. P. Robinson, A comparison of block and recurrent codes for the correction of independent errors, IEEE. Trans. Info. Theory, 11 (1965) 445-449 [1].
[459] С. V. Freiman and A. D. Wyner, Optimum block codes for noiseless input restricted channels, Info, and Control, 7 (1964) 398-415 [1].
[460] A. H. Frey and R. E. Kavanaugh, Every data bit counts in transmission cleanup. Electronics, (Jan. 22 1968) 77-83 [1].
[461] G. Frobenius, Uber die Charaktere der mehrfach transitiven Gruppen, Sitzungberichte Ak. Berlin, (1904) 558-571 [20].
[462] C. Fujiwara, M. Kasahara, Y. Tezuka and Y. Kasahara, On codes for burst-error correction, Electron. Commun. Japan, 53-A (7) (1970) 1-7 [10].
G
[463] H. F. Gaines, Cryptanalysis, (Dover, New York, 1956) [1].
[464] R. G. Gallagher, Information theory and reliable communication (Wiley, New York, 1968) [Intro., 1,9,17].
[465] R. G. Gallager, The random coding bound is tight for the average code, IEEE Trans. Info. Theory, 19 (1973) 244-246 [17].
[466] D. Garbe and J. L. Mennicke, Some remarks on the Mathieu groups, Canad. Math. Bull., 7 (1964) 201-212 [20].
[467] B. Gardner, Results on coverings of pairs with special reference to coverings by quintuples, in: Proc. Manitoba Conf. Num. Math., (Dept, of Computer Sci., Univ, of Manitoba, Winnipeg, 1971) pp. 169-178 [А].
[468] M. Gardner, The curious properties of the Gray code..., Scientific American, 227 (August) (1972) 106-109 [Intro.].
[469] P. R. Geffe, An open letter to communication engineers, Proc. IEEE, 55 (1967) 2173 [1,14].
[470] P. R. Geffe, How to protect data with ciphers that are really hard to break, Electronics, 46 (Jan. 4) (1973) 99-101 [1,14].
[471] S. I. Gelfand, R. L. Dobrushin and M. S. Pinsker, On the complexity of coding, in: B. N. Petrov and F. Csaki, eds., 2nd Internal. Symp. Info. Theory, Akad. Kiado, Budapest, 1973 pp. 177-184 [Intro.].
[472] W. M. Gentleman, Matrix multiplication and fast Fourier transforms, Bell Syst. Tech. J., 47 (1968) 1099-1103 [14].
[473] A. V. Geramita, J. M. Geramita and J. S. Wallis, Orthogonal designs, Linear and Multilinear Algebra, 3 (1976) 281-306 [2].
[474J A. V. Geramita, N. J. Pullman and J. S. Wallis, Families of weighing matrices, Bull. Aust. . Math. Soc., 10 (1974) 119-122 [2].
[474a ] A. V. Geramita and J. H. Verner, Orthogonal designs with zero diagonal, Canad. J. Math., 28 (1976) 215-224 [2].
[475] A. V. Geramita and J. S. Wallis, Orthogonal designs II. Aequat. Math.. 13 (1975) 299-313 [2].
[476] A. V. Geramita and J. S. Wallis, Orthogonal designs III; weighing matrices, Utilitas Mathematics, 6 (1974) 209-236 [2].
[476a] A. V. Geramita and J. S. Wallis, A survey of orthogonal designs, in: Proc. 4th Manitoba Conf. Num. Math., (1974) pp. 121-168 [2].
[477] A. V. Geramita and J. S. Wallis, Orthogonal designs IV; existence questions, J. Combin. Theory, 19A (1975) 66-83 [2].
[478] J. E. Gibbs and H. A. Gebbie. Application of Walsh functions to transform spectroscopy. Nature, 224 (1969) 1012-1013 [2].
[479] E. N. Gilbert, A comparison of signalling alphabets. Bell Syst. lech. Jnl., 31 (1952) 504-522 [1].
[480] E. N. Gilbert, Unpublished notes, 1953 [14].
[481] E. N. Gilbert, Gray codes and paths on the n-cube, Bell Syst. Tech. J., 37 (1958) 815-826 [Intro.].
[482] E. N. Gilbert, Synchronization of binary messages, [EEE Trans. Info. Theory, 6 (1960) 470-477 [1].
[483] E. N. Gilbert, Cyclically permutable error-correcting codes, [EEE Trans. Info. Theory, 9 (1963) 175-182 [17].
[484] E. N. Gilbert, F. J. MacWilliams and N. J. A. Sloane, Codes which detect deception, Bell Syst. Tech. J., 53 (1974) 405-424 [1].
[485] A. Gill, Linear Sequential circuits; Analysis, Synthesis, and Applications (McGraw-Hill, New York, 1966) [3].
[486] A. M. Gleason, Weight polynomials of self-dual codes and the MacWilliams identities, in: Actes Congres [nternl. de Mathematique, 3 1970 (Gauthier-Villars, Paris, 1971) 211-215 [19].
[487] K. R. Godfrey, Three-level m-sequences, Electronics Letters. 2 (1966) 241-243 [14].
[488] J.-M. Goethals, Analysis of weight distribution in binary cyclic codes, IEEE Trans, [nfo. Theory, 12 (1966) 401-402 [8].
[489] J.-M. Goethals, Cyclic error-locating codes, [nfo. and Control, 10 (1967) 378-385 [18].
[490] J.-M. Goethals, Factorization of cyclic codes, [EEE Trans, [nfo. Theory, 13 (1967) 242-246 [18].
[491] J.-M. Goethals, A polynomial approach to linear codes, Philips Res. Reports, 24 (1969) 145-159 [11, 13].
[492] J.-M. Goethals, On t-designs and threshold decoding, Institute of Statistics Mimeo Series, No. 600.29, (Univ, of North Carolina, Chapel Hill, N.C., June, 1970) [16].
[493] J.-M. Goethals, On the Golay perfect binary code, J. Combin. Theory, 11 (1971) 178-186 [2, 15, 16].
[494] J.-M. Goethals, Some combinatorial aspects of coding theory. Ch. 17 in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory, (North-Holland, Amsterdam, 1973) [I. 13).
[495] J.-M. Goethals, Two Dual Families of Nonlinear Binary Codes, Electronics Letters, 10 (1974) 471-472 [15, А].
[496] J.-M. Goethals, Nonlinear Codes Defined by Quadratic Forms Over GF(2), Information and Control, 31 (1976) 43-74 [15, А].
[497] J.-M. Goethals, The extended Nadler code is unique, IEEE Trans. Info. Theory, 23 (1977) 132-135 [2].
[498] J.-M. Goethals, personal communication [15].
[499] J.-M. Goethals and P. Delsarte, On a class of majority-logic decodable cyclic codes, IEEE Trans. Info. Theory, 14 (1968) 182-188 [13].
[500] J.-M. Goethals and J. J. Seidel, Orthogonal matrices with zero diagonal, Canad. J. Math., 19 (1967) 1001-1010 [2]. ‘
[501] J.-M. Goethals and j. J. Seidel, A skew Hadamard matrix of order 36, J. Aust. Math. Soc., 11 (1970) 343-344 [2].
[502] J.-M. Goethals and J. J. Seidel,. Strongly regular graphs derived from combinatorial designs, Canad. J. Math., 22 (1970) 597-614 [21].
[503] J.-M. Goethals and J. J. Seidel, The regular two-graph on 276 vertices. Discrete Math., 12 (1975) 143-158 [21].
[504] J.-M. Goethals and S. L. Snover, Nearly perfect binary codes. Discrete Math., 3 (1972) 65-88 [15, 17].
[505] J.-M. Goethals and H. C. A. van Tilborg, Uniformly packed codes. Philips Research Reports, 30 (1975) 9-36 [15].
[506] M. J. E. Golay, Notes on' digital coding. Proc. IEEE, 37 (1949) 657 [1,2. 20, А].
[507] M. J. E. Golay, Multi-slit spectrometry, J. Optical Soc. America. 39 (1949) 437-444 [2].
[508] M. J. E. Golay, Static multislit spectrometry, and its application to the panoramic display of infrared spectra. J. Optical Soc. America, 41 (1951) 468-472 [2].
[509] M. J. E. Golay, Binary coding. [EEE Trans. Info. Theory, 4 (1954) 23-28 [2, A).
[510] M. J. E. Golay, Notes on the penny-weighing problem, lossless symbol coding with nonprimes, etc.. IEEE Trans. Info. Theory. 4 (1958) 103-109 [7].
[511] M. J. E. Golay, Complementary series, IEEE Trans. Info. Theory, 7 (1961) 82-87 [14].
[512] M. J. E. Golay, Note on lossless coding with nonprimes. IEEE Trans. Info. Theory, 14 (1968) 605 [7].
[513] M. J. E. Golay, A class of finite binary sequences with alternate autocorrelation values equal to zero, IEEE Trans..Info. Theory, 18 (1972) 449-450 [14].
[514] M. J. E. Golay, Hybrid low autocorrelation sequences, [EEE Trans, [nfo. Theory. 21 (1975) 460-462 [14].
[514a] M. J. E. Golay, Anient codes, priorities, patents, etc., Proc. IEEE, 64 (1976) 572 [1].
[515] R. Gold, Characteristic linear sequences and their coset functions, J. SIA.M A.ppl. Math., 14 (1966) 980-985 [14].
[516] R. Gold, Maximal recursive sequences with 3-valued recursive cross-correlation functions, IEEE Trans. Info. Theory, 14 (1968) 154-156 [14].
[517] M. Goldberg, Augmentation techniques for a class of product codes, IEEE Trans. [nfo. Theory, 19 (1973) 666-672 [18].
[518] H. D. Goldman, M. Kliman, and H. Smola, The weight structure of some Bose-Chaudhuri codes. [EEE Trans. Info. Theory, 14 (1968) 167-169 [9, А].
[519] J. Goldman and G.-C. Rota, The number of subspaces of a vector space, in: W. T. Tutte, ed., Recent Progress in Combinatorics, (Academic Press, New York, 1969) pp. 75-83 [15, В].
[520] A. J. Goldstein, A residue operator in formal power series, preprint [19].
[521] R. M. Goldstein and N. Zierler, On trinomial recurrences, IEEE Trans [nfo. Theory. 14 (1968) 150-151 [14].
[522] S. W. Golomb, ed.. Digital Communications with Space Applications, (Prentice-Hall, Englewood Cliffs, NJ, 1964) [1,2, 14].
[523] S. W. Golomb, Shift Register Sequences, (Holden-Day. San Francisco, 1967) [Intro., 3,9, 14].
[524] S. W. Golomb, A general formulation of error metrics, [EEE Trans, [nfo. Theory, 15 (1969) 425-426 [5,6].
[524a] S. W. Golomb, Irreducible polynomials, synchronization codes, and the cyclotomic algebra, in: R. C. Bose and T. A. Dowling, eds.. Combinatorial Mathematics and [ts Applications, (Univ. North Carolina Press. Chapel Hill, NC, 1969) pp. 358-370 [4].
[525] S. W. Golomb. Sphere packing.1 coding metrics, and chess puzzles, in: Proc. Second Chapel Hill Conf, on Combin. Math. A.pplic., (Univ, of North Carolina, Chapel Hill, NC, 1970) pp. 176-189 [5.6].
[526] S. W. Golomb et al.. Synchronization, [EEE Trans. Commun.. 11 (1963) 481-491 [1].
[527] S. W. Golomb and B. Gordon, Codes with bounded synchronization delay. Info, and Control, 8 (1965) 355-372 [1].
[528] S. W. Golomb, B. Gordon and L. R. Welch. Comma-free codes. Canad. J. Math., 10 (1958) 202-209 [Intro.].
[529] S. W. Golomb and E. C. Posner. Rook domains. Latin squares, affine planes, and error-distribution codes, [EEE Trans. Info. Theory, 10 (1964) 196-208 [5,6].
[530] S. W. Golomb and R. A. Scholtz, Generalized Barker sequences, IEEE Trans. Info. v Theory. 11 (1965) 533-5.37 [14].
(53 1J S. W. Golomb and L. R. Welch, Algebraic coding and the Lee metric, in: H. B. Mann, ed., Error Correcting Codes, (Wiley, New York, 1968) pp. 175-194 [5,6].
[532] S. W. Golomb and L. R. Welch, Perfect codes in the Lee metric and the packing of polyominoes. S'MM J. Appl. Math., 18 (1970) 302-317 [5,6].
[533] I. J. Good, Generalizations to several variables of Lagranges’s expansion, with applications to stochastic processes, Proc. Camb. Phil. Soc., 56 (1960) 367-380 [19].
[534] R. M. F. Goodman, Binary codes with disjoint codebooks and mutual Hamming distance, Electronic Letters, 10 (1974) 390-391 [8].
[535] R. M. F. Goodman and P. G. Farrell, Data transmission with variable-redundancy error control over a high-frequency channel, Proc. IEE, 122 (1975) 113-118 [1].
[536] V. D. Goppa, A new class of linear error-correcting codes, Problems of Info. Transmission, 6 (3) (1970) 207-212 [12, А].
[537] V. D. Goppa, Rational representation of codes and (L, g)- codes, Problems of Info. Transmission, 7 (3) (1971) 223-229 [12].
[538] V. D. Goppa, Codes constructed on the basis of (L, g) - codes, Problems of Info. Transmission, 8 (2) (1972) 165-166 [12, 18].
[538a] V. D. Goppa, Binary symmetric channel capacity is attained with irreducible codes, Problems of Info. Transmission, 10 (1) (1974) 89-90 [12].
[539] V. D. Goppa, Correction of arbitrary error patterns by irreducible codes, Problems of Info. Transmission, 10 (3) (1974) 277-278 [12].
[540] V. D. Goppa, On generating idempotents of cyclic codes, preprint [8].
[541] B. Gordon, On the existence of perfect maps, IEEE Trans. Info. Theory, 12 (1966) 486-487 [18].
[542] Y. Gordon and H. S. Witsenhausen, On extensions of the Gale-Berlekamp switching problem and constants of („-spaces, Israel J. Mathematics, 11 (1972) 216-229 [14].
[543] W. C. Gore, Generalized threshold decoding and the Reed-Solomon codes, IEEE Trans. Info. Theory, 15 (1969) 78-81 [9, 10].
[544] W. C. Gore, The equivalence of L-step orthogonalization and a Reed decoding procedure, IEEE Trans. Info. Theory, 15 (1969) 184-186 [13].
[545] W. C. Gore, Generalized threshold decoding of linear codes, IEEE Trans. Info. Theory, 15 (1969) 590-592 [13].
[546] W. C. Gore, Further results on product codes, IEEE Trans. Info. Theory, 16 (1970) 446-451 [18].
[547] W. C. Gore, Transmitting binary symbols with Reed-Solomon codes, Proc. 7th Annual Princeton Conf. Information Sciences and Systems, (Dept, of Electrical Engineering, Princeton University, Princeton, NJ, 1973) pp. 495-499 [9, 10].
[548] W. C. Gore and A. B. Cooper, Comments on polynomial codes, IEEE Trans. Info. Theory, 16 (1971) 635-638 [13].
[549] W. C. Gore, and С. C. Kilgus, Cyclic codes with unequal error protection, IEEE Trans. Info. Theory, 17 (1971) 214-215 [Intro.].
[550] D. C. Gorenstein, W. W. Peterson, and N. Zierler, Two-error correcting Bose-Chaudhuri codes are quasi-perfect, Info, and Control, 3 (1960) 291-294 [9].
[551] D. C. Gorenstein and E. Weiss, An acquirable code. Info, and Control, 7 (1964) 315-319 [14].
[552] D. C. Gorenstein and N. Zierler, A class of error-correcting codes in p“ symbols, J. Soc. IndusC Applied Math., 9 (1961) 207-214 [7].
[553] R. L. Graham and F. J. MacWilliams, On the number of information symbols in difference-set cyclic codes, Bell Syst. Tech. J., 45 (1966) 1057-1070 [13].
[554] D. H. Green and I. S. Taylor, Irreducible polynomials over composite Galois fields and their-applications in coding techniques, Proc. IEE, 121 (1974) 935-939 [4].
[555] J. H. Green, Jr., and R. L. San Souci, An error-correcting encoder and decoder of high efficiency. Proc. IEEE, 46 (1958)* 1741-1744 [13].
[556] M. W. Green, Two heuristic techniques for block-code construction, IEEE Trans. Info. Theory, 12 (1966) 273 [2].
[557] R. R. Green, A serial orthogonal decoder, JPL Space Programs Summary, Vol. 37-39-IV (1966) 247-253 [14].
[558] R. R. Green, Analysis of a serial orthogonal decoder, JPL Space Programs Summary, Vol. 37-53-111 (1968) 185-187 (14].
[559] P. Greenberg, Mathieu Groups, (Courant Institute of Math. Sci., NY, 1973) [20].
[560] C. Greene, Weight enumeration and the geometry of linear codes, Studies in Applied Math., 55 (1976) 119-128 [5].
[561] L. D. Grey, Some bounds for error-correcting codes, IEEE Trans. Info. Theory, 8 (1962) 200-202 and 355 [17].
[562] J. H. Griesmer, A bound for error-correcting codes, IBM J. Res. Develop., 4 (1960) 532-542 [17].
[563] A. J. Gross, Some augmentations of Bose-Chaudhuri error correcting codes, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory, (North-Holland, Amsterdam, 1973) Ch. 8 [10].
[564] E. J." Groth, Generation of binary sequences with controllable complexity, IEEE Trans. Info. Theory, 17 (1971) 288-296 [Intro.].
[565] B. R. Gulati, On maximal (k, t)-sets, Annals Inst. Statistical Math., 23 (1971) 279-292 and 527-529 [11].
[566] B. R. Gulati, More about maximal (N, R)-sets, Info, and Control, 20 (1972) 188-191 [11].
[567] B. R. Gulati, В. M. Johnson and U. Koehn, On maximal t-Iinearly independent sets, J. Comb. Theory, 15AT (1973) 45-53 [11].
[568] B. R. Gulati and E. G. Kouriias, On bounds useful in the theory of symmetrical fractional designs, J. Roy. Statist. Soc., Ser. B, 32 (1970) 123-133 [11].
[569] B. R. Gulati and E. G. Kounias, Maximal sets of points in finite projective space, no t-linearly dependent, J. Comb. Theory, 15A (1973) 54-65 [11]. '
[570] R. C. Gunning, Lectures on Modular Forms, (Princeton Univ. Press, Princeton, NJ, 1962) [19].
[571] R. K. Guy, Twenty* odd questions in combinatorics, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ. N. Carolina Press, 1970) [Intro.].
H
[572] J. Hadamard, Resolution d’une question relative aux determinants, Bull. Sci. Math., (2) 17 (1893) 240-248 [2].
[573] D. Hagelbarger, Recurrent codes; easily mechanized burst-correcting binary codes, Bell Syst. Tech. J., 38 (1959) 969-984 [10].
[574] W. Hahn, Uber Orthogonalpolynome, die q-Differenzengleichungen geniigen, Math. Nachr., 2 (1949) 4-34 [21].
[575] S. L. Hakimi and J. G. Bredeson, Graph theoretic error-correcting codes, IEEE Trans. Info. Theory, 14 (1968) 584-591 [18].
[576] S. L. Hakimi and J. G. Bredeson, Ternary graph theoretic error-correcting codes, IEEE Trans. Info. Theory, 15 (1969) 435-437 [18].
[577] S. L. Hakimi and H. Frank, Cut-set matrices and linear codes, IEEE Trans. Info. Theory; 11 (1965) 457-458 [18].
[578] M. P. Hale, Jr. and E. E. Shult, Equiangular lines, the graph extension theorem, and transfer in triply transitive groups, Math. Zeit., 135 (1974) 111-123 [21].
[579] A. D. Hall, Jr., The ALTRAN system for rational function manipulation - A survey, Comm. Assoc. Comput. Mach., 14 (1971) 517-521 [19].
[580] J. I. Hall, Bounds for equidistant codes and partial projective planes, Discrete Math., 18 (1978) to appear. [1].
[581] J. I. Hall, A. J. E. M. Janssen, A. W. J. Kolen and J. H. van Lint, Equidistant codes with distance 12, Discrete Math., 18 (1978) to appear. [1].
[582] M. Hall, Jr., The Theory of Groups (Macmillan, New York, 1959) [В].
[583] M. Hall, Jr., Hadamard matrices of order 16, Research Summary, No. 36-10 (Jet Propulsion Lab., Pasadena, CA, Sept. 1, 1961) Vol. 1, pp. 21-26 [2].
[584] M. Hall, Jr., Note on the Mathieu group M12, Arch. Math., 13 (1962) 334-340 [20].
[585] M. Hall Jr., Block designs, in: E. F. Bechenbach, ed., Applied Combinatorial Mathematics, (Wiley, New York, 1964) pp. 369-405 [2].
[586] M. Hall, Jr., Hadamard matrices of order 20, Technical report 32-761, (Jet Propulsion Lab., Pasadena, CA, Nov. 1, 1965) [2].
[587] M. Hall, Jr., Combinatorial Theory (Blaisdell, Waltham, MA, 1967) [Intro., 2,5, А, В].
(588] M. Hall, Jr., Automorphisms of Hadamard matrices, SIAM J. Appl. Math., 17 (1969) 1094-1101 [2, 16].
1589] M. Hall, Jr., Difference sets, in: M. Hall, Jr., and J. H. van Lint, eds., Combinatorics. (Reidel, Dordrecht, Holland 1975) pp. 321-346 [13].
[590] M. Hall, Jr., Semi-automorphisms of Hadamard matrices. Math. Proc. Camb. Phil. Soc., 77 (1975) 459-473 [2, 16,20].
[591] N. H,amada, On the p-rank of the incidence matrix of a balanced or partially balanced incomplete block design and its applications to error correcting codes, Hiroshima Math. J., 3 (1973) 153-226 [13].
[592] R. W. Hamming, Error detecting and error correcting codes. Bell Syst. Tech. J., 29 (1950) 147-160 [1, А].
[593] P. Hammond, Perfect codes in the graphs Ob, J. Comb. Theory, 19B (1975) 239-255 [6].
[594] P. Hammond, Nearly perfect codes in distance-regular graphs, Discrete Math., 14 (1976) 41-56 [6].
[595] H. Hanani, On quadruple systems, Canad. J. Math., 12 (1960) 145-157 [2, 17].
[596] M. Hanani, The existence and construction of balanced incomplete block designs, Annals Math. Stat., 32 (1961) 361-386 [2, 17].
[597] H. Hanani, On some tactical configurations, Canad. J. Math., 15 (1963) 702-722 [2, 17].
[598] H. Hanani, A balanced incomplete block design. Annals Math. Stat., 36 (1965 1 711 [2,17].
[599] H. Hanani, On balanced incomplete block designs with blocks having five elements, J Comb. Theory, 12A (1972) 184-201 [2, 17].
[600] H. Hanani, Balanced incomplete block designs and related designs. Discrete Math., 11 (1975) 255-369 [2,17, А].
[601] G. H. Hardy, J. E. Littlewood and G. Polya, Inequalities, (Cambridge Univ. Press, Cambridge, 1959) [2].
[602] G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, (Oxford University Press, Oxford, 3rd edition, 1954) [4].
[603] H. F. Harmuth, Applications of Walsh functions in communications, IEEE Spectrum, 6 (November, 1969) 81-91 [2].
[604] H. F. Harmuth, Transmission of Information by Orthogonal Functions, (Springer, New York, 1970) [2].
[605] L. H. Harper, Combinatorial coding theory; in: R. C. Bose and T. A. Dowling, eds.. Combinatorial Mathematics and its Applications, (Univ, of North Carolina Press, Chapel Hill, NC, 1970) pp. 252-260 [Intro.].
[606] M. A. Harrison, Introduction to Switching and Automata Theory, (McGraw-Hill. New York, 1965) [13].
[607] C. R. P. Hartmann, A note on the decoding of double-error-correcting binary BCH codes of primitive length, IEEE Trans. Info. Theory, 17 (1971) 765-766 [9].
[608] C. R. P. Hartmann, A note on the minimum distance structure of cyclic codes, IEEE Trans. Info. Theory, 18 (1972) 439-440 [7].
[609] C. R. P. Hartmann, Decoding beyond the BCH bound, IEEE Trans. Info. Theory, 18 (1972) 441-444 [9].
[610] C. R.. P. Hartmann, Theorems on the minimum distance structure of binary cyclic codes, in: B. N. Petrov and F. Csaki, eds., 2nd Internal. Sympos. on Info. Theory, (Akad. Kiado, Budapest, 1973) pp. 185-190 [7].
[611] C. R. P. Hartmann, J. B. Ducey and L. D. Rudolph, On the structure of generalized finite-geometry codes, IEEE Trans. Info. Theory, 20 (1974) 240-252 [13].
[612] C. R. P. Hartmann, L. Kerschberg andJM. A. Diamond, Some results on single erroi correcting binary BCH codes, Tech. Rep? 6-74, Syracuse Univ., 1974 [9].
[613] C. R. P. Hartmann, J. R. Riek, Jr. and R. J. Longobardi, Weight distributions of some classes of binary cyclic codes, IEEE Trans. Info. Theory, 21 (1975) 345-350 [8].
[614] C. R. P. Hartmann and L. D. Rudolph, An optimum symbol-by-symbol decoding rule for linear codes, IEEE Trans. Info. Theory 22 (1976) 514-517 [16].
[615] C. R. P. Hartmann and К. K. Tzeng, Generalizations of the BCH bound, Info, and Control, 20 (1972) 489-498 [7]..
[616] C. R. P. Hartmann and К. K. Tzeng, A bound for cyclic codes of composite length, IEEE Trans. Info. Theory, 18 (1972) 307-308 [18].
[617] C: R. Р. Hartmann, К. К. Tzeng and R. T. Chien, Some results on the minimum distance structure of cyclic codes, IEEE Trans. Info. Theory, 18 (1972) 402-409 [18].
[618] C. R. P. Hartmann and К. K. Tzeng, On some classes of cyclic codes of composite length, IEEE Trans. Info. Theory, 19 (1973) 820-822 [18, А].
[619] C. R. P. Hartmann and К. K. Tzeng, Decoding beyond the BCH bound using multiple sets of syndrome sequences, IEEE Trans. Info. Theory, 20 (1974) 292-295 [9].
[620] W. E. Hartnett, ed., Foundations of Coding Theory, (Reidel, Holland, 1974) [Intro.].
[621] J. T. Harvey. High-speed m-sequence generation, Electronics Letters, 10 (1974) 480-48Г [14].
[622] M. Harwit, P G. Phillips, T. Fine and N. J. A. Sloane, Doubly multiplexed dispersive spectrometers, Applied Optics, 9 (1970) 1149-1154 [2].
[623] A. A. Hashim, New families of error-correcting codes generated by modification of other linear binary block codes, Proc. IEE, 121 (1974) 1480-1485 [18].
[624] A. A. Hashim and A? G.. Constantinides, Class of linear binary codes. Proc. IEE. 121 (1974) 555-558 [18].
[625] A. A. Hashim and A. G. Constantinides, Some new results, on binary linear block codes, Electronics Letters, 10 (1974) 31-33 [18, А].
[625a] A. A. Hashim and V. S. Pozdniakov, Computerized search for linear binary codes. Electronics Letters, 12 (1976) 350-351 [А].
(626] T. R. Hatcher, On minimal distance, shortest length and greatest number of elements for binary group codes, Report TM-6-3826, Parke Math. Labs., Inc., Carlisle, Mass., Sept. 1964 [17].
[627] T. R. Hatcher, On a family of error-correcting and synchronizable codes, IEEE Trans. Info. Theory, 15 (1969) 620-624 [1].
[628] O. Heden, Perfect codes in antipodal distance-transitive graphs, Math. Scand., 35 (1974) 29-37 [6]. *
[629] O. Heden, A generalized Lloyd theorem and mixed perfect codes, Math. Scand., 37 (1975) 13-26 [6].
[630] O. Heden, A new construction of group and nongroup perfect codes, Report 2, Mat. Institut., Stockholm Univ., 1975 [6].
[631] H. J. Helgert, Srivastava codes, IEEE Trans. Info. Theory, 18 (1972) 292-297 [12, А].
[632] H. J. Helgert, Noncyclic generalizations of BCH and Srivastava codes, Info, and Control, 21 (1972) 280-290 [12].
[633] H. J. Helgert, Alternant codes, Info, and Control, 26 (1974) 369-380 [12, 18, А].
[634] H. J. Helgert, Binary primitive alternant codis, Info, and Control, 27 (1975) 101-108 [12].
[635] H. J. Helgert, Alternant Codes, Talk given at Information Theory Workshop, Lenox, Mass., June 1975 [12].
[636] H. J. Helgert and R. D. Stinaff, Minimum-distance bounds for binary linear codes, IEEE Trans. Info. Theory, 19 (1973) 344-356 [2, 17, 18, A].'
[637] H. J. Helgert and R. D. Stinaff, Shortened BCH codes, IEEE Trans. Info. Theory, 19 (1973) 818-820 [18, А].
[638] J. A. Heller and I. M. Jacobs, Viterbi decoding for satellite and space communications, IEEE Trans. Commun. Theory, 14 (1971) 835-848 [1].
[639] M. E. Hellman, On using natural redundancy for error detection, IEEE Trans, on Computers, 22 (1974) 1690-1693 [1].
[640] M. E. Hellman, Error detection in the presence of synchronization loss, IEEE Trans. Commun., 23 (1975) 538-539 [1].
[640a] M. E. Hellman and W. Diffie, New directions in cryptography, IEEE Trans. Info. Theory, 22 (1976), 644-654 [1].
[641] U. Henriksson, On a scrambling property of feedback shift registers, IEEE Trans. Commun., 20 (1972) 998-1001 [14].
[642] I. N. Herstein, Nonconimutative rings, Carus Monog. 15, (Math. Assoc. America and Wiley, N.Y., 1968) [В].
[643] M. Herzog and J. Schonheim, Linear and nonlinear single-error-correcting perfect mixed codes, Info. Control, 18 (1971) 364-368 [6].
[644] M. D. Hestenes, On the use of graphs in group theory, in: F. Harary, ed., New Directions in the Theory of Graphs, (Academic Press, New York, 1973) pp. 97-128 [21].
[645] M. D. Hestenes and D. G. Higman, Rank 3 groups and strongly regular graphs, in:
SIAM-AMS Proc. Vol. IV, Computers in Algebra and Number Theory, (Amer. Math. Soc., Providence, 1971) pp. 141-159 [21].
[646] D. G. Higman, Finite permutation groups of rank 3, Math. Zeit., 86 (1964) 145-156 [21].
[647] D. G. Higman, Intersection matrices for finite permutation groups, J. Algebra 4 (1967>= 22-42 [21].
[648] D. G. Higman, Characterization of families of rank 3 permutation groups by the subdegrees, I and II, Archiv. Math. 21 (1970) 151-156 and 353-361 [21].
[649] D. G. Higman, Combinatorial Considerations about Permutation Groups, Lecture notes. Math. Inst.. Oxford, (1972) [21].
[650] D. G._ Higman, Coherent configurations and generalized polygons, pp. 1-5 of Combinatorial Mathematics, Lecture Notes in Math. 403, Springer-Verlag N.Y. 1974 [21].
[651] D. G. Higman, Invariant relations, coherent configurations, and generalized polygons, in: M. Hall, Jr., and J. H. van Lint, eds., Combinatorics, (Reidel, Dordrecht, 1975) pp. 347-363 [21].
[652] D. G. Higman, Coherent configurations, part I: ordinary representation theory, Geometriae Dedicata, 4 (1975) 1-32 [21].
[653] D. G. Higman, Coherent configurations, part II: weights, Geometriae Dedicata, to appear [21].
[654] D. Hilbert and S. Cohn-Vossen, Geometry and the Imagination, (Chelsea, N.Y. 1952) [17].
[655] J. W. P. Hirschfeld, Rational curves on quadrics over finite fields of characteristic two, Rendiconti di Matematica, 3 (1971) 772-795 [11].
[656] C. F. Hobbs, Approximating the performance of a binary group code, IEEE Trans. Info. Theory, 11 (1965) 142-144 [1, 14].
[657] M. Hochster and J. A. Eagon, Cohen-Macaulay rings, invariant theory, and the generic perfection of determinantal loci, Amer. J. Math., 93 (1971) 1020-1058 [19].
[658] A. Hocquenghem, Codes correcteurs d’erreurs, Chiffres (Paris), 2 (1959) 147-156 [7].
[659] C. W. Hoffner and S. M. Reddy, Circulant bases for cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 511-512 [16].
[660] J. K. Holmes, A note on some efficient estimates of the noise variance for first order Reed-Muller codes, IEEE Trans. Info. Theory, 17 (1971) 628-630 [14].
[661] S. J. Hong and D. C. Bossen, On some properties of self-reciprocal polynomials, IEEE Trans. Info. Theory, 21 (1975) 462-464 [7].
[662] S. J. Hong and A. M. Patel, A general class of maximal codes for computer applications. IEEE Trans. Comput.. 21 (1972) 1322-1331 [1].
[663] J. A. van der Horst and T. Berger, Complete decoding of triple-error-correcting binary BCH codes, IEEE Trans. Info. Theory. 22 (1976) 138-147 [9].
[664] M. Horstein, Sequential transmission using noiseless feedback, IEEE Trans. Info. Theory, 9 (1963) 136-143 [Intro.].
[665] H. Hotelling, Some improvements in weighing and other experimental techniques. Annals Math. Stat., 15 (1944) 297-306 [2].
[666] M. Y. Hsiao, On calling station codes, IEEE Trans. Info. Theory, 15 (1969) 736-737 [17].
[667] M. Y. Hsiao, A class of optimal minimum odd-weight-column SEC-DED codes, IBM J. Res. Dev., 14 (1970) 395-401 [7].
[668] M. Y. Hsiao, Incomplete block design codes for ultra high speed computer applications, Discrete Math., 3 (1972) 89-108 [1, 18].
[669] M. Y. Hsiao and D. C. Bossen, Orthogonal Latin square configuration for LSI memory yield and reliability enhancement, IEEE Trans, on Computers, 24 (1975) 512-516 [1, 18].
[670] M. Y.’ Hsiao, D. C. Bossen and R. T. Chien, Orthogonal Latin square codes, IBM J. Res. Devel.. 14 (1970) 390-394 [1, 18].
[671] H. T. Hsu and T. Kasami, Error-correcting codes for a compound channel, IEEE Trans. Info. Theory, 14 (1968) 135-139 [1].
[672] X. L. Hubaut, Strongly regular graphs. Discrete Math., 13 (1975) 357-381 [21].
[673] D. R. Hughes, t-designs and groups, Amer. J. Math.. 87 (1965 ) 761-778 [2].
[674] D. R. Hughes and F. C. Piper, Projective Planes, (Springer, New York, 1973) [В].
[675] D. R. Hughes and F. C. Piper, Block designs, in preparation [2].
[676] B. Huppert, Endliche Gruppen I, (Springer, New York, 1967) [12, 16].
[677] W. J. Hurd, Efficient generation of statistically good pseudonoise by linearly intercon-, nected shift registers, Report 32-1526, vol. XI, Jet Propulsion Labs, Pasadena, 1973 [ 14],
1678] IBM Journal of Research and Development, Special issue on Coding for Error Control, 14 (July 1970) [Intro.. I].
£679] IEEE Trans. Commun. Technology, Special Issue on Error Correcting Codes, 19 (October 1971, Part II) [Intro., 1].
.'[680] IEEE Transactions on Electromagnetic Compatibility, Special Issue on Applications of Walsh functions, 13 (August 1971) [2].
[681] T. Ikai and Y. Kojima, Two-dimensional cyclic codes. Electron Commun. Japan, 57-A (No. 4. 1974) 27-35 [18].
[682] H. Imai, Two Dimensional Fire Codes, IEEE Trans. Info. Theory, 19 (1973) 796-806 [18].
[683] I. Ingemarsson, Commutative group codes for the Gaussian channel IEEE Trans. Info. Theory, 19 (1973) 215-219 [Intro.].
[684] Y. Iwadare, A unified treatment of burst-correcting codes, Electron. Commun. Japan, 52-A (No. 8, 1969) 12-19 [10].
[685] Y. Iwadare, A class of high-speed decodable burst-correcting codes, IEEE Trans. Info. Theory, 18 (1972) 817-821 [10].
*
J
[686] I. M. Jacobs, Practical applications of coding, IEEE Trans. Info Theory, 20 (1974) 305-310 [1]. . '
[687] N. Jacobson, Lectures in Abstract Algebra, (Van Nostrand, Princeton, New Jersey; Vol. 1, 1951; Vol. 2, 1-953; Vol. 3, 1964) [4. 19].
[688] A. T. James, The relationship algebra of an experimental design, Ann. Math. Stat., 28 (1957) 993-1002 [21].
[689] G. D. James, The modular characters of the Mathieu groups, J. Algebra, 27 (1973) 57-111 [20].
[690] F. Jelinek, Probabilistic Information Theory, (McGraw-Hill New York, 1968) [1, 10].
[691] F. Jelinek, Fast sequential decoding algorithm using a stack, IBM J. Res. Devel.. 13 (1969) 675-685 [I].
[692] В. H. Jiggs, Recent results in comma free codes, Canad. J. Math., 15 (1963) 178-187 [Intro.].
[693] S. M. Johnson, A new upper bound for error-correcting codes, IEEE Trans. Info. Theory. 8 (1962) 203-207 [17].
[694] S. M. Johnson, Improved asymptotic bounds for error-correcting codes, IEEE Trans. Info. Theory, 9 (1963) 198-205 [17]. '
[695] S. M. Johnson, Unpublished tables, 1970 [17, А].
[696] S. M. Johnson, On upper bounds for unrestricted binary error-correcting codes, IEEE Trans. Info. Theory 17 (1971) 466-478 [17, A]
[697] S. M. Johnson, Upper bounds for constant weight error correcting codes. Discrete Math 3 (1972) 109-124 [17]
[698] S. M. Johnson, A new lower bound for coverings by rook domains, Utilitas Math., 1 (1972) 121-140 [6].
[699] W. Jonsson, On the Mathieu groups M22, M23, Л/22 and the uniqueness of the associated Steiner systems, Math. Z., 125 (1972) 193-214 [20].
[700] D. D. Joshi, A note on upper bounds for minimum distance bounds, Info. Control, 1 (1958) 289-295 [1,17].
[701] D. Julin, Two improved block codes, IEEE Trans. Info. Theory, 11 (1965) 459 [2, А].
[702] H. W. E. Jung Uber die kleinste Kugel die eine raumliche Figur einschliesst, J. reine angew. Math., 123 (1901) 241-257 [6].
1703] R. R. Jurick, An algorithm for determining the largest maximally independent set of vectors from an r-dimensional vector space over a Galois field of n elements, Tech. Rep. ASD TR-68-40, Air Force Systems Command, Wright-Patterson Air Force Base, Ohio, September 1968 [II].
t[704] J. Justesen. A class of constructive asymptotically good algebraic codes?IEEE Trans. Info. Theory, 18 (1972) 652-656 [10].
[7u5] J Justesen, New convolutional code construction and a class of asymptotically good time varying codes, IEEE Trans. Info. Theory, 19 (1973) 220-225 [10].
[706] J. Justesen, On the complexity of decoding Reed-Solomon codes, IEEE Trans. Info. Theory, 22 (1976) 237-238 [Intro., 12].
К
[707] D. Kahn, The Codebreakers, (Macmillan, New. York, 1967) [ij. *
[708] J. G. Kalbfleisch and R. G. Stanton, Maximal and minimal coverings of (k - l)-tuples by к-tuples, Pacific J. Math.. 26 (1968) 131-140 [17. А].
[709] J. G. Kalbfleisch and R. G. Stanton. A combinatorial problem in matching, J. London Math. Soc.. 44 (1969 ) 60-64 [A],
[710] J. G. Kalbfleisch, R. G. Stanton and J. D. Horton. On covering sets and error-correcting codes, J. Combinat. Theory, 11A (1971) 233—250 [А].
[711] J. G. Kalbfleisch and P. H. Weiland, Some new results for the covering problem, in: W. T. Tutte, ed.. Recent Progress in Combinatorics, (Academic Press, New York, 1969) pp. 37-45 [А].
[712] H. J. L. Kamps and J. H. van Lint, The football pool problem for 5 matches, J. Comb. Theory. 3 (1967) 315-325 [7].
[713] H. J. L. Kamps and J. H. van Lint, A covering problem, Colloquia Math. Soc. Janos Bolyai, Vol. 4: Combinatorial Theory and its Applications, (Balatonfured, Hungary, 1969) pp. 679-685 [7].
[714] W. M. Kantor, Automorphism groups of Hadamard matrices, J. Comb. Theory, 6 (1969) 279-281 [16].
[715] M. Karlin, New binary coding results by circulants, IEEE Trans. Info. Theory, 15 (1969) 81-92 [ 16, А].
[716] M. Karlin, Decoding of circulant codes, IEEE Trans. Info. Theory, 16 (1970) 797-802 [16].
[717] M. Karlin, personal communication [16, А].
[718] M. Karlin and F. J. MacWilliams, On finding low weight vectors in quadratic residue codes for p = 8m - 1. SIAM J. Appl. Math., 25 (1973) 95-104 [16].
[719] S. Karlin and J. L. McGregor, The Hahn polynomials, formulas and an application, Scripta Math., 26 (1961) 33-46 [21].
[720] M. Kasahara, H. Nakonishi. Y. Tezuka and Y. Kasahara, Error correction of data using computers. Electron. Commun. Japan, 50 (1967) 637-642 [1].
[721] M. Kasahara, Y. Sugiyama, S. Hirasawa and T. Namekawa, A new class of binary codes constructed on the basis of BCH codes, IEEE Trans. Info. Theory, 21 (1975) 582-585 [18, A],
[722] M. Kasahara. Y. Sugiyama, S. Hirasawa and T. Namekawa, New Classes of Binary Codes constructed on the basis of concatenated codes and product codes, IEEE Trans. Info. Theory, 22 (1976), 462-468 (18, А].
[723] T. Kasarni, Optimum shortened cyclic codes for burst-error correction, IEEE Trans. Info. Theory; 9 (1963) 105-109 [10].
[724] T. Kasarni, Error-correcting and detecting codes. Electron. Commun. Japan, 46 (9) (1963) 90-102 [1].
[725] T. Kasarni, A decoding procedure for multiple-error-correcting cyclic codes, IEEE Trans. Info, theory, 10 (1964) 134-138 [9, 16].
[726] T. Kasarni, Some lower bounds on the minimum weight of cyclic codes of composite length, IEEE Trans. Info. Theory, 14 (1968) 814-818 [18].
[727] T. Kasarni, Weight distributions of Bose-Chaudhuri-Hocquenghem Codes, in: R. C. Bose and T. A. Dowling, eds.. Combinatorial Math, and its Applications, (Univ, of North: Carolina Press, Chapel Hill, NC, 1969) Ch. 20 [8,9, 15,21].
[728] T. Kasarni, An upper bound on kin for affine invariant codes with fixed d/n, IEEE Trans. Info. Theory, 15 (1969) 174-176 [7,9].
[729] T. Kasarni, The weight enumerators for several classes of subcodes of the 2nd order binary Reed-Muller codes, Info, and Control, 18 (1971) 369-394 [8, 15].
[730] T. Kasarni, A Gilbert-Varshamov bound for quasi-cyclic codes of rate 1/2, IEEE Trans.. Info. Theory, 20 (1974) 679 [16].
1731] T. Kasami, Construction and decomposition of cyclic codes of composite length, IEEE Trans. Info. Theory, 20 (1974) 680-683 [18].
[732] T. Kasami and S. Lin, On majority-logic decoding for duals of primitive polynomial codes, IEEE Trans. Info. Theory, 17 (1971) 322-331 [13].
[733] T. Kasami and S. Lin, The construction of a class of majority-logic decodable codes, IEEE Trans. Info. Theory, 17 (1971) 600-610 [13, 18].
[734] T. Kasami and S. Lin, Some results on the minimum weight of BCH codes, IEEE Trans. Info. Theory, 18 (1972) 824-825 [9].
[735] T. Kasami and S. Lin, Coding for a multiple-access channel, IEEE Trans. Info. Theory, 22 (1976) 129-137 [1].
[736] T. Kasami, S. Lin and W. W. Peterson, Some results on weight distributions of BCH codes, IEEE Trans. Info. Theory, 12 (1966) 274 [11].
,[737] T. Kasami, S. Lin and W. W. Peterson, Linear codes which are invariant under the affine group and some results on minimum weights in BCH codes, Electron. Commun. Japan, 50 (No. 9, 1967), 100-106 [9].
[738] T. Kasami, S. Lin and W. W. Peterson, Some results on cyclic codes which are invariant under the affine group and their applications. Info, and Control. 11 (1968) 475-496 [8, 13].
.[739] T. Kasami, S. Lin and W. W. Peterson, Generalized Reed-Muller codes, Electron. Commun. Japan, 51-C(3) (1968) 96-104 [13].
[740] T. Kasami, S. Lin and W. W. Peterson, New generalizations of the Reed-Muller codes, Part I: Primitive codes, IEEE Trans. Info. Theory, 14 (1968) 189-199 [13].
{741] T. Kasami, S. Lin and W. W. Peterson, Polynomial codes, IEEE Trans. Info. Theory, 14 (1968) 807-814 and 16 (1970) 635 [13, А].
[742] T. Kasami, S. L?h and S. Yamamura, Further results on coding for a multiple-access channel, Trans, of Colloquium on Info. Theory, (Keszthely. August 25-29, 1975) [1].
[743] T. Kasami and S. Matora, Some efficient shortened cyclic codes for burst-error correction, IEEE Trans. Info. Theory, 10 (1964) 252 [10].
[744] T. Kasami and N. Tokura, Some remarks on BCH bounds and minimum weights of binary primitive BCH codes, IEEE Trans. Info. Theory, 15 (1969) 408-413 [9, А].
[745] T. Kasami and N. Tokura, On the weight structure of Reed-Muller codes, IEEE Trans. Info. Theory, 16 (1970) 752-759 [15].
[746] T. Kasami, N. Tokura and S. Azumi, On the Weight Enumeration of Weights Less than 2.5dof Reed-Muller codes, (Faculty of Engineering Science, Osaka University, Osaka, Japan, June 1974) [15].
[747] T. Katayama, Enumeration of linear dependence structures in the n-cube, Electron. Commun. Japan, 55-D(2) (1972) pp. 121-129 [5]. ,
[748] G. О. H. Katona, Combinatorial search problems, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory, (North-Holland, Amsterdam, 1973) pp. 285-308 [7].
[749] W. H. Kautz, Codes and coding circuitry for automatic error correction within digital systems, in: R. H. Wilcox and W. C. Mann, eds., Redundancy Techniques for Computing Systems, (Spartan Books, Washington, 1962) pp. 152-195 [16].
1750] W. H. Kautz, ed„ Linear sequential switching circuits: Selected papers. (Holden-Day, San Francisco, 1965) [3,14].
[751] W. H. Kautz, Fibonacci codes for synchronization control, IEEE Trans. Info. Theory, 11 (1965) 284-292 [1].
[[752] W. H. Kautz and B. Elspas, Single-error-correcting codes for constant-weight data words, IEEE Trans. Info. Theory, 11 (1965) 132-141 [17].
.[7 53] W. H. Kautz and K. N. Levitt. A Survey or progress in coding theory in the Soviet Union, IEEE Trans. Info. Theory, 15 (1969) 197-244 [1].
[754] D, Kelly and G.-C. Rota, Some problems in combinatorial geometry. Ch. 24 in: J. N. Srivastava et al., eds.. A Survey of Combinatorial Theory, (North-Holland, 1973) [17].
[755] J. G. Kemeny, H. Mirkil, J. L. Snell and G. L. Thompson, Finite Mathematical Structures, (Prentice-Hall, Englewood Cliffs, N.J., 1959) [13].
[756] M. G. Kendall and A. Stuart, The Advanced Theory of Statistics, Vol. 1, (Hafner, New York, 1969) [8,19].
[757] B. L. N. Kennett, A note on the finite Walsh transform, IEEE Trans. Info. Theory, 16 (1970) 489-491 [2].
[758] A. M. Kerdock, A class of I*v.-iate nonlinear codes, Info, and Control, 20 (1972) 182-187.. [15, А].
[759] A. M. Kerdock, F. J. MacWilliams and A. M. Odlyzko, A new theorem about- the Mattson-Solomon polynomial and some applications, IEEE Trans. Info, and Theory, 20j (1974) 85-89 [8].
[760] С. C. Kilgus, Pseudonoise code acquisition using majority logic decoding, IEEE Trans.. Comrnun., 21 (1973) 772-774 [14].
[761] С. C. Kilgus and W. C. Gore A class of cyclic unequal-error-protection codes, IEEE Trans. Info. Theory, 18 (1972) 687-690 [Intro.].
[762] Z. Kiyasu, Information Theory, Electron. Commun. Japan, 50(10) (1967) 109-117 [1].
[763] G. K. Kladov, Majority decoding of linear codes, Problems of Info. Trans., 8(3) (1972)' 194-198 [13].
[764] V. Klee, Long paths and circuits on polytopes, in: B. Griinbaum et al., eds., Complex Polytopes, (Wiley New York; 1967) Ch. 17 [Intro.].
[765] V. Klee, A method for constructing circuit codes, J. Assoc. Comput. Math., 14 (1967) 520-528 [Intro.].
[766] V. Klee, What is the maximum length of a d-dimensional snake? Amer. Math. Monthly, 77 (1970) 63-65 [Intro.].
[767] V. Klee, The use of circuit codes in analog-to-digita!_ conversion, in: B. Harris, ed., Graph Theory and its Applications, (Academic Press, New York, 1970) pp. 121-131 [Intro.].
[768] F. Klein, Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree, 2nd rev. ed., 1913. New York: Dover, 1956, 1st German ed., 1884 [19].
[769] T. J. Klein and J. K. Wolf, On the use of channel introduced redundancy for error correction, IEEE Trans, on Commun. Tech., 19 (1971) 396-402 [1].
[770] D. Knee and H. D. Goldman, Quasi-self-reciprocal polynomials and potentially large minimum distance BCH Codes, IEEE Trans. Info. Theory, 15 (1969) 118-121 [9].
[771] K. Knowlton, private communication [18].
[772] D. E. Knuth, The Art of Computer Programming, Vol. 1, Fundamental Algorithms* (Addison-Wesley, Reading, MA, 1969) [4, 11, 14].
[773] V. D. Kolesnik, Probabilistic decoding of majority codes, Problems of Info. Trans., 7(3) (1971) 193-200 [13].
[774] V. D. Kolesnik and E. T. Mironchikov, Cyclic Reed-Muller codes and their decoding, Problems of Info. Trans., 4 (1968) 15-19 [13].
[774a] A. N. Kolmogorov, Three approaches to the quantitative definition of information, Problems of Info. Trans., 1(1) (1965) 1-7 [Intro.].
[775] Y. Komamiya, Application of logical mathematics to information theory, Proc. 3rd Japan. Natl. Cong. Applied Math., (1953) 437 [I].
[776] T. H. Koornwinder, Homogeneous spaces, spherical functions and association schemes, unpublished notes, 1974 [21].
[777] V. I. Korzhik, The correlation between the properties of a binary group code and those of its null space, Problems of Info. Trans., 2(1) (1966) 70-74 [5].
[778] V. 1. Korzhik, An estimate of dmin for cyclic codes, Problems of Info. Trans., 2(2) (1966) 78 [7].
[779] V. N. Koshelev, On some properties of random group codes of great length, Problems of Info. Trans., 1(4) (1965) 35-38 [17].
[780] Y. I. Kotov, Correlation function of composite sequences constructed from two M-sequences, Radio Eng. Elect. Phys., 19 (1974) 128-130 [14].
[781] M. V. Kozlov, The correcting capacities of linear codes, Soviet Physics-Doklady, 14 (1969) 413-415 [17].
[782] M. Krawtchouk, Sur une generalisation des polynomes d’Hermite, Comptes Rendus, 189-(1929) 620-622 [5].
[783] M. Krawtchouk, Sur la distribution des racines des polynomes orthogonaux, Comptes Rendus, 196 (1933) 739-741 [5].
[784] R. E. Krichevskii, On the number of errors which can be corrected by the Reed-Muller code, Soviet Physics-Doklady, 15(3) (1970) 220-222 [13].
[785] J. B. Kruskal, Golay’s complementary series, IEEE Trans. Info. Theory, 7 (1961) 273-276-[14].
(786, V. S.'Kugurakov, Redundancy of linear codes with orthogonal and Л-connected checks, Problems of Info. Trans., 8(1) (1972) 25-32 [13].
[787] H. Kuroda, Note on error-control systems using product codes. Electron. Commun. Japan, 57-A(2) (1974) 22-28 [18].
[788] R. P. Kurshan, What is a cyclotomic polynomial? preprint [7,8].
[789] R. P. Kurshan and N. J. A. Sloane, Coset analysis of Reed-Muller codes via translates of finite vector spaces, Info, and Control, 20 (1972) 410-414 [14].
L
:[790] T. Y. Lam, The Algebraic Theory of Quadratic Forms, (Benjamin, Reading, MA, 1973) [1].
[791] H. J. Landau, How does a porcupine separate its quills?, IEEE Trans. Info. Theory, 17 (1971) 157-161 [Intro.].
[792] H. J. Landau and D. Slepian, On the optimality of the regular simplex code, Bell Syst. Tech. J., 45 (1966) 1247-1272 [I].
[793] S. Lang and A. Weil, Number of points of varieties in finite fields, Amer. J. Math., 76 (1954) 819-827 [9].
[794] V. S. Lapin, The problem of grouped errors on magnetic tape, Problems of Info. Trans., 4(1) (1968) 28-34 [1].
[795] B. A. Laws, Jr., A parallel BCH decoder, (Technical Report, Bozeman Electronics Research Lab, Montana State Univ., June 1970) [9].
[796] B. A. Laws, Jr. and С. K. Rushforth, A cellular-array multiplier for GF(2"’), IEEE Trans. Computers, C-20 (1971) 1573-1578 [3].
[797] R. J. Lechner, Affine Equivalence of Switching Functions, Ph.D. Thesis, Applied Mathematics, Harvard University, January 1963 = Report BL-33, “Theory of Switching” Computation Laboratory of Harvard University, December 1963 [I, 14].
[798] R. J. Lechner, A correspondence between equivalence classes of switching functions and group codes, IEEE Trans. Computers, 16 (1967) 621-624 [1, 14].
[799] R. J. Lechner, Harmonic analysis of switching functions, in: A. Mukhopadhyay, ed., Recent Developments in Switching Theory, (Academic Press, New York. 1971) pp. 121-228 [1.14].
[800] P. Lecointe, Generalisation de la notion de reseau geometriques et application a la construction de codes correcteurs, Comptes Rendus, (A) 265 (1967) 196-199 [181.
[801] C. Y. Lee, Some properties of non-binary error-correcting codes. IEEE Trans. Info. Theory, 4 (1958) 77-82 [5].
•[802] Y. L. Lee and M. C. Cheng, Cyclic mappings of product codes, IEEE Trans. Info. Theory. 21 (1975) 233-235 [18].
[803] J. Leech, Some sphere packings in higher space, Canad. J. Math.. 16 (1964) 657-682 [Intro., 2, 16]. 1
[804] J. Leech, Notes on sphere packings, Canad. J. Math., 19 (1967) 251-267 [Intro., 19,20].
[805] J. Leech, Five-dimensional nonlattice sphere packings, Canad. Math. Bull., 10 (1967) 387-393 [Intro., 19].
[806] J. Leech, A presentation of the Mathieu group Ml2, Canad. Math. Bull.. 12 (1969) 41-43 [20].
[807] J. Leech, Six and seven dimensional nonlattice sphere packings, Canad. Math. Bull., 12 (1969) 151-155 [Intro., 19].
[808] J. Leech and N. J. A. Sloane, New sphere packings in dimensions 9-15, Bull. Amer. Math. Soc., 76 (1970) 1006-1010 [Intro., 19].
[809] J. Leech and N. J. A. Sloane, New sphere packings in more than thirty-two dimensions, in: Proc. Second Chapel Hill Conference on Comb. Math, and Applic., (Chapel Hill, NC, 1970) pp. 345-355 [Intro., 19].
[810] J. Leech and N. J. A. Sloane, Sphere packings and error-correcting-codes, Canad. J. Math., 23 (1971) 718-745 [Intro., 2, 19,20].
[811] E. Lehmer, On the magnitude of the coefficients of the cyclotomic polynomials. Bull. Am. Math. Soc., 42 (1936) 389-392 [7].
[812] P. W. H. Lemmens and J. J. Seidel, Equiangular lines, J. Algebra, 24 (1973) 494-513 [21].
[813] A. Lempel, Analysis and synthesis of polynomials and sequences over GF(2), IEEE' Trans. Info. Theory, 17 (1971) 297-303 [8].
rgj4] A. Lempel, Matrix factorization over GF(2) and trace-orthogonal bases of GF(2n), SIAM J. Comput., 4 (1975) 175-186 [4].
[815] H. W. Lenstra, Jr., Two theorems on perfect codes. Discrete Math., 3 (1972) 125-132 [6].
[816] V. K. Leont’ev, A conjecture about Bose-Chaiidhuri codes, Problems of Infor. Trans., 4(1) (1968) 83-85 [9].
[817] V. K. Leont’ev, Error-detecting encoding, Problems of Info. Trans., 8(2) (1972) 86-92 [1].
[818] T. Lerner, Analysis of digital communications system using binary error correcting codes, IEEE Trans. Commun., 15 (1967) 17-22 [I].
[819] V. I. Levenshtein, The application of Hadamard matrices to a problem in coding, Problemy Kibemetiki, 5 (1961) 123-136. English translation in Problems of Cybernetics, 5 (1964) 166-184 [2, А].
[820] V. 1. Levenshtein. Binary codes capable of correcting spurious insertions and deletions of ones, Problems of Info. Trans., 1(1) (1965) 8-17 [I].
[821] V. I. Levenshtein, Binary codes capable of correcting deletions, insertions, and reversals,. Soviet Physics-Doklady, 10(8) (1966) 707-710 [1].
[822] V. I. Levenshtein, A method of constructing quasilinear codes providing synchronization in the presence of errors. Problems of Info. Trans., 7(3) (1971) 215-222 [1].
[823] V. 1. Levenshtein, Upper-bound estimates for fixed-weight codes, Problems of Info. Trans., 7(4) (1971) 281-287 [17].
[824] V. 1. Levenshtein, Minimum redundancy of binary error-correcting codes, Problems of Info. Trans., 10(2) (1974) 110-123; and Info, and Control, 28 (1975) 268-291 [17].
[825] W. J. LeVeque, Topics in Number Theory, 2 vols., (Addison-Wesley, Reading, MA., 1956) [2, 16].
[826] N. Levinson, Coding theory: a counterexample to G. H. Hardy’s conception of applied mathematics, Amer. Math. Monthly, 77 (1970) 249-258 [7].
[827] K. N. Levitt and W. H. Kautz, Cellular arrays for the parallel implementation of binary error-correcting codes, IEEE Trans. Info. Theory, 15 (1969) 597 -607 [3].
[828] K. N. Levitt and J. K. Wolf, A class of nonlinear error-correcting, codes based upon-interleaved two-level sequences, IEEE Trans. Info. Theory, 13 (1967) 335-336 [18].
[829] J. E. Levy, Self synchronizing codes derived from binary cyclic codes, IEEE Trans. Info. Theory, 12 (1966) 286-291 [1].
[830] J. E. Levy, A weight-distribution bound for linear codes, IEEE Trans. Info. Theory. 14 (1968) 487-490 [17].
[831] Shen Lin, personal communication [А].
[832] S. Lin, Some codes which are invariant under a transitive permutation group, and their connection with balanced incomplete block designs, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ, of North Carolina Press, Chapel Hill, NC, 1969) pp. 388-401 [8].
[833] S. Lin. On a class of cyclic codes, in: H. B. Mann, ed.. Error correcting codes, (Wiley, New York, 1969) pp. 131-148 [13].
[834] S. Lin, An Introduction to Error-Correcting Codes, (Prentice-Hall, Englewood Cliffs, N.J. 1970) [Intro.].
[835] S. Lin, Shortened finite geometry codes, IEEE Trans. Info. Theory, 18 (1972) 692-696 [13].
[836] S. Lin, On the number of information symbols in polynomial, codes, IEEE Trans. Info. Theory, 18 (1972) 785-794 [13].
[837] S. Lin, Multifold euclidean geometry codes, IEEE Trans. Info. Theory, 19 (1973) 537-548 [13].
[838] S. Lin and E. J. Weldon, Jr., Long BCH codes are bad, Info, and Control, 11 (1967) 445-451 [9].
[839] S. Lin and E. J. Weldon, Jr., Further results on cyclic product codes, IEEE Trans. Info. Theory, 16 (1970) 452-495 [9, 18].
1840] S. Lin and K.-P. Yiu, An improvement to multifold euclidean geometry codes, Info, and Control, 28 (1975) 221-265 [13].
[841] J. Lindner, Binary sequences up to length 40 with best possible autocorrelation function, Electronics Letters, 11 (1975) 507 [14].
[842] B. Lindstrom, On group and nongroup perfect codes in q symbols, Math. Scand., 25 (1969) 149-158 [6].
1843] В. Linstrom, Group partition and mixed perfect codes, Canad. Math. Bull., 18 (1975) 57-60 [6].
[844] K. Lindstrom, The nonexistence of unknown nearly perfect binary codes, Ann. Univ. Turku., Ser. A, No. 169, (1975), 3-28 [17].
[844a] K. Lindstrom, All nearly perfect codes are known, Info, and Control, to appear [15].
[844b] K. Lindstrom and M. Aaltonen, The nonexistence of nearly perfect nonbinary codes for 1 ==e==10, Ann. Univ. Turku, Ser. Al, to appear [15].
[845] J. H. van Lint, 1967-1969 Report of the Discrete Mathematics Group. Report 69-WSK-04 of the Technological University, Eindhoven, Netherlands (1969) [6].
[846] J. H. van Lint, On the nonexistence of perfect 2- and 3-Hamming-error-correcting codes over GF(q), Info, and Control, 16 (1970) 396-401 [6].
[847] J. H. van Lint, On the Nonexistence of Perfect 5-, 6-, and 7-Hamming-Error-Correcting Codes over GF(q), Report 70-WSK-06 of the Technological University, Eindhoven, Netherlands, 1970 [6].
[848] J. H. van Lint, Coding Theory, (Springer, New York, 1971) [many references],
[849] J. H. van Lint, On the nonexistence of certain perfect codes, in: A. O. L. Atkin and B. J. Birch, eds., Computers in Number Theory, (Academic Press, New York, 1971) pp. 227-282 [6].
[850] J. H. van Lint, Nonexistence theorems for perfect error-correcting-codes, in: Computers in Algebra and Number Theory, Vol. IV, (SIAM-AMS Proceedings, 1971) [6].
[851] J. H. van Lint, A new description of the Nadler code, IEEE Trans. Info. Theory, 18 (1972) 825-826 [2].
[852] J. H. van Lint, A theorem on equidistant codes, Discrete Math., 6 (1973) 353-358 [1].
[853] J. H. van Lint, Combinatorial Theory Seminar Eindhoven University of Technology, Lecture Notes in Mathematics 382, (Springer, Berlin, 1974) [2].
[854] J. H. van Lint, Recent results on perfect codes and related topics, in: M. Hall, Jr. and J. H van Lint, eds., Combinatorics, (Reidel, Dordrecht, Holland, 1975) [6].
[855] J. H. van Lint, A survey of perfect codes, Rocky Mountain J. of Mathematics, 5 (1975) 199-224 [6,7].
[856] J. H. van Lint and J. J. Seidel, Equilateral point sets in elliptic geometry, Kon. Ned. Akad. Wetensch. Proc. A 69 (= Indag. Math. 28) (1966) 335-348 [2,21].
[857] D. E. Littlewood, A University Algebra, 2nd ed, (Dover, New York, 1970) [19].
[858] C. L. Liu, B. G. Ong and G. R. Ruth, A construction scheme for linear and nonlinear codes, Discrete Math., 4 (1973) 171-184 [2].
[859] S. P. Lloyd, Binary block coding. Bell Syst. Tech. J., 36 (1957) 517-535 [6].
[859a] S. J. Lomonaco, Jr., private communication [А].
[860] R. J. Longobardi, L. D. Rudolph and C. R. P. Hartmann, On a basic problem in majority decoding, Abstracts of papers presented at IEEE International Symposium on Information Theory, October 1974, IEEE Press, N.Y., 1974 p. 15 [13].
[862] M. E. Lucas, Sur les congruences des nombres Euleriennes, et des coefficients differentials des functions trigonometriques, suivant un-module premier, Bull. Soc. Math. France, 6 (1878) 49-54 [13].
[863] V. Lum, Comments on “The weight structure of some Bose-Chaudhuri codes”, IEEE Trans. Info. Theory, 15 (1969) 618-619 [7].
[864] V. Lum and R. T. Chien, On the minimum distance of Bose-Chaudhuri-Hocquenghem codes, SIAM J. Appl. Math., 16 (1968) 1325-1337 [9].
[865] H. Liineburg, Uber die Gruppen von Mathieu, J. Algebra, 10 (1968) 194-210 [20].
[866] H. Liineburg, Transitive Erweiterungen endlicher Permutationsgruppen, Lecture Notes in Math. 84, Springer-Verlag, N.Y. 1969 [20].
[867] F. E. Lytle, Hamming type codes applied to learning machine determinations of molecular formulas, Analytical Chemistry, 44 (1972) 1867-1869 [7].
[868] J. E. MacDonald, Design methods for maximum minimum-distance error-correcting codes, IBM J. Res. Devel., 4 (1960) 43-57 [17].
[869] H. F. MacNeish, Four finite geometries, Amer. Math Monthly, 49 (1942) 15-23 [В].
[870] F. J. MacWilliams, Error correcting codes for multiple level transmission, Bell Syst. Tech. J., 40 (1961) 281-308.[8].
[871] F. J. MacWilliams, Combinatorial problems of elementary group theory, Ph.D. Thesis, Department of Math., Harvard University., May 1962 [5,6,8].
[872] F. J. MacWilliams, A theorem on the distribution of weights in a systematic code. Bell Syst. Tech. J., 42 (1963) 79-94 [5,6].
[873] F. J. MacWilliams, Permutation decoding of systematic codes. Bell Syst. Tech. J., 43 (1964) 485-505 [16].
[874] F. J. MacWilliams, The structure and properties of binary cyclic alphabets, Bell Syst. Tech. J., 44 (1965) 303-332 [8].
[875] F. J. MacWilliams, An example of two cyclically orthogonal sequences with maximum period, IEEE Trans. Info. Theory. 13 (1967) 338-339 [4].
[876] F. J. MacWilliams, Error-correcting codes-An Historical Survey, in: H. B. Mann, ed., Error-Correcting Codes, (Wiley New York, 1969) pp. 3-13 [1,2].
[877] F. J. MacWilliams. Codes and ideals in group algebras, in: R, C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ. North Carolina Press, Chapel Hill, 1969) Ch. 18 [18].
[878] F. J. MacWilliams, Orthogonal matrices over finite fields, Amer. Math. Monthly, 76 (1969) 152-164 [15; 16].
[879] F. J. MacWilliams, On binary cyclic codes which are also cyclic codes over GF(2’), SIAM J. Applied Math., 19 (1970) 75^95 [10].
[880] F. J. MacWilliams, Binary codes which .are ideals in the group algebra of an Abelian group. Bell Syst. Tech. J., 49 (1970) 987-1011 [18].
[881] F. J. MacWilliams, Orthogonal circulant matrices over finite fields, and how to find them, J. Comb. Theory, 10 (1971) 1-17 [16].
[882] F. J. MacWilliams, Cyclotomic numbers, coding theory, and orthogonal polynomials, Discrete Math., 3 (1972) 133-151 [8].
[883] F. J. MacWilliams, C. L. Mallows and N. J. A. Sloane, Generalization of Gleason’s theorem on weight enumerators of self-dual codes, IEEE Trans. Info. Theory, 18 (1972) 794-805 [5, 19].
[884] F. J. MacWilliams and H. B. Mann, On the p-rank of the design matrix of a difference set, Info, and Control. 12 (196.8) 474-488 [13].
[885] F. J. MacWilliams and N. J. A. Sloane, Pseudo-random sequences and arrays, Proc. IEEE 64 (1976) 1715-1729 [18].
[886] F. J. MacWilliams, N. J. A. Sloane and J.-M. Goethals, The MacWilliams identities for nonlinear codes. Bell Syst. Tech. J., 51 (1972) 803-819 [5].
[887] F. J. MacWilliams, N. J. A. Sloane and J. G. Thompson, Good self-dual codes exist, Discrete Math., 3 (1972) 153-162 [19].
[888] F. J. MacWilliams, N. J. A. Sloane and J. G- Thompson, On the existence of a projective plane of order 10, J. Comb. Theory, 14A (1973) 66-78 [19].
[889] G K. Maki and J. H. Tracey, Maximum-distance linear codes, IEEE Trans. Info. Theory, 17 (1971) 632 [17].
[890] V. K. Malhotra and R. D. Fisher, A double error-correction scheme for peripheral systems, IEEE Trans. Info. Theory, 25 (1.976) 105-114 [1].
[891] C. L. Mallows, A. M. Odlyzko and N. J. A. Sloane, Upper bounds for modular forms, lattices, and codes, J.. Algebra, 36 (1975) 68-76 [19].
[892] C. L. Mallows, V. Pless and N. J. A. Sloane, Self-dual codes over GF(3), SIAM J. Applied Math., 31 (1976) 649-666 [19,20].
[893] C. L. Mallows and .N. J. A. Sloane, An upper bound for self-dual codes, Info, and Control, 22 (1973) 188-200 [19].
[894] C. L.. Mallows and N. J. A. Sloane, On the invariants of a linear group of order 336, Proc. Camb. Phil. Soc., 74 (1973) 435-440 [19].
[895] C. L. Mallows and N. J. A. Sloane, Weight enumerators of self-orthogonal codes, Discrete Math., 9 (1974) 391-400 [5, 19].
{896] D. Mandelbaum, A method of coding for multiple errors, IEEE Trans. Info. Theorv, 14 (1968) 518-521 [9,10].
[897] D. Mandelbaum, Note on Tong’s burst-trapping technique, IEEE Trans. Info. Theory, 17 (1971) 358-360 [10].
[898] D. Mandelbaum, On decoding of Reed-Solomon codes, IEEE Trans. Info. Theory, 17 (1971) 707-712 [10].
[899] D. Mandelbaum, Some results in decoding of certain maximal-distance and BCH codes, Info, and Control, 20 (1972) 232-243 [9,10].
[900] D. M. Mandelbaum, Synchronization of codes by means of Kautz’s Fibonacci encoding, IEEE Trans. Info. Theory, 18 (1972) 281-285 [1].
[901] D. M. Mandelbaum, Unequal error-protection derived from difference sets, IEEE Trans. Info. Theory, 18 (1972) 686-687 [Intro.].
[902] D. M. Mandelbaum, On the derivation of Goppa codes, IEEE Trans. Info. Theory. 21 (1975) 110-111 [12]. *’
[903] D. M. Mandelbaum, A method for decoding of generalized Goppa codes, IEEE Trans. Info. Theory, 23 (1977) 137-140 [12].
[904] C. Maneri and R. Silverman, A vector-space packing problem, J. Algebra, 4 (1966) 321-330 [П].
[905] C. Maneri and R. Silverman, A combinatorial problem with applications to geometry, J. Comb. Theory, 11A (1971) 118-121 [11].
[906] H. B. Mann, On the number of information symbols in Bose-Chaudhuri codes, Info, and Control, 5 (1962) 153-162 [9].
[907] H. B. Mann, Addition Theorems, (Wiley, New York, 1965) [5,7].
[908] H. B. Mann, Recent advances in difference sets, Amer. Math. Monthly, 74 (1967) 229-235 [13].
[909] H. B. Mann, ed.; Error Correcting Codes, (Wiley, New York, 1969) [Intro.].
[910] H. B. Mann, On canonical bases for subgroups of an Abelian group, in: R. C. Bose and T_ H. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ, of North Carolina Press, Chapel Hill, NC, 1969) pp. 38-54 [4].
[911] D. E. Maracle and С. T. Wolverton, Generating cyclically permutable codes, IEEE Trans. Info. Theory, 20 (1974) 554-555 [17].
[912] A. S. Marchukov, Summation of the products of codes, Problems of Info. Trans., 4(2) (1968) 8-15 [18].
[913] A. B. Marcovitz, Sequential generation and decoding of the P-nary Hamming code, IEEE Trans. Info. Theory, 7 (1961)- 53-54 [7].
[914] M. Marcus, Basic Theorems in Matrix Theory. National Bureau of Standards Applied Math. Ser. No. 57, U.S. Department of Commerce, Washington, D.C., 1960 [2, 14].
[915] M. Marcus and H. Mine, A Survey of Matrix Theory and Matrix Inequalitities, (Allyn and Bacon, Boston) 1964 [21].
[916] M. A. Marguinaud, Application des algorithms rapides au decodage de codes polynomiaux, Journee d'Etudes Sur les Codes Correcteurs d’Erreurs, Paris, 10th March, 1971 [Intro.].
[917] R. W. Marsh, Table of Irreducible Polynomials over GF(2) Through Degree 19, Office of Technical Services, Dept, of Commerce, Washington D.C., October 24, 1957 [4].
[917a] P. Martin-Lof, The definition of random sequences, Info, and Control, 9 (1966) 602-619 [Intro.].
[918] J. L. Massey, Threshold decoding, (MIT Press, Cambridge, MA, 1963) [131
[919] J. L. Massey, Reversible codes. Info, and Control, 7 (1964) 369-380 [7].
[920] J. L. Massey, Step-by-step decoding of the Bose-Chaudhuri-Hocquenghem codes. IEEE Trans. Info. Theory, 11 (1965) 580-585 [9].
[921] J. L. Massey, Advances in threshold decoding, in: A. V. Balakrishnan, ed.. Advances in. Communication Systems, vol. 2, (Academic Press, N.Y., 1968) pp. 91-115 [13].
[922] J. L. Massey, Shift-register synthesis and BCH decoding. IEEE Trans. Info. Theory, 15 (1969) 122-127 [9,12].
[922a] J. L. Massey, Notes on Coding Theory, (Waltham Research Center, General Telephone and Electronics, Inc., Waltham, Mass., 1969) [Intro., 9].
[923] J. L. Massey, On the fractional weight of distinct binary n-tuples, IEEE Trans. Info. Theory, 20 (1974) 131 [10].
[924] J. L. Massey, D. J. Costello and J. Justesen, Polynomial weights and code constructions,, IEEE Trans. Info. Theory, 19 (1973) 101-110 [13,18].
(925] E. Mathieu, Memoire sur 1’etude des fonctions de plusiers quantites, J. Math. p. et a., 6 (1861) 241-323 [20].
[926] E. Mathieu, Sur la fonction cinq fois transitive de 24 quantites, J. Math. p. et a., 18 (1873) 25-46 [20].
[927] H. F. Mattson, Jr. and E. F. Assmus, Jr., Research program to extend the theory of weight distribution and related problems for cyclic error-correcting codes. Report AFCRL-64-605, Air Force Cambridge Res. Labs., Bedford, Mass., July 1964 [16].
[928] H. F. Mattson, Jr. and G. Solomon, A new treatment of Bose-Chaudhuri codes, J. Soc. Indust. Appl. Math., 9 (1961) 654-669 [8].
[929] M. V. Matveeva, On the 3-error-correcting Bose-Chaudhuri codes over the field GF(3), Problems of Info. Trans., 4(1) (1968) 20-27 [9].
(930] M. V. Matveeva, On a solution of a cubic equation in a field of characteristic 3, Problems of Info. Trans., 4(4) (1968) 76-78 [9].
[931] E. A. Mayo, Efficient computer decoding of pseudorandom radar signal codes, IEEE Trans. Info. Theory, 18 (1972) 680-681 [14].
[932] L. E. Mazur. A class of polynomial codes. Problems of Info. Trans., 8(4) (1972) 351-533 [9].
[933] L. E. Mazur, Minimum code distance of a particular subcode class of Reed-Solomon codes. Problems of Info. Trans., 9(2) (1973) 169-171 [9, 11].
[934] L. E. Mazur, Codes correcting errors of large weight in the Lee metric. Problems of Info. Trans., 9(4) (1973) 277-281 [5].
[935] E. J. McCluskey, Introduction to the Theory of Switching Circuits, (McGraw-Hill, New York, 1965) [13].
[936] R. J. McEliece, Quadratic forms over finite fields and second-order Reed-Muller codes, JPL Space Programs Summary, 37-58-III (1969) 28-33 [15].
[937] R. J. McEliece, Factorization of polynomials over finite fields, Math. Comp., 23 (1969) 861-867 [9].
[938] R. J. McEliece, On the symmetry of good nonlinear codes, IEEE Trans. Info. Theory, 16 (1970) 609-611 [9].
[939] R. J. McEliece, On periodic sequences from GF(q), J. Comb. Theory, 10A (1971) 80-91 [15].
[940] R. J. McEliece, Weights modulo 8 in binary cyclic codes, JPL Technical Report 32-1526, XI, (Jet Propulsion Lab., Pasadena, Calif. Oct. 1972) pp. 86-88 [8].
[941] R. J. McEliece, Weight congruences for p-ary cyclic codes, Discrete Math.. 3 (1972) 177-192 [8,15].
[942] R. J. McEliece, A nonlinear, nonfield version of the MacWilliams identities, unpublished notes, 1972 [5].
[943] R. J. McEliece, Comment on “A class of codes for asymmetric channels and a problem from the additive theory of numbers”, IEEE Trans. Info. Theory, 19 (1973) 137 [1].
[944] R. J. McEliece, An application of linear programming to a problem in coding theory, unpublished notes, 1973 [17].
[945] R. J. McEliece, Irreducible cyclic codes and Gauss sums, in: M. Hall, Jr. and J. H. van Lint, eds., Combinatorics, (Reidel, Dordrecht, 1975) pp. 185-202 [8].
[946] R. J. McEliece, E. R. Rodemich, H. C. Rumsey, Jr. and L. R. Welch, unpublished tables, 1972, [А].
[947] R. J. McEliece, E. R. Rodemich, H. C. Rumsey, Jr. and L. R. Welch, New upper bounds on the rate of a code via the Delsarte-MacWilliams inequalities, IEEE Trans. Info. Theory, 23 (1977), to appear [17].
[948] R. J. McEliece and H. C. Rumsey, Jr., Sphere-Packing in the Hamming Metric, Bull. Amer. Math. Soc., 75 (1969) 32-34 [17].
[949] R. J. McEliece and H. C. Rumsey, Jr., Euler products, cyclotomy, and coding, J. Number Theory, 4 (1972) 302-311 [8].
[950] R. L. McFarland, A family of difference sets in non-cyclic groups, J. Comb. Theory, ISA (1973) 1-10 [14].
[951] P. Mecklenburg, W. K. Pehlert, Jr. and D. D. Sullivan, Correction of errors in multilevel Gray-coded data, IEEE Trans. Info. Theory, 19 (1973) 336-340 [Intro.].
[952] J. E. Meggitt, Error correcting codes for correcting bursts of errors, IBM J. Res. Devel., 4 , (I960) 329-334 [13].
1953] С. М. Melas, A cyclic code for double error correction, IBM J. Res. Devel., 4 (1960) 364-366 [7].
[954] A. M. Michelson, Computer implementation of decoders for several BCH codes, in: Proc, of Symp. on Computer Processing in Communications, (Polytech. Inst. Brooklyn, New York, 1969) pp. 401-413 [9].
[955] G. A. Miller, H. F. Blichfeldt and L. E. Dickson, Theory and Applications of Finite Groups, (Dover, New York, 1961) [19].
[956] W. H. Mills, Some complete cycles on the n-cube, Proc. Am. Math. Soc., 14 (1963) 640-643 [Intro.].
[957] W. H. Mills, On the covering of pairs by quadruples, J. Comb. Theory, 13A (1972) 55-78 and ISA (1973) 138-166 [А].
[958] W. H. Mills, Covering problems, in: Proc. 4,h S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnipeg 1973) pp. 23-52 [А].
[959] W. H. Mills, On the covering of triples by quadruples, in: Proc. 5‘h S-E Conf, on Combinatorics, Graph Theory and Computing, (Utilitas Math. Publ., Winnipeg, 1974) pp. 563-581 [А].
[960] W. H. Mills, Continued fractions and linear recurrences, Math. Comp., 29 (1975) 173-180 [12].
[961] W. H. Mills and N. Zierler, On a conjecture of Golomb, Pacific J. Math., 28 (1969) 635-640 [9].
[962] J. Milnor and D. Husemoller, Symmetric Bilinear Forms, (Springer, Berlin, 1973) [19].
[963] N. Mitani, On the transmission of numbers in a sequential computer, delivered at the National Convention of the Inst, of Elect. Engineers of Japan, (November, 1951) [13].
[964] M. E. Mitchell, Simple decoders and correlators for cyclic error-correcting codes, IEEE Trans. Info. Theory, 8 (1962) 284-292 [16].
[965] H. Miyakawa, H. Imai and I. Nakajima, Modified Preparata codes-optimum systematic nonlinear double-error-correcting codes, Electron. Commun. in Japan, 53A,(10) (1970) 25-32 [18].
[966] H. Miyakawa and T. Kaneko, Decoding algorithms for error-correcting codes by use of analog weights, Electron. Commun. Japan, 58A(1) (1975) 18-27 [16].
[967] H. Miyakawa and T. Moriya, Methods of construction of comma-free codes with fixed block sync patterns, Electron. Commun. Japan, 52A(5) (1969) 10-18 [Intro.].
[968] P. S. Moharir, Ternary Barker codes, Electronics Letters, 10 (1974) 460-461 [14].
[969] P. S. Moharir and A. Selvarajan, Optical Barker codes, Electronics Letters, 10 (1974) 154-155 [14].
[970] P. S. Moharir and A. Selvarajan, Systematic search for optical Barker codes with minimum length, Electronics Letters, 10 (1974) 245-246 [14].
[971] T. Molien, Uber die Invarianten der linear Substitutions-gruppe, Sitzungsber. Konig. Preuss. Akad. Wiss., (1897) 1152-1156 [19]. '
[972] A. M. Mood, On Hotelling’s weighing problem, Ann. Math. Stat., 17 (1946) 432-446 [2].
[973] S. Mossige, Table of irreducible polynomials over GF(2) of degrees 10 through 20, Math. Comp., 26 (1972) 1007-1009 [4].
[974] T. Muir, A Treatise on the Theory of Determinants, (revised by W. H. Metzler, Dover, New York, 1960) [7,12,16].
[975] D. E. Muller, Application of Boolean algebra to switching circuit design and to error detection, IEEE Trans. Computers, 3 (1954) 6-12 [13].
[976] D. Mumford, Geometric Invariant Theory, (Springer, N.Y. 1965) [19].
[977] B. R. N. Murthy, An efficient parity checking scheme for random and burst errors, IEEE Trans. Commun., 24 (1976) 249-254 [1].
[978] J. Mykkeltveit, A note on Kerdock codes, Technical Report 32-1526, Vol IX., June 15, 1972, pp. 82-83, Jet Propulsion Lab, Pasadena, Calif. [15].
[979] J. Mykkeltveit, C. Lam and R. J. McEliece, On the weight enumerators of quadratic residue codes, JPL Technical Report 32-1526, Vol. XII, pp. 161-166, Jet Propulsion Laboratory, Pasadena, Calif., 1974 [16].
[980] E. Myravaagnes, On maximum-weight codes, IEEE Trans. Info. Theory, 9 (1963) 289-290 [17].
[981] E. Myrvaagnes, The weight distribution of two cyclic codes of length 73, IEEE Trans. Info. Theory, 11 (1965) 316 [9].
N
[982] M. Nadler, A 32-point n = 12, d = 5 code, IEEE Trans. Info. Theory, 8 (1962) 58 [2].
[983] G. Nakamura, N. Ikeno and K. Naemura, Optimality of constant-weight codes. Electron. Commun. Japan, 55-A(7) (1972) 32-37 [17].
[984] K. Nakamura and Y. Iwadare, Data scramblers for multilevel pulse sequences, NEC Research and Development? (26) (July 1972) pp. 53-63 [14, 18].
[985] M. Nesenbergs, Comparison of the 3-out-of-7 ARQ with Bose-Chaudhuri-Hocquenghem coding systems, IEEE Trans. Comm., 11 (1963) 202-212 [9].
[986] P. G. Neumann, A note on cyclic permutation error-correcting codes, Info, and Control, 5 (1962) 72-86 [17]
[987] P. G. Neumann, On a class of cyclically permutable error-correcting codes, IEEE Trans Info. Theory, 10 (1964) 75-78 [17].
[988] P. M. Neumann, Transitive permutation groups of prime degree, in: Proc. Second. Internal Conf, on Theory of Croups, (Springer-Verlag, N.Y. 1975) pp. 520-535 [16,19].
[989] P. M. Neumann, Transitive permutation groups of prime degree (IV). Proc. London Math. Soc., 32 (1976) 52-62 [16, 19].
[990] S. W. Ng, On Rudolph’s majority-logic decoding algorithm, IEEE Trans. Info. Theory, 16 (1970) 651-652 [13].
[991] P. J. Nicholson, Algebraic theory of finite Fourier transforms, J. Computer and Syst. Sci., 5 (1971) 524-547 [14].
[992] H.-V. Niemeier, Definite Quadratische Formen der Dimension 24 und Diskriminante 1, J. Number Theory, 5 (1973) 142-178 [19].
[99.3 ] Y. Niho, On maximal comma-free codes, IEEE Trans. Info. Theory, 19 (1973) 580-581 [Intro.].
[994] H. Nili, Matrixschaltungen zur Codierung und Decodierung von Gruppen-Codes, Archiv fiir Elekt. Ubertragung, 18 (1964) 555-564 [16].
[995] I. Niven and H. S. Zuckerman, An Introduction to the Theory of Numbers, 2nd ed., (Wiley, New York, 1966) [10, 12].
[996] S. Niven, On the number of /с-tuples in maximal systems m(k, I, n,), in: R. K. Guy et al., eds., Combinatorial Structures and their Applications, (Gordon and Breach, New York, 1970) pp. 303-306 [17].
[997] E. Noether, Der Endlichkeitssatz der Invarianten endlicher Gruppen, Math Ann., 77 (1916) 89-9? [19].
[998] T. Nomura ,’md A. Fukuda, Linear recurring planes and two-dimensional cyclic codes, Electron. Commun. Japan, 54A(3) (19'71) 23-30 [18].
[999] T. Nomura, H. Miyakawa, H. Imai and A. Fukuda, A method of construction and some properties of planes having maximum area matrix, Electron. Commun. Japan, 54A(5) (1971) 18-25 [18].
[1000] T. Nomura, H. Miyakawa, H. Imai and A. Fukuda, Some properties of the у/3-plane and its extension to three-dimensional space, Electron. Commun. Japan, 54A(8) (1971) 27-34 [18].
[1001] T. Nomura, H. Miyakawa, H. Imai and A. Fukuda, A theory of two-dimensional linear recurring arrays, IEEE Trans. Info. Theory, 18 (1972) 775-785 [18].
[1002] A. W. Nordstrom and J. P. Robinson, An optimum nonlinear code. Info, and Control, 11 (1967) 613-616 [2, A],
[1003]
[1004]
[1005]
[1006]
О
S Sh Oganesyan, V. 1. Tairyan and V. G. Yagdzyan, Decomposition of cyclic codes into equal-weight classes, Problems of Control and Info. Theory, 3(2) (1974) 13-21 [8].
S. Sh. Oganesyan and V. G. Yagdzhyan, Weight spectra of certain classes of cyclic correcting codes. Problems of Info. Trans., 6(3) (1970) 21.3-218 [8].
S. Sh. Oganesyan and V. G. Yagdzhyan, Class of optimum cyclic codes with base p, Problems of Info. Tran., 8(2) (1972) 167-169 [8]. .
S Sh Oganesyan, V. G. Yagdzhyan and V. I. Tairyan. On a class of optimal cyclic codes, in: B. N Petrov and F. Csaki, eds., 2"’ International Symposium on Information Theory, Mkademiai Kiado, Budapest, 1973) pp. 219-224 [8].
[1007] M. Ogasawara, A necessary condition for the existence of regular and symmetrical PB1B designs of T„ type. Inst, of Stat. Mimeo. Ser. No. 418 (Univ, of North Carolina, Chapel Hill, NC, Feb. 1965) [21].
[1008] J. Ogawa, The theory of the association algebra and the relationship algebra of a partially balanced incomplete block design, Institute of Stat. Mimeo. Ser. No. 224 (Univ, of North Carolina, Chapel Hill, NC, April 1959) [21].
[1009] K. Ohno, H. Nakanishi and Y. Tezuka, A method for combining several codes and its application to data transmission. Technical Report of the Institute of Electronics and Communication Engineers of Japan, AL 73-56, Nov. 27, 1973 [18, А].
[1010] G. B. Olderogge, On some special correcting codes of matrix type. Radiotechniques, 18(7) (1963) 14-19 (See Denes and Keedwell [371, p. 356]) [18].
[1011] 1. B. Oldham, R. T. Chien and D. T. Tang, Error detection and correction in a photo-digital storage system, IBM J. Res. Devel., 12 (1968) 422-430 [1].
[1012] J. K. Omura, A probabilistic decoding algorithm for binary group codes (Abstract), IEEE Trans. Info. Theory. 16 (1970) p. 123 [16].
[1013] J. K. Omura, Iterative decoding of linear codes by a modulo-2 linear program, Discrete Math., 3 (1972) 193-208 [16].
[1014] A. Ong, A note on the nonbinary BCH code, IEEE Trans. Info. Theory, 15 (1969) 735-736 [9].
[1015] O. Ore, On a special class of polynomials. Trans. Amer. Math. Soc., 35 (1933) 559-584 36 (1934) 275 [4].
[1016] O. Ore, Contributions to the theory of finite fields, Trans. Amer. Math. Soc., 36 (1934) 243-274 [4].
[1017] R. Ottoson, Group codes for phase- and amplitude-modulated signals on a Gaussian channel, IEEE Trans. Info. Theory, 17 (1971) 315-321 [Intro.].
P
[1018] L. F. Paige, A note on the Mathieu groups, Canad. J. Math., 9 (1956) 15-18 [6,20].
[1019] R. E. A. C. Paley, On orthogonal matrices, J. Math, and Phys., 12 (1933) 311-320 [2].
[1020] J. W. di Paola, J. S. Wallis and W. D. Wallis, A list of (u, b, r, к.Л) designs for rs30, in: Proc. 4'h S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math., Winnipeg 1973) pp. 249-258 [2,17].
[1021] J. H. Park, Jr., Inductive proof of an important inequality, IEEE Trans. Info. Theory, 15 (1969) 618 [10].
[1022] Parke Mathematical Laboratories Staff, Annotated Bibliography on Error Correcting Codes, Report AFCRL-62-101, Parke Math. Labs., Carlisle, Mass., Dec. 1961 [Intro.].
[1023] E. T. Parker and P. J. Nikolai, A search for analogues of the Mathieu groups, Math. Comp., 12 (1968) 38-43 [16].
[ 1024] M. В. Pursley and D. V. Sarwate, Bounds on aperiodic crosscorrelation for binary sequences. Electronics Letters, 12 (1976) 304-305 [14].
[1025] R. H. Paschburg, Software implementation of error-correcting codes, Coordinated Science Lab, Report R-659, University of Illinois, Urbana, III., 1974 [13].
[1026] R. H. Paschburg, C. L. Chen and D. V. Sarwate, Comparison of various software coding systems, Abstracts of papers presented at IEEE Internat. Symposium on Info. Theory, October 1974, IEEE Press, N.Y. 1974 p. 80 [13].
[1027] A. M. Patel, Maximal group codes with specified minimum distance, IBM J. Res. Devel., 14 (1970) 434-443 [17]
[1028] A. M. Patel, Maximal q-nary linear codes with large minimum distance, IEEE Trans. Info. Theory, 21 (1975) 106-110 [17].
[1029] A. M. Patel and S. J. Hong, Optimal rectangular code for high density magnetic tapes, IBM J. Res. Devel., 18 (1974) 579-588 [1, 18].
[1030] N. J. Patterson, The algebraic decoding of Goppa codes, IEEE Trans. Info. Theory, 21 (1975) 203-207 [12].
[1031] N. J. Patterson, A 4-dimensional Kerdock set over GF(3), J. Comb. Theory, 20A (1976) 365-366 [15].
[1032] S. E. Payne, On maximizing det (ArA), Discrete Math., 10 (1974) 145-158 [2].
[1033] W. К. Pehlert, Jr., Design and evaluation of a generalized burst-trapping error control system, IEEE Trans, on Comm. Theory, 19 (1971) 863-868 [10].
[1034] R. L. Pele, Some remarks on the vector subspaces of a finite field, Acta Math. Acad. Sci. Hungar., 20 (1969) 237-240 [4].
[1035] O. Perron, Bemerkungen fiber die Verteilung der quadratischen Reste, Math. Zeit., 56 (1952) 122-130 [2, 16].
[1036] W. W. Peterson, Encoding and error-correction procedures for the Bose-Chaudhun codes, IEEE Trans. Info. Theory, 6 (1960) 459-470 [9].
[1036a] W. W. Peterson, Error-Correcting Codes, (MIT Press, Cambridge, MA, 1961) [Intro.].
[1037] W. W. Peterson, Bounds for error-correcting codes, IEEE Trans. Info. Theory, 8 (1962) 60 [17].
[1038] W. W. Peterson, On the weight structure and symmetry of BCH codes, J. Inst. Elec. Commun. Engrs. Japan, 50 (1967) 1183-1190 (in Japanese). For English version see Scientific Report AFCRL-65-515, Air Force Cambridge Research Labs., Bedford, Mass., July 1965 [8,9].
[1039] W. W. Peterson, Some new results on finite fields with applications to BCH codes, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ. North Carolina Press, Chapel Hill, NC, 1969) Ch. 19 [9].
[1040] W. W. Peterson and E. J. Weldon, Jr., Error-Correcting Codes, 2nd ed., (MIT Press, 1972) [many references].
[1041] G. H. Pettengill, Radar astronomy, in: M. I. Skolnik, ed., Radar Handbook, (McGraw-Hill, New York, 1970) [14].
[1042] P. G. Phillips, M. Harwit and N. J. A. Sloane, A new multiplexing spectrometer with large throughput, in: Proc. Aspen Internal. Conf. Fourier Spectroscopy, (Air Force Systems Command, 1970) pp. 441-444 [2].
[1043] H. R. Phinney, personal communication [А].
[1044] J. N. Pierce, Limit distribution of the minimum distance of random linear codes, IEEE Trans. Info. Theory, 13 (1967) 595-599 [17].
[1045] J. R. Pierce, Synchronizing digital networks, Bell Syst. Tech. J., 48 (1969) 615-636 [1].
[1046] W. H. Pierce, Linear-real codes and coders, Bell Syst. Tech. J., 47 (1968) 1065-1097 [16]. [1046a] M. S. Pinsker, On the complexity of decoding, Problems of Info. Trans., 1(1) (1965) 84-86 [Intro.].
[1047] P. Piret, Good block codes derived from cyclic codes, Electronics Letters, 10 (1974) 391-392 [18, А].
[1048] P. Piret. On a class of alternating cyclic convolutional codes, IEEE Trans. Info. Theory, 21 (1975) 64-69 [18].
[1049] P. Piret, Structure and constructions of cyclic convolutional codes, IEEE Trans. Info. Theory, 22 (1976) 147-155 [18].
[1050] P. Piret, Some optimal AMC codes, IEEE Trans. Info. Theory, 22 (1976) 247-248 [18].
[1051] V. Pless, Power moment identities on weight distributions in error correcting codes, Info, and Control, 6 (1963) 147-152 [5].
[1052] V. Pless, Weight Distribution of the Quadratic Residue (71; 35) Code, Air Force Cambridge Research Lab. Report 64-697 (1964) [16].
[1053] V. Pless, The number of isotropic subspaces in a finite geometry, Rend. Cl. Scienze fisiche, matematiche e naturali, Accad. Naz. Lincei, 39 (1965) 418-421 [19].
[1054] V. Pless, On the uniqueness of the Golay codes, J. Comb. Theory, 5 (1968) 215-228 [19,20].
[1055] V. Pless, On a new family of symmetry codes and related new five-designs, Bull. Am. Math. Soc., 75 (1969) 1339-1342 [16].
[1056] V. Pless, The weight of the symmetry code for p = 29 and the 5-designs contained therein, Annals N.Y. Acad. Sci., 175 (Article 1) (1970) 310-313 [16].
[1057] V. Pless, Symmetry codes over GF(3) and new five-designs, J. Comb. Theory, 12 (1972) 119-142 [16].
[1058] V. Pless, A classification of self-orthogonal codes over GF(2), Discrete Math., 3 (1972) 209-246 [19].
[1059] V. Pless, Formulas and enumeration theorems in coding: origins and uses, Proc. 4th Manitoba Conf. Numerical Math., 1974 pp, 29-51 [19].
[1060] V. Pless, Symmetry codes and their invariant subcodes, J. Comb. Theory, 18 (1975) 116-125 [16]
[1061] V. Pless and J N. Pierce, Seif-dual codes over GF(q) satisfy a modified Varshamov bound. Info, and Control, 23 (1973) 35-40 [19].
[1062] V. Pless and N. J. A. Sloane, Binary seif-dual codes of length 24, Bull. Amer. Math. Soc., 80 (1974) 1173-1178 [19].
[1063] V. Pless and N. J. A. Sloane, On the classification and enumeration of self-dual codes, J. Combin. Theory, 18A (1975) 313-335 [19,20].
[1064] M. Plotkin, Binary codes with specified minimum distances, IEEE Trans. Info. Theory, 6 (1960) 445-450. (This paper had already appeared as a research report in 1951.) [2].
[1065] F. Polkinghorn, Jr., Decoding of double and triple error-correcting Bose-Chaudhuri codes, IEEE Trans. Info. Theory, 12 (1966) 480-481 [9].
[1066] G. Polya and G. L. Alexanderson, Gaussian binomial coefficients, Elemente der Ma-thematik, 26 (1971) 102-109 [15].
[1067] G. Polya and G. Szego, Aufgaben und Lehrsatze aus der Analysis, 2 vols., 2nd ed., (Springer, Berlin, 1964) [11].
[1068] E. C. Posner, Nonbinary codes and projective planes, JPL Calif. Inst. Tech., Space Programs Summary, 37-16-IV (Pasadena, California, August 1962) pp. 42-45 [11].
[1069] E. C. Posner, Simultaneous error-correction and burst-error detection using binary linear cyclic codes, SIAM J. Appl. Math., 13 (1965) 1087-1095 [10].
[1070] E. C. Posner, Properties of error-correcting codes at low signal-to-noise ratios, SIAM J. Appl. Math., 15 (1967) 775-798 [1].
[1071] E. C. Posner, Combinatorial structures in planetary reconnaissance, in: H. B. Mann, ed., Error Correcting Codes, (Wiley, New York, 1969) pp. 15-46 [1, 14].
[1072] K. A. Post, Nonexistence theorems on perfect Lee codes over large alphabets, Info, and Control, 29 (1975) 369-380 [6].
[1073] A. Potton, Implementing an error locating code. Electronics Letters, 5(6) (1969) 121-122 [1]
[1074] E. Prange, The following technical notes issued by Air Force Cambridge Research Labs, Bedford, Mass: Cyclic Error-Correcting Codes in Two Symbols, TN-57-103, (September, 1957) [7].
[1075] Some cyclic error-correcting codes with simple decoding algorithms, TN-58-I56, (April 1958) [7].
[1076] The use of coset equivalence in the analysis and decoding of group codes, TN-59-164, (1959) [7].
[1077] An algorism for factoring x" — 1 over a finite field, TN-59-175, (October 1959) [7,8].
[1078] E. Prange, The use of information sets in decoding cyclic codes, IEEE Trans. Info. Theory, 8(5) (1962) pp. S5-S9 [16].
[1079] W. K. Pratt, J. Kane, and H. C. Andrews, Hadamard transform image coding, Proc. IEEE, 57 (1969) 57-68 [2].
[1080] F. P. Preparata, Weight and distance structure of Nordstrom-Robinson quadratic code, Info, and Control, 12 (1968) 466-473; 13 (1968) 172 [15].
[1081] F. P. Preparata, A class of optimum nonlinear double-error correcting codes, Info, and Control, 13 (1968) 378-400 [15, А].
[1082] F. P. Preparata, A new look at the Golay (23, 12) code, IEEE Trans. Info. Theory, 16 (1970) 510-511 [15].
[1083] F. P. Preparata and J. Nievergelt, Difference-preserving codes, IEEE Trans. Info. Theory, 20 (1974) 643-649 [Intro.].
[1083a] G. Promhouse and S. E. Tavares, private communication [А].
R
[1084] А. О. H. Racsmany, Perfect single-Lee-error-correcting code, Studia Sclent. Math. Hung., 9 (1974) 73-75 [6].
[1085] D. Raghavarao, Constructions and Combinatorial Problems in Design of Experiments, (Wiley, New York, 1971) [2,5, 11, 13,21].
[1086] M. Rahman and I. F. Blake, Majority logic decoding using combinatorial designs, lEEc Trans. Info. Theory, 21 (1975) 585-587 [16].
[1087] S. J. Rallis, New and old results in invariant theory with applications to arithmetic groups, in: W. M. Boothby and G. L. Weiss, eds., Symmetric Spaces, (Dekker, New York, 1972) pp. 443-458 [19].
[1088] J. D. Ralphs, Limitations of error-detection coding at high error rates, Proc. [EE, 118 (1971) 409-416 [1].
[1089] R. A. Rankin, On the closest packing of spheres in n dimensions, Annals of Math., 48 (1947) 1062-1081 [17].
[1090] R. A. Rankin, The closest packing of. spherical caps in «-dimensions, Proc. Glasgow Math. Assoc., 2 (1955) 139-144 [17].
[1091] R: A. Rankin, On the minimal points of positive definite quadratic forms, Mathematika, 3 (1956) 15-24 {17].
[1092] C. R. Rao, Cyclical generation of linear subspaces in finite geometries, in: R. C. Bose and T. A. Dowling, eds.. Combinatorial Mathematics and [ts Applications, (Chapel Hill, NC, 1969) [13].
[1093] T. R. N. Rao, Error Coding for Arithmetic Processors, (Academic Press, New York, 1974) [1].
[1094] V. V. Rao and S. M. Reddy, A (48,31,8) linear code, IEEE Trans, [nfo. Theory, 19 (1973) 709-711 (18, А].
[1095] R. Rasala, Split codes and the Mathieu groups, J. Algebra, 42 (1976) 422-471 [20].
[1096] S. M. Reddy, A note on decoding of block codes, [EEE Trans, [nfo. Theory, 15 (1969) 627-628 [9].
[1097] S. M. Reddy, On decoding iterated codes, [EEE Trans, [nfo. Theory, 16 (1970) 624-627
[18] . '
[1098] S. M. Reddy, On block codes with specified maximum distance, [EEE Trans. Info. Theory, 18 (1972) 823-824 [17].
[1099] S. M. Reddy, Further results on decoders for q-ary output channels, IEEE Trans. Info. Theory, 20 (1974) 552-554 [18].
[1100] S. M. Reddy and J. P. Robinson, Random error and burst correction by iterated codes, IEEE Trans. Info. Theory, 18 (1972) 182-185 [18].
[1101] G. R. Redinbo, Generalized bandpass filters for decoding block codes, IEEE Trans. Info. Theory, 21 (1975) 417-422 [13].
[1102] G. R. Redinbo and J. R. Wolcott, Systematic construction of cyclically permutable code words, IEEE Trans. Commun., 23 (1975) 786-789 [Intro.].
[1103] G. R. Redinbo and G. A. Wolf, On minimum mean-square error linear block codes when the data have q-adic weighting, Info, and Control, 26 (1974) 154-177 [1].
[1104] I. S. Reed, A class of multiple-error-correcting codes and the decoding scheme, IEEE Trans. Info. Theory, 4 (1954) 38-49 [13].
[1105] 1. S. Reed, k,h order near-orthogonal codes, IEEE Trans. Info. Theory, 17 (1971) 116-117 [Ю].
[1106] I. S. Reed and G. Solomon, Polynomial codes over certain finite fields, J. SIAM, 8 (1960) 300-304 [10].
[1106a] 1. S. Reed and R. M. Stewart, Note on the existence of perfect maps, IEEE Trans. Info. Theory, 8 (1962) 10-12 [18].
[1107] I. S. Reed and С. T. Wolverton, The systematic selection of cyclically equivalent codes, IEEE Trans. Info. Theory, 18 (1972) 304-307 [10].
[1108] C. Reid, Hilbert, (Springer, New York, 1970) [19].
[1109] С. T. Retter, Decoding Goppa codes with a BCH decoder, IEEE Trans. Info. Theory, 21 > (1975) 112 (12]. • ’
[1110] С. T. Retter, Correcting burst and random errors with Goppa codes, IEEE Trans. Info. Theory. 22 (1976) 84 [12].
[1111] P. Ribenboim, Algebraic Numbers, (Wiley, New York, 1972) (2, 16].
[1112] J. R. Riek, Jr., C. R. P. Hartmann and L. D. Rudolph, Majority decoding of some classes of binary cyclic codes, IEEE Trans. Info. Theory, 20 (1974) 637-643 [13].
[1113] J. Riordan, An Introduction to Combinatorial Analysis, (Wiley, New York, 1958) [5].
[1114]'J. Riordan, Combinatorial Identities, (Wiley, New York, 1968) [1].
[1115] W. E. Robbins, Weighted-majority-logic decoding using nonorthogonal parity checks-an application, in: Proc. 12"' Allerton Conference on Circuit and System Theory, (Dept, of Elect. Engin., Univ. Illinois, Urbana, IL, 1974) pp. 567-573 [13].
[1116] P. D. Roberts and R. H. Davis, Statistical properties of smoothed maximal-length linear binary sequences. Proc. IEE, 113 (1966) 190-196 [14].
[1117] P. Robillard, Some results on the weight distribution of linear codes, IEEE Trans. Info. Theory, 15 (1969) 706-709 [8].
[1118] P. Robillard, Optimal codes, IEEE Trans. Info. Theory, 15 (1969) 734-735 [11].
[1119] J. P. Robinson, Analysis of Nordstrom’s optimum quadratic code, Proc. Hawaii Intern. Conf. System Sciences, (1968) pp. 157-161 [2].
(1120] E. Y. Rocher and R. L. Pickholtz, An analysis of the effectiveness of hybrid transmission schemes, IBM J. Res. Devel., 14 (1970) 426-433 [1].
[1121] W. F. Rogers, A practical class of polynomial codes, IBM J. Res. Devel., 10(1966) 158-161 [1].
[1122] B. Rokowska, Some new constructions of 4-tuple systems, Colloq. Math., 17 (1967) 111-121 [2,17].
[1123] J. E. Roos, An algebraic study of group and nongroup error-correcting codes, Info, 'and Control, 8 (1965) 195-214 [6].
(1124] J. Rosenstark, On a sequence of subcodes of the quadratic residue code for p — 8m + 1, SIAM J. Appl. Math., 28 (1975) 252-264 [16].
[1125] G.-C. Rota, Combinatorial theory and invariant theory. Lecture notes, Bowdoin College, Maine, Summer 1971 [19].
[1126] H. H. Roth, Linear binary shift register circuits utilizing a minimum number of mod-2 adders, IEEE Trans. Info. Theory, 11 (1965) 215-220 [4].
[1127] O. S. Rothaus, On “bent” functions, J. Comb. Theory, 20A (1976) 300-305 [14].
[1128] B. L. Rothschild and J. H. van Lint, Characterizing finite subspaces, J. Comb. Theory, 16A (1974) 97-110 [13].
[1129] B. Rudner, Construction of minimum-redundancy codes with an optimum synchronizing property, IEEE Trans. Info. Theory, 17 (1971) 478-487 [1].
[ИЗО] L. D. Rudolph, A class of majority-logic decodable codes, IEEE Trans. Info. Theory, 13 (1967) 305-307 [13].
[1131] L. D. Rudolph, Threshold decoding of cyclic codes, IEEE Trans. Info. Theory, 15 (1969) 414-418 [13].
[1132] L. D. Rudolph and C. R. P. Hartmann, Decoding by sequential code reduction. IEEE-Trans. Info. Theory, 19 (1973) 549-555 [13].
[1133] L. D. Rudolph and M. E. Mitchell, Implementation of decoders for cyclic codes, IEEE Trans. Info. Theory, 10 (1964) 259-260 [16].
[1134] L. D. Rudolph and W. E. Robbins, One-step weighted-majority decoding, IEEE Trans. Info. Theory, 18 (1972) 446-448 [13].
[1135] С. K. Rushforth, Fast Fourier-Hadamard deciding of orthogonal codes, Info, and Control, 15 (1969) 33-37 [14].
[1136] H. J. Ryser, Combinatorial Mathematics, Carus Monograph 14, Math. Assoc. America, 1963 [2].
S
[1137] R. A. Sack, Interpretation of Lagrange’s expansion and its generalization to several variables as integration formulas, J. SIAM, 13 (1965) 47-59 [19].
[1138] R. A. Sack, Generalization of Lagrange’s expansion for functions of several implicitly defined variables, J. SIAM, 13 (1965) 913-926 [19].
[1139] R. A. Sack, Factorization oi Lagrange’s expansion by means of exponential generating functions, J. SIAM, 14 (1966) 1-15 [19].
[1140] G. E. Sacks, Multiple error correction by means of parity checks, IEEE Trans. Info.-Theory, 4 (1958) 145-147 [1,17].
[1141] M. K. Sain, Minimal torsion spaces and the practical input/output problem. Info, and Control, 29 (1975) 103-124 [12].
[1142] C. Saltzer, Topological codes, in: H. B. Mann, ed., Error-Correcting Codes, (Wiley, New York, 1968) pp. 111-129 [18].
[1143] P. V. Sankar and E. V. Krishnamurthy, Error correction in nonbinary words, Proc. IEEE, , 61 (1973) 507-508 [7].
[1144] D. V. Sarwate, Weight Enumeration of Reed-Muller Codes and Cosets, Ph.D. Thesis, Dept, of Elec. Engin., Princeton, N.J, August 1973 [1,14, 15].
[1145] D. V. Sarwate, On the complexity of decoding Goppa codes, IEEE Trans. Info. Theory, 23 (1977), to appear. [Intro., 12].
[1147] N. Sauer, On the existence of regular n-graphs with given girth, J. Comb. Theory, 9 (1970) 144-147 [18].
[1148] J. E. Savage, Some simple self-synchronizing digital data scramblers, Bell Syst. Tech. J., 46 (1967) 449-487 [14].
[1149] J. E. Savage, The complexity of decoders: I-Classes of decoding rules, IEEE Trans. Info. Theory, 15 (1969) 689-695 [Intro.].
[1150] J. E. Savage, Three measures of decoder complexity, IBM J. Res. Devel., 14 (1970) 417-425 [Intro.].
[1151] J. E. Savage, A note on the performance ot concatenated codes, IEEE Trans. Info. Theory. 16 (1970) 512-513 [10].
[1151a] J. E. Savage, Coding efficiency and decoder complexity, JPL Space Programs Summary, 37-62-11 (1970) 73-75 [Intro.].
[1151b] J. E. Savage, The asymptotic complexity of the Green decoding procedure, JPL Space Programs Summary, 37-64-11 (1970) 29-32 [Intro.].
[1152] J. E. Savage, The complexity of decoders: II-Computational work and decoding time, IEEE Trans. Info. Theory, 17 (1971) 77-85 [Intro.].
[1152a] J. A. Savage, Computational work and time on finite machines, J. ACM, 19 (1972) 660-674 [Intro.].
[1153] J. P. M. Schalkwijk, A class of simple and optimal strategies for block coding on the binary symmetric channel with noiseless feedback. IEEE Trans. Info. Theory, 17 (1971) 283-287 [Intro.].
[1154] J. P. M. Schalkwijk and T. Kaiiath, A coding scheme for additive noise channels with feedback, IEEE Trans. Info. Theory, 12 (1966) 172-189 [Intro.].
[1155] J. P. M. Schalkwijk and K. A. Post. On the error probability for a class of binary recursive feedback strategies, IEEE Trans. Info. Theory, 19 (1973) 498-511 and 20 (1974) 284 [Intro.].
[1156] F. D. Schmandt, Coding need: A system’s concept, in: J. N. Srivastava et al., eds., A Survey of Combinatorial Theory, (North-Holland, Amsterdam, 1973) Ch. 32 [1].
[1157] K. S. Schneider and R. S. Orr, Aperiodic correlation constraints on large binary sequence sets, IEEE Trans. Info. Theory, 21 (1975) 79-84 [14].
[1158] J. Schonheim, On maximal systems of к-tuples. Stud. Sci. Math. Hungar.. 1 (1966) 363-368 [17].
[1159] J. Schonheim, On linear and nonlinear single-error-correcting q-nary perfect codes, Info, and Control, 12 (1968) 23-26 [6].
[1160] J. Schonheim, Semiiinear codes and some combinatorial applications of them. Info, and Control, 15 (1969) 61-66 [6].
[1161] J. Schonheim, On the number of mutually disjoint triples in Steiner systems and related maximal packing and minimal covering systems, in: W. T. Tutte, ed.. Recent Progress in Combinatorics, (Academic Press, New York, 1969) pp. 311-318 [17].
[1162] J. Schonheim, A new perfect single error-correcting group code. Mixed code, in: R. Guy et al., eds.. Combinatorial Structures and their Applications, (Gordon and Breach. New York, 1970) p. 385 [6].
[1163] R. A. Scholtz, Codes with synchronization capability, IEEE Trans. Info. Theory, 12 (1966) 135-142 [1].
[1164] R. A. Scholtz, Maximal and variable word-length comma-free codes, IEEE Trans. Info? Theory, 15 (1969) 300-306 [1].
[1165] R. A. Scholtz and R. M. Storwick, Block codes for statistical synchronization, IEEE Trans. Info. Theory, 16 (1970) 432-438 [1].
[1166] R. A. Scholtz and L. R. Welch, Mechanization of codes with bounded synchronization delays, IEEE Trans. Info. Theory, 16 (1970) 438-446 [1].
[П67] P. H. R. Scholefield, Shift registers generating maximum - length sequences, Electronic Technology, 37 (1960) 389-394 [14].
[1168] M. R. Schroeder, Sound diffusion by maximum - length sequences, J. Acoustical Soc. Amer., 57 (1975) 149-150 [18].
[1169] J. W. Schwartz, A note on asynchronous multiplexing, IEEE Trans. Info. Theory, 12 (1966) 396-397 [17].
(1170| В. Segre, Curve razionali normali e fc-archi negli spazi finiti, Ann. Mat. Рига Appl., 39 (1955) 357-379 (11].
[1171] B. Segre, Ovals in a finite projective plane, Canad. J. Math., 7 (1955) 414-416 (11].
11172] B. Segre, Le geometric di Galois, Annali di Mat., 48 (1959) 1-97 [11].
[1173] B. Segre, Lectures on Modem Geometry, (Edizioni Cremonese, Rome, 1961) [11,B],
[1174] G. Seguin, On the weight distribution of cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 358 [8].
[1175] J. J. Seidel, Strongly regular graphs, in: W. T. Tutte, ed., Recent Progress in Combinatorics, (Academic Press, New York, 1969) pp. 185-198 [2,21].
[1176] J. J. Seidel, A Survey of two-graphs, in: Colloq. Intemaz. Teorie Combinatoric, Atti dei Convegno Lincei 17, Tomo 1, Roma 1976, pp. 481-511 [2,21].
[1177] J. J. Seidel, Graphs and two-graphs, in: Proc. 5'b S-E Conf. Combinatorics, Graph Theory and Computing, (Utilitas Math. Winnipeg, 1974) pp. 125-143 (2,21].
[1178] E. S. Selmer, Linear recurrence relations over finite fields, (Dept, of Math., Univ, of Bergen, Norway, 1966) [14].
[1179] N. V. Semakov and V. A. Zinov’ev, Equidistant maximal q-ary codes and resolvable balanced incomplete block designs, Problems of Info. Trans., 4(2) (1968) 1-7 [2].
[1180] N. V. Semakov and V. A. Zinov’ev, Complete and quasi-complete balanced codes, Problems of Info. Trans., 5(2) (1969) 11-13 [2,6].
[1181] N. V. Semakov and V. A. Zinov’ev, Balanced codes and tactical configurations, Problems of Info. Trans., 5(3) (1969) 22-28 [2,6,15].
[1182] N. V. Semakov, V. A. Zinov’ev and G. V. Zaitsev, A class of maximum equidistant codes, Problems of Info. Trans., 5(2) (1969) 65-68 [2].
[1183] N. V. Semakov, V. A. Zinov’ev and G. V Zaitsev, Uniformly packed codes, Problems of Info. Trans., 7(1) (1971) 30-39 [15].
[1184] J. P. Serre, Cours d’arithmetique, (Presses Univ, de France, Paris, 1970, English translation published by Springer, Berlin, 1973) [19].
[1185] J. P. Serre, Representations Lineaires des Groupes Finis, 2nd ed., (Hermann, Paris, 1971) [19].
[1186] D. Shanks, Solved and Unsolved Problems in Number Theory, Vol. I, (Spartan Books, Washington, 1962) [16].
[1187] J. L. Shanks, Computation of the fast Walsh-Fourier transform, IEEE Trans. Computers, 18 (1969) 457-459 [2,14].
[1188] С. E. Shannon, A mathematical theory of communication, Bell Syst. Tech. J., 27 (1948) pp. 379-423 and 623-656. Reprinted in: С. E. Shannon and W. Weaver, eds., A Mathematical Theory of Communication, (Univ, of Illinois Press, Urbana, Illinois, 1963) [1].
[1189] С. E. Shannon, Communication in the presence of nbise, Proc. IEEE, 37 (1949) 10-21 [1].
[1190] С. E. Shannon, Communication theory of secrecy systems, Bell Syst. Tech. J., 28 (1949) 656-715 [1].
[1191] С. E. Shannon, Probability of error for optimal codes in a Gaussian channel, Bell Syst. Tech. J., 38 (1959) 611-656 [Intro.].
[1192] С. E. Shannon, R. G. Gallager and E. R. Berlekamp, Lower bounds to error probability for coding on discrete memoryless channels, Info, and Control, 10 (1967) 65-103 and 522-552 [17].
[1193] E. P. Shaughnessy, Codes with simple automorphism groups, Archiv der Math., 22 (1971) 459-466 [16].
[1194] E. P. Shaughnessy, Automorphism groups of the (I + 1, (/ + l)/2) extended QR codes for I and (1 — l)/2 prime, 5</<4079 Abstract 722-A5, Notices Am. Math. Soc., 22 (1975) A-348 [16].
[1195] E. P. Shaughnessy, Disjoint Steiner triple systems, Preprint [6].
[1196] G. C. Shephard and J. A. Todd, Finite unitary reflection groups, Canad. J. Math., 6 (1954) 274-304 [19].
[1197] J. Shimo, H. Nakanishi and Y. Tezuka, Word synchronization for data transmission using cyclic codes, Electron. Commun. Japan, 55-A(l) (1972) 17-24 [1].
[1198] S. G. S. Shiva, Certain group codes, Proc. IEEE, 55 (1967) 2162-2163 [18].
[T199] S. G. S. Shiva, Some results on binary codes with equidistant words, IEEE Trans. Info. Theory, 15 (1969) 328-329 [1].
[1200) S. G. S. Shiva and P. E. Allar , A ew useful etails about a known technique for factoring 1 +X2’ IEEE Trans. Info. Theory, 16 (1970) 234-235 [7].
[1201] S. G. S. Shiva and К. C. Fung, Permutation decoding of certain triple-error-correcting binary codes, IEEE Trans. Info. Theory, 18 (1972) 444-446 [16].
[1202] S. G. S. Shiva, К. C. Fung and H. S. Y. Tan, On permutation decoding of binary cyclic double-error-correcting codes of certain lengths, IEEE Trans. Info. Theory, 16 (1970) 641-643 [16].
[1203] G. S. S. Shiva and G. Seguin, Synchronizable error-correcting binary codes, IEEE Trans. Info. Theory, 16 (1970) 241-242 [1].
[1204] S. G. S. Shiva and C. L. Sheng, Multiple solid burst-error-correcting binary codes, IEEE Trans. Info. Theory, 15 (1969) 188-189 [10].
[1205] S. G. S. Shiva and S. E. Tavares, On binary majority-logic decodable codes, IEEE Trans. Info. Theory, 20 (1974) 131-133 [13].
[1206] S. S. Shrikhande, A note on minimum distance binary codes, Calcutta Statistical Assoc. Bull., (1962) 94-97 [18].
[1207] V. M. Sidel’nikov, Some к-valued pseudo-random sequences and nearly equidistant codes, Problems of Info. Trans., 5(1) (1969) 12-16 [14].
[1208] V. M. Sidel’nikov, Weight spectrum of binary Bose-Chaudhuri-Hocquenghem codes, Problems of Info. Trans., 7(1) (1971) 11-17 [9].
[1209] V. M. Sidel’nikov, On the densest packing of balls on the surface of an n-dimensional Euclidean sphere and the number of binary code vectors with a given code distance, Soviet Math. Doklady, 14 (1973) 1851-1855 [17].
[1210] V. M. Sidel’nikov, Upper bounds for the number of points of a binary code with a specified code distance, Problems of Info. Trans., 10(2) (1974) 124-131; and Info. Control, 28 (1975) 292-303 [17].
[1211] M. Simonnard, Linear Programming, (Prentice-Hall, Englewood Cliffs, N.J., 1966) [17].
[1212] G. J. Simmons, A constructive analysis of the aperiodic binary correlation function, IEEE Trans, on Info. Theory, 15 (1969) 340-345 [14].
[1213] J. Singer, A theorem in finite projective geometry, and some applications to number theory, Trans. Amer. Math. Soc., 43 (1938) 377-385 [13].
[1214] R. C. Singleton, Maximum distance q-nary codes, IEEE Trans. Info. Theory, 10 (1964) 116-118 [1,11].
[1215] R. C. Singleton, Generalized snake-in-the-box codes, IEEE Trans. Computers, 15 (1966) 596-602 [Intro.].
[1216] D. Singmaster, Notes on binomial congruences: I - A generalization of Lucas’ congruence, J. London Math. Soc., 8 (1974) 545-548 [13].
[1217] D. Slepian, A class of binary signaling alphabets, Bell Syst. Tech. J., 35 (1956) 203-234 Г1].
[1218] D. Slepian, A note on two binary signaling alphabets, IEEE Trans. Info. Theory, 2 (1956) 84-86 [1].
[1219] D. Slepian, Some further theory of group codes, Bell Syst. Tech. J., 39 (1960) 1219-1252 [1].
[1220] D. Slepian, Bounds on communication, Bell Syst. Tech. J., 42 (1963) 681-707 [1].
[1221] D. Slepian, Permutation modulation, Proc. IEEE, 53 (1965) 228-236 [Intro.].
[1222] D. Slepian, Group codes for the Gaussian channel, Bell Syst. Tech. J., 47 (1968) 575-602 [Intro.].
[1223] D. Slepian, On neighbor distances and symmetry in group codes, IEEE Trans. Info. Theory, 17 (1971) 630-632 [IntrQ.].
[1224] D. Slepian. ed.. Key Papers in The Development of Information Theory, (IEEE Press, New York, 1974) [Intro., 1].
[1225] N. J. A. Sloane, A survey of constructive coding theory, and a table of binary codes of highest known rate, Discrete Math., 3 (1972) 265-294 [1, А].
[1226] N. J. A. Sloane, Sphere packings constructed from BCH and Justesen codes, Ma-thematika, 19 (1972) 183-190 [Intro.].
[1227] N. J. A. Sloane, Is there a (72,36) d = 16 self-dual code? IEEE Trans. Info. Theory, 19 (1973) p. 251 [19].
[1227a] N. J. A. Sloane, A short course on error-correcting codes (Lectures given at International Centre for Mechanical Sciences, Udine, .1973), Springer-Veriag, N.Y. 1975 [Intro.].
[12281 N. J. A. Sloane. Weight enumerators of codes, in: M. Hall. Jr. and J. H. van Lint, eds.. Combinatorics. (Reidel Publishing Co., Dordrecht. Holland. 1975) pp. 115-142 [19].
[1229] N. J. A. Sloane. An introduction to association schemes and coding theory, in: R. A. Askev. ed.. Theory and Application of Special Functions, (Academic Press. New York, 1975) pp. 225-260 [21].
[1230] N.J. A. Sloane. A simple description of an error-correcting code for high density magnetic tape. Bell Syst. Tech. J.. 55 (1976) 157-165 [1. 18].
[1231] N. J. A. Sloane, Error-correcting codes and invariant theory: new applications of a nineteenth-century technique, Amer. Math. Monthly. 84 (1977 ) 82-107 [19].
[1232] N. J. A. Sloane and E. R. Berlekamp, Weight enumerator for second-order Reed-Muller codes. IEEE Trans. Info. Theory, 16 (1970) 745-751 [15].
[1233] N. J. A. Sloane and R. J. Dick, On the enumeration of cosets of first order Reed-Muller codes, IEEE Intern. Conf, on Commun., 7 (Montreal 1971) 36-2 to 36-6 [1, 14].
[1234] N J. A. Sloane, T. Fine and P. G. Phillips, New methods for grating spectrometers, Optical Spectra, 4 (1970) 50-53 [2, 18].
[1235] N. J. A. Sloane. T. Fine, P. G. Phillips and M. Harwit, Codes for multislit spectrometry, Applied Optics, (1969) 2103-2106 [2, 18].
[1236] N. J. A. Sloane and M. Harwit, Masks for Hadamard transform optics, and weighing designs. Applied Optics, 15 (1976) 107-114 [2,14. 18].
[1237] N. J. A. Sloane, S. M. Reddy and C. L. Chen, New binary codes, IEEE Trans. Info. Theory, 18 (1972) 503-510 [18, А].
[1238] N. J. A. Sloane and J. J. Seidel, A new family of nonlinear codes obtained from conference matrices, Annals N.Y. Acad. Sci., 175 (Article 1, 1970) 363-365 [2, A],
[1239] N. J. A. Sloane and D. S. Whitehead, A new family of single-error-correcting codes, IEEE Trans. Info. Theory, 16 (1970) 717-719 [2, А].
[1240] D. H. Smith, Bounding the diameter of a distance-transitive graph, J. Comb. Theory. 16B (1974) 139-144 [21].
[1241] D. H. Smith. Distance-transitive graphs, in Combinatorics, edited by T. P. McDonough and V. C. Mavron, London Math. Soc., Lecture Notes No. 13, Cambridge Llniv. Press, Cambridge, 1974, pp. 145-153 [21].
[1242] D. H. Smith. Distance-transitive graphs of valency four, J. London Math. Soc.. 8(2) (1974} 377-384 [21].
[1243] K. J. C. Smith, On the rank of incidence matrices in .finite geometries, Univ, of North Carolina. Institute of Statistics Mimeo Series No. 555, Chapel Hill N.C., 1967 [13].
[1244] K. J. C. Smith, Majority decodable codes derived from finite geometries, Univ. North Carolina, Institute of Statistics Mimeo Series No. 561, Chapel Hill, N.C., 1967 [13].
[1245] K. J. C. Smith, An application of incomplete block designs to the construction of error-correcting codes, Univ, of North Carolina, Institute of Statistics Mimeo Series No. 587, Chapel Hill. N.C., 1968 [13].
[1246] K. J. C. Smith, On the p-rank of the incidence matrix of points and hyperplanes in a finite projective geometry, J. Comb. Theory, 7 (1969) 122-129 [13].
[1247] S. L. Snover, The Uniqueness of the Nordstrom-Robinson and the Golay Binary Codes. Ph.D. Thesis, Dept, of Mathematics, Michigan State Univ., 1973 [2, 15,20].
[1248] G. Solomon, A note on a new class of codes. Info. Control, 4 (1961) 364-370 [16].
[1249] G. Solomon. A weight formula for group codes, IEEE Trans. Info. Theory, 8 (1962) S1-S4 [8].
[1250] G. Solomon, Self-synchronizing Reed-Solomon codes, IEEE Trans. Info. Theory, 14 (1968) 608-609 [10].
[1251] G. Solomon, Algebraic coding theory, in: A. V. Balakrishnan, ed., Communication Theory. (McGraw-Hill, New York, 1968) Ch. 6 [Intro.].
[1252] G. Solomon. The (7,5) R-S code over GF(2’) is a (21, 15) BCH code, IEEE Trans. Info. Theory, 15 (1969) 619-620 [10].
[1253] G. Solomon, Coding with character, in: R. C. Bose and T. H. Dowling, eds., Combinatorial Mathematics and its Applications, (Univ, of North Carolina Press, Chapel Hili, NC, 1970) pp. 405-415 [2].
[1254] G. Solomon, A note on alphabet codes and fields of computation, Info, and Control, 25 (1974) 395-398 [10].
11255] G. Solomon, Unified theory of block and convolutional codes, Preprint [16].
[1256] G. Solomon and R. J. McEliece, Weights of cyclic codes, J. Comb. Theory, 1 (1966) 459-475 (8, 15].
[1257] G. Solomon and J. J. Stiffler, Algebraically punctured cyclic codes, Info, and Control, 8 (1965) 170-179 [17].
[1258] R. Spann, A two-dimensional correlation property of pseudorandom maximal-length sequences, Proc. IEEE, 53 (1965) 2137 [18].
[1259] J. Spencer, Maximal consistent families of triples, J. Comb. Theory, 5 (1968) 1-8 [17].
[1260] W. Stahnke, Primitive binary polynomials. Math. Comp., 27 (1973) 977-980 [4].
[1261] R. Stanley, Moments of weight distributions, JPL Space Programs Summary, 37-40-IV (Pasadena, California, 1966) pp. 214-216 [5].
[1262] R. P. Stanley, Private communication [19].
[1263] R. P. Stanley and M. F. Yoder, A study of Varshamov codes for asymmetric channels, Report 32-1526, Vol. 14, pp. 117-123, Jet Propulsion Labs., Pasadena, Calif., 1973 [1].
[1264] R. G. Stanton, The Mathieu groups, Canad. J. Math., 3 (1951) 164-174 [20].
[1265] R. G. Stanton, Covering theorems in groups (or: how to win at football pools), in: W. T. Tutte, ed., Recent Progress in Combinatorics, (Academic Press, New York, 1969) pp. 21-36 [7,A],
[1266] R. G. Stanton and R. J. Collens, A computer system for research on the family classification of BIBDs, in: Colloq. Intemaz. Teorie Combinatorie, Atti del Convegni Lincei 17, Tomo 1, Roma 1976, pp. 133-169 [2,17].
[1267] R. G. Stanton, J. D. Horton and J. G. Kalbfleisch, Covering theorems for vectors with special reference to the case of four or five components, J. London Math. Soc., 2 (1969) 493-499 [7, А].
[1268] R. G. Stanton and J. G. Kalbfleisch. Covering problems for dichotomized matchings, Aequationes mathematicae, 1 (1968) 94-103 [А].
[1269] R. G. Stanton and J. G. Kalbfleisch, Intersection inequalities for the covering problem, SIAM J. Appl. Math., 17 (1969) 1311-1316 [А].
[1270] R. G. Stanton and J. G. Kalbfleisch, Coverings of pairs by к-sets, Annals N.Y. Acad. Sci., 175 (1970) 366-369 [17, А].
[1271] R. G. Stanton, J. G. Kalbfleisch and R. C. Mullin, Covering and packing designs, in: R. C. Bose et al., eds., Proc. Second Chapel Hill Conference on Comb. Math, and Applic., (Chapel Hill, NC, 1970) pp. 428-450 [А].
[1272] H. M. Stark, An Introduction to Number Theory, (Markham, Chicago, 1970) [12].
[1273] J. M. Stein and V. K. Bhargava, Equivalent rate 1/2 quasi-cyclic codes, IEEE Trans. Info. Theory, 21 (1975) 588-589 [16].
[1274] J. M. Stein and V. K. Bhargava, Two quaternary quadratic residue codes, Proc. IEEE, 63 (1975) 202 [16].
[1275] J. M. Stein, V. K. Bhargava and S. E. Tavares, Weight distribution of some “best” (3m, 2m) binary quasi-cyclic codes, IEEE Trans. Info. Theory, 21 (1975) 708-711 [8].
[1276] J. P. Stenbit, Table of generators for Bose-Chaudhuri codes, IEEE Trans. Info. Theory, 10 (1964) 390-391 [9].
[1277] R. F. Stevens and W. G. Bouricius, The heuristic generation of large error-correcting codes, IBM-JRgs. Memo.. (Yorktown Heights, New York, August 1, 1959) [2].
[1278] J. J. Stiffler, Ciomma-free error-correcting codes, IEEE Trans. Info. Theory, 11 (1965) 107-112 [1].
[1279] J. J. Stiffler, Rapid acquistion sequences, IEEE Traps. Info. Theory, 14 (1968) 221-225 [1].
[1280] J. J. Stiffler, Theory of Synchronous Communication, (Prentice-Hall, Englewood Cliffs, N.J., 1971) [1, 14].
[1281] L. R. Stirzaker and С. K. Yuen, A note on error-correction in nonbinary words, Proc. IEEE, 62 (1974) 1399-1400 [7].
[1282] J. J. Stone, Multiple-burst error-correction with the Chinese remainder theorem, J. SIAM, 11 (1963) 74-81 [10].
[1283] P. T. Strait, A lower bound for error-detecting and error-correcting codes, IEEE Trans. Info. Theory, 7 (1961) 114-118 [17].
[1284] M. Sugino, Y. lenaga, M. Tokura and T. Kasami, Weight distribution of (128,64) Reed-Muller code, IEEE Trans. Info. Theory, 17 (1971) 627-628 [15].
[1285] Y. Sugiyama and M. Kasahara, A class of asymptotically good algebraic codes bring second-order concatentation, Electron. Commun. in Japan, 57-A (2) (1974) 47-53 [10].
[1286] Y. Sugiyama and M. Kasahara, Personal communication [10].
[1287] Y. Sugiyama, M. Kasahara, S. Hirasawa and T. Namekawa, A modification of the constructive asymptotically good codes of Justesen for low rates, Info, and Control. 25 (1974) 341-350 [10],
[1288] Y. Sugiyama, M. Kasahara, S. Hirawawa and T. Namekawa, A method for solving key equation for decoding Goppa codes. Info, and Control, 27 (1975) 87-99 [12].
[1289] Y. Sugiyama, M. Kasahara, S. Hirasawa and T. Namekawa, Some efficient binary codes constructed using Srivastava codes, IEEE Trans. Info. Theory, 21 (1975) 581-582 [12, A], [1290] Y. Sugiyama, M. Kasahara, S. Hirasawa and T. Namekawa, An erasures-and-errors decoding algorithm for Goppa codes, IEEE Trans. Info. Theory, 22 (1976) 238-241 [12].
[1291] Y. Sugiyama, M. Kasahara, S. Hirawawa and T. Namekawa, Further results on Goppa codes and their applications to constructing efficient binary codes, IEEE Trans. Info. Theory, 22 (1976) 518-526 [12,18, А].
[1292] D. D. Sullivan, A fundamental inequality between the probabilities of binary subgroups and cosets, IEEE Trans. Info. Theory, 13 (1967) 91-95 [1].
[1293] D. D. Sullivan, A branching control circuit for Berlekamp’s BCH decoding algorithm IEEE Trans. Info. Theory, 18 (1972) 690-692 [9].
[1294] J. D. Swift, Quasi-Steiner systems, Accad. Nazionale dei Lincei. Rend. Cl. Sci. fis. mat. e nat., (8) 44 (1968) 41-44 [17].
[1295] J. D. Swift, On (k, [)-coverings and disjoint systems, pp. 223-228 of Proc. Symp. Pure Math., 19 Combinatorics, (Amer. Math. Soc., Providence 1971) [A],
[1296] J. J. Sylvester, Thoughts on inverse orthogonal matrices, simultaneous sign successions, and tesselated pavements in two or more colors, with applications to Newton’s rule, ornamental tile-work, and the theory of numbers, Phil. Mag., 34 (1867) 461-475 [2].
[1297] G. Szego. Orthogonal Polynomials, Colloquium Publications, Vol. 23; New York: Amer. Math. Soc., revised edition 1959, pp. 35-37 [5,17,21].
[1298] Z. Szwaja, On step-by-step decoding of the BCH binary codes, IEEE Trans. Info. Theory, 13 (1967) 350-351 [9].
T
[1298a] M. H. Tai, M. Harwit and N. J. A. Sloane, Errors in Hadamard spectroscopy or imaging caused by imperfect masks. Applied Optics, 14 (1975) 2678-2686 [14].
[1299] H. Tanaka and S. Kaneku, A fuzzy decoding procedure for error-correcting codes, Electron. Commun. Japan, 57-A (7) (1974) 26-31 [16].
[1300] H. Tanaka, M. Kasahara, Y. Tezuka and Y. Kasahara, Computation over Galois fields using shift registers. Info, and Control, 13 (1968) 75-84 [3].
[1301] H. Tanaka, M. Kasahara, Y. Tezuka and Y. Kasahara, An error-correction procedure for the binary Bose-Chaudhuri-Hocquenghem codes, Electron. Commun. Japan, 51-C (1968) 102-109 [9].
[1302] H. Tanaka and T. Kasai, Synchronization and substitution error-correcting codes for the Levenshtein metric, IEEE Trans. Info. Theory, 22 (1976) 156-162 [1].
[1303] H. Tanaka and F. Nishida, A construction of a polynomial code, Electron. Commun. Japan, 53-A (8) (1970) 24-31 [10].
[1304] H. Tanaka and F. Nishida, A decoding procedure for polynomial codes, Systems, Computers, Controls, 1(3) (1970) 58-59 [9].
[1305] H. Tanaka and F. Nishida, Burst-trapping codes constructed by connecting error-correcting block codes. Electron. Commun. Japan, 55-A (6) (1972) 17-23 [10].
[1306] D. T. Tang and R. T. Chien, Cyclic product codes and their implementation, Info, and Control, 9 (1966) 196-209 [18].
[1307] D. T. Tang and C. N. Liu, Distance-2 cyclic chaining of constant-weight codes, IEEE Trans. Computers, 22 (1973) 176-180 (Intro., 17].
[1308] R. M. Tanner, Contributions to the simplex code conjecture, Report 6151-8, Center for Systems Research, Stanford Univ., Dec. 1970 [1].
[1309] R. M. Tanner, Some content maximizing properties of the regular simplex, Рас. J. Math., 52 (1974) 611-616 [1].
[1310] G. L. Tauglikh, A polynomial weighted code correcting multiple group errors, Problems of Info. Trans., 8(2) (1972) 93-97 [10].
[1311] S. E. Tavares, V. K. Bhargava and S. G. S. Shiva, Some rate-p/(p + 1) quasi-cyclic codes, . IEEE Trans. Info. Theory, 20 (1974) 133-135 [16].
[1312] S. E. Tavares and M. Fukada, Matrix approach to synchronization recovery for binary cyclic code, IEEE Trans. Info. Theory, 15 (1969) 93-101 [1].
[1313] S. E. Tavares and M. Fukada, Further results on the synchronization of binary cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 238-241 [1].
[1314] S. E. Tavares and S. G. S. Shiva, Detecting and correcting multiple bursts for binary cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 643-644 [10].
[1315] Y. Tezuka and H. Nakanishi, Personal communication [18].
[1316] J. A. Thas, Normal rational curves and к-arcs in Galois spaces. Rendiconti di Matematica, 1 (1968) 331-334 [11].
[1317] J. A. Thas, Normal rational curves and (q + 2) - arcs in a Galois space S„.2g (q = 2h), Atti Accad. Naz. Lincei. Rend. Cl. Sc. Fis. Mat. Natur., (8) 47 (1969) 115-118 [11].
[1318] J. A. Thas, Connection between the Grassmannian Gkand the set of the к-arcs of the Galois space S„.q, Rendiconti di Matematica, 2 (1969) 121-134 [11].-
[1319] J. A. Thas, Two infinite classes of perfect codes in metrically regular graphs. Preprint [6].
[1320] R. Thoene and S. W. Golomb, Search for cyclic Hadamard matrices, JPL Space Programs Summary, 37-40-IV (1966) 207-208 [2].
[1320a] J. G. Thompson, Weighted averages associated to some codes, Scripta Math., 29 (1973) 449-452 [19].
[1321] A. Tietavainen, On the nonexistence of perfect 4-Hamming-error-correcting codes, Ann. Ac. Sci. Fennicae, Ser., A. I, No. 485, 1970 [6].
[1322] A. Tietavainen, On the nonexistence of perfect codes over finite fields, SIAM J. Appl. Math., 24 (1973) 88-96 [6].
[1323] A. Tietavainen, A short proof for the nonexistence of unknown perfect codes over GF(q), q > 2, Annales Acad. Scient. Fennicae, Ser. A, (1. Mathematica), No. 580, (Helsinki, 1974) pp. 1-6 [6].
[1324] A. Tietavainen and A. Perko, There are no unknown perfect binary codes, Ann. Univ. Turku, Ser. A, I 148 (1971) 3-10 [6]. r
[1325] H. C. A. van Tilborg, On weight in codes, Report 71-WSK-03, Department of Mathematics, Technological University of Eindhoven, Netherlands, December 1971 [15,16].
[1326] H. C. A. van Tilborg, Binary uniformly packed codes, Thesis, Tech. Univ. Eindhoven, 1976 [15].
[1327] H. C. A. van Tilborg, All binary, (n, e, r)-uniformly packed codes are known, Preprint [15].
[1328] J. A. Todd, A combinatorial problem, J. Math, and Phys., 12 (1933) 321-333 [2].
[1329] J. A. Todd, On representations of the Mathieu groups as collineation groups, J. London Math. Soc., 34 (1959) 406-416 [20].
[1330] J. A. Todd, A representation of the Mathieu group as a collineation group, Ann. Mat. Рига Appl., Ser. 4, 71 (1966) 199-238 [20].
[1331] N. Tokura, K. Taniguchi and T. Kasami, A search procedure for finding optimum group codes for the binary symmetric channel, IEEE Trans. Info. Theory, 13 (1967) 587-594 [18].
[1332] N. Tokura and T. Kasami, Shortened cyclic codes for multiple burst-error correction, Electron. Commun. Japan, 48(1) (1965) 77-84 [7].
[1333] S. Y. Tong, Synchronization recovery techniques for binary cyclic codes, Bell Syst. Tech. J., 45 (1966) 561-596 [1].
[1334] S. Y. Tong, Correction of synchronization errors with burst-error-correcting cyclic codes, IEEE Trans. Info. Theory, 15 (1969) 106-109 [1,10].
[1335] S. Y. Tong, Burst-trapping techniques for a compound channel, IEEE Trans. Info. Theory, 15 (1969) 710-715 [1,10].
[1336] S. Y. Tong, Performance of burst-trapping codes, Bell Syst. Tech. J., 49 (1970) 477-519 [1, 10].
[1337] R. L. Townsend and R. N. Watts, Effectiveness of error control in data communication over the switched telephone network, Bell Syst. Tech. J., 43 (1964) 2611-2638 [1].
[1338] R. L. Townsend and E. J. Weldon, Jr., Seif-orthogonal quasi-cyclic codes, IEEE Trans. Info. Theory, 13 (1967) 183-195 [16].
[1339] S. A. Tretter, Properties of PN2 sequences, IEEE Trans. Info. Theory, 20 (1974) 295-297
r [14].
[1340] K. Trondle, Die Verbesserung der Gerauschwelle pulscodemodulierter Signale durch-Anwendung fehlerkorrigierender Codes, Arch. Elektron Ubertr., 26 (1972) 207-212 [1].
[1341] S. H. Tsao, Generation of delayed replicas of maximal-length linear binary sequences, Proc. IEE, 111 (1964) 1803-1806 [14].
[1341] H. W. Turnbull, Theory of Equations, (Oliver and Boyd, Edinburgh, 1947) [8].
[1343] R. J. Turyn, The correlation function of a sequence of roots of 1. IEEE Trans. Info. Theory. 13 (1967) 524-525 [14],
[1344] R. J, Turyn, Sequences with small correlation, in: H. B. Mann. ed„ Error Correcting Codes, (Wiley, New York, 1969) pp. 195-228 [14].
[1345] R. J. Turyn, Complex Hadamard matrices, in: R. Guy et al., eds.. Combinatorial Structures and Their Applications, (Gordon and Breach, New York, 1970) pp. 435-437 [2].
[1346] R. J. Turyn, On C-matrices of arbitrary powers, Canad. J. Math., 23 (1971) 531-535 [2].
[1347] R. J, Turyn, Hadamard matrices, Baumert-Hall units, four-symbol sequences, pulse compression, and surface wave encodings, J. Comb. Theory, 16A (1974) 313-333 [2].
[1348] R. Turyn and J. Storer. On binary sequences, Proc. Amer. Math. Soc., 12 (1961) 394-399 [14].
[1349] С. C. Tseng and C. L. Liu, Complementary sets of sequences, IEEE Trans. Info. Theory, 18 (1972) 649-652 [14].
[1350] К. K. Tzeng and C. R. P. Hartmann, On the minimum distance of certain reversible cyclic codes, IEEE Trans. Info. Theory, 16 (1970) 644-646 [7].
[1351] К. K. Tzeng and C. R. P. Hartmann, Generalized BCH decoding. Preprint [9].
[1352] К. K. Tzeng, C. R. P. Hartmann and R. T. Chien. Some notes on iterative decoding. Proc. Ninth Allerton Conf, on Circuit and Systems Theory, October. 1971, pp. 689-695 [9].
[1353] К. K. Tzeng and C. Y. Yu, Characterization theorems for extending Goppa codes to cyclic codes, Preprint [12].
[1354] К. K. Tzeng and K. Zimmermann, On full power decoding of cyclic codes. Proc. Sixth Annual Princeton Conference on Info. Sci. and Syst., (Princeton. 1972) pp. 404-407 [16].
[1355] К. K. Tzeng arid К. P. Zimmermann, On extending Goppa codes to cyclic codes, IEEE Trans. Info. Theory, 21 (1975) 712-716 [12].
[1356| К. K. Tzeng and К. P. Zimmermann, Lagrange’s interpolation formula and generalized Goppa codes. Preprint [12].
u
[1357] J. D. Ullman, Decoding of cyclic codes using position invariant functions, IBM J. Res. Devel., 9 (1965) 233-240 [9].
[1358] J. D. Ullman, Near optimal, single synchronization error-correcting codes, IEEE Trans. Info. Theory, 12 (1966) 418-425 [1].
[1359] J. V. Uspensky and M. A. Heaslet, Elementary Number Theory, (McGraw-Hill, New York-1939) [2, 10,12].
V
[1360] S. Vajda, Patterns and Configurations in Finite Spaces, (Hafner, New York, 1967) [2].
[1361] S. Vajda, The Mathematics of Experimental Design, (Hafner, New York, 1967) [2].
[1362] R. R. Varshamov, Estimate of the number of signals in error correcting codes, Dokl. Akad. Nauk SSSR, 117 (1957) 739-741 [1].
[1363] R. R. Varshamov, Some features of linear codes that correct asymmetric errors. Soviet Physics-Doklady, 9(7) (1965) 538-540 [1].
[1364] R. R. Varshamov, On the theory of asymmetric codes, Soviet Physics-Doklady, 10(10) (1966) 901-903 [1].
[1365] R. R. Varshamov, A class of codes for asymmetric channels and a problem from the additive theory of numbers, IEEE Trans. Info. Theory, 19 (1973) 92-95 [1].
[1366] J. L. Vasil’ev, On nongroup close-packed codes (in Russian), Probl. Kibemet., 8 (1962) 337-339, translated in Probleme der Kybemetik, 8 (1965) 375-378 [2].
[1367] J. L. Vasil’ev, On the length of a cycle in an n-dimensional unit cube, Soviet Math. Doklady, 4 (1963) 160-163 [Intro.].
[1368] O. Veblen and J. W. Young, Projective Geometry, 2 vols., (Ginn and Co., Boston,. 1916-1917) [В].
[1369] G. Venturini, Construction of maximal linear binary codes with large distances, (in - Russian) Probl. Kibem., 16 (1966) 231-238 [17].
(137OJ D. Vere-Jones, Finite bivariate distributions and semi-groups of nonnegative matrices, Q. J. Math. Oxford, (2) 22 (1971) 247-270 [5].
[1371] I. M. Vinogradov, Elements of Number Theory, (Dover, New York, 1954) [16].
[1372] A. J. Viterbi, Error bounds for convolutional codes and an asymptotically optimum decoding algorithm, IEEE Trans. Info. Theory, 13 (1967) 260-269 [1].
[1373] A. J. Viterbi, Convolutional codes and their performance in communication systems, IEEE Trans. Commun. Theory, 19 (1971) 751-772 [1].
[1374] A. J. Viterbi, Information theory in the Sixties, IEEE Trans. Info. Theory, 19 (1973) 257-262 [1].
W
[1375] D/G. Wadbrook and D. J. Wollons, Implementation of 2-dimensional Walsh transforms for pattern recognition. Electronics Letters, 8 (1972) 134-136 [2].
[1376] B. L. van der Waerden, Modern Algebra. 3rd ed., 2 vols., (Ungar, New York, 1950) [3,4,8].
[1377] T. J. Wagner, A remark concerning the minimum distance of binary group codes, IEEE Trans. Info. Theory, 11 (1965) 458 [18].
[1378] T. J. Wagner, A search technique for quasi-perfect codes. Info, and Control, 9 (1966) 94-99 [18, А].
[1379] T. J. Wagner, A remark concerning the existence of binary quasi-perfect codes, IEEE Trans. Info. Theory. 12 (1966) 401 [18].
[1380] T. J. Wagner, Some additional quasi-perfect codes, Info, and Control, 10 (1967) 334 [18].
[1381] S. Wainberg, Error-erasure decoding of product codes, IEEE Trans. Info. Theory, 18 (1972) 821-823 [18].
[1382] S. Wainberg and J. K. Wolf, Burst decoding of binary block codes on Q-ary output channels, IEEE Trans. Info. Theory, 18 (1972) 684-686 [10].
[1384] S. Wainberg and J. K. Wolf, Algebraic decoding of block codes over a q-ary input, Q-ary output channel, Q > q, Info, and Control, 22 (1973) 232-247 [10].
[1385] J. S. Wallis, Families of codes from orthogonal (0, 1, —I)-matrices. Proc, of the Third Manitoba Conf, on Numerical Math., (Winnipeg, Man., 1973), pp. 419-426. (Utilitas Math., Winnipeg, Man., 1974) [18].
[1386] W. D. Wallis, A. P. Street and J. S. Wallis, Combinatorics: Room Squares. Sum-Free Sets, Hadamard Matrices, Lecture Notes in Mathematics 292, Springer, Berlin, 1972 [2].
[1387] H. N. Ward, Quadratic residue codes and sympletic groups, J. Algebra, 29 (1974) 150-171 [16].
[1388] H. N. Ward, A form for M„, J. Algebra, 37 (1975) 340-361 [20].
[1389] H. N. Ward, A restriction on the weight enumerator of a self-dual code, J. Comb. Theory, 21A (1976) 253-255 [19].
[1390] W. T. Warren and C. L. Chen, On efficient majority logic decodable codes, IEEE Trans. Info. Theory, 22 (1976) 737-745 [13].
[1391] N. Wax, On upper bounds for error detecting and error correcting codes of finite length, IEEE Trans. Info. Theory, 5 (1959) 168-174 [17].
[1392] G. D. Weathers, E. R. Graf and G. R. Wallace, The subsequence weight distribution of summed maximum length digital sequences, IEEE Trans. Commun., 22 (1974) 997-1004 [14].
[1393] J. H. M. Wedderburn, Lectures on Matrices, (Dover, New York, 1964) [21].
[1394] A. Weil, On some exponential sums, Proc. Nat. Acad. Sci. USA, 34 (1948) 204-207 [9].
[1395] S. B. Weinstein, In Galois fields, IEEE Trans. Info. Theory, 17 (1971) 220 [4].
[1396] E. Weiss, Generalized Reed-Muller codes, Info, and Control, 5 (1962) 213-222 [13].
[1397] E. Weiss, Linear codes of constant weight, J. SIAM Applied Math., 14 (1966) 106-111; 15 (1967) 229-230 [8].
[1398] L. R. Welch, Computation of finite Fourier series, JPL Space Programs Summary, 37-37-IV (1966) 295-297 [14].
[1399] L. R. Welch, R. J. McEliece and H. C. Rumsey, Jr., A low-rate improvement on the Elias bound, IEEE Trans. Info. Theory, 20 (1974) 676-678 [17].
[1400] E. J. Weldon, Jr., Difference set cyclic codes, Bell Syst. Tech. J., 45 (1966) 1045-1055 [13].
[1401] E. J. Weldon, Jr., New generalizations of the Reed-Muller codes, Part П: Nonprimitive codes, IEEE Trans. Info. Theory, 14 (1968) 199-205 and 521 [13].
[1402] E. J. Weldon, Jr., Euclidean geometry cyclic codes, in: R. C. Bose and T. A. Dowling, eds., Combinatorial Mathematics and Its Applications, (Univ, of North Carolina, Chapel Hill, NC, 1969) Ch. 23 [13].
[1403] E. J. Weldon, Jr., Some results on majority-logic decoding, in: H. B. Mann, ed., Error-Correcting Codes, (Wiley, New York, 1969) pp. 149-162 [13].
[1404] E. J. Weldon, Jr., Decoding binary block codes on q-ary output channels, IEEE Trans. Info. Theory, 17 (1971) 713-718 [16,18].
[1405] E. J. Weldon, Jr., Justesen’s construction - the low-rate case, IEEE Trans. Info. Theory, 19 (1973) 711-713 [10].
[1406] E. J. Weldon, Jr., Some results on the problem of constructing asymptotically good error-correcting codes, IEEE Trans. Info. Theory, 21 (1975) 412-417 [10].
[1407] L.-J. Weng, Decomposition of M-sequences and its applications, IEEE Trans. Info. Theory, 17 (1971) 457-463 [14,18].
[1408] L.-J. Weng and G. H. Sollman, Variable redundancy product codes, IEEE Trans. Commun., IS (1967) 835-838 [18].
[1409] H. Weyl, Invariants, Duke Math. J., 5 (1939) 489-502 [19].
[1410] H. Weyl, The Classical Groups, (Princeton University Press, Princeton, NJ, 1946) [19].
[1411] N. White, The critical problem and coding theory, JPL Space Programs Summary, 37-66-Ш (December 31, 1970), 36-42 [17].
[1412] T. A. Whitelaw, On the Mathieu group of degree twelve. Proc. Camb. Phil. Soc., 62 (1966) 351-364 [20].
[1413] A. L. Whiteman, Skew Hadamard matrices of Goethals-Seidel type, Discrete Math., 2 . (1972) 397-405 [2].
[1414] E. T. Whittaker and G. N. Watson, A Course of Modem Analysis, 4th ed., (Cambridge Univ. Press, 1963) [19].
[1415] H. Wielandt, Finite Permutation Groups, (Academic Press, New York, 1964) [20,21].
[1416] M. C. Willett, The minimum polynomial for a given solution of a linear recursion, Duke Math. J., 39 (1972) 101-104 [14].
[1417] M. C. Willett, The index of an m-sequence, SIAM J. Appl. Math., 25 (1973) 24-27 [14].
[1418] M. C. Willett, Cycle representatives for minimal cyclic codes, IEEE Trans. Info. Theory, 21 (1975) 716-718 [8].
[1419] K. S. Williams, Exponential sums over GF(2"), Рас. J. Math., 40 (1972) 511-519 [10].
[1420] R. M. Wilson, An existence theory for pairwise balanced designs, J. Comb. Theory, 13A (1972) 220-273 [2, 17].
[1421] R. M. Wilson, The necessary conditions for t-designs are sufficient for something, Utilitas Math., 4 (1973) 207-215 [2,17].
[1422] R. M. Wilson, An existence theory for pairwise balanced designs: III-Proof of the existence conjectures, J. Comb. Theory, 18A (1975) 71-79 [2,17].
[1423] E. Witt, Die 5-fach transitiven Gruppen von Mathieu, Abh. Math. Sem. Hamb., 12 (1938) 256-265 [2,17,20].
[1424] E. Witt, Uber Steinersche Systeme, Abh. Math. Sem. Hamb., 12 (1938) 265-275 [2,17,20].
[1425] J. K. Wolf, On codes derivable from the tensor product of check matrices, IEEE Trans. Info. Theory, 11 (1965) 281-284 [18].
[1426] J. K. Wolf, Decoding of Bose-Chaurhuri-Hocquenghem codes and Prony’s method for curve fitting, IEEE Trans. Info. Theory, 13 (1967) 608 [9].
[1427] J. K. Wolf, Adding two information symbols to certain nonbinary BCH codes and some applications, Bell Syst. Tech. J., 48 (1969) 2405-2424 [10].
[1428] J. K. Wolf, Nonbinary random error-correcting codes, IEEE Trans. Info. Theory, 16 (1970) 236-237 [9,18].
[1429] J.K. Wolf, A survey of coding theory 1967-1972, IEEE Trans. Info. Theory, 19 (1973) 381-389 [1].
[1430] J. K. Wolf and B. Elspas, Error-locating codes-a new concept in error control, IEEp Trans. Info. Theory, 9 (1963) 113-117 [18].
[1431] M. J. Wolfmann, Formes quadratiques et codes a deux poids, Comptes Rendus, (A) 281 (1975) 533-535 [15].
[1432] С. Т. Wolverton, Probability of decoding error for the (7,2) Reed-Solomon code, Proc. IEEE, 60 (1972) 918-919 [10].
[1433] J. M. Wozencraft and I. M. Jacobs, Principles of Communication Engineering, (Wiley, ' New York. 1965) [1].
1434] E. P. G. Wright, Error correction: Relative merits of different methods, Electrical Commun., 48 (1973) 134-145 [1].
1435] W. W. Wu, New convolutional codes-Part I, IEEE Trans. Commun., 23 (1975) 942-956 \ [И-
[1436] W. W. Wu, New convolutional codes-Part II, IEEE Trans. Commun., 24 (1976) 19-33 [1].
[1437] A. D. Wyner, Capabilities of bounded discrepancy decoding. Bell Syst. Tech. J., 54 (1965) 1061-1122 [1].
[1438] A. D. Wyner, Random packings and coverings of the unit n-sphere, Bell Syst. Tech. J., 46 (1967) 2111-2118 [1].
[1439] A. D. Wyner, On coding and information theory, SIAM Review, 11 (1969) 317-346 [I].
[1440] A. D. Wyner, Note on circuits and chains of spread к in the n-cube, IEEE Trans ( Computers, 20 (1971) 474 [Intro.].
X
[1441] F. Xu-Ning and D. Zong-Duo, Studies in finite geometries and the construction of incomplete block designs V, Acta Math. Sinica, 15 (1965) 664-652 [В].
Y
er
[1442] S. Yamamoto, Some aspects of the composition of relationship algebras of experimental designs, J. Sci. Hiroshima Univ., Ser. A-I, 28 (1964) 167-197 [21].
[1443] S. Yamamoto and Y. Fuji, Analysis of partially balanced incomplete block designs, J. Sci. Hiroshima Univ., Ser. A-I, 27 (1963) 119-135 [21].
[1444] S. Yamamoto, Y. Fujii and N. Hamada, Composition of some series of association algebras, J. Sci. Hiroshima Univ., Ser. A-I, 29 (1965) 181—215 [21].
[1445] С. H. Yang, A construction for maximal (+1, — l)-matrix of order 54. Bull. Amer. Math. Soc., 72 (1966) 293 [2].
[1446] S. S. Yau and Y.-C. Liu, On decoding of maximum-distance separable linear codes. IEEE Trans. Info. Theory, 17 (1971) 487-491 [10].
[1447] P.-W. Yip, S. G. S. Shiva and E. L. Cohen, Permutation-decodable binary cyclic codes, Electronics Letters, 10 (1974) 467-468 [16].
[1448] С. K. Yuen, The separability of Gray codes, IEEE Trans. Info. Theory, 20 (1974) 668 [Intro.].
[1449] С. K. Yuen, Comments on “Correction of errors in multilevel Gray coded data”. IEEE Trans. Info. Theory, 20 (1974) 283-284 [Intro.].
z
[1450] L. A. Zadeh, ed., Report on progress in information theory in the U.S.A. 1960-1963, IEEE Trans. Info. Theory, 9 (1963) 221-264 [1].
[1451] G. V. Zaitsev, V. A. Zinov’ev and N. V. Semakov, Interrelation of Preparata and Hamming codes and extension of Hamming codes to new double-error-correcting codes, in: B. N. Petrov and F. Csaki, eds., 2nd International Symposium on Information Theory, (Akademiai Kiado, Budapest, 1973) pp. 257-263 [15, 18].
[1452] S. K. Zaremba, A covering theorem for abelian groups, J. London Math. Soc.. 26 (1950) 70-71 [7].
[1453] S: K. Zaremba, Covering problems concerning abelian groups, J. London Math. Soc., 27 (1952) 242-246 [7].
[1454] O. Zariski and P. Samuel, Commutative Algebra, 2 Vols. (van Nostrand, Princeton, New Jersey, 1960) [4].
[1455] L. H. Zetterberg, Cyclic codes from irreducible polynomials for correction of multiple errors, IEEE Trans. Info. Theory, 8 f!90fe) 13-20 [7].
[1456] L. H. Zetterberg, A class of codes for polyphase signals on a bandlimited gaussian channel, IEEE Trans. Info. Theory, II (1965) 385-395 [Intro.]. ,
[1457] W. Zhe-Xian, Studies in finite geometries and the construction of incomplete block desighs I, Acta math. Sinica, 15 (1965) 354-361 [19, В]. i
[1458] W. Zhe-Xian, Studies in finite geometries and construction of incomplete block designs, II, Acta Math. Sinica, 15 (1965) 362-371 [21, В]. )
[1459] W. Zhe-Xian, Studies in finite geometry and the construction of incomplete block designs III, Acta Math. Sinica, 15 (1965) 533-544 [21, В].
[1460] W. Zhe-Xian, Studies in finite geometries and the construction of incomplete block designs VI, (In Chinese), Progress in Math., 8 (1965) 293-302 [В]. I
[1461] N. Zierler, Linear recurring sequences, J. Soc. Indust. Appl. Math., 7 (1959) 31-48 [14].
[1462] N. Zierler, On decoding linear error-correcting codes-I, IEEE Trans. Info. Theory, 6 (1960) 450-459 [16].
[1463] N. Zierler, On decoding linear error-correcting codes-II, in: C. Cherry, ed., Fourth London Symp. Info. Theory, (Butterworths, London, 1961) pp. 61-67 [16].
[1464] N. Zierler, A note on the mean square weight for group codes, Info, and Control, 5 (1962) 87-89 [5].
[1465] N. Zierler, Linear recurring sequences and error-correcting codes, in: H. B. Mann, ed., Error Correcting Codes, (Wiley, New York, 1969) pp. 47-59 [14].
[1466] N. Zierler, Primitive trinomials whose degree is a Mersenne exponent, Info, and Control, 15 (1969) 67-69 [4].
[1467] N. Zierler, On x" + x+ I over GF(2), Info, and Control, 16 (1970) 502-505 [4].
]1468] N. Zierler, On the MacWilliams identity, J. Comb. Theory, ISA (1973) 333-337 [5].
[1469] N. Zierler and J. Brillhart, On primitive trinomials (mod 2), Info, and Control, 13 (1968) 541-554; 14 (1969) 566-569 [4].
[1470] V. A. Zinov’ev, Generalized concatenated codes, Problemy Peredachi Informatsii, 12(1) (1976) 5-15 [18, А].
[1471] V. A. Zinov’ev and V. K. Leont’ev, On perfect codes, Problems of Info. Trans., 8(1) (1972) 17-24 [6].
[1472] V. A. Zinov’ev and V. K. Leont’ev, The nonexistence of perfect codes over Galois fields, Problems of Control and Info. Theory, 2(2) (1973) 123-132 [6].
[1473] Yu. S. Zlotnikov and I. Z. Kaiser, Computer simulation of decoding algorithms for error-correcting cyclical codes, Telecommun. Radio Eng., 26 (1972) 54-57 [16].
[1474] D. Zong-Duo and F. Xu-Ning, Studies in finite geometries and the construction of incomplete block design IV, Acta Math. Sinica, 15 (1965) 545-558 [В].
[1475] V. V. Zyablov, An estimate of the complexity of constructing binary linear cascade codes, Problems of Info. Trans., 7(1) (1971) 3-10 [10]. .
[1476] V. V. Zyablov, Optimization of concatenated decoding algorithms, Problems of Info. Trans., 9(1) (1973) 19-24 [10].
[1477] R. Mathon, Symmetric conference matrices of order pq’ + l, preprint [2].
[1478] F. J. MacWilliams, A. M. Odlyzko, N. J. A. Sloane, and H. N. Ward, Self-dual codes over GF(4), J. Comb. Theory, to appear [19].
СПИСОК ЛИТЕРАТУРЫ НА РУССКОМ ЯЗЫКЕ
4. Абрамсон Н. Кодирование и декодирование группы циклических кодов. -Проблемы передачи информации. 1970, т. 6, вып. 2, с. 73—81, [18].
6а*. Афанасьев В. Б. Быстрое кодирование и обнаружение ошибок кодом Рида Соломона.—В кн.: Третий международный симпозиум по теории информации. Тезисы докладов. Ч. II. М,—Таллин. 1973, с. 13—17, [12].
56. Бэр Р. Л-инейная алгебра и проективная геометрия: Пер. с англ./Под ред. Е. Г. Шульгейфера. М.: Иностр, лит., 1955.
76. Бассалыго Л. А. Новые верхние границы для кодов, исправляющих ошибки.— Проблемы передачи информации. 1965, вып. 4, с. 41—44, [17].
76а. Бассалыго Л. А. Обобщение теоремы Ллойда на случай произвольного алфавита.— Проблемы управления и теории информации. 1973, вып. 2, с. 133— 137, [6].
\77. Бассалыго Л, А. Необходимое условие существования совершенных ко-кдовв, метрике Ли.— Математические заметки. 1974, вып. 2, с. 313—320, [6].
78. Бассалыго Л. А., Зайцев Г. В., Зиновьев В. А. О равномерно упакованных кодах.— Проблемы передачи информации. 1974, вып. 1, с. 9—14, [15].
79. Бассалыго Л. А., Зиновьев В. А. Замечание о равномерно упакованных родах.— Проблемы передачи информации. 1977. вып. 3, с. 22—25, .[15].
94. Беккенбах Э., Беллман Р. Неравенства: Пер. с англ./Под ред. В. И. Лерина. М.: Мир, 1965.
102. Белов В. И., Логачев В. Н., Сандимиров В. П. Построение класса линейных двоичных кодов, достигающих границы Варшамова—Грайсмера.—Проблемы передачи информации. 1974, вып. 3, с. 36—44, [17, А].
I 135. Берман С. Д. К теории групповых кодов.— Кибернетика. 1967, вып. 1, с. 31—39, [18].
136. Берман С. Д. Полупростые циклические и абелевы коды II. — Кибернетика. 1967, вып. 3, с. 21—30, [18].
137. Берман С. Д., Юданина А. Б. Коды с обобщенным мажоритарным декодированием и сверточные коды. — Проблемы передачи информации. 1970, вып. 1, с. 6—19, [13].
164. Блох Э. Л. О методе декодирования для кодов Боуза—Чоудхури, исправляющих тройные ошибки. — Известия АН СССР. Техническая кибернетика. 1964, № 3, [9].
165. Блох Э. Л., Зяблов В. В. О существовании линейных двоичных каскадных кодов с оптимальными корректирующими свойствами. — Проблемы передачи информации. 1973, вып. 3, с. 3—10, [10].
166. Блох Э. Л., Зяблов В. В. Кодирование обобщенных каскадных кодов.— Проблемы передачи информации. 1974, вып. 3, с. 45—50, [10].
184. Боуз Р. К., Рой-Чоудхури Д. К. Об одном классе двоичных групповых кодов с исправлением ошибок. — В кн.: Кибернетический сборник. М.: 1961, вып. 2, с. 83—94, [7].
190. Бурбаки Н. Элементы .математики. Группы и алгёбры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли: Пер. с франц./ Под ред. А. А. Кириллова и А. И. Кострикина. М.: Мир, 1976, [19].
207. Брусиловский К. А. Аппаратурное моделирование псевдослучайных двоичных последовательностей. — Автоматика и телемеханика. 1975, вып. 5, с. 836— 845, [14].
321. Кэртис Ч., Райнер И. Теория представлений конечных групп и ассоциативных алгебр: Пер. с аигл./Под ред. С. Д. Бермана. М.: Наука, 1969, [8].
337. Давыдов А. А. Повышение надежности хранения информации с помощью программно реализуемых корректирующих кодов. — Автоматика и телемеханика. 1973, вып. 1, с. 7—12, [1].
338. Давыдов А. А., Тененгольц Г. М. Коды, исправляющие ошибки при обмене информацией между вычислительными машинами. — Известия АН СССР. Техническая кибернетика. 1971, вып. 4, с. 5—11, [1].
351. Дельсарт Ф. Четыре основных параметра кода и их комбинаторное значение. — В кн.: Кибернетический сборник. М., 1977, вып. 14, с. 46—77. [5, 6, 17].
352. Дельсарт Ф. Алгебраический подход к схемам отношений теории кодирования: Пер. с англ./Под ред. В. А. Зиновьева и И. И. Грушко. М.: Мир, 1976, [5, 6, 17, 21].
392а 4. Думер И. И. Замечания о кодах в тактических конфигурациях.— Математические заметки, в печати, [6].
3926 *.. Думер И. И., Зиновьев В. А. Некоторые новые максимальные коды над полем Галуа GK(4). — Проблемы передачи информации. 1978, вып. 3, с. 24—34, [19, 20].
392в 4. Думер И. И. Некоторые новые равномерно упакованные коды. — В кн : Труды МФТИ. Серия «Радиотехника и электроника». М.: МФТИ, 1976, с. 72—78, [15].
397. Дынькин В. А., Тененгольц Г. М. Об одном классе циклических кодов с мажоритарной схемой декодирования. — Проблемы передачи информации. 1969, вып. 1, с. 3—15, [13].
406. Элайес П. Безошибочное кодирование. — В кн.: Коды с обнаружением и исправлением ошибок. М., 1956, с. 59—71, [18].
415. Фано Р. Передана информации. Статистическая теория связи: Пер. cl англ./Под ред. Р. Л. Добрушина. М.: Мир, 1965, [10]. J
427. Феллер В. Введение в теорию вероятностей и ее приложения: Пер. с англ./Под. ред. Ю. В. Прохорова. М.: Мир, 1967, [9].
436. Форни Д. Каскадные коды: Пер. с англ./Под ред. С. И. Самойленко М.: Мир, 1970, [10, 11, 18].
462а*. Габидулин Э. М., Сидоренко В. Д. Об одной общей границе для объема кода. — Проблемы передачи информации. 1976, вып. 4, с. 31—35, [17].
464. Галлагер Р. Теория информации и надежная связь: Пер. с англ./Под ред. М. С. Линекера и Б. С. Цыбакова. М.: Советское радио, 1974, [17].
489. Геталс Дж. М. Циклические коды с локализацией ошибок. — В кн.: Некоторые вопросы теории кодирования. М.: 1970, с. 91—100, [18].
499. Геталс Дж. М. и Дельсарт П. Один класс циклических кодов с мажоритарным декодированием. — В кн.: Кибернетический сборник. Новая серия. М., вып. 6, 1969, [13].
536. Гоппа В. Д. Новый класс линейных корректирующих кодов.— Проблемы передачи информации. 1970, вып. 3, с. 24—30, [12, А].
537. Гоппа В. Д. Рациональное представление кодов и (L, £)-коды. — Проблемы передачи информации. 1971, вып. 3, с. 41—49, [12].
538. Гоппа В. Д. Некоторые коды, построенные на базе (A, g) -кодов. — Проблемы передачи информации. 1972, вып. 2, с. 107—109, [12, 18].
538а. Гоппа В. Д. На непроходимых кодах достигается пропускная способность ДСК. — Проблемы передачи информации. 1974, вып. 1, с. 111—112, [12].
539. Гоппа В. Д. Об исправлении произвольных шумов непроводимыми кодами.— Проблемы передачи информации. 1974, вып. 3, с. 118—119, [12].
540. Гоппа В. Д. Удлиненные двоичные (L, g)-KOgbi.— В кн.: Второй международный симпозиум по теории информации (тезисы докладов). М.—Ереван, 1971, с. 51—53, [12].
540а . Гоппа В. Д. О декодировании (L, g) -кодов. — ДАН СССР. 1975, т. 222, вып. 6, с. 1309—1310, [12].
550. Горенстейн Д., Питерсон В., Цирлер Н. Квазисовершенность кодов Боуза—Чоудхури с исправлением двух ошибок.— В кн.: Кибернетический сборник. М., 1963, вып. 6, с. 20—24, [9].
552. Горенстейн Д., Цирлер Н. Класс кодов .из р™ символов с исправлением ошибок. — В кн.: Кибернетический сборнцк. М., 1963, вып. 7, с. 80—89, [7].
553. Грехем Р. Л., Мак-Вильямс Дж. О числе информационных символов циклических кодов, задаваемых разностными множествами. — В кн.: Некоторые вопросы теории кодирования. М., 1970, с. 22—35, [13].
582. Холл М. Теория групп: Пер. с англ./Под ред. Л. А. Калужнина. М.: Иностр, лит., 1962, [В].
585. Холл М. Комбинаторный анализ. Пер. с англ./Под ред. К- А. Рыбникова. М., Наука, 1963, [2].
587. Холл М. Комбинаторика. Пер. с англ./Под ред. А. О. Гельфонда и В. Е. Тараканова. М.: Мир, 1970, [Введ. 2, 5, А, В].
592. Хэмминг Р. Коды с обнаружением и исправлением ошибок. М., 1956, с. 7—22, [1, А]. '
704. Юстесен. Класс конструктивных асимптотически хороших алгебраических кодов. — В кн.: Кибернетический сборник. Новая серия. М., 1973, вып. 10, с. 39—50, [10].
706а *. Кабатянский Г. А. О существовании хороших циклических почти линейных кодов над непростыми полями. — Проблемы передачи информации. 1977, вып. 3, с. 18—21, [16].
728. Касами Т. Верхняя граница для kin аффинно инвариантных кодов с фиксированным d/n.— В кн.: Кибернетический сборник. Новая серия. М., 1971, вып. 8, с. 5—11, [7, 9].
749. Кауц У. Коды с исправлением' ошибок и их реализация в цифровых системах — В кн : Методы введения избыточности для вычислительных систем. М., \1966, с. 179—229, [16].
756. Кендалл М. Дж., Стюарт А. Теория распределений, т. 1: Пер. с англ./ Под; ред. А. Н. Колмогорова. М.: Наука, 1966, [8, 19].
758. Кердок А. М. Класс нелинейных двоичных кодов с низкой скоростью передачи. — В кн.: Кибернетический сборник. Новая серия. М., 1973, вып. 10, с. 33—38, [15, А].
763. Кладов Г. К. Мажоритарное декодирование линейных кодов. — Проблемы передачи информации. 1972, вып. 3, с. 21—26, [13].
773. Колесник В. Д. Вероятностное декодирование мажоритарных кодов.— Проблемы передачи информации. 1971, вып. 3, с. 3—12, [13].
773а*. Колесник В. Д., Мирончиков Е. Т. Декодирование циклических кодов. М.: Связь, 1968, [13].
774. Колесник В. Д., Мирончиков Е. Т. Циклические коды Рида—Маллера и их декодирование. — Проблемы передачи информации. 1968, вып. 4, с. 20—25, [13].
774а . Колмогоров А. Н. Три подхода к определению понятия «количество информации». — Проблемы передачи информации. 1965, вып. 1, с. 3—11.
777. Коржик В. И. Взаимосвязь свойств двоичного группового кода и его нуль-пространства.— Проблемы передачи информации. 1966, вып. 4, с. 91—95, [5].
778. Коржик В. И. Оценка ймип для циклических кодов. — Проблемы передачи информации. 1966, вып. 2, с. 78, [7].
779. Кошелев В. Н. О некоторых свойствах случайных групповых кодов большой длины. — Проблемы передачи информации. 1965, вып. 4, с. 45—48, [17].
780. Котов Ю. И. Функция корреляции последовательности, построенной по двум М-последовательностям. — Радиотехника и электроника. 1974, № 19, с. 128—130, [14].
781. Козлов М. В. Корректирующая способность линейных кодов. — ДАН СССР. 1969, вып. 14, с. 413—415, [17].
784. Кричевский Р. Е. О числе ошибок, исправляемых кодом Рида—Маллера.—ДАН СССР. 1970, т. 191, вып. 3, с. 544—547, [13].
786. Кугураков В. С. Об избыточности линейных кодов с ортогональными и Х-связанными проверками. — Проблемы передачи информации. 1972, вып. 1, с. 36—44, [13].
789а *. Кузнецов А. В., Цыбаков Б. С. Кодирование в памяти с дефектными ячейками. — Проблемы передачи информации. 1974, вып. 2, с. 52—60, [1].
794. Лапин В. С. К вопросу автоматического исправления сгруппированных ошибок на магнитной ленте. — Проблемы передачи информации. 1968, вып. 1, с. 28—34, [1].
816. Леонтьев В. К. Об одной гипотезе о кодах Боуза—Чоудхури. — Проблемы передачи информации. 1968, вып. 1, с. 83—85, [9].
817. Леонтьев В. К. Кодирование с обнаружением ошибок. — Проблемы передачи информации. 1972, вып. 2, с. 6—14, [1].
819. Левенштейн В. И. Применение матриц Адамара к одной задаче кодирования.— Проблемы кибернетики. 1961, вып. 5, с. 123—136, [2, А].
820. Левенштейн В. И. Двоичные коды с исправлением выпадений и вставок символа 1. — Проблемы передачи информации. 1965, вып. I, с. 12—25, [1].
821. Левенштейн В. И. Двоичные коды с исправлением выпадений, вставок и замещений символов. — ДАН СССР, т. 163, вып. 4, с. 707—710, [1].
822. Левенштейн В. И. Об одном методе построения квазилинейных кодов, обеспечивающих синхронизацию при наличии, ошибок. — Проблемы передачи информации. 1971, вып. 3, с. 30—40, [1].
823. Левенштейн В. И. О верхних оценках для кодов с фиксированным весом векторов. — Проблемы передачи информации. 1971, вып. 4, с. 3—12, [17].
824. Левенштейн В. И. О минимальной избыточности двоичных кодов, исправляющих ошибки. — Проблемы передачи информации. 1974, вып. 2, с. 26—42, [17].
859. Ллойд С. П. Бинарное блочное кодирование. — В кн.: Кибернетический сборник. М„ 1960, вып. 1, с. 206—226, [6].
873. Мак-Вильямс Дж. Перестановочное декодирование систематических кодов. — В кн.: Кибернетический сборщик. Новая серия. М„ 1965, вып. 41, с. 35—57, [16].
874. Мак-Вильямс Дж. Структура и свойства бинарных циклических алфавитов.— В кн.: Кибернетический сборник. Новая серия. М., 1967, вып. 4, с. 7—42, [8].
906. Манн Г. Б. О числе информационных символов в кодах Боуза—Чоудхури.— В кн.: Кибернетический сборник. М., 1964, вып. 8, с. 33—41, [9].
918. Месси Дж. Пороговое декодирование: Пер. с англ./Под ред. Ю. Л. Сегаловича. М.: Мир, 1966, [13].
924. Месси Дж. Л., Кастелло Д. Дж., Юстесен И. Веса многочленов и кодовые конструкции. — В кн.: Кибернетический сборник. Новая серия. М., 1974, вып. 11, с. 24—47, [13, 18].
928. Мэттсон X., Соломон Г. Новая трактовка кодов Боуза—Чоудхури,— В ин.: Теория кодирования. М., 1964, с. 7—29, [8].
929. Матвеева М. В. Об исправлении тройных ошибок в кодах Боуза— Чоудхури над полем GF(3). — Проблемы передачи информации. 1968, вып. 1, с. 20—27, [9]. v
930. Матвеева М. В. О решении уравнений третьей степени в поле характеристики 3. — Проблемы передачи информации. 1968, вып. 4, с. 76—78, [9].
932. Мазур Л. Е. Об одном классе полиномиальных кодов. — Проблемы передачи информации. 1972, вып. 4, с. 99—101, [9].
933. Мазур Л. Е. О минимальном кодовом расстоянии одного класса подкодов кодов Рида—Соломона. — Проблемы передачи 'информации. 1973, вып. 2, с. 104—106, [9, 11].
934. Мазур Ji. Е. Коды, исправляющие ошибки большого веса в метрике Ли. — Проблемы передачи информации. 1973, вып. 4, с. 11—16, [5].
976. (Имеется русский перевод части книги в кн.: Дьедонне Ж., Керрол Дж., Мамфорд Д. Геометрическая теория инвариантов: Пер. с англ./Под ред. А. И. Паршина. М., 1974), [19].
986. Нейман П. Заметки о циклически перестановочных кодах, исправляющих ошибки. — В кн.: Теория кодирования. М., 1964, с. 65—82, [17].
1003. Оганесян С. Ш., Таирян В. И., Ягджян В. Г. Разбиение циклических кодов на равновесные классы. — Проблемы управления и теории информации. 1974, вып. 2, с. 117—125, [8].
1004. Оганесян С. Ш., Ягджян В. Г. Весовой спектр для некоторых классов корректирующих циклических кодов. — Проблемы передачи информации. 1970, вып. 3, с. 31—37, [8].
1005. Оганесян С. Ш., Ягджян В. Г. КЛасс оптимальных циклических кодов с основанием р. — Проблемы передачи информации. 1972, вып. 2, с. 109— Ш, [8].
1010. Ольдерогге Г. В. О некоторых специальных корректирующих кодах матричного типа. — Радиотехника. 1963, вып. 7, с. 14—19 (см. Денеш и Кидвелл [371, с. 356]), [18].
1036. Питерсон У. Кодирование и исправление ошибок для кодов Боуза— Чоудхури. — В кн.: Кибернетический сборник. М., 1963, вып. 6, с. 25—54, [9].
1036а . Питерсон У. Коды, исправляющие ошибки: Пер. с англ./Под ред. Р. Л. Добрушина М.: Мир, 1964.
1040. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ./ Под ред. Р. Л. Добрушина и С. И. Самойленко. М.: Мир, 1976, [много ссылок].
1044. Пирс Дж. Н. Предельное распределение для минимального расстояния в случайном линейном коде. — В кн.: Кибернетический сборник. Новая серия. М„ 1970, вып. 7, с. 5—17, [17].
1064. Плоткин М. Двоичные коды с заданным минимальным расстоянием.— В кн.: Кибернетический сборник. М., 1963, вып. 7, с. 60—73, [2].
1081. Препарата Ф. П. Класс оптимальных нелинейных кодов с исправлением двойных ошибок. — В кн.: Кибернетический сборник. Новая серия. М., 1970, вып. 7, с. 18—42, [15, А].
1104. Рид И. С. Класс кодов с исправлением нескольких ошибок и схема кодирования. — В кн.: Кибернетический сборник. М., 1960, вып. 1, с. 189—205,
1106. Рид И. С. и Соломон Г. Полиномиальные коды над некоторыми конечными полями. — В кн.: Кибернетический -сборник. М., 1963, вып. 7, с. 74—79, ЕЮ].
1113. Риордан Дж. Введение в комбинаторный анализ: Пер. с англ./Под ред. Л. Я- Куликова. М.: Иностр, лит., 1963, [5].
1136. Райзер Г. Дж. Комбинаторная математика: Пер. с англ./Под ред. К- А. Рыбникова. М.: Мир, 1966, [2].
1179. Семаков Н. В., Зиновьев В. А. Эквидистантные q-e коды с максимальным расстоянием и разрешимые уравновешенные неполные блок-схемы. —-Проблемы передачи информации. 1968, вып. 2, с. 3—10, [2].
1180. Семаков Н. В., Зиновьев В. А. Совершенные и квазисовершенные равновесные коды —Проблемы передачи информации. 1969, вып. 2, с. 14—18, [2, 6].
1181. Семаков Н. В., Зиновьев В. А. Равновесные коды и тактические конфигурации.— Проблемы передачи информации. 1969, вып. 3, с. 28—36, [2,6,15].
1182. Семаков Н. В., Зиновьев В. А., Зайцев Г. В. Класс максимальных эквидистантных кодов. — Проблемы передачи информации. 1969, вып. 2, с. 84— 87, [2].
1183. Семаков Н. В., Зиновьев В. А., Зайцев Г. В. Равномерно упакованные коды. — Проблемы передачи информации. 1971, вып. 1, с. 38—50, [15].
1183as. Семаков Н. В., Зиновьев В. А., Зайцев Г. В. О взаимосвязи кодов Хэмминга, Препараты и Голея и о расширениях кодов Хэмминга. — В кн.: Второй международный симпозиум по теории информации (тезисы докладов). М.—Ереван, 1971, с. 227—230, [18, А].
1184. Серр Ж. П. Курс арифметики: Пер. с фра(нц./Под ред. А. В. Малышева. М.: Мир, 1972, [19].
1185. Серр Ж. П. Линейные представления конечных групп: Пер. с франц./ Под ред. Ю. И. Манина. М.: (Мир, 1970, [19].
1188. Шеннон К. Е. Математическая теория связи. — В кн.: Работы по теории информации и кибернетике. М., 1963, с. 243—332, [1].
1189. Шеннон К. Е. Связь при наличии шума. — В кн.: Работы по теории информации и кибернетике. М., 1963, с. 433—460, [1].
1190. Шеннон К. Е. Теория связи в секретных системах. — В кн.: Работы по теории информации и кибернетике. М., 1963, с. 333-—402, [1].
1191. Шеннон К. Е. Вероятность ошибки для оптимальных кодов в гауссовском канале. — В кн.: Работы по теории информации и кибернетике. М., 1963, с. 540—586.
1192. Шеннон К. Е., Галлагер Р. Г., Берлекэмп Е. Р. Нижние границы вероятности ошибки для кодирования в дискретном канале без памяти — Зарубежная радиоэлектроника. 1968, вып. 2, 6, [Г7].
1207. Сидельников В. М. О некоторых /г-значных псевдослучайных последовательностях и кодах, -близких к эквидистантным. — Проблемы передачи информации. 1969, вып. I, с. 16—22, [14].
1208. Сидельников В. М. О спектре весов двоичных кодов Боуза—Чоудхури—Хоквннгема. — Проблемы передачи информации. 1971, вып. 1, с. 14—22, [9].
1209. Сидельников В. М. О плотнейшей упаковке шаров на поверхности n-мерной евклидовой сферы и числе векторов двоичного кода с заданным кодовым расстоянием. — ДАН СССР. 1973, т. 213, вып. 5, с. 1029—1032, [17].
1210. Сидельников В. М. Верхние оценки числа точек двоичного кода с заданным кодовым расстоянием. —Проблемы передачи информации. 1974, вып. 2, с. 43—51, [17].
1217. Слепян Д. Класс двоичных сигнальных алфавитов. — В кн.: Теория передачи сообщений. М., 1957, с. 82—113, [1].
1225. Слоэн Н. Дж. А. Обзор конструктивной теории кодирования и таблица двоичных кодов с наибольшими известными скоростями. — В кн.: Кибернетический сборник. Новая серия. М., 1973, вып. 10, с. 5—32, [1, А].
1248. Соломон Г. Заметка о новом классе кодов. — К кн.: Теория кодирования. М„ 1964, с. 30—39, [16].
1278. Стифлер Дж. Дж. Коды без запятой, исправляющие ошибки. — В кн.: Кибернетический сборник. Новая серия. М., 1968, вып. 5, с. 34—46, [1].
1280. Стифлер Дж. Дж. Теория синхронизации сообщений: Пер. с англ./ Под ред. Э. М. Габидулина. М.: Связь, 1976, [1, 14].
1297. Сегё Г. Ортогональные многочлены: Пер. с англ./Под ред. Я. Л. Ге-ронимуса. М.: Физматгиз, 1962, [5, 17, 21].
1310. Тауглих Г. Л. О полиномиальном весовом коде, исправляющем кратные групповые ошибки. — Проблемы передачи информации. 1972, вып. 2, с. 15—20, [10].
1333. Тонг С. Я- Методы синхронизации при передаче сообщений двоичными циклическими кодами. — В кн.: Некоторые вопросы теории кодирования. М., 1970, с. 101—141, [1].
1338. Таунсенд Р. Л., Велдон И. Дж. Собственно ортогональные квази-циклические коды. — В кн.: Некоторые вопросы теории кодирования. М., 1970, с. 36—67, [16].
1362. Варшамов Р. Р. Оценка числа сигналов в кодах с коррекцией ошибок.—ДАН СССР. 1957, т. 117, вып. 5, с. 739—741, [1].
1363. Варшамов Р. Р. О некоторых особенностях линейных кодов, корректирующих несимметрические ошибки. — ДАН СССР. 1964, т. 157, вып. 3, с. 546—548, [1].
1364. Варшамов Р. Р. К теории несимметрических кодов. — ДАН СССР. 1965, т. 164, вып. 4, с. 757—760, [1].
1366. Васильев Ю. Л. О негрупповых плотно упакованных кодах. — В кн.: Проблемы кибернетики. М., 1962, вып. 8, с. 337—339, [2].
1367. Васильев Ю. Л. О длине цикла в n-мерном единичном кубе. — ДАН СССР. 1963, т. 148, вып. 4, с. 753—756, [Введ.].
1369. Вентурини Дж. Построение максимальных линейных двоичных кодов в случае больший расстояний. — В кн.: Проблемы кибернетики. М., 1966, вып. 16. с. 231—238, [17].
1371. Виноградов И. М. Основы теории чисел. М.: Наука, 1965, [16].
1372. Витерби А. Границы ошибок для сверточных кодов и асимптотически оптимальный алгоритм декодирования. — В кн.: Некоторые вопросы теории кодирования. М., 1970, с. 142—165, [1].
1376. Ван дер Вардеи Б. Л. Алгебра: Пер. с нем./Под ред. Ю. И. Мерзля-. кова. М.: Наука, 1976, >[3, 4, 8].
1400. Велдон И. Дж. Циклические коды, задаваемые разностными множествами;^— В кн.: Некоторые вопросы теории кодирования. М., 1970, с. 9—21, [13].
1410. Вейль Г. Классические группы, их инварианты и представления: Пер. с англ/Под ред. Д. А. Райкова. М.: Иностр, лит., 1947, [19].
1414. Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа. Ч. 1: Пер. с англ./Под ред. Д. В. Широкова. М.: Физматгиз, 1963, [19].
1433. Возенкрафт Дж., Джекобс И. Теоретические основы техники связи: Пер. с англ./Под ред. Р. Л. Добрушина. М.: Мир, 1969, [1].
1451а *. Зайцев Г. В., Зиновьев В. А., Семаков Н. В. Быстрое корреляционное декодирование блочных кодов. — В кн.: Кодирование и передача дискретных сообщений в системах связи. М.: Наука, 1976, с. 74—85, [14].
1454. Зарисский О., Самюэль П. Коммутативная алгебра. (В двух томах): Пер с англ./Под ред. А. И. Узкова.. М.: Иностр, лит., 1963, [4].
1455. Цеттерберг Л. X. Циклические коды, исправляющие кратные ошибки л построенные с помощью непроводимых полиномов. — В кн.: Теория кодиро-завия. М., 1964, с. 40—64, [7].
1461/ Цирлер Н. Линейные возвратные последовательности. — В кн.: Кибернетический сборник. М.. 1963, вып. 6, с. 55—79, [14].
1469а *. Зигангиров К. Ш. Некоторые последовательные процедуры декоди- эования.— Проблемы передачи информации. 1966, вып. 4, с. 13—25, [1].
14696 *. Зигангиров К. Ш. Процедуры последовательного декодирования. М.: Связь, 1974, [1].
1470. Зиновьев В. А. Обобщенные каскадные коды. — Проблемы передачи, информации. 4976, вып. 1, .с. 5—15, >[18, А].
1470а*. Зиновьев В. А. Алгебраическая теория блочных кодов, исправляю-цих независимые ошибки. — Итоги науки и техники. Серия Теория вероятно-
стей. Математическая статистика. Теоретическая кибернетика. МГ,ВИНИТИ, 1976, т. 13, с. 189—234, [1].
1471. Зиновьев В. А., Леонтьев В. К. О совершенных кодах. — Проблемы передачи информации. 1972, вып. 1, с. 26—35, [6].
1472. Зиновьев В. А., Леонтьев В. К. Несуществование совершенных кодов над полями Галуа. — Проблемы управления и теории информации. 1973, вып. 2, с. 123—132, [6].
1472а*. Зиновьев В. А., Леонтьев В. К. Теорема о несуществовании совершенных кодов над полями Галуа. — Препринт ИППИ АН СССР. М., 1972, [6].
УТОЧНЕНИЯ К СПИСКУ ЛИТЕРАТУРЫ, ПРИСЛАННЫЕ АВТОРАМИ К РУССКОМУ ПЕРЕВОДУ
80] S. A. Butman and R. J. McEliece...
83] L. D. Baumert and J. Mykkeltveit...
99] D. A. Bell and...
, (104] Автор: В.—F. Yang.
Discrete Math., 17 (1977) 235—245.
24 (1978) 81—93
См. также Discrete Math., 17 (1977) 247—269.
... of Galois fields
5 (1976) 525—528
Sur les idempotents des codes, C. R. Academ. Sci. Paris, Ser. A—В
103
139
140
200
223
236
297
284 (1977) A509—A512
323] Math. Proc. Cambridge Phil. Soc. 81 (1977) 185—192
330 См. также Addendum, 44 (1969) p. 378
355] P. Delsarte, Bilinear Forms over a Finite Field, with application to Coding Theory, J. Combinatorial Theory, 25A (1978) 226—241 (21]
SIAM J. Appl. Math., 34 (1978), 167—166'
Изменить гл. 8 на гл. 18
17 (1977) 85—94
17 (1977) 71—83
Information and Control, 34 (1977), 314—323
5 (1976) 413—424
Trans. Info. Theory.
[357 563 580 581 630 653 759 844a] 35 (1977) 40—47" 844b] Ser AI, No. 172 (1976), pp. 1—19 947] pp. 157—166 1145................
13191
T441 [1457 1459 1474' 1478
pp. 515—516
J. Combinatorial Theory, 23B (1977) 236—238.
Авторы: X.-N. Feng and Z.-D. Dai
, (1458], (1460] Автор: Z.-X. Wan
Авторы: Z.-X. Wan and B.-F. Yang.
Авторы: Z.-D. Dai and X.-N. Feng.
25A (1978) 288—318
предметный указ егч^
Автокорреляция 398
Автоморфизм группы 232
- — поля 116
Алгебра Боуза—Меснера 632
— групповая 135
Алгебраическая независимость 589
Алгоритм Евклида 352
Антикод 530
— оптимальный 536
Базис дополнительный 120
— инвариантов 579, 589
— нормальный 122
— полиномиальный 590
----хороший 594
Бивесовой спектр или бивесовая
функция 149
Биномиальный коэффициент 23
----оценка для 302, 303
Блок 67
— индексы пересечений 69
Блок-схема 67
— дополнительная 70
— симметричная 69
Булева функция 359
Валентность 630
Вероятность ошибки на символ 30 Вес 19, 247 — действительный 384 •— минимальный 20
— связь с многочленом МС 248
— Хэмминга 119, 147
Весовой план 60
Весовой спектр или весовая функция 49, 127
----—--------дуального кода 128, 145
-------------кода Дельсарта — Геталса 46'1
-------------кода, дуального коду
БЧХ, исправляюшего две ошибки 434—436 ---------------- Кердока 440 ----------------МДР 311, 312 ----------------Препараты 451 ----------------РМ 429 --------------------------------РМ второго порядка 426 ----------------РМ первого порядка 444 ----------------с двумя ненулевыми весами 226
-------------кодов Голея 75, 613, 614
-------------Ли 147
Весовой спектр или весовая функция минимального кода 225 ---------- полная 143 ---------- разделенная 151 ----------— смежного класса 139, 171 ----------смежных классов по ^(1, т) 402 ---------- совместная 149 --------------------точная 148 ----------Хэмминга 147 ----------экстремальная 583, 603
Внутренний спектр 644, 647 Выбрасывание 39 Выкалывание 39
Гауссовский коэффициент 427
Геометрия аффинная 667
— дезаргова 670
— евклидова 667
— проективная 667
Гиперплоскость 667, 669
Гипотеза Артина 504
Граница БЧХ 2011, 244
— Вакса 547
— Варшамова—Гилберта 44, 539
— Грайсмера 528
— Грея—Рэнкина 526
— Джонсона 506, 513
— для двоичных кодов 513
--- кодов постоянного веса 506
--- самодуальных кодов 608
— Зяблова 307
— Карлица—Ушиямы 275—277
— квадратного корня 465
— линейного программирования 517, 524
— Мак-Элиса 547
— Мак-Элиса и др. 541, 546
— Плоткина 50, 51, 513
— Синглтона 43, 310, 526
— сферической упаковки 29, 513, 540
— Хартманна—Тзенга 206
— Хэмминга 29, 513, 540
— Чернова 308
— ’ Элайса 541
Граф регулярный метрический 638
сильно 638
График границы Варшамова—Гилберта 304, 547 --- Зяблова 304
---Мак-Элиса и др. 547
— кодов МДР 319
— пропускной способности 32
— энтропии 302
1 Авторским указателем является библиография, так как библиографическая ссылка сопровождается указанием номера главы, к которой она относится.
Группа автоморфизмов 117
---кода 227, 236
-------БЧХ 233
— -----Голея 616, 627
---— Гоппы 336
-------КВ 473—477
— -----линейного 456
—------недвоичного 235
-------Нордстрома—Робинсона 462
-------РМ387
— — циклического 231
— аффинная 233
— Галуа 117, 236
— диэдра 263, 593
— коллинеаций 672
— Конвея 629
— матриц Адамара 504
— Матье 613, 614, 616, 627
— полная аффинная 233, 388
---линейная 229, 388
--- проективная линейная 341
— проективная специальная линейная 473
— простая 629
— симметрическая 228
— транзитивная 230, 446
— тривиальная 228
— циклическая 108
Двоичная арифметика 13
Двойственная программа 517
Двувесовые коды 226, 387
Декодер Меггита 384
Декодирование алгоритмом Берле-
кэмпа 270, 272
---Рида 375, 393
— альтернаптного кода 354
— в ближайшее кодовое слово 20
— взвешенное мажоритарное 384
— Витерби 45
— вылавливанием ошибок 497
— кода БЧХ 265—272
--- Гоппы 354
--- полученного произведением 575
---РМ 377—385
---PC 299
---циклического 505
— мажоритарное в один шаг 379
---в L шагов 379
— неполное 21
— перестановочное 457
— покрывающими полиномами 498
— полное 21, 272
— по максимуму правдоподобия 19
— последовательное 45
— пороговое 384
— с использованием схем 501
— — ограниченным расстоянием 46
Диаметр графа 638
— кода 174
Длина 46
Додека да 76, 613
Единственность 620, 625, 628
Задача о взвешивании монет 214
Идеал 190
— главный 190
— минимальный 218
Идемпотенты 215—224
— алгебры Боуза—Меснера 632
— кода Голея 467, 469
---КВ 446
— — неприводимого 218
--- произведения 551
---РМ 372
---PC 290
---симплексного 219
---Хэмминга 221
---циклического 224
— примитивный 218, 632
Изоморфизм полей 106
— колец 239
Изотропный вектор 46
Инвариант 579, 588
— однородный 579, 589
Информационный символ 14
Канал двоичный симметричный 12
— действительный 45
— су-ичный симметричный 22
Квадратичный вычет 53
— закон взаимности Гаусса 503
Код 12
— абелев групповой 575
— Адамара 57
— альтернантный 321
— арифметический 45
— биортогональный 41, 371
— блоковый 46
— БЧХ 202, 253—287
---двоичный 203
---в узком смысле 253
---исправляющий две ошибки 193
-------t ошибок 201
---непримитивный 203
---примитивный 203, 253
— Васильева 85
— вложенный 563
— внешний 301
— внутренний 301
— вырожденный 222, 429
— Габидулина 686
— Гёталса 460
— Голея 73, 205, 465, 613
— Гоппы 322, 327—347
---двоичный 331—335
— — комулятивный 335
---неприводимый 328, 334
— — сепарабельный 332
— — циклический 328, 340—347
— дважды циркулярный 480, 491
— двумерный 575
— Дельсарта—Геталса 445
— для вычислительных машин 35
Код для гауссовских каналов 11
— — классификации документов 285
— дуальный 36, 127, 195
-----альтернантному 331
•----КВ-коду 470
-----РМ-коду 365
—----циклическому 189
— евклидово-геометрический 387
— избыточный вычетный 299
— из слов четного веса 14, 18
— исправляющий две ошибки 567
-----одну ошибку 566
-----три ошибки 282
-----t ошибок 201
— каскадный 301
-----обобщенный 572
— квадратично-вычетный 57, 463
----расширенный 470
— квазисовершенный 29
— квазициклический 489
— Кердока 440
— линейный 12, 14
— матрично-конференсный 65, 66
— МДР 44, 308
— Меласа 206
— минимальный 218*
— Надлера 520
— нелинейный 47
— неприводимый 218
— Нордстрома—Робинсона 81, 82
— оптимальный 309
— ортогональный 36, 127
— Плесе симметричный 493
— плохой 294
— подкод над подполем 207
— почти совершенный 515
— Препараты 449
— — укороченный 455
— проективно-геометрический 387
— произведение 575
— прямая сумма 84
— прямое произведение 548
— равновесный 71
— равномерно упакованный 188
— разделимый с максимальным расстоянием — см. код МДР
— разностный циклический 385
— реверсивный 206
— регистровый 39, 96, 395
— РМ — см. код Рида—Маллера
— Рида—Маллера 362
-----выколотый 365
-----первого порядка 41, 362
-----порядка г 362
— PC — см. код Рида—Соломона
— Рида—Соломона 288
-----обобщенный 296, 297
расширенный 289
— слабодуальный 37, 576
слабо 37, 609
-----формально 576
четный 577, 578
Код сепарабельный 332
— симплексный 40, 41
— совершенный 29
— с повторением 14, 18
— Сривэставы 346
---обобщенный 347
— хороший 288
---альтернантный 326
---Гоппы 339
---дважды циркулянтный 489
---квазициклический 488
---самодуальный 609
---случайный 540
---Юстесена 287
— Хэмминга 34, 192
---недвоичный 194
— Цеттерберга 206
— циклический 188—215
— — вырожденный 222
---— укороченный 194
— Ченя—Чоя 350
— Шонгейма—Линдстрема 188
— эквивалентный 34, 47
— Юстесена 300, 305
Кодирование .12
— кода РМ 374—382
— кода PC 295
— систематическое 295
Кодовое слово 12
Коллинеация 672
Кольцо 189
— централизаторов 650
Конструкция д+х, 6+х, а+Ь+х 568
— Андрианова—Сасковца 564
— звезды 556
— Зиновьева 571
— кронекеровского произведения 549
— Пирета 569
— прямого произведения 548
— прямой суммы 84
— с добавлением суффиксов 562—563
— склеивания 23, 58, 561
— следа 208, 553
— Соломона—Стиффлера 533
— и, и-1-и 84, 87, 363
— Хельгерта—Стинаффа 574
Конфигурация Дезарга 537
— когерентная 650
— тактическая 67
Корень из единицы 196
Критерий Гаусса 502
— Эйлера 502
Критическая проблема 547
КВ — см. код квадратично вычетный
Лемма о рандомизации
Линейное программирование 517
Логарифм 92
— Зеча 97
Локаторы вектора 241, 254
Максимально-нелинейная функция
411
Матрица Адамара 52
— • альтернантная 357
— Вандермонда 120
— Джекобстола 55
— индуцированная 592
— инцидентности 70
— конференс- 63, 64
— Коши
— мономиальная 235, 626
— Пейли 56
— порождающая 15, 16
— проверочная 13, 14
— Сильвестра 53
— симплектическая 419
— смежности 631
— сопровождающая 110
— циркулянтная 484
Многочлен аннулирующий 168
— аффинный 39-1
— взаимный 112
— Гоппы 328
— значений ошибок 243, 355
— Кравчука 131, 1132, 152
— линеаризованный 121
— Ллойда 177
— локаторов ошибок 241, 255, 355
— минимальный 105, -197
— неприводимый 89
— покрывающий 498
— порождающий 190
— примитивный 91, 405
— проверочный 194
— Хана 650
— циклотомический 214
— Эберлейиа 627, 644, 650
Многочлен Мэттсона—Соломона 236, 244—248 --- кода Гоппы 337
-------РМ 389
--- минимального идеала 244
---циклического кода 559
Множество сигналов 42
Моменты 133
МС-многочлен — см. многочлен Мэттсона—Соломона
Невычет 53
Ненуль кода 199
Неравенстве Дельсарта 186
— среднего арифметического и среднего геометрического 186
— треугольника 23
— Фишера 71
Нормальное распределение 277
Нуль кода 199
Овал 321
Однородное пространство 650
Октада 76, 613
Опорное множество 178
Отношение 629, 630
Отображение Мэттсона — Соломона 240
Орбита 617
Ортогональные векторы 36
— многочлены 1153
— собственные значения 633
Ортогональная таблица 141, 319
Ошибка 12, 21
— вектор 18
— вероятность 28
— обнаружение 21
Пакет 294
— исправление 294
Пересечение 19
Перестановка 47, 48, 227
— сопряженная 617
Плоскость аффинная 68, 671
— проективная 67, 68, 672, 673
Подпространство 667
Показатель многочлена 410
Покрытие 72
Поле конечное 88, 101
— Галуа 88, 91
— разложения 196
Порядок поля 88, 102
— элемента 102
— q по модулю п 196
Пополнение 39
Последовательная редукция кода 382
Последовательность де Брейна 416
— псевдошумовая ,(ПШ) 396 — псевдослучайная 394—400 Преобразование Адамара 62, 129, 401 быстрое 408, 417
— быстрое Фурье 407
— дискретное Фурье 62, 237
— Мак-Вильямс 139
Примитивный элемент 91, 105
— корень из единицы 196
Проверка 14
— общая на четность 37
— ортогональная 379
Проверочный символ 13
Произведение векторов 22
-скалярное 36
— Кронекера 407
— символическое 123
— покомпонентное 238
Пропускная способность 32
Процедура Ченя 271
Пси-функция Эйлера 104
Радиус покрытия 174
Разложение Кравчука 154, 169
— циклических кодов 559
Размерность 17
— кодов БЧХ 258
Разностное множество 386
Ранг группы 650
Расстояние 19, 20
— Боуза 205
— в графе 638
— внешнее 156, 158
— дуальное 141, 158
Расстояние инвариантность 49, 156, 161
— истинное кода БЧХ 255—257
— конструктивное кода БЧХ 260
— минимальное 20
— спектр 49
— Хэмминга 19
Расширение 38
Регистр сдвига 96
синтез 267
Редукция кода 498
Рекуррентное соотношение 153
Ряды Молина 580 РМ — см. код РМ PC — см. код PC
Свойства альтернантных кодов 324
— кода Гоппы 328
---Кердока 440
----КВ 464
----РМ 365
----PC 296
---Сривэставы 347
— — Препараты 454
— — Хэмминга 36
•---Ченя—Чоя 3§0
— симметричного кода Плесе 493 — ПШ-последовательности 396—399 Секстет 621
Серия линейная 260
— круговая 260
Сизигия 590
Символ Лежандра 54 — сообщения 12, 13 Симплекс 43
Синдром 27
Система Штейнера 68
Систематический кодер 295
Скорость 17, 538
След 119
Сложность 11
Смежный класс 25
---- весовой спектр 139, 166
---- лидер 26
----по коду БЧХ 172
—--------Голея 77
----— — Нордстрома—Робинсона 172, 173
----------Хэмминга 170, 171
----------РМ 405
— цнклотомический 315
Собственное значение 632
— пространство 632
Сопряженный .138
Стабилизатор 616
Стандартное расположение 26
Сумма Гаусса 468
Суперканал 301
Схема декодирования Грина 408
Схема отношений 630
----Джонсона 643
-- метрическая 638
— — симплектических форм 640
Схема отношений Хэмминга 634
Таблица истинности 360
— границ 546, 652
— дважды циркулярных кодов 493
— делителей многочлена 198
— индексов блоковых пересечений
76, 77
— кодов БЧХ 204, 256
---Дельсарта—Геталса 446
---КВ 466
---РМ 364
— конечных полей 106, 114, 115
— линейных кодов 651
— лучших кодов 652, 653
— постоянного веса 661
— минимальных многочленов 142
— неприводимых многочленов 116, 126
- — оптимальных линейных кодов 538
— примитивных идемпотентов 220
— 5-схем 495
— разделенных весовых функций 602
— расширенных кодов КВ 466
— самодуальных кодов 605
— смежных классов по <%(1, т) 405
— циклотомических классов 109
Тактическая конфигурация 67
Теорема Адамара 60
— Ассмуса—Мэттсона 179, 476
— Бормана—Лагранжа 606
— Вентурини—Пейтла 535
— Глизона 581
— Глизона—Пирса-—Турина 576
— Глизона—Прэнджа 474, 476
— двойственности 518
— Дедекинда Н 8
— Дельсарта—Геталса 646
— Диксона 422
— Касами—Токуры 430
— китайская об остатках 298
— Кристофеля—Дарбу 542
— Левенштейна 58, 513
— Ллойда 178. 180
— Лукаса 393
— Мак-Вильямс 128, 139, 147, 148
— Мак-Вильямс—Манна 373
— Мак-Элиса 431
— Молина 580, 591
— Нетер 590
— о дополнительной нежесткости 518
— о нормальном базисе 125
— Парсеваля 403
— Перрона 503
— Титвайнена—Ван Линта 181
— Ферма 102
— фундаментальная проективной геометрии 674
— центральная предельная 282
— Шеннона 32
Теория инвариантов 578, 586
Тетрада 621
Тождества Мак-Вильямс 129
— Ньютона 241—248
— Плесе 134
Удлинение 40
Укорочение 40
Уравнение квадратное над GT’(2™) 272
Форма 419
— альтернированная 419
— билинейная 419
— дизъюнктивная нормальная 360
— квадратичная 419
— линейная 419
— симплектическая 419, 640
Формула Стирлинга 302
Функция Мебиуса 118
Футбольный тотализатор 118
Характер 136—'137, 144
Характеристика поля 102
Централизатор 650
Циклотомические классы 197
— — представители И09, 197
Шар 20
Шаровая упаковка 612
Эквивалентные коды 227
Элемент примитивный 103
— порядок 102
сопряженный 108
— след 149
Энергия 42
Энтропия 302
3^ (а> у) — см. код альтернантный
0% (т, d) — см. код Дельсарта — 1 еталса
EG(m, q)—см. геометрия аффинная GA (т) — см. группа полная аффинная
GF — см. поле Галуа
GF(32) 114
GF (46) 114
GF(9) 115
GF(8) 106
Ж (m) — см. код Кердока /i-множество 317 (т, d)-множество 645 р-многочлен 123
р-полиномиальная схема 639
^(т) —см. код Препараты
PG(m, q)—см. геометрия проективная
PGLn (q) — см. группа полная проективная
PSL (р) — см. группа проективная специальная линейная
PPLm+i (q) — см. группа коллинеаций
Q-полиномнальная схема 639
gi (г, т) — см. код Рида — Маллера. /схема 67, 670
ОГЛАВЛЕНИЕ
Стр.
Предисловие авторов к русскому изданию.............................. 5
Предисловие переводчиков к русскому изданию ........................ 5
Введение . . .................................... 8
ЧАСТЬ I
Глава 1. Линейные коды . . . .12
1.1. Линейные коды................................................. 12
1.2. Свойства линейного кода....................................... 15
1.3. На приемном конце............................................. 18
1.4. Немного подробнее о декодировании линейного кода . 25
1.5. Вероятность ошибки . 28
1.6. Теорема Шеннона о существовании хороших кодов 32
1.7. Коды Хэмминга, . . . 33
1.8. Дуальный код.................................................. 36
1.9. Построение новых кодов из заданных кодов (II) 37
1.10. Некоторые общие свойства, линейного кода......................43
1.11. Краткое содержание гл. 1 ... .................44
Замечания к гл. 1 . -.........................................45
Глава 2. Нелинейные коды, матрицы Адамара, /-схемы и код Голея 47
2.1. Нелинейные коды........................................ . 47
2.2. Граница Плоткина.............................................. 50
2.3. Матрицы Адамара и коды Адамара 52
2.4. Конференс-матрицы 63
2.5. /-схемы....................................................... 67
2.6. Введение в двоичный код Голея . . .< .................73
2.7. Система Штейнера S(5, 6, 12) и нелинейные коды, исправляющие одну ошибку......................................................78
2.8. Введение в код Нордстрома—Робинсона .... 81
2.9. Построение новых кодов из заданных кодов (III) . 84
Замечания к гл. 2 .................................. 86
Глава 3. Введение в коды БЧХ и конечные поля . . . . 87
3.1. Коды БЧХ, исправляющие две ошибки (I) . 87
3.2. Построение поля GE(16).........................................88
3.3. Коды БЧХ, исправляющие две ошибки (II) . 92
3.4. Вычисления в конечном поле 95
Замечания к гл. 3 . . 99
Глава 4. Конечные поля..............................................99
4.1. Введение...................................................... 99
4.2. Конечные поля: основы теории..................................101
4.3. Минимальные многочлены............................... . . 104
4.4. Как находить неприводимые многочлены..........................111
4.5. Таблицы малых полей..........................................113
4.6. Группа автоморфизмов поля GF(pm) ...... 116
4.7. Число неприводимых многочленов...............................1'18
4.8. Базисы GF(pm) над GF(p) .....................................1119
Стр.
4.9. Линеаризованные многочлены и нормальные базисы - • • - 121
Замечания к гл. 4................................................ 126
Глава 5. Дуальные коды и их весовые спектры .........................127
5.1. Введение................................ .............. 127
5.2. Весовой спектр кода, дуального к двоичному линейному коду . 127
5.3. Групповая алгебра ... .135
5.4. Характеры.................................................136
5.5. Теорема Мак-Вильямс для нелинейных кодов...............138
*5.6. Обобщенные теоремы Мак-Вильямс для линейных кодов . . . 143
5.7. Свойства многочленов Кравчука ..................................152
Замечания к гл. 5 .......... . 155
Глава 6. Коды, схемы и совершенные коды .............................156
6.1. Введение...................................................... 156
6.2. Четыре фундаментальных параметра кода...........................157
6.3. Явная формула для спектра весов и расстояний....................159
6.4. Построение схем из кодов при s^cT...............................161
6.5. Дуальный код также порождает схемы..............................165
6.6. Весовой спектр кода, полученного в результате сдвига . . . 167
6.7. Построение схем из нелинейных кодов при s'<d . • . . . . 175
6.8. Совершенные коды................................................177
'6.9. Коды над GF(q).................................................178
*6.10. Не существует неизвестных совершенных кодов . .... 181
Замечания к гл. 6...............................................187
Глава 7. Циклические коды ...........................................188
7.1. Введение.......................................... 188
7.2. Определение циклического кода..................... 189
7.3. Порождающий многочлен....................................190
7.4. Проверочный многочлен.....................................194
7.5. Делители многочлена хп—1..................................196
7.6. Коды БЧХ, исправляющие t ошибок . ........ 201
7.7. Использование матрицы над GF(qm) для задания кода над GF(q) . 206
7.8. Кодирование циклических кодов.............................209
Замечания к гл. 7 .... . ........................214
Глава 8. Циклические коды (продолжение): идемпотенты и многочлены Мэттсона—Соломона................................................215
8.1. Введение . 215
8.2. Идемпотенты.................................................215
8.3. Минимальные идеалы, неприводимые коды н примитивные идемпотенты . . .......................................... . 218
8.4. Весовой спектр минимальных кодов............................225
8.5. Группы автоморфизмов кода ...............................227
8.6. Многочлен Мэттсона—Соломона.................................236
8.7. Некоторые весовые спектры...................................248
Замечания к гл. 8........................................ ... 252
Глава 9. Коды БЧХ....................'...........................253
9.1. Введение....................................................253
9.2. Истинное минимальное расстояние кода БЧХ...................255
9.3. Число информационных символов кодов БЧХ...................258
9.4. Таблица кодов БЧХ...........................................262
9.5. Длинные коды БЧХ............................................264
9.6. Декодирование кодов БЧХ.....................................265
9.7. Квадратные уравнения над GF(2m).............................272
9.8. Квазисовершенность кодов БЧХ, исправляющих две ошибки . 274
9.9. Граница Карлица—Ушиямы.......................-............ 275
9.10. Асимптотическая нормальность некоторых весовых спектров
9.11. Коды не-БЧХ, исправляющие три ошибки......................
Замечания к гл. 9..........................................
Глава 10. Коды Рида—Соломона и коды Юстесена....................
10.1. Введение..................................................
10.2. Коды Рида—Соломона.............................. .
10.3. Расширенные коды PC . . .
10.4. Идемпотенты кодов PC...................... . . . .
10.5. Отображение кодов над GF(2m) в двоичные коды
10.6. Исправление пакетов ошибок . .
10.7. Кодирование кодов Рида—Соломона ................
*10.8. Обобщенные коды Рида—Соломона ...................
10.9. Избыточные вычетные коды ... . .
10.10. Декодирование кодов PC ...
10.1-1. Коды Юстесена и каскадные коды . . .
Замечания к гл. 10 . .
Глава 11. Коды МДР .............................................
11.1. Введение........................................
11.2. Порождающая и проверочная матрицы ......
11.3. Весовой спектр кода МДР ... ...................
11.4. Матрицы, у которых все квадратные подматрицы невырождены
11.5. Коды МДР, полученные из кодов PC . ................
11.6. «-множеству ...........
11.7. Известные результаты................
11.8. Ортогональные таблицы
Замечания к гл. 11 . .
Глава 12. Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ . ..................................
*12.1. Введение . . .
12.2. Альтернантные коды
12.3. Коды Гоппы............................. ..................
12.4. Дальнейшие свойства кодов Гоппы...........................
* 12.5. Цикличность удлиненных кодов Гоппы, исправляющих две ошибки
* 12.6. Обобщенные коды Сривэставы................... .
* 12.7. Обобщение Ченя—Чоя кодов БЧХ ,
12.8. Алгоритм Евклида....................
12.9. Декодирование альтернантных кодов .
Замечания к гл. 12 .
ЧАСТЬ II
Глава 13. Коды Рида—Маллера.....................................
13.1. Введение................ .... . .
13.2. Булевы функции .... . .
13.3. Коды Рида—Маллера ......
13.4. РМ коды и геометрии.......................
13.5. Векторы минимального веса порождают код
13.6. Кодирование и декодирование (I)
13.7. Кодирование и декодирование (II)
13.8. Другие геометрические коды
13.9. Группы автоморфизмов РМ кодов ....
13.10. Многочлены Мэттсона—Соломона для РМ кодов •..............
13.11. Действие полной аффинной группы на многочленах Мэттсона—Соломона ...................................................... .
Замечания к гл. 13 .... . .
Глава 14. Коды Рида—Маллера первого порядка.....................
14.1. Введение..................................................
Стр.
14.2. Псевдошумовые последовательности . ....................394
14.3. Смежные классы по коду Рида—Маллера первого порядка . . 400
14.4. Кодирование и декодирование кода Й? (1, zn).................405
14.5. Максимально-нелинейные функции..............................411
Замечания к гл. 44...........................................416
Глава 15. Коды Рида—Маллера второго порядка, Кердока и Препараты 417
15.1. Введение....................................... 417
15.2. Весовой спектр кода Рида—Маллера второго порядка 418
15.3. Спектр весов произвольных кодов Рида—Маллера................429
15.4. Подкоды размерности 2т в кодах ^*(2, т) и <%(2, т) 431
15.5. Код Кердока и его обобщения.................................437
15.6. Код Препараты...............................................449
15.7. Обобщение Геталса кодов Препараты...........................460
Замечания к гл. 15 ......................................461
Глава 16. Квадратично-вычетные коды ................462
16.1. Введение....................................................462
16.2. Определение квадратично-вычетных кодов 463
16.3. Идемпотенты квадратично-вычетных кодов ............ 466
16.4. Расширенные квадратично-вычетные коды 470
16.5. Группа автоморфизмов КВ-кодов . ................473
16.6. Двоичные квадратично-вычетные коды ... . . 477
16.7. Дважды циркулянтные и квазициклические коды . . 489
16.8. Квадратично-вычетные и симметричные коды над GF(3) 493
16.9. Декодирование циклических и некоторых других кодов .... 496
Замечания к гл. 16 ......................................502
Глава 17. Границы для объема кода ......... 505
1.7. 1. Введение............ . . . . .............505
17.2. Границы для А(п, d, w)......................................506
17.3. Границы для А(п, d).........................................513
17.4. Границы линейного программирования..........................517
17.5. Граница Грайсмера........................................ . 528
17.6. Построение линейных кодов; антикоды.........................529
17.7. Асимптотические границы.....................................538
Замечания к гл. 17 ................ . 547
Глава 18. Методы комбинирования кодов..........................548
18.1. Введение . ....................................... 548
I. Произведение кодов и их обобщения.........................548
18.2. Прямое произведение кодов...................................548
18.3. Не все циклические коды являются прямыми произведениями циклических кодов............................................ . 552
18.4. Другой способ представления неприводимых циклических кодов в виде произведения кодов ........................................... ... 553
18.5. Каскадный коды: (*)-конструкция .... 556
18.6. Общий подход к разложению циклических кодов 559
II. Другие методы комбинирования кодов . 561
18.7. Методы построения, которые увеличивают длину ... 562
18.7.1. Конструкция X: добавление суффиксов к кодовым словам 562
18.7.2. Конструкция Х4: комбинирование четырех кодов . . 565
18.7.3. Коды, исправляющие одиночные и двойные ошибки . 566
18.7.4. Конструкция | а + х | b+х | а+b+х | . . 568
18.7.5. Конструкция Пирета.............................. . 569
18.8. Конструкции, связанные с каскадными кодами.............. 570
18.8.1. Метод улучшения каскадных кодов .... 570
18.8.2. Обобщенные каскадные коды Зиновьева . 571
18.9. Методы укорочения кодов ....................................573
18.9.1. Конструкции Y1—Y4.........................................573
18.9.2. Конструкции Хелгерта и Стинаффа...........................
Замечания к гл. 18 ................................
Глава 19. Самодуальные коды и теория инвариантов..................5
19.1. Введение.................... 5*
19.2 Введение в теорию инвариантов 5
19.3 Основные теоремы теории инвариантов 5
19 4 Обобщения теоремы Глисона.................... 5
19.5. Несуществование некоторых очень хороших кодов 6(
19.6. Хорошие самодуальные коды существуют . 6
Замечания к гл. 19 ... . . 6
Глава 20. Коды Голея . . . .61
20.1. Введение ...... 61?
20 2. Группа Матье М24 . 61
20 3 Группа Л<24 5-транзитивна ................ 6
20.4 Порядок группы М24 равен 24 23-22 21-20-48 61
20.5 Система Штейнера S (5, 8, 24) единственна 62 .
20.6. Коды Голея g?2a и ^24 единственны . 62.
20.7. Группы автоморфизмов троичных кодов Голея 62с
20.8. Коды Голея g?n и gH2 единственны ..........................62 .
Замечания к гл. 20 62.
Глава 21. Схемы отношений ........................................62
21 1 Введение ... 62
21.2. Схемы отношении 63
21 3 Схема отношений Хэмминга .... 63-
21.4. Метрические схемы . 631
21.5. Симплектические формы 640
21.6. Схема Джонсона .... 643
21.7. Подмножества схем отношений.............................. 644
21.8. Подмножества симплектических форм 645
21.9. /-схемы и ортогональные таблицы . .... 648
Замечания к гл. 21 649
Приложение А. Таблицы наилучшнх известных кодов . 650
1. Введение ................... 650
2. Небольшая таблица значений А(п, d) '(Рис- ПАЛ) .... 651
3. Расширенная таблица наилучших известных кодов (рис. ПА.2) 652
4. Таблица значений А (п, d, w) (рис. ПАЗ) ................. 659
Приложение В. Конечные геометрии 667
1. Введение.......................................................667
2. Конечные геометрии PG(m, q) и EG(m, q) ... 667
3. Свойства геометрий PG(m, q) и EG(m, q) 670
4. Проективные и аффинные плоскости 672
Замечания к приложению В ............. 6^1
Список литературы................. 674
Список литературы на русском языке................................
Уточнения к списку литературы, присланные авторами к русскому переводу...................................................... 733
Предметный указатель..............................................73
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр. j Строка Напечатано | Следует читать
24 4-й абз., „(а + Ь)п, (а + Ь)п, ... (а + Ь)П» (а + Ь)п,
2-я, 3-я св. (а + Ь) ”, ... («+&)",..
24 2-я сн. / fT \ ••S =° т=1 'т ! ...^(_1Г П-о,... т>
48 Рис. 2.1. 01110001011 01110001011 10111000101
85 6-я св. ...[2 max {«1, Лг}, — .. [zii+max {/ii, Л2},...
85 21-я си. ...(„, п—т—1, 3).. . [n, п—т—4, 3]...
ПО 12-я сн. ..., что = р. ..., что |3pd = p.
111 5-я сн. ...порядка рц. ... порядка рй.
л h
121 6-я сн.
4=0 i=O
136 8-я св. ,..^= X г“... S zu...
wt(u)=i wt(u)=z
137 10-я св. •••С = Sue<gZU’-" ...C=y ^zu,... zj ue'6
137 14-я сн. ... любой гомоморфизм Q ... ... любой гомоморфизм G ...
147 18-я св. ...(1 а+а4 а2+а2)... ...(1 а+а4 а2+а3)...
158 22-я св. ... A'i — весовой спектр ... ... A'i=B't—весовой спектр ...
164 4-я св., 5-я св. 0. .+£зО>-». <6i°> r=0
209 6-я св. ...® = ^н... д 'll д
234 6-я св., 7-я св. .. .и а*2 v = а22 ... иа1г -{- ч = а7’2
296 Рис. 10.6, .. К—7V- .-6 +1, ... ...К=М—6 + 1,...
4-я св Г RN (2т — s) „ s) Г
305 13-я сн. ...К- т , * • = .. ,К — | I »• • • т 1
325 15-я св. ii’tyj й о
331 14-я св. W .../a(z) = S П W ••4 W = 2 П(г-«г/)..-
1=1 /¥=1
336 15-я св. ... GF(qm) {оо}. ... GF(qm) [J {оо}.
340 2-я сн., 11-я СН, ,„Г(Е, G) ... ...Г(Е, G)...
20 я сн. 72т- 1 1
390 10-я сн. ... z2m= 1.'
390 2-й абз. ... Тш (Xj, 2), ... ... 7пг (^j^) г •••
св. 2-я ... z4
392 14-я св.,
412 18-я св. 11-я СВ. 2?П/2 2»П/2—1. 2m-l 2m/2-1.
418 455 467 22-я сн. 9-я св. 7-я св. (2m, 22m“2, 2,u~1... векторами 1, 2 и 3... ...Е,(а)‘=... 1 (2?w, 22m, 2m 1 ... векторами весов 1, 2 и 3 ... ...£Да‘)=...
Зак. 96