А. И. Субботин
ОБОБЩЕННЫЕ
РЕШЕНИЯ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
ПЕРВОГО ПОРЯДКА
Перспективы
динамической оптимизации
Andrei I. Subbotin
Generalized Solutions
of First-Order PDEs
The Dynamical Optimization Perspective
Birkhauser
Boston • Basel • Berlin
А. И. Субботин
ОБОБЩЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
ПЕРВОГО ПОРЯДКА
Перспективы динамической оптимизации
Перевод с английского Н. Н. Субботиной
Москва ♦ Ижевск
2003
УДК 515.353
Р
И
Издание осуществлено при финансовой поддерж-
ке Российского фонда фундаментальных исследо-
ваний по про екту №02-01-14123.
Субботин А. И.
Обобщенные решения уравнений в частных производных первого поряд-
ка. Перспективы динамической оптимизации. — Москва-Ижевск: Институт
компьютерных исследований, 2003, 336 стр.
С уравнениями Гамильтона - Якоби и другими типами уравнений в частных производных
первого порядка имеют дело многие разделы математики, механики, физики и их приложений.
Как правило, функции, имеющие содержательный смысл в рассматриваемых задачах, не яв-
ляются достаточно гладкими, чтобы удовлетворять этим уравнениям в классическом смысле.
Таким образом, возникает необходимость вводить понятие обобщенного решения и развивать
теорию и методы построения этих решений. Такие теории активно создаются и развиваются
в течение последних 50-ти лет. Среди получивших признание и стремительно развивающих-
ся в последнее время концепций: энтропийные решения С. Н. Кружкова, вязкостные решения
М. Крэндалла и П. Л. Лионса, обобщенные решения на базе идемпотентного анализа, предло-
женные В. П. Масловым.
В книге излагается созданная А. И. Субботиным теория минимаксных решений, кото-
рая имеет истоки в теории позиционных дифференциальных игр Н. Н. Красовского, и может
рассматриваться, как неклассический метод характеристик, где минимаксное решение должно
быть слабо инвариантным относительно характеристических дифференциальных включений.
Приведены теоремы существования, единственности и корректности минимаксных ре-
шений, иллюстрационные модельные примеры и приложения к теории оптимального управ-
ления и дифференциальным играм, конструктивные и численные методы построения мини-
максных решений, а также необходимые факты из теории дифференциальных включений,
негладкого анализа и теории классических решений уравнений Гамильтона-Якоби.
Для специалистов в области теории дифференциальных уравнений, динамической оп-
тимизации, негладкого анализа и их приложений, а также для преподавателей, студентов и
аспирантов соответствующих специальностей.
ISBN 5-93972-206-7
© Институт компьютерных исследований, 2003
http://rcd.ru
Оглавление
Введение ................................................... 7
Глава I. Обобщенные характеристики уравнений в частных про-
изводных первого порядка................................. 12
1.	Классический метод характеристик................... 12
2.	Характеристические включения....................... 19
3.	Верхние и нижние полунепрерывные решения........... 27
4.	Критерии слабой инвариантности минимаксных решений . . 37
5.	Кусочно-гладкие решения............................ 54
Глава II. Задачи Коши для уравнений Гамильтона-Якоби . ... 67
6.	Минимаксные решения уравнений Гамильтона-Якоби .... 67
7.	Единственность минимаксного решения задачи Коши для
уравнения Гамильтона-Якоби ............................. 74
8.	Существование минимаксного решения задачи Коши для
уравнения Гамильтона-Якоби.............................. 81
9.	Единственность при ослабленных предположениях....... 99
10.	Конструктивные и численные методы...................ПО
Глава III. Дифференциальные игры............................130
11.	Основные понятия теории дифференциальных игр........130
12.	Доказательство существования функции цены дифференци-
альной игры.............................................141
13.	Стабильные мосты и экстремальные стратегии ........150
14.	Некоторые замечания................................164
15.	Смешанные позиционные стратегии и контрстратегии .... 179
16.	Конструктивные и численные методы теории дифференци-
альных игр............................................  195
Глава IV. Краевые задачи для УЧП первого порядка...........220
17.	Задача Коши для уравнений Гамильтона-Якоби с дополни-
тельными условиями в форме неравенств...................220
18.	Разрывные решения краевой задачи типа Дирихле......240
19.	Дифференциальные игры на оптимум времени...........259
6
Оглавление
20.	Кусочно-линейные приближения минимаксных решений для
уравнений Гамильтона-Якоби.............................274
Приложение.................................................284
А1.	Доказательство классического метода характеристик.284
А2.	Многозначные отображения.........................  287
АЗ.	Полунепрерывные функции ...........................289
А4. Выпуклые функции.................................... . 290
А5. Контингентные конусы, производные по направлениям, суб-
дифференциалы .....................................291
А6. Об одном свойстве субдифференциалов.................298
А7. Дифференциальные включения .........................302
А8. Критерии слабой инвариантности......................305
Литература.................................................315
Предметный указатель.......................................334
Введение
С уравнениями типа Гамильтона-Якоби и другими типами уравнений
в частных производных (УЧП) первого порядка имеют дело многие раз-
делы математики, механики и физики. Эти уравнения обычно нелинейны,
а функции, имеющие содержательный смысл в рассматриваемых задачах,
не являются достаточно гладкими, чтобы удовлетворять этим уравнениям в
классическом смысле.
Пример такой ситуации доставляет функция цены в дифференциаль-
ной игре или задаче оптимального управления. Известно, что во всех точках
дифференцируемости эта функция удовлетворяет соответствующему урав-
нению Гамильтона-Якоби-Веллмана-Айзекса. С другой стороны, хорошо
известно, что функция цены, как правило, дифференцируема не всюду и
потому не является классическим глобальным решением. Таким образом, в
этом случае, как и во многих других, где используются УЧП первого по-
рядка, возникает необходимость вводить понятие обобщенного решения, а
также развивать теорию и методы построения таких решений.
В 50-е-70-е годы задачи, связанные с изучением негладких решений
УЧП первого порядка, исследовались в работах Бахвалова, Эванса, Флемин-
га, Гельфанда, Годунова, Хопфа, Кузнецова, Ладыженской, Лакса, Олейник,
Рождественского, Самарского, Тихонова и многих других математиков. Сре-
ди исследований этого периода отметим результаты С. Н. Кружкова, которые
были получены для уравнений Гамильтона-Якоби с выпуклым гамильто-
нианом. Обзор работ этого периода лежит вне пределов данной книги. До-
статочно полная библиография может быть найдена в работах [58,126, 128,
141].
В ранние 80-е М. Крэндалл и П. Л. Лионе ввели понятие вязкостного
решения (viscosity solution). За первыми публикациями [54, 57, 58] последо-
вала все расширяющаяся серия статей многих авторов. Теория вязкостных
решений продвинула исследования УЧП первого порядка и эллиптических
уравнений. В рамках этой теории были доказаны теоремы существования
и единственности для различных типов уравнений и краевых задач, а так-
же изучены некоторые приложения к задачам управления и дифференци-
альным играм. Обзор результатов теории вязкостных решений дан в [56].
Ниже мы напомним определение вязкостного решения, а также приведем
некоторые факты теории вязкостных решений.
8
Введение
Однако в этой книге мы развиваем другой подход, который может быть
рассмотрен, как неклассический метод характеристик. Следуя этому под-
ходу, обобщенное решение (называемое минимаксным) должно быть ин-
вариантно относительно потока, порождаемого так называемыми характе-
ристическими дифференциальными включениями. Термин «минимаксные
решения» имеет истоки в теории дифференциальных игр. В ранние 70-е
Н. Н. Красовский и автор настоящей книги ввели в рассмотрение понятие
^-стабильных и ^-стабильных функций, которые мажорировали и мигри-
ровали функцию цены (см., например, [118, 120,122]). Функция цены диф-
ференциальной игры является единственной функцией, которая одновре-
менно ^-стабильна и ^-стабильна. Известно также, что в точках дифферен-
цируемости функция цены удовлетворяет УЧП первого порядка (уравнению
Айзекса-Веллмана). Таким образом, упомянутые свойства определяют од-
но и только одно обобщенное (минимаксное) решение уравнения Айзекса-
Веллмана. Эти свойства гб-стабильности и ^-стабильности могут быть фор-
мализованы различными способами, в частности, с помощью неравенств
для производных по направлению. Такие неравенства были введены в ста-
тьях [192, 203], которые были опубликованы в 1978 и 1980 годах. Вполне
вероятно, они были первыми работами, где понятие обобщенного решения
УЧП первого порядка определялось путем замены этого уравнения парой
дифференциальных неравенств.
Использование термина «минимаксные решения» объясняется посто-
янным присутствием операций минимакса в исследованиях этих решений,
включая хорошо известные формулы Хопфа [90], и в исследованиях, ба-
зирующихся на идемпотентном анализе, которые проводились в последние
годы В. П. Масловым, В. Н. Колокольцовым и С. Н. Самборским. Концепция
обобщенного решения, предложенная в работах этого направления (см., на-
пример, [102, 147]), подобна классическим подходам к определению обоб-
щенного (слабого) решения в математической физике. Основное отличие
состоит в том, что традиционная структура поля над R с операциями а + Ь
и а 'Ь заменяется структурой полукольца с операциями а © b = min(a, 6),
а 0 b = а Ч- Ь. Следуя этому подходу, «скалярное произведение» функций f
и д определено равенством (/, д) = inf (/(ж), #(ж)). С помощью этого под-
хех
хода были развернуты исследования УЧП с выпуклым гамильтонианом и
их приложений к задачам математической физики.
Настоящая книга представляет собой наиболее полное изложение те-
ории минимаксных решений. В нее включены теоремы существования и
единственности этих решений, примеры их численного моделирования, их
применение в теории управления и в теории дифференциальных игр. В ис-
следованиях минимаксных решений используются методы негладкого ана-
лиза, функций Ляпунова, динамической оптимизации и теории дифферен-
Введение
9
циальных игр. В то же время, эти исследования вносят свой вклад в развитие
упомянутых разделов математики. На инфинитезимальном уровне следует
отметить дуальность в различных подходах к определению обобщенных ре-
шений. Это подтверждается замечанием Л.Янга [227]: «.. .Действительно,
гамильтонианы неотделимо сплетены с понятием выпуклости и, в особен-
ности, с двойственностью выпуклых фигур».
Книга состоит из 4-х глав и содержит 20 параграфов и приложение.
Каждый параграф начинается с аннотации. Структура книги видна в разделе
содержание, и мы не будем пересказывать её в данном разделе.
Опишем кратко путь, которым мы вводим понятие минимаксного ре-
шения уравнения
F(x, и(х\ Du(xY) = 0, ж Е G С Г,	(1)
где G — открытое множество в Rn, Du — градиент скалярной функции и.
Классический метод характеристик немедленно привлекает к рассмотрению
обыкновенное дифференциальное уравнение
z(t) — {x(t\ s} — F(x(t), z(t), s).	(2)
Минимаксным решением УЧП (1) называется непрерывная функция
и: G R, график которой слабо инвариантен относительно уравне-
ния (2) (синонимы: график которой инвариантен относительно потока (2);
в графике которой выживают (viable) траектории (2)), т. е. для любых
(to,#o) С gr и := {(ж,гл(ж)): х € G} и s € Rn существуют: число г > 0 и
липшицевые функции (ж(-),г(-)): [0,т] ^Gxl, такие, что (ж(0),^(0)) =
— (xo,u(xq)), z(t) = u(t,a:(t)), и уравнение (2) удовлетворяется при почти
всех t е [0, т].
Это определение в чем-то перекликается с упомянутыми выше идея-
ми дуальности, преобразованием Лежандра и некоторыми конструкциями
динамической оптимизации, введенными в работах Кларка, Флеминга, Кра-
совского, Кротова и Рокафеллара.
Среди результатов из теории дифференциальных игр, приведенных в
данной книге, упомянем конструкции субоптимальных стратегий, которые
подобны понятиям оптимальных стратегий, хорошо известным в рамках
классического метода динамического программирования в случае, когда
функция цены дифференциальной игры является гладкой. Различие состоит
в том, что градиент функции цены (который может не существовать) заме-
няется квазиградиентом. Понятие квазиградиента базируется на результатах
теории обобщенных решений УЧП первого порядка. Этот результат явля-
ется примером использования теории обобщенных решений и негладкого
анализа в теории дифференциальных игр.
10
Введение
В разделе приложение в конце книги собраны факты, необходимые для
изложения книги, в основном — из негладкого анализа и теории дифферен-
циальных включений. Упомянем, в частности, один новый критерий слабой
инвариантности (выживаемости), который, в отличие от хорошо известных
результатов, вместо конуса Булигана использует его выпуклую оболочку.
В приложении мы также формулируем и доказываем одно свойство
субдифференциала, которое является существенным в исследованиях ми-
нимаксных решений. Заметим, что это свойство может быть рассмотрено
как еще один пример, отражающий взаимное влияние исследований в те-
ории дифференциальных игр, теории УЧП первого порядка и негладкого
анализа. Результат, близкий к этому свойству, был получен впервые в рабо-
те [84], которая относится к области теории дифференциальных игр (лем-
ма 4.3 была доказана В. Н. Ушаковым). Далее этот результат был развит в
статьях [205, 196] в связи с исследованиями минимаксных решений. Позже
статья [196] оказалась подлинным стимулом появления важного результата
негладкого анализа для средних значений — неравенств, полученных недав-
но Ф. Кларком и Ю. С. Ледяевым [49, 48]. Их результат является «много-
мерным» обобщением классической теоремы о среднем для «негладкой», к
тому же, функции.
Книга содержит также краткие библиографические комментарии. Они
касаются работ, наиболее тесно связанных с результатами, представленны-
ми в монографии. Мы не претендуем на полноту этих комментариев.
Настоящая книга может быть рассмотрена, как продолжение и развитие
предыдущей монографии автора «Минимаксные неравенства и уравнения
Гамильтона-Якоби», вышедшей на русском языке в издательстве «Нау-
ка» (Москва, 1991 г.). Данная книга содержит также некоторые результаты
из совместной монографии Н. Н. Красовского и автора «Game-Theoretical
Control Problems», Springer, New York, 1988.
Я хотел бы выразить глубокую признательность моему учителю
Н. Н. Красовскому. Его внимание и значимые советы были существенны-
ми для моих исследований и очень полезными в работе над этой книгой.
Я признателен также А. Б. Куржанскому за его благожелательное отно-
шение к моим результатам и его предложение подготовить эту книгу для
публикации в издательстве Birkhauser.
С. А. Брыкалов внимательно прочел всю рукопись, и его математиче-
ские замечания были очень полезны для более ясного представления ре-
зультатов. Он перевел первую главу на английский язык и корректировал
многочисленные ошибки при переводе других разделов книги. Я очень при-
знателен ему за его интенсивную работу.
Некоторые результаты этой книги были получены в статьях, напи-
санных совместно с Н. Н. Субботиной, А. М. Тарасьевым, В. Н. Ушаковым.
Я консультировался с ними во время работы над этой книгой, и эти обсу-
Введение
11
ждения были существенными для меня. Я благодарен А. Г. Иванову за его
помощь при подготовке графических иллюстраций.
Обозначения
Ниже приняты следующие обозначения:
Rn — n-мерное евклидово пространство с элементами х =	,..., хп);
п
(х,у) = YlXiyi
i=l
— скалярное произведение векторов ж, у е Rn; ||ж|| = (ж, ж)1/2 — евклидова
норма вектора ж € Rn.
Замыкание, граница и выпуклая оболочка множества G С Rn обозна-
чаются через G, 3G и со G соответственно;
В(?/; г) = {.т 6	: ||ж — у\\ г}
— евклидов шар радиуса г с центром в точке у; символ Вг обозначает
шар {ж € Rn: ||ж|| г}. Мы обозначаем отрезки прямой R1, соответствен-
но, — открытый, замкнутый и полуоткрытые через (а, 6), [а, Ь], (а, 6], [а, Ь).
Мы также используем обозначение = [0, оо).
Для вещественной функции э ж н-» Л (ж) е R и множества X с
мы обозначим через Arg min h(x) и Arg max h(x) множества минимизиру-
хех	хех
ющих и максимизирующих элементов, т. е.
Arg ттЛ(ж) = {жо € X: ^(жо)	/г(ж) Уж е X},
хЕХ
Arg тах/г(ж) = {жо € X: ^(жо) /г(ж)Уж е X}.
хех
Символами sup/z(X) и inf Л(Х) обозначены
sup/z(X) = sup Л (ж), inf/i(X) = inf h(x).
хЕХ	хЕХ
Символы gr и (соответственно, epi и, hypo и) обозначают график (со-
ответственно, надграфик и подграфик) функции и: G ь-> R. А именно,
gr и = {(ж, z): z = га(ж), ж € G},
epi и = {(ж, z): z и(х), х € G},
hypo и — {(ж, z): z < и(х), ж е G}.
Работа выполнена при финансовой поддержке Российского Фонда фун-
даментальных исследований, грант №93-011-16032.
Глава I
Обобщенные характеристики уравнений
в частных производных первого порядка
1. Классический метод характеристик
В данной главе мы вводим понятие минимаксного решения уравне-
ния в частных производных первого порядка. Предлагаемое определение
базируется на свойстве слабой инвариантности графика обобщенного ре-
шения относительно системы дифференциальных включений, которые мы
будем называть характеристическими включениями. Это свойство может
быть описано с помощью различных по форме критериев, которые сфор-
мулированы ниже в параграфах 2 и 3. Эквивалентность этих критериев и
эквивалентность минимаксных и вязкостных решений доказаны в парагра-
фе 4.
В силу того, что предлагаемый в этой книге подход можно рассмат-
ривать как обобщение и развитие классического метода характеристик, в
данном параграфе мы напомним факты, связанные с этим классическим
методом, которые будут стартовой точкой и смогут подсказать разумные
идеи, необходимые для определения минимаксного решения. Мы приведем
здесь схему построения классического решения в задаче Коши с помощью
метода характеристик. Рассмотрим также пример, в котором классический
метод дает локальное решение, непродолжимое на все пространство. Этот
пример иллюстрирует необходимость рассмотрения обобщенных (неглад-
ких) решений.
1.1. Задача Коши для уравнений в частных производных первого
порядка
Напомним постановку задачи Коши в классической теории диффе-
ренциальных уравнений в частных производных первого порядка. В (п +
+ 1)-мерном пространстве переменных (ж, z) мы фиксируем (п — 1)-мерное
начальное многообразие Со, заданное параметрически с помощью уравне-
ний
х = Хо(у), Z = z0(y), у е R”-1,
1. Классический метод характеристик
13
где у н-> хо(у): Л н-> Rn и у ь-> zo(y): R™-1 н-> R — непрерывно
дифференцируемые функции. Для простоты изложения мы предполагаем,
что многообразие Со взаимнооднозначно проектируется на евклидово про-
странство Rn-1. В общем случае многообразие Со снабжено системой ло-
кальных координат (атласом карт).
Задача Коши формулируется следующим образом: найти непрерывно
дифференцируемую функцию х н-> и(х\ определенную на открытом мно-
жестве X С Rn, такую, что
F(x,u(x\Du(x)) = 0, х е X,	(1.1)
{(ж,и(яг)): х & X} D Са = {(.т0(у), г0(?/)): У б R”-1}.	(1.2)
Здесь F(x. z, s) — вещественная функция, определенная на Rn х R х Rn.
Напомним, что
Du [ди/дх\,..., ди/дхп)
— градиент функции и.
При использовании метода характеристик, мы предполагаем, что
в Rn х R х Rn существуют непрерывные производные
DXF := (dF/dxu ..., dF/dxn), DZF := dFldz.
DSF := (dF/ds^ ..., dF/dsn).
Заметим, что основные результаты для обобщенных решений будут
получены при существенно более слабых предположениях об уравнении и
начальном условии.
1.2.	Характеристическая система
Один из основных результатов классической теории уравнений в част-
ных производных первого порядка утверждает, что при определенных пред-
положениях решение задачи Коши (1.1), (1.2) может быть сведено к инте-
грированию характеристической системы обыкновенных дифференциаль-
ных уравнений
х = DsF(xy г, $),
s = —DxF(x,z,s) — DzF{x^z^s)s^	(1.3)
z = (s, DsF(x, z, s)}.
Заметим, что функция F является интегралом системы (1.3), т. е. она
сохраняет постоянное значение F(x(t), z(t), s(t)) = const вдоль любого
решения t i—> (x(t), z(t), системы (1.3).
14
Глава I
Предполагается, что для любого значения параметра у е R71”1 суще-
ствует единственный вектор s = so(y), удовлетворяющий системе п урав-
нений
F(^o(i/),^o(?/),5o(i/)) = О,
dz^(y) /дх^у) \	-----
"И ’ •el'’‘~L	(L4)
Более того, функция у ь-> 8о(у): Rn-1 Rn предполагается достаточно
гладкой.
Рассмотрим решения (#(£), z(t), s(t)) системы (1.3), которые удовле-
творяют условию
Gr(0),z(0),s(0)) = (xo(y),zQ{y),so{y)).
Обозначим эти решения, зависящие от параметра у е R71”1, через
(x(t, у), z(t, y)ys(t, у)). Отображение
(t,y)	(x(t,y).z(t,y),s(t,y))
определено на некотором открытом множестве D С Rn, которое содержит
гиперплоскость {(0,1/): у е Rn-1}.
Предположения, используемые в методе характеристик, влекут, что
функции х и z дважды непрерывно дифференцируемы на множестве D,
а отображение (t,у) н-» x(t,у): D X взаимно однозначно, так что мы
можем ввести функцию
и(х) = z{t(x)^(x))^ xtX,	(1.5)
где X := {x(t,y): (t,y) 6 D}, x t-» (т(я), £(#)): X i-> D — обратное
отображение к отображению х.
Функция и(х\ сконструированная таким образом, является решением
задачи (1.1), (1.2). Доказательство этого факта приведено в приложении,
в параграфе А1, где также указаны книги, которые содержат подробное
изложение классического метода характеристик.
Напомним следующий геометрический факт. Рассмотрим
gr и := {(х,и(х)): х G X},
т. е. график сконструированной функции и(х). Из приведенных построе-
ний видно, что для любой точки (#*,£*) G gr и существует единственное
значение параметра у*, такое, что траектория (#(•, 1/* ),?(•, 1/*)) проходит че-
рез точку (x*,z*). Таким образом, можно сказать, что график функции и
1. Классический метод характеристик
15
составлен с помощью параметризованного семейства графиков траекто-
рий
Хорошо известно, что во многих приложениях, связанных с задачей
Коши и другими краевыми задачами для уравнений в частных производ-
ных первого порядка, классического решения не существует. Как правило,
метод характеристик не приложим к таким задачам, потому что отображе-
ние (t, у) x(t, у) не является взаимнооднозначным (характеристики пере-
секаются). Имеются различные подходы к определению и методам исследо-
вания обобщенных решений. Конструкции, предложенные в данной книге
для определения обобщенного (минимаксного) решения, могут рассматри-
ваться как обобщение и развитие классического метода характеристик.
1.3.	Задача Коши для уравнений Гамильтона-Якоби. Метод
характеристик
Рассмотрим следующую задачу: найти непрерывную функцию u(t, ж),
определенную в области G := [0,0] х Rn, непрерывно дифференцируемую
в открытой области G := (0,0) х Rn, удовлетворяющую уравнению
^ + H(t,x,u,Dxu) = 0, (t,x)eG	(1.6)
и условию
и(0,х) — сг(ж), х € Rn.	(1.7)
Здесь
Dxu = (ди/дх^ ..., ди/дхп)
— градиент функции и относительно переменной х. Функция H(t, х, z,s)
называется гамильтонианом. Она определена и непрерывна для (t, ж, z, s) €
G [0,0] х х R х Rn. Более того, в настоящем параграфе функции Н и ст
предполагаются дважды непрерывно дифференцируемыми. Эти предполо-
жения используются в классическом методе характеристик.
Заметим, что с недавних пор термин «уравнение Гамильтона-Якоби»
часто используется для всех уравнений в частных производных первого
порядка. Мы подразумеваем под уравнением Гамильтона-Якоби уравнение
вида (1.6). Отметим также, что решение задачи Коши должно удовлетворять
начальному условию
и(0, х) = <т(ж), х € Rn.
Мы в данной книге предполагаем, что задано терминальное условие (1.7)
(что более удобно для предлагаемых конструкций).
16
Глава I
Напоминаем, что, согласно методу характеристик, классическое реше-
ние задачи (1.6), (1.7) может быть сконструировано следующим образом.
Рассмотрим систему обыкновенных дифференциальных уравнений
х = DsH(x, t) z, s),
s = —DxH(x, z, s) — DzH(x, t, z, s)s,	(1.8)
z — (s, DsH(x, г, s)) — Hix, г, s).
Здесь x e Rn, s e Rn, z e R, т. e. система (1.8) состоит из 2n + 1 уравне-
ний. Эта система называется характеристической системой для уравнения
Гамильтона-Якоби. Для задачи Коши (1.6), (1.7) решения характеристиче-
ской системы должны удовлетворять при t = в условиям
x(ff)=y, s(ff) = Da(y), z(ff) =	(1.9)
где у е Rn — значение параметра.
Пусть
11-> (J(£,^),s(t, ?/),?(£,?/)): [0,0] и-> Rn х Rn х R
— такое решение характеристической системы (1.8), которое удовлетворяет
условию (1.9).
Основным предположением, при котором классический метод характе-
ристик применим для конструирования решений задачи (1.6), (1.7), является
предположение о том, что отображение у x(t, у) взаимно однозначно. Та-
ким образом, предполагается, что существует достаточно гладкая функция
(t, X) ьч- y(t,x),
такая, что
x(t,y(t,x)) = х, \/(t,x) Е [0,0] х Rn.
Если это предположение выполняется, то функция
u(t, х) =z(t,y(t)X))) (t,x) Е [0,0] хГ	(1-Ю)
является решением задачи (1.6), (1.7) (см. приложение, параграф А1, содер-
жащий доказательство классического метода характеристик).
Однако указанное предположение, как правило, не выполняется. Ни-
же, в простом примере, отображение у н-> x(t,y) взаимнооднозначно
для £, близких к 0, но это свойство не выполняется для достаточно боль-
ших 0 — t.
1. Классический метод характеристик
17
1.4. Пример
Пусть
х, z^ s) = д/1 + s2, сг(ж) =	,
О t 0 = 2, х е R, s е R. Таким образом, рассмотрим следующую
задачу Коши
t + \/1 + (t)2 = “- ”М = Т' <1Л1’
Характеристическая система (1.8) для этой задачи имеет вид
X = ——===, 3 = 0, Z — .......; ..1..
л/1 + s2	л/1 + я2
В силу (1.9), решения рассматриваемой системы должны удовлетворять
краевым условиям
у2
х(0)=У,	8(0) = у, z(0) = ~,
где у е R — параметр. Следовательно, решения характеристической систе-
мы с указанными краевыми условиями описываются формулами
x(t,y) - у +
(t - 2)7/
д/1 +у2’
V
8(^У)=У, z(t,y) = -^
(t-2) .
д/1 + У2
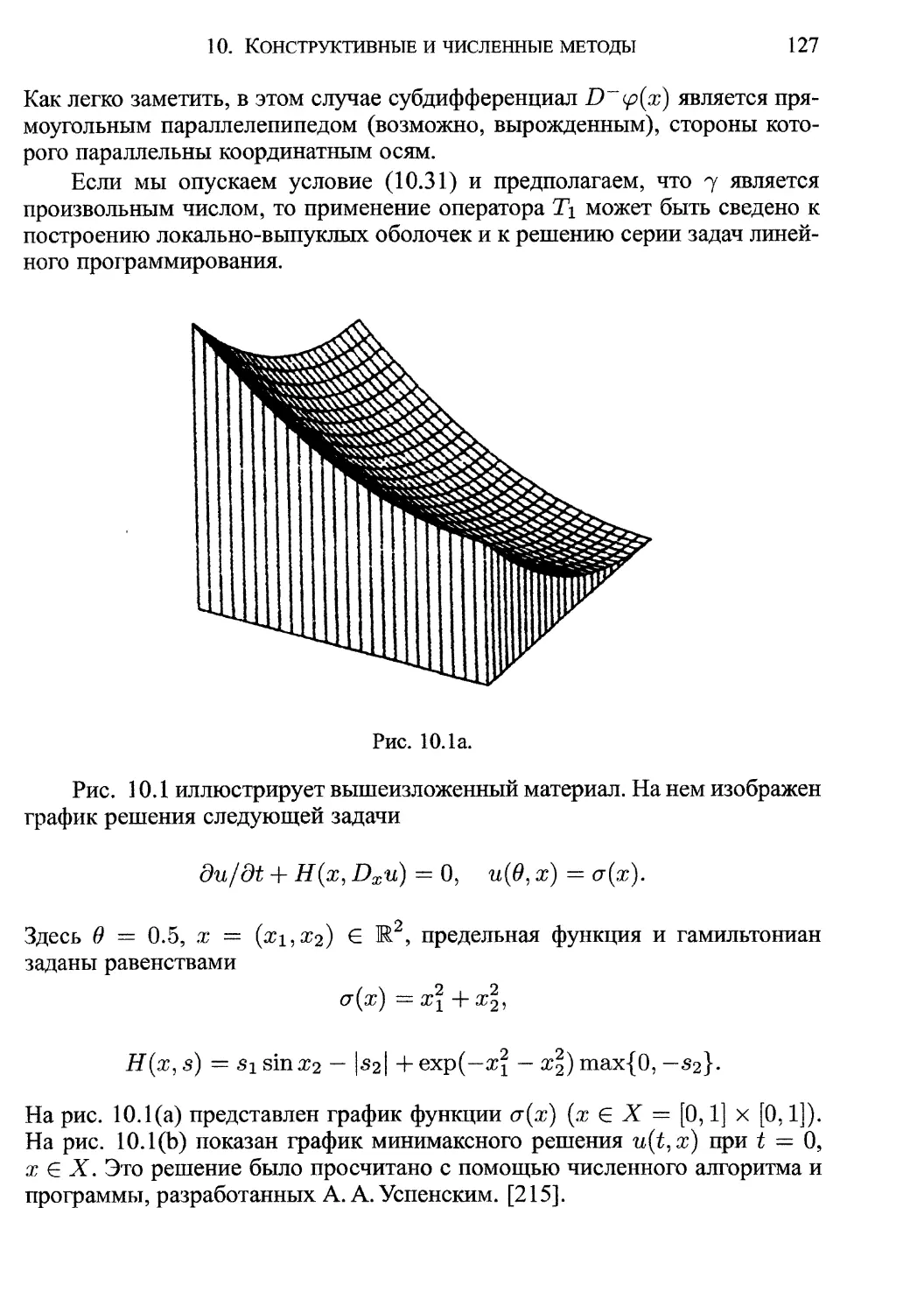
На рис. 1.1 изображены характеристики t —* x(t, у) для значений пара-
метра yi — —1.9 + i8, i Е 0,30, 8 = 1.9/15.
Видно, что эти характеристики не пересекаются при 1 < t 2. В об-
ласти D = {(t,x): 1 < t С 2, х Е R} уравнение х = x(t,y) имеет един-
ственное решение y(t.x). Функция u(t, х) = z(t,y(t,x)) непрерывно диф-
ференцируема в области D. В соответствии с методом характеристик, эта
функция является локальным классическим решением задачи Коши (1.11).
На рис. 1.2 изображена поверхность (ласточкин хвост), описываемая
параметрическими равенствами
х = x,(t,y) :=у +
(t ~ 2)у
д/1 + У2
Z = z(t,y)
У2
2	д/1 + у2
(1-12)
(1-13)
18
, а ЧвСТг
ep^oCTlt filtc-1.2
Ре^£^е^
^Ия * or
& 9^еГс;
гт^ lcJ
^So?i'
2. Характеристические включения
19
является самопересекающейся в [0,1) х R. Отметим, что верхняя часть
(верхняя огибающая) этой поверхности совпадает с графиком обобщен-
ного (минимаксного) решения, определенного ниже в пунктах 4.4, 6.3.
Как видно из рис. 1.2, минимаксное решение u(t,x) недифференцируе-
мо при х = 0, t е [0,1). Известно (см. пункт 4.7 ниже), что классическое
решение (если оно существует) совпадает с минимаксным. В рассматрива-
емом примере минимаксное решение является негладким. Таким образом,
глобального классического решения в задаче (1.11) не существует.
Это геометрическое описание соответствует следующей формальной
конструкции функции u(t, х). Обозначим через Y(t, х) множество решений
уравнения (1.12) (заметим, что в данном примере множество Y(tbx) может
содержать от одного до трех элементов). Определим функцию и с помощью
равенства
u(t, х) — max v),	(1.14)
y€Y(t,x)
где величина z(t,y) определяется из (1.13). Эта конструкция обосновыва-
ется в пункте 10.4.
В пункте 10.1 будет показано, что минимаксное решение задачи (1.11)
можно также описать с помощью формулы Хопфа
u(i, х) = max[rrs + (2 — t)\/l + s2 — s2/2].	(1.15)
Нетрудно видеть, что формулы (1.14)и(1.15) описывают одну и ту же функ-
цию. Действительно, пусть у — значение параметра з, которое доставляет
максимум в (1.15). Как известно, необходимым условием, которому долж-
но удовлетворять такое значение у, является равенство нулю производной
по s у функции, стоящей в квадратных скобках в формуле (1.15). Таким
образом, максимизирующее значение параметра у удовлетворяет (1.12). Ра-
венство (1.13) может быть получено подстановкой (1.12) в выражение в
квадратных скобках. Итак мы видим, что максимум в (1.15) равен вели-
чине, определяемой формулой (1.14).
2.	Характеристические включения
Как было сказано выше, существенным свойством обобщенного (ми-
нимаксного) решения является инвариантность его графика по отношению
к семейству дифференциальных включений. Мы назовем эти включения
характеристическими. В данном параграфе мы определим понятия характе-
ристических включений и минимаксных решений. Будет показана совмести-
мость классических и минимаксных решений. Мы определим свойства, ко-
торые описывают характеристические включения для заданного уравнения
20
Глава I
в частных производных (УЧП) первого порядка. Эти свойства определяют
характеристическое включение не единственным образом, так что любое из
таких включений может быть использовано при определении минимаксного
решения. Это дает нам возможность рассматривать понятие минимаксного
решения с различных точек зрения. Эквивалентность различных определе-
ний будет доказана в параграфе 4.
2.1.	Основные предположения
Рассмотрим следующее уравнение в частных производных первого по-
рядка
F(x,u(x),Du(x)) =0, х е G С Rn,	(2.1)
где G — открытое множество в Rn. Мы предполагаем, что функция
(ж, z, <§) н-> F(x, z, s): G x R x Rn i—> R непрерывна и удовлетворяет усло-
вию Липшица по переменной s
\F(x, z, s') - F(x, z, s")l	z)||s' - s"|| Vs', s" E Rn, (2.2)
где функция p(x. z) непрерывна на G x R. Предполагается, что функ-
ция z F(x, z, s) — невозрастающая, т. e.
F(x, s) > F(x, z", s) V /	z”, (x, s)EG^n. (2.3)
Предположение (2.2) позволяет нам упростить определение минимак-
сного решения, но оно может быть ослаблено (см. пункт 4.11 ниже). Пред-
положение (2.3) применяется при доказательстве различных форм опреде-
ления минимаксного и вязкостного решений, оно используется также при
доказательстве базовых теорем существования и единственности. Заметим,
что это условие выполняется в большинстве проблем, возникающих в тео-
рии оптимального управления и дифференциальных играх.
2.2.	Определение
Функция и: G R называется минимаксным решением уравне-
ния (2.1), если для него выполняется следующее условие’, для любых точ-
ки (#о, ^о) £ gr и := {(х, и(х)): х 6 G} и вектора s Е Rn существуют чис-
ло г >0 и липшицевая функция (ж(-), z(-)): [0, т] G х R такие, что
(ж(0), z(0)) = (x$,zq), z(t) = u(x(t)) для всех t Е [0,т], и справедливо
z(t) = (x(t), s) — F(x(t), z(t), s)	(2.4)
при почти всех t E [0, т].
2. Характеристические включения
21
Как было сказано выше, минимаксное решение может быть определено
в различных формах. Приведенное определение 2.2 не требует никаких
предварительных построений, так что мы начнем с него.
Определение 2.2 — обобщение и развитие классического метода харак-
теристик. Напомним, что функция F является интегралом характеристи-
ческой системы (1.3). Более того, функция F равна нулю вдоль решений
этой системы. Таким образом, третье уравнение системы (1.3) может быть
переписано как
z — {D3F(x, z, s), s) — F(x^ z, s).
Принимая во внимание уравнение x = DsF(x, z, s) (cm. (1.3)), мы заключа-
ем, что уравнение (2.4) совпадает с третьим уравнением характеристической
системы (1.3).
Ограничим здесь объяснения высказанной ремаркой. Ниже мы обсу-
дим различные аналогии в предлагаемом подходе и классическом методе
характеристик и различные аспекты их внутренней взаимосвязи.
2.3.	Характеристические дифференциальные включения
Доказательства теорем существования и единственности минимаксных
решений базируются на свойстве слабой инвариантности (выживаемости)
графиков этих решений относительно характеристических дифференциаль-
ных включений, определяемых следующим образом.
Пусть
E^x.z.s) := Ш.д) € Rn xl: ||/||	p(x,z), д = (f,s)-F(x,z,s)} (2.5)
для (x,z,s) е G х R х Rn. Рассмотрим дифференциальное включение
(±(t), i(t)) е Е(х(€), z(t\ s),	(2.6)
где s — вектор в Rn. Это дифференциальное включение (2.6) может быть
переписано в виде системы
||±||	p(x,z),
z = (±, s) — F(x, z, s).	(2.7)
Ниже в параграфе 4 будет показано, что определение 2.2 эквивалентно
следующему определению.
Минимаксное решение уравнения (2.1) определяется как непрерывная
функция и: G ь-> R, которая слабо инвариантна относительно дифференци-
альных включений (2.6), т. е. такая функция, что для всех s е Rn и xq € G
22
Глава!
существуют число т > 0 и траектория (#(•), z(-)): [0,т] н» GxR дифферен-
циального включения (2.6), которые удовлетворяют соотношениям ж(0) =
= xq, z(t) = для всех t € [0, т].
Напомним, что множество W С называется слабо инвариантным
по отношению к дифференциальному включению
£(*) е £7(y(*)) С Rm,	(2.8)
если для произвольной точки уо G W существуют число т > 0 и траек-
тория t *-> y(t) дифференциального включения (2.8), такая, что ?/(0) = у о
и y(t) е W для всех t е [0, т]. Такая траектория называется выживаю-
щей во множестве W. Если упомянутое условие выполняется, то говорят,
что множество W является множеством выживаемости. Слабо инвариант-
ные множества и связанные с ними задачи управления рассматривались
многими авторами (см. приложение, параграф А8, где приведены ссылки и
результаты теории слабо инвариантных множеств).
Таким образом, график минимаксного решения слабо инвариантен от-
носительно дифференциального включения (2.6). Заметим, что рассмотрен-
ное определение может быть «спроецировано» на соответствующее свой-
ство классического решения.
Напомним (см. пункт 1.2), что классическое решение задачи Коши
для уравнения (2.1) было определено параметрическими уравнениями х =
= x(t, у), и = z(t, у). График функции и сформирован с помощью парамет-
рического семейства траекторий (#(•,?/), ?(•, у)).
Сравним системы (2.7) и (1.3). Первое уравнение
х = DsF(x, z, s)
характеристической системы (1.3) соответствует неравенству
11*11
в системе (2.7). Как было отмечено выше, третье уравнение
z = (DsF(x,z,s))S)
системы (1.3) эквивалентно уравнению
z = (±, s) — F(x, z, s).
Второе уравнение системы (1.3)
s = —DxF(xy г, s) — DzF(x, z, s)s
2. Характеристические включения
23
не имеет аналогичного составляющего в системе (2.7). Это может быть
отнесено за счет того факта, что в классическом методе характеристик пере-
менная s(t) совпадает с Du(x(t)), градиентом функции и, который вычисля-
ется вдоль характеристики x(t). Минимаксное решение может быть недиф-
ференцируемым, поэтому система (2.7) не содержит никакого дифференци-
ального уравнения или неравенства для s. Вместо этого предполагается, что
график минимаксного решения слабо инвариантен относительно (2.7) при
любом выборе параметра s. Наконец, вместо регулярного семейства траек-
торий, покрывающих график классического решения и проектирующегося
на семейство непересекающихся характеристик, мы рассматриваем здесь
те траектории дифференциального включения (2.7), которые выживают во
множестве gr и. Эти траектории могут благополучно пересекаться.
Ниже мы называем дифференциальные включения вида (2.5), (2.6) ха-
рактеристическими. Траектории (ж(£),г(£)) этих включений, выживающие
во множестве gr и, называются обобщенными характеристиками. Заметим,
что это отклонение от принятой терминологии, следуя которой, характе-
ристика— это функция t и-» x(t), которая принимает значения только в
фазовом пространстве.
2.4.	Совместимость минимаксного и классического решений
Проверим совместимость определения минимаксного решения с поня-
тием классического решения. Отметим прежде всего, что
Е(х, z,p) Q Е(х, z,q) / 0
(2.9)
для всех (ж, z,p, q) е G х R х Rn х Rn. Действительно, при р ф q это
пересечение содержит элемент вида
А := (р ~ Я)
Е(х, г, р) — F(x, z, q)
Ир - я112
9* =	- F(x,z,p) =	- F{x,z,q).
Пусть и — классическое решение уравнения (2.1), т. е. функция и
непрерывно дифференцируема и удовлетворяет уравнению (2.1) всюду в
области определения. Покажем, что эта функция является минимаксным
решением этого уравнения. Выберем произвольно xq е G, s е Rn. Ис-
пользуя (2.9), можно проверить, что существуют число т > 0 и реше-
ние t н-» (x(t). z(t)): [0, т] н-> G х R дифференциального включения
(±, z) е Е(х, и(х), Du(x)) П Е(х, и(х), s),	(2.10)
24
Глава!
которое удовлетворяет начальному условию (x(0),z(0)) = (хо,и(хо))-
Из (2.5) и уравнения F(x, и(х), Du(x)) = 0 следует, что
/ч ,тл , /чч / чч du(x(t))
z(t) = {Du(x(t)),x(t)) = ———.
Принимая во внимание начальное условие z(0) = и(ж(0)), мы получим,
что z(t) = и(х(1)). В силу (2.10), (ж(£),г(£)) является решением диффе-
ренциального включения (2.6). Таким образом, доказано, что классическое
решение является также и минимаксным решением.
Обратное утверждение также верно: если минимаксное решение урав-
нения (2.1) дифференцируемо, то оно является и классическим решени-
ем этого уравнения. Действительно, пусть и — минимаксное решение,
дифференцируемое в точке xq е G. Предположим, что s = Du(xq). Из
определения 2.2 следует, что существует абсолютно непрерывная функ-
ция 1i-> (x(t), z(f)): [0, т] м G х R, такая, что
и(х(8У) — z(5) = u(xq) + ($, ж(5) — жо) — ^(жо, гл(жо), з)8 + «1(5)5,
где «1(5) —* 0 при 5 X 0. С другой стороны, дифференцируемость функции
и в точке жо и равенство s — Du(xq) влекут
г/(ж(5)) = z(3) = и(жо) + («,ж(5) — жо) +«2(5)5, lim«2(5) = 0.
Следовательно, /Джо, 1Джо), Ри(жо)) = «1(5) — «2(5). Переходя к пре-
делу при 5 J, 0, получаем ожидаемое равенство К(жд, гх(жо), Du(xq)) = 0.
Заметим, что доказательство этого равенства использует только диф-
ференцируемость функции и в точке жо. Тем самым доказано, что мини-
максное решение удовлетворяет уравнению (2.1) в каждой точке ж, где оно
дифференцируемо.
Другое доказательство совместности минимаксного и классического
решений получено в пункте 4.7 как прямое следствие определения мини-
максного решения в инфинитезимальной форме с помощью контингентного
конуса к графику минимаксного решения.
2.5.	Допустимые многозначные отображения Е
Заметим, что многозначное отображение Е вида (2.5) не является един-
ственным из тех, что могут быть использованы в качестве характеристи-
ческих включений. Для некоторых типов УЧП 1-го порядка удобнее вво-
дить характеристические дифференциальные включения специального ви-
да, принимая во внимание свойства этих уравнений. Рассмотрим условия,
которым должны удовлетворять допустимые многозначные отображения.
2. Характеристические включения
25
Пусть Ф — некоторое непустое множество. Мы назовем многозначное
отображение
G х R х Ф э (ж, z, ф) Е(х, z, VO С х R
допустимым, если оно удовлетворяет следующим условиям:
(i) для всех (ж, z, V>) £ G х Rх Ф множество Е(х, z, ф) выпукло и компактно
в Г х R;
(ii)	для каждого ф 6 Ф многозначное отображение G х R э (ж, z)
н-> Е(х, z, ф) полунепрерывно сверху;
(Ш+) при любых ф Е Ф, х Е G, z' С z" и (f,gf) Е E(x,z' ,ф) существует
такой элемент (J,g") Е Е(х, z" ^ф), что д" д';
(Ш) при любых ф Е Ф, х Е G, z' < z" и (/, р") е Е(х, z", ф) существует
такой элемент (/, д') Е Е(х, z\ ф), что д' < д";
(iv+) для любых (ж, z, s) Е G х R х Rn найдется ф° Е Ф такое, что
F(x,z,s) = s) - д: (J,д) е Е(х, z, 0°)}
>min{(/,s) — д: (f,g) ё E(x,z,ip)}
при всех ф Е Ф;
(iv~) для любых (ж, z, s) Е G х R х Rn найдется фо Е Ф такое, что
F(x,z,s) =max{(/,s) - д: (f,g) € E(x,z,^0)}
max{(/,s) -д: (f,g) & Е(х,г,-ф)}
при всех ф Е Ф.
Очевидно, что многозначное отображение Е вида (2.5), где Ф = Rn,
удовлетворяет предположениям (i) and (ii). Условие (2.3) влечет, что это
многозначное отображение удовлетворяет (iii+) и (iii~). Нетрудно показать,
что многозначное отображение Е вида (2.5) удовлетворяет (iv+).
Действительно,
maxmin{(/,s) - д: (f,g) е E(x,z,p)}
> min{(/,s) -д: (f,g) G E(x,z,s)} = F(x,z,s).
26
Глава!
С другой стороны, (2.9) влечет, что
max inin{ (/, .s) ~9-	^E(x,z,p)}
рЕ^п
< тах{(/, s} — д: (J\g) € Е(х, z,p) А Е(х, z, 5)} = F(x, z, s).
pERn
Равенство (iv_) может быть установлено подобным образом.
В параграфе 4 будет показано, что минимаксное решение может быть
определено как непрерывная функция и: G н-> R, такая, что для каждо-
го гр 6 Ф ее график слабо инвариантен относительно дифференциального
включения
(±(t),i(t)) е E(x(t),z(t)^,	(2.11)
где Е — произвольное многозначное отображение с указанными выше свой-
ствами. Это определение эквивалентно определению 2.2.
2.6.	Минимаксные решения линейных уравнений
Рассмотрим линейное УЧП вида
(/(ж), Du(x)} ~ д(х, и(х)) = 0.	(2.12)
Мы предполагаем, что функции G Э х н-> /(ж) 6 Rn, G х 1 э (:гл) м
д(х, z) е R удовлетворяют условию Липшица и функция д(х, •) — неубы-
вающая.
Пусть
z, V’) = {(/(ж), д(х, Z))}.	(2.13)
Множество Ф параметров гр здесь может быть определено произвольно, т. к.
на самом деле Е(х,г,гр) не зависит от параметра гр. В рассматриваемом
случае F(z,z,s) = (f(x),s) — g(x,z). Легко показать, что многозначное
отображение Е вида (2.13) удовлетворяет условиям (i)-(iv), перечисленным
в пункте 2.5. Характеристическое включение (2.11) превращается в систему
обыкновенных дифференциальных уравнений
x = f(x), z = g{x,z).
(2.14)
Таким образом, в силу замечания из пункта 2.5, минимаксное реше-
ние уравнения (2.12) может быть определено как непрерывная функ-
ция Сэ ж ф) € R, график которой инвариантен относительно систе-
мы (2.14), т. е. при произвольном выборе точки х$ € G равенство z(t) ~
= u{x(t)) имеет место при 0 < t < т, где (ж(-),^(-)): [0,т] мКпх1-
траектория системы (2.14) с начальными условиями ж(0) = xq, z(Q) —
= u(xq), т — некоторое положительное число.
3. Верхние и нижние полунепрерывные решения
27
Данное определение эквивалентно определению 2.2, а также другим
упомянутым выше определениям минимаксного решения. Эта эквивалент-
ность будет следовать из теоремы 4.6. Заметим, что данное определение
согласуется с классической теорией линейных УЧП 1-го порядка.
3.	Верхние и нижние полунепрерывные решения
Минимаксное решение может быть также определено как функция, ко-
торая одновременно является верхним и нижним решением уравнения (2.1).
Эти понятия являются существенными в теории обобщенных (минимакс-
ных и вязкостных) решений УЧП 1-го порядка. В частности, единственность
обобщенного решения проверяется с помощью доказательства справедли-
вости неравенства и v, где и и v — произвольные верхнее и нижнее
решения соответственно. Этот параграф посвящен определениям верхних
и нижних решений, которые базируются на свойствах слабой инвариант-
ности надграфика (соответственно подграфика) верхнего (соответственно
нижнего) решения относительно характеристических включений.
3.1.	Определение
Верхним (соответственно нижним) минимаксным решением урав-
нения (2.1) называется полунепрерывная снизу (соответственно сверху)
функция и: G R, такая, что для любых (x$,zq) Е epi и (соответ-
ственно, для любых (жо, zo) 6 hypo и) и любых s 6 существуют лип-
шицевые функции (ж(-), z(-)): [0, г] G х R, определенные на интерва-
ле [0, г] (г — положительно), которые удовлетворяют начальному усло-
вию (а:(0),^(0)) = (xq^zq) и неравенству (3.1) (соответственно неравен-
ству (3.2))
t
z(t) = zo + f[(x(£),s} - К(Ж),Ж),з)]< > u(x(t)),	(3.1)
О
t
z(t) =z0 + J[(Ж), s) - ^(Ж), Ж), s)] d( u(x(t))	(3.2)
0
для всех t e [0, т].
Напомним, что символы epit/, := {(x,z): x G G, z^ u(x)} и
hypo и := {(x,z): x 6 G, z u(x)} обозначают надграфик и подграфик
функции и. Рассмотрим также следующее определение.
28
Глава I
Верхнее (соответственно нижнее) минимаксное решение уравне-
ния (2.1) определяется также как полунепрерывная снизу (соответствен-
но, сверху) функция ш G н-> R, такая, что для всех xq е G, zq и(х$)
(соответственно zq ^(^о)) и всех s е Rn существуют число т > 0 и тра-
ектория (ж(-),г(-)): [0, т] G х R дифференциального включения (2.6),
которая удовлетворяет начальному условию (.т(0), z(0)) = (xq,zq) и нера-
венству z(t) u(x(t)) (соответственно неравенству z(t) u(x(t))) при
всех t е [0, т].
В силу последнего определения, верхнее минимаксное решение по-
нимается как полунепрерывная снизу функция и: G R, такая, что ее
надграфик слабо инвариантен относительно дифференциального включе-
ния (2.6) для любого значения параметра s 6 Rn. Аналогично, нижним
минимаксным решением называется полунепрерывная сверху функция и9
такая, что ее подграфик слабо инвариантен относительно дифференциаль-
ного включения (2.6).
Если некоторая функция и является верхним (нижним) решением в
смысле последнего определения, тогда она, очевидно, является верхним
(нижним) решением в смысле определения 3.1. Ниже, в теореме 4.3 будет
установлено и обратное заключение, так что эти два определения — экви-
валентны. В следующем параграфе мы дадим также определения верхнего
и нижнего решений, в которых используется аппарат негладкого анализа
(контингентные конуса, производные по направлениям, субдифференциалы
и супердифференциалы). В силу теоремы 4.3, все эти определения эквива-
лентны.
Минимаксное решение может быть определено как функция, которая
одновременно является верхним и нижним решением. Если рассматривае-
мые решения определены с помощью слабой инвариантности их графиков,
надграфиков и подграфиков по отношению к характеристическим включе-
ниям (2.6), тогда факт эквивалентности данных выше определений следует
из теоремы 3.2. Для других определений такое доказательство проводится
в параграфе 4.
Замечание. Пусть щ и U2 — верхние решения. Рассмотрим функ-
цию и = min{tzi, щ}. Отметим, что epi и = epi и± U epi U2- Из опреде-
лений, данных выше, немедленно следует, что эта функция и является
верхним решением. Аналогично, если и± и U2 — нижние решения, то функ-
ция и = max{tzi,tZ2} наследует это свойство, т.е. она является нижним
решением.
Нетрудно проверить, что справедливость подобного замечания может
быть установлена и в следующем, более общем случае: пусть I — непустое
множество, и для любого i € I функция щ является верхним (нижним)
решением.
3. Верхние и нижние полунепрерывные решения
29
Предположим, что нижняя огибающая и := inf щ (верхняя огибаю-
iEl
щая и := sup щ) является функцией, полунепрерывной снизу (сверху), и
iei
для любого х е G существует i* е I такое, что и(х) = Тогда
функция и является верхним (нижним) решением.
Можно также доказать дальнейшее обобщение, в котором предположе-
ние относительно полунепрерывности снизу (сверху) функции и опускает-
ся, и не требуется чтобы инфимум (супремум) по множеству I достигался
(смотри ниже утверждение 8.7).
3.2.	Теорема
График непрерывной функции и: G » К. слабо инвариантен относи-
тельно дифференциального включения (2.6) тогда и только тогда, когда
надграфик и подграфик этой функции слабо инвариантны относитель-
но (2.6).
Доказательство. Очевидно, что из слабой инвариантности графика и
следует слабая инвариантность надграфика и подграфика этой функции.
Докажем обратное утверждение: если надграфик и подграфик непре-
рывной функции слабо инвариантны относительно дифференциального
включения (2.6), то и график ее также слабо инвариантен относительно
этого дифференциального включения. Приведенное ниже доказательство
базируется на свойстве связности множеств достижимости для этого диф-
ференциального включения.
Пусть xq е G, zq = u{xq), s e Rn. Выберем число e > 0 такое, что
2?(.т0; с) := {х 6 Rn: Ца; — ж0|| s} С G. Предположим, что
В(^о; в) х [zq — г, zq 4- е],	:=	E(x,z^s),
h'= . “ax Vll/IP + ff2, T := f •
Напомним, что
E(x, z, s) := {(/,#) G Rn x R: \\f\\ p(x, z), g = [f, s} - F(x, z, $)}.
Пусть t* e [0,т], (ж*, z*) e B\ Обозначим через Sol (£*, ж*, г*, s) мно-
жество всех абсолютно непрерывных функций [t*,r] Э t (rr(t),^(i)) 6
е Rn х R, которые удовлетворяют дифференциальному включению
(±(£),i(t)) G Е(х(Ё)^(1)^8}
и начальному условию: (ж(^),г(^*)) = (a?*,z*).
30
Глава I
Параграф А7 в приложении содержит некоторые результаты теории
дифференциальных включений, из которых вытекает, в частности, что
Sol(0,£o,£o,s) / 0-
Из определения числа т следует, что
[0,т] х D W :=	t 6 [0, т], (ж(-),г(-)) G Sol (0, то, г0, §)}.
Пусть	G W, z* = и(х*), t* е [£*,т]. Из слабой инвариант-
ности надграфика функции и следует, что существует траектория
(ж+(-), Z+(-)) е Sol(t*,£*,Z*,s),
такая, что z+(t*)	и(х+(1*У). Аналогично, слабая инвариантность подгра-
фика влечет, что существует такая траектория
(ж”(-), ^"(-)) € Sol(£*,£*, z*,s),
для которой справедливо z~(t*)	Из того, что функция и непре-
рывна, а множество
{(x(t*\z(t*Y): (ж(-),г(-)) € Sol(t*,x*,z*,s)}
односвязно (см., например, [60]), получаем, что существует такая траекто-
рия
(ж(-), г(-)) е Sol (£*, х*. z*, s),
для которой z(t*) = и(х(1*У).
Выберем произвольно число 6 е (0,т). Положим ti := iS9 г 6 0, [т/5],
где [т/<5] означает наибольшее целое число, меньшее или равное т/8.
Для i = 0 мы имеем (£0,	^о) € W, zq = и(х0). Приведенные выше рас-
суждения доказывают существование траектории
е Sol(^o,^o,^0,s)5
такой, что
Для г = 1 мы получаем
3. Верхние и нижние полунепрерывные решения
31
Таким же образом доказывается, что существует траектория
для которой z^fa) = п(же2\^2))« Если мы продолжим этот процесс, шаг
за шагом, для i = 2,3,..., [т/5], то придем к заключению, что существует
такая траектория
(^(•),^(-)) е Sol (0,^о, г0, з),
для которой справедливо
z$(i6) = и(х$(г$)) г € 0, [т/<5].	(3.3)
Итак, для любого 5 G (0, т) существует такая траектория (ж<$ (•),£$(•))>
которая удовлетворяет равенствам (3.3). Рассмотрим последовательность
чисел которая стремится к нулю, и соответствующую последова-
тельность траекторий {(ж^(-),	(-))}1°- Как известно (см. параграф А7),
указанная последовательность траекторий содержит подпоследовательность,
сходящуюся к некоторой предельной траектории (ж(-). г(-))е Sol (0, х0. zq. з),
и для предельной траектории условие z(t) = u(z(ty) справедливо
при t е [(), г]. Таким образом, мы видим, что график функции и слабо ин-
вариантен относительно дифференциального включения (2.6). Теорема 3.2
доказана.
3.3.	Верхние и нижние характеристические дифференциальные
включения
Как уже было упомянуто в пункте 2.5, существует большая свобода
выбора многозначных отображений Е для характеристических включений,
участвующих в определении минимаксных решений. Подобная же ситуа-
ция имеет место и для верхних и нижних решений. Это обстоятельство
оказывается полезным во многих случаях. Оно делает возможным выбрать
дифференциальное включение, наиболее удобное для каждого конкретного
случая уравнения в частных производных первого порядка.
Рассмотрим следующее дифференциальное включение
(±(t),z(£)) е E+(x(t), z(t)^\	(3.4)
где Е+ — произвольное многозначное отображение, удовлетворяющее усло-
виям (i), (ii), (iii+), (iv+), определенным в пункте 2.5.
Ниже, в теореме 4.3, будет доказано, что верхнее решение урав-
нения (2.1) может быть определено, как полунепрерывная снизу функ-
ция и: G и-> R, такая, что для любого е Ф ее надграфик слабо инва-
риантен относительно дифференциального включения (3.4).
32
Глава I
Аналогично, нижнее решение может быть определено как полунепре-
рывная сверху функция и: G R, подграфик которой слабо инвариантен
относительно дифференциального включения
(i(Z),i(t)) G	(3.5)
для любого е Ф. Здесь Е~ — произвольное многозначное отображение,
обладающее свойствами (i), (ii), (iii“), (iv_).
Эти определения эквивалентны определению 3.1.
3.4.	Уравнения, выпуклые относительно производных
Рассмотрим характеристические включения для случая, когда функ-
ция F(#,z,s) выпукла относительно переменной s. Чтобы определить
верхние, нижние и минимаксные решения, можно использовать общие
определения, в частности, использовать характеристические включения ви-
да (2.5), (2.7). С другой стороны, выпуклость функции F(x, z. •) позволяет
ввести конструкции, более удобные для данного случая, и демонстрирует
некоторые связи с динамической оптимизацией.
Определим сопряженную функцию к функции Р(ж, z, •)
F*(x, z, f) := sup [</, s) - F(x, z, s)].
А также определим эффективное множество функции F*(ж, z, •) с помощью
соотношения
£>(ж, z) := dom F*(x, z, •) = {/ e : F*(x, z, f) < oc}.
Из условия Липшица (2.2) следует, что
sup 11/11 < p(x,z).
f€D(x,z)
Заметим, что множество Р(ж, z) выпукло. Предположим дополнительно,
что существует такая непрерывная действительная функция г(ж, z)9 для ко-
торой
Р*(ж, г, /) г(ж, г), V/ 6 D(x, z).
Считаем также, что функция г(ж,^) является неубывающей по перемен-
ной z.
Введем в рассмотрение множество
E~(x,z) = {(f,g): f G D(x,z), F*(x,z,f) g < r(x,z)}-
Это множество является частью надграфика функции Р*(ж, z, •), а неравен-
ство g^r(x, z) выделяет некоторое ограниченное множество в epi F* (х, z,-).
3. Верхние и нижние полунепрерывные решения
33
Покажем, что многозначное отображение (ж, г) Е~(х, z) удовлетво-
ряет условиям (i), (ii), (iii“), (iv~).
Действительно, функция F*(x,z,f) является верхней огибающей се-
мейства непрерывных функций. Следовательно, она является полунепре-
рывной сверху. Значит многозначное отображение (ж, г) н-» Е(х, z) полуне-
прерывно сверху. Из того, что функция F* (х, z, •) выпукла, следует, что мно-
жество Е~ (х, z) выпукло тоже. Условие монотонности влечет за собой, что
функция z н-> F*(rr, г, /) — неубывающая, а значит, Е~(х, z") С Е~(х, zf)
для z' z". Таким образом, многозначное отображение Е~ удовлетворяет
условию (iii“). Так как функция F(x,z, •) выпукла, то, вследствие извест-
ного факта выпуклого анализа, имеет место равенство
sup [(/, s) - F*(x, z, f)] - F(x, z, s).
f€Rn
Это равенство может быть переписано в следующем виде
max	— д] = F(x, z, s).
^д)еЕ-(Х,г)^	J
Так как в рассматриваемом случае многозначное отображение Е~ не зави-
сит от параметра то последнее равенство показывает, что многозначное
отображение Е~ удовлетворяет условию (iv~).
Итак, мы доказали, что многозначное отображение Е~ удовлетворяет
всем условиям (i), (ii), (iii-), (iv_). Следовательно, нижнее решение мо-
жет быть определено как полунепрерывная сверху функция и: G R,
надграфик которой слабо инвариантен относительно дифференциального
включения
(±, z) G Е~(х, z).	(3.6)
Для дифференциального включения (3.6) можно сформулировать зада-
чу динамической оптимизации таким образом, что функция оптимального
результата для нее совпадет с минимаксным решением следующей краевой
задачи
F(xfu,Du) — 0, х G G, и(х) = а (ж), х G 5G,	(3.7)
где 8G — это граница области G, а ст(х) — заданная краевая функция.
Опуская детали, опишем эту задачу следующим образом. Пусть траек-
тория (rr(£), z(t)) (0 t т) дифференциального включения (3.6) удовле-
творяет начальному условию rr(O) = xq G G и терминальному (конечному)
условию z(t) = <т(ж(т)). Здесь т — момент времени, в который впервые вы-
полняется условие х(т) G dG. На множестве траекторий, которые удовле-
творяют упомянутым краевым условиям, мы определим функционал вида
7(^(-),г(-)) := ^(0) = о-(^(т)) - [ z(t)dt.
О
34
Глава I
Пусть u(xq) — максимальное значение этого функционала на рассматривае-
мом множестве траекторий. Таким образом, определена функция G Э xq
«-> u(xq) G R, которая оказывается минимаксным (и вязкостным) решением
в задаче (3.7).
Отметим еще раз, что это описание является только схемой и некоторые
детали требуют дальнейших разъяснений. С другой стороны, множество
типичных краевых задач и задач Коши хорошо укладываются в эту схему
(они будут рассмотрены в последующих параграфах).
В предложенных конструкциях можно выбрать любую функцию г(ж, г),
которая удовлетворяет сделанным выше предположениям. Величина u(xq)
не зависит от выбора допустимой в этом смысле функции г (ж, г). Мы
ввели ограничение д г (ж, г), чтобы иметь дело с дифференциальным
включением с компактным множеством E~(x,z) в правой части, в дей-
ствительности же в качестве этого множества рассматривается надграфик
функции F*(x. г, •).
3.5.	Уравнения, линейные по части производных
Линейные уравнения вида (2.12) и уравнения Гамильтона-Якоби (1.6)
являются специальными случаями уравнений вида
т
i=l
Здесь £ е Rm, х е Rn. Предполагается, что функции G э (£, х) а?))
непрерывны, G — открытая область в Rm+n; функция Н непрерывна
на G х R х Rn, не возрастает по переменной z и удовлетворяет условию
Липшица
\H(g,x,z,p) — H(£,x,z,q)\ p(£,z,z)||p-g||	(3.9)
для всех (р, g) G Rn х Rn, где р(£, х, z) — непрерывная функция на G х R.
Пусть х := (£, х) е Rm х Rn, s:= (£, s) е Г х Rn.
Ясно, что при названных условиях функция
F(x,z,s) = У hj(£, х)& + Я(С, х, z, s)
i=l
удовлетворяет предположениям, сформулированным в пункте 2.1. Заметим,
что функция F удовлетворяет условию Липшица
(F^z,?7) — Ftfc, г, S'") I P&x>z) 11^
где p(g,x,z) = ||Л(£,я:)|| +p(£,x,z).
x) + Я(£, x, z, Dxu) = 0.	(3.8)
3. Верхние и нижние полунепрерывные решения
35
Для уравнения (3.8) мы можем рассмотреть следующее дифференци-
альное включение
G E(£,x,z,C,s),
Е^,х, z, С, з) = е Г х Г х R: Vll^ll2 + II/II2	Р& х, z),
9 = (С, h} + (s, f) - Н(&, х, z, s)}.
Эта конструкция следует из общей схемы, предложенной в пункте 2.3. Од-
нако, принимая во внимание структуру уравнения (3.8), мы можем ввести
для этого уравнения более удобное характеристическое включение вида
£, = h(£,x),
(ж, i) G Е(£, х, г, ^).	(3.10)
Верхнее решение уравнения (3.8) может быть определено как такая
полунепрерывная снизу функция G э (£, х) н-> и(& х) G R, у которой при
каждом ф € Ф подграфик слабо инвариантен относительно дифференци-
ального включения (3.10), где многозначное отображение Е удовлетворяет
условиям (j), (jj), (jjj+), (jv+)> данным ниже (они аналогичны соответству-
ющим условиям из пункта 2.5).
Таким же образом нижнее решение уравнения (3.8) может быть опре-
делено как полунепрерывная сверху функция и(£,я), такая, что при лю-
бом 0 Е Ф ее подграфик слабо инвариантен относительно дифференци-
ального включения (3.10), где многозначное отображение Е удовлетворяет
условиям (j), (jj), (jjj“), (jv~).
График минимаксного решения должен быть слабо инвариантен отно-
сительно дифференциального включения (3.10), в котором Е удовлетворяет
условиям (j), (jj), (jjj+), (jv+), (jjj“), (jv~).
Итак, пусть (£, x, г, VO •-* z, ф) C Rn xR - многозначное отоб-
ражение, определенное для всех (£, х) G G, z е R, ф G Ф, где Ф — некото-
рое непустое множество. Упомянутые выше требования к многозначному
отображению Е формулируются следующим образом:
(j) для любых (£, х) е G, z G R, ф G Ф множество Е(£, х, г, ф) выпукло и
компактно в Rn х R;
(jj) для любого ф G Ф многозначное отображение (£,ж,г)	Е(£,х^ф)
полунепрерывно сверху;
(jjj+) для любого ф G Ф, (£, х) е G,z' z'' и любых (/, д') е Е(£, х, z', ф)
существуют (/, д") G Е(£, х, z'\ ф), такие, что д" д';
36
Глава I
(jjj ) для любого С Ф, (£, ж) € G, г' г" и любых (J\g'') €
G Е(£, х, z", ф) существуют (/, д') € Е(£, х. z', ф), такие, что д" д';
(jv+) для любых (£, х) € G, z € R и s е Rn найдется ф° € Ф такое, что
H(£,x,z,s) = min{(/,s) - д: (f,g) е Е(£, х, z, ^°)} >
> min{(/,s) — д: (f,g) 6 Е(£,х, z,tp)}
при всех ф ё Ф;
(jv) для любых (£. х) Е G, z Е R и s Е Rn найдется фо Е Ф такое, что
H(£,x,z,s) = max{(f,s) - д: (f,g) е E(£,x,z, ф0)} С
< max{(/,$) — д: (f,g) е Е(£,х,г,ф)}
при всех ф Е Ф.
Если многозначное отображение Е удовлетворяет свойствам (j), (jj),
(jjj+) (соответственно, (j), (jj), (jjj-)), тогда, очевидно, многозначное отоб-
ражение Е, определенное равенством
Е(х, z, ф) := {h(£, ж)} х Е(£, х, г, ф)
удовлетворяет условиям (i), (ii), (iii+) (соответственно, (i), (ii), (iii“)), сфор-
мулированным в пункте 2.5.
Нетрудно установить, что (jv+) (соответственно (jv~)) влечет выпол-
нение (iv+) (соответственно (iv~)). Действительно, пусть х = (^,х) Е G,
z Е R, з = (С, я) Е Rm х Rn. Следуя (jv+), мы имеем
maxmin{(/z, 0 + (/, s) — д: (h,f,g) Е E^c.z.s)} =
= {h(^,x),Q) + maxmin{(/, s) -g-. (J,g) e Е^,х,г,ф)} = F(x,z,s).
Заметим в заключение, что множество E(j^ х^ г, з) вида
E(£,x,z,s) := {(f,g) eRnxR: ||/||	p(£,x,z), д = {f,s)-H^,x,z,s)}
(3.1i)
удовлетворяет всем условиям (j), (jj), (jjj+), (jjj ), (jv+), (jv ). В этом слу-
чае ф = s Е Rn = Ф.
4. Критерии слабой инвариантности минимаксных решений 37
4.	Критерии слабой инвариантности минимаксных
решений
Исследования минимаксных решений существенно опираются на ме-
тоды негладкого анализа и, одновременно, обогащают последний новыми
результатами. На инфинитезимальном уровне можно заметить двойствен-
ность различных форм определений при различных подходах к определе-
нию понятия обобщенного решения, включая двойственность определений
минимаксного и вязкостного решений. Так, ниже, мы дадим определения
минимаксных решений в инфинитезимальной форме, использующие кон-
тингентные конуса и неравенства для производных по направлению. Дока-
зана эквивалентность определений в различных формах. Доказано также,
что вязкостные решения, введенные М. Дж. Крэндаллом и П.Л.Лионсом,
эквивалентны минимаксным решениям.
4.1.	Определения
Напомним некоторые концепции негладкого анализа и приведем необ-
ходимые нам определения. Эти конструкции более подробно представлены
в приложении, в параграфе А5.
Пусть и: G I—> R — некоторая вещественная функция, определенная на
открытом множестве G С Rn. Символ Т((ж, z);epi и) обозначает контин-
гентный (тангенциальный) конус к надграфику epi и в точке (ж, г) (см. при-
ложение, параграф А5). Аналогично, символ T((rr, z); hypo и) обозначает
контингентный (тангенциальный) конус к подграфику hypo и в точке (ж, z).
Мы обозначаем через Т(и)(х) контингентный (тангенциальный) конус
к графику функции и в точке (rr, и(х)) G G х R, т. е., следуя (А5.12), (А5.13)
мы полагаем
Т(и)(х) \= {(f,g) eRnxR: liminf 5-1 dist ((rr+^/5гб(ж)+^);gr и) = 0},
цо
(4.1)
где gr и := {(ж, и(х)): х € G} — график функции и.
При формулировке критериев, характеризующих минимаксные реше-
ния, мы используем также следующее определение
Г(я, z. s) := G Rn х R : д = {f, s) - F(x, z, $)}.	(4.2)
Напомним определения верхних и нижних производных по направле-
нию, субдифференциалов и супердифференциалов. Рассмотрим величины
d~u(x;f) := liminf{5“1[tz(j;-|-5/')~?z(a:)]:	(0,е), \\f~f'W (4-3)
ЦО
d+u(x^f) := limsup{5“1[tz(rr-b5/,)~'u(:r)]:	(4-4)
цо
38
Глава!
Эти соотношения определяют нижнюю и верхнюю производные функции и
в точке х € G по направлению f € Rn.
Множество D~u(x) (соответственно множество D+u(x))), определен-
ное равенством (4.5) (соответственно равенством (4.6)),
D-u(x):={se^n: (з, /) - d~u(x‘ /) < О, V f € Rn},	(4.5)
D+u(x) := {s e Rn: (s,f) - d+u(x;f) ^0, V/бГ}	(4.6)
называется субдифференциалом (соответственно супердифференциалом)
функции и в точке х € G. Элементы множества D~u(x) (множе-
ства D+u(x)') называются субградиентами (соответственно суперградиен-
тами).
4.2.	Эквивалентные критерии
Рассмотрим различные определения верхних, нижних и минимаксных
решений. Ниже приведены три списка. Первый (соответственно, второй и
третий) список содержит различные определения верхнего (соответствен-
но, нижнего и минимаксного) решения. Теорема 4.3 утверждает, что все
критерии в этих списках эквивалентны. Определения в различных (двой-
ственных) формах позволяют нам взглянуть на одно и то же понятие с
различных точек зрения и выработать дополнительные представления для
изучения обобщенных решений.
Рассмотрим следующие свойства полунепрерывной снизу функ-
ции и: G R.
Определения верхних решений:
(U1) для любых xq € G, zq и(хо) и s е Rn существует липшицевая
функция (ж(-),г(-)): [0,т] xR, определенная на интервале [0, т]
(где т — некоторое положительное число), такая, что выполняется на-
чальное условие (ж(0),г(0)) = (#о> го), и неравенство
t
z(t) = z0 + У s) - F(x(£), z(C), s)]dC u(x(t^ (4.7)
0
имеет место для t G [0, г];
(U2) для произвольно выбранного параметра w 6 Ф надграфик функции и
слабо инвариантен относительно дифференциального включения
(±(£),г(£)) € E+(x(t\z(t\i/;)>
(4.8)
4. Критерии слабой инвариантности минимаксных решений 39
здесь и в (U3), (U4), (U6) мы обозначаем через Е+ произвольное мно-
гозначное отображение, которое удовлетворяет условиям (i), (ii), (iii+),
(iv+), сформулированным в пункте 2.5;
(U3) Т((ж, epi и) П Е+(х, u(x),i/j)	0 для всех х G G и 6 Ф;
(U4) со T((x,tt(x));epi и) И Е+(х, и(х),	0 для всех х G G и <ф G Ф;
(U5) F(x, и(х). s) 0 для всех х € G и s € D~u(x);
(U6) и(х\ f) -- g: (f,g) G E+(x, u(x), VO} 0 для всех x G G
и ф G Ф;
(U7) inf{d“ u{x\ f) — (s,f) + F(x. u(x), s): f G Rn} 0 для всех x G G
и s e Rn.
Аналогично, для полунепрерывной сверху функции и: G н-» R мы
рассмотрим следующие свойства, которые определяют нижнее решение.
Определения нижних решений:
(L1) для любых хо € G, zq < u(xq) и s G Rn существует липшицевая
функция (gt(-), ^(-)): [0, г] GxR, определенная на некотором ин-
тервале [0,т], т > 0, такая, что (rr(O), z(0)) = (жо5 £о)> и неравенство
t
z{t) = zo + J"[(ж(С), s) - Г(ж(С), г(С), s)]c?C u(x(t))	(4.9)
О
имеет место для t G [0, г];
(L2) для произвольно выбранного параметра -0 G Ф подграфик функции и
слабо инвариантен относительно дифференциального включения
(x(t),z(t)) е E~(x(t)iz(t'),^)i	(4.10)
здесь и в (L3), (L4), (L6) символ Е~ означает произвольное многознач-
ное отображение, которое удовлетворяет всем условиям (i), (ii), (iii~),
(iv~), перечисленным в пункте 2.5;
(L3) Т((ж, п(ж)); hypo и) П Е~(х, и(х\ з для всех х G G и € Ф;
(L4) со Т((ж, и(х))\hypo и) П Е'~(х^ u(x)^)	0 для всех х G G и ф G Ф;
(L5) F(x, и(х)^ s) 0 для всех х G G и s G D+u(x);
40
Глава I
(L6) sup{d+^(:r; У) — g: (f^g) E E (#, u(x), VO} 0 для всех x e G
и ф e Ф;
(L7) sup{d+tz(x” f) — {s,f} + F(^u(x),s): f G Rn} > 0 для всех x G G
Наконец, пусть и: Gm 1 - непрерывная функция. Рассмотрим свой-
ства, каждое из которых может быть принято за определение минимаксного
решения.
Определения минимаксных решений:
(Ml) для любых (xq,zo) £ gr и и s G Rn существует число т > 0 и
липшицевая функция (ж(-), ^(-)): [0? т] н-> GxR, которая удовлетворяет
уравнению
z(f) = (x(t), s) — F(x(t), z(t\ s),
начальному условию (ж(0), z(0)) = (xq, zq) и равенству z(t) = u(x(t))
для всех t e [0, т];
(М2) при произвольном выборе вектора G Ф график функции и слабо
инвариантен относительно дифференциального включения
(±(t), z(t)) G E(x(t), z(t), ф),	(4.11)
здесь и в (М3), (М4) символ Е означает произвольное многозначное
отображение, которое удовлетворяет всем условиям (i)-(iv), перечис-
ленным в пункте 2.5;
(М3) Т(и)(х) А Е(х, и(х), ф) 0 для всех х G G и ф G Ф;
(М4) со Т(и)(х) А Е(х, и(х),ф)	0 для всех х G G и ф G Ф;
(М5) функция и — одновременно верхнее и нижнее решения;
(Мб) Т(и)(х) А Г(ж,u(x\s) / 0 для всех х е G и s Е Rn (напомним,
что конус Т(п)(ж) и гиперплоскость Г (ж, z, s) определены равенства-
ми (4.1) и (4.2));
(М7) со Т(и)(х) А Г(ж, и(х), s) 0 для всех х е G и s G Rn.
Заметим, что в параграфе 2 мы рассматривали определения минимакс-
ных решений с помощью условий (Ml) and (М2). Аналогично, в парагра-
фе 3 мы рассматривали определения верхних (нижних) решений с помощью
условий (U1) и (U2) ((L1) и (L2)).
4. Критерии слабой инвариантности минимаксных решений
41
4.3.	Теорема
Для полунепрерывной снизу функции и: G t—> R условия (Ul), (U2),
..., (U7) эквивалентны. Аналогично, для полунепрерывной сверху функ-
ции и: G н-» Rсвойства (LI), (L2),..., (L7)эквивалентны. Для непрерывной
функции и: G № условия (Ml), (М2), ..., (М7) эквивалентны.
Отметим, что указанные условия эквивалентны, если рассматривают-
ся для всех х в открытой области G. Если мы рассмотрим эти условия
в фиксированной точке х9 то некоторые из них не эквивалентны. Напри-
мер, если условие (U4) имеет место для некоторой фиксированной точки х,
тогда, очевидно, условие (U3) может не выполняться. В дифференциаль-
ных включениях (4.8) и (4.10) можно использовать многозначное отображе-
ние вида (2.5), которое удовлетворяет всем условиям, сформулированным в
пункте 2.5.
Теорема 4.3 доказана в пункте 4.6. Следуя этой теореме, любое из упо-
мянутых условий (U1)-(U7) (соответственно (L1)-(L7) или (Ml)-(М2))
может быть принято за определение верхнего (соответственно нижнего или
минимаксного) решений. Таким образом, мы приходим к следующим опре-
делениям.
4.4.	Определения
Верхним решением уравнения (2.1) называется полунепрерывная сни-
зу функция и: G R, которая удовлетворяет любому из эквивалентных
условий (U1)-(U7). Аналогично, нижним решением уравнения (2.1) назы-
вается полунепрерывная сверху функция и'. G 1, которая удовлетворя-
ет любому из эквивалентных условий (L1)-(L7). Минимаксным решением
уравнения (2.1) называется непрерывная функция и: G н-> R, которая удо-
влетворяет любому из эквивалентных условий (М1)-(М7).
Приведем еще одно доказательство совместности понятий минимакс-
ного и классического решений. Мы используем при этом определение ми-
нимаксного решения с помощью условия (Мб). Пусть функция и диффе-
ренцируема в точке х. Тогда
Г(«)(ж) = {(/,5) е К" х R: g =
т. е. здесь контингентный конус Т(и)(х) совпадает с касательной гипер-
плоскостью (точнее, с касательным подпространством). Если s /= Du(x\
то гиперплоскости Т(и){х) и Г(т,и(т),«) пересекаются. Таким образом,
если функция и дифференцируема в точке т, то условие (Мб) эквивалентно
условию
{(/,д): 9 = П {и,дУ- д = (f,s) - F(x,u(a:),s)} / 0
42
Глава 1
для s — Du(x). Очевидно, что последнее условие эквивалентно равенству
F(x,u(x),Du(x)) = 0.
Следовательно, мы получаем, что минимаксное и классическое решения
совпадают.
Отметим, что соотношение (Мб) может быть рассмотрено как «геомет-
рическая» интерпретация уравнения F(x, и(х), Du(x)) = 0.
Как было только что показано, в точках х € G, где функция и диффе-
ренцируема, рассмотренное уравнение и условие (Мб) эквивалентны. Если
функция и недифференцируема в точке х, то тогда условие (Мб) является
естественным обобщением уравнения (2.1).
4.5.	Вязкостные решения
Напомним определение вязкостного решения, которое было введено
М. Дж. Крэндаллом и П. Л. Лионсом (см. [57, 58]).
Непрерывная функция называется вязкостным суперрешением (суб-
решением), если имеет место следующее условие', пусть точка xq 6 G
является точкой локального минимума (максимума) для и(х) — р(х), и
функция р дифференцируема в этой точке, тогда имеет место неравен-
ство (4.12) (неравенство (4.13))
F(x0,u(x0),Dp(xq))	0,	(4.12)
F(x0,u(xq),Dp(xq)) 0.	(4.131
Функция называется вязкостным решением, если она одновременно явля-
ется суперрешением и субрешением.
В теории вязкостных решений для определения супер- и субрешений
были введены также соотношения вида (U5) и (L5) (см. [54] (4.12) и (4.13)
соответственно). Заметим, что знаки в неравенствах (4.12) и (4.13) проти-
воположны знакам неравенств в соответствующих соотношениях опреде-
ления, данного в работах М. Дж. Крэндалла, Л. С. Эванса и П.Л.Лионса.
Дело в том, что в этих работах были рассмотрены неубывающие функ-
ции z > F(x, z, s). Для конструкций, предлагаемых в этой книге, более
подходят невозрастающие функции z i-> F(x, г, s).
Согласно теореме 4.3, минимаксное и вязкостные решения эквивалент-
ны. Более того, если верхние (нижние) решения рассматривать в классе
непрерывных функций, то они эквивалентны вязкостным суперрешениям
(субрешениям).
4. Критерии слабой инвариантности минимаксных решений 43
4.6.	Доказательство теоремы 4.3
Сначала мы докажем эквивалентность условий (U1)-(U7). Мы рас-
смотрим импликации в следующем порядке
(U2) & (U3) & (U4), (U5) & (U6), (U3) & (U6),
(U6) => (U7), (U7) => (U5), (Ul) & (U2).
Доказательство эквивалентности (U2) о (U3) о (U4).
Пусть и: G R — полунепрерывная снизу функция. Согласно след-
ствию А8.1 (см. параграф А8), множество epi и слабо инвариантно отно-
сительно дифференциального включения (4.8) тогда и только тогда, когда
имеет место следующее условие
Т((я. z)\epi и) А Е+(х, z, ф) 0, V(x, z) е epi и (4.14)
или выполняется следующее эквивалентное условие
со Т((х\ z); epi и) А Е+(х, z, ф) 0, V(z, z) е epi и. (4.15)
Так что мы имеем
(U2) & (4.14)	(4.15).
Заметим, что (х,?/(ж)) € epi и. Таким образом,
(4.14) => (U3), (4.15) => (U4).
Пусть имеет место (U3). Выберем произвольные х е G и ф € Ф.
Условие (U3) влечет существование
(«/*><?*) С Т((ж,и(ж));ер1 и) А Е+(х,и(х),
Используя соотношение (А5.9) (см. пункт А5),
Т((ж, и(ж));epi и) С Т((ж, г); epi и) Vz гл(ж),
мы получаем (f*9g*) € Т((ж, г); epi и) для любой точки (ж, z) е epi и.
Так как (Д,д*) € Е+(х,и(х),ф>) и z и(х)9 и вследствие условия (iii+)
(см. пункт 2.5) мы видим, что существуют £ Е+(х, z,t//)9 для кото-
рых р" > д*. Так как (f*,g*) € Т((ж, z); epi и) и д" д*9 то из определения
конуса Т((ж, z);epi и) следует, что (J*,g") € Т((ж, z): epi и) (см. (А5.7)).
Следовательно
€ T((x,z)-,epi u)r\E+(x,z,tli).
44
Глава 1
Таким образом, мы получаем
(U3) => (4.14) & (4.15).
Аналогично, мы имеем (U4)=>(4.15). Эквивалентность (U2) о (U3) <=> (U4)
доказана.
Доказательство эквивалентности (U5)44>(U6).
Пусть имеет место условие (U6). Выберем произвольный вектор seD~u(x).
Согласно условию (iv+) (см. пункт 2.5), существует такой параметр е Ф,
что
F(x, u(x),s) — min{($,/) — д: (f.g) С Е+(х, и(х), ^°)}«	(4-16)
Отметим, что функция /	полунепрерывна снизу, а множе-
ство Е+(х, и(х\ ^°) замкнуто и ограничено. Тогда из условия (U6) вытека-
ет существование таких (f\g') 6 Е+(х, и(х), ^°)> которые удовлетворяют
неравенству
d~u(x; f') - д' 0.
Из (4.16) следует, что
F(x,u(x),s)	(s.f) - д'.
Из определения субдифференциала (см. (4.5)) вытекает неравенство
d~u(x;f') -	0.
Комбинируя приведенные выше неравенства, мы приходим к неравен-
ству F(x, п(ж), $)	0. Импликация (U6)=>(U5) доказана.
Докажем импликацию (U5)=>(U6). Пусть имеет место (U5), и предпо-
ложим, от противного, что
nnn{d~u(x0;f) - д: (f,g) 6 Е+(х0, w(xo)/0)} > 0
для некоторой точки (жо,^) С G х Ф. Так как f н-> d~u(xQ;f) — полу-
непрерывная снизу функция, то существует такое положительное число а,
что
тт{сГгфо; /) ~ 9' (J,g) 6 Еа} > 0,	(4.17)
где Еа — «-окрестность множества £+(ж0, гг(жо), V0-
Используем теорему А6.1. Полагаем
у = (х, z) е Y = G х R, v(x, z) = и(х) — г,
h = (/,д) е Rn х R, Н = Еа, уо = (я0,0).
Заметим, что d~v(y\h) = d~v(x, г; /, д) = d~u(x; f) — д.
4. Критерии слабой инвариантности минимаксных решений
45
Пусть D~v(x,z) С Rn х R — субдифференциал функции v, а век-
тор (s. а) е D~v(x, z) — субградиент этой функции. Согласно определени-
ям последнего (см. (4.5)), имеют место соотношения
(s, f) + ад - d~v(x, z; f, д) = {s, f) + ag- (Гu(x; f) + g 0
для всех (/, g) € Rn x R. Следовательно,
a = —1, s e D~u(x).	(4.18)
Из условия (4.17) вытекает, что функция v удовлетворяет условиям теоре-
мы А6.1. Напомним, что многозначное отображение (ж, z) Е+(х, z^)
полунепрерывно снизу, и, значит, можно подобрать такое число е > 0, что
имеет место неравенство
Е{х',^.ф) С Еа, Vх* е B(x§\e), Vz1 е [u(#o) — 2е,и(хо) 4- 2е].
Согласно теореме А6.1, существуют такие точка у£ = (x£,z£) е Y и суб-
градиент (s£J —1) € D~v(y£), что
||х0 - х£|| < е, |ze| < с, |u(^o) - ифх^ + Z£\ < е,
min{(se,/) ~д: (f,g) е Еа} > 0.	(4.19)
Так как Е+(х£,и(х£),ф) С Еа, мы получаем из (4.19) и (iv+) (см.
пункт 2.5), что
F(j:£,u(xe),.se) inin{(se,f) - д: (f,g) е Е+(х£, и(хе), •ф)}
> min{(se,f) — д: (f,g) 6 Еа} > 0.
Вследствие (4.18), мы имеем s£ е D~u(x£). Последнее неравенство проти-
воречит предположению о выполнении всюду условия (U5). Этим противо-
речием, с помощью метода reductio ad absurdum, завершено доказательство
импликации (U5)=>(U6).
Доказательство эквивалентности (U3)o(U6).
Докажем сначала импликацию (U3)=>(U6). Пусть
(J\gf) С T((rc,tz(a;);epi и) П Е+(х, и(х).
Из (А5.5) следует, что выполняется также неравенство d~и(х\ f') — д' 0,
так что из условия (U3) вытекает условие (U6).
Теперь докажем импликацию (U6)=>(U3). Обозначим
Е := {/ € Rn: Эд е R такое, что (/, д) е Е+(х, и(х), ф)},
46
Глава I
т. е. множество Т7 является проекцией Е+(х, на Вп. Возможны два
случая.
Случай 1. Предположим, что d~u(x;f) > —оо для любого / € Т7.
Согласно (U6), существуют такие (f\gf) € Е+(х, и(х), гр), что
d~u(x; f) -д' ^0.
Из (А5.5) и из того, что конус Т((х, и(х))\epi w) замкнут, мы имеем, что
(/', d~u(x; /')) С Т((х,и(х)); epi и).
Согласно (А5.7), справедливо (J\g') € T((x,u(x));epi и). Следовательно,
(J',gf) С T((x,u(#));cpi и) П Е+(х,и(х),'ф).
Случай 2. Предположим, что существует такой вектор f Е F,
что d~u(x;f') = — оо. Из условий (А5.5) и (А5.7) мы получаем, что
(/',$) С Т((ж, и(х)); epi и) для всех д € R. В частности, мы получа-
ем, что (J',g') € T((x,u(x));epi и) для всех чисел д' Е R, так что
(f\gf) С Е+(х, и(х),ф). Импликация (U6)=>(U3) доказана.
Доказательство импликаций (U6)=>(U7), (U7)=>(U5).
Пусть выполняется условие (U6). Выберем произвольно s Е Rn. Соглас-
но (iv+) (см. пункт 2.5), существует такой вектор ф° Е Ф, что
F(x,u(x),s) = min{(s,f) -д: (f,g) е E+(x,u(x),tp0)}.	(4.20)
Заметим, что функция f н-» d~u(x;f) полунепрерывна снизу, а множе-
ство Е+(х, и{х), гр°) компактно. Тогда, используя условие (U6), мы получа-
ем, что существуют такие (f',gf) Е Е+(х,г1(х),ф°), которые удовлетворя-
ют неравенству
d~u(x; /') - д' 0.
Из (4.20) мы получаем
(<*,/') - д' F{x,u{x),s).
И тогда
d~ и(х\ f') — (s, f') 4- F(x, u(x). s) 0.
Импликация (U6)=>(U7) доказана.
Пусть имеет место условие (U7). Выберем произвольно s Е D~u(x).
Согласно определению субдифференциала (см. (4.5)), неравенство
d~и(х\ f) — {s, f) 0 имеет место для всех / Е Rn. Таким образом, из (U7)
следует (U5).
Доказательство эквивалентности (U1)o(U2).
Импликация (U2)=>(U1) очевидна.
4. Критерии слабой инвариантности минимаксных решений
47
Пусть полунепрерывная снизу функция и: G м 1 удовлетворяет усло-
вию (Ш). Ясно, что такая функция удовлетворяет и условию (U7). Как было
показано выше, (U7)=>(U5), (U5)o(U2). Импликация (U1)=>(U2) доказана.
Таким образом, доказана эквивалентность условий (U1)-(U7). Эквива-
лентность условий (L1)-(L7) может быть доказана аналогичным образом.
Сейчас мы докажем эквивалентность условий (М1)-(М7).
Эквивалентность (М2), (М3) и (М4) вытекает сразу из следствия А8.1
(см. параграф А8). Эквивалентность условий (Мб) и (М7) очевидна. Импли-
кация (М2)=>(М1) также очевидна. Таким образом, нам осталось показать
следующее
(М2)	(М5), (М5)	(Мб),
(Мб) => (М5), (Ml) => (М5).
Доказательство эквивалентности (М2)<4>(М5).
Пусть Ef — многозначное отображение, которое удовлетворяет всем услови-
ям, перечисленным в пункте 2.5. В соотношениях (U2) и (L2) мы полагаем
Е± — Е — Е', и обозначим модифицированные таким образом свойства
(U2) и (L2) как (U2') и (L2') соответственно. Свойство (М2) эквивалентно
паре свойств (U2') и (L2'). Доказательство этого факта для многозначной
функции Е вида (2.5) дано в пункте 3.2. Это доказательство может быть
распространено и на случай, когда вместо Е используется произвольное
многозначное отображение Е', которое удовлетворяет всем условиям пунк-
та 2.5. Как было показано вьппе, свойство (U2') (соответственно (L2')) эк-
вивалентно каждому из условий (Ui) (соответственно (Li)) (i = 1,2,..., 7).
Итак, мы получили, что (М2)4=>(М5).
Доказательство импликации (М5)=>(М6).
Предположим, что имеет место условие (М5). Тогда справедливы и усло-
вия (U6) и (L6). Пусть
СхКхФ'э (ж,г,^)н- E+(a?,z,V>) cRn xR
— некоторое многозначное отображение, которое обладает свойствами (i),
(ii), (iii+), (iv+) из пункта 2.5. Аналогично, пусть
G х R х Ф" э (х, z, н-» Е~ (х, г,^) с Rn х R
— многозначное отображение, которое обладает свойствами (i), (ii), (iii~),
(iv~).
Выберем произвольный вектор s € Rn. Согласно (iv+) и (iv ), суще-
ствуют такие ”0° е Ф' и € Ф", что
F(.r, и(х), s) = miii{(s,/) — д: (J,g) € Е+(ж, п(ж),-0°)},	(4.21)
F(x,u(x),s) = max{(s,/)-д: (f,g) € Е”(ж, и(х). ^о)}«	(4.22)
48
Глава I
Докажем, что существуют такие
(f,g')eT(u)(x),	(f",g")&T(u)(x),
ЧТО
(s, f') -д' > F(x,u(x),s), {s,f")-g"^F{x,u(x),s).	(4.23)
Сначала предположим, что d~u(x;f) > —ос для всех / е Rn. Соглас-
но (U6) и (4.21), существуют £ Е+(х. и(х\ -0°), такие, что д' :=
= d~и(х\ ff) С д* < ос, и
<5, /') - д' (s, f'} - д* F(x, u(x),s).
Используя (А5.14), мы получаем, что (f',gf) € Т(и)(х).
Теперь рассмотрим оставшийся случай. Предположим, что суще-
ствует такой вектор f е Rn, что d~u(x;f) = —ос. Полагаем /' —
= 0 и д' = — |F(a;,u(a;),s)|. Используя утверждение А5.1, мы получа-
ем (J',gf) е Т(и)(х). Ясно, что (f',gf) удовлетворяют первому из нера-
венств в (4.23). Аналогичным образом мы можем показать, что существу-
ют С Г (и) (ж), удовлетворяющие второму неравенству в (4.23).
Полагаем
,пп._ Г(-АЛ-АУ) для А е [-1,0],
I (А/ ,Хд") для А € [0,1].
Так как Т(и)(х) — конус, то (f(A),#(A)) е Т(и)(х) для всех А е [—1,1].
Из непрерывности функции А н-> (/(А),^(А)) и неравенств (4.23) вытекает
существование такого числа А е [—1,1], что
(s, /(А)) - д(Х) = F(x, и(х), з).
Таким образом, мы получаем (/(А), д(Х)) G Т(и)(х) Г) Г (ж, и(х)^ з). Импли-
кация (М5)=>(М6) доказана.
Доказательство импликации (М6)=>(М5).
Пусть имеет место условие (Мб), т. е. существуют (J\gf) € Т(и)(х)Г[
ПГ(ж,гх(ж), s). Согласно (А5.16), справедливы оценки
d~u(x;f) д' d+u(x',f'\
а значит, и
d и(х\ f') — (s, /') + F(x, u(x), s) 0,
d+u(x; ff) — (s, /') 4- F(x, u(x), s) 0.
4. Критерии слабой инвариантности минимаксных решений
49
Мы получили, что из (Мб) следует (U7) и (L7). Поэтому функция и является
одновременно и верхним, и нижним решением. Таким образом, имплика-
ция (М6)=>(М5) доказана.
Доказательство импликации (М1)=>(М5).
Пусть непрерывная функция и: G н-> R удовлетворяет условию (Ml). Тогда
неравенства (U7) и (L7) для этой функции справедливы. Поэтому мы сно-
ва получаем, что эта функция является одновременно верхним и нижним
решением.
Теорема 4.3 доказана.
4.7.	Ослабленные предположения1
Рассмотрим определение минимаксного решения уравнения (2.1) для
случая, когда не предполагается выполнение условия Липшица (2.2). Мы
предполагаем только, что функция F(.r, z, s) непрерывна на G х 1 х Rn, не
возрастает по переменной z и удовлетворяет следующему условию. Пусть
Вд •= {(#, 2:) 6 G х R: ||ж|| < A, \z\ < А}.
Напомним, что символом Вд := {seRn: ||s|| А} обозначается замкну-
тый шар. Предполагается, что для любого А > 0 существует такое ^(А) > О,
что оценка
\F(x, z, s) - F(x, z,p)\	^(A)(l 4- ||s - p\\)	(4.24)
имеет место для всех р е s G Вд, (х, z) е Вд.
Пусть
E(x,z,s,a,p) := {(f,g) 6 R” х R: ||/|| С р, \д - (s,f)+F(x,z,s)\ С а}.
(4.25)
4.8.	Определение
Полунепрерывная снизу (сверху) функция и: G н-> R называется верх-
ним (нижним) решением уравнения (2.1), если для любых чисел А > О
и а > 0 существует такое число р > 0, что в области D\ надграфик
(подграфик) этой функции и слабо инвариантен относительно дифферен-
циальных включений
(±, z) Е Е(х, z, s, а, р)	(426)
при любых s G Вд. Непрерывная функция и называется минимаксным ре-
шением уравнения (2.1), если для любых чисел А > 0 и а > 0 существует
1 Материал пунктов 4.7-4.9 будет использован только при доказательстве теорем 9.3 и 9.4,
которые стоят особняком. Этот материал при первом чтении может быть опущен.
50
Глава I
такое число р > 0, что в области график функции и слабо инвариантен
относительно дифференциальных включений (4.26) для любых s е Рд.
Следуя этому определению, полунепрерывная снизу функция и: G н> R
называется верхним решением, если она удовлетворяет следующему усло-
вию. Для любых чисел А > 0, а > 0 (где А — сколь угодно большое число,
а а — сколь угодно малое), можно указать такое число р = р(А, а) > 0,
что при любых (жо, ^о) € epi и А Рд и s е В\ существуют число т > 0
и абсолютно непрерывная траектория (#(•), ^(-)): [0?	|~> Rn х которая
удовлетворяет начальному условию (х(0), z(0)) = (xq, zo), дифференциаль-
ному включению (4.26) и неравенству z(t) u(x(t)) при t е [0, т].
Можно показать, что из локальной инвариантности надграфика вы-
текает его глобальная инвариантность в области Рд в следующем смыс-
ле. Пусть число р(А, а) выбрано согласно рассмотренному определению.
Пусть (я?о, zq) е epi и П Рд и я е В\. Тогда существует число т е [0, оо]
и траектория (х(-), г(-)): [0, т) Rn х R, которая удовлетворяет начально-
му условию (ж(0), г(0)) = (жо,го), дифференциальному включению (4.26)
и неравенству z(t) u(x(t)) при t е [0,т). Кроме того, если т < ос, то
(ж(т), z(r)) € «ЭРд U dG.
Подобные замечания справедливы также для нижнего и минимаксного
решений.
4.9.	Теорема
Полунепрерывная снизу (сверху) функция и: G н-> Rявляется верхним
(нижним) решением уравнения (2.1) тогда и только тогда, когда усло-
вие (427) (условие (4.28))
Т((х, и(х))\epi и) А Г(ж. и(х), я) ф 0,	(4.27)
Т((ж, и(х))\hypo и) А Г(ж, и(х), я) &	(4.28)
имеет место при всех х G G и я е Rn. Непрерывная функция и: G i—> R
является минимаксным решением уравнения (2.1) тогда и только тогда,
когда условие
Т(и)(х) А Г(ж, и(х), я) / 0	(4.29)
имеет место при всех х G G и s Е Rn.
Доказательство. Пусть функция и является верхним решением в
смысле определения 4.8. Выберем произвольно х € G и я G Rn. А за-
тем выберем число А так, что х е ||s|| А. Согласно определению 4.8,
для любого а > 0 существует такое р > 0, что в области Рд надграфик
4. Критерии слабой инвариантности минимаксных решений
51
функции и слабо инвариантен относительно дифференциального включе-
ния (4.26). Из следствия А8.1 мы имеем
Т((ж, и(х)),epi и) А Е(х, и(х), з, а, р) 0.
Полагаем
ra(x,z,s) := {(f,g) е Rn х R: \д - <з,/> 4- F(x,z,s)\	a}.	(4.30)
Заметим, что
E(x, г, s, си, p) С Га(х, z, s).
Поэтому
Т((ж, w(a;));epi и) А Га(ж, гг(ж)5 s) ф 0.	(4.31)
Покажем, что из этого соотношения, которое имеет место при
всех а > 0, вытекает (4.27). Обозначим = F(x^u(x)1s). Возможны два
случая: F* 0 и F^ > 0.
Рассмотрим случай F^ С 0. Принимая во внимание определение гипер-
плоскости Г (4.2), мы можем видеть, что (/о? 9о) С Г(ж, и(х). з), где /0 = 0?
g0 = -F\ С другой стороны, из определений надграфика и контингентного
конуса вытекает, что (/о,р) € T((a?,u(x));epi и) для любых д 0. Таким
образом, мы получаем, что в рассматриваемом случае
(/о,Ро) е Т((х, гх(ж)); epi и) А Г(ж, и(х\ s),
т. е. условие (4.27) выполняется.
Рассмотрим случай F^ > 0. Выберем 0 < а < F\ Из условия (4.31)
вытекает, что
(/а, Ра) е Г((ж,?1(я;));ер1 и) А Г°=(ж, и(х), з).
Из (4.30) следует, что
- д<*~
Полагаем
(/(А), 5(А)) := (А/а, Хда), /г(А) := (/(A), s) - 5(А) - F*.
Заметим, что /г(0) = — F^ < —а < 0, h(l) —а, так что функция h(A)
возрастающая. Следовательно, для некоторого А > 0 имеет место /г(А) = 0,
т. е.	~	~
ША)^(А))еШ^);з).
52
Глава 1
Из того, что
(/(1),	€ Т((ж,гф));ер1 и),
а множество Т((ж, гх(ж)); epi и) является конусом, мы получаем
(/(А), ^(А)) е и(х))] epi и) А Г(ж, и(х), з).
Таким образом, доказано, что условие (4.27) является необходимым для
того, чтобы функция и была верхним решением в смысле определения 4.8.
Докажем теперь, что условие (4.27) является достаточным для того,
чтобы надграфик полунепрерывной снизу функции и был слабо инвариан-
тен относительно дифференциального включения (4.26).
Выберем произвольно А > 0 и а > 0. Полагаем
г \F(x, z,s) — F(x.z.p)\ -an
Ро — sup ] I....V.	\---------------}	(4.32)
(x,z,s,p)	||S	p||	>
для (x, z) e D&, ||s|| € Вд, p e Rn, p ф s. Из оценки (4.24) и непрерывности
функции В(ж, z, з) вытекает, что ро < сю.
Покажем, что
В(ж, z, 5, а, ро) А Г(&, z.p) ф 0	(4.33)
для любых (ж, z) € Вд, s е Вд, р € Rn. Ясно, что это соотношение имеет
место для s = р. Таким образом, нам осталось рассмотреть случай s р.
Полагаем
г =	~	+°-
IIs -р\\
Из (4.25) мы получаем, что	€ Е(х, z, s, се, ро). А из определе-
ния величины ро вытекает, что
Р* - (р,/*) + E(x,z,p) = (/*,s-р) + F(x,z,p) - F(x,z,s) +а =
= Po||s ~р|| + F(x, z,p) - F(x, z, s) + (у 0.
Аналогично, для
Л
Ро
(p-g)
ff* := {s, f*) - F(x, z, s) - a
следует, что € E(x,z,s,a) и p* — (p,f*) + В(ж, z,p) 0. Так как
E(x, z, s, a) — выпуклое множество, оно содержит такую точку (/0? Ро), что
Ро — (р? /о) + Р(ж, 2,р) = 0. В итоге мы получаем, что (/о, Ро) € Г(ж, z.p).
Соотношение (4.33) доказано.
4. Критерии слабой инвариантности минимаксных решений
53
А сейчас докажем справедливость соотношения
со Т((ж, z)\epi и) П Е(х, г, 5, а, ро) ф 0	(4.34)
для всех (.т, г) е Од, з € В\. Предположим противное, пусть существуют
такие (х. z) Е D& и s G что
со Т((ж, z); epi и) А Е(х, г, s, а, ро) — 0-	(4.35)
Тогда, согласно теореме Хана-Банаха, существуют такие (р, a)eRn xR
и число е > 0, что
(р, /') - ад' + £ < (р, /") - ад" - е	(4.36)
для всех
(/', У) е СО Г((ж, г); epi и), (J", д") ё Е(х, z, s, а, р0).
Заметим, что (/' = 0, д') 6 со Т((х, z); epi и), где д' — произвольное поло-
жительное число. Поэтому а 0.
Покажем теперь, что а > 0. Предположим противное, т. е. пусть имеет
место а — 0. Подставим в (4.36) вектора
(J',91) б со Т((я;, z); epi и) (J1 = 0, д' > 0),
(/",д") е Е(х, z, S, а, р0) (J" = 0, д" = -F(.t, z, а)).
Мы получаем е < —е, что, очевидно, является неверным. Таким образом,
мы доказали, что а > 0.
Полагаем
р := max{(p, f) - д: (f,g) ё со T((x,z);epi и)},
v := min{(p,/) - д -. (f,g) ё E(x,z,s,a,p0)},
где р = р/а. Докажем следующее:
0 = р < v.	(4.37)
Действительно, из того, что множество со ^); epi и) является конусом,
вытекает либо р = 0, либо р — оо. Однако равенство р — оо противоречит
оценкам
р < и < оо,
первая из которых следует из (4.36), а вторая — из ограниченности множе-
ства Е(х, z^ s, а, ро). Таким образом, соотношения (4.37) доказаны.
54
Глава I
Используем сейчас (4.27). Пусть
(/',#') £ со г); epi и) ПГ(ж, z,p).
Из (4.2) получаем д' = {р. f) — F(x,z,p). Из равенства г/ — 0 вытекает
оценка (р, /') — д' 0. Поэтому
F(x,z,p)^Q.	(4.38)
С другой стороны, из (4.37) следует оценка v > 0. Далее, используя (4.33),
можно выбрать (f",g") € E(x,z,s,a, р0) П V(x,z,p). Из (4.37), (4.2) мы
получаем, что
F(x, z,p) = (р, f"} — д" р > 0.
Это неравенство противоречит неравенству (4.38). Таким образом, предпо-
ложение (4.35) приводит к противоречию. Соотношение (4.34) доказано.
Согласно следствию А8.1, из соотношения (4.34) вытекает, что над-
график функции и слабо инвариантен относительно дифференциального
включения (4.26), где р — ро-
Подобным же образом можно доказать, что полунепрерывная сверху
функция и\ G н-» R является нижним решением уравнения (2.1) (в смысле
определения 4.8) тогда и только тогда, когда имеет место условие (4.28).
Теми же рассуждениями, что и в теоремах 3.2 и 4.3, мы получим, что и
в рассматриваемом случае минимаксное решение является одновременно
верхним и нижним решением уравнения (2.1). Непрерывная функция и
удовлетворяет паре условий (4.27) и (4.28) тогда и только тогда, когда вы-
полняется условие (4.29). Теорема 4.9 доказана.
Заметим, в заключение, что вязкостное решение и минимаксное реше-
ние (в смысле определения 4.8) эквивалентны.
5.	Кусочно-гладкие решения
Определение 4.4 рассматривает минимаксные решения в классе непре-
рывных функций. В то же время известны условия, при которых обобщен-
ное (минимаксное и/или вязкостное) лежит в более узком классе функций.
Например, известно, что решение задачи Коши для уравненшг Гамильто-
на-Якоби является липшицевой функцией, если гамильтониан и началь-
ная функция удовлетворяют условию Липшица. Известно также, что для
большого числа задач обобщенные решения оказываются кусочно-гладки-
ми. При этом область определения разбивается на гладкие подмногообразия,
и сужения рассматриваемой функции на эти подмногообразия дифференци-
руемы. Ниже показано, что кусочно-гладкая функция является обобщенным
5. Кусочно-гладкие решения
55
решением (в минимаксном и/или вязкостном смысле) тогда и только то-
гда, когда на всех упомянутых многообразиях эта функция удовлетворяет в
классическом смысле некоторым, определенным ниже, дифференциальным
уравнениям в частных производных первого порядка.
5.1.	Кусочно-гладкие функции
Пусть и: G R — некоторая непрерывная функция. Мы полагаем, что
эта функция является кусочно-гладкой в следующем смысле.
Предполагается, что открытая область G разбита на дифференцируе-
мые подмногообразия Mi (i е I), т. е.
G =	= если i / j.	(5.1)
iEl
Здесь I — конечное множество индексов, нумерующих подмногообра-
зия Mi.
Обозначим
J := у е I: Mi является n-мерным многообразием}. (5.2)
Так как G ~~ открытое множество в Rn, то существует по крайней мере одно
/i-мерное подмногообразие Mi, т. е. J / 0. Если i Е I \ J, то символ Mi
обозначает к -мерное подмногообразие, где к € 0,п — 1.
Введем множество
<7(я) := {j Е J: х eMj,	(5.3)
где Мj обозначает замыкание Mj. Поясним, что запись J(x) — {г} означает,
что х Е Mi, i Е J. Мы требуем, чтобы
J(xf) = J(.t") для любых х', х" е Mi для любых i е I. (5.4)
Обозначим
□ J(x)= Q J(z)	(5.5)
xEMi	x^Mi
(последнее равенство следует из (5.4)).
Чтобы проиллюстрировать это требование, рассмотрим два разбиения
на плоскости R2, которые показаны на рис. 5.1(a) и 5.1(b). Разбиение, кото-
рое представлено на рис. 5.1(a), не удовлетворяет условию (5.4). Действи-
тельно, для точек xf Е М± и х" Е М± мы имеем J(xf) = {1,2}	J(x") =
= {1,3}. На рис. 5.1(b) показано другое разбиение. В отличие от первого
случая, многообразие М4 разбито на 1-мерные подмногообразия М6, М7
56
Глава I
и О-мерное подмногообразие (точку) М8. Это второе разбиение удовлетво-
ряет условию (5.4).
Пусть i G J, и пусть щ — сужение функции и на множество Mi.
Предполагается, что функция щ непрерывно дифференцируема на множе-
стве Mi, т. е. существует такая непрерывная функция : Mi X*, что
щ(у) - щ(х) = (sw(a:),y - х) + o(||i/ - ж||),
о(||г/— ж||)	—
Нт —------г— = 0, когда у -+ х, у е Mi
\\у
(s<0 = Вщ — градиент щ). В этом параграфе символ X* означает про-
странство, сопряженное к пространству X — Rn. Мы используем также
обозначение М {Mi}iEi для разбиения, определенного для рассматри-
ваемой функции и.
Функцию и: G н-> Rn, удовлетворяющую приведенным выше требова-
ниям, будем называть кусочно-гладкой.
5.2.	Утверждение
Кусочно-гладкая функция и дифференцируема по любому направлению,
т. е. для любых х G G и f Е X существует предел
, /	, u(x + 5f}—u(x}
du(x-,f) := Inn	(5.6)
5. Кусочно-гладкие решения
57
Пусть М — разбиение, определенное для функции и, и пусть Mi Е Ad —
одно из ненульмерных многообразий, принадлежащих к этому разбиению.
Обозначим через Li (ж) касательное подпространство к этому многообра-
зию Mi в точке х Е Mi. Если х Е Mi и f Е Li(x), то
du(x; f) = (Du^x), f) = (Du^x), f)	(5.7)
для любых p.u E J(x) сужение и на Mi непрерывно дифференцируемо
на М^ (Напомним, что множество J(x) определено соотношением (5.3).)
Заметим, что в этом определении кусочно-гладкой функции требуется,
чтобы для каждого n-мерного многообразия Mj (j Е J) сужение функ-
ции и на множество Mj было непрерывно дифференцируемым на этом
множестве. Согласно утверждению 5.2, сужение функции и на многообра-
зие Mi произвольной размерности непрерывно дифференцируемо на этом
многообразии.
Доказательство.
Пусть заданы х Е G, f Е X. Покажем, что значения
₽ и{х + 5f) - и(х)
а и(х/, f) := Irnimf-----=------
совпадают.
Выберем величину с > 0 так, чтобы J(y) С J(x) для любых
у Е В(х\Е). Выберем также сходящиеся к нулю последовательности
{ak Е (О, I)}?0, {Д/с € (0,1)}?°, такие, что имеют место равенства
,+ /	и(х + akf) - и(х)
cTu(x;f) = hm ---------—--------,
k—>ос	k
+ 0kf) - и(х)
d u(x;f)= lim ------------------,
k-^OQ	Д&
и включения x + akf E B(x’1e), x 4- 0k f E B(x*,e) имеют место для
всех k Е N (здесь N — множество всех целых положительных чисел). Так
как множество J(x) конечно, то существуют р Е J(x) и v Е J(x), такие,
что множества
{UN: x + akf&M,,}, {k € N: x + 3kf &MV}
58
Глава I
являются счетными. Можно предположить, без потери общности, что
x + akfeM^, x + (3kf£M„ Vk е N.
Докажем, что
=	(5.8)
где и— градиенты функций : Мм R ии^: Mv 1вточкех.
Для определенности, предположим, что < (Зк- Числа 7(fc,m) (m =
= 0,1,..., rfc) определены следующим образом. Полагаем
?(&, 0) := ак, у(к, 1) := тах{7 е [у(к. 0), 0к] '• х + 7/ е Мм}.
Так как [х 4- 7/: 7 е [се^,^]} С В(х\е), то существует индекс
j(fc, 1) е J(x) такой, что
j:H-7(fc, 1)/ еМлПМ7-(^1).
Далее, полагая,
?(М) := тах{7 е [7(^,1),^]: х + 7/ е
имеем	___ ________
х + ?(&, 2)/ € ^J(fc,i) ^j(fc,2) >
где 2) € J(x). Продолжая эти построения, мы получим
х 4- 7<Л, По)/ = х + (3kf е М^Гк_1} П Ми.
Заметим, что величина гк не превосходит наибольшего из элементов мно-
жества J(x).
Из приведенной конструкции следует, что
М j^k,Vk)	Му)
X + 7(^4	j(k^n—1)	? X Q Мj{k,rn)
для всех m = 1,2,..., г^.
Непрерывная дифференцируемость сужений функции и на множе-
ства Mj влечет
и(х 4- 7(fc, m)/) — и(х) = [(s(fc, т — 1), f) 4- hi(k, т)]^(к, m),
и(х 4- 7(А;, ш)/) — и(х) =	т), f) 4- h^k, т)]у(к, m),
5. Кусочно-гладкие решения
59
где hi(k, т) 0 при ^(к, т) —> 0, a s(k, т) — градиент в точке х сужения
функции и на множество Mj^kjriy Мы приходим к соотношениям
(s(k, 0), Г) = (ф, 1), f) + h(k, 1) - {s(k. 2), /НЖ 1) + Ж 2) = •.. =
= (s(k, rk),f) + h(k, 1) 4- h(k, 2) 4-------------------h h(k. rk),
где h(k,m) = h2(k,m) — h\(k,m). Так как s(fc,0) = s(k,rk) = s^y\
то, переходя к пределу при к —> оо, получаем равенство (5.8).
Напомним, что х е М^, х е Мр, х 4- akf € и х 4- &kf Е Му.
Таким образом,
и{х + akf) - и(х) = [(s^\ f} + hi(k)]ak,
и(х + М) - и(х) = [<s(p), f) + h2(k)][3k,
где hi(k) -> 0 при к —> оо. Требуемое равенство d+u(x, f) = dru{x;f)
следует из равенства (5.8). Итак, доказано, что функция и дифференцируема
по направлениям.
Докажем теперь равенство (5.7). Пусть х е Mi и f € ТДж). Соглас-
но определению касательного вектора, для любого ^ > 0 найдется такой
вектор h($) е X, что
х 4- (/ 4- Д(5))5 е lim \\h{5)\\ = 0.
3—>о
Выберем произвольно j е J(.t). При выполнении условия (5.4) существует
такой вектор h' (S) € X, что
+	lim 11^(5)11 = 0.
о—>0
Так как х е Mj и сужение и на Mj непрерывно дифференцируемо, то
и(х 4- 5(/ 4- Ъ/(8У) - и(ж)
1ПП -----------;------------
(Ц+0	о
здесь — градиент в точке х сужения функции и на множество Mj. Функ-
ция и удовлетворяет условию Липшица, поэтому этот предел совпадает с
производной по направлению du(x; f). Этим равенство (5.7) доказано.
Пусть щ — сужение и на М^. Требуется доказать, что функция щ
непрерывно дифференцируема на дифференцируемом многообразии Mi.
Пусть т — размерность многообразия М^ Рассмотрим функцию
Rm D Y Э у Ui^(y)) е R, где Y — некоторое открытое множество

60
Глава I
из Rm, и -0: Y и-> Mi C Rn — непрерывно дифференцируемая функция, ко-
торая определяет систему локальных координат на Mi. Пусть f =
где г) € Rm, и Пуф (у): Rm —> Rn — производная функции -0 в точке у. Заме-
тим, что f — это касательный вектор к многообразию Mi в точке £ = 'ф(у).
Выберем произвольно индекс у Е Ji (множество Ji было определено выше
условием (5.5)). Полагаем	(?/)). Как было доказано выше, мы
имеем
Um Цг(^(У + ^))	=
<510	5
= lim + Sf + 5Н(5У) ~ и№(УУ>
510	6
Таким образом мы получили, что линейное отображение
еГ
является производной функции у щфффу)). Оно может быть переписано
в следующем виде
\ дУз /
где
---я	= XCfe(y)—л->
дУз-------------------дУЗ

Преобразование этого выражения, соответствующее изменению локальных
координат на М^ является тензором типа (0,1) (см., например, [156]).
Поэтому последнее равенство определяет компоненты градиента функ-
ции у н-> щфффу)). Отметим также, что этот градиент непрерывен по па-
раметру у е Y.
Утверждение 5.2 доказано.
5.3.	Утверждение
Пусть х е М^ Li (ж) — касательное пространство к многообразию Mi
в точке х, щ — сужение кусочно-гладкой функции и на М^ Ещ(х) —
градиент функции щ: Mi н-» R в точке х. Введем следующие обозначения
Е" := {§ е Г: (з, /) = 0, V/ е Li(x}},	(5.9)
где Е' — алгебраическое дополнение Е" в X*. Пусть р' G Ef, s" G Е” и
pf + s” е D~u(x) U D+(x). Тогда pf = Dui(x).
5. Кусочно-гладкие решения
61
Так как либо субдифференциал D~u(x), либо супердифференци-
ал D+u(x) кусочно-гладкой функции и не пуст, то его проекция на подпро-
странство Е' состоит из единственного элемента Ещ(х), который является
градиентом функции щ в точке ж.
Доказательство.
Пусть р' е Е', s" е Еп, f' е Li(x) и р' + s" е D~u(x). Соглас-
но определению подпространства Е", мы имеем (pf +	— (p',f).
Из дифференцируемости по направлению функции и и дифференцируемо-
сти щ на Mi вытекает, что
du(x; f') = {Dui(x), f'), Vf' 6 Li(x).
Более того, в определении субдифференциала содержится, что
{р' + s”, f} - du(x, /) < О, V/ е X - Rn.
Таким образом,
(р'; /') - du(x-, Г) = <р', Г) -	Г) О V/' е Ц(х).
Из последнего соотношения вытекает требуемое равенство рг =
5.4.	Утверждение
Если D~u(x) 0 и D+u(x) 0, тогда D~u(x) = D+u(x) = {s^},
где — некоторый элемент пространства X*.
Доказательство.
Пусть <$* € D~u(x), s* е D+u(x). Из определений субдифференциала
и супердифференциала следует, что
sup[(s*,/) - du(x;f)] = 0, inf [(s,,/) - du(x;f)] = 0.
feX	feX
Таким образом,	du(x; f) C (s*,/) для всех f e X. Поэтому
для всех f e X, Из последнего неравенства вытекает
равенство .s* = s*.
5.5.	Обозначения
Пусть, как и прежде, х € Mi, и множества Е' и Е" определены, как в
утверждении 5.3. Полагаем
S~ {/' е Е": Е' + s" П D~и(х) 0},
:= {s" Е Е”: Е' + s" П D+u(x) ф 0},
т. е. S~ и S+ — проекции субдифференциала D~u(x) и супердифференци-
ала D+u(x) на подпространство Е".
62
Глава I
Ниже мы используем следующие обозначения [r]+ := max{r, 0},
[r]“ := min{r, 0}, где г е [—ос, 4-ос]. Для вещественной функ-
ции А э а г(а) полагаем maxr(a) = —ос, min г(а) — ос, если А' — 0.
й^А^	йСА^
Определим функцию
(ж, z, s') i—> Fj (ж, z, s') :=
:= I" max F(x, z, s' 4- s")l 4- [ min F(x, г, s' 4- s")l . (5.10)
Ls"gS- v	A [S"ES+	A
Здесь z e R, x e s' e T*(x), а Т*(ж) — это касательное пространство к
многообразию Mi в точке х.
Заметим, что в случае dimM^ = п (где символ dimMz обозначает
размерность многообразия Mi), мы имеем Е' = X*, D~u(x) — D+u(x) =
= {Du(x)}, Е" = {0}, Fi(x, z, s) = F(x, z, s).
- Если размерность Mi равна нулю, то полагаем Е' — {0}. В этом случае
Е' — {0}, Mi = {£}, Т*(£) = {0}, где £ — единственный элемент, принад-
лежащий многообразию Mi, 0 — нулевой элемент пространства X*. При
этом, следуя определению функции Ft, мы имеем
FAFz, 0) := Г max F(F z, s)] 4-[ min Ftt.z, s)l .
v	ls€D~u(x) v J LseD+u(X) v	A
5.6.	Теорема
Пусть и: G —» R — кусочно-гладкое минимаксное (и/или вязкостное)
решение уравнения (2.1). Тогда сужение щ функции и на каждое из много-
образий Mi удовлетворяет (в классическом смысле) уравнению
Fi{x,Ui{x)^Dui{x)) — 0.	(5.11)
Наоборот, пусть и — кусочно-гладкая функция, такая, что ее сужение
на любое из многообразий Mi удовлетворяет уравнению (5.11). Тогда
эта функция является минимаксным (и/или вязкостным) решением урав-
нения (2.1).
Доказательство.
Пусть и — кусочно-гладкое решение уравнения (2.1). Предположим,
что D~u(x) Ф 0, D+u(x) — 0. В этом случае
Fi(x,Ui(x),Dui(x)) = [ max F(x, щ(х), Ощ(х) 4- $")] =
Ls,,G<S'—	-I
Г	1 +
= max F(x,u(x),s)\ =0.
LseD-u(x)	J
Последнее равенство следует из условия (U5) (см. пункт 4.2), которому это
решение и удовлетворяет.
5. Кусочно-гладкие решения
63
f,es-
Аналогично можно проверить условие (5.11) и для случая
D~u(x) = 0, D+u(x) Ф 0.
Если D~u(x) 0 и D+u(x) 0, тогда, согласно утверждению 5.4,
получаем
Fi(x. щ(х), Dui(x)) = [F{x^u{x\s^ F[F{x^u(x)^s^]~ — F(x,u(x), s^).
Из неравенств (U5) и (L5) (см. пункт 4.2) видно, что F(x,u(x),s^) = 0.
Поэтому условие (5.11) снова справедливо. Наконец, в случае D~u(x) = 0
и D+u(x) = 0 мы имеем
S
min F(x, щ(х), Dui(x) 4- s,f) = оо.
s"eS+
Принимая во внимание, что [—оо]+ = [оо]~ = 0, мы получаем равен-
ство (5.11). Тем самым доказана необходимость выполнения условия (5.11)
для кусочно-гладкого минимаксного решения уравнения (2.1).
Покажем теперь достаточность условия (5.11). Пусть
D~u(x) 0, D^u(x') = 0.
Из определения функции Fi и условия (5.11) следуют равенства
Г	"1 +
Fdx. Ui(x). DuAxX) = max F(x,u(xYs)\ = 0.
lsED~u(x)	j
Следовательно, F(x, u(x). s) 0 для всех s 6 D~u(x), т. e. функция и удо-
влетворяет неравенству (U5). Из того, что D+u(x) = 0, вытекает, что усло-
вие (L5) также выполняется.
Если D~u(x) = 0, D+u(x) 0 или D~u(x) — 0, D+u(x) — 0, то,
аналогичным образом, получаем, что из равенства (5.11) вытекают усло-
вия (U5) и (L5).
Теорема 5.6 доказана.
5.7.	Пример
Рассмотрим задачу Коши для уравнения Гамильтона-Якоби
д£+У1+(Ж) =0’	=	<5-12)
64
Глава I
Напомним, что эта задача была рассмотрена в пункте 1.4, чтобы проиллю-
стрировать классический метод характеристик. Известно, что минимаксное
(и вязкостное) решение этой задачи определяется с помощью формулы Хоп-
фа
u(t,x) = maxims 4- (2 — t)\/l 4- s2 — |г-"|	(5.13)
seR L	2 J
(проверка формулы Хопфа приведена в пункте 10.2). Заметим, что функ-
ция и является кусочно-гладкой в области G = (0,2) х R в смысле опреде-
ления, приведенного в пункте 5.1. Можно показать, что при этом
М = {Mi,M2,M3}, Mi = {(t,z): 0 < t < 1, х - 0},
М2 - {(t = 1, х = 0)}, М3 = G \ (Mi U М2).
Поэтому область G = (0,2) х R разбита здесь на 2-мерное открытое мно-
гообразие М3, 1-мерное многообразие Mi и 0-мерное многообразие М2.
Функция и непрерывно дифференцируема на М3. Легко получить, что в
окрестности многообразия Mi функция и имеет вид
u(t, х) — ui(t) + max{u2(t,x),U3(t,x)},
где
U1 (t) = ———1, U2(t, х) = ху/(2 -t)2 -1,
U^(t,x) = —U2(t,x). Ясно, что
D~u(x) = {(t — 2, $"): |s"| 5/(2 ~ 02 “ 1}, D+u(x) = 0
ддя (t,x) € Mi.
Функция ui(t) является сужением функции и на многообразие Mi
и является непрерывно дифференцируемой на этом многообразии. Прове-
рим, что ui удовлетворяет соответствующему уравнению вида (5.11). Значе-
ние (5.10) для рассматриваемой функции определяется следующим образом
Fi(t, s') = s' 4- тах{д/1 4- (s")2\ |s"|	у/(2 - t)2 — 1} = s' 4- 2 - t.
Требуется, чтобы функция ui(t) удовлетворяла уравнению
=0.
\ от /
Действительно, это условие здесь выполняется.
5. Кусочно-гладкие решения
65
5.8.	Библиографический комментарий к главе I
Классический метод характеристик представлен во многих монографи-
ях и учебниках по уравнениям математической физики и теории обыкно-
венных дифференциальных уравнений (см., например, [52, 167, 190]).
Как уже было упомянуто выше, истоки предлагаемого подхода к по-
нятию обобщенного решения связаны с теорией позиционных дифферен-
циальных игр. Понятия верхних и нижних решений уравнения Айзекса-
Беллмана, рассматриваемого в теории дифференциальных игр, совпадают с
понятиями так называемых u-стабильных и ^-стабильных функций, введен-
ных Н. Н. Красовским и автором настоящей книги в поздних 60-х-ранних
70-х (см., например, [118, 119]). Теория позиционных дифференциальных
игр, которая базируется на этих понятиях, представлена в монографии [122]
(исправленная и дополненная версия этой книги была издана на английском
языке [123]). В главе III приведены основные понятия теории дифференци-
альных игр и обсуждается их связь с теорией минимаксных решений.
Свойства стабильности могут быть развиты в различных направлени-
ях, в частности, в дифференциальной форме, например, с помощью нера-
венств для производных по направлению. Эти неравенства были введены
в [192, 203], чтобы определить обобщенное (минимаксное) решение урав-
нения Айзекса-Веллмана. Среди различных форм определений (включая
использующиеся в теории вязкостных решений), которые базируются на
паре дифференциальных неравенств, эти, по-видимому, были введены пер-
выми.
Как было показано позднее (см., например, [195]), предложенный под-
ход может быть использован при изучении широкого класса краевых за-
дач и задач Коши для различных типов уравнений в частных производных
первого порядка, т. е. не только для уравнений Айзекса-Веллмана. И при
этом не нужно менять конструктивную основу подхода, следуя которому
минимаксное решение должно быть слабо инвариантным относительно ха-
рактеристических включений.
Характеристические включения вида (2.5), (2.7) имеют прототипы в
теории дифференциальных игр и были введены в работах [3, 112, 218]
при рассмотрении вопросы так называемой проблемы унификации диф-
ференциальных игр. Эта проблема состоит, по существу, в доказательстве
следующего факта: если совпадают гамильтонианы управляемых систем, то
функции цены дифференциальных игр для этих систем также совпадают.
Позднее этот факт был обнаружен также и в теории обобщенных (мини-
максных и вязкостных) решений уравнений Гамильтона-Якоби. Среди ра-
бот, развивающих минимаксный подход, упомянем работу [204], в которой
были введены понятия сопряженных производных и показана эквивалент-
ность задач конструирования стабильных мостов и стабильных функций.
66
Глава!
Отметим также, что конструкции, подобные упомянутым характеристиче-
ским включениям, вводились также в других многочисленных работах (см.,
например, [70, 77]), где рассматривались вопросы реконструкции диффе-
ренциальных игр, чьи гамильтонианы совпадают с заданной функцией.
Исследования, базирующиеся на результатах негладкого и выпуклого
анализа, теории дифференциальных включений и динамической оптими-
зации имеют особую значимость для теории минимаксных решений. Эта
техника подробно представлена в монографиях [5, 6, 47, 62, 74, 178], а фак-
ты, которые понадобятся ниже, приведены в приложении к данной книге.
Вязкостные решения уравнений в частных производных первого по-
рядка были введены в ранних 80-х М. Дж. Крэндаллом и П.Л.Лионсом
[57, 58]. Отдельные понятия теории вязкостных решений были пересмотре-
ны и упрощены в работе [54]. Теория вязкостных решений имеет продви-
нутые исследования в области уравнений в частных производных первого
порядка и эллиптических уравнений. В рамках этой теории доказаны те-
оремы существования и единственности для различных типов уравнений
и краевых задач, изучены некоторые приложения к задачам управления и
дифференциальным играм. Обзор результатов теории вязкостных решений
можно найти в [56].
Необходимые и достаточные условия для кусочно-гладких решений
уравнений Айзекса-Веллмана были получены в форме неравенств для про-
изводных по направлению в работе [203]. Отдельные результаты для ку-
сочно-гладких решений были получены и в теории вязкостных решений,
например в статье [58], где рассматривается склейка двух функций, которая
является вязкостным решением. Заметим также, что в теории оптимального
управления и в дифференциальных играх большое внимание уделяется ис-
следованиям сингулярных множеств, в точках которых гладкие куски функ-
ции цены склеиваются между собой (см., например, монографию Р. Айзекса
[92], а также работы [29, 31, 148, 163, 184]).
Глава II
Задачи Коши для уравнений
Гамильтона -Якоби
6.	Минимаксные решения уравнений Гамильтона-Якоби
В рамках предложенного подхода, существование и единственность
минимаксного решения могут быть доказаны для широкого класса гранич-
ных задач и задач Коши. Задачи Коши для уравнений Гамильтона-Якоби
рассматриваются в данной главе. Доказательство соответствующих теорем
существования и единственности базируется на свойстве слабой инвариант-
ности минимаксного решения относительно характеристических включе-
ний. Такие включения вводятся в данном параграфе. Ниже мы формулиру-
ем также эквивалентные определения минимаксных решений для уравнений
Гамильтона-Якоби. Теоремы единственности и существования доказаны в
последующих параграфах. Как видно из доказательств, эти теоремы факти-
чески содержат также критерии устойчивости минимаксных решений отно-
сительно малых возмущений гамильтониана и краевой функции.
6.1.	Уравнения Гамильтона-Якоби
Напомним, что уравнение Гамильтона-Якоби -- это уравнение вида
^ + H(t,x,u,Dxu) = 0, (г,ж) е G := (0,0) х	(6.1)
Предположим, что функция s) н-> H(t,x, z, s) (которая называет-
ся гамильтонианом) непрерывна на (0,0) х х R х Rn и удовлетворяет
условию Липшица по переменной р
z,p) — H(t,x,z,q)\ С p(t,x,z) \р — q |	(6.2)
для всех (р, q) Е х 1П. Здесь функция p(t, x,z) предполагается непре-
рывной на G х R. Предполагается также, что функция z H(t, х, z, s) не
возрастает, то есть
H(t^X) zf ,s) H(t)X,z",s)	(6.3)
для z' z".
68
Глава II
Сформулированные условия позволяют упростить определения мини-
максных решений и доказательства теорем существования и единственно-
сти в задачах Коши для уравнений Гамильтона-Якоби. Эти условия можно
ослабить таким же образом, как это сделано в пункте 4.7.
6.2.	Характеристические включения для уравнений
Гамильтона - Якоби
Анализ минимаксных решений в задачах Коши для уравнений Гамиль-
тона-Якоби основан на свойстве слабой инвариантности графиков этих ре-
шений относительно характеристических дифференциальных включений.
Как легко заметить, уравнение (6.1) — это специальный случай уравне-
ния (2.1). Поэтому здесь может использоваться общее определение 4.4.
В то же время, принимая во внимание, что производная du/dt является
аддитивным членом в уравнении (6.1), удобно использовать характеристи-
ческие включения, в которых переменная t удовлетворяет уравнению t = 1.
Чтобы подтвердить это замечание, используем конструкции пункта 3.5.
Уравнение Гамильтона-Якоби (6.1) имеет вид (3.8). В данном случае мы
имеем т = 1, hi = 1, £ = t. Поэтому уравнение £ — hf£,x), входящее в
соотношения (3.10), превращается в уравнение 1 — 1. Для многозначного
отображения
(0,0) х Rn х R х Ф э (t, х, г, ^) Eft, х, z, ф) С Rn х R
свойства (j)-(jv) пункта 3.5 формулируются следующим образом:,
(j) для всех (t, х) € G = (0, в) х Rn, г е R, Е Ф множество Eft. ж, г, ?/;)
выпукло и компактно в Rw х R;
(jj) для любого ф е Ф многозначное отображение ft,x,z) Eft,x,z^i)
полунепрерывно сверху;
(jjj+) для любых ф € Ф, ft, х) Е G, z' z" и (/, д') € Eft, х, z', ф)
существует вектор (/, д") € Eft, х, z", ф), такой, что д" д';
для любых ф е Ф, ft, х) Е G, z' z" и ff, д") е Eft,x,z" ,ф),
существует вектор ff, д') € Eft, х, z', ф), такой, что д" > д';
(jv+) для любых ft, х) е G, z е R и s е найдется значение парамет-
ра ф° е Ф, такое, что
H(t,x,z,s) = min{(/,s) — д: (f,g) е E(t,x,z,^0)}
s) - д: (/, д) е E(t, х, z, чр~)}
при всех ф е Ф;
6. Минимаксные решения уравнений Гамильтона-Якоби
69
(Jv ) для любых (t, х) е G, z е R и s 6 Rn найдется значение парамет-
ра фо С Ф, такое, что
Нф х, z, s) = тах{(/, s) — д: (f,g) Е E(t, х, z, фо)}
тах{(/, s) — д: (J,g) е E(t,<x, z,^}
для всех ф е Ф.
Отметим, что многозначное отображение вида
E(t,x,z,s) := {(/,#) eRnxR: ||/|| p(t,x,z\ д = {f,s} - H(t,x,z,s)}
(6.4)
обладает всеми вышеперечисленными свойствами. Здесь з = ф € Ф = Rn.
Опуская уравнение i = 1, мы получаем следующее характеристическое
включение
(ж, z) G E(t, х, z, ф).	(6.5)
Минимаксное решение уравнения (6.1) может быть определено как
непрерывная функция G Э (t,x) н-> u(t,x) Е R, такая, что для любо-
го ф Е Ф ее график слабо инвариантен относительно дифференциального
включения (6.5), для которого многозначное отображение Е удовлетворяет
всем условиям (j) - (jv).
Аналогично, верхнее (нижнее) решение уравнения (6.1) определяется
как полунепрерывная снизу (сверху) функция G Э (t,x) н-> u(t, х) € R,
такая, что для любого ф Е Ф ее надграфик (подграфик) является слабо
инвариантным относительно дифференциального включения (6.5), для ко-
торого многозначное отображение Е удовлетворяет условиям (j), (jj), (jjj+),
(jv+) (условиям (j), (jj), (jjj-), (jv“)).
Для нестационарного дифференциального включения (6.5) слабая ин-
вариантность графика gr и := {(t, x,z): (t,x) € Г, z = u(t,x)} влечет
следующее свойство: для всех (to, #о, ^о) С gr и и ф € Ф существуют чис-
ло т Е (to,#) итраектория (я(-), z(-)): [to,г] н> RnxR дифференциального
включения (6.5), которая стартует из начального положения (ж0, ^о) и удо-
влетворяет равенству z(t) = u(t, x(t)) при всех t е [to, г].
Слабая инвариантность надграфика и подграфика функции и опреде-
ляются подобным образом.
6.3.	Критерии для минимаксных решений для уравнений
Гамильтона - Якоби
Как и в случае уравнений общего вида (2.1), верхние, нижние и мини-
максные решения уравнений Гамильтона-Якоби могут быть определены в
нескольких эквивалентных формах. Приведем эти определения.
70
Глава II
Сначала мы рассмотрим условия (U1)-(U5), которые продуцируют
определения верхнего решения. Функция (0.0) х Э (t, х) u(t, х) € R
предполагается, по умолчанию, полунепрерывной снизу.
Определения верхнего решения.
(U1) Для любых (to,xo) £ G = (0,0) х Rn, zo u(to,^o), s С Rn суще-
ствуют т € (to, 0) и липшицевые функции (х(-), *(•)): [to, т] х R,
которые удовлетворяют равенству (х(to), z(to)) = (хо, zq)9 уравнению
z(t) = (x(t), s) — H(t, x(t), z(t), s)	(6.6)
при почти всех t € [to, г] и неравенству z(t) u(t,x(t)) при
всех t e [to? t]-
(U2) При любом выборе элемента 0 бФ надграфик функции и слабо
инвариантен относительно дифференциального включения
(x(t), z(t)) е E+(t, x(t). z(t),i/j).	(6.7)
Здесь и в условии (U3) символом Е+ обозначается любое многознач-
ное отображение, которое удовлетворяет условиям (j), (jj), (jjj 4), (jv4),
сформулированным в пункте 6.2.
(U3) inf{d~u(t,x; l,f)-g: (f, g) e E+(t, x, u(x), 0)} 0, для всех (t, x) e G
и 0 e Ф.
(U4) a + H(t,x, u(x),s)	0, для всех (t,x) e G и (a, s) e D u(t,x).
(U5) inf {d~u(t, x\ l,f) - (s,f) + H(t, x, u(x), s): f e Rn} 0, для
всех (t, x) C G и s e Rn.
Поясним понятия d~u(t,x;l,f) и D~u(t,x), использованные
в (U3)-(U5). Согласно общему определению нижней полупроизводной по
направлению, мы имеем
d u(t,x;a,f) := lim	inf	ru(t + 8a', x 4- 8ff) — u(t, x) i л
£10	L	О	J
(6-8)
Здесь (f, х) G G, {а, /) € R х Rn,
Д£(t, х, а, /) := {(<5, o',/') € (0,г) х R х Rn :
|а - а'| + ||/ - Г||	£, t + а'8 е (0,0)}. (6.9)
6. Минимаксные решения уравнений Гамильтона-Якоби
71
Полагаем а = 1. Тогда величина d~u(t, х; 1, /) обозначает нижнюю полу-
производную функции и в направлении (1, /).
Как и в общем случае, символ D~~u(t, х) обозначает субдифференциал.
Элементы этого множества — субградиенты, т. е. пары (a, s), где а — число
и s — n-мерный вектор s. Согласно общему определению, мы имеем
D~u(t, х) := {(«<<§) С R х Rn :
аа + ($, f) - d~u{ty х; а, /) ^ О У(а, /) € R х Rn}. (6.10)
Теперь рассмотрим нижние решения уравнения (6.1). Функция u(t, х)
в условиях (L1)-(L5) предполагается полунепрерывной сверху.
Определения нижнего решения.
(L1) Для любого (to,xo) G Г (0,0) х Rn, zq С u(to,xo) и s G Rn
существуют липшицевые функции (#(•),£(•)): [to,r] > Rn х R, опре-
деленные на некотором интервале [to,r], to < т < 0, которые удовле-
творяют начальному условию (ж (to), z(to)) = (#о, го), уравнению (6.6)
и неравенству z(t) < tz(t, x(t)) при всех t G [to, г].
(L2) При любом выборе элемента ф G Ф подграфик функции и слабо ин-
вариантен относительно дифференциального включения
(±(t),z(t)) G E~(tyx(t),z(t),^).	(6.11)
Здесь и в условии (L3) символ Е~ соответствует произвольному много-
значному отображению, которое удовлетворяет условиям (j), (jj), (jjj-),
(jv~), сформулированным в пункте 6.2.
(L3) sup{d+,u(t, х\	(J\g) eE~(t)X,u(x)^)}	0, для всех (t, x) G G
и С Ф.
(L4) a 4- H(t,x, u(x), s) 0, для всех (t, x) E G и (a, s) G D+u(t,x).
(L5) sup{d+zz(t,x\ 1,/) - (s,f) 4- H(t,X)U(x),s): f G Rn} > 0, для
всех (t, x) G G и s G Rn.
В (L3)-(L5) символы d+u(t, x; 1, /) и x) обозначают верхнюю
полупроизводную функции и в направлении (1, /) и субдифференциал и в
точке (t,a?). Они определены равенствами
lim sup
(6.12)
D+tz(t, ж) := {(a, s) G R х Rn :
аа 4- (s, /) - e/+tz(t, ж; а, /)	0, V(a, /) G R х Rn}, (6.13)
u(t 4- Sa', х 4- Sf') — u(t) x)
.	8
u(t)X; a, /)
72
Глава II
где множество Ae(t, ж, а, /) задано соотношениями (6.9). Заметим, что
d+u(t, х\ a, f) = — d~{~u(t, х: а, /)),
D+u(t, х) = — D~~(—u(t. ж)).
Рассмотрим теперь условия (Ml)-(М3), которые определяют минимак-
сное решение уравнения (6.1). Мы предполагаем, что функция u(t, х) в этих
условиях непрерывна.
Определения минимаксного решения.
(Ml) Для любых (to,^o,^o) € gr и и s е Rn существуют некоторое чис-
ло т е (0,0) и липшицевые функции (ж(-), z(-)): [to,'?"] ln xR,
которые удовлетворяют начальному условию (#(to), ^(to)) = (жо,^о),
уравнению (6.6) и равенству z(t) = u(t, x(t)) при всех t € [to, т].
(М2) При любом выборе элемента ф € Ф график функции и слабо инвари-
антен относительно дифференциального включения
(±(t),z(t)) е E(t, x{t),z(t),^),	(6.14)
где Е — произвольное многозначное отображение, которое удовлетво-
ряет всем условиям (j)-(jv), сформулированным в пункте 6.2.
(М3) Функция и является одновременно верхним и нижним решением
уравнения (6.1), то есть и удовлетворяет паре условий (Ui), (Lj) для
некоторых i,j = 1,5.
6.4.	Теорема
Для полунепрерывной снизу функции (0,0) х Rn Э (t, ж) i—> u(t, х) Е R
условия (U1)-(U5) эквивалентны. Аналогично, для полунепрерывной сверху
функции и условия (L1)-(L5) эквивалентны. Для непрерывной функции и
условия (Ml)-(М3) эквивалентны.
Вышеупомянутые условия (Ui), (Li) и (Mi) могут рассматриваться как
специальные случаи соответствующих условий, сформулированных в пунк-
те 4.2. Поэтому теорема 6.4 следует из теоремы 4.3. Опираясь на теоре-
му 6.4, мы представляем следующие определения верхних, нижних и ми-
нимаксных решений.
6.5.	Определения
Полунепрерывная снизу функция (0,0) х Rn Э (t, х) u(t,x) Е R, ко-
торая удовлетворяет одному из вышеупомянутых {эквивалентных) усло-
вий (U1)-(U5), называется верхним решением уравнения (6.1). Аналогично,
6. Минимаксные решения уравнении Гамильтона-Якоби
73
полунепрерывная сверху функция	которая удовлетворяет одному из
условий (L1)-(L5), называется нижним решением уравнения (6.1). Непре-
рывная функция u(t)X), удовлетворяющая одному из условий (Ml)-(М3),
называется минимаксным решением уравнения (6.1).
6.6.	Дополнительные замечания
Минимаксные решения уравнений Гамильтона-Якоби могут быть
определены в терминах контингентных конусов для графиков, надграфи-
ков и подграфиков функций u(t, х) так же, как это было сделано в общем
случае для уравнения (2.1). Принимая во внимание вид уравнения (6.1), мы
можем рассматривать вместо контингентных конусов производные много-
значных отображений.
Приведем необходимые понятия и определения. Пусть г е (0,0), и
пусть W — некоторое множество в (0,0) х Rm. Полагаем
W(r):={yeRm-. (r,y)ewj.
Рассмотрим многозначное отображение
(0,0)	сГ.
Мы определяем правостороннюю производную по т этого многозначного
отображения в точке (t, w) Е W равенством
WV», w) :={/,.€ R” : limtaf Jist (m +	И-’(8 + ЭД =
Пусть (0,0) х Rn э (t, х) u(t,x) е R — полунепрерывная сверху
функция и W = epi и. Тогда правосторонняя производная многозначного
отображения
т н-> epi и(т, •) := {(ж, z)) € Rn х R: z и(х)}
в точке (t, х, z) Е epi и обозначается символом (Dt epi u)(t, х. z). Ясно, что
(Dt epi u)(t, x, z) := {(/, g) € Rn x R :
. dist ((x + 8f,z + 8g); epi u(t + 6, •))	)
Inn mi--------------------------------= 0 >.
8	J
74
Глава II
Аналогично, производные многозначных отображений т н-> hypo zz(r, •)
и т и-> gr и(т, •) мы определяем равенствами
(Dt hypo n) (t, x,z):= (f, g) E Rn x R :
dist ((a? 4- Sf^z + Sg); hypo u(t + 8, •)) i
hm mf-----------------~-----------------= 0 >,
6X0	8	J
(Agr u)(t,x,z) := e R" x R :
dist ((ж + 5/, z + fy); gr w(t + 5, •)) „1
lim mi--------------------------------— 0 >.
Я0	8	J
Если функция и полунепрерывна снизу, то, согласно результатам, при-
веденным в параграфе А8 (см., в частности, утверждение z\8.1), усло-
вие (U2) эквивалентно следующему соотношению
со (Dt epi tz)(t, ж, z) П E+(t, х, z. ф) 0,	(6.15)
где (t, ж, z) Е epi и, Е Ф и Е+ — произвольное многозначное отображе-
ние, удовлетворяющее условиям (j), (jj), (jjj+), (jv+).
Аналогично, для полунепрерывной сверху функции и условие (L2) эк-
вивалентно соотношению
со (Dt hypo u)(t, х, z) П E~(t, x. z, 0,	(6.16)
где (/;, ж, z) е hypo и, ф Е Ф и Е~ — произвольное многозначное отобра-
жение, удовлетворяющее условиям (j), (jj), (jjj“), (jv“).
Если функция и непрерывна, то условие (М2) эквивалентно соотноше-
нию
со (Dt gr ti)(i, х, z) П E(t, x, z, 05	(6.17)
которое справедливо для всех (t, ж, z) € gr zz и е Ф, где Е — произволь-
ное многозначное отображение, удовлетворяющее всем условиям (j)-(jv)
пункта 6.2.
Обратим внимание на то, что достаточно проверять условия (6.15),
(6.16) только для z = u(t, х).
1. Единственность минимаксного решения задачи Коши
для уравнения Гамильтона-Якоби
Теоремы о единственности минимаксных решений могут быть дока-
заны в рамках единой схемы на базе метода функций Ляпунова. Эта схе-
ма пригодна для различных типов уравнений и краевых задач. В данном
7. Единственность минимаксного решения. ..
75
параграфе мы начнем с применения этой схемы к одной из наиболее про-
стых задач, а именно, к задаче Коши для уравнения Гамильтона-Якоби с
гамильтонианом х, z, s), удовлетворяющим условию Липшица по пе-
ременным х и s. Задача Коши при более слабых предположениях будет
рассмотрена в параграфе 9.
7.1.	Определение
Непрерывная (соответственно, полунепрерывная снизу или сверху)
функция (t,x)	u(t9x): (0,0] х Rn н-> R называется минимаксным
(соответственно, верхним или нижним) решением задачи Коши
^ + H(t,x,u,Dxu)=0, (t,x) €G:=(O,0) xRn, (7.1)
u(0,x) = a{x), a?€Rn,	(7.2)
если она удовлетворяет условию (7.2), а ее сужение на G := (0,0) х Rn
является .минимаксным (соответственно, верхним или нижним) решением
уравнения (7.1).
7.2.	Предположения
Ниже мы доказываем единственность минимаксного решения в зада-
че (7.1), (7.2). Предполагаем, что гамильтониан Н и граничная функция о
удовлетворяют следующим условиям:
(Н1) гамильтониан H(t, х, s) непрерывен на D := (0,0) х Rn х R х Rn,
функция z H(t, х, z. s) невозрастающая;
(Н2) выполняется условие Липшица по переменной s
\H(t^x^z^s^) — H(t,х, z, s(2))|	p(a?)||s(^ —	||	(7.3)
для всех (t, x. z, s^) e D,n имеет место следующая оценка
\H(t, х, z, 0)|	(14-|И|4- \z\)c, \/(t.x,z) e (0,0) xRn xR, (7.4)
где р(ж) := (1 -Ь ||^||)c, а число с положительно;
(НЗ) для любого ограниченного множества М С Rn существует такая кон-
станта А(М), что
|Я(£, х', z. s) - H(t, х", z, s)|	А(М)(1 4- |к||)||ж' - х"\\,	(7.5)
для всех xf. х" е М9 (t, z, s) G (0,0) x R x Rn;
(H4) функция x (j(x): Rn R непрерывна.
76
Глава II
7.3.	Теорема
Пусть условия (Н1 )-(Н4) выполнены. Тогда для любого верхнего реше-
ния и в задаче Коши (7.1), (7.2) и любого нижнего решения v в этой задаче
справедливо неравенство и v.
Как нетрудно видеть, из теоремы 7.3 вытекает единственность мини-
максного решения. Действительно, пусть и± и U2 — два минимаксных ре-
шения. Согласно свойству (М3), функция u± является верхним решением,
а функция U2 — нижним решением в задаче (7.1), (7.2). Поэтому из теоре-
мы 7.3 вытекает неравенство и± U2. Меняя местами и± и U2, мы получим
противоположное неравенство U2 и±. Следовательно, = U2-
Доказательство теоремы 7.3 дано ниже в параграфе 7.5.
7.4.	Предварительные конструкции
Рассмотрим многозначное отображение E{t, х. z, s) вида (6.4). При сде-
ланных выше предположениях мы можем его представить как
E(t,x,z,s) := еГ xR: ||/|| р(х\ д = (/, s) - H(t.x,z.s)},
(7.6)
где р(х) = (14- ||ж||)с. Из оценок (7.3), (7.4) вытекает
\H(t, х. z,s)\	р(#)||$|| 4- |#(£, z, 0)|
р(:г)|И| 4- (1 4-И 4- |г|)с < с(1 4- |И + |<1 + И).
Поэтому для всех (t, x,z,s) Е (0,0) х Rn х R х Rn, (f,g) Е E(Tx,z,s)
имеют место следующие неравенства
||/||	(1 4- \\х\\)с, \д\	2с(1 4- М 4- Н)(1 + \\s\\).	(7.7)
Пусть и — какое-то верхнее решение уравнения (7.1). Следуя определе-
нию (U2) (см. пункт 6.3), надграфик функции и локально слабо инвариантен
относительно дифференциального включения
(±, i) Е E(t, х, z, s),	(7.8)
т. е. для любых s Е Rn, (йь^о) С (0,0) х Rn, z0 u(tQ,xo) существует
траектория (x(t), z(t)) этого дифференциального включения, выходящая из
начальной точки (xq,zo) и удовлетворяющая неравенству z(t) u(t9x(t))
на некотором промежутке времени [£о,т] С [£о>0)« Известно, что в случае
выполнения оценок (7.7) решения этого дифференциального включения мо-
гут быть продолжены до конечного момента времени t — 0. Известно также,
7. Единственность минимаксного решения ...	77
что в рассматриваемом случае можно найти траекторию, которая удовлетво-
ряет неравенству z(t) u(tbx(t}) при всех t е [to,0) (см. параграф А8).
Так как функция и полунепрерывна снизу на (0,0\ х Rn, это неравенство
имеет место и для t = 0.
Таким образом, в рассматриваемом случае, верхнее решение в за-
даче (7.1), (7.2) обладает следующим свойством: для любых s е Rn,
(to,#o) € (0,0) х Rn, z0 w(to,^o) существует такая траектория
[t0, 0] Э t (j?(t), z(t)) е Rn х R дифференциального включения (7.8), что
(®(t0),2:(t0)) = (x0,Z0),
z(t) u(t, x(t)) для всех t G [to, #]	(7.9)
Рассмотрим теперь дифференциальное включение
(±(t),i(t)) € E(t, x{t\z(f)^s(t)\
в котором (0,0] Э t s(t) е Rn — кусочно-постоянная функция. Ес-
ли и — верхнее решение уравнения (7.1), то, как и выше, существует
траектория этого дифференциального включения, удовлетворяющая усло-
вию (7.9). Аналогичное замечание справедливо и для нижнего решения
уравнения (7.1).
Пусть и (соответственно, v) — верхнее (соответственно, нижнее) реше-
ние уравнения (7.1). Выберем произвольные непрерывные функции
(t, х, у) p(t, х, у): (0, х Г х Г М Г,
(t, х, у) н-» g(t, х, у): (0,0] х Г х Г н. Г.
Мы докажем сейчас, что для любых (to, , У о) € (0,0] х Rn х Rn существует
решение системы дифференциальных включений
(i,£) е E(t,x,^,p(t,x,y)),	eE(t,y,y,q(t,x,y)),	(7.10)
которое удовлетворяет начальному условию
Mto),£(*o)) = CEo,u(io,zo)), (у(*о)л(*о)) = (з/о, Жо)) (7.11)
и неравенствам
£(i) > u(t,x(t)), j?(t)	v(t,y(t))	(7.12)
для всех to t 0.
Как следует из приведенных выше рассуждений, для любого 8 е (0,0—
— to) существует решение
М') = (жд(-), €<s(')5 2/5(')> ^О)
78
Глава II
системы дифференциальных включений
(ж, 4) е E(t,x,ps(t)), (y,rj) & E(t,y,qs(t)),
которое удовлетворяет начальному условию (7.11) и неравенствам
&(*) > u(t,xs(t)\ < v(t,ys(t))	(7.13)
при всех to С t С 0. Здесь
P^t) =	Q<s(t) =
при t € [t», ti+i), ti — t0 + i8, i e 0, Ng, a. Ng — целая часть числа (в —t0)/6.
Отметим, что из оценок (7.7) вытекают неравенства
ll^wil (I + 1Ы0||)с,	||М*)Н (1 + Ы(*)И>.
Поэтому найдется такое число К > 0, что ||^(t)|| К, ||?м(£)||	К для
всех S е (0,0 — to) и t е [to? 0]- Предположим, что
r(t, х,у)~ max{\\p(t, х, у) ||, 11q(t, х, у) ||},
М := max{r(t, ж. у): t е [to, &], ||ж|| К, ||у||	К}.
Из оценок (7.7) следует, что
i6(t)i^2C(i+K + i^(t)i)(i+^)?
|^(t)|	2с(1 + К + |^(t)|)(l 4- М)
для всех 5 G (0, в — to) и t е [to, 0]. Поэтому |&(t)|	2, где Е — это
положительное число, не зависящее от 5 е (0,0 — to) и t G [t0,0].
Таким образом, из того, что для любого значения параметра 5 Е (0,0 —
— to) функции
(Ы-ХЫ-))
и их производные удовлетворяют предыдущим оценкам, можно, в силу те-
оремы Арцела, выбрать такую, стремящуюся к нулю, последовательность
значений параметра 8^ (к = 1,2,...), что соответствующая последователь-
ность
W (•) = (xSk (•),	(.-),Убк (•), У8к (•))
стремится к пределу
»(•) = (ж(-),С(-)),(у(-), »?(•))
равномерно на [to, 0].
Предельная функция w(-) удовлетворяет условию Липшица, поэтому
она дифференцируема почти всюду. Более того, эта функция является ре-
шением системы (7.10) (этот факт следует из утверждения А7.1). Так как
функция и полунепрерывна снизу, а функция v полунепрерывна сверху, то
из (7.13) вытекает (7.12).
7. Единственность минимаксного решения ...	79
7.5.	Доказательство теоремы 7.3
Предположим, от противного, что существуют такое верхнее реше-
ние и задачи Коши (7.1), (7.2), такое нижнее решение v этой задачи, такая
точка (to, жо) € (0, в] х Rn и такое число d > 0, что ?z(to, жо) < ж? (to, жо) — d.
Обозначим через Х(^,жо) множество абсолютно непрерывных функ-
ций ж(-) : [to,0] Rr\ которые удовлетворяют дифференциальному нера-
венству ||±(tj|| р(ж(^)) и условию ж(£о) = жо- Пусть Л — константа
Липшица в условии (7.5) для множества М, определяемого как
М := t е [t0, #], ж(-) G Х(^,ж0)}.
Введем обозначения
_____________ (f>	-
ге(х,У) ~ л/е4 + ||а;-у||2, ae(t) :=------g----,
we(t,x,y) := ae(t)re(x,y),	(7.14)
Le(t, х, у, £, г?) := we(t, х,у)+£-т),	(7.15)
где (t, х, у, С, т/) е [0, х F х х R х R. Выберем такое число е > 0, что
неравенства 0 < e2az{t) < d справедливы при всех t € [0,0].
Рассмотрим производную функции Ляпунова L£ в силу системы диф-
ференциальных уравнений и дифференциальных неравенств
||х|| < р(ж), £, = (х,р) - H(t,x,£,p),	(7.16)
1Ы1	Р(.У), г)= (У,д) ~H(t,y,ri,q),
/ X (Ж
= -ae(t)—
ге
Полагаем, что решения этой системы удовлетворяют начальному условию
Ж^о) = T/(to) = Жо, £(t0) = Со ~ u(t0, Жо), 7?(to) = 7?о •= ^(t0, Ж0).
Заметим, что
(жо,2/о,Со,?7о) € N :==	е М х М х R х R: у}.
Пусть траектория (x(t), y(t), £(t), r;(t)) системы (7.16) проходит внутри
множества N на интервале [to, т] с [to, #]. Пусть
Ls[t] := L£(t,a;(t),7/(t),^(t),7?(t)).
р = q - DyWe(t, х, у) = -Dxw£{t, х, у)
80
Глава II
Используя условия (6.3), (7.5), получим
d>L£ [t] dw£ \ / т~\	* \ \ / п • \ I /
= ~gj- + (Dxw£,x) + (Dyw£, у) + £, - у =
p-Ai
-X^-re(x,y) - H(t,x,£,p) + H(t,y,£,p)
С -Х^-гЕ{х,у) + А(1 + ||р||)||а; - у|| С Хге(х, у) [-^7- + 1 + ||р||] =
= Аг£(х,У)[-— + i + asW___J^
Г Z3 — At
< Хг£(х,у)-------h 1 + a£(t) = 0.
Из того, что Le[to] = e2a£(to) 4- Со — Уо < £2a%(to) — d < 0 и L£[t] < 0
для почти всех t € [to, т]> вытекает, что траектории системы (7.16) не поки-
дают области N при всех t € [йъ #]•
Как было показано в пункте 7.4, существует траектория
(жг(’)> ^(‘)> CsV’G)? ^Д’))
системы (7.16), такая, что
£е(0) > и(0,хе(0У) = a(x£(0)), у£(0)	v(0,y£(0)) = <т(у£(0)). (7.17)
Неравенство L£ [t] 0 имеет место для любого решения системы (7.16).
В частности, оно справедливо для решения, которое удовлетворяет неравен-
ствам (7.17). Поэтому справедливо
L£[t0] = €2a£(t0) +ii(^o,^o) - v(tQ,x0) L£[0]
a£{0)r£(x£(ff),ye(0)) + (т(®£(0)) - <т(уе(0))	<т(ж£(0)) - <r(j/e(0)).
Заметим, что
lim e2a£(0') = 0, lim a£{0) —» oo.
s—^0	s—^0
Очевидно, что
|<т(же(0)) -	, max Иж) - CT(y)l := K < oo-
(х,у)ем xM
8. Существование минимаксного решения. ..	81
Поэтому из неравенства
а£(в)т£(х£(в),у£(в))	£2a£(t0) 4-п(£0,ж0) -v(to,xo) А-К
следует
||же(0) ~ Z/e(0)|| ~> 0? когда е 0.
Далее, переходя к пределу при е 0 в оценке
£2a£(t0) + «(*о, жо) - хо) > <t(xs(0)~) - <т(з/е(0))
получаем неравенство u(to, xq) v(te, xq). Таким образом, предположение
о том, что	< ^(£о?^о) приводит к противоречию. Теорема 7.3
доказана.
Примечание. Функция ш£ вида (7.14) удовлетворяет условию (А4),
введенному в работе [55] (это условие сформулировано также в пункте 9.2).
Из доказательства теоремы 7.3, приведенного выше, ясно, что условие (НЗ)
может быть заменено условием (А4).
Модифицируя доказательство теоремы 7.3, мы можем оценить раз-
ность и — где и — верхнее решение в задаче Коши
—+ Я1 (t, х. и, Dxu) — 0, и(в, х) = <71 (ж),
a v — нижнее решение в задаче Коши
+ Я2(Л х, v, Dxv) = 0, v(6, х) = ст2(ж).
Таким способом мы можем получить оценки, которые позволяют анализи-
ровать проблемы корректности минимаксных решений. Заметим, что в те-
ории уравнений Гамильтона-Якоби этим проблемам уделяется много вни-
мания.
8. Существование минимаксного решения задачи Коши
для уравнения Гамильтона-Якоби
В этом параграфе мы приводим результаты, из которых следует суще-
ствование минимаксных решений в задаче Коши для уравнений Гамильто-
на-Якоби. Эти результаты вместе с теоремой 7.3 из предыдущего парагра-
фа доставляют критерии существования и единственности минимаксных
решений. Мы даем два варианта доказательств.
8.1.	Теорема
Если условия (Н1)-(Н4) из параграфа 7.2 выполняются, то в задаче
Коши (7.2) существует единственное минимаксное решение и.
82
Глава II
Как показано выше, единственность минимаксного решения следует из
теоремы 7.3. Нетрудно видеть, что существование минимаксного решения
в задаче (7.1), (7.2) может быть выведено из факта существования таких
верхнего решения и и нижнего решения v этой задачи, что и С v. Дей-
ствительно, согласно теореме 7.3, здесь невозможно строгое неравенство.
Поэтому мы получаем, что существует функция, которая является одновре-
менно верхним и нижним решением задачи (7.1), (7.2). Согласно определе-
нию (М3) (см. пункт 6.3), эта функция является минимаксным решением в
рассматриваемой задаче Коши. Таким образом, доказательство теоремы 8.1
может быть сведено к доказательству следующего утверждения.
8.2.	Теорема
Если условия (Н1)-(Н4) выполнены, то существуют такие верхнее
решение и и нижнее решение v задачи Коши (7.1), (7.2), что и v.
Доказательство может быть схематически очерчено следующим обра-
зом. Рассмотрим нижнюю огибающую множества всех верхних решений за-
дачи Коши (7.1), (7.2). Затем проверим, что функция ио, полученная таким
образом, удовлетворяет определению верхнего решения. Далее, докажем
что верхнее замыкание этой функции ио, определенное равенством
uo(t,x) := limsup{uo(r, £): ||£ — ж|| е, \т — t\ < г, т G (0,0]},
£10	'
удовлетворяет определению нижнего решения. Ясно, что v := ио uq.
(Здесь удобнее проводить все рассуждения в классе локально ограничен-
ных функций.) В конце доказательства применяются операции нижних и
верхних замыканий, которые обеспечивают полунепрерывность рассматри-
ваемых функций снизу и сверху.
Этот метод имеет истоки в теории позиционных дифференциальных
игр, где подобные конструкции были использованы при доказательстве су-
ществования цены игры. Позже этот метод применялся в теории вязкост-
ных решений. А именно, верхние (соответственно, нижние) огибающие г
классах субрешений (соответственно, суперрешений) использовались, что-
бы доказать существование вязкостного решения (см. библиографический
комментарий в конце этой главы).
8.3.	Предварительные конструкции
Пусть W — множество в Rm. Функция w: W R называется локалык
ограниченной, если для любого уо € W существует такое число в > 0, что
sup |w(y)| < оо, для у е В(уо', е) П
у
Ясно, что sup |wQ/) | < оо для любого компактного множества YcW.
yeY
8. Существование минимаксного решения. ..
83
Выберем и зафиксируем т 6 (0,0], s е Rn. Рассмотрим следующие
величины
/Г(^о,жо,го) := sup{^(z(r)) - z(r): (ж(-),г(-)) € Sol (t0, х0, z0,5)},
g*(to,xo,zo) := ш£{^(ж(т)) - г(т): (#(•), z(-)) € Sol (ж0, t0, ^0, $)}•
Здесь (to,^o5^o) С (0,т] х Rn х R, $ е Rn и <р: Rn н-> R — локально
ограниченная функция. Символ Sol (t0, ж0, z0, з) обозначает множество всех
решений
(х(-),г(.)): [О,0]н»ГхК
характеристического включения
(±, г) € E(t, х, г, 5),	(8.1)
которые удовлетворяют условию ж (to) = х$, z(to) = z0. Напомним, что
многозначное отображение Е определено равенством
Е(Е х, z, я) := {(/, д): ||/|| р(х), д = (F, s) - H(t, х. z, $)}	(8.2)
и удовлетворяет оценкам (7.7). Обращаем внимание, что гамильтониан Н
и многозначное отображение Е не определены при t — 0 и t = 0. Однако
траектории дифференциального включения (8.1) могут быть непрерывно
продолжены на весь интервал [0,0].
Пусть М — компактное подмножество множества (О, й] х Rn х R. По-
лагаем
Sol(M, $):=	Sol(£o5£o?^o?s)-	(8.3)
(t0,x0,zQ)eM
Известно, что, если имеют место оценки (7.7), то множество Sol (М, 5) ком-
пактно в пространстве С([0,0]. Rn+1) (см. параграф А7, утверждение А7.3).
Поэтому локальная ограниченность функции <р влечет за собой оценки
sup	ж0,г0)| < 00,
(to,xo,zo)eM
sup |/Z*(<0, х0, z0)| < 00.
(tQ,xo,zo)eM
Следовательно, /i* и д* локально ограничены. Покажем, что
li*(t0,x0,z0 + /г)	(j,*(t0,x0,zo) - h,
М*(^О)^о,-го +/i)	-/i-	(8.4)
84
Глава II
Докажем первую оценку. Очевидно, можно ограничиться случа-
ем h 0. Выберем произвольное число е > 0 и найдем такую траекто-
рию (ж^(-), г^(-)) G Sol (ж0,t0, zq + h, $), что
/z*(to,®o,^o + h) - £	^(жДт)) - zh(r).
Функция удовлетворяет дифференциальному включению
zh(t) = {xh(t), s) - H(t, xh(t), zh(t\ s)
и начальному условию Zh(to) = zQ + h zq. Поэтому существует такое
решение z*(-) дифференциального уравнения
z*(t) = (xh(t),s) - H(t,xh(t),z*(t),s),
что z*(to) = zq и z*(t) < Zh(t) — h для t E [to, 0]. Напомним, что гамиль-
тониан H(t, x, z, s) не возрастает по переменной z. Принимая во внимание,
что т t0, получаем
zh(r) - z*(r) = л + J [H(t,xh(t),z*(t\s) —H(t,xh(t),zh(t),s)] dt h.
io
Согласно (8.1), (8.2) мы имеем
(®л(-),г*(-)) G Sol(i0,a:o,2to,s).
Таким образом, окончательно,
/j*(t0,x0,z0 + h) - е ^(жДт)) - zft(r)
9?(о:я(т)) - г*(т) - h p*(x0,t0,z0) - h.
Вторую из оценок (8.4) можно доказать подобным образом.
Обозначим символом Su множество всех локально ограниченных
функций (0,0] х Rn Э (t, х) ь-> u(t, х) Е R, которые удовлетворяют ра-
венству (7.2) и неравенству
ш£{[и(т,ж(т)) - г(т)]: (ж(-),г(-)) Е Sol (t0, xq, zq, s)}	0,	(8.5)
при всех (to,a:o) (0,0] x Rn, zq > u^q.xq), t E [t0,0], s E Rn.
Точно так же символ Sz обозначает множество всех локально ограни-
ченных функций и: (0,0] х Rn н-> R, удовлетворяющих равенству (7.2) и
неравенству
sup{[tz(r, х(т)) — г(т)]: (ж(-),г(-)) Е Sol (to, xq, zq, s)} ^0,	(8.6)
при всех (t0, ж0) E (0,0] x Rn, zq < u(tQ, xq), t E [t0,0], s E Rn.
8. Существование минимаксного решения. ..	85
Отметим, что в этих определениях функции и Е Su и и е S1 не
предполагаются полунепрерывными сверху или снизу Результаты, приве-
денные ниже, показывают, что полунепрерывная снизу (соответственно,
сверху) функция и является верхним (соответственно, нижним) решени-
ем задачи (7.1), (7.2) тогда и только тогда, когда и е Su (соответствен-
но, и Е S1).
Доказательство теоремы 8.2 опирается на утверждения 8.4-8.7.
8.4.	Утверждение
Пусть выбрано и зафиксировано s G Rn. Определим
P^q.xq.zq) := ш£{(т(т(0)) - z(0): (ж(«), z(-)) G Sol (t0, т0,г0, s)},
n_(t0,T0) •= inf{C C	0}-
Справедливо следующее. Функция u_: (0,0] x Rn i—> R локально ограничена
и оценивает снизу функции и Е Sw, т. е.
u(t0,xQ) tz_(t0,T0)
при всех и ESU и (to, ^о) С (0,0] х Rn.
Доказательство. Величина р_ удовлетворяет оценке вида (8.4), т. е.
p^(to,XQ,zo -Eh) //_ (t0, т0, z0) - h, V h^0.	(8.7)
Полагаем h > |//-(to,0)1- Из (8.7), где z0 = 0, получаем, что
//,„(.т0, to, h) < 0, и поэтому u_(to, xq) h.C другой стороны, полагая z0 =
= —h, из (8.7) извлекаем, что /i_(t0, х0,-h) p_(t(y т0, Q)+h > 0. Из (8.7)
следует, что //_(to, тд, —hf) > 0 для всех h' h. Поэтому u_(to, xq) —h.
Следовательно, \и_(t0, #о)I |//-(to, т0,0)|. Из того, что функция
(t,z) i-+/z_(t,z,0): (0,0] xRnMt
локально ограничена, вытекает, что функция также локально ограниче-
на.
Для любого и Е Su из равенства х) — о(х) и условия 8.5, в ко-
тором мы полагаем т = 0, следует неравенство //_(t0, х0, zq) 0. По-
этому из определения функции и_ мы получаем, что zq u_(to,To)-
Эта оценка справедлива при любых zq > w(to,To). Следовательно,
?z(to,xo) tz_(to,To). Утверждение 8.4 доказано.
86
Глава II
u(Iq,xq) :=
8.5.	Утверждение
Пусть выбраны и зафиксированы s* € Rn, t* С (0, 0], и е Su. Опреде-
лим
p*(to.xo,zo) := sup{u(t*,z(t*)) - z(t*): (ж(-),г(-)) € Sol (t0, ж0, ^о, <%)},
(8.8)
sup{C е R: fj,*(t0,x0X) > 0}, toe(O,t,],
u(t0,x0),
Тогда функция и принадлежит множеству Sn.
Сначала покажем, что существует такая траектория, что
6 Sol (to,xo,zo,s) nSol(to,a;o,^o,s*).
Этот факт будет использоваться при доказательстве утверждения 8.5. Слу-
чай s = s* очевиден. Пусть s^s^. Полагаем
.	.H(t,X)Z)3) — H(t, х, z,s*)
, х, z, s, 8* ):= (s - sf)----------------—,
l|s-M
<7q(t, x. z, s, s*) := x, z, s, s*), s} — H(t, x, z, s').
Из условия (7.3) извлекаем
X, z, s, s*)||	p(x).
Отметим, что
g^(t, x. z,s, s*) = (f\t,x,z, $,$*),$*) — H(t,x,z,s*).
Поэтому
(/^(t, ж, z, s, s*),g^(t, x, г, s, 5*)) € E(t, x, г, <s) A E(t. x, z, s^).
Следовательно, траектория (a^(-), z^(-)), которая удовлетворяет системе
уравнений
ж = f\t,x,z^s, s*), z — g\t,x,zys,s^
и условию (ж(£о), ^(£о)) = (^о?^о), принадлежит пересечению мно-
жеств Sol (to, ^o, zq, s) и Sol (to, жо, ^o, s*).
Доказательство утверждения 8.5. Если t* = 0, то /1*(0,жо,го) =
= и(0,Х$) — Zo — ст(жо) - ZQ. Поэтому и(0,Хо) = ст(жо). Если t* < 0,
8. Существование минимаксного решения. ..
87
то и(0, жо) = u(0,xq) = <т(хо). Таким образом, функция и удовлетворяет
условию u(0,xq) — сг(хо). Локальная ограниченность функции и может
быть проверена подобно тому, как это было сделано для функции и- в
доказательстве утверждения 8.4.
Остается доказать, что для любых (to, жо) С (0,0] х Rn, zq > u(to, жо),
secure [to, 0] имеет место следующее неравенство
inf{S(r, ж(т)) - z(r) : (ж(-), z(-)) € Sol (t0, xq, zq, $)}	0.	(8.10)
Возможны три случая: (i) to t*, (ii) r < t*, (iii) to < t* < t.
Случай (i). Если to > t*, то неравенство (8.10) следует из условия (8.5)
(которое имеет место для функции и) и из равенства (8.9). Заметим, что
для t0 — (согласно (8.8) и (8.9)) справедливо /z*(t*, ж0, z0) = w(t*,x0) —
— zo и u(C,xq) = u(t*,xo). Поэтому неравенство (8.10) имеет место не
только для t0 > t*, но также и для to = t*.
Случай (ii). Полагаем
SolT {(ж(-), z(-)) е Sol (t0, ж0, ^о,^*)<
O(t),^(0) =	te [£0,т]},
Solr := Sol (т, ж^(т), 2^(т), <s*),
где (жк(-), zq(’)) е Sol(to^o,zo,s)ASol(to^o,zo,s*)-TaKKaKZo > ^о,жо),
из (8.9) следует, что /i*(t0, жо, ^о) < 0. Согласно (8.8), имеем
0 > ;/*^о,жо,го) > sup{n(t*^(t*)) - z(t*): (ж(-),г(-)) € SolT} =
= sup{?i(t*,ж^*)) - z(t*): (ж(-),г(-)) е SolT} = //*(т,ж^(т), z^(r)).
Поэтому из (8.4) и (8.9) вытекает S(t, ж^(т))	г^(т). Таким образом, нера-
венство (8.10) доказано в случае (ii). Отметим, что для т — t* справедливо
0 > //(t*^b(t*),^(t*)) = ^(^,ж^(^)) - z\t*).
Случай (iii). Полагаем
Solo := Sol (to, жо, Zq, s),
Sol* := Sol(t*,ж^*),zq(t*),s),
Solb := {(z(-),z(-)) e Sol0:	z’(t)), t 6 [t0,t*]}.
88
Глава II
Справедливы соотношения
inf{w(T,x(r)) - г(т): (ж(-),г(-)) Е Sol0}
(= inf{n(r, ж(т)) — z(r): (ж(-),г(-)) С Solo}
(b)
inf{zz(r, ж(т)) — z(f):	E Sol^}
(c}	(d)
—; inf{tz(r), ж(т)) — z(r): (ж(-),г(’)) C Sol*} 0.
Равенство (а) следует из равенства ia(t, x) — u(t, x); неравенство (b) являет-
ся следствием включения Sol * C Sol о; равенство (с) следует из определения
множества Solq. Последнее неравенство (d) следует из условия и Е Su и
соотношения (8.5), которое выполняется для функции и. Условие (8.5) здесь
применимо, так как выше было показано, что z*[t*) > w(£*, ж* (£*)).
Таким образом, мы получаем (8.10). Утверждение 8.5 доказано.
8.6.	Утверждение
Множество Su содержит локально ограниченную функцию
и+', (0/У] х Rn R, определенную равенством
u+(to,xo) := sup{< Е R: /z+(to,^o?C) > 0},	(8.11)
где
//+(to,^o,^o) := зир{(т(ж(0)) - z(&): (ж(-),г(-)) £ Sol (£0, ж0, ^о? s*)},
us* — вектор из Rn.
Доказательство. Локальная ограниченность функции может быть
доказана таким же образом, как это было сделано для функции и- в утвер-
ждении 8.4. Для to = 0 имеет место равенство /z+(0, жо, zo) = сг(жо) —zo. По-
этому жо) = <т(ж0), так что функция и+ удовлетворяет условию (7.2).
Кроме того, функция удовлетворяет условию (8.5), что можно показать
так же, как это было сделано в случае (й) при доказательстве утвержде-
ния 8.5.
8.7.	Утверждение
Пусть S — непустое подмножество множества 8й. Тогда функ-
ция (0,0] х Rn Э (t, х) н-> х) Е R, определенная равенством
u*(t,x) supinf{u(r, £): (т, £) Е B^(t, х), и € S},	(8.12)
£>0
8. Существование минимаксного решения. ..	89
является верхним решением задачи (7.1), (7.2). Здесь и ниже
:= {(т,0 е (0,0] х Мп: ||£ - ж|| С е, |т - t\ < с}.	(8.13)
Аналогично, пусть S С Sl, S 0. Тогда функция и*: (0,0] х Rft н* R,
определенная равенством
u*(t,x) inf sup{ia(t, £): (т, £) G B^(t, ж), и е S},	(8.14)
€>0
является нижним решением задачи (7.1), (7.2).
Доказательство. Покажем, что и* — верхнее решение задачи (7.1),
(7.2). Введем следующее обозначение
r*(j;,t,£,S) := inf{?/(£, т): (т, £) G B^!(t, ж), и G S}.
Заметим, что	г*(т, t, е", S), когда 0 < г' е". Поэто-
му u*(t,х) r*(#,t, 1,S). Согласно утверждению 8.4, для любой функ-
ции и е 8 С Sw справедлива оценка и и_. Следовательно
u*(t,x) -> inf{tz_(r,£): (т,£) € В\(Тх)}.
Из того, что функция и- локально ограничена, на любом ограниченном
множестве М с (0,0] х Rn для нее справедливо следующее отношение
inf и*(Т х} > —ос.
С другой стороны, согласно (8.12), справедливо w* и, где и — функция
из множества S. Напомним, что функция и локально ограничена. Следова-
тельно, доказана и локальная ограниченность функции и*.
Теперь покажем, что функция и* полунепрерывна снизу. Выберем про-
извольно точку (t0, жо) С (0,0] х и число а > 0. Согласно (8.12), суще-
ствует такое число £ > 0, что г*(i0, то, e,S) -> u*(t0, То)—(т. Из определения
величины г* вытекает, что неравенства
r*(t, t,e/2,S) n(to,TO,c, S)
справедливы для любой точки (t, х) е (0,0] х Rn, такой, что
||т-т0|| <е/2, \t - to| < е/2.
Поэтому, согласно (8.12), справедливо
u*(t, х) r*(t, ж, e/2,S) > r^(to,To,e, S) -> u*(to, то) — а.
Таким образом мы доказали, что функция полунепрерывна снизу.
90
ГЛАВА II
Выберем произвольную точку ж* € Rn. Покажем, что и*(0,#*) ~
= сг(ж*). Из того, что и(0,х*) = ст(х*) для всех и Е S, вытекает, что
г/*(0,ж*)	сг(ж*). Остается доказать, что ж*)	сг(х*).
Согласно (8.12), можно выбрать такую последовательность
(tkyXk^ Zk, Uk) Е (0,0] х Rn х R х S (к = 1, 2,...),
что zk := Uk(tk,Xk) + 1/fe,
lim (tk^Xk) — (0->x^)b lim zk = u*(0,^*).
к—->oo	к—»oo
Функции Uk удовлетворяют условию (8.5). Выберем произвольно s Е Rn.
Заметим, что Zk > Uk(tk,Xk)- Поэтому существует такая траектория
(^(•),z^(-)) € Sol(xk,tk)Zk,s), что
а(х^(0)) = Uk&x^tf)) z^k\0) 4- 1/к.
Перейдем к пределу при к —> оо. Принимая во внимание, что
z^k\0) —»г/*(0, х*), а функция ст — непрерывна, получаем и*(0, х*)	а(х*).
Таким образом, равенство и*(0, х*) — сг(х*) доказано.
Докажем теперь, что надграфик функции и* слабо инвариантен отно-
сительно характеристического включения (8.1).
Пусть (tfb^o) С (0,0] X Rn, Zq U*(tO,Xo), т Е [t0,#], $ С Rn.
Согласно (8.12), можно выбрать такую последовательность (tkE^k^k) Е
G (0,0] xRnxS (/с = 1,2,...), что
(tk,xk) -» (to,^o), uk(tk,Xk) -> n*(to,^o), когда к -> ос.
Полагаем а zq~u*(to, xq)9 Zk := Uk(tk, Xk)+a+l/k. Из того, что a 0,
вытекает, что Zk > Uk(tkl Xk)- Ясно, что Zk —> zq, когда к —> ос. Функции ик
удовлетворяют условию (8.5), поэтому можно выбрать такую последова-
тельность траекторий (х^(•), ^^(-)) Е Sol (£&,zk, -§) (к = 1,2,...), что
z^(r) uk(T,xSk\r)) - 1/к.	(8.15)
Извлечем сходящуюся подпоследовательность последовательности
(ж^(-), (к = 1,2,...). Предел этой подпоследовательности обозна-
чим через (ж*(-), г*(-)). Этот предел принадлежит множеству Sol(to,
(см. параграф А7, утверждение А7.3). Без потери общности можем полагать,
что существуют пределы
(г) , т) —> а, когда к оо.
8. Существование минимаксного решения. ..	91
Из (8.12) следует, что и*(т, ж*(т)) С а. Переходя к пределу при к —> ос в
неравенствах (8.15), получаем
г/*(ж*(т).т) < а г*(т).
Таким образом, доказано, что для любых (to, жо, ^о) С epi и*, т G [to, 0]
и s е имеет место следующее неравенство
тш{и*(х(т),т) - z(t): (ж(-),г(-)) € Sol (t0, xQ, zQ, $)}	0.
Из этого неравенства вытекает, что существует траектория (жт(-), гг(-)) G
G Sol (t0,3Co,zo, s), такая, что (т,х(т), z(r)) е epi и*. Следовательно, над-
график функции и* является слабо инвариантным относительно дифферен-
циального включения (8.1) (см. замечание А8.1 в параграфе А8).
Таким образом, доказано, что функция и* является верхним решением
задачи (7.1), (7.2). Точно так же может быть доказано, что функция гх*
вида (8.14) является нижним решением задачи Коши (7.1), (7.2).
8.8.	Доказательство теоремы 8.2
Рассмотрим функции uq и гщ, которые определены на (0,0] х Rn ра-
венствами
Uo(t,x) supinf{?z(r, £): (т,£) G B^(t, ж), и G Sw}, (8.16)
€>0
uo(t,x) := inf sup{tzo(T, С): (ТЛ) е B^(t, ж)}.	(8.17)
£>0
Заметим, что, согласно утверждению 8.7, функция uq является верхним
решением задачи (7.1), (7.2). Ясно также, что uq — минимальный элемент
множества SU9 т. е.
uq G Su, uq Viz G Su.	(8.18)
Докажем, что функция гщ является нижним решением задачи (7.1),
(7.2).
Функция uq полунепрерывна сверху. Этот факт может быть установлен
таким же образом, как была доказана полунепрерывность снизу функции и*
в утверждении 8.7. Покажем, что подграфик функции йо является слабо
инвариантным относительно дифференциального включения (8.1).
Пусть (to,xo,zo) е hypo t* £ (to,0], s* G Rn. Покажем, что
max{zz0(t*, a?(t*)) - z(t*): (rr(-), г(-)) G Sol (t0, x0, z0, <§*)}	0.	(8.19)
92
Глава П
Согласно (8.17), можно выбрать такую последовательность
(tk.Xk) € (0,0] х Вп [к — 1,2,...), что
(tk,Xk) -> (to,a?o), uQ(tk,Xk) -> Uo(to,xo), когда к оо.
Без потери общности можно полагать, что tk < t* для всех к — 1,2,...
Пусть
Zk '= Zq -Uq^q.Xq) +u0(tk,Xk) - ^/к.
Из неравенства zq ^о(^о?^о) следует Zk < UQ(tk,Xk)- Кроме того,
lira Zk = Zq.
к—*оо
Теперь определим функцию и, используя равенства (8.8), (8.9), в ко-
торых мы полагаем и = uq. Из утверждения 8.5 и соотношений (8.18)
вытекают соотношения
u0(tk,Xk) С u(tk,xk) := sup{C б R: /j,*(tk,xk,C)	0}.
Поэтому из неравенств (8.4) и неравенств zk < uo(tk, хк), uq uq получаем
0 < ix*(tk,xk,zk) := sup{'U0(**,T(t*)) -z(t*): (х(-), z(-)) б Solfc} С
s? sup{uo(t.,a?(t.)) -z(t*): (т(-),г(-)) б Solfc},
где используется обозначение Sol к = Sol (tk,xk, zk, s,).
Следовательно, существует такая последовательность траекторий
б Sol(tfc,Tk,Zk,s*) (к — 1,2,..
что
xw(t*) С uo(tt.,x^\t^.	(8.20)
Без потери общности можно полагать, что
(х^(-),г^(-))	(ж*(-),г*(-)) б Sol (to, то, zo,s,)
когда к —> ею.
Поэтому, переходя к пределу в неравенствах (8.20) при к > сю, полу-
чаем неравенство (8.19), из которого следует, что подграфик функции uq
слабо инвариантен относительно характеристического включения (8.1) (см.
замечание А8.1).
Наконец заметим, что гщ(0,я) = а(х). Этот факт может быть прове-
рен таким же образом, как и равенство г/*(0, х) = а(х) в доказательстве
утверждения 8.7.
Таким образом мы заключаем, что uq является нижним решением за-
дачи (7.1), (7.2). Выше было доказано, что uq является верхним решением
задачи (7.1), (7.2). Из определения (8.17) функции uq следует, что uq uq.
Таким образом, теорема 8.2 доказана.
8. Существование минимаксного решения ...	93
8.9.	Операторные уравнения для минимаксных решений
В данном разделе содержатся конструкции и результаты, имеющие ис-
точником метод программных итераций, который был развит в рамках те-
ории дифференциальных игр и предназначен для нахождения функции це-
ны (соответствующие библиографические комментарии приведены в конце
этой главы).
Введем некоторые некоторое обозначения. Символ LB будет обозна-
чать множество локально ограниченных функций (0,в] х Rn Э (t, х) i->
u(t, х) G R. Множество полунепрерывных снизу (соответственно свер-
ху) функций w: (0,0] х I будет обозначаться символом LSC (соот-
ветственно символом USC).
Пусть и е LB, (/щ^о) С (0,0] х Rn, (£,т, 8) е Rx [to, 0] х Rn-
Определим величины
Г*(и)(*о,^о,Ст,«) := inf{u(T,ar(r)) - z(r): (ж(-),х(-)) е Sol (t0, х0,£, s)},
:= sup{w(t,x(t))-x(t): (x(-),z(-)) € Sol (£0,аг0, £,«)}•
(8.21)
Очевидно, что оценки (8.4) могут быть переписаны следующим образом
^*(u)(tQ,XQ,C + h,r,s) <	- h,
i^*(u)(tQ,XQ,C + h,T,s) < ^*(u)(to,£o,C,T, s) - h. (8.22)
Пусть
v*(u){Iq, xq,t, s) := inf{C e R: ^(u)(£0, С'Л s) < 0},	(8.23)
v*(u)(tQ,XQ,r, s) := sup{< € R: ^*(u)(tQ, xq, Q, t, s) 0}.
r*(u)(to,^o) •= sup sup и,(и)(£о,.то,т,s),	(8.24)
sG'Rn
r*(u)(to,^o) •= inf inf V*(u)(tQ, Xq, T, s).
Заметим, что для любого и С LB и для любого (Iq,xq) Е (0,0] х Rn
справедливы оценки
Г*(п)(^о,жо) u(Iq,xq), r*(u)(to,^o) u(Iq,xq). (8.25)
Выберем и зафиксируем вектор s* С Rn. Напомним, что для любо-
го з е Rn найдется такая траектория, что
(#*(•),£*(•)) е So\(tQ,XQ,C,s) П Sol (to, Xq, £, 8*)
94
Глава II
(см. доказательство утверждения 8.5). Из (8.21) следует, что
^*(^)^о,^о,С,т, s) и(т,ж*(т)) - z*(f) <
< sup{w(r, я(т)) - z(t): (#(•), г(-)) е Sol (t0, ж0, С, «*)} =
= *0* (?z) (t0, а?о, т, <$*).
Заметим, что для
С = 0, h = '0*(w)(to,^o,O,r, s*),
согласно предыдущему неравенству и оценке (8.22), справедливо
^(u)(tQ,XQ,h,r, s) ^*(^)(to,^o,0,s) - h =
= ^(w)(to,rro,0,5) - V>*(^)(to,^o,0,T, s*)	0
при всех т e [to, 0] и s e Rn. Поэтому, привлекая (8.23) и (8.24), получим
^(to,^O,T,<s)	^*(^)(£о,^О,О,Т,<8*)5
r*(u)(to,rEo) sup ^*(^)(£o,^O,0,T, s*).
tO^T^0
Пусть D — некоторое ограниченное множество в (0,0] х Rn, и пусть М
:= {(t? х, z): (t, х) е D, z — 0}. Из того, что и е LB, а множество Sol (М, з*)
вида (8.3) компактно в С([0,0], Rn+1), имеем оценку
sup r*(u)(tQ,X()) < 00.
(to,xo)ED
Объединяя эту оценку с первым неравенством в (8.25), заключаем, что функ-
ция (t0,x0)	Г*(u)(to, хо) локально ограничена.
Точно так же можно проверить, что для любой локально ограниченной
функции и функция вида (to, ^о) Г*(u)(to,жо) также локально ограни-
чена. Эти факты могут быть выражены соотношениями
Г*(ЬВ) С LB, Г*(£В) С LB.
Сначала предположим, что и е LBPiLSC, то есть функция и локально
ограничена и полунепрерывна снизу. Докажем полунепрерывность снизу
функции (t,х) н-> r*(u)(t,#).
Определим множество
М := {(t, х, т, С, s) е (0,0] х Rn х (0,0] х R х Rn :
г t,	(w) (^ С,s) 0}
8. Существование минимаксного решения. ..
95
Пусть
{(tfc, Хк, Ткч Скч С М.
— это последовательность, которая сходится к точке (to, жо, то, Со? so)- Ес-
ли to > 0, то (to? ^о? То, Со? so) С М. Действительно, из полунепрерывности
снизу и и определения (8.21) вытекает, что существует такая последователь-
ность (ж/Д-),^-)) £ Sol(tk,XkXk,Sk), ЧТО и(тк,Хк(тк)) - zk(Tk) 0. Эта
последовательность содержит подпоследовательность, которая сходится к
пределу (ж*(-), £*(•)) G Sol(to,£o?Co?so)« Из полунепрерывности снизу и
следует неравенство п(то, ж*(то)) — z*(tq) < 0. Из определения (8.21) по-
лучаем, что ^(u)(to, жо, Со? то, so) 0, что и требовалось доказать.
Теперь пусть {(tfc, хк, 7fc)}i° С (0,0] х Rn х R — это такая последова-
тельность, что ук = rj,u)(tk'Xk) и lim (tkiXk^k) = (to^o,7o), t0 > 0.
к—*оо
Чтобы доказать полунепрерывность снизу функции (t, х) r*(u)(t, ж),
достаточно показать, что Г*(u)(to, х$) С 70.
Выберем произвольное число е > 0. Из (8.24) следует, что существует
такая пара (т£,$£) € [to, в] х Rn, что Г* (u) (to,#о) v*(tt)(to, жо,т£, s£) Те.
Пусть {taJJ0 — такая последовательность, что тк Е [tk, 0] и lim тк = т£.
к—+оо
Рассмотрим также последовательность {Cfc}?°?> определенную равенством
£к = vJ^u^tk^Xk'TkiSEy Без ограничения общности можно полагать, что
последовательность {Cfc}i° сходится к пределу Со- Заметим, что ук Ск>
следовательно, 70 Со-
Из включения (t&, ж/-, Са?, Л,, s£)	€ М, следует включение
(to, жо, Со? т£, se) Е М. По определению множества М и из (8.23) получаем
неравенства
7о > Со > ш(и)^о,ж0,т£,5£) Г*(гб)^о,жо) - е.
Из того, что выбор е был произволен, заключаем, что справедливо неравен-
ство Г*(^,жо)	7о- Таким образом, функция (^ж) н-> Г*(и)(^ж) полуне-
прерывна снизу.
Аналогичным образом можно проверить, что функция (t, ж) н->
н-> T*(u)(t, ж) полунепрерывна сверху. При этом используется, что и локаль-
но ограничена и полунепрерывна сверху. Эти свойства могут быть записаны
следующим образом:
Г*(£В П LSC) с LB(~] LSC,
Г* (LB A USC) с LBn USC.	(8.26)
Отметим, что верхние и нижние решения задачи Коши (7.1), (7.2) ло-
кально ограничены. Слабая инвариантность надграфика (соответственно,
96
Глава II
подграфика) полунепрерывной снизу (соответственно, сверху) функции и
эквивалентна неравенству (8.27) (соответственно, неравенству (8.28))
Г*(гг)(^о,^о)	^(£(ъ#о), V(^o,^o) € (0,0] х Rn,	(8.27)
r*(7i)(to^o)	u(tQ,x0\ V(to^o) е (0,0] х Rn.	(8.28)
Используя (8.25), получаем следующее утверждение.
8.10.	Теорема
Функция и е LBCiLSC является верхним решением задачи Коши (7.1),
(7.2) тогда и только тогда, когда эта функция удовлетворяет условию (7.2)
и является неподвижной точкой оператора Г*. Точно так же функция
и € LB P\USC является нижним решением задачи Коши (7.1), (7.2) тогда
и только тогда, когда эта функция удовлетворяет условию (7.2), и являет-
ся неподвижной точкой оператора Г*. Непрерывная функция и является
минимаксным решением задачи Коши (7.1), (7.2) тогда и только тогда,
когда эта функция является решением системы операторных уравнений
Г* (и) = и, Г* (и) = и
и удовлетворяет условию (7.2).
Теперь вернемся к теореме 8.2. Приведем еще одно доказательство
теоремы 8.2, в котором мы будем использовать операторы, введенные в
пункте 8.9.
Рассмотрим последовательность
щ :-Г*(и+),	:=Г*(зд), к -1,2,...,	(8.29)
где функция и+ определена соотношением (8.11).
8.11.	Утверждение
Последовательность	вида (8.29) сходится поточечно
на (0,0] х Rn к нижнему решению и* задачи (7.1), (7.2). Функция и*, опре-
деленная соотношением
u*(t, х) :— зиртЦиЦт,^): (г, £) е B^(t, х), к = 1,2,...},	(8.30)
£>0
является верхним минимаксным решением этой задачи (напомним, что
множество B^(t^x) определено соотношениями (8.13)).
8. Существование минимаксного решения. ..
97
Доказательство. Сначала докажем следующий факт. Пусть vw е Su
для любого си е Q, где Q — некоторое непустое множество. Тогда нижняя
огибающая v, определяемая соотношениями
v(t,x) := inf ^(t, ж), (t, х) Е (0,0] х Rn,	(8.31)
принадлежит Su. Напомним, что множество было определено в пунк-
те 8.3.
Из жД0, х) = сг(ж) следует и(0, х) — сг(.т). Из утверждения 8.4 получа-
ем, что функция v локально ограничена. Остается показать, что функция v
удовлетворяет условию (8.5).
Пусть (t0, жо, го) ~ такая точка из (0,0] х х R, что z0 > v(to, жо). Из
определения функции v следует, что существует такой элемент cj* Е Q, что
(to, Жо) < Zq. Из того, что Е Sw, выводим, что для любых Т Е [to, 0]
и s Е Rn имеет место следующее неравенство
mf{[vo>.(-r,^(r)) -z(r)]: (x(-),z(-)) G Sol(f0,a:o,^o,s)} < 0.
Имея в виду, что v , заключаем, что функция v удовлетворяет усло-
вию (8.5). Таким образом, получаем, что v Е Su.
Пусть Q (0,0] х Rn, и пусть для любой точки ш	Е Q
соответствующая функция определена равенством — и, где функция и
задана соотношениями (8.9). Согласно утверждению 8.5, имеем Е Su.
Из определений (8.24) и (8.9) вытекает, что
Г* (u) = inf v„.
(л)
Поэтому получаем следующий результат: если и Е Su, то Г*(u) Е Su.
Это свойство может быть выражено соотношением
r*(Su) С Su.	(8.32)
Теперь рассмотрим последовательность вида (8.29). Напомним, что,
согласно утверждению 8.6, функция и+ принадлежит множеству Su. Мож-
но проверить, что функция и+ является полунепрерывной сверху (доказа-
тельство этого факта проводится совершенно так же, как было проведено
доказательство соотношений (8.26)). Из Е SUE\USC следуют соотноше-
ния (8.26) и (8.32), так что справедливо Uk Е SUE\USC для всех к = 1,2,...
Для любой функции Uk утверждение 8.4 доставляет оценку Uk и_.
Таким образом, согласно (8.25), последовательность (8.29) удовлетворяет
следующим соотношениям
UkESuE}USC, Uk^u_, Uk±i С Uk.	(8.33)
98
Глава II
Поэтому существует поточечный предел
u*(t, х) lim Uk(t, х) (t,x) G (0,0] х Rn.	(8.34)
/с—>оо
В силу того, что и* является нижней огибающей последовательности
полунепрерывных сверху функций Uk, функция и* также полунепрерывна
сверху. Отметим также, что множества hypo Uk удовлетворяют соотноше-
ниям
сю
hypo Uk+i С hypo ик, hypo и* = Q hypo ик. (8.35)
fc=i
Из вышесказанного следует, что lim Г*(иь) — и*. Покажем, что
/с—* сю
lim Г*(зд) =Г*(«*)-	(8.36)
к^оо
Полагаем С/с •—	С •= u*(to,#o)- Выберем произвольно
т G [to,0] и s G Rn. Согласно определению Г* и полунепрерывности свер-
ху ик> существует такая траектория (ж/с(-), ^(-)) G Sol (to, .то, C/c+i? s), что
(г, гпс(т),27с(т)) G hypo Uk. Последовательность {(#&(•), ^(-))}i° содер-
жит подпоследовательность, которая сходится к пределу (х*(•), г*(•)) G
G Sol (to, #о, С?$). Из (8.35) следует, что (т, ж*(т), г*(т)) G hypo и*. Та-
ким образом, согласно определениям (8.21) и (8.24), мы получаем
V’*(w*)(to,^o,C,/r,0, Vr € [to,0], Vs G Rn,
Г*(и*)>С =u*(t0,^0).
Принимая во внимание (8.25), видим, что Г*(^*) = iz*. Кроме того,
и* G LB A USC. Таким образом, из теоремы 8.10 вытекает, что и* — ниж-
нее минимаксное решение задачи (7.1), (7.2).
С другой стороны, из (8.33) и теоремы 8.7 следует, что функция ги,
определенная соотношениями (8.30), является верхним минимаксным ре-
шением задачи (7.1), (7.2). Утверждение 8.11 доказано.
Из (8.30), (8.34) следует, что и* С и*, т. е. из утверждения 8.11 выте-
кает теорема 8.2. Кроме того, используя теорему 7.1, получаем равенство
и* = и*. Таким образом, последовательность вида (8.29) сходится к мини-
максному решению задачи (7.1), (7.2) сверху. Точно так же можно показать,
что последовательность вида
w(1) :=Г*(«_), u(fc+1) :=r,(ww), к = 1,2,...
сходится к минимаксному решению снизу.
9. Единственность при ослабленных предположениях	99
9. Единственность при ослабленных предположениях
Теоремы существования и единственности обобщенных решений со-
держат наборы предположений, касающихся гамильтониана и терминаль-
ной (начальной) функции. Ослабляя некоторых из этих условий и усиливая
другие, можно получать различные варианты таких теорем. Например, мож-
но доказать теорему о единственности минимаксного решения, в которой
требования к гамильтониану ослаблены, а условия для краевой функции
усилены, и в которой введены некоторые дополнительные предположения о
верхних и нижних решениях. В данном параграфе сформулированы утвер-
ждения такого типа, взятые из статьи [55] М. Дж. Крэндалла, Х.Ишии и
П.Л. Лионса. Доказательство, предложенное ниже и основанное на мето-
де функций Ляпунова, проведено тем же способом, как и доказательство
теоремы 7.3. Заметим, что при построении функций Ляпунова здесь ис-
пользуются некоторые конструкции работы [55].
9.1.	Определение
Полунепрерывная снизу (сверху) функция и: G R называется верх-
ним (нижним) решением уравнения
^ + H(t,x,u,Dxu) = 0, eG.= (0,6>) xRn, (9.1)
если для любых чисел Л > 0 и е > 0 существует число р(Л, е) > 0 такое,
что в области
Da ;={(t,x,z) е (0,0) хГх1: ||ж|| < Л, |г| < Л}
надграфик (подграфик) функции и слабо инвариантен относительно диф-
ференциального включения
(х, z) е E(t, х, z, s, с, р(Л, с))	(9.2)
для любого s G Вд. Здесь
E(t, х, z, s, е, р(А, в)) := {(/, g) € Rn х R :
11/11 р(Л,г), Ii?- {f.s) -Я(4,ж,г,з)|	г}. (9.3)
В данном параграфе не предполагается, что гамильтониан удовлетво-
ряет условию Липшица по переменной s. Поэтому прежнее определение
не может применяться непосредственно, и мы используем данное только
что определение 9.1. Напомним, что похожее определение было введено в
пункте 4.8 для уравнения (2.1).
100
Глава II
Можно доказать, что верхнее (нижнее) решение в смысле определе-
ния 9.1 удовлетворяет условиям (U4) и (U5) (условиям (L4) и (L5) из
пункта 6.3). Поэтому верхнее (нижнее) решение в смысле определения 9.1
является также верхним (нижним) решением в вязкостном смысле. Обрат-
ное утверждение имеет место для случая, когда гамильтониан х, z, s)
непрерывен, и выполняется следующее условие: для любого А > 0 суще-
ствует v(А) > такое, что оценка
\H(t, х, z,s) — H(t,x,z,p)\ С z/(A)(l + ||s — p\\)	(9.4)
справедлива при всех р е Rn, s е 5д, (t, х, z) е D\. Таким образом, если
названное условие выполняется, и полунепрерывная снизу (сверху) функ-
ция и удовлетворяет условию (U4) или (U5) (условию (L4) или (L5)), то эта
функция является верхним (нижним) решением в смысле определения 9.1.
Этот результат следует из теоремы 4.9.
Из свойств локальной инвариантности надграфика верхнего решения
и подграфика нижнего решения можно получить следующее утверждение.
Пусть
[0, й] х Вл х Вд э (£, х, у) p(t, х, у) е ВА,
[О, X Вд х Вд Э (t, х, у) i-> q(t, X, у) G ВА
— непрерывные функции. Рассмотрим систему дифференциальных включе-
ний
(ж,4) € E(t,x,^,p(t,x,y'),e,p(A.,e)'),
(у, у) е E(t, у, у, q(t, X, у),е, p(N, е)),
которая эквивалентна системе дифференциальных неравенств
||i|| < р(А,е),	|£- {x,p(t,x,y)) + H(t,x,i,p(t,x,yy)\ sj е,
||у|| sj р(Л, е),	|у — (y,q(t,x,y)) + #(t, у, у,у(Аж, у))| < е.
Пусть и (соответственно, v) — верхнее (соответственно, нижнее) решение
уравнения (9.1) в смысле определения 9.1. Предположим, что
(io,^o,Co) € £>л, Со = u{ta,x0),
(tfhyfh'no) € Da, у0 = v(t0,x0).
Тогда существует решение системы (9.5), которое удовлетворяет начально-
му условию
(ж(4о),С(*о)) = (жо,Со), (y(to),y(to)) = (Уо,%)
9. Единственность при ослабленных предположениях
101
и неравенствам
e(t) u(t,x(t)), ??(t)	v(t,y(t))	(9.6)
для всех to t < т, где
т := min{t & [£0,0]: (t,ar(t), y(t),£ (£),G dS},
S := [0,0] x B\ x B\ x [—А, А] x [—Л,Л].
Это утверждение может быть доказано так же, как это было сделано в
подобной ситуации в пункте 7.4.
9.2.	Предположения
Рассмотрим задачу Коши для уравнения Гамильтона-Якоби (9.1) с
конечным условием
х) = а (ж), х е Rn.	(9.7)
Сформулируем предположения о гамильтониане Н.
(АО) Гамильтониан H(t, x.t z, s) непрерывен на (0,0) х Rn х R х Rn.
(Al) Отображение z н-> H(t^x^z^s) не возрастает для каждого
(U,s) е (0,0) хГ х Rn.
(А2) Существуют липшицевая, всюду дифференцируемая функция д: Rn н->
н-> R4" и непрерывная функция R+ х R+ н-> R+, которая не убыва-
ет по обоим своим аргументам, удовлетворяет равенству 99(0, R) = 0
при R > 0, и неравенство
Я(С ж, г, з + XD^(x)) — H(t, х, z, s) C <p(A, ||s||)	(9.8)
имеет место при (t,x,z,s) e (0,0) x Rn x R x Rn и 0	A 1.
Предполагается также, что
lim /i(x) = oo, sup ||D/z(ar)|| < оо.
INHOO
(АЗ) Существуют липшицевая, всюду дифференцируемая функция v: Rn 1—>
R+, и для каждого h > 0 постоянная Сд, такая, что
Н(С ж, z,s 4- XDv{x)) — Н(С ж, г, s) Ch	(9.9)
при х е Rn, t е (0,0), s е Ва и А е [0, h] (напомним, что Вь '=
:= {8 е Rn: ||8||	h}). Кроме того
v(x) ||ж||, для больших ||ж||.	(9.10)
102
Глава II
(А4) Существует число го > 0, и для каждого е > 0 существует непрерыв-
ная функция Г м R+ (где Г := {(£,ж,у) Е (0,0) х х Rn: |ж —
~ У I < П)}), которая дифференцируема в любой точке области Г и
удовлетворяет дифференциальному неравенству
+ H(t, у, z, Dywe) - H(t, X, z, -DxWe) 0,	(9.11)
V g Г, z g R
и соотношениям
w£(t,x,x)^e, V(£,rr) G (0,0) хГ,	(9.12)
w£(t,x,y)	1/s, при ||rr - ?/|| = r0.	(9.13)
Кроме того,
\\Dxwe(t,x,y)\\	d£. \\Dyw£(t,x,y)\\	d£,	(9.14)
при всех (t, x, у) G Г,
liminf{w£(0, x, y): ||rr — г/|| > r} = oo,	(9.15)
sio
для r G (0, r0].
(A5) Функция a: Rn н-> R равномерно непрерывна.
Эти предположения фактически совпадают с предположениями из ра-
боты [55]. Единственное различие состоит в том, что в упомянутой работе
рассматривается задача с начальным условием п(0,ж) = сг(гг), заданным в
левой граничной точке интервала [0,0]. Из-за этого знак неравенства в отно-
шении (9.11) противоположен знаку соответствующего неравенства в [55].
9.3.	Теорема
Пусть условия (АО), (Al), (А2) и (А4), (А5) выполняются. Пусть и,
v являются, соответственно, верхним и нижним решениями задачи (9.1),
(9.7). Предположим, что Ci и С2 — такие константы, что неравенство
v(t,x)~u(t,x) Си \/(t,x) G (0,0] х Rn,	(9.16)
а также либо неравенство
|ц(£,я) — u(t,y)\ С (?2, либо |г(£,ж) — v(t.y)\ < (?2	(9.17)
9. Единственность при ослабленных предположениях 103
имеют место при t Е (0,0], ||ж — у\\ С г о (где г о — число, указанное в
предположении (А4)). Тогда v.
Доказательство. Предположим противное, т. е. предположим, что су-
ществуют верхнее решение и, нижнее решение v и точка (£о,#о) €
е (0.0) х Rn такие, что
а := v(t0, хо) - u(t0, х0) Е (0, Ci].	(9.18)
Рассмотрим функцию
Ls(t, х, у, rf) := ws(t, х, у) + С - П +	(9.19)
Здесь /2 и w£ — функции, определенные в условиях (А2) и (А4). Непрерывно
дифференцируемая функция gr: R+ н-> R+ имеет следующие свойства:
„ , //ч dgr(z)	pr(z)
0 gr(z) := —: 	1, lim —-— = 1,
arV 7 dz	>оо Z
gr(C) = 0, при 0 С О-	(9.20)
Выберем такие положительные числа г, е и Д, что
R	Х/е > С := Ci + С2 + 1,
е + Зе0<я, de) < г.	(9.21)
Напомним, что <£>, С\, С2 и d£ — это величины, определенные в оценках
(9.8), (9.16), (9.17) и (9.14).
Функция Le будет рассматриваться в области
W := {(t, х, y,£,rf) : to t 0,	(t, x, у) 6 Г,
w£(t,x,y)+/3grMy))<C, -С<е-т?<0}.	(9.22)
Полагаем Co := «(to, xo), % := «(to, xq). Заметим, что
(to,Хо, Хо, Co, %) G W, L£(to, Xo, x0, Co, %) < s - «•
Действительно, согласно (9.18) и (9.12), имеем —С < —С\ Со — % =
= —а < 0 и w£(to,xo,xo) е. Из определения функции gr и числа г
следует, что ,gr(/i(x0)) = 0. Принимая во внимание неравенство s+ЗеО < а,
получаем we(xo,xo,to) + Ддг(//(х0)) е < а < С. Очевидно также, что
(to,xo,Xo) G Г.
104
Глава II
Заметим, что для некоторого Л1 > 0 неравенства
IkKAx, Ы1^А1
имеют место в любой точке (t, х. у, G 77) € W. Полагаем
p(t,x,y) •= -Dxws(t,x,y),
q(t, х, у) := Dyws(t, х) + 0g'r(y(y))Dyp,(y),	(9.23)
rf(t, ж, 3/) := max{||p(t, x, y)||, \\q(t, x, y)||},
A2 := sup{d(t, x, y): t & (0, 0), ]|»|| Лъ ||y|| Лх}.
Так как функция и (функция v) — полунепрерывна снизу (сверху), то при
некотором Лз > 0 справедливы оценки
u(t, х) -Лз, v(t, у) Лз,
для всех (t, х, у, G ту) 6 W. Полагаем
Л := тах{Лх, Л2, Лз + С + 1}.
Рассмотрим теперь систему (9.5), в которой функции р(£, х, ?/), q(t, х, у)
и числа е, Л выбраны, как указано выше. Пусть
Wr := {(t х, у, д) е W: |£| < Л, \rj\ < Л}.
Согласно замечанию, данному в конце пункта 9.1, существует решение
(же(-), 2/е(*)9	^(О) системы (9.5), которое удовлетворяет начальным
условиям xe(t0) = уе(1о) = xq, GW) — G> ?feW) - % и неравенствам
u(t,x£{f)\ rj£(t) v(t,y£(tX), \/te [to,т],	(9.24)
где
т.- min{£ G (W]: W х£ (t),y£ (t), GW> q£ W) e dWf}.
Если t г, то из (9.22), (9.24) следует
GW W xeW) Лз < Л, GW ~c > —Л,
то есть IGWI < Л. Точно так же получается оценка \r}£ (t) I < Л- По опреде-
лению момента т, точка (т, хе(т), ys(r), G(TL ^Д7")) принадлежит границе
множества Wf. Принимая во внимание, что |G(T)I < А, |7?е(т)| < Л, полу-
чаем, что эта точка принадлежит границе множества W, т. е. имеет место
одно из следующих равенств
1МТ) “Ыт)11	(9.25)
w£(Trx£(r)ry£(r^)-+ /Здг(/х(у£(т))) = С,
GW)-^(т) = “^ GW)-^W)=o, т = в.
9. Единственность при ослабленных предположениях
105
Покажем, что первые четыре равенства ложны и справедливо только по-
следнее равенство т = 6.
Оценим производную функции L£ вдоль рассматриваемого решения.
Согласно (9.19), (9.5) и (9.23), имеем
= Zfit + lxDxWs' + (Dyw^y} +	У) + С - т) <
<	- H(t, х, С, р) + H(t, y,q,q) + 2e.
Из условия (9.8) и неравенства de) < е получим
H(t, у, y.q) = Н (t, у, у, Dyw£ + (3g'rDyid) Н (t, у. у, Dyw£) + е.
Так как H(t, ж, г, з) — невозрастающая функция по z, то из неравен-
ства £ < у (справедливого для точек (х, t, у, £, у) 6 W) следует, что
&(t, у, у, Dyw£) H(t, у, Dyw£).
Используя условие (9.11), получим
Зе для почти всех t € [to, т].	(9.26)
Отметим, что Le(to, xq, xq, £о, 7о) с — а. Функция L£ непрерывна
на W U 9W, поэтому из (9.26) и (9.21) следует
Le(T,xs{T),ys{r\£,e{r'),ris{T')) < £ - а + 3£0 < 0.	(9.27)
Предположим, что справедливо первое равенство в (9.25). Тогда, со-
гласно (9.13), (9.24), (9.16), (9.17) и (9.21), получаем
L£(t,®£(t),1/£(t),^(t),77£(t)) > | +£е(т) - %(т)
> I + и(т, Ж(т)) - v(r, у(т)) > | - G - С2 > 0.
Это противоречит (9.27). Поэтому первое равенство в (9.25) оказывается
неверным.
Рассмотрим второе равенство. Из (9.27), (9.24) и (9.22) вытекает
И4(же(т),у£(т),т) + /Здг(ц(уе(т)')') < %(т) - ^е(т) s? С.
Поэтому второе равенство в (9.25) неверно.
106
Глава II
Из (9.24), (9.16) и (9.17) следует £е(т) - ^(т) -Сх - С2 > -С. Так
как w£ 0 и дг 0, то из (9.27) вытекает, что £е(т) — ?уе(т) < 0. Поэто-
му третье и четвертое равенства в (9.25) также неверны. Таким образом,
доказано, что т = 0.
Принимая во внимание, что <?г(м(жо)) = 0, Со — По = ^(^о^о) —
- ъ’(ж0, t0), из (9.26) получаем
b£(to,^o,^o,Co,^o) = w£(to,^o5^o) + u(tO}£o) ~ v(tG,xo)
>	- 3е0 =
= Ш£{0,Х£(0\у£(0)) + &(#) -	- 3с0
we(0,xe(0\y£(0^ + ££(0) - г/г(0) - 3е0
сг(х£(0)) - сг(у£(0У) - 3е0.
Последняя оценка есть следствие соотношений (9.24), (9.7) и w£ 0. Из
неравенства
w£(0,x£(0),y£(0)) we(to,rro,xo) + w(t0,x0) - v(t0,rr0)-
- &(0) + Ъ(0) + 3s0 е - а + С + 3е0
и условия (9.15) вытекает
1К(0) ~ Ы#)11 °, когда е -> 0.
Напомним, что функция а равномерно непрерывна в Rn. Поэтому
<т(яе(0)) — (j(y£(0)) —» 0, когда е —> 0. Принимая во внимание (9.12) и
переходя к пределу при е —» 0 в неравенстве
е - а w£(to,a;o,^o) + u(tQ,xQ) - v(to,^o) сг(ж£(0)) - а(у£(0)) - 3е0,
приходим к противоречию.
Теорема 9.3 доказана. Отметим, что в работе [55] использовались пред-
положения, что верхнее и нижнее решения непрерывны. Приведенное выше
доказательство использует более слабое предположение о полунепрерывно-
сти решений.
9.4. Утверждение
Пусть предположения (АО), (А1), (А3)-(А5) выполнены. Пусть и —
верхнее решение задачи (9.1), (9.7), a v — нижнее решение этой задачи.
Предположим, что существуют такие константы С2 и К, что следующая
оценка
v(t, х) u(t, х) + К(1 + ||ж||), V (t, х) е (0,0] х Rn (9.28)
и одна из оценок (9.17) справедливы. Тогда верна оценка (9.16).
9. Единственность при ослабленных предположениях 107
Таким образом, в этом утверждении заявлено, что оценка (9.16) из
теоремы 9.3 может быть заменена условием (АЗ) и оценкой вида (9.28).
Доказательство. Без потери общности можно принять, что выполня-
ется первая из оценок (9.17), т. е.
\u(t. х) ~u(t,y)\^ С2	(9.29)
для t е (0.0], ||ж — у\\ го (где г0 — число, используемое в предположе-
нии (А4)). Полагаем
(3 К + 1, /г(е) d£ 4- Д M(s) := Ch(e) + 2,	(9.30)
где К, d£, Ch — константы из оценок (9.28), (9.14) и (9.9). Определим
следующие величины
т := sup{|cr(z) - а(у)\: (х,у) Е х Rn, ||ж - у\\	г0},
где С2 — константа из оценки (9.29). Далее, полагаем
ip(t. х, в. г) := w(t, х) — v(t, х) 4- m 4-1 4- /Здг^^х)) + M(s)(0 — t);
а	х € Rn, t € (0.0], 0 < в < со, г > 0}.	(9.32)
Здесь дг — функция, которая удовлетворяет условиям (9.20), а функция v
используется в предположении (АЗ).
Рассмотрим два случая: (i) — 2 а < оо; (ii) —оо < а < —2.
В случае (i) для любой точки (t, х) € (0,0] х Rn имеем
п(Л х) — v(t, х) 4- inf (3gr(i/(x)) 4- M(eo)(0 — t) 4- т 4-1 =
г>0
= u(t, х) — v(t, х) 4- М(со)(0 - t) 4- пН О а —2.
Поэтому
v(t, х) — u(t, х) < Ci := М(со)0 4- т 4- 3.
Следовательно, в этом случае оценка (9.16) справедлива.
Остается доказать, что случай (ii) невозможен. Предположим обрат-
ное. Выберем параметры е е (0, s0] и г > 0 такими, чтобы выполнялось
следующее неравенство
b inff^t, ж, £, г): t Е (0,0], х Е < —2.
108
Глава II
Из (9.28), (9.10) и неравенства 0 > К (см. (9.30)) следует, что Ъ > —сю.
Выберем такую точку (to, xq) € (0,0] х Rn, что -0(^0, г) < 6 Ч-1 < —1.
Определим функцию
Le(t,x,y,£,Tf) :=	(9.33)
которая будет рассматриваться в области
W := {(t, ж, у, £, rf): to t (t, х, у) € Г,
- С2 - 1 - К(1 + М)	< 0}. (9.34)
Пусть
p(t,x,y) := —Dxwe(t,x,y),
q(t, х, у) := Dywe(t, х) + fy'.(^(y))Dyiy(y).
Определим числа Ai, Л2, Л3 таким же образом, как и в доказательстве
теоремы 9.3. Полагаем
Л := max{Ai, Л2, Л3 + 1}.
Рассмотрим систему (9.5), в которой функции p(t, х, у), q(t, х, у) и чис-
ла s, Л выбраны как указано выше. Полагаем £0 ’= ^(to, xq), t]q := г (to, х*о).
Из оценки -0(to, xq, в, г) <-1 вытекает, что £0~ Ло =	#о) - '^(to, -/‘о) < 0.
С другой стороны, из (9.28), (9.29) следует
Со - % = u(io,^o) - <*o,®o) > -К(1 + ||ж0||) > -С2 - 1 - /<(1 + ||ж0||).
Таким образом, доказано, что (to,x0,xq,Со, %) € W. Заметим также, что
u(tQ,x0) -Л3, v(to,xo) < Л3. Поэтому |Со| < Л, |%| < Л.
Полагаем
Wf {(t,x^,e,7?) е W: |С| < Л, \у\ < Л}.
Согласно замечанию в конце пункта 9.1, существует решение
^(^^(ОЛеСО^сС*)) системы (9.5), которое удовлетворяет начальным
условиям rr£(to) = z/£(to) = Хо, £e(to) = £0, 77e(t0) = Т]о И неравен-
ствам (9.24).
Если t т, то из (9.34), (9.24) вытекает
СеЮ %(*) v(t,ys(tY) Л3 < Л,
%(t) Ce(i) > u(t,xs(t)) -Л3 > -Л.
9. Единственность при ослабленных предположениях 109
Поэтому из условия (г, ж£(т),?/е(т),^(т),г/£(т)) е 8W' получаем, что
справедливо одно из равенств
||же(т) - у£(т)|| = Го, &(т) - 77£(т) = 0,
££(т)-7?£(т) = -С2-1-^(1 + |Ыт)||), Т = 6.	(9.35)
Вычислим производную функции L£ вдоль указанного решения
(М-МгС), £е(Т%(-))-
Покажем, что
< 0, при почти всех t е [to, т].	(9.36)
Согласно (9.5) и выбору функций p(t, ж, у), q(t, х, у), справедливы оценки
DLr dwr , „	..
~dt ~dt + \DxW^xf + \Dyw^y)+
+ 4 - f) + (3g'r{Dyv, у) - M(e)
«S	X' +	У^~М(«0 + 2e.
Из условия (9.9) и равенств h(e) = d£ + /3, M(e) =	4- 2 (см. (9.30))
вытекает
H(t, у, у, q) = H(t, у, у, Dyw£ + fig'rDyv)
H^y^DyWs) +Cft(£) = H(t,y,r),DyWe) +M(e) - 2.
Из условия (Al) и неравенства < ту, которое выполняется для
(/z, .т, у, ту) € W, следует, что
Hit.y.ri.DyWe) H(t,y^,DyW£).
Используя условие (9.11) и неравенство £ < 1, получаем (9.36).
Отметим, что
b£(to,^o,^o,^o,^o) = w£(to,^o,^o) + ^(to,xo,£,r) < 6 4-2 < 0.
Функция L£ непрерывна на W U dW. Поэтому из (9.36) получаем
££(т,же(т),?/£(т),^(т),т/е(т)) < Ь + 2 < 0.
(9.37)
ПО	Глава II
Предположим, что справедливо первое равенство в (9.35). Тогда, со-
гласно (9.13), (9.24), (9.17), получаем
Ls (г, Х£ (г), уе (т), С (г),	(г) ) >
1/е — Ci +'ф{у£(т),т,е,г')	1/е - С2 + Ь Ь + 2.
Приходим к противоречию с (9.37). Следовательно, первое равенство
в (9.35) неверно. Величины w£, /?, дг и М{е) неотрицательны. Тогда из (9.37)
вытекает, что второе равенство в (9.35) не выполняется. Третье равенство
противоречит (9.28), (9.29). Рассмотрим четвертое равенство. Если т — 0.
то из (9.37) следует, что
<т(®е(0)) - сг(з/е(^)) = u(0,X£(0)'} - v(0,ye(ff)) < £,£(ff) - у£(0) < -т - 1.
Из того, что ||#е(0) — 2/е(0)|| го, приходим к противоречию с (9.31). Таким
образом, заключаем, что случай (ii) невозможен.
10. Конструктивные и численные методы
В этом параграфе содержатся несколько результатов из области кон-
структивных и численных методов решения задачи Коши для уравнений
Гамильтона-Якоби. Сначала рассматриваются формулы Хопфа и показы-
вается, что они определяют обобщенное решение в минимаксном и вяз-
костном смысле. Приведено прямое доказательство этого факта^ которое
основано на результатах выпуклого и негладкого анализа. При этом исполь-
зована также теорема о минимаксе. Далее приведены результаты для случая,
когда гамильтониан H(t,x,s) является выпуклым по переменной s. Пока-
зано, что при этом условии минимаксное решение в задаче Коши совпадает
с функцией цены некоторой задачи динамической оптимизации. Если, в до-
полнение к упомянутому условию выпуклости, гамильтониан достаточно
гладок, то для получения негладких минимаксных решений можно моди-
фицировать классический метод характеристик. В заключение приводятся
отдельные результаты по применению конечно-разностных операторов и
сеточных методов.
10.1.	Формулы Хопфа
Рассмотрим задачу Коши для уравнения Гамильтона-Якоби
+ H(Dxu) = 0, (£, ж) е Г := (0,6») х R",	(10.1)
и(в, ж) = <т(ж), ж € R”.
(10.2)
10. Конструктивные и численные методы
111
Заметим, что в этой задаче гамильтониан не зависит от переменных t, х, z9 в
отличие от общего случая, рассматривавшегося в предыдущих параграфах.
Если предельная функция а в рассматриваемой задаче выпукла, то для
минимаксного решения справедлива следующая формула
u(t.x) := sup inf [а (у) + (s,x — у} + (0 — t)H(s)].	(10.3)
Если гамильтониан является выпуклым, то минимаксное решение задается
формулой
u(t. х) sup inf [сг(?/) — (5, у — х} 4- {0 — t)H(s)].	(10.4)
y€Rns^Rn
Формулы (10.3) и (10.4) были получены в 1965 г. Э.Хопфом [90]. Он
доказал, что эти формулы определяют обобщенные решения в том смысле,
что функции вида (10.3) и (10.4) удовлетворяют уравнению (10.1) в каж-
дой точке, где эти функции дифференцируемы, то есть почти всюду. Кроме
того, эти функции удовлетворяют краевому условию (в работе [90] рассмат-
ривалась задача Коши с начальным условием). Позже, в 1985 г. М. Барди
и Г. Эванс [17] доказали, что функции, определенные формулами Хопфа,
совпадают с вязкостными решениями задачи Коши (10.1), (10.2). В теории
же дифференциальных игр показано, что функция вида (10.3) совпадает с
функцией цены дифференциальной игры с так называемыми простыми дви-
жениями (см., например, статью Б. Н. Пшеничного и М. И. Сагайдак [177]).
10.2.	Утверждение
Предположим, что выполняются следующие условия:
(С1.1) гамильтониан удовлетворяет условию Липшица
\H^-H{q)\^X\\p-q\\, Vp,q&^n-,
(С 1.2) функция a: Rn н~> R выпукла.
Тогда функция
u(t. х) := sup [(s, х) + (в — t)H(s') — cr*(s)],
(10.5)
(t,x) e (0,0] хГ
является минимаксным решением в задаче (10.1), (10.2).
112
Глава II
Здесь <7* — сопряженная функция к функции <7, т. е.
a*(s) := sup [($,х) — сг(ж)].	(10.6)
Доказательство. Как известно из выпуклого анализа, для выпуклой
функции а справедливо равенство
а(х) = sup [(s, х} — сг*($)].
Поэтому функция u(t, х) вида (10.5) удовлетворяет краевому условию (10.2).
Сопряженная функция Э s cr*(s) € (—оо,оо] является полуне-
прерывной снизу и удовлетворяет оценке cr*(s) а — <т(0). Предполо-
жим сначала, что множество
dom ст* := {seBn: cr*(s) < оо}	(10.7)
ограничено. Известно (см., например, [178]), что это предположение спра-
ведливо, если функция <7 удовлетворяет условию Липшица. Нетрудно дока-
зать, что в этом случае множество
S0(t,rr) := {.so 6	{s0,x} + (0 -	- a*(s0) = u(t,x)}	(10.8)
является непустым и компактным в Rn. Функция u(t, х) дифференцируе-
ма по направлению, и имеет место следующая формула (см. приложение,
параграф А5)
du(t. х\ 1, /) = max{(s, f) — H(s): s e 5o(t, #)}.	(10.9)
Докажем, что функция и вида (10.5) удовлетворяет условиям (L5), (U5),
сформулированным в пункте 6.3. Таким образом, требуется доказать, что
имеют место следующие неравенства для производных по направлению
sup{dw(t,х\ 1,/) — (s, f) + H(s): f e Rn}	0,	(10.10)
inf{dw(£,x\ l,/)~ fsr, f) + f e Rn}	0,	(10.11)
при всех (t, x) € (0, в) x Rn и s € Rn.
Докажем неравенство (10.10). Справедливы следующие соотношения
sup [du(t, х; 1, /) — (s, f) + H(s)] =
fe^n
= sup max [(so — s, f) — H(sq) 4- H(s)] =
fe^n soeso(t,x)
= max sup [($o — s, f) — Я($о) + H(s)] = max «(s, s0).
so€So(t,x)	soGSo(t,:r)
10. Конструктивные и численные методы
113
Здесь
( 0,	если s —
4s,$o) = s	/
( оо,	если s ф s§.
Таким образом неравенство (10.10) доказано.
Докажем теперь неравенство (10.11). Зафиксируем точку (t, х) €
€ (0.0) х!п. Обозначим через Sq = So(t,x), П = rpm(So), т.е. П —
набор вероятностных мер, нормализованных на компактном множестве Sq.
Введем обозначение
St, J sir (ds) (тг е П).
s0
Заметим, что So С dom <т* и dom <т* — выпуклое множество, поэтому
St, е dom ст*. Из определения множества So (10.8) следует справедливость
неравенства
(s,x) + (0 - t)H(s) - a*(s)	{8т,,х) + (0 - t)H(s7r) - СГ*^)
при всех .s e So и тг e П. Если проинтегрировать это неравенство по мере тг,
получим
(0 — t) J H(s)ir(ds) — J cr*(s)7r(ds) > (0 — t)H(S7,) — cr*^).
Sq	Sq
Функция ст* выпукла, поэтому
J CF*(s)7r(d<s) > CT*(<S7r).
So
Принимая во внимание, что 0 — t > 0, получаем неравенство
У Я(в)тг(Ж?) > Я(в^), 7Г € П.	(10.12)
So
Используя (10.9), получаем соотношения
inf [du(t, ж; 1, /) — (s, /) + H(s)] =
= inf max [(s0 — s, f) — H(sq) + H(s)] =
f «0
114
Глава II
(а)	= inf max (s^ — s, f) — / H(so)ir(dso) + H(s) ~
f * L	J	J
So
(b)	= max inf — s,f) — J B(so)7r(dso) + #(*)]
s0
(c)	max inf [(s^ - s,f} - H(s^ 4-Я(5)] =
(d)	= max[—«(s%, so)]	0
7Г
(здесь f € Rn, so 6 So? 7г € П).
Объясним соотношения (a)-(d). Нетрудно проверить, что для любой
непрерывной функции Sq Э s н-> r(s) € R справедливо следующее равен-
ство
max{r(s): s е So} = max^^r(s)?r(ds): л E П^.
So
В частности, функция
So Э So r(s0) = (so - S,f) - H(s0) + H(s)
удовлетворяет равенству (а). Рассмотрим равенство (b). Выражение в квад-
ратных скобках зависит линейно от переменных f и л. Эти переменные
принимают значения из выпуклых множеств 1П и П соответственно. По-
этому здесь можно использовать теорему о минимаксе (см., например.
[98, 162]) и поменять местами операции inf и max. Неравенство (с) сле-
дует из (10.12). Наконец, неравенство (d) следует из (10.12) и определения
величины к (s, so).
Таким образом, доказано, что функция и вида (10.5) удовлетворяет
условию (10.11).
Итак, показано, что формула (10.5) описывает минимаксное решение в
задаче (10.1), (10.2) согласно определению 6.5. Этот результат был получен
для случая, когда множество dom а* ограничено.
Докажем, что функция и вида (10.5) является минимаксным решением
в общем случае, без этой дополнительной гипотезы. Введем следующие
обозначения
стЦя) := max{(s,#) — <t*(s): s e B/J, к = 1,2,...
Uk(t, x) max{(s, x) + (0 — t)B(s) — cr*(s): s e Bk}
(напомним, что В/. := {s € Rn: ||s||	к}). Из доказательства, приведенного
выше, следует, что функция является минимаксным решением в задаче
10. Конструктивные и численные методы
115
Коши
+ H(DxUk) = 0, иь(0,х} = ак{х).
Последовательность Uk(t, х) — возрастающая, поэтому существует предел
lim Uk(t, х) — u(t, х).
к—>оо
Нетрудно проверить, что предельная функция и есть минимаксное реше-
ние рассматриваемого уравнения Гамильтона-Якоби (см. доказательство
утверждения 8.7). Легко заметить также, что предельная функция удовле-
творяет условию (10.2). С другой стороны, формула (10.5) справедлива и
для предельной функции. Утверждение 10.2 доказано.
Заметим, что, согласно (10.6), справедливо
-<7*(s) = - sup [(s,y)-<т(у)] = inf [<т(у) - (s,y)].
Поэтому формула (10.5) может быть переписана в виде формулы Хоп-
фа(Ю.З).
10.3. Утверждение
Предположим, что выполняются следующие условия:
(С2.1) гамильтониан является выпуклым и удовлетворяет условию Лип-
шица
\H(jp)-H(q)\^X\\p-q\\,
(С2.2) функция a: Rn н-» R непрерывна.
Тогда функция
u(t, х) := sup \а(х + (0 — t)f) — (0 —	(10.13)
является минимаксным решением в задаче (10.1), (10.2).
Здесь функция
sup [(s, Л-Я(«)]	(10.14)
— сопряженная к гамильтониану.
116
Глава II
Доказательство. Пусть
dom Я* := {/еГ: Я*(/) < оо}.
Известно, что dom Я* С В\ := {/ е Rn: ||/||	А}.
Предположим сначала, что функция не только непрерывна но также
и непрерывно-дифференцируема. Заметим, что функция
Вх Э f ~ [а(х + (0 “	- (0 -
является полунепрерывной сверху, поэтому множество
W := {w е ВХ' а(х + (0 - t)w) - (О -
+	v/еГ1} (ю.15)
является непустым и компактным.
Известно (см., например, приложение, параграф А5), что величина
du(tbx; 1,/) — max[(s(w), f) —	+ H*(w)]	(10.16)
wEW
совпадает с производной функции и вида (10.13) по направлению (1,/).
Здесь s(w) := Da(x + (0 — t)w).
Докажем, что функция и вида (10.13) является минимаксным решением
в задаче (10.1), (10.2). Из определения функции и видно, что она непрерывна
и удовлетворяет равенству (10.2). Проверим, что эта функция удовлетворяет
условию (L5), приведенному в пункте 6.3.
Выберем произвольный вектор р € Rn. Согласно (10.16), имеем
sup [du(t, х; 1, /) - (р, f) + Н(р)] =
= sup max[(s(w),/) - (s(w), w) +H*(w) - (p, f} + H(p)]
fe^n W^w
sup [(s(w*), f} -	+ Я*(ш*) - (p, f) + я(р)] >
Я*(ш*) - {w*,p} + Я(р) > 0.
Здесь w* — элемент множества W и аргумент последнего неравенства, вы-
текающего из (10.14). Таким образом, доказано, что функция и вида (10.13)
является нижним решением в задаче (10.1), (10.2).
Проверим, что эта функция является верхним решением рассматрива-
емой задачи. Докажем сначала, что s(w) — субградиент функции Я*.
10. Конструктивные и численные методы
117
Пусть h Е Rn, 6 > 0. Согласно (10.15), имеем
а(х+(9 —t)w) — (в —	— —	—
— (у{х + (0 — t)w) -к (0 - t)(s(w), 8ti) — (0 — t)H*(w 4- 8h) + о(5)5,
где q(5) —> 0, когда S —> 0. Получаем
{s(w),8h) H\w + 8h)-H*(w) + a(6)8.
Поэтому s(w) — субградиент функции Я*. Из выпуклого анализа известно,
что
(s(w), w) =	(10.17)
Теперь проверим условие (U5) (см. пункт 6.3). Выберем произвольный
вектор р е Rn. Согласно (10.16) и (10.17) имеем
inf х-	+ H(р)] =
J
= ,ipf max[(s(w), f) - (s(w),w) + H*(w) - (p, f) +H(p)] =
fEkn weW
= Дп£п max[(/, s(w) - p) + H(p) - #(s(w))].
Подобно тому, как это было сделано при доказательстве утверждения 10.2,
полагаем II = rpm (И/). Введем обозначение
Sn = J	7Г е П.
W
Из выпуклости функции Н вытекает неравенство
#(^7г) у* H(s(w))?r(dw).
w
Используя это неравенство, получаем
fERn wEW
= Дчп “еап [/~	- {f,p} + Я(р)]
W
f&R" “III ~	~	+	=
= max iirf [(/, sn - р) -	+ Я(р)]	0.
J ЕК
118
ГлаваП
Таким образом, для случая, когда ст непрерывно дифференцируема,
показано, что функция и вида (10.13) является минимаксным решением в
задаче (10.1), (10.2).
Если функция ст непрерывна, то она может быть приближена непрерыв-
но дифференцируемыми функциями, и дедуктивно выводится, что формула
(10.13) определяет, как прежде, минимаксное решение в задаче (10.1), (10.2).
Утверждение 10.3 доказано.
Формула (10.13) может быть преобразована в (10.4). Действительно,
из (10.14) следует, что
-(0 -	= inf [-(^ -1)(5, f) + (е - i)H(s)].
Поэтому
u(t, x) sup inf \a(x 4- (0 — t)f) — (0 — t){s,	+	t)H(s)].
seRn
Если ввести обозначение у = х + (0 — t)/, то последнее равенство факти-
чески совпадет с формулой Хопфа (10.4).
10.4.	Пример
Используем формулу (10.5), чтобы получить выражение для минимак-
сного решения в задаче Коши
S + V1+(^ =0’	=	(10.18)
dt у	\ох /	2
Здесь 0^Н^ = 2, Напомним, что этот пример рассматривался в
пункте 1.4.
Определим сопряженную функцию ст* к функции а(х) = х2/2. Соглас-
но общему определению, имеем
<т*($) = sup \sx — х2/2\ — s2/2.
Используя формулу (10.5), получаем, что функция
u(t, х) = maxjsrr — (2 — t) -^/1 4- s2/2 — s2/2]	(10.19)
является минимаксным решением в задаче (10.18).
В рассматриваемой задаче гамильтониан и предельная функция яв-
ляются гладкими. Но функция и, заданная равенством (10.19), является
негладкой. Верхняя огибающая поверхности, представленной на рис. 1.2,
является графиком этой негладкой функции.
10. Конструктивные и численные методы
119
10.5.	Задача Коши с гамильтонианом, выпуклым по производным
Формула (10.13) связана с задачей динамической оптимизации на мак-
симум функционала
о
чШД')) = <^(£(0)) - У
t
по множеству всех траекторий (£(•)> С(*)):	xl дифференциаль-
ного уравнения
£ = /, £ = #*(/), /Gdomr,
с начальным условием £(£) = х и терминальным условием £(0) = <т(£(0)).
Это замечание может быть применено и в более общем случае.
Рассмотрим задачу Коши
^+H(t,x,Dxu) = 0, и(0,х)=<т(х).	(10.20)
Предположим, что гамильтониан Н удовлетворяет условиям (Н1)-(НЗ),
приведенным в пункте 7.2. Кроме того, предположим, что функция
<sh» Я(у;,.$‘) выпукла. Определим сопряженную функцию к функ-
ции Н(1, х, •)
Н* (t, х, f) = sup [(/, s) - H(t, X, 5)].
Полагаем
D(t,x) = dom #*(U,’) -{/ЕГ: H*(t,x,f) < oc}.
Из условия Липшица (7.3) следует, что
sup II/II <! р(ж).
Множество D(t, х) выпукло. Помимо этого, мы предполагаем, что суще-
ствует такая непрерывная функция r(t, х), что
H*(t, х, f) < r(t, х), V/ е D(t, х).
Эта гипотеза и предположение, что гамильтониан H(t, х, z. s) независим от
переменной z, — несущественны и введены для простоты изложения.
120
Глава II
Рассмотрим множество
E~(t,x) = {(f,g): f е D(t,x),	r(t,x)}.
Отображение (t, x) E~~(t, x) удовлетворяет условиям (j), (jj), (jjj“), (jv~)
из пункта 6.2. Проверка этих условий подобна проверке аналогичных усло-
вий в пункте 3.4.
Согласно схеме, описанной в пункте 3.4, рассмотрим следующую за-
дачу для дифференциального включения
(±,i) €	(10.21)
Обозначим через S (to, жо) множество траекторий (ж (•), z (•)): [0,0]
xR дифференциального включения (10.21), которые удовлетворяют
условиям ж (to) = жо и z(0) = <т(х(0)). Определим функционал платы
е
7(t0, х(-), z(-)) = ст(а:(0)) - У z(t)dt.
to
Далее, найдем максимум этого функционала на множестве 5(^,жо). Обо-
значим это максимальное значение символом u(to, жо), т. е. мы полагаем
u(t0,x0) = max {7(4о,ж(-),г(-))}.	(10.22)
(cc(-),2(-))G5(to,^o)
Докажем, что функция (0,0] х!п э (^,жо) u(to,xo) €R является
минимаксным и вязкостным решением в задаче (10.20).
Пусть zo = u(to,xo). Пусть (ж°(-),^°(-)) € 5(^,жо) — оптимальная
траектория, которая обеспечивает максимум функционалу 7. Справедливо
е
y(to,x°(-),z°(-)) = <т(аго(0)) - У z°(t)dt = z0
to
Выберем произвольный момент т G [to, 0]. Очевидно, что (ж°(-), г°(-)) €
6 5(т,ж°(т)). Поэтому
и(т,ж°(т)) = max {7(т,ж(-), z(-))}
в
> 7('Г,Ж°(-),2О(-)) =<т(х°(0)) - [z°(t)dt =
= <7(ж°(0)) - г°(0) + г°(т) = г°(т).
10. Конструктивные и численные методы
121
Таким образом, мы получаем, что подграфик функции и слабо инвариан-
тен относительно дифференциального включения (10.21). Следовательно,
функция и удовлетворяет критерию L2, сформулированному в пункте 6.3.
Поэтому, согласно определению 6.5, эта функция является нижним реше-
нием задачи (10.20).
Докажем, что функция и — максимальный элемент среди всех нижних
решений. Пусть v — какое-то нижнее решение задачи (10.20). Выберем про-
извольную точку (to,^o) € (0,0] хГ.Из определения нижнего решения
следует, что существует траектория (z*(f),z*(£)) (0 t < О') дифференци-
ального включения (10.21), которая удовлетворяет условиям
x*(tQ) = .То, z*(t0) = v(t0,x0),
z*(0)	т(0,т(0)) — сг*(х(0)).
Последнее неравенство может быть переписано следующим образом
о
= v(tQ,x0) <т(т*(0)) - / z*(t)dt = 7(to,^*(-)^*(’))-
to
По определению функции и (10.22) имеем
u(to,XQ) 7(t0, £*(•), £*(•))•
Таким образом, заключаем, что функция и — максимальное нижнее решение
задачи (10.20).
Напомним, что, согласно определениям 6.5 и 7.1, минимаксное реше-
ние в задаче (10.20) является одновременно верхним и нижним решением
этой задачи. Принимая во внимание теорему 7.3, получаем, что минимакс-
ное решение в задаче (10.20) совпадает с максимальным нижним решением.
Таким образом, доказано, что функция и, определенная равен-
ством (10.22), совпадает с минимаксным решением в задаче (10.20).
10.6. Обобщение классического метода характеристик
Установим результат, связанный с вариационным исчислением, прин-
ципом максимума Понтрягина, классическим методом характеристик и те-
орией обобщенных решений уравнений в частных производных (УЧП) пер-
вого порядка.
Рассмотрим задачу Коши (10.20). Здесь предполагаем, что функция
s H(t,x,s) выпукла при всех (t, х) е (0,0] х Rn, функция H(t, x.s)
122
Глава II
непрерывно дифференцируема по t, х, з, и что существуют производ-
ные D^XH, DlsH. Предполагается также, что функция а(х) непрерывно
дифференцируема.
Через
(ж(-, у), $(-, у), z(', у)): [0, м 1п х Rn х 1
обозначим решение характеристической системы
х = DsH(t, х, s), s = —DxH(t, х, s), z = (s, DsH(t, x, s)} — H(t^ x, s),
которое удовлетворяет условию
x{0,y) - у, s(0,y) = Dv(y), z(0,y) = a(y).	(10.23)
Определим множество
y(t, 0 = fe er: x(t, y) = £}, (t, e) e cl G. (10.24)
Во-первых, напомним следующий известный результат (см., например,
[52,167] и параграф 1): если для любого (t, £) е [0,0] xRn множество У (t, £)
одноэлементно, т. е. У(£, £) = {y(t, £)}> а отображение (£,£) н-> ?/(/;,£) до-
статочно гладкое, то задача (10.20) допускает классическое решение и, и
справедлива формула
=	(t,C)GciG.
Классический метод характеристик может использоваться и для по-
строения обобщенного решения (в минимаксном и вязкостном смысле) с
помощью равенства
u(t, £) — max{z(t, у): у е У (t, £)} V (t, £) е (0,х
Впервые такая формула была представлена и проверена С. Миричей
(см., например, [149]). Независимо этот же результат был получен Н. Н. Суб-
ботиной [208, 209]. Мы опускаем здесь доказательство и адресуем читателя
к цитируемым работам, где приведены также некоторые обобщения этой
формулы.
10.7. Конечно-разностные операторы и сеточные методы для
уравнений Гамильтона-Якоби
Опишем кратко конечно-разностные операторы и сеточные методы,
которые можно использовать для аппроксимации решений в задаче Ко-
ши (10.20). Предположим, что гамильтониан удовлетворяет условиям (Н1),
(НЗ), введенным в пункте 7.2. Усилим условие (Н2) и предположим, что
|Я(Ха;,5(1))-Я(*,ж,8^)|	— s(2)||	(10.25)
10. Конструктивные и численные методы	123
при всех (t, х) е [0,0] х Rn,	е Rn. Функция ст удовлетворяет
условию Липшица. Чтобы упростить изложение, предположим также, что
гамильтониан H(t, х. г, s) не зависит от переменной z.
Введем следующие обозначения
ew =
ГО,	если i j,
Oi ?' — i	•	•
,J [ 1,	если г = j,
т. е. — координатные единичные вектора. Полагаем
h = (/z0, /zi, • • •, /zn), ho > 0, hi 0, i e 0, n,
Tfc = 0 — kho, к G 0Д.
где К — целая часть числа 0//zo.
Пусть w(-): Rn R — вещественная функция. Определим оператор
Tfc(t, /z, w(-))(a?) = w(x) + hoHit, x, s),
где s — конечно-разностный «градиент» функции w(-), задаваемый следу-
ющим образом
s — (si,... ,sn), Si = (w(x + hie^) - wfx))}^1, i e l,n.
Рассмотрим классическую конечно-разностную схему
w0(x) = ст(ж), Wk+i(x) = Tt’(iA;,/z,w/e(-))(x), к e 1,K - 1.
Полагаем
uh(t,x) = wk(x) для tk+1 < t tfc.
Если в задаче (10.20) существует дважды непрерывно дифференцируемое
решение u(t, ж), то описанная разностная схема сходится к этому решению,
т. е. lim Uh(t, х) = u(t, х). Этот предел является равномерным в любой
ограниченной области.
Однако мы интересуемся обобщенными решениями (в минимаксном
и/или вязкостном смысле), которые могут быть негладкими. Ясно, что клас-
сическая разностная схема не подходит для приближения негладких реше-
ний. Нетрудно привести примеры, в которых функции иь, сконструирован-
ные, как было сказано вътше, не сходятся к требуемому решению.
124
Глава II
В то же время, в работах М. Дж. Крэндалла, П. Л. Лионса и П. Е. Су-
ганидиса (см., например, [59, 188]) доказано, что условие монотонности
гамильтониана H(t, х, s) = х, S2,..., sn) относительно перемен-
ных Si, i € 1, n (вместе с некоторыми дополнительными условиями, которые
даются ниже) является достаточным для сходимости функций ин к вязкост-
ному решению и задачи (10.20). Монотонность гамильтониана может быть
обеспечена с помощью следующего простого преобразования
v(t, х) := u(t, х + (0 — t)f),
где f е —• фиксированный вектор. Можно проверить, что функция u(t, х)
является обобщенным решением задачи (10.20) (в вязкостном и/или ми-
нимаксном смысле) тогда и только тогда, когда функция v(t,x) является
обобщенным решением задачи
+ H(t, X + (О - t)f, Dxv) + (f, Dxv) = 0,
x) — cr(x).	(10.26)
Можно считать, что функция
является, например, неубывающей по каждой из переменных Si, i =
= 1,..., п, если вектор f = (/i,..., /п) выбран подходящим образом.
Итак, без потери общности, можно полагать, что функция s i—*
н-> H(t, х, s) не убывает относительно каждой переменной Si. В этом случае
оператор классического приближения можно использовать при следующих
предположениях
/г0 > 0, hi > 0, Цп + 1)/г0 <Ы, ie Т^п. (10.27)
Здесь L — константа из условия Липшица (10.25). Как было доказано в
работах [59, 188], сходимость
lim Uh(t,x) = u(t,x)
IH-»o	'
функций ин к вязкостному решению и задачи (10.20) имеет место, если вы-
полнены предположения (10.27). Таким образом, использование классиче-
ской разностной схемы для приближения обобщенных решений в принципе
возможно.
Однако в описанной выше разностной схеме для выполнения усло-
вия (10.27) может потребоваться, чтобы шаг сетки был «очень мал».
10. Конструктивные и численные методы
125
Ниже приведены результаты, направленные на преодоление этой трудно-
сти. Более детальное изложение содержится в ряде работ (см., например,
[19, 158, 188, 210, 211, 214, 212]).
Чтобы получить обобщенное решение в задаче Коши (10.20), можно
использовать также численные методы, разработанные в теории дифферен-
циальных игр для построения функции цены и стабильных мостов (см.
параграф 16). В общем случае, это решение невыпукло по х. В работе [218]
В. Н. Ушаков представил конструкцию, в основе которой лежат локальные
выпуклые оболочки, и продемонстрировал ее эффективность для числен-
ных методов. Используя эту идею, он и его коллеги разработали вычис-
лительные алгоритмы и программы для построения стабильных мостов и
функции цены. Опишем аппроксимирующие операторы, которые развивают
упомянутый подход.
Пусть w(-): Rn R — непрерывная функция. Рассмотрим три следу-
ющих аппроксимационных оператора
71 (t, 6, w(-))(x) := <р(.т) 4- supmax[577(t,x, s) 4- <р(у) — ip(x) — (s, у - ж)],
у s
(10.28)
где у е В^(х), S е D~tp(y)-,
T2(t, 6, щ(-))(ж) := ip(x) + inf min[5H(t, х, s') + V>(y) — ^'(т) — (s, у — ж)],
у «
(10.29)
где у е BL/i(x), s е D+t[>(y);
T3(t, d,w(-))(x) :=:= a1(x)T1(t,6,w(-))(x)+a2(x)T2(t,6,w(-))(x). (10.30)
Здесь <^(y): Br$ i—> R — локально-выпуклая оболочка функции w(y) в за-
мкнутой окрестности Brg(x) точки х, имеющей радиус г 6, г > L,
П-+ 1	п+1	п+1
<р(у) := mi[^/3kw(yk): ук G BrS(x), (Зк 0, ^(ЗкУк = у, ^2+ = 1|-
fc=l	к=1	к=1
Множество D~<p(y) — субдифференциал выпуклой функции ср в точке у,
т. е.
D~tp(y) := {в € R": <p(z) - ip(y) (s,z-y), Vz £ Br$(x)}.
Функция y‘j(y)’. Br$(x) н-> R — локально-вогнутая оболочка функции w(y),
множество D+'ipfy) — супердифференциал функции ф в точке у. Величи-
ны «1, «2 определены равенствами
_ $(х) - w(x)	w(x) - tp(x)
Х -ф(х) - (р(х) ’ а2 Х -ф(х) - (р(х) ’
126
Глава II
Ясно, что
О!1(х) 4" Q2(^) = 1,	2 = 1,2.
Операторы Т2, Т3 были введены в работе [210, 211, 214] А. М. Та-
расовым, В. Н. Ушаковым и А. А. Успенским. Заметим, что эти операто-
ры обобщают конструкции Хопфа, Лакса-Фридрихса, Годунова, которые
применялись для построения вязкостных решений уравнений Гамильтона-
Якоби в работах М. Барди, С. Ошера и К. Шу [19, 158]. Используя результа-
ты, полученные в статьях [59, 188], в работе [210, 211] было доказано, что
упомянутые аппроксимационные схемы с операторами Ti, Т2, Тз сходятся,
и оценка погрешности имеет порядок 61/2 .
Следует отметить, что операторы Ti, Т2, Тз достаточно сложны. Од-
нако их формулы могут быть существенно упрощены в случае кусочно-ли-
нейных функций, узлы которых совпадают с узлами сетки. В частности, в
работах [210, 211] приведена такая конечно-разностная формула для опера-
тора Ti на элементарной окрестности
п
г=1
точки х по прямоугольной сетке фазового пространства с шагом 7J, где
параметр 7 удовлетворяет ограничению
^>Ly/n.	(10.31)
В этом случае оператор Т\ может быть определен равенством
Ti(t, 5, w(-))(#) = <р(х) 4- 8 max H(t,x,s).
sED~
Здесь
r	w(x 4- 7<feW) 4- w(x — убе^) )
<p(x) = min< w(x), min--------------------------->,
1 iEl,n	J
D~<p(x) = co : m € 1,2n},
s(m) =
(m)	, w(x ± 7<5е;) - <^(x)	.	_—
s,-	= ±-----------?-------, г e l,n.
’	y6
10. Конструктивные и численные методы
127
Как легко заметить, в этом случае субдифференциал D~cp(x) является пря-
моугольным параллелепипедом (возможно, вырожденным), стороны кото-
рого параллельны координатным осям.
Если мы опускаем условие (10.31) и предполагаем, что 7 является
произвольным числом, то применение оператора Ti может быть сведено к
построению локально-выпуклых оболочек и к решению серии задач линей-
ного программирования.
Рис. 10.1а.
Рис. 10.1 иллюстрирует вышеизложенный материал. На нем изображен
график решения следующей задачи
du/dt + Н(х, Dxu) = 0, и(0, х) = ст (ж).
Здесь 0 = 0.5, х = (a?i,a:2) € R2, предельная функция и гамильтониан
заданы равенствами
ст (ж) = ж2 4- ж2?
H(x,s) = 5i sin— |s2| +ехр(—ж2 — х%) тах{0, —з2}.
На рис. 10.1(a) представлен график функции <т(ж) (х € X = [0,1] х [0,1]).
На рис. 10.1(b) показан график минимаксного решения u(t, х) при I = 0,
х е X. Это решение было просчитано с помощью численного алгоритма и
программы, разработанных А. А. Успенским. [215].
128
Глава II
Рис. 10.1b.
10.8. Библиографический комментарий к главе II
Доказательство неравенства и v, где и и v — верхнее и нижнее
решения, базируется на идее взаимного отслеживания двух характеристи-
ческих траекторий, одна из которых проходит внутри надграфика верх-
него решения, а другая лежит в подграфике нижнего решения. Эта идея
восходит к конструкции процедуры управления с поводырем, предложен-
ной Н. Н. Красовским в теории дифференциальных игр (см., например,
[122, 121, 123]). В случае, когда гамильтониан H(t,x,z,s) положительно
однороден по переменной s, функция Ляпунова может быть определена
простым равенством L = ||х — ?/||2. Такое предположение не является стес-
нительным, поскольку многие задачи могут быть сведены к этому случаю
[194,195]. В доказательстве приведенной выше теоремы 7.3 функция Ляпу-
нова определена равенством L == w£(t,x, у)—ту Функция w£ удовлетво-
ряет условию (А4) введенному в работе [55] (это условие сформулировано
в пункте 9.2).
Доказательство теоремы 8.2 также основано на идеях, связанных с по-
зиционными дифференциальными играми, а именно, с альтернативой для
игр преследования-уклонения и существованием функций цены в диффе-
ренциальных играх (см., например, [118, 122, 123]). Как было установлено
при доказательстве теоремы об альтернативе, фазовое пространство игры
состоит из двух частей: 1) объединения всех ^-стабильных мостов, и 2) до-
полнения к этому объединению, которое оказывается, к тому же, максималь-
10. Конструктивные и численные методы	129
ным г/-стабильным мостом. Эта конструкция подобна определению функ-
ции цены как верхней (нижней) огибающей класса f-стабильных (и-ста-
бильных) функций. Напомним, что u-стабильные (f-стабильные) функции
являются верхними (нижними) решениями соответствующего уравнения
Айзекса-Веллмана. Краткое доказательство существования функции цены
(минимаксного решения) дифференциальной игры, основанное на выше-
упомянутой схеме, приведено в работах [8, 193]. Обращаем внимание так-
же на то, что позже, в работе [94], верхние (нижние) огибающие класса
вязкостных субрешений (суперрешений) использовались, чтобы доказать
существование вязкостного решения.
Операторные уравнения и метод итераций из пунктов 8.9-8.11 под-
сказаны методом программных итераций, разработанным в теории диффе-
ренциальных игр А. Г. Ченцовым (см., например, [41, 200]). Независимые
результаты по программным итерациям были получены С. В. Чистяковым в
работе [44].
Библиографические комментарии относительно параграфов 9-10 вклю-
чены в текст этих параграфов.
Глава III
Дифференциальные игры
11. Основные понятия теории дифференциальных игр
Исследования дифференциальных игр начались в 1950-60-е годы. Сна-
чала, главным образом, рассматривались математические модели конфликт-
ных ситуаций (см., например, известную монографию Р. Айзекса [92]).
В этих моделях движениями управляемых систем руководят два игрока-ан-
тагониста. Типичным примером антагонистической дифференциальной иг-
ры является задача преследования-уклонения. Однако задачи такого типа
достаточно экзотичны. В то же время есть многочисленные инженерные
проблемы, а также задачи в экономике, экологии и т. д., в которых требу-
ется построить управление по принципу обратной связи, гарантирующее
какой-то результат в присутствии неконтролируемых возмущений. В каче-
стве иллюстрации можно упомянуть задачу управления посадкой и взлетом
самолета в присутствии так называемого ветрового возмущения (windshear),
когда самолет подвергается воздействию порывов ветра. Анализ дифферен-
циальных игр может помочь в разработке алгоритмов эффективного управ-
ления для этой и подобных ей задач.
Как было сказано во введении, происхождение предложенного в данной
монографии подхода и методы исследования минимаксных решений связа-
ны с теорией позиционных дифференциальных игр (игр, использующих
управления по принципу обратной связи), разработанной Н. Н. Красовским
и его коллегами (см., например, [110, 122]). Краеугольным камнем этой
теории является концепция //-стабильных и //-стабильных функций. Напом-
ним, что //-стабильные (//-стабильные) функции мажорируют (минорируют)
функцию цены дифференциальной игры. Функция цены — это единствен-
ная функция, которая обладает одновременно свойствами //-стабильности
и //-стабильности. Известно также, что функция цены удовлетворяет УЧП
первого порядка (уравнению Айзекса-Веллмана) в точках, где она диф-
ференцируема. Указанные свойства определяют одно и только одно обоб-
щенное (минимаксное) решение уравнения Айзекса-Веллмана. Свойство
//-стабильности (//-стабильности) — это то же самое, что слабая инвари-
антность надграфика (подграфика) функции цены относительно некоторых
дифференциальных включений.
11. Основные понятия теории дифференциальных игр 131
Эти свойства могут быть выражены с помощью различных техниче-
ских средств, включая различный аппарат негладкого анализа: производ-
ные по направлению, субдифференциалы, контингентные касательные ко-
нуса и т. д. Методы позиционных дифференциальных игр оказываются при-
годными для исследований широких классов краевых задач и задач Коши
для различных типов УЧП первого порядка. С другой стороны, как демон-
стрируется в этой главе, техника теории обобщенных решений УЧП нахо-
дит хорошее применение при конструировании оптимальных стратегий по
принципу обратной связи.
В этой главе приведены основные понятия и результаты теории пози-
ционных дифференциальных игр. Изложение начинается со случая, когда
функционал платы имеет вид (11.2). Некоторые дифференциальные игры
других типов будут рассмотрены в главе IV. Настоящая глава включает
также короткое обсуждение проблемы устойчивости решений дифференци-
альных игр и некоторые результаты относительно численных и конструк-
тивных методов. Позиционные дифференциальные игры рассматриваются
более подробно в книгах [122, 123] и статьях, цитируемых ниже.
11.1. Управляемая система и функционал платы
Рассмотрим дифференциальную игру, в которой динамика управляемой
системы описывается обычным дифференциальным уравнением
i(t) = f{t,x(t\p(t),	(11.1)
Здесь p(t) e P и q(t) & Q — управления игрока P и игрока Q соответствен-
но; множества Р и Q компактны. Эти управления выбираются на основании
обратной связи, т. е. в зависимости от текущей позиции	Игрок Р
стремится минимизировать функционал платы:
о
7(*о,ж(-)>Р(-),«(-)) '•= ФДО) - У g(t,x(t),p(t),q(t))dt,	(11.2)
to
где to £ [0, #] — начальный момент времени. Игрок Q, напротив, желает
максимизировать этот функционал.
Функции f,gna удовлетворяют следующим предположениям.
(А1) Функции /: [0,^j х Г х Р х Q м Г, [0,^] х Г х Р х Q wR
и а: Rn и-> R являются непрерывными и удовлетворяют ограничениям
||/(Ж,Р,«)|| С (1 + |к||)Я/, \g(t,x,p,q')\ (1 + |H).Rff,
|Ж)1 < (1 + 1И)Дг	(П.З)
132
Глава III
для всех (t, х^р, q) € [0,0] х Rn х Р х Q (здесь Rf, Rg и Ra — поло-
жительные числа).
(А2) Функции / и д удовлетворяют условию Липшица по переменной х
\\f(t,x + y,p,q) - f(t,x,p,q)\\ + \g(t,x + y,p,q) - g(t,x,p,q)\	A||p||
(H.4)
для всех (t, x.p, q) e [0,0] x Rn x P x Q, у e Rn.
(АЗ) Для любых s € и (t, x) € [0,0] x Rn имеет место равенство
min max[(s, f(t, x, p, q)) - g(t, x, p, g)] =
pEP q^Q
= maxmin[(s,/(t^x.p, q)) — g(t, x,p, q)] = H(t, x. s). (11.5)
qeQ pep
Предположение (АЗ) называют условием седловой точки в маленькой
игре, оно также носит название условия Айзекса. Величина Н, опреде-
ленная равенствами (11.5), называется гамильтонианом дифференциальной
игры (11.1), (11.2). В параграфе 15 будут рассмотрены дифференциальные
игры без предположения о выполнении условия (11.5).
Покажем, что при выполнении вышеупомянутых предположений га-
мильтониан Н удовлетворяет условиям (Н1)-(НЗ), сформулированным в
пункте 7.2. Нетрудно видеть, что гамильтониан Н непрерывен по пере-
менным (t х, s). Покажем, что выполняется условие Липшица (7.3). Пусть
(t.x) Е [0,0] х Rn, sf,s" е Rn. Выберем такие вектор р' е Р и функ-
цию Р Э р н-» qff(p) е Q, что
р' е Arg minimax [(s', f(t,x,p,q)) - p(t,®,p,g)]},
PEP Iq^Q	J
<f(p) € Arg max[(s",/(t,a:,p,g)) - g(t,x,p,q)].
q^Q
Напомним, что Arg minpep g{p) и Arg maxQeq v(q) — множества
минимизирующих и максимизирующих элементов, т. е.
Argmin/z(p) := {ро е Р: д(ро) ^/*(Р) Vp € Р},
рер
Arg maxzy(^) := {qQ е Q: p(qo) v(q) \/q E Q},
qeQ
где P Э p g(p) 6 R и Q Э q u(q) ER- произвольные непрерывные
функции.
11. Основные понятия теории дифференциальных игр 133
Справедливо
H(t,x,s') = min max [(/, f(t, x, p,q)) - g(t,x,p,q)] =
PEP q^Q
= т^[к'^(*,яУ,д)>-0(Лж,р',д)]
> {s’,f(t,x,p',q"(p'))) - g(t,x,p',q"(p')),
H(t,x,s") = minmax[(s",/(t,^,p, q)) — g(t,x,p,q)]
pGP q^Q
«С ^-^l{s'',f(t,x,p',q)} - g(t,x,f,q)] =
q^Q
= (s",f(t,x,p,,q"(.p')')) -gtt,x,p',q"tp'))-
Следовательно
H(t,.r..s') - Htt,x,s") > (s' - s''J(t,x,p',q"(p'-))) >
> -Ik' - *"ll ||М*УЛ'))11 -Ik' - s"|| (1 + Ikliw
Последнее неравенство следует из оценки (11.3). Точно так же получается
оценка
х, У) — Н(С ж, s/z) С ||У — s"|| (1 -Т ||ж||)Д/.
Таким образом, мы получили, что гамильтониан Н вида (11.5) удовлетво-
ряет условию (7.3).
Немедленно, из (11.5) и (11.3) следует, что гамильтониан удовлетворяет
оценке (7.4).
Теперь покажем, что гамильтониан удовлетворяет условию Липшица
по переменной х. Выберем
р' е Arg mini max [(з,/(£, ж',р, </)) - gtt,x',p,q)]\,
р£Р I qeQ	J
ftp) € Arg max [(s, f(t, x",p, q)) - g(t, x",p, q)].
q^Q
Справедливо
H(t, x', s) — H[t, x", s)
> k,	,p',q"tp'))) - g^x',p',q”(p'))-
- к,/к,ж",р/,9"(р/))Н9к^">р'л"(р')) >
- [П/(Л x',p'’ q'^P1)) - /k, x”,p', ftp')) II +
+ \g(t,x',p',q"tp')) ~p(t,:r",p',<7"(p'))|](l+ Ikll) >
— АЦгг'— x"|| (1 + |kll).
Последняя оценка следует из условия (11.4).
134
Глава III
Таким образом, доказано, что гамильтониан Н вида (11.5) удовлетво-
ряет условиям (Н1)-(НЗ) пункта 7.2.
11.2.	Стратегии по принципу обратной связи и пошаговые процедуры
управления
Пусть задана начальная позиция (to,rro) 6 [0,#] х Rn. Симво-
лом S (to, #о) обозначим множество, элементами которого являются тройки
(®(-)>Р(-), ?(•)), гдер(’) € L([t0,0], Р), g(-) е L([t0,0], Q), а ж(-): [t0, 0] R”
является абсолютно непрерывной функцией, удовлетворяющей уравне-
нию (11.1) и условию х(to) = Напомним, что символами L([to,#],F)
и L([to,#],Q) обозначаются множества всех измеримых функций [to,#] Э
Э t и-» p(t) е Р и [t0,#] Э t i-> g(t) € Q. Тройка (#(•), р(-), #(•)) Е S(to,^o)
называется управляемым процессом. Функция ж(-) называется движением
системы (11.1), порождаемым управлениями р(-) и д(-). Заметим, что из
предположений (А1) и (А2) следует, что при любых р(-) Е L([to,#],F)
и g(-) Е L([to,#],Q) существует единственное решение уравнения (11.1),
продолжаемое до конечного момента времени t = 0.
Игроки выбирают стратегии, которые формируют управления на осно-
вании обратной связи. Произвольная функция
[0,0] хГ Э (t,x) U(t,x) Е Р
называется стратегией по принципу обратной связи (позиционной страте-
гией) для игрока Р.
Точно так же произвольная функция
[0,#] хГ э (t,z) V(t,z) Е Q
называется стратегией по принципу обратной связи (позиционной страте-
гией) для игрока Q. Подчеркнем, что функции U(t, х) и V(t, х) могут быть
разрывными.
Пусть игрок Р выбрал некоторую стратегию U и некоторое разбиение
Д = {ti: i Е 0, т + 1}, t0 < й < • • • < tm+1 = 0.	(11-6)
Символом S(to,^o, Е7, Д) обозначим множество троек
Е S(to,a?o)» таких, что <?(•): [to,#] Q — произвольная измеримая функ-
ция, а р(-) — кусочно-постоянное управление, которое сформировано по
следующему правилу на основе обратной связи
p(t) = U(ti, x(ti)\ ti < ti+1, i = 0,1,... ,m.	(И.7)
11. Основные понятия теории дифференциальных игр 135
Согласно концепции гарантированного результата, качество пошаговой
процедуры управления ([7, Д), выбранной игроком Р, оценивается величи-
ной
Г1(^,ж0,Р, A) :=sup7(to,S(to^o,P, А)) =	01.8)
= sup{7(i0,z(-),p(-),<?(•)): (ж(-), ?(•),?(•)) е S(t0,x0,U, Д)}.
Оптимальный результат в классе пошаговых процедур управления игрока Р
определяется следующим образом
П(^,ж0) := mfri(to,*o,tf,A).	(Н.9)
Точно так же оптимальный результат в классе пошаговых процедур
управления для игрока Q определяется формулами
Г^0,ж0) := supF2(t0,x'0, У, А),	(11.10)
Г2(to, ж0, V, A) inf 7(to, S(t0, ж0, V, A)).	(11.11)
Здесь V и Д — стратегия и разбиение, выбранные игроком Q, S(to, жо, V, А) —-
все такие тройки (ж(-),р(-), <?(•)) Е S(to, Жо), что q(-) — кусочно-постоянное
управление игрока Q, формируемое на основе обратной связи и имеющее
вид
q(t) =	ti^t< ti+1, i = 0,1,... ,m,
x(-) — траектория системы (11.1), порождаемая некоторым измеримым
управлением р(-): [to, 0] н-> Р игрока Р и управлением #(•), сформиро-
ванным, как указано выше.
Заметим, что
S(t0, ж0, U, Дх) AS(to^o, V, Д2) Ф 0
для любых стратегий U9 V и разбиений Д1, Д2. Поэтому имеют место
неравенства
Ti(to, жо, tf, Al) T2(to, жо, V, Аг),
Г^о,жо)^Г^о,жо).	(11.12)
Последнее из этих неравенств подобно известному неравенству для макси-
мина и минимакса. В тех случаях, когда в (11.12) имеет место равенство,
это равенство определяет цену Vai * (to, жо) дифференциальной игры в клас-
се пошаговых процедур управления. Таким образом, эта цена определяется
равенствами
УаГ(^,ж0) :=Г1^о,жо) = Г2^0,ж0).
Цена игры зависит от начальной позиции. Поэтому может быть определена
функция цены игры
(^,ж0)н+ Val*(to,^o): [0,0] хГ-^R.
136
Глава III
11.3.	Цена позиционной дифференциальной игры
Основные понятия теории дифференциальных игр могут быть форма-
лизованы несколькими способами. Ниже в параграфе 14 мы даем краткое
описание некоторых из этих подходов. Отметим, что основные формали-
зации оказываются эквивалентными в том смысле, что цена игры во всех
этих постановках — одна и та же.
Сейчас изменим несколько определение цены дифференциальной иг-
ры, данное в предыдущем подразделе. Цель этой модификации — сфо-
кусировать внимание на главном вопросе, а именно, на конструкции оп-
тимальных (или е-оптимальных) стратегий по принципу обратной связи.
Предлагаемые ниже способы построения позиционных стратегий таковы,
что в соответствующих пошаговых процедурах управления фиксированная
стратегия по принципу обратной связи может быть использована в паре с
произвольным разбиением Д (11.6) достаточно малого диаметра
diam Д = max{ti+1 — ti: i е 0, м.}.	(11.13)
Итак, введем следующие величины
Г1(£о>£(ъ^) •= limsup Г1(£о, #о5 U, Д),	(11.14)
diam А Щ
^2(to,xo,V) := liminf Г2(<о!^o, V, А).	(11.15)
diam АЩ
Эти величины используются как качественные характеристики для по-
зиционных стратегий игроков. Оптимальные результаты игрока Р и игро-
ка Q, гарантированные в классе стратегий по принципу обратной связи,
определяются следующим образом:
r?(to,^o) := inf Г1(^0,ж0,Е7),
:= supr2(to,^o, V).	(11.16)
v
Позиционная стратегия U° (стратегия U£) называется оптимальной
(е-оптимальной) для игрока Р, если справедливо равенство Г1Ц0, ^о, ^°) =
= Г$(^о,жо) (неравенство ГЦ^о,	r5(to,^‘o) + е)« Оптимальная и
s-оптимальная стратегии игрока Q определяются аналогичным образом.
Как и в (11.12), здесь имеет место
r?(fo,®o) > Г2^о,«о)-
(11-17)
11. Основные понятия теории дифференциальных игр 137
Если в (11.17) имеет место равенство, то это равенство определяет цену
дифференциальной игры в классе стратегий по принципу обратной связи
Val(to,®o) =r°1(t0,x0) = rO(to,xo).	(11.18)
Заметим, что это определение цены эквивалентно определению, данно-
му в пункте 11.2, т. е. можно показать справедливость равенства Vai * = Vai.
11.4.	Теорема
При выполнении предположений (А1)-(АЗ) существует цена пози-
ционной дифференциальной игры (11.1), (11.2), т. е. справедливо равен-
ство (11.18). Функция цены совпадает с минимаксным решением задачи
Коши
^+H(t,x,Dxu)=0, и(в,х) =а(х),	(11.19)
где гамильтониан H(t, ж, s) определен равенством (11.5).
Заметим, что УЧП, рассматриваемое здесь, называется уравнением Ай-
зекса-Веллмана. Его называют также основным уравнением теории диф-
ференциальных игр.
Доказательство теоремы 11.4 будет дано в параграфе 12. Отметим, что
это доказательство сведено к доказательству следующего ключевого со-
отношения между верхними (нижними) решениями уравнения Айзекса-
Веллмана и результатами, гарантированными для игрока Р (для игрока Q)
в классе позиционных стратегий. Пусть и — это верхнее решение зада-
чи (11.19); тогда для любого е > 0 можно построить стратегию по принципу
обратной связи Ue ддя игрока F, такую, что
£4) u(t0,xG) + 8.	(11.20)
Точно так же для любого нижнего решения и задачи (11.19) и для любо-
го 8 > 0 можно построить позиционную стратегию V£9 такую, что
Г2(^о,жо,Ю > w(to,^o) -8.	(11.21)
Как было показано в предыдущей главе, существует и единственно ми-
нимаксное решение и в задаче Коши (11.19). Как мы знаем, минимаксное ре-
шение является одновременно верхним и нижним решением задачи (11.19).
Поэтому из (11.16), (11.20) и (11.2-1)-вытекают неравенства
Г?(£(Ъ^о)	u(t0,X0) +8 Г^о^о) +28.
138
Глава III
Так как эти оценки справедливы для любого положительного, числам и
имеет место оценка (11.17), получаем
Val(t0,x0) =r?(to,^o) =Г2(йц^о) = u(t0,x0').
Таким образом, из указанного результата следует, что функция цены диф-
ференциальной игры (11.1), (11.2) существует и совпадает с минимаксным
решением задачи Коши для соответствующего уравнения Айзекса - Беллма-
на.
11.5.	Оптимальные стратегии в случае гладкой функции цены
Предположим, что существует решение в задаче Коши (11.19), которое
является непрерывно дифференцируемым в области (0,0) х Rn. Хотя эта
гипотеза выполнена в довольно редких ситуациях, полезно рассмотреть кон-
струкции оптимальных стратегий в этом случае, поскольку эти конструкции
понятны и могут быть использованы, как отправная точка для построений
в общем случае.
Итак, пусть функция и: [0,0] х Rn н-> R является классическим реше-
нием задачи Коши для уравнения Айзекса-Веллмана, т. е. и удовлетворяет
следующим требованиям. Эта функция непрерывна, и для нее выполняется
конечное условие и(в,х) = а (ж). В области (0,0) х Rn функция и непре-
рывно дифференцируема и удовлетворяет уравнению Айзекса-Веллмана в
классическом смысле. Известно, что в этом случае оптимальные стратегии
игроков могут быть построены следующим образом.
Определим функции
h(t,x,s,p,q) := (s, f(t, х,р, q)) - g(t,x,p,q),	(11.22)
Po(t,x,s) e Arg min max/i(f, x,s,p, q) ,	(11.23)
pePLqeQ	J
qo(t.xys) E Arg max min/z,(£, rr, s,p, q) .	(11.24)
qeQ LpeP	J
Ясно, что в общем случае функции р0(Л ж, s) и qo(t, х, s) могут быть опре-
делены из соотношений (11.23) и (11.24) неединственным образом. Для
предложенных конструкций можно использовать любые функции, кото-
рые удовлетворяют вышеупомянутым условиям. Функция pQ(t, х, <$) (функ-
ция qofa х, б*)) будет называться здесь предстратегией игрока Р (игрока Q).
Далее, определим стратегии игроков по принципу обратной связи с
помощью равенств
Uo(t,£) = po(ty х^ Dxu(t, х)\	(11.25)
Vo(t, х) = qo(t,x,Dxu(t,xy).	(11.26)
11. Основные понятия теории дифференциальных игр 139
Здесь u(t, х) — классическое решение задачи (11.19). Поэтому стратегии Uq
и Vg определены как суперпозиции предстратегий и градиентов функции и
(которая совпадает с функцией цены, как это будет показано ниже).
Докажем, что стратегия Uo оптимальна для игрока Р. Сначала предпо-
ложим, что функция (70 непрерывна. Выберем произвольную траекторию
управляемой системы
x(t) = f(t,x(t\	to ^t 0,	(11.27)
где [to, 0] Э t*-+ q(t) E Q — некоторое измеримое управление игрока Q. Это
управление может быть сформировано игроком Q на основании обратной
связи, например, согласно равенству q(t) = V(t,rr(t)), где V — некоторая
стратегия игрока Q, или согласно некоторому другому правилу.
Теперь оценим производную функции u[t] — u(t, x(t)). Используя при-
мечание (11.22) при s(t) = Dxu{t,x(t)) и p0[t] = Uo{t,x{t)). из определе-
ния стратегии Uq получаем
Duft] .	9u(t, x(t))	у 7 XX P7 7 X r -1	7 XXK
+ (Dxu(t,x(0),f(t,x(0,po{t],q(t))) =
du(t,x(t)}	, ,	7 X 7 X Г 1 X
----л;---------- +max/i(t,®(t),s(t),p0[t],9)4-5[t] =
(Jt--------q(~~Q
=	+ H(t, x(t), s(t\) + g[t] = s[t],
где g[t] := g(t, ж(£),роИ, q(t)). Поэтому
e
u(0,x(0)) u(to,xo) + jg(t,x(t),po[t],q(t))dt.
to
Так как и(0,ж(0)) = а(х(0))9 то, согласно (11.2), получаем
7(to,x(-),po[-],g(-)) u(to,xo).
Аналогичную оценку получим и для случая, когда непрерывность стра-
тегии Uq не предполагается. Обозначим символом X(to,^o) множество
траекторий ж(-): [to,#]	которые удовлетворяют начальному усло-
вию ж (to) = хо и дифференциальному включению
±(t) 6 co{/(t,rr,p,Q): р € Р, q € Q}.
140
Глава III
Полагаем
D := {(t, x(t)) G [t0,0] x Rn: ж(-) G X(t0, ж0)}.
Заметим, что множество D замкнуто и ограничено. Пусть
А := тах{||/(^ж,р,q)\\: t G [to,#], x G D, p G P, q G Q}.
Ясно, что
\\x(t') - x(t")\\ ^A|t'-t"|	(11.28)
ДЛЯ любого ж(-) G X(to, Xq) И Любых t', t" G [to, #].
Рассмотрим пошаговую процедуру (Ро,Д). Выберем произвольный
управляемый процесс (ж(-),р(«), #(•)) £ S(t0, жо, Fo, Д). Будем использо-
вать следующее обозначение
_z х du(t.x(t)) , z . ч ч х
Ol	qeQ
где s(t) := Dxu(t^x(t)) и величина h(t, х, s,p, q) определена соотношени-
ем (11.22). Из равенства p(t) — p(ti) = Uo(ti,x(ti)) для t G [t^.t^-i) и
соотношений (11.5), (11.19), (11.23) и (11.25) следует, что £(F) ~ 0. Теперь
производная функции u[t] — u(t,x(t)) на интервале [t^t^i) может быть
оценена следующим образом
Pu[t] du(t, x(t))	. ..	. z .	....
-5Г- = -------^7-^ +	=
CLb	(Jv
=	+ h(t,x(t),s(t'),p(ti),q(t')') +g[t]
CW +рИ = C(i) + g(t,x(t),p(ti),q(t)).
Функции (t, х) н-> Dxu(t, х) и (t, х) н-> du(ty x)/dt являются равномерно
непрерывными на множестве D. Рассматриваемая траектория ж(-) принад-
лежит множеству X(to, жо) и удовлетворяет оценке (11.28). Напомним так-
же, что ((ti) = 0. Поэтому для любого е > 0 можно выбрать 8 > 0 так,
что для любого управляемого процесса (ж(-),р(-)л(*))	S(t0, жо, Fo, Д),
удовлетворяющего условию diam Д < 8 верна оценка (^(t) С £ для
всех t G [tf,ti+i), ti е Д. Таким образом, получили
о
а(ж(#)) = и(#,ж(#))	и(^,ж0) + У g(t,x(t),p(t),q(t))dt + (# - t0)s.
to
12. Доказательство существования функции цены ...
141
Согласно (11.2), (11.14), заключаем
Г1^о,2!о,^о)	U(*o,^o)-
Точно так же можно показать, что
^(*0,^0, И)) > u(to,xo).
Согласно (11.17), (11.18), приходим к следующему выводу.
Если существует классическое решение и в задаче (11.19), то позици-
онная стратегия Uq (стратегия Vq), определенная, как суперпозиция пред-
стратегии (11.23) (предстратегии (11.24)) и градиента функции и, — опти-
мальна для игрока Р (игрока Q). Функция и совпадает с функцией цены
дифференциальной игры (11.1), (11.2).
12.	Доказательство существования функции цены
дифференциальной игры
В этом параграфе рассматриваются конструкции с-оптимальных пози-
ционных стратегий. Построения, предложенные ниже, подобны конструк-
циям оптимальных стратегий, которые определены в пункте 11.5 с помо-
щью суперпозиции предстратегий и градиентов минимаксного решения. Но
в отличие от случая, рассматриваемого в пункте 11.5, здесь не предполагает-
ся гладкость минимаксного решения уравнения Айзекс а-Веллмана. Таким
образом, желаемые стратегии конструируются с помощью суперпозиции
тех же самых предстратегий и неких квазиградиентов, определения кото-
рых вводятся в пункте 12.2. Из результатов, представленных в настоящем
параграфе, вытекает справедливость теоремы 11.4 о существовании цены
дифференциальной игры (11.1), (11.2). Следует сказать, что представленные
ниже построения подсказаны конструкциями универсальных субоптималь-
ных стратегий, предложенными Н. Н. Красовским [113, 114].
12.1.	Стабильные функции
Определим следующие многозначные отображения
E+(t, х, q) со{(/(£,ж,р, g),g(t, ж,р, g)) ElnxR: р Е Р},	(12.1)
E~(t,x,p) := co{((t, ж,р, q),g(t,x,p, q)) E Rn x R: q e Q}.	(12.2)
Напомним, что в дифференциальной игре (11.1), (11.2) функции f и д
удовлетворяют условиям (А1)-(АЗ), приведенным в пункте 11.1. Поэто-
му многозначные отображения Е+ и Е~ имеют следующие свойства. Для
142
Глава III
любых (t, х) е [0,в] х Rn, р е Р, q G Q множества E+(t, х, q) и E~(t. х, р)
выпуклы и компактны. Многозначные отображения (t,x,q) i—> E+(t. х, q)
и (t, х,р) E~(t, х,р) непрерывны и удовлетворяют равенствам
maxmin{(f,s) - д: (f,g) G E+(t,x,q)} = H(t,x,s),
q£Q
minmax{(/, s) - g: (J,g) G E~(t,x,p)} - H(t,x,s).
pep
Заметим, что эти соотношения следуют из условия (11.5) и равенств
min l(w) — min Z(w), maxZ(w) = max Z(w),
wf~W	wGco W	v)EW	wEco W
которые справедливы для любого компакта W С Rm и любой линейной
функции Rm Э w I—> Z(w) € R.
Таким образом, многозначные отображения (12.1) и (12.2) удовлетво-
ряют всем требованиям (j)-(jv), сформулированным в пункте 6.2.
Согласно определениям 6.5 и 7.1, можно принять следующие форму-
лировки. Полунепрерывная снизу (сверху) функция (t, х) ?i(t, х): [0,0] х
xRn R является верхним (нижним) решением задачи Коши (11.19), если
и удовлетворяет конечному условию и(0, х) = ст (ж), и для любого векто-
ра q е Q (р е Р) надграфик (подграфик) и слабо инвариантен относительно
дифференциального включения (12.3) [(12.4)]
(ж, z) е E+(t, х, q),	(12.3)
(ж,г) е E~~[t^x^p),	(12.4)
Если множество {(/(t,	g), g(t, x^p^q)) e Rn x R: p e P} является
выпуклым, то свойство слабой инвариантности для верхнего решения эк-
вивалентно следующему условию: для любой точки (to.xo) е [0,0] х Rn
и для любого постоянного управления q е Q игрока Q существует такое
измеримое управление р(-): [to, 0] Р игрока F, что траектория
t
x(t) = х0+ J f(r,x(T),p(r),q)dT,
to
t
z(t) =u(to,xo) + У з(т,ж(т),р(т),д)</-г
to
удовлетворяет неравенству z(t) u(t, x(t)) при всех t0 C t в. Аналогич-
ный факт справедлив и для нижнего решения.
12. Доказательство существования функции цены ...	143
Замечание. В теории позиционных дифференциальных игр (см.,
например, [122, 123]) используются другие термины для рассмотрен-
ных свойств. Функции, чьи надграфики (подграфики) слабо инвариантны
относительно дифференциального включения вида (12.3) ((12.4)), называ-
ются //-стабильными (//-стабильными). Таким образом, любая //-стабиль-
ная (//-стабильная) функция является верхним (нижним) решением зада-
чи (11.19) и наоборот. Эти понятия являются ключевыми для теории пози-
ционных дифференциальных игр.
12.2.	Конструкции е-оптимальных стратегий
Согласно утверждению 8.4, любое верхнее решение и задачи Коши для
уравнения Гамильтона-Якоби удовлетворяет неравенству u(t, х) и_ (t, х)
(функция и-, была определена в названном утверждении). Используя усло-
вия (А Г)-(АЗ), можно показать, что в рассматриваемой задаче функция и~
удовлетворяет оценке u_(t, х) — К(1 + ||гг||), где К — положительное
число. Таким образом, для любого верхнего решения задачи (11.19) выпол-
няется следующая оценка
u(t, х) > -К(1 + И) V (Л х) е [0,0] х Rn. (12.5)
Пусть и: [0,0] х R — верхнее решение задачи (11.19). Рассмотрим
для этой функции и преобразование вида
u£(t,x) := min [u(t, у) 4- w£(t, х, //)],	(12.6)
yERn
где функция w£ определена следующим образом
z>	_ С* ___________
(t,x,y):=--------Vs4 + ||ж - y||2.	(12.7)
Здесь A — константа из оценки (11.4), аг — положительный малый параметр.
Отметим, что та же самая функция w£ использовалась в доказательстве
теоремы 7.3 о единственности минимаксного решения в задаче Коши для
уравнения Гамильтона-Якоби (см. (7.14)).
Нетрудно проверить, что функция w£ удовлетворяет неравенству
^ + H(t,x,Dxwe)-H(t,y,-Dyws) ^0.	(12.8)
Действительно, справедливо
Dxw£(t,x,y) = -Dyw£(t,x,y) = a£(t) ———,
г£&У)
144
Глава III
где
rs(x,y) := у/е4 + ||ж - у||2,
Используя следующее условие Липшица (см. (7.5))
\H(t, x^.s) — H(t,x(2\s)\ < А(1 Н- |M>(1) — ж(2)||,
получаем
H(t,x,Dxwe) - H(t,y,-Dywe) А(1 +	4^) ||х - у\\
\ ге(х,у) /
A(l + ae(t))re(x,j/) = A^-^rf(ar,y) = —-р
с	UI
Таким образом получаем, что неравенство (12.8) справедливо.
Выберем теперь такое достаточно малое число е > 0, что имеет место
следующее неравенство
£(е) := е ..£ . £ > К.	(12.9)
Отметим, что
u(t,y) + ws(t,x,y) -К(1 + ||у||) + Ь(е)||ж - у||	00,
когда ||t/|| -+ оо. Принимая во внимание, что функция у н-» и(1,у) 4-
4- w£(t, х,у) полунепрерывна снизу, заключаем, что минимум в (12.6) до-
стигается.
Выберем
t/£(t, rr) G Arg min [u(t, у) 4- w£(^, х, у)].	(12.10)
Покажем, что
lim ||t/£(t, х) — rr|| = 0.	(12.11)
Из определений (12.6), (12.7) вытекает, что
u£(t, х) u(t,x) 4- w£(t,x,x) u(t, х) 4-	(12.12)
12. Доказательство существования функции цены. ..	145
Чтобы упростить обозначения, полагаем т] := y£(t, х). Справедливы оценки
u£(t,x) = н- w£(t,x,rf) -K(l 4- н- £(с)||£ - у\\
> (L(e) - К)\\х - tjII - К(1 + И)-
Принимая во внимание соотношения (12.12), получаем неравенства
(L(e) - К)||х - т/|| - 7<(1 4- ||г||)	u£(t,x) u(t, х) 4- е,
из которых следует оценка
aw)
{L{£) - К)
Из условия L(e) —> оо, когда е J, 0, получаем требуемое соотноше-
ние (12.11).
Обозначим
ss(Lx) := Dxw£(t,x,y£(t,x)) = -Dyw£{t.x,y£(t,x)).	(12.14)
Если функция у н-> u(t,y) — непрерывно дифференцируема в некоторой
окрестности точки г, то для достаточно малого е эта окрестность содержит
точку y£(t, х), и можно использовать необходимое условие экстремума
Dyu(t. y£(t, х)) 4- Dyw£(t, X, y£(t, х)) = 0.
Поэтому s£(t, х) := Dyu(t,y£(t,x)). Принимая во внимание (12.11), полу-
чаем
lim s£(t, х) — Dxu(t, х).
€—>0
Наличие этой взаимосвязи позволяет назвать вектор s£(t. х) квазиградиен-
том функции и по переменной х.
Теперь позиционную стратегию игрока Р определим с помощью ра-
венства
u£(t, х) := po(t, х, s£(t, #)),	(12.15)
где pQ(t, х, s) — предстратегия (игрока Р), определенная в (11.23).
Если в данных конструкциях функция и — это минимаксное решение
задачи (11.19), то, как показывается ниже, соответствующая стратегия U£
субоптимальна для игрока Р. Это означает, что такая стратегия гарантирует
игроку Р результат, который является сколь угодно близким к оптимально-
му, при условии, что параметр е выбран достаточно малым. Отметим еще
146
Глава Ш
раз, что, в отличие от случая, рассматривавшегося в пункте 11.5, здесь не
предполагается, что функция и дифференцируема.
Точно так же конструируется стратегия V£ игрока Q.
А именно, пусть и: [0,0] х Rn R — нижнее решение задачи (11.19).
Выберем произвольную точку
х) € Arg max[w(t, у) — w£(t, х,у)],	(12.16)
где функция w£ определена с помощью (12.7). Полагаем
s^(t,x) := — Dxwe(tbx^y^(t^ ж)),	(12.17)
K(t,х) qo(t,x,s^(t,x)),	(12.18)
где qo(t,x^s) — предстратегия игрока Q, определенная соотношени-
ем (11.24).
12.3.	Теорема
Пусть и - верхнее (нижнее) решение задачи (11.19). Пусть стра-
тегия U£ (стратегия V£) определена как суперпозиция предстратегии
Pofax^s) вида (11.23) (предстратегии qs(t,x,s) вида (11.24)) и квазигра-
диента s£(t, х) вида (12.14) (квазиградиента s^(t,x) вида (12.17)). Тогда
для любого компактного множества D С [0,0] х Rn и любого положи-
тельного числа С существуют такие е > 0 и 8q > 0, что оценка (12.19)
(оценка (12.20))
Г1(^о,£о, U£, A) u(tQ,xo) + С,	(12.19)
Г2(£о,#о,К, А) > u(to,xo) - С	(12.20)
справедлива для всех (to, ^о) € D и любых разбиений А, удовлетворяющих
условию diain А do-
Доказательство. Пусть
(to,xo) € D, (x(-\p(-),q(-)) Е S(to,xQlU£.A), ti.ti+г е А.
Используем обозначения
t*=r3 ti+i=r + d, x(ti) = ^ U£(r,£)=p*.
Доказательство утверждения (12.19) основано на оценке
т+5
и£(т + 3,х(т + 8)) - [	(12.21)
12. Доказательство существования функции цены ...	147
Здесь (д (5) —> 0, когда 6 —> 0. Из доказательства будет видно, что величи-
на (д и величины используемые ниже, зависят только от 8 и являются
независимыми от выбора начальных точек (to,^o) £ D, разбиений Д и
управляемых процессов (ж(-),р(-)> #(•)) £ S(to, жо5 Us, Д).
Из оценки (12.21) следует, что
о
ие(0,х(0У) - Jд(т,х(т),р(т),д(т)У1т	u£(t0, х0) + С2(<5),	(12.22)
to
где £2(£) ~> 0, когда 8 := diam Д 0. Согласно (12.10) и (12.11), имеем
-ие(0,ж) = u(0,ye(0,x)) + we(0,x,ys(O,x)) > а(у£{0,х'}).
Непрерывность функции ст и оценки (12.6), (12.13) влекут за собой, что для
любого ограниченного множества М С Rn существует такое число v(e),
что
и£(0, х) сг(х) — limz/(s) = 0.	(12.23)
£10
Комбинируя оценки (12.12), (12.22) и (12.23), заключаем, что
о
7(x(-),p(-),q(-)) = <r(x(0)) - Jg(t,x(t),p(t),q(t))dt <
to
< «(to, Хо) + <2(<j)) + S + Ь'(е).
Поэтому из оценки (12.21) получается желаемое неравенство.
Таким образом, остается доказать соотношение (12.21). Ниже исполь-
зуются также следующие обозначения
s*=se(r,£), 7/ = уе(т,£), q* = qo(r,T],s*),
т+6
/* = | f f(t,x(t),p*,q(t))dt,
т+д
/7* = | f g(t,x(t),p*,q(ty)dt,	(12.24)
где #o(T,£,s) — предстратегия, определенная соотношением (11.24).
148
Глава III
Согласно (12.6) и (12.10), имеем
We(r, О = и(т, ту) + we(r, 7/).	(12.25)
Из определения верхнего решения (а именно, из свойства слабой инва-
риантности его надграфика по отношению к дифференциальному включе-
нию (12.3)) вытекает, что существует такой вектор (f*,g*) 6 xR, что
dist((/*,5r*),I?+(T,77,Q*))	Сз(<5),
w(r, 77) 4- g*8 u(r 4- 5,77 4- /*5).	(12.26)
Пусть h := w£(r 4- 8, £ 4- /*5,77 4- f*8) — w£(r, 77). Из соотношений (12.25)
и (12.26) следует, что
ие(т,£) и(т + 3,д + fJP) + w£(r,^g) - д*8 =
= и(т + 8,д + f*8) + w£(t 4- 5, £ 4- Г8, д 4- f*8) - h ~ д*8
и£(т 4- 8. £ 4- Г8) - h - д*8.
Последняя оценка вытекает из (12.6). Из того, что £ 4- f*8 = х(т 4- 8),
получаем
и£(г, £) и£(т 4- 8, х(т 4- 5)) — h — д*8,	(12.27)
Теперь оценим величину h. Функция w£ дифференцируема, поэтому
h [dw£(r, g)/dt + Г) - (s\ f*)]6 + G(8)8,	'
где s* = Dxw£(r,^g) = -Dyw£(r,^ g).
Напомним, что p* = U£(r,^) = Po(x, s*). Согласно (11.23), имеем
{s\f(T,^p*,q)) -g(r,^p\q)	Я(т,С,5*) ДОЯ всех q € Q.
Следовательно,
Отметим также, что q* = qo(r, 77, s*). Поэтому из (11.24) следует
G*,/(r,77,p,^)) ~ д(т^РЛ*) > H(r,g,s*) ядяжжрЕ Р.
Таким образом,
(s\U}-g^H(r,g,s^-QQ(8).
Принимая во внимание (12.8), получаем
h<g4-g^8-V(^(8)-V^(8))8,
12. Доказательство существования функции цены. ..
149
Подставляем эту оценку в (12.27) и приходим к неравенству
ш(т,0 и£(т + 8, х(т + 5)) - (д* - <5(5) - С6(6))8.
Напомним, что величина д* определена равенством (12.24). Таким образом
мы получили требуемую оценку (12.21).
Утверждение относительно верхних решений и стратегий игрока Р
доказано. Точно так же может быть доказано второе утверждение теоре-
мы 12.3.
Отметим, что по определению величин, которые оценивают качество
стратегий по принципу обратной связи (см. (11.14), (11.15)), неравен-
ства (12.19) и (12.20) можно переписать следующим образом
Г1(40, х0, U£) u(t0, жо) + С,	(12.28)
Г2(4о,ж0, К) > u(t0,x0) - С-	(12.29)
Замечание. Штрафная функция w£ вида (12.7) — не единственная сре-
ди тех функций, которые могут использоваться в предложенных конструк-
циях. Для некоторых типов дифференциальная игр удобнее рассматривать
штрафные функции специального вида. Рассмотрим случай, когда функци-
онал платы не содержит интегрального члена, т. е. д(1,х,р,о) — 0. В этом
случае гамильтониан H(t,x.s) положительно однороден по з, т. е.
H(t, х, as) = aH(t, х, s),
и удовлетворяет следующему условию Липшица по переменной s
\H(t,x,sw)- Я(4,ж,з(2))| sj A||s(1) - s(2)||	(12.30)
для всех (f, ж) € [0.0] х R”,	6 R”. В этом случае в преобразова-
нии (12.6) можно использовать функцию
/. ч 11Ж-у||2
где e(t) = coe2At, so — положительное число, А — константа из условия
Липшица (12.30). Заметим, что равенство
г	11X — у 11 2 1
ue(t, х) :=	у) + w£(t, х, у)] = min [u(t у) +	j
описывает преобразование, известное в выпуклом анализе (в некоторых
работах оно называется преобразованием Иосиды-Моро). Если функ-
ция u(t, •) выпукла, то, как известно, функция u£(t, •) непрерывно диффе-
ренцируема, т. е. рассмотренное преобразование является «сглаживающим».
150
Глава III
12.4.	Доказательство теоремы 11.4
Нетрудно видеть, что из теорем 8.1 и 12.3 следует справедливость тео-
ремы 11.4. Действительно, как показано в пункте 11.1, в задаче Коши (11.19)
удовлетворены все требования теоремы 8.1, согласно которой минимаксное
решение и этой задачи существует и единственно. Так как функция и являет-
ся одновременно верхним и нижним решением задачи (11.19), то, применяя
теорему 12.3, получаем оценки (12.28) и (12.29). Согласно определению
оптимальных результатов (11.16), имеем
Г?(^о,^о)	Г1(*о,^о,С4)	u(t0,x0) + С
Г2(£о, ^о, К) -Г 2£ r^to, .т0) + 2£.
Эти неравенства справедливы для любого положительного числа следо-
вательно,
Г?(й),жо) и(1о,хо) Г2^о,то).
Принимая во внимание неравенство (11.17), заключаем, что
Г?(£0,ж0) =	= r^to^o) = Vai (t0, то).	(12.31)
Теорема 11.4 доказана.
13.	Стабильные мосты и экстремальные стратегии
В 12-м параграфе было приведено относительно компактное доказа-
тельство существования цены для дифференциальных игр в классе пози-
ционных стратегий. Однако практическое применение предложенных кон-
струкций возможно либо если функция цены задана явной формулой, либо
если ее можно с высокой точностью приблизить численно. Класс таких
задач довольно узок в обоих случаях. Поэтому важно знать конструкции,
которые являются более грубыми в том смысле, что они не требуют точного
вычисления функции цены и менее чувствительны к ошибкам в измерении
текущей позиции (фазового вектора) системы. Одна из таких конструкций
рассматривается в этом параграфе. Обсуждение проблемы устойчивости ре-
шений в классе стратегий по принципу обратной связи будет продолжено в
разделах 14.4 и 14.5.
13.1.	Устойчивые мосты в задачах М-сближения
Задача М-сближения, обозначенная в заголовке, состоит в следую-
щем. Пусть заданы начальная позиция (/щжо) € [0,0] xF и замкнутое
13. Стабильные мосты и экстремальные стратегии
151
множество М С Rn. Игрок Р стремится гарантировать выполнение усло-
вия x(ff) € М. Предполагается, как и в предыдущих разделах, что игрок Р
знает текущую позицию (£, x(t)) и формирует свое управление p(t) на осно-
вании обратной связи. Как и прежде, динамика управляемой системы опи-
сывается уравнением
х = f(t,x,p,q).	(13.1)
Функция /: [0, 0] хКпхРх$мКп предполагается непрерывной. Она
удовлетворяет условию Липшица
||/(£,ж(1\р,д)-/(£,я(2\р,д)|| А||а:(1) -ж(2)||	(13.2)
для всех (t,p, q) е [0,0] х Р х Q, х^ е Rn. Кроме того, предполагаем,
что имеет место следующее равенство
minmax(s, f(t, х,р, q)} = maxmax(s, /(t^x^p^q)} = H(t,x,s) (13.3)
p(=F qp.Q	q€Q peP
для всех (t. x, s) e [0,0] x F x Rn.
Заметим, что в задаче М-сближения игрок Р стремится добиться того,
чтобы фазовая точка достигла целевого множества в фиксированный, апри-
орно заданный момент времени t = 0. В параграфе 19 будет рассмотрена
другая дифференциальная игра, а именно, игра на оптимальное время, в ко-
торой игрок Р минимизирует время достижения цели, т. е. время до первого
попадания траектории управляемой системы на целевое множество.
Теперь введем одно важное понятие, которое будет использоваться для
решения задачи М-сближения.
Многозначное отображение
[О;0]	СГ
называется стабильным мостом в задаче М-сближения, если W(ff) С М, а
график этого многозначного отображения
W := {(i,w): t Е [0,0], w е W(t)}
замкнут в [0,0] хГ и слабо инвариантен относительно дифференциального
включения
х € со /(£, ж, F, q)	(13.4)
при любом q Е Q. Здесь и ниже используется обозначение
f(t,x,P,q) := {f(t,x,p,q): р 6 Р}.
152
Глава III
Условие слабой инвариантности означает, что для любых q € Q
и (^,жо) € W существует выживающая траектория ж(-): [to, 6^] Rn, ко-
торая удовлетворяет дифференциальному включению (13.4), начальному
условию x(to) = хо и следующему условию выживаемости: x(t) е W(t)
для всех t е [to, 0]. В теории позиционных дифференциальных игр это
свойство было названо условием //-стабильности.
Замечание. Пусть множество f(t)X,P,q) выпукло для всех
(t, ж, q) € [0,0] х Rn х Q. Тогда свойство //-стабильности подразумевает
выполнение следующего условия: для любой точки (to, жо) Е W и любого
измеримого управления [to, 0] Э t >-» q(t) € Q существует измеримое управ-
ление [to,0] Э t p(t) е Р такое, что соответствующая траектория ж(-)
дифференциального уравнения
*(£) = /(*,£(£),?(*),?(£))
с начальным условием ж (to) = xq проходит внутри стабильного моста Ж,
то есть x(t) € W(t) при всех t € [to, 0]. Вышеупомянутый факт следует из
теоремы Филиппова (см., например, [72, 225]).
Свойство слабой инвариантности множества W относительно диффе-
ренциального включения (13.4) (свойство //-стабильности) может быть вы-
ражено с помощью различных средств математического аппарата. Ниже
рассматриваются некоторых из них.
Определим индикаторную функцию множества W
z ч f 0, если х € W(t).
u(tyX) := <	(13.5)
( 1, в иных точках.
Отметим, что функция и полунепрерывна снизу. Покажем, что функция и —
верхнее решение уравнения
+H(t,x,Dxu) = 0.	(13.6)
Полагаем
E(tyXyq) := со{(/(^ж,р, g),0) x R: p e P}.
Очевидно, что
maxmin{(s,~ 9- (f,9) G E(t,x,q)} = H(t,x,s)
qeQ
для любых (t, ж, q) e [0, Й] xln x Q. Множество E(ty ж, q) выпукло. Много-
значное отображение (t, ж) t—> E(ty ж, q) непрерывно. Следовательно, отоб-
ражение Е удовлетворяет всем условиям (j), (jj), (jjj+), (jv+), сформулиро-
ванным в разделе 6.2.
13. Стабильные мосты и экстремальные стратегии
153
Пусть (io5^o) С [0,0] х Rn, q Е Q. Нужно доказать, что существует
траектория (x(t), z(t)\ t Е [t0,0], которая удовлетворяет включению
(ж, г) Е E(t, х, q),	(13.7)
начальному условию х(to) = xq9 z(to) — u(to,xo) и неравенству
z(t) = zo = u(to, xo) u(t, x(t)), при t E [to, 0].	(13.8)
Возможны два случая: u(to, xo) = 1 и u(to,xo) — 0. Если u(to,xo) = 1, то
очевидно, что неравенство (13.8) справедливо, т.к. функция и принимает
только значения 0 или 1. Если u(to, хо) = 0, то xo Е W(to). Из определения
стабильного моста следует, что существует такая траектория дифференци-
ального включения (13.7), что x(t) Е IF(t). Из этого факта и вытекает
требуемое условие (13.8). Таким образом, показано, что функция и удо-
влетворяет критерию (U2) в определении 6.5. Следовательно, функция и
является верхним решением уравнения (13.6).
Согласно теореме 6.4, критерии (U2) и (U5), приведенные в пункте 6.3,
эквивалентны. Поэтому рассматриваемая функция и удовлетворяет следу-
ющему условию
inf {(Г u(t, ж; 1, /) — {s, Г) + H(t, х, s): f Е Rn} < 0	(13.9)
при любых s Е Rn, (t,x) Е (0,0) х Rn. Отметим, что и — индикаторная
функция замкнутого множества. Если (t, ж) W, то существует окрест-
ность точки (£,ж), в который функция принимает значение 1. Поэтому
d ~u(t, ж: 1,/) — 0 для всех f Е Rn. Следовательно в этом случае имеет
место условие (13.9) (при f = Ks, где К — достаточно большое число).
Таким образом, требуется проверить условие (13.9) только для (t, ж) EW.
В этом случае u(t, ж) = 0, и из (13.5) вытекает, что d~u(t^ х\ 1, /) Е {0, оо}.
Поэтому неравенство (13.9) эквивалентно следующему условию: для любой
точки (t, ж) Е W, t < 3 существует вектор f Е Rn, такой, что
d~u(t, ж; 1, /) = 0, (s, /) > H(t, ж, $).
Из определения производной d~u(t, х, 1, /) (см. (6.8)) следует также равен-
ство
{/ Е Г: d~u(t, X' 1, /) = 0} = AW*; ж*),
где множество
DtW(t-, х) := (f е R”: liminf dlSt + W^t + S)l = (J J	(13.10)
является правосторонней производной по t многозначного отображения
[0,0] Э 11—> W(t) с в точке (t, ж) Е W.
154
Глава III
Таким образом, приходим к следующему условию
DtW(t; х) П {/ е Г: (s, f} H(t, х, 5)} ф 0,	(13.11)
для любых t е [0,0), х € V7(£), s € Rn. Легко заметить, что здесь мно-
жество DtW(fix) может быть заменено его выпуклой оболочкой. Данные
условия эквивалентны первоначальному определению свойства стабильно-
сти.
Точно так же можно доказать, что для рассматриваемой индикатор-
ной функции и условие (U3) в определении 6.5 может быть переписано
следующим образом
со DtW(t;x) Псо/(£,ж,Р, </)	0,	(13.12)
для любых t € [0,0), х Е W(t), q е Q.
13.2.	Экстремальная стратегия
Ниже будут использоваться следующие обозначения
We(t,x) = Arg min ||a:-w||,
wEW(t)
Se(t, x) — {se = we — xi we e We(t, x)}.
Если iy(t) = 0, то полагаем формально Se(t, x) = {0}. Выберем произ-
вольно se(t,x) e Se(t,x) и
Ue(t.x) e Arg max[min(/(f,£,p, g), se(£, ж))].	(13.13)
peP LqeQ	J
Определенную таким образом функцию Ue: [0,0] х Rn Р будем называть
стратегией, экстремальной к стабильному мосту W.
Поясним идею, мотивирующую такую конструкцию стратегии Ue. Со-
гласно определению, We(t< х) — это подмножество точек из W(t), кото-
рые являются ближайшими к точке ж. Поэтому можно сказать, что век-
тор se (t, х) соединяет точку х и множество VE(t) самым коротким путем.
Условие (13.13) означает, что управление Ue(t^x) выбрано так, чтобы на
маленьком интервале времени [/, 14- J] это управление гарантировало мак-
симальный сдвиг фазовой точки в направлении множества W (£).
Ниже сформулирован основной результат относительно стратегий, ко-
торые являются экстремальными к стабильным мостам. Формулировка это-
го результата имеет более компактную форму, если вместо кусочно-посто-
янных управлений р(£) = Ue(ti^x(ti))9 t €	E Д и соот-
ветствующих пошаговых движений рассматривать предельные процедуры,
в которых diam (Д)	0. Упомянутые конструкции вводятся следующим
образом.
13. Стабильные мосты и экстремальные стратегии
155
Пусть задана начальная позиция (to, >го) С [0, #] xRn Пусть (С7, Д) — по-
шаговая процедура, выбранная игроком Р (здесь U: [0, #] xln Р -стра-
тегия по принципу обратной связи, и Д := {to < ti <• •• < tm+i = 0} —
разбиение интервала времени [to,#]). Обозначим символом X(to,^o, U, Д)
множество абсолютно непрерывных функций ж(-): [to,#] v которые
удовлетворяют начальному условию ж (to) = жо и дифференциальному
включению
±(t) € co{/(t^(t),p(t),tf): q Е Q}
для почти всех t е [to, #], где
p(t) =	ti < t < ti+i, i e 0,m.
Далее, введем
X(tQ. ж0, U) := limsup X(to, жо, t/, Д),	(13.14)
diam AJ.0
где символ lim sup обозначает верхний топологический предел (см. прило-
жение, параграф А2). Согласно этому определению, функция ж(-): [to, #] »->
Rn является элементом множества X(to, жо, U) тогда и только тогда, ко-
гда существуют такие последовательности Д& и ж&(-) Е X(t0, ж0, U, А&)
(к — 1,2,..что
lim diam Д^ = 0, lim max |^(t) — x(t) || — 0.
к—»оо	к—*оо tE[to,0]
Множество Х(^,ж0,С/) называется пучком предельных траекторий,
порожденных стратегией U.
13.3,	Теорема
Пусть W — стабильный мост в задаче М-сближения, и пусть Ue — по-
зиционная стратегия, которая является экстремальной к множеству W.
Предположим, что начальная позиция (^,жо) принадлежит множе-
ству W. Тогда
(M(t)) е W, Vx(-) eX(t0,x0,Ue), Vt е [t0,#],
и, в частности, x(ff) Е W(0) С М, т.е. стратегия Ue гарантирует сбли-
жение с множеством М в фиксированный конечный момент времени t = 0
при условии, что начальная позиция (^,Жо) лежит на стабильном мосту.
Доказательство будет дано ниже. Прежде всего прокомментируем это
утверждение.
156
Глава III
Напомним, что множество W называется слабо (сильно) инвариантным
относительно динамической системы, если для любого начального состоя-
ния, которое принадлежит этому множеству, по крайней мере одна траекто-
рия (любая траектория) проходит внутри множества W. Поэтому, согласно
теореме 13.3, слабая инвариантность множества W относительно диффе-
ренциальных включений (13.4) порождает сильную инвариантность этого
множества относительно управляемых процессов, генерируемых позицион-
ной стратегией, которая экстремальна к множеству W.
Следующее замечание касается задачи М-сближения, в которой иг-
рок Р имеет информационное ^-преимущество. А именно, рассмотрим иг-
ру, в которой игроки выбирают их управления согласно следующим прави-
лам. В начальный момент времени t = to игрок Р знает заранее управле-
ние q(t), которое будет выбрано противником на интервале времени [t0, £i),
t± = tQ -у б. Базируясь на этой информации и знании начального со-
стояния, игрок Р выбирает управление p(t) на первом интервале [£0,й)-
В момент времени t\ игрок Р знает текущую позицию игры cr(ti))
и управление q(t) игрока Q на интервале времени [£i,£2)> *2 = й + 6 и
так далее. Предположим также, что множество f^t.x^P.q) выпукло для
всех (t,x,q) е [0,0] х Rn х Q. Пусть начальная позиция (to,#o) принад-
лежит стабильному мосту W. Согласно вышеупомянутым предположени-
ям, игрок Р может выбирать управление р(-): [Ль ^г+i) Р так, чтобы
€ W ддя любого ti, включая tk = 0, и поэтому игрок Р гаран-
тирует сближение x(ff) eW(ff) С М при любом выборе игроком Q управ-
ления g(-): [^,^+1) Q- Этот факт следует немедленно из определения
стабильного моста.
Вышеизложенная постановка вряд ли является реалистичной, ио мож-
но полагать, что информация об управлении противника q(r) на предстоя-
щий интервал времени [^, ^+i)> t^ = ti + 5 может быть заменена инфор-
мацией об управлении на предшествовавшем интервале [ti — 5, ^). Действи-
тельно, известно, что для некоторого класса управляемых систем различие
между этими двумя постановками не является существенным в следующем
смысле. Если параметр 5 мал, то результат, гарантированный для игрока Р
при наличии информационного ^-преимущества, близок к результату, ко-
торый гарантирован в указанной модификации. Однако, и эта измененная
постановка также неприменима к реально существующим задачам управле-
ния, т. к. фактически невозможно измерять управления (или помехи) д(т),
т е [ti — S,ti), с необходимой точностью.
Поэтому предлагаемая постановка задачи в классе стратегий по прин-
ципу обратной связи кажется более предпочтительной в этом отношении.
Построение позиционной стратегии, которая является экстремальной к дан-
ному стабильному мосту, — относительно простая задача. Главная вычис-
лительная проблема — построение соответствующего стабильного моста.
13. Стабильные мосты и экстремальные стратегии
157
Некоторые результаты, связанные с такими проблемами, будут рассматри-
ваться в параграфе 16.
13.4.	Доказательство теоремы 13.3
Рассмотрим индикаторную функцию для множества W, определяемую
равенством (13.5). Напомним, что эта функция является верхним решением
уравнения (13.6). Полагаем
w(t,x,y) = e~2Xt Ц® - у||2,
v(t, х) min [n(t, у) + w(t, x, у)].
yew1
Определим стратегию [7* подобно конструкции из раздела 12.2. А именно,
выберем точку
y(t, х) е Arg min [u(t, у) + w(i, ж, у)]
уе^п
и определим вектор
s(L х) := Dxw(t, X) y(t9 х)) = 2е~~2Аг(ж — y(t, ж)).
Напомним, что А — коэффициент из условия Липшица (13.2). Стратегия 77*
задается соотношением
U*(t,x) е Arg min[max(s(7, ж), f(t, х^р, д))],	(13.15)
pep qeQ
которым завершается это определение.
Отметим, что в области
N := {(t,®) е [0,0] х Г1: v(t,®) < е“2А(}
экстремальная стратегия Ue, определенная в пункте 13.2, совпадает со стра-
тегией вида U* (13.15). Действительно, если (t, ж) е N, то y(t, ж) — точка из
множества W(7), ближайшая к точке ж. Ясно также, что вектор s(t, ж), рас-
сматриваемый здесь, и вектор se(t, ж), определенный в разделе 13.2, связа-
ны равенством х) = —2e~2Atse(t,x). Поэтому условия (13.13) и (13.15)
эквивалентны. Заметим еще, что функция w(t, х, у) удовлетворяет условию
+ H(t, х, Dxw) - H(t, у, -Dyw) 0.
После вышеизложенных предварительных замечаний докажем теперь
теорему 13.3.
158
Глава Ш
Пусть жо £ W(to). Рассмотрим движение ж(-) е X(to,xo, Ue, Д). Из
того, что жо € W(to), следует г(^о,жо) — 0 < e“2Ato. Предположим, что
неравенства v(ti, x(ti)) < e~2Xti выполнены для каждого z = 0.1. .. .,к^т
(здесь ti е Д; напомним, что Д = {^: i € 0, т 4- 1, tm+i = 0}.
Следовательно, (^,ж(^)) 6 N и Ue(ti, x(ti}} = (7*(^,ж(^)), i € 0, к.
Принимая во внимание, что в рассматриваемой задаче интегрант д равняет-
ся нулю, и повторяя оценки, представленные в доказательстве теоремы 12.3,
получаем
v(ti,x(ti)) С £(<5), где lim ((5) = 0, 6 = diam А, (13.16)
б~>о
для каждого i € 0, к 4-1.
Выберем достаточно малое число S > 0, такое, что выполняется нера-
венство ((6) < е"2А6>. Тогда предположение v(ti,x(ti)) < e~2Xti выполнено
при всех U е Д. Следовательно, оценки (13.16) также выполнены для каж-
дого ti е Д. Нетрудно видеть, что для каждого ti е Д и всех t е [ti, t^ i]
справедливы оценки
dist ((t,ж(£)); ^dist((ti,a;(ti));lV) + c<J^eAev/C(5)+c^ (13.17)
где с — некоторая константа. Переходя к пределу при S 0, приходим к
требуемому утверждению.
13.5.	Оптимальность стратегий, экстремальных к множествам уровня
функции цены
Оптимальные стратегии в дифференциальных играх с платой ви-
да (11.2) могут быть сконструированы в форме стратегий, которые являются
экстремальными к соответствующим стабильным мостам. Сначала рассмот-
рим случай, когда функция g(t, х,р, q) тождественно равна нулю. Поэтому
равенство (11.2), которое определяет функционал платы, имеет здесь вид
7(Ж(.)) = а(Ж(0)),	(13.18)
где сг: Rn R — непрерывная функция (ограничение вида |сг(ж)|	(14-
4- Цж^Ясг не будет использоваться). Как и выше, движение управляемой
системы описывается уравнением (13.1), в котором предполагается, что
функция / удовлетворяет всем требованиям, указанным в разделе 13.1.
Рассмотрим задачу Коши
4- H(t, х, Dxu) = 0, и(0, ж) = а (ж),	Д 13.19)
СП
13. Стабильные мосты и экстремальные стратегии
159
где Н — гамильтониан, определенный равенствами (13.3). Отметим, что га-
мильтониан Н и краевая функция а удовлетворяют предположениям, сфор-
мулированным в теореме 8.1. Поэтому, согласно этой теореме, существует
единственное минимаксное решение в задаче (13.19).
Пусть и — минимаксное решение рассматриваемой задачи. Выберем
число с, и определим для функции и соответствующее множество Лебега,
т. е.
Wc := {(t, х) € [0,0] х Rn: u(t. х) с}.	(13.20)
Так как функция и — верхнее решение, ее надграфик является слабо инвари-
антным относительно дифференциального включения (13.7). Это свойство
подразумевает, что множество Wc слабо инвариантно относительно диф-
ференциального включения (13.4), поэтому Wc — стабильное множество в
задаче Мс-сближения, где Мс = {х €	: <т(х) <5 с}.
Пусть задана начальная позиция (to, жо). Полагаем с = u(to, xq). В этом
случае очевидно, что начальная позиция принадлежит множеству Wc. Пусть
Uo — позиционная стратегия, которая является экстремальной к множе-
ству Wc. Теорема 13.3 утверждает, что x(ff) 6 Мс ддя любой траекто-
рии х(-) е X(to, жо, Uq). Следовательно, 7(ж(-)) С с = u(to, ж0). По опреде-
лениям пучка траекторий X(to, жо, Uq) (см. раздел 13.2) и гарантированного
результата (11.14), получаем
Г1^о,жо, Uq) ^г/^о,жо).
Точно так же можно определить стратегию То для игрока Q, которая
является экстремальной к множеству
Wc := {(t, ж) 6 [0,0] х : ti(t, ж) с — u(to, Жо)}.
Из того, что для любой траектории ж(-) € Х(^,жо, То) справедлива оцен-
ка 7 (ж (•)) > u(to, жо), результат, гарантируемый стратегией То, оценивается
неравенством
Г2(^,Ж0,ТЬ) u(to,T(j).
Используя соотношение (11.17), приходим к равенствам
Vai (to, жо) = Ti(to, жо, Uq) = r2(to, жо, То) = w(to, xq).
Таким образом, доказана оптимальность стратегий Uq и То, которые
являются экстремальными к множествам Wc и Wc соответственно. Эти
стратегии формируют седловую точку в рассматриваемой дифференциаль-
ной игре.
160
Глава III
Сравним полученное решение с решением, представленным в парагра-
фе 12. В силу теоремы 12.3, стратегии Us, определенные в пункте 12.2,
гарантируют оценки
Ti(to,xo,U£) u^q.xq) +С,
где и = Vai — минимаксное решение в задаче (13.19) и одновременно
цена рассматриваемой игры. Из того, что число С > 0 может быть выбрано
произвольно малым, вышеупомянутые оценки означают, что стратегии U£
субоптимальны (почти оптимальны) для игрока Р. Однако, в общем случае,
эти стратегии могут не быть в точности оптимальными.
В этом отношении качество конструкции, представленной в парагра-
фе 12, оказывается, формально, хуже, чем у рассмотренной здесь.
С другой стороны, конструкция из параграфа 12 обладает важным свой-
ством универсальности, которое определяется следующим образом.
Позиционная стратегия U игрока Р называется универсальной (-оп-
тимальной в области D С [0,0] х Rn, если она гарантирует выполнение
неравенства
Г1(*о..то^°) Val(fo,zo) + C, V(t0,s0)e£>.	(13.21)
Точно так же определяются универсальные ^-оптимальные стратегии игро-
ка Q.
Согласно теореме 12.3 (где и равно Vai), для любого ( >,()и для лю-
бого ограниченного множества D, стратегии U£ и V£, определенные как
суперпозиции предстратегий и квазиградиентов, являются универсально
(-оптимальными в области D.
Стратегии Uq и Vo, которые являются экстремальными к множествам
Лебега функции цены, могут не быть универсальными в данном смысле.
13.6.	Экстремальное прицеливание к надграфику функции цены
Напомним кратко определения устойчивых мостов и экстремальных
стратегий в дифференциальной игре (11.1), (11.2). Пусть Val(t, х) — функ-
ция цены дифференциальной игры (11.1), (11.2). Полагаем
:= epi Vai — {(t, x, z) G [0,0] x Rn x R: z Vai (t, x)}.
Так как надграфик функции цены слабо инвариантен относительно диффе-
ренциального включения
(x,z) € co{(f(t,x,p,q),ff(t,x,p,q)); р € Р},
13. Стабильные мосты и экстремальные стратегии	161
то множество является стабильным мостом для управляемой системы
z(t) = g(t,x(t),p(t),q(t)).	(13.22)
Рассмотрим задачу -сближения для этой системы, где
:= epi су = {(x,z) е Rn х R: z су(х}.
Применяя конструкции, описанные в разделе 13.2, определим для иг-
рока Р стратегию, которая является экстремальной к множеству WX
Для (t, ж, z) е [0,0] х Rn х R полагаем
W\t) := {(м,г/) еГ xl: (t,w,t/) G W*},
W^(t, x, z} := Arg min [Цж - w||2 + (z - y)2] ,
Sl(t,x,z) := {(se,Ce) = (we - x, ye - z): (we,?/e) G W^(t,x,z)}.
Выберем произвольно (se, £e) C x, z) и
lP(t)X,z) G Arg max min(se,/(t, x,p, q)) — Ce9(t^iP^) •
peP LqeQ	J
Пусть задана начальная позиция (to,#o) G [0,0] x Rn и пусть zq =
= Vai (to, ^o)« Обозначим символом Xb(t0, #o, ^o, А) множество абсо-
лютно непрерывных функций (ж(-), г(-)): [to, 0] н-> Rn x R, которые удовле-
творяют начальному условию (x(t0), ^(to)) = (^o,^o) и дифференциально-
му включению
е co{(/(f,x(t),p(t),Q),5(^®(*),P(i),9): 9 G <2}>
где
p(t) = ^(^,а?(^),г(^)), ti t < ti+1, i — 0,1,... ,т.	(13.23)
Далее, определим (см. подобную конструкцию в (13.14))
V^(to,rco,^o,^e) := limsup Vb(to, xq, го, А).	(13.24)
diam AJ,0
Равенство г0 = Val(to,#o) подразумевает, что (to,^o,^o) Так
как множество является стабильным мостом для системы (13.22), стра-
тегия обеспечивает движение системы внутри множества W\ и, поэтому,
гарантирует выполнение условия
(ж(0),г(0)) С W\9) = М*	(13.25)
для любых (ж(-), г(-)) € X^(t0, жо, zq, U^).
162
Глава III
Последнее утверждение фактически следует из теоремы 13.3. Обратим
внимание, что теорема 13.3 была доказана в предположении, что выполня-
ется (13.3). Для рассматриваемой здесь системы (13.22) имеем
H\t,x,s,C) = minmax[(s,/(t,a;,p,g)) - Qg(t,x,p,q')] =
реР qeQ
= maxmin[(s, f(t,x,p,qj) - Cg(t,x,p,q)] = (H(t,x,s/Q (13.26)
qeQ peP
для ( > 0 и для любого s е Rn. Здесь минимакс равен максимину в силу
условия (11.5). Переходя к пределу при С | 0, получаем, что это равенство
справедливо и для С — 0. Условие (13.26) может быть нарушено для £ < 0.
Однако, для конструкции, предложенной здесь, достаточно, чтобы гамиль-
тониан х, s, £) был определен для £	0. Чтобы подтвердить это заме-
чание, отметим, что множество обладает следующим свойством: если
(w, у) е H^(t), то (w, у + г) е H^(i) для любого О 0. Следовательно,
||we - rr||2 + (уе - z)2 ||we - ж||2 + (уе + Г - z)2
для каждой точки (we,ye) в W^(t, х, z). Следовательно, 2г(з/е — г) + г2 > 0.
Так как последнее неравенство справедливо для любого г 0, приходим
к оценке £e(t, x,z) := уе ~ z 0. Используя это неравенство и обраща-
ясь к доказательству теоремы 13.3, заключаем, что стратегия ведет по-
рождаемые ею движения системы внутри множества и обеспечивает
включение (13.25).
Обозначим символом S(to,^o, ^о, Д) все тройки (.т(-),р(-),#(•)),
где р(-) — управление, сформированное в соответствии с правилом (13.23),
g(-): [io, 0] |—> Q — произвольная измеримая функция, #(•) — траектория, ко-
торая удовлетворяет первому уравнению системы (13.22) и условию x(ty)
— xq. По определению множества = epi <7, имеем г(0)	для
любых (#(•), г(-)) С X\tQ, ха, zq, 1/|). Из (13.24) и (13.25) следует, что
limsup sup7(io,S(to,#o,£(bC^,A) —
diam Д|0
— lim sup sup
diamAlO («(•),₽(•),?())
p(t,a;(t),p(i), (£))<&
C z0 = Val(to,®o),
где (x(-),p(-),g(-)) e S(t0,x0,z0,U%, Д).
Таким образом, получили, что стратегия гарантирует для игрока Р
оптимальный результат. Заметим, что, в отличие от субоптимальной стра-
тегии Ue, определенной в параграфе 12, стратегия U,; зависит не только
13. Стабильные мосты и экстремальные стратегии
163
от переменных (t,x), но также и от переменной z, которая удовлетворяет
второму уравнению системы (13.22).
В заключение этого параграфа напомним известное преобразование
дифференциальной игры с платой (11.2) в дифференциальную игру с функ-
ционалом платы вида (13.18). Полагаем
х := (х1,х2^.^хп,хп+1),
где функции fi(t,x,p,q) — это компоненты вектор-функции f(t,x,p,q),
стоящей в правой части уравнения (11.1), a g(t, х,р, q) — функция, проин-
тегрированная в функционале (11.2) относительно управляемого процесса.
Рассмотрим вспомогательную управляемую систему
=7(Mt),p(f), </(£))•	(13.27)
Введем следующий функционал платы
7(х(-)) := а(ж(0)) - Я!п+1(0).	(13.28)
Предполагаем, что траектории системы (13.27) подчинены начальному
условию х(£0) = ХО, жп+1(4о) = о. Ясно, что 7(t0, т(-),р(-), ?()) = 7(ж(-)).
Таким образом, вводя дополнительную фазовую переменную xn+i(t),
получаем, что функционал платы в преобразованной дифференциальной
игре не содержит интегрального члена.
Пусть Vai (£, х,	) — функция цены дифференциальной игры (13.27),
(13.28). Пусть [0, в] х Rn э (£, х) u(t, х) е R — это минимаксное решение
в задаче Коши (11.19). Как мы знаем, это решение существует, единственно
и совпадает со значением функции цены дифференциальной игры (11.1),
(11.2). Нетрудно показать, что
Vai (£, х, xn+i) = Vai (i, х) — xn+i = u(t, х) — хп+±.
Полагаем
Wc := {(£, ж, жп+1) е [0,х Rn х R: u(t, х) — хп±\ с = u(t0^ ж0)}
и определим стратегию Uo(t, х, xn+i)9 которая является экстремальной к
множеству Wc. Для заданной начальной позиции (£o,^o,0) эта страте-
гия гарантирует игроку Р оптимальный результат в дифференциальной
164
Глава III
игре (13.27), (13.28). Для начальный позиции (to, a-о) та же самая стра-
тегия гарантирует игроку Р оптимальный результат в дифференциальной
игре (11.1), (11.2).
Отметим, что для стратегии Uq требуется дополнительная информация
о текущих значениях переменной жп+1- Эта информация не используется,
когда мы применяем субоптимальные стратегии, определенные в разде-
ле 12.2.
14.	Некоторые замечания
В данном параграфе приведено краткое описание нескольких различ-
ных концепций стратегий игроков и цены дифференциальной игры. Дано
сравнение постановок задач, используемых в теории дифференциальных
игр. Показано, почему необходимо рассматривать разрывные стратегии по
принципу обратной связи и использовать пошаговые процедуры управле-
ния. Обсуждается также проблема устойчивости позиционных стратегий,
и описываются процедуры управления с поводырем, которые порождают
решения, устойчивые к информационным шумам.
14.1.	Многошаговые аппроксимации
Первое строгое определение цены дифференциальной игры было вве-
дено У. X. Флемингом (см., например, [75, 76]). Его подход был основан
на аппроксимации дифференциальной игры некоторыми многошаговыми
играми. Далее кратко описаны эти конструкции.
Рассмотрим дифференциальную игру вида (11.1), (11.2). Пусть xq —
= х(to) — начальное состояние управляемой системы в начальный момент
времени to- Интервал времени [to, 0] разбит множеством точек
ti — to 4- iSk,	— to)2~fc, i e 0, m, m -- 2k.
Многошаговая аппроксимация вводится следующим образом. Управляемая
система (11.1) и функционал платы (11.2) заменяются их конечно-разност-
ными приближениями
z(tz+i) = x(ti) 4- f(ti, x(ti\pi, (li^ki i = 0,1,..., m - 1,
m—1
7(to,2!0,PO,90, • • 	“ 4 У g(ti,	Qi).
i=O
Игроки P и Q выбирают управления pi e P и qi E Q соответственно. Иг-
рок P стремится минимизировать плату, а игрок Q хочет максимизировать
14. Некоторые замечания
165
ее. У. X. Флеминг рассмотрел два типа аппроксимаций, а именно, мажорант-
ную и минорантную многошаговые игры.
В мажорантной игре игрок Р в момент времени to знает начальную
позицию (to,^o). Зная эту информацию, игрок Р выбирает свое управле-
ние ро. Игрок Q также знает начальную позицию (йь#о)> помимо этого
он/она в момент времени to знает управление ро выбранное его/ее против-
ником. Используя эту информацию, игрок Q выбирает управление qo Е Q.
В момент времени ti (i Е l.m — 1) игрок Р получает информацию
о текущей позиции	он/она имеет также полную информацию о
предыдущих позициях (tj,x(tj)) и управлениях (pj.qj) (j Е 0,i — 1), вы-
биравшихся до текущего момента времени ti этим игроком и противником.
Используя эту информацию, игрок Р выбирает управление pi Е Р. В до-
полнение к информации, доступной игроку Р, игрок Q в момент времени ti
знает управление pi выбранное противником. Опираясь на эту информацию,
игрок Q выбирает управление qi. Поэтому в мажорантной игре максимизи-
рующий игрок имеет информационное преимущество.
Естественным путем определения цены Vai(to, жо) мажорантной
игры на разбиении
= {ti = to + iSk: г = 0,1,..., т = 2к}
является следующий. Эта величина задается формулой
Vai дДЛь^о) := min max • • • minmax7(t0, ^о,Ро, 4о, • • •
Pm-1 Qm — 1 Po QO
где min берется по р^ изменяющимся в Р, a max берется по q^ изменяю-
Pi	Qi
щимся в Q.
Точно так же можно рассматривать минорантную игру, в который ми-
нимизирующий игрок Р имеет информационное преимущество. Цена в ми-
норантной игре задается формулой
Val7 (t0,x0) = max min • • •maxmin7(t0,®o,Po,Qo, • • •
'	Qm —1 Pm — 1	QO PO
Ясно, что Vai (to, zq) Vai(to, жо)- Если
lim Valt (to,zo) = Um Уа1д (*0,ж0) = ValFi(to,zo), (14.1)
к—>OC	й	к—»OC
то величина ValFi(^o,^o) называется ценой дифференциальной игры в
смысле Флеминга.
Подход, основанный на многошаговых приближениях, был развит и
расширен в ряде работ (см., например, [83, 166, 220]) для различных типов
166
Глава III
дифференциальных игр. В рамках этого подхода, модификации определения
цены дифференциальной игры базировались на соотношениях вида (14.1).
При этом рассматривались управляемые системы общего вида и различные
типы функционалов платы. Исследовались мажорантные и миноратные иг-
ры, в которых игроки принимают свои решения в дискретные моменты
времени ti и выбирают кусочно-программные управления. Отметим, что,
в отличие от первых работ [75, 76] (имевших дело с конечно-разностной
динамикой в мажорантных и минорантных играх), в последующих работах
исследовались, главным образом, многошаговые игры, динамика которых
описывается дифференциальными уравнениями.
Отметим, что в случаях, когда обе величины: цена в смысле Флемин-
га Valpi (14.1) и цена Vai (11.18) позиционной дифференциальной игры,
определенная в параграфе 11, существуют, -- они совпадают, т. е. справед-
ливо равенство
Vai (t0, хо) = Vaifi (to, #o)«	(14.2)
Аппроксимирующие многошаговые игры фактически имеют дискрет-
ную природу, и стратегии игроков определяются только для выбранного
разбиения Д интервала времени. Дискретно-временной характер многоша-
говых моделей затрудняет применение аппарата математического анализа.
Важное отличие формализации позиционных дифференциальных игр
состоит в том, что стратегии определены, как функции U(t. х) и V(t, ж),
которые не зависят от разбиений, выбираемых игроками. Исследования по-
зиционных дифференциальная игр базируются на различных результатах
выпуклого, негладкого, и многозначного анализа. Как было продемонстри-
ровано выше, эта теория близко связана с теорией обобщенных решений
УЧП первого порядка. Доказательство существования цены и седловой точ-
ки дифференциальной игры не является единственной целью этой теории.
Много внимания уделяется конструктивным методам вычисления функции
цены и субоптимальных стратегий по принципу обратной связи. Этот под-
ход весьма удобен и для того, чтобы связать вместе различные абстрактные
модели и практически реализуемые конструкции управлений.
Следует упомянуть, что в 60-70-е (когда были сформированы основ-
ные направления исследований в области теории дифференциальных шр),
исследования, выполненные Л. С. Понтрягиным и Б. Н. Пшеничным, были
определяющими для развития этой теории. Л. С. Понтрягин предложил пря-
мой метод и метод альтернированного интеграла для решения задач пре-
следования. Он разработал также оригинальную теорию задач уклонения.
Эти и другие результаты, полученные Л.С.Понтрягиным и его коллегами,
представлены в недавнем обзоре [155]. Б. Н. Пшеничный разработал опе-
раторные конструкции для определения цены дифференциальной игры. Он
получил явные решения для ряда интересных задач преследования и укло-
нения. В своих исследованиях Б. Н. Пшеничный разработал новые подходы,
14. Некоторые замечания
167
основанные на методах выпуклого анализа и негладкой оптимизации (см.,
например, [174, 176, 177]).
14,2.	Квазистратегии
Во многих работах, имеющих дело с дифференциальными играми, ис-
пользуется следующее определение стратегии.
Пусть Р и Q — множества всех измеримых функций [0,0] 91 p(t) е Р
и [0, 0] Э t ь-> q(t) е Q соответственно. Отображение
a:Q^p	(14.3)
называется квазистратегией игрока Р, если оно является неупреждающим,
т. е.
(#i(t) — Q2(Xh Для почти всех t е [0,т]) =>
=> (pi(t) = р2С0?Для почти всех t е [0,т]),
где pi(-) ~ <*(//*(•)), i = 1,2. Аналогично, отображение 5: Р м Q на-
зывается квазистратегией игрока Q, если оно является неупреждающим.
Наиболее вероятно, что такое понятие стратегий берет начало из работ
С. Р. Нардзсвского [153].
Обозначим множество всех неупреждающих отображений а вида (14.3)
символом А. Множество всех квазистратегий игрока Q обозначим симво-
лом В.
Цена дифференциальной игры в классе квазистратегий определяется
следующим образом. Пусть S(tQ, q) — это множество всех таких троек
(ж(‘),р(-), #(•))> что Q(0	2, р(-) = а(д(-)), ж(-) — решения уравнения
удовлетворяющие условию ж (to) = жо- Множество 5(^,жо,/3) определяет-
ся аналогично. Пусть
Г'1(^о,ж0,а) := sup7(t0, S(t0, ж0,«)),
П^0,ж0) := inf Г1(^о,жо,а),
аеА
•= inf 7(to,S'(to,^o,/3)),
Г2^о,жо) := supF2(t0^0,/3).
рев
Если имеет место равенство
Г*(^,ж0) = Г2(^,ж0) := Vah(to^o),	(14.4)
то игра, рассматриваемая в классе квазистратегий игроков Р и Q, имеет
цену, равную VaU(t0, ж0).
168
Глава III
Р. Дж. Эллиотт и Н. Дж. Калтон доказали существование цены Vai * для
широкого класса дифференциальная игр (см., например, [67, 66]). В частно-
сти, известно, что при выполнении условий (А1)-(АЗ), сформулированных
в разделе 11.1, существует цена Vai * дифференциальной игры (11.1), (11.2)
в классе квазистратегий.
Квазистратегии являются инструментом, популярным при изучении
свойств функции цены. Дифференциальные игры в рамках этой форма-
лизации были исследованы во многих работах. Как показано в ряде статей,
функция цены Vai * совпадает с вязкостным решением соответствующего
уравнения Айзекса-Веллмана (см., например, [70]).
Обратим внимание, что в случае, когда существуют обе цены: це-
на Vai (11.18) в классе позиционных стратегий и цена Vai* в классе ква-
зистратегий, — они совпадают, и справедливо
Val(to,^o) = Vai *(t0, я0).	(14.5)
Рассмотрим частный случай квазистратегий, которые определяются с
помощью измеримых по Борелю функций U: [0,0] х Q Р и V: [0, в] х
хР Q. Эти функции U и V называются контруправлениями. Заметим,
что они также называются стробоскопическими (stroboscopic) стратегиями
(см., например, [88]).
Пусть U: [0,6?] х Q м Р - контруправление игрока Р. Введем опера-
тор а, отображающий функции g(-) е Q в функции [0, 0] Э t p(t) =
= U(t, q(t)) € F. Этот оператор является квазистратегией. Действи-
тельно, так как функция U измерима по Борелю, то для любой изме-
римой по Лебегу функции </(•): [0,0] Q, соответствующая функция
р(.) — q(q(-)) — измерима [101]. Ясно, что отображение а является неупре-
ждающим. Аналогично, любое контруправление V представляет собой ква-
зистратегию /3: Р Q.
Отметим, что произвольная пара квазистратегий а и (3 может оказаться
несовместной. Пусть, например, Р = Q = [—1,1],
а(О W = -sign (5(f)),
/?(?(•))(*) =sign(p(t)).
В этом случае нет никаких управлений p(t) и q(t), удовлетворяющих систе-
ме равенств
p(t) = a(q(-))(t), g(t) = ^(p(-))(i).
Так как квазиуправления представляют собой специфический тип ква-
зистратегий, заключаем, что, вообще говоря, невозможно определить диф-
ференциальную игру в так называемой нормальной форме на прямом про-
изведении А х В множеств квазистратегий игроков Р и Q. Следует так-
же упомянуть, что квазистратегии неприменимы в физически реализуемых
14. Некоторые замечания
169
конструкциях, потому что управление p(t) — a(g(-))(t) определяется в за-
висимости от помехи (или управления противника) q(-), реализовавшейся
до текущего времени t, но фактически эта информация недоступна.
14.3.	Непрерывные позиционные стратегии
Ясно, что при математических постановках позиционных дифференци-
альных игр было бы желательным сузить класс стратегий и рассматривать
только непрерывные функции, если это возможно. В этом случае не нуж-
но вводить пошаговые процедуры управления с кусочно-постоянными ре-
ализациями управлений вида (11.7) и предельные процедуры (11.14). Итак
объясним необходимость введения разрывных позиционных стратегий. Рас-
смотрим пример, в котором оптимальный результат не только недостижим в
классе непрерывных стратегий по принципу обратной связи, но и не может
быть аппроксимирован этими стратегиями (последнее является наиболее
важным).
Пример. Пусть движение фазовой точки x(t) е R2 описывается урав-
нением
x(t) = p(t) + (2 — i)q(t), 0 = to С t С в = 2,
и пусть .то = О е >2 — начальное состояние в фиксированный началь-
ный момент времени £0 = 0- Здесь p(t) и q(t) — управления игроков Р
и Q, соответственно, которые удовлетворяют ограничениям p(i) е Р = В
и q(f) е Q = В, где В = {у € R2: ||?/||	1}. Игрок Р (игрок Q) желает
минимизировать (максимизировать) плату
0<ж(-),р(-), </(•)) := “IkWII-
Пусть [0,2] х R2 э (t, х) I—> U(t, х) & В — непрерывная функция,
удовлетворяющая условию Липшица по х. Выберем точку q е Q = В, и
рассмотрим уравнение
t
ж(0 = J[и(т,х(т)) + (2 - r)q]dr.
О
Это уравнение имеет единственное решение, которое обозначим симво-
лом т(-, q). Полагаем
2
?/(?) =	- 9 = У U(r,x(r))dr, q е В.
О
170
Глава III
Отметим, что функция y(q) непрерывна и удовлетворяет оценке ||?/(g)|| < 1,
'iq е В. Таким образом, получаем, что непрерывная функция q i—> y(q) отоб-
ражает шар В на себя. Согласно известной теореме Брауэра (см., например,
[225]), заключаем, что существует такая точка д* е В, что g* — и,
следовательно, ж(2, #*) = 0.
Обозначим символом SC(U) множество всех троек (х(-),р(-), #(•)), где
#(•): [0,2] В — произвольная измеримая функция,
t
j>(t) =
= / [рСг) + (2 - r)q(r)]dr.
О
Из вышеизложенного следует, что
n(B):-sup7(5c(B))-0.	(14.6)
Напомним, что здесь 7(ж(’)>р(')> #(’))	~||ж(2)||.
В рассматриваемом случае предполагалось, что функция U(А, х) непре-
рывна и удовлетворяет условию Липшица по х. Можно показать, что ра-
венство (14.6) остается справедливым для любой непрерывной функции U,
т. е. условие Липшица может быть опущено. Можно заметить также, что
Г1(В, Д) = 0 для любой непрерывной стратегии U и для любого разбие-
ния Д. Здесь Г1 (С7, Д) — результат, гарантированный пошаговой процедурой
управления (U, Д) (см. (11.8)).
Теперь рассмотрим разрывную позиционную стратегию
Ц*(х) =
X 7^ 0,
х = 0.
(14.7)
Заметим, что при ЦжЦ = 0 в качестве значения В* (ж) может быть выбран
любой единичный вектор. Покажем, что
Г1(г7,) = -1	(14.8)
где Г1(С7*) — результат, гарантированный стратегией U* (напомним, что эта
величина определяется согласно (11.8), (11.14)).
Пусть выбрано разбиение Д {0 — to < ^1 < ‘	— 2}.
Рассмотрим тройки (ж(-),р(-), #(•)) Е 8(С7*,Д). Здесь #(•): [0,2] н-t В —
измеримая функция, траектория ж(-) удовлетворяет начальному усло-
вию ,т(0) = О и уравнению
i(t) = p(t) + (2 - t)g(f),
14. Некоторые замечания
171
где p(t) — U*(x(tiY), ti t < ti+i, г = 0,1,..., т. На любом из интерва-
лов [4,4+1] справедливо равенство
x(ti+1) = x^ti) + (ti+i -	+
tl+l
J (2 — t)q(t)dt.
Поэтому
11^(^41)11	l№) + Й1 - 4)ГЛ(ж(4))||
По определению U* имеем, что
ti+l
I (2-t)q(t)dt
ti
+ (ti+1 - ti)U*(x(ti))\\ = ||ж(4)|| + (^+1 ~ ^).
Справедливо также неравенство
^i+l
sC 2(£i+i - is) -
/2	_ f2
4+1 Li
2
Таким образом, приходим к следующему неравенству
t? _ t2
lk++i)ll > lk(«i)|| +	~ ~ (ti+1 ~
Успешно используя это неравенство, начиная с некоторого момента време-
ни tj и до конечного момента tm+i = в — 2, получаем
^2	__^2	^2
||ж(2)|| — ||x(tm+i)|| >	- — (tm+i — tj) = tj —
Выберем число tj из условия |1 — tj| = mini|l — ti\ для i е 0,m + l.
Полагаем а 1 — t}, тогда предшествующее неравенство может быть
переписано как
7к(-),Р(-),9(-)) = -Ik(2)ll
1 — а2
2
172
Глава III
Это неравенство справедливо для любой тройки (ж(-),р('),9(-)) е
6 S(C7*, А). Отметим, что |а| diamA. Таким образом, получено, что
результат Г1(С7*), гарантированный позиционной стратегией t/*, удовле-
творяет неравенству Г1((Д)	Прослеживая путь предшествующих
рассуждений, можно проверить, что полученная оценка точна, т. е., в дей-
ствительности, имеет место равенство (14.8).
Сравнивая (14.6) и (14.8), заключаем, что результат, гарантированный
разрывной стратегией U*9 не может быть аппроксимирован непрерывными
стратегиями. Непрерывные стратегии не используют в полной мере воз-
можности управляемой системы при данном объеме информации.
Обсудим кратко другой подход к определению дифференциальных игр.
Пусть U: [0,2] х R2 i-4 В - некоторая функция (возможно непрерывная).
Следуя по хорошо известному пути (см., например, [73, 74]), введем мно-
гозначное отображение
~ Q сб{С7(т,С): (т,£) 6 Oe(t,x)},
е>0
где O£(t, х) := {(т,£) С [0,2] xl2: (f — т)2 4- ||ж - £||2	е2}. Обозначим
символом S(LP) множество всех троек (#(•), р(-), </(•))> гДе
t
x(t) ~ f Ь(т) + (2 ~ ТМТ)ИТ> 0^2,
о
р(-) — измеримая функция, удовлетворяющая включению p(t) G М (£,#(£))
при почти всех t G [0,2], и #(•): [0,2] 1-4 В — произвольная измеримая
функция, как это было выше. Пусть
Г^) := 8ир7(ЭД).
Можно показать, что Г1(М) = 0 при любом выборе позиционной страте-
гии U. Поэтому та формализация разрывных стратегий по принципу обрат-
ной связи, которая базируется на технике дифференциальных включений,
также оказывается неудачной. Она наследует недостатки непрерывных стра-
тегий по принципу обратной связи.
Также уместно отметить, что в случае, когда функция цены является
выпуклой по фазовой переменной, использование техники дифференциаль-
ных включений для формализации стратегий по принципу обратной связи
обеспечивает оптимальный результат игроку Р (минимизирующему плату).
Оценки результатов, гарантированных в классе непрерывных позиционных
14. Некоторые замечания
173
стратегий и в классе многозначных стратегий, изучались в ряде работ (см.,
например, статьи [9, 10], которые непосредственно связаны с задачами,
обсуждавшимися в данном разделе). Более детальное изложение представ-
ленных результатов содержится в книге [123].
14.4.	Проблема устойчивости позиционных стратегий
Выше предполагалось, что для формирования управления с помощью
пошаговой процедуры, доступна точная информация о реализовавшейся по-
зиции. Однако, в действительности, информационный шум является неиз-
бежным. Как оказалось, в некоторых ситуациях даже небольшие инфор-
мационные помехи могут разрушить предложенное управление по прин-
ципу обратной связи. В этих случаях решения теоретико-игровых проблем
управления являются неустойчивыми по отношению к информационным
помехам, и возникает задача регуляризации этих решений.
Рассмотрим простой пример, в котором информационный шум раз-
рушает идеальное решение. Пусть три точки у, z^ и z^ движутся на
плоскости. Для ясности полагаем, что точка у — позиция собаки, a z^
и z^ — позиции двух зайцев. Уравнения движения имеют вид
y(t) = p(t), z(1)(f) =	= Q(2)(i)-
Полагаем, что скорости точек у, z^ и z^ ограничены, т. е. выполняются
неравенства
||p(i)Ha, lk(i)(t)l| < в, (г = 1,2), а>/3.
Рассмотрим следующую позиционную стратегию для собаки
	z^ — у а——	, ||г(1) — у\\	0< ||г(1) - у\\	||г(2) -у\\,	
и0(ж) := <	z^ — у ||г<2) -у||’	0 < ||г(2) -у|| < ||г(1) -у||,	(14.9)
	. °,	min{||z(1) - з/||, ||г(2) - у\\} = 0.	
Здесь х = Q/, z^\ z^) е R6, О = (0,0) е R2. Если функционал платы
имеет вид
7(ж(-)) = тш{||г(1)(6») - у(0)||, ||г(2)(0) - у(0)Н},
174
Глава III
то стратегия U° оптимальна для собаки. Заметим, что эта стратегия также
является оптимальной и для случая, когда функционалом платы является
время, необходимое для того, чтобы точка y(t) встретилась с одной из
точек z^(t) (£ = 1,2).
В пошаговой процедуре (С7°, Д) управление p(t) сформировано следу-
ющим образом. В момент времени t = ti € Д собака определяет самого
близкого из двух зайцев и направляет вектор своей скорости на этого зайца.
Этот вектор остается неизменным на полуинтервале [^,й+1)- Такой метод
управления обеспечивает s-оптимальный результат для собаки.
Это заключение справедливо при условии, что расстояния между соба-
кой и зайцами измерены точно. Если же они измерены с ошибками, то этот
информационный шум может разрушить предложенный способ управления.
Действительно, пусть движению собаки сформировано следующим
способом
p*(t)	ti <ti+1 =ti + 6.	(14.10)
Здесь x*(ti) — результат измерения фазового вектора x(ti). Пусть ошибки
измерения удовлетворяют ограничению
- ж(44)||	(14.11)
Согласно концепции «гарантированного результата», следует принять
во внимание ситуацию, когда этот информационный шум реализуется наи-
более неблагоприятным образом. Рассмотрим следующую ситуацию: пусть
точка ?/о находится в малой окрестности линии АВ, одинаково отдаленной
от точек Zg1) и zo^- Пусть зайцы z^(t) и z(2\t) стартуют из этих позиций
и двигаются по лучам A±Br и А2В2 соответственно, оставаясь всегда на
равном расстоянии от оси АВ. Из-за неправильного определения самого
близкого из зайцев в моменты времени t = ti, может иметь место движение
собаки вблизи луча АВ. Это может произойти в результате альтернативно-
го прицеливания то на ложную точку z^fa), то на ложную точку z*2\ti).
Такое движение собаки не будет сближаться ни с одним из зайцев.
Отметим, что такое скользящее движение может появиться в случае, ко-
гда число 6 в соотношении (14.10) и число £ в ограничении (14.11) связаны
неравенством S 5о(£)> где величина 5о(£) имеет тот же порядок малости,
что и как величина £. Поэтому возможна следующая рекомендация: для
того, чтобы ошибки не разрушали пошаговую процедуру управления, сле-
дует ограничить снизу расстояние между моментами разбиения ti. Однако
такая рекомендация страдает тем дефектом, что требование ti+1 — ti > <S(£),
i e 0,m, может привести к ненужной грубости пошаговой процедуры. Та-
ким образом, эту рекомендацию следует отклонить.
14. Некоторые замечания
175
Рис. 14.1
В рассмотренном примере можно попытаться заменить разрывную
стратегию UQ (14.9) некоторой непрерывной стратегией, определенной сле-
дующим образом. В начальный момент времени t — to выбирается одна
из двух точек ^(to) и z*2\to), та, которая ближе к y*(to). И в течение
времени t е [£о> #] собака целится только на эту точку. Нетрудно видеть,
что пошаговая процедура управления, выработанная в соответствии с такой
стратегией, оказывается устойчивой относительно информационного шума.
Однако такую регуляризацию, основанную на переходе к непрерывной
стратегии, не всегда возможно осуществить. Возможны также ситуации,
когда решение задачи доставляет разрывная стратегия, которая не может
быть аппроксимирована или подходящим образом заменена непрерывной
стратегией (этот фундаментальный факт был проиллюстрирован простым
примером в разделе 14.3).
В заключение обратим внимание на то, что стратегии, определенные в
пунктах 12.2, 13.2, и 13.5, могут, в общем случае, также оказаться неустой-
чивыми по отношению к информационному шуму. С другой стороны, мож-
но показать, что информационные погрешности не могут разрушить дей-
ствие стратегий минимизирующего игрока, если функции х u(t, х) или
множества W(t), рассмотренные в упомянутых разделах, являются выпук-
лыми. Более полное обсуждение этих вопросов приведено в [123].
176
Глава III
14.5.	Процедура управления с поводырем
Перейдем теперь к описанию регуляризаций позиционных стратегий,
которые приводят к решениям, устойчивым по отношению к информаци-
онным шумам. Рассмотрим процедуру управления с поводырем для задачи
М-сближения. Пусть движение управляемой системы описывается уравне-
нием
£(*) = /(t,®(i),p(t),?(t))-	(14.12)
Полагаем, что функция ft [0,х R” х Р х Q ь-» Rn удовлетворяет условиям,
сформулированным в разделе 13.1.
Рассмотрим пошаговую процедуру, в который управление p(t) сфор-
мировано в соответствии со следующим правилом
p(t) =	ti t < ti+1, i e 0,m.	(14.13)
Здесь U: [0,0] x Rn x	н-> P — функция, ti e А, где A — разбиение
интервала [to, #]* Функция U и разбиение А выбраны игроком P.
Таким образом, управление p(t) (14.13) выбирается в зависимости от
векторов x*(ti) и С(^г)- Первый из этих векторов — результат измерения
позиции управляемого объекта. Предполагаем, что погрешности измерения
удовлетворяют ограничению
|]ж*(*г) - ЛМН С-	(14.14)
Второй вектор называется фазовым состоянием поводыря в момент вре-
мени t = ti. Он получается в результате моделирования движения вспо-
могательной системы на компьютере. Алгоритмы, которые оценивают век-
тор £(ti), описаны ниже.
Теперь обратимся к формальной конструкции процедуры управления с
поводырем в задаче М-сближения. Сначала определим функции t/°(£, х, w)
nV(t,x,w), удовлетворяющие условиям
UQ(t. х, w) е Arg max min (/(t,	g), w — x} ,	(14.15)
PEP LqEQ	J
V(t, ж, w) e Arg min max(/(t,	g), w — x) .	(14.16)
qeQtpeP	J
Заметим, что, вообще говоря, эти условия определяют функции U° и V
не единственным образом. Для успешных построений можно использо-
вать любую пару функций U° и V. удовлетворяющую указанным выше
условиям. Пусть W — стабильный мост в задаче М-сближения. Выберем
разбиение А = {^: i е 0,т+ 1} интервала [to,#]. В начальный момент
14. Некоторые замечания
177
времени t = to игрок Р производит измерение вектора начального состо-
яния жо = ж (to). Пусть — результат этого измерения. Определим
точку £(to) Е Rn из условия
(to) Е Arg min ||ж*(to) - w\\.	(14.17)
wGW(to)
Таким образом, £(t0) — точка из множества W(to), ближайшая к точке ж* (t0)
(если есть несколько таких точек £(to), то можно взять любую из них).
На первом временном интервале [to, ti) управление игрока Р, p(t) =
= P°(to, ж*(^),£(^)), вместе с некоторым измеримым управлением q(t)
для игрока Q, порождают движение управляемой системы (14.12). На пер-
вом временном интервале генерируется также движение поводыря. Для этой
цели выбирается постоянное управление $Ь = V(to, ж* (to) >£(to)) и рассмат-
ривается дифференциальное включение (см. (13.4))
е со	(jo).
Напомним, что (to Л (to)) Е W. Поэтому, согласно определению стабиль-
ного моста W, среди решений дифференциального включения существует
решение £(t), удовлетворяющее условию (ti.^(ti)) Е W. Возьмем это ре-
шение дифференциального включения в качестве движения поводыря на
интервале [to,ti]«
Пусть ж(^) и £(ti) — фазовые состояния управляемой системы и пово-
дыря в момент времени t = ti. Пусть x*(ti) — результат измерения фазо-
вого состояния x(ti). На следующем интервале [t?-,t^+i) игрок Р выбирает
постоянное управление p(t) = Р°(^,ж*(^),£(^)). Это управление, вме-
сте с некоторым измеримым управлением q(t) игрока Q, порождают дви-
жение ж^), которое удовлетворяет уравнению (14.12). Чтобы определить
движение поводыря £(t), t е [t«, t*+i], выберем постоянное управление qi =
— V(ti, x*(ti), £(t*)) и рассмотрим дифференциальное включение
4(t) е co/(t,C(t),P,^)-
В результате построений на предшествующих интервалах времени, имеем,
что (t^,^(tj)) Е W. Тогда, согласно определению стабильного моста, это
дифференциальное включение имеет решение £(t), которое удовлетворяет
условию (t^+i? £(t*+i)) € W. Возьмем это решение в качестве движения
поводыря на интервале [ti, t^i].
Наконец, обращаем внимание на то, что формирование движения £(t)
может интерпретироваться как дифференциальная игра, в который игрок Р
обладает информационным преимуществом, т. е. в момент времени t =
— ti он/она знает не только реализовавшуюся позицию (ti, £(t*)), но также
178
Глава III
и постоянное управление которое будет использовано противником на
интервале [^,^+1) (напомним, что подобные игры обсуждались в разде-
лах 13.3 и 14.1). Фактически, в этой игре игрок Р играет сам с собой и
назначает управление qi согласно равенству qi = V(ti,x*(ti)^(ti)). Его/ее
противником является фиктивный игрок.
Можно показать, что эти конструкции обеспечивают взаимное отсле-
живание движений управляемой системы и поводыря. Ясно, что е
е W(0) С М. Процедура управления, описанная выше, доставляет реше-
ние задачи М-сближения, которое устойчиво относительно информацион-
ных погрешностей. Справедливо следующее утверждение.
Пусть (to, #о) С W, где W — стабильный мост в задаче М-сближения.
Тогда для любого е > 0, можно выбрать такие 6 > 0 и £ > 0, что процедура,
описанная выше, гарантирует выполнение условия dist(x(#);M) С е для
любого измеримого управления игрока Q, любого разбиения Д, удовлетво-
ряющего ограничению diam Д <5, и любых информационных погрешно-
стей, удовлетворяющих ограничению (14.14).
Следует подчеркнуть, что здесь не требуется, чтобы diamA > д\((),
т. е. для заданной величины связанной ограничением (14.14), расстояние
между моментами времени ti может быть произвольно малым.
Очевидно, что свойство стабильности предложенного решения может
быть описано в традиционных выражениях: «... для любого в > 0 мож-
но выбрать такие <5 > 0 и ( > 0, что...». Однако, с практической точки
зрения, значения параметров 5 и £, которые являются допустимыми для дан-
ного значения s, могут оказаться сколь угодно малыми. Основная причина
этого состоит в следующем. Оценка расстояния между фазовыми состояни-
ями х(в) и управляемой системы и поводыря имеет вид (см. подобную
оценку в (13.17))
1Ж -£(0)|| eXf>h(8,<X
где h(6yQ) 0, когда <5 —> 0 и £ —* 0. Эта оценка содержит экспоненциаль-
ный коэффициент, который может принимать достаточно большие значения,
если интервал времени [t0,0] велик.
Упомянем кратко подход, который позволяет преодолеть этот недоста-
ток. Охарактеризуем процедуру с поводырем, используя понятия и термино-
логию теории устойчивости и теории стабилизации (см., например, [146]).
Определим разность s(t) = x(t) — £(t), которая будет называться возму-
щением. Процедура построения управления, описанная выше, может быть
рассмотрена как один из методов стабилизации возмущенного движения
$(•) = #(.)_£(.). Чтобы оценить эти возмущения, используем функцию
s и-> w(t, s) — e“2At||s||2, которая играет роль функции Ляпунова. Соглас-
но (14.15) и (14.16), управления p(ti) и выбирались из условия, кото-
рое обеспечивало как можно меньшее значение производной dw(t. s(t)}/dt.
15. Смешанные позиционные стратегии и контрстратегии 179
Функция w(t, s) := e~2Af||s||2 — вероятно, самая простая функция Ляпу-
нова, которая может использоваться для этой цели. Усовершенствование
процедуры управления с поводырем может быть достигнуто выбором бо-
лее подходящей функции Ляпунова. А это, в действительности, одна из
задач теории стабилизации движений. Некоторые результаты, полученные
в этом направлении, представлены в работах [122, 123].
В данном параграфе была рассмотрена процедура управления с пово-
дырем для задачи М-сближения. Подобные конструкции могут использо-
ваться и в дифференциальной игре с функционалом платы (11.2), а также в
дифференциальных играх других типов.
15.	Смешанные позиционные стратегии и контрстратегии
В дифференциальных играх, рассмотренных в предыдущих парагра-
фах, предполагалось, что позиция (t, x(t)), реализовавшаяся в текущий мо-
мент времени t, известна обоим игрокам. Если один из игроков получает ин-
формацию об управлении, реализованном противником в текущий момент
времени, то можно заметить, что эта дополнительная информация не влия-
ет на оптимальный гарантированный результат. Это положение имеет место
в случае, когда управляемая система удовлетворяет предположению (11.5)
(условию седловой точки в маленькой игре). Однако, если это условие нару-
шено, то постановки и решения дифференциальных игр в большой степени
зависят от того, обладает ли действительно игрок дополнительной информа-
цией об управлении, выбранном противником. В пунктах 15.2-15.4 будет
исследован случай взаимно независимого выбора игроками своих управ-
лений. В разделах 15.5 и 15.6 будут рассмотрены случаи, когда один из
игроков обладает информационным преимуществом.
15.1.	Предварительные соображения
Рассмотрим управляемую систему, движение которой описывается
уравнением
x(t) = f(t, x(t),p(t), g(t)).	(15.1)
Функционал платы определен равенством
е
= с(х(0У) - У g(t,a:(t),p(t),q(t))dt.	(15.2)
to
Предполагаем, что функции /,диа удовлетворяют условиям (А1) и (А2)
(см. раздел 11.1). Подчеркнем еще раз, что теперь условие (АЗ) не тре-
180
Глава III
буется. Изучим следующие три варианта распределения информации об
управлениях, выбираемых игроками.
Случай I. В текущий момент времени t игрок Р знает управление q(t),
выбранное игроком Q, в то время как игрок Q не знает управления p(t),
реализованного игроком Р.
Случай II. Ни один из игроков не знает управление, используемое против-
ником в текущее время.
Случай III. В текущий момент времени t игрок Q знает управление p(t),
выбранное игроком F, в то время как игрок Р не знает управления q(t),
выбранного игроком Р.
Во всех описанных выше случаях каждый из игроков знает реализовав-
шуюся позицию игры (t, x(t)). Ясно, что первый и третий случаи отличают-
ся переменой местами игроков Р и Q. Помимо этих трех случаев возможны
также и другие варианты распределения информации о выборе управлений
игроками. Однако ниже рассматриваются только основные случаи Т-Ш.
Чтобы пояснить различие между этими тремя типами дифференци-
альных игр, рассмотрим следующий простой пример. Пусть управляемая
система описывается уравнением
±1 = cos(p-hg), ±2 = sin(p4-g),	(15.3)
IpI < 7Г, kl 7Г-
Пусть функционал платы определен равенством
7(Ж(-)) = М0)-	(15.4)
В рассматриваемом примере условие (11.5) не выполнено. Действи-
тельно, имеет место
min maxis 1 cos(p 4- (?) 4- s2 sin(p 4- q)] = \ s? 4- s%,
P Q	V
maxmin[si cos(p 4- q) 4- $2 sin(p 4- q)] = — \ si 4- s^.
q p	v
Рассмотрим три типа дифференциальных игр для данных управляемой си-
стемы и функционала платы.
Случай I. Пусть функция U: Q Р определена равенством
тт, '	.	( х	f 7Г-«,
15. Смешанные позиционные стратегии и контрстратегии 181
Предположим, что игрок Р формирует своё управление согласно правилу
P°(t) =	= 7Tsign(g(t)) - q(t),	(15.5)
где q(t) — управление, выбранное игроком Q. В рассматриваемом случае
игрок Р знает управление q(t), выбранное противником в текущее время t,
что делает допустимым вышеизложенный метод управления. Как следует
из (15.3), (15.5), ±i(t) = — 1 для любого допустимого управления игрока Q.
Следовательно,
TOG)) = xi(t0) ~ (0-to).
Ясно также, что если игрок Q выбирает постоянное управление q(t) =
— q* G [—7г, 7г], то для любого допустимого управления игрока Р выполня-
ется неравенство 7(^('))	^i(^o) — (0 — to). Таким образом получаем, что
Vali(to^o) = #i(*o) — (О - to), где Vali(to,^o) — цена рассматриваемой
дифференциальной игры.
Второй тип дифференциальной игры будет рассмотрен чуть ниже. Сна-
чала получим решение в случае, когда информационное преимущество име-
ет игрок Q.
Случай III. Определим функцию V(p) = —р (р е Р). Полагаем, что
игрок Q формирует своё управление согласно правилу
(t) = v (p(t)) =	(15.6)
Такой метод управления допустим, так как игрок Q знает управление p(t),
выбранное игроком Р в момент времени t. Из (15.3), (15.4) и (15.6) получа-
ем, что игрок Q может обеспечить выполнение равенства
тИ’)) = zi(to) 4- (0 -to).
С другой стороны, если игрок Р выбирает любое постоянное управление,
то для любого допустимого управления игрока Q, справедливо неравенство
7(ж(-)) xi(t0) 4- (# - to). Следовательно, Val3(to, #о) = ^i(^o) 4- (0 - tQ),
где Уа1з(й),жо) — цена дифференциальной игры (15.3), (15.4), в случае
информационной дискриминации игрока Р.
Теперь вернемся к дифференциальной игре второго типа. Сначала рас-
смотрим формальное решение этой игры в классе смешанных стратегий, а
затем определим стохастическую процедуру, которая будет аппроксимиро-
вать это решение.
Случай II. Рассмотрим множества
Р = rpm (F), Q = rpm (Q).
182
Глава III
Напомним, что здесь Р = Q = [—%, тг], а символ rpm (S') обозначает множе-
ство всех регулярных вероятностных мер, нормированных на множестве S.
В общем случае игроки Р и Q могут выбирать смешанные управле-
ния Hi и в зависимости от реализовавшейся позиции (t, x(t}). В частно-
сти, они могут использовать программные смешанные управления
[to, $] 3 t Е Р. [to? О] Э t ь-> Pf G Q.
Формально полагаем, что движения управляемой системы, порожденные
программными смешанными управлениями, определяются обычными диф-
ференциальными уравнениями
cos(p + q)m(dp)i>t (dq),
±2(0 = У j sm(p + g);zt(dp>t(<0).	(15.7)
Таким образом, рассматривается дифференциальная игра для уравне-
ния (15.7) и функционала платы вида (15.4). В уравнении (15.7) управления
игроков Р и Q удовлетворяют ограничениям € Р и pt 6 Q. Отметим,
что в рассматриваемом теперь случае, условие седловой точки в маленькой
игре выполнено, т. е.
min max / / (^ cos(p 4- q) 4- s2 sin(p 4- q))p(dp)p(dq) =
veQ J J
= max min / / (si cos(p 4- q) 4- s2 sin(p 4- q))n(dp)p(dq) = 0. (15.8)
ueq J J
Легко проверить что дифференциальная игра (15.4), (15.7) имеет цену
Vai 2(to? xq) = ^i(to). Действительно, пусть /zq — вероятностная мера, скон-
центрированная в двух точках pi = —тг/2 и р2 = тг/2 с равными весами,
т. е. /z({pi}) = //({р2}) = 1/2. Точно так же пусть pQ е Q — такая мера, что
z/({qi}) =	= 1/2, где Qi = —тг/2, q2 = тг/2. Выбирая //0, игрок Р
обеспечивает выполнение равенств х± = 0 и 7(#(•)) — #i(to) при любом
управлении игрока Q. Таким же образом, выбирая z/0? игрок Q обеспечивает
равенство 7(^6)) — Отсюда получается, что Val2(to..To) = ^i(t0).
15. Смешанные позиционные стратегии и контрстратегии
183
Более того, как было показано, пара смешанных управлений (//q?^o) со-
ставляет седловую точку.
Итак, вернемся к управляемой системе (15.3). Рассмотрим следующую
процедуру управления этой системой. Пусть игрок Р выбирает смешанное
управление /zq, а игрок Q выбирает произвольное смешанное управление vt.
Обратим внимание, что чистое (не вероятностное) управление q(t) может
рассматриваться как специфический случай смешанного управления vt, ко-
торое сконцентрировано с вероятностью 1 в точке q(t). Пусть задано разби-
ение А интервала времени [to, #]• В каждый момент разбиения t = ti е А
игроки принимают решения и выбирают случайные управления pi и qi.
Случайное управление Pi принимает значения —7г/2и7г/2с вероятностя-
ми, равными 1/2, в то время, как управление принимает значения из ин-
тервала [—л, 7г] с вероятностью, определяемой с помощью меры vt.. Важно
отметить, что случайный выбор управлений р^ и qi производится взаимно
независимо. Согласно процедуре, описанной выше, получаем множество
движений системы (15.3), на котором вероятностное распределение может
быть определено естественным образом.
Можно показать, что для любого в > 0 существует такое число 6 > О,
что для любого разбиения А, удовлетворяющего diam А 6, и для
любого случайного или детерминированного управления игрока Q, сто-
хастическое управление игрока Р обеспечивает выполнение неравенства
70г(«)) eX’i(to) + в с вероятностью, не меньшей, чем 1 — е. Аналогич-
ным образом можно определить стохастическую процедуру управления для
игрока Q, и получить, что она гарантирует оценку 7(ЖС)) xi(to) ~ £ с
вероятностью, сколь угодно близкой к единице.
Таким образом, стохастические процедуры управления, описанные вы-
ше, приближают оптимальный результат, который был формально опреде-
лен для дифференциальной игры (15.7), (15.4). Далее в разделе 15.4 бу-
дут рассмотрены аппроксимационные свойства стохастических процедур
управления для общего случая нелинейной дифференциальной игры. Заме-
тим, что эти свойства являются следствием известного в теории вероятно-
стей закона больших чисел. Подчеркнем еще раз, что использование сме-
шанных стратегий и их приближений возможно только тогда, когда каждый
из игроков выбирает управление независимо от управления, осуществляе-
мого в данный момент времени его противником.
Таким образом, рассмотрены три типа дифференциальных игр с тремя
вариантами распределения информации об управлениях, выбираемых иг-
роками. Для этих дифференциальная игр определены их цены и получены
следующие соотношения
Vali(to,®o) = ®i(to) - (ff- t0) < Val2(to,^o) =	<
< Val3(to,^o) = xi(t0) + (ff - t0),
184
Глава III
которые демонстрируют, что решения дифференциальная игр зависят от
того, обладает или нет игрок дополнительной информацией об управлении,
выбранном противником.
15.2.	Смешанные позиционные стратегии
Обратимся теперь к формализации дифференциальной игры в классе
смешанных стратегий по принципу обратной связи. Введем некоторые поня-
тия и определения. Напомним, что символы rpm (F) и rpm (Q) обозначают
множества регулярных вероятностных мер, нормированных на компактных
множествах Р и Q, соответственно. Элементы множеств rpm (Р) и rpm (Q)
будут обозначаться буквами /х и v. Пусть
(t, х, //, р) € [0,0] х Rn х rpm (Р) х rpm (Q).
Полагаем
f(t, X, р, v) ~J J Ж х,р, q)n(dp)v(dq),
р Q
(15.9)
Справедливо
min max (s, f(t, x, v)} — g(t, x, v) =
jzGrpm (P) z/Grpm (Q) L	J
= max min (s, f(t, x, /1, p)) — g(t, x, g, p) — H(t, ж, s). (15.10)
z/Grpm (Q) /xGrpm (P) L	J
Отметим, что здесь можно использовать теорему о минимаксе (см., напри-
мер, [98, 162]) и поменять местами операции min и max. Величина Н
называется гамильтонианом дифференциальной игры в классе смешанных
позиционных стратегий.
Напомним, что функция [£о?0] Э t gt € rpm(P) называется слабо
измеримой, если для любой непрерывной функции Р э р h(p) G R,
функция
[to,0] Э t J h(p)gt(dp) G R
р
является измеримой (см., например, [225]). Аналогичным образом опреде-
ляются слабо измеримые функции [to, 0] Э t н-» vt е rpm (Q).
15. Смешанные позиционные стратегии и контрстратегии 185
Символами L([to,0],rpm(P)) и L([tg,0],rpm(Q)) будут обозначать-
ся множества всех слабо измеримых функций у,(.у. [to, 0] rpm(P)
и z/q : [to, 0] rpm(Q) соответственно. Для заданной начальной пози-
ции (to,rro) Е [0,0] х Rn, обозначим символом S(to,x‘o) множество всех
троек (ж(-),//(.),;/(.)), где д(.) е L([to,0],rpm(P)), pq е L([io,0],rpm(Q))
и ж(-): [to, 0] ь-» Rn — абсолютно-непрерывные функции, удовлетворяющие
уравнению
±(t) = /(t,^(t),/l£,Z/£)	(15.11)
и начальному условию х(to) = xq. Функционал платы определен следую-
щим образом
о
:= cr(x(ff}) - У g(t,x{t),gt,ut)dt. (15.12)
to
Функции
U: [0,0] х Rn ^rpm(P), V: [0,0] х Rn ^rpm(Q)
называются смешанными позиционными стратегиями игроков Р и Q соот-
ветственно.
Будем требовать, чтобы эти функции были измеримы относитель-
но х в следующем смысле. Пусть /xtiX = U(t,x) и = V(t,x). Пред-
полагаем, что для любого t G [0,0] и для любых непрерывных функ-
ций Р Э у ip(p) е R, Q Э q н-» ^(q) G R, отображения
Rn Э x у* <y{p}yttyX(dp) e R,
Rn Эжн> f ^{q)vt^dq) G R
Jq
измеримы по Борелю. Отметим, что это требование нужно для того, что-
бы дать строгие определения вероятностным пространствам, порожденным
стохастическими процедурами управления, которые аппроксимируют пози-
ционные смешанные стратегии.
Пусть игрок Р выбирает некоторую смешанную стратегию по прин-
ципу обратной связи U и некоторое разбиение Д интервала времени [to, 0].
Пусть S(to,^o,P, Д) — множество троек (ж(-),//(.),z/(.)) G S(t0,x0), где
z/(.) 6 L([to, 0], г pm (Q)) — произвольная слабо измеримая функция, а //(.) —
186
Глава III
кусочно-постоянное смешанное управление игрока Р, которое формируется
согласно правилу
IM =	ti e A.	(15.13)
По аналогии с в пунктом 11.2, где были введены показатели качества
чистых стратегий по принципу обратной связи, определим показатель каче-
ства пошаговой процедуры управления (Р, А), выбранной игроком Р, как
величину
Г1(£0)ж0,Р, A) :=sup7(to,S(to,^o,P, А)).	(15.14)
Следует отметить, что 7(й),ж(-),//(.), */(.)) и Г1(£о?жо, Р, А) выглядят как
детерминированные величины, которые не зависят от случайных событий.
Пошаговая процедура управления, определенная здесь, основана на мате-
матической идеализации, которая допускает, что значения управлений сме-
шиваются мгновенно. Ниже в пункте 15.4 будет определена физически осу-
ществимая аппроксимация смешанных стратегий, в которой смешивание
значений управлений занимает какое-то время.
Далее, мы полагаем
Г1(£о, ж0, Р) := limsup Г1(^о? жо, Р, А).	(15.15)
diam Д J.0
Оптимальный гарантированный результат в классе смешанных позицион-
ных стратегий игрока Р определен следующим образом
Г1(*о,жо) := ш£Г1(^о,жо,Р).	(15.16)
и
Аналогично, пусть (V,A) — пошаговая процедура управления, вы-
бранная игроком Q. Здесь V — смешанная стратегия по принципу обратной
связи, А — разбиение интервала времени [tQ, в]. Качество этой процедуры
характеризуется величиной
Г2(t0, х0, V, А) := inf 7(t0, S(t0, ж0, V, А)).	(15.17)
Оптимальный гарантированный результат в классе смешанных стратегий
по принципу обратной связи для игрока Q определен как
r^iojXo) := supr2(t0,a:o, V),	(15.18)
v
где	~
Г2(*о,хо,Г) := liminf r2(f0,rr0,V,A).	(15.19)
diam ДЩ
Справедливо следующее утверждение.
15. Смешанные позиционные стратегии и контрстратегии
187
15.3.	Теорема
Пусть выполнены предположения (А1) и (А2) (см. раздел 11.1). То-
гда существует цена дифференциальной игры (15.11), (15.12), рассмат-
риваемой в классе позиционных смешанных стратегий, т. е. имеет место
равенство
Vai (t0? хо) := f?(to,£o) = Г^о^о)-
Функция цены Vai совпадает с минимаксным решением задачи Коши
^ + H(t,x,Dxu) = 0, и{9,х} — а{х),	(15.20)
где H(t.x,s) — гамильтониан дифференциальной игры (15.11), (15.12),
определенный равенством (15.10).
Доказательство этого утверждения приводится ниже, в пункте 15.7.
Отметим еще раз, что в этой теореме рассматривается идеализиро-
ванное решение дифференциальной игры в классе смешанных стратегий
по принципу обратной связи. Согласно этой идеализации, пошаговые дви-
жения конструируются с помощью управлений, смешиваемых мгновенно;
обычные управления р е Р и q е Q заменены управлениями-мерами
(обобщенными управлениями) р Е rpm(P) и и е rpm(Q), а дифференци-
альная игра (15.1), (15.2) заменена дифференциальной игрой (15.11), (15.12).
Однако в реальной жизни управляемый объект, мгновенно смешивающий
значения управления, невозможен. Итак, нужны физически осуществимые
процедуры управления, которые аппроксимируют формальные решения.
15.4.	Стохастические процедуры управления
Пусть игроки Р, и Q выбрали смешанные позиционные стратегии U
и V. Пусть задано также разбиение Д интервала времени [to, 0]. В каждый
из моментов t = ti е Д игроки производят взаимно независимый выбор
случайных значений своих управлений p(t) = p(ti) € Р, q(t) = q(ti) е Q,
ti C t < ti-f_i. Распределения этих постоянных управлений задаются веро-
ятностными мерами p(dp) = U(ti, x(ti)), v(dq) = У(^,ж(^)).
Стохастическая процедура управления, определенная выше, будет обо-
значаться символом SCP(U. V, Д). Эта процедура порождает вероятност-
ное распределение кусочно-постоянных управлений р(-), д(-) и траекто-
рий х(-) системы (15.1). Следующие утверждения являются следствием за-
конов больших чисел, хорошо известных в теории вероятностей.
188
Глава III
Для любой пары U, V позиционных смешанных стратегий игроков Р
и Q и для любого положительного числа s можно выбрать такое положи-
тельное число 3 > 0, что для любой стохастической процедуры управле-
ния SCP(U, V, Д), удовлетворяющей оценкам diam Д <5, неравенства
Г2(«о,я:о, V) - £	Г1(40,ж0, U)+e
выполнены с вероятностью, не меньшей, чем 1 — е.
Пусть Ua и VQ — а-оптимальные смешанные позиционные стратегии Р
и Q, т. е.
Г1(^о,жо,^) Vai (to, я0) + а,
Гг(£о, ^о, V&) Vai (t0, ж0) - а.
Тогда для любого s > 0 существует такое число д > 0, что для любого раз-
биения Д, удовлетворяющего оценке diam Д 6 и для любой позиционной
смешанной стратегии V игрока Q, неравенство
7(ж(-),р(-),«(•)) Vai (*о,жо) + а + е
выполняется с вероятностью, не меньшей, чем 1 — е, где вероятностное
распределение порождено процедурой SCP(Ua^ V. Д).
Аналогично, для любого е > 0 можно найти такое число (5 > 0, что для
любого разбиения Д, удовлетворяющего условию diam Д 5, и для любой
смешанной позиционной стратегии U игрока F, неравенство
7(х(-),р(-),«О)) > Vai(*о,х0)-а-£
выполняется с вероятностью, не меньшей, чем 1 — г, где вероятностное
распределение определяется процедурой SCP(U. Уа, Д).
Согласно этим утверждениям, рассмотренную выше математическую
формализацию, качество которой оценивается величинами (15.14)-(15.19),
и предполагающую идеальное, т. е. мгновенное смешивание значений
управлений, можно аппроксимировать физически реализуемой процедурой,
формирующей кусочно-постоянные случайные управления игроков. Еще
раз подчеркнем важность того требования, что на каждом шаге ti е Д в
рассматриваемой стохастической процедуре игроки выбирают свои случай-
ные управления независимо в стохастическом смысле.
В случае, когда разбиения Дх и Д2, выбранные игроком Р и игро-
ком Q, не совпадают, можно, как и выше, использовать предположение, что
игрок Р (игрок Q) выбирает случайное управление, независимое от теку-
щего управления, выбранного противником. Это предположение особенно
15. Смешанные позиционные стратегии и контрстратегии
189
важно при наличии информационных погрешностей в измерениях текущих
позиций. Строгие постановки и доказательства результатов относительно
упомянутых здесь стохастические процедур, даны в [123, 124].
15.5.	Контрстратегии
Теперь рассмотрим постановку дифференциальной игры в случае I
(см. пункт 15.1). Мы полагаем, что в текущий момент времени t игрок Р
знает управление q(t), выбранное игроком Q, в то время как игрок Q не
знает управления p(t), реализованного игроком Р. Предполагается также,
что каждый из игроков знает реализовавшуюся позицию игры (t, x(t)).
Определим дифференциальную игру в классе контрстратегий игрока Р
и позиционных (чистых) стратегий игрока Q. Контрстратегии игрока Р
вводятся следующим образом.
Пусть заданы функции
[0,0] х Rn х Q Э (t.x.q) Ucs(t,x,q) е Р.
Полагаем, что для всех (t, х) Е [0,0] х Rn функции Q Э q t—> Ucs(t, x,q) E P
измеримы по Борелю. Верхний индекс cs используется здесь, чтобы отли-
чить контрстратегии от позиционных стратегий (t, х) н-> U(t, х).
Пусть задана начальная позиция (to, жо) 6 [0,0) х Rn, и пусть игрок Р
выбирает разбиение Д интервала времени [to, 0]. Пусть <?(•) е L([to, #], Q) —
измеримая функция. В пошаговой процедуре управления контрстрате-
гия Ucs формирует управление игрока Р согласно правилу
p[t) — U(ti^x(ti)^q(t))^ t* t < t*+i, H0,m,	(15.21)
где ti е Д. Как известно (см., например, [101]), функция t p(t),
определенная этим равенством, является измеримой, т. к. на каждом ин-
тервале [tz,^+i) эта функция является суперпозицией борелевской функ-
ции q (7С5(^,ж(^), q) и измеримой (в смысле Бореля или Лебега) функ-
ции t и-> g(t).
Напомним (см. пункт 11.2), что символом S(to,xo) обозначается мно-
жество всех троек (#(•),р(-), q(*))> гдер(-) € L([to,0],P), #(•) е £([to,0],Q),
ж(-): [to ,0] —» Rn — абсолютно непрерывные функции, которые удовле-
творяют уравнению (15.1) и условию x(to) = ж0. Обозначим симво-
лом S(to, ж0, Ucs, Д) множество всех троек	е 8(<о,жо),
где q(-) Е L([to,#],Q) — произвольные измеримые управления игрока Q,
а р(-) — управления игрока Р, которые сформированы контрстратегией Ucs
согласно правилу (15.21).
Качество пошаговой процедуры управления (Pcs, Д), выбранной игро-
ком Р, оценивается величиной
Г!(to, ЖО, Ucs, Д) := sup7(t0, S(t0, ж0, Ucs, Д)).	(15.22)
190
Глава III
Далее, определяем показатель качества для контрстратегии следующим об-
разом
ri(to,^o,t7cs) limsup Г1(£о, «т0,	А).	(15.23)
diam AJ.0
Оптимальный результат, гарантированный игроку Р в классе контрстрате-
гий, вводится с помощью равенства
ГГ(^о^о) := inf	(15.24)
Ucs
Ниже будет сформулирована теорема существования ситуации равно-
весия в классе контрстратегий игрока Р и позиционных стратегий игрока Q.
Чтобы установить этот результат, следует ввести некоторые понятия.
Обозначим через Ucc множество всех измеримых по Борелю функ-
ций Q Э q p(q) Е Р. Напомним, что функции р(-) € Ucc называются
контруправлениями (или стробоскопическими стратегиями) игрока Р. Га-
мильтониан рассматриваемой теперь дифференциальной игры определяется
равенствам
min тах[(в,/(^я,р(9),?)) - g(t,x,p(q), g)] =
Р(-)еи
сс q^Q
= max min [(s, f(t,x,p(q'),q')} - g(t,x, p(q),q)] =
geQ p(.)eu cc
= max min [(s, f(t, x^p, q)} — g(t, x,p, #)] = Hcs(t, x, s)., (15.25)
qeQ peP
Напомним также, что символом Г^о^о) обозначается оптимальный
результат, гарантированный в классе чистых позиционных стратегий игро-
ка Q (см. пункт 11.3, (11.15), (11.16)).
15.6.	Теорема
Пусть выполнены предположения (А1) и (А2) (см. раздел 11.1). Тогда
существует цена дифференциальной игры (15.1), (15.2), рассматриваемой
в классе контрстратегий игрока Р и позиционных стратегий игрока Q,
т. е. справедливы равенства
Valcs(t0,^0) := qs(t0, ж0) = Г^о.жо)-
Функция цены Vaics совпадает с минимаксным решением задачи Коши
4- Hcs(t, х. Dxu) = 0, и(0, х) = сг(х),
(15.26)
15. Смешанные позиционные стратегии и контрстратегии
191
где Hcs(t. х, з) — гамильтониан рассматриваемой дифференциальной игры,
который определен соотношениями (15.25).
Подобная же теорема верна и для дифференциальных игр, рассматрива-
емых в классе позиционных стратегий игрока Р и контрстратегий игрока Q.
Опустим доказательство этого результата, т. к. оно может быть получено из
доказательства сформулированной выше теоремы путем обмена ролей у
игроков Р и Q.
15.7.	Доказательство теорем 15.3 и 15.6
Существование цен для вышеупомянутых типов дифференциальных
игр можно доказать в рамках общей схемы, которая приведена в парагра-
фе 12.
Опишем кратко, как эта схема может применяться к дифференциаль-
ной игре в классе смешанных стратегий по принципу обратной связи. Напо-
мним, что в рассматриваемом случае может быть нарушено так называемое
условие седловой точки в маленькой игре (11.5). Вместо этого условия в
доказательстве теоремы 15.3 будет использовано равенство (15.10).
Предлагаемые конструкции субоптимальных смешанных стратегий по-
добны конструкциям чистых стратегий по принципу обратной связи из
раздела 12.2. А именно, определим субоптимальную стратегию U£: [0,0] х
xF rpm (Р) игрока Р как суперпозицию экстремальной предстратегии
и квазиградиента.
Напомним, что предстратегия, используемая для построения позици-
онной (чистой) стратегии, была определена соотношениями (11.23). Что-
бы сконструировать субоптимальную смешанную стратегию по принципу
обратной связи, используем здесь пред стратегию, которая определена сле-
дующими соотношениями
Po(t, х, з} 6 Arg min max h(t,x.s,p. v} ,	(15.27)
jzGrpm (P) li/Grpm (Q)	J
h(t, x, s, p> v) := (s, jf(i, x, p, p)) — g(t, x, /z, p),	(15.28)
где используются обозначения (15.9).
Определим позиционную смешанную стратегию U£ формулой
U£(t, х) := Po(t, х, s£(t, ж)).	(15.29)
Здесь s£(p х) — квазиградиент, определенный соотношениями вида (12.10),
(12.14), в которых и — это верхнее решение в задаче Коши (15.20). Отметим,
что согласно теоремам об измеримых селекторах, стратегия U£(t, х) может
192
Глава III
быть выбрана так, что отображение х U£ измеримо по Борелю (см.,
например, [4, 39, 131, 225]).
Следующее утверждение является аналогом теоремы 12.3.
Пусть и — верхнее решение задачи (15.20). Пусть смешанная позици-
онная стратегии U£ определена соотношением (15.29). Тогда для любого
компактного множества D С [0,0] х Rn и любого положительного числа £
существуют такие положительные числа е > 0 и Jo > 0, что оценка
Г1(^о,жо, U£. A) u(t0,xQ) + <	(15.30)
справедлива для всех начальных позиций (£0, хо) 6 D и всех разбиений А,
удовлетворяющих условию diam А Jq.
Уточним некоторые различия в доказательствах утверждений, сфор-
мулированных выше, и теоремы 12.3. Вместо р* е Р, q* G Q и
использовавшихся при доказательстве теоремы 12.3, здесь используются,
соответственно,
М* :=^(т,0),
14 е Arg max min Л(т, ту, s*,//,//) ,
z/Grpm (Q) L^Grpm (P)	J
r+6
7* = | /
g* = | j
Из определения верхнего решения задачи (15.20) следует, что суще-
ствует такой вектор (f*,g*) xR, что
dist((/*,g*);S+(r,77,j/*))	<3(5),
u(t,?j) +д*й и(т + 5,т} + f»S).	(15.31)
Здесь вместо (12.1) используется
£'+(£,я,р) := х, р,, г/), g(t, х, д, г/)): р G rpm(F)}.
Остальная часть доказательства совпадает с доказательством теоремы 12.3.
15. Смешанные позиционные стратегии и контрстратегии 193
Точно так же позиционную смешанную стратегию V£ игрока Q можно
сконструировать как суперпозицию экстремальной предстратегий
vntL х, s) е Arg max min h(t, x. s, u, z/)
z/Erpm (Q) t^erpm (P)	J
и квазиградиента s(s\t,x), определенного соотношениями вида (12.16),
(12.17), в которых и — это нижнее решение задачи Коши (15.20). Стра-
тегия К гарантирует оценку
Г2(Ль^(ьК5 A) > u(to,%o) ~ С	(15.32)
Здесь ( — произвольное положительное число, diam Д <5, а е, 6 достаточно
малы.
В случае, когда и — минимаксное решение задачи (15.20) (т. е. когда
оно одновременно является и верхним, и нижним решением этой задачи),
оценки (15.30) и (15.30) доставляют справедливость теоремы 15.3.
Опишем очень кратко основные конструкции, используемые при дока-
зательстве теоремы 15.6.
Чтобы определить субоптимальную контрстратегию игрока F, введем
пред стратегию вида
€ Arg min [{s,f(t, х,p,q)) - g(t,x,p,q)].	(15.33)
peP
Далее полагаем
Ufs(t, x.q) := pQS(t,x,s£(t,x),q).	(15.34)
Здесь s£(t, x) — квазиградиент, определенный соотношениями вида (12.10),
(12.14).
Субоптимальную позиционную стратегию V£ игрока Q определим со-
отношениями (12.16)-(12.18). Заметим, что функция и, используемая в со-
отношениях (12.10), (12.14), (12.16) и (12.14), — это минимаксное решение
задачи Коши (15.26). Используя теоремы об измеримом выборе, можно вы-
брать предстратегию р™ такой, что отображение q pgs(t, ж, s, q) будет
измеримым по Борелю (см., например, [4, 39, 131, 225]).
Очевидно, что управление pQS(t, х, s, q) можно рассматривать как опти-
мальный выбор игрока Р в так называемой маленькой игре, определенной
на множестве Ucc х Q (напомним, что Ucc — это множество всех контру-
правлений игрока Р). Величина
{s, f(t, x,p(q), q)} - g(t, x,p(qj, q)
194
Глава Ш
— это плата в маленькой игре. Элементы множеств Ucc и Q — стратегии иг-
роков Р и Q в маленькой игре. Дифференциальные игры, которые происхо-
дят в процессе реализации предложенных пошаговых процедур управления,
могут рассматриваться как развертывание во времени последовательности
принятия решений в статических маленьких играх с указанной выше функ-
цией платы, и где s — квазиградиенты функции цены дифференциальной
игры.
Данная интерпретация может применяться ко всем типам дифференци-
альных игр, рассмотренных в этом параграфе. Если маленькая игра имеет
седловую точку, то существует цена дифференциальной игры, которая опре-
делена для соответствующих классов стратегий игроков.
В заключении этого параграфа обращаем внимание на то, что кон-
струкции, описанные для дифференциальных игр с платой вида (15.2), мо-
гут применяться и к другим типам дифференциальных игр. Например, эти
конструкции могут использоваться для построения решений игр преследо-
вания-уклонения с функционалом платы вида
7(^(-)) := min{t > to-	G М},
где М — замкнутое множество в [0, оо) х Rn. Особенностью этих игр являет-
ся то, что их функции цены могут быть разрывными. Игры преследования -
уклонения будут рассматриваться в параграфе 19.
В исследованиях некоторых типов дифференциальных игр возникает
необходимость использовать полную информацию о движении управляемой
системы, т. е. игрокам нужно знать траекторию х(-): [to, £] ]Rn, реализо-
вавшуюся ранее до текущего момента времени t. В таком случае вводятся
так называемые стратегии с памятью. Если для управляемой системы вы-
полнено условие
min max(/(t, ж, р, g), s} — maxmin(/(t, р, g), s),
рЕР qEQ	qEQ рЕР
то дифференциальная игра с любым непрерывным функционалом плазы
#(•)	?(#(*)) имеет седловую точку в классе стратегий с памятью. Если
вышеупомянутое условие может быть нарушено, то можно доказать су-
ществование седловой точки в классе смешанных стратегий с памятью.
Может быть доказано также существование цены этой игры в классе кон-
трстратегий с памятью у одного из игроков и классе чистых стратегий с
памятью у другого игрока. Субоптимальные стратегии для этих игр могут
быть сконструированы в виде суперпозиций экстремальных предстратегий
и соответствующих квазиградиентов функции цены. Некоторые результаты,
полученные для дифференциальных игр с памятью, представлены в моно-
графии [123].
16. Конструктивные и численные методы ...	195
16.	Конструктивные и численные методы теории
дифференциальных игр
Большое внимание в теории дифференциальных игр уделяется раз-
работкам конструктивных и вычислительных методов. К этому направле-
нию относятся, во-первых, исследования отдельных типов дифференциаль-
ных игр, для которых удается получить явные аналитические выражения
для функции цены или оптимальных стратегий; во-вторых, изучение диф-
ференциальных игр, решение которых сводится к относительно простым
вычислительным задачам; в-третьих, разработки специальных алгоритмов
вычисления функции цены, построения стабильных мостов и экстремаль-
ных стратегий. Исследования и разработки в этой области представлены
обширной библиографией. Приведенные в данном параграфе результаты
могут дать некоторое представление об этих исследованиях. Вместе с тем,
этот параграф не следует рассматривать как обзор, претендующий на ка-
кую-либо полноту.
16.1.	Экстремальное прицеливание
Рассмотрим предложенный Н. Н. Красовским метод экстремального
прицеливания. Пусть движение управляемой системы описывается урав-
нением
i(i) = A(t)x(t) + ?(i,p(t),	(16.1)
Предполагается, что х G Rn, £: [0,0] х Р х Q н-* Rn — непрерывная функция,
A(t) — п х п-матрица, элементы которой зависят непрерывно от параметра t.
Управления игроков удовлетворяют ограничениям p(t) G F, q(t) G Q, где
P и Q — компактные множества.
Сначала рассмотрим случай, когда функционал платы задается равен-
ством
е
7^о,ж(-),р(-), <?(•)) =	(16.2)
to
Здесь s G Rn — фиксированный вектор, ст* — число, е: [0,0] н-> Rn
и (/?: [0,0] х Р х Q и-> R — непрерывные функции. Предполагаем, что
равенство
/t(tV’) :=maxmin[(^,C(t,p,g)) -<p{t,p,q)] =
qeQ рЕР
= minmax [(</>,£(t,p,q)) -p(t,p,q)] (16.3)
pEP qEQ
выполняется при всех C Rn и t G [0,0].
196
Глава III
Пусть s) — это решение уравнения
S- = -AT(t)^(t, s) + e(t),	(16.4)
удовлетворяющее условию ^(0, s) = s (символ т обозначает транспониро-
вание).
Определим функцию
е
r(t, а;) := (^(t, s), ж) + J /г(т, ^(т, <§))с?т — ст*. (16.5)
t
Проверим, что v — это функция цены дифференциальной игры (16.1), (16.2).
Ясно, что v(0.fx) = (s,x) — ст*. Функция r(t,х) непрерывно дифференци-
руема. Поэтому достаточно проверить, что эта функция является решением
(в классическом смысле) соответствующего уравнения Айзекса-Веллмана.
Нетрудно посчитать
= (х, -AT(t)ip(t, s) + e(i)) - h(t, s)),
Dxv —	s).	(16.6)
Для рассматриваемой дифференциальной игры уравнение Айзекса-
Веллмана имеет вид
-h (A(t)x, Dxu) - (e(t), х) + h(t, Dxu) = 0.
Из (16.3), (16.6) следует, что функция v удовлетворяет этому последнему
уравнению. Следовательно, эта функция является функцией цены диффе-
ренциальной игры (16.1), (16.2).
Теперь рассмотрим случай, когда функционал платы имеет вид
о
7(*0,ж(-),р(-),д(-)) = с(^(0)) ~ Jx(t)) +	q(t))]dt. (16.7)
io
Предположим, что a: Rn н-> R — выпуклая функция, которая удовлетворяет
условию Липшица
— ст(ж^)|	АН^1) — я/2)||
(16.8)
J h(r^(r, s))dr — (?*(s)
16. Конструктивные и численные методы ...	197
при всех х^\х^ G Rn. Напомним, что имеет место следующее равенство
ст (ж) = sup — ct*(s)],	(16.9)
sERn
где
<t*(s) t— sup — <т(ж)]
— это функция, сопряженная к функции а (см. теорему А4.1).
Очевидно, что функция ст*: Rn н-> (—ос, ос] является полунепрерыв-
ной снизу. Из условия Липшица (16.8) следует, что множество
dom ст*	{s € Rn: cr*(s) < ос}
ограничено.
Определим функцию
uv(t, х) := maxt?(t, х, $).	(16.10)
seRn
Здесь используется обозначение
о
v(t. х, s) := (^(t, s), x) +
t
где, как и выше, ^(-,s) — это решение уравнения (16.4), удовлетворяю-
щее условию ф(0,з) = з; величина определена равенствами (16.3).
В формуле (16.10) пишется «тах», т.к. множество dom ст* ограничено, а
функция v{t. х, •) полунепрерывна сверху, и поэтому супремум по Rn отно-
сительно з достигается. Докажем следующее утверждение.
Пусть для любого t Е [0,0] функция
е
Э s н-> у* /г(т, ^’(т, s))dr — ст*s)) G [—ос, ос) (16.11)
t
вогнута. Тогда ир — это функция цены дифференциальной игры (16.1),
(16.7).
Доказательство. Покажем, что ир — минимаксное решение в задаче
Коши для уравнения Айзекса-Веллмана
+ (A(t)x, Dxu) - х) + h(t, Dxu) = 0,	(16.12)
u(0, x) — a(x).	(16.13)
Краевое условие up(0, x) = a(x) следует из (16.10), (16.9) и равенства
0(0, s) = в.
198
Глава П1
Как было показано выше, для любого фиксированного вектора sedom ст*
функция (t. х) н-> v(t. х. s) удовлетворяет уравнению (16.12) в классическом
смысле. Поэтому, функции (t,x) v(t,x,s) являются нижними решени-
ями уравнения (16.12). Согласно замечанию, сделанному в пункте 3.1, их
верхняя огибающая ир является нижним решением этого уравнения.
Таким образом, остается проверить, что функция ир является верхним
решением уравнения Айзекса-Веллмана (16.12). Покажем, что ир удовле-
творяет условию (U3) (см. определение 6.5). Чтобы проверить это условие,
обратимся к утверждению А5.2. Согласно этому утверждению, производная
функции ир в точке (t, ж) G (0,0) х Rn по направлению (1, /) существует и
определена равенством
dup(t,x, 1,/) = max J(Dxv(t, х. s), f)] =
seSo(t,x)L ot	j
= max	(16.14)
s(=S0(t,x)
где
So(t^x) := {s G Rn: v(t,x, s) = up(t. ж)},	(16.15)
J(t,x,s,f) := (ж,-AT(tyi[)(t, s) + e(t)) - h(t, s)) +
Пусть
E+(t, x,q) := со{(А(£)ж + ^(t,p,q), (e(t),x) A	p E P}.
Ясно, что многозначное отображение Е+ удовлетворяет требованиям (j)-(j v),
сформулированным в пункте 6.2. Итак, установим неравенство
d := minmax [J(t, х, s, f) — g] < 0,	(16.16)
(f,9) s
где C E+(t,x,q)9 s G 50(^,ж).
Очевидно, что множество 5Ь(Лж) выпукло и компактно. Покажем вы-
пуклость функции Sg(t, ж) э s и-» h(tb s)) G R. Из (16.15) получаем
о
У /i(r, ^(т, s))dr —	$)) = ж) —	s), ж)
t
при любых з G So(t.x). В соответствии co сделанными предположениями,
функция
е
Rn э s «-> У h(r^(T,s))dT —
16. Конструктивные и численные методы ...	199
является вогнутой. Так как функция V?(t, •) линейна, получаем, что функция
So(t, х) Эзм J h(T^(T,s))dr
t
является выпуклой для любого S е (0,0 — t]. Следовательно, функция
s I—» h(t, ^(t, s)) выпукла на Sq(1, х).
В формуле (16.16) выражение в квадратных скобках зависит линейно
от (/? </) и выпукло относительно s. Поэтому, в соответствии с теоремой о
минимаксе [71, 98, 162], операции min и max можно поменять местами. Из
определения множеств E+(t, х, q) следует равенство
d := max min [J(t, x, s, f)—g] = max min[—h(t, ф(1, $)) + {^(t, s),£) — 9?],
s (/,<?) s (£,¥>)
где
s G S0(t, ж), (/, g) G E+(t, x, q),
(£,<?) e co{(£(p,q),p(p,q): p G P}.
Согласно (16.3), справедливо
min [(V>(t, s), C) - y>] < h(t, ipit, s)).
Неравенство (16.16) доказано.
Мы таким образом показали, что ир является функцией цены диффе-
ренциальной игры (16.1), (16.7).
Приведем некоторые замечания. Пусть Р с Rfc, и Q с Rz. Предполо-
жим, что
Жрл) = B(t)p + C(t)q,
4>(t,P,q) = (b(t),p) + (c(t),q).	(16.17)
Здесь b(t) G Rfe, c(t) G P(t) и C(t) — матрицы размерности к x n
и I x n соответственно; предполагается, что функции &(•), с(-) и компоненты
матриц непрерывны на [0,0]. Определим программный максимин
Up(tG, xQ) := sup inf 7(t0, x[-; t0, ^Q,p(’),q(-)],p(-), q(-)).	(16.18)
P(.) q(-)
Здесь p(-) e L([O,0],F), q(-) 6 L([0,0],Q), символ x[-;tQ,XQ,p(-),q(-)] обо-
значает решение x(-): [0,0] 1-» Rn уравнения (16.1), удовлетворяющее усло-
вию ж (to) = Xq.
200
Глава III
Нетрудно проверить, что в рассматриваемом случае для программного
максимина справедлива формула (16.10). Как показано выше, если функции
вида (16.11) вогнуты при всех t е [0,0], то программный максимин совпа-
дает с функцией цены рассматриваемой дифференциальной игры. Поэтому
игрок Q (максимизирующий плату) вместо позиционной стратегии может
выбрать оптимальное (максиминное) программное управление (т. е. управ-
ление, на котором достигается супремум в формуле (16.18)). Для любой
фиксированной начальной позиции (£о,^о) оптимальные результаты игро-
ка Q в классе позиционных стратегий и программных управлений совпада-
ют.
Кроме рассмотренного здесь условия вогнутости функций вида (16.11),
известны другие условия, при которых программный максимин совпадает
с ценой позиционной дифференциальной игры.
Если выполнено рассмотренное условие вогнутости, то вычисление
функции цены можно провести, используя формулу (16.10), т. е. это вычис-
ление сводится к решению относительно простой задачи выпуклого про-
граммирования.
Более того, если предположить, что функции вида (16.11) строго вогну-
ты, тогда So(t, х) = {$о(£, х)} (т. е. всякое множество вида (16.15) является
одноэлементным), и оптимальную стратегию игрока Р можно определить
следующим образом
U°(t,x) & Arg min(max[(s0(t,a:),C(t,P,</)) -	<?)]}.
pep i qeQ	j
Заметим, что в этом случае функция цены будет гладкой, и вектор so(t, х)
будет ее градиентом.
Отметим, что формула (16.10) определяет программный максимин не
только в случае, когда выполняются соотношения (16.17). Однако в более
общих случаях требуется иное определение программных управлений иг-
роков.
Первые работы, относящиеся к методу экстремального прицеливания,
были опубликованы начале 60-х годов (см., например, [107, 116, ПО]).
В последующие годы, в рамках этого метода, были изучены различные
типы задач (в том числе и нелинейные дифференциальные игры). Сле-
дуя этому подходу, построение стабильных мостов, функций цены и син-
тез оптимальных стратегий можно свести к решению задач программного
поглощения. Полученные в этом направлении результаты представлены в
книгах [122, 123, 200]. В результате введения стохастических программных
конструкций удалось существенно расширить возможности этого подхода
[114, 115].
Рассмотренные в этом параграфе дифференциальные игры обычно на-
зывают линейными. В этом названии отражено то, что правая часть урав-
16. Конструктивные и численные методы ...	201
нения движения зависит от фазовой переменной х линейно (если не при-
нимать во внимание позиционные способы управления). Вместе с тем этот
термин не означает, что линейность наследуется стратегиями игроков. На-
против, оптимальные позиционные стратегии, как правило, нелинейны; бо-
лее того, они могут быть разрывными. В этом отношении эти задачи су-
щественно отличаются от линейно-квадратичных дифференциальных игр,
в которых оптимальные стратегии игроков оказываются линейными функ-
циями фазовых векторов.
16.2.	Стабильные дорожки и стабильные многообразия
Как было показано в параграфе 13, решение задач позиционного управ-
ления может быть сведено к построению соответствующих стабильных мо-
стов. Однако, в общем случае, численное построение этих мостов является
довольно трудной проблемой. Поэтому важным становится (при изучении
специфических типов дифференциальных игр) развивать специальные, ме-
нее сложные, методы построения стабильных мостов. Простейшие методы
такого типа рассматриваются в данном разделе.
Рассмотрим сначала дифференциальную игру, в которой движение
управляемой системы описывается уравнением
X = f(t,x,p,q),	(16.19)
а функционал платы имеет вид
?(*(•)) = сг(ж(0)).	(16.20)
Функция f непрерывна по (t^x.p^q) и удовлетворяет условию Липшица
по х. Будем предполагать, что оценка
,	А(1 + 1Ы|)	(16.21)
и равенство
H(t. ж, s) := minmax(s,q)) = max min(s. f(t. x,py q))	(16.22)
pGF q€Q	q€Q p€P
имеют место при всех (t,x) Е [0,0] х Rn, s Е Последнее равенство
определяет гамильтониан рассматриваемой игры.
Предположим, что существует линейная мажоранта функции
т. е. существует Д Е Rn такой, что
> H(t,x,s\ \/sE^n.
202
Глава Ш
Определим множество всех векторов /*, обладающих указанным свойством.
Полагаем
H*(t, X, f) :=	[(s, f) - H(t, x, 6-)],
:= {f e R”: H*(t,x,f) > -oo}.	(16.23)
Поскольку функция H(t, x, •) положительно однородна, то сопряженная
функция ж, •) может принимать лишь одно из двух значений 0 и —оо.
Учитывая это замечание, получаем, что F*(t, х) является искомым множе-
ством. Будем предполагать, что F*(t, х) 0 при всех (t, х) Е [0,0] х Мп.
Нетрудно проверить, что множество F*(t, х) — выпуклый компакт, бо-
лее того, для любых f Е F*(t, х) справедлива оценка ||/||	А(1 + ||^||), где
А — коэффициент в условии Липшица (16.21). Отметим также, что много-
значное отображение (t, х) F* (t, х) полунепрерывно.
Пусть (to,^o) ~ заданная начальная позиция. Пусть [to- 0] Э t н->
w(t) Е -- некоторая траектория дифференциального включения
w(t) Е F*(t,w(ty),	(16.24)
проходящая через начальную точку (to, xq). Рассмотрим множество
W {(t,w(t)): t Е [to, #]},	(16.25)
которое является графиком этой траектории. Покажем, что это множество
обладает свойством стабильности, сформулированным в пункте 13.1. Вы-
берем произвольно s е Rn, (t,w) Е W. Воспользуемся критерием ста-
бильности в форме условия (13.11). В рассматриваемом случае, для мно-
жества W вида (16.25) имеем DtW(t;w) 0 и DtW(t\w) С F*(t, w).
Из определения множества F*(t,w) следует, что (s,f) H(t,w,s) для
любого / Е F*(t,w). Следовательно, рассматриваемое множество W удо-
влетворяет условию (13.11), и поэтому оно и-стабильно.
Множество W, определенное соотношениями (16.24), (16.25), называ-
ется стабильной дорожкой. Согласно конструкции (13.13), определим стра-
тегию Ue, экстремальную к стабильной дорожке. Очевидно, что в рассмат-
риваемом случае
WQ(t, х) := Arg min ||.т — w\\ = {w(t)}.
wevr(t)
Поэтому
Ue(t, x) E Arg max[min(/(i, x,p, q),w(t) — x)].	(16.26)
peP qeQ
Из теоремы 13.3 следует, что в данном случае пучок траекторий X (to, xq
порожденный стратегий Ue и любыми управлениями игрока Q, состоит из
16. Конструктивные и численные методы ...
203
единственной траектории w(t). Поэтому результат, гарантированный игро-
ку Р в дифференциальной игре (16.19), (16.20), равен величине a(w(0)).
Поскольку игрок Р стремится минимизировать плату, то из стабильных
дорожек он выбирает ту, для которой значение a(w(0)) минимально.
Таким образом возникает следующая задача оптимального управле-
ния. Пусть W(io^o) — множество траекторий дифференциального вклю-
чения (16.24), удовлетворяющих начальному условию w(to) = xq. Требу-
ется определить траекторию w°(-) G W(to,M> на которой достигается
минимум
a(w°(0)) = mina(w(0)) при w(-) € W(t0,M-
w(-)
Получаем, что стратегия вида (16.26), где полагаем w(t) = wo(t), гаранти-
рует игроку Р результат 70 = <r(w°(0))-
Определим стабильное многообразие. Будем предполагать, что в диф-
ференциальной игре (16.19), (16.20) гамильтониан х. s) является вогну-
тым по переменной з. Пусть, по-прежнему, множество х) определено
равенством (16.23). Полагаем
W := {(t, w(t)): to 0, w(-) е W(t0, ML
W(t) — {w 6Г: (t,w)eW}.
В теории дифференциальных включений множество W называется инте-
гральной воронкой дифференциального включения (16.24). В теории диф-
ференциальных игр множество ТУ, определенное указанным образом, на-
зывается стабильным интегральным многообразием.
Покажем, что для любого р G Р многозначное отображение t W(t)
слабо инвариантно относительно дифференциального включения
х е co{f(t,xyp,q): q е Q}.
Полагаем
/J, W(t, >) := {/ е Г: lim mt j*»*^**)) = о}.
Если (t, ж) е W, то из определения множества W и непрерывности много-
значного отображения F* следует, что F*(t,x) С DtW(t;x).
Покажем, что
F* (t, х) П со {/(t, х,p,q):qeQ}^0	(16.27)
204
Глава III
для любых (t,x,p) е [0,0] х Rn х Р. Допустим противное, тогда, со-
гласно теореме Хана-Банаха, существует такой вектор s Е Rn, что
неравенство (з,/*) > (s, f) справедливо для любых € F*(t, х)
и / € со {/(t, х,р, q): q € Q}. Получаем
H(t,x,s} = min (з,/*) > тах(з, f(t,x.p,qY)
f*eF*(t,x) ' qeQx y
minmax(s, fit. x.p)) = H(t.x.s)
pep qeQ v /z v ‘	-
(первое равенство следует из вогнутости функции H(t, ж, •)). Итак, получа-
ем противоречие, которое доказывает соотношение (16.27).
Таким образом, имеем
DtW(t;x) Clco{/(t, ж,р, g): q е Q} 0
для любых (t. х) е W иреР. Используя рассуждения, аналогичные тем,
что приведены в пункте 13.1 для обоснования критериев (13.11), (13.12),
получаем, что множество W слабо инвариантно относительно дифферен-
циального включения (16.24).
Рассмотрим Ve — стратегию игрока Q, экстремальную к множе-
ству W. По определению стабильного интегрального многообразия име-
ем (to,a?o) € W. Стратегия Ve обеспечивает движение системы по стабиль-
ному многообразию W, т. е. (t, x(t)) е W для всех t е [to, 0] и всех траекто-
рий ж(-) е X(to,^o,I4)« Определение стратегии Ve и обоснование упомя-
нутого результата проводятся подобно тому, как это сделано в параграфе 13
(с учетом того, что роль игрока Р теперь исполняет игрок Q). Стратегия Ve9
выбранная игроком Q, обеспечивает выполнение условия (0, х(0)) е W.
Из определения стабильного многообразия W следует, что результатом,
который гарантирует стратегия Ve, является величина
7о = min{<7(w((9)): w(-) G W(to,^o)}-
Учитывая, что такой же результат может гарантировать себе игрок Р при вы-
боре указанной выше стратегии [7е, заключаем, что в рассматриваемом слу-
чае этот результат является ценой дифференциальной игры (16.19), (16.20),
а стратегии Ue и Ve оптимальны и образуют седловую точку.
Опишем совсем кратко некоторые детали аналогичного подхода к ре-
шению дифференциальной игры, в которой движение управляемой системы
по-прежнему описывается уравнением (16.19), а функционал платы имеет
16. Конструктивные и численные методы. ..
205
вид
е
:==0'(®(6')) “У(16.28)
to
Будем предполагать, что выполняется условие (11.5) (условие седловой точ-
ки в маленькой игре). Пусть H(t,x,s) — гамильтониан рассматриваемой
дифференциальной игры, определенный равенством (11.5).
Полагаем
H*(t, X, f) := inf [<s, f) - H(t, X, s)],
sCR17'
K(M :={/€Г:	> -oo}.
Отметим, что функция x, •) вогнута. Поскольку гамильтониан H(t, ж,з)
удовлетворяет условию Липшица по переменной з, то множество F*(t,x)
ограничено. Рассмотрим многозначное отображение
E(t,x) := {(f,g): f е dom/7*(t,(r, •), д H*(t,x, /)}.
Пусть [to, 0] Э t нн> (x*(t), G Rn x R - некоторая траектория диффе-
ренциального включения
(x,z) G E(t,x),	(16.29)
удовлетворяющая начальному условию ж* (to) = %о, z*(to) = 0- Таким
образом, предполагается, что, по крайней мере, вдоль этой траектории мно-
жество E(t,x) не пусто.
Рассмотрим функцию
/ х (	если х —
u(t.x):=<	а	_±	(+\	(16.30)
[ К 4- L\p — t), если ж / ж* (t),
где К и L — достаточно большие числа, такие, что
К> max z*(t\ L> max H(t, x*(t), 0).
te[toj]	te[t0,e]
Можно проверить, что в некоторой окрестности траектории {(t, x*(t)):
t G [to, 0]} функция и является верхним решением соответствующего урав-
нения Айзекса-Веллмана.
Далее можно определить позиционную стратегию Ue игрока Р, экс-
тремальную к надграфику функции и. Эта стратегия гарантирует игроку Р
206
Глава III
выполнение оценки 7(t0,х(-),р(-), #(•))	а(х*(0У) — z*(0). Среди траек-
торий дифференциального включения (16.29) игрок Р может выбрать тра-
екторию, которая минимизирует функционал ст(х*(0У) — Если функ-
ция H(t, х. •) вогнута при всех (t,x) е [0,0] х >п, то в рамках предла-
гаемой конструкции можно определить оптимальный результат игрока Р,
равный цене Vai (to, а?о) рассматриваемой игры. Можно определить также
стабильное многообразие и экстремальную к нему стратегию, которая будет
в рассматриваемом случае оптимальной позиционной стратегией игрока Q.
Конструкции, описанные в этом разделе, являются достаточно простым
методом решения дифференциальных игр. Согласно этому методу, постро-
ение позиционных стратегий сводится в основном к выбору подходящих
траекторий дифференциальных включений или построению интегральных
воронок. Стабильные дорожки и стабильные многообразия можно исполь-
зовать для решения дифференциальных игр с различными типами функцио-
налов платы. Вместе с тем необходимо отметить, что условия, при которых
возможны предлагаемые построения, являются весьма жесткими и выпол-
няются для узкого круга дифференциальных игр.
Основные идеи этого метода были предложены в 60-х годах в рабо-
тах Л. С. Понтрягина и Н. Н. Красовского [108, 170]. К этому направлению
относится серия работ, опубликованных, в основном, в 60-х-70-х годах
(см., например, [130, 154, 216]). Более подробное изложение рассмотрен-
ных выше конструкций можно найти в книгах [122, 123]. Приведенное в
этом разделе изложение, по существу, следует результатам указанных работ,
но отличается от них по форме тем, что опирается на конструкции теории
обобщенных решений уравнений Гамильтона-Якоби.
16.3.	Минимаксные рекуррентные аппроксимации
В этом разделе будут рассматриваться дифференциальные игры ви-
да (16.19), (16.20). Будем предполагать, что выполняется условие (16.22).
Напомним следующие обозначения f(t,x,P,q) := {/(t, q): р 6 Р}.
Для t* е [0,0], ж* G Rn, q 6 Q и т е [£*, 0] обозначим символом X(t*, я?*, q)
множество решений [0,0] э 1t-> x(t) е дифференциального включения
x(t) е co/(t,#(t),P,q),	(16.31)
удовлетворяющих условию x(t*) = х*. Для т е [t*,0] множество
A(t*,x*,r,q) = {ж(т): #(•) 6 Х(р,х*,д)}	(16.32)
называется областью достижимости дифференциального включе-
ния (16.31).
16. Конструктивные и численные методы ...
207
Опишем оператор программного поглощения, рекуррентное примене-
ние которого позволяет определить функцию, близкую к функции цены.
Пусть Д ==	= то > ti > • • • >	= 0} — разбиение отрезка [0,
(моменты времени т* занумерованы здесь в порядке их убывания). Опреде-
лим функцию [0, #] х tn Э (t, х) ид(£, х) следующим образом. Полагаем
ид(0,я) = ид (то, ж) = а(х), Ухе Rn.
Пусть функция ид определена в области [t*,to] х Rn. Тогда в обла-
сти [тг+1,Тг) х Rn функцию ид определим равенством
ид (£*,#*) = тахтт{ид(т^,ж): х € A(t*,#*, г*, </)}.	(16.33)
q£Q
Используя соотношение (16.33) последовательно при i — 0,1, ... ,fc — 1,
получаем функцию ид, определенную во всей области [0,0] х Rn. Известно,
что
lim ид (t, х) = u(t, х) = Vai (t, х), когда diam Д •—> 0.
Здесь Vai — функция цены дифференциальной игры (16.19), (16.20), и — ми-
нимаксное решение задачи Коши для уравнения Айзекса-Веллмана. Функ-
ции ид сходятся к функции цены равномерно в каждой ограниченной об-
ласти G* С [0,0] xRn. Известно также, что ид Vai, т.е. функции ид
аппроксимируют функцию цены снизу.
Отметим, что величина ид (£*,#*) является оптимальным результатом
в игре, которая рассматривается на промежутке времени [£*, Т{] и осуще-
ствляется по следующим правилам. Игрок Р минимизирует функционал
платы 7г(гг-) — ид(тг, ж(тг)) на множестве траекторий дифференциального
включения (16.31), где q — постоянное управление, выбранное игроком Q.
Игрок Q выбирает управление q € Q, которое максимизирует этот минимум
тт{7Д.т(-)): .т(-) € Х(£*,ж*,з)}.
Заметим также, что соотношение (16.33) может быть переписано следую-
щим образом
и д (t* < х*) = max inf и д (т$, х [т^ t*, х*, р( •), д]),
q^Q р(’)
где х[т^ t*,q] — решение дифференциального включения
i(t) =
удовлетворяющее условию x(t*) = ж*, а инфимум берется по множеству
программных управлений игрока F, т. е. по множеству всех измеримых
208
Глава III
функций р(-):	Р. Согласно этому равенству, величина ?/д(£*,ж*)
называется программным максимином. Понятно, что эти конструкции мож-
но рассматривать как определение цены минорантной игры (см. пункт 14.1).
Эти построения можно ограничить построениями на компактном мно-
жестве D С [0,0] х Rn, которое сильно инвариантно относительно диффе-
ренциального включения
х G со/(£, ж, Р, Q).
Другими словами, множество D должно обладать следующим свойством:
любая траектория этого дифференциального включения хф): [0,0] н-> Rn,
стартующая на множестве D:
(о,ж(о)) е D,
не покидает этого множества
(t, x(t)) Е D, при всех t G [0,0].
Соотношение (16.33) допускает некоторые модификации. Например,
вместо множеств достижимости А(£*, ж*, т, q) можно использовать множе-
ства вида
А*(/*,я*,т,д) := {х* + (г - t*)f: f G со f(t*,x*, P,q)}.
Далее вместо (16.31) можно использовать дифференциальное включение
х G F(t, х, фф
где многозначное отображение
[0,0] х Г х Ф Э (t, ж, '0) F(t, х, VO € conv (Rn)
непрерывно и удовлетворяет условиям
maxmin{(s, f): f Е F(t, х, ф)} — maxmin(s, f(t, х,р, g)),
veQ реР
II/II К(1 + ||ж||), V(t, х, ф) Е [0,0] х Rn х Ф, / G F(t, х, ф).
Функцию цены можно аппроксимировать сверху функциями нл, кото-
рые определены следующей рекуррентной операцией
= minmax{wA(7i, х): х Е Аф^х^т^р)},	(16.34)
16. Конструктивные и численные методы ...
209
при (t*. ж*) е Ti) х Rn. Здесь A(t^,x*,n,p) — область достижимости
дифференциального включения
x(t) е со f(t,x(t),p,Q).
Для функций цл имеем оценки
?/А > Vai, lim uA (t, x) — Vai (t, x) при diam A —> 0,
где предел является равномерным в каждой ограниченной области G* С
С [0, в] х Rn.
Аппроксимации функций цены дифференциальных игр с помощью
операторов программного поглощения и другой соответствующей техники
рассматривались многими авторами. Результаты, полученные в этой обла-
сти, представлены в большом числе работ. Отметим только, что некоторые
из названных конструкций были использованы в репрезентативных фор-
мулах для вязкостных решений уравнений Гамильтона-Якоби, а именно,
для аппроксимации этих решений с помощью рекуррентных минимаксных
(и/или максиминных) операторов (см., например, [24, 189]).
16.4.	Построение стабильных мостов
Рассмотрим построение стабильного моста в задаче М-наведения,
сформулированной в пункте 13.1. Будем предполагать, что движение управ-
ляемой системы описывается уравнением (16.19), функция / удовлетворяет
условиям, указанным в пункте 11.1. Напомним, что в задаче наведения
требуется определить стратегию игрока Р по принципу обратной связи, ко-
торая обеспечивает выполнение условия х(0) е М. Согласно результатам
параграфа 13, если в задаче М-сближения известен ^/-стабильный мост, то
решение этой задачи можно определить в форме стратегии, экстремальной к
стабильному мосту. Известно также, что решение многих типов дифферен-
циальных игр можно свести к построению соответствующих стабильных
мостов для соответствующих задач сближения.
Опишем операторы программного поглощения, которые используются
для приближенного построения стабильных мостов. Пусть 0	< т С в,
и пусть М* — некоторое компактное множество в пространстве Rn. Опре-
делим
М*(£*,т,д,М*) = {х* е Rn: A(t*,x*,T, q) А Ж 0},
g^Q
210
Глава III
где	q) — область достижимости, определенная соотношени-
ем (16.32). Оператор М* н-> М*(£*,т,М*) называется оператором про-
граммного поглощения. Его значение М*(t*, т, М*) называется множеством
программного поглощения для исходного множества М*.
Пусть по-прежнему А = {в = т0 > п > • • • > Тк = 0} — некоторое
разбиение отрезка [0, в]. Определим множества
ТУд(то) = М, И7д(п) = М*(п,то,1Уд(то)),
ММ = ЛштЛ(<
Жд = {(^,w): W € Жд(Тг), t € (Тг+1,Тг], i е О, к ~ 1}.
Известно, что при некоторых условиях невырожденности (см. например,
[176, 213, 218]), которые не очень ограничительны, данная процедура опре-
деляет систему множеств, которая аппроксимирует максимальный стабиль-
ный мост Wq в рассматриваемой задаче М-сближения (максимальность
множества Ио означает, что это множество является объединением всех
стабильных мостов для этой задачи), т. е.
dist [Ид, Ио] —> 0, когда diam А —> 0.
Здесь dist [•, •] — хаусдорфово расстояние между множествами.
Отметим, что вместо т, qy М*) можно использовать более про-
стой оператор (конечно-разностный вариант оператора программного по-
глощения), который определяется следующим образом
q. М*) = {х* е Rn: х* + (т — t*) со f(t*,x*)P, q) П М* 0],
т.е. ж* е М(£*,т,д,М*) тогда и только тогда, когда существуют Д е
е со/(£*,ж*,Р, д) и m* е М*, такие, что ж* + (г — t*)/* = m*.
Для реализации в вычислительных программах необходимы дальней-
шие модификации рассматриваемых операторов. Например, операторы про-
граммного поглощения могут быть определены на семействе многогран-
ников (вообще говоря, невыпуклых и несвязных) и имеющих значениями
многогранники из этого семейства. Вычислительные алгоритмы и програм-
мы для аппроксимации стабильных мостов многогранниками разработаны
В. Н. Ушаковым, В. А. Вахрушевым и А. П. Хрипуновым [212, 213]. В этих
алгоритмах основная задача, которая решается на каждом шаге ti е А, за-
ключается в построениях объединений и пересечений невыпуклых много-
гранников. Понятно, что вычислительные алгоритмы и программы, предна-
значенные для решения нелинейных дифференциальных игр, оказываются
гораздо более сложными и требуют больших вычислительных ресурсов.
16. Конструктивные и численные методы. ..
211
В качестве иллюстрации рассмотрим пример задачи М-сближения, в
котором движения управляемой системы описываются уравнениями
±1 = Ж2,
±2 — —0.1бж2^ — 10.15 sina?i
|р|	10, q 6 [0,1], 0 = 5, терминальное множество М состоит из единствен-
ной нулевой точки х\ — 0, х-2 = 0. Чтобы построить множество Жд, которое
аппроксимирует максимальный стабильный мост Жо в этой задаче, была
использована вычислительная программа, разработанная А. Хрипуновым.
Рис. 16.1
На рис. 16.1 изображены сечения Жд(^) множества Жд в моменты
времени € [0,5].
Следует упомянуть, что этот очень краткий обзор не вмещает целого
ряда важных моментов теоретического обоснования алгоритмов и описания
вычислительных программ.
16.5.	Построение поверхностей переключения для позиционных
стратегий
Рассмотрим линейную дифференциальную игру, в которой движение
управляемой системы описывается уравнением (16.1), а функционал платы
имеет вид
7(ж(-)) = сг(я(0)), ст: Rn н-> R выпукла.	(16.35)
Опишем сначала известное преобразование этой игры. Пусть t X(t) —•
п х n-мерная матрица-функция, удовлетворяющая уравнению

(16.36)
212
Глава III
и условию X(ff) — I, где I — единичная матрица. Продифференцируем
равенство y(t) — X(t)x(t), где x(t) — решение уравнения (16.1). Получаем
y = &t,p,q),	(16.37)
где £(t,p,q) = X(i)^(t,p,^), р G Р, q G Q. Пусть u(t0,y0) — цена диффе-
ренциальной игры (16.37) с функционалом платы
%/(•)) = «’(у(б')),	(16.38)
т. е. функционал платы здесь такой же, как в игре (16.1), (16.35). Пусть
Vai (to, жо) — Цена дифференциальной игры (16.1), (16.35). Нетрудно заме-
тить, что справедливо равенство
u(t0,X(t0)x0) = Val(t0,x0)	(16.39)
для всех (to, ^о) € [0,0] х Rn. Таким образом достаточно рассмотреть диф-
ференциальную игру (16.37), (16.38). Отметим, что в тех случаях, когда
функция су не зависит от части компонент фазовых векторов х или у. в си-
стеме уравнений (16.37) следует оставить лишь уравнения для тех компо-
нент, от которых фактически зависят значения функции а. Таким образом,
в этих случаях, указанное преобразование позволяет уменьшить размер-
ность фазового пространства. Отметим также следующее. Хорошо известно
(см., например, [123], стр. 87-89), что для дифференциальной игры (16.37),
(16.38) из выпуклости краевой функции а следует выпуклость функции
цены по фазовой переменной у.
Ниже будет описано построение множеств уровня функции цены в
дифференциальной игре (16.37), (16.38), а также построение позиционной
субоптимальной стратегии игрока Р, гарантирующей ему результат, близ-
кий к оптимальному. В этих построениях используется оператор программ-
ного поглощения. Отметим, что для системы (16.37) из выпуклости входных
данных задачи следует, что множество программного поглощения будет вы-
пуклым. Здесь уместно заметить, что техника опорных функций множеств
программного поглощения была развита в 60-х годах Н. Н. Красовским (см.,
например, [109, 110]). Некоторые пионерские результаты в этом направле-
нии были получены Б. Н. Пшеничным (см., например, [173]).
В дальнейшем будет использоваться конечно-разностный вариант опе-
ратора программного поглощения, который определяется равенством
W(t*, т, М) := Q W(t*, т, q, М\	(16.40)
16. Конструктивные и численные методы ...
213
Здесь
W(t*. т, д. М) : — {х* € Rn: х* + (т — t*) со £(£*, F, q) П М ^0} —
— М ~ (т — со £(£*, Р, q)
О < t* < т < 0, q Е Q, М С Rn. Понятно, что эта конструкция является
частным случаем конструкции, определенной в пункте 16.4.
Предположим, что множество М — выпуклый компакт. Определим
опорную функцию множества W(t*. т, М). Рассмотрим на первом шаге
опорную функцию vq(s) множества IV(7*, т, д, М). Имеем
l/q('s) niax{(.s, w): w € W(t*. т, g, M)} =
— max(s, y) + (t - ^)max(s, -£(£*, p,g)) =
уем	peP
— y(s-M) — (г — t*)mm(s,£(t*,p, g)),
pep
где u(--M) — опорная функция множества M. Точка у содержится в пере-
сечении (16.40) тогда и только тогда, когда выполняется неравенство
0 JE maxmax[(s,v) — ^o(s)l = max[(s. у} — ^(^)].
qeQ scRn	4 seRn ' v /J
Здесь
v(s) p,(s; M) — (r — t*) maxmin(s, g)).
qeQ peP
Функция z/(-) положительно однородна. Если эта функция выпукла, то, как
известно из выпуклого анализа, z/(-) является опорной функцией некоторого
выпуклого множества. Из построений следует, что таким множеством будет
множество W(t*.r, М). Однако функция ?/(•) может быть невыпуклой, в
этом случае опорной функцией множества W(£*, т, М) является выпуклая
оболочка функции ?/(•), которая определяется следующим образом. Пусть
N := epiz/(«) = {(s.z): z z/(s), s Е Rn},
coz/(s) := inf{z E R: (5, z) E co^.	(16.41)
Итак, определенная здесь функция со р(-) положительно однородна и
выпукла. Из определения функции р(-) следует, что со ^(-) является опорной
функцией множества W(t*, т, М).
Указанные соотношения используются для построения множеств уров-
ня функции цены дифференциальной игры (16.37), (16.38). Выберем неко-
торое число с и определим множество уровня функции платы
Мс:= {y&Rn-.a(y)^c}.
Отметим, что множество Мс выпукло и замкнуто. Будем предполагать так-
же, что оно ограничено. Рассмотрим построение стабильного моста в задаче
214
Глава III
о приведении системы (16.37) на терминальное множество Мс. Пусть А =
= {0 = то > и > • • • > тк = 0} — некоторое разбиение отрезка [0,0].
Полагаем ИдДто) = Мс. Пусть
/щ(з) := max{(s, w): w е W&iC(tq)}
— опорная функция множества РИдДто). Предположим, что определена
опорная функция ^щ(-) множества РИдДтД Опорную функцию /^+i(-) сле-
дующего множества W^c(ri+i) определим следующим образом. Полагаем
Pi+i(s) :=я(«) - (T»+1 -Ti)m£ucmm(s,C('ri,p,Q)).	(16.42)
geQ реР
Mi(’) := со^+1(«),	(16.43)
т. е. /1^+1 (5) •= inf{z е R: (s,z) 6 coepi^+i(-)}-
Таким образом получаем набор опорных функций //$(•) и соответству-
ющую систему множеств ИдДтД (г € ОД). Эти множества аппрокси-
мируют множества уровня функции цены, т. е. dist [РИдДтД РИс(тг)] —> 0
при diam А —» 0. Здесь
Wc(r) := {х G Rn: п(т, х) с}
— множество уровня функции цены дифференциальной игры (16.37),
(16.38). Данное соотношение справедливо в невырожденном случае, ко-
гда множества РИс(тг) имеют непустую внутренность, т. е. Wc(ri) =
= clint Wc(ri); здесь символы int А и cl В означают внутренность мно-
жества А и замыкание множества Б.
В рассматриваемой процедуре возможен случай, когда РИдДтг) = 0
при некотором е А. В этом случае указанные построения проводятся
до первого (в порядке их нумерации) момента т*, для которого РИдДтг) =
= 0. Понятно, что достаточно полную информацию о функции цены можно
получить, имея множества ее уровня (или аппроксимации этих множеств)
для некоторого достаточно плотного набора чисел Cj (j G 1, J).
Основная вычислительная проблема, которую нужно решать на каждом
шаге рассматриваемой процедуры (т. е. для каждого момента времени Ti и
для каждого числа с/), состоит в построении выпуклой оболочки положи-
тельно однородной функции.
Ряд эффективных вычислительных алгоритмов построения выпуклых
оболочек был разработан В. С. Пацко и его учениками (см., например,
[93, 230, 231]). В этих алгоритмах максимально используется вся априор-
ная информация о задаче (в том числе, о входной функции, чьи выпуклые
оболочки нужно построить). Опишем их кратко.
16. Конструктивные и численные методы ...	215
В этих алгоритмах множества 1Уд}С(тг) и со£(т?;, F, q) задаются как
выпуклые многогранники. Предполагается, что
£(t,P, Q) = B(t)p + C(t)q,	(16.44)
где B(t), C(t) — матрицы, a Q — выпуклый многогранник.
Пусть Q" — множество всех вершин многогранника Q. Определим
^+1(«) := M(s) - (т»+1 -Тг)тах1шп(в,С(т»,р,д)).
qeQ^ Р^Р
Ясно, что ^+i(s) = i'h-i(s) (напомним, что величина была опре-
делена соотношением (16.42)). Очевидно, что в рассматриваемом случае
функции //*(•) и — z'h-iG) являются кусочно-линейными.
Заметим, что предположение (16.44) не является существенным. В слу-
чае, когда это предположение не выполняется, можно выбрать конечное
множество Qq, такое, что функция будет кусочно-линейной и доста-
точно близкой К функции
Из выражения, определяющего функцию	можно извлечь ин-
формацию о лучах Sq, в окрестности которых эта функция может оказаться
локально невыпуклой. Поэтому построение выпуклой оболочки (глобаль-
ной) начинается с построения локальных выпуклых оболочек в упомянутых
окрестностях лучей . Этот прием позволяет существенно сократить объем
вычислений. Эффективные (быстрые) алгоритмы разработаны для случая
п = 2, п = 3 (п — это размерность фазового вектора управляемой систе-
мы (16.37)). Их можно использовать также в случае п 4, однако следует
сказать, что в этом случае необходимо хранить и обрабатывать огромные
массивы информации, необходимой для аппроксимации рассматриваемых
стабильных мостов с помощью многогранников. Подробное описание этих
алгоритмов приведено в упомянутых выше работах.
После того, как определены множества Пд,сДтг), можно построить
стратегии игроков, близкие к оптимальным, конструкции которых базиру-
ются на этих данных. Опишем построение поверхности переключения для
позиционной стратегии игрока Р в случае, когда
Жрл) = b(t)p + C(t)q, реР= [-1,1],
b(t) — вектор в Rn. Этот случай выбран для простоты изложения.
Пусть Ti G Д, Cj < Cj+i. Рассмотрим множество
TAj :=	(тг) \
216
Глава III
Разобьем его на три части D^-, и Sij следующим образом. Для точ-
ки у G Dij обозначим через wo ее проекцию на множество РИд^Дтг), т- е.
Ily-w-’oll = min Ну —w||,
wewA)Cj.(rj
пусть
Ar(wo) := < s G Bi: (5, wq) = max (5, w) >,
I	w€W&,Cj(Ti) )
и напомним, что Bi — {5 e Rn: ||s||	1}. По определению s e N(wo)
вектор s является внешней нормалью к множеству	в точке Wq.
Отметим, что для осуществления рассматриваемых алгоритмов требует-
ся информация об этих множествах 7V(wq). Множество D~\j определено
условием
(s, Ь(Тг)) >0, Vs е N(wo),
т. е. точка у G Di j принадлежит множеству D~j тогда и только тогда, когда
ее проекция wq удовлетворяет приведенным выше неравенствам. Аналогич-
но, у € D+j тогда и только тогда, когда (s, Ь(тг)) < 0 для всех я G 2V(wo).
Оставшаяся часть множества Dij обозначается через Sij, т. е.
Sid := Ditj\ (D+ и Д7.).
Определим позиционную стратегию С/д (С, у) игрока Р в области
D := {(t,y) G [0,0] х R”:
t & [77,77-1), у & Dij U	i&l.k, j G 1, m}.
Пусть
D := {(t, у) G [0,0] x Rn: t G [тй т»_1), у e Did, i e l,k, j e 1, m},
D+ := {(t,y) e [0,0] x Rn: i e [77,7;_1), у G	i eP/k, j £ 1“^},
Sa := e [0,0] xRn:
te [Тг,Тг_1), ye Sij и ТУд)С1(тг), ? G 1, k, j G 1, m}.
'+1, yeD+,
Ub(t,y) =<-l, у G D~,
p, ye S&,
16. Конструктивные и численные методы ...
217
где р — любое число из отрезка [—1,1]. Таким образом, множество 5д
является «поверхностью переключения» позиционной стратегии игрока Р.
Подробное описание и обоснование предложенных конструкций при-
ведено в работах В. С. Пацко и его сотрудников (см., например [34, 35, 36]).
В частности, в этих работах показано, что стратегия t/д обеспечивает игро-
ку Р результат, достаточно близкий к оптимальному (т. е. к цене дифферен-
циальной игры (16.37), (16.38)) в предположении, что diam А достаточно
мал, а набор чисел Cj (j € 1, m) достаточно плотен.
В работах [164, 33] описано применение этих методов для решения
задач об управлении самолетом на взлете и при посадке в условиях так
называемого «сдвига ветра или микровзрыва» (windshear) — метеорологи-
ческого явления, когда происходят резкие порывы ветра, изменяющие его
направление и скорость.
16.6. Построение функции, сопряженной к функции цены
Рассмотрим еще один подход к решению линейной дифференциаль-
ной игры (16.37), (16.38). Целью этого метода является построение функ-
ций ?1д(т? , •), сопряженных К выпуклым функциям ?2д(тг, •), где и — функ-
ция цены дифференциальной игры (16.37), (16.38). Во многом этот подход
имеет аналогии с построениями множеств уровня функции цены, которые
рассматривались в пункте 16.5.
Будем предполагать, что терминальная функция а удовлетворяет усло-
вию Липшица
|<т(1/(1)) - <т(у(2))|	А||у(1) - ?/(2)||
для всех у^\у^ € Rn.
Рассмотрим сопряженную функцию ст* к функции ст, и ее эффективное
множество dom ст, а именно, определим
cr*(s) := sup [(s, х) — <т(х)],
dom ст* := {sGl’7: сг*(<$) < оо}.
Напомним, что dom ст* С В\. Как отмечалось выше, функция цены диффе-
ренциальной игры (16.37), (16.38) выпукла по фазовой переменной у. Более
того, известно, что
dom п* (£,•)=== dom ст*, ViG[O,0],
где
и* (t, s) := sup [(s, x) — u(t, .t)] ,
и — функция цены дифференциальной игры (16.37), (16.38).
218
Глава III
Аппроксимируем функцию u*(tys) с помощью функций ид(тг,$), ко-
торые определяются следующим образом. По-прежнему, возьмем некоторое
разбиение А = {0 = tq > п > • • • > Т& = 0}. Полагаем
^(т0,з) = cr*(s), VseRn.
Пусть уже построена функция (77, •). Тогда функцию (r^i, •) постро-
им следующим образом. Определим величину
VA(ri+i,,9) := uX(ri+i,s) - (т<+1 - Ti)maxmin(s,C(Tt,p,Q)).
qeQ реР
Затем полагаем
«д(-Гг+1,-) “ «Д (Тг+1,’),
где и**(-) формально определена как вторая сопряженная функция, т. е.
и* (ж) := sup [(s,х} — u(s)],
u**(s) := sup [(s,#) — v*(ж)].
Из выпуклого анализа известно, что и**(-) совпадает с выпуклой оболочкой
функции г;(-).
Отметим также, что для дифференциальной игры (16.37), (16.38) функ-
ции v*(ri,x) совпадают с функциями ид (г*, ж) вида (16.33). Дальнейшие
построения следуют схеме конструкций, описанных в разделе 16.3. А имен-
но, полагаем ид (то, у) = <?(?/) и
ид(т»+1,з) =тгсстт{ыд(тг,в + /): /е - ъ+1)со£(ъ, P.q)}.
qeQ
Доказательство равенства v*(Ti,y) — ид(т^у) базируется на выпуклости
функции ид(т^, •) и теоремах о минимаксе.
Практически описанную процедуру можно реализовать следующим об-
разом. На ограниченном множестве dom ст* выбирается некоторое конечное
множество точек Sk, к е 1,К. Предполагается, что при некотором ма-
лом е > 0 эти точки образуют е-покрытие множества domст*, т. е.
к
B£(sk) Э domст*.
fc=l
Вместо описанных выше функций ид(тг,з), ид (77,3) рассматриваются их
кусочно-линейные аппроксимации, значения которых вычисляются лишь
16. Конструктивные и численные методы ...
219
в точках sk. Основная вычислительная проблема, которую требуется ре-
шать в рамках этого алгоритма, состоит в построении пересечения полу-
пространств
к
V(ri+i) := Р) Hk{ri+1)
k=l
где	{(ж, z) е Rn х R: z (sk,x) - цд(т^+1, ^.)}, и в опреде-
лении полупространств
Hk(ri+i) = {(x.z) 6 Rn х Ж: г > {skyx) -	kel,K,
опорных к этому пересечению V(ri+\). Другими словами, требуется опре-
делить числа так, чтобы
V(t^i) С Hfc(ri+i), V(ri+i) П Д(т^+1)	0. k е 1,К.
Эти числа Vi+ifk аппроксимируют значения искомой функции ид(т$+1,-)
в точках s — sk. Отметим, что множество V(t£+i) является графиком
кусочно-линейной аппроксимации функции и(т^+1,«) (и — функция цены
дифференциальной игры (16.37), (16.38)). Пересечения полупространств и
определения полупространств, опорных к этому пересечению, суть задачи
линейного программирования. Для решения этих задач можно использовать
известные методы.
Более подробное изложение этой процедуры приближенного построе-
ния функции цены и ее обоснование приведено в работе [185]. В этой работе
приведены также некоторые результаты вычислений с помощью програм-
мы, разработанной для случая, когда п = 2 (п — размерность фазового
пространства).
Глава IV
Краевые задачи для УЧП первого
порядка
17.	Задача Коши для уравнений Гамильтона-Якоби с
дополнительными условиями в форме неравенств
Концепция минимаксного решения может использоваться для изучения
обобщенных решений различных типов уравнений в частных производ-
ных (УЧП) первого порядка с различными граничными и терминальными
(или начальными) условиями. Во второй главе были представлены результа-
ты такого применения к задачам Коши для уравнений Гамильтона-Якоби.
В данной главе рассмотрены некоторые другие приложения этого подхода.
Отличительная особенность задач для уравнений Гамильтона-Якоби,
рассматриваемых в данном параграфе, — это то, что их решения подчинены
ограничениям, заданным в форме неравенств. Помимо этого, и само уравне-
ние Гамильтона-Якоби в некоторой области заменено дифференциальным
неравенством. Доказаны существование и единственность минимаксного
решения этой задачи. Эти результаты проиллюстрированы дифференциаль-
ная игрой, функция цены которой является минимаксным решением задачи
такого типа.
17.1.	Постановка задачи
Пусть заданы непрерывная функция и: (0,0] xRn R и уравнение
Гамильтона-Якоби. Обозначим
Q := {(t, ж, z) е (0,0) х Rn х R: z <	х)}.
(17.1)
Рассмотрим задачу: найти функцию и: (0,0] х R, удовлетворяющую
следующим соотношениям
u(t, х) cj(t, х) V (t, х) 6 (0,0] х Rn;
и(в, х) = cj(0, х) \/жбКп;
(17.2)
(17.3)
17. Задача Коши для уравнении Гамильтона-Якоби ...	221
+H(t, x.u,Dxu)	0, если (t, х, u(t, ж)) е Q;	(17.4)
~ + H(t,x,u,Dxu) ^0, V(£,z) €Г:= (0,0) xRn.	(17.5)
Отметим, что неравенства (17.4) и (17.5) должны рассматриваться в
обобщенном (минимаксном и/или вязкостном) смысле. Строгие определе-
ния даются ниже. Как будет следовать из этих определений, обобщенное ре-
шение и удовлетворяет соотношениям (17.4)и(17.5)в классическом смысле
в тех точках, где функция и — дифференцируема.
Проиллюстрируем эту задачу следующим простым примером. Пусть
х G R, 0 < t 0 = 1, cv(t,x)=x2. Н(1^х, z. s) ~ s.
Нетрудно проверить, что функция
{ж2,	х^о, t е (0,1],
о,	t-i^x<o, t е (0,1],
(х + 1 — t)2, х < t — 1, t G (0,1]
является непрерывно дифференцируемой и удовлетворяет соотношени-
ям (17.2)-(17.5). Поэтому эта функция является классическим решением
рассматриваемой задачи. Из результатов, полученных ниже, будет следо-
вать единственность этого решения.
Однако, в общем случае, возникает необходимость рассматривать
негладкие решения задачи (17.2)-(17.5). Для такой задачи понятия верх-
них нижних и минимаксных решений вводятся следующим образом.
17.2.	Определение
Верхним решением задачи (17.2)—(17.5) называется полунепрерывная
снизу функция и: (0, 0] х Rn R, такая, что и(0, х) = си (0, х), и множе-
ство epi и П Q слабо инвариантно относительно верхних характеристиче-
ских включений.
Нижним решением этой задачи называется полунепрерывная сверху
функция и: (0,0] х Rn и-> R такая, что и ш и множество hypo кП
П (G х R) слабо инвариантно относительно нижних характеристических
включений.
Минимаксным решением задачи (17.2)-(17.5) называется непрерыв-
ная функция, которая является одновременно верхним и нижним решением
этой задачи.
222
Глава IV
Напомним, что включение
(ж,г) € Е[фх^ф)
называется верхним (нижним) характеристическим включением для уравне-
ния Гамильтона-Якоби, если многозначное отображение Е удовлетворяет
условиям (j), (jj), (jjj+), и (jv+) (условиям (j), (jj), (jjj“), и (jv )), сформули-
рованным в пункте 6.2.
Свойство слабой инвариантности множества epi означает, что для
произвольных ф е Ф и (tg, Аъ ?о) С epi wPiQ существует число т € (to, 0) и
такая траектория (rc(t),^(t)) верхнего характеристическое включения, что
(#(to),z(to)) — (^о,^о) и (t,rr(t),z(t)) e epiw П Q для всех t e [to,г].
Можно показать, что для полунепрерывной снизу функции и это свойство
и сформулированные ниже условия (U3')-(U5') являются эквивалентными
(доказательство этого факта совпадает с доказательством подобных утвер-
ждений в параграфе 4).
(U3Z) Для любого ф € Ф и любого (t, х) е (0,0) х Rn таких, что
u(t, х) < cu(t, ж), справедливо
]ni{dTu{t, х\ 1,/) — д: (f,g) Е E+(t,xfu(t,x)^)}	0,
где Е+ — произвольное многозначное отображение, удовлетворяющее
условиям (j), (jj), (jjj+), (jv+);
(U4') a 4- H(t, x. u(t) x), s) 0, для любых (t, x, u(t, ж)) e Q и любо-
го (a, s) € D~u(t,x);
(U5Z) для любых (t, ж, u(t, ж)) 6 Q и любого s e Rn:
in^Jd~u(t,x; 1,/) — (5,/) 4- Н(ф x,u(t. ж), 5)]	0.
Аналогично, для полунепрерывной сверху функции и свойство слабой
инвариантности множества hypo и П G относительно нижнего характери-
стического включения эквивалентно условиям (L3')-(L5Z).
(L3Z) Для любых ф € Ф и (t, ж) е G справедливо
sup{d+u(i,®; 1,/) -д- (f,g) е	о,
где Е~ — произвольное многозначное отображение, удовлетворяющее
условиям (j), (jj), (jjj~), (jv~);
(L4') a 4- Н(фх,и(ф ж),§)	0, для любых ^,ж) € G и любого (a, s) €
6 P+w(t, ж);
17. Задача Коши для уравнений Гамильтона-Якоби ...
223
(L5') для любых (t, х) G G и s G
sup [d+u(t, х, 1, /) — (s, f) + H(t, x, u(t, x), s)]	0.
Заметим, что эти условия совпадают с условиями (L3)-(L5), сформу-
лированными в пункте 6.3. Ниже будет доказано следующее утверждение.
17.3.	Теорема
Пусть в задаче (17.2)-(17.5) функция иг. (0,0] х Rn непрерывна, а
гамильтониан Н удовлетворяет предположениям (Н1)-(НЗ), сформули-
рованным в разделе 7.2. Тогда существует и единственно минимаксное
решение и задачи (17.2)-(17.5).
Прежде, чем перейти к доказательству этой теоремы, опишем диф-
ференциальную игру, у которой функция цены совпадает с минимаксным
решением задачи (17.2)-(17.5).
Рассмотрим дифференциальная игру, в которой движение управляемой
системы описывается уравнением
±(t) — f(t. x(t),p(t),q(t)), to^t^0, x(to) — xq G Rn. (17.6)
Здесь p(t) G P и q(t) G Q — управления первого и второго игроков со-
ответственно, Р и Q — компакты. Первый игрок стремится обеспечить
минимальное значение функционала платы
t
:= min к(Лж(<))- /
to
(17.7)
Второй игрок, напротив, пытается гарантировать максимальное значение
этого функционала. Полагаем, что функции fug удовлетворяют услови-
ям (А1)-(АЗ) (см. пункт 11.1). Полагаем также, что функция ок (0,0] х
xRn н-> R непрерывна и удовлетворяет оценке
\u(t,x)\ Ко(1 + |И), \/(t,x) G (0,0] х Rn,
где Ко — положительное число. Напомним, что из предположения (АЗ)
следует справедливость равенства
mmmax[(s. f(t,X,p,q)) -g(t,x,p,q)\ =
реР qeQ
= maxmin[(s,/(t, ж,р, q)} — g(t, x,p, q)] = H(t, ж,з). (17.8)
qeQ peP
224
Глава IV
Величина H(t.x,s) называется гамильтонианом дифференциальной иг-
ры (17.6), (17.7).
Заменяя функционал платы (11.2) функционалом (17.7), определим
величины r^(to,xo) и Г^о^о) таким же образом, что и в разде-
ле 11.3 (см. (11.16)). Эти величины являются оптимальными гарантиро-
ванными результатами первого и второго игроков. Известно (см., напри-
мер, [122, 123]), что в рассматриваемом случае справедливо равенство
Г1(£(ь #о) — жо)- Общее значение оптимальных гарантированных ре-
зультатов первого и второго игроков называется ценой дифференциальной
игры (17.6), (17.7). Итак, определена функция цены
(to, жо) •—> Vai (to, xo): (0,0] х м R.
Также известно, что функция цены является одновременно и-стабильной и
f-стабильной. Для рассматриваемой игры свойство ^-стабильности форму-
лируется следующим образом.
Функция и: (0,0] х Rn н-» R называется ^/-стабильной, если для лю-
бых (to, жо) € (0,0] х Rn и q е Q существует такое решение дифференци-
ального включения
€ co{(f(t,x(t),p,q),g(t,x(t),p,q)): р е Р},	(17.9)
что ж (to) = жо, z(to) = u(to,xo), и справедливо либо z(t) u(t,x(t))
для всех t е [to, 0], либо z(r) ш(т,х(т)) ддя, по крайней мере, одно-
го т е [to,0]. Очевидно, что многозначное отображение Е+, определенное
равенством
E+(t, ж, z, q) := со {(f(t, х,р, q),g(t, х,р, q)): р е Р}
удовлетворяет требованиям (j), (jj), (jjj+), (jv+), сформулированным в раз-
деле 6.2, где гамильтониан определен равенством (17.8). Ясно, что функция
цены удовлетворяет краевому условию Val(0, ж) = си(0,ж). Принимая во
внимание непрерывность функции цены, получим, что эта функция являет-
ся верхним решением в задаче (17.2)-(17.5) с гамильтонианом, определен-
ным в (17.8).
Подобным же способом можно показать, что Vai (t, х) — это нижнее
решение задачи (17.2)-(17.5). Поэтому заключаем, что функция цены диф-
ференциальная игры (17.6), (17.7) совпадает с минимаксным решением за-
дачи (17.2)-(17.5).
Теперь вернемся к доказательству теоремы 17.3. Сначала докажем спра-
ведливость следующей теоремы.
17. Задача Коши для уравнений Гамильтона-Якоби ...	225
17.4.	Теорема
Пусть в задаче (17.2)-(17.5) функция (□,#] х Rn непрерывна,
а гамильтониан Н удовлетворяет предположениям (Н1)-(НЗ), сформу-
лированным в разделе 7.2. Тогда для любого верхнего решения и зада-
чи (17.2)-(17.5) и для любого нижнего решения v этой задачи справедливо
неравенство и v.
Доказательство этой теоремы подобно доказательству теоремы 7.3. По-
этому приведем только схему основных этапов доказательства.
Допустим, что справедливо противное: пусть существуют верхнее ре-
шение и задачи (17.2)-(17.5), нижнее решение v той же самой задачи, точ-
ка (to, жо) € (0,0] х Rn и число d > 0 такие, что w(t0, ^о) < v(to, жо) — d.
Как и в доказательстве теоремы 7.3, здесь используется функция Ля-
пунова вида
Ls(t, х, у, rf) := w£(t, х,у)+£-гр	(17.10)
где (t, х, у, С, rj) € (0,0] х Rn х Rn х R х R,
w£(t,x,y) := ae(f)re(x,y),	(17.11)
Ге(ж,2/) — i/e4+ ||z-?/||2, M*) := (e~At -
Число c > 0 выбрано так, чтобы удовлетворить неравенствам 0 < е2а£ (t) < d
при всех t е [0,0].
Рассмотрим систему, включающую дифференциальные неравенства и
дифференциальные уравнения
||i||	р(х), £ = {x,p)-H(t,x,£,p),
||у||	р(у), У = (y,q) - H(t,y,y,q),
p-.= q = Dyws(t,x,y) = -Dxwe(t,x,y) = -a£(t) ——(17.12)
Используя рассуждения, подобные тем, что были приведены в разде-
ле 7.4, можно показать, это существует траектория (x£(t), y£(t),%£(t), %(t))
(to t 0), которая удовлетворяет системе (17.12), начальному условию
x(t0) = y(io) = ХО,
£(to) = Со ~ u(xQ, t0),	»?(to) = % := v(x0, t0)
и неравенствам
£e(t) > u(t,Xe(t)),
T]£(t) ^v(t,ye(t)) при to ^t^T£.	(17.13)
226
Глава IV
Здесь
т£ = min{t 6 [to, 0]: (t, x£(t), £e(t)) □}.
Если т£ < 0, то из определений множества Q и момента времени т£ следует,
что ££(т£) = ш(т£. ж£(т£)). В случае, когда т£ = 0, из (17.13) и определения
верхнего решения и, получаем ££(0)	^(0, х£(0)) =	ж£(0)). Поэтому в
обоих случаях неравенство £е(те) и>(т£, х£(т£У) выполняется.
Напомним, что, по определению нижнего решения, имеем v < си. Сле-
довательно, 7/£(т£)	и(т£,у£(т£У). Таким образом, заключаем, что имеет
место оценка
Се(т£) - т?е(т£) ^а>(г£,х£(т£))-ш(т£,у£(т£)).	(17.14)
Введем обозначение
Le[i] := Le(t,a;e(t),ye(t),^(0,%(<))•
В доказательстве теоремы 7.3 было показано, что L£[t] -С 0. Следовательно,
L£[t0] = s2Q£(to) + u(to,^o) - ^(to,^o)
L£[t£]	а£(т£')г£(х£(т£\у£(т£)') + и(т£,х£(т£)) - си(т£.у£(т£))
ш(т£,х£(т£У) -ш(т£,у£(т£)).
Заметим, что
€2а£(т£) —> 0, о£(т£) —> сю,	когда е —» 0.
Напомним (см. раздел 7.5), что рассматриваемые траектории удовле-
творяют ограничениям x£(t) G М, y£(t) е М при всех t0 t < 0, е > 0, где
М — ограниченное множество. Следовательно, имеет место также оценка
|^(т£,ж£(т£)) - ш(т£,у£(т£У)\ max |w(i, х) - w(t, ?/)| := Ко < оо.
(х,у)€МхМ
t€[W]
Поэтому из неравенства
аг(т£)г£(о;£(т£),7/£(т£))	e2a£(t0) + u(to,xo) - v(t0,x0) + KQ
вытекает, что
||я;£(т£) - у£(т£)|| -» 0, когда г 0.
Далее, переходя к пределу при е —> 0 в неравенстве
о20!£(«о) + u(to,xo) - v(t0,x0)	w(t£,x£(t£)) - ш(тЕ,уЕ(т£)),
получаем оценку u(to,^o) v(tQixo). Таким образом, получено противо-
речие с исходным предположением, что u(to,xo) < f(to,^o). Теорема 17.4
доказана.
17. Задача Коши для уравнении Гамильтона-Якоби ...	227
17.5.	Теорема
Пусть в задаче (17.2)-(17.5) функция (0,0] х Rn н-> R непрерывна,
а гамильтониан Н удовлетворяет предположениям (Н1)-(НЗ), сформули-
рованным в пункте 7.2. Тогда существует верхнее минимаксное решение и
задачи (17.2)-(17.5) и нижнее минимаксное решение v этой задачи, такие,
что и С V.
Ясно, что утверждение теоремы 17.3 следует из теорем 17.4 и 17.5.
Доказательство теоремы 17.5 приводится ниже. Оно основано на вспомога-
тельных утверждениях 17.6-17.9, которые подобны утверждениям 8.4-8.7.
Введем некоторые обозначения. Определим функционал
7(ж(-), z(-); to, г) := min \w(t,x(t)) — z(t)].	(17.15)
Выберем и зафиксируем т е (0,0], s G Rn. Определим величину
^(to,xo,zo) := inf тт{(р(я(т)) - z(r), у(х(-), z(-);tQ, г)}.
О(-)Х-))
Здесь р: R"' i—> R — локально ограниченная функция, операция inf
(#(.),<’))
берется по множеству Sol (to, xq, zq, s), (to,%o, zq) € (0, t] x Rn x R. Напо-
мним, что символ Sol (to, xo, zq, s) обозначает множество всех решений
(ж(.), £(•)): (to,0] Rn xR
характеристического включения
(x, z) € E(t, x, z, s),	(17.16)
удовлетворяющих условиям x(to) — xq, z(to) — zq. Здесь многозначное
отображение E задается равенством
E(t,x,z,s) :=	\\f\\ < p(x), 9 = (f,s) - H{t,x,z,s)}.
Отметим, что /i* — локально ограниченная функция. Этот факт следует
из локальной ограниченности функции </?, непрерывности функционала 7 и
компактности множества Sol (М, s) (см. (8.3)).
Покажем, что имеет место оценка
H*(to,xo,zo Л-h) p*(to,XQ,zo) - h.	(17.17)
Можно принять, без потери общности, что h > 0. Выберем произвольное
число с > 0 и такую траекторию (ж*(-), z*(-)) € Sol (to, xq, zq, s), что
^*(to,xo,zo) +e imn{p(x^(r)) - z^(r), y(x^(-), z*(-)',to,r)}.
228
Глава IV
Можно показать, это существует траектория (х*(-), ^(-)) С Sol (to, ^o, zo +
+ h,s) такая, что Zh(t) z*(t) + h при t E [to,0] (см. доказательство
аналогичной оценки в пункте 8.3). Поэтому получаем
/i*(to,xo,£o) + £ > min{^(x*(T)) - £*(т), 7(х*(-),z^^t^.r)}
> min{p(x * (т)) —zh(r), 7(х*(«), г^(-); t0, т)} + Л > /i*(t0, х0, г0+ /?>) +/а.
Оценка (17.17) доказана.
Обозначим символом Sw множество локально ограниченных функций
(0,0] xRn Э (t, х) н-> -u(t,x) Е R, удовлетворяющих равенству и(0, х) ~
= о;(0, х), и таких, что для любых (to,xo) Е (0,0] х Rn, z^ > n(to.xo),
т е [to, 0], в е Rn справедливо
inf min{u(r, х(т)) — z(r\ 7(х(-), z(-); to, т)}	0,	(17.18)
где операция inf берется по множеству Sol (t0, х0, z0, s).

Символом S1 обозначим множество всех локально ограниченных функ-
ций (0,0] х Rn э (t,x) н-> u(t.x) Е R, удовлетворяющих неравенству
u(t,x) < cc(t,x) и следующему условию: для любых (to,xo) Е (0,0] х Rn,
z0 < u(to,xo)9 т е [to, 0], s Е Rn справедливо неравенство
sup	[u(r, х(т)) — z(r)]	0.
(o?(-),2;(-))^Sol (to,xo,zo,s)
(17.19)
17.6.	Утверждение
Выберем и зафиксируем s Е Rn. Пусть
^_(£о,жо,2о) := inf{7(a:(-),2:(-);to,0): W’MG)) € Sol(to,x0,^o,s)},
u_(to,^o) := inf{C G R:	xq, 0}.
Тогда функция u_: (0, в] x Rn >—> R является локально ограниченной, и она
ограничивает снизу любую функцию и Е Su, т.е.
u(I^Xq) iz_(to,xo)
для любых и е Su и (to, хо) Е (0,0] х Rn.
ДОКАЗАТЕЛЬСТВО. Чтобы показать локальную ограниченность функ-
ции w_, используем оценку (17.17) и обратимся к доказательству подобного
свойства для функции определенной в утверждении 8.4.
17. Задача Коши для уравнений Гамильтона-Якоби ...	229
Пусть и Е Sn, (to,£o) £ (0,0] х Rn и z0 > u(tG,xo). Заметим, что
и(в, х) = ш(0,х). Используя условие (17.18), в котором полагаем т = 0,
получаем неравенство /i_.(to, жо, £о)	0. Из определения функции и- и
оценки (17.17) следует, что z$ u_(to,#o)- Из того, что это неравенство
справедливо для любых zq > u(to,xo), заключаем, что требуемая оценка
u(t0,.T0) > u_(to,xo) имеет место.
17.7.	Утверждение
Пусть произвольно выбраны и фиксированы s* Е Rn, t* Е (0,0]
и и Е Su. Тогда функция и, определенная соотношениями
( sup{< Е R: /1 (t0,x0,C) > 0},
u(to,xo):=<
I u(x0,t0),
to £ (0,t*),
to £ [t*? 0],
(17.20)
является элементом множества Su. Здесь
//(to, £0, ^o) •=	sup	[iz(t*, z(t*)) - z(t*)]	(17.21)
(z(’),z(-))€Sol(fo,a:o,zo,s*)
Это утверждение формулируется так же, как и утверждение 8.5, но их
смысл различен, потому что множество Su, рассмотренное в разделе 8.3,
отличается от множества Su, которое рассматривается здесь. Поэтому до-
кажем утверждение 17.7 отдельно.
Равенство /(0, х) = й?(0, х) и локальная ограниченность функции и мо-
гут быть получены так же, как и в случае утверждения 8.5. Таким образом,
остается только показать, что для любых (to, xq) е (0,0] xRn, zq > u(to, Хо)>
я Е Rn и т Е [to, 0] справедливо неравенство
.	с .	-Z(T\ 7M-),z(-);io,T)} ^0	(17.22)
(a(-),z(-))eSoio
Здесь и ниже Solo = Sol (to, #o, все-
возможны следующие три случая: (i) to > t*, (ii) т t*, (iii) to < t* < r.
В случае (i) неравенство (17.22) следует непосредственно из равенства
u(t,x) = u(t, х), справедливого для t Е [t*,0], и из условия (17.18), кото-
рому удовлетворяет функция и. В случае (ii) выполнено неравенство (8.10),
из которого вытекает (17.22). Как было показано при доказательстве утвер-
ждения 8.5, в случае, когда т = t* и z^ > u(to,xo), существует такая
траектория (хч(-), ^t,(-)) Е Solo, что
z\t*) > u(t*, ^(t*)).
(17.23)
230
Глава IV
Рассмотрим случай (iii). Введем обозначения
Sol* := Sol(t*,^(t*),^(t*),s);
SoP := {(ж(-),г(-)) е Sol0: (a:(t), z(t)) = (x\t), z\t)), t € [W*]},
где (жч(-),г^(-)) e Solo — это траектория, удовлетворяющая неравен-
ству (17.23). Справедливы следующие соотношения
, 1/ПД о , min[u(T,x(r))-z(r), 7(x(-),2:(-);to,-r)]
(»(•), 2(-))eSoi0
(а)
< inf minWr. х(т)) — z(r), 7(жМ, z(0;t*,r)]
(a(.),*C))eSoi0
inf min[^(r,ж(т)) — z(t), 7(ж(-), z(-);t*,т)]
= , ,, inf o , min[u(r, x(r)) — z(r), y(x(-), z(-); t*, r)]	0.
Здесь неравенство (а) следует из равенства и(т, х) — и(т, х) и неравенства
7(^(*)^(-);^о?т) тМ-М(-);^т),
которое имеет место при to t* т. Из включения Solь С Sol о выте-
кает неравенство (Ь). Равенство (с) следует из определений множеств Sol
и Sol*. Неравенство (d) справедливо, потому что функция и удовлетворяет
условию (17.18), и справедлива оценка (17.23).
Таким образом, утверждение 17.7 доказано.
17.8.	Утверждение
Множество Su содержит локально ограниченную функцию и\ опре-
деленную следующим образом
^(to^o) := min{w+(t0, я0), ^(to,^o)},
где
^+(to,^o) := sup{< е R: /i+(to,^o?C) 0},
/i+(t0, xq, zq) :=	sup	[cj(0, x(0)) - z(ff)]
(:r(-),2:(-))GSol(to;ao,-Zo,s*)
s* — некоторый вектор в Rn.
17. Задача Коши для уравнений Гамильтона-Якоби ...	231
Доказательство. Согласно утверждению 8.6, функция и+ удовлетво-
ряет условию
inf{u+(r, ж(т)) — г(т): (ж(-),г(-)) С Sol (to, xq, zq, 5)}	0
для любых (to,^o) £ (0,0] x Rn, zq > u+(to,xo), r e [to,0], s C Rn.
Поэтому из определений функции и функционала 7 (17.15) следует, что
функция удовлетворяет условию (17.18). Также очевидно, что функция
локально ограничена, и выполняется равенство х) —	х).
17.9.	Утверждение
Пусть S — непустое подмножество множества Su. Тогда функция
(0,0] х R™ э (t, х) I—> u(t, х) Е R, определенная равенством
u(t. х) := supinf{?/(T, £): (т, £) Е B^(t, х), и Е S},	(17.24)
£>0
является верхним решением задачи (17.2)-(17.5). Здесь
;= {(т,е) е (0,0] х ИГ: ||£ - х|| £, |t-/|O}.	(17.25)
Аналогично, пусть S С Sl, S 0. Тогда функция и: (0,0] х Rn н-> R,
определенная равенством
u(t. x) inf sup{u(r, £): (г, £) Е В^,ж), и Е S},	(17.26)
£>0
является нижним решением задачи (17.2)-(17.5).
Доказательство. Чтобы показать полунепрерывность функции и свер-
ху (функции й снизу), можно применять те же аргументы, что и при до-
казательстве утверждения 8.7. Так, тем же путем, которым подобное соот-
ношение было установлено при доказательстве утверждения 8.7, получим
равенство и(в,х} = си(0,ж). Так как любая функция и Е S1 удовлетворяет
неравенству и < сс, получаем, что й < си.
Покажем, что в области Q = {(t,x,z) Е (O,0)xRnxR: z < cu(t,ж) мно-
жество epi и слабо инвариантно относительно дифференциального включе-
ния (17.16).
Пусть (to,^o) £ epitt П Q, s E Rn. Можно выбрать т* Е (to,0) та-
ким образом, чтобы гарантировать неравенство z(г) < са(т, х(т)) для лю-
бых т е [tg, т*] и (ж(-), г(-)) Е Sol (to, xq, zq, s). Согласно (17.24), можно вы-
брать такую последовательность (tk,Xk,Uk) Е (0,0] х Rn х S (к = 1,2,...),
что
(tfc, хк) (to, ж0), Uk(tk) Xk) w(to, Жо), когда к -» оо.
232
Глава IV
Пусть Zk := Uk(tk, Xk) + Zq — u(t0, Xq) + 1/fc и пусть T e (t0, т*). Очевидно,
что Zk > Uk(tk,Xk) и Zk —* zq, когда к —> ос. Без потери общности, мо-
жем полагать, что z(t) < cj(t,x(t)) для всех (x(-),z(-)) € Sol (t/~, Xk, Zk, s\
к = 1,2,..., и при всех t G [to,r]. Функции Uk удовлетворяют усло-
вию (17.18), поэтому можно выбрать такую подпоследовательность тра-
екторий z^^)) G Sol (tk.Xk, Zk, s) (fc = 1,2,...), что
г{к\т^ик(т,х^(т))-1/к.
(17.27)
Теперь так же, как и при доказательстве утверждения 8.7, выводим,
что существует траектория (х* (•),£*(•)) Е Sol (to, хо, ^о, з), удовлетво-
ряющая соотношению (г, х(т), z(r)) G epi и. Следовательно, множество
epi и A Q слабо инвариантно относительно характеристического включе-
ния (17.16). Итак доказано, что функция и является верхним решением
задачи (17.2)-(17.5).
Подобным же образом можно доказать слабую инвариантность множе-
ства hypo й относительно дифференциального включения (17.16). Утвер-
ждение 17.9 доказано.
17.10.	Доказательство теоремы 17.5
Рассмотрим функции Uq и йо, определенные на (0,0] х равенствами
u0(t,x) := supinf{w(r,£): (т,£) GB^(t.x), и G Sw}, (17.28)
£>0
uq(1,x) := inf sup{zz0(r, £): (т, £) G B^(t,x)}.	(17.29)
Согласно утверждению 17.9, функция Uq является верхним решени-
ем задачи (17.2)-(17.5). Отметим также, что и0 — минимальный элемент
множества S'u, то есть
UqESu, Uq^u, VugS\
(17.30)
Из утверждения 17.8 следует, что и0 Так как функция ш непрерывна,
получаем неравенство uq С Далее, повторяя рассуждения из доказатель-
ства теоремы 8.2 (см. раздел 8.8), в которых мы ссылаемся на утвержде-
ние 17.7 вместо утверждения 8.5, и приходим к заключению, что функция й0
является нижним решением задачи (17.2)-(17.5). Очевидно, что Uq ^о-
Теорема 17.5 доказана.
17.11.	Пример
Рассмотрим задачу (17.2)—(17.5) для случая, когда гамильтониан Н
независим от переменных t, х и z. Также предполагается, что функция cj
17. Задача Коши для уравнений Гамильтона-Якоби ...	233
независима от переменной t и выпукла или вогнута по х. Таким образом,
рассмотрим следующую задачу: найти функцию и: (0,0] х Rn i-» R, удо-
влетворяющую соотношениям
u(t.x) ^cj(x), V(t,x) е (0,0] хГ;	(17.31)
и(0, х) = ш(х), Vx е Rn;	(17.32)
~ + H(Dxu) 0, если (t,x,u(t,x)) G Q; (17.33)
+ H(Dxu) > 0, У((,ж) € G := (0,0) xRn.	(17.34)
Здесь Q := {(Л ж, z) е (0,0) х Rn х R: z < ш(х)}.
Напомним, что в утверждении 10.2 была доказана справедливость од-
ной из формул Хопфа при выполнении следующих предположений:
(С 1.1) гамильтониан удовлетворяет условию Липшица вида
|Я(р) - H(q)\	A||p-g||, Vp,<zGR";
(СТ .2) функция w: Rn i—> R выпукла.
Теперь мы сформулируем и докажем утверждение, которое может быть
рассмотрено как модификация и обобщение формулы Хопфа (10.5) на слу-
чай задачи (17.31) — (17.34).
Пусть выполнены предположения (С 1.1) и (С 1.2). Тогда функция
u(t, х) := sup [(s, х) 4- (0 —	— u>*(s)],	(17.35)
V(£,x) e (0,0] хГ
является минимаксным решением задачи (17.31) —(17.34). Здесь
Н~(з) := тш{Я(з), 0}.	(17.36)
Напомним также, что
u>*(s) = sup [(s,х) — и>(ж)]
— это функция, сопряженная к функции си.
234
Глава IV
Доказательство. Так как функция cj выпукла, то справедливо равен-
ство
ш(х) = sup [(s, х) — о>*($)].
Вследствие (17.36) и (17.35) имеем Н~ $0и u(t,x) < ш(х). Из (17.35) и
вышеупомянутого равенства следует также и(0, х) = cj(.r). Поэтому функ-
ция и удовлетворяет условиям (17.31) и (17.32).
Теперь покажем, что для функции и выполняются условия (17.37)
и (17.38), стоящие ниже:
f) — {s, f) + H(s)] ^0,	(17.37)
для всех (£, х, u(t, ж)) € Q и з е Rn;
sup [du(t, x\ 1,/) — (syf) + H(s)]	0,	(17.38)
/GRn
для всех (t. x) e G и 5 € Rn.
Таким образом, переписаны условия (U5') и (L5'). Примем также
во внимание, что функция и дифференцируема по направлениям, т. е.
d~u(t, х; 1, /) = d+u(t, х; 1, /) = du(t, х\ 1, /).
Сначала предположим, что множество dom w*:={s 6 ln: cj*(.s) < ос}
ограничено. Определим множество
S0(t,x) {.sq е Rn: (s0, х} + (9 -	- cu*(s0) = u(t. ж)}. (17.39)
Это множество непусто и компактно. Для производной функции и в точ-
ке (t, х) е G по направлению (1, /) имеем формулу (см. аналогичную фор-
мулу (10.9))
du(£, ж; 1,/) = max [(so,/)-Я-(,s0)].	(17.40)
«о es0{t,x)
Рассмотрим условие (17.38). Справедливы следующие соотношения
sup [du(t, х\ 1, /) - ($, /) + H(s)] =
fe^n
= sup max [($o ~	- H~(sq) + H(s)] =
f^n> soeso(t,x)
— max sup [(s0 — 5,/) - H~(sq) + H(s)] = max «(s, «o)>
soeSo(t,x)	s0GS0(t,a?)
17. Задача Коши для уравнений Гамильтона - Якоби. ..
235
где
.	. Г Н(з) — Н~(з)	0, если s = 50,
ф,50) = <	,
(ос,	если s Ф з0.
Здесь использованы условия (17.40) и (17.36). Таким образом, приходим к
заключению, что функция и (17.35) удовлетворяет условию (17.38), т. е. эта
функция является нижним решением задачи (17.31) — (17.34).
Остается проверить, что функция и удовлетворяет условию (17.37).
Введем обозначение
/1(5, t) := cu*(s) - (0 -	sdn,te (0,0).	(17.41)
Пусть //**(-, t) — вторая сопряженная функция к функции /г(-Д). Отметим,
что функция s и-> /z**($,£):	(—ос, ос] выпукла и полунепрерывна
снизу. Функция //**(•, t) является выпуклой оболочкой функции д(-,£), т.е.
д**(-Д) — co/i(-,t) — наибольшая выпуклая миноранта функции /х(-,£).
Имеют место следующие соотношения
/фД), ser, £е(О,0),	(17.42)
tz(t, х) — max[(s, х) —	£)] = max[(s, х) — //**(5, £)].	(17.43)
Рассмотрим
S*(t. х) := {s* е Rn: (s*,x) —	= u(t,x)}.	(17.44)
Для любых (£, х) е (0,0) х Rn множество S*(t,a?) непусто, выпукло, ком-
пактно и содержится в domcj*. Справедливо включение
S0(M С S*(t,x), V(t,x) е (0,0) х Rn. (17.45)
Здесь So(t, х) — множество, определенное в соответствии с (17.39).
Выберем точку (t,x) € (0,0) х Rn. Возможны два случая: (j) суще-
ствует такой вектор 5* € S*(t}x), что H(s*) > 0; (jj) H(s) С 0 при
всех я е S*(t,x).
Рассмотрим случай (j). Функция Н(я) непрерывна, поэтому
Я(з) > 0 для s С B(s*; s),
где е > 0 — достаточно малое число. Принимая во внимание (17.42), полу-
чаем
/z**(5,t)	cj*(s), s е В(5*;е).
236
Глава IV
Из (17.36) и (17.41) вытекает
[i(s. t) cu*(s), s е Rn,
т. е. является выпуклой минорантой функции /л (•,£)• По определе-
нию //**(-,£), эта функция — наибольшая выпуклая миноранта функ-
ции //(•,£). Поэтому
^cZ(s), ser.
Таким образом, получаем равенство
= w*(s), s е В(з*;е).	(17.46)
Принимая во внимание, что s* 6 5*(£, ж), выводим из (17.46) и (17.43)
u(t,x) = тах[(«,ж) — /i4**(s,t)] =
= max )[(s,#) — /i**(s,t)] =
= max [(s, x) — o/(s)] = (<$*. x) — cj* (s*).
seB(s*;s)
Функция s h-> [(s,.r) — ct?*(s)] является вогнутой и достигает своего макси-
мума в центре шара B(s*; е). Значит, это глобальный максимум, т. е.
(s*, х) — cj*(s*) = max[(s,£) — cj*(s)] = cj(x).
Таким образом, в случае (j) имеем равенство u(t, х) — си(.т). Следовательно,
в этом случае, (С х. u(t, х)) Q, и неравенство (17.37) проверять не нужно.
Рассмотрим случай (jj). В этом случае для всех з € S*(t, х) справедли-
во неравенство Н(з) Z 0. Из (17.36) и (17.45) следует, что = H(s)
для всех з е So(t. х). Следовательно, формула (17.40) совпадает с форму-
лой (10.9). Поэтому, таким же образом, как при доказательстве утвержде-
ния 10.2, получается неравенство (17.37).
По предположению, множество domcj* ограничено. Мы установили,
согласно этому предположению, что функция и (17.35) удовлетворяет усло-
виям (17.31), (17.32), (17.37) и (17.38). Следовательно, эта функция — мини-
максное решение задачи (17.31)-(17.34). В общем случае, когда не предпо-
лагается ограниченность множества domа/, формула (17.35) может быть
доказана с помощью предельного перехода, как это было сделано при до-
казательстве утверждения 10.2.
17. Задача Коши для уравнений Гамильтона-Якоби ...	237
Можно также проверить следующее утверждение. Пусть гамильтони-
ан Н(<§) удовлетворяет предположению (С 1.1), и пусть функция ш: R™ R
вогнута. Тогда функция
u(t, х) :=	“ 7)Я~(«$) ~	(tS)]5
(t,x) е (0,0] xRn	(17.47)
является минимаксным решением задачи (17.31)-(17.34). Здесь
w,(s)= inf [<«,ж> - w(a#
Проверка этого факта опущена, так как она подобна доказательству утвер-
ждения 10.2 и формулы (17.35).
17.12. Некоторые замечания
Минимаксные решения задачи (17.2)—(17.5) также связаны с диффе-
ренциальная играми на оптимум времени, которые определяются здесь сле-
дующим образом.
Пусть движение управляемой системы описано уравнением (17.6), где
функция f удовлетворяет предположениям (А1)-(АЗ) (см. пункт 11.1).
Здесь мы полагаем д = 0, 0 = 1. Пусть задано замкнутое множе-
ство М С [0,1] х Rn. Рассмотрим функционал платы вида
( п ,= 1 если М*))	€ М,	(1748)
[ min{7 е [to, 1]: (t, x(t)) G М}, в иных случаях,
где 0^ — произвольное число, большее 1, а функция #(•): [7о,1] |~> Rn
описывает движение системы (17.6). Как известно, для любой начальной
точки {to.xo) дифференциальная игра (17.6), (17.48) имеет цену T(to,xo)
(см., например, [122, 123]).
Рассмотрим также дифференциальную игру (17.6) с платой вида (17.7),
где полагаем
о?(7, х) = dist ((7, х): М), g(t, х,р, q) = 0, 0^1.	(17.49)
Предположим, что цена дифференциальной игры (17.6), (17.7), (17.49) рав-
няется нулю. Тогда оптимальная стратегия игрока, который минимизирует
плату (17.7), (17.49), обеспечивает встречу точки (7,х(7)) с множеством М
не позже, чем за время 7 = 0. Обратное утверждение также верно. Если в
238
Глава IV
дифференциальной игре (17.6), (17.48) существует стратегия преследовате-
ля, которая обеспечивает встречу не позднее, чем за время t = 0	1, то
цена дифференциальной игры (17.6), (17.7), (17.49) равна нулю.
Пусть u(t, х, 0) —минимаксное решение задачи (17.2)—(17.5), где функ-
ция и определена соотношением (17.49), а гамильтониан задан равенством
H(t,x,s) = minmax(s, f(t, х^р, q)} = maxmin(s, f(t. x,p, q)).
peP qeQ	qeQ peP
Заметим, что здесь 0 — это параметр, который изменяется на интерва-
ле (0,1]. Чтобы отметить, что решение задачи (17.2)-(17.5) зависит от этого
параметра, включаем его в определение. Из вышесказанного следует
T(to,xo) = 0\ если u(to,XQ,0) О, 40 е [tQ, 1],
T(to, xo) = min{0 € [to? 1]' жо? 0) = 0}, в ином случае.
Заметим, что функционал платы 7 вида (17.7), (17.49) и соответствую-
щая функция цены (минимаксное решение задачи (17.2)-(17.5)) непрерыв-
ны, в то время, как в дифференциальной игре на оптимум времени, функци-
онал платы и функция цены только полунепрерывны снизу. Поэтому диффе-
ренциальная игра с платой вида (17.7), (17.49) (и/или задача (17.2)- (17.5),
(17.49)) может рассматриваться как регуляризация дифференциальной игры
на оптимум времени до встречи с целевым множеством М.
Отметим, что Е. Н. Баррон в работе [23] развил исследования диффе-
ренциальных игр вида (17.6), (17.7) на случай платы вида
7^о,Ц-),7’(-)л(-)) min
t e [to 1
где (jj и g — непрерывные функции. Как показано в его работе [23], функ-
ция цены этой дифференциальной игры может быть разрывной, и она удо-
влетворяет в вязкостном смысле уравнению Гамильтона-Якоби-Айзекса,
связанному с этой дифференциальной игрой.
В заключении раздела заметим, что для решения задач вида (17.2)-(17.5)
был разработан ряд вычислительных алгоритмов и компьютерных про-
грамм. В качестве иллюстрации рассмотрим следующий пример. Пусть
77,-2, 0 = 6, tu(t, х) = у х\ 4- х|,
H(t.x,s) = (х2 — 5)$1 4- |si| — (sina?i — 1.91)s2 — |^а|-
На рис. 17.1 изображены линии, которые выделяют множества {х € Rn:
u(ti^ х) = 0} и {х е Rn: u(ti, х) > 0}, ti = 0.1,0.2, ..., 6.0. Здесь u(t, х) —
17. Задача Коши для уравнений Гамильтона-Якоби ...
239
Рис. 17.1
минимаксное решение задачи (17.2)-(17.5) с указанными функциями о; и Я.
Пример моделировался с помощью компьютерной программы, разработан-
ный А. Хрипуновым.
Заметим, что этот пример связан с дифференциальная игрой ви-
да (17.6), (17.7), (17.49), в которой движение управляемой системы описано
уравнениями
±1 = х2 + q,	— 6 q < -4,
±2 = — sin Xi + р, 0.91 С р 2.91.
Терминальное множество задается выражением
М = {(t,X1.X2):	0, Xi = Х2 = 0}.
Ранее в статье [217] вышеупомянутый пример дифференциальной иг-
ры использовался в качестве иллюстрации применения численных методов
для решения следующей задачи: сконструировать такую область D, что для
любой начальный точки (х^х®) е D существует стратегия U преследова-
теля (игрока, который выбирает управление р), которая гарантирует встречу
с терминальным множеством за конечное время. Линии, ограничивающие
множество на рис. 17.1, покрытое построенными линиями уровня цены
игры, совпадают с частью границы области D.
240
Глава IV
18.	Разрывные решения краевой задачи типа Дирихле
В этом разделе изучаются минимаксные решения для краевой задачи
типа Дирихле, которые могут быть разрывными. Введение таких решений
мотивировано некоторыми проблемами теории оптимального управления
и, особенно, теории сингулярно возмущенных эллиптических уравнений.
Главный результат этого параграфа — теорема 18.6 о существовании и един-
ственности минимаксного решения краевой задачи типа Дирихле. Этот ре-
зультат проиллюстрирован простым примером, в котором демонстрируется
сходимость решений в задаче Дирихле для сингулярно возмущенных эллип-
тических уравнений к разрывному минимаксному решению. В следующем
параграфе будет рассмотрена дифференциальная игра на оптимум времени
(игра преследования-уклонения), функция цены которой совпадает с ми-
нимаксным решением задачи Дирихле для уравнения Айзекса-Веллмана.
18.1.	Постановка задачи
Рассмотрим дифференциальное уравнение в частных производных пер-
вого порядка
F(xy и, Du) = 0, х G G С Rn,	(18.1)
с граничным условием
и(х) = <т(х), х Е 8G.	(18.2)
Здесь G — открытое множество в Rn. Напомним, что символом 8G обо-
значается граница G, и(х) — вещественная функция, определенная на G :~-
= G U 3G. Вещественные функции (ж, г, s) F(x, z, s) и х а(х) опре-
делены на G х R х Rn и 3G соответственно.
В последующем будем полагать, что функция z F(x.z.s) строго
убывающая. Тогда можно вместо вышеупомянутой задачи рассматривать
следующую
Я (ж, Du)-и = 0, жеСсГ,	(18.3)
и(х) = <т(ж), х Е dG.	(1^-4)
Отметим, что конструкции, представленные ниже, могут применяться и к
уравнениям вида
Н(х, и, Du) — и = 0,
с убывающими функциями z i—> H(x,z,s). Однако, чтобы избежать несу-
щественных деталей, ограничимся изучением случая, когда УЧП первого
порядка записано в виде (18.3).
Задача (18.3), (18.4) будет рассматриваться при следующих предполо-
жениях:
18. Разрывные решения краевой задачи типа Дирихле
241
(Н1) Функция Я(-,0) ограничена, т. е.
|Я(.т,0)|^с, V.teG.	(18.5)
(Н2) Для всех х € G и pi, Р2 € имеет место неравенство
|Я(ж,Р1) - Я(ж,р2)| «S pO)IIpi -Р2||,	(18.6)
где р(х) = (1 4- ||.т||)д, д — положительное число.
(НЗ) Для любого ограниченного множества Д С G существует константа А,
такая, что
|Я(а:1,р) -Н(х2,р)\	Л||Ж1 - аг2||(1 + ||р||)	(18.7)
для всех р Е и xi, Х2 Е А.
(Н4) Граничная функция <г(х) непрерывна на dG и удовлетворяет оценке
|сг(х)| с, MxEdG.	(18.8)
Заметим, что предположение (НЗ) можно заменить на более слабое
условие (НЗ*), введенное М. Дж. Крэндаллом, X. Ишии и П.Л.Лионсом в
работе [55]. Это условие формулируется следующим образом.
(НЗ*) Пусть Д ~ открытое ограниченное множество из G. Рассмотрим
множество
г = {(.Т,у) € Д х Д: ||ж - у|| < 1}.	(18.9)
Предполагается, что для любого е > 0 и для любого открытого ограни-
ченного подмножества Д С G существует функция w£: Г —» R+, отве-
чающая следующим требованиям: we — липщицева на Г и непрерывно
дифференцируема на Г; для любых (ж, у) Е Г справедливо неравенство
ws(x, у) - Н(х, -Dxw£(x, у)) 4- Н(у, DyWs(x, у))	0;	(18.10)
и выполняются оценки
w£(x,x)^e. \/хеД;	(18.11)
liminf{w£(o:, у): ||ж — у\\ г} = оо,
Vre(0,l].	(18.12)
242
Глава IV
Проверим, что при выполнении вышеупомянутого условия (НЗ) функ-
ция
удовлетворяет требованиям (18.10)- (18.12). Здесь предполагается, что
0 < 2z7 < min{l,l/A}, sA < 1 — 2Az/,	(18.14)
где A — константа из условия Липшица (18.7). Обозначим Dxw£(x, у) бук-
вой s. Ясно, что Dyw£(x, у) — —s и
s = 2р(е2/" + ||ж - yll2)^1^ - у)/е.
Очевидно, что для любых (z, у) е г
||s|| • ||ж - у|| 2vws(x,y), w£(x,y) > \\х - у\\2и/е,	(18.15)
Здесь последнее неравенство следует из оценок ||.т — 2/||	1 и 2и < 1.
Условие (18.7) и оценки (18.15) получаются следующим образом
We(®,y) - Н(х, -Dxwe(x,y)) + H(y,Dy(x,y)) =
= Ws(x, у) - Н(х, -s) + Н(у, -з) >
> w£(x,y) - А||ж - 2/||(1 + ||s||)
> (1 - 2Xv)we(x, ?/) - А||ж - 2/|| >
>(l-2Xu)\\x-y\\2l'/e-X\\x-y\\^
(1 — 2Xv — Ае)||т — 2/||/е 0.
Таким образом, получено, что для функции w£ вида (18.13) условие (18.10)
выполнено. Легко заметить, что функция w£ удовлетворяет также и требо-
ваниям (18.11) и (18.12).
18.2.	Предварительные замечания
Напомним, что в предшествующих разделах мы имели дело с верх-
ними и нижними решениями УЧП. Предполагалось, что верхние (нижние)
решения полунепрерывны снизу (полунепрерывны сверху). Минимаксные
решения были определены как функции, которые обладали одновременно
свойствами верхних и нижних решений. Таким образом, согласно преды-
дущим определениям, минимаксные решения предполагались непрерывны-
ми. В этом параграфе рассматривается обобщенное (возможно разрывное)
18. Разрывные решения краевой задачи типа Дирихле
243
решение задачи (18.3), (18.4). Здесь не требуется, чтобы такое решение
совпадало одновременно с некоторым верхним решением (18.3) и с некото-
рым нижним решением этого уравнения. Вместо этого, минимаксные реше-
ния определяются, как поточечные пределы последовательностей верхних
и нижних минимаксных решений (см. ниже определение 18.3).
Предложенный подход имеет истоки в теории позиционных диффе-
ренциальных игр (см., например, [122, 123, 193]) и связан с конструкциями
функции цены, определяемой как верхняя огибающая г-стабильных функ-
ций или нижняя огибающая u-стабильных функций.
Следует упомянуть, что исследованиям разрывных решений УЧП пер-
вого порядка уделяется в последние годы много внимания. Так, в рабо-
тах [182, 195] были доказаны существование и единственность разрывных
минимаксных решений в задаче Коши для уравнений Айзекса-Веллмана.
Результаты, представленные в этом параграфе, были опубликованы пред-
варительно в статьях [197, 198]. Соответствующий подход использовался
также в недавних работах М. Барди (см., например, [15, 16]).
В случае, когда функция s н-> F(x,z,s) является выпуклой, непре-
рывные и разрывные решения задач типа Дирихле (18.1), (18.2) были рас-
смотрены в ряде статей, посвященных, главным образом, исследованиям
функции цены в задачах быстродействия, т. е. в задачах управления на оп-
тимум времени (см., например, [14, 26, 22, 20, 21, 69, 54, 58, 96, 103, 141] и
библиографию в них).
В данном параграфе не требуется выпуклость функции F(x, z, •). Сфор-
мулированные ниже предположения на F и а охватывают краевые задачи
типа (18.3), (18.4), возникающие в играх преследования-уклонения. Хо-
рошо известно, что для игр преследования-уклонения разрывная функ-
ция цены является типичной. Будет показано, что функция цены такой
игры совпадает с минимаксным решением соответствующей краевой за-
дачи (18.3), (18.4).
В нескольких работах также были получены результаты для разрыв-
ных вязкостных решений, введенных X. Ишии (см. например, [94]). Однако
введенное понятие не подходит для решения некоторых проблем, возника-
ющих в теории оптимального управления и теории дифференциальных игр,
таких, как задачи на оптимум времени (см. ниже пункт 18.16 и параграф 19).
18.3.	Определение
Верхним решением задачи (18.3), (18.4) называется полунепрерывная
снизу функция и: G 1, которая удовлетворяет следующим требовани-
ям'.
(i)	ее сужение на область G является верхним решением уравне-
ния (18.3);
244
Глава IV
(ii)	для нее выполняются граничное условие (18.4) и ограничение
\и(х)\^с, \/хеа	(18.16)
Нижним решением задачи (18.3), (18.4) называется такая полунепре-
рывная сверху функция и: G R, что
(j) ее сужение на область G является нижним решением уравне-
ния (18.3);
(jj) для нее выполняются граничное условие (18.4) и ограниче-
ние (18.16);
(jjj) функция и непрерывна в каждой точке х Е BG.
Минимаксным решением в задаче (18.3), (18.4) называется функ-
ция и: G R, удовлетворяющая соотношениям
lim u^k\x) = и(х) = lim w/Дж), Vх е G. (18.17)
к—к—>оо
где	— последовательность верхних (нижних) минимакс-
ных решений задачи (18.3), (18.4).
Здесь для введения понятий верхних и нижних решений уравне-
ния (18.3) адаптировано определение 4.4. Ясно, что для уравнения (18.3)
характеристические включения (2.5), (2.6) должны иметь вид
(ж, z) Е Е(х, z, s),	'	(18.18)
E(x,z,s) := {(/, g) € R” x R: ||/|| < p(x), g = (f,s) - H(x,s) + .7}.
(18.19)
где p(x) = (1 + ||ж11)м (cm- условие (18.6)).
Поэтому можно использовать следующие определения. Полунепрерыв-
ная снизу (сверху) функция w: G м 1 называется верхним (нижним) реше-
нием уравнения (18.3), если для любого s е Rn ее надграфик (подграфик)
слабо инвариантен относительно дифференциального включения (18.18).
В случае, когда минимаксное решение непрерывно, предельные соотно-
шения (18.17) эквивалентны требованию для gr и быть слабоинвариантным
относительно дифференциальных включений (18.18). Нетрудно видеть, что
любое классическое решение задачи (18.3), (18.4) (если такое решение су-
ществует) является минимаксным. С другой стороны, ниже будет показано,
что минимаксное решение и удовлетворяет уравнению (18.3) в каждой точ-
ке х е G, где оно дифференцируемо.
Заметим, что для любых (ж, z,p, q) е G х R х Rw х Rn справедливо
Е(х, z,p) А Е(х, г, q) 0.	(18.20)
18. Разрывные решения краевой задачи типа Дирихле
245
Это соотношение будет использоваться ниже. Оно следует из условия (18.6)
(Напомним, что подобные соотношения рассматривались в пункте 2.4 и в
доказательстве утверждения 8.5).
При выполнении предположений (Н1)-(Н4) справедливы следующие
теоремы.
18.4.	Теорема
Пусть существуют нижнее решение задачи (18.3), (18.4). Тогда суще-
ствует верхнее решение uq и такая поточечно сходящаяся последователь-
ность нижних решений что
lim иДх) иДх\ Vх eG.	(18.21)
к—»эс
18.5.	Теорема
Для любого верхнего решения и и для любого нижнего решения v верно
неравенство
u(x)^v(x), VxtG.	(18.22)
18.6.	Теорема
Предположим, что существует нижнее решение задачи (18.3), (18.4).
Тогда существует единственное минимаксное решение в задаче (18.3),
(18.4). Это минимаксное решение совпадает с минимальным верхним ре-
шением.
Теорема 18.6 — главный результат этого параграфа. Она следует из те-
орем 18.4 и 18.5, которые будут доказаны в разделах 18.8-18.14. Согласно
теореме 18.6, минимаксное решение является минимальным верхним реше-
нием задачи (18.3), (18.4), поэтому оно является полунепрерывным снизу.
Это свойство совместно с полунепрерывностью снизу функции цены в за-
дачах управления и в дифференциальных играх на оптимум времени.
Однако, когда требуется иметь дело с полунепрерывным сверху реше-
нием задачи (18.3), (18.4), можно изменить определение 18.3, перемещая
условие (jjj) (непрерывность нижних решений в точках х Е 8G) в опреде-
ление верхних решений. В соответствующей модификации теоремы 18.6,
вместо существования нижнего решения, будет предполагаться существо-
вание верхнего решения задачи (18.3), (18.4).
Из конструкций и результатов, представленных в разделах 18.8-18.15,
можно увидеть, что верно также следующее утверждение.
Пусть выполнены гипотезы теоремы 18.6 и пусть существует верх-
нее решение, которое является непрерывным в каждой точке х € 8G.
246
Глава IV
Тогда существует непрерывное обобщенное решение задачи (18.3), (18.4)
(в минимаксном и/или вязкостном смысле).
В случае, когда G = Rn, граничное условие (18.4) заменяется требова-
нием ограниченности решения и(х) на Rn. Используя условие (18.5), можно
проверить, что, в этом случае, функции и+(.т) = с и и~(х) = —с являются
верхним и нижним решением соответственно. Таким образом, согласно вы-
шеупомянутому утверждению, существует единственное непрерывное ми-
нимаксное решение уравнения (18.3).
Следует отметить, что результаты о единственности и существовании
для ограниченных вязкостных решений уравнения (18.3) были предвари-
тельно установлены в [55, 58, 94] для случая, когда G — Rn. Эта задача и
ее приложения к теории оптимального управления и теории дифференци-
альных игр были также исследованы в [1, 38, 54] и других работах.
18.7.	Пример
Чтобы проиллюстрировать понятие разрывного минимаксного реше-
ния и утверждений вышеупомянутых теорем, рассмотрим следующий про-
стой пример.
В задаче (18.3), (18.4) полагаем п = 1, G = (0,1),
Н(х, з) = з 4-1, 0 < х < 1, s Е R, сг(О) — сг(1) = 0.
Таким образом, в этом случае имеем краевую задачу для обычного диффе-
ренциального уравнения
- и + 1 - 0,
ах
0 < х < 1, н(0) = п(1) = 0.
(18.23)
Задача (18.23) не имеет непрерывных решений и(х) (0 х I). Одна-
ко легко увидеть, что функция и_(х) = 0, (х Е [0,1]) является нижним
решением этой задачи. Поэтому, согласно теореме 18.6, существует един-
ственное минимаксное решение задачи (18.23). Можно проверить, что это
решение задается формулой
w(.r) =	/	1 \
[ 1 — ехр(ж — 1),
х — 0,
0 < х 1.
Отметим, что минимаксное решение совпадает с асимптотикой реше-
ний следующих краевых задач для сингулярно возмущенных «эллиптиче-
ских» уравнений
d2u£ du£ .	~
г—v + -Е- - us +1 = о,
dx2 ах
18. Разрывные решения краевой задачи типа Дирихле 247
О < х < 1, us(0) — w(l) = 0, г > 0. Решения этих задач имеют вид
exp(Asx + /ie) -exp(/is£ + Ае) - exp Asx + ехрд£я
us(x) = 14----------------------------------------------,
exp As - exp
Ae := (-1 + vT+4^)/2e	1,
це := (—1 — л/l + 4e)/2e	—оо, когда s J, 0.
Таким образом, для каждого х е [0,1] имеем ие(х) и(х), когда е | 0.
На рис. 18.1 показаны графики решений us для е = 0.1 и е = 0.05.
Верхняя кривая является графиком минимаксного решения.
Хотя сходимость решений задачи Дирихле для сингулярно возмущен-
ных эллиптических уравнений к минимаксному (возможно разрывному) ре-
шению в задаче (18.3), (18.4) может быть установлена при довольно уме-
ренных предположениях, мы не будем стремиться получить подобные ре-
зультаты, а ограничимся этим очень простым примером.
18.8.	Предварительные конструкции
Идея доказательства теоремы 18.4 имеет много общего с приведен-
ным в параграфе 8 доказательством существования минимаксного решения
в задаче Коши для уравнения Гамильтона-Якоби, которое, в свою оче-
редь, тесно связано с приведенным в работах [8, 193] доказательством
существования цены дифференциальной игры. А именно, в цитируемых
248
Глава IV
статьях функция цены была получена, как верхняя огибающая так назы-
ваемых v-стабильных функций (т. е. нижних решений уравнения Айзекса -
Веллмана).
Для xo Е G символ Х(а?о) означает множество всех непрерывных
функций t x(t):	Rn, которые являются абсолютно непрерыв-
ными на любом ограниченном интервале [0,0], удовлетворяют начальному
условию х(0) = хо и дифференциальному неравенству
||z(t)||	p(a?(i)) := (1 + ||ж(«)||)м
при почти всех t 6 R+ (напомним, что р — константа из условия (Н2)).
Ниже используются также следующие обозначения:
dist (х; dG) := inf{||ж — £||: £ е 0G},
M£:={xeG: dist (х; dG) s},
тг(х(-)) := min{t е R+: x(t) e M£}.
То(ж(-)) •— min{Z e R+: x(t) e OG}^
M^o) •= min{r£(x(-)): x(-) e X(x0)},
(IS.24)
I {0},	xo e M£.
Если x(t) £ M£ для всех t 0, то полагаем r£ (#(•)) — ос. Точно так же,
если x(t) 9G для всех Q0, то то(х(-)) = ос.
Для (xq,zo) €ОхКи$е1п символом Sol (х0, г0, я) обознача-
ется множество всех непрерывных функций (ж(-),^(-)):	х
которые являются абсолютно непрерывными на любом ограниченном ин-
тервале [0,т] С R+, удовлетворяют начальному условию (х(0), z(0)) ~
= (xq.zo) и дифференциальному включению (18.18), (18.19) при почти
всех t е Т(а?(-)) := [O/ToiX’)))-
Для функции и: G R обозначим
W+£(u)	{(х, z): х е G \ М£1 z > и{х)}^
W~(u) := {(х, z): х 6 G, z < и(х)},	(18.25)
Пусть v* — некоторое нижнее решение задачи (18.3), (18.4). Напомним,
что его существование постулировано в теоремах 18.4 и 18.6.
18. Разрывные решения краевой задачи типа Дирихле 249
Обозначим символом множество всех функций и: G R, которые
удовлетворяют ограничению (18.16), равенству
и(х) = Vх G	(18.26)
и следующему условию:
(с+) для любых (<т0,г0) € W+£(u), 0 G ©е(^о)? s G Rn,
inf{u(x(0)) — z(0): (x(-), z(-)) G Sol (ж0, г0, s)}	0.	(18.27)
Точно так же символом Sls обозначается множество всех функ-
ций и: G R, которые удовлетворяют соотношениям (18.16), (18.26) и
следующему условию:
для любых (xq,zq) е W~(u), 0 е ©о(^о)5 $ G Rn,
sup{iz(.r(0)) - z((T): (ж(-), z(-Y) G Sol (ж0, zq, s)} > 0	(18.28)
Заметим, что для е = 0 величина ©о(жо) определена условием (18.24).
Подчеркнем, ч\л в этих определениях не требуется, чтобы функ-
ции и G S£ или и G Sl£ должны были быть полунепрерывными сверху
или снизу.
Определим функцию v£, как верхнюю огибающую функций v G Sl£,
т. е.
v£(x) := sup{v(z): v G Sls}.	(18.29)
Нетрудно проверить, что
v£ G Sg, v£(x)	v*(#), VxeG.	(18.30)
Теперь покажем, что v£ G S£.
Пусть и G S£, xq G G, C G R, t G @£(xq), и s* G Rn. Определим
t*(il)(xq,Q,t,s*) := inf{w(x(r)) - z(r): (х(-),г(-)) G Sol (a?0, s*)};
{д(х0,т)} := {C G R: гД^)(ж0, r, s*) = 0}:
w(xq) := sup{/z(a?o, г): r G ©е(ж0)}-	(18.31)
Очевидно, что функция t—> г*(и)(ж0,	s*) непрерывна и строго моно-
тонна в следующем смысле:
г*(?1)(ж0, т, s*) С г^(и)(ж0,С“ Q,r, s*) - а, \/а > 0.	(18.32)
Поэтому величина /1(жо, т) определена корректно.
Чтобы показать, что v£ G S^, нужно проверить следующее утвержде-
ние.
250
Глава IV
18.9.	Утверждение
Пусть и Е Sls и s* Е Rn. Тогда для функции w, определенной соотно-
шением (18.31), справедливо w Е S£.
Доказательство. Ясно, что
Афо, 0) = и(х$), w(x0) u(xq).
(18.33)
Если xq Е М£, то 0£(жо) = {0} и w(xq) = и(х$) = v*(xq). Таким образом,
функция w удовлетворяет условию (18.26). Из (18.16) и (18.33) следует, что
w(xq) u(xq) —с для каждого xq Е G.
Теперь покажем, что w(xq) с. Выберем
(ж(-)Д(-)) Е Sol(ж0?£,<$*) А8о1(жо,С,0).
Согласно (18.20), это пересечение непусто. Из (18.31), (18.16) имеем
г*(^)(ж0,С,т,5*) < и(х(т}) - z(r) с- г(т). Из (18.18), (18.19), (18.5)
вытекает, что г(т) ег (£ — с) + с. Следовательно, полагая £ = с, получим,
что г*(^)(жо, с, т, 5*)	0. Принимая во внимание условие (18.32), выводим
/1(жо, г) с. Так как эта оценка верна для любого т Е 0е(то), заключаем,
что w(xq) 'С с.
Остается доказать, что функция w удовлетворяет условию (Сг). Пусть
(xq^zq) Е H/-(w), 0 е ©о(^о), s Е Rn. Выберем такое т Е 0-(х'о), что
£0<//(ж0,т).
СЛУЧАЙ (1). Пусть 0 С т. Определим множество
Sol# := {(ж0,г(-)) G Sol(£0jzo,s*):
(x(t),z{t)) — (xjj\z*(t)') при t Е [0,0]}.
где (#*(•)>'М’)) С Sol (370,^0,3*) П Sol (жо,£(),<$). Напомним, что, соглас-
но (18.20), это пересечение непусто. Так как zq < /Джсгт), то из непре-
рывности функции С |~» r*(u)(xo)C)T,s*) и соотношений (18.31), (18.32)
следует, что
0 < г*(^)(ж0,г0,т,^)	ш£{1/(ж(т)) - г(т): (ж(-),г(-)) Е Sol^} =
=	— 0, s*).
Из (18.31) и (18.32) получаем, что р(х*(0),т — 0) — z*(0) > 0. Отметим,
что т — в Е 0е(ж*(0)). Поэтому из (18.31) вытекает w(x^{0) — z*(ff) > 0.
Напомним, что (ж*(-),^*(-)) Е Sol(жо,^). Таким образом, в случае (1)
функция w удовлетворяет неравенству (18.28).
18. Разрывные решения краевой задачи типа Дирихле 251
Полагая 0 = т, получаем также
ш£{ад(ж(т)) - г(т): (ж(-),г(-)) € Sol^} = и(х*(т)) — z*(r) > О
и, следовательно, (ж* (г), г* (г)) е W~(u).
Случай (2). Пусть 0 > т, а а — некоторое положительное число.
Отметим, что 0 — т € 0о(^*(т)). Так как и С Sl£ и (ж*(т), z*(t)) € W~(u)9
то существуют такие (ж*(-), £*(♦)) Е Sol (ж*(г), z*(t), s), что
и(х*(0 — т)) — z*(0 — т) > —а.
Полагаем
Из (18.33) следует, что
w(x(0)) — z(ff) и(х(0)) — z(0) = и(х*(0 — т)) — z*(0 — т) > —а.
Так как (ж (•), ?/(•)) С Sol (жо, zq, з), это неравенство означает, что w удовле-
творяет условию (С7). Утверждение 18.9 доказано.
Пусть
{Мг(®о,т)} := {С е R: r*(v£)(x0, (, т, s*) = 0},
w£(a:o) := sup{jUs(2;o,г): т & 0£(жо)},	(18.34)
где функция vs определена соотношением (18.29). Согласно (18.30) и утвер-
ждению 18.9, имеем
w£ е S^.	(18.35)
Теперь просто доказать следующее утверждение.
18.10.	Утверждение
Справедливо следующее соотношение'.
«ees“ns^.	(18.36)
Доказательство. Так как имеет место (18.30), то остается доказать,
что функция ve принадлежит множеству S^. Чтобы установить этот факт,
252
Глава IV
нужно проверить, что функция v£ удовлетворяет условию (С+). Предполо-
жим противное. Предположим, что существуют такие	Е W+£(y£),
г Е 0£(жо) и s* Е Rn, что r*(v£)(#o,zo,T, $*) > 0. (Мы используем здесь
замечание (18.31).) Из непрерывности функции Q r*(v£)(x‘o, С?Л $*) и
соотношений (18.31) и (18.32) следует, что /ге(#о,т) > и w£(xq) > 2о-
Так как (то,^о) Е lV+(ve), имеем г0 > v£(#0). Поэтому получаем, что
wff(^o) > vs(xq). С другой стороны, согласно (18.35) и (18.29), имеет место
неравенство we(xo) С v£(x0)- Полученное противоречие доказывает, что vs
удовлетворяет условию (С+).
18.11.	Утверждение
Пусть и Е Sl£. Тогда его верхнее замыкание, определенное формулой
й(х) := inf sup{u(£): £ Е G, ||т — £|| < J},	(18.37)
<5>0
является нижним решением задачи (18.3), (18.4).
Доказательство. Из формулы (18.37) с необходимостью вытекает, что
функция й полунепрерывна сверху и удовлетворяет ограничению |й(т)| < с.
Из того, что функция и непрерывна в каждой точке х Е 9G, следует, что
функция й также непрерывна в каждой точке х Е 9G и удовлетворяет
граничному условию (18.4). Поэтому остается доказать, что функция й удо-
влетворяет требованию (j) из определения 18.3.
Пусть (x0,z0) Е hypolZ, в Е 0о(жо), s Е Rn. Нужно показать те-
перь существование такой траектории (#*(•)?г*(’)) С Sol(ж0,«), что
(яД#),^#)) Е hypoй.
Можно выбрать такую последовательность {(£&, С W~(u), что
(£bCfc) (>о,^о), когда к —> оо.	(18.38)
Напомним, что 0о(жо) '= [О,0о(#о)), где 0о(^о) определено соотношени-
ем (18.24) при с = 0. Отметим, что функция xq $о(^о) полунепрерыв-
на снизу. Следовательно, можно считать, что 0 < #o(£fc) (к = 1,2,... ).
Так как функция и удовлетворяет условию (С~), то существуют такие
(М‘), М’)) Е Sol (£ь s), что
u(xk(0)) - zk(ff) ~l/k, k = 1,2,...	(18.39)
Отметим, что для последовательности {(#&(•),	существует подпо-
следовательность, равномерно сходящаяся на интервале [0,в]. Чтобы упро-
стить обозначения, полагаем, что начальная последовательность была вы-
брана сходящейся, т. е.
lim (xk(t),zk(t))	(^(t),^(t))
k—>оо
18. Разрывные решения краевой задачи типа Дирихле 253
для любых t е [0,0]. Также известно, что предельная траектория
t н-» (x*(t), удовлетворяет дифференциальному включению (18.18)
при почти всех t е [0,0]. Переходя к пределу в неравенствах (18.39),
получаем И(х*(0)) — z*(0)	0. Из полученного результата следует, что
множество hypo й слабо инвариантно относительно характеристического
включения (18.18). Утверждение 18.11 доказано.
Определим функцию uq : G i—> R
ио(я) = sup inf {v£ (£):
S>0
0 < e < 5, e e G, ||ж - CH < ^},	(18.40)
где функция v£ определена соотношением (18.29).
18.12.	Утверждение
Функция uq является верхним решением задачи (18.3), (18.4).
Доказательство. Пусть {(^/c,wo(a?fc))}i° — последовательность, схо-
дящаяся к точке (ж*, г). Согласно (18.40), существует такая последователь-
ность {(cfc,^)}i° С (0,1) х G, что
\u0(xk) -v£k(Cfc)l Ж
—> 0,	||;г.-&||-*0 когда А; —> оо.
Следовательно, получаем г = lim	«о (•£*)• Таким образом, пока-
к—»оо
зано, что функция uq является полунепрерывной снизу.
Теперь покажем, что функция uq удовлетворяет краевому усло-
вию (18.4). Так как v£(x) = а(х) для каждого е > 0, и х е 9G, то из (18.40)
немедленно следует, что uq(x) < а(х) при всех х С dG. С другой сторо-
ны, имеется оценка (18.30), в которой функция непрерывна в каждой
точке х е 9G и удовлетворяет равенству v*(x) = сг(ж). Поэтому для любо-
го х е 9G верна оценка uq(x) <у(х). Таким образом, для х е 8G доказано
равенство uq(x) — су(х).
Остается доказать, что функция uq удовлетворяет требованию (i) из
определения 18.3. Для заданных (xq,zq) е epiu0, 0 е ©о(^о), s е Rn, нуж-
но доказать существование такой траектории (ж*(-),2*(-)) е Sol (х0, z0, s),
что (x*(0),z*(0)) е epiw0.
Согласно (18.40), существуют последовательности еь > 0 и
(€fc,Cfc) е W+£k(ySk) (к = 1,2,...), такие, что
||Ы^жо,
Cfc Zq, v£fc(^fc) —> Uo(xo), когда А: —> оо.	(18.41)
254
Глава IV
Отметим, что функция (ж, г) >—> 0£(х}, определенная соотношением (18.24),
полунепрерывна снизу. Из неравенства 0 < 0о(^о) следует, что 0 < 0£к(£к)
для достаточно больших к. Чтобы упростить изложение, полагаем, что
О < 0£к (£к), для всех к = 1,2,...
Так как v£ Е	, то существует такая последовательность (хк (•), £&(•)) 6
е Sol(^,Cfc^), к = 1,2,..., что
v£k (хк(0У) - zk(ff) I/к, к = 1,2,...
и, подобно тому, как это было сделано при доказательстве утвержде-
ния 18.11, из предшествующего неравенства получаем, что существует тра-
ектория
(ж*(’),г*(’)) е Sol(rEo,^o5s),
удовлетворяющая требованию (х*(&), z*(0)) Е epitt0.
18.13.	Доказательство теоремы 18.4
Пусть гк 1/к, к = 1,2,.... Как следует из (18.26), (18.29), справед-
ливо v£k < t?£fe+1. Определим функции
Ufe(z) := inf sup{u£fe(£): £ G G. ||ж - £|| < 5}.
d>0
Согласно (18.36) и утверждению 18.11, функции ик (к — 1,2,...) являются
нижними решениями задачи (18.3), (18.4). Ясно, что и/ь-н ик. Поэтому
существует предел
и\х) := lim ик(х).
к-^-оо
С другой стороны, для каждого 6 > 0 и вк < 5 имеем
inf{ve(£): 0 < в < 5, £ Е G, ||ж - £|| < v£k(x) ик(х) ??(х).
Поэтому, согласно (18.40), имеет место неравенство
и0(х) С и\х), Ух Е G.
Напомним, что, на основании утверждения 18.12, г/о является верхним ре-
шением задачи (18.3), (18.4). Таким образом, теорема 18.4 доказана.
18.14.	Доказательство теоремы 18.5
Пусть функция и (функция v) — верхнее (нижнее) решение зада-
чи (18.3), (18.4). Нужно показать, что и v. Предположим противное:
18.	Разрывные решения краевой задачи типа Дирихле 255
пусть существует такая точка ,т0 € G, что
а := v(xq) - и(х0) > 0.	(18.42)
Выберем такое число 0 > 0, что выполняется неравенство
с • ехр(-0) < а/2.	(18.43)
Здесь с — константа, определенная в условиях (18.5) и (18.8).
Обозначим символом Х<?(жо) множество всех абсолютно непрерыв-
ных функций я(-): [0,0] н-> Rn, удовлетворяющих начальному условию
х(0) = х0 и дифференциальному неравенству ||±(t)|| ^(14- ||x(t)||)/i при
почти всех t € [0,0]. (Напомним, что д — константа из условия (Н2).)
Пусть D — ограниченное открытое множество из Rn такое, что D D {x(t):
t е [0,0], х(-) е Хб>(жо)}-Полагаем, что в условии (НЗ) выбрано А := GC\D
(см. (18.9)).
Рассмотрим следующую систему дифференциальных уравнений и
неравенств:
< (1 + |к||)м, 4 = <Р(£М -	+ С;
111/11 (1 + Ы)м, V = («(е),у} -	) + у;
= -Dxwe, - Dyws,	(18.44)
где функция w£ определена равенством (18.13).
Обозначим через
решение системы (18.44), удовлетворяющее соотношениям
хе(0) = Уе(0) = х0, £е(0) = и(^о), %(0) = г>(ж0);
&(*)	w(®e(t)), 7?e(t)	v(ys(t)'), 0 t < t£.	(18.45)
Здесь момент t£ определен следующим образом:
t£ := min{t 0: (x£(t),y£(t)) Г},	(18.46)
где
Г = {(х. у) е А х А: ||ж — у\\ < 1}.
Если (x£(t),ys(t)) е Г для всех t 0, то полагаем t£ = ос. Очевидно, что
существование решения
(Жг(-),е£(-),Уе(-),%(-))
256
Глава IV
следует из определения 18.3 (см. доказательство подобного факта в разде-
ле 7.4).
Определим функцию
Ls(t, х, у, С, ??) е-*[адг(ж, ?/)+£- 77],	(18.47)
где t G R+, (х, у) S Г, (£, ij) £ R х R. Чтобы упростить изложение, обозна-
7e(t) := Ls(t,xe(t),ys(t),^s(t),Tje(t)).	(18.48)
Из (18.10), (18.44) и (18.47) имеем 7£(t)	0 при почти всех t G [0,t£).
Принимая во внимание (18.11), получаем
7sW^7s(0)^s, Vte[o,^).	(18.49)
Выберем последовательность 6k > 0, к = 1,2,..., сходящуюся к нулю.
Ниже будут использоваться следующие обозначения
t(fe)=t£fc, ж^(-) = жеД-),
Без потери общности, можно полагать, что существует предел
lim е (0, оо].
к—-»оо
Случай (1). Пусть
lim № > 0.	(18.50)
к—»ос
Из (18.45), (18.47) и (18.49) имеем
yfe)(0) = w^k\xo,xo) + w(®0) - v(x0) 'У('к\в') =
= e-e[w^^k\o\y^k\0)-) +£(fe)(0) - ^k}(0)] >
Из (18.45) и ограничений |u| c, |v| с получаем ^к\в') — T](k\0)	—2c.
Согласно (18.13) имеем u№(x(),xo) = Следовательно, u(xa) — v(xq)
— 2ce~e — Ek- Переходя к пределу и принимая во внимание (18.43), полу-
чаем п(жо) — г?(жо) > — а. Это неравенство противоречит условию (18.42).
Таким образом, в случае (1) полученное противоречие доказывает, что
и(х0) v(xo).
18. Разрывные решения краевой задачи типа Дирихле	257
Случай (2). Пусть
lim t(fc) < 0.	(18.51)
к—»оо
Без потери общности, можно предполагать, что существуют пределы
lim	lim
k—^oo	k—*oo
Покажем, что
lim ®(fc)(*(fe)) = lim	e dG.	(18.52)
k-^oa	k—*oo
Неравенства (18.45), (18.49), |u| с и |v| с доставляют оценки
(T(fc) (fW), yW (t^))) rC
ei<fe>[u;/c-)(жо,жо) + u(xq) — ж(жо)] —
< ee[Efc + 2c] + 2c.
Следовательно, ввиду (18.12), заключаем, что
lim ||xw(t<fe)) - т/(А;)(t(fc))|[ = 0.	(18.53)
к—*oo
Напомним, что № = tSk. Из (18.9) и (18.46) имеем
едГ = [ад х ад] и{(ж,у) G Д х Д: ||ж-7/|| = 1}.
Из определения множеств Д = G Г) D и D следует, что
(ж<^(^),у^(^)) е dG х dGU {(ж, у) G Д х Д: Цж-J/Il = 1}.
Поэтому, используя (18.53), получаем (18.52).
Из (18.49) и (18.45) имеем оценку
efc + «(ж0) - ц(жо) > e“t<fc> [и(ж(/г)(t(fe))) - v(j/(fe)(t(fc)))]-
Напомним, что функция и (функция г?) полунепрерывна снизу (сверху) на
множестве G. Функции и п v удовлетворяют краевому условию и(х) =
= ж (ж) = (ж) при всех х € dG. Следовательно, переходя к пределу в
вышеупомянутой оценке и принимая во внимание (18.52), получаем u(xq) —
— v(xq) 0. Это противоречит (18.42). Полученное противоречие доказы-
вает теорему 18.5.
258
Глава IV
18.15.	Теорема
В каждой точке х Е G непрерывности минимаксного решения и
задачи (18.3), (18.4), это решение удовлетворяет условиям (U3)-(U7)
и (L3)-(L7), сформулированным в разделе 4.2, где полагается F(x^z^s) =
= Н(ж, s) — z. Минимаксное решение и удовлетворяет уравнению (18.3) в
каждой точке х Е G, где оно дифференцируемо.
Доказательство. Пусть и — минимаксное решение задачи (18.3),
(18.4). По теореме 18.6 функция и является верхним решением уравне-
ния (18.3). Поэтому, по теореме 4.3, оно удовлетворяет условиям (U3)-(U7)
во всех точках х Е G.
Рассмотрим его верхнее замыкание, определенное формулой
й(ж) := inf sup{w(£): £ е G, ||ж - <|| < 5}.	(18.54)
о>0
Утверждается, что функция й удовлетворяет условиям (L3)-(L5).
Действительно, пусть (жо,го) Е hypoE, 0 < 0 < $о(хо)> s G Rn.
Пусть выбрана такая последовательность {(£fc,Cfc)}i° с W‘~(u)9 что для
нее выполняются соотношения (18.38). Из (18.17) следует, что для каждо-
го к = 1,2,... существует нижнее решение Vk, удовлетворяющее оцен-
ке \и(£к) — vk(£k)\ и^Як) — Ck- Подобно тому, как это было сдела-
но при доказательстве утверждения 18.11, можно показать, что существу-
ет траектория (#*(•)> ^*(*)) е Sol (хо, го, s), удовлетворяющая требованию
(ж*($), г*(0)) Е ЬурогГ Следовательно, множество hypo 17 слабо инвари-
антно относительно характеристического включения (18.18). Функция й яв-
ляется полунепрерывной сверху, поэтому, по теореме 4.3, свойство слабой
инвариантности множества hypoti эквивалентно условиям вида (L3)-(L7).
в которых функция и заменена на й и F(x, г, s) = Н(ж, з) -- г.
Если и непрерывна в точке х Е G, то
и(ус) = и(х), d+u(x, f) = d+u(x\ f),
T((x,E(^));hypoE) = Т((ж, u(x)); hypott),
D+u(x) = D+u(x).
Следовательно, минимаксное решение удовлетворяет условиям (L3)-(L7)
в точках непрерывности. Если минимаксное решение дифференцируемо
в точке х Е G, то D~u(x) = D+u(x) = {Du(x)}> где Du(x) — гради-
ент и. В таком случае, пара неравенств (U5) и (L5) эквивалентна равенству
Н(ж, Du(xY) — и(х) = 0.
Таким образом, теорема 18.15 доказана.
19. Дифференциальные игры на оптимум времени	259
18.16.	Дополнительные замечания
Здесь уместно упомянуть о расширении определения вязкостных ре-
шений, предложенном Х.Ишии. Согласно определению, приведенному в
работе [94], функция и(х) (возможно разрывная) называется вязкостным
решением уравнения (18.3), если она удовлетворяет условиям
Н(ж, s) — и(х)	О, х С G, s е D~u(x),	(18.55)
Н(ж, s) — и(х)	0, х е G, s е D+u(x),	(18.56)
где и и й — нижнее и верхнее замыкания и.
Из доказательства теоремы 18.15 очевидным образом следует, что ми-
нимаксное решение, определенное соотношением (18.17), удовлетворяет
условиям (18.55) и (18.56). Однако, минимаксное решение может быть не в
состоянии удовлетворить равенствам
и(х) = и(х) = v(x) на dG	(18.57)
(см. пример 18.7). Поэтому, в таком случае, вязкостного решения, опре-
деленного условиями (18.55) —(18.57), не существует. С другой стороны,
ясно, что множество функций, удовлетворяющих условиям (18.55), (18.56)
и (18.4), — бесконечно.
19. Дифференциальные игры на оптимум времени
В этом параграфе рассматривается дифференциальная игра быстро-
действия. Платой в этой игре является время, за которое фазовая точка
достигает терминального (целевого) множества. Приведено доказательство
существования цены в этой игре. Функция цены игры при этом может быть
разрывной и может допускать бесконечные значения. Определены e-оп-
тимальные стратегии игроков. Структура этих стратегий подобна хорошо
известным конструкциям оптимальных стратегий в случае, когда функция
цены непрерывно дифференцируема. Различие состоит в том, что в пред-
ложенной здесь конструкции градиент функции цены, (который может не
существовать), заменен соответствующим квазиградиентом. В построени-
ях, представленных ниже, используются результаты, полученные в предше-
ствующем параграфе.
19.1.	Дифференциальные игры преследования-уклонения
Сначала напомним постановку задачи преследования-уклонения.
Пусть заданы две управляемые системы с уравнениями движения
e(t) = /p(e(i),p(t)),	(i9.i)
= fE(T}(t),q(t)).	(19.2)
260
Глава IV
Здесь £ и ?? — Z-мерный и m-мерный вектора, соответственно. Полагаем, что
первый игрок, преследователь, управляет движением системы (19.1), в то
время как движением системы (19.2) управляет второй игрок, убегающий.
Как и в случае игры с фиксированной продолжительностью, (определенной
в параграфе 11), управления игроков удовлетворяют ограничениям
p(i) € Р, q(t) € Q,
где Р и Q — компактные множества. Предполагается, что функции
/pzR'xPwK1, fE-.Rm xQ^Rm
являются непрерывными и удовлетворяют условиям Липшица относитель-
но фазовых переменных.
Рассмотрим задачу преследования, в которой требуется обеспечить,
чтобы первые h координат точек £(t) и T}(t) совпали (здесь h — такое целое
число, что h < min{Z, m}). Первый момент, в который выполняется условие
&(£) =	1? fo), называется временем поимки. Преследователь хочет,
чтобы поимка произошла как можно раньше. Убегающий, напротив, стре-
мится или избежать поимки, или, по крайней мере, оттянуть ее, насколько
это возможно. Можно также рассматривать другие варианты определения
условия поимки. Например, можно предполагать, что поимка происходит,
когда впервые реализуется неравенство
52о) -%w)2 г2
i=l
(здесь г — заданное число, называемое радиусом поимки).
19.2.	Дифференциальные игры быстродействия. Основные
предположения
Обратимся теперь к более общему случаю. Пусть движение управляе-
мой системы описывается уравнением
i(t) = /(□?(*), p(t), g(t)),	(19.3)
где x(t) Е Rn - это фазовый вектор системы, p(t) е Р и q(t) е Q являются
управлениями преследователя и убегающего, Р и Q — компактные множе-
ства. Предполагается, что функция /: Rn х Р х Q н-> Rn непрерывна и
удовлетворяет условию Липшица
||/(ж(1),р,д) - f(.x{2\p,q)\\	(19.4)
19. Дифференциальные игры на оптимум времени	261
при всех х^\х^ Е Rn, р Е Р, q Е Q. Предполагается также, что
minmax(s, f(x,p, q)} = maxmin(s, f(x,p, q)) :~'H(x,s)	(19.5)
peP qeQ '	' q^Q p^P
для всех s e Rn и x E Rn. Заметим, что (19.5) называется условием Айзек-
са, его называют также условием седловой точки в маленькой игре. Функ-
ция s), определенная равенством (19.5), называется гамильтонианом в
дифференциальной игре быстродействия (игре на оптимум времени). Со-
гласно сформулированным выше предположениям, для любой начальной
точки xq Е и при любом выборе измеримых управлений р(-): R+ н-» Р,
q(-):	н-» Q, соответствующее решение уравнения (19.3) существует,
единственно и может быть продолжено на всю полуось R+ := [0, оо).
Пусть задано замкнутое множество М С Rn. Определим функционал
платы на пространстве С(R+; Rn) всех непрерывных функций #(•):	Rn
с помощью равенства
т(.т(-)) min{t € R+: x(i) Е М}.
(19.6)
Если x(t) £ М при всех t Е R+, то полагаем т(я(-) = ос.
Функционал т полунепрерывен снизу. Это свойство состоит в следую-
щем. Пусть ж/с(-) Е C(R+;Rn), #/-(•) —> #*(•) и т(а^(-)) —> г* при к оо,
тогда т(х*(У) < г*. Здесь	#*(•) означает равномерную сходимость
на любом интервале [0,в], т. е., для любого 0 > 0:
max ||#fc(£) — x*(t)|| —* 0, когда к —* оо.
Отметим, что предельная функция х* (•) непрерывна на R+. Отметим также,
что г* и	могут быть бесконечными.
Ясно, что описанные выше игры преследования-уклонения являются
частными случаями дифференциальной игры быстродействия вида (19.3),
(19.6). Чтобы заметить это, достаточно вместо пары уравнений (19.1), (19.2)
рассмотреть одно уравнение (19.3), в котором полагается
п — I + гп.
х = (xi, Х2, ...,Хп) = (€1,£2,- • •	 • ,Т]т),
и определить терминальное множество с помощью одного из следующих
равенств
М = {х Е Xi = xi+i, i E 1, h},
h
— Xi+i)2 r2|.
2=1
262
Глава IV
19.3.	Цена дифференциальной игры быстродействия
Введем позиционные стратегии игроков и цену в дифференциальной
игре быстродействия.
Функция U:	Р (функция V: Rn Q) называется стратегией
по принципу обратной связи или позиционной стратегией преследователя
(убегающего). Отметим, что, в отличие от случая, рассмотренного в пара-
графе 11, функции U и V не зависят от переменной t (от текущего времени).
Пусть задана начальная точка х$ е Пусть преследователь выбрал
позиционную стратегию U и разбиение
Д '.= {О = to < ti < • • • }, ti —> оо, когда i —> оо.
Обозначим символом Х(а?о, U, множество пошаговых движений диффе-
ренциального включения
i(t) е со {f(x(t), и	qeQ}	(19.7)
ti < t < ti+i, i — 0,1,2,.... Элементами множества Х(жо, U. Д) являются
непрерывные функции ж(-): R+ ь-> Rn, которые удовлетворяют начальному
условию х(0) = xq. Для любого 0 > 0 их сужения на отрезок [0,0] абсо-
лютно непрерывны и удовлетворяют дифференциальному включению (19.7)
при почти всех t е [0,0].
Точно так же пусть убегающий игрок выбрал позиционную страте-
гию V: н* Q и свое разбиение Д. Символом Х(ж0, У, Д) обозначается
множество пошаговых движений дифференциального включения
x(t) е со {f(x(t),p, V(x(ti))): р е Р)	(19.8)
ti t < ti+i, i = 0,1,2,.... Очевидно, что для любой пары (С7, V) страте-
гий по принципу обратной связи преследователя и убегающего эти страте-
гии совместимы в следующем смысле: для произвольных разбиений Д^1)
и Д^2\ выбранных преследователем и убегающим, существует (и един-
ственно) движение системы (19.3), где
p(t) = иt <
г =0,1,2,...;
q(t) -	tP^t<t^,
^2)ед(2)5 j = 0,1,2,....
Поэтому X(.tq, U, Д(^) П Х(а?о> V, Д®) ф 0-
19. Дифференциальные игры на оптимум времени
263
Ниже будут использоваться обозначения
diam (Д) := sup(ti+i — ti) для i — 0,1,2,....	(19.9)
i
Так как функционал платы (19.6), вообще говоря, может быть разрыв-
ным, то для того, чтобы определить цену в дифференциальной игре быстро-
действия, будут нужны некоторые дополнительные конструкции. Введем
функционал
т£(ж(-)) := min{t € R+: x(t) € М'}.	(19.10)
Если x(t) £ Ме для всех t € R+, то полагаем те(ж(-)) := ос. Здесь е —
положительное число, М£ — г-окрестность терминального множества М, а
именно,
М£ := (х + у: х е М, \\у\\	с}.
Далее, введем величины
Tf(^0,/7,A)	sup{r£(x(-)): я(-) € Х(ж0, U, Д)}5
Т£(хъ,иу.= limsup Tf(x0,U,A\
diam (Д)|0
Tf(z0) := inf Т?(х0,IP),
T°(xo):=limTl(Xo,U).	(19.11)
40
Очевидно, что T^' (xq)	Tf” (xо) для s' s". Из этой монотонности сле-
дует, что предел в последнем из приведенных соотношений существует.
Величина ТР(^о) называется оптимальным результатом для пресле-
дователя в классе стратегий по принципу обратной связи. Предполо-
жим, что T®(xq) < ос. Согласно определению, получаем немедленно,
что для любых е > 0 и 0 > Т®(х0) могут быть найдены такая позици-
онная стратегия U* и число 3 > 0, что для любого пошагового движе-
ния х(-) е X(x0,U*, Д), где diam(A) 5, точка x(t) достигает s-окрест-
ности множества М не позже, чем за время 0.
Аналогично определяется оптимальный результат для убегающего. По-
лагаем
T^x0,V,A) :=inf{r^(.)): х(-) € Х^о, V. Д)},
T^xQ,Vy= liminf Т|(ж0,^,Д),
diam (АДО
Т2г(Ж0) := sup Т^х0, V),
v
T^(xq) := limTfC^o, V).	(19.12)
264
Глава IV
Величина Т^хо) называется оптимальным результатом для убегающего
в классе стратегий по принципу обратной связи. Из этого определения
вытекает следующее: для любого 0 < T^xq) существуют 8 > 0, по-
зиционная стратегия К и 6 > 0, такие, что любое пошаговое движе-
ние ж(-) 6 Х(#о5 К, А) избегает на интервале времени. [0,0] встречи с
s-окрестностью множества М, если diam (Д)	6.
Для произвольных пошаговых процедур управления (Б^Д^) и (КД^2)),
выбранных преследователем и убегающим, справедливы неравенства
Tf(x0,U, AW) >	> Т2£(.г0, V, Д(2)),
где
ж»(.) е X(ar0, С7, Д(1)) ПХ(ж0, V, Д(2)).
Поэтому > ГР(а:о).
Известно, что, при сделанных в разделе 19.2 предположениях, це-
на Val0 в дифференциальной игре быстродействия существует, так что
справедливо равенство
Val(zo) :=T°(z0) =Т2°(гс0).	(19.13)
Доказательство этого факта содержится, например, в книгах [120, 122, 123].
Доказательство, приведенное ниже, основано на теореме 18.6.
Следует упомянуть, что формализация дифференциальной игры бы-
стродействия, представленная выше, не является единственно возможной.
В теории дифференциальных игр известны различные определения цены
в игре на оптимум времени и различные доказательства ее существования
(см., например, [67, 166, 174]).
19.4.	Уравнения Айзекса-Беллмана в дифференциальных играх
быстродействия
Рассмотрим следующую краевую задачу
Н(х, Dv(x)) + 1 = 0, х е G := Rn \ М,	(19.14)
г(ж)=0, xedG,	(19.15)
где H(x.s) — гамильтониан, определенный в (19.5). Для рассматриваемой
дифференциальной игры уравнение (19.14) называется уравнением Айзек-
са-Беллмана. Напомним один хорошо известный результат (см., напри-
мер, [92]).	_
Пусть непрерывная функция v: G ь-> R+ удовлетворяет краевому уело-
вию (19.15). Пусть эта функция непрерывно дифференцируема в области G
19. Дифференциальные игры на оптимум времени	265
и удовлетворяют уравнению (19.14). Тогда функция v совпадает с функцией
цены дифференциальной игры быстродействия.
Более того, в этом случае оптимальные позиционные стратегии Uq и V®
преследователя и убегающего могут быть сконструированы следующим об-
разом. Определим экстремальные предстратегии с помощью соотношений
Ро(х, <s) G Arg min max(s, f(x,p, q)) ,	(19.16)
pePtqeQ	J
qo(x,s) € Arg max max(s, f(x,p, q)} .	(19.17)
qeQ tpeP	J
Оптимальные позиционные стратегии Uq и Vq можно определить как су-
перпозиции предстратегий и градиента Dv, т. е.
Uq(x) := Ро(х, Dv(x)\ Щх) := q$(x, Dv(x)).	(19.18)
Доказательство этого утверждения опущено. Оно имеет много общего
с доказательством подобного факта для игры с фиксированной продолжи-
тельностью, приведенным в пункте 11.5.
Известно, что функция цены является дифференцируемой всюду в ис-
ключительно редких ситуациях. Однако, будет показано, что, в общем слу-
чае, соотношения вида (19.18), в которых вместо градиента Dv(x) исполь-
зуются квазиградиенты, определяют субоптимальные (почти оптимальные)
стратегии.
19.5.	Конструкции е-оптимальных стратегий преследователя в общем
случае
Намереваясь применить результаты, полученные в предшествующем
параграфе, используем при этом преобразование Кружкова [127]
и(х) := 1 — ехр(—v(x)).	(19.19)
Можно заметить, что функция v удовлетворяет (19.14) и (19.15) тогда и
только тогда, когда соответствующая функция и удовлетворяет уравнению
Du(x)) 4-1 - и(х) = 0, х е G := Rn \ М	(19.20)
и краевому условию
и(х) = 0, хе dG.	(19.21)
Это заключение, очевидно, справедливо для функций v и и, дифференци-
руемых в области G.
266
Глава IV
Ниже рассматривается минимаксное решение краевой задачи (19.20),
(19.21). Отметим, что функция Я(ж, s) = 7i(x, s) 4-1 удовлетворяет требо-
ваниям (Н1)-(НЗ), сформулированным в пункте 18.1. Краевая функция ст
равняется нулю, поэтому условие (Н4) также выполнено. Ясно, что констан-
та с в оценках (18.5) и (18.8) может быть выбрана равной с = 1. Отметим
также, Что функция
щ(х) = 0, V.r € G
является нижним решением задачи (19.20), (19.21).
Таким образом, согласно теореме 18.6, существует единственное ми-
нимаксное решение и : G [0,1] задачи (19.20), (19.21). Напомним также,
что функция и полунепрерывна снизу, и ее надграфик слабо инвариантен
относительно верхних характеристических включений, введенных в разде-
ле 2.5.
В частности, надграфик минимаксного решения слабо инвариантен от-
носительно следующего дифференциального включения
(±(t), z(t)) е E(x(t), z(t), q).	(19.22)
Здесь многозначное отображение Е определено как
Е(х, z,q) := со {(/(rr,p, #), д) € Rn х R: р Е Р, д == z — 1}.
где xeG, z el,qeQ. Легко проверить, что многозначное отображение Е
удовлетворяет всем условиям (i), (ii), (iii+), и (iv+), сформулированным в
пункте 2.5. Например, проверим условие (iv+). Из (19.5) вытекает
maxmin{(s, f) -д: (f.g) € E(x,z,q)} =
q^Q
= max min(s,/(ж, p, q)} — z + 1 =	4-1 — z = H(x,s) — z.
qeQ peP
Так как в рассматриваемом случае F(x, z, s) = H(x, s) — z, то из приве-
денных равенств следует, что отображение Е удовлетворяет условию (iv+).
Выполнение других требований (i), (ii) и (iii+) очевидно.
Отметим, что в соотношении (19.22) для переменной z(t) имеет место
уравнение z — z — 1, которое влечет выполнение равенства z(t) — (z(0) -
— 1)е^ 4-1.
Пусть г/ е G, q* е Q, т > 0. Пусть символом Y(p, q*) обозначено
множество траекторий р(-): [0,т] Rn дифференциального включения
y(t) € co{/(3/(t),p,g*): р £ Р},
(19.23)
19. Дифференциальные игры на оптимум времени	267
удовлетворяющих начальному условию у(0) = rj. Предположим, что y(t) € G
для любой у(-) G Y(^g*) и при всех t е [0, т]. Тогда существует такая тра-
ектория ?/(•) е Y(?y, q*), что
- 1)ет и(у(т)) - 1.	(19.24)
Этот факт следует из слабой инвариантности надграфика минимаксно-
го решения и относительно (19.22). Здесь полагаем (жо,^о) =	€
€ epi и и используем равенство z(r) =	— 1)егЧ-1. Важно отметить, что
указанное выше свойство есть форма проявления так называемого условия
//-стабильности для дифференциальной игры быстродействия (см., напри-
мер, [122, 123]).
Покажем, что функция цены дифференциальной игры быстродействия
и минимаксное решение задачи (19.20), (19.21) связаны равенством
и(х) = 1 — ехр(—Vai (ж)), х € G.	(19.25)
Более того, применяя результаты, полученные для минимаксных решений,
построим с-оптимальные стратегии игроков по принципу обратной связи
следующим образом.
Пусть и: G н-> [0.1] — минимаксное решение в задаче (19.20), (19.21).
Введем следующее преобразование функции и
иа(х) := min[u(y) + wa(x, у)].
У EG
Здесь
(19.26)
(19.27)
(19.28)
v = (2 + 2А)-1,
0 < а < min{l/3, [А(1 + А)]~ х},
где А — коэффициент из условия Липшица (19.4). Отметим, что wa — это
та же самая функция, что и в (18.13), которая использовалась в предыду-
щем параграфе при доказательстве единственности минимаксного решения.
Очевидно, что функция wa удовлетворяет неравенству
H(x,Dxwa(x,yy) - H(y,-Dywa(x,y)) -wa(x,y) 0	(19.29)
при любых (ж, у) G G х G таких, что ||ж — у 11	1. Фактически это неравен-
ство было проверено в разделе 18.1.
268
Глава IV
Покажем, что минимум в (19.26) достигается в точке уа, такой, что
||ж “ Уа\\ 2а. Очевидно, что иа(х) С и(х) 4- wa(x,^) = и(%) 4- а С 1 +
4- а < 1 -Г 1/3. С другой стороны, для любого у G G такого, что |k — х/||	1,
имеем и{у) 4- wa(ж, у) wa (х,у) 3. Так как функция у ь-> и(у) 4- wa(ж, у)
полунепрерывна снизу, минимум в выражении (19.26) достигается в точ-
ке уа, такой, что Ik — Ра|| 1- Далее, имеет место wa(x,yQ) =	—
— и(уа) иа(х) С 14-а. Из (19.27), (19.28), и последней оценки получаем
[<?/" +||ж - у||2г	(1 + а)а,
||® - у||2 < [(1 + а)а]1/р - a2/v [(1 + а)а]2 < 2а2.
Таким образом, имеем оценки
иа(х) С и(х) 4- а, |к — Уа\\ 2а.	(19.30)
Определим позиционную стратегию Ua: G н-> Р преследователя ра-
венством
Ua{x) = р0(х,за(х)).	(19.31)
Здесь функция ро — это экстремальная предстратегия, определенная
в (19.16), вектор sa(x) задается соотношениями
sa(x) := (Dxwa)(x,ya(x)) = ~(Dywa)(x,ya(x)'),	(19.32)
где
уа(х) е Arg min[u(y) + wa(a:,7/)].	(19.33)
y^G
Если функция и непрерывно дифференцируема в окрестности точ-
ки х € G, то из (19.26) и (19.33) следует, что
Du(pQk)) 4- (jDywa)(x,ya(x)) = 0.
Вследствие (19.32) и (19.30), имеем за(х) Du(x), когда а —> 0. Прини-
мая во внимание это соотношение, будем называть за(х) квазиградиентом
функции и в точке х.
Заметим также, что стратегию Ua можно определять при помощи ра-
венства
Ua(x) = p0(x,sia(x)'),
где s^k) = sQk)(l — uk))-1. В силу выполнения (19.19), разумно назы-
вать квазиградиентом функции цены дифференциальной игры быстро-
действия.
19. Дифференциальные игры на оптимум времени	269
19.6.	Теорема
Пусть х$ — точка области G, удовлетворяющая неравенству и(х$) < 1.
Пусть £ и 0 — произвольные числа, такие, что £ > 0 и 0 > — 1п(1 — и(х$У).
Тогда существуют числа а > 0 и <5о > 0, для которых выполняется оценка
T^xOyUa^)^0,	(19.34)
если diam (A)	5q. Здесь Ua — позиционная стратегия преследова-
теля, определенная (19.31), а величина Tf (#о> А) задается равен-
ством (19.11).
Доказательство. Обозначим через Х(#о) множество всех траекто-
рий х(-): R+ дифференциального включения
x(t) е со{f(x(t),p,q): ре Р, qeQ},
удовлетворяющих начальному условию ж(0) = х$. Определим
К := {x(t) е JRn: ж(-) G Х(ж0), t G [0,0]},
т := sup{||/(£ + h,p,q)\\: х е К, р е Р, q Е Q, 1}.	(19.35)
Отметим, что множество К ограничено, и т < эо. Выберем числа а > О
и д0 > 0, удовлетворяющие оценкам
За е, 8$т а, За < 1.	(19.36)
Ниже будет доказано следующее утверждение.
Пусть
^)еХ(^7а,Д).
Пусть ti е A, ti < 9, и пусть dist (ж(^); М) > За. Тогда для любо-
го т е	А [0,0] справедливо неравенство
ма(я(т)) 1 — [1 — иа(х(и)]ет~и + (т — и)ег~иН{8).	(19.37)
Здесь 8 — diam (A), h(8) —> 0, когда 5 —> 0. Величина /г (5) зависит только
от 8 и не зависит от #(•) е X(^o, Ua, А).
Помимо (19.36), будем требовать, чтобы параметры а и 8 удовлетворя-
ли неравенству
ее[а 4- 0 • h(8)] < ев~ш - 1,	(19.38)
где через ш обозначена величина — 1п(1 — и(ж0)). Отметим, что 0 > ш по
предположению. Следовательно, (19.38) выполняется для достаточно ма-
лых а и 8,
270
Глава IV
Покажем, что приведенные выше оценки доставляют требуемое нера-
венство (19.34). Рассмотрим следующие два случая: (i) существует е Д
такой, что ti < в и dist (т(£г); М) За; (ii) противоположное неравен-
ство dist (x(ti),M) > За имеет место при всех ti € Д, удовлетворяющих
ограничению ti < 0.
Из того, что За С s, в случае (i) мы немедленно получаем (19.34).
Рассмотрим случай (ii). Из рекуррентных оценок (19.37) можно получить
иа(х(0))	1 — [1 — иа(хо)]е0 4- 0eeh(S).
Так как ш = — 1п(1 — и(хо)), из (19.30) следует, что
na(.ro) u(xQ) + а = 1 — е~~^ 4- а.
Поэтому
иа(х(6»)) < 1 — [1 — иа(х0)]ев + eef)h(d) 1 - ев~ш + ева + ee0h(6) < 0.
Последнее неравенство следует из (19.38). Таким образом, в случае (ii) при-
ходим к неравенству иа(х(в)) < 0. С другой стороны, из (19.26) вытекает
иа{х(в)) > 0. Таким образом, получено противоречие, из которого следует,
что случай (ii) невозможен.
Чтобы завершить доказательство, остается получить оценку (19.37).
Напомним, что рассматривается пошаговое движение ж(-) е Х(ж0, U&. Д).
Предполагается, что ti € Д, ti < 0,t € [^,	0] и dist (rr(^); Af) > За.
Введем следующие обозначения
С =	7? = yQ(C), 5* = «а(£),
р* = Ua(g} =po(^st), q* = qo(j),s*).	(19.39)
Так как функция /(х,р, q) и позиционная стратегия Ua не зависят от пере-
менной t, можно полагать ti = 0. Пусть /* определено равенствами
Г = £(lL 6 = 1
о
(19.40)
где x(t) € со {/(#(£)./>*,#): q Е Q}. Нужно показать справедливость нера-
венства
1 - uQ(C) е~г[1 -	+ Гт)] 4- rh(r). (19.41)
Из неравенства dist(£;Af) > За и второй оценки в (19.30) вытекает,
что dist (т/, М) > а. Напомним, что $отп < а. Эта оценка и определение m
19. Дифференциальные игры на оптимум времени
271
(см. (19.35)) влекут за собой, что y(t) £ М для любой траектории диффе-
ренциального включения (19.23) и при всех t е [0,т]. Из (19.24) следует,
е~т[1 — и(т} + Гт>)]-	(19.42)
Здесь
А = у(-Т\~ 71 = 1 jy(t)dt,	(19.43)
О
y(t) е со {f(y(t),p,q*): р е Р}.
Вспоминая обозначение у = из (19.26), (19.33) получаем
МС =	+™а(£, »?)•
Это равенство вместе с (19.42) влечет за собой
1 - Ua(C) е”Т[1 - u(rl + f*T)] ~ wa(.C, П)-
Добавляя и вычитая в правой части последнего неравенства величи-
ну e~Twa(£, + /*т,Т) + /*т), получаем
1 - ««(£) < е~т[1 - и(»7 + /*т) -	+ Гт,г) + Гт)]+
+ e~Twa(£ +	+ f*r) -wa(^,q).
Из определения (19.26) функции uQ вытекает неравенство
«Д + рт) u(l) + Дт) + Wa(£ + /*Т, Т) + /*т).
Следовательно,
1 - «а(€) < е~т[1 - wa(£ + Гт)]+
+ e~Twa^ + f*T,‘n + f*T)-wa^,T)). (19.44)
Оценим величину
e~Twa(£ + Гт, Г) 4- Гт) - wa(T if).
Функция wa непрерывно дифференцируема. Напомним, что, согласно
(19.32)и (19.39), имеем s* =	rf)- Поэтому
e^Twa(£, + /*т, г] + Гт) - wa(£, rj)
e~T[wa(^,i]) + (s,,/*)r - (з*,Г)т] - wa^,Tj) + Л1(т)т
[(«*, Г) -(s»,r)~ wa(&, т]) + Н2(т)]т.
272
Глава IV
Здесь и ниже hi (т) —> 0, когда т —* 0. Эти величины зависят только от г и
не зависят от рассматриваемого движения ж(«) Е Х(хо, Ua, Д).
Из условий (19.16) и (19.39) имеем
V/eco{Mp*,g):9eQ}.
Поэтому вектор /*, определенный (19.40), удовлетворяет неравенству
Точно так же, из (19.17), (19.39) и (19.43), получаем
О?*, /*) > Я(ту, 5*) - /i4(r).
Вышеприведенные оценки влекут за собой
e~rwa(£ + /*т, т] 4- /*т) - wa(& 77)
Я(£,$*) -	- wa(£,rf)
где s* = Dxwa(& rf) = -Dywa(J^ rf). Используя (19.29), получаем
e~rwa(£ + Гт,т] + f*r)	/z5(r)r.
Подставляя это неравенство в (19.44), получаем требуемую оценку (19.41)
для /г(т) —	где /г5(т) —> 0, когда т -+ 0. Более того, из
вышеупомянутой оценки следует, что можно выбрать независимой
от ж(-) е X(x0,Ucn Д).
Таким образом, теорема 19.6 доказана.
19.7.	Построение е-оптимальных стратегий уклонения
Аналогичным образом можно построить е-оптимальную стратегию
убегающего. Пусть заданы начальная точка хо Е G и число в Е (0,о>).
Здесь ш — 1п(1 — и(хоУ), и: G н-> [0,1] — минимаксное решение в зада-
че (19.20), (19.21). По определению 18.3, существует нижнее решение
этой задачи, такое, что
— 1п(1 - щ(хоУ) Е
Напомним, что функция щ полунепрерывна сверху, и ее надграфик слабо
инвариантен относительно характеристических включений. В частности,
множество hypowt; слабо инвариантно относительно дифференциальных
включений вида
(i(t), z(t)) € co{(f(x(t),p,q),z - 1): q G Q}.
19. Дифференциальные игры на оптимум времени
273
Введем следующее преобразование функции щ
и“(х) := max[«i](y) - wa(x, у)],	(19.45)
yeG
где функция wa определена соотношением (19.27).
Выберем
уа(х) е Arg max[u^(y) - wa(x,y)].
уев
Определим позиционную стратегию Va: G > Q для убегающего с
помощью равенства
Va(x) = q0(x,sa(x)),	(19.46)
где функция qo — экстремальная предстратегия, определенная равен-
ством (19.17), вектор sa(x) задается соотношениями
sa(x) := -(DxWa)(x,ya(xy) = (Dywa)(x,ya(x)).	(19.47)
19.8.	Теорема
Пусть хо — точка области G, и пусть 3 — положительное число,
удовлетворяющее неравенству
3 < ш — 1п(1 — u(xq)\
где и: G [0,1] — минимаксное решение задачи (19.20), (19.21). Тогда су-
ществует нижнее решение этой задачи, удовлетворяющее неравенству
3 < — 1п(1 - г^(ж0)),
и такие числа е > 0, а > 0, до > 0, что оценка
T^x0,Va^)>3	(19.48)
имеет место, если diam(A) Jq. Здесь Va — позиционная стратегия
убегающего, определенная соотношением (19.46), величина	А)
задается равенством (19.12).
Это доказательство подобно доказательству теоремы 19.6, и, поэтому,
оно опущено.
Отметим, что из теорем 19.6 и 19.8 вытекает то, что цена Vai дифферен-
циальной игры быстродействия и минимаксное решение и задачи (19.20),
(19.21) связаны равенством
Vai (я?о) = — 1п(1 — и(хоУ).
Глава IV
274
Заметим также, что стратегии U& вида (19.31) является субоптимальной для
преследователя, а стратегий Va вида (19.46) субоптимальна для убегающего
(в последнем случае предполагается, что функция щ выбрана так, чтобы
разность u(xq) — щ(ж0) была достаточно малой).
20.	Кусочно-линейные приближения минимаксных
решений для уравнений Гамильтона-Якоби
В этом параграфе рассматривается задача Коши для уравнения Гамиль-
тона-Якоби, в которой гамильтониан не зависит от времени и фазовой
переменной. В отличие от в разделов, где рассматривались формулы Хоп-
фа (см. пункты 10.1-10.3), здесь не требуется, чтобы гамильтониан или
граничная функция были выпуклыми или вогнутыми. Вместо этого пред-
полагаем, что гамильтониан и граничная функция кусочно-линейны. При
выполнении этих предположений и в случае, когда фазовое пространство
двумерно, предложен конечный алгоритм для точного вычисления минимак-
сного решения. Полученное решение также оказывается кусочно-линейной
функцией. Результаты, представленные в этом параграфе, могут применять-
ся как при построении кусочно-гладких решений уравнений Гамильтона-
Якоби общего вида, так и для изучения бифуркаций этих решений.
20.1.	Положительно однородные решения
Рассмотрим задачу Коши
^+Я(Д7;и)=0, f<l, xeir,	(20.1)
и(1,ж) = <т(я), я?€Кп,	(20.2)
где гамильтониан Rn Э s ь-> H(s) 61 и краевая функция 1П Э хм <т(ж) е R
являются непрерывными и удовлетворяют условиям
|#(s(1)) - tf(s(2))| «5 A||s(1> - в(2> ||,	(20.3)
(т[ах) =	(20.4)
для любых e ln, х е Rn, а 0. Ниже будет показано, что минимаксное
решение задачи (20.1), (20.2) положительно однородно в следующем смысле
u(t,x) = (1 -i)u(o,	1<1,жеГ.	(20.5)
20. Кусочно-линейные приближения минимаксных решений ...	275
Используя это соотношение, будет сформулирована редуцированная задача
нахождения функции гг(О, х) (см. ниже задачу (20.10), (20.11)). Мотивации
для рассмотрения этой задачи будут приведены в пункте 20.2.
Итак, проверим соотношение (20.5). Пусть и: (—ос, 1] х Rn R — ми-
нимаксное решение в задаче (20.1), (20.2), и пусть выбрано положительное
число S. Определим функцию v как
v(t,x) = ц(1 + <^~ ~	, К1, геГ.	(20.6)
Так как функция и непрерывна, функция v — также непрерывна. Из ра-
венств (20.6), (20.4) следует, что и(1,ж) = <т(ж). Из определений производ-
ных по направлениям имеем
= d+u(r,£;l,f), d~v(t,x;l,f) = d~u(r,£;l, f),
где подразумевается, что т = 1 4- St — S, £ = Sx. Функция и удовлетворяет
уравнению (20.1) в минимаксном смысле, т. е. она удовлетворяет неравен-
ствам
тт[<ГИ(т,£; 1,/) - (f, s) + H(s)] < 0,	(20.7)
пж[Л(г, £; 1, /) - (/, s') + Я(з)] 0	(20.8)
J CK
в любой точке (г, £) е (—ос, 1) х Rn. Следовательно, функция v удовлетво-
ряет аналогичным неравенствам
тт[сГ<£,ж;1,/) - (f,s) + H(s)] 0,
max[</+i;(t, х; 1, /) — (/, s') + Я(з)]	0.
Таким образом, функция v является минимаксным решением в зада-
че (20.1), (20.2). Из единственности минимаксного решения следует ра-
венство u(t, х) = v(t, х). Полагая в (20.6) 5 = (1 — t)-1, получаем (20.5).
Используя соотношение (20.5), можно заменить задачу (20.1), (20.2)
следующей редуцированной задачей нахождения функции
р(х) :=и(0,х), хеТ.	(20.9)
Покажем, что функция ср является минимаксным решением следующе-
го УЧП первого порядка
Я(Р^(у)) + {D<p(.y), у) - у>(у) = 0, у е R",	(20.10)
276
Глава IV
которое рассматривается наряду с предельным соотношением
\iraa(p(y/a) =	(20.11)
аЦО
Это предельное соотношение следует немедленно из непрерывности и
и равенств (20.2), (20.5). Если функция и дифференцируема в точке (t, ж),
то из (20.5) и (20.9) следует
ди^ = ~<р(у) + (Dy<p(y), у), Dxu(t, ж) = Dy<p(y),
где у = х/(1 — t). Поэтому уравнение (20.1) преобразуется в уравне-
ние (20.10).
Минимаксное решение уравнения (20.10) определено согласно общей
схеме, т. е. согласно свойству слабой инвариантности его графика, кото-
рое, как мы знаем, может быть выражено в различных формах. Например,
под минимаксным решением уравнения (20.10) можно понимать непрерыв-
ную функцию р: >п н-> R, которая удовлетворяет паре дифференциальных
неравенств
- (s,f - у) +H(s) - <р(у)]	0,	(20.12)
max[d+y>(j/;/) - (s,f - у) + H(s) - <р(у)] > 0	(20.13)
f
при любых у е Rn, з е Rn.
Можно проверить, что из (20.5) и (20.9) вытекают соотношения
d~u(t, х\ 1, h) = d~ р(у, h + y) — р(у),
d+u(t, х; 1, h) = d+p{y\ h + у) — р(у),
где у = ж/(1 — t), t < 1, h € Rn. Следовательно,
(20.7)	<=> (20.12), (20.8) о (20.13).
Напомним, что на основании теоремы 8.1 минимаксное решение в за-
даче (20.1), (20.2) существует и единственно. В силу этой теоремы,
из (20.9) следует, что существует единственное минимаксное решение в
задаче (20.10), (20.11).
В некоторых случаях известны точные формулы для решения зада-
чи (20.10), (20.11). Например, если гамильтониан Н или краевая функция сг
выпуклы или вогнуты, то можно непосредственно применять формулы Хоп-
фа. Ниже, в пункте 20.3, будет описан алгоритм для построения минимак-
сного решения в задаче (20.10), (20.11), в случае, когда функции Н и сг
кусочно-линейны, и размерность п фазового пространства равна 2.
20. Кусочно-линейные приближения минимаксных решений ...	277
20.2.	Локальное разложение минимаксных решений
Задача (20.1)-(20.4) интересна сама по себе. С другой стороны, ре-
шения задач этого типа могут быть использованы как при изучении би-
фуркаций кусочно-гладких решений УЧП общего вида, так и для развития
численных методов. Обсудим некоторые результаты, связанные с этой те-
мой.
Рассмотрим задачу Коши для уравнения Гамильтона-Якоби
+ H\t,x,Dxv) =0, (t,x) е (0,(9) xRn, (20.14)
v(0, х) = <ть(аг), х е	(20.15)
Здесь предполагается, что гамильтониан удовлетворяет требовани-
ям (Н1)-(НЗ), сформулированным в пункте 7.2. Предполагается также, что
краевая функция сгс удовлетворяет условию Липшица
|сгь(а^1)) — сгь(ж(2))|	— а/2)||,
при любых	е Rn. Согласно теореме 8.1, существует единственное
минимаксное решение v в задаче (20.14), (20.15).
Выберем и зафиксируем точку (т,£) е (0,0] х Rn. Рассмотрим задачу
Коши
+ H(Dxu) = 0, t € (0, г) х Rn,	(20.16)
и(т, х) — и(т,х),	(20.17)
где H(s) =	Обозначим минимаксное решение этой задачи че-
рез щ (t. х). Ясно, что для любых t е [т — е, т], х е В£(£) и ||з|| К имеет
место оценка
-Я(§)|
где К — произвольное положительное число и /3± (е, К) 0, когда е —> 0.
Используя это соотношение, можно показать, что минимаксные решения v
и и\ вышеупомянутых задач Коши достаточно близки в малой окрестности
точки (т, £), т. е. справедлива оценка
\v(t. х) — Ui(t. a?)| ai(s)s, V (t,x) е [г - s, т] х В(£; е),
где од (е) —> 0, когда е —> 0.
Далее, предположим, что для любого у е существует производная
по направлению, равная
/	ч	+ &у) ~	£)
dv(r, 0, у) = Пт ------------------.	(20.18)
278
Глава IV
Рассмотрим задачу Коши для уравнения (20.16) с краевым условием
u(r, х) — v(r, £) + а(х — £),
где полагаем <т(у) dvfaZy^y). Обозначим минимаксное решение этой
задачи через U2(t> х). Можно снова показать, что
\v(t, х) — U2(t. х)|	V (t, х) е[т — г, т] х В(£; е),
где а2 (е) -» 0, когда е —> 0.
Наконец, рассмотрим минимаксное решение из(Т х) уравнения (20.16)
с краевым условием из(т, х) = <т(ж). Очевидно, что U2(t, £ -Кт) = v(r. £) +
4-х) ииз(г — 6, Sy) = iz(l — S, Sy), где и — это минимаксное решение в
задаче (20.1), (20.2). Поэтому предыдующая оценка может быть переписана
следующим образом
|г(т - 5,£ + 8у) -v(r,g) - w(l - S,Sy)\
^a(S)S, VyGRn,	(20.19)
где a(S) —> 0, когда S —> 0. Вследствие (20.5) и (20.9), справедливо
u(l - 8, бу) = 8ip(y).
Таким образом, получено следующее утверждение.
Пусть [0,0] х Э (t, х) *—> v(t. х) G R — минимаксное решение в
задаче Коши (20.14), (20.15), где гамильтониан удовлетворяет требо-
ваниям (Н1)-(НЗ), сформулированным в пункте 7.2, и краевая функция
удовлетворяет условию Липшица. Пусть (т, £) 6 (0,0] х Rn, и пусть для
любого вектора у 6 Rn существует производная dv(r,&{), у) по направле-
нию (0, ?/) (см. (20.18)). Тогда имеет место локальное разложение (20.19),
и существует производная по направлению (—1,1/)
v(r — S, £ 4- Sy) — v(i\ £) z .
dv(r, С; -1, у) = Пт---------:— = у>(у),	(20.20)
где р—минимаксное решение в задаче (20.10), (20.11) и а (у) ~ dv(r,^Q, у).
Оценка (20.19) и формула (20.20) разъясняют суть локальной структуры
минимаксного решения, что может быть использовано для решения зада-
чи (20.14), (20.15) в классе кусочно-гладких функций. Выделим одно из воз-
можных приложений представленных результатов. Так как (20.14), (20.15) —
терминальная краевая задача, то построение ее решения происходит в
20. Кусочно-линейные приближения минимаксных решении ...
279
обратном времени. Предположим, что ее минимаксное решение v яв-
ляется кусочно-гладкой функцией. Пусть это решение построено в об-
ласти [t, 0]xRn. Рассмотрим кусочно-гладкую функцию х
Эта функция сконструирована при помощи склейки конечной сово-
купности гладких функций Mi(t) Э х х) Е R (г 6 !,&(£)), где
Mi{t) cRn - дифференцируемые многообразия. Семейство многообра-
зий Mi(t) (iEl,k(t)) формирует клеточное разбиение M.(t) фазового
пространства Мп. При уменьшении параметра t, деформация многообра-
зий Mi(t) и функции vi(t. •) может оказаться негладкой в некоторые момен-
ты времени, которые называются здесь моментами бифуркации.
Пусть т — один из таких моментов бифуркации. Тогда существует чис-
ло с > 0, такое, что для любых tf Е (г — s, т) и t,f Е (т,т + с) клеточные
разбиения A4(i') и — не изоморфны. Желая продолжить построение
минимаксною решения при t < т, можно использовать формулу (20.20)
и рассмотреть сингулярные точки (т, £), в окрестности которых кусочно-
линейная структура решения изменяется. В рассматриваемом случае функ-
ция а (у) =	0, у) кусочно-линейна и положительно однородна. Если
получено решение <р(у) соответствующей задачи (20.10), (20.11), то, со-
гласно формуле (20.20), определена и производная dv(r,£; — 1,?/). Поэтому
структура кусочно-линейной функции у н-> ср (у) dv(r, £; — 1, у) извест-
на. Эта информация достаточна как для дальнейшего построения гладких
компонент минимаксного решения, так и для определения клеточного раз-
биения M(t) при t Е (т — 6, т).
20.3.	Построение кусочно-линейных решений
Теперь рассмотрим схему построения решения задачи (20.10), (20.11).
Как было отмечено в конце раздела 20.1, если функция сг выпукла или
вогнута, то для решения этой задачи имеются довольно простые форму-
лы. Согласно вышеизложенным соображениям, важно знать, как решить
проблему в случае, когда функция сг только кусочно-линейна. Если, по-
мимо этого, гамильтониан H(.s) также кусочно-линеен, можно догадаться,
что решение v задачи (20.10), (20.11) должно быть кусочно-линейным. Эта
догадка подтверждается в случаях, когда сг выпукла или вогнута. Ниже рас-
сматривается другой случай, в котором эта гипотеза также подтверждается.
Более того, для рассматриваемого случая был разработан и описан ниже
конечный алгоритм для построения точного решения.
Отметим, что, для многих задач оптимального управления и диффе-
ренциальных игр, гамильтониан х, $) в соответствующем уравнении
Айзекса- Веллмана оказывается кусочно-линейным по s. Ясно также, что
любой непрерывный гамильтониан может быть приближен функцией, ко-
торая является кусочно-линейной по s.
20. Кусочно-линейные приближения минимаксных решений ...	281
Задачи 1 и 2. Пусть заданы некоторые линейно независимые вектора а
и Ь. В задаче 1 (в задаче 2) требуется построить минимаксное решение
задачи (20.10), (20.11), (20.21) при <7 = <7+ (при ст = а~).
Можно показать, что решениями этих задач являются функции
9?+ (у) = max (у),	<р-(у)= min W (у),
ZG[a,o|
где
[а,b] — {Аа -+- (1 - А)Ь: Хе [0,1]},	= (1,у}+Н(Г).
Задачи 3 и 4. Пусть заданы некоторые линейно независимые векто-
ра а, Ъ и число г > 0. Пусть
= тах{ </>а(у), <Му)}>	= тт{<у?а(у), <^ь(?/)},
G” = {у € R2: <^(у) < г}, Gt = {у € R2:	< г}.
В задаче 3 требуется построить непрерывную функцию <р°: G ь-» R, удо-
влетворяющую следующим соотношениям
< г, \/у е Gb; = г, \/у е dG\
и уравнению
H(DkpQ(y)) + (D(^°(у), у) - (p°Q/) = 0, у е G\
которое понимается в минимаксном смысле. Точно так же в задаче 4 тре-
буется построить непрерывную функцию : G^ t—> R, удовлетворяющую
соотношениям
=r\fy e dG^
и уравнению
Я(£>Ы?/)) + (Dp0(y\y) - <р0(у) = 0, у e G^
которое понимается в минимаксном смысле.
Решением задачи 3 является функция
<^°(у) = max</?s(y) при s е Sr(a, Ь),
S
где
Sr(a, Ь) = {s е con (a, b): (ps[wo) = г},
con (а, 6) := {Аа -h /ib: А 0, у 0},
280
Глава IV
В последующем материале описывается конечный алгоритм построе-
ния решения в задаче (20.10), 20.11) при следующих предположениях
Я(-)еРЬ, a(’)ePL+, п-2.	(20.21)
Здесь символ PL обозначает множество положительно однородных ку-
сочно-линейных функций, а символом PL+ обозначено множество всех
неотрицательных функций из PL. Обращаем внимание на то, что для лю-
бого сг* е PL справедливо сг* — с^ - сг2 и (^* — (^ - где сг1? сг2 6 РЬ4 ,
а у?*, и (/?2 — минимаксные решения задачи (20.10), (20.11) при сг — сг*,
сг = сг! и сг — сг2 соответственно.
Функция сг, согласно (20.21), сформирована с помощью «склейки» ко-
нечной совокупности линейных функций
О-Ду) =	i е 1,71^.
Полагаем	_____
Z := {si: i 6 Ln^}, Z^ co (Z U 0}),
где 0 обозначает нулевой вектор.
Рассмотрим кусочно-линейную функцию Н. Обозначим через Q мно-
жество точек, в которых функция Н не дифференцируема. Таким образом,
множество Q состоит из точки 0 и точек, в которых функция Н склеена из
двух линейных функций.
Справедливо следующее утверждение.
Пусть выполняются условия (20.21). Тогда решение р в задаче (20.10),
(20.11) формируется при помощи склейки линейных функций
= (1,У) + Н(Г), I € L,
где множество L состоит из конечного числа элементов, и
ZCL, (L \ Z) С (Z* П Q).
Это утверждение следует из предлагаемого алгоритма построения ре-
шение. Алгоритм состоит, в сущности, из последовательного решения эле-
ментарных задач, которые возникают в определенном порядке. Эти задачи
могут быть сформулированы следующим образом.
Пусть
<т+(г/) = тах{{а,у), (Ь,у)}, ст~(у) = min{(a,y), (b,y)},
где а, Ъ и у — вектора из R2.
282
Глава IV
а точка wq является решением системы двух линейных уравнений
(a, wo) + Н(а) = г, (6, w0) + H(b) = г.
Решение <р0 задачи 4 в общем случае (т. е. для произвольных а, Ь и г)
может не существовать. Однако в рассматриваемых случаях решение
существует и имеет вид
V’ofe) = <Ыу) = ™{<ро(у), 9?ь(у)}.
Алгоритм построения решения ср в задаче (20.10), (20.11), (20.21) состо-
ит из конечного числа шагов, на каждом из которых конструируются так на-
зываемые простые кусочно-линейные функции (ПКЛФ). Мы опускаем здесь
формальное определение ПКЛФ (это сделано в работах [183, 195, 201]).
Упомянем только главное свойство ПКЛФ. Если — ПКЛФ, то, для про-
извольной точки у* из ее области определения, существует ее окрест-
ность В (у*, в который имеет одно из следующих трех представлений
'Ф(у) =	+
V'(y) = тах{(зйу) + 1ц, (sj,y) + hj},
V'(y) = min{(si,у) + hi, (sj,y) + hj},
где Si, Sj — некоторые векторы из R2, a hi, hj — некоторые числа. Таким
образом, можно сказать, что область определения ПКЛФ не содержит точек,
в малой окрестности которых эти функции представимы в виде склейки из
трех или более линейных функций.
В первом шаге мы строим ПКЛФ <pi, которая принимает значения
из (ci,oo). В конечном счете, функция epi оказывается сужением искомой
функции (р на некоторую область. Функция <pi получается в результате
склейки решений элементарных задач типов 1 и 2.
На г-м шаге (г е 2, т) очередная ПКЛФ epi конструируется из решений
элементарных задач типов 3 и 4. Она определена в области Di — {у е R2:
d < (pi(y) < Ci-i}, ив Di эта ПКЛФ совпадает с искомым решением (р.
Число шагов заранее неизвестно. Построение завершено, когда про-
исходит одно из двух событий: или ст — 0, или замыкания областей Dt.
i е 1, ш, покрывают полностью всю плоскость R2.
Полагаем
Ио — 0, Wi — Wi-i U Di, i е 1, rn.
Тогда минимаксное решение задачи (20.10), (20.11), (20.21) может быть
20. Кусочно-линейные приближения минимаксных решений ...	283
записано в следующем виде
¥>(у) =
<0,
у е Di, i е 1,т,
у е dWi, i е 1, m,
У € R2 \ Wm.
Числа i е 1, m, которые называются критическими уровнями, опре-
делены следующим условием: Di ~ максимальная область в R2 \ W i-\,
на которой <fi является неотрицательной и ПКЛФ. Это означает, что или
^(?у) = 0 для у е dWi, или найдется сингулярная точка у$ е dWi, такая, что
для произвольного г > 0 функция <р на множестве В(?у0; £) П Di получается
в результате склейки не менее чем трех линейных функций. Чтобы вычис-
лить критические уровни а, необходимо рассмотреть решения rJ),
j е 1,1, конечного числа систем из трех линейных алгебраических уравне-
ний. Эти системы и их количество I определены функцией А именно,
Ci = max{0, г1,..., г1}, и, когда a = rq, q е 1,1, точки (wf, являются
точками сингулярности.
Полное описание и обоснование алгоритма приведены в работах
[183, 201], где показано, что число шагов т конечно, а значит, конечно
и число арифметических операций, используемых при реализации алгорит-
ма. Заметим также, что структуры, используемые в этих статьях (матрицы
смежности, клеточные разбиения и т.д.) являются несколько упрощенны-
ми и модифицированными версиями известных понятий из теории графов
и комбинаторной топологии (см., например, [2, 89, 180]). Они оказались
удобными при разработке данного алгоритма и соответствующих вычисли-
тельных программ.
Приложение
Al. Доказательство классического метода характеристик
В параграфе А. 1 приводится доказательство хорошо известного резуль-
тата классической теории УЧП первого порядка, согласно которому реше-
ние задачи Коши
F(x,u(x),Du(x)) = О, х е X С Rn,	(AlЛ)
{(ж, «(ж)): х е X} D Со := {(ж0(у), z0(y)): у £ Rn-1}	(А1.2)
может быть сведено к решению характеристической системы
х = DsF(x, и, $),
s = —DxF(x, и, s) — DzF(x, и, s) • s,	(A1.3)
z — (s, DsF(x^ и, s)).
Решения (x(t),	этой системы подчинены условиям
(ж(0), s(0), 2(0)) = (жо<2/), s0(y), zo(y)\	(А1.4)
где х$(у) и zq(у) — функции, использующиеся в определении начального
многообразия С$ (А 1.2). Напомним также, что $$(у) — это вектор, удовле-
творяющий системе из п уравнений
F(a:o(?/),zo(y),So(?/)) = 0,
оу г	\ ду.t	'/
i е l5n - 1.	(Al.5)
Предполагается, что для любого значения параметра у е R71”1 век-
тор sn(y) существует и единственен. Помимо этого, предполагается, что
функции у н-> so(y): Rn-1 н-> Rn должны быть достаточно гладкими.
Al. Доказательство классического метода характеристик 285
Для каждого значения параметра у е Rn~x обозначим через t
(x(t, у),'sit, y).zit, у)) решение системы (А1.3), (А1.4). Отображение
(t, у) (x(t, у), s(t, у), z(t, у))
рассматривается в некоторой открытой области D С Rn, которая содержит
гиперплоскость {(0, у):у€ Rn-1}. В методе характеристик постулируется,
что функции х и z дважды непрерывно дифференцируемы в области D.
Согласно методу характеристик, решение задачи (А 1.1), (А 1.2) получается
в форме параметрических равенств
x=x(t.y). U — zit.y).
Отображение it, у) н-* xit, у): D —> X должно быть взаимно однозначным.
Предполагается также, что
Со С {(z(t,y),z(f,y)): (£,у) е D}.
Решение задачи (А 1.1), (А 1.2) может быть получено также в виде явной
функции и(х), заданной равенством
u(x) = zirix).r]ix)). х е X,	(А1.6)
где X := {xit,у): it,у) Е Р}, а отображение х (т(х), у{х)): X D —
это обратное отображение кж(«).
Проверим эту конструкцию. По определению функции и (А1.6), она
удовлетворяет условию (А 1.2). Справедливо
dx/dt — DsFix, z,s),
ds'/dt = —DxF(x,z,s) — DzF(x,z,s)s'7	(Al.7)
dz/dt = (s, DsFix, z,'s)},
(ж(0, y),z(0, y),s(0,y)) = ($'o(y),2'o(?/),Sb(y)).	(A1.8)
Так как функция F является первым интегралом характеристической си-
стемы, то из первого уравнения системы (А1.5), вместе с соотношения-
ми (А1.7), (А1.8), следует
F(x(t, у), z{t, у), sit, у)) = 0, it, у) е D.	(А1.9)
Подставляя t = rix) ny = rj{x), получаем
Fix, uix),'sirix), у(х))) = 0, х С X.
286
Приложение
Следовательно, остается проверить равенство
s{r{x),T]{x}} = Du{x), х е X,
которое может быть также записано следующим образом
s(t,y) = Du(x(t,y)), {t,y} Е D.	(Al.10)
Так как z{t, у) — и(ж(£, у}}, то справедливо, что
dz/dyt — {Du, dx/dyt) — 0, i e 1, n — 1,
d'z/di — {Du, dx/dt} = 0.
Полагаем	_______
Ui = dz/dyi — {s, dx/dyi}, i E l,n — 1,
V = dz/dt - {s, dx/dt}.	(Al. 11)
В методе характеристик постулируется, что якобиан
<9£(t,T/l,...,?/n-l)
d{t,y1,...,yn-1)
не равен нулю при всех (t,y) Е D. Поэтому требуемое равенство (А 1.10)
следует из равенств V = 0, Ui = 0, i Е 1, п — 1.
Равенство V = 0 непосредственно следует из первого и третьего урав
нений системы (А 1.7). Докажем равенство Ui = 0. Будем использовать
соотношение
dUi/dt — dV/dyi — {ds/dyi, dx/dt} — {d's/di, dx/dy/).
Из того, что V{t,y) = 0 для всех (t,y} Е D, имеем dV{t,y}/dyi = 0.
Используя уравнения (А 1.7), получаем
dUi/dt = {{DXF + DzFs), dx/dy^ + {DSF, ds/dyi}.
Дифференцируя (Al.9) относительно yi, получаем
{DXF, dx/dyi} + DzFdz/dyi + {DSF, ds/dyi} = 0.
В результате имеем уравнение
dUi/dt = ~DZF • Ui.
(Al. 12)
А2. Многозначные отображения
287
Согласно (А1.5), (А1.8) и (Al.l 1), получаем С7ДО, у) — 0 для всех у е Rn-1.
Из (А1.12) следует, что Ui(t, у) = 0 для всех (t, у) Е D.
Таким образом, показано, что функция и (А 1.6), построенная с помо-
щью классического метода характеристик, является решением задачи Ко-
ши (А1.1), (А1.2).
Отметим, что решение и построено в некоторой (возможно малой)
окрестности X множества {^о(?/): у Е Rn-1}.
Описанная конструкция обоснована при условии, что отображение
(t,у) x(t,у): D X взаимно однозначно. Как правило, эта гипотеза
не выполняется, если решение рассматривается не локально, а в достаточ-
но большой области.
Доказательство, приведенное в этом параграфе, заимствовано из книги
Р. Куранта и Д. Гильберта [52]. Более подробное описание классического
метода характеристик можно найти также во многих других учебниках (см.,
например, [167, 190]).
А2. Многозначные отображения
Пусть X и Y — два метрических пространства, метрики в кото-
рых будут обозначаться с помощью символов dist (•,•)• Для подмноже-
ства С С У и точки у Е Y, обозначим символом dist (у; С) величину, рав-
ную inf{dist (?/, т?): у Е С}. Ддя е 0 обозначаем через С£ замкнутую
г-окрестность множества (7, т. е.
С£ := {у Е Y: dist (у; С) е}.
Под Ф: X 2У подразумевается многозначное отображение (отобра-
жение, значениями которого являются множества элементов), которое со-
поставляет точке х Е X множество Ф(х) С Y. Рассмотрим множества
:= {(х,у): х Е X, у Е Ф(ж)},
dom$ := {х Е X : Ф(я) / 0},
которые называются, соответственно, графиком и эффективным множе-
ством (или областью определения) многозначного отображения Ф. Для под-
множества D с X обозначим через Ф(Р) множество (J Ф(?/).
Для заданных многозначного отображения Ф: X н» 2У и точки xq Е X,
верхним топологическим пределом называется множество
limsupФ(х) := {у EY: liminf dist (у; Ф(.т)) = 0}.
х—+Хо	X-^XQ
288
Приложение
Точно так же нижним топологическим пределом многозначного отображе-
ния Ф: X н-> 2y в точке xq е X называется множество
lim inf Ф(х) := {у е Y: lim sup dist (?/, Ф(ж)) = 0}.
Х~*ХО	X—+XQ
Можно проверить, что верхний и нижний топологические пределы являют-
ся замкнутыми множествами. Ясно также, что
liminf Ф(ж) С 1пп8ирФ(х).
Х—*Хо	X_+XQ
Многозначное отображение Ф называется полунепрерывным сверху
(снизу) в точке xq е X, если выполняется включение (А2.1) ((А2.2)):
Пт8ирФ(х) С Ф(хо),	(А2.1)
X—>Xq
Ит^Ф(х) D Ф(жо).	(А2.2)
X—+XQ
Многозначное отображение Ф называется замкнутым, если оно полунепре-
рывно сверху в любой точке х е X. Отметим, что Ф замкнуто тогда, и
только тогда, когда его график замкнут. Многозначное отображение называ-
ется непрерывным (в смысле Какутани) в точке ж, если оно одновременно
является полунепрерывным сверху и снизу в этой точке.
Многозначное отображение Ф называется полунепрерывным сверху
(снизу) в смысле Хаусдорфа в точке х0 Е X, если для любого г > 0
существует такое б > 0, что для каждого х Е В(х$\б) выполняется вклю-
чение (А2.3) ((А2.4)):
Ф(т) С Фг(т0),	(А2.3)
Ф(#о) С Фе(т).	(А2.4)
Многозначное отображение Ф называется непрерывным в смысле Хаусдор-
фа, если это одновременно является полунепрерывным сверху и снизу в
смысле Хаусдорфа.
Многозначное отображение Ф: X н-> 2У называется локально ком-
пактным в точке xq Е X, если существует такое б > 0, что множе-
ство Ф(В(#о; б)) компактно в Y.
Как правило, многозначные отображения, рассматриваемые в этой кни-
ге, локально компактны, и множества Ф(ж) замкнуты при каждом х Е X.
Для таких многозначных отображений определения полунепрерывности по-
средством топологических пределов и в смысле Хаусдорфа оказываются
эквивалентными. А именно, нетрудно проверить следующий факт.
АЗ. Полунепрерывные функции
289
Пусть многозначное отображение Ф: X 2У локально компактно
в точке xq Е X, и пусть множество Ф(хо) замкнуто. Тогда соотноше-
ние (А2.1) ((А2.2)) эквивалентно полунепрерывности сверху (снизу) Ф в
точке xq в смысле Хаусдорфа.
Принимая во внимание это замечание, обычно мы не различаем выше-
упомянутые понятия полунепрерывности. Также просто доказать следую-
щее утверждение.
Пусть многозначное отображение Ф: X н-> 2У полунепрерывно сверху
(снизу) в смысле Хаусдорфа, и Ф(ж) компактно для каждого х Е X. Тогда
для любого компактного множества D С X его образ &(D) является
компактным подмножеством Y.
Подробное изложение понятий и результатов многозначного анализа
можно найти в многих книгах (см., например. [7, 39, 151]).
АЗ. Полунепрерывные функции
Пусть р: X н-* R — функция, со значениями из расширенной числовой
прямой, где X — метрическое пространство, R := R U {—сю} U {оо}
:= [—ос, сю] — расширенная числовая прямая.
Для такой функции символ gr р обозначает множество {(x,z) Е X х R:
z — р(х)}, которое называется графиком функции р. Символом epi р
обозначается множество {(x,z) Е X х R: z р(х)}, которое назы-
вается надграфиком функции р; символом hypo р обозначается множе-
ство {(x,z) Е X х R: z С р(х)}9 которое называется подграфиком функ-
ции р.
Функция р: X R называется полунепрерывной снизу в точ-
ке х* Е X, если, для любого г < р(х*)9 существует 6 > 0, такое, что
из dist (х*<х) < S следует р(х) г. Функция р называется полунепрерыв-
ной снизу, если она полунепрерывна снизу в каждой точке х* Е X.
Наряду с вышеупомянутым определением может использоваться любое
из следующих эквивалентных условий:
(1)	liminf р(х) р(х*);
(2)	для любого г Е R множество {х Е X: р(х) С г} замкнуто;
(3)	epi р — замкнутое множество.
Функция р: X и-> R называется полунепрерывной сверху, если функ-
ция —р полунепрерывна снизу. Отметим, что функция р: X R непре-
рывна тогда, и только тогда, когда она является полунепрерывной и сверху,
и снизу.
Справедливо следующее утверждение (теорема Вейерштрасса).
290
Приложение
Полунепрерывная снизу (сверху) функция р: X R достигает своего
минимума (максимума) на любом компактном множестве D С X.
Вещественная функция р: X R. называется локально ограниченной,
если supx.eD |^(^)| < оо для любого ограниченного подмножества D С X.
Для локально ограниченной функции р ее нижнее замыкание р: X i—> R
определяется следующим образом
р(х) := supinf{(/>(£): £ е В(х‘б)}.	(А3.1)
£>0
Пусть х* — произвольная точка из X, и пусть г < р(х*). Выберем 8 > 0,
такое, что inf{<^(£): £ е В(х*;28)} > г. Тогда для любого х е В(х*;5)
имеем
> inf{<p(£): £ е В(х;6)}	inf{<^(C): £ G В(гг*;25)} > г.
Поэтому нижнее замыкание р является полунепрерывной снизу функцией.
Аналогично, для любой локально ограниченной функции р: X R
ее верхнее замыкание р, определенное формулой
:= inf sup{<p(£): С 6 В(ж; е)},	(А3.2)
является полунепрерывной сверху функцией.
А4. Выпуклые функции
Функция р: Rn R называется собственной, если dom 92 {х е ЛГ1:
р(х) < ос} 0 и р(х) 7^—оо для всех х е Кп. Функция р называется вы-
пуклой (замкнутой), если множество epi р выпукло (замкнуто) в простран-
стве х R. Если р — собственная функция, то условие выпуклости этой
функции эквивалентно следующему неравенству:
+ (1 — А)ж(2))	A(/?(x^^) + (1 — А)(/?(ж(2)),
которое удовлетворяется при всех х^\х^ € Rn и А Е [0,1].
Функция </?* : Rn н-> R, определенная равенством
<^*(s) := sup [(ж,з) — </>(#)],	(А4.1)
называется сопряженной к функции р. Справедливо следующее утвержде-
ние относительно взаимосвязи между функцией р и сопряженной к ней
функцией р*.
А5. Контингентные конусы, производные по направлениям. ..
291
А4.1. Теорема Фенхеля-Моро
Пусть р\ Rn н-> R — собственная выпуклая функция. Тогда сопря-
женная функция р* является собственной, выпуклой и замкнутой. Для
любого х G Rn справедливо равенство
р(х) = (/?**(ж) := sup [(ж, s} — <p*(s)].	(А4.2)
seRn
Отметим, что функция р* выпукла и замкнута для произвольной функ-
ции р и-> R.
Для выпуклой функции р справедливо следующее утверждение.
Пусть е > 0, р(х*) < оо и р(х) р(х*) для всех х Е В(х*,е), тогда
р(х) р{х*) для всех х е Rn.
Таким образом, любая точка локального минимума выпуклой функции
является точкой ее глобального минимума.
Упомянем еще один факт. Пусть выпуклая функция р: Rn R удо-
влетворяет условию Липшица равномерно во всем пространстве Rn, т. е.
— р(х^)\ С A||x^ — ж(2)||, Vх^\х^ е Rn.
Рассмотрим функцию </>*, сопряженную к р. Для эффективного множества
функции р* справедливо соотношение dom<p* С В\.
Вышеупомянутые определения и утверждения можно найти фактиче-
ски в любой книге, имеющей дело с основами выпуклого анализа (см.,
например, [97, 175, 178, 191]).
А5. Контингентные конусы, производные по
направлениям, субдифференциалы
Контингентный тангенциальный конус
Пусть W — непустое множество в Rm. Напомним, что для заданной
точки у Е Rm символ dist (y;W) обозначает расстояние от у до множе-
ства W, т. е.
dist (у; IV) := inf \\у - w||.
wEW
Заметим, что
|dist (у^\ W) — dist IV) |	\\у^ — у^\\	(А5.1)
для любых у^ у^ Е Rm.
292
Приложение
Множество
ТЫ W) := {/. е Rm :	g?‘ (u~ +	№) = о} (A5.2)
называется контингентным (тангенциальным) конусом к множеству W в
точке w, (оно называется также конусом Булигана, верхним тангенциаль-
ным конусом, для этого множества используются также и некоторые другие
термины).
Легко проверить, что конус T(w; W) замкнут. Действительно, если А> О
и h е T(w;W)9 то, согласно (А5.2), имеем Xh € T(w;W). Пусть
hk € T(w*,W) (к = 1,2,...), hk —* Л*, когда к оо. Выберем такое
$к € (0,1/к\ что dist (w + 8khk\ W) < 8k/k. В силу (A5.1), справедливо
dist (w+$kJi*,W)	dist (w + ^/zfe; iy) + ^||/z*-/zfc||	(\\h*-hk\\ + l/k)8k°
Следовательно, h* € T(w; W). Это доказывает, что T(w; W) — замкнутый
конус в Rm.
Производные по направлениям
Пусть G Э х и(х) El- вещественная функция, определенная
на открытой области G С Rn. В данной книге используются следующие
определения и обозначения для нижних и верхних производных функции и
в точке х е G по направлению /
d~u(x-,f) := limmf{M^ +	' е	(А5.3)
40 kO	J
d+u(x-, f) := Umsup{	: (5, /') e Де(ж, f)|,	(A5.4)
где
Ae(x, /) := {(6, f') e (0, £) x Г: \\f - f'\\ e, x + 8f € G}.
Эти (возможно бесконечные) величины называются в литературе также
нижней и верхней производными Дини по направлению, или производными
Хаддада по направлению.
Ниже будет введено эквивалентное определение этих производных с
помощью контингентных конусов к надграфику и подграфику функции и.
По определению контингентного конуса, имеем
(/^) e T((x,iz(x));epiiz)	С (0,1) хГ х R,
А5. Контингентные конусы, производные по направлениям. ..
293
где
zk u(x + 5kfkh
Zb — и(х}
Зк -> о, /к	/, ----7-------> д, когда к -> оо.
Ок
Используя это замечание, получаем, что определение (А5.3) эквивалентно
следующему определению
d~u(x;f) := inf{д е R: (f,g) € Т((ж, и(х))\epi u)}.	(А5.5)
Полагаем, что d~ и(х-, f) = оо, если
{д е R: (/,#) е T((.r,iz(x));epiu)} = 0.
Точно так же справедливо
d¥u(x; f) := sup{# € R: (/,<?)€ T((x, u(x)): hypoiz)}. (A5.6)
Отметим также, что имеют место соотношения
[(.f.g) е T((x,zy,epiu), д' .9] => (/, д') & Т((ж, г); epiu);	(А5.7)
[(/•.?) € T((a:,z);hypou), д' < 9] => (J,g') G T((x, z);hypou). (А5.8)
Ясно, что из неравенства zn z' следует
dist ((#, /); epiiz) dist ((я, zn)\ epiu),
dist ((ж, /); hypoiz) dist ((ж, z”)\ hypoiz).
Поэтому для любых x e G и — оо < / z" < оо имеют место следующие
соотношения
Т((х, z');epitz) с T((x,z");epitz),
Г((.т, /); hypoiz) D T((rr, г"); hypoiz).	(А5.9)
Рассмотрим отображение Э /	d~u(x\	€ [—ос,оо]. В си-
лу (А5.5) и (А5.7), справедливо
ep\d 'u{x\ •) := {(/,^) 6 Rn х R: д d~u(x; /)} = T((ir,п(ж));epiiz).
(А5.10)
Точно так же
hypo d+u(x: •)	{(/, д') € Rn х R: д d+u{x', /)} = Т{{х^ u(x))\hypow).
(A5.ll)
Так как конус Т((ж, и(ж)); epi и) (конус Т((х, u{x))\hypo и)) замкнут, вы-
водим, что функция d~и{х\ •) (функция d+u{x\ •)) полунепрерывна снизу
(полунепрерывна сверху).
294
Приложение
Некоторые соотношения между производными по направлениям и
контингентными конусами к графику функции
Будем использовать следующее обозначение
Т(и)(х) := T((a?,n(rr));grn).	(А5.12)
Таким образом,
П«)Ы ₽ {(/,.«) е R" х R:	+	= (>}.
(А5.13)
По определениям конуса Т(и)(х) и производных по направле-
нию d~ и(х\ f), d+u(x; f)9 имеем
[—оо < d~u(x-,f) < оо] => [(/,d~u(x; /)) е Т(и)(ж)];	(А5.14)
[—оо < d+u(x;f) < оо] => [(/,d+u(x] /)) е Т(и)(х)];	(А5.15)
l(f,g) 6 Т(и)(х)] => [сГ^ж;/) si д si d+u(x; /)].	(А5.16)
В параграфе 4 также используется следующее утверждение.
А5.1. Утверждение
Пусть и: G н-> R — полунепрерывная снизу функция. Пусть для
некоторых х Е G и f Е R имеет место dru(x;f) — —оо. Тогда
{0} х (—оо,0] С Т(и)(х).
Точно так же пусть и: G н-> R — полунепрерывная сверху функция.
Пусть для некоторых х Е G и f Е R имеет место d+u(x; f) = ос. Тогда
{0} х [0, оо) С Т(и)(х).
Здесь О — нулевой вектор в Rn.
Доказательство. Из двух подобных утверждений этой теоремы дока-
жем второе. Как следует из равенства d+u(x\ f) = оо, существует такая
последовательность (Sk,fk) £ (ОД) х (к = 1,2,...), что
\\f-fk\\+5k^l/k,
и(х + 5kfk) ~ и(х)
9к :=--------ё--------- к.
Ок
Обозначим
dk := и(х + 5kfk) - и(х). fk :=
dk
А5. Контингентные конусы, производные по направлениям ...	295
Можно принять, без потери общности, что dk > 0, для всех к = 1,2,..и
существует предел lim dk € [0, сю]. Из полунепрерывности сверху функ-
fc—>оо
ции и вытекает, что
lim dk — 0.
к—>оо
Так как Д —» / и 0 < dk/dk < 1Д, заключаем, что f'k = fk$k/dk —> 0.
Кроме того,
(х + dkf'kjutx) + dfe) - (х + 6kfk,u(x + 4/fc)) egru.
Тогда справедливо, что (0,1) € T(u)(x). Множество Т(гб)(я) является кону-
сом. Следовательно, (О, г) € Т(п)(х) для всех г 0. Утверждение доказано.
Производные по направлениям верхней огибающей семейства
гладких функций
Функция u: G	R называется дифференцируемой в точке х € G С Rn
по направлению f € Rn, если существует и конечен предел
,1,^ п = lim +	(А5.17)
Очевидно, что из равенства d~u(x, f) = d+u(x; f) 6 (—oo, oo) следует
существование производной по направлению du(x\ f).
Рассмотрим один часто используемый класс функций и, обладающих
производными по направлениям du(x\ f) в любой точке ж, и по любому
направлению f е Rn. Пусть функции G Э х н-» и(х) е R определены
равенством
и(х) := sup y>(x,s).	(А5.18)
Предполагается, что выполнены следующие условия:
(а)	<р(ж, s) = 9?i (х, $) - <р2 (^);
(Ь)	функция : G х Rm R непрерывна; для любого s е Rm функ-
ция 9?i(-,s) дифференцируема на G; функция (x.s) 1—> Dxip\(x.s) непре-
рывна на G х Rm;
(с)	функция 992:	н-» [а, оо] полунепрерывна снизу (здесь а — конеч-
ное число); эффективная область функции 992, т. е.
dom 992 := {s € Rm: 992(5) < 00},
является непустым и ограниченным множеством.
296
Приложение
Ясно, что для любого х G G, величина и(х) конечна. Рассмотрим
следующее множество
БЛх) = Arg max р(х, s)	(А5.19)
и покажем, что Sq(x) 0 для любого х е G. Пусть Si е Rm (i ~
= 1,2,...), lim<p(x, Sj) = и(х). Можно принять, что si е dom 922 (« ~
i
= 1,2,...) и lim Si = 5*.
г—>оо
Так как функция s н-> <p(x,s) является полунепрерывной свер-
ху, справедливо и(х) = lim tp(x, Si) < <р(х, $*). Строгое неравенство
г—>оо
и(х) < (p(x,s*) противоречит равенству (А5.18). Таким образом, получе-
но, что <р(х, <$*) = и(х), т. е. е So{x).
Точно так же можно проверить, что множество Sq(x) замкнуто, а мно-
гозначное отображение х Sq(x) полунепрерывно сверху.
А5.2. Утверждение
Пусть выполнены условия (a)-(c). Тогда функция и: G R, опре-
деленная равенством (А5.18), удовлетворяет условию Липшица в каждой
ограниченной выпуклой области X С G. В каждой точке х е G функция
и дифференцируема по направлениям. Более того, для любого х е G и
любого f € Rn имеют место следующие соотношения
d~ и(х\ f) — d+u(x, f) = du(x', f) = max (Dx (pi(x, s), /).	(A5.20)
ses0(x)
Доказательство. Пусть X — ограниченное выпуклое множество из G.
В соответствии с условием (Ь), справедливо
||£>ж9?1(2г)в)|| А < ос,
для всех х 6 X, s е dom 992 • Поэтому, используя теорему о среднем, полу-
чаем
s) - <р(х2,з)\ sC А|[Ж1 - ж2||
для всех жх,я;2 £ X, s е dom<^2- Пусть s, е So(Xi) (г = 1,2). Из (А5.18),
(А5.19) вытекает, что
u(®i) > u(®2) + <p(x1,s2') - <p(x2,s2)	u(x2) - АЦ.Т1 - x2|.
Тем же путем можно получить, что 71(^2)	и(х±) — A||a?i — Таким
образом, выполнение условия Липшица проверено.
А5. Контингентные конусы, производные по направлениям ...	297
Пусть х е G, f Е Кп. Рассмотрим такие последовательности 5к > О,
fk е Rn (fc = 1,2,...), что Зк 0,	-> У, когда к ос и
сГи^х; f) = lim ST/^ufx 4- Skfk) ~ ^(^)]«
к—+оо
Из (А5.18) и (А5.19) следует, что
u(x + Skfk) -и(х) > <pi(x + Skfk,s) - <pi(x,s),
где s Е So (х). Из теоремы о среднем вытекает, что
Vi+ Skfk,s) -	= 5k{Dx(p1(x +	fk)
для некоторого 5к € [0,5&]. Принимая во внимание условие (Ь), получаем
неравенство dru(x. f) {Dxip±fx, s), f). Это неравенство справедливо для
всех s е So (ж), поэтому
d~u(x, f) max (Dx(pi(x, s), f).	(A5.21)
sGSo(a;)
Рассмотрим такие последовательности /Зк > 0, hk Е Rn (& = 1,2,...),
что Зк ~* 0, hk —» /, когда к —> оо и
d+u(x; f) = lim	+ (3khk) - w(rc)].
к—>oo
Из (А5.18) и (А5.19) следует, что
и(х + Pkhk) -и(х)	^1(х + Pkhk,Sk) -pi(x,sk)
для sk G Sq(x 4- /3khk). Так как Sk E dom<p2, а множество dom<p2 ограни-
чено, можно принять, что Sk s*, когда к оо. Из полунепрерывности
сверху многозначного отображения So вытекает, что s* Е So (ж). Исполь-
зуя теорему о среднем, и принимая во внимание условие (Ь), приходим к
неравенствам
d+u(x,f) < lim (DxPitx + 0khk,8k), hk) =
k—^ao
= {Dx<p!(x,st), f) max	s),/).
s(=S0(x)
Здесь f3k E [0, /Зк]. Эта оценка вместе с неравенством (А5.21) влечет за
собой справедливость (А5.20). Утверждение доказано.
298
Приложение
Субдифференциалы и супердифференциалы
Теперь напомним определения субдифференциала и супердифферен-
циала. Пусть
D~u(x):={peRn: {р, f) - d~u(x; f) О, V f еГ},	(А5.22)
D+u(x) := {peW1: {р. f) - d+u(x- /) > О, V / e Г}.	(A5.23)
Множество D~u(x) (множество D+u(x)) называется субдифференциа-
лом (супердифференциалом) функции и в точке х е G. Элементы мно-
жеств D~u(x) (D+u(x)) называются субградиентами (суперградиентами).
Обращаем внимание на то, что D~u(x) и D+u(x)} — замкнутые и
выпуклые множества (которые могут быть и пустыми). Если функция и
дифференцируема в точке х € G, то можно легко проверить, что D~u(x) =
= D+u(x) = {Du(x)}> где Du(x) — градиент функции и в точке х.
Подробное изложение понятий и результатов, связанных с негладким
анализом, может быть найдено во многих книгах (см., например, [47, 61,
62, 151]).
А6. Об одном свойстве субдифференциалов
Доказательство эквивалентности минимаксного и вязкостного решений
базируется на следующем утверждении.
А6.1. Теорема
Пусть Y Э у > ф) 6 I - полунепрерывная снизу функция, опреде-
ленная на открытом множестве Y С Rm, и пусть Н — выпуклое компакт-
ное множество в Rm. Пусть для некоторой точки уо Е Y выполняется
неравенство
d~v(yQ-,h)>0, VheH.	(А6.1)
Тогда для любого в > 0 существуют точка у£ е Y и субгради-
ент s£ е D~v(y£) такие, что
\\уо-у£\\<г; (s£,h}>Q, VheH,	(А6.2)
Нуо) - <Уе) | < е-	(А6.3)
Импликация (А6.1) =Ф (А6.2) была доказана в работе [196], как раз-
витие результатов, полученных в работах [84, 205]. В данном параграфе
приведено другое доказательство теоремы А6.1, заимствованное из статьи
А6. Об одном свойстве субдифференциалов
299
Ф. Кларка и Ю. С. Ледяева [49], где этот результат был получен как инфини-
тезимальная версия одного из неравенств для средних значений. Это ведет
к более компактному изложению и позволяет получить оценку (А6.3), кото-
рая упрощает доказательство эквивалентности минимаксных и вязкостных
решений.
Приведем формулировку упомянутого результата об оценке конечных
разностей, который установленный в [49] (см. также [48], где подобные
неравенства были получены для функций в гильбертовых пространствах).
А6.2. Теорема Ф. Кларка и Ю. С. Ледяева
Пусть Э у у (у) 6 (—сю, оо] — полунепрерывная снизу функ-
ция, и пусть Q — выпуклое компактное множество в Rm. Пусть в неко-
торой точке у$ € и для некоторого а > 0 функция у ограничена
снизу на [уо, Q\ + [символ [уо, Q] означает выпуклую оболочку множе-
ства {?/□} UO). Тогда для любых
г <г0 := min[?j(y) - у(уо)]	(А6А)
y^Q
и /3 > 0, существуют г* е [уо, Q\ Ч- Вд и s* е D~v[z*) такие, что
г < (<§*, у — t/o), для всех у е Q.	(А6.5)
Важно отметить, что классическая теорема о среднем значении «одно-
мерна» в том смысле, что, фактически, участвующая в ней функция рассмат-
ривается на отрезке числовой прямой. Принципиальное новым в приведен-
ном выше неравенстве для средних значений является то, что оно является
«многомерным» в следующем смысле. Оно оценивает разность у (у)—^(г/о),
где у пробегает по компактному и выпуклому множеству Q С Rm. Кроме
того, этот факт установлен в негладкой постановке, для полунепрерывной
функции. Отметим также, что в цитируемой работе был получен несколько
более сильный результат. А именно, было установлено, что я* — прокси-
мальный субградиент, который удовлетворяет следующему условию: для
некоторого у 0 и для всех у из некоторой окрестности у$ справедлива
оценка
- v(yo) + р]\у ~ УоII2 > О5*, У ~ Уо)-
Ясно, что d^v^yo) С D~v(yo), где д^у^уо) — множество проксимальных
субградиентов функции у в точке г/о, и D~y(yo) — субдифференциал, опре-
деленный в параграфе А5. Также ясно, что, в общем случае, д'*у (уо)
/ D~v(yo).
300
Приложение
Доказательство теоремы А6.2. Можно принять без потери общности,
что /3 < а и уо = 0. Выберем компактное множество
D С [0, Q] + Ва := {ty + у: t € [0,1], у eQ, ||г;||	а},
такое, что внутренность D содержит множество [0,0]. Зафиксиру-
ем г* 6 (г, го), и определим, для любого положительного целого числа к,
функцию (pk на [0,1] х Q х D следующим образом:
Pk(t,y,z) := v(z) 4- k\\ty - £||2 - r*t.	(А6.6)
Пусть
(Ъс, Ук, zk) е Arg min{<^(t, у, z): (t, у, z) е [0,1] х Q х D}.
Можно принять, без потери общности, что
(tk,yk,Zk) (t,y,z), когда к оо.
Тогда неравенство
(pk(tk, Ук, zk) < Ркф, у, 0) == v(0)	(А6.7)
приводит к тому, что z = ty, т. е. z е [0, Q]. Следовательно, для любо-
го (3 > 0 и для достаточно большого числа к, справедливо, что zk Е [0, Q\ +
+ Вр и Zk — внутренняя точка множества D.
Теперь покажем, что tk < 1 для достаточно больших к. Достаточно
проверить, что t < 1. Предположим обратное. Тогда имеем z ---у. Вслед-
ствие полунепрерывности снизу функции v и выбора числа г*, получаем
liminf^fe^fe,^,^) > v(y) -r*> г(0),
к—+00
что противоречит (А6.7).
Теперь зафиксируем такое число к, что Zk Е ([0, Q] + Bp) A D и tk < 1.
Предположим, что tk > 0. Поскольку (tk,yk,Zk) — точка минимума функ-
ции pk, и множество Q выпукло, получаем, что для достаточно малых Л > 0
и для любого у Е Q имеет место следующее неравенство
У^к^к “Ь А, у , Zk) Pk(tk<) Укч Zk) 0,
где ух = ук + А(у - yk)/tk-
Деля это неравенство на А и переходя к пределу при А | 0, получаем
неравенство
{sk,y) — г* 0, для любого у Е Q,	(А6.8)
где sfc = 2h(tkyk - Zk').
А6. Об одном свойстве субдифференциалов	301
В случае, когда tk = 0, соотношение (А6.8) может быть получено из
неравенства
<Рк(\ У, Zk) - <pfc(0, у. zk) 0,
которое справедливо для всех Л 6 [0,1] и у е Q.
Для всех z из некоторой окрестности zk справедливо
v(z) 4- k\\z - tkykII2 v(zk) 4- k\\zk - 4^||2-
Поэтому
v(z) v(zk) + (sk, z- zk) - k\\z - zk\\2,
что приводит к требуемому заключению, в силу определения проксималь-
ного субградиента, для z* — zk и s* = sk. Теорема А6.2 доказана.
Доказательство теоремы А6.1. Можно снова принять, без потери
общности, что уо = 0. Так как функция h н-» d~v(0il h) полунепрерывна
снизу, а множество Н компактно, из условия (А6.1) вытекает, что
D~v(tyh)>p, VheH,	(А6.9)
для некоторого положительного числа р.
Зафиксируем г > 0. Из (А6.9) и полунепрерывности снизу функции v
следует, что существуют такие а € (0, г/2) и г > 0, что рт < в, В2а С У,
тН С Ва и для любого h е Н, t е (0, г], у е В2а справедливо
v(th) > v(0) 4- tp, v(y) > v(0) — e.	(A6.10)
Пусть Q = тН и (3 < а. Тогда из первого соотношения в (А6.10)
вытекает т0 > тр. Применяя теорему А6.2, выводим существование
ys € [0, Q] 4- Bp С В£ и s£ € D~v(y£) таких, что
(s£, Th) >тр, \/heH.
Следовательно, соотношение (А6.2) доказано.
Чтобы получить оценку (А6.3), сошлемся на доказательство теоре-
мы А6.2, которая справедлива для D — [0, Q] 4- при у е (0, а) и
для г* Е (рт, s). Отметим, что D с В2а. Точка у£ введена в текущем доказа-
тельстве, как zki (ддя некоторого к, см. доказательство теоремы А6.2), где zk
минимизирует функцию (pk(tk, Ук, •) на множестве D. Из (А6.7) вытекает
wfcfe) - Г* v(zk) - r*tk < <Pk(tk,yk,Zk) u(0).
Поэтому v(zk) ~ v(y£) w(0) 4- е. Таким образом, эта оценка, вместе со
вторым неравенством в (А6.10), доставляет (А6.3). Теорема А6.1 доказана.
302
Приложение
А7. Дифференциальные включения
Рассмотрим многозначное отображение [0,0] х э (t, у)
E(t, у) С Rm, удовлетворяющее следующим условиям:
(a)	E(t, у) — выпуклое компактное множество в Rm при всех (t, у) е [0,0] х
xRm;
(b)	многозначное отображение Е полунепрерывно сверху в смысле Хаус-
дорфа.
Пусть (to, Уо) £ [0,0] х Rm. Для у > 0 полагаем
Л/(to) :== [to — *6 tg + у\ П [0,0].
Известно, что существуют положительное число у и абсолютно непрерыв-
ная функция ?/(•): 4/(to) •-> Rm, которая удовлетворяет условию у (to) = У о
и дифференциальному включению
y(t)eE(t,y(t))	(А7.1)
при почти всех t е Л, (to).
Этот факт будет доказан ниже. Для этого удобно ввести некоторые
обозначения. Для е е (0,2] и (t, у) 6 [0,0] х Rm обозначим через O£(t,t/)
множество
{(т, у) е [0,0] х Rm: \t - т\ е, \\у - у\\	г}.
Определим множество
E(t,y;e) := со{е + 6: е е Е(т,у), (т,у) е O£(t,y), ||6|| < е}.
Выберем и зафиксируем точку (to, уо) € [0,0] х Rm. Пусть
Ё* := E(t0, уо' 2), А := гпах{||е||: е € Е^}, у := А"1.
Обозначим через Sol £ множество абсолютно непрерывных функций
у(-): 7p(t0) Rm, которые удовлетворяют условию y(tQ) ~ Уо ™ Диф-
ференциальному включению
y(t) е E(t, y(t)] е), для почти всех t е /p(to).	(А7.2)
А7.1. Утверждение
Пусть вк (0,1], Ук(') £ Sol£fc (к = 1,2,...) и —+ 0, когда к —> оо.
Тогда из последовательности {t/fc(-)}i° можно извлечь сходящуюся подпо-
следовательность, предел у(-) которой удовлетворяет включению (А7.1)
при почти всех t G /P(to).
А7. Дифференциальные включения
303
Доказательство. Нетрудно проверить, что ||s/fc(t) — 2/о||	1 для
всех t е и к = 1,2, ... Предположим противное: пусть ||^(i*) —
— 2/о|| > 1 Для некоторого к и t* € Предположим, что t* > to-
Тогда существует такой момент т G [to, to + v), что 1Ы(Т) ~ 2/о|| = 1
и ||?/& (t) — 2/о ||	1 Для любого t е [t0, т]. Справедливо, что
0,Ы0) е Oi(t0,y0),
E(t,yk(t)-,ek) с E(t0,y0;l + ek) с E(t0,у0; 2),
||^fe(t)ll \ для почти всех t е [£о,т].
Поэтому ||2/fc(r) - 2/о|| =% А(т - t0) < Az/ 1. Следовательно, |)2/*(-г) -
— Уо II < 1, что противоречит выбору т.
Таким образом, получили, что
max ||yfc(t) - уо|| < 1,	||^fc(i)|| < А
t&Iv \^0/
ддя почти всех t € Л,(to). Согласно теореме Арцела, последователь-
ность {2/Ц-)}1° содержит подпоследовательность, которая равномерно на
интервале 4, (to) сходится к пределу ?/(•). Чтобы упростить обозначения,
полагаем
lim max \\yk(t) - y(t)|| = 0.
fc-^oo te/t/^o)
Предельная функция y(/): Л, (to) i-> Rm удовлетворяет условию Лип-
шица, поэтому она абсолютно непрерывна. Пусть т — внутренняя точ-
ка 1У(t0), в которой функция 2/(-) является дифференцируемой. Выберем
положительное число а. Так как многозначное отображение Е полунепре-
рывно сверху в смысле Хаусдорфа, заключаем, что для достаточно большого
номера К и для достаточно малого 5 > 0 выполняется
E(t, yk(t); ек) С Е(т, у(т]) + BQ,
'ik'ZK, \/t€	+
Тем самым получено, что yk(t) С Е(т, у(т)) + Ва для почти всех t € [т —
— т+$]. Пусть т' е [т—T-j-5], т' г. Из вышеупомянутого соотношения
и выпуклости множества В(т, 2/(т)) + Ва следует, что
Ыг-):ЫТ)£Д(Г|!<(Г))+Во
Очевидно, что, переходя здесь к пределу при к оо, получаем
?/(т') - у(т)
------------€ Е(т, у(тУ) + Ва.
304
Приложение
Множество Е(т, у(т)) 4- Ва замкнуто, следовательно, у(т) G Е(т. у (т)) 4-
4- Ва. Из того, что а — произвольное положительное число, заключаем, что
у(т) G Е(т, у(т)). Таким образом, утверждение А7.1 доказано.
Используя это утверждение, можно доказать существование реше-
ний дифференциального включения (А7.1). Пусть задана точка (to,i/o) £
G [0,0] xRm. Как и в утверждении А7.1, определим интервал време-
ни Выберем последовательность положительных чисел 8к (к ~
= 1,2,...), которая сходится к нулю, когда к —> оо. Введем последователь-
ность кусочно-линейных функций ^(-): 4, (to) следующим образом:
Z/fc(^o) = 2/о;
yk(t) = yk(to + i8k) 4- e^k\t -to- iSk),
при t G [to + i8k, t0 + (i 4- l)8k).
где E E(t0 4- гбк, yk(t0 4- г^)), и
Ук(^) “ Ук(^О ^k) 4" Ci^k(t tg 4"
при t G (to - (i 4- l)5fe, to - i8k\)
где е^к G E(to—i8k, yk(to~i8k)). Как и в доказательстве утверждения А7.1,
получаем, что
||z/fc(t') - ЫО1 W - t"\ Для любых t',t" G Iy(t0).
По определению, для t G (t0 4- i8k, t0 4- (г 4- 1)<5&), имеем
yk(t) = е(гЛ) е E(to + i8k, yk(to 4- i8k)) C E(t, yk(t); efc),
где ek ~ X8k (отметим, что Л > 2). Точно так же, yk(t) G E(t, yk(t); ek)
для почти всех t G [to — to] П [0, to]- В силу утверждения A7.1, после-
довательность ук(-) содержит сходящуюся подпоследовательность, предел
которой ?/(•) удовлетворяет условию (А7.1) при почти всех t G Iu{to). Таким
образом, доказана справедливость следующего утверждения.
А7.2. Утверждение
Пусть многозначное отображение (t, у) E(t, у) удовлетворя-
ет условиям (а), (Ь). Тогда для любой точки (to^yo) £ [0,0] х Rm
существуют положительное число и и абсолютно непрерывная функ-
ция у(-): ly (to)	которая удовлетворяет условию у (to) ~Уо и диф-
ференциальному включению (А7.1) при почти всех t G /^(to).
А8. Критерии слабой инвариантности
305
А теперь предположим, что, в дополнение к условиям (а), (Ь), много-
значное отображение Е удовлетворяет следующей оценке
max{||e||: е G E(t, у)}	r(£) (1 + ||у||),	(А7.3)
где [0,0] 9 t н-> r(t) G Ж+ — некоторая интегрируемая функция. Отме-
тим, что это условие гарантирует, что решения дифференциального вклю-
чения (А7.1) могут быть продолжены на весь интервал [0,0]. Условие про-
должимости решений может быть сформулировано различными способами.
Например, неравенство (А7.3) может быть заменено неравенством
тах{(ж, е): е G E(t, у)} r(f)(l + ЦуЦ2),
где, как и выше, г(-) — интегрируемая функция.
Пусть (to.yo) е [0,0] х Rm. Обозначим через Sol (to, З/о) множество
абсолютно непрерывных функций ?/(•): [0,0] Rm, которые удовлетворя-
ют условию у (to) = уо и дифференциальному включению (А7.1) при почти
всех t е [0,0].
Из приведенных выше утверждений можно получить справедливость
следующей теоремы.
А7.3. Утверждение
Пусть многозначное отображение Е удовлетворяют условиям (а), (Ь),
и оценке (А7.3). Тогда, для любой точки (to,#o) € [0,0] х множе-
ство Sol (to, Уо) непусто и компактно в С([0,0]; Rm).
Пусть (rk,r}k) € [0,0] х yk(-) е Sol (rk,rjk) (k = 1,2,...) и
(Ткбдк) (to, %о), при к —> оо. Тогда из последовательности функций Ук{‘)
(к = 1,2,...) можно извлечь сходящуюся подпоследовательность, предел
которой содержится в Sol (to, уо\
Пусть М С [0,0] х — компактное множество. Тогда множество
Sol(M):= (J Sol (г, т?)	(А7.4)
(т,г/)бМ
компактно в С([0,0]; Rm).
Дифференциальные включения изучались многими авторами (см., на-
пример, [6, 32, 60, 229]). Доказательство утверждений А7.1 и А7.2 позаим-
ствовано из книги [74].
А8. Критерии слабой инвариантности
Пусть W — локально компактное, непустое множество в Rm, т. е. для
любого w е W существует такое число е > 0, что пересечение W С\В(ик г)
306
Приложение
замкнуто в Rm. Рассмотрим многозначное отображение
W Э у Р(у) С W
с локально компактным графиком
grF := {(y,w): w е P(t/), У € ТУ}.
Будем также предполагать, что многозначное отображение Р является ре-
флексивным и транзитивным, т. е. оно удовлетворяет следующим условиям:
х Е Р(х) С ТУ, Уже ТУ,	(А8.1)
Р(у) С Р(ж), \/х eW,\/ye Р(х).	(А8.2)
Это многозначное отображение Р порождает на множестве ТУ предпоря-
док >: следующим образом
w h у о w Е Р(?/).
Пусть многозначное отображение
ТУ Э у Y(y) е conv (Rm)
полунепрерывно сверху в смысле Хаусдорфа, т. е. для любых у G ТУ и с > 0
существует 8 > 0, такое, что Y (у') С Y{y) + В£ для всех yf е В (у; <5) П ТУ.
Напомним, что символ conv(Rm) означает совокупность всех непустых,
выпуклых и компактных множеств в Rm. Рассмотрим дифференциальное
включение
y{t) е У(у(4)).	(А8.3)
Будем использовать следующие понятия. Множество ТУ С Rm на-
зывается слабо инвариантным относительно дифференциального включе-
ния (А8.3), если для любой точки yQ е ТУ существуют положительное
число 0 и абсолютно непрерывная функция (выживающая траектория)
у(-): [0,#] н-> W, удовлетворяющая начальному условию 2/(0) — уо и диф-
ференциальному включению (А8.3) при почти всех t е [0,0]. (В этом случае
говорят также, что множество ТУ обладает свойством выживаемости.)
Абсолютно непрерывная функция ?/(•): [0,0] ТУ называется моно-
тонной траекторией дифференциального включения (А8.3), если она удо-
влетворяет (А8.3) при почти всех t Е [0,0], и обладает следующим свой-
ством монотонности: y(t) У у(з) всех (s, t) Е @+, т. е.
y(t) е РШ), V(s,t)6 0+,	(А8.4)
где
:= {(s,t) е [0,0] х [0,6»]: s t}.	(А8.5)
А8. Критерии слабой инвариантности
307
Следует упомянуть, что исследования слабо инвариантных множеств
формируют большой раздел теории дифференциальных уравнений и вклю-
чений и, в значительной степени, связаны с приложениями к теории управ-
ления и теории дифференциальных игр (см., например, [5, 45, 53, 84, 87,
134, 152, 186] и библиографию в этих работах).
Ниже мы докажем следующие утверждения.
А8.1. Теорема
Пусть W С — локально компактное множество. Пусть много-
значное отображение Y: W convRm полунепрерывно сверху в смысле
Хаусдорфа. Пусть W Э у Р(у) G W — многозначное отображение, гра-
фик которого локально компактен. Предположим также, что выполнены
условия (А8.1) и (А8.2). Тогда эквивалентны следующие три условия'.
(al)	Т(т/; Р(у)) П Y(y) ^0,УуЕ W,	(А8.6)
где Т{у'. Р(уУ) — контингентный конус к множеству Р(у) в точке у,
т. е.
=0};
(Ы)	соТ(^;Р(з/)) ПУ(г/) Ф 0, Му Е W;	(А8.7)
(cl) для любой точки у$ 6 W существуют число 0 > 0 и монотонная
траектория ?/(•): [0,0] W дифференциального включения (А8.3),
удовлетворяющая начальному условию y(fd) = у®.
А8.1. Следствие
Пусть Y: W —> conv (Rm) — полунепрерывное сверху многозначное
отображение, и пусть W С — локально компактное множество. Тогда
эквивалентны следующие три условия'.
(а2)	Т(у‘ ТУ)) П Y(y) / 0, V у eW;	(А8.8)
(Ь2)	соТ(у; ТУ)) П Y(y) ^0,Mye W;	(А8.9)
(с2) множество W слабо инвариантно относительно дифференциального
включения (А8.3).
Эти утверждения расширяют и усиливают известные критерии слабой
инвариантности (см., например, работу Дж. Хаддада [87]). Отметим, что
в [87] предполагалось, что многозначное отображение Р непрерывно. Здесь
это предположение заменено более слабым условием полунепрерывности
308
Приложение
сверху. Заметим также, что теорема Хаддада не содержит критерия для
монотонности и инвариантности в форме соотношений (Ы) и (Ь2).
Доказательство теоремы А8.1. Без потери общности, можно предпо-
лагать, что множество W замкнуто в Rm.
Импликация (cl)=4*(al) следует немедленно из определений кону-
са Т(у\и монотонной траектории. Импликация (al)=4>(b 1) также оче-
видна. Доказательство импликаций (bl)=>(al)=>(cl) состоит из нескольких
шагов.
Шаг 1. Введем следующие обозначения
Ty°(?/) := Arg min \\у - w||;
w<~W
E{y)-.= COY(WG(y)).	(A8.10)
Отметим, что многозначное отображение Э у Е(у) е conv (Rm)
полунепрерывно сверху в смысле Хаусдорфа.
Выберем точку у о € W. Далее используются конструкции, подобные
тем, что были введены в параграфе А7. Итак, определим множества
Е(у;г) со{е + Ь: ее E(rf), у G ||Ь||	е};	(A8.ll)
Еь := Е(у0;2)
и числа
А := шах{||е||: е G 0 = А-1.
Пусть С £ [0,0] и у е В(у&, А0. Обозначим через Sol £(С, ту) множество аб-
солютно непрерывных функций ?/(•): [0,0] ь-> Rm, которые удовлетворяют
условию ?;(С) = у и дифференциальному включению
y(t) е E(y(t)', е), для почти всех t е [0,0].	(А8.12)
В частности, используем обозначение Sol о (С,/?) в случае е = 0. Из утвер-
ждений А7.1 и А7.2 следует, что
Sol£(C,77)^0, Vs G [0,1], < € [0,0], у е В(у0; А0.
Шаг 2. Рассмотрим индикаторную функцию множества gr Р
/ \ _ (°’ е ®гР’
eRm xRm\grp.
(А8.13)
А8. Критерии слабой инвариантности
309
Обратим внимание, что функция v:	х Rm {0,1} полунепрерыв-
на снизу. Обозначим символом 77; /1) нижнюю производную функ-
ции 77н-> v(y, rf) по направлению Н, т. е.
<Г	t е (0,<Я, f е B(h: J)}.
Полагаем также
D~v(y,y) := {реГ: (р, h) - d~v(y,rT,h) 0, Vh € Rm}. (А8.14)
Ясно, что условие (А8.6) эквивалентно следующему
{h е Rm: d~v(y, у; h) 0} П Е(у) ф 0,	(А8.15)
VpeRm.
Отметим также, что условие (А8.7) эквивалентно условию
со {h е Rm: d~v(y, у; h) 0} П Е(у) ф 0.	(А8.16)
VpeRm.
Таким образом, справедливы импликации (а1)о(А8.15), (Ы)о(А8.16).
Шаг 3. Теперь докажем эквивалентность
(А8.15)	(Л8.16).	(А8.17)
Импликация (А8.15)=>(А8.16) очевидна. Докажем импликацию
(А8.16)=>(А8.15). Пусть выполнено условие (А8.16). Предполагаем обрат-
ное: пусть существует такая точка у Е Rm, что d~v{y^y\K) > 0 для
всех h € Е(у). Из полунепрерывности снизу функции h 1—> d~v(x,x;h)
получаем, что
d~v(y, у; К) > 0, V h Е Е(у) + By,
где /3 — некоторое положительное число. Так как многозначное отобра-
жение Е полунепрерывно сверху, то существует такое число 6 > 0, что
E(rf) С Е(у) + В@ для всех 77 6 В(у, 5). Согласно теореме А6.1, существу-
ют также точка у е В (у; 6) и субградиент р е D~v(y,y), такие, что
(р, К) > 0, УН е Е(у) + By.	(А8.18)
Рассмотрим два случая: (i) 77 е Р(р), (ii) 77 Р(у)-
310
Приложение
Случай (i). Покажем, что
v(y, р 4- 6f)	+ V/ Е Rm, V(5 > 0.	(А8.19)
Напомним, что v(y. rj) G {0,1} для всех у,т) Е Rm. Если ?;(р, y-ySf) — 1, то
неравенство (А8.19) выполнено. Пусть v(ry т] 4- 8f) = 0, т. е. т) 5f G P(rf).
Тогда из условия у Е Р (у) и свойства транзитивности (А8.2) вытекает, что
7] + Sf Е Р(у)9 т. е. v(y, rj 4- 6f) = 0. Таким образом, неравенство (А8.19)
доказано.
Так как у Е Р(у)9 а многозначное отображение Р рефлексивно
(см. А8.1)), справедливо ?;(р, р) = 0 и у) = 0. Из этих равенств и
неравенства (А8.19) получаем оценку
d~v(y, у; h) С d"~v(jy ту h), Vhdm.	(А8.20)
Согласно (А8.14), имеем
(y,h) ^d~v(yyryh\ V/7€Rm.	(А8.21)
Поэтому (р, К) С d~~ v(ry ту h) при всех h Е Rm и
со {h Е Rm: d~v(ry р; h) 0} С {h Е Rm: (р, h) 0}.
Теперь из (А8.18) и соотношения Е(р) С Е(у) + В@ следует, что
со {h Е Rm: d~v(ry р; h) С 0} А Е(р) — 0,
что противоречит (А8.16).
Случай (ii). В этом случае v(p,p) = 1. Из полунепрерывности снизу
функции v вытекает, что г(р, w) = 1 для всех w Е В (ту. а), где а > 0 —
достаточно малое число. Поэтому d~v(y, р; К) — 0 для всех h Е Rm. В си-
лу (А8.21), для всех h Е Rm имеет место (р,/г) > dTv(y,7yh) — 0, что
противоречит (А8.18).
Эти противоречия доказывают эквивалентность (А8.17).
Шаг 4. Докажем теперь, что из условия (А8.15) вытекает следующее
условие (dl): для любых (^,т) е ©+, р G В(р0;К) П W и £ Е (0,1]
существует такая траектория р(-) Е Solе(С? 77), что У(т) P(ji)-
Пусть выполнено условие (А8.15). Предположим обратное к (dl), т. е.
пусть существуют (£, т) 6 0+, р Е В(уо;ХС) П W и е Е (0,1] такие, что
у(т) P(rj)) для всех р(-) Е So\£(C^rj). Полагаем
*°(з/(-)) := max{t е [с, т]: y(i) е
г* := max{t°(y(-)): у(-) 6 Sole«,7?)}.
А8. Критерии слабой инвариантности
311
Так как множество Р(т]) замкнуто в Rm, а множество Sole(£, 77) компактно
в пространстве C([O,0];Rm), то стоящие выше максимумы достигаются.
Выберем
;(/*() е Arg max{£° (?/(•)): у(-) е Sole«,77)}.
Обозначим ?7* := ж*(т*). Очевидно, что ту* € Р(т?) С W. В силу (А8.1),
справедливо, что ту* G Р(^*). Отметим также, что т* < т.
Согласно (А8.11) и (А8.15), можно выбрать такие число 5 е (0, т — т*),
вектор / € Rm и траекторию ?/*(•) С So1£(t*, т/*), что
y*(t) = у*СО, при t е [о, т*],
+ 5f е Р(й / е Р(^) + В£, ||5/|| е,
y*(t) = f при t е [т*, т* + 5].
Поскольку у*(т* 4- 5) е Р(?7*)> у* С Р(т/), и многозначное отображение Р
транзитивно, получаем, что у* (т* + 5) Е Р(у), а это противоречит выбору г*.
Шаг 5. В заключение, докажем импликацию (dl)=>(cl).
Выберем (£,т) Е Q+, у Е В(у0’, А() A W и последовательность
s/c G (0,1) (fc = 1,2,...), которая сходится к 0. Согласно условию (dl),
существует такая последовательность уь(-) € Sol£fc (£, ту), что ук(т) Е Р(у),
к = 1,2,... Можно выбрать подпоследовательность (не переименовывая
ее), чтобы получить, что Ук(-) —> У*(-)> когда к —> ос. В силу утвержде-
ния А7.1, получаем, что ?/*(•) е Sol о (С У)- Так как множество Р(т?) замкну-
то, то выполняется т/*(т) Е Р(у). Следовательно, для любых (С, г) € ©+
и tj Е В(т/0; AC) A W, можно выбрать такую траекторию ?/*(•) Е Solo(C?]),
что г/*(т) 6 Р(?7).
Пусть 5 Е (0, 0), Ti 15 (i = 0,1,..., [В/5], где [0/5] — целая часть
числа 0/5), Используя рекуррентно приведенные выше рассуждения, по-
лучим, что существует такая траектория у$(-) Е So1q(0, уо), для которой
Wthi) Е P(y$(Ti)), i = 0,1,2,..., [0/5] — 1. Из того, что многозначное
отображение Р транзитивно (см. (А8.2)), вытекает, что
ysirj) Е P(y6(Ti)), для любых 0 i j [0/5].	(А8.22)
Выберем последовательность {5fc}i° С (0,0), которая сходится к нулю, ко-
гда к —> оо, и выберем последовательность {у^к\’) = ж(’)}1°> удовлетво-
ряющую условиям вида (А8.22). Далее можно выбрать подпоследователь-
ность (не переобозначая ее), чтобы получить ук(-) —> ?/(•) Е Sol о(0, уо),
когда к —> ос.
Пусть (s,t) Е 0+. Согласно вышеизложенным рассуждениям, суще-
ствует такая последовательность {($k,tk) £ ©+}i°, что
y(k4tk) е P(yW(Sk)), (Sk,tk)	когда к —> оо.
312
Приложение
Поскольку график многозначного отображения Р замкнут, получаем, что
2/(0 € Р(з/(б))-
Таким образом, получаем, что существует такая траектория
?/(•) G Sol о(О, что y(t) Е Р(у($У) для любых (s,t) Е ©+. Вследствие вы-
полнения условий (А8.10) и (А8.11), справедливо Е(у) = Y(у), для у е W.
Так как Р(у) С W и y(t) Е P(y(t})9 для всех t Е [0,0], выводим, что
y(t) Е W, E(y(t)) = Y(y(t)), и y(t) Е Y(y(t)) для почти всех t Е [0,0].
Следовательно, ?/(•): [0,0] i-+ W — монотонная траектория дифференциаль-
ного включения (А8.3), удовлетворяющая начальному условию ?/(0) = у$.
Теорема А8.1 доказана.
Ясно, что в случае, когда Р(у) — W для всех у G W, следствие А8.1
следует непосредственно из теоремы 8.1.
Замечание А8.1. Пусть Rm э у Е(у) Е conv(Rm) — полунепре-
рывное сверху многозначное отображение. Рассмотрим дифференциальное
включение
Ш Е	(А8.23)
Согласно вышеприведенному определению, локально компактное множе-
ство W С называется слабо инвариантным относительно этого диф-
ференциального включения (А8.23), если для каждого у о Е W существуют
число 0 > 0 и абсолютно непрерывное решение ?/(•): [0,0] включе-
ния (А8.23), такое, что у(0) = у0 и y(t) Е W для всех t Е [0,0]. Ясно, что
это определение является эквивалентным следующему: для каждого уц Е W
существует число 0 > 0, такое, что для любого т Е (0,0] существует такая
абсолютно непрерывная функция ?/(•): [0, т] i—»	которая удовлетворя-
ет (А8.23), начальному условию у(о} = уо и включению у(т) Е W.
Замечание А8.2. Известны различные условия, которые обеспечива-
ют продолжимость локально выживающих траекторий. Например, одно из
таких условий может быть сформулировано следующим образом.
Пусть выполняются требования следствия А8.1, и пусть многозначное
отображение W Э у Y(y) Е conv (Rm) удовлетворяет оценке
PH с(1 + PH), У у Е W, h Е Y(y\	(А8.24)
где с — положительное число. Тогда для любой точки уо Е W существует
по крайней мере одна выживающая траектория ?/(•): [0,0) W дифферен-
циального включения (А8.3), которая удовлетворяет начальному условию
7/(0) = уо и определена на интервале времени [0,0), где либо 0 = оо, либо
у (О) W. Если W — замкнутое подмножество из и выполняется оцен-
ка (А8.24), то любая выживающая траектория может быть продолжена на
всю полуось [0, ос).
А8. Критерии слабой инвариантности
313
В заключение, сформулируем необходимые и достаточные условия для
того, чтобы множество W С [0, t4) х Rm было слабо инвариантным относи-
тельно дифференциального включения, зависящего от времени и имеющего
вид
j(t)6y(t,j/(t)).	(А8.25)
Предполагаем, что множество W локально компактно в [0, ft) xRm, а много-
значное отображение W Э (t,y) н-> Y(t, у) Е conf(Rm) — полунепрерывно
сверху в смысле Хаусдорфа. Здесь $ — или положительное число, или 4-ос.
Заметим, что множество W может рассматриваться как график многознач-
ного отображения
[0,^)	с Rm,
где W(t) := {w Е Rm: (t,w) E W}.
Множество W C Rm называется слабо инвариантным относительно
дифференциального включения (А8.25), если, для любой точки (to, Уо) € W,
существуют число т Е (to, t^) и абсолютно непрерывная функция (выжива-
ющая траектория) ?/(•): [t0,r] i—> Rm, такая, что y(to) = т/о, y(t) Е Hz(t)
для всех t Е [to, т], а включение (А8.25) удовлетворяется при почти
всех t Е [to, г].
Чтобы сформулировать критерий слабой инвариантности множества,
определим производную многозначного отображения t н-> W (t) следующим
образом:
х (7	dist (w + 6h: W(t + £)) 'i
(Djy)(t, w) := Ih E R : lim inf---k - c k " = 0 k
l	S	J
Множество (DtW)(t, w) называется правосторонней производной много-
значного отображения 1i—> W(t) в точке (t, w) E W.
A8.1. Утверждение
Локально компактное множество W С [0,^) х Rm является слабо
инвариантным относительно дифференциального включения (А8.25) тогда
и только тогда, когда выполняется условие
(AHQ(t;w) ny(t,w) 0,	е W. (А8.26)
Этот критерий эквивалентен условию
со (Z^iy)(t, w) П Y(t, w) 7^ 0, V (t, w) E W.
(A8.27)
314	Приложение
Доказательство этого утверждения фактически содержится в доказа-
тельстве теоремы А8.1. Ясно, что условия вида (А7.3) обеспечивают про-
должимость локально выживающих траекторий дифференциального вклю-
чения (А8.25). Отметим, что критерий слабой инвариантности в виде усло-
вия (А8.27) был получен в работе [84].
Литература
[1]	Р. А. Адиатуллина, А. М. Тарасьев. Дифференциальная игра неограни-
ченной продолжительности. Прикл. матем. механ., 51(4): 531-537,
1987. (English transl. in J. Appl. Math. Meeh. 51, 415-420, 1987).
[2]	П. С. Александров. Комбинаторная топология. Гостехиздат, Моск-
ва-Ленинград, 1947. (Translated, Vol. 1, 2, 3, Graylock Press, Albany,
NY, 1956, 1957, 1960.)
[3]	M. И. Алексейчик. Дальнейшая формализация основных элементов
антагонистической дифференциальной игры. В сб. Математический
анализ и его приложения, т. 7, стр. 191-199. Ростовский-на-Дону го-
суниверситет, Ростов-на-Дону, 1975.
[4]	В. И. Аркин, В. Л. Левин. Выпуклость значений векторных интегра-
лов, теоремы измеримого выбора и вариационные задачи. Успехи
мат. наук, 27(3): 21-77, 1972.
[5]	J.-P. Aubin. Viability Theory. Birkhauser, Boston, 1990.
[6]	J.-P. Aubin and A. Cellina. Differential Inclusions. Springer-Verlag, Berlin,
Heidelberg, 1984.
[7]	J.-P. Aubin and H. Frankowska. Set Valued Analysis. Birkhauser, Boston,
1990.
[8]	M. Байбазаров, А. И. Субботин. Об одном определении цены диффе-
ренциальной игры. Дифференциальные уравнения, 20(9): 1489-1495,
1984.
[9]	Н. Н. Барабанова, А. И. Субботин. О непрерывных стратегиях уклоне-
ния в игровых задачах о встрече движений. Прикл. матем. механ.,
34(5): 796-803, 1970.
[10]	Н. Н. Барабанова, А. И. Субботин. О классах стратегий в дифферен-
циальных играх уклонения. Прикл. матем. механ., 35(3): 385-392,
1971.
316
Литература
[11]	Е. А. Барбашин. К теории обобщенных динамических систем. Учен,
записки Москов. универе., математика, 135: 110-133, 1949.
[12]	Е. А. Барбашин. Введение в теорию устойчивости. Наука, Москва,
1967.
[13]	Е. А. Барбашин, Ю. И. Алимов. К теории релейных дифференциаль-
ных уравнений. Известия Вузов, математика, 1(26): 3-13, 1962.
[14]	М. Bardi. A boundary value problem for the minimum time function. SIAM
J. Control Optim., 27: 776-785, 1989.
[15]	M. Bardi, S.Bottacin, and M. Falcone. Convergence of discrete schemes
for discontinuous value functions of pursuit-evasion games. In Michele
Breton and Georges Zaccour, editors, Sixth International Symposium
on Dynamic Games and Applications, pages 79-92, St. Jovite, Quebec,
Canada, 1994.
[16]	M. Bardi and I. Capuzzo-Dolcetta. Optimal Control and Viscosity Solutions
of Hamilton-Jacobi-Bellman Equations. Birkhauser, Boston, 1988.
[17]	M. Bardi and L. C. Evans. On Hopf’s formulas for solutions of Hamilton-
Jacobi equations. Nonlinear Analysis, Theory, Methods, AppL, 8(11):
1373-1381, 1984.
[18]	M. Bardi and M. Falcone. An approximation scheme for the minimum time
function. SIAM J. Control and Optim., 28: 950-965, 1990.
[19]	M. Bardi and S. Osher. The nonconvex multi-dimensional Riemann
problem for Hamilton-Jacobi equations. SIAM J. Math. Anal., 22:
344-351, 1991.
[20]	M. Bardi and P. Soravia. Hamilton-Jacobi equations with singular
boundary conditions on a free boundary and applications to differential
games. Trans. Amer. Math. Soc., 325: 205-229, 1991.
[21]	M. Bardi and V. Staicu. The Bellman equation for time-optimal control of
non-controllable, nonlinear systems. Acta Appl. Math., 31: 201-223,1993.
[22]	G.Barles and B. Perthame. Discontinuous solutions of deterministic
optimal stopping time problem. Model. Math. Anal. Num., 2: 557-579,
1987.
[23]	E.N. Barron. Differential games with maximum cost. Nonlinear Analysis,
Theory, Methods, Appl., 14(11): 971-989, 1990.
Литература
317
[24]	E.N. Barron, L. C. Evans, and R. Jensen. Viscosity solutions of Isaacs’
equations and differential games with Lipschitz controls. J. Different.
£^.,53:213-233,1984.
[25]	E.N. Barron and R. Jensen. The Pontryagin maximum principle from
dynamic programming and viscosity solutions to first order partial
differential equations. Trans. Amer. Math. Soc., 298(2): 635-641, 1986.
[26]	E.N.Barron and R.Jensen. Semicontinuous viscosity solutions of
Hamilton-Jacobi equations with convex Hamiltonians. Comm. Partial
Differential Equations, 15: 1713-1742, 1990.
[27]	T. Basar and P. Bernhard. H°°-Optimal Control and Related Minimax
Design Problems. Birkhauser, Boston, 1991.
[28]	R. Bellman. Dinamic Programming, volume 1, 2. Princenton Univ. Press,
Princenton, NJ, 1957.
[29]	L. D. Berkovitz. A variational approach to differential games. In Advances
in Game Theory, number 52 in Ann. Math. Stud., pages 127-174.
Princeton University Press, Princeton, New Jersey, 1964.
[30]	L. D. Berkovitz. Characterization of the values of differential games. Appl.
Math. Optim., 17: 177-183, 1988.
[31]	P. Bernhard. Singular surfaces in differential games: An introduction. In
Differential Games and Applications, Lecture Notes in Control Inf. Sci.,
pages 1-33, 1977.
[32]	В. И. Благодатских, А. Ф. Филиппов. Дифференциальные включения
и оптимальное управление. Труды математического института им.
Стеклова, 169: 194-252, 1985.
[33]	Н.Д. Боткин, В. М. Кейн, В. С.Пацко. Модельная задача об управле-
нии боковым движением на посадке самолета. Прикл. матем. механ.,
48(4): 560-567,1984. (Translated in J. Appl. Math. Meeh. Vol. 48 (1984),
No. 4, 395-400.)
[34]	N. D. Botkin, V S. Patsko. Universal strategy in a differential game with
fixed end duration. Probl. Contr. and Inform. Theorv, 11(6): 419-432,
1982.
[35]	Н.Д.Боткин, В.С.Пацко. Позиционное управление в линейной диф-
ференциальной игре. Изв. Акад, наук СССР, Техн, кибернетика, (4):
78-85, 1983. (Translated in Engineering Cybernetics, Vol. 21, No. 4,
69-76, 1984.)
318
Литература
[36]	N. D. Botkin, V. S. Patsko. Numerical solution of linear differential game.
In Differential Games — Developments in Modelling and Computation,
vol. 156 Qi Lecture Notes in Control Inf. Sci., pp. 226-434. 1991.
[37]	I. Capuzzo-Dolcetta. On a discrete approximation of the Hamilton-Jacobi
equation of dynamic programming. Appl. Math. Optimiz., 10(4): 367-377,
1983.
[38]	I. Capuzzo-Dolcetta and H. Ishii. Approximate solutions of the Bellman
equation of deterministic control theory. Appl. Math. Optimiz., 11:
161-181, 1984.
[39]	Ch. Castaing and M.Valadier. Convex analysis and measurable
multifunctions. Springer-Verlag, New York, Berlin, 1977.
[40]	А. Г. Ченцов. О структуре игровой задачи сближения. ДАН СССР, 16:
1404-1406, 1975.
[41]	А. Г. Ченцов. Об игровой задаче сближения в заданный момент вре-
мени. Матем. сборник, 99(3): 394-420, 1976. (Translated in Math, of
the USSR Sb. Vol. 28 (1976), 353-376.)
[42]	А. Г. Ченцов. Итерационная программная конструкция для дифферен-
циальной игры с фиксированным моментом окончания. ДАН СССР,
240(1): 796-800, 1978. (Translated in Soviet Math. Dokl. Vol. 19 (1978),
No. 3, 559-562.)
[43]	Ф. Л. Черноусько, А. А. Меликян. Игровые задачи управления и поис-
ка. Наука, Москва, 1978.
[44]	С. В. Чистяков. К решению игровых задач преследования. Прикл. ма-
там. механ., 41(5): 825-832, 1977.
[45]	F. Н. Clarke. Generalized gradients and applications. Trans. Amer. Math.
Soc., 205: 247-262, 1975.
[46]	F.H. Clarke. Optimal control and true Hamiltonian. SIAM Review, 21:
157-166, 1979.
[47]	F. H. Clarke. Optimization and Nonsmooth Analysis. Wiley Interscience,
New York, 1983. Second edition 1990, Vol. 5 in Classics in Appl. Math.
Series, SIAM.
[48]	F. H. Clarke and Yu. S. Ledyaev. Mean value inequalities in Hilbert space.
Trans. Amer. Math. Soc., 344: 307-324, 1994.
Литература
319
[49]	Ф. Кларк, Ю. С. Ледяев. Новые формулы конечных приращений. Докл.
Российск. акад, наук, 331(3): 275-277, 1993.
[50]	F. Н. Clarke and R. В. Vinter. Local optimality conditions and Lipschitzian
solutions to Hamilton-Jacobi equations. SIAM J. Control Optim., 21:
856-870, 1983.
[51]	E. D. Conway and E. Hopf. Hamilton’s theory and generalized solutions of
the Hamilton-Jacobi equation. J. Math. Meeh., 13: 939-986, 1964.
[52]	R. Courant and D. Hilbert. Methods of Mathematical Physics, volume I
and II. John Wiley & Sons, New York, 1953, 1962.
[53]	M. G. Crandall. A generalization of Peano’s existence theorem and flow
invariance. Proc. Amer. Math. Soc., 36(1): 151-155, 1972.
[54]	M.G. Crandall, L. C. Evans, and P. L. Lions. Some properties of viscosity
solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc., 282(2):
487-502, 1984.
[55]	M. G. Crandall, H. Ishii, and P. L. Lions. Uniqueness of viscosity solutions
revisited. J. Math. Soc. Japan, 39: 581-596, 1987.
[56]	M. G. Crandall, H. Ishii, and P.L. Lions. A user’s guide to viscosity
solutions. Bulletin A.M.S., N.S., 27: 1-67, 1992.
[57]	M.G. Crandall and P.L.Lions. Condition d’unicite pour les solutions
generalisees des equations Hamilton-Jacobi du ler ordre. C. R. Acad.
Sci. Paris Ser. A-B, 292: 183-186, 1981.
[58]	M.G. Crandall and P.L. Lions. Viscosity solutions of Hamilton-Jacobi
equations. Trans. Am. Math. Soc., 277(1): 1-42, 1983.
[59]	M.G.Crandall and P.L.Lions. Two approximations of solutions of
Hamilton-Jacobi equations. Math. Comput., 43: 1-19, 1984.
[60]	J. L. Davy. Properties of the solution set of the generalized differential
equation. Bull. Austral. Math. Soc., 6(3): 379-398, 1972.
[61]	В. Ф. Демьянов. Минимакс, дифференцируемость no направлениям.
Издательство Ленинградского госуниверситета, Ленинград, 1974.
[62]	В. Ф. Демьянов, А. М. Рубинов. Основы негладкого анализа и квази-
дифференциальное исчисление. Наука, Москва, 1990.
320
Литература
[63]	A.Douglis. The continuous dependence of generalized solutions of
nonlinear partial differential equations upon initial data. Comm. Pure Appl.
Math., 14: 267-284, 1961.
[64]	A.Douglis. Solutions in the large for multidimentional nonlinear
differential equations of first order. Ann. Inst. Fourier, 15: 2-35, 1965.
[65]	В.Я. Джафаров. Об устойчивости гарантированного результата в за-
даче позиционного управления. ДАН СССР, 285(1): 27-31, 1985.
[66]	R. J. Elliott and N. J. Kalton. The existence of value in differential games.
Mem. Amer. Math. Soc., 126, 1972.
[67]	R. J. Elliott and N. J. Kalton. The existence of value in differential games
of pursuit and evasion. J. Different. Equat., 12(3): 504-523, 1972.
[68]	L. C. Evans. On solving certain nonlinear partial differential equations by
accretive operator methods. Israel J. Math., 36: 225-247, 1980.
[69]	L. C. Evans and M. R. James. The Hamilton - Jacobi - Bellman equation for
time optimal control. SIAM J. Control Optim., 27: 1477-1489, 1989.
[70]	L.C. Evans and P. E. Souganidis. Differential games and representation
formulas for solutions of Hamilton-Jacobi-Isaacs equations. Indiana
Univ. Math. J., 33: 773-797, 1984.
[71]	K. Fan. Minimax theorems. Proc. Nat. Acad. Sci. USA, 39(1): 42-47,1953.
[72]	A. F. Filippov. On certain questions in the theory of optimal control. SIAM
J. Control, 1: 76-84, 1962.
[73]	A. F. Filippov. Differential equations with discontinuous right-hand side.
Amer. Math. Soc. Transl. Ser. 2, 42: 199-231, 1964.
[74]	А. Ф. Филиппов. Дифференциальные уравнения с разрывной правой
частью. Наука, Москва, 1985.
[75]	W. Н. Fleming. A note on differential games of prescribed durations. In
Contributions to the Theory of Games, vol. Ill of Ann. Math. Stud., pp.
407-416. Princeton University Press, Princeton, New Jersey, 1957.
[76]	W. H. Fleming. The convergence problem for differential games. J. Math.
Anal, and Appl., 3: 102-116, 1961.
[77]	W. H. Fleming. The Cauchy problem for degenerate parabolic equations.
J. Math. Meeh., 13(6): 987-1008, 1964.
Литература
321
[78]	W. Н. Fleming. The convergence problem for differential games. II. In
Advances in Game Theory, number 52 in Ann. Math. Stud., pages
195—210. Princeton University Press, Princeton, New Jersey, 1964.
[79]	W. H. Fleming. The Cauchy problem for a nonlinear first order partial
differential equation. Differential Equations, 5: 515-530, 1969.
[80]	W.H. Fleming and H. M. Sonner. Controlled Markov Processes and
Viscosity Solutions, vol. 25 of Applications of Mathematics.
Springer-Verlag, New York, 1993.
[81]	H. Frankowska. Lower semicontinuous solutions of Hamilton-Jacobi -
Bellman equations. SIAM J. Control Optim., 31: 257-272, 1993.
[82]	A. Friedman. The Cauchy problem for firs order partial differential
equations. Indiana Univ. Math. J., 23: 27-40, 1970.
[83]	A. Friedman. Differential games. Intersci., New York, 1971.
[84]	H. G. Guseinov, A. I. Subbotin, V. N. Ushakov. Derivatives for multivalued
mappings with applications to game-theoretical problems of control. Probl.
Contr Inform. Theory, 14(3): 155-167, 1985.
[85]	X. Г. Гусейнов, В. H. Ушаков. Дифференциальные свойства интеграль-
ных воронок и стабильных мостов. Прикл. матем. механ., 55(1):
72-78, 1991.
[86]	П. Б. Гусятников, М. С. Никольский. Об оптимальности времени пре-
следования. ДАН СССР, 184(3): 518-521, 1969. (Translated in Soviet
Math. Dokl, Vol. 10 (1969), 103-106.)
[87]	G. Haddad. Monotone trajectories of differential inclusions and
functional-differential inclusions with memory. Israel J. of Math., 39:
83-100, 1981.
[88]	O. Hajek. Pursuit Games. Academic Press, New York, 1975.
[89]	F. Harary. Graph Theory. Addison-Wesley, MA, 1969.
[90]	E. Hopf. Generalized solutions of nonlinear equations of first order. J.
Math. Meeh., 14: 951-973, 1965.
[91]	E.Hopf. On the right weak solution of the Cauchy problem for a
quasilinear equation of first order. J. Math. Meeh., 19: 483-487, 1969/70.
[92]	R. Isaacs. Differential Games. John Wiley, New York, 1965.
322
Литература
[93]	Е. А. Исакова, Г. В. Логунова, В. С. Падко. Построение стабильных мо-
стов в линейной дифференциальной игре с фиксированным моментом
окончания. В сб. Алгоритмы и программы решений линейных диффе-
ренциальных игр, стр. 127-158. Уральский научный центр АН СССР,
Свердловск, 1984.
[94]	Н. Ishii. Perron’s method for Hamilton-Jacobi equations. Duke Math. J.,
55: 369-384, 1987.
[95]	H. Ishii. A simple, direct proof of uniqueness for solutions of Hamilton-
Jacobi equations of eikonal type. Proc. Amer. Math. Soc., 100(2): 247-251,
1987.
[96]	H. Ishii. A boundary value problem of the Dirichlet type for Hamilton-
Jacobi equations. Annali Scuola Normale Superiore Pisa, Ser. XVI, pages
369-384, 1989.
[97]	А. Д. Иоффе, В. M. Тихомиров. Теория экстремальных задач. Наука,
Москва, 1979.
[98]	L. V. Kantorovich and G. Р. Akilov. Functional Analysis. Pergamon Press,
Oxford, second edition, 1982.
[99]	M. M. Хрусталев. Необходимые и достаточные условия оптимально-
сти в форме уравнения Беллмана. ДАН СССР, 242(5): 1023-1026,
1978.
[100]	А. Ф. Клейменов. Неантагонистические позиционные дифференци-
альные игры. Наука, Уральское отделение Российск. акад, наук, Ека-
теринбург, 1993.
[101]	A. N. Kolmogorov and S.V. Fomin. Introductory Real Analysis. Prentice
Hall, Englewood Cliffs, New Jersey, 1970.
[102]	В. H. Колокольцов, В. П. Маслов. Задача Коши для однородного урав-
нения Беллмана. ДАН СССР, 296(4): 796-800, 1987.
[103]	В. А. Комаров. Необходимые и достаточные условия оптимальности
в задаче быстродействия с фазовыми ограничениями. Дифференци-
альные уравнения, 26(11): 1906-1913, 1990.
[104]	А. Н. Красовский. Дифференциальная игра для позиционного функ-
ционала. ДАН СССР, 253(6): 1303-1307, 1980. (Translated in Soviet
Math. Dokl. Vol. 22, No. 1, 251-255, 1980.)
Литература
323
[105]	А. Н. Красовский. Построение смешанных стратегий на основе сто-
хастических программ. Прикл. матем. механ., 51(2): 186-192, 1987.
(Translated in J. Appl. Math. Meeh. Vol. 51.)
[106]	A. H. Красовский. Управление на минимакс интегрального функцио-
нала. ДАН СССР, 320(4): 785-788, 1991. (Translated in Soviet Math.
Dokl. Vol. 44 (1991), No. 2, 525-528.)
[107]	H. H. Красовский. Об одной задаче преследования. Прикл. матем. ме-
хан., 27(2): 244-254, 1963.
[108]	Н. Н. Красовский. К задачам преследования в случае линейных одно-
типных объектов. Прикл. матем. механ., 30(2): 209-225, 1966.
[109]	Н. Н. Красовский. Теория управления движением. Наука, Москва,
1968.
[110]	Н. Н. Красовский. Игровые задачи о встрече движений. Наука, Моск-
ва, 1970.
[Ill]	Н.Н.Красовский. Дифференциальная игра сближения-уклонения.
Изв. АП СССР, Техн, кибернетика, (2): 3-18,1973. (Translated in Engrg.
Cybernetics, vol. 11, No. 2, 189-203.)
[112]	H. H. Красовский. К задаче унификации дифференциальных игр. ДАН
СССР, 226(6): 1260-1263, 1976.
[113]	Н. Н. Красовский. Дифференциальные игры. Аппроксимационные и
формальные модели. Матем. сборник, 107(4): 511-571, 1978.
[114]	Н. Н. Красовский. Управление динамической системой. Наука, Моск-
ва, 1985.
[115]	N. N. Krasovski! and A. N. Krasovski!. A differential game for the
minimax of a positional functional. In Advances in Nonlinear Dynamics
and Control: A Report from Russia, No. 17 in Progress in Systems and
Control Theory, pp. 41-75. Birkhauser, Boston, 1993.
[116]	H. H. Красовский, Ю. M. Репин, В. E. Третьяков. О некоторых игровых
ситуациях в теории управляемых систем. Изв. АН СССР, Техн, кибер-
нетика, (4): 1-11, 1965.
[117]	Н. Н. Красовский, А. И. Субботин. Смешанное управление в диффе-
ренциальной игре. ДАН СССР, 188(4): 745-747, 1969. (Translated in
Soviet Math. Dokl., 10(5): 1180-1183, 1969.)
324
Литература
[118]	Н. Н. Красовский, А. И. Субботин. Альтернатива для игровой задачи
сближения. Прикл. матем. механ., 34(6): 1005-1022, 1970. (Translated
in J. Appl. Math. Meeh. 34: 948-965, 1971.)
[119]	H. H. Красовский, А. И. Субботин. О структуре дифференциальных
игр. ДАН СССР, 190(3): 523-526, 1970.
[120]	Н. Н. Красовский, А. И. Субботин. О структуре игровых задач дина-
мики. Прикл. матем. механ., 35(1): 110-122, 1971.
[121]	Н. Н. Красовский, А. И. Субботин. Аппроксимация в дифференциаль-
ных играх. Прикл. матем. механ., 37(2): 197-204, 1973.
[122]	Н. Н. Красовский, А. И. Субботин. Позиционные дифференциальные
игры. Наука, Москва, 1974.
[123]	N. N. Krasovski! and A. I. Subbotin. Game-Theoretical Control Problems.
Springer-Verlag, New York, 1988.
[124]	H. H. Красовский, А. И. Субботин, В. Ф. Россохин. Стохастические
стратегии в дифференциальных играх. ДАН СССР, 220(5): 1023-1026,
1975. (Translated in Soviet Math. Dokl., 16(1): 198-201, 1975.)
[125]	V.F. Krotov. Global methods in optimal control theory. In Advances in
Nonlinear Dynamics and Control'. A Report from Russia, No. 17 in
Progress in Systems and Control Theory, pp.76-121. Birkhauser, Boston,
1993.
[126]	H. H. Кружков. Обобщенные решения нелинейных уравнений первого
порядка со многими независимыми переменными, I. Матем. сборник
(новая серия), 70(112)(3): 394-415, 1966.
[127]	С. Н. Кружков. Обобщенные решения уравнений Гамильтона-Якоби
типа эйконала, I. Матем. сборник, 27: 406-446, 1975.
[128]	С. Н. Кружков, Н. С. Петросян. Асимптотическое поведение решений
задачи Коши для нелинейных уравнений первого порядка. Успехи
матем. наук, 42(5): 3-40, 1987.
[129]	А. В. Кряжимский. К теории позиционных дифференциальных игр
сближения и уклонения. ДАН СССР, 239(4): 779-782, 1978.
[130]	Л. А. Кун, Ю. Ф. Пронозин. О сведении дифференциальной игры к за-
даче оптимального управления. Автоматика и телемеханика, (12):
5-11, 1971.
Литература
325
[131]	K.Kuratowski and C. Ryll-Nardzewski. A general theorem on selectors.
Bull. Acad. Polon. Sci.; Ser. Sci. Math. Astr. Phys., 13: 397-403, 1965.
[132]	А. Б. Куржанский. Управление и наблюдение в условиях неопределен-
ности. Наука, Москва, 1977.
[133]	А. Б. Куржанский. Об аналитическом описании пучка выживаю-
щих траекторий дифференциальной системы. ДАН СССР, 287(5):
1047-1050, 1986.
[134]	А. В. Kurzhanskii and Т. F. Filippova. On the theory of trajectory tubes — a
mathematical formalism for uncertain dynamics, viability and control. In
Advances in Nonlinear Dynamics and Control: A Report from Russia,
No. 17 in Progress in Systems and Control Theory, pp. 122-188.
Birkhauser, Boston, 1993.
[135]	H. H. Кузнецов. К точности некоторых аппроксимационных методов
вычисления слабых решений для квазилинейного уравнения первого
порядка. Журн. вычислит, матем. и мат. физики, 1(6): 1489-1502,
1975.
[136]	Н. Н. Кузнецов, А. А. Шишкин. Об одной многомерной задаче теории
квазилинейных уравнений. Журн. вычислит, матем. и мат. физики,
4(4): доп. «Численные методы решения дифференциальных и инте-
гральных уравнений и квадратурные формулы», 192-205, 1964.
[137]	P.D. Lax. Hyperbolic systems of conservation laws II. Communs pure
appl. Math., 10: 537-566, 1957.
[138]	Ю. С.Ледяев. Теоремы о неявно заданном многозначном отображе-
нии. ДЛЯ СССР, 276(3): 543-546, 1984.
[139]	Ю. С. Ледяев. Принцип максимума для оптимальных стратегий в диф-
ференциальных играх. ДАН СССР, 308(1): 41-45, 1989.
[140]	Ю. С. Ледяев, Е. Ф. Мищенко. Экстремальные задачи в теории диффе-
ренциальных игр. Труды математического института им. Стекло-
ва, 185: 147-170, 1988.
[141]	Р. L. Lions. Generalized solutions of Hamilton-Jacobi equations. Pitman,
Boston, 1982.
[142]	P.L. Lions. Existence results for first order Hamilton-Jacobi equations.
Ricerche Mat., 32: 1-23, 1983.
326
Литература
[143]	P.L. Lions. Neumann type boundary conditions for Hamilton-Jacobi
equations. Duke Math. J., 52(3): 793-820, 1985.
[144]	P.L. Lions and B. Pertame. Remarks on Hamilton-Jacobi equations with
measurable time dependent Hamiltonians. Nonlinear Analysis. Theory,
Meth. Appl., 11(5): 613-621, 1987.
[145]	P.L.Lions and P.E.Souganidis. Differential games, optimal control and
directional derivatives of viscosity solutions of Bellman’s and Isaacs’
equations. SIAM J. Control Optim., 23: 566-583, 1985.
[146]	И.Г. Малкин. Теория устойчивости движений. Наука, Москва, 1966.
[147]	В. П. Маслов, С. Н. Самборский. Существование и единственность ре-
шений стационарных уравнений Гамильтона-Якоби и Веллмана. Но-
вый подход. Докл. Акад, наук, 324(6): 1143-1148, 1992.
[148]	A. A. Melik’jan. Method characteristics for constructing of singular paths
and manifolds in optimal control and differential games. In Differential
Games — Developments in Modelling and Computation, vol. 156 of
Lecture Notes in Control. Inf Sci., pp. 81-90. 1991.
[149]	S.Mirica. Extending Cauchy’s method of characteristics for Hamilton-
Jacobi equations. Stud. Cere. Mat., 37(6): 555-565, 1985.
[150]	Е.Ф. Мищенко. Задачи преследования и уклонения от встречи в те-
ории дифференциальных игр. Изв. АН СССР, Техн, кибернетика, 5:
787-791, 1971.
[151]	Б. Ш. Мордухович. Аппроксимационные методы в задачах оптимиза-
ции и управления. Наука, Москва, 1988.
[152]	M.Nagumo. Uber die Laga der integralkurven gewohnlicher differential
Gleichungen. Proc. Phys. Math. Japan, 24: 399-414, 1942.
[153]	C. R.Nardzewski. A theory of pursuit and evasion. In Adv. in Game
Theory, No. 52 in Ann. Math. Studies. 1964.
[154]	M. С. Никольский. О применении первого прямого метода Понтряги-
на в играх преследования. Изв. АН СССР, Технич. кибернетика, 10(6):
51-56, 1972.
[155]	М. С. Никольский. Краткий обзор работ Л. С. Понтрягина по диффе-
ренциальным играм. Вестн. Моск, университета, сер. 15, вычисл.
матем., киберн., (3): 3-8, 1993.
Литература
327
[156]	С. П. Новиков, А. Т. Фоменко. Элементы дифференциальной геомет-
рии и топологии. Наука, Москва, 1987.
[157]	О. А. Олейник. Разрывные решения нелинейных дифференциальных
уравнений. Успехи матем. наук, 12(3): 3-73, 1957.
[158]	S.Osher and С. W. Shu. High-order essentially nonoscilatory shemes for
Hamilton-Jacobi equations. SIAM J. Numer. Anal., 28: 907-922, 1991.
[159]	Ю.С. Осипов. Альтернатива в дифференциально-разностной игре.
ДАН СССР, 197(5): 619-624, 1971.
[160]	Ю. С. Осипов. К теории дифференциальных игр в системах с распре-
деленными параметрами. ДАН СССР, 223(6): 1314-1317, 1975.
[161]	А. И. Панасюк, В. И. Панасюк. Об одном уравнении, порожденном
дифференциальным включением. Матем. заметки, 27(3): 429-437,
1980.
[162]	Т. Parthasarathy and Т. Raghavan. Some Topics in Two-Person Games,
vol. 22 of Modern Analytic and Computational Methods in Science and
Mathematics. American Elsevier, New York, 1971.
[163]	A. G. Pashkov and S. D. Terekhov. Differential game of approach with two
pursuers and one evader. J. Opt. Theory Appl., 55(2): 303-311, 1987.
[	164] V. S. Patsko, N. D. Botkin, V. M. Kein, V. L. Turova and M. A. Zarkh.
Control of aircraft landing in windshear. J. Opt. Theory Appl., 83(2):
237-267, 1994.
[	165] H. J. Pesch and R. Bulirsch. The maximum principle, Bellmans’s equation,
and Caratheodory’s work. J. Opt. Theory Appl., 80(2): 199-225, 1994.
[166]	H.H. Петров. О существовании значения игры преследования. ДАН
СССР, 190(6): 1289-1291, 1970. (Translated in Soviet Math. Dokl., 11:
292-294, 1970.)
[167]	И. Г. Петровский. Лекции по теории обыкновенных дифференциаль-
ных уравнений. Наука, Москва, 1964.
[168]	Е. С. Половинкин, Г. В. Смирнов. Об одном подходе к дифференци-
рованию многозначных отображений и необходимые условия опти-
мальности для решений дифференциальных включений. Дифференц.
уравнения, 22(6): 944-954, 1986.
328
Литература
[169]	Л. С. Понтрягин. К теории дифференциальных игр. Успехи матем.
наук, 21(4): 219-274,1966. (Translated in Russian Math. Surveys, Vol. 21
(1966), 193-246.)
[170]	Л. С. Понтрягин. О линейных дифференциальных играх. I. ДАН
СССР, 174(6): 1278-1281,1967. (Translatedin Soviet Math. DokL, Vol. 8
(1967), 769-771.)
[171]	Л. С. Понтрягин. О линейных дифференциальных играх. 11. ДАН
СССР, 175(4): 764-766, 1967. (Translated in Soviet Math. DokL, Vol. 8
(1967), 910-912.)
[172]	Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе, Е.Ф. Мищенко.
Математическая теория оптимальных процессов. Наука, Москва,
1961.
[173]	Б. Н. Пшеничный. О линейных дифференциальных играх. Киберне-
тика, (1): 65-78, 1968. (Translated Automat. Remote Control (1968)
No. 1, 55-67.)
[174]	Б. H. Пшеничный. Структура дифференциальных игр. ДАН СССР,
184(2): 285-287,1969. (Translated in Soviet Math. DokL, Vol. 10 (1969),
70-72.)
[175]	Б. H. Пшеничный. Выпуклый анализ и экстремальные задачи. Наука,
Москва, 1980.
[176]	Б. Н. Пшеничный, В. В. Остапенко. Дифференциальные игры. Наукова
думка, Киев, 1992.
[177]	Б. Н. Пшеничный, М. И. Сагайдак. О дифференциальных играх с фик-
сированным временем. Кибернетика, 2: 54-63, 1970. (Translated in
Cybernetics, Vol. 6 (1970), 72-83.)
[178]	R. T. Rockafellar. Convex Analysis. Princeton University Press, Princeton,
New Jersey, 1970.
[179]	R. T. Rockafellar. Proximal subgradients, marginal values and augmented
Lagrangians in convex optimization. Math. Operations Res., 6: 424-436,
1981.
[180]	C.P. Rourke and B. J. Sanderson. Introduction to Piecewise Linear
Topology. Springer-Verlag, Berlin, 1972.
[181]	E.Roxin. The axiomatic approach in differential games. J. Opt. Theory
Appl.,3: 153-163, 1969.
Литература
329
[	182] И. Розыев, А. И. Субботин. Полунепрерывные решения уравнений Га-
мильтона-Якоби. Прикл. матем. и механ., 52(2): 179-185, 1988.
[183]	Л. Г. Шагалова. Построение кусочно-линейного решения уравнения
Гамильтона-Якоби, 1991, деп. в ВИНИТИ, No. 2952-В91.
[184]	J. Shinar, М. Medinah, and М. Biton. Singular surfaces in a linear
pursuit-evasion game with elliptical vectograms. J. Opt. Theory Appl.,
43(1): 431-456, 1984.
[185]	E. В. Сидорова, H. H. Субботина. Алгоритм вычисления функции це-
ны линейной дифференциальной игры с выпуклой платой. В сб. По-
зиционное управление с гарантированным результатом, 62-74, АН
СССР, Уральское отделение, Свердловск, 1988.
[186]	G. Sonnevend. Existence and numerical computation of extremal invariant
sets in linear differential games. In Leet. Notes in Control Inf. Set, Vol. 22,
pp. 251-260. Springer-Verlag, 1981.
[187]	G. Sonnevend. Constructing feedback control in differential games by use
of «central» trajectories. Report 385, Institut fur Angewandte Mathematik
und Statistic, Universitat Wurzburg, Wurzburg, 1992.
[188]	P. E. Souganidis. Approximation schemes for viscosity solutions of
Hamilton-Jacobi equations. J. of Different. Equat., 59: 1-43, 1985.
[189]	P. E. Souganidis. Мах-min representations and product formulas for
the viscosity solutions of Hamilton-Jacobi equations with applications
to differential games. Nonlinear Analysis. Theory, Meth. Appl., 9(3):
217-257, 1985.
[190]	В. В. Степанов. Курс дифференциальных уравнений. Физматгиз, Моск-
ва, 1959.
[191]	J. Stoer and С. Witzgall. Convexity and Optimization in Finite Dimensions
I. Springer-Verlag, Berlin, Heidelberg, New York, 1970.
[192]	А. И. Субботин. Обобщение основного уравнения теории дифферен-
циальных игр. ДАН СССР, 254(2): 293-297,1980. (Translatedin Soviet
Math. Dokl., Vol. 22, No. 2, (1980), 358-362.)
[193]	А. И. Субботин. Generalization of the main equation of differential game
theory. J. Opt. Theory Appl., 43(1): 103-133, 1984.
[194]	A. I. Subbotin. Existence and uniqueness results for Hamilton-Jacobi
equations. Nonlinear analysis, 16: 683-689, 1991.
330
Литература
[195]	А. И. Субботин. Минимаксные неравенства и уравнения Гамильтона -
Якоби. Наука, Москва, 1991.
[196]	А. И. Субботин. Об одном свойстве субдифференциала. Матем. сбор-
ник. 182(9): 1315-1330, 1991. (Translated in Math. USSR Sbomik., Vol.
74 (1993), 63-78.)
[197]	А. И. Субботин. Непрерывные и разрывные решения краевых задач
для уравнений с частными производными первого порядка. Докл.
Акад. наук. 323(1): 30-34, 1992.
[198]	A. I. Subbotin. Discontinuous solutions of a Dirichlet type boundary value
problem for first order PDE. Russ. J. Numer. Anal. Math. Modelling. 8:
145-164, 1993.
[199]	A. I. Subbotin. A theory of generalized solutions to first-order PDEs with
the emphasis on differential games. In Advances in Nonlinear Dynamics
and Control: A Report from Russia. Vol. 17 in Progress in Systems and
Control Theory, pp. 189-238. Birkhauser, Boston, 1993.
[200]	А. И. Субботин, А. Г. Ченцов. Оптимизация гарантии в задачах управ-
ления. Наука, Москва, 1981.
[201]	А. И. Субботин, Л. Г. Шагалова. Кусочно-линейные функции, исполь-
зуемые для построения решений уравнения Гамильтона-Якоби, 1990,
Свердловск, деп. в ВИНИТИ, No. 5627-В90.
[202]	А. И. Субботин, Л. Г. Шагалова. Кусочно-линейное решение задачи
Коши для уравнения Гамильтона-Якоби. Докл. Российской акад, на-
ук. 325(5): 932-936,1992. (Translated in Russian Acad. Sci. Dokl., Math.,
Vol. 46(1993), 144-148.)
[203]	А. И. Субботин, H. H. Субботина. Необходимые и достаточные усло-
вия для кусочно-гладкой цены дифференциальной игры. ДАН СССР.
243(4): 862-865, 1978. (Translated in Soviet Math. Dokl., Vol. 19 (1978),
1447-1451).
[204]	А. И. Субботин, A. M. Тарасьев. Сопряженные производные функции
цены дифференциальной игры. ДАН СССР. 283(3): 559-564, 1985.
(Translated in Soviet Math. Dokl., Vol. 32 (1985), 162-166.)
[205]	A. I. Subbotin and A. M. Tarasyev. Stability properties of the value function
of a differential game and viscosity solutions of Hamilton-Jacobi
equations. Problems Control Inform. Theory. 15(6): 451-463, 1986.
Литература
331
[206]	Н. Н. Субботина. Универсальные оптимальные стратегии в позицион-
ных дифференциальных играх. Дифференциальные уравнения, 19(11):
1890-1896, 1983.
[207]	N.N. Subbotina. Maximum principle and superdifferential of the value
function. Problems Control Inform. Theory, 18(3): 151-160, 1989.
[208]	H. H. Субботина. Метод характеристик Коши и обобщенные реше-
ния уравнений Гамильтона-Якоби-Веллмана. ДАН СССР, 320(3):
556-561, 1991.
[209]	N. N. Subbotina. Necessary and sufficient optimality conditions in terms
of characteristics of the Hamilton-Jacobi-Bellman equation. Report 393,
Institut fur Angewandte Mathematik und Statistic, Universitat Wurzburg,
Wurzburg, 1992.
[210]	A. M. Tarasyev. Approximation schemes for construction of the
generalized solution of the Hamilton-Jacobi (Bellman-Isaacs) equation.
Report 371, Institut fur Angewandte Mathematik und Statistic, Universitat
Wiirzburg, Wurzburg, 1992.
[211]	A. M. Тарасьев. Аппроксимационные схемы построения минимакс-
ных решений уравнения Гамильтона-Якоби. Прикл. матем. механ.,
58(1): 22-36, 1994.
[212]	А. М. Тарасьев, В. Н. Ушаков, А. П. Хрипунов. Об одном вычислитель-
ном алгоритме для решения игровых задач управления. Прикл. ма-
тем. механ., 51(2): 216-222, 1987.
[213]	А. М. Тарасьев, В. Н. Ушаков, А. П. Хрипунов. О построении мно-
жеств позиционного поглощения в игровых задачах управления. В сб.
Труды Инет, матем. механ. УрО РАН, 1: 160-177, 1992.
[214]	А. М. Tarasyev, A. A. Uspenskii, and V.N. Ushakov. On construction of
solving procedures in a linear control problem. In IMACS. The Lyapunov
functions method and applications, pages 111-115, 1990.
[215]	A. M. Тарасьев, А. А. Успенский, В. H. Ушаков. Аппроксимационные
операторы и конечно-разностные схемы для построения обобщенных
решений уравнений Гамильтона-Якоби. Известия РАН, Техн, кибер-
нетика, (3): 173-185, 1994.
[216]	С. И. Тарлинский. Об одной дифференциальной игре наведения в
классе смешанных стратегий. Известия АН СССР, Техн, кибернетика,
(4): 64-70, 1973.
332
Литература
[217]	В. Л. Турова. Нелинейная дифференциальная игра качества на плоско-
сти. В сб. Исследования задач минимаксного управления, рр. 91-116,
Уральский научный центр, Свердловск, 1985.
[218]	В. Н. Ушаков. К задаче построения стабильных мостов в дифференци-
альной игре сближения-уклонения, 1980. Известия АН СССР, Техн,
кибернетика, (4): 29-36, 1980. (Translated in Engineering Cybernetcs,
Vol. 18, no. 4, 16-23.)
[219]	P. Varaiya. On the existence of solutions to a differential game. SIAM J.
Control and Optim., 5(1): 153-162, 1967.
[220]	P. Varaiya and J. Lin. Existence of saddle points in differential games.
SIAM J. Control, 7(1): 142-157, 1969.
[221]	R. B. Vinter. A characterization of the reachable set for nonlinear systems.
SIAM J. Control Optim., 18: 599-610, 1980.
[222]	R. B. Vinter and P. Wolenski. Hamilton-Jacobi theory for optimal control
problems with data measurable in time. SIAM J. Control Optim., 28:
1404-1419, 1990.
[223]	В. С. Владимиров. Уравнения математической физики. Наука, Моск-
ва, 1988.
[224]	А. И. Вольперт. Пространства BV и квазилинейные уравнения. Ма-
тем. сборник, 73(2): 255-302,1967. (TranslatedinMath. USSR-Sbornik,
2, (1967), 225-267.)
[225]	J.Warga. Optimal Control of Differential and Functional Equations.
Academic Press, New York, 1972.
[226]	T.Wazewski. Sur une generalisation de la notion des solution d’une
equation au contingent. Bull. Acad. Polon. Sci.; Ser. Sci. Math. Astr. Phys.,
10: 11-15, 1962.
[227]	L. C. Young. Lectures on the calculus of variations and optimal control
theory. Sanders, Philadelphia, 1969.
[228]	L. S. Zaremba. Existence theorems for games of survival. J. Optim. Theory
andAppl., 341-346, 1986.
[229]	S.Ch.Zaremba. Sur les equations au paratingent. Bull. Sci. Math.,
Deuxieme 2 Ser., 60: 139-160, 1936.
Литература
333
[230]	М. А. Зарх, А. Г. Иванов. Построение функции цены в линейной диф-
ференциальной игре с фиксированным моментом окончания. В сб.
Труды Инет, матем. механ. УрО РАН, 2: 140-155, 1992.
[231	] М. А. Зарх, В. С. Пацко. Численное решение дифференциальной игры
наведения третьего порядка. Известия АН СССР, Техн, кибернетика,
(6): 162-169, 1987.
Предметный указатель
Верхний топологический предел 287
Верхняя производная по направле-
нию 292
Выживающая траектория 22, 306,
313
Вязкостное решение 42
—	субрешение 42
—	суперрешение 42
Гамильтониан 67
График многозначного отображения
287
—	функции 289
Дифференциальное включение 302
Задача М-сближения 150
Замкнутое многозначное отображе-
ние 288
Игра преследования-уклонения 259
Квазиградиент 145
Квазистратегия 167
Контингентный (тангенциальный)
конус 292
Контр-управления 168
Контрстратегия 189
Конус Булигана 292
Многозначная функция 287
Многозначное отображение 287
Множество достижимости 206
Монотонная траектория 306
Надграфик функции 289
Нижний топологический предел 288
Нижняя производная по направле-
нию 292
Обобщенные характеристики 23
Подграфик функции 289
Позиционная стратегия 134
Полунепрерывная сверху функция
289
— снизу функция 289
Полунепрерывное сверху много-
значное отображение 288
— снизу многозначное отображение
288
Предстратегия 138
Производная Дини по направлению
292
— Хаддада по направлению 292
Проксимальный субградиент 299
Свойство выживаемости 22,306,313
Слабо инвариантное множество 22,
306,313
Смешанная позиционная стратегия
185
— стратегия по принципу обратной
связи 185
Сопряженная функция 290
Стабильная дорожка 202
Стабильный мост 151
Стратегия по принципу обратной
связи 134
Субградиент 298
Предметный указатель
Субдифференциал 298
Суперградиент 298
Супердифференциал 298
Универсально оптимальная страте-
гия 160
Уравнение Айзекса-Веллмана 137,
264
Условие Айзекса 132, 261
—	седловой точки в маленькой игре
132,261
335
Характеристическое включение 21,
68
Цена дифференциальной игры 137
Экстремальная предстратегия 265
—	стратегия 154
Эффективное множество многознач-
ного отображения 287
Интересующие Вас книги нашего издательства можно заказать почтой
или электронной почтой:
subscribe@rcd.ru
Внимание: дешевле и быстрее всего книги можно приобрести через
наш Интернет-магазин:
http://shop.rcd.ru
Книги также можно приобрести:
1.	Москва, ФТИАН, Нахимовский проспект, д. 36/1, к. 307,
тел.: 332-48-92 (почтовый адрес: Нахимовский проспект, д. 34).
2.	Москва, ИМАШ, ул. Бардина, д. 4, корп. 3, к. 414, тел. 135-54-37.
3.	МГУ им. Ломоносова (ГЗ, 1 этаж).
4.	Магазины:
Москва: «Дом научно-технической книги» (Ленинский пр., 40)
«Московский дом книги» (ул. Новый Арбат, 8)
«Библиоглобус» (м. Лубянка, ул. Мясницкая, 6)
С.-Пб.: «С.-Пб. дом книги» (Невский пр., 28)
Субботин Андрей Измаилович
Обобщенные решения уравнений
в частных производных первого порядка
Перспективы динамической оптимизации
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Компьютерная верстка С. В. Высоцкий
Корректор М. А. Ложкина
Подписано в печать 09.01.03. Формат 60 х 84У16.
Печать офсетная. Усл.печ.л. 19,53. Уч. изд. л. 20,12.
Гарнитура Таймс. Бумага офсетная №1.
Тираж 1000 экз. Заказ №94.
АНО «Институт компьютерных исследований»
426034, г. Ижевск, ул. Университетская, 1.
Лицензия на издательскую деятельность ЛУ №084 от 03.04.00.
http://rcd.ru E-mail: borisov@rcd.ru