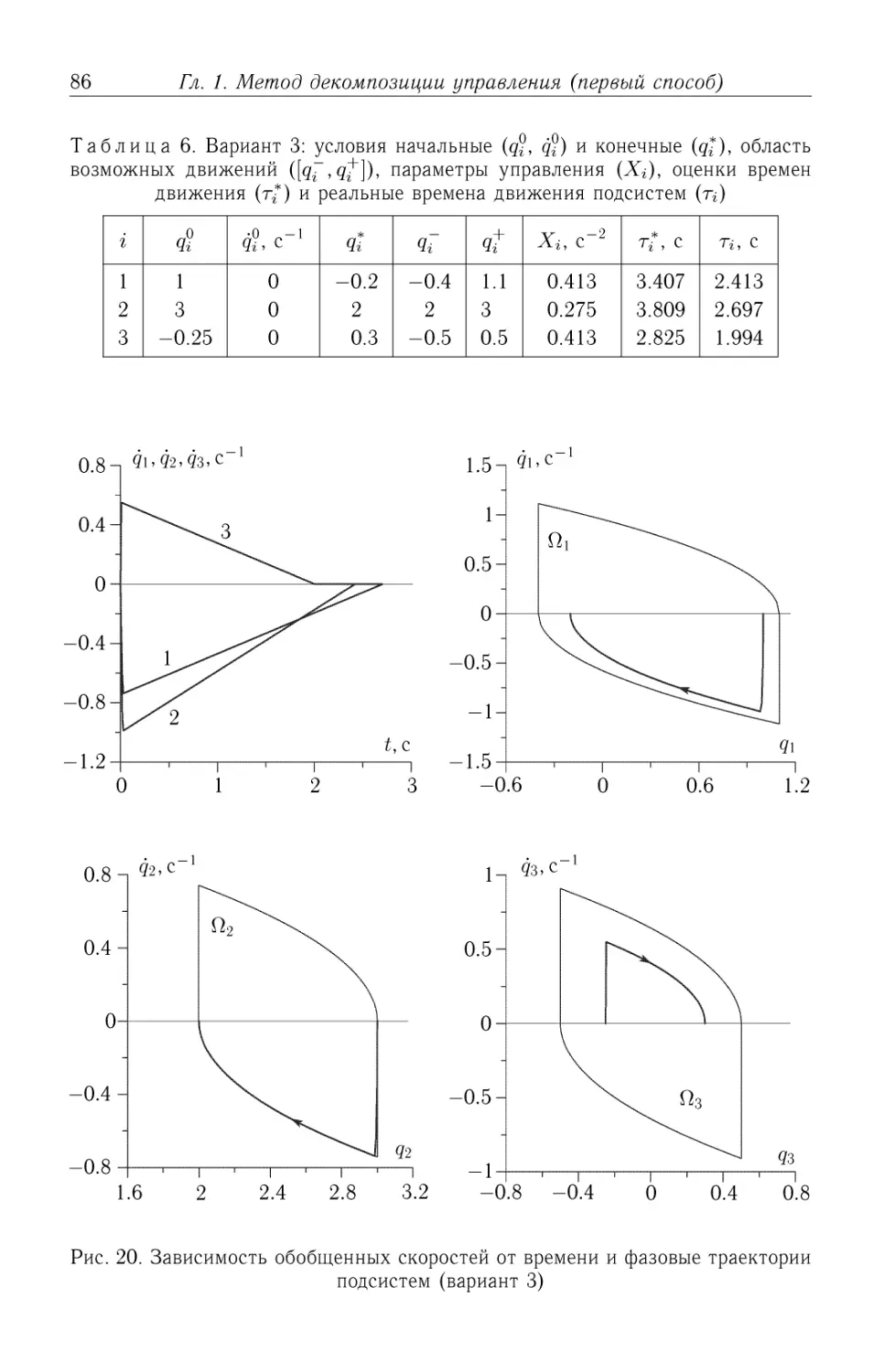
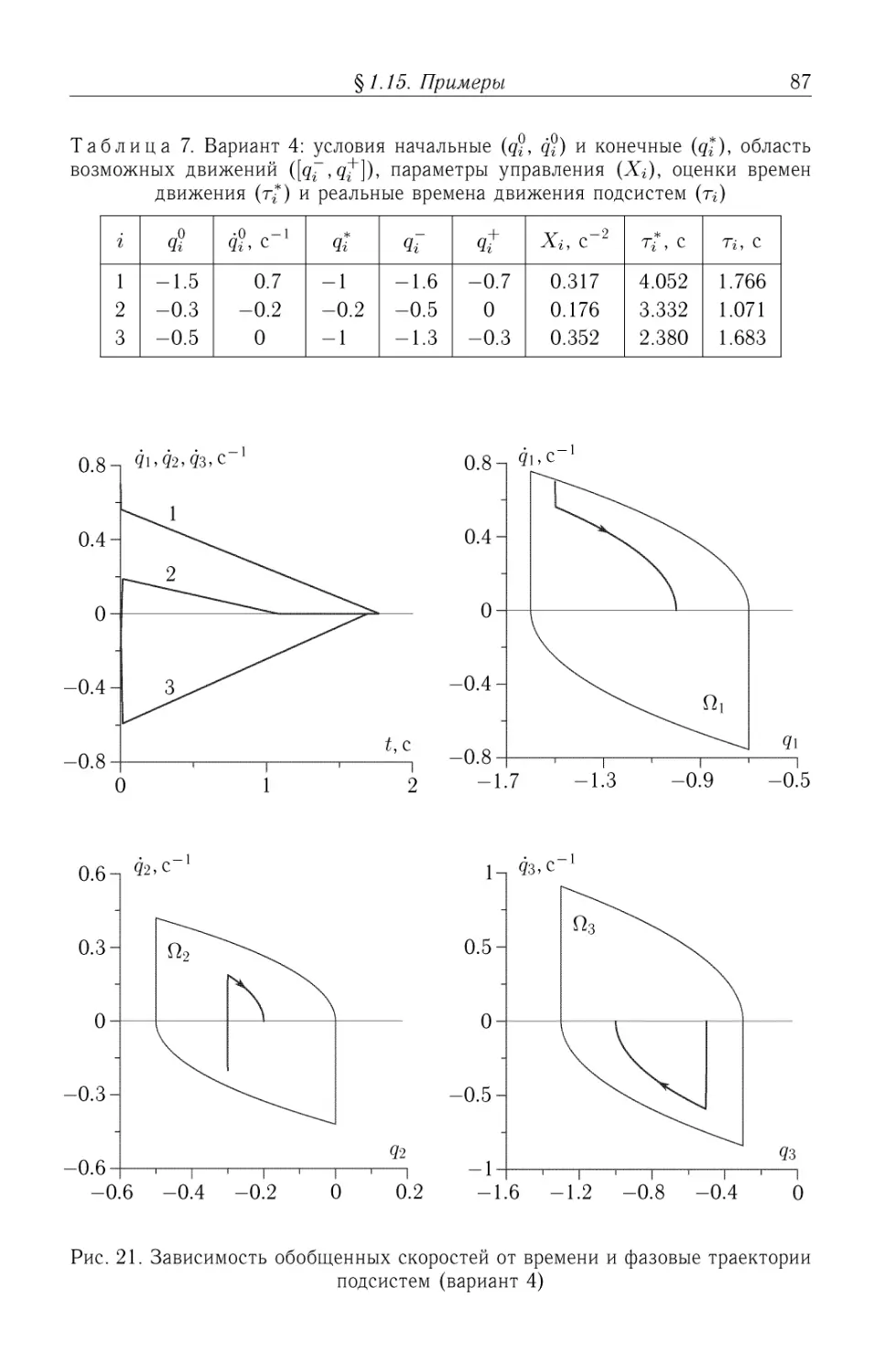
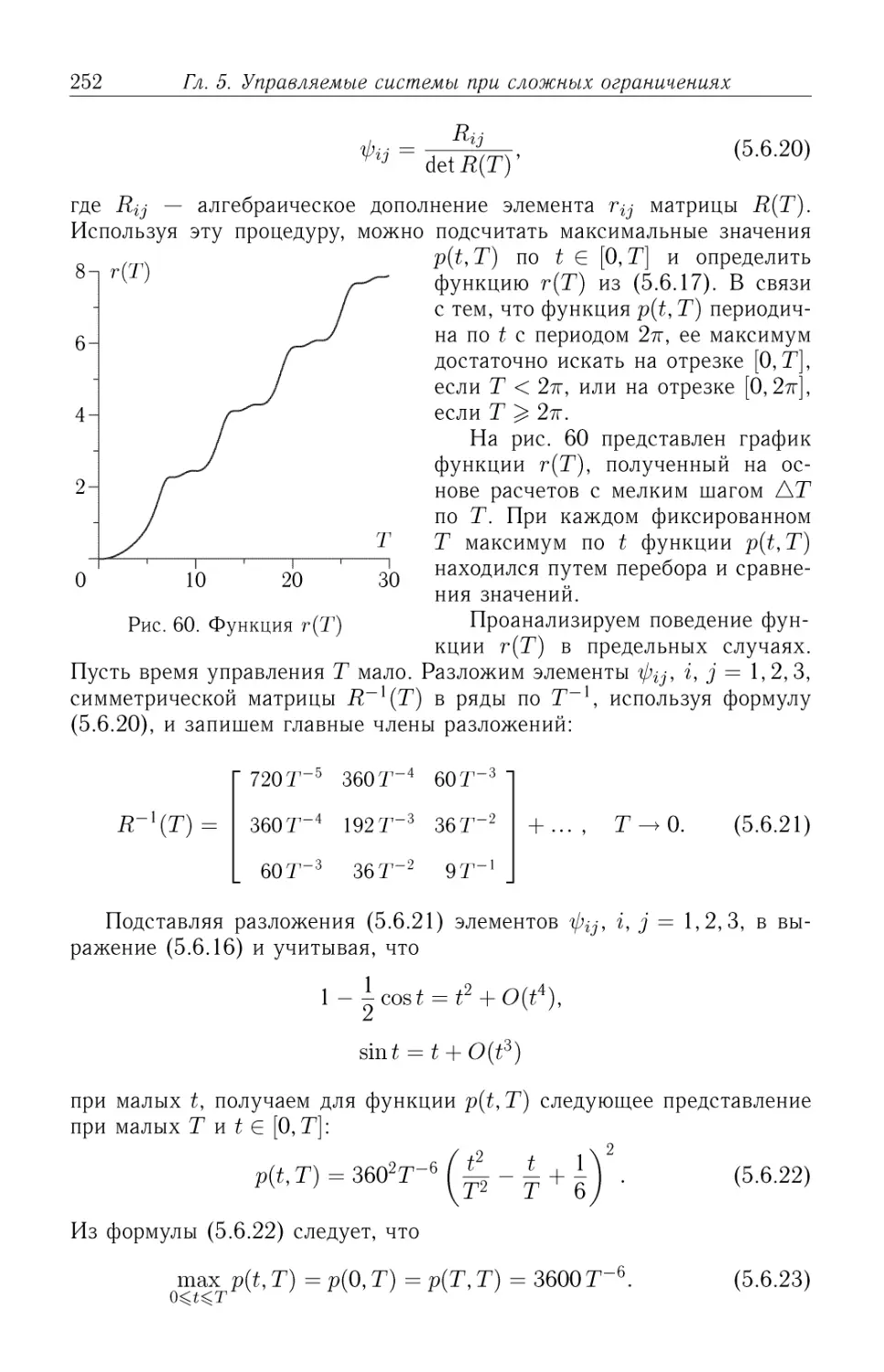
Автор: Черноусько Ф.Л.
Теги: динамика кинетика механика теория автоматического управления
ISBN: 5-9221-0678-3
Год: 2006
Текст
УДК 531.36
ББК 22.21
4 49
Черноусько Ф. Л., Ананьевский И. М., Решмин С. А.
Методы управления нелинейными механическими системами. — М.:
ФИЗМАТЛИТ, 2006. - 328 с. - ISBN 5-9221-0678-3.
Книга посвящена разработке эффективных методов управления сложными
механическими системами на основе математических моделей, отражающих
основные особенности таких систем: высокую размерность системы, динами-
динамическую зависимость между ее степенями свободы, наличие нелинейностей (в
том числе разрывных зависимостей типа сухого трения), сложные совместные
ограничения на управляющие воздействия и фазовые переменные, неполноту
информации о внешних возмущениях и собственных параметрах системы,
требование о приведении системы в терминальное состояние за конечное
время. Эффективность предложенных в монографии методов продемонстриро-
продемонстрирована путем построения законов управления для конкретных механических и
электромеханических систем, а также компьютерного моделирования динамики
этих систем.
Для научных работников и инженеров — специалистов по механике систем,
теории управления и их приложений, а также для студентов и аспирантов.
© ФИЗМАТЛИТ, 2006
© Ф. Л. Черноусько, И. М. Ананьевский,
ISBN 5-9221-0678-3 С. А. Решмин, 2006
ОГЛАВЛЕНИЕ
Предисловие 7
Введение 9
Глава 1. Метод декомпозиции управления (первый способ) 19
§ 1.1. Управляемая механическая система 19
§ 1.2. Постановка задачи управления 20
§ 1.3. Декомпозиция 23
§ 1.4. Оптимальное управление подсистемой 25
§ 1.5. Упрощенное управление подсистемой 29
§ 1.6. Сравнительный анализ результатов 33
§ 1.7. Управление исходной системой 39
§ 1.8. Модификация метода декомпозиции 40
§ 1.9. Анализ управляемых движений 42
§ 1.10. Определение параметров 45
§1.11. Подсистема с нелинейным сопротивлением 52
§ 1.12. Управление нелинейной подсистемой 54
§ 1.13. Приложение к робототехническим системам 69
§ 1.14. Синтез управления двузвенным манипулятором с безредуктор-
ными приводами 73
§ 1.15. Примеры 79
Глава 2. Метод декомпозиции управления (второй способ) 89
§2.1. Управляемая механическая система 89
§2.2. Постановка задачи 91
§2.3. Управление при отсутствии внешних сил 92
§2.4. Декомпозиция 94
§2.5. Построение синтеза управления 99
§2.6. Управление в общем случае 100
§2.7. Обобщение на случай ненулевой конечной скорости 104
§2.8. Задача об отслеживании траекторий механических систем .... 111
§2.9. Приложения к робототехническим системам 118
§2.10. Примеры 123
Оглавление
Глава 3. Кусочно-линейное управление механическими системами
в условиях неопределенности 133
§3.1. Постановка задачи для склерономной системы 133
§3.2. Вспомогательное рассуждение 135
§3.3. Описание алгоритма управления 136
§3.4. Обоснование алгоритма 138
§3.5. Оценка времени движения 144
§3.6. Достаточное условие приведения 146
§3.7. Результаты моделирования динамики двузвенника 148
§3.8. Управление двухмассовой системой с неизвестными параметрами 151
§3.9. Первый этап движения 156
§3.10. Второй этап движения 161
§3.11. Система «груз на тележке» 164
§3.12. Система «физический маятник на тележке» 165
§3.13. Результаты моделирования 177
§3.14. Кусочно-линейное управление реономными механическими
системами. Постановка задачи 179
§3.15. Описание алгоритма для реономных систем 180
§3.16. Обоснование алгоритма для реономных систем 181
§3.17. Результаты моделирования 191
Глава 4. Управление системами с распределенными параметрами 194
§4.1. Управление системой осцилляторов 194
§4.2. Задача быстродействия 195
§4.3. Постановка задачи управления системой с распределенными
параметрами 201
§4.4. Декомпозиция 203
§4.5. Уравнение первого порядка по времени 206
§4.6. Уравнение второго порядка по времени 207
§4.7. Анализ ограничений и построение управления 209
§4.8. Примеры 213
§4.9. Условия разрешимости в общем случае 220
Глава 5. Управляемые системы при сложных ограничениях 225
§5.1. Постановка задачи 225
§5.2. Обобщение метода Калмана 227
§5.3. Управление системой осцилляторов 232
§5.4. Маятник с управляемой по ускорению точкой подвеса 238
§5.5. Маятник с управляемой по ускорению точкой подвеса (продол-
(продолжение) 243
§5.6. Маятник с управляемой по скорости точкой подвеса 249
Оглавление
§5.7. Модель электромеханической системы 256
§5.8. Анализ упрощенной модели 259
§5.9. Управление электромеханической системой четвертого порядка 263
§5.10. Активный динамический гаситель 272
Глава 6. Некоторые задачи оптимального управления при слож-
сложных ограничениях 281
§6.1. Введение 281
§6.2. Постановка задачи оптимального быстродействия при смешан-
смешанных и фазовых ограничениях 282
§6.3. Оптимальное быстродействие при ограничениях на скорость
и ускорение 283
§6.4. Задача управления электродвигателем 289
§6.5. Постановка задачи оптимального быстродействия при ограниче-
ограничении на скорость изменения ускорения 294
§6.6. Программное оптимальное управление 295
§6.7. Синтез оптимального управления 298
§6.8. Постановка задачи оптимального быстродействия при ограниче-
ограничениях на ускорение и скорость его изменения 306
§6.9. Возможные типы управлений 309
§6.10. Построение траекторий 312
Список литературы 320
Предисловие
Предлагаемая монография посвящена ряду новых методов управ-
управления механическими системами со многими степенями свободы.
Рассматриваются, как правило, нелинейные системы при наличии
различных ограничений, наложенных на управляющие воздействия
и фазовые координаты, а также на их совокупности. В значительной
части книги принимается во внимание наличие неопределенностей
различной природы, в том числе воздействие неизвестных, но огра-
ограниченных возмущений, а также наличие неопределенных параметров
системы.
При этих условиях, которые отражают реальные свойства многих
управляемых систем, встречающихся на практике, построение управ-
управления встречает большие трудности.
В книге изложен ряд достаточно общих методов, позволяющих
эффективно, часто в явном виде, построить искомые управления. Пред-
Представлены методы, основанные на декомпозиции нелинейных управ-
управляемых систем, кусочно-линейные алгоритмы управления по обратной
связи, а также другие методы, использующие и развивающие подходы,
известные в теории линейных управляемых систем и в теории опти-
оптимального управления.
Построенные управления удовлетворяют всем наложенным огра-
ограничениям и приводят динамическую систему, подверженную неиз-
неизвестным, но ограниченным возмущениям, в заданное терминальное
состояние за конечное время. Получены явные оценки сверху времени
процесса управления. Во всех случаях дается строгое обоснование
алгоритмов управления и полученных оценок.
В большинстве случаев не ставится и не решается задача оптималь-
оптимального управления для рассматриваемых нелинейных систем. Однако при
построении управлений используются элементы теории оптимальных
процессов и проводится оптимизация времени движения по парамет-
параметрам, так что предложенные методы можно назвать субоптимальными
по быстродействию. Впрочем, в последней главе дается также точное
решение ряда новых задач оптимального управления.
Изложение методов иллюстрируется большим количеством
задач управления для различных механических и электромехани-
электромеханических систем: манипуляционных роботов, маятниковых систем,
Предисловие
электроприводов, многомассовых систем с сухим трением, активных
гасителей колебаний. Во всех случаях решение доводится до конца:
получены законы управления, проведен анализ динамики систем,
оценено время движения, приведены результаты компьютерного
моделирования.
Книга основана на работах авторов, опубликованных в последние
15 лет и приведенных в списке литературы. Авторы надеются,
что предлагаемая монография послужит полезным дополнением
к обширной литературе по теории и методам управления динамичес-
динамическими системами. Книга представляет интерес для научных работников
и инженеров — специалистов по механике систем, теории управления
и их приложений, а также для студентов и аспирантов.
Авторы выражают признательность Российскому фонду фундамен-
фундаментальных исследований (грант 02-01-14072) за финансовую поддержку
публикации этой книги.
Введение
Как известно, существуют различные методы построения управ-
управления динамическими системами.
Классические методы теории автоматического регулирования,
применимые к линейным системам, представляют управление в виде
линейного оператора от текущего фазового состояния системы.
Недостатки такого подхода проявляются как в окрестности заданного
терминального состояния, так и вдали от него. Вблизи терминального
состояния управление становится малым, и не используются все его
возможности. В результате, время процесса управления оказывается,
строго говоря, бесконечным, и можно рассчитывать лишь на асимпто-
асимптотическое стремление фазового состояния к заданному терминальному
состоянию. Вдали же от терминального состояния управление
оказывается большим по величине и может нарушать ограничения,
которые обычно накладываются на управляющие воздействия. Поэтому
учет наложенных ограничений при использовании линейных методов
затруднен и часто невозможен. Кроме того, применение этих методов,
основанных на линейных моделях, к нелинейным системам обычно
оказывается неоправданным.
Для управления нелинейными системами могут быть использованы
методы теории оптимального управления. Эти методы учитывают
различные ограничения, наложенные на управление, а также, хотя
и ценой значительного усложнения, и на фазовые координаты. Данные
методы позволяют привести управляемую систему в терминальное
состояние оптимальным, в том или ином смысле, образом, например,
за минимальное время. Однако построение оптимального закона
управления для нелинейной системы — задача весьма сложная,
и ее точное решение возможно сравнительно редко. Особенно
трудным является построение оптимального синтеза управления,
т.е. управления по принципу обратной связи.
Существует целый ряд других общих методов управления: метод
систем переменной структуры [31,58,59,98,99], метод линеаризации
по обратной связи [86, 87, 91] и различные их обобщения. Эти методы,
однако, обычно не учитывают ограничения, наложенные на управления
и фазовые координаты. Кроме того, в силу большой общности, данные
методы не принимают во внимание специфику механических систем,
10 Введение
например, законы сохранения или структуру уравнений движения
в форме Лагранжа или Гамильтона. Некоторые другие методы управ-
управления, применимые к нелинейным механическим системам, развиты
в работах [48, 51, 52, 60, 84, 85, 88, 90, 100].
В данной книге предлагаются методы управления нелинейными
механическими системами при наличии возмущений, неопределен-
неопределенностей и различных ограничений, наложенных на управляющие
воздействия и фазовые координаты. Использование механической
природы уравнений движения позволяет продвинуться по сравнению
с методами, рассчитанными на системы общего вида, описываемые
обыкновенными дифференциальными уравнениями.
Авторы поставили цель разработать методы, которые обладали бы
следующими свойствами.
1. Методы применимы к нелинейным механическим системам,
описываемым уравнениями типа Лагранжа.
2. Методы применимы к системам со многими степенями свободы.
3. Методы позволяют учитывать ограничения, наложенные
на управляющие воздействия, а в ряде случаев — также на
фазовые координаты и на совокупность управлений и фазовых
координат.
4. Методы обеспечивают приведение системы в заданное терми-
терминальное состояние за конечное время, для которого имеется
эффективная верхняя оценка.
5. Методы позволяют строить управление при наличии неопреде-
неопределенных, но ограниченных внешних возмущений и при неопреде-
неопределенности параметров системы. Тем самым, эти методы обладают
свойством робастности.
6. Имеется эффективный алгоритм построения искомого управления
по обратной связи.
7. Во всех случаях дается строгое математическое обоснование
методов.
Ясно, что перечисленные свойства весьма важны и полезны как
с точки зрения теории управления, так и для практических ее прило-
приложений.
В монографии предложен и разработан ряд методов, и не все из них
обладают всеми свойствами 1-7, перечисленными выше. Свойства
3, 4, 7 выполнены всегда, но для некоторых из излагаемых методов
свойства 1, 2, 5, 6 могут не иметь места.
В первых двух главах книги рассматриваются нелинейные управля-
управляемые механические системы со многими степенями свободы, описыва-
описываемые уравнениями Лагранжа вида
Т^~^ = иг + Яг, г=1,...,п; @.1)
at oqi oqi
Введение 11
здесь qi — обобщенные координаты системы, Щ — управляющие
обобщенные силы, Qi — все прочие обобщенные силы, включая
неконтролируемые возмущения, п — число степеней свободы системы,
t — время, точкой обозначаются производные по времени, T(q, q) —
кинетическая энергия системы, заданная в виде симметрической
положительно-определенной квадратичной формы от обобщенных
скоростей qf.
T(q, q)=X- {A(q)q, q) = | ? ajk(q)qjqk- @.2)
j,k=\
через q и q обозначаются п-мерные векторы обобщенных координат
и скоростей соответственно, а скобками (•, •) — скалярное произведение
векторов.
Квадратичная форма @.2) удовлетворяет условиям
m\\q\\2^(A(q)q,q)^M\\q\\2, @.3)
где т и М — положительные постоянные, М > т > 0. Из @.3)
следует, что собственные числа матрицы A(q) при всех q лежат в ин-
интервале [т,М]. В главах 1, 2 коэффициенты а^ квадратичной формы
считаются известными функциями координат: а^ = cijk(q). В гл. 3
зависимости ajk(q) могут быть неизвестны, требуется лишь знание
постоянных т и М в неравенствах @.3).
Предполагается, что на управляющие воздействия в каждый момент
времени наложены геометрические ограничения вида
\Щ^Ц?, г=1,...,п, @.4)
где U® — заданные постоянные.
Неуправляющие обобщенные силы Qi могут зависеть от координат,
скоростей и времени достаточно произвольным образом, требуется
лишь, чтобы эти силы были ограничены по величине:
\Qi(q,q,t)\^Q°i, i=\,...,n. @.5)
Постоянные Q® считаются заданными, и при построении управления
на них накладываются сверху определенные ограничения.
Задача управления системой @.1) формулируется следующим
образом.
Построить управление по обратной связи Ui(q,q), г = 1,...,п,
которое переводит систему @.1) при наложенных ограничениях
@.3)-@.5) из заданного начального состояния
q(to)=q°, q(to)=q° @-6)
12 Введение
в заданное терминальное состояние с нулевыми обобщенными
скоростями
q(U) = q*, q(U)=O @.7)
за конечное время. Момент t* не предполагается фиксированным.
Во многих приложениях желательно осуществить перемещение
системы из состояния @.6) как можно быстрее, т. е. минимизировать
время ?*. Однако точное решение задачи оптимального быстродей-
быстродействия для нелинейной системы, особенно в части построения синтеза
управления, представляет большие трудности. Предлагаемые методы
построения не приводят к оптимальному синтезу, но включают ряд
процедур оптимизации времени процесса. Поэтому их можно называть
субоптимальными.
Основные проблемы, возникающие при решении задач управления
рассматриваемой системой @.1), обусловлены тем, что она представ-
представляет собой существенно нелинейную динамическую систему высокого
порядка. Ее отличает наличие динамического взаимодействия между
различными степенями свободы, которое характеризуется элементами
ctjk(q) матрицы кинетической энергии A(q). Другим осложняющим
фактором выступает то обстоятельство, что размерность вектора управ-
управляющих сил в системе в два раза меньше ее порядка.
Примером механических систем, описываемых уравнениями @.1),
могут служить манипуляционные роботы, которые являются важ-
важнейшей составной частью автоматизированных производственных
систем. Манипуляционные роботы обладают гибкостью перестройки
на выполнение самых разнообразных технологических операций,
а также широкими функциональными возможностями. В отличие
от автоматов, они способны воспроизводить или имитировать движения
человека. Манипуляционный робот — это управляемая механическая
система, которая содержит один или несколько манипуляторов
(исполнительных органов), систему управления, приводы, захватные
устройства (рабочие органы). Манипулятор — механическая система
с программным управлением, доставляющая объекты в заданную
область пространства внутри рабочей зоны. В конструкции мани-
пуляционного робота используются различные виды приводов —
электромеханические, пневматические, электрогидравлические. Наи-
Наибольшее распространение получили электромеханические приводы,
состоящие обычно из электродвигателя и редуктора. Приводные
двигатели могут быть расположены в шарнирах, соединяющих звенья
манипулятора, или в соседних с шарнирами звеньях.
Для манипуляционных роботов в качестве обобщенных коор-
координат qi обычно выбираются относительные углы или смещения
между звеньями. Интенсивность взаимовлияния между различными
звеньями задается элементами матрицы A(q). Если учитывается
динамика приводов, то функции а^ включают массо-инерционные
Введение 13
параметры электродвигателей и редукторов. Уравнения движения
манипуляционного робота (в форме Лагранжа) содержат составляющие
обобщенных сил Qi, обусловленные силами веса, сопротивления,
которые бывают известны лишь в общих чертах и могут существенно
изменяться в процессе эксплуатации манипулятора. Компоненты Ui
имеют физический смысл сил или моментов сил, развиваемых
исполнительными устройствами.
Необходимость рассмотрения задач управления манипуляционными
роботами именно в нелинейной постановке (без перехода к упрощен-
упрощенному линеаризованному описанию) связана с несколькими причинами.
Так, область допустимых возмущений для систем управления, постро-
построенных на основе линейных моделей, часто не охватывает возмущений,
которые встречаются в реальных эксплуатационных режимах. Кроме
того, при изменении цели управления изменяются как структура,
так и параметры алгоритмов управления. Указанные причины также
затрудняют синтез универсальных систем управления.
В главах 1 и 2 развиты методы декомпозиции для решения постав-
поставленной задачи управления. Суть этих методов состоит в преобразо-
преобразовании исходной нелинейной системы @.1) с п степенями свободы
к совокупности п независимых линейных подсистем вида
Здесь xi — новые (преобразованные) обобщенные координаты, щ — но-
новые управляющие воздействия, V{ — возмущающие силы, включающие
как внешние силы Qi, так и нелинейные члены, описывающие взаи-
взаимодействие различных степеней свободы в системе @.1). Возмущения
Vi в системе @.8) трактуются как неопределенные, но ограниченные
воздействия, которые можно рассматривать как противодействие про-
противника.
Исходные ограничения @.3)-@.5), наложенные на обобщенные
силы и кинетическую энергию системы, при определенных условиях
сводятся к следующим нормализованным ограничениям на управ-
управления щ и возмущения vf
щ\ < 1, Ы < Рь pi < 1, г=1,...,п. @.9)
Если к системе @.8) с ограничениями @.9) применить подход
теории дифференциальных игр [2,43], то для синтеза гарантиро-
гарантированного управления получим выражения Ui{xi,Xi), решающие постав-
поставленную задачу при pi <\.
Наряду с игровым подходом возможен и более простой подход,
в котором возмущения Vi в системе @.8) вообще игнорируются на этапе
построения управления, и в качестве управления Ui(xi,Xi) выбирается
синтез оптимального по быстродействию управления системой
Xi = Ui, г = 1,..., п.
14 Введение
Показано, что данный упрощенный подход приводит к цели, т. е.
обеспечивает приведение системы @.8) при наличии возмущений
в заданное терминальное состояние тогда и только тогда, когда число
Pi в @.9) не превосходит «золотого сечения»:
Pi < Р* = | (\/5 - 1) «0.618.
Другими словами, возмущения можно игнорировать при построе-
построении управления, если их интенсивность, отнесенная к интенсивности
управляющего воздействия, не превосходит величины р*.
Два варианта метода декомпозиции, изложенные в первых двух
главах, несколько отличаются друг от друга по сделанным предполо-
предположениям и по полученным результатам. Допущения второго способа
менее ограничительны, однако время движения системы, управляемой
по первому способу, оказывается обычно меньше времени движения,
рассчитанного по второму способу управления.
В результате обоих вариантов метода декомпозиции получены
в явном виде законы управления для исходной системы @.1)
по принципу обратной связи. Эти законы вида Щ = Ui(q,q), г = 1,...
..., п, удовлетворяют наложенным ограничениям @.4) и обеспечивают
приведение системы в терминальное состояние @.7) при любых
допустимых возмущениях Qi(q,q,t), удовлетворяющих условиям @.5).
Время приведения оказывается конечным, и для него получены явные
оценки сверху.
В главах 1, 2 представлены также некоторые обобщения и моди-
модификации предложенных методов декомпозиции. Так, рассмотрены
возможности редукции исходной системы с п степенями свободы
@.1) к совокупности подсистем более сложного вида, чем @.8), как
линейных, так и нелинейных. Метод декомпозиции распространен
на задачу о приведении системы @.1) в заданное состояние с ненулевой
конечной скоростью, а также на задачу об отслеживании заданной
траектории движения.
В качестве примеров приложения методов декомпозиции приведены
задачи управления движением манипуляционных роботов с несколь-
несколькими степенями свободы. При этом рассмотрены как чисто механи-
механические модели манипуляторов, в которых отыскиваются управляющие
моменты двигателей, так и манипуляторы с электромеханическими
приводами, в которых принимаются во внимание процессы в электри-
электрических цепях.
В гл. 3 разработан метод управления системой @.1)—@.7),
основанный на использовании кусочно-линейной обратной связи.
Искомый вектор управляющих сил отыскивается в виде
U = -p{q-q*)-aq, U = (Uu ..., Un), @.10)
Введение 15
где а и /3 — скалярные коэффициенты, являющиеся кусочно-
постоянными функциями времени. Эти коэффициенты в процессе
движения увеличиваются по определенному алгоритму и стремятся
к бесконечности по мере приближения системы к терминальному
состоянию. Однако управляющие силы @.10) при этом остаются
ограниченными и удовлетворяют наложенным на них условиям @.4).
Переключение коэффициентов обратной связи происходит на эллипсо-
эллипсоидальных поверхностях в 2п-мерном фазовом пространстве. Алгоритм
управления обосновывается при помощи второго метода Ляпунова.
Доказывается, что предложенный способ управления обеспечивает
приведение системы @.1) в терминальное состояние @.7) за конечное
время, для которого получена оценка сверху.
Метод гл. 3 позволяет строить управление не только при наличии
возмущающих сил, удовлетворяющих ограничениям @.5), но и при
неопределенности матрицы кинетической энергии @.2). Требуется
лишь, чтобы удовлетворялись ограничения @.3).
Подход гл. 3, основанный на использовании кусочно-линейных
обратных связей, применен для управления реономной системой,
т. е. системой, кинетическая энергия которой представляется в виде
полного полинома второй степени по обобщенным скоростям с коэф-
коэффициентами, явным образом зависящими от времени и обобщенных
координат. В этом случае также предполагается, что коэффициенты
полинома неизвестны и на систему действуют ограниченные возму-
возмущения. Построен закон управления, приводящий систему в заданное
терминальное состояние за конечное время с помощью ограниченной
силы.
В гл. 3 рассмотрен ряд примеров управляемых механических сис-
систем с несколькими степенями свободы, содержащими неизвестные па-
параметры: массы, жесткостные характеристики, коэффициенты трения.
Для этих систем построены законы управления, приводящие их в за-
заданные состояния посредством ограниченных управляющих сил.
Отметим, что наряду с обсуждаемыми в книге подходами
к построению управления для механических систем существует ряд
других подходов, которые обеспечивают асимптотическую устойчи-
устойчивость заданного состояния системы, т. е. приведение ее в терминальное
положение за бесконечное время. Несмотря на то, что на практике
приведение системы всегда осуществляется лишь в некоторую окрест-
окрестность заданного состояния и, следовательно, алгоритмы, гарантиру-
гарантирующие асимптотическую устойчивость, также обеспечивают конечное
время процесса, постановка задачи о приведении за конечное время
имеет смысл. При уменьшении размеров терминальной окрестности
время движения системы под действием управления, обеспечивающего
асимптотическую устойчивость, стремится к бесконечности, тогда как
время движения системы при законе управления, гарантирующего
конечность процесса, остается ограниченным. Следовательно, с точки
зрения быстродействия последний подход эффективнее.
16 Введение
Выше речь шла о системах с конечным числом степеней свободы,
описываемых обыкновенными дифференциальными уравнениями.
Проблемам управления системами с распределенными параметрами,
описываемыми дифференциальными уравнениями в частных произ-
производных, посвящена большая литература, см., например, книги
и обзоры [23, 30, 45, 57, 59, 89]). Оказалось, что методы декомпозиции,
изложенные в главах 1 и 2, можно перенести на случай систем
с распределенными параметрами.
В гл. 4 рассматриваются управляемые системы с распределенны-
распределенными параметрами, описываемые уравнениями в частных производных,
разрешенными относительно первой или второй производной по вре-
времени. Первый случай охватывает в частности, уравнение теплопровод-
теплопроводности, а второй — уравнения распространения волн. Системы предпо-
предполагаются линейными, а управление осуществляется посредством рас-
распределенных воздействий, описываемых соответствующими членами
в правой части уравнения. Управление предполагается ограниченным
по величине. Ставится задача о приведении управляемой системы
в нулевое состояние за конечное время. Предложен способ управления,
основанный на декомпозиции исходной системы и применении опти-
оптимального по быстродействию управления для каждой моды движения,
полученной в результате разложения решения по методу Фурье.
Особенностью данной задачи управления является наличие бес-
бесконечного (счетного) числа мод, что потребовало проведения спе-
специальных оценок. Получены достаточные условия разрешимости по-
поставленной задачи управления. Дано представление искомого закона
управления в виде обратной связи, выведены оценки сверху для време-
времени процесса управления. Приведены примеры.
Последующие главы 5 и 6 снова посвящены управляемым системам,
описываемым обыкновенными дифференциальными уравнениями. При
этом, в отличии от глав 1-3, здесь рассматриваются линейные системы.
Однако на них наложены различные ограничения, а именно, ограни-
ограничения на управления, фазовые координаты и смешанные ограничения.
Хотя исходные системы линейные, но рассматриваемые задачи управ-
управления, особенно при наличии сложных ограничений, обладают суще-
существенной нелинейностью и не поддаются решению при помощи тра-
традиционных линейных методов. Целью этих глав является разработка
методов управления и решение ряда характерных задач управления при
сложных ограничениях.
В гл. 5 рассматривается линейная управляемая система общего вида
при наличии ограничений на управление и смешанных ограничений,
наложенных в каждый момент времени на фазовые координаты, управ-
управляющие воздействия, а также на некоторые интегралы, зависящие
от этих переменных. Заметим, что фазовые и смешанные ограничения
встречаются во многих прикладных задачах управления. Часто к ним
добавляются интегральные ограничения, отражающие энергетические
и другие требования. Так, при наличии в системе управляющего
Введение 17
электропривода обычно следует учитывать ограничения, наложенные
на угловую скорость вращения вала, на управляющий момент двига-
двигателя, а также на эти величины в совокупности. Как известно, учет
фазовых и смешанных ограничений в рамках теории оптимального
управления приводит к существенным трудностям даже для линейных
систем.
Описываемый в гл. 5 подход представляет собой обобщение извест-
известного подхода Р. Калмана [38,39], предложенного им для управления
линейными системами в отсутствие ограничений на управление и осно-
основанный на формировании управляющего воздействия в виде линейной
комбинации собственных движений неуправляемой системы. В гл. 5
метод Калмана распространен на случай наличия ограничений. По-
Построены в явном виде законы управления различными колебательными
системами, в том числе системой осцилляторов, управляемых одним
ограниченным воздействием. Для некоторых систем второго порядка
построенные законы управления сравниваются с управлениями, опти-
оптимальными по быстродействию. Построены законы управления также
для некоторых систем более высокого порядка, в частности, для систем
четвертого порядка со смешанными ограничениями. Рассмотренные
системы представляют собой модели механических и электромеха-
электромеханических систем, содержащих колебательное звено и электрический
двигатель. Сформулированы дополнительные достаточные условия, при
выполнении которых указанный способ управления обеспечивает при-
приведение системы в заданное состояние за конечное время при удовле-
удовлетворении наложенных смешанных ограничений.
В гл. 6 представлены решения трех задач управления для простей-
простейшей динамической системы, описываемой вторым законом Ньютона.
Постановки задач отличаются наличием различных ограничений.
Во всех трех случаях система приводится в начало координат фазовой
плоскости.
В первых разделах гл. 6 рассматривается одна задача оптимального
быстродействия при наличии смешанных ограничений, наложенных
на управляющие воздействия и фазовые координаты. Построен синтез
оптимального быстродействия. В качестве примера рассматривается
задача управления электродвигателем постоянного тока.
Далее в нескольких разделах этой главы изучается движение инер-
инерционного объекта под действием управляющей силы с ограниченной
скоростью изменения. Сначала построено программное управление си-
системой, оптимальное по быстродействию. Далее в замкнутой форме да-
дано решение задачи синтеза оптимального управления. Построение оп-
оптимального синтеза проведено с применением инвариантно-групповых
методов, что позволило сократить число существенных независимых
переменных, от которых зависит управление.
В заключительной части гл. 6 предполагается, что величина силы
может наращиваться постепенно, с конечной скоростью, и мгновен-
мгновенно выключаться. При этих ограничениях, моделирующих реальные
18 Введение
системы приводов, построено управление, приводящее систему в нача-
начало координат и имеющее простейшую возможную структуру.
Таким образом, в книге изложен ряд новых методов построения
управления в механических системах. Наряду с описанием алгоритмов
и их строгим математическим обоснованием приводятся решения ряда
конкретных задач управления динамическими системами, иллюстриру-
иллюстрирующие эффективность предлагаемых методов.
Монография основана на результатах, полученных авторами
в Институте проблем механики Российской академии наук и опубли-
опубликованных в течение последних пятнадцати лет.
Глава 1
МЕТОД ДЕКОМПОЗИЦИИ УПРАВЛЕНИЯ
(ПЕРВЫЙ СПОСОБ)
§ 1.1. Управляемая механическая система
Рассматривается нелинейная управляемая система, динамика кото-
которой описывается уравнениями Лагранжа
d дТ дТ тт , п . 1 п 1 п
^7я^"я~ = ^ + ^' *=1,...,п, A.1.1)
at oqi oqi
где q= (q\,...,qn) — обобщенные координаты системы, п — число
ее степеней свободы, точкой обозначены производные по времени t.
Обобщенные силы состоят из управляющих сил Щ, подлежащих опре-
определению, и из слагаемых Qi, включающих все остальные внешние
и внутренние силы, в том числе неконтролируемые возмущения.
Кинетическая энергия системы Т задана в виде квадратичной
формы
\ Е к* A-1-2)
j,k=l
где ajk — элементы симметрической положительно-определенной мат-
матрицы A(q) размером п х п. Подставляя A.1.2) в A.1.1), приведем
уравнения движения к виду
A(q)q = U + S(q,q,t), A.1.3)
где U = (U\,..., Un) — вектор управляющих сил, S = (S\,..., Sn) —
вектор-функция
з,к=\
где Tjk = (rijfc,... ,Tnjk) — n-мерные векторы с компонентами
dciij \8ajk
1 ijk — ~т^ о ~^—•
J dqk 2 %
20 Гл. 1. Метод декомпозиции управления (первый способ)
На управляющие силы наложены ограничения
\Щ^и1 i=l,...,n, A.1.6)
где U® > 0 — заданные постоянные.
Начальные условия для системы A.1.3) имеют вид
q(to)=q°, q(to)=q° A-1.7)
и лежат в некоторой заданной области п в 2п-мерном фазовом про-
пространстве: {q,q} G О.
§ 1.2. Постановка задачи управления
Сформулируем задачу управления.
Задача 1.1. Найти управление по принципу обратной связи
U = U(q,q), удовлетворяющее ограничению A.1.6) и приводящее
систему A.1.3) из произвольного начального состояния A.1.7)
из области О в заданное состояние с нулевыми скоростями
q(t*) = q*, q(U)=0 A.2.1)
за конечное время (момент времени ?* > to не фиксирован).
Упрощающие предположения. Задача 1.1 будет решаться при
некоторых упрощающих предположениях (условиях), которые форму-
формулируются ниже.
Представим матрицу A(q) в следующем виде:
= B(q)A*,
A.2.2)
B(q) = E+ [A(q) - А*]А-' = A(q)A~\
где А* — некоторая постоянная симметрическая положительно-
определенная матрица размера п х п, Е — единичная матрица размера
п х п. Матрица B(q) является неособенной, поэтому обратная матрица
B~x(q) существует. Умножим обе части уравнения A.1.3) на B~x(q)
и, пользуясь соотношениями A.2.2), преобразуем A.1.3) к виду
XU). A.2.3)
Здесь введено обозначение
V = V' + V", V = B-l(q)S(q, q, t),
A.2.4)
V" = [B-\q)-E]U.
Уравнение A.2.3) с учетом обозначений A.2.4) эквивалентно исход-
исходному уравнению A.1.3).
§/.2. Постановка задачи управления 21
Предполагаем, что выполнены следующие условия:
A.2.5)
при всех t ^ to, всех {q,q} G О и всех С/, удовлетворяющих A.1.6).
Здесь V® > О и Ai > 0 — некоторые постоянные. Если все А^ = 0, то
условие A.2.5) переходит в более простое условие:
\Vi\ ^Vt° <U?, i= l,...,n, A.2.6)
при всех t ^ to, всех {q,q} gDh всех U, удовлетворяющих A.1.6).
Приведем лемму [64], позволяющую судить о выполнении условия
A.2.6). Далее через || • || будем обозначать евклидову норму вектора
или матрицы (под нормой матрицы понимается норма соответствую-
соответствующего линейного оператора в евклидовом пространстве).
Лемма 1.1. Пусть для любого п-мерного вектора z при всех
t ^ to и всех {q, q} G О выполнены условия
\Si(q,q,t)\ <:VU?, i= l,...,n, A.2.7)
0 < /JL < /X*, V > 0,
где /i*, /i, v — постоянные. Тогда для компонент вектора V из
A.2.4) при всех t > to, всех {q,q} G О и всех U, удовлетворяющих
A.1.6), имеют место оценки
г = 1,... ,п,
A.2.8)
?/° = ([/[>,...,[/°).
Отметим, что так как А* — положительно-определенная матрица,
то в качестве /i* можно принять любое положительное число, не пре-
превосходящее ее наименьшего собственного значения.
Доказательство. Из первого неравенства A.2.7) имеем
\\A-lz\\^fi-l\\zl A.2.9)
Здесь и далее z — любой n-мерный вектор. Введем обозначение
L = [A(q) - A.]Af. A.2.10)
Из A.2.9) и второго неравенства A.2.7) следует
HizKwC'lNI- A.2.11)
22 Гл. 1. Метод декомпозиции управления (первый способ)
Соотношение A.2.2) для В с учетом A.2.10) перепишем в виде
Bz = z + Lz. A.2.12)
При помощи A.2.12), A.2.11) получим оценку
\\Bz\\Z \\z\\ - \\Lz\\ ^ (\ - w-l)\\z\\. A.2.13)
Из условия A.2.7) леммы следует, что A —/i/i) > 0. Полагая
z = B~xzf в A.2.13), получим
\\B-xz'\\^(\-w-x)-x\\z'\\. A.2.14)
Неравенства A.2.11), A.2.14) дают
\\LB-xz\\^fi{^-fi)-x\\z\\. A.2.15)
Положим z = B~xzf в равенстве A.2.12):
В~хz' = z' - LB~Xz'. A.2.16)
Используя равенство A.2.4) для V и соотношение A.2.16) при
z' = S, представим компоненту V[ вектора V в виде
V( = (B~xS)i = Si-(LB-xS)i, i= l,...,n. A.2.17)
Нижние индексы обозначают компоненты векторов. Из A.2.17)
при помощи третьего условия A.2.7) и неравенства A.2.15) получим
-n)~lv\\U°\\, i= l,...,n. A.2.18)
Здесь использовано обозначение A.2.8) для вектора С/0. В соотношение
A.2.4) для вектора V" подставим равенство A.2.16) при z1 = U. Имеем
V(' = (B~XU -U)i = -(LB-xU)i, i= l,...,n. A.2.19)
Отсюда при помощи неравенств A.2.15) и A.1.6) получим
|У/'| < \(LB-lU)i\ < \\LB~]U\\ < MM* " МГ'Ш <
-1л)-1\\и°\\, i=l,...,n. A.2.20)
Из полученного неравенства и A.2.18) следует утверждение A.2.8).
Лемма доказана. ?
§ 1.3. Декомпозиция 23
Из леммы вытекает следствие.
Следствие. Если в условиях леммы v <\ и ц достаточно мало,
то выполнено условие A.2.6).
Отметим, что в качестве матрицы А* следует взять некоторое
«среднее» для области О значение матрицы A(q). В частности,
можно выбрать в качестве А* матрицу A(q) при некотором значении
вектора q, например, A(q*), A(q°) или A((q° + q*)/2). Тогда, если
область О достаточно мала, то на всех рассматриваемых движениях
матрица A(q) будет мало отличаться от А* и число \± в условии A.2.7)
леммы будет достаточно малым. Таким образом, согласно следствию
для данной нелинейной системы A.1.3) можно обеспечить выполнение
условия A.2.6), если, во-первых, повысить возможности управления,
т.е. увеличить постоянные U® в A.1.6), чтобы имело место условие
v < 1, и, во-вторых, уменьшить область О так, чтобы A(q) было близко
к А*, т.е. уменьшить число /i.
Ниже, в § 1.13, показано, что принятая постановка задачи 1.1
и условие A.2.5) являются естественными и часто выполняются для
манипуляционных роботов с электромеханическими приводами.
§ 1.3. Декомпозиция
Обратимся к решению задачи 1.1 при выполнении условия A.2.5).
Предполагаем, что все рассматриваемые движения системы A.1.3)
лежат в области п.
При условии A.2.5) система A.1.3) может быть согласно A.2.3)-
A.2.5) представлена в виде
(A*q)i + \i(A*q)i = иг + Vit Vi = V? + V(\ i = 1,..., п. A.3.1)
В системе A.3.1) сделаем замену переменных
A.(q-q*)=y, A-3.2)
где q* введено в A.2.1). Получим
ш + \гт = щ + ^, i = i,...,n. A.3.3)
Для слагаемых в правых частях A.3.3) согласно A.1.6), A.3.1)
и A.2.5) имеем ограничения
Ш^и?, |U|<V?<C/?, г=1,...,п. A.3.4)
Начальные условия A.1.7) и граничные условия A.2.1) после
замены A.3.2) примут вид
y(to) = Мя° - Я*1 Ш = А,Я°, A.3.5)
y(U) = y(U) = 0. A.3.6)
24 Гл. 1. Метод декомпозиции управления (первый способ)
Задача 1.1 сводится, таким образом, к построению управления
U(у, у), приводящего систему A.3.3) из произвольного начального со-
состояния A.3.5) в состояние A.3.6) при ограничении A.3.4). Система
A.3.3) состоит из п подсистем с одной степенью свободы каждая.
В каждой из подсистем имеется свое скалярное управление Щ, удо-
удовлетворяющее ограничению A.3.4). Функцию Vi в этой подсистеме бу-
будем рассматривать как возмущение, стесненное ограничением A.3.4),
а в остальном — произвольное. Тогда полученный результат можно
подытожить в виде следующего утверждения.
Теорема 1.1. Пусть выполнено условие A.2.5) и все рассматри-
рассматриваемые движения системы A.1.3) лежат в области п. Тогда для
решения задачи 1.1 достаточно решить и задач управления для ли-
линейных подсистем A.3.3) с одной степенью свободы. В каждой
из этих задач требуется построить скалярное управление Ui(yi, щ),
удовлетворяющее ограничению A.3.4) и переводящее г-ю подсисте-
подсистему A.3.3) из произвольного начального состояния A.3.5) в начало
координат A.3.6) за конечное время при любых допустимых возму-
возмущениях Vi, удовлетворяющих ограничению A.3.4).
Излагаемый подход к декомпозиции управления был впервые пред-
предложен в работе [63] для случая Л = 0 и в работе [64] — в общем случае
при А > 0.
Игровая задача. Рассмотрим г-ю подсистему A.3.3) и положим
в ней _
yi = U?x, Щ = Ц?и, Vi = U?v. A.3.7)
Тогда эта подсистема вместе с ограничениями A.3.4) примет стандарт-
стандартный вид
х + \х = u + v, \u\^l, \v\^p<\, A.3.8)
а граничные условия A.3.5) и A.3.6) запишутся в форме:
ж@)=?, х@) = г), х(т)=х(т)=0. A.3.9)
В A.3.8) и A.3.9) введены обозначения
A.3.10)
Без нарушения общности начальный момент времени принят равным
нулю.
§/.4. Оптимальное управление подсистемой 25
Рассмотрим задачу о приведении системы A.3.8) в начало коор-
координат за кратчайшее время, т.е. при минимальном г в A.3.9). Эту
задачу будем рассматривать как дифференциальную игру, в которой
один из игроков (управляющая сторона) выбирает управление и,
а второй игрок (противник) выбирает возмущение v. Воспользуемся
подходом теории дифференциальных игр [43] и построим управление
по обратной связи (позиционное управление) и(х,х), приводящее
систему A.3.8) в начало координат за минимальное гарантированное
время г при любом допустимом возмущении v.
Заметим, что данная дифференциальная игра A.3.8), A.3.9)
представляет собой линейную дифференциальную игру однотипных
объектов. Ее решение, как известно [43], сводится к решению задачи
оптимального быстродействия для системы
х + Хх = A — р)и, \и\^\, г —> min A.3.11)
при граничных условиях A.3.9). Искомое управление и(х,х) и мини-
минимальное гарантированное время г в игровой задаче A.3.8), A.3.9)
совпадают, соответственно, с синтезом оптимального управления
и временем оптимального быстродействия для задачи A.3.11), A.3.9).
Отметим, что система A.3.11) получается из A.3.8) при возмущении,
равном v = — ри, которое представляет собой оптимальное управление
«противника», выбирающего возмущение v. Иными словами, наихуд-
наихудшее возмущение в данной задаче можно принять в виде v = — ри.
Таким образом, в результате декомпозиции решение задачи 1.1
сведено к построению синтеза оптимального по быстродействию управ-
управления в системе A.3.11), A.3.9).
§ 1.4. Оптимальное управление подсистемой
Задачу оптимального быстродействия A.3.11), A.3.9) перепишем
в виде
Х\ = Х2, X2 = —XX2+W, W = (I — р)и, \и\ ^ 1, A-4.1)
XI @) = f, ж2@) = г], хх(т) = х2(т) = 0,
A.4.2)
0^р<1, А^О, г —> min, (х\ = х, Х2 = х).
Решение задачи A.4.1), A.4.2) легко получается при помощи прин-
принципа максимума [50]. Приведем здесь необходимые соотношения.
Функция Гамильтона для системы A.4.1) равна (р\, р2 — сопряжен-
сопряженные переменные)
Н = р\Х2 Ч- Р2 [A — Р)и — ХХ2], \и\ < 1.
26 Гл. 1. Метод декомпозиции управления (первый способ)
Согласно принципу максимума получим отсюда
и = signp2 = ±1. A.4.3)
Сопряженная система имеет вид
р\ = О, р2 = —р\ + \р2.
Интегрируя ее, получим
р2 = С\ + C2ext при А > 0,
Р2 = С\ + C^t при А = 0,
где Сь G2 — произвольные постоянные. Отсюда следует, что p2(t) —
монотонная функция при А ^ 0, поэтому управление A.4.3) имеет
не более одной точки переключения.
Общее решение системы A.4.1) при постоянном w = const имеет
вид
A.4.4)
х2 = \-{w + (В2 - \-{w) е-Л(*-г)
при А > 0;
х\ = В\ + В2(* - г) + - ^(t - гJ,
2 AА5)
Ж2 = ^2 + w(t — г)
при А = 0.
Здесь и далее все соотношения даются отдельно для случаев А > 0
и А = 0. Отметим, что случай А = 0 может быть получен предельным
переходом при А —> +0. Произвольные постоянные В\, В2 в A.4.4),
A.4.5) выбраны так, чтобы при В\ = В2 = 0 удовлетворялись нулевые
граничные условия A.4.2) при t = г. Исключая ? — г из соотношений
A.4.4), A.4.5), получим уравнения фазовых траекторий
xi =Bf -\-lx2-\-2w\n\l -Aii;"^21, A>0, A.4.6)
xi=B' + Bw)-lxl, A = 0. A.4.7)
Здесь В1 — новая постоянная, выражающаяся через В\ и В2.
При выводе соотношения A.4.6) предполагалось, что А?>2 ф w. Если
же А^2 = w, то из A.4.4) получим уравнение фазовой траектории
в виде
x2 = \~1w. A.4.8)
Фазовые траектории A.4.7) при А = 0 суть параболы, симметричные
относительно оси х\ и получающиеся одна из другой путем параллель-
параллельного переноса вдоль оси х\.
§ 1.4. Оптимальное управление подсистемой
27
О
ФР<о
Х\
Рис. 1. Фазовые траектории подси-
подсистемы при w = const, Л > О
Рис. 2. Оптимальные фазовые тра-
траектории
Рассмотрим траекторию A.4.6) при Л > 0, и = 1 и В1 = 0.
Привлекая еще уравнения A.4.1), из которых следует w =
= 1 — р, получим следующие свойства этой кривой х\(х2)'.
• когда Х2 растет от —оо до 0, то х\ убывает от оо до 0 и достигает
нулевого минимума при х% = 0;
• в интервале х% е @, A-1(l — р)) величина х\ растет от 0 до оо,
а в интервале (А-1A — р), оо) величина х\, убывает от оо до —оо.
Таким образом, кривая х\(х2) состоит из двух ветвей, приближаю-
приближающихся к асимптоте х% = A-1(l — р). Эта асимптота согласно A.4.8)
сама также является фазовой траекторией при и = 1. Зависимость
х\(х2) при и = 1, В' = 0 изображена на рис. 1, где стрелками показано
направление роста t. Фазовые траектории, отвечающие и = I и произ-
произвольным В1 в A.4.6), получаются из описанной выше кривой переносом
вдоль оси х\.
Если в соотношениях A.4.4)—A.4.8) одновременно изменить знаки
у х\, Х2, w, В\, ?>2, В', то эти соотношения не нарушаются. Следо-
Следовательно, фазовые траектории, отвечающие и = — 1, получаются путем
центральной симметрии из описанных выше траекторий, отвечающих
и=\.
Единственными фазовыми траекториями, приводящими при росте t
в начало координат, являются кривые A.4.6) и A.4.7) при В1 = 0 и при
и = ±1. Движения вдоль этих кривых описываются соотношениями
A.4.4) и A.4.5) при Б1=Б2=0иг^ = ±1. Пара этих полутраекторий
(A.4.4) при А > 0 и A.4.5) при А = 0) составляет кривую переключений
оптимального управления: на ней происходит единственно возможная
вдоль каждой траектории смена знака управления и. В результате
приходим к полю оптимальных фазовых траекторий, изображенному
28 Гл. 1. Метод декомпозиции управления (первый способ)
на рис. 2 для Л > 0. Здесь жирная кривая изображает линию пере-
переключений, стрелки указывают направление роста t. Поле оптимальных
траекторий при Л = 0 хорошо известно, см., например, в книге [50].
Синтез оптимального управления, соответствующий описанному
выше характеру переключений, можно представить в виде
и(х\, Х2) = sign/0p(xi, X2) при фр^О,
A.4.9)
u(x\, X2) = signal = —sign X2 при фр = 0,
где фр(х\,Х2) — функция переключений, равная
+ А~2A — р) 1п[1 + АA — р)!^!] signal, А > 0, A.4.10)
фр(х\,Х2) = —х\ — #21^21 [2A — р)}~1, А = 0.
Определим еще время, необходимое для попадания в начало
координат в силу оптимального синтеза при произвольных начальных
условиях A.4.2). Пусть, для определенности, начальная точка лежит
в области фр ^ 0, а единственно возможное переключение происходит
в момент s G [0, г]. Точка x\(s), X2(s) лежит, с одной стороны, на фазо-
фазовой траектории, отвечающей и = —I и проходящей через начальную
точку, а с другой стороны — на кривой переключений при и= 1.
Приравнивая соответствующие выражения A.4.5) (на кривой переклю-
переключений имеем В\ = Е>2 = 0), получим при Л = 0
Xl(s) = в, - в2е - \ A - Р)о2 = I A - р)е\
1 1 A.4.11)
x2(s) = В2 + A - рH = -A - р)9, 0 = t-s>0.
Запишем еще условие A.4.2) прохождения фазовой траектории
A.4.5) при и = — 1 через начальную точку:
A.4.12)
г] = В2 + A -р)т.
Исключив из уравнений A.4.11) и A.4.12) постоянные В\ и В2,
получим два уравнения для 0, т. Решая их, найдем
х ,2
A.4.13)
§/.5. Упрощенное управление подсистемой 29
Здесь учтено свойство симметрии фазовых траекторий. Функция
фр определена в A.4.10). На кривой переключений, т.е. при фр = 0,
в качестве 7 в A.4.13) можно взять любое из чисел 7 — =Ы — значение
т(?, 7/) при этом будет одним и тем же.
Аналогично получается время оптимального быстродействия
при Л > 0. При этом вместо A.4.5) используются формулы A.4.4).
Окончательно имеем (см. [5]):
М = ехр[-(Ат7 + Л2^OA - /о)], A.4.14)
7 = signup, Л > 0,
где фр дано формулой A.4.10) при Л > 0.
Соотношения A.4.9), A.4.10) и A.4.13), A.4.14) определяют синтез
оптимального управления и минимальное гарантированное время г
в игровой задаче A.3.8), A.3.9). Отметим, что если возмущение v
отличается от наихудшего (г; ^ —ри), то фазовые траектории также
будут отличаться от оптимальных. Однако время приведения системы
в начало координат не будет превышать г из A.4.13), A.4.14). Заметим,
что после попадания фазовой траектории на кривую переключений
движение будет проходить по этой кривой вплоть до начала коор-
координат при любых допустимых возмущениях. При этом, если v ^ —ри,
то реализуется скользящий режим движения по кривым переключений.
Так, если v = 0 на кривой переключений, то управление принимает
значения и = ±1 с бесконечно частыми сменами знака, так что
«в среднем» имеем и = 1 — р или и = — A — р) на соответствующих
ветвях кривой переключений.
§ 1.5. Упрощенное управление подсистемой
В приведенном в § 1.4 способе управления подсистемой не пред-
предполагается известным возмущение, т. е. не предполагается известной
функция v в системе A.3.8). Однако его максимально возможное
значение (р в ограничении A.3.8)) считается известным, и синтез
управления в форме A.4.9), A.4.10) зависит от этого максимального
значения.
Возможен и другой подход к построению управления в системе
с возмущениями, при котором возмущения вообще игнорируются на
этапе построения управления и учитываются лишь при моделировании
и отработке управления. Такой подход, вполне естественный в случае
малых возмущений, будем называть упрощенным.
Ниже сравниваются оба подхода и выясняется, в какой мере оправ-
оправдано игнорирование возмущений при построении управления.
30
Гл. 1. Метод декомпозиции управления (первый способ)
Поскольку при условии A.2.5) согласно теореме 1.1 рассматривае-
рассматриваемая система в форме A.1.3), A.2.3) или A.3.3) распадается на п подси-
подсистем вида A.3.8), то указанное сравнение обоих подходов достаточно
провести для системы A.3.8).
Если пренебречь возмущением v в системе A.3.8), то она примет
вид
Хх = и,
1.
A.5.1)
Приведем синтез оптимального быстродействия для системы A.5.1)
при граничных условиях A.3.9). Так как система A.5.1) совпадает
с системой A.3.11) при р = 0, то искомый синтез определяется форму-
формулами A.4.9), A.4.10), в которых нужно положить р = 0. Получим
и(х\, х2) = sign-00
при Фо
и(х\,х2) = signal = — signal при фо = 0,
фо(х\,х2) = —х\ — \~хх2
A > 0,
фо(х\,х2) = -х\ - -х2\х2\, А = 0.
Кривая переключений фо = 0 для синтеза A.5.2) показана на
рис. 3 жирной штриховой линией. Здесь же для сравнения жирной
сплошной линией изображена
кривая переключений фр = 0
для синтеза управления A.4.9),
A.4.10) при 0 < р < 1. Обе
эти кривые симметричны относи-
относительно начала координат. Урав-
Уравнение кривой ^о = О может быть
представлено в виде
х\ = ф(х2), A.5.3)
где ф(х2) — монотонно убыва-
убывающая нечетная функция свое-
своего аргумента. Система A.3.8)
при законе управления A.5.2)
примет вид
= -\
Х\
Рис. 3.
Кривые переключений при
р>0ир=0
Х\ = Х2, Х2 = — \Х2 + и(х\, Х2) +17, А
р < 1, (х\ = х, х2 = х).
0,
A.5.4)
Чтобы оценить возможное влияние возмущений на движение
системы A.5.4), поставим задачу о нахождении «наихудшего» возму-
возмущения.
§/.5. Упрощенное управление подсистемой 31
Задача 1.2. Найти оптимальное управление системой A.5.4)
в форме синтеза v(x\,x2), удовлетворяющее ограничению \v\ ^ р
и такое, что фазовая траектория этой системы первый раз
пересекает кривую переключений (фо = 0 или х\ = ф{х2), см. A.5.2),
A.5.3)) как можно дальше от начала координат, т.е. при макси-
максимально возможном \х\\ или, что то же самое, при максимально
возможном \х2\.
Примем для определенности, что начальная точка (?,7/) лежит
в области фо < 0. Тогда согласно A.5.2) имеем на всей рассматриваемой
траектории и = — 1. Фазовая траектория системы A.5.4) при этом
впервые пересечет ту ветвь кривой переключений, на которой х\ >
> 0, Х2 < 0 (см. рис. 3). В результате задача 1.2 будет описываться
следующими соотношениями:
Х\ = Х2, %2 = —А^2 — 1 + V, \v\ < р < 1,
А>0, O^t^r, zi@)=?, х2@) = г], A.5.5)
х\(т) = ф(х2(т)), х\(т) > 0, Х2(т)<0, xi(r)
Здесь г — момент окончания процесса, который не фиксирован. Функ-
Функция ф(х2) в A.5.3), A.5.5) получается из уравнения гро = 0 (см. A.5.2)),
при р = 0 и Х2 < 0:
0Ы = -А^ - А~21пA - Хх2), А > 0,
= |4 А = 0.
Из этих соотношений следует
ф(х2)^0, ф'(х2) =х2A - Хх2)~1 <0, х2<0. A.5.6)
Заметим, что максимизация х\(т) в A.5.5) эквивалентна миними-
минимизации следующего интегрального функционала:
г
\(-x2)dt^min. A.5.7)
о
Применим принцип максимума [50] к задаче 1.2. Функция Гамиль-
Гамильтона для задачи A.5.5), A.5.7) имеет вид
Н = р\х2 +p2(v — \х2 — 1) + х2, \v\ < p, A.5.8)
где р\, р2 — сопряженные переменные, удовлетворяющие следующим
сопряженным уравнениям:
Pi=0, р2 = \р2-р\-\ A.5.9)
32 Гл. 1. Метод декомпозиции управления (первый способ)
и условиям трансверсальности
Р1(т)Ф'(х2(т)) +р2(т) = 0, Н(т) = 0. A.5.10)
Найдем р\(т) из первого условия A.5.10) и подставим его во второе
условие A.5.10), пользуясь выражением A.5.8) для гамильтониана Н.
Получим
P2[(v- Хх2 - 1)ф'(х2) -х2] + х2ф\х2) =0, t = r. A.5.11)
Подставляя ф'{х2) из A.5.6) в A.5.11), получим после некоторых упро-
упрощений
x2[p2(v - 2) + х2] =0, t = r. A.5.12)
Так как согласно A.5.5) имеем \v\ ^ р < 1 и х2(т) < 0, то из соотно-
соотношения A.5.12) следует, что
Р2(т)<0. A.5.13)
Из принципа максимума и равенства A.5.8) вытекает, что опти-
оптимальное управление выражается в виде
v(t) = psignp2(t). A.5.14)
Интегрируя систему A.5.9), получим
Р\ = Си р2 = A-^Ci + 1) + С2ех\ Л > 0,
A.5.15)
Pi=Cu P2 = С2 - (Ci + l)t, Л = 0,
где С\, С2 — постоянные. Из A.5.15) следует, что p2(t) — монотон-
монотонная функция, следовательно, оптимальное управление A.5.14) имеет
не более одной точки переключения.
Так как система A.5.5) автономна, то ее гамильтониан Н постоянен
вдоль оптимальной траектории и в силу A.5.10) равен нулю. Тогда
согласно A.5.8) получим
H{t) = ipx + \)х2 +p2(v - Хх2 - 1) = 0. A.5.16)
В момент переключения согласно A.5.14) имеем р2 = 0, а тогда
из A.5.16) следует, что в этот момент либо р\ = — 1, либо х2 = 0.
Рассмотрим сначала первую возможность. Из A.5.15) следует, что
если р\ = — 1, то p2it) не изменяет знака вдоль траектории, и поэтому
переключение при р\ = — 1 не может иметь места.
Вторая возможность х2 = 0 означает, что управление переключа-
переключается, когда траектория пересекает прямую х2 = 0. Так как р2(т) < 0
согласно A.5.13), то оптимальное управление A.5.14) отрицательно
§1.6. Сравнительный анализ результатов 33
при Х2 < 0 и положительно при х% > 0. Итак, оптимальное управление
имеет вид
v(x\, X2) = psigna^. A.5.17)
Оптимальный синтез в области фо < О построен. Заметим, что
система A.5.5) вместе с соотношениями A.5.2) инвариантна относи-
относительно замены х\ —> —х\, х% —> —#2> ^ ~^ —^- Следовательно, опти-
оптимальный синтез v(x\,X2) обладает свойством центральной симметрии,
а синтез A.5.17) удовлетворяет этому условию. Таким образом, соот-
соотношение A.5.17) дает решение поставленной выше задачи 1.2 во всей
фазовой плоскости х\, х^
§ 1.6. Сравнительный анализ результатов
Используем построенное решение A.5.17) задачи 1.2 для анализа
возможных движений системы A.5.4) при упрощенном управлении
A.5.2). Сначала предположим, что возмущение v дается соотношением
A.5.17). Все траектории системы A.5.4) при и, заданном в виде A.5.2),
и v, заданном в виде A.5.17), состоят из дуг парабол, соответствующих
постоянным и = ±1 и v = ±р. Уравнения этих парабол определяются
формулами A.4.4)—A.4.7), в которых нужно положить в соответствии
с A.5.2) и A.5.17)
w = и + v = sign фо + р sign X2. A.6.1)
Одна из траекторий для закона управления A.5.2) при возмущении
A.5.17) показана на рис. 3 тонкой штриховой линией. Здесь же тонкой
сплошной линией показана оптимальная траектория для управления
A.4.9) при v = — ри. Стрелки указывают направление роста времени.
Заметим, что дуги оптимальных траекторий для обоих законов управ-
управления совпадают в областях, где следующие три функции: ф$, фр
и (~Х2) — имеют одинаковые знаки. Жирные сплошные и штриховые
кривые на рис. 3 изображают кривые переключений фр = 0 и ф$ = 0
для управлений A.5.2) и A.4.9) соответственно.
Для определенности построим оптимальную фазовую траекторию
для закона управления A.5.2), начинающуюся в точке (?,7/) на кривой
переключений фо = 0 при г] > 0 и оканчивающуюся в точке (?*,7?*)
на другой ветви кривой переключений, т. е. при ?* > 0, ту* < 0.
Рассматриваемая траектория лежит в области фо < 0 и состоит из двух
участков, которые непрерывно сопрягаются при х^ = 0. На первом
участке, где х% > 0, имеем согласно A.5.2), A.5.17) и = — 1, v = р.
На втором участке х% < 0, поэтому в силу A.5.2), A.5.17) имеем здесь
и = — 1, v = —р.
Первый участок траектории проходит через начальную точку (?,??),
и на нем согласно A.6.1) w = и -\- v = — \ -\- р. Следовательно, его
уравнение согласно A.4.6), A.4.7) представляется в виде @ ^ х^ ^ rj)
2 Ф. Л. Черноусько и др.
34 Гл. 1. Метод декомпозиции управления (первый способ)
В[ = ? + А-'т? - АA -
приА>0; A.6.2)
хх=В\- [2A - р)]-'4 B\=Z+[2(\- p)]~W
при Л = 0.
Второй участок траектории проходит через конечную точку (?*,?7*),
и на нем w = и -\- v = — 1 — р. Поэтому из A.4.6), A.4.7) получим
для второго участка (ту* ^ х^ ^ 0)
В'2=С+ \-1г]* - А-2A
приЛ>0; A.6.3)
X! = В'2 - [2A + p)]-i4 BJ = Г + [2A + Р)]-Чч*J
при Л = 0.
В точке сопряжения участков имеем х% = 0, а значения #i для обоих
участков совпадают. Из A.6.2), A.6.3) тогда получим
В[ =В'2. A.6.4)
Точки (^, ту) и (^*,гу*) принадлежат соответствующим ветвям кривой
переключений ^о = 0, причем ту > 0, ту* < 0. Следовательно, на основа-
основании формул A.5.2) получим:
Г = -A-V-A-2ln(l-Ar/*), А>0; A65)
В равенство A.6.4) подставим выражения A.6.2), A.6.3) для В[, В'2,
а также формулы A.6.5), выражающие ?, ^* через ту, ту*. В результате
после упрощений получим соотношения
1+рA-Хг)*), А>0; A.6.6)
p)-\r1*J, A = 0,
где г] > 0, г]* <0.
§1.6. Сравнительный анализ результатов 35
Равенства A.6.6) связывают значения ту* и г]. Рассмотрим сначала
случай Л = 0. При этом связь A.6.6) приводится к виду
"<'<'¦
Нетрудно убедиться, что к монотонно возрастает от 0 до оо при
изменении р от 0 до 1, причем к = 1 при значении р, равном
р* = ^(л/5 - 1) «0.618. A.6.8)
Число р* представляет собой отношение «золотого сечения». Таким
образом, если Л = 0, то при р < р* в силу A.6.7) будет \rj*/rj\ < 1,
при р = р* имеем \г]*/г]\ = 1, а при р > р* имеем \г]*/г]\ > 1.
В случае Л > 0 соотношение A.6.6) определяет неявную зависи-
зависимость ту* от г]. Для исследования этой связи положим
Хг] = Х>0, -\rj*=Y>0 A.6.9)
и представим зависимость A.6.6) в виде
ФР(Х) = Фр(У), Х>0, У>0, 0 < р< 1,
ФР(Х)= [1 + A-р)-1Х]1-рA+Х)-\ A.6.10)
Отметим некоторые свойства функций Фр, Фр из A.6.10). Функция
Фр определена при всех 1H и стремится к нулю при X —> оо,
а функция Фр определена на отрезке [0, 1 + р] и обращается в нуль
при Y = \ + р. Обе функции равны единице при X = У = 0. Непо-
Непосредственным дифференцированием функций A.6.10) убеждаемся, что
Ф'р{Х) < 0, Фр(У) < 0, так что обе функции Фр, Фр монотонно
убывают. Подсчитаем еще производную
A.6.11)
Заметим, что выражение р — 1 + р2 в A.6.11) неположительно
при р ^ р* и положительно при р > р*. Следовательно, при р ^ р*
отношение Фр/Фр монотонно убывает на отрезке [0, 1 + р], и поэтому
Фр(Х) < Фр(Х) при 0 < X < 1 + р. Если же р > р*, то ФР(Х) > ФР(Х)
36
Гл. 1. Метод декомпозиции управления (первый способ)
Рис. 4. Функции ФР(Х) и
при р < р*
р> р*
фр
О X У
Рис. 5. Функции ФР(Х) и
при р> р*
на некотором отрезке 0 < X < X* < 1 + р, однако ФР(Х) < ФР(Х)
вблизи X = 1 + р, так как
На рисунках 4 и 5 изображены графики функций Фр(Х),
для случаев р ^ р* и р > р* соответственно. На этих рисунках пред-
представлена графически связь между значениями X, Y, которая устанав-
устанавливается соотношениями A.6.10). Из этих соотношений и отмеченных
свойств функций Фр, Фр вытекают следующие выводы для случая
А>0:
• если р ^ р*, то всегда Y < X и, согласно A.6.9), \r]*/r]\ ^ 1;
• если р > р*, то при достаточно малых X имеем Y > X, то есть
|гу*/гу| > 1, а при достаточно больших X выполняется Y < X,
то есть \г]*/г]\ < 1. При этом всегда имеет место неравенство
Y < 1 + р, то есть |?7*| < A +р)Л-1.
Траекторию, начавшуюся в произвольной точке (?, ту) фазовой плос-
плоскости, можно неограниченно продолжать и после ее пересечения
с кривой переключений ф$ = 0 в точке (?*,?7*)- Для этого нужно
принять точку (?*,77*) за начальную и продолжить движение в силу
системы A.5.4), подставляя в нее управление и из A.5.2) и оптималь-
оптимальное возмущение v из A.5.17). Полученная таким образом траектория
бесконечное число раз пересекает обе ветви кривой переключений, при
этом значения ординат х^ в двух последовательных точках пересечения
кривой переключений ^0 = 0 находятся в отношении \rf /г)\, которое
дается формулой A.6.7) при Л = 0 и определяется равенствами A.6.9),
A.6.10) при Л >0.
§ 1.6. Сравнительный анализ результатов
37
Рис. 6. Фазовая траектория при
Р<Р*
Характер движения существен-
существенно зависит от параметров р, А.
Положим сначала Л = 0. Если
р < р*, где р* определено равен-
равенством A.6.8), то к < 1 в A.6.7).
При этом значения \х2\ в момен-
моменты пересечения траекторией кривой
переключений ф$ = 0 убывают в
геометрической прогрессии со зна-
знаменателем к < 1. Поэтому фазовая
траектория стремится к началу ко-
координат и попадает в него за конеч-
конечное время, хотя и после бесконечно-
бесконечного числа переключений.
Если р = р*, то к = 1 в A.6.7),
и фазовая траектория будет перио-
Рис. 7. Фазовая траектория при
Р = Р*
Р> Р*
Рис. 8. Фазовая траектория при
Р > Р*
дической. Она проходит через одни и те же точки фазовой плоскости
через равные промежутки времени. В этом случае траектория остается
в ограниченной области, но не стремится к началу координат.
Если р > р*, то к > 1 в A.6.7). При этом фазовая траектория уходит
на бесконечность, раскручиваясь как спираль.
Поведение фазовых траекторий изображено на рисунках 6, 7, 8
для случаев р < р*, р = р* и р > р* соответственно.
Обратимся к случаю Л > 0. Если при этом р ^ р*, то согласно
проведенному анализу имеем \г]*/г]\ < 1. В этом случае фазовая
траектория стремится к началу координат и попадает в него за конеч-
конечное время при р < р*. Можно показать, что при р = р* фазовая точка
приходит в начало координат лишь асимптотически при t —> оо.
38 Гл. 1. Метод декомпозиции управления (первый способ)
При р > р* фазовая траектория не стремится к началу координат,
но остается в ограниченной области. Начиная с некоторого момента
времени, имеем \х%\ ^ А-1A + р) (вследствие неравенства Y < 1 -\- р).
Охарактеризуем теперь возможные движения системы A.5.4)
при законе управления A.5.2) и произвольном возмущении \v\ ^ р.
Если отношение максимально возможного значения возмущения
к максимально возможному значению управления меньше отношения
«золотого сечения» A.6.8), т.е. р < р*, то при любом допустимом
управлении и при любом А ^ О закон управления A.5.2) обеспечивает
приведение системы A.5.4) в начало координат за конечное время.
Это следует из того, что такое приведение осуществляется даже при
«наихудшем» возмущении A.5.17), максимально удаляющем систему
от начала координат.
Если р = р*, то при Л = 0 закон управления A.5.2) обеспечивает
удержание системы в ограниченной области, а при Л > 0 — также
и приведение в начало координат при t —> оо.
Если же отношение максимально возможного возмущения к мак-
максимально возможному управлению превышает отношение «золотого
сечения» (р > р*), то существуют возмущения, при которых приведение
системы в начало координат невозможно. Возмущение A.5.17) в слу-
случае Л = 0 уводит систему сколь угодно далеко от начала координат,
а в случае Л > 0 выводит ее из некоторой окрестности начала коорди-
координат, хотя система и остается в ограниченной области.
Таким образом, упрощенный закон управления A.5.2), не учиты-
учитывающий вообще наличия возмущений, достигает цели управления —
приведения системы в начало координат — лишь в том случае, когда
уровень возмущений достаточно мал. А именно, этот уровень, отне-
отнесенный к максимальному уровню управления, не должен превышать
отношения «золотого сечения» (р < р*).
Иными словами, игнорировать наличие возмущений при построе-
построении управления можно, лишь если отношение максимальных уровней
возмущения и управления не превышает отношения «золотого сечения»
р*^ 0.618.
Напомним, что оптимальное управление, основанное на игровом
подходе и заданное соотношениями A.4.9), A.4.10), обеспечивает
приведение системы A.3.8) в начало координат за конечное время
при любом допустимом возмущении, если р < 1. Таким образом,
игровой подход, описанный в § 1.4, имеет более широкую область
применимости, чем упрощенный подход, изложенный в § 1.5. Кроме
того, игровой подход обеспечивает минимальное гарантированное
время приведения системы в начало координат, что вытекает из исполь-
использования синтеза управления, оптимального по быстродействию. Однако
игровой подход, в отличие от упрощенного, требует знания макси-
максимально возможного уровня возмущений, т. е. параметра р. По своей
структуре оба метода сходны, имеют релейный характер и отличаются
лишь кривыми переключений, см. рис. 3.
§/.7. Управление исходной системой 39
§ 1.7. Управление исходной системой
Перейдем к решению исходной задачи 1.1. Синтез управления
в этой задаче получим на основе соотношений A.3.7), A.3.2) в следу-
следующем виде:
хх=х = (С/0)-1^ = (U?)-l[A.(q - q*)]i, A-7.1)
x2=x = (U?)-[yi = (U?)-[(A*q)i, г,...,п.
Здесь, в случае использования оптимального управления из § 1.4,
функция и(х\,Х2) определена формулами A.4.9), в которых фр дается
соотношениями A.4.10). Параметры Л, р, фигурирующие в формулах
A.4.10), выражаются равенствами A.3.10), т.е.
V0
А = Лг, Р=^о<1, г=1,...,п. A.7.2)
Построенное управление A.7.1) является релейным и принимает
предельные допустимые значения Щ = ±^г°, г = 1,...,п. Опишем
характер движения при этом управлении. Сначала предположим, что
возмущения Vi в системе A.3.1) или A.3.3) принимают в каждый
момент времени оптимальные («наихудшие») значения, максимально
задерживающие приведение системы A.3.3) в начало координат.
В терминах системы A.3.8) это означает, что v = — ри, а в терминах
системы A.3.1) с учетом равенств A.3.7), A.7.1), A.7.2) имеем
Vi = -pU?u = -V?(U?)-lUi(q,q), i = 1,..., п. A.7.3)
При возмущении A.7.3) движение системы A.3.3) по каждой
координате г/i происходит по траекториям оптимального быстродей-
быстродействия системы A.3.11) или A.4.1), т.е. по траекториям рис. 2
при Xi > 0. Связь исходных координат q с переменными yi и перемен-
переменными х\, Х2 дается соотношениями A.3.2), A.7.1).
Если же возмущения Vi отличаются от наихудших A.7.3), как это
обычно имеет место, то фазовые траектории для каждой г-й степени
свободы в плоскости х\, Х2 отклоняются от оптимальных. При этом
движение по кривым переключений происходит в скользящем режиме.
Время U приведения системы A.1.3) (или A.2.3), A.3.1), A.3.3))
в заданное состояние A.2.1) не превосходит максимального из времен
оптимального быстродействия для каждой из подсистем A.3.3)
(или A.3.8), A.3.11), A.4.1)). Имеем:
40 Гл. 1. Метод декомпозиции управления (первый способ)
t, < to + max т(&, щ), & = (C/f) [A,(g° - с/*)]*,
A74)
7?i = (C^)-1(A,g°)i, г=1,...,п.
Здесь использованы формулы A.3.10) для ?, ту. Функция т(?, 7/)
определена соотношениями A.4.13) для тех г, для которых Л^ = О,
и соотношениями A.4.14) для таких г, при которых А^ > 0.
Подытожим результаты в виде теоремы.
Теорема 1.2. Пусть выполнено условие A.2.5) и все рассматри-
рассматриваемые траектории лежат в области п. Тогда синтез управления
U(q,q), решающий задачу 1.1, дается соотношениями A.7.1), в ко-
которых функция и(х\,Х2) определена равенствами A.4.9), A.4.10).
Данное управление приводит систему A.1.3) в конечное состояние
A.2.1) не позже, чем к моменту времени ?*, определяемому соотно-
соотношениями A.7.4), A.4.13), A.4.14). Параметры А, р в указанных фор-
формулах для каждой степени свободы даются соотношениями A.7.2).
Построенное управление можно назвать субоптимальным, так как
оно близко к оптимальному по быстродействию и превращается в него
при «наихудших» возмущениях.
При использовании упрощенного подхода, изложенного в § 1.5,
следует в соотношениях A.7.1) заменить функцию и(х\,Х2) ее выра-
выражением согласно формулам A.5.2). В остальном процедура построения
управления исходной системой сохраняется той же, что и для игрового
подхода.
§ 1.8. Модификация метода декомпозиции
Способ декомпозиции, изложенный в § 1.3, привел к построению
управления, решающего исходную задачу 1.1. Это управление пред-
представлено в явном виде в § 1.7. Основным допущением, позволившим
осуществить декомпозицию, было предположение о существовании
такой области п в 2п-мерном пространстве q,q, в которой лежат все
рассматриваемые движения и где выполнены неравенства A.2.5).
Неравенства A.2.5) и их частный случай — неравенства A.2.6) —
в силу формул A.2.4) для V накладывают ограничения на неуправ-
неуправляемые силы Q и на инерционные слагаемые, входящие в S. Как
видно из A.1.4), инерционные слагаемые квадратично зависят от обоб-
обобщенных скоростей q. Поэтому неравенства A.2.5), A.2.6) ограничи-
ограничивают область п по q; в то же время построенное управление может
приводить систему в область больших q.
С одной стороны, ясно, что для решения поставленной зада-
задачи 1.1 необходимо наложить ограничения на неуправляемые силы Q,
иначе ограниченные управления U не смогут преодолеть действие
сил Q. С другой стороны, из сказанного выше следует, что жела-
желательно гарантировать ограниченность величин Si во время процесса
§1.8. Модификация метода декомпозиции 41
управления. Указанные соображения легли в основу модификации спо-
способа декомпозиции, предложенной в работах [55,56].
Снова обратимся к системе, описываемой соотношениями A.1.1)-
A.1.7), A.2.1).
Область D, в которой могут происходить движения рассматрива-
рассматриваемой системы, зададим в виде независимых ограничений на коор-
координаты qf.
D = {q: qr<qi<qt}- A-8.1)
Сделаем некоторые упрощающие предположения относительно
кинетической энергии и обобщенных сил Qi. Предполагаем, что
матрица A(q) из A.1.3) представима в виде
A(q) = J + A(q), J = diag(Jb ..., Jn), J{ = const > 0, A.8.2)
где A(q) — симметрическая матрица, такая, что для любого п-мерного
вектора z выполнено неравенство
\\A(q)z\\ ^ fi\\z\\, /i>0, VqeD. A.8.3)
Здесь /i — достаточно малый параметр, возможные значения которого
указаны ниже.
Кроме того, предполагаем, что
да.
jk
С, С = const > 0, г, j, fc= l,...,n, A.8.4)
и что обобщенные силы Qi представляются в виде суммы
Qi = Gi + Fi, A.8.5)
где Gi(q,q,t) — ограниченные силы, величины которых удовлетворяют
ограничениям
{Gil^G®, г=1,...,п. A.8.6)
Величины постоянных G® не превосходят постоянных [/? в ограниче-
ограничениях A.1.6) на управляющие силы Щ, т.е.
G^KU®, г=1,...,п. A.8.7)
Отметим, что если для некоторых г имеет место неравенство
G? > С/?,
обратное A.8.7), то система может быть неуправляемой.
42 Гл. 1. Метод декомпозиции управления (первый способ)
Через Fi(q,q,t) в A.8.5) обозначены силы, которые достаточно
малы при малых скоростях и удовлетворяют ограничениям
1^К^°(Ш, i = l,...,n. A.8.8)
Здесь F°(iy) — некоторая монотонно возрастающая непрерывная
функция, определенная при 1/Hи такая, что F°@) = 0. Точный вид
функций Gi(q,q,t), Fi(q,q,t) в A.8.5) может быть неизвестен.
Умножим обе части уравнения A.1.3) на JА~х (матрица J была
введена в A.8.2)). Получим
Jiqi = Ui + Vit A.8.9)
Vi = Si- [AA-\U + S)]i. A.8.10)
Система A.8.9), A.8.10) эквивалентна исходному уравнению
A.1.3). Из соотношений A.1.4), A.8.4)-A.8.6), A.8.8) следует огра-
ограничение на компоненты вектора S:
2
Предположим, что имеют место неравенства
\Vi\<:piUV, pi<l, A.8.12)
где pi — некоторые постоянные. Функции Vi будем рассматривать
в A.8.9) как независимые ограниченные возмущения, не превосхо-
превосходящие допустимых значений управлений. Тогда исходная нелинейная
система распадается на п линейных подсистем (г-я подсистема описы-
описывается г-м уравнением A.8.9)), подверженных возмущениям с одной
степенью свободы каждая. Таким образом, для решения задачи 1.1
достаточно решить п более простых задач управления для подсистем
второго порядка.
§ 1.9. Анализ управляемых движений
Скалярное управление Ui, переводящее г-ю подсистему A.8.9)
за конечное время из произвольного начального состояния (q^ffi)
в конечное состояние (</*,0) при любом допустимом возмущении Vit
удовлетворяющем A.8.12), зададим, как это было сделано ранее,
в форме синтеза A.7.1), A.4.9), A.4.10). При этом нужно в A.7.1)
вместо матрицы А* подставить матрицу J и в A.4.10) положить Л = 0.
После всех преобразований получим
§ 1.9. Анализ управляемых движений
43
sign qi
q{ =
A.9.1)
<rf1I/2 sign
Здесь JQ — положительный параметр управления, связанный с кон-
константой pi из A.8.12) соотношением
A.9.2)
Выразим в неравенствах A.8.12) постоянные pi через параметры
управления Xi, используя A.9.2). Получим
\Vi\ < Ui — JiXi, г=1,...,п. A.9.3)
Чтобы конкретизировать закон управления A.9.1), надлежит выбрать
значения параметров Xi > О так, чтобы выполнялись неравен-
неравенства A.9.3)
Напомним, что указанное управ-
управление получено как оптимальное по
быстродействию управление в игро- ^^^*^^^г+(^)
вой задаче, в которой Щ и Vi рас-
рассматриваются как управления двух
игроков [43]. Это управление релей-
но и принимает свои предельно до-
допустимые значения:
Кривая переключений
Яг = Ф*(Яг)
Рис'9' Множ™ ^ и
переключении
состоит из двух параболических
ветвей, которые симметричны отно-
относительно точки (д*,0).
Зададим в двумерном фазовом пространстве г-й подсистемы множе-
множество ui (рис. 9):
^i = {fe> Qi) : Чл ^Яг^ Qi"» Ф7 ^ Чг ^ ^t}'
A.9.4)
44 Гл. 1. Метод декомпозиции управления (первый способ)
Опишем характер движения подсистемы A.8.9) в случае, когда
управление Щ задано в виде A.9.1), возмущение Vi удовлетворяет
ограничению A.9.3), а начальная точка (($,($) лежит в Qf.
(9?.«?)efli. A.9.5)
Процесс управления разбивается на два основных этапа. На первом
этапе движение совершается при постоянном управлении до тех пор,
пока фазовая точка подсистемы не попадет на кривую переключений.
Для определенности считаем, что щ > V>*fe); тогда согласно A.9.1)
имеем Щ = —U^. При этом из A.8.9), A.9.3) следует
ft < -Хг. A.9.6)
Заметим, что из равенств A.9.4) и A.9.1) вытекает
В области fli вдоль траектории рассматриваемой подсистемы имеем,
согласно A.9.4), сц < ipf. Поэтому при сц > О, учитывая A.9.6)
и A.9.7), получим
dqi qi фт d(h
При qi < О имеем согласно A.9.6)
^ = ^>0, qt<0. A.9.9)
dqi qi
Из неравенств A.9.8) и A.9.9) вытекает, что фазовая траектория
рассматриваемой подсистемы при любых возмущениях не пересекает
кривую qi = i^f(c[i) и обязательно за конечное время, в силу
A.9.6), попадает на кривую переключений, не выходя из области Г^.
При qi < ф* этот факт доказывается аналогично.
Попав на кривую переключений, фазовая точка продолжает
двигаться по ней в терминальное состояние. Параболические ветви
кривой переключений совпадают с фазовыми траекториями подсистемы
A.8.9) при управлении Ui, выбранном согласно A.9.1), A.9.2),
и при Vi = —piUi. Если же Vi ф —piUi, то движение все равно
происходит вдоль параболического участка, но в скользящем режиме.
Управление Щ в этом случае принимает значения ±?7г° с бесконечно
частыми сменами знака, так что «в среднем» qi = Xi или qi = — Xi
для соответствующих ветвей кривой переключений.
Таким образом, если в начальный момент времени условия A.9.4),
A.9.5) выполнены для всех подсистем A.8.9), то их фазовые траек-
траектории целиком лежат в соответствующих областях Г^, при этом
выполняются ограничения A.8.1), а также имеют место неравенства,
вытекающие из A.9.4), A.9.1):
§1.10. Определение параметров 45
max
Вводя новые обозначения и используя выражение A.9.1) для ф*, пере-
перепишем полученное неравенство в виде
У* = ГгЫг) = BЗД1/2, di = qt - q~. A-9.10)
На рис. 9 изображена некоторая возможная фазовая траектория
подсистемы A.8.9). Стрелками указано направление роста времени t.
Как показано в § 1.4, время движения г-й подсистемы A.8.9)
максимально при «наихудшем» возмущении Vi = —piUi и, с учетом
обозначений A.9.2), равно (см. A.4.13))
r*fe°, ф = хг1 Ь ГIШ - хгD - e?)
1 J A.9.11)
Поскольку время г приведения исходной системы A.1.1) в тер-
терминальное состояние A.2.1) определяется максимальным из времен
управления для каждой из подсистем A.8.9), то получаем оценку
г <т* =тахДт*), г=1,...,п. A.9.12)
§ 1.10. Определение параметров
Применение управления A.9.1) возможно только при выполнении
неравенств A.9.3) (или A.8.12)) в течение всего процесса управления.
Найдем такие параметры управления JQ, при которых указанные соот-
соотношения действительно выполняются.
Сначала оценим модули величин Vi из A.8.10). Используя соотно-
соотношения A.8.3), A.8.11), A.9.10), получим
(t/ + ^)||, У = (УЬ...,УП). A.10.1)
Из A.8.2) и A.8.3) для любого n-мерного вектора z имеем
Az = Jz + Az, \\Az\\ ^ Jmin\\z\\ - n\\z\\ = (Jmin - vl)\\z\\; A.10.2)
здесь Jmin — наименьшая из величин J^. Положим z = A~xz' в нера-
неравенстве A.10.2). Тогда при /i < Jmin получим
\\A~xzf\\ < ^ ^ . A.10.3)
46 Гл. 1. Метод декомпозиции управления (первый способ)
Из A.1.6), A.8.11) и A.9.10) вытекают соотношения
\(U + S)i\ < \Щ\ + \Si\ ^U? + Got+ S°(Y) = (U° + G%
U° = (С/?,..., ?/°), G° = (G?,..., G°n). A.10.4)
Комбинируя A.10.1), A.10.3) и A.10.4), найдем окончательную оценку
для возмущений:
?
G? + f 1 + /П'^2 ) ^°(Г) + —if—||С/<> + G0||^ A ю 5)
\Щ < G
В неравенствах A.9.3) заменим величины \Vi\ их оценками
из A.10.5). После преобразования получим
S°(Y) < С/о _ Go _ _L||?/0 + G0||^
A.10.6)
Система неравенств A.10.6) задает допустимые параметры управле-
управления Xi и является нелинейной, так как величины Yi связаны с Xi
при помощи равенства A.9.10):
A.10.7)
Если параметр \± достаточно мал, так что выполнено условие
- G») Jmin
min
то выражения в правых частях неравенств A.10.6) положительны.
Поскольку согласно A.8.11) S°(Y) —> 0 при Xi —> 0, то всегда найдутся
положительные значения Xit при которых выполняются неравенства
A.10.6), а следовательно, и неравенства A.8.12).
Подытожим полученные результаты в виде теоремы.
Теорема 1.3. Пусть выполнено условие A.10.8). Тогда синтез
управления Ui(qi,qi), решающий задачу 1.1 в области A.9.4),
задается соотношениями A.9.1), в которых параметры Xi долж-
должны выбираться так, чтобы выполнялись неравенства A.10.6). Это
управление переводит систему A.1.1) из начального состояния
A.1.7) в заданное терминальное состояние A.2.1), если в начальный
момент времени выполнено условие A.9.5). При этом движение
системы q(t) лежит в области D из A.8.1), а время процесса управ-
управления г не превосходит величины г*, определяемой выражениями
A.9.11), A.9.12).
§1.10. Определение параметров 47
Укажем один из возможных способов выбора допустимых значе-
значений Xi. Будем искать их в виде
Xi = Z2di, A.10.9)
где di определено в A.9.10), а величина Z пока неизвестна. Подставим
A.10.9) в неравенства A.10.6), учитывая при этом A.10.7), A.8.11).
Выбрав максимальное допустимое значение Z
Z = ZQ, A.10.10)
удовлетворяющее полученным неравенствам, вычисляем по формулам
A.10.9) параметры управления Xi. При этом хотя бы одно из нера-
неравенств A.10.6) обращается в равенство.
Пусть, например, ограничение A.8.8) имеет вид
|F,KF° (№||) =a\\q\\+b\\q\\\
где а, Ъ — положительные постоянные. Тогда неравенства A.10.6)
приводятся к виду
Z2 + 2gtZ^hu A.10.11)
где gi, hi — положительные коэффициенты, явный вид которых непо-
непосредственно получается из A.10.7), A.8.11), A.10.6). Решение системы
неравенств A.10.11) можно записать в виде
Z < Zo = mini[(g? + hi)l/2 - дг], г = l,...,n. A.10.12)
Условия A.10.6), определяющие множество допустимых парамет-
параметров Xi, и ограничение A.10.8) на параметры системы A.1.1) являются
достаточными и далеки от необходимых. Для конкретных систем
часто удается произвести более точные оценки возмущений, чем
A.10.5). Подставляя эти оценки в неравенство A.9.3) вместо Vi, можно
получить более широкое множество допустимых параметров управ-
управления. Увеличение же значений Xi позволяет расширить области Г^
из A.9.4), которые ограничивают выбор начальных скоростей для под-
подсистем (см. A.9.5)), и существенно уменьшить время управления т.
Это дает возможность также в ряде случаев ослабить ограничения
на параметры системы.
Построенное управление достаточно просто и не требует точного
знания нелинейных членов и возмущающих сил в уравнениях
движения. Оно мало чувствительно к незначительным вариациям
параметров системы и дополнительных возмущений: для того чтобы
их учесть, достаточно уменьшить параметры Xi, создав некоторый
запас в возможностях управлений соответствующих подсистем.
Случай нулевых начальных скоростей. При построении решения
задачи 1.1 предполагалось, что начальное состояние каждой подси-
подсистемы — произвольная точка в области Г^, см. A.9.5). Рассмотрим
частный, но важный случай нулевых начальных скоростей q° = 0.
48 Гл. 1. Метод декомпозиции управления (первый способ)
При использования закона управления A.9.1) в рассматривае-
рассматриваемом случае координаты qi всех подсистем ограничены неравенствами
min(q^,q*) ^ qi(t) ^ max(<^,g*). Поэтому можно максимально ограни-
ограничить область возможных движений, положив в A.8.1)
q-=min(qlq*), q+ = maxfa?,^) A.10.13)
для всех г = 1,...,п. При таком задании области D величины di =
= qf — q^ минимальны, следовательно, оценки, полученные для обоб-
обобщенных скоростей в A.9.10) и для возмущений в A.10.5), наиболее
точны. Будем считать, что границы q~, qf области движения заданы
в виде A.10.13). Оценка A.9.11), A.9.12) в этом случае примет вид
г<г*=тах»«), r*=2\/^' i = l---,n. A.10.14)
В соответствии с A.10.9), A.10.10) и A.10.14) имеем одинаковые
оценки времен приведения подсистем A.8.9) в терминальное состояние:
т*=т*=т*0, ro*=2V- A.10.15)
Покажем, что при управлении A.9.1) с любыми другими допустимыми
параметрами Xi, удовлетворяющими A.10.6), но не связанными между
собой равенствами A.10.9), A.10.10), оценка времени движения т*,
подсчитанная с использованием A.10.14), будет больше, чем Tq .
Действительно, для того, чтобы уменьшить г*, требуется согласно
A.10.14) и A.10.15) увеличить Xi при всех г = 1,... , п. Тогда, в силу
строгой монотонности левых частей неравенств A.10.6) по Xi, все
левые части возрастут, и по крайней мере одно из неравенств A.10.6),
которое обращалось в равенство при выборе Z = Zo согласно A.10.10),
нарушится. Таким образом, величина т* = Tq , полученная в A.10.15),
минимальна при q° = 0 и управлении A.9.1).
Видоизмененный закон управления. В случае q° = 0 мож-
можно видоизменить закон управления A.9.1) так, чтобы новая
(соответствующая видоизмененному закону управления) оценка
времени движения была
меньше, чем полученная
в A.10.15). Для этого
переопределим функции ф*
в A.9.1) так, чтобы кривая
переключений ^ = ip*(qi)
(см. рис. 10) состояла из
ветви параболы (при \qi —
~ Ял\ ^ d*) и прямолинейного
участка (при d* < \qi — q*\ ^
Рис. 10. Видоизмененная кривая переклю- ^ di). Здесь d* должно быть
чений выбрано так, что d* < di/2.
Чг
-Yi
(tf.
ч
0)
ы
(в?.
J
/
0)
/
Чг
§1.10. Определение параметров 49
Зададим функции ф* в виде
ГгЫ = ~ {^г\Чг ~ tf|I/2sign(ft - (/?), \Qi ~ tf | < dj;
V>* Ы = ii sign (ft - ?*)> < < \Qi ~ Q*\ < *;
^г* = 2Х' d*^2di' A.10.16)
Здесь Xi, Yi — положительные параметры нового закона управления,
которые уже не связаны между собой равенством A.10.7).
Если во время движения выполняются соотношения A.9.3) (или
A.8.12)), то управление A.9.1), A.10.16) гарантированно приводит
систему в терминальное состояние. При этом скорости движения под-
подсистем ограничены и выполняются неравенства |<^| ^ Yi, а следова-
следовательно, верна и оценка A.10.5) максимальных абсолютных значений
возмущений \Vi\. Подставляя A.10.5) в A.9.3), получим неравенства,
полностью совпадающие с A.10.6). Следовательно, если Xi, Yi удовле-
удовлетворяют неравенству A.10.6), то управление A.9.1), A.10.16) решает
задачу 1.1 при q° = 0.
Справедливы следующие оценки времени движения:
г < г* =тахДт*), г* = -^ + —?-, г=1,...,п, A.10.17)
где т* — оценка времени движения для г-й подсистемы. Докажем
эти соотношения. Время движения г-й подсистемы максимально при
наихудшем возмущении Vi = —piUi. Все движение распадается на три
этапа. Сначала, согласно A.8.9), A.9.1), A.9.2) и A.10.16), движение
будет происходить с постоянным ускорением
до тех пор, пока фазовая точка не попадет на кривую переключений
Qi = Ф{{Aг)- Далее фазовая точка движется вдоль прямолинейного
участка кривой переключений с постоянной скоростью:
а затем — вдоль параболического участка кривой переключений
с постоянным ускорением
Длительности первого и последнего этапов одинаковы и равны
Длительность второго этапа равна (di — 2d*)/Yi. Суммируя длительно-
длительности всех трех этапов и учитывая, что d* = Y?/2Xi, приходим к оценке
A.10.17) для г.
50 Гл. 1. Метод декомпозиции управления (первый способ)
Покажем, что видоизмененный закон управления A.10.16) позволя-
позволяет уменьшить оценку времени движения по сравнению с A.10.15). Для
этого рассмотрим конкретный выбор параметров Ij и 7j в A.10.16),
полагая
ft = d* = id<- AЛ0Л8)
Отметим, что соотношение A.10.18) отличается от использованной
ранее формулы A.10.7). В этом случае при наихудших возмуще-
возмущениях прямолинейный участок движения отсутствует и соотноше-
соотношения A.10.17) переходят в A.10.14). Будем искать параметры Xi
в виде A.10.9), как это было сделано ранее, а параметры Yi выражать
согласно формуле A.10.18). Выберем максимальное значение Z:
Z = Z'^ A.10.19)
удовлетворяющее A.10.6). Получим, в силу монотонной зависимости
левой части A.10.6) от параметров Yi и равенства A.10.18) значение
Zq, большее, чем Zq, cm. A.10.10). Поэтому в силу формул A.10.14)
получим новое значение Tq* оценки времени движения т*:
которое будет меньше, чем полученное в A.10.15). Таким образом,
видоизмененный закон управления действительно позволяет умень-
уменьшить оценку времени движения.
Для этого закона управления A.9.1), A.10.16) укажем числен-
численную процедуру поиска оптимальных допустимых параметров Xi, Yi,
не связанных соотношениями A.10.18), A.10.9), при которых оценка
времени движения т*, определяемая согласно A.10.17), минимальна.
Будем использовать следующее утверждение.
Если параметры Xi и Yi оптимальны, то величины т* в A.10.17)
одинаковы, т. е.
т*=т*, i=l,...,n, A.10.21)
а неравенства A.10.6) переходят в точные равенства
Y _L ЪГ Q°(V\ — Л ЪГ — (\ _L ^П \ Т~1
Xi + Лго [У ) - /\i, Ki - I 1 + т _ I Ji ,
A.10.22)
Л / Г7-0 /nrO /^ || у7-0 i /nf0|| \ т—1 • 1 ^
А{= [Ui -Gi~ -\\U +G || J. , г=1,...,п.
Этот факт доказывается рассуждениями, аналогичными тем, которые
использовались ранее и приведены после формулы A.10.15).
§1.10. Определение параметров 51
Процедура поиска оптимальных параметров Xi и Yi видоизменен-
видоизмененного закона управления состоит в следующем. В соответствии с равен-
равенствами A.10.17), A.10.21) положим в системе A.10.6)
Xi = Y?{Yij*-di)-\ A.10.23)
Получим
Y2
4 +KS°(Y)^A A.10.24)
Выберем некоторое начальное значение т* (например, т* = Tq*
из A.10.20)) и найдем численно некоторые значения параметров
Yi, удовлетворяющие A.10.24). Множество \Y~ ,Y+], г = 1,...,п,
в^ котором можно производить этот поиск, легко получить, положив
S0 = 0 в неравенствах A.10.24). В результате получим
Если какое-либо решение неравенств A.10.24) для Yi найдено, то
нужно уменьшить значение т* в A.10.24) на некоторую величину
5т* и повторить поиск допустимых параметров Yi при новом т*.
Минимальное значение т*, при котором неравенства A.10.24) имеют
решение Yi > 0 для всех г = 1,...,п, определяет вместе с формулой
A.10.23) оптимальные параметры Xi, Yi.
Покажем также, что найденная ранее оценка времени движения Tq*
не является минимальной и может быть улучшена с использованием
предложенной численной процедуры. Для этого требуется показать,
что если в качестве начального значения оценки т* было выбрано т^*,
то при достаточно малом шаге 5т* предложенный алгоритм на второй
итерации обязательно найдет значения параметров Xi, Yi, обеспечива-
обеспечивающие еще меньшую оценку времени движения
Допустим обратное. Пусть т* = Tq* из A.10.20) — минимальная оценка
времени движения. Тогда, как указано выше, должны быть выпол-
выполнены соотношения A.10.21), A.10.22). Выберем некоторое значение г
A ^ г ^ п) и, используя равенство A.10.17), подсчитаем производную
dr*/dYi, считая, что параметр Xi связан с Yi при помощи первого
равенства в A.10.22):
дт* _ di I YtdXt
щ--у? + тг-^!Щ- AЛ0-25)
При данном г из равенств A.10.22), в силу монотонности S°(Y) no Yi,
см. A.8.11), имеем
52
Гл. 1. Метод декомпозиции управления (первый способ)
Значения Xi, Yi, обеспечивающие оценку т* = Tq*, связаны равен-
равенством A.10.18). Поэтому знак производной из A.10.25) положителен:
дт* _ Yi дХг
Л- Oli
dYj
A.10.27)
Yi на некоторую достаточно
остаются фиксированными)
Xi, г = 1,...,п, для всех
При выбранном г уменьшим параметр
малую величину 5Yi (все Yj, j ф г,
и одновременно увеличим параметры
подсистем, причем так, чтобы равенства A.10.22) не нарушились.
Очевидно, что при такой вариации новые значения параметров
будут удовлетворять ограничениям Y^/Xi < di, что и требовалось
в A.10.16). При этом в силу
A.10.17) и A.10.27) оценки вре-
времен движения всех подсистем
уменьшатся. Таким образом, мы
пришли к противоречию, и Tq* не
может быть минимальным значе-
значением оценки г*.
Отметим, что управление
A.9.1) с видоизмененной функци-
функцией переключений A.10.16) может
быть использовано также и в
случае, когда q° ф 0. Соответ-
Соответствующая область ?li, задающая
возможные начальные состояния
п 1( Л, ~ для г-й подсистемы, описы-
Рис. 11. Область ili для видоизме- /1 ^ ,ч
немного закона управления вается соотношениями A.9.4)
и изображена на рис. П.
§ 1.11. Подсистема с нелинейным сопротивлением
Изложенный в § 1.3-1.7 способ решения задачи 1.1 состоит из двух
этапов: 1) декомпозиции исходной нелинейной системы A.1.3) на под-
подсистемы A.3.3); 2) построения управления для подсистем на основе
игрового подхода. При этом в качестве подсистем с одной степенью
свободы рассматривались системы с линейным сопротивлением A.3.8).
Как было показано, возможны видоизменения предложенного
подхода на обоих этапах. На первом этапе можно приводить систему
к совокупности других подсистем, как более простых, чем A.3.8),
так и более сложных. Наиболее простой подсистемой с одной
степенью свободы будет, очевидно, система A.3.8) при Л = 0. Этот
случай охватывается приведенными выше формулами, которые при
этом значительно упрощаются. В случае Л = 0 наложенное условие
A.2.5) заменяется более простым условием A.2.6), которое можем
непосредственно проверить при помощи леммы 1.1 из § 1.2. На втором
§1.11. Подсистема с нелинейным сопротивлением 53
этапе необязательно использовать игровой подход для построения
управления подсистемами (см. § 1.5).
Рассмотрим подробнее видоизменение изложенного подхода, когда
в качестве подсистемы с одной степенью свободы исследуется система
с нелинейным сопротивлением. Следующее ниже рассмотрение пред-
предложено в работе [65].
Пусть динамика системы с одной степенью свободы описывается
уравнением
,t)- A.11.1)
Здесь q — обобщенная координата системы, т > О — постоянный
инерционный коэффициент (масса), R(q) — сила сопротивления, U —
управляющая сила, V(q,q,t) — возмущающая сила; точка означает
производную по времени t.
Предполагаем, что сила сопротивления R(q) направлена против ско-
скорости, а ее величина строго возрастает с ростом скорости и обращается
в нуль в состоянии покоя. Функцию R(q) считаем гладкой. Таким
образом, имеем
qR(q)<0, ^J^<° Й^О), Д(О) = О. A.11.2)
Управляющую и возмущающую силы предполагаем стесненными
геометрическими ограничениями, причем максимальная величина воз-
возмущения строго меньше максимальной величины управления. Имеем
\U\^U0, \V(q,q,t)\^pU0, р<1, A.11.3)
где Щ > О и р < 1 — постоянные. В остальном возмущение V(q, q, t)
может быть произвольной функцией своих аргументов.
Требуется построить управление по принципу обратной связи
U(q,q), приводящее систему A.11.1) из произвольного начального
состояния
q(to)=q°, q(to)=q° A-11.4)
в заданное конечное состояние с нулевой скоростью
q(U) = q*> q(U)=0 A.11.5)
за конечное время. Здесь to, q°, q°, q* — некоторые заданные числа,
время ?* не фиксировано.
Пусть / > 0 — некоторая величина размерности координаты q.
Введем безразмерные переменные
q — q* ,/ t — to и ? R
x = —> t=^T' u=w f = -Tr0'
A.11.6)
V (ml
V =
54 Гл. 1. Метод декомпозиции управления (первый способ)
После замены A.11.6) уравнение A.11.1) примет вид
x + f(x) = u + v(x,x,t). A.11.7)
Здесь и далее точкой обозначены производные по безразмерному
времени t', которое в A.11.7) и ниже обозначено просто через t.
Гладкая функция f(x) в A.11.7) обладает согласно A.11.2) и A.11.6)
следующими свойствами:
zf(z)>0, /'(*)> 0 (z^O), /@)=0. A.11.8)
На величины и и v в A.11.7) наложены ограничения (см. A.11.3),
A.11.6))
\u\^l, \v\^p, p<\. A.11.9)
Начальные условия A.11.4) и конечные условия A.11.5) после
замены A.11.6) примут вид
х@)=?, x@)=ri, A.11.10)
ж(т)=0, ?(т)=0; A.11.11)
здесь обозначено
° % t*-t0
c=qq =q% r=
4
Поставленная задача управления теперь может быть сформули-
сформулирована следующим образом.
Задача 1.3. Построить управление по принципу обратной связи
и(х,х), удовлетворяющее ограничению A.11.9) и переводящее си-
систему A.11.7) при произвольном возмущении v, стесненном огра-
ограничением A.11.9), из произвольного начального состояния A.11.10)
в заданное конечное состояние A.11.11) за конечное время.
Отметим, что как рассматриваемая постановка задачи, так и приме-
применяемый ниже подход к ее решению аналогичны тем, которые изложены
в § 1.3-1.6, и представляют собой их обобщение.
§ 1.12. Управление нелинейной подсистемой
Игровой подход. Рассмотрим уравнение A.11.7) с точки зрения
теории дифференциальных игр, полагая, что и и v — управления
двух противников, стесненные ограничениями A.11.9). Будем искать
такое позиционное управление и(х,х), которое переводит систему
A.11.7) из состояния A.11.10) в состояние A.11.11) за минималь-
минимальное гарантированное время г при любом допустимом возмущении v.
§1.12. Управление нелинейной подсистемой 55
Это управление и(х,х), полученное в результате решения дифференци-
дифференциальной игры, будет, как нетрудно видеть, давать решение поставленной
выше задачи 1.3. С другой стороны, решение рассматриваемой диффе-
дифференциальной игры сводится [43, 44] к решению задачи оптимального
быстродействия для системы
x + f(x) = A - р)и;
A.12.1)
\и\ ^ 1, 0 ^ р < 1, г —> min
при граничных условиях A.11.10), A.11.11). Уравнение A.12.1) полу-
получено из A.11.7) при условии v = — ри, что соответствует наихудше-
наихудшему для и управлению противника: оптимальные управления игроков
таковы, что и = ±1, v = ТР в любой момент времени.
Искомое в задаче 1.3 управление и(х,х) и соответствующее ему
время г получим, решая задачу синтеза оптимального быстродействия
для уравнения A.12.1) при граничных условиях A.11.10), A.11.11).
Указанную задачу быстродействия перепишем в виде
Х\ = Х2, Х2 = —/(#2) + A — P)u'i \и\ ^ 1> 0 < р < 1,
#i@)—?> ^2@)=^, х\(т) = Х2(т) = 0, г —> min,
(xi =ж, ж2 = х). A.12.2)
Оптимальное быстродействие. Воспользуемся принципом мак-
максимума [50] для решения задачи A.12.2). Функция Гамильтона для
задачи A.12.2) имеет вид
Я = VXX2 +р2[A - Р)и - f(x2)], \u\ < 1, A.12.3)
где pi, P2 — сопряженные переменные.
Сопряженная система имеет вид
Р\ =0, P2 = -Pi+//(^2)P2. A.12.4)
Так как система A.12.2) автономна, то для рассматриваемой задачи
оптимального быстродействия имеем первый интеграл
Я = Р1х2 +ра[A - р)и - /(х2)] = Л ^ 0, A.12.5)
где h — постоянная.
Согласно принципу максимума при ограничении |гх| < 1 из A.12.3)
получим
и = signp2- A.12.6)
56 Гл. 1. Метод декомпозиции управления (первый способ)
Отдельно рассмотрим вопрос о возможности особых участков
оптимальной траектории, на которых р2 = 0. На таком участке согласно
второму уравнению A.12.4) имеем р\ = 0. Следовательно, при нали-
наличии такого участка на всей траектории имеем р\ = const = 0. Тогда
на всей траектории второе уравнение A.12.4) становится однородным,
и, так как р2 = 0 на особом участке, имеем р2 = 0 на всей траекто-
траектории. Однако на оптимальной траектории согласно принципу максимума
сопряженный вектор не равен тождественно нулю. Полученное проти-
противоречие доказывает отсутствие особых участков оптимальной траек-
траектории. Итак, равенство р2 = 0 может иметь место лишь в отдельные
моменты времени (моменты переключения) и, согласно A.12.6), почти
всюду имеем и = ±1.
Рассмотрим сначала участки оптимальной траектории, на которых
Р2 > 0, и = 1. Из уравнений A.12.2) получим для этих участков
^=x2[(l-p)u-f(x2)}-\ A.12.7)
Из A.12.7) следует, что участки оптимальной траектории в плос-
плоскости х\, Х2 при Р2 > 0 суть дуги следующих кривых:
хх=ф+(х2)+с+9 A.12.8)
где с+ — произвольная постоянная, а функция ф+(х2) определена
равенством
у
lZp^f{zy 0 <р< 1. A.12.9)
Отметим некоторые свойства функции ф+(у), вытекающие
из соотношений A.12.9), A.11.8) и необходимые для дальнейшего. При
изменении у от —оо до 0 функция ф+ положительна и строго убывает,
обращаясь в нуль при у = 0. Точка у = 0 является единственным
экстремумом функции ф^(у) и притом ее минимумом.
Если трансцендентное уравнение для z+
f(z+) = l-p A.12.10)
не имеет решения, т.е. f(z) < 1 — р при всех z, то функция ф+(у)
строго возрастает при всех у ^ 0. В этом случае ф~^(у) > 0 при
всех у ^ 0.
Если же уравнение A.12.10) имеет корень z+, то этот корень
положителен и единственен в силу условий A.11.8). В этом случае в
интервале у G @, z+) функция ф^(у) строго возрастает от 0 до оо, а
при у > z+ она строго убывает. Типичный график зависимости A.12.8)
§1.12. Управление нелинейной подсистемой
57
в плоскости х\, х2 при с+ = О пред-
представлен на рис. 12 для случая, когда
уравнение A.12.10) имеет корень
z+ > 0. Направление роста времени
t вдоль траектории, вытекающее из
первого уравнения A.12.2), указано
на рис. 12 стрелками.
Совершенно аналогично рас-
рассматриваются участки траекторий
при р2 < 0, которые являются дуга-
дугами кривых
х\ = фр(х2)+с
A.12.11)
Здесь, аналогично A.12.8), с —
произвольная постоянная, а функ-
функция ф~ определена равенством,
подобным A.12.9):
О
Х\
Рис. 12. Фазовая траектория при
с+ = 0, z+ > 0
zdz
-(l-p)-f(z)
, 0</9< 1.
A.12.12)
Введем трансцендентное уравнение для z , аналогичное A.12.10):
/ОО = -(! ~ ?)- A.12.13)
Если уравнение A.12.13) не имеет решения z~, то есть j[z) > р— 1
при всех z, то функция ф^(у) из A.12.12) строго возрастает при у < 0
и строго убывает при у > 0. При этом ф^(у) < 0 при всех у ф 0.
Если же корень z~ уравнения A.12.13) существует, то он единстве-
единственен и отрицателен (z~ < 0) в силу условий A.11.8). В этом случае
функция ф~р(у) строго убывает при у ? (—oo,z~), строго возрастает
при у е (z~,0) и вновь строго убывает при у е @, оо). При у —> z~ эта
функция стремится к —оо, а при у = 0 она имеет локальный нулевой
максимум. Типичный график функции ф~(у) можно получить из гра-
графика функции ф+(у), изображенного на рис. 12, путем преобразования
центральной симметрии (или, что то же самое, путем одновременного
изменения направлений обеих осей х\, х2).
Описанные выше кривые представляют собой траектории, отвечаю-
отвечающие р2 > 0 и р2 < 0 и проходящие через начало координат в плоскости
х\, х2. Другие кривые, дуги которых могут служить участками опти-
оптимальных траекторий, получаются согласно A.12.8) и A.12.11) из ука-
указанных кривых путем параллельного переноса на с+, с~ вдоль оси х\.
Отметим, что если трансцендентные уравнения A.12.10), A.12.13)
имеют решения, то система A.12.2) допускает соответствующие
решения
x2 = z+ (р2>0), x2 = z~ (р2<0). A.12.14)
58 Гл. 1. Метод декомпозиции управления (первый способ)
Решениям A.12.14) в плоскости х\, х2, отвечают фазовые траек-
траектории — прямые, параллельные оси х\. Эти прямые — асимптоты
кривых A.12.8), A.12.11) соответственно (см. рис. 12).
Таким образом, искомые оптимальные траектории состоят
из участков кривых A.12.8) и A.12.11) с различными с+, с~,
а также, возможно, из участков прямых A.12.14), если разрешимы
соответствующие уравнения A.12.10), A.12.13).
Покажем теперь, что на каждой оптимальной траектории имеется
не более одной точки переключения управления, т.е. функция p2(t)
обращается в нуль не более одного раза.
Предположим противное. Пусть функция p2(t) обращается в нуль
в два момента времени t', t", между которыми она положительна. Тогда
имеем
P2(t) > 0, te (*',*"); P2(t') = P2(t") = 0. A.12.15)
Из первого интеграла A.12.5) для моментов времени t', t" в силу
A.12.15) получим
Pix2(t') = p\x2(t") = h^0. A.12.16)
Если р\ = const = 0, то из A.12.4) получим для p2(t) линейное одно-
однородное уравнение, которое при нулевых условиях A.12.15) в моменты
t', t" имеет тождественно нулевое решение p2(t) = 0. Но это противоре-
противоречит принципу максимума, утверждающему существование ненулевого
сопряженного вектора. Следовательно, р\ = const ф 0, и из A.12.16)
получим x2{tr) = x2{t"). Однако на всех фазовых траекториях, кроме
прямых A.12.14), переменная х2 либо строго возрастает, либо строго
убывает с ростом времени t. Это следует из приведенного выше
анализа фазовых траекторий и видно на рис. 12. Значит, равенство
x2(t') = x2(t") возможно лишь в случае, если рассматриваемый участок
траектории принадлежит прямой A.12.14), т.е.
x2(t) = z+, te (?',?"). A.12.17)
Подставляя A.12.17) во второе сопряженное уравнение A.12.4), полу-
получим линейное уравнение с постоянными коэффициентами
Ш =-Pi + fa, k = f(z+)>0,
где к > 0 согласно A.11.8). Общее решение полученного уравнения
имеет вид
Р2&) = т-+Сеы, A.12.18)
к
где С — произвольная постоянная. Но решение A.12.18) монотонно
по t и ни при каких р\ ф 0 и С не может удовлетворять условиям
A.12.15). Таким образом, участок оптимальной траектории, на кото-
котором выполняются условия A.12.15), не может быть отрезком прямой
§1.12. Управление нелинейной подсистемой
59
A.12.17). Тем самым доказано, что оптимальная траектория не может
включать участок вида A.12.15).
Совершенно аналогично доказывается, что оптимальная траектория
не может также содержать участок, на котором функция P2(t) отрица-
отрицательна, а на его границе обращается в нуль.
Следовательно, функция P2(t) на каждой оптимальной траекто-
траектории обращается в нуль не более одного раза, т. е. управление имеет
не более одного переключения.
Единственными фазовыми траекториями, которые входят в начало
координат при возрастании времени, являются ветвь кривой A.12.8)
при с+ = 0, лежащая в квадранте х\ ^ 0, х% ^ 0 (см. рис. 12), и ветвь
кривой A.12.11) при с~ = 0, лежащая в квадранте х\ < 0, х2 > 0. Эти
ветви кривых отвечают управлениям и = 1 и и = — 1 соответственно.
Совокупность указанных ветвей образует кривую переключений, урав-
уравнение которой представим в виде
здесь введено обозначение
A.12.19)
A.12.20)
и = -\
В силу отмеченных выше свойств функций A.12.9), A.12.12)
функция фр(у) из A.12.20) строго убывает при всех у, а при у = 0 она
обращается в нуль и имеет точку перегиба.
Теперь нетрудно дать описание всего поля оптимальных траек-
траекторий. Оптимальная траектория, начинающаяся в произвольной
точке фазовой плоскости х\, х2,
состоит из отрезка кривой одного
из семейств A.12.8) или A.12.11)
и отрезка кривой переключений
A.12.19).
Качественно поле оптимальных
траекторий показано на рис. 13
для случая существования корней
уравнений A.12.10), A.12.13). Жир-
Жирной линией на рис. 13 изображе-
изображена кривая переключений A.12.19),
а стрелками указано направление
роста времени t. Отметим, что по-
построенная картина поля оптималь-
оптимальных траекторий подобна той, кото-
которая имеет место в случае линейного рис 13. Оптимальные фазовые
сопротивления, см. § 1.4, рис. 2. траектории
и= 1
60
Гл. 1. Метод декомпозиции управления (первый способ)
Синтез оптимального управления, отвечающий построенному полю
фазовых траекторий, может быть представлен в виде
up(xi,x2) = sign^p^) -х\], х\ ф фр(х2),
Up(x\fx2) = signal = -signx2, x\ = фр(х2),
(х\ =х, х2 = х), A.12.21)
где функция фр определена соотношениями A.12.20), A.12.9),
A.12.12).
Полученный закон управления A.12.21) по построению дает реше-
решение задачи 1.3. Это решение можно назвать субоптимальным, так как
оно оптимально по быстродействию (неулучшаемо), если возмущение
v является «наихудшим», что предполагается при игровом подходе.
При наихудшем возмущении v = — ри движение системы происходит
по оптимальным траекториям, см. рис. 13. Если же возмущение v
отличается от наихудшего (г; ^ —ри), как это обычно имеет место,
то траектория движения отличается от оптимальной. При этом дви-
движение по кривой переключений происходит в скользящем режиме,
а время до попадания в начало координат может лишь уменьшиться.
Упрощенный подход. Выше возмущение не предполагалось извест-
известным, однако его максимально возможная величина была задана, и пос-
построенное управление от него существенно зависит. В безразмерных
переменных ограничение на возмущение имеет вид \v\ ^ р, см. A.11.9),
и полученный синтез управления A.12.21) зависит от параметра р.
Нередко используется другой
подход к построению управления
при наличии возмущений, когда
возмущения просто игнорируются.
Этот подход, названный упро-
упрощенным (см. § 1.5), в рассмат-
рассматриваемом случае просто означает,
что параметр р при построении
управления полагаем равным нулю,
т. е. возмущениями пренебрегаем.
Полученное таким образом управ-
управление щ(х\,Х2) определяется со-
соотношениями A.12.21), A.12.20),
A.12.9), A.12.12) при р = 0. Кри-
Кривая переключений для упрощенно-
упрощенного управления задается формулой
A.12.19) при р = 0. Она изображена
на рис. 14 жирной линией.
Рис. 14. Кривая переключений при
р = 0 и траектория для упрощен-
упрощенного подхода
§1.12. Управление нелинейной подсистемой 61
Сравним два способа построения управления — игровой и упро-
упрощенный. Для этого исследуем динамику системы A.11.7) при неко-
некотором р G @,1) под действием упрощенного управления щ(х\,Х2).
Эту систему представим в виде
Х\ = Х2, Х2 = -f{x2) +Щ(Х\,Х2) + V,
A.12.22)
\v\ ^ р < 1, (х\ = X, Х2 = Х).
Поставим для системы A.12.22) следующую вспомогательную зада-
задачу о нахождении наихудшего возмущения (см. аналогичную задачу 1.2
в§ 1.5).
Задача 1.4. Найти оптимальное управление v(x\,X2) системой
A.12.22), удовлетворяющее ограничению \v\ ^ p и такое, что любая
фазовая траектория этой системы первый раз пересекает кривую
переключений х\ = фо(х2) как можно дальше от начала координат,
т.е. при максимально возможном \х\\ или, что то же самое,
максимально возможном \х2\.
Предположим сначала, что начальная точка лежит в области
х\^фо(х2)- Тогда согласно A.12.21) для рассматриваемой траекто-
траектории имеем щ = — 1. При этом фазовая траектория системы A.12.22)
впервые пересечет ту ветвь кривой х\ = ^ofe)» на которой х\ > 0,
Х2 < 0 (см. рис. 14, где принято, что начальная точка (?,7/) лежит
на кривой х\ = фо(х2)). Поставленная задача 1.4 при этом описывается
соотношениями
Х\ = Х2, Х2 = —/(#2) — 1 + ^, \v\ < р < 1,
*i@)=?, x2@)=ri, ZZMri), A.12.23)
х\(т) = фо(х2(т)), х\(т)>0, х2(т) < 0, xi(r)
Момент г окончания процесса не фиксирован. Максимизация х\(т)
эквивалентна в силу A.12.23) минимизации следующего интегрального
функционала:
\(-x2)dt ^min. A.12.24)
о
Применяя принцип максимума к задаче A.12.23), A.12.24), соста-
составим функцию Гамильтона
Я = Plx2+P2[v - 1 - f(x2)}+x2, A.12.25)
где р\, р2 — сопряженные переменные. Они удовлетворяют сопряжен-
сопряженной системе
Pi=0, p2 = f'(x2)p2-Pl-l A.12.26)
62 Гл. 1. Метод декомпозиции управления (первый способ)
и условиям трансверсальности, отвечающим граничным условиям
A.12.23):
Р2=О, Я = 0, t = r. A.12.27)
Из первого условия A.12.27), применяя соотношения A.12.20),
A.12.9) при р = 0 и учитывая, что х2(т) < 0 согласно A.12.23),
получим
Рх = -Л}-Шг t = r. A.12.28)
Подставим A.12.28) в A.12.25) и воспользуемся вторым условием
трансверсальности A.12.27). После упрощения получим
Н = p2(v - 2) + х2 = 0, t = r.
Так как х2(т) < 0 и \v\ ^ р < 1, то из полученного равенства следует
Р2(т)<0. A.12.29)
Оптимальное управление находим из условия максимума Н из
A.12.25) по Н <р:
v = psignp2. A.12.30)
Особые участки траектории здесь невозможны. В самом деле, если
Р2 = 0 на некотором интервале времени, то на этом интервале р\ = — 1
согласно второму уравнению A.12.26). Но р\ = const, следовательно,
р\ = — 1 на всей траектории. Тогда второе уравнение A.12.26) стано-
становится линейным и однородным для р2, и его решение при начальном
условии A.12.29) не может обращаться в нуль.
Следовательно, особые участки отсутствуют, и равенство A.12.30)
означает, что управление v(t) имеет точки переключения там, где
P2(t) = 0.
Найдем кривую переключений в плоскости х\,х2. В силу авто-
автономности системы A.12.23) ее гамильтониан A.12.25) вдоль опти-
оптимальной траектории сохраняет постоянное значение, равное нулю
согласно A.12.27):
Я = (р! + \)х2 +P2[v - 1 - f(x2)} = 0.
Отсюда следует, что в момент переключения, т. е. при р2 = 0 имеем
либо р\ = — 1, либо х2 = 0. Но из равенства р\ = — 1, как показано
выше, вытекает, что р2 нигде не обращается в нуль. Следовательно,
в момент переключения имеем х2 = 0, так что кривая переключений
здесь есть луч х2 = 0, х\ > 0.
Для того чтобы определить знак управления при х2 < 0 и х2 >
> 0, достаточно найти этот знак хотя бы в одной точке. В момент
окончания процесса г имеем х2(т) < 0 согласно A.12.23) и р2(т) < 0
в силу A.12.29). Следовательно, v = — р при х2 < 0.
§1.12. Управление нелинейной подсистемой 63
В результате имеем
v(x\, X2) = psign?2- A.12.31)
Оптимальный синтез в области х\ > ^0(^2) построен. Для его
построения в области х\ < фо(х2) отметим некоторые свойства
симметрии. При замене f(z) на g(z) = —f(—z) согласно A.12.9),
A.12.12) имеем
Ф~р {у) —> ~Фо~(~у\ Фр~{у) —> ~Фр {~у)- A.12.32)
Из A.12.20) и A.12.32) следует, что при указанной замене
фр{у) -* -фР{-у). A.12.33)
Сделаем теперь в системе A.12.22) замену
х\ —> —х\, Х2 —> —Х2,
A.12.34)
v^-v, f(z)^-f(-z).
При этом согласно A.12.33) и A.12.21) щ заменится на —г^о,
и система A.12.22) останется инвариантной. Отсюда следует, что
в области х\ < фо(х2) поле оптимальных траекторий и синтез опти-
оптимального управления будут теми же, что и в области х\ > фо(х2),
но с заменой f(z) на g(z) = —f(—z). Так как синтез A.12.31)
не зависит от конкретного вида функции f(z), то он имеет место
и в области х\ < V>o(#2)- Таким образом, равенство A.12.31) определяет
решение задачи 1.2 во всей плоскости х\,Х2.
Анализ фазовых траекторий. Рассмотрим движение системы
A.12.22) под действием упрощенного управления щ(х\,Х2), опре-
определяемого соотношениями A.12.21), A.12.20), A.12.9), A.12.12)
при р = 0, и наихудшего возмущения v из A.12.31). Пусть начальная
точка ?, г] лежит на той ветви кривой переключений х\ = ^0(^2)»
где х\ < 0, Х2 > 0 (см. рис. 14). Исследуем фазовую траекторию вплоть
до следующего ее пересечения с той же ветвью кривой переключений.
Рассматриваемый отрезок траектории состоит из четырех участков,
на каждом из которых щ и v постоянны. Эти участки характеризуются
следующими граничными точками и управлениями (см. рис. 14):
о = — 1, v = р;
о = — 1, v = —р;
A.12.35)
о=1, v = -р;
1)
2)
3)
(?.
(*?
(?'.
г,)-
.0)-
.*?')¦
>(х?
-(?
->(а
,0),
f,rf),
64 Гл. 1. Метод декомпозиции управления (первый способ)
Параметры граничных точек A.12.35) удовлетворяют соотноше-
соотношениям, отражающим их расположение на кривой переключений и осях
координат (см. рис. 14):
'), r/<0, <f>0; xt < 0; A.12.36)
, ^*>0, Г<0.
Подставляя щ и v из A.12.35) в уравнения A.12.22) и интегрируя
их вдоль соответствующих участков траектории, имеем
, zdz
[_
-1-р-Я*)'
Г7 О
О 77*
TJ'
В полученных соотношениях заменим ?, ^х, ^* их выражениями
A.12.36) и используем формулы A.12.20), A.12.9), A.12.12) при р = 0.
Получим
J 1-Я*) J -i-/(^) ~J i
0
?7 ?7 ?? 77
J -i-/(*)-J T^7M = J -\ + p+f(z) + \ г
J Я) J Я) J +p-Я*)"
0 0 0
A.12.37)
Напомним, что т/ < 0, r\ > 0, 77* > 0 согласно A.12.36). Положим
г]' = —ту0, г]° > 0 и преобразуем соотношения A.12.37) так, чтобы
они содержали интегралы лишь по отрезкам положительной полуоси.
После упрощений получим
Ф4(Г]0) = К2(р)Ф]G1),
A.12.38)
§1.12. Управление нелинейной подсистемой 65
Здесь введены обозначения
±A
A-12.39)
Рассмотрим трансцендентные уравнения A.12.38), определяющие
?70 и ту* по заданным г\ > 0 и р G @, 1). Для этого отметим некоторые
свойства функций Ф^, г = 1,...,4, из A.12.39). Напомним, что согласно
A.11.8) имеем f(z) > 0 при z > 0 и /(г) -> 0 при ^ -^ 0.
Знаменатели подынтегральных выражений для функций <3>i и Фз
в A.12.39) положительны при всех z > 0. Следовательно, функции Ф\
и Фз определены и ограничены при всех у ^ 0.
Если уравнения
/B2)=1+/о, <7Ы = -/(-^4) = 1+Р A.12.40)
для Z2, z\ имеют решения, то знаменатели подынтегральных выраже-
выражений соответствующих функций Ф2, Ф4 в A.12.39) обращаются в нуль
при конечных значениях Z2, Z4, равных корням уравнений A.12.40).
В этом случае функции Ф2, Ф4 монотонно возрастают и обращаются
в бесконечность при у = Z2, у = z\ соответственно. Если же уравнения
A.12.40) не имеют решений, то функции Ф2, Ф4 определены при всех
у > 0. В обоих случаях знаменатели подынтегральных выражений
для функций Ф2, Ф4 имеют максимумы по / ^ 0 и д ^ 0, равные
B + рJA +р)-1/4. Следовательно, справедливы неравенства
Таким образом, во всех случаях функции Ф2 и Ф4 положительны и
строго возрастают, принимая при изменении у ^ 0 все значения от 0
до оо.
Отсюда вытекает, что трансцендентные уравнения A.12.38) при
любых г] > 0 и р G @, 1) имеют единственные положительные решения
?70 > 0 и г]* > 0. Эти решения являются непрерывными и монотонными
функциями от г].
3 Ф. Л. Черноусько и др.
66 Гл. 1. Метод декомпозиции управления (первый способ)
Продифференцируем равенства A.12.38) по г]. После простых
преобразований получим
drf _
Из соотношений A.12.39) и свойств A.11.8) функции f(z) выте-
вытекают неравенства
*M ад, у>0
У
<i
Используя второе из этих неравенств, получим из A.12.41)
Можно проверить, что функция >с2(р) из A.12.39) строго возрастает
от 0 до оо на отрезке р е [О, 1], причем к = 1 при значении р, равном
(см. § 1.6)
р* = |(л/5 - 1) «0.618. A.12.43)
Предположим сначала, что р < р* и, следовательно, к2(р) < ot,
где а < 1 — некоторое положительное число. Тогда из A.12.42)
вытекает
Т2Шу V>0, A.12.44)
Т<-Шу V>0,
drj <?f>(rf)
и, следовательно,
Ф2(^*) <а2Ф1(г]), г]>0. A.12.45)
Докажем, что ту* < г]. Предположим противное, а именно, что
г]* ^ г]. Из A.12.39) следует <&2(y) > Ф1 (г/) при всех у > 0. Тогда,
учитывая монотонность функции <&2(y), имеем цепочку неравенств
которая приводит к противоречию с неравенством A.12.45). Следова-
Следовательно, Г]* < Г].
Преобразуем неравенство A.12.44), подставляя в него выражения
для производных Ф[, Ф'2 согласно A.12.39) и учитывая положитель-
положительность функции f(z):
§1.12. Управление нелинейной подсистемой 67
ат?[1+/(*?)][!q+PO(*?)] ar?[l+/(if)]
*[1+/()][1 + A)'/()] Г[1+/()]' ^ '
Упростим последнее неравенство, учитывая, что f(rf) < f(rj) ввиду
монотонности функции f(z) и неравенства ту* < г]. Получим
drj* a2ri
-j- < ~-L, г]>0.
drj rj*
Интегрируя данное неравенство при условии ту* = 0 при г] = О,
получим (ту*J < а2г]2 или iff jr\ < a.
Итак, если р < р*, где р* определено в A.12.43), то vf jif] < a,
т. е. фазовая траектория приближается к началу координат, при этом
расстояние до начала координат убывает не медленнее, чем в геомет-
геометрической прогрессии. Поэтому система приходит в заданное состояние
за конечное время, хотя и после бесконечного числа переключений
управления.
Предположим, что система попала в малую окрестность начала
координат, так что г] достаточно мало. При этом rf и ту* также будут
малыми ввиду их непрерывной зависимости от г\. Так как f(z) —> О
при z —> 0 в силу A.11.8), то в интегралах A.12.39) при малых у можно
опустить члены f(z), g(z), после чего получим в пределе
фг(у)~2у2' У^°> 2=1,...,4.
Следовательно, трансцендентные уравнения A.12.38) при малом г]
примут вид
Отсюда получим
^- =я2(р). A.12.46)
Пусть р > р* и, следовательно, я2(р) > 1. Тогда вследствие A.12.46)
получим rj* > г], и фазовая траектория, даже попавшая в малую окрест-
окрестность начала координат, удаляется от него. Система в этом случае
не приходит в заданное состояние.
Итак, в случае произвольной функции f(z), удовлетворяющей усло-
условию A.11.8), упрощенный подход приводит к управлению щ(х\,Х2),
определяемому соотношениями A.12.21) при р = 0 и обладающему
следующими свойствами:
• если р < р* « 0.618, то при любом допустимом возмущении
\v\ ^ p система попадает в начало координат. Время движения
при этом конечно, хотя число переключений, вообще говоря,
бесконечно;
68 Гл. 1. Метод декомпозиции управления (первый способ)
• если же р > р*, то существует такое допустимое возмущение v,
определяемое равенством A.12.31), при котором система никогда
не попадает в начало координат.
Следовательно, упрощенное управление гарантирует решение
задачи 1.3 лишь в случае р < р*, т.е. при условии, что отношение
максимальных возможных величин возмущения и управления
не превосходит отношения золотого сечения.
Конкретизируя вид функции f(z), можно получить более деталь-
детальную картину движения. Отметим, что изложенные здесь результаты,
полученные впервые в [65], обобщают результаты работ [63] и [64],
где рассмотрены случаи отсутствия сопротивления и линейного сопро-
сопротивления соответственно, см. § 1.4-1.6.
Заключение. Предложенный закон управления A.12.21), основан-
основанный на игровом подходе, гарантирует приведение рассматриваемой
системы A.11.7) в начало координат за конечное время при любом
виде нелинейности f(z) и при любом неопределенном возмущении,
если р< 1. Этот закон управления не требует знания возмущения;
необходимо лишь знать его возможное максимальное значение, которое
не должно превосходить максимального значения управления.
Подчеркнем различие в требованиях к функциям f(z) и v(x,x,t).
Обе эти функции могут быть произвольны в рамках соответствующих
условий — A.11.8) для f(z) и A.11.9) для v. Однако функция нели-
нелинейного сопротивления f(z) должна быть известна при построении
управления, а возмущение v(x,x,t) знать не требуется.
Упрощенный подход к построению управления, при котором
возмущение вообще игнорируется, оказывается менее эффективным.
Он заведомо приводит систему в начало координат лишь при
р < р* « 0.618. Если же р > р*, то существует такое возмущение,
при котором попадание в начало координат оказывается невозможным.
В то же время по своей структуре оба подхода сходны и различа-
различаются лишь кривыми переключений.
Предложенный способ управления обладает малой чувствительно-
чувствительностью к различным возмущениям и вариациям параметров. Эти факторы
нетрудно учесть, если увеличить предполагаемый уровень возможных
возмущений, т. е. параметр р, создавая определенный запас по этому
параметру.
Отметим, что построенное управление субоптимально по быстро-
быстродействию в том смысле, что оно оптимально при наихудшем возможном
возмущении.
Полученные результаты могут применяться к различным дина-
динамическим системам, например, для управления электроприводами
робототехнических систем. При этом открывается возможность учесть
различные законы сопротивления, часто встречающиеся на практике.
§ 1.13. Приложение к робототехническим системам 69
§ 1.13. Приложение к робототехническим системам
Остановимся на приложении полученных результатов к задачам
динамики роботов. Покажем для этого, что постановка задачи 1.1
и условия A.2.5), A.2.6) типичны и часто выполняются для роботов.
Рассмотрим манипуляционный робот, имеющий п степеней свободы
и состоящий из п звеньев, соединенных цилиндрическими или приз-
призматическими шарнирами. Каждое звено робота является абсолютно
твердым телом. Положение г-го звена относительно (г — 1)-го харак-
характеризуется относительным углом поворота (в случае цилиндрического
шарнира) или относительным смещением (в случае призматического
шарнира). Эти углы и смещения примем в качестве обобщенных
координат (q\,...,qn), определяющих положение робота. Уравнения
движения робота можно представить в виде уравнений Лагранжа
A.1.1), где кинетическая энергия имеет вид A.1.2). Роль обобщенных
сил играют моменты сил относительно осей цилиндрических шарниров
и силы вдоль направлений смещения в призматических шарнирах.
При этом силы Щ в A.1.1) — это управляющие моменты или силы,
создаваемые двигателями (приводами), a Qi включают все остальные
внешние и внутренние силы и моменты: силы тяжести, сопротивления,
трения, разные возмущения и др.
Рассмотрим теперь динамику робота с учетом динамики приво-
приводов. Предположим, что каждый управляющий момент или сила Щ
создается отдельным электродвигателем постоянного тока, г= 1,...
...,п, а силы Qi представимы в форме A.8.5)—A.8.8). Кинетическая
энергия робота Т складывается из кинетической энергии движения
звеньев Tl(q,q) и кинетической энергии движения роторов электро-
электродвигателей T2(q,q, N), здесь N = GVb ..., Nn) — передаточные числа
редукторов, рассматриваемые как параметры. Считаем, что Ni ^ 1,
инерцией подвижных частей редукторов пренебрегаем. По теореме
Кёнига [3] кинетическая энергия г-го ротора Tf равна сумме кинети-
кинетической энергии, которую имела бы материальная точка массы, равной
массе ротора, расположенная в его центре инерции, и кинетической
энергии вращения ротора, т. е.
Thq,q,Ni) =T?(q,q)+T?{q,q,Ni).
Пусть Ji, J[ — моменты инерции г-го ротора соответственно
относительно оси вращения и перпендикулярной к ней оси, проходящей
через центр инерции. Тогда, если вектор угловой скорости статора г-го
электродвигателя имеет проекцию на ось вращения ротора, равную щ,
и перпендикулярную составляющую, равную и[, то
T?(q, q, Ni) =
70 Гл. 1. Метод декомпозиции управления (первый способ)
Угловые скорости uii, ио[ — линейные комбинации обобщенных
скоростей q\,...,qn с коэффициентами, зависящими от q. Поэтому
кинетическую энергию робота можно представить в виде
Т =^YjJi{Niqif + ^Nm^{Bq,q), A.13.1)
г=1
где B(q,N) — ограниченная симметрическая матрица, такая, что при
произвольном векторе z выполняется неравенство
\\B(q,N)z\\ < \\\z\\, А = const. A.13.2)
Здесь и далее через A^max, Nm[n обозначены, соответственно, наиболь-
наибольшее и наименьшее из передаточных чисел N\,...,Nn, а Л не зависит
от N{.
Подставим A.13.1) в уравнения Лагранжа в форме A.1.1). Получим
NfJiQi + Nmax[B(q, N)q\i = Щ + Si(q, q, t, N). A.13.3)
Разделим г-е уравнение A.13.3) на Ni и сделаем замену переменных
Pi = Niqi. A.13.4)
В результате получим
п
JiPi + N^Nr^BijN^pj = N-\U% + Si). A.13.5)
i=i
Учитывая, что N~lUi = Mi, где Mi — момент сил, создаваемый
электродвигателем, приведем систему A.13.5) к виду
M + S*. A.13.6)
Здесь
J = diag(Jb ..., Jn), В = NmaxH~lBH-\ M = (Мь ..., Mn),
S* =H~lS, # = diagGVb...,ATn). A.13.7)
Следовательно, уравнения движения с учетом замены A.13.4)
и обозначений A.13.7) представлены в виде A.1.3), A.8.2), причем
согласно A.13.2) и A.13.7) имеем неравенство
\\Bz\\^fi\\z\l ц = Nm^N~l\ A.13.8)
аналогичное ограничению A.8.3). Начальные и конечные условия пред-
ставимы в форме A.1.7), A.2.1).
§ 1.13. Приложение к робототехническим системам 71
Рассмотрим различные варианты постановок задач управления.
1°. Пусть на создаваемые электродвигателями управляющие момен-
моменты сил Mi наложены ограничения
|MiKM°. A.13.9)
В этом случае для построения управления можно применить
результаты, полученные в предыдущих разделах и подытоженные
в теореме 1.3. Неравенство A.10.8), переписанное в обозначениях
системы A.13.6), определяет допустимые значения параметра /i.
Подставив в это неравенство вместо /i его значение из A.13.8),
получим ограничение на возможные величины передаточных чисел
редукторов
Nmax Jmin V ППщ(М° ~ N^G®)
A.13.10)
Здесь Jmin — наименьший из моментов инерции роторов
Ji,...,Jn; величины G® введены ранее, см. A.8.5)—A.8.7), причем
предполагается, что
G°i < NiM^
для всех г = 1,..., п.
2°. Пусть роль управляющих воздействий играют электрические
напряжения, подаваемые на обмотки роторов электродвигателей.
Дополним уравнения движения A.13.6) уравнениями баланса
напряжений в цепях роторов и соотношениями, связывающими
моменты Mi с токами [76]:
1 dt г г г г г, г % г г г
Здесь Li — коэффициент индуктивности, Щ — электрическое сопро-
сопротивление, kf jkf4 — постоянные коэффициенты, щ — электрическое
напряжение в цепи ротора г-го двигателя, член Ъфг представляет собой
момент сил механического сопротивления. Первый член в первом урав-
уравнении A.13.11) обычно мал по сравнению с остальными. Опуская его,
имеем из A.13.11) выражение
подставляя которое в A.13.6), получим
72 Гл. 1. Метод декомпозиции управления (первый способ)
(J + В)р = U* + S**, S**=S*-Ap,
fffefJRf1+6b...)CfefJR-1 +bn), A.13.12)
Пусть на управляющие напряжения наложены ограничения
Ы<«?. A.13.13)
Ограничения A.13.13) преобразуются в ограничения на компоненты
вектора U* из A.13.12):
\U*\ <: Uf = k^R^ul A.13.14)
Уравнения движения A.13.12) снова приведены к форме A.1.3),
A.8.2).
Неравенства A.13.14) имеют тот же вид, что и соотношения A.1.6).
Очевидно, что в этом случае применим рассматриваемый способ
управления. Согласно теореме 1.3 получим ограничение, аналогичное
A.13.10):
A.13.15)
Итак, если передаточные числа приводов и параметры робота
таковы, что удовлетворяются неравенства A.13.10), A.13.15), то
можно построить управление, переводящее рассматриваемую систему
из начального состояния в заданное состояние за конечное время.
Управление учитывает наличие возмущений и конструктивных
ограничений.
Замечание 1.1. Рассматривая непосредственно систему A.13.3)
и переписывая в ее терминах условие A.10.8), можно получить
ограничения на параметры системы в другом виде. Имеем
NmaxA
для случая 1° ограниченных электромагнитных моментов и
mini(NfJi) \\HU*°-
TVmaxA mmi(NiUri
— для случая 2° ограниченных электрических напряжений.
Использование этих условий для проверки возможности применения
§1.14. Синтез управления двузвенным манипулятором 73
метода декомпозиции кажется более целесообразным в случае,
когда моменты инерции роторов Ji, г = 1, ...,п, сильно отличаются
друг от друга, а эффективные моменты инерции NfJi отличаются
не очень сильно.
Замечание 1.2. Если элементы матрицы Л велики, то для
уменьшения времени управления целесообразно приводить уравне-
уравнения движения A.13.12) к форме A.3.1), где в качестве матрицы А*
выбрана матрица J, а в качестве коэффициентов А^ — соответ-
соответствующие элементы матрицы Л. Для управления полученными под-
подсистемами с линейным сопротивлением можно применить подход,
изложенный в § 1.3-1.7.
3°. В последнее время получили распространение безредукторные
приводы. Для них имеем Ni = I и Ji = 0, так что в соотношениях
A.13.6), A.13.7) нужно положить J = О, Н = Е. Уравнения движения
и ограничения снова приводятся к виду A.1.3), A.1.6). Однако выбрать
матрицу А* в виде A.8.2), A.8.3) уже нельзя, так как J = 0. Эта
матрица должна быть выбрана по-иному, например, в виде А* = A(q*)
(см. замечания в конце § 1.2). Для применения полученных результа-
результатов требуется проверить условия A.2.5) или A.2.6), что нужно делать
в каждом конкретном случае. В следующем параграфе рассмотрена
задача построения синтеза управления двузвенным манипулятором
с безредукторными приводами.
Таким образом, полученные результаты могут быть при определен-
определенных условиях применены для построения управления манипуляцион-
ными роботами.
§ 1.14. Синтез управления двузвенным
манипулятором с безредукторными приводами
В данном параграфе рассматривается управляемая динамическая
система заданной структуры, которая представляет собой упрощен-
упрощенную модель механического двузвенного манипуляционного робота
с абсолютно жесткими элементами конструкции. Двузвенник может
совершать движения в горизонтальной плоскости и управляется
моментами сил, которые создаются в его шарнирах. На величины
управляющих моментов сил наложены геометрические ограничения.
Строится ограниченное управление, переводящее систему за конечное
время из заданного начального состояния в заданное конечное
состояние покоя. Для построения управления применяется метод
декомпозиции, который изложен в § 1.8. Указываются достаточные
условия, при которых исходную нелинейную систему удается
разбить на подсистемы с одной степенью свободы каждая. Затем
управление строится отдельно для каждой из подсистем, при этом
алгоритм расчета управления по существу аналогичен тому, который
приведен в § 1.13, где накладываются ограничения на величины
74
Гл. 1. Метод декомпозиции управления (первый способ)
передаточных чисел редукторов. Главное отличие состоит в том,
что система, рассматриваемая в данном параграфе, моделирует
движение манипулятора с безредукторными приводами. Поэтому здесь
накладываются ограничения на другие параметры системы.
Описание системы. Постановка задачи. Рассмотрим механиче-
механическую двузвенную систему (рис. 15), состоящую из неподвижного
основания Go и двух абсолютно жестких звеньев G\, G^. Элементы
конструкции соединены между собой двумя идеальными цилиндриче-
цилиндрическими шарнирами О\, 0% таким образом, что оба звена могут совер-
совершать движения только в горизонтальной плоскости.
Уравнения Лагранжа A.1.1), описывающие движение данной сис-
системы, имеют вид [73]:
(m2l\ +1\
0\
0\02 -
lgi cos #2) 0.2 —
ot =
+Q\,
A.14.1)
lg2 CO8O2) 0\
02
Q2-
Здесь введены следующие обозначения:
G\ относительно основания Gq
о\
звена
угол поворота
02 — угол между прямыми О\О2
и О2С2, характеризующий положе-
положение звена G2 относительно звена G\
(С2 — центр масс звена G2)] 1\ —
длина отрезка О\О2\ 1д2 — длина
отрезка О2С2; ni2 — масса звена
G2\ 1% — момент инерции г-го звена
относительно оси шарнира 0^; М^
Qi — моменты управляющих и про-
прочих сил, создаваемые в шарнире С^,
соответственно; здесь и всюду далее
i= 1,2.
На управляющие моменты на-
накладываются ограничения
\Mi\^Mf, A.14.2)
где Мг° — заданные постоянные.
Перейдем к безразмерным переменным
Рис. 15. Двузвенный манипулятор
t' =
м\
1/2
+ ТТ — г ТТу — i
' 1~ -"' ' "м20>
м20'
а =
A.14.3)
, /5 =
§1.14. Синтез управления двузвенным манипулятором 75
Если у новых переменных t', Q\ опустить штрих, то уравнения A.14.1)
примут вид
(а + /3 + 2 cos q2) q\ + (/3 + cos g2) #2 - B<?i<?2 + q2) sin 42 =
= Ui+Qu A.14.4)
(/3 + cos q2) q\ + /3 g2 + g? sin g2 = U2 + Q2,
а неравенства A.14.2) перепишутся в форме A.1.6). Заметим, что
в силу введенных обозначений A.14.3) выполняются соотношения
а/3>\, ?/2° = 1.
Таким образом, мы можем рассматривать задачу 1.1 (см. § 1.2)
применительно к системе A.14.4) с ограничениями A.1.6) на новые
управления Щ, считая, что область возможных движений задается
соотношениями вида A.8.1). В этом параграфе считаем, что внешние
силы и возмущения отсутствуют, т. е.
Q\ =Q2 = 0.
Упрощающие предположения и декомпозиция системы. Для
решения рассматриваемой задачи управления манипулятором восполь-
воспользуемся методом декомпозиции.
Разрешим систему A.14.4) относительно вторых производных q\,
q2 и умножим левые части полученных выражений на некоторые
положительные коэффициенты J\, J2. Тогда система примет вид
A.8.9), в которой функции Vi оказываются равными
ар — cos q2
/3(q\ + q2J sin q2 + g| sni 42 cos 42
a/3 — cos2 g2
. a + /3 + 2cosg2 Л 7 TJ
= U2[ J2 « 1 - J2U\
a/3 — cos2 q2 J a/3 — cos:
-J:
a/3 — cos2 q2
A.14.5)
Предположим, что имеют место неравенства A.8.12). Если Vi рас-
рассматривать как независимые ограниченные возмущения, то исходная
76 Гл. 1. Метод декомпозиции управления (первый способ)
нелинейная система распадается на две линейные подсистемы с одной
степенью свободы каждая.
Управление для каждой из этих подсистем можно задать
соотношениями A.9.1), A.9.2). Ниже показано, что условия A.8.12)
действительно выполняются при некоторых ограничениях на пара-
параметры системы и константы J{.
Нахождение параметров управления Х\ и Х2. Применение
управ-
управления A.9.1), A.9.2) возможно только при выполнении в процессе
управления соотношений A.8.12).
Наложим на параметры системы A.14.4) некоторые ограничения
и покажем, что существуют такие Xi, входящие в закон управления
A.9.1), при которых соотношения A.8.12) действительно выполняются.
а). Будем предполагать, что имеет место неравенство
/?< 1. A.14.6)
Например, если звено G2 представляет собой тонкий стержень длины
I2 < h с произвольным распределением плотности р(х), то имеем
h h / х \
C = —— p(x)x2dx= —— xd\ p(y)ydy\ =
m2l\lg2 J m2l\lg2 J I J /
\ 0 0 /
б). Потребуем, чтобы величины q^, q^ в A.8.1) были ограничены
следующими неравенствами:
— arccos(—C) < #2~, q? < arccos(—C). A.14.7)
Так как при управлении A.9.1) выполняется ограничение
— +
(см. § 1.8), то из A.14.7) следует, что в течение всего процесса управ-
управления
cosq2 > -C. A.14.8)
в). Будем считать, что величина U®, ограничивающая управ-
управление U\, удовлетворяет неравенствам
/3+ 1 0 Q + /3 + 2
C 1 C + 1
1.14. Синтез управления двузвенным манипулятором
77
Поскольку
а + /3 + 2 /3+1 а/3-1
/3+1
/3
то выполнения соотношений A.14.9) можно всегда добиться, наклады-
накладывая более жесткие ограничения на величину одного из моментов Mi
в A.14.2). Отметим, что в силу A.14.6) и A.14.9) имеем U® > 2.
г). Константы Ji в системе A.8.9) будем выбирать согласно нера-
неравенствам
ар- 1
< 1,
A.14.10)
ар - 1
Используя сделанные допущения а)-г), оценим модуль величины V\
из A.14.5). Учитывая неравенства A.1.6), A.14.8), A.14.10), получим
а/3 — cos2 ^2
- 1
9
— cosz
g2|
z ^2
q\
— 1
= c/,0 + J.-
9
ар — cosz
J\
Используя неравенства A.9.10), A.14.9), будем иметь
a/3- 1
1 ар ' a/3-1
Аналогично получим оценку для величины V<i'.
A.14.11)
ар — cos^
78 Гл. 1. Метод декомпозиции управления (первый способ)
Далее, используя соотношения A.9.10), A.14.9) и U® > 2, получим
IT/ <\+i W+l)-tt-/?-2 ,
\V2 ^1+^2 о 1"
ар
(а + \)Y? + (/3 + 1) (Y\ + У2J
+ J2 — . A.14.12)
а/3-1
В неравенства A.9.3) вместо величин \Vi\ подставим их оценки
A.14.11), A.14.12):
х У22+/3(У!+У2J ^ J/O/3-/3-1
а/3-1 а/3
A.14.13)
В силу A.14.9) выражения в правых частях неравенств A.14.13)
положительны. Выберем Yi согласно A.10.7). Тогда 1^ —> 0 при Xi —>
-^ 0, поэтому всегда найдутся положительные Х\, Х^ удовлетворяю-
удовлетворяющие неравенствам A.14.13), а следовательно, и неравенствам A.8.12).
Заметим, что константы Ji не входят непосредственно в ограничения
A.14.13), поэтому их конкретные значения не играют роли.
Подытожим полученные результаты.
Пусть выполнены условия A.14.6), A.14.7), A.14.9). Тогда синтез
управления Ui(qi,qi), решающий задачу 1.1 применительно к системе
A.14.4), задается соотношениями A.9.1), в которых параметры Xi
должны выбираться так, чтобы выполнялись неравенства A.14.13).
Это управление переводит систему A.14.4) из начального состояния
A.1.7) в заданное терминальное состояние A.2.1), если в начальный
момент времени выполнено условие A.9.5). При этом движение
системы лежит в области D, заданной A.8.1), а время процесса управ-
управления г не превосходит величины г*, определяемой выражениями
A.9.11), A.9.12).
Укажем способ выбора допустимых значений Х^. Будем искать их
в виде A.10.9). Неравенства A.14.13) в этом случае принимают вид
аC
§1.15. Примеры
79
x d2
Найдя максимальное значение Z, удовлетворяющее полученным нера-
неравенствам, вычисляем по формулам A.10.9) параметры JQ.
Отметим, что множество возможных значений параметров управ-
управления Xi для рассматриваемой системы можно существенно расши-
расширить. Для этого следует получить более точные оценки величин \Vi\
в A.14.11), A.14.12).
§ 1.15. Примеры
1°. Численное моделирование движений трехзвенного робота-
манипулятора. В качестве примера для расчета управления с исполь-
использованием метода, который описан в первой главе, выбран трехзвенный
механизм с заданными параметрами
(рис. 16), который при соответ-
соответствующих допущениях может опи-
описывать динамику руки робота-
манипулятора. Рука манипулятора,
у которого плечо и предплечье
лежат в вертикальной плоскости,
крепится к вертикальной колонке,
которая опирается на основание.
Момент инерции вертикальной
колонки относительно оси враще-
вращения равен if. Звенья руки пред-
представляют собой стержни масс Ш2,
тз и длин I2, /з соответственно.
Центры масс плеча и предпле-
предплечья расположены точно посере-
посередине соответствующих звеньев.
Рис. 16. Трехзвенный манипулятор
Главные центральные моменты
инерции звеньев относительно осей, перпендикулярных стержням,
и относительно продольных осей стержней соответственно равны
/f,/f,i = 2,3.
Вертикальная колонка, плечо и предплечье снабжены приводами,
включающими электродвигатели постоянного тока с независимым
возбуждением и редукторы. Считаем ради простоты, что ось
и направление вращения ротора в каждом электроприводе совпадают
с осью и направлением вращения соответствующего шарнира.
Массы роторов электродвигателей равны raf, г = 1,2,3. Инер-
Инерцией вращающихся частей редукторов пренебрегаем. В качестве
обобщенных координат q\,q2,Q3 выбираем углы поворота в трех
80 Гл. 1. Метод декомпозиции управления (первый способ)
цилиндрических шарнирах манипулятора: угол поворота колонки
вокруг вертикальной оси q\ и углы поворота плеча д2 и предплечья д3
вокруг соответствующих горизонтальных осей (рис. 16).
При сделанных допущениях подсчитаем элементы матрицы кинети-
кинетической энергии A(q) из A.1.2)
Получим
аи =
+ \ [Ы1\ + II - I?) cos2g2 + {1$ - I») cos2(g2 + g3)
ra3/2/3[cosg3 + cos (g3 + 2g2)] + /«f + jf + /f + 73^
1 + cos2g2) + m3/|[cos2(g2 + g3) + 1]},
a22 = J2Nl + J3 + il + /35 +
-m2j +m3/3u2cosg3 + -
s 1 I 1
з 233\v2 3 2
Здесь использованы обозначения для моментов инерции роторов J^, J[
и передаточных чисел редукторов 7Vb введенные ранее в § 1.13.
В качестве обобщенных сил Qi в A.1.1) будем рассматривать
только моменты, создаваемые в шарнирах силой тяжести (силы вязкого
и сухого трения не учитываем)
Qi=0,
1
Q2 = —9.81 /2@.5га2 + raf + m3)cosg2 — 9.81 • - ra3/3cos(g2 + g3),
g3 = -9.81 • - m3/3 cos (g2 + g3).
Будем рассматривать случай, когда ограничения накладываются на
величины управляющих напряжений (см. § 1.13, случай 2°).
§1.15. Примеры 81
Ниже представлены четыре варианта расчетов A,2, 3,4) управления
в форме A.9.1) для рассматриваемой системы. Для каждого случая
в таблицах 1-7 приведены исходные данные: параметры звеньев
и электроприводов, начальные и конечные условия, область возможных
движений. Представлены результаты расчетов: значения параметров
управления, оценки времени движения для каждой из трех подси-
подсистем, реальные значения времени движения, графики зависимости
обобщенных скоростей q\, q%, qs от времени, фазовые траектории
подсистем. Для первого набора параметров робота-манипулятора
дополнительно проведены три расчета Aа,16, 1в) с использованием
способа управления, описанного в конце § 1.10. При выполнении
расчетов 1а, 16, 1в состояния подсистем определялись в дискретные
моменты времени (с конечным шагом). В результате движение вдоль
кривой переключений происходило с конечной частотой смены знака
управления.
2°. Численное моделирование движений двузвенного манипу-
манипулятора с безредукторными приводами. Расчеты проводились при
следующих размерных характеристиках системы A.14.1):
1\ = 1 м, lg2 = 0.5 м, 1\ = 1% = 3.33 кг-м2,
A.15.1)
ш2 = 10 кг, М° = 2.9 Н-м, М2° = 1 Н-м.
В этом примере полагаем Q\ = Q2 = 0 (см. § 1.14). Начальные
и конечные условия, а также величины qf, задающие допустимую
область движения, были выбраны следующим образом:
gf = q°i = -0.1 рад, q% = q2 = -0.05 рад,
В этом случае а = 2.66, C = 0.66 < 1, и неравенства A.14.7), A.14.9)
принимают вид
-2.3 < q~, q+ < 2.3, 2.5 < UQX < 3.2.
Очевидно, параметры системы удовлетворяют этим ограничениям. Вы-
Выберем безразмерные значения величин JQ, удовлетворяющие неравен-
неравенствам A.14.13). При Х\ = 1.82- 10~2, Х2 = 9.13- 10~3 получилась
размерная оценка времени управления г* = 4.68 с, а реальное время
процесса равно г = 3.64 с. На рис. 22 показана зависимость ско-
скоростей q\, q2 от времени. На заключительном этапе скорости q\, q2
меняются линейно, что соответствует движениям фазовых точек под-
подсистем A.8.9) вдоль параболических участков кривых переключений.
На рис. 23, 24 показаны фазовые траектории подсистем. Прекращение
движения по двум степеням свободы происходит в разное время.
82
Гл. 1. Метод декомпозиции управления (первый способ)
Таблица 1. Параметры звеньев (варианты 1-4)
г
1
2
3
1
2
3
1
2
3
1
2
3
ГПг, КГ
-
5
5
-
5
4
-
5
4
-
5
4
U, м
-
0.8
0.8
-
0.8
0.64
-
0.8
0.64
-
0.8
0.74
Igi, M
-
0.4
0.4
-
0.4
0.32
-
0.4
0.32
-
0.4
0.37
if, кг-м2
-
0.25
0.25
-
0.25
0.20
-
0.25
0.17
-
0.25
0.18
tN 2
Ii , КГ-М^
-
0.01
0.01
-
0.01
0.01
-
0.01
0.086
-
0.01
0.009
/f, кг-м2
0.2
-
-
0.2
-
-
0.2
-
-
0.2
-
-
Таблица 2. Параметры электроприводов (варианты 1-4)
г
1
2
3
1
2
3
1
2
3
1
2
3
fcf,
Н-м/А
0.04
0.04
0.04
0.04
0.04
0.04
0.113
0.1
0.1
0.08
0.06
0.06
Ki »
Н-м/А
0.04
0.04
0.04
0.04
0.04
0.04
0.109
0.09
0.09
0.07
0.06
0.05
Ом
1
1
1
0.7
0.6
0.6
0.7
0.6
0.6
0.7
0.6
0.6
Щ,
В
27
27
27
27
27
27
42
36
36
27
27
27
mf-,
кг
0.5
0.5
0.5
0.4
0.25
0.25
0.4
0.25
0.25
0.4
0.25
0.25
Л,
кг-м2
0.00079
0.00079
0.00079
0.00069
0.00039
0.00039
0.00069
0.00039
0.00039
0.00039
0.00039
0.00039
Л
кг-м2
0.00041
0.00041
0.00041
0.00036
0.00022
0.00022
0.00036
0.00022
0.00022
0.00022
0.00022
0.00022
160
250
150
120
180
150
150
250
200
120
180
150
§1.15. Примеры
83
Таблица 3. Вариант 1: условия начальные (q®, <$) и конечные (#*), область
возможных движений ([g~,g^]), параметры управления (Xi), оценки времен
движения (г*) и реальные времена движения подсистем (п)
г
1
2
3
ей
-1
-0.3
-1
1
0
0
0
0
0
яГ
-1
-0.35
-1
яГ
0
0.05
0
Y г~2
1.060
0.424
1.060
т*, с
1.413
1.682
1.942
Тг, С
1.382
1.263
1.467
2-. уь v
1-
-1-
-1.2 -0.1
-0.4
I
0.4
0.8п ^2
0.4-
-0.4-
I ¦ i ¦ I ¦ i ¦ I
-0.4 -0.3 -0.2 -0.1 0 0.1 -1.2 -0.8 -0.4 0 0.4
Рис. 17. Зависимость обобщенных скоростей от времени и фазовые траектории
подсистем (вариант 1)
84
Гл. 1. Метод декомпозиции управления (первый способ)
Таблица 4. Варианты 1а-1в: область возможных движений i\qi ,qf]), усло-
условия начальные (д®, <$) и конечные (#*), времена движения подсистем (п)
г
1
2
3
1
2
3
1
2
3
-1
-0.3
-0.9
-1
-0.35
-1
-1
-0.35
-1
0
0
0
0
0.05
0
0
0.05
0
-1
-0.3
-0.9
-1
-0.3
-1
-1
-0.3
1
0
0
0
0.5
0
0
0.5
0
-0.3
0
0
0
0
0
0
0
0
-0.1
п, с
1.22
1.35
1.27
1.27
0.97
1.07
1.18
1.01
1.20
1.2 -|
1.2 п
0.8-
0.4™
0.4 0.8 1.2 1.6
1.6
О 0.4 0.8 1.2 1.6
Рис. 18. Зависимость обобщенных скоростей от времени (варианты 1а-1в)
§1.15. Примеры
85
Таблица 5. Вариант 2: условия начальные (q®, $) и конечные (#*), область
возможных движений {[q~,qf\), параметры управления (Xi), оценки времен
движения (г*) и реальные времена движения подсистем (п)
г
1
2
3
-0
-0
-1
.8
.3
ql с
1
-0.2
0
Ял
0
0
0
<к
-0.85
-0.35
-1
0.05
0.05
0
Хг
1.
0.
1.
о
392
619
547
Ъ
1.
1.
1.
*» с
145
788
607
т
1.
1.
1.
г, С
109
023
172
21
1-
.-1
1-
—2™
L2 -1
.2 -0.8 -0.4 0 0.4
0.8п
0.4-
0"
-0.4-
08
42
\
\
1
1 1 ' 1 ' 1
2 ¦ ¦ ¦ ¦ ¦ ¦ ¦ ¦ ¦
-0.4 -0.3 -0.2 -0.1 0 0.1 -1.2 -0.8 -0.4 0 0.4
Рис. 19. Зависимость обобщенных скоростей от времени и фазовые траектории
подсистем (вариант 2)
86
Гл. 1. Метод декомпозиции управления (первый способ)
Таблица 6. Вариант 3: условия начальные (q®, q®) и конечные (#*), область
возможных движений {[q~ ,qf\), параметры управления (Xi), оценки времен
движения (г*) и реальные времена движения подсистем (п)
г
1
2
3
<й
1
3
-0.25
0
0
0
Ял
-0.2
2
0.3
*7
-0.4
2
-0.5
it
l.i
3
0.5
Xi9 с
0.413
0.275
0.413
г* у с
3.407
3.809
2.825
Тг, С
2.413
2.697
1.994
0.8-, ^ь ^2,?з, с
0.4-
0
-1
-0.4-
-0.8™
-1.2
t, с
-0.6
0.8 п
0.4-
-0.4-
-0.8
0.5-
-0.5-
2.4 2.8 3.2 -0.8 -0.4 0 о'.4 о'.?
Рис. 20. Зависимость обобщенных скоростей от времени и фазовые траектории
подсистем (вариант 3)
§1.15. Примеры
87
Таблица 7. Вариант 4: условия начальные (q®, q?) и конечные (#*), область
возможных движений {[q~,qf\), параметры управления (Xi), оценки времен
движения (г*) и реальные времена движения подсистем (п)
г
1
2
3
-1.5
-0.3
-0.5
0.7
-0.2
0
-1
-0.2
-1
-1.6
-0.5
-1.3
Qt
-0.7
0
-0.3
Ъ, с
0.317
0.176
0.352
т*, с
4.052
3.332
2.380
П, С
1.766
1.071
1.683
О.8П
0.4-
-0.4-
-0.8
t,c
0.8п ^'с
0.4-
-1.7 -1.3
-0.9 -0.5
0.6 п
о.з-
о-
0.3"
0.6-
42
С
i I i | i i
0.5-
-0.6 -0.4 -0.2
0.2
-0.5-
Рис. 21. Зависимость обобщенных скоростей от времени и фазовые траектории
подсистем (вариант 4)
0.06п
0.04™
0.02™
Гл. 1. Метод декомпозиции управления (первый способ)
0.08 и
0.04™
-0.04™
-0.08
-0.12 -0.08 -0.04
Рис. 22. Зависимость обобщенных Рис. 23. Фазовая траектория под-
скоростей от времени системы 1
0.04
0.02™
-0.02 -
-0.04 -i . 1 . 1 . 1 . 1
-0.06 -0.04 -0.02 0 0.02
Рис. 24. Фазовая траектория подси-
подсистемы 2
Глава 2
МЕТОД ДЕКОМПОЗИЦИИ УПРАВЛЕНИЯ
(ВТОРОЙ СПОСОБ)
§ 2.1. Управляемая механическая система
Снова обратимся к системе, рассмотренной в § 1.1, но сделаем
несколько иную совокупность допущений. Рассматривается нелиней-
нелинейная динамическая система, описываемая уравнениями Лагранжа
±ж_дт_
т. г\ . <-, — ^г т Ц;г, о — 1,...,/б. yz,. 1.1)
at oqi oqi
Здесь и далее точкой обозначены производные по времени t, q = (q\,...
..., qn) — вектор обобщенных координат, Т — кинетическая энергия
системы, Qi — неуправляемые обобщенные силы, Щ — управляющие
обобщенные силы. Будем предполагать, что все рассматриваемые дви-
движения системы B.1.1) происходят в некоторой области D в п-мерном
пространстве Rn, так что всегда q G D. Область D, в частности, может
совпадать с Rn.
Сформулируем исходные допущения относительно кинетической
энергии системы
T(q,q) = \ {АШЛ) = \ J2 азкШзЯк B-1.2)
и обобщенных сил. Здесь A(q) — симметрическая положительно-
определенная (п х п)-матрица с элементами ajk, являющимися непре-
непрерывно дифференцируемыми функциями q при q G D. Здесь и далее
в этой главе скобками (•, •) обозначено скалярное произведение век-
векторов. Предполагаем, что при любом q G D все собственные числа
матрицы A(q) лежат на отрезке [тп, М], где М > m > 0. Таким образом,
для любого n-мерного вектора z
m(z,z) < (A(q)z,z) < M(z,z), Vq e D. B.1.3)
Кроме того, предполагаем, что
daJk s n w^n n = const > 0, B.1.4)
90 Гл. 2. Метод декомпозиции управления (второй способ)
и что неуправляемые обобщенные силы Qi в B.1.1) состоят из трех
слагаемых, на которые наложены различные ограничения:
Qi = Pi + Ri + Gi. B.1.5)
Здесь Pi(q,q,t) — силы, заданные в виде известных функций обобщен-
обобщенных координат и времени.
Через Ri(q,q,t) в B.1.5) обозначены диссипативные силы. Точный
вид функций Ri(q,q,t) может быть неизвестен. Требуется лишь, чтобы
эти силы обладали свойством диссипативности и чтобы они были
достаточно малы при малых скоростях. Первое свойство означает, что
мощность диссипативных сил неположительна, т. е.
п
^Riqi^O B.1.6)
г=1
для всех q G D, всех q и всех t ^ to, где to — начальный момент
времени. Второе свойство сформулируем следующим образом: суще-
существует такое достаточно малое число щ > 0, что если \q^\ ^ v ^ щ
для всех г, то
?. B.1.7)
Здесь Щ(и) — некоторые монотонно возрастающие непрерывные
функции, определенные на отрезке v е [0, щ] и такие, что Щ@) = 0.
Через Gi(q,q,t) в B.1.5) обозначены неопределенные внешние
возмущения, вид которых неизвестен, предполагается лишь их ограни-
ограниченность:
|Gi|<G? B.1.8)
при всех q e D, всех q и t > to. Здесь G® > 0 — заданные постоянные.
Относительно управляющих Щ в B.1.1) предположим, что они
могут полностью компенсировать заданные внешние силы Pi, и, кроме
того, остаются еще возможности выбирать управление в некоторой
области. Таким образом, силы Ui представляются и виде
Ui = -Pi(q,q,t)+wi. B.1.9)
Вектор w = (w\,..., wn) может выбираться из некоторого множе-
множества W, зависящего, вообще говоря, от q, q, t, то есть,
w e W(q,q,t) cRn. B.1.10)
Предполагаем, что множество W при всех q e D, всех q и всех
t ^ to содержит некоторую окрестность Wo начала координат:
W(q,q,t) dW0, 0eW0. B.1.11)
§2.2. Постановка задачи 91
Множество Wo будем задавать в виде шара радиуса г > О:
W0 = {w: \\w\\ <г}, B.1.12)
или в виде прямоугольного параллелепипеда, отвечающего независи-
независимым ограничениям на силы wf.
W0 = {w: \Wi\ <ги?}. B.1.13)
В случае ограничений B.1.13) полагаем
° B.1.14)
§ 2.2. Постановка задачи
Подставляя равенства B.1.5), B.1.9) в систему B.1.1), получим
-T.WT- - ^— = Ri + Gi + Wi. B.2.1)
at oqi oqi
Пусть заданы начальные условия
q(to)=q°, q(to)=q° B.2.2)
и терминальные условия, отвечающие состоянию покоя:
q(U)=q*, <?(**)= О, B.2.3)
причем q° е D, q* G D, ?* > to. Сформулируем задачу управления.
Задача 2.1. Найти управление w(q,q), формируемое по принципу
обратной связи, удовлетворяющее ограничению
weW0 B.2.4)
и переводящее систему B.2.1) из любого начального состояния
B.2.2) в заданное терминальное состояние B.2.3) за конечное
(нефиксированное) время. Здесь множество Wq задано в виде
B.1.12) или B.1.13) и в обоих случаях, в силу B.1.14), содержит
шар \\w\\ ^ г. Кинетическая энергия системы B.2.1) определена
соотношением B.1.2) и удовлетворяет условиям B.1.3) и B.1.4),
а силы Ri и Gi в B.2.1) удовлетворяют ограничениям B.1.6)—B.1.8).
Отметим, что если построенное управление w удовлетворяет огра-
ограничению B.2.4), то в силу включения B.1.11) оно удовлетворяет также
исходному ограничению B.1.10).
Решение поставленной задачи 2.1 сначала построим в частном
случае отсутствия диссипативных сил и возмущений в системе B.2.1),
т. е. при Ri = Gi = 0. Затем будет рассмотрен общий случай.
92 Гл. 2. Метод декомпозиции управления (второй способ)
§ 2.3. Управление при отсутствии внешних сил
Система B.2.1) при Щ = Gi = 0 принимает вид
d_§T_dT =
dt dqi dqi
Зададимся некоторым положительным числом г > О и обозначим
через ?1\ множество всех точек 2п-мерного фазового пространства
(q,q), в которых q е D и \щ\ > г хотя бы для одного г. Через О2
обозначим множество таких точек (g, q), в которых q G D и \q^\ ^ ? для
всех г. Таким образом,
^1 = {{я.Л) '• q € D\ Зг, |^| > г},
B.3.2)
^2 = {(^>^) '• q € D\ \/г, |^| ^ ^}-
Ниже построен синтез управления w(q,q) отдельно для областей
Oi и ^2, а также указано число г. Согласно теореме об изменении
кинетической энергии для системы B.3.1) имеем
лт п
-^=y?rvigi = (w,q). B.3.3)
г=1
Выберем управление w в области ?1\ так, чтобы удовлетворить огра-
ограничениям B.2.4) и обеспечить отрицательность производной B.3.3).
Для этого полагаем
w =—rq\\q\\~l, Wi =—w® sign \qi\, г=1,...,п, B.3.4)
для случаев B.1.12) и B.1.13) соответственно. Подставляя формулы
B.3.4) в B.3.3), получим соответственно
dT dT v^ о •
Учитывая обозначение B.1.14), для обоих случаев B.1.12) и
B.1.13) получим
— = 2Т1/2 —— < -r\\q\\. B.3.6)
Из верхней оценки B.1.3) для кинетической энергии B.1.2) имеем
'2
B.3.7)
Подставим B.3.7) в правую часть неравенства B.3.6) и учтем, что
Т > 0 в области Оь см. B.3.2). Получим
< -ГГ2М)-1/2. B.3.8)
at
§2.3. Управление при отсутствии внешних сил 93
Интегрируя неравенство B.3.8), будем иметь
Ti/2 _ Т\/2 ^ _rBM)~^\t - t0), B.3.9)
где То — значение кинетической энергии в начальный момент
времени to. Из B.3.9) следует, что за конечное время кинетическая
энергия станет сколь угодно малой. Следовательно, в некоторый
момент времени t\ система выйдет на границу областей Oi и О2.
Получим нужные для дальнейшего оценки для времени t\ и обоб-
обобщенных координат q(t\). Согласно B.1.3) и B.3.2) имеем для кинети-
кинетической энергии Т\ в момент t\ оценку снизу
Т\ >^m(q,q)>\™?. B.3.10)
Из неравенств B.3.9) и B.3.10) находим искомую оценку для t\
Для того чтобы оценить q(t\), запишем очевидные неравенства
и и
\qi(ti)-q?\<\\qi\dt^^\\q\\dt. B.3.12)
to t0
Воспользуемся неравенствами, вытекающими из B.1.3) и B.3.9):
Подставляя B.3.13) в B.3.12), получим после интегрирования
1/2
Функция ф(т), как можно проверить непосредственно, строго воз-
возрастает на интервале [0,т\], где т\ определено в B.3.11). Так как
t\ — to ^ т\ согласно B.3.11), то ф{Ь\ —to) ^ Ф(т\), поэтому из неравен-
неравенства B.3.14) при учете B.3.11) получаем
^o) B.3.15)
94 Гл. 2. Метод декомпозиции управления (второй способ)
§ 2.4. Декомпозиция
Итак, в момент t\ система окажется на границе областей ?1\ и Г^2.
Построим управление в Г^2 так, чтобы система, попав в область Г^2,
уже не выходила из нее и попадала за конечное время в терминальное
состояние B.2.3).
Запишем уравнения Лагранжа B.3.1) в развернутом виде, подстав-
подставляя в них Т из B.1.2):
п п
^2aij<ij + Y1 Г^МзЯк = Щ- B.4.1)
j=\ j,k=\
Выражение для Г^& дано в A.1.5), причем Г^& можно рассматривать
как компоненты n-мерных векторов
Tjk = (Tljk,...,rnjk). B.4.2)
Перепишем уравнение B.4.1) в векторной форме и разрешим его
относительно q. Получим
q = U' + V. B.4.3)
Здесь
п
Uf = A~lw, Vf = ~Y, А-%кЫк- B-4-4)
j,k=\
Из условия B.1.3) вытекает, что собственные числа обратной мат-
матрицы А~х лежат на отрезке [М~\т~1]. Следовательно, для любого
n-мерного вектора z имеем
\\Az\\ < М||^||, \\A~xz\\ < ггг1|^||. B.4.5)
Наложим на компоненты U[ вектора V ограничения
l^il^^o, U0 = rM-ln-l/2. B.4.6)
Выполнение ограничений B.4.6) влечет за собой выполнение нера-
неравенства ||С/'|| ^ гМ~\ из которого в силу B.4.4), B.4.5) следует
||гу|| = ЦАс/'Ц < МЦС/'Ц < г. Следовательно, вектор w удовлетворяет
наложенному ограничению B.2.4) в обоих случаях множества Wo,
задаваемого в виде B.1.12) или B.1.13). Поэтому ограничение B.4.6)
обеспечивает выполнение условия B.2.4).
Оценим вектор V из B.4.4), пользуясь вторым неравенством B.4.5)
ыш*|. B-4-7)
3,к=\
§2.4. Декомпозиция 95
Из неравенств B.1.4) следуют оценки для величин Г^ь введенных
в A.1.5): \Tijk\ < C/2)С. Отсюда и из B.4.2) имеем
1/2
Полученные оценки для Г^, а также неравенства |^| < ?, имеющие
место в области О2 в силу B.3.2), подставим в неравенство B.4.7).
В результате получим \\Vf\\ ^ C/2)Crn5/2m~1?2. Следовательно, для
компонент V( вектора V имеем оценки
\V(\ < Vo, Vo = | Сп^2т-1г2. B.4.8)
Уравнения B.4.3) и ограничения B.4.6), B.4.8) перепишем в виде
& = С// + F/, |С//| < Uo, \Vf\ < Fo, B.4.9)
причем С/о, Vo определены в B.4.6), B.4.8).
Потребуем, чтобы имело место неравенство
B.4.10)
и построим управление U[ отдельно для каждой степени свободы
системы B.4.9).
При этом будем исходить из того, что V( могут быть произвольными
функциями, удовлетворяющими наложенным в B.4.9) ограничениям.
Таким образом, используем минимаксный (гарантированный) подход,
характерный для теории дифференциальных игр [43].
Рассматривая г-е уравнение B.4.9), положим
qi - q* =x, qi=Xi = у,
B.4.11)
U[ = и, V( = v
и перепишем соотношения B.4.9), B.4.10) в форме
х = у, у = и + v,
B.4.12)
и\ < С/о, Н < рЩ, 0< р< 1.
В момент t\, по предположению, система находится на границе
областей Oi и О2 из B.3.2). С учетом B.4.11) имеем следующие
начальные условия для системы B.4.12):
x(U) = х[ = q{(ti) - ql y{U)=y{=qi{t{), \yX\^e. B.4.13)
Терминальные условия B.2.3) примут вид
x(U) = 0, y(U)=O. B.4.14)
96 Гл. 2. Метод декомпозиции управления (второй способ)
Для того чтобы система, попав в момент t\ в область Г^2, уже
не выходила из этой области, потребуем
\y(t)\^e, t>U. B.4.15)
Система B.4.12) подобна системе A.3.3) при Л = 0. Отличие состо-
состоит в дополнительном фазовом ограничении B.4.15).
Таким образом, в области &2 имеет место декомпозиция задачи 2.1:
вместо этой задачи для исходной системы с п степенями свободы
получаем п аналогичных задач для систем с одной степенью свободы
каждая. Поэтому для решения задачи 2.1 в области О2 достаточно
решить следующую задачу.
Задача 2.2. Для системы B.4.12) найти управление и(х,у),
удовлетворяющее ограничениям B.4.12) и B.4.15) и переводящее
эту систему из начального состояния B.4.13) в терминальное
состояние B.4.14) за конечное время при любом допустимом v,
удовлетворяющем ограничению B.4.12).
Для построения управления можно, как и в § 1.4, воспользоваться
игровым подходом и найти решение соответствующей дифференциаль-
дифференциальной игры с фазовым ограничением. Вместо этого предлагается более
простое, хотя и не оптимальное управление вида
и(х, у) = Uo sign [ф(х) -у], у^ ф(х),
B.4.16)
и(х,у) = Uo sign х = -Uosigny, у = ф(х),
где функция ф(х) определена соотношениями
B.4.17)
ф(х) = —5signx, \x\ > х*.
Здесь 5 > 0 — любое число из интервала 0 < 5 < г, а параметр х*
определен из условия непрерывности функции ф(х). Согласно этому
условию из B.4.17) получим
x*=62[2Uo(l-p)]~l. B.4.18)
Кривая переключений у = ф(х) для управления B.4.16), B.4.17)
симметрична относительно начала координат и состоит из двух дуг
парабол и двух лучей. Она изображена на рис. 25 жирной линией.
Отметим, что параболические дуги кривой переключений те же,
что и для кривой переключений, построенной в § 1.4, см. формулы
A.4.10) при Л = 0. Так как 5 < г, то кривая переключений целиком
лежит в полосе \у\ ^ г и делит ее на две симметричные части:
область Х+, где у < ф(х) и и = Щ, и область Х~, где у > ф(х),
u = -U0, см. B.4.16).
Докажем, что управление B.4.16), B.4.17) решает задачу 2.2.
В момент t\ выполнены начальные условия B.4.13).
§2.4. Декомпозиция
97
Согласно уравнениям B.4.12) и
закону управления B.4.16), имеем
Рис. 25. Кривая переключений и
фазовые траектории
y^-U0(l-p), (х,у)еХ~.
B.4.19)
Ширина каждой из областей
Х+, Х~ вдоль оси у не превышает
е + 5 (рис. 25), а скорость движе-
движения вдоль этой оси согласно B.4.19)
конечна и направлена к линии пере-
переключений. Следовательно, фазовая
точка никогда не выйдет из полосы
\у\ ^ г и в некоторый момент t^ > t\
попадет на кривую переключений
у = ф(х).
Пусть фазовая точка в момент t^ попала на прямолинейный
участок у = ±5 кривой переключений у = ф(х). После этого точка
будет двигаться вдоль прямолинейного участка в скользящем режиме.
Это вытекает из того, что по обе стороны данного участка фазовые
скорости конечны и направлены к кривой переключений. Движение
вдоль указанных участков будет происходить с соответствующей
постоянной скоростью у = х = ±5 в сторону уменьшения \х\. Следо-
Следовательно, в некоторый момент t% > ?2 фазовая точка попадет в одну
из точек (±х*,=р5) на границе прямолинейного и криволинейного
участков кривой переключений. Криволинейные (параболические)
участки являются фазовыми траекториями системы B.4.12) при и,
выбранном согласно B.4.16), и при v = — ри. Если v ^ —ри,
то движение при выбранном управлении B.4.16) все равно будет
происходить вдоль этих участков парабол, но в скользящем режиме.
Поэтому в некоторый момент ?* фазовая точка попадет в начало
координат.
На рис. 25 тонкими линиями изображены некоторые возможные
фазовые траектории. Стрелками указано направление роста времени t.
Всё движение от момента t\ до момента ?* распадается на три
этапа: движение в области Х+ или Х~, движение по прямым у = ±5
и движение по параболам. Некоторые из этих этапов могут отсут-
отсутствовать. Например, в начальный момент t\ фазовая точка может
лежать на кривой переключений или она может попасть из области
Х+ или Х~ сразу на параболический участок этой кривой. Но во всех
случаях время движения ?* —1\ конечно.
Для оценки этого суммарного времени будем предполагать наличие
всех трех этапов, что приведет к искомой оценке сверху. Длительность
^2 — t\ первого этапа (движение в области Х+ или Х~) оценим,
4 Ф. Л. Черноусько и др.
98 Гл. 2. Метод декомпозиции управления (второй способ)
разделив максимальную ширину е + 5 этих областей вдоль оси у
на минимальную по модулю скорость у из B.4.19). Получим
h ~ U < (е + 5)[U0(l - /о)]. B.4.20)
Оценим еще координату xfo), используя ограничение B.4.15) и
начальное условие B.4.13)
Отсюда при учете B.4.20) получим
B.4.21)
Длительность t$ — ?2 второго этапа (движение по прямым у = ±
±5) найдем, разделив расстояние вдоль оси х на скорость, равную по
модулю 5:
h-t2=[\x{t2)\-x*]5-x.
Подставляя в данное неравенство соотношения B.4.18), B.4.21),
получим
Ч - h < \xl \5~l + e(e + 5)[U0(l - pM]~l - 5[2U0(l - p)]~l.
B.4.22)
Длительность t* — ?3 третьего, последнего, этапа (движение по
параболе) можно найти, разделив максимальную по модулю скорость 5
в начале этого этапа на минимальное (по модулю) ускорение, опреде-
определяемой согласно B.4.19). Получим
U-t3 = S[U0(\-p)}-\ B.4.23)
Суммируя соотношения B.4.20), B.4.22) и B.4.23), получим оценку
сверху полного времени движения в задаче 2.2
U-h < \xl\5-l + Be2+4e5 + 352M-l[2U0(l-p)]-1. B.4.24)
Полученный результат подытожим в виде теоремы.
Теорема 2.1. Управление и(х,у), определяемое равенствами
B.4.16), B.4.17), в которых число х* определено равенством
B.4.18), а 5 — любое число из интервала @, г), доставляет
решение задачи 2.2, т.е. удовлетворяет ограничениям B.4.12),
B.4.15) и переводит систему B.4.12) из начального состояния
B.4.13) в терминальное состояние B.4.14) за конечное время ?* —t\,
удовлетворяющее оценке B.4.24).
§2.5. Построение синтеза управления 99
§ 2.5. Построение синтеза управления
Обратимся теперь к решению исходной задачи 2.1 в рассматрива-
рассматриваемом случае Ri = Gi = 0. Искомое управление w(q,q) в области ?1\
определено соотношениями B.3.4), а в области Г^2 оно может быть
получено из решения и(х,у) задачи 2.2. Для этого достаточно восполь-
воспользоваться соотношениями w = AUf из B.4.4), а также обозначениями
B.4.11). В результате получим
w(q,q) = A(q)U'(q,q), C^fe.ft) = и(Яг - q*,&)• B-5.1)
Напомним, что решение и(х,у) задачи 2.1 получено при условии
р < 1, см. B.4.10), которое при учете обозначений B.4.6) и B.4.8)
приводится к неравенству на г:
¦ B-5-2)
Для оценки полного времени движения ?* — to нужно сложить
времена движения в областях Oi и О,^- При вычислении ?* — t\
учтем, что вместо \хх\ в B.4.24) нужно подставить максимальную
по г из разностей \qi(t\) — q*\, см. B.4.13), так как система попадает
в терминальное состояние тогда, когда все координаты примут терми-
терминальные значения. Используя оценку B.3.15), получим
= max \qi(t\) — q*\ ^ max(|<^(?i) — q®\ + \q® — q*\) ^
г i
1/2
Подставим это выражение в неравенство B.4.24), которое затем
сложим с неравенством B.3.11):
i\l/2
б-1 max|ft(*i) qt\ + BМI/2г~1
+ Bг2 + 4е5 + 352)Г 1[2[/0A - р)]~1. B.5.3)
Параметры Щ и р определены соотношениями B.4.6), B.4.8),
B.4.10), причем р < 1 при условии B.5.2).
Сформулируем полученный результат.
Теор ема 2.2. Задача 2.1 для системы B.3.1), т.е. при
Ri = Gi = 0,
всегда имеет решение.
100 Гл. 2. Метод декомпозиции управления (второй способ)
При любом е е @, ?о)> где ?о задано формулой B.5.2), управление
w(q,q), определяемое соотношениями B.3.4) в области ?1\ (для слу-
случаев B.1.12) и B.1.13) соответственно) и соотношениями B.5.1)
в области 0,2, доставляет решение этой задачи, т. е. переводит
систему B.3.1) из любого начального состояния B.2.2) в заданное
терминальное состояние B.2.3) за конечное время ?* — to, удовле-
удовлетворяющее неравенству B.5.3), при этом функция и(х,у) в B.5.1)
определена соотношениями B.4.16), B.4.17), в которых параметры
Щ, р, ж* заданы формулами B.4.6), B.4.8), B.4.10), B.4.18), а 5 -
любое число в интервале @,г).
Отметим, что с точки зрения уменьшения времени движения
целесообразно выбирать 5 как можно ближе к е. Однако при 5 =
= г уже нельзя гарантировать, что система, попав на границу об-
областей п\ и О2, останется в области О2. Поэтому 5 выбирается из
интервала @,г). Построенные решения задач 2.1 и 2.2, конечно, не
являются единственными. В частности, для построения синтеза в
одномерной системе B.4.12), полученной в результате декомпозиции,
можно воспользоваться другими подходами.
§ 2.6. Управление в общем случае
Перейдем к решению задачи 2.1 в общем случае системы B.2.1).
При этом ход решения в основном остается тем же, что и в § 2.3-2.5.
Зададимся некоторым г > 0 и снова введем в рассмотрение области
Oi и ^2, определяемые соотношениями B.3.2). Теорема об изменении
кинетической энергии для системы B.2.1) в силу условия диссипатив-
ности B.1.6) для сил Щ примет вид, аналогичный B.3.3):
^wi + Gi)*. B.6.1)
г=1
Управление w в области п\ выберем из условия минимума
скалярного произведения (w,q) при ограничении B.2.4). Для двух
случаев множества Wo, заданного в виде B.1.12) или B.1.13), получим
снова выражения B.3.4) соответственно. Подставим эти выражения
в неравенство B.6.1) и воспользуемся ограничениями B.1.8), а также
неравенством Коши-Буняковского. Для случая множества Wo B виде
шара B.1.12) получим
^^-rMW + ^CfiSil^-riMW, B-6.2)
г=1
где
ri=r-||G°||>0, G° = (G?,...,G?). B.6.3)
§2.6. Управление в общем случае 101
Для множества Wo B виде прямоугольного параллелепипеда B.1.13)
найдем
п
^ ~~ У^С^? + ^чЖг| ^ ~Г2||^||- B.6.4)
г=1
Здесь
Го = \\W
¦°-G°||, «/> = («;?,...,«?), B.6.5)
причем предполагается выполненным условие
ги?><7?, i= l,...,n. B.6.6)
Таким образом, при выполнении неравенств B.6.3) в случае шара
B.1.12) и B.6.6) — в случае параллелепипеда B.1.13), неравенства
B.6.2) и B.6.4) переходят в неравенство B.3.6) с заменой постоянной
г > 0 на га > 0. Здесь и далее значения индекса а = 1,2 отвечают
случаям B.1.12) и B.1.13) соответственно. Поэтому все соотноше-
соотношения § 2.3, относящиеся к области п\, остаются в силе с точностью
до указанной замены.
Обратимся к области Г^2. Наложим условие
е < щ, B.6.7)
при котором в этой области справедливы оценки B.1.7). Уравнения
Лагранжа B.2.1) снова преобразуем к виду B.4.3), разрешенному
относительно производных
q = U' + V*, B.6.8)
причем для V имеет место прежнее соотношение B.4.4). Вектор V*
в B.6.8) есть
V* = Vf + A-l(R + G). B.6.9)
Величина V дается формулой B.4.4), a R и G — векторы с компонен-
компонентами Ri и Gi соответственно.
Используя неравенства B.4.5) для А~\ B.1.7) для Ri, и B.1.8)
для Gi, получим оценку
B.6.10)
В соответствии со сделанными в § 2.1 допущениями относительно
функций R®, см. B.1.7), R^(s) — монотонно возрастающая непрерыв-
непрерывная функция от г, причем R®@) = 0.
102 Гл. 2. Метод декомпозиции управления (второй способ)
Из неравенств B.4.8) и B.6.10) вытекает оценка для вектора V*
из B.6.9):
. B.6.11)
J
Наложим на Vq условие, аналогичное B.4.10)
р* = ^-<1. B.6.12)
Процедура построения управления в области Q.2, а также
все проведенные оценки в этой области, остаются теми же, что
и в § 2.4, 2.5. Единственные изменения состоят в замене р на р*,
а также г на га в оценках B.5.3) для времени. В формуле B.4.6)
для Щ параметр г нужно оставить без замены: он здесь определен
соотношениями B.1.12) и B.1.14) для случаев B.1.12) и B.1.13)
соответственно. Кроме того, изменяются ограничения на выбор г.
Вместо неравенства B.5.2) имеем теперь два условия: B.6.7) и B.6.12).
В развернутом виде с учетом соотношений B.4.6) и B.6.11) получим
е < I/O, I Спъ/2е2 + ||Д°(е) + G°|| < mM^1/2. B.6.13)
Итак, предлагаемая процедура построения управления приводит
к решению задачи 2.1, если выполнены следующие условия: неравен-
неравенства B.6.3) или B.6.6) в случаях а= 1,2 соответственно, а также
оба ограничения B.6.13) на г. Число г, удовлетворяющее условию
B.6.13), заведомо существует, если возмущения отсутствуют (G0 = 0)
или достаточно малы:
||G°|| <mM-lrn-{/2. B.6.14)
Это вытекает из непрерывности функции ||Д°(б:)||: ||i?°|| —> 0 при г —> 0.
Заметим, что для диссипативных сил, пропорциональных скоростям,
функции Щ из B.1.7) и ВР из B.6.10) линейны по е.
Подытожим полученные результаты.
Теорема 2.3. Пусть число а равно 1 или 2 соответственно
для случаев множества Wq в виде шара B.1.12) или параллелепи-
параллелепипеда B.1.13). Предположим, что выполнены условия B.6.3), B.6.6)
для а = 1,2 соответственно и существует г > 0, удовлетворяющее
обоим условиям B.6.13).
Тогда управление w(q,q), определяемое соотношениями B.3.4)
в области ?1\ (для а = 1,2, соответственно) и соотношениями
B.5.1) в области Г^2, доставляет решение задачи 2.1 для системы
B.2.1), т.е. переводит эту систему из любого начального
§2.6. Управление в общем случае 103
состояния B.2.2) в заданное терминальное состояние B.2.3).
При этом функция и(х,у) в B.5.1) определена соотношениями
B.4.16), B.4.17), в которых параметры Щ, х* заданы формулами
B.4.6), B.4.18). Параметр р в формуле B.4.18) следует заменить
на р* согласно формулам B.6.12), B.6.11), причем при наложенных
условиях имеем р* < I, а в качестве 5 можно взять любое число из
интервала @, г). Время движения ?* — to конечно и удовлетворяет
неравенству B.5.3), в котором г следует заменить на га
(см. B.6.3), B.6.5)), а р на р*.
Отметим, что полное время движения зависит от величины г.
Во-первых, с увеличением числа г уменьшается время достижения
траекторией множества &2- Во-вторых, во множестве Г^2 прямоли-
прямолинейные участки траектории вдоль лучей у = ±5 из B.4.16), B.4.17)
система проходит со скоростью \q\ = 5 < г. Следовательно, чем
больше г, тем большим может быть выбрано число 5 и тем выше
будет скорость движения по этим участкам. Согласно B.6.13) выбор
числа г определяется, в частности, постоянными Мига, огра-
ограничивающими в B.1.3) максимальное и минимальное собственные
числа матрицы A(q), и константой С из неравенства B.1.4). Поэтому
в качестве области изменения вектора обобщенных координат q целе-
целесообразно брать не всю область D, а некоторую ее подобласть D' с D,
в которой будет лежать траектория движения. Область D' зависит
от начальных и терминальных условий задачи. С уменьшением области
D' константы М и С, вообще говоря, убывают, а константа га растет,
что и позволяет увеличивать параметр г.
В предложенном подходе величины га, М, С, г, 5, р и х* выбраны
заранее, общими для всего процесса движения. Ясно, однако, что
в реальных механических системах собственные числа m(q), M(q)
и производные элементов daij(q)/dqk матрицы A(q) далеко не всегда
выходят на границы неравенств B.1.3), B.1.4). Поэтому представляет
интерес модифицированный закон управления, по которому величины
га, М, С выбираются в каждый момент времени в зависимости
от текущего состояния матрицы A(q). Таким образом, если в момент
времени t вектор фазовых координат системы равен q, то управление
формируется по закону B.3.4) в области п\ и B.4.16), B.4.17)
в области ^2, где
га = m(q), М = M(q), С = max
а числа г, 5, p и х* выбраны в соответствии с B.4.6), B.4.18),
B.6.11)—B.6.13). Моделирование, подробное описание которого
приводится в § 2.10, показало, что управляемая по модифицированному
закону система приходит в терминальное состояние быстрее, однако
для определения области применимости такого подхода необходимы
дополнительные исследования.
104 Гл. 2. Метод декомпозиции управления (второй способ)
§ 2.7. Обобщение на случай ненулевой конечной
скорости
Обобщим предложенный подход на случай ненулевых терминаль-
терминальных скоростей.
Задача 2.3. Требуется построить управление w(q,q), удовле-
удовлетворяющее ограничению B.2.4) и приводящее систему B.2.1)
из произвольного начального состояния B.2.2) в заданное терми-
терминальное состояние
q(U) = q*eD, q(U)=q*, U > t0, B.7.1)
за конечное нефиксированное время.
Не нарушая общности, мы можем считать, что в конечном состоя-
состоянии B.7.1) из всех фазовых координат q*, q* лишь одна q* — первая
компонента вектора скорости — не равняется нулю. Действительно,
существует такая ортогональная матрица В, ВТВ = Е (Е — единич-
единичная матрица), что линейное преобразование q i—> B(q — q*) приводит
условия B.7.1) к виду
q*= 0, дГ = Н?1. ??=0, г = 2,..., п. B.7.2)
При этом константы, которые ограничивают компоненты матриц
dA/dqk и векторов G и w, а также функции Щ, ограничивающие
компоненты вектора R, изменятся не более, чем в п1/2 раз.
Для простоты изложения будем полагать, что неравенства B.1.4),
B.1.6)-B.1.8), B.1.12) имеют место в системе координат, полученной
после указанного преобразования.
Допустим с самого начала, что параметры задачи удовлетворяют
соотношениям B.6.14), а модуль конечной скорости q* достаточно
мал, так что число г удается выбрать, исходя из условий B.6.13)
и дополнительного ограничения
\4*\<е. B-7.3)
Следуя методике § 2.3-2.6, решение задачи 2.3 разобьем на два
этапа.
Цель первого этапа — понизить фазовую скорость до значений,
при которых возможна декомпозиция системы, а именно, \qi\ ^ г.
Для достижения цели первого этапа воспользуемся управлением,
построенным в § 2.3, 2.6 в области О,\, определенной согласно B.3.2).
В области малых скоростей ^ в фазовом пространстве (q, q)
исходная нелинейная система 2п-го порядка B.2.1) сводится к сово-
совокупности п управляемых подсистем второго порядка B.6.8), в которых
нелинейные члены трактуются как возмущения. Цель второго
этапа — построить для каждой подсистемы B.6.8) во множестве
§2.7. Обобщение на случай ненулевой конечной скорости 105
\q_i\ ^ е фазового пространства qi, qi управление по обратной
связи U[, удовлетворяющее ограничению \U[\ ^ Щ и приводящее
соответствующую подсистему из некоторого начального состояния
(q\,q\) в момент t = t\ в заданное терминальное состояние (q*,q*)
за конечное время. При этом начальное состояние и вся траектория
должны принадлежать множеству \qi\ ^ е. В § 2.4-2.6 данная задача
решена для случая нулевых терминальных условий подсистем. Это же
управление можно использовать для приведения каждой подсистемы
B.6.8) с индексами г = 2,..., п в начало координат и удержания ее там.
Теперь построим управление для первого уравнения B.6.8), отве-
отвечающего компоненте q\ вектора q. Терминальное значение скорости
у этой компоненты не равняется нулю. Обозначим
х = qi> У = % = <1и и = U[, v = V*
и приведем рассматриваемое уравнение к виду B.4.12). Об определе-
определении констант Щ и р, фигурирующих в ограничениях на функции и и v
в B.4.12), см. § 2.3-2.6. Рассмотрим вспомогательную задачу.
Задача 2.4. Построить управление и(х,у), переводящее систему
B.4.12) из начального состояния
x(U) = qi(U), y(U) = qi(U), \y(U)\ < e, B.7.4)
в терминальное состояние
x(U) = 0, y(U) = у' B.7.5)
за конечное время при любом допустимом v (фазовые ограничения
B.4.15) пока опущены).
Будем решать задачу 2.4, рассматривая ее как дифференциаль-
дифференциальную игру, на основе минимаксного подхода. В данной игре сторона,
выбирающая управление и, стремится уменьшить время ?* достижения
терминального состояния, а вторая сторона — увеличить это время
с помощью управления v. В [43] показано, что оптимальное управ-
управление и в этой игре совпадает с оптимальным по быстродействию
управлением для системы
х = у, y = (l-p)u, \u\^U0. B.7.6)
Система B.7.6) получена подстановкой оптимального для второго
игрока (и наихудшего для первого) управления v = — ри в систему
B.6.8). Построим синтез оптимального по быстродействию управления
для системы B.7.6) с терминальными условиями B.7.5). Известно
[50], что в фазовом пространстве х, у оптимальные по быстродействию
траектории системы B.7.6) состоят из участков двух семейств парабол:
106
Гл. 2. Метод декомпозиции управления (второй способ)
х =
У
х = — -
2(\-p)U0
У2
Ъ,
B.7.7)
2A-р)Щ "'
где Ъ — произвольная постоянная. Движение по параболам первого
семейства происходит в плоскости х, у вверх в сторону возрастания у,
а по параболам второго — вниз в сторону убывания у (см. рис. 26).
Нетрудно видеть, что лишь две
параболы проходят через точку
(О,у*) — конечное состояние си-
системы. Следовательно, кривая пере-
переключений состоит из дуг этих пара-
парабол и описывается соотношениями
= -U0
X = —
X =
у2 - у*2
у2 - у*2
У<У •
Рис. 26. Кривая переключений и
фазовые траектории
B.7.8)
Так как на каждой оптималь-
оптимальной траектории существует не более
одного переключения управления,
то синтез оптимального управления
состоит в следующем: справа от кривой переключений B.7.8) и на ее
верхнем участке (там, где у ^ у*) имеем и(х,у) = —Щ, а во всех
остальных точках фазового пространства и(х,у) = Щ. Каждое опти-
оптимальное движение системы B.7.6) состоит из двух этапов: сначала
изображающая точка движется по одной из парабол B.7.7) до кривой
переключений B.7.8) (см. рис. 26), а затем по этой кривой до точки
@, у*). Если в начальном положении система находится на кривой
B.7.8), то первый этап отсутствует.
Напомним, что движение системы B.4.12) подчиняется уравнениям
B.7.6) в том случае, если v = — ри, т. е. если второй игрок действует
оптимальным для себя образом. Если же управление v выбирается
как-то иначе, то и движение до кривой переключений B.7.8) проис-
происходит по иным траекториям, а на участках этой кривой, где у > у*
или у < 0, возникают скользящие режимы. Кроме того, на участке
кривой переключений, где 0 ^ у < у*, траектория может покинуть эту
кривую, вернувшись на нее вновь при у > у*. Затем система придет
в терминальное состояние B.7.5) по верхнему участку кривой B.7.8).
Отметим, что если второй игрок действует неоптимальным способом
(г; т^ —ри), то время движения до терминального состояния может
лишь уменьшиться.
§ 2.7. Обобщение на случай ненулевой конечной скорости
107
Используя решение задачи 2.4, построим синтез управления
(уже неоптимального) для системы B.4.12) с учетом фазовых
ограничений B.4.15). Пусть числа 5, х* таковы, что
* < 5 < е,
х =
B.7.9)
2A-p)U0'
Зададим непрерывную кривую К, расположенную в полосе п? =
= {(х,у) : \у\ < г} фазового пространства х, у и проходящую через
точку @, у*). Кривая К состоит из двух лучей
L\ = {(х, у) : х < -ж*, у = 5}, L2 = {(х, у) : х^ х*,у = -5},
а также участка кривой B.7.8), за-
заключенного между прямыми у = ±5
(рис. 27).
Разобьем полосу О? на два мно-
множества. Через О~ обозначим мно-
множество точек О?, которые лежат вы-
выше и справа от кривой К или на
том ее участке, где у > у*. Через
О+ обозначим дополнение множе-
множества п~ до п?. Определим в полосе
п? управление и(х,у) следующим
образом:
Г -С/о, (х,у)еп~,
и(х,у) = {
{ и0, (х,у)еп+.
е
0+
-6
—е
У
6
у*
ж* ж
i
Рис. 27. Модифицированная кри-
кривая переключений
B.7.10)
В силу B.4.12), B.7.10) производная у на множестве п~ удовлетво-
удовлетворяет неравенству
у^ -A - p)U0 <0, B.7.11)
а на множестве О+ — неравенству
у^(\ - р)Щ >0. B.7.12)
Неравенства B.7.11), B.7.12) аналогичны неравенствам B.4.19).
Следовательно, величина у на прямой у = е отрицательна,
а на прямой у = —г — положительна. Поэтому траектория, попав во
множество О?, уже не покинет его, и условие B.4.15) будет выполнено.
Покажем, что предложенное в форме B.7.10) управление приводит
систему B.4.12) в терминальное состояние за конечное время,
и проведем оценку этого времени. Пусть в момент времени t = t\
траектория системы B.4.12) находится во множестве О~ (или О+),
то есть (x\yl) G О~ (или (x\yl) G О+). Принимая во внимание
108 Гл. 2. Метод декомпозиции управления (второй способ)
неравенство B.7.11) (для множества О+ — B.7.12)), можно заключить,
что траектория достигнет кривой К за время т\, не превосходящее
отношения максимальной ширины множества О~ (или О+) вдоль оси у
к минимальной по модулю производной у:
? + L B-7.13)
A -p)U0
За это время координата х изменится не более, чем на ет\, так как
\х\ = \у\ < е. Поэтому
где (x(t2),y(t2)) — точка, в которой траектория впервые попадет
на кривую переключений. Оценки B.7.13), B.7.14) аналогичны
B.4.20), B.4.21).
Если |ж(^2)| > х*, т.е. точка (ж(^2), 2/(^2)) лежит на одном из лучей
L\ или 1/2, то далее движение будет происходить вдоль этого луча
в сторону уменьшения \х\ с постоянной скоростью х = ±5. Этот
участок траектории система будет проходить в скользящем режиме,
потому что по обе стороны от него фазовые скорости конечны
и направлены к кривой переключений. Время движения Т2 по лучу
от точки (x(t2),y(t2)) до точки Е\ или Е2 с абсциссой ±ж* (рис. 27)
равно Т2 = (|ж(^2)| —х*)/5. С учетом B.7.14) получаем оценку, анало-
аналогичную B.4.21):
-1. B.7.15)
Описанный этап движения вдоль лучей L\ и 1/2 отсутствует, если
\у{^2)\ ^ 5, т.е. если точка (ж(^2),2/(^2)) лежит на части кривой B.7.8),
заключенной между прямыми у = ±5.
Из точки Е\ система движется, возможно в скользящем режиме,
вдоль участка у* < у < 5 кривой B.7.8). Время тз прохождения этого
участка определяется следующим образом:
тз= п5~(тт • B-7.16)
A -p)U0
Из точки Е2 движение происходит в течение времени т\ вдоль
кривой B.7.8) до точки Е$, лежащей на оси х, и имеет место равенство
Т4= п \П. B.7.17)
A ~ Р) Uo
Наконец, из точки Е% система может двигаться по кривой B.7.8)
до терминального состояния (если v = — р Щ), а может сойти с нее
(если v^—pUo). Во втором случае траектория вновь попадет
на кривую переключений в некоторой точке Е\ (которая лежит либо
§2.7. Обобщение на случай ненулевой конечной скорости 109
на луче L\, либо, как показано на рис. 27, на участке у > у* кривой
B.7.8)), после чего вдоль кривой переключений придет в терминальное
состояние. Время движения т$ на этом отрезке пути достигает
максимума, если управление v является оптимальным с точки зрения
второго игрока, т. е. v = —рЩ. Тогда в силу B.7.12) получаем
т5< п У\п . B.7.18)
A р)Щ
Из B.7.16) и B.7.17) вытекает, что тз < т^ и, следовательно,
из точки Е\ траектория попадет в терминальное состояние заве-
заведомо быстрее, чем из точки Е^ поэтому для оценки т\ полного
времени движения системы B.4.12) из начальной точки (xl,yl)
в терминальное состояние @, у*) достаточно просуммировать правые
части соотношений B.7.13), B.7.15), B.7.17), B.7.18). После некоторых
преобразований с учетом B.7.9) получим
Г1= 2A -p)U06 +^' X
Отметим, что построенное выше управление может быть использо-
использовано также для приведения г-й подсистемы, г > 2, в нулевое терминаль-
терминальное положение и удержания ее там. Для этого нужно положить у* = 0
и и@,0) = 0 (при этом получим управление, предложенное в § 2.4).
Оценку т* времени прихода г-й подсистемы B.6.8) или B.4.12) в нуль
можно получить, положив у* = 0, хх = qi(t\) в B.7.19):
Д* + 2(е + Д)* ММ i>2 B720)
г " 2A-/3I/0* <5 ' * '
Пусть г* = тах^ т*, г = 2,..., п. Тогда
2A — /о) С/Од 5
В оценки B.7.19)—B.7.21) входят значения координат qi{t\)
в момент t\ выхода системы на границу между множествами ?1\ и Г^2.
Эти координаты могут быть оценены аналогично тому, как это сделано
в B.3.15). Получим
Оценку B.7.22) можно подставить в соотношения B.7.19)—B.7.21).
В отличие от других подсистем, подсистема, отвечающая первой
компоненте вектора q, не может постоянно удерживаться в терминаль-
терминальном состоянии @,у*). Поэтому при г = 1 система B.4.3) не остано-
остановится, однако ее траектория будет возвращаться в точку @, ?/*) через
промежутки времени, не превышающие т^.
ПО Гл. 2. Метод декомпозиции управления (второй способ)
Вернемся к решению задачи 2.3. Из приведенных рассуждений
вытекает, что управление, заданное в форме B.3.4) во множестве О,\,
приводит систему B.2.1) из начального состояния B.2.2) на границу,
разделяющую множества ?1\ и Г^2, в некоторый момент времени t\,
для которого имеет место оценка B.3.11). Множества п\ и U2 опреде-
определены в B.3.2), а число г задается соотношениями B.6.13).
Во множестве Г^2 система распадается на п независимых подсистем
B.6.8) или B.4.12). С помощью управления вида B.7.10) каждая
из этих подсистем B.4.12) с номером г, большим единицы, приводится
в начало координат не позднее, чем в момент t\ +т*, и удерживается
там. Отметим, что для г > 1 при построении множеств п~ и О+ следует
положить у* = 0.
Подсистема B.6.8) с г = 1 будет впервые приведена в терминаль-
терминальное состояние @, у*) не позже, чем в момент t\ +т*. Если т* < г*,
то вся система в целом в этот момент окажется в заданном терми-
терминальном состоянии. Если же т* > т^, то первая подсистема выйдет
из терминального состояния и будет снова приведена в это состояние
с помощью того же управления B.7.10). Таким образом, для времени ?*
приведения всей системы в заданное терминальное состояние имеем
оценку
U <?i+t*+t;\ B.7.23)
где т* и т* определяются соотношениями B.7.19), B.7.21) соответ-
соответственно.
Итак, если параметры исходной системы B.2.1) удовлетворяют
ограничениям B.1.3), B.1.4), B.1.6)-B.1.8), B.1.12), B.6.14),
то система может быть за конечное время переведена из произвольного
начального состояния B.2.2) в ненулевое терминальное состояние
(q*>Q*)> если выполнены условия B.6.13) и B.7.3). Эти условия
ограничивают выбор параметра г: с одной стороны, он должен
быть достаточно мал, чтобы выполнялись неравенства B.6.13),
с другой стороны, требуется выполнение неравенства B.7.3). Таким
образом, реализация предложенного способа управления возможна
лишь в случае достаточно малой терминальной скорости q*. Закон
управления по обратной связи, решающий поставленную задачу,
задается соотношениями B.3.4) во множестве ?1\ и соотношениями
B.5.1), B.7.10) во множестве Г^2. Этот закон управления обеспечивает,
при оговоренных выше условиях, приведение системы системы B.2.1)
в терминальное состояние в момент времени ?*, для которого имеет
место оценка B.7.23). Замечания относительно выбора параметра е,
приведенные в конце § 2.6, сохраняются справедливыми и для случая
ненулевой терминальной скорости, при одном ограничении: здесь
должно выполняться условие B.7.3).
§2.8. Задача об отслеживании траекторий механических систем 111
§ 2.8. Задача об отслеживании траекторий
механических систем
Постановка задачи. Следуя [17], применим метод декомпозиции
к задаче отслеживания заданной траектории механической системы.
Рассматривается система, динамика которой подчиняется уравнениям
B.1.1), B.1.2), в которых силы Qi состоят из заданных обобщенных
сил Pi(t) и неизвестных обобщенных сил Gi(q,q,t), называемых
в дальнейшем возмущениями:
/О Т> _1_ Г^ /ООП
Считается, что возмущения Gi(t,q,q) удовлетворяют условиям
\(jri[t, q, q)\ ^ Ст^, yZ.o.Z)
а на управляющие силы Щ накладываются ограничения
\ТТ I ^ Т Т 0 ' 1 /О О О\
\Ui\^Ui, г=1,...,п, (z.8.o)
где С/?, G® — заданные постоянные, причем
U? > G°{ > 0. B.8.4)
Предполагается, что собственные числа положительно-
определенной симметрической матрицы A(q) при любых q G Rn лежат
на отрезке [тп,М], где 0 < m ^ М, т.е. выполнено условие B.1.3).
Предполагается также, что матрица A(q) дважды дифференцируема
и ее частные производные первого и второго порядков равномерно
ограничены по норме, т. е.
д2А ,
:С2, Cl,C2>0, i,j = l,...,n.
B.8.5)
Здесь через || • || обозначена евклидова норма матрицы, т.е. норма
соответствующего линейного оператора в евклидовом пространстве.
Как и раньше, векторы обобщенных координат и скоростей q, q
предполагаются доступными измерению в каждый момент времени.
Пусть вектор-функции q(t),q(t) задают траекторию движения,
которая начинается в момент времени t = to в точке
и реализуется в результате действия на невозмущенную систему
заданных обобщенных сил Pi(t) при
Ui(t)=O, Gi(t)=O, t^t0.
Такую траекторию будем называть в дальнейшем номинальной.
112 Гл. 2. Метод декомпозиции управления (второй способ)
Обозначим через х, х отклонения фазовых координат и скоростей
возмущенной траектории по отношению к номинальной, т. е.
x(t)=q(t)-q(t), x(t) = q(t)-Q(t)< B-8.6)
и пусть
х° = x(t0) = q° - f, х° = хAо)=о_0-^ B.8.7)
— начальное отклонение траектории системы от номинальной, где
Задача 2.5. Построить управление U = (U\,..., Un) как вектор-
функцию фазовых переменных q, q, удовлетворяющую условию
B.8.3), и указать такую область пх с R2n допустимых началь-
начальных отклонений х°,х°, что любая траектория возмущенной
управляемой системы B.1.1), B.1.2), B.8.1), начинающаяся в этой
области, через конечное время выйдет на номинальную траекторию
и в дальнейшем система будет двигаться вдоль этой траектории,
каковы бы ни были возмущения G = (G\,..., Gn), подчиняющиеся
ограничениям B.8.2).
Уравнения в отклонениях. Запишем уравнения движения вдоль
номинальной траектории в виде
п п
$>уЩ- = - Y, Тт(ЩЯк + Р№ B-8.8)
j=l j,k=l
а уравнения движения вдоль возмущенной траектории — в виде
Tijk(q + хЩ + Xj)(qk + хк) +
з=\ зЛ=\
+ Pi{t) + Ui + Gi, i=l,...,n. B.8.9)
Здесь символы Г^к определены равенствами A.1.5). Применяя
формулу Тейлора с остаточным членом в форме Лагранжа
/~ \ /-\ s~^ daijCq)
aij{q + х) = aij{q) + > —^ xm,
m=\ °qm
где q = q-\- Ox, 0 < в < 1, преобразуем левую часть B.8.9) к виду
?<
¦Хп) =
v-^ daijjq) ~ B 8 10)
§2.8. Задача об отслеживании траекторий механических систем 113
Используя равенство
= Yljk{q) + V
приведем выражение, стоящее в правой части B.8.9), к виду
j,k=\
j,k=i j,k=\
+ E
j,k,m=l
Принимая во внимание соотношения B.8.8)—B.8.11), запишем уравне-
уравнения в отклонениях следующим образом:
j=\ j,m=\ Чт j,k,m=\ Чт
п
- Y Г^(^+ х) [Ъз±к + QkXj + XjXk^j + Gi + Uif
j,k=\
а затем в векторной форме:
ж,ж) ) +G + U. B.8.12)
114
Гл. 2. Метод декомпозиции управления (второй способ)
Оценим отдельные слагаемые в правой части уравнения B.8.12).
Будем считать, что фазовые скорости и ускорения вдоль номинальной
траектории подчиняются ограничениям
ш
В силу B.8.5), B.8.13) и неравенства
п
?
т=\
справедливы оценки
( v дА® _
1 / о Хгт
\ m=i ^Ут
)'
/
1
м.
п
?тг=1
п
\—>
П г
v—>
¦Xfe Ж
fc=l ^ 7 м fe=l
dA(q + x)^\.
к=\
B.8.13)
B.8.14)
q\ < х/^С^гЦхЦ,
B.8.15)
Из условий B.8.5), неравенства B.8.14) и неравенства Коши выте-
вытекают соотношения
?тг=1
q,q
(A(q
771=1
ж|| , г = 1,..., п,
§2.8. Задача об отслеживании траекторий механических систем 115
откуда получаем
\д_
2 да
dA(q)
x)q, х) + ± (A(q + х)х, х)
B.8.16)
Здесь использовано утверждение, справедливое для произвольного век-
вектора z G Rn: если \zi\ ^ h, г = 1,..., п, то ||z|| ^ л/nh.
Вновь применяя соотношения B.8.5), B.8.14), оценим оставшееся
слагаемое в B.8.12) следующим образом:
d4(q)
)Q
k,m=\
z ^
771=1
IE 1«»
к=\
пС2\\х\\ \q\ < nC2Q\\\x\\. B.8.17)
Обозначим через v сумму всех слагаемых, стоящих в правой части
B.8.12), за исключением управляющих сил U и возмущений G, и
запишем уравнения в отклонениях B.8.12) в виде
A(q + х)х = v + G + U.
Из соотношений B.8.15)—B.8.17) вытекает оценка
B.8.18)
|^l|2- B.8.19)
Декомпозиция системы. Разрешим уравнение B.8.18) относи-
относительно х. Получим
х = U' + V. B.8.20)
Здесь
Uf = A~lU, Vf = A~\v + G). B.8.21)
Будем рассматривать Ur как новый управляющий вектор и наложим
на его компоненты ограничения
\Щ\ ^Щ, Щ^гМ-хп-^\
B.8.22)
г = min
1
г ^ п.
116 Гл. 2. Метод декомпозиции управления (второй способ)
Выполнение ограничений B.8.22) обеспечивает выполнение исходных
ограничений B.8.3).
Управление Uf, удовлетворяющее B.8.22), зададим подобно тому,
как это было сделано ранее в § 1.9, в форме синтеза A.9.1):
U- = -U0 Slgn(Xi - фг), Xi ^ фг]
U< = -Uosignxi, Хг = фи B.8.23)
фг(хг,Хг) = -(/
Здесь Xi — некоторые положительные параметры управления, подле-
подлежащие определению.
Область О,х будем задавать в виде, аналогичном A.9.4):
Пх = Щ х ... х «?, Щ = {(xit х{) : х~ < х{ < х+,
B.8.24)
Здесь величины х~ < 0, xf > 0 неизвестны и тоже подлежат опреде-
определению.
Если в процессе управления выполнены условия (xi,Xi) ? Of для
всех г, то имеют место соотношения
Ы^сЦ, |i<|<Vf. di=xt-xr, tf = ilH(-di,Xi). B.8.25)
Используя методику § 1.10, получим систему неравенств (анало-
(аналогичную A.10.6)) для определения допустимых параметров Xi и di, г =
= 1,..., п, в виде:
Xi + m-lv°(d,il;d) < U0-m-l\\G°\\, i= l,...,n,
d=(di,...,dn), фЛ = {ф*,...,ф*), B.8.26)
Отметим, что при одном и том же с^ значения х~, xf могут быть
выбраны неоднозначно; нужно лишь, чтобы выполнялись условия
х~ < 0, xf > 0, xf — х~ = di, г = 1,..., п.
Выражения, стоящие в левой части системы неравенств B.8.26),
монотонно возрастают по di, Xi и при di = Xi = 0 обращаются в нуль.
Поэтому решение di > 0, Xi > 0 существует, если возможности кор-
корректирующего управления достаточно велики и выполнено условие
U0^m-l\\G°\\, г=1,...,п. B.8.27)
§2.8. Задача об отслеживании траекторий механических систем 117
Подытожим полученные результаты. Пусть выполнено условие
B.8.27) и найдены положительные параметры di, Xi, г = 1,...,п,
удовлетворяющие неравенству B.8.26). Тогда синтез управления
U(q,q), решающий поставленную задачу, задается соотношениями
U(q,q) = A(q + x)U'(x,x), B.8.6) и B.8.23). Это управление переводит
систему B.1.1), B.1.2), B.8.1) за конечное время на номинальную
траекторию, если начальное отклонение (х°,х°) лежит в области пх,
задаваемом ограничениями B.8.24).
Отметим, что если нижняя граница т для собственных чисел
матрицы A(q) мала, то ограничение B.8.27) может оказаться
слишком жестким по сравнению с B.8.4). В этом случае целесо-
целесообразно использовать другую модификацию предложенного способа
управления. Введем обозначение
у = A(q)x B.8.28)
и представим систему B.8.18) в виде
v- [A(q + x) - A{q)} A~l(q + x) (U + G + v)
A 8A(q) ^ \
\k,m=l
Учитывая, что
dqkdqm
B.8.29)
получим, аналогично B.8.19),
\Vi\ < G^ + v°(x,x) + d
(x,i) + ||t/°|| + ||G0||)
х\\. B.8.30)
Здесь U0 = (U°,...,U%) и G° = (G?,...,G°) - векторы с компонен-
компонентами, введенными в B.8.2), B.8.3). В силу введенного обозначения
B.8.28) и ограничения B.1.3) верны следующие соотношения:
--U
\\x\\ =
т
/im-2C,Q,||j/||. B.8.31)
118 Гл. 2. Метод декомпозиции управления (второй способ)
Заменим величины ||ж||, ||ж|| в неравенствах B.8.30) их верхними
оценками B.8.31). Получим
Конкретный вид функции v°(y,y) определяется из B.8.30), B.8.31).
Применим закон управления B.8.23) к системе B.8.29), заменяя
в нем Xi, U[ на yi, Щ соответственно. Для нахождения допустимых
параметров Xi и di = yf — у~, г = 1,...,п, получим аналогичную
B.8.26) систему неравенств
Xi + v°(d,^d) < С7? - G?f i= l,...,n. B.8.32)
В неравенствах B.8.32) выражения, стоящие в правых частях, поло-
положительны, а функция v°(d,ipd) монотонно возрастает по переменным
di, Xi и при di = 0, Xi = 0 обращается в нуль. Поэтому решение di > 0,
Xi > 0 системы неравенств B.8.32) существует всегда.
Выбрав параметры Xi > 0, di > 0, которые удовлетворяют
B.8.32), определяем соответствующие значения yf < 0, у~ > 0
и допустимое множество ?1У начальных значений (у®, у®). Отметим,
что при одном и том же di значения у~, yf могут быть выбраны
неоднозначно; нужно лишь, чтобы выполнялись условия у~ < 0,
yf > 0, yf — у~ = di, г = 1,..., п. Множество Qy определяется теперь
соотношениями B.8.24), в которых х нужно заменить на у. Далее,
используя замену B.8.28) и переходя к исходным переменным х,
получаем множество Qx допустимых начальных отклонений (х^,х^)
от номинальной траектории.
§ 2.9. Приложения к робототехническим системам
Построенные выше методы управления могут быть применены
к различным управляемым механическим системам. Наиболее
интересным представляется приложение этих методов к робото-
робототехническим системам и, в первую очередь, к манипуляцонным
роботам. Робот-манипулятор имеет несколько степеней свободы,
каждая из которых, как правило, управляется своим двигателем.
Поэтому число управляющих функций здесь равно числу степеней
свободы, как и предполагается в системе B.1.1). Уравнения
движения манипуляционного робота можно сформировать разными
способами, в частности, воспользовавшись уравнениями Лагранжа
или Гамильтона. Составление системы уравнений вручную сопряжено
с громоздкими вычислениями, требующими больших затрат времени
и усилий, и не гарантировано от ошибок. Поэтому в настоящее
время широко распространено применение методов компьютерной
алгебры для составления уравнений движения систем связных тел
[40]. Разработан целый ряд программных комплексов, позволяющих
§2.9. Приложения к робототехническим системам 119
автоматически формировать уравнения движения систем многих тел
[32,33,95,96].
Ниже приводится описание схемы формирования уравнений
движения голономных систем [28]. Отметим, что для ее реализации
не требуется составлять программы на специализированном языке
символьных вычислений. Достаточно воспользоваться каким-либо
универсальным программным средством, которое позволяет создавать
значительно упрощенный пользовательский интерфейс, зачастую
не предполагающий специальных знаний по программированию.
Формирование уравнений движения систем связанных твердых
тел методами компьютерной алгебры
Вычисление кинетической энергии. Пусть состояние механиче-
механической системы с п степенями свободы описывается обобщенными коор-
координатами qi, г = 1,..., п.
Движение системы N твердых тел рассматривается в неподвиж-
неподвижной системе координат OXYZ. Введем последовательно N локальных
систем координат OiXiyiZi, г-я из которых жестко связана с г-м телом
так, что оси OiXi, Oiyi и О^ являются главными осями инерции
г-го тела, г= \,...,N. Положение трехгранника OiXiyiZi в системе
координат OXYZ определяется следующим образом.
Пара {ro^i— 1} задает координаты тог = {хОг,УОг,%о^) точки Oi
в системе Oi-\Xi-\yi-\Zi-\, т.е. в предшествующей локальной системе.
Случай г — 1 = 0 соответствует заданию координат точки О\ в непо-
неподвижной системе OXYZ.
Ориентация относительно O^_ia^_i^_i^_i трехгранника OiXiyiZi
задается последовательностью пар {j\,K\}, {72^2}» {7з>^з}>
которая определяет последовательность поворотов трехгранника
Oi_\Xi_\yi_\Zi_\, переводящих его в положение, когда его оси
становятся параллельны осям OiXiyiZi. Параметр Kj, j = 1, 2, 3,
принимает значения 1, 2, 3, условно обозначающие ось, относительно
которой осуществляется поворот. Значениям К\ = 1, К^ = 2, К% = 3
отвечают оси Oi-\Xi_\, Oi-\yi-\, Oi-\Zi_\ соответственно. Первый
поворот выполняется относительно оси К\ на угол 7ь второй
поворот — относительно нового положения оси К% на угол 72» третий —
относительно нового положения оси К% на угол 7з-
Для каждого г-го тела формируется матрица перехода из системы
координат OiXiyiZi в систему координат OXYZ:
9г\\ 9г\2 9г\3
Гг =| 9г2\ 9i22 9i23
9%3\ 9%32 9%33
Формирование матрицы 1\, а также вычисление абсолютной угловой
скорости трехгранника OiXiyiZi осуществляется последовательно для
задаваемой тройки параметров вычисления J7j, Kj, i — 1}, j = 1, 2, 3:
120 Гл. 2. Метод декомпозиции управления (второй способ)
Шаг 1. К\ = 1. Рабочей переменной А присваивается значение
/10 0
Д = I 0 cos 71 — sin 71
\ 0 sin 7i cos 71
Рабочей переменной иог присваивается значение
где 7i означает производную по времени от 71 • Переход к шагу 4.
Шаг 2. Къ = 2. Рабочей переменной А присваивается значение
(cos 72 0 sin 72
0 1 0
— sin 72 0 cos 72
Рабочей переменной ujr присваивается значение
иг = @,72,0).
Переход к шагу 4.
Шаг 3. К% = 3. Рабочей переменной А присваивается значение
(cos 73 — sin 73 0
sin 73 cos 73 0
0 0 1
Рабочей переменной иг присваивается значение
иР = @,0,7з).
Переход к шагу 4.
Шаг 4. Вычисляются новые значения Г^ иц:
При первом обращении к процедуре в качестве Г^ и Ui выбираются
IV1 и Ui-\, полученные для предыдущего тела, причем для первого
тела (когда г = 1) формально полагаем Го = diag(l, 1, 1), uoq = @,0,0).
Вычисление абсолютной скорости центра масс г-го тела проводится
по формуле
V T^ + T^ B9Л)
где вектор гсг задает координаты центра масс г-го тела в системе
§2.9. Приложения к робототехническим системам 121
Предполагая моменты инерции г-го тела в системе координат
hi = {Vi + 2?) drrii, Iy. = \ (xj + zj) drrii, hi = \{х\ + yj) drrii
B.9.2)
известными, вычислим элементы матрицы тензора инерции в системе
OXYZ. Из B.9.2) следует, что
jdrrii = - AУ. + Iz. -IXi), yjdrrii = g (h, + IZi -Iyi),
Вводя обозначения
Xi = дщХг + gu2Vi
где gijk, j, к = 1,2,3 — элементы матрицы перехода Г^ для г-го тела,
получим искомые величины:
их = \ [(<?!, + gi)(lVi + lZi - lXif
\ M\ + gl)(iVi + izt - iXif + {g\2 + <?з22)D, + izt - ivtf
hz = \ [(g2u + <&i)(ivt + izt - iXlf + (g2l2 + 9k)(ixt + ht - ivtf
122 Гл. 2. Метод декомпозиции управления (второй способ)
hxz = 2 biWfi^y. + hi ~ hi? + gfahihi + hi ~ hi? +
h, - iVlf
Кинетическая энергия г-го тела вычисляется по формуле
T^^miV^ + ^iiOiJaOi), B.9.4)
где nii — масса г-го тела; vct — абсолютная скорость центра масс
г-го тела, вычисляемая по формуле B.9.1); uoi — абсолютная угловая
скорость трехгранника OiXiyiZi, U — матрица тензора инерции г-го
тела в системе координат OXYZ
hx hxY hxz
= I IiXY IiY IiYZ
hxz hyz hz
элементы которой представлены в B.9.3).
Кинетическая энергия системы N тел равна
N
Таким образом, процедура вычисления суммарной кинетической
энергии подразделяется на несколько шагов.
На первом шаге для каждого тела определяются матрицы перехода
из локальной системы координат OiXiyiZi в неподвижную OXYZ.
Затем вычисляется кинетическая энергия г-го тела по формуле B.9.4).
На последнем шаге в соответствии с B.9.5) определяется выраже-
выражение для кинетической энергии системы Т.
Формирование уравнений Лагранжа второго рода. Движение
системы связанных твердых тел может быть описано уравнениями
Лагранжа:
AdT_dT=Qh i=1>_>n> B.9.6)
dt dqi dqi
где обобщенная сила Qi определяется следующим выражением:
к о
§2.10. Примеры 123
Здесь Fj, j = l,..., к — действующие на систему силы, точки прило-
приложения которых определяются их радиусами-векторами г\,...,г^.
Вычисляя производные
дТ_ дТ_ d дТ _ А / д дТ . д дТ .. \
dqi' dqi' dt dqi ^ \ dqj dqi J dqj dqi J J
формируем уравнения Лагранжа. Алгоритм получения выражения
кинетической энергии Т приведен выше.
Формирование уравнений Гамильтона. Если обобщенные силы
выражаются через функцию потенциальной энергии П:
Qi = - —,
то уравнения B.9.6) можно записать в виде
_d_aL_9L_0 B97)
dt dqi dqi
где L = Т — П — функция Лагранжа. Уравнения B.9.7) преобразуются
к уравнениям Гамильтона
4г = ^Я, д = -М i = !,...,„. B.9.8)
dpi' г dqi'
В уравнениях B.9.8) переменные pi, вычисляемые как
= 9L
суть обобщенные импульсы,
функция Н есть функция Гамильтона, определяемая соотношением
г=1
§2.10. Примеры
1°. Численное моделирование управления
двузвенным механизмом (с тремя степенями свободы)
Описание динамической системы. Применим рассмотренный
в § 2.7 закон управления к системе, описывающей динамику
двузвенного механизма, моделирующего транспортные движения
манипуляционного робота. Звенья двузвенника соединены между
124
Гл. 2. Метод декомпозиции управления (второй способ)
собой цилиндрическим шарни-
шарниром, а сам двузвенник при-
прикреплен к неподвижному осно-
основанию с помощью двухстепенно-
двухстепенного шарнира (рис. 28), подвиж-
подвижная ось которого параллельна
оси шарнира, соединяющего зве-
звенья. Предполагается, что зве-
звенья представляют собой однород-
однородные тонкостенные прямолиней-
прямолинейные стержни кольцевого попе-
поперечного сечения с массами т\
и т2, длинами 1\ и /2, сред-
средними радиусами поперечных се-
сечений R\ и i?2. Главные цен-
центральные моменты инерции зве-
звеньев относительно их продоль-
продольных осей и относительно осей,
им перпендикулярных, соответ-
соответственно равны Jx\ и JX2, J\ и J2.
Составление кинетической энергии и уравнений движения.
Система обладает тремя степенями свободы. В качестве первых двух
обобщенных координат q\ = ф, q% = 0 выбраны углы поворотов во-
вокруг осей двухстепенного шарнира, третья координата q% = /3 — угол
между осями звеньев. Управление осуществляется независимо по каж-
каждой из степеней свободы, управляющие моменты приложены к осям
соответствующих шарниров. Кроме того, на двузвенник действуют из-
известные моменты сил тяжести и неопределенные внешние возмущения
Gi9 г = 1,2,3.
Для определения матрицы кинетической энергии А, собственных
чисел А^ матрицы А и составления уравнений Лагранжа двузвенника
использовалась система компьютерной алгебры Maple. Процедура по-
получения этих уравнений приведена в § 2.9.
Матрица А имеет вид
аи О О
А = ( 0 а22 а23
О
Рис. 28. Двузвенный механизм с тремя
степенями свободы
где
«32 «33
1
- Jx2) cos 2F» + /3)
Jx + J2
[cos2(<9 + /3)
§2.10. Примеры 125
«22 = J\ + ^2 + l\ (™>2 + T
-m2h f/icos/3+ i/2) ,
«23 = J2 + q 77I2/2 ( /l COS/3 + — /2 j , «32 — «23, «33 = ^2 + T 7712/2-
Собственные числа матрицы А равны
/+ 17711/?) cos
+ т Ш2/2) cos 2((9 + /3) + m2/i/2 [cos /3 + cosB(9 + /3)] +
+ Ji + J2 + Л1 + Jx2 + m2/f + ^ (mi/? + 7712/2)} '
A2 = I [Ji +2J2 + m2/i(/i
+ ^ |(Ji +m2/i/2 cos/3J + BJ2 + 7712/1/2COS/3J +
+ — m\l\(J\ + 7712/? + 7712/1/2 cos/3) + 2m2h(hJ2 + ^2^1 cos/3) +
1 /9
+ 2m2l\J\ + 16m?/f + ^ m|/| + ml/i (/? + /| cos /3)
A3 = I [ji +2J2 + 77i2/i(/i +/2cos/3) + 17712/2 + 7т1г?] -
- ^ |"(Ji +7712/1/2COS/3J + BJ2 + 7712/1/2COS/3J +
+ — m\l\(J\ + 7712/2 + 7712/1/2 cos/3) + 2t712/2(/2^2 + 7712/? cos/3) +
1
+ 277i2/?Ji + 16m?/f + I mlZ| + tti^i (l\ + l\ cos/3)
Уравнения
J"i + J2 +
Лагранжа
T 1 T 1
+ (V
ДЛЯ
рассматриваемой
9 1 9
1 + T (ml/f + m2/
4
1 9\
H— 7712/9 cos2(^
4 /
системы
+ Й +
имеют
вид
126 Гл. 2. Метод декомпозиции управления (второй способ)
- JxX + m2l\ + j
sin 2@ + /3)
- Jx\ + m2l\ + т^М?) sin2(9J -
-Рф1 (j2 - Jx2 + ^ m2lf\ sin 2F» + /3) +
+ |m2/i/2[sin/3 + sinB(9 + /3)] j = Мф + Gi
Z (mi^i + m2^2 ) + m2l\(l\ + /2 cos/3) + Ji + J2 +
+ /3 [^2 + X m2^2 (o ^2 + ^icos/3)j - I (9/3- ^- J m2/i/2sin/3 +
i sin2F» + /3) + m2lxl2 sinB6> + /3)+
— Jjci + m2l\ + — m\l\) sin20\ = M^ + G2,
4 / J
•• / 1 2\ ** Г 1 /1 M
/3 ( ^2 H ^2^2 ) + 0 «72 + ^ ^2^2 [~^ h + h COS /3 ) +
+ 02 j-m2l\l2smf3+ %- \ih- JX2 + j т^Л sin2((9 + /3)+
+ im2/i/2[sin/3 + sinB(9 + /3)l) = M0 + G3. B.10.1)
2 L J J
Приведение в ненулевое терминальное состояние. Моделиро-
Моделирование проводилось для следующих параметров системы: массы стерж-
стержней т\ = 8 кг, тп2 = 2 кг, длины стержней /i = 0.4 м, 12 = 0.5 м,
средние радиусы колец поперечных сечений R\ = R2 = 0.05 м.
Рассмотрим один из вариантов начального и конечного состояний:
д° = @.78; -0.52; -1.74), q° = (\с~1; -0.7с~1; 0.5с-1),
д* = @; 0; -1.39), q* = @.1 с; 0; 0).
§2.10. Примеры
127
0.5-•
*1 3
¦¦Gi
¦--0.5
Рис. 29. Проекции фазовой тра-
ектории системы на плоскости
(qi, qi), i = 1, 2, 3
0.5"
-Ь
-0.005
1—
1 0.005
-0.5 f
Рис. 30. Поведение фазовой
траектории вблизи терминального
состояния
Возмущения Gi были заданы в виде
G\(t) = cosA0tt?), G2(?) = 2cos(8tt?),
(t) = 3cosF7rt),
(размерность моментов Gi(t) — Н-м).
Область D изменения обобщенных координат в рассматриваемом
случае имеет вид:
0 < qx
Напомним, что
2тг, —тг/2
тг/2, -тг
Собственные числа матрицы A(q) при изменении q по всей обла-
области D лежат между
т = 2.5 • 1СГ2 кг-м2 и М=1.4кг-м2.
Производные dctij(q)/dqk элементов матрицы A(q) в области D удовле-
удовлетворяют неравенству B.1.4) при С = 1.3 кг-м2. Число г в ограничениях
B.4.6) и параметры г, 5 выбраны с учетом B.6.13), B.7.3), B.7.9)
равными
г = 6.5-102 Н-м, ? = 0.19с-1, 5 = 0.17с-1.
Согласно B.4.6), B.6.11), B.6.12), B.7.9) при таких значениях величин
т, М, С, г и г получаем р = 0.96, ж* = 1.4 • 10~3 рад. Рисунки 29
и 30 иллюстрируют поведение фазовой траектории системы B.10.1),
управляемой во множестве ?1\ по закону B.3.4), а во множестве О2 —
по закону B.7.10).
128
Гл. 2. Метод декомпозиции управления (второй способ)
На рис. 29 показано поведение всех фазовых координат в целом
(на всем интервале движения t ? [0, ?*]), а на рис. 30 в другом
масштабе изображено их поведение вблизи терминального состояния.
Каждой обобщенной координате соответствует кривая, помеченная
номером координаты. Из рис. 29 видно, что во множестве п\ компо-
компоненты вектора обобщенной скорости q быстро убывают по абсолютной
величине. Модуль \q\\ = \ф\ первой компоненты достигает величины г
последним, после чего траектория попадает во множество Г^2, а закон
управления B.3.4) меняется на закон B.7.10). Далее каждая из кривых
представляет собой фазовую траекторию соответствующей подсистемы
вида B.4.12) и ведет себя так, как описано в п 2.7 (см. рис. 30). Время
достижения первой координатой терминального состояния с момента
начала движения равно 4.67 с, второй координатой — 3.12 с, третьей —
2.07 с. Таким образом, общая продолжительность процесса состав-
составляет 4.67 с.
Моделирование динамики двузвенника, управляемого по предло-
предложенному закону, было проведено также для случая, когда в качестве
области D выбран параллелепипед
-0.61 < q2 < 0.09, -1.83 < q3 < -1.3, 0 < qx < 2тг
(от переменной q\ = ф собственные числа матрицы A(q) не зависят).
В этом параллелепипеде неравенства B.1.3), B.1.4) выполнены при
т = 0.12 кг-м2, М = 1.08 кг-м2, С = 0.84 кг-м2.
Число г было взято равным 0.34 с, а константу г оказалось возмож-
При таких значениях перечисленных
параметров поведение траектории
системы качественно не измени-
изменилось, однако время перехода из на-
начального состояния в терминальное
сократилось до 2.63 с.
На рис. 31 представлены ре-
результаты моделирования движения
системы B.10.1), управляемой по
модифицированному закону (см. за-
замечание в § 2.7). В отличие от ри-
рисунков 29 и 30, здесь отсутствуют
прямолинейные участки движения,
что объясняется зависимостью ве-
величины 5 от времени. Как и следо-
следовало ожидать, данный способ управ-
управления привел к цели быстрее преды-
предыдущих: полное время перемещения
двузвенника из начального положе-
положения в конечное составило 1.8 с.
ным уменьшить до 1.3 • 102
0.5
-0.5
1
Рис. 31. Проекции фазовой траек-
траектории системы при модифициро-
модифицированном законе управления
§2.10. Примеры 129
Приведение в нулевое терминальное состояние. В этом случае
были выбраны следующие параметры системы:
1\ = h = 1 м, т\ = тп2 = 20 кг, R\ = Щ = 5 • 10~2 м,
М^ = М^° = Ml = г = 200 Н-м.
Моменты инерции и величины, входящие в выражение для управления,
оказались равными:
Jx = J2 = 1.67 кг-м2, Jxi = Jx2 = 2.5 • 10~2 кг-м2,
га = 7.5 • 10~2 кг-м2, М = 58.67 кг-м2,
С = 53.26 кг-м2, ? = 9.8 • 10~3 с,
5 = 8.82- Ю-3 с, Uo= 1.97 с-2,
р = 0.81, ж* = 1.04- 10~4.
По построению, для всех трех степеней свободы выбраны одина-
одинаковые значения параметров 5 и ж*. Поэтому кривые переключений
для трех управляющих моментов в области О2 также одинаковы,
и на этих кривых переключений лежат заключительные участки
фазовых траекторий для всех трех степеней свободы.
Некоторые типичные фазовые траектории системы изображены
на рисунках 32 и 33, где различным степеням свободы (углам ф, в, C)
отвечают соответственно сплошные, штриховые и штрих-пунктирные
линии. Здесь показаны заключительные участки траекторий — внутри
области ^2 и вблизи нее.
На рис. 34 представлены зависимости угловых скоростей ф, в, /3
от времени для одного из вариантов расчета. На заключительном
этапе движения угловые скорости меняются линейно, что соответ-
соответствует движению по параболическим участкам кривых переключений
в области &2- Приход в терминальное состояние для разных степеней
свободы происходит в разное время.
2°. Численное моделирование управления двузвенным
механизмом с двумя степенями свободы
Отслеживание заданной траектории. Моделировалась динами-
динамика системы A.14.1) с параметрами, которые уже использовались ра-
ранее и приведены в A.15.1). В этом примере полагаем Q = P(t) +
+ G, где P(t) — заданные силы, G — неизвестные силы и воз-
возмущения (см. § 2.8). После перехода к безразмерным переменным
A.14.3) исходная система A.14.1) приняла вид A.14.4). Номинальная
5 Ф. Л. Черноусько и др.
130
Гл. 2. Метод декомпозиции управления (второй способ)
1
1 1 1 \
-0.159 -ж*-0.053
-0.281
-0.562
-0.843
—?
-1.124
— E
-0.
-о.
-о.
\0
-\
-
_-
0,$ (q)-K
843
562
I
0.053
)-2, c-1
1 ' i I
ж* 0.159 0.212
Рис. 32. Проекции фазовой траектории в случае нулевого терминального со-
состояния
- 1.124
- ?
-0.843
-0.562
-0.281
-0.159 -ж* -0.053 0
] -0.281
-0.562
-5
-1.124
, с
ч-з
ж* 0.159 0.212
Рис. 33. Проекции фазовой траектории в случае нулевого терминального со-
состояния
§2.10. Примеры
131
1.124 J
0.562 г
ФЛ
L Г
» /
V*
0
IP Й)-ю-
*x
*x#
! 1 1
0.012
2, с
0.024 „
X
X
X
X
X
X
X
"X i
-^0.036
! 1
0.048
-0.562 -
-1.124
Рис. 34. Зависимость угловых скоростей от времени
траектория (Дг^Чг) была получена в результате численного интегриро-
интегрирования системы A.14.4) при
Ui=U2= 0, Gx = G2 = О,
Px(t) = 1 - qx(t) - Ш, P2(t) = 1 - Ш ~ Ш>
Й@) = q2@) = 0.8, ^@) = 0.45, q2@) = 0.15.
Также были найдены конкретные значения констант, введенных
в B.1.3), B.8.5), B.8.13). Оказалось, что для такой траектории
= 0.13, M = 5.87,
\q\^Qi= 0.47, |
Q2 = 0.28.
Затем были изменены начальные значения обобщенных координат
и скоростей:
qi@) = q2@) = 1.8, ^@) = 1.45, q2@) = 1.15.
Система A.14.4) была проинтегрирована при управлении, построенном
в соответствии с методикой, предложенной в конце § 2.8 при Xi = U®.
При таком упрощенном управлении полностью игнорируются нелиней-
нелинейности и возникающие в системе возмущения:
G\ = -(q\ -q\) - (q\ -qx),
G2 = ~(q2 -q2) ~ (q2 -q2).
132
Гл. 2. Метод декомпозиции управления (второй способ)
3-
О
I
10
_9
-1-
Рис. 35. Зависимость фазовых
координат от времени
О
Рис. 36. Зависимость фазовых
скоростей от времени
Тем не менее, применение такого упрощенного подхода оправдано,
поскольку во многих случаях позволяет привести систему на номи-
номинальную траекторию.
На рис. 35 изображены графики зависимости от времени
фазовых координат системы, а на рис. 36 — фазовых скоростей.
Штриховые линии соответствуют движению вдоль номинальной
траектории, а сплошные — движению возмущенной системы. Видно,
что приблизительно через 7 с после начала процесса система вышла
на номинальную траекторию и в дальнейшем двигалась вдоль нее
в скользящем режиме. Таким образом, описанный алгоритм позволяет
достигать цели управления и в случаях, когда достаточные условия
B.8.32) не выполнены.
Глава 3
КУСОЧНО-ЛИНЕЙНОЕ УПРАВЛЕНИЕ
МЕХАНИЧЕСКИМИ СИСТЕМАМИ В УСЛОВИЯХ
НЕОПРЕДЕЛЕННОСТИ
§ 3.1. Постановка задачи для склерономной системы
В третьей главе рассматривается лагранжева механическая систе-
система @.1) в предположении, что матрица кинетической энергии A(q)
неизвестна и на систему действуют неизвестные ограниченные силы.
Предложен закон управления, переводящий систему из произвольного
начального состояния в заданное терминальное состояние за конечное
время с помощью ограниченной по модулю силы. В предлагаемом
законе используется линейная обратная связь с кусочно-постоянными
коэффициентами: коэффициенты увеличиваются и стремятся к бес-
бесконечности по мере приближения системы к терминальному состоя-
состоянию, однако управляющие силы остаются ограниченными и удовле-
удовлетворяют наложенным на них ограничениям. Алгоритм обосновывается
с помощью второго метода Ляпунова.
На примере некоторых двухмассовых колебательных систем пока-
показано, что предложенный подход может быть использован для управле-
управления системами, у которых число степеней свободы больше размерности
вектора управляющих сил. В заключительной части гл. 3 кусочно-
линейное управление применено к реономным системам.
Результаты, изложенные в гл. 3, получены в работах [8-10, 13, 14].
В первом разделе данной главы рассматривается, как и ранее,
склерономная управляемая механическая система, кинетическая
энергия которой представляется в виде квадратичной формы
по обобщенным скоростям q с коэффициентами, зависящими от
обобщенных координат q:
T{q,q) = \{A{q)q,q), C.1.1)
где A(q) — положительно-определенная симметрическая матрица
инерции системы.
Динамика системы описывается уравнениями Лагранжа второго
рода
?w-T = u+Q' (ЗЛ-2)
at oq oq
134 Гл. 3. Кусочно-линейное управление механическими системами
где U — управляющие силы, Q — другие силы, действующие
на систему. Предполагается, что на n-мерные векторы обобщенных
сил U и Q наложены ограничения
< С/о, U0>0, C.1.3)
^Qo, Qo>O, C.1.4)
причем вектор-функции Q(t,q,q) и U(t,q,q) таковы, что решения
системы уравнений C.1.2) существуют.
Силы Q будем считать неизвестными и трактовать как возмущения.
Наряду с ними на систему могут действовать и другие силы, величины
которых известны. Однако предполагается, что ресурсы управления
достаточно велики, чтобы компенсировать эти известные силы, а вели-
величина Uq — это максимальная допустимая интенсивность управления,
оставшегося после такой компенсации.
Будем считать, что непрерывно дифференцируемая матрица A(q)
неизвестна, ее собственные числа при любых q лежат на отрезке
[т,М], О < т ^ М, а частные производные матрицы A(q) равномерно
ограничены по норме, т. е.
zeRn, C.1.5)
mz $
OA(q)
%
: (A(q)z,
D
<
>
Mz2,
0, i
,...,n. C.1.6)
Фазовые переменные q, q считаются доступными для измерений
в каждый момент времени.
Задача 3.1. Пусть даны начальные условия q@) = q*, q@) = q*
и константы т, М, D, Щ, Qq. Построить управление, удовлетво-
удовлетворяющее ограничениям C.1.3) и приводящее систему C.1.2) в задан-
заданное терминальное положение (q, 0) за конечное время.
Отметим, что терминальное состояние представляет собой состоя-
состояние покоя невозмущенной системы C.1.2). Не ограничивая общности,
будем считать, что q = 0, т. е. терминальное состояние совпадает
с началом координат фазового пространства (для этого достаточно
взять в качестве вектора обобщенных координат вектор q — q).
Наглядным примером задачи в данной постановке может служить
задача об управлении системой связанных твердых тел, массо-
инерционные характеристики которых известны неточно. В этом
случае неизвестна не только матрица инерции системы, но и
действующие на тела силы тяжести. Кроме этих сил на систему могут
действовать и другие возмущения.
Задача о перемещении манипулятором груза неизвестной массы
представляет собой частный случай рассматриваемой задачи.
§3.2. Вспомогательное рассуждение 135
§ 3.2. Вспомогательное рассуждение
Рассмотрим частный случай Q = О и предположим, что управление
системой осуществляется на основе ПД-регулятора, т. е. управляющая
функция имеет вид линейной обратной связи по фазовым перемен-
переменным q, q:
U = -aq-Cq, a, C > 0. C.2.1)
Известно, что если а, C — произвольные положительные постоян-
постоянные, то начало координат фазового пространства представляет собой
глобально асимптотически устойчивое положение равновесия рассмат-
рассматриваемой системы. Действительно, уравнения движения в этом случае
принимают форму
JtM~lTq=-aq-^ C-2-2)
Первое слагаемое в правой части C.2.2) выступает в качестве дисси-
пативной силы, а второе — потенциальной. Полная энергия системы
представляет собой положительно-определенную функцию Ляпунова,
производная которой в силу системы C.2.2) удовлетворяет неравенству
Ё = -aq2 < 0.
Множество {(q,q) ? R2n • E(q,q) = 0}, очевидно, не содержит
целых положительных полутраекторий, за исключением положения
равновесия q = q = 0. Следовательно, по теореме Барбашина-
Красовского [18,41] начало координат фазового пространства
глобально асимптотически устойчиво, т. е. любая траектория приходит
в терминальное состояние за бесконечное время.
Помимо простоты управление в виде ПД-регулятора C.2.1)
обладает рядом других важных достоинств. Оно имеет форму синтеза,
для его реализации достаточно знать лишь текущее состояние
фазового вектора. Это управление робастно, так как не зависит
от параметров системы и может быть применено для стабилизации
положения равновесия системы C.2.2) с любой матрицей кинетической
энергии A(q).
В то же время закон управления по обратной связи с постоянными
коэффициентами имеет существенный недостаток: вдали от терминаль-
терминального состояния управляющие силы велики и могут не удовлетворять
ограничениям C.1.3), а вблизи него они малы и стремятся к нулю
по мере приближения траектории к терминальному состоянию. В малой
окрестности терминального состояния ресурсы управления, определен-
определенные условиями C.1.3), используются не в полной мере, что и приводит
136 Гл. 3. Кусочно-линейное управление механическими системами
к бесконечному времени движения. Кроме того, наличие возмущающих
сил Q ф 0, вообще говоря, нарушает устойчивость рассматриваемого
состояния равновесия.
Для повышения эффективности управления и для ускорения
движения системы будем увеличивать скачкообразно коэффициенты
а, C по мере приближения траектории к терминальному состоянию.
Таким образом, в предлагаемом ниже законе управления используются
линейные обратные связи вида C.2.1), коэффициенты усиления
которых представляют собой кусочно-постоянные функции времени.
Коэффициенты увеличиваются и стремятся к бесконечности, однако
управляющие силы остаются ограниченными и удовлетворяют нало-
наложенным на них ограничениям. Траектория системы при этом приходит
в терминальное состояние за конечное время даже при наличии
некоторых ограниченных силовых возмущений.
§ 3.3. Описание алгоритма управления
Переформулируем исходную задачу следующим образом.
Задача 3.2. Пусть даны начальные условия q@) = q*, q@) = q*
и константы m,M,D,Uo,Qo. Требуется указать такой закон
изменения коэффициентов обратной связи а, C в управлении C.2.1),
чтобы при любых внешних возмущениях Q, удовлетворяющих
условиям C.1.4), траектория системы C.1.2), C.2.1) приходила
в состояние @,0) за конечное время и вдоль траектории выполня-
выполнялись ограничения C.1.3) на управление U.
Введем в рассмотрение функцию
W(q, q) = Mq2+(M2qi+l^-qA . C.3.1)
Величина W(q, q) имеет размерность энергии и характеризует
удаленность точки (q, q) от терминального состояния @,0): множество
уровня W(q, q) = С функции W в фазовом пространстве R2n
представляет собой эллипсоид ACMq2 + U^q2 = 2С2, который
стягивается к началу координат @,0) при С —> 0. Положим
MUp Wo
Wk = w, C.3.2)
и зададим совокупность эллипсоидов
{{q,q)eR2n: W(q,q) = Wk},
где индекс к пробегает множество целых чисел (см. рис. 37).
Пусть точка (q*,q*), отвечающая фазовому состоянию исходной
системы в начальный момент времени t = 0, лежит на эллипсоиде
§3.3. Описание алгоритма управления
137
{(q,q) eR2n : W(q,q) = WkJ или
внутри него, но вне эллипсоида
{(q,q) e R2n : W(q,q) = Wj^ + i},
т. е.
Обозначим через t^+i момент
времени, когда траектория систе-
системы впервые попадет на эллипсо-
эллипсоид с индексом fc* + 1: {(q,q) G
е R2n : W(q,q) = Wk# + i}. Ниже
будет показано, что при выбран-
выбранном алгоритме управления траек-
траектория системы стремится к нача-
началу координат, поэтому такой момент
существует.
Положим g(?/c*+i) = (Zfc*+b (?(?fc*+i) = ^*+ь Обозначим через tk^+2
момент времени, когда траектория системы впервые попадет на эллип-
эллипсоид с индексом к* +2: {(q,q) E R2n : W(q,q) = Wk^+2}- Положим
Последовательность {?&}, к = fc* + 1, fc* + 2,..., определяет
моменты изменения коэффициентов обратной связи а, C в управ-
управлении C.2.1). Зададим значения этих коэффициентов на полуинтервале
времени [tk,tk+\) следующим образом:
и*
Рис. 37. Семейство эллипсоидов и
фазовая траектория
а{ = т(Зк.
C.3.3)
Начальные значения коэффициентов определим по формулам C.3.3)
при к = к*.
В фазовом пространстве q, q траектория движения рассмат-
рассматриваемой механической системы, таким образом, будет состоять
из отрезков траекторий различных систем дифференциальных
уравнений (рис. 37): к-и отрезок соединяет точки (qk,qk) и (фс+ьФс+i)
и отвечает системе вида C.1.2), C.2.1), в которой коэффициенты
усиления а = ctk, ft = Pk постоянны и определяются формулами
C.3.3). Все точки (qk,qk) лежат на соответствующих эллипсоидах
{(q,q)GR2n: W(q,q)=Wk}, к Ж.
Замечание 3.1. Траектория системы, как показано ниже, стре-
стремится к началу координат @,0), однако функция W, вообще
говоря, не является монотонно убывающей вдоль этой траектории.
Поэтому наряду с точками (qk,qk) траектория может иметь
и другие точки пересечения с эллипсоидами рассматриваемого
семейства. Предположим, например, что после назначения новых
коэффициентов в момент времени tk траектория системы стала
138 Гл. 3. Кусочно-линейное управление механическими системами
«удаляться» от терминального положения (О,0) и вновь пересекла
эллипсоид с номером к — 1 при некотором t' > tk. В момент t' индекс
к и коэффициенты од, /3 k не изменятся. Они примут новые значения
лишь тогда, когда траектория достигнет эллипсоида W(q, q) =
= Wfc+i: индекс к возрастет на 1 и, согласно формулам C.3.2),
C.3.3), коэффициент а увеличится в у/2 раз, а коэффициент C —
в 2 раза.
Замечание 3.2. Сформулированный закон управления не пред-
представляет собой синтеза, так как для нахождения управляющей
силы в каждый момент времени необходимо знать не только
текущее фазовое состояние системы, но и поведение траектории
в прошлом. При заданной матрице кинетической энергии
и сформулированном алгоритме изменения коэффициентов обрат-
обратной связи в законе управления C.2.1) траектория системы C.1.2)
определяется начальным состоянием и поведением возмущающей
силы Q(t,q,q). Однако для вычисления управления в каждый
момент времени достаточно знать лишь величину индекса к.
Действительно, зная индекс к, можно найти по формулам C.3.2),
C.3.3) коэффициенты од,/^, а затем и управляющую силу U
согласно C.2.1). Таким образом, управление представляет собой
функцию фазовых переменных q,q и целого числа к:
U(q,q,k) = -akq-Ckq. C.3.4)
Для реализации предложенного закона управления достаточ-
достаточно измерять фазовое состояние системы и хранить в памяти
вычислительного устройства лишь текущее значение индекса к.
В каждый момент времени индекс к равен номеру минимального
по размеру эллипсоида, на котором уже побывала траектория.
Всякий раз, когда происходит изменение коэффициентов, индекс к
увеличивается на 1.
§ 3.4. Обоснование алгоритма
Изучим поведение траектории к-и системы при некотором к > к*.
Интересующий нас участок этой траектории начинается в точке (дьФс)
в момент времени tk и заканчивается, в соответствии с алгоритмом,
в момент tk+\ на эллипсоиде W(q,q) = Wfc+i. Так как существо-
существование точки пересечения траектории с (к + 1)-м эллипсоидом пока
не доказано, будем считать tk+\ = оо, если такого пересечения нет.
Ниже будет показано, что tk+\ < оо.
Введем в рассмотрение семейство функций Ляпунова
Vk{q, q) = T{q, q) + ^q2 + ек(A(q)q, q), C.4.1)
где к — целое число, а параметр гк > 0 будет определен ниже.
§3.4. Обоснование алгоритма 139
Выражение для функции Vk(q,q) содержит матрицу инерции
A(q), которая предполагается неизвестной. Оценим через известные
величины значение этой функции в точке (q,q) фазового пространства.
Предположим, что число гк удовлетворяет условию
C.4.2)
Оценим функцию Vk(q,q) снизу с помощью соотношений C.1.5)
и неравенства
ekM\\q\\\\q\\ <^ Ч +-гЧ
следующим образом:
Отсюда, учитывая C.4.2), получаем неравенство
V*{q, q) < Vk(q, q), Vk(q, q) = I (pkq2 + mf). C.4.3)
Оценим теперь функцию Vk(q,q) сверху, используя соотношения
C.1.5) и неравенство
следующим образом:
f e
Так как m < 4M, то из C.4.2) вытекает е\М < [3k, откуда получаем
неравенство
Vk(q, q) < Vk(q, q), Vk(q, q) = /3kq2 + Mq\ C.4.4)
Установим соотношения, связывающие квадратичную форму
V+(q,q) и функцию W(q,q), множества уровня которой порождают
определенное выше семейство эллипсоидов. Покажем, что при любых
целых к справедливо равенство
2Vk(qk,qk) = Wk. C.4.5)
Для доказательства подставим выражение для коэффициента /3*. из
C.3.3) в выражение C.4.4) для функции Vk. Получим
<3-4-6)
140 Гл. 3. Кусочно-линейное управление механическими системами
По построению точка (qk,4k) лежит на эллипсоиде с номером к.
Отсюда и из определения C.3.1) функции W вытекают соотношения
Wk = W(qk, qk) = Mq\ + (мЩ + Ц- q\
Из C.4.6) и последнего равенства получаем C.4.5).
Равенство C.4.5) означает, что при любом к эллипсоид с номером к
совпадает с множеством уровня квадратичной формы V+(q, q), отвеча-
отвечающим значению Wk/2.
Пусть в момент времени t, tk <t < tk+\, система находится в состо-
состоянии (q,q). Оценим значение квадратичной формы V+(q,q) в момент
времени t через ее значение V+(qk,qk) в момент времени tk, т.е.
в момент первого пересечения рассматриваемой траектории системы
с fc-м эллипсоидом. Напомним, что в силу немонотонного поведения
функции W вдоль траектории точка (q, q) может лежать как внутри,
так и снаружи fc-ro эллипсоида (см. замечание 3.1 в § 3.3). Однако
в соответствии с алгоритмом и в силу условия t < tk+\ точка (q,q)
лежит вне (к + 1)-го эллипсоида, а точка (qk+\,qk+\) — на нем,
поэтому с учетом C.4.5) получаем
В силу C.3.2), C.3.3) и определения C.4.4) функции Vf имеют место
равенства
следовательно,
Из приведенных соотношений вытекает
Л/Т 1 Wh
v+(q>q) ^ fikq2 + -^- <f = о ^++1(^'^) ^ ~5~- C.4.7)
Отсюда, учитывая C.4.5), получаем следующую оценку значения квад-
квадратичной формы V+(q,q) в момент времени t через ее значение
qk) в момент времени tk'.
v+ (b Я) > 7 V+(qk, qk). C.4.8)
§3.4. Обоснование алгоритма 141
Обратимся теперь к вычислению производной Vk. Продифференцируем
функцию Vk в силу системы C.1.2), C.3.4). Получим
= -ekf3kq2-
п о Л
ак1 - ekA(q) - — 2^ Чг -щ_ \q, q) ~
- ekak(q, q) + (Q, ekq + q), C.4.9)
где / — единичная матрица.
Оценим отдельные слагаемые в выражении C.4.9). В силу C.1.5),
C.1.6) и C.3.2) имеют место неравенства
\\ekA(q)\\^ekM,
II п я л II C.4.10)
\\?к v^ 94 L nll и
Используя условия C.1.4), C.4.2) и соотношения C.4.4), C.4.5),
C.4.8) оценим последнее слагаемое в выражении C.4.9) следующим
образом:
+ q\\ < QE22 l2I 2
(a 2 ,
\Pkq -\-
*_(q,q) jMV*(qk,qk)
C.4.11)
Подставив C.4.10), C.4.11) в выражение C.4.9) и воспользовав-
воспользовавшись неравенством
\\ekak(q,q}\\ < e2kakq2 + °j q2,
приходим к оценке
(q, q) < -ek Ck - ekak y=== qz
?ky/MWk )
.2
142 Гл. 3. Кусочно-линейное управление механическими системами
Зададим параметр ек формулой
= mm < „;. ft , ^y™U(L==\ C.4.13)
W' из a
и введем в рассмотрение область
2>/2Wk
Лемма 3.1. Пусть выполнено условие
min
16л/ЮМ
2\/Ю
C.4.14)
в тех точках траектории, что лежат в области G, произ-
производная функции Vk(t) = Vk (q(t),q(t)) в силу системы C.1.2), C.3.4)
удовлетворяет неравенству
Vk(q,q) < _^^g2- ^«f. C.4.15)
Доказательство. Из определения C.4.13) параметра Sk вытекает
условие C.4.2), поэтому справедливы соотношения C.4.3), C.4.4),
C.4.11) и C.4.12).
Используя формулы C.3.3) и C.4.13), получаем
m/3k < fa
AM ^ 4 '
C.4.16)
* 8х/Щ 4 4
Из условия C.4.14) и формул C.3.3) вытекает
2 '
C.4.17)
л/Щ 16л/Щь 8
Из равенства C.4.13) и определения области G следует
4 *
C.4.18)
I\j V 'Ь1 V '*-'
Подставив неравенства C.4.16)—C.4.18) в оценку C.4.12), получим
C.4.15). Лемма доказана. ?
§3.4. Обоснование алгоритма 143
Лемма 3.2. Пусть выполнены условия C.4.14). Тогда участок тра-
траектории, отвечающий полуинтервалу времени [tk,tk+\), целиком
лежит в области G.
Доказательство. Проверим, что начальная точка траектории
{ЧкЛк) лежит в области G. По построению точка (qk,4k) принадлежит
эллипсоиду с номером к, т. е.
= Wk.
Следовательно, q\ < 2W%/Uq, откуда вытекает (дьФс) ? G.
Предположим, что утверждение леммы не выполнено, и пусть t' —
момент времени, когда траектория впервые достигла границы области
G, tf > tk. В силу леммы 3.1 функция Vk в области G строго убывает
вдоль решений системы C.1.2), C.3.4). Отсюда и из C.4.4), C.4.5)
получаем
V" (q(t),q(t)) < Vk(qk,qk) = Vk(q(tk),q(tk)) < V*(qk,qk) = -f.
С другой стороны, из соотношений C.4.3) вытекает неравенство
Vk{q{t'),q{t'))>\
По предположению точка q(t') лежит на границе области G. В силу
определения этой области имеем q2(tf) = 8W%/Uq. Отсюда, из C.3.3)
и последнего неравенства следует
Полученное противоречие и доказывает лемму. ?
Согласно неравенству C.4.3) при любом к функция Ляпунова
C.4.1) положительно определена, а из оценки C.4.15) вытекает,
что вне (к + 1)-го эллипсоида ее производная отрицательна и отделена
от нуля. Из этого можно заключить, что существует такой
момент времени tk+\ < оо, когда траектория попадет на эллипсоид
с номером к + 1.
Убедимся, что на участке траектории, отвечающем полуинтер-
полуинтервалу времени \tk,tk+\)> управляющая сила C.3.4) подчиняется
ограничениям C.1.3). Оценим с этой целью норму вектора U,
используя формулу C.3.3) для коэффициента а& и неравенство C.4.3),
следующим образом:
\\U(q,q,k)\\2 = \\Pkq + akqf < 2(C2kq2 + a\q2) =
144 Гл. 3. Кусочно-линейное управление механическими системами
Выше было показано, что функция Vk вдоль рассматриваемого
участка траектории не возрастает, следовательно, Vk(q,q) ^ Vk(qk,qk).
Учитывая соотношения C.3.3), C.4.4) и C.4.5), получаем
\\U(q,q,k)\\2 < 8CkVk(qk,qk) < 8/3kVk(qk,qk) = 4CkWk = t/02.
Ограничение выполнено C.1.3).
§ 3.5. Оценка времени движения
Из соотношений C.3.3), C.4.13) вытекает
ак V™ Щ Мгк
Воспользовавшись этой оценкой, продолжим неравенство C.4.15)
следующим образом:
Проинтегрируем данное неравенство на полуинтервале \ЬкЛк+\)-
Получим
A Y^\ C.5.1)
Оценим выражение, стоящее под знаком логарифма. Числитель
этого выражения, очевидно, удовлетворяет неравенству
В силу определений C.4.3), C.4.4) квадратичные формы Vk и Vk
связаны соотношением
откуда, учитывая C.4.5) и равенства /Зк = [Зк+\/2, Wk+\ = Wk/2,
получаем следующую оценку знаменателя:
Vk(qk+\,qk+\) >Vk(qk+uqk+i) ^ -^rVk(qk+uqk+i) =
т
_ mWk
~ 32М'
С помощью полученных оценок числителя и знаменателя неравен-
неравенство C.5.1) может быть продолжено следующим образом:
§3.5. Оценка времени движения 145
*fe+i-*fe<-ln—, C.5.2)
ek m
где число бк определено формулой C.4.13).
Нетрудно видеть, что выражения, стоящие под знаком min в
C.4.13) совпадают при к = 0. Если точка (quAk) лежит вне эллипсоида
с номером 0, т.е. к < 0, то
гп Щ у/т Uq
SMy/Щ \6DiWkV2Wk
а если точка (дьФс) лежит внутри нулевого эллипсоида или на нем,
т. е. к ^ 0, то имеет место обратное неравенство.
Предположим сначала, что к < 0. Подставим выражения для ек
и Wk в C.5.2). Получим следующую оценку времени движения вдоль
fc-ro отрезка траектории:
¦ln-^-. C.5.3)
m
Следовательно, время движения т\ системы от точки (qk,4k)
до точки (qo,qo), т-е- от эллипсоида с номером к до эллипсоида
с номером 0, не превышает величины
-1 B\/2\~к — 1
п-. — гт- \ Л о—Зг/2 _ 9л/9 ^ ^ (Ъ К А\
I \ — / > А, — I А\ А — . уО.0.4:J
i=k
Предположим теперь, что к ^ 0. В этом случае неравенство C.5.2)
принимает вид
-/- -/- <^ п- О — к>/Z /о с с\
Т>к-\-\ — ьк ^ Т ' Z ' , ^O.O.Oj
а время движения Т2 от эллипсоида с номером 0 до терминального
положения @,0) не превосходит суммы ряда
оо /~
^~"':/2 V -. C.5.6)
к
До сих пор предполагалось, что к > к*, и рассматривался
отрезок траектории, концы которого лежат на двух соседних
эллипсоидах из совокупности эллипсоидов, определенных выше.
Неравенства C.5.3), C.5.5) дают оценку времени движения системы
C.1.2), C.3.4) на таком отрезке. Пусть теперь к = к*. В точке
(#*>(/*)> отвечающей начальному состоянию системы, функция W
удовлетворяет неравенству
Поэтому точка (#*,(/*) не лежит, вообще говоря, на эллипсоиде
с номером к*. Тем не менее, в начальный момент времени t = 0
146 Гл. 3. Кусочно-линейное управление механическими системами
определим коэффициенты а& и /3& в управлении C.3.4) по формуле
C.3.3) при к = к*. С помощью рассуждений, аналогичных проведен-
проведенным выше, можно показать, что траектория системы C.1.2), C.3.4)
попадет на эллипсоид с номером fc* + 1, а время движения до этого
эллипсоида удовлетворяет неравенству C.5.3), если к* < 0, и нера-
неравенству C.5.5), если к* ^ 0. Полное время т* движения системы из
точки (#*,(/*) до терминального положения @,0) удовлетворяет нера-
неравенству т* < т\ +Т2, где величины т\ и т^ вычисляются по формулам
C.5.4), C.5.6) при к = к*.
§ 3.6. Достаточное условие приведения
Обратимся теперь к ограничениям, наложенным на внешние воз-
возмущения Q. Нетрудно видеть, что при к ^ 0, т. е. внутри эллипсоида
с номером 0, условие C.4.14) равносильно неравенству
C.6.1)
а вне нулевого эллипсоида C.4.14), т.е. при к < 0, эквивалентно
неравенству
2"^U° C.6.2)
Вдоль траектории, начинающейся в точке (#*,#*), наименьшее
значение индекса к равняется к*. Поэтому если точка (q*,q*) лежит
внутри нулевого эллипсоида или на нем самом, то к* ^ 0 и неравенство
C.6.1) представляет собой достаточное условие приведения рассматри-
рассматриваемой системы из этой точки в начало координат за конечное время
с помощью сформулированного выше закона управления. Если же
(q*,q*) лежит вне нулевого эллипсоида и к* < 0, то такое достаточное
условие дает неравенство C.6.2) при к = к*.
Предложенные достаточные условия приведения системы в начало
координат таковы, что максимально допустимая интенсивность
внешних возмущений Qo зависит от начального состояния системы:
чем дальше точка (#*,(/*) находится от точки @,0), тем меньше
должна быть величина Qq. Однако эти условия можно ослабить,
если модифицировать закон управления. Покажем, что для перевода
системы из (q*,q*) в начало координат достаточно выполнения лишь
условия C.6.1).
Выше было отмечено, что в качестве терминального состояния
может быть выбрана любая точка вида E,0) в фазовом пространстве
системы. При этом совокупность эллипсоидов, на которых происходит
изменение коэффициентов усиления, окажется сдвинутой на вектор
q, параметры же эллипсоидов останутся прежними. Предположим
§3.6. Достаточное условие приведения
147
сначала, что в начальный момент времени скорость системы удовле-
удовлетворяет неравенству
^ / /Л
C.6.3)
т.е. точка (q*,q*) лежит на эллипсоиде W(q — q*,q) = Wo или внутри
него (это нулевой эллипсоид, центр которого помещен в точку (#*,0)).
Применим изложенный алгоритм управления и переведем систему
в состояние (</*,0). Из сказанного выше вытекает, что для осуществ-
осуществления такого перевода достаточно выполнения условия C.6.1).
Выберем конечную последовательность точек (cjj,O) таких, что
% = q*,qj = O и
м
C.6.4)
Перевод системы из точки (#*,0) в начало координат осуществим за
J шагов, применяя каждый раз алгоритм управления заново. На j-м
шаге начальному состоянию си-
системы отвечает точка Ej_i,0),
а терминальному — точка (qj,O)
(см. рис. 38). Неравенство C.6.4)
означает, что при любом j точка
(<2j_i,0) лежит на нулевом эллип-
эллипсоиде с центром в (cjj,O) или внут-
внутри него. Следовательно, для осу-
осуществления перевода из Ej_i,0)
в (<2j,0) достаточно, чтобы вели-
величина Qo удовлетворяла условию
C.6.1).
Допустим теперь, что в на-
начальный момент неравенство
C.6.3) не выполнено. К постро-
построенному алгоритму управления
добавим еще один этап, который
предшествует всем остальным. Цель этого предварительного этапа —
снизить скорость движения системы до величины, удовлетворяющей
неравенству C.6.3).
Определим область
G\ = < (q, q):
Рис- 38- Пошаговый перевод системы
и зададим в ней управление следующим образом:
148 Гл. 3. Кусочно-линейное управление механическими системами
Из теоремы об изменении кинетической энергии системы, условия
C.6.1) и определения области G\ вытекает, что в G\ имеют место
оценки
гр( л ^ т .2 .
T{q,q) >-z-qz
Следовательно, система покинет область G\ за конечное время.
В момент достижения траекторией границы области G\ заканчивается
предварительный этап управления и начинается реализация описан-
описанного выше алгоритма пошагового перевода системы в терминальное
состояние.
Таким образом, неравенство C.6.1) представляет собой достаточное
условие приведения системы из произвольного начального состояний
(q*,q*) в начало координат.
Замечание 3.3. Сформулированный закон управления не зависит
от величины Qo, поэтому он может быть формально применен
и в случае, когда неравенство C.6.1) не выполняется. Компью-
Компьютерное моделирование динамики различных систем показывает,
что предложенный закон управления эффективен далеко за
пределами достаточных условий C.6.1). Это объясняется тем,
что условие C.6.1) гарантирует монотонное убывание функций Vk
вдоль траектории системы C.1.2), управляемой по закону C.3.4).
Однако функции Vk могут быть немонотонными, а траектории
системы будут при этом по-прежнему приходить в терминальное
состояние. Приведенные ниже результаты моделирования иллю-
иллюстрируют такое поведение системы.
§ 3.7. Результаты моделирования динамики
двузвенника
Предложенный закон управления был применен при численном
моделировании управляемых движений двузвенника на неподвижном
основании (рис. 15). Предполагалось, что двузвенник перемещает-
перемещается в горизонтальной плоскости, т.е. в отсутствие силы тяжести.
В качестве обобщенных координат системы были выбраны шарнирные
углы звеньев в неподвижной системе координат.
Матрица кинетической энергии двузвенника имеет вид
(А\
A3cos(qi-q2)
§3.7. Результаты моделирования динамики двузвенника 149
Расчеты проводились при следующих значениях параметров:
Ах = 13.9 кг-м2, А2 = 2Л кг-м2, А3 = 4 кг-м2.
Собственные числа матрицы инерции оказались заключены между
константами т = 1.8 кг-м2 и М = 14.2 кг-м2, а частные производ-
производные матрицы ограничены по норме постоянной D = 3. Максимальная
допустимая величина вектора управляющих моментов была выбрана
равной Щ = 500 Н-м. При моделировании вектор возмущающих момен-
моментов задавался постоянной вектор-функцией Q(t) = @; 30) Н-м.
Двузвенник переводился из начального состояния
q*\ = 0.5 рад, д*2 = 1 рад, g*i = <?*2 = 0 рад/с
в положение «горизонтально вытянутой руки»:
Ч\=Ч2 = Ч\=Ч2 = 0.
Значение функции W в точке, отвечающей начальному состоянию
системы, оказалось равным W(q*,q*) = 395, а величина, определяющая
нулевой эллипсоид, равна Wo = 837. Так как Wo/4 < W(q*,q*) < Wo/2,
то первое значение индекса к равно 1. Начальная точка траектории
лежит внутри нулевого эллипсоида, поэтому предварительные этапы
управления (торможение и последовательный перевод системы внутрь
нулевого эллипсоида с центром в начале координат) отсутствуют.
Достаточное условие приведения C.6.1) в данном случае принимает
вид Qo ^ 3.47 и при выбранным векторе возмущающих моментов
не выполняется. Тем не менее, двузвенник приходит в терминальное
состояние за конечное время (см. замечание 3.3 в § 3.7).
Система уравнений интегрировалась методом Рунге-Кутта.
Интегрирование прекращалось, когда в фазовом пространстве q, q
евклидово расстояние
/
между текущим состоянием системы и терминальным положением
становилось меньше 0.01.
На рисунках 39, 40 представлены графики зависимости фазовых
переменных системы от времени. Сплошная линия отвечает обобщен-
обобщенным координатам (рад), штриховая — скоростям (рад/с). Рисунок 39
описывает движение первого звена, рис. 40 — второго.
Сплошная линия на рис. 41 иллюстрирует поведение функции W
вдоль траектории. Из рисунка видно, что функция W не зависит
монотонно от времени.
На рис. 42 показана зависимость абсолютной величины вектора
управляющих моментов от времени (тонкая линия), а также величина
коэффициента усиления а (ступенчатая функция). За время интегри-
интегрирования уравнений коэффициенты обратной связи в управлении C.3.4)
изменились 12 раз.
150
Гл. 3. Кусочно-линейное управление механическими системами
Рис. 39. Первое звено
О 0.5 1 1.5
Рис. 40. Второе звено
800-
600-
5001
0 0.5 1
Рис. 41. Функция W
250-
0 0.5
1
1.5
Рис. 42. Модуль управляющего
момента и коэффициент а
В соответствии с алгоритмом коэффициенты обратной связи
аь и /3k выбираются так, чтобы при любых допустимых реали-
реализациях неизвестных параметров — элементов матрицы инерции
и компонент вектора возмущающих моментов — вдоль получающейся
траектории движения выполнялись ограничения на управление
C.1.3). Для конкретной механической системы область изменения
этих параметров значительно сужается и выбор коэффициентов
усиления может оказаться заниженным. Видно, что в рассматриваемом
случае реализовавшиеся управляющие моменты существенно меньше
максимальной разрешенной величины Щ. Поэтому было проведено
моделирование движения двузвенника, управляемого по тому же
закону, но с коэффициентами а^ и Ck, вдвое превышающими
§3.8. Управление двухмассовой системой
151
предписанные алгоритмом. На рис. 41 штриховой линией изображен
график зависимости функции W от времени, а на рис. 42 также
штриховой линией — абсолютная величина вектора управляющих
моментов при таком способе управления. Время достижения системой
терминального состояния сократилось почти вдвое, а управление
по-прежнему удовлетворяет ограничению C.1.3) со значительным
запасом.
ТП\
ТУТ
XXXXXX
Рис. 43. Двухмассовая упругая
система
§ 3.8. Управление двухмассовой системой
с неизвестными параметрами
Одну из важных областей теории управления механическими
системами составляют задачи об управлении системами, содержащими
так называемые структурные возмущения. Под структурными возму-
возмущениями понимают возникновение дополнительных степеней свободы,
непосредственно не управляемых, оказывающих влияние на движе-
движение всей системы в целом и ее управляемой части. При этом целью
управления, как правило, являет-
является лишь приведение управляемых
координат в заданное терминаль-
терминальное множество, значения же пере-
переменных, отвечающих этим дополни-
дополнительным степеням свободы, несуще-
несущественно.
В нескольких следующих па-
параграфах рассматриваются некото-
некоторые простые системы указанного
вида. Первая представляет собой
две массы, расположенные на го-
горизонтальной прямой и соединен-
соединенные пружиной (рис. 43). Обе мас-
массы испытывают действие сил сухого
трения с переменными, зависящи-
зависящими от положения, коэффициентами.
Предполагается, что массы, жест-
жесткость пружины и коэффициен-
коэффициенты трения неизвестны, но лежат
в заданных пределах. К первой
(несущей) массе приложена ограни-
ограниченная управляющая сила. Требует-
Требуется за конечное время привести несу-
несущую массу в заданное терминаль-
терминальное положение (состояние другой
массы в этот момент произвольно).
ТП\
Рис. 44. Груз на тележке
х
\
X X
Рис. 45. Маятник на тележке
152 Гл. 3. Кусочно-линейное управление механическими системами
Вторая система отличается от первой лишь тем, что здесь одно тело
лежит на другом (груз на тележке, рис. 44).
Третья исследуемая система также состоит из двух масс:
к несущему телу, перемещающемуся вдоль горизонтальной прямой,
подвешено другое тело (маятник на тележке, рис. 45). Исходные
предположения и цель управления — те же, что и в первом случае.
Во всех рассматриваемых случаях из-за наличия сухого трения
имеются зоны застоя. Вследствие этого существуют участки
траекторий, на которых исходную систему можно рассматривать
как систему, имеющую лишь одну степень свободы.
Применяемые законы управления основаны на описанном выше под-
подходе и используют линейную обратную связь с кусочно-постоянными
коэффициентами.
Рассмотрим систему из двух тел, расположенных на горизонтальной
прямой и соединенных пружиной. Массы тел т\ и Ш2, а также жест-
жесткость пружины со считаются неизвестными, но лежащими в заданных
пределах:
га< mi, га2 <М, C.8.1)
с < с0 < С. C.8.2)
Первое тело, массы гп\, будем называть несущим, а второе,
массы Ш2, — несомым. К первому телу приложена управляющая
сила и. Зафиксируем на прямой неподвижную систему координат
и обозначим через х координату первой массы в этой системе. Пусть
переменная ф описывает положение второй массы относительно первой,
причем положение ф = О отвечает недеформированному состоянию
пружины. Таким образом, в каждый момент времени величина ф
равняется удлинению пружины.
Предположим, что оба тела испытывают действие сил сухого
трения с переменными коэффициентами, зависящими от положения
(«шероховатость» прямой в различных местах неодинакова).
Обозначим силу трения, действующую на несущее тело, через /ь
а через /2 — силу трения, действующую на несомое тело.
В обобщенных координатах х, ф уравнения движения системы
имеют вид
ТП\Х = Соф + U + /ь
C.8.3)
Здесь
/2 = -si
§3.8. Управление двухмассовой системой 153
g — ускорение свободного падения. Коэффициенты трения j\(x) и
72(х + ф) будем также считать неизвестными, но удовлетворяющими
условиям
О < 7 < 71 (х)> ъ(х + Ф) < 7»
где 7 и 7 ~~ постоянные. Отсюда вытекают соотношения
I/,!, |/2KF, F = -?Mg. C.8.4)
Предполагается, что на управляющую силу и наложены ограничения
\и\ < Uo, C.8.5)
причем
Щ > 3F. C.8.6)
Фазовые координаты х, ф и скорости х, ф системы считаются
доступными измерению.
Задача 3.3. Пусть в начальный момент t = О система находится
в состоянии
х@)=х0, х@)=х0, Ф(О) = фо, ф@) = 0о-
Требуется за конечное время перевести систему C.8.3) на терми-
терминальное множество
х = х*, х = 0.
Не ограничивая общности, будем предполагать, что терминаль-
терминальному положению несущей массы соответствует точка х* = 0. Этого
можно добиться, выбрав с самого начала на прямой систему координат
с полюсом в той точке, в которую должна быть переведена первая
масса.
Управление будем строить на основе линейной обратной связи
по обобщенным координатам и скоростям (ПД-регулятора)
и =-ах-fix, C.8.7)
коэффициенты а, C > 0 считаем пока постоянными. Применение такого
закона управления эквивалентно введению в систему пружины жест-
жесткости /3 и вязкого трения с коэффициентом а. Эта пружина соединяет
несущее тело с неподвижным основанием, причем пружина недефор-
мирована, когда х = 0.
Полная энергия системы с учетом упругой энергии «фиктивной»
пружины имеет вид
Е(х, х, ф,ф) = - (mix2 + т2(х + фJ + (Зх2 +
154 Гл. 3. Кусочно-линейное управление механическими системами
Для краткости полную энергию в момент времени t на рассматри-
рассматриваемой траектории будем обозначать через E(t). Продифференцируем
E(t) в силу системы C.8.3), C.8.7). Получим
= -ах2 - ъ(х)т1д\х\ - 72 (ж + ф)т2д\х + ф\.
Нетрудно видеть, что полная энергия вдоль траектории системы
неотрицательна и не возрастает. Из-за наличия сил сухого трения
система имеет зоны застоя, т. е. состояния покоя, в которых обе массы
неподвижны, а пружины деформированы. В таких состояниях полная
энергия системы E(t) положительна, а ее производная E(t) равна
нулю. Отсюда вытекает соотношение
lim E(t) = E*, E* >0. C.8.8)
t^oo
Докажем несколько вспомогательных утверждений.
Лемма 3.3. Имеют место равенства
lim x(t) = 0, lim <fi(t) = 0. C.8.9)
t^oo t^oo
Доказательство. Заметим, что вторые производные х и ф
ограничены вдоль траектории, начинающейся в точке {xq,xq, фо, фо).
Действительно, полная энергия системы удовлетворяет неравенству
E(t) < ^@), t > 0, поэтому траектория системы лежит внутри
эллипсоида Е(х,х,ф,ф) = Е@), а фазовые координаты и скорости
ограничены. Следовательно, ограничены правые части уравнений
C.8.3), а с ними и вторые производные х и ф, т.е. существует такое
число D > 0, что
\х\, \ф\ ^D. C.8.10)
Убедимся, что справедливо первое из равенств C.8.9). Предполо-
Предположим противное. Пусть существуют такие число 5 > 0 и последователь-
последовательность {tk}, tk —> 00 при к —> оо, что |ж(?&)| ^ 5. Отсюда и из C.8.10)
вытекает, что на отрезках времени Ik = \ркЛк + VB-D)], к = 1,2,... ,
выполнено соотношение \x(t)\ > 5/2, а производная полной энергии
здесь удовлетворяет неравенству
Следовательно, полная энергия неограниченно убывает, что
противоречит равенству C.8.8). Первое из соотношений C.8.9)
доказано, второе доказывается аналогично. ?
§3.8. Управление двухмассовой системой 155
Лемма 3.4. Справедливо неравенство
, F_
" с0
(число F определено в C.8.4)).
Доказательство. Предположим противное. Пусть существуют
такие число 5 > О и последовательность {tk}, tk —> оо при к —> оо, что
со
Выберем произвольное число г; > 0. В силу леммы 3.3 найдется такое
t1 > 0, что \(j)(t)\ ^ v при t > t1. Тогда при tk > t1 на отрезках времени
1к = [tk,tk + 5/v] выполнено неравенство
Ш)\ ^ — + 5. C.8.11)
со
Отсюда и из условий C.8.2), C.8.4) получаем, что для достаточно
больших к при t ? Ik справедлива следующая оценка правой части
второго уравнения системы C.8.3):
-CO0 + /2| > Со\Ф\ ~ Ш > С
Сила /2 и, следовательно, правая часть второго уравнения C.8.3)
не являются непрерывными функциями времени, а функция </>(?)
непрерывна. В силу C.8.11) при достаточно больших к на каждом
из отрезков Ik знак непрерывной функции </>(?) постоянен. Из C.8.12)
вытекает, что знак правой части второго уравнения C.8.3) совпадает
со знаком функции </>(?) и, следовательно, постоянен на каждом
из этих отрезков. Следовательно, не меняется здесь и знак производной
x(t) + (j)(t) (которая является, вообще говоря, разрывной функцией
времени).
В силу C.8.3), C.8.12) имеет место соотношение
1712 ( x{t) + ф(ъ) I ^ Cq5, t ? Ik, tk > t . C.8.13)
Поэтому при достаточно больших к на отрезке времени Ik ско-
скорость x(t) + (f)(t) изменится не менее, чем на величину cq52/'(m^v).
Выбирая число v достаточно малым, приходим к выводу, что неравен-
неравенство C.8.13) выполняется на сколь угодно большом отрезке времени,
а модуль скорости второй массы \x(t) + <j)(t)\ может быть сколь угодно
велик. Это противоречит ограниченности полной энергии системы.
Лемма доказана. ?
Лемма 3.5. Справедливо неравенство
2F
lim x(t)|
156 Гл. 3. Кусочно-линейное управление механическими системами
Доказательство. Предположим противное. Пусть существуют та-
такие число 5 > О и последовательность {tk}, tk ~^ °° ПРИ k ~^ °°> что
Выберем число v из условия О < v < C5/а. В силу лемм 3.3 и 3.4
найдется такой момент времени t' > О, что при t > t1 выполнены
неравенства
|?(*)| <v<^,
C.8.14)
со
Тогда при tk > t1 на отрезках времени Ik = [?&,?& + S/v] справедливо
соотношение
9F
\x(t)\ ^^ + 35. C.8.15)
Оценим с помощью C.8.4), C.8.14) и C.8.15) правую часть первого
уравнения C.8.3) в момент времени t ? Ik, tk > t', следующим образом:
\соф + и + /i | = |со0 - аж - /Зж + /i | >
^ /3|ж| - а|ж| - со\ф\ - |/i| > /35. C.8.16)
Следовательно, при tk > t' на каждом из отрезков времени Ik верна
оценка
\т\>^- C-8.17)
Сила /i и, следовательно, правая и левая части первого уравнения
C.8.3) не являются непрерывными функциями времени, а функция
x(t) непрерывна. В силу C.8.15) при достаточно больших к на каждом
из отрезков Ik знак переменной x(t) постоянен. Из C.8.16) вытекает,
что знак правой части первого уравнения C.8.3) совпадает со знаком
переменной x(t) и, следовательно, постоянен на каждом из этих
отрезков. Поэтому знак функции x(t) также постоянен на каждом
из этих отрезков. Отсюда и из C.8.17) получаем, что скорость х
на каждом из отрезков Ik изменяется не менее, чем на величину
C52/(m\v). Выбирая v достаточно малым, приходим к выводу,
что скорость первой массы может быть сколь угодно велика
по модулю, что противоречит ограниченности полной энергии системы.
Лемма доказана. ?
Приведение системы в заданное терминальное множество
осуществим в два этапа. Сначала переведем первую массу в некоторую
окрестность точки х = 0 на прямой, одновременно уменьшив
полную энергию всей системы до достаточно малого уровня. Затем,
§3.9. Первый этап движения 157
рассматривая только первое из уравнений C.8.3), в котором упругую
силу соф будем трактовать как возмущение, приведем первую массу
в точку х = 0. При этом на каждом из этапов коэффициенты а, C
в управлении C.8.7) выбираются как кусочно-постоянные функции.
§ 3.9. Первый этап движения
Проведем некоторые вспомогательные построения. Положим
G(x, ф, ф) = Мх2 + М(х + фJ + Сф2
и рассмотрим функцию
И(т т rh rh) — О + (О2 + 9Т12т2) Х12 И Q П
Функция Н исполняет ту же роль, что и функция W при
построении управления в § 3.3. Величина Н вычисляется вдоль
траектории системы, и при достижении функцией Н некоторых заранее
заданных значений Нь происходит изменение коэффициентов усиления
в управлении. Отличие от описанной в § 3.3 процедуры изменения
коэффициентов состоит в том, что последовательность Нь не стремится
к нулю при к —> оо, как это было с последовательностью W&.
Пусть
Введем обозначения
t - ср2 п-— Н - 3^ И 9 2)
с1 Uo 1 — r]z
В силу C.8.6) число г] удовлетворяет неравенству г] < 1.
Предположим сначала, что в момент времени t = 0 выполнено
условие
Н0>Н*. C.9.3)
Зададим числовую последовательность Н^:
Hi - ? + (?2 + п2Н2 V/2 к - 1 2 И9 4)
Лемма 3.6. Числа Нк удовлетворяют соотношениям
Но > Н\ > Н2 > ... , lim Нк = -—Цг.
к^оо 1 - Г}2
Доказательство. Положим
158 Гл. 3. Кусочно-линейное управление механическими системами
и рассмотрим на полупрямой {z G R : z ^ z*} функцию
Легко убедиться, что h(z*) = z*. В силу определения C.9.2)
числа Н* и условия C.9.3) справедливо неравенство Щ > z*.
Используя определение C.9.2) величины г], условие C.8.6)
и неравенство (^2 -\-rj2z2y/2 > rjz, оценим производную функции h(z)
следующим образом:
Отсюда вытекает, что отображение h(z) сжимающее, а последова-
последовательность точек Щ, Н\ = h(Ho), B.^ = h(H\),... монотонно стремится
к неподвижной точке z* отображения h(z). Лемма доказана. П
Опишем алгоритм изменения коэффициентов в управлении C.8.7)
на первом этапе движения системы. Зададим в начальный момент
времени t = 0 коэффициенты усиления а^ и /Зо формулами
U2
ао = Л/^фо C.9.5)
Обозначим
Urn H(t) = Щ, H(t) = H(x(t), x(t),
Здесь предел вычисляется вдоль начинающейся в точке (жо,хсь 0о> 0о)
траектории системы C.8.3), управляемой по закону C.8.7) с коэффи-
коэффициентами C.9.5).
Лемма 3.7. Справедливо соотношение
Щ<нх.
Доказательство. В силу определения функции G(t) =
= G(x(t)^(t),<])(t)), утверждений лемм 3.3-3.5, условия C.8.2)
и обозначений C.9.2) имеет место неравенство
lim G(t) < ?, G(t) = G(x(t),
Отсюда, из определений коэффициента /Зо и числа г], а также в силу
утверждения леммы 3.5 получаем
V2
Лемма доказана. ?
§3.9. Первый этап движения 159
Убедимся, что вдоль начинающейся в точке (хо,хо,фо,фо)
траектории системы C.8.3), управляемой по закону C.8.7) с коэф-
коэффициентами C.9.5), выполнено ограничение C.8.5) на управляющую
функцию. Введем для этого обозначения
Е+(х, х, ф,ф) = - (Мх2 + М(х + фJ + /Зо^2 + Сф2) ,
C.9.6)
Е°_ (х, х, ф, ф) = — ( mi:2 + mix + 0J + /Зо^2 + о/>2 ) .
2 V /
В силу C.8.1), C.8.2) полная энергия Е° системы с учетом упругой
энергии «фиктивной» пружины жесткости /Зо вдоль рассматриваемой
траектории подчиняется соотношениям
E°_(t) < E°(t) < E+(t). C.9.7)
Положим Go = G(xo, фо, Фо)- Из определений функции Н и числа
Яо вытекает
т. е. число Яо — корень уравнения z2 — 2Gqz — 2UqXo2 = 0, рассмат-
рассматриваемого как уравнение относительно z. Следовательно, справедливо
равенство
Н2 - 2G0H0 - 2U2x02 = 0.
Разделим это равенство на Яо и преобразуем его, используя формулу
C.9.5) для коэффициента /Зо, к виду
=Я0.
Отсюда и из определений функций G и Е+ получаем
о)=Но. C.9.8)
Оценим теперь управляющую силу и, используя соотношения
C.9.5), C.9.6) и C.9.7), следующим образом:
\и\2 = \аох + (Зох\2 < 2(а20х2 + $х2) =
= 2C0(тх2 + C0х2) < ЩЕ°_ (х, х, ф, ф) < ЩЕ°(х, х, ф, ф).
Так как полная энергия E°(t) вдоль траектории системы не возрастает,
то оценка может быть продолжена с помощью C.9.7), C.9.8) так:
4C0E°(t)
Следовательно, ограничение C.8.5) выполнено.
160 Гл. 3. Кусочно-линейное управление механическими системами
В выражение C.9.1) для функции Н(х,х,ф,ф) входят только
известные параметры задачи, а все фазовые координаты и скорости по
условию доступны измерению. Следовательно, значение функции H(t)
может быть вычислено в любой момент времени. Обозначим
через t\ первый момент времени, когда значение функции H(t)
на рассматриваемой траектории станет равным Н\. Из определения
числа Щ и утверждения леммы 3.7 следует, что такой момент
существует.
Пусть
x(t\)=x\, x(t\)=x\, ф(и)=ф\, ф(и)=ф\.
Изменим в момент t\ коэффициенты усиления в управлении C.8.7).
Положим
А = ^, а{ = ^ф, C.9.9)
п\
и введем обозначение
ИтЯ(О = Я1*.
Рассуждая как и выше, можно показать, что вдоль начинающейся
в точке (х\,х\,ф\,ф\) траектории системы C.8.3), управляемой
по закону C.8.7) с коэффициентами C.9.9), выполнены ограничения
C.8.5) на управляющую функцию и и имеет место соотношение
Щ <Я2. C.9.10)
Замечание 3.4. Так как при определении величин Н^ и Щ
пределы функции H(t) вычисляются вдоль траекторий с различ-
различными начальными состояниями и различными коэффициентами
обратных связей в управлении, то эти величины, вообще говоря,
не совпадают.
Согласно C.9.10) найдется такой момент времени ?2, когда
значение функции H(t) на рассматриваемой траектории впервые станет
равным Я2. Изменим в этот момент коэффициенты в управлении
C.8.7), определив их формулами
я2
и т.д.
Траектория движения системы, таким образом, состоит из отрезков
траекторий различных систем дифференциальных уравнений:
fc-й отрезок соединяет точки (хк,хк,фк,фк) и (хк+\,Хк+\,Фк+\,Фк+\)
и отвечает системе C.8.3), управляемой по закону C.8.7) с коэф-
коэффициентами, задаваемыми выражениями
§3.10. Второй этап движения 161
Числа Нк определяются рекуррентными формулами C.9.4), причем
Нк = Н(хк,хк,фк,фк)=Н(гк), к = 0,1,... •
С помощью рассуждений, аналогичных проведенным выше для
к = О, можно показать, что при любом к > О на fc-м отрезке траектории
управляющая сила удовлетворяет ограничению C.8.5).
Теорема 3.1. Пусть выполнено условие C.9.3). Тогда существует
момент времени то, когда на траектории системы C.8.3), управ-
управляемой с помощью изложенного выше алгоритма, функция H(t)
примет значение Я*.
Доказательство. Функция H(t) непрерывна. В силу условия
C.9.3) в начальный момент t = О справедливо неравенство Я* < Яо,
а в силу леммы 3.6 имеют место соотношения
lim Hk < Я*, Яо > Hi > Я2 > ... .
Следовательно, найдется такое число к, что H(tk) > Я* > H(tk+\)
и функция H(t) на fc-м отрезке траектории примет значение Я*.
Теорема доказана. ?
Обозначим через то первый момент времени, когда функция H(t)
примет значение Я*. В момент времени то заканчивается первый этап
движения.
Если условие C.9.3) в начальный момент не выполнено, то первый
этап отсутствует. В этом случае Я(то) < Я*, и, полагая то = 0, пере-
переходим сразу ко второму этапу.
§ 3.10. Второй этап движения
На втором этапе движения применим закон управления, предло-
предложенный в § 3.3 для приведения в заданное положение лагранжевой
системы общего вида с неизвестной матрицей кинетической энергии.
Рассмотрим отдельно движение первой массы. Оно подчиняется
уравнению
/i. C.10.1)
Величину Q будем трактовать как возмущение.
Как и прежде, будем управлять движением первой массы
с помощью закона C.8.7), в котором коэффициенты усиления являются
кусочно-постоянными функциями. Опишем алгоритм изменения этих
коэффициентов.
Введем в рассмотрение функцию
W(x,x) = Мх2 + (М2х4 + 2?/0VI/2
и положим
Wn
Wo = W(x(to),x(to)), Wk = ^, k^ 1,2,... .
6 Ф. Л. Черноусько и др.
162 Гл. 3. Кусочно-линейное управление механическими системами
Зададим в момент времени tq коэффициенты а и /3 с помощью формул
Пусть т\ — первый момент времени, когда функция W{t), вычис-
вычисленная вдоль траектории, станет равной W\. Положим
обозначим через т^ первый момент времени, когда функция W(t)
станет равной W^ и т.д. Таким образом, последовательность т&,
к = 0,1,..., задает моменты изменения коэффициентов. В момент
времени т& функция W(t) впервые принимает значение Wk, а сами
коэффициенты определяются формулами
то есть, каждый раз коэффициент /3 увеличивается в 2 раза, а коэф-
коэффициент а — в у/2 раз.
Замечание 3.5. В §3.3 при описании закона управления последо-
последовательность Wk, задаваемая соотношениями C.3.2), зависела толь-
только от параметров задачи D, М и Щ. Следовательно, семейство
эллипсоидов, на которых происходило изменение коэффициентов,
также определялось лишь этими параметрами. В данном случае
применяется модифицированный закон управления. Отличие состо-
состоит в том, что теперь эллипс с индексом 0 совпадает с множе-
множеством уровня функции W, отвечающим значению этой функции
в начальный момент времени. Таким образом, семейство эллипсов,
на которых происходит изменение коэффициентов обратной связи,
определяется начальным состоянием системы, а траектория управ-
управляемого движения на втором этапе всегда начинается на эллипсе
с индексом 0.
В соответствии с результатами § 3.6 для приведения первой массы
в начало координат за конечное время с помощью данного алгоритма
достаточно выполнения условия
^Щ C.10.2)
При этом вдоль траектории сохраняется ограничение C.8.5).
Проверим, что условие C.10.2) выполнено. Оценим для этого
полную энергию Ек всей системы C.8.3) на каждом из отрезков
второго этапа движения. Обозначим через Е энергию первой массы
§3.10. Второй этап движения 163
на fc-м отрезке траектории с учетом упругой энергии «фиктивной»
пружины жесткости /3k'.
С помощью алгебраических преобразований нетрудно убедиться в
справедливости соотношений
~Ек{х, х) < Я+(ж, х), АЁк+(тк) = Wk,
C.10.3)
Е+(х,х) = У- (Мх2 + (Зкх2), к = 0, 1,... .
В силу определения C.9.1) функции Н и условий C.8.1), C.8.2) в
момент начала второго этапа энергия всей системы без учета упругой
энергии «фиктивной» пружины удовлетворяла неравенствам
а в силу C.10.3) упругая энергия «фиктивной» пружины — неравен-
неравенствам
Р0 2/ \ —^ / \ ^0
—- х (то) < EAtq) = ——.
2 4
Следовательно,
На каждом из промежутков времени [rb%i), /с = 0, 1,...,
коэффициенты усиления в управлении C.8.7) постоянны, поэтому
полная энергия всей системы не возрастает. В момент r^+i жесткость
«фиктивной» пружины /3 испытывает скачок, увеличиваясь в 2 раза,
поэтому упругая энергия «фиктивной» пружины в этот момент изме-
изменяется на величину
пк+1 = !(&+, - (Зк)х\тк+Х) =
k
В силу определения полной энергии Е и соотношений C.10.3)
величина тг/c+i удовлетворяет неравенству
164 Гл. 3. Кусочно-линейное управление механическими системами
Суммарное приращение упругой энергии «фиктивной» пружины,
происходящее за счет мгновенного изменения жесткости, не превосхо-
превосходит суммы ряда
1^ 2^+4 ~ 16 '
/с=1
Отсюда и из C.10.4) вытекает, что при любом t ^ то полная энергия
всей системы E(t) подчиняется ограничению
Из определений функций W и Н получаем
Wo = W(t0) < Я(г0) = Я,.
Учитывая данные соотношения и условие C.8.2), приходим
к заключению, что деформация пружины, соединяющей массы т\
и ni2, удовлетворяет неравенству
Следовательно, величина возмущений Q в уравнении C.10.1) на про-
протяжении всего второго этапа подчиняется ограничению
и, учитывая выражения C.9.2) для ? и ту, ограничению
о /о
Подставив в неравенство C.10.2) вместо \Q\ величину Qq, получим
следующее достаточное условие приведения первой массы в начало
координат:
Таким образом, справедлива следующая теорема.
Теор ема 3.2. Пусть параметры задачи т, М, с, С, F, Щ удовле-
удовлетворяют условию C.10.5). Тогда предложенный алгоритм управле-
управления приведет первую массу в начало координат за конечное время.
§3.11. Система «груз на тележке» 165
§ 3.11. Система «груз на тележке»
Рассмотрим механическую систему, состоящую из двух тел, соеди-
соединенных пружиной. Первое тело перемещается вдоль горизонтальной
прямой, а второе расположено на первом и также может совершать
горизонтальные перемещения (рис. 44). Уравнения движения такой
системы имеют вид
ГП\Х = СОф + U + /i - /2, Ш2(ж + ф) = -СОф + /2.
Здесь х — координата первой массы, ф — координата второй массы
относительно первой, причем положение ф = 0 отвечает недеформиро-
ванному состоянию пружины. Через f\ и /2 обозначены силы трения
между несущим телом и основанием и между телами соответственно:
i:Oi(x)(mi + m2)
/2 = -s
Предположения относительно масс, жесткости пружины и коэффици-
коэффициентов трения остаются прежними. Ограничение C.8.5) на управляю-
управляющую силу также остается, однако теперь будем считать
U0>2V5F. C.11.1)
Требуется за конечное время привести несущее тело в положение
х = х = 0.
Рассуждая как и выше, можно доказать справедливость следующих
утверждений:
lim x(t) = 0, lim <fi(t) = 0,
, , SF
-, lim |x(t)K ^
Co t^oo p
Применим к системе описанный выше алгоритм управления.
Учитывая новые ограничения C.11.1) на величину F, положим
Выражения для ? и Н* остаются прежними. На первом этапе система
приводится во множество
{(х,х,ф,ф) eR4: Н(х,х,ф,ф)^Н*},
на втором этапе несущее тело достигает терминального положения.
Динамика несущего тела на втором этапе по-прежнему описывается
уравнениями C.10.1), однако возмущения Q принимают вид
166 Гл. 3. Кусочно-линейное управление механическими системами
Величину Q теперь можно оценить так:
Достаточные условия приведения несущего тела в терминальное поло-
положение принимают вид
§ 3.12. Система «физический маятник на тележке»
Перейдем теперь к управлению механической системой, состоящей
из движущегося вдоль горизонтальной прямой тела массы т\ и под-
подвешенного к нему тела массы тп2 (рис. 45). Рассматривается плоское
движение.
Введем прямоугольную систему координат, ось абсцисс которой
лежит на данной прямой. Динамика системы описывается уравнениями
(mi + m^x + m^l cos фф = и + т^^шфф2 + f(t,x),
C.12.1)
2 /i(t, ф).
Здесь ж — координата первой массы на прямой, ф — угол между
вертикалью и прямой, соединяющей точку подвеса и центр инерции
второго тела, / — расстояние от точки подвеса до центра инерции, J —
момент инерции второго тела относительно центра инерции.
Через f(t,x) обозначена сила сухого трения, действующая со сторо-
стороны неподвижного основания на первое тело, а через /i(t, ф) — момент,
обусловленный сухим трением в точке подвеса. Предполагается, что /
и \i неизвестны и удовлетворяют условиям
C.12.2)
По-прежнему считаем, что массы тел гп\ и тп^ неизвестны, но лежат
в заданных пределах C.8.1), что на управляющую силу и наложены
ограничения C.8.5), C.8.6) и что все фазовые переменные х, х, ф, ф
доступны измерению. Требуется за конечное время привести несущее
тело в положение х = х = 0.
Пусть в начальный момент t = 0 система находится в состоянии
х@)=х0, х@)=х0, Ф(О) = фо, ф@) = 0о-
Как и в предыдущем случае, управление ищется в виде линей-
линейной обратной связи C.8.7) с кусочно-постоянными коэффициентами.
Введем «фиктивную» пружину жесткости /3, соединяющую первое тело
§3.12. Система «физический маятник на тележке» 167
и неподвижное основание, причем положение х = О отвечает ее неде-
формированному состоянию. Полная энергия системы с учетом упругой
энергии «фиктивной» пружины имеет вид
i + т2)х2 + (ш2/2 + 3)ф2 + 2т21хфcos ф + (З
а производная i? в силу системы C.12.1) — вид
Е = —ах2 — \fx\ —
С помощью рассуждений, аналогичных проведенным в § 3.8, можно
доказать справедливость следующих соотношений:
lim
C.12.3)
lim x(t) = 0, lim 6(t) = 0.
t^oo t^oo
Лемма 3.8. Имеет место неравенство
м , F
Доказательство. Предположим противное. Пусть существуют та-
такие число 5 > 0 и последовательность {?&}, tk ^ оо при /с —> оо, что
|a:(tfc)|> | + 45. C.12.4)
Обозначим через Ф(?) левую часть первого уравнения C.12.1):
Ф(?) = (mi + rri2)x + Ш2/0 cos 0.
Выберем число г; из условий
C5 2 /35
0< v < —, v2 < —-.
В силу C.12.3) найдется такое tr > 0, что |0(?)|, \x(t)\ ^ v при t > t''.
Подставим выражение C.8.7) для управления и в первое уравнение
C.12.1) и оценим слагаемые в правой части на отрезках времени
h= \tk,tk + ^\ , tk>t',
учитывая C.12.4), следующим образом:
\/Зх\ > F + 3/35, |аж| < av < /35, \гп21ф2 sin 0| < Ш2/^2 < /35.
168 Гл. 3. Кусочно-линейное управление механическими системами
Отсюда и из C.12.2) вытекает
|Ф(?)| > C5 > О, t e Ik, tk>tf,
следовательно,
г /ЯЛ2
C.12.5)
/352
Функция Ф(?) не является непрерывной, однако на каждом из
отрезков Ik, tk > t', знак функции Ф(?) постоянен, так как совпадает
со знаком переменной x(t), которая непрерывна и не обращается в нуль
в силу условия
\Cх\
Поэтому
sin c/)dt+( (mi + т,2)ж + гп21ф cos <
tk+5/v
tk
Ik
Оценим слагаемые в выражении для интеграла от Ф(?) следующим
образом:
(mi
<С 4Mv,
тп^гф cos 0
tk+5/v
tk
2Mlv,
sin фdt
MISv.
Следовательно,
что противоречит неравенству C.12.5) при достаточно малых v. Лемма
доказана. П
Перевод несущего тела в заданное терминальное положение осуще-
осуществим, как и прежде, в два этапа. Положим
G(x, ф,ф) = \
М(\х\ + 1\ф\J
Mgl(\ - cose
§3.12. Система «физический маятник на тележке» 169
и рассмотрим функцию
/ тт2 \ 1/2
Н(х, х, ф, ф) = G + ( G2 + -^ х2 ) . C.12.6)
Пусть
Я(жо, #о> 0о, 0о) = Щ, G(io» 0о, 0о) = Go.
Зададим в начальный момент времени коэффициенты усиления ао и /Зо
в управлении C.8.7) формулами
2//о
Введем обозначения
Е5.(ж, х, ф, ф) = G(x, ф, ф) + у х2,
C.12.7)
?° (ж, ж, 0, ф) = | ("mi:2 + J02) + шр/( 1 - cos ф) + у ж2.
Нетрудно видеть, что полная энергия Е° системы с учетом
упругой энергии «фиктивной» пружины жесткости /Зо подчиняется
соотношениям
E°_(t) < ?°(?) < El(t). C.12.8)
В силу C.12.6) число Но является корнем квадратного уравнения
U2
Но — 2GoHo —— х0 = 0,
рассматриваемого как уравнение относительно Щ. Разделив это урав-
уравнение на Но и воспользовавшись формулой для /Зо и выражением
C.12.7) для Е+, получим равенство
2Е1(хо,хо,фо,Фо)=Но- C.12.9)
Рассуждая как и выше, покажем с помощью соотношений C.12.7)-
C.12.9), что вдоль начинающейся в точке (хо,хо,фо,фо) траектории
системы C.12.1), C.8.7) с коэффициентами ао, /Зо выполнены ограни-
ограничения C.8.5):
и\2 < 2(а2х2 + C2х2) = 2{30{тх2 + C0х2) < АC0Е°_ (х, х, ф, ф) <
0) = 2/30Я0 =
170 Гл. 3. Кусочно-линейное управление механическими системами
Введем обозначения
^f Ц C.12.10)
^о 1 - Т
В силу C.8.6) число г] удовлетворяет неравенству г\ < 1. Предполо-
Предположим сначала, что в начальный момент выполнено условие
Н0>Н*. C.12.11)
Из вида C.12.6) функции Н(х,х,ф,ф), утверждения леммы 3.8,
соотношений C.12.3) и формулы для коэффициента Д> вытекают нера-
неравенства
ТЕГ Я (i) < ? + (> + Щ j < i + (С2 + ^2
Положим
Обозначим через t\ первый момент времени, когда значение функции
H(t) на рассматриваемой траектории станет равным Н\. Изменим
в момент t\ коэффициенты усиления в управлении C.8.7). Положим
и т.д.
Траектория движения системы, как и в случае двухмассовой
упругой системы, состоит из отрезков траекторий различных систем
дифференциальных уравнений: к-и отрезок отвечает системе C.12.1),
управляемой по закону C.8.7) с коэффициентами, задаваемыми
формулами
Ык = \/т(Зк,
н*~2Нк'
причем на каждом из отрезков выполнено ограничение C.8.5).
Числа Нк определяются рекуррентно с помощью формул
11)*, fc=l,2,...,
и удовлетворяют соотношениям
Но > Нх > Н2 > ... , lim Нк = -^ < Я,.
к^оо 1 — TJZ
Следовательно, справедлива следующая теорема.
Теор ема 3.3. Пусть выполнено условие C.12.11). Тогда существу-
существует момент времени то, когда на траектории системы C.12.1),
управляемой с помощью изложенного выше алгоритма, функция
H(t) примет значение Я*.
§3.12. Система «физический маятник на тележке» 171
В момент времени tq начинается второй этап движения. Если
условие C.12.11) в начальный момент не выполнено, то мы полагаем
т0 = 0 и переходим сразу ко второму этапу.
Выделим из системы C.12.1) уравнение движения первой массы.
Умножим для этого второе уравнение на га2/ cos ф/(га2/2 + J) и вычтем
его из первого. Получим
/.. , ~ , , m2l2 cos2 ф
17lX = U-\-Q, 171 = 171 \ + 1712 — 1712 ~, То 7V >
{17121 + J)
/«2 TTl2gl
г- COS ф ~\- 7Т126 Sin ф[ф + -, о г COS ф
C.12.12)
Величину Q будем трактовать как неизвестную возмущающую
силу.
На втором этапе используем предложенный в § 3.3 алгоритм управ-
управления склерономной механической системой. Исследуемая в данный
момент система представляет собой систему с одной степенью свободы.
В отличие от случая, рассмотренного в § 3.3, в уравнении C.12.12)
величина т', выступающая в роли матрицы кинетической энергии,
зависит от переменной ф(г). Переменная ф(г) является фазовой пере-
переменной для исходной системы C.12.1), однако не является таковой для
системы C.12.12), поэтому возможность применения указанного алго-
алгоритма требует дополнительного обоснования. Приведем кратко такое
обоснование.
По предположению, величина ф измеряется в каждый момент
времени, поэтому в дальнейших рассуждениях функция ф(?) считается
известной. В силу C.8.1) тг удовлетворяет неравенствам
т < шх < 2М.
Введем в рассмотрение функцию
/ г/2
W(x, х) = 2Мх2 + 4М2х4 + -? х2
и положим
Wo = W(x(to),x(to)), Wk = ^, k= 1,2,... .
Пусть Tk — первый момент времени, когда функция W(t),
вычисленная вдоль траектории, станет равной W&. Зададим в момент
времени т^ коэффициенты а и C с помощью формул
U2
172 Гл. 3. Кусочно-линейное управление механическими системами
Множества уровня W(x, x) = Wk функции W представляют собой
семейство эллипсов в фазовой плоскости (х,х), стягивающихся
к началу координат @,0) при к —> оо.
Положим
х(тк) = хк, х(тк) = хк.
Убедимся, что траектория, начинающаяся в момент тк в точке (хк,хк),
попадет на эллипс с номером к + 1.
Рассмотрим функцию Ляпунова
тгк/ .\ т' .о Рк 9 / •
V {х,х) = —-х +^-ж +?ктхх, ек =
При г/с ^ t < Tfc+i имеют место соотношения:
т//с/ • \ _ ± i о 2 , -2 V^(t г) - Bur2 + 2Mrz-
т/~к ( ' \ \^ к> ОТ/"^ / * А Т/Г/" 7 М 1
+ 8 ' + fc' fc fc' »»••••
C.12.13)
Для доказательства последнего соотношения заметим, что число
1/2
Wk = W(xk, xk) = 2Мх\ + (Ш2х\ + ^ х2
очевидно, является корнем квадратного уравнения
рассматриваемого как уравнение относительно Wk. Разделив это урав-
уравнение на Wk и воспользовавшись формулами для (Зк и V+, получим
требуемое равенство.
Выражение для производной функции Vk в силу системы C.12.12)
и закона управления C.8.7) имеет вид
Vk(x, х) = -екCкх2 + (ектг - екак)хх -
- (ак - ekmf -%\x2 + Q(skx + x). C.12.14)
§ 3.12. Система «физический маятник на тележке»
173
Справедливы неравенства
ekakxx\ < e{akxz + —
Пусть величина Q удовлетворяет условию
32V5M
C.12.15)
C.12.16)
Оценим последнее слагаемое в выражении C.12.14) следующим
образом:
\Q(?kX-
1/2
0 V
1/2
I 8M
1/2
2Мх2)
2V2M
Z2MJW,
Подставив полученное неравенство и неравенства C.12.15)
в C.12.14), получим
-?к Рк ~ ?/сОД -
-4ек\т'\)х2-
-гкт -
9\т'
х\
V 4 ^ 16л/Щ 16
Потребуем, чтобы производная т! подчинялась ограничению
:у. C.12.17)
Так как а^ < од, /с = 1,2... , то |mx| ^ од/8. Принимая во внимание
C.12.13) и соотношения
4 '
= X
~ 4'
mC/0
174 Гл. 3. Кусочно-линейное управление механическими системами
приходим к оценке
VK{x,x) < —xz - —xz <
< _Z^ (я, Ж2 , 2Mi;2>l - -7—Vk(t) < -7—Vk(
64 V f У 64 +^ ' 64
Следовательно,
^ 64 , Vk(rk)
В силу C.12.13) числитель под знаком логарифма удовлетворяет нера-
неравенству
Используя равенство /3&+1 = 2/3^ и соотношения C.12.13), знаменатель
оценим следующим образом:
= i (/3fcx2fc+1
Отсюда вытекает, что время движения от fc-ro до (к + 1)-го эллипса
удовлетворяет оценке
64 , 16М Мд/Щ o9-fc/21n 16M
^ Ш = ———— Z I 1П ,
i?k rn 7 у/т Uq m
а общее время движения системы до начала координат не превосходит
суммы ряда из правых частей полученного неравенства. Этот ряд
сходится, поэтому время движения конечно.
Найдем условия, при которых на протяжении всего второго этапа
движения выполнено неравенство C.12.16). В силу определения
функции G и условия C.8.1) в момент то начала второго этапа энергия
всей системы без учета упругой энергии «фиктивной» пружины
удовлетворяла неравенствам
п\ + тп2)х1(то) + (ш2/2 -
§3.12. Система «физический маятник на тележке» 175
а в силу C.12.13) упругая энергия «фиктивной» пружины — неравен-
неравенствам
А) 2/ ч^1 т/0/ ч W0
На каждом из промежутков времени [т&,т&+1), /с = 0, 1,... , коэффици-
коэффициенты усиления в управлении C.8.7) постоянны, поэтому полная энер-
энергия всей системы не возрастает. В момент т&+1 жесткость «фиктивной»
пружины C испытывает скачок, увеличиваясь в 2 раза, поэтому упругая
энергия «фиктивной» пружины в этот момент изменяется на величину
nk+l = |(/3fc+1 - Ck)x2(Tk+l) = ^±V(Tfc+i)-
В силу соотношений C.12.13) величина тг/c+i удовлетворяет неравен-
неравенству
1 к\ Wk+X Wo
Суммарное приращение упругой энергии «фиктивной» пружины, про-
происходящее за счет мгновенного изменения жесткости, не превосходит
суммы ряда
2^ 2k+4 16 '
Следовательно, при любом t ^ tq полная энергия всей системы E(t)
подчиняется ограничению
В силу определений функций G, W и Н имеем
Мх2
( U2 \
W(x, х) < 2G + ( AG2 + -j- х2 \ < 2Н(х, х, ф, ф).
Так как в момент то начала второго этапа Я(то) < Я^, то
откуда получаем, что при любом t ^ tq полная энергия всей системы
E(t) подчиняется ограничению E(t) ^ 9Я*/8, а угловая скорость ф —
ограничению
12 ^ 2E(t) 9H*
J \\m2l1 + J)
10 1 ял
176
Гл. 3. Кусочно-линейное управление механическими системами
Оценим отдельные слагаемые в выражении для возмущений Q
в уравнении C.12.12) следующим образом:
т2
l2g cos ф sin ф
sim
9га2/Я*
m2l2 + J
m2g < Mg,
< 9ff«
" ^ 4/ '
т21ц cos ф
m2l2 + J
Подставив полученные неравенства, а также формулу C.12.10) для Н*
в выражение для Q, после некоторых преобразований приходим
к соотношению
Подставив в неравенство C.12.16) вместо \Q\ величину Q\, получим
C.12.19)
Выведем теперь условия, которые гарантируют выполнение неравен-
неравенства C.12.17). Оценим для этого производную т! с помощью соотно-
соотношений C.12.12) и C.12.18), а величину ао/8 — с помощью формул для
коэффициентов ао, /?о и неравенства Wq ^ 4Я* следующим образом:
= 2-
Шп!
) cos ф sm (
m2/2 + J
2(ml2 + J)
1/2
8
8
Для выполнения условия C.12.17) достаточно потребовать
J)
^
Подставив в последнее неравенство выражение C.12.10) для Н*, после
некоторых преобразований получим следующее соотношение, которое
гарантирует выполнение условия C.12.17):
U2 m(ml2 + J)
(Ц2 - 9F2J ^ 2uM4g2l2 '
C.12.20)
Таким образом, справедлива следующая теорема.
Теор ема 3.4. Пусть параметры задачи удовлетворяют условиям
C.12.19), C.12.20). Тогда предложенный алгоритм управления при-
приводит несущую массу в заданное положение за конечное время.
§3.13. Результаты моделирования 177
Замечание 3.6. Неравенства C.12.19), C.12.20) — достаточ-
достаточные условия приведения системы в заданное терминальное мно-
множество — накладывают довольно сильные условия на исходные
параметры задачи. Это объясняется грубостью некоторых оценок,
использованных в ходе обоснования алгоритма, а также тем,
что всегда предполагалось «наихудшее» поведение системы в рам-
рамках наложенных ограничений. Кроме того, данные неравенства
гарантируют монотонное убывание функций Vk вдоль траекто-
траектории системы, тогда как функции Vk могут быть немонотонными,
а траектории при этом могут по-прежнему приходить в терми-
терминальное состояние. Заметим, однако, что в сам алгоритм управ-
управления приведенные достаточные условия не входят, поэтому алго-
алгоритм может быть формально применен для решения задач с любым
соотношением параметров. Численное моделирование показывает
эффективность данного закона управления для гораздо более широ-
широкого класса систем, чем те, что удовлетворяют условиям C.12.19),
C.12.20).
§3.13. Результаты моделирования
Проиллюстрируем работу предложенного алгоритма управления.
Приведем сначала результаты компьютерного моделирования ди-
динамики системы, изображенной на рис. 43. Ее уравнения движения
C.8.3) интегрировались методом Рунге-Кутта при следующих значе-
значениях параметров:
М = mi = 10 кг, т = т^ = 5 кг,
С = с0 = 10 Н/м, 7 = 71 = 72 = 0.2.
Величина Щ была выбрана равной 100 Н. Система переводилась
из начального состояния
хо = 1 м, фо = —0.5 м, хо = фо = 0 м/с
в терминальное множество х = х = 0, т. е. требовалось остановить
первую массу в начале координат. Интегрирование уравнений прекра-
прекращалось, когда величина (х2 + i;2I/2, равная евклидову расстоянию
от проекции текущей точки фазовой траектории системы на подпро-
подпространство (х,х) до начала координат, становилась меньше 0.001.
Нетрудно убедиться, что при выбранных соотношениях параметров
условия C.10.2) — достаточные условия приведения системы в терми-
терминальное положение — не выполнены. Тем не менее траектория системы
C.8.3), управляемой с помощью предложенного алгоритма, приходит
в терминальное множество за конечное время.
178
Гл. 3. Кусочно-линейное управление механическими системами
Основные характеристики дви-
движения, вычисляемые при реализа-
реализации алгоритма, оказались равными:
Яо = 143.9 кг-м2/с2,
Я* = 706.8 кг-м2/с2.
Так как Яо < Я*, первый этап
движения отсутствует.
Рис. 46 описывает поведение фа-
фазовых переменных системы. Жир-
Жирные кривые соответствуют первой
(несущей) массе, тонкие — второй
массе. Сплошные линии представ-
представляют собой графики зависимостей
координат х, ф обеих масс от вре-
времени, штриховые — графики скоро-
скоростей. Из рисунка видно, что график скорости первой массы х и график
скорости ф второй массы относительно первой имеют изломы, обуслов-
обусловленные разрывным поведением управляющей силы.
Тонкой линией на рис. 47 изображен график зависимости абсолют-
абсолютной величины управляющей силы от времени, а жирной — поведение
коэффициента а (ступенчатая функция). Несмотря на то, что коэффи-
коэффициенты усиления а, C в управлении C.8.7) неограниченно возрастают
(за время интегрирования уравнений коэффициенты обратной связи
в управлении изменились 16 раз), величина управляющей силы и,
как видно из рисунка, удовлетворяет условию C.8.5) со значительным
запасом.
-1
-1.5
Рис. 46. Зависимость координат и
скоростей от времени
120 п
80 ¦
40 ¦
0
0.5
1
Рис. 47. Управляющая сила и коэф-
коэффициент а
1 -
0.5 -
n
-0.5-
-1 ¦
/
/
/
/
/
\
\
\
0.5
\
V
1
* t
f*
.5
Рис. 48. Система «груз на тележке»:
координаты и скорости
§ 3.14. Управление реономными системами
179
На рис. 48 приведены результаты моделирования системы «груз
на тележке». Как и выше, сплошные линии отвечают координатам
масс х, ф, штриховые — скоростям х, ф, жирные кривые соответствуют
первой (несущей) массе, тонкие — второй.
Как уже отмечалось, из-за присутствия сил сухого трения систе-
система имеет зоны застоя. Из рисунка видно, что в процессе движения
вторая масса «залипает» и на протяжении некоторого отрезка времени
остается неподвижной относительно первой, вновь приходя в движение
на заключительном этапе.
§3.14. Кусочно-линейное управление реономными
механическими системами. Постановка задачи
В следующих параграфах рассматривается реономная механическая
система, т. е. система, кинетическая энергия которой представляется
в виде полного квадратичного полинома с коэффициентами, явным
образом зависящими от времени
T(t, ЧА) = \ (A(t, q)q, q) + (a(t,
ao(t, q).
C.14.1)
Предполагается, что положительно-определенная симметрическая мат-
матрица A(t, q) G С1 неизвестна, ее собственные числа при любых t, q
принадлежат отрезку [т,М], О < т ^ М, а частные производные
равномерно ограничены по норме, т. е.
mz2 < (A(t, q)z, z) < Mz2, \/zeRn,
dA
dA
dt
C.14.2)
D2, i= l,...,n, D\, D2 > 0.
Вектор-функция a(t,q) G С1 и функция ao(t,q) G С1 также счита-
считаются неизвестными и удовлетворяющими условиям
да\Т _ да
dq) dq
да0
dq
да
~di
D3, D4
C.14.3)
Динамика рассматриваемой системы описывается уравнениями
C.1.2).
По-прежнему предполагается, что система управляется непосред-
непосредственно по каждой степени свободы и на n-мерный вектор управляю-
управляющих сил U наложено ограничение
Щ,
> о,
C.14.4)
180 Гл. 3. Кусочно-линейное управление механическими системами
а обобщенные силы Q неизвестны и удовлетворяют условию
Qo, Qo>O. C.14.5)
Фазовые переменные q, q считаются доступными для измерений в
каждый момент времени.
Задача 3.4. Пусть даны постоянные т, М, Щ и Dj (j = 1,...
...,4). Требуется построить управление, подчиняющееся ограниче-
ограничению C.14.4), и указать область допустимых начальных состояний,
из которой система C.1.2) придет под действием этого управления
в заданное терминальное состояние покоя (q, 0) за конечное время,
каковы бы ни были матрица Д вектор а, функция а^ и возмуще-
возмущения Q, удовлетворяющие условиям C.14.2), C.14.3) и C.14.5).
§ 3.15. Описание алгоритма для реономных систем
Не ограничивая общности, будем считать, что терминальное состо-
состояние совпадает с началом координат, т. е. q = 0 (этого можно добиться
с помощью соответствующей замены переменных).
Построим управление в форме линейной обратной связи по обоб-
обобщенным координатам и скоростям с коэффициентами усиления в виде
ступенчатых функций:
U=-akq-f3kq, ak, /3k > 0. C.15.1)
Опишем поведение этих функций, т. е. зададим последовательность
значений коэффициентов а& и /3&.
Пусть qo = q@), go = <?@) — начальное состояние системы. Введем
в рассмотрение функцию
1 /9
W(q,q) = Mq2 + (мЦ4 + U$q2) . C.15.2)
Величина W(q, q) имеет размерность энергии и характеризует удален-
удаленность точки (q,q) от терминального положения @,0): множество
уровня W(q, q) = С функции W в фазовом пространстве q, q G R2n
представляет собой эллипсоид 2CMq2 + U^q2 = С2, который сжимает-
сжимается к началу координат @,0) при С —> 0.
Положим
Wo = W(qo,qo), Wk = ^, A; =1,2,.... C.15.3)
Множества уровня функции W(q,q), отвечающие постоянным Wk,
составляют семейство эллипсоидов, стягивающихся к нулю с ростом к.
Обозначим через t\ момент времени, когда траектория системы впервые
попадет на эллипсоид W(q,q) = W\ и положим q\ = q(t\), q\ = q(t\).
Ниже будет показано, что при выбранном алгоритме управления
§3.16. Обоснование алгоритма для реономных систем 181
траектория системы стремится к началу координат, поэтому такой
момент времени существует. Обозначим через t^ момент времени,
когда траектория системы впервые попадет на эллипсоид W(q,q) = W%.
Положим <22 = qfo), 42 = qfo) и т- Д-
Последовательность {tk} определяет моменты изменения коэф-
коэффициентов а&, /3k в управлении C.15.1). Зададим значения этих
коэффициентов на полуинтервале времени [tk,tk+\)> к = О, I,... следу-
следующим образом:
/3fc = ^-, а2к = трк. C.15.4)
В фазовом пространстве R2n траектория движения рассматриваемой
механической системы состоит из отрезков траекторий различных
систем дифференциальных уравнений: к-и отрезок соединяет точки
(qkAk) и (qk+i,qk+i) и отвечает системе вида C.1.2), C.15.1),
в которой коэффициенты усиления а&, /3k постоянны и определяются
формулами C.15.4). Все точки (дьФс) лежат на соответствующих
эллипсоидах W(q,q) = Wk, к = 0, 1,... (рис. 37).
Замечание 3.7. Как и в рассмотренном выше случае склероном-
склерономной системы, функция W, вообще говоря, не является монотон-
монотонно убывающей вдоль траектории, несмотря на то, что траекто-
траектория стремится к началу координат. Поэтому траектория может
иметь более одной точки пересечения с некоторыми эллипсоидами
{см. замечание 3.1 в § 3.3). Кроме того, в отличие от использован-
использованного выше для склерономной системы подхода, семейство эллипсо-
эллипсоидов в данном случае с самого начала выбирается так, что началь-
начальное состояние системы лежит на эллипсоиде с индексом 0.
Таким образом, для реализации алгоритма достаточно измерять
текущие значения фазовых переменных системы q,q и хранить
в памяти текущее значение индекса к, равное номеру минимального
эллипсоида, на котором уже побывала траектория системы. Так как
в выражение C.15.2) для функции W помимо фазовых переменных
входят только известные параметры задачи, то значение функции
W(q(t), q(t)) может быть вычислено в любой момент времени.
Каждый раз, когда значение W уменьшается вдвое, индекс к
возрастает на единицу, коэффициент а увеличивается в л/2 раз,
а коэффициент /3 — в 2 раза.
§ 3.16. Обоснование алгоритма для реономных систем
Для обоснования алгоритма воспользуемся вторым методом
Ляпунова. Рассмотрим к-и отрезок траектории при некотором
фиксированном к ^ 0. Этот отрезок начинается в точке (qk,qk)
в момент времени tk и отвечает системе C.1.2), C.15.1) с постоянными
коэффициентами обратной связи, задаваемыми формулами C.15.4).
182 Гл. 3. Кусочно-линейное управление механическими системами
Покажем, что существует такой момент времени tk+\, когда траектория
системы попадет на эллипсоид W(q,q) = VF/c+i-
Функция Ляпунова. Положим
и введем в рассмотрение функцию Ляпунова
Vk(t, q,q) = \ (A(t, q)q, q) + ^ q2 + sk(A(t, q)q, q). C.16.2)
Выражение для функции Vk содержит матрицу кинетической
энергии A(t,q), которая предполагается неизвестной. Оценим через
известные величины значение этой функции в произвольной точке
(?, q, q) расширенного фазового пространства. В силу неравенства Коши
и выражения C.16.1) справедливы соотношения
\ek(Aq,q)\ < | (Aq, q) + 2e2k(Aq, q) = Х- ((Aq,q) + ^ (Aq,q)),
а из условий C.14.2) вытекает
Подставив полученные неравенства в соотношение C.16.2) и вновь ис-
используя условия C.14.2), получим следующие оценки для функции Vk\
Vk(q,q) < Vk(t,q,q) < Vk(q,q), C.16.3)
где
Vk(q,q) = - (mq2 + Ckq2), V+(q,q) = - [Mq2 + Ckq2). C.16.4)
Установим соотношения, связывающие функции V+(q,q) и W(q,q).
Подставив формулу для коэффициента /3k из C.15.4) в выражение
C.16.4) для функции V+, получим
C.16.5)
По построению точка (qk,4k) лежит на эллипсоиде с номером к.
Отсюда и из определения C.15.2) функции W следует
Wk = W(qk, qk) = Mq2k + (M2q4k + U$q2k) '/2.
С помощью данного равенства числитель в выражении C.16.5) приво-
приводится к виду 5W|, откуда вытекает соотношение
У+(<1кЛк) = y^Wk, C.16.6)
1Ь
§3.16. Обоснование алгоритма для реономных систем 183
которое связывает функции Vk(q,q) и W(q,q) и означает, что при
любом к эллипсоид с номером к является множеством уровня квадра-
квадратичной формы V+(q,q), отвечающим значению 51^/16. В соответствии
с алгоритмом точка (q(t),q(t)) при t ? \ЬкЛк+\) лежит вне (к + 1)-го
эллипсоида, т. е. вне множества уровня
{(q,q) : V?+l(q, q) = ^ Wk+X},
поэтому
^W) > 7^ Wk+\ = м Wk, tk^t< tk+\.
В силу формул C.15.3), C.15.4) имеет место равенство /Зк+\ =
из которого вытекает соотношение
Следовательно, на fc-м отрезке траектории справедлива оценка
^ Wk. C.16.7)
Производная функции Ляпунова. Обратимся теперь к вычисле-
вычислению производной Vk. Введем обозначения
*«•«>=(!ЧТ-?«•«>¦
C.16.8)
дао да
frl-fc^ q\ = (ff q\ (t^ q\
dq dt
и продифференцируем функцию Vk в силу системы C.1.2), C.15.1).
Получим
\/кD. Л _ / т А | 1 9A ?k V^ д
\[ % dt 2 i={ д
',q) + (Q + b,q + ekq) - ek(Bq, q), C.16.9)
где / — единичная матрица.
Оценим отдельные слагаемые в выражении C.16.9). С помощью
соотношений C.14.3), C.16.8) получаем
C.16.10)
184 Гл. 3. Кусочно-линейное управление механическими системами
Используя неравенство
\2ek(q,q)\^±q2 + l6etq\
выражение C.16.1) для г^ и соотношение C.16.7), оценим величину
||(/ + ?fc(Z|| следующим образом:
Отсюда с учетом второго выражения C.16.4) получаем
C.16.11)
В силу C.14.2) и неравенства YH=\ \Чг\ ^ л/^lkll справедливо соот-
соотношение
гк ^ дА\
C-16.12)
Подставив неравенства C.16.10)—C.16.12) в выражение C.16.9)
и воспользовавшись условиями C.14.2), C.14.3) и C.14.5), приходим
к следующей оценке производной функции Vk вдоль fc-ro участка
траектории:
C.16.13)
Покажем, что при некоторых дополнительных предположениях про-
производная Vk будет отрицательно определена. Положим
1
и введем в рассмотрение множества
§3.16. Обоснование алгоритма для реономных систем 185
G = {(q,q)eR2n: W(q,q)^i}},
§^}, к = 0,1....
Из определения C.15.2) функции W вытекает неравенство
из которого в силу соотношений C.15.3) следует, что точка (дьФс)
лежит в области G&.
Лемма 3.9. Пусть начальная точка (дьФс) k-го отрезка принад-
принадлежит множеству G, матрица А, вектор-функции a, Q и функция
ао удовлетворяют условиям C.14.2), C.14.3), C.14.5) и
Тогда на участке траектории, который начинается в точке
(я.кАк), лежит вне эллипсоида W(q,q) = VF/c+i и во множестве G&,
производная функции Vk в силу системы C.1.2), C.15.1), C.15.4)
удовлетворяет неравенству
^k(t,q,q). C.16.15)
Доказательство. По условию леммы W(qk,4k) ^ ^. следовательно,
2
Отсюда и из определений C.15.4), C.16.1) чисел Sk,ak,Ck вытекает
Из условия C.16.14) и формул C.15.4) получаем
ak я I 17 (гл , п^ akf3k
C.16.17)
В силу соотношений C.15.4), C.16.1) имеем
д ч д C.16.18)
186 Гл. 3. Кусочно-линейное управление механическими системами
Из условия
вытекает
Так как рассматриваемый участок траектории лежит во множестве
, то
и, следовательно,
2~?fe"g" ^ ~64^ C.16.19)
Подставив неравенства C.16.16)—C.16.19) в C.16.13) и воспользо-
воспользовавшись равенствами C.16.4), приходим к соотношениям
откуда в силу оценок C.16.3) вытекает утверждение леммы. ?
Лемма 3.10. Пусть матрица А, вектор-функции Q, а и функ-
функция clq удовлетворяют условиям C.14.2), C.14.3), C.14.5), C.16.14)
и {ЧкЛк) ? G. Тогда на к-м отрезке траектории выполняется
неравенство C.16.15).
Доказательство. Выше было установлено, что (qkAk) ? Gk-
В силу леммы 3.9 для доказательства леммы 3.10 достаточно показать,
что fc-й отрезок траектории целиком лежит в области G&.
Предположим противное. Пусть t' — первый момент времени, когда
на рассматриваемом отрезке траектория покинет область G&, т.е.
С другой стороны, из определения C.16.1) коэффициента ?*. и
соотношений C.16.3), C.16.4) вытекает
§3.16. Обоснование алгоритма для реономных систем 187
Так как рассматриваемый участок траектории при tk ^ t < t' лежит
в области Gk, то в силу леммы 3.9 функция Vk вдоль него убывает
и с помощью соотношения C.16.6) оценка может быть продолжена так:
e2kq2(t') ^ ^ ^
Следовательно,
5mWk 5W?
<
3C/-2
что противоречит условию C.16.20). Лемма доказана. ?
Из утверждений лемм 3.9 и 3.10 вытекает, что вне эллипсоида
W(q,q) = Wk+\ функция Vk строго убывает вдоль траектории систе-
системы C.1.2), C.15.1), C.15.4), а в силу соотношений C.16.3)-C.16.6)
существует такой момент времени tk+\, когда траектория попадет на
эллипсоид с номером к + 1.
Нетрудно видеть, что если начальное состояние системы (qo,qo)
принадлежит множеству G, то в этом множестве целиком лежит
нулевой эллипсоид W(q,q) = Wo, а вместе с ним и все осталь-
остальные эллипсоиды W(q,q) = Wk, к = 1,2,.... Следовательно, все точки
(ЧкАк) также принадлежат G и утверждения лемм 3.9 и 3.10 приме-
применимы для любого из отрезков, составляющих траекторию движения
системы.
Оценка времени движения. Покажем, что система придет в на-
начало координат за конечное время. Для оценки времени движения
вдоль fc-ro участка траектории проинтегрируем неравенство C.16.15).
Получим
^ 40М Лп Vk{tk,qk,qk) /qiaoh
tk+\ ~tk<: -^ [nY7ku : v C.15.21)
Sak Votfqq)
В силу соотношений C.15.4), C.16.3)—C.16.6) имеем
Vk(tk+i,qk+i,qk+i) ^ Vk(qk+l,qk+l) =
3 / ,2 , о Л \ ^ 3m
3m лгк+\/ • \ 3m JJT
188 Гл. 3. Кусочно-линейное управление механическими системами
Подставив эти соотношения и выражение C.15.4) для ак в нера-
неравенство C.16.21), получим следующую оценку времени движения от
точки (qk,qk) ДО точки (qk+uqk+i):
. Л Л 40M^/Ш0 20М
к = 0, 1,... , г = Z- In ——.
З га Uq Зга
Полное время движения системы до терминального состояния Т*
не превосходит суммы ряда:
Т* < т]Г2"*/2 = -p^-. C.16.22)
Следовательно, предложенный алгоритм управления приводит систему
C.1.2) в начало координат за конечное время.
Проверим, что вдоль траектории движения выполнено условие
C.14.4). Оценим для этого модуль вектора управляющих сил на fc-м
отрезке траектории, используя соотношения C.15.1), C.15.4), C.16.3)
и C.16.4), следующим образом:
C2kq2) = 2Ck(mq2
f PkVH{q,q)^™ PkVk{t,q,q).
Так как функция Vk на полуинтервале \ЬкЛк-\-\) убывает, то, используя
соотношения C.16.6), оценку можно продолжить так:
откуда вытекает неравенство C.14.4).
Модификация алгоритма. Из приведенных рассуждений выте-
вытекает, что система придет в точку @,0) за конечное время, если началь-
начальное состояние принадлежит эллипсоиду G. Отметим, что в качестве
терминального состояния может быть выбрана любая точка вида (q, 0)
в фазовом пространстве системы. При этом совокупность эллипсоидов,
на которых происходит изменение коэффициентов усиления, окажется
сдвинутой на вектор q, параметры же эллипсоидов останутся преж-
прежними. Покажем, что, используя это обстоятельство и модифицировав
предложенный алгоритм, можно существенно расширить множество
допустимых начальных состояний.
§3.16. Обоснование алгоритма для реономных систем 189
Пусть
{22^y C.16.23)
Переведем сначала систему в точку q = qo, q = 0. Сделаем для этого
замену переменных q' = q — qo. В новых переменных qf,qf множество
аналогичное рассмотренному ранее множеству G, представляет собой
эллипсоид с центром в точке q1 = q1 = 0. Начальное состояние
системы — точка qf0 = 0, qf0 = qo — в силу включения C.16.23)
и определения C.15.2) функции W принадлежит множеству G'.
Следовательно, закон управления
U = -akqf - f3kqf
с указанным выше алгоритмом изменения коэффициентов ак, Рк при-
приведет систему за конечное время в центр этого эллипсоида, т. е. в точку
q = %, 4 = о.
В фазовом пространстве q, q выберем конечную последовательность
точек (gJ,0), j = 1, 2,..., J, таких что ql = qo, qJ = 0 и
qj-qj-l\\<jj-. C.16.24)
Uo
Перевод системы из точки (q\0) = (qo,O) в точку (qJ,0) = @,0), т.е.
в начало координат, осуществим за J — 1 шагов, применяя каждый
раз алгоритм управления заново. На j-м шаге начальному состоянию
системы отвечает точка (gJ, 0), а терминальному — точка (gJ+1,0).
Из неравенства C.16.24) и определения C.15.2) функции W вытекает,
что при любом j точка (gJ,0) принадлежит эллипсоиду
с центром в (gJ+1,0). Этот эллипсоид представляет собой множе-
множество допустимых начальных состояний системы для приведения ее
в терминальное состояние (gJ+1,0) на j-м шаге. Следовательно, закон
управления
U = -akq-Ck(q-qj+[)
с указанным выше алгоритмом изменения коэффициентов а^, /3k
переведет систему за конечное время из точки (qi, 0) в центр этого
эллипсоида, т.е. в точку q = gJ+1, q = 0. Таким образом, через J — 1
шагов система C.1.2) окажется в терминальном состоянии @,0).
190 Гл. 3. Кусочно-линейное управление механическими системами
Следующая теорема подводит итог проведенным выше рассуж-
рассуждениям.
Теорема 3.5. Пусть матрица А, вектор-функции Q,a и функ-
функция ао удовлетворяют условиям C.14.2), C.14.3), C.14.5), C.16.14)
и (qq>Qq) ? G*. Тогда предложенный закон управления переведет
систему C.1.2) из начального состояния (qo,Qo) 6 начало координат
фазового пространства за конечное время. При этом управляющие
силы будут удовлетворять ограничению C.14.4).
Замечание 3.8. Как уже отмечалось выше, изложенный подход
является распространением на реономные механические системы
подхода, примененного ранее к склерономным системам. В случае
склерономных систем множество допустимых начальных состо-
состояний совпадает со всем фазовым пространством, т. е. система
приводится из произвольного начального положения в заданное
терминальное состояние. Для реономных же систем множество
допустимых начальных состояний C.16.23) представляет собой
«полосу» в фазовом пространстве R2n, так как на начальные
скорости накладывается условие
2 ^ ft
Замечание 3.9. В определение множества G* и в выражения
для функции W и коэффициентов усиления од, /3 k входят только
известные параметры задачи. Для реализации алгоритма доста-
достаточно знать величины га, М, С/о, а также значения фазовых пе-
переменных системы в каждый текущий момент времени. Постоян-
Постоянные D\, D2, Дз присутствуют только в условиях, определяющих
множество допустимых начальных состояний G*. Эти условия,
как и ограничения на вектор-функцию a(t,q), функцию ao(t,q)
и возмущающие силы Q в соотношениях C.16.14), представляют
собой лишь достаточные условия приведения системы в терминаль-
терминальное состояние и гарантируют монотонное убывание функций Vk
вдоль траектории системы C.1.2), C.14.1), управляемой по за-
закону C.15.1). Однако функции Vk могут быть немонотонными,
а траектории системы будут при этом по-прежнему приходить
в терминальное состояние {см. замечание 3.3 в § 3.6). Поэтому
предложенный алгоритм управления может быть формально при-
применен и в случаях, когда ограничения C.16.14) не выполняются,
а начальное состояние системы не принадлежит множеству G*.
Компьютерное моделирование динамики различных механических
систем показывает, что алгоритм эффективен и за пределами
приведенных достаточных условий.
§3.17. Результаты моделирования
191
§3.17. Результаты моделирования
Проиллюстрируем работу алгоритма с помощью численного
моделирования вращения тела с изменяющимся во времени
моментом инерции. Рассмотрим систему, состоящую из невесомого
стержня и материальной точки, перемещающейся вдоль стержня
(рис. 49). Стержень вращается в го-
горизонтальной плоскости вокруг одного
из концов под действием управляющего
момента U. Предполагается, что мас-
масса точки то и закон движения точки
вдоль стержня неизвестны. Кроме то-
того, на стержень действует неизвестный
возмущающий момент Q в шарнире.
Обозначим через q, q угловые ко-
координату и скорость стержня, через
l(t) — расстояние от оси вращения до
материальной точки. В принятых вы-
выше обозначениях отдельные слагаемые
в выражении C.14.1) для кинетической
энергии системы принимают вид
Рис. 49. Стержень и материаль-
материальная точка
A(t) = mo/2(t), a = 0, ao(t) = | mo/2(t),
а уравнения движения — вид
m0l2(t)q + 2m0l(t)i(t)q =
C.17.1)
В качестве неизвестной обобщенной силы Q в данном случае выступа-
выступает момент сил сухого трения, действующий на стержень. Постоянные
га, М, Щ, а также неизвестные по предположению масса гао, возму-
возмущения Q и закон движения материальной точки вдоль стержня l(t) при
моделировании принимались такими:
т = 0.25 кг, М = 2.25 кг, Uo = 10 Н-м,
Q = —0.1 sign(g) Н-м, то = 1 кг, l(t) = 1 + - sinuit м.
С помощью предложенного закона управления стержень переводил-
переводился из начального состояния qo = 1 рад, qo = 1 рад/с в терминальное
состояние q = q = 0. Интегрирование уравнения C.17.1) прекращалось,
когда евклидово расстояние от текущей точки траектории до терми-
терминального состояния в фазовом пространстве (q, q) G R2 становилось
меньше 0.01.
192 Гл. 3. Кусочно-линейное управление механическими системами
0.5 -
-0.5 J
Ю 1
Р\
Ю 1
max | U |
|
Рис. 50. Угол поворота стержня Рис. 51. Модуль управляющего
момента
Результаты моделирования для случая и = 1с представлены
на рисунках 50, 51. Сплошными линиями изображены: на рис. 50 —
зависимость от времени угла поворота стержня q, а на рис. 51
(разрывная кривая) — график модуля управляющего момента \U\.
Полное время движения оказалось равным Т* = 3.98 с.
Из рис. 51 видно, что огра-
ограничение C.14.4) выполняется
со значительным (двукратным)
запасом. Поэтому было проведено
моделирование движения системы,
управляемой по закону C.15.1),
но с коэффициентами обратной
связи ak, /3/с, в два раза большими,
чем предписывается алгоритмом
C.15.4). Штриховыми линиями
на рисунках 50, 51 изображены за-
зависимости от времени угла поворота
стержня и модуля управляющего
момента \U\ при таком законе
управления. Время движения в этом
случае сократилось до Т* = 2.53 с,
а управление U по-прежнему удо-
удовлетворяет ограничению C.14.4).
Для оценки работоспособности алгоритма в случае нарушения
условия (qo,qo) E G* сформулированной выше теоремы было проведено
моделирование динамики системы C.17.1) при различных значениях ио.
На рис. 52 сплошной линией изображена зависимость от параметра и
5 ¦
0
0
10
15
20
Рис. 52. Время
максимум модуля
движения и
управляющего
момента
§3.17. Результаты моделирования 193
полного времени движения Т* системы до терминального состояния,
где оо е [0,20]. В этом случае
A(t) = niouj 11 + — sinuit) cosuot
и постоянные D2 из ограничений C.14.2) удовлетворяет неравенству
и ^ D2. Следовательно, О ^ ttiUq/32uj2 и при выбранных значениях
параметров системы для большей части отрезка 0 ^ и ^ 20 с
начальное состояние до = 1 рад, % = 1 рад/с не лежит в области G*.
Тем не менее предложенный закон управления приводит систему
в терминальное состояние.
Штриховой линией на рис. 52 представлена зависимость от
параметра и максимума абсолютной величины управляющего
момента U, реализовавшегося при применении алгоритма. Из рисунка
видно, что ограничения C.14.4) выполнены для всех рассматриваемых
значений и.
7 Ф. Л. Черноусько и др.
Глава 4
УПРАВЛЕНИЕ СИСТЕМАМИ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
§4.1. Управление системой осцилляторов
Прежде чем переходить к задачам управления системами с рас-
распределенными параметрами, имеющими бесконечное число степеней
свободы, рассмотрим управляемую колебательную систему с конеч-
конечным числом степеней свободы. Результаты данной главы основаны
на результатах работ [67, 79, 83].
Рассматривается система с п степенями свободы, описываемая
уравнениями
Ax + Cx = Bv + f(x,x,t)\ v(t) e V, f(x,x,t) eR D.1.1)
Здесь х е Rn — вектор обобщенных координат, А и С — постоянные
симметрические положительно-определенные п х n-матрицы кинетиче-
кинетической и потенциальной энергий, соответственно, В — постоянная п х га-
матрица (га ^ п), / — заданный n-вектор, содержащий нелинейные
члены, и uG Rm — вектор управлений. Значения v и / ограничены
заданными множествами V С Rm и F С Rn, соответственно. Будем
искать управление по обратной связи v(x,x), которое удовлетворяет
наложенным ограничениям и переводит систему D.1.1) из заданного
начального состояния
х@)=х°, х(О)=х° D.1.2)
в нулевое терминальное состояние х(Т) = х(Т) = 0 за конечное заранее
нефиксированное время Т. Перейдем к нормальным координатам q =
= (q\> ••• >Цп)> которые определяются заменой переменных [24]
x = Hq. D.1.3)
Здесь обратимая п х п матрица состоит из столбцов h\,..., hn, которые
являются собственными векторами в задаче на собственные значения:
(C-\A)h. D.1.4)
§4.2. Задача быстродействия
195
Известно [24], что задача D.1.4) имеет п положительных собственных
значений Аь ..., Ап, удовлетворяющих характеристическому уравнению
det(C -XkA) = 0, к= 1,...,п.
D.1.5)
В случае кратных корней уравнения D.1.5) среди чисел Ai,...,An
будут одинаковые, причем число одинаковых А^ равно кратности
соответствующего корня. Собственным значениям отвечают линейно-
независимые собственные векторы h\,...,hn, причем кратному корню
отвечает столько векторов, какова его кратность. При замене пере-
переменных D.1.3) уравнения D.1.1) преобразуются в систему линейных
осцилляторов
к = 1,... ,n.
D.1.6)
Здесь иок — собственная частота fc-ro осциллятора, a wk и (к —
компоненты n-векторов w и (, определяемых соотношениями
w = H-lA~lBv, С = H-lA~lf.
D.1.7)
Осцилляторы в D.1.6) связаны между собой посредством управляющих
и нелинейных членов. В силу D.1.1) векторы w и ? принадлежат
следующим множествам в Rn\
w eW = H-lA~lBV, (e Z = H-lA~lF. D.1.8)
Из D.1.2), D.1.3) имеем начальные условия для системы D.1.6):
<fc@) =q°k = (Н~1хо)к, qk@) = q°k = (Н~хх\. D.1.9)
§ 4.2. Задача быстродействия
Будем рассматривать wk и (к в каждом уравнении D.1.6) как
управления двух независимых игроков. Первый игрок выбирает wk
и стремится привести fc-e уравнение D.1.6) в нулевое терминальное
состояние qk = qk = 0 за конечное время, в то время как второй
игрок противодействует ему, выби-
выбирая (к. Предполагаем, что управля-
управляющая сторона, т. е. первый игрок,
знает функцию / в системе D.1.1)
и, следовательно, ему известно зна-
значение вектора ? в каждый момент
времени. Таким образом, приходим
к следующим условиям. Пусть при
некотором г выполнено включение
(см. рис. 53) Рис. 53. Включение D.2.1)
196 Гл. 4. Управление системами с распределенными параметрами
Z + S?CW, D.2.1)
где S? — n-мерный шар радиуса г с центром в начале координат. При
условии D.2.1) положим
w = -? + u, D.2.2)
где и — новый n-мерный вектор управлений. Подставляя D.2.2)
в D.1.6), получим
lUk, к=1,...,п. D.2.3)
Включение D.2.1) гарантирует существование n-мерного прямоуголь-
прямоугольного параллелепипеда
U : \ик\ ^Uk, к= 1,...,п, D.2.4)
такого, что любое значения и G U является допустимым. Это означает,
что при любом и G U и любом С G Z вектор ги из D.2.2) удовлетворяет
ограничениям D.1.8). Иными словами, для любого «G [/ и любого
(GZ существует вектор г; G V такой, что соответствующий вектор w
из D.1.7) удовлетворяет ограничению D.1.8) и может быть представлен
в виде D.2.2).
Итак, включение D.2.1) может рассматриваться как достаточное
условие управляемости для системы D.1.1). При этом условии синтез
управления для системы D.1.1) сводится к управлению простыми
линейными подсистемами D.2.3) с одной степенью свободы каждая
при помощи независимых управляющих сил ик, ограниченных неравен-
неравенствами D.2.4).
Рассмотрим задачу управления, оптимального по быстродействию,
для одного из уравнений D.2.3) при ограничении D.2.4) и начальных
условиях D.1.9). Имеем
^ Uк, LUk ^> U,
Qk(O)=ql Ш = я1 D-2.5)
Чк{Тк) = qk(Tk) = 0, Tfe^min.
Введем безразмерные переменные и параметры
t = ик г, qk = Ukuk у, qk = Ukuk z,
D.2.6)
ик = ики, Tk = wr'T*, T* -
После замены D.2.6) соотношения D.2.5) примут нормализованный
вид:
§4.2. Задача быстродействия 197
dy dz
»@)=»0, *(<>)= *°, D-2-7)
2/(Т*) = z(T*) = О, Т* ->min.
Решение задачи оптимального быстродействия D.2.7) известно [50].
Синтез оптимального управления для задачи D.2.7) может быть пред-
представлен в виде
и(у, z) = sign [ф(у) -z], z^ <ф(у);
D.2.8)
u(y,z) = sign у = -sign^, z = ф(у).
Здесь функция ф(у) задана равенствами
у<-2; D.2.9)
Кривая переключений z = ф(у), определяемая соотношениями
D.2.8), D.2.9), обладает центральной симметрией и состоит из
полуокружностей единичного радиуса с центрами в точках
z = 0, г/ = ±Bг+1), г = 0, 1,.... D.2.10)
Знаку плюс в D.2.10) отвечают полуокружности, лежащие в четвертом
квадранте, а знаку минус — во втором квадранте фазовой плоско-
плоскости y,z.
Оптимальные фазовые траектории, соответствующие синтезу
управления D.2.8), состоят из дуг окружностей с центрами в точках
у = ±1, z = 0. При этом в области z > ф(у), где и = — 1, центр
этих окружностей находится в точке у = —\, z = 0, а в области
z < ф(у), где и = 1, — в точке у = 1, z = 0. Полуокружности кривой
переключений с центрами в точках у = ±1, z = 0 сами являются
отрезками фазовых траекторий.
На рис. 54 жирной линией изображена кривая переключений,
а тонкой линией — одна из оптимальных траекторий. Стрелками
указано направление роста времени.
Оценим время движения T*(y,z) по оптимальной фазовой тра-
траектории, начинающейся в некоторой точке у, z. Эта оценка будет
использована в дальнейшем. Пусть для определенности точка y,z
лежит в области z > ф(у). Сделаем сначала некоторые вспомогатель-
вспомогательные построения.
198 Гл. 4. Управление системами с распределенными параметрами
Рис. 54. Кривая переключений и оптимальная фазовая
траектория
Обозначим через г, в полярные координаты начальной точки у, z
в случае, если за полюс принята точка у = — 1, z = 0. Имеем
у = г cos в — 1, z = r sin в.
D.2.11)
Начальный участок фазовой траектории есть дуга окружности
г = const. Продолжим эту дугу в обратном времени до пересечения
ее с кривой переключений z = ф(у). Пусть точка пересечения Р
находится на г-й (считая от начала координат) полуокружности кривой
переключений (см. рис. 54, где г = 4). Это означает, что координаты
точки Р можно представить в виде
уР = —2г + 1 + cos a, zP = sin а,
D.2.12)
г = 2,3,... , а е [О,тг).
Угол а отвечает дуге, отсекаемой точкой Р от полуокружности кривой
переключений, на которой она лежит. Отметим, что такие же дуги
а оптимальная траектория отсекает от всех полуокружностей кривой
переключений, которые она пересекает. Заключительная дуга фазовой
траектории также имеет угловую меру а (см. рис. 54).
Так как точка Р с координатами D.2.12) лежит на окружности
г = const, то имеем
= (уР + IJ + 4 = 4(г - IJ + 1 - 4(г - 1) cosa.
D.2.13)
Обозначим через R длину радиуса-вектора фазовой точки у,
Используя соотношения D.2.11), получим
R2 = у2 + z2 = (г - IJ + 2r(l - cost
D.2.14)
§4.2. Задача быстродействия 199
Из D.2.14), D.2.13) следуют неравенства
R^r-l^ [4(г- IJ — 4(г — 1) + 1]1/2- 1 = 2г - 4. D.2.15)
Время движения по любой дуге оптимальной траектории, как
нетрудно видеть, равно угловой мере этой дуги. Каждая дуга между
соседними переключениями управления либо равна тг, либо (для пер-
первого и последнего участков) не превосходит тг, а общее число участков
равно целому числу г, введенному выше. Поэтому имеем Т* < ттг.
С учетом неравенства D.2.15) получим оценку
D.2.16)
Оценка D.2.16) справедлива для всех R ^ О, однако из нее не
следует стремление Т* —> 0 при R ^ 0. Поэтому получим еще одну
оценку для достаточно малых R.
Пусть г = 2, т. е. имеется только одно переключение управления,
см. рис. 54. В этом случае оптимальная траектория состоит из дуги
радиуса г с угловой мерой 9 + 5 и дуги радиуса 1 с угловой мерой а,
совпадающей с участком кривой переключений. Через 5 обозначен угол
между осью у и лучом, проведенным из точки у = — 1, z = О в точку
траектории, где происходит переключение. Таким образом,
Т* = в + 5 + а, D.2.17)
где, как можно определить при помощи рис. 54, имеем
sin5 = г sina, 5 е [о, ^1 . D.2.18)
Получим несколько вспомогательных соотношений, нужных для
оценки времени D.2.17). Полагая г = 2 в D.2.13), найдем
1 /9
r=\l +8sin2 (|)j . D.2.19)
Равенства D.2.18) и D.2.19) определяют зависимость угла 5 от а.
Исследование этой зависимости показывает, что при изменении угла
а в пределах D.2.12) угол 5 изменяется в пределах [0,тг/6], причем
всегда 5 < а. Таким образом, имеем
0<(К^, (К а, 0^а<тг. D.2.20)
о
Отметим следующее неравенство:
^, 7е[О,тг]. D.2.21)
тг
Полагая 7 = ^ в неравенстве D.2.21), получим из D.2.19) неравенство
rXl+STr-VI/2, ae [О,тг),
200 Гл. 4. Управление системами с распределенными параметрами
которое перепишем в виде
2 ? = 8тг-2а2, ?е[0,8). D.2.22)
Так как д{?) — вогнутая функция, на рассматриваемом интервале
удовлетворяется неравенство
Ш) - 5@)] Г' > \ [5(8) - 5@)], ? е [0,8].
Подставляя в последнее неравенство значения д@) = 1 и д(8) = 3
согласно D.2.22), получим
что дает возможность упростить соотношение D.2.22)
г > 1 + 2тг~V, а е [О, тг). D.2.23)
Преобразуем теперь соотношение D.2.14), используя неравенство
D.2.21) при 7 = 0. Имеем
R2 = (г- lJ+4rsin2(|) ^ (г- 1J+4тг-2г<92.
В последнее неравенство подставим D.2.23). Получим
Отсюда вытекают следующие два неравенства:
R ^ 2тг-V, R ^ 2тг-1\0\. D.2.24)
Преобразуем теперь равенство D.2.17) для Т*, используя неравен-
неравенства D.2.20) и D.2.24)
Т* = в + 5 + а < 2а + 0 < 2\а
D.2.25)
Сопоставим оценки D.2.16) и D.2.25). Напомним, что оценка
D.2.25) получена при г = 2, а оценка D.2.16) — при всех г ^ 2. Но при
г > 3 согласно D.2.15) имеем R > 2. Из D.2.16), D.2.25) следует,
что T°(R) < Tl(R) при R^ 2. Следовательно, при всех г > 3 имеем
Т°(Д)
§4.3. Постановка задачи управления 201
Таким образом, установлено, что оценка D.2.25) времени быстро-
быстродействия
'R
Т
D.2.26)
справедлива при любых у, z.
Возвращаясь к исходным размерным переменным D.2.6), получим
оценку времени оптимального быстродействия для задачи D.2.5) в виде
Pk =
/-0Л2
\Як)
D.2.27)
1/2
, k=l,2,..., и>к>0.
Время Т приведения в начало координат всей системы D.2.3)
с п степенями свободы равно максимальному из времен Т&, т.е.
T = m&xTk(q°k,q°k), k= \,...,п. D.2.28)
Полученное неравенство D.2.27) позволяет оценить время Т сверху.
§ 4.3. Постановка задачи управления системой
с распределенными параметрами
Перейдем к рассмотрению управляемых систем с распределенными
параметрами, описываемых линейными уравнениями в частных произ-
производных. Будем параллельно рассматривать уравнение
wt = Aw + v, D.3.1)
разрешенное относительно первой производной по времени, и уравне-
уравнение
wtt = Aw + v, D.3.2)
разрешенное относительно второй производной.
В уравнениях D.3.1) и D.3.2) w(x,t) — скалярная функция
n-мерного вектора х = (х\,... ,хп) пространственных координат и вре-
времени t, характеризующая состояние системы, v — искомое управление,
А — линейный дифференциальный оператор, содержащий частные
производные по координатам Xi, i= I,..., п. Коэффициенты оператора
А не зависят от t, а его порядок oidA считаем четным и равным 2т.
Наиболее важными и распространенными примерами уравнений
D.3.1) и D.3.2), которые рассматриваются в дальнейшем, являются:
202 Гл. 4. Управление системами с распределенными параметрами
• уравнение теплопроводности, которое получается из D.3.1), если
т = 1, А = А — оператор Лапласа;
• волновое уравнение, получаемое из D.3.2) при т = 1, А = А;
• уравнение колебаний упругого стержня или пластины, получае-
получаемое из D.3.2) при т = 2, А = —А2 и п = 1,2 соответственно.
Уравнения D.3.1), D.3.2) описывают также процессы теплопроводности
и колебаний в неоднородной среде, если
9 Г -dw m=\,
где а(ж) — заданная функция, характеризующая неоднородность среды.
Уравнения D.3.1), D.3.2) рассматриваются в некоторой открытой
ограниченной области изменения пространственных переменных х G
Ell и при t > 0. На границе Г области п должно удовлетворяться
однородное граничное условие вида
Mw = 0, М = (МЬ...,МШ), хеТ. D.3.3)
Здесь Mj — линейный дифференциальный оператор порядка ordMj <
< 2m (j = 1,... ,га) с коэффициентами, не зависящими от t. В частно-
частности, при m = 1 оператор М — скалярный и имеет вид
где bo(x), b\(x) — заданные на Г функции. Условие D.3.3) может,
в частности, превращаться в условие Дирихле (при bo = \, b\ = 0) или
Неймана (при 60 =0, Ь\ = 1).
Начальные условия имеют вид
w(x, 0) = wo(x), x ей, D.3.4)
для уравнения D.3.1) и
w(x, 0) = wo(x), wt(x, 0) = wto(x), x G О, D.3.5)
для уравнения D.3.2).
На управляющую функцию v(x,t) в уравнениях D.3.1), D.3.2)
наложено ограничение
v(x,t)\^v°, хеп, t > 0, D.3.6)
где г>° > 0 — заданная постоянная.
§4.4. Декомпозиция 203
Сформулируем задачу управления.
Задача 4.1. Требуется построить управление v(x,t), удовлетво-
удовлетворяющее ограничению D.3.6) и такое, что соответствующее ему
решение уравнения D.3.1) или D.3.2) с граничным условием D.3.3)
и с соответствующими начальными условиями D.3.4) или D.3.5)
обращается в нуль в некоторый конечный {нефиксированный)
момент Т > 0. Точнее, всюду в ft должны быть выполнены условия
w(x,T) =0
для уравнения D.3.1) и
w(x,T) =wt(x,T) =0
для уравнения D.3.2).
Очевидно, что если положить v = 0 при t ^ Т, то решение останется
тождественно равным нулю при t > Т.
Граница области п предполагается кусочно-гладкой. Требования к
начальным функциям и функциональные классы, которым принадле-
принадлежат решения поставленных задач в различных случаях, рассматрива-
рассматриваются в § 4.9.
Отметим, что задачам управления системами с распределенными
параметрами посвящено большое число работ, например, [23, 30, 45,
57,59,89]. Предлагаемый ниже способ управления отличается от из-
известных. Он позволяет построить управление с учетом ограничений в
замкнутой форме и обеспечивает приведение системы в заданное состо-
состояние за конечное время. Этот способ, опубликованный ранее в [61, 78],
использует декомпозицию исходной системы на простые подсистемы и
в этом смысле близок по идее к подходам, изложенным выше в данной
книге для систем с конечным числом степеней свободы.
§ 4.4. Декомпозиция
Решение поставленной задачи будет опираться на метод Фурье. Для
его применения рассмотрим сначала следующую задачу на собствен-
собственные значения, отвечающую начально-краевым задачам D.3.1)—D.3.5)
при v = 0.
Задача состоит в определении функций <р(х), х G 1), удовлетво-
удовлетворяющих при соответствующих постоянных Л линейному однородному
уравнению и граничному условию:
А(р = -\(р, хеп; М(р = 0, хеГ. D.4.1)
Как известно, при определенных условиях (для самосопряженных
эллиптических уравнений и, в частности, для уравнения Лапласа,
т.е. при А = А), задача на собственные значения D.4.1) обладает
следующими свойствами.
204 Гл. 4. Управление системами с распределенными параметрами
Имеется дискретный счетный спектр положительных собственных
значений А&, которые могут быть пронумерованы в неубывающем
порядке: Ai ^ А2 ^ ... , причем А& —> оо при к —> оо. В некоторых слу-
случаях, например, для оператора Лапласа А = А при условии Неймана
имеется также нулевое собственное значение А = 0. Этот случай также
будем включать в рассмотрение. Указанным собственным значениям
отвечает ортогональная система собственных функций (fk(x), которая
является полной в области п. Нормировав эти функции, получим
ортонормированную систему функций (fk(x), обладающих следующими
свойствами:
А(рк = -XkVk, х ей; М(рк = 0, х е Г;
Г D.4.2)
(<Рь Ч>%) = (Pk(x)(pi(x) dx = 5ы.
Q
Здесь 5ы — символ Кронекера. Индекс к в D.4.2) и далее, если
не оговорено специально, пробегает значения от 0 до оо при наличии
нулевого собственного значения Ао = 0 и от 1 до оо при его отсут-
отсутствии. Суммирование в дальнейшем будет проводиться по к также
в указанных выше пределах.
Воспользуемся теперь методом Фурье для разделения временной
(от t) и пространственной (от х) зависимостей. Решения уравнений
D.3.1) и D.3.2) будем искать в виде разложений по собственным
функциям
w(x,t) = У
где qk(t) — некоторые функции времени. Управление v в D.3.1), D.3.2)
также представим в виде разложения
k(t)<pk(x), D.4.4)
где Uk(t) — пока неизвестные функции времени.
Подставляя разложения D.4.3) и D.4.4) в уравнение D.3.1),
получим
^2 Qk(t)ipk(x) = ^(qkA(pk + иксрк).
Здесь и далее точки означают производные по времени.
Воспользуемся уравнением Асрк = —Хкфк из D.4.2), а также усло-
условием ортогональности функций tpk. В результате получим систему
уравнений
Чк + ХкЧк = Uk. D.4.5)
Аналогично, подставляя разложения D.4.3), D.4.4) в уравнение
D.3.2), получим
^ v>k. D.4.6)
§4.4. Декомпозиция 205
Здесь и далее иок — частоты собственных колебаний, равные
шк = Х1к/2, 0 = соо < шх < со2 < ... . D.4.7)
Отметим, что решение в виде D.4.3) по построению удовлетворяет
однородному краевому условию D.3.3), так как этому условию удовле-
удовлетворяют все собственные функции согласно D.4.2).
Подставим решение D.4.3) в начальные условия D.3.4) и D.3.5)
и воспользуемся свойствами ортонормированности собственных функ-
функций D.4.2). Получим начальные условия для задачи D.4.5) в виде
Qk(O) =ql= \wo{xL>k{x)dx D.4.8)
п
и для задачи D.4.6) в виде
Qk(O) = Як=\ wo(x)ipk(x)dx,
D.4.9)
<Ы°) = (Фс)° = wto(x)(pk(x)dx.
п
Таким образом, исходная задача управления для уравнений в част-
частных производных D.3.1) и D.3.2) свелась к задаче управления для
линейных управляемых систем бесконечного порядка D.4.5) и D.4.6).
На управляющие функции Uk этих систем наложим ограничения
\uk(t)\^Uk, i>0. D.4.10)
Значения постоянных Uk должны быть выбраны так, чтобы удовле-
удовлетворялось наложенное ограничение D.3.6).
Из D.4.4) и D.4.10) вытекает оценка
Следовательно, для выполнения исходного ограничения D.3.6)
достаточно потребовать, чтобы при всех х G О удовлетворялось
неравенство
A xeQ. D.4.12)
Введем обозначение
Мх)\- D-4.13)
206 Гл. 4. Управление системами с распределенными параметрами
Неравенство D.4.12) заведомо выполнено при условии
Ю°. D.4.14)
Итак, для решения поставленной задачи управления уравнениями
D.3.1), D.3.2) (задача 4.1) достаточно решить следующие задачи
управления системами D.4.5), D.4.6).
Задача 4.2. Требуется построить управления по обратной связи
u>k(qk) в системе D.4.5) и Uk(qk,qk) в системе D.4.6) при к = 0, 1,... ,
удовлетворяющие ограничениям D.4.10) и приводящие эти системы
в нулевое состояние (qk = 0 для D.4.5) и qk = qk = 0 для D.4.6))
за конечное время при любых начальных условиях вида D.4.8) или
D.4.9) соответственно. При этом постоянные Uk в D.4.10) должны
удовлетворять неравенству D.4.12) при всех х, или, что является
достаточным, более сильному неравенству D.4.14).
Заметим, что в результате применения метода Фурье достигнута
декомпозиция системы: каждая мода движения описывается своим
уравнением D.4.5) или D.4.6) с соответствующим управлением щ.
Таким образом, задача 4.1 сведена к задаче 4.2, которая для систем
второго порядка рассматривалась в § 4.2 (см. систему D.2.3) с огра-
ограничениями D.2.4)). Однако постоянные Uk в ограничениях D.4.10)
связаны неравенствами D.4.12) или D.4.14), что представляет собой
основную трудность при решении задачи.
Для каждого уравнения D.4.5) или D.4.6) будем строить управле-
управление по обратной связи щ, оптимальное по быстродействию при огра-
ограничении D.4.10) с произвольным фиксированным Uk. Эти управления
хорошо известны, для систем второго порядка они приведены в § 4.2.
Ниже проводится анализ данных управлений, оптимальных по
быстродействию, с точки зрения удовлетворения неравенств D.4.12)
или D.4.14). При этом используются оценки, полученные в § 4.2.
§ 4.5. Уравнение первого порядка по времени
Рассмотрим сначала уравнение D.3.1), содержащее первую произ-
производную по времени от искомой функции w(x,t). Для этого уравнения в
результате декомпозиции получена система уравнений D.4.5) первого
порядка.
Рассмотрим задачу оптимального по быстродействию попадания
в нуль для одного из уравнений D.4.5) при ограничении D.4.10)
и начальном условии D.4.8). Имеем
uk, \uk(t)\^uk, Xk > о,
D.5.1)
Qk(O)=q°kt qk(Tk)=0, Tk
§ 4.6. Уравнение второго порядка по времени 207
Решение задачи D.5.1) получим элементарным путем. Интегрируя
уравнение D.5.1) и удовлетворяя начальному условию, найдем
Qk(t) =
t
.0
+ uk(r)exp(Xkr) dr
exp(-Afct). D.5.2)
Отсюда следует, что для скорейшего обращения решения qk(t)
в нуль управление ик должно быть максимально по модулю и проти-
противоположно по знаку начальному значению q%, или, что то же самое,
решению qk(t).
Таким образом, синтез оптимального по быстродействию управле-
управления имеет вид
-Uksignqk, qk^0,
uk(qk) = { D.5.3)
0, qk = 0.
Управление D.5.3) постоянно вдоль любой фазовой траектории.
Подставляя его в D.5.2) и интегрируя, получим
Qk(t) = {\qk\ ~ UkX^[exp(Xkt) - 1]} exp(-Afe*) signgg. D.5.4)
В конечный момент согласно D.5.1) имеем qk(Tk) =0. Из D.5.4)
находим момент окончания процесса:
Tfe = Afc1ln(l + Afe|(/O|C/fc-1), \k>0, k>l;
D.5.5)
T0=\q°0\U-\ A0 = 0.
Решение задачи оптимального быстродействия D.5.1) для всех
к ^ 0 представлено в форме синтеза оптимального управления
D.5.3). Фазовая траектория и время быстродействия даны формулами
D.5.4) и D.5.5) соответственно. Таким образом, определено решение
задачи 4.2 для системы D.4.5). Выбор постоянных Uk будет пред-
представлен в § 4.7.
§ 4.6. Уравнение второго порядка по времени
Обратимся теперь к уравнению D.3.2), содержащему вторую про-
производную по времени от функции w(x,t). В этом случае декомпозиция
приводит к системе уравнений D.4.6) второго порядка.
Рассмотрим задачу оптимального управления для одного из уравне-
уравнений D.4.6) при ограничении D.4.10) и начальных условиях D.4.9).
208 Гл. 4. Управление системами с распределенными параметрами
В случае иок > 0, к ^ 1, воспользуемся результатами, полученными
в § 4.1, 4.2 при рассмотрении конечной системы осцилляторов. Синтез
оптимального управления uk(qk,qk) ПРИ к ^ 1 в безразмерных пере-
переменных определен соотношениями D.2.8), D.2.9), в которые нужно
подставить формулы замены D.2.6).
В результате искомый синтез управления, оптимального по быстро-
быстродействию, имеет вид
Uk(Qk, Qk) = sign [ф(у) -z], z^ ф(у);
D.6.1)
ик(ЧкАк) = sign у = -sign^, z = ф(у).
Здесь функция ф(у) определена соотношениями D.2.9) и введены обо-
обозначения
y = 4UklQk, z = ukU^lqk. D.6.2)
Отдельно рассмотрим случай нулевого собственного значения
к = 0, uoq = 0. В этом случае синтез оптимального управления для
задачи D.2.5) неоднократно приводился выше (см., например, A.9.1)).
Имеем
,4о) = и0sign [V>o(?o) - qo], qo
o) = ^o signg0 = -Uosignqo, q0 = i/jo(qo); D.6.3)
= -[2[/oko|]1/2signgo, V^o(O) = 0.
Время оптимального быстродействия при к = 0, uoq = 0 определяется
формулой, приведенной, например, в A.9.11):
Т0(м) = ЦТ1!2]"! Ш2 ~ Uoqocr] ~ qoA,
Здесь и далее верхний нулевой индекс у qk, qk, к = 0, 1,... , опущен.
Применяя к приведенному соотношению неравенство
получим оценку
To(qOyqo) < (у/2 + l)U-1\q0\+2U-l/2\q0\^2. D.6.4)
Таким образом, получены необходимые в дальнейшем соотноше-
соотношения в задаче оптимального быстродействия для системы D.4.6) при
всех к ^ 0. Оптимальные фазовые траектории также хорошо известны,
см. § 4.2, рис. 54. Для времени оптимального быстродействия получены
§ 4.7. Анализ ограничений и построение управления 209
оценки D.2.27) в случае к ^ 1 и D.6.4) при к = 0. Тем самым найдено
решение задачи 4.2 для системы D.4.6). Выбор постоянных Uk обсуж-
обсуждается ниже.
§4.7. Анализ ограничений и построение управления
В полученных в § 4.5, 4.6 соотношениях фигурируют постоянные
Uk — ограничения на управления для к-и моды движения. Эти посто-
постоянные выберем так, чтобы уменьшить полное время движения, равное
T = maxTfc, к > 0 или к > 1, D.7.1)
к
при выполнении ограничения D.4.12) или D.4.14). Индекс к в D.4.12),
D.4.14) и D.7.1) принимает значения 0,1,... при наличии нулевого
собственного значения Ао = 0 у задачи D.4.2) и значения 1,2,... при
его отсутствии.
Так как все Т& монотонно возрастают с ростом Uk, a в ограни-
ограничения D.4.12), D.4.14) все Uk входят линейно с положительными
коэффициентами, то естественно выбрать Uk из условия равенства
всех Tk'. То = Т\ = .... При этом получится минимально возможное
(при ограничениях D.4.12) или D.4.14)) значение времени Т в D.7.1).
Следуя указанному предложению, положим для уравнения первого
порядка D.3.1) в соответствии с D.5.5)
Тк = Afc1 ln(l + Хк\дк\ик-1) = Го = \qo\U^1 = Т.
Здесь Т — пока неопределенная постоянная, верхний индекс «°» у qk
опущен.
Отсюда найдем искомые значения постоянных Uk'.
Uk = ХкШ [exp(AfcT) - I], к > 0. D.7.2)
Формула D.7.2) справедлива при всех А& > 0, при к = 0 — в пределе
при Ао —> 0. Подставляя D.7.2) в неравенство D.4.14), получим
^Afc[exp(AfcT)- l]~Vl$/c < v°. D.7.3)
Как известно, при весьма общих предположениях собственные
значения А& и максимумы собственных функций Ф& возрастают
не быстрее, чем некоторые степени номера к при к —> оо. Модули
коэффициентов Фурье \qk\ по крайней мере не возрастают с номером к
при к —> оо для любой ограниченной начальной функции wo(x).
Следовательно, из-за наличия экспоненциального множителя ряд
в левой части неравенства D.7.3) сходится при любом Т > 0. Когда Т
пробегает значения от 0 до оо, сумма ряда монотонно убывает от оо
до 0. Следовательно, всегда существует такое Т > 0, при котором
неравенство D.7.3) выполняется. Таким образом, поставленная задача
210 Гл. 4. Управление системами с распределенными параметрами
управления (задача 4.1) для уравнения D.3.1) всегда разрешима
предложенным методом. Время процесса Т можно выбрать из условия
выполнения неравенства D.7.3).
Оценку сверху для времени Т получим, используя неравенство
Хк[ехр(ХкТ) - \]~1 ^Т-1. D.7.4)
Из D.7.3) и D.7.4) следует, что если Т выбрано из условия
Т=-^-, Q\ = y2\qk\$k < oo, D.7.5)
то неравенство D.7.3) заведомо выполнено. Следовательно, при схо-
сходимости ряда Q\ время Т можно выбрать согласно простой формуле
D.7.5).
Обратимся к уравнению второго порядка по времени D.3.2). В этом
случае вместо формул для времен Тк имеются лишь оценки сверху
D.2.27) и D.6.4), поэтому условие равенства всех Тк нельзя выполнить
точно. Имея это в виду, а также для упрощения последующих формул
предлагается выбрать Uk в виде
Uk = срк, с > О, к =1,2,...,
D.7.6)
Uo = max(c\\qo\,C2\qo\), c\ > 0, с2 > 0.
Здесь с, с\, С2 — постоянные. Подставляя Uk из D.7.6) в D.2.27),
получим
Тк^п\Bс)-1 +л/2(здс)-1/2! , к= 1,2,... .
Последнее неравенство не нарушится, если в нем заменить
на и\ ^ Uk. Получим оценку
'/2]. D.7.7)
При подстановке выражения D.7.6) для Щ в неравенство D.6.4)
будем различать два случая. В первом случае, при
получим из D.6.4) и D.7.6)
c2\qo\,
< (л/2 +I)cf42c^1/2. D.7.8)
Во втором случае при ci|</o| < С21<7о| аналогичные оценки приводят
точно к такому же результату D.7.8). Выберем постоянные с\, с2 так,
чтобы оба слагаемых в правых частях неравенств D.7.7) и D.7.8)
совпадали почленно, т. е.
§ 4.7. Анализ ограничений и построение управления
211
пBс)-1 = (л/2 + ljcf1, W2 (с^с)-1/2 = 2с~1/2.
Отсюда находим искомые постоянные
с\ = z/ic, C2 = ^с,
i/i = 2(л/2 + Отг-1 « 1.53, щ = 2u;i7r-2.
Формулы D.7.6) при учете равенств D.7.9) запишем в виде
U fc^l, Uo = с
D.7.9)
2ko|)- D.7.10)
Величины z/i, z/2 определены в D.7.9) и не зависят от с. Так как
в силу выбора постоянных с\ и С2 правые части неравенств D.7.7)
и D.7.8) совпадают, то оценка D.7.7) справедлива при всех к ^ 0.
Таким образом, для времени процесса управления D.7.1) во всех
случаях имеем оценку
Т < тг [Bс)-1 + л/2 (^ic)-1/2] . D.7.11)
Осталось выбрать постоянную с так, чтобы удовлетворить ограни-
ограничению D.4.12). Подставляя D.7.10) в D.4.12), получим
D.7.12)
Здесь введены обозначения
Q* = supQ2(x),
-\-max(ui\qo\,u2\qo\)\(po(x)\,
D.7.13)
и использованы формулы D.2.27) для р^. Неравенство D.7.13) запи-
записано для случая наличия нулевого собственного значения. При его
отсутствии следует просто опустить последнее слагаемое (max) в фор-
формуле D.7.13) для Q2.
Таким образом, достаточным условием разрешимости поставленной
задачи управления (задачи 4.1) для уравнения D.3.2) при помощи
предложенного подхода является равномерная ограниченность ряда
Q2(x) из D.7.13) в области п. Для этого достаточно потребовать
равномерной ограниченности в О следующих двух рядов:
D-7.14)
212 Гл. 4. Управление системами с распределенными параметрами
Используя обозначение D.4.13), условие ограниченности Q* из
D.7.13) можно заменить более сильным условием сходимости числово-
числового ряда
Х> Ш2}[/2, D.7.15)
или условием сходимости двух рядов
Qe = ^ШкЫФк < оо, Q7 = Y, Ш$к < оо. D.7.16)
Подытожим полученные результаты. Для обоих уравнений D.3.1),
D.3.2) указаны условия разрешимости задачи 4.1 и даны оценки сверху
времени процесса управления Т.
Задача D.3.1) всегда разрешима, время Т для нее может быть
выбрано из условия D.7.3) или, в случае сходимости ряда Q\, из более
простого условия D.7.5).
Задача D.3.2) заведомо разрешима, если выполнено одно из условий
сходимости рядов D.7.13)—D.7.16): Q2, или д3 и д4, или д5, или дб
и Qj. Для времени Т имеется оценка D.7.11), в которой постоянная с
должна быть выбрана из условия D.7.12). Здесь число Q* определяется
соотношениями D.7.13) или одним из следующих соотношений:
g* = supQ3(x) + supQ4(x), g* = g5, g* = g6 + g7
в случае выполнения условий сходимости рядов D.7.14)—D.7.16) соот-
соответственно.
Отметим, что при равномерном стремлении к нулю начальных
функций г^о, wto все их коэффициенты Фурье стремятся к нулю,
и при этом все ряды в D.7.3), D.7.5), D.7.13)—D.7.16) также стремятся
к нулю. Из оценок D.7.5), D.7.11), D.7.12) следует, что при этом для
обоих уравнений D.3.1), D.3.2) время процесса Т может быть сделано
сколь угодно малым: Т —> 0.
В общем случае, при указанных условиях разрешимости задачи 4.1,
сначала определим время Т. Для уравнения D.3.1) воспользуемся
формулой D.7.5), а для уравнения D.3.2) сначала найдем с из условия
D.7.12), а затем время Т из условия D.7.11).
После определения времени Т и постоянной с найдем Uk из соотно-
соотношений D.7.2) и D.7.10) для уравнений D.3.1) и D.3.2) соответственно.
Коэффициенты Uk искомого закона управления D.4.4) определены
в виде синтеза, т. е. в зависимости от текущих значений q^ и фс
для уравнений D.3.1) и D.3.2) соответственно, см. § 4.5 и § 4.6.
Поскольку для систем D.3.1) и D.3.2) известны оптимальные траек-
траектории, то управления, полученные в форме синтеза, могут быть пред-
представлены и в виде программ Uk(t), т.е. в виде релейных функций
времени с точками переключения, зависящими от начальных условий.
§4.8. Примеры 213
Таким образом, управление D.4.4) может быть представлено
либо в виде программного управления для заданных начальных
условий, либо в виде синтеза, если используются управления
Uk в зависимости от qk и qk- Во втором случае управление
формируется в виде v = v(x;w(-,t)) для системы D.3.1) и в виде
v = v(x;w(-,t),wt(-,t)) Для системы D.3.2). Приведенная запись
означает, что управление v в точке х G О в момент t есть функционал
от функций w(y,t) и wt(y,t) при у е О. Однако при этом сохраняется
и зависимость от начальных функций wo, wto посредством постоянных
Uk, которые зависят от начальных данных, см. D.7.2), D.7.10). В этих
формулах постоянные Тис также зависят от начальных условий.
Полученное управление D.4.4) по построению таково, что
все краевые и начальные условия, а также ограничения D.3.6)
автоматически удовлетворяются. Это управление не является
оптимальным, но имеет некоторые свойства оптимальности: во-первых,
оптимальными по быстродействию являются управления для каждой
подсистемы и, во-вторых, ограничения Uk выбраны так, что времена
управления для подсистем равны или близки друг к другу.
Ниже рассматриваются некоторые конкретные примеры, в которых
анализируются условия сходимости рядов D.7.5), D.7.15), D.7.16).
Получены условия разрешимости задачи 4.1 в виде требований
к начальным функциям. В § 4.9 даны некоторые общие условия
разрешимости задачи 4.1 для уравнения D.3.2).
§ 4.8. Примеры
Одномерные задачи (п = 1; А = А). Рассмотрим сначала уравне-
уравнения теплопроводности и колебаний в случае одной пространственной
переменной х. Уравнения D.3.1), D.3.2) имеют вид
Wt = Wxx+v, wtt=wxx+v. D.8.1)
Область О представляет собой интервал @, а) оси х, а ее граница
состоит из двух точек х = 0, х = а. Будем параллельно рассматривать
условия D.3.3) типа Дирихле и Неймана
w@) = w(a) = 0, wx@) = wx(a) = 0. D.8.2)
Собственные функции (fk(x), отвечающие задачам D.8.1), D.8.2),
удовлетворяют уравнениям
^ = -Afepfe, 0 < х < а, D.8.3)
где штрихи означают производные по х, и условиям Дирихле или
Неймана
= 0. D.8.4)
214 Гл. 4. Управление системами с распределенными параметрами
Собственные значения задач D.8.3), D.8.4) таковы:
л 2 Кк n Qrx
Ак = ик, иок = — D.о.о)
а
причем к ^ 1 для задачи Дирихле и к ^ 0 для задачи Неймана.
Ортонормированные собственные функции для задач Дирихле
и Неймана равны соответственно
(\ /q / \1/2 ' ( \ 7 1 О
X ) — [Zj I d J Sill \UJkX J, t\i — 1, Zj ... ,
D.8.6)
<Po(x) = a/2, ipk(x) = B/aI/2 cos(cokx).
Величины Фк из D.4.13) в данном случае ограничены:
1 \ 1 /R _, —1/2 //1 О 7\
/с ^ 1, Фо = ft 7 . D.о./)
Вычислим коэффициенты Фурье D.4.8), D.4.9), предполагая
начальные функции wq(x), Wto(x) достаточное число раз дифферен-
дифференцируемыми по х и применяя интегрирование по частям. При помощи
D.8.6) получим
а
Г
Qk(O) = wO(pkdx =
^2
Г Г
Ц [(-wo) cos(o;fca;)] + \w'o cos
aj у lo J
2\1/2 f Г 1
- I ukxl [(-w0) cos^x)] - o;fc 4 г^о sin(u)kx)dx \ =
aJ I ° J J
2\ ^2 Г а
) ^ j [(^o + ЦГ2Ч') co]
для задачи Дирихле и
1 /2
a
^Jv sin(a;fca;)da; 1 D.8.8)
- j ^^ [о (k)]
aj I lo J
2\ Г
J 2| [D -
a
I w% sin(u;kx)dx 1, fc > 1, D.8.9)
§4.8. Примеры 215
для задачи Неймана. Из соотношений D.8.8), D.8.9) можно вывести
оценки коэффициентов Фурье в зависимости, во-первых, от степени
гладкости начальной функции wo и, во-вторых, от дополнительных
условий в граничных точках х = 0, х = а, т. е. на Г. Аргумент О
у функции qk опускаем. Через Bj всюду далее обозначены некоторые
положительные константы, а через Сг — классы функций, имеющих
на отрезке [0, а] непрерывные производные до г-го порядка включи-
включительно. Для задачи Дирихле при помощи D.8.8) получим:
\qk\ < В\ио^х при woe С1;
\qk\ ^ ^>2^/Г2 при wq Е С2, wq = 0 на Г;
D.8.10)
\qk\ ^ Дз^3 при г^о Е С3, г^о = 0 на Г;
\qu\ < В/^ио^А при г^о Е С4, wo = w'q = 0 на Г.
Аналогично для задачи Неймана из D.8.9) имеем
\qk\ < Въио^х при woe С1;
\qk\<: В^2 при w0 eC2;
D.8.11)
\qk\ < ^7^3 при w0 Е С3, Wq = 0 на Г;
|фс| < В$ои^4 при г^0 Е С4, w'0 = 0 на Г.
Очевидно, оценки вида D.8.10), D.8.11) можно продолжать неогра-
неограниченно. Для коэффициентов Фурье фс(О) из D.4.9) имеют место
оценки, аналогичные D.8.10), D.8.11), с заменой wo на wto.
Переходя к исследованию сходимости рядов из D.7.5), D.7.16),
заметим, что величины Фк согласно D.8.7) не зависят от к. Учитывая
еще соотношение D.8.5), получим следующие условия сходимости
рядов.
Ряд D.7.5) для задачи Дирихле сходится при условиях
w0 E С2, wo = O на Г, D.8.12)
а для задачи Неймана — при условии
woe С2. D.8.13)
Ряды D.7.16) для задачи Дирихле сходятся при условиях
wo е С3, wt0 е С2, w0 = wt0=0 на Г, D.8.14)
216 Гл. 4. Управление системами с распределенными параметрами
а для задачи Неймана — при условиях
w0 ? С3, wt0 е С2, ^=0 на Г. D.8.15)
on
Отметим, что условия сходимости D.8.12), D.8.14) рядов D.7.5),
D.7.16) для задачи Дирихле включают, помимо требований гладкости,
условия Дирихле для начальных функций г^о, wtQ. Эти условия, вообще
говоря, не являются обязательными при постановке начально-краевых
задач, и их нужно накладывать дополнительно. В случае же задачи
Неймана условия D.8.13), D.8.15) менее ограничительны: для ряда
D.7.5) никаких условий, кроме условий гладкости, не накладывается,
а для рядов D.7.16) накладывается условие Неймана только на началь-
начальную функцию г^о (но не на функцию wto).
Напомним, что задача управления для первого уравнения D.8.1)
(уравнения теплопроводности) всегда разрешима, и условия D.8.12),
D.8.13), обеспечивающие сходимость ряда D.7.5), служат лишь
основанием для простой оценки времени процесса управления в D.7.5).
Для второго уравнения D.8.1) (уравнения колебаний струны) условия
D.8.14), D.8.15) являются достаточными условиями разрешимости
задачи управления предложенным методом.
Замечание 4.1. Если условия типа D.8.14) или D.8.15) на Г
в начальный момент t = 0 не выполнены, то, тем не менее, предло-
предложенный метод управления всё равно можно применить. Для этого
заметим, что эти условия будут обязательно выполнены при сколь
угодно малом t = At > 0 в силу наложенных краевых условий
(при любом управлении v(x,t) на интервале t ? [0, At]). Поэтому
при t ^ At можно применять предложенный метод управления.
Следовательно, эти условия на Г при t = 0 являются несуществен-
несущественными. Таким образом, достаточными условиями разрешимости
задачи управления для уравнения колебаний струны при условиях
Дирихле и Неймана являются условия
w0eC3, wt0eC2. D.8.16)
Указанное выше соображение будем использовать и в дальнейшем,
опуская несущественные условия на границе Г при t = 0.
Управление колебаниями стержня (п = 1; А = —А2). В каче-
качестве примера уравнения четвертого порядка рассмотрим управление
поперечными колебаниями упругого стержня. Уравнение D.3.2) этом
случае имеет вид
wu = ~wxxxx + v. D.8.17)
Рассмотрим сначала граничные условия шарнирного опирания на
обоих концах стержня длины а, т. е.
w = wxx = 0 на Г, Г = {х = 0, х = а}. D.8.18)
§4.8. Примеры 217
Задача на собственные значения D.4.1) для системы D.8.17),
D.8.18) имеет вид
(?>IV = \(р, xGfl = @,a), (р = (р" = 0 на Г. D.8.19)
Как известно, собственные значения задачи D.8.19) положительны
и таковы:
къ х 7 = 1,2,... , D.8.20)
где uok имеют смысл частот собственных колебаний стержня. Соответ-
Соответствующие собственные функции задачи D.8.19) могут быть представ-
представлены в виде группы равенств D.8.6). Поэтому оценки D.8.7), D.8.8)
и D.8.10) остаются справедливыми для рассматриваемой задачи,
однако всюду в D.8.6), D.8.8), D.8.10) частоты и^ определяются
теперь формулами D.8.20) (вместо D.8.5)). Используя указанные
оценки, получим аналогично D.8.14) следующие достаточные условия
сходимости рядов D.7.16) в рассматриваемой задаче:
woeC\ wt0eC2. D.8.21)
Несущественные условия на Г при t = 0 опускаем, в соответствии
с приведенным выше замечанием 4.1. Можно показать [79], что точно
такой же вид D.8.21) имеют достаточные условия сходимости рядов
и для других наборов краевых условий в задаче управления колебани-
колебаниями упругого стержня, а именно для условий:
w = wx = 0 при х = 0, х = а;
w = wx = 0 при х = 0, w = wxx = 0 при х = а;
w = wx = 0 при х = 0, wx = га^ж = 0 при х = а;
г^ = г^ж = 0 при ж = 0, га^ = wxxx = 0 при ж = а;
w = и>жж = 0 при х = 0, и>ж = и>жжж = 0 при х = а.
Двумерные и трехмерные задачи (п = 2,3; А = А). Перейдем
к рассмотрению уравнений
wt = Aw + v, wtt = Aw + v; n = 2,3, D.8.22)
в двумерном и трехмерном случаях. Пусть область О представляет
собой прямоугольник при п = 2 и прямоугольный параллелепипед при
п = 3, т. е. задается в виде
U:0<xi<ai; /=1,2 или /=1,2,3. D.8.23)
218 Гл. 4. Управление системами с распределенными параметрами
Решения задач на собственные значения D.4.2) для уравнений
D.8.22) в областях D.8.23) при условиях типа Дирихле и Неймана
известны и получаются методом разделения переменных. В двумерном
случае (п = 2) для задачи Дирихле получим аналогично D.8.5), D.8.6)
V
г, fc = 1,2,...
D.8.24)
sm
\
sin
Для задачи Неймана собственные значения задаются соотношени-
соотношениями D.8.24) при г, к = 0, 1,... , а собственные функции имеют вид,
аналогичный D.8.6):
2) = 2(aia2)
(
V а\
COS
ь^2) = 2(aia2) 1/2
cos
( -j
D.8.25)
\у x2) = 2(aia2
~1/2
cos (
i, к = 1,2 ... .
Величины D.4.13) в силу D.8.24), D.8.25) ограничены и таковы:
гк = Baia2
1-1/2.
г, к= 1,2,... .
D.8.26)
Перейдем к оценкам коэффициентов Фурье D.4.8), D.4.9), пред-
предполагая начальные функции г^о, wto достаточно гладкими. Заменяя
кратные интегралы по области п повторным интегрированием по х\,
х2, а затем, применяя интегрирование по частям, получим аналогично
D.8.8)—D.8.11) следующие оценки:
¦) при
\q%k\ < В2(гк)-2 при
\Qik\ < B3(ik)~3 при
для задачи Дирихле и
г^о = 0 на Г;
г^о = О на Г
D.8.27)
„ 219
I to
\qik\
D.8.28)
\qik
для задачи Неймана. В соотношениях D.8.27), D.8.28) всюду г, к =
= 1,2,... , а С(г) — класс функций w, имеющих в замкнутой области
О непрерывные частные производные вида
яр+q
O^p^r, O^q^r. D.8.29)
§4.8.
^ B§i~l при
< Бдг~2 при
^ В\2%~ При
Примеры
qi0\ < Б5/С-1;
Qok ^ В%к~2;
w0 G СЮ;
ко*: < ВцА;;
Wo е С(з) ^о
ах^х«' "^^^" "¦**¦*'•
Для коэффициентов Фурье щк из D.4.9) имеют место оценки,
аналогичные D.8.27), D.8.28), с заменой г^о на wtQ.
При помощи соотношений D.8.24), D.8.26)-D.8.28) получим
искомые достаточные условия сходимости рядов D.7.5), D.7.16).
В рассматриваемых здесь случаях суммирование в этих рядах
проводится по двум индексам г, к в пределах от 1 до оо для задачи
Дирихле и от 0 до оо для задачи Неймана.
Оказывается, что ряд D.7.5) сходится для задачи Дирихле при
условиях
w0 e CB), wo = O на Г, D.8.30)
а для задачи Неймана — при условии
w0eCB). D.8.31)
Ряды D.7.16) сходятся для задачи Дирихле при условиях
w0 e CC), wm e CB), w0 = wm = 0 на Г, D.8.32)
а для задачи Неймана — при условиях
wto e С^2\ ^=0наГ. D.8.33)
on
220 Гл. 4. Управление системами с распределенными параметрами
Условия сходимости D.8.30)-D.8.33) вполне аналогичны соответ-
соответствующим условиям D.8.12)—D.8.15) для одномерной задачи.
Опуская несущественные условия на Г при t = 0 в соответствии со
сделанным замечанием 4.1, получим, что ряд D.7.5) для задач Дирихле
и Неймана сходится при условии D.8.31), а ряды D.7.16) для этих же
задач сходятся при условиях
w0eC{3\ wtoeC®. D.8.34)
В трехмерном случае (п = 3), который рассматривается совершенно
аналогично двумерному, собственные значения определяются равен-
равенствами, подобными D.8.24):
Здесь г, j, к ^ 1 для задачи Дирихле и г, j, к ^ 0 для задачи Неймана.
Для собственных функций и коэффициентов Фурье имеют место
формулы и оценки, аналогичные D.8.24)-D.8.26). В итоге приходим
к точно таким же условиям сходимости D.8.30)-D.8.34), как и в дву-
двумерном случае. При этом под С^ в этих условиях следует понимать
аналогично D.8.29) класс функций w, имеющих в замкнутой области п
непрерывные частные производные вида
§ 4.9. Условия разрешимости в общем случае
Как указано в § 4.7, для разрешимости задачи управления в слу-
случае уравнения D.3.1) не требуется никаких дополнительных условий,
а в случае управления D.3.2) достаточно, например, чтобы были рав-
равномерно ограничены в п функции Q%(x) и Q±(x) из D.7.14). Проана-
Проанализируем эти условия.
Всюду ниже предполагаем достаточную гладкость коэффициентов
операторов А из D.3.2) и М из D.3.3), а также границы Г и начальных
функций г^о, wto из D.3.5).
Заметим, что ряды D.7.14) содержат, во-первых, собственные функ-
функции (fk(x) задачи D.4.2) и, во-вторых, коэффициенты Фурье qk, qk
начальных функций г^о, wto. Поэтому представляется целесообразным
использовать следующие оценки рядов D.7.14), вытекающие из нера-
неравенства Коши-Буняковского и позволяющие разделить вклады соб-
собственных функций и коэффициентов Фурье:
§4.9. Условия разрешимости в общем случае 221
D.9.1)
4(x) [? V ? 2] V2
Здесь /З и 7 — пока произвольные числа, которые должны быть выбра-
выбраны так, чтобы все ряды в D.9.1) были ограничены.
Будем рассматривать дробные (положительные и отрицательные)
степени дифференциального оператора А. Оператор А порядка 2т
определяет преобразование
Aw = f.
Его область определения Da есть класс функций w, определенных
в области О, имеющих в этой области суммируемые с квадратом част-
частные производные порядка до 2т включительно (этот факт можно запи-
записать в форме Da С Я2ш(О), где Я2ш — соответствующее пространство
Соболева), а также удовлетворяющих краевым условиям D.3.3).
Согласно теореме Агмона о ядре [77], оператор A~s при 2ms > п
является интегральным оператором с непрерывным ядром, равным
К(х,у) = ^2\kaipk(x)ipk(y).
Полагая х = у, т. е. рассматривая ядро на диагонали, получим
равномерную ограниченность ряда
y^X^s(fl(x) < const < oo, 2ms > п.
Отсюда следует, что для равномерной ограниченности первых
сомножителей в правых частях D.9.1), т.е. рядов, зависящих от х,
достаточно, чтобы
C>пBт)-\ j>nBm)-{. D.9.2)
Отметим, что условия D.9.2) при т = 1 впервые даны в работе
[36]. Вторые сомножители в правых частях D.9.1) (ряды, зависящие
от коэффициентов Фурье) в силу равенства Парсеваля можно предста-
представить в виде
D.9.3)
222 Гл. 4. Управление системами с распределенными параметрами
Ряды D.9.3) сходятся, если функции A^^^^wo и A7^2wto сум-
суммируемы с квадратом в области О, т.е. принадлежат классу 1/2@).
Другими словами, функции wq и wto должны принадлежать областям
определения соответствующих операторов:
wo e DA(i+f3)/2, %gDA7/2. D.9.4)
Из результатов работы [97] следует, что область определения Das
при s G (О, 1) лежит в i^2ms(^) и выделяется теми из краевых условий
D.3.3), порядок которых ordMj = Tj < r = 2ms — 1/2. В случае, если
для некоторого j имеем rj = г, то соответствующее граничное условие
понимается в некотором интегральном смысле.
В рассматриваемом случае согласно D.9.4) имеем
s = i(l+/3), r = m(l+/?)-i для w0,
D.9.5)
s = - 7, г = Ш7 - х Для wto,
причем s может быть и больше единицы.
Пусть, например, s = 1 + <т, где сг е (О, 1). Тогда, представляя
результат действия оператора As в виде Asw = т4°"(т4г(;) и применяя
теорему Сили [97], придем к следующему утверждению. Область опре-
определения Das лежит в i^2ms(^) и выделяется краевыми условиями
D.3.3), а также теми из краевых условий MjAw = 0, для которых
ordMj < 2та - -.
Другими словами, при s G A,2) на функцию w, помимо краевых
условий D.3.3), накладываются еще те из условий вида MjAw = 0, для
которых
ord (MjA) < r = 2ms - -.
Аналогичные результаты следуют также из лемм, приведенных
в приложении 2 книги [37].
Таким образом, для сходимости рядов D.9.3) функции г^о и wto
нужно подчинить условиям, зависящим от параметров s, r, причем эти
условия тем жестче, чем больше s, r. Отметим, что в ограничениях
Tj < г на порядки операторов, так как дробная часть числа г несуще-
несущественна, Tj — целые числа.
Определим при помощи соотношений D.9.2), D.9.5) для каждой
из функций г^о, Wto Два числа: нижнюю грань 5* возможных значений
s и целую часть г* от нижней грани возможных значений г. Значения
и* = 2ms* и г* для различных пар п, т при п ^ 3, т ^ 2 сведены
в табл. 8.
§4.9. Условия разрешимости в общем случае
223
Таблица
п,т
1Д
1,2
2,1
2,2
3,1
3,2
3/2
5/2
2
3
5/2
7/2
^*(wto)
1/2
1/2
1
1
3/2
3/2
г* (w0)
1
2
1
2
2
3
r*(wto)
0
0
0
0
1
1
При помощи найденных значений z/*, r* можно ответить на вопрос
о сходимости рядов D.9.1) и тем самым указать достаточные условия
разрешимости рассматриваемых задач управления. Для этого доста-
достаточно потребовать выполнения следующих условий.
Во-первых, функции wo, wtQ должны принадлежать классам HV(Q),
где v — любое число, большее соответствующего и*. В частности,
v можно выбрать целым, и тогда это требование будет означать
существование у функций г^о, wto, суммируемых с квадратом частных
производных порядка до v включительно.
Во-вторых, функции wq, wto должны удовлетворять на Г тем
из краевых условий D.3.3), для которых ordMj ^ г*, и тем из краевых
условий MjAw = 0, для которых oid(MjA) < г*. Так как ordMj <
< ord A = 2га, то наложение условий MjAw = 0 может потребоваться
лишь при г* ^ 2га.
Из табл. 8 видно, что неравенство г* ^ 2т имеет место только
при п = 3, т = 1 для функции wq. В этом случае для задачи Дирихле
(ordM = 0) имеем oidMA = 2 = r*(wo), и на функцию г^о нужно
наложить дополнительно условие Aw = 0 на Г.
В случае же задачи Неймана (ordM = 1) при п = 3, т = 1, а также
для любых задач при остальных значениях n, m дополнительных
условий не возникает.
Появление дополнительного краевого условия можно пояснить сле-
следующим образом. Предлагаемый закон управления D.4.4) обращается
в нуль на Г в случае задачи Дирихле, так как при этом (fk = 0 на Г.
Это снижает возможности управления на границе области, и может
требовать дополнительных условий на начальные функции на Г.
В то же время некоторые из краевых условий D.3.3) для разреши-
разрешимости задачи накладывать необязательно. Например, при п = 2, т =
= 1 имеем r*(u>o) = 1, r*(wto) = 0. Следовательно, для оператора А
второго порядка в случае задачи Дирихле (ordM = 0) функции г^о, wto
должны удовлетворять условию Дирихле, а в случае задачи Неймана
(ordM=l) функция г^о должна удовлетворять условию Неймана,
а функция Wto может ему и не удовлетворять.
224 Гл. 4. Управление системами с распределенными параметрами
Сопоставляя данные табл. 8 с результатами анализа примеров
в § 4.8, видим, что в примерах условия сходимости оказались менее
ограничительными при п = 1, т = 2 и п = 3, m = 1. При п = 1,
т = 2 в примере не требуется накладывать условие -ш^ = 0 на Г,
которое фигурирует в табл. 8: r*(wo) = 2. При п = 3, m = 1 в примере
для задачи Неймана не требуется условие dwto/dn = 0, а для задачи
Дирихле — условия Аг^о = 0 на Г, которые следуют из табл. 8.
Следует также иметь в виду, что, в соответствии с замечанием
из § 4.8, условия на Г при t = 0 оказываются несущественными для
решения задачи управления, если они автоматически выполняются
при t = At > 0 в силу наложенных краевых условий.
Глава 5
УПРАВЛЯЕМЫЕ СИСТЕМЫ
ПРИ СЛОЖНЫХ ОГРАНИЧЕНИЯХ
В данной главе предлагается способ построения управления
в линейной системе при наличии ограничений на управление
и смешанных ограничений, наложенных в каждый момент времени
на фазовые координаты, управляющие воздействия, а также на неко-
некоторые интегралы, зависящие от этих переменных. Предложенный
способ управления представляет собой обобщение известного способа
Калмана, распространенного на случай наличия ограничений.
Построен в явном виде закон управления как системой осцилляторов,
управляемой одним ограниченным воздействием, так и другими
колебательными системами. Для некоторых систем второго порядка
построенный закон управления сравнивается с управлением, опти-
оптимальным по быстродействию. Построены законы управления также
для некоторых систем более высокого порядка, в частности, для
систем четвертого порядка со смешанными ограничениями, которые
представляют собой модели механических и электромеханических
систем, содержащих колебательное звено и электрический двигатель.
§ 5.1. Постановка задачи
Рассмотрим линейную управляемую систему
E.1.1)
Здесь х = (х\,... ,хп) — n-мерный вектор фазовых координат,
и = (и\,... ,ит) — m-мерный вектор управляющих воздействий.
Матрицы A(t) и B(t) размера п х п и п х т соответственно, а также
n-мерный вектор /(?) — заданные кусочно-непрерывные функции
времени t.
Предположим, что на фазовые координаты и управления системы
E.1.1) наложены ограничения типа неравенств, выражающие ограни-
ограниченность абсолютных величин или компонент некоторых линейных
комбинаций переменных х, и и интегралов от них. Для определенности
будем рассматривать ограничения следующих двух типов:
226 Гл. 5. Управляемые системы при сложных ограничениях
D\t)u{t) +
Т
&Ц,т)х(т) + Н%т)и(т)]Aт + №)\\ < 1,
i=l,...,r, E.1.2)
dr
1,
j= 1,...,5. E.1.3)
Здесь и далее скобками (•, •) обозначены скалярные произведения век-
векторов.
Ограничения E.1.2), E.1.3) должны выполняться при всех t G
G [to,T], где to и Т — начальный и конечный моменты времени
соответственно. Начальный момент to считаем фиксированным, а Т
пока не фиксировано. Через С\ G1 в E.1.2) обозначены матрицы
размера / х п, через D1, Нг — матрицы размера / х га, через цг —
/-мерный вектор, где / — некоторое целое число. Через pJ, gi
в E.1.3) обозначены n-мерные векторы, через qi, Ь? — га-мерные
векторы. Матрицы и векторы С\ D1, {1г, pJ, qi суть заданные
кусочно-непрерывные функции t на отрезке [to,T], а матрицы
и векторы G1, Нг, gi, h? — заданные кусочно-непрерывные по каждому
аргументу функции t, r при t, r e [to,T].
Ограничения E.1.2), E.1.3) включают как частный случай
различные часто встречающиеся ограничения на управления, фазовые
координаты и интегралы от них. Так, если D1 — единичная матрица
размера га х га, а остальные матрицы и векторы С\ G1, Нг, \il
в E.1.2) равны нулю, получим из E.1.2) ограничение на модуль
управления ||^(t)|| ^ 1. Если вектор gJ имеет одну отличную
от нуля компоненту, а все остальные векторы pJ, gi, h? в E.1.3)
равны нулю, получим из E.1.3) ограничение на одну компоненту
управления. Приравнивая нулю все введенные в E.1.2), E.1.3)
матричные и векторные коэффициенты, кроме С\ _pJ, получим фазовые
ограничения. Аналогично, при обращении в нуль всех введенных
матриц и векторов, кроме Нг, Ь?, получим интегральные ограничения
на управление и т. д.
Поставим задачу о построении управления u(t), удовлетворяющего
ограничениям E.1.2) и E.1.3) при t G [to,T] и переводящего систему
E.1.1) из заданного начального состояния
x(to)=x° E.1.4)
§5.2. Обобщение метода Калмана 227
в заданное конечное состояние
х(Т)=х\ E.1.5)
где х°, хх — n-мерные векторы.
Обозначим через Ф(?) фундаментальную матрицу однородной
системы E.1.1). Имеем
Ф(*0)=Дп, E.1.6)
где Еп — единичная матрица размера п х п. Запишем решение системы
E.1.1), удовлетворяющее начальному условию E.1.4), в виде
t
x(t) = Ф(*)|ж° + J ф-[(т)[В(т)и(т) + /(т)] dr\. E.1.7)
Подставляя решение E.1.7) в краевое условие E.1.5), получим условие
на управление:
т
<&-l(t)B(t)u(t)dt = x*. E.1.8)
Здесь введено обозначение
т
х* =ф-1(Т)х1 -х°- \<&-l(t)f(t)dt. E.1.9)
to
Таким образом, искомое управление должно удовлетворять ограни-
ограничениям E.1.2), E.1.3) и условию E.1.8).
§ 5.2. Обобщение метода Калмана
Воспользуемся методом управления, предложенным в работе [38]
для случая отсутствия ограничений. Будем искать управление в виде
u = QTc, E.2.1)
где с — n-мерный постоянный вектор, Q(t) — матрица размера п х тп,
равная
E.2.2)
а символ «т» означает транспонирование. Подставляя E.2.1) в E.1.8),
получим уравнение для вектора с:
= x\ E.2.3)
228 Гл. 5. Управляемые системы при сложных ограничениях
Здесь введено обозначение
t
R(t)= \Q{r)QT(r)dr. E.2.4)
to
Из E.2.4) следует, что R(t) — симметрическая неотрицательно-
определенная матрица размера п х п при t ^ to. Будем предполагать,
что матрица R(t) — положительно-определенная при t ^ to, что, как
известно (см. [42]), означает полную управляемость линейной системы
E.1.1). В этом случае векторное уравнение E.2.3) имеет единственное
решение
c = R~\T)x\ E.2.5)
Обратимся к условиям E.1.2), E.1.3). Сначала подставим управ-
управление E.2.1) в решение E.1.7). Пользуясь обозначениями E.2.2)
и E.2.4), получим
t
ж(«) = Ф(*)[:сО + Д(*)с+ 1ф-1(т)/(т)с1т]. E.2.6)
*0
Преобразуем E.2.6) с помощью соотношений E.1.9) и E.2.5):
т
x(t) = \\1
J J E.2.7)
R{{t,T) = R{t)R~\T) - Еп.
Теперь подставим в ограничения E.1.2) и E.1.3) выражение E.2.7) для
х и выражение
u(t) = Q1\t)R~\T)x* E.2.8)
для и, вытекающее из E.2.1), E.2.5). Ограничения E.1.2) приводятся
к виду
||F*(*,T)z*+<?*(*,Т)|| < 1, г= 1,...,г. E.2.9)
Здесь матрица F1 размера / х п и /-мерный вектор фг равны соответ-
соответственно
W(t,r)QT(r)R-\T)]dr,
§5.2. Обобщение метода Калмана 229
Т
г= 1,...,г. E.2.10)
Аналогично, ограничения E.1.3) приводятся к виду
(^(*,Г),ж*)+х'(*,Г)< 1, j= l,...,s. E.2.11)
где n-мерный вектор ^ и скаляр %J равны
Xj(?,T) =
t
т
j=l,...,8. E.2.12)
Отметим, что функции F1, фг, фэ, xJ\ определяемые соотноше-
соотношениями E.2.10), E.2.12), выражаются через заданные функции
и поэтому могут считаться известными. Чтобы наложенные огра-
ограничения E.1.2), E.1.3) удовлетворялись, необходимо и достаточно,
чтобы неравенства E.2.9) и E.2.11) были выполнены при заданном х*
и всех t ? [to,T]. Это накладывает условия на время процесса Т
и на вектор х*, что в силу E.1.9) приводит (при заданном конечном
состоянии хх) к условиям на время Т и на начальное состояние
х°. Мажорируя и упрощая левые части неравенств E.2.9), E.2.11),
можно получить достаточные условия на Т и х°, обеспечивающие
выполнение наложенных ограничений E.1.2), E.1.3). Тем самым
получим достаточные условия управляемости при ограничениях.
Приведем возможные варианты таких условий. Предположим, что
при всех Т ^ to и всех t ? [to,T] выполнены неравенства
230
Гл. 5. Управляемые системы при сложных ограничениях
E.2.13)
г = 1,..., г, j = 1,..., s,
где фг0, Хо — положительные постоянные. Неравенства E.2.9) заведомо
выполнены, если
— фп, i — 1,..., г.
E.2.14)
Пользуясь неравенством Коши-Буняковского, оценим сверху левую
часть неравенств E.2.14):
El
_j=\ 4=1
1/2
/ п
1/2
г= 1,...,г. E.2.15)
Подставляя E.2.15) в E.2.14), получим достаточное условие выполне-
выполнения неравенств E.2.9):
min< A—
/ п
j=\ к=\
г=1,...,г, te[to,T]. E.2.16)
Аналогично, неравенства E.2.11) будут заведомо выполнены, если
mini A-XJO) [max |
3 I
-1
j=
o,T]. E.2.17)
Итак, при выполнении условий E.2.16) и E.2.17) управление
E.2.8) удовлетворяет всем наложенным ограничениям E.1.2) и E.1.3)
при te[to,T] и переводит систему E.1.1) из заданного начально-
начального состояния E.1.4) в конечное состояние E.1.5). Поэтому условия
E.2.16) и E.2.17) можно рассматривать как достаточные условия
управляемости за конечное время Т. Отметим, что в силу равенства
E.1.9) эти условия связывают начальное и конечное состояния х°, хх
и время окончания процесса Т. Условия E.2.16), E.2.17) наложены
на абсолютную величину вектора ж*.
Ниже в данной главе, следуя работам [12,29,54,62,69], рассмот-
рассмотрим способы построения управления для различных линейных систем
со сложными ограничениями.
§5.2. Обобщение метода Калмана 231
Следующая теорема [62] дает простые достаточные условия, обес-
обеспечивающие выполнение ограничения (а — положительная постоянная)
|Н?)|| <а E.2.18)
для закона управления E.2.8) в случае /(?) = 0.
Теорема 5.1. Пусть при некотором Т > to матрица R(T)
неособая, т. е. выполнено условие полной управляемости, и пусть
для любого п-мерного вектора v выполнены неравенства
\\QT(t)K(T)v\\ ^ Xi(T)\\v\\, t e [to,T], E.2.19)
\\R(T)K(T)v\\ > \2(T)\\v\\. E.2.20)
Здесь К(Т) — некоторая неособая матрица размера п х п,
Ai(T),A2(T) > 0 — положительные скаляры, v — произвольный
постоянный п-мерный вектор, причем неравенство E.2.19) должно
иметь место для всех t G [to,T]. Тогда, если выполнено условие
\\х*\\ ^а\2{Т)\-\Т), E.2.21)
то управление u(t), заданное равенством E.2.8), переводит
систему E.1.1) из состояния E.1.4) в состояние E.1.5) в момент Т
и удовлетворяет ограничению E.2.18) при всех t G [to,T].
Доказательство. Управление E.2.8) построено так, что условия
E.1.4), E.1.5) выполнены. Согласно E.2.8) имеем
|И*)|| = \\QT(t)R-\T)x*\\ = \\QT(t)K(T)K-\T)R-\T)x*\\.
Воспользуемся неравенством E.2.19):
Положим здесь х* = R(T)K(T)v и применим сначала неравенство
E.2.20), а затем E.2.21). Получим
|И?)|| < А,(Т)|М| < \{{T)\-\T)\\R{T)K{T)v\\ =
= Л1(Г)А2-1(Т)||х*|Ка.
Тем самым установлено, что ограничение E.2.18) выполняется, что
доказывает теорему. ?
Замечание 5.1. Неособая матрица К"(Т) в E.2.19), E.2.^20) может
выбираться произвольной, в частности, и единичной К = Еп. Про-
Произвол в выборе К(Т) может быть полезен, так как расширяет
232
Гл. 5. Управляемые системы при сложных ограничениях
область применимости приведенных достаточных условий. В слу-
случае единичной матрицы К = Еп число М{Т) согласно E.2.20) есть
оценка снизу наименьшего собственного числа матрицы R(T).
Замечание 5.2. Расчет управления E.2.1) требует решения
линейной алгебраической системы уравнений E.2.3) в отличие
от случая оптимального по быстродействию управления, для
определения которого нужно решить систему трансцендентных
уравнений. Кроме того, управление E.2.1) — непрерывная функция
времени, тогда как оптимальное по быстродействию управление,
вообще говоря, разрывно.
Ниже при рассмотрении примеров различных механических систем
получены более тонкие достаточные условия управляемости, в кото-
которых отдельно учитывается вклад различных компонент вектора х*.
G
т/
7
А.
§ 5.3. Управление системой осцилляторов
Рассмотрим, следуя работе [62], систему гармонических осцилля-
осцилляторов, управляемых посредством скалярного управления
Zi+u>Ui = u- E-3.1)
Здесь ^ — обобщенные координаты, постоянные uoi > О — собствен-
собственные частоты осцилляторов, г = 1,...,п, и — скалярное управление,
на которое наложено ограничение
и E.2.18), т.е. \и\ < а.
^^^^^^_^^^^^^_ В качестве механической моде-
модели системы E.3.1) может служить
система математических маятников,
подвешенных к несущему телу G,
перемещающемуся горизонтально с
ускорением и (рис. 55). При этом ^ —
малые линейные отклонения маятни-
маятников от точек подвеса, равные /^, где
li — длина, & ф{ — угол отклонения
маятника от вертикали.
Другая механическая модель си-
системы E.3.1) представляет собой
совокупность масс, присоединенных
пружинами к несущему телу G. Вся
система перемещается поступательно
и горизонтально, причем ^ — удли-
удлинения пружин, и — ускорение тела G
(рис. 56).
(Л
Рис. 55. Система математических
маятников
Рис. 56. Система осцилляторов
§5.3. Управление системой осцилляторов 233
Поставим задачу определения управления u(t), удовлетворяющего
ограничению E.2.18) и переводящего систему E.3.1) из произвольного
начального состояния при to = О
Ш=& ?i@) = V°i E-3.2)
в заданное конечное состояние
&(Т) = ?', ti(T) = vl E-3.3)
Будем предполагать, что частоты Ui положительны и различ-
различны. Не нарушая общности, пронумеруем их в порядке возрастания,
положим ujq = 0 и введем обозначение
О = min (uok+\ — оок) > О, 0 = uoq < ио\ < ... < иоп. E.3.4)
Отметим, что при О > 0 система E.3.1) вполне управляема [72].
Если же некоторые частоты совпадают, то система становится неуправ-
неуправляемой. В самом деле, если начальные состояния двух осцилляторов
с равными частотами различны, то никаким управлением нельзя
добиться одновременного гашения колебаний этих двух осцилляторов:
разность фаз их колебаний будет оставаться постоянной.
С помощью замены переменных
ii = Vu ii = uj~xZi E.3.5)
приведем систему E.3.1) к виду
Уг = -UJiZi +U, Zi= UJiVi. E.3.6)
Фазовым вектором системы E.3.6) является 2п-мерный вектор-
столбец, составленный из компонент векторов у, z. Можно убедиться,
что фундаментальная матрица однородной системы E.3.6), определен-
определенная в E.1.6), ортогональна и имеет вид
diagfcos и it) diag(— sin Uit)
diag(sini^t) diag(cosc^t)
ф-*(?) = ФТ(?).
E.3.7)
Символом diag(a^) обозначены диагональные матрицы размера п х п
с диагональными элементами а^.
Матрицы B(t) и Q(t) для системы E.3.6) — 2п-мерные векторы-
столбцы. Согласно E.2.2), E.3.6), E.3.7) их элементы таковы:
Bi = 1, Bn+i = О,
E.3.8)
Qi(t) = cos Uit, Qn+i(t) = - sin u^.
234
Гл. 5. Управляемые системы при сложных ограничениях
Из соотношений E.2.4), E.3.8) вытекает
[ Q°
R1 R°
R°T R2
Rk =
1
lQkdt,
E.3.9)
fe = 0, 1,2.
Здесь Qk, Rk — матрицы размера п х п. Их элементы вычислим с
помощью формул E.3.8), E.3.9) (всюду далее г, j = 1,...,п):
^ = — COS UJit SmCJjt, Q\j = COS UJit COS Ldjt,
• • = sin uj it
0 cos 2щТ - 1
Raa —
E.3.10)
12 _
T
i>2 _ s
Отметим, что в силу условия E.3.4)
г О, ооi -\- ujj ^ 30, г т^ j.
E.3.11)
При учете E.3.11) получим следующие оценки элементов E.3.10)
матрицы R(T):
Т
2
1
40'
30'
E.3.12)
§5.3. Управление системой осцилляторов
235
В условиях E.2.19), E.2.20) положим К(Т) = Е^п и определим
величины Ai(T), ^(T). Оценим левую часть неравенства E.2.19),
применяя неравенство Коши-Буняковского и используя выражения
E.3.8) для компонент вектора Q(T), следующим образом:
||QT(*H<||QT(t)|||H|=n1/2|H|.
Следовательно, в E.2.19) можно положить
Ai(T) = n1/2. E.3.13)
Оценим левую часть неравенства E.2.20). Для любого вектора v
имеем
E.3.14)
- —Ьоп\У
М = R(T) - | Е2п.
Здесь введена симметрическая матрица М размера 2n x 2п. Для ее
элементов, используя соотношения E.3.9), E.3.12) для матрицы R(T),
получим оценки
±
2
—,
4
—,
E.3.15)
Согласно неравенству Коши-Буняковского, имеем (здесь и в
E.3.17) суммирование ведется от 1 до 2п)
Учитывая оценки E.3.15) и симметрию матрицы М, получим
2п
16O2
(п2 - п)
2п
32(п2 - в) _ 5вF4п - 55)
236 Гл. 5. Управляемые системы при сложных ограничениях
Из неравенств E.3.16), E.3.17) следует
f\ „>,. E.ЗЛ8)
Используя неравенства E.3.14) и E.3.18), получим
\\R{T)v\\ ^(f-^)lHI- <5-3-19)
Следовательно, условие E.2.20) выполнено, если Т ^ 2кп/О,. При этом
условии, сравнивая E.2.20) и E.3.19), получаем
А2(Т) = (| - ^ > 0. E.3.20)
Подставляя в неравенство E.2.21) выражения E.3.13), E.3.20) и раз-
разрешая его относительно Т, получим
ж*|| + ^. E.3.21)
Вектор х* задан соотношением E.1.9), в котором последнее слага-
слагаемое в правой части равно нулю в силу тождества fit) = 0. Векторы
ж0, х\ согласно E.3.5), E.3.2), E.3.3), таковы:
E.3.22)
= {r1l,uHeiy.
В закон управления E.2.1) подставим элементы Q(t) из E.3.8):
u(t) = У^(сг cos LJit — cn+isimjit). E.3.23)
На основе теоремы 5.1 получаем следующий результат [62].
Теор ема 5.2. При выполнении условия E.3.21) управление E.3.23),
в котором вектор с определяется формулой E.2.5), где матрица
R(T) задана соотношениями E.3.9), E.3.10), удовлетворяет
ограничению E.2.18) и переводит систему E.3.6) {или E.3.1))
из начального состояния E.3.2) в конечное состояние E.3.3)
за время Т.
Заметим, что требуемое время Т растет при увеличении ||ж*||,
при уменьшении возможностей управления (т. е. а) и при сближении
собственных частот, т. е. при уменьшении О.
§5.3. Управление системой осцилляторов 237
Рассмотрим поставленную задачу в частном случае гашения
начальных колебаний, т. е. задачу приведения системы в состояние
равновесия. В этом случае имеем хх = 0 и, учитывая, что /(?) = О,
из равенств E.1.9) и E.3.22) получим (E(t) — энергия колебаний)
II*!2 = Ё [fo°J +".W] = 2?о, ?о = Е@). E.3.24)
г=1
S(*) = s?(k(*)]2 + ".2k(*)]2)- E-3.25)
г=1
Условие E.3.21) с учетом E.3.24) перепишем в виде
2BпЗ>)'/* + 2^ з.26)
При условии E.3.26) управление E.3.23) переводит систему E.3.1)
из начального состояния E.3.2) в состояние равновесия ^ = ^ = 0.
В частном случае п = 1 минимальное время, удовлетворяющее
условию E.3.26), равно (учитываем второе соотношение E.3.18))
E.3.27)
ио\
Сравним время E.3.27) с временем оптимального быстродействия
при условии
е=-гЙ—<1, E-3.28)
означающем относительную малость управления. В этом случае
приближенное оптимальное управление системой E.3.1) при п = 1
и ограничении \и\ ^ 1, построенное в [72] с помощью методов малого
параметра [20], имеет вид
и = —a sign ?i, E.3.29)
а фазовые координаты представляются в виде
a), f 1 = -BЕI/2 sm(u>it + а). E.3.30)
o;i
Здесь энергия Е и фаза а — медленные переменные.
Продифференцируем по t энергию Е из E.3.25) и воспользуемся
равенствами E.3.1), E.3.29), E.3.30):
238 Гл. 5. Управляемые системы при сложных ограничениях
В соответствии с методом усреднения [20] усредним по t правую
часть полученного равенства, считая Е и а постоянными. Получим
уравнение первого приближения, которое проинтегрируем:
Отсюда следует, что время Т°, необходимое для гашения колебаний
(т.е. для выполнения условия Е(Т°) = 0), равно
Т° = ^BЕ0У/2. E.3.31)
Формулы E.3.27), E.3.31) следует сравнивать при условии E.3.28),
при котором получено приближенное выражение E.3.31). При этом
второе слагаемое в E.3.27) много меньше первого, а главные части
формул E.3.27), E.3.31) различаются множителями. Имеем
^«-« 1.273 (е<1).
Данное соотношение дает оценку близости результатов, получае-
получаемых при рассматриваемом способе управления и оптимальном быстро-
быстродействии.
§ 5.4. Маятник с управляемой по ускорению точкой
подвеса
Рассмотрим системы, изображенные на рисунках 55 и 56, в случае
одного осциллятора (п = 1), но при учете смещения <^о несущего тела
G. Уравнения движения и ограничение E.2.18) примут вид
?i+o;i?i='M, io = u, \u\^a. E.4.1)
Здесь все обозначения — те же, что и в § 5.3. Отметим, что
смещения <^о и ?i отсчитываются в противоположные стороны, так
что абсолютное смещение осциллятора равно ?о ~?ь Рассмотрим еще
видоизмененную постановку задачи, в которой управление системами,
изображенными на рисунках 55 и 56, осуществляется не с помощью
ускорения тела G, а с помощью силы F, приложенной к телу G
и ограниченной по величине постоянной Fq. В этом случае вместо
соотношений E.4.1) имеем уравнения и ограничение
-mi?i =F, \F\ < Fo, E.4.2)
где mo — масса тела G, m\ — масса осциллятора.
Введем координату центра масс системы
mo + тп\
§5.4. Маятник с управляемой по ускорению точкой подвеса 239
и преобразуем соотношения E.4.2) к виду
F
т0 + т\
Замена переменных и постоянных
то то
E.4.3)
F
? -1- I 7~~1 I ^ 7~~1
, _ (mp + mi)^ /2 _ (mp + mi)^ _
s — ' — ' —
Шо Шо Шо
приводит соотношения E.4.3), с точностью до обозначений, к виду
E.4.1). Таким образом, соотношения E.4.1) описывают также системы,
управлямые с помощью ограниченной силы.
Для упрощения соотношений E.4.1) сделаем в них замену пере-
переменных
?i =-о> ^о = ^, t=—, u = au. E.4.4)
UJ\ UJ\ UO\
После замены E.4.4) соотношения E.4.1) примут вид
у-\-у = и, z = и, \и\ ^ 1. E.4.5)
В дальнейшем рассматриваем систему в виде E.4.5) и обозначаем
точками производные по новому времени t', причем штрихи у t' и uf
в E.4.5) и далее опускаем.
Поставим задачу построить управление u(t), удовлетворяющее огра-
ограничению \и\ ^ 1 и переводящее систему E.4.5) из заданного началь-
начального состояния
у(О) = у°, y@) = v°, z@) = z°, z(O) = w° E.4.6)
в заданное конечное состояние
у(Т) = у\ y{T) = v\ z{T) = z\ z(T) = w[. E.4.7)
Величины в правых частях равенств E.4.6), E.4.7) — постоянные,
Т > 0 — пока неизвестное время окончания процесса.
Решение данной задачи получено в работах [29,62].
Фазовый вектор системы E.4.5) образуют переменные у, у, z, z.
Следуя общей схеме построения управления, изложенной в § 5.2,
найдем фундаментальную матрицу Ф(?), определяемую соотношениями
E.1.6), и обратную к ней матрицу Ф-1(?):
240
Гл. 5. Управляемые системы при сложных ограничениях
cost
— sint
0
0
" cost —
sint
0
0
sint
cost
0
0
sint
cost
0
0
0
0
1
0
0
0
1
0
о -
0
t
1 _
о -
0
-t
1
E.4.8)
Матрица Q(t) из E.2.2) в данном случае есть четырехмерный
вектор-столбец
QT(t) = (- sint, cost, -t, 1), E.4.9)
а управление E.2.1) представляется в виде
u(t) = —с\ sint + С2 cost — c$t + С4. E.4.10)
Выражение для матрицы R(T), определяемой равенствами E.2.4)
и E.4.9), а следовательно, и решение векторного уравнения E.2.3)
значительно упрощаются, если положить Т = 2ттк, к = 1,2,.... Тогда
матрица R(T) примет вид
R(T) =
Т/2
0
-т
0
0
Т/2
0
0
-т
0
Т3/3
-Т2/2
0
0
-Т2/2
т
E.4.11)
Случай произвольного Т ф 2пк рассмотрен далее в § 5.5.
Выразим компоненты вектора х* через краевые условия E.4.6),
E.4.7) с помощью соотношений E.1.9), E.4.8) и учитывая тождество
№ = 0:
х\=У
Хо = V — V
x$=zx- Twx - z°, x%=wx- w° (T = 2тгА;).
Разрешая уравнения E.2.3) с учетом полученных выражений для мат-
матрицы R(T) и вектора ж*, получим
с\ =
Т(Т2 - 24)
-z°)-6T(w
w
%
§5.4. Маятник с управляемой по ускорению точкой подвеса
241
Т(Т2 - 24)
[Чу1 - у
- (Т2 + 12)™1 - 2(Т2 - 6)гу°], E.4.12)
Осталось выбрать натуральное к в соотношении Т = 2тг& так, что-
чтобы управление E.4.10), E.4.12) удовлетворяло ограничению
при t e [0,Т]. Имеем в силу E.4.10), E.4.12)
\U(t)\
- 24)
I2\zl - z°\ + 6T\w
(Т2 -
- v°
- y°\ \T - 2t\ +3\zl-z°\\T-
= |(T2
2(T2 - 6)^;° - 3Tt(wl + w°)\.
E.4.13)
Здесь T = 2тгк, к > 1, поэтому Т2 > 24.
Линейная функция ip(t) принимает наибольшее значение на одном
из концов интервала [0, Т], следовательно,
(Т2 -
- w°)\} = |
I (T2 -
— w
Отметим еще, что \Т -2t\^T при t e [0,Т].
Учитывая сделанные оценки, из неравенства E.4.13) получим
-y°\+ 2\vl - v°\ + f2(T)
w°
— w
+
z'-z0
, E.4.14)
2T2 + 12T
T2-24 '
ЗТ2 + 12Т
Т2-24 *
242
Гл. 5. Управляемые системы при сложных ограничениях
В правой части E.4.14) заменим функции /i(T), /2^), которые
строго убывают при Т ^ Т\ = 2тг, их максимальными значениями
при Т = Т\ ив полученное неравенство подставим Т = 2тг&, Т\ = 2тг.
Придем к неравенству
u(t)\
Вк
~2
А =
7Г + 3
г;1-!;0
2(тт2 - 6)
2
"
-О =
3(тг
2(тг2 - 6)
Из E.4) следует, что ограничение
к2 -Ак-В
т. е. при условии
Т = 2тгк, к
E.4.15)
1 выполняется, если
1
r = ^U-
0,
+ 4Б
E.4.16)
Формулы E.4.10), E.4.12) вместе с соотношениями E.4.16) для Т
и E.4) для А, В полностью определяют искомое управление u(t)
в явном виде через начальное и конечное состояния.
Рассмотрим частный случай краевых условий E.4.6), E.4.7):
000 01 1 1 гл /с л 1 г7\
у =v =z = w =у =v = w =u, @.4.11)
отвечающий перемещению всей системы, показанной на рисунках 55
и 56, из одного состояния равновесия в другое на расстояние zl.
В случае E.4.17) оптимальное по быстродействию управление и = ±\
релейно и имеет три точки переключения [72]. Время быстродействия
Т° — единственный положительный корень уравнения
i(T°J-2(arccos(cos2(!
причем справедливы соотношения
Т°
1 11/2
т°
1/2
при
00.
E.4.18)
Сравним этот результат с временем перемещения для закона управ-
управления E.4.10). По формулам E.4)—E.4.17) имеем (ent /с* — целая часть
числа к*):
1/2
Т = 27r(ent к* + 1), к* = Б1/2 = 0.7965
Отсюда при больших l^1] получим
Т - 5.005
1/2
00.
E.4.19)
§5.5. Маятник с управляемой по ускорению точкой подвеса
243
Если же воспользоваться непосредственно оценкой E.4.14) в слу-
случае E.4.17) при \zx
оо, то найдем
1
Т ~ B/2(оо)|^1|I/2 = V6\zl\l/2 = 2A49\zl\l/'\ \zl\ -> оо.
E.4.20)
Сравнивая формулы E.4.18)-E.4.20) для Т°, Т, видим, что
при Iz1]—>оо они различаются коэффициентами, что обусловлено
как отличием управления E.4.10) от оптимального, так и способом
мажорирования, проведенного при выводе оценки E.4). Заметим, что
оценка E.4.20) значительно ближе к E.4.18) по сравнению с оценкой
E.4.19) именно за счет уменьшения «потерь» при мажорировании.
Отметим также, что при произвольных краевых условиях оптималь-
оптимальные по быстродействию управления для рассмотренных в § 5.3-5.4
задач неизвестны.
§ 5.5. Маятник с управляемой по ускорению точкой
подвеса (продолжение)
В § 5.4 для упрощения выкладок сделано предположение, что
безразмерное время процесса управления кратно 2тг, т. е. Т = 2тг&.
В данном параграфе, следуя работе [29], откажемся от этого допуще-
допущения и будем рассматривать задачу при произвольном Т.
Поставим задачу построить управление u(t), удовлетворяющее
\\ 1 и переводящее систему E.4.5) из начального
ограничению \и
состояния
z(T)=xl
E.5.1)
в состояние покоя
у(Т) = О, у(Т) = О, z(T)=0, z(T) = 0.
Матрица R(T) при произвольном Т примет вид
E.5.2)
R(T) =
(T-sc)/2 -s2/2 s-Tc с-1
-s2/2 (T+sc)/2 l-c-Ts s
s-Tc l-c-Ts T3/3 -T2/2
c-1
-T2/2
T
E.5.3)
здесь введены обозначения s = sinT, с = cos Т.
244
Гл. 5. Управляемые системы при сложных ограничениях
Пусть фц, i, j = 1,...,4, — элементы обратной матрицы R 1(Т)
из E.5.3). Тогда выражение для управления E.4.10) с учетом E.2.5)
примет вид
u(t) = ^2 {Фих°1 sin t - «
COS ?
E.5.4)
Итак, управление E.5.4) при любом Т > О переводит систему E.4.5)
из начального состояния E.5.1) в терминальное состояние покоя E.5.2)
за время Т. Однако это управление, вообще говоря, не удовлетворяет
ограничению \и\ < 1. Для того чтобы учесть это ограничение, приме-
применим к соотношению E.5.4) неравенство Коши-Буняковского
1/2
Е'
г=1
\—фи sint
cost -
г=1
Введем вспомогательные функции
4
p(t, Т) = >^ (—фм sin t + Фъ. cos t — «
г=1
r(T) = \ max
Lo^t^7
-1/2
1/2
E.5.5)
E.5.6)
E.5.7)
Тогда неравенство E.5.5) перепишется в виде
t(T)'
E.5.8)
Будем выбирать время окончания процесса, исходя из условия
E.5.9)
Из E.5.8) следует, что при выборе Т согласно E.5.9) наложенное
ограничение на управление будет удовлетворено при всех t ? [0, Т].
Таким образом, приходим к следующей процедуре построения
управления u(t). Сначала найдем элементы ф^(Т) обратной матрицы
R~l(T) и подсчитаем функции p(t,T) и г(Т) с помощью равенств
E.5.3), E.5.6) и E.5.7). Эти построения выполняются один раз для
данной системы (см. ниже).
Когда они выполнены, для любого начального вектора х° можно
построить искомое ограниченное управление, переводящее систему
в начало координат. Для этого сначала определим время Т из условия
E.5.9), а затем найдем управление и из E.5.4).
§5.5. Маятник с управляемой по ускорению точкой подвеса
245
Для определения функции г(Т) воспользуемся языком символьных
вычислений Reduce и найдем на компьютере аналитические представ-
представления элементов ф^, г, j = 1, ...,4, матрицы R~l(T), обратной к E.5.3).
Выражения для фц получились довольно громоздкими. Приведем для
примера один элемент матрицы R~l(T):
фп = 2[Т5 + Т4 sinTcosT - 8Т3 sin2Т + 24Т2 sinT(l - cosT) -
- 24ТA - cosTJ] / [T6 - T4(8cosT + sin2 T + 16) +
8T3sinTE-2cosT)+48T2(l -cosT)(l +2cosT)-
-240TsinT(l -cosT) + 192A -cosTJ]. E.5.10)
Используя формулу E.5.6) и
найденные выражения для ф^
вида E.5.10), можно подсчитать
численно максимальные значения
p(t,T) no t e [0,Т]. Таким обра-
образом определена функция г(Т) из
E.5.7). Ее график представлен на
рис. 57.
Проанализируем поведение
функции г(Т) в предельных
случаях.
Пусть время процесса Т —>
—> 0. Разложим функцию p(t, T)
из E.5.6) в ряд Маклорена
(используем Reduce) по текущему
времени
б -
4
2 \
0
г(Т)
т
0 10 20 30 40
Рис. 57. График функции г(Т)
p(t, Т) =
Н)
ф24J + @23
+ @24 + Фи? ~ 2Ь[ф12(Фп + 013 + 022 + 024) +
01з@14 + 023 + 034) + 014@11 + 024 + 044)
'22
+ 024 + 033) + 034@24 + 033 + 044)] + ... . E.5.1 1)
Далее разложим числители и знаменатели элементов 0^-,г, j = 1,... ,4,
симметрической матрицы R~l(T) в ряды по Т. Получим
246 Гл. 5. Управляемые системы при сложных ограничениях
/ / Г16
1
Y V 180 630 '" I V 18144000 '
E.5.12)
_ /Г10 11Г12 \ / / Г16
^12 ~ ^360 ~ 18900 + '") I 1^18144000 ~
Остальные элементы имеют аналогичные представления.
Оценки порядков разложений по Т в числителях и знаменателях
функций фц из E.5.12) показывают, что для получения главного члена
разложения функции p(t,T) согласно E.5.11) достаточно сохранить
лишь главный член (порядка Т16) в знаменателях формул E.5.12).
При этом в числителях выражений E.5.12) следует учитывать члены
различных порядков. В результате приведения подобных членов оказы-
оказывается, что имеет место представление
p(t,T) = 1411200Т-8/(т). E.5.13)
Здесь обозначено
/(г) = 1 - 24т + 204т2 - 760т3 + 1380т4 - 1200т5 + 400т6,
т = |е[0,1]. E.5.14)
График полинома /(т) изображен на рис. 58.
Нетрудно видеть, что наибольшего значения /(т) достигает
на границах интервала изменения т, причем /@) = /A) = 1. Тогда
из E.5.13) и E.5.14) следует, что
maxp(t,T) = 1411200Т-8.
Подставляя этот результат в E.5.7),
получим
г(Т) = 8.4 • 10~4Т4, Т -> 0.
E.5.15)
Равенство E.5.15) для расчета
функции г(Т) при малых Т подтвер-
подтверждается и результатами численного
0 1 \У ^\у^ \У t' построения зависимости г(Т).
0 0.5 1 Пусть теперь время процес-
процесса управления Т —> оо. Подста-
Рис. 58. График полинома /(г) вим в равенство E.5.6) выражения
фц, i,j = 1,...,4, подсчитанные по
формулам E.5.10), и разложим функцию p(t,T) в ряд по обратным
степеням Т. Преобразования, проведенные с помощью языка Reduce,
дают следующее разложение:
§5.5. Маятник с управляемой по ускорению точкой подвеса 247
p(t,T) = AT-2{9(t/TJ - 12(t/T) + 5 +
+ Т [12(Т - 2t)T~l sin(T -t)- sin2(T -t)- sin2t -
-l2BT-3t)T-1smt]}+O(T-4), T -> oo. E.5.16)
Перепишем разложение E.5.16) в виде
po(r) = 9т2- 12т+ 5,
Pi(t,T) = 12A -2r)sinT(l -r)-sin2T(l - т) -
-sin2TT- 12B-Зт) sinТт, t = | e [0,1]. E.5.17)
Перейдем к отысканию максимума E.5.7) при Т —> оо, пользуясь
представлением E.5.17). Нетрудно видеть, что квадратный трехчлен
Ро(г) достигает максимума на отрезке [0, 1] при т = 0. Так как
при Т —> оо вклад второго слагаемого в E.5.17) мал, то имеем
с точностью до малых величин высшего порядка
max p(t,T) =p@,T) = 20Т~2 + 4T-3A2sinT - sin2T), T -^ оо.
E.5.18)
Здесь используется разложение E.5.16). Подставляя E.5.18) в E.5.7)
и разлагая результат в ряд по Т~\ получим
10T-12sinr + sin2r ,
20V5
Продифференцируем E.5.19) по Т:
B-cosT)(l-cosT)
=
5л/5
Следовательно, г(Т) — монотонно возрастающая функция при
Т ^ оо.
Из приведенных расчетов и аналитических разложений вытекает,
что функция г(Т) монотонно возрастает от 0 до оо при изменении Т
от 0 до оо. Следовательно, уравнение E.5.9) при любом ||ж°|| имеет
единственное решение.
Приведем результаты численного моделирования. Процедура рас-
расчета управления уже описана выше. Остановимся подробнее на способе
248
Гл. 5. Управляемые системы при сложных ограничениях
практического численного решения уравнения E.5.9). Весь полубеско-
полубесконечный интервал изменения Т разбиваем на три части [0,То], [To,Ti]
и [Ti,oo), которым соответствуют три интервала изменения функции
г(Т): [0, го], [го,п] и [гьоо). Здесь п = r(Ti), г = 0, 1. На отрезке [0,Т0]
используется асимптотическое представление E.5.15) для малых Т,
на отрезке [T0,Ti] — таблица числовых значений г(Т), а на интервале
[Т\,оо) — асимптотическое представление E.5.19) для больших Т.
Вначале по заданному х° определяем путем сравнения ||ж°|| с го и г\,
в каком из трех отрезков лежит искомое Т. Затем определяем Т
следующим образом. Если Т G [0,То], то согласно E.5.15) имеем
Т =
0.00084;
1/4
Если Т G [To,Ti], то находим Т путем линейной интерполяции
по таблице значений г(Т), хранящейся в памяти компьютера. Если
Т G [Т\, оо), то пользуемся представлением E.5.19). При этом Т удобно
искать в виде
J||+#. E.5.20)
Подставляя E.5.20) в E.5.19), получим для в уравнение
F{9) = 100- 128тBл/5||х0|| +0)+ sin[2B>/5 ||ж°|| + 0)] =0.
Это уравнение решается каким-либо численным методом, например,
методом деления отрезка пополам.
Когда для заданного начального вектора х° определено время Т,
управление u(t) в любой момент t может подсчитываться по формуле
E.5.4). При этом используются аналитические выражения вида E.5.10)
для функций фц, г, j = 1,...,4. Вы-
Вычисляемое таким образом управле-
управление подставляется теперь в правые
части системы E.4.5), которая инте-
интегрируется численно при начальных
условиях E.5.1).
Некоторые результаты моделиро-
моделирования при х° = (—1,2,0.5, 1) пред-
представлены на рис. 59. Жирной ли-
линией показана проекция фазовой
траектории x(t) на гиперплоскость
{у, у), а тонкой — ее проекция
на гиперплоскость (z, z). Время
прихода системы в терминальное
Рис. 59. Проекции фазовых траек- состояние в данном случае оказа-
торий лось равным Т = 13.116.
У (у)
§5.5. Маятник с управляемой по скорости точкой подвеса 249
§ 5.6. Маятник с управляемой по скорости точкой
подвеса
Рассмотрим систему, содержащую колебательное звено и управляе-
управляемую по скорости посредством скалярного управления
|i+u;2(?i-?o) = O, ?0 = и. E.6.1)
Здесь <^о> Ci ~~ обобщенные координаты, и > О — собственная частота
осциллятора, и — скалярное управление, на которое наложено ограни-
ограничение E.2.18).
Уравнения E.6.1) описывают движение систем, изображенных на
рисунках 55 и 56, в случае одного осциллятора (п = 1), но при учете
управления скоростью несущего тела G. В частности, это может быть
двухмассовая система, состоящая из несущего тела и присоединенного
к нему с помощью пружины груза. Вся система перемещается посту-
поступательно и горизонтально, причем ?0 — смещение несущего тела, и —
его скорость, ?i — абсолютное смещение груза.
Другая механическая модель системы E.6.1) представляет собой
математический маятник, подвешенный к несущему телу, перемеща-
перемещающемуся горизонтально со скоростью и. При этом <^о — смещение
несущего тела, ?i = —1\ф\ +^о ~~ абсолютное смещение груза маятника
(здесь 1\ — длина маятника, ф\ — угол его отклонения от вертикали,
причем отклонения предполагаются малыми). Соотношения E.6.1),
E.2.18) моделируют также другие механические системы, в кото-
которых в качестве управляющего воздействия выступает ограниченная
по модулю скорость [72].
Поставим задачу определения управления u(t), удовлетворяющего
ограничению E.2.18) и переводящего систему E.6.1) из произвольного
начального состояния при t = О
?о(О)=?о°. ??@) = ??, 6@) = ?? E.6.2)
в заданное конечное состояние покоя
0. E.6.3)
Время окончания процесса Т нефиксировано.
С помощью замены переменных
ay
UJ
3.1),
E
у-
o =
.2
a;
18) к
/ = z,
\u ^
t =
виду
z =
; i.
f
—, и = аи
UJ
и,
E
E
E
.6
.6
.6
¦4)
.5)
.6)
250
Гл. 5. Управляемые системы при сложных ограничениях
Будем рассматривать систему в форме E.6.5), E.6.6), обозначая
точками производные по новому времени, причем штрихи у tr и и'
опускаем. При замене переменных E.6.4) условия E.6.2) и E.6.3)
примут вид
2/@)= ж?, 2/@) =4 *@)=4 E.6.7)
у(Т)=0, у(Т)=0, z(T)=0;
E.6.8)
величины х\у х®, х® — заданные постоянные, Т > 0 — неизвестное пока
время окончания процесса.
Таким образом, поставленная задача сводится к построению управ-
управления u(t), переводящего систему E.6.5) из заданного начального
состояния E.6.7) в конечное состояние E.6.8) и удовлетворяющего
ограничению E.6.6).
Изложенное ниже решение получено в работе [54].
Воспользуемся подходом, изложенным в § 5.2. Обозначив через
х = (y,y,z) фазовый вектор, приведем систему к виду E.1.1), где
А =
0
1
0
1
0
0
0
1
0
, в =
0
0
1
, / =
0
0
0
E.6.9)
Начальные E.6.7) и конечные E.6.8) условия запишутся в форме
E.6.10)
х(Т) = 0.
Матрица, обратная к фундаментальной матрице однородной систе-
системы, имеет вид
cos t — sin t — cos t "
sint cost — sint , E.6.11)
0 0 1
а матрица Q из E.2.2) представляет собой трехмерный вектор-столбец
QT(t) = {l-cost, -sint, 1}. E.6.12)
Подставляя E.6.12) в выражение E.2.1) для управления и, получаем
u(t) = с\(\ — cost) — C2sint + сз, E.6.13)
где с\, С2, сз — компоненты вектора с, задаваемого уравнением E.2.3).
§5.5. Маятник с управляемой по скорости точкой подвеса
251
Найдем матрицу R(T) из E.2.4) с помощью E.6.12)
1
R(T) =
c-l T-s
1 2 Т \
2S +C~l ~2 ~2SC C~l
T-s
с-1
Т
где, как и раньше, s = sinT, с = cosT, и обозначим элементы обратной
к ней матрицы R~l(T) символами ф^, г, j = 1,2,3. Тогда выражение
для управления E.6.13) с учетом E.2.5) примет вид
u(t) =
- COSt)
E.6.14)
г=\
При любом заданном Т > О управление E.6.14) переводит систему
E.6.5) из произвольного начального состояния E.6.7) в конечное
состояние покоя E.6.8) за время Т, но, вообще говоря, не удовле-
удовлетворяет ограничению E.6.6). Для того чтобы учесть это ограничение,
применим к соотношению E.6.14) неравенство Коши-Буняковского:
1/2
E.6.15)
E.6.16)
E.6.17)
E.6.18)
1/2
1
' 3
I
Введем вспомогательные
3
р(Ь,Т) = ^2[ф
г=\
г(Т)-
>
1
Ьи{\ — cost) -
функции
нA — cost) — ф$
max p(t, T)
1-1/2
и перепишем неравенство E.6.15) в виде
Если теперь время окончания процесса управления будет выбрано
из условия
||ж°|| =г(Т), E.6.19)
то ограничение E.6.6) будет выполнено при всех t G [О, Т].
Значения функции p(t, T) могут определяться численно по формуле
E.6.16). При этом элементы ф^, i, j = 1,2,3, симметрической матрицы
R~l(T) подсчитываются по формуле
252
Гл. 5. Управляемые системы при сложных ограничениях
Фа =
Rj
deti?(T)'
E.6.20)
4-
г(Т)
где Rij — алгебраическое дополнение элемента Гц матрицы R(T).
Используя эту процедуру, можно подсчитать максимальные значения
p(t,T) по t ? [О, Т] и определить
функцию г(Т) из E.6.17). В связи
с тем, что функция p(t, T) периодич-
периодична по t с периодом 2тг, ее максимум
достаточно искать на отрезке [О, Т],
если Т < 2тг, или на отрезке [0,2тг],
если Т ^ 2тг.
На рис. 60 представлен график
функции г(Т), полученный на ос-
основе расчетов с мелким шагом ЛТ
по Т. При каждом фиксированном
Т максимум по t функции p(t, T)
находился путем перебора и сравне-
сравнения значений.
Проанализируем поведение фун-
функции г(Т) в предельных случаях.
Пусть время управления Т мало. Разложим элементы ф^, г, j = 1,2,3,
симметрической матрицы R~l(T) в ряды по Т~\ используя формулу
E.6.20), и запишем главные члены разложений:
Т
0
10
20
30
Рис. 60. Функция г(Т)
720 Т 360 Т 60 Т п
360 Т 192 Т 36 Т~2
60 Т 36 Т~2 9Т
Подставляя разложения E.6.21) элементов
ражение E.6.16) и учитывая, что
= ?2 + О(?4),
E.6.21)
^, г, j = 1,2,3, в вы-
выsint =
при малых t, получаем для функции p(t, T) следующее представление
при малых Т и t ? [0,Т}\
2т-6
= збо2т
Из формулы E.6.22) следует, что
max p(t, T) = р{0, Т) = р(Т, Т) = 3600 Т.
0<t<T
E.6.22)
E.6.23)
§5.5. Маятник с управляемой по скорости точкой подвеса 253
Подставляя E.6.23) в E.6.17), получим
г{Т) = ±-Т\ Г^О. E.6.24)
Пусть теперь время Т велико. Подставим в равенство E.6.16) для
функции p(t,T) выражения ф^, г, j = 1,2,3, подсчитанные по формуле
E.6.20), и произведем разложение в ряд по обратным степеням Т:
p(t, Т) = АТ~2 [po(t) + T~lpx(t, Т)] + О(Т~А), Т -> оо. E.6.25)
Здесь введены обозначения
po(t) = cos2t + cost + -,
Pi(t,T) =9A -cost) (sinT+ ^8m2T) -8sinT- |sin2T +
\ Zj / Zi
+ sin2 tsin2T + (-5 + 5cosT - 7 sin2 T) sint -
-2A -costJ(sinT + sin2T) +
+ 2A -cost) A -cosT + 3sin2T)sint. E.6.26)
Пользуясь разложением E.6.25), нетрудно отыскать максимум
по Т функции p(t,T) при Т —> оо. Функция po(t) из E.6.26), очевидно,
достигает максимума на отрезке [О, Т] при t = 0. Так как при Т —>
—> оо вклад второго слагаемого в E.6.25) мал, то имеем с точностью
до малых величин высшего порядка
max p(t, T) = р@, Т) =
= 13T~2 - 32T~3 sinT - 10T-3sin2T, T -+ oo. E.6.27)
Подставляя E.6.27) в E.6.17) и разлагая результат в ряд по Т~\
получим
r(T)= f(T) + O(T-1), T^oo. E.6.28)
Здесь введено обозначение
т +1|sinT + Asin2T)
Продифференцируем функцию /(Т) по Т:
v, _ 20cos2T+ 16cosT + 3
/( j" 13л/13
254
Гл. 5. Управляемые системы при сложных ограничениях
/СО
т
Г"
7Г
I
2тг
Производная /'(Т) обращается
в нуль при cosT = —0.5 и
cosT = —0.3. Расчеты показы-
показывают, что при Т = —2тг/3 +
+ 2тгп и Т = arccos(-0.3) + 2тгп
функция /(Т) имеет локальные
максимумы, а при Т = 2тг/3 +
+ 2тгп и Т = -arccos(-0.3) + 2тгп
— локальные минимумы. Харак-
Характерный вид этих слабозаметных
экстремумов виден на рис. 61, где
представлен график функции /(Т).
Для большей наглядности один
участок графика с расположенными
на нем максимумом и минимумом
показан с увеличением в 100 раз
по оси ординат. Таким образом, функция г(Т) не является монотонно
возрастающей при изменении от 0 до оо, и уравнение E.6.19) при
любом х° имеет, вообще говоря, неединственное решение.
Опишем процедуру построения управляющей функции u(t).
Сначала решаем численно уравнение E.6.19) и находим Т. Для этого
весь полубесконечный интервал изменения Т разбиваем на три
части: [0, То], [To,Ti] и [Ti,oo), при этом То и Т\ выбираем
так, чтобы на отрезке [0, То] было справедливо асимптотическое
представление E.6.24) для малых Т, а на полуинтервале [Т\,оо) —
асимптотическое представление E.6.28) для больших Т. Величинам То
и Т\ соответствуют значения го и г\ функции г(Т). Заданную величину
||ж°|| сравниваем с го и г\ и определяем Т следующим образом. Если
||ж°|| G [0,го], то согласно формуле E.6.24) имеем
Рис. 61. Функция /(Г)
= FО|
1/3
Если ||ж°|| G [ro,ri], то Т находим с помощью таблицы значений
функции г(Т), подсчитанных на отрезке [Tq,Ti] (при неоднозначности
решения выбираем наименьшее найденное значение Т). Если ||ж°|| G
G [ri,oo), то пользуемся асимптотическим представлением E.6.28).
При этом Т ищем в виде
Т = л/Тз||х°|| + <9. E.6.29)
Подставляя E.6.29) в E.6.28), получаем для в уравнение
F@) = 136» + 16sin(VT3||a;0|| + в) + 5sin[2(VT3
Это уравнение решаем численно, причем если корень не один, то
находим наименьшее значение 9, чтобы сократить время управления Т.
§5.5. Маятник с управляемой по скорости точкой подвеса
255
После того как для заданного начального вектора х° определено
время движения Т, управляющую функцию u(t) в каждый момент
t подсчитываем по формуле E.6.14), в которой значения функций
ф-, it j = 1,2,3, находим по формуле E.6.20). Вычисленное управ-
управление подставляем в правую часть исходной системы, которую затем
интегрируем численно при начальных условиях E.6.10). Построенное
управление не оптимально по быстродействию, но достаточно просто
для расчета и практической реализации. В табл. 9 приведены резуль-
результаты сравнения времени Т с временем оптимального по быстродей-
быстродействию процесса Т*, которое найдено в [35, 72] для различных значений
вектора х° = (х^х^х®).
Таблица 9. Расчет времени Т и сравнение с оптимальным значением Т*
Х°2
т
т*
т/т*
0
0
1.0471
5.4
3.1415
1.7
0
0
6.2831
24.2
6.2831
3.9
-5
-4
-1
24.5
9.8362
2.5
-4.9015
3.5253
-2.7750
24.8
8.0612
3.1
0.0245
-1.9302
1.5452
10.7
3.7410
2.9
-0.2070
0.5441
-1.0979
5.7
1.0979
5.2
На рисунках 62 и 63 представлены результаты численного модели-
моделирования при х° = A, 1/2,-1). Для этого случая Т = 6.0. На рис. 62
показана зависимость и = u(t), а на рис. 63 — траектория x(t),
т.е. зависимость величин у, у и z от времени.
-1-
t = T
0 2 4 6
Рис. 62. Функция u(t)
0
Рис.63. Зависимость величин у,у
и z от времени
256 Гл. 5. Управляемые системы при сложных ограничениях
§ 5.7. Модель электромеханической системы
Рассмотрим двухмассовую систему, управляемую электродвигате-
электродвигателем постоянного тока с независимым возбуждением. Уравнения дви-
движения системы возьмем в виде
E.7.1)
Здесь ?ь ?2 ~~ координаты системы, mi и т^ — постоянные инер-
инерционные коэффициенты, с — постоянная жесткость упругой связи,
F — управляющее воздействие (си-
F ла или момент), создаваемое элек-
электродвигателем. На рисунках 64-66
изображены некоторые конкретные
Ш2
TYT
с
7П\
системы, описываемые уравнениями
~^ E.7.1).
^ На рис. 64 показана система
Рис. 64. Система двух тел двух тел массы mi и m2, перемеща-
перемещающихся поступательно вдоль оси ?.
Здесь ?i и ^2 — координаты тел, с — жесткость пружины, F —
управляющая сила, приложенная к первому телу.
На рис. 65 изображена тележка массы т\, перемещаемая силой F
вдоль оси ?. К тележке присоединен математический маятник массы
7П2 и длины /, совершающий малые колебания.
Составим уравнения движения системы рис. 65:
(mi + m2)?i — т^гф = F,
Здесь ф — угол отклонения маятника от вертикали, д — ускорение
силы тяжести. Первое уравнение E.7.2) — это уравнение изменения
количества движения вдоль оси ?, а второе уравнение описывает изме-
изменение момента количества движения относительно оси маятника.
Введем обозначения
Уравнения E.7.2) с учетом обозначений E.7.3) преобразуются
к виду E.7.1).
Система, изображенная на рис. 66, представляет собой электро-
электродвигатель, к оси которого присоединен упругий стержень с массой
m на конце. Пренебрегая массой стрежня по сравнению с массой
m и обозначая через с его крутильную жесткость, снова придем к
уравнениям E.7.1), где переменные и постоянные имеют следующий
§5.7. Модель электромеханической системы
257
>
о /
/
Ш2 У ф
о ,
Рис. 65. Маятник на тележке
Рис. 66. Электродвигатель и
упругий стержень с массой
смысл: т\ — момент инерции ротора электродвигателя и вращающихся
частей редуктора, тп^ — момент инерции стержня с массой на конце,
(i и B - абсолютные углы поворота вала двигателя и массы m отно-
относительно оси вращения, F — момент, развиваемый электродвигателем.
К системе E.7.1) приводятся уравнения движения двигателя с упругим
стержнем и в том случае, когда масса стержня сопоставима с га, если
ограничиться учетом основного (низшего) тона упругих колебаний.
При этом систему, изображенную на рис. 66, можно рассматривать как
простейшую модель упругого манипулятора.
Управляющее воздействие F в системе E.7.1) пропорционально
(или равно) моменту, создаваемому электродвигателем и, следова-
следовательно, пропорционально силе тока / в цепи ротора
F = k\I,
E.7.4)
где к\ — постоянный коэффициент. Уравнение баланса электрических
напряжений в цепи ротора имеет вид
LI + RI +
= U.
E.7.5)
Здесь L — коэффициент индуктивности, R — электрическое сопро-
сопротивление, &2 — постоянный коэффициент, U — управляющее элек-
электрическое напряжение. Член fc2?i B E.7.5), равный противо-э.д.с,
пропорционален угловой скорости вращения вала двигателя, которая,
в свою очередь, пропорциональна (или равна) ?i. Первое слагаемое
в левой части уравнения E.7.5) обычно мало по сравнению с другими
слагаемыми, и им можно пренебречь. Тогда из E.7.4), E.7.5) получим
F =
ki(U-k2ji)
R
E.7.6)
9 Ф. Л. Черноусько и др.
258 Гл. 5. Управляемые системы при сложных ограничениях
Рассмотрим ограничения, наложенные на управление и фазовые
координаты системы E.7.1). Управляющее напряжение ограничено по
величине постоянной
\U\ < Щ. E.7.7)
Силу тока / и пропорциональный ей момент двигателя также
следует считать ограниченными по величине, что в силу E.7.4) приво-
приводит к ограничению
\F\ < Fo, E.7.8)
где Fo — постоянная. Кроме того, угловую скорость вращения вала,
пропорциональную ?i, также считаем ограниченной, притом таким об-
образом, чтобы при максимальном по величине напряжении U = zLC/q
и максимальной угловой скорости управляющий момент не мог приво-
приводить к дальнейшему разгону двигателя. Это ограничение в силу E.7.6)
можно записать в виде
Совокупность ограничений E.7.7)-E.7.9), учитывая E.7.6), пред-
представим как
К
ко.'
F +
R
E.7.10)
Перейдем к новым (безразмерным) переменным по формулам
./ . ГП\?.\ + ГП2&
t = иг, х\ = ¦ --, х2 =
«=
2
2 c(mi+m2) F0mim2 /c7n\
о; = , /о =-7 : чо- E.7.11)
ГПГП С{ТП\ + Ш2)^
(т\
Тогда уравнения E.7.1) примут вид, не содержащий параметров:
Х\ = Х2, Х2 = U, Хо, = Х4, Х4 = —Хо, + U. E.7.12)
Здесь и далее точкой обозначаются производные по безразмерному
времени t', причем штрих у переменной t1 опускается. Сделаем замену
E.7.11) также в ограничениях E.7.10). Получим
qu\ ^ 1, E.7.13)
§5.8. Анализ упрощенной модели 259
где обозначено
Щ kiU0 т\
Для системы E.7.12) с ограничениями E.7.13) поставим задачу
о построении допустимого управления u(t), переводящего ее из началь-
начального состояния
xi@)=x°u х2@)=х°2, х3@)=х°3, х4@)=х°4 E.7.15)
в нулевое конечное состояние
хх(Т)=0, х2{Т)=0, ж3(Т)=0, ж4(Т)=0; E.7.16)
здесь Т — пока нефиксированное время окончания процесса.
Поставленная задача является частным случаем более общей за-
задачи, сформулированной в § 5.1. Рассмотрим сначала ее упрощенный
вариант, описываемый системой второго порядка.
§ 5.8. Анализ упрощенной модели
Положим ni2 = 0 в E.7.1). Получим систему с одной степенью
свободы, которая в безразмерных переменных E.7.11) описывается
уравнениями
Х\ = Х2, Х2 = U. E.8.1)
В ограничениях E.7.13) при rri2 = 0 следует, согласно E.7.14), поло-
положить \i = 0. Число параметров в ограничениях можно уменьшить с
помощью замены переменных
t=p-Hf, xi=p~2x\, X2=p~lxf2. E.8.2)
Сделав замену E.8.2) в системе E.8.1) и опуская штрихи у новых
переменных, придем к прежней системе E.8.1), а ограничения E.7.13)
при этом примут вид
и\^\, \х2\ < 1, \x2 + qu\^l, q>0. E.8.3)
Вместо граничных условий E.7.15), E.7.16) имеем
хх @) = х°{, х2@) = х°2, хх(Т) = х2(Т) = 0. E.8.4)
Применим подход § 5.2 к задаче E.8.1), E.8.3), E.8.4). В обозна-
обозначениях E.1.1), E.1.6) имеем для системы E.8.1)
А =
0 11 ГО] ГО
оо • Н. ¦ Но
E.8.5)
260
Гл. 5. Управляемые системы при сложных ограничениях
С помощью E.8.5) найдем обратную матрицу Ф l(t), а затем мат-
матрицы Q(t) и R(t), определяемые равенствами E.2.2) и E.2.4):
l -t 1 Г -t
. Q(t) =
о l i
3* 2*
Л''
t
E.8.6)
здесь принято to = 0 в соответствии с E.8.4). Найдем еще, пользуясь
E.8.6), обратную матрицу
"б ЗТ "
9 • E.8.7)
ЗТ 2Т2
Используя равенства E.8.4), E.8.6) и E.1.9), получим
х1 =0,
= -х°.
E.8.8)
С помощью соотношений E.8.5)-E.8.8) представим фазовый вектор
E.2.7) и управление E.2.8) в виде
x(t) = Ф(г)[Е2 - R(t)R-l(T)]x° = X(t,T)x°,
u(t) = -QT(t)R-\T)x° = (w(t,T),x°)\
E.8.9)
здесь E<i — единичная матрица размера 2x2. Элементы матрицы
X(t,T) размера 2 х 2 и двумерного вектора w(t,T) равны
Xn(t,T) = 1 -Зт2 + 2т3, Xi2(t,T) = Тт(\ -
X2i(t,T) =
6r(r-
X22(t,T) = 1 -4r + 3r2,
E.8.10)
Каждое из ограничений E.8.3) можно представить в виде
-f3u\ < 1, (Ка<1, /?^0, E.8.11)
где а, /3 — постоянные коэффициенты. Подставим в E.8.11) выражения
для Х2 и и из E.8.9), E.8.10) и проведем оценки сверху левой части
неравенства E.8.11):
\ах2 + (Зи
/?|ги2|) |
E.8.12)
§5.5. Анализ упрощенной модели
261
Так как
по г G [0, 1]
в E.8.12):
t G [0,Т], то т ? [0,1]- Оценим
абсолютных величин элементов
1*
21
сверху максимумы
E.8.10), входящих
E.8.13)
Подставим оценки E.8.13) в E.8.12):
За
2Т
Т2
т0|
х\\
а
E.8.14)
Рассмотрим теперь каждое из наложенных ограничений E.8.3)
в отдельности. Сравнивая неравенства E.8.3) и E.8.11), положим а =
= 0, /3=1 для первого ограничения E.8.3), а = 1, /3 = 0 — для второго
и а = I, Р = q — для третьего ограничения. Тогда получим из E.8.1),
E.8.14) следующие неравенства:
E.8.15)
Так как q > 0 согласно E.8.3), то второе неравенство E.8.15) вытекает
из третьего. Поэтому совокупность двух неравенств
2Т Т2
ж?| +
E.8.16)
\4
1
представляет собой достаточные условия разрешимости поставленной
задачи управления E.8.1), E.8.3), E.8.4). Эти условия, связываю-
связывающие начальное состояние и время процесса, можно рассматривать как
достаточные условия управляемости системы из заданного начального
состояния х° за время Т.
Проанализируем условия E.8.16). Пусть начальное состояние х\, х\
задано. Если \х^\ > 1, то условия E.8.16) не выполнены, что вполне
естественно, так как при этом начальное состояние нарушает нало-
1. Если же
< 1,
женное в E.8.3) фазовое ограничение \х2\ ^
то условия E.8.16) заведомо выполняются при достаточно большом Т.
Представляет интерес минимальное время Т*, при котором выполня-
выполняются оба неравенства E.8.16). Разрешая квадратные относительно Т~х
неравенства E.8.16), получим
262
Гл. 5. Управляемые системы при сложных ограничениях
Fai
= \х°г
г =1,2,
E.8.17)
_ [Cai
- a2)]1/2 -
Z2 2Aqax '
Итак, если \x\\ < 1 и Т ^ Т*, то предложенный способ управле-
управления обеспечивает приведение системы E.8.1) в заданное состояние
при выполнении наложенных ограничений E.8.3). Фиксировав любое
Т ^ Т*, находим искомое управление u(t) и фазовую траекторию x(t)
по явным формулам E.8.9), E.8.10). Тем самым поставленная задача
решена.
Сопоставим построенное решение с полученным в [69] (см. гл. 6)
решением задачи оптимального быстродействия для системы E.8.1)
с ограничениями E.8.3) и краевыми условиями E.8.4). Ограничимся
случаем нулевой начальной скорости х\ = 0 и положим для определен-
определенности q = 1/2 в E.8.3). Тогда из E.8.17) получим
T*(a) = max
12а
(9а2 + 48аI/2-За
FаI/2 при ае [о,-
12а
а =
2
E.8.18)
Из E.8.18) найдем асимптотику зависимости Т*(а) при a —> оо:
Т*(а) = у + 0A), а ^ оо. E.8.19)
(а) = у + 0A),
Отметим, что принятому значению параметра g = 1/2 отвечает,
согласно E.8.3), множество допустимых значений переменных (х2,и)
в виде шестиугольника, изображенного на рис. 67. Этим ограничениям
соответствует зависимость времени Т° оптимального быстродействия
от a = |а^|, задаваемая соотношениями [69]:
2а1/2
Т°(а) =
приае
[о,|],
_3
§5.9. Электромеханическая система четвертого порядка
263
4 -
Рис. 67. Множество допустимых
значений переменных (х2,и)
О
Рис. 68. Зависимости величин Т* и
Т° от параметра а
При а ^ 1/4 зависимость Т°(а) задана в параметрическом виде,
где г> ^ 1/2 — параметр. Найдем асимптотику зависимости Т°(а) при
а —> оо, для чего устремим г; —> 1. Получим из E.8.20)
9
а
оо.
E.8.21)
Сравнивая зависимости E.8.18) и E.8.20), видим, что при малых а
время Т*(а) превосходит оптимальное время Т°(а) примерно на 22%.
Для больших а, как видно из E.8.19) и E.8.21), время Т*(а)
на 50% превосходит оптимальное. Зависимости Т*(а) и Т°(а) показаны
на рис. 68. Таким образом, предложенный способ управления приводит
систему в заданное состояние за время, не очень сильно отличающееся
от оптимального.
§ 5.9. Управление электромеханической системой
четвертого порядка
Применим предложенный подход к системе E.7.12) при ограниче-
ограничениях E.7.13)) и краевых условиях E.7.15) и E.7.16). В обозначениях
E.1.1) имеем для системы E.7.12)
А =
0
0
0
0
1
0
0
0
0
0
0
-1
о -
0
1
0
' в-
- о -
1
0
1
, / =
- о
0
0
0
E.9.1)
264
Гл. 5. Управляемые системы при сложных ограничениях
Запишем для рассматриваемой системы фундаментальную матрицу
E.1.6) и обратную к ней
*-'(*) =
1
0
0
0
1
0
0
0
t
1
0
0
-t
1
0
0
0
0
cost
— sint
0
0
cost
sint
о -
0
sint
cost _
0
0
— sint
cost
E.9.2)
Пользуясь соотношениями E.9.1) и E.9.2), составим матрицу Q(t)
из E.2.2):
Q(t) = (-t, l,-sint,cost)T. E.9.3)
Составим матрицу R(t) из E.2.4), используя соотношение E.9.3)
и принимая to = 0:
R(t) =
— — sint—t cost 1—cost—t sint
sint—t cost cost—1
1—cost—t sint sint
cost—1
2t-sin2t
4
cos 2t-1
sint
cos2t-l
4
2t+ sin 2t
E.9.4)
С целью упрощения выкладок, как и в § 5.4, положим Т = 2тг&, к =
= 1,2,... . Тогда согласно E.9.4) матрица R(T) и обратная к ней
примут вид
R(T) =
3
2
-Т
0
2
Т
0
0
-т
0
г
2
0
0
0
0
г
2 -
§5.9. Электромеханическая система четвертого порядка
265
R-\T) =
1
Т2-24
12 с 24
jr 6 -
12
2Т
О
24
— 12
Г
О
О
О
О
О
2(Г2-24)
Т
E.9.5)
Используя равенства E.7.15), E.7.16), E.9.2) и E.1.9), получим
аналогично E.8.8)
хх = О, ж* = -х°. E.9.6)
С помощью E.9.6) представим фазовый вектор E.2.7) и управление
E.2.8) в виде, аналогичном E.8.9):
x(t) = X(t, Т)х°, u(t) = (w(t,
Здесь X(t,T) — матрица размера 4x4, равная
X(t,T) = Ф(?) - «ЗДД-'СГ), Ф,(*) =
a w(t,T) — четырехмерный вектор, равный
w(t,T) = -QT(t)R~\T).
E.9.7)
E.9.8)
E.9.9)
Обратимся к анализу ограничений E.7.13). Прежде всего отметим,
что так как согласно E.7.14) коэффициенты р, q положительны, то
для выполнения этих ограничений достаточно потребовать выполнения
следующих двух неравенств:
1, р\х2
+q\u
E.9.10)
Подставим соотношения E.9.7) в неравенства E.9.10). Получим
4
?|<1, E.9.11)
г=1
V
г=1
1.
E.9.12)
г=1
Вычислим компоненты вектора w(t,T) из E.9.9), используя равен-
равенства E.9.3) и E.9.5). Получим
W\ =
12Tsint
Т(Т2 - 24)
24*-
- 24)
-2 cost
т(т2 _
E.9.13)
266
Гл. 5. Управляемые системы при сложных ограничениях
Для вычисления элементов матрицы X(t, T) из E.9.8) сначала
перемножим матрицы Ф(?) из E.9.2) и R(t) из E.9.4):
Г
" 9
sint—t I —cost
cost—1 sint
sin t—t
cost—1
tcost— sint
2
tsint
1 — cos t
sint
tsint
2
t cos t+ sin t
E.9.14)
Теперь вычислим те элементы матрицы X(t,T), которые фигурируют
в ограничениях E.9.12). Для этого подставим в равенство E.9.8) для
X(t,T) соотношения E.9.2) для Ф(?), E.9.14) - для <?>i(t) и E.9.5) -
для R~l(T). Получим
_ 6t(t-T)+24(l -cost)
21 - Т(Т2 _ 24) '
TCt2 - 4tT + Т2) + 12Bt-T)- 12Tcost
2 - 24)
12t(t-T)+2T2(l -cost)
^24 =
- 24)
-2 sint
E.9.15)
^43 —
_ 12A -cost) + 6Bt-T) sint
41 " T(T2 - 24) '
6T( 1 - cos t) - 4(T2 - 6) sin t + 6Tt sin t
T(T2 - 24) '
24A - cost)+TA2 + tT-T2) sint
X44 =
2 - 24)
(T-t) cost-sint
§5.9. Электромеханическая система четвертого порядка
267
Неравенства E.9.11), E.9.12) должны выполняться при всех
t ? [О, Т]. Сначала оценим сверху максимальные по t ? [О, Т] значения
величин \wi\, фигурирующих в E.9.11), E.9.12). Имеем
te
\24t- 12T + 2T2sint| < 12Т + 2Т2,
ЫТ - 4Т2 + 24 + 12Tsint < 2Т2 + 12Т + 24,
E.9.16)
6?T-4T2
12Tsint > -4Т2 - 12Т + 24.
Так как Т = 2тг&, к > 1, то Т2 > 24. Тогда из последних двух нера-
неравенств E.9.16) следует
+ 12Tsint <
< max{2T2 + 12T + 24,4T2 + 12T - 24} =
= 4T2+ 12T-24. E.9.17)
Подставляя оценки E.9.16), E.9.17) в E.9.13), получим
\wi(t,T)\ ^ Ait г = 1,... ,4, te[0,T\; E.9.18)
здесь обозначено
6(Т + 4) 4(Т2 + ЗТ - 6)
A^ =
2 - 24)'
2(Т-
- 24)
E.9.19)
T2-24 '
АА = ^.
Переходя к неравенству E.9.12), отметим, что элементы Х22, X43
и Х44 из E.9.15) не стремятся к нулю при Т —> оо. С целью наиболее
точной оценки главных при Т —> оо членов в неравенстве E.9.12),
оценим первое слагаемое в этом неравенстве следующим образом:
г=1
Здесь введены обозначения
В{ = |Х2,
= [(Х
23
+В3
В2 = \Х22
+ (Х24 + м
E.9.20)
E.9.21)
268 Гл. 5. Управляемые системы при сложных ограничениях
Перейдем к оценкам величин Bi, г = 1,2,3. Учитывая очевидные
оценки
\2t-T\^T, -—<?(?-Т)<0, te[O,T]. E.9.22)
получим из E.9.15)
Т(Т2 - 24)(Х21 + fiX4l) < Ы{Ь - Т) + 48 +
+ 24/х + 6/хТ < 24B + /х) + 6/хТ,
Т(Т2 - 24)(Х21 + /iXn) > 6t(t - Т) - 6/хТ > -^ - 6/хТ.
Отсюда находим оценку для величины 5i из E.9.21):
я<л max{3T2/2,24B + /i)} + 6/iT
Bi^Di = Т(Т2 _ 24) * E.9.23)
Далее, на основе E.9.15) получим
Т(Т2 - 24)(Х22 + iiXA2) = TCt2 - AtT + Т2) +
+ 12Bt - Т) + 6/iT - 6ТB + /i) cost +
+ 2/iTCt - 2T) sin ? + 24/i sin t. E.9.24)
Нетрудно видеть, что
|3?2-4?T + T2| <Т2, |3t-2T|<2T, ?e[0,T]. E.9.25)
С учетом соотношений E.9.24), E.9.25), E.9.22), получим оценку
для величины Б2 из E.9.21):
в, < ft . T3
Пользуясь формулами E.9.15), сделаем следующее преобразование
с целью выделения членов, главных при Т —> оо:
»(t-T)smt ,
А23 + /iA43 = у Ь А3,
, _ 12t(tT) + BT + 24/i)(l -cost) + 12/iBt-T)sint
3~ Т(Т2 - 24) '
§5.9. Электромеханическая система четвертого порядка 269
у +„х MT-t)coat ,
Л 24 + МА44 = Tf, г Л4>
VY4 — — . \O.V.±I)
Подставляя E.9.27) в выражение E.9.21) для В%, получим
2_/i2(T-?J 2{i(T-t)(X'4cost-X^smt) /2 y,2
/9 9\ 1/2 9 9
< /i2 + 2/i ^Xf + X'i) + Х'ъ1 + X[\ E.9.28)
Для величины Х'ъ из E.9.27) с учетом E.9.22) имеем оценки
Т(Т2 - 2А)Х^ < №(t - Т) + 4(Т2 + 12/х) + 12/хТ <
Т(Т2 - 24)Х^ > 12t(t - Т) - 12/хТ > -ЗТ2 - 12/хТ.
Отсюда вытекает неравенство
1Хз|< Т(Т2_24) ¦ E-9-29)
Для Х4 получим из E.9.27)
\Х'А\ < ^. E.9.30)
Подставляя неравенства E.9.29), E.9.30) в E.9.28), найдем
|^з|$Ь>з-/х+|Т2(Т2-24JГ2
Обратимся теперь к анализу неравенств E.9.11), E.9.12), представ-
представляющих собой достаточные условия разрешимости задачи управления
за время Т = 2ттк, к= 1,2,.... Подставляя оценки E.9.18) в E.9.11),
получим условие
4
5^| < 1. E.9.32)
270 Гл. 5. Управляемые системы при сложных ограничениях
Подставляя E.9.18), E.9.20) в E.9.12) и используя оценки E.9.23),
E.9.26) и E.9.31) для Bi, получим
E.9.33)
»=i
Условия E.9.32) и E.9.33) представляют собой достаточные
условия управляемости системы E.7.12) за конечное время Т =
= 2ттк, к = 1, 2,.... Другими словами, если эти условия для некоторого
начального состояния х° и времени Т = 2ттк выполнены, то система
E.7.12) может быть переведена из этого начального состояния E.7.15)
в заданное конечное состояние E.7.16) за время Т. Найденный
закон управления u(t) и фазовая траектория x(t) системы заданы
соотношениями E.9.7), в которых матрица X(t,T) и вектор w(t,T)
определены равенствами E.9.15) и E.9.13) соответственно. Таким
образом, все искомые величины определены в явном аналитическом
виде, если найдено время процесса Т.
Осталось выбрать время Т = 2пк, к = 1,2,... , так, чтобы при
заданном начальном состоянии х° удовлетворялись неравенства
E.9.32) и E.9.33). Для этого будем придавать числу к последовательно
значения к = 1,2,... , подсчитывать коэффициенты Ai, г = 1,...,4,
по формулам E.9.19) и Dj, j = 1,2,3, по формулам E.9.23),
E.9.26), E.9.31), а затем проверять неравенства E.9.32), E.9.33).
Отметим, что
Ai^O, г = 1,... ,4; D\ -> 0, D2 -> 1, D3 -> /х
при Т —> оо. Следовательно, неравенство E.9.32) всегда выполняется
при достаточно большом Т. Неравенство E.9.33) также выполняется
при достаточно большом Т, если
22I/21 1. E.9.34)
Таким образом, неравенство E.9.34) представляет собой достаточное
условие разрешимости поставленной задачи управления за конечное
время.
Если в системе E.7.12) имеется лишь ограничение на управле-
управление \и\ ^ 1, а остальные (фазовое и смешанное) ограничения E.7.13)
отсутствуют, то время Т должно выбираться так, чтобы удовлетворить
только одному условию E.9.32). В этом случае задача управления
всегда разрешима за конечное время.
Отметим, что хотя закон управления u(t) представлен в форме
программы E.9.7), он может быть использован и для коррекции
управления по обратной связи. Для этого нужно через определенные
промежутки времени определять текущий фазовый вектор х
§5.9. Электромеханическая система четвертого порядка 271
-1-
Рис. 69. Зависимости величин и,
р(х2 + /ах а) и р(х2 + /ах a) + qu от
времени
Рис. 70. Проекции фазовой траек-
траектории
и рассматривать его в качестве начального вектора х в соотношении
E.9.7), пересчитывая каждый раз время до окончания процесса Т
по описанному выше алгоритму. Ввиду наличия явных соотношений
такой пересчет не будет трудоемким.
В качестве иллюстрации приведем пример численной реализации
описанного алгоритма управления системой E.7.12) при ограничениях
E.7.13). Безразмерные параметры E.7.14) принимались равными
а начальные данные E.7.15) задавались в виде
то _ с о _ а то _ с о _ а
E.9.35)
E.9.36)
Нетрудно проверить, что параметры E.9.35), E.9.36) удовлетворяют
условию E.9.34) управляемости за конечное время.
В результате численной реализации описанного в § 5.9 алгоритма
управления было сначала найдено минимальное целое к, при котором
удовлетворяются условия E.9.32) и E.9.33), а затем построено управ-
управление u(t) и фазовая траектория x(t). Оказалось, что к = 3, Т = бтг.
На рис. 69 кривыми 1-3 соответственно изображены в зависимости
от времени величины
и,
2 + /ах 4)
фигурирующие в ограничениях E.7.13). Видно, что эти ограничения
всюду удовлетворяются. На рис. 70 кривыми 1,2 показаны проекции
четырехмерной фазовой траектории x(t) на плоскости (х\,Х2) и (х$,Х4)
соответственно.
272
Гл. 5. Управляемые системы при сложных ограничениях
§ 5.10. Активный динамический гаситель
Рассмотрим задачу о гашении колебаний груза, закрепленного
на конце упругой балки, с помощью активного динамического гасителя
с поступательно перемещающейся массой. Управляющей величиной
служит сила взаимодействия между гасителем и грузом. Системы
такого типа используются, например, на космических летательных
аппаратах, где измерительные приборы располагаются на платформе,
удаленной от корпуса аппарата на значительное расстояние с помощью
длинной штанги. Проведение измерений требует высокой точности
позиционирования и стабилизации измерительных приборов, поэтому
гашение колебаний штанги представляет собой существенную пробле-
проблему, которую приходится учитывать при конструировании космических
аппаратов (КА). Одним из способов ее решения является использова-
использование управляемого гасителя, расположенного на самой платформе (П)
(рис. 71). Гаситель состоит из направляющей 1, перпендикулярной оси
штанги 2, и подвижной массы 3, которая может перемещаться вдоль
направляющей посредством электропривода. Такая схема применяется
для гашения поперечных колебаний штанги.
Особенностью данной задачи является наличие двух естественных
ограничений на различные переменные системы: одно — на управ-
управляющую силу, обусловленное ограниченными возможностями привода,
другое — на величину смещения подвижной массы относительно плат-
платформы, вызванное конечностью хода массы гасителя (направляющая
гасителя имеет конечные размеры).
//гт\
Рис. 71. Штанга с грузом и актив-
активным динамическим гасителем
Рис. 72. Упрощенная модель
При некоторых упрощающих предположениях [6] моделью
описываемых конструкций может служить следующая управляемая
двухмассовая механическая система, содержащая колебательное
звено (рис. 72). Два тела, массами т\ и Ш2, перемещаются вдоль
горизонтальной прямой. Первое тело соединено с неподвижным
основанием пружиной жесткости с > 0. Второе тело соединено
с первым посредством привода, который генерирует силу и. Уравнения
движения такой системы имеют вид
ГП\у + Су = — U, TT12Z = U.
E.10.1)
§5.10. Активный динамический гаситель
273
Здесь у — координата первого тела, z — координата второго тела на
прямой. На управляющую силу и наложено ограничение
u(t)\^a, а>0,
E.10.2)
а на величину смещения второго тела относительно первого — условие
\z(t)-y(t)\ <d, d>0. E.10.3)
Требуется построить управление u(t), удовлетворяющее ограничению
E.10.2) и переводящее систему E.10.1) из заданного начального
состояния
у(О) = у°, у(О) = у°, z@) = z°, z@) = z
в состояние покоя
y(T) = z(T) = 0, y(T)=z(T) = 0.
°
E.10.4)
E.10.5)
При этом координаты y(t) и z(t) должны удовлетворять условию
E.10.3) на протяжении всего процесса движения, время окончания
которого Т нефиксировано.
Введем новые переменные
х\ = -у,
а
тп\а
z,
t, и' = —аи.
E.10.6)
В новых переменных система E.10.1) и ограничение E.10.2) примут
вид
х\+х\ =и, хз = и, E.10.7)
М<1, E.10.8)
полностью аналогичный E.4.5). Здесь и всюду в дальнейшем точками
обозначены производные по новому времени t', а штрихи у величин t'
и и' опущены. Ограничение E.10.3) перепишется в виде
ТП2
\-х\
cd
а '
Положим х\ = Х2, хз = х\ и обозначим через х = {х\,Х2,хъ,х?)
фазовый вектор системы E.10.7). Введем в рассмотрение постоянный
вектор р= A,0, m\/ni2,0) и перепишем последнее неравенство следу-
следующим образом:
^. E.10.9)
274
Гл. 5. Управляемые системы при сложных ограничениях
Условия E.10.4), E.10.5) после замены переменных E.10.6) пере-
перепишутся в виде
хг@)=х°г, Xi(T)=0, i=
E.10.10)
здесь х® — некоторые заданные постоянные, Т > 0 — неизвестное пока
время окончания процесса.
Поставленная задача сводится к построению управления, удовле-
удовлетворяющего ограничению \и\ ^ 1 и переводящего систему E.10.7)
из заданного начального состояния E.10.10) в начало координат
с соблюдением ограничения E.10.9) на протяжении всего процесса
движения. Присутствие фазового ограничения E.10.9) составляет
главное отличие данной задачи от задач, рассмотренных в § 5.4, 5.5.
Кроме того, на некоторых этапах приведенных ниже рассуждений
использованы иные способы оценивания, чем ранее.
Представленное далее решение задачи получено в работе [12].
Перепишем систему E.10.7) в векторной форме
х = Ах -\-bu, A =
0
1
0
0
1
0
0
0
0
0
0
0
о -
0
1
0 _
, ь =
- о -
1
0
. 1 _
E.10.11)
Начальные и конечные условия E.10.10) запишем следующим образом:
х@)=х°, х(Т)=0. E.10.12)
Как и в случае маятника с управляемой по ускорению точкой
подвеса фундаментальная матрица решений однородной системы
и обратная к ней матрица имеют вид E.4.8), а матрица Q(t) из E.2.2)
в данном случае есть четырехмерный вектор-столбец вида E.4.9).
Выражение для управляющей функции u(t), переводящей систему
E.10.11) из начального состояния х° в начало координат фазового
пространства, запишем теперь так:
u(t) =
V(t,T) = -R~\T)Q(t)-
E.10.13)
матрица R(T) задается выражением E.5.3).
Покажем, что выбирая время окончания процесса Т достаточ-
достаточно большим, можно гарантировать выполнение ограничений E.10.8)
на управление u(t). Оценим для этого функцию u(t) следующим
образом:
E.10.14)
§5.10. Активный динамический гаситель
275
Через || • Цоо и || • ||i обозначены нормы в пространствах R^ и R\
соответственно, которые для произвольного вектора q имеют вид
Iklloo = max \qi\, ||
Введем вспомогательную функцию
1 =
г=1
и перепишем оценку E.10.14) следующим образом:
max \u(t)\
0<t<T
E.10.15)
E.10.16)
Предложим два способа определения момента окончания
движения Т, обеспечивающие выполнение ограничений E.10.8).
Первый основан на аналитических оценках функции v(T), второй —
на численном построении этой функции.
Аналогично тому, как это сделано в § 5.4, будем сначала
выбирать в качестве времени окончания процесса величину Т = 2ттк,
где к — натуральное число. В этом случае матрица R(T) упрощается
и задается соотношением E.4.11), а обратная к ней матрица имеет вид
2Т О
2Л
Т
24
Т
о ==
12
О
О
24
Т
0
12
Т
12
0
6
4(Т2-6)
Л = Т2 - 24.
E.10.17)
Выпишем компоненты вектор-функции V(t,T), используя выраже-
выражения E.10.17) и E.4.9) для матрицы R~l(T) и вектора Q(t), и оценим
их, учитывая неравенство Т ^ 2тг, следующим образом:
2TZ sin
2 cos 11
T
-24 sin
t + 24t
ТЛ
2
- 12T
. 4T
* Л '
t- 12t + 6T| ^
ТЛ
-12Tsin?-6T? + 4T2
/ 2T+12 .
" Л "
6T + 24 ^
ТЛ ^
- 24 | ^ 4T
4T
Л '
4T
Л '
ТЛ
Л
276
Гл. 5. Управляемые системы при сложных ограничениях
Из полученных оценок и определения E.10.15) функции v(T) вы-
вытекает неравенство
AT
v(T) * f ¦
Отсюда и из соотношения E.10.16) получаем оценку для управляющей
функции u(t):
AT
max \u(t)\
- 24
г
E.10.18)
Так как Т = 2тг&, к = 1,2... , то при достаточно больших /с будет
выполнено условие
AT ^ 1
Т2-24
го
E.10.19)
Неравенства E.10.18), E.10.19) гарантируют выполнение ограни-
ограничения E.10.8).
Укажем еще один способ, как выбирать время окончания
процесса Т, чтобы обеспечить выполнение ограничения E.10.8)
для управляющей функции E.10.13). Построим для этого функцию
v(T) численно, используя соотношения E.5.3), E.10.13) и E.10.15).
Функция v(T) целиком определяется матрицей А и вектором Ъ системы
E.10.11), поэтому такое построение может быть выполнено для данной
системы заранее один раз.
На рис. 73 представлен график функции v(T) для случая
р = A,0, 10,0). Как и следовало ожидать, эта функция убывает
с ростом Т, так что максимальная величина управляющей силы
оказалась тем меньше, чем больше
время движения системы до тер-
терминального состояния. В качестве
времени окончания процесса могут
быть выбраны любые значения Т,
при которых
30-
2(Ь
0
1
Т
0 5 10 15
Рис. 73. Функции v(T) и w(T)
E.10.20)
Обратимся теперь к вопросу
о выборе величины Т, обеспечи-
обеспечивающей выполнение ограничений
E.10.9). В принятых обозначениях
решение системы E.10.11), начи-
начинающееся в момент времени t = 0
§5.10. Активный динамический гаситель
277
в точке х°, имеет вид
Подставим сюда выражение E.10.13) для управляющей функции u(t) и
воспользуемся выражением E.5.3), задающим матрицу R(t). Получим
x(t) = Ф(«) х° - Q(t) \^т(т)К-1(Т)х0^ dr =
x° -
Q(r)QT(r)dr
Lo
R-l(T)x° =
W(t,T) = <&(t)[R(T)-R(t)].
= W(t,T)x°,
(Т). E.10.21)
Как и в случае с ограничением E.10.8), предложим два способа
определения величины Т, гарантирующие выполнение условия E.10.9).
Будем сначала выбирать время окончания процесса в виде Т = 2тг&,
к = 1,2.... Оценим евклидову норму вектора x(t) через евклидовы
нормы матриц, стоящих в правой части последнего равенства E.10.21).
Известно [25], что величина ||Ф(?)||2 равна максимальному соб-
собственному числу (j)(t) матрицы
г 1 0 0
ФТ(?)Ф(?) =
0 1
0
te
Нетрудно вычислить, что ф(г) ^ t2
0
+ 1 t
t I
2, откуда получаем
E.10.22)
Матрица R~l(T) является симметрической и положительно-
определенной, следовательно, ее собственные числа положительны,
а максимальное из них равно норме матрицы. Кроме того [25],
сумма всех собственных чисел равна следу матрицы R~l(T). Из вида
E.10.17) матрицы R~l(T) можно заключить, что число 2/Т является
одним из ее собственных значений и
tr
2Г2- 15
Т(Т2-24)
2_
Т'
278 Гл. 5. Управляемые системы при сложных ограничениях
Следовательно, число 2/Т не является максимальным собственным
значением и
tr Д-'(Т) - | = т1т~24)' Т = 2пк- E-10-23)
В силу управляемости системы E.10.11) матрицы R(t), R(T) и
т
t
являются симметрическими и положительно-определенными. Кроме
того,
R(T) - R(t) < R(T), 0<t^T E.10.24)
(неравенство X < Y для симметрических матриц X и Y означает, что
матрица Y — X положительно определена). Так как норма симметри-
симметрической положительно-определенной матрицы равна ее максимальному
собственному числу, а неравенство E.10.24) влечет [25] соответству-
соответствующее неравенство для собственных чисел матриц R(T) — R(t) и R(T),
то справедливо соотношение
Для оценки ||Д(Т)|| воспользуемся рассуждением, аналогичным
проведенному выше в отношении матрицы R~l(T). Из вида E.4.11)
матрицы R(T) можно заключить, что число Т/2 — немаксимальное
собственное значение R(T), поэтому
Из E.10.21)—E.10.23), равенства ||р|| = (m\ + m\)x/2/m2 и последнего
соотношения вытекает
\(p,x(t))\ < \\p
т2(Г2-24)
0
Следовательно, в качестве времени окончания процесса можно выби-
выбирать такие значения Т = 2тг&, чтобы выполнялось неравенство
m2cd
Т2-24
§5.10. Активный динамический гаситель
279
10
Рис. 74. Проекции фазовых траек- Рис. 75. Управляющая функция
торий u(t) и величина \(р,x(t))\
Рассмотрим еще один способ определения величины Т, обеспечива-
обеспечивающий выполнение ограничений E.10.9). Из E.10.21) вытекает
w(T) = max \\WT(t,T)p\\.
Построим функцию w(T) численно. Эта функция целиком опре-
определяется матрицей А и векторами Ъ и р, поэтому такое построение
достаточно выполнить один раз.
На рис. 73 представлен график функции w(T). Видно, что с увели-
увеличением продолжительности процесса Т величина w(t) растет, хотя
и немонотонно. В качестве времени окончания движения могут быть
выбраны любые Т, при которых значение функции w(T) удовлетворяет
неравенству
E.10.26)
cd
Таким образом, предлагается следующая процедура построения
управляющей функции u(t). Сначала для заданного вектора начального
состояния х° выбираем величину Т — момент окончания процесса.
Величину Т можно искать в виде Т = 2тг&, где натуральное число к
должно быть таким, чтобы выполнялись условия E.10.19) и E.10.25).
Еще один способ нахождения времени Т заключается в численном
построении функций v(T) и w(T) и выборе такого значения Т,
при котором выполняются неравенства E.10.20) и E.10.26).
280 Гл. 5. Управляемые системы при сложных ограничениях
После определения момента окончания процесса Т управляющая
функция u(t) вычисляется аналитически согласно E.10.13). Как уже
отмечалось в § 5.5, выражение для обратной матрицы R~l(T), полу-
полученное с помощью компьютерной программы символьных вычислений,
оказывается довольно громоздким. Приведенный в качестве примера
левый верхний элемент этой матрицы имеет вид E.5.10).
На рис. 74 представлены результаты численного моделирования
динамики системы E.10.11). Система переводилась из начального
состояния х° = A/2,-1/2,1/2,1/2) в начало координат. Время
окончания процесса было выбрано равным Т = 10. Жирной линией
показана проекция фазовой траектории на плоскость х\, Х2 = х\,
а тонкой — ее проекция на плоскость х%, х\ = х%.
На рис. 75 сплошными линиями изображены графики зависимости
от времени управляющей функции u(t) и величины
\(p,x(t))\ =
— х3 +х\
1712
из ограничения E.10.9) для случая m\/ni2 = 10. Для сравнения штри-
штриховыми линиями приведены графики тех же функций, но для времени
окончания процесса Т = 5. Видно, что величина \(р,x(t))\ при этом
уменьшилась, а максимум модуля управляющей силы u(t) возрос.
Глава 6
НЕКОТОРЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ ПРИ СЛОЖНЫХ
ОГРАНИЧЕНИЯХ
§ 6.1. Введение
Простейшая динамическая система с одной степенью свободы
m'( = F F.1.1)
неоднократно служила моделью в теории управления. Здесь ? —
обобщенная координата, ? — обобщенная скорость, т — постоянная
инерционная характеристика (масса или момент инерции), F — управ-
управляющее воздействие (сила или момент силы), точки означают произ-
производные по времени t. С одной стороны, на этой модели отрабатывались
и демонстрировались постановки и методы решения задач управления.
С другой стороны, система с одной степенью свободы использовалась
как элемент в схемах декомпозиции нелинейных систем со многими
степенями свободы на более простые подсистемы (см. главы 1,2).
В данной главе представлены решения ряда задач о приведении
системы F.1.1) в начало координат фазовой плоскости при различ-
различных ограничениях. Эти результаты были получены в работах [69-71,
74, 75].
Во многих практических задачах управления встречаются
смешанные ограничения, наложенные в каждый момент времени
на управляющие воздействия и фазовые координаты. Так, при наличии
в системе электропривода обычно следует учитывать ограничения,
наложенные на управляющий момент двигателя, на угловую скорость
вращения вала, а также на эти величины в совокупности. Наличие
смешанных ограничений в задачах оптимального управления приводит,
как известно, к существенным трудностям даже для линейных систем.
В § 6.2, 6.3 излагается постановка и решение задачи оптималь-
оптимального быстродействия для системы F.1.1) при смешанных и фазовых
ограничениях. При отсутствии фазовых ограничений рассматриваемая
задача сводится к задаче быстродействия, для которой в [21] построен
регулярный синтез. В указанных параграфах дано непосредственное
доказательство оптимальности построенного синтеза, не опирающееся
на [21]. В § 6.4 в качестве примера рассмотрена задача оптимального
по быстродействию управления электродвигателем постоянного тока
с независимым возбуждением.
282 Гл. 6. Задачи оптимального управления при сложных ограничениях
В § 6.5-6.7 рассматривается случай, когда движение системы
F.1.1) совершается под действием управляющей силы с ограниченной
скоростью изменения. Построено программное управление системой,
оптимальное по быстродействию. В замкнутой форме дано решение
задачи синтеза оптимального управления.
В § 6.8-6.10 рассматривается случай, когда система F.1.1) управ-
управляется посредством ограниченной по величине силы. Кроме того,
предполагается, что величина силы может наращиваться постепенно,
с конечной скоростью, и мгновенно выключаться. При этих ограниче-
ограничениях, моделирующих реальные системы приводов, построено управле-
управление, приводящее систему в начало координат и имеющее простейшую
возможную структуру.
§ 6.2. Постановка задачи оптимального
быстродействия при смешанных и фазовых
ограничениях
Введем обозначения
w = — F.2.1)
и перепишем F.1.1) в виде
x = v, v = w. F.2.2)
Будем рассматривать управляемую систему второго порядка F.2.2),
где х, v — фазовые координаты (координата и скорость), w — управля-
управляющее воздействие (ускорение). На управление и фазовые координаты
наложены ограничения
v\ ^v ^ v2, v\ < 0, v2> 0, F.2.3)
где v\, v2 — заданные постоянные, и смешанное ограничение
fi(v)^w^f2(v), ve[vuv2]. F.2.4)
Здесь f\(v) и f2(v) — заданные на отрезке [^ь^] кусочно-непрерывные
функции, причем
/i(«)<0, /2(v)>0, v?(vltv2). F.2.5)
Функции f\(v) и f2(v) могут обращаться в нуль лишь на границах
интервала [^ь^]. Область в плоскости (v,w), ограниченная условиями
F.2.3), F.2.4), изображена на рис. 76.
§6.3. Ограничения на скорость и ускорение
283
Поставим задачу об определе-
определении управления в форме синте-
синтеза w(x,v), переводящего систему
F.2.2) с ограничениями F.2.3),
F.2.4) из любого (в области v\ ^
^ v ^ V2) начального фазового со-
состояния
v(t0) = v0 F.2.6)
x(t0) = х
в состояние
х(Т) = О, v(T) = О
F.2.7)
V2 V
Рис. 76. Область допустимых зна-
значений (v, w)
за кратчайшее время (Т —> min). Если заменить управление w на новое
управление и по формуле
w =
Mv) =
f2(v)~fl(v)
то система F.2.2) с ограничениями F.2.3), F.2.4) преобразуется к виду
х = v, v = h(v)u + f±{
\и\ ^ 1, V\ ^ V ^ V2-
F.2.8)
Здесь смешанное ограничение отсутствует. Если опустить фазовое
ограничение v\ < v < V2, то полученная задача быстродействия
для системы F.2.8) с граничными условиями F.2.6), F.2.7)
окажется частным случаем более общей задачи быстродействия,
для которой в [21] построен регулярный синтез. Наличие фазового
ограничения приводит к некоторому видоизменению этого синтеза.
Ниже приведен синтез оптимального управления для поставленной
задачи быстродействия в исходной форме F.2.2)-F.2.7) и дано
непосредственное доказательство его оптимальности, не опирающееся
на принцип максимума.
§ 6.3. Оптимальное быстродействие при ограничениях
на скорость и ускорение
Полагая w = fi(v), i = 1,2, получим из F.2.2)
dx
dv
i= 1,2.
F.3.1)
284 Гл. 6. Задачи оптимального управления при сложных ограничениях
Интегрируя F.3.1), получим уравнения фазовых траекторий, отве-
отвечающих управлениям w = fi(v), в виде {С{ — постоянная)
x = Xi(v) + Ci, г =1,2, F.3.2)
где v
[^г, г =1,2. F.3.3)
В силу F.2.5) функции F.3.3) обладают следующими свойствами.
Функция X\(v) монотонно возрастает при v < 0 и монотонно убы-
убывает при v > 0, а Х2(у), наоборот, монотонно убывает при v < О
и монотонно возрастает при v > 0. При v = 0 функция Xi(u) имеет
нулевой максимум, а функция -^(г?) — нулевой минимум. Согласно
уравнениям F.2.2), движение по траекториям F.3.2) с г = 1 происходит
в сторону убывания v, а по траекториям F.3.2) с г = 2 — в сторону
возрастания v. Если fi(vj) = 0 при некоторых i, j = 1,2 и интеграл
Xi(vj) в F.3.3) расходится, то соответствующая фазовая траектория
F.3.2) имеет горизонтальную асимптоту v = Vj. В противном случае,
т. е. когда либо fi(vj) ^ 0, либо fi(vj) = 0, но интеграл Xi(vj) сходится,
кривая х = Xi(v) пересекает прямую v = vj в точке ж = Xi(vj).
Опишем сначала предлагаемый синтез управления, а затем дока-
докажем его оптимальность. В фазовой плоскости (x,v) определим кривую
переключений равенствами
х = X(v) = < F.3.4)
{ Хх(у), ve[0,v2].
В силу свойств функций Xi(v), г = 1,2, функция X(v) монотонно
убывает и интервале [^ь^], причем Х@) = 0. В начале координат
кривая переключений F.3.4) имеет точку перегиба. Кривая переклю-
переключений изображена на рисунках 77 и 78 жирной кривой. Она разделяет
полосу г; 1 < v < V2, допускаемую фазовыми ограничениями F.2.3),
на две области: D\ (справа и сверху от кривой F.3.4)) и D^ (слева
и снизу от этой кривой) (см. рисунки 77 и 78). Положим в открытых
областях Di
w = f\(v) при x>X(v), v?(v\,V2) (в D\),
F.3.5)
w — /2(^0 ПРИ x < X(v), v € (v\,V2) (в D2).
Определим управление на границах областей D\, D%. На кривой
переключений F.3.4) полагаем
w — f\{v) ПРИ х = X\(v), v^[0,V2],
F.3.6)
w = h(v) при х = Х2(у), и Е^ьО].
§6.3. Ограничения на скорость и ускорение
285
Рис. 77. Кривая переключений и
фазовые траектории (X\(v\) и
^2) неограничены)
Рис. 78. Кривая переключений и
фазовые траектории (все Xi(vj)
ограничены)
На прямых v = v\, v = v2 положим
w = О при v = v\, x>X2(v\),
w = f2(v{) при v = vu x<X2(vi),
W = 0 ПрИ V = V2, X < X\(v2),
F.3.7)
= f\(v2) При V =
X>X\(v2).
Соотношения F.3.7) имеют смысл, если f2(v\) ф О, f\(v2) ф О
и, следовательно, величины X^ivx) и X\(v^) ограничены. Если какая-
либо из них (X<i{v{) или X\{v<if) неограничена, т.е. соответству-
соответствующий интеграл F.3.3) расходится, то кривая переключений имеет
горизонтальную асимптоту v = v\ или v = V2 соответственно. В этом
случае на этой прямой (г; = v\ или v = v2) управление не определено.
При этом с данной прямой нельзя попасть в область v\ < v < v2,
и задача управления неразрешима, если начальная точка (xq,vq) лежит
на соответствующей прямой. Если же величины Xi(^i) или X2(v2)
неограничены, то это означает, что фазовые траектории, начинающиеся
внутри областей D\ и D2 соответственно, не достигают соответствую-
соответствующих прямых г; 1 и v2, а обязательно пересекают кривую переключений.
Если же начальная точка (xq,vq) лежит на одной из этих прямых,
то она согласно F.3.7) движется по данной прямой с управлением
w = 0 вплоть до попадания на кривую переключений.
Фазовые траектории, отвечающие построенному синтезу управле-
управления F.3.5)-F.3.7), изображены на рис. 77 для случая ограничен-
ограниченных значений X\(v2) и X2(v\) и неограниченных значений X\(v\)
286 Гл. 6. Задачи оптимального управления при сложных ограничениях
), а на рис. 78 — для случая, когда все величины Xi(vj)
при г, j = 1,2 ограничены (в обоих случаях /2(^1) ф 0, jxiv^) ф 0).
Стрелками на рисунках 11 и 78 показано направление движения.
Траектории плотно заполняют всю полосу v\ ^ v ^ v^. Каждая фазовая
траектория состоит не более чем из трех участков, отвечающих трем
различным управлениям. Рассмотрим для определенности фазовую
траекторию, начинающуюся в точке F.2.6) области D^ и заканчиваю-
заканчивающуюся в начале координат F.2.7).
На первом участке имеем w = /2A7), и движение происходит
по кривой семейства F.3.2) с г = 2, а именно по кривой
х = X2(v) - X2(v0) + х0 F.3.8)
от точки (хо,Уо) до некоторой точки на прямой v = V2. Согласно F.3.7)
координаты этой точки равны
х = Х2 = ^2(^2) — Х2(г>о) + %о, v = V2- F.3.9)
На втором участке w = 0, и движение происходит по прямой v = V2
от точки F.3.9) до точки
x = Xi(v2), v = v2 F.3.10)
на кривой переключений х = X(v). На третьем участке имеем
w = f\(v), и движение происходит по кривой переключений х = X\(v)
от точки F.3.10) до попадания в начало координат.
Второй участок отсутствует, если Х2(у2) или X\(v2) неограничены,
а также если точка F.3.9) лежит правее точки F.3.10), т.е. при
Х2 > X\(v2). В этих случаях переход с первого на третий участок
происходит в точке пересечения кривой F.3.8) с кривой х = X\(v).
Если же начальная точка лежит на прямой v = V2, причем X\(v2)
конечно и жо < X\(v2), то отсутствует первый участок. Наконец,
если начальная точка лежит на кривой переключений, то отсутствуют
первый и второй участки. Аналогичную структуру имеют фазовые
траектории в области D\.
Сопоставим времена движения по двум траекториям построенного
синтеза, начинающимся в точках (x'0,vq) и (x'q,vq) области D2,
лежащих на одной прямой v = vq. Если х'о < x'q, to из структуры
фазовых траекторий следует, что первая траектория, начинающаяся
левее (при xq = х'о), содержит по крайней мере все те же участки, что
и вторая (с началом при xq = Xq). При этом протяженность участков
и время движения по ним для первой траектории заведомо не меньше,
чем для второй. Поэтому полное время движения по первой траектории
больше, чем по второй. Это свойство монотонной зависимости времени
движения от абсциссы xq начальной точки будет использовано ниже.
Перейдем к доказательству оптимальности предложенного синтеза.
Для этого наряду с какой-то фазовой траекторией построенного
синтеза, которую будем называть исходной, рассмотрим произвольную
§6.3. Ограничения на скорость и ускорение 287
пробную траекторию, удовлетворяющую ограничениям F.2.3), F.2.4).
Пробная траектория начинается в момент t = to в той же точке (xq,vq),
что и исходная траектория, и заканчивается в момент t = Т* в начале
координат. Для доказательства оптимальности построенного синтеза
достаточно показать, что Т* > Т.
Прежде всего отметим, что пробная траектория может иметь
самопересечения, т.е. содержать замкнутые петли. Время движения
по каждой петле положительно. Если удалить все петли из пробной
траектории, соединив начала и концы каждой петли, то полученная
новая пробная траектория допустима, а время движения по ней будет
меньше, чем по пробной траектории с самопересечениями. Поэтому,
не нарушая общности, достаточно рассматривать в дальнейшем лишь
пробные траектории без самопересечений.
Сначала предположим, что точка (#о,гК)) лежит на кривой пере-
переключений х = X\{v). Согласно F.2.2), времена движения по исходной
и пробной траекториям равны соответственно
о о
dv „ , (dv F3П)
Если скорость v вдоль пробной траектории строго убывает (как это
имеет место вдоль исходной траектории), то в силу F.2.4) dv < 0,
f\(v) < w < 0, и поэтому из F.3.11) следует, что Т < Т*. Если
же вдоль пробной траектории v изменяется немонотонно, то второй
интеграл в F.3.11) следует понимать как криволинейный. Заметим,
что отклонение от монотонности убывания v приводит к появлению
участков пробной траектории, на которых dv > 0, w > 0 и которые дают
дополнительный положительный вклад во второй интеграл F.3.11).
Во всех случаях имеем Т ^ Т*.
Таким образом, если фазовая точка (начальная или текущая)
попала на кривую переключений, то дальнейшее оптимальное
движение происходит по этой кривой. Поэтому пробные траектории,
пересекающие кривую переключений, в дальнейшем можно не рас-
рассматривать и считать, что конечный участок пробной траектории,
входящей в начало координат, лежит на кривой переключений.
Пусть теперь начальная точка (жо>^о) лежит в области D<z, причем
^о > 0. Предположим сначала, что пробная траектория не пересека-
пересекает ось х при t ^ to. Тогда координата х монотонно возрастает как
на исходной, так и на пробной траекториях. Времена движения по этим
траекториям можно согласно F.2.2) представить в виде
F.3.12)
7^, о
v{x)
Xq Xq
288 Гл. 6. Задачи оптимального управления при сложных ограничениях
Зависимость v(x) для исходной траектории согласно изложенному
выше состоит не более чем из трех участков: возрастания от vo до г?2,
движения с максимально возможной скоростью v = v2 и убывания от v2
до 0 (некоторые из этих участков могут отсутствовать). Зависимость
v*(x) для пробной траектории удовлетворяет согласно F.2.4) и F.3.1)
неравенствам
ЛЫ^А^ЛЫ „ф>0. F.з.13)
v* ах v*
Знаки равенства в F.3.13) достигаются на исходной траектории.
Из F.3.13), ограничения v* < v2 и граничных условий v*(xo) = ^о
и г;*@) = 0, общих для исходной и пробной траекторий, вытекает, что
зависимость v*(x) (при каждом фиксированном v) растет не быстрее,
а убывает не медленнее, чем v(x). Другими словами, график функции
v*(x) лежит не выше, чем график зависимости v(x), т.е. v*(x) ^ v(x)
при х е [жо,О]. Тогда из F.3.12) следует, что Т < Т*.
Теперь предположим, что пробная траектория, начинающаяся в точ-
точке (xq,vq) области D2 ПРИ ^о ^ О, пересекает ось х при некотором
t\ > to. В точке пересечения имеем х\ > xq, после чего скорость меняет
знак, и х начинает убывать. Однако пробная траектория должна в кон-
конце концов попасть в область v > 0. При этом может либо произойти
самопересечение пробной траектории, что исключено выше, либо проб-
пробная траектория попадет в точку с координатами (x2,vo), где х2 < xq,
после чего траектория останется в области г>о ^ 0. Время движения Ц
по пробной траектории от точки (жг^о) Д° точки @,0), по доказанному
выше, не меньше, чем соответствующее время t^ для исходной траекто-
траектории с началом в той же точке (#2>^о)- В силу же зависимости времени
движения вдоль исходных траекторий от координаты начальной точки
имеем ^2 > Т — to, ибо х% < х$. Следовательно, имеем Т* — to > Ц >
> ^2 > Т — to. Таким образом, Т < Т* в рассматриваемом случае.
Итак, если фазовая точка попадает на ось х при х < 0, то дальней-
дальнейшее оптимальное движение идет по исходной траектории, проходящей
через данную точку оси х. Поэтому можно считать, что пробная
траектория в полуплоскости v > 0 совпадает с исходной.
Осталось рассмотреть случай, когда начальная точка (#2,г;о)
в области D2 такова, что ^о < 0. Как пробную, так и исходную траекто-
траектории представим в виде двух участков, лежащих в полуплоскостях v < 0
и v > 0 соответственно. Времена движения по первым участкам (v < 0)
сопоставим между собой аналогично тому, как это сделано для на-
начальной точки на кривой переключений (см. F.3.11)). Получим, что
пробная траектория достигает оси х не раньше, чем исходная. Оценки
вида F.3.13) позволяют установить, что точка х = х*, где пробная
траектория пересекает ось х, лежит не правее соответствующей
точки х = х\ пересечения оси х исходной траекторией, т.е. х* ^х\.
В силу доказанной выше монотонной зависимости времени движения
по исходной траектории от абсциссы начальной точки заключаем,
§6.4. Задача управления электродвигателем 289
что длительность второго участка пробной траектории не меньше,
чем для второго участка исходной траектории. Тем самым доказано,
что Г ^ Г* и в данном случае. Таким образом, полностью доказана
оптимальность по быстродействию построенного синтеза управления,
заданного соотношениями F.3.5)-F.3.7).
§ 6.4. Задача управления электродвигателем
В качестве примера рассмотрим простейшую модель электродви-
электродвигателя постоянного тока с независимым возбуждением. Момент М,
развиваемый электродвигателем, пропорционален силе тока / в цепи
ротора
M = kMI, F.4.1)
где км — постоянный коэффициент. Уравнение баланса электрических
напряжений в цепи ротора имеет вид
LI + RI + кЕи = и, кЕ > 0. F.4.2)
Здесь L — коэффициент индуктивности цепи ротора, R — ее электри-
электрическое сопротивление, и — управляющее электрическое напряжение,
и — угловая скорость вращения ротора, кЕи — противо-э.д.с, кЕ —
постоянный коэффициент. Первое слагаемое в левой части F.4.2)
обычно мало по сравнению с остальными слагаемыми, и им можно
пренебречь. Тогда, выражая / при помощи F.4.2), получим из F.4.1)
М = kMR~\u - kEou). F.4.3)
Управляющее напряжение ограничено по величине:
\и\ < щ, F.4.4)
где щ — постоянная. Из F.4.3), F.4.4) вытекает, что момент М
ограничен неравенствами
-kMR-{(u0 + кЕи) < М < kMR-{(u0 - kEuu). F.4.5)
Кроме F.4.5), часто накладываются еще ограничения на величину
тока /, а также на величину момента М, обусловленные требованиями
со стороны редуктора. И те, и другие ограничения сводятся согласно
F.4.1) к ограничению вида \М\ ^ Mq, где Mq — постоянная. Угловую
скорость ограничим по модулю величиной uoq = г^о (кЕ) . При этом
ограничении левая и правая части неравенства F.4.5) имеют разные
знаки, т.е. момент М при |о;| < uoq может быть как ускоряющим,
так и тормозящим. В результате приходим к совокупности ограничений
-к(ы0 + и) < М < к(ы0 - и), \М\ < Мо, И < ujo,
F.4.6)
к = kMR~lkE, uoq = щ (кЕ)~1 .
10 Ф. Л. Черноусько и др.
290 Гл. 6. Задачи оптимального управления при сложных ограничениях
Уравнения вращения ротора электродвигателя имеют вид
а = и, Ju = M + Mi. F.4.7)
Здесь а — угол поворота ротора, J — момент инерции ротора и других
вращающихся частей редуктора, М\ — момент всех внешних сил,
кроме электромагнитного момента М, который можно рассматривать
как управляющее воздействие в системе F.4.7). На систему F.4.7)
наложены ограничения F.4.6), среди которых есть смешанное ограни-
ограничение, ограничение на управление и на фазовую координату. Введем
безразмерные переменные t', х, v, w и параметр к соотношениями
t = J(JoM^ltff a = JljqM^~1x,
F.4.8)
и = ujqv, M = Mqw, к = 1
Тогда уравнения F.4.7) при М\ = 0 и ограничения F.4.6) преобразу-
преобразуются к виду
х = v, v = w,
F.4.9)
\w\ < 1, \v\ < 1, -x(l+vL:w4:x(l-v),
где точкой обозначена производная по безразмерному времени tr из
F.4.8). В дальнейшем штрих у переменной tr опускаем. Уравнения
F.4.9) совпадают с F.2.2), а ограничения F.4.9) приводятся к виду
F.2.3), F.2.4), причем
!—хA + v) при — 1 ^ v ^ vc,
-1 при vc^v^l, F.4.10)
Vc = K~X — 1, V\ = — 1, 172=1.
Таким образом, функции /ь /2 здесь кусочно-линейны и имеют точки
излома при v = ±г>с соответственно, причем /1A*2) 7^ 0 и /2(^1) 7^ 0-
Если х ^ 1/2, то точки излома лежат вне интервала (—1, 1).
В этом случае функции /ь /2 линейны на отрезке [—1, 1], ограничение
\w\ ^ 1 выполняется автоматически и становится несущественным. То-
Тогда система F.4.9) приводится к виду линейной управляемой системы
с новым управлением w\
x = v, v = —xv -\-w\,
\w\ I ^ x, |u| ^ 1.
Здесь смешанное ограничение отсутствует.
При к > 1/2 точки ±i>c лежат внутри интервала (—1, 1), причем
при к G A/2, 1) точки vc и — vc лежат в интервалах @, 1) и (—1,0)
соответственно, а при к > 1 — в интервалах (—1,0) и @, 1) соответ-
соответственно.
§6.4. Задача управления электродвигателем
291
к> 1
Область в плоскости (v,w), до-
допускаемая ограничениями F.4.9),
представляет собой в общем случае
шестиугольник, обладающий цен-
центральной симметрией относительно
начала координат. Он изображен на
рис. 79 для случая к = 2.
Рассмотрим задачу оптималь-
оптимального быстродействия для описан-
описанной модели электродвигателя. В
безразмерных переменных F.4.8)
эта модель задается соотношения-
соотношениями F.4.9), которые представляют
собой частный случай соотноше-
соотношений F.2.2)-F.2.4), в которых вве-
введены обозначения F.4.10). Усло-
Условия F.2.5) для функций /ь /2 из
F.4.10) выполнены. Граничные условия по-прежнему имеют вид
F.2.6), F.2.7). Конкретизируем общее решение задачи синтеза опти-
оптимального быстродействия для системы F.2.2)-F.2.7) применительно
к системе F.4.9).
Подставим F.4.10) в F.3.3) и вычислим соответствующие инте-
интегралы, рассматривая отдельно случаи к < 1/2, к е [1/2, 1] и к > 1.
Получим
Xx{v) = -k-\v
Рис. 79. Область допустимых зна-
значений (v,w)
Xi(v) =
—к l[v — ln(l + г;)] при v?[—l,vc],
- A — v2 — я~2) — к~х lnx при ve[vc,l],
l),
Xl(v) =
при v e [— 1, vc
— - v2 при v e [vc, 1],
X2(v) =-Xi(-v),
F.4.11)
10*
292 Гл. 6. Задачи оптимального управления при сложных ограничениях
Кривая переключений х = X(v), задаваемая равенствами F.3.4),
разделяет полосу \v\ ^ 1 на области D\, где х > X(v), и D2, где
х < Х{у). Синтез оптимального управления определяется равенствами
F.3.5)-F.3.7), в которых и 1 = — 1, 172 = 1, а функции fi, Xi, опреде-
определены равенствами F.4.10), F.4.11) соответственно, г = 1,2. Отметим,
что в силу F.4.11) кривая переключений и всё поле оптимальных
траекторий обладает центральной симметрией относительно начала
координат. На рис. 77 показано поле оптимальных траекторий для слу-
случая к = 2, vc = —1/2.
Так как величины Х\(\) и Х2(—1) ограничены (см. F.4.11)),
то согласно замечанию в § 6.3 синтез оптимального управления
определен во всей полосе \v\ ^ 1, включая ее границы. С другой
стороны, из F.4.11) следует, что величины Х\{— 1) и Х2{\) неограни-
чены. Поэтому согласно § 6.3 фазовые траектории, начавшиеся внутри
полосы, т.е. при \v\ < 1, не попадают на границы полосы, а пересекают
кривую переключений (см. рис. 77). Следовательно, каждая из этих
траекторий состоит не более чем из двух участков; средний участок,
описанный в § 6.3, отсутствует. Если же начальная точка лежит
на границе полосы, то фазовая точка движется по границе с управ-
управлением w = 0 до кривой переключений, если v = — 1 и х > Х2(— 1)
или если v = 1 и х < Х\(\). В остальных случаях, т.е. при v = — 1
и х < Х2(— 1) или при v = \ и х > Х\(\), фазовая точка сразу попадает
внутрь полосы (см. рис. 77).
Подсчитаем время движения по оптимальной фазовой траектории,
начинающейся при t = 0 в точке (жо,О) оси х, где xq < 0. Согласно
построенному синтезу и сделанным выше замечаниям оптимальная
траектория начинается в области D2 и состоит из двух участков.
Первый участок — это дуга кривой F.3.8), т.е. кривой
x = X2(v)+x0 F.4.12)
от точки (xq,0) до некоторой точки (xm,vm), в которой кривая
F.4.12) пересекается с кривой переключений х = X\(v). Поэтому
имеем следующие соотношения для определения координат (xm,vm):
хт = X\(vm) = X2(vm) + х0. F.4.13)
Второй участок фазовой траектории — это дуга кривой х = Х\ {у)
от точки (xm,vm) до начала координат. Скорость v возрастает от 0
до vm на первом участке, где w = f2(v), и убывает от vm до 0 на втором
участке, где w = f\(y). Полное время движения представим в виде
Vm 0
\AJ (J / f\ л ч л \
Ш
§6.4. Задача управления электродвигателем
293
Ограничимся для определенности случаем х> 1 и обозначим
? = -жо>О, q = -vc = 1 -к~х >0, к>\. F.4.15)
Вычислим интегралы F.4.14), подставив в них выражения F.4.10)
и пользуясь обозначениями F.4.15). Получим
Т = 2vm при vm < q,
vm-(l-q)ln
\-q
F.4.16)
при vr
Подставляя F.4.11) при х> 1 в F.4.13) и пользуясь обозначениями
F.4.15), получим соотношения, связывающие vm и ?:
= v
при
< q,
\-vm
\-q
при
F.4.17)
Соотношения F.4.16), F.4.17) определяют зависимость Т(?) в пара-
параметрическом виде. Придавая параметру vm значения от 0 до 1, получим
при каждом фиксированном q искомую зависимость Т(?). Отметим,
что из F.4.16), F.4.17) следует
/2 2. F.4.18)
оо. Для этого устремим
при
Найдем асимптотику функции Т(?) при
vm -^ 1 и получим из F.4.16) и F.4.17)
Т = -A - q) ln(l - V
¦q+ 1 + A -g)ln(l — g) + 0A -'
^2 + l ,
+ (l-q)\n(l-q)+O(l-v
Из F.4.19) находим искомую асимптотику
9
F.4.19)
F.4.20)
Отдельно рассмотрим предельный случай к —> оо. Согласно F.4.15)
имеем при этом vc = — 1, g = 1, и ограничения F.4.9) определяют
квадрат \v\ ^ 1, |гу| ^ 1 в плоскости (v,w). В этом случае (см. F.4.11))
Xi(v) = -X2(v) = -V— при
F.4.21)
294 Гл. 6. Задачи оптимального управления при сложных ограничениях
Все фазовые траектории состоят из дуг парабол F.3.2), F.4.21) и
отрезков прямых v = ±1, как показано на рис. 78.
Подсчитаем полное время движения Т от начальной точки (жо,О),
где xq = — ? < 0, до начала координат. Если vm < 1, то справедливо
соотношение F.4.18), если же vm =
= 1, то время движения складыва-
складывается из времен движения по ду-
дугам парабол и времени движения по
прямой v = 1. В безразмерных пе-
переменных время движения по каж-
каждой из парабол равно 1, а время
движения по прямой v = 1 равно
? — 1 — длине проходимого отрезка
этой прямой. В результате получим
при q = 1
при
1 при
1.
1 е
Рис. 80. Зависимость Т(?) при раз-
различных q
Результаты численных расчетов
зависимости Т(?) при различных q
представлены на рис. 80.
Таким образом, построено пол-
полное решение поставленной задачи.
§ 6.5. Постановка задачи оптимального
быстродействия при ограничении на скорость
изменения ускорения
Рассмотрим систему с одной степенью свободы, описываемую
уравнением F.1.1). При постановке задач оптимального управления
обычно предполагают, что сила F по абсолютной величине ограничена
постоянной Fq, т. е. \F\ ^ Fq. В случае задачи оптимального быстродей-
быстродействия это ограничение приводит, как известно, к релейному характеру
оптимального управления. При этом сила F(t) принимает крайние
значения ±Fq и мгновенно переключается с одного из этих значений
на другое. Такое управление не всегда осуществимо на практике,
например, при реализации управления при помощи электропривода.
В данном параграфе примем более реалистическое ограничение
на скорость изменения управляющей силы вида
\F\ < v0,
F.5.1)
где г>о > 0 — заданная постоянная. Будем также полагать, что ограниче-
ограничение на абсолютную величину силы не достигается и всегда \F(t)\ < Fq.
§ 6.6. Программное оптимальное управление 295
При помощи замены переменных
? = — x, ? = — у, F = voz
m m
приведем уравнения F.1.1) и ограничение F.5.1) к виду
х = у, у = z, z = и, \и\^\. F.5.2)
Теперь переменные х, у, z являются фазовыми координатами, а и
играет роль ограниченного управления.
Зададим начальные условия для системы F.5.2) в виде
х@) = х0, у(О) = Уо, z(O) = zq, F.5.3)
где начальный момент времени без ограничения общности принят
равным нулю.
Поставим задачу о построении управления u(t), удовлетворяющего
ограничению \u(t)\ ^ 1 при t ^ 0 и переводящего систему F.5.2)
из произвольного начального состояния F.5.3) на заданное конечное
многообразие
ж(Г)=0, у(Т)=0 F.5.4)
при произвольном z(T) за кратчайшее время Т.
Помимо определения программного управления будет также решена
задача построения синтеза управления, оптимального по быстродей-
быстродействию для системы F.5.2). Это управление u(x,y,z), выраженное как
функция текущих (или начальных) фазовых координат х, у, z, обеспе-
обеспечивает приведение системы F.5.2) на заданное конечное многообразие
F.5.4) за кратчайшее время.
§ 6.6. Программное оптимальное управление
Применим принцип максимума к поставленной задаче оптимального
быстродействия F.5.2)-F.5.4). Составим функцию Гамильтона
Н = рху +pyz + pzu F.6.1)
и запишем сопряженные уравнения
Рх =0, ру = -рх, pz = -py. F.6.2)
Здесь рх, Ру, Pz — сопряженные переменные. Проинтегрируем систему
F.6.2) при условии трансверсальности pz(T) = 0, отвечающем условию
нефиксированности z(T). Получим
Рх = сх, ру = су + схт, pz = сут + - схт2. F.6.3)
296 Гл. 6. Задачи оптимального управления при сложных ограничениях
Здесь г = Т — t — время, отсчитанное от конца процесса («обратное»
время), сх и су — произвольные постоянные. Условие максимальности
гамильтониана F.6.1) по и при ограничении \и\ < 1 из F.5.2) дает
u(t) = sign pz(t).
Из формулы F.6.3) для pz следует, что функция pz(t) меняет знак
при t < Т, г > 0 не более одного раза. Следовательно, оптимальное
управление u(t) = ±1 имеет при t ^ T не более одного переключения.
Обозначим через 9\, 6% длительности двух возможных участков
постоянства управления u(t), а через а = ±1 — значение u(t) на первом
из этих участков. Тогда оптимальное управление можно представить
в виде
{а при te (O,0i),
F.6.4)
-а при teF>i,T), 01+02= Т.
Подставим управление F.6.4) в систему F.5.2) и проинтегрируем
ее при начальных условиях F.5.3). Получим
x(t) = х0 + yot + - z0t2 + - crt3,
z(t) = zq + at при t G @, 0\),
26 F.6.5)
1
2(t) = 2:0 + cr6»i -cr(t-6»i) При teFuT).
Подставляя решение F.6.5) в условия F.5.4), придем к двум соот-
соотношениям, разрешая которые относительно хо, у0, получим
F.6.6)
§ 6.6. Программное оптимальное управление
297
Введем обозначения
с - ~-3„
F.6.7)
), У(Л)=Л2-|.
Тогда соотношения F.6.6) примут вид
F.6.8)
п-2
.-1
= aY(X).
При ^о = О соотношения F.6.6) дают
гу. гр—3 st Y{ \\ о/ T'—'Z srV{ \\ (Сл Сл О\
XQJ. — иУ\.\Л), УО — ^ V /* ^U.U.C/^
Когда параметр А изменяется от 0 до 1, точка с координатами
Х(Х), Y(X) пробегает дугу кривой, соединяющей точки А\ и А^ с
координатами A/3,-1/2), (—1/3,1/2) соответственно. Точки с коор-
координатами аХ(Х), crY(X) при A G [0, 1] и а = ±1 образуют замкнутую
кривую Г, симметричную относи-
относительно начала координат и име- А\
ющую угловые точки А\ и А%
(см. рис. 81). Кривая Г ограничи-
ограничивает выпуклую область, содержа-
содержащую начало координат.
Решение поставленной про-
программной задачи оптимального
быстродействия F.5.2)-F.5.4)
можно представить следующим
образом.
Предположим сначала, что z$ ^
7^ 0. По заданным начальным дан-
данным xq, y0, zq из F.5.4) опреде-
определим ?, г], ( согласно F.6.7). Левые
части соотношений F.6.8) задают
координаты некоторой точки Р, за-
зависящей от параметра s G [0, оо).
При изменении s от оо до 0 точ-
точка Р перемещается по гладкой по-
полубесконечной кривой из начала
координат (при s —> оо) на беско-
бесконечность (при s —> 0). Эта точка
V
-0.4
Ч 0.4
Л
а= 1
-0.4
aY
а =
°\
\
-1
аХ
^г 0 4
\
\\
А9
Рис. 81. Плоскость параметров
аХ, aY
298 Гл. 6. Задачи оптимального управления при сложных ограничениях
хотя бы один раз попадет на замкнутую кривую Г, окружающую
начало координат. Найдем численно наименьшее значение s = s*, при
котором Р G Г. Время оптимального быстродействия согласно F.6.7)
равно Т = l^ol5*- Положение точки Р при s = s* на кривой Г опреде-
определяет значения параметров а = ±1 и А ? [0, 1]. Длительности участков
постоянства управления в силу F.6.7) равны в\ = A — Х)Т и #2 — AT.
При ^о = 0 вместо соотношений F.6.8) рассмотрим равенства
F.6.9). Левые части этих равенств задают координаты точки Р,
зависящей от параметра Т. Когда Т изменяется от оо до 0,
точка Р перемещается по полукубической параболе из начала
координат (при Т —> оо) на бесконечность (при Т —> 0). Наименьшее
значение параметра Т, при котором Р е Г, есть время оптимального
быстродействия. Значения параметров а, А, 9\, 6% определяются
по положению точки Р на Г так же, как и при zq ^ 0.
Когда величины а, 9\, 6% определены, оптимальное управление u(t)
и соответствующая оптимальная траектория задаются равенствами
F.6.4) и F.6.5). Таким образом, изложенный алгоритм полностью
определяет решение программной задачи оптимального быстродей-
быстродействия. По построению это решение единственно.
В качестве примера приведем результаты определения оптимального
управления для начальных данных
х0 = -72 + 27л/3 « -25.2, у0 = 3, z0 = 1.
Для этого случая получено
Т = 5 = 6, сг=1, 01 = 6 - Зл/3 « 0.80, 6>2 = Зл/3 « 5.20.
Соответствующая траектория точки Р при изменении Т от оо до 0
изображена на рис. 81.
§ 6.7. Синтез оптимального управления
Для построения синтеза оптимального управления достаточно
найти в фазовом пространстве xyz поверхности переключений,
на которых меняется знак управления и = ±1. На этих поверхностях
обращается в нуль длительность одного из участков постоянства
управления, т. е. в\ = 0 либо 6% = 0. В соответствии с F.6.7) имеем
здесь Л = 0 или Л = 1. Этим значениям Л отвечают согласно F.6.7)
значения X и Y, равные ±1/3 и =f1/2 соответственно. Из F.6.8)
получим условия
F.7.1)
aVs-2+s- ~
§ 6.7. Синтез оптимального управления 299
выполняемые в плоскости ?т? на кривых переключений при zq ф 0.
Однако соотношений F.7.1) недостаточно для определения кривых
переключений; для этого потребуется непосредственный анализ соот-
соотношений F.6.8), что будет проведено ниже.
Отметим, что при построении синтеза начальные данные xq, y0, zq
можно рассматривать так же, как текущие значения фазовых
координат х, у, z. Соотношения F.6.7) будем рассматривать как
формулы замены переменных
^ = z~3x, г] = z~l\z\-ly, C=sign^ F.7.2)
в фазовом пространстве. Эта замена, вводящая автомодельные пере-
переменные ?, г], позволяет при z ^ 0 понизить на одну единицу размер-
размерность фазового пространства и вести построение синтеза оптимального
управления в плоскости ^rj.
Рассмотрим сначала отдельно случай z = 0. Аналогично F.7.1)
получим из F.6.9) условия
жГ = ±|а, уТ~'1 = т\о, F.7.3)
которые выполняются на пересечении поверхностей переключений
с плоскостью z = 0. Условия F.7.3) определяют при z = 0 две половины
полукубических парабол, которые образуют кривую переключений
в плоскости z = 0, описываемую уравнением
-у(х,у) = Зж + 22/I22/I1/2 = 0. F.7.4)
Анализ знаков а на ветвях кривой переключений F.7.4) позволяет
определить знаки управления с разных ее сторон. В результате
получаем синтез оптимального управления при z = 0 в виде
!— sigwy(x,y) при 7 7^0,
F.7.5)
sign х = — sign у при 7 = 0-
При z Ф 0 замена переменных F.7.2) преобразует первые два урав-
уравнения F.5.2) к виду
F.7.6)
f] = \z\~\\ - 2u(r]).
Разделив первое уравнение F.7.6) на второе, получим линейное отно-
относительно ? уравнение
f^ a = «C = ±l. F.7.7)
300 Гл. 6. Задачи оптимального управления при сложных ограничениях
Вдоль оптимальных траекторий, не пересекающих плоскость z = 0, па-
параметр а сохраняет постоянное значение. Интегрируя уравнение F.7.7)
при постоянном а, найдем его общее решение
? = Ф(т/, а,А)=аг)-\+А\\- 2аг]\3/2, F.7.8)
о
где А — произвольная постоянная. Отметим, что второе уравне-
уравнение F.7.6) позволяет определить направление движения вдоль опти-
оптимальных траекторий. Если а = 1, то движение при г\ < 1/2 происходит
в сторону роста т\ и при т\ > 1/2 — в сторону убывания т\. Если же
а = — 1, то движение происходит в сторону убывания т\ при т\ < —1/2
и в сторону роста т\ при т\ > —1/2.
Перейдем к непосредственному построению синтеза оптимального
управления. Для этого, как указано выше, достаточно установить знак
управления и = а в начальный момент времени t = 0 в зависимости
от начальных данных xq, y0, zq. Переходя к автомодельным пере-
переменным и обращаясь к соотношениям F.6.8), задачу синтеза можно
сформулировать так: найти значение а = ±1, которое соответствует
решению соотношений F.6.8) (при фиксированных ?, rj, ?, где ? = ±1)
с наименьшим s, причем s > 0, Л G [0, 1].
Изложим алгоритм решения в краткой форме, а затем поясним его
наиболее существенные элементы.
Прежде всего отметим, что при одновременной замене знаков
у С и а соотношения F.6.8) сохраняют свой вид. Следовательно, при
замене ? на —? искомая величина а также меняет знак. Поэтому доста-
достаточно построить решение в случае ? = 1 при произвольных ?, rj, а затем
для С = — 1 просто поменять знак в полученной зависимости а({;,г]).
Итак, положим без ограничения общности (= 1 и исключим Л
при помощи второго из уравнений F.6.8). Получим
1 /9
Л= [!+<7(V~2 + 5~1)] ' <т = ±1. F.7.9)
Так как Л G [0, 1], то из F.7.9) при фиксированных а = ±1 и ту опре-
определяются интервалы изменения s, в которых Л вещественно и Л ^ 1.
Подставим Л из F.7.9) в первое уравнение F.6.8) и найдем зависи-
зависимости ? от s, г] и а = ±1. Эти зависимости при фиксированном ту
будем обозначать через ^(s) и ?~(s) для а = ±1 соответственно. При
условии Л G [0, 1] они определяют в плоскости s, ? две кривые, каждая
из которых состоит, вообще говоря, из конечного числа дуг. Исследуем
эти кривые, а именно найдем их области определения и экстремумы
во всем диапазоне изменения аргумента s и параметра rj, после чего
проанализируем их взаимное расположение. Затем проведем мысленно
в плоскости s, ? прямую ? = const и найдем минимальное значение
абсциссы s > 0, при котором эта прямая пересекает одну из указанных
кривых. Значение а = ±1, отвечающее той кривой, с которой имеет
место это пересечение, определяет искомое управление и = а при
§5.7. Синтез оптимального управления 301
данных ?, г] и ? = 1, а значение 5, отвечающее этой точке пересечения,
равно нормированному времени быстродействия: 5 = Т|^|-1 (нормиро-
(нормированной функции Беллмана).
Теперь опишем указанные операции подробнее, причем следует
учесть, что все последующие построения верны только при 5 > 0. Из
F.6.8) имеем
?*(*) = тЬ3 - i s2 - sr) ± \ (s2/2 ±г)± sK/2. F.7.10)
Если s -> +оо, то ?±(s) « ±(-1 + 1/л/2)з3/6 -> Too.
Рассмотрим функцию ?+(s). В случае а = 1 условие Л < 1 выделяет
множество s е @,52] U [si,+oo), где s\$ = 1 ± \/1 + ^rj. Выражение
для ?,+(s) определено, если s e [sb,+oo), где 55 = —1 + д/1 — 2т?.
Производная d^ /ds обращается в нуль в точках 55 и 57 = — 1 +
/ — 2гу), если 55 и 57 существуют, причем 55 ^ 57. Кроме того,
s2 < 0 при s = 57, т.е. 57 — точка максимума. Можно показать,
ЧТО, еСЛИ 5ь 52, 55 И 57 Существуют, ТО 52 ^ 57 ^ 5i, a 52 ^ 55-
Если г] > 0, то 52 < 0 и dt;+/ds < 0 при s ^ s\, т. е. функция ^(s)
задана при 5 G [s\, +00) и убывает от ^+Ei) до —оо. Если —1/2 ^ г] <
< 0, то 55 > 0, т.е. функция ^(s) определена при 5 G [55,52] U [si,+oo).
Она имеет нулевую производную при 5 = 55, возрастает на отрезке
[55,52] и убывает от ?+Ei) до —оо при sg[si, +00). Если г] < —1/2, то
55 > 0, а значение 52 не определено. Тогда функция ^+(s) задана при
5 G [55, +oo), df^/ds = 0 при 5 = 55, C+(s) возрастает до максимума в
точке 5 = 57, после чего убывает от ^{sj) до —оо.
Теперь перейдем к функции ?~(s). Потребуем, чтобы Л ^ 1 в F.7.9).
Получим, что 5 G [55,+оо), где 55 = — 1 + д/1 — 2г]. Если 5 G @,52] U
U [si,+oo), то функция ?~(s) из F.7.10) определена. Ее производная
обращается в нуль в точках s\, 52 и 53 = 1 — д/2A + 2rj), если они
существуют, причем s$^ s\. Кроме того, d2?>~/ds2 > 0 при 5 = 5з, т.е.
5 = 5з — точка минимума.
Если г] ^ 0, то 52 ^ 0 и функция ?~(s) задана при 5 G [si,+oo),
причем d^~/ds = 0 при s = s\. Функция ?~(s) убывает от ?~(s\)
до точки минимума 5 = 5з, после чего возрастает от ^~Eз) до +оо.
Если —1/2 ^ г] < 0, то 55 > 0, т.е. зависимость ?~(s) определена
при 5 G [55,52] U [«ь+оо). Функция ?~(s) возрастает при изменении 5
от 5 = 55 до 5 = 52, причем dt;~/ds = 0 при 5 = 52, и убывает при
s G [5ь 5з], причем dt;~/ds = 0 при s = s\ и 5 = 53. Далее ?~(s)
возрастает от ^~Eз) до +оо. Если г] < —1/2, то 55 > 0, значения s\,
52 и 5з не определены, a dt;~/ds > 0 при 5 > 55, т.е. функция ?~(s)
задана при 5 G [55,+сю) и возрастает на всем этом интервале до +оо.
Сделаем два замечания о взаимном расположении пары кривых
(по одной из обоих исследованных семейств) для одного и того же
значения параметра г\.
302 Гл. 6. Задачи оптимального управления при сложных ограничениях
Во-первых, найдем точки пересечения кривых ^+(s) и ?~(s), что
требует решения уравнения
Возведем обе части уравнения F.7.11) в квадрат и приведем
подобные члены, затем снова возведем обе части уравнения в квадрат
и получим уравнение относительно s:
Анализ корней уравнения F.7.12) показывает, что только s\, s^ и 55
являются корнями уравнения F.7.11), причем положительными хотя
бы при одном значении г]. Совпадающие значения <^+ = <^~ в указанных
точках будем обозначать через ?>±.
Во-вторых, устанавливаем, что ^(«б) > ^(^l) Т0ГДа и только
тогда, когда —л/3/4 < г] < 0.
В результате, оказывается удобным выделить четыре диапазона
значений параметра г], соответствующих различным взаимным рас-
расположениям кривых ^(s) и ?~(s), которые и определяют искомое
управление для всех ? и 77, за исключением ^(si), ^(«г) и ^(^б)-
При г] ^ 0 для любого ? < ^(si) минимальная допустимая абсцисса
5 достигается на кривой ^+(s). При ? > ^(si) тот же результат имеет
место для ?~(s).
При —л/3/4 < ту < 0 к кривым ^+(s) и ?~(s), имеющим те же
характерные особенности, что и в предыдущем случае, добавляется
замкнутая изолированная кривая для 55 < s < 52, причем кривая ?~(s)
лежит выше кривой ?+(s), a ^(s^) < ^(«2)- Кроме того, ^(si) <
< ^(^б)» т-е- ^(^l) лежит ниже самой нижней точки замкнутой
изолированной кривой. Следовательно, искомое управление задается
так же, как и в предыдущем случае.
При —1/2 ^ т\ ^ — л/3/4 выполняется неравенство ^(si) > ?(^5),
и для любого ^ < ^(«б) минимальная допустимая абсцисса s дости-
достигается на кривой <^+(s). При ^ > ^(^б) то же самое утверждение
справедливо для ?~(s).
Замкнутая изолированная кривая исчезает при г] < —1/2, и искомое
управление задается так же, как и в предыдущем случае.
Определим управление на кривых ^(si^)), ?,±(s2(r])) и ^(s^rj))
в плоскости ^г]. Напомним, что зависимости s\, s^ и 55 от г]
приведены выше. В соответствии с F.7.9) на кривой ^E1G7))
имеем Л = 0 при а = — 1, т.е. временной интервал, в котором надо
применять и=\, равен нулю. Следовательно, на кривой ^E1G7))
надо применять и = —\, и она является кривой переключений при
77 > —л/3/4. Аналогично, на кривой ^E2G7)) следует использовать
и = — 1 при —1/2 ^ ту < 0, но кривой переключений она не будет.
§ 6.7. Синтез оптимального управления 303
Тем же способом нетрудно показать, что на кривой ^(s^rj)) имеем
и = 1 при г] < 0. Она служит кривой переключений.
Приведем полностью результаты построения синтеза оптимального
управления. Примем для определенности z > 0, ? = 1. Кривая пере-
переключений в плоскости ^г] определена равенствами
F.7.13)
?7>7f; rj* = ——,
где использовано обозначение F.7.8). В точке К с координатами
?* = 1/12, ту* = —л/3/4 кривая переключений непрерывна и имеет
излом. Эта кривая изображена жирной линией на рисунках 82 и 83.
В связи с тем, что масштаб на рис. 82 меньше, чем на рис. 83,
точки К и R, показанные на рис. 83, практически неразличимы
на рис. 82 и потому не обозначены. С другой стороны, масштаб
рис. 82 позволяет изобразить все характерные фазовые траектории,
существенная часть которых отсутствует на рис. 83. В остальном
обозначения на рис. 82 и рис. 83 идентичны. Для определенности
в дальнейшем будем ссылаться в основном на рис. 82. Ветви кривой
переключений, отвечающие г] < ту* и г] > т?*, обозначены буквами М
и N, соответственно. В плоскости ^rj имеем
и=<
1 при ? <
1 при ? = ф(ц,1,-\ т? < О, F.7.14)
— 1 в остальных точках плоскости ?г?.
Таким образом, и = 1 слева и снизу от кривой переключений F.7.13),
на ее участке КМ справа и снизу от точки К, а также на дуге
кривой ? = Ф(?7, 1, 1/3), соединяющей начало координат и точку К
(см. рис. 83), причем эта дуга является частью кривой переключений.
В остальной части плоскости ^rj имеем и = — 1.
При z < 0, ( = — 1 кривая переключений остается той же,
а в соотношениях F.7.14) множества точек ^г], где и = 1 и и = —\,
следует просто поменять местами. Итак, синтез оптимального
управления u(x,y,z) полностью определен соотношениями F.7.2),
F.7.4), F.7.5), F.7.8), F.7.13), F.7.14) при всех х, у, z.
Опишем теперь множество оптимальных траекторий, которые
в переменных ?, г] состоят из дуг кривых F.7.8). Пусть задана
начальная точка х, у, z, причем для определенности примем z > 0.
Согласно формулам F.7.2) найдем ?, г\ и ? = 1.
304 Гл. 6. Задачи оптимального управления при сложных ограничениях
-4 -2
/ -м
V /
У 2
\\ Him.
\м\\
Рис. 82. Кривая переключений и оптимальные траектории
7] -0.6
Рис. 83. Кривая переключений и оптимальные траектории вблизи
начала координат
§ 6.7. Синтез оптимального управления 305
Если точка ?т? лежит на кривой ? = Ф(г], 1, 1/3), причем г] ^ 0,
то движение происходит вдоль этой кривой МКО с управлением и = 1
до попадания в начало координат.
Все остальные оптимальные траектории приходят в начало коорди-
координат также по этой кривой. Исключение составляет отрезок R0 кривой
? = Ф(?7, — 1, 1/3) при г] е [—1/2,0]: этот отрезок сам является фазовой
траекторией для и = — 1, начинающейся в точке R с координатами
A/6,-1/2) и входящей в начало координат. На рис. 82 и рис. 83
фазовые траектории изображены тонкими линиями, стрелки указывают
направление движения.
Если начальная точка лежит в криволинейном угле R0K
(см. рис. 83)
1'!) <?<ф(г/,-1,|), F.7.15)
то оптимальная траектория состоит из участка с и = — 1 до попадания
на кривую ? = Ф(?7, 1, 1/3) и из последующего движения по ней с и = 1.
Если начальная точка лежит в области ? < f(rj), то сначала
движение происходит с и = 1 до пересечения с кривой Ф =
= ?G7, —1, —1/3), являющейся частью KN кривой переключений
F.7.13) (см. рис. 82), а затем с и = — 1 по этой кривой, уходящей
на бесконечность. Согласно F.6.7) в бесконечно удаленной точке
плоскости ^г] имеем z = 0. На бесконечности z меняет знак, и затем
z < 0, С = — 1. Фазовая траектория продолжается, приходя при и = — 1
из бесконечности по кривой ? = Ф(г], 1, 1/3), и входит по этой
кривой в начало координат. Отметим, что движение через бесконечно
удаленную точку происходит без смены управления и занимает
конечное время.
Осталось рассмотреть начальные точки в области ? > /(??),
но вне криволинейного угла F.7.15). Здесь имеем сначала и = —\,
и траектория ? = Ф(г},—\,А) уходит на бесконечность, причем
А > —1/3. Затем движение происходит при ? = — 1, и = — 1
по кривым ? = Ф(ту, 1,— А) со сменой знака А. Эти кривые лежат
в области ? < f(r]) и упираются в ветвь KN кривой переключений
? = Ф(?7, — 1, —1/3). По этой кривой траектория с и= 1 уходит
на бесконечность, где снова меняется знак z. Далее при ( = 1 движение
происходит при и = 1 по кривой ? = Ф(?7, 1, 1/3) вплоть до попадания
в начало координат.
Отметим, что некоторые фазовые траектории содержат отрезки
прямых ? = ±т? — 1/3 и г] = ±Bа)~\ которые отвечают значениям
А = 0иА = оов F.7.8) соответственно. При уходе на бесконечность
по этим прямым одновременно с z обращается в нуль также пере-
переменная х (для прямых с А = 0) или у (для прямых с А = оо), в
чем легко убедиться при помощи F.7.2). В остальном эти прямые
рассматриваются так же, как остальные траектории F.7.8).
306 Гл. 6. Задачи оптимального управления при сложных ограничениях
Рис. 84. Линии уровня функции s(?,rj)
4
3
s 2
1
0
-0.1
0.2
-0.2
-0.4
-0.6
Рис. 85. Зависимость s(?,rj)
§6.8. Ограничения на ускорение и скорость его изменения 307
Таким образом, для любой начальной точки х, у, z движение
полностью описывается траекториями, представленных на рисунках 82
и 83, и содержит не более двух участков постоянства управления.
При этом знак z может меняться не более двух раз.
Приведем результаты исследования нормированного времени опти-
оптимального быстродействия s как функции ?, г]. Изучается зависимость s
от ? при различных фиксированных г], причем s\, 52, 55 снова рассмат-
рассматриваются как введенные выше функции от г]. При г] ^ 0 функция s(?, 77)
убывает с ростом ?, если ? < ^(si), и имеет разрыв, если ? = ^
При переходе от ? < ^(si) к ? > ^(si) и при росте ? от ? =
до +оо она растет.
При — л/3/4 < ту < 0 функция s(?,rj) убывает с ростом ?, если
? < ^(si), и имеет разрыв, если ? = ^(si). При переходе от ? < ^
к ? > ^(si) она растет. Еще один разрыв имеет место при ? = ^
При переходе от ? < ^(ss) K С > ^(^б) функция s(?, ту) убывает, а при
^(^б) ^ С ^ С±E2) растет. При ? = ^(^г) опять происходит разрыв.
При переходе от ? < ^(^г) к С > С±E2) и при росте ? от ? = ^(^г)
до +оо функция s(^,rj) также растет.
При —1/2 ^ г] ^ —л/3/4 функция s(?,r]) убывает с ростом ?,
если ? < ?^E5), и имеет разрыв, если ? = ^(s^). При переходе
от С < ^(^б) к С > ^(^б) она убывает, а при ^(s^) < ? < ^(^2)
растет. При ? = ^(^г) происходит следующий разрыв. При переходе
от С < С±E2) к ? > s (^2) и ПРИ росте ? от ? = ^E2) до +00 функция
s(?,rj) растет.
При г] < —1/2 функция s(^,rj) убывает с ростом ? при ? <
и имеет разрыв, если ? = ^E5). При переходе от ? < ^(
к ? > ^E5) она убывает, а при росте ? от ? = ^(ss) Д° +00 растет.
Результаты расчета нормированного времени быстродействия s(?, ту)
представлены на рисунках 84 и 85. На рис. 84 тонкие кривые — линии
уровня функции s(?,rj), а жирные — линии разрыва этой функции.
Остальные обозначения те же, что и на рис. 83. Трехмерный график
функции s(?, г]) показан на рис. 85, причем чем темнее фон, тем меньше
соответствующее значение.
§ 6.8. Постановка задачи оптимального
быстродействия при ограничениях на ускорение
и скорость его изменения
При постановке задачи в § 6.5 предполагалось, что ограничение
|F| < Fq не достигается. Теперь снимем это предположение. Будем рас-
рассматривать систему F.1.1) при ограничениях на величину управляю-
управляющей силы и скорость ее изменения, т. е. при следующих ограничениях:
308 Гл. 6. Задачи оптимального управления при сложных ограничениях
\F\ < v0,
F.8.1)
F.8.2)
F
t
где Fq, vq — постоянные.
Будем исследовать задачу о приведении системы F.1.1) в нулевое
конечное состояние ? = ? = 0.
Как известно, при отсутствии ограничения F.8.2) оптимальное
по быстродействию управление является релейным и имеет не более
одной точки переключения. Типич-
Типичная зависимость от времени для
этого управления изображена на
рис. 86.
С другой стороны, решение зада-
задачи быстродействия при отсутствии
ограничения F.8.1) дано в § 6.5-
6.7. Решение задачи оптимального
быстродействия для системы F.1.1)
при учете обоих ограничений F.8.1)
и F.8.2) ранее не встречалось в
литературе.
Далее задача управления систе-
системой F.1.1) рассматривается в следу-
следующей постановке. Предполагается,
что управляющая сила ограничена
условием F.8.1), и условие F.8.2)
выполняется лишь в случае, когда
величина силы увеличивается, т. е.
когда d\F\/dt > 0. В то же время си-
сила может выключаться мгновенно.
Эти ограничения можно записать в
виде совокупности неравенств
-Fr
Рис. 86. Релейное управление
Рис. 87. Область ограничений
F < v0 при F > 0, F.8.3)
F > — vq при F < 0.
Область, задаваемая ограничениями F.8.3) в плоскости (F,F),
изображена на рис. 87.
Ограничения F.8.3) моделируют следующую ситуацию: управляю-
управляющую силу можно наращивать только постепенно, с конечной скоро-
скоростью, а выключать — мгновенно. Такая картина нередко имеет место
на практике, так как торможение часто осуществляется иными сред-
средствами, чем разгон.
§6.9. Возможные типы управлений 309
Введем следующие безразмерные переменные:
t' = v0F-lt, x = mv^F'3^
F.8.4)
у = mv0F-2i z = F~lF, u = v~lF.
Уравнение F.1.1) и ограничения F.8.3) в переменных F.8.4)
примут вид
х = у, у = z, z = и, F.8.5)
1*1 < 1;
и < 1 при z > 0, F.8.6)
и ^ — 1 при z ^ 0.
Здесь и далее точками обозначаем производные по новому (безразмер-
(безразмерному) времени. Штрих у безразмерного времени далее опускаем.
Начальные условия для системы F.8.5) зададим в виде
ж@) = ж0, у(О) = уо, z@)=0, F.8.7)
а конечное состояние — в виде
х(Т) = 0, у(Т) = 0. F.8.8)
Отметим, что значение z(T) в конечный момент может быть всегда
сделано равным нулю за счет скачка силы z(t) в момент t = Т,
что допускается ограничениями F.8.6). Поэтому можно считать, что
условие z(T) = 0 всегда выполнено.
Поставим следующую задачу.
Найти управление u(t) и соответствующую траекторию,
т.е. функции x(t), y(t), z(t), удовлетворяющие уравнениям F.8.5),
ограничениям F.8.6), начальным условиям F.8.7) и конечным усло-
условиям F.8.8) в некоторый {нефиксированный) момент времени Т > 0.
Ниже строится управление, решающее поставленную задачу и
имеющее наиболее простую структуру, допускаемую ограничениями
F.8.6). По-видимому, это управление является оптимальным в смысле
быстродействия.
§ 6.9. Возможные типы управлений
Возможные типы законов изменения безразмерной силы z(t) пред-
представлены на рис. 88. Здесь показаны участки постепенного роста или
убывания силы, на которых z = ±1, и участки постоянства силы,
на которых z = ±1. Эти законы обладают следующими свойствами.
310 Гл. 6. Задачи оптимального управления при сложных ограничениях
Рис. 88. Типы зависимостей z(t)
1°. В начале процесса имеем z@) = 0 в соответствии с начальными
условиями F.8.7).
2°. Законы 1-6 на рис. 88 удовлетворяют ограничениям F.8.6).
3°. Непосредственно перед окончанием процесса имеем z(t) < 0
при t —> Т. Это условие принято для определенности и не ограничивает
общности, так как наряду с законами, изображенными на рис. 88,
можно аналогично рассмотреть симметричные им относительно оси t
законы z\t) = —z(t).
4°. Законы на рис. 88 имеют не более одного скачка и одной смены
знака силы z(t).
5°. Закон 6 на рис. 88 является непосредственным обобщением
релейного закона рис. 86 на случай постепенного наращивания вели-
величины силы, т.е. на случай ограничений F.8.6).
6°. Остальные законы 1-5 на рис. 88 являются частными случаями
закона 6. Действительно, в законе 5 не достигается ограничение
z = — 1; в законе 4 не достигается ограничение z = 1; в законе 3
не достигаются оба ограничения z = ±1; в законах 1 и 2 отсутствует
скачок зависимости z(t), причем в законе 2 ограничение z = — 1
достигается, а в законе 1 оно не достигается.
Как будет показано ниже, при помощи законов для z(t) вида
1-6, а также симметричных им законов z'(t) = —z(t), можно привести
систему F.8.5) из любого начального состояния F.8.7) в конечное
состояние F.8.8).
§6.9. Возможные типы управлений 311
Введем в рассмотрение область D плоскости ху, задаваемую нера-
неравенствами
{х < -ц>(-у) при у < О,
(х,у): F.9.1)
х < (р(у) при у > 0.
Здесь функция <р(у) определена следующим образом:
F.9.2)
Нетрудно проверить, что соотношения F.9.2) определяют <р(у)
как гладкую функцию, монотонно убывающую от 0 до —оо на полуоси
у ? [0, оо). В точке у = 1/2 имеем ц>(у) = —1/3, ip'(y) = — 1.
Кривые Г и Г', определяемые для у > 0 и у < 0 соотношениями
ж = </?(?/) и ж = —<р(—у) соответственно, изображены на рис. 89
жирными линиями. На этих кривых, симметричных друг другу
относительно относительно начала координат, отмечены точки
А=(—1/3, 1/2) и А7 = A/3, —1/2), в которых гладко сопрягаются
участки, определяемые соотношениями F.9.2).
Кривые Г и Г' образуют границу области D, причем, согласно
F.9.1) кривая Г, лежащая во втором квадранте плоскости ху,
принадлежит D, а кривая Гх, лежащая в четвертом квадранте,
не входит в D. Если область D дополнить областью D', симметричной
ей относительно начала координат, то получится вся плоскость ху
с выброшенной точкой О — началом координат. Согласно F.8.7)
эта точка является конечной и поэтому не представляет интереса
в качестве начальной точки: если х = у = 0 при t = 0, то процесс
управления является излишним.
Ниже будет построено управление и траектории, т. е. функции
u(t), x(t), y(t), z(t), для всех начальных точек (xq, y0) G D.
Если же (хо, уq) G Df, то искомое решение задается функциями
{—u(t), —x(t), —y(t), —z(t)}, где набор {u(t), x(t), y(t), z(t)} соответ-
соответствует начальной точке (—хо, ~Уо) ? D, симметричной (хо, Уц) ? D'.
При этом уравнения F.8.5) и ограничения F.8.6) выполняются,
полученные траектории из точки (хо,уо) е D1 будут симметричны
траекториям из точки (—xq, — у0) ? D и также придут в начало
координат, причем за то же время.
Таким образом, поставленную задачу управления достаточно ре-
решить для начальных точек (хо, у0) е D. Это будет реализовано при
помощи законов 1-6, изображенных на рис. 88.
312 Гл. 6. Задачи оптимального управления при сложных ограничениях
§6.10. Построение траекторий
Для каждого из законов на 1-6 на рис. 88 построим соответ-
соответствующие траектории и в области D найдем области Di, г = 1,...,6,
начальных значений хо,уо, из которых данный закон приводит систему
в конечное состояние х(Т) = у(Т) = 0. Множества Di отмечены соот-
соответствующими цифрами г = 1,...,6 на рис. 89.
Рис. 89. Разбиение плоскости ху на множества Di
Закон 1. Согласно рис. 88 имеем и = — 1 при t е [О,Т]. Интегрируя
уравнения F.8.5) при начальных условиях F.8.7), получим
х =
1 я
- -t.
F.10.1)
Положим t = Т в соотношениях F.10.1) и подставим их в конечные
условия F.8.8). Исключая Т, найдем
F.10.2)
F.10.3)
§6.10. Построение траекторий 313
Неравенство Т < 1 следует из того, что ограничение z = — 1
для закона 1 не достигается, см. рис. 88. Из F.10.3), F.10.2) вытекают
неравенства
-| <хо<О, 0<у0<^. F.10.4)
Таким образом, закон 1, задаваемый соотношениями F.10.1),
реализуется, если начальная точка (хо,уо) лежит на дуге кривой, опре-
определенной уравнением F.10.2) и неравенствами F.10.4). Следовательно,
множество D\ — это дуга кривой Г, см. F.9.2), отмеченная цифрой 1
на рис. 89 и заключенная между точкой О и точкой А = (—1/3, 1/2).
Все фазовые траектории, начинающиеся на этой дуге, приходят
в начало координат, если применяется закон 1. Траектории задаются
соотношениями F.10.1), а время движения — формулой F.10.3).
Все эти траектории, как нетрудно проверить, заключены в области
между кривой Г и параболой Го, определяемой соотношениями
То : х = сро(у) =-^у\ у^0. F.10.5)
Отметим, что парабола Го является кривой переключений
и одновременно фазовой траекторией, входящей в начало координат,
для задачи оптимального быстродействия, если ограничения F.8.6)
заменить простым ограничением
1.
Закон 2. Имеем
u = -l, z = -\ при 0< t < 1,
F.10.6)
и = 0, z = -\ при 1 < t < Т.
Движение на первом участке траектории (t < 1) задается соотно-
соотношениями F.10.1). При t = 1 получим из F.10.1)
2/A) = 2/0"^ жA)=жо + 2/о-|. F.10.7)
Интегрируя уравнения F.8.5) с учетом равенств F.10.6) и началь-
начальных условий F.10.7) на втором участке движения (t > 1), найдем
y(t) = y(\)-(t-\),
1 „ F.10.8)
x(t)=x{\)+y{\){t-\)-l-{t-\f.
Подставим выражения F.10.8) в конечное условие F.8.8) и исклю-
исключим Т. Получим
F.10.9)
314 Гл. 6. Задачи оптимального управления при сложных ограничениях
Таким образом, точка (х(\), ?/A)) лежит на параболе Го из F.10.5),
и согласно F.10.6) движение на втором участке (при t ? [1>^])
происходит по этой параболе вплоть до попадания в начало коорди-
координат. Подставляя выражения F.10.7) в соотношения F.10.9), получим
условия
*о = -^о-|уо + 2^ Уо>\- F.10.10)
Соотношения F.10.10) определяют множество D<i начальных
условий, для которых закон 2 обеспечивает попадание в начало
координат. Множество D% представляет собой часть кривой Г
(см. F.9.2)) от точки А = (—1/3, 1/2) включительно до бесконечности.
Все траектории, начинающиеся на этом множестве, заключены между
Г и Го, причем их второй участок (при t > 1) лежит на параболе Го.
Типичные траектории для законов 1 и 2 изображены пунктирными
линиями на рис. 89.
Таким образом, если начальная точка (хо,уо) лежит на кривой Г,
то поставленную задачу решают законы управления 1 и 2, причем
закон 1 имеет место, если точка (хо,уо) лежит между О и А,
а закон 2 — если она лежит слева от А на рис. 89.
Обратимся теперь к законам 3-6 на рис. 88 и обозначим через 9
момент скачка функции z(t), 9 G @,Т). Нетрудно видеть, что зави-
зависимости z(t) при t > 9 для всех законов 3-6 на рис. 88 совпадают
с зависимостью z(t) при t > 0 для одного из законов 1 или 2, причем
для законов 3 и 5 — с законом 1, а для 4 и 6 — с законом 2.
Поэтому отрезки траекторий для законов 3-6 при t > 9 совпада-
совпадают с траекториями для одного из законов 1 или 2. Следовательно,
точка х(9),у(9) для законов 3-6 должна принадлежать множествам
начальных условий для соответствующих законов 1 и 2, а именно:
{х(в), у (в)} ? D\ для законов 3, 5;
F.10.11)
{х@), у(9)} е ?>2 для законов 4, 6.
Для вычисления значений х(9), у{9) отметим, что, с точностью
до знаков, законы изменения z(t) при t < 9 в случаях 3 и 4 совпадают с
законом 1, а в случаях 5 и 6 — с законом 2. Поэтому, изменяя соответ-
соответствующие знаки и полагая t = 9, получим из F.10.1) для законов 3 и 4
F.10.12)
х(9)=хо + уо9 + ^9\ 9< 1.
Пользуясь формулами F.10.7) и F.10.8), получим аналогично для
законов 5 и 6
§6.10. Построение траекторий 315
х(в) = х0 + у0 + i + (у0 + |) (9 - 1) + | (б» - IJ =
= хо + уо9+\^-):9 + \, 0>\. F.10.13)
z z о
Найдем области Di в плоскости ж?/, в которых лежат начальные
данные xq, у0 для соответствующих законов, г = 3,..., 6. Для этого вос-
воспользуемся соотношениями F.10.11)—F.10.13) и приведенными выше
определениями множеств D\ и D^.
Закон 3. Подставим в уравнение F.10.2) и неравенства F.10.4),
определяющие множество D\, вместо хо, у0 выражения F.10.12)
для х(в), у (в). Получим
° F.10.14)
0< 2уо + в2 < 1, 0 < в < 1.
Найдем границы множества Дз> заданного в параметрическом виде
соотношениями F.10.14). Для этого, как нетрудно показать, доста-
достаточно рассмотреть четыре случая, отвечающих достижению равенства
в каждом из четырех неравенств F.10.14).
Положим сначала 2у0 + О2 = 0 и исключим 0 из полученного
равенства. Имеем 0 = (—2у0I/2. Подставляя найденное значение О
в равенство F.10.14), найдем
х0
= | (-2уоK/2, -|<у0<0. F.10.15)
Соотношения F.10.15) определяют согласно F.9.1) и F.9.2)
отрезок кривой Гх от начала координат до точки А! = A/3,-1/2)
(см. рис. 89).
Полагая 2у0 + в2 = 1, найдем в = A — 2^/qI/2. Подставляя 0
в равенство F.10.14), получим
4^
F.10.16)
0 < Уо < \-
Соотношения F.10.16) определяют в плоскости ху дугу кривой
Гь соединяющую точки А = (—1/3, 1/2) и В = (—1/2,0). Эта дуга
показана на рис. 89.
316 Гл. 6. Задачи оптимального управления при сложных ограничениях
Полагая 0 = 0, получим из F.10.14)
*о = 4BуоK/2, 0<у0<1-.
Этот участок границы множества Дз, согласно F.9.2), совпадает
с множеством D\, т.е. с дугой О А кривой Г.
Наконец, полагая 0=1, получим из F.10.14)
жо = -|-Уо-|B2/о + 1K/2. -|<2/о<О. F.10.17)
Соотношения F.10.17) определяют в плоскости ху дугу кривой, соеди-
соединяющей точки В и А'. Эта кривая Г2 в точке А! касается кривой V
(см. рис. 89).
Таким образом, множество Дз представляет собой криволинейный
четырехугольник ОАВА1, ограниченный дугами кривых Г (от точки О
до А), ГЬГ2 и Г' (от А1 до О).
Закон 4. Подставляя в соотношения F.10.10), определяющие
множество D2, выражения F.10.12) для хF),уF) вместо хо,уо,
получим
_ 1 У1 УрО2 . Уо 0А О3 О2
0 ~~ 9А 9 9 ^° 9 ft ft A '
24 2 2 2 8 5 4 F.10.18)
2уо + О2^ 1, О<0< 1.
Границы множества ?>4 найдем, поочередно заменяя равенством
каждое из трех неравенств в F.10.18).
Положим сначала 2у0 + О2 = 1 и исключим из данного равенства 0:
Подставляя полученное значение 0 в равенство F.10.18), придем после
упрощений к соотношениям F.10.16), определяющим дугу Гь
Полагая 0 = 0 в F.10.18), получим, как легко проверить, соот-
соотношения F.10.10), определяющие множество D2, т.е. дугу кривой Г
от точки А до бесконечности.
Полагая 0 = 1 в F.10.18), будем иметь
хо = -^-2уо-±, у0>0. F.10.19)
Кривая Гз, определяемая соотношениями F.10.19), начинается в точке
В = (—1/2,0) и уходит на бесконечность, см. рис. 89.
В результате, множество D\ ограничено множеством D<2, кривой Т\,
по которой оно граничит с Дз> и кривой Гз.
§6.10. Построение траекторий 317
Закон 5. Подставим в уравнение F.10.2) и неравенства F.10.4),
определяющие множество D\, выражения F.10.13) для х(в),у(в)
вместо хо,уо. Получим
1 z D 6 F.10.20)
Найдем границы множества D$, рассуждая аналогично преды-
предыдущим случаям и заменяя поочередно каждое из трех неравенств
F.10.20) равенством.
Полагая у0 + в = 1/2, найдем в = \/2 — у0. Подставляя найденное
значение в в равенство F.10.20), получим
В соответствии с F.9.2), эти соотношения определяют дугу кривой
Г' от точки А! = A/3,-1/2) до бесконечности; эта дуга симметрична
множеству L>2 относительно начала координат.
Полагая у0 + 0 = 1, получим 0 = 1 — ?/0. Подставляя это соотно-
соотношение в равенство F.10.20), получим
*о = у1-Ц-\, Уо^О. F.10.21)
Соотношения F.10.21) определяют кривую Г4, начинающуюся
в точке В = (—1/2,0) и уходящую на бесконечность (см. рис. 89).
Полагая 0 = 1 в F.10.20), придем к соотношениям F.10.17),
определяющим кривую Гг.
Таким образом, множество D$ ограничено дугой Гг, по которой оно
граничит с множеством D%, кривой Г4 и дугой кривой Гх от точки А!
до бесконечности.
Закон 6. Подставим в соотношения F.10.10), определяющие
множество D2, соотношения F.10.13) для х(в), у {в) вместо xq, y0.
Получим
F.10.22)
2 2
Заменяя равенством первое из неравенств F.10.22), найдем
0= I—2/q. Подставляя это выражение в равенство F.10.22), придем
к соотношениям F.10.21), определяющим кривую Г4.
Полагая 0= 1 в F.10.22), получим соотношения F.10.19), опреде-
определяющие кривую Гз.
318 Гл. 6. Задачи оптимального управления при сложных ограничениях
Таким образом, множество D§ граничит с множествами D\ и D$
по кривым Гз и Г4 соответственно, и лежит снизу и слева от этих
кривых, имеющих общую точку В = (—1/2,0).
Заметим, что кривые Г2,Гз и кривые ГьГ4 имеют попарно общие
касательные в точке В.
Решение поставленной задачи управления можно описать
следующим образом. По заданному начальному состоянию F.8.7),
лежащему в области D плоскости ху, определим, в какой из областей
Di, i= 1,...,6, оно находится. Границы между областями заданы
кривыми Г, V, Г\, Г2, Гз, Г4, определенными соотношениями F.9.1),
F.9.2), F.10.16), F.10.17), F.10.19), F.10.21). Границей между
множествами D\ и D2 служит точка А = (—1/3, 1/2).
1°. Если (хо,уо) ? D\, то полагаем и = — 1 при ? > 0. Система
попадает в заданное состояние х = у = 0 за время Т < 1.
2°. Если (хо,уо) ? D2, то полагаем и = — 1 при ? ? @, 1) и и = 0
при ? ^ 1. Система попадает в конечное состояние за время Т ^ 1.
3°. Если (xq, у0) ? Дз> то и= I при ? ? @, 0), где момент 9 < 1 опре-
определяется условием {х(9),у(9)} ? D\. В момент ? = 0 скачком делаем
z равным нулю, что допускается ограничениями F.8.6). При t > в
полагаем и = — 1 до конца процесса. Траектория при t > 0 — такая же,
как для закона 1.
4°. Если (хо,уо) ? D4, то и = 1 при t ? @,9), где момент 0 < 1
определяется условием {х@), у (в)} ? D2. В момент t = в скачком
делаем z равным нулю. Далее полагаем и = — 1 при t ? (9,9+ 1)
и г^ = 0 при t ? (9+ 1,Т).
5°. Если (хо,уо) ? D$, то и = 1 при t ? @, 1) и и = 0 при ? ? A,9),
где момент 0 > 1 определяется условием {х(9), у(9)} ? D\. В момент в
скачком делаем z равным нулю, после чего и = — 1 при t? (9,T)
до конца процесса.
6°. Если (хо,уо) ? Dq, то и = 1 при ? Е @, 1) и м = 0 при t ? A,9),
где момент 9 > 1 определяется условием {х(9), у(9)} ? D2. В момент 0
скачком изменяем z до нуля. Далее полагаем и = — 1 при ? ? (9, 9 + 1)
и г^ = 0 при ? G (9+ 1,Т).
Заметим, что Т < 1 в случае 1, Т > 1 в случаях 2, 4, 5 и Т > 2
в случае 6.
Все траектории, начинающиеся в области D, лежат в области,
ограниченной кривыми Го и Гх (слева и снизу от этих кривых,
см. рис. 89). При этом они входят в начало координат, касаясь
в точке О кривой Го (для законов 1, 3, 5) или совпадая с Го на своем
последнем участке (для законов 2, 4, 6, см. пунктирные кривые
на рис. 89).
§6.10. Построение траекторий 319
Если начальная точка (#о»2/о) лежит в области D', симметричной D
относительно начала координат, то управление следует брать равным
по величине и противоположным по знаку тому управлению, которое
отвечает точке (—хо, —i/q) ? D.
По-видимому (хотя это не доказано), построенное управление
является оптимальным по быстродействию при начальных условиях
F.8.7), которые предусматривают z@) = 0. В общем случае начальных
условий
х@) = х0, 2/@) = 2/о, *@) = z0
можно в начальный момент t = 0 скачком изменить z, сделав его
равным нулю, что допускается ограничениями F.8.6). После этого
можно воспользоваться построенным управлением для начальных
условий F.8.7). Тем самым будет достигнуто выполнение терми-
терминальных условий F.8.8), однако на оптимальность по быстродействию
уже нельзя рассчитывать.
Список литературы
1. Аветисян В. В., Лкуленко Л. Д., Болотник И. И. Оптимальное управление
электроприводами промышленных роботов // Препринт / ИПМ АН СССР.
№ 283. - М., 1986.
2. Айзеке Р. Дифференциальные игры. — М.: Мир, 1967.
3. Айзерман М.А. Классическая механика. — М.: Наука, 1974.
4. Акуленко Л. Д. Асимптотические методы оптимального управления. —
М.: Наука, 1987.
5. Акуленко Л. Д., Болотник И. И. Синтез оптимального управления транс-
транспортными движениями манипуляционных роботов // Изв. АН СССР. Мех.
тв. тела. - 1986.- № 4.- С. 21-29.
6. Акуленко Л. Д., Болотник И. И., Кумакшев С. А., Чернов А. А. Активное
гашение колебаний крупногабаритных несущих конструкций посредством
перемещения внутренних масс // Изв. РАН. Теор. и сист. упр. — 2000.-
№ 1.- С. 135-145.
7. Ананьева Е. Г., Клебанова О. И., Нахапетян Е. Г. Динамические испы-
испытания промышленного робота второго поколения // Экспериментальное
исследование и диагностирование роботов. — М.: Наука, 1981.
8. Ананьевский И.М. Управление механической системой с неизвестными
параметрами посредством ограниченной силы // Прикл. матем. и мех. —
1997.- Т. 61, вып. 1.- С. 52-62.
9. Ананьевский И. М. Ограниченное управление механической системой в
условиях неопределенности // Докл. РАН. — 1998.- Т. 359, № 5.- С. 607-
609.
№. Ананьевский И.М. Управление двухмассовой системой с неизвестными
параметрами// Изв. РАН. Теор. и сист. упр. — 1998.- № 2.- С. 72-82.
11. Ананьевский И.М. Игровая задача управления материальной точкой неиз-
неизвестной массы // Изв. РАН. Теор. и сист. упр. — 2000.- № 4.- С. 19-27.
12. Ананьевский И.М. Управление линейной системой четвертого порядка при
смешанных ограничениях // Прикл. матем. и мех. — 2000.- Т. 64, вып. 6.-
С. 901-908.
Список литературы 321
13. Ананьевхкий И.М. Управление реономными механическими системами с
неизвестными параметрами // Докл. РАН. — 2001.- Т. 377, № 4.- С. 459-
463.
14. Ананьевсшй И.М. Ограниченное управление реономными механическими
системами в условиях неопределенности // Прикл. матем. и мех. — 2001.-
Т. 65, вып. 5.- С. 809-821.
15. Ананьевхкий И.М. Два подхода к управлению механической системой с
неизвестными параметрами // Изв. РАН. Теор. и сист. упр. — 2001.- № 2.-
С. 39-47.
16. Ананьевский И.М., Добрынина И. С, Черноусько Ф.Л. Метод декомпо-
декомпозиции в задаче управления динамической системой // Изв. РАН. Теор. и
сист. упр. — 1995.- № 2.- С. 3-14.
17. Ананьевский И.М., Решмин С. А. Метод декомпозиции в задаче об от-
отслеживании траекторий механических систем // Изв. РАН. Теор. и сист.
упр. - 2002.- № 5.- С. 25-32.
18. Барбашин Е.А., Красовский И. И. Об устойчивости движения в целом //
ДАН СССР. - 1952.- Т. 86, № 3.- С. 453-456.
19. Бербюк В.Е. Динамика и оптимизация робототехнических систем. —
Киев: Наукова думка, 1989.
20. Боголюбов Н. Н., Митрополъский Ю.А. Асимптотические методы в теории
нелинейных колебаний. — М.: Наука, 1974.
21. Болтянский В. Г. Математические методы оптимального управления. —
М.: Наука, 1969.
22. Бурков И. В., Фрейдович Л. Б. Стабилизация положения лагранжевой си-
системы с упругими элементами при ограничениях на управление с измере-
измерением и без измерения скорости // Прикл. матем. и мех. — 1997.- Т. 61,
вып. 3.- С. 447-456.
23. Бутковский А. Г. Теория оптимального управления системами с распреде-
распределенными параметрами. — М.: Наука, 1965.
24. Гантмахер Ф.Р. Лекции по аналитической механике. — М.: Наука, 1966.
25. Гантмахер Ф.Р. Теория матриц. — М.: Наука, 1967.
26. Трошева М. В., Климов Д. М. Опыт использования аналитических преоб-
преобразований на ЭВМ в задачах механики // Препринт / ИПМ АН СССР.
№ 296. - М.: 1987.
27. Добрынина И. С. Моделирование динамики манипуляционных роботов с
применением метода декомпозиции управления // Изв. РАН. Техн. кибер-
нет. - 1995.- № 4.- С. 246-256.
28. Добрынина И. С, Карпов И. И., Черноусько Ф. Л. Компьютерное модели-
моделирование управления движением системы связанных твердых тел // Изв.
РАН. Техн. кибернет. - 1994.- № 1.- С. 167-180.
11 Ф. Л. Черноусько и др.
322 Список литературы
29. Добрынина И. С, Черноусько Ф. Л. Ограниченное управление линейной
системой четвертого порядка // Изв. РАН. Техн. кибернет. — 1992.- № 6.-
С. 94-100.
30. Егоров А. И. Оптимальное управление тепловыми и диффузионными про-
процессами. — М.: Наука, 1978.
31. Емельянов С. В. Системы автоматического управления с переменной струк-
структурой. — М.: Наука, 1967.
32. Ефимов Г. Б., Погорелое Д. Ю. «Универсальный механизм» — комплекс
программ моделирования динамики систем твердых тел // Препринт
/ ИПМ РАН. № 77. - М.: 1993.
33. Ефимов Г. Б., Погорелое Д. Ю. Некоторые алгоритмы автоматизированного
синтеза уравнений движения системы твердых тел // Препринт / ИПМ
РАН. № 84. - М.: 1993.
34. Журов А. П., Карпов И. П., Шингарева И. К. Основы Maple. Применение
в механике // Препринт / ИПМ РАН. № 536. — М.: 1994.
35. Заремба А. Т. Синтез управления маятником // Изв. АН СССР. Мех. тв.
тела. - 1981.- № 1.- С. 60-68.
36. Ильин В. А. О равномерной сходимости разложений по собственным функ-
функциям во всей замкнутой области // Мат. сб. — 1958.- Т. 45 (87), № 2.-
С. 195-232.
37. Ильин В. А. Спектральная теория дифференциальных операторов. —
М.: Наука, 1991.
38. Калман Р. Об общей теории систем управления // Труды 1-го Конгр.
Международной федерации по автоматич. управлению (IFAC). —
М.: Изд-во АН СССР, 1961.- Т. 2.- С. 521-547.
39. Калман Р., Фалб П., Арбиб М. Очерки по математической теории
систем. — М.: Мир, 1971.
40. Климов Д. М., Руденко В. М. Методы компьютерной алгебры в задачах
механики. — М.: Наука, 1989.
41. Красовский П. П. Некоторые задачи теории устойчивости движения. —
М.: Физматгиз, 1959.
42. Красовский П. П. Теория управления движением. — М.: Наука, 1968.
43. Красовский П. П. Игровые задачи о встрече движений. — М.: Наука, 1970.
44. Красовский П. П., Субботин А. И. Позиционные дифференциальные
игры. — М.: Наука, 1974.
45. Лионе Ж.-Л. Оптимальное управление системами, описываемыми уравне-
уравнениями с частными производными. — М.: Мир, 1972.
46. Матюхин В. И. Непрерывные универсальные законы управления манипу-
ляционным роботом // Автомат, и телемех. — 1997.- № 4.- С. 31-44.
Список литературы 323
47. Матюхин В. П., Пятницкий Е. С. Управление движением манипуляцион-
ных роботов на принципе декомпозиции при учете динамики приводов //
Автомат, и телемех. - 1989.- № 9.- С. 67-81.
48. Мирошник И. В., Никифоров В. О., Фрадков А. Л. Нелинейное и адаптив-
адаптивное управления сложными динамическими системами. — С.-Пб.: Наука,
2000.
49. Москаленко В. В. Автоматизированный электропривод. — М.: Энергоатом-
издат, 1986.
50. Понтрягин Л. С, Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф.
Математическая теория оптимальных процессов. — М.: Наука, 1983.
51. Пятницкий Е.С. Синтез управления манипуляционными роботами на
принципе декомпозиции // Изв. АН СССР. Техн. кибернет. — 1987.- № 3.-
С. 92-99.
52. Пятницкий Е. С. Принцип декомпозиции в управлении механическими
системами // ДАН СССР. - 1988.- Т. 300, № 2.- С. 300-303.
53. Пятницкий Е. С. Критерий полной управляемости классов механических
систем с ограниченными управлениями // Прикл. матем. и мех. — 1996.—
Т. 60, вып. 5.- С. 707-718.
54. Решмин С. А. Ограниченное управление линейной системой третьего
порядка // Изв. РАН. Теор. и сист. упр. — 1996.- № 1.- С. 22-26.
55. Решмин С. А. Синтез управления двузвенным манипулятором // Изв. РАН.
Теор. и сист. упр. - 1997.- № 2.- С. 146-150.
56. Решмин С. А., Черноусько Ф.Л. Синтез управления в нелинейной динами-
динамической системе на основе декомпозиции // Прикл. матем. и мех. — 1998.—
Т. 62, вып. 1.- С. 121-128.
57. Сиразетдинов Т. К. Оптимизация систем с распределенными параметра-
параметрами. - М.: Наука, 1977.
58. Уткин В. И. Скользящие режимы и их применения в системах с перемен-
переменной структурой. — М.: Наука, 1974.
59. Уткин В. П., Орлов Ю. В. Теория бесконечномерных систем управления на
скользящих режимах. — М.: Наука, 1990.
60. Фомин В. П., Фрадков А. Л., Якубович В. А. Адаптивное управление дина-
динамическими объектами. — М.: Наука, 1981.
61. Черноусько Ф.Л. Динамика управляемых движений упругого манипу-
манипулятора // Изв. АН СССР. Техн. кибернет. — 1981.- № 5.- С. 142-152.
62. Черноусько Ф. Л. О построении ограниченного управления в колебатель-
колебательных системах // Прикл. матем. и мех. — 1988.- Т. 52, вып. 4.- С. 549-558.
63. Черноусько Ф. Л. Декомпозиция и субоптимальное управление в динами-
динамических системах // Прикл. матем. и мех. — 1990.- Т. 54, вып. 6.- С. 883-
893.
и*
324 Список литературы
64. Черноусько Ф. Л. Декомпозиция и синтез управления в динамических
системах // Изв. АН СССР. Техн. кибернет. - 1990.- № 6.- С. 64-82.
65. Черноусько Ф. Л. Синтез управления системой с нелинейным сопротивле-
сопротивлением // Прикл. матем. и мех. — 1991.- Т. 55, вып. 6.- С. 883-894.
66. Черноусько Ф. Л. Синтез управления нелинейной динамической системой
// Прикл. матем. и мех. — 1992.- Т. 56, вып. 2.- С. 179-191.
67. Черноусько Ф. Л. Ограниченное управление в системах с распределенными
параметрами // Прикл. матем. и мех. — 1992.- Т. 56, вып. 5.- С. 810-826.
68. Черноусько Ф. Л. Декомпозиция и синтез управления в нелинейных дина-
динамических системах // Тр. Мат. ин-та РАН. — 1995.- Т. 211.- С. 457-472.
69. Черноусько Ф. Л. Задача оптимального быстродействия при смешанных
ограничениях // Изв. РАН. Теор. и сист. упр. — 1995.- № 4.- С. 103-113.
70. Черноусько Ф. Л. Управление системой с одной степенью свободы при
ограничениях на управляющую силу и скорость ее изменения // Докл.
РАН. - 1999.- Т. 368, № 4.- С. 464-466.
71. Черноусько Ф.Л. Управление системой с одной степенью свободы при
сложных ограничениях // Прикл. матем. и мех. — 1999.- Т. 63, вып. 5.-
С. 707-715.
72. Черноусько Ф.Л., Акуленко Л. Д., Соколов Б.Н. Управление колеба-
колебаниями. — М.: Наука, 1980.
73. Черноусько Ф. Л., Болотник Н. Н., Градецкий В. Г. Манипуляционные
роботы: динамика, управление, оптимизация. — М.: Наука, 1989.
74. Черноусько Ф. Л., Шматков А. М. Синтез оптимального быстродействия
в одной системе третьего порядка // ДАН СССР. — 1997.- Т. 354, № 2.-
С. 174-177.
75. Черноусько Ф. Л., Шматков А. М. Оптимальное по быстродействию управ-
управление в одной системе третьего порядка // Прикл. матем. и мех. — 1997.—
Т. 61, вып. 5.- С. 723-731.
76. Чиликин М. Г., Ключев В. И., Сандлер А. С. Теория автоматизированного
электропривода. — М.: Энергия, 1979.
11. Agmon S. On kernels, eigenvalues and eigenfunctions of operators related to
elliptic problems // Comm. Pure a. Appl. Math. — 1965.- V. 18, № 4.-
P. 627-663.
78. Chernousko F. L. The decomposition of controlled dynamic systems // Ad-
Advances in Nonlinear Dynamics and Control. / Ed. A. B. Kurzhanski. — Boston:
Birkhauser, 1993.- P. 1-40.
79. Chernousko F. L. Control of elastic systems by bounded distributed forces //
Appl. Math, and Сотр. - 1996.- V. 78.- P. 103-110.
80. Chernousko F.L., Reshmin S.A. Decomposition and synthesis of control in
a nonlinear dynamic system // Proc. International Conference on Informatics
and Control (ICI&C97), St.Petersburg, June 9-13. - 1997.- P. XLV-LII.
Список литературы 325
81. Chernousko F.L., Reshmin S.A. Decomposition of control for nonlinear
Lagrangian systems // Proc. 4th IFAC Nonlinear Control Systems Design
Symposium (NOLCOS'98), Enschede, The Netherlands, July 1-3. - 1998.-
P. 209-214.
82. Chernousko F.L., Reshmin S.A. Decomposition of control for robotic manip-
manipulators // Proc. 4th ECPD International Conference on Advanced Robotics,
Intelligent Automation and Active Systems, Moscow, August 24-26. — 1998.-
P. 184-189.
83. Chernousko F. L. Control of oscillations in systems with many degrees of
freedom // Proc. IUTAM Symposium of Recent Developments in Non-linear
Oscillations of Mechanical Systems, N.Van Dao, E.J.Kreuzer (eds.). —
Kluwer Academic Publishers, 2000.- P. 45-54.
84. Corless M., Leitmann G. Adaptive control of systems containing uncertain
functions and unknown functions with uncertain bounds // J. of Optimiz. Th.
and Appl. - 1983.- V. 42, №. 1.- P. 155-168.
85. Corless M., Leitmann G. Adaptive controllers for a class of uncertain systems
// Ann. Found, de Broglie. - 1984.- V. 9.- P. 65-95.
86. Isidori A. Nonlinear Control Systems. — 3rd ed. — New York: Springer-
Verlag, 1995.
87. Isidori A. Nonlinear Control Systems. Vol. II. — New York: Springer-Verlag,
1999.
88. Leitmann G. Deterministic control of uncertain systems // Acta Astronau-
tica. - 1980.- V. 7.- P. 1457-1461.
89. Lions J. L. Exact controllability. Stabilization and perturbations for distributed
systems // SIAM Review. - 1988.- V. 30, № 1.- P. 1-68.
90. Nijmeijer H., Rodriguez-Angeles A. Synchronization of mechanical sys-
systems // World scientific series on nonlinear science. — World Scientific
Publishing Co. Pte. Ltd., 2003.
91. Nijmeijer H., van der Schaft A.J. Nonlinear Dynamic Control Systems. —
New York: Springer-Verlag, 1990.
92. Reshmin S.A. Control of robots with flexible joints // Proc. 2nd International
Conference «Control of Oscillations and Chaos» (COC2000), St.Petersburg,
July 5-7. - 2000.- P. 177-178.
93. Sato O., Shimojima H., Kitamura Y. Minimum-time control of a manipulator
with two degrees of freedom // Bull. JSME. - 1983.- V. 26, № 218.-
P. 1404-1410.
94. Sato O., Shimojima H., Kitamura Y., Yoinara H. Minimum-time control of a
manipulator with two degrees of freedom (Part 2, Dynamic characteristics of
gear train and axes) // Bull. JSME. - 1985.- V. 28, № 239.- P. 959-963.
95. Schiehlen W. (Ed.) Multibody Systems Handbook. — Berlin: Springer-Verlag,
1990.
326 Список литературы
96. Schiehlen W. (Ed.) Advanced Multibody System Dynamics - Simulation and
Software Tools. - Dordrecht: Kluwer Acad. Publ., 1993.
97. Seeley R. Interpolation in Lp with boundary conditions // Stud. Math. —
1972.- V. 44, № 1.- P. 47-60.
98. Utkin V. I. Sliding Modes in Optimization and Control. — New York: Springer-
Verlag, 1992.
99. Utkin V., Guldner J., Shi J. Sliding Mode Control in Electromechanical
Systems. — London: Taylor & Francis, 1999.
100. Van der Schaft A. L2-gain and Passivity Techniques in Nonlinear Control. —
London: Springer, 2000.
Научное издание
ЧЕРНОУСЬКО Феликс Леонидович
АНАНЬЕВСКИЙ Игорь Михайлович
РЕШМИН Сергей Александрович
МЕТОДЫ УПРАВЛЕНИЯ
НЕЛИНЕЙНЫМИ МЕХАНИЧЕСКИМИ СИСТЕМАМИ
Редактор И.Л. Легостаева
Оригинал-макет: О.А. Кузнецов
Оформление переплета: А.Ю. Алехина
Подписано в печать 16.01.06. Формат 60x90/16. Бумага офсетная.
Печать офсетная. Усл. печ. л. 20,5. Уч.-изд. л. 23,0. Тираж 100 экз.
Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Московская типография № 6»
115088, г. Москва, Ж-88, ул. Южнопортовая, 24
ISBN 5-9221-0678-3
9 785922' 106788