Н. В. Баиичук И. И. Карпов Д. М. Климов А.П.Маркеев Б. Н. Соколов А.В.Шаранюк
МЕХАНИКА
БОЛЬШИХ КОСМИЧЕСКИХ
KOI 1СТРУКЦИЙ
РОССИЙСКАЯ АКАДЕМИЯ НАУК
ИНСТИТУТ ПРОБЛЕМ МЕХАНИКИ
. Баничук И. И. Карпов Д. М. Климов
. Маркеев Б. Н. Соколов А. В. Шаранюк
МЕХАНИКА БОЛЬШИХ КОСМИЧЕСКИХ КОНСТРУКЦИЙ
«Факториал»
Москва, 1997
УДК 539.3
М55 Механика больших космических конструкций/Н. В. Бани-чук, И. И. Карпов, Д. М. Климов и др. — М.: Изд-во «Факториал», 1997, —302 с, —ISBN 5-88688-021-6.
В монографии изложены основные методы анализа механического поведения больших космических конструкций. Проанализировано действие внешних и внутренних силовых факторов. Значительное внимание уделено инженерному анализу конструкций, методам идентификации и оптимизации, анализу орбитального движения. Рассмотрены вопросы управления большими космическими объектами и обеспечения точности рабочих поверхностей.
Для специалистов в области проектирования больших космических систем, инженеров, аспирантов, студентов высших учебных заведений.
Библиогр. 166.
рфи
Издание осуществлено при финансовой поддержке Российского фонда фундаментальных исследований. Проект № 95-01-02896.
Научное издание
Механика больших космических конструкций.
Формат 60 х 90/16. Усл. печ. л. 19. Бумага офсетная № 1. Гарнитура литературная. Подписано к печати 11.09.1997. Тираж 1000 экз. Заказ № 2185
Издательство «Факториал», 117449, Москва, а/я 331; ЛР № 063537 от 22.07.1994.
Отпечатано во 2-й типографии издательства «Наука». 121099, Москва Г-99, Шубин-ский пер., 6.
© Коллектив авторов, 1997.
ISBN 5-88688-021-6	©Факториал, 1997.
Предисловие
Предлагаемая вниманию читателей книга посвящена теории и методам анализа механического поведения больших космических конструкций (БКК). Работы в области проектирования крупногабаритных космических конструкций в настоящее время привлекают значительный интерес ученых, инженеров и конструкторов в связи с решением актуальных проблем создания перспективных образцов космической техники, проектированием многоэлементных крупногабаритных космических систем, предназначенных для эксплуатации в течение продолжительного времени.
Создание больших космических конструкций сопряжено с решением ряда технических и механических проблем, обусловленных уникальностью объектов, характерной особенностью которых является сочетание противоречивых требований увеличения геометрических размеров и обеспечения достаточной жесткости при весьма ограниченной массе материала силового каркаса. Для преодоления этих трудностей и обеспечения надежной эксплуатации больших космических систем требуется подробный анализ условий функционирования объекта, определения внешних и внутренних силовых факторов и воздействий, анализ температурного режима, тщательный подбор конструкционных материалов. Анализ орбитального движения больших космических конструкций, выполнение маневров ориентации требуют учета в уравнениях движения возникающих упругих деформаций, которые оказывают существенное влияние на динамические характеристики аппарата. Громадное значение приобретают методы идентификации упруго-массовых характеристик конструкции и методы оптимизационного моделирования, предназначенные для построения адекватных математических моделей, используемых при вычислительном эксперименте для моделирования движения и деформаций свободного гибкого объекта.
Во Введении обсуждаются современные проблемы астронавтики и связанные с ними задачи механики больших космических конструкций. Рассматриваются основные аспекты проектирования больших космических конструкций, порождающие новые механические задачи, специфика которых требует разработки новых подходов и концепций проектирования крупногабаритных космических систем.
В первой главе книги обсуждаются общие вопросы механики больших космических конструкций. Проведен анализ условий функционирования, действия внешних и внутренних силовых факторов, определяющих
4
ПРЕДИСЛОВИЕ
деформации конструкции и изменяющих ее пространственную ориентацию. Кратко рассматриваются механические характеристики конструкционных материалов, применяемых при создании больших космических систем. Проведен анализ теплового воздействия на элементы конструкции, находящейся в условиях космического полета. Получена система уравнений, описывающая орбитальное движение конструкции с учетом возникающих упругих деформаций.
Вторая глава посвящена инженерным методам анализа упругого поведения свободных космических конструкций. Особое внимание уделено численным методам, в частности, методу конечных элементов как наиболее универсальному методу определения напряженно-деформированного состояния сложных многоэлементных составных конструкций.
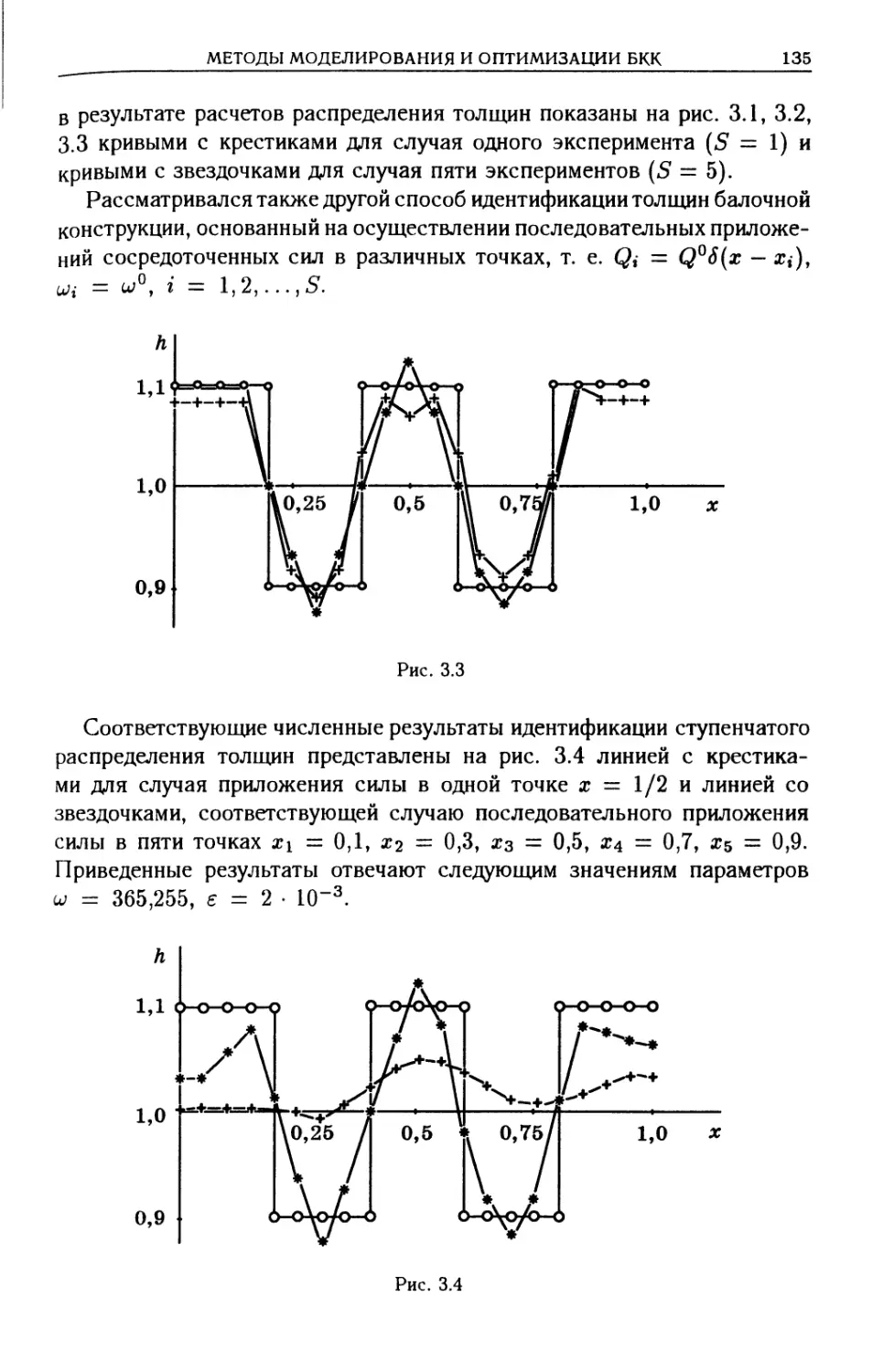
В третьей главе излагаются методы оптимизационного моделирования свободной конструкции, идентификации ее упруго-массовых параметров. На основе разнообразных моделей демонстрируются подходы к решению задач оптимизации конструкции, учитывающие всевозможные внешние воздействия.
В четвертой главе книги рассмотрены общие вопросы движения упругих космических конструкций относительно центра масс под действием моментов сил гравитационного поля. Основное внимание уделено вопросам существования и устойчивости относительного равновесия, стационарных вращений и периодических движений космического аппарата. Рассмотрены также вопросы эволюции быстрых вращений аппарата относительно центра масс на круговой и эллиптических орбитах.
Пятая глава посвящена вопросам оценки влияния конструктивных и эксплуатационных факторов па точность функциональной поверхности БКК, а также обеспечению максимальной гарантированной точности угловых параметров ее ориентации относительно заданного пункта на поверхности планеты при движении конструкции по кеплеровской орбите. Рассмотрена также задача минимизации средней интенсивности расхода топлива при заданной гарантированной точности ее угловой ориентации.
В Приложении рассматриваются вопросы применения систем компьютерной алгебры для построения и аналитического исследования математических моделей упругих механических объектов. Приведены примеры, иллюстрирующие технологию использования этих программных средств применительно к механическим конструкциям.
Авторы выражают свою благодарность сотрудникам Института проблем механики РАН и Центрального аэрогидродинамического института принявшим участие в работе над книгой и предоставивших свои материалы: Войтышену В.С., Ивановой В.Ф., Ивановой С.Ю., «Пущину Л.П., Макееву Е.В., Синицыну Е.В. Авторы выражают свою благодарность Саурину В.В. и Шматкову А.М., без конструктивного участия которых книга не вышла бы в свет.
ПРЕДИСЛОВИЕ	5
Особую признательность авторы выражают Заксону М.Б. и Медз-мариошвили Э.В., с которыми на протяжении ряда лет авторы вели плодотворное сотрудничество и чье влияние определило в значительной степени интерес авторов к рассмотренным проблемам и во многом стимулировало их деятельность.
Авторы надеются, что книга будет полезна научным работникам, инженерам, конструкторам космических аппаратов, преподавателям, аспирантам и студентам высших учебных заведений.
Авторы выражают глубокую признательность Российскому фонду фундаментальных исследований за финансовую поддержку издания этой книги.
Введение
ПРОБЛЕМЫ АСТРОНАВТИКИ И МЕХАНИКИ БОЛЬШИХ КОСМИЧЕСКИХ конструкций
Важные проблемы современной астронавтики связаны с изучением процессов на планете Земля и в Солнечной системе, разработкой энергетических систем космического базирования для накопления солнечной радиации и использования этой энергии человечеством, созданием эффективных систем космической связи, дистанционного зондирования и экологического мониторинга, а также с получением новых материалов в условиях невесомости. Проведение научно-исследовательских и конструкторских работ в этих перспективных областях требуют единения и больших усилий со стороны академической, вузовской и отраслевой науки, а также развития новых инженерных подходов и разработку ключевых технологий. При этом роль новых инженерных конструкций и порождаемых технологий не ограничивается собственным развитием астронавтики и решением ее актуальных задач, но оценивается влиянием на смежные «наземные» области человеческой деятельности и на прогресс цивилизации в целом. В этом смысле астронавтика может сравниваться с вы числительной техникой, возникшей в связи с необходимостью решения научных (главным образом в области механики и физики) и технических проблем, и пронизывающей в настоящее время практически все области деятельности людей.
Отметим вкратце задачи, решение которых тесно связано с развитием астронавтики. Прогресс астронавтики определяет возможности наблюдения за процессами, происходящими на звездах, в Солнечной системе и на планете Земля из космоса. Важными представляются наблюдения и исследования, выполняемые в целях разработки моделей мелкомасштабных явлений и крупномасштабных процессов, определяющих глобальные изменения на Земле. Здесь требуются долгосрочные и краткосрочные осреднения измеряемых параметров физико-химического состояния атмосферы, океанов, поверхности Земли. При этом важную роль играют наблюдения за разрушением озоновых слоев и нагревом планеты.
Развитие астронавтики и техники дистанционного зондирования делают принципиально возможным микроволновый зондаж с адекватным
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
7
пространственным разрешением с геосинхронной орбиты. Разработка соответствующих космических систем позволяет осуществить мониторинг таких мелкомасштабных явлений, как дожди и штормы. Известно, что около половины всех дождевых осадков выпадают в виде мелкомасштабных (с радиусом действия не превышающем десяти километров) и короткодействующих бурь и штормов. Для осуществления космического мониторинга отдельного дождя может быть применена космическая радиоантенна миллиметрового диапазона с апертурой в несколько десятков метров. Космическая техника дистанционного зондирования представляет уникальные возможности для различных аспектов человеческой деятельности. Ее можно эффективно использовать, например, как для обнаружения косяков рыб в океане, так и для наблюдения за распространением пожаров. Чрезвычайно важным в наше время оказываются потенциальные возможности астронавтики в части создания систем экологического мониторинга. Широкое применение для контроля окружающей среды находят карты загрязненности городов и сельских районов, полученные фотографированием из космоса. Для создания систем экологического мониторинга могут эффективно использоваться радиоантенны космического базирования, работающие в миллиметровом (30—300 ГГц) и субмиллиметровом (300—3000 ГГц) диапазонах.
Разрабатываемые космические системы обеспечат возможность решения таких актуальных задач, как измерение характеристик нефтяных пятен на морской поверхности, обнаружение и наблюдение за динамикой границ вулканических извержений, определение границ континентальных ледников и наблюдение за состоянием ледяного покрова морей.
Важное направление работ в области астронавтики связано с созданием систем глобальной связи. Предполагается, что использование больших космических радиоантенн, размещенных на геосинхронной орбите, позволит значительно расширить число абонентских каналов и существенно уменьшить энергетические потери, характерные для кабельной телефонной связи. Космическая телефонная сеть обеспечит, в частности, устойчивую связь с движущимися объектами (автомашинами, самолетами, надводными судами).
Среди других возможностей использования астронавтики в ближайшем будущем отметим проекты создания больших космических платформ, несущих солнечные батареи. Отметим, что для эффективности рассматриваемых энергетических систем потребуются платформы с огромными размерами рабочих поверхностей, чтобы собрать и накопить достаточно большую энергию солнечного излучения, которая поступает на платформу с очень низкой плотностью. Вероятно, что энергетические платформы будут наиболее крупными сооружениями будущего (имеются проекты платформ размерами с десятки километров) и при их создании возникнет
8
ВВЕДЕНИЕ
необходимость разработки новых конструктивных подходов и оригинальных концепций. При разработке космических платформ следует учесть, в частности, такие аспекты, как вывод конструкции на космическую орбиту, сборку конструкции из конструктивных элементов или раскрытие конструкции из сложенного состояния; характеристики платформы, необходимые для функционирования, обеспечение требуемых показателей во время длительной эксплуатации; многоцелевая оптимизация платформы по критериям прочности, жесткости и устойчивости; активное гашение колебаний, возникающих в гибкой конструкции; управление ориентацией и обеспечение точности поверхностей.
Перейдем теперь к рассмотрению некоторых проблем механики, которые возникают в астронавтических приложениях в связи с созданием энергетических платформ, космических радиоантенн, космических телескопов и других типов конструкций. Данные конструкции характеризуются большими размерами и относительно малой массой, лимитируемой стоимостными ограничениями, связанными с расходами по доставке конструкции на заданную орбиту. Поэтому данные конструкции оказываются весьма гибкими, что и порождает множество проблем, нетипичных для таких относительно жестких систем как самолет или космический аппарат многоразового использования «Буран». В то же время к указанного типа конструкциям предъявляются высокие требования по жесткости, обусловленные необходимостью точной ориентации конструкции и обеспечением точности функциональных поверхностей. Приводя дальнейшие пояснения и обсуждая остальные аспекты механических проблем, будем считать, что большая космическая конструкция (БКК) является космической радиоантенной или радиотелескопом. Главными параметрами радиотелескопа (радиоантенны), определяющими его функциональную эффективность, являются чувствительность радиотелескопа и его угловое разрешение. Увеличение размеров апертуры радиотелескопа приводит к двум принципиально важным следствиям. Первое заключается в том, что увеличивается площадь поверхности рефлектора, собирающего энергию, и, тем самым, увеличивается эффективная площадь, определяющая мощность принимаемого сигнала. Второе следствие увеличения размеров рефлектора состоит в повышении разрешающей способности телескопа. Для радиотелескопа с эффективной площадью рефлектора Seff и диаметром рефлектора L среднеквадратичное пороговое значение сгр плотности потока излучения (чувствительность) и ширина диаграммы направленности выражается через величины Seft, L в виде
<7F = cls;^, ф = с2ь~х.	(1)
Не зависящие от размеров диаметра рефлектора L и его эффективной площади величины Ci и Сг определяются значениями температуры
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
9
шумов Г, константой Больцмана к, полосой частот Ai/, рабочей длиной волны А и временем накопления сигнала А/.
Как это видно из (1), уменьшение ширины диаграммы направленности ф при заданном диапазоне волн возможна за счет увеличения диаметра антенны L. Уменьшение же среднеквадратичного порогового значения плотности потока излучения, которое воспринимается радиотелескопом, может быть получено за счет увеличения эффективной площади Seft отражающей поверхности. Заметим, что другие параметры, от которых зависит чувствительность радиотелескопа, близки к своим предельным значениям (для современных радиотехнических приборов), и поэтому их допустимые изменения не могут существенно повлиять на чувствительность радиотелескопа. Так шумовая температура применяемых радиометров мало отличается от температуры космического фона, время накопления сигнала может измеряться сутками, а полоса частот не может превышать рабочей частоты. Заметим, что увеличение площади антенны на Земле существенно затрудненно из-за наличия значительных гравитационных сил и неоднородности атмосферы.
Другое важное обстоятельство, влияющее на качество радиотелескопа, является наличие неровностей на отражающей поверхности и отклонение поверхности рефлектора от идеальной формы. Появление неровностей может быть обусловлено неточностью изготовления элементов рефлектора, ошибками, допущенными при сборке радиоантенны, неравномерным тепловым расширением элементов силового каркаса вследствие солнечной радиации и различного рода внешних воздействий. Если поверхность рефлектора имеет неровности, отстоящие друг от друга не менее чем на величину рабочей длины волны А, произойдет смещение фаз для потоков (сигналов), отражаемых различными частями рефлектора. При этом поток, излучаемый антенной с неидеальным рефлектором в заданном направлении, станет меньше, чем для антенны с идеальной формой отражающей поверхности. Обозначим через (р2)^2 среднеквадратичную фазовую ошибку, а через (w2)1^2 среднеквадратичное отклонение возмущенной отражающей поверхности от идеальной поверхности рефлектора. Квадраты этих величин связаны соотношением
^2) = C3(w2),	(2)
где константа Сз зависит от геометрии конструкции рефлектора и пропорциональна А-2. Следовательно, для практической реализации большого радиотелескопа нужно, чтобы «неточность» отражающей поверхности была достаточно мала. Данная характеристика оказывается в ряде случа-ев(см. [139]) пропорциональной сумме (wf 2+о;^2 + ...), гдеш i,o>2,... —
10
ВВЕДЕНИЕ
ненулевые частоты упругих колебаний конструкции. Собственные же частоты, рассматриваемые часто в качестве меры динамической жесткости, обратно пропорциональны квадрату характерного размера конструкции. Следовательно, с увеличением характерного размера рефлектора будет быстро возрастать «неточность» отражающей поверхности и ухудшаться функциональные характеристики радиотелескопа.
Таким образом, одной из наиболее трудных и важных проблем механики, рассматриваемых на начальной стадии разработки космического радиотелескопа, является разрешение противоречия между требованиями увеличения размеров рабочих поверхностей и обеспечением приемлемой жесткости конструкции. Для обеспечения динамической жесткости конструкции могут использоваться конструктивные подходы, разработанные в строительной механике, и принципиально новые концепции создания больших космических конструкций. Традиционные способы повышения жесткости связаны, однако, с увеличением массы конструкции, что оказывается неэффективным вследствие высокой стоимости доставки грузов на орбиту. Поэтому в настоящее время развиваются комбинированные подходы к решению проблемы обеспечения жесткости, основанные на разработке пассивных средств парирования возмущений (повышение удельной жесткости, увеличение вязкостных свойств конструкции, рациональная компоновка антенны) и активных систем гашения колебаний и обеспечения точности рабочей поверхности. Эти системы включают в себя сенсорные устройства, определяющие состояние отражающей поверхности, подсистемы обработки данных в реальном времени и эффективные устройства (актьюаторы), служащих для приведения поверхности к идеальной форме. Реализация данного подхода к созданию больших космических антенн основывается на концепции одновременного оптимального проектирования конструкции и системы управления. Заметим, что в предшествующей практике создания самолетов и ракет проектирование конструкции и системы управления в основном осуществлялось автономно и затем разработанные проекты «адаптировались» друг к другу для удовлетворения некоторым основным интегральным критериям и ограничениям. Процесс взаимной коррекции конструкции и системы управления заключался в уточнении ряда их функциональных характеристик и занимал обычно значительное время.
Полный спектр возмущений, прикладываемых к конструкции космической антенны, можно условно разделить на коротковолновый и длинноволновый. При этом динамические воздействия на конструкцию, обусловленные, например, работой двигателей переориентации конструкции, столкновениями с метеоритами или космическим мусором, можно отнести к коротковолновым возмущениям, а температурные деформации, происходящие из-за неравномерного солнечного нагрева, следует
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
11
отнести к длинноволновым возмущениям. Если для гашения колебаний и устранения деформаций, вызванных коротковолновыми воздействиями, целесообразно создание в конструкции повышенного уровня вязкостных свойств и разработка активных демпфирующих систем, то для устранения тепловых и других «квазистатических» деформаций требуется разработка иных методов. Вероятно, что наибольшие искажения рабочих поверхностей космических радиоантенн, функционирующих на околоземных орбитах, вызывает солнечная радиация. Искажение поверхностей прежде всего связано с наличием градиентов температур, т. е. неравномерным подводом тепла к конструкции, неоднородностью конструкции антенны, состоящей из большого числа элементов, выполненных из материалов с различными коэффициентами теплового расширения и различными коэффициентами теплопроводности, а также самой геометрической структурой конструкции, у которой одни элементы находятся под непосредственным воздействием солнечной радиации, а другие защищены от солнечного воздействия другими частями конструкции и нагреваются медленней. Для решения проблемы снижения уровня температурных искажений поверхности антенны в настоящее время рассматриваются различные концепции создания структур, деформирование которых в значительной степени происходит дилатационным способом (сдвиговые деформации отсутствуют или минимальны), обеспечивающим геометрически подобное изменение поверхности рефлектора. Другой перспективный подход к решению данной проблемы заключается в оптимальном подборе материалов отдельных элементов с учетом усилий совместного деформирования конструкции. Существенные продвижения при решении данной проблемы получаются при использовании новых композиционных материалов с малыми или даже нулевыми коэффициентами линейного расширения.
Для решения актуальных задач астронавтики по созданию БКК (телескопов, радиоантенн, энергетических платформ и различных конструкций транспортных систем типа «космический парус») требуется проведение научных исследований и разработок в части развития методов математического моделирования таких конструкций. Необходимость проведения этих работ определяется следующими обстоятельствами:
1.	БКК представляют собой многофункциональные и многоэлементные системы, состоящие из десятков тысяч взаимосвязанных между собой отдельных элементов. Взаимодействие этих элементов в условиях космоса определяется градиентами температур, прикладываемыми воздействиями статической и динамической природы, структурными особенностями соединения элементов конструкции, топологией конструкции и точностью изготовления отдельных элементов. Эти конструкции доставляются на космические орбиты в сложенном состоянии или в виде отдельных секций и дальнейшее приведение их в рабочее состояние связано с реализацией
12
ВВЕДЕНИЕ
процесса раскрытия или сборки. Соответствующие стадии реализации проекта представляются чрезвычайно ответственными и обеспечение их надежности связано с решением трудных задач механики конструкций. Поэтому без применения разрабатываемых комплексных моделей процессов раскрытия складных конструкций и сборки отдельных частей в общую комплексную структуру вряд ли возможно обеспечение высоких показателей надежности проектируемой механической системы. Такие факторы, как неточность в изготовлении элементов, разброс свойств применяемых материалов и тип структуры собираемых космических конструкций, могут иметь здесь важное значение. Так, при одних и тех же допусках на неточность изготовляемых деталей, как показано в работе [137], одни рассматриваемые структуры БКК удовлетворяют ограничениям, а другие оказываются функционально непригодными для реализации предписываемого конструкции назначения.
2.	Неполнота информации о внешних воздействиях на БКК и условиях их функционирования также обусловливает необходимость разработки эффективных моделей и новых подходов к анализу и проектированию. Прежде всего здесь следует отметить такие факторы неопределенности, как флуктуации солнечной активности, столкновения БКК с космическим мусором, непредусмотренные разрушения элементов сложной конструкции, динамические процессы, возникающие из-за жесткой стыковки БКК с различными космическими транспортными средствами или из-за ударов метеоритов, отказ систем жизнеобеспечения в случае БКК, обслуживаемых космонавтами. Для учета этих и других факторов и повышения надежности функционирования разрабатываемой системы требуется точный анализ влияния возможных внешних воздействий, основанный на предварительной статистической обработке имеющихся экспериментальных данных и других астрофизических наблюдений. Поэтому для реализации «гарантированного» подхода требуется проведение большого объема различных оценок. Реализация данной системы, по-видимому, также невозможна без создания математических моделей конструкции и ее взаимодействия с внешней средой. Заметим, что для гарантированного или минимаксного подхода к анализу и проектированию конструкций характерно принятие решений в расчете на наихудший случай, а это влечет за собой необходимость эффективного просмотра множества различных ситуаций и выработку соответствующих рекомендаций. Отметим также, что применение гарантированного подхода, не встречающее возражений со стороны проектировщиков и конструкторов, ведет в некотором смысле к переутяжелению конструкций. Вероятностный же подход, приводящий к более оптимистическим результатам и, в частности, к меньшим значениям весовых характеристик, нуждается в определенной статистике и по своей природе не исключает возможность разрушения конструкции и не гарантирует функциональную пригодность проектируемых БКК.
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
13
3.	В практике создания новых сложных изделий значительная роль отводится натурному эксперименту Для этого создаются испытательные полигоны, проводятся многочисленные эксперименты, имеющие целью получение необходимой статистики, при этом результаты проводимых экспериментов и испытаний являются основным критерием надежности и функциональной пригодности разрабатываемых систем. Для конструкций, предназначенных для эксплуатации в околоземных условиях, таких, как самолеты или ракеты, разработаны методы экспериментальной проверки их функциональной пригодности и конструктивного совершенства. Испытания транспортных средств на экспериментальных полигонах, летательных аппаратов в аэродинамических трубах и пробных полетах, являются гарантией надежности, комфортности и безопасности.
Для БКК, функционирующих в космическом пространстве, важными факторами становятся невесомость, отсутствие или значительная разреженность атмосферы и значительная солнечная радиация. Чтобы воссоздать эти условия в наземных экспериментах, требуются дорогостоящие установки обезвешивания БКК, уникальные по размерам вакуумные камеры и сложные облучательные системы. Очевидно, что проведение полномасштабных физических экспериментов в этих условиях оказывается чрезвычайно дорогостоящим делом. Поэтому математический эксперимент, использующий разрабатываемые механические модели БКК с идентифицированными параметрами, по-видимому, является альтернативной возможностью проверки и обоснования функциональной пригодности проектируемого изделия. Например, при определении собственных частот и мод свободных колебаний в наземных экспериментах получаемые частоты и формы колебаний отличаются от соответствующих величин в космосе. Это происходит из-за наличия присоединенных масс, обусловленных ненулевой плотностью атмосферы. Для пологих параболический антенн, превосходящих в диаметре 3 м, получающееся отличие частот от соответствующих частот колебаний в вакууме достигает 20%, что конечно делает невозможным непосредственное использование результатов наземных экспериментов. Применяя же математическое моделирование и решая совместные задачи о колебаниях упругой конструкции в бесконечной среде, а также проводя анализ влияния присоединенных масс, можно, в частности, определить искомые значения собственных частот колебаний в вакууме.
Для математического моделирования БКК наиболее часто используются методы Рэлея — Ритца, методы Бубнова — Галеркина и методы конечных элементов (МКЭ). Для того, чтобы пояснить наиболее важные возникающие здесь проблемы предположим, для конкретности, что при моделировании рассматриваемой эволюционной системы
52и
—+ Lu = q(x,i)	(3)
14
ВВЕДЕНИЕ
применяется метод Бубнова — Галеркина, использующий в качестве координатной системы функций собственные моды свободных колебаний, описываемых однородной системой
Через L в (3) и (4) обозначен матричный оператор дифференцирования по пространственным координатам, а через q(#,/) — воздействия на систему, роль которых могут играть управляющие воздействия и внешние возмущения. Собственные моды и частоты свободных колебаний определяются из решения спектральной задачи
= Xupi (Ai=u>2),	(5)
получаемой при подстановке в (4) представления решения в виде u = u, = epi exp(iwit). С использованием найденных собственных частот нижней части спектра (г = 1,2,..., АГ) и представления для функций состояния, описывающих поведение конструкции, и воздействий, прикладываемых к системе
N	N
U=	q =	(6)
i=l	г=1
приближенное описание поведения исходной бесконечномерной системы (3) сводится к анализу редуцированной конечномерной системы fi 4- Xifi = qi, (г = 1,2, ...,7V). Отметим некоторые особенности поведения систем, описывающих динамику БКК. Первые несколько частот свободных колебаний БКК (в трехмерном случае их шесть) оказываются нулевыми, а отвечающие им моды колебаний соответствуют движениям БКК как твердого целого. Частоты свободных колебаний БКК располагаются очень плотно и концентрируются в нижней части спектра. Это обстоятельство характерно для гибких систем с большим числом степеней свободы. Для того, чтобы промоделировать низкочастотные формы движения конструкции, требуется в ряде случаев рассчитать около ста и более частот и форм свободных колебаний. Это оказывается необходимым для решения задач отстройки от резонанса при адаптации систем управления, а также для минимизации последствий внешних воздействий на конструкцию. Трудная практическая задача отстройки БКК от возможных резонансов решается с привлечением современных методов оптимизации. Заметим, что из опыта решения аналогичных задач для более жестких конструкций ракет вытекает достаточность учета двух-трех десятков мод и частот нижней части спектра.
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
15
Другое обстоятельство, затрудняющее адекватное моделирование динамики БКК и разработку методов комбинированного проектирования конструкции и системы управления, обусловлено плотностью низкочастотной части спектра свободных колебаний. Для исключения возможности пропуска отдельных собственных частот и форм колебаний предъявляются повышенные требования по точности к применяемым численным алгоритмам. Известны примеры из области ракетной техники, когда допущенные ошибки приводили к разрушению конструкций или к неэффективности систем управления.
Для сложных конструкций, таких как БКК, работающих в экстремальных условиях на пределе возможностей, т. е. с относительно малыми коэффициентами запаса, возникают и другие осложнения, обусловленные методами конечномерного моделирования. Так упоминавшийся выше метод Бубнова — Галеркина, а также МКЭ и многие другие методы, сводят моделирование конструкции к представлению функций состояния низкочастотными гармониками. Поэтому механико-математические модели конструкции точно описывают ее динамические свойства только в нижней части спектра колебаний. Высокочастотные составляющие внешних нагрузок или воздействий системы управления могут взаимодействовать с неучтенными высокочастотными модами и приводить к резонансным явлениям. Кроме того, возможно возникновение явлений взаимодействия низкочастотных и высокочастотных мод колебаний конструкции и неконтролируемых перетоков энергии как к учитываемым в модели формам колебаний так и к формам колебаний неучитываемой высокочастотной части спектра. При этом возможны возрастания амплитуд отдельных мод колебаний, что на практике приводит к недопустимым отклонениям рабочих поверхностей БКК. По-видимому, данная проблема моделирования сложных систем с учетом перетоков энергии является одной из самых актуальных для разрабатываемых БКК, для которых требуется обеспечить прецизионную точность функциональных поверхностей и высокую точность ориентации в космосе. Оценкам указанного эффекта и выработке практических рекомендаций по устранению причин его возникновения в современных исследованиях уделяется значительное внимание.
Для динамических процессов поведения БКК характерны относительно низкие коэффициенты демпфирования. Во многом это связано с масштабными эффектами. Так с увеличением характерного размера конструкции L объем конструкции возрастает как L3, а площади сечений стыковочных узлов и поперечные сечения контактирующих ферменных элементов увеличивается как L2, При этом коэффициенты демпфирования ведут себя как L”1, т. е. роль демпфирования уменьшается с возрастанием размеров БКК. Известные предложения осуществлять дополнительный подогрев конструкции, а также использовать новые композиционные материалы (полимерные накладки) с повышенными или даже
16
ВВЕДЕНИЕ
резонансными свойствами демпфирования лишь частично решают возникающие здесь проблемы. Заметим, что для описания внутренней вязкости материалов конструкции существует множество различных физических теорий, учитывающих структурные свойства материалов и механизмы диссипации энергии. Анализ различных механизмов внутреннего трения проводился в ряде исследований. Отметим важную работу X. Эшли [115], посвященную анализу процессов демпфирования применительно к БКК- Однако в настоящее время данная проблема механики находится в начальной стадии разработки, и полученные теоретические решения не полностью подтверждаются экспериментами, а в ряде случаев находятся в противоречии с опытами.
Актуальными являются проблемы синтеза матриц демпфирования для конечноэлементных моделей БКК. Если аналогичные процедуры синтеза матриц масс и жесткостей полностью автоматизированы в МКЭ, то получение матриц демпфирования не является стандартной операцией и требует от исследователя определенного «искусства» [141, 152, 160]. В этой области существует множество в основном эвристических подходов, хорошо зарекомендовавших себя в строительной механике наземных сооружений. Наиболее распространенные рекомендации относятся к представлению матриц демпфирования пропорционально матрицам масс или жесткости (пропорциональное демпфирование), или в виде линейной комбинации указанных матриц. Используются и более сложные степенные зависимости между матрицами демпфирования D, масс М и жесткости К:
р
D = M^ak[M-1K]':,	(7)
k=o
включающие в себя коэффициенты а^, которые должны определятся из динамических экспериментов.
В связи с тем, что механико-математическое моделирование БКК и проводимые на ЭВМ вычислительные эксперименты занимают определяющее место в рамках реализации космических программ, большое внимание в этих работах следует уделять адекватности применяемых моделей реальным изделиям и условиям их функционирования. В этом направлении важная роль отводится методам идентификации параметров и коррекции моделей. Важность этих операций обусловлена, как уже отмечалось, наличием таких «эвристических» параметров, как, например, коэффициенты в формуле (7), а также разбросом свойств материалов, неидеальностями реализации изделия. При этом возникают задачи точного нахождения всех определяющих параметров и более сложные проблемы коррекции структуры операторов модели, определяющих взаимодействие степеней свободы конструкции и влияние внешних воздействий. Наиболее эффективными методами решения задач идентификации
ПРОБЛЕМЫ АСТРОНАВТИКИ И БКК
17
шт я юте я различные спектральные и резонансные методы, а также методы, основанные на использовании данных о вынужденных гармонических колебаниях. Сложности, возникающие при использовании этих методов, связаны с тем, что естественные формулировки проблем идентификации приводят к некоторым математическим задачам, и требуется проведение специальных исследований для регуляризации этих задач и поиска их решений. Многие задачи идентификации формулируются как обратные или оптимизационные задачи (см. главу 3). Однако в отличие от многих других вариационных проблем, возникающих при оптимальном проектировании, они оказываются невыпуклыми и характеризуются наличием многих экстремумов. В настоящее время имеющиеся здесь трудности преодолены применительно к таким типам структурных элементов и конструкций, как балки, стержни, рамы и фермы. Для пластинчатых и оболочечных конструкций, а также для трехмерных деформируемых тел эти методы нуждаются в дальнейшем усовершенствовании. Имеющиеся здесь перспективы обусловлены как более рациональными постановками задач для расширенных функционалов, учитывающих различного типа «штрафы», так и новыми подходами к оценке чувствительности разрабатываемых моделей.
Для описания орбитального движения искусственных спутников и других недеформируемых объектов характерным является декомпозиция на движение центра масс объекта и движение вокруг центра масс. Последнее в известной степени влияет как на само результирующее движение, так и на устойчивость динамического процесса. С увеличением характерных размеров конструкции, сложности ее структуры и наличии упругих деформаций элементов существенно осложняется описание динамики. Многоплановый сценарий сложного деформирования элементов и поведения всей конструкции в целом зависит от многих факторов. Для решения возникающих здесь механических проблем применяются различные подходы. Так, в механике систем твердых тел разрабатываются методы учета влияния упругости элементов на орбитальную динамику конструкции как жесткого целого и учета упругости связей между отдельными жесткими элементами БКК. Это позволяет более реалистично оценить орбитальную устойчивость и другие существенные характеристики движения конструкции на орбите. При этом существенную роль играют моды собственных колебаний отдельных частей и системы в целом. В ряде случаев оказывается существенным взаимодействие гравитационных сил и сил упругости, приводящее к явлениям стабилизации или дестабилизации движения объекта по орбите.
Наряду с анализом орбитальной динамики, учитывающей в некотором приближении деформируемость аппарата, для проектирования БКК требуется также детальный расчет упругой динамики многоэлементной конструкции. Подробные данные о модах колебаний многоэлементной
18
ВВЕДЕНИЕ
упругой системы, состоящей из нескольких тысяч элементов, необходимы для решения основной задачи обеспечения точности рабочих поверхностей и точности расположения относительно этих поверхностей облучателей и регистрирующей сигналы аппаратуры, а также для достижения максимальной точности ориентации БКК на орбите. Полный расчет внутренней динамики системы упругих элементов, составляющих БКК, сводится к определению форм свободных колебаний и последующему расчету вынужденных колебаний упругой системы, вызываемых воздействием вращения конструкции вокруг центра масс, перемещение масс внутри конструкции и другими динамическими факторами. Для учета влияния этих и других силовых факторов на упругие деформации БКК в настоящее время разработаны специальные алгоритмы и программы.
Однако применяемый анализ и декомпозиция связанной проблемы на задачу динамики твердого тела с учетом элементов упругого поведения и на задачу о колебаниях сложной конструкции, совершающей заданное орбитальное движение, являются в известной степени условными и не во всех случаях приводят к исчерпывающим результатам. Только для отдельных типов конструкции и видов движения это разделение является обоснованным и позволяет получить гарантированные оценки полных динамических эффектов. В остальных ситуациях необходимо моделирование связанной динамики упругого деформирования конструкции и ее движения на орбите. Здесь перед механикой БКК возникает целый ряд сложных проблем, требующих своего решения. В общем случае произвольных орбитальных движений БКК для получения на основе динамического анализа адекватной информации необходимо учитывать такие факторы, как неинерциальность связанной с конструкцией координатной системы (при этом усложняется расчет упругих вибраций), большие колебания конструкции в целом и геометрически-нелинейные деформации ее отдельных элементов. Для решения этих задач и других комплексных нелинейных проблем динамики оказываются весьма эффективными асимптотические методы механики, методы компьютерной алгебры, а также МКЭ нового поколения.
Глава 1
БОЛЬШИЕ КОСМИЧЕСКИЕ КОНСТРУКЦИИ И ЗАДАЧИ МЕХАНИКИ
Проектирование и создание БКК порождает ряд задач, связанных с особенностями эксплуатации столь уникальных космических аппаратов. К традиционным задачам механики, которые решаются при создании новых образцов космической техники, добавляются проблемы, связанные с относительно низкой жесткостью и большими размерами БКК. Крупногабаритные конструкции, предназначенные для эксплуатации на околоземных орбитах, испытывают действие разнообразных нагрузок и при их проектировании предъявляются повышенные требования к выбору конструкционных материалов, анализу внешних и внутренних силовых воздействий, определению жесткостных характеристик конструкции. Уникальность и высокая стоимость БКК порождает необходимость в проведении всестороннего наземного механического и технологического эксперимента. Сложности, возникающие при моделировании в наземном эксперименте условий эксплуатации в космосе, требуют создания дорогостоящего крупногабаритного прецизионного оборудования. Важную роль здесь играет методика проведения наземного эксперимента, которая позволяет с наименьшими затратами косвенно определить некоторые механические параметры проектируемой БКК- Поэтому особое значение имеет определение внешних и внутренних силовых воздействий на элементы БКК в условиях эксплуатации. Такие уникальные и дорогостоящие объекты, как БКК, предназначены для длительного пребывания в космосе, что определяет выбор конструкционных материалов, допускающих продолжительную эксплуатацию в неблагоприятных условиях космического полета.
Особое значение при проектировании БКК приобретает разработка математической модели конструкции, адекватно описывающей ее механические свойства, что возможно при тщательном анализе условий функционирования БКК в сочетании с наземным экспериментом и методами идентификации параметров конструкции.
В последние годы внимание исследователей как у нас в стране, так и за рубежом, привлекают задачи, связанные с проектированием и созданием крупногабаритных космических конструкций. По-видимому, впервые
20
ГЛАВА 1
исследователи столкнулись с проблемами, возникающими при создании БКК, на рубеже 70-х годов, когда возникли проблемы управления и ориентации спутников, имеющих протяженные упругие элементы [45, 134]. В процессе развития космической техники возникла потребность в увеличении мощности источников энергии, т. е. увеличении площади солнечных батарей, которые являются весьма гибкими и протяженными элементами конструкции. Решение практических задач астрономии, связи и навигации выдвинуло на передний план проблему создания больших космических радиоантенн. Наличие протяженных гибких упругих элементов в составе космического летательного аппарата значительно усложняет решение задачи ориентации, управления и стабилизации спутника. Система уравнений, описывающая движение летательного аппарата, становится «гибридной», т. е. включает в себя как уравнения орбитального движения спутника, так и уравнения, описывающие упругие деформации его элементов. Свободная БКК в процессе орбитального движения в силу своего функционального предназначения должна ориентироваться в пространстве определенным образом по отношению к Земле. Это значит, что непрерывно должна функционировать система ориентации, которая посредством импульсов тяги реактивных двигателей осуществляет разворот конструкции в заданное положение. Нестационарные воздействия, обеспечивающие большие пространственные развороты конструкции, приводят к деформации аппарата, смещению его центра масс, искажению формы рабочих поверхностей. Описание пространственных движений, при которых упругие деформации конструкции приводят к изменению динамических параметров аппарата, таких, как положение центра масс, главные моменты инерции, ориентация главных осей, требует разработки специальных подходов к решению совместных задач динамики пространственного движения конструкции и ее упругих деформаций.
Подобные подходы, основанные на введении специальных систем координат и разнообразных способах описания упругого поведения конструкции, рассматривались в ряде работ [43, 63, 145, 147].
Для обеспечения максимально точного и подробного описания упругих характеристик конструкции используется расчетная модель, построенная на основании МКЭ. Использование метода конечных элементов обусловлено его универсальностью и гибкостью при описании сложных составных конструкций.
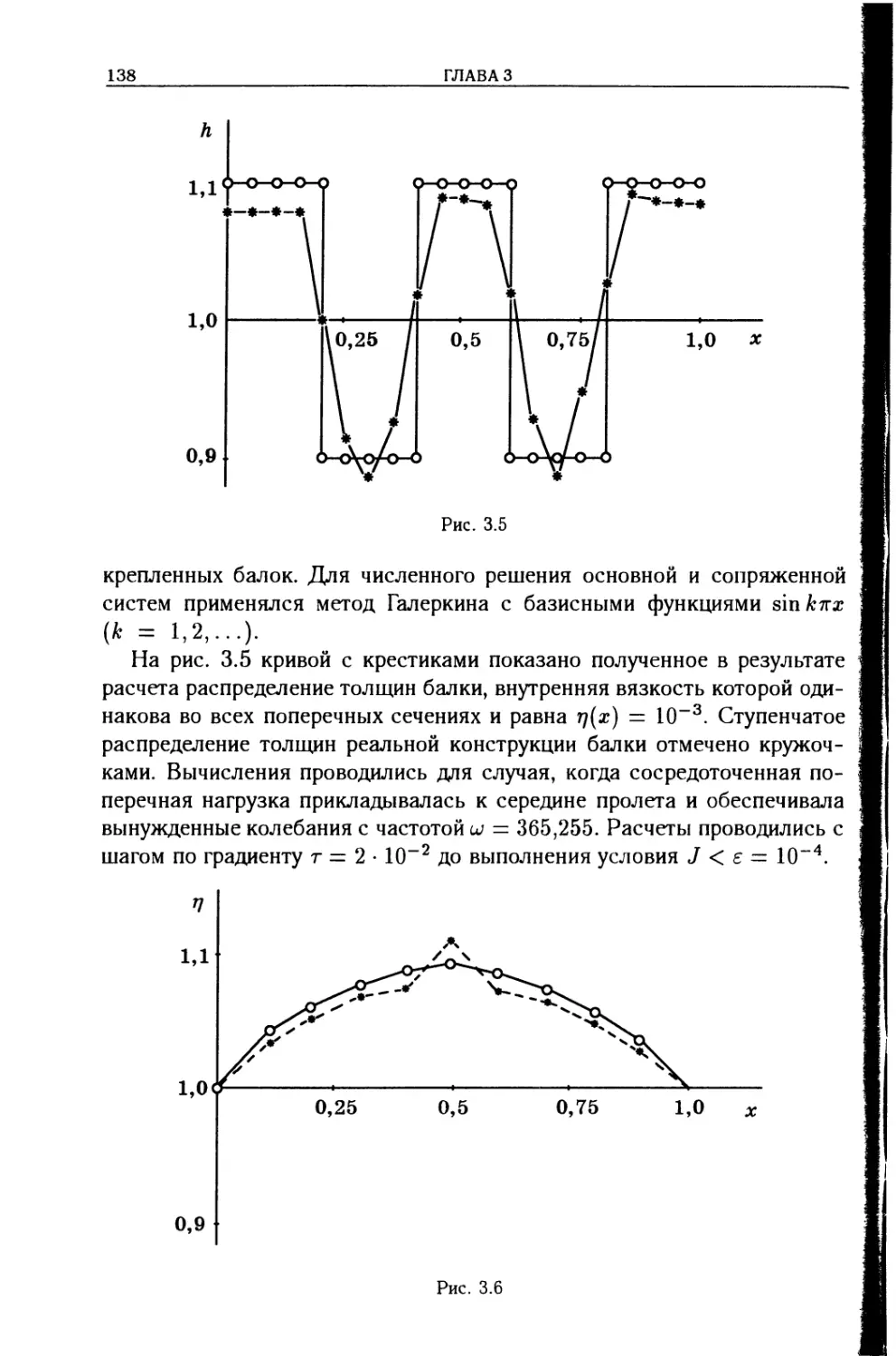
Обеспечение высокой точности рабочих поверхностей — одна из основных задач при проектировании БКК, конструировании системы управления ориентацией и стабилизацией движения. Решение указанной задачи может быть получено за счет построения эффективного алгоритма оценки влияния различных возмущающих факторов на точность рабочей поверхности в процессе функционирования БКК на орбите. К возмущающим факторам можно отнести инерционные нагрузки, гравитационные
БКК И ЗАДАЧИ МЕХАНИКИ
21
силы и моменты, солнечный ветер, управляющие силы и моменты, влияние атмосферы на низких околоземных орбитах. Все эти воздействия вызывают деформации БКК и искажают форму рабочих поверхностей. Для оценки влияния возмущающих факторов на точности рабочих поверхностей БКК необходимо построение достаточно подробной и точной математической модели БКК с использованием МКЭ. Точность модели обеспечивается за счет большого числа элементов, с помощью которых моделируются упругие и массовые характеристики БКК, и большого числа степеней свободы модели. В дальнейшем требуется согласование конечноэлементной модели БКК с уравнениями движения свободной деформируемой конструкции, инерционные характеристики которой в процессе движения изменяются. Адекватная математическая модель и численный эксперимент позволяют выполнить построение системы управления, обеспечивающей в процессе своего функционирования требуемую точность рабочих поверхностей БКК.
Отметим некоторые особенности рассматриваемой задачи. Во-первых, математическая модель движения должна быть согласована с конечноэлементной моделью БКК. Иными словами, вывод уравнений движения должен базироваться на представлении БКК с помощью ее конечноэлементной модели. Во-вторых, математическая модель движения должна быть проста и удобна для численного интегрирования. Это уменьшает объем проводимых вычислений и снижает вероятность появления ошибок.
Проблемы обеспечения точности рабочих поверхностей БКК, таких как зеркала параболических радиоантенн, требуют проведения исследований, связанных с вопросами стабилизации и демпфирования упругих механических колебаний. В настоящее время рассматриваются как активные системы гашения колебаний [117, 149], так и пассивные [115,132].
Ввиду сложности, а в ряде случаев и невозможности проведения наземных экспериментов, уделяется большое внимание вопросам математического моделирования БКК [43, 82, 111 ]. Построение математических моделей БКК, адекватно описывающих ее механические свойства, позволяет в вычислительном эксперименте проанализировать специфические особенности деформирования силового каркаса. Помимо широко используемого способа построения математической модели БКК, основанного на МКЭ [23, 112, 138, 140], применяются методы построения аналитических моделей, т. е. моделей, описываемых достаточно простой системой Дифференциальных уравнений [133, 150]. Сочетание разрабатываемых моделей с подробным анализом условий эксплуатации позволяет проектировать БКК с заданными функциональными параметрами.
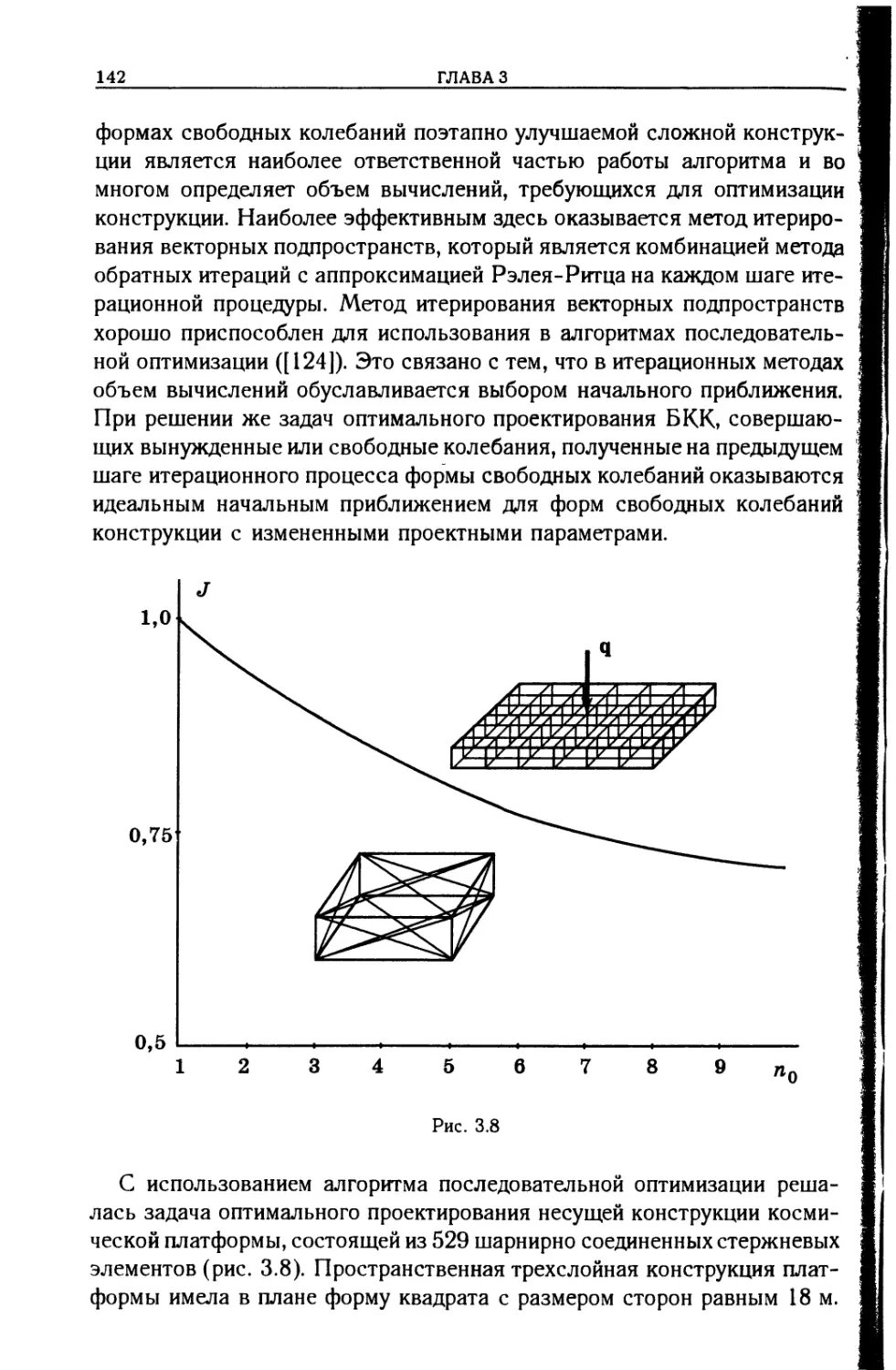
22
ГЛАВА 1
1.1.	НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА БКК
Движение БКК на околоземных орбитах и выполнение ими заданных функций происходит при наличии воздействий на конструкцию различного рода внешних квазистационарных и существенно нестационарных нагрузок, которые могут оказывать влияние на ориентацию и стабилизацию БКК, приводить к значительным внутренним усилиям, обусловливать упругую деформацию конструкции и, в частности, вызывать недопустимые искажения формы рабочих поверхностей.
Анализ величин и характера внешних воздействий на БКК, создаваемых окружающей средой, указывает на необходимость всестороннего учета этих воздействий при рассмотрении компоновки и конструктивносиловой схемы. Выбор рациональной компоновки БКК, ее формы и размеров конструкционных элементов, рациональное распределение неконструктивных масс и органов управления может привести к значительному снижению уровня нагруженности конструкции, меньшим энергетическим затратам при маневрировании аппарата на околоземной орбите.
К внешним нагрузкам, действующим на БКК, можно отнести аэродинамические нагрузки, связанные с наличием остатков атмосферы на низких орбитах; градиенты гравитационных сил; солнечный ветер; световое давление; удары микрометеоритов. Несмотря на относительную малость величин сил и моментов, создаваемых этими внешними воздействиями, они оказывают существенное влияние на стабилизацию положения конструкции, т. е. на ее функциональную пригодность. Если при проектировании традиционных относительно жестких космических аппаратов влиянием этих видов внешних воздействий на нагруженность конструкции, как правило, можно пренебречь, то для крупногабаритных космических конструкций, в силу их размеров и малой жесткости, эти воздействия оказывают существенное влияние на внутреннее напряженное состояние и деформации. Отметим, что в силу того, что природа перечисленных внешних воздействий различна, то и значения их различны для разных высот орбит, разных участков траектории полета и существенно зависят от размеров и формы конструкции.
Рассмотрим каждое из перечисленных внешних воздействий.
Аэродинамические нагрузки. На высотах полета более 150 км в верхних слоях атмосферы Земли требуется учитывать взаимодействие элементов БКК с потоком свободных молекул газа. Приближенное значение величины аэродинамической силы F®, действующей на БКК, можно вычислить по следующей формуле:
Fxa = CaxqS, q=^pv2,	(1.1)
БКК И ЗАДАЧИ МЕХАНИКИ
23
где — коэффициент лобового сопротивления конструкции, который зависит от формы БКК, расположения ее элементов и ориентации самой конструкции относительно направления набегающего потока; q — величина скоростного напора; р — плотность газа; v — скорость набегающего потока; S — эффективная площадь сечения конструкции в плоскости, перпендикулярной направлению вектора скорости. При несовпадении центра аэродинамического давления с центром масс конструкции аэродинамическая сила сопротивления, обусловленная столкновением свободных молекул газа с элементами БКК, приводит к возникновению аэродинамического момента, стремящегося изменить ориентацию конструкции в пространстве. Величина аэродинамического момента М“ может быть вычислена по приближенной формуле:
M°=C£,qS,	(1.2)
где — коэффициент аэродинамического момента. Величины коэффициентов аэродинамических сил и момента зависят от геометрических параметров и конфигурации космического аппарата, а также от характера взаимодействия свободных молекул газа с твердой поверхностью элементов БКК- Кроме того, на величины аэродинамических сил и моментов оказывают влияние такие факторы, как различные значения плотности атмосферы около различных участков конструкции и наличие собственных тепловых скоростей молекул газа. Если вторым фактором в принципе можно пренебречь, то для протяженных в направлении градиента гравитационных сил конструкций, неоднородность плотности по высоте может оказать существенное влияние. Зависимость плотности воздуха от высоты полета h над поверхностью Земли можно получить из следующей формулы:
(h	\
I 
J ^7 (У) I о	/
где д, Т, ро,То — молекулярная масса воздуха и его абсолютная кинетическая температура на высоте h и у поверхности Земли соответственно; д — ускорение силы тяжести; 3? — универсальная газовая постоянная. Изменение р и Т по высоте зависит от множества геофизических факторов и активности Солнца, чем обусловлена цикличность изменения этих параметров. Для практических расчетов используются приближенные модели атмосферы, учитывающие суточные изменения плотности, Циклы солнечной активности, геомагнитную активность и множество
• других факторов [2].
24
ГЛАВА 1
При получении оценок величин аэродинамических сил и моментов используются различные приближенные теории обтекания тела в разреженной космической среде. Приведем формулу, которая для высот полета от 130 км до 600 км дает погрешность порядка 10% [117],
С“ = 2
9
1 + ,(1 о
(1.3)
Здесь е — коэффициент зеркальности; v — коэффициент упругости отражения молекул газа от твердой поверхности. При абсолютно упругом (е — 1, и — 1) и абсолютно неупругом {у — 0) взаимодействии формула (1.3) дает значение коэффициента сопротивления = 2. Это значение коэффициента как правило используется для получения предварительных оценок величин аэродинамических сил на первоначальном этапе проектирования БКК. Оценка коэффициента аэродинамического момента в этом случае имеет вид:
Сат = с°Уа,
(1.4)
где уа — величина расстояния проекции центра давления аппарата от проекции центра масс на плоскости перпендикулярной вектору скорости набегающего потока.
Световое давление. БКК, движущаяся по околоземной орбите, освещается солнечным светом, который оказывает давление на ее элементы. Это явление, экспериментально открытое и исследованное выдающимся физиком П. Н. Лебедевым (1900), представляет собой давление, оказываемое электромагнитным излучением на тела, которые поглощают или отражают излучение. Солнце, освещающее БКК на орбите, является мощным источником электромагнитного излучения. Видимая часть спектра солнечного излучения обуславливает световое давление. Давление изотропного равновесного излучения на систему, с которой оно находится в состоянии термодинамического равновесия, равно р0 = <тТ4/3, где а — постоянная Стефана — Больцмана, Т — абсолютная температура. Вблизи земной орбиты средняя величина солнечного давления равна 0,45 • 10“5 Н/м2 [92] на поверхности, перпендикулярной солнечным лучам. Величина солнечного давления при условии полного поглощения энергии может быть вычислена по формуле [110]:
2
Рс = Ро
Но \ "й J
(1.5)
БКК И ЗАДАЧИ МЕХАНИКИ
25
где Ro — средний радиус орбиты Земли, R — расстояние космического аппарата от Солнца. Величина силы солнечного давления вычисляется следующим образом:
Fc = kcpcS,	(1.6)
где кс — коэффициент, характеризующий отражательную способность БКК. Значение коэффициента кс лежит в диапазоне от 1,0 до 1,44. Величина момента солнечного давления вычисляется по формуле:
Мс — Fcyc,
где ус — расстояние от центра масс до центра светового давления. При эксплуатации БКК величины сил и моментов, обусловленных световым давлением, существенно зависят от непрерывно изменяющейся ориентации аппарата по отношению к Солнцу. Немаловажным фактором также является процесс входа и выхода из тени Земли при движении БКК на низких орбитах. Подробное описание воздействий светового давления на искусственные спутники Земли можно найти в [2].
Гравитационные нагрузки. Гравитационные нагрузки оказывают существенное влияние на компоновку БКК, т. к. возникающий гравитационный момент, обусловленный распределением массы в конструкции и ее ориентацией относительно Земли, стремится развернуть БКК в определенное положение, которое может не соответствовать необходимой ориентации аппарата в пространстве, связанной с его функциональным назначением. Природа возникновения гравитационного момента обусловлена взаимодействием БКК с гравитационным полем Земли. Постоянно действующий гравитационный момент является возмущающим фактором, влияющим на динамические характеристики БКК как объекта управления. При вычислении гравитационных сил и моментов предполагается, что гравитационное поле Земли является ньютоновским центральным полем сил, т. е. не учитывается сжатие Земли, а также неоднородность и неравномерность распределения ее массы. Гравитационный потенциал Земли определяется формулой:
и=-,	(1.7)
Г
где rj = уМ — геоцентрическая гравитационная постоянная, равная 3,98602 • 1014 м3/с2 (7 = 6,672 • Ю-11 Н • м2/кг2 — гравитационная постоянная, М — масса Земли), г — расстояние до центра масс Земли.
26
ГЛАВА 1
Для вычисления величины гравитационного момента рассмотрим элементарную массу dm космической конструкции. Гравитационная сила, действующая на массу dm, определяется по формуле:
dFg = ~rdm,	(1.8)
где г — радиус-вектор, определяющий положение выделенного объема относительно центра масс Земли. Гравитационный момент относительно центра масс, порожденный приложенной к выделенному объему силой равен:
dMg = р х dFg = — (р х dm,	(Г9)
а полное значение момента вычисляется интегрированием по всему объему конструкции:
М5 = у rfMg = - У (рх ^rjdm,	(1.10)
V	V
где р — вектор с началом в центре масс, оканчивающийся в элементе dm. При вычислении величины гравитационного момента для реальных конструкций формула (1.10) весьма мало пригодна ввиду громоздкости необходимых вычислений. Однако если ввести в рассмотрение тензор инерции конструкции J, то при выборе связанной системы координат, в которой оси направлены вдоль главных центральных осей инерции БКК, тензор инерции приобретает диагональный вид с диагональными членами •71, Л, Л- Величина гравитационного момента Мд зависит от ориентации связанной с БКК системы координат по отношению к абсолютной системе координат, начало которой расположено в центре масс Земли. Для задания ориентации связанной системы координат по отношению к абсолютной можно воспользоваться углами Эйлера , #2, #з [63]. Тогда можно показать, что величина гравитационного момента, действующего на БКК, для малых угловых отклонений может быть вычислена по приближенной формуле:
Мэ =	( - А)^1з] • (1.11)
где i2, i.3 — единичные векторы, направленные1 вдоль осей связанной системы координат. Формула (1.11) позволяет провести предварительный
БКК И ЗАДАЧИ МЕХАНИКИ
27
анализ устойчивости БКК на начальном этапе проектирования [3]. Допустим, что конструкция обладает осевой симметрией и Д = J3, Д / J2. Пренебрегая малыми второго порядка и полагая — 02 = 0, получим:
м3 = ^(л-л)^з,
т. е. при J2 > Л продольная ось БКК будет разворачиваться под действием гравитационного момента в направлении местной вертикали.
Величина гравитационной силы земного притяжения с учетом (1.7) может быть вычислена следующим образом:
Fg = -f ^(p + r)dm,	(1.12)
V
где р — вектор, характеризующий расстояние от элемента конструкции dm до центра масс. В формуле (1.12) г — вектор, соединяющий начало абсолютной системы координат с центром масс конструкции. Для спутников, размеры которых относительно невелики, разницей величины гравитационного потенциала для различных элементов конструкции можно пренебречь. Однако для БКК этот эффект может иметь существенное значение, приводя к возникновению дополнительных напряжений в конструкционных элементах аппарата.
Взаимодействие с электромагнитным полем. Измерения геомагнитного поля показали, что в среднем оно близко к полю простого магнитного диполя, расположенного в центре Земли, с осью, наклоненной к оси вращения примерно на 11 градусов [97]. Однако это поле весьма неоднородно ввиду наличия крупномасштабных и мелкомасштабных аномалий (например, Курская магнитная аномалия), взаимодействия с солнечным ветром — высокоскоростным потоком солнечной плазмы. Кроме того, магнитное поле Земли непостоянно, т. к. в ионосфере и выше текут электрические токи, создающие дополнительную переменную компоненту поля. При движении БКК по околоземной орбите происходит взаимодействие его магнитного поля и магнитного поля Земли. Оценить величину возникающего вращающего магнитного момента можно по следующей формуле:
=dh х В,	(1.13)
где d/j — вектор эквивалентного магнитного диполя БКК, В — век-гор индукции геомагнитного поля. Дипольный магнитный момент Земли d = 8,06 • 109 Тл • м3. В конструктивно-силовой схеме БКК могут использоваться ферромагнитные материалы, которые могут иметь начальную
28
ГЛАВА 1
собственную намагниченность, либо намагничиваться в процессе взаимодействия с геомагнитным полем. Кроме того, функционирование БКК может быть сопряжено с протеканием электрических токов в приборах и сервомеханизмах. Все эти аспекты объясняют причину электромагнитного взаимодействия БКК с геомагнитным полем. Величина и направление вектора эквивалентного магнитного диполя может быть вычислена для каждой конкретной БКК-
Движение БКК по орбите Земли часто сопряжено с вращением БКК относительно некоторой оси. Если конструктивно-силовая схема БКК выполнена из токопроводящего материала, то в геомагнитном поле в ней возникают вихревые токи, которые создают момент М^, противодействующий вращению и уменьшающий кинетический момент БКК. Для оценки этого момента токопроводящие элементы БКК приближенно моделируют замкнутым круговым контуром. Геометрия контура такова, что создаваемый им момент может иметь составляющую, перпендикулярную кинетическому моменту БКК, и вызвать ее прецессию. Тормозящий момент вихревого тока может быть описан с помощью формулы:
Mb = -kbBfa,	(1.14)
где kb — коэффициент, зависящий от геометрии БКК и свойств токопроводящего материала, Во — составляющая вектора геомагнитной индукции, нормальная к оси вращения, о? — вектор угловой скорости вращения БКК. Заметим, что В является функцией времени в связи с изменением параметров орбиты БКК, геомагнитными аномалиями, вращением магнитного поля Земли.
В ферромагнитных материалах, используемых в БКК, также имеются потери магнитной энергии вследствие гистерезиса. Эти потери также способствуют торможению БКК. Однако создаваемые ими магнитные тормозные моменты несравнимо меньше моментов, создаваемых вихревыми токами.
Удары метеоритных частиц. Одним из важнейших источников возникновения сил и моментов, действующих на БКК, может быть попадание микрометеорных частиц в аппарат. В настоящее время нет достоверных источников, позволяющих характеризовать величину этого взаимодействия. Опыт эксплуатации современной космической техники показывает, что возмущающие факторы, возникающие вследствие попадания метеорных частиц в космические аппараты, весьма малы, и ими можно пренебречь. При оценке надежности функционирования БКК, тем не менее, должна учитываться вероятность попадания крупных метеоритов в аппарат, влекущая разрушение его элементов. Причем вероятность попадания метеоритов растет с увеличением геометрических размеров конструкции.
БКК И ЗАДАЧИ МЕХАНИКИ
29
Реактивные двигатели. Силы и моменты, действующие на БКК, могут возникать в результате работы реактивных двигателей системы разгона, ориентации и стабилизации. Газовая струя, истекающая из реактивного двигателя, действует на БКК с силой
Fr = CVeff> С = -^,	(1.15)
at
где С — массовый расход газа за единицу времени, Veff — эффективная скорость истечения. Если линия действия вектора реактивной тяги не проходит через центр масс БКК, а находится на расстоянии Z, то возникает дополнительный момент, величина которого равна
Mr =lx Fr.	(1.16)
При выполнении орбитальных маневров вектор тяги реактивного двигателя должен проходить через центр масс БКК. Однако вследствие неточности изготовления конструкционных элементов, погрешностей монтажа, смещения центра масс и по другим причинам возможно отклонение линии действия тяги от расчетного направления, что приводит к возникновению момента силы, раскручивающего БКК- Этот фактор является существенным при выполнении орбитальных маневров крупногабаритной конструкции ввиду того, что в силу своих размеров и относительно малой жесткости при работе реактивного двигателя происходит деформация конструкции. Поэтому выбору места расположения разгонных двигателей и двигателей ориентации придается особое значение. Так, для выполнения разгона БКК двигатель следует располагать в том месте конструкции, которое менее всего деформируется в результате действия силы тяги и момента, создаваемых струей реактивного двигателя. Двигатели системы ориентации и стабилизации с целью уменьшения потребной тяги, величина которой связана с расходом топлива, следует располагать на возможно большем удалении от центра масс БКК.
Движущиеся массы. При выполнении научных и прикладных задач на околоземной орбите к точности ориентации БКК предъявляются очень высокие требования. Как правило, для ориентации БКК используется инерциальная система отсчета, например, связанная со звездами. Требования к точности ориентации могут лежать в диапазоне от нескольких градусов до сотых долей градуса. При выполнении орбитальных маневров, таких как разгон и торможение, также предъявляются высокие требования к точности ориентации БКК- Если переориентация БКК или другие маневры выполняются с использованием реактивных двигателей, то система должна определять положение центра масс аппарата. Так,
30
ГЛАВА 1
например, если при разгоне БКК направление вектора тяги реактивного двигателя не проходит через центр масс, кроме разгона при работе двигателя возникает и вращательное движение. Для изменения направления вектора тяги двигателя используется карданный подвес. Маневрирование с использованием поворотного сопла реактивного двигателя эффективно, если конструкцию спутника можно считать абсолютно твердым телом. Однако для БКК это предположение не справедливо. Жесткость крупногабаритных конструкций весьма низкая и может проявиться заметное влияние внутренних моментов, возникающих в результате деформации и изменения взаимного положения отдельных частей аппарата. Дефор-мативность БКК при неудачном расположении реактивных двигателей может привести к динамической форме потери устойчивости. Вследствие изменения направления вектора тяги реактивного двигателя при деформации конструкции могут возникнуть незатухающие колебания, которые ведут к разрушению аппарата. Кроме того, причиной возникновения внутренних моментов в БКК может служить перемещение ее частей, таких как антенны, научная аппаратура, вращающиеся элементы, перемещающаяся по трубопроводам жидкость, движение членов экипажа для пилотируемых аппаратов.
Для решения задач ориентации БКК можно также использовать перемещения отдельных массивных элементов конструкции или устанавливать массивные вращающиеся элементы, не изменяющие моменты инерции аппарата и положение его центра тяжести.
Выражение для внутреннего момента имеет весьма громоздкий вид [3] даже для упрощенной модели аппарата, которая предполагает, что имеется жесткая связь между недеформируемым корпусом и носимыми элементами. В уравнениях, описывающих пространственное движение БКК, добавляются члены, обусловленные изменением тензора инерции при смещениях масс и изменении конфигурации аппарата, что приводит к возникновению дополнительных сил, деформирующих конструкцию аппарата.
Тепловые воздействия. Одним из важнейших внешних факторов, создающих поле внутренних напряжений конструкции является ее нагрев. Чередование затемненных и освещенных Солнцем участков траектории при орбитальном движении конструкции, вращение конструкции вокруг своей оси приводит к непрерывному изменению температурного режима элементов БКК. Любые материалы, из которых изготовляются элементы БКК, нагреваются под действием солнечного излучения, что приводит к возникновению тепловых деформаций, искажению формы БКК, появлению поля внутренних напряжений. Нестационарное тепловое поле, обусловленное движением БКК и изменением условий освещенности, медленно изменяется ввиду слабого теплового излучения элементами
БКК И ЗАДАЧИ МЕХАНИКИ
31
конструкции аппарата, относительно малыми тепловыми потоками, возникающими за счет теплопроводности.
При создании конструкции космических аппаратов часто используются металлы. Температура металлических элементов конструкции, подверженных солнечному облучению, при неизменных условиях этого облучения принимает некоторое стационарное значение, зависящее от формы, теплопроводности и излучательных характеристик поверхности этих элементов. Существование стационарного температурного режима обусловлено тем, что радиационные потери тепловой энергии нагретого тела растут с ростом его температуры и, естественно, ограничены величиной потока энергии, поступающей к телу от Солнца. Равенство излучаемой и поглощаемой телом энергии и является условием, позволяющим определить стационарный тепловой режим тела. Но само по себе определение стационарного теплового режима еще не достаточно для понимания реальных процессов нагрева конструкции. Необходимо также определить условия его реализации, а это, в свою очередь, требует ответа на вопросы — можно ли пользоваться равновесными излучательными характеристиками элементов конструкции при нагреве их Солнцем, при каких условиях температурное поле может считаться однородным, как быстро устанавливается стационарная температура, как соотносятся интенсивности теплопереноса излучением и теплопроводностью конструкционного материала? Обсуждению этих вопросов будет посвящен один из следующих параграфов.
Предварительные напряжения. Тепловые воздействия, связанные с солнечным излучением, приводят к возникновению тепловых деформаций элементов БКК. При определенном выборе конструктивносиловой схемы каркаса и нагреве конструкционных элементов возможно возникновение внутренних напряжений, величина которых существенно зависит от используемого конструкционного материала, его коэффициента теплового расширения, качества обработки поверхности, коэффициента теплопроводности и т. д. Кроме того, компоновка каркаса БКК может допускать такое расположение и сочленение элементов конструкции, при котором возникновение деформаций в одном из узлов аппарата приводит к возникновению дополнительных внутренних напряжений в остальных элементах конструктивно-силовой схемы. Наглядным примером могут служить статически неопределимые стержневые конструкции. Поле внутренних усилий и напряжений, возникающее в силовых элементах БКК, может изменяться по мере изменения условий освещенности, г. е. при орбитальном движении аппарата и его переориентации. Поле напряжений, создаваемое тепловыми воздействиями, может накладываться на поле предварительных напряжений, специально созданное в конструкции на этапе ее сборки. Если в конструкции силового каркаса
32
ГЛАВА 1
БКК используются элементы, хорошо воспринимающие растягивающие усилия, но не достаточно хорошо работающие на сжатие (тонкостенные протяженные трубчатые элементы), либо элементы, совсем не воспринимающие сжимающих усилий — ванты, то при проектировании БКК учтя все внешние силовые воздействия, приводящие к возникновению внутренних напряжений в элементах конструкции, можно создать такое распределение предварительных напряжений, которое заведомо при деформациях каркаса БКК не приведет к потере устойчивости сжатых элементов или провисанию вант. Однако заметим, что БКК — свободные механические системы, в которых система внутренних усилий должна быть самоуравновешенной. Это значит, что усилия, которые специально создаются в растянутых силовых элементах, должны уравновешиваться системой усилий в сжатых элементах. Кроме того, предварительные напряжения в конструкции оказывают некоторое влияние на динамические характеристики БКК, что необходимо учитывать при разработке систем управления, ориентации и стабилизации.
Нагрузки, возникающие при монтаже БКК. Одним из наиболее ответственных этапов при создании крупногабаритных космических конструкций является доставка на околоземную орбиту конструкции в целом или ее элементов для последующей сборки. Как правило, размер контейнера, в котором располагается полезная нагрузка ракеты носителя, весьма ограничен и не допускает возможности размещения крупногабаритных элементов, составляющих основу каркаса БКК- Поэтому конструкционные элементы должны доставляться либо раздельно с последующей сборкой на орбите, либо в упакованном виде, допускающем трансформацию конструкции из сложенного состояния в развернутое.
При проектировании БКК, собираемых из отдельных частей, раздельно доставляемых на орбиту, необходимо учитывать ударные нагрузки^ которые неизбежно возникают при монтаже на орбите или при стыковке отдельных фрагментов аппарата.
Особый класс БКК образуют так называемые трансформируемые конструкции, т. е. конструкции, схема которых допускает автоматиче-' ское изменение конфигурации. Конструкции такого типа доставляются на околоземную орбиту в сложенном упакованном состоянии. При достижении необходимых параметров рабочей орбиты осуществляется раскрытие конструкции, или ее трансформация. Размеры трансформируемой конструкции в сложенном и развернутом состоянии могут отличаться в десятки раз. Очевидно, что конструктивная схема трансформируемой конструкции содержит в себе множество элементов, соединенных цилиндрическими и сферическими шарнирами, которые устанавливаются на замки, т. е. жестко фиксируются по завершении процесса трансформации. Сама процедура развертывания конструкции происходит под воздействием силовых приводов, в качестве которых могут использоваться
БКК И ЗАДАЧИ МЕХАНИКИ
33
сжатые или растянутые пружины, электродвигатели и т. д. Поскольку при изготовлении шарнирных соединений и элементов конструкции существует технологический разброс размеров, при трансформации конструкции замковые соединения могут сработать не одновременно, каждое срабатывание замка — это дополнительные динамические нагрузки на конструктивные элементы, то при проектировании трансформируемых БКК необходимо учитывать возникающие при трансформации нагрузки, которые носят ударный характер. Кроме того, для обеспечения заданной точности конфигурации БКК и ее жесткости необходимо выбрать зазоры в шарнирных соединений. Это может быть достигнуто либо использованием замков специальной конструкции, либо искусственным созданием поля предварительных напряжений в силовой схеме каркаса БКК-
1.2. МАТЕРИАЛЫ, ИСПОЛЬЗУЕМЫЕ ПРИ СОЗДАНИИ БКК
К разрабатываемым крупногабаритным космическим конструкциям в силу их функционального назначения и высокой стоимости, определяемой как требованиями к статическим и динамическим характеристикам, так и условиями транспортировки элементов БКК на околоземную орбиту и сборки элементов в единое целое, предъявляются повышенные требования к их жесткости, прочности и долговечности. Если БКК обслуживается и управляется людьми, то в числе наиболее важных требований включается обеспечение безопасности и надежности. Наряду с традиционными требованиями
БКК должны удовлетворять специфическим для протяженных и незакрепленных конструкций повышенным требованиям к жесткости. Это относится и к конструкциям больших космических телескопов, используемых для наблюдения звезд, и к конструкциям больших космических антенн, применяемых для земного мониторинга, и к протяженным конструкциям солнечных батарей, точно ориентируемым в космосе.
Для удовлетворения указанным требованиям необходимы теоретическая и конструкторская проработка общих концепций компоновки БКК, тщательный анализ эффектов воздействия внешних и внутренних нагрузок, точный анализ механического поведения элементов и конструкции в целом, а также разработка рационального проекта конструкции с наилучшим использованием свойств конструкционных материалов. Имеющийся опыт разработки конструктивно-силовых схем летательных аппаратов подтверждает исключительную важность рационального выбора материалов для создаваемых конструкций.
Отметим, что при выборе материалов, которые следует использовать для создания БКК, необходимо учитывать весьма специфические условия эксплуатации конструкции в космосе, воздействие различного вида нагрузок и требования, предъявляемые к режимам функционирования.
2 - 2185
34
ГЛАВА 1
Особенно важны требования, относящиеся к стойкости материала и отсутствию деградации его механических свойств в условиях эксплуатации в космосе и, в частности, к неразрушаемости структуры материала под действием солнечной радиации.
К выбору конструкционных материалов, используемых при создании БКК, предъявляются весьма специфические требования. Эти требования могут быть объединены в различные группы, определяющие выбор того или иного материала. Одна группа требований относится к стойкости материала в условиях космоса, неизменности его механических характеристик в процессе эксплуатации, неразруШаемости поверхностного слоя материала, находящегося под непосредственным воздействием солнечного излучения. Другая группа требований включает в себя традиционные условия на механические характеристики конструкционных материалов, которые учитываются при проектировании летательных аппаратов. Это прежде всего требования, накладываемые на такие приведенные характеристики, как удельные константы прочности и модуль Юнга, отнесенные к плотности материала, ресурсные ограничения, учитываемые при циклических нагружениях. В эту группу включаются также и требования технологичности обработки материала.
Специфика БКК порождает особые требования, которым должны удовлетворять конструкционные материалы. Так, например, для обеспечения высокой точности рабочих поверхностей БКК при нестационарных воздействиях требуется наличие активных и пассивных систем демпфирования колебаний, снижающих амплитуду деформаций силового каркаса аппарата. К пассивным средствам демпфирования можно отнести как специальные устройства, поглощающие энергию механических колебаний, так и использование конструкционных материалов, рассеивающих энергию в процессе деформирования.
Говоря о конструкционных материалах, которые могут быть использованы при создании БКК, следует отметить, что параллельно с проектированием конструкции могут разрабатываться и материалы, обладающие некоторыми заданными свойствами, которые могут эффективно использоваться при изготовлении отдельных элементов аппарата. Прежде всего это относится к композиционным материалам, механические и тепловые характеристики которых варьируются в достаточно широких пределах. Применение таких специализированных материалов может привести к снижению массы конструкции, уменьшению ее стоимости и улучшению ее механических параметров, таких как жесткость и прочность.
Выбор конкретного конструкционного материала для изготовления того или иного элемента конструкции является весьма сложной задачей, поскольку требования, предъявляемые к конструкционному материалу,
БКК И ЗАДАЧИ МЕХАНИКИ
35
часто являются противоречивыми. Сравнение материалов и оценка возможности применения того или иного материала производится на основании анализа некоторых основных характеристик материалов, таких как параметры, характеризующие прочностные и жесткостные свойства, тепловые и электропроводные характеристики, технологичность в обработке. Остановимся на некоторых аспектах, определяющих выбор конструкционных материалов.
Традиции проектирования космической техники тесно связаны с традициями проектирования авиационной техники. Поэтому конструкционные материалы, применяющиеся в самолетостроении, достаточно широко используются и при создании космической техники. Как правило, в самолетостроении для изготовления силовых конструкционных элементов применяются металлы. Прежде всего это сплавы на основе алюминия и титана, высокопрочные стали, магниевые сплавы. Неметаллические и, в частности, композиционные материалы применяются значительно реже. Приведем таблицу 1.1, в которой содержатся некоторые характеристики основных конструкционных материалов. В таблице 1.1 Е — модуль Юнга, сгв — предел прочности, р — плотность материала, а — коэффициент теплового расширения.
Таблица 1.1
Материал	Е (ГПа)	<Тв (ГПа)	а -10® (1/°С)	р  ю-3 (кг/м3)	Е/р (Х1О“6)	оъ!р (Х1О~4)
Алюминиевые сплавы	72,0	0,42	20,0	2,8	2,5	1,5
Титановые сплавы	120,0	1,0	8,5	4,5	2,7	2,2
Стали	210,0	1,2	11,0	7,8	2,7	1,5
Магниевые сплавы	42,0	0,28	27,0	1,7	2,5	1,6
Бериллиевые сплавы	310,0	0,6	—	1,8	17,2	3,3
Используемые для создания элементов БКК материалы должны в рамках выбранной конструктивно-силовой схемы обеспечить максимально возможную стабильность геометрических параметров конструкции при действии внешних и внутренних силовых факторов. Действительно, при проведении прецизионных измерений необходимо точно ориентировать БКК в пространстве. Классические методы ориентирования по звездам применительно к БКК имеют некоторую специфику. Астродатчики могут
2*
36
ГЛАВА 1
располагаться в разных частях конструкции и каждый из них определяет пространственную ориентацию того участка конструкции в котором он расположен. Так как крупногабаритные конструкции в силу своих размеров могут значительно деформироваться, то неизбежно возникает неопределенность в ориентации аппарата. Следовательно, материалы, из которых изготовляются основные силовые элементы, должны обладать повышенной жесткостью. Для изготовления основных силовых элементов каркаса БКК должны применяться высокомодульные сплавы металлов или композиционные материалы. Ввиду того, что срок эксплуатации БКК предполагается весьма продолжительным, используемые материалы не должны иметь скрытых внутренних дефектов, таких как трещины и поры, не должны разрушаться под действием длительного солнечного облучения. В то же время применяемые материалы должны хорошо выдерживать высокие и низкие температуры, циклический нагрев и охлаждение. Кроме того, при движении БКК по околоземной орбите существенно изменяются условия воздействия космической среды на материалы. Изменяется интенсивность ультрафиолетового облучения, интенсивность воздействия заряженных частиц космических лучей, интенсивность облучения в рентгеновском диапазоне — все это существенно влияет на способность материалов сохранять свои первоначальные механические свойства. Ультрафиолетовое облучение способствует разрушению неметаллических компонентов материала, вакуум приводит к выделению газов и, как следствие, изменению размеров элементов, изготовленных из пористых материалов. Циклическое изменение температуры в широких пределах вызывает образование микротрещин. Атомарный кислород, присутствующий в космической среде, вызывает эрозию органических веществ. Наконец, микрометеориты фрагментарно разрушают структуру конструкционных материалов. Перечисленные воздействия особенно губительны для органических соединений, например эпоксидных смол, которые часто используются в качестве связующих в композиционных материалах, термопластичных материалов, смазок и покрытий на основе органических соединений, вязко-упругих материалов, которые используются для пассивного демпфирования механических колебаний.
Применение правильно подобранных конструкционных материалов для изготовления элементов БКК дает возможность прежде всего уменьшить массу конструкции при сохранении ее жескостных характеристик, что при весьма ограниченных возможностях ракет носителей доставлять на околоземную орбиту полезную нагрузку даст возможность размещать на БКК Дополнительное оборудование, сделать конструкцию более жесткой, т. е. способной меньше деформироваться при неблагоприятных динамических воздействиях, что в свою очередь может привести к снижению требований к системам управления точностью рабочих поверхностей.
БКК И ЗАДАЧИ МЕХАНИКИ
37
В последнее время при создании космических летательных аппаратов стали применяться сплавы на основе бериллия. Эти материалы очень легки и обладают уникальными характеристиками удельной жесткости, которая в несколько раз выше чем у сталей и традиционных металлических сплавов на основе титана и алюминия. Перспективность применения этой группы материалов при создании БККочевидна. Однако технологические сложности обработки бериллиевых сплавов тормозят широкое применение этих материалов для изготовления силовых элементов для БКК-
Традиционными материалами, используемыми для создания спутниковых систем, являются металлы и их сплавы. Металлические материалы достаточно хорошо изучены, подробно изучены их механические свойства, известна их способность переносить тяжелые условия длительного пребывания в условиях космического полета, отработана технология их обработки. Металлы и их сплавы широко применяются при создании космических аппаратов. Однако их применение при разработке крупногабаритных космических конструкций имеет некоторые особенности, которые следует отметить.
Прежде всего значительный перепад температур, который возникает при эксплуатации БКК, в силу большого коэффициента теплового расширения металлов может привести к заметному искажению геометрических характеристик силового каркаса, что является совершенно недопустимым при создании таких конструкций, как, например, крупногабаритные космические антенны. До некоторой степени смягчить проблему теплового деформирования конструкций удается применением термокомпенсаторов — специальных устройств, включаемых в силовую систему БКК, уменьшающих свой размер при нагреве как пассивно, так и с использованием активных систем. Однако введение термокомпенсаторов в конструкцию приводит к ее утяжелению, усложнению и удорожанию. Эффект, получаемый применением пассивных термокомпенсаторов, не всегда может оказаться удовлетворительным, а активные системы снижения деформации конструкции вследствие нагрева или охлаждения предполагают дополнительные затраты энергии. Кроме того, поскольку металлы — хорошие электрические проводники, при движении их в неоднородном магнитном поле могут возникать нежелательные силы и моменты, приводящие к изменению пространственной ориентации БКК-
Металлы — почти изотропные материалы, т. е. их механические, тепловые и прочие характеристики практически одинаковы во всех направлениях. Поскольку основу разрабатываемых конструктивно-силовых систем БКК составляют протяженные конструкционные элементы, работающие в условиях одноосного напряженного состояния, представляется нерациональным использование металлов и их сплавов для изготовления этих элементов конструкции.
38
ГЛАВА 1
Существует широкий класс конструкционных материалов, механические и тепловые свойства которых варьируются в широких пределах, допускающий целенаправленное изготовление материала для создания конкретного элемента конструкции в зависимости от условий его эксплуатации. Это — композиционные материалы.
Структура композиционных материалов образована матрицей, выполненной из относительно легкого материала с малыми пределом прочности и модулем упругости и высокопрочных армирующих волокон, концентрация которых и ориентация при укладке в основном и определяют уникальные механические характеристики композиционных материалов. В таблице 1.2 приведены некоторые основные характеристики наиболее распространенных композиционных материалов. Здесь приняты обозначения: Ei — модуль упругости вдоль волокон; Е2 — модуль упругости поперек волокон; — предел прочности при растяжении вдоль волокон; а2 — предел прочности при растяжении поперек волокон; сг3 — предел прочности при сжатии.
Таблица 1.2
Материал	Еь ГПа	#2, ГПа	G, ГПа	<71, ГПа	аг, ГПа	аз, ГПа	Р  Ю“3, (кг/м3)
Стеклопластик	57,0	9,0	5,2	1,75	0,034	0,65	2,1
Углепластик	180,0	6,2	5,0	1,1	0,033	0,45	1,5
Боропластик	210,0	19,0	6,2	1,6	0,065	2,4	2,0
Органопластик	72,0	4,9	2,0	1,8	0,028	0,28	1,38
Возможность создания композиционного материала с ярко выраженными анизотропными свойствами и рекордными прочностными и жесткостными характеристиками все более привлекает проектировщиков БКК. Широкие возможности по варьированию структуры укладки волокон в композиционном материале позволяет создавать элементы конструкции БКК с уникальными свойствами.
Так, например, в таблице 1.3 приведены значения коэффициента теплового расширения углепластика для разных значений температуры из рабочего диапазона температур эксплуатации БКК. Как видно из таблицы 1.3 значение коэффициента теплового расширения углепластика значительно ниже, чем у металлов, причем может принимать и отрицательные значения. Это уникальное свойство позволяет проектировать конструктивно-силовые схемы БКК, минимально деформирующиеся при изменении температурного режима и условий освещенности аппарата.
В настоящее время при проектировании БКК все чаще рассматриваются композиционные материалы на основе металлической матрицы.
БКК И ЗАДАЧИ МЕХАНИКИ
39
Таблица 1.3
t °C	а  106
-60 4- -40	5,8
-40 4- —20	2,8
-20 4-	0	0,32
0 4-40	-1,2
40 4- 80	“3,7
80 4- 120	-2,5
120 4- 140	-1,9
которые имеют ряд преимуществ по сравнению с композиционными материалами на основе органической матрицы. Такие материалы, как бор — алюминий, упрочненный волокнами титан, углерод—алюминий, имеют повышенную деградационную стойкость, сохраняют работоспособность до более высоких температур, устойчивы к атомарному кислороду, потерям газа, хорошо выдерживают циклический нагрев и охлаждение, радиационное облучение. В этих материалах наилучшим образом сочетаются достоинства металлических конструкционных материалов и композиционных материалов. Удельные характеристики композиционных материалов, такие как удельная прочность и удельная жесткость, за счет использования высокопрочных и высокомодульных волокон, несмотря на относительно низкие удельные характеристики матрицы, оказываются выше чем у металлических материалов, чем и объясняется привлекательность использования композиционных материалов при проектировании БКК-
Гетерогенная структура композиционных материалов, сочетание разномодульных компонентов в одной структуре объясняет высокую демпфирующую способность композиционных материалов, которая может достигать 15% в пассивном поглощении энергии. Это поглощение осуществляется за счет преобразования энергии механических колебаний в тепло за счет внутренних свойств деформирующегося конструкционного материала и использования специальных вязко-упругих поглотительных элементов.
Как видим, все разнообразие современных конструкционных материалов может найти применение при проектировании БКК. Технологичность металлов и уникальные жесткостные и тепловые свойства композиционных материалов, их разумное сочетание — все это позволит создавать дешевые, высокоэффективные БКК, удовлетворяющие требованиям своего функционального предназначения.
40
ГЛАВА 1
1.3. АНАЛИЗ ТЕМПЕРАТУР ЭЛЕМЕНТОВ БКК
Температура металлических тел, находящихся вне атмосферы и подверженных действию солнечного облучения при неизменных условиях этого облучения, принимает некоторое стационарное значение (или распределение) зависящее от формы, теплопроводности и излучательных характеристик поверхности этих тел. Существование стационарного температурного режима обусловленотем, что радиационные потери тепловой энергии нагретого тела растут с ростом его температуры и, естественно, ограничены величиной потока энергии, поступающей к телу от Солнца. Это равенство потоков излучаемой и поглощаемой телом энергии и является условием для определения стационарного температурного режима тела. Но само по себе определение стационарного режима еще недостаточно для понимания реальных процессов нагрева тел. Необходимо также определить условия его реализации, а это, в свою очередь, требует ответа на вопросы — можно ли пользоваться равновесными излучательными характеристиками металлических тел при нагреве их Солнцем, при каких условиях температурное поле может считаться однородным, как быстро устанавливается стационарная температура, как соотносятся интенсивности теплопереноса излучением и теплопроводностью в металле? Имея ясность по этим вопросам, можно быть уверенным, что найденные стационарные режимы действительно соответствуют телам, для которых они рассчитаны.
Как известно, излучательные характеристики материалов, особенно в оптическом диапазоне и для качества поверхности соответствующего реальным техническим объектам, не поддаются расчету и могут быть получены только экспериментальным путем. В таких экспериментах обеспечиваются условия, близкие к термодинамическому равновесию излучения с исследуемым веществом, и устраняются градиенты температуры внутри тела. Использование полученных таким образом излучательных характеристик в расчетах неравновесных, хотя и стационарных состояний металлических тел, требует своего обоснования. Если в поверхностном слое тела, в котором происходит поглощение энергии электромагнитной волны, градиент температуры достаточно мал, то, очевидно, не будет большой ошибки, если в расчете этого неравновесного процесса будут использованы экспериментальные (равновесные) излучательные характеристики поверхности. Но прежде чем сделать оценку градиента температуры в поверхностном слое металлического тела необходимо оценить толщину этого слоя.
Электромагнитная волна, достигнув поверхности металла, воздействует на электроны проводимости, индуцируя в нем ток. Порождаемое этим током электромагнитное поле воспринимается вне тела как отраженная
БКК И ЗАДАЧИ МЕХАНИКИ
41
волна, а внутри тела это поле суммируется с приходящим извне, ослабляя последнее, и порождая явление затухания напряженности поля (и тока) по глубине, известное как скин-эффект. Основную часть излучения Солнца составляет видимое излучение, которому соответствуют следующие диапазоны длин волн Xs и частот Xs = 0,38 х 10-6 4- 0,76 х 10“6 м, vs = 8 х Ю14 т4х 1014 сек"1.
Для высокочастотного нормального скин-эффекта толщина слоя поглощения [99] 6 = 5 х 10“7 м. Для получения верхней оценки перепада температуры в слое поглощения излучения будем полагать, что все тепловыделение происходит на поверхности тела, а вглубь тела теплота передается за счет теплопроводности. Тогда, по определению,
п dT
где Q — плотность теплового потока, Т — температура тела, х — глубина, х — теплопроводность. В данном случае Q ~ S = 1400 Вт/м2 — солнечная постоянная, Дж ~ J ~ 10“7 м, х ~ 102 Вт/(м х К), AT ~ SS/x ~ Ю-6оК. Градиент температуры в слое поглощения солнечного излучения:
dT dx
$
---10°К/м.
X
Таким образом, распределение температур в слое поглощения солнечного излучения близко к равновесному.
Оценка размеров тел, для которых температурное поле имеет заданное изменение. Рассмотрим некоторое тело, характерное сечение которого в плоскости перпендикулярной направлению солнечного излучения, имеет величину F. По разные стороны от этого сечения тело имеет различные абсолютные температуры Т\ и Т2. Характерный размер тела вдоль направления излучения равен I (рис. 1.1).
Составим приближенные уравнения энергетического баланса и теплопроводности:
FaT? + FaT? = SF,
FaT^ = FX^—^-,
(3.1)
42
ГЛАВА 1
где а — постоянная Стефана — Больцмана. Полагая в (3.1), что 71	72 гчу 71, 71 — 72 — Д7\ найдем
I =
Задавая изменение Д71 температурного поля в теле, можно получить оценку характерного размера I.
В таблице 1.4 приведены значения I для некоторых материалов (ДТ = 1°К).
Таблица 1.4
Материал	Коэффициент теплопроводности (вт/м-град)	Характерный размер (м)
Медь	386	0,5
Алюминий	193	0,3
Сталь	40	0,05
Титан	15	0,03
Таким образом, большинство типичных металлических конструкционных элементов БКК можно считать находящимися при однородном распределении температуры.
Определение мощностей поглощения и излучения тепла телом с однородным полем температуры. Мощность поглощения телом теплового излучения Солнца равна: оо	оо
Wn = У axoJx cos a dX dF — Qs J* cosct J* a\aIx dXdF, (3.2) Fn 0.	Fn 0
где 7д — средняя спектральная интенсивность излучения Солнца, Qs — телесный угол, в котором виден солнечный диск с орбиты, Fn — поверхность тела, поглощающая солнечное излучение, а — угол между нормалью к Fn и направлением на Солнце (угол падения), ада — спектральная угловая поглощательная способность поверхности. Преобразуем внутренний интеграл в (3 2):
БКК И ЗАДАЧИ МЕХАНИКИ
43
где рха — спектральная угловая отражательная способность поверхности, — интегральная угловая отражательная способность поверхности для излучения Солнца. Следовательно,
jyn = у (1 - psa) cos adF =S j (1 - psa) cos a dF, Fn	Fn
(3.3)
где S — солнечная постоянная. Для металлических поверхностей с размером шероховатости h < А, что для видимого излучения соответствует 8— 14 классам чистоты обработки, согласно [77] экспериментально установлена следующая зависимость:
s _ / Рп>
- I pi < ri < 1,
Рис. 1.2
a € [0,7г/6], a € [тг/6,7г/2],
где р„ — интегральная нормальная от-
ражательная способность поверхности. На основании этих данных построим приближенную аналитическую зависимость (см. рис. 1.2):
1-Pa = (1-Pn)cos2a.	(3.4)
Используя эту зависимость в (3.3), окончательно получим:
Wn = S(1 - р„) j cos3 adF. Fn
(3.5)
Мощность теплового излучения, испускаемого телом, равна:
Wu
ОО 27Г
Ей О О
cos /3 dQ dX dF = eaT4
dF,
(3.6)
Fn
где lx — спектральная интенсивность излучения абсолютно черного тела с той же температурой, dtt — телесный угол в окрестности направления /3 от нормали к поверхности, Ги — излучающая поверхность тела, £хр — спектральная угловая излучательная способность поверхности, s — интегральная полусферическая излучательная способность поверхности, Т — абсолютная температура тела, а — постоянная Стефана — Больцмана (<т — 5,67 • 10“8 Вт/(м2К4)).
44
ГЛАВА 1
Следует отметить, что для входящей в (3.5) интегральной нормальной отражательной способности поверхности тела для излучения Солнца (р£), ее зависимость от температуры тела не учитывается. Это объясняется тем, что реально наблюдаемые температуры тел на орбите Земли, по крайней мере, на порядок ниже характерной температуры излучения Солнца (6000 °К). Напротив, для входящей в (3.6) интегральной полусферической излучательной способности поверхности тела е учитывается ее зависимость от температуры тела. Эта зависимость определяется как материалом тела, так и состоянием его поверхности. Несмотря на обилие теоретических кривых, достоверные данные о зависимости s(T) для конкретных условий могут быть получены пока только экспериментально. Значение (р^) также получается из эксперимента. В качестве хорошего приближения к (р^) можно использовать рдп для А = 0,46 х 10-6 м, Т ~ 500°К. Сведения, касающиеся определения рдп и е(Т), можно почерпнуть из [51], где также приведено большое количество экспериментальных данных.
Стационарная температура тел, находящихся под действием солнечного излучения. Условием для определения стационарной температуры тела является равенство мощностей излучения и поглощения тепла телом, т. е.

(37)
Подстановка (3.5) и (3.6) в (3.7) приводит к следующему уравнению для стационарной температуры тела:
е(Т)аТ4
Fvt
dF = S(i-psn) j cos3 adF, Fn
которое можно записать в виде:
е(Т)74 =	(3.8)
а
где
L cos3 adF j__ J rn________
fF dF ’	.
J ги
Вычислим множитель J для некоторых простых форм конструкционных элементов (при этом введем векторы: S — направление на Солнце, i — ось элемента, п — нормаль к поверхности элемента):
БКК И ЗАДАЧИ МЕХАНИКИ
45
а)	стержень круглого сечения (рис. 1.3)
_ 2 sin3 ps
Зтг
б)	стержень квадратного сечения (ребром к Солнцу) (рис. 1.4)
_ sin3 /3S
4>/2
в)	стержень квадратного сечения (гранью к Солнцу) (рис. 1.5)
_ sin3 0S
4
г)	тонкая пластинка (рис. 1.6)
J — cos3 as 2
Рис. 1.5
После того, как для элемента будут также определены р„ и б(Т), уравнение (3.8) может быть решено аналитически или численно. Так, доя стержня круглого сечения (fts = л/2) из алюминиевого сплава (р„ = 0,7, s(T) = 8 х 105 • Т, см. [51J), уравнение (3.8) дает стационарную температуру Тс = 456аК.
46
ГЛАВА 1
Процесс установления стационарного режима тел с однородным полем температуры. На основании ранее полученных соотношений может быть составлено уравнение, описывающее процесс нагрева тела. Действительно, пусть сит — удельная теплоемкость и масса тела соответственно, тогда согласно первому началу термодинамики
cm AT =	— 1УиА/,
где Af — малый промежуток времени. Поделив это уравнение на А/ и перейдя к пределу А/ -> 0, получим дифференциальное уравнение процесса нагрева тела
стТ — 1Уп — IVh,
где точкой обозначено дифференцирование по времени. Подставляя сюда выражения для мощностей поглощения и излучения тепла телом (3.5) и (3.6), получим:
стТ + <те(Т)Т4 j dF = 5(1 - psn) j cos3 a dF, Fvi	Fn
или, в новых обозначениях
А= — [ dF, В= S^~p^ f cos3 adF, cm J	cm J
Fn	Fn
имеем
T + Ae(T)T4 = B.	(3.9)
Очевидно, что уравнение (3.9) имеет два интеграла:
В-Л£(Т)Т‘ = О,	=	(3.10)
Первый из них есть не что иное, как стационарная температура тела, уже найденная в предыдущем пункте, второй — действительно описывает процесс нагрева тела во времени. Согласно (3.10) время г нагрева тела от температуры То до стационарной температуры Тс равно
(3.11)
О То
Функция б(Т) для металлов в диапазоне температур Т = 0 4- 500° К не убывает [4], поэтому при Т -+ТС знаменатель (3.11) стремится к нулю как
БКК И ЗАДАЧИ МЕХАНИКИ
47
Тау где а > 1, и, следовательно, интеграл (3.11) расходится. Таким образом, время установления стационарной температуры тела бесконечно, а физический смысл имеет только интеграл следующего вида:
тс-дт
Г dT
=	5	(3.12)
J Ае(Т)Т4	v 7
То
определяемый как время нагрева тела от температуры Tq до температуры ниже стационарной на ДТ. Для стержня круглого сечения из алюминиевого сплава, при ДТ = 0,01 Тс, тд = 2,5 суток.
Стационарное распределение температуры внутри толстой пластины. Для оценки соотношения интенсивностей те-плопереноса излучением и теплопроводностью в толще металлической пластины выделим в этой пластине слой (рис. 1.7), толщина которого равна длине свободного пробега тепловых фотонов. Очевидно,
что эта длина равна толщине скин-слоя для теплового излучения внутри пластины. Согласно закону смещения Вина [98] АтахТ = 2,9 х 10-3 м • К, где Атах — длина волны, на которую приходится максимум спектральной плотности излучения тела с температурой Т, кроме того, толщин скин-слоя 6 ~ \/Х [99], поэтому если для Солнца Ts = 6000°К, 6s = 5 х 10”7 м, то для тела с температурой Т = 600°К: 6 «	= 15 х 10“7 м.
Плотность потока излучения тепла в J-слое за счет излучения равна
Сизл — 4aT3dT,
то же за счет теплопроводности,
Утепл — X j •
Для металлов (х ~ Ю2 Вт • м”1 • К"1) получим оценку:
Физ л _ 4crT,3J _Ю""7
фтепл X

QS
Рис. 1.7
6(Т2)<тТ*
поэтому для температур порядка 100°К перенос тепла излучением можно не учитывать.
48
ГЛАВА 1
Стационарные температуры г1\ и 72 поверхностей пластины определяются из уравнений энергетического баланса и теплопроводности:
б(7;)<тТ14 + е(Т2)<тТ4 = Q„
(3.13)
е(Т2)<тТ* = х
Т,-Т2 Н
где Qs = 5(1 - р„) cos3 as, Я — толщина пластины. Решение системы уравнений (3.13) позволяет определить стационарные температуры поверхностей толстых пластин, изготовленных из различных материалов и освещенных Солнцем под разными углами.
Стационарные температуры тонких пластин в пакете. Спектральная плотность потока потока тепла с первой пластины на вторую (с учетом многократных отражений излучения) может быть вычислена следующим образом (рис. 1.8):
Q}X-Q^X--pti^lxQ\x-p2XP\XP'2XOl\xQ\x—P2XplXP2XP\XP2>O,YxQ\x------
— Q?a[1 ‘ Р2Л«1л( 1 4- Р\ХР2Х 4- р\хР2Х + Р1АР*2А + •••)]“ _ ПО Л а1ЛР2Л \ — Чи X I J ~ ---------------------- 1 ?
\ I — P\Xp2Xj
Рис 1 8
где Q®x — спектральная плотность потока тепла с первой пластины в пустое полупространство, а бд, ад, рх — спектральные излучательная, поглощательная и отражательная способности пластин соответствен -но, являющиеся функциями температуры соответствующей пластины. Пластины непрозрачны, поэтому
рх = 1 - «д, а2Х
Q?a = aiA 4- а2д — а1да2д £1Аа2д
АСЛ), атд 4- а2д - а1да2л
где /д(71) — спектральная плотность потока излучения абсолютно черного тела при температуре Тр Согласно закону Кирхгофа в условиях
БКК И ЗАДАЧИ МЕХАНИКИ
49
равновесии!п теплообмена ад = €д, что при тепловых потоках порядка 5	1400 Вт/м2 имеет место для металлов. Тогда
С?!А - —— ----------------1х(7\) =
£1Л 4- &2Х — £1Д£2Л	£1ЛХ + £2Л - 1
Аналогично. для тепла, переносимого со второй пластины на первую,
получим оценку
Q1X —
1х(Т2)
£Га + £2А - 1 ’
Результирующий теплоперенос равен:
Qx — Q1X Qr2Xi со	ос
Q / Qx dX = I —:-——-----dX.
J { ^W+e^TJ-l
(3.14)
(лационарныс температуры пластин определяются из уравнений энергетического баланса:
ei(7i)<rt? + е2(Т2)<тТ? = Qs,
— Q(Ti,T2),
(3.15)
где Qs - 5( 1 -Рп ') cos3 <*s- Если спектр излучения материала пластин по-добей спектру абсолютно черного тела (как, например, у алюминия [51])-, (о можно избавиться от спектральных зависимостей в знаменателе (3.14):
£ix — £1,
-2Л = £?,
югда
Q -	. = еп^, Т2)(аТ4 - <т7’4),
£1 (11) + £2 (z2) “ 1
где
£п (71 > 7г) =	—7 >
£1 (11) 4-	(/г) — 1
и система уравнений (3.15) примет вид:
=QS, ^(Т2)Т^ =£п(Т2,Т2)(Т4 -7’4).
(3.16)
50
ГЛАВА 1
Стационарные температуры Т\ и Т2 пластин получаются путем решения системы (3.16). Для материала со слабо выраженной зависимостью е(Т) в некотором интервале температур (например, для меди [51] при Т = 373 4- 673/\, 8 — 0,03) решение (3.16) дает:
2ei — £162 + ^2	\
£1 (2^1 - £162 4- 25г)	/
/	1	Qs\1/4
\2б1 — £162 4" 2^2 & /
Если при этом имеется пакет из п пластин, изготовленных из одного материала, то £1 = 82 — • • • = е, £п = 8/(2 —8). Система уравнений энергетического баланса для п пластин строится аналогично случаю двух пластин
Qs = еаТ4 + е<тТ4, гпО’Т4 - еп^4 = ецагТ^ - ЕпоТ34,
еп^Л4-1 ~	= епо’Т* -
епо’Т4.! - еп<гТ4 = еп^Г4.
Отсюда температура к-ой пластины (считая от источника излучения) вычисляется по следующей формуле:
= f(n-k)(3-e)-(n-k-l)Qs\l/4
к \ (п - 1)(3 - б) - (п - 3)	8а)
Для металлов с гладкой поверхностью 8	1, поэтому
_ /2(n-fc) + iQs\1/4 к \ 2п 8а)
Для самой дальней от источника излучения пластины стационарная температура равна:
т -р ОЛ1'*
1п ~ I п I
\2п 8а /
В заключение отметим, что приведенный анализ справедлив только в тех случаях, когда температура нагретых металлических тел определяется
БКК И ЗАДАЧИ МЕХАНИКИ
51
только излучением и теплопроводностью. В тех случаях, когда в состав конструкции входят газонаполненные элементы или емкости с жидкостью, возникает необходимость в учете конвективного теплообмена между освещенной и затененной частью поверхности элемента конструкции.
1.4. ДВИЖЕНИЕ СВОБОДНОЙ УПРУГОЙ БКК
При исследовании движения и деформаций свободной упругой конструкции значительного упрощения уравнений движения можно добиться путем удачного выбора связанной с упругой БКК системы отсчета. Существует по крайней мере шесть [31,43,63] способов задания подвижной связанной системы координат. Иногда систему отсчета связывают жестко с каким-либо элементом конструкции [63]. Такой подход удобен, когда в качестве этого элемента выбран приборный отсек БКК, который можно условно считать недеформируемым. Условия выбора подвижной системы координат могут иметь нелинейный характер (например — система Тиссерана [43]), могут быть выражены дифференциальной зависимостью (такой подход был предложен В. Г. Вильке [31]). Ниже будет предложен один из способов выбора связанной системы координат — так называемой «средней» системы, или трехгранника Вейля [162]. Будет показано, что использование средней системы отсчета наиболее удобно при использовании метода конечных элементов для определения поля перемещений деформируемой конструкции. При использовании этой системы отсчета уравнения движения получены в виде системы обыкновенных дифференциальных уравнений, что позволяет использовать различные известные методы численного интегрирования подобных систем.
Рассмотрим произвольную деформируемую космическую конструкцию, занимающую в недеформированном состоянии область Q трехмерного пространства. В недеформированном состоянии свяжем с ней, как с твердым телом, систему координат	таким образом, что С —
центр масс недеформированной конструкции, а оси Сх{ — главные оси инерции. Заметим, что сонаправленность осей Cxi (г = 1,2,3) с главными осями инерции не существенна и возможно использование любого трехгранника, жестко связанного с недеформированной конструкцией, с началом в ее центре масс.
Положение любой частицы массы dm в этой системе координат определяется ее радиус-вектором р, заданным своими проекциями на оси Cxi
52
ГЛАВА 1
Так как оси Cxi — главные центральные оси инерции, выполнены равенства
J pdm — ^, ! XiXj dm = 0	(4.2)
о	о
Первое из равенств (4.2) означает, что С — центр масс недеформирован-ного тела, второе — равенство нулю центробежных моментов инерции.
Перейдем к рассмотрению произвольного движения деформируемой конструкции, включающего в себя как поступательно-вращательное движение так и процесс деформирования.
Введем в рассмотрение инерциальную систему координат OCiGCa-Предположим, что в начальный момент времени трехгранники Сх^хз и ОС1С2С3 совпадали, и конструкция была недеформирована. Это предположение не ограничит общности дальнейших рассуждений и использовано для наглядности. В произвольный момент времени положение произвольной точки dm тела по отношению к системе	определим ее
радиусом вектором £
6(р,0
£г(р, <) £з(р>0

6 («1,«2, «3,0 €г(«1, «2, «3,0 €з(«1, «2, «3, 0
заданный своими проекциями на оси О&; р — положение частицы dm в начальный момент времени. Вектор £(р, 0 при Р € П определяет положение каждой точки конструкции в момент времени t.
Опишем способ введения связанной с конструкцией средней системы координат. Из теории движения абсолютно твердого тела известно, что возможно представление (для недеформируемой конструкции)
6
Ъ
Сз
«2(0
«з(0
+ 0(0
«1(0 «2(0 «з(0
где R = (T?i,/?2, «з) — радиус-вектор начала подвижной системы ко-ординат, жестко связанной с твердым телом (рис. 1.9); О(£) — ортогональная матрица, задающая вращение трехмерного пространства и определяющая переход от системы, жестко связанной с телом, к осям инерциальной системы координат. Матрица 0(2) обладает свойством
От(/) = О-1(0-
БКК И ЗАДАЧИ МЕХАНИКИ
53
Матрицу О(/) можно определить с помощью трех независимых параметров, зависящих от времени (например: углы Эйлера, углы Крылова и т. д.), можно воспользоваться кватернионами (четыре параметра и одна связь) или направляющими косинусами (девять параметров и шесть связей). В любом случае независимыми являются только три параметра. Предпочтительным является запись О(/) с помощью направляющих косинусов единичных векторов осей, жестко связанных с телом в инерциальной системе отсчета, и использование кватернионов, так как в этом случае гарантирована взаимно однозначная связь между параметрами, определяющими ориентацию системы координат, и углами между соответствующими осями координатных систем.
Три координаты вектора R и три параметра матрицы 0(1) полностью определяют положение жестко связанного с телом трехгранника и самого тела.
В случае деформируемого тела можно записать
6(р,<) Ыр>о Ыр,0
Л1(*> «2(0 «з(0
+ о(0
а?1(0 ж2(0а *з(0
«1(р,0 и2(р,0 «з(р, о
(4.3)
В выражении (4.3) R и О(/) определяют шесть обобщенных координат, задающих положение некоторой, связанной с деформируемой конструкцией системы отсчета: R(Z) — положение начала этой системы отсчета, О(/) — направляющие косинусы ориентации осей связанной системы координат относительно инерциальных осей; и(р,/) = (ui,U25^3)T — некоторое векторное поле, появляющееся в связи с деформируемостью конструкции. Поле u(Z) в дальнейшем будем называть полем перемещений. Выбор этой подвижной системы отсчета (то есть выбор шести
54
ГЛАВА 1
обобщенных координат) будем осуществлять из условий
u(p, t)dm = Q, р х u(p,t)dm = 0.	(4.4)
Условия однозначно (4.4) определяют положение так называемой средней системы координат (или трехгранника Вейля) в любой момент времени.
Условия (4.4) выбора шести обобщенных координат запишем в виде шести скалярных уравнений
j ui(#i, х2, X3,t)dm = 0, о
У u2(x1,X2,X3,t)dm = 0, п
из(ж1, х2, X3)t)dm = 0, о
У (x2U3(xi,X2)X3,t) — X3U2(xi, х2, x3,t))dm = 0, о
У	- хгиз(хх, х2,хз, t})dm = 0,
о
у*— X2Ui(xi, х2, X3,t))dm = 0, п
где как и раньше (см. (4.2), (4.4)) dm = <t(#i, х2, X3)dxidx2dx3, а(р) — плотность недеформированного тела в точке с радиус-вектором р.
Покажем, что соотношения (4.3), (4.4) однозначно определяют вектор
R(/), матрицу 0(2) и поле перемещений и(р,/).
Пусть £(р, Z) — известное векторное поле. Проинтегрируем левую и правую части (4.3) по области Q с весовой функцией а. Получим
о
6 & £з
Я2
Н3
*1
Х2
Хз
U1
U2 из
dm.
Преобразуем правую часть полученного выражения. Первое слагаемое
примет вид
о
R2
R3
Ri Ri Rs
Ri
R2
Rs
dm =
dm ~
n

БКК И ЗАДАЧИ МЕХАНИКИ
55
где М — масса конструкции. Далее, второе слагаемое (с учетом того, что матрица О не зависит от a?i, #з) преобразуется к виду
«1
*2
*3
Так как в силу (4.2) и
U1
^2
^3
*1
*2
Хз
(4.4) выполнены равенства
Xi dm = О, о
щ(х1, х2, X3)dm = О, о
U1
U2 из
dm.
i = 1,2,3,
о
правая часть полученного выражения равна нулю. Следовательно,
dm = R.
Таким образом, точка С (начало связанного с конструкцией трехгранника) является ее центром масс.
Умножим левую и правую части равенства (4.3) на О-1. Умножая векторно слева на р и интегрируя по области Q, получим
*2
•Гз
хО'1
6
6 Сз
*1
Х2
ХЗ
х О"1
Ri н2 Rs
Х1
Х2 хз
щ
U2 из
Преобразуем правую
часть этого равенства
Х2
Хз
xi
Х2
ХЗ
О"1
хСГ1
R1
R2
R3
Ri
Я2
Rs
Х1
Х2
ХЗ
U1
U2 из
Х1
Х2
Хз
dm =
Х1
х х2
Хз
о
Л?1
Х2
Хз
U2 из
dm.
X
+

11ервое слагаемое полученного выражения
о
Х1
Х2
ХЗ
х О"1
6
£з
dm = — О 1
Ri
R2
Rs
п
XI
Х2
ХЗ
dm = О
56
ГЛАВА 1
в силу (4.2). А так как р х р = 0 и выполнены условия (4.4), то второе и третье слагаемые также равны нулю. Следовательно,
о
х О
6
£2 dm — 0.
Сз
(4.5)
Выражение (4.5), записанное в скалярной форме, представляет собой три уравнения относительно трех параметров, определяющих матрицу О. После нахождения 0(2) и R(/) согласно описанной процедуре из уравнения
U1		6		Ri		Xi
^2	= о-1	£2	—	«2	—	Х2
		&		Кз		хз
находим поле перемещений и(/) в проекциях на оси Cxi. Это уравнение получено с использованием уравнения (4.3). Замел им, что вопрос о разрешимости (4.5) относительно трех параметров, определяющих матрицу О, не рассматривается. Это связано с тем, что в процессе построения алгоритма оценки влияния возмущающих факторов на точность рабочих поверхностей предстоит решать обратную задачу. Обратная задача сводится к следующему: из уравнений движения (вывод которых будет производиться ниже) путем численного интегрирования будут определяться величины 0(2), R(Z), u(f). Подстановкой последних в (4.3) находим векторное поле С(р,/), то есть положение каждой частицы деформируемой конструкции, движущейся под действием внешних сил и моментов.
Заметим также, что соотношения (4.4) не являются уравнениями связи, так как никаких ограничений на движение системы не накладывается. Эти соотношения — условие выбора подвижной системы отсчета (обобщенных координат, описывающих движение). Следовательно, в уравнения движения не нужно вводить новые переменные — неопределенные множители Лагранжа.
Трехгранник Cxi, х2, хз носит название «средней» системы координат. Этот трехгранник получил широкое применение как благодаря достигнутому в результате упрощению уравнений движения, так и благодаря тому, что описание деформации при помощи собственных форм колебаний тела подразумевает использование именно такой системы отсчета. Последнее утверждение будет подробно разобрано в дальнейшем.
Обоснование выбора «средней» системы координат. Покажем, что описание движения деформируемой конструкции при помощи собственных форм колебаний тела предполагает использование средней системы координат.
БКК И ЗАДАЧИ МЕХАНИКИ
57
Рассмотрим незакрепленную деформируемую конструкцию. С неде-формированным состоянием конструкции свяжем как с твердым телом систему координат Cxix2x3. Как и раньше, будем считать, что эта система осей — система главных центральных осей инерции недеформи-рованного тела. Положение частицы dm деформированной конструкции определяется ее радиусом-вектором г
г = р +w(pj),
где w — поле перемещений деформированной конструкции. Предполагается, что |w(p, t)|/|р|	1 и справедлива теория малых деформаций. При
исследовании линейных колебаний упругих систем обычно применяют метод разложения по собственным формам. Суть его заключается в следующем. Решение ищется в виде ряда по некоторым вектор-функциям (собственным формам), являющимися собственными функциями однородной краевой задачи
А^ + С„ = 0, ot2
где А и С соответственно инерционный и упругий линейные операторы [43]. Так как рассматриваемая система является положительно полуопределенной (свободная механическая система), то выполняются следующие неравенства:
(Aw,w) > 0, (Cw,w) > О
для w, не равного тождественно нулю (скобками обозначено скалярное произведение). Равенство нулю во втором из выписанных соотношений встречается, например, когда w соответствует движению всей конструкции как твердого целого (без деформаций). Разложение поля смещений w по собственным формам свободных колебаний имеет вид:
3	3	оо
w(p,<) = ^wk(t)<pk(p) + '}Гок(1)'фк(р) + ^2 9n(*)U(n)(p),	(4.6)
/с = 1	k = l	n = l
где ч>к(р), 'Фк(р), (к = 1,2, 3); U(n)(p) (n = 1,2,...) — полная система функций, являющаяся базисом в конфигурационном пространстве системы (пространстве вектор-функции, интегрируемых с квадратом и удовлетворяющих определенным граничным условиям). Wk(t), Ok(t), qn(t) —
58
ГЛАВА 1
обобщенные нормальные координаты. Собственные формы в проекциях на оси системы координат	имеют вид:
<рк{р) =
?к
Фк
фк(р) =	,
v(n\p) =
и[п) ut} и-п}
и удовлетворяют условиям ортонормированности:
где 6ik — символ Кронекера.
Первые шесть форм колебаний соответствуют шести степеням свобода недеформированной конструкции, движущейся как твердое тело. Для определенности положим, что формы <рк(р) соответствуют перемещениям системы по трем взаимно ортогональным направлениям (в этом случае (г = 1, 2, 3) не зависят от р), а формы фк(р) — элементарным поворотам вокруг трех взаимно ортогональных осей (фгк (г = 1,2,3) — линейные функции от a?i, а?2, а?з).
Частоты свободных колебаний, соответствующие этим шести формам, равны нулю, то есть
С<р*=0, С^=0 (6 = 1,2,3).
Частоты колебаний Qn, соответствующие формам отличны от нуля и являются решением следующего уравнения:
CU(n) =	AU("\ (fi? < Q?, i < j).
Покажем, что каждая из собственных форм удовлетворяет со-отношениям:
I U^din = 0, У р х U^dm = 0.	(4.8)
п	о
Рассмотрим первое равенство (4.8). Из покоординатной формы записи получаем:
У [J<n)dm = o, (г =1,2,3).
БКК И ЗАДАЧИ МЕХАНИКИ
59
Последний интеграл перепишем в виде:
J^U^dm — е, о	о
(4.9)
где е, (г = 1,2,3) — орт оси Cxi. Вектор е, также является собственной формой и соответствует перемещению системы вдоль оси Cxi. Собственная частота, отвечающая е3, равна нулю. Так как векторы <рь представляют собой базис в подпространстве конфигурационного пространства задачи, отвечающем перемещениям системы как твердого тела, то имеет место представление:
з
е> = ХХ*’*> А*
к = 1
У(е, • <Pk)dm. о
Подставим в (4.9) вместо вектора е, выписанную линейную комбинацию векторов ipk и, используя условия ортонормированности (4.7), получим:
что и доказывает первое равенство Перейдем ко второму равенству
(4.8).
(4.8). Оно эквивалентно трем со-
отношениям:
j ~ хз^2П^ dm —
h
dm — О,
П
dm = 0.
Докажем справедливость первого из выписанных выражений (остальные два доказываются аналогично). Перепишем его в виде:
/	— x^U^1^ dm — Л • U^dm,
Q	О
0
х2
(4.10)
60
ГЛАВА 1
где вектор А соответствует элементарному повороту системы вокруг оси Cxi как твердого целого. Проводя рассуждения, аналогичные приведенным выше, получаем,
3	f
*=1	о
Подставляя эти соотношения в (4.10), получим:
j А • V^dm = f №^k \ •	Pk j* fa - U^dm = 0,
П	n \/c--l	/	^ = 1 Q
что следует из условий ортонормированности (4.7).
Три слагаемых, стоящих в правой части (4.5), представляют собой проекции поля смещений w(p, t) на три взаимно ортогональных подпространства, каждое из которых является собственным подпространством операторов А и С).
Из полноты базиса и (4.8) следует, что система собственных форм U(n)(p) является базисом в подпространстве конфигурационного пространства задачи, определяемого соотношениями (4.4). Таким образом, поле перемещений и(р, /) из (4.3) можно представить в виде ряда
оо
u(p,/) = 52<?„(OU(")(p),	(4.11)
71 = 1
где — собственные формы колебаний незакрепленной конструкции, отвечающие ненулевым частотам свободных колебаний, заданные в проекциях на оси средней системы координат:	^зП^||Т-
Удобство использования последней обусловлено как раз этим обстоятельством.
Соотношения (4.3), (4.11) полностью определяют введение обобщенных координат, при помощи которых описывается динамика свободной БКК. Это — шесть обобщенных координат, описывающих движение связанного с телом трехгранника Сх 1X2^3» и обобщенные (нормальные) координаты qn (п = 1.2,...).
Уравнения движения упругой конструкции выводятся исходя из вариационного принципа Даламбера —Лагранжа. Эта вариационная постановка задачи служит затем естественной отправной точкой для рассмотрения конечноэлементной аппроксимации уравнений движения тела.
БКК И ЗАДАЧИ МЕХАНИКИ
61
Принцип Даламбера—Лагранжа, Абсолютное ускорение произвольной точки dm конструкции в проекциях на оси инерциальной системы координат получим двукратным дифференцированием по времени выражения (4.3):
6
С2
Hi
Ъ
Яз
*1
*2
Х3
Щ
U2 из
4-20
и>2 йз
U1
U2 из
(4.12)
+ 6
+ О
где &, Ri — проекции векторов £(р, t) и R на оси инерциальной системы координат, a Xi и щ — проекции векторов р и u(p, t) на оси средней системы. Поскольку в дальнейшем предполагается использование для всех векторов только средней системы, введем следующее обозначение для произвольного вектора b — под Ь° будем понимать столбец из трех чисел ||6?, 6°,^з||т, где Ь® — проекции b на орты неподвижной системы отсчета, а запись b будет означать столбец ||6i,62,/>з||Т» где bi — проекции b на оси подвижной системы координат.
Справедливо равенство:
ь° = оь.
Производную по времени от зависящего от времени вектора будем обозначать штрихом, если она вычислена в инерциальной системе координат, и точкой будем обозначать производную по времени компонент вектора в подвижной системе Сх1X2X3 и производные от скалярных величин. Справедливо равенство:
b' = b + wxb,	(4.13)
где о; — угловая скорость средней системы отсчета.
Абсолютное ускорение точки dm (4.12) перепишем в проекциях на оси CZ1J?2^3-
£ = bfuc + u> х vc х (p+bfu) + 2о> xii4-wx(wx (p+u)) 4-й, (4.14)
где v0 = R 4 wR — скорость точки С (центра масс конструкции) в проекциях на оси средней системы координат.
Возможное перемещение точки dm конструкции получим, проварьи-ровав соотношение (4.3):
^2°
^3°
3R°X				Щ		d’ui
	+ <50	Х2	4-	U2	) +о	
SR°3		Хз		из		Su3
62
ГЛАВА 1
умножив левую и правую части полученного равенства на О \ получим выражение для вектора 3£:
J£ = JR + О"1ЗО(р + u) + Ju.
Обозначим через 11^1,72,7з11 вектор-столбец трех обобщенных координат, определяющих матрицу О. Тогда
3	3
°_1<уо = 520-1	= 52 а,<У7’’
так как оператор	• а = а, х а кососимметричен и эквивалентен
операции векторного умножения. В случае, когда 7,- — углы Эйлера, — единичные векторы осей, относительно которых осуществляются
повороты на углы Эйлера. Обозначим через
з
6(1 = (Xi6^i i=i
и запишем возможное перемещение в виде
6£ = JR 4- бос х (р 4- u) + Ju.	(4.15)
В дальнейшем предполагается использовать представление (4.10) для поля перемещений u(p, t), поэтому для Ju в (4.15) имеет место выражение
00
П = 1
так как собственные формы U(n)(p) — фиксированные вектор-функции.
При выводе уравнений движения с помощью принципа Даламбера — Лагранжа нам понадобятся выражения для элементарных работ внутренних упругих и диссипативных сил на возможных перемещениях.
В рамках теории малых деформаций потенциальная энергия упругих деформаций представляется в виде квадратичного функционала
П. = l(w,Cw),
где w(p,/) — поле перемещений, С — самосопряженный линейный оператор, характеризующий упругие свойства конструкции. Подставив
БКК И ЗАДАЧИ МЕХАНИКИ
63
в выражение для II* разложение w(p, t) по собственным формам колебаний (4.5), получим:
1 / 3 ос	Г 3 оо
п. = 1 Ёя£иМдя,С £>+Е<7пи(п)
\/с = 1	п = 1	,к — 1	п = 1
оо	1 00
^qnQ2nV^ dm=-^^2nq2n,
(4.16)
/? = wkq>k + Оь'фь-
При выводе (4.16) использовались условия ортонормированности (4.6), а также тот факт, что собственные формы являются собственными функциями оператора С с соответствующими собственными значениями (собственные значения для форм (ркз'Фк равны нулю).
Элементарная работа сил упругости на возможных перемещениях задается в виде
00 ЯП	00
М. = - 22	= - 12 Qn4nSqn.
п = 1	П = 1
Предположим, что силы внутреннего вязкого трения определяются квадратичным по скоростям диссипативным функционалом Ф, пропорциональным функционалу потенциальной энергии упругих деформаций
Ф = x&(w, Cw).
(4.17)
Такое описание внутренней диссипации соответствует модели Кельвина— Фойгта линейной теории вязкоупругости. В (4.17) х — безразмерный параметр, b — константа. Выполняя выкладки, аналогичные проделанным выше, получаем выражение:
оо ф = х612п"’"’ П = 1
подобное диссипативной функции Рэлея. Элементарная работа диссипативных сил имеет вид:
SD = -X-^-S<in=-2xbYtQ2nqn6qn.	(4.18)
п = 1	П = 1
Помимо внутренних сил, действующих в системе, на крупногабаритную космическую конструкцию действует поле внешних активных сил F. Силы
64
ГЛАВА 1
F зададим пока в общем виде и будем считать, что F зависят от времени, положения и скорости точек конструкции:
F = F R + р + u, bfR + й + о> х (R + р + и)) .
В выражение для F подставим разложение (4.10) и с учетом линейных по qn членов получим,
оо
F = F. + ^(f(n)<7„+f'(n)<7„),
71 = 1
(419)
где
f(n> -
В дальнейшем под F подразумеваем совокупность всех внешних сил, действующих на конструкцию, включающую в себя объемные (например, гравитационные), поверхностные (например, солнечный ветер и аэродинамические нагрузки), линейно распределенные и сосредоточенные (управляющие) воздействия, приходящиеся на единицу массы. F* обозначает то значение, которое имело бы F в абсолютно твердом теле; f(") и f(,n) зависящие от R, R, р, ш векторы, задание которых связано с рассматриваемой задачей.
Вариационный принцип Даламбера — Лагранжа представим в форме:
У (ё - FS£)dm — 8Л — 8D = 0,	(4.20)
то есть сумма работ сил инерции, внешних сил и внутренних упругих и диссипативных сил на возможном перемещении равно нулю (так как система свободная, возможные перемещения совпадают с виртуальными).
Интеграл в (4.20) применяется в смысле «нагруженного интеграла» [63] (это понятие тесно связано с интегралом в смысле Стильтеса).
С учетом (4.14)—(4.16), (4.18), (4.19) уравнение (4.20) перепишем
в виде:
У|vc + W X vf	х (р + u) + W х (w х (р + и))+
п
4-2си х и + и - F. - ^(f(n)</n + f'(n)<7n)| х п =1	'
s	х	ОО	ОО
х< «УК + <У<« х (р + п) + «Уи У dm + 57 ^пЯп8дп + 2 уб 57 ^п9п«У?п = 0.
'	Г) —]	П = 1
БКК И ЗАДАЧИ МЕХАНИКИ
65
Окончательно, подставив разложение (4.10) в выражение для Ju, получаем:
У -^vc + ы х vc + Ш X fp+52	+ ш х (w х ^р+У2 9nU(ny^ +
ОО	ОО	ОО	х
+2о> х £2 U(n)7n + 52 U(n)?” - F* - I2(f(n)<?” + f'(n)<7")} x 71=1	71 = 1	71=1	'
x f <5R + Ja (p +	<5?nU(r,y + J U* Jg* pm+
71 = 1	' k = l	'
OQ	OO
+ ^Q2nqn6qn+2Xb'^Q2nqn6qn = 0. (4.21) n = l	n — 1
Уравнение (4.21) представляет собой развернутую запись вариационного принципа Даламбера — Лагранжа. Вариации JR, Ja, 6qn независимы, поэтому, приравняв нулю выражения при независимых вариациях, получим уравнения движения системы.
Уравнения движения. Получим уравнения движения, разрешенные относительно старших производных. Поскольку рассматриваются только малые деформации, в уравнениях движения сохраняются лишь линейные относительно qn члены.
Используя векторное равенство
а • (Ь х с) — (с х а) ♦ Ь, преобразуем (4.21) к виду:
+2ш х 52 и(п)<7„ +52 U<n)g„-F# -52(f (n)g„+f'(n)g„) > • <SRdm+ 71=1	71 = 1	71 = 1	)
p+^qnV^] +
71 = 1	'
3 — 2185
+wx (wx fp+52?nU(n)H + 2w X J2U(n)gn+
4	X	71 = 1	71 = 1
ОС	OO	x
+52 и<п^п - f. - 52(f(n)?n+f/(n)<zn) >
• 6cidm+
66
ГЛАВА 1
оо	оо	'l оо
+2о> х 22 u(n)<7n + 12 и(П)’" ( • 12 U(fc)^rfm+
n = l	n = l	) к = 1
оо	оо
+22«п?п^п+2хб22пп^" = 0- <4-22)
П = 1	П=1
Так как JR, Ja, 6qn не зависимы между собой и не зависят от р, их можно вынести за знак интеграла, и, приравнивая нулю стоящие при них выражения, получить уравнения движения
р+52 9"и(п) ) +wx
п = 1	/
оо
р+22<?пи(п)
. П = 1
+2о> х J2 U(n)g„+22 U("’g„-Ft -n = l	n = l
dm=0 (4.23)
х
n=l	J
*>х (р+12 9"и(п) ) +
\ П = 1	/
+«Х U ( р+22 ?яи(л)) ) +2wx22 U(n’<?n+22 \	\ П=1	/ /	П = 1	П = 1
dm=0 (4.24)
-F
/ < Vc+wxvc+wx I p+22 9nu(n) j +wx I I p+52 9"u(n) I I +
n	\ n=l /	\	\ n=l //
+2^x22 и<п)<7„+£ U(n)g„ }u<*)dm+22 i^<?n+2x6 £ a2nqn3=0. n = l	n = l	'	n = l	n = l
(4.25)
Уравнения (4.23)-(4.25) — точные уравнения движения деформируемой конструкции в рамках линейной теории вязкоупругости. Они справедливы для деформируемой конструкции произвольной формы. Уравнения (4.23), (4.24) описывают поступательное и вращательное движение системы Cxix-2^3 соответственно, (4.25) — процесс деформирования. Использование средней системы координат значительно упрощает уравнения (4.23)-(4.25). Произведем это упрощение для каждого уравнения в отдельности.
БКК И ЗАДАЧИ МЕХАНИКИ
67
Рассмотрим уравнение (4.23). Заметим, что это уравнение может быть получено из теоремы о движении центра масс системы. Используя (4.2) и (4.7), получаем:
р + XJ^ri^qn j dm = си х п = 1	/
л
Введем обозначения:
Ф = у F,c/m, п
Уравнение (4.23) можно переписать в следующем виде:
М (ус + о; х vc) = Ф	,
П = 1
(4.26)
где М — масса конструкции. Уравнение (4.26) совместно с уравнением
R = vc - о; х R	(4.27)
описывает движение начала средней системы отсчета.
Рассмотрим уравнение (4.24). Проводя рассуждения, аналогичные тем, которые были использованы при выводе (4.15), получаем:
/ ( р +	j х (vc + ш х vc) dm = 0.
h '	n='	'
Так как в окончательных уравнениях предполагается учитывать только линейные по qn и qn члены, то, используя (4.7), получаем:
з*
68
ГЛАВА 1
Далее, используя определение тензора инерции, получаем:
где J — тензор инерции конструкции в центре масс тела
Е p+^U(n)gn • p + £u<")g„
n L х п~1	7 х n_1
/ оо	\	/ оо
- р+£и<")9„ : р+£и(">9„
= Jo+J1 + 0(72), (1.28)
где знаком (:) обозначено диадное произведение двух векторов, точкой, как и раньше, — скалярное произведение, Е — единичная матрица размера (3 х 3), Jo — тензор инерции в точке С недеформированной конструкции. Так как оси Cxi — главные центральные оси инерции недеформированного тела,
J
(”) о
А О О
О О В О
О С
где Л, В, С — главные центральные моменты инерции, Ji — линейная
по дп часть тензора инерции:


Р '
dm,
ИЛИ
	'н^ + н^	гг(п) ^12		
J<n) =	П12	еДл) । Ет(л) ^33 + //11		(4.29)
	—/у(п) L 771з	-Н$	Ни1 +	
где — J^XiUj^dm.
БКК И ЗАДАЧИ МЕХАНИКИ
69
Заметим, что в силу соотношения (4.7) коэффициенты удовлетворяют условию симметрии	. Эти коэффициенты постоянны и
являются характеристиками конструкции.
Аналогичным образом находим:
оо	\ \	/	оо	\
P+J>u(n)) х p+^9nU(") dm =
. П = 1	/ /	\	71 = 1	/
dm = w х Jo;.
При выводе последнего соотношения было использовано векторное равенство:
а х (Ь х с) = Ь(а, с) — с(а, Ь).
Введем следующие обозначения:
m* = — j р х F*c/m, p!^n>i = j р х n	n
д(”) = У (p x f(n) + U(n) x F,) dm. n
С использованием введенных обозначений уравнение (4.24) можно переписать в виде:
Jeb Jo; + о; х Ju? = m* +	•	(4.30)
n = l
Уравнение (4.30) является уравнением относительно о; и описывает вращательное движение конструкции как целого. Это уравнение не разрешено относительно ci;. Необходимо разрешить (4.30) относительно
70
ГЛАВА 1
так как уравнения, разрешенные относительно старшей производной, наиболее удобны для численного интегрирования.
С этой целью необходимо умножить левую и правую части уравнения (4.30) на матрицу J-1. С учетом линейных по qn членов J-L представляется в виде:
J-1 = Jq 1 —	1 +
Тогда из (4.30) получаем:
ш -j- Jo Jeu -j- Jg (cu х Jeu) Jg JjJg (eu x Joeu) —
oo
= (Jo 1 - Jo‘J^o + Jo"1 52 (м(п)<7„	•
n = l
Поскольку поле сил F зависит от положения всех частиц drn конструкции, оно зависит от ориентации трехгранника	относительно инерци-
альных осей. Обозначим через а, (3, 7 орты осей в проекциях на оси Сxi, Сх2 и Сх3 соответственно. Для замыкания уравнений движения к системе необходимо добавить кинематические уравнения
а = сг х ей, /3 = /3хш, 7 = 7 х ей.	(4.31)
В скалярной форме (4.31) представляют собой 9 уравнений относительно величин Qi, Д, 7,- (проекций векторов а, /3, 7 на оси С&) связанных между собой шестью тривиальными интегралами
ot-/3 = Q, а-7 = О, /3-7 = 0, а-а=1, /3-/3=1, 7-7=1.
То есть среди девяти величин а3, Д и 7, только три независимых (три параметра, определяющих матрицу О).
Перейдем к рассмотрению последней группы уравнений, описывающих деформации конструкции (уравнения относительно (?п).
Справедливы следующие вспомогательные равенства:
[ (ус 4- W х vc) U<n>dm = 0, f ( U<n)gn ) U^dn, = ijk.
n	n ^=1	'
Ггсли ввести обозначение	U-^U^dm , то
•J	J a I • J
U<") X U(fc)rfm =

БКК И ЗАДАЧИ МЕХАНИКИ
71
Тогда справедливы равенства:
] j V^dm = n = l	/ /
x U^dm = d> • Qn n = l
oo p + £u<")g„ <	n = l
x U^dm =
OO
X n = l
x XJ^dm.
При выводе этих соотношений использовались соотношение (4.7) и векторное равенство
а • (b х с) = b • (с х а).
Далее с учетом введенных обозначений
си у (w х р) х U^dm = 2	4-	4- Я^и^з) —
- (Я2*2 + Нк3) о,2 - (Н33 + Нкп) ш2 - (Нкп + Нк2) ш2,
qn xV^dm = -wf (L$ + ^22 )-^2 (Ьзз + Ln
п
~ш3 (^11+^22 )+wlw2 (•^12+^'21')+и'1шЗ (^1з+^31 )+W2W3 (-^гз+^32 ) •
Положим:
дк = у F,U<*)dm, п
9кп f(n)V{k)dm +q„l f'^U^dm = qnrnk + qnr,nk.
72
ГЛАВА 1
Уравнение (4.25), описывающее изменение со временем обобщенных координат qk, примет вид
Як +	4" &kQk + $к + $пк — 9к 4- 9пк, (4.32)
п=1	п = 1
где
Ф* = 2(Я*>1“2 4- Н^3<л>1<л>з 4- #23^2^3) —
~(^22 + Нзз)ш1 ~ (^33 + ^11)ш2 ~ (^11 + ^22)ш3> Фпк = 2q„ (W1(L?3fe - L%) 4- W2(LS* - L\3} + W3(L?2* - L^)) 1-
+<?„ й!(L?* - L32) + w2(L5* - L™3) 4- w3(I?2fc - L^)-
4- L33) -	+ Ln) ~ “з2(Ь?1 + ^)+
4-wiw2(£<12 4- L"i) + ш1шз(Ь™3 4-	) 4-w2w3(L23 + ^32) 
Система уравнений (4.26), (4.27), (4.30)-{4.32) представляет собой замкнутую счетную систему обыкновенных дифференциальных уравнений. Обычно при исследовании динамики упругих систем учитывают N первых форм колебаний. Таким образом, систему уравнений при помощи полученного ранее оператора J-1 и введения новых переменных рп — qn можно привести к следующему виду:
ys = fs(ys,t),
где S = 1,2,..., К\ К = N 4-12 — порядок системы уравнений; у — (/?1, Я2, R3, Vic, V2c, Узе, О>1, Шз, di, &2, ^3, Я1,--^Яп)\ 5г- (г = 1,2, 3) — три независимых параметра из девяти аг, Д, 7,.
Полученную систему в дальнейшем предполагается исследовать численными методами. Использование при ее выводе средней системы отсчета позволило существенно упростить правые части. Внешние воздействия входят в полученную систему через коэффициенты Фг,
9т г?к, г\пк (i = 1,2,3) и через Ь™к, Нк-. Нахождение этих коэффициентов будет предметом специального рассмотрения.
Глава 2
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
Большие космические конструкции, такие, как орбитальные космические станции, трансформируемые радиотелескопы, протяженные антенные системы, космические платформы, солнечные энергетические установки — уникальные объекты, создание которых возможно при тщательном анализе условий эксплуатации и действующих внутренних и внешних силовых факторов, определении напряженного и деформированного состояния силового каркаса, анализе взаимодействия элементов конструкции. Проведение комплексного исследования орбитального функционирования БКК в условиях наземного эксперимента не всегда представляется возможным. Поэтому особую роль при проектировании крупногабаритных космических конструкций приобретают вопросы разработки математических моделей, позволяющих эффективно выполнять проектировочные расчеты, анализировать различные варианты компоновки БКК. Разрабатываемые математические модели должны базироваться на эффективных вычислительных алгоритмах, позволяющих выполнять расчет сложных составных многоэлементных конструкций для различных условий их нагружения, допускать изменение проектных параметров конструкционных элементов, изменять конструктивно-силовую схему и компоновку проектируемого аппарата в широких пределах.
Помимо задачи анализа напряженно-деформированного состояния и динамического поведения конструкции на передний план выдвигаются вопросы коррекции параметров расчетной модели БКК по результатам наземного эксперимента. Это связано с тем, что проблемы управления, ориентации и стабилизации БКК могут быть решены при наличии эффективной упруго-массовой модели конструкции и эффективного алгоритма расчета деформаций аппарата, находящегося под воздействием управляющих силовых факторов. В значительной степени преодолеть противоречие между необходимостью выполнять расчет напряженно-деформированного состояния быстро и эффективно и необходимостью использовать наиболее подробную математическую модель с высокой степенью дискретизации конструкции для достижения максимально возможной точности расчета удается на основании инженерного опыта и
74
ГЛАВА 2
интуиции, приобретенных при проектировании существующих образцов летательной техники.
2.1.	КОНЕЧНОЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ
Опишем используемый в данной книге подход к моделированию конструкций, основанный на представлении конструкций в виде системы конечных элементов. Предположим, что для заданной конструкции выбрано конечноэлементное разбиение и получающаяся модель имеет г узловых точек. Количество степеней свободы, соответствующих каждому конкретному узлу (соответственно, вектор приведенных узловых усилий), определяется пространственной размерностью рассматриваемой конструкции (одномерные, двумерные и трехмерные конструкции), типом элементов, состыкованных в данном узле, а также условиями их стыковки (шарнирный узел, жесткий узел). В простейшем случае, когда необходимо обеспечить равенство только линейных перемещений в узловых точках, используются шарнирные узлы. Тогда число степеней свободы соответствует числу возможных перемещений вдоль осей выбранной глобальной системы координат. Для пространственной конструкции J-ый узел характеризуется тремя степенями свободы и его перемещения описываются вектором UJ с компонентами /7^, и (7/. В случае, если элементы, сходящиеся в узле J, соединяются жестко, что, в частности, имеет место для элементов, работающих на изгиб, необходимо обеспечивать не только непрерывность перемещений, но и равенства углов поворотов концевых сечений элементов, примыкающих к данному узлу. Узел j в данном случае характеризуется шестью степенями свободы, а вектор U наряду с компонентами (7/, и Щ содержит также три угловые компоненты Ф£, Ф^ и Ф^. Эти компоненты представляют собой углы поворота плоскостей, проходящих через данный узел и параллельных координатным плоскостям, относительно соответствующих осей. Очевидно, что между элементами, соединенными жесткими узлами, действуют как силы, так и моменты, а между шарнирно соединенными элементами — только силы. Заметим, что при построении более сложных элементов возможно использование дополнительных степеней свободы в узлах.
Обычно при конечноэлементном описании конструкции поле перемещений uW в каждом отдельном элементе определяется через перемещение его узлов. Обозначим вектор узловых перемещений г-ого элемента с узлами ;Д,/,... через = (UJ*, U**, Uu). Тогда выражение для упругих перемещений г-ого элемента может быть записано в виде:
u(0 = N^UW,	(1.1)
где N(’) — матрица функций формы. Элементы этой матрицы зависят как от пространственных координат, так и от параметров элемента.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
75
При этом упругие деформации и напряжения в элементе будут описываться соотношениями:
е(») - д(’)и(»)? а(») =	= С^А^и^,	(1.2)
где — матрица упругих констант, а А^ — матрица, получаемая при использовании соотношений Коши, связывающих деформации и перемещения. Получение матрицы сводится к выполнению операций дифференцирования элементов матрицы функций формы по пространственным координатам.
Определение матриц жесткости К<’) и матриц масс м(’) для рассматриваемого элемента сводится к выполнению операций перемножения введенных матриц	и интегрирования произведений по
области Q,, занимаемой этим элементом,
К<’> = У	М<’> - У	(1.3)
Здесь — плотность материала для г-ого элемента. Для вектора приведенных усилий соответственно имеем:
q<’) = У A^V dfi, + У A<’>q’ dQi.	(1.4)
Через qv и q5 обозначены векторы объемных и поверхностных сил. Если выполнить интегрирование в (1.3), то матрицы и можно представить в блочном виде:
	Г/С-’ 11	тА1) “jk			
К<*"> =	KS	Пкк nlk	/<(«•) /<(*)		(1.5)
				• _	
Аналогичное представление справедливо для матрицы масс г-ого элемента. Введем также расширенные матрицы жесткости Ю’) и масс W’)
для рассматриваемого		элемента:						
	’0	0	0	0	0	0	...	О’	
	0	кФ 11	0		0	Ajl   	0	
	0	0	0	0	0	0. ...	0	
K(i) =	0 0	0	0 0	/<(’) JXkk 0	0 0	lXkl 0	...	0 0	(1.6)
	0	А’(<)	0	А’(<)	0	А'(,) Ли	0	
	.0	0	0	0	0	0	...	0.	
76
ГЛАВА 2
Расширенная матрица масс записывается в аналогичном виде. Тогда глобальные матрицы жесткости и масс, соответствующие моделируемой конструкции, могут быть получены непосредственным суммированием соответствующих расширенных матриц отдельных элементов
К = £К<’), М = £м(‘\
(1.7)
Матрицы жесткости и масс обычно удобно вычислять в некоторой локальной системе координат, связанной с рассматриваемым элементом. Обозначим оси локальной системы координат через х^г\ , z^ и введем матрицу направляющих косинусов данной системы координат относительно осей х, уу z:

cos(a?, х^) cos(«r, у^) cos(a?, z^)
cos(t/, xty cos(z/, y^) cos(z/, z^)
cos(z, x^) cos(£, y^) cos(£, Z^)
(1.8)
Если известны матрицы жесткости и масс рассматриваемого элемента в локальной системе координат, то определение матриц жесткости и масс в глобальной системе координат сводится к выполнению следующих преобразований поворота:
К<!') -	M(i) = О<*')‘М|(1’’О(,),	(1.9)
1ОС ’	1ОС ’	V '
где матрица преобразования (Уг) имеет следующий вид:
а вид блочных матриц Е(г) зависит от типа соответствующих узлов. Например, для шарнирных узлов Е(г) = а для жестких узлов матрица Е(’) имеет вид:
Е(,) -
‘S(O
О
О S(‘)
(1.11)
Отметим, что К и М являются симметричными разреженными матрицами. Данные свойства являются крайне важными и должны максимально использоваться для повышения эффективности процедур анализа и
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
77
разработки компактных схем хранения данных матриц. Матрицы жесткости и масс имеют одинаковую внутреннюю структуру (расположение ненулевых элементов), которая полностью определяется заданной конечноэлементной схемой.
Отметим также, что для закрепленных конструкций матрица жесткости является положительно определенной и становится вырожденной для свободных конструкций. При этом порядок вырождения равен числу степеней свободы конструкции как жесткого тела. Так, степень вырождения матрицы жесткости для свободной трехмерной конструкции равна шести. В случае же двумерных пластинчатых или оболочных конструкций степень вырождения равняется трем. Матрица масс конструкции обычно является положительно определенной матрицей, за исключением тех случаев, когда при ее формировании используются некоторые специальные методы конденсации. В дальнейшем будем предполагать, что матрица масс М является положительно определенной.
2.2.	ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ БКК
Учет температурных факторов при проектировании БКК оказывает существенное влияние на выбор конструктивно — силовой схемы, выбор конструкционных материалов, построение активных систем управления точностью рабочих поверхностей. Как показано в предыдущих разделах, БКК работают в условиях неравномерного и нестационарного нагрева, связанного с орбитальным движением аппарата и изменением его ориентации по отношению к Солнцу, которое является основным источником тепловой энергии, накапливаемой конструкцией. Кроме того, в составе БКК могут находиться собственные тепловыделяющие элементы, изменяющие поле распределения температур конструкции. Нагрев или охлаждение силовых элементов БКК приводит к возникновению дополнительных тепловых напряжений и деформаций, величины которых могут Достигать значений, превышающих критические величины. Это ограничивает работоспособность конструкции.
Тепловые поля, возникающие в силовых элементах БКК при движении по околоземной орбите, могут носить как стационарный характер, так и нестационарный. Предположение о стационарности распределения температур в элементах БКК нуждается в дополнительном обосновании, т. к. изменение условий освещенности при движении конструкции по орбите приводит к перераспределению тепловых потоков как вне, так и внутри конструкции. Однако если изменение температуры элементов конструкции носит длительный характер, тепловое поле можно считать стационарным. Если же условия освещенности изменяются достаточно быстро, или интенсивно начинают работать внутренние источники тепла,
78
ГЛАВА 2
то предположение о стационарности температурного поля утрачивают силу Кроме того, нестационарные изменения теплового поля конструкции приводят к возникновению динамических эффектов.
Термоупругие эффекты, возникающие в БКК, описываются с использованием классической теории упругости и термодинамических соотношений, которыми характеризуются процессы переноса тепла за счет теплопроводности в элементах конструкции при стационарном и нестационарном теплообмене посредством переизлучения энергии. Важнейшим следствием возникновения градиентов температуры в элементах конструкции БКК является возникновение дополнительного поля напряжений. Анализ величин этих напряжений является одним из важнейших моментов при проектировании БКК-
Для вычисления величин тепловых напряжений, возникающих в процессе эксплуатации БКК, используются традиционные расчетные методы, в частности — метод конечных элементов. Не останавливаясь на подробном описании всех этапов процедуры построения системы уравнений МКЭ, остановимся лишь на особенностях, характерных для решения термоупругих задач. Предполагая распределение температур в элементах конструкции стационарным и заданным, учтем в системе уравнений МКЭ дополнительные деформации, возникающие вследствие нагрева, которые складываются с упругими деформациями
а = С(е-е') ,	(2.1)
где <т — вектор напряжений; С — матрица упругости; е, е* — вектора упругих и тепловых деформаций. Вектор е* имеет следующую структуру
е* = {ai/,a2/, q3*,0, 0,0},	(2.2)
где t — приращение температуры элемента; ai, а2, »з — коэффициенты теплопроводности (предполагается, что материал — ортотропный). Следуя традиционной схеме МКЭ, дополнительные узловые усилия, действующие в узлах расчетной модели, даются соотношением
qf = yN*Ce(<to,	(2.3)
n
где N — матрица функций формы. По аналогичной формуле вычисляются и узловые моменты, если при разработке математической модели БКК используются элементы типа балок, пластинок и оболочек, т. е. узлы расчетной модели допускают шесть степеней свободы — три перемещения и три поворота. Использование подобных элементов при расчете
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
79
термоупругого поведения БКК особенно важно, т. к. характер тепловых воздействий на БКК обуславливает возникновение не только сжимающих и растягивающих усилий в элементах конструкции, но и возникновение распределенных моментов. Примером такого рода тепловых воздействий может служить пластинка, освещенная Солнцем с одной стороны. На освещенной стороне пластинки выделяется тепло солнечного излучения, и поверхность нагревается до некоторой температуры /р Если толщина пластинки достаточно большая или мал коэффициент теплопередачи, то затененная сторона будет иметь некоторую температуру /2 < /р Предполагая, что процесс передачи тепловой энергии стационарен, температуры (л и /2 будем считать постоянными. Энергетический баланс обуславливается рассеянием энергии в виде излучения с обоих сторон пластинки. В силу того, что температуры ti и /2 различны, а коэффициент теплового расширения постоянен по толщине пластинки, возникают распределенные моменты, искривляющие пластинку.
Аналогичные рассуждения можно провести и для балочных элементов. Заметим, что использование традиционной гипотезы плоских сечений для описания деформации балки приводит к необходимости введения дополнительного параметра в систему конструктивных параметров — высоты сечения балки.
Важнейшим этапом в анализе термоупругого поведения БКК является определение поля температур в силовых элементах конструкции. Для определения распределения температур в конструкции и анализа тепловых потоков необходимо построить решение уравнения, описывающего нестационарные процессы распределения тепла в элементах БКК
ср— = АД/ + q, ОТ
(2.4)
где с — удельная теплоемкость материала, р — плотность, А — коэффициент теплопроводности, q — мощность внутренних источников тепла, символом А обозначен оператор Лапласа. Начальным условием для уравнения (2.4) является распределение температур в момент т = 0. В зависимости от условий функционирования БКК краевые условия могут быть заданы различными способами. Пусть на участке поверхности St задано распределение температур t = t(r). На участке поверхности Sqi где известен тепловой поток, имеем dt/dn + qn = 0. Здесь п — нормаль к поверхности Sq. Решение уравнения (2.4), как правило, строится численно с использованием метода конечных элементов. Следуя традиционной процедуре МКЭ выпишем функционал, стационарное значение
80
ГЛАВА 2
которого достигается на решении (2.4):
(2.5)
Задавая систему функций формы в виде матриц Ny и аппроксимируя с их помощью поле распределения температур, подставим полученные выражения в функционал (2.5), проварьировав который получим окончательные выражения для матриц элементов задачи теплопроводности. Матрица теплопроводности j-го элемента, построенная с использованием матриц производных функций формы Aj, имеет вид:
Т,=
ЛА* А,-J J
<Klj.
(2.6)
я,
Матрица теплоемкости записывается следующим образом:

(2.7)
С использованием матриц Ту и Qj строится глобальная матрица системы разрешающих уравнений МКЭ. Вектор правых частей системы уравнений образован векторами
Rj = - J N*q dQ.j -I- J N*gn dSj.
Sj
(2.8)
Таким образом, стандартная процедура метода конечных элементов позволяет свести решение задачи теплопроводности к интегрированию системы обыкновенных дифференциальных уравнений:
Qt + Tt = R(r)
(2.9)
с начальными условиями
t-r=O — tо ,
(2.10)
где t — вектор узловых значений температуры.
Тем не менее, учет всех внешних и внутренних факторов, влияющих на распределение температур в БКК представляет собой весьма сложную
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
81
задачу. При анализе теплового поведения сложных многоэлементных конструкций можно ограничиться некоторыми предельными случаями. Действительно, в процессе эксплуатации БКК условия освещенности, т. е. ориентация конструкции относительно Солнца, могут непрерывно изменяться. Анализ всех возможных распределений температур в силовых элементах БКК, которые приводят к изменениям геометрических параметров конструкции, возникновению дополнительных усилий и напряжений — практически неразрешимая задача. Поэтому при проектировании БКК возможно применение подходов, сложившихся в традиционной практике проектирования летательных аппаратов. С этой целью производится предварительный анализ режимов полета с оценкой возможных предельных значений температур и характера их распределения. Выбирается группа расчетных случаев, при реализации которых возможно достижение наибольших напряжений в элементах БКК и максимальное искажение геометрических характеристик конструкции. Для выбранных расчетных случаев производится подробный тепловой расчет. Естественно, что такой подход к анализу теплового поведения БКК в значительной степени опирается на интуицию проектировщика и зависит от накопленного опыта проектирования и эксплуатации аппаратов аналогичного класса.
Рис. 2.1
Рассмотрим в качестве примера расчет тепловых деформаций космической радиоантенны, схематически изображенной на рис. 2.1. Конструкция антенны выполнена из алюминиевого сплава. Силовой каркас антенны образован трансформируемым кольцом диаметром 30 метров, соединенного вертикально расположенными балочными элементами второго кольца, образующего внешний контур отражающей поверхности.
82
ГЛАВА 2
Центральная часть конструкции антенны, предназначенная для формирования параболической поверхности, образована системой вантов, стержней и тонкостенных лепестковых элементов, на которые натянуто сетеполотно, образующее отражающую поверхность зеркала. Подробная структура силового кольца не приводится ввиду его сложности и наличия множества элементов, обеспечивающих трансформацию из сложенного состояния в развернутое.
Конструкция зеркальной части антенны состоит из 48 идентичных секций. К силовому кольцу антенны прикреплены четыре трансформируемые опоры, соединяющие зеркало антенны с фокальным контейнером, образуя пространственный силовой каркас космического аппарата.
В качестве предельного расчетного случая для оценки тепловых деформаций конструкции антенны и искажения формы отражающей поверхности рассмотрено боковое освещение космического аппарата Солнцем. Предполагалось, что половина антенны относительно оси симметрии нагревается, а другая половина охлаждается. На основании проведенных оценок для конструкционных элементов, изготовленных из алюминиевого сплава, в расчете принят перепад температуры в 120°С. Проведенный расчет тепловых деформаций показал, что величина среднеквадратичного отклонения формы рабочей поверхности зеркала антенны даже при столь неблагоприятных тепловых воздействиях не превышает 0,2% величины характерного размера конструкции.
2.3.	ОЦЕНКА ЖЕСТКОСТИ БКК. СТАТИЧЕСКИЙ АНАЛИЗ
Разрабатываемые БКК в силу своего функционального предназначения должны удовлетворять жестким ограничениям, накладываемым на характеристики их механического поведения. Одним из главных показателей оказывается жесткость конструкции. Обеспечение повышенной жесткости — существенное требование, учитываемое при проектировании космических платформ, несущих лазерные установки, и космических антенн как радио, так и оптического диапазона. Однако требование максимизации жесткостных характеристик вступает в конфликт с тенденциями увеличения размеров БКК и условиями не превышения массой конструкции установленных пределов. Весовые лимиты обусловлены возможностями транспортных систем, используемых для доставки БКК на околоземные орбиты. Даже увеличивающиеся мощности современных носителей не позволяют эффективно решать задачи обеспечения жесткостных характеристик за счет увеличения массы силового материала. Утяжеление конструкции приводит к повышению расходов на транспортировку, а в случае раздельной посекционной доставки отдельных частей изделия на орбиту обуславливает необходимость последующего проведения дорогостоящих сборочных работ в космосе. Поэтому для
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
83
решения проблемы обеспечения жесткости БКК требуется применение таких средств, как активные и пассивные системы контроля жесткости и парирования деформации, а также использование в конструкции высокомодульных композиционных материалов. При проектировании таких конструкций высокие требования естественным образом предъявляются к статическому и динамическому жесткостному анализу. Опишем некоторые подходы статического анализа, причем начнем с метода, позволяющего получить качественные оценки.
Предположим, что конструкция, моделируемая стержневой системой с шарнирными соединениями, описывается следующей системой уравнений равновесия:
As = q,	(3.1)
где символами А и q обозначены, соответственно, матрица равновесия системы и вектор внешних воздействий, приложенных к узлам системы, а через s — вектор неизвестных реакций и внутренних усилий в стержнях. Через тип обозначены число уравнений равновесия и число входящих в них неизвестных внутренних усилий и реакций, а через г а и га+я — ранги матрицы равновесия А и расширенной матрицы, дополненной столбцом q. В зависимости от вида конструкции может реализоваться, вообще говоря, один из следующих трех случаев:
а) т = п, Ь) т < п, с) т > п.
Рассмотрим последовательно каждый из этих случаев:
а)	Пусть т = п, т. е. число уравнений равновесия совпадает с числом неизвестных. Если при этом ранг системы уравнений также совпадает с их числом, т. е. гд = т, то рассматриваемая система уравнений имеет единственное решение для любого вектора нагрузки. Конструкция в этом случае статически определима и геометрически неизменяема.
Если же га < т, то свойства конструкции определяются соотношением между га и гд+д. В случае, когда г а гд+д, система уравнений равновесия, очевидно, несовместна. Это означает, что конструкция представляет собой механизм (мгновенно изменяема). Для того, чтобы определить, к какому из двух указанных типов относится рассматриваемая конструкция, необходимо исследовать уравнения равновесия в возмущенном состоянии. Если при смещениях системы из исходного состояния, не противоречащих связям, уравнения равновесия имеют решение, то конструкция мгновенно изменяема. В противном случае конструкция представляет собой механизм.
При га = ГА+q (га < т) система уравнений равновесия имеет решение, но не единственное. Это означает, что конструкция, которая является
84
ГЛАВА 2
мгновенно изменяемой или механизмом, при некоторой нагрузке ведет себя как неизменяемая статически неопределимая конструкция.
Ь)	Пусть теперь т < п, т. е. число уравнений равновесия меньше числа неизвестных реакций и внутренних усилий. При гд = т система уравнений равновесия имеет не единственное решение и, следовательно, конструкция является геометрически неизменяемой и статически неопределимой. Степень статической неопределимости конструкции равна п — т. Для единственности решения системы уравнений равновесия в рассматриваемом случае к этой системе следует присоединить условия совместности перемещений. При гд < т (т < п) реализуется один из двух случаев: либо конструкция в целом геометрически изменяема, но часть ее статически неопределима, либо конструкция мгновенно изменяема, причем часть ее, по-прежнему, статически неопределима. При гд = гд+<? рассматриваемая система уравнений не имеет решения.
с)	В случае m > п и гд / rA+q система уравнений равновесия не имеет решения, а конструкция геометрически изменяема. Если же гд = гд±я (т > п), то система уравнений оказывается непротиворечивой и, следовательно, имеет решение. Это означает, что рассматриваемая геометрически изменяемая конструкция ведет себя при некоторой нагрузке как неизменяемая.
Рис 2 2
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
85
В качестве примера применения описанного анализа рассмотрим один из возможных проектов трансформируемой радиоантенны, общий вид которой схематически изображен на рис. 2.2. Модель фрагмента вантовой части орбитальной радиоантенны показан в плане на рис. 2.3. Центральная часть антенны считается твердым телом, а ее вантовая часть моделируется стержневой системой (фермой), скрепленной с центральной частью и внешним силовым кольцом. Одна из секций исходного проекта вантовой системы изображена на рис. 1.3 в перпендикулярной к кольцу плоскости. Вантовая система крепится в 288 точках к центральной части, а в 144 — к кольцу. Общее число рассматриваемых уравнений равновесия т = 1296 + 6 состоит из 1296 уравнений, отвечающих условиям равновесия во внутренних узлах вантовой системы и точках закрепления, и 6 уравнений, отвечающих условиям равновесия центральной части как твердого целого (условия равенства нулю проекций сил и моментов, действующих на центральную часть). Количество неизвестных в этих уравнениях п — 864 4- 432 = 1296, где 864 — число искомых усилий в элементах системы, а 432 — число неизвестных реакций в точках закрепления.
В результате получаем т > п, т. е. для исходного проекта вантовой системы конструкция изменяема и не может сохранять заданную геометрию при действии произвольной нагрузки. Существенным недостатком такой конструкции является ее повышенная деформативность и возникновение значительных усилий при относительно небольших нагрузках. Это, очевидно, неприемлемо для конструкций космических радиоантенн, основным требованием к которым является поддержание заданной точности рабочих поверхностей.
Для обеспечения жесткости требуется модификация проекта вантовой системы. На рис. 2.4 изображена проекция одной секции исходного ва
86
ГЛАВА 2
рианта компоновки вантово-стержневой системы, для которой проведен предварительный анализ.
Для модификации исходного варианта конструкции введены дополнительные вантовые элементы, соединяющие узлы 4—5, 6—7, 7—9 (см. рис. 2.5). В этом случае п = 1584, т. е. т < п. Выполняется также условие га > т- Следовательно, модифицированный вариант представляет собой геометрически неизменяемую и статически неопределимую конструкцию.
Как бы ни была важна описанная начальная часть анализа, она еще не достаточна для оценки статической жесткости проектируемых систем и, в особенности, таких конструкций, как космические платформы и антенны, к которым предъявляются особые требования по жесткости.
Для того, чтобы оценить жесткость конструкции в величинах достигаемых упругих перемещений и запасаемой энергии деформаций, следует использовать уравнения равновесия в перемещениях
Ku = q,	(3.2)
где и — вектор узловых перемещений конструкции, q — вектор внешних нагрузок, а К — глобальная матрица жесткости конструкции, ретвля-ющая собой составляемую по известным правилам композицию матриц жесткости отдельных элементов. При данных нагрузках в результате решения линейной системы алгебраических уравнений (3.2) определяется вектор узловых перемещений и, характеризующий деформативность конструкции. Для оценки жесткости могут рассматриваться как максимальные смещения узлов (компоненты вектора и), так и некоторые «интегральные» характеристики: полная энергия упругих деформаций, энергия искажения формы конструкции и др. Воспользуемся следующим представлением критерия жесткости:
J = (u,x),	(3.3)
где х — некоторый заданный вектор, а круглыми скобками обозначено скалярное произведение векторов и и х- Если в качестве
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
87
= (0,0,..., 0,1,0,..., 0) принимается вектор, имеющий единственную ненулевую единичную компоненту с номером г, то величина J будет равна соответствующей компоненте глобального вектора перемещений. В этом случае жесткость оценивается выбираемой из соображений симметрии, структуры конструкции и характера нагружения величиной компоненты перемещения некоторого узла. Если же в качестве вектора х принять вектор нагрузок q, т. е. положить х = <7, то величина J будет характеризовать производимую нагрузками работу, или, что то же, энергию упругих деформаций, запасаемую конструкцией. Обратная величина J*"1 называется интегральной жесткостью и часто используется для установления эффективных оценок.
Обычно конструкция рассчитывается не на одну фиксированную нагрузку, а на множество возможных воздействий. Это соответствует реальным условиям функционирования конструкции и ее многоцелевому назначению. К допущению при анализе и проектировании большого числа внешних воздействий приводит и неполнота имеющейся информации о реальных воздействиях. Эти характерные причины обуславливают множественность принимаемых к рассмотрению внешних воздействий и большой объем вычислений проводимых при анализе жесткости. При данных обстоятельствах чрезвычайно эффективным оказывается следующий способ выполнения расчетов. Наряду с системой уравнений (3.2) в рассмотрение вводится дополнительная сопряженная система уравнений K*v — х, где К* — матрица транспонированная к матрице жесткости К, a v — вектор сопряженных перемещений. Для рассматриваемых в данной книге конструкций и нагрузок матрицы жесткости являются симметричными и поэтому К* = К. Имеем,
Kv = х.	(3.4)
Для вектора реальных перемещений конструкции и и для введенного вектора сопряженных перемещений справедливо следующее замечательное свойство:
(и, х) = (и, Kv) = (v,Ku),	(3.5)
позволяющее представить меру жесткости J в следующем чрезвычайно удобном виде:
J=(v,q).	(3.6)
Как видно из формулы (3.6) и соотношения (3.4) при выполнении полного анализа жесткости конструкции для целого множества воздействий не требуется решать многократно систему уравнений (3.2) с различными
88
ГЛАВА 2
правыми частями и после этого находить величину J по формуле (3.3). Достаточно один раз решить сопряженную систему уравнений (3.4), которая отличается от исходной только видом правой части, и при помощи найденного вектора сопряженных перемещений v определить по формуле (3.6) значения J для различных нагрузок q. Таким образом, за счет предельного сокращения числа решаемых систем уравнений достигается значительное уменьшение объема проводимых вычислений, что, в свою очередь, позволяет учитывать при анализе достаточно широкие классы внешних воздействий.
2.4. ЧАСТОТНЫЙ АНАЛИЗ. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЧАСТОТ И МОД СВОБОДНЫХ КОЛЕБАНИЙ
Упругие колебания БКК, происходящие как в космосе при орбитальном движении конструкций, так и при наземных (стендовых) испытаниях, происходят при воздействии многих внешних и внутренних силовых факторов. Это и температурные градиенты, и гравитационные моменты, и различной природы демпфирующие силы и другие факторы. И тем не менее динамическая жесткость БКК определяется во многом ее внутренней структурой. Поэтому примем во внимание сначала только упругие и массово-инерционные характеристики конструкции и обсудим вытекающие отсюда следствия, полезные как при проектировании, так и при интерпретации результатов. С целью сокращения записей и придания рассматриваемым соотношениям большей простоты будем пользоваться матричной формой записи определяющих уравнений. Пусть свободные колебания конечноэлементной модели конструкции описываются уравнением
М6 + Ки = 0	(4.1)
с симметричными положительно определенными матрицами масс М и жесткости К. Точками обозначено дифференцирование по времени. Разделение временной и пространственной переменных и представление решения в виде суммы произведений синусов и косинусов аргумента wt (cv — частота, t — время) на неизвестные векторы пространственных координат приводит к задаче на собственные значения:
Кф = ХМф,	(4.2)
где под собственным значением Л понимается квадрат частоты: А = и;2, а ф — амплитудный вектор перемещений.
Допустим, что имеется $ собственных векторов ф1, ф2,..., ф3, соответствующих собственному значению А. Тогда их любая линейная комбинация a-Та2</>2 Ч----\-а8ф3 (cii —постоянные) является собственным
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
89
вектором, соответствующим этому собственному значению. Это утверждение проверяется непосредственно:
к (а^') = 12aiK^ =Ам (Z2 а*^‘ \1 = 1	/ i=l	\i=l
Из симметричности (К = К*, М = М*) и строгой положительности операторов К и М следует положительность собственных значений А. Действительно, пусть А и ф — собственное число и собственный вектор уравнения (4.2). Умножим левую и правую части этого уравнения на вектор ф. В результате получим
' (Кф,ф)
(4.3)
С использованием свойств скалярного произведения векторов и симметричности матриц жесткости и масс, а также положительности этих матриц приходим к выводу, что А > 0.
Собственные формы колебаний ф1 и ф2, отвечающие различным собственным значениям Ai = ш2, Аг = (Ai Аг), ортогональны относительно матрицы масс М. Для доказательства данного утверждения достаточно умножить скалярно левые и правые части уравнений Кс/»1 = AiMc/»1, К</>2 = АгМ</>2 соответственно на ф2 и ф1 и получающиеся уравнения вычесть одно из другого. В результате этих операций получим соотношение
(Ai - Х2)(Мф\ф2) = (Кф^ф2) - (Кф2,фг) = 0.
Так как Ai 7^ Аг, то
(М^1,^2) = 0.	(4.4)
Если одному собственному значению А отвечает несколько собственных форм колебаний, то их можно ортогонализовать, применяя к собственным формам процедуру ортогонализации. Собственные векторы для удобства обычно нормируются. Поэтому в дальнейшем считаем, что совокупность всех собственных векторов (форм колебаний) образует ортонормиро-ванную систему.
Отметим, что собственные моды свободных колебаний конструкции ортогональны также и относительно матрицы жесткости. Действительно, предположим, что ф1, ф2 — собственные векторы (моды), отвечающие собственным числам Аь Аг и умножим обе части матричного уравнения Кс/»1 = AiMc/»1 скалярно на собственный вектор ф2. С учетом (4.4) будем иметь
(Кф1, ф2) = Ai (М^1, ф2) = 0.	(4.5)
90
ГЛАВА 2
Рассмотрим упругую конструкцию, совершающую собственные колебания, и отметим некоторые свойства, относящиеся к наложению или снятию механических связей. Наложение механических связей может выражаться в задании дополнительныхусловий, отвечающих более жесткой системе закрепления конструкции, задании односторонних условий типа неравенств (контактных условий), описывающих способ подкрепления конструкции другими упругими или жесткими объектами. Отдельно могут рассматриваться односторонние и двусторонние связи, соответствующие заданию ограничений на перемещения. Снятие механических связей происходит при «отлипании» контактирующих частей конструкции, ее разрушении, приводящему к появлению трещин и полостей, отколов и расслоений в изделиях из композитов и структурно неоднородных материалов. С математической точки зрения введение связей означает задание дополнительныхусловий, налагаемых на класс допустимых переменных, которые составляют область определения функционалов. Таким образом, введение дополнительной связи должно сужать класс допустимых переменных и, тем самым, приводить к увеличению минимального значения или уменьшению максимальной величины рассматриваемого функционала. Наоборот, снятие связей означает расширение допустимого множества переменных, на котором разыскиваются минимумы или максимумы соответствующих функционалов. При этом, очевидно, происходит «опускание» минимумов и «поднятие» максимумов. Подобные соображения лежат в основе многих фундаментальных теорем сравнения, широко используемых в анализе и при проектировании механических систем. Сформулируем здесь некоторые основные утверждения.
Если на механическую систему наложить дополнительные связи, то основной тон (фундаментальная форма колебаний и соответствующая ей минимальная частота) и все собственные тона (обертоны) системы могут измениться лишь в сторону повышения частот. Обратно, если освободить систему от ряда связей, ограничивающих ее колебания, то как основной тон, так и все обертоны системы могут измениться лишь в сторону понижения частот.
Приведем теперь некоторые утверждения общего характера, связанные с разъединением конструкции на подконструкции и сопоставлением собственных частот колебаний целой конструкции и частот колебаний ее отдельных частей. Заметим, что вопросы представления конструкций как объединения некоторого числа подконструкций и вопросы декомпозиции спектра собственных значений оказываются важными как при анализе жесткости конструкций, так и в теории их оптимального проектирования. Пусть механическая система Q представляет собой совокупность отдельных не связанных между собой конструкций Qi. Q2, • • • Тогда совокупность собственных значений и собственных векторов колебаний механической системы состоит из совокупности всех собственных значений
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
91
и собственных векторов составляющих ее конструкций. Для того, чтобы пояснить сформулированное утверждение, достаточно заметить следующее. Собственные моды (амплитудные векторы) свободных колебаний, каждая из которых относится к одной из конструкций Q,, составляющих систему, являются одновременно собственными для всей рассматриваемой механической системы. Справедливо и обратное. Собственная мода колебаний для всей механической системы является собственной модой по крайней мере для одной из входящих в эту систему конструкций. Другими словами, сказанное выше означает только то, что если составляющие систему конструкции не контактируют между собой, то колебания этих конструкций происходят независимо.
Приведем и другое общее свойство колеблющихся конструкций. Предположим, что конструкция Q состоит из подконструкции Q,, контактирующих между собой. Предположим, что конструкция закреплена, и что количество собственных частот колебаний конструкции и подконструкций, не превышающих величины А, обозначены, соответственно, через Q(A) и Q,(A) (г = 1,2,...). Тогда справедливо следующее неравенство:
fi(A)>£fi,(A),
1 = 1
В заключение заметим, что достаточно часто проектируемые БКК представляют собой циклически симметричные конструкции (см. например рис. 2.1, 2.2). При вычислении частот и форм свободных колебаний циклически симметричных конструкций возникают специфические особенности, обусловленные прежде всего кратностью частот свободных колебаний и вытекающими из этого вычислительными особенностями.
2.5. ПРИМЕНЕНИЕ ЧАСТОТНОГО АНАЛИЗА В МЕХАНИКЕ БКК ДЛЯ ОЦЕНКИ ДИНАМИЧЕСКОЙ ЖЕСТКОСТИ
Пожалуй, одними из наиболее эффективных и часто используемых в инженерном анализе аэрокосмических конструкций, в частности, при анализе и проектировании БКК являются частотные методы. В литературе эти методы называются также методами свободных колебаний и спектральными методами. Независимо от использования в практических приложениях той или иной терминологии эти методы основываются на рассмотрениях малых гармонических колебаний ненагруженных конструкций и решении возникающих задач на собственные значения
К</> = АМ</>.	(5.1)
Здесь К и М матрицы жесткости и масс, получаемые при конечноэлементном моделировании конструкции, ф = {</>1, </>2, • • •, Фт} — вектор
92
ГЛАВА 2
узловых перемещений, а А = w2 — квадрат частоты свободных колебаний. Для рассматриваемых на практике конструкций матрицы масс и жесткостей обычно являются симметричными и разреженными. Собственные частоты, определяемые из решения задачи (5.1), составляют спектр частот свободных колебаний
(5-2)
который характеризует жесткостные свойства, а также выявляет и другие важные специфические особенности конструкции. Так области сгущения спектра, приводящие к резонансным явлениям при наложении на них частотного диапазона нагрузок, должны учитываться как при анализе динамики конструкции, так и при проектировании систем управления размещаемых на конструкции. Отметим возникающие здесь проблемы разноса частот и отстройки от резонанса. В свою очередь соответствующие частотам моды или формы свободных колебаний, описываемые векторами ф1, ф2,..., фт, характеризуют допустимые типы движений, которые могут возбуждаться в процессе движения конструкции на орбите и зачастую приводить к нежелательным последствиям.
Чем же наиболее характерны БКК и в чем особенности применения к ним частотного анализа? Отметим здесь два главных момента, обуславливающих основные трудности проведения частотного анализа.
Во-первых, БКК в отличии от привычных наземных сооружений являются свободными конструкциями. Под свободными здесь понимаются незакрепленные конструкции, а не конструкции, к которым не приложены внешние воздействия. Для свободных конструкций возможны движения как твердого целого, при которых не происходит деформирования ее упругих элементов и в конструкции не возникает напряжений. Так, без приложения конечных внешних усилий возможны трансляционные перемещения свободной конструкции вдоль осей координат и ее повороты относительно этих осей. Эти особые формы движения как твердого целого могут реализоваться квазистатически и соответствующие им частоты равняются нулю. Таких мод в общем случае пространственных конструкций будет шесть: три соответствуют параллельным переносам, а три вращениям относительно трех осей. В частных случаях их может быть меньше. Так, для пластинчатой модели БКК, используемой для анализа изгиба и поперечных колебаний, таких мод три. Две из них отвечают поворотам относительно осей, расположенных в плоскости пластинки, а одна мода соответствует смещениям в направлении, нормальном к плоскости пластинки. Наличие у конструкции указанных мод движения как твердого целого и соответствующих им нулевых частот означает, что имеется определенное количество (равное числу степеней
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
93
свободы абсолютно жесткой конструкции) линейно независимых собственных векторов фг 0, i — 1,2,..., к < 6, отвечающих нулевым собственным значениям, т. е. А, = О, К</>* = 0. Таким образом матрица жесткости БКК оказывается вырожденной:
detK = 0,	(5.4)
причем степень вырождения является в общем случае шестикратной. Это приводит к известным сложностям при проведении расчетов, т. к. матрица К не допускает непосредственного обращения. Для регуляризации задачи спектрального анализа применяется следующий прием. Проводится построение «смещенной» матрицы жесткости
Кк = К + кМ,	(5.4)
где к > 0 — достаточно малое число. Поскольку параметр смещения к выбирается положительным, то, очевидно, «смещенная» матрица Кк будет положительно определенной. Для «смещенной» (регуляризованной) матрицы жесткости формулируется задача на собственные значения
ККф = ш2Мф,	(5.5)
которую можно также записать в виде
Кф = (w2 - к)Мф,	(5.6)
Непосредственное сопоставление задач (5.6) и(5.1)с A =w2 позволяет утверждать, что собственные векторы регуляризованной «смещенной» задачи (5.5) совпадают с собственными векторами исходной сингулярной задачи (5.1), а собственные значения этих задач связаны соотношением
у2=и24-/с.	(5.7)
Таким образом, у регуляризованной задачи отсутствуют нулевые частоты колебаний и устраняется сингулярность матрицы жесткости, что позволяет, в частности, выполнять операции обращения.
Вторая важная особенность механического поведения БКК связана с плотностью спектра собственных частот колебаний и, в особенности, низшей части этого спектра. Специфика проектирования БКК и ряда других протяженных гибких конструкций заключается в том, что необходимо весьма точное знание нижней части спектра и часто при этом требуется находить более сотни частот. Заметим, что согласно накопленному опыту проектирования более жестких крупногабаритных конструкций,
94
ГЛАВА 2
таких как ракеты-носители, это требование не является критическим и обычно при расчетах этих изделий ограничиваются отысканием нескольких десятков частот. При этом частотный спектр сравнительно жестких ракет-носителей не является особенно плотным и не возникает серьезных опасений «пропустить» в расчетах какую-либо частоту свободных колебаний. Для того, чтобы повысить надежность вычислений при выполнении частотного анализа БКК, требуется применять специальные процедуры контроля.
Опишем один такой прием, называемый проверкой Штурма. Предполагается, что в результате проведенных вычислений найдены первые (низшие) р частот колебаний и соответствующие им собственные векторы. Проверка основана на свойствах последовательности Штурма характеристического полинома «смещенной» задачи
(Кл-туМ)</> = ^2М(/>,
где ту — А, а А — является «приближением справа» к полученному значению квадрата р-ой частоты ш?. Используемое свойство заключается в том, что при разложении Кк — туМ в произведение трех матриц L^D^L*, где — нижняя треугольная матрица, a — диагональная матрица, получающееся число отрицательных элементов в диагональной матрице D^, равно числу собственных значений меньших А. Если вычисления проведены верно, т. е. не пропущены какие-либо из собственных значений и собственных векторов, то число отрицательных элементов на диагонали матрицы Dr/ будет равняться р+рг, гдерг — количество степеней свободы конструкции как жесткого тела. Данное утверждение справедливо, если р-ая частота не является кратной. Если же р-ая частота имеет кратность к, то число отрицательных элементов в будет равно р + рг + к — 1.
В практике расчетов частот и мод свободных колебаний БКК использовались различные вычислительные методы и их специальные модификации. Однако накопленный при проведении частотного анализа опыт позволяет утверждать, что одним из наиболее эффективных методов является метод итерирования векторных подпространств, который представляет собой комбинацию обратных (блочных) итераций с аппроксимацией Рэлея — Ритца на каждом шаге итерационной процедуры. Приведем кратко используемый в дальнейшем алгоритм этого метода, который сводится к выполнению следующих операций.
1.	Вычисляются М — ортонормированные моды (ф'Мфэ = <5,7), соответствующие перемещению конструкции как жесткого тела, и полагается: Фг = [ф^ ф%,...f фя], где q < 6 (для вычисления достаточно знания лишь геометрических характеристик конструкции). Вычисляется Sr = МФГ.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
95
2.	Выбираегся величина параметра к и вычисляется матрица = К + «М смещенной задачи.
3.	Выбираются s начальных векторов для итерационной процедуры, являющиеся столбцами матрицы Ф^\ где s > р, р — число собственных векторов и собственных значений, которые необходимо определить.
4.	Выполняется разложение Холецкого матрицы К* на треугольные множители Кк = LL*, где L — нижняя треугольная матрица.
5.	Выполняются итерации (г = 1,2,...), на каждом шаге которых с номером i следует вычислять матрицу Ф^ размерности т х s, столбцы которой являются текущими аппроксимациями мод собственных упругих колебаний:
а)	Формируется правая часть = МФ^ для шага обратной итерации. При i > 2 матрица получается следующим образом: = S^T(i). (Матрицы S(i) и Т(г) вводятся ниже).
Ь)	Проводится коррекция матрицы SW с учетом того, что ф(’) должна быть М — ортогональна к Фг:
=	S$ = St*) - SrX(<)‘.
с)	Расчет матричной системы линейных алгебраических уравнений
кЛ(<+1) = s<?
осуществляется при помощи последовательного решения двух матричных систем линейных уравнений с треугольными матрицами:
Ьф(>') = s^, Ь*Ф<’+1) = ф(’).
d)	Вычисляются проекции Кл и М на подпространство, генерируемое ф(Ж)
Kw = ¥(i+1)*K„¥(,+1) =
М<г) = ф^+1^МФ^+1^Ф^+1^*8^+1\
s(<+1) = МФ<’+1>.
е)	Решается задача на собственные значения
96
ГЛАВА 2
с диагональной матрицей собственных значений 0^^ и матрицей собственных векторов, ортогональных по отношению к матрице f) Вычисляется улучшенная аппроксимация собственных векторов
ф(«+1) _
g) Проверяются условия сходимости.
6) Осуществляется проверка Штурма.
7) Определяются собственные значения исходной задачи
J = 1,2, • ••,?•
Заметим, что описанное выше и используемое в алгоритме смещение (сдвиг) полезно применять и для закрепленных конструкций. Это обусловлено тем, что асимптотическая скорость сходимости для J-oro собственного вектора «смещенной» задачи пропорциональна выражению
(J2 •
KJ кз
и? + к
j = 1,2,...,s.
В том случае, если для нормы вектора х используется выражение 11х112 = (х,М-1«), то невязка для J-oro собственного вектора на г-ой итерации определяется величиной
О
uj + к
wf + к
Таким образом, сходимость итерационного процесса существенно зависит от выбора начального сдвига к. Для свободных конструкций максимальная эффективность алгоритма будет достигаться при к - е, где е > 0 — малое число, позволяющее применять стандартные вычислительные процедуры для разложения матрицы Кк на множители Холецкого и решения получаемых треугольных систем. Для закрепленных конструкций из соображений сходимости целесообразно выбирать к =	+ е.
Отметим также, что на шаге 5—с) решаются системы алгебраических уравнений с заведомо плохо обусловленными матрицами коэффициентов. Ошибки при решении таких систем могут быть одного порядка с величиной точного решения. Пусть для ф^ имеем. ~ф^ — ф^ + где
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
97
ту07 — точное решение системы линейных уравнений на шаге обратной итерации для J-oro вектора, фь — ошибка, возникающая вследствие округлений. Существенным является следующее свойство, которому удовлетворяют все векторы (J = 1,2,...,$).
Если величинам близка для некоторого А’ к собственному значению^, то ошибки решения системы линейных алгебраических уравнений на шаге 5—с) будут полностью сосредоточены в направлении А-ого собственного вектора. Поэтому плохая обусловленность матрицы Кк не приведет к ошибкам при вычислении собственных векторов.
Описанный выше метод итерирования векторных подпространств применялся для решения многих задач частотного анализа БКК. В частности, этот метод использовался для определения собственных частот и собственных форм свободных колебаний модифицированной конструкции космической радиоантенны, изображенной на рис. 2.2, а также при рассмотрении ее вариантов с усиленной центральной частью и усиленным кольцом.
На рис. 2.6 представлены значения частот нижней части спектра в зависимости от номера моды колебаний. Кружочками на этом рисунке
4 — 2185
Рис. 2.6
98
ГЛАВА 2
показаны полученные в результате расчетов собственные частоты колебаний модифицированной конструкции. Частоты, получающиеся дл? данной конструкции при десятикратном увеличении жесткости внешнего кольца, показаны звездочками. Из сопоставления приведенных значений следует, что усиление кольца не приводит к значительному изменению жесткостных характеристик. Аналогичные расчеты проводились также для конструкции с десятикратно увеличенной жесткостью центральной части. Полученные при этом значения частот, показанные треугольниками на рис. 2.6, существенно превышают значения частот модифицированной конструкции и ее варианта с усиленным кольцом. Таким образом, данные проведенного анализа показывают, что жесткость радиоантенны может быть значительно увеличена при увеличении жесткости центральной части, а повышение жесткости внешнего кольца влияег на нижнюю часть спектра антенны в меньшей степени.
В качестве другого примера приведем вкратце результаты частотного анализа конструкции космической платформы, показанной на рис. 2.7.
Рис. 2.7
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
99
Конструкция имеет периодическую решетчатую структуру и состоит из 529 стержневых элементов соединенных шарнирами. Ячейка периодичности рассматриваемой ферменной конструкции отдельно изображена на рисунке. Полная конструкция характеризуется 294 степенями свободы. В расчетах свободных колебаний, которые проводили по описанному методу, площади поперечных сечений стержней полагались одинаковыми и равными 50 мм2. Полученные в результате проведенных расчетов частоты нижней части спектра показаны на рисунке звездочками.
Анализ частот и форм свободных колебаний БКК позволяет на начальном этапе проектирования конструкции сделать предварительные выводы об эффективности выбранной конструктивно-силовой схемы, скорректировать значения некоторых конструктивных параметров, уточнить компоновку БКК, оценить эффективность применения тех или иных конструкционных материалов. В качестве примера такого анализа рассмотрим радиоантенну, изображенную на рис. 2.1. Результаты вычисления низших частот свободных колебаний конструкции приведены в таблице 2.1.
Таблица 2.1
	1	2	3	4	5	6	7	8
Вариант 1	0,65	0,69	0,69	0,71	0,96	0,96	1,23	1,75
Вариант 2	0,85	0,85	0,86	1,12	1,12	1,29	1,66	1,66
Вариант 3	0,91	1,49	1,49	1,58	1,66	1,68	1,99	1,99
Вариант 4	1,21	1,50	1,50	1,68	1,75	1,88	1,99	1,99
Вариант 5	1,21	1,49	1,49	1,56	1,88	2,11	2,24	2,24
Вариант 6	1,72	1,88	1,97	1,97	2,63	2,77	3,09	3,09
Первый вариант конструкции — базовый, исходный. Во втором варианте в два раза увеличены величины предварительных растягивающих усилий в центральной части зеркала. Вариант 3 отличается от исходного тем, что крепление опор фокального контейнера перенесено с нижнего силового кольца на верхнее. Четвертый вариант отличается от предыдущего увеличенными усилиями в лепестковых элементах зеркала. В пятом варианте конструкции радиоантенны при увеличенных предварительных напряжениях в лепестковых элементах центральной части зеркала радиоантенны изменена конструкция опор фокального контейнера, масса которых уменьшена вдвое и крепление перенесено на верхнее силовое кольцо. В шестом варианте конструкции в силовых элементах алюминиевый сплав заменен композиционным материалом — углепластиком.
4*
100
ГЛАВА 2
Рис. 2.8
На рис. 2.8 приведены некоторые характерные формы свободных колебаний. Анализ таблицы 2.1 позволяет на предварительном этапе проектирования БКК выбрать наилучшие параметры конструкции, уточнить компоновку и оценить влияние на динамические характеристики изделия применения разных конструкционных материалов.
2.6. НЕСТАЦИОНАРНАЯ ДИНАМИКА БКК
При анализе и проектировании БКК важная роль отводится моделированию процессов нестационарной динамики. Возникновение нестационарных колебаний характерно для различных режимов функционирования конструкций в космосе. Неустановившиеся упругие колебания возникают в конструкциях космических платформ и радиоантенн при включении двигателей с целью переориентации конструкции и при выполнении других определенных маневров. Коротковолновые возмущения конструкции могут быть также вызваны ударными нагрузками при ее соударениях с дру!ими космическими телами (метеориты, космический мусор и т. д.), а также нестационарными нагрузками, возникающими при перемещениях по БКК расположенных на ней аппаратов или при «немягком» причаливании к космической станции различных транспортных средств.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
101
Для того, чтобы оценить динамический отклик конструкции на нестационарные воздействия и разработать активные и пассивные методы парирования возникающих нестационарных процессов в конструкциях, требуется разработать модели, адекватно описывающие нестационарную динамику БКК, и эффективные вычислительные алгоритмы, позволяющие с требуемой точностью интегрировать описывающие динамику конструкции системы уравнений высокой размерности. Успешное продвижение в этом направлении возможно только при условии, что вопросы разработки модели и методов расчета динамического поведения конструкции решаются комплексно. Одним из наиболее эффективных методов, позволяющих рассчитывать динамические характеристики многоэлементных конструкций, является метод конечных элементов. Очевидно, что при использовании конечноэлементных моделей необходимо ориентироваться на применение специальных методов для разреженных матриц, что в значительной степени ускоряет вычисления и позволяет рационально использовать память вычислительных машин.
Рассмотрим сложную составную конструкцию, подверженную внешнему нестационарному нагружению. Динамика конструкции описывается системой обыкновенных дифференциальных уравнений с начальными условиями:
Mu + Dii -I- Ku = q,	(6.1)
и(0) = и0, й(0) = й0,	(6.2)
где и(/) = {иДО,... ,un(t)} — вектор обобщенных перемещений; q = q(t) — вектор нагрузок; М и К — симметричные матрицы масс и жесткостей конструкции; D — матрица демпфирования, структура и свойства которой зависят от выбранной модели демпфирования; uo, uQ — заданные векторы перемещений и скоростей, характеризующие начальное состояние конструкции в момент времени t — 0.
Для свободных (незакрепленных) конструкций вектор-функция и(/) декомпозируется на вектор упругих перемещений и вектор nr(t) перемещения конструкции как жесткого целого, т. е.
u(f) = u/(/) +ur(t).	(6.3)
Заметим, что система дифференциальных уравнений (6.1) записана в предположении о малости вектора перемещений. Это, в частности, накладывает определенные ограничения на вид вектор-функции q(/) внешних нагрузок. Заметим также, что в случае неуравновешенных малых внешних воздействий, действующих в течение достаточно большого интервала времени [0, /у], указанное предположение о малости вектора
102
ГЛАВА 2
перемещений может оказаться невыполненным. Поэтому применительно к БКК динамические уравнения (6.1) могут использоваться на ограниченном интервале времени при рассмотрении случаев приложения к конструкции уравновешенных и слабо неуравновешенных воздействий, когда движение конструкции как твердого целого мало отличается от равномерного поступательного движения. Для описания динамического поведения конструкции удобно пользоваться инерциальными системами координат. Система уравнений (6.1) также применима для определения динамического поведения незакрепленных конструкций по отношению к неинерциальным системам отсчета, связанным с недеформированной конструкцией в случае, если движение медленное и силами инерции можно пренебречь при проводимых расчетах.
Предполагается, что для рассматриваемых свободных многоэлементных конструкций конечноэлементные модели характеризуются большим числом степеней свободы. Чтобы эффективно применить к этим моделям численные процедуры целесообразно использовать редуцированный модальный анализ. Применительно к сказанному сделаем некоторые пояснения. Как уже отмечалось, при нестационарном нагружении анализ динамики конечноэлементной модели сводится к решению задачи Коши для системы линейных обыкновенных дифференциальных уравнений второго порядка. Размерность данной системы определяется числом степеней свободы выбранной модели и для рассматриваемых конструкций оказывается весьма значительной. Поэтому непосредственное интегрирование уравнений динамики во многих случаях оказывается неэффективным и для анализа поведения конструкций применяется метод разложения перемещений по собственным формам колебаний конструкции и формирование редуцированной аналитической модели для определения вектора нормальных координат меньшей размерности р (р < т). Данный подход позволяет существенно снизить размерность системы уравнений, описывающей динамическое поведение конструкции, и является основой эффективного проведения анализа.
Перейдем непосредственно к формированию редуцированной модели. Используем суперпозицию (6.3) и следующие представления векторов упругих и жестких перемещений:
П/^Ф/W/, Ur — Фг\¥г,	(6.4)
U — Фу W/ -Ь Фг1¥г,
где wy — {ur(. юС . •• u'p}, wr ~ {^1,	...,	— векторы нормаль-
ных координат; Фу = {ф\. ф2, •• •, Ф'р } — модальная матрица, составленная из р нижних мод свободных упругих колебаний; Фг — матрица,
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
103
столбцами которой являются векторы представляющие собой моды движения абсолютно твердого тела. Для применяемой конечноэлементной модели принимается, что число мод свободных упругих колебаний много меньше числа степеней свободы т исходной модели (р т).
Моды упругих колебаний и соответствующие им частоты являются собственными векторами и собственными значениями алгебраической задачи:
К</?
фгМф> = hj, i,j = 1, 2,... ,р.
(6.5)
Моды перемещений конструкции как твердого целого являются собственными векторами этой задачи, отвечающими нулевому собственному значению (ш? — 0, j — 1,2,..., 6). В общем случае незакрепленного тела нулевое собственное значение является шестикратным. Учитывая, что собственные векторы, отвечающие различным собственным значениям, ортонормированы относительно матрицы М, будем иметь:
Ф}МФГ = 0.
(6.6)
Так как собственные векторы, представляющие собой моды движения конструкции как твердого целого, соответствуют нулевым собственным значениям, то
ф;кфг = о.
(6.7)
11одставляя представление (6.4) в (6.1), умножая получающееся соотношение слева на матрицу Фу и учитывая свойства (6.6), (6.7), получим:
ФуМФ/wy -|- ФуВФу\¥у 4- ФуВФглуу 4- Ф^КФ/Wy = Фуд. (6.8)
Заметим, что в силу ортонормированности рассматриваемых собственных векторов упругих колебаний справедливо равенство:
ФуМФу = Е,
(6.9)
где Е — матрица тождественного преобразования, диагональные элементы которой равны единицам, называемая единичной матрицей. Из (6.9) с учетом (6.5) следует также равенство:
ФуКФу = diag(c^f).
(6.10)
104
ГЛАВА 2
Здесь diag(o/f) — диагональная матрица, вдоль диагонали которой стоят собственные значения задачи (6.5). Предположим, что матрица демпфирования D удовлетворяет условию:
ФуПФг — 0.	(6.11)
С учетом соотношений (6.9)—(6.11) и обозначения Q — ФуЦ уравнение (6.8) запишется в виде:
Wy -I- ФуВФ/Мг/ -|- diag(u7)w/ — Q.	(6.12)
Аналогично, подставляя представление (6.4) в (6.2) и умножая получающиеся соотношения на матрицу ФуМ, получим равенства:
ФуМФуУУу(О) -I- ФуМФг1¥г(0) ФуМио, ФуМФ/wy(0) + ФуМФгитг(0) - ФуМй0.
С учетом равенств (6.6), (6.9) приходим к начальным условиям для редуцированной системы:
wy(0) — ФуМио, wy(0)--ФуМйо-	(6.13)
Порядок системы дифференциальных уравнений (6.12) ниже, чем порядок исходной системы (6.1). Заметим также, что дифференциальные уравнения системы (6.12) не являются независимыми и должны решаться совместно. Связь между уравнениями обусловлена вхождением в них демпфирующих членов.
Часто рассматриваются случаи пропорционального демпфирования, когда матрица демпфирования пропорциональна матрице масс:
D ~ z/M,	(6.14)
или матрице жесткости конструкции'
D —//К,	(6.15)
где и и ц — заданные коэффициенты. При расчетах применяются также более общие комбинированные матрицы демпфирования, которые представляют собой линейную суперпозицию матриц жесткости и масс с заданными коэффициентами Ум, ук'-
D “ умМ -I- z/AK.
(6.16)
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
105
В этих случаях матрица демпфирования ФуО^у, фигурирующая в уравнениях (6.12), оказывается диагональной:
ФуБФ/ ~ д/д/Фу МФ/ + д/дгФ/КФ/ = д/д/Е + i//< diag^2).
и поэтому в система (6.12) декомпозируется на отдельные несвязанные между собой уравнения, которые могут интегрироваться независимо. При этом декомпозированная система записывается следующим образом:
w + ^mw 4-diag(w2)(w + i//<w) = Q.	(6.17)
В общем случае система уравнений (6.12) декомпозируется, когда матрицы демпфирования, жесткости и масс связаны между собой следующим равенством ({12]):
р-1
D = M^2afc[M“‘K]fc.	(6.18)
А=0
Для определения коэффициентов а>к (к ~ 0,1,..., р — 1) в (6.18) обычно используются механические эксперименты и идентификационные процедуры. Заметим, что матрица демпфирования D сложной конструкции не может быть в общем случае составлена из матриц демпфирования подконструкций или отдельных элементов, как это обычно делается для матриц жесткости и масс составной конструкции. Имеющиеся трудности построения глобальной матрицы демпфирования носят принципиальный характер. Не вдаваясь в различные аспекты данной проблемы, упомянем только, что трудности построения матриц демпфирования для сложных конструкций и конструктивных соединений еще во многом не преодолены. Поэтому большая часть практических рекомендаций основана на построении глобальной матрицы демпфирования с использованием различного рода аппроксимаций диссипируемой энергии для главных мод колебаний.
Система уравнений (6.1), (6.2) представляет собой систему обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами. Для прямого интегрирования подобных систем разработаны специализированные вычислительные процедуры [18], ориентированные на использование в методе конечных элементов. В принципе для интегрирования системы уравнений (6.1) и (6.2) возможно применение стандартных вычислительных процедур. Однако в связи с плохой обусловленностью матриц коэффициентов и большой размерностью задачи эти процедуры становятся малоэффективными. К процедурам прямого интегрирования относятся такие метода, как метод центральных разностей, метод Хаболта, 0-метод Вилсона, метод Ньюмарка и множество других.
106
ГЛАВА 2
He останавливаясь на вопросах точности интегрирования, устойчивости вычислительной схемы и сравнении разных методов интегрирования, опишем подробнее метод Ньюмарка [151], хорошо зарекомендовавший себя при решении задач анализа динамики БКК.
Отрезок времени Т, на котором вычисляется движение конструкции, разбивается на п равных интервалов AL Для вычисления обобщенных перемещений и их скоростей используются следующие соотношения:
Ut+zv — Н- UjA/ 4-
1
2 ~Q
u( 4- au(+At A/2,
(6.19)
и«+д« = u( + [(1 - /?)«t +	Ai,
где нижним индексом t и А/ обозначаются моменты времени, для которых вычисляется вектор обобщенных перемещений, скоростей или ускорений. Числовые параметры вычислительной схемы а и /3 определяют точность и устойчивость метода. При значениях а = 1/6 и /? = 1/2 соотношения (6.19) аналогичны соотношениям метода линейного ускорения [95]. При интегрировании по методу Ньюмарка принимаются значения о = 1/4 и (3 — 1/2, что обеспечивает безусловную устойчивость вычислительной схемы. Дополняя соотношения (6.19) уравнениями равновесия
Mut+At 4- Diif+Af 4- Kut+At = qt-|-At,	(6.20)
получаем замкнутую систему алгебраических уравнений, позволяющую определить й^+де, st и ие+дг по заданным й^, ии(. Таким образом, задавая начальные условия йо, й0 и ио, определяющие состояние механической системы в момент времени t — 0, решая последовательно систему алгебраических уравнений (6.19) и (6.20), для любого момента времени можно определить обобщенные перемещения, скорости и ускорения. Заметим, что точность метода интегрирования существенным образом зависит от выбора шага по времени А/ и обусловленности матриц коэффициентов М, D и К. Устойчивость метода Ньюмарка определяется параметрами а и /?, значения которых должны удовлетворять следующим соотношениям: (3 > 0,5, а > 0,25(/? 4- 0,5)2.
Для приведенного описания динамического поведения конструкции вектор упругих перемещений u/(Z) характеризует гибкость конструкции. Обычно при оценке динамической жесткости представляют интерес отдельные компоненты вектора узловых перемещений ну и их максимальные значения, достигаемые в процессе функционирования конструкции на фиксированном временном интервале [0,//], где tf — заданное значение времени. В ряде случаев для оценки жесткости используются некоторые комбинации компонент иу, характеризующие, например, значения потенциальной энергии упругих деформаций отдельных частей конструкции.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
107
Обозначая через д заданную функцию или функционал от \ можно выразить естественную меру динамической жесткости конструкции в следующем виде:
J— max	(6.21)
tG[O,tz]
Критерии жесткости вида (6.21) используются не только при анализе процессов нестационарной динамики, но и при оптимальном проектировании БКК.
Заметим здесь, что естественная формулировка задач анализа жесткости и проектирования конструкций часто предполагает использование векторов истинных перемещений отдельных точек, а не вектора узловых значений и/. Рассмотрим способ задания жесткостного критерия в этом случае. Пусть на поверхности оболочки, моделирующей динамическое поведение БКК, задан конечный набор точек pj (j = 1, 2,..., /3). Определим вектор естественных упругих перемещений U = [U1*, U2*,..., U^*], где UJ — вектор естественных упругих перемещений для точки с номером j. Векторы естественных перемещений отдельных точек pj могут быть выражены через вектор нормальных координат w/ посредством соотношения
и-7 = BjU/ = BjSywy.
где В7 (J = 1,2,...,/?) — матрицы перехода от обобщенных перемещений к естественным перемещениям в точках pj. Тогда величина упругого перемещения точки pj в момент времени t =	< tf, характеризуемая
величиной скалярного произведения (UJ, Uj)t=tk t находится по формуле:
J/ =
В качестве меры жесткости может рассматриваться величина максимального упругого перемещения, определяемая выражением
I2 zz maxjkJj •
В качестве примера расчета динамической жесткости конструкции рассмотрим деформацию центра зеркала радиоантенны, изображенной на рис. 2.1.
Свободная антенна нагружается импульсным включением четырех реактивных двигателей, расположенных симметрично на силовом кольце. Вектор тяги двигателей направлен вдоль вертикальной оси симметрии
108
ГЛАВА 2
конструкции. Значение тяги каждого двигателя равно 20 Н, продолжительность импульса равна 0,1 с. Вертикальное смещение центра зеркала антенны в начальный промежуток времени изображены на рис. 2.9.
Заметим, что рассмотренный в настоящем параграфе подход к решению задач анализа динамики свободных конструкций при нестационарных динамических воздействиях имеет весьма ограниченную применимость ввиду того, что накладываются ограничения на допустимые движения свободной конструкции. Тем не менее, при решении ряда задач рассмотренный подход оказывается эффективным.
2.7. ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ АНАЛИЗА ДИНАМИКИ СВОБОДНЫХ КОНСТРУКЦИЙ
Определение поля перемещений и деформаций свободной крупногабаритной космической конструкции представляет собой весьма сложную задачу. Представляется целесообразным использование приближенных численных методов, в частности, метода конечных элементов, который получил в последнее время широкое распространение. Это в значительной мере объясняется наличием высокоэффективных вычислительных программ, обладающих высокой степенью автоматизации трудоемких операций. Рассмотрим применение МКЭ для определения деформаций свободной БКК в процессе орбитального движения под действием нестационарных внешних нагрузок.
Область П, занимаемая конструкцией, представляется в виде совокупности конечных элементов Q, (г = 1, 2,..., М), связанных между собой в узловых точках. В качестве неизвестных принимаются узловые значения искомой вектор-функции перемещений w(p,/). Число узловых точек, помноженное на число неизвестных в каждом узле, определяет число степеней свободы, от которого зависит точность определения искомой функции w(p, t) в области П.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
109
Предположим, что выбраны интерполирующие полиномы г-го конечного элемента и можно записать соотношение, связывающее поле перемещений внутри элемента с узловыми значениями
w('> = nW(p)u<’\ pen,,	(7.1)
где w(!) — поле смещений г-го конечного элемента, N(’)(p) — матри-ца размера [k х г], элементами которой являются известные функции координат	& — количество узловых переменных, г — об-
щее число степеней свободы элемента. Вид интерполирующих функций определяется геометрией элемента, классом задачи и содержанием вектора и(г\ — вектор-столбец, состоящий из г узловых неизвестных г-го конечного элемента.
Соотношения (7.1) позволяют аппроксимировать искомую функцию w(p, t) во всей области П. Заметим, что матрицы функций формы приведены к общей (глобальной) системе координат. Для обеспечения непрерывности w(p, t) будем использовать согласованные элементы, т. е. элементы, обеспечивающие одинаковую аппроксимацию вдоль границ. В s-ой узловой точке определяется вектор неизвестных U5. Совокупность этих векторов образует вектор неизвестных в общей системе координат ансамбля конечных элементов
U = ||U1,U2,...,Uf||T,
где t — число узлов; N — число неизвестных во всей области. Перейдем к описанию конечноэлементной трактовки собственных форм колебаний упругой незакрепленной конструкции и коэффициентов, входящих в уравнения движения.
Деформации в каждом конечном элементе вычисляются с помощью вектора w^)(p, t) по формулам:
(,) _ dwV dw2} dw3} дх} ’ дх-2 ’ дхз
1 / dw^ dw^\ 1 / dw^	dw^\ 1 / dw[^	dw^
2 \ dx2	dxi I ’ 2 I dx3	dx? / ’ 2 I dx3	dxi
т
где /) — проекция на ось Cxj, ae^ — вектор-столбец, составленный из композитов тензора малых деформаций. Из представления
через вектор следует, что
е(з)
110
ГЛАВА 2
где ДМ — известная матрица производных функций формы.
Напряжения в материале каждого г- го элемента связаны с деформациями линейными соотношениями:
где — матрица упругих постоянных; — вектор-столбец, составленный из компонентов тензора напряжений.
Вычислим потенциальную энергию упругих деформаций:
п = | f £2	1=
П ’•>=1	‘=ln,
= 1 £ /	= ^UTKU,
'=4
где К — неотрицательная матрица жесткости, вычисленная для незакрепленной конструкции, U — глобальный вектор неизвестных. Матрица К вырождена и дефект ее равен шести (П = 0 для векторов U, которые соответствуют движению гела как жесткого целого).
Кинетическая энергия деформируемой конструкции записываются в виде:
Т=^ f wT(р, £)w(p,/) t/m —	и^тД^тЛ'^и^ ^UMU;
n	l~lnt
где M — матрица масс конструкции. Матрица М всегда положительно определена.
Уравнение, описывающее свободные упругие колебания конструкции (включающие малые движения тела как целого), можно получить, например, из уравнения Лагранжа второго рода. Это уравнение имеет вид:
MU+KU = 0.	(7.2)
Одним невырожденным линейным преобразованием матрицу М можно привести к единичной матрице, а матрицу К к диагональной. Иными словами, существует N векторов Е/с (k — 1,..., 6), En (n = 1,..., N — 6) таких, что
Ё^МЁ,- = 6ki, E^MEj = 6nj, Ё£МЕП = О, (7.3) E*KEj=0, Е„КЕ,- = Sl2n6nj, Ё^КЕП = 0.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
111
Соотношения (7.3) означают, что система векторов Ед, (к = 1,..., 6), (n =	— 6) ортонормирована относительно матрицы М и
образует базис, вектора Ед и Е являются собственными векторами задачи на собственные значения (7.2), причем Ek соответствуют нулевым собственным значениям.
Перейдем к рассмотрению движения свободной упругой конструкции. Предположим, что модель конструкции состоит из совокупности конечных элементов и вектор U характеризует смещение узлов. Сделаем замену переменных:
6	N—6
и = Ё/сА/с +
к = 1	п = 1
где Аь qn — новые переменные. Если ввести в рассмотрение обобщенную матрицу функций формы для всей конструкции [49] N, то аппроксимацию вектор-функции перемещений можно построить следующим образом
6	АГ-6
w(p,Z) = ^NEfeAfc+J2NEng„.	(7.4)
к = 1	п = 1
Таким образом, для форм колебаний, соответствующих шести степеням свободы недеформированной системы, движущейся как твердое тело, фк(р), Фк(р) (& = 1?2,3) мы получили их конечноэлементную аппроксимацию — N(p)Ef (г = 1,..., 6); для форм которым соответствуют ненулевые частоты свободных упругих колебаний — аппроксимацию N(p)En (см. параграф 4 главы 1);	— приближенное выражение для
частот собственных колебаний Пп.
Проводя рассуждения, аналогичные приведенным в § 4 первой главы, нетрудно показать, что
У N(p)En dm = О, У р х N(p)En dm = 0.	(7.5)
n	n
Если для некоторой конкретной конструкции построена ее конечно-элементная модель, построена матрица N(p) и найдены вектора Еп, можно конкретизировать систему уравнений динамики (4.26), (4.27), (4.30)-(4.32) § 4 главы 1 для этой конструкции.
Чтобы построить приближенное решение уравнений движения БКК, необходимо вычислить ряд коэффициентов, в частности, (1.2.18) и L-j1 (см. § 4 главы 1). Покажем, как можно вычислить коэффициенты (г, j — 1,2,3; п = I, 2,..., N — 6) наиболее простым способом.
112
ГЛАВА 2
Во первых, из (7.5) следует, что H-j — и для каждого п надо вычислить 6 коэффициентов Н-j. Используя конечноэлементную аппроксимацию собственных форм получаем, например,
= J {^1,0, 0}N(a?i, х2, dm — j . 0, 0}N(.rL.	,r3) dmEn.
Г2	Q
Проводя аналогичные рассуждения для i,j - 1,2,3, получаем, что если вычислить шесть интегралов
Иц = у (z>i,0,0)NJrn, п
Н33 = у (0,0,x3)Ndm,
Н1з = y^O.OJNchTi,
Н22 ~ у (0,.r2,0)Ndm,
Hi2 = y\.c2,0,0)N</m, Q
н23 = J (O.r3.0)Ndm, О
(7.6)
все коэффициенты найдутся по формулам.
ЯП ___ ТТ ЕЧ
ij —
(7.7)
то есть операцией вычисления скалярного произведения векторов. Это операция очень проста для реализации на ЭВМ.
Перейдем к рассмотрению конечноэлементной трактовки коэффициентов L1-”. Эти коэффициенты обладают свойством симметрии: L^J1 — Lj?. Из условий ортонормированности (4.7) (гл. I, § 4) и (3.3) следует, что
г кп _ г т кп г кп
п33 ~ °кп “	~ ь22
(7.8)
Рассмотрим
j х U^n)
У e£nt • ( 0
• (l,0,0)NE„ dm =
Nr
О
О NrfmE„. (7.9)
1 О
О
О
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК
113
Проводя аналогичные рассуждения для i,j = 1,2,3, получаем, что вычислив восемь интегралов
	N7'	1 0 0 0	0 0 0 0	0 0 0 1	N dm,	Ll2= 1 h	NT	0 0 0 0	1 0 0 0	0 0 0 0	N dm,
Ln = У	NT	0	0	0	N dm,	L?i = У	NT	1	0	0	N dm,
и		0	0	0				0	0	0	
		0	0	0				0	0	0	
L»23 = У	NT	0	0	1	N dm,	L22 = У	NT	0	1	0	N dm,
и		0	0	0				0	0	0	
		0	0	0				0	0	0	
L»31 = У	NT	0	0	0	N dm,	l32 = у	NT	0	0	0	N dm,
п		1	0	0				0	1	0	
Все коэффициенты L^J1 найдутся по формулам:
2# = E?L0E„.	(7.10)
Полученные при помощи (7.7) и (7.10) коэффициенты Я™ и необходимо подставить в систему (4.26),(4.27), (4.30)-^4.32). Коэффициенты Яг” и L^J1 постоянны и для каждой конкретной конструкции вычисляются один раз.
Как уже отмечалось, вычисление коэффициентов, входящих в уравнения движения деформируемой конструкции и характеризующих внешние воздействия, представляет собой самостоятельную задачу. Однако для поля гравитационных сил, например, никаких дополнительных вычислений не потребуется, так как все необходимые коэффициенты выражаются через Я^,	[67]. Для вычисления параметров, характеризующих силы
активного управления (двигателей переориентации), понадобятся только значения собственных форм в точках приложения нагрузки.
Таким образом, в настоящем параграфе уравнения движения выписаны в наиболее простой и удобной для применения ЭВМ форме, достигнуто согласование уравнений движения свободной упругой конструкции с конечноэлементной моделью БКК
Глава 3
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
Особенности проектирования БКК имеют определенную специфику, связанную с тем, что крупногабаритные космические конструкции экс -плуатируются в условиях орбитального полета, т. е. в невесомости. Поэтому применение традиционных подходов к созданию новых образцов техники, которая предназначена для эксплуатации в наземных условиях, не всегда возможно. Это связано с тем, что проведение наземного натурного эксперимента, допускающего моделирование условий эксплуатации в космосе, является весьма дорогостоящим и не всегда возможным. Следовательно, необходима разработка построения математических моделей БКК, адекватно описывающих механические свойства и поведение конструкции. Причем практически невозможно создать уни версальную математическую модель, пригодную для анализа всех возникающих в процессе функционирования БКК ситуаций. Кроме того, построение экспериментальной установки часто является очень сложной задачей, соизмеримой по сложности и затратам с созданием БКК. Основной упор в анализе механического поведения БКК переходит на математическое моделирование с применением высокоэффективных вычислительных программ и алгоритмов.
БКК, развертываемые в космосе, в силу своих размеров имеют относительно большую массу, что порождает трудности с доставкой, развертыванием или монтажем. Несомненно, является актуальной задача оптимального проектирования конструкции с целью снижения ее массы, увеличения жесткости, улучшения функциональных характеристик. Решение задачи оптимизации, как правило, строится на основании математической модели реального прототипа конструкции. В связи с этим особенно важной в процедуре проектирования и создания БКК становится задача идентификации массовых и жесткостных параметров конструкции на основании результатов натурного эксперимента, проводимого в наземных условиях с фрагментами БКК или всей конструкцией. Решение задачи идентификации позволяет в вычислительном эксперименте промоделировать механическое поведение конструкции, определить динамические характеристики аппарата, построить эффективную систему
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
115
ориентации и стабилизации, уточнить рациональную компоновку аппарата. Решение вышеперечисленных задач идентификации и оптимизации конструкций производится с применением процедур оптимизационного моделирования, рассмотрению которых посвящена настоящая глава.
3.1.	ОПТИМИЗАЦИЯ И АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ
В теории оптимального проектирования сложных конструкций важная роль отводится анализу чувствительности. Основная задача анализа чувствительности при моделировании и оптимизации конструкций заключается в установлении эффективных соотношений между рассматриваемыми изменениями в проектах конструкций и результирующими изменениями в их функциональных характеристиках. Получению этих соотношений и применению их при моделировании и проектировании уделяется существенное внимание во многих работах, поскольку это способствует выявлению наиболее эффективных способов оптимизации и рационального конструирования БКК. Обычно при проектировании БКК имеется широкий выбор переменных проектирования, варьированием которых можно повлиять на величину критерия качества. Например, уменьшение веса БКК может быть достигнуто в результате рационального распределения толщин, управления анизотропией материалов, армирования, создания предварительного напряженного состояния, эффективного расположения демпфирующих слоев и т. д. Важно знать, какие способы оптимизации или их комбинации приводят к более значительным изменениям рассматриваемых характеристик (функционалов) и каким образом может быть достигнут максимальный выигрыш по оптимизируемому функционалу. На указанные вопросы можно дать ответ, если получены характерные для анализа чувствительности соотношения. Отметим сначала некоторые характерные аспекты анализа чувствительности. Будем предполагать, что динамическое поведение конструкции описывается некоторой системой уравнений относительно вектор-функции перемещений и с коэффициентами зависящими от вектора параметров проектирования h. Для большей ясности и компактности изложения простейших схем анализа чувствительности воспользуемся операторными представлениями и запишем рассматриваемые уравнения в виде
£(u,h) = 0.	(1.1)
Нелинейное в общем случае операторное соотношение (1.1), устанавливающее функциональную зависимость между переменными проектирования и состояния, включает в себя уравнения динамики, начальные и граничные условия. Соответствующее линеаризованное уравнение, связывающее малые вариации Jh и Ju, запишем следующим образом:
LuJu + LAJh = 0,	(1.2)
116
ГЛАВА 3
где Lu, Lh —линейные относительно Ju и Jh операторы, коэффициенты которых, вообще говоря, могут зависеть от и и h. Зависимость вариаций функционалов 6Ji от вариаций переменных проектирования и состояния Jh, Ju получается непосредственно при помощи линеаризации вы раже ний Ji - Ji(u,h) и представления величин JJ2 в виде суммы линейных относительно Jh и Ju функционалов:
J J,-= (xUh) + (xU4	(1-3)
Круглыми скобками в (1.3) обозначены скалярные произведения векторов <*Ь,Хл = xUu.h) и векторов 6u,xi = хЦи.Н
Принципиальный интерес в теории проектирования заключается в установлении эффективной непосредственной зависимости JJ2- от Jh. Для исключения явной зависимости вариаций функционалов J./, от вари аций переменных состояния Ju и получения основной формулы анализа чувствительности в виде
JJ3 = (elA,Jh)	(1.4)
могут использоваться следующие два метода.
Первый метод (прямой метод) основан на построении обратного оператора L~l и нахождении решения задачи (1.2):
<Уи= -L^LhSh.	(1.5)
Последующее исключение Ju из (1.3) приводит к соотношениям анализа чувствительности
8Jt = (xUh) + (xl-^Wh) = Щ - [ь;ЩГхиН (1.6)
Второй метод (метод сопряженных переменных) установления зависимостей между J Ji и Jh вида (1.4), который находит широкое применение в современных работах по оптимальному проектированию (см. также [7, 121), основан на введении сопряженных переменных v1 (г — 1,2,..., г) и решении сопряженных краевых задач, служащих для их определения. Опишем схематично данный метод. С этой целью умножим скалярно выражение, записанное в левой части равенства (1.2), на сопряженную переменную vz и выполним следующие преобразования
О - (v*, LuJu + LhJh) = (£>1\ Ju) + (L£v’, Jh). (1.7)
Почленное сложение (1.3) с (1.7) приводит к равенству
U = (х’л + iftvUh) + (xt + Ь>’Ли).	(1.8)
МЕТОДЫМОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
117
Определяя сопряженную переменную v2 как решение сопряженной задачи
L*uv' = -Xu	(19)
и обращая тем самым в нуль второе скалярное произведение в (1.8), приходим к искомому выражению вида (1.4)
^• = (xk + b;vUh).	(1.10)
Существуют другие различия в получении соотношений (1.4) ,(1.10), обусловленные в основном характером зависимости от переменных проектирования определяющих соотношений, моделирующих динамику поведения конструкции. Переменные проектирования могут входить в коэффициенты уравнений или ими может определяться форма области, в которой заданы эти уравнения.
3.2.	КОНЕЧНОЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ И АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ
Для моделирования динамического поведения конструкций и проведения анализа чувствительности эффективно используются как континуальный, так и конечноэлементный подходы. Для континуального (недискретного) подхода характерно, что определяющие уравнения включают операции дифференцирования как по времени, так и по пространственным коэффициентам. При этом формулируемые задачи динамики содержат как начальные условия для вектор-функции и ее производной по времени (скорости), так и краевые условия, характеризующие способы закрепления и нагружения конструкции. Если же при моделировании динамического поведения конструкции вместо системы с распределенными параметрами используется конечноэлементное представление, то частные производные по пространственным переменным исключаются из рассмотрения. Динамическое поведение конструкции в этом случае описывается задачей Коши для системы обыкновенных дифференциальных уравнений
Mu + Du+Ku = F	(2.1)
u(0) = u°, ii(0) = u°,	(2.2)
где и(/) = {^1(0, ^2^), • • •,	— искомая вектор-функция,
описывающая напряженно-деформированное состояние конструкции; h = {hi, h?, ..., hn} — вектор параметров проектирования; u°, й° — заданные векторы. Матрицы М, К, D, характеризующие инерционные, жесткостные и демпфирующие свойства конструкции, предполагаются зависящими от вектора параметров проектирования и положительными.
118
ГЛАВА 3
Кроме того, предполагается, что матрицы масс и жесткостей симметричны, т. е. М* = М, К* = К.
Основные функциональные характеристики представим в виде
Ч
Jv - у/р(/,и.Ь)Л, Р=1,2...,г.	(2.3)
О
Из выражений (2.3) непосредственно следует, что вариации интегральных функционалов вариации вектор-функций состояния и вариации параметров проектирования связаны следующим образом
<5Л = f	4-	dt.
J L \	J \ 5h J
о
(2.4)
Для исключения из (2.4) вариаций переменных состояния Ju и установления «прямой» связи Jh с выполним следующие операции. Проварьируем соотношения (2.1), (2.2) и после умножения обеих частей проварьированного уравнения (2.1) на вектор-функцию сопряженных переменных vp =	(£),	(t),..., i^(/)} выполним интегрирование в
пределах от t — 0 до t — if. Имеем
Ч
о = у [(v", Мйи + D<fa + К<5и) + (С", <5h)] dt =
О
ч
= у [(Ju, Mv" - D*vp + Kv") + (С", Jh)] dt+
-Kv^, MJu)(=t/ - (v", MJu)t=t, 4- (v", DJu)t=t/. (2.5)
Через С" в уравнении (2.5) обозначен вектор с компонентами С-(г — 1,2,... ,п), определяемыми следующим образом
сг =
( v ЗМ .. 3D . ЗК Г 'ai?', + aS“'Xu
dhi)
При помощи соотношения (2.5) и наложения условий vt/(/y) = +4tf) = о выражение для вариации функционала Jy (2.4) может быть записано в виде
w'=/[0h’^+c")
+ ( <Ju, + Mv" - D*v^ 4- Kvp
\ 5u
dt.
о
(2.6)
AU:ГОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
119
Определяя затем вектор-функцию v^(Z) как решение задачи Коши
Mv" - D*v" + Kv" +	= 0,	(2.7)
(7U
v^tf) = Q, vI/(<z) = 0	(2.8)
с условиями в конечный момент времени t = tj, приходим к результирующей формуле анализа чувствительности
/ \
= Uh, [ (|^ + CJ л) •	(2.9)
\	о	/
Для того, чтобы воспользоваться формулами анализа чувствительности (2.9) и определить вариации функциональных характеристик 6Jy, z/ — ], 2,..., г, обусловленные вариацией вектора параметров проектирования Jh, или построить улучшающие вариации переменных проектирования, требуется найти соответствующие вектору h переменные состояния и(/) и сопряженные переменные v^(/). С этой целью при заданном h интегрируется на отрезке времени [ОД/] система уравнений (2.1) с начальными условиями (2.2) при t — 0 и определяется вектор-функция состояния u(Z), а затем в обратном направлении от момента времени t = tf интегрируются сопряженные системы уравнений (2.7) с условиями (2.8) и находятся сопряженные вектор-функции v^(Z). Если вектор-функции и(/) и уД/) найдены, то отыскание вариаций сводится к выполнению операций дифференцирования и интегрирования по формулам (2.9).
Выполнение анализа чувствительности существенно упрощается в случае недемпфируемой конструкции. В этом случае вектор-функция состояния и(2), описываемая задачей Коши
Mii + Ku=F,	(2.10)
u(0) = 0, ik(0) = 0,	(2.11)
представляется в виде разложения
з
u(f) = £ a,W = *«(<)	(2.12)
i=i
по собственным векторам фг обобщенной задачи на собственные значения
Кф‘ = ш?Мф*, (ф*,Мф>) = 6ц, i,j = 1,2,...,s.
(2.13)
(2.14)
120
ГЛАВА 3
Здесь а(/) — вектор с компонентами at(/), / = 1,2,...,5,аФ — матрица, столбцами которой являются собственные векторы ф3. Подстановка представления (2.12) для и(/) в (2.10), (2.11) и умножение (2.10) слева на Ф* приводит к задаче Коши с трансформированными матрицами М и К и вектором F:
Ма + Ка F,	(2.15)
<*(0) = О, <i(0) = 0.	(2.16)
Матрицы М, К и вектор F связаны с соответствующими матрицами и вектором исходной задачи (2 10),(2.11) преобразованиями
М^Ф’МФ, К^ФКФ, F^*F	(2.17)
Условия нормировки (2.14) и соотношения (2.13) показывают, что трансформированные матрицы М и К являются диагональными. Матрица М — единичная, а вдоль диагонали матрицы К расположены собственные значения w? задачи (2.13),(2.14). Таким образом, построение решения задачи Коши для связанной системы уравнений (2,10),(2.11) сводится к решению обобщенной задачи на собственные значения и интегрированию расщепленной системы уравнений

(2,18)
at(()) _~r0,	ot(0) = 0,
(2.19)
Решение задач (2.18),(2.19) находится в квадратурах
Ч
о
(2.20)
Сопряженная система в случае отсутствия демпфирования допускает аналогичные упрощения. Применение для сопряженной системы
> < • . ГЛ- 5Л Mv + Kv —	,
(7U
v(/z) = 0, v(//)=0
(2.21)
(2.2?)
разложения решения по собственным векторам задачи (2.13),(2.14)
= £>,(0^ = W)
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
121
приводит к расщепленной системе уравнений и начальных условий для функций
Д+ч2Д = -(^,</),	(2.23)
\ ди у
А(//) = 0, Д(//) = 0.	(2.24)
Это обстоятельство позволяет представить в квадратурах функции Д (/)
Ч
Pi = —- [sin[w,(< - г)] (	) dr.
J	\ OU J
t
Аналогичные упрощения возможны и для демпфируемых систем, если матрица демпфирования пропорциональна матрице масс или жесткост-ной матрице или является их линейной комбинацией. Подробнее способы построения матрицы демпфирования будут обсуждаться в последующих параграфах.
3.3.	О КОРРЕКЦИИ МОДЕЛЕЙ
Одной из основных целей моделирования БКК является получение относительно простых и надежных моделей конструкций для использования как в процессе проектирования, так и разработке систем управления. Эти модели предназначаются для решения таких сложных проблем как управление точностью поверхностей, ориентация и устойчивость гибких конструкций в космосе. При том требуется, чтобы модели были адекватны проводимым экспериментам и были бы к тому же свободны от всех несущественных особенностей. На раннем этапе анализа и проектирования конструкции уточнение и приспособление (адаптация) моделей выполнялось при помощи метода «проб и ошибок», который в значительной мере зависит от накопленного опыта и интуиции. С возрастанием сложности конструкций применение этого метода для адаптации моделей становится затруднительным и необходима разработка более систематических и эффективных подходов.
Отметим некоторые трудности, с которыми приходится сталкиваться при практическом моделировании. Так, при разработке и применении в практике проектирования сложных моделей характерно отсутствие необходимых данных о геометрических и физических параметрах конструкции. 11еполнота информации обусловлена не точностями в изготовлении конструкции, разбросом физико-механических характеристик применяемых материалов, несовершенствами соединительных узлов и многими
122
ГЛАВА 3
другими факторами. Для упрощения же моделей часто отсутствуют объективные данные о неучитываемых рассматриваемой моделью эффектах. Применение этих моделей oi раничено также неточностью задания геометрических и механических характеристик. Эти обстоятельства объясняют расхождения, возникающие при проектировании и оптимизационном моделировании между теоретическими решениями, получаемыми на основе математических моделей, и данными физических экспериментов на изделиях. Поэтому представляются важными вопросы разработки методов учета экспериментальных данных о поведении реальной конструкции для построения адекватной математической модели. Перспективным в этом направлении является подход, заключающийся в доопределении и уточнении геометрических и механических параметров модели на основе минимизации «невязок» между рассчитываемыми функциями состояния и функционалами, характеризующими динамику конструкции, и соответствующими величинами, получаемыми экспериментальным способом. Скорректированные, таким образом, математические модели становятся пригодными для использования при решении задач анализа и оптимизации динамических характеристик реальных конструкций.
Таким образом, задачи оптимизации при проектировании возникают как из естественных требований улучшения характеристик конструкции, так и из необходимости использования адекватных математических моделей. Для решения оптимизационных задач идентификации параметров моделей обоснованным представляется применение эффективных методов оптимизации и анализа чувствительности, основанных на введении сопряженных переменных и сопряженных систем уравнений, получивших широкое применение в оптимальном проектировании конструкций.
Уделим ниже основное внимание параметрической идентификации конструкций, рассчитываемых на динамические воздействия. При этом заметим, что с разнообразными аспектами параметрической идентификации механических систем можно ознакомиться по имеющейся литературе
Важнейшими характеристиками механических систем, подверженных действию нестационарных нагрузок, являются частоты и формы свободных колебаний, формы вынужденных периодических колебаний, декременты затухания. 11ри расчете динамических реакций конструкций, подверженных действию нестационарных нагрузок, часто используются модальные методы, основанные на приведении матриц системы уравнений (матриц жесткости, масс и в ряде случаев матриц демпфирования), описывающих математическую модель конструкции, к каноническому виду. Этот прием позволяет значительно упростить вычисления за счет снижения размерности задачи. Во многих случаях движение динамически нагруженных конструкций описывается следующей системой
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
123
дифференциальных уравнений
J2u du
M^+D^+Ku=^’ (31>
где, как обычно, М — матрица, характеризующая инерционные свойства конструкции; К — матрица жесткости, зависящая от коэффициентов упругости (модуль Юнга, коэффициент Пуассона, модуль сдвига, модуль объемного сжатия и другие коэффициенты); D — матрица демпфирования, внутренняя структура которой существенно зависит от рассматриваемого механизма диссипации энергии (аэродинамическое демпфирование, внутреннее трение, обусловленное механизмами вязкого и вязкопластического демпфирования и др.); q(£) — вектор-функция внешних нагрузок. Матрицы М, К и D зависят от параметров конструкции h = (/ii,/i2, •.. ,hn), значения которых необходимо уточнить в процессе моделирования. Определение наилучших в некотором смысле параметров математической модели конструкции обычно сводится к минимизации функционалов вида
J= J(e,h),
(3.2)
где е(/) — вектор, характеризующий обобщенную ошибку или рассогласование расчетных характеристик конструкции и ее математической модели. Выбор структуры функционала (3.2) является важнейшим этапом решения задачи коррекции параметров модели. Способы построения функционалов рассматривались в [13, 82, 113, 123].
Во многих случаях задачи коррекции параметров математической модели конструкции можно свести к задаче минимизации функционала среднего значения квадрата обобщенной ошибки. В этом случае функционал (3.2) принимает вид
где t/ — граничное значение рассматриваемого временного интервала, а e(Lh) для конструкции, описываемой уравнением (3.1), имеет вид
с/2й	с/й
e(/,h)-M—+D—+ Ku-q, atz	at
где u, q — обозначают рассогласование расчетных и экспериментальных характеристик конструкции. При решении задачи минимизации функционала (3.3) в силу сложной зависимости динамических характеристик
124
ГЛАВА 3
конструкции от параметров hi используются, как правило, методы, применяемые при решении задач оптимизации динамически нагруженных конструкций. Эффективными в этом случае оказываются также методы анализа чувствительности.
Для получения информации о динамических характеристиках конструкции используются специальные целенаправленные эксперименты. Значительную роль при решении задач идентификации параметров и коррекции математической модели играет планирование эксперимента. При проведении активного эксперимента конструкция нагружается разнообразными силовыми воздействиями, которые должны возбуждать все исследуемые частоты и формы свободных колебаний конструкции. В случае применения для идентификации параметров конструкций метода, основанного на рассмотрении вынужденных установившихся колебаниях, появляется возможность управлять в эксперименте как частотами, так и точками и областями приложения вынуждающих колебания нагрузок. При этом возникает возможность эффективной идентификации вязкостных характеристик конструкции.
Отметим, что близость частот и форм свободных колебаний конструкции, или установившихся амплитудных значений прогибов в случае вынужденных гармонических колебаний, полученных в эксперименте и вычисленных для математической модели, является одним из важнейших критериев адекватности построенной модели реальной конструкции. Кроме того, существует хорошо разработанная методика частотного эксперимента. Поскольку решение задач оптимизации конструкций часто связано с обработкой большого количества информации, значительное упрощение расчетов достигается благодаря применению модального метода, т. е. приведения системы уравнений (3.1) к каноническому виду и представления приближенного решения в виде ряда по собственным формам колебаний. При этом матрицы М и К станут диагональными, и на диагонали матрицы М будут стоять квадраты частот свободных колебаний. Отсюда видно, сколь важным является соответствие частот и форм свободных колебаний конструкции и ее математической модели и поэтому при решении задач идентификации параметров конструкции в качестве минимизируемого функционала часто используется функционал квадратичной невязки частот и форм свободных колебаний.
3.4.	ЧАСТОТНЫЙ МЕТОД ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ КОНСТРУКЦИИ
I (елью излагаемого ниже подхода является установление рациональных процедур, служащих для получения уточненных параметров конструкции, которые наиболее точно соответствуют проводимым частотным экспериментам. Для эффективного вычисления вариаций рассматриваемых функционалов невязок в зависимости от вариаций массовых и
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
Г25
жесткостных характеристик здесь применяется метод анализа чувствительности. Метод основывается на введении сопряженных переменных и сопряженных систем уравнений (см. [13]). Данный подход, получивший развитие в теории оптимизации механических систем и конструкций, оказывается чрезвычайно эффективным и в случае его применения к задачам идентификации параметров и коррекции разрабатываемых моделей и позволяет, в частности, определить области в конструкции, где «пере-моделирование» (этот термин введен в теории оптимального проектирования и получил широкое распространение в современных публикациях) оказывается наиболее эффективным. На основе данного подхода был разработан ряд методик, которые применялись для ряда конкретных задач [12]. Другие родственные подходы, которые основаны на производимых модификациях аналитических матриц и прямых сопоставлениях результатов экспериментов и предсказаний опубликованы в [154,161]. Обзор полученных результатов по решению конкретных задач и разработанных методик идентификации содержится в [154].
Предположим, что модель идеальной конструкции характеризуется вектором h = {Ai, /12, • • • , hn} переменных проектирования. Эти переменные в случае континуального (непрерывного) описания конструкции зависит от пространственных переменных, которые принимают значения в некоторой области Q с границей Г, занимаемой конструкции. Собственные частоты (А, = и собственные моды свободных колебаний Ч? — {<£>*,	, <р'т} определяются из решения задачи, получаемой при
подстановке в уравнения динамики Ku 4- Mu = 0 функции и в виде u = ipexp(iwt). Имеем
Ltf = (К - А,М)<^ = 0, (Gu*)r = 0,	(4.1)
где L, G — операторы дифференцирования по пространственным переменным, коэффициенты этих операторов зависят аналитически от компонент вектора h, т. е. L = L(h) и G = G(h). Операторы задачи М и К являются самосопряженными операторами при рассматриваемых граничных условиях и поэтому оператор L также оказывается самосопряженным. Вектор переменных проектирования h* = {AJ, А^,. -., А* }, отвечающий реальной конструкции, неизвестен заранее и его отыскание составляет предмет рассмотрений. Задача моделирования реальной конструкции заключается в определении вектора h* с использованием методов идентификации.
Предположим, что частотные эксперименты выполнены с высокой точностью и в результате определены соответствующие конструкции моды и частоты свободных колебаний. Другими словами, считается, что собственные значения и собственные векторы А*, А^,..., А*; <р1+, <^2*,..., заданы для реальной конструкции.
126
ГЛАВА 3
В качестве меры рассогласования между характеристиками реальной конструкции, соответствующей неизвестному и требующему своего определения вектора h* и характеристиками, получаемыми в результате решения задачи (4.1) с заданным вектором примем функционал
г	г
j =	- А’)2 + £ W -	- ^’)П,	(4.2)
j=l	j=l
где скалярные произведения векторов и нормализованнные величины определяются выражением
<Д’ = 	--ГГ-,	(К1.	(4.3)
п
Коэффициенты о,-, /% — заданные неотрицательные величины (весовые множители), которые характеризуют вклад соответствующих мод колебаний в функционал рассогласования J. Множители ту в (4.2) выбираются при помощи операции минимизации скалярного произведения (4.2) Для получения адекватной модели реальной конструкции, сформулируем задачу отыскания вектора переменных проектирования h, минимизи-руещего функционал рассогласования J и удовлетворяющего системе интегральных ограничений
(!,/,)« = i — 1,2,(4.4)
Здесь Ci — заданные константы, — заданные функции. Накладываемые на переменные проектирования ограничения (4.4) могут содержать такие изопериметрические условия, как например, требование постоянства объема. Применяя описанную выше методику анализа чувствительности и используя преобразование содержащееся в работе [123], получим основное соотношение анализа чувствительности для вариации функционала невязки обусловленное вариацией Jh вектора переменных проектирования
6J= Rh, Е{В*vj +R>[2«j(A, -A*)+(v>,	)n]}+E I • <4-5)
\	= 1	1 = 1	/П
Формула (4.5) определяет чувствительность оптимизируемого функционала невязки к вариациям параметров модели h и обеспечивает возможности развития эффективных вычислительных процедур. Величины vJ (сопряженные переменные) определяются из решения неоднородной краевой задачи
(К - AjM)v' V)r/rflcl2[^’ -- (^, ^’W], (4.6)
(G,v>) = 0.
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
127
Вектор R?, фигурирующий в (4.5), находится по формуле
RJ = В*----------
(4.7)
Оператор В* определяется в результате выполнения стандартной операции интегрирования по частям
О = (v< L6^ -	+ BJh)n =
= LvJ)n - JAj(v< M^’)n + (Jh, B*vJ)n, (4.8)
где оператор M находится в результате варьирования определяющего уравнения
J(L^) =	- (JAjM^ + BJh = 0.
Отметим, что приведенные соотношения неоднократно применялись для решения задач оптимизации и идентификации. В результате проводившихся работ были разработаны и опробованы различные вычислительные алгоритмы. На основе накопленного опыта можно утверждать, что градиентный алгоритм последовательной оптимизации представляется одним из наиболее эффективных методов, которые можно рекомендовать для практического использования.
В качестве примера решения задачи коррекции расчетной модели рассмотрим задачу идентификации массовых и жесткостных характеристик консольной балки совершающей изгибно-крутильные колебания. Пусть балка с прямолинейной осью направлена вдоль оси OZ, а ее деформации характеризуются амплитудной функцией перемещений U(z) и амплитудным распределением угла поворота сечений балки Ф(г) относительно ее упругой оси. Уравнения, описывающие изгибно-крутильные колебания балки, имеют вид
rf2 A d2U\ LXrr _ л
I “ hXU + ЛеАФ = 0, dz* \ dz* J
d (। d$ A _	. n x
----- i A?;— I + heXU — /гг2АФ = 0, dz \ dz J
(4.9)
где Ar#, ka — жесткости балки на изгиб и кручение; h(z) — распределенная масса балки; г — радиус инерции поперечных сечений; е — расстояние между упруюй осью и осью инерции, А — квадрат частоты свободных колебаний (собственное число). Балка защемлена одним концом (z = 0), а другой конец свободен (z = /).
128
ГЛАВА 3
Допустим, что для реального изделия, расчетную математическую модель которого необходимо создать, известны частоты и формы свободных колебаний нескольких тонов, полученные в результате проведения частотного эксперимента. Построим функционал, характеризующий величину рассогласования математической модели и реального изделия, т. е. характеризующий степень несовпадения частот и форм свободных колебаний. Одним из возможных видов этого функционала может быть следующий:
т	т
i=l	:=1
~ I	I
I (щи{-и*)2+1 (№Ф^Ф*)2^
-О	о
(4.10)
где А* — квадраты частот свободных колебаний конструкции, полученные в эксперименте; Д*, Ф* — экспериментальные формы колебаний, соответствующие изгибу и кручению. Индекс i показывает, что рассматриваемая величина соответствует г-тому тону колебаний, а положительные коэффициенты Д- (г = 1,2,..., т) характеризуют вклад соответствующего тона в функционал невязки. Значения этих коэффициентов зависят от степени достоверности полученных экспериментальных результатов. Чем меньше вероятность ошибки в измерении частот и форм свободных колебаний, тем большее значение должно задаваться для соответствующих коэффициентов аг, Д-. При решении задачи (4.9) собственные функции Uj, Фг обычно нормируются определенным образом. При этом формы свободных колебаний, замеренные в эксперименте могут иметь отличную нормировку, определяемую удобствами измерений и обработки экспериментальных данных. Поэтому в выражение для функционала J введены множители тц и //,, которые подлежат определению, например, из условия минимума (4.10), как это указывалось выше. Выбранный таким образом функционал является неотрицательным и достигает своего нулевого минимума только тогда, когда совпадают частоты и формы свободных колебаний реальной конструкции и ее математической модели.
Частоты и формы свободных колебаний балочной конструкции зависят от распределения массовых и жесткостных характеристик. Для рассматриваемой типа балочной конструкции распределения жесткостных и массовых характеристик связаны линейными зависимостями. Поэтому, в качестве переменной проектирования /г(г), отыскание которой составляет предмет задачи идентификации, может быть принято распределение масс. (Следовательно, для коррекции математической модели необходимо решить задачу минимизации функционала невязки (4.10) за счет соответствующего выбора распределения масс. Для численной минимизации функционала невязки необходимо задать начальное приближение для h(z) и решить систему уравнений для амплитудных функций колебаний
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
129
и соответствующих частот, а затем используя приведенные соотношения анализа чувствительности построить выражение для улучшающей вариации 6h(z) распределения масс. Итерационный процесс последовательного улучшения распределения масс продолжается до выполнения необходимых условий экстремума с заданной точностью. Соответствующий алгоритм последовательного улучшения идентифицируемых параметров был разработан в Институте проблем механики РАН и в Центральном аэрогидродинамическом институте и реализован в виде пакета программ. Для удобства проведения расчетов, иллюстрирующих эффективность алгоритма, использовался следующий подход. Рассматривалась балочная конструкция с постоянными по размаху массово-инерционными и жест-костными характеристиками. Для этого варианта конструкции рассчитывались частоты и формы низших шести тонов свободных колебаний. Полученные значения частот, приведенные в таблице 3.1 в первой строке, и соответствующие им моды колебаний принимались в качестве экспериментальных данных отвечающих реальной конструкции. После этого распределение массовых и жесткостных характеристик искажались при условии неизменности общей массы балочной конструкции. Рассматривались два варианта искажения — по косинусу и в виде ступеньки. Косинусоидальное и ступенчатое распределение массы принимались в качестве начальных параметров модели, которая должна была корректироваться. Решение задачи минимизации функционала рассогласования между «экспериментальными» частотами и модами и соответствующими величинами, определяемыми для искаженной модели (искаженная модель, естественно, изменяется в процессе выполнения улучшающих вариаций) должно было устранить внесенные искажения и привести к постоянному распределению масс, т. е. к модели реальной конструкции. Результаты расчетов показали, что искомое постоянное распределение масс находится после 10—15 итерации, причем получающиеся частоты скорректированной модели совпадают с их «экспериментальными» значениями с точностью до четвертого знака после запятой.
3.5.	ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Для получения адекватной математической модели конструкции с использованием экспериментальных данных часто требуется идентифицировать не только массовые и жесткостные параметры, но и такие важные характеристики конструкции, как параметры внешнего и внутреннего трения. Для идентификации вязкостных параметров и других характеристик моделей, учитывающих демпфирование, пригоден предложенный в [119] метод, основанный на анализе вынужденных колебаний. Ниже изложим вкратце этот метод и приведем примеры отыскания распределений
5 — 2185
130
ГЛАВА 3
массовых и жесткостных характеристик демпфируемых конструкций и идентификации вязкостных характеристик.
Пусть модель конструкции характеризуется вектором переменных проектирования h = {Ai, , hn}. Вектор h определен в области Q с границей Г занимаемой конструкцией, т. е. его компоненты являются функциями пространственных координат, характеризующими распределение по конструкции погонных масс, жесткостей, вязкостных свойств и т.д. Предположим сначала, что трение отсутствует. В этом случае вынужденные гармонические колебания конструкции под действием гармонической нагрузки q = Qcoswt (Q — амплитудная функция нагрузки, w — частота, t — время) описываются линейным неоднородным дифференциальным уравнением
Ки + Мй = д,
где считается, что жесткостной и инерционный операторы зависят от переменных проектирования, т. е. К = Л”(Л), М = М(Л). При этом упругие смещения конструкции изменяются синхронно с внешней нагрузкой и — U cos и / (U — амплитудная функция) и находятся из решения уравнения
L(h,u>)U = Q,	(5.1)
(NU)r = 0	(5.2)
с граничными условиями (5.2), отвечающими способу закрепления конструкции. Здесь L — К — ш2М и N — линейные дифференциальные операторы по пространственным координатам. Операторы М и К предполагаются самосопряженными и, следовательно, L также является самосопряженным оператором. Пусть U = U'(x) — решения данной граничной задачи для случаев и = ы', Q = Qi(x) (г = 1,2,..., S).
Рассматриваемая ниже задача идентификации заключается в определении вектора h*(z) с использованием данных экспериментов. Предполагается, что для реальной конструкции, характеризуемой искомым вектором переменных проектирования h*(z), проведенные «точные» эксперименты позволили определить амплитудные функции 17**, соответствующие и = о?, Q = Qi(x) (г = 1,2,..., S). В качестве меры рассогласования между характеристиками действительной конструкции, описываемой вектором h*(#), и характеристиками, получаемыми при решении граничной задачи (5.1), (5.2) с h = h(x), применим функционал
s л
J =	/ (^J’ - Uj*)2 dQ,	(5.3)
>=1 я
a/1 =S I (Uj*)2dQ.
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
131
Коэффициенты aj — заданные неотрицательные величины, играющие роль весовых множителей. Эти множители характеризуют вклад соответствующих мод колебаний в функционал рассогласования. Для отыскания математической модели реальной конструкции рассмотрим задачу определения вектора переменных проектирования из условия минимума функционала рассогласования
Л = min 7(Л)
(5.4)
при дополнительном ограничении, наложенном на переменные проектирования
Jc = У f(h)dQ = с,	(5.5)
п
где с — заданная константа, a f — заданная функция. При помощи ограничения (5.5) могут быть заданы такие изопериметрические условия, как, например, условия постоянства объема или веса конструкции. Для получения эффективных соотношений, используемых при численном решении сформулированной задачи минимизации функционала рассогласования, применим анализ чувствительности. С этой целью сконструируем расширенный функционал Лагранжа, соответствующий задаче (5.1)—(5.5)
+к I / /(Л) dQ—с I .
\п	/
J=^ aj f (uj-Uj*)2 dtt+ f ^(LlP-Q^dQ
J=1 Ln	n
(5.6) Здесь v'^x) — сопряженные переменные, а к — множитель Лагранжа, соответствующий изопериметрическому условию (5.5). Допуская малые вариации 6h и 6U' в (5.1), (5.2), и выполняя необходимые преобразова
ния с учетом малости указанных величин, приходим к линеаризованным соотношениям, связывающим вариации переменных проектирования с вариациями функций состояния
ЦН)би{ + B(U\h)6h = О, (NlhjSU* +Т(СЛ,Л)£Л)Г = О.
Через В(иг, Л), T(U', h) обозначены линейные операторы, применяемые к вектору 6h, Далее мы выразим вариацию минимизируемого функционала, через вариацию 6h. Для этого используем описанный выше метод анализа чувствительности, основанный на введении сопряженных переменных vl и исключении зависимости варьируемого функционала Jl от
5*
132
ГЛАВА 3
вариаций переменных состояния 6U1. Подчиняя сопряженные переменные vl дополнительным соотношениям
Lvj =	- С/’’*),
(5.7)
(W)r = 0, i=l,2,...,S,
(5.8)
составляющим сопряженную граничную задачу, приходим к основному соотношению анализа чувствительности, связывающему непосредственно вариации параметров проектирования и вариацию функционала
У B‘(t7’»? + «^- Shdtl.
(5.9)
Данная формула позволяет применить для решения задачи идентификации численные алгоритмы оптимизации, основанные на последовательном построении улучшающих вариаций вектора h. Различные вычислительные методы могут использоваться в рамках алгоритмов последовательной оптимизации для обеспечения надежного и достаточно быстрого продвижения к локальному минимуму, однако градиентные методы оказываются наиболее эффективными с практической точки зрения. При применении градиентной процедуры формула для улучшающей вариации имеет вид
6h = -r У В*(и*,Ь)е + &- , oh
(5.10)
где константа т > 0 — шаг по градиенту. Множитель к определяется при помощи уравнения
n
df
dh
6h dQ. = 0.
(5.П)
Используя соотношения (5.9) и (5.10) будем иметь
\п 1=1	/ \п
А = В^. (5.12)
Алгоритм последовательной оптимизации, использующий выведенные соотношения анализа чувствительности, применялся для численной идентификации параметров балочных и пластинчатых конструкций. Данный
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
133
алгоритм основан на выполнении последовательных коррекций переменных проектирования (толщин балок и пластин) и решении граничных задач для переменных состояния и сопряженных переменных, улучшающие вариации находятся при помощи метода проектирования градиентов (формулы (5.9) и (5.11)). При последовательном улучшении вектора h переменные состояния (прогибы) и сопряженные переменные определяются методом Галеркина. В качестве базисных функции метода Галеркина в проводимых расчетах брались <pj = sinjTnr для опертых балок, <pj = x^+1 для консольных балок и (fij = sinjTr# sin iirx для опертых по краям пластин. Вычисления проводились до тех пор пока не выполнялось условие J < е, где е > 0 — достаточно малая величина.
В качестве примера приведем результаты численной идентификации распределения толщин балки прямоугольного поперечного сечения. В рассматриваемом случае
LU' = (EIU'XX)XX - ты2и\
(5.13)
Qi = Q°6	- 5) ,
EI(x) = Ebh^, т(х) = pbh(x),
где Е, р, m, 1, 6, h — модуль Юнга материала балки, плотность, погонная масса, момент инерции поперечного сечения, ширина и толщина балки; 6 — дельта функция, описывающая сосредоточенную нагрузку, приложенную к середине балки (х = 1/2) длины I (Q° — заданная константа).
Рис. 3.1
134
ГЛАВА 3
Частоты вынужденных гармонических колебаний брались в виде
^1 = ^(“1 +^г), «2 =	+ ш£),	+ w{)> •••
Здесь — собственные частоты колебаний. В расчетах полагалось = 365,255 для случая одночастотного эксперимента с S = 1 и cvi = 365,255 S“1,	= 949,663 S~1, w3 = 1826,276 S~1, и4 = 2995,092 S'-1,
— 4456,112 S'-1 для случая S = 5.
Рис. 3.2
Следующие безразмерные величины и обозначения использовались при проведении вычислений х' = x/l, h' = h/ha, U' = U/Uha, p' = 12pl4u%/Eha, = w/cva, (Q0/ = 12Q°l4/Eh^uaba. При этом бралось I = 1 м, ba = 10“2 м, Ua = 10"3 м, ша = IS~\ p =2,7 • 10“3 кг/м3, E = 7,1 • IO10 Н/м2. Численные результаты решения задач идентификации для шарнирно закрепленных по краям балок представлены на рис. 3.1, 3.2, 3.3 соответственно, для случаев, когда искомое распределение толщин имеет параболическое, синусоидальное и ступенчатое очертание (отмеченные кружочками). В каждом из случаев постоянное распределение толщин бралось в качестве начальной аппроксимации переменной проектирования теоретической модели. Итерационный процесс последовательной оптимизации начинался с этого приближения и выполнялся вплоть до выполнения условия J < s с 8 = 10“4. Найденные
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
135
в результате расчетов распределения толщин показаны на рис. 3.1, 3.2, 3.3 кривыми с крестиками для случая одного эксперимента (S = 1) и кривыми с звездочками для случая пяти экспериментов (5 = 5).
Рассматривался также другой способ идентификации толщин балочной конструкции, основанный на осуществлении последовательных приложений сосредоточенных сил в различных точках, т. е. Qi =	— я,),
= CJ°, i = 1,2,...,5.
Соответствующие численные результаты идентификации ступенчатого распределения толщин представлены на рис. 3.4 линией с крестиками для случая приложения силы в одной точке х = 1/2 и линией со звездочками, соответствующей случаю последовательного приложения силы в пяти точках = 0,1, х? = 0,3, хз = 0,5, х4 = 0,7, х$ = 0,9. Приведенные результаты отвечают следующим значениям параметров о/ = 365,255, е = 2 • 10"3.
Рис. 3.4
136
ГЛАВА 3
Перейдем теперь к изложению метода идентификации для случая демпфируемой конструкции. Ограничимся рассмотрением вынужденных поперечных колебаний балки, описываемых следующим уравнением и граничными условиями
( Е I'(•£)	\
(EI(x)uxx)xx ---------7](х)ихх +m(x)utt = Q(x) cos cvf,
\ “	Jxxt	(5.14)
u(0) = (EIuxx)x=o = u(l) = (EIuxx)x=i — 0.
Распределение динамических прогибов может быть представлено в виде
и(х, t) = U(х) cos(cut — Ф(а?)).
Здесь т](х) — коэффициент вязкости, U(x) — амплитудная функция прогибов, Ф(я) — фазовая функция. Распределение прогибов можно записать в более удобном виде
и(х, £) = Uc(x) cos(wt) 4- Us(x) sin(o;f),	(5.15)
если ввести в рассмотрение вспомогательные функции Uc(x) и Us(x) при помощи соотношений
и(х) = м*)[1 +	(516)
Ф(г) = arctg [t7s(«)/trc(«)] •
Введенные переменные удовлетворяют следующей системе уравнений
(EI(x)UCxx)xx - m(x)^Uc 4- (El(x)r}(x)USxx)xx = Q(x), (5.17)
(EI(x)Usxx)xx - m(x)u2Us + (E1(x)t}(x)Ucxx)xx = 0 (5.18)
и однородным граничным условиям (5.14).
Предположим, что в результате проведенного динамического эксперимента определены амплитудная и фазовая функции U*(x) Ф*(я) для реальной конструкции. Тогда в качестве меры рассогласования между характеристиками U*(x), Ф*(я) реальной конструкции с неизвестной переменной проектирования h*(x) и характеристиками U*(x), Ф*(я) теоретической модели с заданной переменной проектирования h(х) примем функционал
/	i
J = а У (U -U*)2dx + /3У (Ф -Ф*)2 dx. (5.19) О	о
Здесь о, 0 — заданные положительные множители. Ниже рассмотрим отдельно задачи идентификации распределения толщин и распределения вязкости вдоль балки. Чтобы решить эти задачи будем минимизировать
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
137
функционал (5.19), соответственно, по переменным h(x) и rj(x). Для идентификации указанных распределений применим анализ чувствительности. С этой целью сконструируем расширенный функционал Лагранжа JL для задачи (5.17)— (5.19), выразим вариации 6U и через вариации SUc, Ms следующим образом
= S~‘Uc + ^~SUs =	+ 7^SUs
due oUs	Uz
и введем сопряженную систему уравнений для сопряженных переменных vc, vs-
(ЕIVCxx)xx ТТИл) V(j	{^Е It^V Sxx') хх —
Ur	Us
= -2a(U - U^-Z- + 2/3(Ф - Ф*)^, (5.21)
(EIvSxx}xx - mw2vs - (ElTJVCxx)xx =
Us	Ur
= -2a(U -1Г)-^-2/?(Ф -Ф*)-^. (5.22)
Граничные условия при х = 0 и х = I для сопряженных переменных vc, vs совпадают с граничными условиями для переменных состояния Uc и Us-Варьируя далее расширенный функционал Лагранжа Jl с учетом соотношений (5.20)-(5.22) и однородных граничных условий для переменных Uc, Us, vc, у а также принимая во внимание обозначения I = 6Л3/12, т = pbh (р — плотность материала, Ъ — ширина прямоугольного сечения балки) приходим к основному соотношению анализа чувствительности
Ucxx^Cxx 4“ Usxx^Sxx ”1" ^){vcxxUSxx
VSxx Uc xx
~pbu2(vcUc + vsUs) ► dx + У Srj^vcxxUsxx - vsxxUcxx^EI dx. (5.23) '	0
Формула (5.23) определяет чувствительность оптимизируемого функционала к вариациям толщин 6h(x) (первый интеграл в (5.23))и к вариациям вязкости 6tj(x) (второй интеграл в (5.23)).
Для численной реализации процесса идентификации h и т) использовался подход аналогичный тому, что применялся выше для идентификации характеристик недемпфируемых конструкции. Расчеты проводились в безразмерных переменных x/l, h/ha, Uc/Ua, Us/Ua, 12pl4w2/Ehai 12Q/4/Eh^Uab, (ha, Ua — отсеченные величины) для шарнирно за-
138
ГЛАВА 3
крепленных балок. Для численного решения основной и сопряженной систем применялся метод Галеркина с базисными функциями sin&7nr (к = 1,2,...).
На рис. 3.5 кривой с крестиками показано полученное в результате расчета распределение толщин балки, внутренняя вязкость которой одинакова во всех поперечных сечениях и равна т](х) = 10-3. Ступенчатое распределение толщин реальной конструкции балки отмечено кружочками. Вычисления проводились для случая, когда сосредоточенная поперечная нагрузка прикладывалась к середине пролета и обеспечивала вынужденные колебания с частотой ш = 365,255. Расчеты проводились с шагом по градиенту т = 2 • 10-2 до выполнения условия J < е — 10“4.
Рис. 3.6
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
139
На рис. 3.6 и 3.7 кривыми с крестиками показаны результаты численной идентификации распределений вязкости т](х) по пролету опертой балки с постоянным распределением толщин (h(x) = 1). Параболическое и ступенчатое распределение балочных конструкций отмечены на этих рисунках кружочками. Все исходные данные, использовавшиеся при численной идентификации вязкостных свойств конструкции, брались теми же, что и в предыдущем примере идентификации распределения толщин демпфируемой балки (рис. 3.5).
3.6.	ОПТИМИЗАЦИЯ ЖЕСТКОСТИ БКК ПРИ НЕСТАЦИОНАРНЫХ НАГРУЗКАХ
При расчете и оптимизации БКК размерность системы определяющих уравнений относительно велика и существенное значение приобретают вычислительные аспекты. В случае коротковолновых (нестационарных) воздействий эффективным оказывается модальный метод, основанный на построении приближенного решения системы уравнений нестационарный динамики с использованием разложения в ряд по формам свободных колебаний
и/ = Ф/w/,	(6.1)
где wy — вектор обобщенных координат, а Ф/ — прямоугольная матрица, состоящая из собственных векторов задач о свободных колебаниях конструкции
K^=cv2M^’, (^,M^) = J,7,	(6.2)
где w2 — квадрат г-ой частоты свободных колебаний; у>' — собственные векторы; — символ Кронекера. Если тп — порядок системы
140
ГЛАВА 3
определяющих уравнений, а р — количество вычисленных собственных чисел задачи (6.2), то, как правило, р т. Производя подстановку (6.1) в уравнения динамики и выполняя умножение слева на Фу, как это делалось в главе 1, приходим к задаче Коши для обобщенных координат
w/ + [ФуВФ/Jw/ + diag(cj2)w; = Ф}д(/),	(6.3)
w/(0) = Ф}Ми°, w/(0) = (Ф*)-1Ми°.
Система обыкновенных дифференциальных уравнений (6.3) имеет значительно меньший порядок, чем исходная система, и для ее решения можно использовать стандартные методы интегрирования. Кроме того, в случае, когда рассматривается идеализированная конструкция без демпфирования, система (6.3) распадается на систему независимых уравнений. Аналогичное свойство сохраняется, когда используются упрощенные модели демпфирования (например, модель Фойгта [12]). Для определения упругих смещений узлов конструкции при действии нестационарной внешней нагрузки необходимо проинтегрировать систему (6.3) и воспользоваться формулой (6.1).
Введем в рассмотрение функционал, представляющий собой некоторую квадратичную форму упругих смещений узлов конструкции, вычисленную в момент времени tk € [0, //]:
Jj = (u/>RjU/)t=u.	(6.4)
где квадратичная матрица Rj в зависимости от свойств структуры определяет физический смысл функционала. Индекс j означает номер узла в конечноэлементной модели конструкций, либо номер элемента. Функционал Jj может означать величину квадрата упругого смещения узлов конструкции, величину потенциальной энергии деформации элемента, интенсивность напряжения и т. д. Во всех рассмотренных случаях функционал Jj является локальным и вычисляется в определенный момент времени /&. Конструкция характеризуется вектором параметров проектирования h, в качестве которых можно рассматривать величины масс и жесткостей элементов, их геометрические характеристики.
Исследуем зависимость величины функционала J!- от малых вариаций параметров проектирования. Для этого зафиксируем определенное значение j и момент времени t = tk и проварьируем систему уравнений (6.3) с учетом того, что коэффициенты этой системы являются функциями параметров проектирования
Jw/ 4- [Ф/ВФу]<Улу/ + diag(o;2)Jwy +
+ > ,	dh~i*fWf + Ф/ dh^fW/) = °’ (6'5)
Jw/(0) = 0, Jw/(0) = 0.
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
141
Умножим вариационное уравнение (6.5) слева скалярно на вектор-функцию сопряженных переменных v(/) и проинтегрируем результат от / — 0 до t = tj. Определив сопряженную переменную как решение задачи Коши системы обыкновенных дифференциальных уравнений
v — [ФуВФy]v diag(o;f)v = О,
v(/fc) = 0, v(M = 2[$tR..$.W/(<fc)],	(6’6)
получим выражение для вариации функционала Jj , зависящее от вариации параметров проектирования:
1. Г, 3D
Г Зк \ / w/ + $,	yvAdtShi,
Г- ^D_ ~}dhi*
(6.7)
Заметим, что система уравнений (6.6) интегрируется в обратном времени от t = tk до нуля. Вариационное соотношение (6.7) характеризует чувствительность значений функционалов Jj в момент времени t = к вариациям параметров проектирования h = hi при заданном динамическом нагружении конструкции. На основании полученной формулы (6.7) можно рассматривать задачи построения улучшающей вариации в задаче минимизации целевого функционала
J = max > min 3 h
(6.8)
с ограничениями на параметры проектирования
/z(h) <ch Z = l,2,...,a,	(6.9)
где fi, ci — заданные константы.
Для решения динамических задач оптимизации БКК применялись описанные выше соотношения анализа чувствительности и метод итерирования векторных подпространств. Соотношения анализа чувствительности позволяют эффективно определять улучшающие вариации Jh вектора параметров проектирования, для которых достигается уменьшение оптимизируемого функционала J. Процесс последовательного уменьшения критерия качества является поэтапным. На каждом шаге этого процесса для «улучшенных» (проварьированных) значений вектора параметров проектирования требуется пересчитывать собственные частоты и формы свободных колебаний и интегрировать уравнения редуцированной модели нестационарной динамики. Решение указанных задач о частотах и
142
ГЛАВА 3
формах свободных колебаний поэтапно улучшаемой сложной конструкции является наиболее ответственной частью работы алгоритма и во многом определяет объем вычислений, требующихся для оптимизации конструкции. Наиболее эффективным здесь оказывается метод итерирования векторных подпространств, который является комбинацией метода обратных итераций с аппроксимацией Рэлея-Ритца на каждом шаге итерационной процедуры. Метод итерирования векторных подпространств хорошо приспособлен для использования в алгоритмах последовательной оптимизации ([124]). Это связано с тем, что в итерационных методах объем вычислений обуславливается выбором начального приближения. При решении же задач оптимального проектирования БКК, совершающих вынужденные или свободные колебания, полученные на предыдущем шаге итерационного процесса формы свободных колебаний оказываются идеальным начальным приближением для форм свободных колебаний конструкции с измененными проектными параметрами.
С использованием алгоритма последовательной оптимизации решалась задача оптимального проектирования несущей конструкции космической платформы, состоящей из 529 шарнирно соединенных стержневых элементов (рис. 3.8). Пространственная трехслойная конструкция платформы имела в плане форму квадрата с размером сторон равным 18 м.
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
143
Толщина конструкции принималась равной 0,5 м. Нестационарная сосре-
доточенная нагрузка прикладывалась в центре конструкции и изменялась во времени, как это показано на рис. 3.9. В качестве целевого функционала была выбрана величина наибольшего квадратичного смещения узлов конечноэлементной модели конструкции. Масса конструкции считалась
неизменной, конструкция — свободной. В качестве переменных про-
ектирования использовались площади поперечных сечений стержневых
элементов. В силу симметрии конструкции переменные проектирования объединялись в 28 групп, т. е. отыскивалось 28 параметров проектирования. На все параметры проектирования были наложены ограничения сверху и снизу. Исходное значение параметров проектирования выбиралось равным hi = 50 мм2, i = 1,2,..., 28. Мак
q
0,2 0,225 t, с
Рис. 3.9
симальные смещения в конструкции
под действием сосредоточенной силы достигались в восьми угловых узлах (для оптимального проекта в момент времени t = 0,0067 с). Зависимость функционала качества от номера итерации п0 оптимизационной процедуры приведена на рис. 3.8. Данные, характеризующие оптимальный проект, приведены на рис. 3.10, 3.11. Жирными линиями на этих рисун-
ках выделены элементы, у которых в ходе перераспределения материала произошло увеличение площадей поперечных сечений.
Рис. 3.11
Для сравнения начальной и оптимизированной конструкции на рис. 3.12 показаны ненулевые значения частот (размерность: сек-1) нижней части спектра, отвечающие формам упругих свободных колебаний. Частоты исходной и оптимальной конструкции на этом рисунке в зависимости от номера моды колебаний п/ и отмечены, соответственно, кружочками и треугольниками.
144
ГЛАВА 3
30 (О
25
20
15
О1-------------
5
10	15 nf
3
Рис 3.12
3.7.	ОПТИМИЗАЦИЯ ХАРАКТЕРИСТИК ДЕМПФИРОВАНИЯ
При проектировании конструкций, рассчитываемых на нестационарные воздействия, нередко используются модели, в которых пренебрегают механическим демпфированием. Такие идеализированные модели позволяют получить вполне удовлетворительное описание поведения конструкций в случае, когда рассматриваемый интервал времени достаточно мал, материал, из которого изготовлена конструкция, является идеально упругим, взаимодействие ее со средой таково, что внешним трением можно пренебречь, а также можно не учитывать потери энергии, происходящие вследствие неидеальности соединения элементов конструкции и т. д.
Если исключить из рассмотрения диссипативные силы не представляется возможным или, наоборот, включение диссипативных элементов в конструкцию предопределено ее назначением и позволяет существенно улучшить ее динамические свойства, то параметры влияющие на диссипацию можно применять в качестве переменных проектирования и рассмотреть соответствующие оптимизационные задачи. Отметим, что здесь речь идет о тех характеристиках демпфирования, которые присущи самой проектируемой конструкции и могут быть изменены в процессе оптимизации.
Уравнения движения конструкции при наличии демпфирования, граничные и начальные условия можно записать следующим образом
__52U	_5u
Md/2‘+Dd? + Ku = Ч’	(7.1)
(Gu)r = g, (Nu)t=0 = х,
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
145
где и — вектор перемещений конструкции под действием заданной внешней нагрузки q; М, D, К — соответственно инерционный, диссипативный и жесткостной операторы, которые здесь считаются линейными; G, N — линейные операторы граничных и начальных условий, Г — граница области занимаемой конструкцией; q, х, g — заданные функции. Здесь и далее зависимость рассматриваемых величин от пространственных переменных не указывается для краткости. Предполагается что материал конструкции является вязкоупругим и характеризуется наследственным трением. Тогда диссипативный оператор D может быть представлен в виде
<7-2>
— оо
где ядро оператора выбирается с учетом свойства материала. Далее рассматриваются тонкостенные конструкции, поведение которых под действием заданных нагрузок описывается соотношениями (7.1). Считается,что конструкция имеет двухслойную структуру, причем основу ее составляет упругий слой, определяющий жесткостные свойства конструкции, а другой относительно нежесткий слой обусловливает диссипативные свойства конструкции. Влиянием малой жесткости второго слоя (полимерной пленки, вязкой накладки) на жесткость конструкции можно пренебречь, также как можно не учитывать диссипацию энергии при колебаниях в жестком слое. Для полимерного материала вязкого слоя ядро можно выбрать в виде
Щ,т) =	(7-3)
где 7 = 70/i, h — функция, характеризующая пространственное распределение вязкоупругих свойств конструкции; R(t,r) = hRo(t,r), константы а, /3 и 7 определяются выбором конкретного материала. Ниже функция
Рис. 3.13
146
ГЛАВА 3
h рассматривается в качестве переменной проектирования. Оптимизационная задача заключается в отыскании такого распределения переменной проектирования h по конструкции, которое доставляет минимум функционалу податливости конструкции при ограничении, что интеграл от h по конструкции задан. В качестве функционала податливости конструкции принимается модуль максимального смещения ее отдельных частей. Соотношения анализа чувствительности для этой задачи оптимизации и метод эффективного интегрирования динамических уравнений приведены в [12].
Рис. 3.14
Приведем вкратце один пример отыскания рационального расположения демпфирующего слоя на пластинчатой конструкции. Предположим, что демпфирующий слой располагается на круглой пластинке в виде кольца, площадь которого 0,785. Отыскивалось такое расположение демпфирующего кольца, чтобы минимизировать значение величины максимального прогиба пластинки опертой по краю. Считалось, что нагрузка q распределена равномерно по пластинке и изменяется с течением времени, как показано на рис. 3.13. Максимальное значение нагрузки равнялось 0,5-10"6, значения параметров задачи считались равными v = 0,3, k — IO-5, 7о = 4,4 - 10" 3. Функция h = 0 вне демпфируемого кольца и h = 10“5 всюду внутри кольца. Толщина пластинки принималась постоянной и равной 10“2. При решении задачи минимизации податливости
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
147
(максимального смещения) использовался численный метод описанный в [12, 36]. Полученные в результате расчетов зависимости максимальных прогибов пластинки от времени (от номера шага по времени) показаны на рис. 3.14 кривыми с номерами 1—7. Кривая 1 соответствует размещению вязкоупругого материала в центре пластинки, кривые 2—6 показывают, как изменяется поведение пластинки по мере перемещения демпфиру-
	...... .............. — 7
—----------------- — в
---—-----------------------—------- 5
------—-----------------—---------4
---------- in.................... 3
...............................   2
-------------- 1
Рис. 3.15
ющего кольца из центральной области к периферии, причем кривая 6 отвечает размещению демпфирующего материала по краю пластинки. Кривая с номером 7 представляет зависимость максимального прогиба от времени при отсутствии демпфирования. Для кривых 2—7 максимальный прогиб достигался в центре пластинки, а для кривой 1 — на окружности малого радиуса. На рис. 3.15 изображено расположение демпфирующего материала соответствующее кривым 1—7. Из рис. 3.15 следует, что для указанного вида нагружения и краевых условий наиболее эффективно размещать демпфирующий материал в центре пластинки. Отметим, что с применением описанного метода аналогичные задачи оптимизации могут быть решены для конструкций пологих оболочек.
3.8.	СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ И ИССЛЕДОВАНИЕ ОПТИМАЛЬНОЙ СТРУКТУРНОЙ АНИЗОТРОПИИ
Современные традиции развития космической техники состоят в обеспечении весового совершенства конструкции и существенном увеличении их габаритов. Функциональное назначение создаваемых конструкций обусловливает необходимость достижения максимальной жесткости,так как одновременное увеличение габаритов и снижение материалоемкости делает конструкции недопустимо гибкими.
Адекватной характеристикой динамической жесткости конструкции является основная частота ее свободных колебаний. Выбор основной
148
ГЛАВА 3
частоты в качестве меры жесткости объясняется, в частности, тем, то при модальном способе анализа динамики конструкции, фундаментальная частота является минимальным ненулевым диагональным элементом матрицы жесткости.
К способам повышения фундаментальной частоты колебаний относится выбор рациональной конструктивно-силовой схемы. Для описания механического поведения таких сложных составных конструкций как протяженные космические фермы, солнечные батареи, космические станции, платформы и антенны с регулярной и нерегулярной структурой могут применяться простые динамически подобные балочные, пластинчатые и оболочечные модели, называемые часто аналитическими моделями сложных конструкций. С учетом сложности конструкций должны применяться аналитические модели с распределенными локальноанизотропными свойствами. В частности, могут использоваться модели с локально-ортотропными или трансверсально изотропными характеристиками, а также модели с другими видами анизотропной структуры, например, с кубической структурой. Наиболее часто используемыми при моделировании различного вида космических конструкций оказываются локально-ортотропные схемы. Эти схемы позволяют моделировать основные направления передачи усилий в конструкции в соответствии с ее структурой. В свою очередь, изменение направлений передачи усилий дают возможность улучшить механические и, в частности, динамические характеристики изделия. Эта возможность управления свойствами приводит к естественной постановке задач оптимизации, состоящих в отыскании наилучших ориентаций осей анизотропии для аналитических моделей конструкции. Решение таких задач выявляет тенденции, позволяющие улучшить конструктивно-силовые схемы и обосновать рациональные проекты конструкций [8].
Приведем основные соотношения, необходимые для решения задач оптимального проектирования с применением модели локальноортотропной пластинки, выражение для амплитудных значений потенциальной энергии тонкой упругой пластинки, совершающей свободные поперечные колебания, запишем в следующей форме:
v=| I {DlU^+D2UxxUyy+D3U^y+D4UxxUxy+D5UyyUxy+D6U^dQ, n
(8.1) где U(x,y) — амплитудное значение прогиба; Рх, D2,..., DQ — коэффициенты изгибной жесткости пластинки в прямоугольной системе координат xyz. Контур пластинки Г ограничивает область Q в плоскости
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
149
ху. Амплитудное значение критической энергии запишем в виде
т=^~ I U2dQ,	(8.2)
п
где w — частота свободных колебаний. Обозначим через £, т) оси ортотропии, лежащие в плоскости срединной поверхности недеформиро-ванной пластинки. В точке с координатами (х,у) Е П положение осей ортотропии зададим с помощью угла а(х,у) (а — угол между осями х,£о). Значение коэффициентов изгибной жесткости D°, D®, D®,	в
локальной системе координат, связанной с осями ортотропии, считаются заданными. Коэффициенты жесткости £>i,	, Dq в фиксированной
системе координат ху связаны с заданными константами в системе £т] известными формулами перехода [62]:
= |(Г>° + £>°) + |(Р€° - Г>°) cos2а - sin2 2а, Z	Z	тс
О2(а) = 2D° + |^sin22a, D°3 = D°( + D° - 2Z>° - 4D°(r),
£>з(а) =	+ D°) - hnf - Z>°) cos 2a - ^sin22a, (8.3)
Z	Z	4
D4(a) = (Z>j - D° + D°3 cos 2a) sin 2a,
D5(a) =	— D° — D3 cos 2a) sin2a, £>6(a) = 4D%„ + £>gsin22a.
Пластинка предлагается свободной. При этом спектр частот свободных колебаний содержит три нулевые низшие частоты, соответствующие вертикальному перемещению пластинки в направлении оси z и ее вращению относительно осей ж, у как твердого целого. При отыскании ненулевых частот собственных колебаний на основе вариационных принципов требуется учесть дополнительное условие ортогональности упругих форм колебаний к формам движения пластинки как твердого тела
ju<Kl = 0, j\uda = Q, jyUdto = 0.	(8.4)
n	n	n
Первое условие (8.4) означает отсутствие внешних сил, действующих в вертикальном направлении, а второе и третье условия (8.4) — отсутствие внешних моментов.
Рассматриваемая задача оптимального проектирования заключается в отыскании ориентации осей ортотропии в каждой точке пластинки
150
ГЛАВА 3
из условия максимизации низшей ненулевой частоты упругих колебаний пластинки:
J* = max и2 = max min a(a7,t/)	a U
(8.5)
Внутренний минимум по 17, отвечающий вариационному принципу Рэлея, разыскивается при дополнительных условиях ортогональности (8.4), а внешний максимум по а определяется на множестве произвольных распределений углов ортотропии. Краевые условия отсутствия моментов и перерезывающих сил на контуре пластинки Г являются естественными (условиями трансверсальности), и их учет при минимизации отношения
Рэлея не требуется.
Численное решение поставленной задачи определения оптимальной структурной анизотропии осуществлялось в работе [9] градиентным методом с применением явных выражений анализа чувствительности (градиентов функционала Рэлея по переменным проектирования). При этом для каждого текущего распределения ориентации осей ортотропии динамическое распределение прогибов U(x, у) рассчитывалось по методу ко-
нечных элементов, для которого ма-Рис. 3.16
трицы жесткости и масс конструировались с использованием одной и той же аппроксимации функций прогиба. Выражения для градиентов функционала Рэлея строились с учетом возможности появления в процессе оптимизации структуры кратных собственных частот. В тех случаях, когда в процессе расчетов две низшие ненулевые частоты собственных колебаний сближались и появлялась кратная частота, согласно применяемому алгоритму осуществлялся переход от вычислений, отвечающим классическим выражениям для градиента, к расчетам учитывающим две линейно независимые колебательные моды. Кроме того, для сокращения объемов вычислений и превышения точности применялся способ декомпозиции прямой задачи расчета форм колебаний, использующей симметрию конструкции. Так, для прямоугольных в плане пластинок решение исходной задачи расчета частот и форм колебаний при фиксированном распределении углов ортотропии а(х,у) сводились к расчету четырех или пяти задач о колебаниях 1/4 части пластинки при соответствующих граничных условиях. Для квадратной в плане пластинки метод декомпозиции позволяет сводить задачу расчета частот и
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
151
форм колебаний к решению пяти задач о колебаниях 1/8 части пластинки. Конкретные расчеты проводились для круглых, квадратных и прямоугольных пластинок. При этом задавались конкретные значения констант изгибной жесткости: = 1;	= 0,33;	= 0,16; DQ = 0,08. Данным
набором констант изгибной жесткости характеризуется такой композиционный материал, как стеклопластик. Приведем результаты расчетов квадратной пластинки единичной площади. В результате оптимизации с использованием начального приближения для а(х, у), показанного на рис. 3.16 и соответствующего значения частоты = 3,50, было получено распределение ориентации ортотропии, незначительно отличающееся от начального распределения и соответствующее значение функционала ,4=^1= 3,53. Таким образом, незначительный эффект от оптимизации обусловлен удачным выбором начального приближения, которое может рассматриваться в качестве квазиоптимального. Приведем также несколько высших частот для пластинки с оптимальным распределением угла ортотропии: = 3,81; с^з = 4,80; и;4 = 7,36 (двукратное значение); с^5 = 13,36 (двукратное значение). Отвечающая низшей ненулевой частоте форма колебаний представляет собой нечетную функцию по обоим аргументам, т. е. U(x,y) = —U(—x,y), U(x,y) = —U(x,—y). Заметим, для сравнения, что для пластинки с углом ортотропии а = 0 во всей области низшая частота колебаний равна значению 2,67, а для пластинки с а = 45° низшая частота равна 2,87. Сопоставление приведенных значений выявляет значительные резервы в увеличении динамической жесткости за счет создания оптимальной анизотропной структуры.
Приведем также результаты расчетов для прямоугольной пластинки единичной площади. В качестве начального приближения бралось распределение осей ортотропии о ° (х, у), приведенное на рис. 3.17, которому соответствует значение ненулевой частоты w = 2,86. Проведенный поиск оптимального решения привел к распределению ориентации осей ортотропии, показанному на рис. 3.18. Этому распределению а*(х,у) отвечает значение функционала Д = оц = 3,04 (двукратное). Последующие значения частот для найденного оптимального проекта пластинки равнялось = 6,89; с^з = 7,75; w4 = 8,14. Для сравнения приведем
152
ГЛАВА 3
значения низшей ненулевой частоты свободных колебаний при распределении угла ортотропии и на всей пластинке, равные, соответственно,
= 2,63 и wi = 1,84. Интересно, что собственная форма колебаний, отвечающая ненулевой частоте при а = 0, представляет собой несимметричную по обоим аргументам функцию U(x, у) = ~U(—x,y), U(x,y) = — U(x>— у), в то время, как для распределения а = тг/2 — симметричную U(ж, у) = U(—ж, у), U(х, у) = U(х, —у). Сравнение оптимальных значений низшей ненулевой частоты для квадратной (о>1 = 3,53) и прямоугольной = 3,04 пластинок единичной площади показывает, что эти значения существенно зависят от формы. Характерной особенностью незакрепленных конструкций является повышение первой ненулевой частоты свободных колебаний с увеличением симметрии конструкции, в то время как для закрепленных конструкций повышение ее симметрии приводит к понижению основного тона колебаний.
3.9.	ПРОЕКТИРОВАНИЕ КОНСТРУКЦИЙ С МИНИМАЛЬНЫМ УРОВНЕМ НАПРЯЖЕНИЙ
Требования предъявляемые к условиям эксплуатации БКК, исключают в большинстве случаев возможность появления в них неупругих деформаций, недопустимых по соображениям надежности функционирования изделия. В качестве критерия, определяющего условия перехода материала конструкции в пластическое (неупругое) состояние может использоваться критерий текучести Губера — Мизеса наибольшей интенсивности касательных напряжений. Очевидно, что тогда из всех допустимых конструкций заданного веса или заданного объема материала будет считаться та, для которой при заданном внешнем воздействии реализуется минимум максимального значения интенсивности касательных напряжений. Для оптимальных в этом смысле конструкций может быть расширен диапазон прикладываемых нагрузок, не нарушающих принятого критерия прочности. В соответствии с конечноэлементными представлениями, изложенными в главе 2, определим вектор напряжений для элемента с номером j в момент времени t = tk
>	(9-1)
где — матрица перехода от вектора обобщенных перемещений к вектору перемещений узлов рассматриваемого элемента. Матрица определена в локальной системе координат.
В общем случае элементы матрицы х^ являются функциями пространственных координат и параметров проектирования. Выражение для
МЕТОДЫМОДЕЛИРО ВАНИЯ И ОПТИМИЗАЦИИ БКК
153
интенсивности касательных напряжений может быть записано в виде
(9.2)
В случае плоского напряженного состояния выражение (9.2) записывается следующим образом
Для стержневых элементов имеем
+ 3гЛ)(=и •
тк —
(9.3)
(9.4)
Выражения (9.2)-(9.4) могут быть преобразованы к стандартной форме
T{kj)	,	(9.5)
\	/t=tk
если определить соответствующим образом матрицы G<A Для стержневого элемента = 1/>/3. В случае плоского напряженного состояния эта матрица записывается следующим образом
G^ =
2
-1
-1 О
2 О
О 6
О
В общем трехмерном случае для матрицы
будем иметь следую-
щее представление
	- 2	-1	-1	0	0	0-
	-1	2	-1	0	0	0
G^’) = —	-1	-1	2	0	0	0
Ve	0	0	0	6	0	0
	0	0	0	0	6	0
	. 0	0	0	0	0	6.
Тогда с учетом представления для х^ выражение (9.5) можно записать в компактной форме
= fwy,	,	(9.6)
t=tk \	' t=tk
154
ГЛАВА 3
где через Р^) обозначена следующая матрица
p(j) _	.	(9.7)
Максимальное значение интенсивности касательных напряжений находится для каждого элемента конструкции в предположении, что определены функции, при помощи которых аппроксимируется решение соответствующее данному элементу и, следовательно, известна матрица Р(Д В ряде случаев (симметричные конструкции) предполагается, что максимальные интенсивности напряжений достигаются в фиксированном числе заранее известных точек. В таких случаях величина находится методом перебора значений, принимаемых интенсивностью напряжений. Существенные упрощения достигаются для элементов с однородным распределением напряжений = const. Более сложным, очевидно, является случай, когда интенсивность напряжений достигает максимума в отдельной точке с индексом 0. Тогда
= (u/,P^u/)	= (wy, $*PqJ)$w/>)	,	(9.8)
х / max х	/ t=tk x	/ t=tk
где P^ — матрица, определенная в точке максимума интенсивности касательных напряжений. В общем случае элементы матрицы Р^ зависят от переменных проектирования.
Ограничиваясь классом конструкций, описываемых конечноэлементными представлениями, сформулируем задачу предельного снижения интенсивности напряжений. Требуется определить вектор переменных проектирования h = {Ai, Лг, • • •, hn}, удовлетворяющий условиям
N
= const,	(9.9)
i=l
hl min < hi < hl max, — 1, 2, . . ., 72,	(9.10)
и такой, что
max -> min,	(9.11)
je[i at] *max h
Л€[1 кт]
(j)
где т^ах — максимальное значение интенсивности касательных напряжений в j-м конечном элементе в момент времени определяемое по формуле
(г?2ах) = (w/.ST^fcw/) .	(9.8)
х /	\	/ t=tk
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
155
Сформулированная задача оптимизации решалась для ряда незакрепленных конструкций. Для построения решения применялись различные оптимизационные алгоритмы и проводились сопоставления эффективности вычислительных процедур. Проведенная статистическая обработка выполненных расчетов показала, что используемые в данной книге алгоритмы последовательной оптимизации оказываются наиболее эффективными. В качестве иллюстрации применение алгоритма последовательной оптимизации приведем результаты расчета оптимального проекта для платформы, показанной на рис. 3.8. Конструкция платформы, имеющая ферменную структуру, представляет собой соединение элементов, работающих только на сжатие и растяжение. Напряженное состояние в элементах конструкции является одноосным, и напряжения не изменяются в пределах отдельных элементов. Тогда для интенсивности касательных напряжений имеем выражение т^2х = |crJ |/л/3, где crJ — напряжение в J-м стержне. Рассматриваемая задача оптимизации сводится к минимизации абсолютной величины максимального напряжения. Значения параметров ограничений в (9.10) полагались равными: ft/min = 20 мм2, hi max = 70 мм2, а в качестве начального распределения площадей поперечных сечений элементов бралось hi = fto = 20 мм2. Максимальные напряжения в конструкции достигались одновременно в 16 элементах. Для исходного проекта максимальные напряжения достигались в момент времени tk = 0,073 сек, а для оптимального решения потребовалось выполнить 16 итераций и выигрыш по функционалу составил 28,1 %. Отметим, что полученное в результате решения задачи оптимизации распределение материала качественно совпадает с распределением, полученным для конструкции, обладающей максимальной жесткостью.
3.10.	ОПТИМИЗАЦИЯ ПРЕДВАРИТЕЛЬНЫХ НАПРЯЖЕНИЙ И УСИЛИЙ
При разработке конструктивно-силовых схем БКК часто возникает необходимость создания предварительно напряженных систем, т. е. в отдельных или во всех элементах конструкции создается начальное предварительное напряжение на стадии монтажа или развертывания трансформируемой конструкции, при сборке ее отдельных фрагментов. В целом, рационально созданные предварительные напряжения могут повысить несущую способность конструкции, что достигается наиболее полным использованием возможностей материала, из которого изготовлены силовые элементы, обеспечить возможность упругого деформирования конструкции при воздействии внутренних и внешних силовых факторов, снизить влияние тепловых напряжений, возникающих в силовых элементах БКК в процессе ее эксплуатации.
Существенно важным предназначением создания поля предварительных напряжений в силовых элементах БКК является требования обес-
156
ГЛАВА 3
печения заданной формы и геометрических параметров аппарата и его Я рабочих поверхностей. Для трансформируемых конструкций по суще- Я ству это единственный надежный способ выбрать люфты в шарнирных Я соединениях. Конструкции, в которых используются силовые вантовые Я элементы должны обеспечить предварительные растягивающие усилия в Я них. Во многих случаях создание предварительных напряжений в кон- Я струкции позволяет повысить ее жесткость.	Я
В настоящем параграфе будут рассматриваться лишь предваритель- Я ные усилия, создаваемые в крупных протяженных элементах конструк- Я ции, таких, как балочные, стержневые, пластинчатые элементы, и не Я будут рассматриваться локальные предварительные напряжения, возни- Я кающие, например, в заклепках, болтах и т. д.	Я
Разрабатываемые в настоящее время БКК представляют собой круп- Я негабаритные сооружения, образованные тонкостенными элементами. Я Основу подобных конструкций, как правило, составляют стержневые Я фермы или рамы. Специфика БКК, в отличие от наземных конструк- Я ций, состоит в том, что система усилий, действующая в элементах кон- Я струкции, должна быть самоуравновешена усилиями в элементах самой Я конструкции. Рассмотрим возможности создания поля предварительных Я напряжений в конструкции на примере свободной шарнирно-стержневой Я фермы. Конструктивно-силовая схема фермы образована протяженными Я стержневыми элементами, соединенными в узловых точках. В каждом Я г-ом элементе действуют растягивающее или сжимающее усилие г,. В Я узлах стержневой системы должны выполняться условия равновесия, В которые можно записать в следующем виде	Я
Аг = 0,	(10.1) Я
где г — вектор усилий в стержневых элементах конструкции, А — ма- Я трица коэффициентов системы уравнений равновесия, которая состоит В из косинусов, проектирующих усилия в элементах на оси координат. Раз- В мерность матрицы А — т х п, где п — количество стержневых элементов, Ж ат — утроенное количество узловых соединений, т. к. в каждом узле Ж должно выполняться три уравнения равновесия. Существование нетри- > виального решения системы уравнений (10.1) указывает на возможность J создания предварительных усилий в стержневых элементах. В преды- Ж дущих параграфах проводился анализ системы (10.1) применительно к ж стержневым конструкциям. Мы будем рассматривать лишь такие кон- J фигурации стержневых систем, для которых существует нетривиальное Ж решение системы (10.1). В этом случае выполняется условие	<
rank А = к < min[m, п].
(Ю.2)
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
157
Крупногабаритные конструкции образованы, как правило, большим числом элементов и, как следствие, размеры матрицы А таковы, что возникают проблемы с вычислением ранга матрицы к, что требует разработки и использования специальных численных методов при исследовании предварительно напряженных систем (например, использование симметрии или цикличности структуры конструкции).
В общем случае можно поступить следующим образом — осуществить сингулярное разложение матрицы А [14]:
AT=UEVT,	(10.3)
где квадратные матрицы U и V размером [п х п] и [т х пг] соответ-ственно, ортогональны, т. е.
UTU = Е, VTV = Е.
Через Е обозначены единичные матрицы соответствующего размера. Прямоугольная матрица Е имеет диагональную структуру, на диагонали которой стоят сингулярные числа. Количество ненулевых сингулярных чисел равно рангу матрицы А. Используя сингулярное разложение систему уравнений равновесия (10.1) можно записать следующим образом
Аг = VETUTr = 0.	(10.4)
В ортогональной матрице U можно выбрать к произвольных столбцов, которые образуют матрицу U размера [n х i], а оставшиеся столбцы образуют матрицу U размером [п х п — к]. В силу структуры матрицы сингулярных чисел Е решение системы (10.4) можно заменить эквивалентной системой уравнений
Ur = 0.	(10.5)
В силу ортогональности матрицы все решения системы (10.5) даются формулой.
г = Uh,	(10.6)
где h — произвольный вектор размера п—к. Следовательно, соотношение (10.6) описывает все возможные распределения предварительных усилий в конструкции. Из соотношения (10.6) видно, что любая допустимая комбинация предварительных усилий, т. е. комбинация, удовлетворяющая уравнениям равновесия (10.1), может быть увеличена или уменьшена в произвольное количество раз и даже допускает изменение знака всех
158
ГЛАВА 3
усилий. Размер вектора h в (10.6) тесно связан со степенью стати- I ческой неопределимости свободной шарнирно-стержневой конструкции. I Количество компонентов вектора h равно степени статической неопреде- 1 лимости. Ясно, что в статически определимой свободной системе (k = n) | предварительные усилия создать невозможно. Возможности создания | предварительных усилий возрастают с возрастанием степени статиче- 1 ской неопределимости.	|
Сделаем замечание. Повышение степени статической неопределимо- 1 сти конструктивно-силовой схемы БКК расширяет возможности проек- | тировицика в выборе предварительных усилий в элементах конструкции. I Таким образом можно расширить, например, диапазон рабочих темпера- | тур БКК или величины динамических воздействий от реактивных двига- | телей систем ориентации и стабилизации. Но технический разброс при I изготовлении отдельных элементов БКК, не соблюдение температурных I режимов на этапе монтажа может привести в статически неопределимой 1 конструкции к возникновению дополнительного поля предварительных усилий, которое необходимо учитывать при проектировании БКК. Если I проектируемая БКК представляет собой трансформируемую систему, то при выборе статически определимой конструктивно-силовой схемы пол- J ное раскрытие всех элементов может может быть гарантированно тем, | что в раскрытом состоянии не возникают усилия в стержневых эле- | ментах и, тем самым, обеспечивается закрытие всех замковых соеди- | нений в шарнирах. Напротив, при выборе статически неопределимой I конструктивно-силовой схемы механизм, обеспечивающий трансформа- 1 цию, должен создавать дополнительные усилия для постановки на замки. I
При расчете шарнирно-стержневых ферм с использованием метода | конечного элемента возникают дополнительные компоненты, входящие 1 в матрицу жесткости, обусловленные наличием в конструкции предва- | рительных напряжений. Поскольку соотношение (10.6) описывает все 1 допускаемые сочетания предварительных усилий в стержневых элемен- ] тах, а величины усилий входят в матрицу жесткости конструкции, то * можно сделать вывод о том, что жесткостными характеристиками БКК можно управлять выбирая поле предварительных усилий.
Рассмотрим задачу о свободных колебаниях БКК, которые описываются следующими соотношениями
(К + В(г) - ы2М) х = 0,	(10.7)
где К — матрица жесткости конструкции, В (г) — дополнительная ма-трица жесткости, учитывающая влияние предварительных усилий г в стержневых элементах, М — матрица масс, ш — частота свободных колебаний, х — собственный вектор —- форма свободных колебаний.

МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
159
Рассмотрим задачу рационального выбора величин предварительных усилий в стержневых элементах, обеспечивающих максимум низшей ненулевой частоты свободных колебаний. Предварительные усилия г удовлетворяют системе уравнений равновесия (10.1) и системе неравенств
щ <ri <bi>	(10.8)
В неравенствах (10.8) значения а,- и 6, являются естественными ограничениями по прочности для растянутых стержней и по устойчивости для сжатых. Очевидно, что система уравнений равновесия (10.1) и система неравенств (10.8) должны быть совместны. Предполагаем, что условия совместности выполняются.
Для решения задачи оптимизации проварьируем систему (10.7), получим вариационное соотношение
(К + В(г) - ш2м) 6х + <SB(r)x - Jw2Mx = 0.	(10.9)
Умножая проварьированное уравнение (10.9) на вектор хт слева учиты-вая свойство симметрии матриц К, В и М, получим следующее выражение для вариации квадрата частоты свободных колебаний
^2=(^М) (хТ’5в(г)х)-	(1010)
Здесь скобками обозначено скалярное произведение векторов. Поскольку структура матрицы В (г) зависит лишь от геометрических параметров конструкции, то для ее вариации можно получить следующее соотношение
<*в(г) = Е
Вариации величин предварительных усилий в стержневых элементах не произвольны, т. к. должна выполняться система уравнений равновесия (10.1). Для исключения из (10.10) вариаций Jr, воспользуемся соотношением (10.6), проварьировав которое Jr = UJh получим выражение для вариации величин усилий в стержневых элементах, выраженных через вариации независимых параметров hj (J = 1,2,..., п - к), которые теперь будут выполнять роль параметров проектирования в рассматриваемой задаче оптимизации. Воспользовавшись соотношениями (10.10) окончательно получим выражение для вариации квадрата частоты свободных колебаний, зависящее от вариации параметров оптимизации hj
(х, Мх)
(10.11)
160
ГЛАВА 3
Решение задачи оптимизации строится численным градиентным методом с использованием выражения для градиента
1 N / Лтэ \ ________
= (1012)
с учетом системы ограничений (10.8).
В качестве примера решения задачи оптимизации рассмотрим свободную шарнирно-стержневую форму, состоящую из 94 стержневых элементов (рис. 3.19). При выбранных геометрических параметрах свободной конструкции после нескольких шагов градиентной процедуры оптимизации было достигнуто ограничение по сжимающим усилиям, что сильно уменьшило возможности изменения целевого функционала (достигнутое увеличение частоты составило 0,5% по сравнению с ненапряженной фермой). На рис. 3.19 приведены значения усилий в стержневых элементах фермы полученные в результате решения задачи оптимизации. Однако, конструктивно-силовые схемы БКК могут допускать такие компоновки, когда мощные силовые элементы сочетаются с тонкими, которые, в свою очередь, определяют величину низшей частоты свободных колебаний (например ванты, тонкие мембраны). Эффективно улучшить динамические характеристики подобных конструкций можно с использованием предварительных усилий в элементах.
Рис. 3.19
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК
161
В заключение заметим, что величины предварительных усилий входят в геометрическую матрицу жесткости В линейно, следовательно можно ввести некоторый параметр р, изменение которого пропорционально изменяет предварительные усилия и уравнение (10.7) примет вид
(К + рВ(г) - о>2М) х = 0.	(10.13)
При этом система уравнений (10.1) не нарушается в силу однородности. Изменяя значения параметра р при фиксированном векторе усилий г можно добиться того, что фундаментальная частота свободных колебаний конструкции станет нулевой и уравнение (10.13) примет вид
(К +рВ(г))х = 0.	(10.14)
Задача (10.14) является задачей на собственные значения, в которой собственное значение р определяет критический параметр статической потери устойчивости конструкции, а собственный вектор х — форма потери устойчивости.
6 — 2185
Глава 4
ДВИЖЕНИЕ УПРУГОГО ТЕЛА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС В ГРАВИТАЦИОННОМ ПОЛЕ
Динамика вязкоупругого тела в центральном ньютоновском гравитационном поле в последние десятилетия получила значительное развитие. Актуальность исследований по этой проблеме обусловлена главным образом их приложениями в динамике крупногабаритных космических конструкций, например, больших космических антенн.
Исторически вопросы динамики вязкоупругих тел возникли в связи с изучением приливной эволюции в движении Луны и планет. В конце прошлого века в фундаментальных работах Дж. Г. Дарвина [40, 128, 129] впервые рассмотрено влияние приливов на движение в системе планета-спутник. Более детальное исследование явлений приливной эволюции было проведено во второй половине XX века [21, 31, 80]. Главным стимулом для этих работ послужило обнаружение резонансных явлений в орбитальных движениях планет и в их вращательном движении вокруг своих осей.
Задачи исследования космического пространства, в которых существенна ориентация спутника, привели к возникновению целой новой области динамики, называемой движением спутника относительно центра масс. На ранних стадиях исследования космоса размеры космического аппарата были небольшими, он был механически простым и по существу недеформируемым. Поэтому в качестве математической модели аппарата принималась модель абсолютно твердого тела. Однако в анализе большой космической конструкции, содержащей легкие развертывающиеся элементы и по существу являющейся гибкой, такое моделирование становится неприемлемым. Появилось много исследований (см. библиографию в [41, 43, 44, 78, 83, 142]) по динамике космического аппарата с учетом его деформируемости.
Во многих работах большие упругие космические конструкции представляются в виде связанных между собой твердых тел или твердого тела, имеющего упругие ответвления. Для анализа динамики крупногабаритной космической конструкции может оказаться более пригодной континуальная модель, когда вся конструкция или некоторые ее деформируемые
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
163
элементы моделируются сплошной вязкоупругой средой. В общем случае эта модель приводит к исследованию системы интегродифференциальных уравнений с обыкновенными и частными производными. Такие системы уравнений иногда называют гибридными. Их исследование представляет собой весьма сложную задачу. Аналитическое исследование возможно при некоторых дополнительных предположениях о форме конструкции, начальных условиях ее движения и физических свойствах материала, из которого изготовлена конструкция.
Если предположить, что коэффициент пропорциональности между функционалом потенциальной энергии упругих деформаций и диссипативным функционалом является малым и рассматривать процесс деформирования как квазистатический, то приближенный анализ можно провести методом, разработанным в [31]. При построении приближенного решения гибридной системы уравнений приходится решать довольно сложные вспомогательные задачи теории упругости.
Плодотворным оказался метод исследования, основанный на синтезе методов модального анализа и малого параметра [54, 67, 87, 155]. В этом методе предполагается, что задача динамики решается в рамках линейной теории упругости, а силы внутреннего трения, возникающие в процессе деформирования, задаются при помощи функции Рэлея, что соответствует модели Кельвина — Фойгта теории вязкоупругости. Компоненты вектора упругого перемещения раскладываются в ряд по формам колебаний, зависящим от пространственных координат и определяемым свободными упругими колебаниями тела в отсутствие внешних сил; коэффициенты ряда (обобщенные, или нормальные координаты) — функции времени, подлежащие определению. Движение вязкоупругого тела при использовании «модального подхода» описывается бесконечной системой обыкновенных дифференциальных уравнений. Естественные физические предположения о том, что наибольший период свободных упругих колебаний тела много меньше характерного времени затухания этих колебаний, которое, в свою очередь, много меньше характерного времени движения тела как целого, позволяют ввести в уравнения движения вязкоупругого тела малые параметры. После этого решение уравнений можно построить асимптотическими методами, разработанными для систем дифференциальных уравнений с малым параметром при старших производных [30]. Регулярная часть асимптотического разложения решений для обобщенных координат, описывающих деформации тела, соответствует квазистатическим деформациям — вынужденным упругим колебанием под действием гравитационных сил и сил инерции.
Описанный модальный подход (при учете упомянутых выше физических предположений), по сути дела, эквивалентен методу приближенного анализа гибридных систем из [31]. Однако модальный подход может
6*
164
ГЛАВА 4
оказаться более предпочтительным, так как он приводит к системе уравнений движения, которая хотя и счетна, но образована обыкновенными дифференциальными уравнениями. При анализе такой системы можно использовать классические методы аналитической механики и современные методы, разработанные для бесконечных систем дифференциальных уравнений [28, 46, 79].
Данная глава посвящена исследованию движения вязкоупругого тела относительно центра масс в центральном ньютоновском гравитационном поле на круговой и эллиптической орбитах. Применяется модальный подход, деформации тела считаются квазистатическими. Одной из целей главы является выяснение влияния упругости и внутреннего трения на известные, хорошо изученные движения абсолютно твердого тела в центральном ньютоновском гравитационном поле: положения относительного равновесия в орбитальной системе координат, регулярные прецессии, периодические колебания и вращения в плоскости орбиты. Рассмотрен также рад задач об эволюции быстрых вращений вязкоупругого тела относительно центра масс.
4.1. УРАВНЕНИЯ ДВИЖЕНИЯ
Динамические уравнения. Пусть	— система координат
с началом в центре масс О тела, деформированного или недеформи-рованного. Оси OxiT Ох2 и Ох3 при отсутствии деформаций тела направлены вдоль главных центральных осей инерции. Соответствующие главные моменты инерции обозначим через А, В и С. В процессе деформирования трехгранник Ох \х2х^ перемещается в теле. Положение произвольной частицы dm тела в системе координат	опреде-
ляется радиусом-вектором
r = p + u(p,t),	(Lt)
где — р — радиус-вектор этой частицы в недеформированном состоянии тела, и — ее упругое смещение.
В качестве системы координат Ох^х2х^ выберем «среднюю» систему координат [43, 127]. Ее движение в деформируемом теле происходит так, что выполняется тождество
J pxudm = O.	(1.2)
v
где интегрирование проводится по всему недеформируемому телу. В средней системе координат нет смещений тела как абсолютно твердого [43, 75, 127].
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
165
Деформацию представим в виде ряда
и = ^gn(*)u(n)(zi,x2,x3).
(1.3)
Здесь	Ц2П\ мз”Ь — собственные формы свободных упругих
колебаний тела в средней системе координат, удовлетворяющие условию ортонормированности
У	dm = 6пк (п, к = 1,2,...),
где 6пк — символ Кронекера.
Зависимость от времени обобщенных (нормальных) координат qn, соответствующих формам u(n\ подлежит определению. Для свободных упругих колебаний функции qn(t) удовлетворяют уравнениям гармонических колебаний
9п + ^пЯп = 0 (п = 1,2,...),
где — n-я частота свободных колебаний упругого тела.
Матрицу тензора инерции тела для точки О в системе координат Ож1,х2,ж3
можно представить в виде
J = Jq + Ji 4“ J2,
где
Jo = diag{A, В, С}, Jx = 2 £ mV0,
ОО
J2 = ^2
v
v
166
ГЛАВА 4
При вычислении элементов матриц принято во внимание, что в средней системе координат, в силу условия (1.2), величины обладают свойством симметрии
(i,j = 1,2,3; п= 1,2,...)
Пусть ш — абсолютная угловая скорость трехгранника Ох^хз. Проекцию о? на ось Oxi будем обозначать через щ (г = 1,2,3). Для кинетического момента К тела относительно центра масс можно получить такое выражение:
К = Jo> + K#,
Здесь
оо
к. = 9fc?<K<fc, к ,1=1
Ktk = [ х u(') dm =	- L(£\L(£} -	\
V
Кинетическая энергия тела вычисляется по формуле
Т =	4-	’ Ju;) + о; • К* + Д,
A	L
где тп — масса тела, vq — величина скорости центра масс, а
оо
П = 1
Пусть OXYZ — орбитальная система координат. Ось OZ направлена вдоль радиуса-вектора Ro центра масс относительно притягивающего центра, а оси OY и ОХ — соответственно по бинормали к орбите и по ее трансверсали в сторону движения центра масс. Единичные векторы осей OX, OY и OZ обозначим соответственно через а, /3 и 7 (их проекции на ось Oxi будем обозначать а,, Д и 7,).
Потенциальную энергию тела можно представить в виде суммы двух слагаемых: П = П* + П^, где П* — потенциальная энергия упругих деформаций, оо
= (L5>
П = 1
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
167
а Пд — потенциальная энергия, обусловленная массовыми силами (силами гравитационного притяжения). Если пренебречь величинами порядка (//Ло)3, где I — характерный линейный размер тела, то
Пз = “ я? “ Й(Jxi + Jx2 + Лз) +	’J7)’
Здесь // — произведение универсальной гравитационной постоянной на массу притягивающего центра.
Уравнения движения центра масс тела можно получить из уравнений Лагранжа второго рода с лагранжианом L = Т — П. Пренебрегая величинами порядка (Z/Ло)2, находим, что
d2 Rq Ro ~di^ =
т. е. орбита центра масс — кеплеровская. Пусть она является эллиптической с эксцентриситетом е. Тогда [71]
2
^ = (тЭр(1 + есо8^ (L6)
Здесь w0 — среднее движение центра масс (w0 = 2тг/ТЬ, где То — период обращения центра масс по орбите), ар — истинная аномалия (угол между радиусом-вектором Ro и направлением из притягивающего центра на перицентр орбиты),
/it	\2	/1 ?\
д =	+		С-7»
Получим еще дифференциальные уравнения движения относительно центра масс, которое представляет собой вращение тела как целого и деформации его отдельных элементов. Это движение определено, если известны движение трехгранника Ох 1X2X3 в абсолютном пространстве и зависимость обобщенных координат qn от времени.
Уравнения, описывающие движение трехгранника	получим
из теоремы об изменении кинетического момента
K + wxK = M,	(1.8)
где М — момент внешних сил (гравитационный момент) относительно центра масс:
н
М = 7 х grad7 П = 3—37 х J7.
168
ГЛАВА 4
Отбросив в обеих частях уравнения (1.8) слагаемые, нелинейные относительно qn, qn, получим векторное дифференциальное уравнение, описывающее вращение трехгранника Oxix2#3 относительно центра масс О тела
оо
JOW 4- W х J0o> = 3-^7 х Jo7 + 6-^ 52 qny х J(jn)7-ко	rto n=1
OO	oo	oo
—2 52 qnu x - 2 52 дп^п)й - 2 52	(1.9)
n = l	n=l	n = l
В скалярной форме это уравнение записывается в виде следующей системы трех дифференциальных уравнений
Acbi 4- (С —	= 3	~ В)727з+
оо
+6^ 52 9п [-7172Я1(з)-(7|-7|)ЯЙ)-727з(Я^з)-Я^))+717з^12)] -
—2	(а^2—й;з)Я23^“й;2^з(Язз^ — Я22Ь+и;1и;3-йГ12^ —
П = 1
—2 £ qn [(Я<"> +	- Н$й2 - Я<^шз] -
П = 1
-2^дп [(Я<!р +	~ Я^3] , (1.10)
П = 1
П = 1
Вш2 4 (А — С)с^зс^1 — 3-^(А — С)7з71-|-
+6^S9n -727з^2)“(7з-7?)Я1(з)-7з71(^и)-Я^з))+7271^23) “ п° n=l	J
-2^g„ -о;2а;зЯ1^)-(а;1-^)Я1(")-а;за;1(Я<7)-Я^))+ш2^1ЯЙ) -
-2 £ g„ [-Я+ (ЯЙ} + Н^2 ~ Я^^з] -
П = 1
-2 52д„ [-Я^х + (Я^} +	- Я^^з], (1.U)
П = 1
П = 1
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
169
Сйз + (В — X)a>ia>2 — 3-^(В ~ -4)71724-
+6Д	-7з71^з)-(7?-722)Я1(2)-7172(Я^")-Я{1))+7з72Я1(з)|-
-2 52	-ш3Ш1Н^-(ш1-ш1)Н^>-ш1Ш2(Н^)-Н^)+шзш2Н^ -
ОО
—2 £ qn [-Я<”>йх - Н%>й2 + (ff<? 4- -ЯЙ^з] -71 = 1
ОО
-2$>„ [-Я^х - Я<”>и2 + (Я<?> + Я^)ш3] . (1.12)
71 = 1
Предположим, что силы внутреннего трения задаются при помощи диссипативной функции Рэлея
Ф =	(1.13)
71 = 1
где х — безразмерный параметр, b — положительная константа. Уравнения для величин qn можно записать в виде уравнений Лагранжа второго рода:
dt (J([r ОЦт О([г
После некоторых преобразований эти уравнения принимают следующий вид:
9г+2х^г?г+^2?г + Фг+52Фгп = gr + уgrn (r=l,2,...). (1.14) 71 = 1	71 = 1
Здесь приняты обозначения
Фг = 2 ^//12^1^2 4" Я^ОЦСОз 4" -^23^2^3^ ~
-(^22^ 4" Нзз)^ — (Язз> 4- Я1^)а/2 -	4-
170
ГЛАВА 4
Фгп = 2qn [W1(4"3r) - 4n2r))+"2(4’Г) - 4зг))+^(M”2r) - <’)] + +дп [^(4зг) - 4п2г))+"2(4"г) - 4зг))+«з(4”2г) - 4"г))--w?(4"r) + 4зг)) - "2Мзг) + 4ir)) - -з2(М1г) + 4п2г))+ 4-WiW2(£i"r) +	+ Ш2^з(^23^ + Ьз"Г)) + w3^1 (Ь3"Г^ + Мз”’)
9т — -^з #i?(37i — 1) + #22\372 — 1) + #зз\373 — 1)+
+6^{2)7172 + бЯ^^Пз + бЯ^’7273
gm =	[41Г)(37? - 1) + 4"Г)(3722 - 1) + 4зГ)(37з2 - 1)+
R3n
+3(112^ + ^21^)7172 4- 3(^23 4" ^32 ))727з 4- 3(£з/^ 4- £13^)7371
Уравнения (1.10)—(1.12) и (1.14) впервые получены П. Сантини [155]. Приведенный выше вывод следует работе [67].
Кинематические уравнения Пуассона. Пусть о;* — угловая скорость трехгранника Ох 1X2X3 относительно орбитальной системы координат, тогда w* = w - vfl. Имеем векторные кинематические уравнения Пуассона '
ос — сх. х о;*, /3 — /3 х о;*, 7 = 7x0;*.	(1-15)
В скалярной форме они запишутся в виде
dl =02^3“О'З^г-^71 ? &2—азШ1 — О11Шз — Р72, <>3—^1^2~^2^1 — ^73>
Л =^3-^2,	Л^З, Зз=Л^2—/^2^15	U-16)
71—72^3—7з^24-^«i, 72=73^1-71^34-^2, 73=71^2-72^14-/>«з-
Уравнения (1.7), (1.10)—(1.12), (1.14) и (1.16) с учетом соотношения (1.6) образуют замкнутую систему дифференциальных уравнений относительно величин о,-, Д, 7,, о;,-, qn, v (i = 1,2,3; п = 1,2,...). В рамках линейной теории упругости и в предположении о том, что движение центра масс не зависит от движения тела относительно центра масс, они описывают движение упругого тела с внутренним вязким трением в центральном ньютоновском гравитационном поле.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
171
Если величины а,-, Д-, 7,, qn найдены как функции /, то тем самым в любой момент времени определено положение каждого элемента деформирующегося тела в орбитальной системе координат (а следовательно, и в абсолютном пространстве, так как движение орбитальной системы координат известно). Действительно, задание величин а,, Д, 7, однозначно определяет ориентацию средней системы координат относительно орбитальной, а положение произвольной частицы тела в средней системе координат при известных функциях qn(t) однозначно определяется из равенств (1.1) и (1.3). Отметим, что для получения уравнений (1.10)-( 1.12), (1.14) надо знать частоты и собственные формы свободных колебаний тела. Их определение является задачей теории упругости. Предполагается, что решение этой задачи известно точно или приближенно.
Углы и кинематические уравнения Эйлера. Уравнения Пуассона (1.16) могут быть заменены тремя независимыми кинематическими уравнениями. Пусть, например, ориентация трехгранника	от-
носительно орбитальной системы координат OXYZ задается углами Эйлера Vs 0, (рис. 4.1).
Рис. 4.1
Тогда
cti = cos V> cos 9? — sin V> sin 9? cos 0,
= — cos V> sin — sin ф cos (p cos 0, аз = sin ф sin 0,
172
ГЛАВА 4
~ sin V’ cos p 4- cos ip sin 9? cos 0,	(1.17)
/?2 = — sin ip sin p -f- cos ip cos p cos 0, fa = — cos V’sin#,
71 = sin 0 sin p, 72 = sin 0 cos 9?, 73 = cos 0,
и вместо уравнений (1.16) можно взять кинематические уравнения Эйлера:
= ip sin 0 sin р 4- 0 cos р 4-	,
^2 = ip sin 0 cos р — 0 sin р 4- у fa ,	(1.18)
о>з = ip cos 0 4- р 4- v fa -
4.2. АЛГОРИТМ ИССЛЕДОВАНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ В КВАЗИСТАТИЧЕСКОМ РЕЖИМЕ УПРУГИХ КОЛЕБАНИЙ
Выписанные в предыдущем параграфе уравнения движения сложны для анализа. Некоторого упрощения можно добиться, введя дополнительные физические предположения. Будем считать, что тело достаточно жесткое, а диссипативные силы малы по сравнению с упругими силами. Более конкретно, введем следующие предположения о характерных временах протекания различных динамических процессов в движении тела. Пусть и — наибольший период свободных колебаний упругого тела (л = 2тг/П1, где fii — наименьшая частота свободных упругих колебаний), т2 — характерное время затухания этих колебаний, т3 — характерное время движения тела как целого, которое предполагаем совпадающим с периодом То обращения центра масс по орбите. Главное предположение, лежащее в основе дальнейшего асимптотического анализа динамики упругого тела, состоит в том, что выполняются неравенства
Л < т2 < т3.	(2.1)
Эти естественные предположения позволяют ввести в уравнения движения малые параметры, после чего, аналогично [106, 109] решение уравнений можно построить асимптотическими методами, разработанными для систем дифференциальных уравнений с малым параметром при старших производных [30].
Пусть т3 — величина порядка единицы измерения времени. Считая тело достаточно жестким, предположим, что величина п/тз имеет порядок е (0 < е 1). Положив Qr = (г = 1,2,...), перепишем уравнения (1.14) в виде
e2gr + 2x6Q°2<Zr + ^%„=e2(Qr + Fr) (г = 1,2,...),	(2.2)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
173
где
оо
Qr — 9г ~ Фг ? Fr —	^(#гп ~ Фгп)-	(2-3)
П = 1
Предельный случай е —> 0 отвечает абсолютно твердому телу.
Если в уравнениях (2.2) отбросить правые части, то получим линейные уравнения
e2qr 4- 2ХШ°2<7Г + Q?29n = 0,	(2.4)
описывающие свободные затухающие упругие колебания тела. Соответствующее (2.4) характеристическое уравнение имеет такие корни
Аг = —Ш°2 ± ^^1-^62Q°2.	(2.5)
Отсюда видно, что характерное время затухания свободных упругих колебаний тела имеет порядок в2х-1 и, следовательно, условие (2.1) запишется в виде
0<х<б« 1.	(2.6)
Если тело абсолютно твердое, то из (2.2) имеем qr =0 (г — 1,2,...). При е / 0 уравнения (2.2) являются дифференциальными уравнениями с малым параметром при старших производных. Такие уравнения можно исследовать при помощи теории сингулярных возмущений [30]. Асимптотическое решение системы (1.10)—(1.12), (2.2), (1.7), (1.16) состоит из регулярной части и части типа погранслоя, отвечающей затухающим упругим колебаниям. На интервалах времени порядка тз и больших свободными затухающими колебаниями можно пренебречь и для описания движения тела учитывать только регулярную часть асимптотического решения, отвечающую квазистатическим режимам движения тела относительно центра масс, когда его упругие колебания являются вынужденными колебаниями под действием гравитационных сил и сил инерции.
Исследование квазистатических режимов движения важно в теоретическом и прикладном отношении. Во-первых, квазистатические режимы дают одну из весьма немногих возможностей анализа динамики в очень сложной проблеме о движении вязкоупругого тела в гравитационном поле. А во-вторых, для космических станций, рассчитанных на длительное время существования (месяцы или даже годы), квазистатические режимы движения являются основными, так как большую часть времени станция проводит в пассивном полете, при отсутствии управляющих воздействий.
174
ГЛАВА 4
Регулярная часть асимптотического решения может быть получена в виде ряда по степеням величин е2 и х- Полагая х ~ е1+<5 (0 < 6 < 1), можно получить [67, 106], следующее приближенное решение для обобщенной координаты qr:
9г = Q2
-2xbQr) + O(e4)
(г = 1,2,...).
(2.7)
Здесь для простоты записи опущен верхний индекс «ноль» у величины Q°.
Отметим, что e2Qr есть «свободный» член в правой части уравнения (2.2). Он не содержит величин qn и qn (п = 1,2,...), а зависит лишь от переменных о^, 7, (г = 1,2,3) и р. Для величин Qr, согласно (2.3) и (1.14), имеем такие выражения:
Qr = Д [я1(;)(з712 -1) + <(3722 - 1) + я«(з7з2 - 1)+
+6Я1(2)7172 + 6Я$7173 + 6Я23^7273 -
—2 ^я{2^1«2 +	4- Я^о^з) +	+ Я33^ w2+
+ (я^ + Я<?)«2 + (я<? + Я^) ш23 (г =1,2,...). (2.8)
Подставив выражения (2.7) для qr в правые части уравнений (1.10)—(1.12), получим три уравнения, отвечающие по форме уравнениям движения абсолютно твердого тела относительно центра масс под действием гравитационных моментов и дополнительных моментов, обусловленных упругостью и внутренней вязкостью тела. Если в этих уравнениях отбросить величины порядка в4 и выше, то их правые части будут содержать величины порядка е2 и х£2- Первые соответствуют внутренним упругим, а вторые — диссипативным силам.
Полученные такие путем приближенные уравнения описывают (с учетом кинематических уравнений (1.16) или (1.17), а также соотношений (1.6), (1.7)) движение тела как целого в квазистатическом режиме его упругих колебаний. Если эти уравнения проинтегрированы (точно или приближенно), то тем самым найдена ориентация трехгранника Ох 1X2X3 в орбитальной системе координат. При известной ориентации трехгранника ОХ1Х2Х3 нахождение деформаций тела не требует операции интегрирования, так как приближенные значения обобщенных координат qr определяются по формуле (2.7), а деформации — по формуле (1.3).
Мы не останавливаемся здесь на математическом обосновании описанного алгоритма приближенного исследования уравнений движения
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
175
упругих тел при наличии внутренней вязкости. Ряд вопросов, связанных с оценкой асимптотики сингулярных возмущений в динамике вязкоупругих тел, рассмотрен в работах [86, 88, 102, 109].
4.3. ПЛОСКИЕ ДВИЖЕНИЯ ТЕЛА
Дифференциальные уравнения плоского движения. Пусть деформации тела происходят в плоскостях, параллельных плоскости 0x^X2, а деформациями вдоль оси Ох^ можно прене-	z
бречь. Тело может двигаться так, что ось Ох^ средней системы координат все время пер-	х
пендикулярна плоскости орбиты центра масс. X. / ** Некоторые вопросы динамики плоского дви-	X.
жения больших космических конструкций, мо- _________Хи 1
делируемых упругой сплошной средой, изуча- х	°
лись в работах [114, 143, 144, 155, 158, 159].	42
Ориентацию средней системы координат
#2^3 относительно орбитальной OXYZ
будем задавать при помощи углов Эйлера 0, у?. Для плоских движений имеем = 7г, 0 = тг/2. Из (1.17), (1.18) тогда следует, что
= 0^2 = 0,	0>з = ip + Z>,
•	П	(3.1)
71 = sin 72 = cos 9?, 7з = О,
где <р — угол между осями 0x2 и OZ средней и орбитальной систем координат (рис. 4.2).
На рассматриваемых движениях величины (1.4), содержащие в нижнем индексе цифру 3, равны нулю.
Принимая еще во внимание равенства (3.1), получаем, что уравнения (1.10) и (1.11) на плоских движениях удовлетворяются тождественно, а уравнение (1.12) принимает вид
оо
Си3=3-£(В-А)7172+6-Д	[(722-7?)Я1(2)7172(И1(^-ЯЙ))] -
^0	n = 1	L	J
—2 £ qn(H^ + ЯЙ^з - 2 £ qn(H^ +	(3.2)
n=l	n=l
Уравнение (1.14) на плоских движениях упростится. Теперь в нем
Фг =	(з.з)
$rn— 2</nw3(^12 ) —^21 )) + 9п
Л /г(пг) r(nr)\ Z ,2/r(nr) I Г (пг)\ ^3(^12 “^21	+ ^22 )
176
ГЛАВА 4
9r =	- 1) + Я^(3722 - 1) +	,
9т =	^пГ\371 — 1) 4-	- 1) + 3(£12Г} 4- £21^)7172] •
Уравнения (3.2), (1.14) и (1.7) с учетом равенств (1.6), (3.1), (3.3) представляют собой замкнутую систему дифференциальных уравнений относительно у?, qn, v (n = 1,2,...), описывающую плоские движения тела относительно центра масс.
Упрощение уравнений в случае квазистатических движений. Введем новое «время» г = ujqI. Тогда уравнения плоского движения (3.2), (1.14), (1.7) примут вид (штрихом обозначено дифференцирование по г):
W + "") + 3(2(^”")’)3(Л “ В) ”” 2<f =
=	[(< -	™ Ъ е» 2У] -
(l-g2) Я=1 L J
-2(^'+И) f;	(3.4)
e2q" + 2xbu0^q'r 4- <r2qr = e2(Qr + Fr) (r=l,2,...),	(3.5)
=(1;ec“r):i- we»
(1 — е2)з
В (3.5) приняты обозначения
£ = Q? = Q?	(37)
+ ^\t 1^3^ |/4i)(3sin2¥’- U + ^(Зсоа2^- 1) + ЗЯ^sin2J . \L e ) L J
Величина Fr в (3.5) — линейная форма относительно qn,qn (п = 1,2,...).
Ее явное выражение в дальнейшем не потребуется.
Будем предполагать, что е ~ е2. Тогда в соответствии с § 4.2 получаем, что в режиме квазистатических упругих колебаний
qr = -(Q*r-2xb^0Q*r') + O(e4), (г = 1,2,...),	(3.8)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
177
где Q* — это функция (3.7), вычисленная при е = 0:
Q*r = (H[r1>+H^/ + i)2+
+| [(#и + H2i) ~ Чнп ~ #22)С08	+ 6Я$ sin 2р] . (3.9)
Из (3.4), (3.6) и (3.8) имеем
v' = 1 + 2е cos т + О(е4), v" = —2е sin т + О(е4) ^(1	= 1 + cos т + О(е4), у>" = -3^^--^sin
Отсюда и из (3.9) следует, что
Q*' = 3 [(Я^ - Я$) sin 292 + 2Я$ cos2y>] /-
-3(Л~ В)(Я<Г? + ЯЙ})(/ + 1) sin 2у> + О(е2),
О
Q*n = 6 [(Я^ - H<r2}) cos 2<р - 2Н$ sin 2^] </-
- 3^2r'g\^ii) + Н22) 4/(9’' + О cos 2р - 3(Л	sin2 2 J -
ZC>	Су	j
_	#). sin 2(р Г(Я|^ — Н^) sin 2<р 2Я^ cos 2^>1 4- О(е2). (3.10)
ZC/	L	J
Дифференциальное уравнение, описывающее изменение со временем угла 9? в квазистатическом режиме движения тела, можно найти из уравнения (3.4), подставив в его правую часть величины qr и q'r (г = 1,2,...), определяемые равенствами (3.8)—(3.10). Отбрасывая величины порядка s4 и выше, получаем уравнение
А — В
<р” 4-3(1 + Зе cos т)——— sin 29? = 2е sin т + гл*, (3.11)
где
т* = Ду'дп [(Я*") - H$)sin2<p+ 2Я1^со8 2у>] +	sin2y>x
О „ L	-* О
п = 1 оо	9	оо
X £ Яп(Н^ + Н^>) -	+ 1) х; + ЯЙ’), (3.12)
П=1	П=1
а величины gn, q'n находятся из (3.8)-(3.10).
178
ГЛАВА 4
Об относительных равновесиях на круговой орбите. На круговой орбите (е = 0) возможны положения равновесия в орбитальной системе координат. В положениях равновесия трехгранник Охухъхз неподвижен в орбитальной системе координат, а упругие смещения частиц тела постоянны: р = <ро = const, qn =	= const, (n = 1,2,...).
Пренебрегая величинами порядка е4 и выше, находим из (3.8)—(3.12) систему уравнений, определяющую равновесные значения <р и qn:
|(А - В) sin 2у> = qn [(Я^ - Н&}) sin 2<р2Н$ cos 2р] ,	(3.13)
n = l
=	[(Я^) + Я^))+2Я^)8т29?-(Я^)-Я^))со82¥>] .	(3.14)
Если из (3.13) при помощи (3.14) исключить qn, то получим уравнение относительно равновесного значения В некоторых случаях, когда недеформированное тело обладает значительной симметрией, это уравнение может удовлетворяться при любом так будет, например, в случае тонкого нерастяжимого однородного кругового кольца, совершающего изгибные колебания в своей плоскости. В общем же случае упомянутое уравнение имеет счетное множество корней. Отличающимся одно от другого положениям тела соответствуют четыре значения р из этого множества. Можно показать, что они отвечают таким положениям деформируемого тела, когда его главные центральные оси инерции направлены вдоль осей орбитальной системы координат.
Рассмотрим частный случай, когда тело в недеформированном состоянии динамически симметрично (А = В). Тогда уравнение для равновесных значений <р имеет вид:
ai sin 29? + аг cos 29? + O3sin4<p + O4cos4<p = 0,	(3.15)
где
оо
а2 = 2^2
П = 1
н[п2\н{? + Н%>)
«3
(Я1(")-Я^))2-4Я1(;)а
04 =
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
179
Для исследования устойчивости положений равновесия <р = <р0 положим в (3.11 )(при е = О)<р = 9?о + я- Если пренебречь величинами порядка е4 и выше, то линеаризованное уравнение возмущенного движения примет вид ж" +	= 0.	(3.16)
Здесь введены обозначения
_ 9е2 ~ [(Я^ - sin 2^0 + 2tf£)cos29?0]2
52 = 3(^-^)_г1) и
где Jx и Jz — главные центральные моменты инерции деформированного тела в его положении равновесия:
Jx = JX1 cos2 ip0 + Jx\X2 sin2^>o + Jx2 sin2 9?0,
Jz = Jxx sin2 (pn - JX1x2 sin 2^o 4- Jx2 cos2 <po,
OQ	00
7	— A -k 2 \ 4	7	— 9 \ ' nQ
JX1 — ZL Z у 4nn22 >	~ z Z "nn12 ’
n=l	n=l
}Ха = В + 2^д°пН^. n=l
Анализ корней характеристического уравнения, отвечающего (3.16), показывает, что при выполнении неравенства Jx < Jz (т. е. когда наименьшая из осей эллипсоида инерции деформированного тела, лежащих в плоскости орбиты, направлена вдоль радиуса-вектора центра масс) положение равновесия неустойчиво.
Если же Jx> Jz, то при Ji = О имеет место устойчивость в линейном приближении, а при Ji / 0 положение равновесия неустойчиво (когда 62 < 0) или асимптотически устойчиво (когда 62 > 0).
Замечание. Отметим следующий интересный факт. Как показывают вычисления, уравнение (3.15) может быть записано в виде
^ = 0, д(р
а выражение для коэффициента 62 уравнения (3.16) можно представить в такой форме
_	1 а2п.
а
180
ГЛАВА 4
Здесь П* — потенциальная энергия упругих деформаций (1.5), вычисленная при значениях gn, отвечающих квазистатическим деформациям, определяемым по формулам (3.14), (1.3).
Отсюда следует, что если в недеформированном состоянии тело динамически симметрично (Л = В), то в положениях его относительного равновесия потенциальная энергия П* упругих деформаций имеет стационарное значение, и, если это значение соответствует строгому локальному минимуму П*, то относительное равновесие неустойчиво по отношению к возмущениям угла <р.
Пусть теперь недеформированное тело не является динамически симметричным. Будем считать, что А > В. В случае абсолютно твердого тела (б = 0) существуют устойчивое (9?^ = 0) и неустойчивое (9?^ = тг/2) положения относительного равновесия тела. При е / 0 равновесные значения угла изменяются на величины порядка е2. Из (3.13) и (3.14) найдем, что
(1) вб2 П = 1
(2) _ я- . бе2
2 + А - В
гг(") гг(п)
.2
00 г/(п) Гг(П)
Е 12Jn +°(g4)-
1 — 1	п
(3.17)
(3.18)
Решение (3.18) при достаточно малых е отвечает неустойчивому положению равновесия тела, так как корни характеристического уравнения линеаризованного уравнения возмущенного движения непрерывны по е, а при 6 = 0 существует положительный корень [3(Л — В)/С]1!2.
Для решения (3.17) линеаризованное уравнение возмущенного движения имеет вид (пренебрегаем величинами О(б4))
х" -I- e2xflx' 4- ш2х — 0,
(3.19)
a w
5	-2
а ~ (^2 /
п = 1
ЗСЯЙ^п’ - н&) + 6СЯ<2)2+
+2(Л - В)(Н[? + ЯЙ’)2 + 3(А - В)Я^)(Я<") 4-
24Ьш0	2
Р ~ ~С2~ Ъ
(А - В)(Н{? + Н^)2 + ЗСН[П/ .
Характеристическое уравнение, отвечающее (3.19), имеет такие корни
А1,2 =	±	+ О(е4).
(3.20)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
181
Так как в общем случае /3 > 0, то отсюда следует, что в рамках уравнений, описывающих квазистатические движения, решение (3.17) отвечает асимптотически устойчивому положению равновесия тела.
Отметим одаако (это важно не только здесь, но и для дальнейшего), что этот вывод об асимптотической устойчивости справедлив и для полной нелинейной системы. Это следует из работы [89] где показано, что строгий вывод об устойчивости совпадает с выводом об устойчивости решений уравнений квазистатических движений, если эти решения отвечают критериям асимптотической устойчивости или неустойчивости по первому приближению.
Эксцентриситетные колебания и их устойчивость. При е / 0 асимптотически устойчивое на круговой орбите положение равновесия (3.17) переходит в 2 я-периодические по г колебания. При о;* / 1 эти колебания можно представить в виде ряда по степеням эксцентриситета:
(1) , 2sinr
(3.21)
Линеаризованное в окрестности решения (3.21)уравнение возмущенного движения имеет вид (величинами О(е4) пренебрегаем)
ж" +	4-w* (1 + 3ecosr)a? = 0.
Для анализа этого уравнения его удобно записать в виде системы двух уравнений первого порядка:
х1 — у, у1 — —^*(1 4-Зе cos т)# - е2х&У-
(3.22)
Если не является полуцелым числом (так как при 6 = 0 имеем < 3, то достаточно, чтобы о/*	1/2, 3/2), то систему (3.22) линейной 2тг-
периодической по т заменой переменных х, у -> zi,z2 можно привести к системе с постоянными коэффициентами. В первом приближении по е эта замена переменных имеет вид
х = 1 4- е-------— cos т hi - е---------—г sm т z2,
\	1 - J 1 -
За;* (2^2 _ 1)	/	3^2	\
У = е— -----—— sinт zi 4- 1 - е------------— cosт z2.
1 - 4а>2	\	1 - 4cu; J
(3.23)
Если отбросить величины О(б4), то в новых переменных система (3.22) примет вид
?1 = z2, 4 =	- ex(3z2.
182
ГЛАВА 4
Характеристическое уравнение этой системы имеет корни (3.20). Следовательно, при достаточно малых е периодические колебания (3.21) асимптотически устойчивы.
Отметим, что в (3.23) появляется нулевой знаменатель при резонансе и* = 1/2; нулевой знаменатель при резонансе и* = 3/2 появится в третьем приближении по е.
Более подробно исследуем устойчивость, когда « 1/2. Положим о;* = 1/2 + Д, где Д ~ е. При помощи линейной 4тг-периодической по т замены переменных приведем (3.22) к системе с постоянными коэффициентами. Искомую замену переменных х,у ух,у2 можно получить в виде следующей последовательности трех замен переменных:
х — R cos
„ . / 1 ' у = u^/tsin I Ф — -т
3	1
R— р — е—р cos (20 — 2т) — -£2y/?psin(20 — т) 16	2
3	3	1
ф = 0 — е- sin т + е — sin(20 — 2т) — -£2x/?cos(20 — т), 4	16	2
z/i^pcos©, z/2 = psin0.
Пренебрегая величинами порядка е4 и выше, получаем преобразованную систему в виде
1	/	3 \
= ~^2ХРУ1 + ( А - ае )У2’ Z	у	о /
/	3 \	1
У? = - Д + -е 2/1 - -€2хРУ2-\	О /	*
Анализ характеристического уравнения этой системы
(А + |е2%/?)2 + Д2 -	= О
показывает, что при выполнении неравенства
|д| < W1-	(з-24)
оу \ де )
периодические колебания (3.21) неустойчивы. Если же неравенство (3.24) выполняется с обратным знаком, то имеет место асимптотическая устойчивость.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
183
Область неустойчивости (3.24) лежит внутри соответствующей области параметрического резонанса для спутника — твердого тела, задаваемой [20] неравенством |Д| < Зе/8 (рис. 4.3).
Отметим, что неустойчивость при резонансе « 1/2 возможна только при достаточно больших значениях эксцентриситета (е > е*). Равенство е* = 4/Зб2х/3 опре
деляет связь между критическим значением
эксцентриситета е*, коэффициентом демп-	Рис. 4.3
фирования и моментами инерции тела. При
е < е* колебания (3.21) асимптотически устойчивы.
В [74, 104] исследованы плоские квазистатические движения вязко-упругого тела, упругие колебания которого происходят вдоль одной из осей средней системы координат, лежащей в плоскости орбиты. Для орбит малого эксцентриситета дан подробный анализ нелинейных колебаний (существование периодических движений, их ветвление и устойчивость), когда период собственных колебаний тела близок периоду движения центра масс по орбите. Для орбит произвольного эксцентриситета в [74, 104] методом усреднения исследовано движение тела, близкого к динамически симметричному, рассмотрен характер нелинейных колебаний и вращения
тела в резонансных и нерезонансных случаях.
4.4. О РЕГУЛЯРНЫХ ПРЕЦЕССИЯХ ПРИ НАЛИЧИИ УПРУГИХ КОЛЕБАНИЙ ВДОЛЬ ОСИ СИММЕТРИИ ТЕЛА1
Системы координат. Уравнения движения. Пусть центр масс вязкоупругого тела движется по круговой орбите. Предполагаем, что в недеформированном состоянии тело динамически симметрично (Д = В). Пусть Oxiх2х3 — система координат, образованная главными центральными осями инерции, ось Ох3 направлена вдоль оси симметрии. Пренебрегая упругими смещениями частиц тела вдоль осей Oxi и Ох2, будем считать, что тело может совершать продольные колебания растяжения и сжатия вдоль оси Ох3. Поэтому в формуле (1.3) полагаем
ч(п) = (0,0,4п))-
Предполагая тело достаточно вытянутым вдоль оси симметрии, можно аппроксимировать свободные упругие колебания тела соответствующими колебаниями тонкого стержня. Полярный и экваториальный моменты инерции С и А недеформированного тела считаем для общности произвольными (О < С < 2Д). Можно показать [69,90], что осиОя, (г = 1,2, 3)
184
ГЛАВА 4
и при наличии упомянутых упругих колебаний остаются главными центральными осями инерции и образуют среднюю систему координат (см. § 4.1). При этом ось Охз остается осью динамической симметрии.
Вычисления показывают [69], что уравнения (1.10)—(1.12), (1.14) движения рассматриваемого вязкоупругого тела относительно центра масс имеют следующий вид;
Awi + (С ~ Л)а>2сиз = Зи>2(С* — Л)727з+ оо	оо
+2(w2W3 - «1 - Зо>о727з) ЧпНзз ~ 2^1 52	(4I)
П = 1	П=1
Аа>2 - (С - А)ш3Ш1 = -За)д(С - А)7з71-ОО	оо
-2(W3W1 + й2 - М1371) 52	- 2^2 52	<4-2)
П=1	П = 1
ш3 = О	(4.3)
Чп 4- 4xb^nqn + S%qn =	+ qn} [w? + wf + «о(37з - 0] • (4-4)
Будем определять ориентацию трехгранника	относительно ор-
битальной системы координат при помощи углов Эйлера. Тогда уравнения (4.1)—(4.4) надо рассматривать совместно с кинематическими уравнениями Эйлера (1.18), в которых z> = Величины 7^ $ (г = 1,2,3) определяются равенствами (1.17).
Из уравнения (4.3) следует, что проекция шз абсолютной угловой скорости трехгранника Ох^хъхз на ось Охз является интегралом движения. Из уравнений (4.1), (4.2), (4.4) при помощи равенств (1.17), (1.18) можно исключить угол <р. Действительно, подставим o/j, о>2 из (1.17) в (4.1) и (4.2). Затем умножим первое из получившихся уравнений на sin 9? и сложим со вторым, умноженным на cos 9?. Далее вычтем из первого уравнения, умноженного на cos 9?, второе, умноженное на siny>. Тогда, вместо уравнений (4.1) и (4.2) получим следующие эквивалентные им два уравнения [69]:
sin0V,,/ 4" 2 cos Оф1— 2 sin 0 cos ip0' — sin 0 sin <ф cos ip — aflP+
2 00
+ A T№P + 51)<7" +	= 0, (4-5)
n = l
0,'+‘2 sin2 0 cos ipip' —sv&0 cos 0'ф* H-cos2 ip sin 0 cos 0—3(a—1) sin 0 cos 0+ 2 00
+«/?/? + - £[(3sin0cos0 - pR + S2}qn + Pq’n]H^ = 0. (4.6) n = l
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
185
Здесь штрихом обозначено дифференцирование по безразмерному «времени» т = ujQt и введены такие обозначения
« = ? (О < а < 2), /?=^,	(4.7)
zl	UJq
Р = 0' + sin R = sin 0ip' 4- cos ip cos 0,
Pi = /? + 2 cos ip sin 0, R2 = Ri — cos ip sin 0,
51 — sin 0ipH -I- 2 cos 0ip'0' — R]0' — sin ipR2,
S2 = 0" — sin 0 cos 0ipf2 4- sin 0R± ip1 4- cos ip cos 0R2.
Уравнения же (4.4) после перехода к безразмерному «времени» т и учета уравнений (1.17) запишутся в таком ввде:
е2Яп + 2xbw0<r2q'n + [<г2 - е2(Р2 + Я2) - е2(3 cos2 в - 1)] qn = е2<Э„ (n = l,2,...),	(4.8)
где
е = £°,	= Qn = Я^)(Р2 + Я2 + Зсо820-1).	(4.9)
all	1Z1
Одно точное частное решение. Уравнения (4.5), (4.6) при любых величинах qn(t) (п — 1,2,...) допускают частное решение
-0 = 7Г, 0 = 7г/2.	(4.10)
Это решение отвечает такому движению тела, когда ось Ох3 во все время движения перпендикулярна плоскости орбиты центра масс. В случае динамически симметричного спутника — абсолютно твердого тела это движение иногда называют (21] цилиндрической прецессией, так как ось симметрии описывает в абсолютном пространстве цилиндрическую поверхность. В рассматриваемом же случае деформируемого тела цилиндрическую поверхность описывает ось Ох3 средней системы координат. Само же тело совершает продольные упругие колебания. Эти колебания определяются формулой (1.3), в которой = (0,0, и^), а величины qn(t) удовлетворяют следующей системе дифференциальных уравнений, получающейся из равенств (4.8), (4.9) при ip = я, 0 = я/2:
e2q,n + Zxbwo<r„q'n + (<г2 +e2)qn = -е2Н^(п = 1,2,...).	(4.11)
Эта линейная система легко интегрируется.
186
ГЛАВА 4
Отметим, что решение (4.10) существует и на эллиптической орбите произвольного эксцентриситета, а также и в случае, когда помимо продольных упругих колебаний тело совершает еще и поперечные колебания [69].
Стационарные квазистатическиерешения. Предположим, что выполнены физические предположения § 4.2, определяемые неравенствами (2.6), и будем рассматривать квазистатические движения тела. Согласно § 4.2, в квазистатическом режиме с погрешностью ~ £4 имеем
6^
qn = — (Qn - 2х^о^) (п = 1,2,...).	(4.12)
<?п
Подставив выражения (4.12) для qn в уравнения (4.5), (4.6), получим приближенные уравнения, описывающие движение оси симметрии тела в орбитальной системе координат. Будет интересоваться их стационарными решениями 0 — 0* = const, ф =	— const.
Стационарные решения отвечают таким движениям тела, в которых оно сжато или растянуто вдоль оси симметрии, занимающей фиксированное положение в орбитальной системе координат. При этом тело вращается вокруг оси симметрии как абсолютно твердое тело с угловой скоростью
^> = О,0 (/? + COS -0* sin 0* ),
а деформации определяются по формуле (1.3), в которой
qn = е2—^-(3cos20„ — sin2 0* cos2 0*).	(4.13)
&п
В абсолютном пространстве стационарные решения отвечают регулярным прецессиям тела. Из (4.5), (4.6), (4.8)—(4.13) имеем систему уравнений, определяющую стационарные значения углов 0*.*
sin0* a/? + sin 0* cos +s2«sin 0* cos V>*(3cos2 0*-sin2 0* cos2 V>*) = 0,
cos 0* а/3cos *0* 4- cos2 *0* sin 0* — 3(ct — 1) sin 0* +
+s2Ksin0*(3 + cos2 “0*)(3со82 0* — sm20* cos2 V;*) = 0,
(4.14)
Эта система имеет три типа решений:
“0* = 7Г, 0* —
’	2
(4.15)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
187
cos *0* = — а/3 — е2ка3/33 4- О(е4), 0* = ^,	(4.16)
,.=0. sl„«. = ^ + 4ewffi^>^ + 0(^ (4.7)
Как показано выше, для существования решения (4.15), отвечающего цилиндрической прецессии тела, не обязательно предположение о квазистатичности движения. Движения (4.16), (4.17) в динамике спутника — твердого тела (б = 0) иногда называют гиперболоидальной и конической прецессиями соответственно [21].
Исследование устойчивости цилиндрической прецессии. Исследуем устойчивость движения (4.15) по отношению к возмущениям величин 0, Ф', 0'. Положим ф = 7г 0 = 7г/2 + х2- Дифференциальные уравнения возмущенного движения запишутся в виде [69]
х” 4- (2 - а6)а/2 4- (аб - l)^i = g^ 4- О5,
а?2 — (2 — аб)^ 4- (аб 4- За — 4)а?2 = 9^ + О5,
где О5 — не зависящая от г совокупность одночленов не ниже пятой степени относительно Xj, x'j (j = 1,2), а = (1 4- е2к)а, b = /3, а через д^ обозначены формы третьей степени относительно Xj, х^:
g{i} = Е	Ц = 1,2).
mi +т2+п1+п2=3
Выражения для коэффициентов форм д^ можно найти в таблицах, приведенных в статье [69], только знак выражения для коэффициента </2100 надо изменить на противоположный [90].
Из характеристического уравнения линеаризованной системы (4.18) следует, что в областях, определяемых неравенствами
(аЬ — 1)(а6 4- За — 4) > 0, а2Ь2 — 2аЬ 4- За — 1 > 0,
(а262 — 2а6 4-За — I)2 — 4(а6 — 1)(а6 + За-4) >0,	(41^
движение (4.15) устойчиво в первом приближении. В этих областях характеристическое уравнение имеет чисто мнимые корни zfciJi, ±г<?2 (<Ji >	> 0):
J4 _ (а2^2 _ 2аЬ + За _ ^2 +	+ За _ 4) = 0	(4.20)
Правда, в одной из точек областей (4.19), в которой а = 1, b = 2, ко’рни уравнения (4.20) непростые (Ji — 62 — 1), но в этой точке линеаризованная система (4.18) имеет вид х" + xj =0 (j = 1,2) и, очевидно, устойчива.
188
ГЛАВА 4
Рис. 4.4
Если хотя бы одно из неравенств (4.19) выполнено с обратным знаком, то у характеристического уравнения есть корень с положительной вещественной частью и, согласно теореме Ляпунова об устойчивости по первому приближению [65 J, невозмущенное движение (4.15) неустойчиво.
Отметим, что с точностью до обозначения параметров а, Ь указанные области неустойчивости и устойчивости в первом приближении совпадают с соответствующими областями для цилиндрической прецессии спутника — твердого тела [21J, показанными на рис. 4.4 в плоскости параметров а, 6, где области неустойчивости заштрихованы, а в областях I и II корни характеристического уравнения чисто мнимые. Для области I существует [107] знакоопределенный интеграл и решение (4.15) для спутника — твердого тела устойчиво согласно теореме Ляпунова об устойчивости [65]. Для области II устойчивость была исследована [68, 70] современными методами теории устойчивости гамильтоновых систем [5, 72, 76]; показано, что (расчеты проводились для /? > —20) движение (4. Неустойчиво для параметров о, /3 из области II, за исключением двух участков (-£,743 < (3 < —1,566 и 0,384 < f3 < 0,45) кривой резонанса четвертого порядка <51 = 3<5г, где имеет место неустойчивость, и еще пяти точек, из которых четыре разделяют резонансную кривую 51 = 3^2 на участки
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
189
устойчивости и неустойчивости (в этих четырех точках устойчивость не исследовалась), а впятой(а = а* = 1,064,/? = /?*•= 0,425) гамильтониан уравнений возмущенного движения является вырожденным при учете в его разложении в ряд членов до шестой степени включительно относительно канонически сопряженных координат и импульсов возмущенного движения; для решения задачи об устойчивости при а — о*, /? = /?* нужно учитывать члены не ниже восьмой степени.
В областях (4.19) устойчивости в первом приближении движения (4.15) вязкоупругого тела имеет место критический случай теории устойчивости, отвечающий двум парам чисто мнимых корней. При исследовании нелинейной задачи используем критерий Каменкова [54, 100].
Предполагая, что ab / 2 (кривая ab 2 изображена в области II рис. 4.4 пунктирной линией), сделаем предварительно в системе (4.18) замену переменных xi, %2, , «2 —> у\, t/2, , ^2 по формулам
Z1 t Z2
Х1 = —7^ +
V <>1 V
x'l = v^Tj/1 + у/^Уъ,
ki к2 х2 =-----7?=У1----7^У2,
V <h	N
«2 ~	+ k2\/S^Z2,
где
'	<5,(ст4 — 2) (об+3.-4)-4? 1	’ л
Новые переменные удовлетворяют следующей системе уравнений:
{ab — 1)(д1 — о2)
..Л> + о5,
Здесь — формы (г = 1,2), записанные в переменных yj, Zj (j = 1,2).
Теперь надо при помощи близкой к тождественной нелинейной по у^ У2, zi, Z2 аналитической замены переменных yj,Zj —> £j, tjj получить нормальную форму[27]системы(4.21)сточностью до членов третьей степени включительно, а затем перейти к полярным координатам pj, 0j по формулам j = pj cos 0j, T]j = pj sin Qj; при отсутствии резонансов третьего и
190
ГЛАВА 4
четвертого порядка (Ji / 2<52, 6 / 3J2) условия устойчивости Каменкова выражаются через коэффициенты правых частей уравнений для pi, р2.
В (4.21) отсутствуют члены второй степени, поэтому наличие резонанса третьего порядка не влияет на структуру упомянутой нормальной формы. Резонанс же четвертого порядка важен в нашей задаче. Кривые, на которых в областях (4.19) выполняется резонансное соотношение Ji = 3<У2, показаны на рис. 4.4 сплошными линиями. Устойчивость движения (4.15) для значений параметров а, 6, принадлежащих этим кривым, не рассматриваем.
Дифференциальные уравнения для pi, р2 можно записать в виде
6 = 6(ai 16 + а12б) + Об, 6 = 6(а216 + «226) 4- Об, (4.22)
где 6 = Pi, 6 = Pi, а Об — совокупность членов не ниже шестой степени относительно pi, р2. Выражения коэффициентов из (4.22)через параметры, входящие в уравнения возмущенного движения (4.18), несколько громоздки и здесь не приводятся, их можно получить из формул работ [69,90]. Отметим, что коэффициенты aij зависят только от коэффициентов диссипативных членов в уравнениях (4.18) (они пропорциональны Х£2), гамильтонова же составляющая правых частей уравнений (4.18) на коэффициенты не влияет.
Согласно критерию Каменкова, при одновременном выполнении трех условий
1)	«11 < О,
2)	а22 < 0,	(4.23)
3)	012 < 0, о21 < О,
или ai2a2i < 0, или ai2 > О, а21 > 0 и Д = аца22 — «i2a2i > О имеет место асимптотическая устойчивость. Если же
оц > 0, или а22 > 0, или ai2>0,a2i>0 и Д < 0,	(4.24)
то невозмущенное движение неустойчиво.
Проверка условий (4.23), (4.24) проводилась на ЭВМ. Установлено [90], что в области I имеет место асимптотическая устойчивость всюду (кроме, быть может, кривых ab = 2, <5i = 3J2), а в области II — неустойчивость (всюду, кроме, быть может, кривой 6 = 3<?2).
В [90] содержится строгое математическое обоснование корректности примененного выше квазистатического подхода при исследовании устойчивости.
Устойчивость гиперболоидальной прецессии. Рассмотрим решение (4.16). Положим *0 = -0* +	0 = тг/2 + я2. Пренебрегая вели-
чинами, порядок малости которых не ниже г4, находим линеаризованные
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
191
уравнения возмущенного движения:
х" — cos ^*(1 + 2f2«sin2 ^*)^2 + sin2 ^*(1 “ 2e2«cos2
— 12хв2кшоЬ(а — 1) sin2 *0* cos ^*#2 = 0,	(4.25)
xf2 + cos faxi + [3(a - 1) + Зе2яа cos2 - 6е2я(а - 1) sin2 ^*]я2+ 4-12x£2«o>o&(a — 1) sin2 il>*xf2 = 0.
Характеристическое уравнение этой системы имеет вид
Л4 + ai А3 + а2А2 + АзЛ + а4 = 0,	(4.26)
СЦ = аз = Г2х£2яа?о6(а — 1) sin2 V>*,
а2 = (За — 2) + Зб2яа cos2 — 6б2«(а — 1) sin2 ,	(4.27)
«4 = sin2 V>*[3(a — 1) + 3e2«acos2 — 6е2я(а — 1)].
В (4.27) отброшены величины порядка е4 и выше.
Из критерия Рауса — Гурвица и теоремы Ляпунова об устойчивости по первому приближению [65] следует, что при выполнении неравенств
>0, аз > 0, аз(а1а2 — аз) — 04а2 >0,	04 > 0	(4.28)
гиперболоидальная прецессия асимптотически устойчива, если же хотя бы одно из неравенств (4.28) выполнено с противоположным знаком, то имеет место неустойчивость.
Использовав явные выражения (4.27) для коэффициентов характеристического уравнения (4.26), несложно получить (считая, что / &тг/2, к = 0,1,2,3), что при a > 1 гиперболоидальная прецессия асимптотически устойчива, а при a < 1 неустойчива, если только е — достаточно малая величина (б / 0).
Если тело абсолютно твердое, то при a > 1 имеет место устойчивость, а при a < 1 неустойчивость [21]. Таким образом, внутренняя вязкость и упругость тела условий неустойчивости не изменили, но превратили обычную устойчивость по Ляпунову в асимптотическую устойчивость.
Устойчивость конической прецессии. Теперь рассмотрим решение (4.17). Положив^ = #1, 0 = 0* +Х2 и произведя линеаризацию уравнений возмущенного движения, придем к следующей системе уравнений:
х" — {(За — 2) — 3б2«[а(3 — 4sin2 0Ф) + 2(а — 2) cos2 0*]}я2—
—{3(а — 1) — 3б2«[а(3 — 4sin2 0Ф) + 2(а — 1) cos2 0*]}#i — -12x£2«a>obcos2 0Ф{[(а - 1) - (а - 2)(3а - 2) sin2 0*]a?i + +(а - 2)(3а - 4) cos2 0*^2} = 0, (4.29)
192
ГЛАВА 4
я" -I- sin2 0*{(3а - 2) £2«[(8 - 9а) + 4(3а — 2) sin2 —
— cos2 0*{(3а — 4) + £2/c[32sin20* — 3а(3 — 4sin2 0*)]}#2—
—48х£2к^о^sin2 0* cos2 0* [(а — 2)х'2 4- (а — l)#i] = 0.
Характеристическое уравнение этой системы имеет вид (4.26), где теперь
ai = 12xe2K^obcos2 0*[3(а - 2) sin2 0* — (а - 1)] 4- О(б4),
02 = 7 — 6а — 9а(1 — а) sin2 0* 4- О(б2),
а&=12х82KWQb(a— 1) cos2 0*[(3а—4)—3(а4-4) sin2 0*]4-О(у£4), а4 = 3(а — 1)(3а — 4) cos2 0* 4- О(б2).
Считая, что 0*	0, тг/2, 7г, и пользуясь выражениями (4.30), получаем, что
при достаточно малых е условия Рауса — Гурвица (4.28) эквивалентны следующей системе неравенств:
3(а — 2)2 sin2 0* — (а — 1) > О,	(4.31)
(а — 1)[(3а — 4) — 3(а 4- 4) sin2 0*] > О,
(а — 1)(3а — 4) > О,
(а — 1) ^3(5 sin 0Ф - 1)а2 — 6(7sin2 0* — 1)а 4-4(6 sin2 0* — l)j < 0.
Можно проверить, что эта система неравенств удовлетворяется только при одновременном выполнении двух условий: 1) а < 1, 2) параметры а, 0* не принадлежат кривой /(а,0*) = 0, задаваемой равенством
sin2 0*
За2 — 6а 4- 4 3(а —2)(5а —4)
(4.32)
Последняя кривая показана на рис. 4.5 сплошной линией. На этом рисунке 0q определяется равенством sin20o = 1/6; в точке 0* = 7г/2, а = (9 — л/21)/6 ~ 0,7 кривая имеет вертикальную касательную.
Таким образом, при а > 1 коническая прецессия неустойчива, а при а < 1 и /(а, 0#) ф 0 асимптотически устойчива.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
193
Отметим, что в случае спутника — твердого тела при а < 1 коническая прецессия устойчива, но не асимптотически; при а > 4/3 существует область устойчивости, но она обеспечена гироскопическими силами [21]; наличие внутренней вязкости в материале спутника разрушило эту устойчивость.
4.5. ДИНАМИКА НЕОДНОРОДНОГО ВЯЗКОУПРУГОГО КОЛЬЦА
Рассмотрим однородное нерастяжимое круговое кольцо постоянного сечения, линейные размеры которого малы по сравнению с радиусом г центральной линии кольца. Пусть ст — плотность, F — площадь поперечного сечения, т0 — масса кольца, a EI — его изгибная жесткость. Предположим, что однородность кольца нарушена тем, что в каком-либо его месте жестко прикреплена точечная масса цт$ (0 < ц 1) (рис. 4.6). Предполагается, что кольцо обладает внутренним вязким трением, задаваемым, как в § 4.1, при помощи функции Рэлея.
Эволюция быстровращающегося однородного кругового кольца на круговой орбите исследована в [87]. Относительные равновесия однородного кольца в орбитальной системе координат в квазистатическом режиме его упругих колебаний изучены в [58, 59]. Задача о существовании и устойчивости положений равновесия кольца с точечной массой в орбитальной системе координат на круговой орбите исследовалась в [84, 85]. Динамика кольца с точечной массой на круговой и эллиптической орбитах рассмотрена в [17, 54, 56, 57]. Устойчивость орбитального
7 — 2185
194
ГЛАВА 4
кольца, образованного упругой нерастяжимой нитью изучалась в [61, 126]. Устойчивость движения жесткого кольца с одной неподвижной точкой в гравитационном поле исследована в [146]. Ряд задач о движении вращающегося упругого кольца рассмотрен в динамике волнового твердотельного гироскопа [47].
В данном параграфе, следуя работам [55, 56], изучается динамика кольца с малой точечной массой на круговой и эллиптической орбитах. Рассматриваются только плоские движения, т. е. предполагается, что во все время движения плоскость кольца лежит в плоскости орбиты его центра масс. Исследуются квазистатические режимы движения. При этом используется методика, изложенная в § 4.1 и 4.2.
Нормальные координаты, частоты и собственные формы колебаний. Свободные упругие колебания однородного нерастяжимого кругового кольца подробно изучены в [64, 93, 95]. Мы будем интересоваться только изгибными колебаниями в плоскости кольца. При помощи изложенного в [93] способа приближенного анализа колебаний упругих тел найдем нормальные координаты, частоты и собственные формы изгибных колебаний при малых значениях параметра р.
Пусть угол а (рис. 4.6) определяет положение точки кольца, awn v — ее радиальное и трансверсальное упругие перемещения. Потенциальная и кинетическая энергии, обусловленные упругими смещениями точек кольца, вычисляются по формулам [95]
n=£/(l^ + W) da' (™2 + ”2) dm, (5.1) в которых интегрирование проводится по недеформированному кольцу.
Учитывая нерастяжимость кольца и исключая его жесткие поступательное и вращательное перемещения, представим упругие перемещения w и v в виде
ОО	ОО 1
w = У^(а; cos + h sin га), v =	-(—сц sin ia 4- 6,- cos га), (5.2)
i=2	i-2 г
где а, и bi — величины, не зависящие от а. Подставив w и v из (5.2) в (5.1), получим
П
Т ~ ~2~ ХЛ 1 + ;2 да + ЬЧ + 2цт° i=2 '	'
(5.3)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
195
После замены переменных
2г2	_ /	2г2
т0(г2 + 1) ”	* у т0(г2 + 1)^’
выражения (5.3) и (5.4) запишутся в виде
Здесь
2
’ <rFr4(i2 + 1)
(«• = 2,3,...),
(5.8)
Q, — частоты свободных упругих колебаний однородного кольца.
При /1 = 0 величины тц — нормальные координаты, а соответствующие собственные формы колебаний легко определяются из (5.2) и (5.5). В силу симметрии однородного кольца двум его формам колебаний (отвечающим нормальным координатам & и т/,) соответствует одна и та же частота Qt, определяемая равенством (5.8).
Чтобы найти частоты колебаний неоднородного кольца (ц / 0), воспользуемся уравнениями Лагранжа второго рода с функцией Лагранжа L = Т - П:
/ оо .	\
( <59>
% + tyli + 2д ( £ /Л Л< ) /J , . = 0 (j = 2,3, • • .)•
Vг + 1 / W + 1
Анализ характеристического уравнения системы (5.9) показывает, что при /1/0 происходит «расщепление» частоты Qj: вместо двух равных частот Qj (отвечающих и ту) появляются две различные частоты cuj и w" (j = 2,3,...), причем
(5.10)
и;г = п?(1-2^?1-г) + о(Л
7*
196
ГЛАВА 4
Если сделать замену переменных по формулам
е Л i2
кП2
'А' nj .. 
3	+О(д2),
(5.Н) 1 +О(М2),
где штрих у знака суммы означает, что при суммировании к / j, то потенциальная и кинетическая энергии, обусловленные упругими смещениями точек кольца, примут вид
1 ОО	1 оо
n = 2^(wiV+w"V))	<5-12)
j=2	j=2
Величины g'-, q" (j = 2,3,...) — нормальные координаты для изгиб-ных колебаний неоднородного кольца; о;'-, о;'-' — соответствующие им частоты колебаний.
Чтобы найти собственные формы колебаний, спроектируем вектор и упругого смещения (рис. 4.6) на оси системы координат Сху, жестко связанной с недеформированным кольцом и имеющей начало в его геометрическом центре. Учтя затем (5.2) и замены переменных (5.5), (5.11), найдем формы колебаний неоднородного кольца в системе Сху. Чтобы получить их в средней системе координат	надо в компонен-
ты найденных форм внести поправки порядка р, учитывая, что точка О должна совпадать с центром масс и должно выполняться условие (1.2). Проведя выкладки, получим, что вектор и упругого смещения точек кольца может быть записан в средней системе координат в виде
оо
u = Е (?пи'(П) + 9пи"(п)) •	(5.13)
п = 2
Компоненты собственных форм колебаний U'(n) и U"(n) с точностью до членов порядка ц включительно будут такими

п2 \	.	.
—-г- п - । 1 — и——- (n cos па cos ct+sin па sin q) + m0(n2 + l) L\	п2+1/
&
+2^nQ2); —-———x——(к cos к a cos a-\-sin к a sin а)-/лп , k=2
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
197
1-^
П2 \
п2+1)
(n cos па sin ct—sin па cos о)+

(к cos ka sin а—sin ка cos а)
[7з(п)=0.
(5.14)
И, соответственно,
и"{п}=
(n sin па cos а—cos па sin а)+
J +2pfi"S (F+1)(Q2-Q2)
(k sin ka cos a—cos ka sin a)+p sin a
тт"(п}— /
2 V rn0(n2+l)
( 1-^- • )
\ n2+iy
(n sin na sin ct+cos na cos a)+
+2/Ш"£ (Р+1ж-ад
(A: sin Ara sin ct+cos ka cos a)— ji(l+cos a)
l/',(n)=0.
(5.15)
Штрих у знака суммы в (5.14) и (5.15) означает, что при суммировании к / п.
Уравнение плоских квазистатических движений. На рис. 4.7
показана средняя система координат в случае недеформированного коль-
ца. Компоненты радиуса-вектора р произвольного элемента dm кольца с погрешностью порядка р2 будут такими:
Xi — r(cos а — р), /	\	(5.16)
Х2 = г sin а, хз = 0.
(Следует отметить, что в случае деформированного кольца точечная масса рт0 не обязательно лежит на оси Oxit ее положение в средней си-
рис. 4 7	стеме координат определяется выра-
жениями (1.1), (5.13)—(5.16), в кото-
рых а = 0, а д^(/), g"(Z) — функции времени, получаемые из решения уравнений (1.7), (1.10)-(1.12), (1.14), (1.16).)
198
ГЛАВА 4
В случае плоских изгибных колебаний кольца величины из (1.4), содержащие в нижнем индексе цифру 3, равны нулю. Для остальных величин Н^п\ Н$п\ определяемых из (1.4), (5.14)-(5.16), получаем, с точностью до членов порядка д включительно, такие выражения:
н'^ =	= О,
*:'1 = тУШ1 + й") •
L у 1U у ±О у
„,(2)_ Зг /	4 \
*22 "“TV W’k
Я"(2) _ „//(2) _ 0	„//(2) _ „//(2) _ ЗГ /й^ А 7 \
"11 -"22 -U, "12 -"21 -2УЮТ+15Р/’
гг'(п) _	n(5Q2 — 2П„) tr'W _ fj'(n) _ л /к i7i
я“ -TVn’ + i ’(n2-n2) ’ Я12 -Я21 -°’ (517)
„/(п) _ Зрг / 2т0 пП2
22 ~	5 V n2 + l(Q2-Q2)’
rri>(n)_ rr"(n)_Pr I 2шд (5Q2	2Q2)
12 - 21 - ToV n2 + 1 (Q|-Q2)
(n = 2,3,...).
В случае плоских движений кольца ось Ох3 средней системы координат направлена по бинормали к плоскости орбиты и выполняются соотношения (3.1), в которых — угол между осями Ох2 и OZ средней и орбитальной систем координат (рис. 4.8). На рис. 4.8 буквой тг обозначен перицентр орбиты, 6 — угол между осью Ох2 и линией апсид.
Из (3.1) и (5.17) находим величины (2.8) в случае плоских движений кольца:
Q2 = - у	cos 2<р + ЭД >
У IV
^2 = Sil12*’ + £л у XU
б?; = О(д), С = О(д) (п = з,4,...).
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
199
Здесь для краткости записи через ш2 обозначена правая часть равенства (1.6).
В дальнейшем считаем, что величины ц и имеют одинаковый порядок малости и для определенности (с учетом условий (2.6)) положим, ЧТО 8 ~ /I3/В * 10, X ~ /I2/5.
Из (5.18) и (2.7) находим, что в случае плоского квазистатического режима движения кольца значения нормальных координат q'n, q„ определяются следующими выражениями:
, __ 9г /т0 ш2
—82 cos 2<р -|-	( — cos 2(р — sin 2<р • ф
+ О(е4),
„ _ 9г /то
92 “ 2 V Ю Q.I
е2 sin 2>р — 4уе26 ( — sin 2<р + cos 2у> • ф \^*
+ О(е4),
9; = О(ре2), 9" = О(ре2) (п = 3,4,...).	(5.19)
Отсюда и из уравнений (1.10)—(1.12) следует, что в случае плоского квазистатического движения наиболее существенно влияние основных форм изгибных колебаний, отвечающих наименьшей частоте Пг свободных колебаний однородного кольца. Величина возбуждения остальных (п > 2) форм колебаний за счет движения кольца как целого на порядок ц меньше величины возбуждений, отвечающих основным формам. В свою очередь, главное влияние на движение кольца как целого оказывают опять же его упругие колебания по основным формам.
Подставив q^ и q„ из (5.19) и о;,-, 7,- из (3.1) в уравнения (1.10)—(1.12) и учтя, что
Л = |т0г2, В = ^т0г2 + ^т0г2 + О(^2), С = т0г2 /im0r2 + О(^2),
получим следующее уравнение плоских движений кольца:
3 и • п	о •
9? — sm 2<р = — х^ к —з Ф — у
2	и0
(	816а>п \
V “ "5ОГ) ’
(5.20)
В (5.20) отброшены члены порядка е4 и выше.
Уравнение (5.20) должно рассматриваться совместно с уравнением (1.7) (и при учете равенства ш2 = w^(l — е2)-3(1 4- ecosp)3).
Если решение 9? = (p(t) уравнения (5.20) получено, то зависимость нормальных координат q'k, qk от t найдется подстановкой 9?(/) в равенства (5.19). Из (5.13) определяется затем форма деформированного кольца.
200
ГЛАВА 4
Движение кольца на круговой орбите, В случае круговой орбиты (е = 0) уравнение (5.20) принимает вид
- ^/*sin2^ += О (r = wo<)-	(5.21)
агЛ 2	ат
На фазовой плоскости <р, ф уравнение (5.21) имеет особые точки Рк = (Аг7г/2,0) (к = 0,1,2,...). Они отвечают положениям относительного равновесия деформированного кольца в орбитальной системе координат. Отличающимся одно от другого положениям кольца отвечают только четыре особые точки, например, Pq, Pi, Р^ Рз- В положениях равновесия оси Ох\ и 0x2 средней системы координат направлены вдоль осей орбитальной системы координат. Деформация кольца может быть найдена из выражений (5.19) и (5.13). При этом
?2 = -е2уУ^'Щ'СО82*’* + °^’	= °<е4)
<1'„=О(це2), 9" = О(де2) (п = 3,4,...).
Равновесные конфигурации кольца схематично показаны на рис. 4.9.
Рис. 4.9
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
201
Из характеристического уравнения линеаризованного в окрестности особых точек Рк уравнения (5.21)
Л2 + Х£2«А — 3/1 cos 2<рк =0 (Лг = 0,1,2,3)
следует, что Ро и Р2 — особые точки типа седла, a Pi и Рз —устойчивые фокусы. Равновесные положения кольца, соответствующие точкам Pq, Р2 и Pi, Рз, неустойчивы и асимптотически устойчивы соответственно.
Уравнение (5.21) представляет собой хорошо изученное [4,16] уравнение движения математического маятника при наличии диссипативного момента. Фазовая плоскость уравнения (5.21) 7г — периодична по у?, она показана на рис. 4.10. Почти все фазовые траектории стремятся к асимптотически устойчивой особой точке. Исключительными являются только две траектории, которые с возрастанием времени стремятся к седловой точке.
Это означает, что на круговой орбите движение кольца при почти всех начальных условиях стремится к асимптотически устойчивым положениям
равновесия, соответствующим конфигурациям кольца Pi и Р3 на рис. 4.9. В этих равновесных положениях точечная масса /imo лежит на прямой,
проходящей через центр масс кольца и притягивающий центр, а само кольцо деформировано и вытянуто вдоль этой линии. В отмеченных вы-
ше исключительных случаях предельными положениями кольца могут быть его неустойчивые положения Ро и Р2 (рис. 4.9).
Эксцентриситетные колебания. На эллиптической орбите равновесные положения кольца в орбитальной системе координат невозможны. При малых значениях эксцентриситета е устойчивые на круговой орбите равновесия переходят в периодические колебания малой амплитуды. Полагая, что е ~ е2, найдем эксцентриситетные колебания упругого кольца и исследуем их устойчивость.
Для этого, использовав соотношение (1.7), перейдем в уравнении (5.20) к новой независимой переменной — истинной аномали у. Уравнение (5.20) тогда запишется в виде
(itp	dtp 0 dip 3
-5—5- — 2esini/-—h ye к-----usuPbp = 2esinp. (5.22)
dyz	dy dy 2
202
ГЛАВА 4
Здесь, как всюду дальше в этом разделе, отброшены члены порядка б4 и выше.
Пусть при е = 0 кольцо находится в положении равновесия Pi (рис. 4.9). Решение 9?*(р) уравнения (5.22), описывающее эксцентри-ситетные колебания, рождающиеся при е / 0 из этого положения равновесия, можно найти в виде ряда по степеням е. Получаем
ip* =	— 2esinp.	(5.23)
Для исследования устойчивости колебаний (5.23) введем возмущение х, положив = 9?* х. Линеаризованное уравнение возмущенного движения будет таким
d?x л . dx dx	„
—г - 2е sin р—	хе2к— + Зрх	= 0.	(5.24)
dv2	dv	dv
Сделаем замену переменных по формулам
dx	dx
zi — х -I- 2esin p —, Z2 = (1 4-2ecosi/) —. dv	dv
В переменных zi, Z2 уравнение (5.24) преобразуется к следующей системе с постоянными коэффициентами:
dz\	dz2	п •>
-г- = Z2, -г- = -Зм^1 - хе kz2.	(5.25)
dv	dv
Корни характеристического уравнения системы (5.25)
А2 4-	4- 3/z == 0
комплексно сопряжены с отрицательной вещественной частью. Следовательно, эксцентриситетные колебания (5.23) асимптотически устойчивы.
Нерезонансные вращения. Если кольцо является однородным (д = 0) и твердым (б = 0) телом, то общее решение уравнения (5.20) запишется в виде
р — — v 4- Qr 4- 0* (т = и>0/),	(5.26)
где а и Q — произвольные постоянные.
Решение (5.26) описывает равномерное вращение кольца в абсолютной системе координат: угол 6 между осью Ох2 и линией апсид орбиты
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
203
(рис. 4.8) возрастает (при П > 0) или убывает (при Q < 0) с постоянной скоростью
Для исследования движения кольца при малых, но отличных от нуля значениях параметров р и е, введем в уравнение (5.20) вместо у новую переменную а, определяемую равенством (5.26), в котором величину Q считаем постоянной. Из (5.20), (5.26) с учетом равенств (1.6), (1.7) находим, что новая переменная удовлетворяет уравнению
d2cr
dr2
3 (1 + ecosz/)3 2М (1-е2)3
sin 2(Qr — р + 0*)+
n (1 + ecosp)6 dv d<r\ л
+x£ «bl--------2Гб2- Q - т + Т = 0 5 27
(1 —	\ dr dr J
Для построения приближенного решения этого уравнения воспользуемся методом усреднения [24, 48].
Пусть 2Q — не целое число и отличается от целого на величину порядка единицы. Тогда усредненное уравнение имеет вид [55]
4- ye2«/i(e)— = -хе2к [QZi (е) - /2(е)],	(5.28)
ат^	ат
где
2ж
7(14-е cos р)6	J_ 7 (14-е cos i/)4	l+3e2+|e4
J (l-e2)6 2тг/ (l-e2)»/2 dV~ (l-e2)9/2 ’ (5'29) 0	0
_	+	l + ^2 + fe44-^e6
rj (l-e2)6
0
(5.30)
(1-е2)6
Уравнение (5.28) линейно и легко исследуется. Для любых начальных условий его решения с возрастанием т асимптотически стремятся к решению
ф(г) = (^-П)г+Ф(о)-
Учитывая замену переменных (5.26), получаем отсюда, что в нерезонансном случае, когда 2Q — не целое число, все движения кольца как целого с возрастанием времени имеют тенденцию приближаться к равномерному в абсолютной системе координат вращению вокруг нормали к плоскости орбиты центра масс. Предельная угловая скорость — функция эксцентриситета и определяется равенством
. _	/2(е) _	1 4-^е2 4-f е4 4-^е6
Шз	~"°(1-е2)3/2(1 + Зе24-|е4)‘
(5.31)
204
ГЛАВА 4
В предельном режиме движения имеем:
^(т) = -1/(т) +	+ у>(0),	(5.32)
а деформации в каждой точке кольца будут функциями времени, определяемыми из (5.13), (5.19) и (5.32).
Отметим, что предельное значение угловой скорости (5.31) ранее было известно в теории вращательного движения планет [21].
Резонансные вращения. Пусть 2Q = т — целое число. В этом случае усредненное уравнение будет таким:
^-^-^p$m(e)sin2<r+xe2K/i(e)^ = -\е2к [^Л(е) - /2(e)] > (5.33) аг* 2	ат	L 2	J
где
2л-
1 f (1 + ecosz/)3
Ме) = 7Г- / —7\------cos(mr- 2i/)dr.	(5.34)
2тг J (1-е2)°
о
При m = 0 имеем Ф0(е) = 0 и уравнение (5.33) переходит в уравнение (5.28). В случае твердого тела (е = 0) уравнение (5.33) получено и исследовано в [108].
Если величины е и р отличны от нуля, то уравнение (5.33) является уравнением движения математического маятника при наличии диссипативного и постоянного моментов. Это уравнение хорошо изучено [4,16]. Пусть выполняется неравенство
I та	I 3
Х£2к |у Л(е) ~ /г(е)| > -ц |Фт(е)|,	(5.35)
т. е. постоянная составляющая момента, возникающая из-за нежесткости кольца, превосходит максимальное значение гравитационного момента, действующего на жесткое кольцо. Тогда все решения уравнения (5.33) с возрастанием времени стремятся к решению, в котором da/dr является я — периодической функцией а.
Движение кольца в этом случае асимптотически стремится к вращению с угловой скоростью, которая мало отличается от постоянной и не зависит от начальных условий. Приближенное значение предельной угловой скорости совпадает [55, 56] с величиной (5.31).
Если неравенство (5.35) выполняется с обратным знаком, то картина движения будет иной. В этом случае уравнение (5.33) имеет особые точки и в зависимости от коэффициентов уравнения возможны два принципиально различных случая.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
205
Случай а). Почти все траектории уравнения (5.33) стремятся к асимптотически устойчивой особой точке (аналогично рис. 4.10). Происходит «захват» почти всех движений кольца в резонансное вращение с угловой скоростью mwo/2 в абсолютной системе координат.
Случай б). Помимо траекторий, стремящихся к асимптотически устойчивой особой точке, есть множество траекторий, стремящихся с возрастанием времени к траектории, на которой da/dr - я — периодическая функция а (рис. 4.11). Поэтому не все движения кольца стремятся к резонансному вращению: существуют движения, которые не «захватываются» в резонанс, а стремятся к равномерному вращению в абсолютной системе координат с угловой скоростью о>з, определяемой равенством (5.31).
Отметим, что в обоих случаях су
ществует ровно по два движения кольца, которые с ростом времени стремятся к неустойчивому резонансному вращению; этим движениям отвечает седловая особая точка уравнения (5.33).
Вращения в случае слабоэллиптической орбиты. Остановимся подробнее на анализе движения кольца на орбите малого эксцентриситета. В [37, 108] получены первые члены разложений функций (5.34) в ряды по степеням эксцентриситета. Найдено, что при т / О
Фт(е)~е'т-2'.
(5.36)
В частности, в случае т = 2, когда угловая скорость жесткого кольца близка к угловой скорости движения его центра масс по орбите, имеем
Ф2(е) = 1-|е2 + О(е4).	(5.37)
Для величин (5.29) и (5.30) при малых е справедливы оценки
h(e) = 1 + ^е2 + О(е4), /2(е) = 1+^е2 + О(е4).	(5.38)
Из (5.36)-(5.38) следует, что если т / 2, то при достаточно малых е выполняется неравенство (5.35). И, следовательно, в этом случае почти
206
ГЛАВА 4
все вращения кольца с ростом времени стремятся к вращению с угловой скоростью, мало отличающейся от значения (5.31).
Пусть теперь т = 2. Сделав в уравнении (5.33) замену переменных
	^=7 + ^, »/= \/ЗрФ2(е)т,
получим, что новая переменная х удовлетворяет уравнению
	d х	,	dx	, Л	-я + sin# + а— = sin 0о,	(5.39) dr]2	dr/
где	а =	= аА (1 + 0(е!)) 5 ЗдФ2(е)	М
Фазовая плоскость х, dx/dr] уравнения (5.39) 2тг — периодична по х. В интервале 0 < х < 2тг существуют две особые точки Qi и Q2, для которых Xi = 0$ и Х2 = л — 0о соответственно. Первая из этих точек — устойчивый фокус, а вторая — седло. Точка Qi отвечает движению кольца, когда при его прохождении через перицентр орбиты угол между осью Oxi средней системы координат и линией апсид орбиты равен 0о/2, для точки Q2 этот угол равен тг/2 — 0о/2.
Выясним, когда в эволюции движения кольца реализуются случаи а) и б), описанные выше. Известно [16], что для уравнения (5.39) существует критическое значение а* параметра а, такое, что при а > а* имеет место случай а), а при 0 < а < а* — случай б). В [16] приведен ряд оценок величины о* сверху и снизу. Мы воспользуемся оценками
2 sin 0q
\/тг(2 sin #о + тг cos 0Q )
< а* < 2 sin . 2
(5.41)
полученными в статье [125].
Для интересующих нас малых значений угла 0$ оценки (5.41) запишутся в виде
2
“00 < <*♦ <00-7Г
(5.42)
Следовательно, при а > 0О реализуется случай а), а при 0 < а < 20о/тг — случай б). Подставив в последние неравенства значения а и 0О из (5.40), найдем, что при выполнении неравенства
е < (Ж - 0,38^, у 1о
(5.43)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
207
все движения кольца (за исключением двух движений, стремящихся к неустойчивому резонансному движению, отвечающему особой точке Q2 уравнения (5.39)) асимптотически стремятся к устойчивому резонансному вращению с постоянной в абсолютной системе координат угловой скоростью о>о (траектории уравнения (5.39) стремятся к особой точке Qi). Вероятность «захвата» движения в резонансный режим в этом случае равна единице.
Если же выполняется неравенство
с>У^=о'48'^’	(5-44>
то существует множество движений кольца, которое с ростом времени стремится к вращению с угловой скоростью (5.31). Вероятность «захвата» движения в резонансный режим в этом случае меньше единицы. Так как при у = 0 уравнение (5.33) переходит в уравнение (5.28), то приходим к выводу, что эта вероятность стремится к нулю при /л —> 0.
Интересно, что неравенства (5.43) и (5.44), являющиеся достаточными условиями осуществимости качественно различных эволюций движения кольца, не содержат параметров, характеризующих упругие и диссипативные свойства материала кольца. Условия (5.43) и (5.44) являются ограничениями на величины эксцентриситета орбиты и параметра характеризующего степень неоднородности кольца.
4.6. ДВИЖЕНИЕ ОДНОРОДНОГО КОЛЬЦА НА КРУГОВОЙ ОРБИТЕ
Рассмотрим движение относительно центра масс тонкого однородного нерастяжимого вязкоупругого кольца в центральном ньютоновском гравитационном поле на круговой орбите. Пусть Ох^хъХъ — система координат, образованная главными центральными осями инерции не-деформированного кольца, ось Ох% перпендикулярна плоскости кольца. Будем рассматривать такие движения кольца относительно центра масс, когда его упругие колебания являются изгибными колебаниями в плоскости кольца.
Дифференциальные уравнения квазистатических движений. Нормальные координаты, частоты и собственные формы колебаний однородного кольца определяются из соответствующих соотношений предыдущего параграфа, где рассматривалось кольцо с малой массой рт$. В соответствующих соотношениях нужно просто положить величину р равной нулю. Можно показать [58], что для однородного кольца система координат Ох^хъхз является средней системой координат (см. § 4.1). Ориентацию трехгранника Ох^Х2Хз относительно орбитальной системы координат OXYZ зададим при помощи углов Эйлера.
208
ГЛАВА 4
В [58] получена система уравнений движения кольца относительно центра масс, включающая уравнения движения кольца как целого (движение трехгранника Ох 1X2X3) и уравнения упругих колебаний кольца в системе координат Ох 1X2X3.
При выполнении физических предположений § 4.2 в [58] получена следующая система дифференциальных уравнений, описывающая движение кольца как целого относительно центра масс в квазистатическом режиме его упругих колебаний:
0" sin 0 4- ф'О' cos 0 — ф1 sin 0 cos 0 — О1 cos 0 sin 0 — (6 4- <р')с =
=	4- ^>cA2)sin20 4- ^[(З/zBi — 2к,В2)а — ЗцВ'з 4-	(6.1)
О" 4- Ф' cos 0 — 3 sin 0 cos 0 4- (b 4- <p')d =
2	1
— sin 0cos 0(цАз 4- -kAi) 4- -[(З^В3 — 2к,В4)а -h 3/гВ£ — 2кВ'2], (6.2) •5	9
<р* — -а! - - sin4 0 — 9 sin3 0 cos 0d — 3 sin2 0 a(c2 — d2)4-
4-6cdsin0 cos 0 0' 4- 3 sin 0 cos 0 d(c2 4- d2) - b(c2 4- </2)2^ (6.3) (д = 27бМ/(10А2), к = 81x^2/?^/(5A2)).
Здесь для удобства через /3 обозначена величина b из (1.13).
В уравнениях (6.1)—(6.3) отброшены величины порядка е4 и выше, штрихом обозначено дифференцирование по переменной т = wot и приняты следующие обозначения:
а — ф' cos 0 — cos 0 sin 0, b = tp' + а.
,	, .	(6.4)
с = 0 4- sin 0, d — 0 sin 0 4- cos 0 cos 0,
Ai--cd, A2 = 3sin2 0<р’ — b(c2 — d2) — 3 sin 0cos 0d,
A3 = 3 sin2 0 4- (c2 — d2), A4 = 2bcd — 3 sin 0 cos 0(0' 4- c),
Bi = —c(3sin2 0 4- c2 4- d2), B2 —	4- A4C,
B3 = d(c2 4- d2 — 3sin2 0),	— —/l2c 4-/Ц(/.
В (6.1)—(6.3) и всюду дальше в этом параграфе введено обозначение Q2 = £-1А2 для наименьшей частоты свободных плоских изгибных колебаний кольца. Отметим (ср. с § 4.5), что в квазистатических режимах движения кольца существенны лишь его плоские изгибные колебания, отвечающие наименьшей частоте Q2* Отметим также [58], что в рассматриваемом приближении по s на квазистатические режимы движения кольца
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
209
как целого не оказывают влияния его изгибные колебания, включающие как перемещения под прямым углом к плоскости кольца, так и кручение.
Движения кольца, соответствующие частным решениям приближенных уравнений. Система уравнений (6.1)—(6.3) допускает следующие частные решения:
ф = 7г,	0 = 7г/2, <р — <р'ое к,	(6.7)
ф = 7Г,	0 = 7г/2, р — О,
(6.8)
ф — тг/2, 0 — 7г/2,	ip1 — 0.
(6.9 ,)
В случае (6.7) кольцо расположено в плоскости орбиты и вращается вокруг нормали к плоскости орбиты с уменьшающейся по величине угловой скоростью.
Решению (6.8) соответствует относительное равновесие кольца в орбитальной системе координат, когда его плоскость лежит в плоскости орбиты.
В случае (6.9) кольцо также находится в положении равновесия в орбитальной системе координат, причем плоскость кольца перпендикулярна вектору скорости центра масс (кольцо расположено в плоскости, проходящей через нормаль к плоскости орбиты и радиус-вектор центра масс кольца относительно притягивающего центра).
Ниже исследуется устойчивость движений кольца, соответствующих решениям (6.7)-(6.9).
Об устойчивости вращения с уменьшающейся угловой скоростью. Для движения (6.7) ограничимся исследованием устойчивости в первом приближении. Положим 0 — тг/2 + а;, ф = л+у, <р’ = <р'ое~КТ +z. Линеаризованная система уравнений возмущенного движения будет такой:
4
х" + 4x + 2<p'Qe~KT(l -p)(yf + *) -	(4ip'Qe~KT + l)(z/- a/) = 0,
У
4
у" + У + 2<p'oe~KT(l + р)(У - *') - 5K^e-KT(Voe-KT + 1)(ж + у') = 0, У
z' = — KZ.
(6.10)
В случае абсолютно твердого кольца (е = 0) эта система уравнений принимает вид
х" + 4х + 2<р'0(у' 4- х) = О, у" 4- у+ 2p'0(j/- ж') = 0, z' =0.
210
ГЛАВА 4
Анализ корней характеристического уравнения этой системы
А [А4 + (4^ 2 + 4р'о + 5)А2 + 2(2^ + 1)(/0 + 2)] = О
показывает, что если р'о < —2 или р'о > -1/2, то оно имеет один нулевой и две пары чисто мнимых корней, поэтому в этих случаях движение (6.7) устойчиво (как следует из [70, 107], в этих случаях для абсолютно твердого тела движение (6.7) устойчиво не только в первом приближении, но и в строгом нелинейном смысле). Если же —2 < р'о < —1/2, то имеет место неустойчивость, так как характеристическое уравнение имеет корень с положительной вещественной частью.
Для исследования устойчивости движения (6.7) в случае вязкоупругого кольца (б / 0, х / 0) воспользуемся теоремой Ляпунова об устойчивости движения [65]. Функцию Ляпунова V берем в виде [58]
V = i (ai х2 + а2у2 + а3х'2 + а4у'2 + Ъаьх'у' + 2a6£J/ + z2),
ai = [2<р'ое~кт + 4 - 2ц(<р'ое~кт + 4)] а4,
а2 = (29?ое~'ст + 1 - 2/^'ое-'ст) а4,
2 а3 = (1 + 2р)а4, а5 = аб = -к (4^ кт + 1) а4.
Ее производная V в силу уравнений возмущенного движения (6.10) имеет вид
V' = ^(а1х2 + а2У2 + bix'2 + Ь2У'2) “ Kz2> bl = (1 + 2^)04, 62 = 04-
Функция а4(т) может быть взята произвольной, но такой, чтобы выполнялись условия а4 > т] > 0, а4 < 0 (ту = const). Если, кроме того, на величину наложить ограничения, задаваемые неравенствами ai > О, а2 > 0, а\ < 0, а'2 < 0, то функция V будет определенно-положительной, а ее производная V' в силу уравнений (6.10) знакопостоянной, противоположного с V знака, и выполняются требования теоремы Ляпунова об устойчивости.
Положим, например, а4 = к + е~т. Тогда анализ указанных неравенств приводит к следующему достаточному условию устойчивости движения (6.7) при малых значениях параметров е, х:
/11/ч
4>п > “2 +	+
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
211
Асимптотическая устойчивость относительного равновесия в плоскости орбиты. Исследуем устойчивость движения (6.8) по отношению к возмущениям, выводящим кольцо из плоскости орбиты, и к возмущениям угловой скорости вращения кольца вокруг нормали к плоскости орбиты (т. е. по отношению к возмущениям величин 0,	>
<р')- Положим 0 = 7г/2 + х, ф = 7Г + у, = г. Уравнения возмущенного движения могут быть представлены в следующем виде:
х" = —4х + ху2 + 2x2j/' + ху'2 + |х3 - 2z(x + у' - ^xj/2-
+ 2/CS-1) + О4, (6.11)
у" = -у + ^у3 + Zxyy1 + 2z(-y + х'+ |j/3 - |х2у + |х2х')+ о	О 2	2
+ о (ЗяЛ 4- 2к^г) + О4, (6.12) у
z* = — ху + эд/ + хх' + х'у' — 2z(xy - хх') - 2pz(xy — хх')—
-|k[3z(1 - 2х2) + 4х2 — у2 + 2х'у + 5xj/ — х'2] + О4. (6.13) о
Здесь О4 — совокупность членов не ниже четвертой степени относительно х, у, х', у', z, а через эд (г = 1,2) обозначены следующие полиномы третьей степени:
/1 = 6z(x + у') + 8xj/2 + 2у2у' - 22хух' - 4х'уу' + 8х3 + 18xV +
+12хз/2 + 14хх'2 + 2у'3 + 2х'2у', gi = 6z2(y - х') + 2у3 - 9у2х' - 19х22/ + 2уу'2 + 4хуу' + 15х'2з/4-
+28х2х' - lOxx'j/ - 5х'у'2 - 8х'3, /2 = 6z(x' - у) + 2у3 - вх'у2 + 2х2у + 4хуу' + 2уу'2 + 6х'2у-
-8х2х' - Юхх'у' — 2х'у'2 — 2х'3, д2 = 6z2(x + у') - llxj/2 - 2у2у' + 22хух' + 4х'уУ - 28х3 - 45х2г/-
— 15xj/2 - 8хх'2 4- х'2у' - 2у'3.
Задача об устойчивости системы (6.11)—(6.13) принадлежит к критическому случаю одного отрицательного и двух пар чисто мнимых корней. Для решения задачи воспользуемся «принципом сведения» в теории устойчивости [65]. Сформулируем этот принцип применительно к рассматриваемому критическому случаю.
212
ГЛАВА 4
Пусть дана система дифференциальных уравнений пятого порядка
= bjixi + bj2x2 + bj3x3 + bj4x4 4- Cjy + Xj (^i, x2, x3, x4,y),
X	'6i4>
— = —Xy + Y(xi, x2, x3, x4, y) (j = 1,2,3,4). at
Здесь Xj, Y — сходящиеся в достаточно малой окрестности начала координат х\ — х2 = х3 = Х4 = у = 0 ряды, начинающиеся членами не ниже второй степени относительно Xi, а?2, х3, Х4, у; A, bj/g, Cj — постоянные; А > 0, а характеристическое уравнение матрицы с элементами bjk имеет две пары чисто мнимых корней.
Наряду с системой уравнений (6.14) рассмотрим «укороченную» систему
= bjiXi + bj2x2 -I- bj3x3 + bj4x4 -I- Xj(x1,x2,x3, ам,0).	(6.15)
«Укороченная» система (6.15) получается из первых четырех уравнений системы (6.14) путем отбрасывания в их правых частых всех членов, зависящих от «некритической» переменной у.
Справедлива следующая теорема (составляющая содержание «принципа сведения» в теории устойчивости). Пусть невозмущенное движение х1 = х2 = х3 — Х4 = 0 «укороченной» системы (6.15) устойчиво, асимптотически устойчиво или неустойчиво вне зависимости от членов степени большей N. Тогда, если разложение функции Yj (х^, х2, х3,	0) начи-
нается с членов, степень которых не ниже N 4- 1, то и невозмущенное движение xi = х2 = х3 = Х4 = у = 0 для полной системы (6.14) соответственно устойчиво, асимптотически устойчиво или неустойчиво.
Чтобы применить сформулированную теорему, сделаем в системе уравнений (6.11)—(6.13) замену переменных z —> £, уничтожающую в правой части уравнения (6.13) члены второй степени, содержащие только критические переменные х, у, х1, у1. Замену переменных ищем в виде
z = £ + иих2 -|- 2^12^1/ + 2i/i3xx' 21/14X7/' -|- и22у2 + 21/232/^'4-
4-21/242/2/' + изз*'2 4- 2и34;гУ 4- и44у'2. (6.16)
После замены (6.16) уравнение (6.13) должно принять вид
— —2(,(ху — xxf) — 2ц£(ху — хх') — /с£(1 — 2х2) 4- О4.	(6.17)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
213
Можно проверить, что величины удовлетворяют некоторой системе линейных уравнений. С погрешностью порядка (хе2)2 решение этой системы имеет
вид [58]
1 и^= 4’
U12 = О,
«23 = о, «24 - 24«,
19 «!3 =
«ЭЭ = -jg,
1 U14 = -,
1 ^34 = 7^) о
5
«22 = J2’
12 т (6.18)
«44 = -^-
1
После замены переменных(6.16)уравнения (6.11 )и (6.12)станут такими
1	2
х" - —4х - 2£(х 4- у') 4- hl + -nFi 4- -kGi + О4,
3	92	(6.19)
V — ~У 4- 2£(—у 4- х1) 4- Лг 4- 0^1*2 4- ок;£'2 4- О4. о	У
где
>	1	9	5 9 /	13 о	In.	5	,2	1	/2	1/3	1 /2 /
hi —	-ху2 — -у2у	+	-z-x3	—	т?х2у	~	^ху +	-хх +	-у + -х у
1	б У 6	6	2	6	8	6	8
h2 - -^У3 +	+ |уу'2 + ^Ух'2 4-	(6.20)
6	6	2	6 о
4-|ж2ж' 4- 2ххУ - ^х'у'2 ~ |«'3,
Fi=^(x + y') + F*,	Gi=6e(y-x') + G*,
F2 = -^(y-x') + F^ G2 = 6e(x + y,) + G*2, .	21 о 9 , ,	,	, ,	19 ч 51 , ,
= ~2ХУ + 2У У ~ П'ХуХ ~ ^Ух У + ух + ух У +
35 ,2 Ю9 /2,3 ,з 13 ,2 , 4--^-^ + ~F-XX + «У + У’
2	о	2 о
GJ = 2у3 - 9у2х' 4- \уу'2 4- ^-хуу' 4- 15уя/2 4- ^-х2х'-4	4	16
313 if 11 / /2 q /3 — ~у$хх У ~ 11* У ~ %х > п* 1 Я ^9/	1 9 /а /	5 .2	51 ,2
F2 = ~^У ~ т:У х 4- -Х2у - 2хуу 4- -zyy 4- -г-ух -2 z	Z	Z	о
13 2 / л II ^//2	19 /3
-~ЪХ х - ^хх У - 2х У - у* , G*2 - -llxy2 - ^-у2у' 4- -^ХУХ' “ ^УХУ - 28ж3 - 45х2?/-
— 15жг/2 - т^хх'2 - 2i/3 4- 1х'2у'.
214
ГЛАВА 4
«Укороченная» система, получающаяся из уравнении (6.19), если в них положить £ = О, имеет вид
х" - —4х +	+ О4, у" = -у + 9?2 4- О4,	(6.22)
<Pi = hi +	+ ^kG* (i = 1,2).
Задача об устойчивости «укороченной» системы (6.22) принадлежит к критическому случаю двух пар чисто мнимых корней. Для ее решения используем критерий Каменкова [54, 100], как это было сделано в § 4.4 при исследовании устойчивости движения (4.13). Сначала нужно получить нормальную форму системы (6.22) до членов третьей степени включительно, а затем перейти к полярным координатам р,, (г = 1,2). В системе (6.22) имеет место резонанс третьего порядка (частоты колебаний линеаризованной системы относятся как 1:2). Но наличие этого резонанса не влияет на структуру нормальной формы, так как в (6.22) нет членов второй степени. Как показывают вычисления [58, 59], уравнения для pi, р2 записываются в виде (4.22), где
35	17	20	1145
®11 —	79^’	оо
/ &	У	У	оо
Согласно критерию Каменкова (4.23), (4.24), «укороченная» система (6.22) асимптотически устойчива и этот вывод не зависит от членов выше третьей степени в ее правых частях. А так как разложение в ряд правой части уравнения (6.17), вычисленной при С = 0, начинается с членов не ниже четвертой степени, то на основании «принципа сведения» можно сделать вывод об асимптотической устойчивости полной системы (6.11)—(6.13) и рассматриваемого движения (6.8).
Отметим, что в случае абсолютно твердого кольца движение (6.8) просто устойчиво по Ляпунову [21,107].
Неустойчивость относительного равновесия в плоскости, перпендикулярной вектору скорости центра масс. Исследуем устойчивость движения, отвечающего решению (6.9). Положим 0 = 7г/2 + х, = ^/2 4- у, ч>' — z. Линеаризованная система уравнений возмущенного движения будет такой:
2	2
х" -F 3(1 - -/z)^ +	= 0,	(6.23)
о	о
2	2	2
у" - (1 - оР)у -	- (2 + дК)г = 0,
О	о	У
4
+ у' 4- д«(2г - у) = 0-
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
215
Характеристическое уравнение системы (6.23) имеет две пары комплексно-сопряженных корней
Ai,2 =	± гл/3(1 - |д) + О(е4),
Аз,4 = -к ± »(1 + м) + О(е4),
и один вещественный положительный корень
А5 = ^к + О(б4), У
поэтому рассматриваемое относительное равновесие кольца неустойчиво.
Об эволюции регулярных прецессий кольца. Как уже отмечалось в § 4.4, для динамически симметричного абсолютно твердого тела, движущегося в центральном ньютоновском гравитационном поле на круговой орбите, существуют три семейства регулярных в абсолютной системе координат прецессий: цилиндрическая, гиперболоидальная и коническая. В случае цилиндрической прецессии ось динамической симметрии тела перпендикулярна плоскости орбиты; в случае гиперболо-идальной — она лежит в плоскости, перпендикулярной радиусу-вектору центра масс, и составляет произвольный угол с нормалью к плоскости орбиты; в случае конической прецессии ось симметрии лежит в плоскости, перпендикулярной вектору скорости центра масс, и составляет произвольный угол с радиусом-вектором центра масс.
Если рассматриваемое тело (однородное кольцо) упруговязкое, то его ось динамической симметрии не может занимать фиксированное положение в орбитальной системе координат, отвечающее гиперболоидальной или конической прецессиям. Наличие внутренней вязкости в материале кольца приводит [58] к медленной эволюции движения оси симметрии. В случае гиперболоидальной прецессии ось динамической симметрии кольца стремится совпасть с нормалью к плоскости орбиты, а коническая прецессия эволюционирует так, что происходит медленное увеличение угла между осью динамической симметрии кольца и нормалью к плоскости орбиты.
4.7. УРАВНЕНИЯ РАУСА ДВИЖЕНИЯ ТЕЛА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
Системы координат. Вспомогательные кинематические соотношения. В некоторых задачах, например, при исследовании быстрых вращений вязкоупругих тел [66,73,87,103], более удобными, нежели уравнения (1.10)-( 1.12), (1.14), могут оказаться уравнения движения тела относительно центра масс в форме уравнений Рауса [71].
216
ГЛАВА 4
Орбиту центра масс считаем эллиптической. Пусть	— сред-
няя система координат, введенная в §4.1. Введем еще кенигову систему координат ОХ1Х2*з- Направление оси ОХ± совпадает с направлением от притягивающего центра к перицентру орбиты, а оси ОХ2 — с направлением вектора скорости центра масс в перицентре, ось ОХ% — перпендикулярна плоскости орбиты.
Рис. 4.12
За гамильтонову часть переменных Рауса примем переменные Андуайе Pi, Ц (г = 1,2,3) [42]. На рис. 4.12 плоскость OMN перпендикулярна кинетическому моменту 12 тела относительно центра масс; смысл угловых переменных р^ ясен из рис. 4.12; /2 — модуль кинетического момента, Л и 7з — его проекции на оси Охз и ОХз соответственно. Имеют место очевидные равенства
cosJi = cosJ2 =	(7.1)
h	h
Величины qn (n = 1,2,...) из (1.3) примем за лагранжеву часть переменных Рауса. Переход от кениговой системы координат ОХ1Х2Х3 к средней системе координат О^1Ж2ж3 осуществляется при помощи пяти последовательных поворотов на углы р3,	<^>2, J2, рг. Первые два по-
ворота (на углы рз и 51) задаются матрицей элементы S-р которой
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
217
определяются равенствами
— siny>3 cosJi, = sin <^3sinJi,
= cos <рз, Sj = — sin рз cos <5 = sin <^3,	— cos у?з cos 5i,
4P = 0,	=sin<fi,
S2V — “ cos sin ^1 > = cos Ji.
Последующие три поворота (на углы <^2, 52, <Р1) вполне аналогичны поворотам, которые определяют ориентацию тела при помощи углов Эйлера *0, 0, Повороты на углы у?2, 52, 9?i задаются матрицей S(2\ элементы которой задаются равенствами, аналогичными (1.17):
2) = COS р2 COS у?1 — sin p2 sin COS 62,
= — COS p2 sin — sin ip2 COS COS 62 ,
5(3) = siny?2sin52,
— sin <^2 cos 4- cos y?2 sin pi cos 52,
= — sin p2 sin -I- cos p2 cos pi cos 52,
= — cos <^2 sin 62, S™ = sin pi sin 52, S32 = cos ^1 s*n ^2, S33 = cos 52 •
Матрица S = S^1) • S^2) определяет ориентацию средней системы координат относительно кениговой: ее элементы Sij суть косинусы углов между осями О Xi и Oxj.
Нетрудно получить, что компоненты 7,- (г = 1,2,3) единичного вектора 7 радиуса-вектора Ro центра масс относительно притягивающего центра в средней системе координат Oa?ia?2#3 вычисляются по формулам
7i = cos v ' Si, 4- sin v • S2i (г = 1,2,3),
где у — истинная аномалия. Последние равенства можно записать в таком виде
7i =«1 sin pi 4-61 cos pi, 72=01 cos pi —bi sin pi,
73z=:(cos /3 sin <^2+sin /3 cos P2 cos Ji) sin 524-sin /3 sin 5i cos 52,	^’^)
ai=—(cos/3sin<^2+sin/?cos p2 cos 5i) cos 524-sin/?sin 5i sin52,
bi=cos /3 cosp2—sin/3sin <p2 cos5i, P—p^—y.	(7.3)
218
ГЛАВА 4
Проекции o>i, о;2, ^1 вектора о? абсолютной угловой скорости трехгранника OxiX2%3 на оси Oxi, 0x2, Ох3 задаются равенствами:
^1 =	+ фз (sinJiS^f + cos Ji <) + Ji -I- j2 cos<pi,
O>2 = ф2$32 + 9?3 fsinJiS^ +COs5iS^) + ^1*512^ “ j2sill9?i,
(7.4)
W3 = <p2S^ + фз (sin^iS^ + cosJ1S^) + <pi + £1513 •
Функция Рауса, Уравнения Рауса, Для функции Рауса имеем [71] выражение
з	з
3? = £	=	- т + п-	(7.5)
»=1	»=1
Выражения для кинетической энергии Т и потенциальной энергии П тела получены в § 4.1. Величины входящие в (7.5), должны быть выражены через переменные Андуайе 71, /2, 73, y?i, у?2, <р3 при помощи равенств (7.1)—(7.4) и формул § 4.1. В рамках линейной теории упругости нелинейные относительно qj, qj (j = 1,2,...) члены не учитываются в уравнениях движения.
Не приводя довольно громоздких выкладок, выпишем окончательное выражение для функции Рауса:
ОО	1 оо	. оо
Я = Я(о) - £ 4nQn - 2 Z ’п + 2	Q"9" +	(7 6)
П = 1	П = 1	П = 1
Здесь
Hm = (IzJ) ("^ +	X (л7; + в-,1 + с7Э.
Z	у /Л.	U J ZL> ZJLq
(7.7) Через Qn в (7.6) обозначены величины (2.8), в которых o>i, о/2, ш3 выражены через переменные Андуайе:
Qn = -gj	- 1) + Я^(3722 - 1) + Я^)(37з2 - 1)+
L
+67712^7172 + бЯхзЧпз + 6Я^з}727з +
1'2	.1/	А2
I у2 nll т п22 _
z/(n) । z/(n)	\
”22 +Нзэ Sin2 - 4^- sin 2рг + Нзэ ±tf11 cos2 ) + АВ	В*	)
/------ / /у(п)	/j(n)	\
Л2-7? ^Sin^ + ^cos^ . (7.8)
*	\ /1U	/
С2
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
219
Символом 5?* в (7.6) обозначена линейная по qn квадратичная форма относительно qni qn (п = 1,2,...) с коэффициентами, зависящими от переменных Андуайе и истинной аномалии р. В пределах точности проводимого ниже асимптотического анализа движения тела явное выражение для не потребуется.
Величины А, В и С в (7.7), (7.8) — моменты инерции недеформиро-ванного тела относительно осей Oxif Ох2 и Ох$ соответственно.
Дифференциальные уравнения движения тела относительно центра масс запишутся в виде
dk_ _д®_
dt dli’ dt д<р{ 1	’ ’’
d	<ЭФ	,	, „ x
~ля-+®?'1 = _Ат“ (n = l,2,...).
(2/ dqn	dqn
(7.9)
(7.Ю)
Здесь Ф — функция Рэлея из (1.13), задающая силы внутреннего трения.
Уравнения (7.9), (7.10) должны быть дополнены соотношениями (1.6), (1.7).
Упрощение уравнений движения. Опишем алгоритм анализа уравнений движения (7.9), (7.10) при помощи асимптотических методов [66]. Этот алгоритм в основных своих чертах близок к соответствующим построениям работ [86, 106].
Как и в § 4.2, считаем, что тело достаточно жесткое, а диссипативные силы, возникающие за счет внутреннего трения, малы. Дополнительно предположим, что вращение тела как целого относительно центра масс является быстрым по сравнению с движением самого центра масс по орбите.
Опишем эти физические допущения более конкретно. Пусть, как и в § 4.2, Т1 — характерный период свободных упругих колебаний тела при отсутствии затухания (и = 2tt/Qi, fii — наименьшая частота колебаний), т2 — характерное время затухания упругих колебаний, тз — характерное время для вращения тела как целого относительно центра масс (т3 = 2тгА//2, 7° — начальное значение модуля кинетического момента), TQ — период обращения центра масс по орбите. Принятые физические допущения означают, что выполняется следующее неравенство, аналогичное (2.1):
Т1 < т2 < т3 <Т0.	(7.11)
Пусть тз — величина порядка единицы измерения времени. Условие (7.11) позволяет ввести малые параметры р и е\
_ Ану _ /2° e~Ani
Малым будет также параметр х в диссипативной функции Рэлея (1.13).
(7.12)
220
ГЛАВА 4
Положив в уравнениях (7.10) Qn = £-1Ап, можно, аналогично § 4.2, получить, что величина Т2 имеет порядок £2х-1, а условие (7.11) можно записать в виде
X <£ г < 1 < /i-1.	(713)
Упрощение уравнений (7.9), (7.10) можно теперь осуществить, как и в § 4.2, асимптотическими методами, разработанными для систем дифференциальных уравнений с малым параметром при старших производных.
Считая, что х ~ £1+<5 (0 < J < 1), можно получить, что регулярная часть асимптотического решения для величин qn (п = 1,2,...) имеет вид
б2
— ~^{Qn
-2y6Qn)+O(64).
(7.14)
Величины Qn — функции переменных Андуайе и времени (время входит в Qn через истинную аномалию). Поэтому
Заменив здесь производные Ц на правые части уравнений (7.9) и учтя, что, согласно (7.14), qn ~ £2, найдем, что
<2п = (<2„Л(0)) + ^ + О(е2),	(7.15)
где — функция (7.7), a (Qn, — скобка Пуассона.
Из (7.14) и (7.15) находим выражение обобщенных координат через переменные Андуайе и время в квазистатическом режиме упругих колебаний тела:
qn = Qn- 2у6 (Qn, Н™) - 2ХЬ^-
+ О(е4) (п=1,2,...).
(7.16)
Подставив qn из (7.16) в правые части уравнений (7.9), получим уравне-
ния, описывающие квазистатические режимы движений тела как целого.
Эти уравнения имеют форму, близкую к гамильтоновой, и могут быть
записаны в виде
 - дн	ЛГ 1	’ dii + 2х	дц п=1 п	L		+ О(г4),(7.17)
лп fyi		+ О(е4)
(г = 1,2,3)
<•2 00 Л)2
=	(7.18)
п = 1 п
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
221
Если решение системы (7.17) получено, то деформации тела могут быть найдены из (7.16) и (1.3). Поэтому основные трудности математического исследования квазистатических режимов движения связаны с анализом системы (7.17).
4.8. ВЛИЯНИЕ ПРОДОЛЬНЫХ УПРУГИХ КОЛЕБАНИЙ ТЕЛА НА ЕГО БЫСТРЫЕ ВРАЩЕНИЯ
Уравнения движения. В данном параграфе при помощи методики, изложенной в § 4.7, исследуется влияние диссипации энергии при квазистатических упругих колебаниях тела на его быстрые вращения относительно центра масс [66]. Предполагается, что в недеформированном состоянии тело динамически симметрично (А = В), а упругие деформации представляют собой продольные колебания вдоль оси симметрии Ох3. Орбита центра масс считается круговой.
Можно показать, что среди величин из (1.4) только величины
(п — 1,2,...) могут быть отличными от нуля, а ось Охз будет осью динамической симметрии и при наличии деформаций. Функция Рауса (7.6) не зависит от ipi. Поэтому, согласно (7.9), имеет место интеграл
/1 =. const.	(8.1)
Уравнения для Д (г = 2,3) в (7.17) образуют замкнутую систему, содержащую Д в качестве параметра. Выпишем эти уравнения. При А = В и = 0 (г, j 3, п - 1,2,...) из (7.7), (7.8) и (1.6) получаем
L f 1	1 \ -2	1 г2 3	л\ 2
1\С ~ а) 1 + 2Л 2 + 2W°(С " )73’ ^(37з2-1) + ^^]^з)-
(8.2)
(8.3)
В правой части равенства (8.2) отброшена несущественная постоянная 3Au>q/2.
Из (8.3) и (7.2), (7.3), (7.12) следует, что производная 5Qn/3/2 имеет порядок единицы, а производные Qn по ^2> <^з, 7з — малые величины порядка р2. Кроме того
(О.,	~
zi	иу?2
&Qn _ д ,3 гг(п) ^73	3
— _-6ШоЯ33 7з^-~^ •
(8.4)
222
ГЛАВА 4
Вводя вместо (рз новую переменную /?, определяемую последним из равенств (7.3), исключим время t из правых частей уравнения (7.17), которые затем будем исследовать методом усреднения. Для определенности последующих оценок будем считать, что
е _ „6	„ _ ..7
(8.5)
Учтя (8.4) и (8.5), получим, что после исключения времени уравнения для (pi, Ц (г = 2,3) можно представить в виде
<9Г	, , /о #73	22\
»” = ал+*г"»“з^735^ + 0<'‘ >• /S _	। v-2. ЛкТ	, z")//.24\
/’-Йз+’"“"',/27з»^№+0^ ’’
ЗГ 2 4 т ( А л/ 24\ 2 = "^"xew° 2v3d^) + 0(fi т	2 4 У 2 ^73 дуз . 24ч
3~	шок^27з^2 5/? +0^
(8-6)
Г=^2-'
А2
(g^)2
А2
2
,(8.7)
(8.8)

Переменные и в системе (8.6) изменяются со скоростями порядка 1 и /2 соответственно, а переменные 7г, 1з изменяются со скоростями ; порядка /А	I
Эволюция быстрых вращений. Правые части уравнений (8.6) з являются суммами гамильтоновых и диссипативных составляющих (пер- J вые задаются частными производными функции Г, а вторые пропорциональны параметру х). Гамильтоновы составляющие не дают эволюции медленных переменных /г, 73, их эволюция определяется диссипативными составляющими в правых частях последних двух уравнений системы (8.6).
Опираясь на метод усреднения и современную теорию возмущений гамильтоновых систем [6], аналогично [87] можно показать, что решения системы уравнений
£
А = -xe2wo«;2
2
;	2 4 г / 2 ^73 дуз \
/3 = -хгшок/2^з^-^,
(8.9)
i
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
223
где угловыми скобками обозначена операция двойного усреднения по переменным у>2 и /?, аппроксимируют функции /2, h с погрешностью ~ /1 на интервале времени ~ (е2;^4)"1 (или, если учесть (8.5), на интервале ~ ^“23).
Проведя указанное в (8.9) усреднение, получим, что эволюция переменных /г, 1з определяется уравнениями
1'2 =	~ Л2)[(3724 + 2/2/2 + 3/34)(/2 - /2)+
+4/2(/2 + 3/2)(/2-/2)], (8.10)
/з =	- 1Г)1з[(123 + /22)(/22 - Л2) + 4Л2(722 - 42)]-
где штрихом обозначено дифференцирование по новой независимой переменной г = хв2ШцкЛ.
Вместо (8.10) удобнее исследовать систему уравнений для углов Ji и $2 кинетического момента с нормалью к плоскости орбиты и с осью симметрии тела (рис. 4.12):
= —-г sinJi cosJi sin2 62 [sin2 £2(1 4- 3cos2 Ji) + 12sin2 5i cos2 J2] 64
6f2 = — sin <?2 cos <5г [sin2 £2(3 cos4 Ji +2cos2Ji + 3) +	(8.11)
4-4 sin2 5i cos2 <5г(1 + 3cos2 5i)].
Постоянная 7i содержится в (8.10) (и в (8.11)) как параметр. Рассмотрим качественно различные случаи Д = 0 и Д / 0. Пусть сначала /1 = 0, т. е. быстрое вращение тела происходит вокруг оси, перпендикулярной его оси симметрии. Тогда 62 = тг/2, a Ji удовлетворяет дифференциальному уравнению
JJ = -1-sinJi cos5i(1 4- 3cos2t?i).	(8.12)
Это уравнение имеет три особые точки: 5j. = 0, тг — неустойчивые и Ji = 7г/2 — асимптотически устойчивую. Для значений Ji, отличных от 0, 7г/2, 7г, из (8.12) имеем (с > 0 — постоянная интегрирования):
—5------------------= се-т/8.	(8.13)
sin2 5i(l 4- 3cos2 5i )3
Из (8.13) видно, что с возрастанием времени угол £i стремится к тг/2. Отсюда следует, что если в начальный момент времени тело быстро закручено вокруг оси, перпендикулярной оси симметрии и не совпадающей
224
ГЛАВА 4
с нормалью к*плоскости орбиты, то с возрастанием времени мгновенная ось вращения тела остается перпендикулярной оси симметрии и стремится расположиться в плоскости орбиты.
При Zi 0 система уравнений (8.11) имеет однопараметрические семейства особых точек: <У2 = 0, тг,	—
произвольная величина (0 <	< тг).
Особые точки из этих семейств асимптотически устойчивы по отношению к переменной <У2 и просто устойчивы по отношению к переменной Ji.
Фазовый портрет системы (8.11)ддя О < Ji < тг (г — 1,2) показан на рис. 4.13 в плоскости Ji, J2. Для случая Zi 0 соответствующий фазовый портрет в плоскости Z3, /2 представлен на рис. 4.14. Угол <У2 с возрастанием времени стремится к значению 0 или тг,
a Ji — к некоторому значению зависящему от начальных условий. Следовательно, при Д / 0 направление оси симметрии тела стремится совпасть с направлением кинетического момента, сам же кинетический момент стремится составить в пределе угол , с нормалью к плоскости орбиты (Jj — arccos(Zg/|Zi|), где/3 —предельное значение величины/3).

Рис. 4.14
Описанная диссипативная эволюция переменных /2, /3 имеет характерный масштаб времени ~ /i“23. На небольших промежутках времени (например, ~ ^~2) величины Z2, Z3 существенно не изменятся, кинетический момент составляет с нормалью к плоскости орбиты угол

ДВИЖЕНИЕ УПРУГОГО ТЕЛА
225
Ji = агссоб(/з//2) и прецессирует вокруг нее. Приближенное значение средней угловой скорости прецессии отвечает эволюции кинетического момента абсолютно твердого динамически симметричного тела под действием гравитационных моментов [21]:
3 2/-	дх42-3Л2г
—Ji—
Здесь /1 — const, a /2, h удовлетворяют дифференциальным уравнениям (8.10).
4.9. БЫСТРЫЕ ВРАЩЕНИЯ ВЯЗКОУПРУГОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Собственные формы и частоты колебаний. Рассмотрим движение тела, имеющего форму цилиндрической оболочки в центральном ньютоновском гравитационном поле [73]. Как и всюду в этой главе, влиянием движения тела относительно центра масс на движение самого центра масс пренебрегаем. Будем считать орбиту центра масс круговой.
Срединная поверхность оболочки — цилиндр радиуса а и длины 2/, толщина оболочки 2А, оболочка однородная, р, Е и а — ее плотность, модуль Юнга и коэффициент Пуассона.
При движении по орбите оболочка может совершать упругие колебания. Считаем, что они не сопровождаются растяжениями и сжатиями. При отсутствии внешних сил такие колебания в рамках линейной теории упругости изучены в [64,93]. Пусть Oxyz — система координат, образованная главными центральными осями инерции недеформированной оболочки, ось Oz (ось оболочки) направлена вдоль оси срединной поверхности. Положение частицы dm недеформированной оболочки задается в системе координат Oxyz радиусом — вектором £ = (a cos у?, a sin tp, z), где <р — угол между проекцией £ на плоскость Оху и осью Ох. При наличии упругого смещения и(£,/) положению частицы dm отвечает радиус-вектор г = £ 4- и. Упругое смещение можно представить в виде ряда по собственным формам колебаний оболочки (т — масса оболочки):
сю
« = Е	+ ?'2)(*)u<n) + g(3’(<)uln) + g<4>(0Uln)] ,(9.1)
п—2
— (п cos тир cos ср 4- sin тир sin <р) — (п cos тир sin ip — sin тир cos (р) О
(9.2)
U'n) = к
п sin тир cos (р — cos тир sin (р п sin тир sin (р 4- cos тир cos <р
0
8 — 2185
226
ГЛАВА 4
U^n) = <5
U^n) = 6
—nz(n cos nip cos ip 4- sin nip sin ip) —nz(n cos nip sin ip — sin nip cos <p) a cos nip
nz(n sin nip cos ip — cos nip sin ip) nz(n sin n<^sin ip 4- cos nip cos ip) , —a sin nip
6
/	2
у m(n2 4- 1) ’
Функции ujn) в (9.1) удовлетворяют условию ортонормированности f	dm = 6ij6nk (i,j = 1,2,3,4; n,k = 2,3,...).
\l Г*> 2  21 2 i 1\721’ Snpalh. m[3a2 4- n2(n2 4- I)/2]
Здесь интегрирование проводится по всей недеформированной оболочке.
Исходя из (9.1) и (9.2), несложно проверить, что центры масс деформированной и недеформированной оболочек совпадают и, кроме того, при всех t выполняется равенство
р х и dm = 0. v
Следовательно система координат Oxyz является средней системой координат (см. § 4.1, где для такой системы координат принято обозначение Ох1Ж2^з)-
Величины (j — 1,2,3,4; п — 2, 3,...) в (9.1) — нормальные координаты при упругих колебаниях оболочки. Координаты q£\ q^ отвечают плоским упругим колебаниям, в этих колебаниях упругие смещения элементов оболочки происходят в плоскостях, перпендикулярных ее оси. Координаты q£\q№ соответствуют пространственным упругим колебаниям, в которых упругие смещения имеют составляющие вдоль оси оболочки.
Выражения для кинетической и потенциальной энергии упругих деформаций записываются в виде
г=1£(е2+е2+йз|2+е2). п=2
. оо
п=I z Н (^1)2+^2)2)+°2 (^з)2+^4)2)] -
п — 2
2 _ Eh2n2(n2 — I)2
Шп = 3/>(1 — <т2)а2(п2 + 1) ’ q2 - ^2 (п2 + 1)[6(1-<т)а2 + гс212] п п За2 + n2(n2 + I)/2
(9.3)
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
227
При относительных смещениях элементов оболочки происходит диссипация энергии. Соответствующие диссипативные силы зададим при помощи функции Рэлея
сю
* = хьХ ["»(й‘)2 + А2’2) + °2- (А3)2 + Й3’2)] •
п=2
где b > 0 — const, х — безразмерный параметр.
Уравнения движения. Для описания движения оболочки относительно центра масс используем уравнения Рауса (7.9), (7.10). В рамках линейной теории упругости для функции Рауса имеем такое выражение:
сю
» = Н- Т+П - £	+ ,<№ + &><№) +
П=1
где задается формулой (8.2), в которой А = 1/6т(За2 4- 2Z2), С = та2; функции Т и П определяются равенствами (9.3);	— линей-
ная по (jn ) квадратичная форма относительно qn Яп\ коэффициенты которой — функции переменных Андуайе и времени. Величины Qnзадаются формулами, аналогичными (7.8). Вычисления показывают, что в рассматриваемом случае колебаний цилиндрической оболочки без растяжений и сжатий имеем
За / ГП п О/ 2	2\	(7о	72) г»
<?2 - уу 10 3wo(72-7i)---------^2—cos2y>i ,
(2) За Гт Г 2	(I? - /j) . „ 1	(9.4)
^2 = у у io р°7172---------Д2— sin 2^] ’
= (&> = 0, Q{nj}=0 (j= 1,2,3,4; n = 3,4,...).
Пусть угловая скорость вращения оболочки как целого относительно центра масс велика по сравнению со средним движением центра масс, но мала по сравнению с величиной и наименьшей из частот упругих колебаний оболочки; кроме того, будем считать, что диссипативные силы малы по сравнению с упругими силами. Эти предположения позволяют ввести в уравнения движения малые параметры. Пусть р = Awo/I®, е = ] Aw, где — начальная величина кинетического момента. Считая, что выполнены неравенства (7.13), а у ~ £1+<5 (0 < J < 1), будем исследовать движение оболочки как целого относительно центра масс в квазистатическом режиме ее упругих колебаний.
8*
228
ГЛАВА 4
Согласно § 4.7, соответствующая приближенная система дифференциальных уравнений будет такой:
(? = 1,2,3).
Здесь Хп = ewn, An = eQn (п = 2,3,...), [Qn , Ж0 J — скобка Пуассона, а
2 оо г 1	1
Н =	- У L [дТ )2 + ^2)2) + дТ (е2 + ^4)2)] • (9.6)
Из (9.4)—(9.6) следует, что пространственные квазистатические упругйе колебания оболочки не влияют на эволюцию движения оболочки как целого, а из плоских упругих колебаний на эволюцию движения оболочки оказывают влияние только колебания, отвечающие собственной форме с наименьшей частотой а>2.
Учитывая, что и>о ~ д, можно получить, что dQ^ppdtu3, а порядок малости скобок Пуассона	(J = 1,2) не превосходит р2. По-
этому при достаточно малых р величинами dQ^/dt в системе уравнений (9.5) можно пренебречь, и с учетом (7.2), (7.3) и (9.4) они запишутся в виде
(9.8)
0U/12 Ут
В дальнейшем полагаем, что е ~ /р/2, X ~ ji2/3.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
229
Быстрая эволюция. Если в правых частях уравнений (9.7) отбросить слагаемые, порядок малости которых равен р2 или выше, то получим следующую систему уравнений:
А — С Т о 9та2 _ . г2 г2ч 20Лр?/1(/2“Л)’
/2 9та2 г . т9 г9ч
л = хе;9'ЛД(С-Л)л(/,_;;)! л = 0 л = 0
(9.9)
Уравнения (9.9) описывают квазистатические режимы движения при отсутствии гравитационных моментов. Если оболочка абсолютно твердая (е — 0), то ее движение является классической регулярной прецессией симметричного твердого тела в случае Эйлера — Пуансо; если оболочка деформирующаяся (б / 0), а внутреннее трение отсутствует (у = 0), то, согласно (9.9), движение оболочки относительно центра масс также будет регулярной прецессией, но угловые скорости прецессии и собственного о вращения изменятся на величины порядка £ .
Если оболочка вязкоупругая (е 0, % / 0), то ее движение будет регулярной прецессией с медленно меняющимися (при А / С) параметрами. Решения системы (9.9) аппроксимируют решения системы (9.7) с погрешностью ~ /?/3 на интервале времени 71 ~ (у£2)-1-
Из третьего, пятого и шестого уравнений системы (9.9) следует, что кинетический момент 12 постоянен по величине и направлению в абсолютном пространстве. Однако имеется эволюция движения оболочки вокруг 12. Из четвертого уравнения системы (9.9) видно, что существуют два типа стационарных движений оболочки: Л = 0 и А = зЕ/г- Первое из этих движений неустойчиво, если А < С, и асимптотически устойчиво, если А > С; стационарные движения второго типа неустойчивы при А > С и асимптотически устойчивы при А < С.
Следовательно, если А > С (I > \/ба/2), то движение оболочки вокруг вектора 12 эволюционирует с возрастанием времени так, что предельным движением является вращение вокруг оси, перпендикулярной оси оболочки, а при А < С (I <	предельным движением будет
вращение вокруг оси оболочки.
Описанную эволюцию вращения оболочки под действием диссипативных сил назовем быстрой эволюцией (в отличие от рассматриваемой ниже медленной диссипативной эволюции, в которой кинетический момент не будет постоянным в абсолютном пространстве). Характерное время быстрой диссипативной эволюции равно Тр
230
ГЛАВА 4
Медленная эволюция (случай I > \/ба/2). Пусть А > С. Тогда на этапе быстрой диссипативной эволюции Ц -> 0. При /1=0 правые части уравнений (9.7) не зависят от <^i, и из них можно выделить подсистему, описывающую изменение переменных <^з, /2, /з- Если вместо <^3 ввести новую переменную (3 из (7.3), то правые части этой подсистемы не будут явно зависеть от t. В результате получим следующие уравнения:
sin2/? sin2 Ji +
; ЯГ г 2
h = -a^-K,h'13
(9.10)
(ЭГ
/з=- ^-«1 ^2?з (sin /3 cos <^2+cos /3 sin p2 cos Ji)
sin2/3sin2Ji +
Здесь Г = H — wq/3, H — функция (9.8), вычисленная при /1 = О, а «1 — 81хе2(л^тпа2ЬС/(5Л2А|). В последних двух уравнениях в (9.10) отброшены слагаемые, пропорциональные
Рассмотрим систему уравнений
/2 = -К!/2 ( 7з
sin2/? sin2 +
(9.11)
/3=—«1/2( 73(sin /3 cos(£?2+cos /?sin <^2 cosJi
sin2 /3 sin2 Ji4-
где угловые скобки означают двойное усреднение по <р2 и /3. Следуя [87], можно получить, что решения системы (9.11) аппроксимируют величины /2, /з с погрешностью порядка у на интервале времени Т2 ~ (у^2//4)"1.
Произведя усреднение, получим систему уравнений
Т —	1 Г _ 9 ^3
/3 — j л 1 /3 I 5	^г2/'
16	\ ц)
(9.12)
Эта система описывает медленную диссипативную эволюцию быстрых вращений оболочки, характерное время эволюции равно Т2.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
231
Из (7.1) и (9.12) получаем усредненное уравнение для угла Ji между кинетическим моментом и нормалью к плоскости орбиты
<У1 — sin Ji cos Ji(13 — 9 cos2 Ji).	(9.13)
Особые точки Ji = 0, тг этого уравнения неустойчивы, а особая точка Ji zz 7г/2 асимптотически устойчива. Для значений Jb отличных от 0, тг/2, тг, из (9.13) получаем
8	(13	9 COS2 <ft)9 _ i3Klt/8
LUo (?1	#	— Cc	,
Sin2b Jl
(9.14)
где c > 0 — постоянная интегрирования.
Из (9.14) видно, что с ростом времени угол Ji стремится к тг/2. Следовательно, на этапе медленной диссипативной эволюции вектор кинетического момента стремится попасть в плоскость орбиты.
Таким образом, если А > С, то предельное движение представляет собой быстрое вращение оболочки вокруг оси, находящейся в плоскости орбиты, причем ось вращения ортогональна оси оболочки.
Медленная эволюция (случай I < у/§а/2). В случае А < С быстрая диссипативная эволюция приводит к движениям, в которых Z1 = ±72. Положив в (9.7) /1 = ±72, получим систему уравнений, правые части которых не содержат угловых переменных <^i, <^2, а уравнения для 72, /3 имеют вид
qv
72 =	---«2^2(1 4- COS2 Jl + cos2/3sin2 Ji)2,
a?	<91S>
/3 =	- 2/c273(l + cos2 Ji + cos2/?sin2 Ji),
dp
где Г = H — о,07з, Н — функция (9.8), вычисленная при Ц = ±72, а к2 = 81хе2^та2Ь/(20СХ1\ В уравнениях (9.15) отброшены слагаемые, пропорциональные х^2^о-
Усредненные по /3 уравнения (9.15) имеют вид
1	/ 7ч /чА
72 = --^2 (3 + 2т| + 3]|/
7з = —2«27з (1 +	.
\	72 J
(9.16)
Решения уравнений (9.16) аппроксимируют 72, Z3 с погрешностью порядка р на интервале времени порядка Т2.
232
ГЛАВА 4
Усредненное уравнение для Ji
Ji = |/c2sinJi cosJi(l -I- 3cos2Ji)
имеет неустойчивые особые точки Jx — 0, тг и асимптотически устойчивую = тг/2. Отсюда следует, что как и в случае А > С, на этапе медленной диссипативной эволюции вектор кинетического момента стремится расположиться в плоскости орбиты.
Таким образом, в случае А < С предельное движение представляет собой вращение оболочки вокруг своей оси, которая расположена в плоскости орбиты.
Эволюция в случае сферической динамической симметрии.
В случае А — С быстрая диссипативная эволюция отсутствует. Можно показать, что в этом случае правые части уравнений (9.7) не зависят от <^1, а усредненные по <^2 и 0 уравнения для Д, /2, /3 имеют вид:
/1 -
-4кзЛ [2 (з + 21! + 3^) - (1 -	(15^ -6^-1)
h — —^3^2
8(3+2l+3i)-16(1-® H+1
l-73) Г7Г 7?
(9.17)
/3 — “4«з/з
/ f2 \	/ f2 \ r2 / r2 \ 2 /	t2\
8(1+4)— 16 (1 — 4 ) -A- (1-4) (З —5-4)
\	12 /	\	12	/	J2 \	12 /	\	l2 /
k3 = 81x£2 om°2 b I (320ЛА2).
Решения системы (9.17) аппроксимируют Л, Z2, /3 с погрешностью порядка у на интервале времени Т2.
Вместо (9.17) удобнее исследовать усредненную систему уравнений для углов Ji и J2 вектора кинетического момента с нормалью к плоскости орбиты и с осью оболочки:
ji = я3 sin Ji cosJi[8(3cos2 Ji + 1) — 16sin2 J2(3cos2 Ji — 1) +
+ sin4 J2(15cos2 Ji — 11)], (9.18)
J2 = —«з sin J2 cos ^[4(3 cos4 Ji — 6 cos2 Jx — 5)+
+ sin2 J2(15cos4Ji — 6cos2 J] - 1)].
ДВИЖЕНИЕ УПРУГОГО ТЕЛА
233
Рис. 4.15
Можно показать, что в квадрате 0 <	< тг (г = 1,2) система урав-
нений (9.18) имеет ровно девять особых точек (Ji,^)’ (kirl2,nir/2\ (к,п = 0,1,2), причем восемь из них неустойчивы, а одна (тг/2, тг/2) асимптотически устойчива. Траектории системы (9.18) представлены на рис. 4.15.
В предельном движении кинетический момент лежит в плоскости орбиты и ортогонален оси оболочки.
Глава 5
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ФУНКЦИОНАЛЬНЫХ ПОВЕРХНОСТЕЙ БКК И УГЛОВЫХ ПАРАМЕТРОВ ИХ ОРИЕНТАЦИИ
Для создания эффективных систем спутниковой связи, систем земного мониторинга требуются большие высокоточные антенны на базе космических конструкций диаметром 100 и более метров. Для развертывания этих конструкций на околоземной орбите необходимы специальные устройства для доставки, сборки или производства в космосе отдельных узлов, а сами конструкции по точности должны удовлетворять жестким требованиям, вытекающим из их функциональных назначений.
Так, в зависимости от типа антенны среднеквадратичная погрешность фронта излучаемой волны не должна превышать 4—12% ее длины [137]. В антенных рефлекторах погрешность фронта волны примерно в два раза больше погрешности рефлектора в направлении нормали к своей поверхности. Поэтому погрешность формы функциональной поверхности антенны не должна превосходить 2—6% длины излучаемой волны.
Наиболее просто можно получить допустимую форму конструкции, если собирать ее из изготовленных с максимальной точностью элементов, размеры которых мало меняются за период функционирования. Это позволило бы упростить дорогостоящий процесс сборки и настройки конструкции в космосе и гарантированно обеспечило требуемую точность без применения сложной системы активного управления формой конструкции. Однако такой способ обеспечения заданной точности требует больших затрат на изготовление каждого элемента конструкции и не всегда приводит к нужным результатам, т. к. все детали изготавливаются с некоторыми допусками, на которые накладываются порожденными внешними условиями деформации. Это ведет к искажению формы функциональной поверхности. Точность функциональной поверхности определяется конфигурацией конструкции и погрешностью составляющих ее элементов. Точность последних зависит от точности заводского изготовления и от влияния внешних факторов: динамических, тепловых и прочих деформаций. Исследование влияния точности отдельных элементов конструкции на точность ее функциональной поверхности представляет несомненный интерес для правильного выбора механической компоновки конструк
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
235
ции на этапе эскизного проектирования, когда вопросы осуществимости проекта рассматриваются одновременно с вопросами его стоимости.
Другим важным аспектом проектирования космической конструкции является обеспечение максимальной точности ее ориентации относительно заданного пункта на поверхности планеты в течение длительного срока эксплуатации. Предполагается, что стабилизация конструкции при ее движении по кеплеровской орбите осуществляется реактивными двигателями с релейными характеристиками. Эти двигатели имеют минимальное количество узлов и поэтому являются самыми надежными и простыми в работе. Одной из характеристик двигателей такого типа является наличие запаздывания в канале управления тягой двигателя — отключение тяги двигателя не может произойти мгновенно. При этом можно считать, что ограничений на момент включения нет, т. е. время выхода тяги на стационарный режим мало по сравнению с временем запаздывания.
Для исследования максимальной эффективности системы стабилизации углового положения космического аппарата с помощью релейных реактивных двигателей с запаздыванием отключения тяги рассмотрена задача нахождения при наихудшей помехе оптимального релейного управления одномерной динамической моделью. С использованием метода фазовой плоскости и подходов теории дифференциальных игр [1, 60] решены задачи перехода системы из произвольного начального состояния в режим с максимальной гарантированной точностью стабилизации и (приближено в предположении о малости помехи по сравнению с величиной управления) задача минимизации гарантированного расхода топлива при заданной точности стабилизации. Наличие запаздывания в канале управления тягой и ее релейный характер приводят к отклонению угловых параметров движения от заданных. Применимость одноканальной модели обусловлена малостью отклонения от программы параметров углового движения [3], что делает возможным декомпозицию [81, 105] исходных уравнений углового движения на линейные модели второго порядка [34, 35].
При написании параграфов 5.1,5.3 и 5.4 существенно использовались результаты работ [137, 139]. В основу параграфов 5.2, 5.5 и 5.6 легли работа [15] и исследования авторов книги.
5.1.	ВЛИЯНИЕ КОМПОНОВКИ КОНСТРУКЦИИ НА ТОЧНОСТЬ ФУНКЦИОНАЛЬНОЙ ПОВЕРХНОСТИ
Для анализа влияния компоновки и точности изготовления элементов конструкции на точность функциональной поверхности рассматриваются развертываемые в космосе параболические антенны, рабочую поверхность которых образует сетеполотно, натянутое и закрепленное на соответствующих элементах конструкции. Материал сетеполотна очень гибок,
236
ГЛАВА 5
имеет малую плотность, является упругим и после монтирования на элементах конструкции позволяет получить поверхность требуемой формы. Рассмотрим следующие три типа конструкций космических антенн.
Основу ферменной конструкции, называемой ниже тетраэдрической, составляют соединенные в общих вершинах стержневые элементы, образующие четырехгранники. Для поддержания требуемой формы линейные размеры элементов конструкции должны быть достаточно неизменны. Шарниры соединений и соответствующим образом расположенные замки позволяют развертывать в космосе жесткую конструкцию. Сетеполотно крепится вдоль стержневых элементов.
Конструкция зонтичного типа с радиальными ребрами жесткости представляет собой большое число радиальных изогнутых стержней, соединенных одним концом с расположенной на оси конструкции ступицей. Сетеполотно крепится непрерывно вдоль радиальных ребер. Таким образом натянутое сетеполотно представляет собой совокупность клиньев.
Ферма, обладающая предварительным натяжением, представлена на рис. 2.1, 2.2. Основу конструкции составляет сооружение, напоминающее велосипедное колесо. Конструкция состоит из центральной мачты и находящегося в напряженном состоянии внешнего силового кольца, соединенных друг с другом с помощью системы стержней и вантов (рис. 2.3, 2.4). Внешнее силовое кольцо состоит из шарнирно-соединенных элементов. Предварительное натяжение кольца обеспечивается пружинами. Шарнирные соединения элементов кольца позволяют трансформировать (раскрывать) конструкцию. Центральная мачта представляет собой развертываемую балку. Вантовая система допускает большое многообразие вариантов складывания конструкции, не требуя сложных соединительных узлов. Однако развернутая конструкция является достаточно жесткой, т. к. создающие натяжение элементы предварительно напряжены. Вантовая система передает эти напряжения на рабочую поверхность антенны, обеспечивая наличие растягивающих сетеполотно напряжений в любой его точке. Сетеполотно крепится вдоль радиальных элементов, жесткость которых повышена за счет натяжения. Напряжение радиальных элементов обусловлено наличием предварительно напряженного внешнего силового кольца и системы оттяжек. Оттяжки обуславливают наличие напряжения конструкции в направлении окружности, что создает необходимое натяжение сетеполотна. Предварительное напряжение в элементах, обеспечивающих натяжение сетеполотна, должно быть достаточным, чтобы предотвратить появление морщин и складок.
Сетеполотно, составляющее рабочую поверхность параболической антенны, имеет очень малую изгибную жесткость, поэтому его можно рассматривать как мембрану. Натяжение сетеполотна обычно выбирают достаточно однородным и изотропным. Закрепленное на ребрах конструкции сетеполотно в параболических антеннах с малой кривизной
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
237
рабочей поверхности должно иметь форму, максимально приближенную к сферической, радиус кривизны которой равен удвоенному фокусному расстоянию F.
Определим степень отклонения сетеполотна от идеальной поверхности следующим образом. Пусть поверхность Р* есть результат смещения u(r) каждой точки поверхности Р. Обозначим через п(г) местную нормаль в точке г поверхности Р и определим среднеквадратическое отклонение we поверхности Р* от Р функционалом:
we =
(1-1)
Здесь через S обозначена площадь поверхности Р, ds — элемент этой площади. Если поверхность Р пологая, т. е. векторы п(г) направлены примерно в одну сторону — вдоль оси Oz, а смещение u(r) также происходит вдоль этой оси, то формула для подсчета we упрощается
we
(1-2)
где Pi — проекция поверхности Р на плоскость хОу, Si — площадь этой проекции. Среднеквадратическое отклонение — один из критериев совершенства поверхности, применяемый в радиотехнике [38] и характеризующий ухудшение свойств рефлектора антенны при его деформации.
Изотропно растянутая в двух направлениях мембрана, не подверженная поперечной нагрузке, должна иметь нулевую среднюю кривизну. Поэтому если кривизна поверхности в одном направлении положительна, то в другом направлении она должна быть отрицательной, а форма поверхности в каждой точке — седлообразная. Таким образом, лучшее приближение к полусферической форме при однородном натяжении достигается при прямых ребрах. Конструкция должна быть спроектирована так, чтобы размещение прямых ребер обеспечивало максимальное сокращение отклонения плоской поверхности от требуемой полусферической. Среднеквадратическое отклонение должно быть предельно малым при заданных размерах граней. Осуществление этого требования для треугольной грани приводит к зависимости
we = 0,01614/2/F,	(1.3)
где we — среднеквадратическое значение отклонения сферы с радиусом 2F от оптимально расположенной плоской грани; F — фокусное расстояние и I —длина стороны грани. Разрешая уравнение (1.3) относительно
238
ГЛАВА 5
/, получим максимально допустимое при заданной точности значение I/D:
Т> =7’87
we\
DJd
(1.4)
где D — диаметр рефлектора и {we/D}d — допустимое при проектировании отношение среднеквадратической погрешности рефлектора к диаметру рефлектора для данного источника погрешностей.
Грани в случае фермы с предварительным напряжением имеют приблизительно прямоугольную форму. Для четырехугольных граней такая же процедура дает соотношение
где b — меньшая сторона прямоугольника, I — большая.
В конструкции с радиальными ребрами жесткости функциональная поверхность представляет совокупность клиньев. Кривизна поверхности в радиальном направлении обусловлена кривизной самих ребер и при малых углах раствора между соседними ребрами эти кривизны примерно совпадают. Процесс седлообразования вызывает отрицательную кривизну в окружном направлении в Nx/Ny раз большую, чем радиальная кривизна, где Nx и Ny — натяжение мембраны в радиальном и в окружном направлениях соответственно. Итоговое среднеквадратическое отклонение можно представить в виде
= 0,01076^	+	(1.5)
где I — ширина клина у обода. В случае изотропного натяжения мембраны Nx — Ny и для клина получим
(L6>
Полученные здесь предельные оценки точности определяются только компоновкой конструкции и не могут быть быть улучшены для конструкций данного типа.
5.2.	ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ КОНСТРУКЦИИ С РАДИАЛЬНЫМИ РЕБРАМИ ЖЕСТКОСТИ
Рассматривается математическая модель антенны зонтичного типа, рабочая поверхность которой в раскрытом состоянии представляет собой
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕР1
239
натянутое на ребра сетеполотно. Сетеполотно, натянутое на два смежные, расходящиеся от центра рефлектора ребра, образует лепесток антенны. Форма отражающей поверхности определяется профилем ребер, их количеством и компонентами тензора натяжения сетеполотна.
Необходимо подобрать профиль ребер и компоненты тензора натяжения сетеполотна, чтобы наилучшим образом приблизить поверхность параболоида вращения с заданным фокусным расстоянием F.
В качестве модели сетеполотна рассмотрим анизотропную мембрану, находящуюся в равновесии поддействием приложенных на бесконечности заданных сил Nx, Nyi Т. Прямоугольную систему координат Оху всегда можно выбрать так, чтобы сдвиговые силы обратились в ноль, поэтому будем полагать Т = 0. В результате прогибов, заданных на границе Г некоторой области Q, мембрана отклонится от нейтрального положения. В случае и /, т. е. когда прогиб мал по сравнению с характерным размером области Q, уравнения равновесия мембраны принимают вид
д2и д2и
= 0.	(2.1)
ох2 * оу2
Требуется подобрать профиль дуг каркаса, определяющих форму лепестка антенны, или, что то же самое, определить прогиб мембраны на границе:	г/)|г = и$(х,у) из условия минимума интегрального ква-
дратичного функционала
Ф(«о) =j\u{x,y)~ f(x,y)]2da,	(2.2)
n
где f(x,y) — функция, задающая приближаемую поверхность.
Замена переменных х' — х, у' — (Nx/NyY^y переводит уравнение равновесия анизотропной мембраны (2.1) в уравнение Лапласа для области Q', которая получается в результате растяжения (сжатия) области Q в направлении оси ординат в (Nu/Ny)1/2 раз. Сохраняя прежние обозначения для новых переменных и новой области будем в дальнейшем полагать, что величина прогиба описывается уравнением Лапласа.
Допустим, что заданы прогибы и(х, у)|г = и0(х, у) на границе Г новой области Q. Тогда имеем задачу Дирихле для уравнения Лапласа
Дм = 0, м|г = и0.	(2.3)
Приближенное решение задачи Дирихле может быть получено прямым методом граничных интегральных уравнений, согласно которому задача
240
ГЛАВА 5
(2.3) сводится к следующему интегральному уравнению
у)и(х,у) + Vp [ u(^7j)^(x,y,Cn)dr =
2л	J
г
= vpf	(2.4)
г
где <р = (2тг)_Чп(Я-1), ф — (27r)~idln(R~i)/dn1 а(х,у) — угол между левосторонней и правосторонней касательными в граничной точке (ж, у), R = [(ж — £)2 + (у — т])2]1/<2 [29]. Знак Vp перед знаком интеграла обозначает его главное значение.
Неизвестной величиной в уравнении (2.4) является нормальная производная v = ди/дп, п — внешняя нормаль к границе области Q (рис. 5.1). После решения интегрального уравнения (2.4) прогиб в любой внутренней точке области Q находится простым интегрированием вдоль границы
«(ж,г/) = У	- У	(2.5)
г	г
Для нахождения приближенного решения интегрального уравнения (2.4) граница Г области Q разбивается на п прямолинейных отрезков, на каждой из которых прогиб предполагается постоянным. Дискретный аналог интегрального уравнения (2.4) имеет вид
; + IpijUj = PijVj, i, j = 1,2,...	(2.6)
<fij = Vpj	^ij = VP/'КХ^У"€’Г1)с1Г,
ri	rj
где Xi, yi — координаты середины г-го отрезка Г3, здесь и далее по повторяющимся индексам производится суммирование.
Рис. 5.1
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
241
Решение системы линейных алгебраических уравнений (2.6) представим в виде
V, = aijUj,
-10г	/ А
— Pik I	J '
(2.7)
Приближенное значение прогиба в любой внутренней точке области Q получаем из уравнений (2.5) с учетом соотношений (2.7)
и(ж, у) = (aji<pj(x, у) - ^i{x, у))щ = Xi(x, у)щ, (2.8)
<Pi(x,y) = У	ipi(x,y) = У t/>(x,y,£,i])dr,
г,	г,
Х,(х, у) = ajitp^x, у) - falx, у).
Теперь можно приступить к минимизации исходного функционала (2.2). Подставляя (2.8) в подынтегральное выражение в правой части (2.2) и интегрируя, получаем вместо функционала (2.2) функцию многих переменных
Ф(г/1, иг,..., ип) = QikUiUk — 20,и, 4- const,


n

Условие минимума функции Ф(м1, u2,..., ип) имеет вид
— = aikuk -0,i = О, 1=1,2,...,п.	(2.9)
О V>i
Решение системы линейных алгебраических уравнений (2.5) завершает приближенную минимизацию исходного функционала (2.2).
В качестве примера рассмотрим изотропную мембрану в кольцевом секторе с углом раствора 7 = тг/12, внутренним радиусом г — 6 м и внешним радиусом R = 10 м. Пусть задан параболоид вращения с фокусным расстоянием F = 12 м.
/(*,2/) =
(Я2 -х2- у2) 4F
(2.Ю)
9 — 2185
242
ГЛАВА 5
Рис. 5.2
Требуется выбором прогиба мембраны на границе сектора минимизировать среднеквадратичное отклонение мембраны от поверхности параболоида. На рис. 5.2 представлено разбиение границы кольцевого сектора на 28 прямолинейных отрезков и соответствующая такому разбиению сетка, выполненная на ЭВМ. На рис. 5.3 а изображена оптимальная форма поверхности мембраны, рассчитанная с помощью изложенного выше метода. Максимальное отклонение рассчитанной поверхности от параболоида вращения не превышает 0,032 м. На рис. 5.3 6 дана увеличенная в десятикратном размере разность между поверхностями натянутой мембраны и параболоида.
В приведенном примере на вариации граничных прогибов накладывалось одно ограничение, именно, прогибы вдоль каждой из дуг кольцевого сектора полагались постоянными, т. к. каждая кольцевая дуга каркаса имеет постоянную кривизну.
Рабочая поверхность антенны зонтичного типа в раскрытом состоянии имеет в каждой точке седлообразную форму, т. е. по меридиану она выпукла, а по окружности — вогнута. Поскольку параболоид есть двояковыпуклая поверхность, ясно, что наилучшее приближение параболоида достигается в предельном случае, когда кривизна мембраны в окружном направлении стремится к нулю. Другими словами, идеальной является анизотропная мембрана, сила натяжения которой в окружном направлении стремится к бесконечности по отношению к силе меридионального натяжения. Но на характер натяжения сетеполотна накладываются некоторые ограничения, связанные с прочностными и структурными свойствами конструкции, и с необходимостью исключить образование ряби на поверхности натянутого сетеполотна.
Тем не менее, задача оптимизации формы анизотропной мембраны в идеальном предельном случае представляет интерес. Дело в том, что этот
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
243
Рис. 5.3
идеальный случай является элементарным и допускает точное аналитическое решение, которое может быть использовано как для тестирования вычислительной процедуры, так и для оценки предельной точностной характеристики конструкции, необходимой на этапе эскизного проектирования. Для упомянутого предельного случая анизотропной мембраны имеем NxNy1 -> 0. Возьмем в качестве области Q равнобедренную трапецию (рис. 5.3в). Пусть приближаемая поверхность,есть тот же параболоид вращения (2.10).
Если NxNy1 = 0, то из уравнения равновесия (2.1) следует д2и/ду2 = 0, т. е. искомая функция не зависит от у ввиду ее симметрии относительно оси абсцисс. Таким образом функционал (2.2) принимает вид
R2 - х2 - у2' 4F
JQ.
(2.Н)
Вводя обозначение
= и(х) —
R2 - х2 4F
(2.12)
функционал (2.11) перепишем в виде
dx dy.
9*
244
ГЛАВА 5
Интегрирование по у дает
Проварьировав по и* последний функционал, получаем
(2.13)
И, наконец, из (2.12) и (2.13) находим поверхность мембраны, доставляющую минимум функционалу (2.11)
и(х) = Пг t3^2 “ ~ x2tg2 (2)] ’
Среднеквадратическое отклонение we найденной поверхности от параболоида вращения определяется формулой (1.2)
1
wP = ----
е 12F
(2.14)
п
Вычисление интеграла (2.14) дает значение we
= ».«44‘8г ©		,215)
что совпадает с формулой (1.5) данной главы при Ny = 00 и г = 0. Полученное значение we — предельная (неулучшаемая) среднеквадратичная точность для параболической антенны зонтичного типа.
5.3.	ВЛИЯНИЕ ТЕХНОЛОГИЧЕСКИХ ДОПУСКОВ НА ТОЧНОСТЬ ФОРМЫ БОЛЬШОЙ КОСМИЧЕСКОЙ конструкции
Для анализа влияния технологических допусков при изготовлении отдельных элементов конструкции на точность функциональной поверхности необходимо знать соотношение между погрешностью размеров отдельных деталей и всей конструкции в целом. Если эти соотношения известны, вычисление точности функциональной поверхности конструкции может быть выполнено на основании знания технологических допусков при изготовлении отдельных деталей. С другой стороны, такая информация может быть использована для выработки требований к
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
245
технологическим допускам исходя из необходимой точности изготовления функциональной поверхности. Изучим эти соотношения для крупных ферменных решетчатых конструкции следуя работе [139].
Определим трехмерную решетчатую конструкцию как совокупность прямолинейных элементов, соединенных в узловых точках. Полная энергия деформации конструкции считается равной сумме энергий продольного растяжения составляющих ее элементов. Это определение исключает из рассмотрения деформации изгиба и сдвига в элементах конструкции, и подразумевает, что узлы не передают воздействий в виде моментов вращения. Допускается наличие жестких элементов, вставок, армирующих балок или колец, а так же свободных границ. Такая трехмерная решетчатая конструкция может иметь различные формы и компоновку, однако далее будем рассматривать лишь конструкцию зеркала антенны, определяющую форму функциональной поверхности.
Ухудшение свойств антенны пропорционально взвешенному среднему квадрату отклонений функциональной поверхности от заданной формы. Взвешенный средний квадрат w1 2 отклонений поверхности от заданной формы выражается через перемещения узловых точек решетки следующим образом.
Пусть и/г — вектор перемещения Ar-го узла, Sk — площадь его поверхности, йк — единичный нормальный вектор этого узла. Тогда
1 К
W2 = •?y'AS’fc(nfc,ufc)2,	(3.1)
д к=1
где S — полная площадь поверхности, Д — весовой коэффициент, нормируемый следующим образом:
1 К -qYlfkSk = 1.
/с = 1
Предполагается, что узловые перемещения обусловлены погрешностями размеров элементов решетки. Пусть число этих элементов равно N и относительная погрешность длины n-го элемента — еп. Нагрузка в n-ом элементе определяется формулой
рп = (ЕА)п (£n(||u||) -еп),	(3.2)
где £п(||и||) — деформация в n-ом элементе, обусловленная перемещением его концов, и (ЕА)п — продольная жесткость n-го элемента. Запись ||и|| используется для обозначения упорядоченного набора векторов перемещений при всех к = 1,2,..К. Функция £п считается линейной и однородной.
246
ГЛАВА 5
Уравнения равновесия в узлах могут быть получены из вариационного принципа
J( WT) = О,
где W — величина энергии деформации, зависящая Ът перемещений ||и||. Таким образом
1 N
W=- Y^(EA) nln [[£n (||u||)]2 - 2e„f„(||u||>],	(3.3)
n=l
где ln — длина n-го элемента.
При вычислении отклонений должны учитываться различные ограничения, обусловленные наличием жестких границ, арматуры и вставок. Минимизация энергии деформации по компонентам вектора перемещений при наличии ограничений приводит к искомым уравнениям равновесия. Решение относительно компонент перемещений и подстановка в выражение (3.1) приводит к искомому результату.
Другим подходом может служить использование модального решения. Преимущество такого подхода состоит в том, что для вычисления взвешенной средней погрешности можно использовать известные методы решения задач на определение собственных частот колебаний. Кроме того, модальный подход позволяет облегчить понимание задач вычисления погрешностей формы путем использования аналогии с соответствующей задачей на определение собственных частот.
Представим вектор перемещений ||и|| в виде суммы ортогональных мод с неизвестными коэффициентами а,
1Н1 = £а,||и||<(	(3.4)
1=1
где запись ||и||, используется для обозначения упорядоченного набора перемещений в £-ом узле по г-ой собственной частоте, I — полное число степеней свободы узлов.
Несколько ортогональных мод получаются следующим образом: для i = 1,2, ...,/С вектор ||и||,- является решением следующего уравнения, обусловленного принципом Рэлея — Ритца:
h "	1я	1
51 2 Е>4)п/„ [^(Н«11)]2 - /52 A^(nfe,Ufc)2 > = 0.	(3.5)
I n = l	2 k=l	J
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
247
Оба члена в этом уравнении представляют собой максимальные значения потенциальной и кинетической энергии при гармонических колебаниях и специальном выборе структуры инерционного оператора. Весовой коэффициент fk соответствует отношению массы к единице площади, а инерционные силы, касательные к поверхности, не учитываются.
Собственные решения, полученные из уравнения (3.5), ортонормиру-ются для получения ортонормированной последовательности векторов ||и||,-. Тогда
1 К q У? fkSk(nk,uki)(hk,ukj) = 6ij,	(3.6)
д /с=1
где 6ij = 0, i / j; Sij = 1, i = j. Собственные векторы также диагонализируют выражение для потенциальной энергии
1 N
- ^(ЕА)п1п£п(||u||,)£n(||u||j) =	(3.7)
d n = l
Число членов ряда собственных векторов равно К — числу узлов поверхности, которое в общем случае меньше числа степеней свободы 7. Ряд векторов ||и||,- является полным для определения нормальных перемещений поверхности, однако, вообще говоря, не может быть использован для определения векторов перемещений во всех узлах. Чтобы сделать общий ряд в выражении (3.4) полным, должны быть определены I — К дополнительных членов. Эти члены должны иметь нулевые нормальные перемещения в узлах поверхности, поскольку К собственных мод составляют полный набор векторов по отношению к этим перемещениям. Кроме того, их можно выбрать ортогональными друг другу относительно потенциальной энергии. Однако эти дополнительные ортогональные моды не дают вклада в выражение (3.1), поэтому здесь нет необходимости их оценивать.
Подстановка разложения (3.4) в выражение для w2 (см. уравнение (3.1)) и использование условия ортонормированности (3.6) дает
к w2 = ^^a2.	(3.8)
Аналогично, подставив разложение (3.4) в выражение для энергии деформаций (3.3) и применив условие ортогональности (3.7), получим
я	IN
+ o Е a^(EA)nln [£n(||u||,)]2-
1 = 1	1=К+1	п = 1
I N
-Еа<Е^л)"/пе"^(1Н1.).
1 = 1 П = 1
248
ГЛАВА 5
При этом использовались свойства линейности и однородности оператора £n(||u||). Минимизация по переменным а,- (г = 1,2,..., К)
1 N
ai = srf	(3.9)
1 n = l
Выражение (jE'AJn^ndlullt) может быть отождествлено с распределенной нагрузкой pni в элементах при отклонении формы поверхности по г-ой моде. Таким образом,
1 N
ai =: Suft Pni^n^n ♦	(3.10)
1 п = 1
Для известного набора технологических погрешностей еп коэффициенты а,- можно получить с помощью выражений (3.9) или (3.10). Последующая их подстановка в (3.8) дает искомый результат.
Рассмотрим случай, когда погрешности еп обусловлены случайными технологическими ошибками при изготовлении и, следовательно, являются независимыми случайными величинами. Пусть каждая из них имеет нулевое среднее и дисперсию сг2п. Тогда математическое ожидание w2 (3.8) есть
к
Mw2 = ^Ма?,	(3.11)
1=1
где М — символ математического ожидания и
1 N
Mai = sw	& (IK)]2 •	(312>
1 n = l
Замена двойного суммирования простым обусловлена отсутствием статистической корреляции между еь и еп. Выражение для Mw2 может быть также записано в виде
1 N	к 2
= <313>
П=1	1 = 1 1
Математическое ожидание Mw2 для известных дисперсий сг2п определяется формулой (3.13). Если дисперсии <т2п удовлетворяют нижеследующему соотношению, результат получается чрезвычайно просто. Пусть ЕА, I и а£ — постоянные величины. Предположим, что
(ЕА)п1п(т2п = ЁА1<т2.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
249
Используя условие нормирования (3.7) и соотношение (3.12), получим
М а2 =
EAla2
Sw2
Подстановка этого равенства в выражение (3.11) дает в итоге
1
S
М w2 —
(3.14)
Следовательно, математическое ожидание среднего квадрата отклонений формы поверхности пропорционально сумме квадратов обратных значений собственных частот конструкции с соответствующим образом выбранными инерционными характеристиками.
5.4.	РАСЧЕТ ВЛИЯНИЯ ТЕХНОЛОГИЧЕСКИХ ДОПУСКОВ НА ТОЧНОСТЬ ОТДЕЛЬНЫХ видов КОНСТРУКЦИЙ
Балки, Предположим, что балка, представленная на рис. 5.4, была собрана из отдельных элементов, длины которых случайны и не имеют систематической ошибки. При выводе соотношений между погрешностью формы балки и погрешностью изготовления ее отдельных элементов были приняты следующие допущения [137].
1.	Величина среднего квадратического отклонения сге относительной погрешности длины каждого элемента является одинаковой для всех элементов.
2.	Длина пролета I балки мала по сравнению с длиной L всей конструкции.
3.	Погрешность формы поверхности определяется по отношению к идеальной балке.
4.	Консольная балка рассматривается как часть радиального ребра жесткости антенны зонтичного типа или предварительно напряженной ферменной конструкции. Поэтому весовые коэффициенты при подсчете взвешенного отклонения от идеальной формы выбирались пропорциональными расстоянию от оси симметрии конструкции в целях адекватного описания точности областей рабочей поверхности антенны вблизи внешнего кольца.
Рис. 5.4
250
ГЛАВА 5
Пусть величина взвешенного среднего квадрата отклонений w2 деформированной поверхности от исходной вычисляется по формуле (3.1). Введем определение: w2p кв = Mw2 — математическое ожидание взвешенного среднего квадрата отклонений. Ниже приведены результаты расчетов wcp кв в зависимости от средней квадратической погрешности а£ длины элементов балки при различных вариантах ее крепления.
В каждом из ниже приведенных выражений первое слагаемое под знаком корня обусловлено погрешностями длин пролетов, направленных вдоль оси балки, тогда как второе слагаемое обусловлено погрешностями диагональных элементов. Первое слагаемое уменьшается при увеличении высоты Я, тогда как второе увеличивается при Н/1 > 0,5. Существует оптимальная высота Яопт, соответствующая минимуму погрешности.
Заметим, что шарнирно закрепленная по обоим концам балка характеризуется значительно меньшей погрешностью формы, чем консольная балка со свободным концом. Значительное увеличение погрешности в случае консольной балки объясняется частично тем, что один из концов свободен, и частично большим весовым коэффициентом при подсчете погрешности на свободном конце.
Шарнирно закрепленная балка. В случае шарнирного крепления балки на обоих концах величина среднеквадратического отклонения мср кв формы балки от прямолинейной определяется формулой
«ср кв _ 0,149 /рУ 15 р\2//	4Я\2
Ь<т£	+ 16\£/	+
НОПТ = 0,51\/П.
Консольная балка. В случае жесткой заделки левого конца балки и свободного правого величина среднеквадратического отклонения вычисляется по формуле
Яопт = 0,69л/£/.
Консольная балка с шарнирным креплением на правом конце и жесткой заделкой на левом. Величина среднеквадратического отклонения определяется формулой
Wcp кв _ 0,169 // I \2	35 / / А 2 / Z 4ДА2
La,	+32\Lj \H + ~L~J ’
Яопт z= 0,49x/Z7.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
251
Трехмерные конструкции. Трехмерную тетраэдрическую конструкцию будем рассматривать как оболочку, поверхность которой составляют треугольные решетки, образующие правильные треугольники. Предположим, что оболочка пологая, состоит из большого числа ячеек и является достаточно тонкой с тем, чтобы деформации могли быть выражены через компоненты перемещений ее срединной поверхности. Тогда частотные характеристики этой решетчатой конструкции могут быть получены из рассмотрения частотных характеристик эквивалентной непрерывной изотропной оболочки, имеющей следующие свойства.
Жесткость оболочки на изгиб:
Мембранная жесткость оболочки:
(Eh), =	(4.2)
У 6	*
Жесткость оболочки на сдвиг:
ЕА Л2	,л
(Gh)s — —------------—.	(4.3)
v ’ Уз(л2 + /2/з)3/2
Коэффициент Пуассона оболочки:
v, =	(4.4)
Масса единицы площади оболочки:
Р> = f-	(4.5)
В этих формулах ЕА — продольная жесткость и I — длина элемента конструкции, h — ширина оболочки, f — весовой коэффициент. В общем случае эти величины могут варьироваться по объему, при этом жесткость Ds и единичная масса ps также будут меняться, однако эти вариации невелики. Соответствующие частотные решения, полученные для равномерно выбранных весовых коэффициентов в сплошной оболочке, могут быть успешно применены для оценки погрешности решетчатой конструкции. Для этого определяются собственные частоты эквивалентной непрерывной оболочки, затем суммируются квадраты их обратных величин и подставляются в выражение (3.14) для определения результирующей погрешности поверхности.
252
ГЛАВА 5
Граничные условия в эквивалентной задаче на собственные частоты ставятся исходя из характерных особенностей оцениваемой конструкции и определения «идеальной» поверхности. Если требуется оценить отклонение деформированной поверхности от исходной недеформированной, то перемещения конструкции как жесткого целого не важны. Поэтому здесь следует взять граничные условия, соответствующие свободным концам, и рассмотреть отличные от нуля собственные частоты.
Если представляют интерес перемещения элементов поверхности относительно отдельных точек на этой поверхности, то оболочку следует считать закрепленной шарнирно в этих точках. Наличие недеформируе-мого идеально выполненного внешнего кольца учитывается требованием на перемещение границ как жесткого целого.
Некоторые сложности возникают вследствие того, что ферменная конструкция при сделанных предположениях относительно механических свойств составляющих ее элементов имеет конечное число собственных частот. Сплошная эквивалентная по жесткости оболочка имеет бесконечное число частот. Поэтому обоснованность полной эквивалентности для больших частот отсутствует. Однако если частоты быстро возрастают, то при оценке точности конструкции это расхождение не важно, и ошибка будет незначительной. Если частоты возрастают медленно, суммирование должно включать конечное число мод. Некоторая ошибка вносится за счет неполной эквивалентности, не совсем обоснован выбор учитываемых мод. Однако для качественного анализа полученные оценки могут быть полезны.
Таблица 5.1
	п = 0	п = 1	п = 2	п = 3
т = 0	-	-	2,292	3,497
т = 1	3,014	4,630	5,937	7,274
т = 2	6,209	7,737	9,160	10,55
т — 3	9,370	10,91	12,41	13,86
В качестве примера рассмотрим тетраэдрическую ферменную конструкцию, представляющую в плане круг радиуса а. Предполагается, что ферма имеет малую кривизну, так что ее можно считать плоской, а толщина фермы мала по сравнению с ее диаметром. Эквивалентная сплошная конструкция представляет круглую пластину постоянной толщины со свободными границами. Пластина достаточно тонкая, так что гипотеза прямых нормалей Кирхгофа предполагается выполненной. Значения собственных частот колебаний такой пластины выражается через безразмерный параметр ктп следующим образом:
2	_ Kmn^3
^тп	а •
Рз^
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
253
Здесь т — число узловых окружностей, п — число узловых диаметров. Подставляя это выражение в формулу (3.14) и используя равенства (4.1), (4.5) при / = 1, получим:
Mw2 _ 2х/3/2 2	1
D2 9тгЛ2 ктп* ’ т,п
(4-6)
где D — диаметр конструкции. При суммировании этого выражения следует учесть, что члены с п = 0 суммируются один раз, а члены с п / О суммируются дважды соответственно модам cosn# и sin пО. Значения ктп для свободной круглой пластины даются табл. 5.1. Используя данные, приведенные в таблице 5.1, можно получить
£>-4„«о,п.
тп
Подстановка этой суммы в равенство (4.6) дает
~D~	£-
Наибольший вклад в сумму квадратов обратных частот дают моды с номером п = 2 (65% всей суммы). Практическая сходимость следует из того, что вклад в эту сумму мод с п = 3 составляет только 13%. Такое преобладание мод с п = 2 означает, что результирующее отклонение деформированной поверхности круглой пластинки определяется в основном этими модами. В работах [137—139] на основании вышеизложенной методики исследована погрешность формы различного вида конструкций, в том числе рефлекторной антенны ферменного типа. Полученные по этой методике оценки точности являются достаточно грубыми, однако могут быть полезны для сравнения эффективности различного вида конструкций на этапе эскизного проектирования.
5.5. МАКСИМАЛЬНАЯ ГАРАНТИРОВАННАЯ ТОЧНОСТЬ РЕЛЕЙНОГО РЕГУЛЯТОРА В ЗАДАЧЕ СТАБИЛИЗАЦИИ
При проектировании системы стабилизации космического аппарата на кеплеровской орбите существенную роль играют вопросы обеспечения максимальной гарантированной точности ориентации этого аппарата относительно выбранной планеты при различных внешних возмущениях, а при заданной точности — необходимость обеспечения минимальной средней интенсивности расхода топлива с целью увеличения сроков функционирования всей системы в целом.
254
ГЛАВА 5
Для длительной стабилизации используют наиболее простые и надежные релейные двигатели, имеющие минимальное количество узлов. Если продолжительность интервалов постоянства тяги двигателей достаточна для затухания возникающих при изменении тяги колебаний конструкции, то использование релейных систем не будет вызывать больших искажений формы конструкции. Поэтому исследование предельных точностных и экономических характеристик релейных систем представляет большой интерес для правильного выбора на этапе эскизного проектирования средств и алгоритмов стабилизации.
Положение космического аппарата будем определять относительно заранее выбранной подвижной системы координат, называемой базовой, направление осей которой выбирается с учетом функционального назначения аппарата и технических возможностей системы управления.
Для спутников, предназначенных для исследования Земли или других планет, в качестве базовой используют одну из орбитальных систем координат с началом в центре масс спутника. Удобной является система, у которой ось Oxq лежит в плоскости орбиты по направлению движения, ось Оуо направлена на Землю, а ось Ozq сориентирована так, чтобы система координат стала правосторонней. Ее абсолютную угловую скорость вращения обозначим через Со спутником, который будем считать твердым телом, жестко свяжем систему координат Oxyz с началом в центре масс спутника и осями, совпадающими с главными центральными осями инерции спутника. Ориентация осей Oxyz, а тем самым и спутника относительно базовой системы координат OxoyoZo задается тремя углами а, /3, у, определяющими последовательность трех поворотов: вокруг оси Ozq на угол тангажа 7 (ось Оуо при этом переходит в линию узлов), вокруг линии узлов на угол рыскания /3 и вокруг оси Ох на угол крена а. Эволюция углового положения спутника относительно базовой системы координат описывается системой кинематических уравнений и динамических уравнений Эйлера
а = шх —	+ [(wy — wot/) sin a + (o>2 - o>oz) cos a] tg /3,
3 = (ijjy — wot/) cos a - (wz - a>oz) sin a,
7 = [(wz - woz) cos a + (wy - cvOjz) sin a] (cos /3)*"1, = i,£WxujyUjzW£ 1	1 +	1,
где i* = (Iy-Iz)I~1,iy = (Iz- Ixjly^iz =	— проекции
абсолютной угловой скорости спутника на оси связанной со спутником системы координат Oxyz, wof — проекции абсолютной угловой скорости базовой системы координат на связанные со спутником оси, Ц — моменты инерции спутника относительно связанной системы координат,
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
255
— проекции управляющего момента на оси Oxyz, — проекции остальных возмущающих моментов на те же оси. Введем обозначения: Ди^ —	1 +	\ F% = —и % =	1>
£ = х,у, z. С учетом введенных обозначений динамические уравнения Эйлера запишутся в виде
Д^ = F^(t) +u{(t) + ^(/), £ = x,y,z.
Будем исследовать задачу оптимальной стабилизации спутника при малых значениях углов: a(t), /3(t), y(t) 1, max^ |Да^(0)| < Q = = const 1 сек-1.
Функции F{(t) — мало меняющиеся функции на характерном периоде стабилизации, поэтому можно положить F^(t) « const. Пренебрегая в правых частях кинематических уравнений слагаемыми, содержащими при малых а, /3, у члены, пропорциональные этим углам, получаем систему уравнений:
d = До;г, (3 = До^, 7 = Д^-
Конструкция реактивных двигателей системы ориентации такова, что отключение тяги может произойти не раньше, чем через Д/ после ее включения. При этом можно считать, что ограничений на момент включения нет, т. е. время выхода тяги на стационарный режим пренебрежимо мало по сравнению с Д/. Таким образом, получаем одноканальную динамическую модель
х — V,
v — F + и + в, />/о,	|б| < б0,
(5.1)
где F = const, фазовая переменная х — одно из угловых отклонений, е(/) — ограниченная помеха, £о = const, u(t) — релейное управление, принимающее одно из трех значений
и = {0, ±uq}, uq = const.
(5.2)
Каждый временной отрезок ta < t < tp с постоянным ненулевым управлением удовлетворяет ограничению
tp — ta > Д/ = Const > 0.
Предполагается, что
|F| + е0 < и0.
(5.3)
(5.4)
256
ГЛАВА 5
Нахождение максимальной гарантированной точности стабилизации. Рассмотрим задачу обеспечения минимального гарантированного отклонения от нулевого положения динамической системы (5.1) с управлением
и = {±uo}> UQ = const > 0,	(5.5)
при условиях (5.3), (5.4) на бесконечном интервале времени.
Замечание 5.1. Если в указанной постановке заменить условие (5.5) на более о0щее условие (5.2), то искомая точность, вообще говоря, повысится. Однако в случае отсутствия помехи (бо = 0), как будет показано ниже, максимальная точность не изменится. Поэтому решение поставленной выше задачи с управлением (5.5) может быть применено в качестве асимптотического приближения по решения более сложной задачи с управлением и = {0; ±и0} при достаточно малых значениях е0.
Введем обозначения: z = {#,v}, zq = z(to). Эффективность управления определим после отбрасывания начального куска фазовой траектории, соответствующего переходу системы из произвольного положения в некоторую окрестность начала координат. Это приводит к функционалу:
J[zq, и(-),б(-)] = infsup |ж(/)|, t > /i,	^i>/o-	(5.6)
t
Точки здесь означают, что функционал зависит от управления и от помехи как от функций. Будем отождествлять возмущение е(-) с игроком, стремящимся выбором помехи максимизировать критерий качества (5.6). Стабилизирующее управление выбирается из условия минимизации функционала (5.6) при наихудшей помехе. Таким образом, приходим к следующей задаче.
Задача 5.1. Найти управление и°(-) вида (5.3)—(5.5) такое, что
sup J[z0,u°(-),6( )] = Jm(zQ) = minsup J[z0,u(),e( )],	(5.7)
e	u e
где функционал J определен формулой (5.6).
Задача 5.1 не является автономной, поэтому управление и0, доставляющее ее решение, должно зависеть как от текущей позиции г, так и от времени г, прошедшего с момента ta = t - г последнего переключения управления в прошлом, и индекса
п = sign u(t - т),	(5.8)
который определяет знак управления, установившийся в момент ta в результате переключения.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
257
Рис. 5.5
Пусть т = minZ9Jm(zQ) — абсолютная максимальная гарантированная точность (Jm(zQ) определено в (5.7)).
Рассмотрим сначала задачу нахождения т.
Задача 5.2. Найти минимум по zq значения функционала (5.7):
Лп(^о) -> min = т.	(5.9)
Введем индексы i = {1; 2}, j = {1; 2}, i / j.
Предположим, при t > ti траектория содержится в некоторой полосе |я| < р. Построим контуры, состоящие из параболических участков (рис. 5.5), точки пересечения которых друг с другом и с осью Ох обозначены через A,-, В,, М, О,. Внешний контур JVi А 17^2^2 имеет ширину 2р. Он является траекторией системы (5.1) при помехе
е(у) = £Osignv.	(5.10)
Внутренние линии А,О,В,, г = 1,2, представляют собой участки траекторий при u(t) = const и возмущении
s(u) = —е0 sign v.	(5.11)
Таким образом, линии A2NiAi и AiOiBi являются траекториями, максимально отклоняющимися влево, a ArN2A2 и А2О2В2 — вправо.
Лемма 5.1. Эквивалентны следующие два свойства: траектория при любом возмущении е(-) не выходит из 1) полосы |я| < р; 2) контура NiAiN2A2.
Доказательство. Предположим, траектория вышла из контура N\AiN2A2. Она может выйти только через дуги A±N2 и A2N\. Пусть выход произошел через A^N2l и далее действует помеха е(—и0) = £о, е(и0) — любые значения. Тогда траектория будет проходить над A\N2 до тех пор, пока не пересечет прямую х = р. Аналогично в случае выхода через А2АТ-
Лемма доказана.
258
ГЛАВА 5
Лемма 5.2. Пусть точка z находится под (над) монотонно убывающей кривой v = v(x) на фазовой плоскости. И пусть при u(t) = const = uq (u(t) = const = —uq) любая траектория, выходящая из точки z, попадает на кривую v = v(x). Тогда время движения от z до v = v(x) достигает минимума при e(t) = const = во sign и.
Доказательство основано на условии монотонности в формулировке леммы и свойстве: для двух траекторий х = иДя) и х = г>2(я) на фазовой плоскости, 0 < i>i(z) < vz(x), xi < х < #2, время движения по траектории х = меньше, чем по траектории х = г>1(я).
Лемма доказана.
Лемма 5.3. Пусть F > 0. Тогда tm(p) = minz>c>i Ti[z, е(-)] = = T2[Bi,e(t) = const = во], z принадлежит дуге AiBj, i = 1,2, где Ti[z, £(•)] — время движения от точки z на дуге AiBj до дуги AjBi с управлением u(t) = const = (—1):uq и помехой е(-).
Доказательство. Введем следующие обозначения: Ц — траектория х = (-l)’(uo + во) + F с началом Bi и концом на границе N1A1N2A2 (рис. 5.5), а, — абсцисса точки пересечения Ц с Ох, хщ — абсцисса точки Oi, ti(x) — время движения по траектории х = (—1)*(и0 + во) + F от AiBj до AjBi через точку х на оси Ox, i = 1,2.
Из леммы 5.2 следует, что для определения искомого минимума достаточно найти значения min/i(z), #01 < я < «ь min^z), а2 < ж < #02, и сравнить их. Функции ti(x) имеют свойство:
t'f(x) <0 (во > 0).
Поэтому
fm(p) = min[ti(a?oi),<i(ai), <2(ах), <2(^02)]-
Из геометрических соотношений и оценок получим, что
<т(р) = <г(а2) -
___________\/2p(uo - F - е0)___________
(г»0 + F + Eq) \/Uq(uq —Eo)(uq — F + Eq)
х < \/(wo + Ео) [(«0 - Ео)2 - F2] +
«0 - Eg + 2Fe0(mq - fig) - F2(u§ + e§) «0
F > 0.
Лемма доказана.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
259
Далее в этом параграфе, не ограничивая общности, будем для определенности считать, что F > 0, если не указано по-другому.
Обозначим через ро корень уравнения
tm(p) = Д/,
где Д/ из (5.3).
Определение. U(p) — множество всевозможных управлений и(-), обладающих следующим свойством: для любого и из U (р) существует начальное условие z0 такое, что при любой помехе e(t) траектория на интервале t > tQ не выходит из полосы |я| < р (или не выходит из контура что эквивалентно вышесказанному в силу леммы 5.1).
Лемма 5.4. Имеет место соотношение ро > m (см. (5.9)).
Доказательство. Утверждение верно, потому что множество U(p) не пусто. Действительно, рассмотрим управление с дугами переключения Л1В2 и Л2В1 для траекторий, начинающихся на этих же дугах. Данное управление имеет вид:
и = u(z, т, п),
(5.12)
где п — индекс (5.8). Под воздействием указанного управления движение будет удерживаться в контуре N1A1N2A2 шириной 2ро при соблюдении ограничения (5.3), что следует из леммы 5.3.
Лемма доказана.
Далее везде в этом параграфе будем полагать р = р0.
Проведем линии KiEiGi, удовлетворяющие условию: из любой точки KiEiGi траектория х = (-l)J(uo + во) + F достигает параболической ветви NjAiHi за время Д/ (рис. 5.6), i = 1, 2. Эти кривые совпадают соответственно с параболами NjAiHi при параллельных сдвигах. В силу леммы 5.3 парабола KiEiGi проходит через точку Bi = Еь а линия K2E2G2 пересекает границу A1N2A2 в точке Е2 не выше точки В2 (В2 = Е2 при F = 0).
Замечание 5.2. Согласно лемме 5.2 при любой помехе время движения по траектории с управлением u(t) = const = (—l)Juo от KiEiGi до NjBjAiHi будет не меньше Д/.
260
ГЛАВА 5
Теорема 5.1. Имеет место равенство m — ро.
Лемма 5.5. Пусть р = pQ. Для любого управления из U(ро) включение u — —uq не может произойти левее кривой AiOi В\.
Доказательство. Предположим, такое включение произошло. В этом случае существует помеха (5.11) такая, что следующее переключение произойдет в той же указанной области, следовательно, выше параболы K\B\G\. Но тогда, согласно определению этой параболы, траектория под воздействием помехи = const = £0 может выйти из контура и, в силу леммы 5.1, из полосы |я| < ро, что противоречит принадлежности управления множеству U(po).
Лемма доказана.
Введем обозначения: Wi — область, остающаяся от криволинейного треугольника K2AiE2 после отбрасывания точек левее кривой AiOiBi, W2 — область, остающаяся от криволинейного треугольника К\А2В\ после отбрасывания Из, Из — подобласть треугольника KiA2Bi, из которой траектории u(t) — const = uq при помехе (5.11) не попадают в Wi (рис. 5.6).
Лемма 5.6 (следует из построения, замечания 5.2 и леммы 5.5). Управление и принадлежит Щро) в том и только в том случае, если его включения u = — uq и и = uq происходят в областях Wi и W2 соответственно.
Доказательство теоремы 5.1. Рассмотрим любое управление и из 1/(р0) и любое соответствующее ему начальное условие, при котором траектория гарантированно остается внутри контура N\A\N2A2. Пусть после некоторого переключения управления в точке Si из W2 (по лемме 5.6) действует возмущение
s(u, v) = £0 sign(tw).
(5.13)
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХ НО СТЕ Й
261
Введем обозначения: S2 — точка пересечения траектории с осью Ох, S3 — точка переключения в PVi, S4 — следующее пересечение с осью Ох, S$ — пересечение траектории с параболической ветвью S2Si (рис. 5.7). Контуры S2S3S4S5 и TVi AiOi Bi построены из одинаковых парабол, толь-
ко на разных основаниях S2S4 и N1O1. Поэтому из того, что ордината 5з меньше ординаты Ai, следует, что ордината 5s больше ординаты Bi, в силу чего 55 не принадлежит 1У2- После очередного переключения в точке 5'б из W2 траектория пройдет ближе к точке АТ, чем в первый раз. Причем в силу отграниченности наклона линии K1B1G1 от нуля отношение |NiS71/1Ni S21, где Si — следующая после 64 точка пересечения с осью Ох, будет отграничено сверху от 1 для всех рассматриваемых траекторий. Таким образом, витки траектории при возмущении(5.13) будут сколь угодно приближаться к точке N\, следовательно, и к Ар Если после очередного переключения в сколь угодно малой окрестности Ai помеха сменится на (5.10), то траектория пройдет сколь угодно близко и от N2. Поэтому, с учетом леммы 5.4, ро = тп.
Теорема доказана.
Назовем контур N1A1N2A2 при р — р0 минимальным контуром.
Следствие 5.1. Для того, чтобы оптимальное значение функционала в задаче 5.2 совпадало с минимумом в задаче 5.1, т. е. для выполнения равенства Jm(zo) = m = ро независимо от zq, достаточно чтобы существовало управление (5.3)-(5.5), стягивающее траекторию (5.1) из любой начальной точки z0 к минимальному контуру и обеспечивающее тем самым выполнение равенства:
max J[z0,u(-),£(-)] = р0.
(5.14)
262
ГЛАВА 5
Приведение системы в минимальный контур. Будем называть управление из следствия 5.1 внешним в отличие от внутреннего управления из С7(ро)«
Покажем на двух примерах, как может быть построен алгоритм внешнего управления вида (5.12), приводящий траекторию через конечное число переключений в минимальный контур и затем удерживающий ее там.
Пример 1. В качестве линий переключения управления выберем кривые NjBjAiLi (рис. 5.8), где Д — бесконечное продолжение параболы OiAi, г = 1, 2, и дугу A2S параболической ветви А2Н2 такую, что любая траектория с управлением u(t) = uQ и началом на A2S попадает на дугу Л1В2В2, причем не быстрее, чем за время Д/.
Замечание 5.3. Согласно лемме 5.3 дуга A2S положительной длины существует при любых uo,6o,F > 0, удовлетворяющих (5.4). Максимально возможная ее длина определена ниже в замечании 5.4.
Пусть на линии N2B2A1L1 включается значение управления и = — и0, а на линиях N1B1A2L2 и A2S — и = и0, если это не противоречит ограничению (5.3). В обратном случае пусть переключение запаздывает до момента t = ta 4- Д£, где ta = / — т из (5.8). Значение u(zo,/o) выберем так, чтобы траектория попала на одну из указанных линий. Тогда начиная максимум с третьего переключения изменения значения внешнего управления будут происходить на кривых переключения. Зафиксируем некоторую точку Н на оси Ох слева от и проведем от нее траекторию с переключениями управления на линиях A^Li и A2L2 до точки G на Ох левее (рис. 5.8). Величина \GNi |/|Н| при помехе (5.10) примет максимальное значение:
к - k(u0, F,e0) =
£о
(ио + бо)2
'(uQ + e0)2-F2' _(uo-6o)2-F2.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
263
Коэффициент к стягивания траектории от витка к витку может быть как меньше 1 (например, если |F| + £о ^о), так и больше 1. В последнем случае траектория может раскручиваться и уходить в бесконечность. При к < 1 введение дуги переключения A2S обеспечивает переход к движению внутри минимального контура через конечное число витков.
Пример 2. Рассмотрим теперь внешнее управление, обеспечивающее приведение в минимальный контур через конечное число переключений при любых u0,£0, F > 0, удовлетворяющих условию (5.4). В качестве кривых переключения выберем HiAiB2E2G2 и H2A2B\G\ (рис. 5.6). Описание алгоритма управления с этими линиями аналогично описанию алгоритма в предыдущем примере с линиями N2B2A\L\ и {N\B\A2L2,A2S} соответственно. Исследуя движение с таким управлением, предположим сначала, что ограничение (5.3) снято. Тогда траектория из любой начальной точки попадает в полосу HiG2H2Gi между кривыми переключения и затем уже не выходит из нее. Покажем, что в этой полосе движение будет стягиваться к NiA\N2A2. Возьмем на AiHi точку Hi и выпустим из нее вниз две траектории с максимально отклоняющей влево помехой (5.13):
х = Uq F + £о sign V, X — — Uq + F — £q sign V (5.15)
до пересечения c BiGi соответственно в точках Gi и Pi (рис. 5.6). Контур МЛ1О1В1 задан теми же формулами (5.15). Поэтому из монотонного убывания функций v = v(x), задающих линии переключения, следует, что Pi правее Gi. Следовательно, при любой помехе б(-) каждая последующая точка переключения на BiGi будет правее предыдущей, причем в силу отграниченности наклона кривых переключения от нуля коэффициент k(Gi) = |PiBi |/|GiBi | стягивания от петли к петле удовлетворяет соотношению:
fc(Gi) < &о = const < 1.
Аналогично в полосе HiG2H2Gi справа от NiAiN2A2 имеет место подобное же стягивание. Только в отличие от левой стороны, где движение при наихудшей помехе (5.13) бесконечно долго стягивается извне к AiAiOiBi, траектория, идущая справа, начинает удерживаться в минимальном контуре после конечного числа переключений. Это следует из существования дуги A2S (см. замечание 5.3).
С помощью леммы 5.2, замечания 5.2 и других геометрических соотношений и оценок можно показать, что ограничение (5.3) в процессе рассмотренного движения в полосе HiG2H2Gi не будет нарушаться.
Замечание 5А. Из последнего утверждения следует, что дуга A2S максимальной длины соответствует траектории с управлением u(t) = = const = uq и помехой (5.11), начинающейся в точке S и приходящей в точку Е2 (рис. 5.6).
264
ГЛАВА 5
Для исключения бесконечно долгого асимптотического стягивания к минимальному контуру можно дополнить алгоритм управления переводом траектории из левой части полосы ЯхСгЯзСч в правую.
В силу примера 2 и следствия 5.1 имеет место
Теорема 5.2. Равенство Jm(z0) = т = р0 верно для любого zQ и при любых uo,£q,F, удовлетворяющих (5.4).
5.6. МИНИМИЗАЦИЯ ИНТЕНСИВНОСТИ РАСХОДА ТОПЛИВА ПРИ ЗАДАННОЙ ТОЧНОСТИ СТАБИЛИЗАЦИИ
В предыдущем параграфе было построено управление, приводящее динамическую систему (5.1)—(5.4) из любого начального положения в полосу |а?| < р, так что
|я(/)| < р — const, £>^i, р > Ро,
(6.1)
где р0 берется из соотношения (5.14). Исследуем теперь задачу минимизации средней интенсивности расхода топлива в системе (5.1)—(5.4) при ограничении (6.1) и условии бо F.
Сначала рассмотрим эту задачу при £ = 0. Множество допустимых управлений определим следующим условием. Именно, решение задачи будем искать среди всех законов управления, обеспечивающих заданную точность стабилизации (6.1) В качестве критерия эффективности стабилизирующего управления выберем функционал
{t	)
lim I \u(r)I dr > , z\— z(ti). t-+oo Hot J	I
(6.2) Из дальнейшего изложения будет ясно, что выражение в фигурных скобках (6.2) при оптимальном управлении и отсутствии помехи от zi не зависит. Функционал (6.2) характеризует относительную продолжительность времени работы реактивного двигателя с релейной характеристикой (5.2), или, что то же самое, среднюю интенсивность расхода топлива за период стабилизации.
Без ограничения общности для определенности положим F > 0. Далее для простоты ограничимся следующим классом управлений. Решение задачи будем искать среди программных управлений, обеспечивающих периодическое движение системы (5.1)—(5.4) в заданных пределах —р < x(t) < р (6.1). Соответствующая фазовая траектория должна представлять замкнутую кривую такую, что фазовая точка возвращается в исходное положение, сделав за период Т один полный оборот вокруг начала
ОБЕСПЕЧЕНИЕТОЧНОСТИ ПОВЕРХНОСТЕЙ
265
координат. Частным видом таких кривых будут траектории, проходящие последовательно через точки (—р, 0) и (р, 0) соответственно. Пусть Ti — время пребывания изображающей точки z в верхней фазовой полуплоскости, Т2 — время пребывания в нижней, так что Т = Ti + Т2. Назовем управления, обеспечивающие указанные выше движения, простыми периодическими. Данный класс управлений не исчерпывает всех возможных вариантов движений в полосе (6.1). Однако он удобен простотой технической реализации. При некоторых соотношениях параметров траектории из этого класса доставляют абсолютный минимум функционалу (6.2). Условие периодичности траекторий имеет вид
z(t + Т) = z(t) V t > /1.
(6.3)
Пример 6.1. Выбором простого периодического управления u(t) в системе (5.1)—(5.4) при s(/) = 0 требуется минимизировать функционал (6.2).
Рассмотрим следующий вид траекторий — замкнутые кривые 1, 2 на рис. 5.9. Эти кривые состоят из участков параболических траекторий динамических систем x = Fhx = F — и0. Фазовые траектории 1, 2 симметричны относительно оси Ох. Такие траектории могут реализоваться лишь при условии
Д< < Д<° = 4./ pF
~	V u0(uq - F)
(6.4)
порождаемом ограничениями (5.3), (6.1), Af° — продолжительность интервала постоянства отрицательного управления u(t) = — uq за период Т при движении по траектории 2 рис. 5.9. Значение функционала (6.2) в этом случае равно
VQ = -
Uq
(6.5)
и является точной нижней гранью этого функционала для любых допустимых движений внутри полосы — р <	< р, т. к. управление знакопосто-
янно, в силу чего нет перерасхода топлива на компенсацию возмущения F.
Будем далее для краткости называть режим управления между двумя последовательными моментами включения ta и выключения tp управления — импульсом управления. Импульс будем называть положительным, если значение управления на интервале (/«,//?) положительно и отрицательным — если значение отрицательно. Рассмотрим траекторию 6 на рис. 5.9. Два параболических участка этой симметричной
266
ГЛАВА 5
относительно оси Ох траектории определяются уравнениями х = F + и0 и х = F — ug. Соответствующее движение обеспечивается двумя последовательными противоположными по знаку импульсами управления. Пусть А/* — продолжительность положительного импульса, A/i — продолжительность отрицательного импульса. Соответствующие интервалы постоянства управления определяются формулами:
л/. _ 9 /2р(цо ~ F)
V и0(и0 + F) ’
/2р(ц0 4- F) у izo(«o - F) ’
(6.6)
Т = ДГ + Д<1, ДГ<Д<1.
Минимальная продолжительность интервала постоянства управления в режиме (6.6) равна продолжительности положительного импульса. Среди всех режимов, обеспечивающих простое периодическое движение динамической системы в заданных пределах — р < x(t) < р (6.1), максимальная продолжительность положительного импульса достигается на режиме (6.6) и соответствует А/*. При А/ > А/о наряду с отрицательными импульсами обязательно должны иметь место положительные. Поэтому при условии
тах(А/*, А/0) < А/	(6.7)
не существует способа управления, обеспечивающего движение в полосе (6.1). Пусть выполнено соотношение:
А/0 < А/ < А/*.
(6.8)
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
267
В этом случае минимум функционала (6.2) в рассматриваемом классе движений достигается в зависимости от соотношений параметров на траектории, принадлежащей к одному из пяти типов 2—6, указанных на рис. 5.9. Это утверждение доказывается сравнением всех порожденных простыми периодическими управлениями движений и здесь не приводится. Предположим, что время запаздывания Д/ (5.3) удовлетворяет условию:
max (Д/° ) < Д/ < Д/*.
V 2 J “
(6.9)
Соответствующая оптимальная фазовая траектория имеет структуру траекторий 4, 5, 6 на рис. 5.9. Обозначим через Ji, 62 продолжительность последовательных интервалов постоянства управления при движении по верхней полуплоскости и через <$з, J4, £5 — продолжительность интервалов постоянства управления при движении по нижней полуплоскости фазового пространства. Таким образом, продолжительность положительного импульса равна <?i +<£5, продолжительность отрицательного импульса — <У2 + за период обращения. На интервале продолжительности 64 управление u(t) = 0. Соответствующие интервалы определяются формулами:
63 = ^(F, Д/ - Ji), 64 = Ж “ <*1 Л),
Отвечающее условию (6.9) минимальное значение функционала (6.2) равно:
F 9?(F, ДГ/2) + 9?(F, Д/ - Д/*/2) + Д/
<p(F, Д/*/2) + <p(F, Д/ - Д/*/2) - Д/ ’
(6.11)
При выполнении условия
(6.12)
268	ГЛАВА 5
оптимальная фазовая траектория имеет структуру траекторий 2, 3, 4 на рис. 5.9. Обозначим через 5Х, <У2, <$з продолжительность последовательных интервалов постоянства управления при движении по верхней полуплоскости и через £4, <^5 — при движении по нижней. Таким образом, продолжительность положительного импульса составляет <У2, продолжительность отрицательного — <$з + 64, на интервале длиной Ji + £5 управление u(t) = 0. Величины интервалов определяются формулами:
_	(u0-F)(4p-2At40)
01 — \ ------————————— — zZXt,
Fu0
62 — At,
_	F(4p-2At*u0)
Аз = \ -----7--------Ь
у uo(uo - F)
Т — А 4- Л -1- А - /«о(4р - 2Д<2и0)
T1_J1+J2+fe J Flua F}
г 9 FP А 9 (u0-F)p 04 —	-7----77Г,	05 — Л/ ----,
у uq(uq - F)	у Fuq
т2 = 64+65 = 2./UoP Т = Тг+Т2.
У F(u0 - F)
Минимальное значение функционала при условии (6.12) равно
2А/	F
И) — „——Ч--
Ti 4- Т2	uq
(6.13)
(6.14)
Замечание. Если кривые 1—6 на рис. 5.9 отобразить симметрично относительно оси Ох, то соответствующие траектории также будут оптимальны.
Таким образом, решение задачи при e(t) = 0 полностью построено.
Рассмотрим теперь систему (5.1)-(5.4) при условии (6.1) и малой помехе
0 < е0 « F.	(6.15)
Определим эффективность управления и( ) функционалом
ф[и(.)] =sup V[u( ),e(Z)]. e(t)
(6.16)
Функционал ^[u(-),s(-)] определен формулой (6.2) и рассматривается на множестве U допустимых управлений u(z,r, п), обеспечивающих
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ПОВЕРХНОСТЕЙ
269
заданную точность (6.1) стабилизации динамической системы (5.1)—(5.4) при произвольной допустимой помехе e(t), смысл аргументов г, г, п при управлении и определен формулой (5.8). Обозначим через и0(/) оптимальное управление, доставляющее минимум функционалу Vo[u(•)] (6.2) в задаче без помехи.
Поставим задачу построения приближенно оптимального управления ueo(z, т, п) е U, для которого разность Ф[и£о(-)] - Уо[^о(•)] есть величина порядка s0. За основу при построении управления и£о возьмем программное движение при управлении uq(/), а именно, один из вариантов траекторий 1—6, изображенных на рис. 5.9 в зависимости от выполнения одного из условий (6.4), (6.9) или (6.12). Не ограничивая общности, разберем лишь случай, соответствующий условию (6.9). Остальные варианты рассматриваются аналогично по следующей схеме.
Рассмотрим частный случай движения, изображенный на рис. 5.10. Это движение задается трубкой возможных траекторий, каждая из которых удовлетворяет условию: — р < x(t) < р. Внешняя (внутренняя) граница трубки траекторий определяется наиболее отклоняющимися влево (вправо) по ходу движения траекториями, аналогично изображенным на рис. 5.5, где эти траектории составляют внешний контур	и
внутренние границы ДО, В,, «=1,2 трубки траекторий. Согласно формуле (5.10) интервалы постоянства управления и(/), обеспечивающего совместно с помехой (5.10)движение по внешнему контуру N\A\N2A2A3, могут быть вычислены по формулам (6.10), где вместо F надо положить В + £о при движении по верхней полуплоскости фазового пространства, и положить F - so при движении по нижней. Таким образом, внешняя и внутренняя границы трубки траекторий составлены из программных движений типа 4-5 рис. 5.9 при различных значениях F. Подобно управлению (5.12), удерживающему движение в контуре	в изображенном на рис. 5.10 контуре	движение также будет
270
ГЛАВА 5
удерживаться, если принять за линии переключения управления иео дуги т41В3, Л2В1, А3В2. Внутренние границы трубки целиком определяется координатами точек A,, i = 1,2,3 внешнего контура.
Управление и(/), обеспечивающее движение по построенной трубке траекторий, должно удовлетворять условию (5.3). Этого можно добиться следующим образом. Обозначая при вычислении внешнего контура величину А/ (5.3) в формулах (6.10) через А/, получим однопараметрическое семейство трубок траекторий, зависящих от А/. Поиск участка траектории с минимальной продолжительностью интервала постоянства отличного от нуля управления иео производится аналогично поиску соответствующего участка при доказательстве лемм 5.2 и 5.3 § 5 настоящей главы. Обозначим продолжительность этого участка через A/m(A/). Трубка траекторий, движение по которой отвечает условию (5.3), определяется решением относительно параметра А/ следующего алгебраического уравнения: А/ = Д/Ш(А/). Аналогично управление и€о следует искать в остальных случаях, т. е. при условии (6.4) и (6.12).
Покажем, что построенное управление иео может рассматриваться как решение поставленной задачи, т. е. как приближенно оптимальное. В силу условия (6.15) и проведенного построения верна оценка |Д/ - А/| ~ £о. Следовательно, границы трубки будут близки к одной из кривых типа 1—6 на рис. 5.9.
Отсюда следует требуемое утверждение:
*[иМ - Vb[u0(-)] < С^о,
где константа С не зависит от e0.
Таким образом в качестве приближенно оптимальных значений функционала (6.16) можно в зависимости от соответствующих соотношений между параметрами u0, e0, F, р, St принять выражения (6.5), (6.11) или (6.14).
Приложение
ПРИМЕНЕНИЕ МЕТОДОВ КОМПЬЮТЕРНОЙ АЛГЕБРЫ В ИЗУЧЕНИИ МЕХАНИЧЕСКИХ СИСТЕМ
Хорошо известно, что компьютер может успешно оперировать не только с числами, но и с математическими символами. Эта быстро развивающаяся область вычислительной математики получила название компьютерной алгебры (или символьных вычислений). Основной чертой языков компьютерной алгебры является то, что они явно или неявно могут оставлять символьные переменные невычисленными (т. е. не заменяют их числами). Кроме того, они “умеют” упрощать и преобразовывать к тому или иному виду символьные выражения.
Существует достаточно большое количество систем компьютерной алгебры. В России наиболее распространены такие системы, как Reduce, Mathematica, Macsyma, Derive, Maple и некоторые другие. Они различаются по целому ряду позиций, таких как универсальность, потребляемые ресурсы компьютера, удобство программирования на языке системы, возможность создания библиотек прикладных программ, эффективность разного рода символьных вычислений, пользовательский интерфейс, эффективность выполнения операций с плавающей точкой, построение графиков, генерация выражений на алгоритмических языках и т. п.
На наш взгляд, системы Reduce и Maple из упомянутых выше лучше всего подходят для приложений в области механики. Они также весьма универсальны для проведения общематематических выкладок и позволяют создавать библиотеки прикладных программ. Язык Reduce известен уже более 20 лет и по нему имеется русскоязычная литература1,2.
Система Maple создана в середине 80-х годов в Канаде в университете Ватерлоо. Прикладные библиотеки системы содержат более 2000 математических операций. Например, дифференцирование, интегрирование, нахождение корней уравнений, разложение полиномов на множители,
1	Климов Д.М., Руденко В.М. Методы компьютерной алгебры в задачах механики. — М.: Наука, 1989. — 214 с.
2	Теоретическая механика. Вывод и анализ уравнений движения на ЭВМ: Учеб, пособие для вузов. В 2 ч. Ч. 1 / В. Г. Веретенников, И. И. Карпов, А. П. Маркеев и др.; Под ред. В. Г. Веретенникова. — М.: Высш, шк., 1990. — 174 с.
272
ПРИЛОЖЕНИЕ
разложение функций в ряд Тейлора, матричные операции и многие другие. Система Maple имеет относительно маленькое ядро (500 КВ), написанное на языке Си, что сделало возможным её внедрение на различных типах ЭВМ. (Например, АТ 386 под MS DOS, AT 386 под Unix и т. д. — всего более 36 реализаций.) Одним из ограничений системы (в настоящее время несущественным) является невозможность эксплуатации на АТ 286.
В настоящем приложении приводится краткое описание основных возможностей системы на примерах её использования в механике. Более подробное описание по системе на русском языке можно найти в препринте1 *.
6.1. УРАВНЕНИЯ ДВИЖЕНИЯ
Вывод уравнений Лагранжа второго рода. Рассмотрим движение голономной системы с п степенями свободы. Обобщенные координаты обозначим через gi,... , qn- На систему действует к активных сил Fj (j = 1,... , к), точки приложения которых определяются радиусами-векторами и,... ,r/f. Под виртуальной работой активных сил понимают следующее выражение:
к
= (1.1)
J=1
где Srj — виртуальные перемещения точек приложения сил.
Поскольку rj = (ij(?i,... , qn,t), можем записать
«=1
и 6А на виртуальном перемещении Jgi,... ,6qn может быть представлена в виде	J
п	*
SA^^Qi^q^qi-	(1.3)
1=1
Величина Qi называется обобщенной силой, соответствующей обобщенной координате д, (г = 1,... , п). Подставляя (1.2) в (1.1), получаем
п к п
SA = lDXF^)s<ii-	U-4)-
1=1 J=1 ч>
Следовательно, для вычисления обобщенной силы имеем формулу
1 Журов А.И., Карпов И.И., Шингарёва И.К. Основы Maple. Применение в механике. —
Препринт № 536. - М, ИПМех РАН, 1995. — 76 с.
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
273
Пусть Т = T(qi,... , qn, <71,... , qn, t) — кинетическая энергия системы. Уравнения движения материальной системы могут быть записаны в форме п дифференциальных уравнений второго порядка
(1.6) dt^dqi dqi
Эти уравнения называются уравнениями Лагранжа второго рода.
Автоматизированное получение уравнений Лагранжа в аналитической форме. В дальнейшем для автоматизированного получения уравнений движения широко используется система аналитических вычислений Maple. Для читателя, не знакомого с этой системой, приводятся пояснения различных команд и операторов, используемых в приводимых текстах процедур.
При составлении программ все операторы будем разделять на два вида: операторы, которые для новой механической системы потребуется переписывать заново, и операторы, которые останутся неизменными. Первой группе операторов всегда будет предшествовать оператор (комментарий):
#	User ;
(далее следуют операторы, которые потребуется переписывать будущему пользователю). Второй группе операторов будет предшествовать комментарий:
#	Computer ;
>	далее процесс вывода уравнений идет без участия пользователя). Символ ; означает конец оператора.
Зададим наименования обобщенных координат д, (г = 1,... , п) и определим проекции активных сил Fxj, Fyj1 FZj, действующих на механическую систему в точках с декартовыми координатами Rxj, Ryj, Rzj (J = 1,... ,fc), в виде
#	User ;
var: =[ql,q2,q3,q4] ;
Fl: = [Rxl,Ryl,Rzl,Fxl,Fyl,Fzl] ;
F2:=[Rx2,Ry2,Rz2,Fx2,Fy2,Fz2];
F3:=[Rx3,Ry3,Rz3,Fx3,Fy3,Fz3];
Force:=[Fl,F2,F3];
Здесь условно n принято равным 4, a k равным 3. Считая кинетическую энергию механической системы T(qi,...	- , gn3) задан-
ной, составим процедуру Lagr на языке Maple, реализующую вывод уравнений (1.6).
10 — 2185
274
ПРИЛОЖЕНИЕ
#	Computer ;
Lagr:=proc(var,Force) # группа операторов A; local n,k, j,i,qt,qtt,dTq,dTqt,k,Rx,Ry,Rz,Fx,Fy,Fz,Q,DT,eqn; n:=nops(var); k:=nops(Force);
#	группа операторов В;
for j from 1 to к do
Rx[j] : =op(l,Force [j] );	Fx[j] : =op(4,Force [j]);
Ry[j]:=op(2,Force [j]);	Fy[j]:=ор(Б,Force [j]);
Rz[j] :=op(3,Force[j]); Fz[j] :=op(6,Force[j]); od;
#	группа операторов С;
for i from 1 to n do qt[i]:=cat(var[i],*1() od; for i from 1 to n do qtt[i]:=cat(var[i],*11 *) od;
#	группа операторов D;
for i from 1 to n do
dTq[i]:=diff(T,var[i]); dTqt[i]:=diff(T,qt[i]) ; od;
#	группа операторов F; for i from 1 to n do
Q: =sum ( 1 Fx [j ] *dif f (Rx [j ] , var [i])+ Fy[j]*diff(Ry[j],var[i])+ Fz[j]*diff (Rz[j] ,var[i])1’ j ,=1. .k);
DT[i] :=sum( >diff (dTqt[i] ,qt[j] )*qtt[j] + diff(dTqt[i],var[j])*qt[j]1,’j >=1..n); eqn[i] :=DT[i]-dTq[i]-Q;
od;
RETURN(normal(convert(eqn,list))) end;
Группа операторов А описывает переменные, которые используются только в теле данной процедуры, и определяет с помощью функции поре число элементов в списках var и Force. Группа операторов В выделяет из списка Force проекции k активных сил Fj (j = 1,... , k) и координаты их точек приложения п,... ,г&. Группа операторов С формирует имена скоростей и ускорений обобщенных координат («приклеивает» к имени обобщенной координаты соответственно один и два апострофа). Подразумевается, что в процессе программирования кинетической энергии были использованы такие же имена. Группа операторов D вычисляет производные dT/dqi, dT/dqi. Группа операторов F вычисляет обобщенные силы и полную производную по времени выражения dT/dqi, используя формулу:
__	/ g	д дТ-\
dt	\&4j	/
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
275
Построение приближений уравнений движения. Пусть gf (г = 1,...,п) — положение механической системы, в окрестности которого требуется провести исследования. Поведение системы описывается системой уравнений (gi,... , gn, Qi, • • • , gn, Qi, • • • , gn, t) = 0 (i = 1,... ,n). Обозначим отклонение от этого положения через yi = qi - (г = 1,... , п). Требуется построить полиномы Р,- ЛГ-ой степени от отклонений, которые с точностью до членов O(N + 1) соответственно совпадают с функциями (gi,... , gn, <ji, • • • , gni gi, • • • ,	0
(г = 1,... ,n). Составим процедуру approx, которая преобразует уравнения (4) к указанному виду. В качестве аргументов процедуры будем передавать список уравнений [fi = 0,/2 = 0, ...,/п = 0], список имен отклонений, имен переменных и заданных точек в виде [yi = gi - Pi, 2/2 = g2 - P2,. «,J/n = gn - Pn], а также степень полиномов N. Процедура будет возвращать список полиномов в отклонениях.
#	Computer ;
approx:=proc(tunc,var,N)
#	группа операторов A;
local local k,n,i,y,dev,q,qt,qtt,eqp,f,eqn;
k:=nops(tunc); n:=nops(var);
#	группа операторов В;
for i to n do y[i]:=op(i,var[i]) od;
for i to n do dev[i]:=op(2,var[i]) od;
for i to n do q[i]:=op(l,dev[i]) od;
for i to n do qt[i]:=cat(q[i],'1 *) od;
for i to n do qtt [i] :=cat(q[i] ,'1 ’ *) od;
for i to n do eqp[i]:=op(l,dev[i])=-op(2,dev[i]) od; for i to k do f[i]:=op(l, func[i]) od;
#	группа операторов С;
readlib(mtaylor);
#	группа операторов D;
for i to k do eqn[i]:= mtaylor(f[i], [eqp[j] $ j=l..n, qt[j] $ j=i. .n,qtt[j] $ j=l..n],N+1);
#	группа операторов F;
for j to n do
eqn[i] :=subs(dev[j]=y [j] ,eqn[i] );
eqn[i] :=subs(qt [j]=cat(y [j] , ‘1 ‘) ,eqn[i] );
eqn[i] :=subs(qtt [j]=cat(y [j] , *11') ,eqn[i] ); od;
od;
RETURN(normal(convert(eqn,list))) end;
io*
276
ПРИЛОЖЕНИЕ
Группа операторов А описывает переменные, которые используются только в теле данной процедуры, и определяет с помощью функции nops число элементов в списках func и var. Группа операторов В выделяет из списка var имена отклонений г/,, разности д,- — Pi, наименования переменных д,, формирует имена скоростей и ускорений переменных (“приклеивает” к имени переменной соответственно один и два апострофа). Подразумевается, что в процессе программирования функций использованы такие же имена. Далее формируются выражения д,- = р, (так обозначаются окрестности разложения в ряд Тейлора в стандартной процедуре). И наконец, выделяются выражения для разложения в ряд. Во всех этих операторах (г = 1,... , п).
В системе Maple ряд основных часто используемых функций загружаются в момент запуска системы, остальные функции можно загрузить из библиотечных файлов системы, например, с помощью функции readlib. Так, группа операторов С осуществляет загрузку библиотечной функции taylorm, предназначенной для разложения функции многих переменных в ряд Тейлора. Группа операторов D осуществляет разложение в ряд Тейлора по переменным g,, д', д". Группа операторов D записывает эти разложения в переменных г/,, р',
6.2. ВЫВОД С ПОМОЩЬЮ ЭВМ УРАВНЕНИЙ ДВИЖЕНИЯ УПРУГОГО ТЕЛА
Предположим, что требуется получить уравнения (1.10) и (1.14) из Главы 4 для конкретного объекта, если для него уже вычислены матрицы и Используем для этого систему аналитических вычислений Maple. Будем полагать, что для задания величин , являющихся элементами матрицы написана процедура h:
#	User ;
h:=proc(n,kl,k2) local work;
присвоение значения переменной work
RETURN(work) end;
а для задания величин , являющихся элементами матрицы — процедура I:
#	User ;
l:=proc(n,r,kl,k2) local work;
присвоение значения переменной work
RETURN(work)
end;
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
277
Для удобства программирования перепишем уравнения (1.10, Глава 4) в следующей форме:
Лз^з + (Л2 - Ai)(Jicj2 =	“ ^1)7172 + У^ 1,2,3"
00	00	00
_9V'<?<n)	-9V<?W	9V^c(")
Z ol,w,1,2,3 z / °2,g,w, 1,2,3 Z / . °2,g,to,l,2,3> n==l	n = l	n = l
А1Ш! + (Л3 - Л2)си2Ыз = -^(Аз ~ ^2)7273 + У? ^1л,2,3,1-
oo	oo	00
“2	^1 J,2,3,1 “ 2 У2 ^2,g,w,2,3,l “ 2 У2 ^2 J,Ш,2,3,11 (2Л )
n=l	n=l	n=l
А2й2 + (Л1 - Л3)«зо>1 = -^(Л - Лз)7з71 +	$2 51?7,з,1,2_
Ло	no п=1
oo	oo	oo
9 \ ' c(n) _ 9 \ л a(n)	9 \ A a(n)
“2 2L °l,tv,3,l,2	2 / > ^2,q,ш,3,1,2 “ 2 Z . °2,g,w,3,l,2>
n=l	n=l	n—1
где
^l,x,kl,k2,k3 ~	“ (xki ~ xk2)^k1k2^~
4-	Нк2к2) +
= xn [-^+ яЦ2)].
Здесь в отличие от (1.10, Глава 4) моменты инерции тела А, В, С для удобства программирования обозначены соответственно 41, А2, Л3. Проекции wi, с^2,0,3 угловой скорости cv на оси Ох\, Ох2, Ох3 обозначим переменными wl, w2, w3, а их производные d>i, о>2, а>3 — переменными wtl, wt2, wt3, проекции вектора 7 на оси Oa?i, Ох2, Ох3 обозначим переменными gl, g2, g3. Величину p/R$ зададим с помощью переменной тгОЗ, величины qniqn — с помощью индексированных переменных qm[n], qmt[n]. В принятых обозначениях процедуры для получения выражений Фг, дГ1 Фгп, д™, входящих в уравнение (1.14, Глава 4), можно записать в виде
# Computer ;
fbl:=proc(r)
global h,wl,w2,w3;local work;
work:=
2*(h(r,l,2)*wl*w2+h(r,1,3)*wl*w3+h(r,2,3)*w2*w3) -(h(r,2,2)+h(r,3,3))*wl**2-(h(r,3,3)+h(r,l,l))*w2**2
278
ПРИЛОЖЕНИЕ
-(h(r,1,l)+h(r,2,2))*w3**2;
RETURN(work);
end;
#	Computer ;
gml:=proc(r)
global mr03,h,gl,g2,g3;local work;
work:=
mr03*(6*h(r,1,2)*gl*g2+6*h(r,1,3)*gl*g3
+6*h(r,2,3)*g2*g3+h(r,1,l)*(3*gl**2-l) +h(r,2,2)*(3*g2**2-l)+h(r,3,3)*(3*g3**2-l);
RETURN(work);
end;
#	Computer ;
fb2:=proc(r,n)
global qm,qmt,l,wl,w2,w3;wtl,wt2,wt3;local work;
work:=
2*qmt[n]*(wl*(l(n,r,2,3)-l(n,r,3,2)) +w2*(l(n,r,3,l)-l(n,r,1,3)) +w3*(l(n,r,l,2)-l(n,r,2,1)))
+qm[n]*(wtl*(l(n,r,2,3)-l(n,r,3,2))
+wt2*(l(n,r,3,l)-l(n,r,1,3)) +wt3*(l(n,r,l,2)-l(n,r,2,1)) -wl**2*(l(n,r,2,2)+l(n,r,3,3)) -w2**2*(l(n,r,3,3)+l(n,r,1,1)) -w3**2*(l(n,r,1,l)+l(n,r,2,2)) +wl*w2*(l(n,r,1,2)+l(n,r,2,1)) +wl*w3*(l(n,r,1,3)+l(n,r,3,1)) +w2*w3*(l(n,r,2,3)+l(n,r,3,2)));
RETURN(work);
end;
#	Computer ;
gm2:=proc(r,n)
global mr03,l,gl,g2,g3;local work;
work:=
mr03*qm[n]*(3*(
(l(n,r,l,2)+l(n,r,2,l))*gl*g2
+(l(n,r,1,3)+l(n,r,3,1))*gl*g3 +(l(n,r,2,3)+l(n,r,3,2))*g2*g3)
+l(n,r,1,l)*(3*gl**2-l)+l(n,r,2,2)*(3*g2**2-l)
+l(n,r,3,3)*(3*g3**2-l));
RETURN(work);
end;
Процедуры для получения выражений S^kx k2 k3 и	BX0^-
щих в правые части уравнений (2.1), можно записать в следующей форме:
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
279
#	Computer ;
sbl:=proc(n,kl,k2,k3,xf)
global qm,h;local work;
work:=
qm[n]*(-xf[k1]*xf[k3]*h(n,k2,k3)
-(xf[к1]**2-xf[k2]**2)*h(n,kl,k2)
+xf[kl]*xfEk2]*(h(n,kl,kl)-h(n,k2,k2))
+xf[k2]*xfEk3]*h(n,kl,k3));
RETURN(work); end;
#	Computer ;
sb2:=proc(n,kl,k2,k3,xf,yf) global h;local work;
work: =
yfEn]*(-xf[kl]*h(n,kl,k3)-xf[k2]*h(n,k2,k3)
+xfEk3]*(h(n,kl,kl)+h(n,k2,k2)));
RETURN(work); end;
Для получения членов, определяющих влияние упругих деформаций на движение трехгранника	в уравнениях (2.1), используем про-
цедуру adnl(k):
#	Computer ;
adnl:=proc(k)
global mr03,qm,qmt,gl,g2,g3,wl,w2,w3,wtl,wt2,wt3;
local work,wrkl,wrk2,wrk3,gg,w,kl,k2,k3,si,s2,s3,s4,nbg; work:=
wrkl:=E1,2,3];wrk2:=[2,3,1];wrk3:=[3,1,2]; gg:=Egl,g2,g3]; w:=[wl,w2,w3];wt:=[wt1,wt2,wt3];
к1:=wrk1Ek];k2:=wrk2Ek];k3:=wrk3[k];
#	User ;
#	Здесь нужно определить локальную переменную nbg,;
#	которая означает верхний индекс (вместо символа оо);
#	в знаках суммирования, входящих в уравнения;
#	Computer ;
sl:=sum(<sbl(n,kl,k2,k3,gg)‘,‘п<=1..nbg);
si:=sum(<sbl(n,kl,k2,k3,w)‘,‘n<=l..nbg);
sl:=sum(‘sb2(n,kl,k2,k3,wt,qm)‘,^‘=1-.nbg);
sl:=sum(<sb2(n,kl,k2,k3,w,qmt) ‘, ‘n^l. .nbg);
work:=6*mr03*s1-2*s2-2*s3-2*s4;
RETURN(work);
end;
где k — порядковый номер уравнения в системе уравнений (2.1);
280
ПРИЛОЖЕНИЕ
Случай квазистатических движений упругого тела. Уравнения движения упрощаются, если сделать дополнительные физические предположения. Введем величину е = о>о/^1, гдео>0 —среднее движение центра масс (а>0 = 2тг/То, а То — период обращения центра масс по орбите); Qi — наименьшая частота свободных упругих колебаний тела. Введем также безразмерное время г — wqI в уравнениях движения и величины til =	^2 =	= ^з/^о, уп = ^/(^о^о)- Разделим
правые и левые части уравнений движения на и;2. После выполненных преобразований в уравнениях (2.1 )u?i, о?2, p/Rq будут соответственно заменены на величины d>i, d)2, о)3, т, а уравнение(1.14, Глава 4) примет вид
S2q" +	+ a2qr = S2
ОО	оо
9г 9гп Фг Фгп
П=1	П=1
(2.2)
где штрихи означают дифференцирование по г, сгг = Qr/Qi (г = 1,2,...), а в выражениях для qr, grn, Фг, ФГп величины o?i, о;2, ^з, p/Ro заменены соответственно на d>i, £2, d)3, т. Если в выражении (2.2) отбросить правую часть, то получится уравнение, описывающее свободные затухающие упругие колебания тела. Соответствующее ему характеристическое уравнение имеет корни
\ *к 2,’0Гг Л fX£ \2
Ar = -sbojQCTr ± г — \ 1 - I —с^осгг ) • е2	е V \ о /
Характерное время затухания свободных колебаний имеет порядок е2/%.
Будем предполагать, что
2тг е2	2тг	_ч
о-«-------«—,	2.3
Hi	хио	uQ
т. е. характерное время затухания свободных колебаний много меньше периода То обращения центра масс по орбите, но много больше наибольшего периода свободных упругих колебаний. Предположим также, что период То обращения центра масс по орбите и характерное время движения тела как целого относительно центра масс имеют одинаковый порядок, т. е. тах(и>1,а)2,а)з) ~ 1.
Условие (2.3) можно записать в виде
1.
В предельном случае (абсолютно твердое тело) е —> 0 и из выражения (2.2) следует, что qr = 0 (г = 1,2,...). При 6 = 0 асимптотическое
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
281
решение уравнений движения можно найти методами, разработанными для систем дифференциальных уравнений с малым параметром при старших производных [9]. Свободные затухающие колебания, отвечающие выражению (2.3), дают часть асимптотического решения типа погран-слоя. В интервалах времени порядка Tq и больших затухающими колебаниями можно пренебречь и рассматривать только регулярную часть асимптотического решения, соответствующую квазистатическим режимам движения твердого тела [106].
Считая, что х порядка £1+<5 (0 < 6 < 1), найдем регулярную часть асимптотического решения в виде рядов по степеням ? и у. С погрешностью О (б4) это решение записывается в виде
9г = Л[£2(5г-Фг)-2хе2Ь0(</г-Фг)/] (г =1,2,...).	(2.4)
0*г
При вычислении qr величины и, (г = 1,2,3) определяются из уравнений (2.1):
й'з =	(^1^2 “ Зп*717г) + О(е2),
Аз
w'i = ~Аз л (“2«з - ЗЙ17273) + О(е2), А1
о»2 = - Л1 . 713 (W3W1 - ЗЙ17371) 4- О(е2).
А2
Зависимость qr, qf от 7, (г = 1,2,3) можно получить с помощью следующих операторов языка Maple:
# Computer ;
df:=proc(expr,x)
global wl,w2,w3,wtl,wt2,wt3,gl,g2,g3;
global mr03,gt1,gt2,gt3,gtt1,gtt2,gtt3;
local work;
work:=
dif f(expr, wl)*wt1+diff(expr,w2)*wt2+diff(expr,w3)*wt3 diff(expr,gl)*gt1+diff(expr,g2)*gt2+diff(expr,g3)*gt 3 diff(expr, gt 1)*gtt1+diff(expr, gt 2 )*gtt2
+diff(expr,gt3)*gtt3;
work:=subs(wtl = -a321*(w3*w2-3*mr03*g3*g2),work); work:=subs(wt2 = -al32*(wl*w3-3*mr03*gl*g3),work); work:=subs(wt3 = -a213*(w2*wl-3*mr03*g2*gl),work);
RETURN(work)
end;
qm[r] : = gml [r] -fbl [r] ;
282
ПРИЛОЖЕНИЕ
qm[r] := eps**2*(qm[r]-xi*2*bmo*df(qm[r],x))/sg[r]**2;
qmt [r] : = df (qm[r] ,x) ;
rel: = adnl(l)/A3;
re2:= adnl(2)/Al;
re3:= adnl(3)/A2;
lei:= wl3+a213*(w2*wl-3*mr03*g2*gl); le2:= wll+a321*(w3*w2-3*mr03*g3*g2); le3:= wl2+al32*(wl*w3-3*mr03*gl*g3);
где дифференцирование по времени введено оператором df(*,х), символ * обозначает дифференцируемое выражение; переменные а213, а321, а132 соответственно обозначают (А2 — AJ/A3, (A3 — A2)/Ai, (Ai — А3)/А2, оператор sg[r] — величину сгг. Выполняя эту программу, получаем уравнения (2.1) для случая квазистатического движения упругого тела. В переменных lei, 1е2, 1еЗ будут храниться не зависящие от х и £2 члены уравнений (2.1), а в переменных rel, ге2, геЗ — зависящие, взятые с такими знаками, что выполняются соотношения lel=rel, 1е2=ге2,1еЗ=геЗ. Переменными wll, wl2, wl3 обозначены wj, w'2, w'3. В правых частях уравнений отброшены величины порядка б4 и выше. Эти уравнения являются приближенными и описывают движения тела как целого относительно центра масс (т. е. трехгранника средней системы координат Ож1Ж2жз вокруг точки О).
Чтобы система уравнений, получаемых с помощью приведенной программы, была замкнутой, к ней необходимо добавить три независимых скалярных кинематических соотношения. Предположим, что ориентация трехгранника ОХ1Х2Х3 в орбитальной системе координат задается углами Эйлера, тогда эти соотношения имеют вид
= ф' sin 0 sin <р + 6' cos ip 4- /?1,
cj2 = sin 0 cos 92 4-0х sin 92 4-(2.5) CV3 = ф' COS0 + <рг + /?3.
Проекции векторов о, /3, у на оси O#i, 0x2, Охз выразятся формулами
Qi = cos cos <р — sin <ф sin <р cos 0,
z	а2 = — cos sin <р — sin <ф cos <р cos 0,
аз = sin ip sin 0,
/3i = sin <ф cos ip 4- cos sin <p cos 0,
/?2 = — sin sin 99 4-cos cos 99 cos 0,	(2.6)
{З3 = — cos ф sin0, 71 = sin (p cos 0, 72 = cos <p sin 0, 73 = cos 0.
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
283
Подставляя полученные значения 7, и в уравнения (2.1), получим систему дифференциальных уравнений второго порядка относительно переменных Vs которую можно разрешить относительно старших производных. При этом с точностью до членов порядка б4 в правых частях уравнений (2.1) величины 0", 9?" можно заменять следующими вытекающими из соотношений (2.5) выражениями
= [(d)2 cos 9? — cos *0 cos 0 + £1 sin 9?)/ sin 0]z, 0" = [£»! cos ip — W2 sin 9? — sini/j]',	(2.7)
9?" = [£3 - cos 0 - /?з]' .
Вычисление собственных форм в средней системе координат. Предположим, что известны собственные формы U(n) = (Uxn\ Uyn\ U^)T, описывающие свободные упругие колебания тела в некоторой декартовой системе координат Oxyz. Найдем выражение для собственных форм, описывающих свободные упругие колебания тела в средней системе координат. Для этого добавим к n-й собственной форме вектор D(n), содержащий шесть произвольных констант cj^
Первые три вектора правой части равенства (2.8) отвечают поступательному движению, а остальные три — вращательному движению тела как абсолютно твердого. Константы определяются из двух условий: 1) начало средней системы координат находится в центре масс тела; 2) относительный кинетический момент в средней системе координат равен нулю.
Проделав необходимые преобразования, получим выражения для соб-
284
ПРИЛОЖЕНИЕ
где
В этих выражениях (i,j = 1,2,3) обозначают величины, вычисленные по формуле (1.9) в системе координат Oxyz, т — масса тела.
В качестве примера использования описанных процедур рассмотрим движение пологой сферической упругой оболочки на круговой орбите. Пусть Ох^хъхз — средняя система координат с началом в центре масс тела. Оси Ох\, 0x2, Охз, при отсутствии деформаций тела направлены вдоль главных центральных осей инерции.
Деформацию и представим в виде ряда
оо
« = L<?’WuW(a;i’^^3),	(2.10)
1=1
где Qi(t) — нормальные координаты; = (ж1,Х2,^з) — собственные формы свободных упругих колебаний оболочки в средней системе координат.
Оболочками в теории упругости называют тела, один из размеров которых — толщина — мал по сравнению с двумя другими. С геометрической точки зрения оболочка определяется ограничивающими ее лицевыми и (если она не замкнута) боковыми поверхностями. Обычно оболочку описывают, задавая срединную (равноудаленную от лицевых) поверхность, ее граничный контур и толщину
Принято делить оболочки на тонкие и толстые в зависимости от величины отношения h/R, где h — толщина; R — наименьший линейный размер срединной поверхности. Обычно оболочку относят к тонким при h/R /20. Эта оценка условная, приблизительная. Теорию тонких оболочек применяют и при h/R ~ 1/5 4-1/31. В теории тонких оболочек при рассмотрении деформации оболочки применяют гипотезы Кирхгофа [13]:
1 Прочность. Устойчивость. Колебания: Справ.: В 3 т. / Под общ. ред. И. А. Биргера, Я. Г. Пановко. T. 3. — М.: Машиностроение, 1968. — 567 с.
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
285
1. Волокно, нормальное к срединной поверхности, до деформации остается нормальным к деформированной срединной поверхности, не меняя при этом своей длины.
2. Нормальными напряжениями на площадках, параллельных срединной поверхности, можно пренебречь по сравнению с прочими напряжениями. Пусть оболочка является однородным изотропным телом. Кроме того, будем предполагать, что она пологая и тонкая и совершает только упругие продольные колебания вдоль оси симметрии (упругие деформации в направлении, перпендикулярном оси симметрии, малы по сравнению с дефор
мациями, параллельными оси симметрии).
Пусть Oxyz — система координат, образованная главными центральными осями инерции недеформированного тела (при отсутствии деформаций система Oxyz совпадает с системой Ох 1X2X3).
В принятых предположениях упругие продольные колебания оболочки описываются в системе Oxyz собственными формами вида (выражение (2.9):

О
о
Fk,l{£) cos 1т1
О О Fkil(£) sin/??
(2.П)
где k, I = 0,1,2,...; угол т) и радиус £ (рис. 2.5) связаны с координатами элемента dm в системе координат Oxyz соотношениями х — £costj, у - ^sin?;.
Функция Fkti(£) является линейной комбинацией степенной функции и функций Бесселя:
Fk,i(C) = Ak,i£l 4- ВкД^Ьк^) 4- Ck,iJi(bk,i£),
где Akj, Bkth Ck,h bk,i — постоянные, определяемые граничными условиями и условиями нормировки.
В средней системе координат ОХ1Х2Х3 собственные формы (2.11) для I = 1 записываются в виде

zDk О (Fk,i(£) -(Dk)cosr]
О zDk (Fkj(£) -$Dk) Sin 7]

286
ПРИЛОЖЕНИЕ
где Dk — постоянные для данной оболочки выражения,
Dk = ^~ J xV^ dm = ^~ J yV^ dm, V	V
где Ai — момент инерции оболочки относительно оси Ох. Для I / 1 собственные формы в средней системе координат будут иметь вид (2.11).
После ортогонализации собственные формы и принимают следующий вид:
= dk
и"^’1) = dk
zhk О (Ф/с,1(£) -^hk)cosT]
О zhk (Ф*,1(£) sin т]
где dk — коэффициент нормировки,
/с-1
hk = Dk - DiSifk (к > 1), hi = Di, i=l
/с-1
Фм(О = я,1Ю-53Ф.,1(е)5<л (л>1), Ф1>1ю = г1>1(е), «=1
Si,k = [	dm (i,j = 1,2,...).
При упругих колебаниях оболочки возникают силы внутреннего трения. Будем полагать, что они описываются с помощью диссипативной функции Рэлея:
оо
Ф = Х6	+ Як,2) +	+ 9?) •
Чс=0	/=1	J
(2.12)
где х — безразмерный параметр; b — положительная константа. Функции Qk,i(t) и Qk,2(t) обозначают соответственно нормальные координаты в выражении (2.10) при собственных формах и Им соответствуют частоты свободных колебаний упругой оболочки; функции и qi(t) обозначают соответственно нормальные координаты в этом же выражении при собственных формах и u,z^’^ для I / 1, и им соответствует частота П, свободных колебаний упругой оболочки.
Рассмотрим случай, когда центр масс оболочки движется по круговой орбите. Пусть То — период обращения центра масс по орбите,
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
287
wq = 2тг/7о, cv — абсолютная угловая скорость трехгранника ОХ1Х2Х3 (проекцию на ось Ох^ обозначим щ). Введем орбитальную систему координат ОХ1Х2Х3: ось ОХз направлена вдоль радиуса-вектора Ro центра масс относительно притягивающего центра, а оси ОХ2 и OXi — соответственно по бинормали к орбите, и по ее трансверсали в сторону движения центра масс. Единичные векторы осей OXi, ОХ2 и ОХз обозначим соответственно а, /3, 7, а их проекции на ось Oxi — а,-, Д-, 7,-.
Дифференциальные уравнения движения оболочки относительно центра масс, которое представляет собой вращение тела как целого (движение трехгранника ОХ1Х2Х3 относительно центра масс), и деформации отдельных его элементов в рамках линейной теории упругости можно записать в виде
2 00
аш3 =	Нк +	+ 71,4^2^1^3 - Зо;2717з)+
1	/с=0
4-72,к (^1 — ^2^3 4- Зо;2727з)] ,
2	°°
о>1 4- (а — 1)(с^2^з — За;2727з) = -д- У^ Нк [72,/с^з 4- 72,л(^з 4- а>10>2“ 1 /с=0
-3^7172) +71лМ “^1 4-3^о(“71 “ 27^ - 1))], 2 00
с^2 4- (а “ 1)(^з^1 — За;27з71) = — У^ Нк [71,/с^з 4- 71 л(^з “ u>iu>24-
4-3^07172) 4- 72,к (^з “	4" 3^o(27i 4" 72 “ 1))] > (2.13)
71,к 4- 2x^1,171,/С 4- 0^171,к 4- ЪНк^шз 4-	“ ^з)“
к=0
“272,^3 4- 72,fc^i^2)^/c — 7i,/c(u;i 4-^1)] = 6о>о727з#л4-
+^о У? [3 (72,^7172 4- 71,л(271 + 7*2 “ 1))^ + 71,л(—З71 “ З72 4- 2)], к=0
72,к + 2x^1,192,к 4- ^1,172,к +	4" У2[(?2,fc(^2 “ ^з) +
fc=o
+2gi,/eW3 + 71^1^2)	- 72,л(^? +^2)] = 6^о717зЯл+
4-о>2 У?[3(дх,л7172 4- 72,/с(272 4" 71 “	4" 92,л(“^71 ~ З72 4- 2)],
fc=o
(к = 0,1,2,...),	(2.14)
288
ПРИЛОЖЕНИЕ
Pi + 2хЬ^р, - Pi(ul + uj) = WqP»(373 - !), iji + 2*6Q?g, -	+ w|) = О>о9,(37з - 1),
(i =1,2,...),	(2.15)
где Яд,, Lk — постоянные, определяемые равенствами
Hk = dkhk j z2dm, Lk = d^hj. J z2 dm.
V	V
Параметр а равен отношению момента инерции оболочки относительно оси Oz к ее моменту инерции относительно оси Ох. Для пологой сферической оболочки а = 2(1 — £i), где 61 < 1.
Чтобы уравнения (2.13)—(2.15) образовывали замкнутую систему дифференциальных уравнений величин 7, w, 92л» 9* (* = 0,1,2,...; i = 1,2,...), к ним необходимо добавить три независимых скалярных кинематических уравнения. Зададим ориентацию связанной с оболочкой системы координат Ох 1X2X3 с помощью углов Эйлера ф, в, <р. Тогда кинематические уравнения будут иметь вид
= ф sin 0 sin 9? 4- 0 cos (р 4- u>o (sin ф cos <p 4- cos ф sin <p cos 0),
UJ2 = sin 0 cos (p — 0sin <p 4- <^o(— sin ф sin 9? 4- cos ф cos <p cos 0),
= ф cos 0 4- p 4- wo(— cos ф sin 0).	(2.16)
Проекции вектора 7 на оси Oxi, Ох2, Ох3 через введенные углы будут выражаться формулами
71= sin <р sin 0, 72 = cos <р sin 0, 73 = cos 0.	(2.17)
Уравнения (2.13)—(2.15) допускают частное решение, в котором все нормальные координаты qitky 92,к, Qi (& = 0,1,2,...; i — 1,2,...), соответствующие продольным колебаниям, равны нулю, 73 = 0, wi = w2 = 0, W3 = const. Это решение отвечает такому движению упругой оболочки относительно центра масс на круговой орбите, когда ось симметрии оболочки перпендикулярна плоскости орбиты и оболочка вращается с постоянной скоростью вокруг оси симметрии.
Квазистатический режим движения пологой сферической упругой оболочки. Введем величину е = ^о/По, i. Будем полагать, что характерное время затухания свободных колебаний много меньше периода То обращения центра масс по орбите, намного больше наибольшего периода свободных упругих колебаний. Предположим также, что
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
289
период То и характерное время движения тела как целого относительно центра масс имеют одинаковый порядок.
Тогда дифференциальные уравнения (2.13)—(2.15) будут эквивалентны с точностью до членов е4 приближенным уравнениям, получаемым с помощью алгоритма и методов, разработанных для систем дифференциальных уравнений с малым параметром при старших производных [106].
В результате дифференциальные уравнения, описывающие движение оболочки как целой относительно центра масс в квазистатическом режиме и ее упругие колебания, можно представить в виде
р" ф" cos 0 — aQ0' ф‘ sin 0 sin# = сг[ао(У1/ 4- ^'У2) 4- ах(^,У1 — У2)], ф" sin 0 4- (a — 2)#' cos ф sin 0 4- (2 — а)0'ф' cos #4-
4-(a — 1) sin 0 cos 0sin 0 — фг cos# sin ф — ф' sin ф =
= cr[2(-a2 4- <p')Y[ 4- a3Yr 4- 2(<Zq 4- a? + a% - ф'2 4- sin2 ф 4- Зсо$2#)У2],
7/	! /2 .	л	,	9л.
#" 4- (1 — a) - sin 2#(cos2 ф — ф'2 4- 3) — 2ф' cos ф cos2 # 4-
4-(2 — а)ф' cos ф 4- aa&p1 —
— <т[2(2ао4-ао —V^^sin2 V>4-6cos2 #—4)У14-2(a2 —^У^азУг],	(2.19)
Pi = qi = 0 (i= 1,2,...).	(2.20)
B выражениях (2.19), (2.20) штрихом обозначено дифференцирование по безразмерной переменной т = и приняты следующие обозначения:
Ух (2#' cos2 ф cos2 # — 2#' cos2 ф 4- cos ф cos2 #sin 2ф—
— cos ф sin 2ф 4- 2ф'0г cos ф sin 2# 4- 4^>,#/ cos ф sin #—
— 2ф'2 cos2 0 sin ф — 2ф,20' cos2 # — 12#' cos2 #—
— кр'ф' cos # sin ф — кр'ф^' cos 0 4- Ф' sin 2ф sin 2#4-
4- 2<pf sin 20 sin 0 — 2<p'2 sin ф — 2<£>'2#' 4- 6#')4-
4- cos2 ф sin 2# — 40' cos ф cos2 # — 2<p' cos ф cos #4-
4- 2ф' cos ф — ф'2 sin 2# 4- 3 sin 2# — 2(р'ф' sin #,
I
J
290 ПРИЛОЖЕНИЕ
У2 =2%6a>o(2 cos3 ip cos3 0 — 2 cos3 cos 0 4- 3?// cos2 ip sin 20+
+ 2^/ cos2 ip sin 20 — 2ip' cos2 ip sin 0 — 6ip'2 cos ip cos3 0+
+ 6 cos ip cos3 0 — S^ip' cos ip cos2 0 — 2<pf2 cos ip cos 0+
+ 4ip'2 cos ip cos 0 — 6 cos tp cos 0 + 4<pfipf cos ip—
— ipf3 cos 0 sin 20 + Zip' cos 0 sin 20 — 2ip,ip,2‘ sin 20+
+ 6<p' sin 20 — 2(p,2ip' sin 0)—
— 20' cos ip sin 0 + 2ipf cos 0 sin ip + 2ipf0f cos 0—
— sin 2ip sin 0 + 2<p' sin ip + 2y>,0/,
ao = cos ip cos 0 + ip1 sin 0, сц = 0' + sin ip,
a2 = 9?'(cos ip sin 0 — ipf cos 0),
a3 = -20' cos ip cos 0 — cos 0 sin 2ip — 2ip’ sin ip sin 0 — 20'ip' sin 0,
Введем следующие обозначения:
CU3=/3cUq, Ip = 7Г + a?i, 0=^+^2,	—	^4=^2-
В этих обозначениях частное решение системы (2.19)
xi = Х2 = хз = Х4 = 0,	/3 = const	(2.26)
соответствует исследуемому движению упругой оболочки, а система уравнений (2.19) может быть записана в виде
/?' = Z(a?i, Х2, хз,Х4,Р),
*i = *з,
4 = *4,
х’з = Pll^l +Р12Я2 +Р13*3 + Р14*4 + *1 (Я1, Я?2, *3, *4, (3),
Х4 =Р21*1 + ?22*2 + Р23ХЗ + Р24Х4 + Х2(хЪ Х2, Х3, Х4,0), (2.27)
где Z, Xi, Х2 — аналитические функции переменных /?,	Х2, хз, Х4,
которые в некоторой не зависящей от времени окрестности начинаются членами не ниже второго порядка. При этом выполняются соотношения
7(0,0,0,0, /3) = Xi (0,0,0,0, /3) = 0 (г = 1,2).
МЕТОДЫ КОМПЬЮТЕРНОЙ АЛГЕБРЫ
291
Коэффициенты Pij (j = 1,2,3,4) имеют следующие значения:
Рп = 8сг/33 + /3ei — 2/3+1,
Р12 — —8o*x^o/2(2/33 + З/З2 + 6/3 + 9),
Р1з = - 16ахЬ^о/?(/?3 + 3/3-3),
Р14 = -4<т/3(2/32 + 3) - /Зех + 2/3-2,
Р21 = 8ах6^о/?2(2/?2 + 3),
Р22 = 4<т(2/33 + З/З2 + 6/3 + 9) + pd + 3si — 2/3 — 2,
Р23 = 4сг/3(2/32 + 3) + /3^1 —2/3+2, Р24 = -8сгхЬ^о(2/34 + З/З2 + 6/3 + 9).
Примем движение, отвечающее решению (2.26), за невозмущенное и исследуем его устойчивость. По теореме Ляпунова — Малкина [65] решение (2.26) системы (2.27) устойчиво, если уравнение
-л	0	1	0	
0	-А	0	1	= 0
Ри	Р12	Р1з - А	Р14	
Р21	Р22	Р23	Р24 - А	
(2.28)
имеет корни только с отрицательными вещественными частями. При этом всякое возмущенное движение, достаточно близкое к невозмущенному, стремится с неограниченным возрастанием времени к одному из установившихся движений однопараметрического семейства (2.26). Определим область значений переменной /3, в которой корни уравнения (2.28) имеют отрицательные вещественные части. Выпишем условия Рауса — Гурвица. Перепишем уравнение (6.28) в виде
cgA4 + С1А3 + С2А2 + С3А + С4 = 0.	(2.29)
Тогда условия Рауса — Гурвица записываются в следующей форме [65]:
ci=fci(4/34+9/32+9)>0,
Сз=Л1(4/34 +6/33 +9/32+18/3- 9)>0,
c4=4/32(1-£i)+/3(2-7£i)-(2-3£i)>0,
Сз(С1С2“С0С3)—С4С4 =
=—18fc2(—8/37+22/Зб—34/35+57/34—66/33+63/32—72/3+18)>0,
где ki = 8&cugcr > 0.
292
ПРИЛОЖЕНИЕ
Первое условие выполняется при любых вещественных /?. С помощью ЭВМ можно проверить, что второе условие выполняется при /3 < -1,9 и /3 > 0,4, третье — при /? < —1(1 + £i) и /? > 0,5(1 + £i), четвертое — при /3 > 0,32.
Следовательно, при /3 > 0,5(1 + £i) корни уравнения (2.28) имеют отрицательные вещественные части и, следовательно, решение (2.26) устойчиво, а при /3 < 0,5(1 + £i) неустойчиво.
Если бы оболочка была абсолютно твердым телом, то [107, 70] рассматриваемые установившиеся ее движения устойчивы при /3 < 0,5 или /3 < — 1 и неустойчивы при —!</?< 0,5.
Литература
1.	Айзекс Р, Дифференциальные игры. — М.: Мир, 1967, 479 с.
2.	Аксенов ЕЛ. Теория движения искусственных спутников Земли. —М.: Наука, 1977, 360 с.
3.	Алексеев К-Б. Бебенин Г.Г. Управление космическими летательными аппаратами. — М.: Машиностроение, 1974, 340 с.
4.	Андронов А. А., Витт А.А., Хайкин С.Э. Теория колебаний. — М.: Гостехиздат, 1959, 915 с.
5.	Арнольд В.И. Малые знаменатели и проблемы устойчивости движения в классической и небесной механике // Успехи мат. наук. 1963, т. 18, вып. 6, с. 91 — 192.
6.	Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики // Итоги науки и техники. Сер. Современные проблемы математики. Фундаментальные направления.—М.: ВИНИТИ, 1985, т. 3, 304 с.
7.	Баничук Н.В. Введение в оптимизацию конструкций. — М.: Наука, 1986, 303 с.
8.	Баничук Н.В. Оптимизация формы упругих тел. —М.: Наука, 1980, 256 с.
9.	Баничук Н.В., Барсук А.А., Трифанова Л.Р., Шаранюк А.В. Структурное моделирование больших свободных конструкций с применением анизотропных моделей. — В кн.: Гагаринские научные чтения по космонавтике и авиации. — М.: Наука, 1991, с. 52—56.
10.	Баничук Н.В., Иванова С.Ю., Шаранюк А.В. Анализ чувствительности и оптимальное проектирование конструкций, рассчитываемых на динамические воздействия // Изв. АН СССР, МТТ, 1985, № 4, с. 166-172.
11.	Баничук Н.В., Иванова С.Ю., Шаранюк А.В. Вопросы оптимального проектирования конструкций при нестационарном нагружении // Прикладные проблемы прочности и пластичности: Статика и динамика деформируемых систем. Горький: Горьк. университет, 1985, с. 73—80.
12.	Баничук И.В., Иванова С.Ю., Шаранюк А.В. Динамика конструкций. Анализ и оптимизация.—М.: Наука, 1989, 262 с.
13.	Баничук Н.В., Лущин Л.П., Макеев Е.В., Шаранюк А.В. Моделирование и проектирование сложных конструкций. Труды Гагаринских научных чтений по космонавтике и авиации.—М.: Наука, 1987, с. 177-179.
14.	Баничук И.В., Макеев Е.В., Филимонов Г.Б., Шаранюк А.В. Численное моделирование свободных конструкций. Труды Гагаринских научных чтений по космонавтике и авиации.—М.: Наука, 1990, с. 192-198.
15.	Бараов А.Х., Соколов Б.И. О предельной точности рабочей поверхности параболической антенны зонтичного типа // Изв. АН СССР, МТТ, 1991, № 5, с. 138-142.
16.	Барбашин Е.А., Табуева В.А. Динамические системы с цилиндрическим фазовым пространством. — М.: Наука, 1969, 300 с.
17.	Бардин Б.С., Маркеев А.П. Плоские резонансные движения вязкоупругого тела на эллиптической орбите // Изв. РАН. МТТ, 1993, № 3, с. 95-102.
18.	Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов. — М.: Стройиздат, 1982, 448 с.
294
ЛИТЕРАТУРА
19.	Белвин У.К., Эдигхоффер Г.Г., Хершторм К.Л. Квазистатическое регулирование формы космической антенны диаметром 15 м // Аэрокосмическая техника, 1990, № 2, с. 60-69.
20.	Белецкий В.В. Движение искусственного спутника относительно центра масс. — М.: Наука, 1965, 416 с.
21.	Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. — М.: Изд-во МГУ, 1975, 308 с.
22.	Белецкий В.В., Бронштейн M.JL, Попирный Г.А. Оценка параметров зеркально-диффузионной модели отражения по движению относительно центра масс спутников серии «Протон» // Космические исследования, 1973, т. 11, К? 2, с. 171-179.
23.	Беннигоф Дж.К. Расчет собственных частот методом итерации составляющих мод // Аэрокосмическая техника, № 2, 1988, с. 85-93.
24.	Боголюбов HJL, Митропольский ЮА. Асимптотические методы в теории нелинейных колебаний.—М.: Наука, 1974. 504 с.
25.	Болотин В.В. Динамическая устойчивость упругих систем. — М.: Гостехтеоретиз-дат, 1956, 600 с.
26.	Болотин В.В. Неконсервативные задачи теории упругой устойчивости. — М.: Физ-матгиз, 1961, 339 с.
27.	Брюно АД. Локальный метод нелинейного анализа дифференциальных уравнений. — М.: Наука, 1979, 253 с.
28.	Валеев К.Г.,Жаутыков О.А. Бесконечные системы дифференциальных уравнений. — М.: Наука, 1974, 415 с.
29.	Васидзу К- Вариационные методы в теории упругости и пластичности. — М.: Мир, 1987, 542 с.
30.	Васильева А.Б., Бутузов В.Ф. Асимптотические разложения решений сингулярно возмущенных уравнений.—М.:Наука, 1973, 272 с.
31.	Вильке В.Г. Аналитические и качественные методы в механике систем с бесконечным числом степеней свободы.—М.: Изд-во МГУ, 1986, 192 с.
32.	Виттенбург Й. Динамика систем твердых тел. — М.: Мир, 1980, 292 с.
33.	Ганиев Р.Ф., Закржевский А.Е. Программные движения деформируемых управляемых конструкций. — М.: Наука, 1995, 213 с.
34.	Гаушус Э.В. Исследование динамических систем методом точечных преобразований. — М.: Наука, 1976, 368 с.
35.	Гаушус Э.В., Смольянинов Н.Д. Исследование релейной системы стабилизации летательного аппарата // Изв. АН СССР, МТТ, 1970, № 2, с. 5-13.
36.	Гловинский Р., Лионе Ж.Л., Тремольер Р. Численное исследование вариационных неравенств.—М.: Мир, 1979, 574 с.
37.	Голдрайх П., Пип С. Динамика вращения планет. В кн.: Приливы и резонансы в солнечной системе.—М.: Мир, 1975, с. 130-167.
38.	Гряник М.В., Ломан В.И. Развертываемые зеркальные антенны зонтичного типа. — М.: Радио и связь, 1987, 71 с.
39.	Гуляев В.И., Кошкин В.Л., Рыраховский Л.А. Оптимальное управление движением в центральном силовом поле системы двух тел, соединенных шарниром // Изв. АН СССР, МТТ, 1989, № 6, с. 30-37.
40.	Дарвин Дж.Г. Приливы и родственные им явления в Солнечной системе. — М.: Наука, 1965, 252 с.
41.	Дегтярев Г.Л., Сиразетдинов Т.К. Теоретические основы оптимального управления упругими космическими аппаратами.—М.: Машиностроение, 1986, 214 с.
42.	Депри А. Изучение свободного вращения твердого тела около неподвижной точки с помощью фазовой плоскости // Механика, Сб. переводов. 1968, № 2, с. 3—9.
ЛИТЕРАТУРА
295
43.	Докучаев Л.В. Нелинейная динамика летательных аппаратов с деформируемыми элементами. —М.: Машиностроение, 1987, 232 с.
44.	Докучаев Л.В. Нелинейная динамика упругого летательного аппарата. В кн.: Итоги науки и техники. Общая механика. —М.: ВИНИТИ, 1982, т. 5, с. 135—197.
45.	Докучаев Л.В. Построение областей устойчивого вращения космического аппарата с упругими штангами // Космические исследования, 1969, т. 7, № 4, с. 523—546.
46.	Жаутыков О.А. Метод бесконечных систем дифференциальных уравнений в задачах колебаний систем с распределенными параметрами // Успехи механики. 1986, т. 9, № 1, с. 65-91.
47.	Журавлев В.Ф., Климов Д.М. Волновой твердотельный гироскоп. — М.: Наука, 19'85, 125 с.
48.	Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. — М.: Наука, 1988, 326 с.
49.	Зенкевич О. Метод конечных элементов в технике. — М.: Мир, 1975, 543 с.
50.	Иванова В.Ф., Соколов Б.Н. Об оптимальной форме пологой мягкой осесимметричной оболочки // Изв. АН СССР, МТТ, 1989, № 3, с. 160-166.
51.	Излучательные свойства твердых материалов. Под общ. редакцией А. Е. Шейнд-лина,—М., 1974.
52.	Ишлинский А.Ю. Механика. Идеи, задачи, приложения. — М.: Наука, 1985, 624 с.
53.	Ишлинский А.Ю. Прикладные задачи механики. —М.: Наука, 1986, Кн. 2: Механика упругих и абсолютно твердых тел. 416 с.
54	Каменков Г.В. Избр. труды. Т.2. — М.: Наука, 1972, 214 с.
55.	Климов Д.М., Маркеев А.П. Динамика неоднородного упругогого кольца в гравитационном поле: Препринт № 331. — М.: Ин-т проблем механики АН СССР, 1988, 42 с.
56.	Климов Д.М., Маркеев А.П. Плоские движения упруговязкого кольца в гравитационном поле // Известия АН СССР. МТТ. 1990, № 3, с. 3—13.
57.	Климов Д.М., Маркеев А.П., Бардин Б.С. Квазистатические движения вязкоупругого кольца с материальной точкой в гравитационном поле: Препринт № 510. —М.: Ин-т пробл. мех. РАН, 1992, 31 с.
58.	Климов Д.М., Маркеев А.П., Холостова О.В. К динамике упруговязкого кольца в гравитационном поле: Препринт № 406. —М.: Ин-т пробл. мех. АН СССР, 1989, 35 с.
59.	Климов Д.М., Маркеев А.П., Холостова О.В. Об устойчивости движения упруговязкого кольца в гравитационном поле // ПММ. 1991, т. 55, вып. 1, с. 20-25.
60.	Красовский И.И. Управление динамической системой. Задача о минимуме гаранти-рованоого результата.—М.: Наука, 1985, 520 с.
61.	Кузьмин П.А. Устойчивость круговой формы нити, имеющей счетное множество степеней свободы // Казань: Тр. КАИ. 1949, т. 22, с. 3-15.
62.	Лехницкий С.Г. Анизотропные пластинки. — М.: Гостехтеориздат, 1947, 355 с.
63.	Лурье А.И. Аналитическая механика.—М.: Физматгиз, 1961, 824 с.
64.	Ляв А. Математическая теория упругости. — М.; Л.: Гостехиздат, 1935, 674 с.
65.	Малкин И.Г. Теория устойчивости движения.—М.: Наука, 1966, 530 с.
66.	Маркеев А.П. Влияние продольных упругих колебаний тела на его быстрые вращения в гравитационном поле // Изв. АН СССР. МТТ. 1989, № 6, с. 38-45.
67.	Маркеев А.П. К динамике упругого тела в гравитационном поле // Космические исследования. 1989, т. 27, вып. 2, с. 163-175.
68.	Маркеев А.П. К задаче об устойчивости одного случая регулярной прецессии твердого тела в центральном гравитационном поле // В кн. Темат. Сб. научн. тр. —М.: МАИ, 1978, № 460, с. 13-17.
296
ЛИТЕРАТУРА
69.	Маркеев А.П. Об одном частном случае движения динамически симметричного упруговязкого тела в центральном ньютоновском гравитационном поле // Космические исследования. 1990, т. 28, вып. 5, с. 643-654.
70.	Маркеев А.П. Резонансные эффекты и устойчивость стационарных вращений спутника // Космические исследования. 1967, т. 5, вып. 3, с. 365-375.
71.	Маркеев А.П. Теоретическая механика. — М.: Наука, 1990, 414 с.
72.	Маркеев А.П. Точки либрации в небесной механике и космодинамике. — М.: Наука, 1978, 312 с.
73.	Маркеев А.П. Эволюция быстрых вращений вязкоупругой цилиндрической оболочки в гравитационном поле// Изв. АН СССР. МТТ. 1990, № 5, с. 139-146.
74.	Маркеев А.П., Холостова О.В. О плоских резонансных движениях и регулярных прецессиях космического аппарата с деформируемыми элементами // Космические исследования. 1991, т. 29, вып. 3, с. 328-339.
75.	Михлин С.Г. Вариационные методы в математической физике. — М.: Гостехиздат, 1957, 476 с.
76.	Мозер Ю. Лекции о гамильтоновых системах. — М.: Мир, 1973, 167 с.
77.	Мучник Г.Ф., Рубашов И.Б. Методы теории теплообмена, ч. 2. — М., 1994.
78.	Набиуллин М.К. Стационарные движения и устойчивость упругих спутников. — Новосибирск: Наука, 1990, 217 с.
79.	Персидский К.П. Бесконечные системы дифференциальных уравнений, дифференциальные уравнения в нелинейных пространствах. В кн.: Избранные труды. Т. 2. — Алма-Ата: Наука, 1976, 248 с.
80.	Приливы и резонансы в Солнечной системе. Сб. статей. — М.: Мир, 1975, 287 с.
81.	Пятницкий Е.С. Принципы декомпозиции в управлении механическими системами // ДАН СССР, 1988, т. 300, № 2, с. 300-303.
82.	Редько С.Ф., Ушкалов В.Ф., Яковлев В.П. Идентификация механических систем. Определение динамических характеристик и параметров. —Киев: Наук, думка, 1985, 216 с.
83.	Рубановский В.Н. Устойчивость установившихся движений сложных механических систем. В кн. Итоги науки и техники. Общая механика. — М.: ВИНИТИ. 1982, т. 5, с. 62-134.
84.	Садов Ю.А., Сидоренко В.В. Равновесные конфигурации упругого кольца в плоскости круговой орбиты // Космические исследования. 1986, т. 24, вып. 5, с. 659-667.
85.	Сидоренко В.В. Исследование устойчивости стационарных движений упругого кольца в плоскости круговой орбиты: Препринт № 108, — М.: Ин-т прикл. матем. АН СССР, 1986, 28 с.
86	Сидоренко В.В. Об эволюции движения механической системы с линейным демпфером большой жесткости // ПММ. 1995, т. 59, вып. 4, с. 562-568.
87.	Сидоренко В.В. Эволюция быстрых вращений упругого кольца в гравитационном поле- Препринт № 93. — М.: Ин-т прикл. матем. АН СССР, 1987, 28 с.
88	Синицын Е.В. Асимптотика сингулярных возмущений в исследовании поступательновращательного движения вязкоупругого тела // Изв. АН СССР. МТТ. 1991, № 1, с. 104-110.
89.	Синицын Е.В. О квазистатическом подходе при исследовании устойчивости решений одного класса механических систем с бесконечным числом степеней свободы // ПММ. 1993, т. 57, вып. 4, с. 12-20.
90.	Синицын Е.В. Об устойчивости цилиндрической прецессии вязкоупругого тела при колебаниях вдоль оси симметрии // ПММ. 1993, т. 57, вып. 2, с. 57—66.
91.	Соколов Б.Н. Оптимизация формы поверхности анизотропной пленки // Изв. АН СССР, МТТ, 1986, № 5, с. 185-186.
ЛИТЕРАТУРА
297
92.	Справочное руководство по небесной механике и астродинамике / Под ред. Дубо-шина Г.Н. -- М.: Наука, 1976, 862 с.
93.	Стретт Дж.В. (Лорд Рэлей) Теория звука. Т.1. —М.;Л.: Гостехиздат, 1940, 499 с.
94.	Субботин А.И., Ченцов А.Г. Оптимизация гарантии в задачах управления.—М.: Наука, 1981, 287 с.
95.	Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле / Пер. с англ. Л. Г. Корнейчука; под ред. Э. И. Григолюка. — М.: Машиностроение, 1985, 472 с.
96.	Усюкин В.И. Строительная механика конструкций космической техники. — М.: Машиностроение, 1988, 392 с.
97.	Физика космоса. Маленькая энциклопедия. Глав. ред. С. Б. Пикельнер. —М.: Сов. энциклопедия, 1976, 655 с.
98.	Физическая энциклопедия. Глав. ред. А. М. Прохоров, т. 1. — М., 1988.
99.	Физическая энциклопедия. Глав. ред. А. М. Прохоров, т. 4. — М., 1994.
100.	Хазин Л.Г., Шноль Э.Э. Устойчивость критических положений равновесия. — Пущино: Научн. центр биологич. исслед. АН СССР, 1985, 215 с.
101.	Хог Э., Арора Я- Прикладное оптимальное проектирование. Механические системы и конструкции. — М.: Мир, 1983, 478 с.
102.	Холостова О.В. Квазистатический подход в задачах динамики вязкоупругого тела в гравитационном поле.—Дисс.... канд. физ.-мат. наук. — М., 1992, 170 с.
103.	Холостова О.В. О быстрых вращениях упругой сферической оболочки в гравитационном поле Ц Изв. АН СССР. МТТ. 1991, № 2, с. 129-139.
104.	Холостова О.В. О плоских квазистатических движениях вязкоупругого тела в гравитационном поле // Космические исследования. 1991, т. 29, вып. 2, с. 183—193.
105.	Черноусько Ф.Л. Декомпозиция и синтез управления в динамических системах // Изв. АН СССР, Техническая кибернетика, 1990, № 6, с. 64-82.
106.	Черноусько Ф.Л. О движении твердого тела с упругими и диссипативными элементами Ц 1978, т. 42, вып. 1, с. 34-42.
107.	Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника // ПММ. 1964, т. 28, вып. 1, с. 155-157.
108.	Черноусько Ф.Л. Резонансные явления при движении спутника относительно центра масс // Ж. вычисл. матем. и матем. физ. 1963, т. 3, № 3, с. 528—538.
109.	Черноусько Ф.Л., Шамаев А.С. Асимптотика сингулярных возмущений в задаче динамики твердого тела с упругими и диссипативными элементами // Изв. АН СССР. МТТ. 1983, № 3, с. 33-42.
НО. Эльясберг П.Е. Введение в теорию полета искусственных спутников Земли. — М.: Наука, 1965, 304 с.
111.	Эшли X. Динамика крупных гибких объектов на орбите // Ракетн. техника и космонавтика, 1967, т. 5, № 3, с. 92-104.
112.	Anderson M.S. Vibration of Prestressed Periodic Lattice Structures // AIAA J., v. 20, No. 4, 1982, pp. 551-555.
113.	Artjukh A.I., Banichuk N.V. Application of optimization methods to identification problems // Proc, of the Workshop on Optimization and Optimal Control. Ber. Univ. Jyvaskyla Math. Inst. 58, 1993, pp. 5-16.
114.	Ashley H. Observation on the dynamic behavior of large flexible bodies in orbit // AIAA J. 1967, v. 5, No. 3, pp. 460-469.
115.	Ashley H. On Passive Damping Mechanisms in Large Space Structures // Journal of Spacecraft and Rockets. Vol. 21, No. 5, 1984, pp. 448-455. (Имеется перевод: Эшли X. О механизмах пассивного демпфирования больших космических конструкций. Аэрокосмическая техника, т. 3, № 6, 1985, с. 18—28).
298
ЛИТЕРАТУРА
116.	Ashley Н., McIntosh S.C. (jr.) Applications of aeroelastic constraints in structural optimization // Proc. XII Intern. Congr. Appl. Meeh. Stanford Univ., 1968, Berlin: Springer, 1969, pp. 100-113.
117.	Balas MJ. Active Control of Flexible Systems // J. of Optimization Theory and Applications, vol. 25, 1978, No. 3, pp. 415-436.
118.	Banichuk N.V. Application of analytical models for the optimization of large structural systems. — In: Optimization of Large Structural Systems (Ed.: G. I. N. Rozvany), vol. II, Dordrecht, Kluwer Academic Publisher, 1993, pp. 1051 — 1072.
119.	Banichuk N.V. Identification of mechanical characteristics of large flexible space structures for modelling of dynamics and control. In: Dynamics and Control of Structures in Space II. Southampton, Computational Mechanics Publications, 1993, pp. 423—439.
120.	Banichuk N.V. Problems and methods of optimal structural design. — N.Y.: Plenum Press, 1983, 313 p.
121.	Banichuk N.V., Barboni R., Peroni I. Composite materials influence on aeroelastic and structural design // Proc. Intern. Count. Aeronaut. Soc. USA, Seatie, 1982.
122.	Banichuk N. V., Larichev A.D. Optimal design problems for curvilinear shallow elements of structures // Optimiz. Control Appl. Meeh., 1984, v. 5, No. 3, pp. 197—205.
123.	Banichuk N.V., Luschin L.P., Sharaniuk A.V. Sensitivity analysis for structural modeling and design. In: Dynamical Problems of Rigid-Elastic Systems and Structures (N. V. Banichuk, D. M. Klimov, W. Schiehlen (Eds.)). Berlin, Heidelberg, Springer-Verlag, 1991, pp. 7-16.
124.	Banichuk N.V., Makeev E.V. Sensitivity Analysis and Optimal Design for Large Unrestrained Structures // Proc. 38 Congress of the International Astronautical Federation, Brighton, United Kingdom, 1987.
125.	Bohm C. Noavi criteri di esistenza di soluzioni periodiche di una nota equazione differenziable non lineare // Annali di matematica pure ed applicata. 1953, Str. 4, v. 35, pp. 343—353.
126.	Brekwell J.V. Stability of an orbiting ring // AIAA Paper, 1980, No. 57.
127.	Canavin J.R., Likins P.W. Flotating reference frames for flexible spacecraft // J. Spacecraft and Rockets, 1977, v. 14, No. 12, pp. 724—732.
128.	Darwin G.H. On the precession of a viscous spheroid and on the remote history of the Earth // Phil. Trans. Roy. Soc. London. 1879, v. 170, pp. 447—530.
129.	Darwin G.H. On the secular change in the elements the orbit of a satellite revolving about a tidally distorted planet // Phil. Trans. Roy. Soc. London. 1880, v. 171, pp. 713—891.
130.	Dinkier D., Hanle U., Kroplin B. Dynamics of flexible elastic structures with geometric nonlinearities. — In: Dynamics and Control of Structures in Space II. Sauthampton, Computational Mechanics Publications, 1993, pp. 61—73.
131.	Dosch J., Leo D., Inman D. Modeling and control for vibration suppression of a flexible smart structure. — In: Dynamics and Control of Structures in Space II. Sauthampton, Computational Mechanics Publications, 1993, pp. 603—618..
132.	Edberg D.L. Mateial Damping of Simple Structures in a Simulated Space Environment // J. Spacecraft, v. 23, No. 3, pp. 288-296.
133.	Flower W.R., Schmidt L.C. Analysis of Space Truss as Equivalent Plate // J. of the Structural Division, ASCE, v. 90, No. ST12, Dec. 1971, pp. 2777-2789.
134.	Gevarter W.B. Basic relations for control of flexible vehicles // AIAA J. 1970, vol. 8, No. 4, p. 666—672.
135.	Haug EJ. Computer Aided Kinematics and Dynamics of Mechanical Systems, Volume I: Basic Methods, Allyn & Bacon, Boston, 1989.
ЛИТЕРАТУРА
299
136.	Haug E.J. Elements and methods of computational dynamics. — In: Computer Aided Analysis and Optimization of Mechanical System Dynamics (Ed.: E. J. Haug), Berlin, Springer-Verlag, 1984, pp. 3-38.
137.	Hedgepeth J.M. Accuracy Potentials for Large Space Antenna Reflectors with Passive Structure // J. Spacecraft, v. 19, No. 3, 1982, pp. 211-217
138.	Hedgepeth J.M. Application of High-Fidelity Structural Deployment Analysis to the Development of Large Depoyable Trusses // Proc. 40th Congress of the International Astronautical Federation, Oct. 7—12, 1989, IAF—89—339.
139.	Hedgepeth J.M. Influence of Fabrication Tolerances on the Surface Accuracy of Large Antenna Structures // AIAA Journal, v. 20, No. 5, 1982, pp. 680-686
140.	Hutton D.V. Modal Analysis of a Deployable Truss Using the Finite Element Method // J. of Spacecraft and Rocets, 1984, v. 21, No. 5, pp. 468—472.
141.	Johnson T.L. Progress in Modelling and Control of Flexible Spacecraft // Journal of the Franklin Institute, v. 315, No. 5/6, 1983, pp. 495—520.
142.	Komkov V. Sensitivity analysis in some engineering applications. — In: Lecture Notes in Mathematics (Eds.: A. Doldand, B. Eckmann), Berlin, Springer-Verlag, 1984, pp. 1-30.
143.	Kumar V.K-, Bainum P.M. Dynamics of a flexible body in orbit // AIAA Paper, 1978, No. 78-1418.
144.	Kumar V.K-, Bainum P.M. Dynamics of a flexible body in orbit // J. Guidance and Control, 1980, v. 3, No. 1, pp. 90—93.
145.	Likins P., Ohkami Y., Wong C. Appendage modal coordinate trunkation criteria in hybrid coordinate dynamic analysis // J. of Spacecraft and Rocets, v. 13, 1976, No. 10, pp. 611-617.
146.	Maxwell J.G. On the stability of the motion of Saturn’s rings. In: The scientific paper of J. G. Maxwell. Paris: Hermann, 1927, v. 1, pp. 288-376.
147.	Meirovich L., Nelson H.D. On the High-Spin Motion of a Satellite Containig Elastic Parts // J. of Spacecraft and Rocets, v. 3, Nov. 1966, pp. 1597—1602.
148.	Modi V.J. Attitude dynamics of a satellite with flexible appendages (a brief review) // J. Spacecraft and Rockets, 1974, v. 11, No. 11, pp. 743-751.
149.	Natori M., Ogura S., Motohashi S. Vibration Control of Truss Structures Using Active Members // Prac. 39th Congress of the International Asronautical Federation, Oct. 8—15, 1988 / Bangalore, India, IAF—88—290.
150.	Nayfeh A.H., Hefzy M.S. Continuum Modeling of the Mechanical and Thermal Behavior of Discrete Large Structures // AIAA J., v. 19, No. 6, 1980, pp. 766-773.
151.	Newmark N.M. A Method of Computation for Stuctural Dynamics // ASCE J. of Engineering Mechanics Division, v. 85, 1959, pp. 67-94.
152.	Nicholson D.W. Stable Response of Nonclassically Damped Mechanical Systems // Appl. Meeh. Rev., v. 40, No. 6, 1987, pp. 733—740.
153.	Pironneau O. Optimal shape design for elliptic systems. — N.Y.: Springer-Verlag, 1984, 168 p.
154.	Rodden W.P. A method for deriving structural influence coefficients from groud vibration tests // AIAA J., v. 5, No. 5, 1967, pp. 991-1000.
155.	Santiny P. Stability of flexible spacecrafts // Acta Astronautica, 1976, v. 3, No. 9-10, pp. 685-713.
156.	Santini P., Betti F., Gasbarri P., Rossi A. Control of flexible multi-body systems by means of intelligent structures. — In: Dynamics and Control of Structures in Space II. Sauthampton, Computational Mechanics Publications, 1993, pp. 585-602.
157.	Schiehlen W.O. Computer generation of equations of motion. — In: Computer Aided Analysis and Optimization of Mechanical System Dynamics (Ed.: E. J. Haug), Berlin, Springer-Verlag, 1984, pp. 183-215.
300
ЛИТЕРАТУРА
158.	Shrivastava S.K., Maharana P.K. Flexural vibration of gravity-stabilized, structurally damped, large flexible satellites // J. Guidance Control and Dynamics, 1985, v. 8, No. 2, pp. 214-222.
159.	Shrivastava S.K., Maharana P.K. Longitudinal vibration of gravity-stabilized, large, damped spacecraft modeled as elactic continua // J. Guidance Control and Dynamics, 1985, v. 8, No. 6, pp. 689-696.
160.	Soni M.L., Kluesener M.F., Drake M.L. Damping Synthesis and Damped Design for Flexible Spacecraft Structures // Computer and Structures, v. 20, No. 1-3, 1985, pp. 563-574.
161.	Taylor J.E. Scaling a discrete structural model to match measured modal frequencies // AIAA J., v. 5, No. 11, 1977, pp. 1647-1649.
162.	Weil H. Das asymptotischc Verteilungsgesetz der Eigenschwingungen eines beliebig gestalteten elastischen Korpors. Rend. Arcolo mat. Palermo. 1915, 39 p.
163.	Wittenburg J. Dual quaternions in the kinematics of spatial mechanisms. - In: Computer Aided Analysis and Optimization of Mechanical System Dynamics (Ed.: E. J. Haug), Berlin, Springer-Verlag, 1984, pp. 129-145.
164.	Wu S.C., Haug E.J., Kim S.S. A variational approach of dynamics of flexible multibody systems // Meeh. Struct. Mash., v. 17, 1989, pp. 3-32.
165.	Yoo W.S., Haug E.J. Dynamics of articulated structures: Part 1. Theory // J. Struct. Meeh., v. 14, 1986, pp. 105-126.
166.	Yoo W.S., Haug EJ. Dynamics of articulated structures: Part 2. Computer implementation and applications // J. Struct. Meeh., v. 14, 1986, pp. 177-189.
ОГЛАВЛЕНИЕ
Предисловие................................................................. 3
Введение.
ПРОБЛЕМЫ АСТРОНАВТИКИ И МЕХАНИКИ БОЛЬШИХ КОСМИЧЕСКИХ КОНСТРУКЦИЙ ................................................................... 6
Глава 1.
БОЛЬШИЕ КОСМИЧЕСКИЕ КОНСТРУКЦИИ И ЗАДАЧИ МЕХАНИКИ.......................... 19
1.1.	Нагрузки, действующие на БКК.......................................... 22
1.2.	Материалы, используемые при создании БКК.............................. 33
1.3.	Анализ температур элементов БКК....................................... 40
1.4.	Движение свободной упругой БКК........................................ 51
Глава 2.
ИНЖЕНЕРНЫЙ АНАЛИЗ БКК...................................................... 73
2.1.	Конечноэлементное моделирование....................................... 74
2.2.	Температурные напряжения и деформации БКК............................. 77
2.3.	Оценка жесткости БКК. Статический анализ.............................. 82
2.4.	Частотный анализ. Некоторые общие свойства частот и мод свободных колебаний................................................................ 88
2.5.	Применение частотного анализа в механике БКК для оценки динамической жесткости................................................................ 91
2.6.	Нестационарная динамика	БКК.......................................... 100
2.7.	Применение	метода	конечных	элементов для анализа динамики свободных
конструкций.......................................................... 108
Глава 3.
МЕТОДЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ БКК.................................... 114
3.1.	Оптимизация и анализ чувствительности................................ 115
3.2.	Конечноэлементное моделирование и анализ чувствительности............ 117
3.3.	О коррекции моделей.................................................. 121
3.4.	Частотный метод идентификации параметров конструкции................. 124
3.5.	Идентификация параметров на основе анализа вынужденных колебаний ....	129
3.6.	Оптимизация жесткости БКК при нестационарных нагрузках............... 139
3	7.	Оптимизация характеристик демпфирования.......................... 144
3.8.	Структурное моделирование и исследование оптимальной структурной анизотропии ............................................................... 147
3.9.	Проектирование конструкций с минимальным уровнем напряжений......	152
3.10.	Оптимизация предварительных напряжений и усилий..................... 155
302
ОГЛАВЛЕНИЕ
Глава 4.
ДВИЖЕНИЕ УПРУГОГО ТЕЛА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС В ГРАВИТАЦИОННОМ ПОЛЕ................................................................... 162
4.1.	Уравнения движения.................................................... 164
4.2.	Алгоритм исследования уравнений движения в квазистатическом режиме упругих колебаний....................................................... 172
4.3.	Плоские движения тела................................................. 175
4.4.	О регулярных прецессиях при наличии упругих колебаний вдоль оси симме-.	трии тела.......................................................... 183
4.5.	Динамика неоднородного вязкоупругого кольца........................... 193
4.6.	Движение однородного кольца на круговой орбите........................ 207
4.7.	Уравнения Рауса движения тела относительно центра масс................ 215
4.8.	Влияние продольных упругих колебаний тела на его быстрые вращения ....	221
4.9.	Быстрые вращения вязкоупругой цилиндрической оболочки................. 225
Глава 5.
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ ФУНКЦИОНАЛЬНЫХ ПОВЕРХНОСТЕЙ БКК И УГЛОВЫХ ПАРАМЕТРОВ ИХ ОРИЕНТАЦИИ................................................... 234
5.1.	Влияние компоновки конструкции на точность функциональной поверхности 235
5.2.	Оптимальное проектирование конструкции с радиальными ребрами жесткости .................................................................... 238
5.3.	Влияние технологических допусков на точность формы большой космической конструкции............................................................. 244
5.4.	Расчет влияния технологических допусков на точность отдельных видов конструкций............................................................. 249
5.5.	Максимальная гарантированная точность релейного регулятора в задаче стабилизации............................................................ 253
5.6.	Минимизация интенсивности расхода топлива при заданной точности стабилизации ................................................................ 264
Приложение.
ПРИМЕНЕНИЕ МЕТОДОВ КОМПЬЮТЕРНОЙ АЛГЕБРЫ В ИЗУЧЕНИИ МЕХАНИЧЕСКИХ СИСТЕМ................................................................ 271
6.1. Уравнения движения.................................................... 272
6.2. Вывод с помощью	ЭВМ уравнений движения упругого тела.................. 276
Литература................................................................. 293