Автор: Лунц Г.Л. Эльсгольц Л.Э.
Теги: математический анализ функциональный анализ математика математическая логика издательство санкт-петербург
ISBN: 5-8114-0457-3
Год: 2002
Текст
Г. Л. ЛУНЦ, Л. Э. ЭЛЬСГОЛЬЦ
функции
КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
с элементами
операционного
исчисления
САНКТ-ПЕТЕРБУРГ
ББК 22.161
Л 82
Лунц Г. Л., Эльсгольц Л. Э.
Л 82 Функции комплексного переменного: Учебник для
вузов. 2-е изд.— СПб.: Издательство «Лань», 2002.—
304 с. — (Учебники для вузов. Специальная литература).
ISBN 5-8114-0457-3
В предлагаемом учебнике излагаются основные элементар-
элементарные факты теории функций комплексного переменного и ряд
приложений этой теории (к электростатике, гидродинамике и
др.), а также элементы операционного исчисления и его при-
приложения к интегрированию обыкновенных линейных диффе-
дифференциальных уравнений с постоянными коэффециентами и
некоторых других типов уравнений.
Книга рассчитана на студентов втузов и инженеров.
ББК 22.161
Оформление
С. ШАПИРО, А. ЛАПШИН
Охраняется законом РФ об авторском праве.
Воспроизведение всей книги или любой ее части
запрещается без письменного разрешения издателя.
Любые попытки нарушения закона
будут преследоваться в судебном порядке.
) Издательство «Лань», 2002
) Г. Л. Лунц, Л. Э. Эльсгольц, 2002
) Издательство «Лань»,
ОГЛАВЛЕНИЕ
Предисловие 6
Глава I. Алгебраические действия над комплексными чис-
числами 7
§ 1. Комплексные числа 7
§ 2. Действия над комплексными* числами i . . . 10
Задачи к главе I 17
Глава II. Основные понятия теории функций комплексного
аргумента 18
§ 1. Функции комплексного аргумента 18
§ 2. Предел последовательности 23
§ 3. Предел функции. Непрерывность 26
Задачи к главе II ." 29
Г лав а III. Основные трансцендентные функции 30
§ 1. Показательная, тригонометрические и гиперболические
функции 30
§ 2. Логарифм и обратные тригонометрические функции . . 35
Задачи к главе III 41
Глава IV. Производная 43
§ 1. Аналитическая функция 43
§ 2. Связь аналитических функций с гармоническими ... 48
§ 3. Аргумент и модуль производной. Конформное отобра-
отображение 51
Задачи к главе IV 56
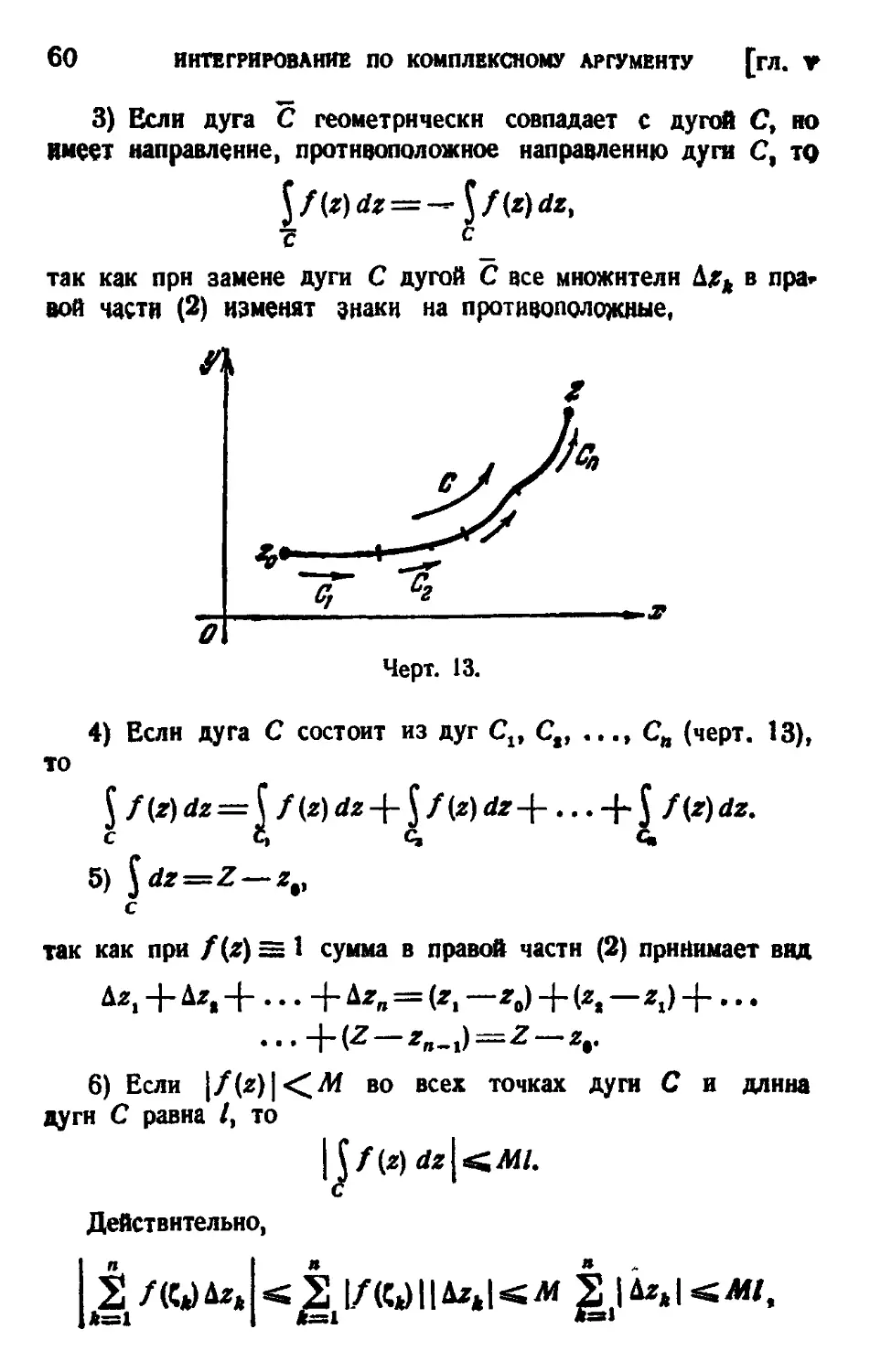
Глава V. Интегрирование по комплексному аргументу . . 58
§ 1. Интеграл от функции комплексного переменного ... 58
§ 2. Теорема Коши 64
§ 3. Вычисление интеграла от аналитической функции . . 67
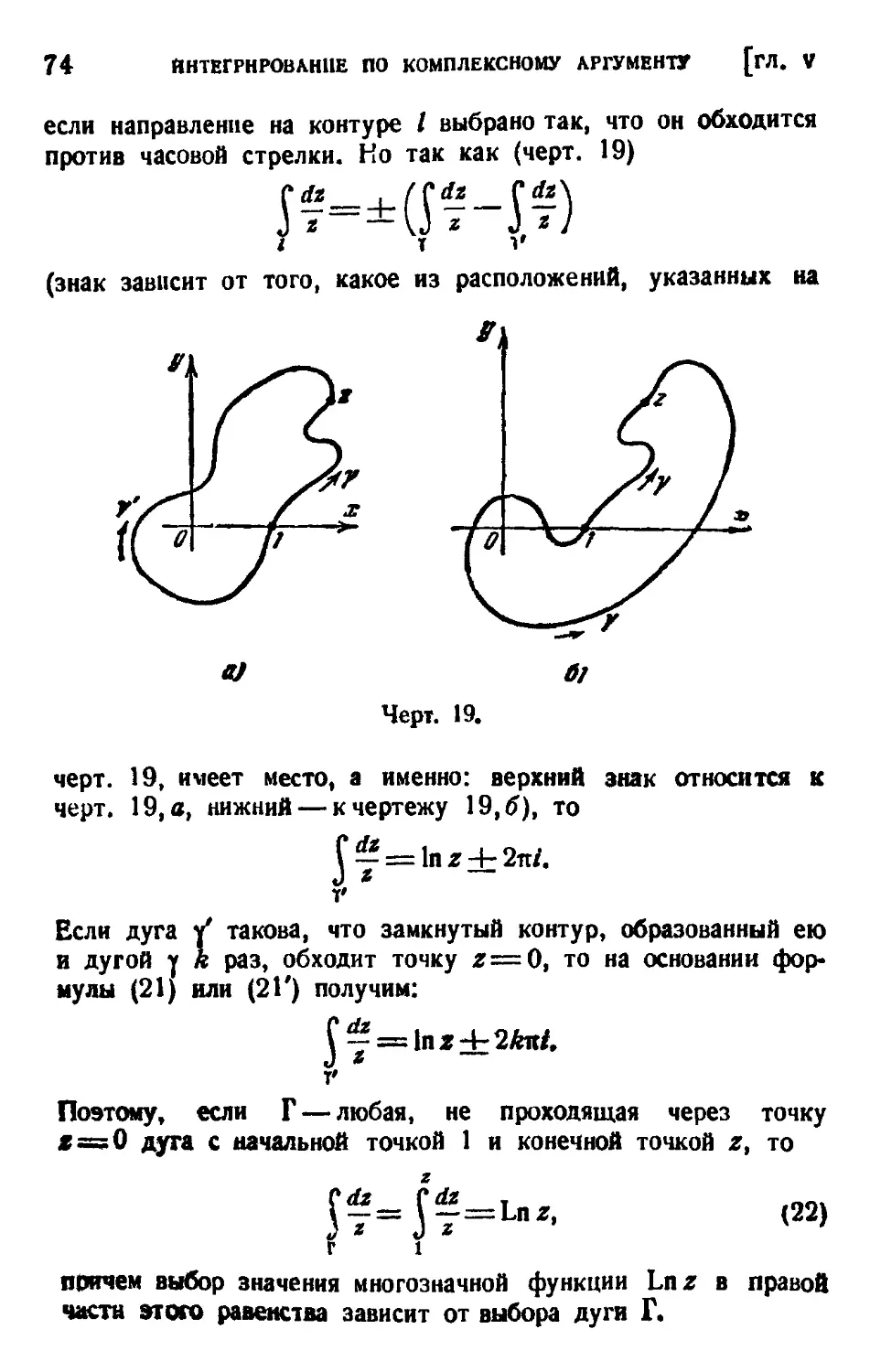
С At
§ 4. Интегралы вида 1 ¦ __ ,„ 71
§ 5. Интеграл Коши 75
§ 6. Производные высших порядков от аналитической функ-
функции 82
V
4 ОГЛАВЛЕНИЕ
§ 7. Теорема Морера 86
Задачи к главе V 88
Глава VI. Ряды , '. . 90
§ 1. Числовые ряды 90
§ 2. Функциональные ряды , . 91
§ 3. Степенные ряды , 98
§ 4. Ряд Тейлора 102
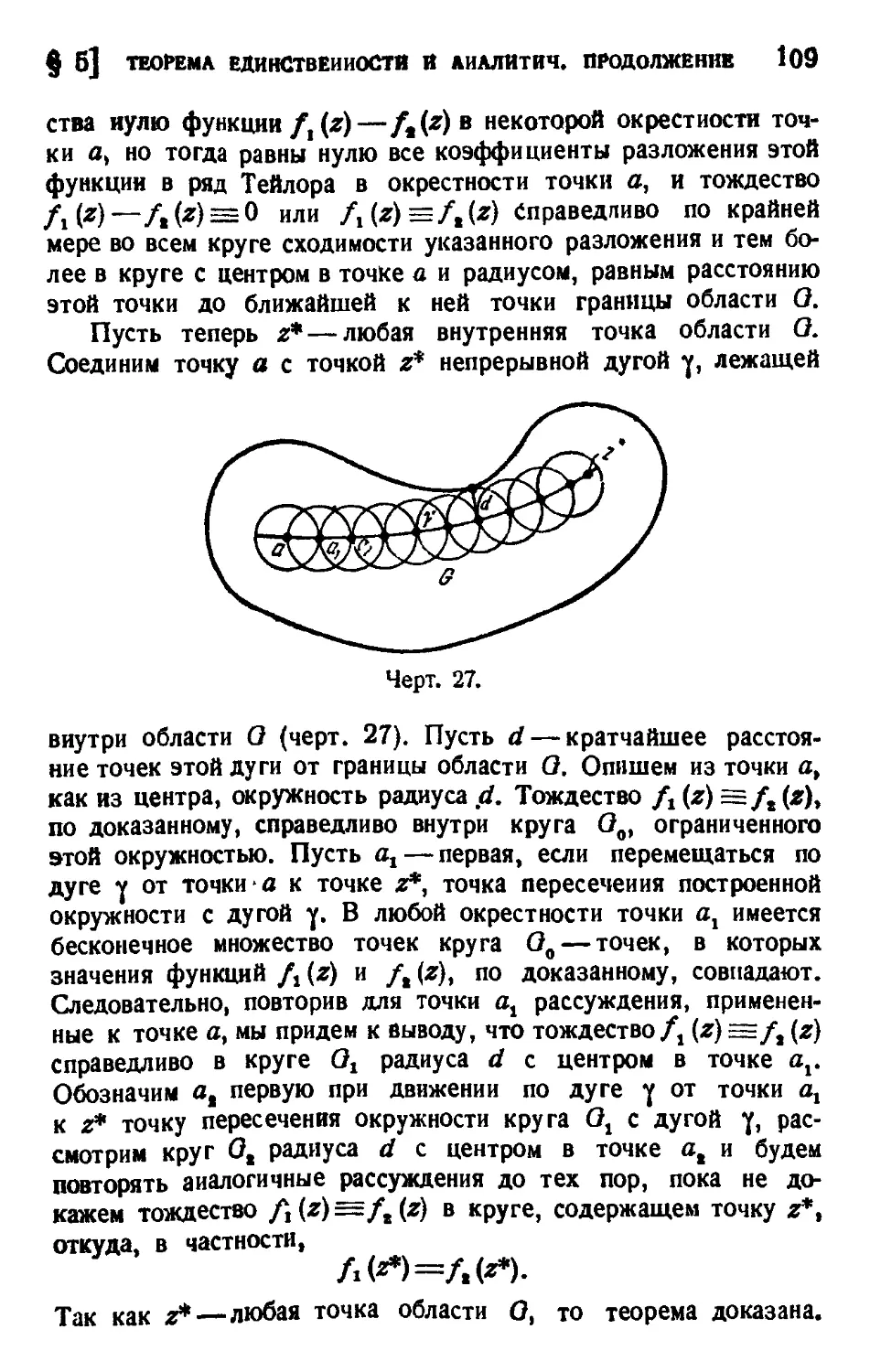
§ 5. Теорема единственности и аналитическое продолжение 108
§ 6. Ряд Лорана , . Ш
§ 7. Изолированные особые точки 121
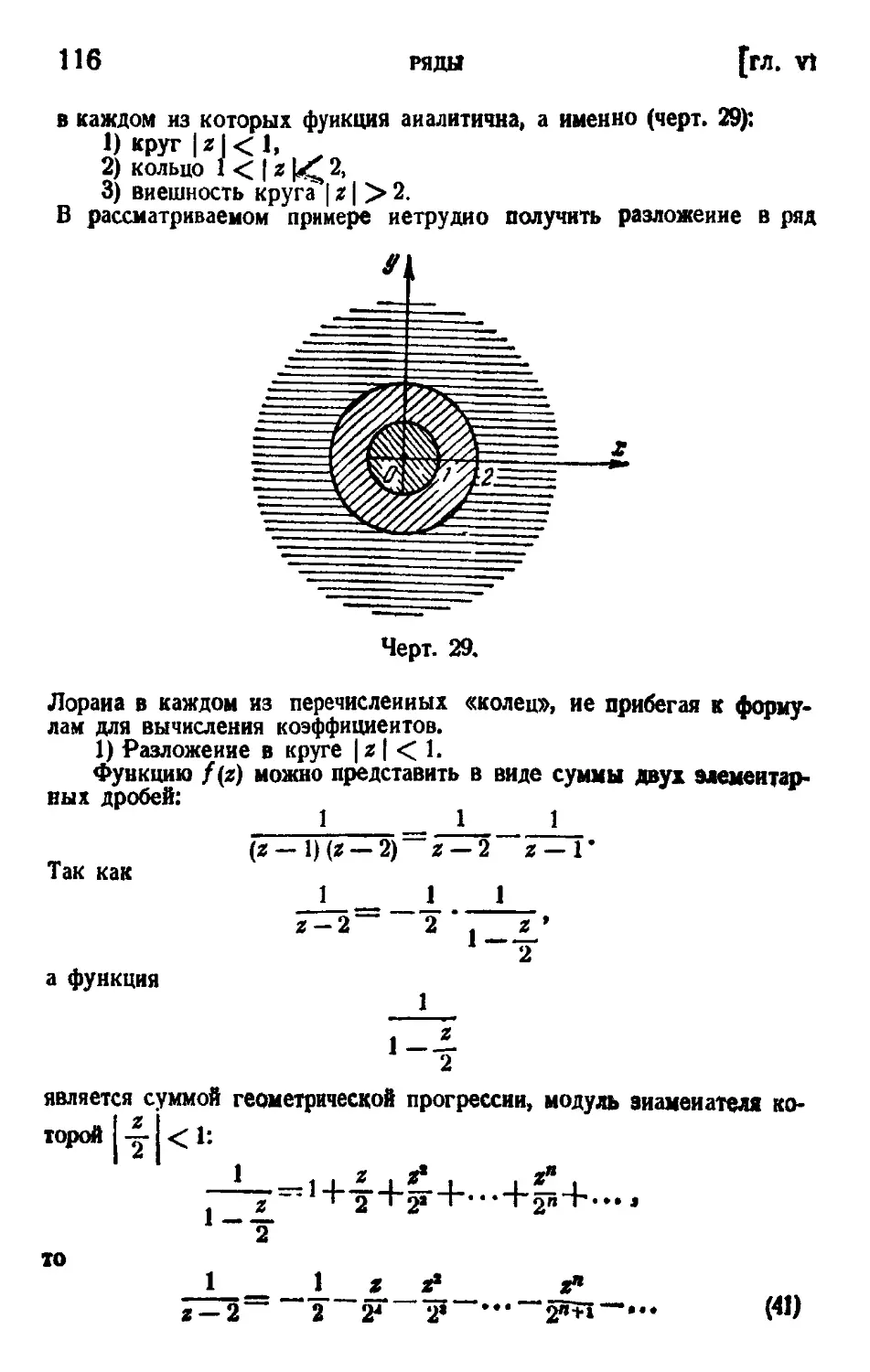
§ 8. Некоторые приемы разложения функций 8 ряд Лорана 129
Задачи к главе VI 130
Глава VII. Теория вычетов -. . Ш
§ 1. Основная теорема о вычетах 133
§ 2. Вычет относительно полюса 136
| 3. Логарифмические вычеты 139
§ 4, Вычисление определенных интегралов с помощью теории
вычетов 144
Задачи к главе VII 156
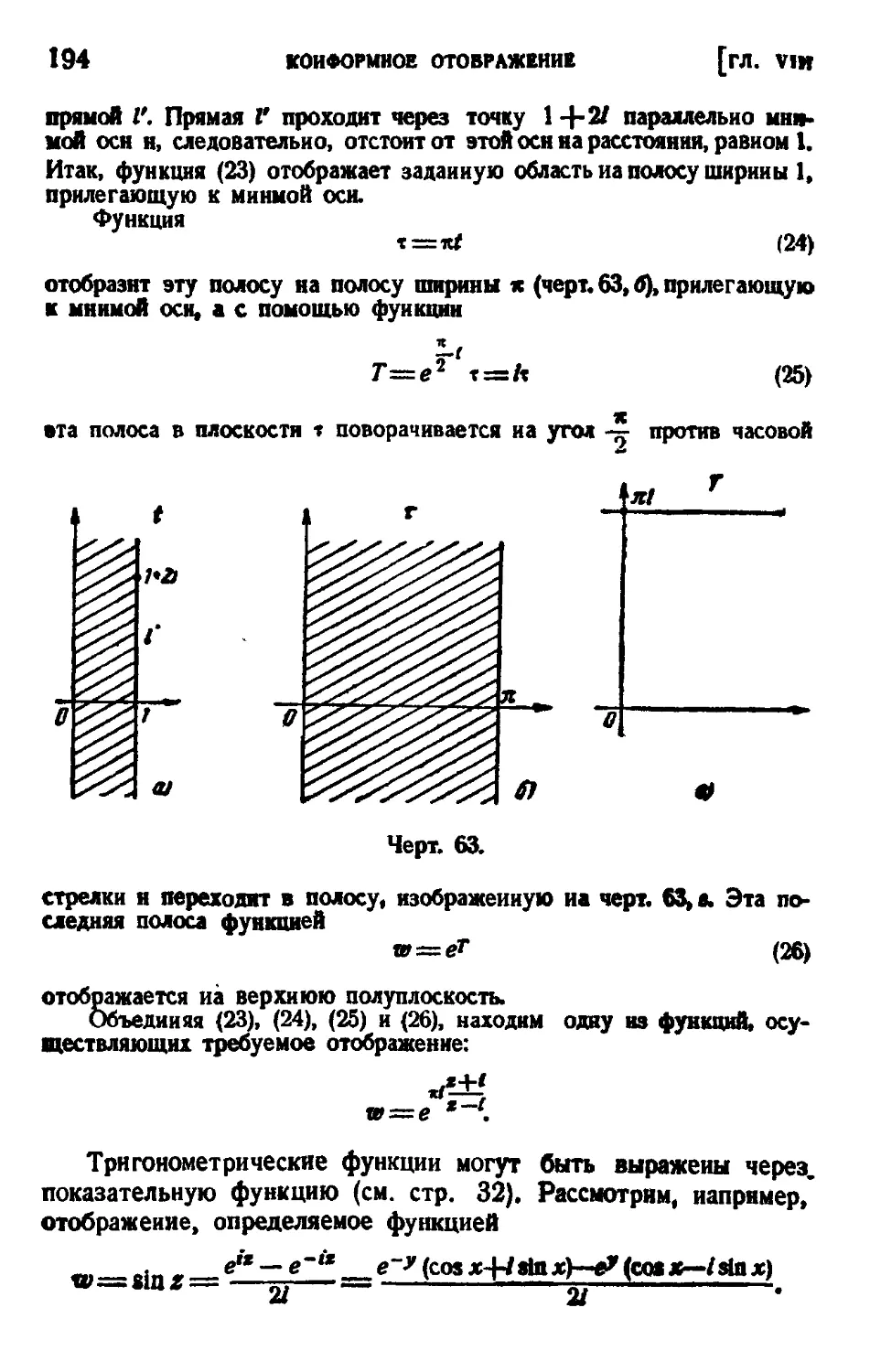
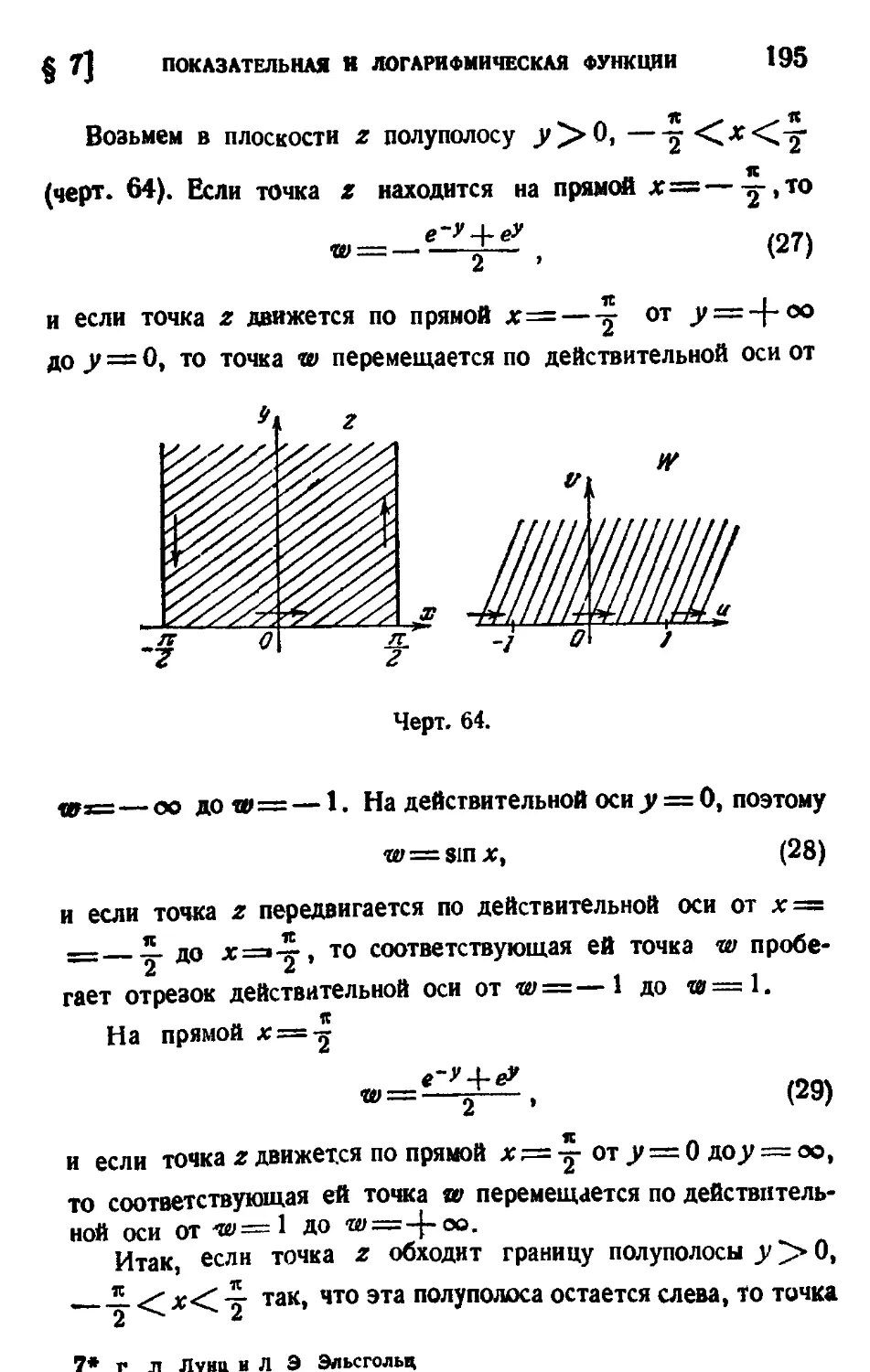
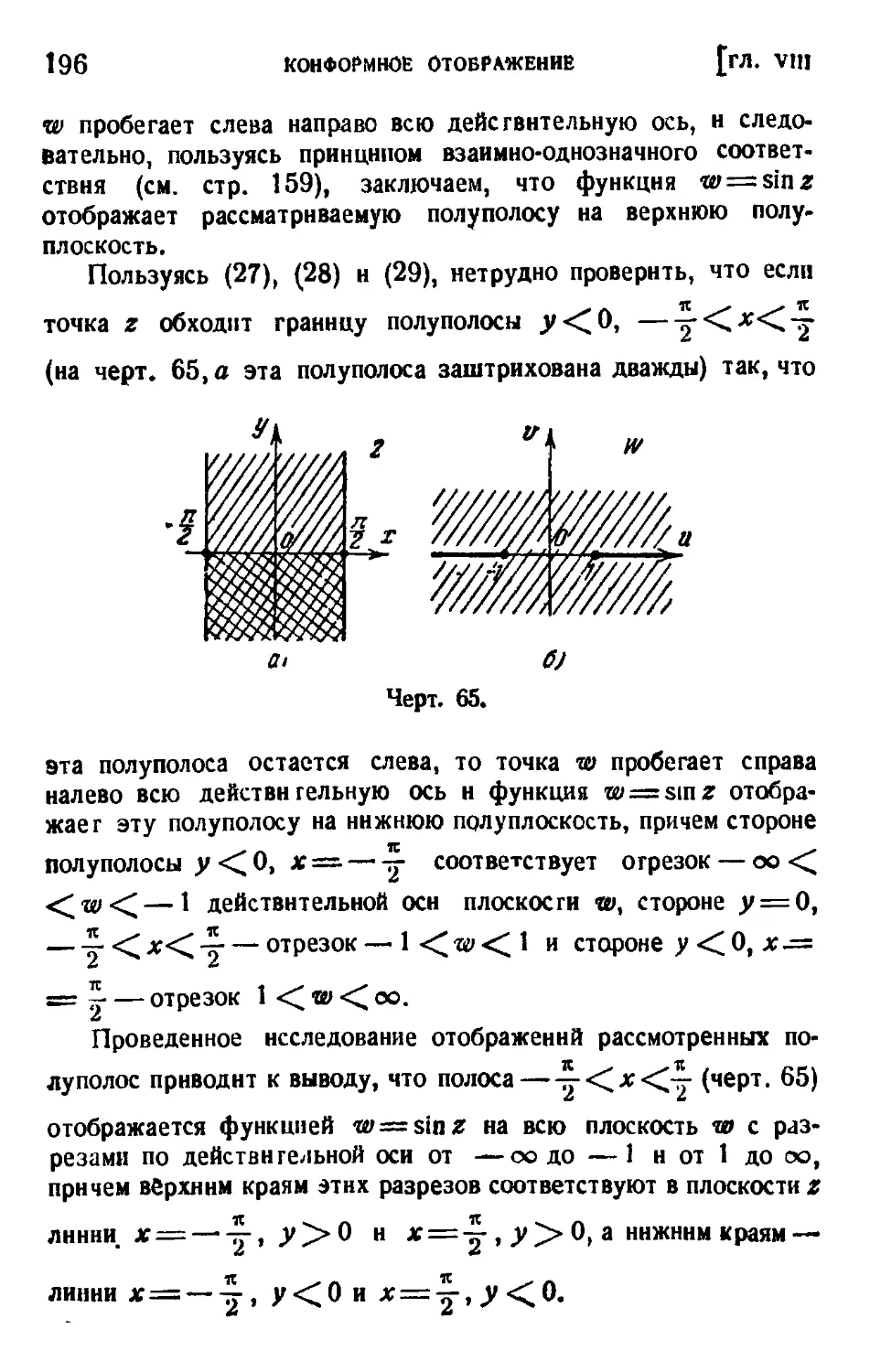
Глава VIII. Конформное отображение 158
§ 1. Некоторые общие теоремы 158
§ 2. Линейная функция 160
§ 3. Функция w=— 163
4. Дробно-линейная функция 164
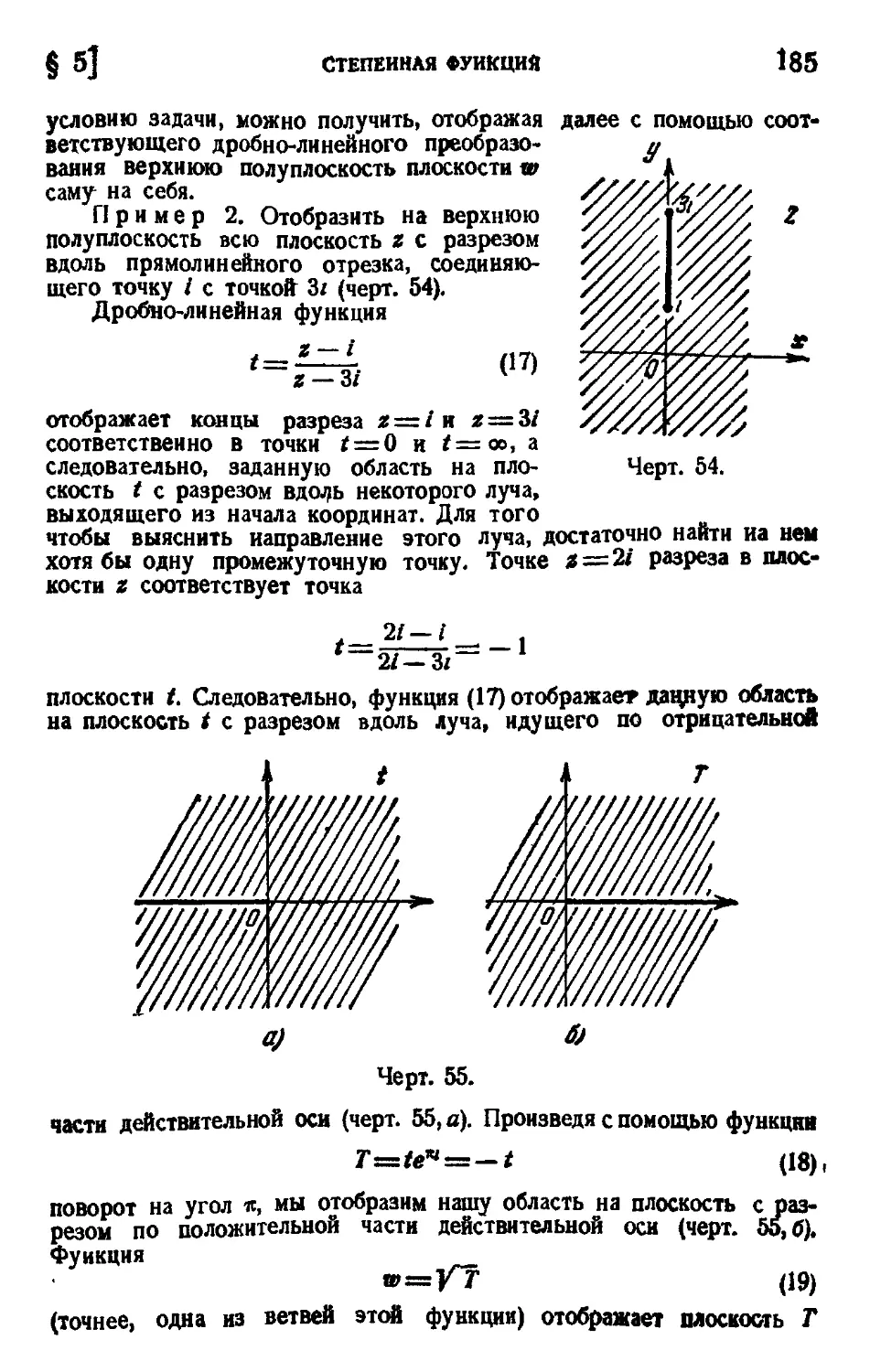
5. Степенная функция 176
i 6. Профили Жуковского 186
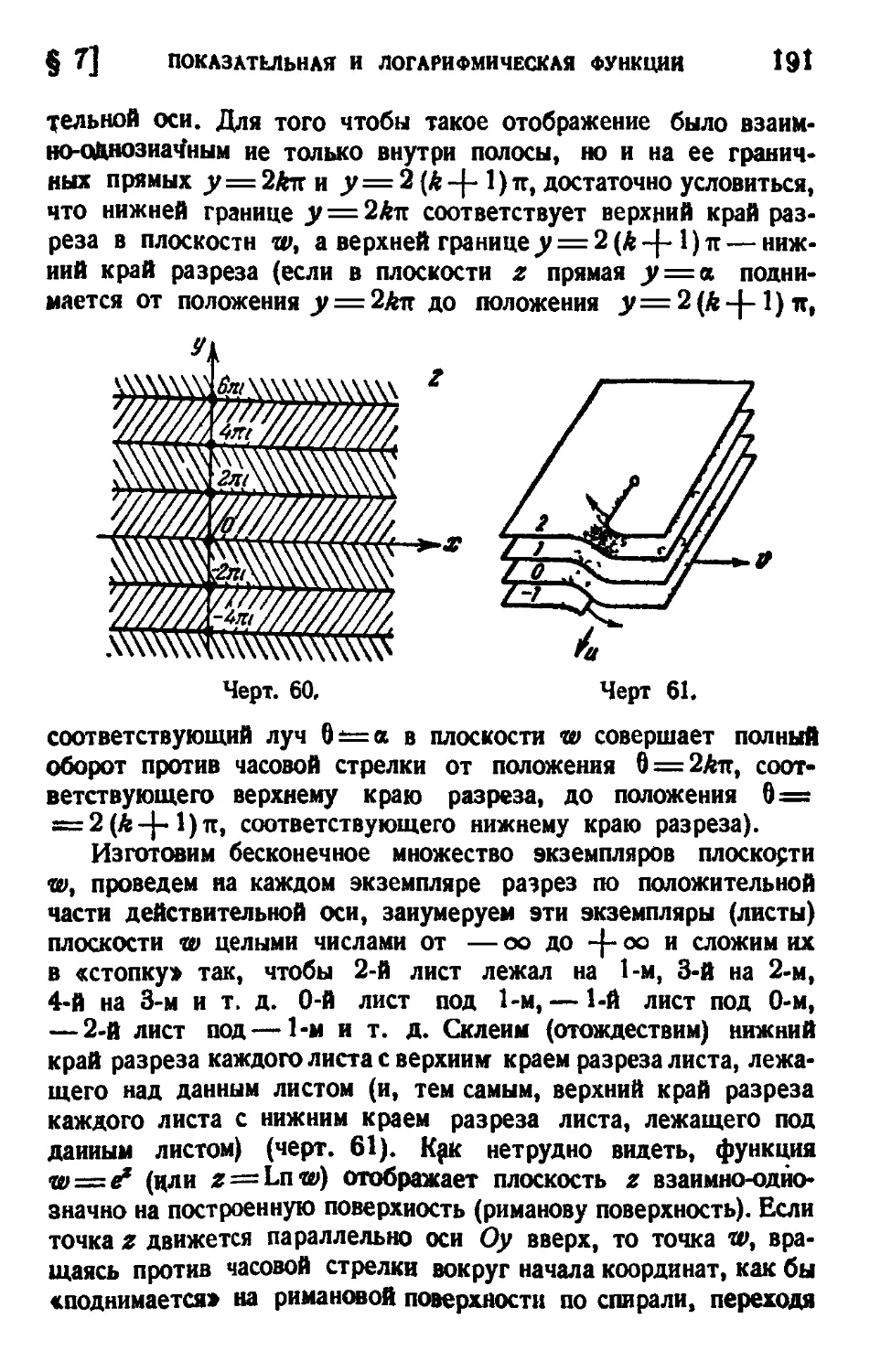
7. Показательная и логарифмическая функции 189
8. Конформное отображение полуплоскости на прямоуголь-
прямоугольник и многоугольник 197
§ 9. Понятие о вариационных методах приближенного кон-
конформного отображения 208
§ 10. Принцип симметрии 213
Задачи к главе VIII 214
Глава IX. Комплексный потенциал 219
§ 1. Плоско-параллельные векторные поля 219
§ 2. Комплексный потенциал 220
§ 3. Комплексный потенциал в гидродинамике 226
§ 4. Задачи на обтекание 232
§ 5. Теорема Н. Е. Жуковского о подъемной силе .... 242
§ 6. Комплексный потенциал в электростатике и термоди-
термодинамике 246
Задачи к главе IX 252
Глава X. Применение теории логарифмических вычетов
к исследованию устойчивости движения 253
§ 1. Основные понятия теории устойчивости 253
§ 2. Признак отрицательности действительных частей всех
корней многочлена , 2$7
ОГЛАВЛЕНИЕ 5
§ 3. Исследование на устойчивость решений дифференци-
дифференциальных «уравнений с запаздывающим аргументом . . . 260
Задачи к главе X 269
Гдава XI. Некоторые сведения из операционного исчис-
исчисления 270
§ 1. Преобразование Лапласа и его основные свойства . . 270
§ 2. Интегрирование обыкновенных линейных дифференци-
дифференциальных уравнений с постоянными коэффициентами . . 280
§ 3. Интегрирование некоторых линейных дифференциаль-
дифференциальных уравнений с запаздывающим аргументом .... 283
§ 4. Интегрирование некоторых дифференциальных уравне-
уравнений в частных производных 284
§ 5. Разложение изображения в асимптотический ряд ... 286
Задачи к главе XI 289
Ответы к задачам 290
Цитированная литература • . . 297
Рекомендуемая литература 298
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателя книга рассчитана на лиц,
имеющих математическую подготовку в объеме курса матема-
математики для технических вузов. Она имеет целью в краткой и по
возможности общедоступной форме ознакомить читателя с основ-
основными понятиями и некоторыми приложениями теории функций
комплексного аргумента.
Для читателей, желающих глубже изучить рассматривав-
мые в этой книге вопросы, на стр. 298 указана рекомендуе-
рекомендуемая литература.
Авторы считают своим приятным долгом выразить благо-
благодарность доцентам Ю. Л. Рабиновичу и А. Г. Свешникову и
редактору книги С. Б. Норкину за ряд- ценных замечаний.
ГЛАВА I
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
§ 1. Комплексные числа
Число
где х и у— любые действительные числа, а / — так назы-
называемая мнимая единица, называется комплексным числом. Дей-
Действительные числа хну называются соответственно действи-
действительной и мнимой частями комплексного числа z и обозна-
обозначаются:
или R{z),
или I(z).
Два комплексных числа считаются равными, если равны порознь
их действительные и мнимые части, т. е. равенство
равносильно двум равенствам:
Так как две точки, определеиные своими координатами в декар*
товой прямоугольной системе координат, совпадаю г тогда и
только тогда, когда они имеют равные абсциссы и равные
ординаты, то можно установить взаимно-однозначное соответ-
соответствие между всевозможными точками плоскости, с одной сто-
стороны, и всевозможными комплексными числами — с другой.
Иначе говоря, будем изображать комплексное число z — x-\-iy
С помощью точки, абсцисса которой равна х, а ордината у;
Тогда всякое комплексное число изобразится с помощью вполне
8 АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ [гл. 1
определенной точки плоскости и обратно всякой точке (х, у)
плоскости будет соответствовать вполне определенное ком-
комплексное число z = x-\-iy (черт. 1). Вместо «точка, изобра-
изображающая число г-» часто говорят короче1 «точка z». Можно
действительной и мнимой частям комплексного числа поставить
в соответствие не координаты точки, а координаты вектора,
т. е. взятые с соответствующим знаком проекции иа коорди-
координатные оси вектора, начало «ото-
рого совмещено, например, с на-
началом координат, и, следователь-
следовательно, изображать комплексные числа
с помощью векторов (черт. 1).
Комплексное число с мнимой
частью, равной нулю х-\-Ю, бу-
будем отождествлять с его действи-
действительной частью: х -(- /0= х, и счи-
считать действительное число частным
случаем комплексного. Действительные числа изображаются
точками, лежащими на оси Ох; эту ось будем называть дей-
действительной осью. Аналогично будем писать 0-}-/у=/у.
Числа, действительные части которых равны нулю (чисто мни-
мнимые числа), изображаются с помощью точек, лежащих на
оси Оу; эту ось будем называть мнимой осью.
Положение точки, изображающей комплексное число г,
можно определять также с помощью полярных координат г
и <р (черт. 1) или, что то же самое, с помощью длины век-
вектора, соответствующего комплексному числу, и величины угла,
образованного этим вектором с положительным направлением
действительной оси. Числа г и у будем называть соответ-
соответственно модулем и аргументом комплексного числа г и поль-
пользоваться обозначениями:
г=\г\,
Черт. 1.
Для действительного числа введенное здесь понятие мо-
модуля совпадает с понятием абсолютной величины. Модулем чисто
мнимого числа является абсолютная величина его мнимой части.
Из определения модуля и аргумента следует, что есл»
Z=x-\-iy, то
*=rcos<p = |*|cos(Arg2)
= rsm <p = |z|sin (Argz)
§ 1] КОМПЛЕКСНЫЕ ЧИСЛА
И
Величина ktgz многозначна и определена лишь с точ-
точностью до целого кратного числа 2л. В качестве главного
значения величины ktgz обычно выбирают значение, опреде-
определенное неравенствами
Главное значение аргумента г обозначают aigz. Если г — дей-
действительное положительное число, то argz = 0; если г — дей-
действительное отрицательное, то argz = ir; если г — чисто мни-
мнимое число с положительной мнимой частью, то axgz=-^, если
i — чисто мнимое с отрицательной мнимой частью, то
ugz =—•?-. При z=0 величина Argz не имеет смысла.
Пользуясь формулами A), можно всякое комплексное число,
отличное от нуля, представить в так называемой тригоно-
метрической форме:
z=x-\-iy = r cos <f-\-ir sin if = г (соз у -\-1 sin <p). B)
Например,
— 2 = 2(cosir-j-/sinn).
С помощью формулы Эйлера e'*=cos<p-f /sinу (см. [1],
п. 135 или здесь гл. III, стр 32) можно перейти от тригоно-
тригонометрической формы B) к показательной:
Например,
10 АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ [гл. I
Два комплексных числа, имеющие одну и ту же действи-
действительную часть, а мнимые части которых равны по абсолютной
величине, но противоположны по знаку, называются взаимно-
сопряженными. Число, сопряженное числу г, обозначается z.
Если z = x-\-iy, то z = x — /у. Из этого определение сле-
следует, что если w = z, то z = w и, следовательно, z — z.
Модули взаимно-сопряженных чисел одинаковы, а аргументы
отличаются только знаком:
Всякое действительное число совпадает с числом, ему сопря-
сопряженным.
Сопряженные числа изображаются точками, взаимно-симмет-
взаимно-симметричными Относительно действительной оси.
§ 2. Действия над комплексными числами
Сложение и умножение комплексных чисел производятся по
правилам сложения и умножения алгебраических многочленов;
последнее из этих правил дополняется требованием замены (*
числом —1 (а следовательно, /* числом —/, i* числом 1, р
числом гит. д.). При записи результата действий, произве-
произведенных над комплексными числами, следует отделить действи-
действительную часть от мнимой, т. е. собрать отдельно члены, не
содержащие множителя /, и члены, содержащие этот мно-
множитель:
У.) = С*. +
Из C), в частности, следует, что произведение двух взаимно-
сопряженных комплексных чисел является действительным чис-
числом, равным квадрату модуля этих чисел:
т. е.
_Ч Так как функция кщг неоднозначна, то равенство
Arg2 = — Arg2 надо понимать в том смысле, что множество зна-
значений, определяемых левой частью этого равенства, совпадает с мно-
множеством значений, определяемых правой частью.
§2]
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
11
Сумма двух взаимно-сопряженных комплексных чисел также
является действительным числом
т. е.
Вычитание определяется как действие обратное сложению,
откуда следует, что
—л)-
Итак, при сложении и при вычитании комплексных чисел
отдельно складываются или вычитаются их действительные и
Черт. 2.
мнимые части. Если изобразить комплексное число с помощью
вектора, то, как мы уже знаем, его действительная и мнимая
части будут являться координатами вектора,-' а так как при
сложении и вычитании векторов их координаты соответственно
складываются или вычитаются, то сложение или вычитание
комплексных чисел сводится к сложению или вычитанию век-
векторов, изображающих эти числа (черт. 2). Модуль комплек-
комплексного числа равен длине соответствующего вектора, поэтому
модуль суммы двух комплексных чисел меньше или равен
сумме модулей этих чисел:
Применяя это неравенство несколько раз, получим:
12 АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ [ГЛ. 1
Знак равенства имеет место только тогда, когда векторы,
изображающие числа г,, zt,... , zn, лежат на одной прямой
и направлены в одну и ту же сторону, т. е. когда
argzl = argzl = ... =argzn.
Модуль разности двух комплексных чисел равен расстоянию
между точками, изображающими эти числа (черт. 2). Следо-
Следовательно, если г, — данное комплексное число (данная точка),
р— данное действительное положительное число, то совокуп-
совокупность точек г, удовлетворяющих уравнению
образует окружность с центром в точке г, радиуса р. Нера-
Неравенство \z — г, | < р определяет множество точек, лежащих
внутри этой окружности («внутренность круга»), а неравен-
неравенство \z — Zj О р — множество точек, лежащих вне окруж-
окружности («внешность круга»).
Деление определяется как действие, обратное умножению.
Пользуясь свойствами сопряженных чисел, удобнее всего деле-
деление комплексных чисел производить следующим образом: сна-
сначала умножить делимое и делитель на число, сопряженное дели-
делителю, после чего делитель станет действительным положительным
числом, а затем произвести деление действительной и мнимой
частей отдельно:
Если воспользоваться тригонометрической формой записи
комплексных чисел:
то получим:
zxzt = rxrt [(cos (р, cos <ft — sin (p, sfn 9f) -f- ' (cos tpj sin tp, -f-
4-etaf,cos«p1)]=rlr1[cosD»1-f-«p1)+/sln(«pl + «p1)]. D).
Следовательно, при умножении комплексных чисел их модуля
§ 2] действия над комплексными числами
перемножаются, а аргументы складываются:
Arg (г^г) = Arg zx + Arg *,')•
Вектор, изображающий произведение zlzt, может быть полу-
полуб
чен из вектора, изображающего
угол <рг образованный вектором zt
число zv поворотом на
с положительным направ-
направу рг
лением действительной оси, и умножением его длины на длину
О
Черт. 3.
вектора zt (черт. 3). Например, число / имеет модуль, равный
единице, и аргумент -я-, поэтому умножение на / сводится
к повороту вектора на 90° в положительном направлении без
изменения его длины.
Число, модуль которого равен единице, имеет вид
cos<p-j-fsin(p, или в показательной форме el<f. Следовательно,
вектор ze'f может быть получен noeqpoTOM вектора z около
начала координат на угол <р.
Деление комплексных чисел, заданных в тригонометриче-
тригонометрической форме:
*! = /•, (cos <р, + /sin tp,),
') Обе части этого равенства многозначны. Множество значений
левой части этого равенства совпадает с множеством значений его
правой части.
14 АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ [гл. 1
приводит к формуле
*=»*[«* (fc - fc) + *sta (fc-*,)],
т. е.
Из правила умножения D) следует правило возведения в
целую положительную степень:
если
2=r(cos y-f-Zsintp),
то
г"=г" (cos лу -[" г sin лср),
т. е.
| = |s|B; Arg (*") = « Arg г1).
Пользуясь правилом деления, нетрудно проверить, что эти
формулы остаются справедливыми и при целом отрицательном л.
Извлечь корень целой положительной степени л из чис-
числа г значит найти такое число w= y/zt л-я степень которо-
которого равна z. В соответствии с правилом возведения в степень
имеем:
Если обозначить:
г=г (cos <р + / sin <p),
w = р (cos 6 -f- г sin в),
то, учитывая, что аргумент комплексного числа содержит не-
неопределенное слагаемое, кратное числу 2п, получим:
(* = 0, ±1, ±2,...).
') Это равенство справедливо с точностью до кратного числа 2я,
т. е. левая часть равенства или совпадает с правой или отличается
от нее на 2кщ к — целое число. Если же иметь в виду все множест-
множество значений аргумента, то равенство неверно, так как />Argz =
= я arg г -|- 2Аял, в то время как Arg (zn)=л arg г -\- 2fac, и таким об-
образом, с какими-либо значениями величины «Argг совпадают не все
значения величины Arg (г"), а только те из них, для которых число
к является кратным числа п.
§ 2] ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 15
Так как г и р — положительные числа, то первое из этих
равенств однозначно определяет р, а именно:
где скобка в правой части обозначает, что берется арифмети-
ческее (действительное и положительное) значение корня. Из
второго равенства находим:
и формула, с помощью которой можно извлекать корень из
любого комплексного числа, принимает вид:
== У г (cos <р —|— * sin (p) =
Хотя k — любое целое число, однако из этой формулы сле-
следует,1 что имеется лишь л различных значений величины у^г,
которые можно получить, полагая k = 0, 1, 2, .. ., л—1,-
Действительно, два значения k, отличающиеся друг от
друга на л, а значит и на любое кратное числа л, дают при
подстановке в формулу E) одно и то же значение, так как если
к' — k = n, то
2У« y + 2fat2(ft'--ft)*__g
п
п
и, следовательно,
я
Как видно из формулы E), все я различных значений ве-
величины у/И имеют один и тот же модуль, равный (^fF[)
А так как
и, следовательно, аргументы двух значений jj^z, соответст-
соответствующих соседним значениям k (k и k 4- 1), отличаются один от
Другого на —, то точки, соответствующие значениям у/И ,
16 АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ [гл. I
являются вершинами правильного л-угольника, вписанного в
окружности радиуса (^\г\) с центром в начале координат.
Поэтому способ построения точек, соответствующих значе.
ниям (/F, таков (черт. 4): из начала координат, как из
центра, описываем окруж-
окружность, радиус которой равен
({/[Т{); пР°веДя из начала
координат луч, направленный
к положительному направле-
направлению действительной оси под
углом в я раз меньшим,
чем угол, образованный с тем
же направлением лучом, иду-
идущим из начала координат в
точку z, мы найдем на ок-
окружности точку, соответст-
Черт. 4. вующую одному из значений
%/z (для этой точки в фор-
формуле E) k = 0); вписав в окружность правильный л-угольних
так, чтобы одной из его вершин была найденная точка, мы
построим точки, соответствующие остальным значениям корня.
Пример. Вычислить все значения у — 8.
Имеем: — 8 = 8 (cos к-f г йп я), откуда
V=i- С/Г) (
При fee Q, 1, 2 получим:,
Если так же, как это принято для действительных чисел,
обозиачшь
то действие возведения комплексного числа в степень окажется
определенным для любого действительного рационального по>
(изателя степени,
§ 2] ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 17
Задачи к главе I
1. Записать в тригонометрической форме числа
аK/, дI+/, и) 2 + 5/,
б)-/, е) —1— /, к) -2 + 5/,
в) 2, ж) УЗ-/, л) 2-5/,
г)-2, зI -/УЗ, м)-2-5/.
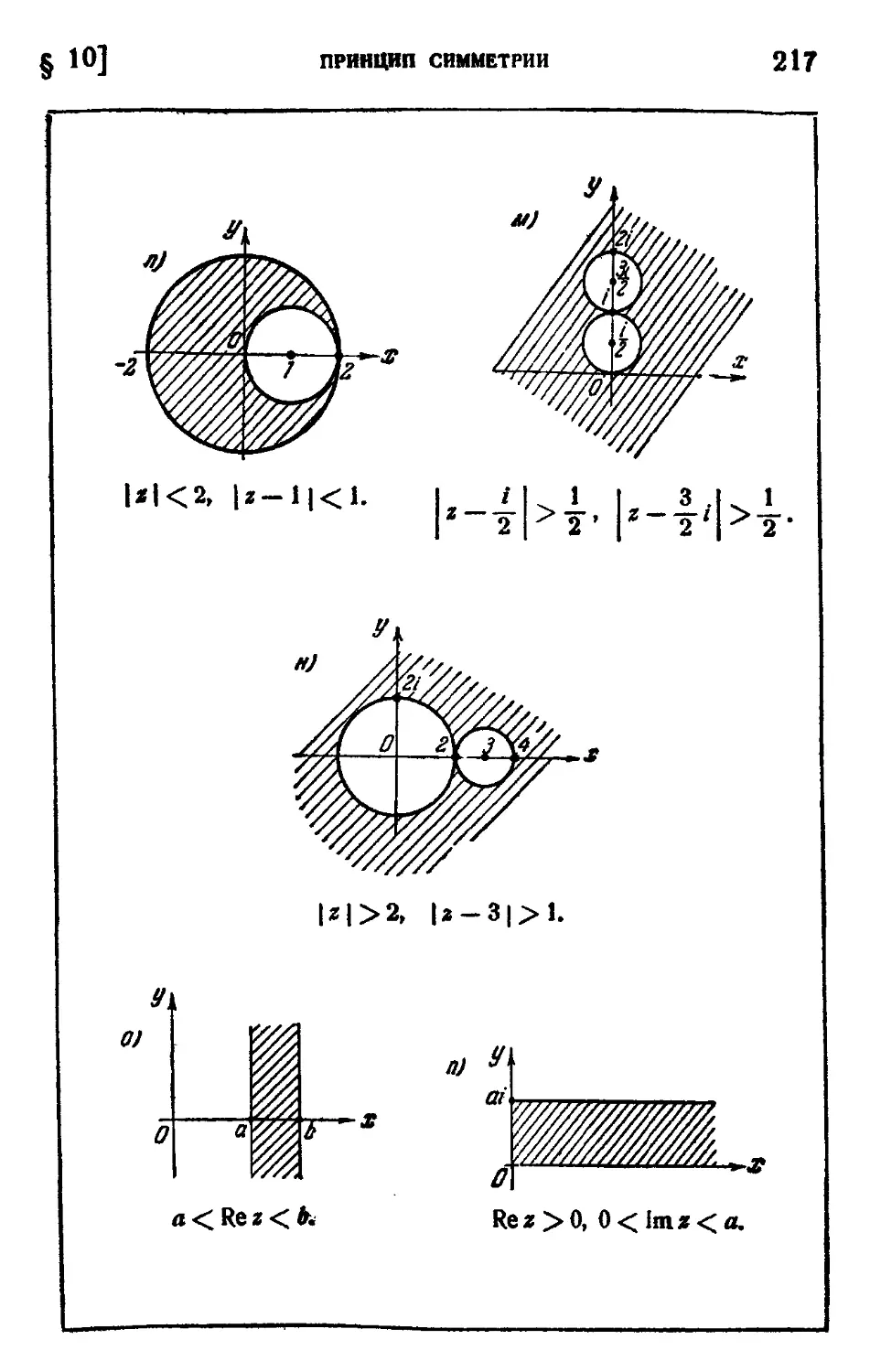
2. Где расположены точки г, для которых:
а)|г|>5, H)|z»-l|=a»
,)|г_3-4<|=5, и)
д) Re г > 3, и) a < argz <
е) Imz<2, о) arg(« — i) = -j-
ж)|г-2| + |г + 2| = 5, п)
8)|*-2|-|z
3. Доказать, что если г,+2,+2,=0 и |г, | = |г,| = |г,| = 1,
то точки Z], z» г, являются вершинами правильного треугольника,
^писанного в круг радиуса 1 с центром в начале координат.
4. Найти:
«I-
б)Г+1'
6. Найти:
а) 1/Т,
ftt */' ft
в) J/T
в)
г)
г)
д)
е)
1^37' ^A +
|/Т=Г/,
^3 + 47,
ГЛАВА II
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФУНКЦИЙ
КОМПЛЕКСНОГО АРГУМЕНТА
§ 1. Функции комплексного аргумента
Основные понятия теории функций комплексного аргумента
являются почти дословным обобщением соответствующих по-
понятий теории функций действительного переменного. Эта глу-
глубокая аналогия в основных определениях влечет за собой столь
же глубокую аналогию во многих теоремах, доходящую в неко-
некоторых разделах, например в излагаемой в этой главе теории
пределов, до полного тождества формулировок основных теорем.
Говорят, что на некотором множестве точек, изображаю-
изображающих значения комплексного переменного г, задана функция
w=/(z), если каждой точке г (каждому значению г) этого
множества поставлено в соответствие одно (в случае однозначной
функции) или большее число (в случае многозначной функции)
значений w.
Множество точек, на котором задана (определена) функ-
функция w=f{z), в дальнейшем будет, как правило, или сово-
совокупностью всех точек плоскости (вся плоскость), илн всей
плоскостью, за исключением отдельных ее точек, или одно-
связной, либо многосвязной областью (см. [2] п. 139), являю-
являющейся частью плоскости, ограниченной одной или несколькими
гладкими или кусочно-гладкими') кривыми, из которой могут
быть удалены отдельные точки.
Так, например, функция w — z* однозначна и ее можно
считать определенной на всей плоскости, так как с помощью
') Дуга называется гладкой, если в каждой ее точке можно про-
провести касательную, непрерывно вращающуюся при движении точки
по кривой; дуга непрерывной кривой, состоящая из конечного числа
гладких дуг, называется кусочио-гладкой.
§ 1] ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА 19
формулы, по которой производится возведение комплексного
числа в степень (стр. 14), всякому комплексному числу 2
соответствует (и притом только одно) значение г*. Функция
w=Avgz многозначна и определена на всей плоскости, за
исключением точки 2 = 0 (см. стр. 8—9).
Так как задание комплексного числа z равносильно заданию
двух действительных чисел хну, являющихся соответственно
Действительной и мнимой частями z (z = x-\-iy), а числу w
точно так же однозначно соответствует пара действительных
чисел а и v (w=a-\-iv), то зависимость w=/(z) между
комплексной функцией w и комплексным аргументом 2 равно-
-сильна двум зависимостям:
« = *(*,».
v—v(x, у),
определяющим действительные величины а и о как функции
действительных аргументов х и у.
Например, если w—z*, то, полагая &=.x-\-iy, w=tt-\-
-\~iv, получим а + iv=(x-\-iy)* = (x%—y*)-\-2ixy и, сле-
следовательно, равенство та»=2* равносильно равенствам:
а=х1 — у\
v = 2xy.
Если значения аргумента z изображать с помощью точек не-
некоторой плоскости («плоскости z»), а значения функции та» с по-
помощью точек другой плоскости («плоскости та»), то функция
да—/(г) устанавливает соответствие между точками пло-
плоскости 2, в которых эта функция определена, и точками
плоскости та», другими словами, функция осуществляет ото-
отображение точек плоскости z на соответствующие точки пло-
плоскости w.
Обозначим символом g множество точек плоскости z, на
котором определена функция w=/(z), а символом G мно-
множество,' состоящее из тех точек плоскости w, на которые с
помощью функции w=f(z) отображаются точки множества g.
Выбрав какую-либо определенную точку множества О, найдем
те точки множества g, которые отобразились в выбранную
точку. Таким образом, каждой точке множества О будет соответ-
соответствовать одна или несколько точек множества g. В соответствии
с определением функции это будет означать, что на множестве О
20 основные понятия теории функций [гл. п
определена некоторая функция z = y(w), которую называют
обратной по отношению к функции w=f(z).
Если функция w=f(z) однозначна, то каждой точке пло-
плоскости z, в которой функция определена, соответствует одна
точка плоскости w. Если при этом некоторое множество то-
точек g плоскости z отображается взаимно-однозначно на неко-
некоторое множество О плоскости w, т. е. если функция w=/(z)
такова, что не только каждой точке множества g соответствует
одна и только одна точка множества О, но и обратно, каждой
точке множества G соответствует в точности одна точка мно-
множества g, то функция z = <р (w), определенная на множестве О
и отображающая его на множество gt обратная по отношению
к функции w=/(z), также является однозначной.
Пример 1. Функция w — zx осуществляет однозначное отобра-
отображение внутренности круга g плоскости г с центром в начале коор-
координат и радиусом, равным 2, на внутренность круга G плоскости w
с центром в начале координат н радиусом, равным 4.
Действительно, точки круга gопределены неравенством I г|<2,
но если и» = г1, то неравенство | г | < 2 равносильно неравенству
|и»|<4, которое определяет совокупность точек, лежащих внутри
круга G. Нетрудно видеть, что это отображение области g на область
О однозначно, но не взаимно-однозначна Действительно, функция
w—z* однозначна н каждой точке z соответствует единственная
точка и», но каждой точке w, лежащей внутри круга G, за исключе-
исключением точки да = 0, соответствуют две точки круга g, симметричные
относительно начала координат, так как если z4=— z, и z\=w, то
z\ = z\ = w. Следовательно, функция z=y~w< осуществляющая
отображение области G на область g, обратная по отношению к фун-
функции w = z*, многозначна (двузначна).
Пример 2. Сектор g, точки которого определены неравен-
неравенствами 0<argz<-j-, |z|<l, в силу того, что arg (z*) = 2arg*
и |22| = |z|\ отображается с помощью функции tp=z' на сек-
сектор G: 0<argt»<-^-, |и»|<1 (черт. 5).
Нетрудно видеть, что это отображение взаимно-однозначно.
Действительно, хотя функция z = Yw, обратная по отношению к
данной, двузначна, все же из двух точек z, и 22(z, = — Zj), соответ-
соответствующих точке и» области G, лишь одна принадлежит области g.
Иными словами, отображение области G на область ^ осуществляется
с помощью однозначной ветви1) функции г—Yw (другая ветвь
функции г = Уи> отображает область G-на область g\ граница ко-
которой на черт. 5 отмечена пунктиром).
') О ветвях многозначной функции см. подробнее в главе VIII.
§ 1] ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА 21
Если в плоскос1и z кривая с задана уравнением
F{x,y) = 0, B)
то для того, чтобы найти уравнение кривой С в плоскости
w, на которую отображается кривая с, с помощью функции
Черт. 5.
>w=f(z), достаточно исключить х и у из уравнений A)
(стр. 19) и B). Если кривая с задана параметрическими урав-
уравнениями:
то, подставляя x(i) и у (t) вместо х и у в A) (стр. 19), получиы
уравнения кривой С также в параметрической форме:
v=v[x(t), y(t)] =
Пример 3. Найти уравнения линий плоскости w, на которые
с помощью функции w = г* отображаются прямые, параллельные коор-
координатным осям плоскости 2.
Как было показано выше (стр. 19), равенство w — z* равносильно
равенствам:
где z=x + iy и w=t +
Образ прямых х = с, параллельных мнимой оси плоскости г, по-
получим, исключая х ъ у кз уравнения х=с к уравнений C):
и = с*-у*,
«=2су,
22
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФУНКЦИЙ
[гл. п
откуда
4?'
Мы получили уравнение некоторого семейства парабол, симмет-
симметричных относительно оси Ои, вершины которых находятся на поло-
положительной части этой оси и которые обращены вогнутостью в
сторону отрицательной части оси Ои
(черт. 6).
Мнимая ось х = 0 плоскости г ото-
отобразится на линию
« = -/,
D)
Второе из этих равенств показывает,
что линия D) расположена на оси Ои, а
из первого следует, что и может прн-
ннмать любые значения, для которых
u=S0, следовательно, минмая ось х = 0
плоскости г отображается на отрицательную часть действительной
оси плоскости w:
Черт. 6.
Аналогичные рассуждения показывают, что семейство прямых у = с,
параллельных действительной оси плоскости г, отобразится в се-
семейство парабол
--?-'
плоскости w,. также изображенное , на чертеже 6, причем действи-
действительная ось jr=O плоскости г отобразится в положительную часть
действительной оси плоскости w.
, 0 = 0.
Следует заметить, что параметрические уравнения линии в
плоскости z
x = x(t),
y=y(t)
могут быть заменены одним уравнением
z=z(t),
Например, уравнение
z=cos /-{- Ша t
§ 2] ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 23
является уравнением окружности радиуса 1 с центром в. начале
координат, так как оно равносильно уравнениям;
X = COS /,
у = sin t.
Уравнение кривой в плоскости w, на которую с помощью
функции w=f(z) отображается кривая z = z(t), имеет вид
Пример 4. Найти образ прямой z — (l-\-i)t при отображении
к» = 2.
Уравнение г = A -f-1) t равносильно системе уравнений
x = t,
и определяет в плоскости г биссектрису первого координатного угла
_1 С помощью функции Wz=zz* эта биссектриса отображается на
линию
ИЛИ
откуда
Исключая параметр t, получим v = — и — уравнение биссектрисы
второго координатного угла плоскости w.
§ 2. Предел последовательности
Окрестностью точки, изображающей комплексное число z0,
называется всякая область, внутри которой лежит точка г0.
В дальнейшем мы будем пользоваться только круговыми окрест-
окрестностями, т. е. будем называть окрестностью точки г0 внут-
внутренность круга с центром в этой точке, при этом ^-окрест-
^-окрестностью точки г0 мы будем называть внутренность круга ра-
радиуса р с центром в точке г0, т. е. совокупность точек,
удовлетворяющих неравенству
Число z0 называется пределом последовательности ком-
комплексных чисел zlt zt, zt, ... , zn, ...:
lim arn:=z0,
П-* 00
24 основные понятия теории функций [гл. и
если для любого положительного числа е, как бы мало оно ни
было, можно подобрать такое число N (N зависит от е), что при
л Э* ЛГ выполнено неравенство \zn — z0\<е. В этом случае
говорят также, что последовательность zlt zt, ... , zn, ...
сходится к числу zv Если среди членов последовательности
нет бесконечного множества одинаковых чисел, то числа
zt, zt, ... , zn, ... определяют бесконечное множество раз-
различных точек. Если
lim zn = z.,
п-юо
то как бы мала ни была е-окрестность точки za, вне этой
окрестности может остаться лишь конечное число точек после-
последовательности, так как все точки последовательности г„,
начиная с той, для которой л = JV, попадут внутрь этой
е-окрестности.
Если zn = xn-{-iyn и *0 = *0-f-/y0, то, учитывая равенство
К - *. I=У К - *„)*+(у« -лI.
нетрудно, исходя из определения предела, заключить, что су-
существование предела
lim zn = z9
л-» оо
равносильно существованию двух пределов:
lim xtt = x0,
л-> оо
lim yn=yv
л-> оо
Если последовательность zv zt, ..., zn, ... такова, что
модули всех ее членов, начиная с некоторого, становятся больше
любого, сколь угодно большого положительного числа (т. е.
если, как бы велико ни было положительное число М, к нему
можно подобрать такое N, что | zn | > М при л ^ N), то хотя
последовательность, очевидно, предела не имеет, однако удобно
и в этом случае писать
lim 2n = oo
и говорить, что последовательность точек *,, гх, ... , zn, ...
сходится к бесконечно удаленной точке или что предел после-
последовательности бесконечен. Окрестностью бесконечно удаленной
$23
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 25
точки будем называть внешность круга достаточно большого
радиуса. Если радиус этого круга равен R, а центр находится
в точке Z—0, то множество точек, образующих окрестность
бесконечно удаленной точки, определяется неравенством
| z | ]> R. Чем больше радиус круга, тем «меньше» окрестность
бесконечно удаленной точки, являющаяся внешностью этого
круга.
Сопоставляя определение равенства Нт гл = оо с опреде-
л-юо
лениеи окрестности бесконечно удаленной точки, мы видим,
что, если последовательность точек сходится к бесконечно уда-
удаленной точке, то, как бы мала нн была окрестность беско-
бесконечно удаленной точки, т. е. как бы велик ни был радиус R
круга, внешностью которого эта окрестность является, все
точки последовательности zv zt, ... , zn, ... , за исключением
конечного их числа (все точки zn, начиная с той, для которой
n=zN), попадут внутрь этой окрестности.
Таким образом, определение предела, по существу, одной
то же как в случае, когда этот предел конечен, так и в том
случае, когда он бесконечен, и в этом смысле бесконечно уда-
удаленная точка вполне равноправна с остальными точками пло-
плоскости.
Равноправность бесконечно удаленной точки по отношению
к другим точкам можно сделать наглядной, если изменить
геометрическую интерпретацию комплексных чисел.
Черт. 7.
Построим сферу (черт. 7), касающуюся в точке ?=0
плоскости z, служившей нам для интерпретации комплексных
чисел. Пусть N—точка сферы, диаметрально противоположная
26 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФУНКЦИЙ [ГЛ. II
точке касания сферы с плоскостью г. Проведем из точки N
луч в любую точку z плоскости z и отметим на сфере точку,
отличную от точки N, в которой этот луч пересекает сферу.
Будем считать эту точку изображением того же самого ком-
комплексного числа г. Любому комплексному числу z ставится
таким образом в соответствие определенная точка сферы, ко-
которую будем так же, как и соответствующую точку плоскости,
называть точкой z. Если на плоскости взята последователь-
последовательность zx, zt, ... , zn, ... точек, сходящаяся к некоторой
точке z0, то соответствующая последовательность точек на
сфере также будет сходиться к точке г„ на сфере (т. е. рас-
расстояние точки zn на сфере от точки z0 на сфере будет стре-
стремиться к нулю).
Если
lira zn — oo,
П-+ОО
то последовательность точек zt, zt, ..., zn, ... на сфере
будет сходиться к точке N, т. е. при л—юо расстояние между
точкой zn на сфере и точкой N будет стремиться к нулю.
Таким образом, точка N (а это «обычная» точка сферы) соот-
соответствует бесконечно удаленной точке плоскости.
Заметим, что в соответствии с введенным нами определением
на комплексной плоскости имеется только одна бесконечно
удаленная точка (соответствующая точке N на сфере), в то
время как, например, во многих разделах геометрии удобно
считать, что существует бесконечное множество бесконечно
удаленных точек: каждому направлению соответствует своя
бесконечно удаленная точка.
§ 3. Предел функции. Непрерывность
Число да0 называется пределом однозначной функции f(z)
при г, стремящемся к z9:
w%= Urn /(*),
если, как бы мала ни была выбранная е-окрестность точки wt,
можно найти такую 5-окрестность точки zt, что для всех то-
точек z этой окрестности (кроме, быть может, самой точки z0)
соответствующие значения функции f(z) будут изображаться
точками выбранной s-окрестности точки wv
.§ 3] ПРЕДЕЛ ФУНКЦИИ НЕПРЕРЫВНОСТЬ 27
В случае, если z0 и w0 — конечные числа, это определение
равносильно следующему. Равенство
wo=lim/(z)
обозначает, что как бы мало ни было положительное число е,
к нему можно подобрать такое положительное число 8, что
для всех значений г(гфга), удовлетворяющих условию
1*-*.|<*. E)
выполнено неравенство
|/(*)~».|<в. F)
Если z0 или w0 или оба эти числа бесконечны, то в соот-
соответствии с определением окрестности бесконечно удаленной
точки неравенства E) или F), или оба эти неравенства
должны быть заменены другими. Так, например, равенство
lim •/ (z) = te»0
z-юо
(w0 конечно) обозначает, что, как бы мало ни было положи-
положительное число б, к нему можно подобрать столь большое по-
положительное число А, что для всех значений z, для которых
функция f(z) будет удовлетворять неравенству
Введенное нами определение предела функции формально ничем
не отличается от определения предела функции действитель-
действительного аргумента, и следовательно, все доказываемые в курсе
математического анализа теоремы о пределах и бесконеч-
бесконечно малых1) остаются в силе для функций комплексного аргу-
аргумента.
Если функция w—f(z) определена в точке z0 и в неко-
некоторой ее окрестности и предел
lim f{z)
') Функция f(t) называется бесконечно малой в окрестности
точки ze, если
Hm /(z) = 0.
28 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФУНКЦИЙ [ГЛ. I
не только существует, но равен значению функции f(z) в
точке zQ:
11ш /(*)=»/(*.),
г-
то функция /(г) называется непрерывной в точке гй. В соот-
соответствии с определением предела это значит, что функция
w=f(z) непрерывна в точке z0, если для любого положи-
положительного числа б, как бы мало оно ни было, можно подобрать
такое число 8>0, что из неравенства
1*-*,|<» G)
будет следовать, что
1/Ю-/(*.) К •• (8)
Если обозначить г—zo — bz, w — wo = Aw (Дг — прираще-
приращение аргумента, Aw—приращение функции), то неравенства G)
и (8) заменяются, соответственно, неравенствами:
(Г)
(8')
и определение непрерывности в точке zt функции w=f(z),
заданной в некоторой окресгности этой точки, сводится к тому,
что в этой точке
lim Дге>=0.
Д2-»0
Так как сформулированное выше определение непрерывности
совпадает с определением непрерывности для функций действи-
действительного аргумента, то доказываемые в курсе математического
анализа теоремы о непрерывности суммы, разности, произведе-
произведения, частного') непрерывных функций, а также непрерывной
функции от непрерывной функции остаются в силе для функ-
функций комплексного аргумента.
Как уже указывалось выше (стр. 19), равенство w=f(z)
равносильно системе равенств:
и — и(х,у),
v=v(x,y),
где w=u-\-iv, z = x-{-iy.
') Если делитель не обращается в нуль.
§ 3] ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ 29
Если *0 = *0 + /ув. то
/ W—/(*•) = [«(*. Л ~ «(*,. У,)] +' [« (*. y)—v С*,, у,)]
я
Из определения непрерывности функции /(г) в точке г следует,
что, если точка (х,у) находится в достаточно малой окрест.
ности точки (дс0, ^0), то выполнено неравенство (8), а следова»
тельно, в соответствии с (9), тем более, удовлетворяются не'
равенства:
|e(x.jr) — u(x,y9)\<6,
которые означают, что функции и{х,у) и v(xty) непрерывны
в точке (х0, yt).
Таким образом, из иепрерывности функции комплексного аргу-
аргумента следует непрерывность ее действительной и мнимой частей"
как функций двух действительных аргументов хну. Справед-
Справедливо и обратное утверждение: из неравенств A0) и равенства (9)
непосредственно следует, что непрерывность функций и(х,у)
и v (x, j|) влечет за собой непрерывность функции f(z).
Заметим, что если вспомнить (см. стр. 21) способ, с по-
помощью которого, зная уравнение некоторой линии в плоскости г,
можно найти уравнение ее образа на плоскости w при отобра-
отображении v>=f\z), то мы легко убедимся в справедливости ут-
утверждения: непрерывная кривая отображается с помощью не-
непрерывной функции на непрерывную кривую (или, если /(г)
постоянна вдоль заданной кривой, в одну точку).
Задачи к главе II
1. На какие линии плоскости w отображаются с помощью функции
цг=— следующие кривые плоскости z (g = x-\-iy, w = u
Za)x«+/=4; г) ,у=0;
б) *'+/=1; д) х=1;
) )A
2. Какие линии заданы уравнениями (t — действительный параметр):
a) g = t A + 0; б) g =
i
i-; г) * = <
ГЛАВА HI
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
§ I. Показательная, тригонометрические и гиперболические
функции
Ряд с комплексными членами
*! + *•+••• +*«+••-. 0)
так же как и ряд с действительными членами, называется сходя-
сходящимся, если существует предел при я—*оо его частичной
суммы
+ ++
Этот предел
s= Иго sn
в-юо
называется суммой ряда.
Очевидно, что ряд A) сходится тогда и только тогда, когда
сходится как ряд
*! + *¦+• ••+*.+ •••. B)
членами которого являются действительные части членов ряда
A), так и ряд
составленный из мнимых частей членов ряда A).
Это утверждение немедленно следует из того, что сходи-
сходимость последовательности комплексных чисел равносильна схо-
сходимости двух последовательностей, одна из которых составлена
из действительных, а другая из мнимых частей членов данной
последовательности. Отсюда, в частности, получаем, что в слу:
чае сходимости ряда A) lim za = 0, так как za = xn-\-iyn,
л-юо
а 11пиев= lim^B = 0 ввиду сходимости рядов B) и C).
в->оо в->оо
§ 1] ПОКАЗАТЕЛЬНАЯ, ТРИГОНОМЕТРИЯ. И ГИПЕРБОЛИЧ. ФУНКЦИИ 31
Если сходится ряд
членами которого являются модули членов данного ряда A),
то ряд A) также сходится и называется абсолютно сходя-
сходящимся. Действительно, из очевидных неравенств
вытекает сходимость рядов B) и C), а следовательно и ряда A).
Определения суммы, разности, произведения двух рядов я
теоремы о сходимости суммы, разности, произведения рядов не
отличаются от соответствующих теорем для рядов с действи-
действительными членами (см. [1], п. 126).
Введем определения основных трансцендентных функций для
комплексных значений независимой переменной. Очевидно, что
когда показатель степени является комплексным числом, опре-
определение степени с?, вводимое в-алгебре, теряет смысл. Точно
так же известные из тригонометрии определения тригонометри-
тригонометрических функций sinz, cosz, igz, ctg? теряют смысл при ком-
ллексных значениях г. Принимая во внимание известные для
действительных значений х разложения функций ех, siax,
cos* в степенной ряд, положим, по определению,
3! Т! •••T"t ' Bn + l)M "•'
Ряды, стоящие в правых частях этих равенств, сходятся, и
притом абсолютно, при любом комплексном значении г. Дейст-
Действительно, рассмотрим, например, ряд D). Если z = r, где г —
любое действительное положительное число, то ряд D), как
известно из курса анализа, сходится, но это и значит, что
ряд D) сходится абсолютно при |,г| = г, а так как г произ-
произвольно, то ряд D) сходится абсолютно в любой точке плоско-
плоскости г. .Аналогичные рассуждения применимы к рядам E) и F).
Следовательно, равенства D), E), F) определяют во всей пло-
плоскости комплексного переменного z функции в*, sin z, cos z,
совпадающие при действительных значениях z с соответствую-
82 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ [гЛ. III
щими функциями, определяемыми в курсах математического
анализа.
Функции ez, sin2, cos* связаны между собой формулой
Эйлера:
е'г = cos г -ft sin г. G)
Действительно, подставив в равенство D) iz вместо z, получим:
е ~ *11 2! 3! ~Г4Г~Г?~'"
Умножив, далее, обе части равенства E) на / и почленно
сложив полученное равенство с равенством F), убедимся в спра-
справедливости формулы Эйлера.
Если в формуле Эйлера заменить г на — Z, будем иметь:
е-"=cos г — / sin г. (8)
Из G) и (8) получим:
?Ц±1*, (9)
* M* . A0)
Как уже указывалось иа стр. 9, формула Эйлера позволяет
преобразовать тригонометрическую форму комплексного числа
в показательную:
z=r (cos <р -{- / sin tp)=re'9.
Если xt я xt—действительные числа, то, как известно,
Принимая во внимание, что
е*~1 +ТГ + 2Г+ '' * +"й+ *'м
получим:
A1)
Если заметить, что сходимость (и притом абсолютная) рядов,
участвующих в равенстве A1), ие нарушится при замене дей-
действительных чисел xt и хх любыми комплексными числами гх и
§ !] ПОКАЗАТЕЛЬНАЯ, ТРНГОНОМЕТРНЧ. И ГИПЕРБОЛИЧ. ФУНКЦИИ 33
zt и что формальное перемножение рядов с комплексными- чле-
членами можно производить по правилам перемножения рядов с
действительными членами, то можно утверждать, что равенство
e*i+r. = e*»e*« A2)
справедливо и при любых комплексных гх и гх. В частности,
если z = x-\-iy, где х и у— действительные числа, то
Но, в силу G),
eiy = cos у -\- i sin у,
следовательно,
e*=e*(cosy-{-isiny). A3)
Отсюда, в частности, следует, что |е*| = е* и одно из значе-
значений Arge2 равно у.
Равенство A3) позволяет вычислять значения показательной
функции при любых комплексных значениях показателя. На-
Например:
««-"^«•(совЗ —/sin3),
е —— I,
Л'
Из равенства A3) следует периодичность функции в' с пе-
периодом 2п/:
Действительно, если z = x-\-iy, то
gt+ы=в*+,«-+»«, _ е* [cos ^ _(_ 2тг) + / sin (у-f 2n)] =
:= е* (cosy -J- / sin_y) = e*.
В частности, е|*я'=в°=1, в"*+1>я' = в«' = _1 (А—целое
¦мо).
Если т — целое число, то из A3) получим:
(e*)m — [е* (cosy -\- i siny)]m=в* (cos у + / slny)m ^=
= етх (cos ту + / sin ту) = ет (*+"> = ет.
Если р — рациональная дробь (р== —, где т и п — целые
числа), то выражение (ezf многозначно (оно имеет п значений)
и только одно из значений этой величины равно е?х.
2 Г. Л. Лунц н Л Э Эльсгольц
84 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ [гл. П1
Формула A3) позволяет вычислять значения показательной
функции, а формулы (9) и A0) могут служить для вычисления
cos г и sin г при любом комплексном г.
Показательная функция имеет период 2тт/, поэтому правые
части равенств (9) и A0) не изменятся при замене г на г-\-Ък,
так как ee«+t*) = ef*+ta=e», *-'<*+*">=*-й-«"'==*-« сле-
следовательно,
cos(z+2*)=cos*, sin(z-|-2*)—sin*,
т. е. определенные с помощью (9) и A0) функции cos г и sin *
периодичны и имеют, как и в случае действительного аргу-
аргумента, период 2гс. Нетрудно убедиться в том, что для функций
sin г я cos г при любых комплексных значениях г сохраняется
основное связывающее их тождество
Действительно,
Г 4 *
Сохраняются также и другие основные тригонометрические
тождества. Например, на основании (9) и A0)
sin г, cos гш -f- cos zx sin zt =
— 2? 2 > 2 S •
я, преобразовав правую часть этого равенства, получим:
sin г, cos zt -f- cos г, sin г,=— j/ == s'n (zi T" zi)«
Функции tgz и tgz определяются с помощью равенств:
§ 2] ЛОГАРИФМ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ **5
Гиперболические функции shz, chz, ihz, cthz опреДеля*
ются равенствами:
sh z= ^ , chz= ^ , thz = EF5, cthz=shi-
Принимая во внимание (9), A0), A4) и A4'), заметим» что
гиперболические функции легко могут быть выражены ^ерез
тригонометрические:
sh z = — / sin iz, ch z = cos iz,
thz = — itgiz, cthz = iz\giz.
Из этих тождеств следует в частности периодичность гипеР"
болических функций, причем периоды sh2 и chz равны 2ш,
a thz и cthz равны т.
Пример 1. Найти cos/.
Принимая во внимание, что cos г = —3^ f получим:
cos / = —~— = ch 1.
Пример 2. Найти sin A + 20-
Принимая во внимание, что sin г = ^. -, получим:
_c">(cos 1 +/sin 1) — c' (cos 1 — / sin 1)_
__ 2/ _
_ cos 1 (e - e1) + isin l(et + e~t)_
__ ^. _
— ~2^~ Sin l +' ^~T~ C0S l ~ ch 2 m l + sh 2 C0S!
(аргумент под знаком синуса и косинуса измеряется, конечно, в Ра*
дианах).
§ 2. Логарифм и обратные тригонометрические
Логарифмическая функция определяется как функция,
ная показательной.
Если e* = z, где гфО, то число w называется
мом числа z и обозначается
о*
86 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ [ГЛ. Ill
Если w=u-\-iv, то, как уже было отмечено выше, из фор-
формулы A3) следует, что |ew| = ee н Kxge"=v. Так как в рас-
рассматриваемом случае ew = z, то e*=\z\, или
(| г | — число действительное» и положительное, и здесь имеется
в виду известное нз курса математического анализа обычное
определение логарифма), и
Итак,
=Hn|*|4-/arg*-|-2*n/ (*=rO, ±1, ±2,...). 05)
Ввиду многозначности величины htgz логарифм является много-
многозначной функцией (действительная часть логарнфма, равная In | z |,
определяется однозначно, а мнимая содержит неопределенное
слагаемое, кратное 2тт).
Главным значением логарифма чнсла г будем называть
то значение, которое соответствует главному значению аргу-
аргумента чнсла г. Следовательно, в формуле A5) главное значе-
значение логарифма получим при k±=0.
Если z—x—действительное положительное число, то
|z[ = x н argz = 0, поэтому, согласно A5), главное значение
логарифма действительного положительного чнсла является чис-
числом действительным и совпадает со значением, обозначаемым
символом \пх, которое и приводится в таблицах логарифмов.
Естественно поэтому символом In г обозначать главное значение
логарнфма любого комплексного числа г; тогда в соответствии
с формулой A5) получим:
lnz = ln|*|-f-/argz. A5')
Пример 1. Найти In (— 1) и Ln (— 1).
Модуль числа — 1 равен 1, а главное значение аргумента равно к,
следовательно,
11) 1
Пример 2. Вычислить In/ и Ln/.
Модуль числа /равен 1, а главное значение аргумента равно
§ 2] ЛОГАРИФМ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 37
следовательно,
ln/=ml + J/=|-/.
Ln/=-J/-f2*n/ (А — О, =fcl. 2:2,...).
Пример З. Найти InC + 4/) и LnC + 4/). Модуль числа 3-f-4/
равен УЗ*+ 4*=5, а главное значение аргумента равно arctg -5-»
следовательно,
4
In C + 4/) = In 5 +/arctg у,
(Аа=0, *1, А2,...).
Так как
Arg (*, *,)=Arg *, -f- Arg *„
^ = Arg^— Aigz
»
Arg j/* = j
(л —целое число, положительное или отрицательное), то из
формулы A5) следует, что обобщенная на случай комп-
комплексных значений аргумента логарифмическая функция обладает
следующими известными свойствами логарифмов действительного
аргумента'):
Ln (ztzt) = Ln zx -f-Ln zv
~=Lnzx—Lnz,,
Ln $/z = ~Lnz.
Формула A3) (стр. 33) служит для возведения в комплекс-
комплексную степень числа е. Чтобы перейти к определению возведе-
возведения в степень любого комплексного числа, заметим сначала,
') Относительно смысла двух последних свойств, следующих из
соответствующих свойств аргумента, следует иметь в виду сказанное
в сноске на стр. 14.
38 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИЯ [ГЛ. UI
что в силу определения логарифмической функции
для любого комплексного ?.
Для действительных Сиг при О 0, очевидно, справед-
справедливо тождество
Будем теперь считать
С» = е*ь»е A6)
для любых комплексных С и z и тем самым определим вели»
чину С* при любых комплексных значениях Сиг.
В силу многозначности логарифма определенное равенст-
равенством A6) выражение С2 многозначно. Его главным значением
будем называть то, которое получим, подставив в правую
часть A6) 1п С вместо Ln?- Только при целых действительных
(положительных, отрицательных или равных нулю) значениях z
формула A6) определяет единственное значение величины ?*,
так как в этом случае неопределенное слагаемое вида 2kni,
входящее в Ln С, будучи умножено на целое число г, дает
в показателе правой части равенства A6) слагаемое вида
2/s'nf, где k—также целое действительное число и значения
правой части A6), соответствующие различным значениям А',
совпадают.
Пример 4. Найти Р:
II
Главное значение величины /' равно е .
Пример 5. Найти 2'+':
21 +1 = eU+0 Ln 2 _ e(l +0 Aп2+2**О _ g A0 ? - 2JSm)+/<ln 2+2 *«> _
= eln 2 - 2*" (cos In 2 + / sin In 2).
Обратные тригонометрические функции определяются как
функции, обратные по отношению к тригонометрическим (см.
определение обратной функции на стр. 19).
Если
г — sin да,
§ 2] ЛОГАРИФМ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИЯ 39
то w называется арксинусом числа г и обозначается
w=Arcsin z.
Аналогично, если
то да называется арккосинусом г и обозначается
w=Arccosz;
если z = tgw, то « называется арктангенсом г и обозна-
обозначается
w=Arctgz
и т. д.
Если z — s\nw, то на основании A0)
*=—ш—•
откуда
elw — liz—e-iw=0
или
ettw—2lzeiw—1 = 0.
Решив это квадратное относительно e'w уравнение, получим:
т. е.
да=Arcsin z = — / Ln (iz + V1 — *')• A7)
В силу многозначности логарифма и двузиачноси корня
в правой части A7) Arcsin z является функцией многозначной.
Если z--число действительное и |z \ < 1, то величина J/ 1 —г*
также является действительной и
\iz + yi—zt\ = l.
Но, в силу формулы A5), все значения логарифма числа, мо-
модуль которого равен 1, являются числами чисто мнимыми, а
') Мы не пишем перед радикалом двойного знака, так как симво-
символом j/7 обозначаем все значения корня.
40 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ [ГЛ. I»
так как перед знаком логарифма в правой части A7) стоит
множитель —i, то все значения Arcsinz будут в рассматри-
рассматриваемом случае, как и следовало ожидать, числами действитель-
действительными; во всех прочих случаях значения A resin г действитель-
действительными быть не могут.
На основании A4), если z = tgw, имеем:
откуда
e"u(l—i
или
Следовательно,
t»=Arctg* = — Tj-Ln-pi-^. A8)
Если г является любым действительным числом, то числа
\-\-iz и 1 — iz будут взаимно-сопряжениыми, поэтому их
модули одинаковы, следовательно, модуль выражения, стоящего
под знаком логарифма в правой части A8), равен 1 и, в силу
A5), все значения этого логарифма чисто мнимы. В этом слу-
случае ввиду наличия в правой части A8) множителя —=- вели-
величина Arctg г, как и следовало ожидать, действительна, в осталь-
остальных случаях эта величина действительной быть не может.
Аналогично можно получить:
Arccos г — — i Ln {z -|- У г* — 1),
Пример 6. Найти Arcsin2. С помощью A7) и A5) получим:
=—/Ln Bi3itVT)=—iLa[B
=- / [ш B а УТ)+/-J
2] ЛОГАРИФМ И ОБРАТНЫЕ ТРИГОНОМЕ1СИЧЕСКИЕ ФУНКЦИИ 41
Пример 7. Найти Arctg B1):
Arctg B/)=_-L Ln (- 4- )=- 4
Функции, обратные shz, chz, ihz, cthz, называются
обратными гиперболическими функциями и обозначаются
соответственно Arsh;s, Arch г, Arihz, Aretha. Обрат-
Обратные гиперболические функции многозначны. Действительно,
если «»= Arsh лг, то г = sh w или г = к > откуда
е11* — 2ze" —1=0. Решая это квадратное относительно е*
уравнение, получим: e*=z-\~Yz*-\-\, откуда w=LnB-|-
-j-K«*-(- l) или Arsh г = Ьп(лг-(-}/«•-(- 1). Многозначность
функции Arsh 2 является следствием многозначности логарифма
и квадратного корня, стоящих в правой части последнего ра-
равенства.
Совершенно так же можно доказать, что Arch 2 =
Задачи к главе 111
1. Найти:
a) Ln(l+0.
2. Найти:
1С
а)#~'7, г);
О * , д) |
в) е'+', е) 3'.
3. Доказать тождества:
a) sin 2г = 2 sin 2 cos 2,
42 ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ [ГЛ. III
4) НаЯти:
а) sin/, г) ch/,
б) cos(l -|-/), Д) sh(— 2-J-0 ,
B)tgB-/), e)sln(x + (y),
ж) cos (х -j- (у).
5. Доказать тождества:
а) sinx=—ishix, г) sin /x = / sh jc,
б) cosx = ch/x, д) cos/jf = chx,
B)tgx = —/thx, e) tgix = /thx.
6. Найти:
a)Arcsln3, r) Arctgy,
QArcsin/, д) Arctg(l+2/),
B) Arcsin (V2~- /), e) Arth /,
ж) Arch(— 1).
ГЛАВА IV
ПРОИЗВОДНАЯ
§ 1. Аналитическая функция
Определения производной н дифференциала функции комп-
комплексного переменного дословно совпадают с определениями
тех же понятий для функций действительного переменного.
Поэтому почти все основные теоремы н формулы дифферен-
дифференциального исчисления без изменения распространяются и на
функции комплексного аргумента.
Однако дифференцируемые функции комплексного перемен-
переменного обладают по сравнению с дифференцируемыми функциями
действительного переменного многими дополнительными свойст-
свойствами, причина появления которых заключается в том, что тре-
требование существования производной функции комплексного
аргумента, как будет видно из дальнейшего, является несрав-
несравненно более ограничительным, чем требование существования
производной функции действительного аргумента.
Дадим независимому переменному z = x-\-iy приращение
kz — kx-\-i\y и вычислим вызванное этим приращением аргу-
аргумента приращение Д«> функции w=/(z):
At»
Если существует предел отношения д— при стремлении йа
к нулю по любому закону, то этот предел называется про-
производной функции /(г) в точке z и обозначается f (z), w',
Ш или 1:
44 производная [гл. tv
Требование существования предела отношения -z-± и его
независимости от закона стремления Дг к нулю накладывает
на функцию f(z) значительно более сильные ограничения, чем
аналогичное требование для функции у = у(х) действительного
переменного х. В самом деле, требование существования про-
производной функции действительного переменного означает су-
существование предела отношения -Л- при приближении точки
х -f- Lx к точке х по двум направлениям, слева (при Дл? < 0)
и справа (при \х > 0), и совпадение этих пределов, а требо-
требование существования производной функции f(z) комплексного
д»
переменного означает существование предела отношения -г-
при приближении точки г-\-Ьл к точке г по любому пути,
по любому из бесконечного множества различных направлений,
и совпадение всех этих пределов.
Пусть
f{) (,y) + (,y) и Дг =
тогда
(x+bx,y+&y) — a(x,y)]+
, у + Ду) — v(x, у)]=Дв -f ibv,
где
Дв = и (х -f Ьх, у + Д^) — в (х, у)
н
Д©=v (х -J- Дл:, У + Ду) — w (х, .у).
В этих обозначениях
A)
Функция, имеющая производную в точке г, называется
дифференцируемой в этой точке.
Если функция /(г) дифференцируема в точке г, то пре-
предел A) существует и не зависит от закона стремления
Дг = Дл:-|-*АУ к нулю; в частности, при Дг = Дл:, т. е. при
приближении точки г -f- Дг к точке г по прямой, параллельной
§ 1] АНАЛИТИЧЕСКАЯ ФУНКЦИЯ
оси Ох (черт 8), получим:
м. . ,, До» „ Д« -f- /До
f(z) = \\m -^- = Цга —J-—=
<Дв , .Д«Л дм
45
B)
Выбрав Az = /Ay, т. е. устремляя точку f
по прямой, параллельной оси Оу (черт. 9), получим:
к точке
42-Ю
4у-»0
ду
C)
Так как предел отношения -г- при
•О не должен за-
о
.2 +42
f
Черт. 8.
Черт. 9.
висеть от закона стремления Ыг к нулю, то из B) и C) сле-
следует, что
,да
или
д» , .до bv_ ,да
ду •
д« Л/
ду' дх
D>
Эти условия, называемые условиями Даламбера—Эйлера или
условиями Коши—Римана, должны быть выполнены в каждой
точке, в которой функция f(z) = n-\-iv дифференцируема.
При некоторых добавочных ограничениях, например, требуя
существования полных дифференциалов функций и(х,у) и
v(x,y), можно доказать, что условия Даламбера — Эйлера не
только необходимы, но и достаточны для дифференцируемости
функции / {z) = a -f- w •
46 производная [гл. пг
Действительно, если функции а(х,у) и v{x,y) имеют
полный дифференциал (см., например, [2], п. 145), то
где
llm 6.= О, llme, = 0, E)
Лл0 Д*0
Лл-»0 Д*-»0
Ду-»0 Ду-»0
И каково бы ни было kz = hx-\-iky, имеем:
Да
Заменив на основании условий Даламбера—Эйлера в числителе
„ да dv dv ди
правой части ^- на — ^, а -д- на ^, получим:
_ди , ;ар , (»,
"-dx^'dx"!
Дх-+-/Ду
Так как | Ддг+/Д> | = /(Дл:I + (ДуI, то
и, в силу E), |е,-{-/6,1 стремится к нулю при Дх—>0 я
Д>—»0, т. е. при Дг—>О.
Следовательно, по какому бы закону приращение Ьл ли
стремилось к нулю, из F) получим:
и достаточность условий Даламбера—Эйлера для существования
/ (z) доказана. Мы снова пришли для вычисления производной
к формуле B), которая показывает, что дифференцирование
функции по комплексному аргументу г (если оно возможно)
равносильно вычислению частной производной по х.
§ 1] АНАЛИТИЧЕСКАЯ ФУНКЦИЯ 47
Вели однозначная функция дифференцируема не. только в
данной точке, но и в некоторой окрестности этой точка, то
она называется аналитической в данной точке.
Функция, дифференцируемая во всех точках некоторой об-
области, называется аналитической1) в этой области.
Точки плоскости z, в которых однозначная функция /(г)
является аналитической, называют правильными точками этой
функции, а точки, в которых функция f(z) не является ана-
аналитической (в частности, точки, в которых /(г) не определе-
определена),— особыми точками.
Пример 1. Выяснить, является ля функция ю=г' аналитиче-
аналитической.
Если »=**, та-\-1о=(х+1у?—х* — у* + Шу яи=х* — у1,
v=2xy, откуда находим:
да - dv
2х
_
ду ~ У~ дх'
Условия D1 выполнены во всех точках плоскости, следовательно,
функция v является аналитической во всей плоскости.
Пример 2. Выяснить, является ли функция ег аналитической.
Если ю=е*,то B-Jpft>=e*+0'=e*(cos.y-t-/sin-y) и л=е*соз.у,
о=е* sin у.
Отсюда
да г до
да х , до
Следовательно, условия Даламбера — Эйлера выполнены в каждой
точке.
Функция е* является аналитической во всей плоскости.
Пример 3. Выяснить, является ли аналитической функция
Если ю=1, то u + lo=sx — iy и в=ж, »=—у, откуда
да , dv ,
д*' ~Зу—~ *
щ следовательно, первое из условий D) не выполнена Функция w=si
¦4 дифференцируема ни в одной точке плоскости.
') Аналитическую функцию называют также голоморфной, моно-
тшой, регулярной.
48 производная [гл. iv
Пример 4. Выяснить, является ли функция w = zRe z анали-
аналитической.
Если w = zRez, то u-\-to = (x-\-iy)x = x*-\-ixy и и=,х\
v—xy, откуда
Условия D) выполнены .только при * = 0 и у = 0. Следовательно,
функция zRe г дифференцируема только в одной точке г = 0 и нигде
не является аналитической.
Так как основные теоремы о пределах сохраняются для
функций, зависящих от комплексного аргумента, а определение
производной функции комплексного аргумента также не отли-
отличается от определения производной для функции действи-
действительного аргумента, то нетрудно проверить, что известные'
правила дифференцирования суммы, разности, произведения,
частного, степени, функции от функции, обратной функции
остаются справедливыми и в случае комплексного аргумента.
Легко проверить, что сохраняются и правила дифферента
рования элементарных трансцендентных функций. Например, если
w=e»=e*+I> = e* (cosy -\- i sin у),
то, пользуясь формулой B) (стр. 45), получим:
С помощью формул (9) и A0) (стр. 32) главы III нетрудно
проверить справедливость известных формул дифференцирова-
дифференцирования тригонометрических функций. Правило дифференцирования
обратной функции приведет нас к известным формулам диф-
дифференцирования логарифма и обратных тригонометрических
функций.
§ 2. Связь аналитических функций с гармоническими
Действительная и мнимая части функции f(z) = u-\-iv,
аналитической в некоторой области D, в той же области
2 Т1
являются решениями уравнения §р~Ь^»:=0. называемого
уравнением Лапласа^ т. е.
§ 2] СВЯЗЬ АНАЛИТИЧЕСКИХ ФУНКЦИЙ С ГАРМОНИЧЕСКИМИ 49
и
Действительно, функции и и v связаны в области D условиями
Даламбера — Эйлера:
ди _ dv
дх ~ ду'
дм до
ду== дх *
Дифференцируя первое из этих тождеств по х, а второе по у
и складывая, получим:
Дифференцируя первое из тех же тождеств по у, а второе
по х и вычитая, будем иметь:
d'v
Решения уравнения Лапласа л^~Ьл~*==^ называются гармо-
гармоническими функциями. Следовательно, действительная и мни-
мнимая части аналитической функции являются гармоническими
функциями.
Однако, если и (х, у) и v {x, у) являются произвольно вы-
выбранными гармоническими функциями, то функция и{х,у)-\-
-f- iv (x, у), вообще говоря, не будет аналитической функцией,
так как условия D), как правило, не будут выполнены.
Аналитическую функцию f{z) = и (х, у) -\- iv (x, у) мы
получим, если, произвольно задав одну из двух гармониче-
гармонических функций и(дг, у) или v(x, у), подберем другую так,
чтобы удовлетворялись условия Даламбера — Эйлера ~ = -^-,
ди dv .
у-= — j- , т. е. определим другую из этих функций по ее
двум частным производным или, что то же самое, по ее полному
дифференциалу. Как известно (см., например, [2], п. 187), по
') Существование и непрерывность частных производных вто-
второго порядка функций и (х, у) и о (х, у) следует из доказываемой в
следующей главе возможности дифференцировать аналитическую
функцию дюбое число раз.
50 ПРОИЗВОДНАЯ [ГЛ. IV
полному дифференциалу функция определяется с точностью
до постоянного слагаемого. Следовательно, аналитическая
функция с точностью до постоянного слагаемого определяется
своей действительной или мнимой частью.
Две гармонические функции и(х,у) и v{x,y), удовлетво-
удовлетворяющие условиям Даламбера — Эйлера и, следовательно, являю-
являющиеся действительной н мнимой частями некоторой аналитиче-
аналитической функции f(z) = и(х, у) -f- iv (x,y), называются сопряженной
парой гармонических функции.
Пример. Найти аналитическую функцию, если известна ее мни-
мнимая часть
v=23?
Так как
ду "
то из условий Даламбера — Эйлера D) находим производные:
й—* m
?=-*¦-1. «9
Воспользовавшись первым из этих уравнений, получим:
а= J— Aydx = — 4ху+ч(у), (9)
где функция <р(у) пока произвольна. Для определения функция у {у)
дифференцируем (9) по у и подставляем в (8):
откуда
Ч'(У) = -1 и
Следовательно,
и=— 4ху —
и окончательно получим:
= Щх? - f + 21 ху) + i(x + 1у) + С=
§ 3] КОНФОРМНОЕ ОТОБРАЖЕНИЕ 51
Многие задачи, связанные с изучением стационарных тепловых и
электрических полей, а также с изучением потенциального течения
жидкости, сводятся к решению уравнения Лапласа.
В простейших двумерных задачах такого типа в некоторой об-
области D требуется определить непрерывное решение уравнения Лап-
Лапласа -r~i-{--s-i = 0, принимающее заданные значения на границе об-
области D. Эта задача называется первой краевой задачей для уравне-
уравнения Лапласа или задачей. Дирихле.
Задача Дирихле и некоторые более сложные краевые задачи для
уравнения Лапласа легко решаются для небольшого числа простейших
областей, например для круга или для прямоугольника.
Для более сложной области D задача Дирихле обычно решается
следующим методом.
Стараются подобрать аналитическую функцию w =/ (г) = и(х,у}-{-
-f- to (х, у), которая отображала бы область D, лежащую в плоскости
х, у, на одну из тех простейших областей, лежащих в плоскости и, «,
для которой задача Дирихле легко решается, например иа круг.
Если удается подобрать такую аналитическую в области D функ-
функцию, то задачу Дирихле можно считать решенной, так как при ука-
указанном преобразовании уравнение Лапласа -t-j -(- -т-j = 0 снова пере-
ходит в уравнение Лапласа -^-j -f- ^-j = 0.
Действительно, Т можно рассматривать как действительную (или
мнимую) часть некоторой аналитической функции ю, = у (г) = Т(х, у) 4-
-f- iQ (x, у). Переходя к новым переменным и и v с помощью преоб-
преобразования w=f{z) = u{x, y)-\-tv(x, у), где / является аналитической
в области D функцией, и предполагая, что функция }(г) имеет одно-
однозначную обратную функцию t = F(w), которая, согласно замечанию
на стр. 48, также будет аналитической функцией в соответствующей
области, можем рассматривать и;, = 74-Л? как функцию ы и tr.
Щ = Ч [F(w))*= Пи, v) + iQ(u, v),
причем сложная функция <f[F(w)} будет аналитической функцией w
(в соответствии со сказанным на стр. 48). Следовательно, Г (в, v) будет
_ . _ дгТ , д*Т
гармонической функцией и jft +
§ 3. Аргумент и модуль производной.
Конформное отображение
Пусть в плоскости г дана некоторая точка г0 и через эту
точку проведены линии уа и ft, причем каждая из них имеет
в точке z0 определенную касательную.
Функция w=f(z), которую мы будем предполагать ана-
аналитической в некоторой области, содержащей точку гЛ,
52
ПРОИЗВОДНАЯ
[гл. п
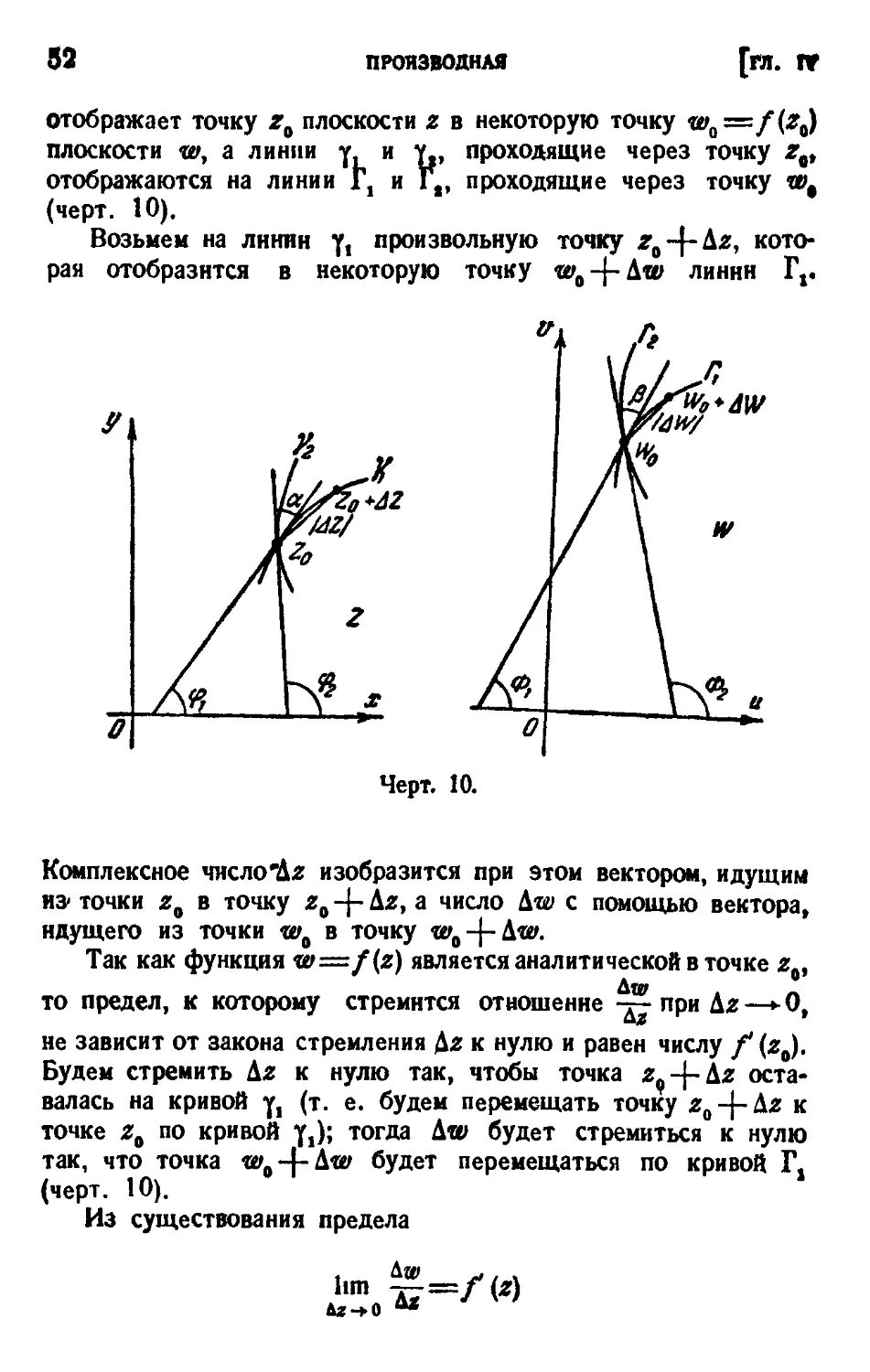
отображает точку z0 плоскости z в некоторую точку wa=f(Zu)
проходящие через точку zv
Yi и Yt»
Г, и Г,,
проходящие через точку да.
плоскости w, а линии
отображаются на линии
(черт. Ю).
Возьмем на линии Yi произвольную точку zu-\-kz, кото-
которая отобразится в некоторую точку «>0-|-Дда линии Г,.
О
Черт. 10.
Комплексное число'Дг изобразится при этом вектором, идущим
ИЗ' точки z0 в точку za -\- Дг, а число Дда с помощью вектора,
идущего из точки w0 в точку я>0-}-Дя>.
Так как функция w=/(z) является аналитической в точке zu,
то предел, к которому стремится отношение ~ при Дгг —»¦ О,
не зависит от закона стремления кг к нулю и равен числу / (#„).
Будем стремить Дз к нулю так, чтобы точка z,.-\-hz оста-
оставалась на кривой Yi (т. е. будем перемещать точку zQ-\-kz к
точке г0 по кривой Yi); тогда Дда будет стремиться к нулю
так, что точка «^-{-Дя» будет перемещаться по кривой Г,
(черт. 10).
Из существования предела
?.?-/<¦»
§ 3] КОНФОРМНОЕ ОТОБРАЖЕНИЕ 53
следует существование предела
Аю
а также, если f{z.)^O, и предела
||т Iтог|=I/M. 0°)
С другой стороны,
Arg ~ = Arg Aw — Arg A*,
где ArgAz и Arg Aw—углы, образованные векторами, изо-
изображающими числа Az и Aw с положительными направлениями
соответствующих действительных осей. При выбранном нами
способе предельного перехода эти векторы направлены по
хордам кривых Yj и Г, (черт. 10) и пределы величин ArgAz
и Arg Aw при Az—»-0 равны соответственно углам <р, и Ф,
между касательными к кривым, у, и Г, в точках z0 и w0 и
положительными направлениями соответствующих действитель-
действительных осей.
Следовательно,
) = Ф, — <fV (Щ
Повторив те же рассуждения для случая, когда точка л\
стремится к точке za по кривой у„ и принимая во внимание,
что величина Arg/'B0), определенная равенством A1), не за-
зависит от закона, по которому Ьа—»-0, получим:
Arg/(*0)^t-<pt, A3)
где (р, и Ф, —соответственно углы между касательными к
кривым у, и Г, в точках z0 и w0 и положительными направ-
направлениями осей Ох и Оа.
Из A2) и A3) получим:
*i —»! = *• — »..
или
Ф.-Ф, = <Р« —?„ A4)
но « = <pt — ft является углом между касательными к кри-
') Здесь символ Arg служит для обозначения одного из значений
аргумента, но не обязательно главного.
54 производная [гл. п
вым Yi и Y* в точке z»> т- е> Углом между этими кривыми е
точке г0, а р == Ф, — Ф! — угол между кривыми Г, и Г,
в точке w0, причем, в силу A4), {J = a. Следовательно, при
отображении, осуществляемом аналитической функцией, угол
между двумя кривыми, пересекающимися в точке, в кото-
которой производная отображающей функции отлична от нуля,
сохраняется как по величине, так и по направлению от-
отсчета {свойство постоянства углов)').
Выясним геометрический смысл аргумента и модуля произ-
производной.
Равенства A2) и A3) показывают, что если совместить
плоскость z с плоскостью w так, чтобы точка z0 совпадала
с точкой w0, а ось Ох была бы направлена параллельно
оси Ои, причем положительные направления этих осей совпали
бы, то угол, на который после этого нужно повернуть вокруг
точки z0 плоскость z для того, чтобы касательная к кривой Yj
(или у,) совпала с касательной к отображенной кривой Г, (со-
(соответственно Г,), равен Atgf'(z0),— таков геометрический
смысл аргумента производной отображающей функции.
Для выяснения геометрического смысла модуля производ-
производной заметим, что | Az | является расстоянием от точки z0 до
точки zo-\~bz, а |Ди»| — расстояние между точками гё>0 и
| А I
| ТС I
и, следовательно, величина -¦¦. .' указывает,в каком
отношении в результате отображения изменяется расстояние
между этими точками. Величину |/(zo)|, являющуюся [см. A0)]
пределом отношения . при Д.г—*0, естественно назвать
коэффициентом растяжения в точке z0 при отображении с по-
помощью функции w=f(z). Если |/(го)|>1, то в достаточно
малой окрестности точки z0 расстояния между точками при
отображении увеличиваются и происходит растяжение; если
I/ (zo) 1 ^ 1 > т0 отображение в окрестности точки zQ приводит
к сжатию.
Так как, в силу аналитичности функции f{z), производная
f'{zj не зависит от того, по какому закону точка zo-\-kz
стремится к точке z0, то коэффициент растяжения в дан-
данной точке постоянен, т. е. одинаков во всех Направле-
') Если бы при отображении углы сохранялись по величине, Но
направление отсчета углов изменялось бы, то равенство A4) заменя-
заменялось бы равенством Ф, — Ф, =—(«у, — <pj.
§ 3] КОНФОРМНОЕ ОТОБРАЖЕНИЕ 55
ниях,— таково второе свойство отображения, осуществляемого
с помощью аналитической функции.
Отображение, обладающее свойством постоянства углов и
свойством постоянства коэффициента растяжения в каждой
точке, называют конформным или, точнее, конформным
отображением 1-го рода. Отображение, осуществляемое ана-
аналитической функцией, является конформным во всех точках,
в которых производная этой функции отлична от нуля. Можно
доказать и обратное утверждение: если отображение, осу-
осуществляемое функцией f(z), конформно в области D, то
функция f(z) является аналитической в области D.
Пример 1. Рассмотрим отображение, осуществляемое функ-
функцией tt>=3z.
Так как -т- = 3 ?? О, то отображение конформно во всей пло-
плоскости и коэффициент растяжения в любой точке равен 3.
Так как
то направление при отображении не изменяется.
Если учесть, наконец, что ю = 0 при 2=0 и, следовательно, на-
начало координат остается при рассматриваемом отображении непо-
неподвижным, то можно утверждать, что ртображение с помощью функ-
функции b> = 3z сводится к преобразованию подобия с центром подобия
в нулевой точке и коэффициентом подобия, равным 3.
Пример 2. Отображение w = z* конформно во всех точках
плоскости г, за исключением точки 2=0.
s/mi .I'm
Действительно, -T- = 2z и лишь при z = 0 -3— = 0. Так как
аг at
Arg w = 2 Arg z, то лучи Argz = a и Aigz —((, выходящие из точки
* = 0 и образующие между собой угол, равный % — о, отображаются
соответственно в лучи Arg w = 2a и Arg w == 2A, образующие между
собой угол 2 (Р — а).
Следовательно, в точке 2 = 0 конформность отображения нару-
нарушается: углы в этой точке не сохраняются, а удваиваются.
Отображение, отличающееся от конформного тем, что углы
сохраняются только по абсолютной величине, но изменяют
направление отсчета на противоположное, называют конформ-
конформным отображением 2-го рода. Таково, например, отображе-
отображение, осуществляемое функцией w=z. Действительно, если
значения z и w изображать точками одной и той же плоскости,
то ввиду того, что точки z и J взаимно-симметричны относи-
относительно действительной оси (черт. 11), это отображение сводится
к симметрии относительно действительной оси, при э/гом не
56 производная [гл. rv
происходит никакого искажения масштаба (коэффициент растя-
растяжения в каждой точке равен 1), а все углы сохраняются по
абсолютной величине, но изменяют направление отсчета на
противоположное.
В дальнейшем, говоря о конформном отображении, мы
всегда будем иметь в виду лишь конформное отображение
1-го рода.
Дифференциалом d/(z) аналитической функции w=/(z)
в точке z называется главная линейная по отношению к Дг
часть приращения Дтю=/(г -j- Дг) —
— f(z) этой функции.
Так как
ТО
где Нт а {г, Длг) = 0. Следовательно,
Дтю =/' (z) bz -j- a (z, Lz) • Д*
и ввиду того, что произведение
а (г, &z) • kz является бесконечно ма-
Черт. 11. лой величиной более высокого поряд-
порядка, чем Д?, дифференциал функции
/(*) равен произведению f\z) Az или j"(z)dz (так как при
f{z) = f t
Задачи к главе IV
¦%, Проверить условия Даламбера — Эйлера для функций
а) w = sin г, г) w = Arcsln z,
б) w — cosz, д) т=-гп (я — целое число).
в) w = Ln г,
2. Найти аналитическую функцию аргумента г, действительная
часть которой равна:
а)х'-3ху», г)_г-р-г_2у,
д) 2ё* sinj».
§ 3] КОНФОРМНОЕ ОТОБРАЖЕНИЕ 57
3. Найти аналитическую функцию аргумента г, мнимая часть ко-
которой равна:
б) 2ху-{-Зх, r) ex{ycosy-\-xsiny)-\-x-\-y.
4. Найти угол поворота и коэффициент растяжения, при отобра-
отображении с помощью аналитических функций ш=г* и » = «' в каждой
из следующих точек:
а)* = 1, r)z = \+i,
вJ=- j,
5. Выяснить, какая часть плоскости аргумента г сжимается и
какая растягивается, если отображение осуществляется функцией:
а)ю=*\ т)хв = ег,
б)ю=—, д) в/ = 1п(г—1).
в) в/ =
ГЛАВА V
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ
Понятие интеграла функции комплексной переменной, ос-
основные свойства этих интегралов и формулы интегрирования
элементарных функций почти не отличаются от аналогичных
понятий и свойств интегралов функций действительного пере-
переменного. Однако определенный интеграл аналитической функ-
функции обладает еще одним замечательным свойством, присущим
далеко не всем криволинейным интегралам дифференцнруемых
функций действительных переменных, а именно: в односвязных
областях интеграл аналитической функции не зависит от пути
Интегрирования. Это свойство влечет за собой далеко идущие
следствия, изложение которых и составляет основное содержа;
ние как настоящей главы, так и главы VII.
§ 1. Интеграл от функции комплексного переменного
Предположим, что в плоскости г дана замкнутая или не-
незамкнутая дуга С, которую будем в дальнейшем считать глад-
гладкой или кусочно-гладкой. Граничные точки кривой С Обозна-
Обозначим z, и Z; если кривая замкнута, то ze=Z. Одну из этих
точек, например z0, будем считать начальной, а другую ко-
конечной и тем самым установим положительное направление на
кривой С, которое на чертеже будем отмечать стрелкой
(черт. 12). Предположим, далее, что функция f(z) комплекс-
комплексного аргумента z непрерывна во всех точках дуги С.
Разобьем дугу С произвольным способом на я «элементар-
«элементарных» дуг и занумеруем точки деления гк в направлении от
начальной точки к конечной, причем zn — Z (черт. 12). Вве-
Введем обозначения:
Число Lzk изображается вектором, идущим из точки Z4_, в
• ч
ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
59
точку zk, a \bzk\—длина этого вектора, т. е. длина хорды,
стягивающей соответствующую элементарную дугу. Внутри
или на одном из концов каждой элементарной дуги выберем
Черт. 12.
по одной точке и обозначим эти точки С„ ?t, ..., Ся (точка СА
находится на элементарной дуге с концами в точках zk_1
и *»).
Составим -сумму
Предел этой суммы, вычисленный при условии, что л—»-оо и
длина наибольшей из элементарных дуг стремится к нулю
(ввиду того, что дуга кусочно-гладкая, это равносильно тому,
что стремится к нулю максимальная из величин | Azft |), назы-
называется интегралом функции f(z) по дуге С:
= 1ш 2
Из этого определения непосредственно получим следующие
свойства интеграла2):
1) $ [/, (#) ± /, W] Л = J /г (г) Л ± J /, (г) dz,
2)
где А — действительная или комплексная постоянная.
*) Существование этого предела при ограничениях, наложенных
выше иа функцию f(z) и дугх С, оуде.т доказано на стр. 62.
*) Свойства 1)—5) могут быть также легко получены из фор-
формулы C) (стр. 62) или из формулы F) (стр. 63).
60
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гл.
3) Если дуга С геометрически совпадает с дугой С, но
имеет направление, противоположное направлению дуги С, то
= -Л f(z)dz,
так как при замене дуги С дугой С все множители \sk в пра-
правой части B) изменят знаки на противоположные,
Черт. 13.
4) Если дуга С состоит из дуг С„ Сг, ..., Си (черт. 13),
то
5) ldz=Z-z9,
с
так как при /(*) = 1 сумма в правой части B) принимает вид
6) Если \f(z)\<C.M во всех точках дуги С и длина
дуги С равна /, то
Действительно,
$ 1] ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 61
п
так как сумма 2 |Л**1 равна длине ломаной, вписанной в
дугу С, и следовательно, эта сумма не больше чем длина /
дуги С.
где символом
обозначен предел
Это свойство становится очевидным, если принять во вннма*
ние, что
14
Вычисление интеграла B) сводится к вычислению криволи-
криволинейных интегралов от действительных функций действительных
аргументов. В самом деле, пусть
z = x-\-iy, f(z)=u-\-iv,
где а и v являются функциямн аргументов хну:
а = а(х,у),
v = v(x,y).
Обозначим
(* = 0, 1, 2, .... , я),
(А=1, 2, ... , р);
тогда
где
а так как
62 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
то
—"E*. ч*)Ду*+
= lim
lim 2 Ь> (**. Ч*) A** + «(E*. 4*) 4У*1
х|Дгд|-»0 ft=0
или в соответствии с определением криволинейного интеграла
(см., например, [2], п. 183)
5 f(z)dz=\ a(x,y)dx — v(x,y) dy-\-i [ v(x,y)dx-\-
c с с
-\-a(x,y)dy. C)
Существование криволинейных интегралов в правой части фор-
формулы C), а следовательно и существование интеграла
f(z)dz,
следует из кусочной гладкости кривой С и из непрерывности
вдоль дуги С функций и (х, у) и v (х, у), являющихся действи-
действительной и мнимой частями непрерывной вдоль кривой С функ-
функции f(z).
Формула C) показывает, что для того, чтобы свести вы-
вычисление интеграла по комплексному аргументу к вычислению
обычных криволинейных интегралов, достаточно выделить из под-
подынтегральной функции действительную и мнимую части
и умножить u-\-iv на
dz — dx-\-idy,
после чего подынтегральное выражение преобразуется к виду
f(z) dz~{a-\- iv) (dx -\-idy) = udx — v dy -f- / (vdx-{-a dy).
Если дуга С задана параметрическими уравнениями:
y=y{t), W
§ 1] ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 63
а начальная и конечная точки дуги соответствуют при этом
значениям параметра t=t9 и t = T:
Z=x(T)-\-iy(T),
то, как известно из правила вычисления криволинейного ин-
интеграла (см., например, [2], п. 183), подставив под знак интег-
интеграла вместо хну функции, стоящие в правых частях урав-
уравнений D), а вместо dx и dy дифференциалы этих функций,
можно свести вычисление криволинейных интегралов в правой
части C) к вычислению определенных интегралов с нижним
пределом tQ и верхним пределом Т. С другой стороны, урав-
уравнения D) равносильны (см. стр. 22) одному уравнению в
комплексной форме
z=z(f), E)
где z(t)=x (t)-\-iy (t), и подстановка в правую часть формулы
C) вместо хну функций, стоящих в правых частях D), а
вместо dx и dy соответствующих дифференциалов равносильна
подстановке в левую часть формулы C) вместо z функции,
стоящей в правой части E), а вместо dz дифференциала этой
функции.
Следовательно, интеграл по комплексному аргументу можно
вычислять, пользуясь формулой
г
/(*)*= J/IXOKW*. F)
U
Пример. Вычислить интеграл
$
С
С Rezdz,
где дугой С является:
1) прямолинейный отрезок, соединяющий точку О С точкой 1 -}- /J
2) ломаная, состоящая из прямолинейного отрезка, соединяющего
точку 0 с точкой 1, и прямолинейного отрезка, соединяющего точку 1
с точкой 1 -f- /.
Решение.
1) Уравнение отрезка, соединяющего точки Он 1 -+-' в парамет-
параметрической форме, имеет вид
x=t,
y-t,
а в комплексной форме
где действительное переменное t изменяется от 0 до 1.
64 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гЛ. V
Находим:
dz = (l+ i)dt
ш
1 1
[ Rezdz = С Ret(l + 01]0+i)dt={l+~l) ^ t dt^i
2) Уравнение отрезка, соединяющего точки 0 и 1 в комплексной
форме:
t = t,
где t изменяется от 0 до 1; уравнение в комплексной форме отрезка,
соединяющего точки 1 и 1 -J- /:
где t изменяется от 0 до 1.
Итак,
1 1
— С Retdt+{Re{l+U)tdt
o
1
— С
§ 2. Теорема Коши
Если /(г) является аналитической функцией на замкну-
замкнутом контуре Сив односвязной области, ограниченной этим
контуром, то
{/пеорема Коши).
Справедливость теоремы Коши немедленно следует из фор*
мулы C), если предположить, что производная f (z) данной
функции непрерывна на контуре Сив области, ограниченной
этим контуром, так как в этих предположениях криволинейные
интегралы \ftdx — vdy и \ vdx-\- a dy, будучи интегралами
с с
по замкнутому контуру от полных дифференциалов, равны
яулю (см. [2], п. 185).
§ 2] теорема коши
Действительно, для того чтобы выражение
где.Л! (х, у) и N(x, у) — непрерывно дифференцируемые функ-
функции, было полным дифференциалом, как известно, необходимо
В
и достаточно,
фф
чтобы -т—=-з-.
применении к интегралам
\udx — v dy и \vdx-^-ady это условие сводится к условиям
Эйлера — Даламбера gp = — ^ и
dv ди
gp ^ ^ = j-, выполненным в силу
аналитичности функции f(z),
а непрерывность произвол-
HOtt/'(z) обеспечивает непре-
рывиость частных производных
функций и (х, у) и v(x,y).
Таким образом, каждый
из двух интегралов в правой
части C) равен нулю, и теоре-
теорема Коши тем самым доказана.
Можно доказать теорему
Коши и без предположения
о непрерывности произво-
производной/' (г) на контуре С и в об-
области, ограниченной этим контуром, однако
зательство значительно усложнится.
Распространим теорему Коши на случай многосвязной обла-
области. Рассмотрим многосвязную область О, ограниченную внешним
контуром Со и внутренними контурами С,, Ct, ... ,С„ (черт. 14);
и предположим, что функция./(z) является аналитической как
в этой многосвязной области, так и на контурах С,, Clt..,, Са.
Пусть
Черт. 14.
при этом дока-
дока\
f(z)dz (jfcssO, 1, 2,
п)
обозначает интеграл по контуру Ск, проходимому против ча-
часовой стрелки. Сложный контур, являющийся границей дан-
данной многосвязной области и состоящий иу контуров
Со, С,, Ct,... , С„, обозначим Г и выберем на нем в качестве
положительного такое направление, при движении по которо-
которому область О остается слева. Иными словами, интеграл по
3 Г. Л Луни, и Л Э Эльсгольц
66 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гл. V
контуру Г будем считать равным сумме интеграла по контуру С,,
проходимому против часовой стрелки, и интегралов по контурам
С,, Ct, ... , С„, проходимым по часовой стрелке:
J/(*)dz = J f(z)dz—[ f{z)dz —
г с, с,
-[f(z)dz-...-\f(z)dz. G)
Теорема Коши будет распространена на случай многосвязной
области, если мы докажем, что при наших предположениях
[f{z)dz = 0.
г
Соединим контуры, образующие сложный контур Г, дугами у,,
Y*' ••• • Тп+и как показано на черт. 14, при этом область О
окажется разбитой на две односвязные области. Контуры, ог-
ограничивающие эти односвяэные области, обозначим, соответ-
соответственно, Г* и Г". Так как функция f(z) является аналити-
аналитической как на контурах Г' и Г", так и в областях, ограниченных
каждым нз этих контуров, то в соответствии с теоремой Коши
для односвязной области
f(z)dz =
Г'
[f(z)dz=0,
г»
а следовательно и
\f(z)dz+\f{z)dz = O. (8)
Г' Г»
Если на каждом из контуров Г, Г" считать положительным
то направление, при котором область, ограниченная этим конту-
контуром, остается слева, то
[f{z)dz + [f(*)dz=[f(z)dz, (9)
Г' Г» Г
так как при сложении интегралов в левой части последнего
§ 3] ВЫЧИСЛЕНИЕ ИНТЕГРАЛА ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 67
равенства интегралы по дугам у,, у,. ••• > у„+, уничтожатся
•виду того, что интегрирование по каждой из этих дуг будет
производится при вычислении суммы (9) два раза в противо-
противоположных направлениях.
Из (8) и (9) следует
$/(*)Л = 0, (Ю)
г
и теорема Коши для многосвязной области доказана.
Учитывая G), можно равенство A0) за-
записать в виде
J/(*)</*= $/(*)</*+$/(*)</*+...+
с, с, с,
+ $/(*)&. (И)
с*
В частности, если функция f{z) является
аналитической на контурах Со и С, (черт. 15) и в двусвя^ноя
области, ограниченной этими контурами, то из (И) при я = 1
получим:
$$ A2)
§ 3. Вычисление интеграла от аналитической функции
Если интеграл от функции f[z) по всякому замкнутому конту-
контуру, расположенному в некоторой области G, равен нулю, то
интеграл по всякой дуге, находящейся
внутри области G, зависит только от
положения начальной и конечной точек
этой дуг и и, следовательно, одинаков для
всех дуг, имеющих общую начальную и
общую конечную точки. Другими сло-
словами, интеграл не зависит от пути ин-
интегрирования. Действительно, если дуги
С, и С, имеют общую начальную точку гь и общую конеч-
конечную точку Z (черт. 16), то величина
\f(z)dz-\f(z)dz A3)
3« с' *
68 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гл V
представляет собой интеграл от функции /(г) по замкнутому
контуру С, состоящему из дуги С, й дуги Ct, геометрически
совпадающей с дугой Ct, но противоположной ей по направле-
направлению Если этот интеграл равен нулю, то равна нулю и раз-
разность A3), откуда
=[f(z)dzl).
Таким образом, из теоремы Коши следует, что есля функция
/(г) аналитична в некоторой односвязной области G, то, какова
бы ни была дуга С внутри этой области, величина
зависит только от начальной точки гь и конечной точки Z
дуги С и, следовательно, для этого интеграла можно пользо-
пользоваться обозначением
$/(*) dz.
Докажем, что если величина г% постоянна, a Z изменяется
в области О, то в этой области функция
F{Z)=]f(z)dz
*»
является аналитической и
Какова бы ни была точка Z внутри области О, можно
взять столь малый круг с центром в этой точке, что все точки
рассматриваемого круга будут также принадлежать области О.
Поэтому, если |AZ| достаточно мал, то можно точку Z соеди-
') Очевидно, справедливо и обратное утверждение если в неко-
некоторой области интеграл от функции f(z) не зависит от пути интегри-
интегрирования, то интеграл по всякому замкнутому контуру, расположенному
в этой области, равен нулю.
§ 3] ВЫЧИСЛЕНИЕ ИНТЕГРАЛА ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 69
нить с точкой Z-J-AZ прямолинейным отрезком, лежащим в
области G (черт. 17). Пусть С—какая-нибудь дуга, лежащая
внутри области О и соеди-
соединяющая точку ?0 с точкой Z;
тогда
** Черт. 17.
причем в A4) можно считать
путь интегрирования состоящим из дуги С и прямолинейного
отрезка у, соединяющего точку Z с точкой Z-f-AZ. Тогда на
основании свойства 4) (стр. 60)
Z+AZ
+
-/7(Z)= J
г
Функция /(«) является функцией аналитической, а следовательно
и непрерывной, в области G и, в частности, иа отрезке у.
Поэтому как бы мало ни было положительное число е для лю-
любой точки z отрезка f> соединяющего точку Z с точкой Z-J-AZ,
выполнено неравенство
если только величина | AZ | достаточно мала. Если учесть, что
длина отрезка у равна |AZ|, то на основании свойства 6)
(стр. 60) получим:
A6)
откуда
70 интегрирование по комплексиому аргументу [гл. v
Но в соответствии со свойствами 2) и 5) (стр. 59—60)
dz=f(Z)l dz=
в неравенство A6) принимает вид
|J|
откуда, учитывая A5), при достаточно малом \LZ\ получим:
Но это неравенство означает, что предел
11»
bZ-*Q
существует и равен /(Z). Утверждение доказано.
Если две функции имеют в некоторой области одинаковые
производные, то в этой области разность между функциями
постоянна. Действительно, если
в
/"!(*) =
то
?'(*) = 0. A7)
Но если
V(z) = a(
• аз A7) получим:
дх ' дх
Отсюда, в силу условий Даламбера — Эйлера в
35=°. %=»¦
Сяедователмо, функции я(х,у), vfay), а значат я функция
§ 4] ИНТЕГРАЛЫ ОТ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ 71
Если Ф (г) какая-нибудь функция, для которой
Ф'(*)=/(*),
где f(z)— аналитическая функция, то по доказанному
г
где С — постоянная. Положив в этом равенстве Z=zt (точ-
(точнее, перейдя к пределу при Z—>г0), получим;
откуда
н
Эта формула совпадает с известной из интегрального исчисле-
исчисления формулой Ньютона — Лейбница.
§ 4. Интегралы вида \ jj-m
Вычислим интеграл
A8)
по замкнутому контуру С в предположении, что п является
целым положительным числом (если целое число я^О, то по
теореме Коши Г .—^-^ = С(z — а)тdz = 0, т — — п^О).
Если точка z = a находится вне области, ограниченной
контуром С, то в соответствии с теоремой Кош*
Предположим теперь, чтд контур С один раз обходит точку а,
и будем считать, что направление обхода выбрано так, что
точка а остается слева. Тогда, в силу теоремы Коши (см. A2)),
величина интеграла A8) не зависит от вида контура С, хотя,
72
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ
[гЛ. V
быть может, и отлична от нуля. Поэтому в качестве контура
С можно взять, например, окружность радиуса R с центром в
точке а. Уравнение такой окружности в комплексной форме
имеет вид
z — a = Re"f,
Отсюда
dz=Rie"fd<?
и на основании F)
При пф 1 (я=2, 3, ...) получим:
Г dz { !_в'«-я)<р
)(z~af~~ й" /A-я)
с
I /fli
так как etrf|I-">=«t=l.
Если же /t=l, то из A9) следует, что
B0)
Итак, если даже точка а находится внутри контура С,
то интеграл A8) отличен от нуля только
при я = 1.
Из B0) следует, что если контур С
И обходит k раз точку а в положительном
направлении (черт. 18), то
Черт. 18. _ . .
если же контур С обходит k раз точку
а Ш отрицательном направлении, то
dz
z —л
=r — 2Ш.
B Г)
Равенства B0), B1), BГ) находятся в тесной связи с оп-
определением логарифмической функции. Действительно, для не-
§ 4] ИНТЕГРАЛЫ ОТ ДРОВНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ 73
определенного интеграла имеем:
Z — I
Подынтегральная функция аналитячна всюду, кроме точки
х==а, и поэтому в любой односвязной области, не содержа-
содержащей точки z=a, интеграл
dz
z-a'
f
где у—дуга, принадлежащая этой области, не зависит от
пути интегрирования, а зависит только от начальной точки z,
и конечной точки zt дуги у-
Допустим для простоты, что а=0, и рассмотрим интеграл
Jf
Пусть 2, = 1 и zt=z являются соответственно начальной и
конечной точками дуги у и пусть дуга у не пересекает отри-
отрицательной части действительной оси и ие проходят через
точку 2=0. Тогда можно дугу у включить в односвязную
область, не содержащую точки 2 = 0 я точек отрицательной
части действительной оси; в такой области функция In* бу-
будет непрерывной и аналитической (отрицательная часть дейст-
действительной осп является для функции lnz = ln|z|-}-/argz ли-
линией разрыва, так как в силу определения главного значения
аргумента величина argz терпит разрыв при действительных от-
отрицательных значениях z). При этих условиях независимо от
формы дуги у будем иметь:
Если теперь соединять точку 1 с точкой z дугой f так, -чтобы
дуги у и у' образовывали замкнутый контур /, один раз ок-
окружающий точку z = 0, то в соответствии с равенством B0)
получим:
74 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
если направление на контуре / выбрано так, что он обходится
против часовой стрелки. Но так как (черт. 19)
(знак зависит от того, какое из расположений, указанных на
а/
Черт. 19.
черт. 19, имеет место, а именно: верхний знак относится к
черт. 19, а, нижний — к чертежу 19,6), то
Если дуга y' такова, что замкнутый контур, образованный ею
и дугой у я раз, обходит точку z = 0, то на основании фор-
формулы B1) или B Г) получим:
Поэтому, если Г — любая, не проходящая через точку
х=0 дуга с начальной точкой 1 и конечной точкой z, то
причем выбор значения многозначной функции Lnz в правой
части этого равенства зависит от выбора дуги Г.
ИНТЕГРАЛ КОШИ
75
§ 5. Интеграл Коши
Предположим, что функция f(z) является аналитической
на некотором контуре Г и в односвязной области О, ограни-
ограниченной этим контуром. Пусть, далее, z— любая точка внутри
области О (черт. 20). Описав из точки г, как из центра, ле-
лежащую в области О окружность у радиуса р, в силу основан-
основанной на теореме Коши формулы
A2) получим:
r/(O<g_r/(Q
г
B3)
Теорема Коши применима, так
как единственной особой точ-
точкой в области О для подынте-
подынтегральной функции является точ-
точка С = 2 и, следовательно, в Черт. 20.
двусвязной области между кон-
контурами Г и у эта функция является аналитической. Заметим, что
в равенстве B3) радиус р окружности у может быть выбран про-
произвольно, лишь бы эта окружность лежала внутри области О.
Так как функция f{z) является аналитической, а следова-
следовательно и непрерывной в области О, то для каждого е>0,
как бы мало оно ни было, и для любой точки ? на окружно-
окружности у справедливо неравенство
1/@-/(*)!< в,
если только радиус р окружности у достаточно мал (напоми-
(напоминаем, что точка z — центр этой окружности и, следовательно,
U—*1=р).
Поэтому
~/B).
, — г
<—• 2тгр = 2тге. B4)
Здесь мы воспользовались свойством 6) (стр. 60) и тем,
что j 5 — z | = р на дуге у«
Так как е можно взять сколь угодно малым, то неравен-
неравенство B4) означает, что
l'm \ т—Г==\т—Т' B5)
76 ИНТЕГРИРОВАНИЕ. ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
Но, как уже было отмечено, величина
¦ z
при уменьшении р не изменяется, поэтому знак предела в ле-
левой части B5) можно опустить. Если учесть также, что
в силу B0)
то из B5) будем иметь:
Сопоставляя последнее равенство с равенством B5), получим
так называемую интегральную формулу Коша:
с-* •
Величина, стоящая в правой части интегральной формулы Кошя,.
называется интегралом Коши. Для вычисления интеграла
Коши нужно знать значения функции f(z) только на нон--
туре Г и, следовательно, интег-
интегральная формула Коши позво-
позволяет находить значения аналити-
аналитической функции в любой точке,
лежащей внутри области О,
если известны значения этой
функции на контуре Г, ограни»
чивающем область О.
Если точка z лежит вне об»
ласти О, то интеграл Коши
равен нулю в силу теоремы
Коши, так как в этом случае подынтегральная функция
является аналитической в области О.
Интегральная формула Коши легко обобщается на случай
сложного контура Г, ограничивающего многосвязную область О.
Действительно, пусть функция /(() является аналитической
на сложном контуре Г, состоящем из простых контуров
С,, Ct, ..., Сш (черт. 21), в в многосвязной области, огра-
§ 5] ИНТЕГРАЛ КОШИ 77
ничейной контуром Г. Пусть, далее, г — любая точка вну-
внутри этой многосвязной области и у — лежащая в этой области
окружность с центром в точке г. Рассмотрим многосвязную
область, границей которой является сложный контур Г, со-
состоящий из простых контуров Со, С,, С„ .... Сп, у. В этой
области и на ее границе функция ^-Н- является аналитиче-
аналитической и, в силу теоремы Коши,
г'
Так как
Но область, ограниченная контуром у, односвязна и для нее
справедливость интегральной формулы Коши доказана, следо-
следовательно,
7
и на основании B6) получим:
Применим интегральную формулу Коши к случаю, когда
контуром Г является окружность с центром в точке z = a,
уравнение которой имеет вид
или
откуда
78
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
На основании интегральной формулы Коши
1 Г /@ dC I ft
2/ 1 t 2/ 1
а+/?в'р
B7)
Для того чтобы выяснить смысл этого равенства, представим
себе, что на окружности Г задана некоторая непрерывная
функция F(y), значения которой
зависят от угла ср (черт. 22) меж-
ду радиусом, идущим из центра а
в данную точку окружности, и по-
положительным направлением дей-
действительной оси. Разобьем окруж-
окружность Г на л равных дуг лучами,
идущими из центра (каждые два
соседних луча образуют между
2тс\
собой угол Д<р = — ), и выберем
на каждой из этих дуг по одной
то.чке, обозначив <р,, cpt, ...,<p« значения угла <р, соответст-
соответствующие выбранным точкам. Величина
Черт. 22.
2^ B8)
является средним арифметическим из значений функции F(<p)
в точках окружности Г, соответствующих углам <рр <р„ ..., <ря.
Предел выражения B8) при я—>оо естественно назвать сред-
средним арифметическим значений функции F(y) на окружности Г.
Из B8) и из определения интеграла следует, что этот предел
равен
2л
Следовательно, формула B7) показывает, что значение анали-
аналитической функции в центре круга равно среднему арифмети-
арифметическому из ее значений на окружности этого круга.
§ 5] ИНТЕГРАЛ КОШИ 79
Если zv zt, ..., г„ — комплексные числа, а п—целое
положительное число, то
т. е. модуль среднего арифметического не больше, чем сред-
среднее арифметическое из модулей. Путем предельного перехода
это неравенство распространяется на среднее арифметическое
из значений функции на окружности Г:
2т 2к
(впрочем, к тому же выводу приводит и свойство 7), стр. 61).
В то же время очевидно, что среднее арифметическое не
скольких действительных чисел не может быть больше, чем
каждое из этих чисел. Путем предельного перехода это свой-
свойство также распространяется на среднее арифметическое зна-
значений непрерывной функции на окружности, если эта функция
принимает в точках окружности только действительные значе-
значения. Учитывая, что модуль аналитической функции является
непрерывной функцией, принимающей только действительные
значения, можно доказать весьма важное свойство аналитиче-
аналитических функций, носящее название принципа максимума модуля:
модуль функции, отличной от тождественной постоянной
и аналитической в некоторой области, не может ни в
одной внутренней точке этой области принять максималь-
максимальное для этой области значение.
Действительно, предположим, что z9 — внутренняя точка
области О, в которой функция /(г) аналитична, и допустим,
что |/(го)| больше, чем |/(z)|, для любой другой точки области.
Опишем из точки z0, как из центра, окружность у столь
малого радиуса, что все точки этой окружности лежат в об-
области О. По доказанному, значение /Ц) равно среднему
арифметическому из значений f{z) на окружности у. Следо-
Следовательно, |/(я„)| не больше, чем среднее арифметическое из
значений \/(z) | на окружности у, и, тем более, не может быть
больше, чем каждое из значений \/(z)\ на этой окружности.
Но это заключение противоречит предположению о том, что зна-
значение |/(*0)| больше, чем значение \/(z)\ во всякой точке
области О, и в частности во всякой точке окружности у. Если
80 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гл. V
бы мы допустили, что значение модуля аналитической функции
f(z) в некоторой внутренней точке z0 больше или равно зна-
значению \/{г)\ в любой друюй точке области О, то можно
было бы доказать, что функция /(г) постоянна (доказательство
мы опускаем).
Пользуясь тем, что действительная и мнимая части анали-
аналитической функции являются функциями гармоническими, можно,
исходя из интегральной формулы Коши, выразить значения
гармонической функции во всякой точке, лежащей внутри
круга, через значения этой функции на окружности круга.
Для этого следует в левой и правой чаетях интегральной фор-
формулы Коши отделить действительную часть от мнимой.
Выберем для упрощения вычислений систему координат
так, чтобы центр круга совпал с началом координат. Тогда
уравиеиие ограинчнвающий окружности будет иметь вид
С=Яе", 0<<р<2п,
откуда
dZ = Re"fidy.
Положив 2=re''(r<#), получим с помощью интегральной
формулы Коши:
— l С
5^
С другой стороны, если в правую часть формулы Кошн
подставить вместо г число, соответствующее точке, лежа-
лежащей вне данного круга, то интеграл, в силу теоремы Коши,
будет равен нулю. Вне данного круга лежит, в частности,
точка z*, определенная равенствами
т. е.
Действительно, из г<# следует, что
•) Точка 2* называется симметричной точке г относительно дан-
данной окружности. Подробнее о симметрии относительно окружности
см. на ста 163.
§ 5] ИНТЕГРАЛ КОШИ 81
Подставляя в правую часть формулы Коши г* вместо г,
получим:
2
или
Вычитая из левой и правой частей {29) соответственно лецук
и правую части C0), получим:
J
о
Разделив числитель и знаменатель дроби, стоящей под знаком
интеграла в правой части последнего равенства на eiii+n,
найдем:
Но
е'«-?» +*-'»- и — 2 cos (« — ^)>,
следовательно,
Отделив действительную часть от мнимой
f(re^) = u{r, b) + tv(r, в),
el<<) = u{R, <f)-\-iv{R, <p)
82 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
я приравняв действительные части в равенстве C1), получим:
Эта формула позволяет найти значение гармонической функции
в любой точке (г, 0), находящейся внутри круга, если известны
значения и (R, <р) этой функции в точках (R, <р) на окружности
круга радиуса R. Правую часть равенства (82) называют
интегралом Пуассона.
Положив в C2) г = 0 и обозначив через и, значение функ-
функции «(г, 6) при г=О, получим:
2к
Следовательно, значение гармонической функции в центре круга
равно среднему арифметическому ее значений на окружности
круга. Так как среднее арифметическое значений u(R, <р) не
может быть больше наибольшего из этих значений и меньше
наименьшего из них, то рассуждения, аналогичные изложенным
на стр. 78—80, приводят к принципу максимума и минимума
для гармонической функции: функция, отличная от тож-
тождественной постоянной и гармоническая в некоторой об-
области, ни в одной внутренней точке этой области не мо-
может принять максимальное или минимальное для этой
области значение.
§ 6. Производные высших порядков от аналитической
функции
Докажем, что производная аналитической функции также
является аналитической функцией.
Пусть /(г) является аналитической функцией на замкну-
замкнутом контуре Сив ограниченной этим контуром области; тогда
в соответствии с интегральной формулой Коши
с
где г — любая точка внутри рассматриваемой области.
§ 6] ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 83
Какова бы ни была внутренняя точка z рассматриваемой
области, величину |Л[ можно выбрать столь малой, что точка
z-j-A будет также лежать внутри этой области. Будем, на-
например, считать, что |А| меньше кратчайшего расстояния
точки z до контура С. На основании той же интегральной
формулы Коши
f(z+h)-f(z)
h
— J Г Г №
или после несложных преобразований
/(г
— buH-z-h)(i:-z
При А—»-0 левая часть этого равенства стремится к /'(г),
а подынтегральная функция в правой части — к ,¦„ _ ^. Сле-
Следовательно, мы приходим к формуле
справедливость которой будет доказана, если будет обоснован
предельный переход под знаком интеграла в правой части C3),
т. е. если будет доказано, что
_f/(C)rfC
Г
J
(f - г - Л) С - г)"" J IT^
Для этого достаточно установить, что разность
(С-г-А)(С-г) J (С-гI
с
стремится к нулю при А—*0.
84
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гЛ. V
Если обозначить буквой 8 кратчайшее расстояние точки г
от контург) С (черт. 23), то кратчайшее растояние точки г-\-h
от этого контура будет во всяком случае не меньше, чем
}_|/,|( f. е. какова бы ни была точка С контура С, спра-
справедливы неравенства
Если, далее, М — наибольшее
значение модуля функции /(г)
на контуре С, то для любой
точки С этого контура
и на основании уже неодно-
неоднократно использованного свойства 6) (стр. 60)
где /—длина дуги С.
Но тогда на основании C5)
при А—*0, и формула C4) доказана.
Составив с помощью C4) отношение
-/'(*)
и перейдя к пределу при h —* 0, можно с помощью аналогич-
аналогичных выкладок доказать, что
-,,_д 2
Так же доказывается, что при любом целом положительном л
' (z' — а« J (i-*/"-1 ''
с
') Для удобства запоминания заметим, что формально формулы
C4), C6), C7) можно получить из интегральной формулы Коши, диф-
§ 6] ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 55
Равенство C7) получено в предположении, что функция /\г)
является аналитической как на контуре С, так и в области,
ограниченной этим контуром. Но если функция f(z) является
аналитической в точке z, то всегда можно провести из этой
точки, как из центра, окружность С столь малого радиус,
что функция f(z) останется аналитической на этой окружное™
я в круге, ею ограниченном, и следовательно, на основании
формулы C7) можно заключить, что в точке г и в любой
другой точке достаточно малой окрестности точки г существует
производная любого порядка п этой функции. Итак, из ансиц.
тичности функции в некоторой точке, т. е. из существо^.
ния первой производной данной функции в какой-либо окресп.
ности этой точки, следует существование в окрестности
той же точки производных данной функции любого порид-
ка, а следовательно и аналитичность этих производньх.
Интегральная формула Коши и формула C7) могут с;у.
жить для вычисления интегралов по замкнутым контурам.
Пример 1. Вычислить интеграл
e*dt
где С —окружность радиуса 2 с центром в точке 3/.
f(z)~— внутри круга, ограниченного окружностью С, аналитич(а,
поэтому, применяя интегральную формулу Коши, получим:
= 2w ^ — w(cos 2 -f / sln2).
Пример 2. Вычислить
f*C08?*S
j (г — 0* '
где С — замкнутый контур, однократно обходящий точку /.
няя формулу C7) к функции /(«)=«»«, получим.
ГсовгЛ_2«;^Мсо??)| __ _я/с08/__ я/fZl+i
С
ференцируя обе ее части по г (в правой части дифференцировали
производится по параметру z под знаком интеграла).
86 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [ГЛ. V
Мы условились называть интеграл вида
$
с
интегралом Коши в предположении, что С—замкнутый контур,
а функция fie) — аналитическая на контуре Сив области G, огра-
ограниченной этим контуром. При этом оказалось, что функция, опреде-
определяемая интегралом C8), совпадает с / (z) внутри области G и равна
тождественно нулю вне контура С. Если считать, что С—произволь-
С—произвольная кусочно-гладкая дуга (или даже совокупность нескольких таких
дуг), а относительно функции /(Q ограничиться предположением,
что «на непрерывна вдоль С, то величину C8) принято называть
интегралом типа Коши. Интеграл Коши является, очевидно, частным
случаем интеграла типа Коши.
Функция, определяемая интегралом типа Коши:
с
определена всюду, кроме точек дуги С, так как в любой точке г, не
принадлежащей С, интеграл типа Коши существует (единственной
точкой разрыва подынтегральной функции является точка t = z).
Дословно повторяя выкладки и рассуждения, с помощью кото-
которых была обоснована формула C4), можно найти производную инте-
интеграла типа Коши в любой точке г, не принадлежащей дуге С:
р.М- * f/ЮД
* 2я* J (К-г)*'
и тем самым доказать, что интеграл типа Коши является функцией,
аналитической в любой точке, не лежащей на дуге С. Для произ-
производной любого порядка л интеграла типа Коши справедлива формула,
аналогичная формуле C7).
:= *' Г /(
2ш J (C-
§ 7. Теорема Морера
Докажем следующую теорему, называемую теоремой
Морера, в известном смысле обратную теореме Коши: если
функция /(г) непрерывна в области О и если для любого
замкнутого контура С, расположенного внутри области О
$/@*5=0,
с
то функция /(г) является аналитической в области О.
7} ТЕОРЕМА МОРЕРА 87
Действительно, в силу условий теоремы, интеграл
не зависит от пути интегрирования, лежащего в области О
в соединяющего точку ?0 с 'произвольной точкой г области О,
и, следовательно, при данном г0 определяет однозначную
функцию F(z). Возьмем величину |А| столь малой, чтобы
круг радиуса |Л| с центром в точке z находился целиком
внутри области О; тогда
*+*
F + *) J
C9)
причем за путь интегрирования в последнем интеграле можно
взять прямолинейный отрезок, соединяющий точку z с точкой
Так как
ТО
и, принимая во внимание C9), получим:
D0)
Пользуясь непрерывностью функции /(*) и учитывая, «о
точка J находится на прямолинейном отрезке, соединяющем
точку z с точкой г -j- Л. иожно утверждать, что при дост*
точно малом [ h I
88 ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ АРГУМЕНТУ [гЛ. V
как бы мало нн было положительное число е. Следовательно,
e|Al «
и на основании равенства D0) получаем:
при достаточно малом [А|. Но это неравенство означает, что
Итак, функция F(z) имеет производную во всякой точке обла-
области О и является в этой области аналитической функцией, а
на основании доказанного в предыдущем параграфе функция
f(z), будучи производной аналитической функции, также ана-
литична в области G.
Задачи к главе V
1. Вычислить
\ lm zdz,
с
если путь интегрирования С:
а) является прямолинейным отрезком, соединяющим точку 0 с
точкой 2+i\
б) состоит из прямолинейного отрезка, соединяющего точку 0
с точкой / и прямолинейного отрезка, соединяющего точку /сточкой
2 + 1.
2. Вычислить
|11 А.
с
если путь интегрирования С является:
а) прямолинейным отрезкой, соединяющим точку —1 с точкой 1;
б) полуокружностью радиуса 1 с центром в начале координат,
лежащей в верхней полуплоскости, причем точка —1 является на-
начальной, а точка 1 — конечной.
В задачах 3 — 8 следует пользоваться теоремой Коши, интеграль-
интегральной формулой Коши н формулами, получаемыми нз интегральной
формулы Коши дифференцированней. Контур С в этих задачах одно-
однократно обходится против часовой стрелки.
§ 7] ТЕОРЕМА МОРЕРА 89
3. Выгадать
если'
а) С — окружность радиуса 3 с центром в начале координат;
б) С — окружность радиуса 1 с центром в начале координат.
4. Вычислить
если- С — окружность радиуса 3 с центром в точке — L
5. Вычислить
dz
если'
а) С — окружность с центром в точке 2/ радиуса %
б) С — окружность с центром в точке —2/ радиуса 2.
6. Вычислить
Г dz
если:
а) С — окружность радиуса 2 с центром в точке ЗД.
б) С — окружность радиуса 2 с центром в точке — 2/.
7. Вычислить
e*dz
ci
если С — замкнутый контур, однократно обходящий точк} —2 в по-
положительном направлении.
8. Вычислить
dz
если
а) С— окружность радиуса /?<2 с центром в точке *« I;
б) С—окружность радиуса й<2 с центром в точке z=— И
в) С - окружность радиуса R > 2 с центром в точке ъ = 1 или
ГЛАВА VI
РЯДЫ
§ 1. Числовые ряды
В главе III были введены основные понятия теории рядов
С комплексными членами. Там было также доказано, что для
сходимости ряда
*»+*•+•••+*»+••• 0)
достаточно, чтобы сходился ряд
Однако ряд A) может сходиться, как известно, и тогда, когда
ряд B) расходится, в этом случае ряд A) называется неабсо-
неабсолютно (условно) сходящимся.
Для исследования сходимости ряда B) можно применять
известные признаки сходимости знакоположительных рядов,
например признаки Даламбера и Коши. Ряд B) сходится, если
в расходится, если
lim ±*Щ
¦ ¦+ 00 I *В I
(признак Даламбера).
Ряд B) сходится, если
hm
я расходится, если
lim УЩ>\
(признак Ковш)!
2] функциональные ряды 91
Бели
или
то расходится не только ряд B), но и ряд A), так как в этом
случае, очевидно,
lim гпф0.
§ 2. Функциональные ряды
Функциональный ряд, членами которого являются функции
комплексного аргумента z:
/,(*)+/,(*)+...+/.<*)+..., C)
может в одних точках сходиться, в других расходиться. Сумма
такого ряда
где
Sn (*) =/, W +/, (*)+... +/. (*).
является функцией аргумента z, определенной в точках, в ко-
которых ряд C) сходится. Множество точек, в которых ряд C)
сходится, будем называть областью сходимости этого ряда..
Остатком ряда C) называется разность
Rn (z)=/(z)-Sn («)=/„, <*)+/.+,
В каждой точке сходимости ряда C)
В-+СО
Другими словами,- если ряд в данной точке z сходится, то для
каждого s>0 можно подобрать столь большое число N, что
при n^>N модуль остатка ряда удовлетворяет неравенству
Наименьшее число N, определяющее номер я, начиная с кото-
которого справедливо неравенство D), вообще говоря, зависит не
92 ряды [гл. vi
только от е, но и от г и не является, следовательно, одинаковым
для всех точек области сходимости ряда; чтобы подчеркнуть
эту зависимость, лучше вместо N писать N (е, г). Может слу-
случиться, что значения N (е, г) для всех точек некоторой
области не превышают некоторого числа N* (е), и тогда, сле-
следовательно, существует такое число N* (8) (N* (е) не зависит
от г, а зависят только от е), что при «>iV* (е) неравенство D)
будет справедливо во всех точках области,— в этом случае
говорят, что ряд C) сходится в данной области равномерно.
Пример 1. Известная формула для суммы л членов геометри-
геометрической прогрессии
a + at + az* + ...+cua=±Zr-±r-l, E)
как видно из ее доказательства, справедлива при любом комплексном
ж(гф\). Принимая во внимание, что Шпгп+1 = 0, если |г|<1, g
n-»ao
11т г*+1= со, если | г \ > 1, получим:
я-юо
если
loo, если |*|>1 и афО.
Но сумма E) является частичной суммой бесконечной геометрической
прогрессии
a + az + azx + . ..+azn+... F)
и, следовательно, ряд F) сходится внутри круга [г|<1, и сумма
этого ряда равна
Вне единичного круга (при | г \ > 1) ряд F), как установлено выше,
расходится; нетрудно видеть, что он расходится и на окружности
|г| = 1, так как в этом случае не выполнен необходимый признак
сходимости
llm /„(*) = О,
В-»ОО
где /„ B) — общий член ряда.
Рассмотрим круг | г К у, лежащий внутри круга \ г |< 1. Под-
Подберем к данной точке г, лежащей в этом круге, и любому • > 0 такое
N (г, г), чтобы при я > N («, 2) остаток ряда удовлетворяя неравен-
неравенству D) |Я„ («) | < е. -г~ -г-
Как указано выше,
§ Щ
откуда
и для того, чтобы удовлетворялось неравенство
-Я+1 I
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Д-Я+1
S(z)
или
аг"
\-z
<«
95
G)
т. е.
достаточно, чтобы
(внак неравенства изменился» так как 1п|г[<0 при
оисуда
я>-ТпТ7Г и
(8)
При достаточно иалон Е не только знаменатель, но и числитель первого
члена в правой часта неравенства (8) отрицателен, поэтому правая
часть (8) тем больше, чем больше абсолютная величина числителя и
чем меньше абсолютная величина знаменателя первого члена. Так как
|1— *ls»l — 1*|и|г|^-д-> т<> наибольшее значение абсолютной
~2 *
величины числителя первого члена в правой части (8) равно In -т—; ,
а наименьшее значение абсолютной величины знаменателя 1 In -к-1, сле-
следовательно, правая часть неравенства (8) во всяком случае не
превышает для всех точек круга | z | sg -^- числа
¦ следовательно, при п > N (е) неравенство G) будет удовлетворяться
94 ряды [гл. vi
во всех точках круга | г \ а? -я-, т. е. ряд F) сходится в Kpyrejjt |«?-у
равномерно.
Очевидно, что ничего бы не изменилось в существе рассуждений
и выклацрк, если бы вместо круга | г К -я- мы рассматривали любой
круг | г | «S 1 — К где S > О, лежащий внутри единичного круга; сле-
следовательно, ряд F) равномерно сходится в круге радиуса 1 — I, т. е.
в круге, радиус которого хотя бы немного меньше единицы. Но в круге
\г |< 1 ряд F), хотя и сходится, но сходится неравномерно. Действи-
Действительно, как было показано выше, для того, чтобы удовлетворялось
неравенство
необходимо, чтобы
правая часть этого неравенства стремится к бесконечности при г -*¦ 1
и, следовательно, нельзя найти величину N ((), превышающую правую
часть этого неравенства во всех точках круга | г | < 1. Иными словами,
нельзя найти такое N (е), не зависящее от г, чтобы при л > N (е)
неравенство | Rn (г)\ < с удовлетворялось во всех точках круга | г |< 1,
а это н означает, что в круге | г }< 1 рассматриваемый ряд сходится
неравномерно.
Часто равномерную сходимость ряда можно установить,
пользуясь следующим признаком: если, в любой точке г обла-
области О модуль каждого члена ряда
/«(*)+/,(*)+. .-+/„(*)+... (9)
не превышает соответствующего члена сходящегося число-
вого ряда
*•+<*,+ • •.+*„+..., О»)
то ряд (9) сходится в области О равномерно.
Пусть Rn (z) — остаток данного ряда (9), а /¦„ — остаток
числового ряда A0):
^п (*)^=/я+, (*)+/„+, W+ ... . О»)
'"B = aB+. + a»+i-h.-- A2)
По условию
следовательно, таким же неравенствам удовлетворяют частичные
суммы рядов (П) и A2), а значит и их пределы:
§ 2] ФУНКЦИОНАЛЬНЫ! РЯДЫ 95
Но, в силу сходимости числового ряда A0), для каждого 6>0,
как бы мало оно ни было, можно подобрать такое N (г) (N за-
зависит, конечно, только от е, так как ряд A0) числовой), что
при л>Л/(е)
Следовательно, тем более при л>А/(е)
во всех точках области G.
Следовательно, ряд (9) сходится равномерно,
Докажем несколько теорем о равномерно сходящихся рядах.
1) Если члены ряда
/.(*>+/,<*)+•••+/.(*)+... О)
являются непрерывными функциями t некоторой области Q
и если ряд сходится в этой области равномерно, то сумма
ряда / (г) также непрерывна в области О.
Пусть Sn (г) — частичная сумма данного ряда, Rn {г) —
остаток ряда (9), гй и z9-\-h — две произвольные точки об-
области О; тогда
и, следовательно,
A)
Так как в области О данный ряд сходится равномерно, то в
соответствии с определением равномернЬй сходимости для любого
8^>0 можно найти такое, не зависящее от г число N* (s),
что неравенство
I/?.(*)!<•
удовлетворяется при л > N* (г) во всех точках области О и,
а частности, в точках z0 и z%-\-h.
Итак, пусть n^>N* (e); тогда
(,)|<6,
96 ряды [гл. vi
каковы бы ни были z0 и А (при условии, что zt и «,~{~Л
принадлежат области О). Функция Sn (z) непрерывна в облает* О,
так как является суммой конечного числа непрерывных функций.
Следовательно, в частности, функция Sn (z) непрерывна в точке г.,
и поэтому для любого 6^>0, как бы мало оно ни было, при
достаточно малом | h | удовлетворяется неравенство
A5)
Пользуясь A4) и A5), мы заключаем, что при достаточно
малом |А| из A3) следует
—/(*,)]< 8в,
а это и означает, что функция / {г) непрерывна в произвольной
точке г, области G.
2) В условиях предыдущей теоремы ряд можно почленно
интегрировать вдоль всякой дуги С, лежащей внутри обла-
области О, причем сумма ряда, полученного в результате та-
такого интегрирования, равна
\f(z)dz,
с
где / (z) — сумма данного ряда.
Пусть, по-прежнему, SB (z) — частичная сумма данного ряда:
и
ее
$
с
Теорема будет доказана, если мы обнаружим, что
1нп an(z)=[/(z)dz.
Но
$/(*) йж-ил (*)= J/(*) dz-\sn (z) dz =
с ее
J & 4шг A6)
» 2Т функциональные ряды 97
где Rn (z)=f(z) —Sn (z) — остаток данного рада. Ввиду равно-
равномерной сходимости данного ряда в области О для любого е >• О
при л^>Л^(е) во всех точках области О и, в частности,
во всех точках дуги С будет выполнено неравенство
если N {€) достаточно велико. Но тогда из A6) при л
получим:
| J / W dz-on (z)\ = \ J Rn {z) dz\<el,
где /—длина дуги С. Так как число е сколь угодно мало, то
из полученного неравенства следует, что
lim <jtt(z)=[/(z)dz.
n-юо ?
3) Если члены ряда
/. (*)+/, (*)+-.. +/„ W+ •. • =/(*)
являЬтся аналитическими функциями в односвязной обла»
спи О и ряд сходится в этой области равномерно, то
сумма ряда f (г) также является функцией, аналитической
внутри области G (теорема Вейерштрасса).
Пусть С — любой замкнутый контур внутри области G. Та*
как данный ряд сходится в области G по условию равномерно,
то его можно вдоль контура С интегрировать почленно и
J/W dz= J/, (г) dz+j /, (z) dz+ ... + $Д (*)<**+...
Так как /0 (z), fx (z), ... , /„ (z), ... являются аналитическими
функциями в области G, то на основании теоремы Коши каждый
из интегралов в правой части последнего равенства равен нулю,
а следовательно,
$/(*)& = 0, A7)
с
при любом выборе контура С в области G. Так как, кроме
того, функция / (z), будучи суммой равномерно сходяще-
сходящегося ряда аналитических, а следовательно и непрерывных,
функций, также, по ранее доказанному, непрерывна, то из A7)
на основании теоремы Морера (стр. 86—87) следует, что функция
/(г) аналитична внутри области О.
4 Г Л ЛуЙЦиЛ Э.Эльсгольц
98 ряды [гл. у,
Теорема Вейерштрасса остается, конечно, справедливой и
в случае многосвязной области О, так как каждая внутренняя
точка za многосвязной области может быть включена в Одно*
связную часть области О, например в достаточно малую окре-
окрестность точки za; по доказанному функция /(г) будет анали-
аналитической в этой односвязной области и, в частности, в данной
точке zt.
§ 3. Степенные ряды
Ряд вида
.., лщ
где С{ — постоянные, называется степенным. Основной теоремой1
теории степенных рядов является теорема Абеля.
Если степенной ряд A8) сходится в точке z0, то он
сходится и притом абсолютно во всех точках, лежащих
внутри окружности С с центром в точке 2 = 0 и прохо-
проходящей через точку гв (т. е. во всех точках z, для которых
|«|-<|го|). При этом во всяком круге |*|*Sp (черт. 24)
радиуса р, меньшего, чем | г91, ряд A8) сходится равномерно.
Из сходимости ряда A8) при z = zt следует, что
lim cnzS = 0,
П-+Х
я следовательно, модули членов ряда A8) ограничены, е.
существует такая постоянная М, что
при любом л. Пусть z—любая точка, лежащая внутри окруж-
окружности С; тогда )г|<\zt\ и — =tf< 1.Общий член ридаA8)
можно преобразовать к виду
Отсюда видно, что
и следовательно, модули членов ряда A8) в точке z мещше
соответствующих членов геометрической прогрессии
СТЕПЕННЫЕ РЯДЫ
99
со знаменателем q, меньшим единицы. Следовательно, ряд A8)
сходится в точке г абсолютно, и первая часть теоремы доказана.
Возьмем теперь произвольный круг (z|^p (черт. 24),
лежащий внутри окружности С (p<t*0|). По доказанному ряд
A8) сходится абсолютно во всякой точке, расположенной внутри
окружности С, и в частности во всякой точке, лежащей на
окружности выбранного нами круга радиуса р. Итак, если z* —
какая-нибудь точка на окружности этого
круга (т. е. |г*1 = р), то числовой ряд У.
сходится. Но для любой другой точки
г, лежащей внутри или на окружности
круга
|1
справедливо неравенство
|p
z*\, следовательно,
A9)
Черт'24-
при любом п. На основании признака равномерной сходи-
сходимости, доказанного на стр. 94—95, из A9) следует, что
ряд A8) равномерно сходится в круге |г\гёр. Этим дока-
доказана и вторая часть теоремы.
Рассмотрим теперь любой луч, выходящий из нулевой точки.
Возможны три случая:
1) Ряд A8) сходится во всех точках этого луча. Тогда,
в силу теоремы Абеля, ряд A8)-сходится внутри круга сколь
угодно большого радиуса, т. е. сходится во всей плоскости.
2) Ряд расходится во всех точках луча, кроме точки 2 = 0
(в точке г-=0 сходится всякий степенной ряд вида A8), так
как при z = 0 все члены ряда, кроме первого, обращаются
в нуль).
В этом случае ряд расходится во всех точках плоскости,
кроме точки z=0.
Действительно, из теоремы Абеля следует, что если ряд A8)
в некоторой точке г расходится, то он расходится и всюду
вне круга с центром в начале координат, окружность которого
проходит через точку 2, так как из сходимости ряда в неко-
некоторой точке вне такого круга следовала бы сходимость его и
в точке г. Следовательно, в рассматриваемом случае ряд расхо-
расходится вне круга сколь угодно малого радиуса с центром в ну-
нулевой точке, т. е. всюду, кроме точки z = Q,
100
РЯДЫ
[гл. vi
3) На луче имеются, как точки сходимости, отличные от
г = 0, так и точки расходимости ряда A8).
Как было указано выше, из теоремы Абеля следует, что
всякая точка сходимости находится ближе к нулевой точке,
чем всякая точка расходимости. Следовательно (черт. 25), на
луче найдется точка г*, отделяющая точки луча, в которых
ряд A8) сходится от точек, в кото-
которых ряд расходится. Сама точка г*
принадлежит или к числу точек схо-
сходимости, или к числу точек расходи-
расходимости ряда A8). Ряд A8) будет
сходиться внутри круга G -с центром
в нулевой точке, окружность которого
проходит через точку г*, и расходиться
вне этого круга.
Круг G называют кругом схо-
сходимости, а его радиус—радиусом
*-<Я
Черт. 25.
сходимости степенного ряда A8). На окружности круга схо-
сходимости могут лежать как точки сходимости^ так и точки рас-
расходимости ряда A8). В рассмотренных выше случаях 1) и 2) мож-
можно считать, что радиус сходимости равен, соответственно,
бесконечности и нулю.
Так как во всяком круге, находящемся целиком внутри
круга сходимости, как было доказано выше, степенной ряд
сходится равномерно, то из теоремы Вейерштрасса следует,
что сумма степенного ряда внутри круга сходимости является
аналитической функцией.
Радиус сходимости степенного ряда можно определять, поль-
пользуясь известными признаками сходимости рядов. Например,
если существует конечный или бесконечный предел
lim
л-юо
то (см. стр. 90—91) ряд A8) сходится, если
л->ео1
т. е. при
1*1<Т
IS-±rl'
с 3] СТЕПЕННЫЕ РЯДЫ 101
и расходится, если
т. е. при
lim \ta±i
Следовательно, в этом случае радиус сходимости г можно опре-
определять по формуле
Д B0)
ТО
т.
н
т.
Если существует
(см. стр.
е. при
90—91J
lim^
п-юо
расходится, если
е. при
Ига ?"]-<
п-кх>
1 —
lim
n-юо
Сп
конечный или бесконечный предел
lim У\
л-юо
ряд A8) сходится, если
7-F]=|*|Uin VK\<h
л-юо
1-1 <Г '
п-»оо
n-юо
В этом случае радиус сходимости г можно определять по фор-
формуле
люо
Ряд
'. + ', (г—a) + ct (г —в)§+ ... +ся (* — а)"+¦.... B2)
где а — любое комплексное число, также называется степенным.
102
РЯДЫ
[гл. vi
Этот ряд подстановкой z—a — t сводится к ряду A8), причем
точке ? = 0 соответствует точка z — a. Следовательно, обла-
областью сходимости ряда B2) является круг с центром в точке
Z — a. Радиус этого круга (радиус сходимости ряда B2))
можно определять по формулам B0), B1).
§ 4. Ряд Тейлора
Рассмотрим однозначную функцию f{z), аналитическую
внутри круга О, ограниченного окружностью С с центром
в точке г = а (черт. 26). Разложим эту функцию в степенной
ряд вида B2).
Пусть z — любая внутренняя
г точка круга О. Проведем внутри
круга О окружность С с цент-
центром в точке а так, чтобы точка
z оказалась внутри этой окружно-
окружности. Тогда в соответствии с интег-
интегральной формулой Коши
О
/(*) =
2*0 С-* *
и
Черт. 26.
Преобразуем один из множителей подынтегральной функции
1 ' ' B4)
где С—любая точка окружности С. Модуль разности |? — а\
равен радиусу окружности С, а так как модуль разности
|г — а\ равен расстоянию точки z от центра окружности
С, то, как бы ни перемещалась точка С по окружности С,
при фиксированном z сохраняет постоянное
величина
х.-а
значение, меньшее единицы (черт. 26).
Следовательно, функция
1
1 —
(.-а
является суммой, сходящейся во всякой точке г внутри окруж-
f 4] HU ТЕЙЛОРА ЮЗ
ности С (см. стр. 92) геометрической прогрессии
1 С-«
Эта прогрессия равномерно сходится на окружности С отно-
относительно С. потому что при фиксированном z величина
t~a. =.q постоянна на этой окружности и, следовательно,
модули членов ряда B5) совпадают с соответствующими чле-
членами сходящегося числового ряда
1+? + ?1+---+?"+---. где ?<1.
Следовательно, подынтегральную функцию в правой части B3)
можно, пользуясь B4) и B5), представить в виде суммы ряда,
равномерно сходящегося на окружности С
/(О _ /ГО 1 (*-fl)/@ i (*-а)'/@ ,
T=l — T:ri~T~ (С-aJ ~i (Г=^р Г---
¦ (г-а)"/(О ¦
••• "Т (f_a)n+i "Г" • ••
и произвести почленное интегрирование, что приводит к раз-
разложению функции /(г) в степенной ряд:
с
с с
(множители {г—а), (г — а)*,..., (г — а)" вынесены за знаки
соответствующих интегралов).
Итак, во всякой точке z, находящейся внутри круга О,
функция /(г) представлена с помощью B6) в виде суммы сте-
степенного ряда
коэффициенты которого вычисляются по формуле
/и —О 1 2 \ (ЧТ\
{п ' •2"' *'• B7)
где С—любая окружность с центром в точке г=а, лежа-
104 ряды [гл. v!
щая внутри круга О, или любой другой простой замкнутый
контур, однократно обходящий точку а в положительном на-
направлении и лежащий внутри круга О, так как, в силу тео-
теоремы Коши, величина интеграла B7) не зависит от выбора
контура С. Полученный ряд называется рядом Тейлора.
Пользуясь интегральной формулой Коши и вытекающей из
нее формулой C7) главы V, можно для коэффициентов ряда
Тейлора получить иное представление:
2*0 С-
C"— 2SJ (С-а)"+1~~^Г (Я"~1>2> "Л
с
н записать разложение в ряд Тейлора в форме, совпадающей
с известной из курса математического анализа для функций
действительного аргумента
B8)
Отсюда, в частности, легко -получить известные разложения
элементарных функций
1„A+*) = *—?+?- .... arctgz=z-?-fJ-...
и другие. Равенства
служившие нам для определения функций е*, sinz, cosz
можно рассматривать, как разложения этих функций в ряд
Тейлора.
Всякая однозначная элементарная функция является анали-
аналитической во всех точках, в которых она определена. Но мо-
может случиться, что ряд Тейлора для какой-либо элементарной
функции сходится и в такой точке, в которой эта элементар-
§ 4] РЯД ТЕЙЛОРА 105
ная функция не определена. Условимся в этом случае припи-
приписывать рассматриваемой элементарной функции в соответствую-
соответствующей точке значение, равное сумме ряда Тейлора в этой точке.
Так, например, разложение
справедливо, как мы знаем, во всей плоскости. Поделив обе части
этого равенства на z, что допустимо, если г Ф 0, получим:
sin ггг ,z4
Это равенство справедливо при любом z Ф 0. Однако ряд, стоящий
в правой части этого равенства, сходится и при z = 0, причем его
сумма при z = 0 равна 1. Условимся поэтому считать, что ^-2-5 = 1
при 2 = 0.
Из предыдущего следует, что при таком условии радиус
сходимости ряда Тейлора для всякой однозначной элементар-
элементарной функции f(z) равен расстоянию р точки г=а, являю-
являющейся центром круга сходимости, до ближайшей особой точки
этой функции.
Действительно, радиус сходимости не может быть больше
указанного расстояния р, так как в противном случае внутрь
круга сходимости попала бы по крайней мере одна особая
точка функции /(г), причем эта точка была бы особой и для
суммы ряда Тейлора (внутри круга сходимости ввиду принятого
условия элементарная функция /(г) и сумма ее ряда Тейлора
тождественны). Это противоречило бы тому, что сумма ряда
является функцией, аналитической во всякой точке, лежащей
внутри его круга сходимости (см. стр. 97, теорема Вейер-
штрасса).
С другой стороны, радиус сходимости ряда Тейлора не
может быть и меньше расстояния р точки г = а до ближай-
ближайшей особой точки функции f{z), потому что внутри круга
радиуса р с центром в точке 2=а функция f(z) аналитична
и поэтому, как было доказано, допускает разложение в схо-
сходящийся ряд Тейлора.
Если R—радиус круга сходимости ряда Тейлора функции
f(z) и эта функция ограничена в круге сходимости, т. е. су-
существует такая посюянная М, что |/(г))<Ж при \z\<R,
то, пользуясь интегральной формулой для коэффициентов ряда
106 гады [гл. vi
Тейлора и выбрав в качестве пути интегрирования в этой
формуле окружность радиуса р с центром в точке z=^a,
уравнение которой |С — я| = Р. получим:
или
Так как радиус р окружности С можно брать сколь угодно
близким к радиусу круга сходимости R, то
1«.1<? (я=0,1,2,...). B9)
Если функция f(z) является аналитической во всей пло-
плоскости, то радиус круга сходимости ряда Тейлора бесконечен,
и следовательно, из неравенств B9) находим, что все коэффи-
коэффициенты с„, кроме с9, равны нулю и, значит, /(г) = с0. Тем
самым доказано, что функция, аналитическая и в то же
время ограниченная во всей плоскости, постоянна (теорема
Лиувилля).
Ряд Тейлора можно почленно дифференцировать. Действи-
Действительно, если f(z) — аналитическая функция, то аналитической
является и ее производная f'(z)\ разложив но формуле B8)
в ряд Тейлора функцию f'(z), получим:
Г (г) =
Но к этому же равенству приводит почленное дифференциро-
дифференцирование равенства B8). Полученный после дифференцирования
ряд имеет тот же круг сходимости, что и исходный ряд, так
как, с одной стороны, при дифференцировании степенного
ряда модули его коэффициентов увеличиваются (коэффициент
с„ умножается на п) и поэтому радиус сходимости не может
увеличиться, а, с другой стороны, радиус сходимости не мо-
может и уменьшиться, так как сумма ряда B8), а следовательно,
и ее производная являются функциями аналитическими во вся-
всякой внутренней точке круга сходимости ряда Тейлора для
функции f(z).
В качестве точки а в формуле B8) можно взять любую
точку, в которой функция f(z) аналитична. Разложение B8)
§ 4] РЯД ТЕЙЛОРА 107
называют разложением функции f(z) в окрестности точки а.
Если /(а) = 0, то точка а называется нулем функции /(г).
Если точка а является нулем функции f{z), то разложение
этой функции в ряд Тейлора в окрестности точки а имеет вид
так как ео=/(а) = О. Если в разложении функции f(z)
в ряд Тейлора в окрестности точки а
с„ = с, = ...=<;„_, =0,
но сп=?0 и, следовательно, разложение имеет вид
/(*)=«„ (z - а)" + еп+1 (z - а)»+1 + ..., C0)
то точка а называется нулем функции f(z) порядка или крат-
кратности л. Если л = 1, то нуль называется простым. Продиф-
Продифференцировав C0), приходим к выводу, что если а — нуль
порядка л функции f{z), то эта же точка является нулем по-
порядка л — 1 для функции /' (z).
Из формул для коэффициентов ряда Тейлора следует, что
если точка а является нулем порядка л функции f(z), то
(ф
Разложение C0) можно переписать в виде
(*-«)"[e1. + «.+i (*-a)+...]=(*-a)e?(*), C1)
где функция <f(z) определяется как сумма степенного ряда
имеющего, очевидно, тот же круг сходимости, что и данный
ряд C0). Для функции f(z) точка а уже не является нулем,
так как <р(а) = е„=?0. Справедливо и обратное утверждение:
всякая функция вида
/() (*_ а)в
где л — целое положительное число, <р (а) ф. 0 и <р (z) анали-
тична в точке а, имеет в этой точке нуль порядка л. Дей-
Действительно, разложив <p(z) в ряд Тейлора в окрестности точ-
точки а, получим: _ _
108 РЯДЫ [ГЛ. 7
где со = <р(а)=?О. Отсюда
f(z) = (z — a)a<f(z) = 70(z — a)n-\-7t(z—a)'*1 ^
Мы пришли к разложению вида C0) и, следовательно, точка
а является нулем порядка я функции /(*).
§ 5. Теорема единственности и аналитнческое продолжение
Докажем следующую теорему о единственности анали-
аналитической функции.
Если значения аналитических в области О функций
/, (г) и /, (г) совпадают на некоторой бесконечной после'
довательности точек
^•ц ^t» • • • i 'в» • • *»
сходящейся к точке а, которая является внутренней точ-
точкой области О, то функции /, (z) a /f (z) тождественны
во всей области О.
Для доказательства этой теоремы заметим сначала, что
если точка а является нулем функции f(z) в функция f{z)
не равна тождественно нулю в некоторой окрестности точки а,
то из C1) следует, что в достаточно малой е-окрестности
точки а функция /{г) других нулей не имеет. Для того чтобы
в этом убедиться, достаточно заметить, что множитель (z — а)"
в правой части C1) отличен от нуля всюду, кроме точки
z — a, а функция <p(z) отлична от нуля в точке а, а следо-
следовательно, в силу непрерывности, н в некоторой окрестности
точки а.
Для функции f1(z)—fl(z) точки zlt zt, ..., *„, ... яв-
являются, по условию, нулями, следовательно, точка а также
является нулем этой функции, так как, если бы в точке а
функция /, (z)—/|(z) была бы отлична от нуля, то в силу
непрерывности она была бы отлична от нуля н в некоторой
окрестности точки в, что невозможно, так как из определения
предела следует, что в любой, сколь угодно малой окрестно-
окрестности точки а находится бесконечное множество точек последо-
последовательности *!, zt, ..., zn, ..., в которых /, (z)—/t{z) = 0.
Итак, точка а является нулем аналитической функции /t (z)—
—ft(z) и в то же время в любой, сколь угодно- малой окре-
окрестности точки а имеются другие нули этой функции, что, как
указано выше, возможно лишь в случае тождественного равен-
§ б] ТЕОРЕМА ЕДИНСТВЕННОСТИ Й АИЛЛИТИЧ. ПРОДОЛЖЕНИЕ 109
ства нулю функции /,(г)—Д(^)в некоторой окрестности точ-
точки а, но тогда равны нулю все коэффициенты разложения этой
функции в ряд Тейлора в окрестности точки а, и тождество
/,(г)—/t(z) = 0 или /1{z)=/t(z) Справедливо по крайней
мере во всем круге сходимости указанного разложения и тем бо-
более в круге с центром в точке а и радиусом, равным расстоянию
этой точки до ближайшей к ней точки границы области О.
Пусть теперь г* — любая внутренняя точка области О.
Соединим точку а с точкой г* непрерывной дугой у, лежащей
Черт. 27.
внутри области О (черт. 27). Пусть d— кратчайшее расстоя-
расстояние точек этой дуги от границы области G. Опишем из точки а,
как из центра, окружность радиуса ,d. Тождество /, {г) =/, (г),
по доказанному, справедливо внутри круга О0, ограниченного
этой окружностью. Пусть а,— первая, если перемещаться по
дуге ^ от точки а к точке г*, точка пересечения построенной
окружности с дугой у. В любой окрестности точки а, имеется
бесконечное множество точек круга О0 — точек, в которых
значения функций /, (z) и ft (z), по доказанному, совпадают.
Следовательно, повторив для точки at рассуждения, применен-
примененные к точке а, мы придем к выводу, что тождество/, (z) =/, (z)
справедливо в круге Gt радиуса d с центром в точке ах.
Обозначим а% первую при движении по дуге f 0T точки at
к z* точку пересечения окружности круга Ох с дугой у, рас-
рассмотрим круг Ot радиуса d с центром в точке at и будем
повторять аналогичные рассуждения до тех пор, пока не до-
докажем тождество /\ (z) =/t (z) в круге, содержащем точку z*,
откуда, в частности,
Так как z*—любая точка области О, то теорема доказана.
110 гады [гл., V»
Из теоремы единственности, в частности, следует, что две
функции, аналитические в некоторой области, тождественны,
если их значения одинаковы на сколь угодно малой площад-
площадке, принадлежащей этой области, и даже на сколь угодно
малой дуге.
В главе III мы определили для комплексных значений ар-
аргумента функции Ln z, ег, sin z, cos z, причем было доказано, что:
1) значения функций ег, sin г, cos г на действительной оси
и главные значения функции Lnz на положительной части дей-
действительной оси совпадают со значениями соответствующих
функций, определяемых в курсе математического анализа для
действительных значений аргумента;
2) функции ег, sin г, cos г являются аналитическими во
всей конечной части плоскости, а функция Lnz всюду, кроме
точек г = Ои г = оо.
Из теоремы единственности следует, что никакие другие
функции, кроме введенных нами, указанными двумя свойствами
обладать не могут.
Всякое тождество (например, sin* z -j- cos* г = 1, sin2.z =
= 2sinzcosz и т. д.), справедливое на действительной оси
(или даже только на некотором отрезке действительной оси),
остается справедливым во всей комплексной плоскости, если
левая и правая части этого тождества являются функциями,
аналитическими во всей плоскости.
С теоремой единственности связано очень важное понятие
аналитического продолжения. Предположим, что в некото-
некоторой области G задана функция /(г), аналитическая в этой об-
области. Встает вопрос, существует ли функция, аналитическая
в области более широкой, чем область G, и совпадающая
в области О с функцией /(г). Если такая функция существует,
то она называется аналитическим продолжением функции f(z).
Если данную функцию /(г) можно аналитически продолжить,
то такое продолжение является единственным в следующем-
смысле: функции Д (г) и /8 (г), аналитические в некоторой об-
области О', частью которой является данная область О, тожде-
тождественны между собой, если они являются аналитическими про-
продолжениями одной и той же функции /(г), аналитической
в области G.
Действительно, так как в соответствии с определением
аналитического продолжения эти функции совпадают с функ-
функцией /(г) в области О, то они совпадают также между со-
§6}
РЯД ЛОРАНА
111
бой в области О, а следовательно, в силу теоремы единствен-
единственности, они тождественны и в области С.
В качестве примера рассмотрим функцию f(z), которую
определим как сумму ряда
Радиус сходимости этого ряда равен 1, и функция f[z) яв-
является аналитической в круге |z|< 1. Вне этого круга ряд
расходится, и функция f(z) вне круга |г|<[1 не определена.
Нетрудно видеть, что функция /, (z) = y^~z • аналитическая
во всей плоскости, кроме точки 2=1, является аналитическим
продолжением данной функции f(z), так как в соответствии
с формулой для суммы геометрической прогрессии f(z) ==у-—
в круге | z | •< 1 и, следовательно, в этом круге функции
/, (г) и f(z) совпадают.
Обычно аналитическое продолжение функции f(z) обозна-
обозначают тем же символом f{z).
§ 6. Ряд Лорана
Предположим, что f(z) является однозначной аналитической
функцией внутри кольца между концентрическими окружно-
окружностями С и С" с центром в точке z — a (черт. 28), и пусть
z — произвольная внутренняя точка этого кольца. Проведем
окружности ГнГ с центром
в точке а так, чтобы каждая
из них находилась внутри данно-
данного кольца и чтобы точка z
оказалась между Г и Г. Поль-
Пользуясь интегральной формулой
Коши для многосвязной об- I II Н V J" i • \С
ласти, получим:
'/ГОЛ
&Ут=7 <32) черт. 2а
(окружности Г и Г* обхо*дятся против часовой стрелки —
черг. 28). Если ; — точка на контуре Г*, ю |; — в|>|г — а\
112
и
ряды
[гл. VI
Ряд в правой части этого равенства сходится на окружности
Г" равномерно (см. совершенно аналогичные рассуждения на
стр. ЮЗ); умножив его почленно на /(С)<?С и проинтегрировав
вдоль Г", получим для первого из интегралов в правой части
C2) разложение
1 Г/(О<К_ 1 Г/Ю
точка
¦
то
С находится на контуре Г',
\z—с|>|С — а\ и, следовательно, 1-^ <1; поэтому для
того, чтобы получить ряд, равномерно сходящийся на Г, пре-
преобразуем _ _ иначе:
1 1 1
С-а , (С-
, С-а , (С-а)« , , ?С-а)"' ,
' z —a ' (z —аI ' * ••~(z —а)" ' "
После такого преобразования для второго из интегралов в пра-
правой части C2) получим:
... C4)
Так как в силу теоремы Коши для двусвязной области вместо
путей интегрирования Г" и Г' в C3) и C4) можно взять лю-
§ 6] РЯД ЛОРАНА 113
бую окружность Г с центром в точке а, лежащую в данном
кольце между С и С", то из C2) получаем следующее раз-
разложение функции f(z), сходящееся во всякой точке г внутри
кольца между С и С" и называемое рядом Лорана:
где
(л=0, 1, 2,...), C5)
l*~* dZ (« = 1,2,...) C6)
и Г — любая окружность в данном кольце, с центром в
точке а.
При замене л на —я правая часть C6) переходит в пра-
правую часть C5), поэтому, обозначив для удобства Ьп = с__а,
разложение в ряд Лорана можно записать в виде
где коэффициенты сп как при л — 0, 1, 2, ... , так и при
л = — 1, — 2, ... определяются формулой
1 г- /юл 3
г
Г — любая расположенная в данном кольце окружность с
центром в точке z = a.
Разложив функцию f(z) в рад Лорана, мы тем самым
представили ее в виде суммы
где
1 я=0 " '
114 ряды [гл. vi
Ряд C8) называется правильной частью, а ряд C9) главной
частью ряда Лорана. Областью сходимости степенного ряда
C8) является, как доказано выше, некоторый круг радиуса R
с центром в точке z = a, на окружности которого имеется
по крайней мере одна особая точка функции /, (<?)• Что ка-
касается ряда C9), то поастановка = * преобразует его
в степенной ряд:
2 c_f. D0)
Областью сходимости степенного ряда D0) является некото-
некоторый круг радиуса р с центром в точке t = 0, на границе ко-
которого находится по крайней мере одна особая точка суммы
этого ряда. С помощью преобразования = 1 или z =
= — -^-а внутренность этого круга плоскости / отображается
на внешность круга радиуса г=— плоскости г с цент-
центром в точке z — a, так как \г — а\ = — при 11\ = р и
\г— в[>^ при |*|<р (см. также стр. 163 и 167); следова-
следовательно, областью сходимости ряда C9) является внешность не-
некоторого круга радиуса г с центром в точке z = a, на границе
которого находится по крайней мере одна особая точка функции
/,(*), являющейся суммой этого ряда. Если учесть, наконец,
что по доказанному ряды C8) и C9) сходятся в концентри-
концентрическом кольце с центром в точке г=а и, что в этом кольце
функция f(z) аналитична, то мы придем к выводу, что об-
областью сходимости ряда Лорана (т. е. областью, в которой
сходятся как ряд C8), так и ряд C9)) является кольцо, огра-
ограниченное окружностями, имеющими центр в точке а, причем
на каждой из этих окружностей имеется по крайней мере одна
особая точка функции /(г). При этом на граничной окружно-
окружности радиуса R (большего радиуса) имеется по крайней мере
одна особая точка функции /, (z), являющейся суммой пра-
правильной части ряда Лорана, в то время как функция /,(*)
(сумма главной части ряда Лорана) на этой окружности
особых точек не имеет, так как она аналктнчна всюду вне
§ 6] РЯД ЛОРЛНА 115
граничной окружности радиуса г (меньшего радиуса) и,
в частности, на граничной окружности радиуса R. Ана-
Аналогично на граничной окружности радиуса г имеется по
крайней мере одна особая точка функции /г(г), но нет осо-
особых точек функции Д (z), так как функция /, (г) аналитич-
на всюду внутри области, ограниченной окружностью ра-
радиуса R.
Если считать, что точка г = а выбрана, то имеется все
же, вообще говоря, несколько колец с центром в этой точке,
в которых функция f(z) аналитична, причем на граничных
окружностях лежат особые точки функции f(z). Каждому из
этих колец соответствует свое разложение функции f(z) в
ряд Лорана: контур Г, по которому производится интегриро-
интегрирование в формуле C7), при вычислении коэффициентов ряда
Лорана должен находиться внутри того кольца, в котором
происходит разложение, и поэтому разным кольцам соответ-
соответствуют различные коэффициенты разложения одной и той же
функции /(г). В частности, если в точке z = a данная функ-
функции f(z) аналнтична (точка а — правильная точка данной
функции), то круг с центром в точке а, радиус которого
равен расстоянию точки а до ближайшей особой точки функ-
функции f(z), также является одним из «колец», в которых можно
произвести разложение в ряд Лорана. Все коэффициенты
Ь„ = с_п такого разложения, как это видно из формул C6),
в силу теоремы Коши, равны нулю, так как функция
/(С) (С — а)"~х> стоящая под знаком интеграла в правой части
формулы для вычисления Ьп, при любом целом положительном
п не^ имеет особых точек внутри окружности Г. Следовательно,
в этом случае ряд Лорана состоит только из правильной ча-
части, а так как формулы для вычисления коэффициентов пра-
правильной части ряда Лорана ничем не отличаются от инте-
интегральных формул для коэффициентов ряда Тейлора (см. стр. 103),
то ряд Лораиа превращается в ряд Тейлора. Итак, ряд Тей-
Тейлора является частным случаем ряда Лорана.
Пример 1. Рассмотрим различные разложения в ряд Лорана
функции
()
выбрав а = 0.
Функция /{*) имеет две особые точки: г = 1 и ж=г2. Сле-
Следовательно, имеется три круговых «кольца» с* центром в точке О,
116
РЯДИ
[гл. vt
в каждом из которых функция аналитична, а именно (черт. 29):
1) круг |zj< 1,
2) кольцо I < | z К ,
3) внешность круга" | г | > 2.
В рассматриваемом примере нетрудно получить разложение в ряд
Черт. 29.
Лорана в каждом из перечисленных «колец», не прибегая к форму-
формулам для вычисления коэффициентов.
1) Разложение в круге | z | < 1.
Функцию /(z) можно представить в виде суммы двух элементар-
элементарных дробей:
111
Так как
а функция
(г-\)(г — 2)~z-2 г-V
1
z-2:
2 -f
'-4
является суммой геометрнческой прогрессии, модуль знаменателе ко-
1орой|||<1:
xo
23
§6] РЯДЛ6РАНА 117
Диалогично
причем ряд в правой части сходится, так как | г \ < 1.
Складывая D1) и D2), получаем:
откуда
^ (« = 0,1,2,...),
Полученное разложение является рядом Тейлора.
2) Разложение в кольце 1 < | г f < 2.
Ряд D1) остается сходящимся, так как |г|<2, во ряд D2) рас-
расходятся, потому 4to|z|>1; поэтому разложение D2) заменяем
следующим:
} _±._!___±Л , 1. ±4-
г
111 ! /44»
T-F-7 — — F~- D3)
В рассматриваемом кольце ряд D3) сходится, так как | г | > 1 и, сле-
следовательно, — I < 1.
Складывая D1) и D3), получим:
!____?1_
ж— 1)(г-2)~ 2 2' 2« "' 2я+| "*
^ 1^ 1
"• г г% р —••••
откуда
ся=-2^п (я = 0, 1, 2,...),
6в = с_„=-1 (я=1, 2,...).
3) Разложение в области | г [ > 2.
Равенство D3) сохраняется, гак как если | г \ > 2, то тем более
|*| > 1; но ряд в правой части D1) расходится, и равенство D1) за-
заменяем следующим:
II»
118
РЯДЫ
[гл. vi
Ряд в правой части D4) сходится, так как | г \ > 2, и следовательно,
< 1. Складывая D3) и D4), получаем:
1
1
(г— \){г — 2)
откуда
(я = 0, 1, 2,...),
ba = c_n = 2»-t-l (r=1, 2,...).
Пример 2. Найдем разложения в ряд Лорана в различных об»
ластях той же функции
1
= <*-1)<*-2)'
выбрав а=\.
В данном случае имеется два круговых «кольца» с центром в
точке 1 (черт. 30):
1) круг, из которого удален центр 0< |z — 11< 1',
2) внешность круга | z — 11 > 1. В каждом из этих «колец»
функция f(z) аналитичиа, а иа грани-
границах имеет особые точки.
Разложим в каждом из этих «ко-
«колец» функцию f(z) по степеням раз-
разности (z — 1).
1) Разложение в области 0 < | z —
Как и в примере 1, получим*.
1 _1 1__
(z — \)(z — 2)
Далее,
1 1
Черт. 30.
z-1~ 1 — (г — 1) —
=-[1 +(*-») + (*-1)' + ...
причем ряд в правой ча«и сходится, так как \z— 1|< 1. Следова-
Следовательно,
откуда
<?„=— 1 (я=0, 1,2,...),
Главная Часть ряда Лорана состоит здесь только из одного члена.
2) Разложение в области [г — 11> 1.
x-2-{z-l)-l-JZri —
причем ряд в правой части равенства сходится, так как | г — 11 > 1
я, следовательно,
< 1. Итак,
(z-l)BT-2) — z-2 z-
Нетрудно доказать единственность разложения функции
ряд Лорана, т. е. в ряд вида
Иными словами, нетрудно доказать, что если функция /(г)
является в некотором кольце с центром в точке а аналити-
аналитической, то не существует двух различных рядов указанного
вида, сходящихся в этом кольце и имеющих своей суммой
функцию f(z).
Действительно, как доказано выше, областью сходимости
рассматриваемого ряда является некоторое кольцо G с центром
в точке а, и во всяком кольце, целиком внутреннем к кольцу
G, ряд сходится равномерно. В частности, он сходится равно-
равномерно и на всякой окружности Г с центром в точке а, распо-
расположенной внутри кольца сходимости, и следовательно, этот
ряд можно почленно интегрировать вдоль такой окружности.
В § 4 главы V было доказано, что интегралы вида
\{z-a)Hdz%
120 ряды [гл. vi
где замкнутый контур Г однократно обходит в положительном
направлении точку а, равны нулю при всяком целом л, кроме
п = — 1, а в этом последнем случае интеграл равен 2тг/.
Следовательно, при почленном интегрировании ряда D5) исчез-
исчезнут все члены, кроме первого члена главной части, и мы получим:
$
откуда
Чтобы определить с_„, достаточно до интегрирования умно-
умножить все члены ряда D5) на (г — а)". Тогда после инте-
интегрирования все интегралы, кроме одного, опять обратятся в
нуль, и мы получим:
откуда
Аналогично, для того чтобы определить сп при я = 0, 1,2, ...,
достаточно, прежде чем почленно проинтегрировать ряд D5),
разделить члены ряда на (z — a)n+1. Тогда после интегриро-
интегрирования получим:
С f(z)dz __Г cndz __c ^
V V
с = * Г fWd*
n 2kI J B— a)a+l'
г
Мы пришли к формулам C5) и C6) для коэффициентов ряда
Лорана И тем самым доказали, что никакое другое разложе-
разложение функции /(г) в ряд указанного вида невозможно. Так как
ряд Тейлора является частным случаем ряда Лорана, то дока-
доказана и единственность разложения в ряд Тейлора.
§ 7] ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ 121
§ 7. Изолированные особые точки
Особая точка функции f(z) называется изолированной,
если в некоторой Окрестности этой точки функция f(z) не
имеет других особых точек. Разложение функции в ряд Ло-
Лорана, сходящийся к этой функции во всех точках круга с
центром в данной изолированной особой точке а, кроме этой
точки а (радиус такого круга равен расстоянию данной особой
точки а до ближайшей другой особой точки суммы ряда),
будем называть разложением функции в ряд Лорана в окре-
стности данной изолированной особой тонки. Так, в при-
примере 2 (стр. 118) первое из разложений является разложением
в окрестности особой точки z = 1.
Выясним, как связано поведение функции f(z) в окрест-
окрестности точки z=a с разложением функции в ряд Лорана в
окрестности этой точки. Предположим сначала, что при раз-
разложении функции в окрестности точки z = a главная часть
ряда Лорана отсутствует, т. е. все коэффициенты с_п равны
нулю, и следовательно, разложение имеет вид
/(*) = «. + «, (*-«)+ • • ¦ + cn(z-a)" + ... D6)
Ряд Лорана превращается в этом случае в степенной ряд, и
его сумма есть функция аналитическая внутри круга сходимо-
сходимости, н в частности в точке z = a, являющейся центром этого
круга (см. стр. 98). Если в точке а функция f(z) аналитич-
на, то равенство D6) дает разложение этой функции в ряд
Тейлора в окрестности точки а; если же точка а является
изолированной особой точкой функции f{z), то сумма ряда
D6) совпадает с функцией f(z) всюду в круге сходимости
этого ряда, кроме самой точки z — a, и так как сумма ряда
в точке а аналитична и, следовательно, непрерывна, а значе-
значение этой суммы при z = a равно с0, то
Следовательно, если изменить определение функции в точке а
и считать /(а) = с0, то функция /(г) станет в точке а аналитиче-
аналитической, а равенство D6) будет разложением этой функции в ряд Тей-
лора.Точку а называютвэтом случае устранимой особой точкой.
Если обратиться к примеру, рассмотренному на стр. 105,
то можно сказать, что точка 2 = 0 является устранимой
122 ряды [гл. vi
особой точкой функции , так как разложение
sin г . г* [ г*
не содержит отрицательных степеней г. Если при *=0 при-
sln z • . sin 1 .
нять ~-=\t то функция -j- станет аналитической в точке
z = 0.
Пусть теперь главная часть разложения функции в ряд
Лорана в окрестности точки z — a содержит лишь конечное
число членов. Следовательно, разложение имеет вид
(i^ <47>
(здесь m — номер последнего из отличных от нуля коэффи-
коэффициентов главной части, т. е. с тф0,с im+v=c_(m+t)=...
...=0).
Если обозначить
<f(z)=(z-ar/(z)t
то из D7) получим:
<?(*) = (* — а) «.(* — «)" + «-,(* —e)"-f +
+ «-,(* —вГ"' + ...+«_„. D8)
Равенство D7), а следовательно, и равенство D8) справед-
справедливы во всей области сходимости ряда D7), т. е. во всех
точках некоторого круга с центром в точке а, кроме точки а.
Т*к как правая часть D8) при z = a принимает значение
f
Но
следовательно,
г-* а г-*а
11т/(*) = 11ш 7-тй = оо.
Итак, если главная часть разложения функции f(z) в окрест-
§ 7] ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ 123
ностй точки а содержит лишь конечное число членов, то
функция f(z) стремится к бесконечности при z—> а. В этом
случае изолированная особая точка а называется полюсом,
а число т (номер последнего из отличных от нуля коэффи-
коэффициентов главной части ряда Лорана) — порядком полюса.
Если т = 1, полюс называется простым.
В примере 2 (стр. 118) вид разложения в ряд Лорана по-
показывает, что точка z=l является простым полюсом рассмот-
рассмотренной в этом примере функции j-г- ^-.
(Z — 1) (Z — Z)
Если в точке z=a функция / (z) имеет полюс порядка т,
то функция jj- имеет в этой точке нуль порядка т. Дейст-
Действительно, как было показано выше, функцию f{z), имеющую
в точке а полюс порядка /га, можно представить в виде
где функция <р {г) определяется как сумма ряда D8) и является ана-
аналитической функцией в точке а, если считать
у (а) = llmtp (*) = с_т ф 0.
г-*а
Отсюда следует, что функция -ут также является аналитиче-
аналитической и отличной от нуля в точке z = a и, следовательно,
разлагается в окрестности точки а в ряд Тейлора:
причем со= — фО. Следовательно,
-a)m+> -f ...
Но такой вид разложения в ряд Тейлора (см. стр. 107) и озна-
означает, что для функции тщ точка а является нулем по-
порядка т.
Справедливо и обратное утверждение: нуль порядка т
функции /{г) является полюсом порядка т функции тт-г ,
124 РЯДЫ [ГЛ. VI
Действительно, еслн точка а является нулем порядка «функции
), то в соответствии с C1) функция /{*) имеет вид
где y(z)—функция, аналитическая в точке а, причем
<р (о)^=0. Но тогда функция <|)(z) = -U также является ана-
аналитической и отличной от нуля в точке а и может быть в
окрестности этой точки разложена в ряд Тейлора
(г -V + <* -'„)*-> + • • • + 7^
Ряд в правой части равенства является рядом Лорана, причем
в главной части этого ряда коэффициент при _ ^ отли-
отличен от нуля, а коэффициенты при {г_[
) ?р
равны нулю, так как соответствующие члены ряда отсутст-
отсутствуют. Следовательно, в соответствии с определением (стр. 123)
точка а является полюсом порядка т функции т-г\.
Если главная часть разложения функции f(z) в ряд Ло-
Лорана в окрестности точки z = a содержит бесконечное мно-
множество членов (т. е. бесконечное множество коэффициентов
с_„ отлично от нуля), то точка а называется существенно
особой точкой функции f(z). Поведение функции в окрест-
окрестности существенно особой точки подчиняется следующей
теореме Ю. В. Сохоцкого, доказательство которой мы опу-
опускаем 1): если точка а является существенно особой точкой
функции f (г), то для любого заданного комплексного числа
А найдется последовательность точек, сходящаяся к тон-
') См. [% гл. VI, § 2, а° 5.
§ 7] ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ 125
лее а, вдоль которой значения /(г стремятся к А, при
том случай А = оо не исключается.
Пример. Найти особые точки функции е* н определить их типы.
Принимая во внимание, что
получим:
^— <49)
причем ряд в правой части сходится всюду, кроме точки 2=0. Ра-
Равенство D9) можно рассматривать как разложение функции ег в ряд
Лорана в окрестности точки z = 0, и так как его главная часть со-
содержит бесконечное множество членов, то точка 2=0 является
существенно особой точкой функции ег .
Рассмотрим поведение функции ег в окрестности точки 2 = 0.
При г —> 0 вдоль положительной части действительной оси получим
——»--|-оо и ег—»-оо; если г—»0 вдоль отрицательной части
действительной оси, то — —*¦— оо и ez —»-0. Пусть теперь А-=ге*
— любое комплексное число, отличное от нуля и от бесконечности. Из
равенства
е7=Л
или
находим:
Полагая k = 0, ± 1, 2:2,i3 получим последовательность точек»
сходящуюся к точке г=0, так как
Шп * =р
причем функция ег не только стремится к А вдоль этой последова-
последовательности, но даже в точности равна А в каждой точке рассматри-
рассматриваемой последовательности.
Других особых точек функция ег не имеет.
126 ряды [гл. vt
Мы рассмотрели все возможные виды главной части рада
Лорана в окрестности изолированной особой точки а (правиль-
(правильную часть ряда мы все время считали произвольной) и усло-
условились называть особую точку а устранимой, если главная
часть разложения в окрестности этой точки отсутствует, по-
полюсом, если главная часть содержит лишь конечное число
членов, и существенно особой, если главная часть представ-
представляет собой бесконечный ряд. Мы установили, далее, что пре-
предел lim f(z) существует и конечен, если особая точка а
z -* a
является устранимой, что этот предел бесконечен, если рас-
рассматриваемая точка является полюсом, и что предел /(г) при
z —> а не существует, если а — существенно особая точка.
Так как были рассмотрены все возможные случаи изолирован-
изолированных особых точек, то справедливы и обратные заключения:
если с — изолированная особая точка функции /(г), то она
является: а) устранимой, если предел lim f(z) существует и
конечен, б) полюсом, если этот предел бесконечен, и в) су-
существенно особой точкой, если lim /(г) не существует.
z -» а
Классификацию изолированных особых точек можно распро-
распространить и на случай, когда изолированной особой точкой является
бесконечно удаленная точка. Назовем бесконечно удаленную
точку изолированной особой точкой функции f(z), если в не-
некоторой окрестности бесконечно удаленной точки, т. е. вне
круга с центром в начале координат достаточно большого ра-
радиуса нет других особых точек функции /(г).
Разложение функции в ряд Лорана, сходящееся всюду вне
круга достаточно большого радиуса с центром в точке z = 0
(кроме, быть может, самой бесконечно удаленной точки), будем
называть разложением в окрестности бесконечно удаленной
точки. Последнее из разложений в примере 1 (стр. 117—118)
является разложением функции , _. _ в рад Лорана в
окрестности бесконечно удаленной точки. Ряд D9) является
разложением функции ег не только в окрестности точки г = 0,
«о также и в окрестности бесконечно удаленной точки. При
разложении функции в ряд Лорана в окрестности бесконечно
удаленной точки следует в соответствии с определением счи-
считать в D5) о = 0. Запишем члены разложения в следующем
? 7] ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ 127
порядке:
... E0)
Назовем ряд
п=1
правильной частью, а рид
00
главной частью разложения в окрестности бесконечно уда-
ленной точки. Такая терминология вполне естественна, если
учесть, что при замене *=— окрестность бесконечно
удаленной точки отображается на окрестность точки г = 0
и разложение E0) превращается в разложение функции
/(—) в ряд Лорана в окрестности точки 5 = 0:
в котором ряд
является правильной, а ряд
CD
главной частью.
Бесконечно удаленную точку будем называть устранимой
особой точкой функции /{г), если в разложении E0), а сле-
следовательно и в разложении E1), отсутствует главная часть.
Нулевая точка является в этом случае устранимой особой точ-
точкой функции /(-f J i и следовательно, предел
Urn /(*) = hmf(-L)
Г-юо - „ \ г 1
128 ряды [гл. V!
существует и конечен. Разложение функции f(z) в этом слу.
чае имеет вид
чае имеет вид
Если предел 1!т/(г)==с0 принять за значение функции f(z)
Z-* 00
в бесконечно удаленной точке, то функцию f(z) можно счи-
считать аналитической в бесконечно удаленной точке. В част-
частности, если Cj = O, то бесконечно удаленная точка будет ну-
нулем функции/(г); при этом если гс = с_, = .. , = с_((П_1)=0,
но с_тф0, то бесконечно удаленная точка будет нулем по-
порядка т функции /(г).
Если главная часть E0), а следовательно и главная
часть E1), состоит лишь из конечного числа членов, т. е.
если D5) имеет вид
где cm=?Ot то бесконечно удаленная точка называется полю-
полюсом порядка т функции f{z). В этом случае
Hm f(z)= lim f(V) = oo.
Если бесконечно удаленная точка является нулем порядка т
функции f(z), то она является полюсом порядка т функции
77-г, и наоборот: нуль z = оо порядка т функции г— является по-
люсом порядка т функции f(z).
Если главная часть E0), а следовательно и главная
часть E1), состоит из бесконечного множества отличных от
нуля членов, то бесконечно удаленная точка называется су-
существенно особой точкой функции f(z). В эгом случае
lim f(z),
z-+ao
t. e
-Ии /(т)
я« существует и справедлива теорема Сохоцкого.
§ 8] НЕКОТОРЫЕ ПРИЕМЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД ЛОРАНА 129
§ 8. Некоторые приемы разложения функций в ряд Лорана
Общие формулы C7) для коэффициентов ряда Лорана
обычно мало удобны для вычислений. В некоторых случаях
могут быть применены более простые приемы.
Для того чтобы разложить в ряд Лорана рациональную
функцию, достаточно воспользоваться представлением правиль-
правильной рациональной дроби в виде суммы простейших дробей,
как это было сделано в § 6 (примеры 1 и 2). Простейшая
дробь вида --_ ¦ разлагается в ряд, являющийся геометри-
геометрической прогрессией, а дробь вида , -л {k > 1 целое) — в
ряд, полученный с помощью (k—1)-кратного дифференцирова-
дифференцирования геометрической прогрессии. Заметим, что всякая правиль-
правильная рациональная дробь может быть разложена в сумму дро-
дробей вида ¦ _ д- , где А, а — комплексные числа.
При разложении в ряд Лорана иррациональных и трансцен-
трансцендентных функций иногда можно использовать разложения в ряд
Тейлора функций е*, sin z, cos z, ln(l -\-z), биномиальный ряд
и другие известные разложения. Так, например, в окрестности
точки z=2
_1 , 1 ¦ ¦ . ..„ 1 ,
C0S2-2 2!B-2)*"Т~** *¦+¦* ' B«)! B-2)'" "Г"*"
При этом иногда следует предварительно преобразовать раз-
разлагаемую в ряд функцию.
Пример 1. Разложить в ряд Лорана в окрестности точки 2 = 1
функцию sin —~г •
Имеем:
sin _ = sin ( 1 -|—^-т J = sin 1 cos ——-? -|- cos 1 sin ——ft
откуда
. г > | I cos' sin 1 cos 1 , ,
2 — 1 — * z 1 2!(z 1)* 3J B — 1)J ~1~' "~*~
, , ,._ sin 1 . . ,._ cos 1 .
Bл)! B — 1) B/i-)-l)!B jj»n+iT^*"
Если бесконечно удаленная точка является правильной (или
устранимой особой) для функции f{z), то разложение в ряд
Б Г. Л. Лунц в Л. Э. Эльсгольц
130 ряды [rh. vt
в окрестности бесконечно удаленной точки сводится подста-
подстановкой z=j- к разложению функции / (j-j B Р"* Тейлора
в окрестности точки 5 = 0.
П ример 2. Разлржить функцию/B) = ^+ в ряд Лорана в
окрестности точки z = oo.
Т
1 1
1 / 1 \ г+2 ГШ
Положив *= =-, получим '[~г)~е ==е f причеи
точка С = 0 является для этой функции правильной точкой. Обозначив
[ -=¦) = ч @, будем иметь;
и т. д. Следовательно, ?{0) = е, <р'@) = — 2е, f"@) = 12e и т.
Отсюда
т. е.
Рад сходится вне единичного круга (т. е. при | г \ > 1), так как един-
единственной особой точкой функшш является точка л=—• 1.
Задачи к главе VI
1. Определить радиусы сходимости следующих рядок
00 л °°
¦ad
& g] НЕКОТОРЫЕ ПРИЕМЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯД ЛОРАНА 131
2. Доказать, что ряд
сходится в своем круге сходимости неравномерно.
3. Доказать, что ряд
сходится во всем круге сходимости равномерна
4. Разложить в ряд_Тейлора в окрестности точки *=1 лю-
любую ветвь функции у z . Каков радиус сходимости полученного
ряда?
5. Разложить в окрестности нулевой точки в ряд Тейлора те
ветви функций Arctgz и Arcsinz, для которых Arctgu = ArcslnO=O.
Каков радиус сходимости полученных разложений?
6. Написать первые четыре члена разложения в ряд Тейлора
в окрестности нулевой точки функций:
а) е*^, б) sinгЛ— , в) 1п<1 -f е%
Каковы радиусы сходимости этих рядов?
7. Разложить в ряд Лорана функцию -. г- т::
а) в кольце \а\< \г\< \Ь\,
б) в окрестности бесконечно удаленной точки,
в) в окрестности точки а.
8. Найти несколько первых членов разложения функции sin
I — Z
в ряд Лорана в окрестности бесконечно удаленной точки. Какова об-
область сходимости этого разложения?
9. Найти особые точки функций и определить их тип (для полю-
полюсов указать порядок):
1 — cos 2
з) ig(*~X)
Z — i
132 ряды [гл. vi
10. Каков характер особенности в бесконечно удаленной точке у
функций:
б>5"="?« ДJ+г+г», з)
1
е) е* +f — ¦*•
П. Является ли точка г=0 изолированной особой точкой для
функций:
a) tg —, б) sin —.
Z Z
12. Является ли бесконечно удаленная точка изолированной осо-
особой точкой функций:
а) «*, б) ctg*.
ГЛАВА VII
ТЕОРИЯ ВЫЧЕТОВ
§ 1. Основная теорема о вычетах
Если точка z — a является правильной точкой или изоли-
изолированной особой точкой^однозначной функции f(z), то можно
выбрать простой контур С, однократно обходящий точку а
в положительном направлении (например, окружность доста-
достаточно малого радиуса), так, чтобы на контуре С и всюду
внутри этого контура, за исключением, быть может, самой
точки а, функция f\z) была аналитической. Величину
будем в этом случае называть вычетом функции f(z) относи-
относительно точки а и писать:
Res[/(*); e] = i[/(,)ft.
Из теоремы Коши следует, что вычет данной функции отно-
относительно заданной точки не зависит от формы и размеров
контура С, если этот контур удовлетворяет указанным выше
требованиям.
Если точка а является изолированной особой точкой функ-
функции f{z), то коэффициент с_, первого члена главной части
разложения этой функции в ряд Лорана в- окрестности точки а
(см. формулу C7) на стр. 113) равен
и, следовательно, вычет функции f(z) относительно точки
134
ТЕОРИЯ ВЫЧЕТОВ
[гл. vii
совпадает с ко-ффициентом с_, разложения этой функции
в ряд Лорана в окрестности точки а:
Res[/(z); o] = *_,.
Если а является правильной или устранимой особой точкой
функции f(z), то все коэффициенты главной части разложе-
разложения в окрестности этой точки равны нулю и, следовательно,
вычет функции относительно
правильной точки или устрани-
устранимой особой точки равен нулю.
Если а — полюс или сущест-
существенно особая точка функции
/(г), то вычет относительно нее
может оказаться отличным от
нуля, но может быть и равным
нулю (если с_, = 0).
Пусть Со — простой замкну-
замкнутый контур, на котором функ-
функция f(z) аиалитичиа. Допустим,
что внутри контура Со функция
f(z) аналитична всюду, за ис-
исключением п изолированных особых точек а,, а,, ..., а„.
Окружим эти точки лежащими внутри Ct окружностями С,,
С,, .... С„ (черт. 31) столь малых радиусов, чтобы внутри
каждой из этих окружностей находилось лишь по одной особой
точке функции f(z) и чтобы никакие две из этих окружно-
окружностей ие имели общих точек. Тогда, в силу теоремы Коши,
для сложного контура получим:
_1_
2ic/
•где при интегрировании все контуры обходятся против часо-
часовой стрелки.
Следовательно, величина 7r—.\/(z)dz равна сумме выче-
тов функции f(z) относительно всех особых точек этой
функции, находящихся внутри контура С, (основная те*-
§ 1] ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ 135
рема о вычетах):
*=i
Вычетом функции относительно бесконечно удаленной точки
естественно считать величину
f(z)dz,
где С — окружность с центром в начале координат столь
большого радиуса, что вне этой окружности нет особых точек
функции f(z), отличных от бесконечно удаленной особой точки.
Направление интегрирования на окружности С следует вы-
выбрать так, чтобы при обходе контура бесконечно удаленная
точка оставалась слева, т. е. направление обхода надо уста*
новить по часовой стрелке. Отсюда следует, что если с_, яв-
является коэффициентом при — в разложении функции f(z)
в ряд Лорана в окрестности бесконечно удаленной точки, то
Res[/(*); oo] = -<r_t.
Вычет относительно правильной (или устранимой особой) бес-
бесконечно удаленной точки функции f(z) не обязательно равен
нулю. Так, например, для функции
точка оо является правильной, если считать /(оо) = 2, но
с_, = 3 и, следовательно,
Res[/(*); ео]=-3.
Из сопоставления определения вычета относительно бес-
бесконечно удаленной точки с основной теоремой о вычетах сле-
следует, что если функция имеет конечное число особых точек,
то вычет относительно бесконечно удаленной точки равен
взятой с обратным знаком сумме вычетов относительно всех
особых точек, расположенных в конечной части плоскости.
Следовательно, сумма вычетов относительно всех особых то-
точек, включая и бесконечно удаленную точку, равна нулю.
136 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. VII
§ 2. Вычет относительно полюса
Если точка а является простым полюсом функции f(z), то
в окрестности этой точки функция f(z) представима в виде
^, A)
где функция <р (г), будучи суммой правильной части разложе-
разложения функции f\z) в ряд Лорана в окрестности точки а, яв-
является аналитической и, тем более, непрерывной функцией
в точке а. Из A) имеем:
и, переходя к пределу при z—>а, получим:
так как вследствие непрерывности функции <p(z) в точке а
существует конечный предел lim <p(z) = <p(a) н
z-*a
lim [(z — a)<p(z)] = 0.
z-*a
Итак, если а простой полюс функции f(z), то
Res[f(z); a] = lim[(z — a)f(z)]. B)
Пример 1. Вычислить вычет функции _„ относительно
ТОЧКИ 2 = 2.
г1
Точка г = 2 является простым полюсом функции ^.
Следовательно, в соответствии с B) имеем:
Пример 2. Вычислить вычет функции -— относительно
sin %
ТОЧКИ 2 = 0.
Точка z = 0 является простым полюсом функции -—, так как
Sin 2
для функции sin 2 эта точка является простым нулем. Следовательно)
Res \4~; о] = lim [г -Д-Л = 1.
Иногда для вычисления вычета относительно простого по-
полюса более удобен иной метод. Предположим, что точка а
§ 2] ВЫЧЕТ ОТНОСИТЕЛЬНО ПОЛЮСА 137
является простым полюсом функции /(г) и что функция /(г)
представлена в виде
где Д (z) и /, (г) — функции, аналитические в точке а, при-
причем для функции /, (г) точка а является нулем первого по-
порядка, a /j (а) ф 0. В соответствии с B) имеем:
2 —а г-ю2 —a
Но так как /,(в) = 0, то в соответствии с определением про-
производной
Итак,
Res[/(*); a]=^gj. B')
Пример 3. Вычислить Res[ctgz; 0].
Имеем ctg2 = ^—. Точка 2 = 0 является нулем первого по-
sin *
рядка для функции sinz, и в соответствии с формулой B') получим:
Пример 4. Вычислить
zdz
где С—окружность радиуса 2 с центром в начале координат.
Так как
то внутри контура С подынтегральная функция имеет два простых
полюса в точках «, = j и г,=— j-.
В соответствии с основной теоремой о вычетах
138 ТЕОРИЯ ВЫЧЕТОВ [и. VII
С помощью B'), учитывая, что fl — sln1*)':*—sta2*, находим:
—¦*¦
Следовательно,
Если точка z = a является полюсом порядка т функция
/(г), то в окрестности этой точки
^ C)
где функция <p(z) является суммой правильной части разло-
разложения в ряд Лорана и, следовательно, аналитична в точке
г = а. Умножив обе части C) на (г — в)*, получим справед-
справедливое в некоторой окрестности точки а (кроме самой точки в)
равенство
Продифферениировав обе части этого тождества т — 1 раз,
получим:
^ ^---l)\c_t. D)
Для функции (г—- а)т<р (г) точка г = а является нулем по-
порядка не ниже, чем т, следовательно, в точке а обращаются
в нуль производные этой функции во всяком случае до по-
порядка т— 1 включительно (см. стр. 107). Отсюда
%"* 9
§ 3] ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ 139
и, переходя в D) к пределу при z—>а, получим:
Пример 5. Определить вычет функции
1
относительно точки 2=/.
Точка 2 = / является полюсом третьего порядка данной функции,
так как
1 _ 1
(«¦+ 1)»-(I-!)•(«+ <Г
В соответствии с E) получим:
4- «m UKz + /)"'] = Tlim К-3)(-4)B
3^
'- 16и
§ 3. Логарифмические вычеты
Если точка а является полюсом порядка т функции f(z),
то, как было указано на стр. 122, функция f(z) представима
в виде
/И-в???
(z-a)m>
где функция if(z) аналитична и отлична от нуля в точке а.
Отсюда
Функция ^-7-т является аналитической в точке а, и следова-
Ф B)
/' B)
тельно, главная часть разложения функции ^-Н в P"A Лорана
в окрестности точки а состоит из одного члена —¦
поэтому
Res I ttti » ° I e—"*• I
140 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. VII
Если точка а является нулем порядка т функции /
то эта же точка является полюсом порядка т функции
F{z)=lhi' Так как
то
^!]' = -5$. G)
Для функции F{z), как было указано выше, точка а является
полюсом порядка т и, следовательно, в соответствии с F)
отсюда на основании равенства G) получим:
; а] =!*. (8)
Итак, вычет логарифмической производной функции f{z) от-
относительно точки, являющейся нулем функции f(z), равен
порядку нуля, а относительно точки, являющейся полюсом
функции f(z),— порядку этого полюса с обратным знаком.
Предположим, что функция f(z) аналитична и отлична от
нуля во всех точках некоторого контура С, а внутри этого
контура имеет конечное число особых точек а„ а„ ,.., ak,
причем все они являются полюсами. Обозначим а,, а„ ..., а„
нули функции f(z), расположенные внутри контура С. При
fi (А
этих условиях особыми точками функции J7-T» расположен-
расположенными внутри контура С, будут только точки в,, о,, ..., ак;
аи ац • • •. а„ и в соответствии с основной теоремой о вычетах
? 158'
Величину, стоящую в левой части этого равенства, называют
логарифмическим вычетом функции f(z) относительно кон-
контура С.
С другой стороны, как указано выше (см. (8)), величина
§ 3] ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ 141
равна порядку нуля функции f{z) в точке ад, в частности,
если нуль простой, то Resfyjjj; aJ = 1-
Если каждый нуль считать столько раз, каков его порядок,
то сумма
будет равна числу нулей функции /(г), расположенных внутри
контура С. Аналогично, если ввести обозначения
я условиться каждый полюс функции f(z) считать столько раз,
каков его порядок, то из формулы F) следует, что Р равно
числу полюсов функции f(z) внутри контура С. Записав
равенство (9) с помощью введенных обозначений в виде
приходим к следующей теореме о логарифмическом вычете:
при указанных выше условиях логарифмический вычет функ-
функции относительно замкнутого контура равен разности
между количеством нулей и количеством полюсов функ'
ции, расположенных внутри данного контура.
В частности, если внутри контура С функция /(г) не имеет
особых точек, то Р=0 и логарифмический вычет
равен числу нулей функции /(г), расположенных внутри
контура С.
Если точка z пробегает дугу С с начальной точкой z* и
конечной точкой zt, то соответствующая ей точка w=/(z)
пробегает некоторую дугу Г плоское! и w с начальной точкой
w =f(z9) и конечной точкой w1=/(zl).
Если аналитическая функция f(z) не обращается в нуль
вдоль дуги С, то в соответствии с правилом вычисления
142 теорий вычетов [гл. vii
интеграла от аналитической функции (см. стр. 71) получим:
) = Lnw1-Lnwu, A1)
С т
причем берется любая, аналитическая вдоль Г ветвь логарифма.
Если С—замкнутый контур (zl = z0), то Г также является
замкнутым контуром («/, = w0), пробегаемым точкой w один
или несколько раз. Однако равенство нулю правой части A1)
следует из того, что w1 = w0 только в том случае, когда
вдоль Г можно определить однозначную ветвь функции Lnw,
а это (см. стр. 73 — 74, а также подробнее дальше на стр. 192)
возможно лишь тогда, когда внутри области, ограниченной
контуром Г, не содержится точка да=0. Если же контур Г
обходит точку w=0, то, как было показано на стр. 74,
к мнимой части логарифма прибавляется приращение, получен-
полученное аргументом w Bтт при обходе против часовой стрелки
и —2л пр» обходе по часовой стрелке). Поэтому, если кон-
контур Г к раз обходит точку «/ = 0, то из A1) получаем:
или
A2)
2WJ
Если обозначить через &cArgf(z) приращение, получаемое
аргументом функции f(z) при обходе точкой z контура С, то
равенству A2) можно придать вид
Сравнивая A2) с A0), приходим к следующей формули-
формулировке теоремы о логарифмическом вычете: разность между
числом нулей и числом полюсов, функции f(z) внутри кон-
контура С равна числу оборотов, которые соверитет в плоско-
плоскости w вектор, идущий из точки w=Q в точку w=f(z),
когда точка z описывает контур С (число оборотов счи-
считается при этом положительным, если вектор вращается
против часовой стрелки, и отрицательным в противопо-
§3]
ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ
143
\W-t\=l
w
ложном случае). В такой форме теорема о логарифмическом
вычете носит название принципа аргумента.
В качестве приложения изложенной выше теории докажем
следующую теорему (теорема Руше): если функции <f(z) и
ф(я) аполитичны на простом замкнутом контуре С и
в области, им ограниченной, функция <f(z) ре обращается
в нуль ни в одной точке контура С а во всех точках
контура справедливо неравенство
IФ (*) КI <Р (*)It mo в области,огра-
области,ограниченной контуром С, функции у (г)
и <p(z)-{-ty(z) имеют одинаковое
число нулей.
Так как функции <р B) и <f(z)-\-
-f-ф (z) являются, по условию, анали-
аналитическими в области, ограниченной
контуром С, и, следовательно, не
имеют полюсов в этой области, то „ _
для доказательства теоремы Руше ^т>
достаточно.в соответствии с принципом аргумента доказать, "что
= дс
A3)
Из тождества
следует, что
I—n-|fg|<i.
. (И)
Когда точка z движется по контуру С, соответствующая ей
точка г»=1-|-Ц-т, перемещается по некоторому контуру Г,
причем в силу условий теоремы
|fg|
Это означает, что контур Г находится внутри круга радиуса 1
с центром в точке / (черт. 32), поэтому контур Г не обходит
точку w=0, а следовательно,
ДгArgW=AcArg [l + Jgj] =0. A5)
Сравнивая A4) и A5), убеждаемся в справедливости равен-
равенства A3), что и доказывает теорему Руше.
144 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. УП
Пример. Найти число корней уравнения
г« _ 5*'-2 = 0,
лежащих в единичном круге |z|< 1.
Функция — 5г* не обращается в нуль на окружности | г \ = 1,
и во всех точках этой окружности справедливо неравенство
так как в каждой точке окружности имеем I г \ = 1 и, следовательно,
| — 5г* | = 5, в то время как | г% — 21 < | г11 -\- 2 = 3. Следовательно,
внутри единичного круга в соответствии с теоремой Руше функция
г' — Ьг* — 2 имеет столько же нулей, сколько их имеет функция — 5z',
а так как функция — 5z* имеет внутри единичного круга три нуля
(один трехкратный нуль в начале координат), то три нуля имеет
внутри единичного круга и функция г* — Ьг% — 2.
§ 4. Вычисление определенных интегралов
с помощью теории вычетов
Основная георема о вычетах позволяет при указанных
выше (см. стр. 134) условиях свести вычисление интеграла
по замкнутому контуру к вычислению вычетов подынтеграль-
подынтегральной функции относительно особых точек, расположенных внутри
данного контура. Иногда этим же методом удается вычислить
интегралы, у которых путь интегрирования не замкнут, и в
частности некоторые определенные интегралы функций дей-
действительного переменного. При этом предварительно эти инте-
интегралы преобразуют в интегралы по замкнутому контуру,
к которым уже применима теорема о вычетах.
Вычислим, например, интеграл
где действительное число а >• 1.
Положим z = elt. При изменении От 0 до 2ц точка z
описывает в положительном направлении окружность С еди-
единичного радиуса. Так как
cosf -
§ 4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 145
и H=Lnz, откуда „"—= — , то
dt С liidz 2 С dt
k—i
где йА — особые точки подынтегральной функции, расположен-
расположенные внутри контура С. В данном случае особыми точками
подынтегральной функции
1
являются простые полюсы в точках z=—а + У а* — 1, из
которых, в силу условия а > 1, только точка — а -)- V^a*— 1
лежит внутри единичной окружности С. Следовательно, получим:
Г ** ;=4irRes
J a + cos t ч [
*-(-«+T/*'-0_
С помощью вычегов вычисляют также некоторые несоб-
несобственные определенные интегралы.
Предположим, что бесконечно удаленная точка является
нулем второго или более высокого порядка функции f(z) и,
следовательно, разложение этой функции в ряд Лорана в окре-
окрестности точка г = оо имеет вид
(случай с_, = 0 не исключается). Допустим также, что f(z)
является аналитической функцией на действительной оси, а в
146 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. УП
верхней полуплоскости Imz>0 имеет лишь конечное число
особых точек в,, а„, ..., в„. Тогда все лежащие в верхней
полуплоскости особые точки функции f(z) можно заключить
внутрь расположенного в верхней полуплоскости полукруга
достаточно большого радиуса R с центром в начале коорди-
_ иат. В соответствии с основной
" * теоремой о вычетах интеграл
взятый по границе L этого по-
-К *- Я лукруга, будет равен числу 2п/,
Черт. 33. умноженному на сумму выче-
вычетов функции f(z) относительно
всех ее особых точек, расположенных в верхней полуплоско-
полуплоскости, причем при дальнейшем увеличении R этот интеграл из-
изменяться не будет, так как никакие новые особые точки при
этом внутрь полукруга ие попадут.
Пусть С—полуокружность, входящая в состав границы L
указанного полукруга (черт. 33); тогда
R
J f(z) dz = J f(z) dz + 5 /(*) dx.
L С -Н
На основании A6) имеем:
где
Для функции <р (г) бесконечно удаленная точка является
правильной (вернее, устранимой особой точкой), причем
lim <p(z) = c_t; следовательно, функция y(z) ограничена в
г-*оа
окрестности бесконечно удаленной точки, и в частности на
полуокружности С, если ее радиус R достаточно велик, т. е.
во всех точках полуокружности С
§ 4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 147
где М — некоторое положительное число. Следовательно,
lim \f(z)dz
R-*aa с
А так как
-R
то тем самым доказано, что если функция f(z) удовлетворяет
указанным выше условиям, то интеграл
со
J f(x)dx
—00
равен произведению числа 2тг/ на сумму вычетов функции
У (г) относительно всех ее особых точек, расположенных
в верхней полуплоскости.
Пример 1. Вычислить иите1рал
со
dx
I
— со
Функция i . . имеет в бесконечности нуль четвертого по-
порядка; особыми точками функции являются полюсы второго порядка
в точках 2 = :+:/, из них только первый находится в верхней полу-
полуплоскости. Имеем:
Res
Г 1 ; Л = lim ' \?=Г] =Ш* \ 1 1 =
- 2 2 1 ,
Следовательно,
со
148 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. VII
Интеграл
J f(x)dx
иногда может быть вычислен с помощью теории вычетов и в
том случае, когда бесконечно удаленная точка не является
нулем второго или более высокого порядка функции /(*).
Докажем следующее предложение, называемое леммой
Жордана:
Если:
1) f(z)=elm*F(z), причем /н>0 и F(z)-+ 0, когда
х—»оо по любому закону, оставаясь, однако, в верхней
полуплоскости или на действительной оси, т. е. так, что
2) на действительной оси функция f(z) аналшпична,
а в верхней полуплоскости имеет не более конечного числа
особых точек аг, ах, ..., ап,
то
оо в
J /(*) Лс=2it/ 2 Res[/(z); ak]. A7)
-00 *=J
Для доказательства построим в верхней полуплоскости по-
полукруг (см. черт. 33) с центром в точке z = 0, выбрав его
радиус R столь большим, чтобы все особые точки функции
f(z), лежащие в верхней полуплоскости, оказались лежащими
внутри этого полукруга. Пусть С—дуга полуокружности, входя-
входящей в состав границы этого полукруга, с направлением обхода
против часовой стрелки. Тогда, в силу основной теоремы' о
вычетах,
f{x)dx+lf(z)dz=2*i 2 Res[/(z); ak],
С *1
-R С *=
причем при дальнейшем увеличении R правая часть этого
равенства не изменяется, а предел первого члена левой части
при R—+oo равен
во
J f(x)dx.
— 00
Следовательно, равенство A7) будет доказано, если мы обна-
§ 4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 149
ружии, что
lira [f{z)dz = 0.
На полуокружности С z = Rei<r = R (cos <p -\~l sin (p) и в
соответствии с правилом вычисления интеграла по комплекс-
комплексному переменному
*
J f(z)dz=\ e"MF(z)dz =
с с
о
It
= //?С е'1»*cos* е'**-**»ta *F (Re1*) dy. A8)
Обозначим M(R) максимальное значение модуля функции F(z)
на полуокружности С, т. е. максимальное значение \F(Rei4)\.
при изменении <р от 0 до it. В силу условий леммы М (R)—*-6
при R—юо. Так как |/| = 1, |в''| = 1 и | е(тК™9\= 1,
то, применяя к A8) обычную оценку для модуля интеграла,
получим:
|$| $ A9)
с о
Так как график функции sin л:, а, следовательно, и функции
симметричен относительно прямой х=-^, то
^ ^ B0)
о о
Пусть i — любое положительное число, меньшее чем ^-; тогда
SI* Г
g-m/JstaT^a^ \ g-mft^nf d<0-\- \ e~m^aia<f d<D. B1)
0 0 5
С помощью B0) и B1) неравенство A9) преобразуется клиду
• B2)
ISO
ТЕОРИЯ ВЫЧЕТОВ
[ГЛ. VII
Если г<?<|-, то sin <pss sinЬ и e~**"°* <г-ж**"|
следовательно,
Г g-mRflnV fa «ge-mR tin* [ fa — ce-mR»lnt B3)
j T j т » » '
s ь
, TO COS (p ^ COS i И ^| ^= 1.
где с — \ — &• Если
Следовательно,
B4)
Интеграл в правой части B4) легко вычисляется:
\ л—
О
«я/f sin 9
= г-
mRcosi
j e
,-mR a\nt
1
mR cos & "^ mR cos t *
и из неравенства B4) следует
ь
B5)
Оценив интегралы, стоящие в правой части B2) с помощью
B3) и B5), получим:
\{
f(z)dz\<2RM{R) (се-*
или
Пользуясь правилом Лопиталя'), легко убедиться а том, что
lim _5— = 0,
>) Си. Ш, п. 73.
§ 4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 151
а так как по условию hmM (/?) = 0, то из неравенства B6)
/?->СО
следует, что
lim
в лемма Жордана доказана.
Пример 2. Вычислить интеграл
00
С xcosxdx
J х»-2х4-Ю'
Функция
/B) = -г- "
как нетрудно проверить, удовлетворяет условиям леммы Жордана.
Здесь т=\ н *Ч*)= г, _ 2* + 10 •
Особыми точками функции f(z) являются полюсы первого по-
порядка z='l 4*3/ н z=\—3/(эти точки являются нулями первого
порядка для функции г* — 2г 4-10). В верхней полуплоскости имеется
единственная особая точка 2=14-3/. Вычислим вычет функции f(z)
относительно точки 1 4- 3/:
Следовательно,
f
J x»-
» — *+*
**"
— GO
= j e~* A4- 3/) (cos 1 4- / sin 1) ==
= je-«(cosl-3sini) 4--|e-»Ccosl4-slnl)/.
Сравнивая i обеих частях этого равенства действительные и мнимые
части и учитывая, что
" С х cos х С xaiax
dx + i ) ^
Г хе" л _ С х c
О x*-2* + 10rfX- 3 ^-
о
2x4-10
-оо
152 ТЕОРИЯ ВЫЧЕТОВ [ГЛ. VII
получим:
— ор
00
I
xsinxdx я _.,_ 1 i _; t\
x*-2x+W=lie 'Pccl-MliiO.
— 00
При доказательстве леммы Жордана предполагалось, что
на действительной оси нет особых точек функции /(г). Если
бы это предположение не было сделано, то интеграл
B7)
мог бы и не существовать. Однако если на действительной
оси расположено конечное число полюсов первого поряд-
порядка функции /(z), то интеграл B7) в смысле главного значе-
значения существует и может быть вычислен с помощью теории
вычетов.
Предположим, что единственными особыми точками функ-
функции f(z) на действительной оси являются простые полюсы
jc,, х1У... , хт(jc, <xt <... <С.хт), а в остальном выполнены
условия леммы Жордана, причем a,, at, ... , ап по-прежнему
являются особыми точками функции ~f{z), расположенными в
верхней полуплоскости.
Интеграл
00
[f{x)dx
— 00
будем понимать в смысле главного значения, ,т. е. будем счи-
считать, что
l/(x)dx+ J /&>"*+••• +
f(x)dx+ J f(x)dx]}. B7')
«*]
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
153
Выберем число R столь большим, чтобы все особые точки
функции f(z), лежащие в верхней полуплоскости, а также
точки xt, xt, ... , хт оказались внутри круга радиуса R с
центром в z = 0, и рассмотрим замкнутый контур, состоя-
состоящий из верхней полуокружности С этого круга, отрезков
действительной оси [ —/?, *, — р], [к, + р, х% — р], ... ,
[mi + P т ?\ [ Р ^] и верхних полуокружностей
радиуса р с центрами в точках хх, xt, ... , хт (черт. 34).
Дуги этих полуокружностей, обходимые по часовой стрелке,
обозначим, соответственно, у,, уг, ... , ут.
Применив к этому замкнутому контуру основную теорему
о вычетах, получим:
*|-р
R
J
*го-!>
*i+P
S
T,
Tm
B8)
Как было доказано в лемме Жордана, условия которой
выполнены на контуре С.
hra \f{z)dz — 0. B9)
Переходя в равенстве B8) к пределу при р—*0 и /?->оо,
154 теория вычетов [гл. vil
учитывая B8) и B9), а также то обстоятельство, что правая
часть постоянна, получим:
$ / (х) dx=2ir/ S Res [/(*); a J - S lira J /(г) dz. C0)
-OB *=l *=> f-*° T*
Если обозначить Res [f{z); xk]=ak, то в соответствии
с правилом вычисления вычета относительно простого полюса
lim [(z-xk)/(z)] = ak
и, следовательно, при достаточно малом р для любой точки г
на у* будет справедливо неравенство
\(z-xk)f(z)-*k\<B
при любом е]>0, как бы мало оно ни было.
Докажем, что
т* т*
Для этого оценим модуль разности
Так как \z — хк\ = р для любой точки z на у*, а длина ду-
дуги у* равна Tip, то
Так как е сколь угодив мало, то равенство C1) доказано.
С другой стороны, т уА *—xk — pe"f «te =
Следовательно,
Т»
§ 4} ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 155
Из равенства C1) получим:
lim
и на основании C0)
as
У f{x) dx = 2то 2 Res [/(z); ak] -{- тс/ 2 «*
— QO
или
т
Напомним, что здесь ак— особые точки функции f(z), рас-
расположенные в верхней полуплоскости, а хк — полюсы первого
порядка функции f(z) на действительной оси.
Пример 3. Вычислить интеграл
Psinx
о
Применим формулу C2) к интегралу
00
С е'* .
\ ~x~dx-
— оо
Если не считать точки z=oo, то единственной особой точкой функ-
функции — является простой полюс, расположенный на действительной
оси в точке z = 0, поэтому на основании C2) получим:
Но
156
следовательно,
Сравнивая в этоы
ТЕОРИЯ ВЫЧЕТОВ
00
f e'x d
J ~x Х~ '
— оо
равенстве ыииыые части, находим:
оо
— оо
stnx
откуда, ввиду четиости функции ,
J x 2 *
0
[гл. vn
Задачи к главе VII
1. Найти вычеты следующих функций относительно каждого из
полюсов:
а) Т=Т' е) Р^
г) -.g _ 1)Л (я > 0 и целое), н) ctg«z.
2. Найти вычеты относительно точки 2 = 0 функций:
-; б) cos-, в) sin-i-.
а) в , Z 2
3. Вычислить
если С —окружность x*-\-yl=.2x, проходимая однократно в поло-
положительной направлении.
4. Вычислить
dz
J (* —
§ 4] ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 157
если С —окружность х*-\-у* = 2х+2у, проходимая однократно в
положительном направлении.
5. Вычислить
dz
\
(z-а)" {*-*)"
(л>0 и целое), если С—однократно проходимая в положительном
направлении окружность |*| = 1, в следующих случаях:
а) |а|<|»|<1,
в)
6. Вычислить с помощью вычетов интегралы:
»>1
00
xainxdx
«J
— ао
ао
XCOSX
^x~+6dx'
- оо
00
sinxdx
аи
7. Найти число корней, находящихся внутри единичного круга
||< 1 для каждого из следующих уравнении (каждый корень сле-
следует считать столько раз, какова его кратность):
б) z'-5**4-z1-2=0,
в) *»-2г* + «*-&»-2=0.
ГЛАВА VIII
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
§ 1. Некоторые общие теоремы
В главе IV было доказано, что отображение, осущест-
осуществляемое аналитической функцией, является конформным во
всякой точке, в которой производная этой функции отлична от
нуля. Справедливо и обратное .утверждение: если функция
w=/{z) отображает конформно и взаимно-однозначно область Gt
на область О,, то она является функцией однозначной и ана-
аналитической в области Glt а обратная ей функция z=<f(w)
однозначной и аналитической в области О,. Приведем без
доказательства некоторые теоремы теории конформных ото-
отображений.
а) Теорема Романа о возможности конформного и взаимно-
взаимнооднозначного отображения одной односвязной области на дру-
другую (см. [9], гл. XII, § 6).
Теорема Римана не дает способа для отыскания аналити-
аналитической функции w=f(z), отображающей взаимно-однозначно
и конформно одну односвязную плоскую область О, на дру-
другую Gt, но утверждает, что такая функция существует всег-
всегда, если только ни оДна из областей О,, О, не принадлежит
к числу двух исключительных. Одним из таких исключений
является вся расширенная (т. е. включающая бесконечно
удаленную точку) плоскость, другим — вся плоскость с од-
одной выключенной точкой (например, вся плоскость с выклю-
выключенной бесконечно удаленной точкой, т. е. вся конечная часть
плоскости).
Можно, далее, доказать, что аналитических функций,
осуществляющих взаимно-однозначное и конформное отображе-
отображение односвязной области О, на односвязную область Ot (если,
конечно, ни одна из них не является исключительной), бес-
§ 1] НЕКОТОРЫЕ ОВЩИЁ ТЕОРЕМЫ 159
конечное множество, и для того чтобы обеспечить единствен-
единственность отображающей функции w=/{z), достаточно в любой
точке z0 области О, задать значения:
Геометрически это означает, что единственность отображения
будет обеспечена, если для некоторой точки гл области О,
будет указан ее образ да0 в области О, и задан угол, на
который при этом отображении поворачивается бесконечно
малая окрестность точки гй.
Для того чтобы найти функцию, отображающую односвяз-
ную область О, на односвязную область Gt, достаточно уметь
отобразить .каждую из этих областей на какую-нибудь область
стандартного вида, например на единичный круг |z|<l.
Если одна какая-либо функция, отображающая взаимноодно-
взаимнооднозначно и конформно некоторую область О на единичный круг
найдена, то все остальные функции найдутся с помощью ото-
отображения этого круга на самого себя. На стр. 174 будет
найдена зависящая от нескольких произвольных параметров
функция, отображающая единичный круг сам на себя. С по-
помощью условий типа A) можно будет однозначно определить
значения этих параметров и, следовательно, зная какую-нибудь
одну функцию, отображающую область О на единичный круг,
можно найти функцию, осуществляющую это же отображе-
отображение и, кроме того, удовлетворяющую заданным условиям.
б) Принцип взаилно-однозначного соответствий (см. [9],
гл. XII, § 2). Пусть область О ограничена гладким или ку-
-сочноггладким контуром Г, и предположим, что функция w—f(z),
аналитическая в О и на Г, отображает контур Г взаимно-
взаимнооднозначно на некоторый контур Г, ограничивающий область <У,
причем, когда точка z обходит контур Г так, что область О
остается слева, соответствующая точка w обходит контур Г
так, что область О' также остается слева. В этом случае,
как утверждает принцип взаимно-однозначного соответствия,
область О отобразится с помощью функции f(z) взаимно-
взаимнооднозначно и конформно на область О'.
Следовательно, в тех случаях, когда этот принцип приме-
применим, для отыскания области, на которую функция w—f(z)
отображает заданную область О, достаточно обойти границу
области О и найти контур, на который эта граница отобра-
160 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [гл. VIII
жается функцией f(z). В дальнейшем принцип взаимно-одно-
взаимно-однозначного соответствия будет неоднократно использован.
Перейдем теперь к изучению отображений, осуществляемых
некоторыми простейшими функциями.
§ 2. Линейная функция
Отображение, осуществляемое линейной функцией
где а и Ь — комплексные постоянные, а=?0, является кон*
формным во всей плоскости, так как производная этой функ-
функции во всех точках плоскости су-
Z, W ществует и отлична от нуля.
Рассмотрим некоторые частные
случаи линейных преобразований,
/у причем для большей наглядности
будем считать плоскость w совме-
х-в щенной с плоскостью г:
0\
Черт. 35. 1О- ™^* + Ъ. B)
Так как сложение комплексных чисел сводится к сложению
векторов, то при отображении B) всякая точка г смещается
в соответствующую точку w с помощью вектора сдвига, изо-
изображающего данное комплексное число Ь (черт. 35). Ввиду
того, что Ь постоянно, вектор сдвига одинаков для всех то-
точек, и мы имеем преобразование параллельного переноса;
где а — действительное число; в"—общий вид комплексного
числа с модулем, равным единице. В соответствии с правилом
умножения комплексных чисел (стр. 13) переход от точки г
к точке w осуществляется с помощью поворота точки г на
угол а около начала координат. Величина а постоянна, сле-
следовательно, рассматриваемое преобразование является преобра-
преобразованием поворота вокруг начала координат (черт. 36);
Зо _„
(г—действительное положительное число).
Так как argr=0, то в соответствии с правилом умноже-
яня комплексных чисел
§2]
ЛИНЕЙНАЯ ФУНКЦИЯ
161
Первое из этих равенств показывает, что точка z и соот-
соответствующая ей точка та» находятся на одном и том же луче
(черт. 37), выходящем из начала координат, а из второго ра-
равенства следует, что отношение расстояния точки w от нача-
начала координат к расстоянию соответствующей точки z от на-
„ чала координат постоянно и
равно г. Следовательно, рас-
\ сматриваемое преобразование
w
Черт. 36.
Черт. 37.
является преобразованием подобия с центром подобия в начале
координат; г — коэффициент подобия.
Общий случай линейного преобразования
w = аг -J- b
сводится к рассмотренным выше простейшим преобразованиям.
Действительно, если г и а — модуль и аргумент числа а
\а==ге1а), то
и переход от точки z к точке w осуществляется путем после-
последовательного применения следующих операций: 1) поворота
около начала координат на угол а, 2) преобразования подобия
с центром подобия в начале координат и коэффициентом по-
подобия, равным г, и 3) параллельного переноса с помощью
вектора сдвига, соответствующего комплексному числу Ь.
Пример. Найти функцию, отображающую равнобедренный
прямоугольный треугольник с вершинами в точках А, В, С, соответ-
соответствующих числам 3-J-2/, 7 + 2/, 5 + 4/, лежащий в плосмюти г,
на равнобедренный прямоугольный треугольник с вершинами в точ-
точках О, В1, С' плоскости w, соответствующих числам 0, — 2/, 1 — /
(черт. 38).
Так как треугольники ABC и ОА'В' подобны, то отображение
может быть осуществлено с помощью линейной функции.
Г. Л. Луиц и А. Э. Эльсгольц
162
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[ГЛ. VIII
Отображение можно разложить на следующие операции:
1) Параллельный сдвиг, смещающий точку А в начало координат.
V
о
?
W
и
Черт. 38.
Этот сдвиг производится вектором АО, соответствующим числу
— C 4-2/), и, следовательно, осуществляется функцией
2) поворот около начала координат на угол — у, соответству-
соответствующий преобразованию
ИЛИ
T——IU
3) Преобразование подобия с центром подобия в начале коорди-
координат и коэффициентом подобия, равным у. Это преобразование осу-
осуществляется функцией
Таким образом, окончательно
—4+{«-
% 3] функция w=j
s
j 163
§ 3. ФуНКЦИЯ
Точки А а В называются взаимно-симметричными отно-
относительно окружности, если (черт. 39):
1) они лежат на одном луче, выходящем из центра окруж-
окружности;
2) произведение их расстояний от центра окружности равно
квадрату радиуса окружности:
v~ • uu _^ . —-иве. ff
или
Отсюда, в частности, следует, что если
точка А приближается к окружности, то церт. 39.
точка В также приближается к окруж-
окружности, и всякая точка, лежащая на окружности, симметрична
самой себе относительно этой окружности. Из C) следует
также, что точкой, симметричной центру окружности, является
бесконечно удаленная точка.
Если центр О окружности совпадает с началом координат
и одна из двух взаимно-симметричных относительно окружности
точек изображает комплексное число z, то другая соответ-
ствует числу -=-. Действительно, модули чисел z и -=• удовлет-
удовлетворяют условию C), так как
'I К1
и, кроме того, числа z и — изображаются точками, лежащими
на одном луче, выходящем из начала координат, так как
? = — kxgz — kigz.
В частности, точки z и -=- взаимно-симметричны относительно
окружности единичного радиуса с центром в начале коорди-
') Построение пары взаимно-симметричных точек показано на
черт. 39: МА — перпендикуляр к ОВ, ЛИ—касательная к окружности.
в*
164
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. vm
нат («единичной окружности»), а так как точки у я — вза-
взаимно-симметричны относительно действительной оси, то пре-
преобразование
w —*~ —
состоит из двух симметричных отражений: относительно еди-
„ ничной окружности и относительно
действительной оси (черт. 40).
Производная
«to _1_
— — -р
функции —существует и отлична
от нуля во всех точках плоско-
плоскости, кроме точки z = 0 (соответст-
Черт. 40. вующей точке да=оо) и точки
z = оо (соответствующей точке
да = 0). Поэтому отображение, осуществляемое функцией
w =— (z — —)» является конформным во всей плоскости,
если условиться считать, что угол между линиями в бесконечно
удаленной точке равен углу между отображениями этих линий
с помощью функции w—— в начале координат.
§ 4. Дробио-лянейная функция
Дробно-линейная функция
сг -f- d'
где а, Ь, с, d — комплексные постоянные и ad —
осуществляет взаимно-однозначное отображение всей расширен-
расширенной плоскости z на всю расширенную плоскость да. Действи-
Действительно, разрешив D) относительно г, получим:
г=
dw — b
*) Если ad—йс=О, то a:cz=b:d я w=k, где А—постоянная.
§ 4] дровно-линейиАя функция 165
Я следовательно, не только всякому z соответствует единствен-
единственное значение да, но и каждому w соответствует единственное
значение г. При этом мы считаем бесконечно удаленную точку
равноправной точкой плоскости. Точке г = — — соответст-
а
вует точка да=оо, а точке а>=— точка z = oo.
Нетрудно непосредственной проверкой убедиться в том,
¦что дробно-линейная функция от дробно-линейной функции яв-
является также дробно-линейной функцией, т. е. если
cz + d
то зависимее™ между да и z также дробио-линейиая:
Произвольное дробно-линейное преобразование D) можег
быть получено с помощью последовательного применения линей-
линейных преобразований и преобразования да=—. Действитель-
Действительно, преобразование D) легко приводится к виду
аг-\-Ь асг -\- be асг -\- ad -\- be — ad
cz-f-rf c(cz-\-d) c(cz-\-d)
a(cz-\-d)-j-(be — ad) a ¦ bc~~ad 1
с (cz -f- d) с ' с ' cz-\-d'
Следовательно, к преобразованию D) можно прийти путем
последовательных преобразований:
i=cz-\- d,
Отсюда следует, что если какое-нибудь свойство справедливо
при линейном преобразовании и при образовании да = —-, то
оно справедливо и при дробно-линейном преобразовании D).
166 КОНФОРМНОЕ ОТОВРАЖЕНИЕ [гЛ. ТЫ
Например, можно утверждать, что отображение, осуществля-
осуществляемое дробно-линейной функцией, конформно во всей плоскости,
так как этим свойством обладают отображения, осуществля-
осуществляемые линейной функцией и функцией w=--.
Дробно-линейное преобразование обладает круговым свой-
свойством, состоящим в том, что с помощью этого преобразова-
преобразования окружность всегда отображается также на Окружность,
если прямую считать частным случаем окружности — окруж-
окружностью бесконечного радиуса.
Для доказательства этого свойства достаточно проверить,
выполнено ли круговое свойство при преобразовании щ/=— ,
так как для всех простейших преобразований, из которых со-
состоит линейное преобразование (стр. 165), круговое свойство
очевидно.
Считая z = x-\-iy,w = u-{-iv, перепишем равенство w=—
в виде
или
откуда
*=— E)
Уравнение произвольной окружности в плоскости z имеет
вид
Aix'+y^+Bx + Cy+D^O F)
(при А = 0 имеем прямую — окружность бесконечного радиуса).
Подставив в F) х и у из E), получим уравнение отображен-
отображенной линии
А , Ви су , п__п
+~ти—и
или
§ 4] Дробно-линейная функция 167
являющееся также уравнением окружности (при D=0 полу»
чим уравнение прямой), и круговое свойство доказано.
Всякая окружность делит всю плоскость на две области:
внутренность круга и внешность круга, если радиус окруж-
окружности конечен, и две полуплоскости, если радиус окружности
бесконечен. При отображении с помощью дробно-линейной
функции каждая из двух областей, ограниченныхокружносгью
в плоскости г, отображается на одну из двух областей, ог-
ограниченных соответствующей окружностью в плоскости w. Так,
например, из сказанного выше относительно отображения, осу-
осуществляемого функцией да=— (стр. 163), следует, что с по-
помощью этой функции единичная окружность |z| = l отобра-
отображается сама на себя (т. е. на такую же окружность плоско-
плоскости w), причем внутренность единичного круга плоскости г
отображается на внешность единичного круга плоскости w,
а внешность единичного круга плоскости г — на внутренность
единичного круга плоскости да. Вообще же, для того чтобы
определить, на какую область плоскости w отображается каж-
каждая из двух областей, ограниченных окружностью в плоскости
г, следует, учитывая, что при конформном отображении углы
сохраняются не только по величине, но и по направлению,
проследить за тем, в каком направлении движется точка w,
когда соответствующая ей точка г непрерывно перемещается
по окружности. При этом та из областей, ограниченных окруж-
окружностью в плоскости г, которая находится, например, влево от
движущейся по окружности точки, перейдет в область плос-
плоскости w, расположенную также влево, если смотреть в сторо-
сторону движения точки да.
Если а, Ь, с, d — действительные числа, то дробно-линей-
дробно-линейная функция
принимает при действительных значениях г действительные
значения и, следовательно, действительная ось плоскости г
отображается на действительную ось плоскости w При этом,
так как действительная ось делит плоскость на две полуплос-
полуплоскости («верхнюю» и «нижнюю»), то верхняя полуплоскость
плоскости г отображается или сама на себя (т. е. на верхнюю
полуплоскость плоскости да), или на нижнюю полуплоскость,
в зависимости от того, в каком направлении при заданных
168
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. viii
а, Ь, с, d движется по действительной оси точка да, если со-
соответствующая точка г перемещается по действительной Оси,
например, слева направо.
Область, ограниченная дугами двух окружностей, в силу
кругового свойства дробно-линейной функции, отображается
этой функцией или на область такого же вида, или на область,
ограниченную дугой окружности и прямолинейным отрезком
(внутренность или внешность кругового сегмента), или на угол
между двумя лучами. Для выяснения того, какой из указанных
случаев осуществляется в некотором конкретном примере, сле-
следует иметь в виду, что если на данной окружности (или пря-
прямой) расположена точка, отображающаяся в бесконечно удален-
удаленную точку плоскости да, то эта окружность (или прямая) ото-
отображается в прямую, в противном случае она отобразится в
окружность конечного радиуса. Поэтому, если, например, об-
общая точка двух окружностей отображается в бесконечно уда-
удаленную точку, to область, ограниченная дугами этих окруж-
окружностей, должна отобразиться в угол.
Пример 1. Найти область плоскости w, иа которую отобра-
отображается с помощью функции
i
заштрихованная на черт. 41,а область плоскости г, ограниченная" ду-
дугами окружностей радиуса У с центрами в точках — 1 и 1.
6).
Черт. 41.
Окружности пересекаются в точках / и — / под прямым уг-
углом, так как радиусы, идущие в точку пересечения окружностей,
взаимно-перпендикулярны. Так как ш=оо при z=s—i, то одна
$ 4] ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ 169
1C общих точек окружностей отображается в бесконечно удаленную
точку плоскости w. Следовательно, заштрихованная область отобра-
отображается на угол.
Другая общая точка отображается в начало координат (tv = O
при г =:), и таким образом, вершина угла, на который отображается
данная область, находится в начале координат. Величина угла равна
-я-, так как отображение конформно, а для того чтобы определить
положение угла, достаточно найти хотя бы одну точку на какой-ни-
какой-нибудь нз его сторон. Точка г = УТ— 1, как это видно из чертежа,
находится на дуге т- При 2 = 1^2—1 имеем:
YT— 1-f/ (у?-I)* 4-1 4-2У2"
2-У1
Эта -точка, как нетрудно видеть, расположена в третьей четверти на
биссектрисе координатного угла (ее координаты одинаковы и отрица-
отрицательны). Следовательно, дуга f отображается в луч Г, идущий из на-
начала координат по биссектрисе координатного угла в третьей четверти
(черт. 41,0). Так как углы сохраняются не только по величине, но и
по направлению, то для того, чтобы получить вторую сторону угла Г',
следует луч Г повернуть около начала координат на угол 90° по ча-
часовой стрелке, потому что в плоскости г при движении по дуге т от
точки / (отображающейся в начало координат плоскости w) заштри-
заштрихованная на черт. 41,а область остается-справа.
Каковы бы ни были заданные окружности в плоскостях г
и w, существует, и притом бесконечное множество дробно-
линейных функций, отображающих одну из этих окружностей
на другую. Действительно, не нарушая общности, можно счи-
считать один из коэффициентов в правой части D) равным еди-
единице (так как числитель и знаменатель правой части D) можно
разделить на этот коэффициент) и представить общую дроб-
дробно-линейную функцию, если, например, а Ф 0, в виде
Задав произвольно три различные точки а, р, у в плоскости
Z и три различные точки а', ?', у' в плоскости w, можно найти
дробно-линейную функцию, отображающую точку z=а в точ-
точку «> = <*', точку z = p в точку да = р' и точку г = у в точ-
точку w=Y> для этого достаточно найти Ь, с и d из системы
170 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [гл. VB1
уравнений
Можно показать, что эта система уравнений имеет единствен-
единственное решение и что, следовательно, существует единственная
дробно-линейная функция, отображающая тРи заданные
точки плоскости Z соответственно на три заданные точ-
точки плоскости w.
Эта функция в неявной форме задается равенством
— а' г — р т —а"
Непосредственная проверка убеждает нас в том, что точки а,
6, у действительно отображаются с помощью G) в точки' а',
Г. i-
Дробно-линейная функция обладает свойством симметрии:
две точки, взаимно-симметричные относительно окруж-
окружности С, отображаются с по-
ff мощью дробно-линейной функции в
точки, взаимно-симметричные осно-
сительно той окружности, на ко-
которую отображается окруж-
окружность С.
Переходя к доказательству этого
свойства, заметим сначала, что если
Черт. 42. окружность Г проходит через точ-
точки А и В, взаимно-симметричные от-
относительно окружности С, то окружность Г ортогональна к
окружности С. Действительно, пусть М (черт. 42) — точка
пересечения Г и С. Тогда, в силу определения симметрии,
Но в силу известной теоремы о касательной и секущей отсюда
следует, что радиус ОМ касается окружности Г и, следова-
следовательно, окружность Г ортогональна к С.
Докажем теперь, что если окружности Г, и Г,, пересека-
пересекающиеся в точках А к В (черт. 43), ортогональны к окруж-
окружности С, то точки А к В взаимно-симметричны относительно
окружности С. Действительно, проведем через одну из точек
пересечения Г, с Т%, например через точку А; луч О А из
ДРОВНО-ЛИНЕЙНАЯ ФУНКЦИЯ
171
центра окружности С, и пусть В*— вторая точка пересечения
этого луча с окружностью Г,. Тогда, в силу ортогональности
окружностей Г, и С, обозначив через М точку пересечения
С н Г,, с помощью теоремы о секущей и касательной получим
Черт. 43.
Черт. 44.
ОА • ОВ* — ОМ* = #*, следовательно, точка В* симметрична
точке А относительно окружности С. Те же рассуждения при-
применимы и к окружности 1\, которая тоже проходит через точ-
точку Л и тоже ортогональна к С. Следовательно, та же самая
точка В*, симметричная точке А относительно С, лежит и на
окружности Г„ а значит точка В* совпадает с точкой В. .
Доказанное свойство сохраняется, если окружность С заме-
заменяется прямой. Читатель без труда докажет, что все окруж-
окружности, проходящие через точки А и В, симметричные отно-
относительно прямой, ортогональны к этой прямой (черт. 44) и
обратно: если две окружности, проходящие через точки А я В,
ортогональны к прямой С, то эти точки взаимно-симметричны
относительно С.
Свойство симметрии дробно-линейной функции следует из до-
доказанных предложений. Действительно, если точки А и В
плоскости z, взаимно-симметрнчные относительно окружности
С (черт. 45), с помощью некоторой дробно-линейной функции
отображены соответственно в точки А' и В1 плоскости w, a
окружность С — на окружность С, то всевозможные окруж-
окружности, проходящие через точки А и В, отобразятся, в силу
кругового свойства дробно-линейной функции, на окружности,
проходящие через точки А' и &. Но окружности, проходя-
проходящие через точки А и В, как было доказано выше, ортогональ-
ортогональны к окружности С, а следовательно, ввиду конформности
172
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. \т
отображения, осуществляемого дробно-лннейной функцией, ок-
окружности, проходящие через точки А' и В', ортогональны к
О\
Черт. 45.
IV
окружности С; отсюда следует, что точки А' н В' взаимно-
симметричны относительно окружности С, н доказательство
свойства симметрии завершено.
Пример 2. Найти дробно-линейную функцию, отображающую
верхнюю полуплоскость на внутренность единичного круга (черт. 46).
При этом отображении какая-то точка а верхней полуплоскости
г отобразится в центр единичного круга (т. е. в начало координат
плоскости w). В силу свой-
свойства симметрии, точка а,
симметричная точке а от-
относительно действитель-
действительной оси, должна отобра-
отобразиться в точку со, симмет-
симметричную точке 0 относи'
тельно единичной окруж-
окружности плоскости w, так
как действительная ось
плоскости 2 по условию
должна быть отображена
да единичную окружность плоскости ю. Дробно-линейная функция,
удовлетворяющая перечисленным условиям (т. е. такая, что а» = 0
при z = в и w = со при г = а), имеет вид
Черт. 46.
где k — комплексная постоянная.
Величина к не вполне произвольна, так как при действительном
г точка w должна находиться на единичной окружности н, следова-
следовательно, | XI) 1 = 1. Так как, с другой стороны, при действительном г
ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
173
I*.—a| = |« —oj , то |ft| = l, т. e k = e"f, где <p—любое действн-
teflbHoe число» Следовательно, отображающая функция имеет вид
— iyz~a
W~e z — ~a'
Как и следовало ожидать, существует бесконечное множество дробно-
линейных функций, осуществляющих требуемое отображение. Каж-
Каждая из этих функций определяется значениями трех действительных
параметров (параметра <р и двух действительных параметров, опреде-
определяющих комплексное число а)
V
Iff
Черт. 47.
Пример 3 Найти дробно-линейную функцию, отображающую
внутренность единичного круга на себя (черт. 47).
Пусть а — точка внутри единичного круга плоскости 2, отобра-
отображающаяся в центр круга (в начало координат) плоскости w. Тогда
точка —, симметричная точке а относительно единичной окружности,
а
должна отобразиться в точку, симметричную с центром круга, т. е.
в бесконечно удаленную точку плоскости и>. Таким образом, п>=0
прн г = о и а» =оо при г = —. Дробно-лииейная функция, удовлет-
удовлетворяющая этим условиям, имеет вид
. 2 — а ._ 2 — а ,tZ — а
1 ааг — 1 1 — 52*
2 ~
а
где*'=— ka.
Постоянная k не произвольна, так как точки единичной окруж-
окружности плоскости г отображаются в точки единичной окружности
плоскости w и, следовательно, |о| = 1 при J2_[=l. Так как, далее,
zz= |2|*i то 22=1 при |2| = 1,_числа 1 — аг и 1 — а? взаимно-
сопряжеиные и [ 1 — azl = | 1 — а~г |. Если |2| = 1, то 11 — «|=з
=г|1 — ai||2|=|2 — azz \ = \ 2 — о |, следовательно, при 121 = 1
1-52
« 1-1
52'-'1
174
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл.
VIII
а так как при этом условии |v| = l, то |*'J = 1, т. е. **=«*, <р —
действительное число. Следовательно, общий вид функции, отобража-
отображающей единичный круг на себя, таков:
Л г — а
1 — аЯ
В этом равенстве также участвуют три действительных пара-
параметра. Произвольность параметра <р связана с тем, что при повороте
на любой угол вокруг центра круг отображается сам на себя (умно-
(умножение на ёг* соответствует повороту на угол у вокруг начала коорди-
координат). Произвольность комплексного числа а (]а| < I), определяемого,
как и всякое комплексное число, двумя действительными числами,
означает, что можно, отображая единичный круг сам на себя, потре-
потребовать еще, чтобы любая заданная точка, лежащая внутри круга,
отобразилась в центр круга.
П р и м е р 4. Найти дробно-линейную функцию, отображающую
двусвязную область, ограниченную окружностями | г — 31 = 9,
| г — 81 = 16 (черт. 48) на концентрическое кольцо между окружнос-
-г*
Черт. 48.
тями с центром в точке о/ = 0, так, чтобы внешний радиус этого
кольца был равен 1.
Точки и>,=0 и t»t = oo взаимно-симметричны одновременно
относительно обеих окружностей, ограничивающих кольцо, на которое
должна быть отображена заданная двусвязная область. В силу свой-
свойства симметрии в эти точки должны отобразиться те точки z,, tt
плоскости z, которые взаимно-симметричны одновременно относи-
относительно окружностей \z — 3| = 9 и \г — 8| = 16. Так как центры
этих окружностей находятся на действительной оси, то точки гх и z,
также должны расположиться на действительной оси, поэтому поло-
положим zt=xv 2,=хг Произведение расстояний этих точек до центра
§ 4] ДРОБНО-ЛННЕЙНАЯ ФУНКЦИЯ 175
каждой из окружностей должно быть равно квадрату раднуса соот-
соответствующей окружности:
(х,-3)(х1-3) = 81, (*,-8)(*,-8)=256.
Решив эту систему, получим х, = — 24, х,=0 (или х, = О, х, = — 24).
Одна из найденных точек должна отобразиться, как было отмечено,
в точку да = 0. а другая в точку w = оо. Пусть, например, » = 0
при 2 = — 24 и ю=оо при 2 = 0. Тогда
(8)
где коэффициент k пока произволен. Так как точка 2 = 0, внутрен-
внутренняя по отношению к данным окружностям, отображается в точку
ГС—со, внешнюю по отношению к- образам этих окружностей, то
преобразование (8) отображает внутренность каждой из данных
окружностей на внешность соответствующего образа. Окружность
|2 —3|=9 находится внутри окружности \г—8| = 16, поэтому ра-
радиус образа окружности \г — 3| = 9 больше, чем радиус образа ок-
окружности |2 — 8| = 16. Следовательно, по условию задачи требуется
коэффициент k подобрать так, чтобы для точек окружности \г — 3] = 9
было |ю| = 1. Рассмотрим, например, точку 2 = 12, лежащую на
окружности 12 — 31 = 9. Соответствующим значением и» из (8) будет
w = 3ft, следовательно, 13* I =1, или | k | =-г-. Итак, искомой фуик-
цией будет
где а — любое действительное число.
Если бы мы потребовали, чтобы ю = 0 при 2=0 и »=ео при
г = —24, то тем же методом получили" другое решение:
A0>
Заметим, что в условии задачи был задан только внешний ради-
радиус кольца. Что касается внутреннего радиуса, то он, как нетрудно
видеть, вполне определен, если внешний радиус задан. Действительно,
подставив в (9) или A0) вместо 2 любую точку окружности, отобра-
отображающейся во внутреннюю окружность концентрического кольца, мы
2
легко найдем, что внутренний радиус равен -а-. Следовательно, задан-
заданную в условии задачи двусвязную область можно отобразить только
на такое круговое концентрическое кольцо, у которого отношение
2
внутреннего радиуса к внешнему равно у.
176
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[ГЛ. VIII
§ 5. Степенная функция
Отображение, осуществляемое степенной функцией
« = *", (И)
где целое положительное число п ^ 2, является конформным
во всей плоскости, кроме точки 2=0, так как производная
этой функции существует и отлична от нуля всюду, кроме
точки г = 0. В точке 2=0, как будет показано ниже, кон-
конформность отображения нарушается. Введя в плоскостях z и
w полярные координаты
получим из A1):
и, следовательно,
'
A2)
Из равенства A2) следует, что окружности г=const с
центром в точке 2 = 0 плоскости z отображаются (черт. 49)
Черт. 49.
на окружности р = const с центром в точке «/ = 0 плоскости
w, причем единичная окружность отображается сама на себя,
а лучи <р = const, выходящие из начала координат плоскости z,
на лучи 6=const,-выходящие из начала координат в плос-
плоскости w. При этом луч tp = O, идущий по положительному
направлению действительной оси, отображается сам на себя,
Т. е, на луч 8 = 0; луч ^> = я плоскости z отображается на
§5]
СТЕПЕННАЯ ФУНКЦИЯ
177
луч 6=лас плоскости w, и угол 0<[<р<[а плоскости г
Bic \
а<[—1 с вершиной в начале координат отображается на
угол 0<[0<[ла плоскости го. Следовательно, конформность
отображения действительно нарушается в точке z = Qi углы
в этой точке увеличиваются при отображении в л раз. В част-
частности, угол 0<(р<-^- величины — плоскости г отобра-
отображается с помощью функции го=2я на верхнюю полуплоскость
@<C6<it) плоскости w. Угол 0 <[<{)•<— величины —
отображается на угол 0<[9<2тт, т. е. на всю плоскость,
Черт. 50.
кроме действительной положительной полуоси (черт. 50). На
эту полуось отображаются обе стороны рассматриваемого
угла плоскости г(<р = 0и <p —JM,
Для того чтобы отображение было взаимно-однозначным
не только внутри угла 0 < <р < -^-, но и на его сторонах,
следует в плоскости w произвести «разрез» по положительной
части действительной оси и условиться считать, что луч у=О
отображается на верхний, а луч <р = —? на нижний край этого
разреза (если луч f — a, вращаясь против часовой стрелки,
приближается к лучу <р = —, то соответствующий луч в
плоскости w приближается к действительной части положи-
положительной полуоси снизу).
Если w=zn, то каждой точке г соответствует единствен-
единственная точка w, но одной к той же точке w (w=?0,
Г. Л. Лунц и Л. Э Эльсгольц
178 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [гл. VIII
соответствует (см. стр. 15) л точек плоскости z, расположенных
в вершинах правильного л-угольиика с цеитром в нулевой точке;
отображение плоскости г на плоскость w не является, следо-
следовательно, взаимнооднозначным. Всякие два значения z, соот-
соответствующие одному и тому же w (т. е. всякие два значения
величины \/w), имеют один и тог же модуль и аргументы,
отличающиеся иа число, кратное —. Если одно из этих чи-
сел z, то другое ze п , где k — целое.
Область плоскости г, ие содержащая никаких различных
точек, соответствующих одному и тому же w, т. е. ие содер-
содержащая никаких двух различных вершин правильного л-уголь-
ника с центром в начале координат, отображается с помощью
функции г»=г" иа соответствующую область плоскости w
взаимно-однозначно. Этим свойством, во всяком случае, обла-
обладает любая область, целиком заключенная внутри угла вели-
чины — с центром в начале координат. В частности, как
2к
указано выше, угол 0 < <р < — отображается взаимно-однознач-
взаимно-однозначно на всю плоскость w с разрезом по положительной части
действительной оси, причем лучу ср = О соответствует верхний,
П_ OflP Aim
а лучу 9 = -jj- нижний край разреза. Угол -^<С.Ч<С— с по-
помощью функции w=z" также отображается взаимио-одно-
2к
зиачно иа плоскость -w с тем же разрезом, причем лучу «р=—
соответствует верхний, а лучу <р=— нижний край разреза.
Такое же отображение получим для каждого из углов, на ко-
торые разбивают плоскость z лучи ср = —, где k — целое
число, причем при отображении на плоскость с описанным
выше разрезом угла д < <р < — (Л = 1, 2,..., л)
лучу у= ' ~ соответствует верхний, а лучу ^ = —
нижний край разреза.
Для того чтобы получить во всей плоскости z взаимно-
взаимнооднозначное соответствие между точками z н точками да,
осуществим следующее геометрическое построение,
§ 5] степенная функция 179
Изготовим плоскость w с разрезом по положительной час-
части действительной оси в л экземплярах и будем считать, что
1-й экземпляр A-й лист) является отображением угла 0 < <р < — ,
2-й экземпляр B-й лист) — отображением угла — <С^<С~
и т. д., л-й экземпляр (л-й лист) — отображением угла
- д <С У <С 2"- Если точка я, перемещаясь по непре-
непрерывной кривой в своей плоскости, пересекает один из лучей
<р = —, соответствующая точка w переходит с одного эк-
экземпляра (листа) плоскости w на другой. Для того чтобы точка
w описывала при этом также непрерывную кривую, а также
для того чтобы отображение было взаимно-однозначным и на лучах
(f = — , соответствующих краям разрезов, следует «склеить»
(отождествить) края разрезов различных экземпляров (листов)
плоскости w, соответствующие одному и тому же лучу плоскости
г, а именно: нижний край разреза на 1-м листе следует скле-
склеить с верхним краем разреза 2-го листа [они оба соответст-
2is\
вуют лучу tp-=— V нижний край разреза 2-го листа с верх-
верхним краем разреза 3-го листа (они оба соответствуют лучу
«р = — J и т. д., нижний край разреза (л—1)-го листа с
верхним краем разреза л-го листа [они оба соответствуют
лучу <р= *я~ *j; наконец, оставшийся свободным нижний
край разреза л-го листа следует склеить с верхним краен
разреза 1-го листа1) (один из них соответствует в плоскости
/ лучу <р==2тг, другой — лучу <р = 0, который геометрически
совпадает с лучом <р = 2тт). Отображение, осуществляемое
функцией w=2", всей плоскости на построенную таким обра-
образом поверхность, называемую римановой поверхностью функ-
функции г = y/w (черт. 51 для л = 4), является взаимно-одно-
взаимно-однозначным.
¦) Такое склеивание, если представить себе каждый экземпляр пло-
плоскости w в виде листа бумаги неограниченных размеров, в трехмер-
трехмерном евклидовом пространстве осуществить без самопересечений нельзя.
180 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VIII
При движении точки z в своей плоскости по непрерывной
кривой точка да движется по иепрерывной кривой на римано-
римановой поверхности, причем, как уже отмечалось, когда точка z пе-
пересекает один из лучей ю = — , точка w переходит по линии
склеивания с одного листа римановой поверхности на другой. Не-
Незамкнутой дуге плоскости z соответствует незамкнутая дуга на
римановой поверхности, замкнутой ду-
дуге соответствует замкнутая. Если бы
значения w изображались не точками
римановой поверхности, а точками
плоскости w, то незамкнутая дуга,
соединяющая точки z и ze " , где
k—целое число, отображалась бы на
замкнутую кривую, так как начальной
и конечной точкам указанной дуги
соответствовала бы одна и та же точ-
точка w. Если точка z обходит по не-
некоторой замкнутой кривой один pas начало координат и воз-
возвращается в исходное положение, то соответствующая точка
плоскости w делает п полных оборотов вокруг начала коор-
координат в том же направлении, а точка w на римановой поверх-
поверхности также возвращается в исходное положение, описав иа
римановой поверхности замкнутую кривую.
Как было отмечено выше, для того чтобы область плос-
плоскости z с помощью функции w=z" взаимно-однозначно ото-
отображалась на соответствующую область плоскости да, необхо-
необходимо и достаточно, чтобы эта область плоскости z не со-
содержала двух различных вершин какого-нибудь правильного
л-угольника с центром в точке z = 0 (т. е. двух различных
уы
точек вида ze " , где k — целое действительное число).
Область, внутри которой находится начало координат или
бесконечно удаленная точка, таким свойством заведомо не
обладает, так как в первом случае область содержит целиком
достаточно малые правильные я-угольники с центром в начале
координат, а во втором случае содержит достаточно большие
л-угольники указанного вида, и следовательно, отображение
такой области с помощью функции да=*я иа соответствую-
соответствующую область плоскости w не является взаимно-однозначным.
§5] СТЕПЕННАЯ ФУНКЦИЯ 181
В любой односвязной области, не содержащей точек га»=0
я да=ор, в частности в достаточно малой окрестности всякой
точки да=г»0, не совпадающей ни с точкой 0, ни с точкой оо,
можно определить однозначные ветви функции г= j/w. Это
означает, что в такой окрестности можно определить несколь-
несколько однозначных аналитических функций, по отношению к
каждой из которых функция w=zn является обратной. Эти
функции и называют однозначными ветвями функции %/w.
Вообще, если функция w=f(z), аналитическая в неко-
некоторой области С и отображающая эту область на область О*,
такова, что обратная функция г=<р (да) многозначна в области О*,
но в то же время существуют однозначные, аналитические в
области Of, содержащейся в G*, функции я = <р, (w), z=
=<pt(z»), , для которых данная функция «/=/" (z) является
обратной, то функции z = <p, (w), z = yt(w), ... называются
однозначными ветвями функции z = <f(w), определенными
в области Of.
Если
z = rei<f, w=pe",
то, имея в виду, что (см. стр. 15)
выберем в точке wa какое-нибудь определенное значение
0=6о (например, будем считать, что б0 — главное значение
аргумента w0) и фиксируем также число А. Если окрестность
точки w0 достаточно мала, то она не содержит нулевой точ-
точки и при непрерывном перемещении точки w в этой окрест-
окрестности можно считать, что величина 6 аргумента w изменяется
также непрерывно, причем разность значений 6 для любых
двух точек w не превышает по абсолютной величине числа 2п.
Тем самым в окрестности точки w0 величина z определена с
помощью равенств A3) как непрерывная и однозначная функ-
функция аргумента w\ эта функция и является ветвью функции z =
= y/w. Различным фиксированным в формуле A3) значениям
k (к = 0, 1,2, ..., п — 1) при одном и том же выборе числа в0
соответствуют различные ветви функции %/!& в окрестности
точки w0.
Если точка w совершает один или несколько полных оборо-
оборотов вокруг начала координат, то непрерывное изменение
182 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [гл. VIII
величины 0 при этом движении точки w приводит к тому,
что точка w возвращается в исходное положение со значе-
значением аргумента б, отличающимся от исходного на величину,
кратную 2тг, а это соответствует изменению значения k во
втором равенстве A3), т. е. переходу на другую ветвь функ-
функции y^W.
Точка, обладающая тем свойством, что обход вокруг этой
точки в ее достаточно малой окрестности влечет за собой
переход от одной ветви многозначной функции к другой, на-
называется точкой разветвления (или точкой ветвления) рас-
рассматриваемой многозначной функции. Точками разветвления
функции 2= y/w являются точки w —0 и «> = оо. Следует
также отметить, что в каждой из этих точек ветвления функ-
функция yrw имеет только одно значение (jJ^O = 0 и у/ оо = оо),
т. е. различные ветви функции в этих точках совпадают. Это об-
обстоятельство связано с тем, что на римановой поверхности точки
да = 0 и «>=оо, будучи конечными точками разрезов на
каждом листе, являются общими для всех листов.
Как уже отмечалось выше, угол величины а (а<—) с
вершиной в точке г = О (соответствующей точке разветвления
w = 0) отображается функцией w = zn на угол с вершиной
в точке гаг=0 величины па, в частности угол с вершиной
.в точке w=0 величины — отображается взаимно-однозначно
на полуплоскость. Это замечание относится и к тому случаю,
когда число п дробное, так как угол с вершиной в начале
координат не содержит никакой окрестности нулевой точки
(а также и бесконечно удаленной точки) и, следовательно,
^внутри такого угла может быть определена однозначная
ветвь отображающей функции. Так как, с другой стороны,
с помощью дробно-линейной функции можно отобразить на
угол область, ограниченную дугами двух окружностей
(или дугой окружности и прямолинейным отрезком)'), то,
Комбинируя дробно-линейную и степенную функции, можно
такую область отобразить на полуплоскость.
') Для этого достаточно взять такую дробно-линейную функцию,
С помощью которой одна общая точка дуг окружностей отображается
в бесконечно удаленную точку. Если другую общую точку отобра-
отобразить в начало координат, то вершина угла будет находиться в нача-
начале координат.
СТЕПЕННАЯ ФУНКЦИЯ
183
Пример !. Отобразить на верхнюю полуплоскость область,
общую двум кругам радиуса 1 с центрами в точках 0 и 1
(черт. 52).
Точки пересечения дуг, ограничивающих заданную область,
соответствуют числам
H*t = T 2
Дробно-линейная функция
*— -=¦
A4)
отображает одну из этих точек
в точку *=«, а
другую f *=у-/^2-) в точку *=0
и, следовательно, данную область в угол
с вершиной в точке t = 0. Величина втого
угла (см. чертеж) равна у • Для того чтобы выяснить, как рас-
расположен в плоскости t этот угол, достаточно найти хотя бы одну
точку на одной из его сторон. Выясним, например, в какую точку
отобразится точка z = l, лежащая иа одной из дуг (Q, ограничиваю-
ограничивающих данную область. При г=\ получим:
.
_ !
- 2
Следовательно, дуга U плоскости г отображается на луч A) плоско-
плоскости w, выходящий из начала координат и проходящий через точку
t—^L + iLl (черт. 53,о). Если идти по дуге I, из точки zf, ко-
которой в плоскости t соответствует точка t = 0, то отображаемая об-
область окажется слева, следовательно, луч B) плоскости t, являющийся
отображением дуги *», может быть получен поворотом луча A) на
угол ^ против часовой стрелки,
4
184
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[ГЛ. VIII
Так как полученный в плоскости t угол предстоит отобразить на
верхнюю полуплоскость, то, прежде чем воспользоваться для этой
цели степенной функцией, следует произвести в плоскости t поворот
на угол -s- по часовой стрелке с тем, чтобы луч A) совместить с по-
VI
Черт. 53.
ложительной частью действительной оси, которая (см. стр. 176) сте-
степенной функцией отображается сама на себя. Такой поворот (см.
стр. 160) осуществляется функцией
T — te 3. A5)
Полученный в результате в плоскости Т угол (черт. 63, б) отобра-
отображается на верхнюю полуплоскость плоскости да одной нз ветвей
функции
W — f1* A6)
/ 2я 2я 3
(угол величины -=• отображается на угол величины -^- • — =
Объединяя A4), A5) и A6), получаем функцию
=г е
или окончательно
аг——
отображающую заданную область плоскости г на верхнюю полупло-
полуплоскость. Это, конечно, только одна из функций, осуществляющих тре-
требуемое отображение. Все множество функций, удовлетворяющих
§5]
СТЕПЕННАЯ ФУНКЦИЙ
185
условию задачи, можно получить, отображая далее с помощью соот-
соответствующего дробно-линейного преобразо-
преобразования верхнюю полуплоскость плоскости w
саму на себя.
Пример 2. Отобразить на верхнюю
полуплоскость всю плоскость г с разрезом
вдоль прямолинейного отрезка, соединяю-
соединяющего точку / с точкой" 3/ (черт. 54).
Дробно-линейная функция
z — i
'z — Zi
A7)
отображает концы разреза г = / н 2 = 3/
соответственно в точки f = 0 и *=оо, а
следовательно, заданную область на пло- Черт. 54.
скость t с разрезом вдоль некоторого луча,
выходящего из начала координат. Для того
чтобы выяснить направление этого луча, достаточно найти на нем
хотя бы одну промежуточную точку. Точке * = 2/ разреза в плос-
плоскости z соответствует точка
плоскости /. Следовательно, функция A7) отображает данную область
на плоскость t с разрезом вдоль луча, идущего по отрицательной
a) &
Черт. 55.
части действительной оси (черт. 55, в). Произведя с помощью функции
T=te« = -t A8),
поворот на угол я, мы отобразим нашу область на плоскость с раз-
разрезом по положительной части действительной оси (черт. 55,6).
Функция
w=VT A9)
(точнее, одна из ветвей этой функции) отображает плоскость Г
186
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гЛ. vrtl
с разрезом вдоль положнтельной действительной полуоси на верхнюю
полуплоскость. Объединяя A7), A8) и A9), получим:
Это, конечно, только одна из функций, осуществляющих требуеное
отображение.
§ 6. Профили Жуковского
Отобразим всю плоскость г с разрезом по дуге I окружности,
концы которой находятся в точках -аи а действительной оси и ко-
которая пересекает мнимую ось в точке hi, на расположенную в пло-
плоскости а» внешность круга G с центром в точке hi, окружность ко-
которого проходит через точки — а и а (черт. 56).
Черт. 56.
Заметим, что если а - угол между касательной ВК к дуге I
в точке а и отрицательным направлением действнтельной оси, то луч,
идущий из точки а в точку hi, образует с отрицательным направле-
направлением действительной оси угол -|. Действительно, если С-центр
дуги I, А, В, D — точки, соответствующие числам — a, a, hi, то
= « и, следовательно, / CDB^ ? DBC= \ - \. Но так как
^j, то IKBD^j, а значит и ?.DBO^\. Отсюда
вытекает, что в плоскости w угол между радиусом, идущим из точки
аГв точку а, и отрицательным направлением действительной оси
также равен ? , а угол между касательной к окружности в точке а
и положительным направлением действительной оси равен 2 —--.
Для того чтобы найтн функцию, осуществляющую требуемое отобра-
отображение, отобразим сначала как плоскость 1С разрезом по данной дуге
§ 6]
профили жлсовского
187
I, так и внешность данного круга G плоскости w на одну и ту же
вспомогательную область.
Функция
отображает плоскость г с разрезом по данной дуге I на плоскость t
с разрезом по лучу, идущему из точки 0 в точку ов (черт. 57, а). Этот
луч наклонен к положительному направлению действительной оси
под тем же самым углом к — а, что и данная (в плоскости г) дуга в
Черт. 57.
точке а. Это утверждение следует из конформности отображения и из
того, что движению точки z по действительной оси от точки а впра-
вправо соответствует движение точки t по действительной оси от точки
О также вправо, так как при г > а
Функция
Т=
B0)
отображает окружность даииого круга плоскости w на прямую пло-
плоскости Т, проходящую через точку 0 (черт. 57,6). При этом дейст-
действительная ось плоскости w отображается на действительную ось пло-
плоскости Г, причем если точка w движется по действительной оси от
точки а вправо, то точка Г движется от точки 0 по действительной
оси также вправо. Отсюда следует, что внешность круга G плоско-
плоскости w отображается на полуплоскость плоскости Г, содержащую ио-
ложительную действительную полуось и ограниченную прямой, на-
наклоненной к этой полуоси под тем же углом -=¦ — -^ . что и каса-
касательная к окружности круга О плоскости w в точке а. Функция
188
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. viii
отображает эту полуплоскость на плоскость t с разрезом вдоль луча,
наклоненного к положительному направлению действительной оси под
AС в \
•=— ¦=-1 = я — а, т. е. на ту же область, на которую с по-
помощью функции
z — a
1~Т+а
была отображена плоскость z с разрезом по заданной дуге I. Следо-
Следовательно, в силу B0), функция,
дающая решение поставленной за-
W дачи и отображающая плоскость
Черт. 58.
с разрезом по дуге I на внешность круга G, может быть определена
равенством
fw — aV_z — a
\w+a) z + a'
Разрешая это уравнение относительно г или ха, получим:
Так как полученная зависимость не содержит величины А, то пло-
плоскость z с разрезом по всякой дуге окружности, соединяющей точ-
точки—а и а, отображается на внешность круга, проходящего через
точки — а и а и имеющего центр в точке, совпадающей с точкой
') В плоскости г с разрезом по дуге I функцию Vz% — а*, как
нетрудно видеть, можно считать однозначной, точнее, каждая из вет-
ветвей этой функции является в этой области непрерывной и однознач-
однозначной. Точки — а и а делят окружность круга G иа две дуги ?, и /.,,
одна из которых соответствует одному краю разреза, идущего пс
дуге I, а другая — другому краю разреза. Выбором определенной ветви
функции yV — а* мы и устанавливаем, какому краю разреза соот-
соответствует дуга Lv а какому — дуга Lr
§ 7] ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 189
пересечения данной дуги с мнимой осью (если плоскости г и «/счи-
«/считать совмещенными).
Внешность всякого круга плоскости w, содержащего круг О и
касающегося окружности этого Kpyia в точке а (черт. 58), отобра-
отображается с помощью найденной функции на область, лежащую вне не-
некоторого замкнутого контура, содержащего дугу I, для которого
точка а является точкой возврата с касательной, совпадающей с ка-
касательной к дуге I. Такой контур носит название профиля Жуков-
Жуковского. Форма контура Жуковского зависит от параметров а и А, а
также от расстояния d центра круга G от центра того круга, отобра-
отображением которого является рассматриваемый профиль.
Существование функции весьма простого вида, отображающей
внешность профиля Жуковского на внешность круга, делает профили
крыльев самолета, входящие в класс профилей Жуковского, весьма
удобными для расчетов при решении задач на обтекание (см. стр. 241К
§ 7. Показательная и логарифмическая функции
Отображение, осуществляемое функцией
т=ег,
конформно во всей плоскости, так как производная этой функ-
функции существует и отлична от нуля во всякой конечной точке
плоскости z. Введя в плоскости г декартовы, а в плоскости w
полярные координаты, т. е. положив z-=s=x-\-iy, w = ре", по-
получим:
1*
Следовательно,
I B1)
Из равенств B1) следует, что прямые, параллельные мнимой
оси Оу (черт. 59) плоскости г (х = const), переходят при ото-
отображении <w=ez в окружности с центром в нулевой точке
плоскости w (р = const), а прямые, параллельные действитель-
действительной оси Ох {у = const), — в лучи, выходящие из начала коор-
координат F =¦ const). Прямоугольник со сторонами y=yl,y=yv
x = xv x~xt, параллельными осям координат плоскости г,
отображается на область, плоскости w, ограниченную лучами
Q—yv Ь=уг и дугами концентрических окружностей р=е*«
р = е*«. Действительная ось плоскости z(y = 0) отображается
на действительную положительную полуось @ = G) плоскости да,
прямая у = а—на луч 6 = а. Следовательно, полоса ширины
ес(а<2тг), прилегающая к действительной оси: 0О^
190
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. vai
отображается конформно и взаимно-однозначно на угол
величины а (в радианах) с вершиной в начале координат, од-
одной из сторон которого является действительная положитель-
положительная полуось. В частности, полоса 0<_у<[1т ширины л ото-
отображается функцией w = ez взаимно-однозначно на верхнюю
If
и
z
X
Черт. 59.
полуплоскость, а полоса 0<_y<2ir ширины 2ц — на всю
плоскость с разрезом по положительной действительной полу-
полуоси: 0<6<2ir.
Отображение всей плоскости г на плоскость w не является
взаимно-однозначным: всякой точке w (кроме точек да—0 и
то=оо) соответствует бесконечное множество точек г:
z = Lnw^=la\w\-\-iATgw=la\w\-\-iatgw-\-2kKi
(k = 0, ±\, ±2,...).
Для того чтобы область плоскости г отображалась функцией
то=е* взаимно-однозначно на соответствующую область пло-
плоскости w, необходимо и достаточно, чтобы она не содержала
никаких двух точек, абсциссы которых одинаковы, а ординаты
отличаются друг от друга на величину, кратную 2ir, так как
е?* = ег* лишь при гг — z1 = 2fati (k = 0, +1, +2,...).
Такому условию, в частности, удовлетворяет всякая область,
заключенная в полосе 2Air <[у <[ 2 {k -\-1) it.
Если плоскость г разбить (черт. 60) на полосы 2kxc<^y<^
<2(*-f-l)'It (* = 0, ±1, ±2,...), то каждая из этих по-
полос отобразится функцией w=e* взаимно-однозначно на всю
плоскость w с разрезом вдоль положительной части действи-
§7]
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
191
тельной оси. Для того чтобы такое отображение было взаим-
но-однозиачным ие только внутри полосы, но и на ее гранич-
граничных прямых у=2Длг и у=2 (k -j- I) ir, достаточно условиться,
что нижней границе y = 2kn соответствует верхний край раз-
разреза в плоскости w, а верхней границе у = 2 (k -j- I) п — ниж-
нижний край разреза (если в плоскости г прямая у = а подни-
поднимается от положения у = 2кп до положения у=2(к-\-Цк,
Черт. 60.
Черт 61.
соответствующий луч 0 —а в плоскости w совершает полный
оборот против часовой стрелки от положения 0 = 2&ir, соот-
соответствующего верхнему краю разреза, до положения 0=
= 2(A-j-l)ir, соответствующего нижнему краю разреза).
Изготовим бесконечное множество экземпляров плоскости
w, проведем на каждом экземпляре разрез по положительной
части действительной оси, занумеруем эти экземпляры (листы)
плоскости w целыми числами от — оо до -{- оо и сложим их
в «стопку» так, чтобы 2-й лист лежал на 1-м, 3-й на 2-м,
4-й на 3-м и т. д. 0-й лист под 1-м, — 1-Й лист под 0-м,
— 2-й лист под — 1-м и т. д. Склеим (отождествим) нижний
край разреза каждого листа с верхним краем разреза листа, лежа-
лежащего над данным листом (и, тем самым, верхний край разреза
каждого листа с нижним краем разреза листа, лежащего под
данным листом) (черт. 61). Как нетрудно видеть, функция
да=е* (или z=tnw) отображает плоскость z взаимноодно-
взаимнооднозначно на построенную поверхность (риманову поверхность). Если
точка г движется параллельно оси Оу вверх, то точка w, вра-
вращаясь против часовой стрелки вокруг начала координат, как бы
«аодннмаетсяэ на римановой поверхности по спирали, переходя
192 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [гл. VIII
с одного листа на другой с ббльшим номером; если точка пло-
плоскости z движется параллельно оси Оу вниз, соответствующая
точка w римановой поверхности, вращаясь по часовой стрелке
вокруг начала координат, как бы «опускается» по спирали,
переходя с одного листа на другой с меньшим номером.
В достаточно малой окрестности всякой точки и/=и/0,
кроме и/0 = 0 и дав = оо, можно определить однозначные ветви
функции z=Lnw. Для этого достаточно, положив w = pel\
фиксировать в формуле
z = Lnw = lnp-\-fi-\-2kTii B2)
целое число k, выбрать в точке w0 какое-либо определенное
значение 0 = 0о (например, положить 0о равным главному зна-
значению аргумента w в точке w0) и считать, что 0 изменяется
непрерывно при движении точки w по непрерывной кривой.
Различным значениям k(k = 0,4^1, 4^2,...) соответствуют
различные ветви функции Ьпи/. Если окрестность точки wt
достаточно мала, то она не содержит точки и/ = 0, и при
указанном способе изменения 0 абсолютная величина разности
значений 0 для любых двух точек этой окрестности не превы-
превышает 2л. Если же точка w совершает в своей плоскости один
или несколько полных оборотов вокруг начала координат, то
она возвращается в начальное положение со значением 0, от-
отличающимся от исходного на величину, кратную 2тт, а э о
равносильно изменению значения k в равенстве B2), т. е. пе-
переходу на другую ветвь функции Lnw. Следовательно, точка
w=0 является точкой разветвления функции Lnw; нетрудно
убедиться, что точкой разветвления является также точка
w = oo. В каждой из этих точек функция Ьпи/ имеет только
одно значение (Ln 0 = оо, Ln оо = оо). Точки w = 0 и w = оо
являются конечными точками разрезов на всех листах римано-
римановой поверхности и, следовательно, являются общими для всех
листов.
Характер точек разветвления функций ?= у w HZ = Lno> раз-
различен. После п-кратного обхода вокруг точки w = 0 мы вернемся
к первоначальной ветви функции у w, точки разветвления, облада-
обладающие таким свойством, называются алгебраическими точками раз-
разветвления порядка я — 1. Иначе обстоит дело с функцией Ln w. Лю-
Любое конечное число обходов (в одном и том же направлении) вокруг
точки ш = 0 не приведет к возвращению к первоначальной ветви
функции Ln or. такие точки разветвления называются логариф-
логарифмическими.
§7]
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
193
Так как с помощью дробно-линейной функции область, ог-
ограниченная двумя касающимися друг друга окружностями (или
окружностью и касающейся ее прямой), может быть отобра-
отображена на полосу между двумя параллельными прямыми (для"
этого достаточно, чтобы точка касания отобразилась в беско-
бесконечно удаленную точку), а полоса ширины тт с помощью по-
показательной функции отображается на верхнюю полуплоскость,
то, комбинируя дробно-линейную и показательную функции,
можно область указанного вида отобразить на верхнюю полу-
полуплоскость.
Пример 1. Найти функцию, отображающую область, ограни-
ограниченную единичной окружностью С и прямой I, касающейся этой
окружности в точке z = i (черт. 62) ~
на верхнюю полуплоскость.
Функция
1ч i
t =
z-i
B3)
отображает общую для окружности
н прямой точку z = i (точку ка-
касания) в бесконечно удаленную
точку плоскости t, следовательно,
в силу кругового свойства дробно-
линейной функции, как окружность
С, так и прямая I отображаются этой
функцией на прямые, параллельные
(окружность С и пря-
Черт. 62.
"-НУ
точку, лежащую на этой прямой. Возьмем,
на окружности С, ей соответствует на прямой С точка
,, „ г> ппптопит чеоез точки * = 0и* = / и, следовательно,
совпадет с3миС„М^Й о'сьГплоГкости" (черт. 63,а). Чтобы определить
положение прямой V плоскости t, на которую функция B3) отобра-
жТет прямуюТдостаточно знать на прямой V одну точку. Точке
z=l + / прямой I соответствует точка
7 Г. Л. Лунц и Л. Э Эльсгольц
194
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. vin
прямой I'. Прямая V проходит через точку 1+2/ параллельно мня*
мой оси и, следовательно, отстоит от этой оси на расстоянии, равном 1.
Итак, функция B3) отображает заданную область на полосу ширины 1,
прилегающую к мнимой оси.
Функция
t=itf B4)
отобразит эту полосу на полосу ширины к (черт. 63, о), прилегающую
к мнимой оси, а с помощью функции
Т=еТ т = Л B5)
•та полоса в плоскости т поворачивается на угол -тг против часовой
1
i
/¦а
Черт. 63.
стрелки и переходят в полосу, изображенную на черт. 63» а. Эта по-
последняя полоса функцией
w=eT B6)
отображается на верхнюю полуплоскость.
Объединяя B3), B4), B5) и B6), находим одну из функций, осу-
осуществляющих требуемое отображение:
w=e *-'.
Тригонометрические функции могут быть выражены через,
показательную функцию (см. стр. 32). Рассмотрим, например,
отображение, определяемое функцией
е —6 i
= 2/ W
§7]
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
195
Возьмем в плоскости г полуполосу у^>0, —г> <^ дг <С"о"
(черт. 64). Если точка z находится на прямой дс=—у>то
w — _ } B()
и если точка г движется по прямой дс=—к от jr = -}-oo
до у = 0, то точка то перемещается по действительной оси от
urs=—оо до да= — 1. На действительной оси у = 0, поэтому
то=sin*, B8)
и если точка г передвигается по действительной оси от х =
— —до х =»-?•, то соответствующая ей точка то пробе-
пробегает отрезок действительной оси от то = —1 до «=1.
На прямой х = 7j
B9)
и если точка г движется по прямой х — -^ от у = 0 до.у = оо,
то соответствующая ей точка w перемещается по действитель-
действительной оси от iiy=l До да=-f °°-
Итак если точка г обходит границу полуполосы у > О,
__ Л <^ x<i -|- так, что эта полуполоса остается слева, то точка
7* г л Луни и Л Э Эльсгольц
196
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. viii
w пробегает слева направо всю действительную ось, и следо-
следовательно, пользуясь принципом взаимно-однозначного соответ-
соответствия (см. стр. 159), заключаем, что функция w = sin г
отображает рассматриваемую полуполосу иа верхнюю полу-
полуплоскость.
Пользуясь B7), B8) и B9), нетрудно проверить, что если
точка г обходит границу полуполосы у<С0, —~2<^X<^~J
(на черт. 65, а эта полуполоса заштрихована дважды) так, что
/////////
/////////
//s/f////
Wm
ш
v/a
w
///A
Ш
7//j
w
7/
7u
О
%
6J
Черт. 65.
эта полуполоса остается слева, то точка w пробегает справа
налево всю действительную ось и функция w=smz отобра-
отображает эту полуполосу на нижнюю полуплоскость, причем стороне
полуполосы у < 0, х ¦=¦ — у соответствует отрезок — оо <
<w<[ — 1 действительной оси плоскости w, стороне у = 0,
— ~ <[х<С-о" — отрезок — 1<да<М и стороне у <С0, jc-=
= J — отрезок 1 < w <[ оо.
Проведенное исследование отображений рассмотренных по-
полуполос приводит к выводу, что полоса — ^r<ix<^- (черт. 65)
отображается функцией да = sin .г на всю плоскость w с раз-
разрезами по действительной оси от —оо до — 1 и от 1 до оо,
причем верхним краям этих разрезов соответствуют в плоскости г
и х = ~, у^> 0, а нижним краям —
линии x = —^-,
линии х =
= — -j, У<Ои x==j,
§8]
КОНФОРМНОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
197
Так как sin (г -f- 2я) =* sin г и sin (гг -f- тг) = — sin z, ro
(черт. 66) все полуполосы А отображаю!ся функцией да=sin*
на верхнюю, а все полуполосы В— на нижнюю полуплоскость
Черт. 66.
плоскости w. Учитывая вышеизложенное, читателю в качестве
упражнения рекомендуется построить риманову поверхность
функции z = Atcs\a w (листы плоскости w с соответствую-
соответствующими разрезами склеить так, чтобы функция z —Arcsin w
отображала полученную поверхность взаимно-однозначно и не-
непрерывно на плоскость г).
§ 8. Конформное отображение полуплоскости
на прямоугольник и многоугольник
Рассмотрим функцию
C0)
где 0 <С к <С 1. Особыми точками подынтегральной функции
/(*) = :
( )
являются точки z1, = ±1 и г, 4==±-^-. Эти точки являются
точками разветвления, так как
VT^VT^kz Vl
а точка w = 0 является точкой разветвления функции j
7*»
198 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VIII
(см. стр. 182). Следовательно, выбор однозначной ветви функции
f(z) возможен лишь в такой области, в которой нельзя обойти
вокруг точек +1 и + -г ¦ Для того чтобы обеспечить выпол-
выполнение указанных условий, будем считать, что точка z в правой
части C0) расположена в верхней полуплоскости или на дей-
стви гельной оси ( но не в точках 4; 1 и + -^ ] и что путь
интегрирования тоже лежит в верхней полуплоскости. Если в
дальнейшем будет необходимо интегрировать по действительной
оси, то потребуем, чтобы точки ±1, +-т-обходились, напри-
например, по верхним полуокружностям с центрами в этих точках.
При этих условиях функция ; = <рB), определенная равенством
C0), будет аналитической и однозначной во всей верхней по-
полуплоскости, а также- на действительной оси, за исключением
точек 4; 1, +• -r .
Для того чтобы функция ? = ср (z) была вполне определена,
нужно договориться о том, какую из двух ветвей функции
/B) мы выбираем. Условимся брать ту ветвь функции /(*),
для которой/@)= 1 (для другой ветви /@) = —1).
Найдем линию в плоскости С> на которую с помощью C0)
отображается действительная ось плоскости 2. Точке 2 = 0
соответствует, очевидно, точка С = 0. Если точка z движется
из положения 2 = 0 по действительной оси вправо, то интег-
интеграл в правой части C0) является обычным определенным ин-
интегралом функции действительного переменного, причем пока
* <С •, подынтегральная функция положительна, а поэтому ?
тоже является положительной величиной, возрастающей при
возрастании 2. При 2=1 интеграл C0) становится несобст-
несобственным, обозначим его —:
«,_Г_ * (82)
Величина й, зависит от А: и может быть найдена по таблицам
эллиптических, интегралов (см., например, [Ю], таблицу 22).
Продолжим теперь движение точки х по действительной оси
в положительном направлении. Точнее, пусть точка г, двигаясь
от точки г = 0 вправо в положительном направлении и несколько
§ 8] КОНФОРМНОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ 199
не дойдя до точки 2=1, обходит точку z=l по верхней
полуокружности радиуса р (впоследствии нужно считать, что
р —> 0), после чего точка г продолжает двигаться по действи-
действительной оси в положительную сторону. При 1 < г < -г- подко-
подкоренное выражение в знаменателе становится отрицательным и
корень мнимым. Выясним, будет ли при этом мнимая часть
знаменателя положительной или отрицательной. Запишем
Y(\—z1){\~ktzt) в вице
— 2«)(i_ jfe«2«) = yT~z УТ+z VT^k
Для последних трех множителей точка 2=1 не является точ-
г
\
О г г г
Черт. 67.
кой разветвления, и поэтому при переходе через эту точку
аргумент каждого из этих множителей не изменяется. Дейст-
Действительно, рассмотрим, например, Vl -\~z. Число \-\-z — z—
— (—1) изображается вектором, идущим из точки —1
в точку z. При 0<2<1 этот вектор (черт. 67) идет
по действительной оси г
в положительную сто-
сторону. Следовательно,
arg A -J- z) = 0. Когда
точка z движется по по- •—•-
луокружности с центром 0 2 / г
в точке 2=1, вектор, Черг. 68.
изображающий число
\-\-z, сначала отклоняется от действительной оси, но после того,
как точка 2, описав полуокружность, вернулась на действитель-
действительную ось, направление вектора опять становится прежним. Таким
образом, обход вокруг точки 2=1 не влияет на аргумент
числа 1 -)-2, а следовательно и числа V \-\-z. Аналогично
Обстоит дело с множителями Y^—kz и ]/Ч-|-Алг.
Рассмотрим теперь первый множитель У \ —2. Число 1—t
изображается вектором, идущим из точки z в точку 1 (черт. 68).
200 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [>Л~ Vt||
При 0 < г <^ 1 этот вектор направлен по действительной оси
в положительную сторону, что соответствует тому, что
arg(l—г) = 0. Но когда точка z обходит по полуокружности
точку 2=1, вектор поворачивается на 180° по часовой стрелке,
следовательно, его аргумент уменьшается на it, и поэтому при
г >¦ 1 аргумент числа 1 — z нужно считать равным — я, а
аргумент числа \^\—z равным, соответственно, —-^-. Так
как аргументы всех остальных множителей в C3) не измени-
изменились и остались равными нулю, то аргумент всего произведе-
произведения также станет при 1 < г <[ -т- равным — -д-, а так как это
произведение стоит в знаменателе подынтегральной функции,
то аргумент подынтегральной функции C1) при 1<[гг<[-т-
следует считать равным-|-у, т. е. величину f(z) нужно счи-
считать чисто мнимой с положительной мнимой частью. Это значит,
что при 1<?<-t- удобнее писать:
-^-^rW-ixi-**)- C4)
причем радикал в знаменателе положителен. Без предшест-
предшествующих рассуждений нельзя было установить, справедливо ли
при 1 < г < — равенство C4) или равенство
Итак, при 1 <*¦<-?¦ имеем:
-0A-*'¦*')
f * о, | у Г dt
JYU -^(l -**¦> ~" 2 "*"' J У(р- i)(i -*V)
Если точка г движется по действительной оси от z—\ к
2 = -?•, то из C5) следует, что действительная часть С остается
постоянной и равной у, i мнимая часть положительна в уве-
§ 8] КОНФОРМНОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ 201
личивается, так как подынтегральная функция в последнем
интеграле правой части C5) положительна. Это значит, что
точка С движется параллельно мнимой оси от точки ? = ^ до
точки J = ^-j_/{oi) где <о, — несобственный интеграл
J
вычисляемый с помощью таблиц эллиптических интегралов.
Рассуждениями, аналогичными приведенным выше, можно
убедиться, что после тою, как точка г обойдет по полуокруж-
полуокружности точку -г-, аргумент f(z) увеличится еще на -»- и станет
равным 7Г, т. е. величина /(г) станет действительной и отри-
отрицательной. Это означает, что при г^>1 следует писать:
-О '
причем радикал в правой части положителен. Следовательно,
при г > 1 будем иметь:
г—Ъ.
<•— 2
Если г —» оо, то
Пользуясь подстановкой ' = ^, Л = —^ и учитывая, что
>0 при t—»оо, получим:
'202 КОНФОРМВОЕ ОТОБРАЖЕНИЕ [ifcl. VIII
в соответствии с C2). Следовательно, если г—к», то
Итак, если точка г движется по действительной оси от
я=— до z = оо, то точка С движется параллельно действи-
действительной оси от C=-?p-j-«|>iW>C = ro>!-
Продолжая аналогичные рассуждения, обнаружим, что когда
точка z движется по действительной оси от z = — оо до
z = — -г, точка С продолжает перемещаться параллельно мни-
мнимой оси от С = Л», ДО С = — -j~b"V Далее, отрезок дей-
действительной оси плоскости- z между z = — -=- и z — — 1 ото-
отобразится на отрезок, параллельный мнимой оси плоскости ?
между точками С = — у"Ь|ш« и ^=—Т1 И| накОнец» отРе"
зок действительной оси между точками z = — 1 и z = 0 ото-
отобразится на отрезок действительной оси между точками
Таким образом, если точка z пробегает слева направо всю
действительную ось (верхняя полуплоскость остается при этом
слева), то соответствую-
соответствующая точка С обходит про-
2-.«г 1(аг т ¦ тив часовой стрелки гра-
* ' +/й* ницу прямоугольника, изо-
изображенного на черт. 69.
-»- Отсюда следует, что функ-
-j- -g ция ; = tp($), определен-
определенная с помощью C0), от-
Черт. 69. ч| ображает конформно и вза-
взаимно-однозначно верхнюю
полуплоскость плоскости z на прямоугольник со сторонами
длины в), и at плоскости ;. Обратная функция z=F{Q ото-
отображает прямоугольник плоскости С на верхнюю полуплоскость
ПЛОСКОСТИ Z.
Если требуется отобразить верхнюю полуплоскость на не-
некоторый заданный прямоугольник, то сначала, пользуясь табли-
таблицами эллиптических интегралов, следует подобрать такое зна-
значение параметра fc, при котором отношение «к^ш, будет равно
§8]
КОНФОРМЙОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
203
отношению сторон заданного прямоугольника. При таком выборе
параметра k функция <р (г), определенная равенством C0), будет
отображать верхнюю полуплоскость на прямоугольник, подобный
заданному. Для того чтобы Этот прямоугольник отобразить на
заданный, достаточно воспользоваться преобразованием подобия,
а также, если это понадобится, параллельным переносом и по-
поворотом плоскости Все эти преобразования осуществляются
линейной функцией. Следовательно, функция w = с,С -f- с„
т. е.'
Cl J V(l-rt(l -*V)
при соответствующем выборе параметров А, с, и с, отображает
верхнюю полуплоскость на любой заданный прямоугольник.
Функция
'...(/— an)an~idt, C6)
действительные числа, а
4
где а,, в,, ..., а„ — произвольные
является, как в этом можно убе-
убедиться, повторяя рассуждения,
аналогичные приведенным на
стр. 197—202, аналитической и
однозначной в верхней полупло-
полуплоскости и отображает верхнюю
полуплоскость на многоуголь-
многоугольник плоскости С с углами, соот-
соответственно равными <х,п, а,тг,...
..., а„п. Вершины многоуголь-
многоугольника являются образами точек
а,,о„..., а„. Функцию C6) на-
называют интегралом Шварца —
Кристоффеля. Отображение
частный случай при
1
а, = 1
C0)
«• = •
получается из C6) как
Обозначим Л,, Аг,...,Ая (черт. 70) вершины много-
многоугольника, а 5,, С,|..ч С„—соответствующие им значения
204 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. Vll i
переменной С- Тогда длина стороны AkAk+l будет равна
о
"с
...(<-а„)«»-'Л|. C7)
Если занумеровать точки а,- так, чтобы о, < о, <... < а„, и
считать, что выбор ветвей функций (z— в*)"*" (к = 1,-2,..., л)
таков, что действительным положительным значениям z — ak
соответствуют действительные положительные значения соот
ветствующих функций, то вместо C7) можно писать:
. • • (t - «*)'»"' («*+1- <)'*+'"l -..(«„- ^~ »Л, C8)
так как интеграл в правой части C8) положителен, н знак
модуля становится излишним.
Покажем, как подбирают параметры alf at,.. .,ап для того,
чтобы многоугольник, на который с помощью C6) отображается
верхняя полуплоскость, был подобен некоторому заданному
многоугольнику со сторонами /,, /4, ... /„.
Для этого достаточно выполнения равенств
1% AtAt — I,
Левые части этих равенств в силу C8) содержат под знаками
ннтегралов неизвестные параметры avat, ...,aa. Для опре-
определения этих параметров имеем п — 1 уравнений C9). Так как
углы многоугольника axir, a,ir,..., anir заданы, то два из этих
уравнений (например, два последних) являются следствием
остальных. В самом деле, если длины всех, сторон какого-либо
8]
КОНФОРМНОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
205
многоугольника, кроме двух (например, кроме Ап_хАп и АпАА),
найдены, jo эти последние стороны можно построить (черт. 71),
пользуясь соответствующими углами. Таким образом, для опре-
определения неизвестных параметров а„ av ..., ап мы имеем лишь
п — 3 независимых уравнений. Следовательно, какие-нибудь
три параметра, например ах,аш и ап, можно выбрать произвольно.
Это вполне естественно, так как полуплоскость можно отобра-
отобразить на себя так, чтобы
какие-либо три точки, на-
например а„ ах и ап, пе-
перешли в любые другие
трн точки на действитель-
действительной оси.
После того как пара-
параметры а„ at, ...,а„ опре-
определены так, что удовлет-
удовлетворяется система C9),
функция C6) будет отоб-
отображать верхнюю полупло-
полуплоскость на многоугольник, подобный заданному многоугольнику,
имеющему стороны /,,/,,...,/„. С помощью функции w =
= CjC-t~ci ПРИ соответствующем выборе ct и сш можно затем
отобразить этот многоугольник на заданный.
Итак, задача об отображении полуплоскости на заданный
многоугольник сводится к определению параметров аа, av... ,а„_,
(параметры a1 = bv at=bt, an = bt считаем выбранными) из
системы уравнений:
•М«*1. UV ¦ • '. an-l) = Vl («2. UV ••'> пП-х)
Jt (at, a,, .... <*„_,) = Vi K. «». • • •. an-x)>
D0>
где XA = -r- — отношения длин соответствующих сторон, а
(см. C8)) '
/4=AxAt = J (t—bj* ~l {bt - 1)"-Ца,-1Г'-*...
206 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VIM
«»-¦
Укажем один из способов для приближенного решения
системы D0). Выберем какую-нибудь начальную систему приб-
приближенных значений параметров а<3°), af\ ..., d®_ l и обозначим
Jf, 40),...,4°L2 значения Jv Jt, ...,/„_, при at=af),
dJ() dJ
a4 = af\ ..., an_1^ a<J>>_ v a -^ значения ^- при тех же
значениях параметров. Пусть, далее,
%) = at-af\ V?> = at-af\ ..., Ь^^а^-а^^.
Разложив левые и правые части уравнений D0) в ряд по сте-
степеням величин д*,1) и, сохранив только первые степени этих
величин, получим:
D1)
Решив эту линейную систему относительно i^1), 8*1),...,
найдем приближенные значения параметров:
Положив, далее, 8^) = а,— а^1), 8J) = at— а^, ..., 8<2>_ (
ее,.,— а^1^, составим для поправок if>, if>, ..., 8®_
§ 8] КОНФОРМНОЕ ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ 207
аналогичную системе D1), и т. д. Этим методом можно вы-
вычислить значения at,av ...,<*„_, с любой точностью.
Применение изложенного метода требует умения приближенно
вычислять несобственные интегралы вида
(подынтегральная функция обращается в бесконечность при
t=ak и при t = ak+u поэтому к ним нельзя применять обыч-
обычные формулы приближенного интегрирования).
Здесь можно воспользоваться следующим методом Л. В. Кан-
Канторовича. Выбираем какое-нибудь число ск между ак и ак+1
и пишем Jb = Ekl-\-EH, где
"к
'... (ft,- /)-~ «
Обозначим подынтегральную функцию F(t). Имеем:
F@ = (<-a^-«T@, D2)
где
Преобразуем D2) следующим образом:
P («*) + ?'(«*)•(<-
208 конформное отображение [гл. yih.
и разобьем интеграл Eki на два интеграла Ek\ и Ек\.
4.= j (t -о*)а"-1[(Р(
?«= $ С - в») "»-* [<р @ - <р («*) - <Р' («*) С - «
Первый из этих интегралов легко вычисляется точно с помощью
неопределенного интеграла; что же касается второго, то он не
является несобственным, так как в соответствии с формулой
Тейлора выражение в квадратных скобках под знаком этого
интеграла имеет вид
где eft<CS<C* и> следовательно,
«к
Отсюда видно, что подынтегральная функция ограничена, ин-
интеграл не является несобственным и может быть вычислен по
какой-нибудь из известных формул приближенного интегриро-
интегрирования. Аналогично вычисляется интеграл Ekt.
Заметим в заключение, что интеграл Шварца—Кристоффеля
используется для приближенных конформных отображений.
Если требуется отобразить полуплоскость (или круг) на неко-
некоторую односвязную область, то подбирают многоугольник с
достаточно большим числом сторон так, чтобы ломаная, огра-
ограничивающая этот многоугольник, была достаточно близка к
границе заданной области, и заменяют приближенно функцию,
отображающую полуплоскость на данную область, интегралом
Шварца — Кристоффеля, отображающим полуплоскость на
подобранный многоугольник. Подробнее о приближенных кон-
конформных отображениях см. [5].
§ ft. Понятие о вариационных методах приближенного
конформного отображения
Конформное отображение области на круг обладает некоторыми
экстремальными свойствами, благодаря которым задачу об отображе-
отображении области на круг можно рассматривать" как вариационную и для
Приближенного решения этой задачи применять различные приближен-
§ 9] ВЛРИЛЦИОН. МЕТОДЫ ПРИБЛИЖЕН. КОНФОРМНОГО ОТОВРАЖ. 209
ные методы решения вариационных задач, например метод Ритца1).
Напомним, что идея метода Ритца в применении к функционалу
V [г (х, у)] = J J F (х, у, z (х, у), р (х, у), q (х, у)) dx dy, где р (х, у) =
D
дг , . dz *
j=-j- и q (x, y)=-^- с какими-нибудь граничными условиями заклю-
заключается в том, что значения функционала V[z(x, у)] рассматриваются
не на произвольных допустимых 'функциях данной вариационной за-
задачи, а лишь на всевозможных линейных комбинациях
л
zn = 2 a№i(x, у) с постоянными коэффициентами а,-, составленных
i=t
из функций некоторой выбранной системы w,{x,у), wt(x,y) wn (x,y).
п
При этом, конечно, предполагается, что функции ^ а,-®,- (х, у) явля-
/1
ются допустимыми в рассматриваемой вариационной задаче. На таких
линейных комбинациях функционал V[z(x, у)] превращается в функ-
функцию V[zn(x, у)] = Ф(а„ аг а„) коэффициентов а„ <xs,.... а„. Эти
коэффициенты выбираются так, чтобы функций Ф(«,, а,, ..., а„) до-
достигала экстремума. Следовательно, если коэффициенты а,, а2, ..., а_
независимы, то они должны быть определены из системы уравнений
^ = 0 ('=1.2 п).
Если при найденных из этой системы значениях а,' функция
Ф (а„ аг а„) достигает максимума или минимума, то
п
2„= 2 afl»i(x, у) дает приближенное решение вариационной задачи.
Для некоторых часто встречающихся классов функционалов при
определенном выборе функций wi(x, у) могут быть указаны оценки
погрешностей при применении метода Ритца (см. [5]).
Докажем следующее экстремальное свойство конформного ото-
отображения области на круг.
При конформном отображении w—f(z) круга \z | < R на не-
которую область G, удовлетворяющем условиям
/@)=0 D3)
/'@)=1, D4)
площадь области G больше или равна площади отображаемого
круга.
Заметим, что условию D3) при отображении круга \z\=R на
некоторую область О всегда можно удовлетворить параллельным пе-
переносом области G, а условию D4) можно удовлетворить путем изме-
') С вариационным исчислением читатель может ознакомиться по
книге [16J, а более подробное изложение приближенных методов кон-
конформного отображения можно иайти в [5J и [IV].
210 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [fJ*. VWI
нения масштаба отображаемой области, т. е. путем соответствующего
выбора радиуса отображаемого круга.
Доказательство. Разложив аналитическую внутри круга
\г | < R функцию /(г) в окрестности точки 2 = 0 в ряд Тейлора, по-
получим:
f() + * + * + + ^ + . D5)
(а.=/@)=0, а1==/'@) = 1).
При конформном отображении w=f(z) элемент площади dx dy или
в полярных координатах в dp dy приобретает множитель |/*(*)!*• так
как при конформном отображении коэффициент линейного растяже-
растяжения в точке 2 равен \f'(z)\. Следовательно, площадь S области G в
полярных координатах равна
J J
о о
J J
о о
где z=pe"t, turn
Л2
Л2«
D6)
Пусть G* — та часть области G, на которую функция /(«) ото-
отображает круг 121<г радиуса г, меньшего чем R. Площадь S* об-
области G* равна
2
J J D6а)
о о
Из D5) получим:
откуда
¦ли, полагая z = («'',
., D7)
Принимая во внимание Dба), D7), D8), получим:
Г 2* 00 00
5"«|» D9)
H
О 0 т=1 л=1
2*
Заметим, что если я /я, то Je/'"-m>V«p=ft если же в=±т, то
о
о
2»
§ 9] ВАРИАЦИОН. МЕТОДЫ ПРИБЛИЖЕН. КОНФОРМНОГО ОТОБРАЖ. 211
Следовательно, интегрируя почленно равномерно сходящиеся при
0<p=Sr (r< R) и 0^<р^2я ряды в D9j сначала по <р, а затем
по р> получим:
/¦оо оо
О я=1 п=2
или, так как а, = 1,
П=2
откуда ^
Принимая во внимание, что г можно выбрать сколь угодно
близким к /? и что площадь S области G больше площади S* облас-
областн G*, получим:
причем величина S может быть равна площади nR* отображаемого круга
лишь, если все д„ = 0 (я = 2, 3, ...), но тогда f(z) = z и отображение
/(z) является тождественным.
Доказанная теорема позволяет утверждать, что при конформном
отображении некоторой области G на область F, осуществляемом ана-
аналитической функцией, удовлетворяющей условиям D3), D4), из все-
всевозможных областей г наименьшую площадь имеет круг.
Действительно, если функции f (г) и ф(г) удовлетворяют услови-
условиям D3) и D4), то и /(z) = <i>[<p(z)] удовлетворяет тем же условиям:
/' @) = f [<р @)] ?' @) = у @) <р' @) = 1.
Поэтому конформное отображение области G на F можно рассматри-
рассматривать как результат двух последовательно совершаемых конформных
отображений <р и <|>, удовлетворяющих условиям D3) и D4), первое нз
которых отображает область О на круг, а второе отображает этот
круг на область F, и так как при втором отображении площадь мо-
может лишь увеличиваться, то наименьшую площадь из областей F бу-
будет иметь круг.
Итак, аналитическая функция f(z), удовлетворяющая условиям
D3) и D4) н отображающая область и на Круг, реализует минимум
интеграла D6), который может быть записан в виде
E0)
Искомую функцию f(z), реализующую минимум интеграла E0),
можно приближенно определить методом Ритца. Выберем систему
п -f 1 аналитических в области G и линейно независимых функция
("о (z), o»i (г), .--, wn (г) так, чтобы хотя бы одна из них, например
w,(z), была отлична от нуля в точке z = 0. Рассмотрим значение
212 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VIII
функционала E0) ие яа произвольных допустимых функциях /'(«), а
лишь на линейных комбинациях функций wk (г):
*=0
с произвольными постоянными комплексными коэффициентами
<*л = рл-|Wf*> подчиненными условию/в@)=1, т. е.
«ош,, @) + «,«;, @) + • • • + <Ы*. @)= 1, E1)
которому, в силу предположения w, @) 9= 0, всегда можно удовлетво-
удовлетворить выбором коэффициента а„:
J
^i'v/" Eia)
Подставляя вместо /' B) под знак интеграла E0) функцию
4=0
получим некоторую функцию комплексных коэффициентов ак
п п
SV»(г)] =[[?«*»*(*)?"*?*<г)rf*rfy = Z7(о.. «„..., «„)
(а0 выражено через а„ а„ ..., а„ с помощью E1а)) или функцию
Ф(Рр Р*. •••. Рп. Ti> T Tn) = ^(ai. ai <*„) действительных ко-
коэффициентов рА и Y* (*=1| 2 я).
Пользуясь основными необходимыми условиями минимума функ-
функции Ф01, Р» .... Р„, Ti. Ti Тв):
эрг*0« S^0 (ft=1>2 п)г
определим рА н т* и тем самым найдем j'n (г). Отсюда, интегрируя,
получим /„(г), причем постоянная интегрирования определится из
условия /„ @) = 0.
Заметим, что вычисление функции Ф(Р„ р„ .... р„, Тит» ••••Тл)
значительно упрощается, если функции wk взаимно-ортогональны в
области G, т. е. если \ \w/p>tdxdy = 0 при k Ф V, чаще всего в ка-
0
честве функций wk берут систему ортогональных в области G поли-
полиномов.
§ щ
ПРИНЦИП СИММЕТРИИ
213
§ 10. Принцип симметрии
Приведем без доказательства формулировку еще одной весьма
полезной теоремы теории конформного отображения, называемой
принципом симметрии (см. (9], гл. XII, § 2).
Если функция f (г), аналитическая в области G и непрерывная
на ее границе, содержащей дугу окружности (или прямолинейный
отрезок) f, отображает область 0 на некоторую область G'
так, что дуга ? Отображается на дугу- f', также являющуюся
либо дугой окружности, либо прямолинейным отрезком, то функ-
функцию f(z) можно аналитически продолжить через дугу т_ и про-
продолженная таким образом функция будет отображать пару то-
точек (из которых одна принадлежит области G) взаимно-симме-
взаимно-симметричных относительно т, в пару точек взаимно-симметричных
относительно •('.
Н
•f
ш
УУ,
/
ШШЛ
Черт. 72.
Пример 1. Найти функцию, конформно отображающую на
верхнюю полуплоскость полосу — -^ < х < -к- с разрезом вдоль от-
отрезка 0 < х < у (черт. 72).
Функция t=slnz отображает, как было показано (см. стр. 194),
полуполосу — %><х<^г,у>Ъ на верхнюю полуплоскость. При
атом отрезок @, -~) оси х переходит в отрезок @,1) действительной
оси плоскости t, отрезок (—^-, 0) оси х — в отрезок (—1, 0) дей-
действительной оси, отрезку 0 < у < оо прямой х = — -^- соответству-
ет отрезок (—оо, —1) действительной оси и отрезку 0<j;<oo
прямой х = ~ — отрезок A, оо) действительной оси плоскости t.
Применим принцип симметрии, выбрав в качестве дуги -(, о кото-
которой идет речь в формулировке принципа и через которую осущест-
214 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VIII
вляется аналитическое продолжение, отрезок —^- < х < О действи-
тельной оси (ему соответствует, как указано выше, отрезок (— 1, 0)
действительной оси плоскости t) На основании принципа симметрии
можно утверждать, что функция f = smz будет отображать нижнюю
полуполосу —5"<*<-5-,j)<0 иа нижиюю полуплоскость плос-
плоскости t (функцией, полученной аиалнтическим продолжеииен из верх-
верхней полуполосы функции sin г через отрезок (—^, 0), будет опять-
таки функция sin 2, так как эта функция является аналитической во
всей плоскости). При этом, в силу принципа симметрии, отрезку
— оо < у < 0 прямой х =—=• будет соответствовать нижний край
отрезка (— ао, — 1) действительной оси плоскости t, отрезку
— оо < у < 0 прямой х = -~— иижиий край отрезка A, оо) действи-
тельиой оси, а нижнему краю отрезка 0 < х < -^- (вдоль этого отрез-
отрезка, как сказано в условии, сделай разрез, т. е. этот отрезок входит
в границу интересующей нас области, в то время как отрезок
— тг- < х < 0, обозначенный на чертеже пунктиром, лежит внутри
этой области) — нижний край отрезка @, 1) действительной оси плос-
плоскости t. Итак, функция t = sinz отображает данную в условии задачи
область иа всю плоскость t с разрезами по действительной оси вдоль
отрезков (— оо, — 1) и @, оо).
Функция
t sinz
«склеивает» эти два разреза (в этом читатель может легко убедиться
самостоятельио) и отображает заданную область иа всю плоскость с
разрезом вдоль _положительиой действительной полуоси Наконец,
функция w = YT, т. е.
sin г -f-1
sin г
отображает заданную в условии задачи область на верхнюю полу-
полуплоскость.
Задачи к главе VIII
1. Найти функцию, отображающую конформно и взаимно-одно-
взаимно-однозначно единичный круг плоскости г иа нижиюю полуплоскость плос-
плоскости w так, что точки г=\,1, — i переходят в точки w~ 1, 0, — 1.
2 Найти функцию, отображающую конформно и взаииио-одно-
значно верхнюю полуплоскость плоскости г на единичный круг
101
ПРИНЦИП СИММЕТРИИ
215
б)
о
*j3
if
о
Im z > 1,
е/
216
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
[гл. viii
Вся плоскость с разрезом по
отрезку, соединяющему
точки 1 -j- / и 2 4- 2/.
Вся плоскость с разрезом по
биссектрисе координатного
угла от 2 = 1 -f /До z = оои
от 2 = — 1— i до 2= оо.
°\
Вся плоскость с разрезом
по отрезку, соединяющему точ-
точки 2 = 0 и t = ai.
Внешность единичного кру- Внутренность единич-
га с разрезом по мнимой оси ного Kpyi а с разрезом
от z = i до 2= оо. по радиусу от 2 = 0
до 2=1.
§10]
ПРИНЦИП СИММЕТРИИ
217
3 .К 1
*~ТК 2 ' Г'1'ri1
218 КОНФОРМНОЕ ОТОБРАЖЕНИЕ [ГЛ. VlU
плоскости. w так, что точке z = i и направлению, идущему из этой
точки параллельно действительной оси в положительную сторону, со-
соответствуют точка о> = 0 и выходящее из точки ш = 0 положи-
положительное направление мнимой оси.
3. Найти функцию w=f(z), отображающую конформно и взаим-
взаимно-однозначно единичный круг на себя и такую, что:
= 0, arg/'@) = ™.
4. Найти какую-нибудь функцию, отображающую взанмно-одио-
вначно и конформно на верхнюю полуплоскость каждую из заштри-
заштрихованных на чертежах а) — п) (стр. 215—217) областей, ограниченных
отрезками прямых и дугами окружностей.
5. На какую область плоскости w отображает функция » = cos г
полосу —y<Re«< у?
6. На какую область плоскости w отображает функция w = tjj«
полосу — -^ < Re*< ^ ?
ГЛАВА IX
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
§ 1. Плоско-параллельные векторные поля
Векторное поле
А = Ах(х, у, г, f)i + Ay(x, у, z, i)j-j-Az(x, у, z, i)k,
где /, j, k — единичные векторы, направленные по осям коор-
координат, t — время, называется плоско-параллельным, если все
векторы поля параллельны некоторой плоскости Р, причем
в точках каждой прямой,
перпендикулярной к этой
плоскости, в любой фи-
фиксированный момент време-
времени i векторы поля равны
(черт. 73).
В дальнейшем мы бу-
будем считать плоскость
XOY параллельной пло-
плоскости Р. Тогда
Ав(х, у, z,t) =
= Ах(х,у,
—?. —=t —*- -*- —•- -^
(х,у, О У.
Черт. 73.
Очевидно, что изучение
плоско-параллельного векторного поля сводится к изучению
плоского векторного поля в плоскость Р или в любой другой
параллельной ей плоскости.
Векторное поле называется стационарным, если оно не из-
изменяется с течением времени.
220 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. IX
В этой главе мы будем рассматривать лишь плоские (или
плоско-параллельные) стационарные векторные поив:
A)
Точку (х, у) в плоскости XOY можно характеризовать
комплексным числом z — x-\-iy, а вектор А = Ах(х, уI-\~
-\-Ay(x,y)j—комплексным числом w = Ax(x, у)-{-iAy(x, у).
Поэтому наряду с записью A) вектор А можно представлять
в виде
A = Ax(x,y) + iAr(x,y). (la)
Следовательно, векторное поле A) можно задать, указав две
функции действительных переменных Ах(х,у) и A, (jc, _у)илн
одну функцию комплексного переменного <f(z) — Ax(x, У)-{-
+ iAy(x,y).
§ 2. Комплексный потенциал
Напомним некоторые понятия векторного анализа (см. [2],
гл. Х111 или [3], ч. И, гл. IV) в применении к плоским ста-
стационарным векторным полям A) или в комплексной форме Aа).
Проекции Ах (х, у) и Ау (х, у) вектора А в области их опре-
определения будем считать непрерывно дифференцируемыми функ-
функциями, за исключением, быть может, конечного числа точек.
Циркуляцией вектора поля А вдоль замкнутого контура С
называется криволинейный интеграл
>.-]¦
где As — проекция вектора А (х, у) на положительное направ-
направление касательной к дуге С в точке (х, у) (положительное
направление на касательной соответствует положительному на-
направлению обхода дуги С), ds— элемент дуги кривой С. Ес-
Если ввести *вектор ds = idx-\-]dy (или в комплексной форме
ds=dx-\-idy), то скалярное произведение
(А• ds) = AJs = Ax(x,y)dx + Ay(x, у)dy
ш
Гс = J (А. if») = J Ах (х, у) dx + Ау (х, у) dy. B)
Если в некоторой односвязной области циркуляция по лю-
любому замкнутому контуру равна нулю, ,то подынтегральное вы-
§ 2] КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ 221
ражение Ах (х, у) dx -\- Ау (х, у) dy в этой области является
полным дифференциалом некоторой функции и(Х, у), называе-
называемой потенциальной функцией. По отношению к функции
и (х, у) вектор А называется градиентом и (х, у) и обозна-
обозначается
(x, у).
Справедливо и обратное утверждение: если в B) подынте-
подынтегральное выражение Ах (х, у) dx -f- Ау (дг, у) dy является пол-
полным дифференциалом некоторой функции а(х, у) в односвяз-
ной области О:
du=Ax(x, y)dx-\-Ay{x, y)dy,
т. е.
то циркуляция по любому замкнутому контуру С в этой об-
области равна нулю.
В рассматриваемом случае, т. е. при A = grauu(x, у),
векторное поле называется безвихревым или потенциальным.
Для того чтобы в B) подынтегральное выражение
Ах (х, у) dx-f- Ay (x, y)dy являлось полным дифференциалом и,
следовательно, поле А = Ах(х, у) i-\-Ay(x,y)j было бы по-
потенциальным, как известно, необходимо и достаточно, чтобы
дАх(х,у) _ дАу (х, у) „
ду = дх ' <3>
Если условие C) выполняется во всех точках рассмат-
рассматриваемого поля, за исключением конечного числа точек zt,
в которых условие C) нарушается или теряет смысл из-за
обращения в бесконечность хотя бы одной из производных
-^?- и -ft*-, то циркуляция по замкнутому контуру С, обхо-
обходящему какую-нибудь из этих точек или группу таких точек,
может быть отличной от нуля. Если циркуляция по контуру С,
ограничивающему область D, внутри которой находится лишь
одна из этих точек zt, отлична от нуля, то точка 2, назы-
называется вихревой точкой. Если при этом контур С однократно
обходит точку г{ в положительном направлении, то число Гс
называется интенсивностью вихря в точке г{.
222 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. ПС
Потоком вектора поля А через замкнутую или незамкну»
тую кривую С называется криволинейный интеграл
где ds — элемент дуги кривой С, а Ап— проекция вектора
А(х,у) на положительное направление нормали к кривой С
в точке (х, у).
Вектор dn, направленный по нормали к кривой С в точке
(х, у) и по длине равный вектору ds = ldx-\-jdy, направ-
направленному по касательной к той же кривой, можно записать
в виде
— jdx).
Выбрав какой-нибудь из двух знаков перед скобкой в правой
части равенства, мы установим положительное направление на
нормали. Условимся в дальнейшем брать знак-j-, тогда dn=
s=ldy—Jdx. При этом условии для замкнутого контура С
с -направлением обхода против часовой стрелки вектор dn
направлен по внешней нормали к коцтуру С.
Так как
Ands = (А ¦ dn) = Ах (х, у) dy — Ау (х, у) dx,
Nc = S Ands = S (Л • dn) = S Ax (x, у) dy - Ay (x,y) dx. D)
с с с
то
Если в некоторой области поток вектора через любой замк-
замкнутый контур С равен нулю, то подынтегральное выражение
Ах{х, y)dy — Ау (х, у) dx в D) является полным дифферен-
дифференциалом некоторой функции v(x, у), называемой функцией
тока (это название связано с гидродинамическим смыслом
функции v, см. стр. 227):
dv = Ах (х, у) dy — Ау (х, у) dx;
дх~==~
В этом случае поле называется соленоидальным.
Необходимым н достаточным условием соленоидальности
поля является
дАу(х,у)_дАх(х,у)
§ 2] КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ 223
или
дАх(х,у} ¦ дАу(х, у) _ 0 ...
дх ' ду ' * '
Если условие соленоидальностн E) выполняется во всех точ-
точках рассматриваемого поля, за исключением конечного числа
точек г„ в которых условие E) нарушается или теряет смысл
из-за обращения в бесконечность хотя бы одной нз производ-
производных ¦—*• ' У' или —^ '^ , то поток вектора поля через
замкнутый контур, внутри которого содержатся точки zt, мо-
может быть отличным от нуля.
Если поток вектора поля Nc через замкнутый контур С,
ограничивающий область, в которой содержится лишь одна нз
этих точек г,, огличен от нуля, то точка г( называется ис-
источником, если Л/с>0, н стоком, если NC<C.O. При этом
предполагается, что контур С обходится в положительном на-
направлении, т. е. при обходе контура С точка z{ остается
слева. Если контур С однократно обходит точку zt в положи-
положительном направлении, то число Nc называется производитель-
производительностью или интенсивностью источника (если Л/с>0) или
стока (если Nc<0). Если в области D, ограниченной конту-
контуром С, не проходящим через точки z{, содержится несколько
точек zt, то поток вектора поля Wc через контур С, одно-
однократно проходимый в положительном направлении, равен алгеб-
алгебраической сумме производительностей всех источников и сто-
стоков, находящихся в области D.
Аналогичная теорема, являющаяся следствием свойств кри-
криволинейных интегралов от полных дифференциалов, конечно
справедлива н для циркуляции по контуру С в потенциальном
поле с конечным числом вихревых точек.
Предположим, что поле Л (х, у\ потенциально и соленон-
дально и, следовательно, существуют потенциальная функция
и{х,у) и функция тока v(x, у), определяемые с точностью
до постоянных слагаемых своими полными дифференциалами:
da = Ах (х, у) dx-\-Ay {x, у) dy
и
dv = Ах (х, у) dy — Ау (х, у) dx.
Рассмотрим функцию комплексного переменного f{z) =
= u(x,y)-\-iv{x,y), называемую комплексным потенциа-
потенциалом. Функции и(х, у) и v(x,y) удовлетворяют условиям
224 комплексный потенциал [гл. ix
Эйлера —Даламбера
ди dv да dv
дх ду ду дх '
так как
dv л I \ dv . . .
¦5? = — ААх>У)'ду =Ах(х> У)-
Следовательно, комплексный потенциал f{z)^=u-\-iv ««-
ляется аналитической функцией..
Весь превосходно разработанный аппарат теории аналити-
аналитических функций может быть использован для изучения по-
тенциально-соленоидальных векторных полей, если их описывать
с помощью комплексного потенциала.
Если известен комплексный потенциал / (z) = и {х, у) -\-
-\-iv{x, у), то соответствующее ему векторное поле А =
г=Ах(х, y)-\-iAy(x, у) легко определяется, так как
Принимая во внимание, что
ох * ох * у
получим:
А = Ах (х, у) + 1Ау (х, у) =7п). F)
Следовательно, \А(х, y)\ = \f(z)\, а аргумент вектора
А (х, у) отличается от аргумента вектора f (z) знаком (так
как arg/(z) = — arg/(z)). Линии уровня функций и и v:
а(х, у) = с, и v(x, y)=ct,
образуют ортогональную сеть, так как их образами в плоско-
плоскости w при сохраняющем углы конформном отображении w=f(z)
являются взаимно-ортогональные семейства прямых, параллель-
параллельных осям координат u = ct и v=ct. Линии уровня функции
и(х, у) ортогональны вектору поля, так как вектор поля А
является градиентом функции и(х, у):
Следовательно, вектор поля А (х, у) направлен по касательным
§ 2] комплексный потенциал 225
к линиям уровня v(x,y) = ct, т. е. линии уровня функции
v {х, у) являются векторными линиями рассматриваемого вектор-
векторного поля.
Заметим, что
/' (z) dz = J [Ах (х, у) - iAy (х, у)] (dx + / dy) =
о
= J К (*, У) dx + Ау (х, у) dy] + / J [Ax (x, у) dy -
с с
где С—замкнутый контур (см. B) и D)).
Во многих прикладных задачах приходится изучать по-
тенциально-соленоидальные векторные поля с изолированными
особыми точками zh т. е. точками, в которых не выполнены
дАх dAv
условие потенциальности -^-=-~^. или условие соленоидаль-
ности -=^--\—л*~~®- Среди то*чек г( могут быть вихревые
точки, источники и стоки. Могут быть вихревые точки, кото-
которые одновременно являются источниками или стоками; такие
точки называются вихреисточниками или вихрестоками. Мо-
Могут быть также и иные особые точки, например особые точки,
получающиеся от слияния источника со стоком равной беско-
бесконечной интенсивности (см. стр. 231).
Заметим, что если условия потенциальности C) и соленои-
дальности E) выполнены в многосвязной области О, то потен-
потенциальная функция и(х,у) и функция тока v(x, у) могут быть
многозначными.
Действительно,
(ж. у)
S Ax(x,y)dx + Ay(x,y)dy, G)
v(x,y)= J Ax(x,y)dy — Ay(x,y)dx, (8)
(«о, У о)
но в случае многосвязной области G криволинейные интегралы
от полных дифференциалов могут до некоторой степени зави-
зависеть от пути интегрирования, соединяющего заданные точки
P(xv У о) и ^(-v> УЬ —9ТИ интегралы совпадают при измене-
изменении пути интегрирования лишь с точностью' до слагаемого,
226 комплексный потенциал [гл. is
равного линейной комбинации с целым» коэффициентами не-
некоторых постоянных, называемых циклическими постоянными
(см [12J, гл. Ill, § 2).
На черт. 74 изображена двухсвязная область: круг, из ко-
которого удалена точка М.
Если точка М является вихревой
точкой, то криволинейные интегралы G),
взятые по путям С, и С8, очевидно, бу-
аут отличаться на не равную нулю
хиркуляцню вектора А по замкнутому
контуру С, однократно обходящему
точку М. Точно также, если точка М
является источником (или стоком), то кри-
криволинейные интегралы (8), взятые по
Черт. 74. путям С, и С1Ч будут отличаться на ве-
величину потока вектора через упомяну-
упомянутый выше замкнутый контур С, т. е. на производительность
источника (или стока), находящегося в точке М.
§ 3. Комплексный потенциал в гидродинамике
Рассмотрим поле скоростей A (х, у) = Ах (х, у) I -\- Ay (x,y)J
стационарного плоско-параллельного движения несжимаемой
жидкости в области, не имеющей источников или стоков жид-
жидкости.
В рассматриваемом случае поток Nc = J Ands вектора ско-
с
рости А(х,у) через некоторую кривую С по абсолютной ве-
величине равен в соответствующих единицах количеству жид-
жидкости, протекающей в единицу времени через кривую С1).
Если в области D, ограниченной замкнутым контуром С, не!
источников и стоков, то, в силу несжимаемости жидкости, ее
количество внутри контура С не может изменяться и, следо-
следовательно, количество втекающей в область D жидкости равно
количеству вытекающей жидкости, т. е. поток вектора скоро-
скорости через замкнутый контур С равен нулю — поле соленой-
дально.
') Точнее, количеству жидкости, протекающей через цилиндричв'
скую поверхность единичной высоты с образующими, параллельный!
оси Oz, проекцией которой иа плоскость Оху является кривая С.
§ 3] КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ГИДРОДИНАМИКЕ 227
Если к тому же рассматриваемое поле скоростей движе-
движения несжимаемой жидкости потенциал ьио, то для его изучения
целесообразно ввести комплексный потенциал
f(z)=u(x,y)-\-iv(x,y).
При этом векторными линиями v=e в данном случае будут
линии тока жидкости, так как касательный к ним вектор Л
является вектором скорости течения. Отсюда и происходит наз-
название 'функции v — «функция тока». Названия «источник»,
«сток», «производительность» источника или стока также заим-
заимствованы из рассматриваемой в этом параграфе гидродинами-
гидродинамической интерпретации векторного поля.
Пример 1. Найти поле скоростей движения несжимаемой жид-
жидкости, комплексный потенциал которого равен ах, где действитель-
действительное число а > 0.
Функция w=az является аналитической во всей плоскости к,
следовательно, ее можно рассматривать как комплексный потенциал
движения несжимаемой жидкости, в котором отсутствуют вихревые
точки, источники, стоки и другие особые точки.
Так как
¦ а — число действительное и положительное, то вектор скорости
параллелей действительной оси, направлен в положительную сторону
¦ по длине равен а во всех точках плоскости.
П р н м е р .2. Найти поле скоростей движения несжимаемой жид-
жидкости, линии тока, линии уровня потенциальной функции (эквипотен-
(эквипотенциальные линии), зная комплексный потенциал
w = Laz.
Для течения жидкости, определяемого комплексным потенциалом
w = Ln z,
особой точкой является начало координат, так как 2=0 являете*
особой точкой функции
~dz~Th
Длина вектора скорости Л в точке г в соответствии с F) равна
•) Предполагается, что при дифференцировании выбирается не-
непрерывная ¦ окрестности точки *(*?0) ветвь функции-Ln ж (см.
стр. 192).
228
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[гл. и
Следовательно, модуль вектора скорости обратно пропорционален рас-
расстоянию точки от начала координат.
Угол а, образованный направлением вектора скорости и положи-
положительным направлением оси Ох, согласно F), равен
Ag
и следовательно, направление вектора скорости в точке г совпадает
с направлением луча, идущего из начала координат в эту точку.
Очевидно, линиями тока являются лучи, выводящие из начала
координат (черт. 75), а ли-
линиями уровня потенциальной
функции — ркружности с
центром в начале коор-
координат.
К тому же выводу мож-
можно было бы прийти, выделив
из комплексного потенциала
потенциальную функцию и
функцию тока:
и -f- iv = Ln г=
откуда (z = ре'4)
и=1п |z| = !np,
v = Arg z = <p.
Следовательно, линии уровня
потенциальной функции р =
Черт. 75 =Ci, а линии тока ? = 0,F, и
с, — постоянные).
Начало координат является источником. Так как других особых
точек нет, то для подсчета количества жидкости, производимого этим
источником в единицу времени, достаточно подсчитать поток через
любой простой замкнутый контур, содержащий начало координат.
Выбрав в качестве такого контура окружность С радиуса г с центром
в начале координат, получим'
с с
/так как на окружности С всюду Ап = \А\=—\.
Пример 3. Найти поле скоростей движения несжимаемой жид-
жидкости, линии тока и эквипотенциальные линии, зная комплексный по-
потенциал w = iLnz.
Для комплексного потенциала
единственной особой точкой является начало координат. Пусть А —
вектор скорости, а а — угол, образованный этим вектором с положи-
§ 3]
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ГИДРОДИНАМИКЕ
229
тельным направлением действительной оси. Тогда
л*1 |Я|-
Модуль вектора скорости обратно пропорционален расстоянию точки
от начала координат, а направление вектора скорости (черт. 76) пер-
перпендикулярно к лучу, соединяющему точку с началом координат, т. е.
совпадает с направлением касательной к окружности с центром вна-
вначале координат, проходящей через данную точку. Отсюда следует,
что линиями тока являются окружно- п
ста с центром в начале координат, а
линиями уровня потенциальной функ-
функции—лучи, выходящие из начала ко-
координат. К этому же выводу можно
бы было прийти, выделив из комплек-
комплексного потенциала потенциальную функ-
функцию и функцию тока.
Начало координат является вих-
вихревой точкой. Для того чтобы вы-
вычислить циркуляцию вектора А по кон-
контуру С, обходящему вихревую точку,
проще всего взять в качестве кон-
контура С окружность с центром в
начале координат произвольного
радиуса г. Вектор скорости карателен
Черт. 76.
этой окружности и
(отрицательный знак указывает на то, что движение происходит по
часовой стрелке). Следовательно,
Г= С Asds=— Г -<& = — 2я.
Г
=— Г -<& =
X Г
Пример 4. Найти линии тока движения несжимаемой жидко-
жидкости, если комплексный потенциал равен (a-\-bi)Lnz.
Из примеров 2 и 3 следует, что в движении, определяемом комп-
комплексным потенциалом
w = (а + Ы) Ln я,
где а и b — действительные постоянные, начало координат является
вихреисточником (если а > 0, b Ф 0) или внхрестоком (если а < 0,
b Ф 0), причем поток через контур, окружающий начало координат,
равен 2тса, а циркуляция равна — 2кЬ.
Линиями тока являются логарифмические синралн (черт. 77). Дей-
Действительно,
w=(a -f- W) Ln г=(о -f- bl) (In p + if) =
, рде ,z = pe'*.
функция тока имеет вид
230
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[гл. *х
и линии тока определяются уравнением
ftlnp-f-a<p=c, где с — постоянная,
или
откуда
Пример 5. Найти линии тока, эквипотенциальные линии я
особые точки движения несжимаемой жидкости, если комплексный
потенциал равен —.
Черт. 77.
Движение, определенное комплексным потенциалом
шеет единственную особую точку 2=0.
Так как
dw _ 1
то в прежних обозначениях получим:
Уравнение семейства линий тока
=c, где с—постоянная,
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ГИДРОДИНАМИКА
231
ВДВ
или
Линиями тока (черт. 78) являются окружности с центрами иа оси Оу,
касающиеся оси их. Аналогичные вычисления показывают, что ли-
линиями уровня потенциальной функции (на черт. 78 они обозначены
пунктиром) являются окружности (х — cf -\- у* = с1 с центрами на оси
Ох, касающиеся оси Оу.
Легко убедиться в
юм, что жидкость дви-
движется по линиям тока в
указанном на черт. 78
направлении. Для этого
достаточно подсчитать ве-
величину угла а между век-
вектором скорости А и поло-
положительным направлением
оси Ох, например для то-
точек, лежащих иа мнимой
оси, т..е. для точек г, у
которых arg г=± -*-.
Заметим, что комп-
комплексный потенциал
La(z + h) — Ln*
Черт. 78.
при действительном положительном h определяет течение жидкости
с источником в точке — я (см. пример 2), производящим в единицу
2я
времени количество жидкости, равное -т- , и стоком в начале коорди-
координат, поглощающим такое же количество жидкости. Так как
llmLn(*-H)-Ln*= (LM, = lt
а-+о я г
то начало координат в течении жидкости, определяемом комплексным
потенциалом а>=—, можно рассматривать как точку, в которой
совмещены сток и источник одинаковой «бесконечно большой» про-
производительности. Такую точку называют диполем1).
") Впрочем, диполь можно рассматривать также, как точку, в
которой совмещены две вихревые точки с одинаковыми бесконечно
большими, но противоположными по знаку циркуляциями, так как ве-
величину h можно считать мнимой (сн пример 3).
232 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. IX
Нетрудно непосредственным вычислением проверить, что поток
через любой замкнутый контур, окружающий диполь и не содержащий
других особых точек, и циркуляция по такому контуру равны нулю,
§ 4. Задачи на обтекание
В задачах на обтекание требуется определить комплексный
потенциал плоско-параллельного поля скоростей безвихревого
течения несжимаемой жидкости, обтекающего заданные покоя-
покоящиеся в жидкости цилиндрические твердые тела, образующие
которых перпендикулярны к плоскости векторного поля (можно
считать также, что эти цилиндрические тела движутся в по-
покоящейся жидкости в направлении, перпендикулярном к обра-
образующим цилиндрических поверхностей).
Очевидно, течение жидкости не определяется одной только
формой обтекаемых тел, поэтому для единственности решения
задачи на обтекание необходимо, кроме формы обтекаемых тел,
задать еще некоторые добавочные условия.
1. Течение в криволинейной полуплоскости. Рассмотрим
самонепересекающуюся гладкую кривую С в обе стороны уда-
удаляющуюся в бесконечность (это означает, что при движении
точки z по кривой С в любую сторону г стремится к беско-
бесконечности). Эта кривая разбивает плоскость на две области
Dx и D% (черт. 79), называемые криволинейными полуплоско-
полуплоскостями.
4
Черт. 79.
Задача заключается в том, чтобы в одной из этих областей
(например, D,) определить комплексный потенциал поля ско-
скоростей безвихревого течения несжимаемой жидкости, в кото-
котором отсутствуют источники и стоки, обтекающего кри-
кривую С.
Так как в точках кривой С вектор скорости должен быть
направлен по касательной к этой кривой, то кривая С должна
быть линией тока искомого поля скоростей v(x%y)=v%t tte-
vt постоянно.
§ 4] ЗАДАЧИ НА ОБТЕКАНИЕ 233
Так как функция тока v(x,y) определяется по своим част-
частным производным:
д?=-Ау(х, у) * ру=Ах(х, у),
то она определяется лишь с точностью до постоянного сла-
слагаемого. Следовательно, можно считать г>0 = 0.
Итак, искомый комлексный потенциал w=u(x,y)-\-iv(x,у)
должен отображать кривую С в
прямую v=0, а следовательно,
область D1 должна отобразить-
отобразиться в полуплоскость г; > 0 (или
Существует (см. стр. 158—159)
бесконечное множество аналити- -я lA A
ческих функций, осуществляю- „ fl
щих указанное отображение. еРт* '
Чтобы задача стала вполне определенной, необходимы добавоч-
добавочные условия.
В задачах гидродинамики такимн условиями обычно являются
задание модуля вектора скорости в бесконечности, т. е. зада-
задание!/ {z)\ при z=oo, и требование /(оо)=оо.
Рассмотрим в качестве примера безвихревое течение жид-
жидкости (без источников и стоков), обтекающей линию, состав-
составленную из луча — оо <[ х «g — /?, верхней полуокружности
радиуса R с центром в точке г=0 и луча /?^*<оо, в
области G (черт. 80), расположенной выше этой линии. В со-
соответствии со сказанным выше комплексный потенциал w=f(z)
такого течения должен отображать границу области О на дей-
действительную ось, а область G—на верхнюю (или нижнюю)
полуплоскость. Скорость в бесконечности будем считать за-
заданной и равной числу v^ («о, — действительное число, так как,
в силу условий задачи, скорость в бесконечности направлена
по действительной оси).
Область G ограничена дугой окружности и частью прямой,
поэтому с помощью дробно-линейной функции, отображающей
одну из общих точек в бесконечно удаленную точку, она отек
бразится на внутренность угла (прямого, так как углы при
отображении сохраняются). Такой функцией является, напри-
например, функция e_ff
(9)
8* Г. Л. Луиц и Л. Э. Эльсгольц
234 комплексный потенцилл [гл. к
отображающая точку R в точку 0, • точку — R в точку оо.
Так как при этом точка z=Ri, лежащая на верхней полу-
полуокружности, переходит в точку
то полуокружность отображается на положительную часть мни-
мнимой оси плоскости t. При движении точки z от точки R (соот-
(соответствующей точке t=0) к точке Ri отображаемая область
остается справа, а так как при этом точка i движется по мни-
ной оси вверх (от t=sO к i=i), то функция (9) отображает
область G на первую четверть плоскости t, а функция
отображает область О на верхнюю полуплоскость. Следова-
Следовательно, функции, отображающие область О на верхнюю (или
нижнюю) полуплоскость, имеют следующий вид (см. стр. 167);
aT+b_
~'T+d~
где a, b, c, d—действительные постоянные. Так как при z—
= оо по условию
das
то степень многочлена, стоящего в знаменателе, должна быть
ниже степени многочлена, стоящего в числителе. Следовательно,
c-\-d=0 (если числитель и знаменатель являются многочле-
многочленами второй степени относительно z, то -г- имеет вид дроби,
числитель которой 3-й степени, а знаменатель 4-Й степени
относительно z и, следовательно, -т- = 0 при z—оо). За-
ыетиы, что при c-f-d=O условие /(оо) = оо будет выпол-
выполнено, если а-\-ЬфО.
§ 4] 8АДАЧИ НА ОВТЕКАНИЕ 235
Итак,
*> 2(d-c)Rz =
где
*__«+*_. й-*~д
*—2(d-c)R' ?-~7=Ът
Отсюда
dw „ aR*
_ = « — ¦р-,
dw
причем, так как — = tf00 при г=оо, то аг^г^.
Если учесть, что комплексный потенциал определяется лишь
с точностью до постоянного слагаемого (так как скорость те-
течения определяется производной комплексного потенциала), то
можно считать р = 0 и окончательно
. A0)
dw f, В*\
Так как jj=t»oof 1 — ?)> т0 модуль вектора скорости
определяется равенством
В точках z=+f? скорость равна нулю; такие точки назы-
называются критическими.
Отделив в (Ю) мнимую часть от действительной, опре-
определим функцию тока:
откуда
Следовательно, семейство линий тока определяется уравнением
236
или
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[гл. я
Линии тока (черт. 81) симметричны относительно оси Оу в
имеют асимптоты, па-
параллельные оси Ох.
2. Течение в кри-
криволинейной полосе.
Рассмотрим криволиней-
криволинейную полосу D(черт. 82),
ограниченную двумя
гладкими кривыми С, и
Черт. 81. Ct, пересекающимися
лиц!ь в бесконечности.
Задача опять заключается в определении в полосе D поля ско-
скоростей стационарного течения несжимаемой жидкости, обтекаю-
обтекающего кривые С, и Ct, или комплексного потенциала этого поля.
Так как кривые С, и С, должны быть линиями тока искомого
течения жидкости, то комплексный потенциал отображает линии
С, и С, на прямые v=v0 и v=vr. Опять без ограничения
общности можно считать vo==O. Следовательно, определение
искомого комплексного потенциала сводится к нахождению ана-
аналитической функции, отобра-
отображающей заданную криволи-
криволинейную полосу D на . прямо-
прямолинейную полосу, ограничен-
ограниченную прямыми v=0 и v=vx.
Конечно, для однознач-
однозначного определения комплекс-
комплексного потенциала необходимы церт 32.
добавочные условия. Такими
условиями в гидромеханике обычно являются задание расхода
жидкости, т. е. потока N вектора скорости, .через кривую у,
соединяющую кривые С, и С, (черт. 82), и требование огра-
ограниченности скорости при Z-* оо.
Заметим, что задание расхода жидкости N определяет
значение •»,. Действительно (см. стр. 222),
Nf= S Ах (х, у) йу— Ау {х, у)их— 5 dv=v1—v0=vt,
так как «,= 0.
§¦]
ЗАДАЧИ НА ОВТЕКАНИВ
237
Пример. Найти комплексный потенциал течения жидкости в
канале, берега которого (черт. 83) имеют форму парабол х=у*—i-
У*
и *=^f — 1. если расход жидкости равен Q.
Функция ю = УТ(см. стр. 22) отображав г криволинейную полосу
между параболами х=у1—j
и х=-т — 1 в полосу между
ПРЯМЫМИ » = тг И 0=1.
Здесь о»—ов=1 — тг — -гг.
Следовательно, функция w =
а= УТявляется комплексным
потенциалом течения жидко-
жидкости в заданном канале, когда
1
расход жидкости равен —.
Функция w—2Q У~2, со-
соответствующая расходу Q,
дает решение поставленной
задачи.
3. Обтекание замкну-
замкнутого контура. Найдем сна-
сначала комплексный потен-
потенциал плоско-параллельного Черт. 83.
течения жидкости, обте-
обтекающей круговой цилиндр радиуса R, предполагая, что в
плоскости, перпендикулярной к, оси цилиндра, течение сим-
симметрично относительно некоторой прямой, проходящей через
центр сечения цилиндра, а скорость в бесконечности направ-
направлена параллельно оси симметрии и равна V&.
Выберем систему координат так, чтобы начало координат
находилось в центре сечения цилиндра, а направление скоро-
скорости в бесконечности совпадало с положительным направлением
оси Ох. (черт. 84). № условий задачи следует, что линия,
составленная из отрезка —оо<*«5—R действительной
оси, верхней полуокружности радиуса R с центром в точке
z = 0 и отрезка R*^x<^oo, должна быть одной из лШшй
тока, и следовательно, дело сводится к задаче, уже решенной
238
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[ГЛ. IX
на стр. 23$—235. Таким образом, комплексный потоптал в
рассматриваемой задаче равен
(?) (Щ
Найдем более рбшее решение задачи. Выше было показано
(пример 3 на стр. 228—229), что функция
является комплексным потенциалом течения с вихревой точкой
в начале координат и циркуля-
циркуляцией, равной —2гс. Линиями
тока в этом случае являются ок-
окружности с центром в начале
координат. Для комплексного
потенциала
Г
Черт. 84 величина циркуляции вокруг вих-
вихревой точки в начале коорди-
координат равна Г, а скорость в бесконечности равна нулю. Так как
цилиндр радиуса R с центром в начале координат обтекается
каждым из течений, определяемых комплексными потенциалами
A0) и A1), то течение с комплексным потенциалом
A2)
будет также обтекать этот цилиндр. Скорость такого течения
в бесконечности параллельна действительной оси и равна г»»,
циркуляция вокруг начала координат равна Г.
Найдем критические точки, т. е. точки, в которых скорость
равна нулю:
вли после преобразований
откуда
A3)
(И)
ЗАДАЧИ НА ОБТЕКАНИЕ
239
.. |ag;R. то радикал в правой части последнего ра-
ренства принимает действительные значения и в критических
точках
Следовательно, в рассматриваемом случае обе критические
точки находятся на окружно-
окружности Jz\ = R, причем, как
видно из A4) и A5),
Г
¦*¦*
где <р —¦ аргумент критиче-
критической точки (черт. 85). В ча-
частности, в случае рассмот-
рассмотренного в начале этого пара-
параграфа потока без циркуляции
(Г = 0) критическими точ-
точками являются точки z = ¦+-/?.
Черт. 85.
Критические точки делят окружность \z\ = R на две дуги
/ и /; в одной из критических точек (точке разветвления)
линия тока разветвляется на две: одна идет по дуге /,, дру-
другая по дуге / ; во второй критической точке (точке схода)
Черт. 86.
эти линии опять соединяются. Если известны величина и на-
направление скорости в бесконечно удаленной точке, то, как
видно из формулы A6), положение точки разветвления (или
точки схода) определяет величину циркуляции Г.
240
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[гл. не
Ml
Если -А— =#, то обе критические точки совпадают (черт.
86,а) и окружность \z\ = R становится замкнутой линией тока.
равенство A4) принимает вид
При
и модуль одного из критических значений больше, чем R.
В силу известного свойства корней квадратного уравнения, из
A3) следует, что произ-
произведение модулей критиче-
критических значений равно R*,
поэтому модуль второго
критического значения
меньше, чем R, и в это»
случае вне цилиндра рас-
расположена только одна кри-
критическая точка. Проходя-
Проходящая через нее замкнутая
Черт. 87.
линия тока отделяет замкнутые линии тока от незамкнутых
(черт. 86, б).
Если С—заданный замкнутый контур (черт. 87), а функ-
функция t=y(z) отображает внешность контура С взаимно-одноз-
взаимно-однозначно и конформно на внешность круга радиуса R с центром
в начале координат, то в соответствии с A2) функция
w=vao[<f(z)+ ^]
является комплексным потенциалом течения, обтекающего С.
С помощью функции t = y(z) линии тока течения, обтекаю-
обтекающего в плоскости г контур С, отображаются на линии тока
течения, обтекающего в плоскости t круг радиуса R; точка
t = oo является при этом общей для всех линий тока. Потре-
Потребовав, чтобы (р(оо) = оо, мы получим в плоскости г течение,
обладающее тем же свойством. Если потребовать еще, чтобы
<р'(оо)=Г), то скорость течения, определяемого комплексный
') Аналитическая функция, отображающая одну односвазную об-
область на другую, определяется однозначно (см. стр. 159), если задать
в какой-либо точке отображаемой области значение отображающей
функции и аргумент ее производной. Поэтому для определения едим»
ственной функции <=<р(г), отображающее внешноегь контура С на
ЗАДАЧИ НД OBtBKAKHB
241
потенциалом A7) в бескшечао удаленной точке, окажется рав-
равной fdo. так как
dw\
dz
dt
dt
<=00
В качестве примера рассмотрим обтекание профилей Жуковского.
На стр. 188 было показано, что функция
08)
отображает внешность профнля Жуковского на внешность круга радиу-
радиуса J?=y"a*-f-Al-f-rf с центром в точке
А я
(черт. 88).
Из A8) имеем;
в .. Г
Следовательно, функция
Черт88
удовлетворяет условиям <р(оо)= со, <у'(оо)= 1 и отображает внешность
профиля Жуковского на внешность круга радиуса у(у a*4-*f-t-d)
с центром в начале координат. Подставив A9) вместо <р (г) в формулу
A7), найдем комплексный потенциал течения, .обтекающего профиль
Жуковского и имеющего в бесконечности скорость «», направленную
по положительному направлению действительной 'оси. Остается толь-
только определить циркуляцию Г. Для этого воспользуемся условием Чап-
Чаплыгина, в силу которого при обтекании контура с острием (т. е. с
внешность данного круга 111 > R, достаточно, кроме равенства <р(оо) =
= оо, задать только аргумент числа <р'(оо), например считать этот
аргумент равным нулю, т. е. считать «р' (да) действительным положи,
тельным числом. Следовательно, вообще говоря, невозможно найти
функцию <f(z), осуществляющую требуемое отображение и удовлетво-
удовлетворяющую условиям
в(оо)=со,
(а)
если считать радиус круга R в плоскости * заданным, но можно найта
такой радиус R, при котором условия (а) будут выполнены. При этом
число К в равенстве A7) определяется из условий (а).
8 Г. Л. Луяц а Л. Э. Эльсгольц
242 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. IX
точкой, в которой усол между касательными меньше, чем it) точка
схода смещается в острие. Так как
aig(a-M)=-arctg-?,
10
а - Ы=
я с помощью функции A9) острие профиля Жуковского (z=a) ото-
отображается в точку
= ^-D-Г.) = 1 (в _
Следовательно, аргумент точки схода в плоскости / равен — arctg —•.
Подставив это значение вместо <? в формулу A6), получим:
ж так как
то окончательно
§ б. Теорема Н. Е. Жуковского о подъемной силе
Выведем сначала формулу С А. Чаплыгина для величины подъем*
ной силы, действующей на крыло самолета. При скоростях, меньших
скорости звука, можно, как известно, воздух считать несжимаемой
жидкостью. Для удобства предположим, что крыло самолета, про-
профиль С которого изображен на черт. 89'), покоится, а окружающий
его воздух движется. Это движение будем считать установившимся
м безвихревым в области G, внешней к контуру С, и на контуре С и
1) Мы считаем крыло, имеющим форму цилиндра; на черт. 89 да-
яо сечение этого цилиндра плоскостью, перпендикулярной к его обра-
образующей. Вычнсдевия ведутся для цилиндра единичной высоты.
ТЕОРЕМА Н. В. ЖУКОВСКОГО О ПОДЪЕМНОЙ СИЛЕ
243
ямеющим в бесконечности определенную скорость. Будем считать
также, что в области G и на контуре С отсутствуют источники в
стоки.
Величина давления вычисляется по формуле Бериулла
где А — постоянная, р — плотность и V — величина скорости в рас-
рассматриваемой точке. Так как дав- ..
ление перпендикулярно к соответ- "
ствующему элеиенту дуги кон-
контура С, то вектор, изображающий
силу, действующую на элемент ду-
дуги контура, будет соответствовать
комплексному числу
('--И
idz
(вектор Idz равен по модулю векто-
вектору dz, но перпендикулярен к нему).
Черт. 89.
Следовательно, комплексное число Р, соответствующее вектору снлн,
действующей на весь контур С, равно
р=~
так как, в салу теоремы Коша,
[Adx=u.
Если /(<) — комплексный потенциал рассматриваемого течения, то
число /' (*) соответствует вектору скорости в точке"«, а ынсло J/'(z)|
равно модулю вектора скорости V:
Следовательно,
B0)
Так как во всякой точке контура С скорость направлена по каса-
касательной к С, то для точек контура С, обозначив
Arg dz —а,
получим:
=— a.
244 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. DC
Отсюда, пользуясь свойствами аргумента, имеем:
Arg \\f (г)]1 dz\ =-2а+«=- а
¦
так как |/'(г)]— положительное действительное число н его аргу-
аргумент равен нулю. Таким образом, во всякой точке контура С аргу-
аргументы величин \f'(i)\*dz и \f'(z)]*dz отличаются только знаком, а
так как модули этих величин одинаковы, то эти величины являются
взаимно-сопряженными. Переходя в обеих частях равенства B0) к со-
сопряженным величинам, найдем комплексное число Р, сопряженное
числу, изображаемому вектором подъемной силы:
Эта формула носит название формулы. С. А. Чаплыгина.
Производная комплексного потенциала является, в силу сделан-
сделанных предположений, функцией, аналитической вне контура С, и сле-
следовательно, Может быть разложение окрестности бесконечно уда-
удаленной точки в ряд Лорана. Если Voo — число, сопряженное числу,
изображаемому вектором скорости в бесконечно удаденной точке, то
в окрестности бесконечно удаленной точки имеем:
B1)
Если Vx н Vy — взятые с соответствующими знаками проекции век-
вектора скорости на координатные оси, то
и следовательно, для всякого замкнутого контура L в области О
имеем в соответствии с правилом вычисления интеграла по комплекс-
комплексному аргументу
J /' (z)dz = С (К, - IV,) (dx + tdy) ¦.
i I
Но, если контур С находится внутри контура L, то ввиду того, что
течение вне контура С безвихревое, а источники и стоки отсутствуют,
в соответствии с формулами B) и D) (стр. 220 и 222) находим.
Vx dx + V, dy = J Vx dx + Vy dy = Г,
с
Vxdy - V, dx=J Vxdy - V,dx = N,
§ 5] ТЕОРЕМА Я. Е. ЖУКОВСКОГО О ПОДЪЕМНОЙ СИЛЕ 245
где Г — циркуляция вектора V по контуру С, а АГ—поток этого
вектора через контур С. Следовательно,
С другой стороны, если контур L лежит в области сходямостн ряда B1),
с помощью формулы для вычисления коэффициентов ряда Лорана
получим:
B3)
В рассматриваемом случае N=0, так как вектор скорости направлен
по касательной к контуру С, и, сравнивая B2) н B3), находим:
с-*—2ы'
Возведя ряд, стоящий в правой части B1) в квадрат (для этого нужно
составить ряд, членами которого являются квадраты членов рассмат-
рассматриваемого ряда и всевозможные удвоенные попарные произведения
его членов), будем иметь:
Отсюда
J [/>(«)]»dz=2Fa> с_1.2«/=2РЬ0Г, B4)
прячем за путь интегрирования в интеграле, стоящем в левой части
этого равенства, можно в соответствии с теоремой Коши выбрать и
контур С, так как функция lf'(z)]% аналитична на контуре С и вне
этого контура. Подставляя B4) в формулу Чаплыгина, получим:
откуда, переходя к сопряженным величинам, получим известную тео-
теорему Н. Б. Жуковского о подъемной силе:
P=—ipV<x>T. B5)
Так как р > 0, то вектор,^ изображающий число, стоящее в пра-
правой части B5), повернут относительно вектора V» на угол -tj-против
часовой стрелки, если Г < 0 (т. е. если обтекание происходит
по часовой стрелке), и на угол — -я- (т. е. на угол -%¦ по часовой
стрелке), если Г>0. Итак, теорема Жуковского может быть сфор-
') Нетрудно видеть,, что это разложение справедливо в той же
окрестности бесконечно удаленной точки, что и разложение B1).
246 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. ИГ
мулирована следующим образом величина подъемной свмг, дейст-
действующей на обтекаемый контур, равна произведению плотности
обтекающей жидкости (или газа), циркуляции и величины ско-
скорости течения в бесконечно удаленной точке, направление же
подъемной силы можно получать, повернув вектор скорости V»
на 90° навстречу циркуляции,
§ 6. Комплексный потенциал в электростатике
и термодинамике
Плоское электростатическое поле, т. е. поле вектора нап-
напряженности Е=Ех (х, у) i -\- Еу {х, у) У, является полем гра-
градиента
E=—gtauv{x, у),
где "О—потенциал электростатического поля, и, следовательно,
это поле потенциально. Во всех точках, в которых нет зарядов
(заряды играют здесь роль источников и стоков в гидродина-
гидродинамике), электростатическое поле соленоидально и для его изу-
изучения целесообразно воспользоваться понятием комплексного
потенциала. Однако в отличие от гидродинамики в задачах
электростатики применяются несколько иные обозначения и
иная терминология. Комплексным потенциалом поля Е назы-
называется функция
где
dv= - [Ex(x, y)dx+E,(x,y)dy],
ш
du— — Ey (х, y)dx + Ex {x, у) dy.
Функция и{х,у) называется силовой функцией, а функция
v(x,y), как уже упомянуто выше, — потенциалом электро-
электростатического поля.
Производная
откуда
Линии уровня потенциальной функции v{x,y) называются
акеипотенциалъными линиями, а линии уровня силовой функ-
функции u(xty)—силовыми линиями.
§ 6] КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ЭЛЕКТРОСТАТИКИ
Циркуляция вектора напряженности Е по замкнутому кон-
контуру С
равна работе поля при перемещении единичного заряда по
замкнутому контуру и всегда равна нулю.
Поток вектора напряженности через замкнутый контур С
в силу известной теоремы Гаусса, равен алгебраической сумме
расположенных внутри контура С зарядов, умноженной на 2я
(рассматривается плоский случай).
Пример 1. Выяснить характер электростатического поля соог -
ветствующего комплексному лотенциалу f{z)=iLat,
Здесь, (см. для сравнения стр. 228—229)
Эквипотенциальными линиями являются окружности
силовыми линиями являются лучи
Argz=G
Найдем модуль и аргумент вектора напряженности:
Arg?=- [i+Arg^j =- [? + J—Aig *] «= Arg *- 1
Это означает, что вектор напряженности направлен вдоль линии
Aig z=C (вдоль силовой линии) к началу координат.
Единственной особой точкой является точка z=0; в ней pas
ложен заряд. Для того чтобы найти величину этого заряда, следует
вычислить поток вектора Е через замкнутый контур С, однократно
обходящий точку z=0. Выбрав в качестве такого контура окруж
ность \z\=r, получим:
t t
откуда
248
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[гл. к
2я
в, в силу теоремы Гаусса, величина заряда равиа — =-=— '• От*
сюда следует, что комплексный потенциал, соответствунций заряду
+ 1 в точке 2=0, имеет вид
/(*)=-/Ln *,
влн
Пример 2. Выяснить характер электростатическою поля, соот-
соответствующего комплексному потенциалу
Здесь (см. для сравнения стр. 230—231)
Эквипотенциальными линиями являются окружиоств (чер. 90) с цент-
Черт. 90.
рами ва оси Ох, касающиеся оси Оу; силовыми лияими — окруж-
окружности с центрами на оси Оу, касающиеся оси Ох. Так >ак
/'(«)=¦
I
§ 6] КОМПЛЕКСНЫЙ ПОТЕН1ЩАЛ В ЭЛЕКТРОСТАТИКЕ 249
то вектор напряженности определяется равенствами
l*|=rjp. AigF=2Arg*.
6 особой точне 2 = 0 расположен диполь. Нетрудно (си. стр. 231)
убедиться в том, что рассмотренное электростатическое поле явля-
является предельный при h—»0 для поля, определяемого двумя зарядам!:
одним — величины ^т , находящимся в точке 2=0, и другим — вела*
чины — — _ в точке г = — А.
in
Вместо гидродинамических задач на обтекание в элект-
электростатике возникают задачи об определении поля Е или его
комплексного потенциала в односвязных или многосвязных об-
областях, ограниченных проводниками. Приведем несколько типов
таких задач.
а) Определение электростатического поля (или его кома*
лексного потенциала) в области, ограниченной проходящим
через бесконечно удаленную точку проводником С, если из*
вестны величина и направление вектора Е в бесконечности
(см. черт. 79, стр 232).
б) Определение электростатического поля (или его ком*
плексного потенциала) в криволинейной полосе, ограниченной
двумя непересекающимися на конечном расстоянии проводин*
ками С, и Сш, в предположении, что разность потенциалов
между проводниками задана (см. черт. 82, стр. 236).
в) Определение электростатического поля во внешности
замкнутого проводника С, если известны величина и направле-
направление вектора Е в бесконечности.
г) Определение поля между двумя замкнутыми непересе-
непересекающимися проводниками, если известна разность потенциалов
между ними.
Эти задачи решаются совершенно аналогично соответствую-
соответствующим задача» на обтекание.
Комплексный потенциал в задачах электростатики находится
так же, как и в задачах гидромеханики, как функция, отобра-
отображающая заданную область на стандартную область, соответ-
соответствующую типу рассматриваемой задачи (полуплоскость, по-
полоса между параллельными прямыми и т. д.).
Пример 3. Найти комплексный потенциал электростатичес-
электростатического пода в кольце между двумя проводниками, имеющими форму
250 КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ [ГЛ. IX
окружностей \г — 3] = 9 и \г — 8| = 16. Потенциал первой (внутрен-
(внутренней) окружности равен Vo, потенциал внешней окружности равен V,.
Комплексный потенциал электростатического поля в кольце между
проводниками, имеющими форму концентрических окружностей с
центром в начале координат, имеет, очевидно, вид
w = aiLnz,
где а — действительная постоянная, так как мнимая часть функции
alLaz равна
v(x,y)=a\a\z\
и постоянна вдоль каждой нз окружностей кольца.
Если задано отношение между радиусами г, и г, окружностей
и разность между соответствующими потенциалами К, и V,, то можно
определить а:
V0 = aln/-0,
V, = alnr,,
откуда
Итак, функция
у
w = ——
B6)
является комплексным потенциалом электростатического поля в кольце
г0 < \г\ < г,, если разность потенциалов между окружностями
\г\ = г, и |г| = г0 равна Vx — Ve. Для решения задачи достаточно
найти функцию С=/(/), отображающую взаимно-одназначно и кон-
конформно кольцо между окружностями \г — 3|=9 и \г — 8|=16на
кольцо г0 < \К\ < г, (причем окружность \г — Щ = 9 должна отобра-
отобразиться в окружность |С| = г,, а окружность |г — 8| = 16 в окружность
|?| = /-,), и подставить найденную функцию f(z) в B6) вместо г. Функ-
Функция, осуществляющая требуемое отображение, имеет вид (см. при-
пример 4 на стр. 174—175)
причем, как было показано на стр. 175, здесь
Функция B7) соответствует, правда, значению г, = 1, поэтому при
произвольном г, следовало бы писать:
§ 6] КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ЭЛЕКТРОСТАТИКЕ 251
где k — некоторая постоянная. Но так как комплексный потенциал
B6) определяется лишь с точностью до постоянного слагаемого, то
введение под знак логарифма постоянного, множителя k излишне.
Можно также отбросить в B7) множитель 2е" и искомый комплекс-
комплексный потенциал записать в виде
В задачах термодинамики часто приходится рассматривать
векторное поле
Д = — kgtaia{x,y,z),
или в плоском случае
A = — kgtada(x,y),
где а — температура соответственно в точке (х,у, г) или (х,у),
k — коэффициент внутренней теплопроводности, который мы
будем считать постоянным. Вектор А называется вектором пото-
потока тепла.
При постоянном * векторное поле
А = — k grad a = grad (— ka),
будучи полем градиента, потенциально. Это поле также и со-
леноидально во всех точках, в которых нет источников и сто-
стоков тепла, потому что стационарный поток тепла через любой
замкнутый контур С, ограничивающий некоторую область D,
в которой нет источников и стоков тепла, должен быть равен
нулю, так как в противном случае количество тепла в области
D изменялось бы и, следовательно, изменились бы с течением
времени температура а и ее градиент, т. е. поле А не было
бы стационарным. Для изучения поля теплового потока
также целесообразно использовать понятие комплексного потен-
потенциала.
Задачи термодинамики, соответствующие основным зада-
задачам на обтекание, формулируются и решаются так же, как
и аналогичные задачи электростатики (стр. 249), только,
говоря о проводниках, мы должны теперь иметь в виду не
проводники электричества, а хорошие проводники тепла, вмес-
вместо разности потенциалов теперь надо задавать разность темпе-
температур.
352 комплексна потенциал [l9. ос
Задачи к главе IX
В задачах 1—4 требуется определить модуль я направленде Мк-
тора поля А, найги уравнения линий тока и линий уровня поте&ВД-
альной функции по заданному комплексному потенциалу w.
4. w=Vt — a (a — действительное число).
О
5. Найти циркуляцию Г по контуру \г —1\ =-у и поток N через
•тот контур, если комплексным потенциалом является
и
6. Найти циркуляцию Г по контуру \г\ =3 и поток N через этот
жонтур, если комплексным потенциалом является функция
ГЛАВА X
ПРИМЕНЕНИЕ ТЕОРИИ ЛОГАРИФМИЧЕСКИХ ВЫЧЕТОВ
К ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ ДВИЖЕНИЯ
§ 1. Основные понятия теории устойчивости
Система дифференциальных уравнений
Л (<)=/, С, Уг (О, У. (О, ...,Л @) ('= 1, 2,.... Я) A)
С начальными условиями yt(tQ)=yjQ, описывающая некоторый
реальный процесс, неизбежно описывает его лишь прибли-
приближенно, так как и система дифференциальных уравнений сое*
тавляется при некоторых упрощающих действительные зависи-
зависимости предположениях, и начальные данные, являющиеся обычно
результатом измерения, определяются с некоторой погрешнос-
погрешностью. Поэтому обычно только те решения системы A) могут,
хотя бы приближенно, описывать изучаемый процесс, которые
при t^st9 лишь мало изменяются при малом изменении правых
частей уравнений A) и при малом изменении начальных зна-
значений.
Теория устойчивости изучает условия, при которых малые
изменения начальных значений или функций /, приводят лишь
к малому изменению решений при t^st0. В дальнейшем мы
рассмотрим первую из этих задач.
Решение У[=<р,У) (' = 1, 2,...,я) системы A) назы-
называется устойчивым (точнее, устойчивым в смысле Ляпунова),
если для каждого в>0 найдется число д>6 такое, что все
решения
,У,Ю (/=1,2,..., я)
системы A), для которых
254 теория логарифмич. вычетов и устойчивость движем, [гл. х
при всех <>*„ удовлетворяют неравенствам
1у,@-?,<0|<в. C)
т. е. если решения, близкие при t = tt, остаются близкими и
для всех значений t>t0.
Решения, не удовлетворяющие этим условиям, называются
неустойчивыми.
Если решение yt = у, (t) (/= 1, 2,..., я) устойчиво и, кроме
того, при достаточно малом Ь из \yt (tu) — ^, (tb)\ < 8 следует, что
hm {у, @ - <р, @) = О (I = 1, 2 л) D)
t-*CO
(т. е. если решения, близкие по начальным значениям, неогра-
неограниченно сближаются с возрастанием 0. то решение у, = <р, (t)
(i = 1, 2,..., л) называется асимптотически устойчивым.
Как уже было пояснено выше, обычно в приложениях имеют
значение только устойчивые решения.
Исследование на устойчивость некоторого решения
*, = ?,№ ('=1. 2 «)
системы A) может быть заменой переменных
*,=У, — «МО ('=!. 2 «)
сведено к исследованию на устойчивость тривиального решения
*{ = 0 (/=1, 2,...,л) системы уравнений
0) ('==», 2 л).
Поэтому в дальнейшем речь будет идти только об исследова-
исследовании на устойчивость решения xt = 0 (<=1, 2 л) системы
уравнений
xt{f)=Fl {t,xt,xt хп) (/=1, 2 л),
при этой неравенства C) и B), входящие в определение ус-
устойчивости, примут вид: |*,(*)|<б при *>*„, если |*,(*в)|<5,
* условие D), входящее в определение асимптотической устой-
*|нвости, переходит в
hm xt(i) = 0 (/ = 1,2,..., л).
Нетрудно проверит];, что тривиальное решение х ~0
l, 2 п) линейной однородной системы днфференциаль-
§ 1]' ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ 255
цы< уравнений с постоянными коэффициентами
я
*/=Ste//*/ (/=1, 2,...,л) E)
асимптотически устойчиво, если все корни характеристичес-
характеристическою уравнения
au — k
'*
"in
= 0
имеют отрицательные действительные части.
Действительно, любое решение системы E) имеет вид
где Pt> (f) — некоторые многочлены, степени которых ниже кратно-
кратности соответствующих корней kf характеристического уравнения,
т — число различных корней характеристического уравнения').
Если действительные части всех корней kj характеристи-
характеристического уравнения отрицательны, то не только решения xt(t)
(/'=1,2,..., л), близкие к Х/~0 (t= 1, 2,..,, я) по начальным
значениям, удовлетворяют неравенствам |лт,(<)|<^8 при *>/„ и
асимптотически приближаются к решению xt = Q (i = 1, 2,..., л),
но даже все без исключения решения
2
/sal
=1.2,.,.,л)
при достаточно больших t неограниченно приближаются к ре-
решению х,эО (/=!, 2,...,л). В этом случае говорят, что
решение xf = 0 (i==l, 2, ...,л) асимптотически устойчи-
устойчиво в целом.
Заметим, что в рассматриваемом случае не только решение
х, = 0 (/= 1, 2,...,л), ной остальные решения системы E)
асимптотически устойчивы.
Если хотя бы один корень ks=p-\-ql характеристи-
характеристического уравнения имеет положительную действительную
•) См., например, A5].
256 теория логарифмич. вычетов и устойчивость движен. [гл. х
часть р>0, то тривиальное решение ^ = 0 системы E) не-
неустойчиво.
Действительно, соответствующее этому корню решение
*/ = «*•*'' (/=1,2...,л),
где с и ait — постоянные, или в действительном виде
х( = CtP1 ($isz.o%qt -j- fissiaqt) (/ = 1, 2,..., л),
где с, Р4> и Y/j — действительные постоянные, при сколь угодно
малых значениях произвольной постоянной с, т. е. при сколь
угодно малых начальных значениях \х{ (?0)|, с возрастанием t
ие только не удовлетворяет условию [*/(*)! <Cei н0 даже не"
ограниченно удаляется от решения ^ = 0 (/=1, 2,...,л).
Одним из основных методов исследования на устойчивость
решения ^ = 0 (/=1, 2,...,л) нелинейной системы является
метод исследования на устойчивость по первому приближению.
Этот метод заключается в том, что, предполагая все функции
/, дифференцируемыми по всем переменным, начиная со вто-
второго, в окрестности точки Xj=0 (/=1, 2,...,л) представ-
представляют систему
в виде
*t @ = St "и @ *у @ + Rt (*, *» W х« @) F)
(*=1, 2 л)
и, отбрасывая члены Rit имеющие порядок выше первого от-
относительно переменных х,, xt,...,xn, исследуют на устойчи-
устойчивость тривиальное решение лг,- = О (/=1, 2,...,л) линейной
системы уравнений
*,-(<) = jkfutoxjto 0*1, 2, .... я),
называемой системой первого приближения для системы F).
Если все пц — постоянные, то система F) называется ста-
стационарной в первом приближении.
Для стационарной в первом приближении системы F) сле-
следующая теорема указывает условия применимости метода
¦сследования по первому приближению:
§ 2] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВИТ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 257
Если все корни характеристического уравнения системы
первого приближения для системы F) имеют отрицатель-
отрицательные действительные части и функции R( удовлетворяют
условию
I Ri it, xlf xt *,) | < M( |^) f+" G)
при t&st0 и |jc;|<8 (/=1, 2, ..., л), где 8>0 и доста-
достаточно мало, а а и N—некоторые положительные посто-
постоянные, то решение х( = 0 (/=1, 2, ..., я) не только си-
системы первого приближения, но и системы F) асимпто-
асимптотически устойчиво').
Если при тех же ограничениях на функции /?, хотя
бы один корень характеристического уравнения имеет по-
положительную действительную часть, то решение х{ = 0
(i=l, 2, ...,п) не только системы первого приближения,
но и системы F) неустойчиво*).
Эта теорема дает весьма удобный признак асимптотической
устойчивости решений широкого класса систем дифференциаль-
дифференциальных уравнений и очень часто применяется в практических
задачах.
Однако вычисление корней характеристического уравнения
при л>2, и особенно при л>4, весьма затруднительно,
поэтому большое значение имеют различные признают отри-
отрицательности действительных частей всех корней многочлена.
Среди таких признаков наряду с признаком Гурвица (см., на-
например, [15]) и признаком Н. Н. Меймана (см. [14]) большое
значение имеют признаки, основанные на теории логарифми?
ческих вычетов.
§ 2. Признак отрицательности действительных частей
всех корней многочлена
Теория логарифмических вычетов, изложенная в гл. VII,.
§ 3, позволяет найти число нулей аналитической функции,
расположенных в области, ограниченной некоторым контуром у;
>) Если функции R{ не зависят от t, то условие G) означает, что
все R; должны иметь порядок выше первого относительно совокуп-
совокупности переменных х„ х„ .... Хп при стремлении всех х{ к нулю.
*) Доказательство этой теоремы можно найти, например, в курсе
дифференциальных уравнении В. В. Степанова или в книге И. Г. Мае-
кина [7].
258 теория догарифмич. вычетов и устойчивость движен. [гл. х
в частности, этим методом можно определить число нулей
многочлена, расположенных в правой полуплоскости Rez^O,
в, потребовав, чтобы это число равнялось нулю, получить
условие того, что все корни многочлена имеют отрицательную
вещественную часть.
Для получения такого условия можно воспользоваться
основной теоремой теории логарифмических вычетов (стр. 141)
или, что обычно оказывается более удобным, ее геометриче-
геометрической интерпретацией — принципом аргумента.
* Рассмотрим при отображении
образ Гв замкнутого контура у,, расположенного
в плоскости переменного z и состоящего из
х отрезка 1% мнимой оси [— iR, iR] и распо-
расположенной в полуплоскости Re*> 0 дуги CR
полуокружности радиуса R с центром в начале
координат (черт. 91).
Если многочлен
/(z) = z-+fllz*-*+...+W+«,, (8)
не имеет нулей на мнимой оси и если при достаточно боль-
большом R число обходов контуром Гв начала координат равно
нулю или, что то же самое, приращение Arg w на контуре Гш
равно нулю, то согласно принципу аргумента в правой полу-
полуплоскости Rez>0 иет корней многочлена /(z).
Заметим, что приращение аргумента функции f(z) на полу-
полуокружности С^ 4С Arg/(z) при достаточно большом R сколь
угодно мало отличается от /от, так как
+Т
где о—^0 при |z|—>-оо. Следовательно, надо вычислить
лишь A,oArg/(z) при достаточно большом R, и если это
приращение при R—юо стремится к —/пг, то в правой
полуплоскости нет нулей мноючлена /(z).
§ 2] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВИТ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 259
Пример 1 Выяснить, имеет ли многочлен
/(г)=г«
корни с положительными действительными частями.
Находим образ мнимой оси г = ty, где j; изменяется от -f- oo до —во,
при отображении w=f{z)
откуда
v =y* — 5y* -f" *У
При достаточно больших зна-
значениях у и < 0, a v > 0, при-
причем
чем
Ьга —=0.
Нулями функции v =
У(У* — 5У + 4) являются.
Вычисляем соответствующие
значения и
и@)=1, и(*1) = -2,
и(±:2) = 1.
Черт. 92.
Если еще учесть четность функции и = и (у) й нечетность
функции v = v(y), то уже можно дать довольно грубый, но достаточ-
достаточный для вычисления A/gArg/(z) иабросок образа мнимой оси (черт. 92).
Образ мнимой оси трижды обходит начало координат в отрица-
отрицательном направлении Следовательно,
ЬтД, Arg f(z) = — 6я
я число нулей в правой полуплоскости
N= lim (
R-юо
Рассматриваемый многочлен не имеет нулей с положительной веще-
вещественной частью.
260 ТЕОРИЯ ЛОГАРИФМИЧ. ВЫЧЕТОВ И УСТОЙЧИВОСТЬ ДВИЖЕН. [ГЛ.Х
§ 3. Исследование на устойчивость решений
дифференциальных уравнений с запаздывающим аргументом
Явления с последствием часто описываются дифференци-
дифференциальными уравнениями с запаздывающим аргументом. Осо-
Особенно часто такие уравнения встречаются в задачах теории
регулирования.
Дифференциальное уравнение с запаздывающим аргументом
первого порядка и первой степени имеет вид
х (t) =/(t,x (t), x{t — xl @), x (t —с, (*)),..., x (*-т„ (*))), (?)
где запаздывания ik(f)^s0 F = 1, 2, ..., л).
Рассмотрим сначала для упрощения изложения случай лишь
одного постоянного запаздывания т:
x{t)=/(t, x(t), x(t—z)). A0)
Обычно требуется определить непрерывное решение x=x(t)
при t^10 уравнения A0), совпадающее при t9 — -c^/^/e
с заданной непрерывной функцией <р(/), называемой начальной
функцией. Эта задача имеет единственное решение, если
функция / непрерывна и имеет ограниченную производную по
второму аргументу в окрестности точки t = L, х (М = <р (М,
*(/„—с) = (р(/в—с).
Решение x(t) называется устойчивым, если для любого
е>0 можно указать такое 8>0, что каждая непрерывная
начальная функция фС). для которой на начальном множестве
t0—-с «S / «^ *ф выполнено неравенство | ф (t) — <р (t) \ < i, опре-
определяет решение x(t), для всех t^t0 удовлетворяющее нера-
неравенству
\x(t)-x(f)l<t,
¦ <р
т. е. в случае устойчивости близкие по начальным функциям
решения остаются близкими при всех значениях t^t0.
Если решение x{t) устойчиво и, кроме того, при доста-
достаточно малом i из j <J>A) — <р@1<С& на начальном множестве
следует, что
lira (x(t)—x(t)) = Q,
t-*ao ф <р
то решение x{f) называется асимптотически устойчивым.
§ 3} УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ 261
Если решение не удовлетворяет указанному выше опреде-
определению устойчивости, то оно называется неустойчивым.
Аналогично определяются устойчивость, неустойчивость и
асимптотическая устойчивость для решений систем дифферен-
дифференциальных уравнений с запаздывающим аргументом и для реше-
решений уравнений я-го порядка, которые почти всегда могут быть
заменены системой уравнений первого порядка').
Заменой переменных у — х—x(t) можно свести исследо-
вание на устойчивость решения х (t) к исследованию на устой-
чивость решения у (t) = 0, поэтому в дальнейшем мы будем
исследовать на устойчивость лишь решения, тождественно рав-
равные нулю.
Частные решения линейных однородных уравнений л-го по-
порядка с постоянными коэффициентами, с одним или несколь-
несколькими постоянными запаздываниями, мо/ут быть найдены в виде
x(t)=eM. A1)
Рассмотрим, например, уравнение
= 0. A2)
Подставляя (И) в уравнение A2) и сокращая на еи, получим
так называемое характеристическое уравнение
k-\-a+be-*l=0. A3}
Аналитическая во всей плоскости функция переменной ft,
стоящая в левой части уравнения A3), называемая характе-
характеристическим квазиполиномом, имеет бесконечное множество
нулей
k k ь
Каждому корню kt уравнения A3) соответствует частное ре-
решение eki' уравнения A2). В силу линейности и однородности
уравнения A2) линейная комбинация
| A4)
') Подробнее об устойчивости решений дифференциальных урав-
уравнений с запаздывающим аргументом см. [15].
262 ТЕОРИЯ ЛОГАРИФМИЧ. ВЫЧЕТОВ И УСТОЙЧИВОСТЬ ДВИЖЕИ. [ГЛ. X
частных решений с произвольными постоянными коэффициен-
коэффициентами ci также является решением уравнения A2). Если при.
некотором выборе постоянных ряд
сходится и допускает почленное дифференцирование, то сумма
этого ряда также является решением уравнения A2).
При действительных коэффициентах а и b уравнения (\2)
комплексным сопряженным корням ks=ps-\-tqs, ks+l=ps—iqs
уравнения A3) соответствуют два действительных решения,
являющихся соответственно мнимой и действительной частями
решения
е*«*= еР** (cos qjt-\- i sin qst).
Если некоторые корни уравнения A3) кратны, то корням kt
кратности а( соответствуют частные решения уравнения A2)
вида
Можно доказать, что если действительные части всех
корней характеристического уравнения отрицательны, то
решение х (t) = 0 уравнения A2) асимптотически устойчиво.
Если же хотя бы один из этих корней имеет положи-
положительную действительную часть, то решение x{t) = 0 урав-
уравнения A2) неустойчиво.
Эта теорема справедлива и для линейных однородных диф-
дифференциальных уравнений л-го порядка с постоянными коэффи-
коэффициентами и с одним или несколькими постоянными запазды-
запаздываниями, а также для систем линейных уравнений с постоянными
коэффициентами и с постоянными запаздываниями.
Справедлива также следующая теорема о возможности ис-
исследования на устойчивость по первому приближению, анало-
аналогичная теореме, изложенной в предыдущем параграфе (см.
стр. 256—257).
Если все корни характеристического уравнения
k-\-a-\-be-kt=0 A3)
имеют отрицательные действительные части, то асимп-
асимптотически устойчиво не только тривиальное решение
§ 3] УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ 263
х (t) = 0 Уравнения
(t — x)=zO, A2)
но и решение х (i) = 0 уравнения
+ R{t,x(t),x(t-x)), A5)
где
lim al(f) = O,
t-*ao
lim ft,(*) = 0,
t-+oo
при t^st0, если \х\ и \у\ достаточно малы, a N и а — не-
некоторые положительные постоянные.
Если же хотя бы один корень ks характеристического
уравнения имеет положительную вещественную часть, то
решения х~0 не только уравнения A2), но и A5) не-
неустойчивы.
Аналогичная теорема справедлива и для линейных однород-
однородных уравнений .я-ro порядка с постоянными коэффициентами
и с постоянными запаздываниями, а также для систем таких
уравнений.
Итак, вопрос об устойчивости решений широкого класса
дифференциальных уравнений связан с расположением нулей
некоторых аналитических функций — левых частей соответ-
соответствующих характеристических уравнений.
Если дифференциальное уравнение с запаздывающим аргу-
аргументом л-го порядка имеет лишь одно запаздывание, то ха-
характеристическое уравнение имеет вид
РЩ + Q (*>*"*= 0, A6)
где степень полинома P(k) выше степени полинома Q(k).
В дальнейшем переменное k будем обозначать буквой г и,
следовательно, характеристическое уравнение A6) .перепишем
в виде
P(z) + Q{z)e-**=0. A7)
Левая часгь этого характеристического уравнения также на-
называется характеристическим квазиполиномом.
264 ТЕОРИЯ ЛОГАРИФМИЧ. ВЫЧЕТОВ И УСТОЙЧИВОСТЬ ДВИЖЕН-. [ГЛ. X
Как и в предыдущем параграфе, применим принцип аргу-
аргумента. Предполагая, что аналитическая функция
e-" A8)
не имеет нулей на мнимой оси, рассмотрим образ Ти при
отображении w=P(z)-{-Q(z)e~rt замкнутого контура у„
состоящего из отрезка мнимой оси (— IR, //?) и полуокруж-
полуокружности \z\=R, Re*>0 (см. черт. 91, стр. 258).
Если при однократном обходе контура уг в положительном
направлении, его образ Гте обходит начало координат в поло*
жительном направлении N раз, то внутри контура у, нахо-
находится N нулей функции A8) (каждый нуль считается столько
раз, какова его кратность). Если при R—> <» число N остается
равным нулю, то в правой полуплоскости Re z ^ 0 не содер-
содержится нулей характеристич/еского квазиполинома Р (z)-\-Q(z)e~u
и, следовательно, действительные части всех нулей этого ква-
квазиполинома отрицательны.
Построить контур rw иногда довольно трудно, поэтому
обычно указанный метод применяется в несколько видоизме-
видоизмененной форме, а именно, вместо функции f{z)=P (z) -{- Q(z)e~v
рассматривают функцию
/(*)_! -<?(«).-»
/>(*)— Р(г) е '
нули-которой совпадают с нулями функции f(z) (если P(z)
и Q(z) не имеют общих нулей) и которая имеет полюсами
нули многочлена P{z).
Обозначим wx (z) — — ^щ в*. Предельное положение при
R —> оо образа контура уг ПРИ отображении wT (z) называется
амплитудно-фазовой характеристикой. Так как
то нулям функции -рт-; соответствуют точки, в которых
w( (г) = 1. Поэтому, применяя принцип аргумента к функции
wr(z), мы должны подсчитать число обходов амплитудно-фа-
амплитудно-фазовой характеристикой не точки z = 0, а точки 2=1. Число
обходов амплитудно-фазовой характеристикой точки г= 1
будет равно разности N—Р между числом N нулей (с уче-
учетом их кратности) квазиполинома PB)-{-QB)e"*=0, распо-
§ 3] УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ 265
воженных, в правой полуплоскости, и числом Р там же распо-
расположенных полюсов функции дат(г) (также с учетом их крат-
кратности). Для того чтобы действительные части всех корней
характеристического уравнения были отрицательными, необхо-
необходимо и достаточно, чтобы N=0, т. е. чтобы число обходов
амплитудно-фазовой характеристикой точки г = 1 равнялось —Р.
Еще раз напомним, что при этом предполагается, что на
мнимой оси нет нулей функции Р (г) -\- Q (г) е"т* и что P{z)
и Q(z) не имеют общ^х нулей, причем оба эти условия
сравнительно легко проверяемы. Заметим, что при отображении
wT(z) образ полуокружности, входящей в контур у, при
R—»-оо, стягивается в точку z = 0 (степень полинома P(z)
выше степени полинома Q(z)) и, следовательно, надо строить
лишь образ мнимой оси, проходимой в отрицательном направ-
направлении.
При построении амплитудно-фазовой характеристики удобно
вначале строить так называемую предельную характеристику,
являющуюся предельным положением образа контура у* при
R—юо при отображении дао(г) = — -р^\'
Для построения образа мнимой оси при отображении
или
уже зная предельную характеристику, достаточно учесть влия-
влияние множителя е'^'У, поворачивающего (без изменения моду-
модуля) радиус-вектор точки предельной характеристики, соответ-
соответствующей значению у, на угол — ту. Заметим, что при построе-
построении амплитудно-фазовой характеристики особое внимание
надо уделить точкам предельной характеристики, лежащим на
окружности |z| = l, так как именно эти точки при повороте
на угол — ту могут попасть в точку г = 1.
В качестве примера найдем область асимптотической устой-
устойчивости в пространстве действительных коэффициентов а и b')
тривиального решения х = 0 уравнения
(t-x) = O. A2)
') Пространством коэффициеитов в даниом случае будет плоскость»
координатами точек которой являются числа а и Ъ.
266 ТЕОРИЯ ЛОГЛРИФМИЧ. ВЫЧЕТОВ И УСТОЙЧИВОСТЬ ДВИЖЕЯ. [ГЛ. i
Характеристическое уравнение имеет вид z-\-a-\-be~v=O.
В рассматриваемом случае
Ье-"
A9)
Предельной характеристикой является образ мнимой оси при
дробно-линейном отобра-
отображении A9). Пользуясь
свойствами дробно-линей-
дробно-линейной функции (см. § 4
гл. VIII), читатель легко
обнаружит, что это ото-
отображение преобразует
мнимую ось в окружность
Ь I
;j- с центром в
Черт. 93.
радиуса
точке z=—2^, уравнение которой имеет вид
(черт. 93).
Предположим, что в>0; тогда функция wx(z) не имеет
полюсов в правой полуплоскости и если |*|<о, то ни при
каком повороте точек окруж-
окружности B0), вызванном нали- У
чием множителя e~vy в выра-
' амплитудно-фазовая харак-
характеристика не будет охваты-
охватывать точки z=l и, следо-
следовательно, все нуля квазипо-
. линома г -\-а-f- be'* распо-
* ложены в левой полуплоско-
полуплоскости ?е*<0.Прн|?|>в>0
¦ (черт. 94) для некоторых Черт. 94.
аначений х точки предельной
характеристики, лежащие одновременно и на окружности | z \=1,
изображенной на чертеже пунктиром, могут перейти в точку
i=l. Наименьшее из таких значении t при заданных а в b
§3]
УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
267
будет значением, при переходе через которое решение х = О
уравнения A2) теряет устойчивость, так как при переходе
через это значение х=х0 амплитудно-фазовая характеристика
начинает охватывать точку z=\.
Нетрудно было бы подсчитать значение т0, однако в этом
нет необходимости, как нет необходимости и в исследовании
этим методом случая а<0, так как, зная уже часть области
асимптотической устойчи-
устойчивости |*|<с (черт. 95),
мы можем уточнить ее
границу, находя в плоско-
плоскости параметров а и Ь ли-
линии, которые при фикси-
фиксированном х соответствуют
чисто мнимым или равным
нулю корням характери-
характеристического уравнения.
Действительно, корни
характеристического урав-
уравнения
z,=zt{a, Ь, х),
Черт. 95.
где -с > 0, являются непре-
рывными функциями пара-
параметров а, Ь и -с и, следовательно, если считать х фиксированным,
то потеря устойчивости решения х = О при перемещении точки
из найденной выше области асимптотической устойчивости по
любому пути в плоскости а, Ь может произойти лишь при
перемене знака у действительной части хотя бы одного корня
характеристического уравнения, т. е. при переходе при задан-
заданном х через точку (а, Ь), соответствующую лежащему на мни-
мнимой оси корню характеристического уравнения. Уравнение
*4-a-|-te~'e = 0 имеет равный нулю корень лишь при
в-)-*=0 и имеет чисто мнимые корни z = iy, если урав-
уравнение
или
u-\-iy-\-b (cos ту — / sin ху) = О
имеет действительные корни в, следовательно, если действи-
268 ТЕОРИЯ ЛОГЛРИФМНЧ. ВЫЧЕТОВ В УСТОЙЧИВОСТЬ ДВНЖЕЯ. ?tifl
тельные корни имеет также система уравнений
o + *cosx> = 0,
у— bsm-zy =0,
откуда
*=-^, д=-У«*х'щ B1)
При 0 <:_у ^ — получаем ближайшую к уже найденной части
области устойчивости ветвь кривой B1), которая вместе с пря-
прямой a -j-ft=0 и ограничивает область асимптотической устой*
чивости (см. черт. 95) *).
Заметим, что в области а>0, |?|<[а, заштрихованной
на черт. 95 горизонтальной штриховкой, решение х = 0 асимп-
асимптотически устойчиво при любом х. Область устойчивости, об*
ладающая таким свойством, называется областью абсолютной
асимптотической устойчивости.
В рассматриваемом случае теорема Руше (см. стр. 143) дает
возможность еще проще провести исследование.
Действительно, рассматривая на том же контуре f- функции
* + а и <р (*) = &-«,
заметим, что при |а|>-|?| и при достаточио большом радиусе
R полуокружности эти функции / и ср удовлетворяют условиям
теоремы Руше, т. е. на контуре уг
| -« B2)
где z = x-\-iy.
В самом деле, на дуге полуокружности достаточио боль-
большого радиуса R справедливость неравенства B2) очевидна,
так как *>0, а на мнимой оси \&-\-a\si> \a\, 1^-^1 = 1 ?|
и, следовательно, при |а|>|&| | дг —[— а | >-1 fre—x* (. При а>0
функция /(«) = «-(- а ие имеет ни одного нуля внутри конту-
контура Yz> следовательно, по теореме Руше нет нулей в области,
ограниченной контуром Y-. и У функции z-\-a-\-be~'a.
Итак> часть области асимптотической устойчивости реше-
решения jc = O уравнения A2) найдена: а>0и |^|<[а, а уточ-
*) Конечно, из приведеииого рассуждения ие следует, что мы
нашли всю область асимптотической устойчивости, однако в этом мож-
можно было бы убедиться, продолжая исследование амплитудио-фазопнм
методом.
§ 3] УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ 269
нить границы этой области асимптотической устойчивости можно
так же, как это сделано выше.
Заметим, что если |a|]>|ft|, но в<^0, то из теоремы
Руше следует неустойчивость решения х = 0 уравнения A2)
при любом т.
Задачи к главе X
1. Исследовать на устойчивость решение дс = О уравнения
Щ) + 2* (*) + Ъх (t) = Xх (t) - Зх« (*).
2. Исследовать на устойчивость решение х =s 0 уравнения
x(t) + 4x (t) + 3jc (t) + x{t) = 0.
3. Исследовать на устойчивость решение х«зО, у^О системы
уравнений
4. Исследовать на устойчивость решение хаО уравнения
х (t) + Зх (t) + x(t)=x*(t) sin t — xl (t) cos t.
В задачах 5—8 величины a, b и х постоянные, х > 0.
5. Найти область устойчивости при изменении коэффициентов
а и Ь решения x==0 уравнения
6. Найти область устойчивости при изменении коэффициентов
а я Ь решения х=»0 уравнения
7. Исследовать на устойчивость решение х=>0 уравнения
8. Имеет ли тривиальное решение х»0 уравнения
x(t) + ax{t -x) + bx(t -x)=0
область абсолютной устойчивости.
ГЛАВА XI
НЕКОТОРЫЕ СВЕДЕНИЯ
ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
§ 1. Преобразование Лапласа и его основные свойства
В основе операционных методов решения обыкновенных
линейных дифференциальных уравнений с постоянными коэф-
коэффициентами или аналогичных уравнений в частных производных
лежит следующая идея: вначале определяется не искомое ре-
решение и дифференциального уравнения, а функция », являю-
являющаяся результатом некоторого преобразования решения и,
причем преобразование выбирают с таким расчетом, чтобы
функцию п можно было найти значительно проще, чем я;
определив н, находят с помощью обратного преобразования
искомое решение а.
Аналогичная идея применяется и в элементарной математике
при переходе от чисел к их логарифмам, после чего вместо
действий умножения, деления, возвышения в степень и извле-
извлечения кория выполняют более простые действия над логарифмами
чисел, а затем по вычисленным логарифмам находят искомые
числа.
В качестве преобразования, позволяющего реализовать
указанную выше идею, в операционном исчислении обычно при-
применяется преобразование Лапласа, при котором функция u(t)
преобразуется в функцию
н (р) = $ e-P'aMdt, A)
и
где /—действительное переменное, a ps=j-{-/« — комплекс-
комплексное переменное.
§ 1] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА 271
Например: а) если и(/) = 1, то при о>0
оо
о . р~Р* °о I
J Р О Р
б) если я (/) = /, то при а>0
ао
я(р)= \ e~pitdt,
о
и, интегрируя по частям, получим:
_ 1
в) если u(t) = tn, где л — целое положительное число),
то, считая о>0, получим:
CD
u(p)=[e-ptt"dt,
'л!
и, интегрируя по частям п раз, будем иметь в(р) = жт;
г) если я(<) = ев', то
оо
о
и при а~^>а получим:
Функция я(^) в A) называется оригиналом, а н(р)—изо-
бражением.
В дальнейшем будем считать, что оригинал и (t) удовлет-
удовлетворяет следующим условиям:
1) a{i) является кусочно-непрерывной и кусочно-гладкой
функцией (т. е. я (t) и u'(t) на каждом конечном отрезке имеил
не более конечного числа точек разрыва и притом только
первого рода);
2) н(/) = 0 при /<0;
3) с возрастанием t модуль функции a(i) растет ие быст-
быстрее некоторой показательной функции; точнее, |я(/)|Л**?
где М и s — постоянные.
272 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ Г?Я. XI
Условие 3) обеспечивает абсолютную сходимость интеграла
00
где p = a-{-i(o при a>s, т. е. для всех точек р, лежащих
провее прямой Rep=s (черт. 96). Действительно, если
o>s, то
В дальнейшем всюду предполагается, что o>s.
Условие 2) не накладывает никаких ограничений на значе-
значения оригинала «(Она полупрямой 0<*<оо, которые только
и оказывают влияние на вид функции
п(р).
Заметим, что в прикладных задачах
решение дифференциального уравнения
обычно требуется определить, лишь на-
начиная с некоторого начального момента
tf = f0, причем без существенного огра-
ограничения общности можно считать t0 = 0.
Докажем несколько основных свойств
преобразования Л атаса.
Черт. 96. 1) ca.(t)—-сп{р), где с — постоян-
постоянная, а знак—«-обозначает переход от
оригинала к изображению.
Доказательство.
00
[(Cpicu (t) dt
00
:c[e-ptu(t)dt = cu(p),
о
2) «,(<) + «, @ — 3,(p) +«,(/>).
Доказательство.
во
§ 1] ПРЕ0ВРА30ВАНИЕ ДАЛЛАСА Н ЕГО ОСНОВШЛ СВОЙСТВА 273
Следствие свойств 1) и 2):
Где с,— произвольные постоянные.
3) и' (t)—*pa(p)—а@). В частности, если д(О) = 0,
то дифференцирование оригинала сводится к умножению
изображения на р.
Доказательство. Интегрируя по частям, получим:
$ =e^a @ Г+р$в-*в Щ dt=PH {р) —e@),
о о
так как при Rep=a>s Um e'^tt (t) = 0.
Применяя свойство 3) два раза (или два раза интегрируя
00
по частям y^u'ii) df), получим:
Применяя свойство 3) л раз, будем иметь:
я<"> @—/>" в (р)—рн~ги @)—/>"-V @) —... ~я'«-1>@).
t
Доказательство. Обозначим ^u(t)dt=v(t); тогда
о
в, интегрируя по частям, получим:
10 ГЛ. Лунц и Л. Э. Эльсгольц
274 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [гЛ. Х|
так как легко обнаружить, что
Действительно, t>@) =
1
о
при s^O (если *=0, то \v(f)\*?Mt), где М — постоянная
(см. условие 3) стр. 271). Следовательно, если s^=0, то
и так как о>*. то lim — ««*-•>*=0.
Читатель без труда проверит справедливость доказанного
свойства при s = 0.
Итак, интегрированию оригинала соответствует деле-
деление изображения на р.
б) tt(t—x)-*e-"H{p)t
где постоянная t>0.
Доказательство.
в (<—т) —. $ e-#a (t—x)dt;
полагая / — *=<ц получим:
00 О»
\е->хи(t — x)dt=\ e-M+^в(/;)
О —т
и, принимая во внимание, что и (tx) = 0 при /j<[ 0, окончатель-
окончательно будем иметь:
09
и (* — т) —¦ e-'T J «-'*•« (/j) rf/, = «-'"й (р).
о
Итак, сдвигу графика функции u(i) в напоавлении оси О/
на отрезок т соответствует умножение изображения «а е~**.
6)
§ 1] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА 275
Доказательство.
полагая af = f,, получим:
о
7) е"'« (/) —»й (р— а) при Re(р
Доказательство.
J e-pteatu(t)dt={ е-*-а*и (9<й = й(р —a).
о о
Непосредственное вычисление изображений различных часто
встречающихся функций-оригиналов и применение более слож-
сложных приемов дают возможность составить приводимую ниже
таблицу, с помощью которой во многих обычно встречающихся
в приложениях случаях легко осуществляется переход от
функций-оригиналов к их изображениям и обратный переход
от изображений к оригиналам.
Таблица изображений и оригиналов
1
2
3
4
5
6
7
Изображение
1
Р
1 , я — целое положнтель-
pn+i ное число.
¦~, где Re а > - 1
1
р-а
1 , п—целое положи-
(р — аУ+1 тельное число.
1
(О ¦"• в)
1
1
ip-a)(p-b)
Оригинал
1
л!
ПаТТ)^
а-*
') Определение гамма-функции Эйлера Г (р) читатель может найти
в [12]. Там же указаны простейшие свойства функции Г(р),
276 НЕКОТОРЫЙ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. XI
= -^=1е-*\*х.
м
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Изображение
1
iP — <»|) (Р — «J (Р — «»)
1
Р
1
р-Ь
[p-bf + a*
f-a*
Р
(p' + a'f
1
Р
Р
Р*
1
1
p(i +VT)
)
Ориганал
(а, - а.Иа, - а,М<»,—<U
sin at
а
cos at
в*' sin at
a
la
1 — cos at
ax
cos at — cos W
1 , at . at
-r Sin -=s Sh -7=r
? У1Г /2
rt h "*
/2" >^J
1
2УТ
j i c^fl^F" II)
^'A _ 4>(V"t)}
y,(at)»)
*) С определением и описанием простейших свойств функций
Бесселя Jn{x) чшатель может познакомиться оо шшв 112J
§ 1] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Н ЕГО ОСНОВНЫЕ СВОЙСТВА
24
25
26
27
7Я
29
30
31
32
33
34
Изображение
1
1 _^ 1
1 • " ^* " 'о
(р -J- в*)
1ПA+?)
У^
3
оо
е^ \e-#dx
р
~р~
_ Кр
с
Р
Opiranu
а»BяI
-^—
cosaVT
2!ЙпаУТ
Г"»
ае At
1"Ф(^рт)
Л (а V Л
1 о»
Более полную таблицу читатель может найти в [4].
Если переход от оригинала к изображению или обратный
переход от изображения к оригиналу не удается осуществить
с помощью таблицы, то для перехода от оригинала к изобра-
изображению пользуются непосредственно формулой A) (стр.
278 некоторые сведения из операционного исчисления [гл. XI
а для обратного перехода от изображения к оригиналу — фор-
формулой обращения интеграла Лапласа:
во+ioo
I
«о —/оо
где символ \ в правой части обозначает, что в качестве пу-
a0,
а0 — loo
ти интегрирования взята прямая Rep = a0, параллельная мнимой
оси, точнее,
eptu (p) dp = Urn J е^'п (р) dp.
•о-loo ш-
Доказательство формулы обращения, требующее знакомства с
теорией интеграла Фурье, мы опускаем, отсылая интересую-
интересующихся этим вопросом читателей к [8].
При доказательстве формулы обращения одновременно уста-
устанавливается и единственность построения оригинала по изо-
изображению.
Вычисление по формуле B) обычно требует применения
теории вычетов и осуществляется методами гл. VII, причем во
многих случаях это вычисление оказывается весьма сложным,
поэтому большое значение имеют теоремы, дающие возмож-
возможность представить некоторые функции п (р) в виде суммы более
простых слагаемых и тем самым, в силу свойства 2) (стр. 272),
упростить задачу перехода от изображения п(р) к оригиналу.
В частности, часто удобно пользоваться следующими двумя
теоремами о разложении.
Теорема о разложении рациональной дроби
В курсе интегрального исчисления при интегрировании ра-
рациональных дробей доказывается, что правильная несократимая
рациональная дробь ^Д может быть представлена в виде
суммы элементарных дробей вида **:
§ 1] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Я ЕГО ОСНОВНЫЕ СВОЙСТВА 279
где рк—действительные или комплексные корни многочле-
многочлена Q(P). ** — кратность корня p^,^ — постоянные величины-,
т —«число различных корней многочлена С? (р).
Для каждого слагаемого правой части оригинал легко на-
находится (см. пример в), стр. 271 и свойство 7), стр. 275 или
№№ 4 и 5' таблицы стр. 275).
Опираясь на теорию вычетов, можно указать очень простой
способ вычисления коэффициентов А^ в том случае, когда все
корни рк простые и, следовательно, разложение C) имеет вид
Действительно, разлагая функцию tjt-t в ряд Лораиа в окрест*
ности полюса первого порядка рк, получим:
так как для всех слагаемых суммы D), кроме ¦¦ _* , точка
рк ие является особой точкой, и поэтому их разложение в ряд
Лорана содержит лишь правильную часть.
Следовательно, Ак является вычетом функции -я— отно-
относительно полюса рк и может быть иайдеио методами § 2 гл. VII:
или
Следовательно, в рассматриваемом случае
Q(P)
280 некоторые сведения из операционного исчисления [гл. xi
Теорема о разложении по отрицательным
степеням р
Если аналитическая в окрестности бесконечно удаленной
точки функция п(р) имеет в бесконечности нуль, то разложе-
разложение в ряд Лорана в окрестности бесконечно удаленной точки
имеет вид
и так как оригиналом для общего члена этого ряда Ц? яв-
ляется . _ . (см. пример в), стр. 271 или 2, стр. 275), то
естественно ожидать, что оригиналом для функции
является сумма ряда
и=1
Сумма ряда F) действительно будет оригиналом функции п(р),
если ряд F) равномерно сходится при 0^t<^oo, так как
в этом случае, умножая F) на e~ptdt и почленно интегрируя
ряд в правой части уравнения в пределах от 0 до оо, полу-
получим E).
§ 2. Интегрирование обыкновенных линейных
дифференциальных уравиений
с постоянными коэффициентами
Для интегрирования линейного уравнения с постоянными
коэффициентами
G)
(f{t) удовлетворяет условиям 1), 2), 3), стр. 271) с начальными
условиями
*<*@) = 0 (А = 0, 1, 2,..., <л-1))
совершаем над левой в правой частями равенства G) пре-
§ 2] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦ. 281
образование Лапласа и, опираясь на свойства 1), 2), 3) (стр.
272—273), получим:
откуда
*(р) = М, где
Пользуясь таблицами или формулой обращения, а иногда пред-
предварительно преобразовав функцию Цтк {например, с помощью
теоремы о разложении), находим по изображению х (р) = -тур-.
оригинал x{f), когорый и является искомым решением при
ех>.
Если искомое решение уравнения G) должно удовлетворять
начальным условиям
*<*'@) = *<*> (* = о, 1,..., (л —1)),
то, применяя к G) преобразование Лапласа, получим:
или
Q{p)x(p)=?{p)+<f{p),
где <р(р) — известная целая рациональная функция р, откуда
Х{Р)~ Q(p) •
и, находя по изображению оригинал, получим искомое реше-
решение x(t).
Пример 1. Найти решение дифференциального уравнения
удовлетворяющее начальным условиям х@) = 0, х@) =
Переходя к изображению, получим:
()
282 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. XI
откуда
2
Разлагая на элементарные дроби (при этом удобно применить теорему
о разложении рациональной дроби — см. стр. 278—279), получим:
1 2.1
+
Принимая во внимание, что eat—<¦ , найдем искомое решение:
Пример 2. Проинтегрировать уравнение
x(t)-4x(t) + 4x(t) = itea, х@) = 0, *{0) = 0.
Переходя к изображению и принимая во внимание формулы
^ a) (8)
(см. стр. 271 и 275), получим:
(р._4/,+4)х(р) = _А!_,
3!
откуда x(p)=z.р_2\*' "' ПОЛЬЗУЯСЬ теми же Двумя формулами (8)
или табличной формулой 5 (стр. 275), найдем:
Ре*
Пример 3. Проинтегрировать уравнение
X(Q + x(O=sinf, x@) = 0, jc(O)=-i.
Пользуясь свойством 3) (стр. 273) и формулой 9 (стр. 276),
переходим к изображениям и получаем:
(^ + 1)*(р)+у ^
откуда
Пользуясь формулой 13 (стр. 276), получим:
... t cos t
x(t)= 2~.
Тем же методом можно интегрировать системы линейных
дифференциальных уравнений с постоянными коэффициентами.
§ 3] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЗАПАЗД. АРГУМЕНТОМ/ 283
Пример 4. Проинтегрировать систему уравнений
*<0)=1, у@) = 1.
Переходя к изображениям, получим:
3* (/>) + (? - 2O (P)=~i + Ь
Решая эту систему линейных уравнений, получим:
откуда
§ 3. Интегрирование
некоторых лииейиых дифференциальных уравнений
с запаздывающем аргументом
Как уже упоминалось на стр. 260, многие процессы с по-
последействием, и в частности многие задачи теории регулиро-
регулирования, описываются дифференциальными уравнениями с запаз-
запаздывающими аргументами. Особенно часто в приложениях
приходится интегрировать линейные дифференциальные уравне-
уравнений с запаздывающими аргументами, с постоянными коэффици-
коэффициентами и с постоянными запаздываниями:
где аы и т, — постоянные, причем
или системы таких уравнений.
Предполагая, что искомое решение x(t) удовлетворяет
условиям 1), 2), 3) (стр. 271) и что лг<*>@) = 01) (* = 0, 1,
..., (п — 1)), переходим в равенстве (9) к изображеиию, поль-
пользуясь при этом свойствами 1), 2), 3), 5) (стр. 272—274):
)
функция
») Это условие и условие 2) стр. 271 означают, что начальная
кция ?@^0 (см. стр. 260 или подробнее [15J).
284 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [гЛ. И
или
*(/>)= гШ • <10>
Переходя с помощью таблиц или формулы обращения к
оригиналу, получим искомое решение x(t).
Заметим, что переход от изображения к оригиналу в рас-
рассматриваемом случае обычно сопряжен с некоторыми затруд-
затруднениями ввиду довольно сложного вида знаменателя в A0),
поэтому операционный метод часто применяет в комбинации
с «методом шагов» (см. [15]).
§ 4. Интегрирование некоторых дифференциальных
уравнений в частных производных
Общая схема интегрирования методами операционного
исчисления линейных уравнений в частных производных с по-
постоянными коэффициентами, например уравнений вида
fl» dF+ 2a»CT+e» d?+ 2fl»Tx+2a» W+
+ а„« =/(t,x), A1)
с некоторыми начальными и граничными условиями сводится
к следующему: считая, что искомое решение а(х, t) по пере-
переменному t удовлетворяет наложенным на оригинал условиям
(см. стр. 271), умножаем тождество A1) на e~ptdt и интегри-
интегрируем по t в пределах от 0 до оо, т. е. переходим в равен-
равенстве (И) к изображениям по переменному t, при этом уравнение
в частных производных A1) переходит в обыкновенное диффе-
дифференциальное уравнение. Переходя к изображению в граничных
условиях, получим граничные условия для решения обыкновен-
обыкновенного дифференциального уравнения, определяющего изображение.
Интегрируя полученное обыкновенное уравнение операционными
или иными методами, получим изображение а(х, р) искомого
решения и с помощью таблиц или формулы обращения находим
искомое решение.
Пример 1. Найти ори х > 0 к t > 0 решение уравнения тепло-
проводностм
ди ,&и /1т
§ 4] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ 285
удовлетворяющее граничному условию
а @, <)=и» A3)
в начальному условию
а(х, 0)=0. A3')
При этом мы решаем задачу о распределении температуры и (х, t)
в полубесконечном однородном стержне, если начальная температура
стержня равна нулю, а на границе стержня все время поддерживается
постоянная температура я„.
Переходя в уравнении A2) к изображениям и принимая при
атом во внимание начальное условие A3'), получим:
Переход к изображению в граничном условии A3) дает
й@,/>)=-^. A5)
Р
Интегрируя уравнение A4), получим:
xVJ xYf
й(х,р) = с1 е а +cte a .
Произвольные постоянные определяются из условий A5) и из вытекаю-
вытекающего из физического смысла задачи требования ограниченности реше-
решения а(х, t), а следовательно и ц (х, р), при х—> оо. Из этих условий
и
получим: ct=0, с, ^-^ и, следовательно,
Пользуясь формулой 32 (стр. 277), находим искомое решение:
X
1л VT
При интегрировании дифференциальных уравнений в част-
частных производных с двумя или большим числом независимых
переменных во многих случаях целесообразно совершать прео-
преобразование Лапласа не по одному, а по нескольким переменным.
Подробнее о применении операционных методов к интегри-
интегрированию дифференциальных уравнений см. [6], [VII], [VIII].
286 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. XI
§ 5. Разложение изображения в асимптотический ряд
В прикладных задачах часто требуется хотя бы прибли-
приближенно определить значение некоторой функции f(f) при боль-
больших значениях аргумента. Такие задачи возникают, например,
при изучении установившихся режимов.
В этих случаях стараются представить функцию/(*) в виде
/(О = <Р (О+ Ж'), A6)
где R(t)—*0 при t—юо. Если f(t) не стремится к нулю
при t—»-оо или если R(t) стремится к нулю быстрее, чем
<р @, то можно для больших значений t приближенно заменить
функцию f(t) функцией <р@, причем такая замена будет тем
более точной, чем быстрее стремится R Щ к нулю при t —юо.
Если t комплексное переменное и речь идет о вычислении
значений аналитической в бесконечности функции f(t) при
бопьших по модулю значениях t, то представление функции
f(t) в виде A6) может быть получено, например, путем раз-
разложения функции f(t) в ряд Лорана в окрестности бесконечно
удаленной точки:
07)
стремится к нулю при
-оо, причем порядок стремления к нулю остатка ряда
Ra(t) не ниже рт» так как
lim ^+1/?я@ =
t-*ao
Следовательно, для больших по модулю значений t можно при-
приближенно заменять функцию f{t) несколькими членами ее
лорановского разложения A7).
Удобный способ получения таких так называемых асимпто-
асимптотических представлений функций даю г методы операционного
исчисления.
Рассмотрим изображение
оо
u{p)=\e'ptu(t)dt
§ 5] РАЗЛОЖЕНИЕ ИЗОБРАЖЕНИЯ В АСИМПТОТИЧЕСКИЙ РЯД 287
в в предположении, что a(t) имеет производные до я-j-1-го
порядка, удовлетворяющие условиям, наложенным на функцию-
оригинал (см. стр. 271), проинтегрируем правую часть по ча-
частям л— 1 раз:
Докажем, что
где Ап — некоторая постоянная.
Действительно,
и так как по предположению
| *<»+•>(*) К л1я+1***,
где Мп+1 — постоянная прн фиксированном я, то при
где Ап — постоянная.
Следовательно, изображение п(р) представлено в виде
где
Если функция обладает производными сколь угодно высо-
высокого порядка, удовлетворяющими условиям, наложенным на
функцию-оригинал» то вместо A8) можно написать для функ-
288 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ [гл. XI
ции и (/>) разложение в так называемый асимптотический ряд:
При разложении в асимптотический ряд вместо знака равен-
равенства пишут знак с/з, так как ряд, стоящий в правой части
A9), может быть даже расходящимся, т. е. гп(р) в A8) мо-
может не только не стремиться к нулю при л—>оо, но может
даже неограниченно возрастать по модулю ввиду возможности
быстрого стремления Ап к бесконечности. Однако при фикси-
фиксированном л /*„(/>)—»0 при \р\—>оо, причем г„(р) стремится
к нулю быстрее, чем остальные слагаемые в правой части A8),
и, следовательно, при больших по модулю значениях р можно
приближенно заменять функцию п(р) суммой нескольких на-
начальных членов ее асимптотического ряда A9).
Заметим, что ряд A9), вообще говоря, не является рядом
Лорана функции п(р), так как для возможности разложения
функции и(р) в асимптотический ряд A9) не требовалось, на-
например, чтобы бесконечно удаленная точка была правильной
или изолированной особой точкой функции п{р).
Пример 1. Разложить в асимптотический ряд функцию
Принимая во внимание, что оршиналом функции B0) является
функция р
(см. 31, стр. 277), согласно A9) будем иметь:
? 1 1 .1.3 ЬЗ-5 .
еР)е
нш
, !у,1-3.5...Bя-1) ,
B1)
§ 5] РАЗЛОЖЕНИЕ ИЗОБРАЖЕНИЯ В АСИМПТОТИЧЕСКИЙ РЯД 289
Р
Представив интеграл \e'tldt в виде разности
о р
и принимая во внимание, что
можно из B1) получить асимптотическое разложение
Пример 2. Разложить в асимптотический ряд функцию sin —.
Рассматриваемая функция является аналитической в бесконечно-
бесконечности. Следовательно, асимптотический ряд можно получить iiyтем раз-
разложения этой функции в ряд Лорана в окрестности бесконечио уда-
удаленной точки
Задачи к главе XI
Проинтегрировать диффереициальные уравнения прн
1. "х-2х+х=±М, х@)=х@) = 0.
2. x'+3x + 3i + * = 6e"t. х@) = х@)=х@) = 0.
3. х-3х + 2х=12е*. х@) = 2, х{0)=6.
4. x-T-4x = 3slnf-f-10cos3f, х@) = — 2, х@) = 3.
6. * — x = 4Mnt + 5cos2t, х@)= -1, х@)=-2.
& x+x=cost, х@)=0, х((^ = а
7. х-2х + 2х = 2в'со8<, х{0) = 0, *@)=0.
8. х+9х.— Э0сЫ, х@)=3. х@)=0.
9. x + 2x + 2y = lje« \ x@)=sl, y@)=3.
10. Разложить в асимптотический ряд функцию е **.
П. Разложить в асимптотический ряд функцию со* у
ОТВЕТЫ К ЗАДАЧАМ
Глава I
в) 2 (cos 0 -f' stn 0); г) 2 (cos тс -j- / sin к);
jO/T^cosj
е) V~2 [cos ^-
и)
к) ]A29[cos^-arctg|-)+/sin^il-arctg-|-)];
л) У29 [cos(-arctg-|-) + /sin(-arctg -|)J;
м) /29 [cos^ + arctg |-) + /sin (it + ardg-|
2. а) Вне круга радиуса 5 с центром в- начале координат; б) вну-
внутри круга радиуса 3 с центром в точке г; в) вне круга радиуса 2 с
центром в точке — 2/ и на окружности этого круга; г) на окруж-
окружности круга радиуса 5 с центром в точке 3+4/; д) направо
от прямой х —3; е) ниже прямой у =2 и на самой этой
прямой; ж) на эллипсе с фокусами в точках —2 и 2 и
большой полуосью •?-; з) внутри левой ветви гиперболы с фокусами
в точках — 2 и 2 и действительной полуосью -у; и) на лемискате
(х* — у* — 1)* -\- 4х*у* = а4; к) на гиперболе х* — у* = а*", л) на перпен-
перпендикуляре к отрезку, соединяющему точки / и — 2, восставленному из
ОТВЕТЫ К ЗАДАЧАМ 291
5
середины этого отрезка; м) на пряной х = у и слева от нее; н) вну-
внутри угла между лучами <р=<* и <р=Р, выходящими из начала коор-
координат; о) на луче, выходящем из точки / под углом -j к положи-
положительному направлению действительной оси; п) внутри угла между
лучами, выходящими из точки — 41 и образующими с положитель-
положительным направлением действительной оси углы, равные соответственно
it it
4. а) -Л в) —/; в) у+|"/; г> - 16(УТ-Ь0; Д) -8.
5. a) I (VT+i), 1(- УГ-ь/), -/; б)
- VT+ft X± (YT+i), - Vii, J^
где ?=^, ~\
_2-/; е) VT(cos9 + /sin9), где ? = |-, Ц?, I??.
Глава II
i; 6)ut + v1=l; b)w=—и; г) t» = 0;
2. а) Прямая y = xr, б) эллипс -1-|-'г«= 1; в) гипербола у^—;
г) ветвь гиперболы у = —, лежащая в первой четверти (х > 0, у > 0).
Глава III
1. a)-i-
B)lo5-/arctg j
Указание. Главное значение аргумента числа — 3Ц-4/ равно
ж — arctg -g .
2, а) - « б) - el; в) e»(cos 1 + /sin 1); г)
/2 — —\
^cosx или chy sinx-J-/shycosxj
sin x или chycosx — iahy sin x.
в. а) BА+1)^-/10C*2 1^-): 6J*«-Пп(/~5-1К
BA + 1) n - /In (VT+1); в) 2b + ardg ^T-1 [In A
, BA+l)il-arctg«/'2-/[ln(</T-l)-f
i-arctg2 + l
= 0, rt 1, rt 2, ...).
Глава IV
2. a) *•+« б) г»+2г+О; вI +О; r) -i- + 2iz+ Cf, д) - 2fe»+Gt
a) j^y + C б) *« + 3/г+С в) 1пг + С; г)
4. а) Углы поворота 0 и 0, коэффициенты растяжения 2 и 3;
б) углы поворота 0 н 0, коэффициенты растяжения 1 и -j-; в) углы
1 3
поворота и и 0, коэффициенты растяжения y ц W Г* углы ПОВО"
рота |i|, коэффициенты растяжения 2 У~2 и 6; д) углы пово-
поворота — -g- и — -g- > коэффициенты растяжения 4 и 12.
& а) Сжимается внутренность круга |z|<-=-, растягивается
внешность круга | % \ > -к \ б) сжимается внешность круга ] г \ > 1,
растягивается внутренность круга | г \ < 1; в) сжимается внутренность
круга | г -\-11 < у, растягивается внешность круга | г -J-11 > J-;
ОТВЕТЫ К ЗАДАЧАМ 293
г) сжимается левая полуплоскость х<0, растягивается правая
полуплоскость х >0; д) сжимается внешность круга |z-A 11 > 1, рас-
растягивается внутренность круга \z— 11< 1.
Глава V
1. a) B±i; б) 2+~. 2. а) 1; б) 2. & а) —8*? б) 0.
5.а,|-; 6)-f *¦)?;*-?. 7. ?.
а) У J б) -^; в) 0.
Глава VI
I. а) % б) 1; в) оо; г) 0; я) е\ е) 1. 4. е - [^1 + i- (z - 1)-|-
где А = 0, 1, 2, ... , ш— 1. Радиус сходимости равен 1.
1.3-5
Радиус сходимости равен 1 в обоих случаях.
б) sin 1+cos Lz-f-(cosl — ^-
() ()
z-a {z-a? , 1
{-bf (a-ft)* r(a-ft)(z-a) *
1 1 5_ 1
* -~T~z* 6z»~2z* *•••
область сходимости | z | > 1.
9. а) Полюсы 1-го порядка z=0 и t—~ \, полюс 3-го порядка
»= 1; б) полюсы 3-го порядка + ^- A-0; в) полюсы 1-го по-
294 ответы к задачам
рядка z = Ли (k=0, -?z 1, -iz 2,...); г) полюсы 2-го порядка z = ^
(* = 0, rtl, ±:2, ...); Я) существенно особая точка z = 2? e) суще-
существенно особая точка z =— Л, ж) полюсы 1-го порядка z=l-f~
2
-j- „. . . - (* = 0, itl, -±.% ...), z=l —предельная точка для по-
2й4-1
люсов; з) z = 1 -| 3-— « — полюсы 1-го порядка, z = 1 — устра-
устранимая особая точка; и) z = 0 — устранимая особая точка; к) z = 0 —
полюс 3-го порядка.
10. а) Устранимая особая точка; б) устранимая особая точка (нуль
3-го порядка); в) существенно особая точка; г) существенно особая
точка; д) полюс 3-го порядка; е) полюс 2-го порядка; ж) устранимая
особая точка; з) устранимая особая точка; и) существенно особая
точка.
11. а) Нет; б) да. 12. а) Да; б) нет.
Глава VII
1. а) 5; б) -я- (fi-f"-j); в) ~ Та (относительно точки /) и -^
(относительно точки - /,; г) ( - 1)»- <Л + 2>(л + ^ • fn ~ »'2п ;
д) —-J-1 относительно точки / |и -j( относительно точки —/);
е) 1 ( относительно точки 0 1 и — -=- ( относительно каждой из
точек d: 1); ж) —1 (относительно каждой из точек B*4-1) -тН!
з) 0 (относительно каждой из точек kit); и) — 1 (относительно каждой
из точек kn) (й = 0, ±1, =?2, ...).
2. а) 1; 6H; в) I. &-¦—, 4. -^.
5. аH;
1 '» 1(л-1)!]»(а-
в. а) к 1^ 2;
"зтз; «) 4^- <4 cos 2+2 sin 2>- 3» * B sin 2~3 со* зх
и) y (cos 1 — e~*Y
г а) 0; б) 4; в) 1.
ОТВЕТЫ К ЗАДАЧАМ 295
Глава VIII
E) w~i
для облаем //, ю= f^+^j+Л для
«масти III, а> = -/2г + ^Д+Л 'длг области /К; г) ю =
/:3) —
и) w=e3 * T=l%
S. На верхнюю полуплоскость.
в. На внутренность единичного круга.
Глава IX
Модуль вектора в точке г:
Угол между вектором в точке г н положительным направлением дей-
действительной осн:
1, — Atgz. 2. 2Arg«-Arg(z*— I). 3. Atgz— j. 4. у Arg(«-a).
i) В каждом ответе указана лишь одна из функций, удовлетво-
удовлетворяющих условию задачи.
396 ОТВЕТЫ К ЗАДАЧАМ
Уравнения линий тока
1. ху=с. 2. у (l — ^ Л = с, в полярных координатах
c. З.р = се-*. 4. р=—¦?—
если полярная систеыа координат выбрана так, что полюс находится
в точке z = а, а направление полярной оси совпадает с положитель-
положительным направлением действительной оси.
Уравнения линий уровня потенциальной функции
1. Xх — у* = с. 2. к !-(- * . , J = с, в полярных координатах
если полярная система координат выбрана так же, как при опреде-
определении линий точка (см. выше).
5. Г=0; #=0.
в. Г = — 6ic;7V=4ic.
Глава X
1. Решение x=sO асимптотически устойчиво.
2. Решение хгО асимптотически устойчиво.
3. Решение х^0, уэО неустойчиво.
4. Решение х==0 асимптотически устойчиво.
5. Область асимптотической устойчивости ограничена прямой
fc=0 и кривой a = t\gxt, b=-!—., 0*?t<?-.
cos тг /т
в. Область асимптотической устойчивости ограничена прямой
*=0 и кривой a = *shitf, Ь = Рсовх1, Q^t^-%-.
7. Решение х == 0 асимптотически устойчиво.
8 Не имеет. См. пример 6.
Глава XI
I. х = ~. 2.х = Ре-*. З.х=2е*. 4.x=slnt + sln2t—2cos3/.
S. *=— 2sinf — cos2*. в. x—i-Zj^-. 7.x = fe'sin<. 8.
гл 00
1 it V t — l)"
ilssO
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1. А. Ф. Берм аи т, Курс математического анализа, т. I, Гостехиз-
дат, 1957.
2. А. Ф. Б е р м а н т, Курс математического анализа, т. К, Гостех-
издат, 1957*
3. И. А. Гольдфайи, Элементы векторного исчисления, Гостехиз-
дат, 1948.
4. В. А. Диткии и П. И. Кузнецов, Справочник по операци-
операционному исчислению, Гостем из дат, 1951.
Б. Л. В. Канторович и В. И. Крылов, Приближенные мето-
методы высшего анализа, Гостехиздат, 1952.
6. X. С Карслоу, Теория теплопроводности, Гостехиздат, 1947.
7. И. Г. М а л к и н, Теория устойчивости движения, Гостехиздат,
1952.
8. М. А. Лаврентьев и Б. В. Шабат, Методы теории функций
* комплексного переменного, Гостехиздат, 1951.
9. И. И. Привалов, Введение в теорию функций комплексного
' переменного, Гостехиздат, 1954.
'10. И. Н. Бронштейн и К. А. Семеидяев, Справочник по ма-
математике, Гостехиздат, 1958.
11. В. И. Смирнов, Курс высшей математики, т. I, Гостехиздат,
1957.
12. В. И. Смирнов, Курс высшей математики, т. II, Гостехиздат,
1957.
13. Л. И. Седов, Плоские задачи гидродинамики и аэродинамики,
Гостехиздат, 1950.
14. Н. Г. Чеботарев и Н. Н. Меймаи, Проблема Рауса —Гур-
вица для полиномов и целых функций, Труды матем. ин-
института им. В. А. Стеклова, XXVI, Изд. АН СССР, 1949.
15. Л. Э. Э л ь с г о л ь ц, Обыкновенные дифференциальные уравне-
уравнения, Гостеиздат, 1954.
16. Л. Э. Э л ь с г о л ь ц, Вариационное исчисление, Гостехиздат, 1958.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
I. А. И.Маркушевич, Краткий курс теории аналитических
функций, Гостехиздат, 1957.
II. М. А. Л а в р е н т ь е в и Б. В. Ш а б а т, Методы теории функ-
функций комплексного переменного, Гостехиздат, 1951.
III. Б. А. Ф у к с и Б. В. Ш а б а т, Функции комплексного перемен-
переменного и некоторые их приложения, Физико-математическая
библиотека инженера, Гостехиздат, 1949.
IV. М. А. Лаврентьев, Конформное отображение, Физико-мате-
Физико-математическая библиотека инженера, Гостехиздат, 1946.
V. И. И. П р н в а л о в, Введение в теорию функций комплексного
переменного, Гостехиздат, 1954.
VI. В. И. Крылов и Л. В. Канторович, Приближенные мето-
методы высшего анализа, Гостехиздат, 1952.
VII. М, И. Канторович, Операционное исчисление и нестацио-
нестационарные явления в электрических цепях, Физико-математи-
Физико-математическая библиотека инженера, Гостехиздат, 1949.
VIII. А. И. Л у р ь е, Операционное исчисление и его приложения к
задачам механики, Физико-математическая библиотека ин-
инженера, Гостехиздат, 1950,
ГРИГОРИЙ ЛЬВОВИЧ ЛУНЦ
ЛЕВ ЭРНЕСТОВИЧ ЭЛЬСГОЛЬЦ
ФУНКЦИИ
КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
ИЗДАНИЕ ВТОРОЕ,
СТКРЕОТИПНОЕ
Генеральный директор А Л. Кноп
Директор издательства О.В.Смирнова
Главный редактор Ю. А. Сандулов
Художественный редактор С. Л. Шапиро
Выпускающие Н. К. Белякова, А. В. Яковлев
ЛР № 065466 от 21.10.97
Гягиеввческий сертификат 78 01.07.953.П.000996.02.01.
от 13.02.2001 г., выдан ЦГСЭН в СПб
Издательство «ЛАНЬ»
lan@lpbl.spb.ru
www.lanpbl.spb.ru
193012, Санкт-Петербург, пр. Обуховской обороны, 277,
издательство: тел.: (812J62-11-78;
pbl@lpbl.spb.ru (издательский отдел),
производственный отдел; тел.: (812J62-24-95;
print@lpbl.spb.ru (производственный отдел),
склад № 1: факс: (812J67-27-92, 267-13-68;
trade@lpbl.spb.ru (торговый отдел),
193029, пр. Елизарова, 1,
склад М 2: (812J65-00-88, 567-54-93, 567-14-45;
root@lanpbl.spb.ru
Филиал в Москве:
Москва, 7-я ул. Текстильщиков, 5,
тел.: @95)919-96-00, 787-59-47, 787-59-48'
Филиал в Краснодаре:
350072, Краснодар, ул. Зиповская, 7, тел.: (8612N2-97-73
Сдано в набор 23.10.99. Подписано в печать 10.02.2002.
Бумага газетная Гарнитура Школьная. Формат 84X108V32-
Уч.-изд. л. 15,18. Усл. п. л. 15,37. Тираж 5000 экз.
Заказ N' 66.
Отпечатано с готовых диапозитивов
вГИПК «Лениздат» (типография им. Володарского)
Министерства Российской Федерации по делам печати,
телерадиовещания и средств массовых коммуникаций.
191023, Санкт-Петербург, наб. р. Фонтанки, 59.