Algèbre
linéaire
Réduction des endomorphismes
• Cours complet
• Commentaires et développements
• Plus de 120 exercices corrigés
Vuibert
A

Roger Mansuy
Avec la participation de Rached Mneimné
ï f*
Réduction des endomorphismes
Cours & exercices corrigés
LICENCE MATHÉMATIQUES
CLASSES PRÉPARATOIRES SCIENTIFIQUES
Vuibert

Déjà parus dans la nouvelle collection de manuels universitaires scientifiques
Éric Canon
Analyse numérique.
Cours et exercices corrigés - L2 & L3, 256 pages
Jérôme Depauw
Statistiques.
Cours et exercices corrigés - Master, 176 pages
Vincent Rivoirard & Gilles Stoltz,
Statistique mathématique en action.
Cours, problèmes d'application corrigés et mises en action concrètes - Master & Agrégation externe,
2e édition, 448 pages
Marc Briane & Gilles Pages,
Analyse. Théorie de l'intégration. Convolution et transformée de Fourier.
Cours et exercices corrigés - L3 & Master 1, 5e édition, 368 pages
Anne Cortella,
Algèbre. Théorie des groupes.
Cours et exercices corrigés - L3 & Master, 224 pages
Bruno Aebischer,
Introduction à l'analyse.
Cours et exercices corrigés - L1, 288 pages
Bruno Aebischer,
Analyse. Fonctions de plusieurs variables & géométrie analytique.
Cours et exercices corrigés - L2,448 pages
Bruno Aebischer,
Géométrie. Géométrie affine, géométrie euclidienne & introduction à la géométrie projective.
Cours et exercices corrigés - L3, 288 pages
Ariel Dufetel,
Analyse. CAPES externe et Agrégation interne.
Cours et exercices corrigés, 672 pages
et des dizaines d'autres livres de référence, d'étude ou de culture
en mathématiques, informatique et autres spécialités scientifiques
www.vuibert.fr
En couverture : Escalier en double spirale de Giuseppe Momo, Vatican.
© Sylvain Sonnet/Corbis
Maquette intérieure, composition et mise en page de l'auteur
Couverture : Linda Skoropad/Prescricom
ISBN 978-2-311-00285-0
Registre de l'éditeur : 610
La loi du 11 mars 1957 n'autorisant aux termes des alinéas 2 et 3 de l'article 41, d'une part, que les « copies ou reproductions
strictement réservées à l'usage privé du copiste et non destinées à une utilisation collective » et, d'autre part, que les analyses et les
courtes citations dans un but d'exemple et d'illustration, « toute représentation ou reproduction intégrale, ou partielle, faite sans le
consentement de l'auteur ou de ses ayants droit ou ayants cause, est illicite » (alinéa 1erde l'article 40). Cette représentation ou
reproduction, par quelque procédé que ce soit, constituerait donc une contrefaçon sanctionnée par les articles 425 et suivants du
Code pénal. Des photocopies payantes peuvent être réalisées avec l'accord de l'éditeur. S'adresser au Centre français d'exploitation
du droit de copie : 20 rue des Grands Augustins, F-75006 Paris. Tél. :01 44 07 47 70
© Vuibert - septembre 2012 - 5 allée de la 2e DB, 75015 Paris

Table des matières
I. Polynômes d'endomorphismes
1. Un morphisme d'algèbre 1
2. Idéal des polynômes annulateurs 2
3. Polynôme minimal 4
4. Utilisation pratique d'un polynôme annulateur 5
5. Commentaires et développements 7
6. Exercices 9
II. Sous-espaces stables
1. Restriction d'un endomorphisme 13
2. Sous-espace stable 15
3. Endomorphisme induit sur un sous-espace stable 16
4. Exemples de sous-espaces stables 16
5. Sous-espaces cycliques 17
6. Commentaires et développements 18
7. Exercices 20
III. Commutation
1. Définitions 25
2. Calculs de commutants 27
3. Endomorphisme adf 28
4. Commentaires et développements 29
5. Exercices 30
IV. Lemme des noyaux
1. Étude de kerP(/) 37
2. Lemme des noyaux 38
3. Décomposition de l'espace en sous-espaces stables 40
4. Commentaires et développements 41
5. Exercices • . 43

iv Table des matières
V. Éléments propres, caractéristiques
1. Définitions 45
2. Polynôme caractéristique 48
3. Commentaires et développements 50
4. Exercices 53
VI. Endomorphismes cycliques
1. Définitions 59
2. Caractérisation avec le polynôme minimal 60
3. Caractérisation avec le commutant 60
4. Matrice compagnon 62
5. Polynôme caractéristique 64
6. Commentaires et développements 65
7. Exercices 67
VII. Théorème de Cayley & Hamilton
1. Énoncé et conséquences 71
2. Preuve par les sous-espaces cycliques 72
3. Preuve par la formule de la comatrice 72
4. Sous-espaces caractéristiques 73
5. Multiplicités 73
6. Commentaires et développements 74
7. Exercices 75
VIII. Diagonalisation
1. Critères de diagonalisation 79
2. Critère de co-diagonalisation 84
3. Commentaires et développements 85
4. Exercices 86
IX. Trigonalisation
1. Critères de trigonalisation 93
2. Fonctions symétriques des valeurs propres 95
3. Commentaires et développements 99
4. Exercices 100
X. Réduction de Jordan
1. Décomposition de Jordan & Dunford 105
2. Réduction de Jordan : cas nilpotent 107
3. Interlude : lire un tableau de Young 113
4. Réduction de Jordan : cas général 114
5. Commentaires et développements 115
6. Exercices 117

Table des matières v
XI. Réduction de Probenius
1. Réduction de Frobenius 125
2. Retour sur la réduction de Jordan 128
3. Commutants et bicommutants 131
4. Commentaires et développements 134
5. Exercices 135
XII. Topologie des classes de similitude
1. Rappels sur la relation de similitude 139
2. Classes de similitude dans M2O&) 140
3. Adhérence d'une classe de similitude 144
4. Connexité d'une classe de similitude 146
5. Commentaires et développements 147
6. Exercices 148
XIII. Localisation des valeurs propres
1. Théorème de Hadamard 153
2. Disques de Gerschgorin 154
3. Rayon spectral 156
4. Théorème de Perron 157
5. Théorème de Perron & Frobenius 159
6. Commentaires et développements 161
7. Exercices 163
XIV. Application aux chaînes de Markov finies
1. Chaînes de Markov 169
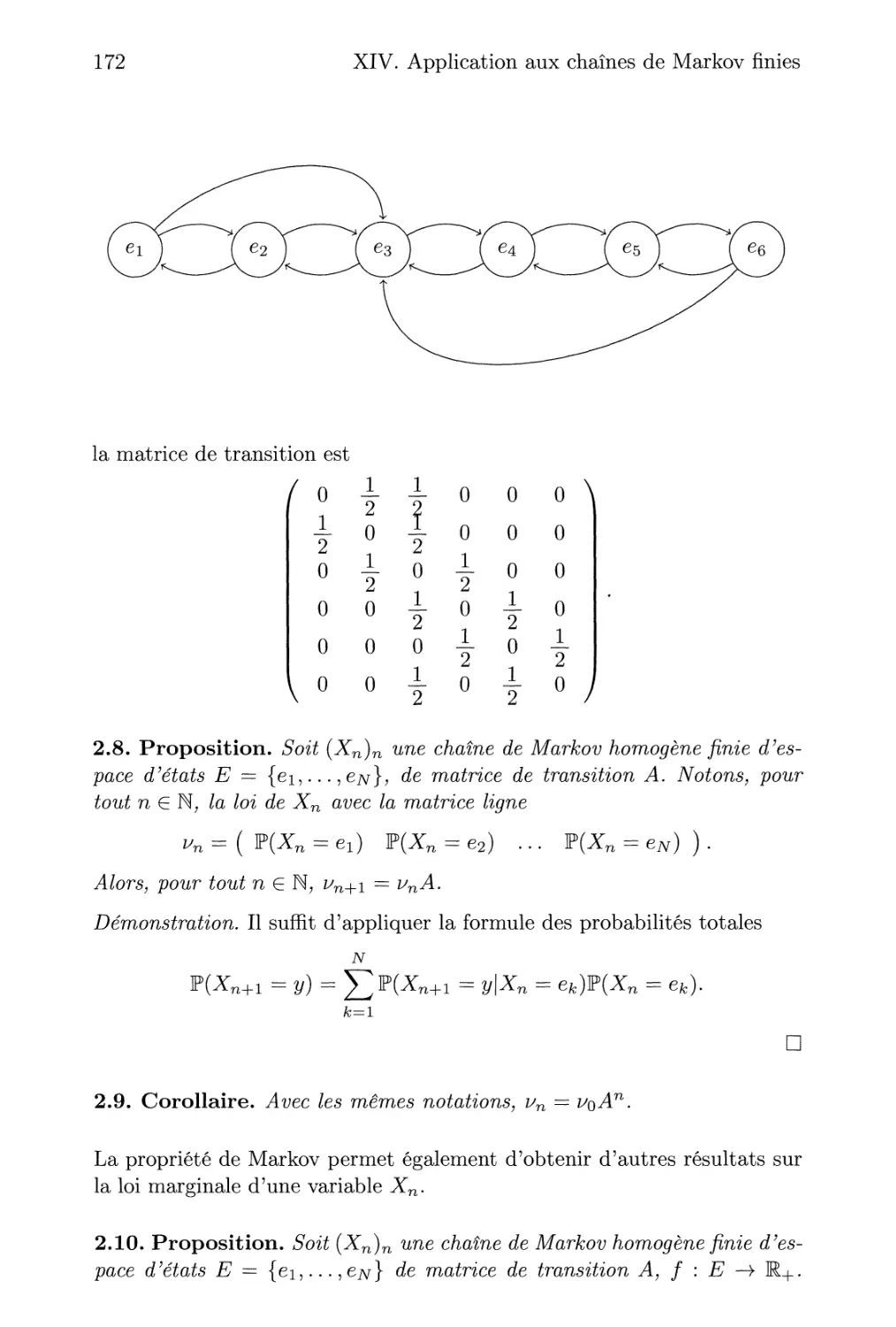
2. Matrice de transition 170
3. Probabilité invariante 173
4. Théorème ergodique 174
5. Commentaires et développements 176
6. Exercices 178
Notations 181
Index 182

Avant-propos
Qu'est-ce que la réduction ?
Dans tout cours d'algèbre linéaire, la réduction des matrices et des endo-
morphismes occupe une place prépondérante. Toutefois, ce terme de
réduction cache de nombreuses réalités et perspectives.
> D'une part, réduire un endomorphisme / d'un espace de dimension finie,
c'est trouver une base dans laquelle l'endomorphisme / est « bien
compris » et « facilement manipulable ». En pratique, cela revient à pouvoir
déterminer une matrice de l'endomorphisme avec une forme particulière :
diagonale (dans le meilleur des cas), diagonale par blocs, triangulaire...
Pour une matrice carrée M, l'équivalent de cette démarche consiste à
chercher une matrice d'une forme particulière semblable à M : en effet, la
formule de changement de bases pour la matrice d'un endomorphisme n'est
autre que la traduction de la similitude de deux matrices.
> D'autre part, réduire un endomorphisme (respectivement une matrice)
c'est comprendre l'ensemble de toutes les matrices qui lui sont associées
(respectivement sa classe de similitude) ; pour ce faire, on cherche une
matrice réduite qui décrit simplement, qui caractérise cet ensemble. En
avançant dans cette direction, on retrouve à la fois les invariants de similitude
(pour la réduite de Frobenius) et les tableaux de Young (pour la réduite de
Jordan).
En théorie, un cours complet comporte les deux aspects imbriqués avec
quelques applications endogènes de l'algèbre linéaire mais aussi exogènes
en provenance de l'algèbre bilinéaire, de la topologie, des probabilités, des
sciences physiques...
Qu'est-ce que ce livre ?
Il existe de nombreux livres pour les étudiants de premiers cycles qui
traitent certains des aspects de la réduction mais aucun ne semble avoir

Vlll
Avant-propos
pris la mesure de la richesse du sujet dans les cours des premiers cycles
(et dans les préparations aux concours de recrutement de l'Éducation
Nationale). Nous avons donc cherché à fournir une introduction raisonnée à
l'ensemble de la réduction. Le livre se découpe grossièrement en cinq
parties.
> Tout d'abord, les sept premiers chapitres présentent dans un ordre assez
classique les outils de la suite du livre. L'algèbre des polynômes en un
endomorphisme (respectivement une matrice carrée) joue évidemment un
rôle essentiel. Nous avons pris le parti de privilégier l'aspect élémentaire
donc de cacher, au moins en apparences, la structure de K[X]-module.
En revanche, nous avons insisté sur l'étude des sous-espaces stables de la
forme kerP(/) trop souvent limitée au lemme des noyaux et aux sous-
espaces propres et caractéristiques. Par exemple, le lemme IV-3.3 établit
l'existence d'un sous-espace cyclique maximal de dimension le degré du
polynôme minimal : ce résultat simple est riche pour la suite.
De même, nous avons choisi de mettre en exergue les endomorphismes
cycliques (chapitre VI) à la fois pour fournir une démonstration simple du
théorème de Cayley & Hamilton mais aussi pour le lemme VI-3.3 qui établit
l'existence du supplémentaire stable d'un sous-espace cyclique maximal.
L'idée est bien évidemment de préparer le terrain aux réductions de Jordan
et Frobenius en se familiarisant avec l'argument des preuves par récurrence.
> Une fois tous ces outils mis en place, deux petits chapitres décrivent les
critères simples de diagonalisation, de trigonalisation, de réduction
simultanée... Il s'agit simplement de combiner tout ce qui a été détaillé
précédemment. Cela constitue un objectif de nombreux cours de premiers cycles
mais ce n'est ici qu'un jalon dans notre parcours.
> Les chapitres X et XI présentent les deux formes réduites normalisées :
celle de Jordan et celle de Frobenius ; nous ne nous arrêtons bien
évidemment pas à l'existence de ces réductions mais nous cherchons à en montrer
l'utilité pratique avec de nombreux exercices sur les tableaux de Young ou
les algorithmes pour passer d'une forme réduite à l'autre. Il apparaît que
ces aspects sont souvent mal compris et qu'une lecture attentive de ces
chapitres serait bienvenue pour de nombreux étudiants.
> Le chapitre XII exploite les différentes caractérisations de la similitude
obtenue jusqu'à présent pour donner dans le cadre réel ou complexe des
descriptions géométriques et topologiques des classes de similitude.
> La dernière séquence du livre répond à un problématique différente : il
s'agit de chercher approximativement où se trouvent les valeurs propres
pour une matrice complexe. Ce sujet est souvent une introduction à des
problèmes d'algorithmique pour le calcul matriciel numérique ; nous avons

Avant-propos
IX
choisi d'en détailler une autre application classique avec les chaînes de Mar-
kov homogènes finies. L'application du théorème de Perron & Frobenius est
alors assez élémentaire et pourtant très parlante sur l'importance de ce
résultat.
Voilà pour le contenu du livre. Passons maintenant à la forme. Il reste
plusieurs rédactions dans ce livre qui correspondent à différents usages. Le
contenu des chapitres est présenté de manière didactique dans une démarche
très conventionnelle parsemant de nombreux exemples (certains étant très
élémentaires) l'enchaînement des propositions et leurs preuves détaillées.
Certaines preuves sont délicates et il peut être astucieux de les sauter lors
d'une première lecture afin de comprendre correctement les énoncés puis
d'y revenir plus tard à tête reposée.
Toutefois, à la fin de chaque chapitre, une section intitulée « Commentaires
et développements » détonne : il s'agit de remarques moins détaillées mais
néanmoins profondes, d'ouvertures pour permettre d'aller plus loin, il ne
s'agit plus pour nous de faire cours mais de suggérer un travail personnel. La
dernière partie de chaque chapitre est bien évidemment constituée
d'exercices ; les corrections sont détaillées pour pouvoir être lues facilement même
si nous préconisons plutôt de ne pas les lire trop vite. Certains exercices
sont relativement classiques, d'autres plus originaux : nous avons choisi de
ne pas indiquer la difficulté pour ne pas biaiser le lecteur dans son effort
de recherche.
Notations
Précisons quelques notations ou conventions (l'ensemble des notations est
détaillé dans l'index en fin d'ouvrage).
Dans tout l'ouvrage, E un ]K-espace vectoriel de dimension finie où K est
un corps quelconque (sauf précisions contraires).
Nous pratiquons abusivement l'identification d'une matrice de A4n(K) à
l'endomorphisme de Kn canoniquement associé ; cela nous amène par exemple
quelquefois à dire qu'une matrice est injective ou qu'elle laisse stable un
sous-espace.
Lorsque que nous manipulerons des matrices par blocs, seuls les blocs non
nuls seront représentés : les espaces « vides » sont à compléter avec des
coefficients nuls.

X
Avant-propos
Remerciements
Un grand remerciement va aux relecteurs (anciens élèves, collègues et amis)
qui ont sacrifié une partie de leurs vacances estivales pour débusquer nos
coquilles et autres imprécisions : Yixin SHEN, Pierre Bayle, Anne-Laure
Biolley, Marc Yuma Chapuis, Mohammed Hawari, Ulysse Mizrahi.

Chapitre I
Polynômes
d ' endomor phismes
Objectifs du chapitre
- Comprendre l'importance de l'algèbre K[f] associée à l'endomorphisme
/•
- Calculer sur des exemples simples le polynôme minimal d'un
endomorphisme.
- Utiliser les polynômes annulateurs pour calculer puissances ou inverse
(s'il existe).
1. Un morphisme d'algèbre
1.1. Définition. Soit / G C{E). Pour tout polynôme P G K[X] de la
N
forme P(X) = Yl akXk, l'endomorphisme P(f) est défini par
k=0
N
p(f) = J2a«fk-
k=0
1.2. Exemple. Par exemple, pour le polynôme P = X3 + 2X — 1 et un
endomorphisme /, l'endomorphisme P(f) vaut /3 + 2/1 — f° — /3 + 2/ —Id.

2
I. Polynômes d'endomorphismes
1.3. Remarque. Pour toute matrice A G Mn(K) et tout polynôme P G
K[X], on définit de même la matrice P(A). Il est important de remarquer
que si A est la matrice d'un endomorphisme / dans une base B, alors P(A)
est la matrice de l'endomorphisme P(f) dans cette même base B.
1.4. Remarque. Attention aux erreurs de notation entre polynômes et
polynômes en /. Par exemple, on veille bien à ne pas mélanger les écritures
suivantes pour P, Q G K[X], f G C(E) et x G E :
- P(f)(x), qui est un vecteur et P{f(x)) qui n'est pas défini;
- (P • Q)(f) = P{f) ° Q(f), qui est un endomorphisme et (P o Q)(f) qui
est un autre endomorphisme.
1.5. Proposition. Soit f G C(E). L'application qui à un polynôme P G
K[X] associe l'endomorphisme P(f) G C{E) est un morphisme d'algebres.
L'image de ce morphisme, notée K[f], est une sous-algèbre commutative
deC(E).
1.6. Proposition. Soit f G C(E) et deux polynômes P et Q. Alors, les
endomorphismes P(f) et Q(f) commutent.
Démonstration. Par linéarité, il suffit de noter que, pour tous m et n G N,
rm rn £m-\-n £n rm
n
2. Idéal des polynômes annulâteurs
2.1. Définition. Soit / G C(E) et P G K[X]. Un polynôme P est annula-
teur de / si l'endomorphisme P(f) est l'endomorphisme nul.
2.2. Remarque. Comme précédemment, cette notion est définie de
manière analogue pour une matrice carrée.
2.3. Proposition. Tout endomorphisme d'un espace vectoriel de
dimension finie admet un polynôme annulateur non nul.
Démonstration. Soit / un endomorphisme d'un K-espace vectoriel E de
dimension n. Alors, la famille (fk)kelo,n2j comporte n2 + 1 vecteurs de
l'espace £(E), lequel est de dimension n2 : elle est alors liée. Il existe donc

2. Idéal des polynômes annulateurs
3
2 il
une famille de (<^/c)/ce[o,n2] £ ^n de scalaires non tous nuls telle que
n2
fc=0
n2
Par conséquent, le polynôme Yl akXk est annulateur de /. □
k=0
2.4. Remarque. Nous verrons plus loin (théorème de Cayley & Hamilton)
qu'en dimension n, on peut déterminer un polynôme annulateur de degré n
(le polynôme caractéristique).
2.5. Exemple. Le seul endomorphisme qui admet aX+b comme polynôme
annulateur avec a ^ 0 est l'homothétie de rapport — —.
En dimension infinie, il existe des endomorphismes qui n'admettent pas de
polynôme annulateur non nul.
2.6. Exemple. La dérivation usuelle D : P H> P' est un endomorphisme
de K[X] qui n'admet pas de polynôme annulateur.
En effet, raisonnons par l'absurde : si D admet un polynôme
annulateur Q, alors, pour tout polynôme P G 1K[X], Q(D)(P) = 0. Or, avec P =
^degQ+i^ Q(D)(P) ^ 0 : contradiction.
2.7. Définition. Un endomorphisme est nilpotent s'il admet un monôme
comme polynôme annulateur.
2.8. Proposition. L'ensemble Xf des polynômes annulateurs de
l'endomorphisme f est un idéal de l'anneau K[X].
Démonstration. L'ensemble Xf est clairement un sous-groupe additif de K[X].
Si P G Xf et Q G K[X], alors QP G !/, car
(QP)(f) = Q(f) ° P(f) = Q(f) ° 0c(E) = 0C(E).
D
2.9. Remarque. Pour / G C(E) et x G E, on peut aussi définir l'ensemble
If,x = {P£K[X], P(f)(x) = 0E}.
C'est encore un idéal de K[X] et il vérifie Xf C Xf^x.

4
I. Polynômes d'endomorphismes
3. Polynôme minimal
Comme l'anneau K[X] est euclidien, il est en particulier principal, donc
chaque idéal de K[X] peut être engendré par un unique polynôme unitaire.
Ceci justifie la définition suivante (conjointement avec l'hypothèse que
l'espace E est de dimension finie donc que l'idéal des polynômes annulateurs
est non réduit au seul polynôme nul).
3.1. Définition. Soit / G C{E). Le polynôme minimal de / est l'unique
polynôme unitaire, noté /z/, qui engendre l'idéal des polynômes annulateurs
de/.
3.2. Remarque. Il est facile de voir que, pour un endomorphisme /, la
dimension de l'algèbre K[f] est le degré du polynôme minimal fif. La
proposition 1-4.4 détaille cette remarque.
Déterminons l'idéal des polynômes annulateurs de quelques endomorphismes
remarquables.
3.3. Exemple. Si / est un endomorphisme nilpotent, il admet un polynôme
annulateur de la forme Xp. Par conséquent, le polynôme minimal est donc
un monôme Xk avec k < p. Cet entier k est appelé indice de nilpotence de
/. Un polynôme est alors annulateur e / si 0 en est une racine d'ordre au
moins k.
3.4. Exemple. Si h est une homothétie de J5, il existe À G K tel que h =
Àldjç. Par conséquent, X — À est un polynôme annulateur de degré 1, donc
minimal. Un polynôme annulateur de h est donc un multiple de X — À,
c'est-à-dire un polynôme admettant À comme racine.
3.5. Exemple. Si p est un projecteur, alors un polynôme annulateur de p
est, par définition, X2 — X. Ce polynôme est le polynôme minimal de p
sauf si p est l'identité ou l'application nulle (en effet, s'il n'est pas minimal,
alors p admet un polynôme annulateur de degré 1, donc est une
homothétie).
3.6. Exemple. De même, le polynôme minimal d'une symétrie vectorielle
qui n'est pas une homothétie (c'est-à-dire différente de ±Id#) est X2 — 1.
3.7. Définition. Soit / G C(E) et x G E. Le polynôme minimal local en x
de / est l'unique polynôme unitaire, noté /x/,œ> qui engendre l'idéal XfiX des
polynômes P G K[X] tels que x G kerP(J).

4. Utilisation pratique d'un polynôme annulateur
5
4. Utilisation pratique d'un polynôme
annulateur
Calcul de l'inverse
4.1. Proposition. Soit f G C(E) admettant un polynôme annulateur P
tel que P(0) ^ 0. Alors, f est inversible. De plus, son inverse appartient à
l'algèbre K[f].
N
Démonstration. Écrivons P(X) = Yl akXk avec N > 0 et ao = -P(O) ^ 0.
k=0
Posons
k=i
Comme P(f) = 0c{e)^ on obtient en isolant le terme en Id^;,
f°g = ^o/ = o£(E).
Ainsi, / est inversible et que f~x — g. □
4.2. Exemple. Soit / un endomorphisme de E qui vérifie
(/ - 2Id) o (/ - 3Id) = 0
sans être une homothétie. Cherchons les réels À tels que h\ = f — Àld soit
non inversible (nous verrons plus loin que ces réels sont, par définition, les
valeurs propres de /). Comme le polynôme (X — 2){X — 3) est annulateur
de /, on en déduit que (X + X — 2)(X-\-X — 3) est annulateur de h\. Donc, si
À ^ {2,3}, l'endomorphisme h\ est inversible, car son polynôme annulateur
n'admet pas 0 pour racine. En revanche, ni /12, ni /13 ne sont inversibles, car
sinon l'autre est nul (et donc / est une homothétie) puisque h^ o /13 = 0.
La réciproque du résultat précédent est bien évidemment fausse avec un
polynôme annulateur quelconque : si P est un polynôme annulateur de /,
alors XP est aussi annulateur et admet 0 pour racine, que / soit inversible
ou non. En revanche, la situation est plus claire avec le polynôme minimal.
4.3. Proposition. Un endomorphisme f G C(E) inversible si, et seulement
si, 0 n'est pas racine de son polynôme minimal.

6
I. Polynômes d'endomorphismes
Démonstration. Avec la proposition précédente, il suffit d'étudier le sens
direct. Supposons que / est inversible et que 0 est racine du polynôme
minimal fMf de /, c'est-à-dire /jif = XP. On en déduit foP(f) = $c(E) \ or? f
inversible et par conséquent P(f) = Oc(e)> ce Qui contredit la minimalité
de fif. Par conséquent, 0 n'est pas racine du polynôme minimal. □
Calculs de puissances
4.4. Proposition. Soit f G C(E) admettant un polynôme annulateur de
degré N. Alors, pour tout entier m G N, fm G vect(/fe)fc€|0,jv-i]-
Démonstration. Soit / G C(E) de polynôme annulateur P de degré N
et m G N. D'après la division euclidienne dans K[X], il existe (Qm,i?m) £
K[X]2 tel que
Xm = Qm(X)P(X)-hRm(X),
avec degRm < degP = N. Alors, on trouve que /m = iïm(/), d'où le
résultat. □
En fait, on peut aussi utiliser en pratique la démonstration de ce
résultat pour obtenir l'expression explicite de fm pour tout entier m G N. Il
suffit pour cela de savoir obtenir le reste dans une division de polynômes.
Détaillons les calculs dans quelques cas particuliers.
4.5. Exemple. Soit (a, b) G C avec a ^ b et / un endomorphisme dont un
polynôme annulateur est
P(X) = (X-a)(X-b).
Déterminons fm pour tout entier m G N. Le reste de la division euclidienne
de Xm par P est un polynôme de degré au plus 1 que nous noterons amX-\-
/3m. Reste à déterminer les valeurs des complexes am et /?m. Pour cela,
spécifions la relation de division euclidienne en a et en b :
( am = a 'dm + Jim
\ 6- = b-am + pm
am _ yn b • am — a - b171
En conclusion, f171 = —/ H Id#.
a — b b — a
4.6. Remarque. Plus généralement, la même méthode permet de traiter
le cas où / annule un polynôme scindé à racines simples Ai,..., Àp. On a

5. Commentaires et développements
7
alors, pour tout m G N,
/m = ]TA^Lfe(/),
fc=0
où Li,..., Lp désignent les polynômes interpolâteurs de Lagrange associés
aux Ai,..., Àp.
Lorsque le polynôme annulateur est scindé mais avec des racines multiples,
le problème est à peine plus compliqué et se ramène à un problème
d'interpolation.
4.7. Exemple. Déterminons les puissances d'un endomorphisme / de
polynôme annulateur (X — a)2.
Soit m un entier. Le reste de la division euclidienne de Xm par (X — a)2
est un polynôme de degré au plus 1 que nous noterons amX + /3m. On a
donc : Xm = Q(X)(X — a)2 + amX + fîm. Reste à déterminer les valeurs
des complexes am et /3m. Pour cela, nous spécifions cette relation en a puis
dérivons cette relation avant de spécifier en a (tous les termes où apparaît Q
s'annulent, car a est racine double de (X — a)2). Nous obtenons :
am = a • am + /3m
m • am_1 = am.
En conclusion, fm — m • am_1/ + (1 — ra) • amId£.
5. Commentaires et développements
5.1. La donnée d'une matrice A met en évidence le morphisme d'algèbre
^ f K[X] -> .Mn(K)
$A\ P ^ P{A)
Son noyau, l'idéal ker <£>a> est non nul, pour des raisons de dimension. Il est
engendré par le polynôme minimal \xa \ l'image im §a — ^{A} est une sous-
algèbre de .Mn(K), dont la dimension se déduit aisément de l'isomorphisme
de K-algèbres
^:K[X}/(fiA)^K[A}.
Ainsi, la dimension de l'algèbre ~K[Â\ est égale à celle de l'espace vectoriel
quotient K[X]/(iia). C'est donc le degré dA du polynôme minimal jjla de la
matrice A. En effet, les vecteurs 1, X, ..., XdA~1 forment une base de cet
espace quotient. Le fait que ces vecteurs soient générateurs provient d'une

8
I. Polynômes d'endomorphismes
simple division euclidienne par le polynôme jjla et le fait qu'ils soient libres
provient du caractère minimal de /j,a-
Cela se traduit au niveau de l'algèbre K[A] par le fait que les matrices In,
A,..., AdA~1 forment une base de l'algèbre des polynômes en A.
5.2. La structure de l'algèbre K[A] est donc celle d'un quotient d'un anneau
de polynômes en une seule variable. Elle dépend uniquement du polynôme
minimal de A. La structure de ces quotients-là, comme celle des anneaux
Z/nZ, est bien connue et son étude se trouve grandement simplifiée par
le théorème des restes chinois, qui montre que cette algèbre est produit
d'algèbres locales, c'est-à-dire d'algèbres ayant chacune un idéal maximal
unique (et pour une telle algèbre le treillis de leurs idéaux est alors une
liane...).
5.3. Précisons donc que si le polynôme minimal est une puissance d'un
polynôme irréductible, soit ha = 7rm avec tt irréductible, l'algèbre quotient
K[X]/(ij,a), tout comme l'algèbre K[A], est une algèbre locale et son idéal
maximal est l'idéal m = (tt) engendré par la classe du polynôme tt. La
démonstration est calquée sur celle de la mise en évidence des idéaux de
l'anneau quotient Z/_pnZ, où p est premier.
5.4. Comme autre application, remarquons que l'algèbre K[A] est réduite
(au sens qu'elle n'a d'autres nilpotents que 0n) si, et seulement si, le
polynôme minimal de A est sans facteur carré. Quand K = C, cela revient à dire
que l'algèbre K[A] est un produit de corps isomorphes à C. On verra une
démonstration de ce fait ultérieurement (chapitre X) avec la décomposition
de Jordan & Dunford.
5.5. Nous avons vu que l'algèbre K[A] contenait l'inverse de A si A est
inversible. On verra plus tard que les composantes semi-simple et nilpotente
dans la décomposition de Jordan & Dunford de A sont aussi dans K[A],
tout d'ailleurs comme les opérateurs de projection sur les facteurs directs
de la décomposition de E en somme d'espaces caractéristiques. Tout cela
pour dire qu'au delà de sa structure elle-même, l'algèbre ~K[A] contient de
part ses divers éléments des renseignements précieux.
5.6. L'idéal des polynômes annulateurs de A en le vecteur x est le noyau de
l'application <&a,x : K[X] —> E, qui, à un polynôme P, associe le vecteur
P(A)(x). Cette application est une simple application linéaire et, pourtant,
son noyau est un idéal ! En fait, cette application est K-linéaire, mais elle
est aussi K[X]-linéaire, au sens que $a,x(PQ) = P{A){§a,x{Q))> C'est en

6. Exercices
9
fait un morphisme de K[X]-modules et son noyau est donc un sous-K[X]-
module de K[X], donc un idéal de K[X].
5.7. Le groupe des inversibles de l'algèbre K[A] est l'ensemble des matrices
Q(A) où Q est un polynôme premier avec /x^.
6. Exercices
6.1. Exercice. Soit A, B G Ain{K) deux matrices semblables et P G K[X].
Montrer que les matrices P(A) et P(B) sont semblables.
D> Eléments de correction. Par définition de la similitude, il existe U G
GLn(K) telle que A = UBU~l. Par une récurrence immédiate, pour tout k G
N, Ak = UBkU~~l ; ainsi, par linéarité P{A) = UP{B)U~l. <
6.2. Exercice. Soit A G Mn(M.) une matrice semblable à une matrice
diagonale diag(Ài,..., An). Montrons qu'il existe P G K[X] tel que A =
P(A3).
> Éléments de correction. Par définition, il existe U G GLn(K) telle que A =
C/diag(Ai,..., An)?7_1 et donc
A3 = Udmg(Xl...,X3n)U-1.
Considérons le polynôme P d'interpolation de Lagrange qui vaut, pour
tout k G [1, n], A/e en A| (ce qui est possible car Aj* — A| entraîne A& = Xj).
Alors, diag(Ai,..., An) = P(diag(A?,..., A3)) et donc A = P(A3). <
6.3. Exercice. Soit f G C(E) ; définissons V endomorphisme de C(E)
associé par composition à gauche Gf : g —>> / o g. Comparer jif et ficf ■
D> Éléments de correction. Remarquons tout d'abord que, pour tout P G
K[X] et tout g G C(E), P(Gf)(g) = P(f) o g. Ainsi, /j,f est annulateur
de G/.
De plus, pour tout g G £(P), /xG/(/) o g = 0C(e) donc ^G/(/) = Oc(E)
et /iG/ est annulateur de /.
En conclusion, /i/ = ncf • <l
6.4. Exercice. Soit n ^ 2 et M e Mn(K) une matrice de rang 1.
7. Montrer que \iM = X2 - tr(M)X
#. En déduire les puissances de M en fonction de M etln.

10
I. Polynômes d'endomorphismes
D> Éléments de correction. On montre facilement qu'il existe des vecteurs
colonnes non nuls X, Y G Mn,i(K) tels que M = iV.
1. La matrice M n'est pas une homothétie donc le polynôme minimal est
au moins de degré 2. De plus,
M2 = XYxY = (Vl)M,
car YX est un scalaire. Or, YX = tr(YX) = tr(XY) = tr(M). Ainsi,
X2-tr(M)X est annulateur de M. En conclusion, /iM = X2-tr(M)X.
2. Pour calculer la puissance Mfc, effectuons la division de Xk par /im-
> Si tr(M) = 0, alors Mk = 0n dès que k ^ 2.
> Sinon, il existe un polynôme Q G K[X] tel que
Xfc = Q(X)Mm(X) + t^M)*"1*.
En effet, le reste dans la division de Xk par \xm est un polynôme de
degré au plus 1, qui est nul en 0 et qui vaut tr(M)fc en trM. Ainsi,
Mk = tv{M)k-lM pour tout k ^ 1.
Remarquons que ce résultat peut aussi être déduit par une simple
récurrence.
<
6.5. Exercice. Déterminer, en fonction de n = dimE ^ 2, le polynôme
minimal de Vendomorphisme
C(E) -+ C(E)
f ^ f + tr(f)ldE
D> Eléments de correction. L'endomorphisme $ n'est pas une homothétie,
donc son polynôme minimal est de degré au moins 2.
Par ailleurs, pour tout / G £{E),
*2(/) = <*>(/)+tr($(/))IdE
= / + tr(/)Ids + tr(/)IdB + ntr(/)Ids
= /+(n + 2)tr(/)IdB
= (n + 2)$(/)-(n + l)Id£(B)(/).
En conclusion, /z$ = X2 - (n + 2)X + (n + 1). <
6.6. Exercice. 5oii / e C{E). Notons, pour tout x £ E, \ijyX le ■polynôme
minimal de f local en x, c'est-à-dire l'unique polynôme unitaire engendrant
l'idéal
lftX = {PeK[x], P(f)(x) = oE}.
Montrer que Vensemble {/i/^, x e E} est fini.
.,{

6. Exercices
11
> Eléments de correction. Remarquons que, pour tout x G E1 fif{f)(x) =
Oe donc /if G Xf^x et par conséquent fif^x divise fif. Comme fif admet un
nombre fini de diviseurs unitaires (et l'on peut calculer ce nombre à partir de
la décomposition en facteurs irréductibles de /x/), l'ensemble {fif,x, % G E}
est fini. <
6.7. Exercice. Soit f G C(E) et P e K[X}. Montrer que P(f) est
inversible si, et seulement si, P est premier avec fif.
> Eléments de correction. Remarquons tout d'abord que si un endomor-
phisme de la forme P(f) est inversible, alors son inverse est aussi dans
l'algèbre K[/].
Soit P G K[X]. L'endomorphisme P(f) est inversible si, et seulement si, il
existe Q G K[X] tel que P(f) o Q(f) = Id^;, c'est-à-dire si PQ — 1 est un
multiple de fif. D'après le théorème de Bézout, cette dernière condition est
équivalente à P et fif premiers entre eux.
On peut noter que Valgorithme d'Euclide (étendu) nous fournit ici Vinverse.
Cet exercice montre donc K[/] est un corps si, et seulement si, le polynôme
minimal fif est irréductible sur K. <
6.8. Exercice. Soit f G C(E) et J = {P G K[X], P(f) est nilpotent}.
Montrer que J est un idéal puis déterminer, en fonction de fif, un élément
générateur.
> Éléments de correction. > Soit P et Q e J. Les endomorphismes P(f)
et Q(f) sont nilpotents et commutent donc l'endomorphisme (P — Q)(f)
est nilpotent d'après la formule du binôme avec pour exposant la somme
des indices de nilpotence : P — Q G J.
> Soit P G J et R G K[X}. L'endomorphisme P{f) est nilpotent et R(f)
et P(f) commutent donc {RP)(f) = R(f)n o P(f)n = 0C(e)- Ainsi, on
obtient RP G J.
En conclusion, J est un idéal.
Enfin, notons que P appartient à J" si, et seulement si, fif divise Pn c'est-
à-dire fif divise P où fïf est le produit des facteurs irréductibles distincts
de fif. Un générateur est donc ce polynôme fif. <
6.9. Exercice. Soit A, B G A^n(K) et un polynôme P G K[X] non
constant tel que P(0) ^ 0 et AB — P(A). Montrer que A est inversible
puis que A et B commutent.
> Éléments de correction. Notons P = P(0)JrXQ(X). La condition AB =
P(A) se récrit A(B — Q(A)) = P(0)In : par conséquent, A est inversible

12
I. Polynômes d'endomorphismes
d'inverse
De plus, B = A~1P(A) commute avec A. <\
6.10. Exercice. Soit f G C(E) tel que
Vf = X[{X-\k)\
k=i
où Ai,..., Xp sont des scalaires deux à deux distincts.
1. Montrer qu'il existe une base (#i,..., H2n) de K2n_i[X] telle que
> pour tout k G [1, n], Hk{Xi) = ôk,i et H'k(Xi) = 0 ;
> pour tout k G fn + 1, 2n\, Hk(Xi) = 0 et H'k(\i) = ôk,i-
2. En déduire en fonction des polynômes (iJi,..., i^2n); un expression des
puissances de f'.
t> Eléments de correction.
1. L'application
/ K2n_x[X] -> K2n
\ P h> (P(A1),P'(A1),...,P(Àn),P'(An))
est linéaire et injective (si P est dans son noyau, alors il admet n racines
doubles et est de degré au plus 2n — 1 donc est nul) : c'est donc une
bijection ce qui établit la propriété désirée.
2. Effectuons la division euclidienne de Xm par fif : il existe Q G K[X]
et R G K2n-i[X] tels que Xm = Q./i/ + R. On vérifie rapidement que
pour tout k G [1,71], P(Afe) = A^ et R'(\k) = mX™"1. Ainsi,
n n
k=l k=l
car la différence de ces deux membres définit un polynôme du noyau de
l'application linéaire de la première question. En conclusion,
n n
r = j2wHk(f) + Y,mXT~lHn+k(f).
fc=i fc=i
<

Chapitre II
Sous-espaces stables
Objectifs du chapitre
- Distinguer les restrictions des endomorphismes induits.
- Calculer dans des cas simples les sous-espaces stables.
- Utiliser les espaces cycliques associés à un endomorphismes.
1. Restriction d'un endomorphisme
1.1. Définition. Soit / G C{E,E') et F un sous-espace vectoriel de E.
La restriction de / à F est l'application linéaire f\p : F —> E' définie
par J\f{x) = f(x) pour tout x G F.
1.2. Exemple. La restriction de l'identité de E à un sous-espace F est
appelée l'injection canonique de F dans E.
1.3. Proposition. Soit f G jC(E,Ef) et F un sous-espace vectoriel de E.
Alors
ker/|F = Fnker/, imf]F = f(F).
Démonstration. Il suffit d'appliquer les définitions.
ker/|F = {xeF, /|F(») = 0js}
= {xeF, f(x) = 0E} = FDkerf,
im/|F = {y G E, 3x e F, y = f\F(x)}
= {yeE,3xeF,y = f(x)}^f(F).

14
IL Sous-espaces stables
□
1.4. Corollaire. Soit f un endomorphisme et un entier k G N. Alors,
dim ker fkJrl = dim ker fk + dim im / D ker /.
Démonstration. L'objectif est d'appliquer la formule du rang à la
restriction g = /,ker r/c+i- Remarquons alors que
ker g = ker fk H ker fk+1 = ker fk
par croissance de la suite des noyaux itérés et img = imfk D fk(ker fk+1).
Comme /fe(ker/fe+1) C ker/, im^C im/fcnker/. Montrons l'inclusion
réciproque. Soit y G im fk Hker/'. Par définition, f(y) = 0^ et il existe x G E
tel que y — fk(x) ; par conséquent, fk+1(x) = 0e et donc y G /^(ker fkJrl).
En conclusion, img = im fk D ker /.
La formule du rang donne alors directement
dim ker fk+1 = dim ker fk + dim ker / D im fk.
D
1.5. Remarque. Cette propriété en apparence anodine permet de
retrouver assez facilement (en exploitant la décroissance de la suite des images
itérées) que la suite des « sauts de dimension dans la suite des noyaux »
décroît.
En effet, on sait déjà que la suite des noyaux itérés (ker fk)k d'un
endomorphisme / est croissante pour l'inclusion (en fait strictement croissante
puis stationnaire). On remarque que, pour tout & G N,
ker / n im fk+1 C ker / H im fk,
ce qui entraîne, avec le corollaire précédent que la suite des sauts de
dimension dans la suite des noyaux itérés
(dimker/fc+1 - dim ker fk)k
est décroissante.
1.6. Exemple. Remarquons que dim ker/2 = 2 dim ker/ si, et
seulement si, ker/ C im/. En effet, d'après le corollaire précédent, la
condition dim ker /2 = 2 dim ker / équivaut à dim ker / = dim ker / n im /, soit
encore à
ker / H im / = ker /
et donc à ker / C im /.

2. Sous-espace stable
15
2. Sous-espace stable
2.1. Définition. Soit / un endomorphisme d'un espace vectoriel E. Un
sous-espace vectoriel F de E est stable par / si f(F) C F.
2.2. Exemple. Pour tout endomorphisme /, im/ et ker f (et plus
généralement kerP(/) pour tout P G K[X]) sont stables par /. Au chapitre
suivant, on relie cette propriété avec la propriété de commutation.
2.3. Proposition. Soit F un sous-espace stable par deux endomorphismes f
et g. Alors, F est stable par f + g et f o g.
Démonstration. Pour tout x G F, f{x) G F et g(x) G F donc f(x)+g(x) G
F et f(g(x)) G F. □
2.4. Proposition. Soit f un endomorphisme, g un automorphisme d'un
espace vectoriel E et soit F un sous-espace stable par f. Alors, g (F) est un
sous-espace stable par g o / o g~l.
Démonstration. Pour tout y G g (F), il existe x G F tel que y = g(x). Alors,
f(x) G F et donc g o / o g-\y) = g(f(x)) G g(F). □
2.5. Exemple. Soit p une rotation de M3 d'axe dirigé par le vecteur u et
d'angle 0 et f une isométrie. Alors, la rotation f o p o f"1 a pour axe la
droite dirigée par f(u).
2.6. Remarque. L'intérêt des sous-espaces stables est qu'ils permettent
d'obtenir une première version plus simple d'un endomorphisme : si l'on
dispose d'une décomposition de E en somme directe de sous-espaces stables
par /, alors l'étude de / est équivalente à l'étude des endomorphismes
induits par / sur chacun de ces sous-espaces.
Dans une base associée à une décomposition en somme directe
e = fx e f2 e • • • e fp
de sous-espaces stables par /, la matrice de / est diagonale par blocs :
mat(/Fl)
mat(/FJ |
V | mat(/Fp) 1 /

16
IL Sous-espaces stables
3. Endomorphisme induit sur un sous-espace
stable
3.1. Définition. Si F est un sous-espace stable d'un espace vectoriel E
par un endomorphisme /, alors l'endomorphisme induit par / sur F est
l'endomorphisme fp ' F -> F défini par /f(x) = f(x) pour tout x G F.
3.2. Remarque. Soit / un endomorphisme et F un sous-espace stable
par /. Il ne faut pas confondre la restriction f\F qui est à valeurs dans E
et l'induit fp qui est à valeurs dans F.
3.3. Proposition. Soit f G C(E) et F un sous-espace stable par f. Alors,
le polynôme minimal de Vinduit fp divise le polynôme minimal de f.
Démonstration. Il suffit de remarquer que fif est annulateur de l'induit fpX2
3.4. Proposition. Soit f G C{E). Supposons que E = F.Ç&G avec F et G
deux sous-espaces stables par f. Alors, le polynôme minimal de f est le
PPCM des polynômes minimaux de fp et fc-
Démonstration. > Comme les polynômes fj,fF et \ifG divisent ///, leur PPCM
divise aussi /if.
> Montrons désormais que fjifF V /i/G est annulateur de / (et donc un
multiple de /j,f). Soit x G E, xp G F et xq G G tels que x — xp -f xq-
Alors,
M/f V M/g(/)W = M/f V M/g(/)(sf) + M/f V VfG(f)(xG)
= M/f V///g(/f)(zf) + M/f vM/g(/g)(^g)
= 0f,
car //yF V fifG est annulateur de fp et /^ en tant que multiple de fj,fF
et nfG. D
4. Exemples de sous-espaces stables
Déterminons tous les sous-espaces stables dans quelques cas particuliers.
4.1. Exemple. Tous les sous-espaces sont stables par une homothétie.
4.2. Exemple. Soit p un projecteur (donc la projection sur imp = ker(p —
Id) parallèlement à kerp). Montrons qu'un sous-espace est stable par un
projecteur p si, et seulement si, il est la somme directe d'un sous-espace
de imp et d'un sous-espace de kerp.

5. Sous-espaces cycliques
17
Soit F un sous-espace stable par p. L'endomorphisme pp induit par p sur F
est un projecteur de F ; par conséquent, F est la somme directe du noyau
de pf et de l'image de pf qui sont, respectivement, des sous-espaces de imp
et de ker p.
Réciproquement, la somme directe d'un sous-espace de imp et d'un sous-
espace de kerp est bien un sous-espace stable, car p laisse invariant tous les
éléments de imp.
4.3. Remarque. De même, les sous-espaces stables par une symétrie
vectorielle s sont obtenus comme somme directe d'un sous-espace de ker(s —Id)
et d'un sous-espace de ker (s + Id).
4.4. Exemple. Soit / un endomorphisme de E, nilpotent d'indice n =
dimE (c'est-à-dire tel que fn = 0 et fn~~l ^ 0). Montrons que les sous-
espaces stables sont les ker fk pour k G [l,n]. Il est immédiat que ces
sous-espaces sont stables d'après la proposition précédente.
Soit F un sous-espace stable par / ; l'endomorphisme fp induit par /
sur F est nilpotent. Notons p son indice. On a alors F = ker fF C ker/p.
Or dim ker fp — p (car les noyaux itérés de / forment une suite strictement
croissante jusqu'au rang n) donc dim F ^ p. Mais comme fp est d'indice p,
alors dim F ^ p (même résultat sur la suite des noyaux itérés).
5. Sous-espaces cycliques
Soit / un endomorphisme d'un espace vectoriel E et x G E non nul. Si
deux sous-espaces F\ et F2 sont stables par / et contiennent x, alors leur
intersection est un sous-espace non réduit au vecteur nul (il contient x) et
stable par /.
5.1. Définition. Soit / un endomorphisme d'un espace vectoriel E et x G
E. Le sous-espace cyclique de / associé au vecteur x, est le plus petit
(pour l'inclusion) sous-espace stable par / contenant x. On le note Ef^x
(ou, plus simplement, Ex s'il n'y a aucune ambiguïté sur l'endomorphisme
considéré).
D'après les remarques précédents la définition, si un sous-espace F de E
stable par / contient x, alors EfyX C F.

18
IL Sous-espaces stables
5.2. Proposition. Soit f un endomorphisme d'un espace vectoriel E
et x G E. Le sous-espace cyclique de f associé à x est le sous-espace
engendré par la famille (fk(x))ken-
Démonstration. Comme vect(fk(x))ken est un sous-espace de E contenant
x et stable par /, alors
EfiX C vect(fk(x))keN.
Réciproquement, pour tout k G N, fk(x) G EfyX (par récurrence, car x G
Ef%x et EfiX est stable par /). D'où E^x = vect(fk(x))keN- D
5.3. Remarque. Il est facile de montrer que la dimension du sous-espace
cyclique Ef^x est en fait le degré du polynôme minimal local de / en x,
noté fifjX et que si cette dimension est notée n, alors la famille
{x,f{x),...Jn~l(x))
est une base de EfjX.
6. Commentaires et développements
6.1. Soit F C E un sous-espace stable pour / G C(E) et fp
l'endomorphisme induit par / sur F. Aux côtés de l'endomorphisme fp, il existe un
autre endomorphisme induit apparaissant dans ce cadre : l'endomorphisme
fp/F> induit par / sur le quotient de E par F
f E/F -> E/F
JE/F '
\El-:
f(x)
L'endomorphisme fp/F recèle, tout comme fp, de renseignements
intéressants sur le couple (/, F). Par exemple, det / = det fp det Je/F- La matrice
M de / dans une base (ei,..., ep, ep+i,..., ep+q) adaptée à une
décomposition E — F 0 G est de la forme f ~ ) ; la matrice de fp/F dans la
base (ep+i,..., ep+q) de E/F est la matrice C qui apparaît en bas à droite
dans la matrice M.
6.2. La situation précédente se généralise comme suit. Un drapeau Q) de
E est une suite croissante de sous-espaces vectoriels de F, soit
® : {0} C Fx C F2 C • • • C Fp C E.
Un drapeau complet de E est un drapeau formé de dim E +1 sous-espaces
Fi vérifiant dim Fi — i. Un drapeau est /-stable si tous ses sous-espaces
sont stables par /.

6. Commentaires et développements
19
Un endomorphisme / est ainsi trigonalisable si, et seulement si, il laisse
stable un drapeau complet ; une matrice est triangulaire en blocs si, et
seulement si, elle laisse stable un drapeau ayant au moins un sous-espace
non trivial.
À un drapeau $) dans E, on associe un espace vectoriel Grad(^, E) (de
même dimension que E), appelé le gradué associé, défini par
Grad(^,£) = Fx 0 (F2/F1) 0 • • • 0 (Fp/Fp^) 0 (E/Fp).
Si le drapeau Q) est /-stable, il s'induit naturellement sur le gradué associé
un endomorphisme
Grad(/) : Grad(^,£) -> Grad(^,£),
qui est la « somme directe » des endomorphismes induits successivement
dans les quotients, soit
Grad(/) - fFl 0 (fF2)F2/Fl 0 • • • 0 fE/Fp-
On a encore det/ = detGrad(/), trGrad(/) = tr/, et plus généralement
l'égalité des polynômes caractéristiques respectifs.
Matriciellement, l'endomorphisme Grad(/) se pense dans une base
convenable comme la matrice diagonale en blocs sous-jacente à une matrice
triangulaire en blocs. Il résume en lui à la fois l'induit sur un sous-espace et
l'induit sur le quotient.
On peut vérifier que si / est diagonalisable, alors Grad(/) l'est également.
6.3. On verra ultérieurement qu'un endomorphisme / cyclique (voir le
chapitre VI pour la définition) admet un nombre fini de sous-espaces stables.
Quand K = C, ces sous-espaces forment un drapeau complet si, et
seulement si, l'algèbre C[/] est locale.
L'endomorphisme gradué associé Grad(/) est dans ce cas une homothétie,
puisque le drapeau s'identifie alors à la suite des noyaux itérés définis par
l'unique valeur propre À :
{0} C ker(/ - AIds) C ker(/ - Ald^)2 C ... C ker(/ - Àld^'-1 C E.
Un endomorphisme n'a pour seuls sous-espaces stables que les deux sous-
espaces triviaux si, et seulement si, son polynôme caractéristique est
irréductible.
6.4. Un sous-espace stable n'admet par en général de supplémentaire
stable (prendre par exemple le bloc de Jordan Jn). Les endomorphismes
qui vérifient que leurs sous-espaces stables ont des supplémentaires stables
s'appellent les endomorphismes semi-simples. Sur C, cela équivaut à dire

20
IL Sous-espaces stables
que l'endomorphisme est diagonalisable. Les endomorphismes semi-simples
réels sont les endomorphismes dont le complexiflé est diagonalisable. Une
matrice antisymétrique réelle est semi-simple.
Dans le cas général, un endomorphisme est semi-simple si, et seulement
si, son polynôme minimal est sans facteur carré1. Cela revient à dire que
l'algèbre K[f] est réduite (sans éléments nilpotents non nuls) ou encore si
elle est produit de corps.
Le gradué associé à un endomorphisme semi-simple relativement à un
drapeau stable est à son tour semi-simple.
6.5. Si F C E est un sous-espace stable par /, l'orthogonal F^ de F dans
l'espace dual E* est stable par l'endomorphisme tf : E* —> E* transposé
de /. La recherche des hyperplans stables par / se ramène en particulier à
la recherche des droites stables par tf.
Une question naturelle vient maintenant à l'esprit, au vu du commentaire
par lequel a débuté cette section : quel est l'endomorphisme %fE* /F± induit
par tf dans le quotient E* /F1- ? On a tout simplement
fE*/F± = fF,
une fois que l'on a identifié E*/F± avec le dual F* de F, comme il résulte
naturellement de l'écriture
F1- <-» E* -^ F\
où pf est l'endomorphisme de restriction à F.
6.6. Un exercice amusant ici est le suivant, lequel est un cas particulier de
ce qui précède : montrer que si le polynôme minimal de / est irréductible,
alors tout sous-espace stable par / admet un supplémentaire stable. L'idée
c'est de munir E d'une structure d'espace vectoriel E^ sur le corps F = K[u],
de caractériser le sous-espaces stables par / comme étant les sous-espaces
du F-espace vectoriel E^ et d'appliquer le fait élémentaire que tout sous-
espace vectoriel d'un espace vectoriel admet un supplémentaire.
7. Exercices
7.1. Exercice. Soit f G C(E). Montrer que ker/ et im/ sont
supplémentaires dans E si, et seulement si, ker / = ker f2.
1. La notion de semi-simplicité se comporte, de ce fait, bien par rapport aux
extensions de corps, puisque le polynôme minimal ne dépend pas du corps de base.

7. Exercices
21
> Éléments de correction. D'après le corollaire II-1.4, la condition ker/ =
ker f2 équivaut à ker /nim / = {0#}. D'après la formule du rang, cette
dernière propriété (ker / et im / en somme directe) se récrit encore en ker / 0
im / = E. <
7.2. Exercice. Soit E un espace vectoriel de dimension n et f G C(E)
nilpotent.
1. Montrer que l'indice de nilpotence de f est n si, et seulement si,
dim-ker / = 1.
2. Montrer que, si Vindice de nilpotence de f est n — 1, alors dimker / H
im/ = l.
> Éléments de correction.
1. (=>) La suite (ker fk)k est strictement croissante pour k G [0,n] et
dimker/77, — dimE = n. Par conséquent, pour tout k G [0, n], on a
dim ker/^ = k.
(<=) La suite (dimker//c+1 — dimker/^)^ est décroissante de premier
terme 1. Ainsi, si un noyau itéré ker fk est de dimension n, alors k ^ n.
Comme un indice de nilpotence est inférieur ou égal à n, l'indice de
nilpotence de / est n.
2. > Remarquons tout d'abord que dimker / > 2 d'après la première
question donc dim im / $J n — 2.
> L'endomorphisme induit /im/ est nilpotent d'indice n — 2, car /
est d'indice de nilpotence n — 1. Ainsi, dimim/ = n — 2 et d'après
la question précédente, dim ker g = 1. Or, ker# = ker/ n im/ d'où
dim ker / D im / = 1.
La réciproque à cette deuxième question est fausse comme on peut le
voir avec la matrice suivante d'indice de nilpotence 2
/ 0 1 0 0 \
0 0 0 0
0 0 0 0
\ 0 0 0 0 /
<
7.3. Exercice. Déterminer les sous-espaces stables de rendomorphisme
Mn(K) -+ Mn(K)
M h-> *M
D> Eléments de correction. L'endomorphisme considéré est l'une des deux
symétries vectorielles associées à la décomposition M.n(K) = Sn(K) 0

22
IL Sous-espaces stables
An(K) (l'autre étant M i-> —lM). Les sous-espaces stables sont donc les
sommes d'un sous-espace de <Sn(K) et d'un sous-espace de An(K) (remarque
II-4.3). <
7.4. Exercice. Soit A G A//n(K) non nulle. Déterminer les sous-espaces
stables de Vendomorphisme
Mn(K) -> Mn(K)
M h-> tr(AM)In
ï> Eléments de correction. > Remarquons tout d'abord que tous les sous-
espaces de Mn(K) contenant In sont stables.
> Soit F un sous-espace de Mn(K) ne contenant pas ïn. Le sous-espace F
est stable par cet endomorphisme si, et seulement si, pour tout M G F,
tr(AM) = 0, c'est-à-dire si F est inclus dans l'hyperplan
H = {M G Mn(K), ti(AM) = 0}.
En conclusion, les seuls sous-espaces stables sont ceux qui contiennent In
ou qui sont inclus dans l'hyperplan H.
L'endomorphisme considéré est de rang 1 (on peut même vérifier que sa
trace est égale à trA). De manière générale, un sous-espace F est stable
par un endomorphisme f de rang 1 si, et seulement si, im/cF ou (non
exclusif) F C ker/. <\
7.5. Exercice. Soit f un endomorphisme. Montrer que si ker/ admet un
supplémentaire S stable par f, alors S = im/.
t> Eléments de correction. Soit S un supplémentaire de ker / stable par /.
Comme ker/ D S = {0^;}, / réalise un isomorphisme de S dans S. Ainsi,
S = /(S)cim/.
Par ailleurs, la formule du rang donne
dim im / = dim E — dim ker / = dim 5.
En conclusion, S = im /. <
7.6. Exercice. Déterminer les endomorphismes de Kn laissant stables
chacun des axes de coordonnées et la droite engendrée par le vecteur (1,1,...,1).
> Éléments de correction. Notons ei, e2, ..., en la base canonique de Kn
et / un endomorphisme de Kn qui vérifie les conditions de l'énoncé. Par
définition, il existe des scalaires Ai, ..., Àn, À G K tels que /(e&) = Àe^
pour tout k G [1, n] et f(e\ + ... + en) = A(ei -f ... + en). Par linéarité,

7. Exercices
23
on a
Àiei + ... + Anen = A(ei + ... + en)
et donc Ai = ... = Àn = À. En conclusion, / est une homothétie.
Réciproquement, il est évident que les homothéties vérifient bien les conditions de
l'énoncé. <\
7.7. Exercice. Montrer qu'un endomorphisme f G C(E) est une
homothétie si, et seulement si, pour tout x G E, dim Ef^x = 1. '
D> Eléments de correction. Remarquons que la condition dim EfiX = 1
équivaut à (x,f(x)) liée et l'on est ramené à un problème classique d'algèbre
linéaire. Comme ce résultat sera utilisé à plusieurs reprises, détaillons-le.
Pour tout x G E, il existe Xx G K tel que f(x) = Xxx.
Soit x et y deux vecteurs de E. Alors, par linéarité de /,
Xx.x + Xy.y = Xx+y.(x + y).
- Si vect(x) = vect(y) =^ {0^;}, alors x et y sont colinéaires non nuls et
XX = Xy.
- Si vect(x) et vect(y) sont en somme directe, alors, par unicité de
l'écriture,
Ax = Ax-\-y — Ay.
<
7.8. Exercice. Déterminer les endomorphismes pour lesquels tous les sous-
espaces sont stables.
D> Éléments de correction. Si tous les sous-espaces sont stables pour un
endomorphisme /, alors toutes les droites sont stables et donc / est une
homothétie (comme on l'a redémontré dans l'exercice précédent).
Réciproquement, tous les sous-espaces sont stables par une homothétie. <
7.9. Exercice. Soit D une droite vectorielle de R3. Déterminer les
endomorphismes de R laissant stables tous les plans de R contenant D.
> Éléments de correction. Considérons e\ un vecteur directeur de D et
complétons-le en une base (61,62,63). Soit / un endomorphisme laissant
stable tous les plans de R3 contenant D.
Dans un premier temps, / laisse stable les plans vect(ei, 62) et vect(ei, 63)
donc laisse stable D qui est leur intersection. La matrice de / dans cette

24
IL Sous-espaces stables
base est donc de la forme
Ensuite, / laisse stable le plan vect(ei, e2) : la matrice est donc de la forme
En procédant de même avec le plan vect(ei, 63), on obtient la forme
Enfin, / laisse stable le plan vect(ei, e2 + 63) et, avec nos notations, f(e2 +
63) = (a + 7)ei + (3e2 + £e3, d'où (3 = ô.
Réciproquement, si un endomorphisme / admet dans la base (ei, e2.es)
une matrice de la forme
À a 7
0/3 0
0 0/3
alors il laisse stable tous les plans contenant D car, pour tous a, b G M,
f(ae2 + 6e3) = (aa + bj)ei + /3(ae2 + be3).
Remarquons qu'avec la notion d'espace vectoriel quotient, on aurait
simplement dit que Vendomorphisme de l'espace quotient R /D associé à f est
une homothétie. <
7.10. Exercice. Soit f G £(]R3) nilpotent d'ordre 2. Montrer les sous-
espaces de dimension 2 stables par f sont ceux qui contiennent im/.
D> Éléments de correction. t> Si un sous-espace F contient im/, alors il
contient f(F) : par conséquent, F est stable.
> Soit F un plan de M3 stable par F. Remarquons que la condition f2 =
Û£(R3) entraîne im/ C ker/ et donc, grâce à la formule du rang dimim/ =
1 et dimker/ = 2.
- Si F = ker /, alors im / C ker / = F.
- Sinon, il existe x G F tel que f(x) ^ 0K3. Comme im/ est une droite,
im/ = vect/(x)c/(F)cF
Dans les deux cas, F contient l'image de /. <

Chapitre III
Commutation
Objectifs du chapitre
- Calculer le commutant de quelques endomorphismes simples.
- Comprendre les sous-espaces stables fournis par une relation de
commutation.
- Savoir calculer avec l'endomorphisme adf associé à un endomorphisme.
1. Définitions
1.1. Définition. > Deux endomorphismes f et g d'un même espace
vectoriel E commutent sifog = gof.
> Soit / un endomorphisme d'un espace vectoriel E. Le commutant de /
est l'ensemble, noté C(/), des endomorphismes de E qui commutent avec /.
> Soit / un endomorphisme d'un espace vectoriel E. Le bicommutant de /
est l'ensemble des endomorphismes qui commutent avec tous les éléments
de C(f).
1.2. Remarque. Encore une fois, ces notions s'étendent pour définir le
commutant et le bicommutant d'une matrice.
1.3. Proposition. Le commutant C(f) d'un endomorphisme f d'un espace
vectoriel E est une sous-algèbre de C(E).
Démonstration. Remarquons tout de suite que C(f) C C(E) et que Id G
C(f). Pour tous g,he C(f) et tout AgKj + A/iG C(f) et g o h G C(f)

26
III. Commutation
car
(g + \h)of = gof + \hof = fog + \foh
= fo(g + \h).
(goh)of = go(hof)=gofoh
= (g°f)°h = fogoh.
D
1.4. Proposition. Soit f un endomorphisme de E et g un automorphisme
de E. Alors,
C(gofo (T1) = sCCOjT1 = {gohog-\ he C(f)}.
Démonstration. Un endomorphisme h G C{E) appartient au commutant
C(g o f o g~l) si, et seulement si,
hogo f og-1 = go f og"1 oh,
soit
g-1 o h o g o f = f o g'1 o h o g,
c'est-à-dire g"1 o ho g appartient au commutant de /. D
Un des intérêts de la propriété de commutation est qu'elle permet de
dégager des sous-espaces stables assez facilement.
1.5. Proposition. Soit f et g deux endomorphismes de E tels que f o g =
g o f. Alors, le noyau et l'image de g sont des sous-espaces stables par f.
Démonstration. > Si x G ker#, alors g(f(x)) — f(g(x)) = /(0#) = 0^,
d'où f(x) G kerg.
D> Si y G img, alors il existe x G E tel que y = g(x). Par conséquent,
f (y) = f (g(x)) =g(f(x)) G im g. D
On a déjà utilisé cette propriété pour g G K[/].
1.6. Proposition. Les seuls endomorphismes qui commutent avec tous les
automorphismes sont les homothéties.
En théorie des groupes, on dit que le centre de GL(i?) est {Aid, A G K*}.
Démonstration. Soit / un endomorphisme qui commute avec tous les
automorphismes. Pour tout x G E, considérons F un supplémentaire de vect(x)
dans E et s la symétrie vectorielle par rapport à vect(x) parallèlement à F.

2. Calculs de commutants
27
Comme / commute avec s donc avec s — Id, / laisse stable ker(s — Id) =
vect(x). Ainsi, pour tout x G E, la famille (#, /(#)) est liée, donc / est une
homothétie. □
2. Calculs de commutants
2.1. Exemple. Déterminons l'ensemble des matrices qui commutent avec
la matrice D = diag(l, 2,..., ri).
t> Si M = {Triij)ij commute avec 12, alors en calculant les produits
matriciels, on obtient que, pour tout (i, j), irriij = jrriij. Par conséquent, pour
tout i ^ j, ra^j = 0 : la matrice M est diagonale. Réciproquement, les
matrices diagonales commutent avec D.
> On peut aborder différemment le problème en remarquant que si M
commute avec D alors M laisse stable tous les sous-espaces ker(D — kln)
avec k G [l,n] donc est diagonale.
2.2. Exemple. Déterminons l'ensemble des matrices qui commutent avec
la matrice
/ 0 1 0 ... 0 \
Jn
V o
0
1
0/
Considérons M = (mij)ij qui commute avec Jn et écrivons les coefficients
des matrices MJn et JnM
Ainsi,
M =
0 si j = 1
rriij-i sinon.
/ mi,i mi,2 mi>3
0
V 0
[JnM]id =
0 si z = n
rrii+ij sinon.
miin \
'• mi>3
0 raM /
Par conséquent, le commutant de Jn est l'algèbre K[Jn] des polynômes
en Jn.

28
III. Commutation
2.3. Remarque. Ce dernier exemple, où le commutant ne contient que des
polynômes en la matrice, est en fait assez générique et nous l'étudierons
extensivement au chapitre VI.
3. Endomorphisme adf
Introduisons ici un exemple d'endomorphisme qui nous servira tout au long
de cet ouvrage.
3.1. Définition. Soit / G C(E). L'endomorphisme adf est défini par
adf :
C(E) -+ C(E)
g »-> f°g-g°f
3.2. Remarques. > Cet endomorphisme nous sert essentiellement à
mesurer le défaut de commutativité. La première remarque dans ce sens est
que le commutant de / est C(f) = ker adf.
> L'application
ad.(L(E) -> £(£(£))
{ f *-> adf
s'appelle représentation adjointe de C{E). Elle vérifie, en plus de la
propriété de linéarité,
adf0g-g0f — adf o adg — adg o adf,
pour tous /, g G C{E).
Calculons les puissances de l'endomorphisme adf.
3.3. Proposition. Pour tout m G N et tous f, g G C{E),
m / \
a^(5) = ^(7J(~1)fe/m~fe°50/fc-
On peut bien entendu établir cette formule par récurrence sur m G N, mais
il est plus raisonnable d'exploiter la structure d'anneau de C(E).
Démonstration. Les endomorphismes G f : g i-> / o g et Df : g H> g o f
commutent, on peut donc appliquer la formule du binôme de Newton pour
calculer les puissances (pour la composition) de adf — Gf — Df et obtenir
le résultat désiré. □

4. Commentaires et développements
29
3.4. Corollaire. Si f est un endomorphisme nilpotent d'indice p, alors adf
est nilpotent d'indice 2p — 1.
Démonstration. > Commençons par remarquer que la formule précédente
avec m = 2p— 1 donne l'endomorphisme nul puisque le terme fm~kogo fk
est nul pour k > p et pour m — k ^ p (c'est-à-dire k ^ p — 1).
> Par ailleurs, pour tout g G £>{E),
adf-2(g) = (-ir-1r-1ogofP-\
De plus, il existe x G E tel que fp~1(x) ■=£ 0^; et g un endomorphisme tel
que g(fp~~1(x)) = x. Avec ces choix, adf~ (g)(x) ^ 0^, donc adf~ n'est
pas l'endomorphisme nul.
En conclusion, l'indice de nilpotence est 2p — 1. □
4. Commentaires et développements
4.1. Le chapitre de la réduction des endomorphismes consiste comme
rappelé dans l'introduction en l'étude de la relation de similitude. Ce chapitre
est l'examen d'une relation d'équivalence définie par l'action du groupe
linéaire GL(E) sur C(E) par conjugaison. Matriciellement, cela revient à
examiner les classes de similitude de matrices, une telle classe étant «
l'orbite » Ûm d'une matrice M sous « l'action » du groupe linéaire GLn(K)
ÛM = {PMP-\ P G GLn(K))}.
Or, on sait que, dans l'étude d'une action de groupe, il y a d'un côté les
orbites, et de l'autre les stabilisateurs. Plus précisément, si l'on pose
Stab(M) = {P G GLn(K), PMP'1 = M},
on a une bijection canonique entre les classes (à gauche) de GLn(K) modulo
Stab(M) et l'orbite ÛM,
GLn(K)/Stab(M) ^ 0(M).
Les stabilisateurs sont des sous-groupes de GLn(K), et il est clair que les
orbites de deux matrices conjuguées (entendre par là, semblables) sont
conjugués, c'est-à-dire
Stab(P0MP_!) = P0 Stab(M) P^1.
Le sous-groupe Stab(M) de GLn(K) coïncide avec le groupe des éléments
inversibles de l'algèbre ^(M) des matrices commutant avec M. Certains
auteurs notent alors 3(M) l'algèbre ^(M) et Z(M) le groupe Stab(M) de
ses éléments inversibles. Nous ne le ferons pas.

30
III. Commutation
4.2. L'algèbre associative ^(M) est plus difficile à étudier que l'algèbre
K[M], ne serait-ce que parce que la première n'est pas commutative alors
que la seconde l'est. Ces deux sous-algèbres coïncident pourtant générique-
ment ; plus précisément, elles sont égales si, et seulement si, la matrice M
est semblable à une matrice compagnon... Lorsque M est, par exemple,
diagonale, il est facile de voir que ^(M) est un produit d'algèbres de matrices,
en l'occurrence l'algèbre des matrices diagonales en blocs de tailles &i,...,
fe/, avec fci H h ki = n (laquelle est de dimension k\-\ \-kf). On voit
déjà ici deux faits, d'autant plus intéressants à relever qu'ils sont valables
pour toute matrice M, diagonale, diagonalisable ou pas : le centre de
l'algèbre ^(M) est réduit à K[M] et la codimension de ^(M) dans Mn(K)
est paire !
4.3. Si M G .A/fn(K), le sous-espace vectoriel ^(M) apparaît comme le
noyau de l'endomorphisme adw De son côté, l'image de adj\4 a une
signification géométrique inattendue : il donne dans le cas réel la direction de
l'espace (affine) tangent en M à l'orbite Û(M), qui s'avère ainsi être une
sous-variété de Mn(R) de dimension paire. L'application linéaire
ad: Mn(K)-ï C(Mn(K))
s'appelle la représentation adjointe de Mn(K) ; elle vérifie
ad[M,N) — adM o adjy — ad^ ° adj\4-
Son noyau est réduit aux matrices scalaires ; quant à son image, on se
contentera de dire qu'elle est formée de dérivations1 (de traces nulles) de
l'algèbre Mn(K).
5. Exercices
5.1. Exercice. Déterminer une condition nécessaire et suffisante pour
qu Jun projecteur p commute avec un endomorphisme f fixé.
\> Eléments de correction. Soit p le projecteur sur F parallèlement à G.
Montrons que p commute avec / si, et seulement si, les sous-espaces kerp
et ker(p — Id) sont stables par /.
> Si p commute avec /, alors F — kei(p — Id) et G = kerp sont stables
par /.
o Réciproquement, si F = ker(p — Id) = imp et G = kerp sont stables
1. Une dérivation de l'algèbre A^n(K) est, par définition, un endomorphisme 0 de
Mn(K) vérifiant 6(XY) = 6{X)Y + X0(Y).

5. Exercices
31
par /, alors pour tout xF G F et tout xq G G,
fop(xF + xg) = f(xF)
p o f(XF + o^) = p{f{xF) -f /(xG)) = /(xF).
donc / op = po /.
<
5.2. Exercice. Montrer que si deux endomorphismes f et g vérifient f +
g = f o g, alors ils commutent.
> Eléments de correction. Remarquons que (/ — Id)o(g — Id) = Id, donc les
endomorphismes / — Id et g — Id sont inverses. Ainsi, (g — Id) o (/ — Id) = Id
et par conséquent,
/O0=(/-Id)o(0-Id)+0 + /-Id
= (0-Id)o(/-Id)+0 + /-Id
= 9°f-
<
5.3. Exercice. Déterminer la dimension du commutant d'une matrice
diagonale.
> Eléments de correction. Notons D la matrice diagonale et soit Ai, A2,
..., Ar les valeurs distinctes sur la diagonale et d\, d2, ..., dr le nombre
de fois où chacune d'elles apparaît. On peut, quitte à utiliser la
proposition III-1.4, supposer la matrice D = diag(AiI^1,..., ArI^r). Une matrice M
qui commute avec D laisse stable les sous-espaces ker(D — \iln) donc est
diagonale par blocs avec la même structure que D.
Réciproquement, une telle matrice commute bien avec D (dont la restriction
à chacun des sous-espaces est scalaire).
En conclusion, la dimension du commutant de D est
i=l
5.4. Exercice. Déterminer le commutant de la matrice diagonale par blocs
\
(
1
0 1
0 0
V
0 1 0
0 0 1
000

32
III. Commutation
> Éléments de correction. Considérons une matrice M du commutant que
l'on écrit en blocs
Alors, la commutation équivaut aux conditions AJ2 — J2A DJ3 = J3D,
CJ2 = J3C et BJ3 = J2B. Les deux premières conditions se résolvent avec
l'exemple III-2.2. On exploite les deux autres « à la main » et l'on obtient
qu'une matrice du commutant est de la forme
a
0
e
0
^ 0
b
a
~T
e
0
0
0
9
0
0
c
0
h
9
0
d
c
i
h
9
avec a, 6, c, d, e, /, g, h et i G K.
La dimension du commutant est donc 9.
Il existe un résultat général exprimant la dimension du commutant d'une
matrice nilpotente comme la somme des carrés des longueurs des colonnes
de son tableau de Young : ici, 22 + 22-fl2 = 9. <
5.5. Exercice. Soit A G .M2Q&) une matrice non scalaire. Montrer que le
commutant de A est K[Â\.
> Eléments de correction. Comme A n'est pas scalaire, il existe un
vecteur X G A42,i(IK) tel que la famille (X,AX) est libre donc une base
deA42,i(K).
Soit M une matrice qui commute avec A. Posons a, j5 G K tels que
MX = aX + f3 AX = (aln + pA)X.
Alors,
MAX = AMX = A{aln + j3A)X - (aln + f3A)AX.
Ainsi, les endomorphismes associés aux matrices M et {aln-\-j3A) coïncident
sur une base donc les matrices sont égales : M = aln + fi A G K[A}.
L'inclusion K[A] C C(A) est évidente, d'où l'égalité.
Ce résultat indique seulement que les matrices de M.2^) non scalaires sont
cycliques. On étudie cette notion au chapitre VI. <
5.6. Exercice. Déterminer l'ensemble des matrices qui commutent avec
toutes les matrices triangulaires supérieures strictes.
O Éléments de correction. Une matrice M = (rriij) commute avec toutes
les matrices triangulaires supérieures strictes si, et seulement si, MEij =

5. Exercices
33
EijM pour tout i < j. En effectuant ce calcul matriciel, on trouve, pour
tous i < j,
rrik,i = 0 si k ^ i, ra^fc = 0 si /c / j, raJ;J- = ra^.
La première condition entraîne que tous les coefficients hors diagonale
des n — 1 dernières lignes sont nuls ; la deuxième que tous les coefficients
hors diagonale des n — 1 premières colonnes sont nuls ; la dernière que tous
les coefficients diagonaux sont égaux. En conclusion, M G vect(In, £i,n).
La réciproque est une simple vérification. <
5.7. Exercice.
1. Existe-t-il une matrice A G Mn(ï
/ o i
Az =
telle que
0 ... 0 \
0
\0
1
0/
2. Déterminer les matrices A G Ms(R) telles que
A2
t> Eléments de correction.
1. Proposons deux solutions pour cette question.
> Soit A une matrice qui vérifie l'équation. Notons Jn la matrice du
membre de droite. La matrice A commute avec A2 = Jn donc est un
polynôme en Jn d'après l'exemple III-2.2. Ainsi, il existe P G ~K[X]
tel que A = P(Jn)\ en reportant dans l'équation, on obtient (P2 —
X)(Jn) = 0n. Comme jijn = Xn divise tout polynôme annulateur
de Jnj on en déduit qu'il existe Q G K[X] tel que P2 = X + XnQ.
Alors, 0 est racine d'ordre pair dans le membre de gauche et racine
simple du membre de droite : contradiction.
> Notons encore Jn la matrice du membre de droite et remarquons
que cette matrice est nilpotente d'indice n. Une matrice A qui vérifie
l'équation est nilpotente. Comme 2(n — 1) ^ n, .A2(n_1) = 0n et donc
J™-1 = 0n ce qui contredit la valeur de l'indice de nilpotence de Jn.
Dans cette seconde solution, on a exploité de Vindice de nilpotence d'une
matrice de taille n était au plus n. Ce résultat est une simple
conséquence de la croissance (plus précisément de la stricte croissance puis
du caractère stationnaire) de la suite des noyaux itérés.

34
III. Commutation
Soit A une matrice qui vérifie l'équation. Comme A commute avec A2,
on en déduit que A est de la forme
A
0
0
a
7
0
P
ô
A
Une fois cette simplification obtenue, on peut reporter dans l'équation
et trouver X = j = 0 et aô = 1.
Réciproquement, pour tout a ^ 0 et tout /3, les matrices
0
0
0
a
0
0
P
1
a
0
vérifient l'équation.
5.8. Exercice. Soit A, B G Mn(R) telles que AB — BA soit de rang 1.
Montrer que B laisse stable k.ei A ou imA
\> Éléments de correction. Remarquons tout d'abord que la droite im(AB—
BA) est incluse dans imA ou en somme directe avec imA
> Si im(AB — BA) c imA, alors, pour tout vecteur X G Mnji(K), il
existe Y G Mn,i(K) tel que ABX ~ BAX = AY^ donc BAX e [mA :
l'image de A est stable par B.
> Si im(AB — BA) fl im^ = {0n5i}, alors, pour tout vecteur X G kerA,
ABX = ABX - BAX G im^ n im(AB ~ BA).
Ainsi, ABX = 0n?i et BX G ker^4 : le noyau de A est stable par B. <
5.9. Exercice. Soit G un sous-groupe fini de GL(E) et F un sous-espace
vectoriel de E stable par tous les éléments de G- Montrer qu'il existe un
supplémentaire de F dans E stable par tous les éléments de G (théorème
de Maschke).
Indication : on pourra, pour un supplémentaire G de F, introduire le
projecteur p sur F parallèlement à G puis le projecteur
]yi geG
> Eléments de correction. Soit G un supplémentaire quelconque de F (qui
existe car E est de dimension finie) et p le projecteur sur F parallèlement
à G. Posons q comme dans l'indication.

5. Exercices
35
> Soit g G G- Remarquons que g (F) — F donc, pour tout x G F, il existe y G
F tel que x = g (y). Alors, gop°g~l(x) = gop(y) = g(y) = x, car F = imp.
Ainsi, tous les éléments de F sont fixes par g ° p ° g~l donc par g; par
conséquent, F C im(g).
Par ailleurs, pour tout x G F, il existe x' G F et x" G G tels que g-1(x) =
x' + x", donc g o p o g~'1(x) = g o p[xf + x") — g(x/) G #(F) = F. En
conclusion, imçcF, d'où imç = F.
> De plus, q est un projecteur. En effet, pour tout x e E, q(x) e F et l'on a
vu que les éléments de F sont fixes par q donc q2(x) = q{x). Ainsi, q2 = q.
> Pour tout h G G->
hoq= -L- Y^ho9°P°g~1
'^' geQ
= -—- 2_] k°P° k~X o h en posant k = h o g
= q o h.
Ainsi, q commute avec tous les éléments de G-
En conclusion, le noyau de q est un supplémentaire de F = img (car q est
un projecteur), stable par tous les éléments de G (d'après la propriété de
commutation). <
5.10. Exercice. Soit X, Y et H G A^C) non nulles telles que
HX-XH = 2X
HY ~YH = -2Y
XY-YX = H
1. Montrer que XetY sont nilpotentes (donc de rang 1).
Indication : on pourra vérifier que trX = trX2 = 0.
2. Vérifier que si kerX = ker Y, alors il existe À G C tel que X = XY ; en
déduire une contradiction.
3. Montrer qu'il existe une même matrice P G GL2(C) telle que

36
III. Commutation
> Éléments de correction.
1. Comme 2X = HX - Xff, 2trX = tr(HX) - tr(XH) = 0 ; de plus,
4X2 = HX2-X2H et donc trX2 = 0. On a, de même, tr Xk = 0 pour
tout k G N*.
Reste à voir que cela entraîne que la matrice X est nilpotente ; ce
résultat sera évident avec le théorème de Cayley & Hamilton mais nous
en proposons ici une démonstration élémentaire. La première étape
consiste à remarquer que X n'est pas inversible en remarquant que
2/j,x(0) = tr(iJ,x(X)) = 0. Ainsi, en considérant une base construite en
complétant une base du noyau de X, la matrice X est semblable à une
matrice de la forme
(!;)■
La condition trX = 0 entraîne alors /3 = 0. La matrice X est donc
semblable à une matrice triangulaire supérieure donc nilpotente.
On montre de même que Y est nilpotente.
2. Supposons ker X = ker Y et considérons une base de A42,1 (C) construite
à partir d'un vecteur directeur de ker X. Alors, il existe une matrice P G
GL2(C) telle que
.v=p(°;)p-, y=p(2i)p-
La condition sur les traces nulles entraîne f3 = ô = 0. Ainsi, X et Y
sont proportionnelles.
Enfin, notons que si X et Y sont proportionnelles, XY — YX = O2 ce
qui entraîne H = O2, cas explicitement exclu par l'énoncé.
3. Nous avons montré à la question précédente que les droites ker X et ker Y
sont supplémentaires dans A^2,i(C). Considérons une base associée à
cette décomposition telle qu'il existe une matrice P G GL2(C) vérifiant
Il reste alors à vérifier les conditions de l'énoncé.
> Avec H = XY — YX, on trouve
> Avec 2X = HX-XH, on trouve a = 1. La condition 2Y = YH-HY
est alors vérifiée et l'on a obtenu la forme désirée.
<3

Chapitre IV
Lemme des noyaux
Objectifs du chapitre
- Comprendre le résultat de finitude de l'ensemble des sous-espaces de la
forme kerP(/).
- Exploiter la décomposition en sous-espaces stables obtenue par le lemme
des noyaux.
- Comprendre l'existence d'un vecteur x tel que le polynôme minimal local
en x soit le polynôme minimal (///)X = ///).
1. Étude de kerP(/)
1.1. Proposition. Soit deux polynômes P et Q de pgcd D et un endo-
morphisme f G C(E). Alors,
kerP(f) HkeiQ(f) = kerD(f).
Démonstration. > Remarquons tout d'abord que D divise P et Q donc
ker D(f) Ckei P(f) D ker Q{f).
> Réciproquement, il existe d'après la relation de Bézout des polynômes U
et V tels que UP + VQ = D. D'où si x G kerP(/) H ker Q(/), alors
£>(/)(*) = U(f) o P(f)(x) + V(/) o Q(f)(x) = 0.
Cela prouve kerP(/) D kerQ(/) C ker D(f) et le résultat annoncé par
double-inclusion. D
Cet exemple est complété par un résultat analogue pour la somme (voir
Exercice IV-5.1).

38
IV. Lemme des noyaux
1.2. Corollaire. Soit f G C{E) et P G K[X]. Posons A = P A ///. Alors,
kerP(/)=kerA(/).
Démonstration. Il suffit d'appliquer la proposition avec Q = jif et de
remarquer que kerfjbf(f) — E. □
1.3. Remarque. Cette proposition permet de limiter l'étude des sous-
espaces de la forme kerP(/) aux seuls cas où P divise \i$.
1.4. Exemple. Revisitons l'exercice 1-6.7. Pour un endomorphisme / G
C(E) et un polynôme P G K[X], P(f) est inversible si, et seulement si,
kerP(/) = {0E}, c'est-à-dire kerP A fif(f) = {0E}- Si F A /// ^ 1,
alors kerPA/i/(/) contient les vecteurs non tous nuls Q(f)(x) pour xG^,
OÙ /Z/ = Q • (P AfJLf).
L'autre implication étant évidente, on obtient kerP A ///(/) = {0#} si, et
seulement si, P A fif — 1.
1.5. Corollaire. Soit / G £(P) et P G K[X] un diviseur de fif. Le
polynôme minimal de l'endomorphisme induit par f sur kerP(f) est P.
Démonstration. Notons F = kerP(/) et \i$ = PQ.
> Comme P(/f) = 0, on a que /i/F divise P.
> Comme P(/) o Q(f) = M/(/) = 0, imQ(/) C kerP(/). Or, kerP(/) C
kerfifF(f)1 donc imQ(f) C ker/i/F(/) et /i/FQ est annulateur de /. Par
conséquent, \±j = PQ divise \ifFQ, soit P divise /i/F.
En conclusion, /i/F = P. D
1.6. Remarque. Si l'on omet la condition P divise ///, le résultat est alors
que le polynôme minimal de l'endomorphisme induit par / sur ker P(f)
est P A /if.
2. Lemme des noyaux
Le résultat suivant est essentiel pour la suite, car il permet de «
décomposer » un espace vectoriel en une somme directe de sous-espaces vectoriels
stables adaptés à la réduction de l'endomorphisme considéré.

2. Lemme des noyaux
39
2.1. Lemme des noyaux. Soit (Pk)ke{i,...,N} une famille de polynômes
deux à deux premiers entre eux et un endomorphisme / G C(E). Alors,
CN \ N
npH^)=0kerw)-
k=i j k=i
/ N \
De plus, le projecteur de ker l Yl Pk ) (/) sur l'un de ces sous-espaces pa-
\fe=i /
rallèlement à la somme des autres est un polynôme en /.
Démonstration. Montrons ce résultat par récurrence sur le cardinal 7V ^ 2
de la famille de polynômes.
> Si Pi et P2 sont deux polynômes premiers entre eux, le théorème de
Bézout garantit l'existence de polynômes U\ et Ui tels que LriPi+£/2P2 = 1,
et donc tels que
U1(f)oP1(f) + U2(f)oP2(f)=IdE.
D'où, pour tout x G ker(PiP2)(/),
X = U^f) O P! (/)(*) + U2(f) O P2(/)(X),
avec U^f) o Pi(/)(x) G kerP2(/) et U2(f) o P2(/)(x) G kerP^/) (en
utilisant la commutation des polynômes en /).
Par ailleurs, si x G kerPi(/) f|kerP2(/), alors x = Ux{f) o Pi(/)(x) +
^2(/) ° P2{f)(%) = ®e- On déduit de ces deux résultats que kerPi(/)
et kerP2(/) sont supplémentaires dans ker(PiP2)(/).
> Soit N > 2. Supposons que le théorème est établi pour toute famille de iV
polynômes deux à deux premiers entre eux. Soit (Pfc)fce|[i,iv+i] une famille
N
de polynômes deux à deux premiers entre eux. Alors, Yl Pk e^ P/v+i sont
fc=i
premiers entre eux et l'on peut appliquer le théorème à cette famille de
deux polynômes ; d'où
(N+l \ N
J] Pk (/) = ker J] Pfe(/) 0ker Pjv+i(/).
fe=l / fe=l
Il suffit désormais d'utiliser l'hypothèse de récurrence pour conclure à la
décomposition.
Passons à la démonstration de la propriété sur les projecteurs associés à
cette décomposition. Revenons à une famille (Pfc)fce[i,jvj de polynômes deux
N
à deux premiers entre eux. Puisque Pj et Yl Pk soirt premiers entre eux,
fe=i

40
IV. Lemme des noyaux
il existe des polynômes Uj et Vj tels que
N
UjPj + V, l[Pk = l.
fc=i
N
Posons pj = [ Vj Yl Pk ) (/) et vérifions que pj est bien le projecteur de
l'espace
fc=i
k^j
kev(f[Pk\(f)
N
sur kerPj(f) parallèlement à ® kerPk(f) — imPj(f). En effet,
fe=i
pour tout x G kerPj(/),
a; = (UjPjXfXx) + {V3 n ft)(/)(*) = P;(*),
pour tout y = Pj(f)(x) GTO Pj(/),
Pj-(y) = Pj {Pj{x)) = Vj(f) o (J] Pfc)(/)(x) = 0B.
3\J )->
N
k=i
k^j
N
L'endomorphisme Pj est donc le projecteur recherché. D
2.2. Remarque. On retrouve ainsi la décomposition naturellement
associée aux projecteurs ou aux symétries vectorielles qui admettent
respectivement les polynômes annulateurs X(X — 1) et (X — 1)(X + 1).
3. Décomposition de l'espace en sous-espaces
stables
3.1. Remarque. Ecrivons la décomposition en facteurs irréductibles de /// :
où les Pk sont des polynômes irréductibles deux à deux distincts et les ak
des entiers non nuls. Le lemme des noyaux entraîne alors que E = ker ///(/)

4. Commentaires et développements
41
est égal à
£ = ®kerP«*(/).
fe = l
On a ainsi obtenu une décomposition de E comme somme de sous-espaces
stables par / (et donc une écriture matricielle de / comme matrice diagonale
par blocs) et l'on verra que cette décomposition a des propriétés utiles.
Rappelons un résultat élémentaire pour la suite des noyaux itérés utile pour
décrire les espaces apparus dans la décomposition.
3.2. Proposition. Soit un polynôme P G K[X]. La suite (keTPk(f))k est
strictement croissante pour l'inclusion puis stationnaire.
Si, de plus, P est irréductible, alors le polynôme minimal local de f en x G
kerPfc(/)\kerP/c~1(/) est Pk.
Donnons une application en terme de polynôme minimal local.
3.3. Proposition. Soit f G C(E). Il existe x E E tel que \i^x — ///.
Démonstration. Reprenons les notations de la remarque ci-dessus et
considérons, pour tout k G [l,p], Xk G kerP^fc \kerP^fc-1 (qui existe d'après
la croissance de la suite des noyaux itérés) et x = X\ -\- X2 + • • • + xp G E.
Alors
p
oE = vfAf)(x) = YlfJ,fAf)(xk)-
fc=l
Pour tout k G [l,p], Hf,x(f){%k) £ kerP^fc(/). Or, les sous-espaces ker Pj?k (f)
sont en somme directe donc, pour tout k G [l,p], fif,x(f)(xk) = 0# et
donc P£k divise fifjX (car P£k est le polynôme minimal de #&). On conclut
avec le lemme d'Euclide que jif divise jj,fiX et donc \i^x — \if.
D
4. Commentaires et développements
4.1. Ce chapitre est l'occasion d'une ouverture plus marquée de l'algèbre
linéaire sur l'arithmétique. Les propriétés de divisibilité dans l'anneau
principal R = K[X], pour IK corps commutatif, jouent ici un rôle crucial. Les
deux propriétés fondamentales d'intersection et de somme de noyaux
kerP(/)nkerQ(/) =ker(PAQ)(/), kerP(/) + kerQ(/) = ker(PVQ)(/)
où l'identité de Bezout joue un rôle primordial sont à comparer avec les

42
IV. Lemme des noyaux
relations concernant les idéaux de R (noter l'inversion des cas
correspondants)
aR + bR=(aA b)R, aR DbR=(aV b)R.
4.2. Les sous-espaces kerP(/) (mais aussi les sous-espaces imP(/)) sont
des exemples prioritaires de sous-espace stables sous l'action de l'endomor-
phisme /. Leur nombre est fini, comme on l'a vu dans la propriété de début
du chapitre.
Il existe en général d'autres sous-espaces stables par / que ceux-là.
Toutefois, il est bon de noter que tout sous-espace stable sous l'action de / est de
la forme kerP(/) si, et seulement si, l'endomorphisme / est cyclique, soit
encore s'il n'existe qu'un nombre fini de sous-espace stables sous l'action de
/. Voir le chapitre VI. Ainsi, lorsque / est cyclique, chacun des sous-espaces
im P(f) est donc de la forme ker P(f). Ainsi, à titre d'exemple, pour le bloc
de Jordan plein Jn, on a im Jn — ker Jn
Attention, un sous-espace quelconque im P(f) peut être de la forme ker Q(f)
sans que / ne soit cyclique. En fait, une condition nécessaire et suffisante
pour que tous les im/fe, où / est endomorphisme nilpotent, soient des
kerQ(f) pour un polynôme Q adéquat est que le tableau de Young de /
soient rectangulaire. Voir page 121 du livre
Réduction des endomorphismes, Rached Mneimné, Calvage & Mounet, 2006.
4.3. Il est intéressant de savoir quels sont les ker P(f) qui ont un
supplémentaire stable, et aussi d'en calculer le nombre. Le lemme suivant est
facile et important.
4.4. Lemme. Le sous-espace ker/ admet un supplémentaire stable si, et
seulement si, ker/ = ker/2; auquel cas ce supplémentaire est im/.
Nous savons déjà que le cardinal des idempotents dans l'algèbre K[f] est
une puissance de 2. En effet, avec le lemme chinois, l'algèbre K[/] s'écrit
comme produit d'algèbres quotients K[f]/(Pk), où P est un polynôme
irréductible. Une algèbre K[f]/(Ph) est alors locale (au sens qu'elle a un seul
idéal maximal, à savoir l'idéal engendré par la classe de P, ou encore que
l'ensemble des éléments non inversibles est un idéal). Dans ce cas, il y a
seulement deux idempotents, 0 et 1.
Calculons maintenant le nombre de sous-espaces kerP(/). On sait que ce
qui compte, ce sont les kerP(/) où P est un diviseur du polynôme minimal

5. Exercices
43
Un fois l'on a écrit l'espace comme somme directe des sous-espaces
caractéristiques, ker P(f) se décompose bien et l'on est ramené à calculer le nombre
de sous-espaces kerP(/) fl ker P^i(f). Mais, ce dernier sous-espace est de
la forme kerPj■ (/), avec 0 ^ fa ^ o^ ; par stricte croissance des noyaux
itérés, il existe exactement a^ + 1. En conclusion, le nombre de sous-espaces
de la forme kerP(/) est égal au produit des c^ -f 1, autrement dit, il y a
autant de sous-espaces kerP(/) que de diviseurs du polynôme minimal.
En particulier, le nombre de sous-espaces kerP(/) est impair si, et
seulement si, le polynôme minimal [if est un carré.
4.5. On comprend maintenant quelles sont les décompositions de l'espace
de la forme ker P(f) 0ker Q(f). Il s'agit seulement des décompositions avec
P • QQ = /x/ avec kerP(/) = kerP(/) et kerQ(/) = kerQ(/) : il y a en a
donc 2S où s est le nombre de facteurs irréductibles de fif.
Si ker P(/)®ker Q(f) = E, alors P et Q sont premiers entre eux et fif divise
PQ. Si l'on suppose, sans perte de généralité avec la proposition IV-1.2,
que P et Q sont des diviseurs de /i, le résultat est clair.
5- Exercices
5.1. Exercice. Soit deux polynômes P et Q de PGCD D et un endomor-
phisme f G C(E). Montrer que kerP(/) +kerQ(/) = kerM(/), où M est
le PPCM des deux polynômes P et Q.
> Éléments de correction. > Comme P divise M, kerP(/) C kerM(/). De
même, kerQ(/) C kerM(/) et par conséquent
kerP(/) +kerQ(/) C kerM(/).
> Notons Q = DQ et remarquons que P et Q sont premiers entre eux.
D'après la propriété de Bézout, il existe U et V G K[X] tels que
UP + VQ = 1.
Alors, pour tout x G kerM(/), on a la décomposition
x = U(f)o P(f)(x) + V(f)oQ(f)(x).
Enfin,
QU){U{f) « P(f)(x)) - [/(/) o D{f) o M(f)(x) = 0E,
P(f)(V(f) o Q(f)(x)) = V(/) o M(/)(x) = 0£.
Ainsi, x £ ker P(/) + ker Q(f). <

44
IV. Lemme des noyaux
5.2. Exercice. Soit f un endomorphisme d'un espace E. Montrer qu'il
existe r G N* tel que E = ker fr ® im/r (décomposition de Fitting).
Indication : on pourra utiliser le résultat, établi à l'exercice II-7.5, que
le seul supplémentaire du noyau d'un endomorphisme g stable par g est
l'image de g.
t> Eléments de correction. Soit P un polynôme annulateur de / et r la
multiplicité de 0 comme racine de P. Notons Q le polynôme tel que Q(0) ^
0 et P(X) = XrQ(X). D'après le lemme des noyaux,
£ = ker/rekerQ(/).
Mais alors, ker<2(/) est un supplémentaire de ker/r stable par fr, qui est
donc égal, d'après l'exercice II-7.5, à im/r.
Le sous-espace ker fr qui intervient ici est le nilespace de f ; on verra plus
loin qu'il s'agit simplement du sous-espace caractéristique de f associé à la
valeur propre 0. Le sous-espace imfr est appelé cœur de f. <
5.3. Exercice. Soit f un endomorphisme d'un K-espace vectoriel E.
1. Soit F un plan de E stable par f. Montrer qu'il existe un polynôme P
non nul de degré au plus 2 tel que F C kerP(/).
2. Soit P un polynôme non nul de degré au plus 2 tel que dimker P(f) ^ 2.
Montrer qu'il existe un plan stable inclus dans kerP(f).
t> Eléments de correction.
1. > S'il existe À G K tel que fp = Aid/?, alors F C ker(/ - Àld).
t> Sinon, il existe x G F tel que la famille (x, f(x)) est libre donc est une
base de F. Mais alors, f2(x) G F, car F est stable par / ; il existe donc a,
b G K tels que f2(x) — af(x) + bx. On vérifie immédiatement que x
et f(x) appartiennent à ker(/2 — af — bld) donc F C ker(/2 — af — Hd).
2. > S'il existe À G IK tel que /kerp(/) — ^Idker p(/)j alors deux vecteurs
linéairement indépendants de ker JP(/) engendrent un plan stable.
> Sinon, il existe x G kerP(/) tel que la famille (x,f(x)) est libre et
définit un plan F de kerP(/). Par ailleurs, F est stable car P(f)(x) =
0e et donc f2(x) G vect(x, f(x)) = F.
<3

Chapitre V
Eléments propres,
caractéristiques
Objectifs du chapitre
- Définir les éléments propres d'un endomorphisme.
- Calculer le polynôme caractéristique et connaître le lien avec les valeurs
propres.
1. Définitions
1.1. Définition. Soit / un endomorphisme de E.
> Une valeur propre A de / est un scalaire tel que / — Aid n'est pas injective,
c'est-à-dire tel qu'il existe x G E non nul qui satisfait f(x) — Xx.
> Un vecteur propre de / associé à la valeur propre A est un vecteur x non
nul tel que f(x) = Xx.
> Le sous-espace propre de / associé à la valeur propre A est le sous-
espace E\(f) — ker(/ — Aid). On le note E\ s'il n'y a pas ambiguïté sur
l'endomorphisme considéré. La dimension de ce sous-espace propre est
notée rrig(X) et appelée multiplicité géométrique de la valeur propre A.
1.2. Proposition. Des vecteurs propres associés à des valeurs propres deux
à deux distinctes forment une famille libre.

46
V. Éléments propres, caractéristiques
1.3. Exemple. Pour tout réel a, les fonctions x H> eax sont des vecteurs
propres de la dérivation (qui est un endomorphisme de C°°(]R,IR)). Par
conséquent, pour tout n-uplet de réels deux à deux distincts (ai,... , an),
la famille (x t-> eaiX)ie^iyTq est libre.
Démonstration. Procédons par récurrence sur le cardinal N de la famille de
vecteurs propres considérée. > Si N = 1, alors la famille ne contient qu'un
vecteur qui est non nul (car vecteur propre) donc la famille est libre.
> Soit iV G N* ; supposons que toute famille de N vecteurs propres
associés à des valeurs propres deux à deux distinctes soit libre et
considérons (xi,...,#jv+i) une famille de N + 1 vecteurs propres associées aux
valeurs propres deux à deux distinctes Ai,..., Ayv+i-
JV+1
Soit (ai,..., ûfjv+i) G K^4"1. Si ^ a^ = 0#, alors
i=l
/N+l \
/ I ]P aiXi ) = °#'
7V+1
c'est-à-dire ]T K&i%i = ®e- En combinant ces deux relations,
2=1
N
y^(A7v+i - XijOiXi = 0E.
i=l
D'après notre hypothèse de récurrence, pour tout i G |l,iV], ai — 0
(car Àjv+i 7^ K par hypothèse). On en déduit que «jv+i est aussi nul, car
xn+i est non nul. Nous avons donc montré la liberté. □
1.4. Corollaire. Soit E un espace vectoriel de dimension n. Tout
endomorphisme de E admet au plus n valeurs propres distinctes.
Démonstration. Une famille constituée de vecteurs propres associés à
chacune des valeurs propres est libre (d'après la proposition précédente) et de
cardinal le nombre de valeurs propres distinctes. Or, le cardinal d'une
famille libre est inférieur ou égal à la dimension de l'espace, d'où le résultat.□
1.5. Remarque. Le nombre de valeurs propres d'un endomorphisme d'un
espace vectoriel de dimension infinie n'est pas borné comme l'on peut le
voir avec les exemples suivants.
D> L'endomorphisme <p de K[X] défini par (f(P) = XP' admet tous les
entiers naturels comme valeur propre puisque (p(Xn) = nXn1 pour tout
entier n G N.

1. Définitions
47
> L'endomorphisme de dérivation sur C°°(R, R) admet tous les réels comme
valeur propre ; en effet, pour tout a G M, t \—> eat est un vecteur propre
associé à la valeur propre a.
1.6. Proposition. Des sous-espaces propres associés à des valeurs propres
deux à deux distinctes sont en somme directe.
Démonstration. Soit E\x,..., E\N des sous-espaces propres associés à des
valeurs propres deux à deux distinctes Ai,..., Xn- Soit x un élément de la
somme de ces sous-espaces propres ; supposons que x admette deux
décompositions distinctes sur cette somme
N N
x = y ^ Xi = y ^ x^
k=l k=l
N
Alors J2 (xi ~~ x'ù ~ ®e ot chacun des termes de cette somme est soit
nul, soit un vecteur propre. D'après le résultat précédent, xi — x\ — 0
pour tout iG[l, N} (sinon on aurait trouvé une combinaison linéaire nulle
non triviale de vecteurs propres associés à des valeurs propres deux à deux
distinctes). On obtient l'unicité de la décomposition de x et, par conséquent,
les espaces £\i,..., E\N sont en somme directe. □
1.7. Exemple. Dans E = C°°(]R., R), le sous-espace vectoriel V des
fonctions paires et le sous-espace vectoriel X des fonctions impaires sont en
somme directe. En effet, ce sont les sous-espaces propres associés aux
valeurs propres 1 et —1 de l'endomorphisme de E défini par / (-» / où
f :x^ f(-x).
1.8. Remarques. Remarquons quelques liens entre sous-espaces propres
et sous-espaces stables.
> Un sous-espace propre est un sous-espace stable, et même plus
généralement, tout sous-espace vectoriel d'un sous-espace propre est un sous-espace
stable.
t> La réciproque est évidemment fausse (il suffit de considérer tout l'espace,
par exemple). En revanche, une droite vectorielle est stable si, et seulement
si, elle est engendrée par un vecteur propre et donc est une droite incluse
dans un sous-espace propre.
1.9. Proposition. Soit f un endomorphisme. Les valeurs propres de f
appartiennent à Vensemble des racines de chaque polynôme annulateur de f.

48
V. Éléments propres, caractéristiques
Démonstration. Soit / un endomorphisme de polynôme annulateur P, A
une valeur propre de / et x un vecteur propre associé à A. On a pour
tout fcGN, fk(x) = Xkx par une récurrence immédiate. Par conséquent,
P(f)(x) = P(X)x. Comme P est annulateur de /, on trouve P{\)x = 0#
puis P(X) = 0, car x est non nul (en tant que vecteur propre). D
1.10. Remarque. La réciproque est bien évidemment fausse. En effet,
étant donné un polynôme annulateur, on peut trouver un polynôme
annulateur admettant d'autres racines arbitrairement choisies en le multipliant
par d'autres facteurs.
1.11. Proposition. Les valeurs propres d'un endomorphisme f sont
exactement les racines du polynôme minimal de f.
Démonstration. > D'après la proposition précédente, les valeurs propres
appartiennent déjà à l'ensemble des racines de fif, le polynôme minimal
de/.
> Réciproquement, soit A une racine de fif et Q le polynôme tel que jif =
(X — X).Q. Alors (/ — AId#) o Q(f) = 0. Si A n'est pas valeur propre de /,
alors / — AId# est inversible et donc Q est annulateur : contradiction avec
la minimalité de jif. D
1.12. Définition. La multiplicité minimale d'une valeur propre A d'un
endomorphisme / est l'entier noté ram(A), multiplicité de A en tant que
racine du polynôme minimal de /.
2. Polynôme caractéristique
2.1. Définition. Le polynôme caractéristique d'un endomorphisme / d'un
espace de dimension n est le polynôme (unitaire) Xf défini par
Xf(X) = (-l)nâet(f-XU).
Le polynôme caractéristique de la matrice A G A4n(K) est le polynôme \A
défini par
XA(X) = (-l)ndet(A-~XIn).
2.2. Remarque. D'après les propriétés du déterminant d'un matrice à
coefficients dans un anneau (ici, IK[X]), \A — Xp~1ap e^ par conséquent le
polynôme caractéristique d'un endomorphisme / est le polynôme
caractéristique de n'importe laquelle de ses matrices.

2. Polynôme caractéristique
49
2.3. Proposition. Soit f G C(E) et F un sous-espace stable par f. Alors,
le polynôme caractéristique XfF de Vendomorphisme induit divise le
polynôme caractéristique Xf de f.
Démonstration. Ecrivons la matrice de / dans une base de E obtenue en
complétant une base de F. La matrice est alors triangulaire par blocs et
le premier bloc est une matrice de fp> Le résultat provient du calcul d'un
déterminant par blocs. □
2.4. Proposition. Soit f G C(E). Supposons que E = F ® G avec F, G
des sous-espaces stables par f. Alors, le polynôme caractéristique de f vaut
Xf X/fX/g '
Démonstration. On procède comme précédemment avec une base de E
obtenue en concaténant une base de F et une base de G. □
2.5. Remarque. On peut comparer ce résultat à l'analogue pour le
polynôme minimal à la proposition II-3.4.
Un des intérêts du polynôme caractéristique est la recherche des valeurs
propres comme l'indique la proposition suivante.
2.6. Proposition. Soit f G C(E) un endomorphisme d'un espace vectoriel
de dimension n. Les racines de Xf sont exactement les valeurs propres de f.
Démonstration. Le scalaire À est une racine de Xf sh e^ seulement si det(/ —
Àld) = 0, c'est-à-dire si, et seulement si, / — Àld n'est pas inversible, ce qui
est la définition de A valeur propre. □
2.7. Remarque. D'après le calcul du déterminant, les racines du polynôme
caractéristique (c'est-à-dire les valeurs propres) d'une matrice triangulaire
sont les coefficients diagonaux.
2.8. Corollaire. Un endomorphisme d'un C-espace vectoriel admet au
moins une valeur propre.
Démonstration. Le polynôme caractéristique est non constant donc admet
une racine d'après le théorème de D'Alembert-Gauss et cette racine est une
valeur propre d'après la proposition précédente. □
Ce résultat implique en particulier que le polynôme minimal et le polynôme
caractéristique ont les mêmes racines. Il est donc important de comprendre
la multiplicité de celles-ci pour mettre en évidence la différence entre ces
deux polynômes dans l'étude de la réduction.

50
V. Éléments propres, caractéristiques
2.9. Définition. Soit / un endomorphisme et À une valeur propre de /.
t> La multiplicité de la valeur propre À est sa multiplicité en tant que racine
du polynôme caractéristique \f '•> on n°te ma(X) cette multiplicité et on
l'appelle multiplicité algébrique.
o Le sous-espace caractéristique de / associé à la valeur propre À est ker(/ —
AId)m«W.
2.10. Remarque. On verra plus loin que la multiplicité ma(X) est
exactement la dimension du sous-espace caractéristique.
2.11. Proposition. Soit f un endomorphisme et X une valeur propre de f.
Le sous-espace caractéristique de f associé à la valeur propre X est stable
par f.
Démonstration. Ces sous-espaces sont stables par / car ce sont les noyaux
de polynômes en / qui commutent donc avec /. □
Les relations entre coefficients et racines donnent pour les coefficients du
polynôme caractéristique les résultats suivants.
2.12. Proposition. Soit f G C(E) de polynôme caractéristique scindé.
Alors, la somme des valeurs propres (comptées avec leurs multiplicités) est
la trace de f, leur produit est le déterminant de f.
On généralisera cette proposition au chapitre IX.
3. Commentaires et développements
3.1. L'existence de n scalaires associés à une matrice carrée complexe A
et qui sont invariants (à l'ordre près) par similitude est un fait
particulièrement frappant. Ces scalaires sont les coefficients diagonaux communs à
toutes les matrices triangulaires de la classe de similitude de A. On verra
plus loin que de telles matrices existent dans la classe de similitude de A
si, et seulement si, le polynôme minimal de A est scindé.
Une manière rapide de les mettre en évidence est de constater que si A et
B sont semblables alors ig(A — AIn) = rg(B — AIn) pour tout scalaire À. Et,
les rangs en question sont toujours égaux à n, sauf pour un nombre fini de
scalaires À en nombre inférieur ou égal à n. Ces scalaires sont les valeurs
propres de A.

3. Commentaires et développements
51
3.2. Dans ce chapitre et les suivants, on met en évidence trois
multiplicités relatives aux valeurs propres. Ces trois multiplicités jouent un rôle
important dans l'étude de la similitude, mais ne sont pas suffisantes pour
caractériser une classe de similitude. Elles sont toutefois suffisantes dans
beaucoup de cas rencontrés en premier cycle.
Il s'agit des multiplicités géométrique, algébrique et minimale. Ces
multiplicités, on le verra dans la suite, vérifient différentes inégalités dont les cas
extrêmes correspondent au cas de la cyclicité et de la diagonalisabilité d'un
endomorphisme.
3.3. La réunion ensembliste dans tous les sous-espaces propres est la
réunion de toutes les droites stables par notre endomorphisme. Cette réunion
définit une configuration remarquable de sous-espaces en somme directe :
les intersections de chacun de ces sous-espaces avec le sous-espace engendré
par la réunion des autres sont réduites à {0}.
3.4. L'existence de valeurs propres sur un corps quelconque est liée à la
« rupturabilité » sur le corps K du polynôme minimal ou du polynôme
caractéristique, qui s'avèrent avoir les mêmes racines (aux multiplicités près).
3.5. Les endomorphismes nilpotents n'ont qu'une seule valeur propre, en
l'occurrence la valeur propre 0 ; cela rend leur étude la même quel que soit
le corps de base. Ces endomorphismes réunissent le gros des difficultés dans
l'étude des cas de réduction délicats. En écrivant la suite des noyaux itérés
{0} Ç ker/ C ker f C ... C ker fr = ker/r+1,
les multiplicités de la valeur propre 0 sont mg(0) — dimker/, mm(0) = r
et raa(0) = n.
On verra plus tard que deux matrices nilpotentes sont semblables si, et
seulement si, les dimensions des noyaux itérés sont les mêmes. On voit
alors combien les trois multiplicités sont loin de caractériser une classe de
similitude.
3.6. Les sous-espaces propres et caractéristiques associés à la valeur propre
À sont donc des sous-espaces de la forme kerP(/) avec P une puissance de
X — À. Sous-espace propres et sous-espaces caractéristiques sont donc des
objets étudiés au chapitre précédent.
3.7. L'application A H> xa qui va de Mn(C) dans l'ensemble des
polynômes unitaires de degré n est remarquable dans la mesure où ses fibres

52
V. Éléments propres, caractéristiques
sont génériquement des classes de similitude et dans les cas singuliers sont
des réunions finies de classes de similitude.
3.8. L'ensemble des polynômes complexes unitaires de degré n admet deux
paramétrages. D'une part, il s'agit d'un sous-espace affine de dimension n,
quand on écrit un tel polynôme comme Xn + an_iJn_1 + • • • H- a\X + clq ;
d'autre part, c'est l'ensemble des orbites sous l'action du groupe symétrique
&n opérant par permutation sur Cn, quand on écrit un tel polynôme comme
(A" - AO • • • (X - An).
Le passage entre les deux situations se faisant grâce aux relations entre
fonctions symétriques élémentaires et sommes de Newton, que nous verrons
plus loin.
3.9. Les valeurs propres de ad a sont un peu délicates à déterminer. On
pourra se reporter à l'exercice 20-101 page 205 de
Réduction des endomorphismes, Rached Mneimné, Calvage & Mounet, 2006.
3.10. L'ensemble des matrices ayant un même polynôme caractéristique
P ~ \\{X — Xi)ai est réunion de classes de similitude, dont seulement une
i
contient des matrices diagonales. On peut calculer le nombre de ces classes
en utilisant les invariants de similitude et en exprimer le nombre à l'aide
des multiplicités c^.
3.11. Il existe une expression simple du polynôme caractéristique d'une
matrice A = (clîj). Le coefficient devant Xk est égal à
{_1)n-k Y^ det(aM)MG/,
ieVn-kdhn])
c'est-à-dire que le coefficient devant Xk est, au signe près, la somme des
mineurs principaux d'ordre n — k. Ce résultat est évident pour les matrices
diagonales (il s'agit des relations coefficients racines) ; il suffit ensuite de
montrer que cette quantité est conservée par conjugaison pour étendre le
résultat aux matrices diagonalisables puis d'utiliser un argument de densité.
Toutefois, on peut remarquer que, dans le cas général, le coefficient de Xn~1
est — ti A et le coefficient constant égal à (—l)ndet A Par exemple, pour
une matrice de taille 3, le coefficient devant X est
«1,1 «1,2
«2,1 «2,2
+
«1,1 «1,3
«3,1 «3,3
+
«2,2 «2,3
«3,2 «3,3

4. Exercices
53
4. Exercices
4.1. Exercice. Soit f G C(E) et des scalaires X, ji G K tels que
im(/ - Aid) + im(/ - /Jd) ^ S.
Montrer que À = /i.
Indication : on pourra utiliser une forme linéaire non nulle, mais nulle
sur im(/ — Aid) -f im(/ — /ild).
> Eléments de correction. Soit (f E E* non nulle telle que, pour tout y G
im(/—Ald)+im(/—/xld), <p(y) = 0 et x G .E tel que (p(x) ^ 0. Comme f(x) —
Xx G im(/ —Aid), on a<p(/(x)) = A^(x). De même, f{x)—jjix G im(/—/ild),
on a (p(f(x)) = /jnp(x). Par conséquent, (A — /x)<p(x) = 0 donc A = /x. <
4.2. Exercice. Soz£ / G £(E) de rang 2. Calculer Xf en fonction de tr f
ettrf2.
> Éléments de correction. Dans une base de E obtenue en complétant une
base de ker/, la matrice de l'endomorphisme / est de la forme
/ 0 ... 0 • • \
: * *
I : : a b \
\ 0 ... 0 c d J
Alors Xf = Xn~2((X — a)(X — d) — 6c). En remarquant que
tr / = a + d, tr f2 = a2 + d2 + 26c,
on obtient
X/ = X^2 (X2 - tr fX + | (tr /)2 - | tr /2) .
<
4.3. Exercice. Soit A G GLn(K). Calculer x a-1 -
> Eléments de correction.
XA-^X) = {-l)nàet(A-l-Xln)
= {-l)nàet{A-l){-X)nàet(-jçln + A)
<

54
V. Éléments propres, caractéristiques
In
A
4.4. Exercice. Soit A G Mn(K). Calculer en fonction de \a le polynôme
caractéristique de la matrice par blocs
B =
> Eléments de correction. Pour effectuer ce calcul, on va raisonner avec des
opérations élémentaires par blocs.
> Commençons avec le cas n = 1 avec des opérations élémentaires pour
comprendre le cas général. Le calcul avec les opérations successives L\ <(—
L\ + XL2, C2 <— C2 + XCi, L2 <-> Li, L\ < L\ donne que la matrice
0 1 W 1 X\(X -A\(\ X
-1 0 j [ 0 1 J l -1 10 1
vaut
1 0
0 X2-a
> Revenons au cas général. Le produit matriciel
ln \ ( ln Xln \(Xln -A\f In Xln
. "In A In A -1- Xln A !™
vaut
' In
X2ln - A
En passant au déterminant, on obtient xb(X) = xa(X2). <
4.5. Exercice. Soit A € M.n(C). Déterminer les valeurs propres de la
comatrice ComA.
Indication : on pourra discuter selon le rang de A.
> Eléments de correction. > Si rg^L ^ n — 2, alors tous les mineurs de A
sont nuls (grâce à la caractérisation du rang comme la taille du plus grand
déterminant extrait non nul) donc Corn .A = 0n : la seule valeur propre
est 0.
d> Si rgA = n, alors A est inversible et ComA = (det A) A"1. Les valeurs
propres de ComA sont donc les —^-— où À est une valeur propre (non
A
nulle car A est inversible) de A donc de tA.
> Si rg A — n — 1, alors (Com A)lA = 0n. En particulier, imVl C kerCom A
et donc
dim ker Com A > rg lA = rg A = n — 1.
À ce stade, nous avons établi que 0 est valeur propre de multiplicité au

4. Exercices
55
moins n — 1. La dernière valeur propre est alors tr Com A d'après la
proposition V-2.12. Notons Ai, ..., Àn_i, Àn = 0 les valeurs propres de A.
Pour t > 0 suffisamment petit, la matrice A + tln est inversible et l'on est
ramené à l'étape précédente :
r, , A t n v^ det(A + tIn)
tr Com( A + tln) = ]T K n)
Afc-ht
fc=i
n n
fc=l J = i
n—1 n—1 n—1 n—1
= E*IKAi+*) + IKAi+')^IIAi-
fc=i j'^1 j=i j=i
n-l
Or, l'application 11-> trCom(A + tIn) est continue donc trCom A = f| À^.
n-l
En conclusion, les valeurs propres de Com A sont 0, 0, ..., 0, \\ Xj.
3 = 1
4.6. Exercice. La matrice de permutation associée à a G <5n est la
matrice Pa = (ôii(T(j))ij G A4n(K). Montrer que deux permutations sont
conjuguées dans &n si, et seulement si, les matrices de permutations associées
sont semblables (ce résultat est issu d'une remarque de Brauer).
> Eléments de correction. (=>) Soit des permutations <r, p G Gn
conjuguées et r G <5n telle que a = r o p o r-1. Comme l'application
&n -+ GLn(K)
a ^ P*
est un morphisme de groupes, on en déduit que PG — PrPpP~x donc que
les matrices PG et Pr sont semblables.
(<=) Soit des permutations a, p £ &n telles que les matrices Pa et PT
sont semblables. Alors, le polynôme caractéristique commun à ces deux
matrices est (en échangeant l'ordre des vecteurs de la base canonique de
sorte à écrire Pa diagonale par blocs)
Y[(xe - i)c*w = Y[(xl - îyw
t £
où ct(a) (respectivement ct(p)) désigne le nombre de cycles de longueur £
dans la décomposition en cycles à supports disjoints de a (respectivement

56
V. Éléments propres, caractéristiques
2J7T
de p). Alors, en étudiant la multiplicité de e £ comme racine de ce
polynôme, on obtient que, pour tout l,
£\d £\d
Par récurrence, on déduit que, pour tout £, ce(cr) = ce(p) ce qui équivaut
classiquement à la conjugaison de a et p. <
4.7. Exercice. Soit A, B e Mn(C). Montrer l'équivalence entre les
propriétés suivantes :
1. les matrices A et B ont une valeur propre commune;
2. il existe une matrice M G Mn(C) non nulle telle que AM — MB ;
S. la matrice Pa{B) n'est pas inversible.
> Eléments de correction. (1 => 2) Soit À G C une valeur propre commune
à A et B. C'est aussi une valeur propre de lB puisque xb = X*b-
Considérons X et Y des vecteurs propres associés à À pour A et lB respectivement
et posons M = iV. Alors,
AM = AX'Y = AXV et MB = XVB = XXV.
Par conséquent, la matrice M de rang 1 vérifie AM = MB.
(2 => 3) Soit M non nulle telle que AM = MB. Remarquons que cette
relation entraîne avec une récurrence facile que P(A)M = MP(B) pour
tout P eC[X]. Alors, pour P = /i#, on obtient Mpa(B) = 0n et donc Pa{B)
est non inversible, car la matrice M est non nulle.
(3 => 1) Le polynôme pa £ C[XT] est scindé. Ecrivons donc
p
^ = [T(X-Aî)ai.
L'hypothèse 3 indique que la matrice
n'est pas inversible. Ainsi, il existe un indice i tel que la matrice B — ÀJn
est non inversible : À^ est donc une valeur propre commune à A et B.
<3
4.8. Exercice. Soit A, B E Mn(C) et r G [l,n|. Montrer l'équivalence
entre les propriétés suivantes :

4. Exercices
57
1. les matrices A et B ont au moins r valeurs propres communes comptées
avec leurs multiplicités;
2. il existe une matrice M G A4n(C) de rang au moins r telle que AM =
MB.
Cet exercice est bien entendu une généralisation du précédent et Ton peut
se poser la question de l'analogue de la troisième propriété.
> Eléments de correction. (1 => 2) Soit Ai, ..., Ar des valeurs propres
communes, (Xi,...,Xr) (respectivement (Yî,..., Yr)) une famille libre de
vecteurs propres de A (respectivement de tB). Alors, la matrice
r
i=l
est de rang r et vérifie AM = MB.
(2 =»• 1) Réciproquement supposons qu'il existe M de rang r' ^ r telle
que AM — MB et écrivons
M = p( n Ir' 0r'>n-r' )q-\
Décrivons de la même manière les matrices A et B
p-iap={aI t)- «-iB«=(t i
Jr' ,n—r'
La relation AM — MB équivaut alors à A3 = 0n_r/,r/, B2 = 0r
et Ai = B\. Ainsi, les matrices P~XAP et Q~1BQ sont triangulaires par
blocs avec un bloc de taille r' en commun : leurs polynômes caractéristiques
ont donc un facteur commun de degré r', ce qui traduit l'existence d'au
moins r' valeurs propres communes. <
4.9. Exercice. Montrer que le sous-espace F de Vespace vectoriel réel
A/(n(C) engendré par les matrices M G A/(n(C) à polynôme caractéristique
réel est Vhyperplan des matrices de trace réelle.
t> Éléments de correction. > Remarquons tout d'abord que F n'est pas égal
à l'espace tout entier, donc sa dimension est au plus 2n2 — 1.
D> Ensuite, les matrices Ekj pour tout entier k et /, les matrices iEkti pour
k y^ l et les matrices iEk,k ~ ^1,1 pour k > 1 forment une famille libre
de 2n2 — 1 éléments de F. Par conséquent, dimF = 2n2 — 1. De plus, ces
matrices appartiennent toutes à l'hyperplan des matrices de trace réelle
(noyau de la forme linéaire non nulle définie par la partie imaginaire de la
trace) donc F est égal à cet hyperplan comme annoncé. <\

Chapitre VI
Endomorphismes cycliques
Objectifs du chapitre
- Définir les endomorphismes cycliques.
- Caractériser les endomorphismes cycliques en termes de polynôme
minimal, de commutant.
- Manipuler les matrices compagnons.
- Montrer qu'un espace cyclique maximal admet un supplémentaire stable.
1. Définitions
1.1. Rappel. Rappelons que le sous-espace cyclique E^x de l'endomor-
phisme / G C(E) engendré par x G E est le plus petit sous-espace stable
par / contenant x. Cet espace est engendré par la famille (p{x))je^ et,
si dimEf:X = p, alors (x, /(x),..., fp~1{x)) est une base de E^x.
1.2. Définition. Un endomorphisme / G C(E) est cyclique s'il existe x G E
tel que E = Ef:X.
1.3. Exemple. Un endomorphisme / d'un espace de dimension 2 est soit
une homothétie, soit un endomorphisme cyclique.
En effet, si / n'est pas une homothétie, alors il existe un vecteur x tel
que dim EfiX > 2 donc Ef^x = E.
1.4. Exemple. Un endomorphisme d'un espace de dimension n qui
admet n valeurs propres distinctes est cyclique.

60
VI. Endomorphismes cycliques
En effet, en notant Xi, X2, • • • > %n des vecteurs propres associés à chacune
des valeurs propres et x = x\ + X2 + • • • + xn, on vérifie immédiatement
que (x, /(x),..., fn~1(x)) est une base de I? car le déterminant de la
matrice de passage entre les familles (x, /(x),..., fn~1(x)) et (xi,X2,... , xn)
est le déterminant de Vandermonde associé aux valeurs propres.
2. Caractérisât ion avec le polynôme minimal
2.1. Proposition. Si f est un endomorphisme cyclique d'un espace E de
dimension n, alors le degré du polynôme minimal /j,f est n.
Démonstration. Considérons x G E tel que E = E^x.
> Supposons que \i$ soit de degré strictement inférieur à n. Alors, fif(f)(x) =
0e donc la famille (x, /(x),..., fn~1(x)) est liée : contradiction. Ainsi
deg/jf ^ n.
> Comme (x, /(x),..., /n~1(x)) est une base de E, il existe P G Kn_i[X]
tel que fn(x) = P(/)(x). Montrons que Q = Xn — P est annulateur de /.
Pour tout j G [0,n - 1],
<?(/)(/'(*)) = P o <?(/)(*) - /'" (/n(x) - P(f)(x)) = f(0E) = 0E.
Par conséquent, Q(f) s'annule sur une base donc Q est annulateur de /
et deg fif ^ degQ = n.
ï> En combinant les deux résultats, deg/i/ — n. D
2.2. Remarque. Si l'on sait que le degré du polynôme minimal est au plus
n, alors on peut donner une preuve plus rapide : le polynôme fifiX est de
degré dim Ef:X = n et divise le polynôme minimal fif donc deg/i/ = n.
2.3. Proposition. Si f est un endomorphisme d'un espace E de
dimension n tel que le degré du polynôme minimal \i$ est n, alors f est cyclique.
Démonstration. Considérons x G E tel que fif = jif,x (qui existe d'après
la proposition IV-3.3). Alors, dim Ef^x = deg/i/^ = deg/i/ = n, c'est-à-
dire Ef^x = E et / est cyclique. D
3. Caractérisât ion avec le commutant
3.1. Proposition. Si f est un endomorphisme cyclique, alors son
commutant C(f) est l'algèbre K[f] des polynômes en f.
Démonstration. > L'inclusion K[f] C C(f) est évidente.

3. Caractérisât ion avec le commutant
61
> Soit g G C(f) et x G E tel que E = Ef:X. Comme (x, /(x),..., /n-1(x))
est une base de E", il existe des scalaires ao, ai ..., an_i tels que
n-l
Mais alors, pour tout j G [0, n — 1],
n—1 n—1
fc=0 /c=0
n-l
Ainsi, les endomorphismes g et J^ ûfc/fc coïncident sur une base donc sont
égaux : g G K[/].
> En combinant les deux résultats, C(f) = K[f]. D
3.2. Proposition. Si f est un endomorphisme tel que son commutant C(f)
est Valgèbre K[f] des polynômes en f, alors f est cyclique.
Commençons par un lemme technique fondamental indépendant de la
notion d'endomorphisme cyclique.
3.3. Lemme. Soit f G C(E) et x G E tel que \ij = /x/}X. Alors, EfiX admet
un supplémentaire stable par f.
Démonstration. Notons p = dim E^x et considérons la base
(ei = x,e2 = /(x),...,ep =/p_1(x))
de EfjX que l'on complète en une base (ei, e2, •.., en) de E.
> Le sous-espace F = {y e E, \/j G N, e*(/J(y)) = 0} est stable par /.
> Écrivons y G Ey^ H F sous la forme
p-i
fc=0
Pour tout je[0,p-l], ep(P(y)) — 0 donc <2j = 0 et donc y = 0^. Ainsi,
les sous-espaces E/)X et F sont en somme directe.
> Calculons enfin la dimension de F. On a rapidement
F = {y € £, Vj G [0,p- 11, e;(/^'(y)) = 0},
car K[/]=vect(Id,/,..., F"1).

62
VI. Endomorphismes cycliques
La famille de formes linéaires (e* o p):?e|0?p„1j est libre ; en effet, s'il existe
des scalaires ao, ai,... ap_i tels que
;?'=0
p-1
alors ]P ajfj(x) G £^/jX H F = {0^}. Par conséquent, ao = ai — ... =
i=o
ap_i = 0 car la famille (x,/(x),... ,fv~l{x)) est libre. Le sous-espace F
est ainsi l'intersection de p hyperplans indépendants donc de dimension
n — p.
En conclusion, F est un supplémentaire stable de EfiX. □
Revenons à la preuve de la proposition VI-3.2.
Démonstration. Comme dans la section précédente, introduisons un
vecteur x G E tel que fif = fj,fjX puis considérons F un supplémentaire stable
de EfjX.
Le projecteur n sur F parallèlement à E^x commute avec / (car les deux
sous-espaces sont stables) donc est un polynôme en / : notons 7r — P(f).
Alors, P(f)(x) = 7r(x) — 0# donc \i^x = \i divise P, qui est annulateur. Par
conséquent, 7r = P(f) est l'endomorphisme nul. En conclusion, F = {0 e}
etE = Ef,x. □
4. Matrice compagnon
4.1. Définition. La matrice compagnon ou matrice de Frobenius d'un
n-l
polynôme unitaire P(X) = Xn — ^ akXk est la matrice
k=0
/O 0 0 a0 \
1 'ai
cP= ° •• '• : ; .
: "-. 0 :
\ '• • "'• 0 an_2 I
\0 0 1 an_i/

4. Matrice compagnon
63
4.2. Remarque. Un endomorphisme / est cyclique si, et seulement si, il
existe une base dans laquelle sa matrice est une matrice de compagnon.
En effet, s'il existe x G E tel que EfiX — E, on considère la base
(xJ(x),...Jn-1(x)).
Réciproquement, si dans la base (ei, e2,. •., en), la matrice de / est
compagnon, alors EfjCl = E.
4.3. Proposition. Le commutant d'une matrice compagnon A est K[A],
c'est-à-dire l'algèbre des polynômes en A.
On peut bien entendu déduire ce résultat de la proposition VI-3.1 mais
nous allons en proposer une démonstration alternative.
Démonstration. > Remarquons dans un premier temps que l'application
linéaire
f C(A) -> Mn,i(K)
\ (rriij) h> (m^i)
est injective. Pour cela considérons M dans le noyau de cette application
linéaire, ce qui se traduit par les conditions sur les colonnes
n
Cn(M4) = 5>fcCfe(M)
fc=i
et pour tout k < n, Ck(MA) = Ck+i(M).
> Montrons par récurrence sur k G [1, n] que Cj(M) = 0n,i pour j G [1, k}.
- L'initialisation vient de l'hypothèse sur M.
- Soit k G [l,n - 1] tel que Cj(M) = 0n,i pour j G [l,fc]. Alors, pour
tout j G [1, fe], ^(M) = ^^(M) = 0n,i mais alors
Cfc+i(M) - Cfc(Mi) = Cfc(M) = 0n,i.
La propriété au rang n indique que M = 0n. En conclusion, l'application
linéaire considérée est injective.
Par conséquent, dimC(A) ^ dim.Mnji(R) = n. Comme K[Â\ est inclus
dans C(A) et de dimension n, on en déduit que C(A) = K[^4]. D
4.4. Remarque. L'idée de cette preuve est que si l'on connaît l'action de
C G C{A) sur le premier vecteur de la base E\, alors on la connaît sur les
autres vecteurs puisque
CAkE1 =AkCE1.

64
VI. Endomorphismes cycliques
5. Polynôme caractéristique
5.1. Proposition. Le polynôme caractéristique de la matrice compagnon
de P est le polynôme P.
Donnons deux preuves de ce résultat.
Démonstration. Notons A(oo,..., an-i)(X) le polynôme caractéristique d'une
telle matrice et calculons-le en développant par rapport à la première ligne
ou la première colonne
A(a0,..., an_x)(X) = (-1)" (-X • A(au..., an^)(X) + (~l)n+1a0)
= -a0 + X • A(ai,..., an-i)(X).
D'où, par récurrence, A(ao,..., an_i)(X) = P. On a donc montré que le
polynôme caractéristique de la matrice compagnon de P est P. □
Pour éviter la récurrence, on peut choisir de calculer le polynôme
caractéristique autrement.
Démonstration. En développant par rapport à la dernière colonne, on
obtient que le polynôme caractéristique est
(-!)" (i^(-l)fc+nafc-iAfc,n + (<*„_! - X)AnA .
Par ailleurs, le mineur Afc,n est le déterminant d'une matrice diagonale par
blocs triangulaires : l'un de taille k — 1 avec —X sur la diagonale, l'autre de
taille n — k avec des 1 sur la diagonale. Ainsi, A^n = (—X)k~l d'où l'on
déduit le résultat pour le polynôme caractéristique. □
En terme d'endomorphisme cyclique cette proposition se récrit comme suit.
5.2. Proposition. Soit f un endomorphisme cyclique, x G E tel que EfjX =
E et ao,<2i, • •., CLn-i £ K tels que
n-l
Alors, le polynôme caractéristique de f est
n-l
Xf = xn-J2^xk.
k=0
Démonstration. Il suffit de considérer la matrice (compagnon) de / dans la
base (x, /(x),..., fn'1(x)) pour se ramener au calcul précédent. □

6. Commentaires et développements
65
Un corollaire direct de ce calcul est que tout polynôme unitaire de degré n
est le polynôme caractéristique d'une matrice de taille n x n.
On obtient également le résultat plus profond suivant qui est un cas
particulier du théorème de Cayley & Hamilton.
5.3. Théorème de Cayley & Hamilton (cas cyclique). Soit / un
endomorphisme cyclique. Alors, le polynôme caractéristique Xf es^ annulateur
de/.
Démonstration. Soit x G E tel que E = EfjX. Il suffit de vérifier que l'en-
domorphisme Xf(f) es^ nul sur ^a base (x, /(x),..., fn~~l(x)) et même,
comme Xf(f) commute avec /, d'avoir Xf(f)(x) = Os- Or, on a établi
ci-dessus que si
n-l
n*) = X>/fc(*),
alors le polynôme caractéristique de / est
n-l
fc=0
Donc,
n-l
k=0
D
6. Commentaires et développements
6.1. La décomposition de E en somme de sous-espaces caractéristiques
met en évidence les endomorphismes induits par / sur ces sous-espaces,
qui sont à leur tour cycliques! De plus, un sous-espace stable F par un
endomorphisme cyclique se découpe bien sur la décomposition de E en
sous-espaces caractéristiques, car les projecteurs sont des polynômes en /
et donc laissent stable F.
Pour déterminer les sous-espaces stables d'un endomorphisme cyclique, on
est ramené à chercher les sous-espaces stables d'un endomorphisme
cyclique ayant comme polynôme minimal la puissance d-ème d'un polynôme
irréductible P. L'affirmation est alors que les sous-espaces stables sont les
sous-espaces qui apparaissent dans la suite des noyaux itérés ker Pk(f) avec
fce|o,dl.

66
VI. Endomorphismes cycliques
Dans ce cas, les éléments de la preuve sont alors les suivants :
- un endomorphisme induit par un endomorphisme cyclique est cyclique ;
- si F est un sous-espace stable, et si le polynôme minimal de
l'endomorphisme induit fp est Ps alors F Ç kerPs(/) et la dimension de F est
celle du polynôme minimal donc dimkerPs(/).
On détaille le premier point dans les commentaires suivants.
6.2. Un endomorphisme / cyclique sur E fait de E un R = K[X)-module
engendré par un seul élément (on dira aussi cyclique) ; autrement dit, le
P-module Ef s'identifie à un quotient R/I, où / est l'idéal annulateur d'un
vecteur x tel que E — Ef:X. Le P-module R/I est engendré par la classe
de 1, est donc bien cyclique. L'action de X dessus correspond à l'action de
l'endomorphisme /.
Il est alors immédiat qu'il existe une base (à savoir les classes des monômes
1, X, X2, ..., Xd~1) de E où la matrice de / est une matrice compagnon.
Par ailleurs, les sous-espaces stables par / correspondent aux sous-modules
de l'anneau R/I.
6.3. L'exercice VI-7.6 fournit une preuve élémentaire que l'endomorphisme
induit par un endomorphisme cyclique sur un sous-espace stable est
cyclique.
Soit / un endomorphisme cyclique de E, x G E tel que EfjX = E et F un
sous-espace stable par /. On considère l'idéal formé des polynômes P tels
que P(f)(x) soit dans F. Si D est un générateur de cet idéal, alors D(f)(x)
est un vecteur cyclique pour l'endomorphisme induit fp.
C'est exactement la même démonstration qui permet d'obtenir que les
idéaux de Z/nZ sont principaux (cycliques). Pour un tel idéal /, on
considère l'ensemble 7r-1(7), où n : Z -> Z/nZ est la surjection canonique, des
entiers m tels que m soit dans I. On conclut en disant que I = 7r(7r-1(/)),
par surjectivité.
De manière plus générale, si A est un anneau principal et / un idéal de A,
les sous-modules du module cyclique A/I sont de la forme J/I où J est
un idéal de A contenant I. Comme J est principal, le sous-module J/I est
cyclique (engendré par la classe modulo / d'un générateur de J).
6.4. La manière savante d'étudier la finitude de l'ensemble des sous-espaces
stables pour l'endomorphisme cyclique / G £(P), dans le cas où le
polynôme minimal est une puissance Pm d'un polynôme irréductible P, est de
dire que E est un IK[X]/(Pm)-module cyclique. L'anneau R = K[X]/{Prn)
est local, notre P-module cyclique est donc isomorphe à un P-module de

7. Exercices
67
la forme R/I, où I est un idéal. Les sous-modules de E sont les idéaux de
l'anneau P//, c'est-à-dire les J/I où J est un idéal de R contenant I. Or,
les idéaux de R sont respectivement engendrés par Pm, Pm_1,..., P, 1. Il
y a donc m + 1 sous-modules donc autant de sous-espaces stables par / et
nous connaissons ces sous-espaces
{0} C kerP(/) C • • • C kerP™-1^) C kerPm(/) - E.
7. Exercices
7.1. Exercice. Soit f G C(E), x, y G E tels que les polynômes /i/?x et fif^
soient premiers entre eux. Montrer que
Ef,x+y = Ef,x ®Ef,y
t> Éléments de correction. > Remarquons tout d'abord que si z G EfiX C\
Ef^y, alors fJ>fiX(f)(z) = fi>fiy(f)(z) = 0e- En écrivant la relation de Bézout
entre \i^x et /i/)3/, on obtient que z — 0#. Les deux sous-espaces cycliques
sont donc en somme directe.
> Soit z G EftX+y ; il existe P G K[X] tel que z = P(f)(x + y) = P{f)(x) +
P(f)(y) €EfiX®Efiy. Ainsi,
Ef,x+y C EfjX ®Efjy.
> Soit z G EfiX@Efiy ; il existe P,Qg K[X] tels que z = P(f)(x)+Q(f)(y).
Comme /jifjX et /x/î2/ sont premiers entre eux, il existe un polynôme R G
K[X] (construit à partir de l'identité de Bézout par exemple) tel que [x^x
divise R — P et \i^y divise R — Q. Avec un tel polynôme P, P(f)(x) =
R(f)(x) et Q(f)(y) = R(f)(y) et donc, z - R(f)(x + y) G £/>ÎB+î/. En
conclusion,
Ef,x+y = EfjX ®Efjy.
<
7.2. Exercice. Déterminer une condition nécessaire et suffisante pour
qu'un endomorphisme nilpotent soit cyclique.
> Éléments de correction. Si / est un endomorphisme nilpotent d'un
espace E de dimension n, alors jif = Xp où p est l'indice de nilpotence de /.
Or, on a vu que / est cyclique si, et seulement si, deg fif = n. En conclusion,
un endomorphisme nilpotent est cyclique si, et seulement si, son indice est
la dimension de l'espace. <

68
VI. Endomorphismes cycliques
7.3. Exercice. Montrer que les endomorphismes suivants de Wn[X] sont
cycliques :
1. P^P'
2. Pk?(I + 1)-P(I)
> Éléments de correction. Ces deux endomorphismes sont nilpotents
d'indice maximal n + 1 = dimMn[X] donc cycliques. <
7.4. Exercice. Montrer qu'une rotation de M3 d'angle 0 ^ ttZ est un
endomorphisme cyclique.
ï> Eléments de correction. Une telle rotation R n'est pas une homothétie
donc son polynôme minimal est de degré au moins 2. Supposons que le
polynôme minimal /jlr soit de degré 2. Alors, 1 est racine de /jlr (car 1 est
valeur propre avec pour sous-espace propre l'axe de la rotation) et donc jir
admet une autre valeur propre réelle. Cette dernière valeur propre ne peut
être que 1 ou — 1 car R conserve la norme (endomorphisme orthogonal). Ce
résultat est contradictoire avec la condition sur l'angle.
En conclusion, le polynôme minimal de R est de degré 3 donc R est
cyclique. <
7.5. Exercice. Montrer que deux matrices A, B G M.2Q&) de trace nulle
et qui commutent sont proportionnelles.
> Eléments de correction. > Si la matrice A est nulle, le résultat est évident
car alors, B = OA
t> Sinon, A est cyclique (car elle ne peut être scalaire à cause de la
condition sur la trace) et la matrice B appartient à son commutant. D'après
la caractérisation de la cyclicité par le commutant, B est un polynôme
en A : il existe des scalaires a, /3 G M tels que B = a A -f /3i2. D'après la
condition tr(jB) = 0, j3 = 0 et l'on obtient B = aA.
<
7.6. Exercice.
1. Montrer que si f est un endomorphisme cyclique, x G E tel que E =
EfjX et F un sous-espace stable par f, alors il existe un diviseur D
de fif tel que F = EfiD(f)(x).
Indication : on pourra considérer l'idéal {P G K[X], P(f)(x) G F}.
2. En déduire qu'un endomorphisme cyclique n'admet qu'un nombre fini
de sous-espaces stables.

7. Exercices
69
3. Supposons le corps de base K infini. Montrer qu 'un endomorphisme qui
n'admet qu'un nombre fini de sous-espaces stables est cyclique.
Indication : on remarquera qu'une réunion finie de sous-espaces stricts
ne peut être égale à l'espace tout entier.
> Éléments de correction.
1. On vérifie rapidement que l'ensemble Xp — {P G K[X], P(f)(x) G F}
est bien un idéal de K[X] car F est stable. Soit D un générateur de cet
idéal.
> Comme fif E Xp, D divise jif.
> Comme D(f)(x) appartient à F (par définition de D) et F est stable
par /, £f,D(/)0r) C F.
> Soit y G F et P G K[X] tel que y = P(f)(x) (qui existe car E =
EfiX). Effectuons la division euclidienne de P par D : P = QD + i?
avec degi? < degD. Alors,
R(f)(x) = P(/)(:r) - Q(/) o £>(/)(*) = y - Q(f) (D(/)(x)) G F.
Par conséquent, i? G Xp et par minimalité de D, jR est le polynôme
nul. En conclusion, y = Q(f) (D(f)(x)) G £?/,d(/)(x)-
Par double inclusion, F = Ef^D(f)(xy
2. Soit / un endomorphisme cyclique. Comme il n'y a qu'un nombre fini
de diviseurs de /i/, il y a un nombre fini de sous-espaces stables, d'après
la description obtenue à la question précédente.
3. Supposons que l'endomorphisme / G C(E) n'admet qu'un nombre fini
de sous-espaces stables et considérons l'ensemble A obtenu par réunion
des sous-espaces stables différents de E. Comme le corps est infini,
A ^ E. Le sous-espace EfiX pour x £ A est stable et n'est pas inclus
dans A donc n'est pas un sous-espace strict de E : par conséquent,
E = EfiX et / est cyclique.
> À la question 1, on a en particulier démontré que l'endomorphisme
induit par f sur F est cyclique (pour le vecteur D(f)(x)).
t> Remarquons que si le corps K. est fini, tous les endomorphismes
n'admettent qu'un nombre fini de sous-espaces stables, car il n'y a qu'un nombre
fini de sous-espaces. La question 3 n'est donc pas pertinente dans ce cas.<\

Chapitre VII
Théorème de Cayley &
Hamilton
Objectifs du chapitre
- Démontrer le théorème de Cayley & Hamilton.
- Comprendre les conséquences du théorème de Cayley & Hamilton sur les
sous-espaces caractéristiques.
- Explorer les liens entre les différentes multiplicités associées à une valeur
propre.
1. Enoncé et conséquences
Pour comprendre le rôle important des sous-espaces caractéristiques pour
la réduction, expliquons que le polynôme caractéristique est annulateur.
1.1. Théorème de Cayley & Hamilton. Soit / G C(E). Le polynôme
caractéristique de / est annulateur de /.
Voici un énoncé équivalent.
1.2. Théorème de Cayley & Hamilton. Soit / G C(E). Le polynôme
minimal jif divise le polynôme caractéristique Xf-
En particulier, degfif < dimE.

72
VIL Théorème de Cayley & Hamilton
2. Preuve par les sous-espaces cycliques
Commençons par une première preuve exploitant les notations de sous-
espaces cycliques.
Démonstration. Soit x G E, g l'endomorphisme induit par / sur le sous-
espace cyclique E^x. On a déjà montré que Xg(d) — ®c(E) (proposition
VI-5.3) donc Xg(f)(x) = °£- Or, Xg divise Xf donc Xf(f)(%) = ®e- Cette
relation étant vraie pour tout x G E, on a bien Xf(f) = 0/:(£;)- ^
3. Preuve par la formule de la comatrice
Donnons une nouvelle preuve en apparence plus naturelle, mais qui illustre
la difficulté à manipuler le morphisme d'algèbre qui à un polynôme P
associe l'endomorphisme P(f).
Commençons par rappeler la formule de la comatrice.
3.1. Proposition. Pour tout M G Mn(A) à coefficients dans un anneau
intègre A, MtCom(M) = det(M)In.
Démonstration. Pour démontrer le théorème de Cayley & Hamilton pour
une matrice M G Mn(K), appliquons la formule de la comatrice à la
matrice M — Xln G À4n(]K[X]) e^ adoptons les notations suivantes :
n
XM(l)^afeeK[l],
k=0
n-1
tCom(M - Xln) = ]T MkXk G Mn(K[X]).
k=0
Alors, le polynôme
n
(M - XIn)tCom(M - Xln) = Y.^MMk ~ Mk-i)X\
k=0
avec la convention M_i = Mn = 0n, coïncide avec XM(X)In. En identifiant
les coefficients, on obtient, pour tout k G [0,n],
M M* - Affc_i =akïn.

4. Sous-espaces caractéristiques
73
Mais alors,
n
XM(M) = Y^akMk
k=0
n
fc=0
= Mn+1Mn - M°M_i = 0n.
n
4. Sous-espaces caractéristiques
4.1. Corollaire. Soit f un endomorphisme de E de polynôme
caractéristique scindé. Alors, E est la somme directe des sous-espaces caractéristiques
def.
En particulier, la dimension d'un sous-espace caractéristique est égale à la
multiplicité algébrique de la valeur propre.
Démonstration. Le premier point est une application du théorème des noyaux
(théorème IV-2.1) au polynôme Xf-
Notons Ai,..., Xp les valeurs propres deux à deux distinctes de /, rai,..., mp
les exposants associés, /i,..., fp les endomorphismes induits par / sur les
sous-espaces caractéristiques. Alors, d'après le premier point,
p
2=1
Or, la seule racine du polynôme scindé Xfi es^ K (car fi annule (X-- A^)mi).
Ainsi degxfi est la multiplicité ra$. On conclut que degx/* est la dimension
d'un sous-espace caractéristique associé à À*. □
5. Multiplicités
Il est temps de comparer les trois notions de multiplicité que nous avons
introduites.
5.1. Rappel. Soit / un endomorphisme et A une valeur propre de /.
> La multiplicité algébrique raa(A) de A est sa multiplicité en tant que
racine du polynôme caractéristique %/•
> La multiplicité minimale ram(A) de A est sa multiplicité en tant que racine
du polynôme minimal fif.

74
VIL Théorème de Cayley & Hamilton
t> La multiplicité géométrique mg(\) de À est la dimension du sous-espace
propre associé E\(f).
5.2. Exemple. Le scalaire 1 est une valeur propre de la matrice
0 0 0 \
10 0
0 11
0 0 1/
Les multiplicités associées sont mm(l) = 2 (car fiA = (X — l)2), raa(l) = 4
(car xa = (X — l)4) et m^(l) = 3 (le sous-espace propre est engendré par
les trois premiers vecteurs de la base canonique).
5.3. Proposition. Soit f un endomorphisme et X une valeur propre de f.
Alors
1 < rrig(X) ^ ma(X), 1 ^ ram(A) < ma(A).
Démonstration. > Le scalaire A est une valeur propre de / donc son sous-
espace propre associé est de dimension au moins 1. Ainsi, mg(X) ^ 1.
> Le sous-espace propre associé à A est inclus dans le sous-espace
caractéristique correspondant, soit en passant à la dimension, mg(X) < raa(A).
t> Le polynôme minimal divise le polynôme caractéristique (car celui-ci est
annulateur d'après le théorème de Cayley & Hamilton) ; par conséquent,
la multiplicité de A en tant que racine de fjbf est inférieure ou égale à la
multiplicité de A comme racine de x/ : à savoir, ram(A) ^ ma(X). □
6. Commentaires et développements
6.1. En dimension 2, le théorème de Cayley & Hamilton peut être mis en
évidence dès le début d'un cours de calcul matriciel : il suffit de calculer
directement A2 — (trA)A.
6.2. On peut consulter d'autres preuves du théorème de Cayley &
Hamilton dans l'ouvrage
Réduction des endomorphismes, Rached Mneimné, Calvage & Mounet, 2006
en page 19 et en pages 26-27. Cette dernière preuve repose sur l'argument
pour la matrice générale X = (Xij) ayant pour coefficients les n2
indéterminées Xij qui est diagonalisable puis sur un argument de spécialisation.
A =
( 1
0
0

7. Exercices
75
6.3. Le théorème de Cayley & Hamilton permet d'établir que la comatrice
d'une matrice A appartient à l'algèbre K[A).
6.4. L'arrivée du polynôme caractéristique met en évidence un ouvert
algébrique important, en l'occurrence l'ouvert des matrices à valeurs propres
distinctes (c'est l'ensemble des matrices qui n'annule pas le discriminant du
polynôme caractéristique). Cet ensemble est un ouvert (algébrique) connexe
dense de .Mn(C). On établit souvent les choses pour ces matrices et l'on
passe au cas général par densité.
Par exemple, on peut établir l'égalité entre formes quadratiques tr((adm)2) =
2ntr(M2) — 2tr(M)2. Il suffit de la vérifier pour une matrice diagonale puis
pour une matrice diagonalisable puis d'exploiter la densité.
6.5. Si l'on dispose d'une preuve du théorème de Cayley & Hamilton
ne passant pas par les endomorphismes cycliques, le calcul du polynôme
caractéristique d'une matrice compagnon Cp s'avère immédiat.
On écrit en effet que le polynôme minimal de Cp en le dernier vecteur de
base en divise le polynôme minimal lequel divise le polynôme
caractéristique. Mais, il est immédiat de donner l'expression du polynôme minimal en
en, lequel est P, et donc en particulier de degré n. C'est donc le polynôme
caractéristique de Cp.
6.6. Récrivons les inégalités de la proposition VII-5.3
1 < rrig(X) < ma(X)
1 < mm(X) ^ ma(\).
Alors,
D> il y a égalité à droite dans la première ligne si, et seulement si, il y a
égalité à gauche dans la seconde (voir l'exercice VII-7.6) ; si cela se
produit pour toutes les valeurs propres d'une matrice complexe, alors elle est
diagonalisable.
> il y a égalité à gauche dans la première si, et seulement si, il y a égalité
à droite dans la seconde ; si cela se produit pour toutes les valeurs propres
d'une matrice complexe, alors elle est cyclique.
7. Exercices
7.1. Exercice. Soit A E .M2OK) de trace non nulle. Montrer qu'une
matrice commute avec A si, et seulement si, elle commute avec A2.
Le résultat est-il toujours vrai si Von ôte l'hypothèse sur la trace de A ?

76
VIL Théorème de Cayley & Hamilton
> Eléments de correction. > Le sens direct est évident. Pour le sens retour,
il suffit de remarquer que, d'après le théorème de Cayley & Hamilton,
A G vect(A2,I2).
> Le résultat n'est plus vrai comme on peut le voir avec la matrice
-Ci)-
Comme A2 = 02, il suffit de remarquer que toutes les matrices ne
commutent pas avec A pour établir le contre-exemple.
<
7.2. Exercice. Soit A, B G M2(K). Montrer que la matrice (AB - BA)2
est scalaire.
> Éléments de correction. Remarquons tout d'abord que le théorème de
Cayley & Hamilton donne l'identité suivante, pour toute matrice M G
M2(K),
M2 = (tiM)M - (detM)I2.
Or, ti(AB-BA) = 0 donc (AB-BA)2 = -det(AB-BA)I2 est scalaire.^
7.3. Exercice. Soit A, B G M2{K).
1. Montrer que
AB + BA = (trB)A + (tr A)B + (tr AB - tr Atr B)l2.
2. En déduire que si tr A = tri? = 0, alors la matrice AB -h BA est
scalaire.
t> Éléments de correction.
1. Remarquons, comme dans l'exercice précédent, que le théorème de
Cayley & Hamilton donne l'identité suivante, pour toute matrice M G
M2(K),
M2 = (trM)M-(detM)I2.
Alors,
AB + BA = (A + B)2 - A2 - B2
= (tr(A + B))(A + J3) - (tr A)A - (tr5)5
+(det A + det 5 - det(A + B))I2
= {tvB)A + (tr A)B + (det A + det 5 - det (A + 5))I2.
Pour conclure, remarquons qu'en prenant la trace, l'identité déduite de

7. Exercices
77
Cayley & Hamilton donne, pour toute matrice M G A^QK),
2 det M = (trM)2 -trM2.
Par conséquent,
det A + det B - àet{A + B) = tr AB - tr Atr 5,
et l'on obtient bien la formule de l'énoncé.
2. Il suffit d'appliquer la formule précédente.
<
7.4. Exercice. Montrer qu'il n'existe pas de matrice M G M$(R) telle
que [iM = (X2 + l)2.
> Éléments de correction. Supposons qu'une telle matrice existe. Son
polynôme caractéristique est de degré 5 donc admet une racine réelle, donc M
admet une valeur propre réelle. Comme toutes les valeurs propres sont
racines du \iMï il faudrait que \im admette une racine réelle ce qui n'est pas
le cas. <\
7.5. Exercice. Soit M G Mn(M). Montrer que hm et xm ont les mêmes
facteurs irréductibles.
\> Eléments de correction. > Remarquons tout d'abord que /xm divise xm
donc les facteurs irréductibles de \im sont des facteurs irréductibles de xm-
> Par ailleurs, remarquons que xm et \im ont les mêmes racines complexes
(les valeurs propres de M). Si P est un facteur irréductible de xm-, ses
racines complexes sont racines de /jlm donc P divise jim-
Ce résultat immédiat ici sera le point de départ de l'étude des invariants de
similitude au chapitre XL
Nous n'avons utilisé le corps R ou C que dans le second point. B. Randé
nous a rappelé le raisonnement élémentaire suivant qui permet d'échapper
à cette contrainte sur le corps de base. D'après les règles de calcul dans
un anneau (plus précisément, la factorisation de an — bn pour a et b deux
éléments qui commutent), il existe un polynôme à coefficients matriciels
Qm tel que
I^M{x)ln = Vm{x)Iti ~ Mm (M) = (xln - M)QM(x).
En passant au déterminant, fiM{%)n = Xm(#) det(QM(^)); donc les
facteurs irréductibles de Xm divisent jjlm- <

78
VIL Théorème de Cayley & Hamilton
7.6. Exercice. Soit f G C(E) et A une valeur propre de f. Montrer
que rap(A) = ma(\) si, et seulement si, ram(A) = 1.
O Éléments de correction. Décomposons l'espace E = F\®G où F\ est le
sous-espace caractéristique associé à A et G est la somme directe de tous les
autres sous-espaces caractéristiques. Par construction, le polynôme minimal
de fc n'admet pas A comme racine donc le polynôme minimal de fpx est
Alors, mrn(X) — 1 si, et seulement si, fpx — AId^A, c'est-à-dire si, pour
tout x G F\, f(x) = Xx : cette condition équivaut à l'égalité entre le sous-
espace propre et le sous-espace caractéristique associé à A et donc étant
donnée l'inclusion triviale entre ces deux espaces, à l'égalité des
dimensions mg (A) = ma(X). <

Chapitre VIII
Diagonalisation
Objectifs du chapitre
- Maîtriser les critères de diagonalisation.
- Comprendre le lien entre co-diagonalisation et commutation.
1. Critères de diagonalisation
Comme les vecteurs colonnes d'une matrice sont les images des vecteurs de
la base, si la matrice M est diagonale, alors la base canonique est une base
de vecteurs propres de M.
1.1. Définition. > Un endomorphisme est diagonalisable s'il existe une
base dans laquelle sa matrice est diagonale, c'est-à-dire s'il existe une base
de vecteurs propres pour cet endomorphisme ou encore si l'espace est la
somme directe des sous-espaces propres.
> Une matrice est diagonalisable si, et seulement si, elle est semblable à
une matrice diagonale.
1.2. Remarque. Avec cette définition et celle de la relation de similitude,
on vérifie immédiatement qu'une matrice est diagonalisable si, et seulement
si, l'application linéaire qui lui est canoniquement associée est
diagonalisable.
Les valeurs propres de / sont alors les coefficients diagonaux de toute
matrice diagonale à laquelle la matrice de / est semblable.

80
VIII. Diagonalisation
1.3. Exemple. Si une matrice M est diagonalisable et n'admet qu'une
seule valeur propre, alors M est scalaire (car elle est semblable à la matrice
scalaire).
L'objectif de ce paragraphe est d'obtenir des conditions nécessaires et/ou
suffisantes pour la diagonalisabilité d'un endomorphisme. Commençons par
un résultat simple.
1.4. Proposition. Si un endomorphisme f d'un espace vectoriel E
admet n — dim E valeurs propres deux à deux distinctes, alors f est
diagonalisable.
Démonstration. Si / admet n valeurs propres deux à deux distinctes, alors
une famille de vecteurs propres associés à chacune de ces valeurs propres
est libre et de cardinal n donc c'est une base. On a trouvé une base de
vecteurs propres de / donc / est diagonalisable. □
1.5. Exemple. Une matrice triangulaire avec des coefficients diagonaux
deux à deux distincts est diagonalisable (car ses valeurs propres sont
précisément ces coefficients diagonaux).
1.6. Corollaire. Soit f G C{E). Si son polynôme caractéristique Xf est
scindé à racines simples, alors f est diagonalisable.
Démonstration. Les racines de Xf sont les valeurs propres de /. L'hypothèse
implique que / admet n valeurs propres distinctes, donc est diagonalisable
d'après la proposition précédente. □
Passons désormais à des critères (c'est-à-dire des conditions nécessaires et
suffisantes) de diagonalisabilité.
1.7. Théorème. Un endomorphisme f est diagonalisable si, et seulement
si, f admet un polynôme annulateur scindé à racines simples.
Démonstration. (=>) Si / est diagonalisable, il existe une base (ei,..., en)
de vecteurs propres; notons (\k)ke\i,m\ les valeurs propres distinctes. Le
m
polynôme f| {X — A&) est annulateur de / : en effet, pour tout i G [l,n],

1. Critères de diagonalisation
81
en notant A/-, la valeur propre associée à e$,
m
P(f)(ei) = Y[(f-XkldB){ei)
fc=l
m
= II (/ - AfeId£) ° (/ - Afc.Ide)(e0 = °£-
fc = l
m
(<=) Soit P(X) = n (X — Àfc), avec À& 7^ Aj dès que k ^ j, un polynôme
fc=i
annulateur de / scindé à racines simples. Puisque les complexes {\k)ke[i,m}
sont deux à deux distincts, les polynômes (X — \k)ke{i,ml sont deux à
deux premiers entre eux. En appliquant le lemme des noyaux, on obtient
la décomposition de
m
E = 0ker(/-Afclds)
fc=i
comme somme directe de sous-espaces propres de /. Par conséquent, / est
diagonalisable. □
Ce résultat admet la réécriture immédiate suivante.
1.8. Théorème. Un endomorphisme f est diagonalisable si, et seulement
si, son polynôme minimal jif est scindé à racines simples.
1.9. Exemple. Les projecteurs et les symétries vectorielles sont diago-
nalisables car ils admettent des polynômes annulateurs scindés à racines
simples (respectivement X2 — X et X2 — 1).
1.10. Exemple. Le seul endomorphisme nilpotent et diagonalisable est
Tendomorphisme nul. En effet, si / est un tel endomorphisme, alors /
admet un polynôme annulateur scindé à racines simples P et un polynôme
annulateur de la forme Xm. D'où, P divise Xm et par conséquent P = X.
D'où / est l'endomorphisme nul.
1.11. Exemple. Soit A G M.n(M) un endomorphisme tel que A5 = In.
> A est diagonalisable en tant que matrice complexe (donc avec une
matrice diagonale et des matrices de passage à priori à coefficients complexes)
puisqu'elle annule le polynôme scindé à racines simples X5 — 1.
D> Si A est diagonalisable sur R, alors le polynôme minimal jjla divise X5 — 1
et est annulateur scindé à racines simples; en conclusion, /aa = X — 1,
donc A = ln.

82
VIII. Diagonalisation
1.12. Exemple. Un endomorphisme de rang 1 est diagonalisable si, et
seulement si, sa trace est non nulle.
En effet, si / est un endomorphisme de rang 1, sa matrice dans une base
quelconque est de la forme M = XV donc M2 = X?YX) Y = (tYX)XtY =
tr(M)M car YX = tr(M) G K. Ainsi, si la trace est non nulle, alors M
annule un polynôme scindé à racines simples donc est diagonalisable ;
sinon M2 = 0n et d' après l'exemple précédent, la condition M diagonalisable
entraîne M = 0n ce qui est contradictoire avec rg(M) = 1.
On peut aussi voir, en notant la dimension de l'espace n, que le noyau est
de dimension n — 1 donc la dimension de l'espace propre associé à la valeur
propre 0 est n — 1 ; alors / est diagonalisable si, et seulement si, / admet
une autre valeur propre (c'est-à-dire une valeur propre non nulle).
1.13. Exemple. Soit A G Mn(R) diagonalisable et G a l'endomorphisme
de Mn(R) défini par Ga(M) = AM (multiplication à gauche par A).
Montrons que G a est diagonalisable.
Comme A est diagonalisable, il existe un polynôme P scindé à racines
simples, annulâteur de A.
Un rapide calcul donne que, pour tout M G Mn(R), P{GA){M) = P{A)M =
0n (c'est-à-dire Gp^A) — P(Ga)), donc P est aussi annulateur de G a qui
est donc diagonalisable d'après la caractérisation précédente.
1.14. Exemple. Soit A G A4n(K) une matrice diagonalisable. Alors, la
matrice
est diagonalisable.
d> En effet, A admet un polynôme annulateur scindé à racines simples P et
P(A) 0,
0„ P(A)
P(B)= ^^ p^ =02n.
> Une autre méthode consiste à écrire A — QDQ 1 avec Q inversible et D
diagonale et à remarquer que
R = ( Q 0n\{ D °n\[Q °n ' ^
' 0n Q M On D A °n Q
Essayons de regarder une réciproque à l'affirmation de cet exemple.

1. Critères de diagonalisation
83
1.15. Exemple. Soit A, B et C E M.n(K) telles que la matrice
est diagonalisable. Montrons que A et C sont diagonalisables.
En effet, M admet un polynôme annulateur scindé à racines simples P et
Par conséquent, P(A) = P{C) — 0n : A et C sont diagonalisables.
1.16. Proposition. La restriction d'un endomorphisme f diagonalisable
à un sous-espace F stable pour f est un endomorphisme (mais de F cette
fois) diagonalisable.
Démonstration. Un polynôme annulateur scindé à racines simples qui
annule / annule aussi fp, donc fp est diagonalisable. □
Après avoir détaillé un critère reposant essentiellement sur /xy, revenons au
polynôme caractéristique.
1.17. Théorème. Un endomorphisme f est diagonalisable si, et seulement
si, Xf es~k scindé et la dimension de chaque sous-espace propre est égale à
la multiplicité algébrique de la valeur propre correspondante (c'est-à-dire la
multiplicité de la valeur propre dans Xf)-
Démonstration. D'après le lemme des noyaux et le théorème de Cayley &
Hamilton, E est la somme directe des sous-espaces caractéristiques. Or
chaque sous-espace caractéristique contient le sous-espace propre associé à
la même valeur propre. Par conséquent, E est la somme directe des sous-
espaces propres si, et seulement si, les sous-espaces propres et
caractéristiques associés à une même valeur propre sont égaux (c'est-à-dire s'ils ont
même dimension). On trouve le résultat annoncé en rappelant que la
dimension d'un sous-espace caractéristique est égale à la multiplicité algébrique
de la valeur propre associée (corollaire VII-4.1). □
1.18. Corollaire. Un endomorphisme f d'un espace de dimension n est
diagonalisable si, et seulement si, la somme des dimensions des sous-espaces
propres est égale à n.
Démonstration. La somme des dimensions des sous-espaces propres est
inférieure à la somme des dimensions des sous-espaces caractéristiques.
L'égalité n'est possible que si chaque espace propre a la même dimension que

84
VIII. Diagonalisation
l'espace caractéristique associé. Le résultat provient alors de la proposition
précédente. D
2. Critère de co-diagonalisation
2.1. Définition. Une famille finie d'endomorphismes (fk)keli,N] d'un
espace vectoriel E est co-diagonalisable s'il existe une base de E dans laquelle
chacun des endomorphismes fk pour k G [1,TV] admet une matrice
diagonale.
D'après les résultats sur les sous-espaces stables déjà montrés, on sait que
les sous-espaces propres d'un endomorphisme sont stables pour tous les
endomorphismes qui commutent avec lui. En fait, ce résultat s'inscrit dans
un cadre plus général et la commutativité entre endomorphismes diagonali-
sables est une condition nécessaire et suffisante pour la co-diagonalisabilité.
2.2. Proposition. Une famille finie (fk)ke\i,N] d'endomorphismes dia-
gonalisables est co-diagonalisable si, et seulement si, pour couple (z, jr) G
Jl,7V]2; les endomorphismes fi et fj commutent.
Démonstration. > S'il existe une base dans laquelle chacun des
endomorphismes fk pour k G [l,iV] admet une matrice diagonale, alors les
endomorphismes commutent deux à deux (car deux matrices diagonales
commutent).
> Réciproquement, montrons par récurrence sur TV que si tous les
endomorphismes d'une famille de N endomorphismes diagonalisables commutent
deux à deux, alors la famille est co-diagonalisable.
> Le résultat est évidemment vrai pour un endomorphisme diagonalisable.
> Soit AT" G N*. Supposons que toute famille de N endomorphismes
diagonalisables qui commutent deux à deux est co-diagonalisable et considérons
une famille (/Oief^jv+ij de N + 1 endomorphismes qui satisfont ces
conditions.
Si tous les fi sont des homothéties alors le résultat est établi ; sinon, il
existe au moins un endomorphisme (que nous supposerons être /jv+i quitte
à réordonner la famille) qui admet au moins deux sous-espaces propres et
donc E = En+i © F avec £W+i un sous-espace propre de /jv+i et F la
somme des autres sous-espaces propres de /jv+i- Chacun de ces deux sous-
espaces est stable par (fk)ke{i,Nj • les N endomorphismes induits sur E^+i
(respectivement sur F) sont diagonalisables et commutent deux à deux donc

3. Commentaires et développements
85
sont co-diagonalisables d'après l'hypothèse de récurrence. En concaténant
les bases ainsi déterminées de jE7/v+i et de F, on obtient une base de E où
chacun des endomorphismes (/i)ie[:L,iv+i] admet une matrice diagonale.
□
2.3. Exemple. Soit A, B <E M.n(M) diagonalisables. Montrons que l'endo-
morphisme
' Mnm -> MJR)
6 : \ M »-* AMB
est diagonalisable.
D'après l'exemple VIII-1.13, les endomorphismes G a ■ M >-> AM et Db :
M i-> MB sont diagonalisables ; or, ces endomorphismes commutent, car
pour toute matrice M G .Mn(]R),
GA o DB(M) = DBo GA{M) = AMB.
La proposition précédente assure l'existence d'une base commune de
vecteurs propres ; dans cette base, la matrice de G = G a ° Db est diagonale
donc 6 est diagonalisable.
3. Commentaires et développements
3.1. Il existe d'autres critères de diagonalisabilité comme le théorème
spectral pour les matrices symétriques réelles ; toutefois ce résultat relève
de l'algèbre bilinéaire même si sa conclusion semble le faire appartenir au
domaine de l'algèbre linéaire.
Remarquons que ce résultat n'est plus vrai pour les matrices symétriques
complexes comme par exemple pour la matrice complexe suivante (avec
pour seule valeur propre 0)
1 i
i -1
3.2. On vérifie facilement que si A = PBP~X, alors ad a et adB sont
semblables avec l'automorphisme 3>p : X H> PXP~1.
Par conséquent, si A est diagonalisable, ad a l'est aussi puisque pour une
matrice D diagonale, ado est diagonale.
La réciproque est vraie comme on le verra plus tard avec la décomposition
de Jordan & Dunford. Toutefois, un argument élémentaire (laissé au
lecteur) peut être obtenu à partir de la remarque évidente suivante : si X est

86
VIII. Diagonalisation
un vecteur propre de A et M un vecteur propre pour ad a, alors MX est
soit nul, soit un vecteur propre de A.
3.3. Attention à ne pas confondre diagonalisation par similitude et
diagonalisation par congruence ! Les matrices congruentes à une matrice
diagonale sont les matrices symétriques. La matrice
(il)
est « diagonalisable au sens de la similitude » (car ses valeurs propres sont
distinctes), mais pas « diagonalisable au sens de la congruence » (car elle
n'est pas symétrique).
3.4. La somme ou la différence de deux matrices diagonalisables n'est pas
en général diagonalisable. Remarquons par exemple l'égalité suivante
(oîM-M;:)-
On peut facilement montrer qu'il existe une base de A4n(M) ou de .Mn(C)
faite de matrices diagonalisables (remarquer que les matrices à valeurs
propres distinctes forment un ouvert).
4. Exercices
4.1. Exercice. Déterminer les matrices M G Mn(^) telles que M2 = M
et tr(M) = 0.
> Éléments de correction. Comme X2 — X est annulateur scindé à racines
simples 0 et 1, M est diagonalisable et sa trace est la somme de ses valeurs
propres (comptées avec leur multiplicité). En conclusion, M est
diagonalisable avec 0 pour seule valeur propre : M est la matrice nulle. <\
4.2. Exercice. Etudier la diagonalisabilité de la matrice M — (rriij) G
M.2n{(£) définie par
f 0 sii=j[2],
,J [ 1 sinon.
> Eléments de correction. Un rapide calcul donne que M2 — nA avec A =
(a>ij) G A42n(C) la matrice définie par
a = f 0 siz^j[2],
M | 1 sinon.
puis que MA — nM. Par conséquent, M3 = n2M. Comme le polynôme

4. Exercices
87
annulateur X3 — n2X est scindé à racines simples, la matrice M est diago-
nalisable. <
4.3. Exercice. Déterminer une condition nécessaire et suffisante sur les
complexes u\,..., un, vi,..., vn pour la diagonalisabilité de la matrice
/ 0 ..." 0 U! \
M
0 ... 0 un
\ Vi ... Vn 0 )
> Éléments de correction. Écrivons la matrice par blocs
M = , tl
On U
V 0
avec [/et Vg A/fn,i(C) les vecteurs de coordonnées iti,..., un et vi,
respectivement. Alors, le calcul des puissances successives donne
n
Ainsi, M admet pour polynôme annulateur X3 — ]P UkVkX.
fe=i
n
> Si ^ itfcf fc ^ 0, ce polynôme est annulateur et scindé à racines simples
fc=i
donc M est diagonalisable.
> Sinon, M est nilpotente donc est diagonalisable si, et seulement si, M =
0n+i-
En conclusion, M est diagonalisable si, et seulement si, M est nulle ou
n
fc=i
Une autre approche de l'exercice serait de considérer d'abord la condition
plus faible M2 diagonalisable qui équivaut à la diagonalisabilité de la
matrice de rang 1 UlV puis de discuter pour se ramener à M. <3
4.4. Exercice. Exhiber une base de Vhyperplan de Ais(C) des matrices de
trace nulle qui soit constituée de matrices diagonalisables.
D> Eléments de correction. Il suffit de montrer que les matrices E\^ — i?2,2,
E\t2 + ^2,1 et les six matrices diagonalisables E\^ H- 22^,2 — 321^3 + Eij,
avec i ^ j forment une famille libre. <

VIII. Diagonalisation
4.5. Exercice. Montrer que la matrice « sous-triangulaire »
( * *\
ai
0
M :
V o
0 an_i • /
elle admet n
avec ai ... an_i ^ 0 est diagonalisable si, et seulement si,
valeurs propres distinctes.
t> Éléments de correction. Le sens retour est évident.
Pour le sens direct, remarquons que, pour tout À G K, rg(M — ÀIn) ^
n — 1 (en considérant le mineur en position (n, n) qui est triangulaire à
coefficients diagonaux non nuls) et donc que les sous-espaces propres sont
de dimension 1. Pour que M soit diagonalisable, il faut donc qu'il y ait n
valeurs propres distinctes.
Remarquons que la matrice « sous-triangulaire » considérée ici est en fait
un exemple de matrice cyclique et que le sous-espace cyclique de M
engendré par le premier vecteur de la base canonique de Mn,i(J&) est Mn,i(K).
Un cas particulier de cet exercice est le critère suivant : la matrice
( a 0 0 0 \
1
0
0
0
dj
est diagonalisable si, et seulement si, les scalaires a, b, c et d sont deux à
deux distincts. <
4.6. Exercice. Soit (a, 6, c, d) G
/ a ab
1 b
0 1
\ 0 0
n'est pas diagonalisable.
Montrer que la matrice
0 \
0
cd
d j
D> Eléments de correction. On montre tout d'abord comme dans l'exercice
précédent que les sous-espaces propres sont de dimension 1.
Par ailleurs, le polynôme caractéristique est
X — a —ab \ X — c —cd
-1 X -b \'\ -1 X -d
X2(X
b)(X
d).

4. Exercices
89
Par conséquent, la multiplicité de 0 est au moins 2 donc ne coïncide pas avec
la dimension du sous-espace propre : la matrice n'est pas diagonalisable. <]
4.7. Exercice. Soit A G Mn(R) telle que A6 = In. Montrer que si A est
diagonalisable sur M., alors A est une matrice de symétrie vectorielle.
> Eléments de correction. Comme A est diagonalisable sur M, son
polynôme minimal est scindé à racines simples sur R. Or il divise le polynôme
annulateur X6 — 1. Ainsi, les seules possibilités sont jia = X — 1, /m = X + l
ou \ia = X2 — l. Dans tous les cas, le polynôme X2 — 1 est annulateur donc A
est une matrice de symétrie vectorielle. <3
4.8. Exercice. Montrer que, pour toute permutation a G @n, la
matrice Pa = (#i,<7(j)) G A4n(C) est diagonalisable.
> Eléments de correction. Remarquons tout d'abord que, pour toutes
permutations (T, p G (Sn, PaPp — Paop-
Soit a G &n et k son ordre ; alors Pk = Pak = In : le polynôme scindé
à racines simples Xk — 1 est annulateur de la matrice Pa qui est donc
diagonalisable. <
4.9. Exercice. Soit f un endomorphisme d'un C-espace vectoriel. Montrer
que f est diagonalisable si, et seulement si, pour tout À G C,
dimker(/ - Aid) = dimker(/ - Aid)2.
> Éléments de correction. > Si / est diagonalisable, les sous-espaces propres
et caractéristiques sont confondus donc, pour toute valeur propre A G C,
dimker(/ - Aid) = dimker(/ - Aid)2.
De plus, si A n'est pas valeur propre, les deux sous-espaces sont réduits
à {0#} car / — Aid est injectif.
> Si, pour tout A G C,
dimker(/ - Aid) = dimker(/ - Aid)2
alors la suite des noyaux itérés (ker(/ — XLd)k)k^i est constante : en
particulier les sous-espiaces propres et les sous-espaces caractéristiques
coïncident : / est diagonalisable. <3
4.10. Exercice. Soit f un endomorphisme d'un C-espace vectoriel tel
que f2 est diagonalisable. Montrer que f est diagonalisable si, et seulement
si, ker / = ker f2.

90
VIII. Diagonalisation
> Eléments de correction. L'endomorphisme f2 est diagonalisable donc il
existe un polynôme jip scindé à racines simples annulateur de f2.
(=>) Si ker / ^ ker /2, alors le sous-espace propre associé à la valeur 0 n'est
pas égal au sous-espace caractéristique : / n'est pas diagonalisable.
(4=) Supposons ker/ = ker/2. Le polynôme np{X2) annule de / et, sa
seule racine multiple possible est 0. D'après le lemme des noyaux, E est
somme de sous-espaces propres associés à des valeurs propres non nulles et
de ker/2 = ker/, le sous-espace propre associé à 0 : ainsi, / est
diagonalisable. <
4.11. Exercice. Déterminer les sous-espaces stables dans Kn de
l'endomorphisme canoniquement associé à la matrice diag(l, 2,..., n).
D> Éléments de correction. Soit / l'endomorphisme associé à cette matrice
dans une base (ei, e2,..., en) et F un sous-espace stable par /. Remarquons
tout d'abord que les sous-espaces propres de / sont exactement les droites
engendrées par les vecteurs de la base considérée.
L'endomorphisme induit fp est encore diagonalisable donc F est la somme
(directe) des sous-espaces propres de fp. Comme ces sous-espaces sont
inclus dans les sous-espaces propres de / et que ces derniers sont des droites,
on en déduit que F est somme directe de sous-espaces propres de / : en
conclusion, il existe une partie / c [l,n] telle que
F = vect(ei)iG/.
Réciproquement, ces sous-espaces conviennent.
On remarque que tous ces sous-espaces stables sont cycliques car le sous-
espace F = vect(ei)iç.i est le sous-espace cyclique associé au vecteur
iei
Si on considère une matrice diagonale avec des coefficients non distincts,
on peut facilement montrer que le sous-espace associé à une valeur propre
multiple est stable sans être cyclique. <\
4.12. Exercice. Soit f G £(K4) qui admet une base (ei, e^ es, e^) formée
de vecteurs propres et un plan stable P en somme directe avec chacun des
six plans engendrés par des vecteurs de la base (ei, e2, ê3, e^).
Montrer que f est une homothétie.
> Eléments de correction. La restriction de / au plan P est diagonalisable ;
il existe une base (x, y) de P formée de vecteurs propres de /. Remarquons
que les vecteurs x et y admettent chacun au plus une coordonnée nulle dans

4. Exercices
91
la base (ei, e2, e3, e4), car sinon, ils appartiendraient à P et à un plan de
coordonnées.
> Si x admet quatre coordonnées non nulles #i, ..., x4, alors
f(x) = xif(ei) + ... -f x4/(e4).
On en déduit que les valeurs propres associées à chaque vecteur de la base
(ei, e2, e3, e4) sont toutes égales à la valeur propre associée à x.
On procède de même si y admet toutes ses coordonnées non nulles.
> Si la coordonnée de x selon e\ est nulle, alors l'argument précédent donne
que les valeurs propres associées à e2, 63 et e4 sont toutes égales.
- Si la coordonnée de y selon e\ est non nulle, alors la valeur propre associée
à ei est égale aux valeurs propres associées à deux autres vecteurs de la
base (ei, e2, e3, e4) donc toutes sont égales : / est une homothétie.
- Sinon, il existe une combinaison linéaire non nulle de x et y dans P et le
plan de coordonnées vect(e3,e4) ce qui contredit l'hypothèse.
<
4.13. Exercice. Déterminer les endomorphismes cycliques diagonalisables.
> Eléments de correction. Soit / un endomorphisme d'un espace vectoriel
de dimension n. Alors, / est cyclique si, et seulement si, jif = Xf- Or
si / est diagonalisable, /j,f est scindé à racines simples. Par conséquent, les
valeurs propres de / sont toutes distinctes. Réciproquement, cette condition
caractérise ainsi les endomorphismes cycliques diagonalisables. <
4.14. Exercice. Soit A une matrice diagonalisable. Montrer que
f Mn(R) -+ Mn(R)
aaA'\ m h* AM-MA
est diagonalisable.
> Éléments de correction. Les endomorphismes G a ' M H> AM et Da '
M v-ï MA sont diagonalisables (car A l'est et qu'ils admettent les mêmes
polynômes annulateurs que A) et commutent. Par conséquent, ils sont co-
diagonalisables. Dans cette base de co-diagonalisation, l'endomorphisme
ad a = G a ~~ Da admet une matrice diagonale. <
4.15. Exercice. Montrer que toutes les matrices d'un sous-groupe G fini
abélien de GLn(C) sont co-diagonalisables.

92
VIII. Diagonalisation
> Eléments de correction. Les éléments de G sont diagonalisables (si un
élément de G est d'ordre k, alors il annule le polynôme scindé à racines
simples Xk — 1) et commutent (car G est abélien) donc sont co-diagonalisables
d'après le théorème de réduction simultanée. <l

Chapitre IX
Trigonalisation
Objectifs du chapitre
- Maîtriser le critère de trigonalisation.
- Savoir utiliser la trigonalisation pour retrouver les fonctions symétriques
des racines.
1. Critères de trigonalisation
1.1. Définition. > Un endomorphisme est trigonalisable s'il existe une
base dans laquelle sa matrice est triangulaire.
> Une matrice est trigonalisable si elle est semblable à une matrice
triangulaire.
Commençons par rappeler le cas simple des endomorphismes nilpotents.
1.2. Proposition. Tout endomorphisme nilpotent admet dans une base
adaptée une matrice triangulaire strictement supérieure.
1.3. Théorème. Un endomorphisme est trigonalisable si, et seulement si,
il admet un polynôme annulateur scindé, soit encore si, et seulement si,
son polynôme minimal est scindé.
Démonstration. Si l'endomorphisme / est trigonalisable, il existe une base
dans laquelle sa matrice est triangulaire. En calculant le polynôme
caractéristique de / écrit dans cette base, on trouve que celui-ci est scindé : il est

94
IX. Trigonalisation
égal au produit des termes (a^ — X) où les a^ sont les termes diagonaux
de la matrice de / dans cette base.
Réciproquement, supposons que / admet un polynôme annulateur scindé
m
D'après le lemme des noyaux, l'espace E est la somme directe des F\i =
ker(/ — Xild)ai et il suffit donc de montrer que l'endomorphisme induit
par / sur chacun de ces sous-espaces F\i est trigonalisable.
Chacun de ces endomorphismes induits est la somme d'une homothétie À Jd
et d'un endomorphisme nilpotent / — À^Id. Il existe donc une base de F\i
telle que / — À^Id s'écrit sous la forme d'une matrice triangulaire
supérieure (Proposition IX-1.2) : l'endomorphisme induit par / sur F\i est
donc trigonalisable. En concaténant les bases obtenues pour chacun de ces
sous-espaces, on obtient une base de E dans laquelle la matrice de / est
triangulaire supérieure (et même diagonale par blocs triangulaires
supérieurs). □
1.4. Corollaire. Un endomorphisme sur un C-espace vectoriel
(respectivement une matrice carrée à coefficients dans C) est trigonalisable.
Démonstration. C'est une application directe du résultat ci-dessus en
remarquant que C est algébriquement clos (théorème de D'Alembert-Gauss),
donc que tous les polynômes non constants de C[X] sont scindés. □
1.5. Corollaire. Si f est un endomorphisme trigonalisable et si F est un
sous-espace stable par f, alors l'endomorphisme induit fp est trigonalisable.
Démonstration. Il suffit de remarquer que /x/F divise le polynôme scindé
/jif donc est scindé. □
1.6. Remarque. En calculant le polynôme caractéristique dans une base
de trigonalisation (quand elle existe), on retrouve que les coefficients
diagonaux sont exactement les valeurs propres (avec la multiplicité). En
particulier, la trace (respectivement le déterminant) d'une matrice trigonalisable
est la somme (respectivement le produit) de ces valeurs propres comptées
avec leurs multiplicités.
On peut également montrer l'analogue de la proposition VIII-2.2 pour la
trigonalisabilité.

2. Fonctions symétriques des valeurs propres
95
1.7. Proposition. Une famille finie (fk)ke{i,N] d'endomorphismes trigo-
nalisables telle que, pour tout pour couple (i,j) G [l,iV]]2; les endomor-
phismes fi et fj commutent, est co-trigonalisable.
Prouvons-le pour deux matrices trigonalisables qui commutent.
Démonstration. Raisonnons par récurrence sur la dimension n de l'espace.
> Le résultat est évident pour les matrices de taille 1.
> Soit n G N* tel que le résultat soit vrai au rang n, A et B G Mn+i (K) deux
matrices trigonalisables qui commutent. Comme B est trigonalisable, B
admet une valeur propre À. Le sous-espace propre ker(J3 — AIn+i) est stable
par A et l'endomorphisme induit par A y admet un vecteur propre. En
considérant une base construite en complétant ce vecteur propre commun
à A et J3, on obtient que les matrices A et B sont simultanément semblables
à
/ M *
0
A
*\
/
( X
0
u
B
\
I
Comme A et B commutent, les matrices A et B G Ain(K) commutent aussi.
Par ailleurs, A et B sont aussi trigonalisables (corollaire IX-1.5). Par
hypothèse de récurrence, il existe une matrice P G GLn(K) telle que PAP^1
et PBP"1 sont triangulaires. En considérant la matrice inversible
GXn+i(K),
on obtient que A et B sont simultanément trigonalisables.
n
2. Fonctions symétriques des valeurs propres
2.1. Définition. Soit Ai, ... ,An G C.
> Soit k G N*. La /c-ème somme de Newton de Ai,
,. ,An est le complexe

96
IX. Trigonalisation
> Soit k G [l,n]. La k-ème fonction symétrique élémentaire de Ai, ..., A„
est le complexe
Gk — 2i^ A^A^g • • • \ik.
l^.ii<...<ik^n
Rappelons les relations entre coefficients et racines pour un polynôme
complexe.
2.2. Proposition. Soit Ai, ... ,An G C. Les coefficients du polynôme
n n—1
P = l[(X - A,) = Xn + ]T a***
s'expriment à l'aide des fonctions symétriques élémentaires
V/cG [l,n], an_fc = (-l)fc(7fc.
2.3. Remarque. Soit A G .Mn(C) et Ai, ... ,An G C ses valeurs propres
(avec leur multiplicité). La matrice A est semblable à une matrice T
triangulaire dont les coefficients diagonaux sont les Ai, ..., An.
> Pour tout k G N*, la matrice Ak est semblable à une matrice Tk
triangulaire dont les coefficients diagonaux sont les Af, ..., A^. Par conséquent,
tr(Ak) — tr(Tk) est la k-ème somme de Newton de Ai, ..., An.
> Les racines du polynôme caractéristique de A sont les Ai, ..., An. Par
conséquent, les coefficients de xa sont (au signe près) les fonctions
symétriques de Ai, ..., An du fait des relations entre coefficients et racines.
Utilisons cette remarque pour établir les formules de Newton qui relient
fonctions symétriques et somme de Newton.
2.4. Exemple. Soit Ai, ..., An G C, (sk)k la suite des sommes de Newton
n n
et P = Y\(X — \j) = Yl ajATJ- Pour toute matrice M de polynôme
3=1 3=0
caractéristique P, P(M) = 0n et donc tr P(M) = 0, ce qui nous donne
l'égalité
J2a3S3 =°i
3=0
car tr MJ = Sj.
Cette première formule de Newton se généralise.

2. Fonctions symétriques des valeurs propres
97
2.5. Proposition. Soit Ai, ..., An G C, (sk)k l>a suite des sommes de
n n
Newton et P = H{X - Xj) = J2 ajxj- Alor$
n
3=0
Comme dans l'exemple précédent, ces formules résulteront d'un judicieux
calcul de trace avec le théorème de Cayley & Hamilton.
Démonstration. Le polynôme P est annulateur de la matrice compagnon * Cp
(théorème de Cayley & Hamilton) donc tr(P(Cp)Cp~~n) — 0 c'est-à-dire
J2a3tr(Ckp-^)=0.
3=0
En remarquant que les valeurs propres de Cp sont Ai, ..., An, on en déduit
n
/ J Ûj^k-n+j — 0.
3=0
n
2.6. Proposition. Soit X\, ..., Xn G C, (sk)k M suite des sommes de
Newton et P = fi (X - A,) = £ a^X?'. .4/ors,
Vfc G [l,n], ^2,an-k+jSj = (n-k)an^k.
j=o
Ces identités peuvent sembler difficiles à appréhender ; il est bon de réécrire
les premières d'entre elles
ctnSi +an_i = 0,
ans2 + an-isi + 2an_i = 0,
ans3 + an_is2 + an-2S2 + 3an_i = 0.
Démonstration. Afin de développer un argument de trace analogue à celui
1. Il n'est pas nécessaire de considérer une matrice compagnon ici (la matrice
diag(Ai,... , An) suffirait); ce choix permet d'unifier les notations avec la preuve de
la proposition suivante.

98
IX. Trigonalisation
de la preuve précédente, introduisons les polynômes
k
Wk G [0,n], Qn-k = Y^an-k+jX3.
3=0
Ainsi, le premier membre de l'égalité recherchée pour l'entier k est tr(Qk(Cp)).
Remarquons que Q0 = xcP, Qn = a<n et que Qn-k - ^Qn-fc+i = an-k
pour tout k G [l,n]. Cette relation permet alors de déduire les égalités
n-l
P(x)In - Qn(CP)xnln + J^(Qk(CP) - CPQk+1(Cp))xkIn
k=0
n—1 n—1
= YJQk+i{Cp)xk+1in - Y,Qk+y{Cp)cPxkin
k=0 k=0
n-l
= (xIn-CP)J2Qk+i(Cp)xkIn.
k=0
Pour tout x £ {Ai,..., Àn},
n-l
J2 ti(Qk+i(CP))xk = P(x) tr ((xln - Cp)-1)
k=0
Or,
n
p(x) tr ((xi„ - cPyi) = p(X) y; -^— = *"(*)•
*—' X — An
j = l J
Par continuité, l'égalité polynomiale
n-l
£>(Qfc+i(Cp))a;fc =/"(*)
fc=0
est vérifiée sur tout C et l'on obtient le résultat désiré en identifiant les
coefficients. □
2.7. Proposition. Soit N G Mn(C). La matrice N est nilpotente si, et
seulement si, pour toutke [l,nl, tr(Nk) = 0.
Démonstration. (=>) Si N est nilpotente, sa seule valeur propre est 0 donc TV
et les puissances Nk sont semblables à des matrices triangulaires
supérieures strictes. Par conséquent, pour tout k G [l,n], tr(Nk) = 0.
(4=) D'après les formules de Newton, toutes les fonctions symétriques des
valeurs propres de TV sont nulles. Par conséquent, le polynôme caractéris-

3. Commentaires et développements
99
tique de N est Xn et le théorème de Cayley & Hamilton assure que N est
nilpotente. D
2.8. Théorème de Kronecker. Soit P G C[X] unitaire à coefficients
entiers dont les racines complexes sont de module inférieur ou égal à 1.
Alors, les racines non nulles de P sont des racines de l'unité.
Démonstration. > Remarquons tout d'abord qu'il n'y a qu'un nombre fini
de polynômes unitaires de degré n, à coefficients entiers et racines dans le
disque unité car les fonctions symétriques des racines (donc le rapport des
coefficients par le coefficient dominant) sont des entiers majorés en valeur
absolue par n!. Ainsi, l'ensemble 7Z des racines des polynômes de degré n,
à coefficients entiers et racines dans le disque unité est fini.
> Soit P un polynôme à coefficients entiers dont les racines complexes de P
sont de module inférieur ou égal à 1 et soit z une racine de P. Rappelons
que z est une valeur propre de Cp, car P = xcP et donc, pour tout /c G N*,
zk est une valeur propre de CP c'est-à-dire une racine de Xck • Par ailleurs,
Cp donc CP sont à coefficients entiers. Ainsi, zk G 1Z.
Comme 1Z est fini et contient {zk, A: G N}, il existe fc>!çN tels que zh —
z1 ; ainsi, z — 0 ou z est une racine de l'unité. D
3. Commentaires et développements
3.1. La théorie de la dimension fait peu de cas des propriétés propres du
corps de base. Il en est de même des questions relatives à l'étude des
systèmes linéaires. La réduction, quant à elle, dépend de la nature du corps,
notamment à travers l'existence ou non dans K de valeurs propres.
L'arithmétique du corps intervient essentiellement peu, et se limite à la nature
des polynômes irréductibles. Quand on cherche à réduire une matrice, et
plus précisément à la trigonaliser, la scindabilité ou non du polynôme
caractéristique (ou ce qui revient au même du polynôme minimal) est la seule
donnée essentielle dont il est importe d'en tenir compte.
En revanche, dans la réduction des formes quadratiques, ou de manière
équivalente, dans l'étude des classes de congruence des matrices symétriques, de
nombreuses propriétés de nature arithmétique du corps sont essentielles et
la théorie est souvent bien dure. Pour simplifier, on pourrait dire que le cas
d'étude qui est « dénominateur commun » à tous les corps de la réduction
est celui fondamental des matrices nilpotentes (cas où le polynôme
caractéristique est scindé avec la racine 0 comme seule racine), et le dénominateur
commun dans le cas des formes quadratiques est le cas des espaces
quadratiques hyperboliques, cas où la forme quadratique admet une base de la

100
IX. Trigonalisation
forme
cas bien pauvre et que l'on évacue assez vite pour pouvoir s'occuper du
reste.
3.2. Trigonaliser une matrice M, c'est trouver un drapeau complet de Kn
stable par M.
3.3. La mise en phase du lemme des noyaux et de la trigonalisation montre
que pour un endomorphisme de polynôme caractéristique scindé sur K, il
existe une base de Kn où la matrice de l'endomorphisme s'écrit comme
matrice diagonale en blocs, avec chaque bloc somme d'une matrice scalaire
et d'une matrice triangulaire supérieure stricte.
Ce résultat est ce que l'on peut faire de mieux à un niveau élémentaire, et
montrer le chemin qui reste à parcourir pour boucler ce qui reste : rechercher
les classes de similitude des matrices nilpotentes triangulaires supérieures.
3.4. L'ensemble des matrices trigonalisables réelles est un fermé. En fait,
c'est l'adhérence de l'ensemble des matrices diagonalisables. Cela résulte
intuitivement de ce que le polynôme caractéristique dépend continûment
des coefficients de la matrice et que la limite d'une suite de polynômes
scindés est scindée.
Cela met en évidence malgré tout l'importance de travailler avec le
polynôme caractéristique, et que l'usage du polynôme minimal n'est pas adaptée
à cette situation puisqu'il ne définit pas une application continue.
4. Exercices
4.1. Exercice. Soit A G Mn(C) de valeurs propres Ai, A2, ..., Xn et P e
C[X). Déterminer le polynôme caractéristique Xp(A)-
> Eléments de correction. La matrice complexe A est semblable à une
matrice triangulaire dont les coefficients diagonaux sont Ai, A2, . •., An. Par
conséquent, la matrice P(A) est semblable à une matrice triangulaire dont
les coefficients diagonaux sont P(Ai), P(A2), . •., -P(An). En conclusion,
n
Xp(A) = l[(X-P(Xk))-
<

4. Exercices
101
4.2. Exercice. Soit A G Mn(M) qui admet le polynôme cumulateur X3 —
X — 1. Montrer que A est de déterminant positif.
> Éléments de correction. Les valeurs propres de A sont parmi les racines
du polynôme annulateur X3 — X — 1 et une rapide étude des variations de
la fonction x H> xs — x — 1 indique une racine réelle À strictement positive
et deux racines complexes conjuguées \i et ~p. Notons a la multiplicité de
la valeur propre À et /3 la multiplicité des deux valeurs propres /x et JL (la
multiplicité est la même pour les deux valeurs propres puisque \A est à
coefficients réels).
Or, le déterminant est le produit des valeurs propres avec leur multiplicité
donc
detA = Aa/iV = Aa|/i|2/3 >0.
<
4.3. Exercice. Montrer que Vensemble des matrices admettant n valeurs
propres distinctes est dense dans Ain(C).
Retrouver le théorème de Cayley & Hamilton.
D> Eléments de correction. > Soit A G «Mn(C). Comme A est trigonalisable,
il existe P G GLn(C) telle que PAP"1 est triangulaire. Par ailleurs, pour p
suffisamment grand, la matrice
PAP-1 + ^diag(l,2,...,n)
est triangulaire avec des coefficients diagonaux deux à deux distincts donc
admettant n valeurs propres distinctes. Par conséquent, la suite
(A + P-1 £diag(l,2,... ,n)p)p
est constituée, à partir d'un certain rang, de matrices à n valeurs propres
distinctes et converge vers A.
En conclusion, l'ensemble des matrices admettant n valeurs propres
distinctes est dense dans Mn(C).
> Le théorème de Cayley & Hamilton est évident pour les matrices
admettant n valeurs propres distinctes et l'application A *-» Xa{A) est continue
(car polynomiale en les coefficients de A). Ainsi, pour tout A G «Mn(C),
XA(A) = Qn. <
4.4. Exercice. Soit A G Mn(£) telle quetr(A) = ti(A2) = ... = tr.^-1).
Montrer que A est diagonalisable ou nilpotente.

102
IX. Trigonalisation
D> Eléments de correction. D'après les formules des sommes de Newton et
les relations coefficients-racines, le polynôme caractéristique est
In + (-l)ndet(A).
Si det(^4) = 0, le théorème de Cayley & Hamilton assure que A est nil-
potente. Sinon, le polynôme caractéristique est scindé à racines simples
donc A est diagonalisable (et d'ailleurs, toutes les valeurs propres ont le
même module). <
4.5. Exercice. Soit A et B G Mn(C) telles que AB — 0n.
1. Montrer que A et B admettent un vecteur propre commun.
2. Montrer que A et B sont co-trigonalisables.
> Éléments de correction. La solution proposée suit la preuve de la
proposition IX-1.7.
1. D> Si B admet un vecteur propre X associé à une valeur propre À ^ 0,
alors BX est à la fois un vecteur propre de B associé à A et de A associé
àO.
> Si la seule valeur propre de B est 0, alors B est nulle (auquel cas,
il n'y a rien à montrer) ou B est nilpotente (d'après le théorème de
Cayley & Hamilton). Si B est nilpotente d'indice p, il existe X tel
que Bv~lX ^ 0n,i et BPX = 0n_i : le vecteur B^X est alors vecteur
propre de A et de B associé à la valeur propre 0.
2. En considérant une base construite en complétant un vecteur propre
commun à A et B, on obtient que les matrices A et B sont
simultanément semblables à
0
\o
\
A
(>
0
Vo
B
\
J
L'hypothèse AB = 0n entraîne AB — 0n_i. On conclut par récurrence.
<
4.6. Exercice. Soit A, B G Mn(C).
1. Supposons qu'il existe a G C tel que AB —
et B sont co-trigonalisables.
2. Supposons qu'il existe a, (3 G C tel que AB
que A et B sont co-trigonalisables.
BA = a A. Montrer que A
- BA = aA + /3B. Montrer

4. Exercices
103
> Éléments de correction.
1. Si a = 0, c'est la proposition IX-1.7.
Supposons a ^ 0.
Une récurrence immédiate donne que, pour tout k G N, AkB — BAk =
akAk. L'endomorphisme de Mn(C) défini par M i-> MB - BM admet
un nombre fini de valeurs propres donc il existe k G N tel que Ak = 0n :
la matrice A étant nilpotente, le noyau de A est un sous-espace non
trivial et stable par B. L'endomorphisme induit par B sur le sous-
espace ker A est trigonalisable donc admet un vecteur propre dans ker A.
Il y a ainsi un vecteur propre commun à A et B. On conclut la preuve
par récurrence sur la dimension comme dans la preuve de la proposition
IX-1.7 ou dans l'exercice précédent.
2. Supposons a^O (sinon, on est dans le cas de la question précédente).
Posons A = ctA + (3B. Alors,
ÂB - BÂ = olÂ.
D'après la question précédente, A et B sont co-trigonalisables ; on en
déduit que A = — (Â — f5B) et B sont co-trigonalisables.
4.7. Exercice. Soit Ni, N2, ..., Nn G A4n(C) nilpotentes qui commutent
deux à deux. Montrer que N\N2- • • Nn — 0n.
> Éléments de correction. Comme les matrices iVi, N2) ..., A^n sont trigo-
nalisables et commutent, elles sont co-trigonalisables. Il existe donc 7\, T2,
..., Tn triangulaires supérieures strictes et P inversible telles que
VzG[l,nJ, Ni = PTip-1.
Montrons par récurrence sur k G [l,n] que les coefficients en position (i, j)
avec i ^ j — k + 1 de la matrice T1T2 • • • X^ sont nuls.
> Pour fc = 1, il s'agit simplement de la définition d'une matrice triangulaire
supérieure stricte.
> Soit k G [1, n—lj telle que les coefficients en position (z, j) avec i > j—fc+1
de la matrice T\T2 • • • T& sont nuls. Soit (i, j) telle que i ^ j — k. Avec des
notations évidentes,
n
[TiT2 • ' -T/e+iJ^j = 2JT1T2 • • •^fe]i,/[îfc + l]/,j
Z=l
= 2^[^i^2 • • •Tfc]i,i[Tfc+i]z)(7-
= 0 car i ^ Z — fc + 1.

104
IX. Trigonalisation
La récurrence est terminée et l'on en déduit en considérant le cas k = n
que la matrice T\T^ ■ • • Tn est nulle. En conclusion,
N±N2 • • • Nn = PT±T2 • • -TnP'1 = 0n.
On pewÊ awssi obtenir une autre solution pour cet exercice en utilisant le
résultat suivant :
Si une matrice M G M.n{K) et une matrice nilpotente N G Mn(K)
commutent, alors vg(MN) < rgM. <
4.8. Exercice. Montrer que tout hyperplan de A^C) contient au moins
cinq matrices nilpotentes linéairement indépendantes.
t> Eléments de correction. Soit H un hyperplan de A^C) et A G Ms(C)
telle que
H = {M G M3(C), tr(AM) = 0}.
La matrice A est trigonalisable donc il existe P inversible et T triangulaire
supérieure telle que A = PTP~l. Alors,
H - {PMP-1 G M3(C), tr(TM) = 0}.
Il suffit alors de montrer que
H' = {M G MS(C), tr(TM) = 0}.
contient au moins cinq matrices nilpotentes linéairement indépendantes. On
remarque déjà que les trois matrices nilpotentes de Eij de la base canonique
avec i < j appartiennent à H' ; en outre, la forme linéaire M H> tr(TM) de
l'espace des matrices triangulaires inférieures strictes admet un noyau de
dimension deux ce qui fournit deux matrices indépendantes des trois déjà
choisies.
Ce résultat est loin d'être optimal. Par exemple, Vhyperplan des matrices
admettant un coefficient nul en position (1,3) admet sept matrices
nilpotentes linéairement indépendantes :
000\/000\/000\/000\
0 0 0,100,000,001,
100/\000/\0 10/\000/
0 1 0 \ / 1 1 0 \ / 0 0 0\
0 0 0,-1-10,0 1 1 .
0 0 0/ \ 0 0 0 / \ 0 -1 -1 /
<

Chapitre X
Réduction de Jordan
Objectifs du chapitre
- Comprendre la décomposition de Jordan & Dunford, en particulier le
caractère polynomial de cette décomposition.
- Savoir construire et exploiter les tableaux de Young d'un endomorphisme
nilpotent.
- Caractériser la similitude avec la réduction de Jordan.
1. Décomposition de Jordan & Dunford
Dans les démonstrations précédentes, on s'est appuyé sur la
décomposition de l'endomorphisme induit par / sur un sous-espace caractéristique
comme somme d'une homothétie et d'un endomorphisme nilpotent. Si l'on
considère l'endomorphisme dans sa globalité, on obtient la décomposition
suivante.
1.1. Proposition. Décomposition de Jordan & Dunford. Soit / un
endomorphisme annulant un polynôme scindé. Alors, il existe un unique
couple d'endomorphismes (d, n) tel que
t> f = n + d;
\> n et d commutent ;
> n est nilpotent ;
t> d est diagonalisable.
De plus, les endomorphismes d et n sont des polynômes en /.

106
X. Réduction de Jordan
Démonstration. > Montrons dans un premier temps l'existence d'un tel
couple.
Sous ces hypothèses,
m
£ = 0ker(/-AfcId)afc;
k=i
de plus, l'endomorphisme induit par / sur ces sous-espaces est la somme
d'une homothétie dk et d'un endomorphisme nilpotent n^. Notons, enfin,
que la projection pi sur ker(/ — ÀJd)Q!i parallèlement à
m
0ker(/-AfcId)a&
fc=l
m
est un polynôme en /. Posons d = Y2 ^kPk et n = / — d et vérifions les
k=i
propriétés de la proposition.
- Par construction, f = d + n.
- L'endomorphisme d est un polynôme en / comme somme de polynômes
en / donc commute avec / et par conséquent avec n = / — d.
- L'endomorphisme n est nilpotent, car l'endomorphisme induit par n sur
chacun des sous-espaces ker(/ — AJd)ai est nilpotent.
- L'endomorphisme d est diagonalisable, car sa matrice est diagonale dans
m
une base adaptée à la décomposition E = 0 ker(/ — A/Jd)0^.
> Montrons maintenant l'unicité de cette décomposition.
Soit (d, n) le couple construit précédemment et (d, n) un couple
satisfaisant aux conditions de la proposition. Chacun de ces quatre
endomorphismes commute avec / donc laisse stable les sous-espaces ker(/ — Afcld)afc
pour k ^ m. Notons (dk,rik) et (dk^nk) les endomorphismes induits par ces
endomorphismes sur le sous-espace ker(/—Afcld)afe. Les endomorphismes n^
et hk commutent (le premier est un polynôme en / et le second
commute avec / = n + d) et sont tous les deux nilpotent s, donc leur
différence est nilpotente (d'indice inférieur au égal à la somme de leurs indices).
Or, rik — fik — dk — Afcld est diagonalisable. Le seul endomorphisme
diagonalisable et nilpotent est l'endomorphisme nul ; d'où dk — A/Jd et rik = n^
et par conséquent d = d et n = h. D
1.2. Remarque. Dans la preuve de cette décomposition, on a en
particulier retrouvé que si un endomorphisme / est diagonalisable de valeurs
m
propres (A^G|1)mj, alors f = Yl ^Pi avec Pi ^e projecteur sur le sous-
2=1
espace propre associé à Xi parallèlement à la somme des autres.

2. Réduction de Jordan : cas nilpotent
107
1.3. Exemple. La décomposition de Jordan & Dunford de la matrice
est I3 + N avec
1.4. Exemple. Déterminons la décomposition de Jordan & Dunford de la
matrice
(l 0 0 0\
0 2 10
0 0 2 1
\0 0 0 2)
Les valeurs propres de cette matrice sont 1 et 2 (avec multiplicité trois).
La décomposition de Jordan & Dunford de la matrice est D -f N avec D —
diag(l,2,2,2) et
TV-
/o 0 0
0 0 1
0 0 0
\0 0 0
°\
0
1
0/
1.5. Remarque. Attention, la décomposition de Jordan & Dunford d'une
matrice n'est pas simplement l'extraction des coefficients diagonaux (même
si elle est triangulaire). Par exemple, la matrice
est diagonalisable, car elle admet trois valeurs propres distinctes (qui se
lisent sur la diagonale de cette matrice triangulaire), donc est sa propre
décomposition de Jordan & Dunford.
2. Réduction de Jordan : cas nilpotent
2.1. Définition. Le bloc de Jordan de taille m£f est la matrice Jm G
A4m(K) dont tous les coefficients sont nuls sauf ceux en position (z, i + 1)

108
X. Réduction de Jordan
pour i G [l,m — Ij qui valent 1, c'est-à-dire
Jm —
/ 0 1 0 0 0 \
0 0 10 0
o o '•. "-. o
0 0 0 0 1
\ 0 0 0 0 0/
2.2. Remarque. On vérifie immédiatement que Jm est nilpotente d'ordre m
et que J™~1 = -£a,m- Plus précisément, le calcul des puissances de Jm donne
que le rang de J^ est m — k pour tout k G [0,777,] et 0 si k > m.
Nous allons établir que toute matrice nilpotente admet une unique (à
permutation près des blocs) écriture sous la forme d'une diagonale par blocs
de Jordan. Commençons par l'unicité.
2.3. Proposition. Soit f un endomorphisme (nilpotent) tel qu'il existe
des entiers d\ = deg jjln ^ <^2 ^ • • • ^ dr et une base dans laquelle la
matrice de f est diagonale par blocs avec les blocs J^, ..., Jdr • Alors,
pour tout k G N*?
#{j e [l,r], dj = k} = 2dimker/fc - dim ker/*-1 - dimker/*+1.
En d'autres termes, le nombre de blocs de Jordan de taille k de f est
2 dim ker fk — dim ker fk~x — dim ker fk+1.
Démonstration. Calculons, pour tout k ^ d\ le rang de la puissance fc-ème
de la matrice diagonale par blocs avec les blocs J^x, ..., Jdr '• il s'agit donc
du rang de la matrice diagonale par blocs avec les blocs J| , ..., J\ qui
est d'après la remarque précédente
j=i
(dj -fc)+.

2. Réduction de Jordan : cas nilpotent
109
Alors, la quantité A& = 2 dim ker fk — dim ker fkl— dim ker fk+l vaut
Afe = rg(/fe+1)+rg(/fe-1)-2rg(/fc)
r
= ]T{{d3 -k-i)+ + (dj -k + i)+-2(dj -k)+)
3 = 1
r
= J2 «dJ - k - !)+ + (dj -k+l)+- 2(d3 - k)+)
3 = 1
dj=k
r
3 = 1
dj=k
car, pour dj < k, les trois termes sont nuls et, pour dj > k,
{dj-k-l)+ + (dj~k+l)+-2{dj-k)+ = dj-k-l+dj-k + l-2(dj-k) = 0
D
Maintenant que nous avons vu l'unicité de l'écriture d'une matrice nilpo-
tente sous la forme d'une diagonale par blocs de Jordan (le nombre de blocs
de chaque taille est intrinsèque à la matrice car défini à partir des noyaux
de ses puissances), passons à la propriété d'existence.
2.4. Proposition. Soit f un endomorphisme nilpotent. Il existe des
entiers d\ = deg /ijv ^ <^2 ^ • • • ^ dr et une base dans laquelle la matrice
de f est diagonale par blocs avec les blocs J^, ..., Jdr • Cette matrice est
appelée réduite de Jordan de f.
Démonstration. Démontrons ce résultat par récurrence.
> Le résultat est évident pour les endomorphismes d'un espace de
dimension 1 ou 2.
> Soit n G N* tel que le résultat soit établi pour tous les endomorphismes
nilpotents d'espaces vectoriels de dimension au plus n ; considérons alors
un endomorphisme / d'un espace vectoriel E de dimension n + 1.
Soit x G E tel que \i$^x = \ij (d'après la proposition IV-3.3) et F un
supplémentaire stable de Ef^x (d'après le lemme VI-3.3).
Appliquons l'hypothèse de récurrence à l'endomorphisme induit fp. Il existe
d2 = deg /ifF ^ • • • ^ dr
et une base de F dans laquelle la matrice de fp est diagonale par blocs
avec les blocs Jd2, ..., Jdr •

110
X. Réduction de Jordan
Complétons la base de EfiX définie par (/dl_1(x), • • • ,/(#),#) avec cette
base de F : la matrice de F dans cette base est alors diagonale par blocs
avec les blocs J^, ..., Jdr •
Pour conclure, remarquons que d\ — dim EfjX = deg \if^x = degfif et
que d>2 = deg fifF < deg///, car /i/F divise /x/, (puisque /ij annule fp)
ainsi d\^ d^- □
Cette preuve est efficace, mais elle dissimule un aspect important : le lien
avec la suite des noyaux itérés. Donnons une seconde démonstration plus
explicite sur ce point. Rappelons que la suite (ker jk\ est strictement
croissante puis stationnaire à partir d'un rang noté p (l'indice de nilpotence).
Commençons la construction de la base avec le lemme suivant.
2.5. Lemme. Soit f un endomorphisme nilpotent d'indice r. Il existe des
sous-espaces Fri..., F\ tels que
- pour tout k G [l,r], Fk est un supplémentaire de ker fk~~1 dans ker fk ;
- pour tout k G [2,r], f(Fk) C Fk-i.
Démonstration. Construisons les sous-espaces Fr,... ,-Fr_fc par récurrence
sur k.
> Pour l'initialisation (k = 0), on construit Fr comme un supplémentaire
de ker/r_1.
> Soit k < r et supposons les sous-espaces Fr,... ,Fr^k construits. Alors,
f(Fr-k) est un sous-espace de ker fr-k~1 en somme directe avec ker fr~k-2.
Pour obtenir un sous-espace Fr-k-i, il suffit alors de compléter f(Fr-k) en
un supplémentaire de ker/r_fc~2 dans ker/r~fe_1. □
Revenons à la preuve de la proposition X-2.4.
Démonstration. Construisons la base récursivement à l'aide des sous-espaces
Fr, ..., Fi associés à / par le lemme X-2.5. On commence par une base
(ej>)je[i,mr] de Fr\ alors (ejir-i = f(zj,r))j£{i,mr} est une famille libre
de jPr_i (car la restriction de f & Fk pour k ^ 2 est injective puisque Fk H
ker/ = {O^}) que l'on complète en une base (ej,r-i)je{i,mr+mr-i] de i^V-i-
De même, une fois construit une base (ej,k)jeii,mr+...+mk] de Fk, on
considère son image par / que l'on complète ensuite en une base de F^-i-
On dispose ainsi, au bout de r étapes d'une base (ej^)j,k de E que l'on
ordonne selon l'ordre lexicographique des couples d'indices. Dans cette base,
la matrice de / a la forme désirée. □

2. Réduction de Jordan : cas nilpotent
111
2.6. Remarque. Essayons de voir les différences entre ces deux preuves à
l'aide d'une matrice semblable à la réduction de Jordan suivante
Râl
J3
h 1
> Dans la première preuve, on commence par construire un sous-espace
cyclique maximal c'est-à-dire par déterminer les vecteurs de la base de
réduction correspondant à l'un des plus « gros » blocs de taille 3 ; encadrons
les colonnes correspondantes dans la matrice réduite.
/
\
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0 0 0 0 0 \
0 0 0 0 0
0 0 0 0 0
0 10 0 0
0 0 10 0
0 0 0 0 0
0 0 0 0 1
0 0 0 0 0/
Ensuite, on passe au bloc suivant.
> Dans la seconde preuve, on commence par construire un supplémentaire
de ker f2 dans ker /3, c'est-à-dire les « derniers » vecteurs de chaque « gros »
bloc de taille 3 ; encadrons les colonnes correspondantes dans la matrice
réduite.
( ° l
0 0
0 0
0 0
0 0
0 0
0 0
\ 0 0
0
1
0
0
0
0
0
0
0 0
0 0
0 0
0 1
0 0
0 0
0 0
0 0
0
0
0
0
1
0
0
0
0 0 \
0 0
0 0
0 0
0 0
0 0
0 1
0 0/
Ensuite, on ajoute les images des vecteurs déjà choisis et l'on complète en
une base d'un supplémentaire de ker/ dans ker/2.
/ o
0
0
0
0
0
0
V o
1
0
0
0
0
0
0
0
0 0
1 0
0 0
0 0
0 0
0 0
0 0
0 0
0
0
0
1
0
0
0
0
0 0
0 0
0 0
0 0
1 0
0 0
0 0
0 0
0
0
0
0
0
0
1
0
\
/

112
X. Réduction de Jordan
2.7. Définition. > Le tableau de Young associé à la suite finie d'entiers
strictement positifs Ai ^ A2 ^ • • • > Ar est un tableau à r lignes (alignées
à gauche), la première comptant Ai cases, la deuxième A2 cases, ..., la
dernière Ar cases. On le note TY(Ai, A2,..., Àr).
> Le tableau de Young conjugué à TY(Ai, A2,..., Ar) est le tableau de
Young TY(/xi,/i2,...,MP), où \i\ ^ ^2 ^ • * * ^ Mp sont les longueurs des
colonnes de TY(Ai, A2,..., Ar). On le note TY(AX, A2,..., Ar)*.
> Le tableau de Young d'un endomorphisme nilpotent / est le tableau
TY(di, c?2> • • • 1 dr), où d\ ^ d,2 > ... ^ dr sont les entiers associés à / dans
la proposition X-2.4 ou de manière équivalente le tableau TY(#i, £2,..., ôp)*
où les entiers ôi > 62 > ... ^ ôp > 0 sont les valeurs distinctes non nulles
de la suite décroissante (dimker/fc+1 — dimker fk)k-
2.8. Exemples. > Le tableau de Young à une seule colonne
correspond à la classe de similitude de la matrice nulle (ici O9).
> Le tableau de Young à une seule ligne
correspond à la classe de similitude d'un bloc de Jordan (ici J9).
2.9. Exemple. Soit TV G M17ÇK) tel que dimker TV = 7, dimker TV2 = 12,
dimker N3 = 14, dimker NA — 16 et dimker TV5 = 17. Son tableau de
Young est alors
Par transitivité de la relation de similitude et l'unicité de la réduction de
Jordan, on obtient la caractérisation suivante des classes de similitude.

3. Interlude : lire un tableau de Young
113
2.10. Proposition. Deux endomorphismes nilpotents sont semblables si,
et seulement si, ils admettent les mêmes tableaux de Young.
2.11. Remarque. On pourrait croire un peu rapidement que deux
endomorphismes nilpotents qui commutent peuvent être réduits simultanément
au sens de Jordan. Ceci est faux comme on peut le voir avec les matrices Jn
et J^ qui commutent mais ne peuvent être simultanément des réduites de
Jordan.
3. Interlude : lire un tableau de Young
On peut lire énormément d'informations sur le tableau de Young d'un en-
domorphisme nilpotent /.
> Par construction, le nombre de lignes (c'est-à-dire le nombre de cases de
la première colonne puisque la suite des colonnes est décroissante en taille)
est la dimension du noyau de / : en effet, la première colonne correspond
à la base du noyau dans la base correspondant à la réduction de Jordan.
Autrement dit, le rang d'un endomorphisme nilpotent / est le nombre de
cases du tableau privé de sa première colonne.
Ainsi, deux endomorphismes nilpotents d'un même espace vectoriel qui ont
des tableaux de Young avec le même nombre de lignes ont le même rang.
> De même, le nombre de cases des j premières colonnes est la dimension
du noyau de p.
Ainsi, deux endomorphismes nilpotents d'un même espace vectoriel ont les
mêmes tableaux de Young si, et seulement si, toutes leurs puissances ont
les mêmes rangs.
> On sait désormais obtenir la dimension des sous-espaces im p. On peut
faire mieux en « localisant » ces sous-espaces sur le tableau de Young à
l'aide de la preuve du théorème de réduction : pour obtenir im/fc, il suffit
de rogner les k dernières cases de chaque ligne du tableau.
De même, le tableau de Young de la restriction de / à im / est simplement
le tableau de Young de / privé de sa première colonne.
3.1. Exemple. Par exemple, pour l'endomorphisme nilpotent de l'exemple

114
X. Réduction de Jordan
précédent dont le tableau de Young est
les sous-espaces im /, im f2 et im f3 sont indiqués ci-dessous (avec le
symbole •)
• # I • I
[ • | I
I • I I
I • I I
• I • I
Le sous-espace im f2 H ker f2 est par ailleurs localisé
• I •
donc est de dimension 4.
> Le nombre de colonnes est la taille du plus « gros » bloc de Jordan donc
l'indice de nilpotence, soit encore le degré du polynôme minimal.
4. Réduction de Jordan : cas général
Dans la partie précédente, on a réduit les endomorphismes nilpotents. Pour
passer au cas d'un endomorphisme quelconque, il suffit de se ramener aux
composantes nilpotentes sur chaque sous-espace caractéristique ; notons
toutefois qu'une hypothèse additionnelle est alors nécessaire pour obtenir
que l'espace est somme des sous-espaces caractéristiques.
4.1. Proposition. Soit
ristique est scindé, Ài7 ,
un endomorphisme dont le polynôme caracté-
., Xm les valeurs propres de f. Il existe des

5. Commentaires et développements
115
suites dj^i ^ ... ^ dj^rj pour j G [l,m] telles que, dans une certaine
base, la matrice de f soit diagonale par blocs avec les blocs
Ce^e matrice est appelée réduite de Jordan de f.
4.2. Remarque. Étant donné que la matrice diagonale par blocs en
conclusion de cette proposition admet un polynôme scindé, l'hypothèse sur le
polynôme caractéristique est bien nécessaire.
Cette proposition permet la caractérisation complète des classes de
similitude sur un corps algébriquement clos (donc, en particulier, sur C) mais ne
permet pas de conclure sur R.
En adaptant la remarque sur la réduite de Jordan pour les nilpotents, on
obtient le cas général.
4.3. Proposition. Deux endomorphismes f et g d'un même espace
vectoriel qui admettent des polynômes caractéristiques scindés sont semblables
si, et seulement si, ils admettent la même réduite de Jordan.
4.4. Théorème de Jordan & Weyr. Deux endomorphismes f et g d'un
même espace vectoriel qui admettent des polynômes caractéristiques
scindés sont semblables si, et seulement si,
VA £ C, V/c e N, rg(/ - Aid)* - rg(<? - AId)fc.
Démonstration. Les polynômes caractéristiques étant scindés, il suffit de
vérifier que les réductions de Jordan sont les mêmes ce qui est le cas d'après
la remarque X-3. □
5. Commentaires et développements
5.1. L'ensemble des matrices nilpotentes est appelé cône nilpotent : la
matrice nulle est son sommet et il est stable par homothétie : si N est
nilpotente, XN l'est aussi.
De surcroît, en dimension 2, cet ensemble se voit bien, car il est contenu
dans l'hyperplan (de dimension 3) des matrices de trace nulle ; et là, c'est
un véritable cône quadratique, c'est-à-dire c'est l'ensemble des zéros d'un
polynôme homogène de degré 2 (indifféremment ici, le déterminant det(M)
ou bien tr(M2). Cette description est détaillée dans le chapitre XII.

116
X. Réduction de Jordan
5.2. Un des résultats fondamentaux, qui irradie ensuite sur le reste, est
que le cône nilpotent contient un nombre fini de classes de similitude, et
plus précisément p{n) classes où p(n) est le nombre de partitions de l'entier
n.
Pour un polynôme caractéristique donné scindé, il y a n^(a0 classes de
i
similitude où les ai sont les multiplicités des racines du polynôme
caractéristique.
5.3. Dans C, on peut paramétrer les classes de similitude : d'abord avec
le polynôme caractéristique puis avec la succession des tableaux de Young
associés à chaque valeur propre.
5.4. La décomposition de Jordan & Dunford est une façon compacte,
incisive et élégante de résumer l'essentiel de ce que l'on peut tirer de la
décomposition en sous-espaces caractéristiques. Elle présente en outre l'avantage
qu'elle survit au cadre matriciel propre, puisqu'elle est encore valable pour
les algèbres de Lie (comme l'espace des matrice triangulaires ou les matrices
antisymétriques).
Ainsi, si A est une matrice triangulaire (respectivement antisymétrique
complexe) de décomposition de Jordan & Dunford A = D + N sa
décomposition de Jordan-Dunford, alors D et N sont encore triangulaires
(respectivement antisymétrique complexe).
5.5. La décomposition de Jordan & Dunford permet de montrer facilement
que le rayon spectral de A est strictement inférieur à 1 si, et seulement si,
la suite des puissances (Ap)p est de limite nulle.
5.6. La décomposition de Jordan & Dunford est effective au sens qu'il
existe un algorithme permettant de l'obtenir (ce qui contraste avec la
question difficile de la recherche des racines du polynôme caractéristique). Voici
les grandes lignes de cet algorithme pour un endomorphisme / :
- Calculons le polynôme P unitaire dont les racines complexes sont celles
de Xf niais avec la multiplicité 1. On l'obtient algorithmiquement en
divisant Xf Par Ie PGCD Xf A x'f-
- On définit une suite de polynômes (Qk)k Par la premier terme Qo = X
et, pour tout k, il existe U G C[X] tel que Xf divise Pr{Qk)U — 1 et
P(Qk+i) = Qk-P(Qk)U.
- La suite (Qk(f))k est stationnaire et sa limite est la partie d de la
décomposition de Jordan & Dunford de /.

6. Exercices
117
La relation de récurrence est l'analogue dans K[X]/(xf) de la méthode de
Newton pour la recherche de zéro d'une fonction réelle.
5.7. L'application qui à une matrice A associe sa partie nilpotente dans
la décomposition de Jordan & Dunford n'est pas en général continue ! Elle
n'est continue en M que si M admet au plus deux valeurs propres égales.
En particulier, elle n'est continue en 0n que si n ^ 2. On pourra consulter
l'exercice 11-18 page 257 de
Éléments de géométrie, Rached Mneimné, Cassini, 1997
5.8. Pour exploiter au mieux les tableaux de Young, il peut être intéressant
de les remplir avec des vecteurs correspondant à la base de réduction de
Jordan. La « localisation » indiquée à la section 3 permet alors d'extraire de
cette base de réduction des bases des différents sous-espaces ker fp P\imfq.
6. Exercices
6.1. Exercice. Déterminer la décomposition de Jordan & Dunford d'une
matrice de M2((£) de trace nulle.
> Éléments de correction. Le polynôme caractéristique d'une matrice A G
.A/Ï2(C) de trace nulle est xa = X2 + det A. Deux cas se présentent :
> si det A ^ 0, alors xa est annulateur scindé à racines simples donc A est
diagonalisable ;
> sinon, A2 = O2 donc A est nilpotente.
Dans tous les cas, A est sa propre décomposition de Jordan & Dunford. <\
6.2. Exercice. Déterminer la décomposition de Jordan & Dunford d'une
matrice de A^C) antisymétrique.
\> Éléments de correction. Une matrice A G M.%{C) antisymétrique est de
trace nulle et de déterminant nul. Son polynôme caractéristique est donc
de la forme xa = X3 + aX ; on conclut comme dans l'exercice précédent :
si ce ^ 0, la matrice est diagonalisable ; sinon, elle est nilpotente. Dans tous
les cas, A est sa propre décomposition de Jordan & Dunford. <
6.3. Exercice. Déterminer la décomposition de Jordan & Dunford de la
matrice
(a c d \
0 a e ,
0 0 6/

118
X. Réduction de Jordan
où a ^b, c, d, e G C.
> Eléments de correction. Notons A = D + N la décomposition de Jordan
& Dunford. Comme D et N sont des polynômes en A, ces matrices sont
triangulaires supérieures. Par ailleurs, la matrice N est nilpotente, donc est
triangulaire strictement supérieure. À ce stade, nous avons montré que les
matrices sont de la forme
/ a a p \ / 0 c-a d-fi \
D==\0a-y\, N=\0 0 e-7 1 .
\ 0 0 6 / \ 0 0 0 /
Comme D est diagonalisable, a = 0 (on peut le voir directement en
considérant l'induit sur l'espace engendré par les deux premiers vecteurs). La
relation ND = DN entraîne alors
<
6.4. Exercice. Soit M antisymétrique complexe de décomposition de
Jordan & Dunford M — D + N. Montrer que D et N sont antisymétriques.
> Éléments de correction. La relation M = — lM se récrit D + N = —lD —
t/V'. Comme — lD et —lN sont des matrices qui commutent, respectivement
diagonalisable et nilpotente, on peut appliquer l'unicité de la décomposition
de Jordan & Dunford, ce qui entraîne le résultat annoncé. <
6.5. Exercice. Soit M G A4n(C). Montrer que la seule matrice nilpotente
de l'algèbre C[M] est la matrice nulle si, et seulement si, M est
diagonalisable.
> Éléments de correction. (=>) Il suffit d'écrire que les termes de la
décomposition de Jordan & Dunford de M sont des polynômes en M. Par
conséquent la partie nilpotente est nulle et M est donc diagonalisable.
(<=) Si M est diagonalisable, alors M est semblable à une matrice diagonale
diag(Ai,...,An).
Pour tout polynôme P tel que P(M) est nilpotente, diag(P(Ài),..., P(Xn))
est nilpotente donc P(Ai) = ... = P(Xn) = 0. Par conséquent, P(M) = 0n.
Ainsi, la seule matrice nilpotente de C[M] est la matrice nulle. <
6.6. Exercice. Soit M G Ain(C) de décomposition de Jordan &
Dunford M — D H- N avec D diagonalisable et N nilpotente qui commutent.
Montrer qu'il existe un polynôme Q G C[X] tel que Q(0) = 0 et N = Q(M).

6. Exercices
119
> Eléments de correction. On sait déjà d'après la décomposition de Jordan
& Dunford qu'il existe un polynôme P G C[X] tel que N = P(M).
> Si /iAf(O) 7^ 0, il suffit de poser
P(0)
Q(X)=P(X) ^m(I).
> Sinon, Pn est annulateur de M donc est divisible par [Im- Ainsi, 0 est
racine de jum donc de P et il n'y a rien à établir.
Le résultat est également vrai pour D avec le polynôme X — Q(X).
On peut alors facilement obtenir que, pour tout vecteur X G ker M2, NX G
kerM. Ce résultat découle directement de la remarque simple suivante : N
et M coïncident sur le sous-espace caractéristique de M associé à 0. <
6.7. Exercice. Soit f un endomorphisme d'un C-espace vectoriel E de
décomposition de Jordan & Dunford f = n + d avec d diagonalisable et n
nilpotent qui commutent. Supposons qu'il existe des sous-espaces
vectoriels G C F tels que f(F) C G. Montrer que n(F) C G.
Indication : on peut utiliser Vexercice précédent.
> Éléments de correction. Comme n = Q(f) avec Q un polynôme à
coefficient constant nul, n(F) C G.
Là encore, le résultat est également vrai avec la partie diagonalisable d. <
6.8. Exercice. Soit f un endomorphisme d'un C-espace vectoriel E.
1. Montrer qu'il existe un endomorphisme g G C{E) tel que la partie nil-
potente n de f dans la décomposition de Jordan & Dunford soit n =
f°9-9°f'
Indication : on pourra commencer par montrer qu'il existe une
matrice M G Mn(C) telle que Jn = JnM - MJn.
2. Montrer le critère de diagonalisabilité de Klarès : f est diagonalisable
si, et seulement si, ker adf = ker ad2*.
D> Eléments de correction.
1. Commençons par montrer le résultat sur Jn. Il suffit de prendre M =
diag(l, 2,... n) (ou toute autre matrice diagonale avec des coefficients
diagonaux en progression arithmétique de raison 1) pour avoir JnM —
MJn = Jn.
Par conséquent, pour tout sous-espace caractéristique Fa associé à la
valeur propre À, il existe g\ G C(F\),
nFx = nFx ogx-gxo nFx = fFx ogx-gxo fFx
car fFx — XldFx + nFx.

120
X. Réduction de Jordan
Définissons alors, g comme l'unique endomorphisme de E coïncidant sur
chaque sous-espace caractéristique F\ avec l'endomorphisme g\
correspondant. Alors, n — fog — go f.
2. (=>) La condition ker adf — ker ad2r est équivalente à ker adf Dim adf =
{0e}- Or, la partie nilpotente n appartient à la fois à ker ad/ (en tant
que polynôme en /, elle commute avec /) et à im adf (d'après la
question précédente). Ainsi, n est l'endomorphisme nul et / est diagonali-
sable.
(4=) Si l'endomorphisme / est diagonalisable, alors adf est diagonali-
sable : ainsi ker adf = ker ad2*.
<
6.9. Exercice. Montrer que N G A4n(C) est nilpotente si, et seulement si,
N et 2N sont semblables.
> Eléments de correction. (=>) Il suffit de vérifier la propriété sur les blocs
de Jordan d'après la réduction de Jordan et le calcul par blocs. Or,
diag(l,2-1,...,2-m+1)Jmdiag(l,21,...,2m-1) = 2Jm.
Ainsi, Jm et 2Jm sont semblables.
(<=) Supposons N et 2Af semblables et considérons une valeur propre À G C
de N. Ainsi 2À est une valeur propre de 2N donc de N par similitude. Une
récurrence immédiate donne que la suite (2/cA)/c est une suite de valeurs
propres de N. Pour que cette suite soit finie (ce qui est nécessaire car
le nombre de valeurs propres de N est fini), il faut que À = 0. Mais alors,
comme 0 est l'unique valeur propre de A", xn = Xn et donc N est nilpotente
d'après le théorème de Cayley & Hamilton. <
6.10. Exercice.
trice
/0 1
0 0
0 0
\ 0 0
de Young correspondant à la ma-
2 3 \
4 5
0 6'
0 0/
Déterminer le tableau

6. Exercices
121
> Eléments de correction. La matrice proposée est nilpotente d'indice
maximal (ici 4) donc son tableau de Young est la ligne
<
6.11. Exercice. Déterminer le tableau de Young correspondant à une
matrice vérifiant ker A = imA. En déduire que toutes les matrices vérifiant
cette condition sont semblables.
ï> Eléments de correction. On trouve que A est nilpotente d'indice 2 et
que dim ker A2 = dim ker A + dim ker A fi im A = 2 dim ker A (proposition
II-1.4). Le tableau admet deux colonnes de même taille.
Ainsi, toutes ces matrices ont le même tableau de Young donc sont
semblables. <
6.12. Exercice. Déterminer le tableau de Young d'une matrice A G A^C)
nilpotente telle que rg(A2) — 2.
t> Éléments de correction. Ilya5 — 2 = 3 cases réparties sur les deux
premières colonnes donc ces colonnes sont
d'où l'on déduit que le tableau complet est
Ainsi, toutes les matrices vérifiant ces conditions ont le même tableau de
Young donc sont semblables. <
6.13. Exercice. Montrer qu'une matrice nilpotente M G M.n(C) est
semblable à la matrice
Jr+l
^n—r—1
si, et seulement si, rgM = r et rgM2 = r — 1.
D> Eléments de correction. > Pour le sens direct, il suffit de faire le calcul
et de remarquer que le rang est préservé sur une classe de similitude.
> Soit M nilpotente telle que rgM = r et rgM2 = r — 1. La première
colonne tableau de Young de la matrice M a n — r = dim ker M cases, les
deux premières ont ensembles n — r + 1 = dim ker M2 cases. Par conséquent,
la deuxième colonne (et donc toutes les suivantes) ne compte qu'une case.

122
X. Réduction de Jordan
Ainsi, le tableau de Young est une « équerre ». Par exemple, pour n
et r = 5, on obtient
Le résultat découle de la caractérisation des classes de similitude par la
réduction de Jordan. <
6.14. Exercice. Déterminer le tableau de Young correspondant à la
matrice B = A2 où la matrice A est nilpotente de tableau de Young
> Éléments de correction. Il suffit de remarquer que keri^ = ker A2k et
Ton obtient donc le tableau de Young de B en regroupant les colonnes deux
par deux, d'où
6.15. Exercice. Déterminer le tableau de Young correspondant à la
matrice
( A A
B-{0n A
où la matrice A est nilpotente de tableau de Young
> Éléments de correction. Il suffit de remarquer que
ryk ( A K,A ^ f In KLn ^ I A Un
0n Ak ) \ 0„ In )\ 0n Ak
donc rg(Bfe) = 2rg(J4fc), c'est-à-dire dimkerBfc = 2dimkerJ4fc. En conclu-

6. Exercices
123
sion, on obtient le tableau de Young de B en multipliant la longueur des
colonnes par deux. Dans notre cas particulier, le tableau de Young de B
est
<
6.16. Exercice. Soit A, B G Mn(C) nilpotentes ayant le même polynôme
minimal et le même rang.
1. Montrer que, si n $J 6, alors A et B sont semblables.
2. Donner un contre-exemple à cette affirmation pour n = 7.
D> Eléments de correction.
1. Il suffit pour ces petites dimensions de dresser la liste des tableaux
de Young puis de vérifier que si on fixe le degré du polynôme minimal
(donc le nombre de colonnes) et le rang (donc le nombre de lignes car on
fixe la dimension du noyau), on n'a qu'un seul tableau correspondant.
> n = 2
> n = 3
t> n = 4
> n = 5

124
X. Réduction de Jordan
> n ■
2. Avec les tableaux de Young suivants à sept cases qui ont le même
nombre de lignes et le même nombre de colonnes (donc même rang
et même polynôme minimal pour des endomorphismes associés)
on obtient le contre-exemple des deux matrices nilpotentes suivantes
non semblables
/
0 1 0
0 0 1
0 0 0
V
1
0 1
0 0
0 1
0 0
0 1 0
0 0 1
0 0 0
0 1 0
0 0 1
0 0 0
L°J/
o
6.17. Exercice.
blables.
Montrer que deux matrices de transvection sont sem-
> Eléments de correction. Il suffit de remarquer que le tableau de Young
associé à l'unique valeur propre 1 est TY(n — 1,1) pour toutes les trans-
vections. <!
1. On peut voir directement que leurs carrés n'ont pas le même rang.

Chapitre XI
Réduction de Frobenius
Objectifs du chapitre
- Comprendre la réduction de Frobenius et identifier une forme réduite
d'une diagonale par blocs compagnons quelconque.
- Savoir passer de la réduite de Jordan à la réduite de Frobenius et
réciproquement.
- Utiliser des calculs sur les matrices compagnons pour obtenir via la
réduite de Frobenius un résultat pour toutes les matrices.
1. Réduction de Frobenius
1.1. Proposition. Soit f un endomorphisme. Alors, il existe une unique
suite finie de polynômes unitaires Pi, P2, ..., Pr et une décomposition
r
1=1
telles que
> pour tout i G [l,r — 1], Pi+\ divise Pi ;
> pour tout i G [1,t]; Vinduit /^ est cyclique de polynôme minimal Pi.
1.2. Remarque. Remarquons tout d'abord que cette réduction ne requiert
pas l'hypothèse d'un polynôme annulateur scindé comme la réduction de
Jordan.
Démonstration. > Prouvons l'existence par récurrence sur la dimension de
l'espace.

126
XL Réduction de Frobenius
- Le résultat est évident pour les endomorphismes d'un espace de
dimension 1 (qui sont tous cycliques).
- Soit n G N*. Supposons le résultat établi pour les endomorphismes des
espaces de dimension inférieure ou égale à n et considérons / un endo-
morphisme d'un espace E de dimension n -h 1.
Introduisons x G E tel que \i^x — fif (qui existe d'après la proposition
IV-3.3) et F un supplémentaire de E\ = EfiX stable par / (qui existe
d'après la proposition VI-3.3).
Appliquons l'hypothèse de récurrence à l'endomorphisme induit fp par /
sur F : il existe une suite finie de polynômes unitaires P2, ..., Pr et une
décomposition
2 = 2
telles que, pour tout i G [2,r — 1], Pz+i divise Pi et l'induit /#. est
cyclique de polynôme minimal Pz. On vérifie alors que /i/F = P2
divise fif (car fif annule fp). Ainsi, la suite P\ = /iy, P2, ..., Pr et la
décomposition
2=1
vérifient les conditions de l'énoncé.
> Montrons désormais l'unicité de la suite de polynômes de cette
proposition en supposant qu'il existe deux telles suites distinctes de polynômes
unitaires Pi, P2, ..., Pr et Qi, Q2, ..., Qs et notons
£ = 0^ = 0*
2=1 2=1
des décompositions associées.
Remarquons que par construction Pi = Qi — \ij. Comme
r s
Y^àegPi = ]Tdeg(2i,
2=1 2=1
il existe j G [2, min(r, s)} minimal tel que Pj ^ Qj.
Étudions P3(f).
- Pour i G [l,j — 1], fpi et Jq1 sont semblables car les deux sont
cycliques de même polynôme minimal Pi — Qi donc Pj(fFi) et Pjifd)
sont semblables.
- Pour i > j, Pi divise Pj donc Pj(fpi) est l'endomorphisme nul.
- Pour i ^ j +1, Qi = Pi divise Pj donc Pj(fci) est l'endomorphisme nul.

1. Réduction de Frobenius
127
Combinant ces résultats, on obtient que Pj{fQô) est F endomorphisme nul
donc Qj = /i/G. divise Pj. Par symétrie, Pj divise Qj et donc Qj = Pj :
contradiction. □
Reformulons cette proposition.
1.3. Proposition. Soit f un endomorphisme. Alors, il existe une unique
suite finie de polynômes unitaires Pi, P2, ..., Pr tels que
> pour tout i G [1, r — 1], P^+i divise Pi ;
t> il existe une base de E dans laquelle la matrice de f est diagonale par
blocs et les blocs diagonaux sont les matrices compagnons des polynômes P\,
P2, :. ., Pr :
(\cPl
Cp2 1
\
\
cPr \)
Cette matrice est appelée réduite de Frobenius de f.
1.4. Définition. Les invariants de similitude d'un endomorphisme sont les
polynômes qui lui sont associés par la proposition XI-1.1.
1.5. Remarque. Si les invariants de similitude de / sont les polynômes Pi,
P2, • • • •> Pr (en gardant l'ordre correspondant à la divisibilité de la
proposition XI-1.1), alors
r
M/ = Pi, Xf = \[Pi-
La justification de l'appellation invariants de similitude provient du
corollaire suivant (immédiat par transitivité de la relation de similitude).
1.6. Corollaire. Deux endomorphismes sont semblables si, et seulement
si, ils ont les mêmes invariants de similitude.
1.7. Exemple. Déterminons la forme réduite de la matrice diagonale par
blocs compagnons Cx^+i et Cx^ •
/
V
0
1
-1
0
0 0
1 0
\
/

128
XL Réduction de Frobenius
Remarquons tout d'abord que cette forme n'est pas la réduite de Frobenius
car les polynômes X2 et X2 + 1 ne sont pas multiples l'un de l'autre. Par
ailleurs, le polynôme minimal de cette matrice est X2{X2 -f 1) (de degré 4)
donc la matrice est cyclique et son seul invariant est X2(X2 + 1).
1.8. Exemple. Déterminons la forme réduite de la matrice diagonale par
blocs compagnons C^a+i, Cx et Cx •
/
0 -1
1 0
V
0
\
Loj /
Le polynôme minimal de cette matrice est X(X2 + 1) et son polynôme
caractéristique est X2(X2 + 1) donc les invariants sont X(X2 + 1) et X
d'après la remarque XI-1.5. La matrice est donc semblable à
/
0 0 0
1 0 -1
0 1 0
\
kl/
2. Retour sur la réduction de Jordan
On dispose de deux caractérisations de la similitude : la forme réduite de
Jordan (si le polynôme minimal est scindé) ou la forme réduite de
Frobenius. Etudions les passages entre ces deux formes réduites. Pour cela
commençons par remarquer qu'il est facile d'obtenir la réduction de
Jordan d'un nilpotent.
2.1. Exemple. Soit / un endomorphisme nilpotent. D'après la réduction
de Frobenius, il existe des polynômes Pi, ..., Pr tels que P^+i divise Pi
pour tout i et f admet une matrice de la forme
/r^n
V
Cp2
\
[çK\)
De plus, les Pi sont des diviseurs du polynôme caractéristique Xf ~ Xn
donc sont des monômes. Alors, pour obtenir la réduction de Jordan, il suffit
de remarquer que CXk = lJk et donc de renverser l'ordre des vecteurs pour
obtenir exactement la forme voulue.

2. Retour sur la réduction de Jordan
129
Proposons une nouvelle preuve de la réduction de Jordan rappelée dans la
proposition suivante.
2.2. Proposition. Soit f un endomorphisme dont le polynôme
caractéristique est scindé, Xi, ..., Àm les valeurs propres de f. Il existe des
suites dj^i ^ ... ^ dj^rj pour j G [l,ra] telles que, dans une certaine
base, la matrice de f soit diagonale par blocs avec les blocs
^lldi,i+^di,iî • • • 5^lIdi,ri+Jdi,riî • • • >^mIdm,i+Jdn
, ^rrJ-dm.rrr, + Jd„
Démonstration. Comme Xf es^ scindé, on peut, via le lemme des noyaux,
se limiter à l'étude de l'endomorphisme induit par / sur chaque sous-espace
caractéristique. Le résultat découle alors directement du calcul précédent
sur les endomorphismes nilpotents. □
2.3. Exemple. La réduite de Frobenius de la matrice (cyclique) ÀIn + Jn
est C(x_A)n.
2.4. Exemple. Soit Ai, ..., Xp G C deux à deux distincts. La réduite de
Frobenius de la matrice par blocs
/ 1 Aiin + jri
V
O V
n(*-Ai)r*
^2Ïr2 + Jr2 1
1 ^P^p ' ^Tp
\
)
Ces exemples laissent croire que le passage de la forme réduite de Jordan
à la forme réduite de Frobenius est élémentaire ; attention toutefois à bien
comprendre les distinctions : la réduction de Jordan se fait valeur propre
par valeur propre alors que la réduction de Frobenius panache les valeurs
propres.
Détaillons les algorithmes pour passer d'une réduite à l'autre en utilisant
l'exemple XI-2.4.
2.5. Algorithme. Considérons un endomorphisme qui admet un polynôme
annulâteur scindé.
Pour passer de la forme réduite de Frobenius à la forme réduite de Jordan,
il suffit de remplacer chaque invariant de similitude (nécessairement scindé)
par des blocs de Jordan associés à chacune de ses racines et dont la taille
est la multiplicité de la racine.

130
XL Réduction de Frobenius
On obtient ainsi une écriture matricielle de / diagonale par blocs de
Jordan : c'est donc la forme réduite de Jordan d'après l'unicité démontrée au
chapitre précédent.
2.6. Exemple. Par exemple, si les invariants sont Pi = X2{X — 2)3,
P2 — X(X — 2) et Ps — X, les blocs de Jordan dans la forme réduite seront
> J2 et 2I3 -f J3 pour l'invariant Pi,
> J\ et 2Ii + J\ pour l'invariant P2,
> J\ pour l'invariant P3.
La forme réduite de Jordan est donc (en remettant les blocs dans un ordre
plus habituel)
2 1 0
0 2 1
0 0 2
2
0 1
0 0
0
0 1
2.7. Algorithme. Considérons un endomorphisme qui admet un polynôme
annulât eur scindé. Pour passer de la forme réduite de Jordan à la forme
réduite de Frobenius, on procède par étapes
> on écrit la liste des polynômes minimaux des blocs de Jordan,
> on retire de la liste les polynômes de plus haut degré pour chacune des
valeurs propres : le produit de ces termes donne un invariant de similitude,
ï> on recommence tant qu'il y a des polynômes dans la liste.
Notons que ceci correspond exactement à l'idée de l'exemple XI-2.4. On
obtient ainsi une écriture matricielle de / diagonale par blocs compagnons
avec des polynômes qui se divisent successivement (car les multiplicités des
racines décroissent au fur et à mesure) : c'est donc la forme réduite de
Frobenius d'après l'unicité démontrée.
2.8. Exemple. Considérons un endomorphisme dont les blocs dans la
réduction de Jordan sont les suivants
2I3 + J3, 2I3 + J3
I3 + J3, Is + ^3, I1 + J1
^2? J\

3. Commutants et bicommutants
131
Les polynômes correspondants sont
(X - 2)3
(X-l)3
X2
Pi
(X - 2)3
(X - l)3
X
p2
X -1
p3
X -1
Pi
Remarquons que la disposition a été choisie de sorte à simplifier l'étape
suivante : une ligne contient tous les termes associés à une valeur propre
par ordre de degré décroissant ; chaque invariant est alors le produit des
facteurs sur une colonne. Ainsi,
P1 = (X- 2)3(X - 1)3X2, P2 = {X - 2)3(X - 1)3X, P3 = P4 = X-1.
On déduit immédiatement de ces algorithmes la propriété suivante.
2.9. Corollaire. Soit f un endomorphisme à polynôme minimal scindé tel
que le nombre de blocs dans récriture réduite de Jordan soit égal au nombre
d'invariants de similitude. Alors, f admet une unique valeur propre.
3. Commutants et bicommutants
3.1. Proposition. Soit f un endomorphisme d'un espace de dimension n
et C(f) son commutant. Alors, dimC(/) ^ n.
Démonstration. D'après la réduction de Frobenius, il existe une base B dans
laquelle la matrice de / est de la forme
\
f[Cp~^\
\
[Çr7\
[Cp7]
Alors, pour toute matrice Ai commutant avec Cp^ l'endomorphisme dont
la matrice dans la base B est
/m
0D
V
\
fol/

132
XL Réduction de Frobenius
commute avec /. Par conséquent,
r r
dimC(/) ^ ]T dimC(CPJ = ^degp* = n-
i=l i=l
D
3.2. Corollaire. 5oi£ / un endomorphisme d'un espace de dimension n
et C(f) son commutant. Alors, dimC(/) = n si, et seulement si, f est
cyclique.
Démonstration. (<=) Montrons que si / admet deux invariants de similitude
alors dimC(/) > n. Pour cela il suffit de montrer que pour P et Q deux
polynômes de degré respectif p > 0 et q > 0, le commutant de la matrice
e M2p+q(K)
contient un élément qui n'est pas diagonal par blocs. Cherchons une telle
matrice de la forme
[CpQ
cP |
1 A
T]
c'est-à-dire A G Mp+qiP(K) telle que ACpq = CpA. Pour cela
considérons les endomorphismes / G C{KP) et g e £(Kp+q) canoniquement
associés à Cp et Cpq. Par construction, la base canonique de Kp est de la
forme (eu /(ei),..., /p-1(ei)) et celle de Kp+q de la forme
(e2,^(e2),...,^^-1(e2)).
Définissons <p G £(Kp+q,Kp) par l'image suivante de la base canonique
de Kp+q
VfcelO.p + 9-11, ip(gk{e2)) = fk(e2).
Il est alors évident que (p o g(gj(e2)) — f o (p(gJ;(e2)) pour j e [0,p -f q — 2].
Calculons le terme analogue pour j = p -f q — 1. Pour cela, notons PQ =
Xp+qf -f R avec P de degré au plus p -\- q— 1.
= ¥>(PQG/)(e2))-¥>(i*(s)(e2))
= —(^(P(#)(e2)) car PQ est annulateur de #
= —R{f)(e\) par définition de y?
= /p+«(e1)-PQ(/)(e1)
= /p+g(ei) car P est annulateur de /.
Par ailleurs, /o<^+9-i(e2)) = /(/P+9-i(ei)) = /P+*(ei). En conclusion,
les applications linéaires ip o g et f o (p coïncident sur une base donc sont

3. Commutants et bicommutants
133
égales. La matrice A de ip dans les bases canoniques vérifie ACpq = CpA
donc fournit une solution de notre problème reformulé. Remarquons au
passage que l'application <p est surjective donc A est de rang maximal p.
(=>) Il s'agit d'utiliser les caractérisations des endomorphismes cycliques :
d'une part C(f) = K[/] ; d'autre part, dimK[/] = deg/// = n. D
L'introduction de la matrice A de rang maximal qui « entrelace » deux
matrices compagnons associées à des polynômes en relation pour la divisibilité
va être reprise dans la démonstration de la proposition suivante.
3.3. Proposition. Soit f un endomorphisme d'un espace de dimension n.
Le bicommutant de f est Valgèbre K[f] des polynômes en f.
Démonstration. > Il est évident que K[/] est inclus dans le bicommutant.
> Soit g un élément du bicommutant de /. Considérons une décomposition
telle que l'endomorphisme induit par / sur Ei correspondent au z-ème
invariant de similitude P{.
- Chaque projecteur sur un espace Ei parallèlement à la somme des autres
espaces appartient à C(f) (car Ei est stable par /) donc commute avec g.
Par conséquent, g laisse stable les sous-espaces Ei.
- L'endomorphisme induit gEt commute avec l'endomorphisme cyclique /^ :
il existe donc un polynôme Qi tel que gEt — Qi(fEi)-
- Si / est cyclique, le résultat est établi car g — Qi(f) ; sinon, il reste à voir
que les polynômes Qi peuvent être choisis égaux. Ecrivons l'argument
pour r = 2 facteurs invariants (la récurrence est immédiate pour obtenir
le cas général). Nous venons de montrer que, dans une base bien choisie,
les matrices de / et g sont
1 Qi(cPl)
Q2(cP2) |
r^n
Cp2 [
Considérons comme dans la preuve précédente A G Md2jd1 fâ) de rang d<i
telle que ACpx = Cp2A (où d\ et ^2 sont les degrés de Pi et P2) ce qui
est possible car P2 divise P\.
Alors, la matrice
A
T]
commute avec la matrice de / donc commute avec la matrice de g.
Le calcul par blocs de ces produits amène l'égalité Q2 (Cp2 )A = AQi (Cp1 )
et, en utilisant la relation ACpx = Cp2A, Q2(Cp2)A = Qi{Cp2)A. Ainsi,

134
XL Réduction de Frobenius
la matrice Q2(Cp2) — Qi(Cp2) G Md2Q&) contient le sous-espace imA de
dimension d,2 dans son noyau donc est nulle. En conclusion, la matrice
de g est
1 Qi(CPl)
Qi(Cft) |
et donc g = Qi(f). On a ainsi établi que tout élément du bicommutant
de / appartient àK[/].
□
4. Commentaires et développements
4.1. La réduction de Frobenius d'une matrice A est le résultat le plus fin
sur la réduction, de part sa généralité et l'essentiel de l'information qu'elle
cumule sur la réduction de la matrice A. La réduction de Frobenius traduit
tout simplement le théorème fondamental sur la structure des modules de
type fini sur un anneau principal, ici, l'anneau est K[X] et le module le
K[X]-module défini par A.
La traduction de ce même théorème dans le cas des groupes abéliens finis,
nous dit qu'un tel groupe est produit (de manière unique) de groupes
cycliques Z jd\ Z (g) • • • (g) Z /dk Z, avec d\ \d2 • • • \dk> Le cas crucial étant celui
d'un p-groupe abélien fini, comme on s'en aperçoit en se ramenant aux
différents p-Sylow de G. Pour ces groupes, l'examen de l'endomorphisme
x i—)► px et de ses noyaux itérés ramène la classification de ces groupes à des
tableaux de Young.
De même que dans ce cas, on montrer que dans un groupe abélien fini, il
y a un élément dont l'ordre est le PPCM des ordres de tous les éléments du
groupe (l'exposant du groupe), de même grâce à la réduction de Frobenius,
il est possible d'y voir l'existence d'un vecteur où est atteint le polynôme
minimal.
De même que dans le cas des groupes abéliens, on peut calculer vite l'anneau
des endomorphismes d'un tel groupe, on peut ici déterminer le commutant
de A grâce à la biadditivité du foncteur Hom et l'on est ramené à calculer
les espaces d'entrelacement entre deux K[X]-modules cycliques, c'est-à-dire
entre deux matrices compagnons dont le polynôme de l'une divise l'autre.
4.2. Les invariants de similitude d'un endomorphisme / de matrice M sont
les facteurs invariants différents de 1 de la matrice M — XIn E A/ln(K[X]).
On les obtient facilement en utilisant des opérations élémentaires (à
coefficients dans K[X]) sur les lignes et les colonnes.

5. Exercices
135
5. Exercices
5.1. Exercice. À quelle condition sur P et Q G K[X] la matrice
compagnon Cpq est-elle semblable à la matrice
\Cp
Cq\
> Éléments de correction. > Si ces deux matrices sont semblables, elles ont
le même polynôme minimal : la première a pour polynôme minimal PQ car
la matrice est cyclique ; la seconde le PPC M de P et Q. Par conséquent,
pour obtenir l'égalité, il faut que P et Q soient premiers entre eux.
> Réciproquement, si P et Q sont premiers entre eux, la matrice par blocs
admet PQ comme polynôme minimal et est de taille degP + degQ =
degPQ donc est cyclique. D'après la réduction de Frobenius, elle est
semblable à Cpq. <\
5.2. Exercice. Déterminer les invariants de similitude de Vhomothétie de
rapport A.
> Éléments de correction. La réduction de Jordan de cette homothétie est
Ali + Ji,..., Ali + J\ (n fois). D'après l'algorithme XI-2.7, les invariants
de similitudes sont P1 = ... = Pn = X — A. <\
5.3. Exercice. Déterminer les invariants de similitude d'un projecteur de
rang r.
> Eléments de correction. t> Supposons r > n — r. Alors, les invariants de
similitude sont au nombre de r et
- {'S1.
r>(Y\-l ^y^~X) si i^n-r,
^W-1 ^ X sinon.
t> Supposons r ^ n — r. Alors, les invariants de similitude sont au nombre
de n — r et
n ) ] X sinon.
5.4. Exercice. Soit \i et \ £ Œ£[X]. Déterminer une condition nécessaire
et suffisante pour qu'il existe une matrice A telle que \±a — \i et \A = X-
> Eléments de correction. > Il est évident que x e^ M on^ ^es mêmes facteurs
irréductibles et que la multiplicité de chaque facteur dans \ es^ supérieure
ou égale à celle correspondante dans jjl.

136
XL Réduction de Frobenius
> Réciproquement, écrivons la décomposition en facteurs irréductibles
i=l
et supposons \i — \\ R^ avec, pour tout % G [l,r], Pi G [l,o^].
2=1
Posons p — max(a^ — fy + 1), P\ = fi et pour tout k G [2,p],
^
n ^
i = l
Alors, pour tout k G [l,p — 1], Pjt+i divise P&. La matrice diagonale par
blocs Cp1, ..., Cp admet les polynômes Pi, ..., Pp comme invariants
p
de similitude donc fi = P\ et % = f| P& comme polynômes minimal et
fc=i
caractéristique.
5.5. Exercice.
1. Soit P G K[X] unitaire. Déterminer le rang de la matrice
compagnon Cp.
2. Soit A G Mn(K). Montrer que deg fiA ^ rgA + 1.
3. Déterminer les matrices A G .Mn(K) £e//es gne deg//,4 = rgA + 1.
> Eléments de correction.
1. Rappelons que la matrice compagnon de P est de la forme
/O 0 0 -P(0)\
Cp =
1
Vo
•. o
"•• o
0 1
/
Par conséquent, si P(0) = 0, la première ligne est nulle et les n —
1 = deg P — 1 suivantes sont indépendantes, sinon les n colonnes sont
échelonnées non nulles. Ainsi
rg CP
degP siP(0)^0,
deg P — 1 sinon.

5. Exercices
137
2. Considérons la réduite de Frobenius de A
( 1 Cf. 1
V
\Cp< 1
\cPr |
avec, pour tout k G [l,r — 1], P/c+i qui divise P&. Rappelons que
Pi = AU-
Alors le rang de A est la somme des rangs des différents blocs
compagnons et Ton déduit successivement
rgA = J2*gCPk
fe=i
£degPfc-#{*£[!,r], Pfc(0)=0}
fc=l
^ degPi + (r - 1) - #{& G [l,r], P,(0) = 0}
^ deg/iA ~ 1,
en minorant degP/c par 1 et en majorant #{& G [l,r], Pfc(0) = 0}
par r.
3. En reprenant les notations de la question précédente, on obtient que
l'égalité équivaut à
r
^degPfe = #{fce[l,r], Pfc(0)=0}-1.
Or, le premier membre est minoré par r — 1 (cas où tous les invariants
restants sont de degré 1) et le second membre est majoré par r — 1
(cas où tous les invariants admettent 0 pour racine). Par conséquent,
les deux termes sont égaux à r — 1 et l'on en déduit que les invariants
de similitude de 1 sont
Pr — X, Pr—i = -X,..., P2 = Jv, P\ — XQ,
avec Q un polynôme unitaire.
Réciproquement, si une matrice a ces invariants de similitude, alors son
rang est degQ et son polynôme minimal est XQ de degré degQ + 1.
<

138
XL Réduction de Frobenius
5.6. Exercice. Soit n ^ 4 et A, B e MnQ&) de rang 2. Montrer que A et
B sont semblables si, et seulement si, \ia — Vb-
> Eléments de correction. Le sens direct est immédiat. Pour établir le sens
direct, montrons que la suite des invariants de similitude d'une matrice A
de rang 2 est uniquement déterminée par le polynôme minimal va • Notons
P\ = Va, P2, ..., .Pr les invariants de similitude de A. Comme
r
t%a = ]CrgC,p* ^rgCfpi = deg^ -1,
car 0 est racine de va, on obtient que degVA ^ 3. Discutons selon la
valeur de degVA en utilisant le calcul du rang d'une matrice compagnon
de l'exercice précédent.
> Si degfiA = 1, alors \ia = X et A est diagonalisable de seule valeur
propre 0 : A = 0n, contradiction.
0 Si degVA — 2, alors va = X(X — a). Le polynôme P2 divise va, est
divisé par X et
r
k=2
Par conséquent, les autres invariants sont P2 = va (car rgCp2 = 1) et
P3 = .. • = Pn_2 = X (car rgCPk = 0 pour k > 2).
> Si deg/i^ = 3, alors /i^ = XQ(X) avec Q de degré 2 et donc rgCMA = 2.
Les autres invariants sont P2 — • • • = Pns = X car les matrices
compagnons associées sont de rang nul.
Dans tous les cas, les invariants de similitude (donc la classe de similitude)
d'une matrice de rang 2 sont uniquement déterminés par le polynôme
minimal. <!

Chapitre XII
Topologie des classes de
similitude
Objectifs du chapitre
- Comprendre la géométrie des classes de similitude de A^M).
- Savoir interpréter en termes topologiques de la classe de similitude la
nilpotence ou la diagonalisabilité d'une matrice.
- Dériver les propriétés de connexité des classes de similitude des propriétés
correspondantes des groupes linéaires.
1. Rappels sur la relation de similitude
1.1. Rappel. > Deux matrices A, B G Mn(K) sont semblables s'il existe P G
GLn(K) telle que B = P^AP.
> La classe de similitude d'une matrice A G Mn(K) est l'ensemble des
matrices semblables à A.
1.2. Remarques. > Deux matrices semblables sont en particulier
équivalentes donc ont même rang (la réciproque est fausse).
> La relation de similitude est une relation d'équivalence sur .Mn(K) et les
classes d'équivalence sont, par définition, les classes de similitude.
> D'après la formule de changement de bases, deux matrices sont semblables
si, et seulement si, elles représentent le même endomorphisme dans des
bases (a priori) différentes.

140
XII. Topologie des classes de similitude
1.3. Exemple. La classe de similitude de ÀIn est réduite à ÀIn car, pour
tout P G GLn(K),
P(AIn)P~1 - XPP-1 = Ain.
On a obtenu deux caractérisât ions de la relation de similitude. Deux
matrices sont semblables si, et seulement si,
> elles ont la même réduite de Jordan, c'est-à-dire les mêmes tableaux de
Young pour chaque valeur propre (chapitre X),
> elles ont la même réduite de Frobenius, c'est-à-dire les mêmes invariants
de similitude (chapitre XI).
2. Classes de similitude dans A^O^)
Commençons dans cette section par une étude « géométrique » des classes
de similitude dans A^W-
Remarquons tout d'abord que les matrices scalaires ÀI2 avec À G M sont
seules dans leur classe de similitude. Par conséquent, nous ne considérerons
pas ce cas dans l'étude géométrique qui suit.
Rappelons que deux matrices non scalaires (donc cycliques) de Ai 2 0^) sont
semblables si, et seulement si, elles ont le même polynôme caractéristique.
Pour rédiger simplement les résultats, introduisons la base suivante de
.M2O&) adaptée à nos considérations
1 0 \ f ° 1\ ( 1 ° ^ ( ° l
o 1 y ' v 1 0 y ' vo-iy' V -1 °
Écrivons toute matrice M sous la forme
t + y x + z
x — z t — y
avec t, x, y et z G 3R les coordonnées de M dans cette base.
2.1. Proposition. Soit A G .M2 W une matrice non scalaire. La matrice
non scalaire
m = ( t+y x+z \&Mi
x — z t — y
est semblable à A si, et seulement si,
( 2t = tiA
x2 + y2-z2 = ~Aj
4

2. Classes de similitude dans A^QK-)
141
où A a = (trA)2 — 4detA est le discriminant du polynôme caractéristique
de A.
Démonstration. Il suffit d'identifier les polynômes caractéristiques \A —
X2 - (tiA)X + det A et Xm = X2 - 2tX + t2 - y2 + z2 - x2. D
2.2. Remarque. D'après ces équations, les classes de similitude des
matrices non scalaires sont donc (essentiellement) des quadriques incluses dans
un hyperplan affine défini par la trace.
Pour tout A G ^2(^)5 la classe de similitude de A est l'image de la classe
tr A
de similitude de la matrice de trace nulle A —12 par la translation
tr A
de vecteur I2. Ainsi, il suffit d'étudier les classes de similitudes des
matrices de trace nulle pour obtenir la géométrie de toutes les classes à
translation près.
Dorénavant, on suppose tr A = 0 et l'on discute selon le signe de A^ pour
déterminer la classe de similitude de A.
Tous les dessins sont réalisés dans l'hyperplan kertr de M2Q&) privé de son
origine qui correspond à la matrice (scalaire) nulle.
- Les trois axes représentent les coordonnées x, y et z correspondant
respectivement aux vecteurs
(° M (l ° ) ( ° M
\i 0 y ' vo-iy' v-10/'
Le plan « horizontal » d'équation z = 0 correspond aux matrices
symétriques de cet hyperplan, l'axe d'équations x = y = 0 aux matrices
antisymétriques.
- La symétrie orthogonale par rapport au plan d'équation z = 0 est la
transposition.

142
XII. Topologie des classes de similitude
2.3. Cas A^ = 0. Les matrices A telles que ti A = 0 et A^ = 0 sont
exactement les matrices nilpotentes.
D'après la proposition précédente, la classe de similitude d'une matrice
nilpotente non nulle est donc le cône d'équation x2 + y2 — z2 — 0 privé de
l'origine (qui est la classe de similitude de O2).
On remarque que cette classe n'est ni bornée, ni fermée (à cause de
l'origine), ni connexe.
2.4. Remarque. L'adhérence de la classe de similitude d'une matrice
nilpotente non nulle est donc le cône complet (avec son sommet) des matrices
nilpotentes. En particulier, la matrice nulle est adhérente à la classe de
similitude d'une matrice nilpotente ; on verra à la section suivante que cette
propriété est en fait une caractérisation des matrices nilpotentes.
2.5. Cas Aa < 0. Dans ce cas, la matrice n'admet pas de valeur propre
réelle : elle n'est donc pas diagonalisable. Réciproquement, une matrice non
diagonalisable de trace nulle admet deux valeurs propres imaginaires pures
conjuguées donc vérifie bien A^ < 0.

2. Classes de similitude dans .M2Q&)
143
La classe de similitude d'une telle matrice est donc l'hyperboloïde à deux
nappes d'équation x2 + y2 — z2 = a avec a < 0. Les deux composantes sont
« intérieures » au cône nilpotent (représenté en grisé sur le dessin suivant).
Cette fois-ci, la classe est fermée mais n'est pas connexe.
Ces classes ne rencontrent pas le plan horizontal ce qui est cohérent avec
le théorème spectral : toute matrice symétrique réelle est diagonalisable et
les matrices de ces classes ne sont pas diagonalisables.
On remarque qu'au sein d'une telle classe, une matrice et sa transposée
n'appartiennent pas à la même composante connexe.
2.6. Cas A^ > 0. Dans ce cas, la matrice A admet deux valeurs propres
réelles distinctes donc est diagonalisable. Réciproquement, si A est
diagonalisable de trace nulle, alors elle admet deux valeurs propres réelles distinctes
donc le discriminant est strictement positif.
La classe de similitude d'une telle matrice est donc l'hyperboloïde à une
nappe d'équation x2 + y2 — z2 = a avec a > 0.
Cette fois-ci, la classe est à la fois fermée et connexe.

144
XII. Topologie des classes de similitude
3. Adhérence d'une classe de similitude
3.1. Proposition. L'adhérence d'une classe de similitude est une réunion
de classes de similitude.
Démonstration. Soit A G A4n(]K) et B dans l'adhérence de la classe de
similitude de A. Par définition de l'adhérence, il existe une suite de
matrices (Ap)p semblables à A qui converge vers B.
Pour tout P G GLn(K), la matrice PBP~1 est la limite de la suite de
matrices (PApP~1)p semblables à A (par continuité du produit matriciel) :
toute matrice semblable à B est donc dans l'adhérence de la classe de
similitude de A.
En conclusion, l'adhérence de la classe de similitude de A est la réunion
des classes de similitude de ses éléments. □
3.2. Proposition. Une matrice de A4n(C) est nilpotente si, et seulement
si, la matrice nulle est adhérente à sa classe de similitude.

3. Adhérence d'une classe de similitude
145
Démonstration. (=>) Soit A G A4n(C) nilpotente et T sa réduite de Jordan.
Notons, pour tout t > 0, Dt = diag(l,t,£2,... , t71"-1) et
Tt = D~xTDt = tT.
Par conséquent, 0n = lim Tt est adhérente à la classe de similitude de A.
£—►0
(<=) Si la matrice nulle est limite d'une suite de matrices (Ap)p semblables
à A, alors le polynôme caractéristique xon est la limite de la suite constante
de polynômes caractéristiques (xa )p \ Par conséquent, xa = Xon — Xn
et A est nilpotente d'après le théorème de Cayley & Hamilton. □
3.3. Remarque. Dans le sens direct de cette preuve, on n'a pas besoin de
considérer la forme réduite de Jordan. Toute matrice triangulaire
strictement supérieure semblable à A suffirait pour notre calcul.
3.4. Exemple. L'adhérence de la classe de similitude de Jn est
l'ensemble M des matrices nilpotentes.
> L'ensemble J\f est fermé comme image réciproque du singleton {0n} par
l'application continue M 1—> Mn. Comme A/* contient la classe de similitude
de Jn, il contient l'adhérence de cet ensemble.
> Réciproquement, considérons une matrice N nilpotente et T une
matrice triangulaire strictement supérieure semblable à N. Considérons la
suite (Tp)p la suite de matrice où l'on a remplacé les coefficients nuls de T
en position (i,i + 1) par le coefficient —.
Chaque matrice Tp est semblable à Jn car nilpotente d'indice n (ou, de
manière équivalente, de rang n — 1) et la suite (Tp)p converge vers T. Ainsi,
T appartient à l'adhérence de la classe de similitude de Jn. En conclusion,
A^ appartient à cette adhérence également.
3.5. Proposition. Une matrice de Ain(C) est diagonalisable si, et
seulement si, sa classe de similitude est fermée.
Démonstration. (=£-) Soit A diagonalisable et (Ak)k une suite de matrices
semblables à A qui converge vers B G Mn(C). Comme A est diagonalisable,
il existe un polynôme P annulateur scindé à racines simples ; ce polynôme
est alors également annulateur de toutes les matrices Ak par la relation de
similitude donc de B : la matrice B est diagonalisable. Par ailleurs, toutes
les matrices Ak ont le même polynôme caractéristique que A donc, par
continuité du déterminant, B aussi. Ainsi B a les mêmes valeurs propres
que A avec les mêmes multiplicités. En conclusion, A et B sont semblables
à la même matrice diagonale donc semblables entre elles.

146
XII. Topologie des classes de similitude
(<=) Soit A G Ain(C) dont la classe de similitude est fermée. En utilisant la
décomposition de Jordan & Dunford, il existe D diagonale et T triangulaire
strictement supérieure telle que D + T soit semblable à A.
En posant encore, pour tout t > 0, Dt = diag(l, t, t2,..., £n_1), on observe
que D^1ADt est semblable à
D^ADt = D-xDDt + D~lTDt = D + D~xTDt.
Or, lim D^1TDt = 0n donc D appartient à l'adhérence de la classe de
similitude de A qui est, par hypothèse de fermeture, la classe de similitude de A.
Ainsi, A est semblable à la matrice diagonale D : A est diagonalisable. D
En fait, nous avons établi un résultat un peu plus élaboré.
3.6. Proposition. Soit A G A/(n(C) de décomposition de Jordan &
Dunford A = D-\- N avec D diagonalisable, N nilpotente et DN = ND. Alors,
la matrice D appartient à Vadhérence de la classe de similitude de A.
4. Connexité d'une classe de similitude
4.1. Proposition. La classe de similitude d'un matrice M G Ain(C) est
connexe.
Rappelons un résultat classique.
4.2. Lemme. Le groupe GLn(C) est connexe.
Démonstration. Montrons en fait que cet ensemble est connexe par arcs.
Soit A, B G GLn(C). L'ensemble
Z = {z G C, àet(zA + (1 - z)B) = 0}
est fini en tant qu'ensemble des racines d'un polynôme non nul et ne
contient ni 0, si 1. Par conséquent, C\Z est un ensemble connexe par
arcs contenant 0 et 1 : l'image d'un chemin continu de C \Z joignant 0 et 1
par l'application z i-> zA + (1 — z)B fournit un chemin continu de GLn(C)
joignant A et B. D
Revenons à la preuve de la proposition.
Démonstration. L'application
GLn(C) -+ Mn(C)
P h-> PMP-1

5. Commentaires et développements 147
est continue et GLn(C) est connexe. Par conséquent, l'image de cette
application, c'est-à-dire la classe de similitude de M, est connexe. □
Passons maintenant au cas réel.
4.3. Proposition. La classe de similitude d'une matrice M G M.2n+\(R)
est connexe.
On admet ici que l'ensemble GL+(R) = {A G Mn(R), detA > 0} est
connexe par arcs (on le démontre, par exemple, en utilisant la
décomposition polaire).
Démonstration. Remarquons que si A est semblable à M alors, il existe une
matrice P G GL2n+i(R) telle que
A = PMP-1 = (-P)M(-P)-1.
Comme l'une des matrices P et — P appartient à GL^+^R) (les
déterminants sont opposés car la dimension est impaire), on obtient que la classe
de similitude de M est l'image de l'application continue
f GL+n+1(R) -> M2n+1(R)
\ P h-> PMP'1
donc est connexe par arcs. □
4.4. Remarque. Le résultat de connexité n'est plus vrai en dimension
paire. En effet, on a établi que les matrices semblables
( -1 0 j ( 1 0 )
appartiennent à deux composantes connexes distinctes de la même classe
de similitude.
5. Commentaires et développements
5.1. La classe de similitude de la matrice M est fermée si, et seulement
si, on l'a dit plus haut, la matrice M est semi-simple. En général, elle est
seulement localement fermée dans .Mn(R), autrement dit elle est ouverte
dans son adhérence. L'exemple du bloc de Jordan Jn est assez suggestif.
Sa classe est exactement l'intersection du cône nilpotent (qui est
manifestement un fermé, car caractérisé par la condition Mn = 0n) et de l'ouvert
des matrices telles que Mn_1 ^ 0n.

148
XII. Topologie des classes de similitude
Le cas général résulte tout simplement du théorème de Jordan & Weyr.
En effet, une classe de similitude sur C est caractérisée parmi les classes de
similitude des matrices ayant un même polynôme caractéristique par des
conditions d'égalité sur le rang des puissances itérés de M — ÀJn et il est
bien connu que les matrices ayant un rang donné est localement fermé.
5.2. L'ensemble des matrices inversibles tout comme celui des matrices à
valeurs propres distinctes sont les complémentaires de l'ensemble des zéros
de fonctions polynomiales non nulles des coefficients d'une matrice. Aussi
sont-ils des ensembles ouverts denses et connexes par arcs dans Mn(C).
Les classes de similitude de matrices complexes sont par conséquent des
parties connexes par arcs, car orbites sous l'action de GLn(C). L'ensemble
des matrices diagonalisables complexes est à son tour clairement connexe
et dense.
5.3. Deux classes de similitude de matrices nilpotentes qui ont même
adhérence sont égales, car, étant toutes deux ouvertes dans cette adhérence,
elles ont donc une intersection non vide et sont dès lors égales. Il est possible
de décrire, en termes de tableaux de Young, les matrices qui sont dans
l'adhérence de la classe de similitude d'une autre. La question étant délicate,
on se contentera de quelques exercices simples et montrerons en exercice
que l'orbite du bloc de Jordan Jn est dense dans le cône nilpotent et que
l'adhérence de la classe de similitude d'une matrice d'indice de nilpotence
n — 1 est l'ensemble des matrices dont la puissance (n — l)-ème est nulle.
6. Exercices
6.1. Exercice. Soit A une matrice diagonalisable. Montrer qu'une
matrice B est semblable à A si, et seulement si, elle a à la fois le même
polynôme minimal et le même polynôme caractéristique que A.
Le résultat reste-t-il vrai si Von enlève l'hypothèse A diagonalisable ?
t> Eléments de correction. > Le sens retour est évident.
Passons au sens direct. La matrice A est diagonalisable donc le polynôme
minimal est scindé à racines simples. Comme /2b = I^Aj la matrice B est
diagonalisable et ses valeurs propres sont celles de A (les racines de /i^).
Par ailleurs, xb — Xa-> donc les valeurs propres ont la même multiplicité
pour A et B. En conclusion, A et B sont semblables à la même matrice
diagonale donc sont semblables par transitivité.
> Avec les invariants de similitude, il est facile de réaliser un contre exemple.
Considérons d'une part la matrice dont les invariants de similitude sont X2

6. Exercices
149
et X2 et celle dont les invariants de similitude sont X2, X et X. On peut,
par exemple, considérer les matrices suivantes
/ 0 1 0 0 \
0 0 0 0
0 0 0 1
\ 0 0 0 0 J
( 0 1 0 0 \
0 0 0 0
0 0 0 0
\ 0 0 0 0 /
Pour ces deux matrices non semblables, le polynôme minimal est X2 et le
polynôme caractéristique est X4. <\
6.2. Exercice. Montrer que les matrices
o o > et
0 0
1 0
sont semblables mais que la matrice de passage est forcément de
déterminant strictement négatif.
> Eléments de correction. Ces deux matrices sont semblables car cycliques
de polynôme minimal X2.
En notant a, b1 c et d les coefficients d'une matrice de passage, on a
0 1
0 0
a b
c d
a b
c d
0 0
1 0
En identifiant les coefficients, on obtient b = c et d = 0 : la matrice de
passage est de déterminant — b2 < 0. <\
6.3. Exercice.
1. Montrer que l'application
j Mn(K)
l A
est continue.
2. Montrer que l'application
j Mn(K)
l A
n'est pas continue.
> Eléments de correction.
-> K[X]
•-» XA
-> K[X]
1. Chaque coefficient du polynôme caractéristique de A est polynomial
en les coefficients de A donc définit une fonction continue. Par suite,
l'application A v-> \A est continue.

150
XII. Topologie des classes de similitude
2. Chaque matrice de la suite {2~pEi^)p admet X2 comme polynôme
minimal. Or, la limite de cette suite est la matrice nulle dont le
polynôme minimal est X. La suite des polynômes minimaux (constante)
ne converge donc pas vers le polynôme minimal de la limite :
l'application A i-> fj,A n'est pas continue.
<
6.4. Exercice. Montrer que la classe de similitude d'une matrice A est
bornée si, et seulement si, A est une matrice scalaire.
> Eléments de correction. (<=) Si A est une matrice scalaire, alors la classe
de similitude de A est {A} donc est bornée.
(=>) Supposons que A n'est pas une matrice scalaire. Montrons que sa
classe de similitude n'est pas bornée pour la norme définie comme la borne
supérieure des modules/valeurs absolues des coefficients. Comme A n'est
pas scalaire, il existe un vecteur X G Mn^i(K) tel que (X,AX) est libre.
Pour tout t > 0, considérons une base obtenue en complétant la famille
libre (tX, AX). Grâce à la formule de changement de bases, A est semblable
à une matrice dont la première colonne est
t
0
w
On peut donc trouver, dans la classe de similitude de A, des matrices de
norme supérieure ou égale à t : la classe n'est pas bornée.
<
6.5. Exercice. Montrer qu'une classe de similitude est d'intérieur vide.
D> Éléments de correction. La classe de similitude de M est incluse dans
l'hyperplan affine M + kertr qui est d'intérieur vide. <
6.6. Exercice. Déterminer les ouverts de Mn(C) contenant les matrices
diagonales et stables par similitude.
> Eléments de correction. Considérons O un tel ouvert. D'après les
hypothèses, O contient la réunion des classes de similitudes de matrices
diagonales donc toutes les matrices diagonalisables.
Soit M e Mn{C) de décomposition de Jordan & Dunford M = D + N
avec D diagonalisable, N nilpotent et DN = ND. La matrice D appartient

6. Exercices
151
à O et est adhérente à la classe de similitude de M : il existe donc une
matrice semblable à M dans O. Comme O est stable par similitude, M
appartient à O.
En conclusion, le seul ouvert qui convient est .Mn(C). <3
6.7. Exercice. Soit n ^ 4. Montrer qu'une matrice nilpotente de tableau de
Young TY(n — 1,1) n'appartient pas à Vadhérence de la classe de similitude
d'un matrice nilpotente de tableau de Young TY(n — 2, 2).
Indication : on pourra montrer que l'ensemble des matrices de rang
strictement inférieur à n — 3 est un fermé puis calculer le rang du carré de
matrices nilpotentes de tableau de Young TY(n — 1,1) ou TY(n — 2, 2) .
> Éléments de correction. t> Soit r G [l,n]. L'ensemble
Ar = {M eMn(K), rgM <r}
est un fermé comme intersection des images réciproques du fermé {0} par
chacune des applications continues définies par un déterminant extrait de
taille r.
> Soit A une matrice nilpotente de tableau de Young TY(n — 2, 2). Alors,
comme calculé au chapitre X, rg A2 — n — 4 et Â1 G An-z- Ainsi, toute
matrice M semblable à A vérifie M2 G An~3-
D'après le premier point, toute matrice M adhérente à la classe de
similitude de A vérifie donc M2 G An-3.
Or, toute matrice M nilpotente de tableau de Young TY(n — 1,1)
vérifie rgM2 = n — 3 donc n'appartient pas à l'adhérence de la classe de
similitude de A. <3
6.8. Exercice. Montrer que l'adhérence de la classe de similitude d'une
matrice nilpotente de tableau de Young TY(n — 1,1) est constituée des
matrices nilpotentes admettant au moins deux blocs de Jordan.
> Éléments de correction. Notons A la classe de similitude d'une matrice
nilpotente de tableau de Young TY(n — 1,1).
> Remarquons tout d'abord que les matrices semblables à une matrice
nilpotente de tableau de Young TY(n — 1,1) sont nilpotentes et donc que
l'adhérence de A est constituée de matrices nilpotentes.
En adaptant la question précédente, on vérifie que la matrice Jn n'est pas
adhérente à A : une suite convergente de matrice de rang n — 2 ne peut avoir
une limite de rang n — 1. Par conséquent, l'adhérence de A est composée
de matrices nilpotentes admettant au moins deux blocs de Jordan.

152
XII. Topologie des classes de similitude
D> Soit k ^ 2 tel que n — k > k. Montrons que l'adhérence de A contient une
matrice nilpotente de tableau de Young TY(n — k, k). Pour cela, établissons
que, pour tout p G N, la matrice
+ 2~pEn -fc+l,n-
est nilpotente de tableau de Young TY(n —1,1) donc appartient à A. En
effet, pour tout j ^ n — k,
(
\
Jn~k
Jk
keiAJp
vect(ei,... ,ej,en),
et pour j G [n — k + 1, n],
ker AJp = vect(ei,..., en_/e, e2n-k+i-j,
où (ei,... ,en) désigne la base canonique de .Mn,i(]K). La suite des sauts
de dimension indique donc que Ap admet le tableau de Young TY(n— 1,1).
La suite de matrices (Ap)p converge vers la matrice
> €-n) 5
( 1 Jn—k
\
Jk
nilpotente de tableau de Young TY(n — k,k) qui est donc dans l'adhérence
de A. Par conséquent, toute matrice nilpotente de tableau de Young TY(n—
k, k) est aussi dans l'adhérence de A.
Terminons l'exercice. Considérons un tableau de Young TY(Ài,..., Xp)
avec p > 2. Comme l'adhérence de la classe de similitude de Jn-\p est
l'ensemble des matrices nilpotentes de taille n — Àp, il existe une suite (Mi)i
de matrices de Mn-\p(K) nilpotentes d'ordre n — Xp qui converge vers
une matrice nilpotente de tableau de Young TY(Ài,..., Ap_i). La suite de
matrices définies pour tout / G N par
([W
\
J\p
de l'adhérence de A (car de tableau de Young TY(n — XP,XP)) converge
vers une matrice nilpotente de tableau de Young TY(Ài,..., Àp, k).
En conclusion, toutes les matrices nilpotentes avec au moins deux blocs de
Jordan sont dans l'adhérence de A.
Remarquons que l'on peut décrire autrement cette adhérence comme
Vensemble des matrices nilpotentes d'ordre au plus n ~ 1.
<3

Chapitre XIII
Localisation des valeurs
propres
Objectifs du chapitre
- Déterminer des localisations des valeurs propres à partir des coefficients
de la matrice.
- Comprendre le disque spectral (centré en l'origine et de rayon le rayon
spectral) pour localiser les matrices.
- Démontrer les théorèmes de Perron et Perron & Frobenius sous
différentes hypothèses de positivité et d'irréductibilité.
1. Théorème de Hadamard
1.1. Théorème de Hadamard. Soit A = (dij) G Mn(C) telle que, pour
tout i G [l,n],
n
WiA >^2\aij\-
3 = 1
3*i
Alors, A est inversible.
Démonstration. Soit X = (xi) G A/(n,i(C) un vecteur du noyau de A et i G
[l,n] tel que
\xA = max \xn\.
jelhn] n

154
XIII. Localisation des valeurs propres
Alors, la i-ème ligne de l'égalité AX = 0n5i donne J2 aiJxj ~ 0 so^
0*1,i%i — / j^i-ij 3 '
j = i
En prenant le module et en utilisant l'inégalité triangulaire, on obtient
n n
3 = 1 3=1
3^i j*i
Si X est non nul, Xi ^ 0 et en simplifiant cette égalité, on obtient une
contradiction avec l'hypothèse du théorème. Par conséquent, X = 0n,i et
la matrice A est injective donc inversible. □
2. Disques de Gerschgorin
2.1. Définition. Soit A = (aij) G A/ln(C) et i G [l,n]. Le i-ème disque
de Gerschgorin de A est le disque (fermé) de centre a^ et de rayon
n
3 = 1
3^i
Le théorème de Hadamard se traduit alors en : si 0 n'appartient pas aux
disques de Gerschgorin de .A, alors A est inversible. Une translation de ce
résultat donne la variante suivante.
2.2. Théorème de Gerschgorin. Les valeurs propres complexes d'une
matrice appartiennent à la réunion de ses disques de Gerschgorin.
Démonstration. Soit À un complexe qui n'appartient à aucun des disques
de Gerschgorin, c'est-à-dire tel que, pour tout i G [l,n],
K* - A| > ^2\aij\.
3 = 1
3^i
D'après le théorème d'Hadamard, A — ÀIn est alors inversible : À n'est pas
valeur propre. □
2.3. Remarque. Une matrice et sa transposée ayant les mêmes valeurs
propres, on peut dire que les valeurs propres de A appartiennent également

2. Disques de Gerschgorin
155
à la réunion des disques de centre djj et de rayon Yl \ai,j\ pour j G [1,
i = l
i^3
Les valeurs propres réelles appartiennent à la fois à Taxe des abscisses et à
tous ces disques donc à l'intersection des deux domaines.
2.4. Théorème. Soit A G A/(n(C) telle que r de ces disques de Gerschgorin
ne rencontrent pas les n — r autres. Alors, la réunion de ces r disques
contient exactement r valeurs propres (comptées avec leur multiplicité).
L'argument proposé pour la preuve suivante consiste à exploiter la connexité
par arcs de domaines du plan complexe.
Démonstration. Soit A la réunion des r disques de Gerschgorin considérés
et B la réunion des n — r autres. Comme ces deux ensembles sont fermés
et disjoints, d(A,B) > 0.
Notons A = (aij) et D la matrice diagonale de A, c'est-à-dire la matrice
de coefficients diagonaux les a^. Considérons l'application
r [o,i] -► Mn(c)
\ t h* D + t(A-D)
Les valeurs propres de J5(0) = D sont exactement les centres des disques
de Gerschgorin de A : il y en a donc r dans A et n — r dans B.
Rappelons, enfin, que les valeurs propres de B(t) définissent des fonctions
continues de la variable t (résultat ici admis mais non trivial). Comme
d(A, B) > 0, une de ces fonctions / telle que /(O) G A (respectivement /(O) G
B) doit vérifier f(l)eA (respectivement /(l) G B).
En conclusion, la matrice A = B(l) admet aussi r valeurs propres dans A
et n — r dans B. D
2.5. Corollaire. Soit A G A4n(C) et D un de ces disques de Gerschgorin
qui ne rencontre pas les autres. Alors, D contient une unique valeur propre
et celle-ci est simple.
2.6. Exemple. En appliquant les résultats précédents à la matrice
e-M3(C),
on obtient trois disques de Gerschgorin en deux zones disjointes : d'une part
la réunion de deux disques qui contient deux valeurs propres, de l'autre un
disque isolé qui contient une valeur propre.
0
-1
0
1 0
i 1
1 3

156
XIII. Localisation des valeurs propres
3. Rayon spectral
3.1. Définition. Soit A G Mn(C). Le rayon spectral de A est le réel
p(A) ^ 0 défini comme le plus grand module d'une valeur propre.
3.2. Remarque. Attention, le rayon spectral d'une matrice n'est pas
forcément une valeur propre.
En revanche, toutes les valeurs propres d'une matrice A appartiennent au
disque fermé de centre 0 et de rayon p{A). Illustrons quelques situations
très différentes.
t> Le rayon spectral de la matrice de permutation associée à une permutation
circulaire de 6n est 1 et toutes les valeurs propres sont des racines n-èmes
de l'unité. Ainsi, toutes les valeurs propres appartiennent au cercle de centre
0 et de rayon 1.
> Le rayon spectral de la matrice dont tous les coefficients sont égaux à
1 vaut n et aucune autre racine n'appartient au cercle de centre 0 et de
rayon n.
Mentionnons sans preuve quelques propriétés élémentaires du rayon
spectral.
3.3. Proposition. Soit A e Mn(C) et || || une norme d'opérateur sur
Mn(C). Alors, p{A) ^ \\A\\ et
p{A)=\im \\Ak\\k.
3.4. Proposition. L'application
Mn(C) -> R+
A k+ p{A)
est continue.

4. Théorème de Perron
157
4. Théorème de Perron
4.1. Définition. Soit A G -Mn,p(C). La matrice A est positive
(respectivement strictement positive) si tous ses coefficients sont des réels positifs
(respectivement strictement positifs).
4.2. Exemple. La matrice I4 -f P(X 2 3 4) (où P(i 2 3 4) désigne la matrice
de permutation associée au cycle (1 2 3 4)) est de puissance strictement
positive sans être strictement positive car
/ 1 0 0 1 \
110 0
0 110
\ 0 0 1 1 )
6
/ 1 1 3 3 \
3 113
3 3 11
V 1 3 3 1 )
4.3. Remarque. Si une matrice A G M.n(M) est strictement positive et
X G A/fn,i(IR) un vecteur positif, alors AX = 0nji si X est nul et AX est
strictement positif sinon.
4.4. Lemme. Soit A G Â4n(C) une matrice strictement positive, À une
valeur propre de module p(A) et X — {pa) un vecteur propre associé. Alors,
> le rayon spectral p(A) est une valeur propre de A,
> le vecteur \X\ = (\xi\) est un vecteur propre associé à p(A),
> il existe 0 G M tel que X = eie\X\.
Démonstration. Par inégalité triangulaire, pour tout i G [l,n],
p(A)\xi\ = \Xxi\ =
^ y^aj,k\xk\
k=l
Ainsi, le vecteur E = A\X\ — p(A)\X\ est positif. Supposons E non nul et,
par conséquent, AE strictement positif. Le vecteur Y = A\X\ est
strictement positif et la condition AE strictement positif entraîne que le vecteur
AY — p(A)Y est strictement positif. Il existe donc un réel p > p(A) tel que
le vecteur AY — pY est positif. Par une récurrence immédiate, pour tout
fcGf, AkY - pkY est positif et donc
p^Yim\\Ak\
k
k
00
P(A),
(où II ||oo désigne la norme d'opérateur associée à la norme uniforme) d'où
la contradiction.
Ainsi, E est nul et \X\ est un vecteur propre associé à p(A).

158
XIII. Localisation des valeurs propres
Pour conclure, il suffit de remarquer que nous avons prouvé l'égalité
/ v Q/i,k%k
fc=l
ce qui entraîne classiquement (cas d'égalité dans l'inégalité triangulaire sur
C) que tous les complexes Xk ont le même argument. □
4.5. Théorème de Perron. Soit A G A4n(K) strictement positive. Alors,
> p(A) est l'unique valeur propre de module maximal.
> Le sous-espace propre Ep(A) es^ une droite dirigée par un vecteur
strictement positif.
Démonstration. > Soit À une valeur propre de module p(A) et X un vecteur
propre associé. D'après le lemme précédent, il existe 9 G R tel que X =
el6\X\ et \X\ est un vecteur propre associé à p(A). Ainsi,
XX = AX=Ael6\X\ = eieA\X\ = ei9p(A)\X\ = p(A)X.
En conclusion, À = p(A).
> Soit X un vecteur propre associé à p(A). D'après le lemme, il existe
0 G M tel que X = eie\X\. Alors, p(A)X = ei0p(A)\X\ = eieA\X\. Or,
X est positif et A strictement positif : ainsi, p(A) ^ 0 (ou de manière
équivalente p(A) > 0) et X n'a pas de coordonnées nulles.
Supposons dim Ep^) ^ 2 et considérons maintenant deux vecteurs propres
indépendants X — {xi) et Y = (^) associés à la valeur propre p(A). Le
vecteur propre x\Y — y\X admet au moins une coordonnée nulle ce qui
contredit la remarque ci-dessus. □
4.6. Corollaire. Soit A G Mn{K) positive. Alors, le rayon spectral p{A)
est une valeur propre et le sous-espace propre associé Ep(A) contient un
vecteur positif.
Démonstration. Définissons, pour tout k G N, la matrice
/i ... i
Ak = A + 2-* : : :
V i ... i
Alors, la suite {Ak)k converge vers A et, pour tout k G N, Ak est strictement
positive : d'après le théorème de Perron, il existe un vecteur propre Xk
strictement positif, de norme 1, associé à la valeur propre p(Ak).
Par continuité du rayon spectral (proposition XIII-3.4), limp(Ak) — p(A).
k
De plus, la suite (Xk)k est à valeurs dans la sphère unité qui est compacte

5. Théorème de Perron & Frobenius
159
donc il existe une sous-suite (X^^k qui converge vers un vecteur X de
norme 1. Alors
AX = lïmA^X^k) = limp(A¥,(fc))Xy)(fe) = p(A)X.
k k
Comme X est positif (comme limite de vecteurs strictement positifs), le
résultat est établi.
D
4.7. Remarque. Attention, dans le cas d'une matrice positive, il peut
exister plusieurs valeurs propres de module maximal et le sous-espace propre
associé au rayon spectral peut être de dimension strictement supérieure à
1 comme on peut le voir avec les exemples suivants de rayon spectral 1
0 1 \ / 1 0
i o J ' V o i
5. Théorème de Perron & Frobenius
5.1. Définition. Une matrice A = (a^) G Mn(C) est réductible s'il existe
une partie J C [l,n] non triviale telle que
Vi E /, Vj i J, aid = 0.
Dans le cas contraire, la matrice est irréductible.
On peut traduire différemment l'irréductibilité d'une matrice.
5.2. Proposition. Une matrice est irréductible si, et seulement si, il n'existe
pas de sous-espace stable non trivial engendré par des vecteurs de la base
canonique.
Démonstration. Une matrice est réductible si, et seulement si, il existe une
partie Je [1, n] non triviale telle que
vi g j, vj i /, aitj = o,
ce qui équivaut à la stabilité du sous-espace vect(J^)^/. D
5.3. Proposition. Toute matrice A telle qu'il existe p G N vérifiant que
AP est strictement positive est irréductible.
Démonstration. Supposons A réductible. Par définition de la réductibilité,
il existe une partie J C [l,n] non triviale telle que vect(Ej)jej est stable
par A. Ce sous-espace est par conséquent stable par Ap : mais alors AP

160
XIII. Localisation des valeurs propres
admet des coefficients nuls en position (i, j) G J x J ce qui contredit
l'hypothèse. □
5.4. Remarque. Là réciproque est fausse : pour toute permutation
circulaire a G <5n, la matrice Pa est irréductible mais aucune de ses puissances
n'est strictement positive.
5.5. Exemple. Si une matrice admet une ligne ou une colonne nulle, alors
elle est réductible.
5.6. Exemple. Une matrice ( , ) G A^QK) est irréductible si, et
seulement si, b 7^ 0 et c 7^ 0. En effet, ces deux conditions équivalent
respectivement à la non-stabilité des sous-espaces vectf^) et vect(^i).
On obtient la caractérisation suivante de l'irréductibilité.
5.7. Proposition. Une matrice positive A G Mn(R) est irréductible si, et
seulement si, la matrice (In + A)n~1 est strictement positive.
Démonstration. > Si la matrice A est réductible, alors la matrice In + A
l'est aussi (avec le même sous-espace stable). Par conséquent, la matrice
(In + A)n~l a des coefficients nuls : par contraposition, le sens direct est
établi.
> Supposons A irréductible et utilisons le lemme suivant démontré à
l'exercice XIII-7.6.
5.8. Lemme. Soit A positive, irréductible. Pour tout vecteur X positif le
vecteur (In + A)X est soit strictement positif, soit positif avec strictement
moins de coordonnées nulles que X.
Il est alors évident que pour tout vecteur de la base canonique Ej, (In -f
A)n"1Ej a tous ses coefficients strictement positifs; ainsi, tous les
coefficients de (In + A)n~l sont strictement positifs (car chaque colonne l'est).□
5.9. Théorème de Perron &; Probenius. Soit A G Mn{K) irréductible
et positive.
> p(A) est une valeur propre de module maximal.
> Le sous-espace propre Ep^) es^ une droite dirigée par un vecteur
strictement positif.

6. Commentaires et développements
161
Démonstration. Comme A est positive, le corollaire XIII-4.6 s'applique :
ainsi, p(A) est une valeur propre de A.
De plus, le sous-espace propre de A associé à p(A) est inclus dans le sous-
espace propre de (In -f A)n~l associé à (1 + p(A))n~'1. Or, la matrice (In +
A)n~~1 est strictement positive donc l'espace propre associé à
p{{ln + A)n-1) = (l + p(A))n-i
est de dimension 1 dirigé par un vecteur propre strictement positif. Par
conséquent, le sous-espace propre de A associé à p(A) est cette même droite
dirigée par un vecteur strictement positif.
□
Dressons un petit bilan de tous ces théorèmes proches.
p(A) est valeur
propre
dimEp{A) = 1
Il existe un vecteur
propre positif
Pour toute valeur
propre À ^ p{A)1
\\\ < p(A)
A
strictement
positive
/
/
/
/
A
positive
/
(iï)
/
A
positive
irréductible
/
/
/
(ïi)
6. Commentaires et développements
6.1. Si la théorie de la réduction des endomorphismes est parfaitement
comprise, la mise en pratique de la réduction se heurte très tôt au problème
de la détermination des valeurs propres, qui sont les racines du polynôme
minimal ou caractéristique. S'il est aisé de déterminer les racines d'un
polynôme de degré deux ou trois, on sait depuis Galois qu'il n'y a pas de
méthode générale pour écrire les racines d'une équation générale de degré
supérieure ou égale à 5 en termes de radicaux dépendant des coefficients de
l'équation. Aussi, il importe en pratique d'obtenir des approximations de
ces racines et de s'atteler en conséquence à obtenir des approximations des
vecteurs propres et au delà des vecteurs figurant dans les différents noyaux
itérés...

162
XIII. Localisation des valeurs propres
6.2. La dépendance des valeurs propres de la matrice M par rapport aux
coefficients de M étant, on le sent bien, continue (idée difficile à mettre
en vérité en forme de façon précise), il importe souvent d'avoir une idée
des régions du plan complexe où vivent les valeurs propres d'une matrice
donnée, le contrôle qui en résulte sur les valeurs propres peut être
extrêmement utile pour des questions de convergence comme le montre en termes
élémentaires le résultat suivant :
La suite (Ap)p tend vers la matrice nulle si, et seulement si, p(A) < 1 si, et
seulement si, la série ]T ^ est convergente.
v
Le chapitre présent s'est ainsi appliqué à donner quelques résultats des plus
simples pour « localiser » les valeurs propres... Il existe des ouvrages entiers
qui traitent de ces questions de localisation et d'approximation... on appelle
cela l'analyse numérique matricielle...
6.3. Un résultat fondamental en localisation est le suivant et dont la
démonstration instructive tient en trois lignes :
6.4. Lemme. Si N(A) < 1, pour une norme matricielle quelconque, alors
p(A) ^ N(A),
comme il résulte simplement du fait que si |A| > N(A), la série de terme
général (A/X)p est alors normalement convergente dans l'espace complet
Mn(C) donc convergente, et sa somme $^^°(^/A)p est (à peu de choses
près) l'inverse de A — AIn, ce qui prouve que A ne peut être alors valeur
propre.
6.5. Un autre aspect abordé dans ce chapitre est le théorème surprenant
et remarquable de Perron, qui dit qu'une matrice à coefficients strictement
positifs admet son rayon spectral comme valeur propre avec une multiplicité
algébrique égale à 1. De surcroît, le rayon spectral est la seule valeur propre
ayant son propre module et les composantes d'un même vecteur propre pour
p sont tous non nuls et de même signe.
Il est bon alors que si A vérifie les hypothèses du théorème de Perron, il en
est de même de sa transposée î
Il importe de saisir que l'information particulière liée à la positivité des
coefficients n'est aucunement une propriété invariante par similitude. Pourtant
elle donne des informations sur l'endomorphisme que définit notre matrice
dans Kn. Cet endomorphisme a une nature contractante, puisque les
vecteurs de base sont envoyés par les puissances itérées de A sur des vecteurs
qui font ensemble des angles solides de plus en plus serrés dans la direction

7. Exercices
163
de la droite propre A associée à p(A). Les puissances itérées de l'opérateur
A/p(A) convergent vers l'opérateur de projection sur A parallèlement à
l'hyperplan orthogonal de la droite propre de lA associée à p(A).
7. Exercices
7.1. Exercice. Soit A G .Mn(C) et D la diagonale de A. Supposons
que D est inversible et qu'il existe une norme d'algèbre N sur Ain(C) telle
que N{D~lA - In) < 1. Montrer que A est inversible.
> Éléments de correction. Notons B — D~XA — In. L'hypothèse sur la
norme de B entraîne que la matrice In + B est inversible d'inverse
oo
k=0
Par conséquent, A = D(ln + B) est inversible.
On remarque qu'en prenant la norme uniforme sur A1n,i(C), la norme
d'algèbre associée pour une matrice A est
\\A\\ =sup]T|ai>i|.
i
0
Dans ce cas particulier, l'exercice donne une variante de la démonstration
du théorème de Hadamard. <
7.2. Exercice. Soit A = (a^) G .Mn(C) telle que, pour tout i G [l,n],
n
Montrer que
|detA|^ jj[
i=l
«m - ^2 \a>i.
3 = 1
3*i
> Éléments de correction. Notons, pour tout i G Jl,n]
n
3*i
et D = diag(|ai5i|—ri, |a2,21 — ^2, • • •, |ûn)n|—rn). La matrice D est inversible
car tous ses coefficients diagonaux sont non nuls. D'après le théorème de
Geschgorin, les valeurs propres de la matrice B = D-1 A appartiennent aux

164
XIII. Localisation des valeurs propres
disques de centre
n
En
et de rayon
Q>i.i\ fi
m.
Par conséquent, toute valeur propre À de B vérifie
\X\>
\CLi,
Ainsi, |det JB| ^ 1 et donc |det^4| ^ |detL>|. En conclusion,
n
|detA| > J||aM-r*|.
2=1
7.3. Exercice. Soit A ~ (a^) G M.n(C). Les ovales de Cassini de la
matrice A sont les ensembles pour i ^ j définis par
Oij = {z G C, \z- aiti\ • \z - ajj\ ^ riTj}
n
oùri= Yl Wi,k\-
k = l
k^i
Montrer qu 'une valeur propre X de A appartient à au moins l'un des ovales
de Cassini (théorème de Brauer).
> Eléments de correction. Soit À une valeur propre de A et X = (xi) un
vecteur propre associé. Considéro
j 7^ i tel que \xj\ = max^ ^ \xk\
vecteur propre associé. Considérons i G [l,n] tel que \x{\ = max \xk\ et
feG[l,n|
kelhn]\{i}
Remarquons que
|A - aM| • \xi\ < ]P K^l ' \Xk\ ^ Ti\xj\
fc=i
n
lA - aJj\ ' \Xj\ < Yl l^l '\Xk\^ rj\Xi\
fc=i
Ainsi,
|A - aiyi\ • |A - a^jH^H^I ^ rirj\xi\\xj\.
Comme \xi\ > 0, on peut simplifier par \xi\. Discutons sur le terme \xj\.
> Si \xj\ = 0, alors |A — a^l-l^l = 0 donc A = a^i G Oij.

7. Exercices
165
> Si \xj\ > 0, alors on simplifie et l'on obtient |À — a^||À — cljj\ ^ r^j donc
XeOitj.
<
7.4. Exercice. Déterminer les permutations a G &n telles que la matrice
de permutation Pa est irréductible.
t> Éléments de correction. Si a admet au moins deux orbites, alors, pour I
l'une de ses orbites, l'espace vect(e^e/ est stable par Pa : la matrice Pa
est donc réductible.
Si a est une permutation circulaire, alors le sous-espace cyclique engendré
par le vecteur de la base canonique contient tous les vecteurs de cette base.
Par conséquent, il n'existe pas de sous-espaces stables non triviaux engendré
par des vecteurs de la base canonique. La matrice Pa est donc irréductible.
<
7.5. Exercice.
1. Soit A une matrice irréductible. Montrer que les valeurs propres de A
appartenant à la frontière de la réunion des disques de Gerschgorin
appartient en fait à Vintersection de tous les disques de Gerschgorin
(théorème de Taussky).
2. En déduire que la matrice tridiagonale
/ 2 1 0 0 \
1 2 :
0 1 :
: '-.10
: -.121
\ 0 0 12/
est inversible.
> Éléments de correction.
1. Soit À une valeur propre de A appartenant à la frontière de la réunion
des disques de Gerschgorin et X = {xi) un vecteur propre associé.
Considérons la partie non vide
/ = {z G [l,n], \xi\ = max|^-|}.
3
> Pour tout % G /, on obtient en copiant la preuve des théorèmes de

166
XIII. Localisation des valeurs propres
Hadamard et de Gerschgorin,
|A -a^Wxi
3 = 1
<
Y \a^
3*i
Ainsi, en utilisant l'hypothèse sur À,
n
|A — «i,i| = Y\aij\-
3 = 1
3*i
Autrement dit, À appartient à la frontière des disques de Gerschgorin
dont l'indice appartient à l'ensemble /.
> Ainsi, pour tout i G J,
n n
Y K^'l W = lA ~ aiA\xi\ ^ Y KilN'
3 = 1
3 = 1
et donc
X^KiKW - N) <o.
Comme tous les termes de cette somme sont tous positifs, ils sont tous
nuls. Pour tout j' ^ /, a^j; = 0.
Comme la matrice est irréductible, il faut / = [l,n] ce qui, avec le
résultat du premier point, entraîne que À appartient à la frontière de
tous les disques de Gerschgorin.
2. La matrice proposée est bien irréductible car un calcul rapide montre
que sa puissance (n — l)-ème est strictement positive.
Elle admet deux disques de Gerschgorin centrés au point d'afflxe 2 et
de rayon 1 et 2. Le complexe 0 appartient à la frontière de la réunion
de ces disques mais n'appartient pas à la frontière de tous les disques
donc n'est pas valeur propre d'après la question précédente.
Remarquons que cette matrice ne vérifie pas l'hypothèse du théorème de
Hadamard puisque |a2,21 = la2,i| + la2,3|-

7. Exercices
167
<3
7.6. Exercice. Soit A une matrice positive, irréductible. Pour tout vecteur
X positif, le vecteur (In + A)X est soit strictement positif soit positif avec
strictement moins de coordonnées nulles que X.
D> Éléments de correction. Notons X — (xi). Alors, pour tout i G [l,n],
n
((In + A)X)i — Xi + J2 ai,k%k ^ Xi. Par conséquent, toute coordonnée de
fc=i
(In -f A)X est positive et une coordonnée de (In + A)X ne peut être nulle
que si la coordonnée correspondante de X est nulle.
Raisonnons par l'absurde en supposant que X et (In + A)X ont le même
nombre (strictement positif) de coordonnées nulles et notons I l'ensemble
des indices de ces coordonnées nulles. Alors, pour tout i G J,
^CLi^Xk = 0.
fc=l
k&I
Cette somme de termes positifs est nulle donc, pour tout k £ J, a^k = 0 :
ceci contredit l'irréductibilité de la matrice. <
7.7. Exercice. Soit A = (a^) G A4n{^) et B = (hj) strictement positive
telles que
Montrer que les valeurs propres de A sont incluses dans la réunion des
disques fermés de centre a^i et de rayon p(B) — 6^.
Indication : on pourra introduire un vecteur propre X = (x^ strictement
positif de B associé à p(B) et appliquer le résultat de Gerschgorin à la
matrice A! = f -^r^ij ) •
> Éléments de correction. > Soit X = (x^ un vecteur propre de B associé à
p(B), strictement positif (ce qui est possible d'après le théorème de Perron
& Frobenius). Alors, pour tout i G [l,n],
n n
^ K/e|Xfc < ]P Kkxk = (P(B) ~~ bi,i)Xi'
fc=i fc=i
k^i k^i
> Appliquons le théorème de Gerschgorin à la matrice A! = (-^rai,j) '•

168
XIII. Localisation des valeurs propres
pour toute valeur propre À de A!, il existe i G [l,n] tel que
n
fc=i
> Pour conclure, remarquons que la matrice A' = f -JrQ'ij ) est semblable
à A avec la matrice de passage diag(#i, #2,..., xn) donc admet les mêmes
valeurs propres que A. Ainsi, pour toute valeur propre À de A, il existe
iG [l,n] tel que
|A- dijl ^ p(B) -&»,*.
Remarquons que le résultat peut être étendu au cas d'une matrice B
seulement positive en approchant B par des matrices strictement positives et en
utilisant la continuité du rayon spectral.
<
7.8. Exercice. Soit A une matrice strictement positive et p(A) son rayon
spectral. Montrer que la multiplicité (algébrique) de p(A) est 1.
Indication : on pourra montrer que la suite (p(A)~pAp)p est bornée et
raisonner par l'absurde en considérant un bloc de Jordan associé à p(A).
D> Éléments de correction. > Notons X = (x^ un vecteur propre associé à
p(A), strictement positif (qui existe d'après le théorème de Perron). Pour
tout i G [l,n],
[X]t = [p(A)-*APX]i = p{A)-*YyA\kxk > p{A)-vY}AkU^xr
k=i k=i 3
Par conséquent, Wp^-PA?^ < —^ H^IU- La suite (p(A)-pAP)p est
Il1111 Jb q
3
donc bornée.
> Supposons que la valeur propre p(A) ne soit pas de multiplicité
algébrique 1. Comme le sous-espace propre associé à p{A) est de dimension 1,
A admet un bloc de Jordan de taille r > 1 associé à p{A). Alors,
llp^-MPlU > \\p(A)-P(p(A)Ir + Jrr|U > pp{A)-\
Ceci contredit alors le point précédent. Ainsi, la multiplicité est 1.
Remarquons que cet argument s'adapte pour les matrices positives dont
une puissance est strictement positive. <\

Chapitre XIV
Application aux chaînes de
Markov finies
Objectifs du chapitre
- Comprendre le lien entre la propriété de Markov et le calcul des
puissances d'une matrice.
- Appliquer le théorème de Perron & Frobenius pour la convergence vers
une loi de probabilité stationnaire.
1. Chaînes de Markov
On suppose connu le formalisme usuel des probabilités, la notion de mesure
de probabilité P, d'espérance E, les probabilités conditionnelles et la formule
des probabilités totales.
1.1. Définition. Une chaîne de Markov est une suite de variables aléatoires
(Xn)n à valeurs dans l'espace d'états E telle que, pour tout n G N, et tous
2/,2/o,---,2/n £ E,
P(Xn+1 = y\X0 = 2/0, • • - , *n = 2/n) = P(*n+1 = y\Xn = 2/n).
Elle est homogène si cette quantité ne dépend pas de n. Elle est finie si
l'ensemble E est fini.
1.2. Exemple. Une suite (Xn)n de variables indépendantes est une chaîne
de Markov (dont l'intérêt est limité) puisque
P(Xn+1 = y\X0 = î/o, • • •, *n = 2/n) = P(*n+i = y) = P(*n+i = y\Xn = yn).

170
XIV. Application aux chaînes de Markov finies
1.3. Exemple. Soit (Yn)n une suite de variables indépendantes
identiquement distribuées. La suite
xn = ï>
\ k=0 / n
est une chaîne de Markov. En effet,
P(Xn+i = y\X0 = y0,...,Xn = yn)
= F(Xn + Yn+1 = y\X0 = y0,...,Xn = yn)
= HVn + Yn+1 = y)
= F(Xn + yn+1 = y\Xn = yn)
= F(Xn+1=y\Xn = yn).
1.4. Exemple. Soit (Fn)n une suite de variables indépendantes
identiquement distribuées à valeurs dans F, X0 une variable à valeur dans E
indépendante de cette suite et / : E x F —» E. La suite (Xn)n définie par
la relation Xn+i = f(Xn,Yn) est une chaîne de Markov. En effet,
P(Xn+i = y\X0 = y0,...,Xn = yn)
= P(/(2/n, ^n) = 2/|^0 = 2/0, • • • , Xn = yn)
= p(/(2/n,yn) = 2/)
= p(/(2/n,yn) = 2/|xn = 2/n)
= F(Xn+1=y\Xn = yn).
1.5. Exemple. Considérons une famille (Yij)ij de variables aléatoires
indépendantes, Xq G N, et pour tout n G N,
Xn+i — y v y^i+i,fc-
fc=i
Alors, la suite (Xn)n est une chaîne de Markov homogène. En effet,
Vn
P(Xn+1 = y\X0 = 2/0, • • • ,-ïn = yn) = P ^ **+!,* = 2/ •
vjfc=l
2. Matrice de transition
2.1. Définition. La matrice de transition d'une chaîne de Markov
homogène finie (Xn)n d'espace d'états E — {ei,... , ejv} est la matrice d'ordre

2. Matrice de transition
171
N dont le coefficient en position (i,j) est
F(X1=ej\X0 = ei).
2.2. Remarque. Si A est la matrice transition d'une chaîne de Markov
homogène finie (Xn)n d'espace d'états E = {ei,..., e^}, alors
[A]i>i=P(Xn+1=ei|Xn = ei)
pour tout n E N.
2.3. Proposition. La matrice de transition d'une chaîne de Markov
homogène finie est stochastique, c'est-à-dire positive et telle que la somme des
coefficients sur l'une quelconque de ses lignes vaut 1.
Démonstration. Il est évident que la matrice de transition est positive car
ses coefficients sont définis comme des probabilités. Par ailleurs, la somme
des coefficients sur la ligne i pour la matrice de transition de la chaîne de
Markov homogène finie (Xn)n dont les états sont ei,..., e/v est
n
Y,HXi=eJ\X0 = ei) = l.
□
2.4. Définition. Une chaîne de Markov homogène finie est irréductible si
sa matrice de transition est irréductible (au sens de la définition XIII-5.1).
2.5. Remarque. Traduisons la propriété d'irréductibilité sur la chaîne : il
n'existe pas de famille non triviale d'états qui soit « stable » par la chaîne.
Par conséquent, l'ensemble des états accessibles depuis un état x fixé ne
peut être différent de E : tous les états sont accessibles depuis chaque état.
C'est d'ailleurs souvent ainsi que l'on définit l'irréductibilité.
2.6. Remarque. Nous disposons donc de deux descriptions pour une
chaîne de Markov homogène finie de loi initiale donnée : d'un côté, la
matrice de transition et de l'autre, le graphe orienté dont les sommets sont les
états et les arêtes (étiquetées par des probabilités) les transitions.
2.7. Exemple. Pour la chaîne décrite par la graphe suivant où chaque arc
correspond à une transition de probabilité —

172
XIV. Application aux chaînes de Markov finies
ei
la matrice de transition est
V
o
j_
2
0
0
0
2
0
J_
2
0
2
0
0
1
2
0
1
2
0
0
0
0
1
2
0
1
0 \
0
0
0
1
2
0 i
2.8. Proposition. Soit (Xn)n une chaîne de Markov homogène finie
d'espace d'états E = {ei,..., ejv}; de matrice de transition A. Notons, pour
tout n G N, la loi de Xn avec la matrice ligne
isn = (nXn = el) P(Xn = e2) ... F(Xn = eN)).
Alors, pour tout n EN, vn+i = vnA.
Démonstration. Il suffit d'appliquer la formule des probabilités totales
N
P(Xn+1 =y) = £>(Xn+1 - y\Xn = ek)F(Xn = ek).
k=i
n
2.9. Corollaire. Avec les mêmes notations, vn = i/qA"
La propriété de Markov permet également d'obtenir d'autres résultats sur
la loi marginale d'une variable Xn.
2.10. Proposition. Soit (Xn)n une chaîne de Markov homogène finie
d'espace d'états E = {ei,...,e/v} de matrice de transition A, f : E —» R+.

3. Probabilité invariante
173
Alors,
N
E(/(Xn+1)|X0, . • •,Xn) = Y^AU^fiej).
3. Probabilité invariante
3.1. Proposition. Le rayon spectral d'une matrice stochastique est égal
à 1.
Démonstration. Soit A = (a^j) une matrice stochastique.
> Remarquons tout d'abord que 1 est valeur propre de A car
1
/ N \
N
J2 aN,k
> Soit À une valeur propre de .A, X = (a^) un vecteur propre associé et
i G [l,iV] tel que \xi\ = max|xfe|. Alors,
AT
iV
\^Xi\ ^ Ylai^Xk\ ^ ^^.fcl^l = \xi\'
fc=l
k=l
Par conséquent, |À| ^ 1.
n
3.2. Définition. Une probabilité invariante d'une matrice stochastique A
est un vecteur 7r G .Mi>n(R) positif et de somme 1 tel que ixA = n.
3.3. Remarque. Une probabilité invariante d'une matrice stochastique A
est donc, à transposition près, un vecteur propre de lA associé à la valeur
propre 1 (ce qui est légitime car 1 est valeur propre de A donc de lA). La
contrainte forte est que ce vecteur doit être positif non nul.
Une récurrence immédiate donne la proposition suivante qui permet
d'interpréter la probabilité invariante de la matrice de transition comme loi
stationnaire de la chaîne.
3.4. Proposition. Soit (Xn)n une chaîne de Markov, de matrice de
transition A. Notons, pour tout n G N, vn la loi de Xn. Si vq est une probabilité
invariante de A, alors, pour tout n GN, vn = uq.

174
XIV. Application aux chaînes de Markov finies
3.5. Proposition. Toute matrice A stochastique et irréductible admet une
unique probabilité invariante i\. De plus, cette probabilité invariante est
strictement positive.
Démonstration. Appliquons le théorème XIII-5.9 de Perron & Frobenius
à la transposée lA. Alors, pi^A) = 1 est une valeur propre (ce que l'on
sait déjà) et le sous-espace propre associé est une droite dirigée par un
vecteur strictement positif. En normalisant ce vecteur directeur, on obtient
le vecteur V recherché. □
3.6. Remarque. La condition d'irréductibilité est essentielle pour Puni-
cité. En effet, si A et Ar sont des matrices stochastiques irréductibles de
probabilités invariantes n et tt', alors la matrice stochastique réductible
pr
A' |
admet tous les vecteurs
( Att (1 - A)tt' )
avec À G [0,1] comme probabilités invariantes.
4. Théorème ergodique
4.1. Proposition. Soit A une matrice stochastique irréductible. Il y a
équivalence entre
> il existe p G N tel que Ap est strictement positive ;
> il existe îq G [1,AT] tel que le PGCD de Vensemble
{n G N, [An]i0ii0 > 0}
vaut 1.
Dans ce cas, la matrice est dite ergodique ou apériodique.
Démonstration. > Supposons qu'il existe p G N tel que AP est strictement
positive. Alors, Ap+1 est strictement positive (car A n'admet pas de
colonne nulle). Par conséquent, pour tout i$ G [1, AT], les entiers p et p + 1
appartiennent à {n G N, |/4n]^ > 0} et le PGCD recherché est 1.
> Supposons qu'il existe îq G [1, A"] tel que le PGCD de l'ensemble
{n G N, [An]i0ii0 > 0}
vaut 1.

4. Théorème ergodique
175
Une utilisation classique du théorème de Bézout (ici admise) permet de
montrer qu'il existe po G N tel que, pour tout k ^ po,
k e {n e N, [An]i0ïi0 > 0}.
Comme la matrice est irréductible, il existe pour tout (i,j) des entiers ai
et bj tels que
[Aa%i0 > 0, [A%0tj > 0.
Par conséquent, pour tout n ^ ai + po + bj,
[Ank3 > [Aa%i0[An~ai-bi\io,io[Abi}i0j > 0.
Posons p = max(aiJrpo-\-bj). Alors, la matrice Ap est strictement positive.□
4.2. Théorème. Soit A une matrice ergodique de probabilité invariante n.
Alors, pour tout (i,j),
lim[An}^=7T3.
Plus précisément, il existe r G]0,1[ tel que
lim r~~n max | [An]ij ~ ttj \ = 0.
Effectuons la preuve dans la cas d'une matrice strictement positive
(l'adaptation des arguments au cas d'une matrice ergodique est relativement
immédiate) .
Démonstration. > Remarquons tout d'abord qu'en vertu du théorème de
Perron (théorème XIII-4.5 et exercice XIII-7.8), la matrice A admet 1
comme unique valeur propre de module 1, que sa multiplicité algébrique
est 1 et que toutes les autres valeurs propres sont de module strictement
inférieur à 1.
Par conséquent, il existe une matrice P inversible telle que
A = P
\T
Bj
où B est la matrice diagonale par blocs de Jordan associés aux valeurs
propres de A de module strictement inférieur à 1. Ainsi, (Bp)p est de limite
nulle et

176
XIV. Application aux chaînes de Markov finies
fT"
r'PBP |
En utilisant que ApJrl = AAP = APA, on obtient que le vecteur C\(P) est
constant et que L\(P~1) est proportionnelle à tt. Ainsi,
Ci(P)Li(P-1) = Ai
1
avec À G R. Comme les matrices Ap et donc Ci(P)Li(P_1) sont
stochastiques, À = 1 et le résultat du premier point suit immédiatement.
> Avec les mêmes notations que précédemment, on remarque, pour tout
r < 1 strictement supérieur aux modules des valeurs propres de A distinctes
de p(A) = 1,
r~p(Ap - C1(P)L1(P'1)) = P
D
4.3. Remarque. Remarquons que la condition de matrice stochastique
irréductible n'est pas suffisante pour cette conclusion. Par exemple, si Ton
considère la matrice stochastique irréductible
0 1
1 0
alors, A2n = I2 et A2n+1 = A. Par conséquent, la suite (An)n ne converge
pas (mais les deux suites extraites (A2n)n et {A2n+l)n convergent). On
remarque que dans ce cas,
PGCD{n G N, [An]iti > 0} = 2.
5. Commentaires et développements
5.1. La majeure partie de notre étude repose sur l'hypothèse
d'irréductibilité de la chaîne de Markov. Il ne faut pas toutefois croire qu'une chaîne
de Markov réductible soit tout à fait dénuée d'intérêts. Considérons, par
exemple, la chaîne de Markov dont la transition est décrite par le graphe
suivant (où chaque arc est étiqueté par l'inverse du nombre d'arcs issus de
cet état) :

5. Commentaires et développements
177
Cette chaîne est issue du paradoxe de Penney : la probabilité de voir
apparaître le motif FPP avant le motif PP-F dans une suite de lancers d'une pièce
équilibrée est de 3/4.
La chaîne n'est pas irréductible car son graphe n'est pas fortement connexe.
Pire, les états e^ et e$ sont « absorbants » : une fois la chaîne dans l'un de ses
états, elle y reste. Les questions ne peuvent donc être celle de la probabilité
stationnaire (il suffit qu'elle charge uniquement l'un des états absorbants)
mais plutôt celle de la probabilité d'être absorbée par e±, celle du temps
avant l'absorbtion par l'un de ces états. Ces calculs, souvent appelés calcul
à un pas, sont détaillés dans le joli petit livre suivant :
Processus aléatoires pour les débutants, Arthur Engel, Cassini, 2011.
5.2. Nous avons défini une chaîne de Markov ergodique avec la propriété
d'apériodicité. De manière générale, la période de l'état e\ de la chaîne de
Markov finie homogène de matrice de transition A est le PGCD de l'ensemble
{n e N, [An]iti > 0}.
Si la chaîne de Markov est irréductible, il est facile de vérifier que tous les
états ont la même période. Lorsque cette période d est différente de 1, la
convergence de la suite ([-Ap]iî<7-)p est remplacée par la convergence de suites
extraites avec des indices en progression arithmétique de raison d.
5.3. Une chaîne de Markov infinie homogène peut admettre une vecteur
propre (de taille infinie) à gauche positif associé à 1 sans qu'il existe une
probabilité stationnaire. Ceci amène à distinguer les chaînes dites
récurrentes positives des chaînes dites récurrentes nulles.
Un exemple simple qui peut faire réfléchir est la marche aléatoire
symétrique simple sur Z.
5.4. Le moteur de recherche Google est initialement basé sur une chaîne
de Markov. Internet est alors considéré comme un graphe dont les sommets
sont les pages web et les transitions sont étiquetées, entre autres, par les

178
XIV. Application aux chaînes de Markov finies
liens entre pages x. La probabilité stationnaire pour cette chaîne sert alors
de repère pour les réponses du moteur de recherche. On trouvera tous les
détails de cette jolie application dans l'article (qui se trouve également sur
la page de l'auteur) :
Comment fonctionne Google ?, Michel Eisermann, Quadrature, 68, avril
2008
6. Exercices
6.1. Exercice. La chaîne de l'exemple XIV-2.1 est-elle irréductible ? er-
godique ?
Déterminer sa probabilité invariante.
> Eléments de correction. > La chaîne est irréductible (on voit facilement
sur le graphe que tous les états communiquent) ; par ailleurs, elle est ergo-
dique car les entiers 2 et 3 appartiennent à l'ensemble {n G N, [^4n]i,i > 0}.
> L'ensemble des solutions de l'équation n — ttA est, après résolution par le
pivot de Gauss, vect ((4 8 12 9 6 3)). La probabilité invariante
est donc, en normalisant,
4r ( 4 8 12 9 6 3 ) .
42 v J
<
6.2. Exercice.
1. Une probabilité réversible d'une matrice stochastique A — (dij) est un
vecteur tc = (7^) G A/(i?n(M) positif et de somme 1 tel que,
V(i,j), itidij =7^-0^.
Montrer qu'une probabilité réversible est invariante.
2. SoitN G N*. Considérons le modèle d'Ehrenfest, c'est-à-dire une chaîne
de Markov homogène finie (Xn)n de transition donnée, pour tout k G
[0, N}, par
P(Xn+1 = k + l\Xn = k) - 1 - P(Xn+1 =k-l\Xn = k) = ^r.
Déterminer la probabilité invariante pour cette chaîne.
D> Éléments de correction.
1. « Entre autres » car il faut modifier cette définition de sorte à assurer le caractère
irréductible.

6. Exercices
179
1. Il suffit de calculer ttA. En effet, pour tout i G [l,n],
n n n
/] ^k^k,i = 2J 7TiCli,k = Kl 2_^ ai,k = Kl.
fc=l fc=l fc=l
2. On peut vérifier rapidement que cette chaîne est bien irréductible (mais
qu'elle n'est pas ergodique). Toutefois, ici nous allons exploiter la
première question et chercher une probabilité réversible, c'est-à-dire un
vecteur n positif de somme 1 tel que, pour tout k E [0, TV],
N
('-*)■
avec la convention 7Ttv+i = 0. Un rapide calcul donne alors TTk
2~N{Nk) pourfceïO.iV].
<3
6.3. Exercice. Soit A une matrice stochastique irréductible et probabilité
invariante n. Notons M la matrice dont toutes les lignes sont tt.
1. Montrer que la matrice In — A + M est inversible.
2. Vérifier que (In + A + ... + A^~l){ln - A + M) = In - A* + pM.
3. En déduire que la suite (Ap)p converge au sens de Cesaro vers M.
> Éléments de correction.
1. Soit X e ker(In - A + M). Alors, 7r(In - A + M)X = 0 mais aussi
7r(In -A + M)X = (tt - nA + ttM)X
= (7T - 7T + 7r)X = TïX.
Ainsi, ttX = 0 et donc MX = 0n)i et AX = X. Comme le sous-
espace propre de A est de dimension 1 (d'après le théorème de Perron
& Frobenius pour la matrice A irréductible positive), le vecteur X est
constant. Mais alors, la condition \iX = 0 entraîne que le vecteur X
est nul.
En conclusion, ker(In — A + M) = {0n>i} et la matrice In — A -f- M est
inversible.
2. Remarquons tout d'abord que AM = M car la somme des coefficients
sur une ligne de A vaut 1. Par conséquent,
(In + A + ... + A*-1)^ - A + M) = In - Ap + (In + A + • . • + AP-^M
-In-Ap+pM.
3. On vérifie que (In - A + M)M = M et donc, (In - A + M)-1 M = M.

180
XIV. Application aux chaînes de Markov finies
D'après la question précédente,
±(ln + A + ... + A?-1) = l(ïn-A + M)-\ln - A?) + M.
La suite (||ylp||)p étant bornée, le second membre tend vers M.
<3
6.4. Exercice. Soit A une matrice stochastique, strictement positive.
Notons d le plus petit coefficient de A et, pour tout vecteur X = (x^,
S(X) = max(xi — Xj).
1. Montrer que, pour tout vecteur X positif, 8{AX) < (1 — 2d)ô(X).
2. En déduire que, pour tout vecteur X positif, la suite (ô(ApX))p converge
vers 0.
On retrouve ainsi une justification heuristique du premier point du théorème
XIV-4-2 pour les matrices stochastiques strictement positives.
> Eléments de correction.
1. Soit X — (x^ un vecteur positif, io et jo des indices tels que
Xîç. —— max Xï, xjn ~=~ ni m Xï,
i i
de sorte que S(X) = Xi0 — Xj0. Alors, pour tous i ^ j,
[AX]i - [AX]j = ^2aijkxk -^2,ajikXk
/c=l k=l
n n
^ / j ai,kxi0 + ai,joXJo ~ / v aj,kxj0 ~~ aj,i0
fc=l k=l
k^j0 k^i0
^ {*- aiJo)Xio < aiJoxjo (-L aj,io)xjo aj,ioXio
^ (1 — CLijQ — aj^0)Xi0 — (1 — OjyiQ — CLi,j0)Xj0
^(l-2d)(xio-xjo) = (l-2d)6(X).
2. Par récurrence, on trouve, pour tout vecteur X positif et tout entier p,
0^S(ApX) ^{l-2d)pô(X).
Comme la matrice A est supposée strictement positive, d > 0 et donc
1 — 2d < 1. Le théorème d'encadrement donne que la suite (Ô(ApX))p
converge vers 0.
<3

Notations
adf endomorphisme de C(E) défini par g^fog — gof
Xf polynôme caractéristique de l'endomorphisme /
C(f) commutant de l'endomorphisme /
Cp matrice compagnon du polynôme unitaire P
EffX sous-espace cyclique de l'endomorphisme / associé au
vecteur x ; aussi noté Ex s'il n'y a pas d'ambiguïté
E\(f) sous-espace propre de l'endomorphisme / associé à À;
aussi noté E\ s'il n'y a pas ambiguïté
f\F restriction de l'application linéaire / au sous-espace F
/f endomorphisme induit par l'endomorphisme / sur le
sous-espace stable F
GL(E) groupe linéaire sur l'espace E
GLn (K) groupe linéaire d'ordre n sur le corps K
Xf idéal des polynômes annulateurs de l'endomorphisme /
XfiX idéal des polynômes annulateurs en x de
l'endomorphisme /
Jm bloc de Jordan de taille m
K[X] algèbre des polynômes à coefficients dans K
K[f] sous-algèbre de C(E) des polynômes en
l'endomorphisme / G C(E)
£(E, F) espace des applications linéaires entre E et F
Mn(K) espace des matrices d'ordre n sur le corps K
A4n,P(IK) espace des matrices d'ordre n x p sur le corps K
Hf polynôme minimal de l'endomorphisme /
fjLftX polynôme minimal local en x de l'endomorphisme /
ma(À) multiplicité algébrique d'une valeur propre A, c'est-à-
dire la multiplicité de A comme racine du polynôme
caractéristique ou encore la dimension du sous-espace
caractéristique associé
mg(X) multiplicité géométrique d'une valeur propre A, c'est-à-
dire la dimension du sous-espace propre associé
mm(A) multiplicité d'une valeur propre A en tant que racine du
polynôme minimal
P A Q PGCD des polynômes P et Q
P V Q ppcm des polynômes P et Q
p(A) rayon spectral de la matrice A
TY(a, 6, c, d) tableau de Young de lignes de longueur a ^ b ^ c ^ d

Index
bloc de Jordan, 1
chaîne de Markov, 169
classe de similitude, 139
co-diagonalisabilité, 84
commutant, 25
critère de Klarès, 119
décomposition
de Fitting, 43
de Jordan & Dunford, 105
diagonalisabilité, 79
CNS, 80
disques de Gerschgorin, 154
drapeau,18
endomorphisme
cyclique, 59
induit, 16
fonction symétrique élémentaire, 95
formules de Newton, 96
indice de nilpotence, 4
interpolation de Hermite, 12
matrice
ergodique, 174
irréductible, 159
positive, 157
strictement positive, 157
matrice compagnon, 62
matrice de transition, 171
multiplicité
algébrique, 50
géométrique, 45
minimale, 48
nilespace, 44
polynôme
annulâteur, 2
caractéristique, 48
en un endomorphisme, 1
minimal, 4
minimal local, 4
probabilité
invariante, 173
réversible, 178
rayon spectral, 156
réduite
deFrobenius, 125,127
de Jordan,109, 115,129
restriction, 13
sl2-tripletde.M2(C),35
somme de Newton, 95
sous-espace
caractéristique, 50, 73
cyclique, 18
propre, 45
stable, 15
tableau de Young, 112
théorème
de Brauer, 55,164
de Cayley & Hamilton, 65, 71
de Hadamard, 153
de Jordan &; Weyr, 115
de Kronecker, 98
de Maschke, 34
de Perron, 158,168
de Perron & Frobenius, 160
de Taussky, 165
trigonalisabilité, 93
valeur propre, 45
vecteur propre, 45
ovales de Cassini, 164
®
Certifié PEFC
PEFC °
10-31-2568 pefc-france.org
Achevé d'imprimer par EMD SAS. (France) - N° éditeur : 2012/0590 - Dépôt légal : septembre 2012 - N° d'imprimeur : 2711>

Roger Mansuy & Rached Mneimné
Algèbre linéaire
Réduction des endomorphismes
Rédigé à l'attention des étudiants en Licence de mathématiques et des classes
préparatoires scientifiques, l'ouvrage est constitué d'un cours complet, de
commentaires et développements et de 120 exercices corrigés.
Afin d'aborder les différents aspects de la théorie de la réduction, les premiers
chapitres détaillent avec soin les objets et concepts de l'algèbre linéaire.
Les chapitres suivants présentent aussi bien les critères pratiques que leurs
utilisations théoriques, à l'appui de nombreux exemples.
Cette approche pédagogique offre également une base solide de révision pour
tous les candidats qui se préparent aux concours de l'enseignement.
Sommaire
1. Polynômes d'endomorphismes
2. Sous-espaces stables
3. Commutation
4. Lemme des noyaux
5. Éléments propres, caractéristiques
6. Endomorphismes cycliques
7. Théorème de Caley-Hamilton
8. Diagonalisation
9. Trigonalisation
10. Réduction de Jordan
11. Réduction de Frobenius
12. Topologie des classes de similitude
13. Localisation des valeurs propres
14. Application aux chaînes de Markov finies
Notations
Index
Ancien élève de l'ENS Cachan, agrégé de mathématiques, Roger Mansuy est professeur de mathématiques
en MPSI, et d'informatique en MP* au lycée Louis le Grand. Membre du jury de l'Agrégation externe, il est
l'auteur de plusieurs ouvrages de référence dédiés à l'enseignement supérieur.
Ancien élève de CENS Saint-Cloud, agrégé de mathématiques, Rached Mneimné est maître de conférences à
l'université Paris-7 Denis Diderot. Plusieurs fois membre du jury de l'Agrégation externe, il est également
l'auteur de nombreux ouvrages universitaires.
ISBN 978-2-311-00285-0
WWW.VUI