Текст
В.А.СВЕТЛИЦНИИ
j
।
ЗАДАЧИ И ПРИМЕРЫ ПО ТЕОРИИ КОЛЕБАНИЙ
’ Часть I
• : ." ” • ‘' •<
' ' . . . ’ > ' i • Г '
Издательство МГТУ им.НЭ. Баумана
В. А. СВЕТЛИЦКИЙ
ЗАДАЧИ И ПРИМЕРЫ ПО ТЕОРИИ КОЛЕБАНИЙ
Часть I
Допущено Учебно-методическим объединением вузов по машиностроительным и приборостроительным специальностям в качестве учебного пособия для студентов высших технических учебных заведений
Москва Издательство МГТУ им. Н. Э. Баумана 1994
ББК 22.23
С24
УДК 534(075)
Рецензенты: кафедра «Сопротивление материалов» Челябинского государственного технического университета; докт. техн. наук. проф. Б. Г. Кеглин — кафедра «Динамика н прочность машин» Брянского института транспортного машиностроения
С24
Светлицкий В. А.
Задачи и примеры по теории колебаний: Учебное пособие. М.: Изд-во МГТУ, 1994. Ч. I. 308 с., ил.
ISBN N? 5-7038-0893-6
Приведены задачи и упражнения по всем основным разделам курса «Теория колебаний», относящиеся к системам с конечным числом степеней свободы. Сформулированы задачи, связанные с определением частот и форм колебаний систем с конечным числом степеней свободы: анализом установившихся и неустановившнхся режимов колебаний; анализом нелинейных колебаний; . определением вероятностных характеристик решений при действии случайных сил; анализом устойчивости параметрических колебаний. Как правило, предложенные в сборнике задачи связаны с конкретными механическими системами, которые могут быть использованы и для курсовых работ по теории колебаний. Учитывая интересы студентов, занимающихся самостоятельным изучением теории колебаний, для большинства задач даны подробные решения или алгоритмы решения.
Для студентов и аспирантов технических вузов и университетов. Может быть полезен преподавателям технических вузов, а также инженерам, использующим теорию колебаний в практической работе. Ил. 305 Библиогр. 11 назв.
По вопросам приобретения книги обращаться по телефону 263-60-45.
ISBN 5-7038 0893-6
1603030000—31 „ 93
095 (2)-94
ББК 22.23
© В. А. Светлицкий, 1994
С
ПРЕДИСЛОВИЕ
Курс «Теория колебаний» широко распространен в высших технических учебных заведениях, а для ряда специальностей он относится к числу основных дисциплин фундаментальной профилирующей подготовки, поэтому предлагаемый сборник задач окажет большую помощь студентам при изучении этой дисциплины, будет способствовать развитию навыков решения прикладных задач с использованием ЭВМ.
Основная особенность сборника — его прикладная направленность. Он содержит задачи по всем основным разделам теории колебаний, включая также разделы, вошедшие в учебные курсы теории колебаний только в последнее время — параметрические колебания, случайные колебания, устойчивость колебаний. По сравнению со «Сборником задач по теории колебаний», вышедшим в 1979 г. [1], в данном издании частично переработаны многие разделы и изъяты задачи, не имеющие отношения к механическим системам. Основная цель сборника — помочь изучающим теорию колебаний глубже овладеть теорией и освоить методы решения прикладных задач. Поэтому в сборнике практически для всех задач даны решения.
Автор с благодарностью примет отзывы, замечания и предложения читателей, которые можно присылать по адресу: 107005, Москва, 2-я Бауманская, 5.
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
A С С, с D £ F Fa F(t) G J J J,, Ц Jp\ h J. У. К k L I M m P Q q R — амплитуда колебаний; — электрическая емкость, конденсатор; — коэффициенты; — жесткость, коэффициент жесткости; — дисперсия; — модуль упругости первого рода; — площадь поперечного сечения; — амплитуда возмущающей силы; — возмущающая сила; — модуль упругости второго рода; — полярный момент инерции массы; — сила тока; — геометрические характеристики поперечного сечения стержня; — функция Бесселя нулевого порядка первого рода; — функция Бесселя нулевого порядка второго рода; — корреляционная функция; — коэффициент жесткости упругого основания; — индуктивность; — длина; — момент силы; — масса; — сила; — собственная частота колебаний; — сила; обобщенная сила; — обобщенная координата; —диссипативная функция Релея; электрическое со-
s T i U V U7 w X, Y, Z противление; — спектральная плотность; — кинетическая энергия; период колебаний; — время; — напряжение электрического тока; — скорость — передаточная функция; — линейное ускорение; — перемещения в направлениях координатных осей х, у, z;
У(.) a — отображение по Лапласу оригинала; — коэффициент вязкого трения;
— логарифмический декремент затухания;
— перемещение точки в направлении i от действия силы по направлению /;
— малый параметр; динамический коэффициент вязкости;
— потенциальная энергия;
— плотность материала;
— нормальное напряжение; среднеквадратичное отклонение;
— время; касательное напряжение;
— угловое перемещение;
— угловая скорость;
— частота свободных затухающих колебаний.
ЗАДАЧИ
Глава 1. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 1. Свободные колебания
1. Для систем, изображенных на рис. 1, определить частоты собственных изгнбных колебаний.
ь
Рис. 2
2. Для систем с постоянной изгибной жесткостью EJX (рнс. 2), используя метод сил, составить дифференциальные уравнения малых свободных колебаний и определить частоты собственных колебаний. При составлении уравнений движения принять, что масса системы по сравнению с массой груза мала; массу груза считать точечной.
3. Для систем, изображенных на рис. 3, составить дифференциальные уравнения малых свободных колебаний, используя метод сил и считая массы т точечными. Определить частоты собственных колебаний.
4. Для систем, изображенных на рис. 4, составить дифференциальные уравнения малых крутильных колебаний маховичка, имеющего момент инерции массы /, и определить частоты собственных колебаний. Считать, что в схемах г и д подшипник длинный, т. е. угол поворота при изгибе равен нулю, a GJh = =0,8 4.
5. Чувствительный элемент (датчик давления) (рис. 5) предназначен для регулировки давления жидкости или пара в некотором объеме. При изменении давления поршень массой /П| смещается и через шток приводит в движение исполнительный
Рис. 4
7
орган. Приведенная масса штока и остальных движущихся элементов прибора равна m2. Определить частоту собственных колебаний датчика давления (поршня), считая, что трение уплотнительных колец о цилиндр весьма мало.
6. Груз массой т закреплен на абсолютно жестком невесомом стержне длиной 3/, связанном двумя одинаковыми пружинами жесткостью с каждая (рис. 6). Определить частоту малых собственных колебаний маятника.
7. Решить задачу 6 при горизонтальном положении стержня.
8. Зубчатое колесо 1 (рис. 7) массой т\ с жестко скрепленным с ним водилом 2 массой т2 лежит на зубчатой рейке 3. К свободному концу водила прикреплены без натяга пружины 4 жесткостью с каждая. Составить дифференциальное уравнение малых свободных колебаний системы; определить частоту собственных колебаний.
9. Тяжелый цилиндр массой maQlg, радиусом г (рис. 8) лежит на вогнутой поверхности, имеющей радиус кривизны /?. К верхней точке цилиндра прикреплены пружины-растяжки жесткостью с каждая. Составить дифференциальное уравнение малых свободных колебаний цилиндра, считая, что проскальзывание цилиндра по поверхности отсутствует. Исследовать влияние радиуса кривизны поверхности R на частоту собственных колебаний цилиндра и, в частности, определить ее, когда поверхность является плоскостью (/? = со).
10. Определить частоту собственных колебаний вертикально установленного маятника массой т (стержень считать абсолютно жестким) .(рис. 9). Жесткость пружин равна с.
8
Рис. 7
11. Определить частоту малых собственных колебаний диска индукционного гальванометра (рис. 10), представляющего собой стальной диск толщиной Л=2 мм, диаметром d=50 мм. Жесткость пружины при кручении с—Л1/ф=0,488 Н-м.
12. Стержень АВ жесткостью на кручение с на одном конце имеет цилиндрический шарнир А, а на другом — диск радиусом /? и массой т (рис. И). Система укреплена на плоскости, наклоненной к горизонту на угол а. Считая, что диск может совершать колебательные движения качения без проскальзывания, составить дифференциальное уравнение его малых свободных колебаний. Исследовать зависимость частоты собственных колебаний и их устойчивость от угла наклона а плоскости.
9
13. Чувствительный элемент уровня (датчик уровня) (рис. 12) состоит из поплавка диаметром d и массой погруженного в жидкость; системы рычагов, пружины жесткостью с и противовеса массой тг. При изменении уровня жидкости Но избыточная выталкивающая сила перемещает поплавок, что передается через систему рычагов регистрирующему или исполнительному механизму. Считая, что плотность жидкости равна р, составить дифференциальное уравнение малых свободных колебаний поплавка и определить- частоту его собственных колебаний, пренебрегая инерцией жидкости.
Рис. 12
14. Диск массой т с моментом инерции массы Jo насажен на ступицу радиусом г (рис. 13). Ступица диска опирается на криволинейную круговую направляющую радиусом R. Составить дифференциальные уравнения малых свободных колебаний диска, считая, что при его движении проскальзывание между ступицей и направляющей отсутствует. Дифференциальное уравнение движения получить двумя методами: по методу Лагранжа и по методу Даламбера.
10
15. На шероховатой наклонной поверхности (рис. 14) установлена тележка массой т, удерживаемая пружиной жесткостью с. Считая, что каждая из двух колесных пар тележки имеет момент инерции массы /, радиус колес R, а движение происходит без проскальзывания колес по поверхности, составить дифференциальное уравнение малых свободных колебаний тележки.
16. Балка массой m = Q/g (рис. 15) лежит на цилиндре радиусом R. Составить дифференциальное уравнение малых свободных колебаний балки относительно положения равновесия. Определить частоту собственных колебаний балки и амплитуду <ро max. при которой возможны колебания, приняв коэффициент трения скольжения равным р..
Рис. 14
Рис. 15
17. Кольцо, имеющее радиус внутренней поверхности R, надето на вал диаметром 2 г (рис. 16). Определить частоту собственных колебаний кольца, считая известными его массу т и момент инерции массы относительно центра тяжести I.
18. Для гашения колебаний маховика (рис. 17), вращающегося с угловой скоростью и, можно применить маятниковый демпфер, представляющий собой специальной формы груз массой m=Q/g, помещенный во внутреннюю полость маховика. Контактная поверхность груза имеет радиус кривизны /?г, поверхность маховика R\ (R\<Rz).
Найти частоту собственных колебаний груза при остановленном маховике (ш^О) (сила тяжести направлена по оси у), а также частоту собственных колебаний груза при <o=const (пренебрегая силой тяжести).
11
Рис. 16
При решении задачи принять, что /?2—/?| = А/? — малая величина; расстояние от точки контакта груза с маховиком до центра тяжести груза равно а; момент инерции массы груза относительно оси, проходящей через центр тяжести груза, равен /«, а расстояние от оси вращения маховика до центра тяжести груза равно г.
19. Массивный диск радиусом R вращается равномерно с угловой скоростью <0. На ободе диска шарнирно закреплен стержень, имеющий длину I и массу т на свободном конце (рис. 18). Считая массу стержня малой по сравнению с массой т, определить частоту собственных колебаний груза в поле центробежных сил.
20. Груз массой т укреплен на гибкой стальной стойке прямоугольного поперечного сечения жесткостью ct=FJx, поддерживаемой двумя пружинами жесткостью с2 каждая (рис. 19). Определить частоту малых собственных колебаний груза, считая массу стойки и пружин по сравнению с массой груза. Влиянием силы тяжести груза на изгиб стойки пренебречь.
21. Для гашения крутильных колебаний на маховиках иногда устанавливают дополнительные массы, представляющие собой маятники в поле центробежных сил. Определить частоту собственных колебаний центробежного маятника (рис. 20), счи
12
тая, что угловая скорость диска со, расстояние от оси вращения диска до точки подвеса маятника г, момент инерции массы маятника относительно точки подвеса JB, масса маятника т.
22. На ободе массивного диска радиусом R жестко защемлен гибкий стержень длиной I, несущий на свободном конце массу т. Диск равномерно вращается с угловой скоростью а (рис. 21). Полагая жесткость стержня при изгибе равной EJX и
Рис. 20 Рис. 21
пренебрегая массой стержня по сравнению с массой груза, определить частоту собственных колебаний груза в поле центробежных сил.
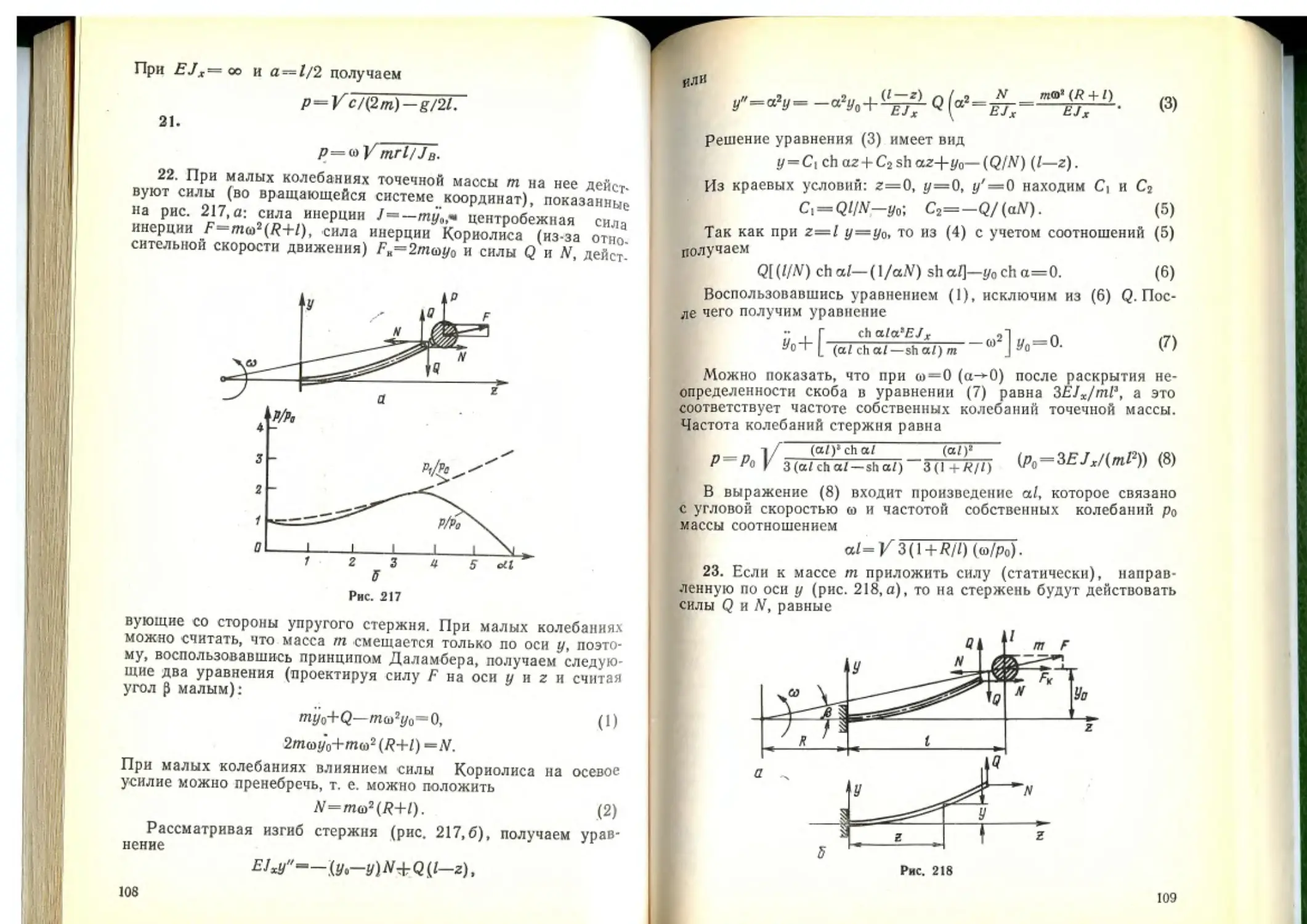
23. Получить приближенное выражение для частоты колебаний массы т (см. задачу 22), 'воспользовавшись выражением для прогибов при продольно-поперечном изгибе в виде
0о=у/(1 + Л7Р»),
где N — осевая растягивающая сила; P^i^EJx/AP—критическая сила; у—прогиб от действия поперечной нагрузки. Построить графики зависимости безразмерной частоты колебаний р/ро в зависимости от al для точного (см. задачу 22) и приближенного решения при R*=l.
24. Стержень АВ (рис. 22) жесткостью EJX закреплен на конце жесткого рычага ВС, вращающегося равномерно с угло
Рис. 22
Рис. 23
вой скоростью со в горизонтальной плоскости. Определить частоту собственных колебаний точечной массы т, закрепленной в точке А стержня (массой стержня пренебречь), считая, что масса т колеблется в плоскости вращения.
25. На ободе тяжелого диска радиусом R (рис. 23) закреплен стержень длиной жесткостью EJX, несущий на конце массу т. Определить частоту собственных колебаний груза при равномерном вращении диска. Полагая /?>I, определить критическое значение угловой скорости диска со, при которой частота собственных колебаний груза равна нулю. При решении задачи массой стержня пренебречь.
26. На массивном диске, вращающемся с угловой скоростью и, закреплен стержень длиной I, жесткостью EJX (см. рис. 23). На свободном конце стержень несет массу т, центр О которой совпадает с центром вращения диска. Определить частоту собственных колебаний груза, пренебрегая массой стержня.
27. Груз массой т укреплен на тонкой абсолютно гибкой нерастяжимой нити длиной 2t. С помощью пружины в нити создается натяжение То (рис. 24). Считая, что натяжение в обоих участках нити одинаково и постоянно, определить частоту малых собственных колебаний груза.
28. Точечная масса т закреплена на струне длиной /, имеющей предварительное натяжение То (рис. 25). Составить дифференциальное уравнение малых свободных колебаний массы. Построить график зависимости частоты собственных колебаний от координаты положения массы х<>. Изменением натяжения струны в процессе колебаний и влиянием силы тяжести пренебречь.
29. Груз массой т укреплен на конце упругого растяжимого безынерционного троса, намотанного на барабан (рис. 26).
14
Составить дифференциальное уравнение малых свободных продольных колебаний груза при равномерном вращении барабана с угловой скоростью св. Диаметр барабана 2г, площадь поперечного сечения троса F, модуль упругости материала троса Е. Определить моменты времени, в которые груз проходит через положение равновесия, считая, что в начальный момент времени t0 длина размотанной части троса равна /0, полная скорость движения v=taR + Дх0, а Дхо = 0 (Дх0 — динамическое удлинение троса).
Получить решение для частного случая w=const, приняв т=100 кг, £=10 ГПа, F=10-5 м2, t» = <i>/? = l м/с, /0=1 с, 1о— = 1 м.
30. Груз, имеющий массу т, укреплен на конце абсолютно гибкого нерастяжимого безынерционного троса, намотанного на
барабан. Составить дифференциальное уравнение малых свободных поперечных колебаний груза при равномерном вращении барабана с угловой скоростью ш (см. рис. 26). Получить зависимость амплитуды свободных колебаний от длины свободного участка троса I и угловой скорости барабана ©. Рассмотреть два случая: а) подъем груза с некоторой начальной длиной троса /0; б) опускание груза. Принять следующие условия: при t~to, фо = О, ф — 0 (ф — угол отклонения троса от вертикали).
31. Стальная безынерционная балка длиной I, имеющая из-гибную жесткость EJX, лежит на упругом безынерционном основании с коэффициентом постели k (рис. 27). Посредине балки закреплена точечная масса т. Определить частоту собственных колебаний системы, если сечение балки представляет собой прямоугольник с основанием 6 см и высотой 1см; длина балки <в2 м; коэффициент постели й=4 кН/м2; масса т=100 кг.
32. На стальной балке длиной /= 1 м, имеющей поперечное сечение 4>ХЛ = 6Х1 см2, закреплена масса т = 20 кг (рис. 28).
Балка защемлена одним концом и лежит на упругом основании, коэффициент постели которого Л— 4 кН/мг. Пренебрегая инерцией поворота массы, т. е. рассматривая ее как точечную, определить частоту собственных колебаний. Массой балки и инерционностью упругого основания пренебречь.
33. Стальная балка длиной 2/=200 см, имеющая поперечное сечение ЬхЛ=6х2 см2, торцевые сечения балки жестко закреплены (рис. 29). Балка лежит на упругом основании, коэффициент постели которого k= 2,5 кН/м2, и нагружена посредине массой т = 50 кг. Определить частоту собственных ко-
лебаний массы т, пренебрегая силой тяжести балки и инерционностью основания.
34. Используя метод Релея, определить частоту собственных колебаний системы (рис. 30) с учетом массы балки. Сосредоточенную массу т считать точечной, т. е. ее моментом инерции
пренебречь. Изгибная жесткость балки £/ж; масса единицы длины балки тл.
35. Используя метод Релея, определить низшую частоту собственных колебаний массы т, закрепленной посредине балки, имеющей изгнбную жесткость EJX и массу единицы длины балки т0 (рис. 31).
Рис. 31
16
36. Для схем, изображенных на рис. 32, определить по методу Релея частоты собственных колебаний, считая массы т точечными, а массу единицы длины стержней равной ггц.
з
Рис. 32
§ 2. Свободные колебания систем с учетом сил сопротивления
37. Определить зависимость частоты собственных крутильных колебаний вала смесителя от вязкости среды, а также время, в течение которого амплитуда колебаний вала смесителя уменьшится в 10 раз после мгновенной остановки мотора, если скорость равномерного вращения перед остановкой равна Q (рис. 33). При решении задачи принять, что масса вала мала по сравнению с массой лопастей. Момент инерции массы лопа
Рис. 34
2—5000
1 7
стей J=0,5 кг м!. Диаметр вала d=0,005 м, длина вала /= = 0,5 м. Коэффициент момента вязкого сопротивления движению лопастей а=1,2 Н-м-с.
38. Для определения коэффициента вязкости масла v можно использовать установку, показанную на рис. 34. Здесь массивный стальной цилиндр высотой Н и диаметром D\ подвешен на тонкой проволоке диаметром d и длиной L в стакане диаметром D. В стакан заливается масло и цилиндр приводится в колебательное вращательное движение. Считая, что момент сопротивления движению можно вычислить по формуле М = =n//Di3<opv/4(D2—D\) (где о = ф— угловая скорость, р — плотность масла), определить кинематическую вязкость v солярового масла, имеющего удельный вес -у = 9 кН/м3, если при
проведении испытания в приборе, размеры которого £)|=0,1 м, Й2=0,12 м, Я = 0,2 м, d=0,001 м, 2=0,5 м, период свободных колебаний был равен то=6,5 с. (Жидкость считать безынерционной).
39. Для системы, изображенной на рис. 35, составить дифференциальное уравнение малых свободных колебаний массы т, считая, что сила сопротивления демпфера прямо пропорциональна скорости движения (Fay).
40. Безударная муфта сцепления (рис. 36) служит для смягчения влияния резких колебаний скорости ведущего вала на ведомый. Муфта представляет собой стальной диск 1, свободно укрепленный на валу 3. Передача усилия от вала к диску осуществляется через пружину 2. Считая, что сопротивление между валом и диском вязкое, определить коэффициент а момента вязкого сопротивления движению в паре диск—вал, если известно, что логарифмический декремент свободных колебаний диска 6=1,5, диаметр диска D=0,I м, толщина Н = 20 мм, диаметр пружины Z)| = 30 мм, диаметр проволоки di=3 мм, число витков пружины 1=9 м, модуль упругости материала пружины 6 = 80 ГПа, плотность стали р=8-103 кг/м3.
18
41. На абсолютно жестком стержне длиной 2/ подвешен груз массой т (рис. 37). К середине стержня прикреплены две упругие растяжки-пружины жесткостью с каждая. Груз помещен в сосуд, заполненный вязкой жидкостью. В процессе малых свободных колебаний груза жидкость оказывает демпфирующее влияние на систему. Определить коэффициент вязкого
сопротивления движению системы, если период затухающих колебаний системы то=1,0 с при следующих параметрах системы: масса груза т=1 кг, длина стержня 21 = 0,3 м, диаметр пружины 7)^20 м, диаметр проволоки пружины d=2 м, модуль упругости материала пружины G=80 ГПа, число витков каждой пружины 1 = 6.
42. Гидравлический демпфер (катаракт) (рис. 38) представляет собой поршень массой т, движущийся в жидкости. Исследовать движение поршня, считая, что в начальный момент времени (/ = 0) поршень отклонен от положения равновесия на г/о“5 мм. Определить время, в течение которого отклонение поршня от положения равновесия уменьшится в два раза, если жесткость пружины с=3 кН/м, диаметр цилиндра /) = 0,1 м, диаметр отверстий d=10 мм, число отверстий г=25, масса поршня ш = 2,73 кг, высота поршня //=50 мм, динамический коэффициент вязкости жидкости ц=6-10'2 Па-с.
43. Прибор представляет собой груз массой т, укрепленный на двух пружинах жесткостью с каждая. Груз находится в трубке, заполненной жидкостью. Сопротивление движению груза может изменяться в зависимости от величины зазора между грузом и стенками трубки и в зависимости от вязкости жидкости (рис. 39). Считая, что сопротивление движению груза
прямо пропорционально скорости движения, т. е. ах, требуется:
Рис. 40
Рис. 39
а) составить дифференциальное уравнение малых свободных колебаний груза;
б) определить время, в течение которого амплитуда свободных колебаний уменьшится в 100 раз, приняв, что при /=0, х = 0, х=х0.
При решении задачи считать т=50 кг, с=1 кН/м, а= = 500 Н е м-1.
44. Груз массой т укреплен на абсолютно жестком безынерционном стержне длиной I (рис. 40), который удерживается в равновесии пружиной и демпфером. Последний имеет линейную характеристику трения /=ах. Определить частоту собственных колебаний системы и логарифмический декремент затухания колебаний, если т—1 кг, /=0,5м, а=0,2 м, диаметр пружины D=
20
=50 мм, диаметр проволоки пружины d=5 мм, число витков 1= = 5, модуль упругости G=80 ГПа, коэффициент вязкого сопротивления движению демпфера а = 3- 102 Н е м-1.
45. Для измерения малых разностей давления газов (или малых колебаний давления) применяют жидкостной [/-образный манометр с наклонной трубкой (тягомер Креля) (рис. 41). Определить частоту малых собственных колебании жидкости, заполняющей трубку тягомера, считая, что ее плотность равна р; сила сопротивления движению жидкости по трубке F"=zx, где х —отклонение уровня жидкости от положения равновесия.
46. В начальный момент времени масса т (рис. 42, о) отклонена от положения равновесия на расстояние х0 и отпущена без начальной скорости. При скольжении по поверхности между
массой т и поверхностью возникает сила трения, которую можно рассматривать как силу «сухого* (кулонова) трения. Зависимость силы кулонова трения Гт от скорости движения х массы т показана на рис. 42,6. Установить закон движения массы т.
47. Диск 1 насажен на вал 2 и удерживается от вращения пружиной 3, закрепленной одним концом на диске, а другим — на опоре (рис. 43). Считая, что система диск—вал—пружина имеет момент инерции массы J, а зазор между диском и поверх-
Рис. 43
21
ностями кулонова трения А и Б весьма мал, составить дифференциальное уравнение малых свободных колебаний диска, приняв, что при /=0 <р = <ро. <ро=О. Выяснить характер движения и закон изменения амплитуды в зависимости от числа периодов колебаний, приняв, что восстанавливающий момент упругости пружины больше момента трения. Определить период колебаний.
Указание. При повороте диска на угол <р длина пружины изменяется и диск прижимается к одной из поверхностей трения А или Б. Сила кулонова трения пропорциональна силе прижатия диска к поверхности трения.
48. Используя метод фазовой плоскости, исследовать свободные колебания системы, изображенной на рис. 43 (см. условие задачи 47).
49. Для механической колебательной системы, состоящей из груза массой т, подвешенного на пружине жесткостью с, составить электрические аналоговые цепи.
50. Поршень масляного демпфера, имеющий массу т, подвешен на пружине жесткостью с (см. рис. 38). Составить электрическую аналоговую цепь малых свободных колебании системы.
§ 3. Вынужденные колебания
51 На рис. 44 приведена схема вибрографа — прибора для регистрации колебаний. На жесткой станине 1 прибора закреплена катушка 2, сердечником которой является магнит 3, подвешенный на пружине 4. При движении магнита внутри катушки в ней возникает электрический ток, который подается на регистрирующий прибор. Считая, что магнит 3 имеет массу т, а пружина 4 — жесткость с, составить дифференциальное уравнение движения магнита и определить, при каком условии иска
Рис. 44
Рис. 45
22
жения записи колебаний будут минимальными (прибор записывает вертикальные колебания основания, происходящие по закону у=yosinwZ).
52. Безрычажный датчик контроля биения поверхности (рис. 45) состоит из измерительного стержня / массой т, укрепленного на двух плоских пружинах 2. Винтовая цилиндрическая пружина 3 служит для прижатия измерительного стержня к контролируемой детали. Если контролируемая деталь 4 имеет биение поверхности относительно линии центров (величина биения определяется эксцентриситетом е), то при вращении детали, угловая скорость которой ы, измерительный стержень получает вертикальные перемещения.
Считая, что при отсутствии эксцентриситета (е=0) усилие прижатия измерительного стержня к детали равно /?0. и пренебрегая массой упругих элементов, определить предельную угловую скорость детали ы. из условия непрерывности контакта при контроле детали, имеющей эксцентриситет е. Чему равно измерительное усилие прибора (усилие, с которым измерительный стержень прижимается к детали) при w = 0,lo.?
При расчете принять: т=0,05 кг, r0=5H, d|=»50 мм, е= = 0,1 мм. Плоские пружины имеют длину /=30 мм и поперечное сечение ЬХЛ™5Х0,5 мм. Диаметр винтовой пружины D— =5 мм, диаметр проволоки d=l мм, число витков i=20. Материал пружин — сталь, Е=200 ГПа, G—80 ГПа.
53. На рис. 46 показан стержень, торцевое сечение которого принудительно поворачивается (0(0 =60coso/). Такое возбуж-
Рис. 46
Рис. 47
дение колебаний называется кинематическим. Считая, что имеют место установившиеся колебания, определить максимальное нормальное напряжение в заделке.
54. Сечение стержня k (рис. 47) имеет заданное вертикальное перемещение yh(t) = t/ocostof Считая, что имеют место установившиеся колебания, определить реакцию в шарнире.
55. Рычажный электроконтактный датчик (профилометр) (рис. 48), предназначенный для автоматического контроля волнистости поверхности, состоит из измерительного стержня /, контактирующего с контролируемой поверхностью, и рычага 3, увеличивающего перемещение измерительного стержня L/1 раз. Измерительный стержень прижимается к контролируемой поверхности пружиной 2, имеющей жесткость С|. Рычаг 3 укреплен на полупружинном шарнире 5, имеющем угловую жест
91
кость Ci. При выходе детали из поля допуска происходит замыкание одного из контактов 4, т. е. поступает сигнал на отбраковку. Производительность контроля пропорциональна скорости и перемещения детали относительно датчика. Однако скорость не может быть как угодно велика, так как при больших скоростях возможно нарушение контакта в точке В|.
При массе измерительного стержня 1, равной т, и моменте инерции J массы рычага 3 относительно шарнира 0, пренебрегая силами трения, определить предельную скорость движения детали v., если уравнение ее поверхности имеет вид x=asin2nz/
Рис. 48
Рис. 49
/А (где А — длина волны неровности). Учесть, что при установке измерительного стержня на контролируемую поверхность пружина 2 имеет предварительный натяг х0, а пружины шарнира 5 — натяг фо-
56. В механизме профилометра (см. рис. 48) при достаточно большой скорости движения контролируемой поверхности относительно прибора возможно нарушение контакта между измерительным стержнем 1 и рычагом 3 в точке В2. Считая, что профиль поверхности представляет собой синусоиду в виде х= определить условие нарушения контакта в точке Вг. Момент инерции массы рычага равен /, угловая жесткость пружины шарнира 5 равна с2. Пружины имеют предварительный натяг фо=Мо/с2, где Л10 — упругий момент в пружине 5 после установки прибора.
57. На рис. 49 приведена схема триммера / руля высоты самолета. Величина момента инерции / массы триммера относительно точки подвеса О известна, но определить жесткость
проводки управления статическим путем практически невозможно. Поэтому частоту собственных колебаний триммера определяют по резонансной частоте колебаний системы. В экспериментальной установке к триммеру прикрепляют дополнительные пружины 2 и 3. Определить частоту собственных колебаний триммера, если резонансная частота системы равна
58. Для уменьшения влияния колебании основания на работу приборов применяется пассивная виброизоляция — подвеска (установка) прибора на мягких податливых амортизаторах. Для схем, изображенных на рис. 50, определить динамический
sin cot
Рис. 50
коэффициент (отношение амплитуды колебаний массы т к амплитуде колебаний основания х0).
59. При работе однофазного электродвигателя развивается переменный крутящий момент Af^Mo+AfiSincot В этом случае в качестве виброизоляции применяют специальную подвеску (рис. 51), выполненною таким образом, что наклонные участ
Рис. 51
ки стальных полос пересекаются в центре подшипника. Такая опора оказывается весьма жесткой в вертикальном и горизонтальном направлениях, что необходимо для обеспечения нормальной работы зубчатого колеса, закрепленного на валу двигателя, и достаточно податливой при повороте двигателя в плоскости чертежа.
25
Определить необходимые размеры поперечного сечения ЬХ Х2Ь полос опор из условия, что динамический коэффициент передачи момента на основание не должен превышать 1/15, /з=100 мм, /2=1600 мм, /|«50 мм, момент инерции массы двигателя J— 20 кг-м2. Определить также коэффициент запаса выносливости при Л1о=5О Н-м, М,=30 Нм, с„=1 ГПа, <о= “105 с'1, О-, = 0,4 ГПа.
60. Для уменьшения воздействия сил инерции, возникающих в машине (двигателе) из-за неуравновешенности вращающихся масс, на основании используются различные системы внброизоляции, например упругие подвески или опоры. Для •схем, изображенных на рис. 52, определить динамический коэф
Рис. 52
фициент передачи силы на основание в местах прикрепления упругих опор жесткостью с. Балки, на которых установлены двигатели, считать абсолютно жесткими.
61. Масса tn (рис. 53) подвешена на пружине жесткостью с=7,2 кН/м. Верхний конец пружины связан с кривошипноползунным механизмом и может совершать возвратно-поступательное движение, описываемое уравнением x=xosina>/, где амплитуда xq=15,5 мм, а угловая скорость кривошипа со равна частоте свободных незатухающих колебаний массы т. Считая, что коэффициент силы вязкого сопротивления демпфера а= =27 Н-с/м, а масса т=9,1 кг, определить максимальную силу, растягивающую пружину, и коэффициент запаса усталостной прочности пружины, считая, что ее диаметр D=50 мм, диаметр проволоки d=5 мм. Пружина изготовлена из стали, имеющей следующие механические характеристики: тя—850 МПа, т, = 600 МПа, т_| = 300 МПа.
62. Масса т (рис. 54) установлена на двух пружинах жесткостью с каждая н связана с кривошипно-ползунным механизмом через демпфер, коэффициент силы вязкого сопротивления
26
которого равен а. Составить дифференциальное уравнение движения массы т. Определить напряжения, возникающие в пружине, приняв диаметр пружины равным D, а диаметр проволоки пружины равным d, для случая, когда угловая скорость кривошипа ш равна частоте незатухающих колебаний массы т на пружинах жесткостью с.
1
Рис. 53 Рис, 54
63. На массу т (рис. 55), связанную с упором пружиной, имеющей жесткость с, и демпфером, коэффициент вязкого трения которого а, действует периодически изменяющаяся сила F^Fosino/. Определить частоту собственных колебаний массы т и те значения частоты возмущающей силы <о, при которых максимальная сила, действующая на пружину, равна амплитуде возмущающей силы.
Рис. 55
64. Мотор массой т, жестко укреплен на станине, имеющей массу т2 (рис. 56). Между станиной и основанием имеется слой смазки; станина укреплена на основании с помощью двух пружин. Ротор мотора имеет массу т0, центр которой смещен относительно оси вращения на величину е. Общая Жесткость пружин равна с. Определить коэффициент вязкого трения смазки, при котором рассеиваемая энергия (работа сил трения) будет наибольшей при равномерном вращении ротора с угловой скоростью со.
07
65. Для системы, изображенной на рис. 56, построить график изменения амплитуды силы, действующей на пружины при установившихся колебаниях, в зависимости от частоты возмущающей силы.
66. На двух стальных балках установлен двигатель, имеющий несбалансированную массу (рис. 57). Для уменьшения амплитуды колебаний, возникающих при работе двигателя, в систему введен демпфер вязкого трения. Считая, что масса двигателя т=50 кг, w=63 с-1, а амплитуда возмущающей си-
Рис. 56 Рис. 57
лы при этом Ро=2000 Н, подобрать характеристику а демпфера таким образом, чтобы коэффициент запаса усталостной прочности балки равнялся п„=2. Балка имеет квадратное поперечное сечение bXh=^500X500 мм и изготовлена из стали СтЗ со следующими механическими характеристиками: =220 МПа, о„=400 МПа, о-|“180 МПа. Длина балки /=1 м. Влиянием концентрации напряжений в заделке, а также влиянием абсолютных размеров и обработки на прочность балки пренебречь.
67. Для виброизоляции машин и приборов в упругую подвеску вводит диссипативные элементы — демпферы вязкого трения. Определить динамический коэффициент для схемы, изображенной на рис. 58. Принять для расчета следующие данные: т=100 кг, <о=100 с-*, а=6 103 Н-с м'1, /=1 м, £/х= =20 кН/м.
Рже 58
28
68. Для регистрации колебательных процессов при наличии различных случайных возмущений (толчки, удары) применяются низкочастотные вибрографы, имеющие для гашения возникающих колебаний демпферы вязкого трения. Принципиальная схема такого прибора приведена на рис. 59. Здесь движение массы т, подвешенной на пружине жесткостью с, демпфируется силой движения груза, т. е. ау, где у — смещение массы относительно основания. Найти смещение, которое фиксирует
Рис. 59 Рис. 60
прибор как функцию времени, есЛи его основание движется по закону t/i = i/o(sin<i)/+2sinl0(i)0. При решении задачи принять, что ро2=с/ш=О,О1<1)2 и n=a/2m—0,02<1).
69. Для записи вибрационных процессов используют магнитоэлектрические осциллографы с петлевыми вибраторами (шлейфами), представляющими собой тонкую ленту 1 (петлю) из немагнитного материала (обычно из бронзы), натянутую между полюсами постоянного магнита. Петля опирается на две ножевые опоры (призмы) 2; в центре ее наклеено зеркальце 3 (рис. 60). Натяжение в ленточках петли создается с помощью пружины 5, оттягивающей натяжной ролик 4. При протекании тока по петле ее ветви в результате взаимодействия с магнитным полем смещаются в разные стороны, и зеркальце поворачивается на угол, пропорциональный току. В связи с требованиями повышенной точности измерения при расчете вибраторов необходимо учитывать момент сопротивления движению (Af = acp),
Составить дифференциальное уравнение малых свободных Колебаний зеркальца петлевого вибратора, считая, что при протекании тока i по одной ленточке на нее действует сила F~Bli №— индукция магнитного поля, I — длина ленточки в преде
лах магнитного поля). Определить частоту собственных колебаний системы. Натяжение в ветвях петли постоянно и равно Q, масса зеркальца т3. расстояние между опорами ленточки
70. На рис. 61 приведена схема рамочного вибратора (шлейфа) осциллографа. В отличие от петлевого вибратора рамочный имеет чувствительный элемент, выполненный в виде рамки 1 из нескольких витков проволоки, помещенной в поле постоянного магнита. Чувствительность такого прибора выше, чем петлевого, так как в магнитном поле расположено больше линий тока. Регистрация колебаний рамки (рамка поворачивает-
Рис. 61
ся на угол <р) при пропускании через нее тока осуществляется лучом света, отражаемого от зеркальца 2, укрепленного на рамке. Растяжки, удерживающие рамку и зеркальце, изготовлены в виде сплошной ленты или стержня круглого поперечного сечения.
Считая момент инерции / зеркальца и рамки относительно вертикальной оси равным 7=1,02-10~“ кг-м1, определить частоту собственных колебаний прибора. Рамка подвешена на сплошной струне из бронзы (d=0,2 мм, G=40 ГПа) длиной /=30 мм. Исследовать зависимость движения зеркальца от величины коэффициента вязкого трения а (считая момент сопротивления равным а<р) при подаче в систему тока I, создающего внезапно приложенный вращающий момент Af“Af0=const. Момент Л1о пропорционален току i, т. е. Mo=if'. Рассмотреть Для указания значений а определить частоты колебаний рам-следующие случаи демпфирования: 1) а-0; 2) а=0,6 Ус/J. ки (с — крутильная жесткость стержня).
71. Для исследования крутильных колебаний вращающихся валов применяют специальные .приборы — торсиографы (рис. 62). В торсиографе системы Гейгера массивный диск (ма ховая масса) 2 с помощью спиральной пружины I закреплен
30
внутри легкого шкива 3, который жестко связан с валиком 4,. вращающимся в подшипниках 5. Шкив 3 с помощью легкого ремня соединяется с валом, движение которого исследуется. Таким образом, вращение шкива 3 с достаточной точностью повторяет вращение исследуемого вала. При равномерном вращении вала маховик 2 также движется равномерно. При изменении угловой скорости вала шкив 3 также изменяет свою скорость, а маховик 2, обладающий значительной инерционностью, продолжает вращаться равномерно. Разность движений маховика и шкива фиксируется специальным механическим устройством (на схеме не показано). Стальной маховик имеет форму
Рис. 62
кольца, размеры которого d=50 мм, 0=100 мм, 6 = 50 мм, и укреплен на пружине с угловой жесткостью с=146 Н-м.
Составить дифференциальное уравнение относительных колебаний маховика при вращении шкива с угловой скоростью G)*=(i)o+ci)icosW. Учесть, что в системе имеется демпфирование, причем демпфирующий момент пропорционален относительной угловой скорости маховика и диска. Коэффициент момента вязкого сопротивления а= 0,73 Н-м-с. Определить сдвиг фаз колебаний маховика и диска, а также логарифмический декремент затухания колебаний прибора при £=50 с-’.
72. Для уплотнения бетона, уложенного в основания фундаментов сооружений, применяют специальные приспособления— вибраторы. Вибратор (рис. 63, а) состоит из тяжелой рамы массой т, на которой смонтированы два диска массами Wi каждый. Диски вращаются в вертикальной плоскости в
Jr
a F
Рис. 63
противоположных направлениях с угловой скоростью со. На дисках закреплены грузы массой то с эксцентриситетом е относительно оси вращения. В конце процесса уплотнения свойства бетонного основания можно приближенно описать реологической моделью, представленной на рис. 63, б.
Составить дифференциальное уравнение установившихся колебаний корпуса вибратора. Определить амплитуду колебаний, считая, что в процессе работы корпус вибратора не открывается от уплотняемой массы.
73. В бесконтактном датчике мембранного типа (рис. 64) замеряется изменение давления в трубопроводе, зависящее от величины зазора между наконечником 2 и деталью /. Регистрация давления производится путем измерения прогибов мемб-
Рис. 64
раны 3 с помощью специального индикатора 4, имеющего подвижный стержень 5.
Считая, что давление на мембрану р изменяется пропорционально изменению зазора Д, т. е., полагая, что
Др/р0= (р/Д) A sinwt
(где ро—номинальное значение давления в камере прибора; е—амплитудная величина изменения зазора Д в процессе контроля детали; со — угловая скорость детали; А — безразмерный коэффициент), построить зависимость показания датчика от угловой скорости детали, т. е. амплитудно-частотную характеристику прибора, если масса стержня 5 равна т, жесткость пружины индикатора, связанного со стержнем, равна с, а коэффициент вязкого сопротивления, возникающего при движении стержня, равен а.
При расчете принять: т=0,05 кг; с=2-10’ Н/м; р.=2Х ХЮ’ Па; Д=1 мм; е=0,1 мм; площадь мембраны Р=300 мм!; Л = 0,5; 0=1, а коэффициент демпфирования, полученный на
основании анализа свободных колебаний прибора, а“= = 10 Н-с-м-1. Массой мембраны пренебречь.
ty к а э а и и е. При изменении давления на Др на стержень действует сила со стороны мембраны, равная Др=рГДр, где р — коэффициент пропорциональности, зависящий от упругих свойств мембраны, F —площадь мембраны.
74. В качестве мультипликатора (увеличителя) в бесконтактных измерительных приборах часто используют гофрированные цилиндры — сильфоны. Незначительное изменение внутреннего давления в сильфоне вызывает относительно большое изменение его длины. На рис. 65 приведена схема сильфонного датчика для автоматического контроля овальности деталей.
В корпусе / прибора на плоских пружинах 2 жесткостью П подвешен цилиндр 4 массой т. Цилиндр 4 жестко соединен с сильфоном 5, имеющим жесткость Сч. Давление в сильфоне связано с давлением в трубопроводе 6, равным ро. Усилие предварительного натяга б0 и регулировка прибора осуществ-
Рис. 65
ляется пружиной 7 жесткостью с3. При выходе контролируемого размера из поля допуска происходит замыкание одного из контактов 8 и дается сигнал на отбраковку.
Для уменьшения времени затухания колебаний прибора при подаче детали на контроль в измерительную систему введен демпфер вязкого трения 3, сила демпфирования которого пропорциональна скорости перемещения: FT — ax.
Считая, что изменение давления в сильфоне пропорционально изменению зазора между измерительным наконечником и Деталью Ap/p,-= (е/Д)A-sin u>t, где е — амплитуда отклонения
33
от цилиндрической формы, Д — зазор между деталью и наконечником, ю — угловая скорость детали, А — коэффициент, построить амплитудно-частотную характеристику прибора. Определить диапазон угловых скоростей со, в котором динамическая погрешность измерения не превышает ±10% измеряемой величины (т. е. такой диапазон ш, в котором амплитуда колебаний массы 4 отличается от статического отклонения не более чем на 10%).
Данные для расчета: т=-0,1 кг; с(=-20 Н/см; сг=5 Н/см; с*=10 Н/см; р0“3-105 Па; Д«=1 мм; Л = 1,0; эффективная площадь сильфона Fe=400 м*. Коэффициент силы вязкого трения, определенный по осциллограмме свободных затухающих колебаний, равен а=7,5 Н с мЛ
75. Прицеп массой т движется по неровной дороге с постоянной скоростью v (рис. 66, а). Считая, что точка крепления прицепа к автомобилю (точка О) не имеет вертикальных перемещений, определить скорость установившегося движения системы, при которой амплитуда колебаний достигает максималь-
ной величины. При решении считать, что жесткость шин весьма велика по сравнению с жесткостью рессор с. Профиль неровностей дороги можно описать уравнением й = относительно точки О равен /». Считать, что в рессорах возникает вязкое трение с коэффициентом трения а. Массой колес прицепа по сравнению с массой т можно пренебречь.
Указание. При решении задачи прицеп можно представить схемой, как показано на рнс. 66, б, причем Л значительно меньше I (т. е. поворот на угол <р приводит только к вертикальному смещению точки Л).
76. К системе, изображенной на рис. 43, приложен внешний возмущающий крутящий момент, изменяющийся во времени по закону M>sin mt. Составить систему дифференциальных уравнений, определяющую установившееся периодическое движение диска.
Указание. Рассмотреть полупернод 7/2= л/А колебаний диска, состоящий из двух участков движения (см. решение задачи 47). Стыкуя эти участки, получить уравнение для определения параметров установившихся колебаний.
77. Считая, что на систему, изображенную на рис. 43, действует периодически изменяющийся крутящий момент Л1 (() = =Afosin о)?, определить амплитуду установившихся колебаний и возмущающей силы.
Указание. При решении задачи заменить кулоново трение вязким, используя условия равенства рассеиваемой энергии за период установившихся колебаний.
78. Решить задачу 47, считая, что на систему действует возмущающий момент Al^Afo-f-Af^in mt, а на диск дополнительно к кулонову трению с коэффициентом трения р действует момент сопротивления, пропорциональный угловой скорости диска и равный а<р. Вычислить амплитуду установившихся колебаний и фазовый угол. При решении воспользоваться указанием к задаче 77.
79. На массу т действует возмущающая сила, изменяющаяся по закону P(/)=P(,|sin (рис. 67). Составить уравнение вынужденных колебаний груза и определить, при какой частоте т возмущающей силы при установившихся колебаниях происходит резонанс (силами сопротивления пренебречь).
Рис. 68
Рис. 07
80. На груз массой т, подвешенный на пружине жесткостью с, действует сила притяжения P(t) электромагнита (рис. 68). Силу притяжения массы т магнитом можно приближенно представить в виде '
(Posino)/ при 2пл<<в/<(2л-}-1) я
(0 при (2n4-l)n<<i^<2(/i-t-l)n.
Составить уравнение вынужденных колебаний груза относительно положения равновесия (силами сопротивления пренебречь). -
81. Исследовать движение массы т, закрепленной на конце консольной балки длиной I, при действии на массу единичного O-f-At
импульса силы ( I P(t)dt=\) (рис. 69). Массой балки по сравнению с массой груза и затуханием при колебаниях пренебречь.
82. Исследовать движение массы т (см. рис. 69) при действии на нее внезапно приложенной силы Q, т. е. считая, что P(0 = Q=const (рис. 70).
83. Исследовать движение массы т, закрепленной на конце консольного стержня (см. рис. 69), при действии на нее силы Р(0, изменяющейся по законам, изображенным на рис. 71.
84. Исследовать движение массы (см. рис. 69) при действии на нее линейно возрастающей нагрузки P(t)—al. Считать, что при (=0 (/=z/“0.
85. На массу т (рис. 72, а) действуют периодические (период равен Т) единичные импульсы силы P(t) (рис. 72,6) одного знака. Исследовать вынужденные колебания массы и найти амплитуды ее отклонения от положения равновесия, а также скорости при этом периодическом движении. Жесткость пружины равна с (с/т=р/); трением между массой и направляющей пренебречь.
Рис 72
86. В задаче 85 исследовать вынужденные колебания массы т при действии на нее периодической импульсной нагрузки переменного знака (рис. 73).
87. Исследовать вынужденные колебания массы т (см. рис. 72, а) при действии на нее периодических импульсов одного знака конечной продолжительности tt и высоты h (рис. 74).
Рис. 73 Рис. 74
88. В задаче 85 найти периодический установившийся режим движения массы т с учетом силы трения (FTp=at/) (см. рис. 72, а).
§ 4. Критические состояния и устойчивость колебаний
89. Скорость движения жидкости по различным трубопроводам влияет на частоту их собственных колебаний. Скорость протекания, при которой частота колебаний системы равна ну
37
лю, является критической. Для системы, изображенной на рис. 75, составить дифференциальное уравнение малых свободных угловых колебаний, считая, что скорость протекающей жидкости vt постоянна. Определить значение скорости протекания 1»„ при котором движение трубки будет апериодическим. Масса трубки та, ее длина /, площадь сечения отверстия Ft, плотность жидкости р'. Трубка может свободно вращаться относительно шарнира А.
90. На тонкостенной горизонтальной шарнирно опертой безынерционной трубе укреплена деталь массой (рис. 76). Через трубу протекает идеальная несжимаемая жидкость со скоростью V. Средний диаметр трубы d, толщина стенки 6, модуль
Рис. .75 Рис. 76
упругости материала грубы Е, момент инерции сечения трубы Jx.
Определить скорость vt протекания жидкости по трубе, при которой частота свободных колебаний системы равна нулю. Начальным прогибом, связанным с действием силы тяжести системы, а также силами инерции переносного движения жидкости при колебаниях (в том числе и силой Кориолиса) пренебречь.
91. Диск разбрызгивателя, имеющий п радиальных отверстий (рис. 77), укреплен на полом валу, имеющем жесткость при кручении с. Скорость истечения жидкости из отверстий диска v0, момент инерции массы диска J.
Составить дифференциальное уравнение малых свободных колебаний диска относительно стационарного равномерного вращения, происходящего с угловой скоростью <о (с учетом влияния протекающей жидкости). Жидкость считать идеальной и несжимаемой.
Определить частоту собственных колебаний диска и скорость v., при которой частота становится равной нулю.
38
92. Решить задачу 90 (см. рис. 76) считая, что масса т подкреплена дополнительно пружиной, имеющей жесткость с.
93. На гибкий стальной вал (рис. 78) диаметром d=5 мм. длиной 2/=0,5 мм насажен диск диаметром D=100 мм и толщиной Л=10 мм. Центр тяжести диска О, расположен на расстоянии е^1 мм от оси симметрии вала О.
Получить дифференциальное уравнение малых свободных колебаний диска в векторной форме при постоянной угловой скорости вала, ограничившись только поступательным движением диска. Массой вала по сравнению с массой диска пренебречь. Определить критическую угловую скорость вала со, и наибольшие напряжения в нем при ш=100 с-*.
Указание. Под критической угловой скоростью понимается скорость, при которой амплитуда колебаний может быть бесконечно большой.
94. Вращающийся консольный вал (рис. 79) длиной I, жесткостью Е]х имеет на свободном конце точечную массу т. Пренебрегая силами сопротивления и массой вала, определить критическую угловую скорость вала.
то
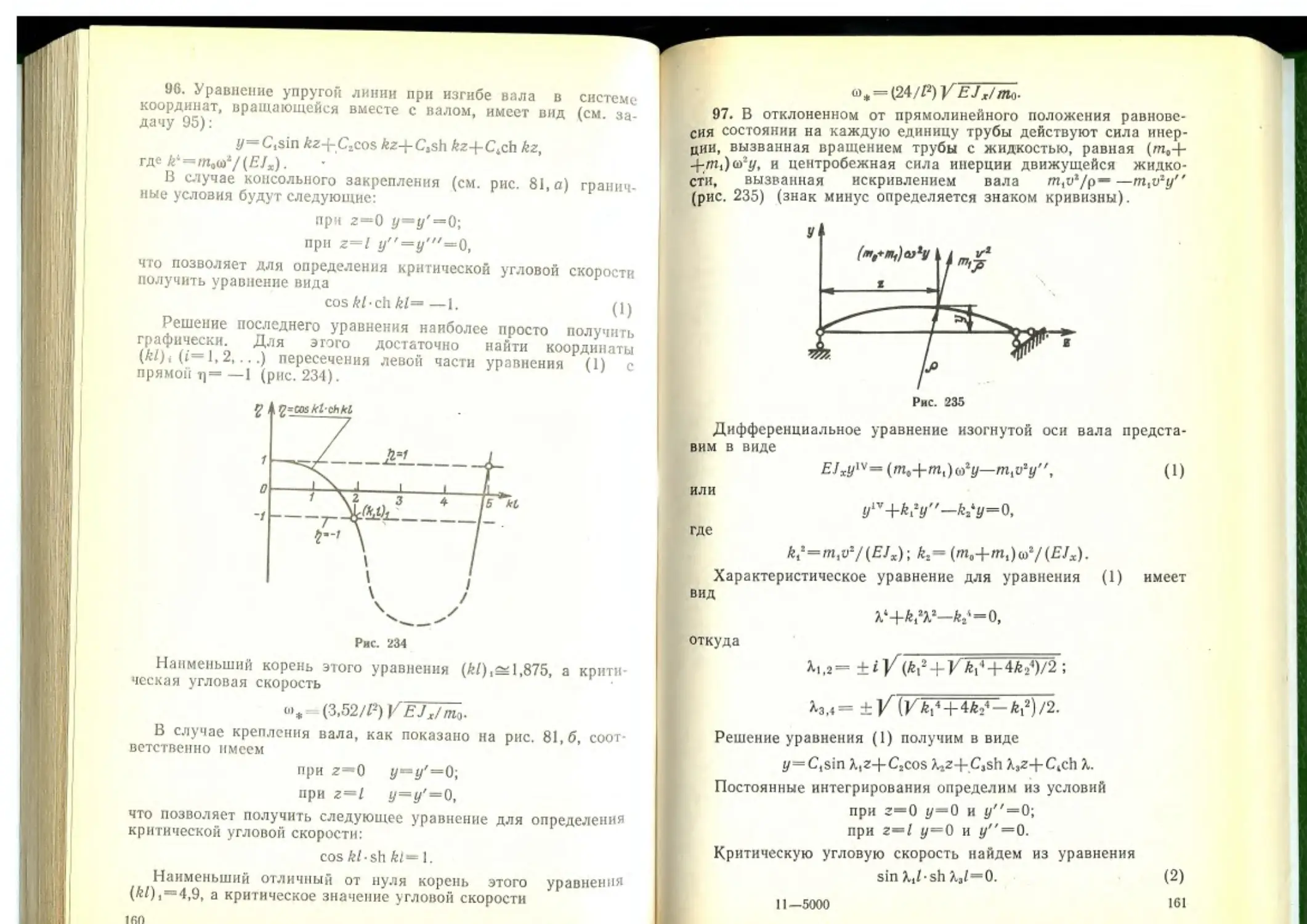
95. Гибкий вал постоянного поперечного сечения, закрепленный концами в коротких подшипниках, можно рассматривать как шарнирно опертую балку длиной I и изгибной жесткостью EJX (рис. 80). Определить критическую угловую скорость вала, при которой прямолинейная форма становится неустойчивой.
96. Определить критическую угловую скорость гибких валов постоянного поперечного сечения, при которой прямолинейная форма становится неустойчивой, для случаев закрепления концов, изображенных на рис. 81.
97. Определить критическую угловую скорость полого вала с учетом движущейся по нему идеальной несжимаемой жидкости (рис. 82). Масса жидкости, приходящаяся на единицу длины трубы ть масса единицы длины трубы т0, скорость движения жидкости в трубе v=const, изгибная жесткость вала EJX. Кориолисовыми силами инерции жидкости пренебречь.
98. Чувствительный элемент прибора (рис. 83) состоит из пружины 1 жесткостью с, рычагов 2 массой т, шанирно закрепленных в точках А, и свободно движущегося штока 3 массой тг. При стационарном режиме работы ((^“const) момент силы инерции рычагов уравновешивается моментами сил тяжести штока и сжатия пружины. Определить частоту собственных колебаний штока и критическую угловую скорость.
40
99. Определить частоту собственных колебаний масс регулятора Уатта (рис. 84) при вращении его с постоянной угловой скоростью со. При выводе дифференциального уравнения малых свободных колебаний системы пренебречь влиянием вертикального смещения масс т, на величину кинетической и потенциальной энергий системы, а также массой стержней по сравнению с массами т, и массой втулки тг. Жесткость пружины сжатия равна с. Втулка, которая передает вращение массам т,, может смещаться в вертикальном направлении.
Рис. 84
100. Решить задачу 8, предполагая, что водило в положении равновесия направлено вертикально вверх, а пружины прикреплены к водилу с некоторым предварительным натягом б ,(см. рис. 7). Определить критическую длину водила т. е. такую длину, при которой частота малых свободных колебаний равна нулю.
101. Однородный стержень постоянного поперечного сечения, имеющий массу т и длину /, прикреплен шарнирно (рис. 85) к оси, вращающейся равномерно с угловой скоростью ы. Исследовать малые свободные колебания стержня относительно положения статического и динамического равновесий (на рис. 85 угол а характеризует состояние динамического равновесия). Определить, при какой угловой скорости ш. состояние равновесия неустойчиво.
102. Невесомый жесткий стержень длиной I с массой т, укрепленной на его конце (рис. 86), шарнирно прикреплен к вращающейся с постоянной угловой скоростью ы втулке. Определить критическое значение угловой скорости а>„ при которой вертикальное положение стержня становится неустойчивым.
41
Рис. 85
Рис. 88
Найти частоту малых свободных колебаний массы относительно вертикального положения равновесия (при со<со.) и частоту ее колебаний относительно положения динамического равновесия (ПОИ (0><0.).
103. Массивный диск (рис. 87) вращается равномерно с угловой скоростью ш. В прорезь диска вставлен груз массой т, удерживаемый двумя одинаковыми пружинами. Каждая пру
жина имеет жесткость с и вставлена с предварительным натягом б„.
Составить дифференциальное уравнение малых свободных колебаний груза. Определить критическую угловую скорость диска со, (скорость, при которой положение груза в центре диска оказывается неустойчивым).
42
104. Жесткая рама вращается в горизонтальной плоскости, с постоянной угловой скоростью со (рис. 88). По радиальному пазу рамы может скользить груз, имеющий массу т, удерживаемую пружиной жесткостью с. Используя метод Лагранжа, составить дифференциальное уравнение малых свободных колебаний груза относительно положения его динамического равновесия, при котором масса т находится на расстоянии х0 от
Рис. 88
оси вращения. Определить частоту собственных колебаний груза и критическую угловую скорость рамы.
105. Тонкая, абсолютно жесткая пластинка толщиной б закреплена на круглом стержне диаметром d и жесткостью v и обдувается воздушным потоком, имеющим скорость v (рис. 89).
Рис. 89
Рис. 90
Считая, что подъемная пластинки на малый угол свободного края пластины
сила1, возникающая при отклонении а, приложена на расстоянии Л/4 от и определяется выражением
(где р — плотность воздуха; S — площадь поверхности пластинки; а — угол атаки), исследовать зависимость частоты собственных колебаний пластинки от скорости потока и определить критическую скорость дивергенции пластинки. Силой лобового сопротивления пренебречь.
Указание. Под критической скоростью дивергенции пластинки понимается скорость, при которой появляется еще одна форма равновесия при ау=0.
43
106. На упругом валике длиной /, имеющем жесткость на кручение с, закреплен массивный рычаг, момент инерции массы которого относительно оси валика равен / (рис. 90). К рычагу приложена сила Ро, линия действия которой проходит через ось валика. Считая, что при повороте рычага линия действия силы перемещается параллельно своему начальному положению, составить дифференциальное уравнение малых свободных колебаний системы. Определить частоту собственных колебаний и критическую силу F,— такое значение силы, при котором частота колебаний становится равной нулю.
107. Груз массой т укреплен с помощью упругих растяжек длиной I в постоянном однородном магнитном поле (рис. 91).
Определить частоту собственных колебаний груза, считая, что в процессе колебаний натяжение растяжек 7. не меняется. Сила притяжения массы магнитом прямо пропорциональна квадрату расстояния до магнита: +*)*]• Опреде
лить также зависимость критического значения Фо от натяжения То, считая критическим такое значение, при котором частота собственных колебаний груза равна нулю.
108. Груз массой т (рис. 92), укрепленный на конце длинного упругого стержня, помещен в постоянное однородное магнитное поле с магнитным потоком Фо. Считая, что при малых отклонениях груза от положения равновесия сила со стороны магнитного поля пропорциональна смещению х (см. задачу 107), определить частоту собственных колебаний груза н критическое значение напряженности магнитного поля. Влиянием массы стержня пренебречь.
109. На шарнирно закрепленной невесомой балке укреплена точечная масса т (рис. 93). По балке с постоянной скоростью v движется сосредоточенная сила Ro. Определить (приближенно) закон изменения вертикального смещения мас-
44
сы т и установить, имеется ли критическая скорость v движения силы /?,, при которой амплитуда колебаний массы т безгранично возрастает.
§ 5. Параметрические колебания
110. Маятник (рис. 94) представляет собой груз массой т, закрепленный на невесомом стержне длиной I. Верхняя точка подвеса маятника совершает периодическое движение по закону yt=t/osin (at. Исследовать устойчивость малых колебаний маятника при to=10 с-1, /“=0,5 м, т=1 кг, г/0= 10 мм.
Рис. 94
Рис. 95
111. На рис. 95 изображена схема астатического маятника. При движении точки закрепления О маятника с некоторой частотой со вертикальное положение груза является устойчивым. Определить наименьшую частоту Ыпвп. при которой система устойчива, если движение точки О совершается по закону у\— *=yosin ы/, /=0,2 м; у«=5 мм.
112. Стальной абсолютно жесткий стержень постоянного поперечного сечения длиной /=0,12 м, массой т=0,2 кг шарнирно закреплен нижним концом на плите, совершающей колеба-
ния с амплитудой г/0= Ю мм (рис. 96). . Считая движение опоры гармоническим (</, = t/osin щ/), определить, при какой наименьшей частоте Umm вертикальное положение стержня становится устойчивым.
ИЗ. Тонкая прямоугольная стальная пластинка размерами &Х/Х6 помещена в воздушном потоке (рис. 97). Один край пластинки закреплен шарнирно, а другой имеет упругое закреп
Рис. 96
Рис. 97
ление с общей жесткостью с. Скорость течения потока изменяется по закону v+v»+V<sin <о/.
Составить дифференциальное уравнение малых колебаний пластинки и исследовать их устойчивость, считая, что Точка приложения подъемной силы находится на расстоянии 1/4 от передней кромки пастинки. Числовые данные для решения задачи: /=6=0,2 м; 6=5 мм; р=0,125 кг/м1; с=2,5 кН/м; ш=100 с-'; ио=ЗО м/с; У(=5...1О м/с амплитудное значение скорости.
Указание. При составлении уравнения малых колебаний можно считать. что подъемная сила
Y=0,5cvEpvi,
где св=2ла— коэффициент подъемной силы; Е=Ы — площадь пластинки; р—плотность воздуха; v—скорость потока; а — угол атаки.
114. Упругий стержень длиной 2 I с шарнирно закрепленными концами подвергается воздействию осевой периодически изменяющейся силы P=P,-}-PiSin со/ (рис. 98).
Составить дифференциальное уравнение движения массы т, закрепленной на стержне, при его малых поперечных колебаниях. Массой стержня по сравнению с массой груза пренебречь. Исследовать устойчивость малых колебаний системы, если длина стержня 2 1=2 м, момент инерции площади поперечного сечения /х=10-’ м‘, модуль упругости материала £=200 ГПа, т=5 кг, Ро=5О Н, Р, = 20 Н, со=10 с"‘.
115. Составить дифференциальные уравнения малых колебаний массы т, закрепленной на стойке длиной 21 (рис. 99), при действии на стойку периодически изменяющейся осевой силы
46
Рис. 98 Ряс. 99
P=Po+Psintt>f. Исследовать устойчивость малых колебаний, считая; 1=1 м, J =10“* м\ Е=200 ГПа, т=5,2 кг, Р„=50 Н, Pi =20 Н, ф=30 с-’.
116. Масса т подвешена на двух струнах-растяжках длиной каждая (рис. 100). Исследовать устойчивость малых вертикальных колебаний груза при изменении усилия натяжения по зако-
ну 7"=Ро+ Т\ sin at. Массой струн и их растяжимостью при решении задачи пренебречь. Принять То=2О Н, Л = 10 Н, о> = =25 с-1, т = 0,25 кг, 1=0,2 м.
117. Стальная балка длиной / имеет на свободном конце точечную массу т (рис. 101). Исследовать устойчивость малых вертикальных колебаний массы т, если длина балки изменяется по закону /=1о—A sin at. При решении задачи массой балки по сравнению с массой т пренебречь. Принять /0=1 м, /| = **=0,2 м, т = 2 кг, ш = 20 с"1, /х=8,310“10 м4, Е=200 ГПа.
118. Масса т подвешена на абсолютно гибкой нерастяжимой нити таким образом, что длина свободного участка нити оавня ‘о (рис. 102). Составить ----
колебаний груза, если точка О (отверстие, из которого выходит нить) перемещается относительно своего среднего положения по закону у\—уоsin и/.
Дифференциальное уравнение колебаний получить двумя методами: 1) используя теорему об изменении момента количества движения; 2) используя принцип Даламбера.
119. Составить дифференциальное уравнение малых колебаний маятника с периодически изменяющейся длиной нити (рис. 103). В произвольный момент времени длина нити маятника равна /=/о-(-/| sin (at.
120. В тяжелой раме массой т\, подвешенной шарнирно в точке 0, установлен кривошипно-ползунный механизм, приводящий в движение массу т (рис. 104). При работе системы положение ее центра тяжести меняется вследствие изменения положения массы т.
Рис. 105
Рис. 104
Составить дифференциальное уравнение малых колебаний системы, считая, что расстояние от точки подвеса до центра тяжести рамы 1\, а при горизонтальном положении кривошипа расстояние от точки О\ до центра массы т равно /о; момент инерции массы рамы относительно точки подвеса У,, угловая скорость кривошипа to, плечо кривошипа х0. Массами ползуна и кривошипа по сравнению с массой т пренебречь.
121. Масса т, укрепленная на маятнике, принудительно перемешается относительно его оси по закону х = х sin (рис. 105). Составить дифференциальное уравнение малых колебаний маятника, пренебрегая массой стержня и рамы по сравнению с массой груза.
122. На вагонетке массой т (рис. 106) закреплен растяжимый трос, конец которого жестко связан в точке А со шкивом радиусом /?. В состоянии равновесия (при х=0) длина троса равна /о, а натяжение в нем Го. Расстояние от рельса до блока
Составить дифференциальное уравнение малых горизонтальных колебаний вагонетки, если шкив совершает двнже-
Рис. юв
Рис. 107
ние по закону <р=<р0 sin <os, а вагонетка в начальный момент времени получает отклонение, равное х0. Исследовать устойчивость малых колебаний вагонетки, если Го=103 И, /п=500 кг, ^о=1 м, фо = 0,1 рад, 1о1иО,7 м, площадь поперечного сечения троса F=10"4 м* /? = 0,1 м, <o=10 с-1, модуль упругости троса £=200 ГПа. Трением в системе пренебречь.
123. Составить дифференциальное уравнение малых колебаний массы т, закрепленной на конце упругого стержня (см. рис. 92), в магнитном поле с переменным магнитным потоком Ф = Фо+Ф1 sin ы/. Амплитудное значение магнитного потока Ф|
4—5000
49
считать малым, т. е. слагаемыми, содержащими Ф|2, можно пренебречь.
Исследовать устойчивость малых колебаний массы, считая т=500 кг, /==0,21 м. Изгибная жесткость стержня £/я= = 2-103 Н-м2; (0 = 200 с-1; а!=10 мм; (Л/си3) Ф02= 10 Н; (^Ф0/а|3)Ф1 = 1 Н.
124. В магнитном поле, создаваемом постоянным током /(, протекающим по бесконечно длинному жесткому проводнику /, помещена шина 2 массой т (рис. 107). По шине 2 пропускается ток 12 = i2o+h\ sin о/. Взаимодействие двух магнитных полей создает силу притяжения шины 2 к проводнику 1, равную F = =2ц/\lilla\t где ц—магнитная проницаемость, ai — расстояние между проводниками в произвольный момент времени.
Составить дифференциальное уравнение поступательного движения шины 2, считая, что жесткость каждой из удерживающих ее пружин равна с, расстояние между проводником и шиной в состоянии покоя (при /2=/2о) равно а0.
125. Полагая, что сила Р, приложенная к рычагу, изменяется по закону P=P0+Pi sin at (см. задачу 106, рис. 90), исследовать устойчивость малых колебаний системы. Принять с= =80 Н-м, Ро=ЮОН, Л = 40 Н, /? = 0,2 м, Д=10 с"1, /= =0,4 кг-м2.
126. Вывести дифференциальное уравнение малых колебаний массы т (см. рис. 25), движущейся с постоянной скоростью v по абсолютно гибкой струне. Натяжение струны То считать постоянным.
127. На абсолютно гибкой нити длиной I подвешен маятник (рис. 108). Считая, что усилие натяжения нити Т = 7"о = const, исследовать устойчивость малых колебаний маятника. Статический прогиб нити в точке подвеса маятника равен уст, длина маятника /ь масса т. Принять, что при / = 0 точка подвеса маятника имеет вертикальное смещение ую, а ее скорость <лю=0;
маятник отклонен на произвольный угол ср. Рассмотреть два случая:
1) координата точки подвеса Si=0,3 I, начальное натяжение т =40 Н, длина маятника /) = 0,3/, масса маятника т = 0,1 кг, 2-0,1
* 2) То" Ю Н, /i=0,i I (остальные параметры те же, что и в варианте 1).
128. Масса ш укреплена на невесомом стержне длиной I (рис. 109). Верхний конец стержня (точка подвеса маятника) соединен с пружиной, имеющей жесткость с. Считая, что точка подвеса маятника О может совершать только вертикальные колебания, и пренебрегая массой ползуна т’ по сравнению с массой т, исследовать устойчивость малых угловых колебаний маятника для двух случаев начальных условий:
1) при /=0 точка подвеса маятника имеет смещение относительно положения равновесия уо=40 мм, а ее скорость уа~0.
2) при (=0 отклонение точки подвеса маятника от положения равновесия уо=О, уо"О,1 м/с, гл=0,2 кг, с=1 кН/м, /= = 80 мм.
§ 6. Случайные колебания
129. Решить задачу о движении прицепа по дороге с неровностями (см. задачу 75, рис. 66), считая, что неровности имеют случайный характер. При решении считать, что в результате статистических исследований получена спектральная плотность воздействия дороги на систему 5л(<й) в зависимости от скорости движения и в предположении, что колебания системы можно рассматривать как случайный стационарный процесс
Sh(<o) =ai7l(<i)2+6u2) 2л],
где v — скорость движения, м/с. ,
Определить среднеквадратичное отклонение о, угла колебаний <р в зависимости от скорости и движения прицепа. Построить график о»(к) при следующих значениях параметров системы: Jo— 5-103 кг-м2; с = 2-105 Н/м; I =2,5 м; а=105 Н-с-м_|; а== 1000 мм2/м; 6 = 2,5-10s м2.
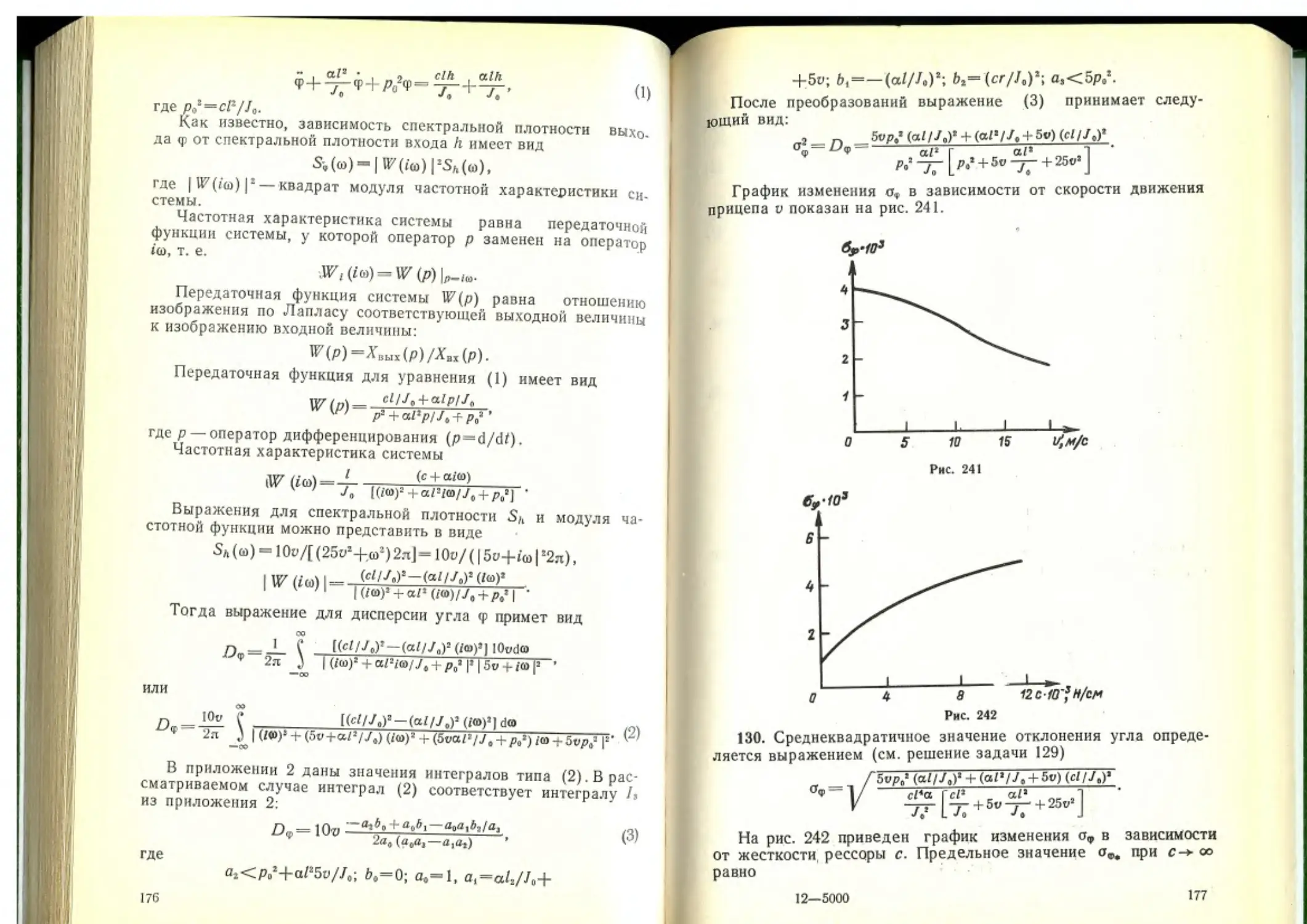
Примечание. Значения интегралов, получающихся при решении задачи, даны в приложении 2.
130. Построить график изменения среднеквадратичного отклонения угла <р колебаний прицепа (см. задачу 129) в зависимости от жесткости рессоры с при скорости движения прицепа v=10 м/с. Числовые данные аналогичны данным, приведенным в задаче 129.
131. Определить среднеквадратичное отклонение tr„ угловой скорости ср колебаний прицепа при движении его по дороге с Неровностями (см. задачу 75), если спектральная плотность воздействия дороги на прицеп
$л (<в) = 10 v/[ (251>2+со2) 2л].
4*
51
Числовые значения параметров системы принять такими же, как в задаче 129.
132. На точечную массу т, закрепленную на невесомой упругой балке длиной 21 (рис. 110), действует случайная возмущающая сила f. Демпфирование колебаний осуществляется демпфером вязкого трепня с коэффициентом трения а. Спектральная плотность случайного возмущения j определяется выражением
S,(<D)=pl/2n(P22-H1)2).
Рис. НО
Определить среднеквадратичное отклонение ускорения перемещения массы у при следующих параметрах системы: т = = 10 кг; /=0,5 м; £=200 ГПа; а = 2000 Н-с-м-1; р, = 105 Н2/с; р2= 100 с-1; 6=20 мм; 6=50 мм.
133. Определить среднеквадратичное отклонение реакций балки (см. рис. НО) и наибольшее нормальное напряжение при колебаниях массы т под действием случайной возмущающей силы f. Спектральная плотность стационарного случайного возмущения f равна S/(<о) =р1/2л(р224-й)2) (числовые данные аналогичны данным задачи 132).
134. В установившемся режиме работы угловая скорость двигателя равна Q (рис. 111,а). При этом момент двигателя Мд уравновешивается моментом сопротивления Л1с.
Считая, что момент сопротивления зависит от угловой скорости 52 (рис. 111,6), определить дисперсию отклонения угловой скорости от номинального значения Йо при действии на систему дополнительного стационарного случайного момента сопротивления ЛЛ1, математическое ожидание которого тлМ и
52
^реляционная функция KAMT~De~a^ известны. При решении задачи считать, что приведенный момент инерции системы равен /, а изменением момента двигателя Мд при малых отклонениях угловой скорости можно пренебречь.
135. В задаче 69 рассмотрены колебания петлевого вибратора магнитоэлектрического осциллографа (см. рис. 60). В реальных условиях протекающий ток имеет случайную составляющую, т. е. он равен t=io+Ai, где i0 — среднее (расчетное) значение протекающего тока, Д/ — случайная составляющая тока. Источником появления случайной составляющей тока может служить, например, беспорядочное тепловое движение электронов в проводниках электрической цепи. Если ограничиться рассмотрением моментов времени работы осциллографа в моменты времени, достаточно удаленные от начала работы, когда все переходные процессы в системе можно считать законченными, то колебания зеркальца, вызванные случайной составляющей тока, можно рассматривать как стационарные колебания.
Считая, что воздействие случайной составляющей тока Дс на систему можно рассматривать как «белый шум» с известной постоянной спектральной плотностью 5Д|(<1))=Л\ найти среднеквадратичное отклонение показаний осциллографа о,.
136. На консольной балке двутаврового поперечного сечеуия установлен электродвигатель массой т (рис. 112). Гашение колебаний осуществляется демпфером вязкого трения, имеющим коэффициент трения а. Пренебрегая массой балки и рассмат-
Рис. 112
ривая двигатель как точечную массу, определить максимальные нормальные напряжения, возникающие в балке при случайных вертикальных смещениях заделки (точка О). Случайное вертикальное смещение точки О(у0) можно рассматривать как стационарную случайную функцию с известной спектральной плотностью Syo(w), равной
Sy. (ш) =20/[(I02+g?) 2л].
Провести числовое решение задачи при следующих значениях параметров системы: Е=200 ГПа; т = 300 кг; а= = 5-104 Н-с-м-1; 1=2 м; сечение балки — двутавр № 10 (/*= «= 1,98-10-» м<; W*=3,97-10-5 м3).
53
137. Определить среднеквадратичное отклонение аи массы т (рис. 113) и дисперсию DM изгибающего момента в заделке при действии на систему случайного стационарного возмущения Р(1). спектральная плотность которого
5р(ю) = аЦ(Ь2+ы2) 2л].
Рис. 113
138. На консольной балке жесткостью EJ закреплен мотор массой т (см. рис. 112). Колебания системы, вызываемые кинематическим возбуждением — вертикальным перемещением заделки — гасятся демпфером жидкого трения, имеющим коэффициент трения а. Кинематическое возбуждение происходит по закону
Уо=Уо\ sin <at+Sy0(t),
где i/oi — амплитуда систематического смещения; Д1/о(/)—случайная стационарная составляющая смещения, имеющая спектральную плотность 5ДУо =а1Д(р24-й)2) 2л].
Определить среднеквадратичное отклонение разности между случайной составляющей смещения массы т(Др) и случайным смещением заделки Ау0.
139. Для замера давления жидкости или пара используется прибор, схематично показанный на рис. 5. Давление Др, действующее на поршень, площадь которого F, имеет наряду с систематической составляющей Др0 случайную составляющую Др| с известной спектральной плотностью S дР1 =а)((Р2-|-(1)2) 2л]. При движении поршня между поршнем и цилиндром возникает сила трения, пропорциональная скорости движения Дг с коэффициентом пропорциональности а.
Определить среднеквадратичную погрешность показания прибора, считая, что его случайное отклонение Azi можно рассматривать как случайную стационарную функцию.
140. В общем случае действия сил поршень прибора для замера давления (см. рис. 5) может иметь случайное перемещение, вызванное действием двух случайных возмущений: составляющей случайного давления &pt (см. задачу 138) и случайных, колебанием основания, к которому прикреплен цилиндр (вертикальное случайное смещение Дз0)- Случайное вертикальное смещение цилиндра эквивалентно кинематическому возмущению системы. Спектральные плотности случайного давления Apt и случайного смещения Дао соответственно равны
54
S^.-ai/KPi2+<>*) 2л] и S^, = a2/[(p,2-f-«2)2n].
Считая, что при движении поршня на него действует сила сопротивления, равная ccAz, и полагая, что корреляция между случайными возмущениями отсутствует, определить среднеквадратичное отклонение од,, погрешности показания прибора (Д2| — случайная составляющая смещения штока).
141. На поршень измерительного прибора (см. рис. 5) действует случайное давление Api в виде <белого шума» со спектральной плотностью 5лр,—М. Прибор прикреплен к основанию, которое совершает случайные вертикальные колебания Дго, спектральная плотность которых 5до,=а2/[(Р22+<о2)2л]. Под действием случайных возмущений Др| и Дг0 шток получает случайное смещение Дгь что вызывает погрешность показаний прибора.
Считая, что корреляция между Др! и Ддо отсутствует, определить оптимальное значение жесткости пружины с, при котором среднеквадратичная ошибка измерения становится минимальной.
142. Масса т подвешена на пружине жесткостью с и связана с демпфером вязкого трения, коэффициент трения которого а (рис. 114). Точка крепления пружины совершает случайные
Рис. 114
стационарные вертикальные колебания у0. Корреляционная функция случайного смещения у0 известна Л\, (т) =*Z\,e_e'’L Определить среднеквадратичное отклонение ускорения массы т.
143. На массу /п==100 кг (рис. 115), подвешенную на конце пружины жесткостью с*=400 Н/м, действует случайная возмущающая сила, ограниченная по модулю. Значения этой силы p(t) заданы полем допуска, внутри которого они могут изменяться во времени произвольным образом.
Установить наихудшнй возможный закон изменения силы P(t), при котором в момент времени /„=2 с смещение массы становится максимальным. Определить максимальное смещение груза. Полученное смещение сравнить со смещением от действия внезапно приложенной постоянной силы, равной максималь
55
но возможному значению P(t). Принять, что при /=0 смещение массы относительно положения статического равновесия и ее скорость равны нулю.
144. Масса т находится под действием силы Р(0, сообщающей ей в момент времени t»=2 с наибольшее возможное смещение (см. задачу 143). Определить скорость массы т.
145. Масса т—100 кг закреплена на горизонтальной плоскости с помощью пружины жесткостью с=400 Н/м (рис. 116, а).
Рис. 116
Между грузом и основанием при движении груза действует сила трения, пропорциональная скорости движения груза (Л=ах; а=400 Н-с-м-1).
Установить закон изменения возмущающей силы F(t), действующей на массу и заданной полем допуска (см. рис. 116, б), при котором смещение массы в моменте времени /*=2 с становится наибольшим (при нулевых начальных условиях).
146. Для определения тяги реактивного двигателя его устанавливают на стенде, состоящем из тележки и силоизмерите-ля — динамометра (рис. 117, а). В связи с неравномерностью горения заряда и его неоднородностью тяга R в процессе работы двигателя может изменяться произвольным случайным образом в пределах /?=/?0±Д/? (рис. 117, б).
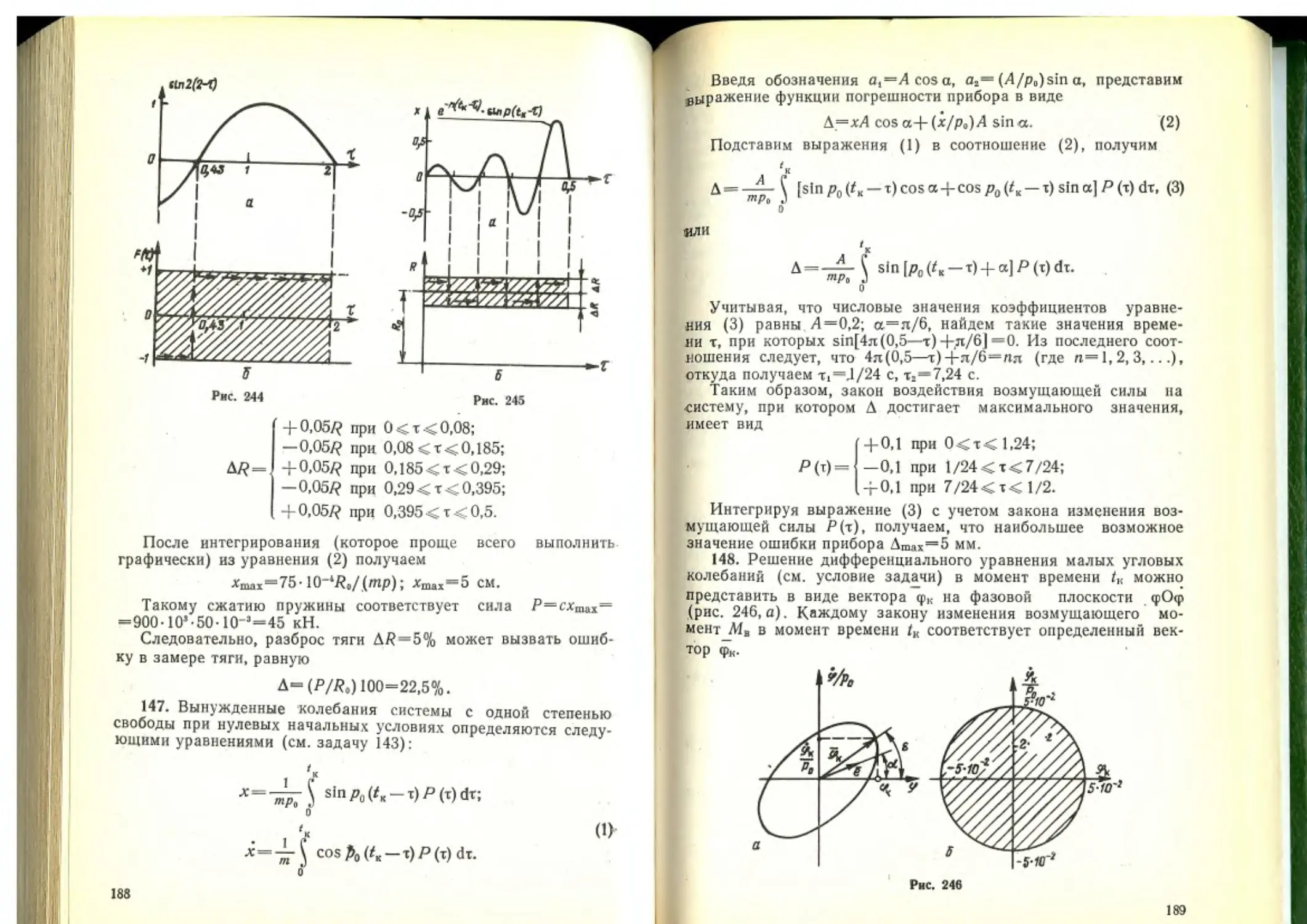
Определить максимально возможную погрешность показаний динамометра в момент окончания работы двигателя при следующих параметрах системы: суммарная масса системы т = = 1000 кг, время работы двигателя 1*=0,5 с, жесткость динамометра с=900 кН/м, коэффициент силы вязкого сопротивления а=4-104 Н-с-м-1. номинальное значение тяги /?0= = 2-105 Н, разброс тяги Д/?=±0,05 Ro. Изменением массы системы в связи с выгоранием заряда пренебречь.
147. Погрешность А прибора, замеряющего параметры колебательного процесса какой-либо системы, линейно зависит от
дополнительного смещения и скорости системы (вызванных действием на систему случайной возмущающей силы P{t):
Д=в]х+а2х,
где Oi и а2— постоянные коэффициенты, а х удовлетворяет уравнению вида mx+cx*“P(t). Случайная возмущающая сила 'p(t) задана полем возможных значений (см. рис. 115, б) с границами, равными ±1 Н.
Определить максимально возможное значение ошибки измерения А в момент /«—0,5 с, если х(0) =х(0) «=0, т=1 кг, с— =0,16 кН/м, а,= 1,73-10~‘, а2—8-10~3 с.
148. Динамически устойчивое движение ракеты может сопровождаться ее малыми колебаниями на траектории полета, которые вызываются в первую очередь разбросом тяги двигателя, линейным и угловым эксцентриситетами тяги и др. Дифференциальное уравнение малых угловых колебаний ракеты (рис. 118, а) по углу тангажа имеет вид
7оф+йф=Л1,,
где Л —момент инерции ракеты относительно оси, проходящей через центр тяжести О; Л1„ — случайный возмущающий момент (вызываемый, в частности, газодинамическими эксцентриситетами тяги), величина которого известна в виде поля допуска (рис. 118, б), имеющего границы ±Ь; а<р — восстанавливающий момент.
Рис. 118
Рис. 119
Определить область возможных значений угла отклонения Ракеты от курса <р и угловой скорости ф (область на фазовой
57
плоскости (<рОф] в момент времени ^“5 с. При решении задачи считать, что при 1=0 ф(0)=ф(0)=0; 10‘ кг-м1; а=1,6Х
Х10‘ Н-м/рад, |Ь|=2 МН/м.
149. В задаче 135 была определена среднеквадратичная ошибка показания осциллографа (см. рис. 60) (среднеквадратичное отклонение угла поворота зеркальца) в предположении, что изменение угла Дф во времени можно рассматривать как случайный процесс. Это предположение справедливо только в случае, когда время затухания переходных процессов мало по сравнению со временем наблюдения и случайный ток Д1 является стационарной случайной функцией.
При малом затухании (малом коэффициенте п) время переходных процессов может быть одного порядка со временем наблюдения, а ток Д1 не является стационарной случайной функцией. Тогда теорией стационарных случайных процессов пользоваться нельзя. Для исследования малых колебаний зеркальца методами теории нестационарных случайных процессов требуется дополнительная информация о случайном токе AZ, получать которую весьма трудоемко (необходимо знать математическое ожидание и автокорреляционную функцию во времени).
Определить максимально возможную ошибку показаний осциллографа при нестационарном случайном токе AZ, если известно только поле возможных значений AZ с границами ±а, где |а| — |А<т»ж| =0to (например, lAZm„l=0,05 10).
150. Масса т закреплена на абсолютно жесткой балке, имеющей момент инерции массы относительно левой опоры /0 (рис. 119, а). Правая опора балки представляет собой пружи ну жесткостью с с демпфером вязкого трения (коэффициент трения а). На массу т действует случайная возмущающая сила P(t), заданная полем допуска (рис. 119, б).
Определить максимально возможное значение динамической реакции, возникающей между массой т и балкой. Установить, как изменяется динамическая реакция с уменьшением коэффициента силы вязкого сопротивления а. При решении задачи считать начальные условия нулевыми.
151. Как изменится выражение для динамической реакции Wmax (при малом <х) в задаче 150, если возмущающая сила P(t), действующая на массу т, изменяется во времени по закону P(t) =asin<i)Z (где u=p0)- т. е. имеет место случай обычного резонанса.
152. Решить задачу 150 о движении балки под действием случайного, ограниченного по модулю возмущения (см. рис. 119), считая, что в начальный момент времени 1=0 балка имеет угловую скорость фо, а ее смещение фО=0. Определить закон изменения во времени возмущающей силы P(t), при котором в момент времени t^^n/Po (где р0 — частота свободных незатухающих колебаний системы) угловая скорость ф(1*) достигает экстремального значения. Считать, что демпфирование колебаний отсутствует (а=0).
5Я
§ 7. Нелинейные колебания
153. Составить дифференциальное уравнение свободных колебаний системы, состоящей из двух дисков массами и т2 (диаметрами D{ и D2 соответственно), связанных жестким стержнем длиной I (рис. 120). Верхний диск может перекатываться по опорной плоскости без проскальзывания. Массой соединительного стержня пренебречь.
154. Жесткий брус постоянного поперечного сечения длиной 21 и массой т шарнирно укреплен в точке А и поддерживается двумя пружинами жесткостью с каждая (рис. 121). Составить дифференциальное уравнение свободных колебаний бруса, считая зависимость силы сопротивления пружины от удлинения
Рис. 120 Рис. 121
155. Жесткий брус длиной 21 постоянного Поперечного сечения массой т подвешен за верхний конец и поддерживается
Рис. 122
RQ
двумя пружинами жесткостью с каждая (рис. 122). Составить дифференциальное уравнение свободных колебаний и определить частоту собственных колебаний бруса.
156. Масса т может свободно (без трения) перемещаться вдоль направляющих (рис. 123). По обеим сторонам груза установлены две одинаковые пружины жесткостью с каждая. Между упорами и пружинами имеется зазор Л. Найти частоту колебаний системы в зависимости от амплитуды х©.
Рве, 123
Рис. 124
157. Решить задачу 156, считая жесткости пружин различными (Ci и с2).
158. Масса т (рис. 124) может свободно (без трения) перемещаться по плоскости, контактируя попеременно с одной или другой пружиной. Пружины не прикреплены к грузу и в положении равновесия (при отсутствии зазора между пружиной и грузом) не напряжены. Жесткости пружин различны и равны Ci и с2. Определить частоту колебаний системы.
159. Для уменьшения влияния вибраций на работу приборов последние устанавливают на амортизаторах, собственная частота которых значительно 1меныпе частоты возбуждения. При этом желательно, чтобы отношение частоты вибраций к частоте малых свободных колебаний для всех объектов амортизации было постоянным вне зависимости от их массы. Определить характеристику такого равночастотного амортизатора (зависимость перемещения от силы), если известно, что при силе Р=Ро перемещение объекта равно Хо.
160. Считая, что правый конец нити закреплен (см. рис. 100), а начальное натяжение равно То, получить уравнение вертикальных колебаний массы т с учетом изменения натяжения в нитях, вызванного смешением массы. Решение изобразить на фазовой плоскости. Принять, что при t=0 х-0, х=х0.
161. К массе т прикреплены свободно (без предварительного натяга) пружины длиной Iq и жесткостью с каждая (рис. 125). Считая, что масса перемещается по плоскости с пренебрежимо малым трением, установить зависимость между частотой и амплитудой свободных колебаний массы, если в начальный момент времени (/=-0) масса отклонена от положения равновесия на величину х©.
60
162. Установить зависимость между частотой свободных колебаний и скоростью движения груза (см. задачу 161, рис. 125), если в начальный момент времени массе т сообщена скорость Хо (отклонение от положения равновесия Хо=О).
163. Используя фазовую плоскость, построить решение задачи о колебаниях массы (см. рис. 125), считая, что трение между опорой и массой отсутствует, а натяжение в пружине при равновесии массы равно То (пружины имеют предварительное натяжение).
Исходные данные для расчета следующие: при t=0 хо=О, Хо=*1О мм; /=50 мм; с=500 Н/м; т=0,1 кг; T0=l Н.
164. Построить траекторию движения массы (см. рис. 125) на фазовой плоскости, считая, что между массой и направляющей возникает кулоново трение, а пружины имеют предварительное натяжение, равное То. При решении задачи принять, что сила сухого трения F = F“=2,5-10-2 Н; Tq— 1 Н; ш=0,1 кг; с=500 Н/м; /о=50 мм. Начальные условия: при /=0 хо=О, Хр= = 10 мм.
165. Масса m закреплена на нелинейном упругом элементе, имеющем характеристику F=cx+C[X3 (рис. 126). Составить дифференциальное уравнение свободных колебаний массы пг (пренебрегая трением) и установить зависимость между частотой колебаний и амплитудой, считая, что в начальный момент времени отклонение массы от положения равновесия равно А, а скорость движения равна нулю.
Исходные данные для расчета: Л = 1 с/м; с—100 Н/м; С| = ®=50 Н/м, т=100 кг.
Указание. При решении задачи воспользоваться методом Ляпунова— Линстедта, ограничившись первым приближением.
61
166. Решить задачу 165, воспользовавшись методом линеаризации, т. е. заменяя нелинейную характеристику пружины линейной из условия минимума квадратичного отклонения линейной характеристики от нелинейной.
167. Получить зависимость частоты колебаний массы (см. задачу 165) от амплитуды, используя метод Галеркина.
168. Используя метод линеаризации по минимуму квадратичного отклонения, определить частоту колебаний массы т (см. задачу 156), считая, что амплитуда колебаний равна А.
169. Масса т (см. рис. 125) укреплена двумя пружинами-растяжками, имеющими начальное натяжение То. Считая, что колебания массы происходят без трения ее о поверхность, определить такое значение начального отклонения х0, при котором частота колебаний массы равна 5 с-1. Задачу решить методом малого параметра (методом Ляпунова—Линдстедта), ограничившись первым приближением. Принять, что т=10 кг; /о= =0,5 м; То=5О Н; с=2 кН/м.
170. Исследовать движение массы т в магнитном поле Фо (см. рис. 92), если в начальный момент времени (/=0) масса отклонена от положения равновесия на величину Хо. При выводе дифференциального уравнения движения массы учесть первый нелинейный член силы притяжения.
Определить критическое значение начального отклонения Хо и построить график зависимости х<> (Фо) - Установить область значений х0 и Фо, при которых колебания массы устойчивы.
171. Определить частот}' колебаний шины В (см. рис. 107 к к задаче 124) при протекании по проводнику и шине постоянных токов /[ и /j одного направления, считая, что при 1=0 х= =Хо, х=0, а расстояние между шиной и проводником в положении равновесия равно а<>. Силу взаимодействия между проводником и шиной .при отклонении последней от положения равновесия [F-=2g/|/2//(ao+-v)l представить в виде ряда, ограничившись разложением его до членов х’ включительно. Решение задачи провести методом малого параметра (методом Ляпунова—Линдстедта), взяв в качестве малого параметра ц> = =хо/а0.
172. Решить задачу 170 в предположении, что точки Л и Jt в проводнике и шине имеют противоположные направления
173. Определить частоту свободных колебаний шины В (см. рис. 107) при протекании по ней и по проводнику А постоянных токов Л и /2 одного направления, считая, что в начальный момент времени (1=0) отклонение шины от положения равновесия равно нулю, скорость движения равна хо, расстояние между проводником и шиной в положении равновесия равно ад, а сила их взаимного притяжения при отклонении от положения равновесия F=2nfJ2l/(d0+x). Решение получить, используя метод малого параметра и ограничиваясь при разложении силы F в ряд членами не выше х3.
174. Известно уравнение свободных колебаний математического маятника
<p+(^+/)sin<p—О,
_де I — длина маятника.
Найти частоту его свободных колебаний, ограничиваясь двумя первыми членами разложения sin ф в ряд. Принять, что в начальный момент времени маятник отклонен на угол ф0. При решении задачи применить метод малого параметра и метод прямой линеаризации и сравнить полученные результаты.
F 175. Определить частоту колебаний рычага (см. рис. 90) при действии на него постоянной силы Ро. Момент инерции массы / рычага равен J, а жесткость вала — с.
Считать, что колебания рычага достаточно велики, поэтому при разложении в ряд считать sin <р = ф—ф3/6. Принять, что в начальный момент времени угол поворота рычага ф(0)=0, а его угловая скорость ф(0)=фо. При решении задачи использовать метод малого параметра и метод Галеркина; полученные решения сравнить.
176. Тяжелый рычаг массой т жестко закреплен на валу длиной I и жесткостью с (рис. 127). Один конец вала защем-
лен, а другой проходит через подшипник. При колебании рычага в подшипнике возникает момент силы трения, пропорциональный квадрату угловой скорости ф вала (МТр=Лф2).
Считая, что момент инерции массы рычага относительно осн нала равен /, а расстояние от оси вращения до центра тяжести Рычага равно /о, установить зависимость между частотой колебаний рычага и начальным его отклонением от положения равновесия на первом и втором полупериодах колебаний, а также значения амплитуд в конце полупериодов (приближенные), используя метод малого параметра, т. е. полагая a=k/J малым
63
177. Масса т закреплена на конце нелинейного упругого элемента (пружины) (рис. 128). Установить зависимость между амплитудой вынужденных колебаний массы и амплитудой гар. ионической возмущающей силы Р= Ро sin со/, считая, что характеристика пружины имеет вид Т=сх+С\Х3, а трение отсутствует. Вычислить амплитуду колебаний, если Ро=20 Н, <!)=□ = 10 с-1, /п= 10 кг, с= 1,5 кН/м, Ci = 2 МН/м3-
Рис. 128
178. Для системы, изображенной на рис. 128, определить, при каком значении частоты возмущающей силы со. возможно существование двух режимов установившихся колебаний. Вычислить амплитуду колебаний на этих режимах (исходные данные см. в задаче 176).
179. Получить приближенное (по методу Дуффинга) решение уравнения вынужденных колебаний массы т (см. задачу 177), считая, что в начальный момент времени масса т имеет максимальное отклонение Хо от положения равновесия. Числовые данные те же, что и в задаче 177.
180. Решить задачу 177 в предположении, что при движении массы т возникает сопротивление, пропорциональное скорости движения, т. е. Л = ах, где а=1000 Н-с-м-1.
181. При решении задач о колебаниях системы с кулоновым трением обычно принимается, что сила трения не зависит от скорости. Однако более точные исследования показывают, что это не всегда отражает физическую сторону явления и может вызвать качественное искажение результатов решения.
На рис. 129, а изображен так называемый маятник Фроуда. Масса т укреплена на конце рычага длиной I. Точка подвеса маятника представляет собой втулку, надетую на вращающийся с постоянной угловой скоростью Q вал. Между втулкой и валом возникают вязкое (момент сил вязкого трения Л1в=аф, где <р — угловая скорость маятника) и сухое трение с нелинейной характеристикой, изображенной на рис. 129,6; величина момента сил сухого трения равна Afc = M(Q—<р).
Ограничиваясь при разложении Л1(Й—<р) в ряд слагаемыми, содержащими <р до третьей степени включительно, получить дифференциальное уравнение свободных колебаний маятника. Исследовать устойчивость малых колебаний (ограничиваясь только линейным членом разложения момента трения). При решении считать, что нормальная угловая скорость вала Q соответствует точке перегиба на графике (см. рис. 129,6).
64
182. Тормозное устройство состоит из кольцевой колодки 1, надетой на вал 2, вращающийся с угловой скоростью Я (рис. 130,я). Тормозная колодка удерживается от вращения с помощью рычага и пружин общей жесткостью с. Между валом и тормозом возникает сухое трение, величина которого зависит от скорости вращения вала (рис. 130,6).
Исследовать устойчивость малых угловых колебаний тормозной колодки относительно стационарного вращения вала. При решении ограничиться линейным членом разложения момента трения в ряд.
183. Исследовать устойчивость малых свободных колебаний маятника Фроуда (см. задачу 181), используя метод Ван-дер-Поля. Принять, что момент инерции маятника / = 0,15 кг-м2, масса т = 5 кг, длина /=0,3 м. Коэффициенты разложения момента сил трения в окрестностях точки перегиба следующие-Л! (Q)=—0,0375 Н м-с, Л1"(й)=0, М'" (Я)-=0,045 Нмс3. Коэффициент момента сил вязкого трения а = 0,015 Н м-с.
184. Провести качественное исследование изменений амплитуды колебаний маятника Фроуда (см. рис. 129), считая, что в некоторый начальный момент времени (/=0) маятник отклонен а угол Ч'о*=0,1 рад (Ч'о^О) от положения равновесия при гэ&0. При исследовании использовать числовые данные и ре
зультаты решения задачи 183. Изобразить характер изменения амплитуды на фазовой плоскости.
185. Определить частоту колебаний маятника Фроуда, соответствующую устойчивому предельному циклу (см. задачу 181).
186. Определить амплитуду предельного цикла колебаний, описываемых уравнением
d2x/d/2+pox = рро[ 1 —x2]dx/d/,
и исследовать его устойчивость при ц>0.
187. Исследовать устойчивость малых продольных колебаний планера массой т, буксируемого самолетом с постоянной скоростью v0 на гибком растяжимом тросе жесткостью с (рис. 131). Силу лобового сопротивления планера считать равной Fc= = cxSpvo2/2, где сх — коэффициент лобового сопротивления; S — площадь миделевого сечения; р — плотность воздуха.
Рис. 131
Глава 2. КОЛЕБАНИЯ СИСТЕМ О НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 7. Свободные колебания*
188. Два груза массами т{ и т2 (рис, 132) скреплены пружиной, имеющей жесткость с. Определить частоты малых собственных колебаний системы.
с
/7^2
ЖЖ
Рис. 132
189. Стальной цилиндр радиусом г и массой М (рис. 133) может кататься без проскальзывания по горизонтальной плоскости. К оси цилиндра подвешен маятник, состоящий из стержня длиной I с массой т на конце.
• Силы сопротивления во всех задачах, если они не указаны, не учи тывать.
66
Считая стержень невесомым, а массу т точечной, составить 1ифФсРснциальныс Уравнения свободных колебаний системы. Определить частоты малых собственных колебаний системы, ес-ли Л1 = 2 кг; г=0,1 м; /=0,5 м; т=0,2 кг.
190. Диск массой т, имеющий момент инерции J, свободно надет на круглый жесткий вал (рис. 134). Диск удерживается на валу пружиной, имеющей средний диаметр витка D, число витков п и угол подъема витка а.
Составить дифференциальные уравнения малых свободных колебаний диска, считая, что J = mD2/2, а жесткости проволоки пружины при изгибе и кручении соответственно равны £/* и G/M.
Определить частоты собственных колебаний и исследовать их зависимость от угла подъема витка а в пределах 0^а^л/8.
191. На натянутой струне закреплены две массы mt и т2 (рис. 135). Натяжение струны То при малых колебаниях масс
Рис. 13S
остается практически постоянным. Силой тяжести, действующей на массы, пренебречь. Определить частоты собственных колебаний системы.
192. На конце консольной балки с жесткостью на изгиб £/* находится электродвигатель (рис. 136). Масса электродвигателя т; момент инерции относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (центр инерции), равен /оь
Вычислить погрешность, которая допускается при определении частоты собственных колебаний системы, если двигатель рассматривать как точечную массу.
5*
67
193. Стальной вал диаметром d=0,l м несет две сосредоточенные массы /nt = 200 кг и rzi2 = 250 кг (рис. 137). Вал укреплен на трех опорах так, что расстояния от опор до каждой массы составляют а=1 м и Ь=2 м. Считая массы точечными и пренебрегая массой вала, определить частоты собственных колебаний системы.
Рис. 137
194. Для систем, изображенных на рис. 138, составить дифференциальные уравнения малых свободных колебаний и определить частоты собственных колебаний.
Рис. 138
195. На стальной балке прямоугольного поперечного сечения (рис. 139) закреплены два груза mi=m и тъ = 2т. Определить частоты и формы собственных колебаний балки, если /п=2 кг, 1=0,5 м; Ь=20 мм, Л=40 мм.
68
Рис. 13»
196. На однопролетной балке жесткостью EJ* закреплены три одинаковые точечные массы пг (рис. 140). Пренебрегая массой балки, определить частоты собственных колебаний системы.
197. Определить частоты и формы собственных колебаний укрепленной на стойке пластины массой т (рис. 141), считая^ что жесткость стойки при изгибе EJX. Момент инерции пластины относительно оси, перпендикулярной плоскости чертежа и проходящей через центр тяжести, равен J.
198. Определить частоты и формы малых собственных колебаний системы (рис. 142), считая массы точечными. Изгибная жесткость всех участков рамы одинакова и равна EJX.
Рис. 141
Рис. 142
199. Определить частоты и формы собственных колебаний рамы (рис. 143). Массой стоек по сравнению пластины пренебречь; жесткость стоек при изгибе равна EJ*. Пластину считать абсолютно жесткой.
200. Длинный стальной вал постоянного поперечного сечения закреплен в коротких подшипниках (рис. 144). Подшипники расположены на швеллерах, заделанных на стенку. На валу имеется диск массой т, момент инерции массы которого относительно диаметра равен /.
Рис. 144
Пренебрегая массами опорных швеллеров, подшипников и вала, определить частоты вертикальных собственных колебаний диска, если гп — 320 кг, /=12,8 кг м2, а=1 м, Ь = 2 м, /=0,6 м, </=0,1 м; балки изготовлены из швеллера № 16.
Указание. Короткие подшипники можно рассматривать как шарнирные опоры. При определении жесткости системы закручивание швеллеров не учитывать.
201. На раме круглого поперечного сечения (рис. 145) закреплены массы т\ = 2т и rti2 = m. Определить частоты и формы вертикальных собственных колебаний системы, считая, что между жесткостями стержней имеется зависимость вида GJK-= 0,8 £/х.
202. Груз массой т закреплен на гибком стержне длиной I (рис. 146). Считая, что момент инерции массы груза относительно его центральной оси, перпендикулярной к плоскости черте-
70
жа, равен J=mP/$, определить частоты и формы собственных колебаний системы в плоскости чертежа. Действием силы тяжести и массой стержня при решении задачи пренебречь.
203. Определить частоты собственных колебаний системы (см. задачу 202) с учетом силы тяжести.
204. Па гибком стержне длиной 21 закреплены две точечные массы т, и т2 (рис. 147). Жесткость стержня на изгиб равна £7*. Пренебрегая действием силы тяжести и массой стержня, определить частоты и формы собственных колебаний стержня в плоскости чертежа.
205. Три точечные массы закреплены на гибком стержне жесткостью EJX (рис. 148). Пренебрегая массой стержня и не учитывая действие силы тяжести, определить частоты и формы собственных колебаний системы в плоскости чертежа.
206. Определить частоты и формы собственных колебаний в плоскости чертежа системы, состоящей из двух масс т, связанных между собой гибким безынерционным стержнем жесткостью EJX (рис. 149). Момент инерции каждой массы относительно центральной оси, перпендикулярной плоскости черте-
71
Рис. 149
жа, равен J = tnl2/4. Влиянием силы тяжести при решении задачи пренебречь.
207. Определить частоты и формы собственных колебаний системы (в плоскости чертежа), представляющей собой коромысло с двумя закрепленными на нем одинаковыми массами т, имеющими момент инерции относительно центральной оси, перпендикулярной плоскости чертежа, равный J = (рис. 150). Влиянием силы тяжести пренебречь.
Рис. 150
208. Два тела массами mi и т2, имеющие моменты инерции /| и /г относительно центральных осей, перпендикулярных плоскости чертежа, соединены упругим стержнем, изгибная жесткость которого EJX (рис. 151). Пренебрегая массой соеди-
Рис. 151
нительного стержня и не учитывая действие силы тяжести, вывести дифференциальные уравнения малых свободных колебаний системы (в плоскости чертежа).
209. Для системы, изображенной на рис. 151, определить собственные частоты колебаний, считая, что mz=2mi; ]2— ^2Jl = m2P/2-, 1\ = 12=1.
210. Определить частоты и формы собственных колебаний системы в плоскости чертежа, состоящей из точечной массы т
и двух грузов массами т, моменты инерции относительно центральной оси, перпендикулярной плоскости чертежа, J=mP/A (рис. 152). Изгибная жесткость соединительных стержней Е1Х. При решении задачи массой стержней и силой тяжести пренебречь; длину стержня и размер / считать равными.
72
Рис. 152
211. На свободном валу постоянного сечения закреплены три маховые массы, имеющие моменты инерции J\, J2, /3 (рис. 153). Составить дифференциальные уравнения малых свободных крутильных колебаний масс и определить частоты их собственных колебаний. Принять, что моменты инерции масс равны: /1я = 203,9 кг-м2, /2=611,8 кг-м2, /3=ЗО5,9 кг-м2; диаметр стального вала d=50 мм, расстояние между массами 4=250 мм, /2 = =400 мм.
Рис. 153
212. Определить частоты собственных колебаний систем 1 и 2 (рис. 154), считая, что моменты инерции шестерен и валиков малы по сравнению с моментами инерции дисков /1 и /2. Жесткости валов на кручение соответственно равны Ci и с2, а передаточное число зубчатой передачи u=z2/zb где z2 и z( — числа зубьев шестерен.
Рис. 154
213. Для систем, изображенных на рис. 155, составить дифференциальные уравнения малых свободных угловых колебаний; определить частоты собственных колебаний. Массами валов и колес по сравнению с массами дисков пренебречь.
Указание. На приведенных схемах г — число зубьев колес, с — кру-’ильная жесткость вала.
73
Рис. 155
214. Система, совершающая крутильные колебания, состоит из трех маховиков (см. рис. 153), моменты инерции которых соответственно равны Js = 3J. Маховики соединены
валами, имеющими крутильную жесткость, равную с каждый.
Рис 156 Рис. 157
Определить частоты и формы собственных колебаний системы (массой валов пренебречь). Произвести проверку правильности полученных форм колебаний, используя свойство их ортогональности.
215. Составить дифференциальные уравнения малых свободных (Л1=0) колебаний системы дисков (рис. 156), считая жесткость участков вала на кручение равной GJP. Определить частоты и формы собственных колебаний.
216. Определить частоты и формы собственных (М = 0) колебаний системы (рис. 157), считая, что жесткость вала на кручение равна GJP.
217. Получить характеристическое уравнение для определс ния частот собственных колебаний системы (см. задачу 212), считая, что моменты инерции маховиков равны Л и Л. а моменты инерции зубчатых колес // и //. Крутильные жесткости ва лов соответственно равны с| и Cj.
218. Судовая двигательная установка состоит из двух одинаковых двигателей, имеющих приведенные к оси вращения мо-74
менты инерции J\ и /2 вращающихся частей (рис. 158). Двигатели имеют одинаковую скорость вращения и приводят во вращение гребной винт, имеющий момент инерции /3.
Считая, что передаточное число редуктора u=Zi!z\, жесткости валов системы равны Ci, с2, а также пренебрегая моментами инерции зубчатых колес редуктора, составить дифференциальное уравнение малых свободных колебаний системы и получить характеристическое уравнение. Затуханием в системе пренебречь.
Рис. 158
219. На стальном валике жесткостью насажены два маховика, моменты инерции которых J\ и /2 (рис. 159). Маховики соединены между собой упругим элементом — легкой конической оболочкой, которая жестко скреплена с правым маховиком и может проскальзывать относительно левого. Крутильная жесткость оболочки равна с2, а момент сил трения пропорционален угловой скорости проскальзывания.
Рис. 160
Считая, что /1 = 5 кг-м2, /2=2 кг-м2, Ci = 600 Н-м, с2= =300 Н-м, а коэффициент вязкого трения а = 5 Н-м-с, составить дифференциальные уравнения свободных затухающих колебаний системы и вычислить значение корней характеристического многочлена.
220. Корпус автомобиля массой т соединен с колесами рессорами, имеющими жесткость с, и с» (рис. 160). Расстояния от центра массы корпуса до подвесок равны Ц и /2. Считая, что момент инерции массы корпуса относительно центральной поперечной оси равен J, и пренебрегая упругостью шин, соста
вить дифференциальные уравнения малых свободных колебаний корпуса автомобиля в продольной плоскости. Определить частоты собственных колебаний, если Ci—200 кН/м; с5= •=250 кН/м; /,-= 1 м; /г=1,5 м; т=1,5Ю’ кг; 7 = 300 кг-м2.
221. Установить, при каком соотношении между параметрами автомобиля (см. задачу 220) его частоты собственных колебаний равны между собой.
222. Составить дифференциальные уравнения малых свободных колебаний автомобиля (рис. 161, а), кузов которого имеет массу и момент инерции относительно центральной поперечной оси т. Масса переднего и заднего мостов колес равна т, и тг, жесткость рессор передней и задней подвески ct и с2, а жесткость шин передних и задних колес с и 2с, соответственно. При
Рис. 161
решении считать, что в рессорах имеется вязкое трение с коэффициентом трения а. Расчетная схема системы изображена на рис. 161,6.
223. Определить частоты собственных колебаний автомобиля (см. рис. 161) для частного случая 1л=таЬ. Принять следующие числовые значения параметров системы: а-2,3 м; Ь= —0,94 м; Л1вб,4‘10* кг; /п, = щ2=650 кг; ct=c2=35 кН/м; а=0. Жесткость шин переднего и заднего колес считать одинаковой и равной с=1200 кН/м.
224. На рис. 162 схематично изображена передача с гибкой связью (привод токарного станка). В установившемся режиме работы момент двигателя уравновешивается моментом сил резания (моментами сил сопротивления можно в первом приближении пренебречь); напряжения в ветвях передачи равны о10 и ом.
76
г
Рнс. 162
Составить дифференциальные уравнения малых угловых колебаний шкивов 1 и 2 и определить частоты собственных колебаний, если /?,==100 мм, /?г=200 мм; момент инерции массы ведущего шкива / и ротора электродвигателя /,=0,08 кг-м2; момент инерции массы ведомого шкива 2 и шпинделя станка /,=0,1 кг-м’; /=0,6 м; площадь поперечного сечения гибкой связи F=2 см2; модуль упругости материала гибкой связи Е= = 100 МПа; угол упругого проскальзывания гибкой связи на шкиве 4)0=150°; коэффициент трения между гибкой связью и ШКИВОМ Щ> = 0,3.
Указание. Удлинения ветвей передачи, вызванные дополнительными напряжениями, возникающими при колебаниях шкивов, соответственно равны
Д/. = Да, [4-+{Й'(,-еМ*Ф’)]=а>Д0‘’ д/,—до, jipr(e>t*y.—о] =в«Дст’-
225. В конструкциях ременного привода станков постоянство усилия натяжения в ветвях передачи часто осуществляется за счет использования массы двигателя. На рис. 163 приведена схема вертикальной ременной передачи, в которой гибкая связь заменена упругими элементами, работающими на растяжение.
Составить дифференциальные уравнения малых свободных колебаний шкивов привода, считая,что момент инерции массы верхнего шкива равен / = 0,1 кг-м2, а его радиус /?,=200 мм; момент инерции массы двигателя и нижнего шкива относительно точки О /'=0,125 кг-м2, их масса т=16 кг, радиус нижнего шкива /?,=0,1 м; момент инерции массы нижнего шкива и ротора двигателя /,=0,08 кг-м2; плечо Л,=0,5 м; жесткость упругих связей EF=2-101 кНм2, их длина /=0,6 м, ф,о=9°40'. Определить частоты собственных колебании системы.
226. В современном машиностроении получили широкое применение самонатяжные передачи. На рис. 164 изображена
77
Рис. 163
Рис. 164
схема самонатяжной передачи. Для упрощения решения гибкая замкнутая связь заменена двумя упругими элементами, работающими на растяжение. Крутящий момент от электродвигателя 1 на ведущий шкив 4 передается через пару шестерен 2, закрепленных на осях двигателя и шкива и связанных между собой кулисой 3.
В статическом положении (как и при установившемся режиме работы передачи с замкнутой гибкой связью) внешний момент М уравновешивается моментом двигателя 1. При увеличении внешнего момента Af возрастает и момент со стороны двигателя, т. е. увеличивается усилие зацепления Р — сила, передающая момент со стороны шестерни двигателя на шестерню ведущего шкива 4. При этом сила зацепления одновременно натягивает передачу, отклоняя кулису 3.
78
Составить дифференциальные уравнения малых свободных одебаний шкивов передачи и определить частоты собственных Копебаний, считая, что шестерня 2 не перемещается. Моменты инерции Движущихся масс, приведенные к осям вращения шкивов. равны It и Ji, масса ведущего шкива с шестерней тс, мо-удь упругости связей Е, а их площадь поперечного сечения F. кассами кулисы и упругих связей пренебречь. Провести числовое решение при следующих значениях параметров системы: / =0,08 кг-м1; /2=0,1 кг-м2; т,=0,16 кг; /=600 мм; ф,о=9040; р=2 см2; £=100 МПа; /?,=100 мм; /?. = 200 мм; г, = 50 мм; Гз=40 мм.
227. Масса т укреплена на двух растяжимых нитях длиной /( и /2 (рис. 165). Считая, что в процессе малых колебаний груза в вертикальной плоскости натяжение Т„ в нитях не изменяется, определить частоты малых собственных колебаний массы т. .Момент инерции массы относительно оси, перпендику-
лярной чертежу и проходящей через центр тяжести груза, равен J, жесткость нитей на растяжение ££„- Статическим смещением, вызванным массой груза, пренебречь.
228. Составить диференцнальныс уравнения малых свободных колебаний вагонетки массой т, движущейся с постоянной скоростью v по натянутому тросу (сила натяжения троса То) (рис. 166). Момент инерции массы вагонетки относи
тельно оси, проходящей через ее центр тяжести перпендикулярно чертежу, равен J. Изменением натяжения То в тросе пренебречь.
229. Точечный груз массой т укреплен на свободной невесомой растяжимой нити, концы которой жестко закреплены на
79
одном уровне на расстоянии lt один от другого. На рис. 167 изображено статическое состояние системы. Все величины, приведенные на чертеже, считать известными. Определить частоты собственных колебаний массы в плоскости чертежа, считая, что жесткость нити при растяжении равна EF.
230. Составить дифференциальные уравнения малых свободных колебаний массы т, движущейся по растяжимой невесомой нити, концы которой закреплены на одном уровне на расстоянии /, один от другого (рис. 167). Скорость движения
массы относительно нити постоянная и равна V. Жесткость нити при растяжении EF. Принять, что в начальный момент времени (/=0) координаты массы равны хо=0, y„=s,a.
231. В качестве возбудителя крутильных колебаний можно использовать магнитоэлектрический вибратор, например шунтовой двигатель с раздельным питанием обмоток якоря и возбуждения (рис. 168). Обмотка возбуждения 1 питается постоянным током, а на обмотку якоря 3 подается переменное напряжение (7=t/„sin ы/, частоту которого можно регулировать. Колебания якоря 2, имеющего момент инерции массы J, вызывают изменением напряжения в цепи якоря на величину aidq>/d/ (где at — коэффициент, зависящий от магнитного но
во
тока якоря; <р— угол поворота якоря). Изменение напряжения в цепи якоря вызывает возникновение тока, создающего электромагнитный момент M—a2i (а, — коэффициент, зависящий от магнитного потока якоря; i — ток в цепи), действующий на якорь-
Составить дифференциальные уравнения свободных колебаний системы, считая, что крутильная жесткость торсиона равна с, индуктивность цепи якоря L, а активное сопротивление его цепи R. Силами сопротивления в механической системе пренебречь. Определить корни характеристического многочлена для частного случая, когда /?«0.
232. Электромеханический прибор, известный под названием конденсаторный микрофон, схематически изображен на рис. 169. Цепь состоит из батареи постоянного напряжения U, катушки самоиндукции L, активного сопротивления R2, конденсатора переменной емкости С и гибкого проводника 2. Конденсатор имеет одну неподвижную пластинку, с которой упруго связана движущаяся пластинка / массой т, которая представляет собой звуковоспринимающую мембрану микрофона. Она колеблется под действием переменного давления р звуковых волн. Система имеет две степени свободы (две обобщенные координаты)—заряд q конденсатора и перемещение х мембраны.
Составить дифференциальные уравнения движения пластинки / (мембраны) и изменения заряда q конденсатора, считая, что жесткость каждой из пружин 0,5 с.
233. Колебательная система состоит из двух дисков с моментами инерции массы и /2, скрепленных между собой валом, крутильная жесткость которого равна с (рис. 170). Опре-
Рис. 170
Делить частоты собственных колебаний системы и установить закон движения дисков, если в некоторый начальный момент времени им сообщены одинаковые по величине, но различные По направлению угловые скорости движения <р0 (считать, что При ( = 0 <р1=<рг=О).
§ 9. Вынужденные колебания
234. Определить максимальные нормальные напряжения, возникающие в балке (см. рис. 139) при действии на массу тх периодической силы P=P„sinci^, где ci)2= 1/(т2622), — значе-
ние амплитуды силы.
6— 5000
81
235. Для систем, изображенных на рис. 171, определить коэффициент динамичности, равный отношению амплитуды возмущающей силы Ре к амплитуде усилия, действующего на массу /п,. Принять ____
c-l'/EI*. т,*=2т2-, ы=Ус/‘т1.
а
Рис. 171
236. Тяжелый электродвигатель массой т закреплен на балке длиной 3/ (рис. 172). При вращении ротора мотора, имеющего эксцентрично расположенную массу mt, развивается центробежная сила инерции Ft=4nt(oze (где е — эксцентриситет массы ротора, о» — его угловая скорость).
Рис. 172
Определить частоты собственных колебаний и амплитуды вынужденных колебаний системы, если расстояние от оси балки до центра массы мотора R=l/b, момент инерции массы мотора относительно центральной оси/0“=т/2/4, угловая скорость й)=2уг Е/х/(те)3. Массой балки по сравнению с массой двигателя пренебречь.
237. На массу т, (рис. 173) действует периодическая возмущающая сила, равная P=Posin(of. Площадь поперечного сечения стержней, соединяющих массы, равна F, а модуль упругости Е. Установить, при каких значениях параметров системы амплитуда вертикальных колебаний массы тг равна нулю.
238. Определить параметры системы, при которых амплитуда колебаний массы тг равна нулю, считая частоту ш возмущающей силы заданной (рис. 174).
239. Две точечные массы т, и тх находятся на шарнирно закрепленной балке (рис. 175). На систему действует возмущающий момент Af=Aiosin ®s. Определить параметры системы, при которых амплитуда колебаний массы mt равна нулю.
82
Рис. 175
240. Для гашения колебаний массы тг, находящейся на конце мачты, используется маятниковый гаситель колебаний (рис. 176). На массу тг действует периодическое возмущение P—Ptsin at. Средняя изгибная жесткость мачты EJX. Определить параметры маятника (т,, Ц), при которых амплитуда колебаний массы т2 равна нулю.
241. Для гашения крутильных колебаний применяется гаситель колебаний Прингла, в котором массы т могут перемещаться в радиальных пазах диска (рис. 177). Определить параметры т и ct гасителя, при которых амплитуда угловых колебаний диска равна нулю (при заданной частоте ы возмущающего момента и угловой скорости диска QJ, если известны: возмущающий момент Af=Afosin ю/, действующий на диск; Жесткость с вала, на котором находится диск, момент инерции массы диска 1 и угловая скорость диска при стационарном режиме Но.
6*
83
242. Рассмотренный в задаче 241 гаситель колебаний Прингла имеет недостаток — массы т с увеличением угловой скорости смещаются из-за деформации пружин, изменяя суммарный момент инерции системы. Указать, как надо изменить конструкцию гасителя, чтобы на интервале изменения Й»(0^Й^ ^Й..) массы оставались относительно диска неподвижными.
243. На рис. 178 показан маятниковый гаситель колебаний, установленный на диске, вращающемся с угловой ско
Рнс. 178
Рис. 179
ростью Q. Определить параметры т и I маятникового гасителя колебаний, при которых амплитуда колебаний диска равна нулю.
244. На систему, изображенную на рис. 145, в сечении закрепления массы тг действует вертикальная периодическая сила P=Posin со/. Определить допускаемое значение амплитуды возмущающей силы Ро, если частота возмущающей силы w=0,8 pt (где pt — первая частота собственных колебаний системы), d=40 мм, 1=1 м, считая, что коэффициент лт=3. Материал стержней — сталь СтЗ (<Ттр=ат.с=240 МПа).
245. Определить наибольшие касательные напряжения, возникающие в стальном валу постоянного поперечного сечения (рис. 179) при действии периодического возмущающего момента ;W=Afosin со/, если Ц=21г, ЛТ,=5Нм, d= 1 см; <d1=2/(/i5ii), 7=20 см, G=80 ГПа. Вычислить коэффициент запаса прочности вала по пределу текучести, если тт=200 МПа.
246. На стальном валу круглого поперечного сечения, имеющем жесткость при кручении G/p, закреплены четыре диска (см. рис. 156). Определить наибольший крутящий момент на валу в установившемся режиме колебаний при действии периодического возмущающего момента Al=Mosin ш/, где ш= = 0,8 рг (рг — вторая частота собственных колебаний системы).
247. Определить наибольшие напряжения, возникающие в вале (см. рис. 157) постоянного поперечного сечения d=40 мм при действии на него периодически изменяющегося крутящего 84
момента Af = Afusin (at, если A40=30O Н м; ш“0,7 р, (р,— вторая частота собственных колебаний системы).
248. Два абсолютно жестких шкива (рис. 180) соединены упругими связями, работающими на растяжение и имеющими предварительное натяжение N0=F(jt.
Определить частоты собственных колебаний шкивов и величину наибольшего возмущающего момента /И», при котором напряжение в упругой связи достигает нуля. Принять, что радиусы шкивов: R,= \0 см, Яг=20см, их моменты инерции У,— =0,08 кг-мг, /1=0,1 кг-м2, длина упругой связи 1=60 см, площадь ее поперечного сечения F=2 смг, модуль упругости £= = 100 МПа, напряжение предварительного натяжения п0=2 МПа, частота возмущающего момента со=О,8 р. (где р2— вторая частота собственных колебаний системы).
249. Определить закон изменения напряжений о( и о- в установившемся режиме колебаний передачи привода токарного станка (см. задачу 224, рис. 162) при действии на ведомый вал периодического возмущающего момента сил резания ДЛ1 = = A'l„sin (at.
250. На стальном валике 1 (рис. 181) диаметром жестко закреплен маховик 2, имеющий момент инерции массы /t. Нижний конец валика жестко защемлен, а верхний поддерживается подшипником. Второй маховик 3 с моментом инерции массы /г свободно надет на валик и прижимается к маховику 2 пружиной 4.
Считая, что к маховику 2 приложен периодически изменяющийся момент M=Af,sin со/, а между маховиками имеется ку-лоново трение с коэффициентом трения ц, составить дифференциальные уравнения движения маховиков 2 и 3. При составлении уравнений учесть, что пружина 4, прикрепленная к Маховику 3 и верхней опоре, имеет предварительный осевой натяг 6о, величина которого изменяется в процессе колебаний.
251. Определить напряжения, возникающие в элементах конструкции при установившихся колебаниях (см. рис. 181), считая, что между маховиками 2 и 3 возникает вязкое трение и момент сил вязкого трения Л1т=а((ср|—ср,).
252. На свободном конце консольного вала жесткостью с закреплен диск (момент инерции диска Jt) с надетым на него
массивным кольцом (момент инерции кольца /2) (рис. 182). Кольцо удерживается на диске ребордами. Между диском и кольцом имеется вязкое трение. Момент трения пропорционален относительной скорости движения диска и кольца =а((р,—ф2), где <pi — угол поворота диска; <рг — угол поворота кольца.
Рис. 181
Составить дифференциальные уравнения малых колебаний диска и кольца при действии на диск момента М=Alosin ш/. Определить амплитуды установившихся колебаний диска и кольца.
253. Составить дифференциальные уравнения движения прицепа по дороге с неровностями (рис. 183), считая, что масса прицепа т, масса колес mit момент инерции массы прицепа относительно поперечной оси, проходящей через точку 0, равен Л, жесткость рессор с, жесткость шин колес скорость буксирования о.
86
При решении задачи принять, что точка крепления прицепа к машине (точка О) не имеет вертикальных перемещений, а профиль дороги описывается уравнением й-=Л0(1—cos 2лх//,), где x^vt. Учесть, что при колебаниях прицепа в рессорах возникают силы трения F1=ia(y—yt), пропорциональные относительной скорости вертикального перемещения кузова и колеса.
Определить частоты собственных колебаний и критические скорости буксирования при отсутствии трения в рессорах.
254. Автомобиль движется по дороге, имеющей периодические неровности (рис. 184). Считая, что профиль дороги описы-
вается уравнением й=Ло(1—cos2;tx/Z»), где х=и/, определить амплитуды углового и вертикального ускорений при установившихся колебаниях системы. Принять, что масса автомобиля щ=6000 кг; момент инерции массы относительно центральной поперечной оси /=1,2-103 кг-м2; жесткости рессор с,= = 200 кН/м и Ci=250 кН/м; расстояния до центра тяжести /(=1 м, /2=1,5 м; скорость движения автомобиля и=25 км/ч; шаг неровностей /0 = 5 м; высота неровностей Л = 0,1 м.
265. Определить критическую скорость движения автомобиля по дороге с неровностями (см. задачу 254), т. е. такую скорость при которой амплитуды вынужденных колебаний достигают максимальных значений.
256. Составить дифференциальные уравнения вынужденных колебаний автомобиля (см. задачу 222, рис. 161) при движении его со скоростью v и по дороге с неровностями, которые приближенно описываются уравнением й = Л„(1— cos 2лх//«).
257. На рис. 185 изображена схема центрифуги, предназначенной для разделения смеси жидкостей по плотностям ее компонентов. При вращении системы с угловой скоростью ш более тяжелые фракции скапливаются у стенок сосуда, а легкие вытесняются в центр (ближе к оси вращения). Слив легких фракций производится через центральную трубку.
Известно, что из-за технологических погрешностей при изготовлении центр масс сосуда с жидкостью находится на расстоянии е (эксцентриситет масс) от оси вращения.
87
Составить дифференциальные уравнения движения центри-фуги, считая угловую скорость о» постоянной, а слив жидкости равномерным, т. е. полагая, что масса тж находящейся в сосуде жидкости изменяется во времени по закону т((1—t/
/t\), где т} — масса жидкости в начальный момент времени, /1 — время, за которое вытекает вся жидкость. Масса сосуда mt намного больше массы трубки. Жесткость трубки при изгибе равна с. Изменением вертикальной координаты центра масс системы и колебаниями жидкости в сосуде пренебречь.
258. На массу т, закрепленную на конце упругого стержня (рис. 186), действует единичный импульс /=тп(0). Считая, что изгибная жесткость стержня EJX, а момент инерции массы относительно центральной осн, перпендикулярной к плоскости чертежа, равен J-mE/b, определить закон движе
ния массы и максимальный изгибающий момент в стержне. В качестве начальных условий принять, что при М горизонтальное смещение, угол поворота и угловая скорость движения груза равны нулю (и(0) =<р(0) =ф(0) =0]. Влиянием силы тяжести на движение системы пренебречь.
259. Демпфер крутильных колебаний (рис. 187) состоит из упругого элемента 4, несущего на своем свободном конце контактное кольцо 1, к которому пружиной 3 прижимается маховик 2.
Считая, что на маховик действует периодически изменяющийся крутящий момент Л1—Afosincof, а момент сил трения между маховиком и кольцом пропорционален скорости их относительного движения (с коэффициентом пропорциональ-
88
Рис. 187
ности at), определить амплитуду установившихся колебаний кольца /. Момент инерции массы валика и маховика равен J. Массой упругого элемента 4, кольца / и пружины 3 пренебречь (С| и С2—жесткости при кручении).
260. Массивный контейнер 2 массой т подвешен на пружине 1 жесткостью Ci (рис. 188). Для ограничения боковых перемещений и смягчения боковых ударных воздействий служат легкие вертикальные направляющие 3, прижимаемые к контейнеру прижинами 4 с изгибной жесткостью Сг каждая. Меж-
Рис. 189
Рис. 188
ДУ контейнером и направляющими возникает вязкое трение с коэффициентом трения а.
Составить дифференциальное уравнение вертикальных колебаний контейнера при действии на него силы /•=/?osin(i>Z. Массой направляющих при составлении уравнения движения пренебречь.
261. При движении по дороге со случайными неровностями Колебания автомобиля вызывают колебания сиденья с водителем. Так как масса автомобиля намного больше суммарной ^ассы водителя и сиденья, то можно считать, что происходит
89
одностороннее воздействие автомобиля на сиденье. На рис. 189 показана схема виброизоляции сиденья водителя от пола автомобиля (точка 0) (т — суммарная масса сиденья и водителя); С|, с2—жесткости пружин упругой подвески сиденья; а — коэф! фициент вязкого трения.
В результате обработки осциллограммы случайного стацно-парного процесса с нулевым математическим ожиданием, возникающего при движении автомобиля с постоянной определен-ной скоростью v, получена корреляционная функция вертикаль, ного смещения точки О вида
где Dy, —дисперсия, си — параметр затухания.
Получить выражения для дисперсий вертикального ускорения водителя с сиденьем (пружины и демпфер можно считать невесомыми).
§ 10. Критические состояния и устойчивость колебаний
262. Диск массой т закреплен на гибком идеально сбалансированном безмассовом валике длиной 21, вращающемся с постоянной угловой скоростью и (рис. 190) .
Считая, что эксцентриситет массы диска относительно оси валика равен нулю, составить дифференциальные уравнения малых колебаний диска в системе координат xyz. вращающейся со скоростью со (ось z является осью вращения). Вследствие симметрии схемы можно считать, что поворот диска в плоскости чертежа отсутствует, т. е, диск совершает только вертикальные колебания. Определить частоты колебаний диска во вращающейся системе координат, пренебрегая действием силы тяжести.
263. Вывести уравнения малых колебаний диска относитель-
90
й0 стационарного режима вращения с учетом эксцентриситета е (сМ. рис. 78). Уравнения получить во вращающейся системе координат.
264. Составить дифференциальные уравнения малых колебаний диска массой т, насаженного без эксцентриситета на вал длиной 2 I (см. рис. 190) при вращении его с постоянной угловой скоростью со.
Определить значение критической угловой скорости <о., €Слн поперечное сечение вала имеет различные осевые моменты инерции, т. с. (например, прямоугольное поперечное се-
чение).
265. На горизонтальном валике диаметром d и длиной 2 I укреплен (без эксцентриситета) массивный диск массой т (см. рис. 190). Составить дифференциальные уравнения малых свободных колебаний диска при равномерном вращении валика с угловой скоростью и. Определить амплитуды установившихся колебаний диска. Массой валика по сравнению с массой диска пренебречь.
266. Составить дифференциальные уравнения малых свободных колебаний вращающего диска массой т, насаженного на горизонтальный валик (см. рис. 190) прямоугольного поперечного сечения bXh. (b<h). Определить амплитуду установившихся колебаний диска и критическую угловую скорость и валика с учетом силы тяжести, действующей на диск.
267. На рис. 191 изображен вращающийся с постоянной угловой скоростью со стальной консольный валик длиной I и диаметром d, несущий на одном конце массивный диск массой т. Момент инерции массы диска относительно оси вращения равен 7.
Считая, что имеется регулярная прецессия, определить критическую угловую скорость валика с учетом (7=А0) и без учета (7=0) гироскопического эффекта, если /=1 м; 7ж=лт/'/64 = =490 см‘; 7=4,05 кг-м2; £=200 ГПа; т=175 кг.
268. Стальной вал диаметром d вращается в длинных подшипниках (рис. 192). На конце вала насажен маховик радиусом /? и толщиной й. Считая, что длинный подшипник можно рассматривать как глухую заделку, составить дифференциальные уравнения малых свободных колебаний диска и вычислить значение критической угловой скорости вала ш., если 7?=0,3 м; /i=80 мм; d=0,1 м; /=1 м. Массой вала по сравнению с массой Диска пренебречь
Полученный результат сопоставить с результатом решения без учета гироскопического эффекта.
269. Определить критическую угловую скорость стального вала, закрепленного в двух коротких подшипниках (рис. 193), Которые можно рассматривать как шарнирные опоры. При расчете принять: £>=0,6 м; й=80 мм, d=0,12 м, а=1 м, 1=3 м, £=200 ГПа.
91
270. Гибкий стальной валик длиной 21 с закрепленным на нем несбалансированным диском, масса которого т, помещен в однородное магнитное поле с постоянной напряженностью Фо (рис. 194). Определить критическую угловую скорость валика со., если изгибная жесткость равна EJX, а эксцентриситет центра массы относительно оси вращения е.
Указание. При положении груза посредине между магнитами их силы притяжения взаимно компенсируются. При отклонении же груза силы, дейст вующие на него со стороны магнитов, оказываются различными и их раз ность не равна нулю (см. решение задачи 107: AF=F,—Д2). При решении принять
Рг=кФ02/(cii—x)2; Г2=/гФ02/(«1+-^)2-
271. Тонкая прямоугольная абсолютная жесткая стальная пластинка массой т, закрепленная на четырех пружинах, помещена в воздушный поток (рис. 195). Составить дифференциальные уравнения малых свободных колебаний пластинки в вертикальной плоскости, считая, что между подъемной силой Fx, скоростью потока v и углом поворота 6 имеется следующая зависимость:
92
hl пл
где Fi — подъемная сила, приложенная в точке 0, находящейся на расстоянии Z/4 от передней кромки пластинки; Cz — коэффициент подъемной силы (производная dC2/d0 считается известной); Р — плотность воздуха.
Исследовать устойчивость малых свободных колебаний
,пластинки.
Рис. 195
272. Определить критическую скорость потока воздуха и., при которой колебания пластинки становятся неустойчивыми (см. задачу 271), считая, что dC2/dO=3, Ci = 0,l кН/м, с2= =0,05 кН/см, р=1,25 кг-м3, /1=20 см, ]v=m?IY2..
273. Горизонтальный полет самолета (рис. 196) всегда сопровождается дополнительными движениями, вызванными различными возмущениями. Ограничившись возмущенным движением самолета в вертикальной плоскости [учитывая только малое смешение по оси у и малый угол поворота <р (рис. 196)], Т. е. рассматривая самолет как систему с двумя степенями свободы, получить уравнения возмущенного движения и соотно-
93
шения, позволяющие исследовать устойчивость невозмущенно, го горизонтального установившегося полета.
При выводе уравнений принять, что на хвостовое оперение действуют только аэродинамические силы Г2о и ДГ2, вектор ско. рости v практически сохраняет свое горизонтальное направле-ние, а вектор тяги R постоянен по модулю и направлен по оси самолета OOt
Указание. При установившемся горизонтальном движении действую-шие на самолет аэродинамические силы г>о; F»°, Mt<y, сила тяжести mgt сила тяги R и сила лобового сопротивления Хо взаимно уравновешены.
При возмущенном движении появляются дополнительные аэродинамические силы Д/чДГг и ДМь которые при малых колебаниях линейно зависят от приращений углов атаки Доц и Да2, т. е. можно .считать
Д/Г1 = С|Д<Х|, ДГ2=С2Да2, ДМ| = СзДаз,
где С, — постоянные числа (/= 1 ... 3).
Для вывода уравнений надо получить выражения для Да, в зависимости от у и ф, характеризующих возмущенное движение самолета.
274. Исследовать устойчивость малых свободных колебаний шкивов передачи относительно установившегося режима ее работы (см. рис. 162, задачу 224), если при колебаниях возникают два возмущающих момента: момент со стороны электродвигателя ДМ1=—£)<Р1 и момент сил резания ДМ2=—£2ф2= =—Юфг (<₽| и <р2 — скорости угловых колебаний шкивов, и Рг — коэффициенты обратной связи).
Определить значения коэффициента при которых колебания системы устойчивы.
275. Механическая система (рис. 197) состоит из вала 1, свободно вращающегося в подшипниках; маховика 2, жестко
94
скрепленного с валом, и упругой муфты 3. На маховик 2 действует внешний крутящий момент М = а<рь величина которого про-лорциональна угловой скорости вала.
Считая, что между маховиком и муфтой действуют силы вязкого сопротивления, пропорциональные относительной угловой скорости с коэффициентом пропорциональности а, и пренебрегая инерционностью муфты, определить область значений коэффициента а, при которых движение маховика является устойчивым. Принять, что суммарный момент инерции массы вала и маховика /=10_‘ кг-м2, угловая жесткость муфты с,= == 1 Н-м, а=0,005 Н м-с.
276. Угловая скорость волчка в установившемся режиме относительно оси симметрии равна Qo (рис. 198). Центр тяжести волчка расположен на расстоянии I от точки О; сила тяжести волчка равна mg. Определить частоты колебаний оси симметрии (ось Ог) волчка относительно вертикального положения. Установить критическую угловую скорость Qo.-
277. Вертикальная ось симметрии гироскопа (рис. 199) может свободно вращаться вокруг точки О и удерживается пружинами в точке О\. Пружины взаимно перпендикулярны и имеют жесткость с. Определить момент количества движения гироскопа, необходимый для его устойчивого вращения.
278. Получить уравнения возмущенного движения оси симметрии гироскопа (см. задачу 277) для случая, когда жесткости пружин различные. Установить, при каком условии ось симметрии гироскопа совершает малые периодические движения. Найти критическую угловую скорость гироскопа Qo«- Принять,
95
что жесткость пружин в направлении оси 0xt равна сь а в направлении оси Oyt равна с2.
279. Масса математического маятника представляет собой гироскоп в карданном подвесе (рис. 200). Наружное кольцо 2, жестко связанное со стержнем 3, несет подшипники внутреннего кольца, имеющего противрвес массой тз. Во внутреннем кольце 1 вращается ротор гироскопа. Сила тяжести ротора Qb его моменты инерции массы Jx,, Jet,Jtt, сила тяжести внутреннего кольца Q?, его моменты инерции массы Jg„ Ju,, Jг,. Угловая скорость ротора относительно оси z равна Qo- Пренебрегая массой стержня 3, определить частоты малых колебаний системы.
280. Устойчивость монорельсовой тележки (рис. 201) достигается с помощью вертикального гироскопа. Ось гироскопа укреплена в точке Oi так, что она может двигаться только в плоскости симметрии тележки (в плоскости xtOzi). Масса тележки m = Q!g, момент инерции тележки относительно оси Oxt равен /л0 (оси Xit/jZt жестко связаны с тележкой, ось z направ-
Рис. 201
лена по оси симметрии гироскопа, ось у совпадает с осью «л, ось х перпендикулярна плоскости zy). Моменты инерции гироскопа относительно осей х, у, z соответственно равны 7Х, /г (вследствие симметрии /х=/„). Сила тяжести гироскопа Q. центры тяжести тележки и гироскопа находятся соответственно в точках С( и С2.
Составить дифференциальные уравнения малых свободных колебаний гироскопа относительно вертикали, считая углы 6 и ф малыми. Получить характеристическое уравнение для определения частот собственных колебаний и соотношение для вычисления критической угловой скорости Qo. гироскопа.
281. Гироскоп в карданном подвесе используется как прибор для измерения угловой скорости (гиротахометр) (рис. 202)-Наружное кольцо гироскопа / закреплено на основании и вра-
96
щается вместе с ним относительно оси у\- Измеряемая угловая сКорость основания й, угловая скорость ротора 2 гироскопа Йо. 0ри вращении наружного кольца гироскопа относительно оси у\ рОтор гироскопа поворачивается относительно оси х на угол 6. ращение колебаний внутреннего кольца 4 гироскопа осуществляется демпфером вязкого трения <“ -----..-
пропорциональности а.
4, имеющим коэффициент
Составить дифференциальные уравнения движения гироскопа относительно угла 6, если суммарные моменты инерции кольца вместе с ротором относительно осей хну, жестко связанных с кольцом, равны /х и момент инерции ротора относительно оси симметрии г равен /0. Определить угловую скорость Й, считая, что она очень медленно изменяется во времени, т. е. й~0.
282. Диск радиусом г, имеющий массу т, катится без проскальзывания по горизонтальной шероховатой поверхности с угловой скоростью й (рис. 203).
Составить дифференциальные уравнения малых свободных колебаний диска в плоскости xOz и исследовать их устойчивость в зависимости от скорости движения Й. Толщиной диска при составлении уравнения движения пренебречь.
7—5000
97
§11. Приближенные методы определения низших частот
283. Воспользовавшись методом Релея, определить низшую частоту колебаний системы (рис. 204). Массы mi и «2 (шг = = 2и1|) считать точечными; массой балки пренебречь.
284. Методом Релея определить низшую частоту поперечных колебаний системы (рис. 205), пренебрегая массой балки.
_____1 _______I
Рис. 205
285. Методом Релея определить низшую частоту колебаний системы (рис. 206). Массой балки пренебречь.
286. Найти низшую частоту колебаний системы (см. задачу 195) по методу Релея.
287. Определить низшую частоту колебаний системы с учетом массы балки, если масса единицы длины балки равна то (см. рис. 206), причем т=2т01.
288. Определить низшую частоту колебаний системы (пренебрегая массой балки), если жесткости пружин с=£/,/2/' (рис. 207).
98
289. Методом Релея определить низшую частоту продольных колебаний системы (рис. 208), состоящей из трех равных масс соединенных безынерционными стержнями. Площадь поперечного сечения стержней F, модуль упругости Е. ' 290. Определить низшую частоту продольных колебаний системы (рис. 209) методом Релея, считая стержни безынерционными.
291. Определить низшую частоту продольных колебаний системы (рис. 210) методом Релея, считая стержни безынерционными.
Рис. 208 Рис. 209 Рис. 210
292. Методом Релея определить низшую частоту крутильных колебаний системы (рис. 211), пренебрегая инерционностью вала.
293. Определить методом Релея низшубо частоту крутильных колебаний системы (рис. 212), состоящей из четырех маховых
Рис. 211 Рис. 212
масс, у каждой из которых момент инерции равен J, соединенных безынерционными стержнями с крутильной жесткостью с.
294. Методом Донксрлся определить низшую частоту колебаний системы в задачах 283 и 285.
295. Методом Донкерлея определить низшую частоту продольных колебаний масс в задаче 288.
296. По методу Донкерлея определить низшую частоту колебаний системы в задачах 290 и 291.
7*
99
ОТВЕТЫ И РЕШЕНИЯ
Глава 1. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 1. Свободные колебания
1.
a) p=^3EJx(a + 6)//na2^:
б) p=V \2EJx/ma2(ba + 3b)\
в) p=y(d+3£Jx/mP).
Указание. Дифференциальное уравнение движения в канонической форме для систем с одной степенью свободы имеет вид (по методу сил) у=бц(—ту), где 6ц — перемещение массы под действием единичной силы, совпадающей по направлению с перемещением, поэтому частота свободных колебаний р=ИУ тбц.
2.
а) р=УEJt/ml?-, б) p=VWEJx/7ml\
в) р=/6£Л//пЛ2(* + *): г) p=V]2EJx/tna2(4a + 3b).
В качестве примера определения коэффициентов податливости для статически неопределимых систем рассмотрим задачу 2, г. Разорвав связь (считая, что связь между массой т и опорной поверхностью двусторонняя), приложим к массе т силу N (реакция связи). В результате имеем раму, нагруженную силой А' и силой инерции J (рис. 213). Методом сил получаем два уравнения относительно перемещения массы т по осям у и z:
IOO
»-d./+6„V;
О=б„/-|-биЛГ;
(1)
(2)
где J=—my.
Исключив N, имеем
У ——Ъ\\ту\ где бц = б11б22 — 6126^/622-
Таким образом, частота колебаний
р= /пб(!1).
Изложенный прием определения бц(|) для статически неопределимых задач не требует традиционных вычислений (как правило, довольно трудоемких) для определения податливости системы би”’ с предварительным раскрытием статической неопределимости и определением перемещения от единичной силы по направлению смещения массы при колебаниях. Если на систему наложено несколько связей (например, система трижды статически неопределима), то столько же можно получить и алгебраических уравнений для определения реакций связей, которые затем исключаются из дифференциального уравнения.
3.
v т/ bnEJx . -]/5,55£7ж
а» К- V а«‘(3я‘-1в); 6> ₽“ V
4. Аналогично решению задачи 2 дифференциальное уравнение малых крутильных колебаний для всех схем имеет вид
ф+т^ф“°-
Следовательно, частоты собственных • колебаний для схем а—г (см. рис. 4) соответственно равны
«> p=V^- *
Указание. В вариантах г и д системы статически неопределимы, и для «олучения б| необходимо сначала раскрыть статическую неопределенность.
5.
т, + mt'
101
7.
P-V1T-
8. Поворот зубчатого колеса на некоторый малый угол ф вызывает перемещение его центра на величину <pD/2. При этом точка А (точка крепления пружин к водилу) смещается на величину 6=ф1—yD/2. Учитывая, что момент инерции массы колеса /, = <71,078, а момент инерции массы водила 12,
найдем кинетическую энергию системы:
(т, 4-m,) D’<₽ , (ггцО* , m/Z* \ <j>* m,ZD<p*
8 _| \ 8 + 3 ) 2 4
Изменение потенциальной энергии системы выразили через деформацию пружин и угол подъема водила:
гт Г, св* , I Ц ч Г It D m,gl п
п = 2—+ — C0S<p)=k(Z — +-у- Ф2-
Используя уравнение Лагранжа второго рода, получаем
" , 19 mJ?Z+4c(/-D/2)’ п
Ф Т 1 z (9m, + 6m,) d* + 8m,/’— 12m,ZD 4 u> откуда частота собственных колебаний
_ 12m,£Z — 48с (/ — D/2)’
Р V (9m, -f-6m,)D* + 8m,Z*—12m,ZD ’
9. В процессе малых свободных колебаний цилиндра его кинетическая энергия складывается из кинетической энергии вращательного движения и кинетической энергии поступательного перемещения:
Т=( 1/2) /фг+( 1/2) т(гчУ,
где J^Qrl/2g — момент инерции массы цилиндра.
С учетом последнего
Т = (3/4) (Qlg)r^.
Изменение потенциальной энергии системы вызвано растяжением (сжатием) пружин и подъемом цилиндра при его движении по вогнутой поверхности. При повороте цилиндра на угол ф верхняя его точка А смещается на величину б=2гф. Потенциальная энергия деформации пружин
П| = 2сб2/2 = 4сг2ф2.
При отклонении цилиндра от положения равновесия на угол ф угловая координата ф центра его тяжести равна
ф = ф/7(Я—г).
В таком случае изменение потенциальной энергии положения цилиндра
102
Цг=Q (/? - г) (1 - cos V) =
Подставляя выражения для кинетической и потенциальной энергии в уравнение Лагранжа, получаем уравнение малых свободных колебаний
~ , /2 if . 16cg\ л
откуда собственная частота колебаний
„=1/2—
г } 3 (R — г)~г 3 Q*
Из полученной формулы следует, что при R—r, р—<х>, т. е. частота колебаний возрастает с уменьшением радиуса кривизны вогнутой поверхности.
10. ______________________________
p=Vc/(2m) — g/(2I).
11.
•р=Гс///п=224 сЧ
12. Для решения задачи удобнее всего воспользоваться уравнением Лагранжа второго рода.
В процессе колебаний при отклонении стержня АВ на некоторый угол ф от положения равновесия диск имеет кинетическую энергию
+ Jm = ^\ (1)
где <р — угол закручивания стержня.
Линейная скорость перемещения диска v и угловая скорость
•ф связаны со скоростью отклонения стержня ф зависимостями
о=/Ф; ф=(///?)ф. (2)
Потенциальная энергия системы равна
П = Сф2/2 + т^,
где у — изменение вертикальной координаты центра тяжести диска.
Очевидно, что
у = 1(1—cos ф) sin а~ (/ф2 sin а)/2. (3)
Подставив эти соотношения в уравнение Лагранжа второго рода, получим
ф. с (///?)» 4-mg/sin а (3/2) ml' т ’
откуда собственная частота колебаний
1 / с (//Л)14- mgl sin а
Р~ Y (3/2)ml*
103
I
Из последнего соотношения следует, что частота р обра. щастся в нуль (система неустойчива) при
sin а.=—сЦ (mgR2).
13. При перемещении поплавка в вертикальном направлении (например, вниз) на величину Дх возникает дополнительная выталкивающая сила, равная (nd2/4)yAx. Дифференциальное уравнение движения можно представить в виде
[miAx+ (л^2/4)уДх]/|4-/п2Дх(/з2//1) +сДх(/22/7|) =0, откуда частота собственных колебаний
р—К(л^/4 + cl?/l |2) («I 4- m-lflHi3).
14. Составим дифференциальное уравнение движения, используя уравнение Лагранжа второго рода.
Кинетическая энергия диска
T=mu2/2+J<p,’.2,
где v—скорость движения диска по направляющей; ф| — угловая скорость диска.
Потенциальная энергия
n = mg(R—г) (1—coscp).
Углы ф И(р| (рис. 214, а), а также скорость v связаны между собой соотношениями
С учетом последнего кинетическая энергия диска Г=[(/?-г)/г,](шг1+/) (ф«/2).
Подставим в уравнение Лагранжа выражения для кинетической и потенциальной энергий:
(тг24-/)ф4-т#[г7(Я—r)]sin<p—0. (2)
104
При рассмотрении малых колебаний (sintp«<p) частота колебаний p-v mgr*/{(R -r)(mr*+J)\.
Получим теперь дифференциальное уравнение движения, используя метод Даламбера. Из рис. 214, б можно записать
тх= —Ncos ф+Feos <р; (3>
m</=Ncos<p4-F sin<p —mg; (4)
/ф = —Fr, (5}
где N— сила нормального давления; F— сила трения между ступицей и направляющей, препятствующая проскальзыванию диска.
Умножив уравнение (3) на cos ф, а уравнение (4) на sin ф и сложив их, получим
т(хС08ф+^51Пф)=Г—/П£5Шф. (6)
Используя уравнения (1) и (5), запишем выражение для силы трения
F----J(R_r)y/r\ (7)
Выразим координаты центра тяжести диска через угол ф:
*=(/?—r)sinq>; y=(R—г) (1—совф). (8)
Подставив выражения (7) и (8) в уравнение (6), получим уравнение (2), выведенное выше по методу Лагранжа.
15. Решение этой задачи аналогично решению задачи 14. Дифференциальное уравнение малых свободных колебаний имеет вид
(mRz -|-2/) ф+с Я2ф=О, где ф — угол поворота колеса.
«л ~ . 3(Я—a) g п.
16- V+ Р + <Р=0:
%m«x = M^+4aW+a2 + 3/?a).
17 л — 1/ mSl<1
Р V (/ + /?’«)(/?-Г)-
18. Рассмотрим произвольный момент движения груза, когда точка контакта смещается в положение В (рис. 215, а). Полное контактное усилие разложим на две составляющие н Л/,. Тогда дифференциальные уравнения движения можно Представить в виде
(Q/g)di=^; (Q/g)Ay=^-Q- (1)
гДе Дх и Ду — смещения центра тяжести груза при колебаниях.
106
Рис. 215
Используя принцип Даламбера, рассмотрим сумму моментов всех сил относительно центра тяжести груза Ci:
—JcA<P=(Л Bcoscpqh—Дх) созДф—Nx (a+Д у). (2)
Учитывая, что ЛВ=^?1Дф1я=/?2(Дф1—Дф), найдем
Aq>.=/?2^; лв=/?1/?2^: Дх=аДФ.
Так как Ду = ЛВДф=/?1/?2^у — величина высшего порядка малости, то, подставляя (1) в (2), получаем дифференциальное уравнение движения
(Jc+a2m) Дф4-/п^(/?1/?2/А7? — а) Дф=0. (3)
Отсюда находим частоту собственных колебаний
p=V[mg/(Jc-1t-a2m)](RlR2/^R—a) .
В случае вращения маховика можно пренебречь ускорением силы тяжести и дифференциальные уравнения свободных колебаний груза представить в виде (рис. 215, б)
тДх=— /Уж+/П(1)2гДЧг (Д'И = (а/r) Дф;
/сДф=Лгжа—т<1)2г(/?|Дф1—Дх), где
Дф|“Дф/?2/Д/? и Дх=аДф.
Исключая из этих уравнений Д^, ДфЬ Дх и N„, получаем 106
(Jc+aIrn)&<f+mrfr[(RtRi—aAR—atbR/r)&R[&<^0
Отсюда находим частоту собственных колебаний груза:
P = V[m^r/(Jc-]-a~rri)] (RiR2/^R — a—al/r).
19. _________________________
p=a>yR/l.
20. На рис. 216, а показано положение стойки в произвольный момент времени. Взяв сумму моментов относительно шарнира, получим
—Pl—mgy+P{a=0. (1)
(2)
Рис. 216
Так как Pi = 2c2(yi—Ду), а у\—уа/l, то после преобразований получим дифференциальное уравнение малых свободных колебаний маятника:
myl+2c2(ya/l—\у)а—mgy=0.
Прогиб Ду (рис. 216, б) равен
Ду-Р (/—а) 2а/ (3£/х) = [а (1-а)'/ (3EJX) ] (my) (при определении величины Ду силой тяжести пренебрегаем, поэтому Р1 = Р1/а).
После преобразований из уравнения (2) получаем
2с,д*// — mg у
У
ж[* + 2с» 3EJX J
Частота собственных колебаний
f 2с,аЧ1—тД
Р I/ П I а*(1—а) г т I + 2с, j
У = 0.
107
При EJх— оо и а —1/2 получаем
p = Vc/(2m)—g/2l.
21.
р=иУ tnrl/J в-
22. При малых колебаниях точечной массы т на нее действуют силы (во вращающейся системе координат), показанные на рис. 217, а; сила инерции /——ту»;* центробежная сила инерции F‘=mu2(R+l), сила инерции Кориолиса (из-за отно-сителыюй скорости движения) FK=2muy0 и силы Q и N, дейст-
вующие со стороны упругого стержня. При малых колебаниях можно считать, что масса т смещается только по оси у, поэтому, воспользовавшись принципом Даламбера, получаем следующие два уравнения (проектируя силу F на оси у и г и считая угол р малым):
туь+Q— m(i>2y0=Q, (1)
2тауо+ты2 (R+l)
При малых колебаниях влиянием силы Кориолиса на осевое усилие можно пренебречь, т. е. можно положить
АГ-/п<»2 (R+1). (2)
Рассматривая изгиб стержня (рис. 217,6), получаем уравнение
EJ*y"---(yt-y)N+Q(l-z),
108
„ ч 2 I (I—г) I 2 N тЯ^(Я+1) ,п\
у^а?у= Q (аг = £7; =---(3)
решение уравнения (3) имеет вид
у = Ct ch az + C2sh az-j-y0— (QIN) (l—z).
Из краевых условий: z=0, y=0, y'=0 находим C} и C2
Ct^Ql/N-yo-, C2=—Q/(aN). (5)
Так как при z—l y=yo, то из (4) с учетом соотношений (5) получаем
Q[(l/N) chal—(\/aN) sha/]—Уо ch a=0. (6)
Воспользовавшись уравнением (1), исключим из (6) Q. После чего получим уравнение
** । Г ch J г о 1 л
[ (aZ chaZ —shaZ) m w ] ^0 ‘ О
Можно показать, что при a>=0 (a->0) после раскрытия неопределенности скоба в уравнении (7) равна ЪЕ1х/т1\ а это соответствует частоте собственных колебаний точечной массы. Частота колебаний стержня равна
Р^Ро V3 (aZ ch az-shaZ)“3(l(+%/) (P0 = ^>EJx/(mP)) (8)
В выражение (8) входит произведение al, которое связано с угловой скоростью и и частотой собственных колебаний ро массы соотношением
а/= рг3( 1+ /?//) (ш/ро).
23. Если к массе т приложить силу (статически), направленную по оси у (рис. 218,а), то на стержень будут действовать силы Q и N, равные
109
Q=P+m<o2i/o; (1)
N=M<S(R + l). (2)
Понимая под жесткостью стержня отношение с-Р/уъ, найдем уо, воспользовавшись приближенной формулой для прогибов при продольно-поперечном изгибе:
y0=y/(l+N/P.), (3)
где y~QP/(3EJx). Подставив в выражение (3) соотношения (1), (2), после преобразований получим
[1 - и/Хэд ] <> + ЛГ/Р,)- Р.
Следовательно, жесткость системы (с учетом центробежных сил инерции) равна с = с0[1 + (4/я2) (а/)2]-т<о2, где с„=3£/х//’; а2=АГ/ (£Л) = те? (/?+О /EJX.
Зная жесткость, находим приближенное выражение для частоты собственных колебаний массы т:
Рх=р0 &
Числовые значения отношений р/р0 и pjpo при R = l приведены ниже:
a/Z . . . . . 0,5 1 2 3 4 5 6 7
Р/Ра • - . . 0.701 1,111 1,382 1.732 2,108 1,443 1.091 0
Р/Ро . . . . 1,031 1,112 1,391 1.761 2,176 2,614 3,066 3,527
Графики изменения отношений р/ро для точного решения [формула (8) в решении задачи 22] и pi/p0 (формула (4) в решении задачи 23] приведены на рис. 218,6. Из графиков следует, что только в интервале значений а/ от 0 до 4 р и р, мало различаются между собой (максимум на 4%). При <х/>4 приближенной формулой (4) при определении частоты пользоваться нельзя.
24. На рис. 219, а показано положение массы т в состоянии равновесия с учетом сил инерции (масса сместилась на yi0) 11 при колебаниях, когда масса т имеет еще дополнительное сме-110
«дение Угк, зависящее от времени. На рис. 219,6 показана масса с действующими на нее силами при колебаниях, где Fiv.
— проекции силы Ft (см. рис. 219,a), J — сила инерции, q и # — силы, действующие на массу со стороны упругого стержня. Кроме приведенных сил на массу будет действовать. сще сила Кориолиса (см. решение задачи 22), которой при малых колебаниях пренебрегаем.
Уравнение движения массы т имеет вид /+En-Q=0 или
т{уы—nt<n2(/i + t/io + l/2*) +Q = 0. (1)
Силы Q и W можно представить в виде
Q = Qo+AQ; NFu-m^l, (2)
где Qo=m<o2(/i+^ю)—сила, действующая на массу в отклоненном состоянии равновесия; AQ — дополнительная сила, вызванная колебаниями.
111
Сила У при малых колебаниях (без учета силы Кориолиса) остается неизменной как в статике, так и при колебаниях.
С учетом соотношения (2) уравнение (1) принимает вид
туги—m(o2y2* + AQ=0. (3)
Дифференциальное уравнение изогнутой оси стержня имеет вид
EJxy"=—N(yll>+yll,—y) + (l—z). (4)
Так как y=yi+y2 (см. рис. 219,6), то, исключив из уравнения (4) слагаемые, характеризующие состояние равновесия, получим
У2’ — агу2 = — а2Угь + (Z — *)• (5)
Решение уравнения (5) имеет вид
у2= С, chaz + C2shaz + y2k— (&Q/N) (!—*) (6)
При Z=0 должны выполняться условия у2 = 0, у2' = 0, что возможно при
Ct-(AQ/N)(l-y2lty, C2=-&Q/(aN). (7)
Из выражения (6) при г=1 получаем (с учетом соотношений (7)) зависимость
ЛО_ RJx (а‘Г ch а/
У2к l‘(alchal —she/’
Окончательно уравнение малых колебаний массы т записываем в виде
~ . Г EJX (aiy ch al л! n
[ ml1 (al cha/— shaZ) •
Частота колебаний массы т равна
। / (al)‘ ch al i a> / 2____3EJX\
P—Po у 3(a/chaZ— shaZ) [p, ) — ml )•
25. Уравнение малых колебаний массы т имеет вид
112
my K—m®2yK+Q=0. (1)
Запишем уравнение изогнутой осн стержня:
EJxy"=N (ук—у)+Q (I—z), или
y"<azy=aiyK<(Q/EJx)(l—z). (2)
После решения уравнения (2) имеем
у=С, cos aZ+Ct sinaZ+yK+(Q/N) (l—z). (3)
Так как при z=0 у=у' = 0, то для постоянных Ci и С2 получаем
Cl = — (yK + Ql/N); C^Q/(aN).
При условии 2 — 1 имеем t/=«/K и из уравнения (3) получаем зависимость
Q=[£’/Xa1 cos a//(sin al—al cos а/)]ук.
Исключив из (1) Q, получим уравнение малых колебаний массы
У к+Ро2 {(«О3 cos a//[3 (sin at—al cos al) ]— (<o/po)2} У к=0.
Частота колебаний равна
р = р0 У (al)3 cos aZ/[3 (sin aZ—aZ cos aZ)] — (o>/p0)2.
26. В этом случае на груз, отклоненный от положения равновесия на величину уо, действует кроме силы инерции ту0 и силы упругости суо еще центробежная сила, равная тш2уо, т. е. дифференциальное уравнение движения имеет вид
шуо+(с—mci)2)yo=O.
Таким образом, частота собственных колебаний p=l/’c/nj. — all,
при elm — ci)2p=0, т. е. движение становится неустойчивым 27.
p=‘K2r0/(/nZ).
28. Рассмотрим отклоненное от положения равновесия состояние массы т (рис. 221, а). В соответствии с принципом Даламбера
ту = — Т оУ1хо — Т оу/(1 —х0) или
У-|~7’oi/Z/[/rexc (Z хо)] = О.
Отсюда частота собственных колебаний
Р = l/ToZ/(znJCo(/—
8—5000
113
График этой зависимости приведен на рис. 221,6.
29. В процессе вертикальных колебаний на груз действуют сила инерции mv, сила тяжести mg и восстанавливающая сила N = aF. Дифференциальное уравнение движения имеет вид
mv+<jF=mg, (1)
где
У = Я(1) + ДХ.
Полное напряжение о в тросе можно рассматривать как сумму статического напряжения и напряжения, вызванного удлинением троса Дх при колебаниях груза:
aF = mg + EFSx/x, (2)
где
x=Rwt = vt
С учетом (2) представим уравнение (1) в виде
тДх +Ax£F/(i'/) = 0. (3)
Дифференциальное уравнение (3) является уравнением Бесселя, общий интеграл которого можно представить в виде
Дх=С1(т|)/1(т)+С1тУ1(т), (4)
где С, и С2 — постоянные интегрирования; т=2рЛ££//ти —-безразмерная переменная; Л и —функция Бесселя первого порядка первого и второго рода соответственно.
Вычислим скорость движения массы т:
114
= dr (c d [т/ (т)] = с2 Х[ТГ (Т)]|2££. (5)
dr dZ [ 1 dr 1 1 ' /J 1 dr 1 1 ' mvt ' '
Используя известные соотношения между функциями Бессе-1Й нулевого и первого порядка, получим
т/о(т)=-^|г/, (т)]; тГ0(т) = -^1гГ, (г)|.
Представим уравнение (5) в виде
ДХ=[С,/0(т) + С2У0(т)][2££/то)]. (6)
Постоянные интегрирования найдем из граничных условий задачи (при t=t0; Дх=0; Дх—Дх0):
С]= —AY। (то); С2 = А\ (Tq);
д___________________________
Л (Хр) У» (то) Л (хр) Y 1 (Хр)
Окончательное решение задачи получим в виде
Дх=Лт[/, (то) У1 (т)—У । (то) U, (т) ]. (7)
Найдем последовательные моменты времени, в которые движущаяся масса проходит через положение равновесия, т. е. моменты времени, в которых Дх=0. Из (7) следует, что эти промежутки времени определяются соотношением
Л (т)/У, (т) =/, (то)/У! (то) = const. (8)
В соответствии с условиями задачи
т0=2 V EFtb/mv=2 У Ю10- 10-sl/(100.1) = 63,2.
Из решения уравнения (2) получаем значения моментов времени тя, в которых удлинение троса равно статическому.
Рассмотрим частный случай начальных условий. Будем считать, что /о=О- В таком случае /о(0) = 1, У0(0)=оо, В связи с ограниченностью скорости из уравнения (6) следует, что С2=0. a Ci = Акту/(2EF) и решение принимает вид
Дх=т/| (т) Дхоти/(2££).
Отсюда следует, что Дх равно нулю при Л(т„)=0. Для нахождения корней т„ воспользуемся справочником [2] (ti = 3,83;
т2 —7,01; tj- 10,17 и т. д.).
Моменты времени tn, в которые Дх равно нулю, равны
t„=tKzmu/ (4EF).
30. Для составления дифференциального уравнения движения груза применим уравнение Лагранжа второго рода. Положение тела в любой момент времени определяется двумя коор-. Динатамн: углом отклонения от положения статического равно-Кесия и длиной размотанной части троса I. Поскольку /= I — известная функция времени, в качестве обобщенной К Координаты выберем угол <р.
8*
115
Кинетическая энергия движущегося груза в декартовы координатах выражается в виде
Т= 0,5 т(х2+у2), где
x=/sin<p, i/ = /cos<p.
С учетом этого кинетическая энергия груза равна
7'«=0,5m[ (/ sin ф+/ф cos ф)2 4- (/ cos ф—/ф sin ф) 2 =
О.бтСР+Рф2)] {|)
Потенциальная энергия груза в отклоненном положении
П=т#/(1—соэф). (2)
Подставляя уравнения (1) и (2) в уравнение Лагранжа
d / дГ \ , <Ш 0 d< ( д<р ) "Г <*Ф
получим дифференциальное уравнение движения в виде
ф+ (2///)ф+ (g/l) зтф = 0.
Полагая отклонения малыми (з1пф«ф) и учитывая зависимость длины размотанной части троса от времени (/=<i>/?0, получим дифференциальное уравнение малых свободных колебаний
ф + 2ф//+Яф/(ы/?/) =0. (3)
В случае подъема груза свободная длина троса в любой момент времени t (полагая Iq^wRtq) равна
I— 4)—(i)/?/ “(о/? (tq—t) = (t\ = tq—t) ,
дифференциальное уравнение движения принимает вид
Фг, — 2ф/ ,/ti 4- ^Ф/(<о/?/,) = 0. (4)
Решение уравнения (3) можно представить в виде
Ф=(С1/т)/1(т) + (С2/т)У,(т), (5)
где Л(т), У1(т) —функции Бесселя первого порядка первого и второго рода соответственно; gt}/(wR),
Постоянные интегрирования найдем из начальных условий задачи (при t*=t0, ф = фо, ф = 0). Дифференцируя уравнение (5) во времени t с учетом известных соотношений [2]:
(где /2(т), У2(т)—функции Бесселя второго порядка первого м второго рода соответственно), получим
116
Ф = -(С,/2(т)/т+С2У2(т)/т).
Из начальных условий находим
= фото Уз (т0)/[-Л (то)Уг(то)— /2(т0) У|(то)];
С2 = —фото/г (то) Д/1 (то) Уг (то) —/а (то) У| (т) ].
Подставив полученные выражения для постоянных интегрирования С| и С2 в уравнение движения (5), получим
т. /,(т)Г,(т,)-Г,(т)/,(ь) ф-фо т /1(т.)Г,(т.)-/,(т.)У1(т.) •
Решение уравнения (4) также можно представить в функциях Бесселя:
Ф=т3[С|/3(т)+С2У,(т)],
где />(т) и У3(т)—функции Бесселя третьего порядка первого и второго рода соответственно.
Постоянные интегрирования определим из начальных условий задачи, подобно тому, как это выполнено в примере 29.
Окончательно получаем
m _ _ т» /1(т)Г,(т.)-У,(т)/г (т.) ф__ф0 г.г Л (т.) У» (г.)-Л (г.)/, (т.) '
Случай опускания груза рассмотреть самостоятельно.
31. Дифференциальное уравнение малых свободных колебаний системы с одной степенью свободы имеет вид
mp4-ct/=0, (1)
где у — вертикальное перемещение груза; с — жесткость системы.
Для определения жесткости системы приложим в точке нахождения массы т к балке единичную силу Р. Тогда жесткость с—1/у, (у, — прогиб от единичной силы).
Дифференциальное уравнение изгиба балки на упругом основании имеет вид
или
4Г+4₽‘!/=О, (2)
где
4р‘-л/(ад.
Представим решение уравнения (2) в виде
У (0) v,+y' (0) v2-j-y" (0) о,+у''' (0) i\, (3)
где (/(0), у' (0),... — значения прогиба и его производных в начале координат (при х=0); оДх)—функции Крылова:
x’i=ch рх cos рх; v2=(ch рхsin рхsh рх cos рх);
117
”»з=sh ₽х sin рх;
-о4 = (ch рх sin рх — sh §х cos рх).
Полагая, что начало, координат находится посредине балки (в точке закрепления массы), запишем граничные условия дЛя определения у(0) и у' (0) и т. д.: при л=0 у'=0, у"'= — \/2EJx, при х=//2 z/ = 0, у"=0
Учитывая, что и/= —4р'у4, р,‘=ыг; v/^v,, найдем
,. /п\ - - 2Р4 р* <Pf/2) v> Ф*/2) — с» Ф'/2) у, (pz/2)
У\У)-Ух- b w1«(P//2)+4P<vJi(p//2)
Вычислим жесткость системы c—\/yt. Сначала определим р:
Р-r Л/(4Е/х); Р“1 М-*
Тогда р//2—I-2/2= 1, с=\/у3. После вычисления у3 получаем с=9,44 кН/м.
Частота собственных колебаний
р = У 77т = У 9440/100^9,7 с"'.
32. Аналогично решению задачи 31, уравнение изгиба балки имеет вид
У= С1о,4-С2у14-С1о,4- С*о4.
Располагая начало координат в левой крайней точке балки, получаем С( = Сг=0. Для сечения х=/ имеем у"=0, Е1ху'" = —1. Используя эти граничные условия, найдем прогиб от единичной силы:
,, /а 1 v.(POv,(pZ)-t>.(p/)v«(PO
** W EJX v,> (pZ) + 4р4уг (pZ) v4 (pZ) •
Учитывая, что р—0,01 см-1 и р/=1, найдем жесткость системы
с=1/у,, или с=3,8 кН/м
и частоту собственных колебаний
р = УсТт = | 3800/20- 13.8 с’1.
33. Жесткость системы определяется так же, как и в задаче 31. Для определения начальных параметров в уравнении (3) решения задачи 31 имеем следующие условия: при х=0 у^ и /=0, при х=/ /=0 и Q=EJxy= —1/2. В таком случае прогиб балки в месте закрепления груза (х=/) от действия единичной силы равен
и и\ — —________v/(pZ) —v,(pZ) и, (PZ)
- 2EJX у, (PZ) v, (pZ) + 4p«va (pZ) У, (pZ) •
В рассматриваемом случае
П«
fil—l у/ k/£Jx, или pZ — 0,25, a частота собственных колебаний груза
р = ---^77—, или р = 87 С-1.
34. Метод Релея основан на равенстве максимальных значений кинетической и потенциальной энергий при колебаниях консервативных систем:
7'тах==Птвх.
Максимальная кинетическая энергия системы
i
7'тах = °>5^Л2+0-5 § tnjfte.
о
Здесь второе слагаемое представляет собой наибольшее значение кинетической энергии балки.
Максимальная потенциальная энергия (энергия изгиба балки)
Птщ —0,5 Cl/i,2.
Здесь
c=3>EJ*/l\
Прогиб балки при колебаниях можно представить в виде
у(6 z)=y1(z)sinpL
Функция y,(z) должна качественно соответствовать ожидаемой форме колебаний и удовлетворять граничным условиям задачи.
В рассматриваемом случае в качестве y,(z) можно взять уравнение прогибов балки от действия некоторой силы Q, приложенной к массе т (рис. 222). При этом
Рис. 222
Эта функция удовлетворяет дачи (при z=0 yl = t/i'=O, при мальное значение кинетической
всем граничным условиям за-г=/ у'^=0). Вычислим макси-энергии системы:
119
т m? ( Ql' \г , ( Ql* К 3 / * у 1./*ГТя,
"*х 2 ! 3tVx I “г 2 I 3EJt I) 2 ( I J 2 I I I Z’
' ' 'o'* ' ' J
или
‘rmiI=-j f $Ejx I
I 2
где И=~^4'(т’) —у f-pYl <12=0,236—коэффициент приве-
0 ' ' х / J
дения массы системы.
Наибольшее значение потенциальной энергии
Пгоа1= (c/2)[QP/(3EJx) j*.
Приравняв Tmax и Птах, находим собственную частоту колебаний системы но формуле
р=У с/(п 4- ц/п^О = } е/|/п + (33/140) тс/]-
35. Решение задачи аналогично приведенному выше. Выберем функцию прогибов балки в виде
i/i (z) =f/0sinnz/2/.
Тогда коэффициент приведения массы 21
Ц = sin2-^-dz, о а собственная частота колебаний
p=Vc/(m+mJ),
где с=ЬЕ1х/1\
После вычислений получаем ц=1.
Если в качестве функции прогибов принять прогибы от некоторой сосредоточенной силы, приложенной к массе т, то коэффициент приведения массы балки ц=34/33=* 1,03.
36. Формула для вычисления собственной частоты колебаний имеет вид
р=Кс/(/п + р/П1).
где с — жесткость системы; т, — коэффициент приведения массы; ц, — распределенная масса системы.
Параметры с и ц для схем, приведенных на рис. 32, а—е, соответственно равны:
c = Gd*/(8D?), р» 0,333;
c=EJx/l3 0,121;
с=96£/х/7/з 0,445;
120
c = 2AEJ ц «0,371;
c = 3EJ х1*/(а№) ц «0,522;
c = nd4G/(66a) g«0,04,
де i — число витков пружины. Коэффициент р. (см. решение задачи 34) определяется" с учетом конкретных краевых усло-вИй схем, приведенных иа рис. 32.
Для схемы, приведенной на рис. 32, е, в формуле для определения частоты собственных колебаний необходимо заменить величину т на / (момент инерции массы).
§ 2. Свободные колебания систем с учетом сил сопротивления
37. Дифференциальное уравнение малых свободных колебаний вала смесителя имеет вид
7<р-|-аф4-сф=0,
или
Ф+2иф4-/>2ф=О,
где
2п=а/1, рг=с[1.
По условнию задаии, п = 1,2/(2-0,5) = 1,2 с-*; ps = Gnd‘/(32G) = = 19,6 с-1, или р=4,43 с-1.
Так как р>п, то наступает затухающий периодический режим и решение уравнения свободных колебаний (1) имеет вид
ф—e-|.»‘(C1COS4,25/+Cssin4,25/). (2)
Постоянные интегрирования Ct и Сг найдем из начальных условий задачи: при О ф=ф0 (фо — угол скручивания вала при его равномерном вращении) и ф=0.
При равномерном вращении вала со скоростью Q угол скручивания
Фо=—aQ/c.
Используя начальные условия, найдем, что С2-=0, Ci ——ай/с. С учетом этого уравнение движения (2) принимает вид
Ф= —/—) е1-21 cos 4,256 I С J
Время t., в течение которого амплитуда колебаний уменьшается в 10 раз, находим из условия е_,-2‘»=0,1, откуда 6—1,9 с.
38. Дифференциальное уравнение движения имеет вид
Ф4-2лф + Ро2Ф-=О.
гДе 2п = pv; J — момент инерции цилиндра.
Вычислим
121
. G/„ 8-10*ж/'32 . „ Ра LJ £-32я£>///р~ 1,02 С
и 2n = 0,046v. Поскольку т0=^ ...2л-..^ = 6,5 с. F Р?-п'
окончательно получаем
л= ]/рг2_^= j/1,0221^ = 0,295 с-1 и v= 12,826 м2/с.
39. Воспользовавшись методом сил, получим следующее диф. ференциальное уравнение малых свободных колебаний массы т:
У~6ц(—^)+б|г(— аук). (1)
Уравнение (1) содержит еще одно неизвестное ук, так как сила сопротивления приложена не к массе т, а к безынерционной балке в точке К, поэтому надо рассматривать еще одно уравнение, связывающее смещение точки К с силами, действующими на систему
По методу сил,
У*=б2|(—ту)+622(—ауж). (2)
Исследование свободных колебаний массы т сводится таким образом к решению системы уравнений (1) и (2). Решение можно искать в виде
Ук=Ве".
В результате получаем характеристическое уравнение третьей степени вида
а № - Г2U3 + Л К+* + гтг- = 0•
Рассмотренная задача относится к задачам с «дробным числом степеней свободы» (в данном случае «полторы степени свободы»).
40. Составим дифференциальное уравнение движения диска. Па диск действует инерционный момент —/<р, момент сил сопротивления пружины —Сф и момент сил вязкого сопротивления демпфера —аф. Поэтому можно записать
7ф-|-осф-4-Сф=О, или
Ф 4-2л<₽-f-/Ар = 0 = 0, где = —зу-^=1.57-10"3 кг-м2; 2n = a/J; pL = clJ. Жесткость пружины
122
с=^тг—^7ГТ> с «0,938 Н-м
nOlt 67D,/
Частота собственных колебаний системы без демпфирования
р=Г c/J, р = 24,3 с-1.
Логарифмический декремент определяется как б = ят0, где то = 2л/К/г —п2. Отсюда приведенный коэффициент силы вязкого сопротивления
п=6 р/Д/ б2 4- 4л2; п — 5,64, а коэффициент момента вязкого сопротивления
a=2n/t = 2-5,64/l,57 10-3 = 7,18-103 Нм-с.
41. Дифференциальное уравнение свободных колебаний запишем в виде
- , a • cl + mg n
<Р + 2^7(Р+^Г*ф = 0’
где а — коэффициент момента вязкого сопротивления движению.
Частота собственных колебаний системы без затухания р = У (cl + mg)/2 ml.
По формуле c=Gd*/(803i) находим с=333 кн/м и, следовательно, р= 14,0 с-1.
Период затухания колебаний
т0 = 2л/|/'р2 — я2, откуда
я = V р1 — 4л2/т02.
После подстановки и вычисления получаем я* 12,5 с-1.
Коэффициент сопротивления движению найдем из условия 2n=a/(2m/), т. е.
a-4nml=4-12,5-10 0,15=75 Нм-с.
42. При движении поршня в жидкости на него кроме силы инерции mdPy/dt2 и силы упругости пружины су действует сила сопротивления, развиваемая демпфером. Эта сила пропорциональна скорости протекания жидкости через отверстия в поршне и, следовательно, скорости движения поршня:
F=ady/dZ.
Воспользовавшись принципом Даламбера, получим дифференциальное уравнение движения поршня
у+2я1/+р21/=0. (1)
123
Учитывая начальные условия задачи (при t=0, У“"Уо, у0= =0), представим решение уравнения (1) в виде
у = у0е~я,со& (V/P-nt-t). (2)
Приведенный коэффициент вязкого сопротивления вычислим по формуле
п=[4лрН / (mz)](D/e)*.
После вычисления получаем п«5,42 с-1 и р2=с/т=3- 10э/ /2,73=1098,9 с-2.
Время t, в течение которого амплитуда уменьшается в два раза, найдем из условия #*=0,5 у0. Подставляя полученные значения п и р в уравнение (2), определим время, в течение которого происходит уменьшение амплитуды колебаний в два раза:
Q,5y0r= уое-п1‘,
откуда находим /1 = 0,14 с.
43. При движении груза на него действуют сила инерции —тх, сила сопротивления пружин 2сх и сила вязкого сопротивления жидкости ах. С учетом этих сил дифференциальное уравнение движения груза представим в виде
х+2пх+р2х=0,
где л = а/2/п = 500/2-50 5 с"’; р2 = 2с//п = 1^=40 с'2.
Учитывая начальные условия, получим решение уравнения движения груза в виде х=xoe~at cos p,s, где /?| = |У-л2= =3,87 с-1. Время затухания колебаний найдем из условия
откуда
In 100 = 1 In 100 = 0,92 с. П О
44. В соответствии с принципом Даламбера составим дифференциальное уравнение движения груза как уравнение равновесия при отклонении стержня на некоторый малый угол <р:
mglq>=ml2<f—с а? у—а2аф=0. (1)
Обозначив 2n=a2a/(m/2), р2= (са2—mgl)/ml2, запишем дифференциальное уравнение (1) в виде
Ф4-2лф+,р2ф=0. (2)
При л = 0 система имеет частоту собственных колебаний
р=У(са2— mgl)/mP.
124
Для определения логарифмического декремента затухания колебаний вычислим жесткость пружины c = Gd*/8D3i. После подстановки числовых значений получим с-=10 кН/м; р2= = 1600 с-2, или р=40 с_|.
Приведенный коэффициент сопротивления демпфера п= ~a2a./(2ml2) = (0,22-3-102)/2-1 0,52=24 с-'.
Частота собственных затухающих колебаний pi = V р2—п2= = 1600—576=32 с-'.
Период затухающих колебаний то=2л/р=6,28/40=0,157 с, откуда логарифмический декремент затухания 6=лт0=24Х Х0,157-3,768.
45. Дифференциальное уравнение колебаний, полученное из уравнения Лагранжа второго рода, при отклонении столба жидкости от положения равновесия на величину х с учетом силы сопротивления имеет вид
у4-2ях-+-р2х=0, где 2« = a/ffi = 4aslnp/[nd2ps(l 4-sinp)J; p2 = (2g/s) sin р, (так как сила тяжести неуравновешенного столба жидкости равна 2xgpnd2/4), откуда частота р1 = Кр2 —л2 и период То = 2л/Р1.
46. При движении массы т из начального положения (справа налево) дифференциальное уравнение движения можно представить в виде
/ИХ! фсх, —FT = 0.
Так как при f=0 х=0, х=хь, то решение уравнения (1) имеет вид
x' = (^-^)cos^ + ^’ (2)
где p—VcTm.
Время /ь соответствующее движению массы справа налево, находим из условия Xi(6)=0. Поэтому
/1=л/р.
Максимальное отклонение массы т от нейтрального положения влево
Х|тах =—Хо+2FТ//Ир2.
При движении массы т слева направо дифференциальное уравнение движения представляется в виде (сила кулонова трения изменяет знак)
тх+сх2+Л=0. (3)
При начальных условиях f—х2=х1т1Х; х2=0 решение уравнения (3) имеет вид
х2= (-«Ь—cos pt — ~r..
\ и тр*/ г (ту)
125
После каждого полупериода амплитуда колебаний уменьшается на 2Fr(mp2), поэтому для n-го полупериода можно записать
х„=[хо— (2п— 1) FT/ (тр2) cos pt + (— 1)1 FT/ (игр2).
Колебания массы т продолжаются до тех пор, пока
Fq<Z С/X(m— |)тах/-
47. При закручивании свободной пружины на некоторый угол ф ее длина изменяется на величину X. В рассматриваемой конструкции осевое смещение диска отсутствует, т. е. Х= =0 и в упорах возникает сила реакции N. Для определения жесткости конструкции составим уравнения перемещений:
ф = Л16||+Л'б|2,
(1)
где бц и б|2 — углы закручивания свободной пружины от действия единичного момента и от единичной силы; 621 и 622 — осевое удлинение свободной пружины от единичного момента и от единичной силы соответственно.
Вычислим коэффициенты Приложим к свободной пружине внешний крутящий момент 6=1, который вызовет в проволоке пружины внутренний крутящий и изгибающий моменты 411,,= Isina, и AfiB=lcosa (a — угол подъема витков пружины). Приложение единичной осевой силы вызовет также внутренние крутящий и изгибающий моменты Л12,,= 1 -fleosa и
— 1 J?sina. В соответствии с методом Мора имеем
2nfli ..2
. С И,и j , С jW1k < л r-./sin’a , cos’ a\
й|,_ ) G77ds4“ ) £77ds —2^ ("ЗУГ + ТТ?)’ 0*0
2л/?/ 2
Л С Л,2и . I С Л,гк ,/с°8г® , Sina\
) 677ds+ ) 3 —+_ , (3)
о 1 о \ р /
2kRI 2nRl
$ ^^d* + $ о ₽ о х
=л/?'2(о77+т^)81п2“: (4)
где j — число витков пружины.
Решение системы уравнений (1) с учетом Х = 0 позволяет получить следующее соотношение:
Ф=с/Л1
где с=б22/(би612—6122); Л1=—фс(;
С1 —612/ (бцб|2—6122) •
126
В соответствии с полученным решением момент сил тре-ния
AJTp = |1Л//?=рс |<р/?=с*ф,
-де с*=|л/?сг, ц — коэффициент кулонова трения; R — радиус трущихся поверхностей.
' В последнем соотношении нет знака минус, так как имеются две поверхности трения и Л1тР не зависит от того, по какой из поверхностей происходит контакт.
Таким образом, в процессе колебаний на диск действуют следующие моменты; момент инерции /<р, момент силы сопротивления пружины cq> и момент силы трення с*ф, который всегда направлен против скорости движения ф. Дифференциальное уравнение движения представим в виде
/ф4-с+,ф+$1£ПфС*ф=0, (5)
где sign ф означает знак скорости движения ф.
По условию задачи при <=0 диск отклонен от положения равновесия на угол ф0.
Для первой четверти периода колебаний (при фо^ф^фо,) дифференциальное уравнение движения имеет вид
ф+ (с/1—с*/7)ф=0.
Для движения диска необходимо, чтобы выполнялось неравенство Сфо>с*фо или Л1>Л17Р, как указано в условии задачи.
Решение уравнения движения для первой четверти периода колебаний имеет вид
Ф=Фосоз£1/,
где
*.= Г (с-с*)/Л-
Zi—л/2&|.
(ф = 0) изменяет*
(6)
(/=Zi; ф=0; ф= в виде
Время движения в первой четверти периода При переходе через положения равновесия ся знак момента силы сопротивления и знак момента инерции. Знак момента силы кулонова трения сохраняется, так как сохраняется знак скорости ф. Поэтому движение во второй четверти периода можно описать дифференциальным уравнением
Ф+(сЧ-с*)ф//=0.
Учитывая начальные условия движения ’=—Фо£|), решение уравнения (6) представим
Ф= — sin£2/,
где У /J. Отсюда следует, что в
Да при t2—n/2ki, / = /|+/2=0,5л(1Д|+1/А2) отклонение диска от Положения равновесия составляет
конце полуперио-
127
%!= — (7)
скорость же движения ф', = 0.
В третьей четверти периода дифференциальное уравнение движения имеет вид (1)п но с начальным углом <pOi. определив-мым выражением (7). В четвертой четверти периода движение описывается дифференциальным уравнением (6).
Проведя решение аналогично предыдущему (см. задачу 46), получим, что в конце первого периода амплитуда угла ново’ рота диска уменьшается до
qx>i=<po(WM2="<Po(c—с*)/(с+с*).
В конце п-го периода колебаний амплитуда равна фоп=фо (ki /k2)2,1=фо[ (с—с*) / (с+с*)
Период колебаний
Т -2 (/, + У -» (Д-+ (/5^+
48. При наличии кулонова трения между диском и упорами дифференциальное уравнение свободных колебаний системы (см. задачу 47) имеет вид
/фН-Сф+sign фС*ф=0. (1)
Будем считать, что в начальный момент времени / = 0 диск имеет некоторое отклонение фо и находится в покое (фо=0). В таком случае в начале движения при изменении угла ф в пределах 0<ф^ф0 уравнение (I) имеет вид
Фь+^2Фо=°- ®
где
V=(c-c*)//.
При переходе диска через положение равновесия изменяется знак силы упругого сопротивления и знак силы инерции, и уравнение (1) принимает следующий вид:
ф2-|-Л22ф2 = 0, (3)
где
V-(c+,c*)//.
В третьей четверти периода будет действительно уравнение (2), в четвертой — уравнение (3) и т. д.
Решение уравнения (2) представим в виде
Ф1 = С! cos&i/ + C2 sin kit.
Учитывая, что при < = 0 ф1 = фо, а ф1 = 0, получаем
ф0 = ф,3СО8 kit, |
Ф1= — А1Фо81пй^ J
128
Выражения (4) на фазовой плоскости (ф; <р) представляются В виде уравнения эллипса (рис. 223):
ф 12/фо2+ф|2/ (Л,фо) 2= 1.
Решение уравнения (3) получим, учитывая, что при ₽л/2^| фг=ф1=0, а фг=Ф1 = —&1фо- Тогда
Фг= Фо sin Аг/. 1 ф2= — Л°ф0СО5 k ,t. ,1
Здесь время t во второй четверти движения изменяется от 0 до /2. Конец второй четверти движения определяем из условия, что при t — t2 Ф2=0, откуда t2=n/2k2.
Система (5) на фазовой плоскости представляется также в виде уравнения эллипса (см. рис. 223):
Подобным же образом находим решения для остальных участков движения. Так как ki<Zk2, то движение системы является затухающим.
49. Дифференциальное уравнение свободных механических колебаний системы имеет вид
тх + сх=0. (1)
Дифференциальное уравнение колебаний тока в контуре представим в виде
+ (2)
Дифференциальное уравнение колебаний напряжения в контуре будет следующим:
CU+U/L=O. (3)
9—5000 129
В соответствии со структурой уравнений (2) и (3) электри-ческая аналоговая цепь является контуром, состоящим из kor. дснсатора емкостью С, катушки индуктивности L и выключателя. Если на обкладках кендснсатора накопить электрический заряд, затем цепь замкнуть, то в ней возникнут колебания электрического тока I и колебания напряжения с частотой р=» =1//тс.
50. Дифференциальное уравнение свободных затухающих колебаний поршня имеет вид
тх4-ах-}-сх = 0.
Дифференциальные уравнения колебаний тока и напряжения в электрических цепях представим в виде
Li'+Ri+I/C=0, (1)
CU+U/R + U/L=0. (2)
Уравнение (2) описывает колебания тока в цепи, состоящей из катушки индуктивности L, сопротивления R и конденсатора С, соединенных параллельно. Уравнение (2) описывает колебания напряжения в контуре, состоящем из тех же элементов, но соединенных последовательно.
§ 3. Вынужденные колебания
51. При движении станины вибрографа по закону у= = j/osin<i)Z магнит совершает колебания, описываемые дифференциальным уравнением
ту=— с(у\—у), (1)
где у\ и у — перемещения нижнего и верхнего концов пружины соответственно; yi—у — величина растяжения пружины, или величина смещения магнита относительно катушки.
Обозначим
г=У1—у. (2)
Тогда
y0=z + 'y = z — y^sin cat (3)
Подставив в уравнение (3) значение у из (1) с учетом (2), получим дифференциальное уравнение малых вынужденных колебаний
z=po2z=y0(a2sin
где ро2=с/т.
Решение последнего уравнения имеет вид
z=p^~ISint0t-
130
Наименьшие искажения колебаний, очевидно, происходят лри ро2<(л2. Тогда z«—j/osino/.
г Знак минус показывает, что колебания магнита относительно колебаний станины противоположны по фазе, т. е. магнит в этом случае остается неподвижным в пространстве.
52. При вращении детали с угловой скоростью ш закон движения измерительного стержня выражается уравнением
х—1 sin wt. (1)
При этом на стержень действуют сила инерции — тх, сила реакции R и сила упругости пружин С|Х+С2(*+бо) (где ct — суммарная жесткость плоских пружин; с2 — жесткость винтовой пружины; б0 — предварительный натяг винтовой пружины). В таком случае дифференциальное уравнение движения имеет вид
ntx+С\Х 4- с2 (х+б0)=/?, или (2)
/пх4-(С14-С2)х4-/?0=/?(
где ct6<,=Ra.
Условие непрерывности контакта заключается в том, что сила реакции R всегда направлена в одну сторону (вверх). Тогда предельную угловую скорость ы. можно найти из условия, что минимальное значение реакции в течение периода хотя бы один раз становится равным нулю.
Подставляя уравнение (1) в (2), находим
(Ро2—св2) sin cof-|-/?o/(me) =R, (3)
где р0= Y (с,+с2)/т — частота собственных колебаний измерительного стержня.
Рассмотрим возможные случаи.
При дорезонансном режиме работы (р02>ы2) минимальное значение реакции достигается в моменты времени, когда sinw/i = — 1- При этом
-р024-ш14-/?0/(те)>0, (4)
или
/?о/ {те) > то2—со2. (5)
Для непрерывности контакта необходимо, чтобы условие (5) выполнялось во всем интервале возможных значений а (0<<о<ро), и если оно выполняется при ш = 0, то и для всех «5^0 оно будет выполняться.
При w-0 /?«> (Ct-f-cje.
Если условие (5) не выполнено, то возможны нарушения контакта, т. е. R=0. Из условия (4) получаем следующее выражение для предельной угловой скорости со:
wi. = flo2— RY {те).
9*
131
Еще один случай нарушения контакта возможен при <ог>.р г (зарезонансный режим). При этом /? = 0 в момент времени, кор-да ы/2=1. Таким образом, еще одно значение предельной уг. ловой скорости определяем по формуле
“2.= Ро + R^(me).
Динамическую реакцию при <о = О,1и2» находим из уравне-ния (2):
Я=/?оЧ-[(С14-с»)—п1(0,1ш:.)’]е sin «’*#„ (6)
Вычислим теперь параметры, входящие в уравнения (3) и (5). Жесткость винтовой пружины
Gd* 10“0,00I« ,
Ci SD4 0,005’-20 — 4 КП/М.
Жесткость двух плоских пружин
= 9.26кН/М.
Предельная угловая скорость
1/ Ci + Ci , Я. 1/4-10*+ 9,26-10’ . 5
V -^—+^7= V----------бдо---- +мПб^=600Лс •
Наконец, измерительное усилие прибора, определенное по формуле (6), равно
/? = 5±1,3 Н.
53. Отбросив шарнир (заменив его реакцией W) и приложив к торцевому сечению неизвестный момент М (рис. 224), согласно методу сил, получаем три уравнения
у=бц(—ту) +б|2Л1 + б|зЛ^;
ft = 62t (—ту) +б22Л1+б2^;
У\"• Sai (—ту) +бзгЛТ+633N,
где fhj — коэффициенты податливости; O=O0cos(i)Z у\ — вертикальное перемещение сечения, связанного с шарниром, i/i = 0.
Рис. 224
132
Выразив из двух последних уравнений этой системы Af и N, досле преобразований получаем следующее уравнение относительно у:
y+ay=bfr0cos <о/, где а, b — коэффициенты, зависящие от бу. При установившихся колебаниях имеем
у =---Ч-cos юг.
’ а—и’
Определив у, находим М и N. Изгибающий момент в заделке (см. рис. 224) равен
Л4из“Л+.2/ЛГ+Л1.
Максимальное нормальное напряжение в заделке равно
Отах — х. ч
где Wx — момент сопротивления сечения.
54. Задачу следует решать аналогично задаче 53. В сечении, перемещение которого задано, прикладываем неизвестную силу Р, отбрасываем опору, вводя еще одну неизвестную силу N, и методом сил получаем три уравнения:
у=бц(—ту)+б,2У + б13^л, (1)
0=бг1(—/nf/J-biWV+iW’*. (2)^
Ук~ 6„ (—ту) + 6,1 Л/ Ч-.бахР*, 13)
где Рк — неизвестная сила, приложенная в точке k, у* — =y0cos a>t.
Из уравнений (2) и (3) находим Рк и У. Выражение для силы У имеет вид
кг(6»16»а—5»1Д») + ба>.</> cos СИ ..,
Исключая У и Рк из уравнения (1), получаем следующее выражение для определения у:
y+p2y=by0cosut, (5)
где р и b — коэффициенты, зависящие от бу.
Определив у из уравнения (5), находим У.
55. Перемещение стержня 1 на некоторую величину х вызывает поворот рычага на угол ф=х//. В этом случае при движении вверх усилие в пружине 2 увеличивается, а в пружинах 5 уменьшается. Таким образом, на стержень 1 действуют сила инерции —тх, сила сопротивления пружины гс^х+хо), реакция опоры R и усилие со стороны рычага 3, равное |7ф+ + с2(ф—фо)//о-
При этом дифференциальное уравнение движения стержня / имеет вид
133
(m4-J//‘)x+ (c.-ct/P)x+ (c.x.+M>o//) = /?,>.
Обозначив mfy/i'-Af, c, = g//s=c, c1x04-c,<pe//=P0( предСТа. вим дифференциальное уравнение движения измерительного стержня в виде
Mr+cx-t-P0=R. (1)
Условие постоянства контакта заключается в том, что реакция в точке В| не изменяет свой знак, т. е. /?^0.
Поскольку профиль поверхности описывается уравнением x=asin2nz/A, уравнение движения измерительного стержня имеет вид
x=asin<i)/, (2)
где
ы1 = 2т/А = (2n/A)vt. (3)
Подставляя уравнение (2) в (1) и учитывая условие /?^0, получаем
(ро2—a2)a sin at + Po/M^O, (4)
где Po—V с/М — частота собственных колебаний рычага прибора.
Возможны два случая нарушения контакта (см. решение задачи 52). При дорезонансном режиме (Ро2>ш2) нарушение контакта возможно при
<о2=Ро2—Ро/аМ.
Если параметры системы выбрать такими, чтобы выполнялось условие Ро > Г|< р С: а = р2Ма, то нарушение контакта не произойдет.
При работе в зарезонансной области (ш2>ро2) значение <о. при котором возможно нарушение контакта, найдем из равенства соотношения (4) нулю (при sin<o/| = l). Тогда
(а2=Ро2+Ро/аМ,
ли с учетом (3) получаем, что предельное значение скорости о» определяется формулой
о» = (Л/2л) +
56, = Vгде (Po=C2/J).
57. Дифференциальное уравнение вынужденных колебаний триммера имеет вид
•f«p+lc4-.(Ci+Ci)^]<p=c1/A(1sin о/.
При резонансе
“>к!=[с+ (с. +,С1) Р\/1=Ро2+ (с,+с») 1г/1,
134
откуда
Ро‘=юк—(с.+с»)/’//.
58. Динамический коэффициент определяется по формуле /гДни=а/х0= 1/| I—<о2/р2|.
Для изображенных на рис. 50 схем а и б соответственно имеем
*днн=1/| 1— тш2/с| и
Адая=1/| 1—4т<о,/3с|
59. Коэффициент динамичности выражается формулой *дки=1/| 1—/й)*/с1-
Так как £Д11и=1/15, а работа мотора происходит в зарезонансной области (р02>ы2), то жесткость системы должны быть равна
с=7<о!=20-105716= 1,38-10‘ Н м.
Будем считать участок А абсолютно жестким, а крепление опор к основанию как заделку. Раскрыв статическую неопределенность и вычислив угловое перемещение опоры двигателя, находим, что жесткость одной опоры
С1=11,ЗЕ/ЯД. Jjl)
Здесь момент инерции площади поперечного сечения /х= = 663/12 = 64/с, а модуль упругости стали £=200 ГПа. Так как с=2с1, то с учетом (1) находим 6=0,654 см. Принимаем 6 = =6,5 мм, тогда 6=26=13 мм.
В этом случае после вычислений получаем с=2с1 = 1,34Х ХЮ‘ Н м, knm= 1/15,1.
Как показывает расчет, наибольший изгибающий момент в стойке Afmax = 0,3 М, следовательно, в опасном сечении действует переменный момент
Л4пих=0,ЗЛ4=0,3(Л40-|-6ди„Л11 sin wf).
Среднее значение наибольшего напряжения в сечении
ат = 0,3 М0Ж, от = 275 МПа.
Амплитуда напряжения
<Та=йдив0,ЗЛ41/1Гх, ав=110 МПа, а коэффициент запаса выносливости
Пв= aa/a.+am/o.’ Л®==1’8<
60. Поскольку возмущающая сила имеет периодический характер, амплитуда вынужденных колебаний системы
а = а„/\ 1—й)2/ро2|.
Амплитуда реакции опоры пропорциональна амплитуде деформации упругой связи
135
R дин = ca = Rct/ 11 —<1>г/Ро21.
Отсюда следует, что динамический коэффициент
^дни —Ramh/Rct = 1/1 1 —<*>2/Ро" I •
Таким образом, для приведенных на рис. 52 схем а—в соответственно имеем
*дии=1/|1—т<о2/с|;
^дни= 1/1I--т<о2/с|;
Лднн = 1/11 —9тсо2/20с |.
61. Обозначим смещение верхнего конца пружины через Х|, а массы — через х2. Тогда сила, действующая на груз пр» движении верхнего конца пружины, F=c(xi—х2).
Дифференциальное уравнение движения массы имеет вид
тх2+аХ2—c(xi— х2) =0, или
x2+2rtx2+p02x2= (cx0/m)sin а/.
Амплитуда колебаний груза относительно положения равновесия (считая о = Ро) равна
х, — 1.55 /7200 , _
xVi=—-Vchn^=- yj~ У -g-f-= 1.615 см.
Сдвиг фаз в резонансном режиме равен л/2, поэтому полное удлинение пружины
Xmax = *«o4-XCT = X„-|-Q/c= 1,615-j-1,26 — 2,875 см,
где Хет — растяжение пружины при статическом действии силы Q = mg.
Максимальная сила, растягивающая пружину,
Ртах = СХтах = 7200 • 2,875 10"2=207 Н.
Найдем теперь среднее и амплитудное напряжение в пружине
_ 8QD _ 8-91-5-10'* nd* 3,14(5-1(H)*
92,74 МПа,
8r,.eD 8-1.615-10-*.7200-5-1(Н nd* — 3,14(5-1(H)*
= 118,5 МПа.
Коэффициент запаса прочности по пределу текучести лт = *т/ Lnax = тг/(тт 4" та) = 92,74 — 118,5 = 2,84.
Наконец, коэффициент запаса усталостной прочности
1/(тв/г_14-тда/т.)= 1+ = 2.22.
136
62. Обозначим вертикальное перемещение штока через Х|, а • перемещение массы через х2. В таком случае на массу действу-еТ передаваемое через демпфер усилие F=a(xi—х2), сила инерции тх2 и сила сопротивления пружин 2сх2.
В соответствии с принципом Даламбера, дифференциальное уравнение движения представим в виде
тх2+2сх2—a (х ।—х2).
Учитывая, что перемещение штока зависит от угловой скорости кривошипа
X\ = r sin at,
получим
mx2-\-ax2-\-2cx2—a<ar cos cat, или
х2 4- 2пх2+рогх2=2л<1)Г cos wt, где
2п = а/т, р* = 2с/т.
Решение этого уравнения имеет вид
х2«= 2псог sin ((at + £)/К(р0! — й)2)2-|-4л2(1)г;
tg£ = 2fto)/(p02 —ю2).
Наибольшие напряжения в пружине возникают при ее наибольшей осадке, т. е. при sin ((of-j-£) = l. Так как по условию (0 = Ро> ТО Х2пих = Г.
Сила, соответствующая этой осадке, будет равна
Pi = cr.
Полная сила в пружине
P=Pi + mg/2^cr+mg/2.
Наибольшее напряжение
Сш.х = 8 (cr+mg/2) D (nd3).
63.
p=V р02—п2 (где р^=с/т, п = а/2т); (ах = 0-, (о2= V 2 (Ро2 —2П2).
64. Дифференциальное уравнение движения системы имеет вид
jc-+-2nx+p02x=F0sinx<, (1)
где х — горизонтальное смещение центра массы системы, от-I считанное от положения статического равновесия; 2п = а/(тх + I +m2); p02—c/(mt+m2)-, Fo=mO(aie/(mi+m2).
Решение уравнения (1) для случая установившегося движения имеет вид
I
137
x=Fosin(w/—e)/l ©y+lnW, (2)
где e — фаза колебаний.
Вычислим работу сил трения (рассеянную энергию) за один период колебаний Т=2л/л>:
2тс,'<.> 2vs/<jt>
^п>= $ a-xdx^ \ <*xdt -= + 4(|1<и .
о о
Значение коэффициента вязкого сопротивления а., при кото-ром рассеянная энергия становится максимальной, найдем из условия <L4Tp/da=0. Дифференцируя уравнение (3) по а и учитывая, что n = a/[2x (/П|4-т2)], получаем
(Ро2—со2)2—a.2co2/ (mi 4- гпч)2=О, откуда
«♦= I (Ро—й>2)/(о| (m( + m2). (4)
Подставив соотношение (4) в уравнение (3), вычислим максимальное значение рассеянной за один период энергии
Лтах= |пРо2(^1 + ^2)/[2(Ро2— <02)] |. (5)
В резонансном режиме (ро=(о) работа сил трения обратно пропорциональна коэффициенту трения а, что следует из уравнения (3).
65. Используя решение задачи 64, из уравнения (2) найдем амплитуду установившихся колебаний:
*о= т^е/\(т.\ + т2) К(ро2—ю2)2+4п2<о2 ].
Усилие, действующее на пружины, F^cx.
Найдем значение угловой скорости, при которой амплитуда усилия, действующего на пружины, равна амплитуде возмущающей силы
Fw = сх$ =---------ст0<о в moUpe
(mi + m,) V (ро*—•’Г + Чп*»’
Учитывая, что ро2=*с/(т.х — тд, получаем
Ро2 = К(Ро2-“2) + «Ч2.
откуда
о», = К 2р02-4л2 = ^2(ро2-2п2).
На рис. 225 изображен график изменения амплитуды силы Fio = cxo в зависимости от частоты возмущающей силы со. Из графика непосредственно следует, что при <o — ®iFio<mo<o2/. а при <о = (о1 Р10>т0ы21.
66. Дифференциальное уравнение движения массы двигателя имеет вид
/nj7-|-ai/4-cz/ = Posin со/,
138
или
y + 2ny-[-p0y = (P0/m)sin<i>t, (1)
где
2п=а/т; pj=c/m\ с~ЗЕ1х/13
Приведем решение уравнения (1) для случая установившегося режима колебаний
у=А sin (cijf+ф),
где А = уС7// (1 — <о2/ро2)2 4- (2nw/p<ff; у„^Р0/с\ tgcp=
*=2пи/(ро2 — о2).
Полный прогиб балки равен у+уо, где уо — прогиб от действия силы тяжести мотора mg.
Таким образом, прогиб балки, а следовательно, и напряжения в ней изменяются по несимметричному циклу.
Вычислим величину напряжения в заделке:
om = mffZ/U7x=6mg//(bftl) = (6• 50-10-1)/(125-10"*) =24 МПа.
Поскольку напряжения пропорциональны прогибам, амплитудное напряжение можно вычислить следующим образом;
а. = аст/ 1/(1-й)2/ро2)2 + (2ло/р02)2, где
аст=Ро// Wx = ^?°;L6 = 96 МПа; д>2 -с/т = 3EJx/(ml3),
1 £>О* I U
ро2-=625О с~2.
Коэффициент запаса усталостной прочности определим по формуле
л° = a./o-i + от/°в ’ ®
в которой единственным неизвестным является коэффициент п. Из формулы (2) определяем п=62,64 с-1, откуда a=2nm= = 2-62,64-50 Н-с-м-'.
67. Динамический коэффициент равен
Адин = 1/К (1 — ^/РоУ + рпи/ро2?.
После подстановки числовых данных получаем йдин = 0,316.
139
68. Дифференциальное уравнение движения массы т относительно станины имеет вид
у+2пу+р02у=у0а>2 (sin со/4-200 sin 10 a>t),
где у — смещение массы т относительно основания, 2n=a/m; Poz=c/m.
Запишем решение этого уравнения для состояния установившегося движения:
Уо<*>2
у = г - sin (соt — а,) + У(№—со2)г + 4п2<ог '
-]— 200(0 у° -------sin (1(W — а2),
V(A2— ЮОо2) + 400n2co2 '
где tga1=2«o)/(to2—Po2); tgcc2=2O/zco/(lOOcd2 — p02).
Учитывая, что po2=0,01 и2 и п=0,02о, окончательно получаем, что относительное смещение массы т, которое записывает прибор, определяется выражением
у—у0 sin (и/—ai)+2f/osin (10 о/—о^).
69. Дифференциальное уравнение малых свободных колебаний зеркальца имеет вид
/ф+аф+сф=Л1 (i), или
ф4-2пф4-рсгф=2И (i)/J,
где возмущающий момент M(i) = F.,a-
Вычислим жесткость системы. Приложим к зеркальцу единичный момент Л1,=£,а=1 (рис. 226, а). При этом зеркальце повернется на угол ф1 относительно вертикальной оси. Считая, что h<^lx (рис. 226,6), найдем
F 1=2рр = 2<2ф1Ц//1.
Рис. 226
140
Отсюда
Л11 = £1а=2С<р1а2//1 = сф1. Следовательно, жесткость системы c=2Qa2/Zi.
Момент инерции массы зеркальца относительно его оси вращения 7=ms62/12.
Таким образом, частота свободных колебаний зеркальца p = K24Qa7(m%b2) ~(a/2J)2.
70. Дифференциальное уравнение движения рамки вибратора имеет вид
/ф-|-аф + СФ=/И0. (1)
Представим уравнение (1) в виде
Ф+2шр+ро2<Р=М, (2)
где
Поскольку возмущающий момент Мо является внезапно приложенным, т. е. удовлетворяет условию м (0 при t<0, 'Ио-рИо при />0, а начальные условия имеют следующий вид: при t=0 ф=0, Ф=0, то решение уравнения (2) будет таким:
Ф=Фст [1 sin (#* + ₽)],
где фст = 7И0/с = у1/с;
Ро=Ус77; n=a/2J; Pi = ]/po2 —л2: tg ₽=Pi /« = Vp02—n2/n .
После вычислений получаем
„ г п 40- 1О’-з,14-16-10-12 .
с = G J р/1=---зг.з.цьг---=21 Н/м;
Ро= Vc/j = у 2,1/(1,02-10-6.10).
При отсутствии демпфирования
Pi=Po=1320 с-1; р = л/2.
При демпфировании (п=0,Зро)
А = 1259 с'1; tgp=3,17; ₽^72°30'.
На рис. 227 приведены графики ф/фст от pit для двух коэффициентов п.
71. Обозначим абсолютную угловую скорость маховика ф. Тогда инерционный крутящий момент, действующий на маховик, равен 7ф (7— полярный момент инерции массы маховика).
141
Сила сопротивления пружины определяется разностью углов поворота маховика и шкива и составляет с(тр—ф), где ф — угол поворота шкива.
Таким образом, дифференциальное уравнение движения маховика имеет вид
/ф=а (ф— ф) 4- (ф— ф) = 0.
Обозначим т = ф— ф. Тогда
Jv-\-av — cv = — /ф.
Учитывая, что ф=о = со0-]- coj cos kt, получаем
v—2nv-\- p02v = k(x>l sinkt,
где 2n = a/J; p(2 = c/J.
Решение последнего уравнения имеет вид v = A sin(£/ — р),
где А = k со, /V —k2)2 + 4/г2Л2.
Сдвиг фаз
Р = arctg \2nk/(p2 — k2)].
Логарифмический декремент затуханий определим по формуле
б = 2лд/У ро2 — п2.
Вычислим момент инерции маховика:
, nD* / . d* \ by *,=='32-(<1 —
После подстановки числовых значений получаем /= = 3,68-10-2 кг-м2.
Частота собственных колебаний (без затухания) и коэффициент сопротивления соответственно равны
Ро=/146/(3,68-IO'2) = 62,92 (Г1, n=a/2J—0,73/(2 - 3,68 • 1 СР2) = 9,92.
Таким образом, получаем 6=1, сдвиг фаз р~53о30'.
142
72. Дифференциальное уравнение движения корпуса вибратора имеет вид
Мх + txx-\-cx = P(t), где
Af = m+2(m0+mi).
Возмущающую силу P(t) находим как проекцию на вертикальную ось сил инерции неуравновешенных масс:
Р (f) = 2т0ы2е sin a>t.
Амплитуда вынужденных колебаний вибратора
*о=XCT/J/ (1 — со2//?о2)2 + (2псо/Ро2)2,
где xCT = 2/ra0®2e/c; п=а/2Л4; р0=Ус/М.
73. Дифференциальное уравнение движения измерительного стержня Индикатора при изменении давления имеет вид т'х-\-+ сх—Р (/) = A/? (Z) Др или
x-\-'2rixA-k2x—BpF^/m=Bs\n(i>t, (1)
где
2n = a/m; k02=c/m\ B=Ap0Fefi/(m&). (2)
Решение уравнения (1) будет следующим:
x=xosin (mt—<р), (3)
где ^чч
x0/xcr = k^/V (k02 — со2)2 +4п2ы2. (4)
Подставляя числовые данные в соотношения (2) и (4), получаем
2п = 200, хСт=1,5 мм.
График изменения Хо/хСТ в зависимости от <о/#о (амплитудно-частотная характеристика прибора) приведен на рис. 228 (кривая 1).
Хо Хот
2
1
° fSlL} 1 г Ро (Pjmu
Рис. 228
143
74. Дифференциальное уравнение движения цилиндра 4 (см рис. 65) имеет вид
/тисоис-}- (С| Сз+ сз) х—bpF,
или
х+2пх-}-р02х— В sin <о/,
где 2n=a/m=0,75-10^70,1 • 10“’=75 с-*; ра2 = (<\+с»+с,)/т=а - (2000+50+1000)/0,1 =3,5-10-‘ с~\ B=poeAF/(тД) = (3,5* ХЮ‘ - Ю-‘ • 1 - 4-10-‘)/(0,1 • 10"*) = 14 м/с2.
Статическое отклонение хст=В/р02 = 14/(3,5-104)=4-10-4 м = =0,4 мм.
Зависимость частоты колебаний цилиндра от амплитуды имеет вид
Хо/хСт=[(1-<о2/Ро2)2+(2пш/ро2)8]-,/*-
В рассматриваемом случае 2п1ръ = 1Ь1У 3,5-104 = 0,4, поэтому
хо/хст=[( 1-о>2/ро2) + (0,4 со/Ро)2]-172-
График этой функции изображен на рис. 228 (кривая 2).
Там же приведено поле допуска на динамическую погрешность измерения (заштрихованная полоса), уравнение которого можно представить в виде
х0/хст= 1±0,1.
Точка пересечения поля допуска и амплитудно-частотной характеристики дает наибольшее допустимое значение угловой скорости контролируемой детали <отах=Ро2/3 = 62,5 с“*.
75. Для решения задачи воспользуемся уравнениями Лагранжа второго рода. Кинетическая и потенциальная энергия, а также диссипативная функция Релся соответственно равны
Т = m.'v2/2-\-J0^/2\
П=с(/ф—Л)’/2;
^ = а(/ф_Л)2/2.
Подставив эти выражения в уравнение Лагранжа
<1 / дт дТ dn dR
At \ а<р ] <>ф а<₽ а<р
получим
J0<p+a/ (/ср —A) + tZ (Z<p —й) = 0,
или
Ф+2Дф + р02Ф= b sin (2nvt/l{ — 7) + p^h0/l,
где
144
ь |/ (—Зу'")*+pv (7'У = Po^i/^nnv);
2n = al2/ J 0; p2 = cl2/ J b.
Решение уравнения (1) можно представить в виде
<р—Л sin (2hvI/Ii— у) +Bcos (2jivt/li—у) +D.
Очевидно, что D-hq/l, а для определения постоянных А и В получим систему уравнений
[ро2— (2л vfl) 2]Л —2п (2л v/h )B = h;
2п {2nv/h) А + (р— (2л v/l\) = О,
из которой находим
л_________»fp/—(2ло//,)г)_______.
“ (р.‘-(2ло//1)*]1 + 4п’(2л«//,Г ’
D_______________2nb (2ЛУ/Ц)________
(р.*-(2ло/1,)’]? 4- 4в» (2лv/Z,)’ •
Решение уравнения движения (1) можно представить в виде Ф=Фо51П (2ло///о +Р) 4*Ло/А где
ф0= и A-’J-B2 = г Ь __________- - .
0 V[p,’-(2nv/lI)’]»+4?(2nv//I)t
Максимальное значение амплитуды колебаний в зависимости от скорости движения прицепа находим из условия
d фо/do—О, или
2 (2п/1) 2Мр0<-2р02и2+«4 -I- 4 л2о)2] + 4[ (2п//) 2ho2<o2+
+р„*(WI (рЛ-^+гп») =0, (2)
[где (1) = 2ло//1.
После преобразований выражения (2) имеем
я2©4+рп4<о2—ро6=О.
При отсутствии затухания (л = 0) из последнего уравнения получаем, что наибольшего значения амплитуда вынужденных колебаний достигает при резонансе w=p0 или и« = р0/|/2л.
При наличии затухания в системе
о) =- V - р04/2л2 ± Кри&/^ + рв6/г?.
Поскольку физический смысл имеет только действительный корень, то
= (*/2л) У — р0*/2п? 4- Кр08/4л4 + р06/п2 -
10—5000
145
76. Аналогично уравнению (5) решения задачи 47 дифференциальное уравнение движения диска представим в виде
/ф -f- сф sign фс*ф=Л40 sin (ui 4- 7),
где с = д22/(б11д)2 —б?2). с* = р/?с|.
Считая, что в некоторый момент времени /О“=0 в режиме установившихся колебаний отклонение системы максимально дифференциальное уравнение на первом участке движения’ представим в виде
ф1+рочФ1“Н81’п (<о/+7), (1)
где р0‘= (с—с*)/], ц—М„/7.
Решение уравнения (1) имеет вид
ф( —CiCOspi/+C2sinpi/+(n/(pi2—со2) Jsin (со/4-f),
где 7 — начальная фаза возмущающего момента.
Уравнение движения на втором участке (см. решение задачи 47) будет следующим:
ф24-р22ф2=ц8т(<1)/4-7), (2)
где р28=(с4-с.)/Л
Запишем решение уравнения (2):
ф2=СзСО5рг/+С451пр2/+[м/(р22—G>2)]sin((oZ+i). (3)
Для определения постоянных интегрирования воспользуемся следующими условиями:
1) при движении системы на первом участке при /=0 имеем ф|™0, ф| = ф|т»х»
2) при движении системы на втором участке при t=t\ имеем ф2 = 0, ф2 = ф|.
В конце второго участка (из условия периодичности) при /=/2=л/<о имеем ф2=0, а ф2=—ф|т„.
Таким образом, для решения задачи получаем следующую систему из шести уравнений с шестью неизвестными
Ci, С2, Сз, С4, 7:
PiC2+[p.<o/ (pi2—(o2)]cos7=0;
Ф1т»х = CiC0sp1/|+C2sinp1/i4-[p/ (pi2—<o2)]sin (co/fF-y);
—PiCiSinpi/|+p1C2cospi/i+[p<o/(pi2—<o2)]cos(<o/1+
+Т)=— P2C3sinp2/|4-p2C4cosp26+[n<i>/(p22—co2)]cos (<0/1+7);
C3cosp2/|+C4sinp2/|+[p/(p22—<o2)]sin (<0/1+7) =0;
Ct+[|x/(p,2-<o2)]sin7=—{C3cosp2n/<o+C4sinp2n/<o+
+[ц/(Рг2—<o2) ]sin (21+7) ];
—p2C3sin (р2л/<o) +p2C4cos (р2л/<о) +[|i<0/ (p22— <o2) cos (л+
7) “CI-
146
71. Точное решение задачи об установившихся колебаниях при наличии в системе кулонова трения оказывается весьма сложным (см. задачу 76). Упрощение может быть достигнуто, если предположить, что и при наличии кулонова трения в системе происходит гармоническое движение по закону
<p=<posin(wf+f).
При этом энергия, рассеиваемая за цикл, может быть определена по формуле
(/=4рМ?фо/2.
В последнем выражении учтено, что сила трения pW прямо пропорциональна углу отклонения системы <р, поскольку N— =С1<р (см. решение задачи 47).
При наличии в системе вязкого трения рассеянная энергия будет равна (см. решение задачи 64)
£Л“алймро2-
Приравняв энергии U и Ut, найдем коэффициент эквивалентного вязкого трения:
а=2рС1/(лс1)).
Амплитуда вынужденных колебаний системы с вязким сопротивлением, эквивалентным кулоному трению, равна
Фо=Фст/1 (1 — w’/До2)8 4- (2пы/р0^, где фст = А40/с — статическое отклонение системы при действии момента Мп; с — угловая жесткость системы;
2л=а//=2цс,/(л<о/);
Угол сдвига фаз у определим из соотношения tgt=2n(o/(po2—ш2).
78. Дифференциальное уравнение движения системы пред-I ставим в виде
/ф+а<р4-Сф+адпфС*ф=.М0-|-Л!15т(1)Л (1)
Уравнение эквивалентной линейной системы имеет вид /ф4-аэф-|-Сф=Л4()-|-Л/151п(й^ (2)
где а» — коэффициент эквивалентного вязкого сопротивления, определяемый из условия равенства энергии, рассеиваемой за I Цикл.
Считая, что установившееся движение гармоническое, т. е. ф=фо+ф|81П(ф/+7), где фо=Л4о/с, вычислим энергию, рассеиваемую в системе, вос-| пользовавшись уравнением (1).
Энергия, рассеиваемая за период в демпфере вязкого трения, равна лаф1Ю, а энергию, рассеиваемую в демпфере куло-
Ю*
147
нова трения, можно определить из зависимости момента сил кулонова трения Л1тр“р.М?=цС|/?<р от угла закручивания дц< ка ср. Выражение для Л41Р показывает, что работа, рассеивае. мая силами трения за половину периода при несимметричном цикле отклонений, равна
[(^И7ртзх+Л11рт1п)/2]2ф|=2цс1/?фй(р|,
Приравнивая энергии, рассеиваемые за период в заданной и эквивалентной системах, получаем
л ааф 12<i)=л аф । св+4 цс ।/?фоф j, откуда
аи=а+(4цС|/?/яш)фо/ф1.
Амплитуду вынужденных колебаний при наличии вязкого трения вычислим по формуле
Ф| ₽ /с ] (1 — ю2/^2)2 + (2яо)/р02)2,
где 2п*=аэ//; рлг—с/1.
Угол сдвига фаз 7 определим, как и при взяком трении: 1§7=2пй)/(р02—ю2).
79. Дифференциальное уравнение движения массы имеет вид
х+рогх=Р(О/т. (I)
Возмущающую силу P(t) можно разложить в ряд Фурье:
ра\_в Г - 4 /fos2<Df соз4ш/ , cos 6®/ , \1
~Т^~ьз~Н ЗЛ5“--^7—h"J]' (2)
Решение уравнения (1) равно сумме решений от каждого лз возмущений (2):
v _ 2Р0 4Р„ ут cos 2лш(
' л£ пт (2п-1)(2лч U’®*)’
Отсюда следует, что гармоническое движение смещено относительно положения равновесия на величину х€Т=2Р„/лс.
Резонанс наступает при pa^2n<o, т. е. при
со=р0/2; р0/4; р0/6;...
80. Решение задачи аналогично решению задачи 79. В рассматриваемом случае возмущающую силу можно представить в виде ряда Фурье
р/А — р I 1 I 1 2 /COS2®f COS 4(0/ ,
Решение уравнения движения груза относительно положе* ния равновесия имеет вид
148
cos 2п<Ы
v= Pt I /%sina>< 2P, лс ' 2m(p0’—co’) пт Xjl (2л — 1) (2л +1) (/>,» — 4-a>*) ’
Полное перемещение груза
81. Дифференциальное уравнение движения массы при действии произвольной возмущающей силы P(t) имеет вид
У+Р^=(1/ш)Р(/), (1)
где р,*=с/т-, c=3EJx/l*.
I Общее решение можно получить, используя преобразование Лапласа. Уравнение для изображения функции У($), соответствующее уравнению (1), представим в виде
{s2-p^)Y (;)=-yos + Уо + f (s)/т,
(2)
Откуда
f/n
I r<s) а» + л«+FT774-т’+ р?) /(*)•
где </о=^#(О), ya- у(0), a /(л) —изображение функции ₽(/)• Переходя к оригиналу, получаем
. <
У (*) = !/о cos sin p(T)slnp0(*—т)(1т.
f о ,n"o
0
I Последний интеграл называют сверткой функций Р(/) и sin р.7. Воспользуемся в данном случае уравнением (2). Так как P(t)—дельта-функция первого порядка, изображение ко-гторой равно единице, и у,=уо=О
ггкуда
Ki(/) = sin pat/(jnp„).
Полученное решение называют реакцией системы на единичный импульс.
Г 82. Гак как P(t)^Q и «/.=«/,—О, то воспользовавшись пре-рбразованием Лапласа, получаем
(s-+poi)y(s) = Q/(rns),
Откуда
Y(s) = Q/[ms (s2+p,)] и тогда
У (0 = LQ/ (траг) I (1 —COS р,0; у (t) =[Q/(mp„) ] sin p,t.
Из полученного решения следует, что при внезапном приложении нагрузки прогиб Утах в два раза больше, чем при статическом действии силы. Действительно.
MQ
ymax = 2Q/(mP<>) -2Q/f“26cr-
83. Рассмотрим силу P(t), действующую на массу т (см. рис. 71). Для случая, показанного на рис. 71, а, в интервале времени 0^/^/, решение имеет вид
У^У«(()Ро,
где у2 = (1— cos р.ОДтРи2).
В интервале времени t^t^oo решение будет следующим:
У~РМ)-У1(‘-Ш
Окончательно получаем:
при 0^/^Л
y=P,(l— cos PuO/(mPoJ), при
у=P„(cos Ро (t—t,) —cos p,t ]/ (mpo‘).
Аналогично для случая, представленного на рис. 71,6, будем иметь: при
//= Ро (1 —cos p,t) /(тр*), при
r/=Pu[2—cos Ро/—COS Р.(/—/,)]/(щро’)
И при 5^4
y=P0[2cos Po(/t—0— cos Po(t—S,)— COS p./]/(mpo‘).
84. Движение системы при однородных начальных условиях Уо=ул=0 имеет вид (см. решение задачи 81)
т
$р wsinp°TdT-о
В рассматриваемом случае
y=a(t—sinp«f/p.)/(mp/); (1)
</—а(/—cos p0/)/(mp,’). (2)
Решение (1) можно получить и операционным методом. Учитывая, что f(s)=a/s2, получаем
У(5)=аД«1(х24-р#г)].
откуда (переходя к оригиналу) имеем
у (t) - а (t—sin Pot/po) I (тр„г).
85. Уравнение движения
//+рЛ/"Л(0/Х
где P(t)—функция, составленная из периодически повторяющихся импульсов, имеет периодическое решение с периодом I
150
вынуждающей силы только при специально подобранных начальных условиях У»=У(Р) и у»=у(О).
Пользуясь правилом отыскания изображения для периодической функции и для дельта-функции, получаем
(s2+P«2) Y(s)—syt—yt~= I/{tn (1—е-«г) ].
Отсюда
у (s) = (syQ+y0) / (s-+p*) + l/[tn (s’+p,*) (1—e-»T)]; (1)
у (/)= y0cos p4 + ~ sin pt/ + 2 sin p0(t - kt) H (t - kT).
^=o
где H(t) —единичная функция Хевисайда.
Из уравнения (1) получаем решение для интервала
y{t) = y„cos p<,t+ {у,/Рв) sin Ро/ +11 / (mp0) ]sin pat. (2)
Для того чтобы решение (2) было периодическим, должны быть выполнены условия периодичности: У»=у(Т), ул=у(Т), которые позволяют получить два уравнения для определения нужных начальных условий:
Уо(1— cos рЛ) — (£/о/Ро)sin р„Т— (l/mp,)sin р„Т;
y„sin Р/Г+ (уо/ро) (I—cos РоТ) = (1 /юр,) cos р,Т.
Определитель D системы равен
0=2(1 —cos р,Т) /р,.
Если T^2kn/pa, т. е. отсутствует резонанс (определить •0*0), то искомые начальные условия имеют вид
j/0 = sin р0Г/[2(1—cos р,Т)трл]; (3)
у,= —1/(2т).
Подставив условие (3) в уравнение (2), получим искомое периодическое решение 0^/^Т:
cos +s,n р°*)-или
У (/)=* (Л/р,) sin (р,/+а),
где Л —l/[m У 2(1—cospoT")]; tga=sin р0Т/(\— cos pj).
Таким образом, амплитуда скорости хшах=Л, а амплитуда перемещения хтах=Л/р,.
86. Решение для периода функции P(t) можно представить в виде
Л(0 = (1/«)[а(0-а(<-Т/2)].
Изображения P(J) и y(t) равны
f(s) = (l—ет«/‘) [hi(1—£?-г»)]-1/[гп(1+е-г»/2)],
. ос ЬТх
Переходя к оригиналу, имеем
У (/)= i/ocos Ро/ sin р</ -I J- V (- 1)Л у р* mp°
4Z . ft kT\ п{, kT\
X sin p() J/-2'] 1 I ?-2~ •
Как и в задаче 85, периодическое решение с периодом р возможно только при специальных начальных условиях уа и у Найдем их из условий
у(Т/2)=-уп- у(Т/2)—ув
0</<°7'/2ЗУеМ АЛЯ нахождения Решен,,я У У) в полупсриоде
У (О = «/«cos р^+Ху./Ро) sin pot+ (l/mp„) sin pj.
После вычисления получаем
> 2Й7. (=“” * - 'ХЙ »’ л'):
y(0=2k(c°spo/4
sin Pn7'/2 , \
Й- cos p,Tl$ S П )*
87. В интервале 0^/^Т функцию P(t) можно в виде
представить
Р(/)=й[Я(/)-//(/-/,)]
и, следовательно, изображения Р(1) и y(t) имеют вид f (s)=Л (1 - е-‘ ч)/[5 (1 - е^)];
Г(s) = + l *0—<~rt‘)
s± + Р«" ms (s'- + р,г) (I —е~т/j
Переходя к ооигичалу, получаем решение у (/) для одного периода:
У (0=Уо cos р0/ -Н v- sin ро/ Ч- |cos ро (/ - /,)- cos ру/]. (1)
Определим р0 и у0. так же как в задаче 85, из условий у(Т) = у0, у(Т)^=у0:
_ Л 1—CQS р„Т 4-cos (Г—/,)— соз
° 2"'Ро! 1 —cos ptT
• _ h sin p„7' —sin pa (T —sin p,t,
;0 2/«P« 1—cosp,r
(21
152
Подставив уравнения (2) в выражение (1), после элементарных преобразований находим искомое решение в интервале
. Л
hsAap -9-
H(t) =-------A-
' ' ' mp„-
cos рп
т
sinpoy
4-2sIn pQ
B интервале T^t^ooy(l) изменяется периодически с периодом Т.
88. Дифференциальное уравнение движения m имеет вид у + 2пу-\-рп2у = (\/т)Р (/), (1)
где 2n=a/m.
Переходя к изображениям, получаем
оо
(s2 + 2ps + Ра2) Y(s) = 2пуа + у0+syQ + 2 е~*"-
t-o
Для одного периода (O^Z^T) в сумме справа следует взять лишь первое слагаемое, приняв k—О. Возвращаясь к оригиналам, получаем решение для первого периода:
.'/(0 = “"' [i/ocos w/-|-5^tbsin sin ц/], .
ГДе <00=^02-/12.
Для того чтобы решение было периодическим с периодом Т, нужно подобрать начальны г значения уй и у0, используя условия периодичности:
Уо=</(Г); yQ^il(T).
(3)
Дифференцируя (2), получаем y(i). Из условий (3) найдем необходимые начальные значения у0 и у0:
е"г sin ci>07’__.
° (А7 —1епГ cos <а„Т 4-1) ’
пт / п I
е1 |cos®0T—sin о,7 I — [
m (е2яГ —2^ cos ®,Г + I)
Подставив уравнения (4) в (2), получим искомое решение в интервале 0^/^Т, которое справедливо и для последующих интервалов.
§ 4. Критические состояния и устойчивость колебаний
89. Рассмотрим элементарный объем жидкости, выделенный из трубки сечениями х и x-(-dx (рис. 229). Масса этого объема dm^pFpdx (здесь Wj—pFo-l масса единицы длины столба жид-кости).
Рис. 229
На рассматриваемый объем действуют сила тяжести (dmtg), касательная составляющая— сила инерции (dmtcpx) и сила Кориолиса (2бт1у0ф). Момент сил относительно точки подвеса равен
dA4 =—(g<p 4-tpx4-2t'*<p) xdm, или
1
dAI— — (/П1/2^ф/2 + /П1ф/3/3-+-‘ио/и№гФ). o'
Запишем момент сил инерции массы трубки и силы тяжести:
Л-fl = — (/поФ/2/3 + fftog<pZ/2).
В соответствии с принципом Даламбера
Д1 + Л12=0,
или
"* . 3/7X|Vq * . 3 ё л
Отсюда находим, что частота собственных колебаний трубки, заполненной движущей жидкостью, равна
P=V 3g/(21) —{3 /п! т>0/|2 (т0 +
Движение является апериодическим при о>,ое, где
х» « = |( то + mi I)/ mt 1 V2g! (31).
154
90. На рис. 230 изображено деформированное состояние системы при ее колебаниях. Изгиб трубы сопровождается появлением центробежных сил инерции в жидкости, величина которых на единицу длины трубы составляет
где ш,— р— масса жидкости, приходящаяся на единицу трубы; р — плотность жидкости; рк — радиус кривизны трубы.
Рис. 230
Дифференциальное уравнение изогнутой оси трубы имеет вид
г!»
(1)
где Jx=nd38/8— осевой момент инерции сечения трубы.
Так как в выбранной координатной системе zOy (см. рис. 230) вторая производная прогиба отрицательна, то
<7=т1у,/рк=—
С учетом последнего уравнение (1) принимает вид
(2)
Решение уравнения (2) представим в виде t/=Ctcos vz-j-Csin vz-j-Gz-j-C,, где v=V mtv2/(EJx).
Постоянные интегрирования определим из граничных условий: 1) при ги0 у=0; 2) при z—0 Л1и=Е/1у"=0; 3) при z=/ !/' = 0; 4) при z-l Q=—Е1ху'"——туа/2.
Последнее условие представляет собой выражение для перерезывающей силы Q, действующей в сечении стержня при
С помощью этих граничных условий представим уравнение Изогнутой оси трубы в виде
у=—[ (ту,,) (2v3E/x)](sin Qz/cos v/—vz).
155
Отсюда следует, что уравнение движении массы при г / имеет вид
yo+2£Vxv3cosv/i/e/[rn(sin vl—vl cos v/)]=0.
Частота колебаний груза' зависит от скорости протекающей жидкости:
Р — V 2£Jjtv3cos v//pn(sfn vZ + vl cos vZ)|. (3)
Если скорость протекания жидкости v=0, то из выражен я (3) получаем известную формулу для определения част* ц собственных колебаний
р=УбЕ7х/(т.1я).
Частота колебаний равна нулю при cosv/=0, т. е. при v/ =л/2. Следовательно, критическая скорость протекания ж ь кости
^♦== v =(л/2/) УEJX/mi.
91. Рассмотрим элементарный объем жидкости, движуще । ся по радиальному отверстию со скоростью с,, (рис. 23! .
Рис. 231
В процессе малых колебаний на него действуют дополниic пая сила инерции переносного движения dni/q и сила Ki риолпса 2dm,c’0<p. Момент этих сил относительно оси врашею1 равен
d/Vf — ——2drnlvll(fr,
где m,— масса жидкости, приходящаяся на единицу длины верстия; tp — отклонение угловой скорости диска от стацион. 1 ного значения со.
Полный момент сил инерции жидкости
- п \ (г2Ф4-2н0фг)/п1<1г =
= — «/И! [ф(гг8—Г)/3 + -Роф (Гл2 —r,2)j.
Кроме того, при колебаниях диска на него действуют мо-йент инерции /ср” и момент упругих сил со стороны вала с«р. ' С учетом всех действующих на диск сил дифференциальное уравнение его малых свободных колебаний можно представить так:
" пу„т, (гэ*~г,»)/3 ।_________£________ л
“ / +л/»1 (Г?—г/)/3 /+nw, (Tj8—г,*)/3 4
Найдем отсюда частоту собственных малых колебаний диска с учетом протекающей жидкости и скорость v* (из условия
А=0): ____________________________________
__ ]/_______£__________I / nv,m, (Г,°—Г,") \‘
I J + nm, (г,’—г,’)/3 4\/ + пт, (г, —r,J)/3j ’
„ _ -[ / tc [J + nm, (егг—г, )/3|
•' ’ пт, (ггг—г,:)
92. Решение этой задачи отличается от решения задачи 90 только определением перерезывающей силы. При наличии пружины следует считать, что
Q-—EJxy'" — — (тул+су,) /2,
откуда выражение для критической скорости протекания жидкости имеет вид
tg vl= (v lc—2EJxy*)/c.
93. Рассмотрим отклоненное состояние диска (рис. 232, а). В этом положении на диск действует упругая восстанавливающая сила
—► —►
-СГ|,
где с жесткость вала при изгибе (с = &EJ
Рис. 232
Так как F{=F— е, то упругая восстанавливающая сила
F, = — с(г-ё).
В этом случае дифференциальное уравнение движения векторной форме имеет вид
где тп —масса диска.
Представим уравнение (1) в проекциях на неподвижны^ координатные оси х и у:
тх-\-сх=се cos wt, ту су = се sin wt.
(2)
При установившемся движении решение системы уравнения (2) будет следующим:
х={ерлг/(рлг—w2)Jcos о/; (3)
'/=[₽Ро7(Р«’—<o2)]sin at,
где p0=V elm.
Из уравнений (3) следует, что амплитуда колебаний неограниченно возрастает при м.-ь-ре^У с/т.
При отклонение центра тяжести диска от оси вращения равно п+е, а при смещение центра тяжести диска происходит в сторону центра вращения, т. ё. центр тяжести диска находится на расстоянии г1—е от оси вращения (рис. 232,6).
Как следует из выражений (3), при весьма высоких скоростях вращения (й>->оо) происходит самоцентрирование диска (смещение г стремится к нулю).
В рассматриваемом случае масса диска
тп=л£)2/гр/4, 771=0,625 кг.
Жесткость вала
с™6Е./х/Р, с—2,35 кН/м
Частота собственных колебаний
Po^Vc/m, po=61,4 с"1.
Отклонение вала от положения равновесия (см. уравнения (3))
Г1=г — е^^хР+у2 — е=*еа2/(р£— о»2), или
П-1.6 мм.
Определим силу, которая отклоняет стержень на 1,6 мм: P=c6=crlt Р-3,77 Н
и вычислим наибольшие напряжения в вале по формуле a=Mu/Wx (где Ma=Pl/2, Wx=ncP/32). Окончательно получаем о=38,4 МПа.
158
94. шж = КЗ£,Л/(/п/3).
96. В отклоненном положении (рис. 233) на вращающийся вал действует инерционная распределенная нагрузка интенсивностью
д=т^гу,
где та — масса единицы длины вала; со — угловая скорость вала; у — прогиб вала.
Составим дифференциальное уравнение изогнутой оси вала в системе координат, вращающейся с валом:
EJsylv=q=m<ta>,y. (1)
Соответствующее характеристическое уравнение имеет вид
Х‘—Л‘= (Xх—*’) (Х‘+^) =0,
где Л‘=тои7(Е/х).
Запишем решение уравнения (1)
y=Ctsin /fz-f-CjCos fcz-f-Cjsh ^z-f-Cch kz
и приведем граничные условия при шарнирном опирании концов вала:
у=у"=0 при z=0;
z/=i/"=0 при z=l.
Для определения постоянных интегрирования имеем систему, состоящую из четырех однородных уравнений:
С, sin£Z-]-C2CosAZ-|-C3sh£Z+C4Ch Л/ = 0;
Cj-f- С4 = 0;
-Л2С2 + й2С4 = 0;
— С)Л2 sin kl— С2k2 cos kl-\-C3k2 sh kl-\-C3k2 chA/=0.
Приравнивая нулю определитель этой системы, находим
sin AZ • sh kl=0.
Наименьший отличный от нуля корень этого уравнения kl=n, т. е. критическая угловая скорость вала равна
*=(л2//2) V EJx/m0.
159
96. Уравнение упругой линии при изгибе вала в системе координат, вращающейся вместе с валом, имеет вид (см. задачу 95):
i/=C,sin Az+Cjcos te-j-Cjsh fcz-(-C4ch kz, где /г‘ = щв(1)7(Е/х).
В случае консольного закрепления (см. рис. 81, а) граничные условия будут следующие:
при 2=0 у=у'=0-,
при 2=/ у" =у"' = Ъ, что позволяет для определения критической угловой скорости получить уравнение вида
c.QSkl-chkl=—1. (j)
Решение последнего уравнения наиболее просто получить графически. Для этого достаточно найти координаты (kl) , (i= 1, 2,...) пересечения левой части уравнения (1) с прямой i]= —1 (рис. 234).
Рис. 234
Наименьший корень этого уравнения (б/)^ 1,875, а критическая угловая скорость
шф = (3,52//2)И£./.с//По.
В случае крепления вала, как показано на рис. 81, б, соответственно имеем
при 2=0 у=у'=0;
при г=1 У=у'=0,
что позволяет получить следующее уравнение для определения критической угловой скорости:
cos kl-sh kl= 1.
Наименьший отличный от нуля корень этого уравнения (W)(=4,9, а критическое значение угловой скорости
wt = (24/Z2) V EJ x/nus-
97. В отклоненном от прямолинейного положения равновесия состоянии на каждую единицу трубы действуют сила инерции, вызванная вращением трубы с жидкостью, равная (т,4--f-tn,) а>гу, и центробежная сила инерции движущейся жидкости, вызванная искривлением вала т,и*/р“= —т,угу" (рис. 235) (знак минус определяется знаком кривизны).
Дифференциальное уравнение изогнутой оси вала представим в виде
EJxylv=(mt+ml)u>iy—mlvIy", (1)
или yiV+kl1y"—k1iy=O, где klt=-m,vt/(EJxy, k,= (т,+т,)(лг/(Е/х). Характеристическое уравнение для уравнения (1) имеет вид
Л‘+ЛД2—V=0, откуда
*1,2 = ± i V(Л|2 + ГА14+4А!2<)/2 ;
Лз.4= ±/(КА144-4Л24-Л12)/2.
Решение уравнения (1) получим в виде j/=C,sin Xtz4-Ctcos M-f-Cjsh M4-Cich X. Постоянные интегрирования определим из условий при г=0 у=0 и у"=0; при ?-/ £/=0 и у"=0.
Критическую угловую скорость найдем из уравнения sin k,/ sh X,/—0. (2)
161
11-5000
Левая часть уравнения (2) равна нулю в следующих случаях: Х,=0, т. е. при ы = 0.
При А=1, т. е. ktl=n, получим значение критической угловой скорости
= Кn*EJx/\l* (/Пи-f- /721)] — л2/П|®2/]/г(/По+ mt)].
98. В соответствии с принципом Даламбсра, уравнение движения рычага 2 можно получить, взяв сумму моментов относительно точки А всех сил, действующих на рычаг:
-/дф+ т&1\2/2-\-с12у/2 — /711(о2/22Ф=О,
где /лф — момент силы инерции рычага при колебательном движении; тгц>1,г — момент силы инерции штока; с//ф»— момент силы сжатия пружины; — момент дополнительной инерционной центробежной силы, возникающей при отклонении рычага при колебании на угол <р;
Отсюда собственная частота колебаний штока
| /с/,-/2 — т.ш1/.* Р Г JA + mtl^r2
При (1)!^(1).гмс/|7(2гп,/г!) малые колебания масс т, становятся неустойчивыми и нормальная работа чувствительного элемента регулятора скорости нарушается, тем самым критическое значение угловой скорости со. является верхним пределом рабочих угловых скоростей регулятора.
99. При малых колебаниях грузов mt их горизонтальные смещения Дг связаны с вертикальным смещением Ду втулки массой тг соотношением
A«/= ](tg a+tg Р) Дг=Мг.
Для составления дифференциального уравнения движения грузов воспользуемся уравнением Лагранжа второго рода
d дТ 0
°* (1)
Составим выражения для кинетической и потенциальной энергий:
т т,Дг/‘ „ицДс? . „ m, (Г + Д«//А)’со3 .
1 2 *> 2 2Л3 п“2 2
п = m2g (Уо + Ду) + С (у0 4- Ду)2/2.
где у0 — сжатие пружины при стационарном режиме работы регулятора.
Принимая на обобщенную координату у смещение Ду, из уравнения (1) получим
/ , 2m, \ . •- . / 2m.со' \ , 2/и.гсо1 Л
(т2 + -*т- | Ду+ (с---р- | Ду-Ь/пг^ + суо------— = 0.
Так как в стационарном режиме Ду=Ду=0, то
162
rnig+cyt—2niir(a2/k=0, u следовательно, дифференциальное уравнение малых колебаний регулятора можно привести к виду
by + р?Ьу =О,
где частота собственных колебаний системы
р=Уг (Л2с—2/п, (О^)/(А2/П2+2 /П|). (2)
Из выражения (2) следует, что существует критическая угловая скорость регулятора
со.*-= klc/(2mt),
при которой собственная частота колебаний равна нулю.
100.
; m,g/(4c) — D -]/’(m,g \2 mtgD
-------2-------+ V ^*8Г J “ ST-
101. При малых колебаниях стержня относительно положения динамического равновесия на стержень действуют момент сил инерции, равный /»ф, сила тяжести Q—tng и центробежная сила инерции, направленная перпендикулярно оси вращения к равная 0,5m/<ij2sin (a-f-ф) (здесь угол а определяет положение динамического равновесия, а ф—малое отклонение от положения динамического равновесия).
Уравнение малых колебаний стержня получим в системе координат, вращающейся с угловой скоростью <о. Стержень может поворачиваться относительно оси, проходящей через шарнир. Для положения стержня, показанного на рис. 85, эта ось перпендикулярна плоскости чертежа и проходит через точку О.
Приравнивая сумму моментов сил, действующих на стержень, и момента инерции стержня относительно этой оси нулют получаем уравнение
Г — Лф+”,- 0>25|п(а4-ф)у 1С05(<х-|-ф)— Q у sln(a-|-q>) = a
Учитывая, что и считая угол ф малым, имеем
Ф4- j -^--р cos а —<о2cos 2a^ф-|-4 y-slna—sin2a = 0. (1) Два последних слагаемых в этом уравнении соответствуют Положению динамического равновесия при ф = ф=0, т. е. их сУМма равна нулю:
1,5g sin a//—0,5<i>2sin 2a=0.
Следовательно, положение равновесия возможно при двух Значениях угла а:
а(=0 и а2*= arccos[3g/(2<o2/)]. (2)
При at“0 из уравнения (1) следует, что колебания будут устойчивыми при
o’< 1,5g//.
Критическая угловая скорость, при которой состояние рац. новесия неустойчиво, равна w.= У i,5g/l.
Подставив в уравнение (1) aJ( получим, что при <»2>3g/(2/)
любое отклоненное состояние равновесия является устойчивым 102.
р=уg/i—ч? и р=а>К1—к/(/й)2)]2 •
103. Кинетическая энергия груза при малых колебаниях равна
7'=0,5тх2-|-0,5тш2х2, где х — смещение груза, отсчитанное от осн вращения. Потенциальная энергия деформации пружин
П=0,5с[ (6,4-х) ’+ (6,-х) ’]=с (б.2 4-х2).
Составляя функцию Лагранжа L—T—П и подставляя ее в уравнение Лагранжа, получаем
х-}- (2с—тш*)х/т=0, откуда собственная частота колебаний р^УЧс/т—а*.
Критическая угловая скорость
w, = K2c/zn.
104. Дифференциальное уравнение относительного движения массы т имеет вид
х-|- (с—т(йг)х/т—0, где х — отклонение массы т от положения динамического равновесия.
Частота колебаний и критическая угловая скорость соответственно равны
р = Ус/т — ы2; со е = Ус/щ.
105. В процессе малых колебаний на пластинку действуют следующие силы: Y — подъемная сила; Мс — момент, создаваемый упругим стержнем, и инерционная нагрузка.
Поскольку площадь поверхности пластинки s = bh, подъемная сила
У=лри,5Ла, где р — плотность воздуха.
164
ирмент Afc = ca, где с — угловая жесткость системы [с= •^G/p/(2/)=nd‘G/(64/)].
Момент сил инерции пластинки /<р, где /в (йй*р,/3) (ЛЦ-_j,3d/2)—момент инерции массы пластинки относительно оси вращения (pi — плотность материала пластинки).
Используя принцип Даламбера, составим дифференциальное уравнение движения в виде суммы моментов всех сил относительно оси вращения:
Ja+ca—У(Зй/3-М/2) =0, или
а-|-[с//—лрц’ййй,/(2/)ja=0, где Ai = 3A/4+^/2.
Отсюда частота собственных колебаний пластинки
р = V dJ — лр'О2йЛЛ1 /(2 J).
Нетрудно видеть, что существует критическая скорость
-о, = 1^2c/{npbh/i^), при которой частота колебаний равна нулю — система теряет устойчивость (происходит дивергенция пластинки).
106. Дифференциальное уравнение малых свободных колебаний рычага имеет вид
/ф4-Сф=Р0/?ф или <р-Ь(с—Р»/?)ф = 0.
Частота собственных колебаний р=У (с—PtR)/J. Критическая сила P.=c/R.
107. Сила притяжения массы т магнитом
Р—кф^/а'.
Если массу сместить в горизонтальном направлении на малую величину x(x<^Oi) (рис. 236), то возникает сила, равная разности сил притяжения:
ДР=Р,—Рг=кфог/ (а,—х)г—йФ01/(а1+х)гл4йФ0х/а1’, где
Р.=йФ,7(а.-х)г; Л-М>.’/(а,+х)1.
Воспользовавшись принципом Даламбера, получим дифференциальное уравнение движения массы:
щх+2Г<,х//=4йФогх/а1’.
Или
х4-[270/(т/)— 4йФв7("И’1’)]*=0-
При малых колебаниях частота собственных колебаний массы в магнитном поле
p=V 2Т0/(т1)—4кФа2/(па}3).
Интересной особенностью полученного выражения для частоты является зависимость ее от Фо, которое эквивалентно по своему влиянию «отрицательной упругости».
1££
Рис. 236
Каждому значению натяжения Та соответствует критическое значение магнитодвижущей силы
при котором частота р равна нулю. При этом значении ф. состояние равновесия массы m является неустойчивым, т. е. колебания невозможны.
108. р=И Ф.-У Mt3£ats/(l6A/»j
109. Воспользовавшись методом сил, получим дифференциальное уравнение движения массы
«/=6U(—my)+d12/?„,
где би=/’/48£/— прогиб балки в точке крепления массы tn от единичной силы; б12 — прогиб в точке крепления массы m от единичной силы, приложенной к балке на расстоянии z от начала координат, или, что то же самое (по теореме взаимности перемещений), прогиб балки на расстоянии г от единичной силы, приложенной в месте крепления массы tn.
Для б|а примем приближенное выражение
612®бп sln^.
Так как z—vt, то окончательно получаем следующее дифференциальное уравнение колебаний массы т;
y+P«2!/=(^o/m)sin nvt/l. (О
При однородных начальных условиях t/(O)=y(O)=O решение уравнения (1) имеет вид
166
Из рассмотрения знаменателя выражения (2) следует, что имеется критическая скорость движения силы /?„ которую можно найти из условия
Po2-(nv.//)*=0, откуда
О* = lpo/п = (I/л) К48EJ/(l3m).
Однако при этом значении скорости v в уравнении (2) имеется неопределенность, раскрывая которую (ло//->р„), получаем
У- —{/?o/(2mpo)](f cos pat—sin pat/pa).
Так как время движения силы по балке конечно, то конечно и смещение массы т, т. е. никакой критической скорости нет.
§ 5. Параметрические колебания
ПО. Для составления дифференциальных уравнений движения воспользуемся методом Даламбера. Спроектируем все силы, действующие на груз, на неподвижные оси xOty (рис. 237): тх=—^sinф, (1)
my=N cos <p—mg. (2)
Рис. 237
Исключим из уравнения (1) силу натяжения JV:
т (х cos ф+у sin ф) = —mg sin ф. (3)
Координаты положения груза выразим через угол отклонения стержня от вертикали ф и смещение точки подвеса yt:
167
y=l—/cos<p+ylt (4)
x*=Z sin cp.
В таком случае
х/ == Z (Ф sin q>4- <f*cos ф) — у0ы2 sin ш/,
х= / (Ф cos ф—ф2 sin ф).
Подставляя выражения (5) в уравнение (3) и считая угол ф малым, т. е. полагая созф=1, з!пф=*ф, ф2=0, получаем
ф+Jg//—(yow7/)sin о)/]ф=0. (6)
Уравнение (6) обычно приводят к форме уравнения Матье t^/dT‘-|-(a4-2<7 cos 2т)ф=0,
где a=4g/(<a‘/); 2q^4ya/l-, т=ш//2.
В зависимости от конкретных параметров системы малые колебания маятника будут устойчивыми или неустойчивыми. Устойчивым колебаниям соответствует положение изображающей точки на диаграмме Аниса—Стретта. в незаштрихован-ных областях (см. приложение 1). Если параметры а и q таковы, что изображающая точка попадает в заштрихованную область, то колебания будут неустойчивыми.
В рассматриваемом случае а=0,784; </—0,04, что соответствует точке на диаграмме (см. приложение 1) в устойчивой зоне.
111. Решение задачи аналогично решению задачи 110. В отличие от него коэффициент а в уравнении Матье отрицателен. Таким образом, движение маятника устойчиво при со^ЗЭб с-’ (при выполнении условия |а| <<?а/2).
112. (ОтьаИгб с"*.
ИЗ. Дифференциальное уравнение малых свободных колебаний пластинки аналогично уравнению движения, полученному в задаче ПО. Если пренебречь силой лобового сопротивления, которая при малых отклонениях пластинки весьма мала, то, считая в указанном решении скорость потока переменной и пренебрегая слагаемыми, содержащими и/, получим дифференциальное уравнение движения в виде
(Рсс/бт2 Д- (а + 2q cos 2т) а = 0, где
4/сР ЗяЫ*рр,*\. „ 4 Зп ь^рУ'У,. . 1
a &\~J 4 J )' “2 J ’ —з*00Р'
При указанных в задаче параметрах и а=1,53 коэффициенты уравнения Матье равны:
при Vi=5 м/с 2q=—0,132, |<?|=0,066;
при п,“10 м/с 2q = —0,264, |?| =*0,132.
168
Из диаграммы Аниса—Стретта (см. приложение 1) следует, что при изменении амплитуды скорости потока в заданных пределах колебания являются устойчивыми.
114. При составлении дифференциального уравнения движения можно воспользоваться приближенной формулой для определения прогибов стержня при продольно-поперечном изгибе
y~yJ(\-P/P9),
где </«=—ту/с — прогиб стержня от действия только поперечной нагрузки, которой в рассматриваемом случае является сила инерции массы; с — жесткость стержня при изгибе; Рэ= *=л1£/*/(4Р)—критическое значение сжимающей силы.
Таким образом, дифференциальное уравнение движения можно представить в виде
У +'(! — P/PJ су/т -= О,
или
у 4- (а+2q со s 2т) у = О, где
а <(^^ = 6,63; 2,—*.^ — 0,39.
/л/, лЧт1 • » * лЧщ
После подстановки числовых значений находим а=6,63; |<?| “0,195. На диаграмме Айнса—Стретта (см. приложение 1) точка с такими координатами характеризует устойчивое движение.
115. В рассматриваемом случае жесткость балки при поперечном изгибе с=24Е1х/Р, а критическая сила Рэ=я2Е1х/Р. Коэффициенты уравнения Матье будут определяться следующими выражениями:
а —
2q =
Pt 4с Р9 ты1'
После подстановки значений получаем а=4,2; |</|=0,02. Точка с такими координатами находится в области неустойчивости на диаграмме Айнса—Стретта (см. приложение 1).
116. Дифференциальное уравнение движения массы т можно представить в виде
у 4-2 (Го-Ь Pt sin wt)y/(ml) = 0, Или
cPy/di? 4- (fl 4- 2q cos 2т) у=О, где
4 2Г, _ 4 2-20 г
“ <0* ml 25» 0,25-6,2 ’
„ 4 27", 4 2 10 „
2? —S* ml — 25*" 0,25-0,2 "=2,061 */2‘
169
Движение массы т является устойчивым, так как точка координатами а™5,12; 9= 1,28 находится в незаштрихованнол области диаграммы Айнса—-Стретта (см, приложение 1). *
117. Дифференциальное уравнение движения груза предста вим в виде к.
У=“ ~6иту,
где б11 = /’/(3£/х) «= (/0—/,sin <of)’/(3£Jx).
Ограничиваясь линейной частью разложения функции 1/6. в ряд по степеням /ь получаем дифференциальное уравнение движения в виде
У+^^+З^п^У-О.
Это уравнение удобно представить в форме уравнения Матье
d2y/dr‘4- (а+2^ cos 2т) У3 О, где
а <о! т/,” ш> и/,’ _ 2 +2т*
Подставив числовые значения параметров системы в выражения для коэффициентов а и 2q, получаем а=2,5; </=0,75.
Решение уравнения Матье будет устойчивым или неустойчивым в зависимости от соотношения между коэффициентами а и q. В рассматриваемом случае изображающая точка на диаграмме Айнса—Стретта (см. приложение 1) попадает в незаштрихованную область, т. е. движение груза при выбранных параметрах системы устойчиво.
118. В произвольный момент времени точка перегиба нити О смещается из своего среднего положения на величину yt, а нить отклоняется от положения равновесия на угол <р (рис. 238).
Используя теорему об изменении момента количества движения, запишем
^1/п(4 + У1)2ф1 = — mg(lo + yi)<9. (О
откуда
Ф-+-2у|Ф/(/о + </1) + £Ф/(4Н-Ю = О- ®
По методу Даламбера рассмотрим равновесие сил, действ)" ющих на груз в произвольный момент времени. Это сила натяжения нити N, сила тяжести mg и силы инерции тх и ту.
Спроецируем все действующие на груз силы на вертикальную и горизонтальную оси:
ту=N cos <р— mg, (3)
тх=— Nsincp. (^
170
Рис. 238
Выразим координаты груза х и у через угол ф и длину *=(^+f/.)sin ф; у= (/,+//,) (1—cos ф).
Подставив эти соотношения в уравнения (3) и (4) и исключив из них силу натяжения У, получим уравнение (2).
119. Дифференциальное уравнение движения матяника имеет вид
где /=/04-/,sin и/.
120. Изменение положения массы т вызывает изменение момента инерции системы. В таком случае для составления уравнения движения удобно воспользоваться теоремой об изменении момента количества движения
^(/оФ)-2Л4О(, (1)
где — полный момент инерции массы системы относительно точки подвеса О; ф — угловое отклонение системы от положения равновесия; Мо(— моменты внешних сил, действующих на систему относительно точки О.
Уравнение движения массы т относительно рамы имеет вид x=xosin (о/.
Момент инерции системы
Л = “О’- (2)
Момент сил тяжести относительно точки подвеса О при отклонении системы на угол ф равен
SMoi= —т^^ф—mg(/.+xosin (о/)ф. (3)
Подставив выражения (2) и (3) в уравнение (1), получаем дифференциальное уравнение движения системы в виде
[J,-|-m(/e4-xosin at)2]ф4-2щх0<1> (/„-f-x.sin w/X
Xcos<o/ <p+g[ml/14-m(/,4-x,sin at)]ф=0.
171
121. Решение аналогично решению, приведенному для задачи 120. Дифференциальное уравнение движения маятника имеет вид
- , 2х,cosat ♦ . g п
/0+х, since/ 6)<* 1 /.+х. since/ ’
где <р — угол отклонения маятника от вертикали.
122. (1ри отклонении вагонетки от положения равновесия на расстояние х и повороте шкива на угол ф изменение длины троса (рис. 239) составит
д/=/?Ф+К/Г+^’-/(Л.
или в случае малых колебаний
Д/=/?ф.
Отсюда следует, что изменение натяжения в тросе \T=MEF/l,=REF(f/la.
Тогда дифференциальное уравнение движения вагонетки можно записать так:
тх= — (T.4-AT)sin а, где а — угол, на который отклоняется трос от вертикали при колебании вагонетки.
При малых колебаниях
sin а=а“х/(0|. (1)
С учетом (1) дифференциальное уравнение движения представим в виде
х+(а-|-2</cos 2т)х=0. (2)
Вычислим числовое значение параметров, входящих в выражение (2):
а=4Т0/(тш’/01) =4-107(500-10*-0,7) =0,114;
2<7=4J?EF<p0/(mM1/o/(,i)=4 0,l-200-Ю’Х
XЮ‘-0,1/(500-102-1-0,7) =2,28; ?=1,14.
Из диаграммы Айнса—Стретта (см. приложение 1) следует, что малые колебания вагонетки неустойчивы.
123. Дифференциальное уравнение движения массы в магнитном поле имеет тот же вид, что и уравнение в задаче 108:
тх+(с—Mf/a,3)x=0, (1)
где c—SEJx/l3\ Ф=Ф(,+Ф181п ш/.
С учетом малости амплитуды магнитодвижущей силы Ф| уравнение (1) принимает следующий вид:
с ЛФ0‘ 2АФ.Ф, Л Л
*4- — — ---£rr-sinw/ -*=0.
1 \ т та^ maf ;
или
dx/dt2 (а 4- 2q cos 2т) х=0, где
4 / с Лф.2 \ о 4 2ЛФ.Ф, а——,[---------Ц- , 2о=---; —^-4-.
со2 т та^ ) со’ тах1
Нанося на диаграмму Айнса—Стретта точку с координатами о=1,03; |q|=0,02, находим, что движение массы устойчиво, так как точка находится в незаштрихованной области.
124. При движении шины ее расстояние от проводника равно а, = а«4-х.
Сила, действующая на шину при ее колебании
\F=-Fa—F2,
где
/=’о=2ц/|/2гХ/<2ю;
Р 2ц//(/„ + /„ sin ©Q 2ц/4,7 . Х\
“5Г (/го + '21 s’n <->0 (J -
В этом случае дифференциальное уравнение движения имеет вид
тх + 2сх=kF,
или
*+2i [1 - йу ('»+'»81• ]* - -s •
125. Дифференциальное уравнение колебаний рычага имеет вид (см. рис. 90)
Ф4- Н-—j------j— sin (di | ф = 0.
173
Обозначив (о/ = п/2Ц-2т, после преобразований получаем коэффициенты уравнения Матье:
(О- J (*)? J
Рассчитав числовые значения коэффициентов а=6,0 и <7=0,4, находим, что движение является устойчивым.
126. В произвольный момент времени положение массы определяется координатой
х,—xM+»/.
Дифференциальное уравнение малых свободных колебаний в таком случае имеет вид (см. решение задачи 28) ~ . _7\_______________________I________ _п
т (I—х,„— vt) (ги + vt) '
127. Пусть в произвольный момент времени точка подвеса маятника смещена относительно положения равновесия на некоторую величину у„, а маятник отклонен от вертикали на угол ф (рис. 240). Тогда дифференциальные уравнения движения массы т имеют вид
тх\= — Arslnq>; (1)
Рис. 240
Подставив в эти уравнения значения координат
xl=s1-|-/lsin <р;
(3)
'Л^ст+'Л+Асоэ ф
и исключив из них силу N, находим
Аф—i/osin(p= —f sin<r
или, полагая угол ф малым,
Ф+fg—£о)ф/А—О- (4)
174
Из условия равновесия узла точки подвеса маятника следует, что
W COS ф 7 (Уо+^ст) /s,+ Л ({/.4-Уст) /$2.
Выражая N через у с помощью выражения (2) и учитывая соотношения (3), получаем
(l/st sj То (у0 4- </„) = mg — m [у —l\ (<p sin ф+ф2 cos ф].
Учитывая, что 1Т<>уст/(sisi)=mg и пренебрегая нелинейными членами в правой части уравнения (поскольку ф — малый угол), представим последнее выражение в виде
Уо^=
или
f/o = P2«/o=°- (5)
где pl=Tol/(msts2).
Решая уравнение (5) с учетом начальных условий (1 = 0, Уо—Уол, Уо—0), получаем уравнение движения точки подвеса маятника
Уо = УооС08 pt.
Подставим это выражение в уравнение (4):
Ч>+-^№ + УоР2<Х)$ рОф=о.
После замены pt=2x получаем уравнение Матье б2ф/(1т2+ (a4-2g cos 2т)ф = 0, где а=47/(р=/,); 2q=4yM/lt.
Подставив числовые значения параметров, находим п= =0,0687; д=0,665, что соответствует устойчивому движению.
Во втором случае получаем а = 0,825; 9 = 2. Точка с такими коэффициентами попадает в область неустойчивых колебаний.
В рассматриваемом случае, конечно, не может быть беспредельно нарастающих угловых колебаний, так как система консервативна. Под неустойчивым движением следует понимать неустойчивость вертикальных колебаний (тенденцию к нарастающим колебаниям по углу ф). Для правильного определения Угла ф следует рассмотреть колебания с учетом нелинейных слагаемых.
128. Решение аналогично решению, приведенному для задачи 127. В первом случае движение маятника будет неустойчивым, а во втором — устойчивым. 1) а=0,0981, 9=0,5; 2) а= =0,0981, 9 = 0,07.
§ 6. Случайные колебания
129. При решении задачи 75 получено дифференциальное Уравнение малых угловых колебаний системы
175
где рог=с/г/Л.
Как известно, зависимость спектральной плотности выхода ф от спектральной плотности входа Л имеет вид
где | IF(idj) р — квадрат модуля частотной характеристики системы.
Частотная характеристика системы равна передаточной функции системы, у которой оператор р заменен на оператор т. е.
Передаточная функция системы W (р) равна отношению изображения по Лапласу соответствующей выходной величины к изображению входной величины:
Г(р)=А'ВЫХ (р)/х„(р).
Передаточная функция для уравнения (1) имеет вид
WV>>- p'+al'p/J. + pT' где p — оператор дифференцирования (p=d/d/)-Частотная характеристика системы
ivz /л \ I (с +
(jw) — ((.q)2 + а/!/с#/Уф + .
Выражения для спектральной плотности S/, и модуля частотной функции можно представить в виде
5Л (о) = 10v/[ (25v*+.®*) 2я]= 10v/(|5о+йо | !2я),
I U7 z/гй I (С^/А)г (g^/A)* (/<>)*
1 * л |(Z®), + aZ’(Z®)//. + />.’| •
Тогда выражение для дисперсии угла ф примет вид
п =J_ С [(с//У,)>—(ст//^0)= (/о»Ч IQvda ф 2л J | (Z®)’ + aZ2Z®/J, + р,« I’ 15v + i<o I1 ’ —оо
или
n _ J°v С ______________((cZ/J,)»-(aZ/J,)3 (Z®)31 dco_____
2л ' |(/®)’-f-(5v+aZs//,)(Z®)’ r (5vaZ’/J, + p0*)Z®-r5vp03 |3’ V
—CO
В приложении 2 даны значения интегралов типа (2). В рассматриваемом случае интеграл (2) соответствует интегралу /» из приложения 2:
= 10-ц -^. + М,-д,дЛ/д, (3)
ф 2a„(atal~alat) '
где
Ог<Рог+а/г5о//0; Ь,=0; а<>=1, at=al2//<>+
+5v; Ь, = —(а//Л>)*; b2= (cr/J,)1; at<5p*.
После преобразований выражение (3) принимает следующий вид:
3_ n 5ир.» (aZ//,)» + («Z»//t + 5v) (clU,У
ф — --------а7гТ аР 1 *
График изменения оФ в зависимости от скорости движения прицепа v показан на рис. 241.
О 5 10 15 I/,м/с
130. Среднеквадратичное значение отклонения угла определяется выражением (см. решение задачи 129)
/5vp.» (aZ/J,)‘ + (aZ*/J, + 5v) (cZ/У.)* cZ4a Ге/» e aZ» 1 “77" Lt7+5v”77' + 25w J
На рис. 242 приведен график изменения о» в зависимости от жесткости рессоры с. Предельное значение при оо равно
12—5000
177
= V + 5z>)/(aZ4).
131. Зависимость спектральной плотности производной функции от спектральной плотности функции имеет вид
S. =‘o2S<p(w). (1)
В этом случае дисперсия скорости
00
£>• = ^ ы25ф (<о) da>. (2)
—оо
Поскольку
|25а(ш).
выражение для дисперсии скорости представим в виде (см решение задачи 129)
Интеграл (3) можно преобразовать к виду
График изменения в зависимости от скорости движения прицепа v приведен на рис. 243.
178
132. Дифференциальное уравнение движения массы т имеет
ВИД
y+ay/m+p^ycfm,
где pj*“c/m\ с=ЪЕ1 X/V=Ebh*/12Р.
Спектральная плотность ускорения S„ (to) = (о).
Учитывая, что спектральную плотность смещения у можно представить в виде
5» = । W Sf = m> |(/®)* + ata/m + pj |* | P. + (/•)*!* 2 л ‘
найдем дисперсию ускорения
D _ 1 р ___________________p,a>*d<n_________________
Из приложения 2 получаем
n _«2 Р. (яМдач-р*1) и у °у 2т [ар1/л1 + р,‘+р»'1 ® ’
После подстановки числовых значений имеем о- =29 м2/с4.
133. В процессе колебаний на массу гп действует сила
F = — ту—ay+f=су.
Вследствие симметрии реакции опор
/?=0,5 F=0,5 су.
Выразим спектральную плотность реакции через спектральную плотность перемещения:
SH (<о) •“0,25c2Sy (ш).
Учитывая, что спектральная плотность перемещения массы связана со спектральной плотностью возмущающей силы соотношением (см. задачу 132)
<, , ._________Sf(«>)
(“J + ако/т + р^'- 2тг’
найдем спектральную плотность реакции
s = ________________0.25с’Р,___________________
R 2тг I (1®)’ + (-J- + ₽*) (/w)’ + ("ST Ь + Z® + | ’2л
Воспользовавшись приложением 2, йайдем
2 р.с3 g/w-bfe ~~ 4т ‘ 2а (ар,/л» + р.‘4-р?)
После подстановки числовых значений получаем ад!=ЗН2, откуда ол=1,7 Н.
19»
179
Максимальное напряжение в балке
Среднеквадратичное отклонение максимального напряжения а?=0я/Л/(/«-2).
После подстановки числовых значений находим о»== = 10,2 МПа.
134. При возмущенном движении системы угловая скорость й = йоЧ_ДЙ.
Если возмущение ДИ мало, то момент сопротивления можно найти как
Мс (й) = Мс (Йв) + (dM<JdQ) о_0, Дй.
Представим дифференциальное уравнение возмущенного движения при действии на систему случайного момента сопротивления ДЛ1С
/бДй/(1/=Л1д—Мс (Йо) —(сШе/дЙо, Дй+ДМс.
Поскольку Мд=Л1с(йо), то
ldMl/dt+ (дМс/д£10, ДЙ=ДМС-
Как известно, зависимость спектральной плотности от корреляционной функции имеет вид
$ /СДм(т)е'“Мт,
или, учитывая выражение для Кьм>
ею
+ С e-(«+to) |д
1 .) I (а’ + ®) л
о J
Спектральная плотность случайной угловой скорости ДЙ равна
где IW (/<о)| = . - 1 .
1 1 / J’Q’ t-(d.Mc/dQ)!
Дисперсия отклонения угловой скорости
n I f Dad®
^да — Т ) Р’4О» 4- (dAtc/dQ)»] (а*+ а’) ’
откуда
л _______________2D____________
^д0 |(<Wc/<H2)(a/ + <LWc/<JQ)] •
180
135. При решении задачи 69 получено дифференциальное уравнение вынужденных колебаний зеркальца осцилографа вида
Ф + 2/г<р-|-ро2ф = Д(, (1)
где n=a//; A — aBl’lQ/gJ.
В случае, когда полный ток / = /0+Д/, угол поворота зеркальца можно представить в виде ф = фв4-Дф. где фо — угол, соответствующий номинальному значению тока i0, а Дф —угол, вызванный случайным током Д/.
Для угла Дф из выражения (1) получаем
Д ф+2пД фРо* Д ф "= Д Д»
Спектральная плотность угла Дф равна
SA,=42S4f/| (1<о)г4-2л1и+Рох|г.
Дисперсия угла Дф (см. приложение 2) равна
п = ? AM8do>_______________лМА'
J |(/w)8 + 2л/со +Рог1’ 2лр0г ’
—оо
Среднеквадратичное отклонение угла Дф будет следующим:
Од<р=(Д/2ро) V2nQ/n.
136. Дифференциальное уравнение движения массы т при кинематическом возбуждении имеет вид
У + 2л^ + Ро2!/ = Ро21/о. где
2л = а//п; ро2 = 6EJ x/(jnl3).
Вычислим спектральную плотность вертикального смещения массы
5„(ш) =p1)‘S1,, (со) Д | (<<o)‘4-2niii)+p()s|t2n].
Наибольший изгибающий момент в балке возникает в заделке и, следовательно, ,
/М = ( — ту — ay) I.
Его спектральная плотность
Sm = Р | — т (iu)2— а/со |2 Sy (co), или
«, 20p‘Z8 [m1 (/co)*—cc8 (/®)8]
d M _ 2л |(/co)8 + 2л/» + p.8|8 | 10 + Zw|a “
=___________20p<,*/8 [m8 (ZIP)*—a8 (/co)8)__
l(Z®)’ + (2л + 10) (Z®)8 + (20л + p.8) Z40 + 10p0‘|’-2n-
Вычистим среднеквадратичное отклонение изгибающего момента М:
1W1
2 С с / xj 5р0«/*[(2л+1О)т‘ + а’1
°* = 2 (“) d“ = n (jin+p? + 100) -•
После подстановки числовых значений получаем оА1!=
=5,4-10* (кН-м)‘, или o.vr=2,32 кН м, Максимальное нормальное напряжение в заделке
Отах"иМ/Р7х,
Поэтому среднеквадратичное отклонение
Олмх-вм/^-г,32/3,97- 1О‘-29,3 МПа.
137. Дифференциальное уравнение движения массы т, составленное по методу сил, имеет вид
У\ = *п {~ту} -at/|)-p12P. (1)
Вычислим спектральную плотность перемещения массы:
о ,<Л__________few
1 7’ “[«fin (/“)* +«61 I’ ’
Тогда дисперсия случайного смещения у, равна
со 9
_ 1 С О|2Л(1®
Dv> — 2п } | жбн (/•)« + (а + bm) d„ (to)’ + (1 + 6а5„) /а + »|" *
Вычислим интеграл (2) (см. приложение 2):
£>У1 = а*!2(а+ bm)/[2ba (1 4- ддпа-|- Z>26nm)J.
Среднеквадратичное отклонение вертикального смещения массы т
Изгибающий момент в заделке
M — Pl-\-2l( — mi/i — ayt). (3)
Воспользовавшись уравнением (1), исключим из уравнения (3) силу Р:
М— (У\ 4-*ц/пУ1 + *n«//i) —21 (ту\ +«!/1)
или
М— (*п/*12 — 2) т1у\ 4- (*п/*|2 —2) o-ly\ 4-^/i/*i2-
Спектральная плотность
5^ = 1^ (MP-Sy, И.
где | UP] (ш) | — модуль частотной функции, равный
U7, (М = [4г—(M24-f4n—2U/tto4-4-.
С учетом значения Wx выражение для Sm принимает вид 182
е дв?я [*.(/«)♦+»! (/«)*+*,]
•5л*= J m6it (i<D}‘ - (а + Ьт) б„ (/со)» + (1 + 6u»a) Z® + 6’ |* 2л '
г де b0 = т?Р (611/612— 2)2;
6,-^f в» _2\_а^л$и._2у:
0ц \ 011 / \ 0ц / \ Си J
Дисперсия момента Л1 (см. приложение 2) будет равна
Dm — 5;И(1® =
(1 4- Ица) b„—тЪцЬ,—&^т (а + bm) bt/b 26^та (1 +бц6а + Ьг6ит)
138. Дифференциальное уравнение случайных колебаний массы т имеет вид (см. решение задачи 136)
Ду+ЗгаДу+р/Ду-р/Ду,. (1)
Для определения среднеквадратичного отклонения разности
Лу—Ьуа=е, (2)
необходимо знать спектральную плотность случайной функции е. Для этого найдем сначала передаточную функцию (2). Передаточная функция системы (1) (при нулевых начальных данных) имеет вид
W (р) =Д Y (р) /Д Го (р) -р.7 (р!+2пр+Ро2), где ДУ(р) и ДУо(р) — изображения функций Ду и Ду0 по Лапласу.
Воспользовавшись преобразованием Лапласа для левой и правой частей уравнения (2), получим
е(р)—ДУ(р)—ДУ.(р).
Передаточная функция системы (9) имеет вид
1Г1-8(р)/ДУ.(р) = 117(р)-1=р(р+2п)/(рг4-2пр4-Рог).
Спектральная плотность равна
S. (<o) = |UZ, (MI’Sa,.. или
О _____________а, [(!»)♦ — 4л(/а>)*|_____
1 | (/<□)• + (2л + 0) (У®)’ + (р.‘ + 2лр) + РРо‘ Г 2л ‘
Вычислим дисперсию разности е (см. приложение 2):
л _ С с mix»-«, (р«* + 2ир + 4л1)
Dl “ J 5е d “ 2л(/>.1+2л0 + 0‘) • — 30
Среднеквадратичное отклонение разности перемещений а8 = У De.
139. Дифференциальное уравнение движения поршня под действием случайной составляющей давления имеет вид
183
A A -L2/iAZ] 4- p(~\z\ ~Fhpi/(m\ -} tni), где щ\— масса поршня; /п2—масса штока. Спектральная плотность смещения поршня $A.1-JWr(M|a$ApI (<->)» ИЛИ
Q _________________________а,/7»__________________
Л,‘— (т, + тг) | (imy 4- (2п + Р) (До)1 + (2Яр + />,*) 1ш + 0р,’ |* 2я ‘
Вычислим дисперсию перемещения \z} (см. приложение 2): о _________ С с _____ в)/7' 2л 4- р
A'- } Лдг.иы («, + „,)»• 4Л«рЯ(2Яр + />.» + рЧ '
—СО
Среднеквадратичная погрешность показаний прибора (или среднеквадратичная ошибка прибора) (Тдг, = |/£)Дг1.
140. Дифференциальное уравнение движения со штоком имеет вид
AZj 4- 2nAzt 4- А2Дг1= ДА^/(tfii + mj) 4- ри2Дг0.
При действии независимых случайных возмущений дисперсия равна сумме дисперсий:
“ D&zt (Да) 4" (kzj).
Дисперсия каждого из возмущений в отдельности равна оо
Вд..(ДА) = (—^w>), $ |^(/ы)|25ДР1дш,
(Lza)~pJ \ | W (гы) pS^dw,
где 1/| (4d))24-2ni<o 4- a2 I-
После вычисления интегралов (см. приложение 2) получим а2 _пд _________(2"+Р.) _ ,
« Ах‘— &г‘ (mt + mty ^ргр.^пр.+рг + Р,*) рога, (2Я 4-р,) 4лР« 4лР« (2Яр, + р,г 4- Р?) ’
'Х141. Дифференциальное уравнение движения поршня со штоком под действием случайных возмущений имеет вид
Дг, 4" 2n^Zj 4* д/ДZ\ ~ FДР\ /(Щ\ 4" т2) 4* P^^zq.
Дисперсия AZj будет равна
(Да)4" 1 (Дг«)-
Здесь
184
СЮ
P VF1
D,t. (ДА)- $ I W
—oo
Охг, (Дг0)
Рог«а (2л + ft,)
4ft’/l (2nft, + />.* + ft,*) •
Оптимальное значение жесткости пружины найдем из условия
[d0a,/do*,=0, где р20,-=с/(т1 +т2).
Для определения р2* получаех« уравнение
ЛАК , *K\-,Q
Ра, вк—дРъ, ВК-А '
где
А
NE’ . г> а« (~п + fti) . JZ__о „я ! Я 2
(4 +*’)*>• ’ A=2np2-:₽2-
Оптимальное значение жесткости пружины существует только при условии ВК — Л > 0 и равно
£»==('П14-'п2) А;, = (от| -Ь т 2)
( АК , 1// ЛК \2 , АК* \
\ ВК-А~ Г (ВК — А) ‘ВК — А )'
142. Представим дифференциальное уравнение малых вертикальных колебаний массы т при кинематическом возбуждении в виде
i/-|-.2nz/-|-PoIy=P»i«/o.
Для определения дисперсии ускорения у найдем спектральную плотность перемещения у0 в зависимости от корреляционной функции 00
$ /Гуо(т)е-г“Чг =
е-<в>-<«)Мг 4- \ e_(“i+i(,>)Tdr
20^, (а,*+ <о2) л ‘
Спектральная плотность вертикального смещения груза определяется выражением «
5у(о)«=|^(М|’^0(о)),
где
| W (iw) | = р02/1 (/ш)2 + 4- р21.
Найдем спектральную плотность ускорения у’.
ЧОиа.^*р,*
S" (<|>) = 0,45Т (lay + 2,цш + рв» |« I <х, -т- /СО |»2л '
Вычислим дисперсию вертикального ускорения по формуле
185
p l С 20^а,«>‘р04(1<о
У ~2л .1 I (1<1>)' 4- (2я + а,) (»ш’) + (2л а, + раг) /<о + <х,р0‘ |* ’
Воспользовавшись приложением 2, получим
=V DyoaiP<?P(?)/[‘2ti (2/KX; -|~/>q2-f-®i2)l •
143. Дифференциальное уравнение движения массы имеет вид
mi+«-P(0. (1)
Представим его решение при действии произвольного возмущения F(/) при нулевых начальных условиях в виде
/к
i (2)
где Pq=Vс/т.
На рис. 244, а изображен график функции sinp0(/K—т), где рс=2 с-‘, /н=2 с.
Для того чтобы отклонение груза было максимальным в момент времени /к“2 с, необходимо, чтобы подынтегральное выражение было знакопостоянным, т. е. значение P(t) в промежутке времени 0</гС0.43 было отрицательным, а при 0,43^ Ст^2 положительным.
Наибольшее значение хк получим при следующем законе изменения силы:
( — 1 при 0<т<0,43;
P^ = U1 при 0,43<т<2. (3)
График изменения возмущения во времени показан на рис. 244, б.
После вычисления интеграла (2) с учетом закона изменения силы Р(т) (3) имеет ХтдХ=58,6 мм.
При действии же внезапно приложенной единичной силы смещение массы в момент /к=2 с равно 37 мм.
144. Скорость движения массы можно получить, продифференцировав по параметру tK выражение для смещения (см. уравнение (2) в задаче 143). В общем случае производную интеграла по параметру можно вычислить так:
Ь а) »(а)
а(а) й(а)
В соответствии с этим скорость движения груза
, 'к
Л = -^- COS Ро(/К — т)Р (т)<1т. о
486
Учитывая закон изменения функции возмущения Г—1 при 0<т<0,43;
ПрИ 0,43<т<2,
получаем 0,« 2
cos 2(2 —т)(—l)dr-|- jj cos 2(2 —т)(-{-1)dr,
О 0ДЗ
или jc(Q=38 мм/с.
145. Дифференциальное уравнение движения массы т имеет вид
тх-\~ах-}-сх=Р (t). • (1)
Запишем его решение:
fK
х = e-',('«"t,sinp(/lt-T)P(T)dT, (2)
/пр J
где п=а/(2/п). j7=Vp02 —«2. Р^с/щ-
Поскольку влияние вязкого трения на частоту колебаний весьма незначительно, можно принять
p = /poi-n2 =K22-(O,2F «2 с-'.
Подынтегральная функция в выражении (2) изменяет свой знак в момент времени 1^0,43 с (см. задачу 143). Следовательно, закон изменения силы F(t), при котором х достигает максимального значения, будет таким же, как и в задаче 143.
146. Дифференциальное уравнение малых колебаний системы относительно положения равновесия, соответствующего номинальному значению тяги /?0, имеет вид
/пх4-ах+сх=ДР, (1)
•откуда 'к
sin Р^к— т) A/?(t)dr, (2)
о
где п=а/(2т), р=У~рог — п*, рйг = с/т.
График подынтегральной функции е-*' _T)sin р(1к(т) (при р~30 с-1, n=2 С"*) (рис. 245, а) имеет нули при т=0,08;
*0,185, 0,29; 0,395 с. Следовательно, закон изменения разброса
тяги Д/? имеет вид (рис. 245, б)
187
tlnifM)
О
Рис. 244
4-0,05/? при 0<т<0,08;
— 0,05/? при 0,08 С г <0,185; 4-0,05/? при 0,185 < т < 0,29; — 0,05/? при 0,29<т< 0,395;
4-0,05/? при 0,395<т<0,5.
После интегрирования (которое проще всего выполнить графически) из уравнения (2) получаем
JCmax = 75- 10-‘/?,/(mp); Xmax-=5 см.
Такому сжатию пружины соответствует сила Р=схтах= =900-10*-50-10"’=45 кН.
Следовательно, разброс тяги Д₽“5% может вызвать ошибку в замере тяги, равную
Д=(Р//?,) 100=22,5%.
147. Вынужденные колебания системы с одной степенью свободы при нулевых начальных условиях определяются следующими уравнениями (см. задачу 143):
'к
sinp0(/,-x)P(T)dr;
"‘го <'
0
cos^0(/K —т)Р(т)бт.
о
(1>-
188
Введя обозначения а,=Лсоза, аг= (4/p0)sin а, представим пряжение функции погрешности прибора в виде
Д=хЛ cos а+(х/р<>)Д sina. (2)
Подставим выражения (1) в соотношение (2), получим
Д = —[sinp0(/K — t)cosa4-cosp0(^ — т) sin a] Р (т) dr, (3) * о
«ли
\ sin[p0(^-T)4-a]P(T)dt. о
Учитывая, что числовые значения коэффициентов уравнения (3) равны А=0,2; а=л/6, найдем такие значения времени т, при которых sin[4n(0,5—т)+,л/6] =0. Из последнего соотношения следует, что 4л(0,5—т)-Ьл/6=пл (где п= 1, 2,3,...), откуда получаем ti=J/24 с, т2”7,24 с.
Таким образом, закон воздействия возмущающей силы на систему, при котором Д достигает максимального значения, имеет вид
Р(т) =
-|-0,1 при 0<т<1,24;
—0,1 при 1/24<т<7/24;
4-0,1 при 7/24<т<1/2.
Интегрируя выражение (3) с учетом закона изменения возмущающей силы Р(т), получаем, что наибольшее возможное значение ошибки прибора Дтах=5 мм.
148. Решение дифференциального уравнения малых угловых колебаний (см. условие задачи) в момент времени tK можно представить в виде вектора <рк на фазовой плоскости <рО<р (рис. 246, а). Каждому закону изменения возмущающего мо-мент_Л1в в момент времени 1К соответствует определенный вектор <рк.
Рнс. 246
189
По-видимому, имеется такой закон изменения момента Л1а> при котором модуль вектора <рк (направленного под углом е к оси <р) достигает своего наибольшего значения (см. рис. 246, а). Если изменять значение угла в в пределах О... 2л и для каждого промежуточного значения е опрсде-лить |<р|шах, то конец вектора <рк опишет на фазовой плоскости некоторую замкнутую кривую (см. рис. 246, а).
Поскольку для каждого значения е определяется |<р|тах, полученная кривая является границей области возможных (наибольших) решений <р и
Для практического определения границ области возможных решений спроектируем вектор <рк на прямую, определяемую единичным вектором е:
<p< = (^l[==e) = UKcosa+-^-sina). (1)
Определив максимальное значение проекции вектора решения <ре для фиксированного значения угла а и закон изменения момента Af„, соответствующий фешах, находим по этому закону значение компонентов вектора фк, т. е. значения <рк и фк, которые являются координатами одной из точек границ области возможных значений решения.
Например, при а=л/6 выражение (1) принимает вид (см. решение задачи 147)
Ф» = sjn |р0(^ — т)4--J-] MadT. (2)
о
Полагая
sin[p0 (/,<—т) +л/6]=0, найдем
Ро (*к—т) 4-л/6=л; р0 (/к—т) +л/6=2л.
Учитывая, что Vа]1л~ 1,26 с-1, получаем Т1 = 0,42 с, т2=2,9 с.
Следовательно, закон изменения Л1В, при котором фе достигает максимального значения, имеет вид
Л1„=
4-й при 0<т<0,42;
— b при 0,42 < г <2,9;
4-6 при 2,9 <т <5.
(3)
Вычислим значение <рк для случая, когда закон изменения возмущающего момента имеет вид (3):
"0.42
- 0
ь
Фк
2.9 sln/70(^ —T)dT4- Sfnpo(/K —T)dr4-0,42
190
5
+ sin р0(/к —x)dr
3.9
Аналогично
2b
1,66.
ФкДРо = [2£/(Уоа/)]1.О9-
Произведя подобные вычисления для угла а, получаем следующие значения:
различных значений?
а.......................... О
.........................5-Ю-*
Ф.Р........................ О
30° 60° 90е
4,1-10-» 2,5 Ю"» 0
2,7-10-» 4,2-10-» 5-10-»
Область возможных значений решений, построенная в соответствии с приведенной таблицей, показана на рис. 246, б.
149. Дифференциальное уравнение возмущенного движения зеркальца имеет вид (см. решение задачи 135):
Дф4-2пДф4-р02Дф=АД1 (/) (О
Запишем решение уравнения (1) при. нулевых начальных условиях:
t
Дф = ') sin pt (t — т) Д/dr,
P> о
где д = )/>02—я».
Для получения максимального значения Лф возьмем верхний предел равным бесконечности, а закон изменения Д1(т) — разрывным, следящим за знаком функции sinpt(l—т). Это позволит вычислить
СО
Афтах = 5у$е"ЛЕ|5,ПЛе1 de# к О
(2)
Интеграл в выражении (2) можно представить в виде
. аА
Афт.,- —
~K/Pi Зк/р,
\ Ф (е) Je — Ф (е) de 4-- о Г./р.
ак/р, <л-Н)«/Р1
4- \ Ф(е) de— ... 4-(— I)4 ®(e)de Зп/Pt knfp,
где Ф(е) =e“n,sin р,е.
После интегрирования получаем
I UZ1
Афтхх^Т/
191
Ряд 7. е р' представляет собой бесконечную геометрц.
вескую прогрессию, сумма которой равна 1 Окончательно находим
—пк
Дфт.х==аМ1+е
\—ер> JJ.
Если п мало (при малом затухании), то, принимая получаем
Афтах « 2аА/ (лпро)...............
150. На рис. 247 изображены масса т и балка в произвольный момент ра, получим балки:
времени. Воспользовавшись принципом Даламбе-дифференциальные уравнения движения массы и
ту + JV — Р = 0; /0ф4-а£2ф4-с£2ф= —NI.
(2)
учитывая,
или
Исключая из системы уравнений реакцию N и
что у~1<р, получаем
(У04'тОф_1'а^1ф+с^'»ф = Р1
ф4-2пф+р02ф = РЧ (Jo+ml1),
где 2n=aZ.7(J(,4-m/2); p0J=cL2/(704-mP).
Решение уравнений (3) представим в виде
t
^=(—+L»)p, $ s,n А “ ’) PdT’
о
где Д —V Р02-л2.
(4)
192
Учитывая связь между у и <р, из уравнения (1) определим динамическую реакцию
М=Р(/)—m/d’qj/d/1.
Учитывая выражение (4), найдем
м-Р(Р~ р т1‘ ц-______—z ---х
X е~п<'~^ sin [a (/ — т) + Р1 о
(5)
где B = F>o44-4«2A2; p = arctg2/iA/fl,2.
Максимальное значение выражения (5) получается при разрывном поведении возмущения Р(т) (аналогично задаче 146), когда функция Р(т) принимает постоянные значения, равные ±а. В этом случае подынтегральная функция берется по модулю.
Моменты разрыва функции Р(т) определяются из условия sin[plTK4-pj = 0 или Р1Тк4-Р=*л, откуда тк=(£л—Р)А-
Интегрируя уравнение (5), полагая t—т=8, получаем следующее выражение для наибольшего значения динамической реакции:
N = j/+*amli----В, [е~м sin (р,е 4- р 4-p,)|S‘ -
—е~м sin (р,е 4- р 4- Pi)|«: 4- • • • 1.
где В, = Вт12а/[рор,(Ц+т1г)\-, tg p, = arctg(pl/n).
Для получения наибольшего значения реакции Лгтах примем верхний предел равным бесконечности. Тогда
оо — Г?(ЛТТ—3)
{-5! sin (Р4-р,)4-2 sin Р, 2 е
дт________—
'Vmox — £, + т1г
Учитывая, что oo —fl) —я(ТС~fl) У e ** =e Pl
Pi
окончательно получаем
Nmax = - Isin P cos pl 4-cos P sin ft 4-
-4(lt-fl)//>, 4-2 sin p, ———— .
1 [__en*IPl
где sin p=2na//Po*4-4«2A2i sinpi = p„/] p024-n’.
При малых значениях коэффициента вязкого трения а (или, что то же самое, при п<£1) можно записать
sin p=2n/p0; cos р® 1, sin р,® 1, cos р,®п/р0.
13—5000
193
Раскладывая e~'mlPt и e“n₽/Pi в ряд и оставляя только линейные члены разложения, из уравнения (6) получаем
•Vra>x = 2arriPp0/[nn (J0-|- mJ2)].
151. При установившихся колебаниях решение уравнения движения (3) (см. задачу 150) имеет вид
т= al з1п(а>/4-Р)
(J. + m/’J V(®-—/>,»)»+ 4я»®»’
где p"=arctg[2Mto/(p02 —ю2)).
Так как <о = р0, то из уравнения (1) следует
<p=a/sln(-J- + ^y [(J0+mP)2np0].
Динамическая реакция
ДГ= _ от/ф+р (<) = _5^'^ sin + pot]4-a sin pot.
Амплитуда динамической реакции при. малых а равна ^т^Р<>ат1г/[2п(]а+тР)].
Максимальное значение реакции Лггаах при разрывном поведении возмущающей силы P(t) (см. задачу 150) на 30% больше, чем при P(t)=a sin p9t.
152. Дифференциальное уравнение малых вынужденных колебании системы имеет вид
(f+pSq^Pl/J, • (1)
где pe2=cL»/(/04-m/2); J=J0-\-mP.
В соответствии с начальными условиями (<р(О)=фо; <р(0)*=0) представим решение уравнения (1) в виде
Фк“<Й) cos PiltK + J- \ cos ро (/« - т) Р (т) От,
6 или
'к
Фк=— % + 7" cos (Зя — рот)Р(т)<1т. (2)
о
Следовательно, фх = фктлх при следующем законе изменения возмущающей силы:
4-а при 0< т<п/(2ро);
— а при л/(2ро)< т<Зл/(2р0):
4-а при Зл/(2р0)< т<5л/(2р0):
— а при 5л/(2ри)<т<Зл/р1>=/1{.
194
Проинтегрировав уравнение (2) с учетом найденного закона 3>)енения возмущающей сил 4 Р(/), получаем
|фш4х| —Фо + 6/а/(/ро).
§ 7. Нелинейные колебания
153. Кинетическая энергия системы складывается из кинетической энергии Г, верхней массы т, и кинетической энергии fs нижней массы т2.
Так как масса mt совершает вращательное движение, поворачиваясь в процессе колебаний на угол <р, и поступательное движение, перемещаясь горизонтально на расстояние х„ то
Масса т, совершает вращательное движение со скоростью ф и два поступательных движения: х2 по горизонтали и у, по вертикали. Поэтому можно записать
+ (2)
Изменение потенциальной энергии системы связано только с изменением вертикальной координаты уг груза т^:
n=m2gy2. (3)
Принимая в качестве обобщенной координаты угол поворота ф, найдем
x1‘=0,5tpDl; x2=Z sin <р—0,50!; </г=/(1—cos ф), (1)
откуда
Xi=0,5£)|<p; л2 = (/созф—0,5О|)ф; f/2 = <p/sin (5)
Подставив выражения (1) — (5) в уравнение Лагранжа второго рода, получим
Ф +______________w*gfsinlp________________=0-
4 ' .3 .73,’ £)’ \
-g-т,©,2 4-m. l-g- + cos <р )
154.
2^ с/2 cos ф cos а /___1_________________1________
3 1 sin q> у у ]—sina sin 2<р У1 + sin a sin 2ф
р = )/ГЗс/Л1С05ф.
155.
а+4т sin а 4-2^ (Kl + sina -y'l-sina =0. p=V(3g/4)|c/(mg)+1//].'
156. Период колебаний системы можно разбить на четыре отрезка: два отрезка времени, в течение которых одна из пру-
1.3» 195
жни находится в контакте с упором, и два отрезка времени течение которых происходит свободное движение груза. ’ 8
Движение груза прн контакте пружины с упором описи вается уравнением
x=(x,/p0)sinpD/, 0)
где х0 — скорость, с которой пружина (груз) входит в сопрц. кос новен ие с упором; р0=Уг с/т.
В соответствии с уравнением (1) время контактирования пружины с упором
ti=*n/pa.
Поскольку пружина входит в соприкосновение с упором со скоростью х0, время движения груза в свободном состоянии (а одну сторону)
Период колебаний
Т=2 (/,+/,) =2 (я/р.+,2ДД). (2)
Представим последнее выражение в зависимости от амплитуды свободных колебаний х0. Наибольшее сжатие пружины, очевидно, равно х0—Д, что в соответствии с уравнением (1) можно выразить через х0:
х0—Д=х#/р(|, или
Xa=p„(xt—Д). (3)
Подставим соотношение (3) в уравнение (2):
Т-(2/р.)(л+2Д/(х.-Д)].
Таким образом, частота свободных колебаний
р=2л/Т=2р0Дл+2Д/(х.-Д) ].
168. При движении груза в одну сторону (например, влево) от положения равновесия дифференциальное уравнение движения имеет вид
А+аЦ—о, (0
где Рх2=схт.
Считая, что в момент прохождения грузом положения равновесия (т. е. при л*] = 0) скорость движения х1=Х|0. представим решение уравнения (1) в виде
^“(^o/AJslnp,/. (2)
Груз будет находиться в контакте с левой пружиной в течение полупериода колебаний (2), т. е. в течение
196
ti^n/pt.
Аналогично время контакта груза с правой пружиной h=n/pt.
Период установившихся колебаний
(P«+Pi)/(PiPi) •
Частота свободных колебаний
Р=2л/Г=2/7а/[К^(К^+ Kg)J.
159. Частота малых свободных колебаний груза
p^VTjm.
Жесткость системы с определяется как отношение нагрузки к вызванному ею перемещению
с—Р/х.
Для обеспечения постоянства частоты свободных колебаний необходимо, чтобы отношение с/т было постоянным. Это возможно в двух случаях: при постоянной нагрузке Р и при нелинейной характеристике пружины. В последнем случае для каждого значения груза Р жесткость пружины
c=dP/dx.
Из условия постоянства частоты свободных колебаний следует, что
p2=(g/P)(dP/dx),
откуда
(g/pt)lnP=x+.C1, или
Р=ехр[(р2/^) (x-t-C,)].
Значение постоянной интегрирования С, найдем из граничных условий задачи. При Р=Р0, х—х0 имеем
G“(g/P2)ln Р.4-хв.
Окончательно выражение зависимости перемещения от приложенной нагрузки принимает вид
*=U/P:)ln Р/Ро+Хо.
160. Кинетическая энергия при движении массы т определяется выражением
Т=/п?/2.
Потенциальная энергия
П-с(\4-в)72,
197
где сЬ,=Тл—начальное натяжение нити; сб=Т1—дополни, тельное натяжение, вызванное колебанием массы; б — У длине" яие нити при колебаниях массы.
Выразим б через отклонение х, ограничиваясь первым нели-ненным членом разложения:
б—2(1—I cos а)=хг/1,
где а=х/1.
Окончательно потенциальная энергия деформации системы равна
П = с(б0+х7/)72.
Подставим выражение для кинетической и потенциальной энергии деформации в уравнение Лагранжа:
i’+ (2c6./m){x//+x7(V)]=0.
Возьмем первый интеграл этого дифференциального уравнения движения, для чего представим
d’x dr I d (ж’> d<» ^dr^ 2 dr
Тогда
4г_ л С
A, ' '
ИЛИ
?=Л t-(4c60/m) [ (x2—Ло2) / (2/) + (х<-Л0«) / (4б0/2) ].
Используя начальные условия (при /=0, х=0, х=х0), находим
_ 9 [сб./г,1—г* । х«*—Х*\1у 21 ' 26./* *
Последнее соотношение можно представить в виде кривой «а фазовой плоскости.
161. При отклонении массы m от положения равновесия на произвольную величину х натяжение в пружинах (рис. 248) составляет
T = cAZ=c(j//7+P-/o)~cx2/(2/0). (1)
Спроектируем на горизонтальную ось силы, действующие на массу:
тх= — 2Гх//о= —CJ&/IJ,
или
£+*лЯ-0, (2)
где k = c/(ml02).
198
Рис. 248
Введем обозначение х=*у- Тогда
• dy_ dy dr_ • dy_ dy dt dr'df dr y dx'
Подставим последнее соотношение в уравнение (2): ydy — — kx3dx. (3)
Интегрируя уравнение (3) с учетом начальных условий (при /=0 х=ха, х=у=0), получаем y2=k(xtk—х‘) /2.
Учитывая, что у=х, из последнего соотношения имеем г __ 1
____Г dr_____________1_ т/ 2 у* de
= J УЛ (г0‘—г*)/2 ~J УГ^в5’
где е=х/х0— безразмерное перемещение.
Поскольку восстанавливающая сила Т [см. уравнение (1)] симметрична, для определения периода колебаний достаточно рассмотреть только одну четверть периода:
Здесь К (а, <р)—полный эллиптический интеграл первого рода, который является частным случаем эллиптического интеграла
первого рода вида
t
К (а, <р)=
СО8ф
________(К_________
1Л1—<’)(<»’ +а’Т*) ’
где a=slna, a=»cosa[3],
В рассматриваемом случае надо положить а = л/4 и ср=л/2. Из таблицы значений эллиптического интеграла [3] при a = 45* находим К 1,8541.
199
Сдедовательно, период колебаний груза
Т = 1,8541 (4Z0/x0) V m/c.
Круговая частота колебаний
р=О,85(хоД) V с/пг.
162. По методу Релея, для консервативной системы применяется равенство наибольшей кинетической и наибольшей потенциальной энергий системы:
Т = П
1 max х max’
где
A^max
Tmax = W/2; Птах= Jj 2Td(AZ).
0
Так как T = сЫ (см. решение задачи 161), а Д/«л2/(2/0), то
Пгаах =сл04/(4Z02).
Следовательно,
тхо/2 = сх03/ (4Z02) и х0=I^ZqXo у/ 2т/с.
Учитывая связь между частотой свободных колебаний и начальным смещением (см. решение задачи 161), находим
р= (O,85/Zo) V loxo /2с/т = 1,02 Vx0/l0 frc/m.
163. Составим дифференциальное уравнение движения подобно тому, как это сделано в задаче 161:
тх+2ТоХ/1й + cxVZq2 = 0.
Переходя к безразмерному смещению e = x/x0, получаем
E + 27\»e/(/nZo)4-ex:ozE3/(mZ02)=O. (1)
Введем соотношение e = ede/de. Учитывая начальные условия задачи, после интегрирования уравнения (1) имеем
е2 = [2с/(т10)] ЦТ0/с) (1 - е2) + (^2/4Z0) (1 - е)4]. (2)
Уравнение (2) описывает движение массы на фазовой плоскости (рис. 249).
164. Рассмотрим произвольный момент движения. Пусть, например, масса движется справа налево, так что х>0, а х<0 (см. рис. 248 к решению задачи 161).
Поскольку сила кулонова трения всегда направлена против скорости движения, дифференциальное уравнение колебании представим в виде (см. задачу 163).
200
mx+2T0x/l0+cx2/l02^F. (1)
Перейдем к безразмерной координате e = x/Xq’.
е + 2Г0е (m4) + cxo2s2/(ml02)==F/(mXo). (2)
Поскольку e = ede/de, из уравнения (2) с учетом начальных условий (при 1 = 0 е = е0, е=0) получаем
Подставляем числовые значения входящих в это уравнение параметров:
е = ± /2 К - 50 (б0- е)+200 (е02 - е) + 50 (е04 - е4). (3)
Исследуем движение массы на первом полупериоде колебаний е0=1, а е<0.
Из решения уравнения (3) имеем:
при /=0 е=1, е=0;
при е=0 из соотношения (3) находим е= —20;
при t=T/2 е= —0,42, е=0.
Для исследования движения на втором полупериоде колебаний можно также использовать решение (3), но при этом следует считать, что ось х направлена влево (это ведет к изменению знаков е и е, что надо учесть в решении).
При е=0 из соотношения (3) получаем е=5,64;
При t—T е=0, е«0,15 (рис. 250).
Аналогично строим решение и на остальных участках движения.
Движение массы т прекратится, если в одном из крайних Положений (левом или правом) восстанавливающая сила пру-
201
жив будет меньше (или равна) силы трения. Из этого условия найдем наибольшее отклонение, при котором невозможно свободное движение массы.
Полагая в уравнении (2) е=0, получаем е.=О,124. Из расчета следует, что движение заканчивается на третьем полупериоде в точке на фазовой плоскости ё=0, е«0,1.
165. Дифференциальное уравнение движения массы т имеет
вид
mx-\-cx+ctx3**0 (1)
или
х+р!х+|лх’=0, (2)
где ц— малый параметр.
Запишем решение уравнения (2) в виде ряда
х=х04-1цх14-ц2х,+ ••• (3)
Положим
P,=Pi±+lial+.gloJ, . (4)
где рь at, аг — постоянные.
Подставим выражения (3) и (4) в уравнение (2). Ограничиваясь слагаемыми, содержащими ц в первой степени, получаем
-Ко + РГ-^Ь + М С*14” Р\?х\ + -’Со 4- -^о3) = 0. (5)
Уравнение (5) должно быть справедливо при любом малом значении ц, поэтому
Хо+йЛо-=0. (6)
Л 4- АЧ “ ~ (А*о+-«о3)- (7)
Учитывая начальные условия (при /=0 х0=Л, х1 = х(=0), решение уравнения (6) представим в виде
х,=Л cos pj.
Подставим это выражение в правую часть уравнения (7):
xt+p*Xt— —(a144-0,7543)cosp1l—0,25Л’со8 3ptt (8)
Решение уравнения (8) должно быть ограниченным, поэтому
а ,А 4-ЗА ’/4=0
(в противном случае частота возмущения равна частоте свободных колебаний и х,->-оо). Отсюда получаем
а,---ЗЛ2/4. (9)
Решение уравнения (8) с учетом начальных условий имеет вид
х1=[Л1/(32р12) J (cos Зр,/—cos p.f).
Следовательно, в первом приближении полное решение дифференциального уравнения (!) можно записать так:
х=А cos PjZ+n^j/tSdp/JKcos 3ptt—cos pj).
Частоту свободных колебаний находим из соотношения (4) с учетом (9)
р,’=р14-ЗиД2/4.
В рассматриваемом частном случае р,= 1,17 с-1.
166. Заменим нелинейную характеристику F—cx+cJt? линейной F=ctx. Для этого необходимо, чтобы
л
[cqX — (£x4-qx3)]2dx = min.
о
Вычисляем интеграл и варьируем полученное выражение по неизвестному параметру с0. Тогда
Со=с+.Зс1Д*/5>
откуда следует, что частота свободных колебаний массы
p = V Co/m = Vc/m-\-3ciA2/(5mY
С учетом числовых значений входящих в уравнение параметров получаем р= 1,14 с-*.
167. Считая движение гармоническим, решение дифференциального уравнения свободных колебаний (см. решение задачи 165)
х4-р!х+.рх’=0 (1)
ищем в виде
х4=Л cos(p^+,a). (2)
Решая уравнение (1) по методу Галеркина, необходимо, чтобы
2п/р,
J (ль + Р2Хо + цхьз)хос1/=О. (3)
о
Подставив выражение (2) в уравнение (3), находим квадрат частоты
P1!=P2+0,75|lA‘.
Полученный результат совпадает с решением задачи 165 по методу Ляпунова—Пуанкаре.
168. Характеристику упругих элементов в рассматриваемом случае можно представить в виде
F—0 при О^х^Д;
F=c(x—Д) при Д<х<Л.
Заменим действительную нелинейную характеристику линейной
Определим среднеквадратичное отклонение линейной характеристики от нелинейной: а л
J = \ + 1е ^х~ С*Х‘
а а
Так как dJ/ck?o = O, то
с0= (2Л2— 2ЛЛ - А2) с/(2Аг + 2ЛД + 5Л2).
Частота колебаний равна
р = К с (2Л2 - 2ЛД - А2)//п (2 Л2 + 2Л А + 5Л2).
Колебания возможны, если 2Аг— 2ЛД—Аг>0, откуда получаем Л>1,36А.
169. Уравнение свободных колебаний имеет вид (см. решение задачи 161)
tnx-\-2Tx/l=0. (1)
Вычислим полное натяжение в пружине:
T=cAZ4-T„ (2)
где AZ«JC*/(2/0). Подставим выражение (2) в уравнение (1), считая х<£1л:
щх + 2Т ох/10 + сх*/1^=О или
л4-р2л-|-рл3==0, (3)
где pz=2T0/(m/e); p=c/(m/,:). Решая уравнение (3) (см. решение задачи 165), получаем
Р12=Р!+.ЗцХо,/4, откуда после вычислений находим х0«91,2 мм. 170. Сила, действующая на массу при отклонении ее на х, равна
F=W/(al-x)2-fe®ol/(a1+x)1«4(W/a1,)(x/al+2xi/ats).
Представим дифференциальное уравнение движения массы в виде mx-\-cx=F или x4-p*x4-jtx‘e0.
Здесь рг=с/т—2кФв3/(та13)-, ц- — 8кФвг/(та,3). (1)
Применяя метод малого параметра (см. решение задачи 165), получаем выражение для основного тона частоты свободных колебаний
204
Р1г=Р!+.3|лх074. (2)
Подставив выражения (1) в уравнение (2), находим критическое значение х,(р,=0)
х,.*- (с—4/W/a.a) (6W/a,s) • (3)
Введем безразмерный параметр, зависящий от магнитного поля и жесткости системы: а=4ЛФ0,/(са1’).
Тогда решение (3) принимает вид
е*“2(1—а)/(3а), (4)
где е=х0./а1.
Уравнение (4) представлено в виде кривой на рис. 251. Поскольку е“Х,./о(<1, заштрихованная область является областью устойчивых значений е и а (областью устойчивых колебаний). Кривая соответствует критическим значениям е и <х.
При а<0,4 е=1,0, т. е. движение происходит с ударами о магниты, и, следовательно, приведенное выше решение становится несправедливым.
171. Дифференциальное уравнение движения шины В имеет вид (см. решение задачи 124)
щх 4- 2сх — (2ц /, 1£/Оь — 2ц/, /2//(ао4-x)J = 0.
Раскладывая 1/(00 4"-^) 11 ряд 11 полагая x=Xq4-x,, получаем /
+ + — И12Р^13 = 0- (О
где ц,=Хо/а»; 0-2ц/1/2//(тапг); р2-2с/т—0; ц,х,=х/а«.
Ищем периодическое решение уравнения (1) и частоту колебаний в виде
X, ₽х,о + Ц1-*ц + НГ-Чг!
Р\2 = Р*4~ С,ц, + С2ц,2, где х1Ф, хи, х,2 и С, и (^ — соответственно функции и постоянные, подлежащие определению.
205
Подставляя выражения (2) в уравнение (1) и ограничиваясь членами, содержащими у,2, получаем систему уравнений;
хю+А’*ю—О; (3)
Л1 +a2jcii=£ijcio—P-vr0; (4)
•*n4"Pi2jfu= Ci-*n + 2^to — 2рЛкрС1|^хуо. (5)
Учитывая начальные условия (при /*=0 х10=1, х|0-0), решение уравнения (3) представим в виде (в такой форме решение можно искать при условии р!>0 или 2с/т—р>0)
х,о= 1 - cos ptt.
Решение уравнения (4) не должно содержать вековых членов, поэтому следует принять £, = 0. Если решение уравнения (4) соответствует однородным начальным условиям (хи= =0=х11(0)“0), то
= -^7 +Ур7 C0S + 6^7 cos 2p,Z + ^не-
подобным же образом получаем решение уравнения (5). Из условия, что коэффициент при множителе cos ptt в правой части решения уравнения (5) равен нулю, следует, что
С2=5р2/(4р,2)—Зр/4.
Подставляя С2 во второе уравнение (2) и учитывая, что С, = 0. находим основную частоту свободных колебаний шины
pJ,=p24-(x0/a)J[5p2/(4pl2)-3p/4]. (6)
Уравнение (6) необходимо решить относительно р,2. Учитывая, что Р12=Р2+,СгР2, можно в правой части этого уравнения принять pi2=p*. Тогда
p,‘=P2+(x,/a»)W/(4p2)-3p/4]= =р02-р+ (х,/а„) 2{5р:/[4 (р.2-р) J-3P/4}, где раг=2с/т.
172. Решение отличается от решения задачи 171 только знаком р.
173. Принимая в качестве малого параметра р1=*тах/о»> получаем уравнение движения в виде уравнения (1) в решении задачи 171. Решение уравнения (3) должно удовлетворять начальным условиям х(0)=0 и х(0)=ях|>, откуда
^-=(-<o/P.)sinp1£
Следовательно, xomai=xo/p,, т. е. ц1=х,/аор,.
Решая далее задачу, аналогично задаче 171, получаем, что основная частота свободных колебаний шины
p12-p2 + (Wa0p)2 (5р7(4р2)- Зр/4].
где p2=2c/m—Р; р—2цЛ/2//(то,г).
206
174. Приведем заданное дифференциальное уравнение к ВИДУ
<p + g<p/Z-g<^/(6/) = 0. (1)
Принимая в качестве малого параметра p=g/(6/), получаем (с точностью до членов первого порядка относительно ц) частоту основного тона колебаний
Pi’= (S/l) (1 -Фо2/8). (2)
Применяя метод прямой линеаризации, представим дифференциальное уравнение (I) в виде
ф4-сф=0.
Согласно этому методу, необходимо, чтобы уклонение линейной характеристики от нелинейной было минимально, т. е.
£ \ 1 2
ф—буф3) —Сф|ф ! бф = О.
Произведя вычисления, находим
с=р,2=р02(1-5ф02/42), (3)
где р<?=8/1-
Сравнивая выражения (2) и (3), получаем
Д=Ро2( 1—5ф02/42) —До2 (1 - Фо2/8) = 0,0О6ро2Фо2.
175. Дифференциальное уравнение колебаний рычага имеет вид (см. решение задачи 106)
ф+р:ф+мф3==о.
где p2 = (c—FR)/J- n=FR/(6J).
Основная частота, определенная по методу малого параметра,
Р.2=Р1+(3/4)(ф0/р,)г[Р/?/(6/)]. (1)
Воспользуемся теперь методом Галеркина. Считая движение гармоническим и полагая ф1=ф0 sin (Pi/4~a), потребуем равенства нулю интеграла
(Ф1 + Р2Ф1 + ИФ13) Ф1б/ = 0. о
Учитывая, что фо = Фо/Рн из последнего выражения найдем Pl2 = P2 + (3/4)(Wp1)2{F/?/(6J)|. (2)
Таким образом, полученные решения (1) и (2) совпадают.
176. Дифференциальное уравнение малых свободных колебаний рычага имеет вид
</Ф4-(/п£/о4-с)Ф4-51§пфЛф2 = О. (1)
Здесь sign <р означает, что знак момента силы трения AfT|>==s = &Ф2 совпадает со знаком скорости ф.
Представим дифференциальное уравнение (1) в виде
ф-}- /Ар = sign фаф2 «= О,
где pt= (rngl0+c)/J, а=й//.
Поскольку необходимо выяснить зависимость частоты колебаний от начального отклонения фо, за начальные условия примем
ф(0) =а, ф(0) =0.
Рассмотрим первый полупериод движения. Здесь sign <р= = — I и уравнение движения имеет вид
ф4-р2ф—аф2=0. (2)
Решение ищем в форме
ф=фо+.а1ф1+а2й)2+..р2”р12+С,а4-С,а2-Ь... (3)
Подставляя выражения (3) в уравнение (2) и пренебрегая членами, содержащими а в степени выше второй, получаем систему уравнений:
Фо4" А2Фо=0;
Ф1 + A2<₽i= Фо2— (4)
Фг4" А2Фг = “ ^1Ф1 - С2Фо + 2^.
В соответствии с начальными условиями решение первого уравнения (4) имеет вид
Фо=а cos р^. (5)
Подставляя это решение в правую часть второго уравнения (4) (при однородных начальных условиях надо принять Ci=0, чтобы нс было вековых членов):
Ф, = (1 /2) а2— (2/3) а2соз Р,/+ (1 /6) a2cos2p,L (6)
Подставим выражения (5) и (6) в правую часть третьего уравнения (4):
Ф2 + а2Ф2= — C^acos — 2t?A2sin А* 1(1/3) sin А^ +
4-(1/3) sin 2а/- (7)
В последнем уравнении содержится произвольная постоянная С2, которую нужно определить из условия отсутствия резонанса. Уравнение (7) можно преобразовать к виду
Фг4- A2Ti = (у A2fl3- С2а j cos pxt — -| Р\2& 4-
+4 Pi2(f-\-^- Pi2a3cos2pit — pfa? cos 3pit. (8) ом О
208
Чтобы решение (8) не содержало вековых членов, должно соблюдаться условие
C2=pt2a2/3.
Из второго уравнения (3) найдем частоту свободных колебаний
P\ = PlV 1 -+-а2а2/3.
При колебаниях (ограничиваясь двумя слагаемыми) <р= =фо+а<рь и при t=nlpi амплитудное значение угла
ф(л//ъ) =а1=—(а—4аа2/3).
Рассматривая уравнение движения на втором полупериоде Ф4-/,2Ф4-«Ф2 = О> можно получить выражение для частоты
P2 = p/Kl-|-a2ai2/3 и значение амплитуды в конце второго полупериода —4(Х|2/3.
Для последующих полупериодов задача решается аналогично.
177. Уравнение движения массы т имеет вид mx-{-cx-|-CiXJ=Posin (1)
Уравнение (1) решаем по методу Галеркина, положив x~X| =xosin о)/. (2)
Подставим (2) в уравнение (1) и потребуем равенства нулю интеграла
2я/ы
I— l/TUq + — Posln off]x1d/ = O,
о
где 2л/ы — период колебаний.
После интегрирования получаем (3/4)clx03+(c—zn<o2)xo—Ро=0. (3)
Корни уравнения (3) удобно определить графически, построив графики функций t]i= (3/4)С|Х03 и т)2=Л)— (с—ты2)х0.
В точке пересечения графиков тр и т]2 получаем значение Действительного корня уравнения (3), равного х© да 2,27 см (рис. 252)
178. В зависимости от значения частоты возмущающей силы изменяются и корни уравнения
(3/4)С|Х034-(с—тю2)х0—Fo=O (I)
[см. уравнение (3) в решении задачи 177].
14—5000
209
Аналитическим условием совпадения двух действительных корней этого кубического уравнения является условие D=0 при Р3=— q2 [2]. Здесь Л = <7г+р3; <?=—2F0/3cr, р=4(с—тш2)/ /(9ci). Отсюда находим
w.2=c/m+[9c1/(4/n)][2F0/(3c1)]2/3.
Используя числовые данные задачи 177, получаем ш*2= = 16,6 с-1. При этом q=—13,33; р=— 5,63. -
Для определения амплитуд корней уравнения (1) следует воспользоваться тригонометрической формой решения кубического уравнения. Корни уравнения (1) будут следующие:
хм=—2r cos ф/3; (х0)ъэ=2г cos[ (л±<р)/3].
Так как r=sign q \ |р] “—2,38, a cos ф=<?|га = 1, то корни уравнения (1) равны x0i=47,6 мм; (х0)2,з=—2,38 мм.
Рис. 253
Тот же результат можно получить графически. С увеличением значения со прямая t]2=F—(с—та)2х0 на графике т)(х0) (рис. 253) поворачивается против вращения часовой стрелки. Искомому значению со. будет соответствовать такое ее положение, при котором она касается левой ветви графика tji и пересекает его правую ветвь.
179. Дифференциальное уравнение движения [уравнение (1) в решении задачи 177] представим в виде
тх+ты2х= (ш®2-с)х—C|X34-F0sin ш/. (1)
Используя метод Дуффинга, примем в качестве первого приближения величину
xt=x0 sin о/. (2)
Подставим Xi в правую часть уравнения (1) и получим уравнение для вычисления второго приближения:
гпх2-|-то)2х2“"[(т<1)г—с)х.— (3/4)qxe'+
-f-F0] sin w/+(l/4)c)Xo2 sin Зю/.
Поскольку рассматривается только периодическое решение, то для исключения векового члена необходимо, чтобы
(тшг—с)х0— (3/4)с1хв34-Го=О. (2)
Это уравнение совпадает с выражением для определения амплитуды вынужденных колебаний хо по методу Галеркина. Если условие (2) выполнено, то второе приближение находим как решение дифференциального уравнения
тхг4-/Пй)гхг= (1/4)с,х#’ sin Зю/, откуда
х2=А sin ю/-|-В cos ®/—[C|Xo3/(32<o2m)] sin Зю/.
Постоянные интегрирования Л и В определяем из начальных условий. Так как при отсутствии трения сдвиг фаз между возмущающей силой и смещением равен нулю, максимальное отклонение массы происходит в момент действия наибольшей силы, т. е. за начало отсчета времени можно принять t=TH, где Т=2л/ю — период. При этом х2=х0 и х2=0.
Используя эти условия, находим А=Хо—с»х03/(32ю2т); В— И=0.
Следовательно, приближенное решение уравнения вынужденных колебаний имеет вид
х=х08Шю/—[cIXo3(32w2m)](sin<i)/—sin3<o/).
Из уравнения (2) вычисляем х<>=2,27 см, тогда х=2,27-•sin 10/ = 0,363-10-1 (sin 10/—sin 30/).
180. Дифференциальное уравнение движения массы т имеет вид
mx-|-ax4-cx+ciX3=FoSin((i)/-[-p). (1)
211
14*
Здесь учтено, что при наличии сопротивления смещение х и сила F имеют рассогласование по фазе (угол сдвига фаз р) Приближенное решение уравнения (I) имеет вид
x=x0sin<ot (2)
Подставляя выражение (2) в уравнение (1) и пренебрегая слагаемыми, содержащими sin3<oZ, получаем
(—mw’xo+cxo+OJSCjXo3—F0cosp) sino)/-|- (а<ох0—
—Fosinp)cos(oZ=0. (3)
Поскольку функции sincoZ и cosw/ линейно независимы, для равенства нулю уравнения (3) необходимо, чтобы
—rn(o2Xo+cxo+0,75ciXo3—F0cosp=x; асохо—Fosinp=0. (4)
Система уравнений (4) определяет амплитуду колебаний х0 и сдвиг фаз р. Исключив из (4) р, получаем
[(с—m<o2)xo4-0,75cixo3]24- (a(BXO)2=Fo2. (5)
На рис. 254 показано графическое решение уравнения (5), в котором
q 1 = [ (с) /по2) Хо+О,75с1хо3]24- (аюхо)2; qz = F02.
Точка пересечения графиков qi и qz позволяет получить значение амплитуды установившихся колебаний Хо=1,65 см. При этом сдвиг фаз p = arcsinaAxo/Fo~54°40'.
181. Предположим, что маятник совершает колебания относительно некоторого отклоненного от вертикали положения. Тогда дифференциальное уравнение его движения имеет вид
J<p-|-a<p + /zi£/sin<p = ./M(fl— <р). (1)
Разложим функцию возмущения Af(Q —<р) в ряд в окрестностях номинального значения Й:
М (Q_ ф) = М (й) - М' (Й) ф+ О.5Л4" (Й) Ф2 — 0,17ЛГ (Й) ф3 + ... .
Ограничиваясь линейной частью разложения, получаем
Уф_|_ [а_|_ М' (Й)] ф4-М (й).
212
Отсюда следует, что при отсутствии колебаний (<p = <p=O) угол отклонения маятника от вертикали равен
q>0=M(Q)/(mgl). (2)
Пусть ф=ф—фо, тогда можно записать
/ф4-[а4-М' (Q)]4+mg/i|)=0.
При a+Af'(Q)>0 система диссипативна, т. с. ее колебания являются затухающими.
При a+ЛГ (£2) <0 система самовозбуждающаяся, т. е. возможны возрастающие во времени колебания.
Вопрос о действительном поведении системы можно решить, если в разложении М (£2—ф) оставить нелинейные члены.
Рассмотрим разложение M(Q—ф), включающее члены третьего порядка. Тогда
/ф+ la+ЛГ (£2) KHmg/t-Af" (QH’/2—М"' (£2)ф76.
Обозначим a-f-M' (£2)=—b\; М'"(£2)/6=&2- Тогда при Alz,(£2) =0 можно записать
/ф — ф -}- доф3 4 mglty = 0.
Полагая po=Vmgl/J; 6 = х=фр0Кд7д1; p = bi/(Jpa), получаем уравнение Релея
хЧ-х= р (1 — х2) х, (3)
где x — dx/dfl.
182. Нелинейное уравнение угловых колебаний тормозной колодки имеет вид
УфЧ-Сф— М (£2 — ф) — 0, (1)
где / — момент инерции тормозной колодки относительно оси вращения вала. Ограничиваясь линейной частью разложения М (£2—ф) в ряд, получаем
Уф4-СФЧ-аф = Л1 (£2'). (2)
где
<Ш | а~ dQ
Так как Сфо=М(£2/), а также полагая ф=фоЧ"Ф1 (где фо — угол поворота тормозной колодки при установившемся режиме, Ф1—дополнительный угол поворота при колебаниях колодки), из уравнения (2) имеем
/ф, ч-сф, 4-a<h== 0. (3)
Из уравнения (3) следует, что угловые колебания тормозной колодки будут устойчивыми, если а>0, что имеет место при значениях |£2'|^|£2.| (рис. 255).
213
183. Как показано при решении задачи 181, уравнение движения маятника при нелинейной характеристике сил трения приводится к уравнению Релея (см. уравнение (3) в решении задачи 181).
х 4- РаХ = цхр0 [ 1 - л’р/о2], (1)
где p=-(a+M'(Q))/(/p0).
Решение уравнения (1) ищем в виде
x=acos(p0^+7).
где а и f — неопределенные, медленно изменяющиеся во времени функции, т. е. такие функции, производные которых по времени имеют тот же порядок малости, что и параметр ц.
Найдем скорость х:
x-acos —aposin (д/4-7) —af sin (р0* 4-1)-
Поскольку в решении имеются две неопределенные функции (а и 7), необходимо, чтобы
acos(p0/4-l)— ai sin(po/4-7)=O. (2)
Тогда
х=—aposin (ро14-Т); (3)
х=—apoSin (ро/4-7) — opo2cos (pot 4- 7) —a^pocos (р0ЬН) (4) Подставим выражения (3) и (4) в исходное уравнение (1):
—aposin (pot+1) —ароч cos (р<>/4-Tf) =
= —ц(1—a’sin2 (pot 4-7) ]ap02sin (pot+t). (5)
Для определения неизвестных a и 7 воспользуемся уравнениями (2) и (5), из которых можно записать
7 = цр0[1—a2 sin2 (р0/4-7)1 sin(p0f4-l)cos(p0r4-7);
(6)
а=ацр0[1 —a2sin2 (ро/4-7)]sin2 (р<+7)
214
По методу Ван-дер-Поля, функции (6) можно заменить их средними за период значениями (при этом f считается параметром, а не функцией времени), т. е.
2п/р, • (* •
jj а(т)<1т.
b
Интегралы (7) удобнее вычислять, перейдя к новой независимой переменной 0=рот4-у. Тогда
d0=podT4-TfdT.
Поскольку 7 имеет тот же порядок малости, что и параметр ц, можно считать, что
d0=podT.
В таком случае
2п
а=^- [1 — a2 sin20] sin2 0d0;
b
2л
7=^- ^(l —a2 sin2 0) sin 0 cos 0d0.
b
После интегрирования получаем
а-фФ(а)-^(1-4*); (g)
Уравнение (8) позволяет определить изменение амплитуды колебаний а во времени. Из общей теории нелинейных колебаний известно, что равенство нулю правой части уравнения (8) свидетельствует о наличии предельных циклов (или состояний равновесия на фазовой плоскости). Найдем корни уравнения а=0. Из (8) следует, что а=0 при at=0 и а2=2/}^3.
Нулевой корень соответствует состоянию равновесия маятника, а ненулевой — периодическому движению.
Исследуем устойчивость равновесия и устойчивость периодического движения маятника. Допустим,
a=a1-f-Aa, (9)
где а{ — корни уравнения Ф(а)=0; Да — отклонения маятника от состояния равновесия или периодического движения. Подставим выражение (9) в (8):
dAa/d/ = (цро/2) Ф (а<4- Да).
215
Разложим правую часть последнего уравнения в ряд, удерживая в разложении только линейные члены
dba/dt = (цро/2) (с/Ф/da,) Да. (10)
Решение уравнения (10) имеет вид
UP. <1ф ( ^а — Се~^’Ла‘ ,
откуда следует, что виджение (или состояние равновесия) маятника устойчиво при с1Ф/дО|С0 (если р>0) и неустойчиво при d®/da(>0. В рассматриваемом случае ц“0,015>0 (см. задачу 181). Следовательно,
a. z \ в /. 3 2\ <1Ф 1 [. 9 «\
ФЮ-7(1—Й--т(1~
При a=ai=0
d®/da( = 1/2>0, т. е. состояние равновесия неустойчиво.
При 0=02=21^3.
6ф/ба2=—1<0.
Следовательно, предельный цикл колебаний является устойчивым, т. е. маятник, выведенный из положения, равновесия, совершает колебания с медленно изменяющейся амплитудой, стремящейся с ростом времени к предельному значению фпред (переходя к амплитуде угловых колебаний ф), равному
4>прея = V Ьу/Ь2, фпре1=0.224 рад.
184. Поскольку начальный угол отклонения маятника фо меньше предельного (фп=0,1 рад, а фПр«д=0,224 рад), амплитуда колебаний маятника непрерывно увеличивается, стремясь к предельной. На рис. 256 пунктиром показана фазовая траектория изображающей точки, характеризующей движение маятни-
Рис. 256
7 1К
ка. Сплошная замкнутая кривая изображает предельный цикл: (установившееся периодическое движение маятника).
Если фо>фп₽ед, то движение маятника происходит с убывающей амплитудой (пунктир снаружи замкнутой кривой).
185. Решение нелинейного уравнения колебаний маятника (см. решение задачи 183) рассматривали в виде
х=а cos(po^+if).
Было получено, что у=0, поэтому частота маятника, соответствующая устойчивому предельному циклу, равна ро.
186. После выкладок, аналогичных выполненным при решении задачи 183, получаем
Ф(а) = (а/8) (4—а2); ф(а)=0.
Приравняв Ф (а) нулю, находим а|=0, а2=2. Первый корень соответствует неустойчивому равновесию системы, второй дает амплитуду предельного цикла.
Продифференцировав выражение Ф(а) по а (см. решение задачи 183) и подставив в него значение а, соответствующее предельному циклу, получим
дФ | 4 3 2 ,
да 8 8 °2 1 ‘По-
следовательно, предельный цикл устойчив. 187. В стационарном режиме сила лобового сопротивления планера уравновешивается силой натяжения троса
cxo=c,SpOo2/2, (1)
где с — жесткость троса при растяжении; х0— удлинение троса при стационарном режиме полета.
Если планер совершает малые продольные колебания, его движение описывается уравнением
тх 4- с (х0+х)=cxS р (ту 0 — х)2/2, где х — отклонение от положения равновесия.
При увеличении х скорость планера уменьшается, поэтому в правой части уравнения (2) стоит знак минус.
Преобразуем уравнение (2) с учетом равенства (1):
х + Рах = - М (2т»о^— х1)=Л.
где р02=с/т\ p=c3pS/(2m).
При колебаниях планера относительно положения равновесия сила сопротивления должна быть симметричной функцией х. Поэтому Fc следует принять равной
Fc= —ц(2о0х-х|х|).
Допустим, что x=acos(po*+<p) =а cos 0.
Считая а и ф переменными и применяя метод Ван-дер-Поля (см. задачу 183), можно записать (достаточно получить уравнение для а)
(2)
2л
НГ=~2г5 [2г>^а-а2р0[ sin 01] sin2 0d0. о
или da/d/ = ®(a), где Ф (д) = — (ац/р0)[2оол—(8/3) ар0].
При Д|=О и а2=ЗУол/(4ро) получаем Ф(а)=0, что соответствует наличию состояния равновесия (а^О) и предельному циклу с амплитудой а2=3оол/4ро.
Найдем производные Ф(а) по а при значении а, равном а, и а2:
d®/da|a_a, = — гъдл/рд < 0;
d®/da|e-a, = З'о0я/(4р0) > 0.
Полученный результат свидетельствует о том, что положение равновесия (установившийся полет планера) является устойчивым.
Глава 2. КОЛЕБАНИЯ СИСТЕМ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 8. Свободные колебания
188. Воспользовавшись принципом Даламбера, получим следующие дифференциальные уравнения движения:
т1х,4-с(х1—х2)=0;
т2х2+с(х2—ху) =0.
Решение системы ищем в виде
X|=4sinp/; х2=В cos pt.
Для определения коэффициентов А и В запишем систему уравнений вида
(с—р2т)А—сВ=0;
—сА + (с—т2р2) В=0.
Так как А и В не равны нулю, то определитель системы должен быть равен нулю:
С— Щур1 —с „ =0 — с С — ГП2К
или
р2 [ту т2р2 — (ту 4- тд d — 0-
Отсюда получаем
Pi = 0, р2=У (ту + т£ c/(mymt).
189. За обобщенные координаты примем угол поворота и**' линдра <р и угол отклонения маятника от вертикали О. Вычисли** кинетическую энергию цилиндра:
<91Я
T,= (J^+Mr^)/2,
где J=*Mr*/2.
Скорость движения массы т складывается из скорости, перпендикулярной стержню (/0) и скорости горизонтального перемещения оси цилиндра (гф). Кинетическая энергия массы т равна
Т2=т(/2О2+г2ф24-2/лОф cos 0)/2.
Изменение потенциальной энергии системы определяется вертикальным смещением массы т:
FI="»g/(l—cos О).
Составляя функцию Лагранжа L = Ti+T2—П и подставляя ее в уравнение Лагранжа
(d/df) (dL/dqt)—dL/dqi=O, получаем
(37Иг2/2 + тг2) <р 4- mJrb cos ft — mlr& sin О=0; .
miry cos О -f- mPb + mgl sin 0=0.
В случае малых колебаний в последних уравнениях следует пренебречь нелинейными членами и принять sinO=<>, cos0=1. Тогда уравнения (1) примут вид
(ЗМ/2 + т) г2ф + mlr§—0;
miry + тРЬ -|- mglft=0.
Для определения собственных частот колебаний положим Ф=Л sin pt, Q = B sin pt. Подставив эти выражения в уравнения (2), из условия равенства нулю определителя системы однородных уравнений найдем
_ П- П 1/ (l,5Af + m)g _
P1=U« Pi— у +
_ 1/ (1-52+0,2)10 _,4 ,
— У (1,5-2 + 0,2)0,5—0,2-0,5 •
190. Применяя метод сил, составим дифференциальные уравнения движения диска:
х==бп(_ — -/ф);
Ф = 6,2 (— отх) + бя( — Уф).
Здесь б./— перемещения диска от единичных сил, приложенных в направлении возможных перемещений. Вычисление 6,/ Показано в решении задачи 47.
Так как жесткость проволоки пружины при изгибе и круче-®Ии соответственно равна EJX и GJt, то можно записать
219
. __nnD‘ /sin’a . cos’a \
°u 4 + /’
л „„г,/cos’a ,sin’a\ ди WlD^ EJx + GJ^ J,
. A ,ялО’ . o / 1 . 1 \
д12=да = -j— sin 2a (-^ +
Подставим эти выражения в уравнения (1) и найдем их решения в виде д/ = Л,81пр/:
2 8(EJ х + GJJ / Г EJxQJ0(\+3cos‘2a) \
Р>.»~ллО’т(1 +3cos’2a) 4 \ 1 (£Jj+GJp)’ J‘
Графики изменения частот pt и р( в зависимости от угла a приведены на рис, 257. При этом принято, что GIf>=0,8EJx, а рлг=Е]ж(ппО3т).
191. Рассмотрим положения масс в произвольный момент времени (рис. 258,а). На массы действуют силы, показанные на рис. 258,6. Воспользовавшись принципом Даламбера, получим следующие дифференциальные уравнения:
+ roai4-7’oaj = O; '
(О
ГП2У2 + Гоа2Ч-7'оа3=0,
где O| = t/i//; а2= (</j—yi)/l, a3=y3/l.
С учетом выражений для at... а3 система уравнений (I) принимает вид
miyi + ToiyJl)—Т0(уг—yi)/l=0-, т2У2-\-Т0(У2—У\)/1+ Тоу2/1 = О.
Отсюда собственные частоты колебаний масс будут равны
Pt,2=F ((mt +т3) Т Vmi'-t-nh2—m\m2/(mimd\.
192. Дифференциальные уравнения движения массы щ, ^оставленные по методу сил, имеют вид
у = (— /п«/) + й12(— /<иф);
Ф=в21 ( — ту) + Й2г(—Л»Ф)-
Решение этой системы уравнений ищем в виде у = А sin pt, <р = В sin pl.
После преобразований получаем следующее уравнение для определения собственных частот колебаний системы:
р‘—(6217ol+61)m)p7(Am/0,)4-l/(AmJol)=0,
где Л=611622—612621-
Отсюда квадраты частот колебаний
„2 _ (6»»Л| + 6цт)Т УГ(вм/о1 + 6нп*)*—4Д/п/0|
^1.2“ 2m АД,
Первая частота колебаний р, при /О1-*0 позволяет получить частоту колебаний точечной массы, равную У 1/(6цт). Найдем поправку к этой частоте, принимая Jot малым, но не равным нулю. Преобразуем выражение для pi2 к виду
/622^ Ji + 26,,ба2т/4]—4/п,Дт
1 + 772
__________________________________
F1 2ДтУ„ ’ •
Разложив корень в ряд и ограничившись только первым членом разложения, после преобразований получаем
Р,2= 1/(611ОТ)-(6^М)/(4Д-/п26п).
Второе слагаемое в этом выражении представляет собой искомую погрешность в определении квадрата частоты, если считать массу т точечной.
193. Для определения собственных частот колебаний многомассовых статически неопределимых систем удобно воспользоваться уравнениями движения, составленными по методу сил. При этом статическую неопределенность системы можно не раскрывать, а заменить лишние связи неизвестными силами Xi.
Выберем основную систему так, как это показано на рис. 259. Силами, действующими на балку, являются силы инерции {—ту\ и —ту2) и неизвестная реакция X.
Перемещения точек приложения этих сил равны
У\ — Wtl^l^ll — ^^13»
у2— — /71|У16д — т2у2Ь22А~ -^23»
Уъ— — т\У\Ъл — /212^2^32+ ^взз-
Полагая y\ = C\sin pt, y2=C2sinpt, X=Xosinpf и учитывая.
221
что i/з" 0. получаем систему из трех однородных уравнений относительно неизвестных Сь С2 и Хо.
Уравнение частот этой системы имеет вид
(1 —mi>%) —/П1Р?Й21 — niiP2^^ 6]з (1 — /Пгр’бгг) бгз = 0
— П'рРЬж ®зз
или
Йц 612 6]3
т\Ш:. 6д dji 623 р4 — 1^11 (бцйзз-6в)4-
631 632 633
— Hl! (622633—623)] р2 —633= 0. 0)
Коэффициенты бу/ определим методом Мора путем перемножения по правилу Верещагина соответствующих эпюр 1, 2 и 3 (см. рис. 259):
а»
а»(1—а)‘. д ь*(1 — ЬУ' А _ Р
: 31EJX ' ’ Озз^48£Л'
61EJ х — Ь2У' 613«=6a = 4£jy ^-5 4-
А А Ь (Ь* 1’\ б2з=о32= 4£77|“з---г)’
б12=6а
где 1=2(а+Ь).
Подставив числовые данные в эти выражения и решив уравнение (1), находим pi = 101 с-1; р2 = 150 с_|-
Рис. 260
999
194. Дифференциальные уравнения малых свободных коле* ($аний. составленные по методу сил, имеют тот же вид, что и в задаче 193.
Собственные частоты колебаний системы равны:
а) а = 3,68КДЛЛтР); р2 = Ю,62КДЛ/(^3) (см. рис. 138, а);
б) А =2,34 р2=3,05 У EJx/(mV) (см. рис. 138, б);
в) a = 2,54F ДЛ/(т/3); р2 = 4,37 /ДЛД/пР) (см. рис. 138, а);
г) px = \WV EJx/(mPy p2=WVEJx/{fnP) (см. рис. 138,г).
195. Дифференциальные уравнения движения системы, составленные по методу сил, имеют вид
«/1=вц(—/»1У1)+б12(—W2);
Аг=6д (— OTiA) + M—
Для определения коэффициентов б,7 к каждой из точек крепления масс приложим единичные силы и построим эпюры /, 2 изгибающих моментов (рис. 260). Перемножив их по правилу Верещагина, получим
б.1=ба=4/’/(9Е/я); б12=б21=7Г/(18Е/х). (2)
Нахождение решения уравнений (1) в виде i/]=Aisinp/, y2=A2sin pt позволяет получить систему однородных уравнений вида
(6umiP2— 1)Я1 + 6]2т2р2Л2=0;
(3)
62i miP2A |-|- (622wi2p2— 1) А2—0.
Отсюда находим уравнение частот
n4 _ р2 = w|6|l + w16» I________!________ Q (4)
WjWlj (б„бг1—-fijij ^б||бг>—62|)
Подставим в уравнение (4) выражения для 6^ из (2):
г 5 ml* 5 [ml* )
откуда
р, = 0,89 yEJx/(ml3Y, Pt=3,7 У EJx/(ml3).
Для определения форм колебаний в уравнениях (3) положим;
1 и р = рь Тогда
Л21 = (1—6nmiPi2)/(6i2m2pi2)
ЙЛЦ после подстановки Д2) = 1,052.
Аналогично при Л|2=1 и р=р2 получаем А22=—0,475.
Формы колебаний 3, 4 изображены на рис. 260.
22S
Числовые значения частот, соответствующие условию зада, чи, равны
р( = 336 с-1, Р2=1400 с-1.
196. Воспользуемся методом сил и запишем уравнения дви-жения
!/> иД1 (— тУ\) 4- б] 2 (—/пУ2) + ^1з(— тУзУ
y2 = f>2i ( — Л1«Л)-]-в?2(—/И^2) + ®2з(— тУз)',
Уз=^л (— тУ}) 4* — /иУг) 4" ®зз (— гпУз),
где бц=25Х; S)2 = 39X; 6)3=17Х; 622 = 81 А; б2з=39Х; 6зз=25Х-А=/’/3888Е/я.
Решение ищем в виде «/,=Д sin р/.
После преобразований, аналогичных приведенным в решении задачи 195, получаем следующее уравнение частот колебаний системы:
2880 р’—1344 ц24-131 ц—1=0, (1)
тде ц=щ/2р!/(3888Е/х).
Решение уравнения (1) ищем графически. На рис. 261 показан график левой части выражения (1). Из графика получаем три значения ц, при которых левая часть уравнения (1) равна
нулю; Ц| = 0,00825; Ц2 = 0,126; ^«=0,334. После подстановки и •соответствующих преобразований находим
A = 5,65F£Jx/(m/3);
рг=22,Q5V EJx/(ml3Y,
Pz—Z&V EJx/(ml3y
197. Положение центра тяжести пластины при колебания* определяется горизонтальным х и вертикальным у смещениям и углом поворота <р пластины. В этом случае дифференциал1*'
224
цые уравнения малых свободных колебаний могут быть представлены в виде
х=611 (— тх) -Ь fit 2 (— /п </) + Й1 з (— -/ф);
y = f>a(~mx)-]-b2i(—ту) + Ъ<д(—J ч)', (1)
Ф=6з1 (— /71Х) + йз2(— /пу)4-6зз(— Ji)-
Коэффициенты б(/ уравнений (1) определим перемножением по правилу Верещагина эпюр изгибающих моментов /, 2, 3 от единичных сил, приложенных к центру тяжести пластинки в направлениях х, у, <р (рис. 262, а—в): би—/7(3£/х); б1г=6г1 = ==Р/(4ЕЛ); 61з=бз1 = /2/(2£/х); б22=/3/(4£Л); 623=6з2 = -=Р/(2Е/Х); 6„-l/(EJx).
Рис. 262
В случае малых перемещений вертикальное перемещение центра тяжести пластинки у=1<р/2. Тогда уравнения (1) принимают вид
х= (— тх) бц + [— тЬ12—(2///) Ifta] у,
У—(— тх) 6д +1 — mi a—(2J/I) б23| у.
Полагая x=A,sinp/; у—Аг sin pt и учитывая, что J = m/J/12, найдем собственные частоты колебаний:
А = 1,185 / EJx/(ml3); р2=4,75 V EJX/(ml*)- (3)
Для определения формы свободных колебаний положим в Уравнениях (2)x=Altsinp^ и y=A2|SinplL Тогда при p=Pi
Л __ I—'n?s!6n д _______1 tC Л
Ля “ (Ьб.,+/«„//)я’ Ап -1 •Al-
Аналогично при р=р2 находим
15—5000
225
А<‘----°'87л-
Проверкой правильности решения может служить услови ортогональности главных форм колебаний:
/П]Л цА 12+/П2Л 21Л 22 = 0.
В рассматриваемом случае при т, = т, = т
АцА J г+Л 21^22 “ 0.
Полагая Лц=Л12, убеждаемся в выполнении условия ортогональности. Формы колебаний рамы показаны на рис. 162, г, д.
198. А=0.97/Ё7л^Р); p2=3,2V EJx/(mP).
Формы колебаний и смещения масс т{ и т2 изображены на рис. 263 а и б соответственно.
199. Центр тяжести пластины может иметь линейные (вертикальные и горизонтальные) и угловые перемещения, т. е. система имеет три степени свободы. Выберем основную статически определимую систему так, как это показано на рис. 264:
Рис. 264
226
Используя метод сил, представим дифферениальные урав-нен«я движения центра тяжести пластины в виде
х= (— тх) й|1 (— ту) ^12 + ( -" JФ)
у-=( — тх) б21 4- (. — ту) 4-/?бм; (1)
Ф = (— тх) ба + (— ту) Йз2 + (~ йзз + #бзз.
где R — неизвестная реакция.
К системе уравнений (1) необходимо добавить уравнение перемещений, учитывающее, что линейное перемещение в направлении неизвестной реакции R равно нулю:
(— тх) бц +(— ту) 642 4" (— J Ф) б4з4-/?б4|=0. (2)
Здесь х, у и ф—горизонтальное, вертикальное и угловое перемещения массы т соответственно.
Для определения коэффициентов уравнений (1) и (2) приложим к основной системе единичные силы и построим эпюры изгибающих моментов подобно тому, как это сделано в задаче 197.
Систему уравнений (1) можно упростить, если учесть, что левый угол пластинки не имеет вертикального перемещения, т. е. что между вертикальным смещением у и углом поворота ф имеется зависимость вида у=/ф/2.
Учитывая что, момент инерции массы пластинки относительно центра тяжести равен 7=/п/2/12, получаем следующую систему уравнений:
х = (— /пх)6п —(/nfi124-^- 613j У4-^?йЫ’
у=(— тх) ба — । m.f>22 4- б231 У 4- (3)
0 == (— тх) б4) — I тб424- б431 у 4- /?б44.
Вычислим коэффициенты б,7, используя эпюры 1, 2, 3 и 4 (см. рис. 264):
б„-Л/(3£/х); б„-б,.-/7(4£/х); б1>=б11 = /7(2Е/х);
Уи“б4,=/7(6£/я); бгг=/7(4£/х); б„=б„=/7(2£/х);
бм=б«=Р/(4£/х); би=2/7(3£/х).
Полагая х=Л181пр^, y=/l2sinp/, R=Rasinpt, определим частоты свободных колебаний системы:
Pi = 1,45 /£Jx/(m/3); р2=5,83 V EJx/(ml3).
Для установления форм свободных колебаний примем х— *=.<4 = 4 nsinpf; y=y(=/l1sinpif Тогда из системы (3) получаем
Л71 = 1,05Ли.
227
15'
Положив Х=Х2“ЛI2sinp2^, !/ = !/-2 = ^22Sinp2t, находим ВТОру10 форму колебаний Л2=—0,95Ли.
Формы свободных колебаний при Лц=Л|2=1 изображены на рис. 264 пунктиром.
200. А—71.2 с1/>2 = 466 с ’.
201. а = 0,685 Г£Л/(/Л А>= 1.4 VEJt/(mP).
Формы колебаний, соответствующие этим частотам, изобра. жены на рис. 265. а и б.
202. Рассмотрим отклоненное от положения равновесия состояние системы (рис. 266, а). Вычислим потенциальную энергию системы как энергию изгиба стержня
П=су2/2.
где c^SEJx/l3 — жесткость при изгибе консольной балки.
Кинетическая энергия груза
Г = /пйо2/2Ч-У<Ро72.
где н0=« + ф74 (см. рис. 266, а).
При рассмотрении малых колебаний
228
у= (ф/—и)С03ф!“ф/—и. Применяя метод Лагранжа, получаем уравнения малых колебаний
тй + /п/ф/4 4- с (и — фО = 0; тй + 5/п/ф/44-4с (ф/ — и) = 0.
Решение этих уравнений ищем в виде u=4icosp/; ф—Лгеозр/, что позволяет получить уравнение частот
I -(т*»+я)
I -(>+£) (*-<*) “ или р4 = 29ср2/(4/п)==0.
Отсюда находим ________
Pi=0; p2^V9>7EJ/(4mP).
Нулевой частоте (pi = 0) соответствует движение системы, как жесткого целого (рис. 266, б); частоте р2 соответствует форма колебаний изгибного характера (рис. 266, в).
Из условия ортогональности форм колебаний можно установить соотношение между амплитудами. Так как "1и0|Н02+/ф11ф12 = 0.
то, полагая и01 = «о2=1 (см. рис. 266,6, в), находим ф„= = 4/(5/); ф12-5//.
203. В отличие от решения задачи 202 потенциальная энергия системы с учетом силы тяжести равна
11==^ — mg 4 I (1 — c°s ф) = С-£ +4 ptff/ф2-
Выражение для кинетической энергии остается таким же, как и в задаче 202.
Уравнения движения груза имеют вид и-\—^-ф — (и — /ф) = 0,
«4-4^+^-(/ф— н)4-б£ф=0.
Из этой системы уравнений после соответствующих преобразований получаем уравнение частот „4_2?^ о , 5с Q т И ' mls откуда ___________
1 /29 с , 1 < /29 с 5cg Р1'2 у 8 т ~ г .,8 т I nil ’
гДе C=3EJ/1‘.
229
204. Рассмотрим положение стержня в произвольный момент времени (рис. 267, а). Кинетическая энергия системы равна
mlui2/2+m2ui2f2.
При определении потенциальной энергии изгиба стержня его можно рассматривать как балку на двух опорах (рис. 267, б). Поскольку изгибающие моменты в верхней и нижней точках равны нулю, то
П=смп2/2,
где с=6Е/х/Р.
Рис. 287
Из рис. 272, а следует, что в случае малых колебаний (cos а~ 1)
мц=а/—Ui; а/=и2/2.
С учетом последнего представим уравнения движения масс в виде
miUj — cut—
Характеристическое уравнение для этой системы имеет вид p2[mim2p2—(сгП|/4+ст2)]=0, откуда
Pi = 0; р2 = V (с/П1-Ь4с/п2)/(4/П1/П2)•
Нулевой частоте соответствует вращение стержня без изгиба, а частоте р2— форма колебаний, изображенная на
рис. 267, в.
205. Рассмотрим положение системы в произвольный момент времени (рис. 268, а). В соответствии с принципом Даламбера система, нагруженная силами инерции, находится в равновесии, поэтому реакция опоры
/? = — тщ- 2гпи2— ти3 (1)
Момент сил инерции относительно шарнира равен нулю, т. е.
+ 4mlu2 + З/п/из=0. (2)
Рис. 268
В уравнения (1) и (2) входят четыре неизвестные величины (/?, Ui, и2, и3). Для получения недостающих уравнений рассмотрим изгиб стержня под действием сил инерции:
EJxy"*=* —Rz + (— тщ)(г — 1)+(—2гпй^(г — 21).
После двукратного интегрирования, учитывая соотношение (I), получаем
EJxy — (miii 4-2/nzz2-|- тй3) з’/б —
— mtii (z — lY/8 — 2mu2(z—2lf/8-\-Cz-\-D. (3)
Постоянные интегрирования С и D находим из граничных условий задачи: при z=0 «/=0; при z=3 {/=0.
Из первого граничного условия имеем 0=0, а из второго —
С= —-\-52Рти2+2712ти3)/18.
Окончательно уразнзние изогнутой осн стержня имеет вид
EJxy = (tnii\ 4-2zratt2-|-/7iU3) । — Цг-j —
“ /(•г—/)* 4Z’Z\ _ - /(г—2/)’ 1гг\ ,,,
mUl ( 6 9 I ^mu'i ( 6 18
Из рис. 268, а следует, что
У1-— y,~i=u3/3—«ь t/2“—У«-2<“2из/3—и2 (5)
231
Используя соотношения (5), из уравнений изогнутой оси (4) получаем два недостающих уравнения:
у /п«1 + у ти2+4ти3+—^ их—р^и3=0; (6)
18W“1 + -9/п«24-у/п«з4-—“2 — у-pi«3=0. (7)
Уравнения (2), (6), (7) образуют полную систему уравнений. После преобразований получаем следующее уравнение для определения частот:
„2Г„4 „2 . I08/£-GVl п
Р + ] = 0’
откуда находим
А=0; р,-1,23 Г £Л/(тР); р3=3,8/£/,/(/nF).
Нулевой частоте соответствует вращение стержня без изгиба, т. е. движение абсолютно жесткого тела (рис. 268, б).
Найдем связь между амплитудами при второй форме колебаний (р=р2). Рассмотрим систему уравнений (2) и (6), в которых примем u(2=A(2sinp2t Тогда
4A22+3A32=—Aj2; 1 1,5А22+7Дз2я=—А[2.
Считая Ацж 1, получаем Аг1=0,61, А„=—1,15.
Аналогично, полагая в уравнениях (2) и (6) uf3=-A(3sinp3;' и считая А|з= 1, находим, что при колебаниях ,по третьей форме А2з =—0,485; Азз=0,31.
Вторая и третья формы колебаний системы приведены на рис. 268, виг соответственно.
206. Формы колебаний системы можно определить из следующих соображений. Система (рис. 269, а) имеет две нулевые частоты, соответствующие поступательному и угловому движениям тела как жесткого целого. Эти формы колебаний изображены на рис. 269,6, в.
Рис. 269
Две другие изгибные формы — симметричную и кососимметричную — можно найти из условий ортогональности.
Пусть «ц, Ui2, Ui3, и14— линейные перемещения левой массы, соответствующие различным формам колебаний; иц, иц, м2з, 024 —линейные перемещения правой массы; фп, <pt2. Ф>з. фн — угловые перемещения левой массы; ф2ь Ф22. фгз, Ф24 — угловые перемещения правой массы.
Третья форма колебаний (симметричная изгибная форма) должна быть ортогональна первой форме (поступательному движению), т. е.
ти,1и„4-щи21и134-/ф11ф„+/ф11ф2л=0.
Поскольку фп = ф12"0, то полагая «n = «2i = l. получаем м|3==и23=0 (случай Ut3=«235^0 относится к первой форме колебаний).
Кроме того, третья форма колебаний должна быть ортогональна второй:
ти,2а,а-|-тииигл-|-/ф1гфи-|-/ф21ф„=0.
Полагая иц=—1, «22=1 и учитывая, что «1з=«»зв0, а ф|2= =ф23=3/(4/) находим, что ф1з=—фгз- На рис. 269,г показана третья форма колебаний.
Аналогично из условия ортогональности четвертой и первой форм колебаний можно записать
т-1 -«,4-|-т-1 •и24-|-/фнО4-/ф«-0=0.
откуда
«14 = —«24=—!•
Учитывая ортогональность четвертой и третьей форм, получаем
т 0 1+т • 0 (— 1) 4-/фифн+/ф1зфа»=0, или
ф14 = ф24
Наконец, из ортогональности четвертой и второй форм колебаний имеем
*3 О
.то.(-1).(-1)4-от.1.1+/Аф14+У^фм=°,
Или
ф,4 = ф24 = —16/(3/).
Четвертая форма колебаний изображена на рис. 269, д.
Частоты колебаний определим, используя найденные формы колебаний. Поскольку третья форма колебаний (см. рис. 269, в) является симметричной, рассмотрим правую часть системы (рис. 269, е).
Для определения жесткости системы при угловых колебаниях приложим к массе единичный момент и найдем угол поворота
0*32
ф|»"в11=/(2Е/<).
Соответствующие частоты колебаний равны
А = 0; рл=Кl/(/d„) = ^8EJx/(mP) = 2,84 У EJx/(mP).
Четвертой частоте колебаний соответствует кососимметричная форма. Поэтому силовую схему можно представить так, как это изображено на рис. 269, ж.
Для определения частот воспользуемся уравнениями Лагранжа. Кинетическая и потенциальная энергия системы соответственно равны
T=jfr/2+mut*/2-, П~су*/2,
где и. — и-Ь/ф/ц; с=24£/ж/Р; у=1у/2— и.
Уравнение движения и уравнение частот имеют вид
(/4-т/716)ф4-т/и/4+с/гф/4—du/2=0;
т/ф/4 + mu—с/ф/2+си=0;
рг[1тр2—9с (1гт+J) /16]=0.
Частоты, соответствующие кососимметричным формам колебаний, равны
Р2 = 0; Р< = V67,5EJx/(mP)= 8,2 VEJx/(mP).
207. Система имеет четыре степени свободы и соответственно четыре формы колебаний: две кососимметричные (рис. 270, а, в) и две симметричные (рис. 270, б,г).
Определение частот кососимметричных форм колебаний аналогично определению, приведенному в задаче 206. После соответствующих преобразований находим
234
А=0; р3=4,7 KfA/tmP).
Для вычисления частот симметричных форм колебаний рассмотрим правую часть системы с жесткой заделкой на одном конце (рис. 270,(?).
Выведем дифференциальные уравнения движения, используя метод сил:
«=би (— /пй)4-6|2(— /ф); ф = б21 (—/пй)4-ди(—/ф).
По методу Мора с применением правила Верещагина определим коэффициенты б,/:
бн=31/7(48£/,); б11=б1|=3/2/(4£/ж); б«-//(£/х).
Таким образом частоты симметричных форм колебаний равны р2 = 1,1 VEJ/(mP\, =6,5 И EJx/(mP).
Полагая И22 = «24=К находим углы ф22 = 0,93//; ф24 = —— 3,3/1.
208. Положение системы в произвольный момент времени определяется четырьмя независимыми координатами у\, у2, ф1 и фг (рис. 271,а).
Кинетическая энергия этой системы равна
Т = + J1Ф12/2-\-J2Ф22/2»
Потенциальную энергию деформации системы удобно выразить через относительные линейные у* и угловые фй перемещения масс. Считая массу пг неподвижной (рис. 271,6), приложим к концу упругого стержня силу Q и момент М. Тогда угол поворота и прогиб стержня будут соответственно равны
*/* = 6nQ + 612М;
Ф* = 62iQ + бг2Л1-
где б.,-/7(3£/х); б«-б„-Р/(2£/х); «„=//(£/,).
Из этой системы уравнений определим Q и М;
Q=(622/A)j/k—(б|2/Д)фк; 1
Л1= — (б21/Д) ук 4- (б„/Д) фк,| где Д = б11б22-б22=[/2/(£Л)]76.
Вычислим потенциальную энергию деформации изгиба стержня:
п Г AfH*dz С (Af + (?.)’ . МЧ QMP , Q’P __
1 J 2Е77 J 2е77 2— 2EJX ’•* 2£/.г 1 6£jt
о о
= ОцФк2-Ь аиЧЛк — ЪгУк- (1)
Здесь
°п =2Л’£УЛ (би “li>'211 + Тб?ЯР)=Т“Г’
Д12 —2д»£уг [^(^ii^22 + ^2) —2бпб]2 612^22] =‘2~pi’
6X22 = 2 А’£/71Ъ* ~ ^12^22 4* -у = У 7*^-
Как следует из рис. 271, а:
Ук = «/2—//I—/2Ф2/2—/|фг/2—/1Ф1/2—/ф! =
= «/2—«/I—/2Ф2/2—//ф|/2; (2)
фк —ф2—фь
где // = /4-/1/2.
Подставив выражения (2) в уравнение потенциальной энергии деформации (1), получаем
П = ^нф]‘4'Ь«»фг:1“Ь^м1/|"4_^4«1/1"_Ь^12ф1фг_|_
+ Ь1 Зф1 УI + Ь14ф I у 2 + 62зф2</ I + 624ф2{/2 + Ь иУ IУ 2, где
6.l=all4-(/t')’a„/4—/,'а„/2; 6„=а114-/2,а22/4—
—/2О12/2; 633 = 644 = 022, 612=—2вц 4-/1'012/24-
+ /2O12/2—///2022/2; 613=012—//022; 614 = —О|2-|“//О22;
623=—O12+/2O22; 624 = 012—1га22\ Ьц — —2а2!.
Воспользовавшись теперь уравнением Лагранжа, запишем систему дифференциальных уравнений движения
J 1Ф4-26пф1 4- 6|2*Pj4- 6|з</| Ь^у2=0;
•/ 2Ф2 4“ 6|/fi 4“ 2622Ф2 4“ 623//14“ 6241/2=
/Л1У14- 6]зФ14- 623Ф2 4" 2ЬззУ) 4- 634У2—
Я*2//2-|- 614Ф1 4~ б24фг4~ 634I/! + 2 644I/2 = О-
209. Решение дифференциальных уравнений малых свободных колебаний, полученных в задаче 208, ищем в виде у^ =At cos pt; q>i=Bisin pt, что позволяет получить следующее уравнение для определения р:
пос
26n-J,p» 6l2 613 *14
612 2 622— J-iP1 Ьгъ bM
Ь1з Ь2з 2Л33—myP1 Ьц
b\i Ьц bn 2£>!4 — тр2
или
JJsm.mjp’+a.p’+^p'+a^+a^O.
Поскольку система имеет две степени свободы, соответствующие движению абсолютно жесткого тела, четыре корня уравнения должны быть нулевыми, т. е. коэффициенты Дз и равны нулю.
Отличные от нуля частоты определим из уравнения
J (1)
Подставив в это уравнение выражения для Ьц, находим
Лу— — 2 (У(У2Т1| Ьц -|- J\J 2/И2633 + JI ttly tnzb22'\~ j 2ftl\ fH'b\ | ] — = -(13/16) m?lFJx,
<h= J\J2(^34 — 4633^44)-}-</l/?l2(^23 — 4 623633) 4"-AWl(^24—4 622644)-]-
4~ Jiffii (46цЬц — 6’4j + J2ГП2 (46ц^гз— -|-
4-/И1/П2 (46ц6й— b22') — (2\/32)(m.EJx/l)r.
Собственные частоты колебаний определим из уравнения (1):
р|>2=0; дз=0,447 У EJx/(mfy р<=3,Ь2У EJx/(ml/(ml*).
210. Система имеет пять степеней свободы (положение каждого из грузов определяется вертикальным смещением и углом поворота, а положение центральной точечной массы—только ее вертикальным смещением).
Двум степеням свободы (движение системы как жесткого целого) соответствуют нулевые частоты Pi = p2 = 0 и формы движения, показанные на рис. 272, а и б.
Третья форма колебаний ортогональна двум первым: т«ци1з+ти21«2з + щиз1«зз+/фпф1з-|-/фз|фзз = 0; (1)
ти1,и134-ти28и„4-ты>1и„4-/фиф1,-|-/ф1хф„=0. (2)
Поскольку фц=фз1 = 0 и Une«2t = «3i = l из уравнения (1) следует, что
Из14-И2з+“зз=0-
Принимая Ц)з=«зз= —1> находим д23=2.
Аналогично, подставляя в уравнение (2) значения и32=1, Ui2=Ui3=Uj3= — 1, ф|2 = фз2=1Д получаем Д22 = 0. Следовательно, третья форма колебаний является симметричной (рис. 272,в).
237
Условие ортогональности четвертой формы колебаний трем первым позволяет получить следующие соотношения:
ам+«м+«м—0; (3)
+ = (4)
— Ut4~l-2U24 — U34 + ~ Ф|ЗФ14 + (РззФз4==О- (5)
Поскольку четвертая форма колебаний должна быть кососимметричной, т. е. uu=—«м=—1, из соотношения (3) полу, чаем uS4=0. Кроме того, фн=фз4 и из уравнения (4), полагая «>*=!, находим фн=фЭ4=— ml/J= — 4/1.
Ulfl Us,= 1
иа=-1
Рис. 272
Четвертая форма колебаний показана на рис. 272, г.
Пятая, симметричная, форма колебаний ортогональная первым четырем. После выкладок, аналогичных предыдущим, принимая u,s“«„=l, получаем фп= —<р15=Зт//(/ф11) = 12/(/<р13); «25=—2. Эта форма колебаний изображена на рис. 272, д.
Частоты колебаний можно определить, используя найденные формы свободных колебаний. Для нахождения частот, соответствующих симметричным формам колебаний, рассмотрим систему как шарнирно закрепленную балку, нагруженную по концам моментами M — и инерционными силами Р„ Рг, Pz (рис. 272, е).
238
Из условия равновесия системы Р|4-Рз=Р2, т. е. u2=2ut. Представим дифференциальное уравнение изогнутой оси балки в виде
Е1ху"=М+muip^z—muiP* (z—l).
После интегрирования и определения постоянных имеем
EJxy<=M + (6)
При z=l
у= — (u,+«2)=—3u(.
Тогда из уравнения (6) получаем
3EJxu^MP/2+muJ3p‘/3. (7)
Поскольку у',=о=—ч>, из уравнения (6) следует
Е/хф=М/+та,/’р72. (8)
Учитывая, что Л4=/ргф, приведем (7) и (8) к виду
(—mPpz/3+3EJx)ul—JpzP(p/2^0;
тРр*иЛ2+,(Лр'-Е1х)ф=Ъ. (9)
Соответствующее уравнение частот будет таким:
р‘-52£/др7 (тР+144 [—£/«/ (тР) ]*-0.
Отсюда находим частоты симметричных форм колебаний:
р3= 1,71 VEJt/lmP); р.=7 V EJx/(mty-
При отыскании форм колебаний остались неопределенными углы <р13 и ф|5. Их можно вычислить, используя одно из уравнений (9) и известные частоты р, и рь. Так, принимая и13=— 1, находим ф|з = —5,5//, а при «is = l <pis=—2,2//.
Частоты колебаний, соответствующие кососимметричным формам колебаний, находим аналогично тому, как показано в решение задачи 206. Значения частот р2 и р* будут следующие:
р2 = 0; рА = 3,83У EJx/(ml3)-
211. Для составления дифференциальных уравнений движения воспользуемся принципом Даламбсра. Рассматривая каждую из масс, найдем, что в процессе колебаний на массу действуют момент сил инерции и момент сил упругости. Считая, что ф1<ф2<фз< (ф<— углы поворота дисков), имеем
—•/1ф1+^,=0;
—73ф2-(- (Мг—Aft) = 0;
или 73ф3—Л13=0,
—/|ф14-С1(ф2—ф,) =0;
—/2ф24-с3(ф3—ф2) —ct (ф3—ф|) =0;
—73ф3—с2(ф3—ф3) =0.
239
Решение последней системы уравнений будем искать в виде <p(=4(sinpt Уравнение частот имеет вид
„6 л4 (С1 + I Cl I С» \ I r r + 2 Л
р Р 1 Т,) c'Ci TJ^Tt Р—
Учитывая, что ci=GJp/li и ct=G]p/lit получаем следующие значения собственных- частот колебаний:
Pi = 0; р2=92,4 с-*; р’-151,6с-'.
212. Пусть ф] — угол поворота левого диска; ф2— угол по-ворота правого диска; ф/— угол поворота шестерни /; <р2' угол поворота шестерни 2.
Вычислим кинетическую и потенциальную энергии системы:
Т = -АФг/2 4-
П = Ci (Ф1 — ф! ')’/2 4- с2 (ф2 — ф/)2/2.
Между.углами поворота шестерен имеется зависимость вида
Ф>' — —ф2Ли.
Исключив из выражения (1) угол ф| и воспользовавшись уравнением Лагранжа, получаем
•I 1ф14-С1 (ф14~иф/) =0;
/2ф2->с2(ф2'—ф2)=0; (2)
ис 1 (ф^Ифа') 4"с2 (ф2Л—фг) =0.
Последнее из этих уравнений означает, что в любой момент времени моменты упругих сил, действующие на шестерни со стороны валов, уравновешены.
Исключив из выражения (2) угол ф2', имеем
7^+7^7<р‘+7^тггф2=°; (3)
гФгЧ- Ф1+ c1U»4-C, Фг-
Уравнение частот для системы (3) будет следующим:
/4лЛр>-С/,«’+Л)-1^4-0.
откуда следует, что собственные частоты колебаний равны А=0; р3==/^-^Л.
213. Уравнения угловых колебаний дисков следует составить аналогично тому, как это сделано в задачах 211 и 212. Частоты колебаний для приведенных на рис. 155 а—д схем соответственно равны:
240
а) Р\₽ 0» Рг — У~2 ~у’*
б) P1 = V c/2J; p2=V2c/J-,
в) pt =0,8 Ус/ J ; рг=\,37 Уc/J \
\ П. .. 1 fJ.U^Ut* + J, с,сгс.и^ . ,
Г) А = О; р2= у -'—p-j—- ,а >с 1и,с +с (щ=г2/гх, и2=
V J । J 2 «1 Ug Cj -f Ug L j -f Cl
г4/г3); ____ ______________
д) Pi = 0,651 Vc/J\ рг— 1,256 У с/J.
214. Уравнения движения систем можно получить по методу Лагранжа. Кинетическая и потенциальная энергии системы соответственно равны
7=/ф,72+2/ф,*/3+3/ф172;
П=с (<р 1—фг) 2/2+с (фз—фг) */2.
Дифференциальные уравнения движения имеют вид /ф1+с(ф1—ф,)=0;
2/фг—с(ф,—фг)4-с(ф,—Ф,)=0; (1)
3/ф,—с(ф1—ф»)=0.
Решение системы уравнений (1) ищем в виде ф<=Л,с05р/, поэтому можно записать
(с—]рг)Ах—сЛ»=0;
—<?Л1+(2с-2/р‘)Л2-сЛ3=0; (2)
—сЛ,+.(с—3/рг)Л3 = 0.
Отсюда получаем уравнение частот
/[/-7^/(3/) +(с//)»]-0.
Следовательно, частоты колебаний системы будут равны р1 = 0; р2=0,755 /7/7; р,-1,33 /с/7.
Найдем связь между амплитудами колебаний для каждой из форм колебаний. При нулевой частоте (первая форма) из системы уравнений (2) получаем Лп—Л„—Л„.
Для второй частоты колебаний имеем
4»,— (с—/р/)Л12/с=0,435Ли; Л„-сЛ„/(с—37р/) 0,615Л12.
Наконец, для третьей частоты колебаний амплитуды колебаний будут следующими:
Л23=—0,77Л13; Лм=0,179Л13.
Формы колебаний показаны на рис. 273. При построении принято
Л ц=Л12=Л |3= 1.
16—5000
2-11
Pro
Проверим полученные формы колебаний, используя условие ортогональности. Представим условие ортогональности форм (например, первой и второй) в общем виде
7Л цЛ11+2/Л21Л1х+3/Лз1Лз2=0. (3)
Подставим в уравнение (3) значения амплитуд Ло первой и второй форм колебаний:
/ (1 • 1+2 • 1 • 0,435—3 • 1 • 0,615) = J (0,025) « 0.
Из условия ортогональности для первой и третьей форм получаем
J (1 1 — 2 1 • 0,77+3 0,179) = J • 0,003 « 0, а для второй и третьей форм —
/ (1 • I—2 • 0,77 • 0,435—3 • 0,615+0,179) = 0.
215. Обозначим c=GJv/\, тогда дифференциальные уравнения движения дисков можно представить в виде
7<р1+с(ф1—<рг)=0;
/<р2 с («р»—фг)+с(ф2—ф1) "0;
/ф,—с(ф2—фа)+с(фз—фч) =0;
2/ф*+с(ф1—фэ) =0.
Принимая ф,=Л(5|‘пр/, получаем уравнение частот
- 7 Т +8 (т)> - 7 (т)’] - °-
Отсюда находим частоты колебаний
А=0, р.=0,656VcTJ\ рг=\3£>УсП\ р± = 1,82FT7+
На рис. 274 показаны соответствующие формы колебаний. Как видно, условие ортогональности форм колебаний выполняется.
216. Уравнение частот системы имеет вид
Р-1Р6 - у j- Р* + 18 (у)2 р-’ - 8 (-U’] = 0.
242
Корни этого уравнения (собственные частоты) следующие: Р-0; p?=0,613 c/J-, p,*=2,26c/J; р?=5,8 c/J.
Формы свободных колебаний характеризуются следующими амплитудами отклонений дисков:
первая форма
фп=1; <р2( = 1; фз1=1; ф41=1;
вторая форма
ф12=1; ф22=0,387; фз2==—0,0375, фчг==—0,455;
третья форма
фн—I; фи= —1,26; ф»з=—0,966; ф^—0,412;
четвертая форма
ф1<=1; ф24 = —4,8; фз4=6,22; ф44=—0,8.
217. Выражение для потенциальной энергии деформации системы остается тем же, что и в решении задач 212, а в выражении для кинетической энергии появляются два новых слагаемых:
Т = У,Vi2/2 + J^/2 4-Л'(Ф1 ')2/2 + J2' (Фз')2/2-
Исключая из выражений для кинетической и потенциальной энергии угол ф1| (см. решение задачи 212) и используя уравнение Лагранжа, получаем следующую систему уравнений:
Лф1+.с1ф1+<'1иф/=о;
(/2/+//Цг)ф2/4-С1«ф1+(с>«!4-Сг)ф2/—Сгф1 = °;
Дфг—Сгфг -Ьс^фа = 0.
16*
243
Принимая <pi=<p(o=sin pt, получаем уравнение частот
РгУ J J ipi—[7 г (CtJ ,) +/,/,£,] Р‘4"
+ (C.G—С|2«г)Л+с.с.Л4-,(с,Сз—£?)/,} = О,
где J3=J\'u2+J2'; cs=C|U2+c2.
218. Кинетическая и потенциальная энергии системы соответственно равны
7-=/1ф12/2+/2ф272+/3фз72
П==С| (ф1—ф1') 2/24-ct (ф2—ф/) 2/2-{-с2 (фз'—фз) 2/2.
Здесь ф/, ф/ и ф/ — углы поворота зубчатых колес редуктора.
На рис. 275 изображена схема работы редуктора, из которой следует
Ф1'= —Фз'^= —«Фз'; <pI'=<p2'-
Исключая с учетом последних соотношений из уравнений (1) углы ф/ и ф/ и используя уравнения Лагранжа, получаем следующие дифференциальные уравнения.движения:
•Лф|+Мф|+“ф/)=0;
Лфг+с1(ф2+«ф>/)=0;
Лфз4-с*(ф*—ф/)=0;
(ф|+ифз') +С|и(ф24-иф3') _|_с2(фз/—ф3) =0.
Выразим фз' из последнего уравнения:
„ г_сгфз ci“ (Ф| + фг)
фз 2е,«> + с,------•
Исключая из уравнений движения угол ф3', получаем следующую систему дифференциальных уравнений:
Л ч1! +аиФ|—2Ф2+Л13Ф2=0;
J2Ф2—Л12Ф1 Ч-^иФа 4_Я1зФз==О; (2)
Лфз + 3Ф1 Ч_о!1зФ2“Ь2аа1зФз==0,
глр а _с11ц, + с1с». п _ . п с,с„и
11 2с,в* 4-е, ’ 12 2с,и- + с* ’ 13 2с,в’ 4- с, ’
Уравнение частот системы (2) имеет вид
On (J,J3+ /2/3)] +
+ [2«Oi3^1l (•/1 + ^2)_"а?з(Л + —а?2А] Р2 —
- 2(Z13 [и (а2 - а2г) - а13(а12+Оц)] = 0.
244
Нетрудно показать, что свободный член последнего уравнения равен нулю. Это следует и из физических соображений — система может вращаться как жесткое тело.
219. Рассматривая динамическое равновесие каждого маховика, получаем два уравнения следующего вида:
Лй+МФ!—Ф2)+«(<₽1-Фз)=0; (О
Лфг — (Ф1 — фр) — Сг (Фз — Ф>) = 0. (2)
где ф| — угол поворота левого маховика, срг — угол поворота правого маховика; <рз— угол поворота контактного кольца демпфера.
Рассматривая равновесие безынерционной упругой оболочки, получаем третье уравнение
а(<Р1 — Фз) — <МФз~ Фг) = 0. (3)
Решение системы уравнений (1) —(3) ищем в виде Ф^Л.е^. что позволяет получить следующее характеристическое уравнение:
(Ал Jj 4-Ла-}-£,) — С]
— С "Ь ^1
Ла Сч
— ра
-Ci
— (Ла + Сг)
= 0,
или
AV 1/го+Л‘/1/2с2Н_.Л:'а (Л+Л) (Ci-f-Cj) 4-Лгс,с1(/i+Л) =0. (4)
Имеем систему с дробным числом степеней свободы. Из уравнения (4) получаем два нулевых корня (Xi.2«0), соответствующие вращению системы как абсолютно жесткого тела. Для нахождения остальных трех корней составим следующее уравнение:
Подставив в него числовые данные, получаем
Л3+60Л24-630Л4-12 600=0, откуда находим
А3=—53,1; Л45=(—3,45±Л6,5).
220. В качестве обобщенных координат выбираем вертикальное смещение центра тяжести копуса у и угол его поворота ср (рис. 276).
Потенциальная и кинетическая энергии системы при колебаниях равны
П=с, (у+ф/,) !/24-с2 (у-ф/2) ’/2;
7’=туг/2+/ф72.
245
mg
Рис. 276
'A*
W
Подставив эти выражения в уравнения Лагранжа второго рода, получаем
mg+ci (р4-фМ +с2(у—ф/2) =0;
Ар+с,/, )сгЦу—<(1г) =0,
или
у+ан{/4-О12ф=0; <р4-а21У4-а22ф=0, (а)
где
«и = (Ci+c2)/m; O|2= (C|/i^-c2/2)/m;
fl2i= (Ci^i Огг~ /J,
Решение системы уравнений (а) ищем в виде у=А sin pt-, Ф=В sin pt. Собственные частоты колебаний
Р1,2 = р^ (#11 4"а2г)/2 + У |(Оц — <>22)/2р 4*^12^21 >
откуда после подстановки числовых значений получаем
Pi = 16,5 с-1; р2=50 с-1.
221. Равенство частот собственных колебаний системы возможно при выполнении следующих условий:
и (с1//+М‘)//=(с,4-сх)/т.
Если ввести обозначение рг=1/т, то эти два условия можно свести к одному
р2=/|*2.
222. За обобщенные координаты выберем вертикальное перемещение центра тяжести кузова у, его угловое перемещение Ф и вертикальные перемещения переднего и заднего мостов у\ и у2 (см. рис. 161). Выражения для кинетической и потенциальной энергий и диссипативной функции Релея имеют вид
П = у (У + Ф b - у, )2 + (у - фа - у2) 2 + -j- ;
^ = -?-(1/ + Й-«/1Р4--у (У-ча-th)2-
24fi
Подставив Т, П и R в уравнения Лагранжа, получаем следующие уравнения движения:
/оф+«(а2 + ^2) Ф + (Wh + clb2)<f>-i-a(b — a)y-l-(cll>—cJa)y —
—abyl-j-aay2—c1byl-l-c2y2a=O;
my + 2ay-j-(cl + c^y + a(6 — a)q>+(clb — c2a)q>—
- «(У\ + Уд — А Ух — с2у2=0;
yt+°ч/1+(с+й) Ух—а й—с\ *ф—аУ—с\ ф=°;
m2y2 -f- а.у2 + (2с + с2) У г+®<*Ф+е^Ф — <*У — Сцу=•0.
223. За независимые переменные (обобщенные координаты) примем перемещения у\ и у2 центров тяжести переднего и заднего мостов. Силы вязкого сопротивления примем равными нулю (а=0).
Введем новые неизвестные ?i и z2, положив Zi=y-j-(pa; z2= =y—tpb. Тогда
y=zib/(a+b) +z2a/(a+b); <p=z1/(a-|-b)—z2/(a-{-b).
Проводя решение подобно тому, как это сделано в задаче 222, получаем две независимые системы дифференциальных уравнении вида
mbzt-l-Ctia-j-bjzt—cia+b) ^=0;
Mt Ух 4“(с + ci) Ух — схгх =0’
лшг2 -г (а + b) z2—с (а -|- Ь) у2 = 0;
т\ У 2+(с 4- Ci) У 2—Ci z2=0.
Частный случай Je=mab эквивалентен расчетной приведенной на рис. 277.
(1)
(2) схеме,
Рис. 277
Система уравнений (1) описывает колебания переднего моста и некоторой массы m2=mb/ (а-Ь-b) при неподвижной массе тз, а система уравнений (2) — колебания заднего моста и некоторой массы тз=та/(а-^-Ь) при неподвижной массе тг.
247
Из системы уравнений (1) после соответствующих преобра, зований и подстановки числовых значений находим р1=а = 8,27 с-1; рз=48,5 с_|, а из системы уравнений (2) получаем Рг=9,9 с~’; р<=48,8 с-1.
224. Удлинения верхней и нижней ветвей передачи при колебаниях шкивов равны
Д/|=/?1ф1— /?2<р; Д/2——(1)
Удлинения A/1i2 можно выразить через дополнительные напряжения по формулам, приведенным в условии задачи:
A/i=aiAci; Д/2=а2До2. (2)
В процессе колебаний на каждый из шкивов действуют момент сил инерции и момент сил натяжения в ветвях передачи. Дифференциальные уравнения свободных колебаний шкивов имеют вид •
ЛФ1 + RiF = 0;
72ф2 + Rf (А°г — Д°1) = 0-
С учетом соотношений (1) и (2) систему уравнений (3) можно представить в виде
ф| 4- fJ\ — R\ Rfa&t/Ji=0;
Фг — R\ Rfatfh / J 2 4- J 2 = 0,
где аз^^ + ^/а^.
Из уравнений (4) после преобразований находим
Pi = 0; />2 = уг/?)/:‘аз(/?1//1+/?2/2). Рг — 146,3 с'1.
225. На рис. 278 изображено положение системы в произ вольный момент времени. Вычислим кинетическую и потенци альную энергии системы:
Рис. 278 Рис. 279
248
T = J^/2+J2^/2-\-Jy'^/2; (1>
H=cAZi2/24-cA/22/24-mg[Ai 51пф + й2(со5ф — 1)].
где c—EF/l.
Удлинения упругих связей равны
Д/| = Я|ф| — Ягфг—х cos <рю;
Д/2 = /?2ф2—/?|ф2—X COS ф|0, или, учитывая, что xszh^,
Д/| = /?|ф|—/?2ф2—Al'l’COS’Plo;
(2) Д/г=/?2ф2—/?|ф|—Ai’picos ф|0.
Подставим выражения (1) с учетом соотношений (2) в уравнения Лагранжа:
- , 2с/?,1 2с/?,/?, п.
Ф1 + -77-Ф1—— Ф2=О;
** ‘IcRtRi । 2cRii . /ч
<й----— <й + — *+0.
- М.’е«Ф.. |ф+«».о.
J1 •* 1
Угол ф можно представить как сумму угла фо от статического приложения нагрузки mg и угла ф| при колебании системы, т. е.
ф=фо+фь
При этом в статическом состоянии (ф=0) справедливо соотношение
2сй12фосоз ф1о+т£Л|=0.
С учетом этого третье уравнение в системе (3) принимает вид
Ф.+.гсЛ/сов ф,0ф///=о.
Алгоритм определения частот аналогичен изложенному в задаче 193. Окончательно получаем, что частоты собственных колебаний системы равны
pt=0; р2=187 с-1; р3=270 с-1.
226. Вычислим кинетическую и потенциальную энергии системы при колебании шкивов (рис. 279):
Т=/1ф,72+/гф,72-|-.т1х1/2; (1)
П=сД/1724-сД/22/2+я11#(Г14-Г2) (1—cos 4’)>
где c=EF/l— жесткость упругих связей; Д/j и Д/2— удлинения упругих связей, равные
Д/| = /?!ф|— /?2ф2—х COS фю;
Д/2 =—Л1ф]-|-/?2ф2—X COS фю-
249
Между углом ф1 поворота ведущего шкива 4 и углом ф по. ворота кулисы 3 имеется зависимость вида
,, v Ф1=’1>(1+',7Г|), (2)
где ф=*/(г14-г2).
Из выражения (2) следует, что ж=Г1ф|. Тогда уравнения (1) принимают следующий вид:
Т — J2ф22/2-}-(Т1 4 /П\Г 12) ф]2/2;
У IWl П COS фо) ф| /?2ф2]24" у [ —(/?! 1 cos Ф10) Ф1 Н~
4- Я2фг1г 4- mx g (Г14- г2) (1 — COS —г±- <й У \ '11'1 /
Используя уравнения Лагранжа второго рода, получаем дифференциальные уравнения движения
+ [(7Г^г,«) z + r«2 CQs2 ‘Pi о) + т^Г\ ] Ф1 -lEFRJh л
(/l + m1rI«)/<₽2“0;
% ^‘Pl + 7J = 0.
Из последних уравнений после соответствующих преобразований и подстановки числовых значений получаем pi=34,6 с-11 р2=179с-'.
277. На рис. 280 изображена масса т в произвольный момент времени t. Поскольку натяжение в нитях То принимается постоянным, горизонтальным смещением массы можно пренебречь.
Дифференциальные уравнения движения имеют вид ту=— (Tosin ai+Tosin a2), /ф —— (Лй^ТЛ).
Учитывая, что sin a,= (</4-*ф/2)/„ sin a2= (у—btp/2)/h, eina2=(«/—Ьф/2)//|, й|= (b/2)sin(a14-a), й2= (й/2)5ш(ф—a2l« а также считая а и ф малыми, получаем
251)
:: , Т'Щ + и r.b(i,-i,} 0
У+ ml, l, 2ml,I, *
" , Wi-U,. Wo _, ±£i±h)<pg ф_|---277л y 1 2/Гн 2 l,l, I4
Из этих уравнений теперь можно записать уравнение частот:
„2 - Г, <*» + '») T,b(i,—i,\
Р 1 ml,l, 2ml ,1, q
W/«-G) d2,/9 + -^-
или
< n Г b , Z, + l, 4 J + mb1 ] T , T,*b b + 2 (I, + Z2)_n
p4_p2^_+_l_---------__jro + __ --------—-------U.
В частном случае при lt=l2=l движения по у и <р независимы и частоты малых собственных колебаний равны
р,--=\'2Т0/(ml); Рг = V(Tob/2J) (2 -f- Ь/Г).
228. В произвольный момент времени положение вагонетки определяется тремя координатами: х, y-(-h, <р (рис. 281). При этом горизонтальная координата является независимой функцией скорости движения вагонетки (x=xo4-t>O« а Две другие связаны между собой следующим образом:
ту = (То sin «j 4- То sin <х2) — mg,
7ф= —ТоЛг + Т'оЛ) •
Учитывая, что
sin ai« (t/4-b<p/2) /si; sin а2« (у—b<p/2)/s2;
Л|«Л+«/—х sin си; Л2«Л+у—(/—x)sin а», получаем
у + [2То/(mb)] Л, (Z) у + (Го/m) А2 (t) Ф = - gl
<₽ + (То//)А2(I) у + (T0b/2J) Ai(t)<^Q.
251
где
Л, (О —Ь (I—b)/[(x0+vt—b/2) (l—Xo—vt—b/2) -2];
Л2(/) =6[/-2(xo4-v/)]/[(xo+»/—b/2) (l—x0—vt-b/2) -2].
229. Рассмотрим произвольное отклоненное от положения равновесия состояние системы (рис. 282, а). В соответствии с
Рнс. 282
принципом Даламбера дифференциальные уравнения движения массы можно представить в виде
тх=—Ticos ai4-T2cosa2; ту=— (Tisin ai+T2sin a2)4-m£. (1)
Из рис. 282, а следует, что
cos ai= (xo+xJ/^to+Asi);
COS Ot2 = [Zi — (хо4-х)]/ ($2oH~As2);
sin ai= (t/o+^)/(sio+Asi)
sin a2= (t/o+f/)/(s2o+As2).
При этом натяжения в ветвях нити равны
Ti = Tio4-ATi; Т2=Т2о+АТ2.
Подставляя эти соотношения в уравнения движения (1) и сохраняя члены, линейно зависящие от приращений номинальных значений, получаем
252
4~ 7'ю —£- AS| — T и о ASj!
S,° 520 (2)
I /п^-Т10^-Т^-ДГ1^-АГ2^-4-
4* T'io ~ ~ AS| 4" 20 2° ASj*
sio S20
Удлинения ветвей нити связаны следующими зависимостями с приращениями усилий:
Asl = ArIS|O/(£F)=Arsio/(c/i); As2=AT2s20/(c/i). (3)
В уравнения (2) и (3) входят шесть неизвестных величин (х, у, Mi, М2, Asi, As2). Дополнительными геометрическими уравнениями могут служить тождества
sin2 <х 14-cos2 ai = l;
sin2 a24-cos2 a2=l,
которые позволяют получить (с учетом выведенных выше соотношений) следующие два уравнения:
As)= (i/o/sio)!/4-(xo/sio)x;
As2 = [(/1—Хо) /$2о]х4- (W«2o) у. (4)
Входящие в систему уравнений (2) статические натяжения ветвей имеют между собой зависимость в виде уравнений равновесия
-Г1О^4-7'2о^=О; Г1о т2-4-7120-р-= mg, *2© *10 *2©
из которых легко получить
T^mg^^-. (5)
•1 У© • 1 £/©
Подставив соотношения (3), (4) и (5) в уравнения (2), имеем
* 4-A i*4-0120=0;
Л (о)
У 4- о-л* 4“ о220 = 0.
Здесь
(Л-
7.0
SIO
012-02!-^
1 аи—— ffl
7|о*о* 1 4
4о
Тi«(/1 —
4, 20
У» m
^0
EFyJ / 1
s3 ’
*20 /
Ти (I,-
S20
1
11 m
4
253
Полагая x=.Asin/tf, i/=Bsinpf, находим уравнение частот |«ц- Р2 «и I 0
«Л «22 /,2|
ИЛИ
Р4 = («И + «22) Р2 — «12 + «II «22 е °-Отсюда
Pi ,2=(«и +«2г)/2 + |(«ц +«21)/2]24-л22-
В частном случае расположения массы т в середине пролета (х0=/1/2, $|0=52o=So) начальные натяжения в ветвях Тю== = Т2о=То‘ При этом система уравнений (6) распадается на дча независимых дифференциальных уравнения:
mx-|-2[To (yo2/s03) +EF (Хо2/$о3) ]х=0;
(7) тУ+2(То (xo2/so3) +EF («/oW]f/=O.
Частоты вертикальных и горизонтальных колебаний соответственно равны.
А = n2/(/ns03)](W+£Fx02);
А = К 12/(«503)](ТЛ24-£^). (8)
Из выражений (7) можно найти частоты колебаний для ряда частных случаев. Полагая хо=0, т. е. рассматривая вертикальные колебания груза на растяжимой нити (см. рис. 282,6) (при этом 5О=1/о; To—mg/2-, /1 = 0), находим
Pi = V g/Sy Pi=V 2EJ/(ns0).
Если во втором уравнении (7) принять уо=0, получаем частный случай колебаний массы т, расположенной посредине упругой нити( рис. 282, в). В этом случае
А =/4^/^/!); Д2=/2Г0'/(Ы,),
где Г/ — натяжение, при котором у<,~0.
230. Дифференциальные уравнения движения массы т аналогичны уравнениям (6), полученным в задаче 229, но в отличие
254
от них величины Х0, Уо, Г10 и Т20 являются, функциями скорости движения массы v и времени t.
В соответствии с начальными условиями задачи масса m начинает двигаться из положения, изображенного на рис. 283, описывая в стационарном движении дугу эллипса. Уравнение эллипса в обозначениях, приведенных на рис. 283, в полярной форме имеет вид
sio=soo/(l— е cos «0=500/(1—exo/si0). (1).
Учитывая, что 5ю=5(х)+ц/, из уравнения (1) получаем
х0=у^е, где
е=А /(^10+Ы=А /($»+]А» + А2) •
Вторая координата массы m при ее стационарном движении равна
У и ~ РЧ -*о2-
Натяжения Гю и Г20. соответствующие стационарному движению, определим из уравнений
/ПХ0 = Г» (/j -(- Хо)/$20— Т\оХй/SjO?
>ny^~T i0y0/5jo+ Т 2йУ0/ 5»— mg-
Решая эту систему уравнений относительно Гю и Г^ с учетом полученных выше соотношений, находим
р ,___________Уо /Г________.
*°~ «((/♦/51<1)(1 +*./(/,—X.)) ’
7" __________У»+ 8_________.
х0)/х,+ 1] ’
где у0=(ф2/Уо)[(1- 1/Z2)-(5io-Vz)WL
231. Изменение напряжения в цепи якоря в произвольный момент времени равно приложенному напряжению, т. е.
Hl4-Wk-|-uv= Uo sin wt. (1)
Учитывая, что UL=Ldil^t, UR=Ri, L/,=«|d<p/d/, представим Уравнение (1) в виде
Adi/d/-|-/?t4-aid(p/dZ = //osin ыЛ (2)
Запишем дифференциальное уравнение вращения якоря: /d2<p/d/24-c<p=a1i, (3)
где a2t — электромагнитный возмущающий момент.
Решение однородных уравнений (2) и (3) ищем в виде i= *=Л]е“‘; ф=.Д2еа‘, что позволяет получить следующее характеристическое уравнение:
255
x*+ (/?/L)XI+[(a,aI4-cL)/(/L) ]%+Rc/(JL) =0.
В частном случае весьма малого активного сопротивления цепи якоря (/?«0) получаем следующие значения корней:
Х,=0;
232. В состоянии равновесия конденсатор имеет заряд <?о, а пружины сжаты на величину х0 (силой, с которой пластины конденсатора притягиваются между собой).
Пои колебаниях заряд и смещение соответственно равны
q=qo+&q, х=х0+Ьх.
Емкость конденсатора С обратно пропорциональна расстоянию между электродами
С=а/(1—х), где а — некоторая постоянная; /—расстояние между пластинами в отсутствие заряда.
При выводе уравнений движения воспользуемся уравнениями Лагранжа. Потенциальная энергия системы (электрическая и упругая)
П = - £/Л<7+с(Дх+х„)72.
Разлагая выражение для потенциальной энергии в ряд и ог-раниичваясь квадратичной частью разложения, получаем
П = Ц^-Д<72-^А7Д^+уД^2+[^К-^)-^]Л7 +
+ [cx° — 2e] Ах + const.
Выражения в квадратных скобках равны нулю из условия равновесия системы. Сумма кинетической и магнитной энергий
Г=тД?/2+£Дд2/2.
Энергия, рассеиваемая системой (из-за активного сопротивления в электрическом контуре),
D=R\q2/2.
Таким образом, дифференциальные уравнения свободных колебаний системы имеют вид
ткх Ч- сДх — kq = 0;
L Д? + Rkq 4- Д</ - £ Дх = 0.
233. Кинетиечская и потенциальная энергии системы соответственно равны
Т-/1ф,,/2+Лф,72; П=с(ф,-Ьрг)72,
где qpi и фг — углы поворота дисков.
9SB
Используя уравнения Лагранжа, запишем дифференциальные уравнения движения дисков:
ЛФ>+^(ф>-(Р2) = 0;
•Афг 4" (Ф2 Ф)) = О-
Представляя решение системы уравнений (1) в виде q>i = e=4isinp/, ф2=Лг sin pt. получаем следующее уравнение частот:
p‘-c(J1+/1)p7(/,A)=0.
Отсюда находим частоты собственных колебаний дисков
Р! = 0; р. = Ус (/| — J^/(J
Закон движения дисков с учетом кратных нулевых корней имеет вид
§ 9. Вынужденные колебания
234. Дифференциальные уравнения вынужденных колебаний, составленные по методу сил, представим в виде
— —ТП\У\ 4*Р) 4“®12 ( Wl>^2)>
02—би (— от ।ух + р) -г Й22 (— т2у-2).
Решение системы уравнений (1) ищем в форме У\=А} sin at, y2=A2sin at Подставив y\ и у2 в уравнения (1), найдем значения амплитуд колебаний А[ и А2:
5ц (1 — + в] 2^®’
=== * Q ’ 9 . I
(1 —бцД1|<1>’) (1 —5}»т,ш2)—6[2,ni,ni®
д =р__________________51!_____________.
2 ° (! —бит,шг) (I —6;2/игшг)—
По условию задачи ш2 = 1 /(m2f>n). Следовательно,
А, = —8JJ7 (9£7J; Аг=—64PJ’ (63£/ж).
или с учетом найденных в задаче 195 соотношений >
Л1 = —8РоР/(9£/1); Д2=—64Р0/3(63£/1).
В процессе колебаний на массы от( и т2 действуют периодические силы fi=—Р—т{у\ и Р2=—т2у2, амплитудные значения которых равны
Fio==O; F20^2^0^22/612-
17—5000 257
На рис. 284 показана эпюра изгибающих моментов, из которой видно, что опасным является сечение закрепления массы т2, в котором действует
Л4гаах=46Р0//21.
Наибольшие напряжения в балке
п = М /U7 — 4P0Z6tl
°max 36^х‘
235. Обозначив через х1 и х2 перемещение массы mi и ^2. соответственно получаем следующие дифференциальные уравнения движения системы:
х, = (Ро sin at — т}х}) бц б,* t >
Х2 — ( /П]Х|) д21 Ц- (— ZTljXo) 6j2.
Для случая, показанного на рис. 171, а коэффициенты уравнений системы (1) равны
6.. =[ 1А+/7 (3£4) ]/2=2/ (Зе);
6,2^6,., = Г/(bFJx) = 1 /(6с); 6„=б12.
В установившемся режиме колебаний решения уравнений (1) ищем в виде x^xiosin wZ; x2=X2osin <at.
Подставив эти выражения в систему уравнений (1), получаем
Р. (1—
Л.]0 -----—— — — “V ,
(I —лцео’бп) (1 —— т1таш11)|,
Ajo -------------------------------~.
(1 —/П|(1)*6|1) (1 —лг
С учетом исходных значений окончательно имеем
X|o=44Po/(45c); х20=—8Р0/(45с).
258
Усилие, передаваемое на массу т2 со стороны массы т}, равно
Pi = 2c(xio—Х20) =2,31Р0.
Коэффициент динамичности передачи силы равен
Лдин = Р1/Ро=2,31.
Для случая, показанного на рис. 171,6, коэффициент динамичности
ЛдИи=4,5.
236. Разложим полную силу инерции Fo на две составляющие: Fr=Fosin со/ и F,=pocos <at, направленные соответственно перпендикулярно осевой линии балки и вдоль нее. Положение центра массы мотора в любой момент времени определяется двумя независимыми координатами — его вертикальным перемещением у и углом поворота <р.
Используя метод сил, можно записать
+ /ф)б12;
Ф= (Fy— ту) ба + (F,/? — /<₽) 622.
где / = /<,4-т/?2 — момент инерции массы двигателя относи-•тельно его основания.
Коэффициенты уравнений (1) определим по правилу Верещагина
бн=4/7(9£/.ж); б11'=б11=2/’/(9£/х); б2г=/*/(3£Л).
Частоты свободных колебаний системы найдем из уравнений (1), приняв в них Fv=Fj=0. Полагая y=ctsinpt, ^=сгз'\пр1, после преобразований получаем две частоты колебаний:
д = 1,43 / EJx/(ml3); д 3,96 К EJx/(mP).
Решение системы уравнений (1) ищем в виде
i/=^,sin (о/Н-ЛгСОв со/;
q)=B|Sin(i)/4-B2COS о/. (2)
Подставляя выражения (2) в уравнения (1) и учитывая связь между компонентами центробежной силы инерции, получаем следующую систему уравнений для определения постоянных Д). Аг, Blt В2:
(1—fn<i)26n)^i—/<i)26i213| =£обц;
(1—Щ(1)26[ j) А 2—I <о26 j2£2== F о£б|2;
( 1-/(D'622) £1—tTl(i)J()\2A 1 =F0612;
(1—/й)2б22)#г—mco26i2^2 = £o£fiM-
17*
259
Решив эту систему уравнений, находим Л.-(Л/Д)[(1—/(о±в„)6114-/<о*в11‘]=-----IO4Fo/7(227£/x);
Л,= (Го/Д)[(1— /П(0гб,<)61,+т<02б„611]=—72F0/J/(227£/±);
В.= (£./?/Д)[ (1-/и262г)5,1+7<ог612б1г]= —18F0P/(227£/x):
Вг= (£./?/Д)[(Г— m<ol6,,)d„4-m<rt*6,asJ =5£ог//227£Л, где Д=(1—Отш’бц) (1—т/ш'бп*.
Из выражений (2) следует, что амплитуды вынужденных линейных и угловых колебаний соответственно равны
Уо = у Л,2 + ^22 =« 0,467£(,£/(£Л);
Фо= V Br'+B22=O,319FOZ2/(£JJ.
237. Дифференциальные уравнения движения масс, составленные по методу сил, имеют вид
-Г1 — ^11 (— f>2 (— П2Хц-{- Р)',
х2 = ^21 ( П}Х\) -f- б22 (— П2Х2 Р).
Решение системы (1) ищем в виде X|=4sinct)/; x2=Bsin<Df. Для определения Л и В получаем следующую систему уравнений:
( 1 б| 1ГТ11 СО2) А—б 12ГП2(1)2В = Pfl6|2J
— m 16214- ( 1 —^22m2(t>2) В = Рд^22-
Отсюда находим амплитуду колебаний массы т2:
д_р _________й?»(1 — 6ц>и,а3)4-/п16^2<»г___
~ ° (1—61|п»1<о*)(1—6гтга>г) — ’
Амплитуда колебаний массы т2 равна нулю при бЯ (1 — dt! Щу (1)2) 4- 6?2(1)2 = 0,
откуда получаем связь между частотой возмущающей силы и параметрами системы
°)2 = б22/ [ т,\ (б] j б22 — б J2)]. (2)
Левая часть выражения (2) представляет собой парциальную частоту колебаний массы mt (частота колебаний массы («1 при жестко закрепленной массе т2). Коэффициенты этого уравнения равны
би=2//(££); б12=б21=//(£F); 6i3=l/(EF).
238. Амплитуда колебаний массы т2 равна нулю при
<1)2 = б22/[/?11 (бцб^п — 6i2)J, где
б„=6г1=4/7(9£/х); б12=7Р/(18£/х).
260
1 239. Воспользовавшись методом сил, запишем дифференциальные уравнения движения масс:
И«=*и (— + т>У1) + ^3М;
(— /П1У1) + б22(— ГП1У1) + (>пМ.
Так как yi должно быть тождественно нулю, то из системы И) получаем
б 12^2^2=6 1зЛ»;
У2 =—б22т2*/2~|-б23'Л'1. (2)
Решение системы (2) будем искать в виде i/2=^sin<oZ. После преобразований получаем
—С1)26|2^2А =Й|зЛ1;
(1—бгг^гЧ)2) А ;=62зА1. (3)
Из системы (3) находим связь между частотой возмущающего момента <> и параметрами системы, при которых амплитуда колебаний массы /П| равна нулю:
Ш2 —613/(^2(622613—623612)].
240. На рис. 285 показано положение системы при колебаниях (мачта заменена стержнем). Координаты массы т( можно выразить через угол <р и смещение массы т2 следующим образом:
x1=x2+/1sin ф; у(=/, (1—со$ф).
Для вывода уравнений малых колебаний масс т, и т2 воспользуемся методом Лагранжа. Запишем кинетическую и потенциальную энергии:
Г = miX^/2 4- т\У^/2 4-
П= тi£(l— cos ф)4-сх22/2,
где с — жесткость балки на изгиб, равная 3EJх/1\
После преобразований получаем систему дифференциальных Уравнений вида
гп2)х2+сх2+m\li‘<i>=Fosin at;
л11^1-*24-'И1/12ф+/П1£/|<Р=О, (1)
Решение этой системы будем искать в виде x2=Asin <о/;<р = p==Bsin at. Амплитуда колебаний массы т2 равна
» = (l/A)[Po(^.-W)mi],
гДе Д — определитель системы алгебраических уравнений, соответствующих (1).
Амплитуда колебаний А равна нулю при
<О* = Я/А,
гДе у g/tt — частота колебаний маятника при неподвижной 1,1 эссе /п2.
261
Рис. 285
241. Составим дифференциальные уравнения малых колебаний системы, воспользовавшись методом Лагранжа. При колебаниях диска угловая скорость равна
где Qo — угловая скорость диска при стационарном режиме; ДЯ=ф — дополнительная угловая скорость диска при колебаниях.
При колебаниях массы т смещаются на величину х от положения динамического равновесия. При динамическом равновесии массы находятся на расстоянии I от оси вращения.
Кинетическая энергия системы
Г=/(Я04-ДЙ)’/2+2т{[(Й0+ДО)(/4-л)Г+^}/2,
потенциальная —
П=с<р2/2-|-2С| (х04-х)2/2,
где х0 — растяжение пружины при стационарном режиме вращения. Обобщенная сила равна М. После преобразований из уравнений Лагранжа второго рода получаем два дифференциальных уравнения вида
ф — У + iml’ + J + 2ml2
X — 2ц/ф+(й / т — ад х=0.
Решение этой системы будем искать в виде ф = Л sin Xs® =Bcos со/.
После преобразований получаем, что амплитуда колебани11 диска
А = (Af 0/Д) [Ci/m—Я02)—и2],
где Д — определитель системы (1).
262
Параметры гасителя колебаний, при которых амплитуда угловых колебаний диска равна нулю, определяются соотношением
ю2=С|/т—SV.
т. е. гашение колебаний происходит в том случае, когда частота возмущающего момента равна частоте колебаний массы т на вращающемся с постоянной угловой скоростью Йо диске.
242. На рис. 286 показана измененная конструкция гасителя Прингла, в которой пружины имеют предварительный натяг * х0. В этом случае массы т будут прижаты к диску до тех пор, пока сила m/ойо2, действующая на массу т, не станет равной силе предварительного сжатия пружины, т. е.
tnl0Q02=x0c{.
243. Для гашения вынужденных колебаний диска, происходящих с частотой со, необходимо, чтобы частота колебаний маятника р равнялась со, т. е. а=р. Следовательно, частота колебаний маятника, находящегося на вращающемся с постоянной угловой скоростью Йо диске, равна
р=Й У~ь/Т.
244. Дифференциальные уравнения вынужденных колебаний системы имеют вид
У\ =6ц (— тгУг-^Р)',
У2 — ^21 ( — fflii/1) + f>22 ( — /П2//2 + Р)>
\ где б11=бп“б11=/7(3£'/ж); 6^=23//(12E/X);zn, = 2m; тг=т\ P=Posin ш/. (При решении считаем 6Д = О,8Е/Я).
Решение системы уравнений (1) будем искать в виде
i/i=4isin u>t\ y2=X2sin at. (2)
Подставив соотношения (2) в уравнения (1), найдем амплитуды вынужденных колебаний:
А, = 1.085PJ7 (£/я); Лг=5,02Ро/7 (£/я).
263
Вычислим теперь силы, действующие в точках закрепления масс:
Fl=—m1y'|=2/n/l|®2sin io/ = 0,8Posin cat;
F2=P—^2!/2== (F2<i> ^)sin и/=2,94Posin u>t.
Опасным сечением рамы является сечение заделки. Амплитудные значения изгибающего и крутящего моментов в этом сечении равны
AfMo=(F<o+f„)/=3,74Po/;
Л1к.-Ло/=2,94 Р,/.
В соответствии с теорией наибольших касательных напряжений эквивалентное напряжение в опасной зоне равно
<г,-(1/Гх)/Afi+ Л12о=4,75 PJW»
где tt7I=nd732 — момент сопротивления при изгибе бруса круглого поперечного сечения.
Из условия прочности (Тэтах <Отр/пт НЗХОДИМ, ЧТО ДОПуСКЗ-емая амплитуда переменной возмущающей силы равна Рв«106 Н.
245. Решение этой задачи аналогично решению задачи 234.
Поскольку б|=61г=//(б/р), а 62!“=26ll=2//(G/p), то амплитуды установившихся колебаний дисков равны
•4,= —-6„Л10; A2=612Af(,.
Рис. 287
Найдем максимальные значения моментов, действующих на вал:
Al|o=Aft-f-A1(0"/4 = —ЗЛТ»;
На рис. 287 изображена эпюра кутящих моментов от действия на вал моментов Af10 и Л4го.
264
Наибольшее касательное напряжение тюа1=Мтаж/(0,2d’) =4М./(0,2<Г) = -=4-5/0,2-10 *= 100 МПа.
Коэффициент
Пт=Тт/Tmai = 200/100 — 2.
вынужденных колеба-колебаний в задаче 215, которое в правой части этой системы
246. Дифференциальные уравнения ций аналогичны уравнениям свободных ja исключением четвертого уравнения, содержит возмущающий момент М. Решение уравнений удобно искать в форме <р,"BjSin что позволяет
получить следующие соотношения:
(с——сВ2=0;
—cB.+ ^c—№)В2— сВ3=0;
—сВ2+ (2с—/<о2)В3—сВ4-=0;
—cBj-f- (с—2/о’) В2=М0.
После решения этой системы получаем следующие значения 1 углов закручивания: В,=0,373А1|)/с; Bt=9,274 М./с; В3*= —0,841 М,/с; Bi=—0,352 М„/с. Отсюда следует, что ампли-
моментов на участках вала равны
тудные значения крутящих
М1г~с(В,—Вг) =0,102 М.;
Мг)=с(В,—В,) = 1,112 М.;
Мц—с(В,—BJ — —1,193 М,.
Таким образом,
Мщах = I М>. |.
247. Решение аналогично решению задачи 256.
Амплитуды вынужденных колебаний дисков имеют следующие значения:
В,-3,08 М./с; В2= 1,135 М./с;
В, = —0,1 М./с; В4= —0,02 М./с.
Отсюда амплитуды крутящих моментов
М12-1,945 М.; М„=1,235 М.; М,4= —0,19 М..
Наибольшее касательное напряжение в вале
Tmai = Мтах/Wp -1,945 М./ 1FP = 1,945 • 300/0,2Х
X64 10-0=45,5.
248. На рис. 288, а изображено произвольное отклонение системы от положения равновесия. Удлинения верхней и нижней ветвей упругой связи соответственно равны
Д/|=/?|ф1—Ягф»; Д/»“= —
265
Рис. 288
Дополнительные напряжения в ветвях связи можно определить из соотношений
Д/.-Ла^/Г; Мг=\сг1/Е.
На рис. 288,6 изображены шкивы с действующими на них дополнительными усилиями. Из рассмотрения равновесия шкивов следует, что
J\4\+R\F — Д<ъ) = °;
Лфг 4- RiF (Дст2 — До()=М.
После преобразований получаем
Tl Ч'^пФ! Ч" .‘Ф’ — 0;
+й22Фг= М/ Ji, гаи
at^2RtEFI (J ,1); an=-2RiRtEF/(Jll)-,
alt---2R>RtEF/(JJ), a,, -2R.REF /
Полагая ф1“=Ле‘Рг и <p2=Be'P', после преобразований (см. задачу 188) находим собственные частоты:
А=0; A=-|/'^(4f + 7r)’
(нулевой корень соответствует малому повороту шкивов в одну сторону; при этом дополнительные напряжения в связях нс возникают).
Для определения амплитуд малых вынужденных колебаний шкивов получаем следующие выражения:
<р.0=----------_______________•
А [(аи—w’) (а«—<•>*)—
(j._________<Д;)___________
Л((вц — и’)—a.id,,)-
После подстановки исходных значений и соответствующих преобразований получаем <j>10=—0,595• 10~‘, ф24=0,51 • 10 * М,.
266
Полные напряжения в ветвях упругой связи равны
о,*=о»+До1=о1>+£(/?,ф1—/?2<р2)//;
Оа=0.+До1 = Оо4-£(Л»ф1—/?1ф1)/Л
или о1=Оо=—0,0269 Af„sin wt; о2=Оо+0,0269 Afosin tot. Напря-
жение в одной из ветвей равно нулю при А1в=73,4 Н м.
249. Дифференциальные уравнения малых вынужденных колебаний имеют следующий вид (см. решение задачи 224):
Ф1 +/? 12£а3ф ।// j—R । R2Fa3(f2/J i = 0;
ф2 — /?,/?1ааф1//,4-/?2,£а,ф,//г=Л1,51П tot.
Решение этой системы уравнений ищем в виде
= <j>toSin tot, фг=фг»зш tot, поэтому
M0R,RtFa,
ф,0-_ \to*—(R,*FU, I RJFUt) a,) ’
m ___________Afo ________
~ /,*«[ш'-(Я,*/7Л \ R^F!Jt)at\
Изменение напряжений в ветвях передачи связано с удлинением ветвей (см. задачу 224):
До. = ^2 = sin tot-,
1 «1 «1
Дст2 = 4£« = *»ф*^*»ф»». sln ш/.
a, а.
Таким образом, законы изменения полных напряжений в ветвях передачи будут следующими:
Oi = Oie+.Ao>(iSin tot',
o2=CT!o+Ao2eSin tot.
250. Дифференциальные уравнения движения маховиков 2 н 3 представим в виде
•Л *Pi Ч-£1Ф| — Mt— jVfoSin u>/;
Мт = 0,
где ф, и фг — углы поворота маховиков; с,ф, и с2ф2— силы упругого сопротивления; Л1Т— момент сил трения между поверхностями маховиков.
Между моментом сил кулонова трения и распределенным нормальным давлением р„ имеется зависимость
Л4Т= J фрярс1Г,
FK
где Fh — площадь поверхности трения (контактная поверхность); pn=N/FK-, р —полярная координата площадки dF, N —
267
сила нормального давления, равная NV+£N; М,=б0/б1| — сила предварительного сжатия пружины; ДМ— динамическая состав-ляющая силы нормального давления.
Вычислим жесткости упругих элементов системы. Жесткость валика
Ci = G/p//l=nd14G/(32/|).
В процессе колебаний нормальное давление периодически изменяется, что связано с удлинением (укорочением) пружины при ее закручивании.
Найдем связь между углом поворота маховика фг и изменением силы нормального давления ДМ. Поскольку высота пружины (ее предварительная осадка 60) при повороте маховика 3 на угол ф, не изменяется, уравнения перемещений представим в виде
б1₽+ДМби=0;
. <2) 6jp+ДМ621 — ф2,
где б1Р и 6(1 —осадка свободной пружины от действия внешнего момента М и единичной осевой силы соответственно; 6гР и 6ц — углы закручивания свободной пружины от тех же сил.
В соответствии с методом Мора
л ___С . f А(|ИЛ</Н .
J ~GJ~ ds + ? ~Ё7Г ds-
3 V 3
Учитывая, что МРк=М sin а, Л1Рп*=Л1 cos а, AfIK=sina, и считая, что длина проволоки пружины s—лО</со5а (где i — число витков пружины), найдем
. л£>8Mi /1.1 X sin 2a
б1Р =
. ___пРЧ ftos8 a . sin1 a \ 1
11 - 4 ! ОУр ~ EJX jeosa ’
Ь.лОЛ!, (';
‘ GJp 1 EJX ! cos a
• ___n£><8 ( 1___IX sin 2a
21 — 4 \<7Ур EJX / cosa ‘
Из уравнений (2) имеем
ДЛ/____б|Р _ _ Л1 (£Уж+ОУр)з1п2а
8,, D EJX cos! a + GJp sin8 a ’
ф2==t>2P - [ EJX shP a +
r . 2 _ £ <EJX 4- GJp)1 sin8 a ] i
pc°s J. £УХcos8 a-f-ОУр sin8 a J cosa'
2C8
Считая угол а малым (sina«a; cos ass 1; sin2a=0), получаем
(f>2=^ яО Mt/(E J л).
Введем обозначения: с2=Л1/ф1; П| = ДУ/фг.
Найдем выражение для момента сил трения:
D,/2
p/MidF = /7„p 2Kp2dp=-^(Dt3—rfj3),
А rf>'2
или
л^иМ+ДЛО^’-^Мз^,2-^2)].
При выводе уравнений движения (1) необходимо учесть, что момент сил кулонова трения AfT всегда направлен против относительной скорости движения маховиков, т. е. знак момента сил трения определяется знаком разности q>i—<р2.
Окончательно дифференциальные уравнения колебаний маховиков имеют вид
/i<Pi+ci<Pi4-s,£n(Tt —<P>)^nE7T<iVo+«i(P2)=^oSin
J+ С2Ф2 — sign (<p, — ф2) у (Wo + «1Ф2) = °-
251. Дифференциальные уравнения движения маховиков представим в виде
JiTi+02(«Pi —<й)4-АФ1 = Д<о81п (0<;
•Л2Ф2 4“ (ф2 — Ф1) 4* ^2Ф2 —
где c,=nd.‘G/(32/,); ct=d'E/(MDi).
Из второго уравнения системы (1) получаем
Ф1 — — (•/2Фг4_ а1Фг 4- ^зФз)- (2)
~~ i
Продифференцируем один раз первое уравнение системы (1) и подставим в него выражение (2):
^ф;+(/14-/2)ф4-^±^-^4-
4-(с14-с2)ф2 + ^ ф2=А1о“со5й)/. (3)
269
Решение уравнения (3) ищем в виде
Ф2 = Л25!п (o^-J-BsCos со/. (4)
Подставив (4) в выражение (3), получаем систему уравнений
- 7'W,C| Л - КЛ + + (с, + с2)(о] В2=О;
/0)4_ A£i±Zi£i (02+£i£l ] в2 -
\ «1 а, ' а, у 2
। Ч~ J 2){,>3 — (С\ + с2)ы] А2= Моы>
из которой определим Л2 и В2 (выполнить самостоятельно).
Амплитудное отклонение маховика 3 от положения равновесия равно
Ф20“ V Е\2-\-В}2.
Используя решение задачи 250, найдем внутренние силы в пружине:
где 6о — предварительный натяг пружины.
Отсюда наибольшие напряжения в пружине:
Отах = Af/ IV Л = Е<р20/(2л) ;
т -Л (£±2GN„
Из уравнения (2) можно записать
Vi = + «ф2 + <W>) dt
т. е.
<jft = A! sin Bi cos wt,
где A1 = (j2w + £l)|i + A2; 51 = B2-p2« + ^)^.
Амплитуда колебаний маховика 2 равна
ф| о — V В^.
а наибольшие напряжения в валике
Ттах = 32с,ф,«/(iw/j’).
270
252. Воспользовавшись принципом Даламбера, получим следующие дифференциальные уравнения малых колебаний диска и кольца:
Лф|+^Ф| + “(Ф1— «hH-AfoSincot
Л’ф + а(Ф2-^) = 0-
Решение системы (1) будем искать в виде
Ф,=Д sin ut+B cos (al', <ps = C sin (at-\-D cos (at.
Для определения произвольных постоянных А, В, С и D составим систему уравнений вида
(С—А—a(aB-j-a(aD=M0;
awA + (с—J,(a2)B—awC“0;
(2)
—cz<»> В—/го/ С—ouaD=0;
—ала А —ан С—Jz^D — 0.
Из системы (2) получаем
А =Л10[(с—Jt(a2) (/г2н‘+а2нг)—Ла2о/]/Д
В=Л10аД2н’/Д;.
С=.'М,)[ (с—/,н2)а3н2—Да‘<о‘]/Д;
D=M„Jza(a' (с—Ди1) /Д,
где
C — J\(a^ — ао> 0 ао)
ан —с —7)0)2 — ао) 0
Л 0 ао — 72“2 —ао)
— ао 0 ан — J2w*
Амплитуды установившихся колебании диска и кольца соответственно равны
Ф10=/Д2+Я2; q^/C-’ + ZX
253. На рис. 289 изображена расчетная схема конструкции. Выражения для кинетической и потенциальной энергии системы и для диссипативной функции Релея имеют вид
_ то1 /„ф1
/ — 2 -Г 2 Т 2 •
п с(/ф—, с, (th—Л)’.
11 2 2
п а(/ф—у,)»
К-------2 ‘
271
Подставив эти выражения в уравнения Лагранжа, имеем: /оФН-а/(/ф—у}) — =
тхУх - а (ф/ - ух) -c(l<p- ух) -J- с, (у, — Л) = О, или
ф+2лф + Р02Ф - у У1 — 7-\1 = 0;
У1 4" 2«1 У\ 4- 4" р2йУ\ — 2«] /ф — Рю/ф = P2oh,
где 2п=а/2//0; 2/z^a/m,; р02=с/г//0; р21й=с/тх\ Р^схтх-
При отсутствии силы трения (а = 0) частоты собственных колебаний
Pl,2 =
1/ рг + Р?о + Л I /7рг + Pio + Рао у 2
V ----2---± | \---2----/ -Ро2Р2о>
а критические скорости буксирования
Vi. = /iPi/(2n); v2, = ltp2/(2n).
254. Потенциальная энергия деформации рессор при движении машины по неровной дороге равна
П=-^(//4-фА-М2 + -7-('/-Ф*2-Лг)2.
где hi и h2 — подъем переднего и заднего колеса при двиЖ-нии автомобиля соответственно.
272
Учитывая, что положение автомобиля на дороге определяется координатой x=vt, а расстояние между осями машины L = = /| + /г, получаем
= cos2nof//o);
Й2“Л0(1— cos 2л (о/+ £)//<>)• * '
Кинетическая энергия системы
Г = /пу2/2+/ф2/24-т®2/2. (3)
Из уравнений (1) —(3) получаем дифференциальные уравнения малых колебаний:
" । ci + ct .. , c4i—(j .
m J ' tn 4 m ctl ,ht + c,lth'
Ф--------7
(4)
ф +ч 4
Уравнения (4) удобнее представить в виде
•• • - , 2ntrf . . . 2л»с.
У 4“ ФйФ——Йо COS j -]-Йз51П у
ф+ам</ + а22ф=^1 cos —----l-’a sin—'
(5)
где
b\ == (f] + Лс/m't l>2= Cj 4- c2 cos —j- j;
&з=-^- c2 sin —; b\' = + Cnlj) h0/ J',
b2'=4- c./2 cos b3' = c2l2 sin Решение системы уравнений (5) будем искать в виде
. . 2nvt . D . 2xvt . !/ = {/0+Дсо5-7—4-Bsin -у—, , . 2ли/ . о 2ло< Ф=Ф04-Д1 cos-,—+ #! sin-^-,
(6)
где
Ул~ (bjOji—bi Д=[О1г^| Ь2(иг1—со) ]/Д,
В = [Ьз(а22—со2),—ацЬэ'1/А« Фо= ОиМ/Дг.
Д1 = [а2)б2—Ь2'(ац—<о2)]/Д; Bi = [&з' (ан—о2)— а21&э]/Д;
Д|=ацО22—а|2а2); Д= (ап—со2) (а22—со2)—а)2а2ь со = 2ли//о-
Выражения (6) можно представить так:
у = у04-/А24-В2 sin (со/ 4- р);
ф=ф04-КА2 4- B|2 sin (со/ 4- ₽)>
18-5000
273
тогда выражения для амплитуд вертикального и углового ускорений будут следующие:
\ * о /
После подстановки числовых значений получаем £/0=7,5м/с2, %«= 0,2 рад/сг.
255. Так как в рассмотренной системе (см. решение задачи 254) затухание не учитывается, критические скорости движения соответствуют случаям резонанса, т. е.
Wi. = /oPi/2n; v2, = lQp2/2n, где pi и р2 — частоты собственных колебаний.
256. При движении автомобиля по неровной дороге пружины с жесткостью с и 2с, характеризующие податливость шин передних и задних колес, получают дополнительные сжатия hi и Л2. Следовательно, в выражении для потенциальной энергии, приведенном в решении задачи 222, последние два слагаемые будут такими: c(yi—h})2 и 2c(y2—h2)2/2.
Так как расстояние между осями автомобиля равно а+& = = /1+4. ТО
1 — cos —L—1; й2=л01 1 —cos —-—j-------L
Дифференциальные уравнения движения автомобиля по дороге с периодическими неровностями совпадают с уравнениями свободных колебаний, полученными в задаче 222, кроме двух последних, которые не являются однородными и правые части которых сооответственно равны chi и 2ch2.
257. Пусть + —<//i)—суммарная масса сосуда и находящейся в нем жидкости. Дифференциальные уравнения движения массы т имеют вид
dr , ,
т-г7- + сх=се cos <о/;
У (I)
dr/ , . ,
т + су=се sin ы/,
где е— отклонение массы т от положения равновесия.
Введем следующие обозначения mH = m(i + mi— суммарная масса при / = 0; т=т11/[(m0+m,)/(] — безразмерное время.
Тогда уравнения (1) можно представить в виде
" .____е_____ ._ ес cos <£>t
+ mH(I—Т) Х~ w„(l—т) ’
•• .___с ______ gesin tot ’
У ’’’ mH(l—т) У — m„ (I — t)’
274
Учитывая, что dZ-mn/dx/m, и рг=с/та, заменим в уравнения системы (2) дифференцирование по t дифференцированием по т:
Переходя к безразмерным координатам хх=х/е и ух = у/е, !кончательно получаем
(1)
258. Дифференциальные уравнения движения груза получены в решении задачи 202 и имеют вид
“+4-’+^-(и_<ро=0:
« + | 4 (<р/ - «) = °-
Решая уравнения (1) при указанных начальных условиях, получаем уравнения движения системы:
и~ 29* +29 sinр^'
ф 29 ml t 29 mlpt slnAA
(2)
где Pi=V29с/(5m).
Движение центра тяжести груза при этом описывается уравнением
«о-«+4-§ 4г1+s,n р^
Вычислим силы инерции, действующие на груз:
F = — /поо*= JP2 sin pd\
М = — J<p= —Jlpz, sin pit.
Наибольший изгибающий момент возникает в сечении А стержня (рис. 290) и равен
Л.„ = М -J- ± Jpl=0,643J
18*
275
259. Запишем дифференциальные уравнения движения маховика и контактного кольца:
•^Pi + Oi (Ф1 —Ф2) + ^2Ф1 =Afosinw/;
«1(Ф2-Ф|) + <ЧФ2 = О.
где (pi и <р2 — углы поворота маховика и кольца.
Решение уравнений (I) можно представить в виде
«Pi = Л1 sin со/+ Bi cos со/;
<p2=A2sin (d/+B2cos<dZ. (2)
Подставив выражения (2) в уравнения (1), находим
л + лл . о с»—У*.»* с
-------о----мо, —
где (c.+g—ЛоТ+ (G—/w’JWCa/w2).
Амплитуда установившихся колебаний
260. Решение аналогично решению задачи 259. Уравнение вертикальных колебаний будет следующим:
хи A |Sina)/4-A2cos(oZ, где
Л । — Fo{[ 14-16с22/ (а2®2) ] (C|—m®2) +4c2)/D;
^2e—Fo16c27(Оа<о); D=4c22(C\—mw2)2/(a2®2) +
+ (ci+4c2—m®2)2.
276
261. На рис. 291 показано положение сиденья с водителем в произвольный момент времени.
Дифференциальное уравнение движения массы т имеет даид
ту2+а(у2 —У1)4-с (у2— У0 = 0. (1)
Второе уравнение получим, рассмотрев равновесие системы подвески (считая пружины и демпфер невесомыми);
Ci (УI— Уо) -с(у2—У') +а(уг—У\). (2)
Систему уравнений (1) и (2) можно представить в виде
Уг+2л у2 4- р<?у2 - 2лу, — р<?ух = 0;
2пу2 + pfy2 - 2nyt - р02у, - р^у, = - pt2y0, где 2п=а/т; р02=с/т; p^^cjtn.
Для нахождения передаточных функций перейдем к изображению по Лапласу. При нулевых начальных данных из уравнений системы (3) получаем
(р2+2лр+р02) Y2(p) — (2пр+р02) Yi{p) =0;
(2np+p02)Y2(p) — (2np+p02+pl2)Yl(p)-—pl2Y0(p).
Передаточная функция между возмущением (вход) и перемещением массы (выход) равна
иу („V _________Pi* (2пр + р,1 + р,*)__
2пр* + (р,г + р,*) р* 4- 2пр,гр + р„* + pSpS '
Спектральная плотность ускорения у2 равна
а спектральная плотность вертикального смещения —
Sp,(a>) = |lF(/<o) р$„».
Для определения спектральной плотности перемещения у2 необходимо найти SVt по известной корреляционной функции
оо
SVt = \ ^о(т)е-'“Мт=
2DP.g-а,г + <1>’
После преобразований выражение для Sr2 можно пред, ставить в виде
Sy2 = -| D^pS [-4лЦ/<1>)«+(М (Рог+А2)]. где Д= |2n(«<o)4+(2rtaI-l-po2+pi2) (»<в)3+ +{ai (Po2+Pi2) +2«pi2] (iw) 2+[p!2 (po2+ +2nai) 4-po4]i<o+ai (po4.+po2Pi2) I*.
277
Вычислим дисперсию ускорения:
“СО
Воспользовавшись приложением 2, получаем
2 Dv «iPi4[4n! ОМ*—— во«8 (Pp’+Pi’)]
(J •• = [_) •* —« ... —— ---------------------
»« а» (аоа,г—ata,at)
где ai = 2nai+p02+pi2; a4=ai (p04+p02pi2); a2=a, (Р.’+аЭ +2лрЛ a,=p/ (р.’+гла,) +p0‘;
a0=2n.
§ 10. Критические состояния и устойчивость колебаний
262. Пусть в произвольный момент времени I положение центра тяжести диска определяется вектором г (рис. 292). Воспользуемся для описания движения диска уравнением Лагранжа второго рода.
Кинетически энергия диска
7’=m(Ox’4-v/)//.<o72, (1)
где иж, vv— проекции абсолютной скорости центра тяжести диска на оси х и у; Jt — момент инерции массы диска относительно оси, перпендикулярной плоскости диска и проходящей через центр тяжести диска (точка О,).
97R
Так как абсолютная скорость движения центра тяжести
диска
г, = л/+<//+[“ X И-
где
[<оХг] =
i j k О 0 <о х у О
i, j, А—орты осей, то проекции скорости на можно определить как скалярные произведения:
vx=(vi) = х — иу,
o, = (W) = ^+w-«-
Потенциальная энергия изгиба вала
П-с/-2/2-с(х2-Н/2)/2,
где с=ЪЕ]х/1* — жесткость вала.
Уравнения Лагранжа имеют вид
0- ± — — — -=0 dt д'х дх ~ ’ dt ду дУ
ОСИ X И у
(2)
(3)
(4)
где L=T—П — функция Лагранжа.
Подставляя в уравнения (4) выражения для потенциальной (3) и кинетической (1) энергий с учетом соотношений (2), получаем дифференциальные уравнения малых колебаний диска во вращающейся системе координат:
х+(ро1 — <о2) х—2ыу ---= 0;
!/+(Ро2 — °>2) =О,
где р<?=с!т.
Приняв х=Ае‘7', y=-Be'ft, получим уравнение частот |(p02-W2)-p2 -2wtp о
I 2uip W-^)-p^
или
((ро2-о>2)-р2]2=4ш2р2. (5)
Из решения уравнения (5) получаем (во вращающейся системе координат) две частоты колебаний диска:
Pi=Po—<о; Р2=Ро+<о.
263. Положение центра тяжести диска (точка Oi) при колебаниях относительно стационарно вращающихся осей уО х определяется вектором г (рис. 293), равным
г=Г|+е,
279
Рис. 293
где г, — вектор, характеризующий смещение оси вала. На рис. 293 показано положение точек О' и О/, соответствующее случаю, когда <о<ш. (см. решение задачи 93). Для показанного расположения точек О и О, в стационарном режиме справедливо уравнение равновесия
т(о2х0=с(х0—е). (1)
Для случая й)>(о. уравнение (1) принимает вид тЛо=с(хо+е).
При стационарном движении диска векторы г и rt коллинеарны (точки О", О и О, находятся на одной прямой О"х). Угол q> характеризует малые отклонения вектора е от оси О"х, ахи у—малые смещения центра тяжести диска по вращающейся системе координат.
Кинетическая энергия системы
Г- т (ох2+о,«) /2+Л (о»+ф) 72,
где vx=x—иу, 1\=#+(ох (см. решение задачи 262); /0 —момент инерции относительно точки О.
Потенциальная энергия изгиба вала
П=сГ|*/2=с[(х—есозф)24-(у—езшф)2]/2.
Таким образом, положение центра тяжести диска (точка 0|) определяется в подвижной системе координат хО'у тремя независимыми переменными х, у и ф. Поэтому при подстановке выражений для кинетической и потенциальной энергий в уравнение Лагранжа получаем три уравнения
т (х — ыу) — (t/ + ox) + c (х—есозф) = 0;
т (у + ох) + ты (х— ыу) + с (у — е sin ф) = 0; (2)
Аф + с (х— есо5ф)е sin ф— с(у—е sin ф) е cos ф=0.
Так как в задаче рассматриваются малые колебания относительно стационарного режима, то можно принять х=хо+Х), 280
у^У\, а также cos<p=l; sing: <р; Х|ф« //|<р~0 (в стационарном режиме считаем, что ось х направлена по прямой, проходящей через точки O"OOi).
Система уравнений (2) после преобразований и исключения уравнений равновесия диска при стационарном режиме вращения принимает вид
х, + (Pg2 - ®2) Xi — 2«Х| = 0;
। + (Po2 — <°2) У1 + - Po2e<P = 0;
ф+Рг-адр-РгУ! =o.
где p'“c/m, рхг=се/]„
Следует отметить, что система (3) справедлива как для случая так и для случая
264. Пусть сх — жесткость вала .при его изгибе в направлении главной оси инерции х, а с, — в то же в направлении оси у. Выражение для кинетической энергии системы имеет такой же вид, как и в решении задачи 262, а потенциальная энергия равна
П=сжх2/24-суу2/2.
Во вращающейся системе координат дифференциальные уравнения малых колебаний имеют вид
х + (Ъ2~ й’2)х ~ 2<оу — 0,
у + (Л у2 — о»2) у + 2(ох =-- 0, где kx2=cx/m; k/--^cy/m-
Принимая х= Ае‘р‘ и y=Belpt, из уравнений (1) получаем
Р4- Р2 (V-W4-2(о2) + (Лх2— оР) (АУ2- о)2) =0, (2)
откуда
Р\,г— |/ --------о----ь г ----4-----Ь2«2(ЛЖ2+ЛУ2).
В соответствии с представлением решения в виде х=Ле'*', j/=Be‘P' движение диска является устойчивым, если р112 являются действительными. Если же р1Я комплексно-сопряженные величины вида pi,2=±»X, то решение содержит функцию еи, неограниченно возрастающую во времени, т. е. при некотором значении угловой скорости со- происходит неограниченный рост амплитуд колебаний и, следовательно, малые колебания являются неустойчивыми. Такая угловая скорость системы и является критической.
Условие появления комплексно-сопряженных корней можно получить из уравнения (2) в виде
kx*4-k/4-2а)2< ^(^Х2-Ау2)+8(1)2(А!.Г2Н М-
19-5000
281
откуда
kx^(O^kt.
Из последнего неравенства следует, что имеется целая об ласть значений критических угловых скоростей.
265. Как и в задаче 262, решение удобно вести во вращающейся системе координат. Однако в отличие от указанной задачи в выражение для потенциальной энергии необходимо добавить слагаемое П(= mgyit где т/i— координата центра тяжести диска в неподвижной системе координат (рис. 294), зависящее от силы тяжести.
Переходя к вращающейся системе координат xOty, получаем
П, — mg (xsinwZ+t/cosw/).
Полная потенциальная энергия будет равна
П=с (x24-t/2) 12+mg (xsinoZ+ycosw/).
где c"=2£nd4/4P.
Выражение для кинетической энергии останется тем же, что и в задаче 262, поэтому дифференциальные уравнения движения будут следующими:
х4-(£- — о>2)л —2wi/+g’sin и/ =0;
у 4~ (k2 -|- о»2) у 4-2(1)х 4- К cos wt = 0, где k2=c!m.
Решение уравнений (1) для установившихся колебаний бу-
дем искать в виде x=/4sin у=В cos со/. (2)
Подставляя эти выражения в уравнения (1), получаем неоднородную систему уравнений для определения А и В, из которой находим А~В=—g/k2.
Критическое значение угловой скорости найдем из условия равенства нулю определителя однородной системы уравнений. Окончательно получаем (о*иА/2.
282
266. Дифференциальные уравнения движения во вращающейся системе координат (см. решение задачи 265) имеют вид x-f-(Ax3 — «»2) х — 2ыу = — Д' sin о>Л
у + ш2) y4-2wx=gcos ыЛ
где kg=4Ebh*/ (ml1), к*=4ЕМА/(тГ).
Если решение уравнений (1) искать в виде x=4sin wt, у = = Bcos(i)Z, то амплитуды установившихся колебаний будут следующими:
. _ л/—to» т
*»**/—2ю* + 2®» (*,» + ам»)’
Критическая угловая скорость валика
о|.=Г W/I2 (М+МЬ
Кроме того, имеется область критических скоростей, полученная при решении задачи 264.
267. При вращении изогнутого валика с угловой скоростью относительно оси АВ (рис. 295) на отклоненный и повернутый
Рис. 295
диск действуют силы инерции, перпендикулярные оси АВ. При этом полная сила инерции, действующая на элементарную массу dm, равна
dF = d/no>2r1.
Учитывая, что г,=г-|-у, представим силу инерции AF в виде суммы двух составляющих:
dF = dF| 4-dF2,
где dFt = d/nw2y, d/^—d/nci^r.
19» 283
Равнодействующа я _сила d/^ равна та^у и направлена вдоль оси Оу. Сила dF2 создает момент относительно оси Ох, препятствующий повороту диска. Поскольку угол поворота диска относительно оси х мал, момент силы dF2 равен
Мх — ы -ф \ iFdm = (iPtpJ, т
где J — моментинерцни массы диска относительно оси вращения.
Таким образом, со стороны диска на валик действуют сила Fi и момент Мх.
Воспользовавшись методом сил, получим уравнения смещений точки крепления диска:
У=бцЩыг1/—612а)г/ф; —б21(й1/<р,
или
(1—дцП1<о2)^-|-б12<о2/ф=0;
(1)
б2( /л (о2 у— (I —|— 5 21<о* J) <р=0,
где 6,.=/7(3S/x), 6,i-6tl=—/7(2£/я), бм~//(Е/х), Jx=nd7
/64 — момент инерции площади поперечного сечения валика.
Из равенства нулю определителя системы (1) найдем уравнение для критической угловой скорости валика:
. . 12£Jr/т1г ,\ , 12 (EJx\i л
откуда
2_6EJr( , т/16/-Л / . m/Sp , Г.! /£/,\2
)+ V ) +т^(—)• <3)
Из второго корня уравнения (2) получаем мнимое значение для угловой скорости валика.
Если момент инерции массы диска мал и им можно пренебречь, т. е. рассматривать диск как точечную массу, то критическую угловую скорость найдем из уравнений (1) при /—0:
<о»=У 1/(/пМ = КЗ£“Л/(т/»). (4)
Числовые значения критических частот со., вычисленные по формулам (3) и (4), соответственно равны 165 и 130 с-1. Таким образом, гироскопический эффект, делая систему более жесткой, сдвигает критическое значение угловой скорости в область более высоких частот.
268. Критическая угловая скорость, вычисленная с учетом гироскопического эффекта, равна <в.«138 с-1. Если гироскопический эффект не учитывать, то со. i ~ 127,8 с-1.
284
269. С учетом гироскопического эффекта критическая угловая скорость ©.*173 с-1, без учета — ®.1*158,6 с-1.
270. Рассмотрим силы, действующие на диск (рис. 296). Пусть гр—прогиб валика, е — эксцентриситет центра массы диска относительно центра вращения, Fynp™—cri— сила упругости, действующая на диск со стороны валика, ДЛ. — суммарная сила притяжения магнитов.
В соответствии с принципом Даламбера дифференциальные уравнения движения при постоянной угловой скорости диска имеют вид
jc-|-p2x=ep2Cos (1)
t/ + p2y=ep2sin ©/, (2)
где рг=*с/т~ЬЕ1х/тГ. Суммарная сила притяжения магнитов bF*~kQJI(a—xF-lrt?f(a+x)*.
Раскладывая последнее выражение в ряд и ограничиваясь линейной частью разложения, находим
Л5м"=4^Ф02х/а\
После подстановки уравнение (1) принимает вид х+[р2—4йф02/(та3)1х=р2есо8 at. (3)
Из уравнений (2) и (3) следует, что система, находящаяся в магнитном поле, имеет две критические угловые скорости = Ир2 — 4АгФ<,2/(/п^);
271. Пластинка имеет три степени свободы: вертикальное перемещение по оси z и два угловых <р и 0.
285
Поворот пластинки на угол 6 приводит к появлению угла атаки относительно потока воздуха. При этом возникает аэродинамическая подъемная сила (см. условие задачи). Кроме того, вертикальные перемещения пластинки создают упругие силы в пружинах. Их равнодействующая
с, (z—е//2+ФЛ/2)—Cj (z—0//2—<рЛ/2) —
—с2 (г+е//2-)-фЛ/2) —с2 (z+61/2—фй/2).
Определим моменты сил упругости относительно центральных осей х и у:
Мх——С[фЛ2—СгфЛ2,
Му - 2с I (г—61/2)1—2с2 (z+61/2) I.
Дифференциальные уравнения движения пластинки имеют вид
/nz 4- 2 (<?, — с2) 0/— jg2 f— A/0=O; (1)
Л о 4- у fa + Ci) +fa - ) lz - у рт>210=°; (2)
Лф + ^(С1 + ^)Ф=°- (3)
Уравнение (3) не зависит от уравнений (1) и (2), поэтому из него можно найти частоту угловых колебаний пластинки относительно оси х:
P=h К(с, 4- с2)/(4Л),
Остальные две частоты определим из уравнений (1) и (2), полагая z=Aept, 6=Bept. Подставив выражение для z и 0 в уравнения (1) и (2), после преобразований получаем определитель D системы однородных алгебраических уравнений:
£) —
2(c,+ct) т ' "
V
где FI0=-^--^-p©2.
I—1f10 m m 10
(C|±c«)/2 I q2— 2JV 1 4Jy
Из условия равенства нулю определителя D получаем характеристическое уравнение вида
р44-а2р24-а4=0,
(4)
где
_ 2(с,+сг) р I (с, +
02-----т--------Л‘° 477^ -----ТГи-’
V О
_ (с, + с,)2 I2 . / <?t—с, .____ 2 р \ с,—с» .________ 2 (с, 4- Сг) Fxtl
mJ у ~ т т l0) Ju 4mJ у
286
Необходимым условием отрицательности действительных частей корней характеристического уравнения (4) является положительность его коэффициентов (для биквадратного уравнения это условие является также и достаточным):
р I । 2(ct+ct) , (с> + с1) I’ п /к\
^10477 +---т----+~2—7;>0’
(с, 4- с,)1 1г / с,—с, _ <1сг pv1 . \ (с,—с») /» _
mJu 1 I т <10 2m J J и
2 (С| + tj) р п /и\
-----т-----Л'°Ч;>0’ <6)
При выполнении условий (5), (6) колебания пластинки устойчивы.
272. Колебания пластинки будут устойчивыми, если корни характеристического уравнения (4) (см. решение задачи 271) имеют отрицательные действительные части. Для этого необходимо, чтобы коэффициенты а2 и а4 в уравнении (4) были положительными.
Значения аэродинамической силы F10, при которых коэффициенты а2 и а4 обращаются в нуль, являются критическими, поэтому критические значения скорости v найдем из условий
а^О; а4=0. (1)
Подставив числовые значения параметров системы, из условий обращения в нуль коэффициентов а2 и а4 соответственно находим о. 1”32,6 м/с, и.2=73 м/с.
273. При «малом> возмущенном движении с индексом нуль сокращаются и уравнения движения, полученные по методу Даламбера, имеют следующий вид (рис. 297):
^4-Д/?1+Д/г24-/?Ф=0, (1)
Мн+ДМ,—Д/^-0, (2)
где FH, А1и — соответственно сила инерции и момент инерции самолета относительно оси, перпендикулярной плоскости чертежа и проходящей через точку О'.
287
(3)
после
(4)
J Jv mv mv Jv '
~m~^~ Jv Jmv +C^‘
Необходимое условие устойчивости невозмущенного движения самолета:
в/>0.
Необходимое и достаточное условие устойчивости нсвозму-щенного движения (критерий Гурвица):
aia2—а3>0.
274. Дифференциальные уравнения движения шкивов имеют вид (см. решение задачи (241))
ф1+вцф1—а12ф2"Р1фь
ф2—а2 1 ф 1+^22ф2 “ —₽2ф2-
288
Получим выражения для приращений углов атаки Дои. и Aoj. Для крыла угол Да, равен углу ф минус угол «скоса» потока, равный y/v, т. е.
Да|=ф—y/v.
Хвостовое оперение при малых ф и у имеет вертикальное смещение
У\=У—<$1,
поэтому можно принять, что приращение угла атаки Да2 зависит только от угла «скоса» потока и равно
Таким образом, имеем следующие выражения для приращений сил ДГ1, Д£2 и момента ДМ,:
^Fi = Ci((p—y/v); ДГ2=С2(ф//и—j//o);
ДМ1 = С3(ф—y/v).
Подставив выражения (3) в уравнения' (1) и (2), преобразований получаем
До + _£l±£l_ до _ _£=£ ф _ + ф = 0;
у 1 mv У mv т т т ’
•• , (С,—С,1) . . С,/’ • С, п
Ф +—7^ Д°у + ^-Ф—7-Ф = 0.
где Дт»у = у.
Полагая Д'оу = Дем, ф = Вем, из системы (4) находим характеристическое уравнение
Л.3 Л- —|— (1/К -| Дд = 0,
. с> + с« . п с> I c’z +С,) С./ (G-C,/).
где ai - : mv аг“------------------------------------------
„ _(С, + Я) «?,-<?,/) С, а3---------------------------
Запишем характеристическое уравнение для этой системы Xs+ (Рг—₽1)Х2+(аи+а22—fhfh)X4" (ai।?2—°22^i) “О, или
V-H10-0,)V+(21 420—10М*+(51 ООО—16 320^)-=0.
Необходимым условием устойчивости движения является условие положительности коэффициентов характеристического уравнения, т. е. {К 10; £,<2142 и 0,<3,1. Следовательно, pi должен быть меньше 3,1.
Достаточным условием устойчивости решения является выполнение критерия Гурвица. Для уравнения третьей степени должно выполняться условие Д2>0:
(10— р,) (21 420— Юр,) — (51 000—16 320Д,)>0,
откуда —оо<р,<34; 48О<0,<со.
Сопоставляя эти неравенства с необходимым условием, получаем интервал возможных значений pt:—оо<р,<3,1.
275. При движении маховика происходит его проскальзывание относительно контактного кольца муфты. Обозначив угол поворота маховика через ф,, а угол поворота контактного кольца через ф2. запишем дифференциальное уравнение движения маховика:
Уф Н-ct, (<Р1 — Ф2) = Л<Ь (1)
где а, (ф,—<р2) —момент сил трения.
Момент сил трения
Мтр=2л/?6а (ф, — ф2) /? = а, (ф, — Фг).
Дифференциальное уравнение движения контактного кольца имеет вид
СС1 (ф2—ф1) Н~С|ф2 = 0. (2)
Приняв ф,=4ед,', ф2=Веч, получаем следующее уравнение для определения параметра X:
Л3 + ~С| ^аа ’ X*+ ^7=^ сЛ = 0- (3)
JU, J О’!
Из решения уравнения (3) получаем три корня:
А‘ = 0’ Л2.э= - —у— ± |/ 2/- j - -j^~ С,.
Движение маховика будет устойчивым, если:
а) корни Х2 и Х3 отрицательны — в этом случае возмущенное движение (ф, и ф2) затухает со временем;
б) корни Х2 и Хз комплексно-сопряженные с отрицательной действительной частью — в этом случае движение (ф, и ф2) имеет периодический характер с уменьшающейся амплитудой.
Необходимым и достаточным условием отрицательности кор
289
ней уравнения (3) является условие положительности его коэффициентов, т. е.
Jci—aai>0, a,— a>0.
(4)
Из второго условия (4) следует, что устойчивое движение происходит при ai>a, т. е. при aai>a2. Подставляя это неравенство в первое условие (4), получаем Jc^aa^a2, откуда
a< K^=110-‘=10-2 Н-м с.
Поскольку при этом должно выполняться условие а<а“ =0,005 Н м-с, окончательно получаем, что движение устойчиво при а<0,005 Нм-с.
276. Дифференциальное уравнение вращения волчка вокруг неподвижной точки имеет вид
dK/dt=M,
где К — главный момент количества движения волчка (кинетический момент) относительно неподвижной точки О.
В общем случае вектор К равен
Л=/(о,
где / — матрица моментов инерции тела (моментов инерции относительно осей х, у, г, жестко связанных с волчком); о — вектор угловой скорости волчка при возмущенном движении.
Матрица / имеет вид
/= •Ar J ху J хг JyX Jy Jух ~ Jzx J гу Jх
Как известно, полная производная вектора К связана с локальной производной в подвижной системе координат соотношением
d^/d< = d'X’/d/-b[w'XX:J> (1)
где го —вектор угловой скорости подвижной системы координат, не-Обязательно жестко связанной с волчком, т. е. в общем случае
Если локальная производная берется в системе координат, жестко связанных с волчком, то a» = w', и получаем уравнения Эйлера
а^/д/4-[(0ХЛ=м
290
Проецируя уравнение (1) на подвижные, но не связанные с волчком оси х', у', г' (рис. 298), находим (не употребляя штрих в локальной производной):
dKx/dt — Ky4>z‘ =
dfCy/dt + Кх(0г' — Кгие==Му1 (2)
dKz'/dt 4- Ky-tox- — Kx'^y' — Mf.
Оси у', z' участвуют в движении волчка (при малых колебаниях), но не участвуют в его собственном вращении. Ось Oz' всегда совпадает с осью симметрии волчка Ог. Поэтому угловые скорости со*', шу и шх' можно рассматривать как малые величины.
При малых движениях оси_ симметрии гироскопа полная угловая скорость волчка Запишем проекции векто-
ра а»' (при малых отклонениях от невозмущенного состояния), (см. рис. 298):
“г «К! <<.а?0; <о^«ф.
Проекции кинетического момента на оси х', у', г', являющиеся главными осями инерции тела, следующие:
Кх' —* J г^дг, Ку* JуЬ)у , z' — Jz^ z>
где шл«0; <Dy«q>; WjWfij-f-i.
291.
Запишем моменты силы тяжести относительно осей х'. у’, z' (при малых углах х'^х и у’— у):
М’»0; My'^mgx', Mj^mgy',
где х7 —/<р, =
Из уравнений системы (2) получаем (вследствие симметрии JX=JV) линейную систему дифференциальных уравнений
Л0-Ь /дф—
/*ф—/Д8—л^ф=О; (3)
<ох = 0.
Из третьего уравнения этой системы следует, что сох= =const—Qo-
Умножив первое уравнение системы (3) на мнимую единицу i и сложив его со вторым уравнением, получаем
7-i = (4)
где Y=0+i<p.
Характеристическое уравнение для (4) будет следующим (решение ищем в виде 7=Сел'):
а его корни равны
Чз-1[^- Ч ± VW*-*]-
Возмущенное движение волчка устойчиво, если (277^0) >7Г*
Следовательно, критическая угловая скорость волчка
277. При малом отклонении оси гироскопа от вертикального положения можно получить следующие дифференциальные уравнения движения (см. решение задачи 276):
0 Н“ / .’"пф/ J X — Mr’ IJxt i-JSkfi/Jx=MU’/jx.
В рассматриваемом случае на гироскоп кроме силы тяжести действуют упругие силы со стороны пружин.
На рис. 299 показано положение точки Dt оси гироскопа в произвольный момент времени.
292
Выражения для моментов имеют вид Mx. = (mg/2—2с/)/0;
(2)
Му• = (mg/2—2d) 1<р.
С учетом выражений (2) дифференциальные уравнения движения (1) можно записать так:
Корни характеристического уравнения системы (3) (см. решение задачи 276) будут следующие:
Л
(3)
Х1(2=/
2Jr
Движение гироскопа устойчиво, если
J > V 2Jxl(mg-4cl).
278. Дифференциальные уравнения движения имеют вид (см. решение задачи 277):
0 + 77 ~ 577 («§—4с2Л 0=°;
ф — 77^9—577 (W?—4с/)Ф=0,
гироскопа
(1)
20—5000
293
Решение системы (1) ищем в виде О—Л«?, ф=Д2е1г. Тогда характеристическое уравнение для системы (1) имеет вид
х<+[(^-Ц))1 — те1+У'+с,) ] +
+ “477-(/пЯ—4cJ)(mg—4с/)=0, (2)
или
V+a2V+a4-0. (3)
Найдем корни уравнения (3):
Аы—'К—а2/2 ± V а£/4—а4.
Если а2>0, о4>0 и, кроме того, а22—а4>0, то корни можно представить в виде
।. 2 = / V аз/2 Т VaJ/b - а4.
т. е. в этом случае движение оси симметрии гироскопа является периодическим.
Из условия а22—4а4=0 находим критическую скорость
Й°* = Т^Г D? — 4с, Z) (zng—4с/)4- ~ (mg—2ctl—2с/ j.
279. Для вывода дифференциальных уравнений малых колебаний воспользуемся уравнением Лагранжа второго рода.
На рис. 300 показано положение системы в произвольный момент времени /. Оси х, у, г жестко связаны с внутренним кольцом 1. При колебаниях прямая 00' всегда находится в плоскости уг.
Рис. зоо
294
Кинетическая и потенциальная энергии ротора равны
i
Л (£12К2)+4 <+4^+4 •*.*’
П1-/Л1£/(1—cos 7).
Кинетическая и потенциальная энергии внутреннего кольца и противовеса будут соответственно равны
п=(?>+&+4 <+4 <+4 < ’•
П2— — cos к);
г,—
Пз=т3£[(/+а)—(/+acos0)cosf)].
Считая, что углы 0 и f малы, вычислим проекции угловой скорости ротора и внутреннего кольца на оси х, у, г и х2, у?, г$
©х=0, ю*,=оо+’Г0;
©», = 0. ©л—т[; ©z,=fQ«O.
Определим координаты центров тяжести всех трех масс:
£i = ^; ^2=^; b“G+a)*G
?i = /; ^а—1', Пз=а0.
Подставляя эти выражения в уравнения Лагранжа
dZ^ дО >00 U’ dZ dy dy'dy ’ получаем
710 — j A fiui+/Пз?а0 = 0;
7 2 If + 72|Qo0+^if = 0,
где
+ ("ii+zn2)/2+zn3(/4-e)2; Л =[(zni+m2)/+
+ (/+a)m3]g.
Решение системы (1) ищем в виде 0=CiCOSpt, Для определения частот получаем уравнение
р] + /,Л + /2О?) = 0
Из уравнения (2) легко найти частоты колебаний pt и р2.
20’
295
280. Кинетические энергии ротора гироскопа и тележки соответственно равны
। J
2 1 2
а потенциальные —
n=Qfli(l— cos 0)—Q(a|-|-a2) (1—cos q>);
По=—Q0/o( 1—cos <p).
Ротор гироскопе получает дополнительные угловые скорости 0 и <j>, вызванные угловыми смещениями ротора и тележки. Вектор угловой скорости ф направлен по оси
Проектируя угловую скорость ф на оси х и z, получаем угловые скорости <ож и сог ротора: о>л = фсо5 0, <ог=£2о+ Ч-Ф sin 0.
Движение ротора в направлении 0 создает угловую скорость, направленную по оси у и равную <оу = 0.
Координаты центра тяжести ротора:
£= (Oi+o»)cos <p4>atcos 0; £= (fli+ejsin ф; Xj—ajsinO.
Воспользовавшись уравнениями Лагранжа второго рода, получаем следующие дифференциальные уравнения движения системы:
(/у+/па,2) 0 — ЛДф—Qai0== 0;
[Лг+т (й) 4- а2)2] Ф4-./— [Q (til -l-flj)-}-Qo/o] ф=0.
Решение системы (1) ищем в виде 0=Д!СО5рЛ ф = = H2sinp/. Тогда уравнение частот имеет вид
4 (ma? + /,) [Q (at •+ a,) + (ДМ—[m (a, 4-as)’+ •/») Qai т
(Jy+mat1} \Jx+m (a, +a,)‘J
I____Qoi IQ (ai + д») ~h Qu/«] __л
' (/y+mai*) Rx+m («,+«!)•] '
ИЛИ p4 — «2^4-04 = 0.
Для устойчивого движения необходимо, чтобы корни уравнения (2) были действительными, а это выполняется при условии a/—4ut>0. Поэтому критическая угловая скорость гироскопа определяется из условия a?=4al.
281. Для вывода дифференциального уравнения движения воспользуемся уравнением Лагранжа второго рода.
Кинетическая энергия системы
7’=/x<Oz724-W/24-A<0z72.
296
На рис. 300 показано положение кольца с ротором в произвольный момент времени. Угловые скорости сох, о, и являются проекциями полной угловой скорости <о на подвижные оси х, у, г (оси х, у, г участвуют в движении кольца, но не участвуют в собственном вращении ротора):
w = £2ц £2+6.
Проектируя w на оси х, у, z, получаем
о>х==б; wy = £2cosfi; <ог —£2о—£2 sin 6.
Выражение для кинетической энергии в случае малости й принимает вид
7'=/I672-)-/vQ72+70Q0—Q6)2/2.
Запишем выражения для потенциальной энергии системы в функции Релея:
П = сР672; /?=аб72.
Уравнение Лагранжа второго рода в рассматриваемом случае следующее:
d_dT = n
dtdb u-
Подставив в это уравнение выражения для Т, П и R, получаем дифференциальное уравнение движения гироскопа:
б + 2лб4-р02д=--£-(Д,.
где 2п=а//х; р*—сР/]х.
Если частота свободных колебаний прибора р» велика, то его движение при ненулевых начальных условиях быстро затухает и угол 6 определяется только правой частью уравнения
б=—М2£2./(с(*).
Следовательно, угловая скорость
£2=— 6c/7(/0Q0).
282. Рассмотрим неподвижную систему координат O,XYZ с центром в точке касания диска с плоскостью (рис. 301).
Пусть в некоторый момент времени плоскость диска отклонилась от вертикали на малый угол 0, а касательная к диску в точке его контакта с плоскостью составляет угол Ф с осью OtY, т. е. оси диска х, у, z составляют с осями X, Y, Z малые углы 0 и Ф. Вектор угловой скорости диска
£2 в + £2^2 -1- Оз₽з,
где et, е2, е2, е3—единичные векторы, направленные по осям х, у, z; Й1 = —OcosO, £22=0. Q3 | £2| — составляющие угловой скорости £2.
297
X
X W |
I
/X
Рис. 301
Вычислим момент количества движения диска относительно точки О:
К = A'lgj 4- К2е2 + К 3е3= — ЛФ cos 0^ + Лвё2 + СИе3,
где А^тгг/4, С=тг*/2— соответственно экваториальный и осевой моменты инерции массы диска.
Используя теорему об изменении момента количества движения, получаем следующие дифференциальные уравнения:
( — (Deos 0) 4-Л0Фз1п 0 + Сй0=О;
Д0 4- СОФ cos 0 4- ДФ2 sin 0 cos 0 = jV,t;
CQ= — Nyr,
где N,hN, — проекции реакции N на оси Oz и Оу.
В случае малых колебаний и постоянной угловой скорости (й-const) имеем
Л0 4-СйФ=^;
(1)
ДФ — CQ0 = O.
Рассмотрим движение центра массы диска. Так как точка О находится в состоянии мгновенного покоя, то ее скорость равна
v — ViCt 4-г12е2 + -Озез==0-е1 4- г<2е24- (—г0)е3,
Выразим составляющие абсолютного ускорения в направлении осей х, у, z через угловые и линейные скорости:
wt = Vi— v,Q»4-v,Qt;
ЛПО
Дифференциальные уравнения движения центра массы диска в таком случае имеют вид
— + mg cos В;
т/ю2~= т (v2 — -уА + pIQ3) — N(2)
т&з= т ('У.з—+ Ог^А) — Мг — mg sin 0.
Используя введенные выше обозначения и пренебрегая нелинейными членами, из последнего уравнения системы (3) получаем
— тг (0 + йф) = Nt— mgQ- (3)
Исключив из уравнений (1) и (3) величины Nt и Ф, имеем
•• . (C + mr^CQ'/A — mgr r
0 +------------------- 0~
где С,—произвольная постоянная, определяемая из начальных условий.
Частота малых колебаний диска
,/ (C±mr>)C&lA-mgr т/ 4
Р~ Г ; Л + mr1 V 5 г Г
Малые колебания диска устойчивы при g/%r-
§ И. Приближенные методы определения низших частот
283. Зададимся некоторой статистической нагрузкой, принимая определяемую ее кривую прогибов за форму колебания системы (рис. 302). В этом случае максимальная потенциальная энергия равна работе внешних сил, т. е.
где у, — прогибы, вызываемые принятой системой нагрузки.
Максимальная кинетическая энергия
йт«х = 4" ^P2ypmt.
Приравняв Ттах и Птах, находим
j^-EP^/Sm^*. (1)
При расчете удобно за Р, принять силы тяжести, т. е. Р<= В этом случае формула для частоты колебаний принимает вид
р'-^Ът.у./^т.у^, (2)
Для определения прогибов yt и уг построим эпюры изгибающих моментов от заданных сил и от единичных сил по на-
299
Рис. 302
правлению yt и yt (рис. 302, эпюры 1 и 2). Перемножая эпюры по правилу Верещагина, находим
у,“11 P,/’/(9EJx); yt-23/>,/*/( 18Е/Х).
Подставив в формулу (2) выражения для у, и уг, получаем /> = 0,891 VEJx/tnl\ '
284. p=G,7\V FJx/(mP),
285. В рассматриваемом случае можно принять следующее приближенное выражение для прогибов:
y=y.sin пг/3/.
Максимальная потенциальная энергия равна
з<
а максимальная кинетическая энергия сосредоточенных масс —
T’mn — Р2 [ту? sin’ -у- + ту? sin’ 2л/з) / 2.
Частота собственных колебаний
/>=1.1 V FJx/(ml2).
286. Перемещения масс будут следующие:
</i=y.=81mffP(3888£Jx); yt= 159mg/3(3888£Jx).
300
Частота собственных колебаний
/7=5,71 V EJx/(mP\
287. Максимальная кинетическая энергия в этом случае (с учетом кинетической энергии распределенных масс балки) будет следующая:
Т'тах
чи
3/
Р2 /и{/о2т + 4'$^2'п<>51пг_ЗГ<1г ' о
Максимальная потенциальная энергия (см. решение зада-285).
Пв.х
П,
Частота собственных колебаний
Л4£/ _ Q. 1 ,/ Г
-----3----------= 0,91 г
108--£- (zn-t-mj) Z, 288. Максимальная потенциальная энергия системы 31
[max=4 EJxyA^ 5 sin«£ (fc +-£- ^(sin’l ' 'о
Максимальная кинетическая энергия
+ sin^).
Низшая частота собственных колебаний системы
р=\,35УЕЗх/(тР).
289. Для определения частоты по методу Релея ауемся формулой (см. решение задачи 283)
з I з P2=g^yimi / 2 mjzA
<-i I i=i
восполь-
(1)
На рис. 303 показаны эпюры осевых усилий 1, 2, 3, необходимых для вычисления прогибов у., у».
После вычисления получаем
^=3/mg/(£F); yt-=5lmg/(EF); y3=6lmg/(EF).
Подставив yt в выражение (1), находим
/>=0,45 VEF/(ml).
290. /7=0,775 V EF/(ml).
291. p=0,65/£F/(/Ti/),
30!
292. При крутильных колебаниях выражение для низшей частоты колебаний можно представить в виде
р’—ЕМ^/ХЛфЛ (1)
где М, — статически приложенные моменты, которые можно взять пропорциональными моментам инерции Л1(=аЛ; ф>— углы поворота маховых масс.
Для определения углов <р< приложим к валу моменты М{ и построим эпюры 1 и 2 (рис. 304) от Mit а также эпюры от единичных моментов. Углы закручивания
Ф<— (Aft4-Af»)/c,; фг=Л!г/с24-(Л4,-|-Л4,)/с1.
Рис. 304
Так как Л11 = а/1, Мг^аЛ, то после преобразований из выражения (1) получаем квадрат низшей частоты:
Л(А+Л) , / Л , А + А\
, * +AV*+“^J
п1= ---------—: Z——г— .
293. р = 0.35/с/Л
294. По методу Донкерлея, низшую частоту колебаний системы найдем по формуле
1/р2=1/р.3+1 /рЛЬ- -+1/РЛ
где Pi — парциальная частота колебаний массы т,.
В задаче 283 парциальные частоты колебаний равны
p,*=l/(m1611); ргг=\/(т,.Ьи),
где би-12Г/(27£/я); ба-= 12/’/(27£/я).
Таким образом, частота р равна
р = 0,865 VEJtlmP.
В задаче 295 имеем mt и mlt поэтому частота колебаний в этом случае будет
р-1,0бК£Л/(да1»).
295. Низшую частоту колебаний найдем из выражения
1/рг-|/рг+1/Р1*+1/рл
где Pi*—l/(m6n); pZ-l/tme,»); р,2 = 1/(тб„);
6„-3Z/(£f); б„=2//(££); 6M-//(£F).
После вычислений находим
р=0,41 VEF/(mJL).
296. р = 0,7VEF/M\ p = Q,58VEF/(ml~).
зоз
СПИСОК ЛИТЕРАТУРЫ
1. Светлицкий В, А., Стасенко И. В. Сборник задач по теории колебаний. М.: Высшая школа, 1979. 368 с.
2. Бронштейн И. Н., Семен диев К. А. Справочник по математике М.: Наука, 1980. 976 с.
3. Янке Б., Эм де Ф. Таблицы функций: Пер. с англ М_: Физматгиз. 1959. 150 с. -г. г
4. Тимощенко С. П. Колебания в инженерном деле. М.: Наука, 1967.
5 Сборник задач по теории колебаний / Под ред. Л. В Постникова и В. И. Королева. М.: Наука, 1978. 271 с.
6. Б и д е р м а н В. Л. Теория механических колебаний. М.: Высшая школа, 1980. 408 с.
7. Сборник задач по аналитической механике/Е. С. Пятницкий, Н. М. Трухан, Ю. И. Ханукаев, Г. Н. Яковенко. М.: Наука, 1980. 320 с.
8. Магнус К- Колебания: Пер. с нем. М.: Мир, 1982. 303 с.
9. Светлицкий В. А. Динамика старта летательных аппаратов. М.: Наука, 1986. 280 с.
10. Светлицкий В. А Случайные колебания механических систем. М.: Машиностроение, 1991. 316 с.
11. Василенко Н. В. Теория колебаний. К-: Вища шк„ 1992. 430 с.
304
ПРИЛОЖЕНИЯ
Приложение 1. ДИАГРАММА АИНСА-СТРЕТТА
Колебания, описываемые уравнением Матье </+(а+2<?cos2т)у=0, устойчивы, если точка с координатами (о, Q) находится в незаштрихованной области диаграммы Айнса—Стретта, и неустойчивы, если в заштрихованной области (рис. 305).
Рис. 305
Приложение 2. ИНТЕГРАЛЫ, ВСТРЕЧАЮЩИЕСЯ
ПРИ ОПРЕДЕЛЕНИИ ДИСПЕРСИЙ
В общем случае интегралы, получающиеся при определении дисперсии случайной функции по известной ее спектральной плотности, можно привести к виду
С С (fto) , Jn~ \ |Л (х<0) I’
— DO где
A (ia) = a, (/<o)n + e, (/а>)л-‘+ ... +ап.
С1 (1<д) = Ьв + bl {Io)11*-* + .. . + bn-f
Для л = 1
f bt n_
J' = J | ati<o + a, |l ~2<h<h
305
Для л=2
, _ С Ro W + Md<0 + „
‘= I о. (««)* + Я, (/®) + в, I* “ 2<цв, 2п-
Для п=3
. Ro(Zm)*+M*®)* + »t]<l«» —gR» + e»*,---—
*= J I во U®)* + «1 (Z®)’ + esZ® 4- Л, |я 2а, (а,а,— а,а,) “00
Для п = 4
С Ro W + 6, (1<о)* + Ь, Ца>)г + ^] dm
) | a, (Z®)4 + а, (№)> + <ц (/©)’ + а, (/в) + a, Is — —оо
6, (— в!Я4 + esa3) — a,aab, + a,a,bt + ~~ (а,а,—а,а2) 2а, (а„а,2 + e,2e4—а)а1в1)
306
ОГЛАВЛЕНИЕ
Предисловие.................................................
Глава 1. Колебания систем с одной степенью свободы . .
§ 1. Свободные колебания................................
§ 2. Свободные колебания систем с учетом сил сопротивления
§ 3. Вынужденные колебания .............................
§ 4. Критические состояния и устойчивость колебаний
§ 5. Параметрические колебания......................
§ 6. Случайные колебания................................
§ 7. Нелинейные колебания...............................
Глава 2. Колебания систем с несколькими степенями свободы
§ 8. Свободные колебания................................
§ 9. Вынужденные колебания .............................
§ 10. Критические состояния и устойчивость колебаний
§ 11. Приближенные методы определения низших частот Список литературы...........................................
Приложения . . . . ...................................
3 6
6
17
22
37
167
175
195
218
218
257
278
299
303
305
307
Учебное издание
Валерий Александрович Светлнцкий
ЗАДАЧИ И ПРИМЕРЫ ПО ТЕОРИИ КОЛЕБАНИЙ Часть I
Редактор Е. Н. Стааицкая Художник С. К. Девин Технический редактор О. В. Рыбина Корректоры Л. И. Малютина, М. Л. Василевская
ЛР № 020523 от 23.04.92
Сдано в набор 25.11.93. Подписано в печать 08.02.94
Формат 60X90 1/16 Гарнитура литературная Бумага тип. № Печать высокая. Усл. печ. л. 19,25. Уч.-изд. л. 22,72.
Тираж 2000 экз. Заказ 5000 Изд. № 71
Издательство МГТУ им. Н. Э. Баумана. 107005. Москва, 2-я Бауманская. 5.
Производственно-издательский комбинат ВИНИТИ 1400010, г. Люберцы 10, Октябрьский пр., 403
В.А.СВЕТЛИЦНИИ
•%
1
ЗАДАЧИ И ПРИМЕРЫ ПО ТЕОРИИ КОЛЕБАНИЙ
Часть I
? . '. ; ; . ' •/ ' '
(' •' V. V'
\ ' / 1 ' 1 •‘н ' ' ’ ’ . V • • - . • • . --V . , , с ’ • • I । ,» . v • ‘ V \ ' t. , ’ ‘ ) . • • ’ .,' ‘ л' и * \ у
Издательство МГТУ им. Н.Э. Баумана