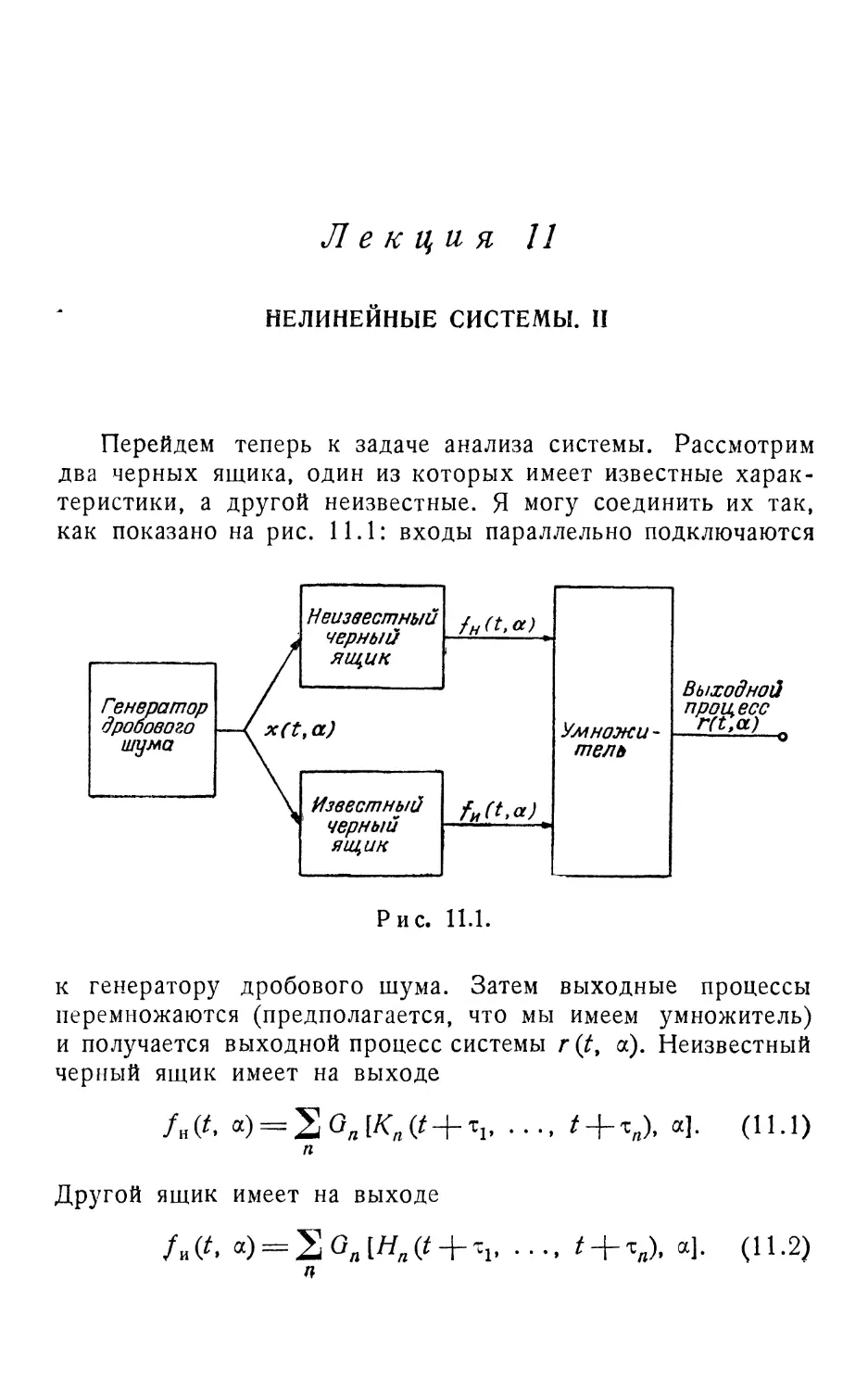
Текст
NORBERT WIENER
Professor of Mathematics
Massachusetts Institute of Technology
NONLINEAR PROBLEMS
IN RANDOM THEORY
The Technology Press of
The Massachusetts Institute of Technology
and
JOHN WILEY & SONS, INC., NEW YORK
1958
Н. Винер
Нелинейные задачи
в теории
случайных процессов
Перевод с английского
Э. М, ХАЗЕН
Под редакцией
Ю, л, КЛИМОНТОВИЧА
ИЗДАТЕЛЬСТВО иностранной литературы
Москва 1 961
Книга представляет собой курс лекций известного
американского математика Н. Винера, прочитанный им
в 1958 году в Массачусетском технологическом
институте. Рассмотрены понятия случайного процесса, меры
в пространстве функций, функционала от случайного
процесса. Большое внимание уделено случайному
процессу типа „броуновского движения" и связанной с ним
мере в пространстве непрерывных функций, введенной
автором в 1923 году и известной под названием меры
Винера.
Рассматриваются возможности применения
изложенных методов к вопросам частотной модуляции,
прохождения случайных сигналов через нелинейные
системы, к задачам статистической механики и др.
Книга будет полезна лицам, занимающимся теорией
случайных процессов и ее применениями в различных
областях.
Редакция литературы
по математическим наукам
ПРЕДИСЛОВИЕ
В течение некоторого времени меня интересовал ряд
явлений, связанных со случайными процессами. С одной
стороны, я заметил, что „дробовой эффект" является
подходящим входным процессом для анализа нелинейных цепей.
С другой стороны, для работы, касающейся природы
электроэнцефалограмм и, в частности, альфа-ритма (которую
выполняли проф. В. А. Розенблит и я), мне пришла в голову
мысль использовать модель системы нелинейных
осцилляторов, возбуждаемых случайными входными сигналами. На
протяжении многих лет я обсуждал свои идеи с проф. И. У. Ли
и с проф. А. Дж. Бозе — сотрудниками электротехнического
факультета и исследовательской лаборатории электроники
Массачусетского технологического института. В начале
1958 г. они обратились ко мне с предложением прочесть
несколько лекций на эту тему для избранной группы
аспирантов-электротехников. Мне предложили любую возможную
noMv>uj,b в технике записи лекций и их обработке в
неизмененном или почти неизмененном виде. По магнитофонной
записи моих слов и фотографиям формул, которые я писал
на доске, были составлены записки, отпечатанные на
гектографе.
Вначале предполагался цикл из четырех или пяти лекций.
Однако мои идеи развивались по мере изложения курса,
и к концу семестра число лекций выросло до пятнадцати.
Несколько последних лекций посвящены приложению моих
идей к задачам статистической механики газов. Эта работа
явлается новой и поисковой, и мне представляется, что
я должен был бы дополнить мой курс, переписав эти лекции
с помощью проф. И. У. Ли.
Я выражаю глубокую благодарность проф. Ли и проф. Бозе
и слушателям курса, имена которых я здесь привожу;
ПРЕДИСЛОВИЕ
Д. А. Чеслер, Д. А. Джордж, И. М. Джейкобе, А. Г. Нат-
толл, С. Е. Уернлайн мл. (сотрудники исследовательской
лаборатории электроники и аспиранты электротехнического
факультета Массачусетского технологического института).
Без их активного содействия и внимания, без их помощи,
освободившей меня от тяжелого труда составления записок,
эта книга никогда не появилась бы или, в лучшем случае,
прошел бы еш,е год или несколько лет до ее появления.
Они также сообш,али мне, какие вопросы были бы
интересны инженерам-электротехникам и работникам родствен-
ных специальностей. Я хочу также выразить признательность
г-же Р. Е. Розенсвейг за выполнение трудной задачи
печатания лекций по магнитофонной записи и перепечатки
рукописи, подготовленной слушателями курса.
Книга написана в разговорном стиле, во многом так, как
я излагал материал на лекциях. В этом есть свои преиму-
ш,ества и недостатки, но я надеюсь, что читатель простит
мне неформальность ради живости, придаваемой материалу
принятым мной способом изложения. Я надеюсь, что
полученные мною результаты будут интересны для специалистов,
работаюш.их в ряде областей: в частности, для инженеров-
электриков, работаюш,их в области теории связи, для
специалистов, изучающих нелинейные электрические цепи, для тех,
кто интересуется устойчивостью электрических
генерирующих систем. Работа представляет интерес для биофизиков,
в частности, для интересующихся всеми типами ритмовых
явлений, для физиков-атомников и для изучающих все ветви
статистической механики. В число последних я включаю
изучающих гидродинамику, так же как метеорологов и
океанографов. Моя книга—запись некоторых положений
развивающегося направления науки, и я искренне надеюсь, что
вскоре она приведет к появлению новых работ, которые
превзойдут ее.
Массачусетский технологический
институт
Кембридж, Массачусетс
2 июня 1958 г.
Лекция 1
случайная функция - ФУНКЦИЯ ВРЕМЕНИ
и состояния ^)
я хочу рассмотреть методы определения случайного про*
цесса и, в частности, методы определения спектра процесса,
хотя эти методы имеют гораздо более общее применение.
Для этого я подвергну разбору броуновское движение. Под
таковым я подразумеваю одномерное броуновское движение.
Рис. 1.1.
Наконец, по крайней мере в первой лекции я буду
рассматривать его на отрезке времени [0,1] (рис, 1.1).
Рассмотрим блуждание некоторой частицы. Пусть с
течением времени эта частица перемещается случайным образом,
так что смещение, которое она получит, отправившись в
данный момент времени из данного положения, к другому
моменту времени имеет гауссовское распределение, и для
неперекрывающихся интервалов времени эти гауссовские
^) Множество состояний, на котором задается эта функция,
в русской литературе по теории вероятностей называют „мнэже-
CTBOiM элементарных событий'*. — Прим. перев.
ЛЕКЦИЯ 1
распределения независимы. Вначале я буду рассматривать
смещения за фиксированные промежутки времени, а затем
на основе рассмотрения движения в фиксированные моменты
времени я найду распределение траекторий этого
движения— сначала на конечном отрезке времени, затем на
бесконечном. Далее я собираюсь рассмотреть процессы, которые
зависят от этого движения линейным и нелинейным
образом.
Нам понадобится формула композиции гауссовских
распределений, которые независимы для непересекаюидихся
интервалов времени. Возьмем величину х, которая имеет
гауссовское распределение. Вероятность того, что эта
величина находится между х^ и Хз, равна
"■I
J
1
-ехр
(27ia)'^2 \ 2а /
\dx, (1.1)
Я еще не сказал, как а зависит от времени; для того чтобы
разумным способом определить эту зависимость, я рассмотрю
сначала композицию двух таких перемещений. Иными словами,
я беру частицу, положение которой к концу некоторого
промежутка времени имеет гауссовское распределение. Новое
смещение частицы из точки, в которую она пришла, также
имеет гауссовское распределение. Каково распределение
для величины смещения по истечении обоих промежутков
времени?
Итак, я отправляюсь от совместной функции
распределения
[-V-p(-^)l(-^expr-i>^=^l) (1.2)
[заметьте, что именно у — х, а не у является аргументом
второй плотности вероятности в выражении (1.2)] и хочу
получить распределение вероятностей для у, если х
принимает все возможные значения; иначе говоря, меня интересует
интеграл
оо
rf>» г —^ ехр (— ~\ —Цр ехр (— ^^ ~ ^^' \ dx. (1.3)
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 9
Легко вычислить интеграл в (1.3); это тривиально, и нам
нет необходимости этим заниматься. Ответ дается равенством
оо
—оо -*
^ "^^ [27. (а + Ь)]''^ ^""^ \ Ji^Tb)) ' ^^'^^
Это и есть закон композиции гауссовских распределений.
Заметим, что при композиции двух гауссовских
распределений значения параметра а суммируются. Если мы теперь
учтем, что блуждания на неперекрывающихся интервалах
гауссовские и независимые и что величина смещения зависит
только от длины интервала времени и не зависит от
начального момента, то мы увидим (так как а я b складываются),
что распределение для величины смещения за некоторое
время t равно
где k зависит от t линейно. Нормируем время так, чтобы k
было равно t:
Заметьте, что при композиции гауссовских распределений
эти временные параметры также складываются.
Теперь я собираюсь сопоставить траектории частиц
со значениями переменной а, где а меняется от О до 1.
Это отображение я хочу провести подробно. Заметим,
во-первых, что все случайные движения частиц где-нибудь
заканчиваются и что траектории частиц отображаются на
интервал а от О до 1. На данном этапе я не отделял
различные области значений а; я взял всю область а от О до 1
и сопоставил ее с множеством всех траекторий.
Рассмотрим броуновское движение в два момента
времени: ^ = V2 и ^=1 (рис. 1.2). Я введу четыре класса
броуновских траекторий. Заметим, что в момент ^ = V2 ^^^ь
две возможности: частица может находиться под осью t
или над осью, вероятность попадания на ось равна нулю.
Это напоминает бросание монеты, при котором вероятность
10
ЛЕКЦИЯ 1
попадания на ребро равна нулю. Мы бросаем монету дважды:
при t = ^l2 и при ^=1. Если иметь в виду, что может
выпасть только герб или решетка, то существует
возможность выпадения комбинаций герб — герб, герб — решетка,
решетка — герб, решетка—решетка. Что это за возможности
выпадения комбинации герб — герб, решетка — решетка и
Рис. 1.2.
т. д.? Величины а и b в уравнении (1.4), соответствуюш.ем
двум бросаниям, равны Vg. Распределение задается
выражением
1
ш\
(У-х)П
■ ехр I — I :—77 ехр I — '-^— 1 dx dv.
[ чФ-т- [ О) \
(1.7)
Выражение (1.7) есть вероятность того, что частица в
момент ^ = 72 находится между х и x-\-dx, а в момент ^ = 1
между у и y-\-dy. Поэтому вероятность того, что частица
находится, скажем, под осью при ^ = 72 С'^- ^- ^
отрицательно при t
о о
72) И X отрицательно при t-
X
1.
равна
ехр
---Ч^-ШГ L Н4)
X
1 г (>' — -^)
гг ехр —
dxdy, (1.8)
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ И
Этот интеграл имеет вполне определенное значение. Возьмем
теперь точку О на оси а, и отложим от этой точки
интервал А8, длина которого равна величине интеграла (1.8)
(рис. 1.3). Скажем, что Л8 соответствует траекториям,
Рис. 1.3.
пересекающим внизу оси ^ = \/2 и ^=1. Затем возьмем
в (1-^) ^ между О и со, а _у между —со и 0. Вероятность
таких значений хну равна
оо о
/ /
Х = 0 У=: -ОО
1
1\^
нш
йгехр
■т
X
X
[^-т
ТГ^^Р
(y-xf
<4)J
dxdy. (1.9)
Отложим на оси а другой интервал, ВС, соответствующий
величине интеграла (1.9) (рис. 1.4). [Заметим, что сумма (1.8)
/
Рис. 1.4.
и (1.9) есть вероятность того, что конец траектории лежит
под осью, и равна 72-1 Затем интегрируем (1.7) следующим
образом:
J /
Г=-оо у
X
ехр
И)
X
1М'''
[K^)J
IT ехр
Hi)
dxdy, (1.10)
12
Л E КЦ И55 I
С D
Рис. 1.5.
Это дает нам третий промежуток, CD, на линии а (рис. 1.5).
И, наконец, четвертый промежуток, DE (рис. 1.6), дает
со со
1
т''=
=0 v=o [2.(1)]
ехр
ш
X
X
1 \п'/^
{'<^\
ТТГехр
(у-^)2
^Ш
^fjc^y. (1.11)
Итак, мы получили четыре сегмента на линии а
соответственно четырем вероятностям, сумма которых равна 1.
Рис. 1.6.
Возьмем более мелкое разбиение множества броуновских
траекторий. Построим такое разбиение, чтобы любое новое
подмножество заключалось внутри одного и только одного
из имевшихся ранее подмножеств и соединение некоторого
определенного числа новых подмножеств составляло прежнее
целое подмножество. Мы получим более мелкое разбиение
Смеш^ение
1
0
х, >
V ^
/
г
<з
J
-
1
Рис. 1.7.
линии а, соответствующее областям блуждания броуновского
движения. Сначала я разделю мельче отрезок времени [О, 1]:
я буду работать с четырьмя моментами времени (рис. 1.7).
Вероятность того, что частица лежит в заданной области
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 13
В каждый из четырех моментов, задается интегралом от
2%
Хехр
ехр
ехр
К1)
ехр
(X2 — X^f
X
<i)j
44)
по соответствующей области.
Далее я рассматриваю вероятность того, что частица
проходит через некоторое отверстие (область значений х),
заданное для каждого из четырех моментов времени. Я беру
теперь четыре момента времени 74» V2> ^/4 и 1 и
рассматриваю по четыре области для каждого момента. В каждый
из этих моментов времени я буду различать не только
положительные и отрицательные значения х, но и значения
от —оо до —1, от —1 до О, от О до 1 и от 1 до оо.
Сколько тогда будет типов траекторий? Имеются 4
возможные области для каждого момента времени и 4
последовательных момента, т. е. 4'* = 25б типов траекторий. Как
определить вероятность каждого из этих типов? Я просто
проинтегрирую выражение (1.12) по соответствующей области
значений различных х. Получится 256 чисел, сумма которых
равна 1. Длина каждого из имевшихся ранее интервалов
на линии а равна сумме 64 из этих чисел. Можно получить
в определенном порядке 256 неперекрывающихся малых
интервалов (неодинаковой длины), по 64 в каждом из прежних
интервалов а. Мы получаем сопоставление классов
траекторий и маленьких областей значений а.
Сделав это, возьмем более мелкое разбиение (рис. 1.8).
Во-первых, число моментов времени вырастет до 8, так что
для плотности вероятности будем иметь выражение
J2.
1
нш \
ехр
т
ехр
(^8 — Xjf
i^
(1.13)
Я буду интегрировать по областям, полученным следующим
способом (этот прием повторяется и в дальнейшем): у нас
теперь имеются 8 моментов времени; сохраним все
предыдущие деления оси х не только для моментов времени,
имевшихся ранее, но и для вновь введенных; затем для
14
ЛЕКЦИЯ I
каждого из интервалов, ограниченных с обеих сторон,
введем новое деление оси х посередине интервала. (Делить
именно пополам не обязательно, но удобно.) Для областей х,
простирающихся к -|-'^^> новое деление берется на единицу
выше, чем прежнее, ограничивавшее эту область снизу;
для областей, простираюш.ихся к —оо, — на единицу ниже,
чем прежнее.
Теперь у нас уже не 4"*, а 8^ интервалов, соответствующих
этим случайным кривым. Каждый из этих интервалов имеет
конечную длину, каждый из них лежит внутри одного
2
1
2
0
0
-/
1
8
1
/
2
/ '
Рис. и
из интервалов предыдущего разбиения, и на интервале
О < а < 1 они образуют еще более мелкое разбиение. Если
продолжать разделять движение в пространстве и во
времени все более и более тонко, то количество рангов для а
будет возрастать. Легко показать, что при таком разделении
(как и при более общем способе разделения) длина каждого
из интервалов а стремится к нулю. Если взять любое
значение а, не принадлежащее счетному множеству наших
делений оси а, то это значение будет лежать в одной
из четырех областей, полученных на 1-м этапе разбиения,
и в одной из 256 областей, полученных на 2-м этапе,
и т. д. Значение а однозначно определяется (за исключением
граничных точек интервалов, которые не учитываются) тем,
в какие интервалы оно попадает на различных этапах
разбиения. Другими словами, мы в состоянии все более и более
СЛУЧАЙНАЯ ФУНКЦИЯ ~ ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 15
ТОНКО отделять те из блужданий, которые соответствуют
данной точке а.
Вообще говоря, неверно, что, проделав это, я получу
некоторую непрерывную кривую, но я покажу, что можно
обойти эту трудность. Можно ввести некоторую величину,
которую я назову „прямизной последовательности делений".
Так как 2^ уже не понадобится, скажу просто, что имеется
ряд отверстий — по одному отверстию в каждый из
произвольного числа моментов времени (рис. 1.9).
Рис. 1.9.
Предположим, что имеется нить ВС, закрепленная в точке О
и продетая через эти отверстия. Пусть она туго натянута.
Существует по крайней мере одна часть нити, которая имеет
наибольший наклон. Наибольший наклон туго натянутой нити
меньше, чем наибольший наклон любой другой кривой,
проходящей через тот же ряд отверстий. Можно назвать
тугую нить кратчайшей из проходящих через данный ряд
отверстий. Эта нить покажет нам „гладкость" этого ряда
отверстий следующим образом. Обозначим кратчайшую (для
данного ряда отверстий) нить x=^s(t)\ каждому ряду
отверстий соответствует своя s(t). Рассмотрим
\s{t + z)^s{t)\
шах
hi
(1.14)
Это максимальное значение назовем „шероховатостью"
данного ряда отверстий. Нет других оснований брать в (1.14)
|т| в степени ^4' ^ро^^^ следующего: степень должна быть
равна некоторому числу, меньшему половины. На каждом
этапе разбиения имеются ряды отверстий, и н^ каждом этап^
16 л E КЦ ИЯ 1
Я выбрасываю все ряды отверстий, для которых
„шероховатость" больше чем Л, т. е.
шах-^—^^—^—^——^-^^ > Л. (1.15)
Теперь я могу доказать следующее: сумма длин
интервалов а, соответствуюш.их рядам отверстий, которые
выбрасываются на каждом из этапов, ограничена. Когда я
выбрасываю ряды отверстий, я имею для каждого этапа одно и то же
выражение 1(Л), ограничивающее сумму длин выброшенных
интервалов. Множество всех выброшенных рядов отверстий
только счетно; сумма длин соответствующих интервалов а
сходится, и соединение этих интервалов образует так
называемое измеримое множество; мера этого множества не
превосходит 1(Л).
Я мог бы доказать (но не имею времени, чтобы сделать
это здесь), что
lim /(Л) = 0. (1.16)
л -> со
Другими словами, сумма длин интервалов, соответствующих
всем рядам отверстий любого из этапов, „гладкость" которых
меньше некоторой величины, ограничена, и, если А растет,
эта сумма стремится к нулю. Разрешите мне выбросить ряды
отверстий, „гладкость" которых меньше определенной
величины. Это значит, что я выброшу определенное множество
значений а, мера которого меньше некоторой малой величины.
Остающиеся ряды отверстий будут содержать непрерывные
траектории; более того, все эти непрерывные траектории
будут удовлетворять одному и тому же условию
равномерной непрерывности. Иными словами, Ах стремится к нулю
быстрее, чем некоторая функция от АЛ
Привлечем следующую математическую теорему:
Пусть дана последовательность кривых, проходящих
через некоторый ряд отверстий и удовлетворяющих
определенному условию равномерной непрерывности.
Предположим, что отверстия сужаются (в пределе к нулю) и что
увеличивается плотность моментов времени, в которые они
заданы. Тогда наше условие равномерной непрерывности
сжимает кривые теснее и теснее во все большем и большем
количестве точек. Последовательность кривых равномерно
сходится к предельной кривой, удовлетворяющей тому же
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 17
условию равномерной непрерывности. Значит., если выбросить
некоторое множество а и 5, такое, что мера множества
выброшенных 5 меньше е, тогда с каждым из остаюш,ихся
значений а будет связана кривая, предельная для всех рядов
отверстий, последовательно соответству1ош.их этому
значению а. Предельная кривая непрерывна; более того, она
удовлетворяет определенному условию равномерной
непрерывности. Итак, с помощью этого процесса мы связали
с каждым значением а (за исключением множества а нулевой
меры) какую-то кривую. Эта кривая удовлетворяет
некоторому условию равномерной непрерывности; и, что еш,е важнее,
каждой из таких кривых, за исключением множества нулевой
вероятности, сопоставлено некоторое значение а. Можно
показать, что предельные кривые единственны. Поэтому
с каждым значением а, за исключением множества а нулевой
меры, будет связана одна и только одна непрерывная кривая.
Назовем ее x{t, а). Это вполне определенная функция t
для почти всех значений а. Если на каждом этапе разбиения
задан процесс упорядочивания отверстий — а это можно
сделать,—то x{t, а) является вполне определенной
функцией / и а, так же хорошо определенной, как любая
математическая функция. Легко показать, что x(t, а) измерима
и ограничена по ^ и а и непрерывна по t для почти всех а.
Итак, я ввел так называемую „стохастическую"
функцию x(t, а).
Что еш.е можно сказать относительно x(t, а)? Я уже
отметил, что x{t, а) непрерывна для почти всех значений а.
Дифференцируема ли она? Не входя в доказательство (для
которого достаточно рассмотреть противные случаи,
объединить их и провести подсчет), отмечу, что справедливо сле-
дуюш.ее утверждение.
Рассмотрим множество кривых, для которых
^^^ (1.17)
имеет предел при А^-> О хотя бы для одного значения t.
Это множество имеет меру нуль, т. е. почти все
кривые x(t, а) нигде не дифференцируемы. (Это важное
свойство. В нашей работе придется использовать непрерывные
недифференцируемые функции.) Более того, предел
выражения (1.18) не суш.ествует ни для одного t ддя почти всех а,
2 Зак. 2305. Н Винер
18 ЛЕКЦИЯ 1
(1.18)
если X > 72» и существует для любого t равномерно для
почти всех а, если X < ^2
^tx (t, а)
(Я пропускаю случай X = Уг» Я излагаю здесь скорее
факты, чем доказательства.)
Функция x(t, а) будет использована в дальнейшем.
Я предполагаю, что мы уже определили x(t, а). Мы назвали
ее стохастической. Выведем теперь некоторые интегральные
свойства x(t, а).
Рассмотрим следующий интеграл:
1
/ = /U(^2. сс) —x(^i. a)fda [t,<t^]. (1Л9)
о
[л:(^2> ^) — -^(^1' °^)1 имеет гауссовское распределение. Это
легко следует из нашего определения, [fg — ^il ^^'^^ параметр
гауссовского распределения и, следовательно,
оо
^-12.аД,)Г/-_/""--Р[-2-^]-^'- [^:< ^.1.(1.20)
Это равенство, конечно, справедливо для двоичных
интервалов, и его легко распространить по непрерывности на все
остальные интервалы. Выражение (1.20) может быть
подсчитано следующим образом. Положим
(1.21)
Тогда
со
'-^'^-'^^"'Т^' /г.«ехр(-^)^г.. (1.22)
— ОО
Заметим, что ехр(—v^l2)—^ четная функция. Если п
нечетно, то
оо
^^'-^'^"'"'ЩГ' fv"txp(-^^yv = 0, (1.23)
— ОО
так как интеграл от —со до + ^^^ от произведения четной
функции на нечетную равен нулю.
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 19
Если п четно, то интеграл (1.22) берется по частям
— V ехр i— -у) ^"^ = ^ ^хр (— -^) • (1-24)
Тогда
оо
'=^^'^-'^^"'-^' /(-1)г.''->^ехр(-^). (1.25)
— ОО
Интегрируя по частям, получаем
'=<'-'.'"" ^{[-'"--(-т)]1+
+ {{n-\)v"-4x^(--^yv\, (1.26)
-оо J
со
l^{t,-t,f"-^{n-\) jv"-4x^(-^yv. (1.27)
^ '^ —СО
продолжая считать этим способом, получаем
/ = (^2-^,)"^(»-1)(»-3)...(1)--^ JtX^[-~-yV.
(2.)Т_^^^'"--'
(1.28)
Последовательность [п—1—2k] дойдет до 1, так как п
четно. Кроме того, можно проверить, что
(2^)
Следовательно,
1
о
О, п нечетно.
Ь /-p(-f)<^.= l. (1.29)
«/9 (1-30)
(^2 —^1Г (Я—1)(Аг —3) ... (1). п четно.
Интересна правая часть (1.30). Пусть имеется п элементов,
и требуется найти число способов, которыми можно разбить
2*
20 ЛЕКЦИЯ 1
их на пары. Если п нечетно, то не существует ни одного
способа. Посмотрим, сколько имеется способов, если п четно.
Возьмем какой-нибудь элемент. С ним можно соединить
любой из п—1 оставшихся. После этого останется п — 2
элементов. Возьмем какой-нибудь из п—2 элементов;
имеется п — 3 возможных соединений с ним. Таким
образом, во всех случаях {п четно или нечетно) справедливо
следующее равенство:
1
о
X (Число способов разбиения п элементов на пары). (1.31)
Это начало исчисления случайных функций.
Рассмотрим следующий интеграл:
1
j f{t)dx{t, а). (1.32)
о
Заметим, что как обычный интеграл Стильтьеса этот
интеграл не будет существовать, так как x(t, а) почти никогда
не дифференцируема. Но можно это обойти. Предположим,
что f(t) дифференцируема и что f^{t) ограничена (в
настоящий момент ограничимся этим). Определим
выражение (1.32) „интегрированием по частям":
1
ff{t)dx{t, a) = f{l)x{\, а) —/(0)^(0. а)—
о
1
~ffit)x(t, a)dt. (1.33)
о
Здесь д:(0, а)==0. Вспомните, что нити, которые я
натягивал, проходили через начало. Поэтому
1 1
f fit)dx(t, a) = f(\)x{\, OL)~f f(t)x{t, a)dt. (1.34)
0 0
правая часть равенства (1.34) есть вполне определенная
функция для почти всех значений а. Функция x(t, а) огра-
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 21
ничена, f {t) ограничена, и, следовательно, интеграл в (1.34)
существует. Кроме того, если заменить x{t, а) на —x(t, а),
то очевидно, что распределение броуновских движений
не изменится. При этом (1.34) сохранится. Интеграл от
выражения (1.34) по а равен нулю.
Оценим следующее выражение:
12
f{t)dx{t, а)
о Lo
(1.35)
Интегрируя по частям и раскрывая, получаем
1 г 1 12
jdAjf{t)dx{t, а) =
о Lo J
1 г 1
= J^a /(1)д;(1, а)-^r{t)xit^ а)
о L о
Отсюда
1 г 1 -|2 1
dt
(1.36)
j da.\j f{t)dx{t, a) = J^a/2(1) д;2(1, a) —
0 Lo Jo
1 1
-2 J^a/(1)A:(1, a)f r{t)x{t, a)dt +
0 0
1 1 1
-i-jdajf(t)x{t, a)dt J f(s)x(s, a)ds. (1.37)
0 0 0
Рассмотрим теперь следующее выражение:
1
j x{t^, a) л: (^2» ^)doL =
0
1
= Jjc(^i, o)\x{t^, а) + д;(^2» a) —^(^i. a)] ^fa. (1.38)
0
Пусть t^ < t^. Прибавлением и вычитанием одной и той же
величины сводим правую часть (1.38) к рассмотренному ранее
выражению. Заметим, что xijt^, а) и [л: (^2» *) — ^(h* ^)1
22 л E к Ц и я 1
имеют независимые распределения. При условии, что одна
из них положительна, другая с одной и той же вероятностью
может быть положительна или отрицательна; среднее
значение произведения равно 0. Так что от (1.38) останется
только
1 1
Jjc(^i, а)л:(^2. а)й?а= Гл:2(^1, a.)d(x = ty (1.39)
о о
Рассмотрим три члена уравнения (1.37). Первый член равен
1
Jйfa/^(l)Jc2(l, а)-:/2(1). (1.40)
о
Предположим, что в оставшихся двух членах изменен
порядок интегрирования. (Легко доказать, что эта перемена
законна.) Тогда для второго члена мы имеем
1 1 1
— 2 J^a/(1)A;(1, OL)jfit)x(t, ci)dt = — 2f(\) f tf {t)dt.
0 0 0
(1.41)
Равенство (1.41) справедливо, так как ^<1. Теперь
рассмотрим оставшийся член (1.37):
1 1 1
j da j fit)x{t, OL)dt j f'is)x{s, a)ds =
0 0 0
1 1 1
= j fit)dtj f{s)ds j x(t, a)jc(s, a)da, (1.42)
0 0 0
Вспомним, что
f x(t, a)x(s, a)da = {^' ^^^' (1.43)
Значит, можно разбить интеграл в (1.42) на два; в одном
из них будет S < ^, в другом ^ < 5. Эти интегралы равны,
так как s и t перестановочны. Подставим (1.43) в (1.42),
взяв S < ^ и умножив на два, чтобы учесть оба случая.
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 23
Тогда правая часть (1.42) примет вид
1 1 1
j f{t)dt jr(s)ds j x(t, а)л:(5, a)da =
0 0 0
1 t
= 2 f f(t)dt j sf(s)ds, (1.44)
0 0
Подстановка (1.40), (1.41) и (1.44) в (1.37) дает
1 г 1 "12 1
fdoi\ff(t)dx{t^ а) =P(\)-2f{l)ftr(t)dt^
о U J о
1 1
-^2 f f{t)dt f sf(s)ds, (1.45)
0 0
Теперь
1 /
2Jf(t)dtfsf{s)ds =
0 0
/ "11 1
}sr{s)dsf(t)\ —2Jtf(t)r{t)dt, (1.46)
0 Jo 0
It 11
2 f f (t) dt J sf (s)ds==:2f{l)f sf (s) ds-2 f tf (t) f (t) dt.
0 0 0 0 (1,47)
Поэтому
1 г 1 -|2 1
f dalj f(t)dx{t, a) ^P{\) — 2Jtf{t)f'{t)dt, П.48)
0 U J 0
Р1меем
Поэтому
ii\tP{t)]=-P{t)-^2tf{t)f'(t).
(1.49)
2 J tf {t) f {t)dt = \tp(01J —jp{t)dt, (1.50)
0 0
1 1
2 j tf{t)f' {t)dt=^P(\)- j f{f)dt. (1.51)
24 л E к ц и я 1
Итак, ^ Г ^ V ^
j da\j f{t)dx(t, а) =fp(t)dt. (1.52)
о U Jo
Заметьте, что если мы предполагали, что f (t)
дифференцируема и принадлежит L^, и пришли к функции от а,
удовлетворяющей уравнению (1.52), то мы имеем унитарное
преобразование. Это позволяет нам распространить определение
интеграла на любую функцию f {t), принадлежащую лебе-
говскому L^, с помощью следующего приема.
Предположим, что имеется последовательность f„{t)
действительных функций, которые принадлежат iL^ и
удовлетворяют условию
1
flfn(^)-f(m'cit^O. (1.53)
о
Ясно, что если задана f^L^, то найдется такая
последовательность. Каждая функция из L^, измеримая по Лебегу и
интегрируемая с квадратом по Лебегу, может быть
аппроксимирована функциями с ограниченными производными.
Это не проблема.
Образуем F^{a), определенные равенством
1
^n(^) = ffn(^)dx(t^ а). (1.54)
о
1
J [Р„(а)-F„(a)l2da=f [/„(t)-/„(t)f dt. (1.55)
0
1
f[f„(i)-fm(O]'dt->0. (1.56)
0
если тип независимо стремятся к бесконечности.
Теперь применим теорему Рисса—Фишера. Если мы имеем
последовательность функций (/^„(а)}, принадлежащих L^,
таких, что
Тогда
а
о
/[^„(«)-
■F„{a)fda-^0, (1.57)
СЛУЧАЙНАЯ ФУНКЦИЯ - ФУНКЦИЯ ВРЕМЕНИ И СОСТОЯНИЯ 25
ТО существует некоторая функция от а, к которой эта
последовательность сходится в среднем
F{a) = \.i.m.F^{o). (1.58)
/г->оо
Можно доказать, что /^(а) не зависит от того, какая
последовательность [Pfi^^)] [^^- (^-54)1 ^^ аппроксимирует,
и будет одной и той же для всех таких
последовательностей.
Пусть теперь, по определению,
1
F(a) = j f(t)dx(t, а). (1.59)
о
Определение (1.59) имеет смысл для почти всех значений а.
F(a) есть функция из L^. Нетрудно убедиться, что
1 1
j F'^(a)doi = j P(t)dt. (1.60)
о о
Итак, мы распространили наш интеграл на все функции,
принадлежащие пространству L^ Лебега.
ЛИТЕРАТУРА
1. Wiener N,, Generalized harmonic analysis, Acta Math., 55»
117—258 (1930).
2. P a 1 e у R. E. A. С. and Wiener N., Fourier transforms in tlie
complex domain, Colloquium Publication № 19, American
Mathematical Society, New York, 1934.
Лекция 2
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ
И ИХ СРЕДНИЕ ЗНАЧЕНИЯ
Предположим, что
Ранее я определил
cp^L2 на [О, 1].
j^(t)dx(t, а).
(2.1)
(2.2)
Как вы помните, x(t^ а) является функцией „броуновского
движения", которую я определил совершенно точно. Затем
я доказал, во-первых, что
1 1
j da j<j^(t)dx(t, а) = 0 (2.3)
и что
J й?а J ср(/) dx {t, oi)\ = j f (0 dt, (2.4)
Здесь cp(^) — действительная функция.
Из лекции 1 следует, что если заданы x(t^, а), Jc(^2' °^). • • •
...,x(t^j, а), где t и а лежат между нулем и единицей,
то для нечетных п
Гх(^1, а)х(^2' ^) • • • ^{^п* 0!,)d(X=::0
(2.5)
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 27
и для четных п
1
г X (^р а) X (^2» ее) , , . д: (^,^, а) йа =
"= S П / ^ (О' ^) ^ (^^' ^) ^^' (2-6)
где сумма берется по всем способам разбиения п элементов
/j, ..., tfj^ на пары, а произведение — по всем парам
данного разбиения. Отсюда сразу следует, что
11 1 1
J й?а J cpi (^i) dx (^1, a) J cp2 (^2) d^ {h> a) • • • / Tn (^J dx (t^^, a)
00 0 0
(2.7)
будет суммой членов, подобной правой части равенства (2.6).
Раскрывая (2.7), получаем
1 1 1
j da j cpi (t{) dx (^1, a) J срз (^з) ^^ ih* ^) • • •
0
1 1
f T. (^J ^-^ (^.> ^) = S П J T; (^) T/^ (^) ^^- (2-^)
0 0
1
0
Допустим, что
^'.(^1. .... ^.) = ?i(^i) ... ТЛ^Л (2.9)
где все ср принадлежат L^. Более общо, я буду пользоваться
суммой таких произведений. Именно
Knih ^„) = 2т,('^1)-.-?„Ю- (2.10)
Тогда для нечетных п
1 1 1
fdaf... J dx (Tj. a) ... dx (x„. a)K, (^^ ',)=. 0, (2.11)
0 0 6
28 ЛЕКЦИЯ2
a для четных
1 1 1
(da J .,. f dxi'z^. a) .,, dxi'z^, ^)f<n(b ^л)=^
0 0 0
1 1
*^2 /^^1 • ' • f^^m^ni'^V h* V Ь ^m» ^m). (2-12)
0 0
где 2m = п. Иными словами, сомножители/C^
перемножаются, а сумма берется по всем способам разбиения на пары.
Будем считать, что /С„ симметричны, так что порядок
интегрирования безразличен. Легко видеть, что если /С;, не
симметрична, то можно получить симметричную /С^ в
выражении этого типа, если взять все перестановки по т,
просуммировать полученные выражения и разделить на число
перестановок. При этом получится тот же самый
функционал, так как я складываю между собой одинаковые
функционалы, только с разными обозначениями. Тогда
1 1 1
j dd j . . . j dx (tj, a) . .. dx (т^, a) K^ (xj x^) =
0 0 0
1 1
=^(2m-~l){2m-3) . . ,{l)fdz,. . J dz^K,{x,^T, t^,tJ.
0 0
(2.13)
Другими словами, в случае симметричной К^ мы разбиваем
все т на пары, отождествляем т в каждой паре, интегрируем
и суммируем по всем возможным способам разбиения.
А сколько всего возможных способов? Ведь все эти
действия одинаковы, если К^ симметрична. Сколькими
способами можно разбить 2п элементов на пары? Я показал это
на прошлой лекции: (2п— \)(2п — 3) . . . (1). Итак, мы имеем
интеграл не просто для линейных функций, но и для
некоторого очень важного класса нелинейных функций.
Теперь разрешите мне взять другое множество
функций ср^(0- Пусть они будут действительные, ортогональные
на [О, 1] и нормированные. Рассмотрим выражения вида
1 г 1
jda\f<^^{t)dx{t^ а)
(2.14)
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ
29
где <p„^Z.^; (р„(0 должны быть ортогональными и
нормированными, и
f(l<i\f%(t)dx(t, а)
= 0 для нечетного v, (2.15)
fda\f:f„(t)dx(t, й)
о Lo
I
= (v—l)(v —3) ... (\)f (flit) di АЛЯ четного v. (2.16)
Ho
f^lit)dt=l.
(2.17)
И потому для четного v
1 Р 1
f da\ Г cp^ (t) dx {t, a)
= (v-l)(v-3) ...(1). (2.18)
Правая часть равенства (2.18) представляет по-прежнему
просто число способов разбиения v элементов на пары,
и если взять
1_ J,.exp(-4)^., (2.19)
(2;:)
ТО получится то же самое выражение, что и (2.18), как
я показал в прошлый раз.
Иными словами, если рассмотреть моменты выражений
f^^{t)dx(t, а).
(2.20)
то окажется, что они в точности равны выражениям (2.19).
Сказанное эквивалентно следующему утверждению: моменты
полностью определяют распределение (как мы знаем), и
распределение для величины (2.20) является гауссовским.
30
ЛЕКЦИЯ 2
Значит, вероятность того, что
«</тЛО^^(^, а)<^ +
da
равна
(27С)
—ту- ехр (— 4-^ du.
(2.21)
(2.22)
Итак, первое, что я установил, это то, что каждое из
выражений (2.20) имеет гауссовское распределение. Теперь
рассмотрим совместное распределение двух или большего числа
выражений вида (2.20). Посмотрим, что получится. Возьмем
I 11
{\f9^(t)dx(t. а) Jcp„(0^^(^, а)
X
X
f^p{t)dx{t^ а)
da, (2.23)
где (D^, ср^^ и ср различны. Мы взяли выражение из трех
членов как типичное; не будем ограничиваться двумя.
Вычислим теперь интеграл (2.23). Вспомним, как это
делается. М-ы разбиваем ср на пары всеми возможными
способами, интегрируем каждую пару и складываем. Но так
как ср ортогональны, интеграл от произведения различных ср
равен нулю. Следовательно, все такие пары, в которые
входят разные ср, выпадут, и останутся только пары,
содержащие одинаковые ср. И мы найдем, что
выражение (2.23) равно произведению моментов отдельных членов.
Иными словами, момент произведения равен произведению
моментов. Это позволяет нам утверждать, что распределения
независимы. Действительно, мы можем просто перемножать
моменты; легко показать, что тогда и распределения
перемножаются. Иными словами, все величины
^^^{t)dxit, а)
(2.24)
имеют одинаковое распределение (гауссовское, с одними и
теми же параметрами) и независимы одна от другой. Это —
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 31
во-первых. Повторяю, величины
1
fc^,{t)dx{t, а)
распределены по-гауссовски и независимы.
Во-вторых, если ср образуют полную систему, то, как
легко показать, многочлены от этих интегралов образуют
полную систему функций от а и любая функция от а может
быть выражена через них. Я пока не вхожу в детали
доказательства. Результат состоит в том, что если задана какая-
либо полная, ортогональная, нормированная система функций
от t, то задача о распределении функций сводится к задаче
о распределении этих интегралов, а они все имеют
одинаковые распределения (гауссовские и независимые, как я уже
объяснял). Это чрезвычайно интересно; вы увидите, что здесь
кое-что напоминает коэффициенты Фурье. Формально
1
f^,(t)dx(t^ а) (2.25)
о
есть коэффициент Фурье для
-^x(t. а) (2.26)
ПО отношению к функционалу ср. Однако он не существует
в обычном смысле
Это недифференцируемая функция. Если бы мы имели
дифференцируемую функцию, скажем F{t), то интеграл
1
j P{t)^^{t)dt (2.27)
о
был бы коэффициентом Фурье для F {t). Обозначим его
через а^, тогда
оо 1
2ИJ^ = J/^^(0^^. (2.28)
о о
Здесь все функции и числа действи'гельные. Пространство
таких последовательностей коэффициентов называется гиль-
32 ЛЕКЦИЯ2
бертовым пространством. Это — действительное гильбертово
пространство. (Позже я перейду к комплексному
гильбертову пространству, но в настоящий момент ограничимся
действительным.) Однако коэффициенты
1
^.(«) = /тЛО^^(^. а) (2.29)
о
не образуют последовательности со сходящейся суммой
квадратов. Они имеют независимые гауссовские распределения.
Вероятность того, что сумма квадратов конечна, равна нулю.
Так что я получаю нечто очень похожее на гильбертово
пространство, но не совпадающее с ним. В гильбертовом
пространстве последовательностей сумма квадратов
коэффициентов конечна. Здесь же коэффициенты имеют
независимые гауссовские распределения. Это пространство я назову
дифференциальным ^).
Существует несколько путей дальнейшего продвижения.
Сначала предположим, что берется другая полная
последовательность ортогональных и нормированных функций {^,^(0}
и рассматриваются
1
j^^{t)dx{t. а), (2.30)
/■
и сравниваются с
1
\^{t)dx{t, а). (2.31)
о
Эти две случайные величины будут иметь одинаковое
распределение, потому что, если ср^^ заменить на ф,^
гауссовские свойства интеграла не изменятся. Зададим
линейное преобразование, которое переводит Т^ ^ Фл " любое
множество ср^ в множество ф^^. Такое преобразование
называется унитарным. (Это преобразования довольно общего
типа, которые не меняют интеграла от квадрата функции.)
Я говорю о действительных функциях и могу писать
ФЛО=^?ЛО. (2.32)
где и—действительное унитарное преобразование. Чему
') Термин „дифференциальное пространство" введен Н.
Винером в работе „Differential space", Journ. of Math. Phys.y 11, № 3,
131—174 {\923У—Прим, перев.
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 33
ЭТО соответствует для а? Я могу вернуться назад от
распределения для
JcpJO^^C^ а) (2.33)
о
к значениям а. Рассмотрим особенную систему функций ср^^СО.
известных под названием функций Уолша. Эти
функции обладают свойством быть линейными комбинациями
всех таких функций, которые равны 1 на интервале
[^/2''. (^ + 1)/2"]. где 0<^<2'', и нулю вне его;
характеристические функции таких множеств в свою очередь
являются линейными комбинациями функций Уолша. Первая
функция Уолша равна 1 на всем интервале (О, 1). Следую-
ш.ая равна 1 на первой половине интервала и —1 на второй.
Она ортогональна первой. Следуюш.ая функция равна 1
на первой четверти, —1 на второй, 1 на третьей и —1 на
четвертой. Она ортогональна обеим предыдущим.
Следуюш.ая функция равна 1 на первой четверти, —1 на второй,
— 1 на третьей, 1 на четвертой. Это и есть функции Уолша;
я укажу обш.ее правило их построения. Я беру функцию,
которая равна 1 на первой 2" -й доле интервала (О, 1),—1 на
второй, 1 на третьей, —1 на четвертой, 1 на пятой и т. д.
Это п-я функция Хаара. Затем я беру произведение
функций Хаара — двух, трех и т. д. Получающиеся функции ср^
и есть функции Уолша. Любая из функций Уолша на
достаточно широком интервале принимает значения 1 и —1,
тогда как другая функция Уолша на этом интервале равна 1
или —1. В результате функции Уолша оказываются
ортогональными друг другу и нормированными.
Заменяя ср функциями Уолша, возьмем
1
j i^(t)dx(t, а), (2.34)
о
где 0) (t) — одна из функций Уолша от t. Отсюда я могу получить
а, так как имею интегралы и приращения х на любых двоичных
интервалах. Тогда можно перейти к процессу, с помощью
которого я получал а. Далее, если я перехожу от некоторой
последовательности ортогональных функций к функциям Уолша, то я
могу сказать, что интегралы вида (2.34) должны соответствовать
3 Зак. 2305. И. Винер
34
ЛЕКЦИЯ 2
интегралам от функций Уолша, и я получаю новую
переменную а, я получаю взаимно однозначное точечное
отображение новых а на старые, и это отображение сохраняет
интеграл по любому интервалу. Другими словами, делая
это преобразование, я получаю следующий результат:
1 1
J и [ср, (01 dx (t, а) = J ф, (t) dx (^, 7а), (2.35)
о о
где Та — сохраняющее меру преобразование. Другими
словами, я могу заменить унитарное преобразование в
пространстве ср сохраняющим меру преобразованием в
пространстве а. Это очень важно.
Нескслъкими, достаточно простыми способами можно
обобщить этот материал. Мне хватит времени на два обоб-
щенля: а) обобщение по области ^, ^ не от О до 1, а
Рис. 2.1.
от —со до оо (что очень важно при рассмотрении
спектральных проблем) и б) переход от действительного
дифференциального пространства к комплексному. Займемся
первым. Возьмем ось t и разделим ее на интервалы (О, 1),
(1, 2), (2, 3), (—1, 0), (—2. —1) и т. д. Предположим,
что мы имеем кривую броуновского движения в каждом
из интервалов (рис. 2.1). Неважно, где именно в каждом
из этих интервалов я начинаю строить кривую броуновского
движения, так что я могу отправляться от начала каждого
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 35
интервала. Действительно, броуновское движение
симметрично, так как приращения симметричны, если мы
отправляемся из начала или из конца интервала. Кривая
броуновского движения определяется последовательностью
функций x{t, а^). Здесь а^ — переменная, лежащая между
О и 1. Я покажу, что можно представить всю эту
последовательность функций с помощью одной переменной а,
лежащей между О и 1, и для этого единственного а будет
определено распределение меры, обобщающее все
распределения мер для всех других а. (Здесь п меняется от —со
до со.) Расскажу, как его получить. Я беру а^, а а^ можно
представить единственным образом в виде двоичной дроби
(за исключением множества а^ меры нуль):
ao = 0.aoi«o2«o3 •••» (^•^б)
и для а^ имеем
aj = 0.aiiai2ai3 ... (2.37)
и т. д. Таким образом, я получаю счетное множество знаков,
расположенных в двойной последовательности. Я могу
переставить их в одну последовательность множеством разных
способов. Я могу, например, двигаться вдоль пунктирной
линии
/ / / ^
«/ = •«// /iz/is^ocj^ ■- (2.38)
и получить
• ^2l^2Z^23y^Z<i '
^»°^01°^02°^11*^21°^12°^03^4°^13°^22 •
Эта последовательность даст мне по-прежнему одно
двоичное число, лежащее между О и 1, и такое соответствие
почти всюду взаимно однозначно. К тому же, если задано
некоторое множество интервалов различных а, то мера
новых а, соответствующих указанному множеству
интервалов, — это просто мера одного определенного интервала.
Так что это преобразование измеримо. И оно сохраняет
меру при переходе от бесконечного числа одномерных
интервалов к одному одномерному интервалу. Обозначим
новое переменное через а без индекса. Раньше я имел
последовательность х^ (t, а), где х^ были различны для разных
36
ЛЕКЦИЯ 2
интервалов. Я привел все а.^ к одному а для интервала t
от О до оо. В случае —оо^^^оо отличие не
существенно.
Теперь из кривой рис. 2.1 я построю кривую рис. 2.2.
Я перенесу кривые в каждом интервале вверх или вниз так,
чтобы начало кривой в одном интервале было в то же
время концом в предыдущем для положительных п, и
наоборот— для отрицательных. Первый интервал оставляется
Рис. 2.2.
без изменений. Теперь, когда я все совместил, я обозначу
эту функцию X{t, а); X{t, а) определяется старыми x^{t, а).
Свойства X{t, а) аналогичны свойствам функции x(t, а).
Ее график выходит из нуля в начале координат, а
распределение для приращения на любом интервале гауссовское.
Интеграл от квадрата приращения на интервале
пропорционален длине этого интервала, и для неперекрывающихся
интервалов приращения независимы.
Пусть теперь имеется функция ср(/), принадлежащая L^
на бесконечном интервале, ср(^) можно разрезать на счетное
множество cp^j. Именно можно взять
О для остальных t,
91 (О =
(2.39)
% W =
fit). i€U. 2],
О для остальных t
(2.40)
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 37
и т. д. Получится бесконечная последовательность. Затем
я образую
и, по определению, считаю эту сумму равной
оо
j ^(t)dX(t, а). (2.42)
В этом нет ничего трудного, это — элементарная операция.
Таким образом, для любой функции из L^ я определяю
интеграл по всему бесконечному промежутку. Получаю
следующий результат:
р с» -1
j (^{t)dX{t, а)
[_—оо
2
dOL
J j (^(t)dX{t, a)\da= j<^'^{t)dt, (2.43)
где a—это новое a, a правая сторона составлена из суммы
частей. Кроме того, мы видим, что выражение (2.42) имеет
гауссовское распределение. Оно представляет собой сумму
большого числа членов с гауссовскими распределениями,
а ряд из средних значений квадратов этих членов сходится.
Выражения этого типа независимы при ортогональных на
бесконечном интервале функциях ср. И все, что мы имели
раньше, можно перенести на бесконечный интервал. Иначе
говоря, нет никакого различия между случаями, когда t
и ср берутся на [О, 1] и на интервале от —оо до со.
Теперь, когда это сделано, перейдем к комплексной
теории (безразлично, для конечного или бесконечного
интервала). В дальнейшем, в технических приложениях, с
которыми я буду иметь дело, я использую действительную
теорию. Комплексная же теория понадобится мне для
квантовой теории. Положим
cp(0 = Ti(0 + %(0. (2.44)
где cpi, ср2 действительны и принадлежат О. Таковы
наиболее общие ср, принадлежащие L^ в комплексном случае»
38
ЛЕКЦИЯ 2
1
(2)V^
г
(2.45)
Теперь построим
- 1 1 -|
J cpi (t) dx (t, a) - J cp2 (0 ^д: (^ P) +
0 0 J
г ^ ^
+ / J cpi (0 6fJC (^, P)+ Гср2(0й?л:(^ a) I
Lo 0
Когда я рассматриваю это комплексное выражение, я
рассматриваю просто действительную и мнимую части по
отдельности. Для перенормировки, так как мы имеем две функции,
а не одну, введен множитель 1/У^2. 1/^2 появляется
просто потому, что мы имеем теперь два нормированных
вектора, расположенных под прямым углом. Будем считать,
что, по определению, выражение (2.45) равно
1
\{t)dy(t, а, р). (2.46)
о
Это первый шаг. С помощью простых вычислений полу-
/■
чаем, что
J й?а J й?р и ср (О dy (t, а, р) Г = J I ср (О Р dt. (2.47)
Заметьте, что здесь присутствует квадрат абсолютной
величины, т. е. складываются квадраты действительной и
мнимой частей. Интегрирование производится по конечному
или бесконечному промежутку. Это просто способ записи.
Можно отделить части и работать с каждой в отдельности,
а затем сложить и найти все, что требуется. Предполагается,
что мы действуем так: мы берем x(t, a)-\-lx(t, р)
[вспомните, что это и есть y(t, а, р)] и сопоставляем. Мы уже
имели отображение для бесконечномерного случая, здесь же —
для двумерного. Можно записать а как двоичную дробь
а^О.а^Озаз . .. (2.48)
а также
и образовать
^0,р1р2рЗ
(2.49)
Это нам дает отображение единичного квадрата ар на y
ОТ О до U Теперь y{t, а, Р) определена как y(t, f) —
ОДНОРОДНЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИОНАЛЫ 39
функция комплексного броуновского движения. Заметьте,
что в каждом случае, переходя от конечного интервала
к бесконечному, или от действительной теории к
комплексной, я провел специальное построение и получил
в каждом случае вполне определенные функции.
Итак, мы имеем
1
fd-ilf^findyit. 7)Г-/19(ОГ'Л (2.51)
О
для конечного или бесконечного интервалов.
Рассмотрим теперь
f<^{t)dx{t, Т)- (^•52)
Что представляет собой распределение этого выражения?
Легко показать, что если взять дейстьительную и мнимую
части этого выражения, то каждая из них имеет гауссовское
распределение; эти гауссовские распределения одинаковы,
но независимы. Другими словами, теорию комплексных
броуновских движений мы свели не к независимым гаус-
совским действительным распределениям, а к комплексным
распределениям. Остается справедливым утверждение, что
унитарное преобразование функций от t порождает
сохраняющее меру преобразование ^ на [О, 1]. Но теперь мы
не ограничиваемся действительными унитарными
преобразованиями. На следующей лекции я вернусь опять к теории
ортогональных функций, определенных с помощью x(t, а),
Я соби ,аюсь построить анализ функций от а с помощью
различных степеней x(t, а); это столь же подходящий метод
анализа для нелинейных задач электротехники и
аналогичных областей, как для линейных задач — гармонический
анализ. Заметьте, что хотя я не входил в некоторые детали
при построении разбиений отрезка а от О до 1 и при
отображениях, которые я производил, я мог бы в каждом
случае проделать все аккуратно. x(t, а) или y{t, 7) — вполне
определенные функции, которые можно использовать так же
просто, как синусы и косинусы, при анализировании спектра;
именно это я и предполагаю сделать. Далее я использую эту
теорию для изучения спектра процесса на выходе системы
нелинейных осцилляторов со случайными входными
возмущениями и получу его в замкнутом виде.
Лекция 3
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ
Я намерен рассмотреть иерархию ортогональных
функционалов. Пусть мы имеем функцию двух переменных
^('^1> '^г)- Д*^^ ^^^^ чтобы у нас было достаточно
рабочих гипотез (часть из которых будет снята в дальнейшем),
возьмем конечную сумму для /C(ti, Т2):
/C(Xi, Т2) = 2а„ср„ЫтЛ^2)- (3.1)
Таким образом мы избежим хлопот, связанных со
строгостью. Теперь я буду работать с выражением вида
J Ja:(ti. ^^)dx(x^, a)dx('z^, a). (3.2)
Функция /C(ti, T2) предполагается симметричной, однако
в этом нет ограничения. Если она не симметрична, я
переставлю Tj, Т2, суммирую полученные выражения и разделю
на 2. Это не изменит функционала (3.2). Аналогичным
образом можно произвести симметризацию для функционала
Г Г Г/С(т1, Т2, Тз)й?х(т1, а)й?л:(т2, а)(1х{т^, а) (3.3)
и т. д.
Заметьте, что сумма двух выражений вида (3.2) — это
выражение того же вида, и аналогично сумма двух
выражений вида (3.3) имеет тот же вид. Функционалы вида (3.2),
(3.3) являются однородными полиномиальными
функционалами от броуновского движения. Однородный функционал
нулевого порядка есть/Cq. Однородный функционал 1-го
порядка равен
//С(т)^^(т, а); (3.4)
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ 41
однородный функционал 2-го порядка задается
выражением (3.2) и т. д. Теперь я могу построить неоднородные
функционалы какой угодно степени. Например,
J/Ci(T)6f^:(T. a) + /Co (3.5)
можно назвать неоднородным функционалом 1-й степени.
Такие функционалы являются функциями от а,
принадлежащими L?. Это нетрудно доказать, если сами ядра
принадлежат L?.
Теперь я поступлю следующим образом: сначала возьму
константу и нормирую ее; затем возьму однородный
функционал 1-й степени плюс константу, сделаю это выражение
ортогональным всем константам и нормирую его; затем
возьму однородное выражение 2-й степени плюс однородное
выражение 1-й степени плюс константу и сделаю его
ортогональным всем константам и всем функционалам 1-й
степени и нормирую его и т. д. Таким путем мы получим
иерархию функционалов различных степеней, каждый из
которых ортогонален всем функционалам низшей степени.
Это важно, так как даст нам возможность выражать
заданную функцию от а через ортогональные функционалы
разных степеней.
Начнем с нулевой степени, т. е. с постоянной /Сл. Сред-
нее значение квадрата Ко, есть /Со и его абсолютная
величина равна 1 (речь идет о действительной области). Итак,
если Kq равна плюс или минус 1, то мы имеем
нормированный функционал нулевой степени. Рассмотрим теперь
выражение 1-й степени типа (3.5). Оно должно быть
ортогонально всем функционалам нулевой степени. Заметьте, что
если броуновское движение заменить отрицательным, то
распределение не изменится. Следовательно, если умножить
первый член (3.5) на константу и усреднить, то среднее
значение будет нулевым. Умножая выражение (3.5) на
константу С и усредняя, мы получим CKq. Оно должно быть
нулем, чтобы выражение (3.5) было ортогонально всем
константам, а это возможно только в случае /Cq = 0.
Следовательно, все однородные функционалы 1-й степени
ортогональны всем функционалам нулевой степени. Постоянный
член должен быть нулем, чтобы выражение (3.5) было
ортогональным. Теперь я нормирую ортогональный функционал
42 ЛЕКЦИЯЗ
1-й степени
J ATj (х) й?л: (т, а). (3.6)
Далее,
1
J^a[J/Ci(T)^x(T, a)J = J/C?(t)^t. (3.7)
о
Итак, мы имеем категорию (однородных) функционалов
первой степени, ортогональных по а всем однородным
функционалам нулевой степени, они имеют вид
fK,{x)dx(z, а). (3.8)
J/C?(T)6fT=l. (3.9)
где
Мы получили уже две категории: нормированные
функционалы нулевой степени и нормированные функционалы первой
степени, ортогональные ко всем функционалам нулевой
степени.
Теперь выкладки станут немного более сложными.
Рассмотрим функционал второй степени вида
J J ^2 (^1. '^2) d^ (^1. ^) dx (Т2, а) + J /Ci (т) dx (т, а) 4- /Cq,
(3.10)
где /^2 симметрична. Предполагается, что /^2 представима
в виде суммы произведений, как в равенстве (3.1).
Требуется, чтобы выражение (3.10) было ортогонально всем
константам; для этого достаточно, чтобы оно было
ортогонально 1. Отсюда
J/C2(t, т)йfт-^-/Co = 0. (3.11)
Требуется также ортогональность выражения (3.10) любому
выражению
JC(T)6fx(T, а). (3.12)
Если умножить (3.10) на (3.12), то первый член — третьей
степени и имеет нулевое среднее; второй член — второй
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ 43
степени, последний член — первой степени и также имеет
нулевое среднее. Мы получаем
jA:i(T)C(T)6fT = 0. (3.13)
Это означает, поскольку (3.13) должно быть верно при
любой С(т), что /Ci(t)^0. а из (3.11) мы получаем
/Со = -//С2(^. ^)d'^' (3.14)
Следовательно, выражение, ортогональное всем
функционалам первой и нулевой степени, есть
I \ K^i'^i, '^2)d^i'^v 0L)dx{i2, а)— I /С2(х, т)й?т. (3.15)
Мы ортогонализировали выражение (3.15) со всеми
выражениями первой и нулевой степени, а теперь нормируем его:
возведем это выражение в квадрат и проинтегрируем по а
от О до 1:
Гй?а ( \ К2(^1, '^2)dx('z^, a)dx{i2, а)— | /СдС'^, '^)d'^\ •
о
(3.16
Получается
1
j d^{J j j j ^2(Ь> ^2)Л^з(^3' ^4)dx{^i, a)dx(T2, a)X
0
X dx (тд, a) dx (T4, a) — 2 j K2 ('c, x) cfx X
Xf f^2(^ub)dx{z,,a)dx(T2,a)+[fK2(^,^)dzJY{3A7j
Вспомним теперь наше правило: попарно отождествить
переменные и интегрировать. Имеется три способа попарного
отождествления переменных т^, Тз, Тд и т^ в первом члене
выражения (3.17): Tj и Tj, Тд и т^; Tj и Тд, Тз и т^; Tj и т^,
Тд и Тд. Вспомним, что /Сз можно сделать симметричной,
Из (3.17) получаем
[/ ^2(^. ^)^^]' + 2 J J К1 (Tj, Т2)^Т, ^Т2 - 2 [/ /^2 ('^. ^) ^^Т +
+ [J/C2(T, T)dzJ' , (ЗЛ8)
44 ЛЕКЦИЯЗ
где два первых члена получены путем отождествления
переменных Tj, Т2, Т3, Т4 различными способами. Суммируя,
получаем
2f JKliT,^ T2)^Ti^T2. (3.19)
Таким образом, мы получили вторую категорию
ортогональных функционалов. К ней относятся функционалы
J f ^2(Ь' Ъ)^х(^1, a)dx{x^, а) —J^2(^. '^)^'^. (3-20)
2j Ja:2(Ti. Т2)й?Т1Й?Т2=1. (3.21)
где
Я построю и третью категорию, чтобы дать это
почувствовать. Затем я перейду к общей теории. Возьмем
J J/л^зС'^!' ^2' '^з)^-^(^1' а)й?х(т2. cC)dx{x^, а) +
+ J Г/C2(ti, 'z^dx{'z^, a)dx{z^, а)-{- f Ki(^) dx (z, a)-\~K,
(3.22)
где /Сз—симметричная функция. Это неоднородный
функционал 3-й степени от x{t, а). Он должен быть ортогонален
константам, функционалам 1-й степени и функционалам
2-й степени. Вначале возьмем константу. Среднее значение
первого члена выражения (3.22) равно нулю, так как он
3-й степени; среднее значение третьего члена также равно
нулю. Остается среднее значение второго члена
J/C2(T, T)dz (3.23)
и константа Kq. Таким образом, мы получаем
J/C2(T, z)dz+Ko = 0. (3.24)
Кроме того, выражение (3.22) должно быть ортогонально
любому выражению
j C{'z)dx{z, а). (3.25)
Умножаем (3.25) на (3.22) и усредняем. Так как К^
симметрична, все способы разбиения т^, Т2, Тд на пары эквива-
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ 45
лентны, и мы получаем
3 J J/CaCTi, Tj. z)C{x)d'zdz^-^ j Ki(x)C(T)dz = 0 (3.26)
для всех С(т). A так как С(т) произвольны, то функция,
ортогональная всем С(т), есть нуль. Следовательно,
^/^з(^1' '^1' T)cfTi-f A:i('c) = 0 для всех т. (3.27)
Это необходимое и достаточное условие для
ортогональности функционала (3.22) линейным функционалам. Далее,
мы умножаем выра кение (3.22) на
J JC(G^, G^)dx(a^, a)dx(G^, a). (3.28)
где C(aj, 02) симметрична, и затем усредняем. Это дает
выражение пятой степени. Первый и третий члены этого
выражения имеют нулевые средние значения. Имеем
Г С (а, а) do Г К^ (т, т) й?т -f- 2 Г Г С (tj, Т2) К2 (^1, ^2) ^'^i ^"^2 +
+ /Co JC(a. G)dG = 0, (3.29)
где первый член получен отождествлением а с а, т с т,
а второй — отождествлением ост. Если использовать
равенство (3.24), то видно, что сумма 1-го и 3-го членов
в равенстве (3.29) равна 0. Какова бы ни была C(aj, 02),
выражение (3.29) должно быть нулем. Но любая
симметричная функция, которая ортогональна всем симметричным
функциям, равна тождественно нулю. Поэтому Л'2 есть
тождественный нуль, а из (3.27) мы получаем
A:i(t) = —3 Г/<'з(т1, Tj, т)й?Т1 для всех т. (3.30)
Подставляя равенство (3.30) в выражение (3.22), находим,
что наш функционал 3-й степени имеет вид
/ J/^з('^1' ^2- Ъ)^^('^1' ^)dx{x^, a)dx{x^, а) —
— 3 J J/^aC^i. ^1. ^)dz,dx{z, a). (3.31)
46 ЛЕКЦИЯЗ
Это выражение ортогонально всем константам, линейным и
квадратичным функционалам, но еще не нормировано.
Должно быть
1
\ = I da 1 1 I K^i^i, Т2, Тз)й?л:(т1, ajdxix^, a)dx('z^, а) —
о
— 3 J J/CaCTi, Tj. 'z)dxidx{x, а)Т. (3.32)
Раскрывая это выражение, получаем
1
l=J^a[J JJ J JJ/C3(Ti. Т2, Тз)/Сз(т4. т^. Тб)^х(т1, а)Х
о
y<^dx(i2, OL)dx(x^, a)dx(x^, a)dx(z^, a)dx(^Q, a) —
— 6 J J J JJ/Cs(ti, Тз, Тз)А:з(а1, Oj, x)dGidx{T, a) X
y(^dx(i^, a)dx{z2, oi)dx{i^, «) +
+-9 J J J J /Сз (tj, Tj, T2) /Сз (тз, Тз, T4) cfTj й?тз й?л: (тз, а) dx (т^, а).
(3.33)
Первый член в правой части равенства (3.33) —
шестикратный интеграл, и мы можем различными способами
отождествлять переменные; мы можем, в частности, отождествить
каждое т первой скобки с каким-либо т из второй. Для
первого т это делается тремя способами, после чего для
второго остается два способа, а для третьего — один, так
что мы получаем
3! J J ^/^3(^1. т<2. Тз)cfTj й?Т2й?Тз (3.34)
для первой комбинации. Во второй комбинации т из первой
скобки выражения (3.33) отождествляется с каким-либо х
из той же скобки, а одно т остается и отождествляется с х
из другой скобки. Тогда получается
////Сз(Т1, Т„ т)/Сз(Т2. Тз. ^)dx,dX2d'Z (3.35)
в качестве типичного члена. Сколькими способами можно
получить этот член? Один элемент из первой скобки может
ОРТОГОНАЛЬНЫЕ ФУНКЦИЙ 47
быть выбран тремя способами; то же и для второй скобки.
Таким образом, мы можем это делать 9 способами. Итак,
первый член в равенстве (3.33) содержит выражение (3.35)
9 раз плюс выражение (3.34). Теперь возьмем
1
о
у(^(1х{%^, a)dx(x2y ^)dx(i^, а), (3.36)
т. е. второй член (3.33). Здесь т можно отождествить только
с одним из Tj, Т2, Тд, и, значит, остающиеся т придется
отождествить между собой, так что мы получим в точности
то же выражение, что (3.35), только множитель будет
—6 X 3. или —18. Остается последний член равенства (3.33).
В нем отождествляются Тз и т^:
9/[//Сз(т1, Tj, x)dx,Jdx. (3.37)
Равенство (3.33) принимает вид
31 J JJ/Ci(Ti, Т2, Тз)й?Т1Й?Т2Й?Тз4-
+ 9 J J J/C3(ti, Tj, т)А:з(т2, T2, t)cfTj й?Т2 й?т—
— 18 f г J/C3(Ti, Tj, т)А:з(т2, Тз, x)dx^d^2d^ +
4- 9 / [ J /Сз (Tj, Tj, t) dz,J dx. (3.38)
Последние три интеграла в выражении (3.38) одинаковы —
стоит только переименовать т. Так что мы получаем
J J/Л^з('^1' ^2> 4)dx{z^, a)dx{z2' ^)dx{x^, а) —
— 3 f j K^i^v h' '^)d'z^dx('z, a). (3.39)
где
31 J J J/C3(Tb ^2, Тз)й?Т1Й?Т2Й?Тз=1. (3.40)
Я построил первые три ортогональных функционала.
Я мог бы построить и четвертый. Функционал 4-й степени
будет содержать члены 4, 2 и 0-го порядка и т. д. Во всех
48' ЛЕКЦИЯ 3
случаях старший член (член высшего порядка) определяет
все остальные, а интеграл от квадрата ортогонального
функционала, если он не нормирован, равен интегралу от квадрата
старшего симметричного члена с соответствующим
множителем (для трех переменных с множителем 3!, для п
переменных с множителем п\).
Рассмотрим еш,е раз функционалы второго порядка
(случай функционалов 3-го порядка аналогичен).
Заметьте, что функции от а (3.15) соответствует
нормированная симметричная функция от Tj, Тз таким
образом, что если разделить К^ в выражении (3.15) на ]/2,
то интеграл от квадрата (т. е. выражение (3.16)) будет
равен интегралу от квадрата, входяш.ему в равенство (3.21),
и будет равен 1. Применим теперь теорему Рисса — Фишера.
Предположим, что имеется последовательность симметричных
функционалов 2-го порядка [K^ni'^i* '^2))- Тогда если
Ит Г Г[/С2т(^1. ^2)-^2.(^1. T2)]2^Ti^T2 = 0, (3.41)
m, /г ->► со *^ «^
ТО функции К2п сходятся В среднем к некоторой функции
K^i'^i, ^^2), а выражения вида (3.2) сходятся в среднем по а
к некоторому пределу, который не зависит от выбора
аппроксимируюш.ей последовательности. Это значит, что мы,
отправляясь от функций /C(ti, Т2) весьма специального вида,
как в равенстве (3.1), где были конечные суммы
произведений функций из L?, и используя сходимость этих функций
в среднем, можем определить некоторый оператор от а,
предельный для приближений в среднем; определим этот
оператор как
^2(^2» а) = //лГ2(т1, T2)cfx(Ti, a)dx{z^, о) — ^ К<^{х, х) dx.
(3.42)
Заметьте, что для каждой функции К^, которая является
симметричной (или может быть сделана симметричной)
и принадлежит L?, я буду определять функционал G2{K2, а).
Мне придется здесь быть осторожнее: это не означает, что
представление (3.42) можно сразу использовать, так как
второй член выражения (3.42) может не суш.ествовать даже
в том случае, когда /^2 принадлежит L^ по обеим
переменным. Поэтому необходимо добавочное условие
/СзСт, т)й?х < оо, ' (3.43)
f'
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ 49
Однако все же можно определить ^/2(^2» ^) ^^^ вполне известную
функцию от а, принадлежащую 1?, если /^2 — симметричная
функция из L^, Аналогично определяются С/з(/Сз, а), G^(Ki, а),
Gq{Kq, а); последний в действительности не зависит от а.
Забегая вперед, предположим, что все это уже доказано
в общем случае любого п, что в действительности я могу
сделать позднее. Итак, имеется иерархия функционалов от а.
Легко видеть, что все функционалы одного уровня образуют
замкнутое множество, т. е. предел в среднем
последовательности функционалов данного уровня принадлежит тому же
уровню. Другими словами, мы получаем последовательность
классов функционалов от а, принадлежащих L?, Любой
функционал данного класса ортогонален любому
функционалу другого класса. Если взять из каждого класса по
определенному /Cq, /Cj, К2 то получится последовательность
функционалов от а. Я утверждаю, что можно доказать, что
наше множество функционалов полно, так что любая
функция от а, принадлежащая L^, может быть приближена
с помощью полиномиальных функционалов из этого
множества, и что, так как G ортогональны, эти приближения
представляют собой проекции функции от а на следующие
друг за другом классы, или пространства, функций от а.
К этому мы перейдем' в следующей лекции.
Любую данную функцию F {а), принадлежащую L^, можно
представить единственным образом в виде
7^(a) = I.i.m.[Go(/Co. a) + Gi(/Ci,a)+...^G;v(/C7v. а)],(3.44)
N ^ оо
причем ранее определенные члены не изменяются при
увеличении числа членов в этом приближенном выражении для F {о).
Это совершенно аналогично обычному ортогональному
разложению, за исключением того, что здесь мы строим
ортогональное разложение по целым классам функционалов —
именно это и позволяет нам получить каноническое
представление для любой функции от а, принадлежащей L?.
Мы увидим, что такое каноническое разложение по
функционалам от случайных функций чрезвычайно удобно; мы
рассмотрим его детально в следующей лекции.
В действительности мы имеем нечто большее, чем
простое сознание того, что возможно разложение, указанное
равенством (3.44). Имеются приемы, с помощью которых
4 Зак. 2305, Н. Винер
50 ЛЕКЦИЯ 3
по заданной функции от а строятся соответствующие
компоненты, т. е. выбираются /Cq, К^, Л'г» • • • • Эгим мы и
займемся. Обратите внимание, что это разложение аналогично
разложению Фурье, т. е. такому разложению, в котором
коэффициенты „представления" по функциям определяются
путем интегрирования. Наше разложение другого типа; оно
зависит от x{t, а). Но x{t, а) — вполне определенная
функция; мы уже ее определили. Наше разложение отличается
от обычного разложения Фурье, поскольку мы имеем
счетное множество функционалов, но тем не менее общая задача
остается той же, а именно найти разложение, если задана
функция от а.
В следующей лекции я покажу, как найти каноническое
разложение для любой функции от а, принадлежащей L^.
Затем мы используем это разложение в различных задачах,
связанных со случайными функциями. В частности, мы
используем его для следующего. Предположим, что имеется
функция не только от а, но и от 7^а, где Г^а получается
в результате замены л: (т, а) на х(^ + т, а). Мы уже видели,
что такое преобразование а сохраняет меру. Я собираюсь
показать, что если делается такое преобразование, то каждый
член разложения F (Т^а) получается из соответствующего
члена разложения F (ol), и они не смешиваются. Тогда
я смогу вычислить
^daF(T^a)F(al (3.45)
о
/'
используя тот факт, что нормированность и
ортогональность G по а переходит в нормированность и
ортогональность G, в ядрах которых сдвинуты значения аргументов
для соответствующего множества переменных. Таким путем
мы сможем находить автокорреляционные функции
нелинейных операторов от броуновского движения и их спектры.
ЛИТЕРАТУРА
Wiener N., Response of а nonlinear device to noise, Report № 129^
Radiation Laboratory, M. I. Т., 1942.
Cameron R. H. and Martin W. Т., Tlie Ortliogonal development
of nonlinear functionals in series of Fourier-Hermite functionalsi
Annals of Mathematics, 43, 1947, pp. 385—389.
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ 51
Wiener N., Seminar in nonlinear networks, Research Laboratory
of Electronics, February, 1949 (не опубликована).
Wiener N.. Mathematical problems of communication theory,
summer session lecture notes, 1953—1954, M. I. T. (не
опубликована).
Возе A. G., A theory of nonlinear systems. Report № 309, Research
Laboratory of Electronics, M. L Т., May, 1956.
В a r r e i t J. F., The Use of functionals in the analysis of nonlinear
p'lysical systems. Statistical Advisory Unit Report № 1/57»
Ministry of Supply, G. B. (дата не указана).
F г i e d г 1 с h s K. O., Integration of functionals. Notes from a course
given at New York University, 1957 (не опубликована).
4*
Лекция 4
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ И АВТОКОРРЕЛЯЦИОННЫЕ
ФУНКЦИИ
Сегодня мы рассмотрим общую теорию разложений,
введенных на прошлой лекции. Мы имеем
^Л^)^/ • •• /^Л^1 ^J^-^(^i. а)...й?х(т^. а) +
+ /.../^.-1(^1 T.-i)^^('^i. а)...
...^х(т,_1. а)+ ... +/Со. (4.1)
Предполагается, что К^ обладает всеми свойствами
гладкости, которые потребуются. Я считаю К^ заданным.
Остальные К должны быть определены так, чтобы /^^(а) была
ортогональна как функция а любому интегралу
J... Jq(Ti, .... tJ^x(ti, а)^х...(т^, а), (4.2)
для которого т <in. При этом условии
1
JFl{o)da (4.3)
о
равен
1 1
JF^ (a)rfa = J[ J. . . jК,{о„ ... o„)dx{o„ a)...cfx(a„. a)] X
0 0
X[/...//C„(x, T„)rfx(T,. a)...rfx(T„. a) +
-4- Члены низшего порядка , (4.4)
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ И АВТОКОРРЕЛЯЦ- ФУНКЦИИ 53
так как все члены низшего порядка ортогональны F^^ (а)
на [0,1]. Чтобы выполнить интегрирование, мы берем все
переменные а и т, отождествляем их попарно всеми
возможными способами, интегрируем и складываем. Заметьте,
что если отождествляются две переменные о, то получается
выражение более низкой степени. Интеграл от произведения
такого члена и Р^^{сС) равен нулю. Поэтому остаются только
те члены, которые получены отождествлением каждой
переменной о с одной из переменных т.
Мы можем отождествить каждую переменную а с
переменной т только в первом члене F^(a)\ это производится п\
способами. Следовательно, я получаю
1
JFl{a)da^n\f ... JKli^zu ..., т J ^ti .. . й? v (4.5)
о
Другими словами, минуя вычисления, я получил формулу
для интеграла от квадрата ортогонального функционала F
степени п, по крайней мере для случая, когда К^ — конечная
сумма произведений функций из L^.
Воспользуемся теперь прежним рассуждением: для того
чтобы выражения вида (4.1) имели предел в среднем,
необходимо и достаточно, чтобы К^ сходились в среднем
к пределу. Равенство (4.5) сохраняется при этих условиях.
Общую функцию, которая получается из равенства (4.1),
я обозначаю через G^ (К^* ol), где К„ — симметричная
функция п переменных. Теперь определение G^ я распространяю
с помощью предельного перехода в среднем на все /С^,
принадлежащие L^ по разным переменным. Любое G^(Kfj, ol)
ортогонально любому G^(K^, ol), для которого тфп.
Следующий вопрос — полнота системы этих функций,
но мы фактически его уже разрешили. Система всех G^^
замкнута, как будет показано. Помните ли вы, как мы
получили наши а? Мы брали x{t, а) и определяли ее с
помощью t, которые задавались двоичными числами.
Предположим, что имеется некоторая функция
ср [х (tj. а) X (Т2, а) ... X (т^. а)], (4.6)
где т^ — двоичные числа некоторого порядка. Вспомните,
что, когда я определял кривую, проходящую через некоторый
ряд „отверстий" (рис. 1.9), я определял ее только через л:.
54 ЛЕКЦИЯ4
Другими словами, я определил меру для а с помощью
функций, которые зависели от значений x{t, а) во все
большем и большем числе двоичных точек. Легко использовать
это для доказательства полноты системы функций от л: (^, а)
в этих точках.
Действительно, ввиду полноты системы функций х'^е"^
легко показать, что ср^можно аппроксимировать полиномами,
проходящими через заданные точки. Следовательно, любая
функция от а, принадлежащая L^, может быть приближена
в среднем полиномами, зависящими от значений х или
разностей значений х в конечном числе точек. Так как эти
приближающие полиномы можно аппроксимировать
ортогональными полиномами, то мы получим по крайней мере
приближение требуемого вида. Следовательно, G^ образуют
полную систему, если К^^ пробегает все функции,
симметричные и принадлежащие L? по п переменным.
Итак, любая функция от а может быть приближена
суммой ортогональных функций G. Кроме того, если взять
сумму двух G П'й степени, получится член /г-й степени.
Если взять проекцию F (а) на множество всех членов
степени, меньшей, чем п, где п — степень старшего члена
в приближении для F, то при увеличении п эта проекция
не изменяется. Проекция проекции остается той же самой
проекцией.
Из предыдущего следует, что если F{a)^U, то мы
можем записать единственным образом
N
/^(а)=:1. i. т.20,(/С„ а), (4.7)
N->oo v = 0
причем улучшение этого представления выбором большего N
не изменяет младших G^, а только добавляет новые.
Теперь перейдем к задаче определения 0^, т. е.
определения К. Предположим, что я беру
0,(Q,, а), (4.8)
где 0^—известное G^^(Q^, а). Любое выражение такого
типа ортогонально всем членам равенства (4.7), кроме [х-го,
и мы имеем
1 1
J daF (а) О^ (Q^. а) = J О^ (К^, а) 0^(Q^, а) da. (4.9)
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ И АВТОКОРРЕЛЯЦ- ФУНКЦИИ 55
Все другие члены обращаются в нуль. Мы уже имели
формулу для атого интеграла
о
... fd^^K^(x„ .... VQ,(Ti. .... тД (4.10)
Чтобы это показать, возьмем сначала (Q^-\-K^^ в равенстве
(4.5), затем {Q^ — К^), результаты вычтем и разделим на 4.
Разделив на р.!, получим
J^ftj ... J^fT^AT^Tj. .... T^)Q^Ti. .... т^)==
= i^J^aF(a)O^Q^. а). (4.11)
о
Уравнение (4Л1) можно использовать для разных целей.
Вот одна из простейших.
Рассмотрим G^{Q^, а) при одном частном Q^, которое
мы определим так:
_ j 1. при любых т^(1 <^<[i). ^ft <^й <^ft + s;
'"^ \ О, при всех остальных '^^(1 ^k ^\i).
Это симметричная функция. Если выбрать такое Q , то
уравнение (4.11) сведется к
1 /i+e ti+e
jlJrfaF(a)0^(Q^, а)= / ... J К^{х, x^dz,...dx^.
О t, t
(4.13)
Из равенства (4.13) мы получаем
1
-±-jdc^F{a)Q^{Q^,a.) (4.14)
как среднее значение К^ на определенном s-интервале. Если
К^^ принадлежит L?-, то можно доказать, что эти средние
значения сходятся в среднем к К^. Следовательно, мы
указали процесс, с помощью которого можно точно
определить К^ и разложение для F (а).
56 ЛЕКЦИЯ4
Вывод: мы получили здесь разложение по членам, такое,
что если F (а) задана, то мы можем, интегрируя F,
умноженное на известные G, и переходя к пределу в среднем,
определить различные К и различные члены разложения.
Это аналогично теории разложения Фурье, в которой для
заданной функции из L^ не только утверждается
существование разложения типа (4.7), но указывается также, как
определить точно коэффициенты с помощью пределов в
среднем от некоторых интегралов. Это разложение так же важно
для нелинейных задач, как интеграл Фурье для линейных.
Есть и другие частные случаи Q^, с которыми можно
работать. Один из важнейших — такой, когда
Q^i^i '^[.) = Ti('^i)T2('^2) ••• ТД^Р.). (4.15)
где ср образуют последовательность ортогональных
нормированных функций. Между прочим, G^ не обязательно
должна быть симметричной. Всегда можно сделать ее
симметричной. Некоторые ср могут быть одинаковыми,
некоторые— разными. Можно получить разложение К по ср. Этим
я воспользуюсь позже.
Теперь предположим, что
оо
F(a) = l.i. т.20„(^„. а) (4.16)
/г = 0
и ЧТО
/С„ = /СЛЬ •••. ^«)- (4.17)
Заменим равенство (4.17) на
Kn^Knii + ^i i-\-\)- (4.18)
Ясно, что такая замена порождается сохраняющим меру
преобразованием а. Ясно также (если вспомнить способ
построения разных членов), что каждое К^ равенства (4.17)
переходит в соответствующее К„ равенства (4.18) при этом
преобразовании, а G^ переходят в G^,
Если обозначить это преобразование а как 7^, то
оо
F(7'cc) = 2g„(C ос), (4.19)
л = 0
где
/С;(х,. .... т„) = /С„(^-|-х, f + x„). (4.20)
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ и АВТОКОРРЕЛЯЦ- ФУНКЦИИ 57
Вначале я рассмотрю действительный случай, затем скажу
несколько слов о комплексном. Имеем
J F{T^a)F(a)da =
о
оо
п = 0
Xfif^i
fifx„.
(4.21)
Если К комплексные, то можно отделить действительную и
мнимую части, а окончательный результат будет
JF{T'a)F(a)da^^nlf ... JKA^i^ .... ^.) X
п = 0
Х/СЛ^ + ^1. .... t + i^)dT,...dT^
(4.22)
Нетрудно это доказать. Выражение (4.22) — это
автокорреляционная функция, полученная усреднением по а; а теперь
мы используем некоторые положения эргодической теории.
Если мы заменяем x{t, а) на x{t-\-G, а) — х(с, а), то мы
X
Рис. 4.1.
изменяем броуновское движение следующим образом
(вспомните, что t меняется от —оо до оо): вместо того чтобы
рассматривать движение от начала, мы относим его к точке Р,
как показано на рис. 4.1. Однако получается броуновское
движение с тем же самым распределением. Это
преобразование можно записать как
x(t-\-G, а) — X (а, а) = X {t, Г^а).
(4.23)
Это — сохраняющее меру преобразование а, порожденное
переносом. Это такое сохраняющее меру преобразование,
58 ЛЕКЦИЯ4
которое обладает свойством, известным под названием
метрической транзитивности.
Вначале я установлю вообще эргодическую теорему,
а затем применю ее для этого случая. Предположим, что
имеется некоторая переменная а и сохраняющее меру
преобразование Т, Рассмотрим группу Т\ такую, что
Т^^Т^2а= V^'rt,^ (4.24)
есть сохраняющее меру преобразование а. Пусть функция
Р(Т^а) принадлежит L^ и измерима по паре переменных
t и а. Эргодическая теорема Биркгофа гласит, что тогда
А
lim —- I f(T^a)dt существует для почти всех а. (4.25)
Л->оо ^ »{
Можно доказать, что множество значений а, для которых
значение этого интеграла лежит между нулем и ее,
измеримо* и инвариантно по отношению к каждому
преобразованию Т^.
Если преобразование Т^ обладает тем свойством, что оно
не имеет никаких измеримых инвариантных множеств меры,
отличной от нуля или 1, то для почти всех а предел
выражения (4.25) один и тот же. Это свойство преобразований Т^
называется метрической транзитивностью. Оно известно также
под названием эргодической гипотезы. Итак, если выполнена
эргодическая гипотеза, то
А
lim \ (f{T^a)dt--=--C (4,26)
для почти всех значений а.
Что такое С? Проинтегрируем по а
1 А 1
{ Cd^ = C=\\m -^ \ dt J daf(T^a). (4.27)
о ^~^°° о о
Так как /(а) абсолютно интегрируема, можно поменять
порядок интегрирования. Интегрируя сначала по t, получим
А 1
С = lim -^ J / (Т^а) dt = ^ f (а) г/а. (4.28)
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ И АВТОКОРРЕЛЯЦ. ФУНКЦИИ 59
Следовательно, для метрически транзитивных
преобразований среднее по времени для почти всех а совпадает со
средним по а.
Отсюда следует, что если требование метрической
транзитивности удовлетворяется, то
1 ■ А
Г F (Г^а) T(^do. = lim -i Г ^ {T^a)F(^da, (4,29)
так как
F{Ta.)F{a\ (4.30)
очевидно, принадлежит L^ как произведение двух функций
из L?^). Поэтому, если мы установим в нашем частном
случае метрическую транзитивность преобразований, мы сможем
определять временную автокорреляцию F {а) для почти всех а.
Вернемся к вопросу о метрической транзитивности.
Я утверждаю, что преобразование а, порожденное переносом
времени для броуновского движения, метрически транзи-
тивно, т. е. если' некоторое множество 5 значений а
инвариантно по отношению ко всем преобразованиям Т\ то его
мера равна О или 1. Изложу доказательство.
Рассмотрим некоторое множество 5 значений а и
предположим, что 5 измеримо. Суш,ествует теорема для
бесконечномерного пространства, в силу которой измеримое
множество значений а можно аппроксимировать конечным числом
интервалов на линии а. Конечное число интервалов в свою
очередь можно аппроксимировать конечным множеством
интервалов, соответствуюш^их двоичным делениям на линии а.
Таким образом, если дано множество 5, то суш.ествует мно-
') Здесь, по-видимому, допущены опечатки: равенство (4.29)
должно иметь вид
1 А
^ F(Pa) F(Tt-'a)doL= lim ~ f F (Pa) F (р-'а) dt.
0 0
Если требование метрической транзитивности удовлетворяется, то
для справедливости этого равенства достаточно, чтобы функция
F (Ра) F {Р-~ а) была интегрируема. Это условие выполняется для
рассматриваемых F{a). — Прим. перев.
60 ЛЕКЦИЯ4
жество S^, заданное с помощью конечного числа точек,
такое, что
m(S^-+-SfS)<e, (4.31)
Если мы берем T^S. и \t\ достаточно велик, то T^S^
не зависит от Sp т. е. если взять логические произведения
множеств (ST^Sy) или (T^SfS), то мера логического
произведения будет как угодно близка к произведению мер. Кроме
того, так как m(S) инвариантна по отношению ко всем 7^,
m{Sf) почти инвариантна. Используя все это в (4.31), мы
получим в пределе, поскольку т(8Л^=:^ m(S), что
т (S) т (Т% + т(T^S) m(S) = 2 [т (5) — [т (5)]^} < е (4.32)
для любого е. Поэтому
w^(5) —w(5) = 0, (4.33)
т. е. мера 5 равна либо О, либо 1.
Следовательно, операторы сдвига действительно
образуют метрически транзитивную, или эргодическую группу
преобразований.
Вывод: мы можем воспользоваться теоремой Биркгофа
и показать, что для почти всех значений о: (это все, что нам
требуется) временная автокорреляция F {а) совпадает с той,
которая получается из наших формул интегрирования как
среднее по множеству состояний.
Теперь мы можем двигаться дальше и получить настоя-
ш.ие спектры некоторых временных рядов, нелинейно
зависящих от x{t, а). В следующих лекциях будут рассмотрены
спектры для двух нелинейных случаев. Этот метод
применим также во многих других случаях, но я изложу довольно
подробно только два.
Один из этих случаев следующий:
ехр[/J/C(^ -т)й?х(т, а)1. (4.34)
По существу функцию такого рода мы получаем физически,
если возьмем часы с вращающейся стрелкой, но стрелка
прикреплена не плотно и подвергается броуновским
возмущениям. На самом деле, выражение (4.34) описывает
вращательное броуновское движение, которое зависит от пара-
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ И АВТОКОРРЕЛЯЦ. ФУНКЦИИ 61
метров к. Мы перейдем к нему в следующей лекции и
рассмотрим спектр случайного движения, описываемого
выражением (4.34).
Физически это очень важное явление; с ним сталкиваются,
например, в том классе задач, которыми занимается в
настоящее время проф. Джеральд Закариас, а именно
создание очень точных часов. У него нет достаточно точного
прибора для измерения времени. Измерение времени зависит
от того, какие используются часы. Если ваш прибор для
считывания времени неточен, но сами часы очень точные,
то как ошибки измерений будут влиять на спектр? Я покажу,
что спектр тогда будет иметь вид рис. 4.2, Я изобразил
ФцСо))
этот спектр с нулевой центральной частотой, но я мог бы
получить такой спектр вблизи любой частоты. Влияние
неточности измерений расширит спектральную линию в полосу.
Вид этой полосы, как мы увидим, в действительности нега-
уссовский.
Второй случай аналогичен, но порядок рассматриваемого
здесь выражения на единицу выше, чем у предыдущего.
Рассматривается броуновское движение, воздействующее
квадратично на скорость стрелки,
ехрГ/ Г Г ATsC^ + 'Ci, t-\-x^)dx{x^, a)dx{x^, а)1. (4.35)
Каков будет спектр? Я опишу его в общих чертах,
впоследствии мы его вычислим.
Выражение (4.35) обладает спектральной линией на
нулевой частоте. Кроме того, появляются боковые полосы. Их
очертание примерно показано на рис. 4.3. Однако я покажу.
62
ЛЕКЦИЯ 4
ЧТО В некоторых особых случаях очертание боковых полос
будет несколько иным. Появится углубление в начале
координат, как показано на рис. 4.4.
Я начал эту работу потому, что натолкнулся на спектр,
обусловленный, конечно, случайными воздействиями, у кото-
Фп (со)
рого были боковые полосы с углублением в центре. Он
получился при изучении мной колебаний биотоков мозга. Как
вы знаете, электроэнцефалограмма выражает напряжение
как функцию от времени. Спектр такой функции можно
найти известными методами и притом с высокой степенью
точности. Я проделал это экспериментально и нашел, что
Фц СО))
Рис. 4.4.
явление углубления здесь имеет место. Я попытался дать
ему возможное объяснение и построить рабочую модель
системы, которая могла бы его воспроизвести. Попытка
получить рабочую модель вовлекла меня в эту работу.
Дело в том, что мы на самом деле получаем нечто
в этом роде. На следующей лекции мы начнем оценивать
эти выражения.
Лекция 5
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. I
Сегодня мы рассмотрим функцию F^{(i), заданную
равенством
y'„(a) = J... Ja'„(t, т„)й?х(т,. а)...й?х(т„. а). (5.1)
Надо представить F^{cl) в виде, который мы называли
каноническим,
п
/^Л^) = 2^Л^Л^1 ^Д °^1. (5.2)
где [Gj^]—ортогональные функционалы. Надо точно
определить /-^(t^i т^). Для этого будет полезна следующая
лемма.
Пусть имеется выражение
п
S/ •• • /^^("^1 ^k)dx{y^. а) ...dx(xj^, а); (5.3)
требуется умножить его на
f '" f ^п (^1. • • . ^п) dx (а,, а) . .dx (а^, а) (5.4)
и проинтегрировать по а от О до 1. Если я введу
интегрирование K^io^, , а^) под знак суммирования, то
выражение, которое надо оценить, примет вид
1 п
fda^f ... fK„(c, a„)/?ft(T„ .... х,)Х
X dx (а^, (х) . , . dx (а^, а) dx (т^, т) . . . dx (т^, а). (5.5)
64 ЛЕКЦИЯ5
Вспомним, как это интегрируется почленно. В каждом члене
имеется k-\-n переменных. Мы разбиваем их на пары всеми
возможными способами, отождествляем переменные каждой
пары и интегрируем. Поскольку п больше или равно k,
ясно, что при попарном отождествлении переменных мы
должны отождествить несколько переменных а друг с
другом, прежде чем перейти к отождествлению а с т, так как
переменных о больше, чем т. Если я это сделаю и
проинтегрирую только по тем переменным а, для которых
парными являются также а, то в каждом члене суммы я получу
выражение вида
j'" j К^ (aj 0^, Xj, Xj, X2, X2 X,, XJ d\.., dl,, (5.6)
где n = k-\-2v. Затем я начну отождествлять а с т и
проведу остальные интегрирования. Ясно, что при таком
двухстепенном интегрировании я получу в точности тот же
результат, какой получился бы, если бы я интегрировал по всем
парам а и т одновременно.
Сколько раз выражение вида (5.6) повторяется в каждом
из членов суммы? Сколькими способами можно выбрать 2v
из п переменных? Ясно, что (^ ) способами; здесь ( ^^\ —
биномиальный коэффициент
&
' (Ъ)\{п — 2^)\'
(5.7)
Но нужно не только выбрать 2v переменных, но и
отождествить их попарно. В результате добавится (2v—l)(2v—3)...(1)
членов. Следовательно, при интегрировании выражения (5.5)
можно заменить ка>1У1ый член
/... J>.(^i ^n)dx{o,, a).,.dx(a„^ а) (5.8)
на
J... J(2"J(2v-l)(2v-3)...(l)/... //С„К •••. ^..
Xj. Xj X,. XJdXj ... dX,dx(a„ a) ... dx{o^, a). (5.9)
Применение к задачам частотной модуляции, i 65
Далее, я могу упростить коэффициент следующим образом:
(2"^)(2v-l)(2v-3)...(l) = ^2^^^^
^' ^ (5.10)
(л —2v)! 2М
Если выражение (5.3) представляет G-функцию, то эта
лемма применяется к интегрированию следующего
выражения:
1
/^а J ... J/C^^i ^J^-^(^i. а) ••• ^-^К. а)Х
ХО,[М,{а„ .... аД а]. (5.11)
Если мы заменим К„ в выражеьли (5.11) выражением (5.9),
то получим как раз то, что должны были получить. Мне
уже известно, что этот интеграл будет равен
^•/•••/(7з|у[^^^(^1 ^..>пД1ЛЛ КЮХ
Xd\ .,, d\M,(x, ^k)d^i ^" dx^. (5.12)
Заметьте, что выражение (5.11) равно (5.12), только если к
и м одинаковой четности. Если k и п разной четности, то
выражение (5.11) тождественно равно нулю.
Из этого легко заключить, что в равенство (5.2) не
входят Lj^, для которых k имеет четность, отличную от
четности п, т. е. Z,^_2^_i тождественно равны нулю, а Z^^_2v
равны
X/•.•//СЛ'^1 -^«-2». =>!. ^1 «V. 3jda, ...da,. (5.13)
Объединяя равенства (5.1), (5.2) и (5.13), можно записать
J ... Ja:„(ti T„)rfx(T,, а) ...dxix„, а) =
Xdo^ ... do,, a], (5.14)
5 Зак. 2305. H Винер
66 л E к Ц и я 5
где 1п/2] равно Аг/2 при четных п и (п—1)/2 при
нечетных п. Я получил разложение по ортогональным
функционалам. Эти ортогональные функционалы той же четности,
что К„, и определяются, например, в случае C/^_2v с
помощью К„, в котором отождествлено v пар переменных и
проведено интегрирование.
Теперь я перейду непосредственно к прямому применению
таких разложений к изучению частотной модуляции (ЧМ).
Я намерен изучить спектральный состав выражения
ехр ]^i j f(t~{~T) dx (т. a)j . (5.15)
Заметьте, что здесь, конечно, имеется два члена: косинус и
синус, которые можно описать с помощью выражения (5.15)
Таким образом, наш сигнал — это реакция линейного
резонатора на броуновский входной процесс, и нас интересует
его спектр. Чтобы получить спектр, как мы видели,
достаточно выразить этот сигнал через фундаментальные
ортогональные функционалы. Проделаем это. Введем комплексное
число а, в которое для удобства включим и множитель /,
под знак экспоненты; функцию / теперь можно считать
нормированной. Тогда выражение (5.15) примет вид
ехр[а Jcp(^ + '^)^-^(^. а)]' (5.16)
где
Jcp2(T)jT=l. (5.17)
Мне нужно разложение выражения (5.16) по
ортогональным функционалам. Это выражение можно представить
в виде суммы однородных полиномиальных функционалов,
используя разложение экспоненты
ехр а Гср(^)^х(т, а) U=
оо
^2 ^ / • • • /^^"i)- • •T(S)^^(^1. ^). . 'dx{^^^ а), (5.18)
/2 = 0
где ср я считал функцией только от т, В дальнейшем я вновь
введу t. Теперь я использую равенство (5.14), чтобы выразить
ПРИД\ЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. I 67
через ортогональные функционалы каждый из членов суммы
(5Л 8), и получу
ехр|^а Jcp(T)Jx(T, a)j::^
оо [j\
= 2^" S 7;rzhr2^^n-2Jf(^i)---9(^^-2.1 «1; (5.19)
n = 0 v = 0 ^ '''
здесь cp были сгруппированы попарно и проинтегрированы
с учетом равенства (5.17). Изменяя порядок суммирования
в (5.19) и полагая \i = n — 2v, получаем
оо оо
2^0,[T(X:)...T(V). «iS^- (5.20)
|х = 0 v = 0
Выражение (5.20) можно существенно упростить. Суммируя
по V, получаем
оо
ехр[а Jfp(T)u?x(x, а)] = 2 ^ехр(-|-)Ор,((р(х,). . .9(хД а].
(5.21)
Я построил разложение по ортогональным полиномиальным
функционалам для случая ЧМ. Я намерен использовать его
в двух целях. Во-первых, немедленно найти спектр ЧМ
сигнала и, во-вторых, использовать как некоторый общий
инструмент при разборе более сложных случаев. Сначала
заменим а на а/. Мы получаем следующую функцию от а:
/(а)=:=ехр ш frf (т) Jx(t, a)j =
оо
Если теперь заменить т на t-j-z, то получится функция от /
и а
/ (t, а) = ехр ai Г ф (^ + т) dx (т, а) =
оо
= S^^^p(-^^^'P(^ + ^i)---T(^+V). «]• (5-23)
5*
68 ЛЕКЦИЯ?)
Затем мы выполняем интегрирование, используя формулу
для интеграла от произведения двух G:
1
о
fit+ 8, a)/(s. (x)da =
a = 0
= exp (— a^) exp a^ Г cp (^ -[- x) cp (т) cfx 1 =
= exp|a2rjcp(^ + T)cp(T)jT— ijj, (5.24)
где f(t, a) — комплексно сопряженное к f(t, a).
Равенство (5.24) определяет среднее значен11е по а, и, как мы
видели, в силу эргодической теоремы оно почти всегда равно
среднему по времени t. Следовательно, выражение (5.24)
точно определяет автокорреляционную функцию в одном из
случаев ЧМ.
Проведем теперь гармонический анализ для этого
случая ЧМ. Раскрывая (5.24), мы получаем ряд по степеням
автокорреляционной функции для ф. Если мы возьмем
преобразование Фурье, то получим спектральную плотность
мощности в виде суммы членов, состоящих из спектра ср
и соответствующих его сверток. Пусть h{t) представляет
автокорреляционную функцию ср и //(о)) — ее спектральная
плотность мощности
/г (^) = J ср (^ + т) ср (т) dz, (5,25)
^^""^^^^ \h{t)e^^4t, (5.26)
(2?:)'' J
Возьмем итерированные Я(а)) ://^(со), //^(со) /У'^ (со),
где
/у1(а)) = Я(а)) (5.27)
и
оо
W(^<s>)= j H'^''^{m-\-^)H{^^)d^. (5.28)
— <-xri
Тогда спектр я получаю в виде ряда по итерированным /У(со).
Таков точный вид спектра в случае частотной модуляции.
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. Т 69
Теперь, я думаю, надо перевести на обычный язык то,
что я сделал. Я рассматривал сигнал, являющийся реакцией
линейного резонатора на входной броуновский процесс.
(Действительно посылаемые сигналы не похожи на этот
сигнал, но их распределения не так уж сильно отличаются.)
Предположим, что я посылаю сигнал с помощью частотной
модуляции. Каков спектр частот, занятых при такой
передаче? Вот задача, которую я решил; она составляет большую
часть всех задач ЧМ. Можно расширить разобранный нами
случай. Пусть передается известный сигнал, причем к нему
добавляются случайно распределенные ошибки по частоте.
Нужно определить, как случайные ошибки в точности
сообщения воздействуют на частотную модуляцию. Эту задачу
можно решить подобными методами. Я это опускаю;
используем полученные результаты для разбора более сложных
случаев.
Рассмотрим
ехрГ/ Г Га:(^ + ^1. t-\-x^)dx{z^, а)й?х(т2, а)1. (5.29)
Этот случай можно назвать „квадратичной ЧМ". Первое,
чем следует воспользоваться, — это тем, что в большинстве
случаев симметричную функцию /С(т^, Xj) можно записать в
виде
^/^(^1. ^2) = 2^Л(^1)?.(^2). (5.30)
где ср„ — собственные функции ядра /C(ti, Тд), а а^ —
собственные значения. Это — билинейная форма. При этом ср^
действительные и ортогональные, а а^ (при некоторых
условиях, которые я допущу вначале) действительные и
неотрицательные Тогда выражение (5.29) становится, по
крайней мере формально,
= nexp{/fl„[Jcp„(^ + T)rfA:(T, a)J|. (5.31)
Первый случай, который следует разобрать — это просто
txp[la„[Jf„it^x)dx(z, a)J}. (5.32)
70 л E к Ц и я 5
Я найду спектр этой функции тем же методом, который
применялся в случае „линейной ЧМ". Затем мы перемножим
функции (5.32). Заметьте одно очень важное обстоятельство.
Если К состоят из произведений различных ср, то
произведения ортогональных функционалов из нашей иерархии
ортогональных функционалов снова принадлежат ей.
Заметим, что
оо
2 «'Я^ (ti) =: ехр ( - -^ + «), (5.33)
где Н^{и) — многочлены Эрмита. Вместе с равенством (5.21)
это приводит к тождеству
Я,[/ср(т)^д:(т. a)]==G^[cp(Ti)..:cp(T^), а]. (5.34)
Лекция 6
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. II
На прошлой лекции я доказал, что
ехр \а \ ^{t)dx (t, а) =
со
= S ^ ^^Р (^) ^' f* ("l)' ■■■•'? ("v). «]. (6.1)
v=0
где
f\f(t)\dt=\ (6.2)
и
Re(a)< 1. (6.3)
Теперь я хочу изучить выражение
exp|^[Jcp(0^x(^. а)]'|, (6.4)
которое равняется
оо
/2=0
Если перейти к G-функциям, то выражение (6.5) равняется
со
1]С2„02„[ф(т,) ср(т2„). а] (6.6)
л = 0
И задача состоит в определении Сз^. Это можно было бы
сделать непосредственно, но я намерен применить метод
производящих функций.
72 ЛЕкцияе
Умножая левую часть равенства (6.1) на выражение (6.4),
а правую — на выражение (6.6) и интегрируя по а, получаем
Г^аехр [а f'f (^)fifjc(^, a)]exp\b\f(j^(t)dx(t, а)| I =•
о
оо
_Va2«exp(^)c,„. (6.7)
п = 0
Правая часть равенства (6.7) получена с учетом равенства
1
JfifaG,[cp(Ti), ..., cp(tj. a]G2jcp(Ti). .... ^(tJ. a] ===
0
f v! при 2n = y,
= \ (6.8)
( 0 в других случаях.
Теперь положим
u = ^{t)dx(t, а) (6.9)
и вспомним,
и
Поэтому
1
что и
имеет гауссовское распределение, причем
1
juda===0 (6.10)
0
1
ju'^da=:l, (6.11)
0
Г da exp \а j (^(t)dx (t, a) exp \b\j(p(t)dx(t, a) > ==
0
1
= j daexp(au)exp(bu'^) =
0
oo
"^ 72^ / ^^P ( "^ "t) ^^P ^^" + ^"^^ ^"' ^^' ^ ^^
— oo
Здесь мы воспользовались тем, что уже знали распределения
для и, и получили выражение, которое можно проинтегри-
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОП МОДУЛЯЦИИ. II
73
ровать. Положим
v^a{\—2bf\
(6.13)
где b следует взять меньшим ^г- Это не вызовет затрудне*
НИИ, так как вообще мы будем рассматривать малые
значения Ь. Если b мнимое, то можно брать и большие
значения Ь. Теперь равенство (6,12) принимает вид
-)''/exp[--+-^^_^J-^^-3^ (6.14)
(2'
И, дополняя его до полного квадрата, мы получаем
1
ехр
Далее, имеем
(211)'/
(1 — 2^)'/^
J
ехр
\ а?- Л dv
^^^L 2(1—2^) J (1-^2^
(1-2^)
dv=\.
(6.15)
(6.16)
так как. и в комплексной плоскости сдвиг v вверх или вниз,
так же как вправо или влево, не меняет значения этого
интеграла. Чтобы это показать, используем теорему Коши.
Мы интегрируем вдоль действительной оси, и ничего не
изменится, если интегрировать вдоль параллельной ей линии,
так как подинтегральное выражение очень быстро стремится
к нулю, когда мы идем к со, и не имеет особенностей
внутри конечной области. Применяем теорему Коши. Интг^
грал становится равным 1.
Следовательно, выражение (6.15) равно
L_^ ехр Г 1. (6.17)
(1_2^)'/2 ^[2(1—2^) J ^
Подставляя выражение (6.17) в равенство (6.7), получаем
оо
/г = 0
(1-2^)'/'
ехр
2(1—2^)
(__Ьа?\
(6.18)
74 ЛЕКЦИЯб
Вспомните, кстати, что
, С2„+, = 0. (6.19)
Раскрывая правую часть равенства (6.18), имеем
оо оо
Приравнивая коэффициенты при а'^'\ найдем
уо А 1 \ /R 91 ^
2«~ (1—2^)'/^ \Т—2Ь ) ~^/
Видите, как, использовав производящую функцию, мы
избежали хлопот, связанных со сложением м'ножества рядов.
Теперь можно записать
expj^y ср(^)^х(^1, а)1 1 =
оо
= 1 ^ (т^) ^2„ W (h) Т (hn). «]• (6.22)
п = 0
Далее, заменим b на lb — в предшествующем изложении
нет ничего, что помешало бы нам это сделать. Случай
мнимого b даже предпочтительнее, чем действительного,
вследствие того, что знаменатель выражения (6.21) становится
неограниченным при неограниченных Ь\ кроме того, мы
можем теперь не беспокоиться о том, не подходим ли мы
к точке, где нарушается сходимость ряда. Итак, мы имеем
exp\lb\j^(t)dx(t, а)Т} =
со
= S Т ( Ь=Ж)" "'^ ^2„ 1т (^i) Т (^2«). «]• (6.23)
/2 = 0
Рассмотрим
ехр!/^ Г \ K(ii, T2)Jx(tj, а)й?х(т2, а) 1, (6.24)
где К (tj, Tg) симметрично. В некоторых случаях (эти случаи
представляют обобщение обычных фредгольмовских ядер)
мы найдем
оо
К{^г. X2)=2^'fv(^i)?v(x2). (6.25)
v = 0
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. II 75
где фДт) — последовательность действительных
ортогональных функций, называемых „характеристическими", а ^^^ —
„характеристические числа" задачи. Тогда выражение (6.24)
примет вид
оо
Zl2[b) ^2;z[?v('^l) 9v(^2/z). °^1. (6-26)
V /г = 0
если подставить равенство (6.25) в выражение (6.24) и
использовать равенство (6.23).
Далее, нам нужно преобразовать этот ряд в ряд по
ортогональным функционалам различных порядков, и мы
встречаемся с некоторыми свойствами G, которыми мы до сих
пор не пользовались. А именно:
<^Л?;Ы ^](Уп\ Сс10^[срд^(т^ + 1) cpft(^;z+m).Ct] (6.27)
является полиномом степени п-\-т, ортогональным ко всем
полиномам меньшей степени. Это ясно благодаря
независимости: всякая функция от одного набора переменных не
зависит от какой-либо функции от другого набора
переменных. Мы также знаем, что выражение меньшей степени
будет содержать по меньшей мере один член меньшей
степени, чем соответствующий член выражения (6.27). Поэтому,
когда мы проинтегрируем по а, то получим 0. Это сразу же
подсказывает нам, как преобразовать выражение (6.26) в ряд
по ортогональным функционалам. Вспомните, что ср^
ортогональны друг другу. Существует довольно простой способ
этого преобразования.
При перемножении двух ортогональных полиномов
получается в точности тот же результат, как в случае
перемножения их старших членов и дополнения получившегося
выражения до ортогонального. Все определяется старшими членами,
так что можно считать, что имеется соответствующая
выражению (6.26) функция, содержащая старшие члены выражения
(6.26), т. е. имеется аналогичный ряд. Мы перемножаем ряды
старших членов и получаем члены, которые нам нужны для
построения G, входящих в искомое разложение. Выражение
оо
76 ЛЕКЦИЯб
соответствует старшим членам выражения (6.26). Члены,
полученные в результате перемножения, являются старшими
членами для G в искомом разложении. Исследуем, что мы
получили. Выражение (6.28) равно
V
Это производяш.ий оператор. Я должен раскрыть этот
оператор и получить сумму однородных операторов различных
порядков. Затем я заменю эти однородные операторы на G
с теми же старшими членами и получу искомый ряд. Но
это приводит к рассмотрению функций
2i:^[/^vW^^(^'«)r- (6.30)
V
Это выражение можно записать как однородное выражение
второй степени
/ Г Г/?(т1, T2)Jx(ti, a)Jx(T2, а) (6.31)
так же, как мы записали равенство (6.25). Тогда
выражение (6.29) принимает вид
Д(1-2/М'/^'''Р['//^^^^' ^2)^-^(^1. а) Jx(t2, а)]; (6.32)
это и есть функция, которая дает искомые коэффициенты
при старших членах.
Теперь остается оценить произведение
II0^- '-''^
По крайней мере формально оно равно
ехр
Вначале возьмем
"-1^1п(1-2/^)'
1М<|-
(6.34)
(6.35)
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ И 77
Тогда
1 ^
2
^\n(\^2ibj=\y[(2lb,)
"|~ 2
+
3
• +
(6.36)
так ЧТО
1 ^
2
V
1 г
2/
V V * J
Вспомним теперь, что
К(^,, ^2) = 2^Tv(^i)?v(^2X (6.38)
где ср^ —последовательность ортогональных и нормированных
функций, а Ь^ вещественны и неотрицательны. Тогда, по
крайней мере формально, имеем
^^-//('(т. t)Jt. (6.39)
^1^1^ j f KH^l, T2)jTiGfT2. (6.40)
2*' = ///'^(^i' Ъ)1<(г,. Тз)/С(тз, x,)dx,dx^dx^ (6.41)
V
и т. д. Поэтому равенство (6.37) можно выразить с помощью К,
по крайней мере при достаточно малых Ь^, но никакая
проблема не возникнет, если Ь^ будут больше, так как
абсолютная величина выражения
5 гг (6.42)
равна
Ц_^, (6.43)
(1 + 4*2)''
И чем больше Ь^, тем лучше сходимость. Следовательно,
выраже 1ие (6.33) — это параметр, зависящий от К\ он не
имеет для нас значения при рассмотрении спектра. Это
78 ЛЕКЦИЯб
просто постоянный множитель при автокорреляционной
функции, и, следовательно, постоянный множитель для
спектральной плотности один и тот же для всех членов. Поэтому мы
можем ограничиться рассмотрением
ехр / Г Г/?(т1, T2)<ix(Tj, a)<ix(T2, a)U=
= 1-f-/ Г I /?(tj, T2)Jx(xi, a)Jx(T2, a) —
—2г////^(^1' ^2)^(^3. "^d^^i^i^ a) . .. Jx(t4, a)4-
(6.44)
Это однородные функционалы; их можно привести к такому
виду, когда ядра симметричны; для этого достаточно
просуммировать по всевозможным перестановкам. После этого
можно построить соответствующие G описанным раньше
способом, и мы получим разложение для
ехрГ/ Г fК(^1, T2)Jx(xi. а)^х(т2, а)| (6.45)
по ортогональным полиномам.
Вы видели, как я избежал трудностей, использовав
производящие функции. Я мог бы прямо складывать ряды. Но
зачем напрасно тратить время, когда есть простой способ?
Лекция 7
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. HI
На прошлой лекции мы установили, что
exp|a[Jcp(OJx(^ a)J}==
v;5](i^r^2^^^"i) ^^^^п\ а]. (7.1)
(1—2л)
^ ^ /2 = 0
где а вещественное или мнимое. Если взять
^(^1. ^2) = 2«v%(VTv(^2). (7.2)
V
где ср ортогональны, то
ехр Г Г/С(т1, t2)^x(ti, ci.)dx{x^, а) =
оо
Вспомним, что если берутся ортогональные функции ср, то
произведение двух полиномов Эрмита снова будет
полиномом Эрмита, степень которого равна сумме степеней
сомножителей. Поэтому
ехрГ Г Г/С(т1, x^)dx{x^, a)Jx(T2, а)Ь=
оо
""f .II (1-2j ^'Ч 2^ 2 ^^'^ '"^^^ ^^^^' "^^^ ^''^^' "^^^ ^''^^' "^^^ ^^^^' ' * '
. • •. Т*„ (^2«-1) ?ft„ (^2«), а] |[ 1^г^ . (7.4)
80 л E к Ц и я 7
где члены суммы по k^ получены отождествлением /г^ с v
всеми возможными способами, а произведение по k — по
тому же множеству 2/г/г,., которые входят в аргумент Gg^.
Я введу небольшое изменение в обозначения. Я
определял 0^ для симметричных функций. 0^ для
несимметричных функций, т. е.
G,[F(T,, .... тД а], (7.5)
где F — несимметричная функция от т^, .... х^, можно
определить как
G,[G(xi тД а]. (7.6)
Величина О получена из F путем всевозможных перест>ано-
вок т в F, суммирования и деления на число перестановок.
Нам удобен такой переход к симметричному ядру.
Выражение для
ехрГ/ Г Г/С(Х1, T2)cfx(Tj, а)й?х(т2, а)] (7.7)
не что иное, как выражение (7.4), где а^ заменены на ia^.
Далее мы симметризуем ядра в равенстве (7.4). Берем
сумму по k^, переставляем члены всеми возможными
способами, складываем и делим на число способов. Получаем нашу
формулу. Меня, однако, особенно интересуют члены низшей
степени Gq и G^^ Так как эти члены уже симметричны, нам
не нужно производить такой операции.
Если ввести е, на которое умножаются все а^, то
ехрГе Г \ K{'z^, T2)^x(tj, a.)dx{x<^, а) =
-f-Члены более высокого порядка по s . (7.8)
Если считать, что s мало,
1—2a,s^l, (7.9)
и что членами высшего порядка по е можно пренебречь, то
exp[s J J/CCxi, -^)dx{x^, a)dx{'2. а)]^1-Нг02 [/С(т1, Xj), a].
(7.10)
ПРИМЕНЕНИЕ К ЗАДАЧАМ ЧАСТОТНОЙ МОДУЛЯЦИИ. ТП 81
В случае /е выражением для главных членов будет
ехр is Г j /C(Ti, T2)Jx(Tj, а)й?х(т2, a)^l-|-ieG2 [ЛГ(т1, Т2), а].
(7.11)
Члены равенства (7.10) или (7.11) представляют члены
нулевой и второй степени в соответствующих разложениях.
Рассмотрим теперь их спектр. Меня интересовала функция от t
ехрГе J Ja:(/-|-'^i. t+ ^^i)dx{'z^, a)dx('z^, a)l. (7.12)
Главные члены (7.12):
ехрГе Г jK{t-\-x^, ^-f-Tg) Ja:(t^, а)й?л:(т2, a)|^
Sl+eG2[/C(^ + Ti. ^ + Т2). a] (7.13)
или, в случае ie
\J^iBG^[K(t + z^, t + T^l a]. (7.14)
Заметим следующее: если некоторую функцию от t,
например, выражение (7.12), я разложил в сумму
ортогональных полиномов, то спектр равен сумме спектров слагаемых
функций. Вспомните, это было показано раньше: каждый
симметричный функционал n-Pi степени G^ ортогонален любому
функционалу другой степени. Следовательно, перекрестные
члены выпадают.
Если взять только главные члены, указанные в (7.13)
или (7.14), то спектр выражения (7.12) дается суммой
спектров 1 и функции еОз [/С(^4~'^1. ^~\~^)^ а]. Спектр 1
сосредоточен в точке а) = 0. Спектр второго слагаемого равен е^,
умноженному на спектр Gg, как для (7.13), так и для (7.14).
Это следует из того, что при вычислении корреляционной
функции перемножаются комплексно сопряженные
выражения. Аналогичным образом можно ввести в спектр члены
высшего порядка.
Найдем теперь спектр G^. Чтобы определить спектр
выражения (7.13), надо взять преобразование от его
автокорреляционной функции. Автокорреляционная функция равна
l+в^JJ/C(^ + Tl, ^ + ^2)^(^1. V^^i^V (7.15)
g ^ак. 2305. Н Винер
82 ЛЕКЦИЯ7
Первый член дает спектральную линию на нулевой частоте.
Если мы определяем Q(tOj, cog) как двойное преобразование
Фурье от /C(ti, Tg), то
/C(Ti. ^2)==^JJQK. C02)^^(^^^^+^^^^)fifa)ififa)2. (7.16)
Преобразование Фурье от /C(^ + '^i, ^ + '^2) определяется
равенством
(7.17)
Поэтому преобразование Фурье от K{t-\-i^, ^ + '^2) вместо
Q(a)j, cDg) равно
Q(a)i. 0)2) ^^(^1+^^)^ (7.18)
Интеграл от произведения функции и ее комплексно
сопряженной (а для действительных функций они совпадают) равен
интегралу от произведения ее преобразования Фурье и
сопряженного ему выражения. Поэтому
в^J//C(^ + Tl. ^ + T2)/C(Ti. Т2)^Т1^Т2 =
= £^J r|Q(a)i, 0)2)^ ^-^ ('^•+^2) ^ fifcoj й?а)2. (7.19)
Делая подстановку
^1 + ^2"^^' Wj = «. (7.20)
получим в правой части (7.19)
e^J J|Q(tt. i^ —и)\^ е'^^Ыи. (7.21)
Следовательно, преобразование Фурье от выражения (7.19)
равно
со
(2it)'''e2 J|Q(«, ш_и)|2с?и. (7.22)
— СО
Это и есть спектр второго слагаемого (7.13).
Лекция 8
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ;
КОЛЕБАНИЯ СВЯЗАННЫХ ОСЦИЛЛЯТОРОВ,
ВОЗБУЖДАЕМЫХ В СЛУЧАЙНЫЕ МОМЕНТЫ ВРЕМЕНИ
Начну с того, как мне пришлось заняться вопросом
о причинах углублений в графике спектральной плотности
мощности. Я впервые с этим столкнулся в одной специальной
задаче, Я интересовался спектральным составом колебаний
биотоков мозга. Как известно, если поместить пару электродов на
кожу головы, то снимаются флуктуирующие напряжения,
которые можно усилить. Их можно записать и по
коэффициентам автокорреляции определить спектр. Нет
необходимости много говорить о техническом осуществлении.
Используется следующий прием: мы берем запись напряжения
колебаний биотоков, но вместо того, чтобы записывать
их на бумаге, записываем на магнитной ленте, и притом
с помощью частотной модуляции. Применение частотной
модуляции важно по следующим причинам. При повторном
проигрывании запись на магнитной ленте немного стирается.
Действие этого стирания менее значительно при частотной
модуляции, чем при амплитудной. Фактически, стирание при
частотной модуляции не имеет значения до тех пор, пока
оно не станет почти полным. Таким образом, ЧМ позволяет
воспроизводить запись несколько раз без искажений.
Используя две считывающие головки, установленные на
некотором расстоянии одна от другой, можно получить при
проигрывании одновременно первоначальную и сдвинутую
во времени записи. Напряжения для двух считывающих
головок соответствуют f (t) и f {t — т). Мы можем сложить
эти напряжения. Нам легче изучать не сами напряжения,
а их средние мощности, пропорциональные средним
значениям квадратов напряжений. Средняя мощность суммы
6*
84 ЛЕКЦИЯ8
напряжений дается уравнением
[f{t)+f{t-^)? = f4t)JrPit-x)-^2f{t)f{t-z\ (8.1)
где черта обозначает усреднение по времени.
Во-первых, величину напряжения легко возвести в квадрат
с помощью квадратичного детектора. Далее, легко
проинтегрировать ее, заряжая конденсатор. Напряжение между
пластинами конденсатора пропорционально количеству
электричества на них, а это последнее пропорционально
интегралу от тока по времени.
Рассмотрим отдельные члены уравнения (8.1):
/2 (/) = /2 (/ _ X) == const. (8.2)
Автокорреляционная функция ==/(^)/(/ — т). (8.3)
Таким образом мы определим автокорреляционную функцию
колебаний биотоков; она-то и будет объектом гармонического
анализа. Задача совсем нетрудная, и я не буду входить
в детали: это предмет общего гармонического анализа.
Между прочим, один из наиболее легких способов
выполнения гармонического анализа колебаний биотоков состоит
Спектральная плотность
мощности
JL
'5 10 Частота f, ги^
Рис. 8.1.
в смешивании этих колебаний с синусоидальным колебанием
какой-то определенной частоты, близкой к наиболее
значительной из их частот, и в проведении затем
последовательного гармонического анализа. Если так делать, то
спектральный состав колебаний определяется с высокой
степенью разрешения.
Уже давно известно, что спектр колебаний биотоков
мозга имеет общий вид, показанный на рис, 8.1. Некоторая
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 85
активность наблюдается вблизи О гц, немного, быть может,
около 5 гц, и очень заметная активность — вблизи 10 гц.
Эта активность вблизи частоты 10 колебаний в сек и есть
так называемый альфа-ритм.
Заметьте, кстати, что при изучении колебаний такого
типа автокорреляционный метод имеет одно преимущество.
Мы изучаем спектральную плотность мощности не только
вблизи некоторой частоты, но и в целом, и если случится,
что вся она сосредоточена вокруг какой-то частоты, то мы
это увидим. Мы следим не за мощностью какой-либо
определенной частоты, а за интегралом от мощности по
частотам, не превосходящим некоторой.
Заметьте также, что при проведении гармонического
анализа встает вопрос о степени разрешения. Чтобы свести
ее к одной десятой герца, надо рассмотреть сто
последовательных колебаний, что соответствует времени 10 сек. Нам
надо знать автокорреляционную функцию за 10 сек. Теория
здесь точно такая же, как в оптике. Большим преимуществом
этого метода является возможность использовать достаточно
широкую временную базу при проведении гармонического
временного анализа. Принцип в точности тот же, какой
применяется в интерферометре Майкельсона для света.
В интерферометре Майкельсона составляется
параллельный пучок световых лучей, который полупосеребренным
зеркалом разделяется на два пучка; затем оба пучка
отражаются и наблюдается их интерференция. Измеряется
освещенность как функция от разности хода обоих пучков.
Такой способ позволяет получить исключительно высокое
разрешение.
Выбор большой временной базы при проведении
гармонического временного анализа совершенно эквивалентен
использованию прибора с высокой разрешающей силой.
Спектральный анализ колебаний биотоков мозга для
нескольких действительных случаев был проведен с высокой
степенью разрешения. Люди бодрствовали, но находились
в покое, с закрытыми глазами. На рис. 8.2 показан (в
увеличенном виде) спектр вблизи 10 гц.
Можно было ожидать, что мы не найдем здесь явления,
подобного тем, которые мы хотим изучить; в таком случае
вся наша работа по определению тонкой структуры спектра
колебаний биотоков пропала бы даром. Однако поскольку
86
ЛЕКЦИЯ 8
МЫ обнаружили этот эффект, мы должны попытаться дать
ему объяснение. Замечательны два факта: первый — очень
узкая линия в центре спектра, и второй — то, что эта линия
поднимается из углубления. Возникает задача — дать
разумное объяснение того, чем вызвано такое строение спектра.
В действительности именно эта задача и привела меня
к большей части той работы, которую я недавно проделал
и изложил на нескольких последних лекциях.
Прежде всего, существует предположение, что в мозгу
имеются осцилляторы некоторого рода и что эти
осцилляторы в некотором смысле образуют в совокупности более
добротный осциллятор, чем по отдельности. Это
предположение заставило меня поинтересоваться, встречается ли где-
Рис. 8.3.
нибудь в электротехнике подобное явление. Ответ был
утвердительным. Приведу пример.
Рассмотрим несколько генераторов, связанных с
нагрузкой через шины, как показано на рис. 8.3. Здесь мы не
только имеем нагрузку, но у нас колеблюплаяся нагрузка.
Люди включают и выключают свет случайным образом. Можно
представить это с помош.ью процесса, тесно связанного
с „дробовым эффектом" или броуновским движением
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 87
Не следует понимать это буквально, но здесь есть нечто
в этом роде. Что же поддерживает частоту на уровне,
скажем, 60 гц'^ Можно полагать, что это делается одним
из нескольких способов. Первый состоит в том, что каждый
отдельный генератор приводится во вращение первичным
двигателем, на котором есть регулятор, так что, если
вращение слишком быстрое, то пар или какой-либо другой источник
силы отключается, если же вращение слишком медленное,
то действующая сила увеличивается. Благодаря этому
поддерживается постоянный режим работы системы. Однако
такие регуляторы, даже очень хорошие, отнюдь не так хороши,
как регулирование системы в целом. Регулировка нашей
электроосветительной системы занимает три минуты в день
или что-то в этом роде, даже если мы не подправляем ее.
Подправлять можно двумя путями. Первый заключается в том,
что мы можем по своему произволу ускорять или замедлять
систему. Другой способ, к которому мы прибегаем, — ввести
в систему один особый генератор, снабженный
регулятором с достаточно широким диапазоном, чтобы
компенсировать как можно полнее влияние больших колебаний
нагрузки. Даже если это осуществить, то незначительные
колебания нагрузки компенсируются инерцией систем и
регуляторами узкого диапазона. Я могу сказать, что на регулятор
широкого диапазона в нашем рассмотрении можно не
обращать внимания, так как он управляет системой, в то время
как регуляторы узкого диапазона в действительности
образуют единый регулятор статистического действия. Как
действует такая система регуляторов? Забудем различие между
регуляторами широкого и узкого диапазонов. Как известно,
если генератор дает более высокую частоту, то он имеет
большую нагрузку, чем при нормальной работе. Тот факт,
что вращение слишком быстрое, означает, что должен
действовать регулятор; регулятор соединяется с возрастающей
нагрузкой и уменьшает ее. Если вращение слишком
медленное, он увеличивает нагрузку и стремится ускорить
вращение. Иными словами, частоты этих различных осцилляторов
(а мы можем рассматривать генераторы как нелинейные
осцилляторы) являются не независимыми одна от другой,
а связанными. Важной особенностью здесь является связь
между частотами генераторов: благодаря этой связи
осуществляется хорошая регулировка частоты.
88 ЛЕКЦИЯ8
Здесь возникает несколько вопросов. L Можно ли
ожидать, что такой метод регулировки даст определенную
среднюю частоту, равную 60 гц, скажем, для генераторов
частоты 60 гг^? 2. Создает ли такая регулировка частоты
полосы по обеим сторонам от центральной частоты, вблизи
нее? 3. Создается ли углубление между этими полосами и
центральной частотой? 4. Применимы ли эти идеи к
изучению колебаний биотоков мозга? Я отвечу утвердительно на
все эти вопросы. Я свяжу их с материалом, который
я излагал на предыдущих лекциях.
Обратимся к биотокам мозга. Известно, что если внезапно
послать в мозг электрический импульс, то последует энер'-
гичная разрядка с частотой примерно 10 колебаний в сек.
Там имеется что-то похожее на локальные осцилляторы.
Это явление в значительной степени является локальным
в мозгу или по крайней мере начинается как локальное.
Таким образом, в мозгу имеются осцилляторы с частотой
колебаний примерно 10 гц, как и требовалось. Кроме того,
это нелинейные осцилляторы.
Доказательство этого утверждения очень простое. Частота
их колебаний зависит от интенсивности возбуждения. Для
линейного осциллятора частота не зависит от интенсивности.
Это наводит на мысль, что частоты осцилляторов в мозгу
могут взаимодействовать. И мы спрашиваем: как они
взаимодействуют? Возможно ли здесь явление затягивания частот,
как для генераторов? Разумно ли это предположение?
Да, разумно.
Мы можем сделать лампу, которая мерцает перед
глазами с частотой примерно 10 ги,. Если мы это осуществим,
то а-ритм мозга будет затягиваться к частоте и фазе
мерцаний. Другими словами, различные частоты сближаются.
Можно сказать, что это зрительное возбуждение, но, конечно,
это и электрическое возбуждение, так как появляются
изменения потенциалов, вызванные этим мерцанием.
Кроме того, уже проведена некоторая работа в
отношении прямого электрического воздействия на мозг. Это
осуществлялось путем введения электродов в мозг животного.
С человеком этот опыт проводился довольно интересным
образом.
К потолку комнаты подвешивается лист жести; этот лист
соединяется с одной клеммой генератора с частотой 10 гц н
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 89
напряжением 400 в. Эта установка вызывает
электростатическую индукцию в любом предмете, находящемся в
комнате. Она действительно воздействует на мозг, вызывая
определенно неприятные ощущения. Другими словами,
это — способ * посылать сигнал в мозг не через органы
чувств, а непосредственно.
Остаются вопросы: что можно сказать о математическом
описании затягивания частот; вызывает ли этот механизм
характерное углубление? Вот это я и собираюсь связать
с тем, что было сделано на предыдущей лекции. Мы
говорили о частотах порядка 10 или 60 гц в соответствии
с тем, относилось ли это к электрической цепи мозга или
к энергетической системе. Должно существовать затягивание
частот, лежащих вблизи центральной по разные стороны от
нее, равное и противоположное, так что если верхние
частоты затягиваются колебаниями биотоков мозга или
колебаниями в электроосветительной системе в одну сторону, то
частоты, настолько же меньшие центральной, затягиваются
таким же образом в другую сторону Вот что мы
подразумеваем под „затягиванием" и „затягиванием в сторону".
В противном случае частоты изменялись бы в одном и том же
направлении, а это не то, что нам нужно. Нам нужно
некоторое действие и противодействие, равные или почти
равные.
Теория не улучшится, если мы будем считать
центральную частоту отличной от нуля. Если мы умножаем
наше колебание на синусоидальное колебание центральной
частоты, скажем 10 гц для биотоков, или 60 гц для
энергетической системы, то вместо ббльших и меньших частот мы
имеем положительные и отрицательные частоты. Иными
словами, надо, чтобы для двух час>тот затягивание одной из них
другой было противоположно затягиванию соответствующих
отрицательных частот. Заметим, что отрицательные частоты
получаются при обращении времени:
^'(-^)^=г^^'«^(-0. (8.4)
Поэтому мы задаем следующий вопрос: если имеется
некоторое затягивание между частотами, равное и
противоположное для частот противоположных знаков или
противоположных знаков времени, то можно ли получить на выходе
такой системы спектр вида рис. 8.4, имеющий пик при
90 л E к Ц и я 8
нулевой частоте и углубление вокруг О? Этот вопрос и будет
рассмотрен в лекции.
Разберем сначала случай, когда центральная частота равна
нулю. Мы рассматривали спектр для
ехрГ/е Г Г/С(^ + Т1, t~\-Z2)dx(z^, a)dx{xc^, а) . (8.5)
Выражение (8.5) означает, что у нас есть входной
случайный процесс; мы хотим, чтобы воздействие этого случайного
процесса заменилось на противоположное при обращении
времени или частот. Совершенно ясно, что если верно
уравнение (8.6), то направление затягивания частот меняется, когда
большие частоты заменяются на меньшие, или меньшие
моменты времени на большие:
/С(—Tj, -T2) = -/C(Ti, тз). (8.6)
Будем считать, что предположение (8.6) выполнено. По
суш.еству это предположение о том, что [если
рассматривать (8.5) с точки зрения взаимодействия частот] действие
положительных и отрицательных частот противоположно по
знаку (т. е. равно и противоположно) действию
соответственно отрицательных и положительных частот. Для
колебаний биотоков мозга это предположение состоит в том, что
для частот, немного больших 10 гг^, и для частот, настолько
же меньших 10 гг^, эффект будет противоположным.
Рассмотрим спектр выражения (8.5), полученный на пре-
дыдуш.ей лекции. В нем были главные члены и члены менее
значительные. Вспомним, что
ехрГ/£ Г Га:(^ + Т1, t-^x^)dx{'z^, a)dx(z^, a)j =
;=:=l+/sj'J/C(^ + Ti, t + x^)dx{'z^, a)dx('Z2, a)+- .... (8.7)
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 91
где остальные члены — второго или еще более высокого
порядка по е и малы при малом е. Первые два члена,
стоящие с правой стороны в уравнении (8.7), можно записать
в виде
l-\-lej I /C(^ + Ti, t-j''z^)dx(x^, а)й?х(т2, а) =
= 14~/sJ/C(t, 'z)dz + isOr^lK(t + 'z^, ^ + ^2). а]. (8.8)
Первые два члена правой части уравнения (8.8) —
постоянные. Автокорреляционная функция правой части (8.8) равна
1Ч-^^[//С(т, т)^х]' +
4-2e2jJ/C(^ + Ti, ^ + T2)/C(xi, i2)dx^dx^, (8.9)
где черта обозначает переход к комплексно сопряженному
выражению. Первые два члена в выражении (8.9) постоянны,
они не содержат t. Если провести гармонический анализ
константы, получится только одна спектральная линия
Спектр
О Частота f 214
Рис. 8.5.
при о гц, так что спектр, который дадут первые два члена
выражения (8.9), сосредоточен на линии О гц, как показано
на рис. 8.5. Далее, мы наложим на этот спектр то, что дает
последний член выражения (8.9).
Определим ту часть спектра, которую дает последний
член выражения (8.9). Надо найти
^ J,-/co/j32j J/C(H-^i. t + 'z^)'K{^~^)dx,dz^]dt. (8.1С)
Преобразование Фурье для двух переменных мы
определяем как
Qi^v ^2) = ^//^(^ ^^)e-^-^^^e-^-^^^d'z^d'z^, (8.11)
92 ЛЕКЦИЯ 8
Записав формально преобразование Фурье, получим
^/(a), + u)2)/Q(a)^^ 0)2) =
==-^jJK{t-^z^, t-^'l^)e-^''^''^e-'^''^''^dx^dx^. (8.12)
Следовательно,
= e2jJ|Q(a)j, a)2)|2^^'K+<^^)^fifa)it/a)2. (8.13)
Сделаем замену переменных
tt = a)j. (8.15)
Тогда
£2 Г J |Q(a)i, а)2)|2^-'("^'+"^2)^йГа)1Й?а)2 =
= e2 J J(Q(tt, CO —w)|2^'"'^fiftt6fa). (8.16)
Ho правая часть уравнения (8.16) есть преобразование
Фурье от
e2jjQ(tt. (О —tt)|2cftf. (8.17)
Следовательно, та часть спектра, которую мы стараемся
получить, оценивая выражение (8.10), определяется
выражением (8.17).
Нетрудно видеть, что спектральная плотность, заданная
выражением (8.17), непрерывна, в отличие от спектральной
плотности, сосредоточенной в О гг^, и существенно
положительна как интеграл от квадрата абсолютной величины.
Всякая спектральная плотность мощности неотрицательна.
Возникает вопрос: как ведет гебя спектральная
плотность, заданная выражением (8.17), при со, близких к О?
В точке (0 = 0 спектральная плотность равна
e2j|Q(tt, •-^-0)1''du. (8.18)
Если Q{u, —и) есть тождегтвенный нуль, то
выражение (8.17), будучи неотрицательным, уменьшается до нуля
При со=^0 и u)==oo. Другими словами, спектральная плот-
ПРИМЕНЕНИЯ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 93
ность имеет углубление в точке О, как и требуется. Тот
факт, что Q(tt, —и) равна О, немедленно следует из
определения Q, если выполняется уравнение
^C^l. ^2) = -Л:(-Х,. -^2). (8.19)
Приведем доказательство
Q(a)i, o)2) = ^/J^-'(-^^^+-^^^)A:(ti. T2)^Ti^T2. (8.20)
Q (coj, 0)2) = ^ / J ^' (-,-.+">,^.)A:(- Tj. - T2) dz, ^T2, (8.21)
Q(«>i> 0)2)= ^//^'^"^^'^^"^'^^1-^(^1' ^2)1 ^^i^V (8.22)
Положим
0), =tt, (8.23)
0)2 = —tt. (8.24)
Тогда уравнения (8.20) и (8.22) примут вид
Q(«. -r/) = ^/J^-'«^^^'-^A:(xi, T2)^Tj^t2. (8.25)
Q(tt. — tt) = — •^JJ^^"^'^-'«^^/C(Ti. Т2)й?Т1Й?Т2. (8.26)
где /С симметричное. Следовательно,
Q (м. --- й) = ^ J J е'и.,^'^^-^К (т,. тз) ^т, б?Т2, (8.27)
Q(«. -tt) = ^~^ J J^'"^^^''^-^/C(Ti, x^)dx,dx^. (8.28)
Ho величина, равная своему отрицательному значению,
должна быть нулем.
Другими словами, мы установили вполне строго, что
существует углубление до нуля в спектральной плотности
(8.17) в точке со = 0.
Рассмотрим теперь выражение
ехр/ Г Г/<:(^ + '^1. ^ + '^2)^-^('^1. ^)dx{x^, а). (8.29)
Совершенно ясно, что существуют и другие члены,
накладывающиеся на его спектр. Главная часть спектра изображена
94
ЛЕКЦИЯ 8
на рис. 8.6 линией а. Следующая часть—Ь.
Остальное— с. Некоторые члены с в действительности имеют пик
в начале, но если е мало, то их влияние незначительно. Для
их изучения необходимо дальнейшее исследование, но мы
видим по крайней мере, что углубление не является
неестественным. Таким образом, я дал по крайней мере
предварительное обоснование для своего предположения о том, что
явление углубления в спектральной плотности мощности
вызывается „затягиванием" частот.
Я думаю, что такое явление углубления встречается
во многих физических случаях. Вероятно, мы найдем в
молекулярных спектрах подобную нелинейную связь между
о
Рис. 8.6.
Частота
частотами. Вот один интересный случай, где оно имеет
место. В конце концов планеты являются нелинейными
осцилляторами, и возмущения их движения—следствие
нелинейной связи. Как известно, кроме больших планет,
существуют малые планеты — астероиды. Их много, и плотность
заселения ими солнечной системы велика, а периоды
обращения до некоторой степени различны. Следовало бы
ожидать, что периоды их обращения распределены непрерывно.
Но это не так. Некоторые полосы значений периодов
обращения астероидов отсутствуют; эти полосы лежат вблизи
периодов, находящихся в простом отношении к периоду
обращения Юпитера. Мощная частота Юпитера вызывает
пертурбацию системы; получается что-то подобное
циклотронному эффекту с частотой, рациональной по отношению
к частоте Юпитера. Совокупное влияние множества
пертурбаций, вызванных Юпитером, может существенным образом
изменить орбиту. Следует ожидать, что вблизи юпитеров-
ских частот стабильность намного меньше. Я думаю, что это
то же самое явление, которое мы обнаружили при изучении
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ КОЛЕБАНИЙ БИОТОКОВ 95
колебаний биотоков; оно-то и вызывает углубление вокруг
спектральной линии. Я полагаю, что если бы мы провели
тщательный математический анализ частот, встречающихся
в циклотроне, то нашли бы, что частоты, близкие, к
ведущей частоте, представлены меньше, чем несколько
удаленные от нее частоты, т. е. что частоты, достаточно близкие
к ведущей в циклотроне, не стабильны.
Лекция 9
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ
Начнем новый раздел, связанный с квантовой теорией.
Для квантовой теории нам нужно взять не действительное,
а комплексное дифференциальное пространство. Я уже
немного говорил о комплексном дифференциальном
пространстве в лекции 2.
Рассмотрим
Jcp„($)dKG. а). (9.1)
где Y — комплексное выражение, представляющее
комплексное броуновское движение. Я пишу I вместо t, так как
время — это нечто более специальное, чем то, что я возьму.
Если ср^ — ортогональная и нормированная
последовательность функций (не обязательно действительных), и если
К имеет производную, то выражение (9.1) представляет
собой комплексный коэффициент Фурье для производной от К.
Но вообще производной от Y не существует. Траектории
броуновского движения, действительного или комплексного,
недифференцируемы, за исключением множества нулевой меры.
Однако формально выражение (9.1) является коэффициентом
Фурье.
Раньше мы видели, что выражение (9.1) может быть
записано в виде
J ф„ (I) dY (5. а) = Л„ (а) + /5„ (а). (9.2)
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПС КВАНТОВОЙ ТЕОРИИ 97
А И Б имеют гауссовские распределения нормального вида.
Если ср^ ортогональны при разных п, то распределения
независимы. Это мы уже видели раньше.
Рассмотрим теперь распределение для абсолютной
величины этих коэффициентов Фурье. Иными словами, нас
интересует распределение для следующего выражения при
различных п:
f ^ri&dYd а)
(9.3)
Рассмотрим две независимые величины хну, распределение
которых задается функцией
^1 (^' ^^ = i ^^р (- 4) ^^р (- Т-) • (^•'^)
Равенство (9.4) задает плотность распределения в точке (х, у)
комплексной плоскости. Рассмотрим теперь Pi(x, у) не
в декартовых, а в полярных координатах. Тогда
распределение примет вид
Р2 (г, 6) drdd=l- ехр (— -J-) г dr dd. (9.5)
Интегрируя по 9, получим
/?2 (г) dr = dr f р2 (Г, Q)db=r ехр (— ^\ dr. (9.6)
о ^ '
Мы видим, что распределение для абсолютной величины
коэффициента Фурье —т. е. выражения (9.3) —дается
равенством (9.6).
Пусть теперь имеются два выражения:
fb&^y{i. a) = ^i(a) + /^j(a) = rig'9i (9.7)
и
J срз (О dV (1 а) === А, (а) + iB^ (а) = г^е^К (9.8)
Меня интересует вероятность
^{к1^1>|^к2}. (9.9)
7 Зак. 2305, Н. BiiHco
98 ЛЕКЦИЯ9
Вопрос вполне определенный, раз мы уже вывели закон
распределения для величин г^ и Гд. Это типичный
вероятностный вопрос в классическом смысле теории меры.
Вероятность (9.9) равна
^[\a\r,>\b\r,]= f f r,exp(-^)x
\a\r,>\b\r, ^
Xr,exp[-~'^jdr,dr,. (9.10)
Равенство (9.10) верно, так как r^ н Гз имеют независимые
распределения. Правую часть равенства (9.10) можно
вычислить с помощью замены переменных.
Положим
2
(9.11)
v=-^. (9.12)
Тогда
P{|fl|ri> |г»|г2)= fj e-"e-''dadv =
|a Ра> I b|'f
a P
^/.-.«/.-^
dv
.J%-«[l_exp(-||[«)]rf,. (9.13,
0
Pl\a\r,>\b\r,} = l
1 +
Поэтому
(9.14)
P{\a\r,>\b\r,\ = j^j^.- (9.15)
Подобное рассмотрение мы хотим распространить на
случайные процессы в пространстве нескольких измерений.
Для этого надо внести существенное изменение в нашу
точку зрения. До сих пор мы рассматривали случайные
процессы, связанные в общем с функцией x{t, а) или некото-
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ 99
рым ее комплексным аналогом, что представляло случайные
процессы во времени. С тем же успехом, можно считать t
пространственной переменной; но она представляется
одномерной. Последнее, однако, не столь существенно, как
кажется. Прием, с помощью которого мы распространяем
нашу теорию случайных процессов на случай /г-мерного
пространства, прост: мы изучаем не аналог x{t, а), который
и в самом деле связан с одномерным t, а некоторый
аддитивный функционал от множеств точек, связанный с а,
который одинаково хорошо определяется для любого числа
измерений.
Пусть имеется измеримое множество 5 значений s. Пусть
S{s) — функция, задающаяся S, равная 1 на 5 и нулю вне
этого множества. Пока мы рассматриваем пространство одного
измерения, но я намерен расширить это рассмотрение.
Функция S{s), очевидно, принадлежит L^, так как множество 5
имеет конечную меру. Рассмотрим выражение
оо
j S{s)dx{s, а), • (9.16)
—ОО
которое представляет массу в том или ином смысле. Это
аддитивный, но не вполне аддитивный функционал от S.
Интеграл (9.16) вполне определяется из того, что мы
проделали ранее. Далее, если взять другое множество T{s),
измеримое и неперекрывающееся с S{s), то имеем выражение
оо
j T{s)dx{s,oi), (9.17)
—ОО
которое ортогонально выражению (9.16), и, как следует из
вышеизложенного, имеет независимое от (9.16) гауссовское
распределение ввиду ортогональности функций S{s) и T{s).
Среднеквадратичное значение выражения (9.17) зависит от
меры множества Т значений 5. Эти свойства верны и для
случая двух или любого числа измерений. Другими
словами, x(s, а) определяет некоторую аддитивную, но не
вполне аддитивную функцию от измеримых множеств S.
Распределение для ее значений всегда является гауссовским, но
в каждом случае параметр гауссовского распределения
зависит от меры множества 5, и для непересекающихся
100 л E к Ц и я 9
множеств распределения независимы. Иными словами,
функцию x(s, а) можно заменить этим функционалом от множеств,
который полностью определяет х (5, а) и полностью
определяется ею. В одномерном случае это не дает никакого
преимущества, но для Аг-мерного случая имеется некоторое
преимущество; и то, что делается для конечной области
плоскости, можно распространить на бесконечную.
Существует сохраняющее меру отображение квадрата на плоскости
на линию или куба в пространстве на линию и т. д. Это
делается следующим образом: мы берем квадрат, делим его
на четыре части и представляем их четырьмя равными
сегментами на [О, 1]. Затем мы делим каждую из четвертей
квадрата на четыре части и представляем их шестнадцатью
равными сегментами на [О, 1] и т. д. Так строится
сохраняющее меру преобразование квадрата с плоской мерой
в отрезок с линейной мерой, и наоборот. Эта методика
распространяется на три и большее число измерений.
Следовательно, если мы имеем некоторый аддитивный
функционал для одного измерения, как, например выражение (9.16).
то мы имеем его и для п измерений. Это очень важно.
Таким образом, в то время как понятие x(s, а) не совсем
подходит для пространства, понятие аддитивного
функционала от множества точек, порожденное им, одинаково
пригодно для п и для одного измерения. Я все это привел,
чтобы показать естественность использования идеи
дифференциального пространства в случае числа измерений,
большего чем 1. Это великолепная идея. Вместо того чтобы
брать x(s, а), мы должны брать аддитивный функционал,
порожденный этой функцией. Другими словами, для любого
числа измерений мы имеем некоторый аддитивный
случайный функционал, причем не только для действительного,
но и для комплексного случая, т. е. для случая, когда мы
имеем сумму двух случайных функционалов, действительного
и чисто мнимого, независимых один от другого. С числом
измерений эта идея не связана. Основанием для
предшествующего рассмотрения служит то, что мы переходим к
квантовой теории, где мы будем иметь дело со случайными
процессами в пространстве и не будем ограничиваться одним
измерением, так как это не соответствует тому, что мы
намереваемся делать. Однако, чтобы избежать усложнения
обозначений, я могу сопоставить a:(s*, а) для п измерений
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ 101
И x(s, а) для одного измерения с помощью сохраняющего
меру преобразования и пользоваться теми же самыми
обозначениями, которые применялись раньше. Это предварительное
замечание важно для наших теперешних целей: ведь мы
переходим к квантовой теории, мы имеем дело с
броуновским движением не во времени, а в пространстве и мы хотим
освободиться от ограничений, связанных с одномерностью.
Перейдем к квантовой теории. Нет необходимости
рассматривать гамильтонианы, так как нас будет интересовать не
вывод уравнений квантовой теории из классической механики.
а тот способ описания, который она дает. Я намерен
рассмотреть случай дискретного спектра, что даст нам основные
идеи настоящей лекции. Не требуется выходить за его рамки
в данный момент.
Состояние вселенной описывается в терминах некоторого
распределения собственных функций, соответствующих типам
колебаний всей вселенной в целом. В некоторый
определенный момент времени состояние вселенной задается с
помощью
2^Л(^). (9.18)
где S принадлежит пространству п измерений, s и а^, вообще
говоря, комплексны, и мы сделали допущение
2laj2=l. (9.19)
Таким образом описывается вселенная в данный момент
времени. Допущение, принятое в квантовой теории,
заключается в том, что вселенная может находиться либо
полностью в одном, либо полностью в другом состоянии,
предположим, что она находится полностью в п-м состоянии.
Квантовая гипотеза состоит в том, что величина \ci^f, в том
или ином смысле, представляет вероятность пребывания в л-м
состоянии. Как видно из уравнения (9.19), сумма этих
вероятностей равна 1. Коэффициент а,^ называется амплитудой
вероятности. Будучи комплексным числом, а^ не может быть
вероятностью. Однако [а^р есть вероятность. В квантовой теории
имеется замечательное взаимодействие комплексных величин,
определяющих вероятность, и вещественных величин,
являющихся вероятностями. Таинственность квантовой теории
возникает главным образом из того, что мы должны получить
действительную вероятность из всего этого комплексного
102 ЛЕКЦИЯ 9
аппарата. Взаимодействие действитечьного и комплексного
было ясно выражено в постулатах, но никогда не было ясно,
почему квадрат комплексного числа должен определять
относительное количество тех случаев, когда система находится
в заданном состоянии.
Уравнение Шреаингера показывает, как меняется
распределение с течением времени. Из него следует, что если ср^ —
собственные функции, ортогональные и нормированные
функции, относящиеся к определенной задаче, то представление
(9.18) в момент t имеет вид
2^.exp(/X,0cp.W- (9.20)
Иными словами, если мы рассматриваем собственные
функции для определенной системы, то абсолютные величины
амплитуд этих собственных функций, выделенных нами, не
изменяются с течением времени, меняются только фазы. \^
называются собственными частотами, а а^ — амплитудами.
Если мы рассматриваем систему с собственными
функциями ср, то
|a„exp(/V)P = l«„P. (9.21)
где t вещественно и, следовательно, вероятность не меняется
со временем. Система стационарна. Я не вижу
необходимости выводить из соображений динамики уравнение Шредин-
гера, имеющее такое решение, так как объектом нашего
рассмотрения является не механика, а феноменология
квантовой теории, те характеристики, которые она определяет.
Для нас необычно то, что, начиная с комплексной теории,
мы приходим к действительной вероятности. Вероятность
п-то состояния равна
так как в силу (9.19)
2|«vP=l. (9.23)
Я не пытаюсь решать какие-либо философские проблемы
оснований квантовой теории; я ставлю вопрос, имеются ли
другие действительные случаи, когда мы получаем
вероятность как частное от деления квадрата абсолютной величины
некоторого комплексного числа на сумму квадратов абсо-
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ ЮЗ
лютных величин аналогичных комплексных чисел. Ответ
положителен, такие случаи существуют. Именно здесь мы
и возвращаемся к идее броуновского движения. Простейшим
примером для рассмотрения может служить случай, когда
имеются две собственные функции, т. е. имеются только
два состояния, взаимно исключающие друг друга. В
действительности общий случай можно свести к этому, если
объединить все остальные состояния в одно с собственной
функцией какого-то вида. Вероятность того, что из двух
собственных функций реализуется какая-либо одна, равна
"^'' или ,, ,l!f'L,2-- (9.24)
В выражении (9.24) обе вероятности — вещественные числа
и их сумма равна 1.
Ограничимся рассмотрением ситуации, подобной данной,
так как при этом будут видны все характерные
особенности. Можно ли указать случаи, когда вероятности
естественным образом получаются в виде квадратов абсолютных
величин, деленных на сумму квадратов абсолютных величин?
Ответ дает, например, равенство (9.15); там был именно
такой случай. Пока я не утверждаю, что это действительно
информация о квантовой теории; я только показал, что
возможна умозрительная модель вероятностей, связанная
с броуновским движением, в которой наблюдается то же
явление. То, что я сказал раньше, показывает, что не
существует коренного различия между случаями пространства
одного и нескольких измерений. Если у нас есть
последовательность ортогональных функций в пространстве двух
измерений, то мы можем отобразить ее сохраняющим меру
преобразованием в последовательность ортогональных
функций в пространстве одного измерения и вся теория
сохраняется с некоторыми формальными усложнениями. Сделав
это замечание, я имею право работать с одним измерением
вместо п измерений. Пусть имеются функции a2cpi(5) и
^гФгС*^) и выражения
А = а^( ^^ (5) dy (5, а), (9.25)
B = a<^j^^{s)dy{s, а). (9.26)
104 л E к Ц и я 9
Величины (9.25), (9.26) комплексные, с распределениями,
заданными с помощью а. Меня интересует вероятность того,
что |Л|;^|5|, т. е. мера множества значений а, для
которых выполняется это неравенство. Это типичный
вероятностный вопрос, относящийся к теории меры Лебега. Вот
ответ, к которому я пришел в уравнении (9.15):
Это есть именно вероятность того же вида, который
встречается в квантовой теории. Иначе говоря, я построил
процесс, который дает мне настоящую вероятность, численно
равную той вероятности, которую мы получаем в квантовой
теории; это может послужить рабочей моделью для
некоторых задач квантовой теории.
Иными словами, мы составили отвлеченную
математическую задачу, решение которой — действительная вероятность.
Имеется действительная мера Лебега множества точек, равная
тому же выражению, что и вероятность, в квантовой
теории, в случае выбора одной из двух собственных функций.
Выражение, полученное в квантовой теории, было физически
интерпретировано как вероятность; но математического
объяснения того, как появляется эта вероятность, не дано. Иначе
говоря, без метафизики мы имеем некоторую рабочую
модель для того случая, который встречается в квантовой
теории при выборе одной из двух собственных функций*
Дальше в настоящий момент я не пойду. Я подчеркиваю,
что все это делалось в пространстве и связывалось с
уравнением Шредингера.
Существует и другая особенность квантовой теории,
которую я хотел бы отметить. Уравнение Шредингера
преобразует выражение
2^Л(5) (9.28)
в выражение
^a,exp(llJ)o^(s). (9.29)
Это преобразование унитарно. Я имею в виду, что
так как собственные функции ортогональны и нормированы.
Действительно, обе стороны равенства (9.30) равны сумме
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ 105
квадратов модулей а^. Другими словами, уравнение Шре*
дингера можно рассматривать, как группу сохраняющих
меру преобразований в пространстве 5.
Теперь позвольте мне рассмотреть
^а^ехр(11^)^^(8) = Ф(8, t) (9.31)
— функцию от времени и пространства. Равенство (9.31)
можно записать в виде
ф(5, t)=:U^Ф{s\ (9.32)
так как это унитарное преобразование, — комплексное
преобразование, которое линейно и сохраняет
/It.WI
|2й?5. (9.33)
Рассмотрим
D -=: J Ф (5, t) dy (5, а) = / ^^Ф (s) dy (s, а). (9.34)
Мы уже видели, что унитарное преобразование пространства
функций от 5 порождает сохраняющее меру преобразование
пространства а. В этом мы убедились раньше. Другими
словами, уравнение (9.34) принимает вид
D=:fф(s)dy(s, Т^а), (9,35)
где Т^а — сохраняюилее меру точечное преобразование.
Группу унитарных преобразований, которая образует
решение уравнения Шредингера для любого момента времени
из решения для какого-то одного момента, можно свести
к группе сохраняющих меру преобразований пространства а
или фазового пространства. Это весьма важно; группы
сохраняющих меру преобразований не являются новыми в
физике. Они возникли в статистической механике Гиббса.
Я имею здесь в виду, что это одна из форм квантовой
теории, которая тесно связана со статистической механикой
Гиббса.
Мне как раз хватит времени, чтобы это установить, и
на этом я заканчиваю сегодняшнюю лекцию. Как вы помните,
в классической физике рассматривается некоторое количество
частиц, имеющих координаты q^^ и импульсы р^. Я не буду
останавливаться на том, как именно связывает их гамильтониан.
106 л E к Ц и я 9
В механике обычна задают координаты и скорости;
компоненты импульса и компоненты скорости, вообще говоря,
не совпадают. Компоненты импульса получаются из
координат и компонент скорости с помощью преобразований,
совершаемых над лагранжевыми переменными.
Преобразование со временем фазового пространства системы частиц
имеет инвариантную меру, т. е. произведение dq^^ и dp^
в данный момент времени равно этому же произведению
в любой более поздний момент. Рассмотрим фазовое
пространство. Если имеется одна координата для задания
положения и одна координата—для импульса, то фазовое
пространство двумерно. Если для положения и импульса имеется
по три координаты, то фазовое пространство шестимерно.
Возьмем двумерный случай. Имеется некоторая область
значений р и q, координат и импульсов, а не координат и
скоростей. По истечении небольшого промежутка времени эта
область изменится. Для статистики Гиббса важно, что, хотя
это не тождественное преобразование, оно сохраняет объем.
Имеется инвариантность для объема в фазовом пространстве.
Таким образом, статистическая теория Гиббса исходит из
того, что система с течением времени претерпевает
некоторую последовательность таких бесконечно малых
преобразований. Если система находится в статистическом равновесии,
группа таких преобразований сохраняет меру. Обстановка
здесь аналогичная. На отрезке а (между О и 1) мы имеем
такое же точечное преобразование, при котором точки любого
множества переходят в точки множества той же меры, и
имеем группу таких преобразований, если мы рассматриваем
решение уравнения Шредингера во времени. Таким образом,
существует довольно точная аналогия между таким способом
построения квантовой теории и традиционным способом
построения статистической механики Гиббса. Гиббс
рассматривал такие же потоки в фазовом пространстве системы.
А именно если вы возьмете малый промежуток времени, то
произойдет перемешивание такого рода. Если удвоить
промежуток времени, то это перемешивание произойдет дважды,
но объем останется прежним и т. д. Я хочу подчеркнуть,
что сопоставление уравнения Шредингера и преобразования,
заданного им, с чем-то весьма сходным в статистической
механике Гиббса, указывает на некоторый важный параллелизм;
я думаю, что в дальнейшем мы поговорим о нем еще.
НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО КВАНТОВОЙ ТЕОРИИ Ю?
Это все, что я хотел рассказать сегодня о квантовой
теории. Здесь еще очень многое надо сцелать. В дальнейшем
на этих лекциях я собираюсь рассмотреть
турбулентность и изложить некоторые свои работы в этом
направлении. Эти работы не закончены, но они связаны с
материалом этой лекции, и я могу многое рассказать о них. Но
чтобы изложить сначала более законченную работу,
проведенную ранее, я думаю на следующей лекции перейти
к исследованиям проф. Амара Бозе и моим, посвященным
применению теории случайных функций к изучению
нелинейных электрических систем, к задачам их анализа и
синтеза. В этой области непосредственно применимы некоторые
из разработанных нами методов.
Лекция 10
нелинейные системы. I
Теперь я собираюсь рассмотреть анализ и синтез
нелинейных цепей. Я 'намерен показать, что мы можем
рассматривать поведение нелинейных цепей при некоторых довольно
общих условиях под действием броуновского входного
процесса или „дробового эффекта". Одно из свойств дробового
эффекта состоит в том, что им можно в некотором смысле
имитировать любой входной процесс. Именно предположим,
Величина сигнала
Рис. 10.1.
что мы имеем конечное число отверстий, например, как на
рис. 10.4. Существует конечная, ненулевая вероятность того,
что траектория броуновского движения пройдет через эти
отверстия. Если эти отверстия сдвинуть ближе и сделать
достаточно узкими, то ряд отверстий будет с наперед
заданной точностью „аппроксимировать" какую-либо непрерывную
кривую, и тем не менее существует конечная вероятность
того, что броуновское движение пройдет через эти
отверстия. Поэтому если только цепь не устроена так, что такая
аппроксимация не может быть хорошей в течение длительного
времени, то реакция цепи на броуновское движение дает
нам по существу реакцию на любое движение.
НЕЛИНЕЙНЫЕ СИСТЕМЫ. I 109
Пока мы будем считать цепь „черным ящиком" с двумя
входами и двуМя выходами. Я не знаю, „черные" ли это
ящики, они „черные" — ех officio. Далее, нетрудно
сделать генератор дробового шума, для которого полное
количество электричества, протекающего за некоторое время,
будет довольно близким к броуновскому процессу.
Следовательно, мы можем изучать выходной процесс черного
ящика с генератором дробового шума на входе.
Предположив, что наши ящики не самовозбуждаются и т. п.
(эти уточнения следует сделать тщательнее), посмотрим, как
представить выходной процесс, когда на входе дробовой шум.
Мы уже видели, что если имеется x{t, а), то любая
функция от а, принадлежащая L^, может быть представлена
выражением
^0„{К„{^, х„). а]. (10.1)
Если на входе используется эффект, меняющийся со
временем, то (это мы также видели) мы просто сдвигаем все т.
Таким образом, выражение (10.2) дает общее представление
для функции от t, определенной всей историей параметра а,
изменяющегося с изменением t, в предположении, что эта
функция принадлежит L^ по а при любом t
^G,\K,{'z,+t х„+0. «]. (10.2)
Теперь нам нужно найти характеристики электрической
цепи, т. е. выразить выходной процесс через входной,
в общем случае для четырехполюсника (двухполюсник
включается как частный случай). Заметьте, что я не требую
сохранения энергии. Усилители—допустимые цепи при
условии, что они не самовозбуждаются и что выходной процесс
является функцией от входного, принадлежащей L?. Важно,
чтобы цепь не была самовозбуждающейся. Мы берем
некоторые цепи и представляем их характеристики с
помощью (10.2). Возбуждающиеся цепи, под которыми мы
подразумеваем и цепи, несамовозбуждающиеся в строгом
смысле, но обладающие внутренними колебаниями, не пред-
ставимы таким образом. Мы рассматриваем нелинейнбте цепи
„спокойного" типа, которые не дают самопроизвольных
колебаний, и для которых выходной сигнал не зависит от
бесконечно далекого прошлого. Если реакция системы зависит
по ЛЕКЦИЯ 10
от удаленного прошлого, то броуновское движение не
является хорошей аппроксимацией, так как мы всегда должны
рассматривать далекое прошлое.
Итак, мы рассматриваем нелинейные цепи со
„спокойным" характером, для которых выходной процесс
асимптотически не зависит от протекания входного процесса в
далеком прошлом и, как функция от а, принадлежит L^.
Выражение (10.2) является, пожалуй, немного более общим,
чем это нужно для характеристики цепи, так как выходной
п[ оцесс зависит только от прошлого и не зависит от буду-
ш,его входного сигнала. Однако это выражение зависит от
входного сигнала; следовательно, наложив ограничение на
вид выражения (10.2), мы сможем получить физически
реализуемый выходной процесс. Я собираюсь сделать это
немного позже.
Я хочу сравнить то, что мы делаем, с тем, что сделано
для линейных систем. Для них стандартным входом является
тригонометрический. Это связано с тем фактом, что если
задать два тригонометрических сигнала на входе линейной
цепи, то реакции на выходе складываются. Мы можем изу^
чать их по отдельности; они не смешиваются. В нелинейной
цепи они смешиваются и разделение на тригонометрические
слагаемые не дает никакого преимуш,ества. Иначе говоря,
тригонометрические функции — это функции, которые
обладают некоторой инвариантностью по времени: именно, за
исключением фазы, ничто не изменяется по сравнению с тем,
что было. Тригонометрические функции обладают линейной
инвариантностью по отношению к группе сдвигов. Броуновское
движение имеет инвариантность по отношению к группе
сдвигов более общую, чем линейная. Иными словами, теперь мы
имеем полную независимость для различных моментов времени.
Если в выражении (10.1) ядра K^i^z^, ..., х^) зависят
только от прошедших значений их аргументов, то мы имеем
такие характеристики, которые действительно могут быть
реализованы для цепи, выходной сигнал которой зависит
только от прошлого входного процесса. Тогда я могу
использовать полную систему функций
{?Л0}. (10.3)
зависящих только от прошедших t. Так как эта
последовательность— полная, то все, что зависит от прошлого, может
НЕЛИНЕЙНЫЕ СИСТЕМЫ. I Щ
быть описано с помощью коэффициентов при этих функциях.
Посмотрите, какие выражения я могу получить. Определение
постоянного слагаемого не вызывает затруднений. Для
линейного члена, если я имею выражение (10.4) при всех я,
то я могу узнать все, что относится к линейной части, если
ср^ — полная система функций на множестве прошедших t.
f^^(t)dx(t, а), п=\, 2 (10.4)
Таким образом, 0^ [/Cj (х), а] в (10.1) можно получить как
линейную комбинацию (10.4). Предположим, что я перехожу
к следующему порядку. Используем обобщение, состоящее
в том, что если функция K^^i'z^, ..., xj не симметричная,
то можно симметризовать ее, сложив все /С„, получающиеся
из первого K;i различными перестановками аргументов, и
разделив на число перестановок. Теперь, если я знаю
то мне известно все о моих квадратичных членах, так как
можно представить все Оз в виде линейной комбинации
членов вида (10.5) в силу ортогональности разложения.
Ведь если ср^(^) образуют полную систему, то функции
вида (10.5) или их симметризации также образуют полную
систему функций с двумя переменными. Аналогично если
я рассмотрю
(10.6)
то буду иметь разложение для кубичных членов. С
помощью (10.6) можно получить любое выражение 3-го порядка.
Возникает вопрос об отыскании подходящей системы
функций для разложения ядер К. Если я могу получить
такую систему, то я имею способ анализа цепей, способ
описания выходного процесса с помощью входного, а также,
как мы увидим в дальнейшем, способ синтеза цепей. Итак,
рассмотрим теперь (и это восходит к одной старой работе
проф. И. У. Ли и моей) одну частную систему
ортогональных функций, которые зависят только от прошлого и
с помощью которых будет строиться наше разложение. Это
так называемые функции Лагерра. Я их опишу двумя спо-
соОами, математически и с точки зрения инженера, т. е.
112 ЛЕКЦИЯ 10
покажу как функции Лагерра от входного процесса в
прошлом можно получить с помощью приборов. Затем я перейду
к разбору синтеза и анализа электрических цепей.
Сначала надо выяснить некоторые простые свойства
однокаскадной ячейки, изображенной на рис. 10.2. Заметим,
что работа с такой разомкнутой цепью не представляет
трудностей, так как существуют приборы, управляющиеся
напряжением, но не нарушающие токов, в частности приборы,
в которых используются катодные повторители. Вопрос
состоит в том, как выражается выходной процесс такой
простой ячейки через входной. Выходной процесс можно
^А V
с Разомкнутая
цепь
Рис. 10.2.
описать на языке частот или времени. Как и в любой
электрической цепи, выходной процесс не может зависеть от
будущего входного сигнала. Далее, если ш — частота, то
Е{(^) 1 + /со (LCy^^ '
Следует отметить, как следствие равенства (10.7), что
простая ячейка дает сдвиг фазы, не не изменяет амплитуду.
Кроме того, входной импеданс ячейки является чистым
сопротивлением, равным (LlC)'\
Компановка аппаратуры, которая будет показана,
по-видимому, предложена проф. Ли. Произошло это примерно
так. Я сказал, что электрические цепи могли бы
реализовать передаточные отношения такого типа, и проф. Ли
заметил, что эти цепи следовало бы присоединять друг
к другу так, чтобы элементы одной цепи могли также
использоваться в следующей, что позволило бы создавать
цепи этого типа весьма компактным и экономным способом.
Полагаю, что это правильное изложение. Рассмотрим две
НЕЛИНЕЙНЫЕ СИСТЕМЫ. I
113
ячейки разомкнутой цепи (рис. 10.3). Заметьте, что в первой
ячейке ничего не изменилось, так как вторая ячейка по
отношению к первой представляет то же самое
сопротивление (L/C)'^^ Поэтому
1 — /со {LC)'f^
£(00)
1 + /О) {LC)'I'
(10.8)
(10.9)
£(00)
Этот процесс может повторяться сколько угодно раз.
Если мы продолжаем заменять сопротивление добавочным
Рис. 10.3.
каскадом, то можем получить передаточную характеристику
вида
Уп{^)
1—/a)(Z,C)'^2
(10.10)
£((0) [ l+/a)(Z,C)'^2
Можно ввести добавочный множитель l/[l \-Ы(1,С^^\ на
который умножается любая передаточная характеристика,
если поместить индуктивность величины L между источником
и первым каскадом, т. е. между клеммами О и 1 (рис. 10.3).
Тогда я получу цепь, реализующую последовательность
функций
t^-^'-(^0'^^i' . (10 11)
Важно отметить, что мы можем одновременно получить любое
число передаточных отношений напряжений вида (10.11).
Чтобы избавиться от (LO)^^, мы выберем наши единицы так,
чтобы это выражение было равно 1. Это по существу выбор
масштаба времени. Тогда мы получаем
(1 — ыу
(1 + /0))«+1
л>0.
(10.12)
g Зак. 2305. Н. Винер
114 ЛЕКЦИЯ 10
Возникает вопрос, что это за оператор во времени?
Чтобы найти этот оператор, возьмем преобразование Фурье
от выражения (10.13). Так как преобразование Фурье любого
оператора, заданного на языке частот, дает его описание
во времени, мы берем
/
(i"+..i?'. ''•"''"■ ('»■•')
Вместо того чтобы вычислять эти интегралы, я укажу
другой подход, а затем сравню результаты. Я изменю знак и
буду работать с положительным ^, а не с отрицательным;
переход снова к отрицательному t не вызовет затруднений.
Я утверждаю, что функции
t^e-\ 0<^<оо, п = 0, 1, 2, ... (10.14)
принадлежат L^, и нетрудно показать, что они образуют
полную систему функций в L?, К этому я перейду позже.
Независимо от того, полна система или нет, фун-кции
принадлежат L?, и их можно нормировать. Имеем
{e-'fdt = \. (10.15)
/ -.
о
Таким образом, если взять (Т)''^ е~\ получим нормированную
функцию. Теперь я перехожу к процессу ортогонализации.
Я беру
{at + b)e-^ , (10.16)
и подчиняю это выражение двум условиям: оно должно
быть ортогонально е~^ и нормировано. Тогда я получаю,
во-первых,
сх>
j (at-i-b)e-'^4t = 0, что дает Ь = — -~, (10.17)
о
и, во-вторых,
a'^f(t — ^Je-^^t=\, что дает а = (~у. (10.18)
о
Таким образом, функция V^4/5 (^ — Уг)^"^ ^^Р^^^Рована и
ортогональна первой функции. Я продолжаю этот процесс
НЕЛИНЕЙНЫЕ СИСТЕМЫ. I 115
неограниченно. Система таких функций будет полной на
[О, сх^), так как получена ортогонализацией полной системы.
Следовательно, любая функция может быть выражена через
них. Они мне дают полное представление о настояш.ем и
прошедшем. Теперь я утверждаю, что эти ортогональные и
нормированные функции совпадают с функциями, заданными
выражением (10.13), с точностью до постоянных
множителей, различных для разных л. Это можно показать. Иначе
говоря, с помощью аппаратуры, состоящей из каскада
простых ячеек и добавочной индуктивности, я получаю
выходные процессы вида (10.4), когда входной процесс —
дробовой шум; 9;^(0 — функции Лагерра.
Я получу соответствующие G следующим образом. Для
начала заметьте, что G — функции только от выходных
процессов лагерровских цепей и, следовательно, G — операторы,
зависящие только от прошлого. Рассмотрим
Ое«ДПт?. ос}. (10.19)
k
Выражение (10.19) дает мне полный базис для О любого
выражения, так как я получаю полную систему
симметричных К. Далее, было установлено раньше, и легко
проверить, что поскольку ср ортогональны, то выражение (10.19)
можно переписать в виде
Ое«ДИ9*Ч а} = П0„,(т*Ч «}• (10.20)
Это так называемые полиномы Эрмита от лагерровских
функционалов. Я могу получить все члены равенства (10.20),
если сумею сцелать следующее: если я смогу получить
в каждый момент времени значение лагерровского
функционала от прошлого, если затем я смогу получить многочлен
от этих значений, который будет многочленом Эрмита, и,
наконец, если я смогу перемножить эти многочлены друг
с другом.
Если учесть законы электротехники, то что надо сделать,
чтобы их получить? Ну, пожалуй, первое, что я могу
сделать— это сложить напряжения; это не трудно. Так как я
должен получить многочлены, мне надо перемножить
напряжения. Тогда, если я могу складывать и перемножать
напряжения, нетрудно получить все эти члены. Как перемножать
8*
116
ЛЕКЦИЯ 10
напряжения? Это очень просто. Предположим, что у меня
есть специальное устройство — квадратичный детектор. Если
имеется напряжение V (t), то требуется прибор, который
преобразовал бы его в напряжение У^(1), Иначе говоря,
мне нужен нелинейный прибор с квадратичной
характеристикой. Есть различные способы их выполнения; общий
„ Выход
Выход
Рис. 10.4.
принцип состоит в использовании двухтактной схемы.
Предположим, что я уже получил характеристику вида,
который изображен на рис. 10.4; точность ее формы не
играет большой роли. Но я могу также получить
характеристику вида, представленного на рис. 10.5, т. е. ту же
характеристику, что на рис. 10.4, но отраженную
относительно вертикальной линии. Нетрудно сделать детектор,
работаюш.ий иным образом. Тогда, используя вакуумные
Выход
Рис. Щб.
лампы или полупроводниковые триоды, нетрудно собрать
двухтактную схему, имеющую характеристику вида,
изображенного на рис. 10.6. Если я буду работать на у^ком
участке этой кривой (чем уже, тем лучше), а затем буду
усиливать, то получу квадратичную характеристику. Чтобы
умножить V^{t) на 1^2W» ^ образую напряжения V\(t)-\-У^^t)
и V^^{f) — V'gCO- Затем с помощью этого квадратичного
устройства я получу [V^i(0 + ^2W1^ и \у ^(t)— V ^(f)\^,
НЕЛИНЕЙНЫЕ СИСТЕМЫ. I 117
Нетрудно вычитать напряжения, так что я вычту и получу
4V^i(0^2(0- Следовательно, я могу перемножать напряжения
с помощью существующей аппаратуры. Перемножив
напряжения, я могу опять умножить их, т. е. могу получить не
только квадрат, но и куб, и четвертую степень. Я могу
получить многочлен конечной степени. Следовательно, могу
получить многочлены Эрмита. Итак, нам нетрудно получать
полиномы Эрмита и их произведения, так как мы можем
перемножать значения лагерровских функционалов от
прошлого. Поскольку я умею складывать различные полиномы
Эрмита, я могу синтезировать все, что только можно
синтезировать из моих симметричных функций; т. е. могу
аппроксимировать сколь угодно точно любую функцию от
прошлого, которая изменяется в зависимости от данной
функции. Другими словами, я могу синтезировать любую
нелинейную характеристику, не связанную с далеким
прошлым, и принадлежащую L^. Следовательно, у меня есть
универсальный метод синтезирования.
Остается вопрос: можно ли анализировать? Если известно,
что функция существует, то как определить коэффициенты
моего разложения? Как мне представить выходной процесс
в виде полиномов Эрмита от значений лагерровских
функционалов и записать характеристики системы? Следует
подчеркнуть, что, если я смогу это сделать для нелинейных
цепей, я получу эквивалент того, что обычно делается для
линейных цепей с помощью передаточных отношений. Иными
словами, если я описал, как цепь реагирует на любой
броуновский входной сигнал, то я знаю, как она будет
реагировать на любой входной сигнал. В дальнейшем я разберу
это подробно.
Сейчас я хочу по крайней мере рассказать, что я делаю.
Я дал полное описание цепи. Я ее проанализировал. Следует
ясно представлять себе, что отношение напряжений, или
импеданс, не является полной характеристикой нелинейной
цепи. Много лет назад, почти сорок лет, я работал с проф.
Ванневаром Бушем над этими задачами, и мы пытались
поставить вопрос: как определить импеданс нелинейной цепи?
Ответ состоит в том, что импеданс нелинейной цепи нам не
нужен. Импеданс не является полной характеристикой цепи,
т. е. поведение цепи нельзя охарактеризовать с помощью
ее реакции только на тригонометрические функции. То, что
118 ЛЕКЦИЯ 10
мы искали, дает реакция цепи на дробовой шум, и мы
получаем теорию, эквивалентную, параллельную теории
импеданса, но не тождественную с ней.
Я смогу получить мои коэффициенты в виде средних
значений. Это будут средние по а. С помощью цепей можно
достаточно просто получать временные средние. Об этом
будет рассказано подробно на следующей лекции. Временное
среднее, вообще говоря, не совпадает со средним по а, но
если верна эргодическая гипотеза, то временные средние
почти всегда равны средним по а. Поэтому все получится,
если есть эргодичность. К тому же эргодическая гипотеза
удовлетворяется броуновским движением: если мы сдвигаем
броуновское движение по времени, то это преобразование
вызывает сохраняющее меру преобразование а и можно
показать, что это сохраняющее меру преобразование не имеет
инвариантных множеств, которые измеримы и мера которых
отлична от О или 1. Иначе говоря, если взять какую-либо
конкретную реализацию входного дробового шума и
образовать временные средние, то можно найти средние по а,
которые требуются нам для определения коэффициентов.
Есть несколько вопросов: 1) как связаны средние по а
с коэффициентами, 2) как действительно получить средние
по а. Мы их обсудим на следующей лекции. Мы почти
закончили задачу синтеза для нелинейных цепей и на
следующей лекции перейдем к задаче анализа.
Лекция и
нелинейные системы, п
Перейдем теперь к задаче анализа системы. Рассмотрим
два черных ящика, один из которых имеет известные
характеристики, а другой неизвестные. Я могу соединить их так,
как показано на рис. 11.1: входы параллельно подключаются
Генератор
дробового
шума
Неизвестный
черный
ящик
x(t,a)
Известный
черный
Я1цик
/H(t,a)
fH(t,a)
Умножитель
Выходной
прои^есс
Рис. 11.1.
к генератору дробового шума. Затем выходные процессы
перемножаются (предполагается, что мы имеем умножитель)
и получается выходной процесс системы r{t, си). Неизвестный
черный ящик имеет на выходе
/At. «)-20«[/C„(f + T, t-\-x„), а]. (11.1)
Другой ящик имеет на выходе
/Л(. «)-=20„[Я„(^+п i + '^n). «1- (11-2)
120 л E КЦ и я и
Произведение выходных процессов систем равно
r(t, a) = 2 20m[^m(^+^l t + ^m). «1 X
Х0„[Я„(^+Х1 ^ + х„). а]. (11.3)
т •
т п
Если я рассматриваю временное среднее этого произведения,
оно равно
т
1
lim -7^^ 1 r{t, (x)dt для почти всех а. (И.4)
7'->сю у.
Но МЫ знаем, что преобразование, которое мы получаем,
прибавляя t к аргументу всех броуновских кривых, является
сохраняющим меру преобразованием броуновских движений,
и это сохраняющее меру преобразование эргодическое.
Мы уже в этом убедились. Поэтому выражение (11.4) равно
1
Jrfa^ 2 G^lK^i-z, Tj, а]0„[Я„(т1 х„\ а]. (11.5)
О т п
В этом содержание эргодической теоремы. Для почти всех а
временное среднее совпадает со средним по состояниям.
Теперь мы используем материал, изученный раньше.
Когда тип различны, интегрирование по а дает нуль.
Когда тип одинаковы, имеем
п\ f ... fK„(x, т„)Я„(т, TjdT, ...rfv (11.6)
Следовательно, если мы знаем среднее значение r(t, а),
мы получаем
т
lim -^^ Г г (t, а) dt =
7'->оо ^^ ^
п
Так как известный ящик можно сделать каким угодно, то,
в частности, можно сделать его „одночленным". Мы можем
Бзять конкретное Н
ЯДх, ^„) = Пт*(^.-). (11.8)
НЕЛИНЕЙНЫЕ СИСТЕМЫ И
121
где cp^^ — функции Лагерра. Если мы имеем множество Н
такого вида, соответствующих произведениям лагерровских
функций, то временное среднее выходного процесса будет
с точностью до п\ совпадать с интегралом по времени от
произведения К^ и известной лагерровской функции. Таким
способом ^мы можем получить разложение /С^ в ряд по
Рис. 11.2.
Рис. 11.3.
произведениям лагерровских функций, и у нас будут
необходимые данные, чтобы синтезировать неизвестный яш.ик. Это
значит, что мы имеем способ анализа и синтеза систем.
Существует один или два простых приема, с помощью
которых можно получить наши средние значения. Я здесь
не буду входить в детали. Оказывается, что если мы
возьмем случайную функцию такого типа, который изображен
на рис. 11.2, и усредним ее за длинный период с весовой
функцией рис. 11.3, т. е. с весовой функцией, убывающей
экспоненциально, или с такой, которая представлена на
рис. 11.4, то средние почти всегда
будут одними и теми же. Я мог бы
прийти к этому путем вычислений;
это легко проверить. Иными
словами, мы можем вычислять
временное среднее в равенстве (11.7),
используя экспоненциальное
ослабление прошлого.
Мы можем произвести умножение и усреднение Д(^ а)
и /и(^ ^) с помощью электрического устройства, как и все
остальное; один из способов получения среднего значения
произведения с некоторой весовой функцией заключается
в использовании ваттметра. Такой ваттметр показан на
рис. 11.5. Вращательный момент катушки пропорционален
произведению входных напряжений V^ и !/„.
Теперь предположим, что мы укрепили на оси катушки
медный диск и поместили электромагнит поперек этого
— f
Рис. 11.4.
122
ЛЕКЦИЯ И
диска, как показано на рис. 11.6. Питается электромагнит
от внешнего источника. Это нам даст усреднение с
экспоненциальным ослаблением прошлого. Чем больше затухание,
тем дальше усреднение распространяется на прошлое.
Мы знаем, что произойдет. Затухание будет мешать оси
свободно поворачиваться. Результатом длительного
воздействия этого будет усреднение с некоторой весовой функцией
предыдуш.их положений оси. Далее, если мы увеличиваем
затухание, заставляя ток в электромагните стремиться
к бесконечности, тогда положение оси асимптотически
приближается к среднему значению произведения !/„ и V^^.
Используя эти устройства, мы мoжe^^ считывать с
ваттметра среднее значение произведения для данного яш,ика-
теста, и это даст нам интеграл в равенстве (11.7) с
вероятностью 1 с той точностью, которую мы сможем технически
г^оШлягч
Рис. 11.5.
Рис. 11.6.
обеспечить. Если мы имеем яш,ик с весовой функцией —
эрмитовским полиномом от функций Лагерра — и какой-то
неизвестный яш,ик, соединяем их указанным способом,
считываем стационарное значение произведения и делим на п\,
то тогда мы получаем интеграл произведения К^ и эрмитов-
ского полинома степени п. Это дает нам представление К^
в виде суммы произведений п-го порядка эрмитовских
полиномов.
Иначе говоря, этот способ позволяет нам использовать
аппаратуру для синтеза, о которой говорилось на предыду-
ш,ей лекции, как аппаратуру для анализа. Все что требуется
для устройства ящиков-тестов — это яш,ики с лагерровскими
весовыми функциями. Я уже говорил, как их получить,
поскольку я говорил о том, как образовать из них
полиномы и как перемножать эти полиномы. Необходимые
ящики-тесты получаются из набора ящиков с лагерровскими
весовыми функциями и умножителей. Мы берем данный
• НЕЛИНЕЙНЫЕ СИСТЕМЫ П |23
неизвестный ящик, подаем дробовой шум на его вход,
считываем величину отклонения при большом затухании и
получаем таким образом один из коэффициентов. Зная эти
коэффициенты, мы можем собрать соответственные члены и
воссоздать устройство.
Таким образом, изложенное является одновременно
теорией и анализа и синтеза нелинейных устройств. Вначале я
описал синтез, но, изложив синтез, я показал, как
произвести анализ и искусственно воссоздать устройство из этих
лагерровских и эрмитовских выражений.
Лекция 12
КОДИРОВАНИЕ
Теперь я перейду к другой задаче — задаче дискретного
кодирования. Рассмотрим временные ряды, которые в
отличие от броуновского движения задаются только в
дискретные моменты времени. Возьмем некоторую функцию /.
действительную и интегрируемую по Лебегу. В данный
момент не требуется, чтобы / принадлежала Z^, но в
дальнейшем мы поставим это условие.
Я рассматриваю /(а), но я рассмотрю также сохраняющее
меру преобразование Т и f (Т^о). Возьмем
последовательность из /(а) и предшествующих ей f{T~^a), /(7~^а) и
т. д. Предполагается, что в этой последовательности нет
полной зависимости последующих членов от предыдущих.
В действительности мы допускаем далеко не полную
зависимость от прошлого.
Между прочим, удобно заменить мое первоначальное а
на а, которое полностью определяется последовательностью
значений /{Т~^а), Это не проблема. Раньше для
броуновского движения мы провели подобное построение;
используется аналогичный прием отображений. Я ввожу новое
переменное а.
Я беру /(а) и вначале беру целый отрезок значений
переменной, скажем, а^. Имеются две возможности: / (а) > О
или /(а)<0 (рис. 12.1 и 12.2). Каждая из них
соответствует определенному случаю. Я ставлю им в соответствие
две части отрезка а^, как показано на рис. 12.3. Затем я
делаю нечто подобное тому, что делал раньше. Я делю
область значений /(а) на четыре части и также делю на
4 части область значений /(7~^а). Это дает 16 случаев, как
КОДИРОВАНИЕ
125
видно из рис. 12.4. предполагается, что они измеримы, так
что я получаю 16 вероятностей. Далее, я делю эти области
все мельче и мельче, одновременно добавляя f\T а), f {Т а)
точно так же, как это делалось в случае броуновского
движения. Таким образом, я получаю а^, которое
представляет /(а) и,ее предыдуш.ие значения в дискретные моменты.
f(oc)
«/
Рис. 12.1.
Рис. 12.2.
Рис. 12.3.
Затем я описываю распределение /(а), f{Т~^а), ... на
языке а^.
Это удобное представление, так как нас интересует
именно дискретный ряд величин. Отдельное значение а
(прежнего) не определяется полностью последовательностью
значений /; однако мы имеем новое а, определяющееся ею
единственным образом.
Итак, я отобразил дискретную временную
последовательность в cp(ai), cp(r~^aj) Я не только получаю
такую последовательность, но и условное распределение
/rr'^ajl
-I
f(OL)
Рис. 12.4.
для cpC^i) при заданном прошлом, что можно показать
следующим образом. Я помещаю значение /(а) в некоторый
ящик, т. е. в некоторое измеримое множество. Кроме того,
я накладываю ограничения на значения /(7"^), /(7~^а), ...
так же, как я делал это раньше. Утверждения: „значения
/(г ^а), /(7~^a), /(7~\), ... лежат в некоторой области"
и „значение/(а) лежит в некоторой области S" — определяют
126
ЛЕКЦИЯ 12
некоторую область а, общую^ всем этим событиям и
имеющую меру. Этим и определяется условное
распределение, когда выполнены условия, наложенные на прошлое.
С помощью математических рассуждений можно показать,
что при почти всех последовательностях „прошлого"
существует определенное условное распределение для значений /.
Вероятность [f(a) ^Х]
Р(Х)
j£
~^Х
Рис. 12.5.
Рис. 12.6.
Итак, мы имеем условное распределение для /(а) при
заданном „прошлом" для почти всех „прошлых" /(а). Оно
задается некоторой неубывающей функцией. Вероятность
того, что при заданном „прошлом" значение /(а) меньше
некоторого числа, • возрастает с ростом этого числа, как
показано на рис. 12.5.
Хорошо известно, что всякую неубывающую функцию
можно составить из трех функций — слагаемых. Первая имеет
счетное число скачков. Ее называют разрывной компонентой
/рМс/л
Р(.х)
Рис. 12.7.
Рис. 12.8.
неубывающей функции; она показана на рис. 12.6. Вторая
может быть представлена в виде интеграла от
положительной функции, например такой, которая показана на рис. 12.7.
Эта функция, пример которой приведен на рис. 12.8,
называется абсолютно возрастающей компонентой неубывающей
функции.
Однако в общем случае неубывающая функция содержит
и третью компоненту (и я приведу пример), непрерывную,
HQ возрастающую на множестве меры нуль. Я приведу этот
КОДИРОВАНИЕ 127
'
/
4
i
i
0
-
. . 1
3
-
-
1 1 1 1
1 •
Пример, чтобы было ясно, что такие случаи возможны. Это
будет непрерывная функция, не имеющая производной,
которая может представлять функцию плотности распределения.
Чтобы построить такую функцию, возьмем отрезок от О
до 1. Рассмотрим его среднюю треть от 7з ^^ ^з ^ будем
считать, что^ наша функция равна ^2 в этой области.
Рассмотрим первую и последнюю трети отрезка, возьмем
средние трети этих третей и на
них положим функцию
равной V4 и ^/4 соответственно.
Затем возьмем средние
трети всех оставшихся
интервалов и на них положим
функцию равной Vs» ^/s» Ve
и 7/8 (см. рис. 12.9).
Я могу продолжать
заполнение такими отрезками.
Заметим, что любой верти- Рис. 12.9.
кальный просвет будет рано
или поздно заполняться. Поэтому функция будет непрерывной
и неубываюш,ей. Однако все возрастание происходит на
множестве нулевой меры. Заметьте, что возрастание не имеет
места на средней трети отрезка. Его нет также на средних
третях двух других третей. Если сложить длины всех
областей нулевого роста, то получим
4-+2(4-)+4(^)+...=1. (12.1)
что составляет полную длину отрезка. Таким образом, эта
функция не возрастает на множестве точек, всюду плотном
на отрезке. Это непрерывная недифференцируемая функция.
Теперь я намерен рассмотреть непрерывные функции,
определенные в области от — сх:> до оо, имеющие или не
имеющие производной. Я наложу на них одно
дополнительное ограничение, исключающее существование „прошлого",
при котором закон условного распределения представляется
функцией, подобной функции на рис. 12.9. Я потребую, чтобы
эти функции были собственно возрастающими (таким
образом, функция „средних третей" не является собственно
возрастающей, так же как и функция, приведенная на рис. 12.10).
128
ЛЕКЦИЯ 12
О Производной я ничего не говорю. Производная может быть
нулем в течение некоторого времени, функция может иметь
одинаковые значения в двух разных точках; меня это не
беспокоит. График этой функции может иметь одну и ту же высоту
Рис. 12.10.
в двух разных точках. Заметьте, что если у меня есть
функция, аналогичная изображенной на рис. 12.9, и если я
прибавлю к ней собственно возрастаюш.ую непрерывную
функцию, то тогда снова получится собственно возрастающая
непрерывная функция.
Я предполагаю, что функция условного распределения
для значений /(а) при заданных значениях /(Г~^а),
/(Т'^а), ... является для почти всех „прошлых" /(а)
собственно возрастающей. Тогда при заданном „прошлом"
я получаю некоторую возрастающую функцию, равную О
^^fCa)
При /(а) = — оо и возрастающую до 1 при /(а) = оо. Эта
функция, изображенная на рис. 12.11, зависит от „прошлого".
Можно преобразовать эту функцию соответственным
образом для каждого „прошлого". Если взять в качестве
аргумента функции условного распределения величину А —
величину площади, лежащей под кривой условной плотности
распределения (рис. 12.12), а не величину /(а), как раньше,—
то получится функция, график которой идет от О к 1 под
углом 45"", как показано на рис. 12.13. Функция распреде-
КОДИРОВАНИЕ
129
ления A(f) зависит от прошлого /(а) и, следовательно,
зависит от значения а для данного распределения; я
обозначу через ^(а) ее значение при данном а.
По построению ^(а) равномерно распределена на
отрезке [О, 1], каково бы ни было прошлое, так как я провел
P[f(OC)'XiJ
Рис. 12.12.
нормировку в зависимости от прошлого. Распределение
для ^(а) имеет вид рис. 12.14 независимо от прошлого.
Рассмотрим теперь g\T V). Функция ^(а) зависит от /(а)
и ее прошлого. Функция g{T ^а) зависит от f[T~^a) и ее
Рис. 12.13.
прошлого; g{T а) также является равномерно
распределенной в интервале [О, 1]. Значения ^(7~^а) и ее свойства не
влияют на распределение ^(а). Поэтому ^(а) и g{T~^(x)
при наших допущениях независимы одна от другой.
Независимо от того, в какую область мы заключим значения
9 Зак. 2305. Н. Винер
130
ЛЕКЦИЯ 12
ОДНОЙ ИЗ НИХ, другая останется равномерно распределенной
в интервале [О, 1].
Аналогично ^(а), g\T V), g\T а), . . . равномерно
распределены и независимы друг от друга. Мы получаем
последовательность независимо меняющихся величин, лежаш.их
между О и 1. Каждая из них представляет (нелинейным
образом) новые сведения о /.
Итак, g определяются с помош.ью „прошлого" /. При
каких условиях определяются / с помощью „прошлого" ^?
Позвольте мне сказать так: значениями g кодируются
значения / и ее прошлого. Можно ли найти /, зная ^? Если
можно, то мы получаем способ построения дискретного ряда
Распределение для дса)
Г\
I
Рис. 12.14.
-д«1)
сигналов, удовлетворяющего заданным условиям в
зависимости от дискретного ряда полностью независимых
сигналов, лежащих на отрезке [О, 1]. Это важная задача
кодирования.
Заметьте следующее: так как функции распределения
являются собственно возрастающими, то если известны
/(7"'а), /(Т'^а), ... и ^(а), можно /(а) выразить через
них. Значения /(Т'^а), /(7~ а), ... определяют функцию
распределения, соответствующую g{p), Si затем частное
значение /(а) определяется значением ^(а). Итак, мы имеем
условное кодирование для /(а), еще не в виде
последовательности ^, а с помощью первого g и остальных /.
Таким же образом можно кодировать /(7~V) с помощью
g{T V) и более ранних /. Следовательно, можно
кодировать /(а) с помощью ^(а), g{T~^a), /(Т~ а), /(Г'^а)
Продолжая этот процесс, получим кодирование /(а) с по-
мощью g(a), g(T-'a). g{T~\) §(7^^), /[Т-^^+^а].
/ [Г-^^+^'а]
КОДИРОВАНИЕ 131
Кодирование, которое мы ранее осуществляли с
помощью g и прошлого / до некоторого момента, можно
осуществить посредством одних только g, но для этого
необходимо одно допущение. Вначале я установлю его,
а позднее мы обсудим, является ли оно естественным.
Рассмотрим а. Это по существу aj, так как нам нужно,
чтобы о* зависело только от последовательности /. Введем
измеримые множества точек а, принадлежащие некоторому
классу, который зависит только от /(/""'^а), /{Т'^^'^^^а),
y:Jj-(«+2)^j ^^^ измеримые множества точек,
которые можно задать с помощью утверждений, относящихся
к /(Т'^'а), f{T~^^'^^^a) Назовем их принадлежащими
классу С^. Любое измеримое множество из класса C^^i
автоматически принадлежит С^, так как утверждение,
относящееся только к членам последовательности /, по номеру
большим или равным п, содержит также утверждения,
относящиеся только к членам последовательности, по номеру
большим или равным п-\-\. Я рассматриваю класс измеримых
множеств, заданных таким образом; они образуют борелев-
ские поля, определенные различными классами. Существует
соотношение
С„зС„+,зС„+2^С„+з--- (12.2)
ДЛЯ этих классов множеств, определенных отдаленным
прошлым.
Существуют некоторые множества 5, принадлежащие
всем С^. Их можно задавать сколь угодно удаленным
прошлым. Такие множества принадлежат Соо. С^ представляют
множества, заданные утверждениями, касающимися только
тех /, которые следуют за п-и и п-го. С^о можно
определить таким же образом при сколь угодно больших п.
Допущение, которое я сделаю, относится к Соо и сходно
с эргодической гипотезой. Класс Соо не пуст. Наибольшее
из всех множеств не задается никакими ограничениями и
может быть определено как соединение наибольшего
множества некоторого класса наибольшего множества
предыдущего класса и т. д. Допущение, которое я сделаю, состоит
в следующем:
Если S измеримо и принадлежит Соо, гпо мера S равна
либо 1, либо О,
132
ЛЕКЦИЯ 12
Мы утверждаем, что измеримые множества, которые можно
задать произвольно удаленным прошлым, имеют меру,
равную О или мере наибольшего множества, содержаш.его все
остальные. Заметьте, насколько тесно Э'го связано с эргоди-
ческой гипотезой. Опять появляется мера О или 1.
Если эта гипотеза верна, то /(а) полностью определяется
с помош.ью g(oL), g{T~^a), g (Т'^^а), ... без учета сколь
угодно удаленного прошлого, за исключением множества
случаев, имеющего нулевую вероятность. Наше допуш,ение
сводится к тому, что отдаленное прошлое несуш.ественно
при определении /(а), что любое утверждение, основанное
Распределение
Распределение
д(а)
дШ
Рис. 12.15.
на отдаленном прошлом, является почти всегда верным или
почти никогда не является верным, или, иначе, что любое
измеримое множество, заданное отдаленным прошлым, имеет
меру либо О, либо 1.
Тогда можно доказать, что задание g определяет /(а)
таким образом, что знание распределения для g дает
распределение для /. Можно кодировать / значениями g в на-
стояш,ем и в прошлом. Я вернусь к этому в следуюш.ей
лекции; результат, который мы получаем, состоит в том, что
мы можем не только кодировать наше сообш,ение
последовательностью независимо меняюш,ихся величин, но и
декодировать его, что, конечно, важно.
Нет никакого смысла кодировать сообш.ение, если нельзя
его декодировать; однако при нашем допуш,ении
декодирование возможно. Этому будет посвяш,ена часть следуюш,ей
лекции. Впрочем, есть одно предложение, достаточно
простое, чтобы рассказать его сегодня. Мы кодировали /
сигналами, значения которых распределены равномерно в
промежутке [О, 1], как на рис. 12.14. Возьмем это распределение
КОДИРОВАНИЕ 133
вблизи середины и изменим его с помощью преобразования
масштаба горизонтальной шкалы, как показано на рис. 12.15.
Втляните, и вы увидите, что можно получить гауссовское
распределение с помош,ью соответствуюш.его преобразования
масштаба шкалы. Поэтому если можно кодировать / с помо-
ш.ью g, распределенных равномерно, то можно кодировать /
и величинами с независимыми гауссовскими распределениями.
Мы рассмотрим это на следуюш.ей лекции: это позволит нам
применить в задаче кодирования дискретный аналог теории
броуновского движения, изложенной раньше.
На следуюш.ей лекции я закончу эти рассуждения и
перейду к гауссовскому кодированию и декодированию.
Я покажу, что теория ортогональных разложений, которую
мы построили для броуновского случая, применима и здесь
и дает нам способ представления сигналов с помош,ью
некоторых основных, независимо распределенных гауссовских
величин в виде ряда по полиномам Эрмита.
Лекция 13
ДЕКОДИРОВАНИЕ
я хочу немножко расширить прошлую лекцию. Мы
отправлялись от
/(а), f{T-\\ f{T-\l ... (13.1)
и получили из этого выражение
g(a). g(7-'a), g{T-\) (13.2)
где jg'(a) зависело от „прошлого* и „настоящего" /(а). Эти g
были независимы и равномерно распределены в
интервале [О, 1]. Вопрос состоит в том, можно ли вернуться
назад, к распределению для / от распределения для ^?
Мы можем выразить /(а) через
^(а). g{T-'a) giT-\). /{Т-"-\). fiT-''-'о,)
(13.3)
Нам надо рассмотреть некоторые утверждения относительно /.
Именно возьмем утверждение о
f(a), f{T-'a) /(Г-*а). (13.4)
Пусть значения этих функций лежат в некоторой области
/г-мерного пространства. Пусть 5(a)—ее характеристическая
функция, измеримая по а. Нам надо знать, можно ли
определить меру, связанную с этой функцией от а, ^ помощью
утверждения, относящегося к
^(а). g{T-\), g{T-'a) (13.5)
Разумеется, это можно сделать с помощью утверждения,
относящегося кр э^ем членам (13.3), так как каждый из
ДЕКОДИРОВАНИЕ
135
членов последовательности (13.4) может быть выражен через
все члены (13.3). Вспомните, что наше а по
построению полностью определяется последовательностью /. Поэтому
какое-либо утверждение относительно 5(a) можно сделать
с помощью утверждений, касающихся конечного числа g и
^прошлого" / до некоторого момента. Последнее множество
можно аппроксимировать множеством, определяемым всеми g
и „прошлым" / до произвольно удаленного момента. Другими
словами, мы можем описать каждую из конечного числа /
в выражении (13.4) с помощью ^(а), g{T~^cf) и т. д. и
бесконечно удаленного прошлого /.
hCa)
Рис. 13.1.
Любое утверждение (в том числе и условное), сделанное
в терминах бесконечно удаленного „прошлого" / и
относящееся к измеримому множеству /, является почти всегда
верным или почти всегда ложным. Следовательно, если
опустить утверждения, которые почти всегда верны или почти
всегда ложны, то все остальные утверждения можно выразить
в терминах g (при любом числе функций /). Бесконечно
удаленное прошлое не имеет значения, так как любой класс,
заданный бесконечно удаленным прошлым, имеет меру либо
О, либо 1. Вспомните, что множества меры О или 1 не влияют
на распределение. Поэтому можно полностью описать на
языке g распределение для любого числа /. Здесь мы и
остановились на прошлой лекции.
Далее, я перехожу от ряда ^(а) к ряду /г (а), который
получается из ^(а) простым преобразование!^, как показано
на рис. 13.1. Точка V2 ^^^ кривой g(a) переходит в центр
для кривой /г (а). Мы сопоставляем равные площади,
находящиеся под гауссовской кривой для /г(а) и под кривой
для ^(а). Таким путем мы получаем бесконечное количество
136 л E к Ц и я - 13
независимых гауссовски распределенных величин
h(cL\ h{T~\), h{T~\) (13.6)
Мы можем узнать все, что нам нужно, о распределении
различных /, считая /(а) функцией от бесконечного множества
переменных (13.6). Первоначальный временной ряд я
выразил через гауссовски распределенный ряд. Теперь
позвольте мне ввести допущение, что функция /
принадлежит /.2. Тогда можно представить /(а) в виде некоторого
разложения с помощью независимых, гауссовски
распределенных величин
f{a)=:F[h{o.\ h[T-\\ ...]. (13.7)
Другими словами, в дискретном случае я сделал нечто
совершенно аналогичное тому, что проделал в непрерывном
случае. В непрерывном случае я описываю временные ряды
с помощью броуновского движения. Здесь же дискретные
временные ряды я описываю с помощью величин,
соответствующих приращениям броуновского движения на
единичном интервале. Амплитуды этих приращений также являются
гауссовски распределенными и независимыми для
независимых интервалов. Используя это, я покажу, что вся теория,
развитая выше для ортогональных полиномиальных
функционалов, так же применима в дискретном случае, как и
в непрерывном.
Введем следующие переменные:
г/о (а), г/Да), г/зС^Х • • • • (13.8)
Все эти величины зависят от а. Далее, мы считаем, что они
первой степени по отношению к броуновскому движению,
т. е. соответствуют первой степени броуновского движения.
Я утверждаю, что можно разложить любую функцию от а
на постоянные члены, члены первой степени, второй степени,
третьей степени и т. д., на такие же члены, как в
непрерывном случае. Это делается точно тем же способом.
Во-первых, постоянная функция /Cq, очевидно, принадлежит L^.
Рассмотрим ^
2«А(«)- (13-9)
О
Если рассматриваемое выражение зависит только от
„прошлого", то п берется от О до оо. Если же оно должно
ДЕКОДИРОВАНИЕ 137
зависеть от „прошлого" и от „будущего", то п берется
от —оо до ОС. Среднее значение выражения (13.9) равно
1 оо
j do.^a,u,{c,) = ^, (13.10)
о о
Выражение (13.9) ортогонально всем константам.
Рассмотрим среднее значение квадрата выражения (13.9)
/ ^^ S ^гг^^п (^)
L о
оо оо у 2 \ со
=-S«^7^;;yr/-р(-тГ«''"'' = 5«^ 03-11)
О ^ ^ -оо ^ ^ О
Перекрестные члены — нули, так как они состоят из
произведений независимых, гауссовски распределенных величин
с нулевыми средними значениями.
Рассмотрим вначале конечную сумму
N
2^А(а) (13.12)
о
и затем используем то же рассуждение, которое
применялось в непрерывном случае. По теореме Рисса — Фишера,
если оо
2^^ сходится, (13.13)
о
то выражение (13.12) сходится в среднем, т. е. интеграл
от квадрата разности /г-й и m-Vi. частных сумм стремится
к нулю. Поэтому суш,ествует предел в среднем /, и я
называю Л^ оо
1. i. m. 2 cinitni^) =^ 2 ««^«W. (13.14)
N ^ оо О О
где выражение в правой части теперь вполне определено.
Это рассуждение проходит при суммировании не только
от О до оо, но и от — (СЮ до оо. Я нахожу функцию от а,
принадлежаш,ую L^, в виде (13.14). Как видите, это вполне
аналогично тому, что я делал в непрерывном случае.
Заметив это, пойдем дальше. Я думаю, что это хорошее
упражнение, чтобы овладеть техникой, примененной в
138 Л E к Ц и я 13
непрерывном случае, так как дискретный случай несколько
проще.
Возьмем квадратичное выражение
22 «шл («)««(«)• (13.15)
Это однородное квадратичное выражение. Вначале возьмем
в (13.15) конечную сумму. Надо оценить среднее и среднее
квадратическое значения для выражения (13.15). Без
ограничения общности можно считать а^^ симметричными,
так как мы получили бы точно то же самое, если бы
заменили а-,- на а а
-^ + -^2^- (13.16)
Если (13.15) — конечная сумма, то среднее равно
1
/^«22] ^гпп^гп («) «л (а) = 2 ^гпт' (13.17)
Перекрестные члены выпадают, как и прежде!
Выражение (13.18), следовательно, будет ортогонально любой
постоянной V ^ / ч / ч Х^
т п т
Выражение (13.18) ортогонально также любой линейной
функции по следующей причине. Произведение линейных
членов и выражения (13.18) содержат члены 1-й и 3-й
степени. Но члены нечетной степени нельзя представить
в виде попарных произведений, и, следовательно, их
средние значения равны нулю. Поэтому выражение (13.18)
ортогонально выражениям нулевого и первого порядка —
в точности как раньше.
Вычислим теперь среднее значение квадрата
выражения (13.18)
1
/^«[22 ^тп^т (а) «л (а) — 2 ^m/Tz] =
О т п т
1
= Jfl?a[2 2 2 2]^mn^p<7«mCa)tt„(«)«p(a)«^(a) —
о т п р q
-2222 «mnV-»(«)"„(«)+ 2 I] «mm«pp]- (13.19)
ДЕКОДИРОВАНИЕ 139
Рассмотрим первый член правой части равенства (13.19).
Члены, отличные от нуля, будут только в случаях, когда
(1) все индексы одинаковы;
(2) какие-то два индекса одинаковы и другие два также
одинаковы.
Возьмем сначала случай, когда все они одинаковы. Так
как u^ip) входит в 4-й степени, то мы получаем
ЗS^^mm. (13.20)
т
3 — ЭТО число способов разбиения 4 элементов на пары.
Другой способ отыскания этого числа состоит в
непосредственном вычислении интеграла
^/«''exp(-^)d.==3. (13.21)
Рассмотрим теперь случай, когда т = п, p = q, но тФр,
Здесь имеется только один способ разбиения на пары.
Штрих у знака суммирования указывает, что индексы
суммирования нигде не равны друг другу
^ f^mmf^pp- (13.22)
т, р
другие два случая: (1) т = р, л = ^, но т Ф п и (2) т = д,
п = ру но т Ф п. Они совершенно одинаковы. Поэтому
мы возьмем удвоенное значение, полученное для одного из
этих случаев
2 2'«L (13.23)
m, п
Таким образом, мы оценили первый член правой части
равенства (13.19). Второй член правой части равенства (13.19)
имеет ненулевые значения только при т=^п и поэтому
принимает вил
т р
Полностью правая часть (13.19) равна
ш fn, р т, п
- 2 2 «„„йрр + 2 ^п^т^рр- (13.25)
Hit р Ш, р
140 л E к Ц и я 13
Последние два члена можно объединить. Можно сократить
некоторые члены, заметив, что
2^mm-h2'^mmS/^ = 2 ^(^тт^рр- (13.26)
т т, р т р
Выражение (13.25) принимает вид
2^^lm + ^Ij^ <п' (13.27)
т т, п
Первый член в (13.27) — сумма по m и д при равных т и
п; второй член — при разных тип. Выражение (13.27)
равно
2 2 !]</.• (13.28)
т п
Следовательно,
1
J ^fa [2 2 Cl^n^m (^) ^п («) — S ^mmj == ^ 2 S "^^
2
mrf
О т п т т п
(13.29)
Результат аналогичен тому, который был получен в
непрерывном случае.
Это сделано для конечного ряда а^^^\ теперь применим
теорему Рисса — Фишера. Пусть множество а^^ бесконечно
и выполняется условие
2 2 ^1гп сходится, (13.30)
т п
Т. е. разность между частными суммами квадратов
коэффициентов стремится к нулю. Тогда, по-прежнему пользуясь
теоремой Рисса — Фишера, мы получаем
N N N
2 2^m««m(a)««(a)— 2 ^п
l.i.m.
„ mm
m = 0 n = 0 m = 0
= cp(a). (13.31)
2
Это верно просто в силу допущения, что двойная сумма Umn
сходится в среднем. Поэтому можно определить ср(а) как
оо оо
9 (а) = 2 2 «.„«т («) И« («) - S ^тт- (13.32)
т = 0 п = 0 т = 0
Иными словами, мы пo^yчили множество неоднородных
функционалов второй степени, ортогональных ко всем членам
первой и нулевой степени.
ДЕКОДИРОВАНИЕ 141
Я не думаю, что мне необходимо углубляться в
дальнейшее рассмотрение. Построение на всех этапах
производится точно тем же способом, который применялся для
непрерывных функций. Ясно, что получится множество
классов функций от а, и функции каждого класса
ортогональны функциям любого другого класса и всем
выражениям меньшей степени. Вспомним, что а полностью
определяется последовательностью /, или g, или h. Легко показать,
что многочлены от этого множества независимых гауссовски
распределенных величин образуют полную систему и любую
функцию из L^ можно аппроксимировать ими в среднем. Эти
многочлены суть многочлены Эрмита и произведения
многочленов Эрмита от независимых переменных м. Здесь мы
имеем полное разложение для любой функции из L^.
Отметим, что это верно, независимо от того, имеем ли мы дело
с односторонним бесконечным набором и или с
двусторонним бесконечным набором. Если рассматривается
„односторонний" случай, получаем „одностороннее" разложение;
в „двустороннем" случае получается аналогичный,
„двусторонний", результат. Другими словами, если некоторая
функция ср(а) принадлежит L^, то ср(а) можно записать в виде
оо
cp(a)~2G„(/Cv, ...V. а). (13.33)
О 1 • • • /I
Такая запись вполне ясна и совершенно аналогична записи,
применявшейся в случае броуновского движения.
Суммирование может идти от — оо до оо, а в случае, когда нам
может быть известно только настояш,ее и прошлое, от О до
оо„ Функция G^ определяется в виде
-(- Члены низшей степени, (13.34)
где члены низшей степени необходимы для того, чтобы
сделать 0^ ортогональной всем выражениям, степень
которых меньше п. Выражение (13,33) дает универсальное
описание для всех функций от а на языке м„, где
a^ = h[T~''a), (13.35)
Это совершенно аналогично тому, что мы делали раньше
142 л E к Ц и я 13
Если я заменяю (13.36) на (13.37)
К, V (13.36)
Avj ± V ^ ^ ^ V^ ± V, (13.37)
то, по существу, я заменяю а на
Г'^'а. (13.38)
(Знак минус обозначает движение назад во времени.)
Поэтому, если я представил / (а) в виде ряда, подобного (13.33),
то я имею также представление для
f{T^\) (13.39)
в виде ряда того же типа. Это дает мне способ
кодирования с помощью „настоящего" и „прошлого" Л. Другими
словами, имеется некоторое выражение стандартной формы,
которым можно представить первоначальный временной ряд,
если это ряд из L^. Если функция условного
распределения для h (при условиях на прошлое) собственно
монотонная, и влияl^иe отдаленного прошлого (борелевского
прошлого) распространяется только на множества событий меры
О или 1, то имеется стандартная форма кодирования и
декодирования сообщения с помощью независимо
распределенных гауссовских величин. Теория вполне аналогична
изложенной раньше, связанной с броуновским движением, и мы
действительно несколько продвинулись в кодировании.
Мне хочется отметить, что в случае непрерывных
временных рядов надо было бы проделать еще много работы,
чтобы получить аналогичные результаты, в особенности для
построения рядов g и h из f. Здесь нам пришлось бы
сделать много дополнительных предположений по той
простой причине, что на малых интервалах времени „настоящее"
не содержит части, независимой от „прошлого", и мы не
имеем возможности выбрать для обработки только новые
сведения. Над этим надо было бы работать. Пока что
я оставлю этот вопрос. Это все, что я хотел сказать о
кодировании и декодировании.
Лекция 14
новый подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. I
Сегодня мне хочется начать с некоторых соображений
по статистической механике. Этой темой мы будем заниматься
до конца курса. Я намерен построить модель для газа или
жидкости. Мы могли бы даже сказать — для твердого тела,
но для твердого тела это не совсем подходит, несмотря на
то, что в твердом теле мы можем в первом приближении
рассматривать молекулы и предполагать, что силы
действуют только между соседними молекулами. Дальнодейст-
вующие силы не столь важны как в случае газа, так даже
и в случае жидкости. В твердом теле имеются силы,
действующие вне зоны отдельной частицы. Будем сейчас
говорить о газе, однако жидкости не исключаются из
рассмотрения. Используем обычную картину газа: имеются частицы;
положения этих частиц заданы тремя координатами х, у
и Z, а скорости заданы тремя компонентами i/^, Vy и v^.
Мы хотим описать газ, причем не столько путем указания
координат для каждой частицы, сколько указанием того,
какое число частиц содержится в определенной области.
Логичный способ такого описания для частиц газа —
выделить шестимерный ящик: сколько частиц лежит в
определенном диапазоне положений и скоростей? Иными словами,
меня интересует не то, где находится частица как
отдельная частица, а другое: если задана некоторая область
положений и скоростей, то сколько частиц в ней находится.
В статистической механике мои результаты являются
поисковыми по сравнению с тем, что было сделано на
предыдущих лекциях, так как в них содержится много
проблем, которые я еще не решил. Я думаю, что область их
144 ЛЕКЦИЯ 14
применения значительна. Я полагаю, что мой подход новый;
насколько он плодотворен, покажет будущее. Он вводит
нас в кинетическую теорию газов (включая теорию
флуктуации), в теорию жидкостей, теорию турбулентности и
многое другое. Я даже надеюсь, что этот подход в конечном
счете найдет применение в квантовой теории. Моя точка
зрения связана с результатами изучения случайных функций,
изложенными в этих лекциях.
Посмотрим, как нам включить теорию полей для газов
в теорию случайного движения. Мы рассмотрим случай,
когда газ состоит из частиц, взаимодействующих только
посредством центральных сил, зависящих от расстояний
между частицами. Я ограничусь изотропным случаем и все
упрощу. Методы, которые я ввожу, в действительности
являются общими, но я изложу только простейшую
формулировку метода. Наше обсуждение посвящено скорее развитию
методологии, чем получению конкретных результатов.
Рассмотрим трехмерный ^) газ с точки зрения Уилларда
Гиббса. Газ состоит из некоторого набора частиц, которые
мы обозначим номерами 1, 2 п д-я частица имеет
координаты х^, у^, z^ и компоненты импульса м^, i/^^, w^.
Полный набор Xj, Х2, . . ., х^ w^, -Шд, ... определяет
точку в том, что Гиббс называет фазовым пространством.
Это пространство, в котором полный набор,
соответствующий газу, распределен способом, аналогичным тому, кото-
оо
рым были распределены выражения 2 ^л [?« ('^i» •••» '^J» ^1
о
в а-пространстве, определенном параметром а, меняющимся
от нуля до единицы. Как и в рассмотренном ранее случае,
нам надо интегрировать по этому пространству (как мы
интегрировали по переменной а), чтобы получить средние
значения и распределения величин, характеризующих газ.
Однако такое описание газа неудобно, если иметь в виду
применение методологии, использованной на предыдущих
лекциях. Поэтому я предлагаю другое описание газа. Пусть
R — область в фазовом пространстве. Тогда R содержит
некоторое число v частиц, лежащих внутри R по отношению
к координатам и к компонентам импульса. Это число — ад-
') То есть газ из частиц, находящихся в трехмерном
пространстве.— Прим. перед.
НОВЫЙ подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. I 145
дитивный функционал от множества /?, характеризующий
распределение газа.
Отметим, что такая характеристика имеет одно
определенное преимущество перед характеристикой Гиббса: она
инварцантна по отношению к любым перестановкам частиц.
С феноменологической точки зрения такие перестановки не
меняют газ.
Нам уже знакомы аддитивные функции от множеств
значений одной переменной, зависящие от параметра
распределения а. Мы их задавали с помощью функции
/(а:, а). (14.1)
Здесь разность [/(Хд, а) — f {х^, а)] при х^^ х^
представляет „массу", лежащую между х^ и х^ при заданном
значении а. Иными словами, если S—некоторое множество
значений х и S{x) — характеристическая функция этого
множества, то „масса", лежащая на S при заданном а, равна
/^/(х, а). (14.2)
Определение „массы", лежащей на множестве 5 при
заданном а с помощью такого интеграла, нетрудно распространить
и на случай распределения „массы" в д-мерном
пространстве, если вспомнить, что интегрирование производится по
отношению к аддитивному функционалу от множества точек,
а не по отношению к функции /(а).
Теперь мы хотим дать стандартное представление для
такого функционала в д-мерном случае. Ограничимся
аддитивными функционалами, которые не меняются при
одинаковом сдвиге положений всех точек, хотя они могут
измениться, и вообще меняются при подобном переносе
импульсов.
Мы уже видели, что любая функция от а,
принадлежащая Z,2, может быть представлена в виде
оо
2 ^ЛтЛ^1 ^Д а]. (14.3)
Возможность такого представления не связана с числом
измерений пространства т^^, так как любое конечномерное
пространство можно отобразить на пространство одного
10 Зак. 2305, Н. Винер
146 ЛЕКЦИЯ 14
измерения с сохранением меры, с сохранением гауссовости
распределения масс на любой заданной измеримой области
и с сохранением независимости распределений масс на
непересекающихся областях. Следовательно, любая функция,
принадлежащая LP' по а, может быть записана в виде
оо
2 <^ЛтЛ-^1. 3^1» ^V «1» '^1' '^V -^2. У2. ^2^ % '^2. Щ\ •••
•••^«» У/г. ^п^ ««. '^п. ^J. о^Ь (14.4)
где Tj^ записаны в развернутой форме как совокупности
координат в фазовом пространстве.
Преобразование
■^* = -^ + ^» / = У + '^» ;г:* = ^ + С.
* * * (14.5)
унитарное. Такое преобразование порождается сохраняющим
меру преобразованием
7^1т;7к (14.6)
где Тх, Ту у Tz перестановочны.
Поэтому любая функция F {х^ у, z, и, V, w, а),
принадлежащая L^ по а при любых л:, у, 2^, и, Vy w и не меняющая
своей статистической природы, когда h прибавляется к х,
7]— к у, С— к Z, а и, V и W остаются неизменными,
может быть представлена в виде
оо
о
Проинтегрировав это выражение, получим линейный
функционал от множества 5 значений л:, у, Zy а, i/, w
Г Г/^(л:, у, 2:, й, 1/, w)dx dydzdadvdw. (14.8)
Такой функционал можно использовать для того, чтобы
представить распределение какой-либо величины в фазовом
пространстве; он инвариантен по отношению к сдвигам по
координатам д:, у н ^. Функционал (14.8) очень похож на
НОВЫЙ подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. I 147
те величины, которые нам нужны для описания газа в
фазовом пространстве. Заметим, однако, что в отличие от
классической теории газа здесь не предполагается, что масса
размещена в счетном множестве отдельных точек в фазовом
пространстве. Описать газ как действительную материю
этим способом невозможно.
Тем не менее такое описание может быть использовано
в теории газа. С одной стороны, как, например, в теории
турбулентности, суш.ествуют задачи, в которых мы не
доходим до размеров молекул. С другой стороны, даже в тех
случаях, когда наша теория неприменима непосредственно,
на основе такого описания можно развить статистическую
теорию, сходную с обычной теорией газа, и можно надеяться,
что в тех случаях, когда эта теория не будет верна, мы
сможем исправлять ошибки, вызванные дискретной
структурой газа, путем введения добавочных членов, специально
определяемых для каждой конкретной задачи.
Введем теперь описание такого типа для газа, состояш,его
из сферически симметричных частиц, взаимодействуюш,их
одна с другой посредством сил, зависящих от расстояния
между частицами и направленных вдоль линии,
соединяющей эти частицы. Пусть jc^, у^, z^ — координаты л-й
частицы; тогда компоненты силы, действующей на нее, равны
2 F [{{х^ - x,f + (у„ - у„)2 + {z^ - г„)2]'/'} X
т
X ^п — Хт П4 9)
2 F I\{х^ - x,f + (у„ - у„)2 + {z^ - z,fi''] X
т
[{Хт - Хп? + {Ут - Уп? + (-fm - ^п?]''' ' ^^
т
X ?nzzlM (14.11)
Если мы заменим координаты частиц функцией
р(л:, у, Z, и, V, W, а), представляющей плотность в фазовом
10*
148 л E к Ц и я 14
Пространстве, то в качестве компоненты силы, действующей
на единичную массу в точке (л:, з^, z), получим следующий
интеграл:
//////^(к--^)^+(^-^)^
По всему фазовому
пространству
+ (^_C)2]V^)p(^, ^, С, X, р., V, а)Х
X ^^^ ^dld^d^(rkd]xd^ (14.12)
и т. д. Здесь р(^, 7], С, X, [JL, V, а) — плотность частиц в
фазовом пространстве в точке с координатами ^, т]. С,
определяющими положение частицы, и X, (л, v, определяющими
импульс, при заданном значении а параметра состояния.
Сейчас мы занимаемся развитием методов, а не
получением результатов. Для этой цели одномерный газ столь же
удовлетворителен, как трехмерный. Сила взаимодействия
между частицами будет иметь только одну компоненту и
запишется в виде
J Jf(a: —Ор(Е, X, o)dld\. (14.13)
Надо отметить, что р(х, у, z, а, v, w, а) дает полное
описание газа в некоторый отдельный момент времена.
Для того чтобы исследовать динамику газа (что означает
описание поведения газа во времени), мы должны ввести
дополнительный параметр t и записать плотность в фазовом
пространстве в момент t как функцию р(^, х, у, z, а, v, w, а).
Чтобы описать поведение р, желательно представить р
в некоторой канонической форме. Положим
оо
р(^, л:, м, a) = 2Gjp^(^tt; x + a:i, Ml x-^x^,u^\ct].
(14.14)
В такой записи подразумевается некоторый фундаментальный
аддитивный броуновский функционал, соответствующий
Х(х, и, а). Однако этот функционал заслуживает
дальнейшего рассмотрения. С течением времени связь между пара-
HOBblPf подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. Т 149
метрами изменяющейся системы и фиксированным Х{х, а, а)
становится все более и более отдаленной. Описать динамику
системы с помощью таких выражений — значит отнести все
случайности к эпохе, непрерывно удаляющейся в прошлое.
Такое описание не совсем подходит для применения теории,
основанной на дифференциальных уравнениях, в которой
задание системы в какой-нибудь отдельный момент времени
является полным, и мы не должны постоянно возвращаться
от одного момента к другому.
Лекция 15
новый подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. И
Рассмотрим движение некоторой частицы газа,
находящейся под действием центральной силы. Разберем подробно
только одномерный случай. Рассмотрение трехмерного газа
не содержит принципиальных трудностей; оно не добавит
ничего нового в отношении методологии; усложняется только
запись. Скорость в точке (jc, и) фазового пространства
равна tt. Поэтому по прошествии времени dt координата х
заменится на
x + udt. (15.1)
Отметим, что здесь и — скорость, соответствующая импульсу
та для массы т. Новое значение скорости равно
•dt
j J F(x — ^)p(l \)dЫK (15.2)
где интеграл берется по всему фазовому пространству ($, X),
а р(^, X) — плотность массы в этом фазовом пространстве.
Это бесконечно малое преобразование можно записать в виде
dx=:^adt, (15.3)
du = dt j f F(x — ^)p(l \)did\, (15.4)
Заметим, что якобиан этого бесконечно малого
преобразования равен
1 dt\
dt J j F'(x — ^)p(l \)dld\ 1
= I - idtf J jF\x — i)p (;, X) dl d\. (15.5)
НОВЫЙ подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. И 151
Заметьте, что dt входит в квадрате. Поэтому якобиан
равен 1 по первому порядку dt. Другими словами, наше
бесконечно малое преобразование фазового пространства
сохраняет меру.
Нам известно, что в случае одного измерения, если
образовать ^^j^^ ^^^ (^5.6)
где Т—сохраняющее меру преобразование, то
j^(t)dx(Tt, а) = Jcp(7'V)fi?A:(^, а), (15.7)
где cp(r~V) отличается от ср(^) только применением
унитарного преобразования. Следовательно, можно написать
J^(t)dx(t, (i) = ^^{t)dx{t, 5а). (15.8)
где 5—сохраняющее меру преобразование. Так как
свойства переменной х (t, а) [которую мы будем обозначать
через X(t, а), чтобы не спутать с переменной х] не зависят
от числа измерений, мы видим, что бесконечно малое
изменение X п а на dx и du (соответственно) порождает
некоторое бесконечно малое измеримое преобразование а. Верно,
что, рассматривая сейчас бесконечно малые преобразования,
мы рассуждаем эвристически, но в нашем представлении
основ статистической механики вся процедура эвристическая.
Рассмотрим теперь изменение функции р(л:, а, t, а) —
плотности нашего распределения по jc и ^/ в момент t при
значении а параметра распределения. Здесь а обозначает
нашу случайную переменную не в момент О, а в момент
времени t, причем а получается из этой случайной
переменной, взятой в момент О в результате применения
бесконечной последовательности бесконечно малых унитарных
преобразований; результирующее преобразование будет само
унитарным преобразованием. Это преобразование будет
фактически зависеть от истории переменной р, что следовало
бы обсудить при полном обосновании нашей процедуры, но
сейчас мы не будем этим заниматься.
Теперь мы рассмотрим бесконечно малое изменение
выражения
J ... /t(a:i, «1 х^, u^)dX{x^, а^, а) .. . dX(x^, а^, а),
(15.9)
152 л E к Ц и я 15
вызванное изменением X со временем. Это изменение
складывается из бесконечно малых приращений, каждое из
которых вызывается изменением отдельного X. Поэтому нам
надо рассмотреть только изменение выражения
Гср(д:. u)dX(x, и, а) (15.10)
со временем. Чтобы указать момент времени, в который
берется X, запишем (15.10) в виде
Гср(л:. a)dX(t, х, и, а). (15.11)
Далее
Гер (л:, а) dX(t -\-dt, х, и, а) =
= Jcp(A:, a)dX{t, x — udt, it — Fdt, a), (15.12)
где F представляет ускорение сил в точке {х, и).
Уравнение (15.12) можно записать в первом приближении по dt
\ ^{x-\-adt, u-\-F dt)dX{t, х, а, а) =
^j^{x, a)dX{t^ а, a)+dt j(a^-^F^yX{t^ й, а).
(15.13)
Теперь вернемся к рассмотрению поведения плотности
[функции р(^, JC, и, а)] во времени. Для нее было дано
разложение
2<^ЛРл(^> X, а, Xj, «1 л:,^. wj, а]. (15.14)
Здесь переменная а—измененная переменная,
соответствующая моменту времени t. Для действительно строгого
изучения желательно использовать именно такое разложение р.
Однако для нашего теперешнего эвристического
рассмотрения лучше ввести разложение
оо
Р (^ л:, ил) = 2 / • • • / ^Л^ ^' -^+-^1. «i; ...; х+х,^^ ujx
y^dX{t, X, «1, а) ... dX(t, х^, а^, а). (15.15)
HOBblV^ подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. II 153
Равенство (15.15) находится в таком же отношении к
разложению по членам р^, как разложение в ряд Тейлора —
к разложению по полиномам Эрмита, и приводит нас к ряду
неприятных и трудных вопросов, касающихся сходимости и
суммируемости. Здесь мы просто обратим внимание на то,
что такие вопросы существуют, но не будем их обсуждать.
Рассмотрим p(t-{-dt, х, а, а) и попытаемся найти
цепочку дифференциальных уравнений, связывающих различные
производные от
Р„(Л а\ x-f--^i. ^i; ...; ^4--^n. ^/г)- (15.16)
Прежде чем приступить к составлению уравнений, не говоря
уж об их решении, надо знать, каких результатов мы от
них ожидаем. Наши уравнения должны дать полное
статистическое описание газа, не обязательно находящегося
в состоянии равновесия. Мы можем надеяться получить
величины, определяющие в каждый момент времени
распределение кинетической и потенциальной энергии (что более
или менее соответствует проблемам температуры), скорость
переноса потенциальной энергии через точку / или, в
трехмерном случае, через единичную площадку (что математически
эквивалентно давлению) и решить различные другие вопросы,
касающиеся, например, флуктуации этих и других величин.
Средняя плотность газа будет вообще задаваться средней
плотностью в нулевой момент, так как наши частицы
двигаются не настолько быстро, чтобы вызвать реальное
изменение массы, содержащейся в большом объеме. Все это
может иметь практическое значение и открывает новые
области в неравновесной статистической механике.
Что касается равновесной статистической механики, то
здесь имеются две возможности. Одна из них состоит в том,
чтобы каждое dPJdt положить равным нулю. Это приводит
к цепочке дифференциальных уравнений только по
переменным X и и. Вторая возможность — сформулировать и решить
неравновесную задачу и изучить асимптотическое поведение
решения при увеличении отрезка времени.
Надо отметить, что равновесная задача при сделанных
здесь предположениях не имеет никакого значащего
решения. Система со многими степенями свободы в равновесии
будет при достаточно общих предположениях иметь
равномерное распределение энергии по всем степеням свободы.
154 л E к Ц и я 15
Таким образом, „непрерывный" газ, строго говоря, не имеет
температуры. Если такому газу дать развиваться самому по
себе, под действием только собственных сил, в течение
длительного времени, то вся энергия уйдет в весьма
мелкомасштабные пульсации и асимптотическое состояние будет
статическим состоянием совершенного покоя.
Все это не означает, однако, что методы такого типа
безнадежны, но просто что их надо усовершенствовать,
учесть какими-то иными способами свойства, вызванные
дискретной структурой газа. Надо наложить на процессы,
уже взятые в расчет, некоторый процесс, который
непрерывно вносит 3 газ новые мелкие случайные воздействия,
подобные тем, что вызываются отдельными индивидуальными
особенностями молекул. Температура и аналогичные понятия
должны быть переопределены таким образом, чтобы они не
обраш,ались в бесконечность при этих мелких случайных
воздействиях. Соответствуюш,ие понятия уже предлагались
Колмогоровым и заслуживают дальнейшего изучениг.
Рассмотрим выражение
p(t-^dt, X, и, а)==
оо
л = 0
XdX(t-\-dt, х^, «1, а) ,,,dX(t-\-dt, л:„, м^, а). (15.17)
Раскрывая уравнение (15.17) мы должны учесть оба
реальных изменения Р^: одно, вызванное динамическим
изменением газа, и другое, вызванное изменением переменной а
со временем. Это даст нам
дРп
дх„
^JJ/C(x, —орел I к a)d^dl)-\-..
XdX{f, Xi, «J, a) ... dX{t. x„, u„, a). (15.18)
НОВЫЙ подход к СТАТИСТИЧЕСКОЙ МЕХАНИКЕ. II 155
Однако величины p(t, $, X, а) сами имеют известные
разложения. Мы имеем
сю
X dX(t. Si. li. а) ... dX(t, S„. X„. a). (15.19)
Следовательно, мы представили (по крайней мере формально)
dp(t, X, Uy OL)/dt в виде суммы членов
J ... JQ(t, X, и, х^. tti л:„. и„, ^1, \ е^^. 'к^)Х
X dX(t, Xj, ttj, а) . .. й?Х(^ х^, и^^, а) X
X dXit, $1, Xj, а) . .. б?;«Г(Л е^, Х^^, а), (15.20)
где Q (t, X, и, х^, а^ х„, а^, S^, \ $^. л: J —
представляемые в конечном виде интегральные выражения,
содержащие /С, Р^ (до некоторого порядка) и их производные.
Можно взять Q, переставить в нем все пары aTj, и^\ aTj, ^2» • • -
...; х^, и^\ ^1, Xj; ...; Sj^, Xj^ всеми возможными способами,
просуммировать эти выражения и разделить на число
перестановок. Если заметить, что симметричное К^ в выражении
/...//СЛ^! S,)dX{S,. a)...dX(S,, а) (15.21)
по существу единственно и что любая сумма таких
выражений различных порядков разлагается на свои слагаемые
единственным образом, и если вспомнить, что
дифференцирование такого выражения по параметру t приводит, по
крайней мере формально, член за членом к подобному
разложению, то мы увидим, что можно прийти по крайней мере
формально к цепочке интегро-дифференциальных уравнений,
в которых каждое dPJdt представлено в виде интегро-диф-
ференциального выражения, содержащего Pj^ (k^n) и их
частные производные по различным переменным х и и.
Можно надеяться решить эти уравнения последовательно,
отправившись от Pq и Р^.
В последних двух лекциях я скорее хотел установить
программу дальнейших исследований, чем получить
определенные результаты, А поэтому, хотя ц н еыцисал подробнд
156 ЛЕКЦИЯ 15
некоторые из интегро-дифференциальных уравнений
указанной цепочки, я думаю, что здесь не стоит их приводить.
Однако несколько общих замечаний, пожалуй, было
бы уместно сделать. Можно ожидать, что эти уравнения
имеют не единственное решение, а систему решений,
зависящих от различных численных и функциональных
параметров. Некоторые из них должны соответствовать величинам,
задание которых необходимо для определения физического
состояния в тех случаях, когда оно не может быть
фиксировано заданием только силы F взаимодействия между
частицами. Среди них находятся такие величины, как
плотность и давление газа, или какие-либо иные две
эквивалентные величины. He^ьзя ожидать, однако, что если эти величины
заданы, то задача становится определенной. Наше
представление случайной системы с помощью членов 0^ не
обязательно должно быть единственным, если учесть корреляции
и величины высшего порядка того же типа, определяющие
статистическое состояние газа. Все, что мы можем надеяться
получить с помощью наших методов, — это найти одно или
несколько статистических представлений для газа. А они
могут содержать достаточно свободных параметров, чтобы
их можно было использовать практически. В этой
практической работе мы вольны накладывать на решения наших
уравнений такие условия, которые облегчат получение
решений в удобной форме, но не будут настолько жесткими»
чтобы исключать интересующие нас явления.
УКАЗАТЕЛЬ
Автокорреляционная функция 50 ,
60 , 57 , 78 . 84
Альфа-ритм 85
Амплитуда вероятности 101
Анализ гармонический 39 , 84 , 91
— системы 107 , 108 , 111 , 119 ,
123
Астероид 94
Биотоки 83 , 84 , 85 , 88 , 89
Бозе А . Д . 5 , 107
Броуновское движение 7 , 9 , 12 ,
21 , 26 , 35 , 41 , 50 , 57 , 60 , 103 ,
108 , 110 , 120 , 136
Буш В . 117
Ваттметр 121 , 122
Газ 143 , 144 , 145 , 147 , 148 , 150 ,
153 , 154
Гамильтониан 101 , 105
Генератор 86 — 88 , 119
Гиббс Дж . В . 105 , 106
«Гладкость» 16 , 17
Давление 153 , 156
Двигатель 87
Декодирование 132 — 134 , 142
Детектор квадратичный 116
Дробовой шум 108 , 115 , 118 , 119
Закариас Д 61
Затягивание частот 89 , 90
Затухание 122
Импеданс 117
Индуктивность 113
Индукция электростатическая 89
Интерферометр Майкельсона 85
Исчисление случайных функций
20
Каноническое разложение 49 , 63
Катодный повторитель 112
Кодирование 124 , 130 — 133 , 142
Колмогоров А . Н . 154
Конденсатор 84
Лагранжа переменные 106
Лента магнитная 83
Ли И . В . 5 , 112
Мера Лебега 104
Мерцание 88
Модуляция частотная 63 , 67 — 69 ,
78
Нагрузка электрической цепи 86
Независимость 30 , 31
Непрерывность равномерная 16 ,
17
Нормирование 41 , 46 , 48
Оптика 85
Ортогональные функции 40 — 46 ,
48 , 50 , 52 , 56 , 63 , 67 , 75 , 79 ,
81 , 96 , 99 , 111 , 114 , 138
Осциллятор 39 , 83 , 87 , 88
Передаточное отношение 113
Перемножение напряжений 115
158
УКАЗАТЕЛЬ
Поле борелевское 131
Полиномы Эрмита 70 , 115 , 117 ,
133 , 141 , 153
Полнота системы функций 54
Преобразования бесконечно
малые 106 , 150 , 151
— метрически транзитивные 58 ,
59
— сохраняющие меру 35 , 38 , 56 ,
100 , 105 , 106 , 120
— унитарные 32 , 34 , 39 , 105 ,
151
— эргодические 58 , 120
Производящая функция 71 , 78
Пространство Гильберта 32
— дифференциальное 32 , 96
— фазовое 106 , 144 , 147 , 148
Разрешающая сила 85
Распределение вероятностей
гауссовское 7 — 9 , 18 , 29 30 ,
31 , 37 , 99 , 137
условное 125 , 126 , 128
Регулятор 87
Резонатор линейный 66
Рисса — Фишера теорема 24 , 48 ,
137 , 140
Ряд Тейлора 153
Ряды временные , дискретные 124 ,
130
Сдвиг фазы 112
Синтез системы 108
Случайный процесс 39 , 98 , 107 ,
119
в пространстве
нескольких измерений 98
Спектр 39 , 60 — 62 82 , 84 , 90 91
— тонкая структура 85
Спектральная плотность
мощности 83 , 94
Статистическая механика 105 ,
141 , 150 , 153
Температура 154
Теорема о равномерном
распределении энергии по степеням
свободы 153
Теория газов кинетическая 144
— квантовая 96 , 101 103 , 104
— эргодическая 58
Турбулентность 107 , 144 , 147
Усилитель 109
Уравнение Шредингера 102 , 104 ,
105
Уравнения дифференциальные
149
— интегро-дифференциальные
155 , 156
Фредгольм Е . И . 74
Функции Gn , определение 48 , 53 ,
80
— измеримые 17 , 125
— интегрируемые по Лебегу 24 ,
25 , 124
— Лагерра 112 , 115 , 121 , 122
— недифференцируемые 31
Функции собственные 69 , 102
— Уолша 33 , 34
— Хаара 33
Функционал аддитивный 99 , 100
— полиномиальный 40 , 44 , 49 ,
67
Фурье коэффициенты 31 , 50 , 96 ,
97
— преобразование 91 , 92
Цепи линейные , нелинейные 108 —
110 , 117
Циклотрон 95
Частоты собственные 102
«Черный ящик» 109 , 119
«Шероховатость» 15 , 16
Энергия 153 , 154
Эргодическая гипотеза 58
Ячейка 112 , 113
ОГЛАВЛЕНИЕ
Предисловие 5
Лекция 1. Случайная функция — функция времени и
состояния 7
Лекция 2. Однородные полиномиальные функционалы и их
средние значения 26
Лекция 3. Ортогональные функции 40
Лекция 4. Ортогональные функции и автокорреляционные
функции 52
Лекция 5. Применение к задачам частотной модуляции. I 63
Лекция 6. Применение к задачам частотной модуляции. II 71
Лекция 7. Применение к задачам частотной модуляции. III 79
Лекция 8. Применение к изучению колебаний биотоков;
колебания связанных осцилляторов, возбуждаемых в
случайные моменты времени 83
Лекция 9. Некоторые соображения по квантовой теории . 96
Лекция 10. Нелинейные системы. I 108
Лекция 11. Нелинейные системы. II 119
Лекция 12. Кодирование 124
Лекция 13. Декодирование 134
Лекция 14. Новый подход к статистической механике. I . . 143
Лекция 15. Новый подход к статистической механике. II . 150
Указатель 157