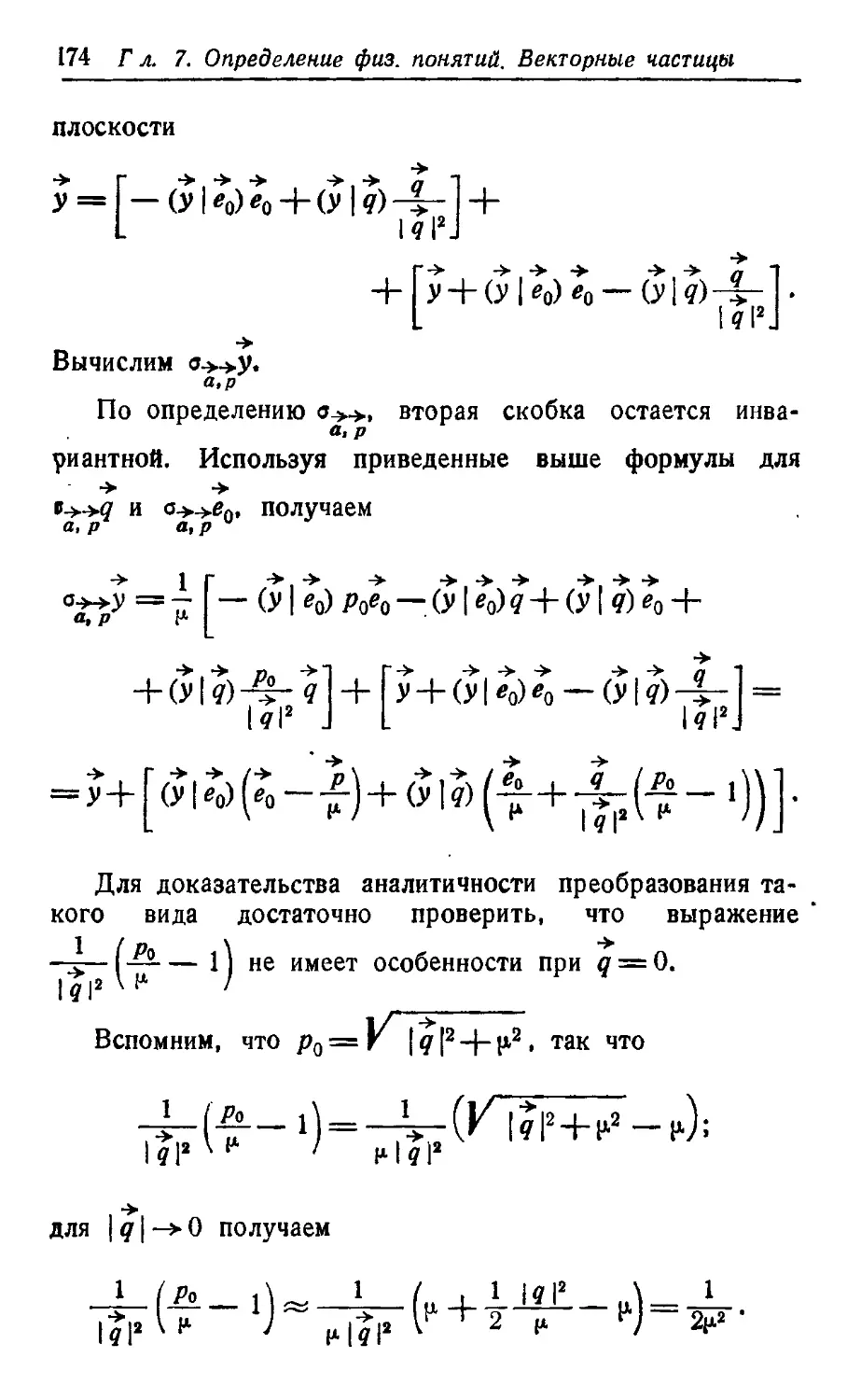Notes taken at the lectures of
LAURENT SCHWARTZ
APPLICATION OF DISTRIBUTIONS
TO THE STUDY OF ELEMENTARY PARTICLES
IN RELATIVISTIC QUANTUM MECHANICS
DEPARTMENT OF MATHEMATICS
UNIVERSITY OF CALIFORNIA
March 1961

БИБЛИОТЕКА СБОРНИКА „МАТЕМАТИКА-
ЛОРАН ШВАРЦ
ПРИМЕНЕНИЕ
ОБОБЩЕННЫХ ФУНКЦИЙ
К ИЗУЧЕНИЮ
ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
В РЕЛЯТИВИСТСКОЙ
КВАНТОВОЙ МЕХАНИКЕ
Перевод с английского
И. Б. АЛЕКСАНДРОВА
и
А. Н. СТАРОСТИНА
Под редакцией
А. А. КИРИЛЛОВА
С предисловием
Н. Н. Боголюбова
ИЗДАТЕЛЬСТВО «МИР»
М о•%к9 а 1964

Настоящая квига является переводом лекций
Л. Шварца, в которых кратко, в доступной форме
излагаются основы теории обобщенных функций
применительно к квантовой механике.
Эта теория, с помощью которой за последние
годы был революционизирован ряд отраслей мате-
матического анализа, уже нашла и в ближайшее
время, безусловно, найдет новые важные приложе-
ния в механике и физике.
Книга Л. Шварца представляет интерес как
для математиков, механиков и физиков-теоретиков,
так и для инженеров-исследователей, применяющих
аппарат математики и физики, а также для студен-
тов старших курсов указанных специальностей.
Редакция литературы по математическим наукам

ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Предлагаемый русский перевод лекций Лорана Шварца—
одного из крупнейших современных математиков — по-
священ получению основных уравнений теории поля мето-
дом обобщенных функций. Лоран Шварц является одним
из создателей теории обобщенных функций, которая воз-
никла в связи с задачами физики и находит в ней все
более широкое применение.
Обобщенные функции по существу использовались еще
в работах Хевисайда и Дирака, хотя предложенный ими
аппарат был далек от строгого математического обосно-
вания. Следует отметить, что первые строгие математи-
ческие исследования по обобщенным функциям принад-
лежат С. Л. Соболеву (см. его работы в ДАН СССР
и в Машем, сборнике).
Математическое обоснование применяемого в физике
аппарата имеет принципиальное значение, так как зачастую
нуждаются в обосновании сами построения, возникающие
в современной теоретической физике. Например, весьма
актуален вопрос о внутренней непротиворечивости элек-
тродинамики, возникший в связи с использованием теории
возмущений, и этот вопрос еще не получил своего раз-
решения.
Рассматривая задачу построения матрицы рассеяния
при помощи явно сформулированных физических условий —
причинности, релятивистской инвариантности и унитар-
ности,— мы получаем возможность обосновать вычисли-
тельный процесс в рамках теории возмущений без обра-
щения к псевдонаглядным ренормировочным представле-
ниям. Вычитание бесконечностей при этом выступает как
составной элемент процедуры получения конечных выра-
жений из произведений некоторого числа несобственных
сингулярных функций. Рассмотрение этой процедуры облег-
чается, как известно, использованием аппарата теории
обобщенных функций.
В настоящих лекциях Лоран Шварц не рассматри-
вает взаимодействия полей, при описании которого как

Предисловие к русскому изданию
раз и проявляются вышеупомянутые трудности. Все изло-
жение проводится для единственной свободной частицы.
Тем не менее книга представляет значительный интерес,
и ее ценность состоит в следующем. Во-первых, в книге
вводятся как раз те классы обобщенных функций, кото-
рые используются в аппарате теории квантованных полей.
Поэтому можно надеяться на дальнейшее развитие идей,
которые здесь излагаются. Во-вторых, четкое и коррект-
ное в математическом смысле построение позволяет полу-
чить строгий вывод уравнения Дирака на основе предпо-
ложений самого общего характера. В-третьих, проводимая
на основе обобщенных функций классификация элементар-
ных частиц и данные автором определения этих частиц,
несомненно, полезны, так что можно надеяться на распро-
странение описываемых методов на случай взаимодействия.
Кроме того, книга полезна в чисто математическом
отношении, так как является прекрасным введением в тео-
рию обобщенных функций для лиц, занимающихся проб-
лемами теоретической физики. В процессе изложения
автор не приводит доказательства всех теорем, а иногда
отсылает читателя к оригинальной литературе и учеб-
никам. В этом отношении можно рекомендовать серию
книг И. М. Гельфанда, Г. Е. Шилова и Н. Я. Виленкина
„Обобщенные функции" (вып. 1—5), которая содержит
все последние достижения в этой области.
Встречающиеся иногда повторения нельзя рассматри-
вать как недостаток книги. Введение различных классов
обобщенных функций по единой схеме представляется по-
лезным для понимания математической теории обобщенных
функций и уяснения приложений, используемых в физике.
Следует указать, что оригинал книги Шварца представ-
ляет собой запись лекций автора, прочитанных в Калифор-
нийском университете в 1961 году. Эта запись содержит
большое количество опечаток и неточностей, которые были
исправлены в процессе подготовки русского издания; при
этом последовательность изложения нисколько не изменена.
В заключение выражаю надежду, что предлагаемая книга
будет с пользой прочитана специалистами и студентами,
как математиками, так и физиками.
Я. Н. Боголюбов

Глава 1
ПОСТАНОВКА ЗАДАЧИ
§ 1. Введение
Квантовая механика занимается описанием движения
частиц. Вся информация, необходимая для полного описа-
ния движения некоторой частицы, содержится в ее волно-
вой функции ф(лг, у, z, t), являющейся комплексной функ-
цией координат (л:, у, z)?R3(R3— трехмерное евклидово
пространство) и времени t. В нерелятивистской квантовой
механике величина |ф(лг, у, z, t)\2 представляет собой
плотность вероятности положения частицы. Вероятность
того, что частица находится в произвольный момент вре-
мени t в некоторой области 4cR3, определяется выраже-
нием Г Г f |<|>(*. У. z, t)\2dxdydz.
А
Заметим, что функция ф при любом t должна быть
функцией с интегрируемым квадратом модуля; предположим,
кроме того, что Г \ \ |ф(*, у, г; t)\2dxdydz = l для
R'
любого t. Если мы определим скалярное произведение
волновых функций с помощью интеграла
///¦
с, у, z, t)ty2(x- У> z< t)dxdydz,
Ra
то функция if будет принадлежать гильбертову простран-
ству для любого t.
В нерелятивистской квантовой механике ф удовлетво-
ряет волновому уравнению Шредингера:
где Ъ — постоянная Планка, деленная на 2те, а Н — само-
сопряженный оператор в гильбертовом пространстве Z.2
функций на R3 с интегрируемым квадратом модуля. Из

Гл. 1. Постановка задачи
уравнения Шредингера следует, что скалярное произведе-
ние двух волновых функций остается постоянным во вре-
мени. В случае свободной частицы имеем
где m— масса частицы, а Д — оператор Лапласа.
В релятивистской квантовой механике пространство
и время неразделимы, поэтому нельзя говорить, что ф есть
функция четырех переменных, если не выбрана лоренцова
система координат. Для одновременного рассмотрения вре-
мени и пространства вводится четырехмерное аффинное
пространство ?, и функция ф определяется на Е4. Опре-
деление аффинного пространства будет дано позднее.
Определение. Частицей ?7в называется гильбер-
тово пространство функций, определенных на Е4.
Определение. Движением ф называется элемент &в
с нормой 1)^1^= 1.
Пусть а—произвольное преобразование Лоренца*в ЕА
и &— группа Лоренца. При преобразовании а функция ф
переходит в функцию оф.
Определение. Если для любого a?G имеем
то частица Зв называется мировой частицей. Короче го-
воря, мировая частица — это частица, которая не изменяется
при лоренцевых преобразованиях.
Определение. Мировая частица ?Ю называется эле-
ментарной, если Sf6 не содержит подпространств, кото-
рые переходят в себя при всех преобразованиях a?G,
т. е. когда пространство S/в минимальнох).
Позднее мы покажем, что пространство Ш зависит от
параметра /ио^-О и некоторого параметра, который может
принимать два значения: ,-f-" и „ —". Последний интерпре-
тируется как заряд частицы, а т0 — как масса покоя частицы.
') В теории представлений групп такие пространства назы-
ваются неприводимыми. — Прим. ред.

§ 2. Элементы теории обобщенных функций 9
Определение. Мезоном называется скалярная
элементарная частица (ей соответствует скалярная волновая
функция ф).
Для системы двух частиц гильбертово пространство оп-
ределяется теми же самыми аксиомами, что и выше; однако
его элементы теперь являются функциями на произведении
ЕА X Б4. В этой книге мы будем рассматривать только
случай одной свободной частицы.
Ради общности мы будем считать, что наше гильбер-
тово пространство есть пространство обобщенных функций.
Поэтому мы начнем с краткого введения в теорию
обобщенных функций.
§ 2. Элементы теории обобщенных функций
Пусть R" означает «-мерное евклидово пространство,
и пусть <2J(R") (или просто ЗУ)— пространство всех ком-
плексных функций (р, определенных в R", имеющих про-
изводные всех порядков и обращающихся тождественно
в нуль вне некоторой ограниченной области в R". Функ-
ции <р будем называть основными функциями. Заметим,
что <2J(R") — линейное пространство.
Введем топологию в пространство S.
Определение. Последовательность основных функ-
ций (ср/*)} стремится к нулю в 35 (обозначается <fj—*-0),
если все функции <pj(x) обращаются в нуль вне одной
и той же ограниченной области в R" и если функции <?j(x)
вместе со своими производными любого порядка равномерно
сходятся к нулю.
Определение. Обобщенной функцией Тназывается
непрерывный линейный функционал на пространстве 33, т. е.
правило, согласно которому каждому элементу ер ?.2? ста-
вится в соответствие комплексное число G\ ср), такое, что
G\ (р2)
и сходимость ср.-—>-0 влечет за собой сходимость
(Г, ?,.)-*0. .

10 Гл. 1. Постановка задачи
Пусть 3)' (R") (или просто 2ВГ) обозначает пространство
обобщенных функций на R".
Пример. Пусть / — локально интегрируемая функция
в R"'). Тогда равенство
(/. 9) = f f{x)<?(x)d* =* f /(*)<?(*)dx (*)
R" A
определяет обобщенную функцию. Здесь А — ограниченная
область в R", вне которой ср обращается в нуль (носи-
тель <р). Таким образом, каждая локально интегрируемая
функция однозначно определяет обобщенную функцию, за-г
данную равенством (*). Очевидно, что fx и /2 определяют
одну и ту же обобщенную функцию тогда и только тогда,
когда /; == /2 почти всюду. Рассматривая соответствующие
классы Лебега (т, е. отождествляя, функции, которые равны
между собой почти всюду), мы заключаем, что классы ло-
кально интегрируемых функций образуют подпространсхво
пространства обобщенных функций.
Другими важными примерами обобщенных функций яв-
ляются дельта-функция Дирака, определенная соотноше-
ниями
(8, <р> = <р(О)
или
(8в, <р> = ?(<*).
и диполь С, определенный равенством
(С. <р> = -<р'(О).'
Определение. Производная обобщенной функ-
ции Т определяется формулой
Из этой формулы следует, что
{D'T. tp) = (-1)"" (Т,
') То есть функция, абсолютно интегрируемая в каждой
ограниченной области из R". — Прим. перев.

§ 2. Элементы теории обобщенных функций 11
где р обозначает набор из л целых чисел р = (Рх, ..., р„).
Таким образом, любая обобщенная функция имеет про-
изводные всех порядков.
Пример. Рассмотрим функцию Хевисайда Y(х),
определяемую равенством
( 1. х>0.
Имеем
00
{Г, <р) = - (К, ср'> = — / К (х) <р' (х) их =
/
о
Поэтому У" = 8.
Определение. Пусть / — непрерывная функция и
пусть
А=[х:
Замыкание А множества А называется носителем
функции /.
Определение. Пусть 2 — открытое множество
в R" и пусть Т?3'. Мы говорим, что обобщенная функ-
ция Т равна нулю в Q, если (Т, ф) = 0 для всех ^Ь
носители которых содержатся в 2.
Например, 8 = 0 в R — {0}.
Теорема. Пусть {2J — некоторая система от-
крытых подмножеств в R"; предположим, что Г = 0
в каждом Ог. Тогда 7 = 0 в Q
Доказательство. Мы должны показать, что
(Т, <р) = 0 для любой функции cp?S, носитель которой
содержится в IIQj. Пусть А — носитель некоторого <f.

12 Гл. 1. Постановка задачи
Так как множество А компактно и покрыто системой {Qt},
существует конечное подпокрытие {2*А}. k = \, 2, .... п.
Пусть {фА}, ft = l, 2 и,—бесконечно дифференци-
руемое разбиение единицы в А, соответствующее покры-
тию B/.|. т. е. для й=1, 2 п выполняются сле-
дующие условия:
2) носитель фА содержится в 2/ ;
з) 2ф* = 1 на А
Тогда
(г, <р>=G\ 2ф*?> ij
Следствие: Л-«я каждой обобщенной функции Т
существует в точности одно максимальное откры-
тое подмножество пространства R", в котором эта,
функция равна нулю.
Доказательство. Рассмотрим все Qt, в кото-
рых Г=0. Тогда М Qt представляет собой требуемое
i
множество.
Определение. Носителем обобщенной функции Т
называется дополнение в R" к максимальному открытому
подмножеству 2, в котором Г = 0.
Введем теперь топологию в пространство обобщенных
функций 35''. Так как 3)' — линейное пространство, то
достаточно определить сходимость к нулю.
Определение. Слабая сходимость: пусть {Tj} —
произвольная последовательность в 3'. Будем говорить,
что tj сходится к нулю в смысле обобщенных функций,
или Tj->0 в 3)', если G^-, <р)-»-0 для каждой основной
функции <р?<2*.
Понятие сильной сходимости включает требование
типа равномерности; соответствующее определение будет
дано позже, когда оно потребуется.

§ 2. Элементы теории обобщенных функций 13
Теорема. Дифференцирование является непре-
рывной операцией в &', т. е. Tj-+O в 3' влечет за
собой T'j-+0e 3'.
(Из слабой сходимости обобщенных функций следует
слабая сходимость их производных.)
Доказательство.
(t'j, <р) = — (Tj, tp')->0 для любой функции <??3.
Замечание. Многие последовательности, расходя-
щиеся в обычном смысле, становятся сходящимися в смысле
введенной здесь слабой топологии. Ряд, сходящийся
в смысле обобщенных функций, можно дифференцировать
почленно, т. е. если Т = 2Т., то т'= У^Т',.
J J
Теорема: Пусть fj->0 почти всюду, пусть,
далее, |/у|<?\ где g — фиксированная положитель-
ная локально интегрируемая функция. Тогда fj-*-0
в смысле обобщенных функций.
Доказательство. Утверждение следует из тео-
ремы Лебега о переходе к пределу под знаком интеграла.
Примеры. Тригонометрический ряд 2 я^21"**
*
сходится 6 смысле обобщенных функций тогда и только
тогда, когда |аА|<^Л?а, где А — константа, а — некото-
рое цело^ положительное число. Таким образом, многие
тригонометрические ряды становятся сходящимися в смысле
обсбщенныхч функций. Чтобы убедиться в достаточности
приведенного выше условия, рассмотрим ряд
a+i
Этот ряд сходится равномерно, так как
А 1
<^——гот"» значит, он сходится и в смысле обобщен-
ия) k
ных функций. Дифференцируя этот ряд почленно a -f- 2 раз,
получаем исходный ряд, который, следовательно, сходится
в смысае обобщенных функций.

14 Гл. 1. Постановка задачи
Ряд 2 е2*'** в обычном смысле расходится. Однако
*=-со
в смысле обобщенных функций он сходится к обобщен-
оо
ной функции 2 Ъ(х — к):
8 8 8 8 8
—2—1 0 1 2
оо
Дифференцируя почленно, убеждаемся, что 2 Bя/А) е2Шх
— оо
оо
сходится к 2 "8У(* — k):
8' 8' 8' 8' 8'
• —2—10 1 2
§ 3. Аффинные пространства. Преобразования
Лоренца
В предыдущем параграфе мы определяли простран-
ство ^'(R") обобщенных функций на евклидовом про-
странстве R". Аналогично можно определить простран-
ство ЗЬ' (Еп) обобщенных функций на и-мерном векторном ¦
пространстве Еп. Однако в физическом пространстве не
существует выделенного начала отсчета, поэтому здесь
у нас нет исходного векторного пространства. По этой
причине мы вводим понятие аффинного пространства.
Определение. Аффинным пространством на-
зывается множество Е и связанное с ним векторное про-
странство Е. Связь между Е и Е определяется отображе-
нием Еу^Е в Е, которое переводит пару элементов а, Ь
из Я в вектор аЬ из Е, причем выполняются следующие
два условия.
A) Соотношение Шаля. Если а, Ь, с — любые
три элемента из Е, то ab-\-bc-\-ca — Q.

§ 3. Аффинные пространства. Преобразования Лоренца 15
B) Пусть о—фиксированный элемент из Е. Отобра-
жение а->оа устанавливает взаимно однозначное соот-
ветствие между Е и Е.
Следует отметить, что соотношение A) можно обоб-
щить более чем на три элемента. Кроме того, трояка
—> —>
элементов а, а, а, согласно A), дает Зал = 0, или аа = О.
а тройка а, а, Ь дает ab-\-ba = 0.
По очевидным причинам весьма удобно обозначение
ab = b — а.
Таким образом, операция .вычитания задает отображение
пары a, b из Е на вектор аЬ из Е, удовлетворяющее
приведенным условиям. Если а— данный элемент из Е,
а х — данный элемент из Е, то существует единственный
элемент Ь?Е, такой, что а-\-х — Ь, причем последнее
эквивалентно равенству х — b — а.
Определение. Пусть Е и F—два аффинных про-
странства. Отображение
называется аффинным оператором, переводящим Е в F,
если существует связанный с ним линейный оператор
такой, что
ab — <за = о ф — а).
Заметим, что линейный оператор о однозначно опре-
деляется оператором о. Далее, произведение двух аффин-
ных операторов является аффинным оператором, и обрати-
мые аффинные операторы образуют группу.
Пример. Оператор сдвига U : х-> х -f- и — аффин-
ный оператор, переводящий аффинное пространство Е
в себя. Связанный с ним линейный оператор сдвига

1в Гл. 1. Постановка задачи
является единичным оператором
Обратно, каждый аффинный оператор является единичным,
если связанный с ним линейный оператор представляет
собой оператор сдвига.
Пусть Е— векторное пространство над полем действи-
тельных чисел и пусть на Е определена квадратичная
¦> -> ¦*¦,"*¦
форма (х у). Мы предположим, что форма (х \ у) били-
¦> -> ¦> ->
нейна, симметрична [т. е. (л: | у) = (у | х)] и невырожденна
(не существует отличного от нуля элемента, ортогональ-
ного ко всему пространству).
->¦*-> • •>.
Пусть ev е2 еа— ортонормированный базис в Е,
т. е. (et | ej) = 0 для I ф j и (et | et) = ± 1. Любое конеч-
номерное векторное пространство, в котором задана невы-
рожденная квадратичная форма, имеет бесконечное числа
ортонормированных базисов. Однако число базисных эле-
-> ¦> ->
ментов е, таких, что (е|е)=1, и число базисных элемен-
¦> ¦> ¦>
тов е, таких, что (е|е) = —1, не зависит от конкретного
выбора базиса.
Определение. Сигнатурой д-мерного векторного
пространства по отношению к данной квадратичной форме
(х\у) называется пара целых чисел (р, q), где p-\-q = n,
р — число элементов ортонормированного базиса е, таких,
->¦ ->¦
что (е\е)=1, a q — число элементов ортонормированного
-> ¦> ->
базиса е, таких, что (е\е) = —1.
Определения. Четырехмерным векторным про-
странством Лоренца называется векторное простран-
ство с квадратичной формой, которое имеет сигнатуру C,1).
Соответствующий ортонормированный базис мы обозначим
ev е2, е3. «о- гДе (ei 1 <?г) = 1 при / = 1, 2, 3 и (е01 е0) = — 1.
Четырехмерным аффинным пространством Ло-
ренца называется такое аффинное пространство ?, для

§ 3. Аффинные пространства. Преобразования Лоренца 17
которого соответствующее векторное пространство ?4 имеет
сигнатуру C,1).
Под галилеевой системой отсчета мы понимаем
выделенную начальную точку 0 в ?4 и выделенный орто-
¦>->¦>-> ¦>
нормированный базис ev e2. ег, е0 в Е4 (выделенная си-
стема координат).
Каждая мировая точка имеет четыре координаты xv
Х2> лг3, х0 — ct (три пространственных и одну временною).
Определение: Преобразованием Лоренца о на-
зывается аффинный обратимый оператор в лоренцевом
аффинном пространстве, сохраняющий его лоренцеву струк-
туру; это значит, что связанный с ним линейный оператор
сохраняет квадратичную форму
(в х | в у) = (х | у).
Преобразования Лоренца образуют группу. Группа О,
содержащая все преобразования Лоренца о, называется
неоднородной группой Лоренца, тогда как группа О,
образованная соответствующими линейными операторами о,
называется однородной группой Лоренца.
Пример. Сдвиги являются преобразованиями Ло-
ренца.
Теперь можно определить пространство 35'' (Е) обоб-
щенных функций на аффинном пространстве Е просто
с помощью выбора начальной точки в Е: этот выбор
превращает Е в векторное пространство (изоморфное Е)
и позволяет определить обобщенные функции на Е, исходя
из уже имеющегося определения обобщенных функций на
->
векторном пространстве Е. Легко видеть, что построен-
ное таким образом пространство обобщенных функций не
зависит от выбора начала координат. В общем случае
можно определить пространство З)' (V) обобщенных функций
(или потоков) на любом многообразии V класса С°°') (част-
ным случаем которого является аффинное пространство).
') Определение многообразия класса С°° см., например,
в книге Ж. де Рам, Дифференцируемые многообразия, М., ИЛ,
1956. — Прим. ред.

18 Гл. 1. Постановка задачи
§ 4. Мировые скалярные частицы
Теперь мы уточним определения скалярной частицы и
мировой частицы.
Определение. Скалярной частицей в мире ?4
называется множество о№, удовлетворяющее следующим
постулатам.
A) &6 есть векторное подпространство пространства
B) вЮ снабжено структурой гильбертова пространства,
т. е. в jsfB существует линейно-антилинейная форма (<|>j [ф2)зс
(линейная по <J)j и антилинейная по <|>2)> которая является
эрмитовой, положительно определенной и такой, что <з№
полно по норме ||ф||Л, = (ф|ф)да..
C) Каноническое вложение ?№ в S' непрерывно, т. е.
«)>;-->0 в ^=^ф;->0 в 35'.
Мы увидим, что 36 представляет заряженные частицы.
Если обобщенные функции в ?4 принимают только дей-
ствительные значения, то S6 описывает нейтральные
частицы.
Определение. Движением частицы называется
элемент (j>?JS/, такой, что ||<|»||w=l.
Мировая частица одинаково наблюдается различными
наблюдателями. Наблюдатель производит свои наблюдения
в некоторой системе отсчета, так что частица вЮ рас-
сматривается им как некоторое пространство обобщенных
функция, определенных в R4, а не в ?4. Если все наблю-
датели наблюдают о№ как одно и то же пространство
обобщенных функций, определенных в R4, то оЮ является
мировой частицей. Более точное определение можно
дать, если описать действие оператора о^О на обобщен-
ные функции.
Преобразование Лоренца о ? О действует не только
в Е4, но также в любой другой структуре, определенной
над ?4. Если <р(х), х?ЕА, — комплексная функция на Е4,
то преобразование ср —> оср определяется равенством

§ 4: Мировые скалярные частицы 19
или, что то же самое,
Из того, что a?G — линейный оператор, следует
Теорема. <р ? S (?4) =ф o<j> ? S (Е4).
Из определения о<р следует
Т е о р е м а. (р„ ->¦ 0 =ф о(рл -> 0.
Таким образом, о осуществляет автоморфизм 35.
Действие оператора о на обобщенные функции опре-
деляется равенством
или, что то же самое,
(о7\ <р> = G\ о-\) = (Ту, 9(ву)>.
Теорема. Оператор а действует на обобщенные
функции линейно и непрерывно.
Доказательство. Линейность:
Непрерывность. Если Г„—>0, то для любой функ-
ции <j?S имеем а~^^3) и
следовательно, оГ„ -> 0.
Легко показать, что последовательное применение опе-
раторов о и х в 3)' равносильно оператору то в 3'.
Отсюда следует, что о является автоморфизмом 3}'.
Если задано аффинное пространство Е и положитель-
ная мера в Е, инвариантная относительно сдвигов, то тем
самым однозначно определена мера в Е. Тогда любая
локально интегрируемая функция / в Е определяет обоб-
щенную функцию
2*

20 Г л. 1. Постановка задачи
Если задана квадратичная форма над Ё, то ей соот-
ветствуют ортонормированный базис и определенным об-
разом нормированная мера Хаара. Ввиду того что любой
> ¦>
оператор о ? О сохраняет квадратичную форму, он сохра-
няет также и выбранную меру Хаара. Следовательно,
а сохраняет установленное с помощью этой меры соот-
ветствие между обычными локально интегрируемыми функ-
циями и обобщенными функциями.
Если заданы скалярная частица |i?cf'(?4) и любой
оператор o?G, мы можем построить пространство <sg№
как совокупность всех зф для ф ? о№. Определив в о$в
скалярное произведение
получим, что Q&6 — также гильбертово пространство.
Определение. Скалярная частица &в называется
мировой, если для всех o?G справедливы соотношения:
A) gSV = SV;
B) ||w|» || ж = || 4» || w для любого ф g т.
Следовательно, ?№ является мировой частицей тогда и
только тогда, когда любой оператор о ? G является уни-
тарным оператором, отображающим ¦?№ на &в.
§ 5. Скалярные и векторные частицы
в произвольном мире
Определение. Миром V называется многообразие
класса С°° конечного числа измерений п. Группу G, эле-
менты которой действуют в мире V, назовем структур-
ной группой мира.
Определение. Скалярной частицей в мире V
называется множество о№, удовлетворяющее следующим
постулатам:
A) &6—векторное подпространство пространства 35' (V)
обобщенных функций, определенных в мире V;
B) $6 снабжено гильбертовой структурой;
C) фу-*0 в <^:фф->0 в SB'(У).

§ 5. Скалярные и векторные частицы в произвольном мире 21
Определение. Скалярная частица $в в мире V
называется универсальной относительно G, если для
всех операторов a?G справедливы соотношения:
A) 0^ = ^;
B) ИНяр^ИфНав Для всех Ф6^-
Отметим, что ранее данное определение мировой частицы
совпадает с определением частицы, универсальной отно-
сительно группы Лоренца.
Пример. Для одной скалярной частицы можно взять
в качестве мира V аффинное лоренцево пространство ?4
с заданной лоренцевой квадратичной формой и в качестве
структурной группы соответствующую группу Лоренца.
Пример. Для двух частиц можно взять V = Ei X EA.
Структурной группой О вновь будет группа Лоренца,
действующая на Е4 X Е4 по. следующему закону: для
(х. У)?Е4ХЕ4 и o?G
(х, у)->о(лг, у) = (ох, су).
Для изучения таких частиц, как электрон, протон и
т. д. мы должны ввести понятие векторных обобщен-
ных функций. Пусть F — конечномерное векторное про-
странство над С1).
Определение. Обобщенной функцией Т, опре-
деленной в мире V и принимающей значения из F,
называется непрерывное линейное отображение Т : <р->G\ <f)
пространства 3(V) в F.
Пространство 3)' (V; F) обобщенных функций, опре-
деленных в мире V и принимающих значения из F, про-
странство J3?{35(y); F) непрерывных линейных отображе-
ний S (V) в F, а также тензорное произведение 3}' (V)(giF
пространств S'(V) и F тождественны между собой:
С обозначает поле комплексных чисел.— Прим. ред.

22 Гл. 1. Постановка задача
Пример. Пусть V = R" —аффинное пространство
с мерой Лебега. Если / (дг) — локально интегрируемая
функция, определенная в R* и принимающая значения
из F, то функции / соответствует обобщенная функция
Если S???)f(V) и f?F, то векторную обобщенную
функцию S/? S'(V; F) можно определить равенством
E/, <?) = <$, ?>/•
Обобщенная функция Sf отождествляется с тензорным
произведением S®f??B'(V)®F.
Если F имеет базис
f\> fi> • • •• /я»
то обобщенную функцию T?3}'(V; F) можно записать
в виде
где Г,, Г2 Г„?,2К0О- Таким образом, для
имеем
(Г. ср) = 2(Г,,
Определение. F-векторной частицей в мире V
называется множество J5?cS'(V; F), удовлетворяющее
постулатам, сформулированным в определении скалярной
частицы в мире V, если заменить в них пространство 3' (V)
пространством 3' (V; F), и, кроме того, следующим допол-
нительным постулатам.
A) Каждый оператор ofG действует не только на V,
-> .>->->.>
но и на F, так что л:?V =фо*?V и f?Fz$of?F.
B) Если а определяет тождественную операцию как
в V, так и в F, то о — единичный оператор группы О.

§ 6. Слабая и сильная сходимость 23
- Таким образом, группа О действует эффективно1) на
произведении V®F, но необязательно на V или F в от-
дельности.
Пример. Для электрона О представляет собой соб-
ственную спинорную группу, V==?4 и F — Двумерное
векторное пространство над С. Существует отображение
G ^ о -> о0- гДе °о принадлежит собственной неоднородной
группе Лоренца, такое, что каждому элементу лоренцевой
группы соответствуют два элемента группы О и действие
каждого о на любой элемент Е4 такое же, как действие
соответствующего оператора о0, заданного этим отображе-
нием. Существует также отображение о->т группы О
в некоторое множество унимодулярных операторов в F,
при котором бесконечное число элементов группы G пере-
ходит в один и тот же оператор в F, и действие любого
•>
оператора о на произвольный элемент из пространства F
такое же, как действие соответствующего оператора т,
заданного этим отображением.
Определение. Действие оператора amT?3B' (V) ® F
определяется равенством
или эквивалентным равенством
{of. <р} = °«7\ 0-1<р» =
Определение. Универсальная F-векторная ча-
стица в мире V определяется точно так же, как миро-
вая скалярная частица в мире V.
§ 6. Слабая и сильная сходимость
Определение. Пусть Е—топологическое векторное
пространство. Множество АсЕ называется выпуклым,
если для любых х, у?А элементы ах-j-A — а)у,
1) Говорят, что группа G действует эффективно на про-
странстве X, если каждому элементу группы, отличному от
единицы, соответствует нетождественное преобразование про-
странства X. — Прим. ред.

24 Гл. 1. Постановка задачи
0^. а^.1, также принадлежат А. Множество Е назы-
вается локально выпуклым пространством, если его топо-
логия может быть определена базой, состоящей из выпу-
клых множеств1).
Пусть Е— локально выпуклое топологическое вектор-
ное пространство, и пусть Е' — дуальное к нему про-
странство непрерывных линейных форм на Е. Определим
слабую и сильную сходимость в Е'.
Определение. Последовательность fe'\сЕ' слабо
сходится к нулю (е'.->0 слабо), если (е'., е\-+0 для
любого е? Е. Скалярное произведение определяется здесь
естественным образом, как значение функционала е' на
элементе е.
Сильная сходимость требует некоторой равномерности
на ограниченных подмножествах пространства Е.
Определение. Подмножество Л из ? называется
ограниченным, если его можно отобразить в любую
окрестность нуля подобным преобразованием с ненулевым
коэффициентом подобия. Например, если Е — банахово
пространство, то подмножество из Е ограничено в том
случае, когда его можно отобразить внутрь любой сферы
при помощи сжатия с ненулевым коэффициентом.
Определение. Последовательность \е'\сЕ' сильно
сходится к нулю (e'j->0 сильно), если (е'.,е}-+0 для
любого е ? Е, и эта сходимость равномерна на любом
ограниченном подмножестве из Е.
Вернемся теперь к пространствам 3) (V) и 3' (V).
Пространство ?B(V)— это пространство основных функ-
ций, определенных в мире V. Если К — компактное под-
множество из V, то пусть 3K(V) обозначает пространство
основных функций, Носители которых содержатся в AT.
В 3K(V) можно ввести норму
||<p||m= sup \D\(x)\,
\р\<т
') Базой топологического пространства называется такой
набор открытых множеств, что любое открытое множество полу-
чается объединением некоторого числа элементов из этого на-
бора.— Прим. ред.

§ 6. Слабая и сильная сходимость 25
где Dp обозначает дифференцирование, определенное в § 2.
Как и ранее, определим сходимость к нулю последова-
тельности {<ря} в ?ЁК(У), потребовав, чтобы для всех m
выполнялось соотношение ||сря||т—*-0.
Элемент Т из 3>' (V) представляет собой линейную
форму на ЗЬ(У), непрерывную на любом ??K(V). Последо-
вательность [ТАсЗ'(V) слабо сходится к нулю (Tj-+O
слабо), если {Tj, ф)->0 для любой функции y??fi(V).
Эта последовательность сходится к нулю сильно
G\->0 сильно), если {Tj, <p)-^-0 для любой функции
ср t; ЗЬ (V) п эта сходимость равномерна на ограниченных
подмножествах ?BK(V) для любого К.
Приведем без доказательства следующую важную
теорему.
Теорема. Пространство 3)' (V; F) обобщенных
функций, определенных на V и принимающих значе-
ния из пространства F, является локально выпуклым
топологическим векторным пространством, которое
полно в сильной топологии.
Далее нашей основной задачей будет отыскание всех
подпространств ?№ пространства 3)' (V, F), таких, что ?№
может быть снабжено структурой гильбертова простран-
ства, так что сходимость в ?№ влечет за собой сходи-
мость в &>' (У; F).

Глава 2
МНОЖЕСТВО ? МИРОВЫХ ЧАСТИЦ
И ЕГО СТРУКТУРА
§ I. Пространство S$
Пусть Е — полное локально выпуклое топологическое
векторное пространство. В изучаемом случае Е является
пространством S'(V; F). Пусть ф обозначает множество
пар {<%%>, (.. .\ .. .)дЛ, состоящих из линейного подпро-
странства ?№ пространства Е и скалярного произведения
в Цв и удовлетворяющих следующим условиям:
(а) <Ш является гильбертовым пространством относи-
тельно скалярного произведения (... | .. .)до!
(б) вложение &в в Е непрерывно, т. е. сходимость в &6
влечет за собой сходимость в Е.
В множестве ф мы можем определить следующие
операции:
A) Умножение на неотрицательный скаляр
.множество ~к&в определяется формулой
, х=о.
Если Т ? ®в и, следовательно, Г ? X ffl, то J Т1^= ~= |) Т [^.
B) Сложение. Множество &6х~{-&6^ определяется
формулой
Норма в Цвх-\-$вч задается равенством
где нижняя грань берется по всем разложениям Т в сумму
Лг Л€#? П€^

§ 1. Пространство ф 27
C) Порядок. Частичное упорядочение определяется в ф
соотношением
3@i-*C &6V если J^?icj!?2 и норма в ?№х не меньше
нормы в J5?2.
D) Топология. Будет показано, что ф представляет
собой замкнутый выпуклый конус в топологическом век-
торном пространстве, которое мы построим.
Определение. Антиядром L называется антили-
нейное непрерывное отображение дуального пространства
Е' в Е [т. е. Е'—*Е, L непрерывно и L(ke') = lL(e')].
Антиядро L называется положительным, если (er, L(e'))^>Q
для всех е'?Е'.
Произведение, устанавливающее дуальность пространств
Е и Е'. определяется выражением
{е\ f) = e'(J) (значение е' на /) для f?E, e'?E'.
Пример. Пусть Е = С (и-мерное комплексное век-
торное пространство), тогда Е' = С. В этом случае анти-
ядро является положительно определенной эрмитовой ма-
трицей L:
где
и
В пространстве положительных антиядер очевидным
образом определяются сложение и умножение на скаляр.
Кроме того,- задается отношение порядка:
;L2, если {e't Lje'X^e', L2e') для всех
Докажем теперь следующий важный результат.
Теорема. Существует взаимно однозначное соот-
ветствие между элементами <3в пространства § и
положительными антиядрами L,

28 Г л. 2. Множество ф мировых частиц и его структура
Каждому Ив ? 4? соответствует ядро') J о /^ о *J,
где J—естественное вложение Ив->Е, fJ — сопря-
женное отображение Е'-> Ив' а 1^ — канонический
антиизоморфизм Ив'-+Ив.
Доказательство. Покажем сначала, что данному Ив
соответствует положительное антиядро L. Пусть е?Е'.
Так как е' — непрерывный линейный функционал на ? и
вложение Ив в Е непрерывно, отсюда следует, что е' —
непрерывный линейный функционал на Ив. По теореме
Рисса о линейных функционалах в гильбертовом прост-
ранстве существует однозначно определенный элемент из Цв',
который мы обозначим Le', такой, что
<«'. ¦ Н) = {Н\и')х. h^&e, e'?E'. A)
Очевидно, что отображение L : ?'-> ШсЕ, определенное
соотношением A), антилинейно. Для того чтобы доказать,
что L непрерывно, предположим, что е^Ов ?' (в смысле
сильной топологии), т. е. (е'., А) -> 0 для любого h ? Е,
равномерно по h на ограниченных подмножествах из Е.
Из непрерывности вложения Ив в Е следует, что огра-
ниченные подмножества из Ив ограничены в Е.
Следовательно, (е1., h\=={h\Le'\ —>0 равномерно на
единичной сфере в Ив. Поэтому \Le'A ->0 и L непре-
рывно. Наконец, полагая в A) h==Lf, получаем
<«'. Lf') = (Lf'\Le')g€; e',f?E'. B)
и если e' — f, то
<«'. Le') = {Le' | Le')^ > 0, е'? Е',
что доказывает положительность L.
Теперь мы должны показать, что данному положитель-
ному антиядру L соответствует элемент Ив из ф. Пусть
Если требуемое Ив существует, то должно иметь место
включение е№0а&6. Согласно равенству B), определим
') Знак о — знак композиции, — Прим. ред.

§ 1. Пространство ф 29
скалярное произведение
^ = </'. Le">- C)
где и, г»?е%?0 и u = Le', v = Lf. Докажем теперь
для З&о следующие утверждения.
(а) Скалярное произведение (и [ v)^ определяется фор-
мулой C) однозначно, т. е. не зависит от выбора е' и /',
таких, что u = Le' и v — Lf. Это немедленно следует
из C), если заметить, что (.u\v)se=0, когда либо и,
либо v равно нулю.
(б) Форма (и | v)^ положительно определена. Так как L
положительно, имеем
(и j a)Xi = («', Le') > 0, и ? J5?o-
Если (е', 1е') = 0, то, согласно неравенству Шварца,
К/', ?*')!<</'. Lf'Lt{e'. Le')'h = 0
для всех /' ^ ?'. Поэтому Le' = и = 0 и (и [ а)^ = 0
тогда и только тогда, когда и = 0.
(в) Топология в J5?o сильнее, чем топология в Е, т. е.
вложение 3&0 в Е непрерывно. Для этого достаточно по-
казать, что единичная сфера в §вй, {Le': (е', Z.e')^l},
является ограниченным подмножеством множества Е, Из
неравенства Шварца
следует, что множество {(/', Le'):{e\ Ie')-<1, ef?E]
ограничено в С для любого f'?E', или что единичная
сфера в Зв§ слабо ограничена в Е. Используя теперь
теорему Макки, которая утверждает, что подмножество
локально выпуклого топологического векторного простран-
ства сильно ограничено тогда и только тогда, когда оно
слабо ограничено, получаем, что .единичная сфера в i№0
ограничена в Е.
Итак, мы показали, что е%?0 = LE' — предгильбертово
пространство, вложение которого в пространство Е не-
прерывно. Мы. ожидаем получить нужное пространство 3€,
соответствующее L, пополняя $6^. Поэтому необходимо
доказать следующее. .

30 Гл. 2. Множество ф мировых частиц и его структура
(I) Если существует <S€, соответствующее антиядру L,
такое, что выполняется равенство A), то е%?0 плотно в ?№.
Пусть элемент Л ? @Н! таков, что (h\Le')g€ = O для всех
е'?Е'. Тогда (h\Le')g€ = (ef, А) = 0 для всех е'?Е', и
по теореме Хана — Банаха Л = 0. Таким образом, элемент
из <36', ортогональный к любому элементу из е%?0, является
нулевым и, следовательно, J#o плотно в ffi'.
(II) Пополнение <$№0 множества <%№$ может быть вло-
жено в Е. Рассмотрим (непрерывное) вложение
J: &въ-+Е
и его однозначно определенное расширение
У: Se0->?(=?).
Мы должны показать, что J по-прежнему является вло-
жением. Пусть Л? Шй и пусть h = Jh?E. Мы утверждаем,
что для любого е'?Е' справедливо равенство
<«'. h) = {h\Le')^. D)
Если A?J5?0, то h = h = Lf, и равенство D) просто
сводится к определению C) скалярного произведения в J5?o.
Рассмотрим теперь последовательность {Av}c^0, такую,
что Л,->А. Тогда
Переходя к пределу и используя непрерывность скалярного
произведения в S@o. а также непрерывность линейной
формы е'', получаем равенство D). Предположим теперь1,
что h = fh = Q. Тогда в силу D) (А [ Le') ^ = 0 для всех
Le'?g%?0, и, поскольку J5?o плотно в ^0, имеем А=0;
"Поэтому операция J взаимно однозначна.
(III) Наконец, положим $%? — ?е%?0 и перенесем гиль-
бертову структуру из $?0 в Ш- Мы должны показать,
что &в — гильбертово пространство, соответствующее анти-
ядру L. Если k^gfe, то существует некоторое Ag^Ql
.такое, что Jh = A==ft, и равенство D) дает

§ I. Пространство ф 31
откуда следует, что L является антиядром, соответствую-
щим sfe.
Приведем теперь другое построение гильбертова про-
странства J5?, соответствующего данному положительному
антиядру L. Это будет построение „сверху", в отличие
от приведенного в доказательстве предыдущей теоремы
построения „снизу".
Теорема. Пустб L — положительное антиядро.
Элемент h?E принадлежит гильбертову простран-
ству &€, соответствующему антиядру L, тогда и
только тогда, когда
.fr?<oo
' (e',Le')i*
и если это условие выполнено, то.
I («', h) |
.= sup
Доказательство. Если A?J#, то, используя A)
и неравенство Шварца, получаем
«', А> | = | (А | Le>) х |< (А 1 Н)% • (Le
' \
для всех ?
Обратно, предположим, что справедливо условие E),
и рассмотрим отображение
Легко убедиться в том, что это отображение является
антилинейным функционалом на J#o, который непрерывен,
так как он ограничен на единичном шаре из &вй. Поэтому
его можно продолжить до непрерывного антилинейного
функционала на пополнении J5? пространства J^o. Следо-
вательно, по теЪреме Рисса, существует элемент k ? $tf,
такой, что
= {e', k)
для всех е'??'. По теореме.Хана — Банаха, h =

32 Г л, 2, Множество ф мировых частиц и его структура
§ 2. Структура ф и j?+ (?'. Е)
Пусть ??{Е', Е) обозначает множество непрерывных
линейных отображений из Е' в Е, J? (?', Е) — множество
непрерывных антилинейных отображений, или антиядер.
из Е' в Е, и ^+ (??', ?) — множество положительных
антиядер. В предыдущем параграфе было показано, что
существует взаимно однозначное соответствие между ф
и J&+ (f, Е), ф х J&+ (?', Е). Упоминалось также, что
как в «g>, так и в ^+ (?', Е) можно определить есте-
ственную структуру (сложение, умножение на скаляр
и т. д.). В этом параграфе будет дано более точное опре-
деление структуры ф и S'+iE', E), а также установлено
соответствие между ними.
Определение. Определим в ??+ (?', Е) следую-
щие понятия.
A) Отношение порядка: L^^L^, если L2 — ij^-0,
т. е. если Ц — Lx — положительное антиядро.
B) Умножение на неотрицательный скаляр X:
C) Сложение: (ii + L2)e' — Lxe' -\-1ге'.
Соответственно определим в § следующие понятия.
A') Отношение порядка: &€х-^Зв^, если &€хс&€г
и норма в &€х не меньше нормы в &вг, ||A||W ^-11^11^^.
B') Умножение на неотрицательный скаляр X.
Пространству &в и неотрицательному числу X соответ-
ствует пространство
с нормой
11*11=11*11*-
C') Сложение: пространствам {Sffv &в? соответ-
ствует пространство ¦ «
с нормой

§ 2. Структура $ и ^+ (?', Е) 33
Следует отметить, что A) и A') в самом деле опре-
деляют отношения порядка, так как
(а) из ^,<^2и &62 < <ШХ следует, что <ШХ = Ж2;
(б) из Z-! <^ Z-2 и L2 < Lj следует, что Lx = Z.2.
Первое тривиально вытекает из того, что в гильберто-
вом пространстве скалярное произведение однозначно опре-
деляется нормой. Второе предположение означает по опре-
делению, что
или
Используя формулу
заключаем, что
(<?', LJ') — {e', LJ') для любых e', f'?E', откуда "по
теореме Хана — Банаха вытекает, что
Следует отметить также, что из требования
' -^ II *11 эс в определении отношения ?№х ^ $ff2
следует, что сходимость в пространстве ^вх влечет за
собой сходимость в пространстве J??2.
Установим теперь соответствие между структурами ф
и JF+(E'. E).
Теорема, (а) Если &6Х соответствует анти-
ядру Lj, а &в2 соответствует антиядру L2, то
&в\ ^. &в2 тогда и только тогда, когда Lx ^ L^.
(б) Если &в соответствует антиядру L, то \&€
соответствует A.L (А.^-0).
(в) Если <ШХ соответствует антиядру Lv а &в2
соответствует антиядру L2, то &вх-\-&€2 соответ-
ствует Li + L2.
Доказательство..
(а) Предположим сначала, что &€х <] <з№2. Тогда
3 Л. Шварц

34 Г л. 2. Множество ф мировых Частиц и его структура
выбирая f' = e', получаем
(в' L е'\'1г
или
(«'. V)IA
или
, <«'. (Z.2
или
Обратно, предположим, что Ьг ^ L2. Тогда для любого
элемента h?E имеем
| (е', h) | 1 («', ft) i
Отсюда следует, что &6хсЖ^ и если h?SWv то
(б) Утверждение следует непосредственно из выбора
нормы в \7в
(в) Прежде всего следует оговорить, чтб мы понимаем
под гильбертовым пространством &6х-\-&6ч! Множе-
ство &в\-\-&в% состоит из всех элементов h из Е,
которые можно записать в виде h = hx -f- h2, где hx ^ ^вх
и A2? J?V Если ^1П^?2 = {°}- то норму в <$?1 + J2?2
можно определить формулой
где A = A1-t-A2 — единственное представление А в требуе*
мом виде. Если, однако, <Цвх П &вч ф {0}, то любой эле-
мент А ? JS?! -\- ?№¦} имеет бесконечное число представле-
ний, поскольку нулевой элемент бесконечным числом спо-

§ 2. Структура S и ?f+ (Ef, Е) 35
собов можно представить в виде а — а, где
а ? &вх П &вг.
Поэтому мы определяем норму равенством
где нижняя грань берется по всем возможным предста-
влениям
Нужно показать, что это выражение действительно задает
норму, т. е. что ее можно определить скалярным произ-
ведением в e%?i~\-е%?2> причем Звх-\-&€2 полно и топо-
логия пространства ?/в\ + &€2 сильнее, чем топология
пространства Е. Так как это довольно утомительная про-
цедура, мы построим гильбертово пространство i№x-\- Sfff2
другим способом.
Пусть еЯ?!®©^ обозначает абстрактную (прямую)
гильбертову сумму пространств ?}6Х и ?}6V Элемен-
том &в\®&вч. является пара (Ах, Л2), где hx^ef6x
и Л2 ^ &в2. Сложение и умножение на скаляр определяются
соотношениями
(A,.
h2) = (Xhv XA2);
скалярное произведение в еЮ\®еЮч определяется соот-
ношением
(Alt Aj) | (ftlf ftj) )Wi ф W2 = (A! | ft^, + (*
Заметим, что Звхх,Зех®Щ и J^2«{0}©J^2. Ото-
бразим абстрактное гильбертово пространство &
в пространство Е:
Пусть т) = {(Aj, Аг): At —(— Л2 = №}} —нулевое пространство
этого отображения.- Очевидно, что т) замкнуто в прямой
сумме е%?1®е%?2- Следовательно, факторпространство
36\®еН>гН стандартным образом превращается в гиль-
бертово пространство, которое отождествляется с орто-
гональным дополнением к i\ в &
3*

36 Г л. 2. Множество ф мировых частиц и его структура
Рассмотрим теперь отображения
Отображение &вх@&€2\г\-^*-Е является вложением,
образ которого — пространство ?№х + е%?2. Мы можем пере-
нести структуру гильбертова пространства из е^чфе^У7!
на e%?i ф е%?2; сразу же видно, что факторнорма на
&в\фе%У]— эт0 норма, определенная выше в &в\-\-Звч
с помощью нижней грани. Этим построением доказано,
что пространство e%?i + <з№2 является гильбертовым про-
странством, содержащимся в Е, топология которого силь-
нее, чем топология пространства Е.
Нам нужно еще показать, что Зв\-\-&€2 соответст-
вует антиядру Lx-\-L2. Пусть L = Z,]-(-L2 и пусть е2Г —
гильбертово пространство, соответствующее антиядру L.
Мы должны показать, что
Так как L~^>LX и L>.L2, отсюда следует, что 1
S@2, а значит, и ^jf з &6Х + ^2- Кроме того,
содержится ^в J5?x +J5?2> так как Le'= LYe'-\-L2er.
Таким образом, получаем
где е^*,, — плотное подмножество множества
Так как и <??, и <ffil-\-362 — полные гильбертовы
пространства, достаточно показать, что норма в ^fu равна
норме в J#i + J#2. Пусть h = Le' = Lxe' -j- V = Aj + A2,
где At = Ljg'? e%?i и Ji2 = L2e'? &в2. Имеем
или
Для того чтобы показать, что в этой формуле имеет
место равенство, достаточно показать, что элемент (hx, A2)

§ 2. Структура ф и Jg>+ (Е1, Е) 37
прямой суммы е%?1®е%?2 ортогонален нулевому простран-
ству t\, потому что в этом случае при переходе от
&в к <гЮх-\-&в2 норма не уменьшается. Если
то имеем .
= <«'. »1 + »2} = (е'> 0> = 0.
Замечание. Если ^?,<^ ^?, то существует един-
ственное гильбертово пространство е%?2> такое, что
<§В\-\-&в<i=*iffl• Это следует из того, что L2 = L — Lt
является положительным антиядром.
Определение. Антиядра Lx и L2 называются
дизъюнктными, если единственное антиядро, которое не
больше каждого из антиядер Lx и L2, есть нуль, т. е. из
L ^ Lt и L^.L2 следует, что L = 0.
Аналогично, гильбертовы пространства е%?! и JS?3
называются дизъюнктными, если из неравенств
следует, что JS? = {0}.
Теорема. J5?j fl J^f2 == {0} тогда и только тогда,
когда 36Х и Шч дизъюнктны (в смысле данного выше
определения).
Доказательство. Если S$\ П е%?2 = {°}• то отсюда
немедленно следует, что 0в\ и &6i дизъюнктны. Обратно,
если e%?! и &в<2, дизъюнктны, то <fflx П &62^= {0}. В самом
деле, предположим противное, т. е. что
Пусть норма в </%* задается формулой
И*1&= 11*111»,+11*11**.
Эта норма больше, чем норма в каждом из пространств if6\
и eft}2. Используя это, легко показать, что <?? — полное
гильбертово пространство, топология которого сильнее,

38 Гл. 2. Множество ф мировых частиц и его структура
чем топология пространства Е, и что ^ <; &вх.
Поэтому е2Г = {0}.
Следствие. ?№х П е%?2== {0} тогда и только
тогда, когда соответствующие антиядра LA и L2
дизъюнктны.
Данное выше определение дизъюнктности можно рас-
пространить на случай более чем двух антиядер или гиль-
бертовых пространств, причем будут справедливы резуль-
таты, аналогичные доказанным выше.
В дополнение к уже введенной структуре в простран-
ствах § и jg>+ (?', Е) можно определить топологии в этих
пространствах. Топология в ?> довольно неинтересна. Однако
мы определим два типа сходимости в jS?+ (Е', Е).
Определение. Сходимость последовательности
антиядер
{Ln}cz^+(E't E)
к некоторому антиядру L называется
(а) поточечной сходимостью, если Lne'->Le' для
всех е' ??';
(б) ограниченной сходимостью, если Lne'->Le' для
всех е' ? Е', и эта сходимость равномерна на огра-
ниченных подмножествах пространства Е'.
Следует заметить, что „g"+ (?', Е) является замкнутым
подмножеством множества J&OE', E) относительно обеих
определенных выше сходимостей.
Далее, это множество является выпуклым конусом.
В самом деле, это конус с вершиной в начале координат,
так как tL — положительное антиядро, если ^0 и i
положительно; этот конус — выпуклый, так как при лю-
бом t, 0 <; t -^ 1, в предположении, что антиядра Lx и L2
положительны, tLx-\~\\—f)L2 представляет собой поло-
жительное антиядро. Таким образом, мы можем сформу-
лировать следующую теорему.
Теорема. Существует взаимно однозначное соот-
ветствие между пространством $> и замкнутым
выпуклым конусом в топологическом векторном про-
странстве. Этот конус не содержит векторных
подпространств, кроме нулевого.

§ 2. Структура f) и ??+ (?', Е) 39
Последнее утверждение этой теоремы выражает тот
факт, что отношение Звх -^ е%?2 действительно является
отношением порядка, а не только частичной упорядочен-
ности.
Перейдем теперь к следующему вопросу. Если дана
система {et} элементов пространства Е, то каковы необ-
ходимые и достаточные условия для того, чтобы эта си-
стема была полной ортонормированной системой некото-
рого гильбертова пространства 36 ? ?>?
Отметим сначала, что элемент е ? Е определяет сле-
дующие отображения:
(а) линейный функционал на Е'\
(б) антилинейный функционал на Е'\
(в) эрмитову форму на Е' X Е'\
(f'.g1) ->(/'¦ e){g',e);
(г) отображение Е' в Е, обозначаемое через ее:
Легко показать, что ее является положительным анти-
ядром. Соответствующим гильбертовым пространством
является &€ = {Хе: Х^С} с нормой ||Хе|| = |Х| и скаляр-
ным произведением (Хе|]хе) = Х]х.
Теорема. Для того чтобы данное множество
{e^rj элементов пространства Е было гильберто-
вым базисом, т. е. полной ортонормарованной си'
стемой гильбертова пространства &в ? ?>, необхо'
димо и достаточно, чтобы
A) ряд антиядер ^е,е, был поточечно сходя-
щимся или чтобы конечные частичные суммы этого
ряда были поточечно ограниченными,
B) множество {^};g/ было линейно независимо
в гильбертовом смысле, т. е. если {ci}lrI — любое

40 Г л. 2. Множество ф мировых частиц и его структура
множество комплексных чисел, таких, что 2|сг12<
< со, и если 2 ciei = 0, то ct = 0 для всех I ? /.
i
Доказательство. Допустим, что {^}г?/ — гиль-
бертов базис в &в'?§ и L—соответствующее антиядро.
Тогда для любого /'?Е' имеем
2Я/ U,{Fl),?
так что Se,e, сходится в смысле поточечной сходимости.;
Далее, так как {6*}*g/ — гильбертов базис, то отсюд^
немедленно следует, что он линейно независим в гильбер-
товом смысле.
Обратно, допуская, что выполняются условия A) и B),
покажем, что {0*}^/—гильбертов базис некоторого i#???>.
Прежде всего заметим, что условие A) означает, что для
любого /'??' частичные суммы ряда 2(ej» f')ei сильно
ограничены в Е, и для любых /' и g* из Е' частичные
суммы ряда 2(ег- f'){ei< ?>') ограничены.
Полагая /' = g' и используя элементарные свойства
рядов с неотрицательными членами, заключаем, что
S
Попытаемся теперь построить гильбертово пространство &6\
Рассмотрим гильбертово пространство Р, элементами ко-
торого являются наборы {-^Лгс/ комплексных чисел, таких,
что %\xt\2 <оо, и пусть /g обозначает подмножество
пространства Р, элементы которого имеют лишь конеч-
ное число координат, отличных от нуля. Существует есте-
ственное отображение из PQ в Е, определяемое формулой
Для того чтобы показать, что это отображение непрерывно,
достаточно показать, что образ единичной сферы ограничен

§ 3. Скалярные частицы 41
или, по теореме Макки, что он слабо ограничен. Это
следует из неравенства Шварца. Пусть [х^^^Щ и
2|*i|2<Cl- Тогда для любого /'??' имеем
Расширим теперь описанное выше отображение на попол-
нение (*, которое можно отождествить с Р
Р-+Е
при помощи формулы
Используя предположение B) о линейной независимости
в гильбертовом смысле, можно показать, что это отобра-
жение является вложением. Пусть ?№— образ этого вло-
жения со структурой, перенесенной из Р. Множество
{6t)i^l является образом канонического базиса из Р и, сле-
довательно, гильбертовым базисом для Sf6.
Следствие. Если L—положительное антиядро, то L
можно бесконечным числом способов представить в виде
§ 3. Скалярные частицы
Вернемся теперь к изучению скалярных частиц в мире V.
Напомним, что мир является многообразием класса С°°
размерности п и что скалярная частица представляет со-
бой гильбертово пространство &в, непрерывно вложен-
ное в пространство обобщенных функций 3' (V), опреде-
ленных на мире V. Локально выпуклое топологическое
векторное пространство 3' (V) дуально пространству ?В (V)
бесконечно дифференцируемых функций на V с компакт-
ными носителями. Элемент Т пространства 3' (V) является
обобщенной функцией, значение которой на элементе ср
пространства 3 (V) обозначается ¦ через (Г, <р): & {V) —
рефлексивное пространство [это означает, что дуальное

42 Гл. 2. Множество ф мировых частиц и его структура
пространство к пространству 3' (V) совпадает с простран-
ством 3 (V)]. Пространства 3 (V) и 3' (V) имеют силь-
ную дуальную топологию по отношению друг к другу.
Применим теперь результаты последних двух параграфов
к случаю, когда E — 3'(V) и E' = 3(V).
Для того чтобы определить в 3' (V) гильбертово про-
странство, мы должны найти антиядро L: 3 (V) -> 3' (V).
Мы начнем с отыскания непрерывных линейных отобра-
жений из 3(V) в 3'(W), где V и W — два многообразия
класса С°° (например, два евклидовых пространства). Пусть
у — общая точка многообразия V, ах — общая точка
многообразия W. Для удобства можно обозначить 3(V)
через Зу а 3' (W) через З'х. Пусть 3' (W X V) или з'х, у
обозначает пространство обобщенных функций на произ-
ведении W X У (обобщенные функции двух переменных).
Теорема о ядрах. Топологическое векторное
пространство 3?ЪC(У)\ 3'(W)) непрерывных линей-
ных отображений из 3(У) в 3' (W) с топологией
ограниченной сходимости канонически изоморфно
топологическому векторному пространству 3'(WXV).
Доказательство. Пусть К — данный элемент про-
странства 3'(W y(V). Он определяет непрерывное линей-
ное отображение v->Ktf из 3(V) в 3 (W) по формуле
{Kv, w) = {K, w®v), w??B(W), A)
где w ® v = w (x) v (у). Прежде всего мы должны убе-
диться в том, что Kv^35'(W). Очевидно, что Kv—ли-
нейный функционал от w. Если w —> 0 в 3 (W), то
И)®г>-»-0 в 3(WXV), и так как K?3'(WXV), то
{Kv, w) = {K, w®v)->0.
Нужно также показать, что v->Kv—непрерывное линей-
ное отображение. Линейность этого отображения очевидна.
Если »->0 в 3(V), то, как легко видеть, {Kv, w)—>0
для любой функции w?3(W), и эта сходимость равно-
мерна, когда w остается ограниченной в 3(W).
Для большей ясности перепишем этот результат,
используя обозначения Зу, Зх, Зй'х, у. и приведем пример
ИЗ теории интегральных уравнений, откуда эти рбозначе-

§ 8. Скалярные частицы 43
ния заимствованы. Пусть Кх, у ? 35Х, у — данная обобщен-
ная функция двух переменных х и у. Она определяет не-
прерывное линейное отображение из 35У в Зх:
* (У)->**,* (У) = (*«)(*). »(У)€#,.
где (Kv) (х) ? 35Х определяется формулой
{(Kv) (х), w (х)) = {Кх, у, w (х) v (у)). w (х) 6 ?ВХ.
Пример. Пусть Vy и Wх — два евклидовых простран-
ства, снабженных мерой Лебега, и пусть К(х, у) — ло-
кально интегрируемая функция, определенная на произве-
дении W X V. Тогда К (дг, у) ? З'х, у — обобщенная функ-
ция двух переменных х и у. Пусть
— значение обобщенной функции Т на основной функ-
ции <р.
Обобщенная функция К (х, у) определяет непрерывное
линейное отображение из Зу в Зх:
K:v(y)->(Kv)(x), v^SBy,
где (Kv) (х) ^ Зх определяется в соответствии с нашей
формулой следующим равенством:
{К. w®v) = J f K(x, y)w(x)v(y)dxdy==
(x. y)v(y)dy]w(x)dx =
, w),
в котором мы использовали теорему Фубини. Таким обра-
зом,
Вторая часть теоремы о ядрах утверждает, что любое
непрерывное линейное отображение из 3(V) в 3'' (W)
однозначно определяет обобщенную функцию, заданную
на произведении W X V. Доказательство этого утвержде-
ния значительно более сложно и будет опущено. Вместо

44 Г л. 2. Множество § мировых частиц и его структура
этого мы обратимся к доказательству эквивалентности
топологий изоморфных пространств JgiSby, Зх) и З'х, у
В этих двух пространствах существует естественная топо-
логия. Рассмотрим сначала в пространстве Зх, у сильную
топологию (равномерную сходимость на ограниченных
подмножествах Зх>у). В пространстве Л?CУ, Зх) мы
имеем ограниченную сходимость и поточечную сходимость.
Пусть J3?b{3y, З'х)—топологическое векторное простран-
ство, полученное из векторного пространства ^[Зу, Зх)
при введении топологийг ограниченной сходимости. В то-
пологическом векторном пространстве ^ЬCУ, Зх) после-
довательность непрерывных линейных отображений из 3
в Зх сходится к нулю в смысле ограниченной сходимости,
если последовательность образов любого элемента из 3V
сходится к нулю в Зх и эта сходимость равномерна на
ограниченных подмножествах пространства 3V. Мы дока-
жем только, что сходимость в Зх, у, влечет за собой схо-
димость в Jg'i, (Зу, З'х). Пусть {Kj} — последовательность
в Зх, v, такая, что Kj->0 сильно, т. е. (Kj, <р(лг, у))->0
для любой функции ср(аг. у)?Зх,у. и эта сходимость
равномерна на ограниченных подмножествах простран-
ства Зх% . Нужно показать, что при фиксированном
v (у) ? Зу имеем (KjV, w) -> 0 для любого w (х) ^ Зх и
что эта сходимость равномерна, когда w(x) пробегает
ограниченные подмножества из 3х. По определению
(K}v, w) = (Kj(x, у), w(x)v(y))-+0,
причем сходимость равномерна, когда w(x) остается огра-
ниченным, так как в этом случае остается ограниченным
w (x) v (у). Доказательство обратного утверждения мы
вновь опускаем.
Замечание. Из теоремы Банаха — Штейнгауза сле-
дует, что любая слабо сходящаяся последовательность в 3'
сходится сильно.
Теперь, когда мы установили, что пространство
??Ь{3(У)\ 3'(V)) непрерывных линейных отображений
из 3 (V) в 3' (V) совпадает с пространством 3' (V X V)
обобщенных функций двух переменных, легко получить

§ 3. Скалярные частицы 45
пространство Л?+ C (V); 3' (V)) положительных анти-
ядер из 3 (V) в 3' (V) и пространство § гильбертовых
пространств 3@ с непрерывным вложением в 3' (V). Обоб-
щенная функция двух переменных KXt у?3' (V ~X[V) опре-
деляет непрерывное линейное отображение из ЗЬ< (V)
в 3'(V):
Поскольку мы хотим получить антилинейное отображе-
ние, мы должны вместо этого взять отображение
где v—комплексно сопряженная функция скалярной функ-
ции vfe3(V). Положительность этого антиядра есте-
ственно определить следующим образом.
Определение. Антиядро v->Kv, определенное
обобщенной функцией Кх> у ? 3' (V X У), называется по-
ложительным, если
(Кх,г <р(*)®?(*))>О
для любой функции
Согласно нашей основной теореме, соотношение между
положительным ?-антиядром L и соответствующим гиль-
бертовым пространством е№ зиписывается в виде
для любого элемента h?e%? и любого е' ? Е. В нашем
случае связь между положительным антиядром К из <& (V)
в Q)' (У) и соответствующим гильбертовым пространством &€
имеет вид
(Г, <$) = (Г\Щ B)
для любой обобщенной функции Т? @f6<z.3i' (V) и любой
функции <p?^(V). Если мы положим в предыдущей
формуле T = Kty, то получим
(Щ, <р) = {К, ср ® ф> = (АГф |/Cf)» C)
для любых (риф, принадлежащих пространству 3(V).

46 Г л. 2. Множество |> мировых частиц и его структура
Замечание. Не совершая ошибки, можно поставить
черту над Т в формуле B). Пространство &6 не инва-
риантно относительно комплексного сопряжения. Про-
странство ?№ = {Т: T?g?6) представляет ту же самую
частицу, что и ?Ю, но с противоположным зарядом.
Определение положительности антиядра, заданного
с помощью Кх> у, берется из теории интегральных урав-
нений. Пусть К(х, у) — непрерывная функция, опреде-
ленная на произведении VY.V. Ядро К(х, у) называется
положительным, если для любого множества элементов
{хх, дг2. •••• xi) B /-мерном пространстве V и любого
множества комплексных чисел \zv z2, ••-, zt] выполняется
следующее неравенство:
i
Можно показать, что определение положительности анти-
ядра, заданного при помощи KXt у ? 2'(УУУ), совпадает
с приведенным выше определением в случае, когда Кх у —
непрерывная функция К (х, у) двух переменных х и у.
Мы объединим окончательные результаты этого па-
раграфа в следующей теореме.
Теорема. Пусть V — многообразие класса Сго.
Пространство § гильбертовых пространств &в
с непрерывным вложением в S>'(V) канонически изо-
морфно подпространству пространства 3'(VX.V),
состоящему из таких обобщенных функций КХ)У
двух переменных, что
(К, <р®?)>0
для любой функции у?д> (V). Связь такого анти-
ядра К с соответствующим пространством <$№
дается формулой
где обобщенная функция Л'ср (^еЮс.®1 (у) определяется
выражением

§ 4. Тензорные произведения 47
§ 4. Тензорные произведения
Чтобы обобщить результаты предыдущего параграфа
на векторные частицы, нужно ввести понятие тензорного
произведения. Мы приведем только основное определение
и основные свойства без доказательств.
Пусть Е и F— два векторных пространства. Для на-
ших целей нет необходимости давать полное определение
тензорного произведения. Тензорным произведением про-
странств Е и F мы назовем новое векторное простран-
ство Е ® F с заданным каноническим билинейным отобра-
жением из EXF в E®F:
Отметим, что E®F не является образом декартова
произведения Е X F при этом отображении. Однако Е® F
¦> -> ->
порождается элементами вида e®f, т. е. любой элемент х
из Е (gi F можно записать следующим образом:
Сформулируем теперь некоторые свойства.
Если Е и F имеют конечные размерности соответст-
венно т и п, то размерность пространства E®F равна т.п.
Если \et) и [fj) являются базисами соответственно
пространств Е и F, то {et®fj\ есть базис простран-
ства E®F, т. е. любой элемент х из E&F может быть
единственным образом записан в виде
Если F — конечномерное пространство с базисом {/,},
то каждый элемент х?E(&F можно единственным обра-
зом записать в виде
Если О — любое векторное пространство над йолем
скаляров С, то Q да G ® С. В этом случае изоморфизмом

48 Гл. 2. Множество $) мировых частиц и его структура
является отображение. g->g® 1, так как {1}—базис
векторного пространства С над С.
Допустим теперь, что Е и F — топологические век-
торные пространства. Мы хотим определить топологию
в E®F. Вообще говоря, в ?®F имеется несколько раз-
личных топологий. Однако если F — конечномерно, то
существует единственная топология, определенная bE®F —
топология покоординатной сходимости: пусть {/у},
У=1 п,—базис пространства F. Любой элемент
может быть записан в виде
x=2
Последовательность [xk] сходится в E®F к нулю,}
если ? * "?**• 0 для всех /. Эта топология не зависит от ба-
зиса в F, Все „хорошие" свойства пространства Е со-
храняются также и в E(g)F. Если Е локально выпукло,
рефлексивно или полно, то Е ® F соответственно локально
выпукло, рефлексивно или полно.
Пусть О — данное векторное пространство. Если
р: EX.F-+G — заданное билинейное отображение, то су-
ществует единственное линейное отображение а: Е® F->Q,
такое, что
р(х, у)'= а (х® у)
для любых (х, у) ?Е X F. Наоборот, если и: Е(& F-+G—
данное линейное отображение, то существует единствен-
ное билинейное отображение |3: Еу. F->О, такое, что
справедливо указанное выше соотношение:
EXF
Если задано а, то fS определяется приведенной выше фор-
мулой. Если задано р, то указанная формула определяет и

§ 4. Тензорные произведения 49
-> ->
на элементах вида х®у, а так как любой элемент про-
странства Е ®F можно представить в виде конечной ли-
нейной комбинации элементов такого вида, то тем самым и
определяется на Е ® F. Этот важный результат показы-
вает, что основное назначение тензорного произведения
состоит в линеаризации билинейных отображений: любое
билинейное отображение C: Е X F -*¦ О может быть заме-
нено линейным отображением u:E®F->0. Если Е и F —
топологические векторные пространства, и пространство F
конечномерно, то отображение а непрерывно тогда и
только тогда, когда непрерывно fi.
Предположим, что Е и F — топологические векторные
пространства, причем F конечномерно. Тогда имеем
т. е. пространство, дуальное к E®F, канонически изо-
морфно и топологически эквивалентно тензорному про-
изведению пространств, дуальных к Е и F.
Топология понимается здесь в смысле сильной дуаль-
ной топологии. Любой элемент z?E ®F можно записать
в виде
а любой элемент z'?(E®F)' — в виде
Дуальное произведение {z, z'} задается формулой
Если [еа] и {/р} — базисы пространств соответственно
Е и F, а [е'Л, \/'Л — соответствующие дуальные базисы,
го
4 Л. Шварц

50 Гл. 2. Множество © мировых частиц и его структура
(z, z') = 2ca/a?.
Здесь использовано соотношение Кронекера (е., е'.\ = Ь1Г
Предположим, что Е и F — топологические векторные
пространства и что пространство F конечномерно. Тогда
jg>b(E; F)^E'®F,
где J?ft(E; F) — пространство всех непрерывных линей-
ных отображений из Е в F с топологией ограниченной
сходимости. В частности,
Любой элемент е' ® f определяет непрерывно линейное
отображение из Е в' F:
*- ¦>
Если z = 2 ^tei ® fi — элемент из Е' % F, то он опре-
деляет отображение
Подобным же образом можно определить тензорные
произведения более чем двух векторных пространств, об-
ладающие теми же самыми свойствами. Для того чтобы
ввести топологию в E®F®Q, нужно предположить, что
два из этих трех пространств конечномерны. Далее,
Е ® F ® G *» Е ® (F ® G) « (Е ® F) ® О.
Если Е и Н конечномерны, то
j?(E®F; G®H)~?>(E; 0)®F'®H;
если, кроме того, О также конечномерно, то
Jg>(E®F;
§ 5. Векторные частицы
->
Пусть F — конечномерное векторное пространство.
->
В этом параграфе мы попытаемся найти все F-векторные
частицы, т. е. все гильбертовы пространства ?№, непре-

S б. Векторные частица 81
рывно вложенные в пространство ?8r (V; F) F-векторных
обобщенных функций, определенных в мире V. Мы будем
следовать тому же плану, что и в случае скалярных ча-
стиц, используя результаты предыдущего параграфа о тен-
зорном произведении.
Локально выпуклое топологическое векторное про-
странство Е определяется в данном случае так:
Любой элемент пространства Е имеет вид 2 ci^ifi> гДе
-> ->
Tt?3 (V) — скалярные обобщенные функции и
Значение этой обобщенной функции на элементе
равно
В соответствии со свойствами тензорного произведения,
дуальное к Е пространство Е' определяется выражением
Е' = 3 (V) ® F' ж 3 (V; F'),
т. е. Е' — пространство бесконечно дифференцируемых
функций с компактным носителем на V, принимающих
значения в дуальном к F пространстве F'. Пусть {/Д —
базис пространства F, a f/J} — соответствующий дуаль-
ный базис пространства F'. Элемент ср пространства Ё'
имеет вид
где y>i(z?fi(V) — скалярные основные функций, а эле-
мент Т пространства Е имеет вид
где Tj??fi'(V) — скалярные обобщенные функции. Значе-
ние обобщенной функции Т на основной функции ср равно
{Т. *)*=
-»¦ ¦*-,
Здесь мы использовали соотношение Кронекера lft, /Л=о4..
4*

62 Гл. 2. Множество ф мировых частиц и его структура
Для того чтобы определить пространство ф гильбер-
товых пространств Ш с непрерывным вложением в Е',
мы должны найти канонически изоморфное пространство
J2?+ (?'; Е) положительных антиядер из Е' в Е. Прежде
всего найдем пространство ^Ь(ЕГ; Е) непрерывных ли-
нейных отображений из Е' в Е. Используя теорему о яд-
рах и свойства тензорного произведения, получаем
Ъ\ 3b')®F®Ftt3b'(yxV)®F®F.
Элемент К пространства J3?b {Е'\ E) выражается через эле-
менты базиса {/[} пространства F при помощи равенства
где (Ktj) — квадратная матрица скалярных обобщенных
функций двух переменных. Значением К на элементе
ср = 2 fif'i пространства Е' = ЗЬ ® F' является элемент
К • <р пространства E = 3b'®F, определяемый равенством
где
Таким образом, элементы К пространства ??ь (Е'; Е) вза-
имно однозначно соответствуют квадратным матрицам ска-
лярных обобщенных функций двух переменных.
Теперь из линейного отображения ср -> К • ср нам нужно
получить антилинейное отображение. В случае скалярных
частиц это делалось при помощи замены ср -> К • <р, так
как ср ? ЗЬ (V) — скалярная функция, для которой имеет
смысл комплексно сопряженная к ней функция ср. Однако
в случае векторных частиц элемент ср ? ЗЬ (V; F') имеет
вид cp = 2cp;/j, где f'{?F', и комплексное сопряжение
не имеет смысла. Для того чтобы обойти эту трудность,
введем понятие антипространства.

§ S. Векторные частицы 53
Определение. Пусть F— топологическое вектор-
ное пространство над полем С комплексных чисел. Ан-
типространством F пространства F называется любое
топологическое векторное пространство, антиизоморф-
ное и топологически эквивалентное пространству F.
Это значит, что существует операция надчеркивания /->/,
переводящая F в F и представляющая собой взаимно од-
нозначное взаимно непрерывное отображение, такое, что
для любого X ? С имеем
Антипространство F пространства F единственно с точ-
ностью до изоморфизма. Не существует никаких преиму-
ществ, связанных с использованием какой-нибудь кон-
кретной реализации пространства F. Мы приведем не-
сколько примеров таких реализаций.
1) Пусть F — данное топологическое векторное про-
странство. Антипространство F совпадает с F как с мно-
жеством, имеет ту же самую топологию, тот же самый
закон сложения, однако операция умножения на скаляр
у них различна:
(kf)F = (Тд, для любого I ? С и / ? F.
Операция надчеркивания в этом случае является тождест-
венным преобразованием.
2) Пусть О' — дуальное пространство к данному то-
пологическому векторному пространству О. Антипростран-
ство G' пространства G' является антидуальным к про-
странству О, т. е. пространством непрерывных антилинейных
функционалов на О. Если g' ? О' и g' задает линей-
ный функционал g': g -> {g', g), то g' задает антили-
нейный функционал g': g -> {g'', g) для любого g^O.
3) В пространствах Z.2, 3 или 3' существует вну-
треннее сопряжение. Соответствующие антипространства
совпадают с исходными пространствами, а операция

54 Гл. 2. Множество $ мировых частиц и его структура
надчеркивания является обычным комплексным сопряже-
UUPM*
нием:
<р->ср
4) Пусть &€ — гильбертово пространство. Дуальное
пространство &6' является реализацией антипростран-
ства §в. Если h^m, то Й?Ж-=<Ш, причем (А, *) =
1 для Л1°б°го k ? J#. Заметим, что
<ХА, *> =
так что \h—J.h.
Приведем некоторые свойства антипространств:
(a) E®F^E®F с соответствием
(б) (?У жР'\
(в) F ж />.
Вернемся теперь к задаче нахождения непрерывных
антилинейных отображений из E' — 3(V; F') в ?" =
= 3' (V; F). После введения понятия антипространства эта
задача становится простой, если заметить, что отображе-
ние из Е' в Е антилинейно тогда и только тогда, когда
соответствующее, отображение из Е' в Е линейно. Таким
образом, ^„(Е'; Е)ж J?b(E'; E). Используя свойства
антипространств, получаем:
и пнрис* рапс id, iiKjJiy част.
r'^3(y)®F'tt3lyj®F &3(У)®РжЗ(У; F).
d терминах базиса {ft\ в пространстве F и соответствую-
щих базисов в пространствах F' и F' имеем:
если
y^^yJ'^E'=*3(V; F')t <ft^3(V),
E
В
то

§ 5. Векторные частицы 55
Используя вновь теорему о ядрах и свойства тензорных
произведений, получаем
': Е) « 3>ь ф ® Т'\ 3' ® F) »
и, окончательно, пространство ^Ь{Е'\ Е) непрерывных
антилинейных отображений из Е' в ? определяется выра-
жением
Теперь нам осталось найти подпространство J2?+ (Е'\ Е)
пространства ^b(E'; E), состоящее из положительных
элементов.
Определение. Антиядро ср->/С? в ^b(E'; E),
определяемое обобщенной функцией
называется суперположительным, если
(АГ, ср^
для любой функции <р ^ ЗЬ (V; F'). Переходя к базису
в пространстве F, получаем
{К. 9 ® ?> = 2 {Кф ъ ® ?у> > 0.
Таким образом, понятие суперположительности предста-
вляет собой комбинацию понятий положительности для
матриц и для ядер.
Мы можем теперь сформулировать основной результат
этого параграфа в следующей теореме.
Теорема. Пространство ф гильбертовых про-
странств ?Ш, непрерывно вложенных в 3'(V; F).
канонически изоморфно подпространству

56 Г л. 2. Множество f) мировых частиц и его структура
ства ?В'(V X V)® F® F, состоящему из обобщенных
функций К, определенных на V X V и принимающих
значения в F ® F, таких, что
{К, ср ® ?) > О
для любой функции cp?i?(V; F'). Связь между обоб-
щенной функцией К и соответствующим простран-
ством Ш дается формулой
для любой обобщенной функции Г^сЛ''(V; F) и
любой функции <????(V; F'). Элемент Ку простран-
ства ?№ определяется формулой
(К>. ф) = <АГ. ф®9>. ф € 36 (V;
Положив Т = Щ, получим
{К.
Эти формулы в точности соответствуют формулам, полу-
ченным для скалярных частиц. Для удобства мы предста-
вим здесь сводку формул, выраженных в терминах базиса
{ft) ?F-
' = 36(У; Ь
W{V; F), Tt?ЗЬ'(V).
=2W

§ 6. Отношения порядка в векторных пространствах 57
§ 6. Отношения порядка в векторных пространствах
и положительность антиядер
Пусть Е — векторное пространство над полем вещест-
венных чисел R. Мы хотим определить отношение по-
рядка ^ в пространстве Е, совместимое с векторной
структурой пространства Е. Это означает, что отноше-
ние порядка должно быть инвариантно относительно сдви-
гов и положительных преобразований подобия, так что
I ¦*¦¦*¦¦*¦¦*¦ ¦> _,
х — с>у — а для всех а(-Е,
1х >¦ Ху для всех X > 0.
Для того чтобы определить отношение порядка в Е,
достаточно определить множество „положительных" эле-
ментов {х : х ^> 0}, так как в этом случае можно положить
-> ->¦ -> ->•
Напомним, что множество ГсЕ называется выпуклым ко-
нусом, если
х, ^Т^ +
х?Г для всех X > 0.
Легко убедиться в справедливости следующей теоремы.
х Теорема. Множество выпуклых конусов ТсЕ,
таких, что Г|"|(—Г)= {0}. взаимно однозначно соот-
ветствует множеству отношений порядка, совме-
стимых с векторной структурой пространства Е.
Это соответствие задается выражением
Отношение порядка замкнутох) тогда и только
тогда, когда замкнут соответствующий конус Г.
Условие ГП(—Г)={0} означает, что если х?Т,
~~ ТО АГ = О.
') Отношение порядка замкнуто, если из хк > у и хк -> х
следует, что х~^у (т. е. если можно переходить к пределу под
знаком неравенства). — Прим. ред.

58 Гл. 2. Множество D мировых частиц и его структура
Отношение порядка в аффинном пространстве естест-
венным образом определяется отношением порядка в соот-
ветствующем векторном пространстве: х ^ у ф==ф х—у-^Т.
Замкнутый выпуклый конус Г при определенных усло-
виях задает дуальное отношение порядка в дуальном к Е
пространстве Е': элемент е' ? Е' положителен, если
{е', е) > 0 для всех е ? Г. Пусть
Г'= {«':(«', е>>0 для всех е?Г].
Очевидно, что Г' является выпуклым конусом, который
слабо замкнут. По теореме Макки конус Г' сильно замк-
нут и поэтому является замкнутым выпуклым конусом.
Следовательно, Г' определяет отношение порядка в Е',
если выполняется условие Г'|"|(—Г') = {0}. Для того
чтобы найти соответствующее условие для Г, нужно ввести
понятие полярных множеств.
Определение. Пусть АаЕ. Полярное множество,
или поляра, АйаЕ' множества А определяется формулой
А^={е' :У??', <Ле)> — 1 для всех е?А).
Заметим, что поляра любого множества всегда выпукла
и слабо замкнута; кроме того, {Ai U Л2H = А\ (] Л\. Если
А — выпуклый конус, то условие {е1, е)^ — 1 для всех
е? А влечет за собой {е1', е)^>0 для всех е? А. Таким
образом, для нашего выпуклого конуса Г имеем Г'==Г°.
Теорема. Условие Г°П(— Г°)= {0} выполняется
тогда и только тогда, когда пространство, натя-
нутое на Г, плотно в Е.
Мы докажем только, что если пространство, натянутое
на Г, плотно в Е, то Г°П(—Г°) ={()}• Допустим, что
е' ? Г° П (— Г°). Тогда е' одновременно неотрицательно и
неположительно на Г и, следовательно, равно нулю на Г.
Так как е' — непрерывный линейный функционал на ? и
пространство, натянутое на Г, плотно в Е, то е' на Е
равно нулю. Отсюда е' = 0.
Следствие. Если пространство, натянутоенаТ,
плотно в Е, то Г° определяет дуальное отношение
порядка в Е'.

§ 6. Отношения порядка в векторных пространствах 59
Так как Г — замкнутый выпуклый конус, то Г°° = Г.
Следовательно, отношение порядка в Е можно определить
через отношение порядка в Е'\ элемент е ? Е положителен
<• -у
тогда и только тогда, когда {е', е)!>0 для всех е'?Г°.
В дальнейшем мы предположим, что Г—замкнутый
выпуклый конус в Е, такой, что Г|"|(— Г)={0} и про-
странство, натянутое на Г, плотно в Е. Таким образом,
Г определяет отношение порядка в Е, а Г° определяет
дуальное отношение порядка в ?".
Вернемся теперь к комплексным векторным простран-
ствам. Пусть Е — векторное пространство над полем
комплексных чисел С. Мы будем считать, что Е является
комплеКсификацией векторного пространства Ео над полем
вещественных чисел, т. е.
так что Е — прямая сумма пространств Ео и 1Е0. Если
задано пространство Е и вещественное подпространство
EoczE, to существует операция надчеркивания г->г (ком-
плексное сопряжение), определенная в Е и обладающая
свойством z = z. Эта операция является каноническим
антиизоморфизмом, т. е. антилинейным взаимно непрерыв-
ным взаимно однозначным отображением из Е на Е:
Подпространство Ео состоит из всех самосопряженных
элементов пространства Е, т. е. E0={z: zf_E, z = z}.
Любой элемент z ? Е может быть единственным образом
записан в виде
2i '
где —^— и —21— принадлежат Ео. Таким образом, струк-
тура операции надчеркивания в Е определяет веществен-
ное подпространство Ео (и в свою очередь определяется
этим подпространством).
Дуальное к Е пространство Е' также имеет структуру
операции надчеркивания. В самом деде, соотношение
X*. *> = <*'. z)

60 Гл. 2. Множество ф мировых частиц и его структура
или
(?/«) = <?, и), z'?E, и?Е,
определяет г'\ элемент г' пространства Е' веществен,
если он самосопряжен, т. е. если он принимает вещест-
венные значения на Еа. Вещественное подпространство
пространства Е' (состоящее из вещественных элементов)
канонически изоморфно (вещественному) дуальному к Ео
пространству E'Q. Итак,
Пусть Г — конус положительных элементов простран-
ства Ео, т. е. Г — замкнутый выпуклый конус в Ео, такой,
что Г|"|(—Г)={ОЬ и (вещественное) пространство, натя-
нутое на Г, плотно в Ео. Тогда T'cE'Q определяется фор-
мулой
T'=:[z':z'€E'Q, {z\ 2>>0 для всех г?Г},
и элемент пространства Е' положителен, если он при-
нимает положительные значения на положительных эле-
ментах пространства Ео.
Применим эти результаты к пространствам, которые
мы изучаем. Рассмотрим сначала пространства 36 и 2)'.
Сопряженная к Г обобщенная функция Т определяется
соотношением
(Г, <Р>=*<7\~?>.
Определение. Обобщенная функция Т?3б' назы-
вается вещественной, если G\ ср) вещественно для лю-
бой вещественной функции ср ? ЗЬ. Обобщенная функция Т
называется положительной, если (Г, ср) ^ 0 для любой
положительной функции ср ? ЗЬ. _
Рассмотрим теперь пространство F ®F, где F — ко-
нечномерное векторное пространство. Структура операции
надчеркивания в F®F определяется так: образом эле-
мента 3>jCj4®g4(-F®F при надчеркивании является"
Элемент 2<^Д®?\- Таким образом

§ 6. Отношения порядка в векторных пространствах 61
Переходя к базису {/4} в F, убеждаемся, что сопряжен-
ным к элементу 2 cijfi ® fj 6 ^ ® F является элемент
mct}7t®f)' Этот элемент инвариантен по отношению
к операции надчеркивания, т. е.
2 ctJft ® /}=2 'ciiSi ® fj=2 cjt/t ® Jj
тогда и только тогда, когда Сц = cjt. Таким образом,
самосопряженные элементы представляются эрмитовыми
матрицами.
Определение. Элемент пространства F®F назы-
вается вещественным, если для любого базиса простран-
ства F он представим эрмитовой матрицей.
Можно дать следующее эквивалентное определение:
элемент пространства F® F веществен, если он является
линейной комбинацией квадратов с вещественными коэф-
фициентами, т. е. если он имеет вид 2 ^v ® gH c вещест-
венными \.
В самом деле, пусть
2^Л®Л=2Х
где \ вещественны и
Тогда
откуда следует, что Сц — с^. Если же су = Сц, то тео-
рема о приведении эрмитовой формы к диагональному
виду обеспечивает существование требуемого представления.
Определение. Элемент пространства F®F назы-
вается положительным, если для любого базиса про-
странства F он представим положительно определенной
эрмитовой- матрицей. Или, что то же самое, элемент про-
странства F®F положителен, если он представим в виде
линейной комбинации квадратов с положительными коэф-
фициентами.
Возможно и другое эквивалентное определение поло-
жительности. Элемент А = 2 с,/, ® ?» ? F ® F определяет

62 Гл. 2. Множество §) мировых частиц и его структура
врмитову форму на F' X F' по следующему правилу:
Эта форма является положительной эрмитовой формой
тогда и только тогда, когда положителен элемент
2*\Ь
Приведенное выше определение положительного эле-
мента устанавливает отношение порядка в пространстве
F®F, так как такое отношение существует для эрмито-
вых матриц. Наконец, мы имеем следующее определение
положительных элементов в дуальном к F ® F простран-
стве F'®F'.
Определение. Элемент пространства F'®F' по-
ложителен, если он принимает положительные значения
на всех положительных элементах пространства F ® /*•
Обсудим теперь понятие положительности для анти-
ядер, определяемых элементами KXi y?2B' (У Y<V)(& F (&F-
Возможны два определения положительности, причем оба
представляются вполне естественными.
Определение. Антиядро, определенное элементом
У XV)®F®F,
называется
(а) положительным, если для любого <р ? 3 (V)
имеем (/С, <р®<р)^-0 в естественном порядке пространства
F®F (здесь {К, <?®y)€F®F);
(б) суперположительным, если для любого ty ? 3(Y; F')
имеем {К, <|>®ф>>0 в С (здесь {К, $®$)?С).
В предыдущем параграфе мы потребовали, чтобы анти-
ядро К, соответствующее гильбертову пространству
$всЗ'(У\ F), было суперположительным (там, однако,
мы называли К просто положительным). Может показаться
странным, что в- определении суперположительности
не участвует естественное отношение порядка в простран-
стве

§ 6. Отношения порядка в векторных пространствах 63
В терминах базиса [fj] пространства F элемент
К 6 ЗУ (V X V) ® F <g> F записывается в виде К =
= 2 Ktjft ® //• где Ки 6 S' (VX V). а элемент <|> ? 5J (К; /")
задается выражением <1' = 2!Р;//> r^e ?/6-^(^)- Теперь
данные выше определения можно сформулировать так:
(а) К положительно, если для любой функции ер ? i$ (V)
матрица
является эрмитовой и положительно определенной;
(б) К суперположительно, если для любого набора
функций
справедливо соотношение
в с.
Легко видеть, что суперположительность влечет
за собой положительность. Однако эти понятия, по-види-
мому, не эквивалентны, и хотелось бы получить противо-
речащий пример '). До сих пор понятия отношения порядка
') Эти понятия действительно не эквивалентны. Простейший
пример положительного ядра, которое не является суперполо-
жительным, можно построить следующим образом. Пусть про-
странство F двумерно. Тогда антиядро К задается матрицей
второго порядка с элементами из ^'(VX V). Пусть <pi н <f2 —
ортогональные функции из L2 (V), нормы которых равны 1.
Тогда ядро
дает требуемый пример. В самом деле, если у — любая функ-
ция из 31 (V), то

64 Гл. 2. Множество 4> мировых частиц и- его структура
в векторном пространстве и (простой) положительности
антиядер не использовались, однако позднее они нам по-
надобятся. Будет показано, что для некоторых антиядер
введенные выше два понятия положительности эквива-
лентны.
где a—(<fi, <?), Ь = {<?2< <?)• Так как эта матрица положительно
определена, ядро К является положительным. С другой сто-
роны, если взять в качестве ф вектор-функцию (<?,, —<р2), то
несложный подсчет показывает, что (/С» ф ® Ф) = ~ 2> Поэтому
ядро К не является суперположительным. — Прим. ред.

Глава 3
МИРОВЫЕ ЧАСТИЦЫ И ИНВАРИАНТНОСТЬ
ОТНОСИТЕЛЬНО СДВИГОВ. УПРОЩЕНИЕ ПО ЯДРУ
§ 1. Тензорные произведения обобщенных функций
Пусть X и Y — многообразия класса С°°, и пусть Зх
и Зу — пространства основных функций, определенных
соответственно на Л" и К. Для любых функций и (х) ? Зх
и v(y)?3y функция u(x)v{y) бесконечно дифференци-
руема по х и у и носитель функции u(x)v(y) компактен,
так как декартово произведение компактных множеств
компактно. Таким образом, u(x)v(y) является элемен-
том 3Xi у пространства основных функций, определенных
на Xy^Y. Следовательно,
Кроме того, можно Показать, что Зх®Зу является плот*
ным собственным подмножеством пространства ?fiXi y.
Тот же результат справедлив для пространств обобщен-
ных функций: З'х ® З'у является собственным плотным под-
множеством пространства Зх, у Мы не будем здесь этого
доказывать. Мы покажем только, что тензорное произве-
дение двух обобщенных функций, принадлежащих Зхн Зу,
определяет элемент, принадлежащий 3XiT
Теорема: Если SX?3X нТу? S'y, mo существует
единственная обобщенная функция S
такая, что
{Sx®Ty, u(x)®v(z)) = {Sx, u(x)){Ty, v(y))
для всех и(х)?Зх, v(y)?3y.
Доказательство. Единственность. Допу-
стим, что существуют две различные обобщенные функции
5 Л, Шварц

66 ' Гл. 3. Мировые частицы и инвариантность
Uv U2?3'Xiy, такие, что
{Uv a(x)®v(y)) = {Sx, u(x)){Ty, v
{U2, u(x)®v(y)) = {Sx, u(x)){Ty, v
Очевидно, что тогда Ul и U2 совпадают на Зх®Зу. Но
так как ?Вх®Зу плотно в 3Xt y и дуальные произведе-
ния непрерывны, значения Ul и U2 совпадают на всем Зх.
Таким образом, Ul = U2-
Существование. Для любой функции tp (л:, у) ^ 3Xi y
мы хотим выяснить, имеет ли смысл выражение
{Sx®Ty, 9(x. У))-
Для всякого фиксированного значения х имеем ср(лг, у)?Зу,
и (Ту, ср(лг, у)) является функцией от лг, которая, оче-
видно, имеет компактный носитель. Можно показать, что
эта функция от х бесконечно дифференцируема по х.
Следовательно,
Теперь можно вычислить
{Sx, {Ту, 9(х, у)));
таким образом, для любой функции <р ^ 3Xi y мы получаем
некоторое число.
Положим, по определению,
{Sx®Ty, 9(x, y)) = {Sx, (Ty. ?(х. у)».
Эта формула задает непрерывный линейный функционал
на ?ВХ> у, но здесь мы не будем доказывать его непрерыв-
ность. Если теперь
ср(лг, y) = u(x)v(y), где
то мы имеем
{Ту, u(x)®v(y)) = ay
и применение оператора S, дает
{Sx®Ty, u(x)®v(y)) = {Sx, {Ty, u
= {SX, u(x)){Ty, tF

§ 1. Тензорные произведения обобщенных функций 67
Тем самым доказательство существования закончено.
Можно было определить Sx ® Ту другим способом:
{Sx®Ty, ?(*. у)) = {Ту, (Sx, 9(х, у))),
но в силу единственности эти определения эквивалентны,
т. е.
(Ту, (Sx, 9(х, y))) = {Sx. (Ty. <р(лг, у))).
Та же самая теорема справедлива для векторных обоб-
щенных функций в случае, когда пространство значений
одной из этих функций конечномерно.
Теорема. Если даны обобщенные функции
X; E), Ty?3'(Y; F)
и хотя бы одно из пространств Е, F конечномерно,
то существует одна и только одна обобщенная
функция
Sx®Ty?3'(X®Y; E®F),
такая, что
{Sx ® Ту, u{x)®v (у)) = {Sx, и (х)) ® {fr v (у)).
Доказательство. Единственность доказы-
вается так же, как и раньше.
-> ->
Существование. Если Е и F конечномерны, то
существование доказывается просто. В самом деле, пусть
тогда, очевидно, Sj. ® Ту можно определить как элемент
пространства Зх ® З'у ® Е ® F. Из предыдущей теоремы
мы знаем, что 3)'х® З'ус Зй'х, у', поэтому
Ь*

68 Гл. 3. Мировые частицы и инвариантность
Таким образом, тензорное произведение Sx®Ty опреде-
лено в S' (X X У. E®F) благодаря каноническому изо-
морфизму этого пространства и пространства 3>х, у® Е ®г.
Допустим теперь, что Е конечномерно, а пространство
F — не обязательно конечномерно. Тогда ох®Ту опре-
деляется равенством
{Sx®fy, 9(x, у)) = {Ту. D 9(х. у))).
Для фиксированного у имеем {Sx, ср(лг, у))?Е, и так
как Е конечномерно, то {Sx, <?(x, у))?Зу®Е. Далее,
{x р ))?
S ( )?ЗуЕ
->->-> ->
7"vf ^'(К; F), т. е. Tv определяет отображение 3V-±F
у у > ^. ^. у
и, следовательно, отображение 3V®E->F®Е. Поэтому
-*¦ -> -> ->
мы можем определить (Г^, EЖ, ср(лг, y)))^E®F.
-> ->
Таким образом, SX®T можно определить отображе-
нием ср(лг, у)->{Ту, {Sx, ср(лг, у))), которое линейно и
непрерывно.
Замечания. Если Е и F оба бесконечномерны, то
тензорное произведение S®T. нельзя определить таким
образом.
Носитель тензорного произведения S®T является де-
картовым произведением А X В носителя А обобщенной
функции S и носителя В обобщенной функции 7".
Это тензорное произведение непрерывно, т. е. если
S->S0 и Т->Т0, то S®T->S0®T0. Доказательство мы
опускаем.
Выбрав базис et?E, f,^F, можно записать тензорное
произведение обобщенных функций S = 2^ Siel и Т = 2j Tjfj
в виде
2l

§ 2. Свертка
§ 2. Свертка
Пусть V — многообразие, на котором задан внутренний
закон композиции (л:, у)-+ху, т. е. отображение из
V X V в V. Допустим также, что этот закон композиции
бесконечно дифференцируем. Тогда в пространстве обоб-
щенных функций 3' (V), определенных на V, можно
определить закон композиции, называемый сверткой.
Определение. Если S и Т — две обобщенные функ-
ции из 3'(V), то их свертка S*T?3r(V) опреде~
ляется равенством
{S*T,
для €0(V)
Замечание. Свертка существует не всегда. Мы скоро
обсудим условия, при которых она действительно сущест-
вует.
Функция (рС?7!)— бесконечно дифференцируемая функ-
ция переменных E, ^^VX^. Однако множество
{(?, ?)): Ь\ принадлежит носителю функции <р в V), являю-
щееся носителем функции ер(?т}) в V X V", не компактно
(за исключением случая, когда ср==О), поэтому пока еще
нельзя определить свертку написанным выше равенством.
Пример. Пусть V = R — вещественная прямая, и пусть
законом композиции является сложение. Если ср (х0) Ф О,
то <р(?+ '»!)=? О для $-(-7| = д;0, т. е. диагональ S-f-7j = jc0
принадлежит носителю функции <р(?-|-'»)) в R X R- Таким
образом, этот носитель не может быть компактным (за
исключением случая, когда ер = О).
Для того чтобы определить свертку, необходимо рас-
пространить определение величины (Т, ср) на некоторые
случаи, когда Т — обобщенная функция, а ср — бесконечно
дифференцируемая функция с некомпактным носителем.
Теорема. Пусть Т — обобщенная функция с но-
сителем А а ср — бесконечно дифференцируемая функ-
ция с носителем В. Если пересечение А[\В компактно,
то можно определить (Т, <р).

70 Гл. 3. Мировые частицы и инвариантность
Доказательство. Возьмем функцию а ? 35 (V), та-
кую, что а = 1 в окрестности множества А(]В. Тогда
G\ яср) имеет смысл, так как окр является основной функ-
цией. Нужно показать, что результат. не зависит от вы-
бора а. Допустим, что C — другая функция, обладающая
тем же свойством, что и я. Тогда я —р = 0 в окрестности
пересечения А[\В, и носитель функции (а — р)ср содер-
жится в дополнении к А П В. Из определения носителя
обобщенной функции Т следует, что G\ (а — C) ер) = 0.
Следовательно, можно положить
(Г. <р> = G\ окр).
и это значение не зависит от выбора а.
Определение. Пусть заданы обобщенные функции
S, T?3'(V) с носителями соответственно A, BcV. Го-
ворят, что носители А и В допускают свертку, если пе-
ресечение множества А X В (носителя тензорного произве-
дения S® Т) с носителем функции ср (S-tj) в V"XV ком-
пактно для любой функции ср ? i$ (V).
Определение. Если Е и F — локально компактные
топологические пространства, то отображение E-+F на-
зывается собственным, когда выполняется любое из сле-
дующих эквивалентных условий.
A) Прообраз любого компактного множества компактен.
B) Образ любого замкнутого множества замкнут, и про-
образ любой точки компактен.
C) Если Е И F компактифицированы добавлением
бесконечно удаленной точки (компактное расширение Алек-
сандрова), то расширенное отображение, при котором оо
переводится в оо, непрерывно.
Дадим теперь другое определение двух носителей, до-
пускающих свертку. Это определение эквивалентно сфор-
мулированному выше.
Определение. Пусть множества А и В являются
носителями двух обобщенных функций. Мы говорим, что
А и В допускают свертку, если выполняется любое из
следующих эквивалентных условий.
A) Для любого компактного множества К с V мно-
жество (АХВ)(\ {(?, •>!): Щ ? К] компактно.

§ 2. Свертка 71
B) Отображение (?, т))->?т), рассматриваемое только
на множестве А * В, является собственным.
Пример.
. Таким образом, 8e * 8ft = 5aft.
Приведем без доказательства следующую теорему.
Теорема. Если имеются две сходящиеся последо-
вательности обобщенных функций
S->S0, Т-> То,
причем
A) носители всех обобщенных функций S содер-
жатся в одном и том же компактном множестве А,
а носители всех Т содержатся в одном и том же
множестве В,
B) множества А и В допускают свертку,
то
(I) 5*7-->50*Г0,
(II) носитель функции So * 7 содержится в мно-
жестве
Пусть V — группа Ли с групповой операцией — произ-
ведением: ($, 7})-Ит).
Определение. Внутренняя свертка трех обоб-
щенных функций R, S, T?35'(V) определяется равен-
ством
{R*S*T, ?> =
для
Определение. Носители А, В, С трех обобщенных
функций R, S, T??B'{V) допускают внутреннюю
свертку, если отображение (?, ч\. С)-»?¦»?, рассматриваемое
на Ау^Ву^С, является собственным.
Возможны и другие эквивалентные определения.

72 Гл. 3. Мировые частицы и инвариантность
Теорема. Пусть R, S, T??8r(V) имеют носите-
лями множества А, В и С. Если (^ЭС = S (¦»?) и А, В
и С допускают внутреннюю свертку, то
(R* S)*T = R*(S*T) = R*S*T.
Доказательства мы- не приводим.
Теорема. Пусть е — единичный элемент группы
Ли V. Тогда
Ье*Т = Т*Ье = Т.
Доказательство.
Теорема. Пусть АаТ — левый сд$иг, определен-
ный элементом a?V, обобщенной функции T??8'(V)
на группе Ли V. Тогда
Аналогично для правого сдвига Ra справедливо
равенство
Доказательство.
(АаТ, ср)^G\ Аа_#
Теорема. Пусть V — векторное пространство
{сложение в нем, разумеется, коммутативно). One-
рация свертки обобщенных функций S, Т?35'(V) ком-
мутативна.
Доказательство.

§ 2. Свертка 73
Теорема. Пусть R — вещественная прямая. Тогда
для обобщенной функции Г?Ф'(Ц) имеем
Ь>
Доказательство.
(Ь'*Т, 9)=|
-G .
= -<7\ <р') = (Г. ср).
Аналогично
(Г*В', ср) = (Г. 9).
Справедливы также следующие равенства:
8С0 * Г = ГС")",
Dpb*T =
где Dp — дифференциальный оператор порядка /> с посто-
янными коэффициентами. В случае более чем одного изме-
рения имеем
Д8 * Т = AT,
где А — оператор Лапласа или Даламбера.
Теорема. Для S, r?S'(R) имеем
E*7')' = 5'*Г = 5*Г.
Доказательство.
Аналогично
Следовательно, для обобщенных функций S, Т ??8' (V),
где V — векторное пространство над полем вещественных
чисел размерности не меньше 2, имеем
д* ,с _ч <?2S T 6S дТ

74 Гл. 3. Мировые частицы и инвариантность
Теорема. Пусть T?3'(V)u a.?35(V) заданы на
векторном пространстве V с мерой Лебега dx. Если
носитель обобщенной функции Т и носитель функции
а допускают свертку, то положим
Тогда р — бесконечно дифференцируемая функция,
определяемая равенством
Доказательство.
Для любого ср ? 3) имеем
{Т*а, ср) =
j
Таким образом, р (л;) = (Г^, а (х — t)).
Согласно предыдущей теореме,
Так как функция а бесконечно дифференцируема, p<m> =
= Т* а<щ) также является обычной функцией, и, следова-
тельно, $(х)— бесконечно дифференцируема.
Теорема. Пусть V = E — векторное простран-
ство с мерой Лебега. Если f и g — локально интег-
рируемые функции на Е и носители функций fug
допускают свертку, то
где
) = ff(t)g(x-t)dt,
') Любая основная функция ? является также н обобщенной,
н свертку Т * <f можно понимать в смысле определенной выше
свертки обобщенных функций. — Прим. перев.

§ 2. Свертка 75
причем h(x) локально интегрируема и определяется
этим равенством для почти всех х.
Доказательство.
Делая замену переменных \ = t, i\ —х — t (при этом яко-
биан равен 1) и применяя теорему Фубини, получаем
<J*g. <P> =
= f9(x)dxff(t)g(x-t)dt.
Пусть
h{x) = j f(t)g(x-t)dt;
тогда
(/**. ?> = (*. ?>•
Теорема. В группе Ли V свертка S*T имеет
смысл (т. е. носители допускают свертку), если хотя
бы одна из обобщенных функций S и Т имеет ком-
пактный носитель.
Доказательство. Нужно показать, что отображе-
ние ($, ¦»))->¦ 51») является собственным для !•? А, ^^5. До-
пустим, что 5 имеет компактный носитель А и Т имеет
носитель В. Пусть 3) — компактное подмножество множе-
ства V. Множество
является ограниченным, так как % содержится в компактном
множестве А, а элемент 7] = $~1($т]) для \?А, \ч\^3)
также ограничен. Следовательно, Н компактно, и поэтому
отображение является собственным.
Замечание. Аналогично, свертка R * S *Т имеет
смысл, если две из этих трех обобщенных функций имеют
компактный носитель.
Пример, Рассмотрим свертку К*5'*1, где У—
функция Хевисайда:
. х<0.
, х>0.

76 Гл. 3. Мировые частицы и инвариантность
Носителями функций Y, 8' и 1 являются соответственно
[О, оо], {0} и R. Отображение ($, ч\, С) -> S -\- ч\ -\- С не
является собственным, и поэтому внутренняя свертка не
допустима. Однако выражения (К * 8') * 1 и Y * (8' * 1)
имеют смысл каждое в отдельности, хотя они и не равны
по величине, т. е. свертка в этом случае не ассоциативна:
(Г*8')*1=8* 1=1,
§ 3. Инвариантность относительно группы сдвигов
В этом параграфе мы попытаемся найти гильбертовы
пространства &6, которые остаются инвариантными отно-
сительно данной группы и, в частности, относительно
группы сдвигов.
Пусть О — группа топологических алгебраических авто-
морфизмов локально выпуклого топологического вектор-
ного пространства Е. Как и ранее, <?> обозначает про-
странство гильбертовых Пространств S6 с непрерывным
вложением в Е, a jg*+ (Е'\ Е) — замкнутый выпуклый ко-
нус положительных антиядер из Е' в Е. Мы видели, что
¦ Элемент a?Q определяет переход из &в ? § в гиль-
бертово пространство oS@(z$> следующим образом:
где в&6 имеет гильбертову структуру, перенесенную из
Так как а действует на Е, этот оператор действует и
на дуальном пространстве Е'. В самом деле,
(?е', ее) = {е', е), е?Е, е'?Е',
и автоморфизм е'->ае' на Е' задается выражением
Следовательно, о действует также и на J3?(E'\ E). В са-
мом деле,

§ 3. Инвариантность относительно группы сдвигов 77
и автоморфизм L->cL множества J?(E'; Е) определяется
выражением вида
Очевидно, что если антиядро L положительно, то анти-
ядро aL также положительно. Используя перенос струк-
туры, нетрудно доказать следующую теорему.
Теорема. Если гильбертово пространство <Ш ? ^
соответствует антиядру L ? _2*+ (Er; E), то про-
странство аЗ€ соответствует антиядру aL для
любого оператора о ? О.
Таким образом, если &€ = <*?№ для всех а?О, то
L = aL для всех o?G, и для того чтобы найти гильбер^
товы пространства S6, инвариантные относительно группы О,
можно искать антиядра L, инвариантные относительно
группы О.
Обратимся теперь к случаю векторйых частиц. Пусть
G — группа автоморфизмов о, которые действуют на мире V
и на конечномерном векторном пространстве F. В этом
случае оператор о действует также и на 3)' (V) и, следо-
вательно, он действует на 36 с 3)' (V) <g) F.
С другой стороны, так как оператор а действует на V,
он действует также на V XV (a(v, w) = (av, aw)) и на
35' (У X V),. а так как о действует на F, он действует
также на F(af = of). Следовательно, о действует на анти-
ядра KXt у 6 3i' (У X V) ® F ® F. В терминах базиса
{/г} пространства F имеем К= 2
Ktl?ay<yxv), и
где аКц — обобщенная функция, определяемая формулой
{вКи, <р(*. y)) — (Ki}, if (ax. ay)).
Используя опять перенос структуры, можно показать,
что если гильбертово пространство &в а ЭЬ' (V) ® F
соответствует антиядру К ? 35' (V X V) ®F®F, то
о JS? соответствует аК для любого оператора о ? Q, и вместо
того чтобы искать пространства $в, инвариантные отно

78 Гл. 3. Мировые частицы и инвариантность
сительно группы G, можно искать суперположительные
антиядра К, инвариантные относительно G.
Будем теперь искать антиядра
инвариантные относительно группы сдвигов на мире V.
Пусть, в частности, V — аффинное пространство Е4 (или ?).
Тогда группа сдвигов G изоморфна векторному простран-
ству Е4 (или Е), связанному с аффинным пространством Е4
(или Е). Мы предполагаем, что элемент группы G дей-
ствует на Е как аффинный оператор и что он действует
на конечномерном векторном пространстве F как единич-
ный оператор.
Допустим сначала, что мы имеем функцию К(х, у).
Для того чтобы К(х, у) была инвариантна относительно
любого сдвига, должно выполняться равенство
К[х— а, у— а)=:К(х, у) для всех а.
В частности, если положить а равным у, то
К{х. у) = К(х — у, 0) = //(* —у).
где Н — функция одной переменной х — у. Итак, в этом
случае, для того чтобы получить функцию К, инвариант-
ную относительно сдвигов, мы можем взять функцию Н
одной переменной и подставить в качестве аргумента х — у.
Обобщим теперь этот способ на случай, когда KXl y —
обобщенная функция, определенная на Е X Е. Рассмотрим
изоморфизм класса С°°
°°
определенный формулой (х, у)-«->•(*, я), гаеи = х — у,
у = х — и. С помощью переноса структуры этот изо-
морфизм определяет взаимно однозначное соответствие
между обобщенными функциями
х, и
определенное соотношениями
(Н ->, ^ (х, и)\ = (Кх>у, ф(л;, х — у)\,

§ 3. Инвариантность относительно группы сдвигов 79
Для удобства мы используем следующее обозначение: если
задано Кх. „, то Н -> = ЛГ ->, а если задано Н +, то
' х, и х, х-и х, и
К =Н —... Для того чтобы описать те обобщенные
¦*' " х, х-у
функции И, которым соответствуют инвариантные относи-
тельно сдвигов функции К, рассмотрим следующую ком-
мутативную диаграмму:
Эта диаграмма порождает коммутативную диаграмму для
обобщенных функций, определенных на соответствующих
пространствах:
Кх v > И ->
**у х, и
I 1
оК >- хЯ
где а — оператор сдвига, действующий на две переменные х
и у функции К, а х — соответствующий оператор сдвига,
действующий только на первую переменную х функции Н.
Таким образом, вместо того чтобы искать обобщенные
функции К?ЗУ (Е X E)®F® F, инвариантные относи-
тельно всех сдвигов, действующих на две переменные, мы
должны найти функции H??8'(EXE)®F®F, инвариант-
ные относительно всех сдвигов, действующих только на
первую переменную.
Воспользовавшись теперь теоремой о ядрах:
3' (ЕХЁ)~ &ь C (?); SB' (Е)) = 3' (?; &' (?)),
мы видим, что
$'(EXE)®F ®Р~жЗУ(Е; 2>r(E)® F ®F).
Таким образом, Н -> является обобщенной функцией,
определенной на Е, принимающей значения в бесконечно-

80 Гл. 3. Мировые частицы и инвариантность
мерном локально выпуклом топологическом векторном
пространстве of = $'(E)®F®F, и мы должны искать
такие Н, которые инвариантны относительно всех сдвигов,
действующих только на Е. Мы будем рассматривать HXtt
как элемент пространства S' (Е, S1")-
Выберем в Е меру Лебега dx. Ответ на наш вопрос
заключен в следующей теореме.
Теорема. Всякая обобщенная функция
Т?3)'(Е, &"), инвариантная относительно всех
сдвигов, действующих на Е, является константой,
т. е.Т==1х®\ где\^^ {или T=dx®t).
Доказательство. Пусть а ? 3) (Е)—бесконечно диф-
ференцируемая функция, такая, что Г а (л;) dx = 1. Тогда
для любой функции <р ? 35 (Е) имеем
= (Г, ср).
Здесь мы воспользовались инвариантностью Т относительно
сдвигов. Таким образом, Т * а = Т. Согласно теореме,
приведенной в предыдущем параграфе, Т является беско-
нечно дифференцируемой функцией, и из инвариантности Т
относительно всех сдвигов следует, что Т — константа.
В рассматриваемом случае если Н -> инвариантно от-
носительно всех сдвигов, действующих на х ? Е, то
Н -> = 1 ,.&//-> /или Н -> = (
х, и и \ х, и
где
®H+\,
и)
Мы показали, что антиядра Кх< у ? 3)' [Е X Е) ® F ® F,
инвариантные относительно группы сдвигов, действующей
в пространстве Е X Е, взаимно однозначно соответствуют
Обобщенным функциям #> ? 3)' (?) ® F ® F, определенным

§ 3. Инвариантность относительно группы сдвигов 81
на ? и принимающим, значения в F(&F. Если задана об-
общенная функция Н+, то соответствующая инвариантная
функция К задается формулой
х,у Ж®*
¦*'* х, х-у * х-у х-у
т. е. для любой функции у?3(Еу^Е) имеем
{Кх,г <?(*, у)) = <1,®Я>,
= /#* , J" ср (л;, л — и) rfx\ = j dx (Нр ср (л;, л; — й)).
(При вычислении (#>, <р(л;, х — а)\ переменная х счи-
тается фиксированной.)
Найдем теперь условия на функцию //>, которые со-
ответствуют положительности или суперположительности
KXi у. Напомним, что обобщенная функция KXt y называется
положительной, если
(Кх,у, ср(лг)®<р(у))>0 в F®F
ци
вие принимает вид
для любой функции у?3(Е). Для функции Я> это усло-
в
F®P
для любой функции у??8(Е). Для того чтобы исключить
из рассмотрения аффинное пространство Е, мы можем
выбрать в Е начальную точку, и тогда (если вспомнить,
что существует взаимно однозначное соответствие между
Е и Е) условие положительности примет вид
)^^>0 в
для любой функции <р ? 35 (Е). Интеграл в этом неравенстве
-> ->¦ -> ->
означал бы свертку, если бы вместо х — и стояло и — х.
Введем обозначения
6 Л. Щв«рп

82 Гл. 3. Мировые частицы и инвариантность
тогда условие на Я, соответствующее положительности
для К, имеет вид
(Я, ср*?>>0 в F®F
для любой функции <р ? 3) (Е). Аналогично условие на Я,
соответствующее суперположительности для К, принимает
вид
(Я, <]* * $) > 0 в С
(E
для любой функции ijj ? S (E; Fr).
Результаты настоящего параграфа объединены в следую-
щей теореме.
Теорема. Пусть Е — {конечномерное) аффинное
пространство и F — конечномерное векторное про-
странство. Гильбертовы пространства Ш'с S' (E; F)
или соответствующие суперположительные антиядра
KXty?3)'(EX,E)®F®F, инвариантные относительно
группы сдвигов, действующей аффинно на Е и то-
ждественно на F, взаимно однозначно соответствуют
обобщенным функциям H+?3)'{E)®F®F суперполо-
жительного типа. Условие положительности функ-
ции Я имеет вид
(Я, ср*ср)>0 в F®F для любой функции <р?3)(Е),
а условие суперположительности имеет вид
(Я, ср*?)>0 в С для любой функции <??3)(E; F').
Вышеприведенные определения положительности в
3' (Е) ®F(g>F являются естественными обобщениями по-
нятия положительности функций в смысле Бохнера.
Определение. Функция /, определенная в /-мерном
векторном пространстве Е, называется положительной
в смысле Бохнера 1), если для любого множества эле-
ментов {хг xt] из Е и любого множества комплекс-
') Обычно такие функции называют положительно опреде-
ленными. — Прим. ред.

§ 3. Инвариантность относительно группы сдвигов 83
ных чисел [zv .... zt) справедливо неравенство
Г / («) du J ср (х) ср (л: — и) dx ^. О
2/(«,)
В том случае, когда скалярное антиядро KXi y задается
непрерывной функцией К(х, у), мы видели, что класси-
ческое определение положительности совпадает с опреде-
лением положительности антиядер ((/С, <р®<р)^>0, <р6^)-
Аналогично в данном случае, если / — непрерывная
функция, то условие положительности в смысле Бох-
нера эквивалентно условию
или
для любой функции ср ?S. Заметим, что если обобщенная
функция #->?D' (E)®F ®F является обычной непрерыв-
ной функцией Я (а), то Я—> = Я(х — у), и мы можем
х— у
обобщить понятие положительности в смысле Бохнера на
пространство 3)'{E)®F®F. К сожалению, здесь воз-
можны два определения.
Определение. Обобщенная функция Н?35'(Е)®
®F ®F называется
(а) положительной в смысле Бохнера, или Б-поло-
жительной, если
(Я, ср*9>>0 в F®?
для любой функции ср ? S (?),
(б) суперположительной в смысле Бохнера, или
Б-суперположительной, если
(Я, ф*ф)>0 в С
для любой функции ф ? S (?, f).
Мы обсудим вопрос об эквивалентности этих двух
определений в одном из последующих параграфов (см. § 5
этой главы).
6*

84 Гл. 3. Мировые частицы и инвариантность
§ 4. Преобразования Фурье
Пусть Я—конечномерное вещественное векторное про-
странство с мерой Лебега dx. Преобразование Фурье 4? f
функции / (х), х ? Е, определяется равенством1)
A)
<- -> <¦
где р принадлежит дуальному к Е пространству Е' и
(х, р) является дуальным произведением. В пространстве Е
можно выбрать базис ev e2, .... е„ таким образом, чтобы
мера Лебега равнялась rfx, dx2 ... dxn. Вектор х = 2j х\е{
i
¦*¦ ,
определяется своими координатами [х^, а вектор р=
i
определяется координатами {рД. В этом случае равен-
ство A) принимает вид
Р2 Рй) =
,х2, ...,xn)dxldx2...dxn.
-*¦ -> ->¦
Если в Е задано скалярное произведение (х | у), то
преобразование Фурье можно определить формулой
T<J)-J>
Однако мы будем придерживаться определения, выражен-
ного равенством A).
') В нашей литературе принято другое определение пре-
образования Фурье:
поэтому преобразование Фурье обобщенных функций опреде-
ляется равенством
В своих лекциях Лоран Шварц придерживается обозначений,
принятых в его книге: Schwartz L., Theorle des distributions,
t. 1, 2, Hermann, Paris, 1950—1951. — Прим. nepee.

§ 4. Преобразования Фурье 85
Если /? L1, то интеграл A) существует и функция g{p)
непрерывна и ограничена; в самом деле,
Если <&~f = g и функция Xjf интегрируема для всякого
/=1, 2, .... п, то существуют непрерывные и ограни-
ченные производные -—-, причем
др
i
Если / быстро убывает на бесконечности, т. е. если для
любого полинома Р произведение Р/ интегрируемо, то
все производные g существуют и ограничены.
Проинтегрируем равенство A) по частям. Получим
xl ... dxj^dxj+1 ... dxnx
Допустим, что / ? L1 и что первые производные ~-
непрерывны и интегрируемы; тогда, как легко видеть,
/ должна стремиться к нулю на бесконечности. Следо-
вательно,
-Ш^-щ dx B)
¦¦ ¦«-
и функция pjg(p) непрерывна и ограничена.
Если / бесконечно дифференцируема и все ее произ-
водные принадлежат L1, то произведение g на любой
полином остается непрерывным и ограниченным.
Определение. Пространством &1 (Е) называется
пространство всех бесконечно дифференцируемых функ-
ций, у которых все производные быстро убывают на бес-
конечности, т. е. для произвольных полиномов Р и Q

86 Гл. 3. Мировые частицы и инвариантность
произведение P{x)Q\-~\f существует и ограничено,
или (эквивалентно) Qy-~\P{x) f существует и огра-
ничено.
Легко доказать следующую теорему.
Теорема.
Распространим теперь понятие преобразования Фурье
на обобщенные функции. Прежде всего заметим, что если
¦> ¦*¦
мера Лебега задана в Е, то она тем самым задана и в ?',
потому что если в пространстве Е выбрать базис так,
чтобы по отношению к нему заданная мера Лебега равня-
<¦
лась dxx dx2 ... dxn, то дуальный базис в Е' определит
меру Лебега dpx dp2 ... dpn.
Для f^L1, у?Зр(Е') рассмотрим дуальное произве-
дение <р на Фурье-образ g(p) функции /:
(*.?) = (<?7. ?> = / ? (Р) dp / е-2'*«• *
где
ф = J е~ш «¦ (
Таким образом, имеем
Ввиду этого можно попытаться определить преобразование
Фурье обобщенных функций следующим равенством:
где <f?3)p, T^Sb'x- Хотелось бы, чтобы <*Гч??$х, но,
к сожалению, ЗГу^З)х, за исключением случая ср^О.
В этот момент на помощь приходит пространство ?Р (Е).
Топология в <§Р определяется следующим образом.

§ 4. Преобразования Фурье 87
Определение. /,->0 в смысле пространства ?Р,
если Р'(#) Qf-gj) 1'] равномерно сходится к нулю для
произвольных полиномов Р и Q.
Пространство ?f'(E) непрерывных линейных функцио-
налов над ?Р(Е) называется пространством обобщен-
¦них функций медленного роста. Заметим, что
/,.->0 в ?D=$fj->0 в &,
так что всякий непрерывный линейный функционал над 4?
является непрерывным линейным функционалом над S.
Таким образом, существует непрерывное линейное ото-
бражение пространства ?f" (E) на подпространство про-
странства 3)'{Е). В действительности это отображение
является вложением, так как 3(Е) плотно в &' (Е). Сфор-
мулируем без доказательства следующую теорему.
Теорема. Пространство 3)(Е) всюду плотно
в &{Е)
Примеры.
A) (f(x) = e~x'^Sp(R.), где R — множество веществен-
ных чисел.
B) Любая локально интегрируемая и измеримая функ-
ция /, такая, что | / (х) \ -< Р (х) для некоторого поли-
нома Р(х), является обобщенной функцией медленного
роста.
C) ех не является обобщенной функцией медленного
роста.
Доказательство. Возьмем ср(л:) = ?-1/*2+1, тогда
а этот интеграл расходится,

Гл. 3. Мировые частицы и инвариантность
Определение. Преобразование Фурье &~Т обоб-
щенной функции Т ? gfx определяется равенством
(STT. «р) = G\<У».
где срб^р-
Так как ср^^гф^ср^^, то преобразование Фурье
существует для всех Т??РХ. Если ср->0 в S?P, то
<^'(р->0 в &'х и
(STT. ср) = (Г, <Г?)->0,
так что <?ГТ — непрерывный линейный функционал и
Замечание. Если обобщенная функция Т совпадает
с обычной функцией f^L1, то Т — обобщенная функция
медленного роста, и определенное выше преобразование
Фурье функции Т совпадает с преобразованием Фурье
функции /, определенным формулой A):
Приведем теперь некоторые основные свойства пре-
образований Фурье обобщенных функций медленного роста;
доказательство многих из этих свойств мы опускаем.
A) #-8=1.
Доказательство.
и аналогично для полиномов Р имеем
C) Формула обращения. Если преобразование #
определить заменой /на —I в определении <sf', то спра-
ведливы следующие соотношения:

§ 4. Преобразования Фурье
V = 3^11 ф==ф U = &"V. (Если одна из обобщенных
функций U или V является обобщенной функцией мед-
ленного роста, то и другая будет функцией медленного
роста и формула обращения имеет смысл.)
D) Ж
E)
и аналогично для полиномов Р имеем
Замечание. Пусть g = &'/ для /?L1. Тогда функ-
ция g непрерывна и ограничена, но не обязательно инте-
грируема. В этом случае обратное преобразование Фурье
f (х)= I е2к! <*¦ &g (p) dp не существует в классиче-
ском смысле, однако в смысле обобщенных функций
обратное преобразование Фурье всегда существует.
G) / ? Z.2 ф==ф о?~/ ^ L2 (здесь функции из Л2 рассма-
триваются как обобщенные функции).
(8) ||<r/||i8= H/II,, "
(9) Если /, g?L2 и /=• = #"/, G = 3Tg, то
J f(x)g(x)dx^ JF{p)O(p)dp,
т. е. S1" является унитарным оператором.
A0) Если Т^$" и Т имеет компактный носитель, то
-<- -> •<-
У(/?)=(ГЖ, 0-2'*<*./я) является бесконечно дифференци-
руемой функцией от р и V {p) = SrT.
Доказательство. Доказательство дифференци-
руемости обсуждалось в параграфе о тензорном произ-
ведении (см. § 1, гл. III). Далее, имеем
= f ср (р) 4 (Т4^-2^<л ^) =

90 Гл. 3. Мировые частицы и инвариантность
Если разрешить переменной р принимать комплексные
значения, то V(p) будет голоморфной функцией.
A1) Если 5, Т??Р', Т имеет компактный носитель
(так что свертка S *Т имеет смысл) и У = q?~S, V = #",
то произведение UV имеет смысл, UV(^&" и UV =
= <sF(S *Т). Таким образом, преобразование Фурье пере-
водит свертку в произведение, а произведение—в свертку.
§ б. Теорема Бохнера
Теорема Бохнера для скалярных обобщен-
ных функций. Обобщенная функция Т на Еа
является положительно определенной тогда и только
тогда, когда Т — обобщенная функция медленного
роста и ее преобразование Фурье является положи-
тельной мерой степенного роста ').
Напомним, что обобщенная функция Т называется по-
ложительно определенной, если G\ <р *cpM>0 для любой
функции <??3)(Е„).
Определение. Пусть М — упорядоченное вектор-
ное пространство. Мы говорим, что обобщенная функ-
ция Т?3)'(Еп)®М является Б-положительной, если
->¦ ~ >
(Т, ср * ср) — положительный элемент пространства М для
¦у
любой функции cpgS (?„).
Теорема Бохнера для векторных обобщен-
->¦
ных функций. Пусть М—конечномерное векторное
пространство. Обобщенная функция ?п
является Ъ-положительной тогда и только тогда,
когда Т—обобщенная функция медленного роста и
') Доказательство теоремы Бохнера можно иайти в книге
Л. Шварца (Schwartz L., Theorie des distributions, т. 2, p. 132),
или в книге И. М. Гельфанда и Н. Я. Виленкина, Обоб-
щенные функции, вып. 4, Фнзматгиз, М., 1961, гл. 2, § 3. —
Прим. ред.

§ 5. Теорема Бохнера 91
ее преобразование Фурье (&~Т?3'(Е„) ®Ж является
положительной мерой степенного роста.
Доказательство. Необходимость. Докажем
сначала, что Т является обобщенной функцией медленного
роста. Пусть Г—замкнутый выпуклый конус, определяющий
-> ¦<-
порядок в М, Г' — дуальный конус в ЛГ. Обобщенная
->¦ ¦>
функция Т, принимающая значения в пространстве М,
является непрерывным линейным отображением 33 (Еп)—>М;
любой элемент ш' ? Г' определяет отображение М -> С.
Таким образом, отображение Т с последующим отобра-
жением т' является скалярной обобщенной функцией
<- ->
т' о Т!):
(m'of, 9) = m'({f,ff)).
->
Так как обобщенная функция Т является Б-положитель-
ной, имеем
(и' о Т, <р * f) = m'((f, «p * i» > 0
для любой функции cp^S(?) и любого вектора т'?Г'.
Следовательно, для любого вектора т' ? Г' выражение
т' о Т является положительно определенной скалярной
обобщенной функцией. По теореме Бохнера для скалярных
обобщенных функций, т'°Т является обобщенной функ-
цией медленного роста. Так как конечные лимейные ком-
бинации обобщенных функций медленного роста являются
также обобщенными функциями медленного роста и так
как пространство М' порождается векторами из дуального
конуса Г', то выражение т'°Т является обобщенной
функцией медленного роста для любого вектора т' ? М'.
') Знак о —знак композиции двух отображеиий (или супер-
позиции двух функций) (/ о g) ¦ (х) = / (g-dx}).-— Прим. перев.

92 Гл. 3. Мировые частицы и инвариантность
->
Отсюда следует, что Т — обобщенная функция медлен-
ного роста.
Чтобы доказать, что р — <1?Т является положительной
мерой степенного роста, заметим прежде всего, что при
любом т' ? Г' композиция
т! о (а = т! о <?ГТ= <?Г(т' о Т)
является положительной мерой степенного роста, согласно
теореме Бохнера для скалярных обобщенных функций.
Так как пространство М' порождается векторами из Г',
<- ->
то ш' о jj, — мера степенного роста для любого вектора
<- <- ->
т' ? М'. Следовательно, (а является мерой степенного роста.
Для того чтобы доказать, что мера (а положительна,
нужно показать, что (|а, <р)?Г для всякой непрерывной
функции <р^>0 с компактным носителем. Достаточно
показать, что т'{Ы, ср))^-0 для произвольного вектора
<- <- -у
т' ? Г'. Но так как композиция т! о (а — положительная
скалярная мера, то
Достаточность. Любая функция ф ^ (^ (fQ, t|» ^- 0,
является пределом в (^ последовательности функций дуф,
где функции о, можно выбрать так, чтобы выполнялись
следующие условия:
(I) ф
A1)<,<
(III) a, — 1 -> 0 равномерно вместе со всеми произ»
водными на любом компактном множестве.
Так как функции а ф непрерывны и имеют компактный
носитель, а \ъ = <&~Т — положительная мера, то (ij., о,ф)^-
^-0 в пространстве М. Переходя к пределу (что возможно^
так как \х имеет степенной рост), получаем
) 0 в пространстве М.

§ 5. Теорема Бохнера 93
Это неравенство справедливо для любой функции
. Положим ф = срср, <р ? (^. Тогда
t
Но с^~<р может быть любой функцией G из пространства
(Е
(п и тогда (^~ср = б. Следовательно, для любой функ-
ции б ? ?Р имеет место неравенство
-*¦ ~ •>
(Г, 6 * 6) ^ 0 в пространстве М.
Исследуем теперь Б-суперположительность.
-у
Лемма 1. Пусть ф — непрерывная функция с ком-
пактным носителем, принимающая значения в ко-
нечномерном упорядоченном векторном простр-ан-
-*¦ -*¦-*¦
cmee N, такая, что 4 ^ 0. Тогда ф можно равно-
мерно аппроксимировать конечными суммами вида
^i а^, г<?е ф^ — неотрицательные векторы в про-
странстве N, а а1 — непрерывные неотрицательные
скалярные функции с компактным носителем.
Доказательство. Пусть ф имеет носитель /С. Вы-
берем любое е ^- 0. Так как носитель К компактен, а ф —
непрерывная функция, существует конечное открытое по-
крытие {2^} носителя К, такое, что колебание функции ф на
каждом из множеств 2^ не превосходит е. Пусть {<хг} — раз-
биение единицы на К, отвечающее покрытию {2г}. Пусть ф/
является значением функции ф в произвольной точке мно-
жества 2г. Имеем ф^ ^- 0, и, кроме того,
Лемма 2. Если (а является положительной мерой
на Е'п, принимающей значения в конечномерном упо-
рядоченном векторном пространстве М, то (|а, ф) ^

94 Гл. 3. Мировые частицы и инвариантность
<
, какова бы ни была непрерывная функция ty с ком-
пактным носителем, принимающая положительные
<¦
значения в М' (е смысле дуального отношения по-
рядка).
Доказательство. В силу леммы 1 любая данная
¦*¦<¦<¦ <-
функция ф ? 3> (Е'\ ® М', такая, что <|> ^- 0, может быть
равномерно аппроксимирована конечными суммами вида
_. <- <- <-
2j m'iair где т^О (в М'), ч.^-О и а. — непрерывные
скалярные функции с компактным носителем. Имеем
так как
(|а, а() ^-0 в пространстве Ж и
/rej ^ 0 в дуальном пространстве М'.
Пусть F — конечномерное векторное пространство.
-у
Теорема. Если (а — положительная мера сте-
пенного роста на Е', принимающая значения в про-
странстве F(g)F, то ее преобразование Фурье Г=
= u?f|A является Ъ-суперположителъной обобщенной
функцией.
В этом утверждении р положительна в смысле „есте-
ственного" отношения порядка в F0F.
Доказательство. Рассмотрим любую функцию
ср ? Sf {E'\ g> F' (F' — пространство дуальное к F). Тогда
?®Т^-0 в F'®F'. По лемме 2, а также в силу того,
что <р является пределом в <?? (Е'„) последовательности
функций из 3(E'n^®F', имеем
+ <- :*"
(р. <р®<р>>0.

§ 6. Свойства «упрощенного» ядра 95
Тогда
¦> <- *
= G\ 6» 6),
ч- <-
где 8 = о? <р может быть любым элементом пространства
Следствие. Для любой обобщенной функции
¦> —
'(En)®F®F следующие деа свойства эквива-
лентны:
->
(а) Т является Б-положительной;
(б) Т является Б-суперположительной.
§ 6. Свойства „упрощенного" ядра
Подытожим коротко наши предыдущие рассмотрения.
Мы имели дело с многообразием класса С°°, так назы-
ваемым миром V, и конечномерным векторным простран-
ством F над полем комплексных чисел С. Мы занимались
определением F-частиц в мире V. Каждая частица является
гильбертовым пространством ЗФаЗ' (V)(g) F (вложение
непрерывно). Движение частицы определяется в этом слу-
чае обобщенной функцией ф ?<=%?, такой, что jj ф Ц^^ ?= 1 •
Мы видели, что
(а) существует взаимно однозначное соответствие между
F-частицами ?76 и положительными .антиядрами, т. е. не-
прерывными положительными антилинейными отображе-
ниями
Это соответствие сохраняет алгебраическую структур}
и отношение порядка.

96 Гл. 3. Мировые частицы и инвариантность
_ _________
(б) Положительным антиядрам взаимно однозначно
соответствуют суперположительные обобщенные функции
Кх< у ? ЗЕ>' (V ® V) <g> F ® F (F — пространство, комплексно
сопряженное к пространству F), т. е. такие обобщенные
функции KXt у, что .
<*_.,-
какова бы ни была функция <??3(V)®Fr.
Если задана обобщенная функция КХ) у, то соответ-
ствующее ей антиядро К определяется формулой
< _
для любых ср, ф ^ 3 (V) ® F'; здесь <р — элемент, комп-
•> 5
лексно сопряженный к ср в смысле сопряжения F-+F, или
«• *
точнее, в смысле транспонированного сопряжения F'->F'.
Опять-таки это соответствие сохраняет различные алгеб-
раические операции и отношение порядка.
Если, кроме того, нам дана структурная группа О,
действующая соответствующим образом на мире V и на
пространстве F, то гильбертово пространство Ж является
G-инвариантным, если обобщенная функция KXi y G-инва-
риантна.
(в) Мы ограничились затем частным случаем, когда
V = _?„, где _•„ —n-мерное аффинное пространство,
а О=?, является группой сдвигов на Еп, действующей
¦>
тождественно в пространстве F.
Мы рассматривали отображение
ЕпХЕп-+ЕпХЕп, (х, У)^(х, я). '
где и = х — у, и образ Нх-> обобщенной функции Кх у
при этом отображении. Обратно, если задана обобщенная
функция

§ 6. Свойства «упрощенного» ядра 97
то можно определить Кх v при помощи равенства
кх, у х,х-у
Если обобщенная функция KXiil инвариантна относи-
тельно сдвигов
(х, у)->(* + о + %
то Их ¦* должна быть инвариантной относительно сдвигов
(х, и)-^-(л; + а, я).
Из инвариантности следует, что Нх •> = 1^® Я^-, где
1^. — единичная функция переменной х (т. е. функция,
тождественно равная 1 на ?п) и Н->?$'{E^®F®F.
Суперположительность обобщенной функции KXt y экви-
валентна Б-суперположительности обобщенной функции
Н-*. Но мы видели, что это эквивалентно Б-положитель-
ности.
Это в свою очередь означает, что Н+ является обоб-
щенной функцией медленного роста и ее преобразование
Фурье является положительной мерой ^ степенного роста
со значениями в пространстве F®F. Обратно, любой
такой мере соответствует Б-положительная обобщенная
функция Н->.
Замечание. Пусть К — антиядро, соответствующее
частице <?№. Тогда
Доказательство. Для любой функции W ? ?S(En)®F'
имеем
что и требовалось доказать.
7 Л.

98 Гл. 3. Мировые чЯстицы и инвариантность
Заметим, что ##cp— свертка обобщенной функции,
определенной на векторном пространстве, с обобщенной
функцией, определенной на аффинном пространстве, свя-
занном с этим векторным пространством. Пусть Е— аф-
финное пространство, Е — связанное с ним векторное
пространство, Sx — обобщенная функция на Е, Т-* —
обобщенная функция на Е (причем по крайней мере одна
из них имеет компактный носитель).
Тогда общее определение свертки Sx * Т+ задается
выражением
(Sx * 7>, ср (*)) = (SE®Т+, <р E + ?)).
Таким образом, S?*7V — обобщенная функция на аффин-
ном пространстве Е. Имеем также:
В последнем члене для определения свертки ср * ср необхо-
дим выбор начала координат, так как ср задана в аффин-
ном пространстве. Заметим, что выбор начала координат
необходимо сделать также для того, чтобы перенести по-
нятие преобразования Фурье обобщенных функций на
аффинное пространство.
Прежде чем сформулировать следующую теорему,
отметим, что если Е— полное локально выпуклое топо-
логическое векторное пространство, то утверждение <s.&6clE
соответствует антиядру L» означает, что L задается при
помощи следующей композиции отображений:
где Ж -+Е — каноническое вложение, Е' —> ?№' — транс-
понированное к нему отображение и 3@'->-е% — канони-
ческий антиизоморфизм гильбертовых пространств.
В дальнейшем нам встретится случай, когда ШаЕхаЕ,
причем все вложения непрерывны. В частности, про-
странству ?№ будет соответствовать антиядро L\: Е\ —>Еь
а также антиядро L : Е' -+Е. Для того чтобы различать эти
два случая, антиядро L1 мы будем называть ?гантиядром,
а антиядро L — Е-антиядром. ч

§ 6. Свойства «упрощенного» ядра
Теорема. Пусть Е, Ех — два полных локально
выпуклых пространства, Е^сЕ, и топология в Ех
сильнее, чем топология, индуцированная топологией
пространства Е. Пусть 3№аЕ — гильбертово про-
странство с более "сильной топологией, чем тополо-
гия, индуцированная из Е, L — соответствующее Ш
Е-антиядро.
Тогда для того чтобы имело место непрерывное
вложение ИваЕ-^, необходимо и достаточно, чтобы L
можно было разложить в композицию отображений'
i i - ¦
с —> с 1 —> Е\ —> с, A)
где Ei-*E — естественное вложение, Ё -+Е\ — транс-
понированное к нему отображение, Е\ —> Е\ — непре-
рывное антилинейное отображение Lx. Если L можно
разложить таким образом, то Lx является Ех-анта-
ядром, соответствующим пространству
Доказательство. Рассмотрим диаграмму
где 3&->Е, Е1—*-Е — естественные вложения, Е'->?№'',
Ё —>Ё\ соответствующие транспонированные отображения
и Ш' —>¦ &в — канонический антиизоморфизм пространства
<&в и дуального к нему гильбертова пространства <?№'.
Допустим теперь, что J{?c:?j, причем вложение непре-
рывно. Тогда можно считать, что пунктирная стрелка
Е1 обозначает естественное вложение
'1
Е[ —¦> Ив' означает
к этому вложению,
в Ev
отображение, транспонированное
a Lv определяется композицией
1*

100 Гл. 3. Мировые частицы и инвариантность
отображений:
Разложение A) следует из коммутативности диаграммы
B) (т. е. из того, что при движении слева направо по
любому возможному пути, указанному стрелками, полу-
чается один и тот же результат). Обратно, предположим,
что имеет место разложение A). Тогда fj-антиядру соот-
ветствует гильбертово пространство ^61аЕ1 с непрерыв-
ным вложением и ?, можно разложить следующим образом:
Отсюда следует, что диаграмма B), в которой ?}в нужно
заменить на ?№\, коммутативна. Следовательно, Ш\
является гильбертовым пространством, непрерывно вло-
женным в ? и соответствующим ?-антиядру L. Но в силу
взаимно однозначного соответствия между ^-антиядрами
и гильбертовыми пространствами, непрерывно вложен-
ными в Е, имеем
<Sv\ == еЮ •
Следовательно, мы получаем опять коммутативную диа-
грамму B).
Эта теорема упрощает наши поиски частиц ?№а
c?B'(E)®F. Частице $в соответствует отображение
/Сер = Н * ср:
ср ? 3 (Е)® Р -+ Н * у ? 3* (Е) ®Р.
Но Н является обобщенной функцией медленного роста и,
следовательно, #*ср не только определяет отображение
из 3)(E)®F' в ?B(E)®F, но также определяет отобра-
жение из Sf{E)®F' в ?f"(E)®F. Таким образом, ото-
бражение Н * ср можно разложить следующим образом:
$(E)®F'-+?P(E)®F' -+ Sf'iE)® F-+3'(E)®F.
Согласно доказанной выше .теореме, если ?№аЗ!)' (F)®F
(вложение непрерывно), то ?№<=.&" (Е)® F (вложение
непрерывно).
Следовательно, наша задача сводится теперь к отыска-
нию частиц в пространстве <&"(E)®F.

§ 7. Гильбертово пространство &в для скалярных частиц 101
§ 7. Гильбертово пространство &в
для скалярных частиц
Случай скалярных частиц выделяется тем, что F = C.
В силу теоремы Бохнера мы можем теперь рассматривать
положительные меры \х степенного роста на' Е' вместо
Б-положительных обобщенных функций <?№ ?ЗУ {Е). Если
<-
на Е' задана такая, мера |а, to можно ввести простран-
ство L2 относительно меры |а. Каждый элемент / про-
су
странства L». является классом ^-измеримых функций /
на Е', совпадающих почти всюду в смысле меры р. и та-
ких, что
п
Скалярное произведение в L^ определяется равенством
L
где fug — любые представители классов соответстве нно
Мы можем связать с пространством 1^ пространство А^
обобщенных функций, определенных на Е', вида /|х, где
/^L^ (заметим, что / — локально интегрируемая функция
относительно меры (а).
Обобщенная функция /jj. определяется равенством
Мы видим, что /ja определяет новую меру, одинаковую
для всех / из одного и того же класса /'. Положим
= f
Это скалярное произведение превращает Л^ в гильбертово
пространство; А^ непрерывно рложено в

102 Гл. 3. Мировые частицы и инвариантность
Теорема. Если у. — положительная мера степен-
кого роста на Е', то пространство Л^ непрерывно
вложено в &" (Ег).
Доказательство.
Для <р?3, / ?lX имеем
Так как мера р имеет степенной рост, любое множество,
ограниченное в ?Р, ограничено в пространстве 1^. Если
<Р ? &?> т0 существует последовательность функций <fy
ив-пространства 3, - сходящаяся к ср в смысле топологии
пространства ?Р и поэтому ограниченная в ?Р. Это озна-
чает, что приведенное выше неравенство остается справед-
ливым для любой функции <р, принадлежащей SP. и когда ср
пробегает ограниченное множество из ?Р, а / — единич-
ную сферу в Lp, величина |(/(а, <?}\ остается ограничен-
ной. Это доказывает теорему.
Пространство Л^. можно рассматривать как пополнение
векторного пространства обобщенных функций вида /ц,
где / пробегает пространство ?рЛ по норме
11/11 А2=
Здесь мы имеем в виду конкретное пополнение в &".
¦ С другой стороны, частица ?№ является пополнением
в 3' (Е) пространства элементов вида Н * <р, где <р пробе-
гает пространство ?Р, по норме
Это означает, что пространство Л2 является преобразо-
ванием Фурье гильбертова пространства ffi:

Глава 4
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И ИНВАРИАНТНОСТЬ
ОТНОСИТЕЛЬНО ВРАЩЕНИЙ
§ 1. Элементарные частицы
Пусть V = Еп и пусть F — конечномерное векторное
пространство над полем С. Структурная группа О дей-
ствует на Еп и на F. Допустим, что О удовлетворяет сле-
дующим условиям (кроме условий, данных в определении
структурной группы):
AH содержит всю группу сдвигов, т. е. для любого
сдвига а?Еп существует элемент g+?G, такой, что дей-~
ствие элемента g+ на Еп является сдвигом а и g-> дей-
& а
ствует тождественно на F. :
B) Любой оператор о?О сохраняет меру Лебега
на Еп. Это эквивалентно утверждению, что любой опера-
тор в на Еп задается матрицей с определителем ± 1.
Пусть О0с:О — подмножество элементов группы О,
действующих как сдвиги на Еп и как единичные опера-
торы на F; О0 является нормальным делителем группы О.
Для того чтобы понять, как о действует на обобщен-
ную функцию Кх,г мы используем обычную „замену
->• ¦*¦
переменных" и = х— у и напишем
К г, v = Н ->
*• ' х, и •
Мы уже показали, что если обобщенная функция Кх,у
инвариантна при преобразовании
(х, у)-хз(х, у)=г(ах, ау)
(причем о действует тождественно на F) для а ? О0,
то обобщенная функция Я, -> инвариантна при

104 Гл. 4. Элементарные частицы и инвариантность
преобразовании
(х, а)-*-(ах, а).
Следовательно, Н ->= 1 ,.<g>//.>; заметим, чтоо?бптож-
х и х и и
х, и
дественно действует на Я_>. Любой оператор а?О дей-
F
ствует, с одной стороны, на F, с другой стороны, — на Еп
-> -> ¦>•>
по закону х-*-ах и на Еп по закону х->- вх.
-*¦
Операция о определяется следующим образом: если
-> ^.
5, ¦»)??„ таковы, что S — у — х, то
Это определение не зависит от выбора 5, ч\?Еп. В самом
деле, пусть I-', irj' — другие элементы Еп, такие, что
разность
также равна л\ Тогда
Г^1' = ^Г^'= а,
или
?' = & — а, 7)' = 7j—а.
Обозначим через te сдвиг х->х — а в Еп. Мы видим, что
о?' = эта$, от)' = otair).
Но так' как Go — нормальный делитель, то существует
элемент $?Еп, такой что ств = Тра; следовательно, для
такого р имеем
0$' = Трв! = 0$ р, ОУ)' = XoOif) = 07) р
и
0|' 07)' =<J$ 07J,
что и доказывает справедливость нашего замечания.

§ 1. Элементарные частицы 105
Оператор a?G действует также на пространстве
Еп X Еп по закону
и на пространстве ?п X ? п по закону
(?, ?)-*(<*, Ъх).
Далее, так как о сохраняет меру Лебега на Еп, этот
оператор сохраняет константы (рассматриваемые как обоб-
щенные функции) и, следовательно, преобразует 1х®#->
в 1х®оЯ->. Инвариантность обобщенной функции KXty
относительно оператора а эквивалентна инвариантности //->
относительно а (действующего на F и на ?„). В действи-
тельности мы можем заменить инвариантность обобщенной
функции //-> относительно группы G инвариантностью этой
обобщенной функции относительно факторгруппы GjGQ,
потому что О0 действует тождественно как на Еп, так .
и на F.
Например, если О—неоднородная группа Лоренца
и Go — группа сдвигов, то GjO^ является однородной
группой Лоренца.
Мы хотим найти свойства инвариантности преобразо-
вания Фурье (t = а?"Я. Действие оператора a?G на |х
определяется его действием, с одной стороны, на F и,
с другой стороны, на Е'„ как контраградиентного опера-
тора к оператору
а-* а а,
Каждая ^-частица на Е„ соответствует положительной
мере степенного роста (t на Еп, принимающей значения
в пространстве F ® F и инвариантной относительно фак-
торгруппы G/Go (или группы G).
Возвратимся вновь к общему случаю, когда заданы
мир V, комплексное векторное пространство F и струк-

106 Г л. 4. Элементарные частицы и инвариантность
турная группа О. Пусть гильбертово пространство
является О-инвариантной /'-частицей
или, другими словами, универсальной /'-частицей (или
еще О — F-частицей).
Определение. Универсальная r-частица Ж назы-
вается элементарной, если любое б-инвариантное гиль-
бертово пространство ЗТв^^Зв (т. е. такое, что З^
и норма в S@ не меньше нормы в S@i) имеет вид
где 0<Х<1.
Теорема. Следующие три свойства универсаль-
ной частицы $в эквивалентны:
(а) Цв — элементарная частица,
(б) ?%? не имеет замкнутых О-инвариантных
линейных подпространств, за исключением {0}
и самого Щ',
(в) если G-инвариантное гильбертово простран-
ство Звх, непрерывно вложенное в W(V)(g)F,
содержится в <§в, то $в\=-Ж и нормы в i№
и &6\ пропорциональны.
Условие (б) можно перефразировать следующим обра-
зом: представление группы О в гильбертовом простран-
стве <§в (т. е. в группе унитарных операторов простран-
ства Ив) неприводимо.
Справедливость соотношений (а)гф(б) и (в)зф(а) про-
веряется тривиально.
Мы докажем, что из (б) следует (а) и из (а) следует (в).
(б)=ф(а). Пусть гильбертово пространство &вх^$в,
gfgx ф {0}, является О-инвариантным. Пространству i№x
соответствует (однозначно) антиядро L\ : $@\~>?$\. Пусть
L — канонический антиизоморфизм $в' ~> $в. Для л: ^ &в
положим х = L 1х. Для у ? <§вх получаем
(У I *)» = (У I Lx')m = <У> х') = (У I V)w
Положим

§ 1. Элементарные частицы 107
-Тогда
Так как всякий оператор a?G действует унитарно и
на Цв и на 3@i> то
(у |
Таким образом, оператор Л коммутирует с О. Следова-
тельно, любое спектральное подпространство оператора А
инвариантно относительно группы О; заметим, что А — огра-
ниченный оператор, действующий в J?\ и А^-0, так как
Йо, согласно (б), не существует нетривиального замкну-
того подпространства пространства <Ш, которое было бы
G - инвар иантным.
Поэтому оператор А должен иметь только одно спек-
тральное подпространство — само пространство $в. Значит,
существует число Х?С, такое, что
для любого вектора х ? &6 и
Возьмем х =* у ? &в\, тогда число
должно быть положительным; следовательно,
(а)=ф(в). Допустим, что J^jCj^ — другое О-инва-
риантное гильбертово пространство с непрерывным вложе-
нием в 35' Q/) ® F. Тогда естественное вложение про-
странства &вх в пространство Ш должно быть непре-

108 Гл. 4, Элементарные частицы и инвариантность
рывным, согласно теореме о замкнутом графике1). Это
означает, что существует константа М<-|-оо, такая, что
для любого элемента л: ? &€х справедливо неравенство
Определим новое гильбертово пространство J^2 сле"
дующим образом: <?№2 совпадает с $вх как множество,
а норма в &6<i определяется равенством
Тогда J#2<J#; в самом деле, &6гсШ и |[*||з
11* Use для х^Ш2- Согласно (а), $вг совпадает с
как множество и существует константа А. ^ 0, такая, что
для любого элемента х ? Зв имеем
Следовательно, ?№х = &€ и
II*Use, = "Af U*Hw
что и требовалось доказать.
Вернемся к частному случаю, когда V = Еп и О удовле-
творяет условиям, приведенным в начале этого параграфа.
Тот факт, что Ш является элементарной частицей, можно
выразить по-разному.
1. В терминах антиядра К, соответствующего про-
странству $в.
•Если КХ^К — другое положительное G-инва-
риантное антиядро, то КХ=\К для некоторого
Х
2. В терминах обобщенной функции Я->.
и
Если Нх—другая Б-положительная (или Б-супер-
положительная) G-инвариантная обобщенная функ-
ция и Нх^Н в смысле положительности по Бох-
неру, то Н1 = ХН.
') По поводу этой теоремы см., например, книгу Дан-
форда Н. и Шварца Дж. Т., Линейные операторы, ч. I,
М., ИЛ, 1962, стр. П. —Прим. ред.

§ 2. Носители экстремальных мер 109
3. В терминах меры (*.
Если (tj —другая положительная О-инвариантная
мера степенного роста и 1*1^A., to (j.j=Ah.
Совокупность всех /'-частиц образует замкнутый вы-
пуклый конус. Набор G- инвариантных частиц образует
подконус. Элементарные частицы являются крайними обра-
зующими этого подконуса1).
§ 2. Носители экстремальных мер
Рассмотрим случай, когда многообразие V представляет
собой «-мерное аффинное пространство Еп над полем
вещественных чисел (F, как обычно, является конечномер^
ным векторным пространством над полем комплексных
чисел). Мы будем рассматривать группу О, действующую
на Еп как аффинная группа и на F как линейная группа,
обладающую следующими свойствами:
A) все элементы группы О сохраняют меру Лебега
в пространстве Еп, т. е. для любого оператора из О как
оператора, действующего на пространстве Еп, справедливо
равенство det=il;
B) группа О содержит все сдвиги, т. е. для любого
-У ->
сдвига «??„ существует элемент g->f G, который дей-
ствует как сдвиг а на пространстве ЕЛ и тождественно на F.
Пусть О0 — подмножество группы О, состоящее из всех
элементов, которые действуют как сдвиги на Еп и как
единичные операторы на F; Go является нормальным
делителем.
Мы ищем G-инвариантные гильбертовы пространства
3@cz$'(En)®F, непрерывно вложенные в 3)'(En)<g)F;
это эквивалентно отысканию всех мер (t степенного роста
') Образующая выпуклого замкнутого конуса называется
крайней, если ее направляющий вектор х нельзя представить
в виде х{ + х2, где хх и хг принадлежат конусу и ие пропор-
циональны х. По поводу общего понятия крайней точки вы-
пуклого множества см., например, книгу ДанфордаН. и
Шварца Дж. Т., Линейные операторы, ч. I, M., ИЛ, 1962,
гл. V, § 8 -Прим. ред.

НО Гл. 4. Элементарные частицы и инвариантность
на Ёп, принимающих значения в пространстве F®F, Поло-
жительных и О-инвариантных. Если мы хотим найти
элементарные частицы, то нам необходимо, чтобы
пространство if6 было экстремальным, т. е. чтобы для
любого другого О-инвариантного пространства &вх, не-
прерывно вложенного в &в, было справедливо равенство
и нормы в этих пространствах были пропорциональны;
или, эквивалентно, если ЁЮХ4^?Ю и &вх G-инвариантно, то
с пропорциональной нормой. Наконец, условие на меру (*
означает, что эта мера является экстремальной, т. е. если
(tj — другая О-инвариантная положительная мера степен-
ного роста, такая, что (*1 <^ [*, то |*j пропорциональна |* ')•
Приведем теперь необходимое условие экстремальности
меры.
Определение. Пусть G—группа, действующая на
топологическом пространстве. G-орбитой называется мно-
жество всех образов одной и той же точки пространства
под действием группы О.
Теорема. Пусть ц — мера, определенная в ло-
кально компактном пространстве X со счетной
базой открытых множеств, а пусть значения меры ц
лежат в конечномерном упорядоченном векторном
пространстве <У. Если [х положительна, G-инва-
риантна {или 0100-инвариантна) и экстремальна
среди всех мер с теми же свойствами, то носитель
меры (t является замыканием одной из G-орбит.
Замечания. В интересующем нас случае X = Е\,
Jf =F®F и Q/Qo действует в пространстве Е4 как
однородная группа Лоренца. Орбиты в этом случае являются
гиперболоидами, так как группа Лоренца сохраняет ква-
дратичную форму
р2=р\+р\+р\-р1
') Такие меры обычно называются крайними (см. преды-
дущее примечание).—Прим. ред.

§ 2. Носители экстремальных мер 111
Таким образом, мы знаем, что носитель экстремальной
меры обязательно является одним из гиперболоидов1). Это
дает нам существенное ограничение, налагаемое на носи-
тели экстремальных мер; нахождение таких мер теперь
не представляет трудности. В действительности мы покажем,
что на каждом гиперболоиде существует только одна
с точностью до константы инвариантная мера.
Заметим, что мы по необходимости должны рассматри-
вать замыкание орбиты, так как носитель всегда замкнут.
Существуют, однако, и не замкнутые б-орбиты. Например,
верхняя часть поверхности светового конуса без вершины
(начала) является такой О-орбитой. Замыканием этой
орбиты является верхняя часть конуса с присоединенной
вершиной, и она может быть носителем меры. Однако
бывают меры, сосредоточенные на конусе без вершины
в следующем смысле.
Определение. Мы говорим, что мера сосредото-
чена на некотором подмножестве, если дополнение к этому,
подмножеству имеет меру нуль.
В нашем примере мера, носителем которой является
конус с вершиной, сосредоточена на конусе без вершины
всякий раз, когда мера вершины равна нулю.
Более сильным, чем приведенная выше теорема, было бы
утверждение о том, что экстремальная мера сосредоточена
на одной из О-орбит. Однако такое утверждение сделать
нельзя.
Прежде всего понятие сосредоточенности не носит
однозначного характера. Например, мера Лебега на прямой
линии сосредоточена на дополнении к любому счетному
подмножеству. Кроме того, теорема была бы неверна,
если бы мы утверждали, что мера всегда сосредоточена
на одной из орбит; это показывает следующий пример.
Пусть X — окружность, а О—группа вращений, поро-
ждаемая поворотом на угол, несоизмеримый с гс. Любая
орбита является плотным счетным множеством, и единствен-
ной мерой, инвариантной относительно группы О, является
мера Лебега на окружности, так как если мера инвариантна
относительно некоторой группы, то она инвариантна также
') Особый случай, когда гиперболоид вырождается в конус,
рассмотрен ниже.—Прим. ред.

112 Гл. 4. Элементарные частицы и инвариантность
относительно замыкания этой группы, которым в данном
случае является группа всех вращений. Таким образом,
в данном случае не существует инвариантной меры, сосре-
доточенной на G-орбите').
Доказательство теоремы. Достаточно пред-
положить, что X является носителем меры ц, поскольку
если (i. инвариантна, то ее носитель также инвариантен.
Мы должны доказать, что существует одна орбита, плот-
ная в X. Возьмем некоторую точку а ? X, и пусть
V — открытая окрестность точки а. Возьмем насыщение V
окрестности V, т. е. объединение образов окрестности V под
действием всех элементов группы О. Множество V открыто
и имеет положительную меру, поскольку всякое непустое
открытое множество имеет положительную меру (в про-
тивном случае носитель меры p не был бы равен X).
Дополнение к V имеет меру нуль; иначе мы могли бы
умножить меру ц на характеристическую функцию мно-
жества V и получить положительную G-инвариантную
меру, не превосходящую р и не пропорциональную р.
Таким образом, V содержит почти все множество X.
Точка а имеет счетную фундаментальную систему окрест-
ностей Vп. Каждое множество Vn содержит почти все
множество X. Тогда f| Vn также содержит почти все
множество X. Другими словами, Ь ? Л Vn для почти всех
Ь?Х.
Если Ь ? П Vn, то Ь ? Vn для всех га; таким образом,
орбита b элемента Ъ пересекает все Vn, т. е. b пересекает
все окрестности точки а.
Следовательно, а принадлежит b (замыканию орбиты Ъ)
для почти всех Ь. Возьмем счетное множество \ak}, плот-
') Это утверждение справедливо только для регулярных мер
(т. е. таких мер (*, что для любого множества А имеем (а (А) =
= inf (а (С?) = sup (a (F), где нижняя грань берется по всем откры-
тым множествам G zd А, а верхняя грань — по всем замкнутым
FcA). Нерегулярные инвариантные меры, сосредоточенные
на G-орбите, в данном случае существуют. Например, мера,
определенная следующим образом: р (А) равно числу точек
G-орбиты, лежащих в А. Отметим, что меры, о которых идет
речь в теореме Бохнера, всегда регулярны. — Прим. ред.

§ 3. Мезоны ПЗ
ное в X. При любом фиксированном k име^м ak ? b для
почти всех Ь. Так как множество \ak} счетно, то отсюда
следует, что ak?b при любом k для почти всех Ь. Сле-
довательно, Ь = Х для почти всех Ь?Х.
§ 3. Мезоны
Мы собираемся теперь применить предыдущие резуль-
таты к теории мезонов. В этом случае V = E4 и F = C;
группа О действует тождественно на F и как собствен-
ная неоднородная группа Лоренца на пространстве ?4.
Напомним, что неоднородная группа Лоренца имеет
четыре связные компоненты. То же самое справедливо
для однородной группы Лоренца 2, которая состоит
из следующих четырех связных множеств:
A) преобразования, сохраняющие направление времени,
с определителем, равным-f-1;
B) преобразования, сохраняющие направление времени,
с определителем, равным — 1;
A') преобразования, которые обращают направление
времени, с определителем, равным-f-1.
B0 преобразования, которые обращают направление
времени, с определителем, равным — 1.
Так как 2 является факторгруппой неоднородной группы
Лоренца по коммутативному нормальному делителю, со-
стоящему из сдвигов, то связные компоненты неоднород-
ной группы Лоренца являются прообразами связных ком-
понент группы 2. Мы берем в качестве группы О прообраз
множества A). (Это множество образует группу, которая
называется собственной однородной группой Лоренца.)
Заметим, что множество A) является единственной связной
компонентой группы 2, которая сама является группой;
это — связная компонента единицы.
Чтб означает сохранение или обращение направления
времени, можно объяснить с помощью светового конуса.
Пусть ось времени направлена вверх.
Световой конус отображается на себя любым опера-
тором а ? 2. Имеются две возможности:
A) о отображает верхнюю часть светового конуса на
верхнюю, а нижнюю часть — на нижнюю. В этом случае
8 Д. Шварц

114 Гл. 4. Элементарные частицы и инвариантность
говорят, что оператор о сохраняет направление вре-
мени.
B) о отображает верхнюю часть светового конуса
на нижнюю, а нижнюю часть — на верхнюю. В этом слу-
чае говорят, что оператор о обращает направление времени.
Вопрос о том, сохраняется ли направление времени,
можно решить, выбирая некоторую систему координат
и представляя оператор в при помощи матрицы. Тогда
преобразованная временная компонента примет вид
Х0 = ^01*1 ~Т" ^02*2 ~Ь C0ZX3 ~Ь ^ОО^О1
где коэффициент % всегда отличен от нуля. Если с00 > 0,
то а сохраняет направление времени, если с^ < 0, то о
обращает направление времени.
Выбор группы О чрезвычайно важен, так как он опре-
деляет, с какими элементарными частицами мы имеем дело.
С математической точки зрения здесь имеется много
возможностей, однако существуют физические соображения
в пользу выбора неоднородной собственной группы Ло-
ренца. Прежде всего физически оправдано задание ориен-
тации пространства и направления времени, по крайней
мере, локально. Это делает естественным выбор собствен-
ной неоднородной группы Лоренца вместо полной неодно-
родной. Далее, если бы мы взяли в качестве О полную
группу Лоренца (или только ее часть, состоящую из
прообразов преобразований типа A) и B')), то мы полу-
чили бы заряженные частицы с неопределенным зарядом,
т. е. частицы, имеющие с некоторой вероятностью тот
или иной заряд.
Однако это не дает еще достаточных оснований для
выбора собственной неоднородной группы Лоренца. Заме-
тим, что это не та группа, которая используется в спе-
циальной теории относительности, где не задана основная
единица длины. В пространстве Е4 нам задана не одна
фиксированная квадратичная форма, а целое семейство
пропорциональных квадратичных форм. Поэтому казалось
бы, что правильно выбранная группа должна включать
в себя все растяжения (в дополнение к собственной группе
Лоренца). Если бы это было так, то элементарные частицы
были бы совсем другими. Существовали бы типы частиц,
у которых масса не фиксирована, а вероятностно распре»

§ 3. Мезоны 115
делена (т. е. известна лишь вероятность того, что при
измерении массы получится результат в заданных пределах).
Оказывается, что физика микромира дает нам основания
для исключения растяжений. Физические частицы, такие,
как электрон или протон, в действительности не имеют
всех возможных масс, и не все длины волн обнаружены
в атомных спектрах элементов. Но если в мире существуют
привилегированные массы или длины, мы должны выбрать
в качестве группы собственную неоднородную группу
Лоренца.
Пусть Go — группа сдвигов. Факторгруппа QfQQ дей-
ствует на E'v и каждая орбита содержится в одном из
гиперболоидов
р* — а, а = const,
так как величина р2 инвариантна относительно группы О/О0.
Имеется три типа гиперболоидов
A) однополостный;
B) двуполостный;
C) световой конус.
О/О0-орбита содержится в одном из этих гиперболои-
дов, но не обязательно совпадает с ним.
Однако любая орбита, лежащая на гиперболоиде
типа A), т. е. однополостном (или связном) гиперболоиде,
обязательно совпадает с самим гиперболоидом. В самом
деле, возьмем любую точку а этого гиперболоида; выби-
рая подходящую систему координат, мы можем считать,
что эта точка имеет координаты (ах, О, 0, а0). Если взята
любая другая точка b = (bv b2, b3, b0), то существует
пространственное вращение р, которое отображает ее
в точку вида (bi, 0, 0, bo). Но в этом случае существует
вещественное число 6, такое, что
Обозначим это преобразование через ав; мы видим, что
отображает b на а, и очевидно, что oep?G/O0.

116 Гл. 4. Элементарные чадтицы и инвариантность
Таким же образом можно показать, что существуют
два типа орбит на гиперболоиде B): верхняя ветвь гипер-
болоида B) и нижняя ветвь гиперболоида B).
С другой стороны, если бы группа О содержала
преобразования, не сохраняющие направление времени
(например, если бы О была полной группой Лоренца),
то на гиперболоиде B) лежала бы только одна орбита,
ибо обе ветви вместе были бы одной орбитой. Для све-
тового конуса C) существуют три типа орбит: верхняя
часть без вершины, нижняя часть без вершины и сама
вершина.
Прежде всего изучим гильбертово пространство, соот-
ветствующее простейшему типу орбит — вершине свето-
вого конуса. Все положительные меры степенного роста,
сосредоточенные в вершине и экстремальные, пропорцио-
нальны 8-функции:
Пропорциональные гильбертовы пространства определяют
одну и ту же частицу, т. е. частица является классом
пропорциональных гильбертовых пространств или целой
образующей замкнутого выпуклого конуса. Поэтому мы
можем положить (х = 8, поскольку все другие меры про-
порциональны этой. Функция Н=1 является Фурье-
образом меры (х. Пространство Ц,. в данном случае можно
отождествить с пространством всех констант. Пространство
л? = ?Г?1в — пространство всех обобщенных функций
вида /8 с произвольной константой / (т. е. / ? /?) и
со скалярным произведением
Обратное преобразование Фурье этого пространства
дает нам пространство &€, которое в данном случае
состоит из постоянных функций. Скалярное произведение
в Ш задается формулой
Физическая интерпретация этого пространства $в не вполне
ясна. Мы будем называть его мезонным вакуумом.

§ 4. Лоренц-инвариантные скалярные обобщенные функции 117
§ 4. Лоренц-инвариантные скалярные обобщенные
функции.
Для отыскания положительных мер степенного роста,
имеющих носители на заданной орбите и экстремальных,
мы используем некоторые результаты П. Д. Метэ. Метэ
нашел общий вид обобщенных функций, инвариантных
относительно однородной расширенной группы Лоренца й.
Первая теорема Метэ. Отображение /(«)->
->-/(Р2) пространства непрерывных функций, опре-
деленных на R1, в пространство непрерывных функ-
ций, определенных на Ei и инвариантных относи-
тельно 2, можно единственным образом продолжить
до линейного топологического изоморфизма Ти->Тг
из SB'(R1) в D'(E'4— {0}). Образ пространства 3'(R1)
при этом отображении состоит аз обобщенных
функций, определенных на Е\—{0} и инвариант-
ных относительно группы й.
Замечания. Здесь мы не будем приводить доказа-
тельство существования указанного отображения. Един-
ственность следует из того, что функции, непрерывные
на R1, плотны в 3>' (R1).
Эта теорема определяет понятие прообраза обобщен-
ной функции при отображении р->р2 из ?^—{0}
в R1 : Tpi—прообраз обобщенной функции Та. Легко
найти носитель любой обобщенной функции Трг: он
является прообразом носителя обобщенной функции Та
при отображении р->р2.
Пример. На множестве Е'А—{0} можно определить
обобщенную функцию Sp*1)- Носителем Ьрг является по-
верхность светового конуса, за исключением вершины.
Эта теорема является частным случаем более общей
теоремы, которая утверждает, что если бесконечно
') Определение обобщенной функции 8р5 приведено в книге
И. М. Гельфандаи Г. Е. Шилова, Обобщенные функ-
ции, вып. 1, изд. 2, М., 1961. — Прим. ред.

118 Г л. 4. Элементарные частицы и инвариантность
дифференцируемое отображение из одного многообразия V
в другое W является отображением постоянного ранга,
то всегда можно определить прообраз обобщенной функции
на W; этот прообраз является обобщенной функцией на V.
Вторая теорема Метэ. Любая обобщенная
функция в Е'4—{0], инвариантная относительно
группы й, имеет вид Тр,, где T^S'CR1) (т. е. изо-
морфизм, указанный в первой теореме, отображает 3' (R')
на все пространство инвариантных обобщенных
функций, определенных на Е\—{0}).
Замечания. Если мы рассмотрим все простран-
ство Е'4 вместо пространства Е\—{0}, то эта теорема
несправедлива.
Для данной обобщенной функции Та эта теорема не
позволяет утверждать, что ей обязательно соответствует
обобщенная функция Т^ во всем пространстве Е\. Более
того, даже если такое соответствие существует, мы не
можем найти никаким определенным способом все лоренц-
инвариантные обобщенные функции на E'v Например^
нельзя получить этим путем ни одной лоренц-инвариант-
ной обобщенной функции с носителем в начале коорди-
нат. Вот почему мы рассматриваем не все E'v а только
дополнительное к началу координат множество Е'4—{0}.
Теперь мы хотим найти обобщенные функции на
Е'4—{0}, инвариантные относительно собственной одно-
родной группы Лоренца 2+ (вместо расширенной одно-
родной группы Лоренца й).
Прежде всего мы должны сформулировать частный
случай первой теоремы Метэ и усиленную, форму второй
теоремы Метэ. Пусть й+ — открытое множество, полу-
чаемое выбрасыванием из E't нижней части светового ко-
нуса вместе с вершиной.
Теорема. Отображение /(«)->¦/ (р2) простран-
ства непрерывных функций на R1 в пространство
непрерывных функций на Et, рассматриваемых

$ 4. Лоренц-инвариантные скалярные обобщенные функции 119
только на 2+ и инвариантных относительно й,
может быть единственным образом продолжено
до линейного топологического изоморфизма Ти-*ТР%
из ^'(R1) в &'(Q+). Образ пространства S'(R!)
при атом отображении содержит все обобщенные
функции на 2+> инвариантные относительно соб*
ственной однородной группы Лоренца.
Замечания. В этом частном случае мы объединили
утверждения, разделенные в случае пространства Е'4 — {0}
на две части (первая и вторая теоремы Метэ). Доказа-
тельство этой теоремы мы здесь не приводим. Справед-
ливы также соответствующие теоремы, в которых
вместо 2+ берется 2_ — открытое множество, получае-
мое вычитанием из Е'А верхней части светового конуса
вместе с вершиной.
Заметим, что 2+ и 2_ инвариантны относительно соб-
ственной однородной группы Лоренца.
Теорема. Пусть Т—обобщенная функция, опре-
деленная на Е'4—{0} и инвариантная относительно
собственной однородной группы Лоренца й^. Тогда
в 2+ обобщенная функция Т является прообра-
зом Тр% обобщенной функции Та на R1, в«2.^
прообразом Т^г обобщенной функции Тп на R1, при-
чем функции TZ и Тп совпадают в области и > 0
в R».
Обратное утверждение. Если даны две обоб-
щенные функции Ти, TZ на прямой R1, которые сов-
падают при и > 0, то их прообразы Т^% и Т^ совпа-
даю/Н на 2+ П 2_ и пара (Тр, Тр) определяет обоб-
щенную' функцию на E't—{0}, инвариантную отно-
сительно собственной однородной группы Лоренца 2+.
Доказательство теоремы. Пусть Г—любая
обобщенная функция на Е'А—{0}, инвариантная относи-
тельно й|; Т определяет обобщенную функцию на 2+,

120 Гл. 4. Элементарные частицы и инвариантность
которая также инвариантна относительно й+. Согласно
частному случаю второй теоремы Метэ, обобщенная функ-
ция Т на 2+ является прообразом 7$ обобщенной функ-
ции Ти на R1. Аналогично Т определяет обобщенную
функцию на 2_, инвариантную относительно й+. Поэтому Т
является прообразом Тр\ на 2. обобщенной функции Тй
на R1. В области Q+ Л 2_ прообразы Тр\ и Трг должны
совпадать. Так как 2+ П 2_ является прообразом области
« > 0 в R1, то обобщенные функции Т% и 7? должны
совпадать при и > 0 в R1.
Доказательство обратного утверждения.
Возьмем две произвольные обобщенные функции Тц и Тц,
совпадающие при и > 0 в R1. Согласно первой теореме
Метэ (частный случай), Та определяет обобщенную функ-
цию Tpi на 2+1 инвариантную относительно 8+. Подоб-
ным же образом Тп определяет обобщенную функцию 7^
на 2_, инвариантную относительно й|. Так как 7"j" и Тй
совпадают при и > 0 в R1, то их прообразы 7^и 7^
совпадают на 2+|"|2_ (прообразе области и > 0). Таким
образом, (Трг, Тр) определяют обобщенную функцию на
Е'ц— {0} =2+ U 2_, инвариантную относительно группы 8?,
Мы видим, что нахождение всех обобщенных функций
на Е'4— {0}, инвариантных относительно собственной одно-
родной группы Лоренца, эквивалентно нахождению всех
пар обобщенных функций на R1, которые совпадают при
и>0.
§ б. Описание всех мезонов
Рассмотрим однополостный гиперболоид A). Он опре-
деляется уравнением p2 = k2, где k2 — положительная
константа. Мы ищем меру с носителем на гиперболоиде A),
инвариантную относительно собственной однородной группы
Лоренца. Согласно результатам, вытекающим из теорем
Метэ, она определяется двумя обобщенными функциями
Tpt, Tp\, являющимися прообразами двух обобщенных

§ 5. Описание всех мезонов 121
функций Г„, Г„, которые совпадают при а>0 в R1.
Согласно сделанному выше замечанию, носители обобщен-
ных функций Ти и Гц состоят из одной точки k2 в R1.
Таким образом, мы получаем две меры Т%, Тп с носи-
телями в точке k2, совпадающие при и > 0 и, следова-
тельно, на всей вещественной прямой.
Изоморфизмы, фигурирующие в теоремах Метэ, сохра-
няют порядок в пространстве обобщенных функций,
поэтому, чтобы получить меру на Е^—{0}, мы должны
взять меру на R1. Единственной с точностью до постоян-
ного множителя положительной мерой с носителем
в точке k2 является обобщенная функция Ьи_кг. Оконча-
тельно мера на Е'А— {0} определяется двумя обобщенными
функциями Метэ 8P2_fta, 8P2_ftJ, а так как они совпадают,
то достаточно только одной обобщенной функции 8pi_jj
для определения нашей положительной меры на Е'А—{0}.
Так как носитель ¦ этой меры является гиперболоидом A),
не содержащим начало координат, то существует только
одна инвариантная обобщенная функция в пространстве E'lt
для которой гиперболоид A) является носителем. Эта
обобщенная функция определяется двумя обобщенными
функциями
Ьр,_к, на %-{0} и 0 на Е'4~Ср:р^Щ.
которые определены на открытых множествах и совпа-
дают на их пересечении, причем E't является объединением
этих открытых множеств. Таким образом, мы определили
в пространстве Е\ обобщенную функцию, которую мы
будем обозначать просто через 8p2_fta.
Из теоремы, доказанной Метэ, следует, что изомор-
физм Гц->ГР1 сохраняет также степенной порядок роста.
Таким образом, обобщенная функция, инвариантная отно-
сительно собственной или полной группы Лоренца,
ярл;ется обобщенной функцией степенного роста тогда
и только тогда, когда соответствующая обобщенная функ-
ция (или пара обобщенных функций) на прямой линии
является обобщенной функцией степенного роста. Поэтому

122 Гл. 4. Элементарные частицы и инвариантность
Sps_ft2—обобщенная функция степенного роста, так как
Ьа-кг—обобщенная функция степенного роста.
Итак, мы знаем теперь, что существует единственная
с точностью до постоянного множителя положительная
мера, а именно 8р»_»з в пространстве Е'А, с носителем на
гиперболоиде A), инвариантная относительно собственной
однородной группы ЛоренЦа. Эта мера «ксрремальна,
потому что она единственна с точностью до постоянного
множителя. Взяв соответствующий класс гильбертовых
пространств, мы увидим, что лйбой однополостный ги-
перболоид определяет одну и только одну частицу.
Эти частицы физически не приемлемы, если принять
постулат о положительной определенности энергии.
Рассмотрим теперь двуполостный гиперболоид B).
В этом случае существуют две орбиты: нижняя ветвь
и верхняя ветвь. По тем же соображениям, что и ранее,
находим, что любая обобщенная функция, инвариантная
относительно собственной группы Лоренца и имеющая
носителем верхнюю ветвь гиперболоида B), определяется
в смысле Метэ двумя обобщенными функциями
», 0.
Аналогично любая обобщенная функция, инвариантная
относительно собственной группы Лоренца и имеющая
носителем нижнюю ветвь, определяется парой функций
О,
В силу сохранения порядка роста при соответствии
в смысле Метэ эти обобщенные функции имеют степен-
ной рост. Таким образом, каждая ветвь двуполостного
гиперболоида B) определяет частицу, т. е. мы получаем
частицы, зависящие от параметра k2 > 0 и знака ±, при-
чем считают, . что минус соответствует верхней ветви,
а плюс — нижней.
Такие частицы изучаются в физике. Физики полагают
Где mQ называется массой покоя частицы, с — скорость
света, h — постоянная Планка. Параметр ± «оответ-
твуег заряду частицы.

§ 5. Описание всех мезонов 123
Для нулевой массы, т. е. когда &2 = 0, задача несколько
усложняется. Верхняя часть поверхности светового конуса
без вершины является одной из орбит. Аналогично, ниж-
няя часть без вершины является другой орбитой. Мера (а
на Е'А— {0} с носителем в верхней части конуса задается
обобщенными функциями Метэ
Мы хотим теперь распространить эту меру на Е'А. Но-
ситель этой продолженной меры, если он существует,
является поверхностью верхней части светового конуса
включая вершину. Продолжение этой меры на Е'А суще-
ствует только в том случае, когда мера любого компакт-
ного множества, содержащего начало координат, конечна.
Оказывается, что мера может быть конечной в том
и только в том случае, когда размерность пространства
не меньше трех. Так как в нашем случае размерность
равна четырем, то рассматриваемую меру можно продол-
жить на с'4. Однако это можно сделать бесконечным чи-
слом способов, так как можно добавить в вершине меру
Дирака 8, умноженную на любую константу. Заметим, что
если п=±2, то не существует частицы нулевой массы.
Меру [х можно единственным способом продолжить
на Е'4, если мы условимся считать," что начало координат
{0} имеет нулевую меру.. Это продолжение определяется
формулой
где интеграл берется по Е'^—{0}; здесь <р—любая не-
прерывная на Щ функция с компактным носителем. К этой
мере можно добавить меру Дирака, умноженную на про-
извольную константу. Однако, если мы потребуем, чтобы}
мера была экстремальной, мы увидим, что верщина дол?.
жна иметь нулевую меру, так как
и, следовательно, мера ^ —J— XS не экстремальна при

124 Гл. 4. Элементарные частицы и инвариантность
Аналогично может быть продолжена на Е'А мера с но-
сителем в нижней части конуса.
Подводя итог, подчеркнем, что существуют три типа
частиц:
1) особая частица — вакуум;
2) частицы, определяемые уравнением р2 = k2, k2 > 0;
3) частицы, определяемые уравнением р2 = — k2,
k? ;> 0, и знаком ±.
Частицы C) физически приемлемы. Заметим, что эти
частицы могут иметь любую положительную массу. Однако
до сих пор известны только мезоны, массы которых при-
надлежат дискретному множеству положительных чисел,
Следовательно, либо требуется дополнительный принцип
отбора масс, либо следует ожидать, что будет открыто
все большее число мезонов с произвольными массами.
§ 6. Описание пространства ?№ в случае мезона
Рассмотрим теперь более детально пространство е%?т„, ±.
Это гильбертово пространство представляет частицу
с массой покоя т0 и зарядом -)- или —. Мы рассматри-
вали гиперболоид в Е[, определяемый уравнением
где
Верхняя и нижняя ветви отвечают соответственно отрица-
тельному и положительному зарядам. На каждой ветви
этого гиперболоида существует единственная с точностью
до постоянного множителя положительная лоренц-инва-
риантная мера. Например, на положительной ветви мера'
определяется по теореме Метэ прообразом пары обобщен-
ных функций
@. 8u+m.)
на R1. т. е. парой
@. V+"*1)'

§ 6. Описание пространства &6 в случае мезона 125
Эту меру можно записать в классических обозначениях
в виде
где Y — функция Хевисайда.
Если мы выберем начало координат в Е4, то имеет
смысл преобразование Фурье <&~еЮ пространства gf6\
<&~&в представляет собой гильбертово пространство Л,?
обобщенных функций на Е4 вида /(а, где / — квадратично
интегрируемая функция по отношению к мере \х.
Скалярное произведение в Л^ записывается в виде
Обобщенная функция H?dr'(E4) задается выражением
Н =
и соответствующее антиядро К определяется формулой
х'у х-у'
Метэ вычислил некоторые прообразы Фурье, которые
можно использовать при нахождении явного выражения
для Я1). Введем обобщенную функцию
B 2 \
где p.v.—главное значение в смысле Коши, Л^ — функ-
ция Неймана, Кг — функция Кельвина.
По определению главного значения, обобщенная функ-
ция p. v. /, где /—приведенное выше выражение в
') Преобразование Фурье функций вида BpI+ej вычислены
также в книге И. М. Гельфанда и Г. Е. Шилова,
Обобщенные функции, вып. 1, изд. 2, М., 1961. — Прим. ред.

126 Гл. 4. Элементарные частицы и инвариантность
квадратных скобках, задается формулой
где ер — основная функция.
Точно так же
= Ж[е (Ро) § (р2 4-^-
где
и У] — функция Бесселя. Тогда можно доказать, что
где
Д' —
Д+
Преобразования Фурье сохраняют четную и нечетную сим-
метрию относительно начала координат и заменяют черту
(комплексное сопряжение) на тильду: у (лг) = <р(—х).
Далее, функция 8 г sis четна, и так как эта функция
Р +NIqC /Л
вещественна, то она инварианта по отношению к операции
тильда. Поэтому Д' является четной обобщенной функцией,
инвариантной относительно комплексного сопряжения,
т. е. вещественной. Аналогично получаем, что /Д — не-
четная чисто мнимая обобщенная функция.
Все элементы ф ? ??в оказываются обычными функ-
циями; напротив, Й — обобщенная функция. Любой эле-
мент ф ? &в удовлетворяет дифференциальному уравнению
Клейна — ГордонаJ).
') Здесь ?—дифференциальный оператор Даламбера:
П=-2 "Пг" — ТТ — ТТ~"^Т- —Прим. ред.

§ 6. Описание пространства &9 в случае мезона 127
Это уравнение выводится с помощью преобразования Фурье
где /t* — мера с носителем на гиперболоиде
= 0.
Эта мера аннулируется при умножении на р2-\~-
т. е.
=о.
Обратное преобразование Фурье этого уравнения дает
уравнение Клейна— Гордона. Поскольку мы получили
оператор Даламбера с помощью преобразования Фурье,
его следует понимать в смысле обобщенных функций;
поэтому функция ф не имеет, вообще говоря, вторых
производных в обычном смысле.
Гильбертово пространство ??в состоит не из всех ре-
шений уравнения Клейна — Гордона. Во-первых, суще-
ствуют решения, не являющиеся обобщенными функциями
степенного роста и поэтому не принадлежащие фв.
Далее, рассмотрим произвольное решение уравнения
Клейна — Гордона, имеющее степенной рост. Преобразо-
вание Фурье этого решения имеет носитель на объеди-
нении двух ветвей двуполостного гиперболоида. Только
в специальных случаях носителем является одна ветвь,
поэтому не все решения уравнения Клейна — Гордона сте-
пенного роста принадлежат &в. Существует, кроме того,
еще дополнительное ограничение на Фурье-образы эле-
ментов пространства J#: они должны быть мерой вида /jj.,
где функция / квадратично интегрируема по отношению
к р.

Глава 5
ВЕКТОРНЫЕ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
И ИХ СВОЙСТВА
§ 1. Векторные частицы
Пусть V = ЕА, a F — конечномерное векторное про-
странство над полем комплексных чисел С. Пусть струк-
турная группа О удовлетворяет следующим условиям.
A) О действует на Е4 как неоднородная собственная
группа Лоренца, т. е. задано представление группы О
в аффинной группе пространства ЕА, образом которого
является неоднородная собственная группа Лоренца.
B) Для любого сдвига a f Е, существует элемент g+ ? О,
который действует как сдвиг а на аффинном простран-
стве Е4 и тождественно на F.
Заметим, что в силу условия A) группа О сохраняет
меру Лебега.
Рассмотрим элементарную частицу $@cz?B' (V; F).
Говоря, что О действует на F, мы подразумеваем, что
в пространстве F задано линейное представление груп-
пы О. Обычно говорят, что обобщенная функция
T^Sb'Q/; F) принимает значения в подпространстве Fx
пространства F, если для любой функции <р ? 3> (V) имеем
Теорема. Пусть ^в—элементарная F-частица.
Сделаем два следующих предположения.
(I) Не существует подпространства Fo прост-
ранства F, F^F, такого, что все элементы ф?е%?
принимают значения в Fo.
(II) Представление группы О в пространстве F
приводимо.
Тогда существует линейное подпространство Fl
пространства F, О-инвариантное и обладающее
следующими свойствами.

§ 1 Векторные частицы 129
(а) Существует изометрия пространства <Ш на
F°-4acmuity S^°, где F° = FIFV
(б) Факторпредставление группы G в F0 непри-
водимо.
Доказательство. Пусть F1 является О-инвариант-
ным собственным подпространством пространства F. Пусть
е%?, — подпространство всех элементов ф ? 36, прини-
мающих значения в F-^ Sf6x — замкнутое линейное под-
пространство пространства ?Ю. Так как пространство F,
О-инвариантно, ?ЮХ также G-инвариантно. Частица S№
является элементарной, поэтому либо $0г = J5?, либо
^, = {0}. Но, согласно (I), равенство е№л = 3в не вы-
полняется. Следовательно, ©>??, = {0}.
Пусть it—каноническая проекция пространства F на
F° = F/Fv Каждая обобщенная функция ф со значениями
в F канонически определяет обобщенную функцию ф со
значениями в F0 по формуле
Для o?G, f^F° положим
"/=("/)¦;
правая часть равенства не зависит от выбора /^/, так
как F1 инвариантно относительно о. Пусть Шй — множе-
ство всех обобщенных функций <{>'• для ф, принадлежащих
пространству &€. Разумеется, $@ос=& (V; F0) и в 3@°
действует группа G. Если ф = 0, то ф принимает значе-
ния в F1 и, следовательно, ф = 0, так как 36г = {0).
Поэтому отображение ф->ф из <!0в на Звй взаимно од-
нозначно.
Можно перенести структуру гильбертова пространства
из &6 в &в*. Если представление группы б в f° при-
водимо, мы можем продолжать таким же образом и при-
менять предыдущие соображения к F0 вместо F. Так как
размерность пространства F конечна, этот процесс при-
ведет после конечного числа шагов к пространству F0,
обладающему свойством (б).
Эта теорема показывает, что можно ограничиться эле-
ментарными F-частицами,, для которых представление
9 Л. Шварц

130 Гл. 5. Векторные элементарные частицы
структурной группы О в F неприводимо. Точнее, теорема
показывает, что если это условие не выполняется, то изу-
чаемую /'-частицу можно рассматривать как /^-частицу,
где F°— некоторое векторное пространство, на котором
группа О неприводима. Следует, однако, отметить, что
в общем случае не существует способа канонического
определения пространства F0.
Мы предположили, что для любого сдвига а?Е4 су-
ществует элемент g-> структурной группы G, действую-
л
->
щий как сдвиг а на ?4 и тождественно на F. Следующая
теорема показывает, что это верно в широком классе
случаев (примером этого является случай электрона, для
которого О — собственная спинорная группа).
Теорема. Пусть F — конечномерное векторное
пространство над полем комплексных чисел С а
О — топологическая группа, действующая неприво-
димо на F. Пусть О действует на F непрерывно,
т. е. отображение
(g. x)?GXF-^gx?F
непрерывно. Пусть О0 — подгруппа группы О, обла-
дающая следующими свойствами:
A) О0 — коммутативная группа, являющаяся нор-
мальным делителем группы О;
B) единственным характером группы О0, инва-
риантным относительно связной компоненты
единицы группы О, является характер -?^1.
Тогда О0 действует тождественно на F.
Замечания. Элементы о ? G действуют на. О0 как
внутренние автоморфизмы
Действие оператора а на характеры нормального дели-
теля Go определяется с помощью переноса структуры,
т. е. если i—характер подгруппы О0, то о^—новый
характер подгруппы Go> определяемый равенством

§ 1. Векторные частицы 131
Покажем, что для электрона условия теоремы выпол-
няются. В этом случае О — собственная спинорная группа,
двукратно накрывающая собственную неоднородную груп-
пу Лоренца. Образом группы О в аффинной группе про-
странства Е4 является собственная неоднородная группа
Лоренца, причем любой элемент группы Лоренца является
образом двух различных элементов группы О. Подгруп-
пой Go в этом случае является связная компонента еди-
ницы прообраза в О группы сдвигов.
Для того чтобы проверить для электрона условие A),
заметим сначала, что группа сдвигов коммутативна и
является нормальным делителем в собственной неоднород-
ной группе Лоренца. Прообраз нормального делителя
также является нормальным делителем. Кроме того, если
подгруппа является нормальным делителем, то тем же
свойством обладает связная компонента единицы. Следо-
вательно, О0 — нормальный делитель группы О. С другой
стороны, подгруппа О0 коммутативна, так как она изо-
морфна группе сдвигов.
Чтобы проверить второе условие для электрона, мы
должны сначала доказать, что единственным характером
->
группы сдвигов Е4, инвариантным относительно собствен-
ной неоднородной группы Лоренца, является характер .
Х=1- Дуальное пространство ?4 канонически изоморфно
пространству характеров на Е4. Собственная неоднород-
ная группа Лоренца связна. Ее действие на Е4 с помощью
внутренних автоморфизмов совпадает с обычным действием
собственной однородной группы Лоренца. Поэтому она
действует на характеры так, как собственная однородная
группа Лоренца действует обыкновенно на дуальном про-
<-/ ¦ '
странстве Е\. Нам нужно только найти те точки про-
<-/
странства Еь которые являются лоренц-инвариантными.
Но такой точкой является лишь начало координат,
а начало координат определяет характер х—*• Отсюда
следует, что условие B) выполняется для электрона, ибо
подгруппа О0 изоморфна группе сдвигов, и элементы
a?G действуют на О0 так же, как элементы собственной
неоднородной группы Лоренца действуют на ЕА.
9*

132 Г л. 5. Векторные элементарные частицы
Доказательство теоремы. Для любого конеч-
номерного комплексного представления абелевой группы
существует по крайней мере один собственный вектор,
общий для всех операторов представления, поэтому для О0
->
существует собственный вектор /:
-> ->
gof = X(go)f Для любого элемента go?Go,
где X (g0) — комплексная функция от g0 ? О0.
Так как представление группы О непрерывно, ска-
ляр х(?о) определяет непрерывную функцию на О0, ко-
торая является характером, поскольку
X (Sogi) = X (tfo) 1 (8i)-
->
Таким образом, для любого собственного вектора / мы
получаем соответствующий характер j(. Несколько соб-
ственных векторов могут соответствовать одному и тому
же характеру у. Пусть FxaF— максимальное подпро-
странство, образованное собственными векторами, та-
кое, что Go действует на Fx как умножение на харак-
тер Х- Пусть [Fj] — набор таких подпространств F%,
где х пробегает множество характеров подгруппы О0.
Число таких подпространств Ft конечно. В самом деле,
достаточно показать, что для любой минимальной линейно
зависимой системы векторов (эта система конечна, по-
скольку пространство F конечномерно), каждый из кото-
рых отвечает своему характеру, эти характеры тожде-
ственны между собой.
Пусть
— минимальная линейно зависимая система векторов, каждый
из которых соответствует своему характеру fa. Любая
система к — 1 векторов et линейно независима, и мы
имеем
для некоторого набора ненулевых комплексных чисел
Применяя операцию ^0 ? О0, получаем

§ 2. Описание всех векторных частиц 133
Если бы числа XiiSo) не все совпадали, можно было бы
скомбинировать эти два равенства и получить в резуль-
тате зависимость между меньшим количеством векторов.
Но это невозможно. Следовательно, характеры
Хл> & Ik
принимают одно и to же значение на g0, и, так как это
верно для любого g0, эти характеры тождественны.
Любой1 оператор о ? О действует на F и на Ga. Так
как О0—нормальный делитель группы G, то а оставляет
инвариантным действие Go на F, Следовательно, опера-
тор о должен оставлять инвариантной совокупность под-
пространств {Fj} (но соответствующие характеры х* могут
при этом переставляться). Если элемент группы О остается
в связной компоненте единицы и действует непрерывно
на этом конечном множестве характеров ул, то он не
может переставить их и оставляет все Хг инвариант-
ными.
Но мы предположили, что единственный характер
в подгруппе, инвариантный относительно связной компо-
ненты единицы,—это характер х —*• Поэтому суще-
ствует только одно максимальное подпространство Ft,
такое, что группа О действует на F1 как умножение на
характер Xi> и этот характер ii должен быть равен 1.
Поэтому группа О оставляет пространство F-y инвариант-
ным.
Так как представление группы О в F неприводимо,
то Fj^ — F, и, следовательно, О0 действует на F тожде-
ственно, что и требовалось доказать.
§ 2. Описание всех векторных частиц
Сформулируем более точно нашу задачу. Нам заданы
многообразие V = Eit конечномерное векторное простран-
ство F над С и группа Ли G, удовлетворяющая следую-
щим условиям:
A) О сохраняет меру Лебега на Е4, т. е. любой опе-
ратор о ? G имеет определитель ± 1 как оператор
->
на Е4;

134 Гл. 5. Векторные элементарные частицы
B) для любого сдвига в аффинном пространстве Е4
существует по крайней мере один элемент груп-
пы О, который действует как этот сдвиг на Е4
и тождественно на F.
Мы ищем экстремальные О-инвариантные гильбертовы
пространства J^ciP(?4; F) с непрерывным вложением
в 3 (Е^, F). Как мы видели, это эквивалентно отысканию
¦*¦
положительной О-инвариантной экстремальной меры р сте-
пенного роста в Е\ со значениями в пространстве F®F.
¦*¦
Мы нашли необходимое условие экстремальности меры (л,
->
которое заключается в том, что носитель меры (а должен
лежать в замыкании одной из О-орбит. В случае мезона
мы взяли в качестве О собственную неоднородную группу
Лоренца и положили F = C. Мы описали положительные
О-инвариантные экстремальные скалярные меры р степен-
ного роста.
Те меры, которые соответствуют физически приемле-
мым частицам, имеют носителями одну из ветвей двупо-
лостного гиперболоида (или одну из ветвей конуса в слу-
чае нулевой массы), и, таким образом, носители зависят
от параметров т0 и ±. Векторная мера ;а также будет за-
висеть от параметров т0, ± и некоторых других. Мы пока-;
жем, что для векторных частиц (когда О является собственной
спинорной группой), если оставаться на двуполостном гипер-
¦*¦
болоиде (т. е. т0 Ф 0), то мера |а должна иметь вид
-»< -> ->¦
р. = AIjj., где (а— найденная для мезона мера, а М — беско-
нечно дифференцируемая медленно растущая на бесконеч-
ности О-инвариантная экстремальная функция на гипер-
болоиде, принимающая значения в пространстве F®F.
Пусть W — многообразие класса С°°, а О — группа Ли,
действующая на U^. Предположим, что (g, x)—>gx—отобра-
жение класса С°° из G \W на U^. Мы покажем, что
любая О-орбита является многообразием в некотором
локальном смысле, который мы сейчас уточним. Позднее
нам понадобится предположение о том, что рассматри-
ваемые О-орбиты являются замкнутыми многообразиями.

§ 2. Описание всех векторных частиц 135
Рассмотрим отображение s—>sa, где s?O, a
. Это отображение принадлежит классу С°°, и, сле-
->¦ ->
довательно, определено касательное отображение X ->Ха,
-> ->
где X — касательный вектор в точке s группы О, а Ха—
касательный вектор в точке sa Многообразия U^. В част-
ности, если X—элемент алгебры Ли © (т. е. касатель-
ного пространства к рассматриваемой группе в единице),
то Ха—касательный вектор в самой точке а. Таким
образом, мы видим, что любой элемент алгебры Ли ®
определяет посредством этого отображения вектерное поле
на W (где а пробегает все многообразие W).
Стало быть, мы имеем линейное отображение из
алгебры Ли ® в векторное пространство всех векторных
полей на U^.
Для данной точки а ? W область ¦ значений отображе-
ния s—>sa является в точности орбитой точки а.
Пусть 3№, Ш'—два многообразия класса С°°, и—отобра-
жение класса С°° из Ш в Ш', ta—касательное отобра-
жение. Для любой точки m многообразия Ш сужение
отображения ta на касательное пространство Г (/и) к Ш.
в точке m является линейным отображением из Т(т)
в касательное пространство Т'{т') к многообразию W
в точке т' = и (т). Размерность образа пространства Т (т)
при этом отображении называется рангом отображения и
в точке т.
Применим это определение к 2№=G, W=W и к отобра-
жению s—>sa, когда точка a?W фиксирована.
Теорема. Отображение s->sa является отобра-
жением постоянного ранга.
Доказательство. .Любая точка s0?G определяет
левый сдвиг на G, который является изоморфизмом группы О
на себя. Следовательно, касательное отображение, соот-
ветствующее такому сдвигу, является в каждой точке линей-
ным изоморфизмом (на) соответствующих касательных про-
странств. В частности, отображение

136 Гл. 5. Векторные элементарные частицы
представляет собой линейный изоморфизм алгебры Ли ©
на касательное пространство группы G в точке s0. Любой
элемент X в касательном пространстве к О в точке s0
может быть записан в виде
где Y — элемент алгебры Ли. Так как G действует на
многообразии W как группа, мы можем написать
для s0, у ? О. Дифференцируя это равенство, получаем,
что этот ассоциативный закон выполняется также и для
касательных векторов
(sf) a = so(Ya).
Таким образом, имеем
Y
Ранг отображения s->sa в точке s0 равен размерности
векторного подпространства Д5о = {Ха : X принадлежит
касательному пространству к О в точке so}= {sQ(Ya): Y ? Щ.
Размерность подпространства
Ae={Ya:Y?®}
равна рангу отображения s->sa в точке s = e (е — еди-,
ничный элемент группы О). Пространство ASl) получается
из Ае с помощью отображения ^0 (касательного отобра-
жения, соответствующего преобразованию s0 : W -> W). Так
как s0—автоморфизм многообразия U^, то ^0 определяет
линейные изоморфизмы (на) касательных пространств.
Следовательно,
dim AS<1 = dim Ae.
Множество Оа элементов s?G, таких, что sa = a
(точка а ? W фиксирована), является подгруппой группы О
и называется стабилизатором (или стационарной под-
группой) точки а.
Пусть точка a?W фиксирована, и пусть р — ранг
отображения s~>sa. Касательное отображение Х->Ха,
рассматриваемое на касательном пространстве к О в произ-

§ 2. Описание всех векторных частиц 137
вольной точке s0, является, как показано выше, линейным
отображением ранга р. Возьмем в качестве $0 точку е—еди-
ничный элемент группы О. Согласно классической теореме
об отображении постоянного ранга, существует окрест-
ность $ точки е в G, такая, что множество {sa : s ? $}
само является многообразием класса С°° размерности р.
Более того, Оа (] $ — также многообразие, размерность
которого равнк разности между размерностями группы О
и орбиты. Стабилизатор Оа представляет собой много-
образие как локально, так и в целом. В самом деле, так
как Оа — замкнутая группа, такая, что ее пересечение
с окрестностью единичного элемента является многообра-
зием, то легко видеть, что Оа — группа Ли, а следова-;
тельно, и многообразие. , •
Касательное векторное пространство к пересечению
Оа[\$ в точке е, которое является алгеброй Ли ®а стаби-
лизатора Оа, представляет собой множество всех ' век-
торов X, для которых Ха = 0.
Любая точка орбиты обладает окрестностью в самой
орбите, которая является многообразием класса С°°. Но
может случиться, что орбита бесконечное число раз про-
ходит вблизи точки а, каждый раз все ближе и ближе,
таким образом, что пересечение любой достаточно малой
окрестности точки а в многообразии W с орбитой всегда
имеет бесконечное число компонент. В этом случае орбита
не может быть подмногообразием многообразия W.
Для того чтобы избежать такой неприятности, мы будем
предполагать, что орбита является замкнутым подмного-
образием многообразия W. Тогда размерность этого
подмногообразия равна постоянной р, потому что оно
является объединением не более чем счетного числа много-
образий размерности р, а, согласно теореме Бэра, объеди-
нение счетного числа многообразий размерности р также
чмеет размерности р. Когда G — группа Лоренца или спи-
норная группа, a W — E'4, рассматриваемые орбиты будут
настоящими гиперболоидами; световой конус исключается,
так как, согласно нашему предположению, орбиты должны
быть замкнутыми.
Чтобы получить дальнейшие результаты, используем
теорему о неявных функциях. Рассмотрим трансверсальное
10 Л. Шварц

138 Гл. 5. Векторные элементарные частицы
многообразие Е, проходящее через единичный элемент
е ? О, т. е. многообразие класса С°°, касательное про-
странство к которому дополнительно к касательному про-
странству стабилизатора Ga.
(Два векторных подпространства называются дополни-
тельными, если любой вектор пространства представим един-
ственным образом в виде суммы двух векторов, принад-
лежащих этим подпространствам').)
Это трансверсальное многообразие Е определяется выбо-
ром подпространства в ©, дополнительного к ©0. Мы
можем ограничить наши рассмотрения многообразием Е,
поскольку точка а ? W инвариантна относительно всех
$ ? Оа. Все пересечение орбиты с окрестностью точки а
можно получить, рассматривая действие на а только
операторов s? E.
Пусть 2 — орбита точки а; рассмотрим уравнение
y = sx, х, у ?2. s?E.
Рассматривая у как функцию от s, мы видим, что матрица
Якоби функции у по отношению к s (в допустимых ло-
кальных координатах для s вблизи е и для х, у вблизи а
в 2) является не чем иным как матрицей касательного
отображения (в базисе, определенном этими локальными
координатами). Для s = e, x = a это касательное отобра-
жение является изоморфизмом касательного пространства
к Е в точке е на касательное пространство к 2 в точке а.
Поэтому якобиан не может быть равен нулю. Ввиду этого
мы можем применить следующий результат.
Теорема о неявной функции. Существуют
окрестность X' точки а в орбите 2 и окрестность Е'
точки е в многообразии Е, такие, что для всех х?Х',
у ? X' уравнение
y = sx
имеет единственное решение s?E'. Это решение
можно записать в виде s = S(x, у), где S — функция
класса С°° на X' X X' со значениями в Е'. Более того.
') То есть если все пространство является прямой суммой
этих двух подпространств. — Прим. ред.

§ 2. Описание всех векторных частиц 139
в силу непрерывности операции (s, x)—>sx суще-
ствуют окрестность X" точки а и окрестность ?"
точки s, где Х"аХ', такие, что для х?Х", s?S"
мы имеем sx ? X'. (Мы можем пойти еще дальше и
найти окрестность ХосХ" точки а и окрестность 20
точки е, такие, что для jc ? Хо, s ? 20 выполняется соотно-
шение s~*x ? X".)
->
Теорема. Пусть Т — обобщенная функция на
многообразии 2 со значениями в пространстве F ® F.
-> ->
Если Т G-инвариантна; то Т — бесконечно дифферен-
цируемая функция.
Замечания. В этом утверждении пространство F® F
можно заменить любым' конечномерным векторным про-
странством.
->
Напомним, что имеют в виду, когда говорят, что Т —
функция класса С°° на 2. Возьмем любое открытое под-
множесгзо U многообразия Q, в котором заданы локаль-
ные координаты. По определению эти координаты задают
бесконечно дифференцируемый гомеоморфизм подмно-
жества U на открытое подмножество U' пространства Rp
(р — размерность многообразия 2). Следовательно, суже-
ние Т на U определяет обобщенную функцию V в U'
(по-прежнему принимающую значения в пространстве
F ® F). Эта обобщенная функция Т' на U' должна быть
функцией класса С°° на U'. Иначе говоря, если мы выберем
в Rp меру Лебега dx, то найдется функции f (х) класса С"
на U', принимающая значения в F ® F и такая, что
{T')
для любой функции cp6-^(Rp) с носителем в U'. Описан-
->
ное свойство обобщенной функции Г не зависит ни от
выбора подмножества U и локальных координат на U,
ни от меры Лебега dx.
Доказательство теоремы. Пусть Ф — представ-
ление группы О в пространстве F®F. Из инвариантности
10*

140 Гл. 5. Векторные элементарные частицы
обобщенной функции Т следует, что
(Г, <р) = Ф(s)(Г, ср(sх)), ч?3B).
Мы должны доказать, что для любой точки а ? 2 обоб-
щенная функция Т бесконечно дифференцируема в неко-
торой окрестности точки а. Мы можем считать, что эта
окрестность совпадает с окрестностью Хо, которую мы
выбрали в теореме о неявной функции. Пусть ср ? 26 (Хо),
в.?3 (Ео). Положим ds — dsl ds2 ... dsp, где s( — кано-
нические координаты на 20. Если
то
(Г, <р> = J a (s) dsQ (s) (T, ср (sjc)>.
По определению тензорного произведения обобщенных
функций имеем
(Г, ср) = (а (Я) Ф (я) ® Тх. ср (sx)) =
Для вычисления интеграла достаточно рассмотреть только
те значения jc, в которых подинтегральная функция от-
лична от нуля, т. е. множество
{jc : sx принадлежит носителю функции ср,
s принадлежит носителю функции а).
Но носитель функции ср содержится в Хо, а носитель
функции а содержится в 20. Полагая sx = у, находим,
что достаточно рассматривать jc в множестве
По теореме о неявной функции это множество содер-
жится в X", так что достаточно рассмотреть х ? X"; для
х^Х" подинтегральное выражение равно нулю. Исполь-
зуем выражение s = S(x, у) для перехода от перемен-
ной s к новой переменной у (при фиксированном jc). Мы
должны проверить, что области интегрирования правильно

§ 2. Описание всех векторных частиц 141
определены как в старых, так и в новых переменных,
и что замена переменных определяет изоморфизм между
этими областями с отличным от нуля якобианом. Отобра-
жение у -> s = S (х, у) при фиксированном х ? X" является
отображением из X' в 2'. Так как это отображение об-
ращается с помощью равенства
образом X' является открытое подмножество окрест-
ности Е'. Таким образом, это отображение определяет
гомеоморфизм класса С°° из X' в открытое подмножество
окрестности Е'.
Теперь мы должны показать, что образ окрестности X'
покрывает всю область интегрирования по переменной s,
т. е. мы должны показать, что носитель функции a (s)
содержится в образе окрестности X'. Если s принадлежит
носителю функции a (s), то s ? 20. Но л^ X", следова-
тельно, sx ? X', а это означает, что образ окрестности X'
при отображении s = S(x, у) при фиксированном х?Х"
покрывает Ео, а значит, и носитель функции a (s). Замена
переменных приводит к равенству
(Т, ?> =
dS
х, у))ФE(дг, у))<р(у) det-5-(jc,
оу
х, аE(дг, у))Ф(Я(*, y))\tet^-{x.
Далее, произведение
n(S(x, у))ФE(дг, у)) det-5—(д:, j
является бесконечно дифференцируемой функцией пере-
менной у в X'. Следовательно,
*. У))ФE(дг, y))
det||-(*,
•—также бесконечно дифференцируемая функция перемен-
ной у. Мы получаем
(Г, ср) = f ср (у) к (у) dy = (к, «р);

142 Гл. 5. Векторные элементарные частицы.
следовательно, Т = х — бесконечно дифференцируемая
функция переменной у.
Применим эту теорему к нашей задаче. Рассмотрим
в многообразии Q О-орбиту, которая является гипербо-
лоидом, и меру [а с носителем Q, которая определяет
обобщенную функцию на Q. По доказанной теореме,
р. — бесконечно дифференцируемая функция на Q. Тот же
самый результат справедлив для скалярной меры {*, т. е.
она является бесконечно дифференцируемой функцией.
Из инвариантности меры р следует, что она не обра-
щается в нуль, так как в противном случае она была бы
равна нулю тождественно. Поэтому мы можем определить
отношение [a|ji = ./W, которое должно быть бесконечно
дифференцируемой функцией на Q. Таким образом, мы
->
получаем, что \х можно записать в виде
где М — бесконечно дифференцируемая функция. Более
того, М инвариантна относительно группы О, так как М\х
преобразуется под действием оператора о ? G в другую
обобщенную функцию, которая определяет ту же самую
меру. Таким образом, М должна переходить в другую
функцию, которая почти всюду (в смысле меры р) равна
-> -> ->
функции М, но так как М непрерывна, то М должна
-*.
всюду совпадать с преобразованной функцией. Если ц
->
положительна, то и Ж должна быть положительной почти
всюду (в смысле меры [а), а так как она непрерывна, то
она всюду положительна.
Таким образом, наша задача свелась к отысканию на
гиперболоиде Q бесконечно дифференцируемой функции М,
принимающей значения в пространстве F®F, которая
была бы О-инвариантной, положительной, экстремальной
и имела степенной порядок роста на бесконечности. Возь-
мем точку а ? 2. Мы уже знаем, что М (а) — положитель-
ный Ов-инвариантный элемент множества F ®F. Обратно,

§ 2. Описание всех векторных частиц 143
-*¦
если положить М(а) равным любому положительному
Оа-инвариантному элементу множества F ® F, то можно
однозначным образом восстановить бесконечно дифферен-
цируемую функцию М на Q, которая принимает значения
в Z7®/7, является О-инвариантной, положительной, экстре-
мальной и имеет степенной рост на бесконечности. Эта
функция определяется формулой
-*¦
где р = <за\ М(р) не зависит от выбора о, так как если
имеется другой элемент о', переводящий точку а в точку р,
то он должен иметь вид <з'= а-\, где f ? Оа, а отсюда
следует, что
а'М (а) — о? Л! (а) = аМ (а)
-*¦
в силу того, что элемент М (а) инвариантен относительно
-*¦
подгруппы Оа. Покажем теперь, что М (р) — бесконечно
дифференцируемая функция. Будем считать, что окрест-
ность Na точки а в Q достаточно мала для того, чтобы
можно было применить теорему о неявной функции.
В этом случае можно взять в качестве о элемент S(a, p),
где 5 определяется теоремой о неявной функции. Таким
образом,
M(p) = S(a, р)М(а),
а так как S(a, p) является функцией класса С°°, мы
видим, что М(р) — функция класса С°° в окрестности Na
точки а. Если мы возьмем теперь любую точку Ь, то
существует элемент о0, такой, что b — oQa. Множество
является окрестностью точки Ъ. Так как любую точку
p?Na можно записать в виде р = ва, где о = 5(а, р),
то отсюда следует, что любую точку q?Nb можно за-
писать в виде
q = o0S (a, p)a = aQS (а, а^д) а;

144 Гл. 5. Векторные элементарные частицы
тогда для q ? Nb имеем
M(q) = a0S(a, c^q)M(a).
-*¦
Поэтому M(q) является функцией класса С°° в окрест-
ности Nb. Мы доказали тем самым, что М является бес-
конечно дифференцируемой функцией на всем множестве 2.
Нам осталось доказать, что определенная таким обра-
зом функция М имеет степенной рост на бесконечности.
Предположим сначала, что О — собственная однородная
группа Лоренца. Рассмотрим систему координат в про-
странстве ?4, в которой точка а имеет вид а = ф, 0, 0, а^).
В равенстве
М(р) = вМ(а), р — аа,
-*¦
действие оператора о на М (а) определяется с помощью
представления Ф группы G. Поэтому для большей ясности
лучше писать
М (р) = Ф (о) М (а), р = <за.
Выберем какую-нибудь норму в пространстве F&F.
Тогда
\\М(р)\\^\\Ф(о)\\\\М{а)\\, р = оа.
Теперь достаточно показать, что ||Ф(о)|| медленно воз-
растает по отношению к р, где р = <за. Допустим, что р
имеет вид
p = (pv 0, 0, р0),
и рассмотрим преобразования Лоренца (б), зависящие от
параметра 6, на плоскости Р первой пространственной
оси и оси времени
A — #ich9-|-?osh9>
Так как за исходную точку принята точка @, 0, 0, а„),
мы получаем
/7, = aosh6,
р0 = а0 ch 6.

§ 2. Описание всех векторных частиц 145
Следовательно,
Ро~ а<Л
и поэтому для некоторой постоянной Cj имеем
I в К
Пусть теперь р — произвольная точка гиперболоида. Мы
можем перейти от точки а к точке р при помощи двух
последовательных преобразований Лоренца. Пусть х —
пространственное вращение (которое принадлежит стаби-
лизатору Ga точки а), переводящее р в плоскость Р;
положим р'=:хр. Пусть F) — описанное выше преобра-
зование в плоскости Р, переводящее а в р'. Имеем:
0 = 1-». (в)
Но пространственные вращения образуют компактную
группу линейных операторов в пространстве Ff&F, по-
этому все их нормы ограничены некоторой фиксирован-
ной константой. Тогда для некоторой константы С2
¦ ||Ф(о)||<С2||Ф((9))||.
Согласно общей теореме о представлении любой одно-
параметрической группы в нормированном пространстве,
которая утверждает, что норма оператора представления
ограничена некоторой экспонентой от параметра, справед-
лива следующая оценка:
где k — некоторое число. Так как |6| <^ logCj||//|[, та
можно записать
IIФ (F)) II < Q** 1о« Cl" *'«== QII/>Т-
Используя еще раз тот факт, чта пространственные вра-
щения образуют компактную группу, получаем оценку

146 Гл. 5. Векторные элементарные частицы
\\рг\\^. С$\\р\\ и> наконец, для некоторой константы Сй
находим
Цф((в))||<св|И*.
откуда следует, что ||Ф(о)|| имеет степенной рост, а зна-
чит, тем же свойством обладает и мера М.
Если G— любая группа, образ которой в линейной
<-,
группе пространства ?4 является собственной однородной
группой Лоренца, то однопараметрическую группу (б)
в этом образе можно „поднять" в группу G. Для этого
достаточно „поднять" соответствующий инфинитезимальный
оператор, и он породит в G однопараметрическую группу,
имеющую (б) своей проекцией. Таким образом, доказа-
->
тельство степенного роста функции М, приведенное выше,
остается справедливым и для группы G.
Тем самым мы показали, что все G-инвариантные гиль-
бертовы пространства <%№ с 3' (Е4; F) (с непрерывным
вложением), связанные с орбитой 2, т. е. с параметрами
/я0 > 0 и ±, взаимно однозначно соответствуют положи-
тельным Оа-инвариантным элементам М (а) ? F <gi F для
фиксированной точки а ? 2. Кроме того, гильбертово
пространство gf6 экстремально тогда и только тогда,
когда соответствующий элемент М(а) экстремален.
Применим теперь теорию ядер. Положительный Оа-ин-
вариантный элемент пространства F®F является положи-
тельным Оа-инвариантным антиядром для F, т. е. поло-
жительным антилинейным отображением F'—>F, которое
(/„-инвариантно. Нахождение этого антиядра эквивалентно
нахождению Оа-инвариантного подпространства Fa <r F,
снабженного эрмитовой структурой. Это подпространство
экстремально тогда и только тогда, когда соответствую-
щий элемент пространства F®F экстремален.
Методы отыскания всех Оа-инвариантных неприводи-
мых подпространств Fa пространства F известны. Допу-
стим, что найдено такое подпространство Fa; мы должны,
если это возможно, наделить Fa Оа-инвариантной эрми-
товой структурой. Пусть Та — образ Ga в линейной группе
подпространства Fa. Заметим, что

§ 2. Описание всех векторных частиц 147
где Gj — подгруппа группы Оа, которая действует то-
ждественно на подпространстве Fa. Наша задача состоит
в том, чтобы выбрать Га-инвариантную эрмитову струк-
туру на Fa. Необходимое и достаточное условие для су-
ществования такой структуры заключается в том, чтобы
группа Га была относительно компактной1). Для того
чтобы доказать это, предположим сначала, что Га оста-
вляет инвариантной эрмитову форму над Fa. Тогда Га
должна содержаться в унитарной группе, соответствующей
этой эрмитовой структуре.
Так как унитарная группа компактна, то группа Га
относительно компактна. Обратно, если Га относительно
компактна, мы можем выбрать на Fa любую эрмитову
форму и, усреднив ее по мере Хаара подгруппы Га, по-
лучить Га-инвариантную эрмитову форму. Эта Га-инва-
риантная эрмитова форма единственна с точностью до по-
стоянного множителя.
Итак, мы нашли все возможные решения нашей задачи,
соответствующие данной орбите Q. Повторим кратко этот
процесс. Мы отыскиваем в пространстве F все возможные
Оа-инвариантные и Оа-неприводимые подпространства Fa.
Для любого такого Fa, если образ Га группы Ga в ли-
нейной группе подпространства Fa относительно компактен,
существует единственная с точностью до постоянного мно-
жителя эрмитова форма, которая является Оа-инвариантной
и определяет векторную частицу. Если же образ Га не
является относительно компактным, это значит, что мы не
нашли никакой частицы.
В качестве примера предположим, что G — собственная
неоднородная группа Лоренца, V — E4 и F — любое
конечномерное векторное пространство. Пусть 2 — любая
ветвь двуполостного гиперболоида (но не конуса) в Е\.
Выберем точку а ? 2 и систему координат такую, что
в ней точка а имеет координаты @, 0, 0, а0). Стабилиза-
тор Ga является просто ортогональной группой в трех-
мерной пространственно-подобной плоскости, определяемой
тремя пространственными осями выбранной координатной
системы. Известно, что пространство F вполне приво-
') Множество Г называется относительно компактным, если
его замыкание Г компактно. — Прим. ред.

148 Гл. 5. Векторные элементарные частицы
димо '). Любому неприводимому подпространству простран-
ства F соответствует /^-частица, поскольку ортогональная
группа компактна. Если в этих неприводимых подпро-
странствах представления группы Ga не эквивалентны, то
такое разложение пространства F на неприводимые ком-
поненты единственно. Но некоторые представления могут
оказаться эквивалентными, и в этом случае мы имеем
бесконечное число возможных неприводимых подпро-
странств. Каждое из них определяет /•'-частицу. Мы не
будем здесь касаться вопроса, определяют ли одну и ту же
частицу два эквивалентных неприводимых представления.
Мы ищем только /^-частицы для одного данного предста-
вления. Наша задача отыскания всех /^-частиц решена
теперь для случая, когда G — собственная неоднородная
группа Лоренца, и легко видеть, что подобным же обра-
вом эта проблема решается, когда , G — собственная спи-
норная группа.
Совершенно иная задача возникает, если рассматривать
однополостный гиперболоид. Если на этом гиперболоиде
задана точка а, то выберем систему координат так, чтобы
координаты точки а имели вид (av 0, 0, 0). Стабилиза-
тор Ga является группой Лоренца по отношению к двум
последним пространственным и временнбй координатам.
Мы должны проверить, имеет ли пространство F непри-
водимые компоненты Fa, на которых Ga действует ком-
пактно (т. е. образ стабилизатора Оа в линейной группе
подпространства Fa является компактной группой). Напри-
мер, может случиться, что Ga тождественно действует на Fa.
Это как раз происходит в случае мезона, когда F — C
и вся группа G тождественно действует на С (и, конечно, Ga
также тождественно действует на С). Оказывается, что,
исходя из однополостного гиперболоида, мы можем полу-
чить только такие /^-частицы, для которых Ga действует
тождественно на Fa, поскольку единственная компактная
факторгруппа группы Лоренца — это группа, состоящая
из одной единицы.
') Пространство называется вполне приводимым (относи-
тельно некоторой совокупности операторов), если всякое инва-
риантное подпространство имеет инвариантное дополнение. —
Прим. ред.

§ 3. Полное описание преобразования Фурье 149
Пространство Fa в случае /и = 0
В случае т = О гиперболоид заменяется световым кону-
сом. Для любой точки а светового конуса (исключая вер-
шину) стабилизатор Ga является группой Лоренца каса-
тельной плоскости, которая изоморфна группе вращений
и сдвигов в двумерной евклидовой плоскости. Эта группа
имеет компактную факторгруппу — ортогональную группу
двумерной плоскости. Таким образом, для некоторых пред-
ставлений можно получить инвариантную функцию М (а),
а для других — нельзя. Например, для фотона и нейтрино
этого нельзя сделать. В физике известно, что фотоны и
нейтрино нельзя представить гильбертовыми простран-
ствами функций, но можно представить неотделимыми
предгильбертовыми полными пространствами (см. ниже § 5).
В таком пространстве движение задается классом ф функ-
ций, Эквивалентных в смысле так называемой калибровоч-
ной инвариантности.
§ 3. Полное описание преобразования Фурье
гильбертова пространства для векторных частиц
Мы сначала опишем функциональное пространство,
а потом покажем, что оно является преобразованием Фурье
гильбертова пространства <§№. Пусть а — заданная точка
на одной из ветвей Q двуполостного гиперболоида. Нам
задана скалярная мера {г с носителем Q и функция М (р),
определенная на 2. Для любой данной точки p?Q вели-
чина М (р) представляет собой положительный элемент
пространства Т7®/7, т. е. положительное антилинейное
отображение (положительное антиядро):
p
где подпространство Fp имеет Ор-инвариантнук> эрмитову
структуру, является Ор-неприводимым и соответствует
антиядру М{р) по теореме об антиядрах. Так как
М(р) = аМ(а)
для любого оператора о, такого, что р = аа, то Fp-=<iFa
для любого такого о, где aFa означает действие опера-
тора о на Fa в представлении группы G в пространстве F.

150 Гл. 5. Векторные элементарные частицы
Квадратичная форма на Fp под действием оператора в
переходит в квадратичную форму на подпространстве Fa.
Таким образом, для любой точки р ? 2 мы получаем под-
пространство FpdF, которое зависит от р и в котором
задана положительно определенная эрмитова форма, также
зависящая от р.
Определение. Пространством V-B, р, Fp, F) назы-
вается пространство, которое состоит из классов эквива-
лентных функций / (т. е. совпадающих почти всюду
в смысле меры р.), заданных на 2, принимающих значения
в F и обладающих следующими свойствами:
A) для любого p?Q имеем f(p)^Fp;
B) как вектор-функция / является ^-измеримой;
C) ||/(/0 ||р квадратично [А-интегрируема.
Обозначим эрмитову форму в F символом ( , )_ и
положим
Введем в Z.2(Q, p., Fp, F) скалярное произведение
(/. g)= ) (/(/>). g(P))pdp(p), f, g?L2(Q' t*. FP' H-
я
Соответствующая норма определяется выражением
\p\
J
Лемма. Если f является 2 -> F-функцией, удовле-
творяющей условиям A) и B) приведенного выше
определения, то неотрицательная функция \\f{p)\\p
^.-измерима.
Фиксируем а ? 2. Существует окрестность 2а точки а
в 2, такая, что для р ? 2а можно рассмотреть функцию
S(a, p) переменной р, принимающую значения вО и опре-
деленную по теореме о неявной функции; S(a, p) является
бесконечно дифференцируемой функцией Q.a—>G. Имеем
а, p)f(p)\\a,
Если /(/?) {г-измерима как функция Qa-*>F, то функция
S~1(a,p)/(p) ^.-измерима как функция Qa->F и как

§ 3. Полное описание преобразования Фурье 151
функция Qa->Fa. Отсюда следует справедливость леммы,
поскольку норма измеримой векторной функции (прини-
мающей значения в конечномерном пространстве) измерима
и измеримость является локальным свойством.
Теорема. L2(Q, ц, Fp, F) — гильбертово про-
странство.
Нам нужно показать лишь полноту этого пространства.
Пусть [fk] — последовательность Коши элементов про-
странства Z,2B, jj., Fp, F). Можно найти подпоследователь-
ность {/и \ (<х=1, 2, ...), такую, что
Положим,
Если мы докажем, что ряд 2 ?<, сходится в L2(Q, {г, F , F)
к элементу g этого пространства, то / = ?-+-/й, будет
пределом последовательности {/ft}.
Ряд
л=1 Я
сходится. Из свойств скалярных функций вытекает, что
существует множество NczQ меры нуль, такое, что ряд
оо
2 и*„ (/он,
сходится, если p^N.
оо
Но отсюда вытекает, что для p^N ряд 2 ?а(Р) схо"
дится в Fp\ пусть g (р) — его сумма. Для р ? N положим
оо
g (р) = 0. Ряд 2 Sa сходится почти всюду (в смысле
а=1
меры |*) к классу функций, эквивалентных g (который мы
также обозначим через g). Так как ga — измеримые функ-
ции из 2 в F, то по теореме Егорова то же верно для g.
Согласно лемме, норма \\g(p)\\p в этом случае измерима;

152 Гл. 5. Векторные элементарные частицы
применяя классический результат для неотрицательных
функций, находим, что
со
Отсюда следует, что g удовлетворяет условиям A), B), C)
определения. Теорема доказана.
Определение. Пространством Л2B, ц., Fp, F)
называется пространство всех мер /[а на сА, где
/?Z,2(9, ц, Fp, F). Пространство A2(Q, ц, Fp, F) снаб-
жено нормой
I
Пусть 3)(Q, F , F) — пространство функций y:Q->F
со следующими свойствами:
(I) для любого p?Q имеем <f(p)^Fp;
(II) tp как функция Q —> F является функцией класса С"
с компактным носителем.
Теорема. 35 (Q, Fp, F) является плотним подпро-
странством пространства L2(Q, (i, Fp, F). Анало-
гично множество {<pjx: (f> ^ 35 (Q, Fp, F)} является плот-
ним подпространством пространства Л2B, ц., Fp, F).
Доказательство. Любая функция
является пределом „срезанных" функций, т. е. функций,
равных / на некотором компактном подмножестве множе-
ства Q и нулю на дополнении к этому подмножеству (можно
взять возрастающую последовательность таких компактных
подмножеств, исчерпывающую Q). Поэтому достаточно
доказать, что любая функция f?L2 с компактным носи-
телем является пределом функций из 35 (Q, ft, Fp, F).
В действительности достаточно доказать, что для
любой точки а ? Q существует окрестность, такая, что
любая функция с компактным носителем, содержащимся
в этой окрестности, является пределом функций из
3)(Q, (л, Fp, F). Если это доказано, то любой компактный
носитель можно покрыть конечным числом таких окрестно-

§ 3. Полное описание преобразования Фурье 153
стей, и из разложения единицы немедленно вытекает, что
любая функция с компактным носителем, принадлежащая L2,
является пределом функций из 3 B, \х, F , F). Далее,
если задана точка a (j Q, то можно выбрать открытую
окрестность Qa в соответствии с теоремой о неявной функ-
ции так, что для любой функции / на Qa можно рассмо-
треть функцию g(p) = S~l (a, p)f(p). Таким образом,
в множестве Qa мы снова приходим к фиксированному
гильбертову пространству Fa с фиксированной нормой]] • |]а.
Однако известно, что функции
плотны в гильбертовом пространстве L2(Qa, \l, Fa).
Следовательно, функции <р (/?) = ? (a, p)ty(p) плотны
в L2(Q, ц., Fp, F). Кроме того, ср является функцией
класса С°°, поскольку ф и S принадлежат этому классу,
и имеет компактный носитель, так как этим свойством
обладает ф. Теорема доказана.
Пространство <зШ является дополнением пространства
всех элементов вида Я*ср, где у?3(E^®Ff, по норме
Мы можем также взять y??P{E^)®F'. Преобразова-
нием Фурье (см. стр. 90) тогда будет
где § = (уПр и <&~Н = Мр. Так как ф = о?"<р, то из
определения преобразования Фурье обобщенных функций
следует, что
= Г
Но М (р) определяет антилинейное отображение
задаваемое равенством
11 Л. Шварц

154 Гл. 5. Векторные элементарные частицы
так что
Положим
/()М(Ц() для
Мы видим, что f(p)(zFp для любой точки p?Q. Если
вместо произвольной функции (р ? S^ взять функцию
<f^S^(Et)®F', такую, что ее преобразованием Фурье
является функция ty?3(Et)(g)F , то мы получим функ-
цию /{л, где / — бесконечно дифференцируемая функция
Q-+F с компактным носителем, принимающая значения
в пространстве Fp; следовательно, fp?A2(Q, (x, Fp, F).
Норма функции /р в <&"?№ определяется равенством
поэтому
Но это последнее выражение имеет вид (е1, ?в'), и из
того, что (е1, Le')=\\Le'\\g€, где ^5?i — гильбертово
пространство, соответствующее антиядру L, следует, что
интеграл
равен норме функции / в пространстве L2(Q, p, Fp, F).
Отсюда мы заключаем, что
таким образом, доказана
Теорема.
то /0?) ?^B, Fp, F) и

§ 3. Полное описание преобразования Фурье 155
Пространство
является плотным подпространством пространства
по норме Л2. Если теперь показать, что это подпростран-
ство совпадает с пространством
которое плотно в Л2 = Л2B, [л, Fp, F), то мы получим,
что efJ$? = A2, так как 4?~?№ будет тогда конкретным
пополнением (т. е. пополнением, вложенным в Л2) плот-
ного подпространства пространства Л2. Для того чтобы
доказать совпадение этих двух множеств, мы докажем сле-
дующую лемму.
Лемма. Какова бы ни была функция / ? 35 (Q, Fp, F),
существует функция g(-35(Q)®F', такая, что
для любого p^Q.
Доказательство леммы. Пусть а—любая точка
пространства Q. Выберем базис в пространстве F'
[е\ ek' ё\ ?¦*}•
такой, что
является базисом пространства Fa. Тогда
является базисом пространства Fp для любого р ? 2.
Можно записать
Компоненты /'(/>) функции f (р) являются функциями
класса С°° на 2 с компактными носителями. Полагая
убеждаемся в справедливости леммы.
11*

156 Гл. 5. Векторные элементарные частицы
Если теперь g — бесконечно дифференцируемая функ-
ция на Q с компактным носителем (принимающая значения
в пространстве F'), то легко видеть, что на Q существует
функция ф? ?6(E'^®F', такая, что ty(p) = g(p) для лю-
бого р ? Q. Вместе с леммой это доказывает, что какова бы
ни была функция
. Fp, F),
существует такая функция ^^3^(E'^\®F', что
для любого />?2. Тем самым доказана
Теорема, t&'effl совпадает (как гильбертово про-
странство) с пространством Л2B, ц., Fp, F).
§ 4. Электрон
Дадим краткое описание случая электрона. В этом
случае F = С2, a G представляет собой накрывающую
группу собственной неоднородной группы Лоренца. Можно
показать, что существует изоморфизм класса С°° двукратно
накрывающей группы для собственной однородной группы
Лоренца (т. е. собственной спинорной группы) на уни-
модулярную группу в С2'). Двум элементам группы спи-
норов, имеющим одну и ту же проекцию в группе Ло-
ренца, соответствуют два преобразования в С2, которые
отличаются только знаком. Образ группы О в аффинной
группе пространства ?4 представляет собой собственную
неоднородную группу Лоренца. Прообраз подгруппы сдви-
гов имеет две связные компоненты. Одна из этих связных
компонент, содержащая единицу, действует в простран-
стве F тождественно, другая действует как оператор
умножения на —1. Таким образом, группа О действует
не эффективно в пространстве Е^, ибо два элемента, имею-
щие одну и ту же проекцию в собственной неоднородной
группе Лоренца, дают на ЕА один и тот же оператор;
') Этот изоморфизм подробно описан в книге Г е л ь-
ф а н д а И. М., М и н л о с а Р. А. и Шапиро 3. Я-, Пред-
ставления группы вращений и группы Лоренца, М., 1958, ч. 2,
гл. I, § \. — Прим. ред.

§ 4. Электрон 157
кроме того, О действует не эффективно и в пространстве F,
поскольку сдвигам соответствуют тождественные преобра-
зования. Тем не менее О действует эффективно на произ-
ведении ?4 X F1).
Возьмем точку а на гиперболоиде в Е'^, соответствую-
щем массе от, и рассмотрим лоренцеву координатную си-
стему, в которой пространственные компоненты точки а
равны нулю. Тогда стабилизатором точки а в группе Ло-
ренца будет ортогональная группа в трехмерном под-
пространстве, определяемом пространственными коорди-
натными осями; Ga является накрывающей группой этой
ортогональной группы; группа Оа компактна, и простран-
ство F Оа-неприводимо. Поэтому на F существует един-
ственная с точностью до постоянного множителя Ов-инва-
риантная эрмитова форма, так что можно, как и выше,
построить пространства Fp и получить две компоненты ф;-,
преобразования Фурье которых имеют вид
=/#• ¦ у = 1. 2;
мы напоминаем, что
Далее, можно доказать, что существует единственный
(с точностью до постоянного множителя) однородный
О-инвариантный дифференциальный оператор D первого
порядка с постоянными коэффициентами, принадлежащим»
Jg (F; F). В нашей системе координат можно написать2)
Аналогично существует единственный (с точностью
до постоянного множителя) однородный О-инвариантный
линейный дифференциальный оператор D первого порядка
с постоянными коэффициентами, принадлежащими Jg' {F\ F\
') См. примечание редактора на стр. 23. — Прим. ред.
г) Символ др означает dfdx^ а^ — матрица Дирака. — Прим.
пере в. - ' . .

158 Гл. 5. Векторные элементарные частицы
Рассмотрим произведения DD и DD. Их можно норми-
ровать так, чтобы для волновых функций /""-частиц вы-
полнялось соотношение
DD = JDDJ=n=m2,
где J—канонический антиизоморфизм F->F, а У: F->F—
обратный к нему антиизоморфизм.
Если <|>— волновая функция некоторой F-частицы, то
?>ф является волновой функцией /^-частицы (т. е. анти-
частицы). Точно так же, если <|> описывает /^-частицу, то
?><]) описывает /^частицу. Введем в рассмотрение пару
которая представляет собой обобщенную функцию со зна-
чениями в прямой сумме F@F, и определим оператор
(D, D) следующим образом:
Тогда мы получим соотношение
известное под названием уравнения Дирака.
Если мы интересуемся только представлениями соб-
ственной неоднородной группы Лоренца, то достаточно
взять F=C2, и пространство F „лучше", чем F®F, так
как оно проще. Заметим, что пространство F@F непри-
водимо относительно расширенной спинорной группы,
а относительно собственной спинорной группы оно рас-
падается на два неприводимых подпространства.
Однако, если мы хотим получить дифференциальное
уравнение в частных производных, в котором участвуют
допускающие внутреннее определение операторы D и А
и использовать представления накрывающей группы для
расширенной неоднородной группы ^Лоренца, то мы должны
взять вместо F пространство

§ 5. Векторные частицы с нулевой массой 159
§ 5. Векторные частицы с нулевой массой
Для фотона и нейтрино миром является аффинное про-
странство ?4, а пространством F — соответствующее век-
горное пространство ?4. Допустим, что мы определили
функцию М (х), выбрав значение М (а) для некоторой
точки а светового конуса. Но в этом случае М обра-
щается в бесконечность в вершине и выражение Мр не
интегрируемо. Таким образом, М\х не является мерой, и
для фотонов и нейтрино не существует гильбертова про-
странства. Вместо этого можно поступить следующим
образом. Рассмотрим гильбертово пространство для малой
массы от Ф 0, затем перейдем к пределу при m -> 0, и
возьмем то, что получится, в качестве пространства для
нулевой массы.
Опишем кратко частицы малой массы от =?0 со спином 1,
а затем устремим от к нулю.
Для незаряженных частиц V = EA и /7 = ?4. Описание
фотона получается при от->0. Рассмотрим соответствую-
щий случай для заряженных частиц, т. е. комплексифи-
цируем F; тогда F = Ei-\-iEi.
Для данной точки а на гиперболоиде выберем лорен-
цеву систему координат, в которой а = @, 0, 0, а0).
Стабилизатор точки а является ортогональной группой на
трехмерной пространственно-подобной гиперплоскости Р,
проходящей через начало координат 0 перпендикулярно
вектору а. Существуют два независимых подпространства,
инвариантных относительно этого стабилизатора:
A) одномерное подпространство Q, натянутое на век-
тор а;
B) пространственно-подобная гиперплоскость Р.
Рассмотрим сначала случай, когда Fa = Q-\-lQ. Тогда
пространство Fx для любого х одномерно, а частицы соот-
ветствуют мезонам. Устремляя m к нулю, получаем, что
для любого х Ф 0 пространство Fх остается одномерным,
а частица соответствует мезону нулевой массы.
Рассмотрим теперь случай, когда Fa = P -\-iP. Про-
странство Fх для любого х является касательным про-
странством к гиперболоиду в точке х и имеет размер-
ность 3. В пространстве F фиксирована квадратичная форма,

160 Гл. 5. Векторные элементарные частицы
являющаяся расширением лоренцевой формы, заданной
на Е4. Квадратичная форма на F порождает квадратичную
форму в пространстве F х, положительно определенную,
поскольку на пространственно-подобном подпространстве
лоренцева квадратичная форма всегда положительно опре-
делена. Пусть т—>0. При этом гиперболоид переходит
в конус. Для любой точки х Ф 0 пространство Fх является
касательной к конусу трехмерной гиперплоскостью,
а квадратичная форма на Fх является вырожденной с сиг-
натурой B, 0), поскольку она обращается в нуль на
образующей конуса. Полученное в результате пространство
не является гильбертовым, потому что норма для ненуле-
вого элемента / может обратиться в нуль. В самом деле,
если значение вектор-функции f (х) в каждой точке х
пропорционально вектору х, то норма функции f(х)
равна нулю. Возьмем теперь обратное преобразование
Фурье этого пространства. Оно является предгильбертовым
пространством, неотделимым и полным. Так как это про-
странство неотделимо, то наша норма является на самом
деле полунормой. Движение такой частицы определяется
классом эквивалентности из соответствующего фактор-
пространства, т. е. бесконечным числом элементов, эк-
вивалентных относительно полунормы. Тот факт, что
ф-функции, эквивалентные относительно этой полунормы,
описывают одно и то же движение, называется прин-
ципом калибровочной инвариантности.

Глава 6
ОПРЕДЕЛЕНИЕ НЕКОТОРЫХ ФИЗИЧЕСКИХ ПОНЯТИЙ.
СЛУЧАЙ СКАЛЯРНЫХ ЧАСТИЦ
§ 1. Оператор эволюции
Пусть р = (р0, q) (где <7 = (<7j, q2, q3) — совокупность
пространственных координат)—переменный вектор про-
странства E'v a Q — нижняя ветвь двуполостного гипер-
болоида р2-\-т2 = 0.
Напомним, каким образом для обобщенных функций Г,
определенных на Q, делается замена переменных
q = q; и = р1 = q2 — р\.
Выше мы установили справедливость равенства
так что мы можем использовать обычные правила замены
переменных. Вычислим якобиан
д(и, q) __
НРо, Я)
Таким образом,
О
О
О
1_
2|Л1
1
0
о
0
1
о
0
о
1
= — 2р0.
dudq = dp0 dq
dudq
lYq^b'
так как | р01 = Yq2 — и и р0 < О.
. Вернемся теперь к случаю скалярных частиц; пусть
S№ — такая частица.
Если ф ^ ?ffl, то преобразованием Фурье этой функции
будет

162 Гл. 6. Определение физ. понятий. Скалярные частицы
где (J. — единичная плотность, сосредоточенная на 2, т. е.
(. = 8(р2 + /Я2)К(-/70),
где К(—р0) — функция Хевисайда, соответствующая
нижней части пространства E'v Тогда
Л»
так что мы можем сказать, что на Q функция ф задается
следующим выражением:
dq
Предложение 1. /7усть х = (х0, у)—набор че-
тырех переменных пространства Е4 и пусть
3)'х^З)'у) — множество обобщенных функций от х0 со
значениями в 3>у.
По определению, З^сЗ'^Зу). В самом деле,
имеем:
где ЪхХ&у)—множество бесконечно дифференцируе-
мых функций от х0, принимающих значения в SPy
Доказательство. В соответствии с общим мето-
дом достаточно доказать справедливость этого утвержде-
ния для функций ср вида ср = а(л;0){3(у), где а
р() ^) Имеем:
Обозначим через S^~y преобразование Фурье, действую-
щее только на три пространственных переменных. Тогда

§ 1. Оператор эволюции
163
Пусть tyx (у)— обобщенная функция от переменной у,
зависящая от параметра х0 и равная ф (д;0, у). Из равенства
а„(у).р(у)>=/<
Rs
мы получаем, что
Тогда
\k
2
o-2ta0 Vq'+m'
Следовательно,
Vq'+m*
Таким образом, преобразование Фурье (с^~у|!>,Г() (у)) (?) при-
надлежит SPq и отображение
является бесконечно дифференцируемой функцией со зна-
чениями в SPq- Поэтому
что и требовалось доказать.
Следствие.
где ф0 — значение обобщенной функции tyx при лг0 = О,
a *q означает, что свертка действует только на
пространственно-подобные переменные q, или, что
то же самое, у.

164 Гл. 6. Определение фаз. понятий. Скалярные частицы
Доказательство. Рассмотрим опять предыдущее
выражение
Применяя оператор 47~q к обеим частям этого равен-
ства, получаем
К (У) = % О *ч?{е-'гш> V*^),
что и требовалось доказать.
Замечания. Для того чтобы однозначно определить
общее решение уравнения Клейна — Гордона
требуются два дополнительных условия: начальные значе-
ния волновой функции и ее производной по времени
ф@. У), ^@, у).
У нас же движение ф полностью восстанавливается по
известному значению ф @, у). Мы вновь приходим к тому,
что движения представляют собой весьма частный случай
общего решения уравнения Клейна — Гордона (ср. гл. 4,
§ 6).
Определение. Оператор
восстанавливающий ф по ф @, у), называется оператором
эволюции.
§ 2. Пространство e№Q представления Гейзенберга
Пусть S@o — совокупность начальных значений фо(у)
движений ф. Тогда из следствия предложения 1 мы заклю-
чаем, что формула
(
устанавливает взаимно однозначное соответствие между
и ?Шй (так как из фо(у) = О вытекает, что ф(л;0, у)^

§ 2. Пространство &е0 представления Гейзенберга 165
С другой стороны, из самого предложения 1 следует, что
Предложение 2. Гильбертова структура в про-
странстве е%!0, перенесенная из <?%> с помощью соот-
ветствия ty(x0. У) —>• ф0 (у), определяет в <Фва более
сильную топологию, чем топология, индуцированная
пространством af'y.
Доказательство. Достаточно выписать определе-
ния этих двух топологий.
Определение пространства Hs. Говорят, что
обобщенная функция Т(у) на R3 принадлежит простран-
ству Hs, где 5 — любое вещественное число, если
(I) T (у) является обобщенной функцией степенного
роста,
(II) f(y) — квадратично суммируемая функция
относительно меры A ~\~ \q\2)sdq.
Норма в пространстве Hs определяется равенством
\\TfH>=*f\f(q)\*(l-\-\q\*fdq.
Предложение 3. Пространство ?№0 совпадает
с Hi/2. (Это, в частности, означает, что нормы этих про-
странств эквивалентны, т. е. существуют два фиксирован-
ных положительных числа А и В, таких, что для любой
функции ф0 ? ??вй имеем
Доказательство. Условие ф0 ? $f6Q эквивалентно
условию
а это в свою очередь означает, что
R»
(ср. доказательство предложения 2) и ф0 является обобщен-
ной функцией степенного роста. Таким образом, условие
эквивалентно условию •'¦ ^ н

166 Гл. б. Определение физ. понятий. Скалярные частицы
Тогда эквивалентность обеих норм очевидна, так как
Итак, пространство $в является множеством
решений уравнения Клейна — Гордона, удовлетво-
ряющих следующим условиям:
1) частоты этих решений отрицательны;
2) начальное значение % принадлежит Я1/г;
3) ()
§ 3. Плотности вероятности координат и скоростей
Предыдущее выражение для квадрата нормы ||фо|1ав,
позволяет написать следующую коммутативную диаграмму:
If 'II'
и,*
где
В самом деле,
, разумеется, представляет собой унитарный оператор),
следовательно, оператор свертки ?/0 * унитарен.
Определим оператор UXa* как произведение следую-
щих изоморфизмов:
Так как эти изоморфизмы унитарны, оператор ?/*„* тоже
унитарен.
Определение. Назовем вероятностью нахождения
частицы с движением ф в момент времени х0 в области Aq

§ 3. Плотности вероятности координат и скоростей 167
следующее выражение:
Предложение 4. Оператор UXo* является опе-
ратором свертки с функцией
UXa = Ж(/2 >V 4-
Следствие предложения 1 дает
с другой стороны, из предыдущей диаграммы и опреде-
ления UXo *. следует, что
^ (q)
что и требовалось доказать.
Предложение 5. (Закон сохранения ча
стиц.) Величина P+(R3. *„) не зависит от х0.
В самом деле,
Замечания. 1. Функция ?/Жо(у) выражается через
функции Кельвина и поэтому очень быстро убывает на
бесконечности. Таким образом, Р$,(А, Xq) зависит глав-
ным образом от значений функции ф вблизи А, но не
только от значений на самом множестве А.
2. Функция UXo определяется из физических сооб-
ражений неоднозначно: выражение в круглых скобках
можно умножить на е"<1?1), где / — любая вещественная
измеримая функция. Если мы потребуем, чтобы выполня-
лось дополнительное условие: комплексное сопряжение
«J» -> ф переводит частицу с параметрами (т. —) в частицу

168 Гл. 6. Определение физ. понятий. Скалярные частицы
с параметрами (от, -(-), то и тогда функция l(\q\) не
определяется однозначно; она может принимать любые
значения вида kit, где k — целое число.
Определение. Назовем вероятностью того, что
частица с движением <^Хо имеет в момент времени х0 ско-
рость q, заключенную в области Дс?3 . выражение
K(?)|22}V + m2 dq.
A
Следовательно,
Ф V 4/ j 1 "I
= г i/ (?) i2 ^
I O 1/ 9 I ™9 "
д
Отсюда вытекает, что
SP~(А, хЛ не зависит от х0 (скорость постоянна);
" ^|(Д л;0) зависит только от значений функции f(q)
в Л.

Г лава 7
ОПРЕДЕЛЕНИЕ НЕКОТОРЫХ ФИЗИЧЕСКИХ ПОНЯТИЙ.
СЛУЧАЙ ВЕКТОРНЫХ ЧАСТИЦ
§ 1. Постановка задачи
Так же, как и в случае скалярных частиц, мы полу-
чаем, что
1) движение ф ? ?ёХо (з'у (F)) на самом деле принадле-
жит пространству &Хе
2) ^¦y^(y)
где / (q) обладает следующими свойствами:
(I)""
(II) f(q)— является tfg-измеримой,
ОН)
Напомним, что совокупность таких функций, снабжен-
ную гильбертовой структурой, определяемой нормой
где
мы обозначаем символом L?{d\>., R3, {Fq}9< F); здесь R3
появилось вместо 2 в результате замены переменных.
12 л. Шварц

170 Гл. 7. Определение физ. понятий. Векторные частицы
Таким образом, величина ||/||2 возникает как непре-
рывная сумма норм, каждая из которых берется в своем
пространстве Fq, тогда как в случае скалярных частиц
величина ||/||2 подсчитывалась только в одном про-
странстве. Поэтому определения еР^ М- *0) и *\ М1 хо)
нельзя непосредственно распространить на рассматриваемый
случай.
Вторая трудность заключается в том, что про-
странство Звй в этом случае уже не является инвариант-
ным относительно операторов о ? О; в самом деле,
где h — гиперплоскость, которая получается из гиперпло-
скости х0 = 0 под действием оператора <з?О; таким
образом,
где S%?o — множество всех начальных значений движений.
Сечение, которое дает коммутативную диаграмму, зависит
от о:
Сечение
Сечение А:
а.Го-0
(гиперплоскость h проходит через начало координат
в пространстве F, так как сдвиги группы G действуют
->
тождественно на F).
Следовательно, для того чтобы в рассматриваемом слу-
чае для наших операторов были справедливы те же фор-
мулы, что и в случае скалярных частиц, необходимо вы-
->
числять норму функции f(q) в одном и том же простран-

§ 1. Постановка задачи
171
стве Fw, не зависящем от q и инвариантном относительно
любого оператора a?G. Для этого нужно, чтобы вектор-
ный аналог преобразования ^(?/0) был оператором вида
где / (q) -> Vf (q) — унитарное отображение пространства
*. R3. {Р<}.П в i^.R3. Fw).
Вместо одного оператора V можно рассматривать набор
операторов Vq ? J? (Fq, Fw), q ? R3. связанный с V ра-
q
венством (Vf)(q) — Vq(J(q))- Операторы V
следующими свойствами:
(I) Vq
(II) диаграмма
обладают
унитарный оператор из Fq на Fw\
w
коммутативна.
Отсюда вытекает, что пространство Fw инвариантно
относительно оператора о, унитарно действующ»го в Fw.
Из этой диаграммы легко определить Vg, если бы мы
могли определить оператор о(а, р), принадлежащий
группе О и действующий на F, такой, что
(I) выбор оператора о зависит только от точек акр
множества 2 (и не зависит, например, от гиперплоскости
(III) о (а, р) — всюду регулярная (т. е. аналитическая)
функция переменной р и о (а. а) = I A — единичный опе-
ратор).
12*

172 Гл. 7. Определение физ. понятий. Векторные частицы
Если такой оператор а построен, то V9 определяется
при помощи следующей коммутативной диаграммы:
Р' М (п\ > р Каноническое р
к"' Ч вложение *" *
о (а. Р) V4 а (а, р)
1 ' I I
pi АЛ (п\ > р Каноническое Р
Г т(п) *Та вложение * г
где а (а, р) — оператор, контраградиентный к а (а, р).
§ 2. Построение оператора <з(а,р) в случае,
когда О/О0 является группой Лоренца или ее
накрывающей группой
В этом случае известно, что О/О0, как множество
операторов в Eit содержит только один элемент аар,
такой, что
(I) оар переводит точку а в точку р;
(II) оар оставляет инвариантной двумерную плоскость,
проходящую через точки 0, а и р;
(III) аар действует тождественно в плоскости, которая
лоренц-ортогональна к плоскости @, а, р).
Возьмем теперь в качестве а (а, р) оператор в про-,
странстве F, который соответствует элементу аа р, со-
гласно определению действия группы GIG0 в F. Это
соответствие аналитическое; поэтому для доказательства
аналитичности отображения р->а(а, р) достаточно дока-
зать аналитичность отображения
Напомним, что вектор р ?Е4 можно записать в виде
-> •> ¦*¦ ->->-> •> ->
Р — (Ро> Я)> где ?6R ¦ или Р— Poeo~*rQ- Пусть а и р—
два элемента орбиты Q, а у — любой элемент про-
странства Ei.

§ 2. Построение оператора о (а, р) 173
Так как а — времени-подобный вектор (в самом деле,
он принадлежит 2), то в качестве е0 можно взять век-
а
тор -qp-.
И
. Теперь доказательство состоит в применении а++
а,р
->•
к вектору у и в проверке того, что координаты этого
вектора преобразуются аналитически. Оператор о» пе-
реводит единичный вектор, пропорциональный а, в еди-
ничный вектор, пропорциональный р:
ар
где
Следовательно,
Отсюда вытекает, что в базисе ^ е0, —^— ] оператор о.»
записывается матрицей
/chcp sh <
\shcp ch <
так что
->¦ -> ->
/Т "^ I /Т I /Т
Теперь разложим вектор у на две компоненты, одна
из которых лежит в плоскости @, а, р), т. е. в пло-
скости ( 0, е0 -Аг- ), а другая — в ортогональной к ней
\ \q\J

174 Г л. 7. Определение физ. понятий. Векторные частицы
плоскости
+ С|> (k)
I?I2J
Вычислим o-»y.
По определению <*-»->, вторая скобка остается инва-
а,р
риантной. Используя приведенные выше формулы для
¦> ¦>
в->->^ и °->->в0, получаем
а, р а,р
11 L
l9l
Для доказательства аналитичности преобразования та-
кого вида достаточно проверить, что выражение
^ I — — 1) не имеет особенности при # = ()•
^
Вспомним, что po=r I^P + t*2- так что
для | ^ | ->• 0 получаем

§ 3. Построение некоторых операторов 175
§ 3. Построение некоторых операторов
и плотностей вероятности
Из сказанного в начале § 1 вытекает, что, вводя обо-
значение
мы получаем следующее:
(I) Хо(<7) является й^-измеримой;
ОН)
Поэтому
что в точности эквивалентно соотношению
где
Положим теперь
«Г (Uo)(q) = V2 Vq*+m> V.
где оператор V определяется набором операторов Vq, удов-
летворяющих коммутативной диаграмме, приведенной на
стр. 171.
Так как оператор о (а, р) аналитичен, он измерим; сле-
довательно, о (а, р) определяет оператор Vq, аналити-
ческий по q и унитарно отображающий Fр на Fa; пре-
образование
из L2(dq,K3, {Fq)r F) на L2(dq,R3.Fa) унитарно.
Теперь мы получаем искомое обобщение формул для
скалярных частиц, заменяя %(q) на V%(q).
Фурье-образ оператора эволюции задается формулой

176 Г л. 7. Определение физ. понятий. Векторные частицы
плотность вероятности скорости частицы принимает вид
А
а плотность вероятности нахождения частицы в области Aq
определяется выражением
где
V
Найдем выражение для оператора энергии, или гамильто-
ниана, Н.
По определению, оператор Гамильтона является Фурье-
прообразом величины
В самом деле, применяя обратное преобразование Фурье
к обеим частям равенства
получаем
Так как
то в результате находим уравнение
Отсюда для гамильтониана Н получается выражение
§ 4. Переход к более общим группам
До сих пор (кроме § 1, гл. 7) от группы О требо-
валось только, чтобы она была группой Ли, обладающей
коммутативным нормальным делителем О0, таким, что GJG0

§ 4. Переход к более общим группам 177
является однородной группой Лоренца 8 или ее накры-
вающей группой. Поэтому желательно распространить ре-
зультаты § 1 этой главы на следующий несколько более
общий случай. Пусть 0 = 2ХЛ где Л —произвольная
группа Ли. Пусть Ф-1A) — ядро представления группы G
в 8(f; F). Обозначим через Г факторгруппу О/Ф A).
В наших рассмотрениях участвует, по существу, только
эта факторгруппа Г и, в частности, отсутствуют сдвиги.
Так как группа 8 не имеет ни одного нетривиального
нормального делителя, проекцией «в [ф A)]ядра Ф-1A)
на 8 является либо сама 2, либо единичный элемент е.
Рассмотрим отдельно два случая.
(I) ^[Ф
В этом случае группа 8 тривиально действует в про-
-> -> ¦>
странстве F, а так как Fp является образом Fa при пре-
образовании, переводящем а в р, то Fp совпадает с Fa.
Тогда можно считать, что F = Fa и пространство F не-
приводимо, так как Fa неприводимо относительно стаби-
лизатора точки а, который в нашем случае совпадает
со всей группой Г.
Это показывает, что в данном случае справедливы те же
самые формулы, что и в случае скалярных частиц.
(Н) ти8[ф-! (!)] = «.
В этом случае группа 8 эффективно действует в про-
странстве F, и
тсй (Г) = «s (О/Ф A)) = щ (8)/я8 [ Ф A)] 1саГ == 8/1 = 8.
Пусть N — ядро гомоморфизма Г— -»8; ядро N яв-
ляется нормальным делителем, и по теореме Леви — Маль-
цева существует подгруппа 8' группы Г (которая не обя-
зательно является нормальным делителем), такая, что
Г = 8'ХМ (полупрямое произведение).

178 Гл. 7. Определение физ. понятий. Векторные частицы
Согласно той же теореме, 2' и 8 имеют одну и ту же
алгебру Ли, откуда вытекают две возможности.
(а) 8'= 8.
Можно показать, что необходимым и достаточным усло-
вием существования плотности вероятности для координат
частицы является равенство
Г = 8' X N ' (прямое произведение).
(б) 8'—однородная спинорная группа группы 8.
В этом случае можно доказать, что необходимым и до-
статочным условием существования плотности вероятности
координат частицы является равенство
Г = (Й' X ЛО/Т (знак X означает прямое произведение),
где у — подгруппа группы 8'XN, состоящая из двух эле-
ментов (е, е) и (е', е). Здесь е — единичный элемент ядра
N, а е и е' — два элемента в 2', соответствующие еди-
ничному элементу в 2 при канонической проекции 8' на 8.
Из этого условия вытекает, что 2' и N коммутируют.
Следовательно, эта коммутативность необходима в обоих
случаях (а) и (б). Это справедливо и в том случае, когда
ядро N конечно.
Достаточность приведенных условий тривиальна.
§ б. Структурная четность частиц
Пусть О — структурная группа рассматриваемой F-чг-
стицы — является подгруппой неоднородной группы Ло-
ренца, сохраняющей направление времени, но не обяза-
тельно сохраняющей пространственную ориентацию. Пусть
Q — ветвь гиперболоида, соответствующая этой частице;
обозначим через Оа стабилизатор точки а ? 2. Он яв-
ляется максимальной компактной подгруппой группы О,
т. е. полной ортогональной группой подпространства Е3,
ортогонального к а. Тогда подпространство Fa простран-
ства F является неприводимой компонентой представления
группы Оа в F.

§ S. Структурная четность частиц 179
Пусть 5 — оператор симметрии относительно начала
¦>
координат в пространстве Е3. Тогда
(I) s?Ga; s2 = \ и s принадлежит центру группы Оа;
(II) Оа определяет (с точностью до постоянного мно-
жителя) положительно определенную квадратичную форму
в пространстве Fa, для которой Оа является ортогональ-
ной группой.
Из (I) и (II) следует (согласно лемме Шура), что опе-
¦>
ратор s в Fa является скалярным оператором, квадрат
которого равен 1'. Таким образом, s = -f-1 или —1
->
во всем пространстве Fa. По определению, этот знак
называется четностью частицы. Разумеется (в силу непре-
рывности), этот знак не зависит от выбранной точки а
на 2.
Рассмотрим теперь вместо группы О, с которой нам
приходилось иметь дело- до сих пор, ее накрывающую
группу, которую обозначим также через О. 'Тогда новая
подгруппа Оа будет накрывающей прежней группы Оа.
Таким образом, в новой группе Оа существует один или
несколько различных операторов, действующих в про-
странстве Е3 как s. Но они не принадлежат центру группы
Оа, поэтому понятие четности теряет смысл. С таким
положением мы встречаемся в случае электрона.
Напомним, что все изложенное относится только к слу-
чаю отсутствия взаимодействия.

ОГЛАВЛЕНИЕ
Предисловие к русскому изданию 5
Г л ава 1. Постановка задачи 7
§ 1. Введение 7
§ 2 Элементы теории обобщенных функций .... 9
§ 3. Аффинные пространства. Преобразования Ло-
ренца 14
§ 4. Мировые скалярные частицы 18
§ 5. Скалярные и векторные частицы в произволь-
ном мире 20
§ 6. Слабая и сильная сходимость 23
Глава 2. Множество ?> мировых частиц и его струк-
тура - 26
§ 1. Пространство §) 26.
§ 2. Структура $ и ^+ (?', Е) 32
§ 3. Скалярные частицы 41
§ 4. Тензорные произведения 47
§ 5. Векторные частицы 50
§ 6. Отношения порядка в векторных пространст-
вах и положительность антиядер 57.
Глава 3. Мировые частицы и инвариантность отно-
сительно сдвигов. Упрощение по ядру. ; . . . 65
§ 1. Тензорные произведения обобщенных функций 65
§ 2. Свертка 69
§ 3. Инвариантность относительно группы сдвигов 76
§ 4. Преобразования Фурье 84
§ 5. Теорема Бохнера 90
§ 6. Свойства „упрощенного" ядра 95
§ 7. Гильбертово пространство dre для скалярных
частиц 101
Глава 4. Элементарные частицы и инвариантность
относительно вращений ¦. 103
§ 1. Элементарные частицы 103
§ 2. Носители экстремальных мер 109
§ 3. Мезоны 113

§ 4. Лоренц-ннвариантные скалярные обобщенные
функции 117
§ 5. Описание всех мезонов 120
§ 6. Описание пространства &е в случае мезона . . 124
Глава 5. Векторные элементарные частицы и их
свойства 128
§ 1. Векторные частицы 128
§ 2. Описание всех векторных частиц 133
§ 3. Полное описание преобразования Фурье гиль-
бертова пространства для векторных частиц 149
§ 4. Электрон 156
§ 5. Векторные частицы с нулевой массой .... 159
Глава 6. Определение некоторых физических поня-
тий. Случай скалярных частиц 161
§ 1. Оператор эволюции 161
§ 2. Пространство &@а представления Гейзенберга 164
§ 3.- Плотности вероятности координат н скоростей 166
Глава 7. Определение некоторых физических поня-
тий. Случай векторных частиц 169
§ 1. Постановка задачи 169
§ 2. Построение оператора а(а,р) в случае, когда
GIGa является группой Лоренца или ее накры-
вающей группой 172
§ 3. Построение некоторых операторов и плот-
ностей вероятности 175
§ 4. Переход к более общим группам 176
§ 5. Структурная четность частиц 178
Лоран Шварц
ПРИМЕНЕНИЕ ОБОБЩЕННЫХ ФУНКЦИЙ К ИЗУЧЕНИЮ ЭЛЕМЕНТАРНЫХ
ЧАСТИЦ В РЕЛЯТИВИСТСКОЙ КВАНТОВОЙ МЕХАНИКЕ
Редактор Н. И. Плужникова Художественный редактор В. И. Шаповалов
Художник И. А. Литвишко Технический редактор А. В. Грушин
Корректор И. И. Казарина
Сдано в производство 21/Х-1963 г. Подписано к печати 7/Ш-1964 г.
Бумага 84x108732-2,9 бум. л., 9,4 печ. л. Уч.-изд. л. 7,5. Изд. № 1/2323.
Цена 53 к. Зак. 1783. (Тем. план 1964 г. изд-ва „ИЛ- пор. № 26)
ИЗДАТЕЛЬСТВО «М И Р»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2 имени Евгении Соколовой
«Главполнграфпрома» Государственного комитета Совета Министров СССР
по печати. Измайловский проспект. 29.