Автор: Пухначев Ю.В. Попов Ю.П.
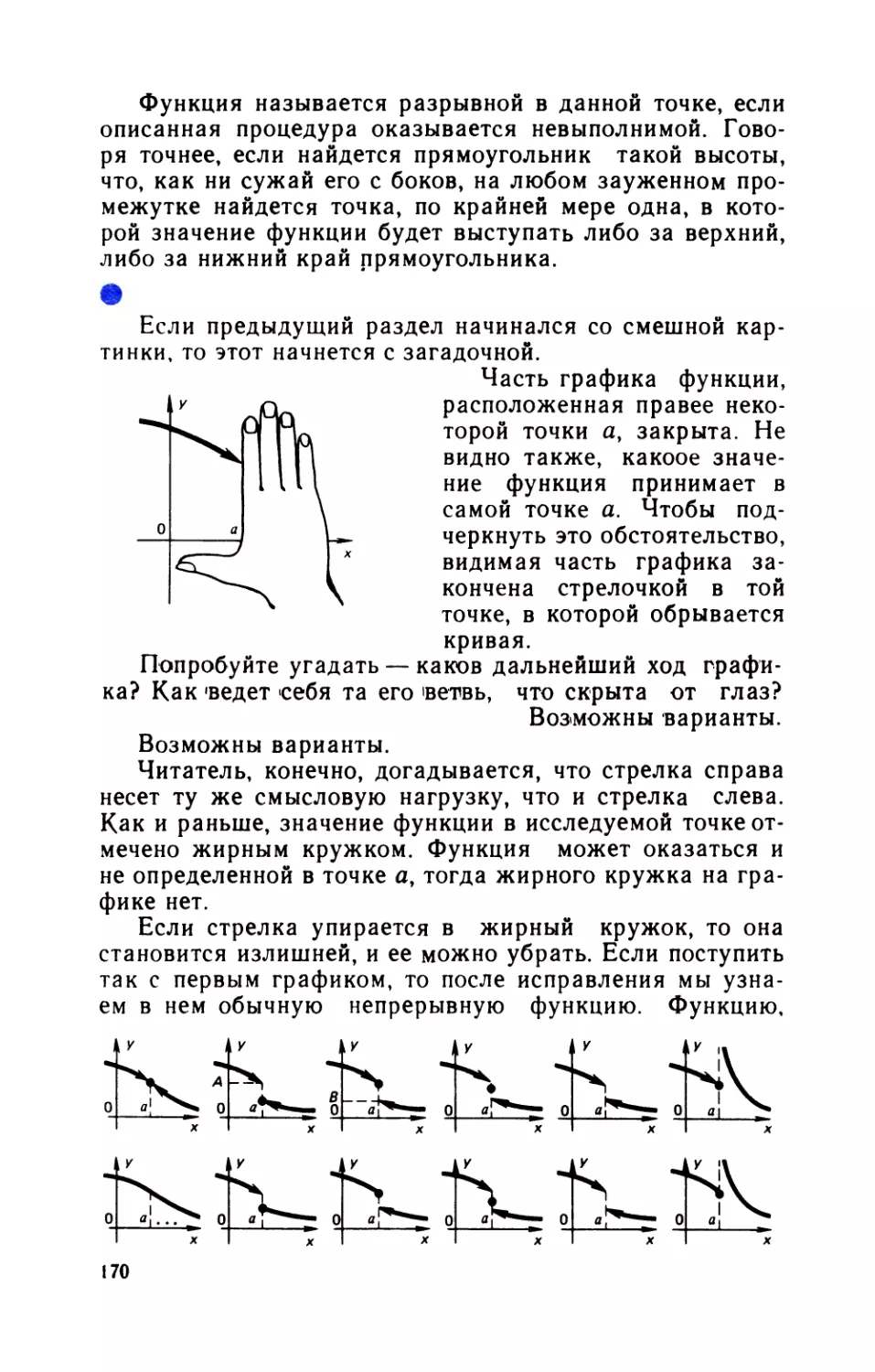
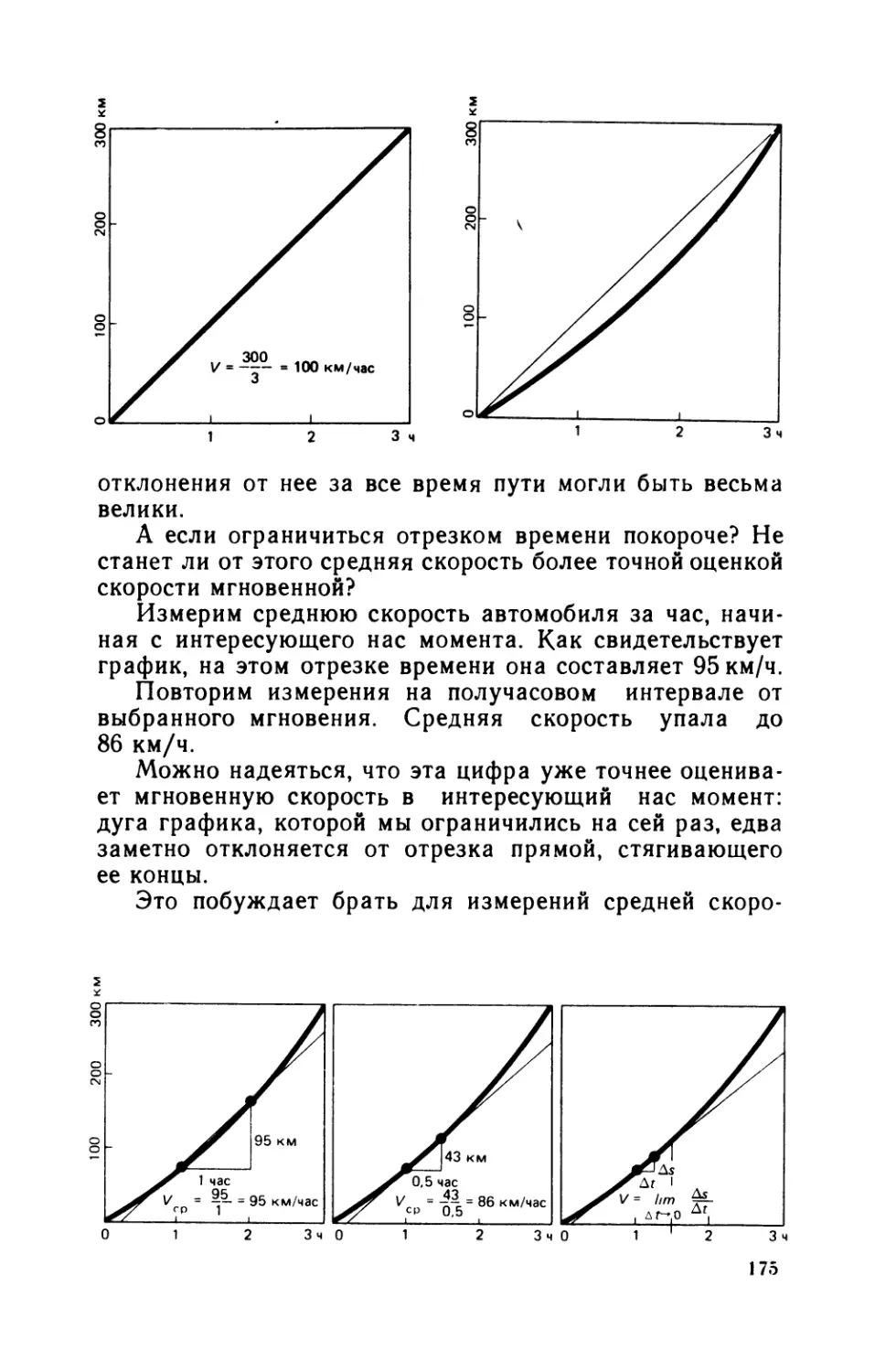
Теги: математика дифференциальное исчисление теория множеств издательство знание математические методы числовые ряды математические формулы
ISBN: 5—07—000096—9
Год: 1989
юппоповкувп^св /И«4ТЕ/Я4ТИК<4 ВОБР43«4Х
НАРОДНЫЙ УНИВЕРСИТЕТ
естественнонаучный факультет
ЮЛ. ПОПОВ. Ю.В. ПУХНАЧЕВ
НАРОДНЫЙ УНИВЕРСИТЕТ
естественнонаучный факультет
Издается с 1961 г.
ЮЛ. ПОПОВ
доктор физико-математических наук
Ю.ВПУХНАЧЕВ
кандидат физико-математических наук
ААХЫАМЫ
ВОБР434Х
Издательство „Знание”
Москва
1989
ScanAAW
ББК 22.1
П 58
ПОПОВ Юрий Петрович — доктор физико-математических
наук, заместитель директора Института прикладной матема-
тики им. М. В. Келдыша АН СССР. Автор многих научных
работ. Лауреат Государственной премии СССР.
ПУХНАЧЕВ Юрий Васильевич — кандидат физико-математи-
ческих наук, доцент Московского физико-технического инсти-
тута. Автор многих научно-популярных книг и статей по ма-
тематике и физике.
Попов Ю. П., Пухначев Ю. В.
П 58 Математика в образах. — М.: Знание, 1989. —
208 с. — (Нар. ун-т. Естественнонаучный фак.).
65 к. 80000 экз.
Математические формулы — лишь удобный язык для изложения
идей и методов математики. Сами же эти идеи и методы можно
описать, используя привычные и наглядные образы из окружающей
жизни.
Следуя этому принципу, авторы в доступной и увлекательной фор-
ме излагают основные понятия теории множеств, числовых рядов,
дифференциального и интегрального исчисления и других разделов
математики.
Книга рассчитана на слушателей народных университетов естест-
веннонаучных знаний И широкий круг читателей.
п 1602010000—007
073(02)—89
17-89
ББК 22.1
ISBN 5—07—000096—9
© Издательство «Знание», 1989 г.
ПРЕДИСЛОВИЕ
Читатель, если вы раскрыли эту книгу — значит, вас не
отпугнуло слово «математика» на ее обложке. Вы, ко-
нечно, представляете, сколь важной стала эта наука се-
годня и как стремительно расширяется сфера ее прило-
жений.
Вместе с тем вам, вероятно, известно привычное мне-
ние, будто математику «выдумывают» этакие отшельни-
ки в академических шапочках, будто математика — на-
ука чрезвычайно абстрактная, сухая, сложная, изучать
ее невероятно трудно, так что человеку средних способ-
ностей удается постичь в ней самые элементарные вещи,
а все остальное, именуемое высшей математикой, — удел
исключительно одаренных людей.
Такое мнение ошибочно. Математика возникла из
практической деятельности человечества, здесь ее кор-
ни, стало быть, основные понятия математики можно по-
яснить на обыденных, общеизвестных примерах.
Авторы книги, которую вы держите в руках, чита-
тель, проводят эту мысль последовательно, демонстри-
руя ряд основополагающих концепций высшей матема-
тики с помощью простых доходчивых образов. Разговор
о множествах начинается с игры в слова (алфавит--это
множество букв), идея координат возникает из рас-
смотрения прямоугольной сети улиц, свойства функций
иллюстрируются пословицами и т. п.
Язык книги свободен и легок. Однако при всей ка-
жущейся нестрогости изложения в его основе лежит
строгая логика предмета. Описываемые понятия появ-
ляются в продуманной последовательности, их образы
соответствуют точным определениям и складываются в
систематическую картину.
Книга будет полезна и школьному учителю матема-
тики, и руководителю математического кружка, и люби-
телю математики.
Член-корреспондент АН СССР
С. П. КУРДЮМОВ
э
ВМЕСТО ВВЕДЕНИЯ —
ДИАЛОГ АВТОРОВ
— Математика в образах? Без строгих доказательств,
без формул? Не перехватили ли мы? Ведь это что-то
вроде географии без карт или оперы без музыки!
— Что ж, опера без музыки в самом деле ничто. А
что касается карт... Разве в них соль географии? Когда
ты смотришь видовой фильм, слушаешь бывалого путе-
шественника или путешествуешь сам — разве ты не по-
полняешь свои географические познания? К тому же
все это гораздо глубже воспринимается и гораздо инте-
реснее, чем карты. Хотя, конечно, те подают информа-
цию в предельно отчетливом, концентрированном виде.
Так же и формулы. При всей их четкости и емкости — не
в них душа математики.
— Ну-ка, ну-ка, в чем же она, эта загадочная душа
математики?
— Не знаю, убедят ли тебя мои собственные слова —
как говорится, нет пророка в отечестве своем. Поэтому
позволь спрятаться за авторитеты. «В математических
работах., главное — содержание, идеи, понятия, а затем
для их выражения у математиков существует свой
язык — это формулы». Заметь: первично — содержание,
идеи, понятия, а форма, формулы — вторично.
— Кто это сказал?
— Софья Ковалевская.
— Ну, хорошо. Формулы — не душа математики. Но
все-таки язык! Родной язык! Тебе приходилось когда-
нибудь читать японские стихи?
— В переводе.
— Вот-вот! В переводе, где короткие слова оригина-
ла приходится заменять многосложными. И — улетучи-
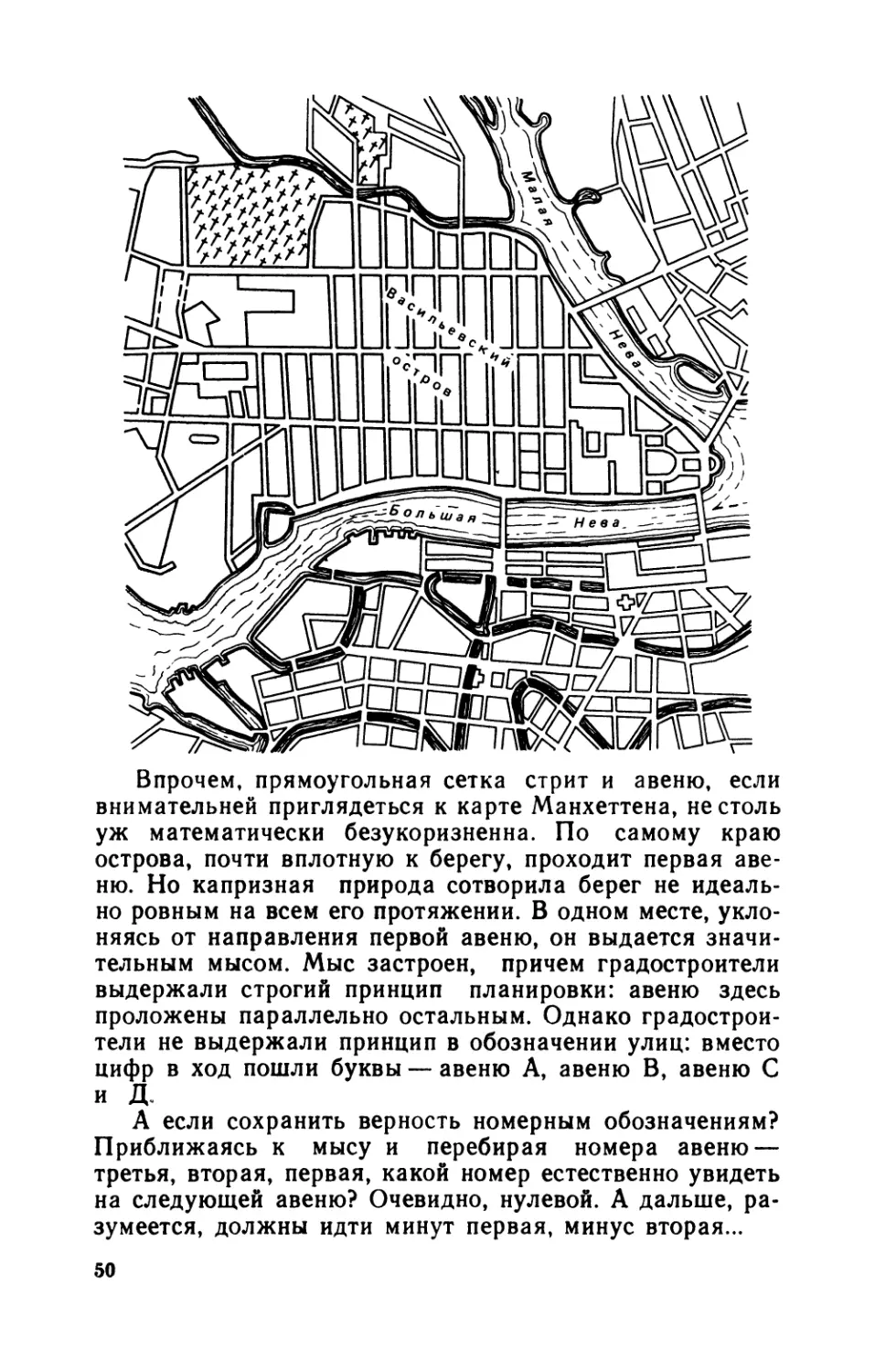
лось своеобразное очарование японской поэзии! Ощутить
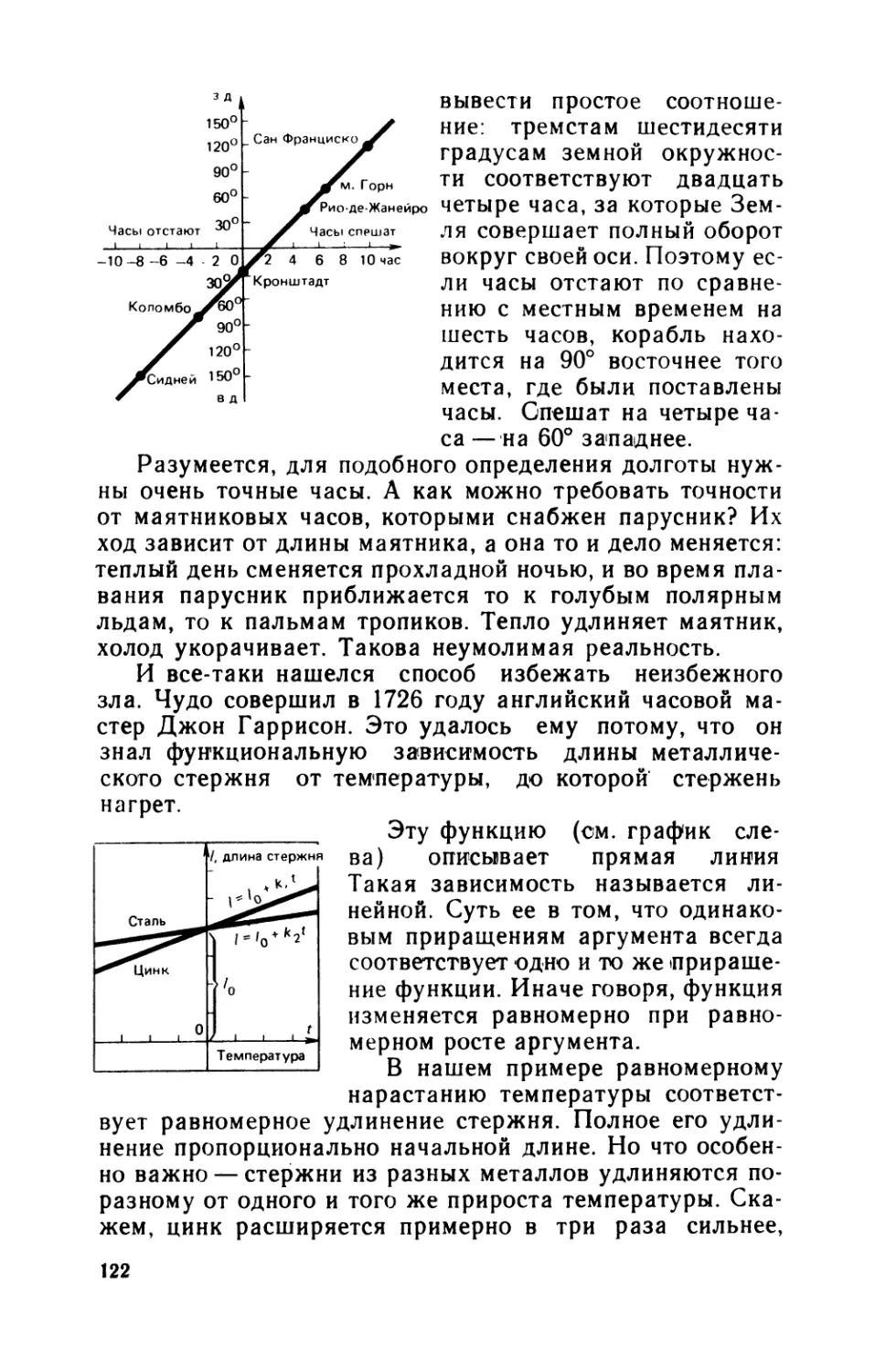
его можно, лишь изучив японский язык и читая стихи в
подлиннике.
— Да, но все мы живем в условиях постоянного
цейтнота. Прежде чем начинать какое-то дело, нужно
знать, ради чего оно предпринимается, видеть конечную
4
цель. Я возьмусь за изучение японского языка лишь
после того, как мне расскажут о неповторимых преле-
стях японской поэзии на моем родном языке. Но если
вместо этого мне дадут свиток с иероглифами... Мате-
матические формулы для непосвященного — те же иеро-
глифы. Да и доказательства для него не понятнее иеро-
глифов. Этот жаргон, эти бесконечные «если... то... для
любого... существует... вообще говоря... по крайней ме-
ре...».
— Ну, уж тут позволь с тобой не согласиться. Есть
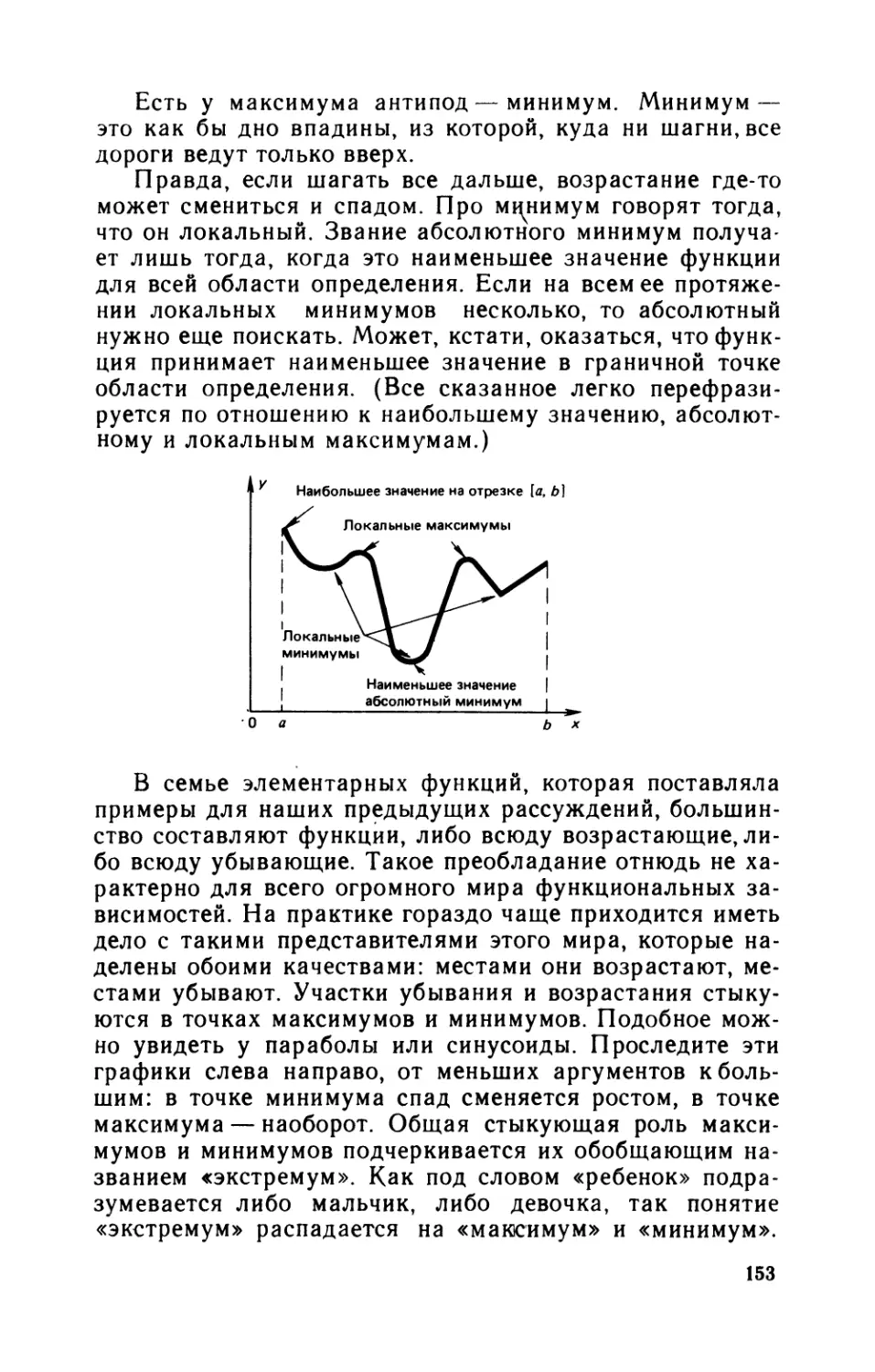
хороший анекдот на эту тему — не возражаешь?
— Давай.
— Рихард Дедекинд, как ты знаешь, умер глубоким
стариком, через много лет после того, как написал свои
классические труды. А о классиках принято думать, что
жили они в давно прошедшие времена. Короче говоря,
где-то в начале нашего века Дедекинд раскрыл какой-
то календарь и прочел там: «Рихард Дедекинд. Умер в
Брауншвейге 4 сентября 1899 года». Дедекинд написал
тогда издателю календаря: «Глубокоуважаемый колле-
га!.. Позвольте обратить Ваше внимание на то, что в да-
те моей смерти неверен по крайней мере год». Так и чув-
ствуется рука математика! А в этом самом «по крайней
мере» заключено все остроумие ответа. Так что стро-
гость и занимательность — вещи вполне совместимые,
можешь меня не разубеждать!
— Не приведи господи! Ведь именно об этом я тебе и
толкую! Анекдоты и приметы, пословицы и детские счи-
талки, картины великих художников и отрывки из клас-
сических произведений, факты истории и нашей повсе-
дневной жизни — вот где нужно искать иллюстрации к
математическим понятиям! И они не могут не найтись.
Разве древо математики поднялось бы до таких высот,
если бы не уходило корнями в глубины общечеловеческой
практики?
— Ив таком духе ты намереваешься изложить всю
математику, и притом совершенно строго?
— Зачем всю? И зачем совершенно строго? Наша
книга не должна быть учебником. Важны основные идеи
и понятия. И если читатель войдет во вкус, — он потом
возьмется и за учебники, за формулы и строгие доказа-
тельства. «Подобно тому, как рою бесчисленных пчел,
поражающему наперебой своими жалами, не удается
отогнать упивающегося медведя, если он хоть немного
5
вкусил приятность скрытого в дереве меда, так нет, разу-
меется, никого, кто, хоть краем губ постигнув сладость
математических доказательств (какая бы масса вели-
чайших трудностей, которыми эти доказательства сопро-
вождаются, ни отталкивала его, точно частыми укола-
ми жал), не стремился бы всеми силами освоить их впол-
не, до полного насыщения». Это сказал Бонавентура Ка-
вальери в своем трактате «Геометрия».
— Ну и что же за книга у нас получится? Если не
учебник — то что? Что-то вроде «Кабаре математики»
Графа? «Математической смеси» Литтлвуда? Развлека-
тельное чтиво?
— Не учебник и не чтиво. Я попытался бы опреде-
лить ее дух иносказательно. Представь себе поток, на
одном берегу которого стоит жаждущий, но не сведу-
щий, а на другом раскинулись райские сады матема-
тики. Книги о математике — словно камни в потоке, по
которым можно переправиться на ту сторону. К берегу
незнания примыкает россыпь анекдотов. У другого бере-
га теснятся глыбы учебников. А в промежутке — не так
уж много для уверенной переправы. Трехтомник «Мате-
матика, ее содержание, методы и значение» А. Д. Алек-
сандрова, А. Н. Колмогорова, М. А. Лаврентьева и дру-
гих. «Что такое математика?» Р. Куранта и Г. Роббин-
са. «Что такое математика?» Л. Геффтера. «Прелюдия
к математике» и «Путь в современную математику»
У. У. Сойера... Где-то здесь мы и должны положить свой
камешек.
— Книгу полусерьезную-полушутливую, как я понял.
Этакий гибрид теоремы и побасенки. А форма книги?
— Есть стиль, на мой взгляд, отлично соответствую-
щий ее содержанию. Фрагменты, связанные друг с дру-
гом не словесными переходами, но одною лишь логикой
предмета.
— Догадываюсь: «Опыты» Монтеня, «Записки у изго-
ловья» Сэй-Сёнагон...
— Высокие примеры! В вольном разбеге пера одна
за другой появляются зарисовки лаконичные и в то же
время детальные, поэтичные и в то же время глубоко-
мысленные, часто проникнутые усмешкой... Вот бы и нам
показать в таких картинах важнейшие области матема-
тики!
— Итак, нечто вроде путеводителя по мате-
матике?
6
— А почему бы и нет? Когда ты едешь в незнакомый
тебе город и предвкушаешь его красоты, ты берешься
не за фолианты по его архитектуре. В таких томах ты
рискуешь споткнуться о фразы типа: «Рустованный пери-
птер фланкируется лучковыми сандриками». От такого
чтения первое свидание с городом наверняка будет ис-
порчено. А интересный путеводитель, хороший гид рас-
скажут тебе то же самое понятным тебе языком, да еще
приведут старинную легенду или отрывок из поэмы, наве-
янной образом этого города. И если все услышанное то-
бою заронит в твою душу чувство любви к замечатель-
ному городу, это заставит тебя взяться потом и за серь-
езные книги о нем, перечитать все те скучные фолианты,
которые иначе только отвратили бы тебя от него.
— Решено. Так в путь же—и пригласим с собою чи-
тателя!
ТЕОРЕМЫ,
АКСИОМЫ,
ОПРЕДЕЛЕНИЯ
Что такое математика?
Задайте этот вопрос своим приятелям, спросите у
взрослых, и в ответ вы скорее всего услышите что-ни-
будь вроде: «Это наука о числах и фигурах».
В самом деле, возьмем наугад любой раздел матема-
тики. Арифметика занимается числами. Они же подра-
зумеваются под буквами в формулах алгебры. В гео-
метрии речь идет о плоских фигурах и пространствен-
ных телах.
Между тем существуют такие отрасли математики,
где ни числа, ни фигуры никакой видной роли не играют.
Вот книга по математической логике. Заглянем в нее.
Формулы, которые встретятся нам тут, напоминают ал-
гебраические. Однако буквы в них обозначают не числа,
а фразы, чаще всего математического содержания. Их
в логике именуют высказываниями. Фигуры же появля-
ются здесь исключительно для иллюстрации.
А вот книга по теории групп. В ее формулах буквы
истолковываются как математические операции. После
таких примеров трудно утверждать, будто в числах и
фигурах заключено нечто самое существенное для ма-
тематики.
Так что же такое математика? Что в ней самое глав-
ное? Что прежде всего характерно для любого из ее раз-
делов, любой ее теории?
Если вообразить математику в виде огромного дома,
то ученых, чьими трудами возведен этот дом, естествен-
но сравнить с каменщиками. И такое сравнение небезос-
новательно. Когда каменщик возводит ётену, то каждый
кирпич прочно укладывается на уложенные ранее и
скрепляется с ними раствором. Точно так же в рассужде-
нии математика каждое утверждение опирается на уже
доказанные. Оно сцементировано с ними законами логи-
ки.
Каждый такой «кирпич» в математической «кладке»,
каждое утверждение математической теории, получен-
8
ное из ранее доказанных на основании правил логиче-
ского вывода, именуются теоремой. Конечно, математики
в своих рассуждениях далеко не каждое умозаключение
отмечают званием теоремы — есть у них и другие наз-
вания. Говорят, например, про признаки делимости чи-
сел, про правила разложения полиномов на множите-
ли. Но если быть строгим в терминологии, каждое такое
правило, каждый признак — одним словом, каждое ма-
тематическое утверждение, получаемое путем логичес-
кого доказательства, есть теорема.
Любая теорема или несколько теорем, в свою очередь,
могут послужить обоснованием для какой-то новой тео-
ремы. И подобно тому как здание складывается из кир-
пичей, любая математическая теория представляет со-
бой совокупность теорем.
Логически последовательная стройность утвержде-
ний — вот самое существенное и характерное свойство
математики. Оно ярко проявилось уже в древнейших ее
разделах — арифметике и геометрии. В числах и фигу-
рах впервые воплотилось это отличительное свойство
точной науки.
Со временем появились в математике и формулы,
этот особый язык для записи выкладок и теорем, язык
удобный, точный и емкий. Скажем, небезызвестную тео-
рему Пифагора можно высказать словами: «Квадрат ги-
потенузы равен сумме квадратов катетов». Но математик
а2 + ь2 = с2
предпочтет этой длинной фразе короткое равенство
а2+в2 = с2.
В любом здании, спускаясь с верхних этажей все ни-
же и ниже, мы в конце концов добираемся до фундамен-
та. Так можно перебирать и теоремы. Занявшись этим,
мы рано или поздно доберемся до утверждений, истин-
ность которых принимается без доказательства. Это ак-
сиомы или постулаты.
9
Раскроем знаменитые «Начала» Эвклида. В тече-
ние многих веков эта книга служила для школьников
учебником геометрии, для ученых — образцом математи-
ческой строгости.
Уже на первых страницах своего трактата Эвклид
перечисляет постулаты, на которые опирается в даль-
нейшем, выводя геометрические теоремы: «1. От всякой
точки можно провести прямую линию. 2. Ограниченную
прямую можно непрерывно продолжать по прямой. 3.
Из всякого центра и всяким раствором может быть опи-
сан круг. 4. Все прямые углы равны между собой. 5. Ес-
ли прямая, падающая на две прямые, образует внутрен-
ние и по одну сторону углы, то эти две прямые, продол-
женные неограниченно, встретятся с той стороны, где уг-
лы меньше двух прямых» (то есть в сумме составляют
меньше 180 градусов).
Посмотрим, как на таком фундаменте возводится зда-
ние эвклидовой геометрии.
С помощью своего пятого постулата Эвклид доказы-
вает, например, теорему о равенстве накрест лежащих
углов при параллельных пря-
мых— р и Р', а также б и
б' на нашем чертеже. В са-
мом деле, сложим паралле-
ли так, как показано на ри-
сунке ниже. Если бы накрест
лежащие углы были не рав-
ны друг другу, то . какие-то
два угла, лежащих по одну
сторону от АВ, тогда оказа-
лись бы в сумме меньше
двух прямых и параллели
встретились бы. Но это не-
возможно. Параллели на то
и параллели, что не пере-
секаются нигде. Значит, на-
крест лежащие углы р и р',
а также б и б' равны.
Следующий чертеж под-
сказывает нам, что углы а,
р' и / в сумме равны двум
прямым. Если заменить в
этой сумме р' и у' равными им
углами треугольника АВС
10
0 и у, то тем самым будет доказана известная теорема
о том, что сумма углов любого треугольника равна двум
прямым, то есть 180 градусам.
Так и получается одна теорема за другой.
Перед вами — малярная кисть, плакатное перо, фло-
мастер и тонко очиненный карандаш . Каким из этих
инструментов вы бы воспользовались, чтобы нарисовать
прямую линию на бумаге?
По-видимому, вы сразу потянетесь за карандашом. И
это понятно: малярная кисть рисует широкую полосу с
неровными краями, с кляксами по сторонам, с торчащи-
ми в разные стороны усами, то есть с теми деталями, ко-
торые не имеют никакого отношения к прямой линии. Не
свободны от подобных недостатков и плакатное перо, и
фломастер. А у следа, оставленного на бумаге тонко очи-
ненным карандашом, таких «довесков» нет. По крайней
мере они не заметны невооруженным глазом.
Но посмотрите на след карандаша через увеличи-
тельное стекло. Он ничем не лучше следа, оставленною
малярной кистью! Та же непостоянная ширина, те же не-
ровные края.
Карандаш нужно заменить инструментом более совер-
шенным. Но где же тот инструмент, который позволит
свести на нет все несущественные подробности? Хоро-
шенько поразмыслив, мы наверняка придем к выво-
ду: такого инструмента не найдешь ни в одной гото-
вальне.
Может быть, мы сплоховали из-за своей неопытности?
Не посоветоваться ли нам в этом щекотливом вопросе с
признанными авторитетами? Как, например, определял
прямую линию отец геометрии Эвклид?
Раскроем вновь его «Начала»:
«Точка есть то, что не имеет частей. Линия же — дли-
на без ширины. Концы же линии —точка. Прямая ли-
ния есть та, которая равно расположена по отношению к
точкам на ней...»
Ну как — все ясно? Нет, пожалуй. Недоуменные во-
просы напрашиваются и после этих слов. Разве только
про прямую линию можно сказать, что она равно распо-
ложена по отношению к своим точкам? Ведь таким же
свойством обладает и окружность. И потом что такое
п
длина? Что такое ширина? Не нуждаются ли эти поня-
тия, в свою очередь, в строгом определении?
Подобные вопросы могут показаться кощунством:
придираться к самому Эвклиду! Что же, мы далеко не
первые, кто упрекает его в нестрогости. Особенно участи-
лись такие придирки на рубеже XIX и XX веков, когда
математики стали задумываться: а такое ли уж стройное
здание геометрии? Начали они, естественно, с фундамен-
та. Вот тут-то и были замечены некоторые погрешности,
допущенные отцом геометрии. Началась кропотливая ра-
бота по их устранению.
Как же выглядят начала геометрии в современном из-
ложении? Возьмем книгу немецкого математика Давида
Гильберта «Основания геометрии»:
«Мы мыслим три различные системы вещей: вещи
первой системы мы называем точками, вещи второй си-
стемы мы называем прямыми, вещи третьей системы мы
называем плоскостями. Мы мыслим точки, прямые и
плоскости в определенных соотношениях и обозначаем
эти соотношения различными словами, как-то: лежать,
между, конгруэнтный (то есть совмещаемый наложени-
ем.— Авт.), параллельный, непрерывный».
Как видно, Гильберт и не собирается определять ос-
новные объекты геометрии — точку, прямую, плоскость.
•
«Нельзя быть математиком, не будучи в то же время
и поэтом в душе», — говорил немецкий математик Карл
Вейерштрасс.
Если геометрия упорно отказывается выдавать исто-
ки своих понятий и представлений, если нам никак не
удается определить их в строгих математических терми-
нах, то, может быть, нам в наших затруднениях помогут
поэтические образы.
«Звезды на небе — как искорки». «Луч света — как
тетива лука». «Равнина — как гладь озера».
Поэтический дар, которым человек наделен от приро-
ды, побуждал его подмечать сходство в различном.
Многократно отмечая то или иное свойство у различных
предметов, человек осознавал это свойство и давал ему
имя.
Тетива лука и луч света прямы. В этом обобщающем
суждении уже явно выражено понятие прямой. Напоми-
ная о тетиве лука и о луче света, оно в то же время уже
12
отделено от них, существует само по себе в нашем созна-
нии.
В нашем сознании... Вот почему мы так и не нашли
подходящего инструмента для проведения прямой на
бумаге. Штрих карандаша, мазок кисти — все это были
реальные образы. Они не способны точно выразить иде-
альный образ прямой.
Так появлялись абстрактные геометрические понятия.
И чем настойчивее искал человек простые, но харак-
терные, немногие, но существенные свойства предметов,
чем смелее отбрасывал при обобщении черты второсте-
пенные и случайные, чем шире был круг предметов, тем
более содержательным и вместе с тем более отчетливым
становилось соответствующее абстрактное понятие, будь
то плоскость или прямая, точка или окружность.
Так складывался набор элементарных геометриче-
ских образов.
Но человек — не только созерцатель и поэт. Чело-
век — прежде всего труженик.
В своей практической деятельности, постигая свой-
ства реальных предметов и их взаимосвязи, человек уста-
навливал свойства созданных им геометрических обра-
зов и отношения между ними.
Старинная легенда рассказывает, как зародилась на-
ука геометрия. Было это в Древнем Египте. Огромная
река течет через всю эту местность—Нил. Разливаясь с
каждой весной, Нил затоплял поля и уничтожал межи,
разделявшие земельные участки. Межи приходилось вос-
станавливать каждый раз заново. Из года в год, из века
в век совершенствовались приемы землемерия. Если про-
изнести это слово на древнегреческом языке, мы узнаем
в нем название науки, о которой рассуждаем: геометрия.
Натягивая межевую веревку между двумя колышка-
ми, древние землемеры не раз имели возможность убе-
диться, что эта несложная операция всегда приводит к
одному и тому же результату. Многократно повторенный
опыт внушал вывод: через две точки можно провести
прямую, и притом только одну.
Так рождались аксиомы, общие для всех, кто трудит-
ся на земле.
И чем настойчивее вскрывал человек устойчивые и
закономерные связи между предметами реального мира,
чем глубже осмыслял их логику, чем чаще узнавал при
самых различных обстоятельствах то или иное соотноше-
13
ние, чем успешнее использовал его в своих рассужде-
ниях и действиях, тем надежнее подтверждала свое зва-
ние соответствующая аксиома: через любые две точки
можно провести прямую; существуют три точки, не ле-
жащие на одной прямой, и так далее.
Аксиом становилось все больше. Они складывались в
единую систему. Математики заботились о том, чтобы
такая система была полной, то есть чтобы из нее можно
было вывести любую из известных геометрических тео-
рем. И еще о том, чтобы она была непротиворечивой,
то есть чтобы из нее нельзя было вывести взаимоисклю-
чающих утверждений.
Взятые вместе, эти аксиомы описывают все свойства
основных геометрических объектов, все соотношения
между ними, используемые при выводе геометрических
теорем. Потому и не нуждаются в определении основные
геометрические понятия —- точка, прямая, плоскость. Их
определения содержатся в аксиомах геометрии.
Если вы знаете азбуку Морзе, то вам не составит
труда прочесть написанное здесь ее знаками слово «ма-
тематика». Но если вы даже совсем не понимаете языка
радистов, для вас, видимо, не секрет, что из этих точек
и тире складываются буквы, из букв — слова, из слов —
фразы, из фраз — тексты, посылаемые в эфир.
Так же и в геометрии: из основных геометрических
объектов, таких, как точка и прямая, конструируются
объекты все более сложные.
Что есть квадрат? Определение гласит: это прямо
угольник, у которого все стороны равны между собой.
Понятие квадрата, как видим, выводится из более обще-
го понятия прямоугольника. А что такое прямоугольник?
Это параллелограмм, у которого все углы прямые. Еще
один шаг к понятию более элементарному. А параллело-
грамм? Это четырехугольник, у которого противополож-
ные стороны параллельны. Понятие четырехугольника, в
свою очередь, основывается на понятии отрезка, а тот
н
определяется как часть прямой, заключенной между дву-
мя лежащими на ней точками, включая их самих.
Так по ходу своего анализа мы добрались до первич-
ных геометрических понятий, о которых идет речь в ак-
сиомах геометрии: «точка» и «прямая», «лежать» и
«между».
Такой способ построения математических понятий из-
ложил еще Аристотель. Великий древнегреческий фило-
соф назвал его так: определение через род и видовое
отличие.
Скажем, прямоугольник относится к роду параллело-
граммов, а его видовое отличие состоит в том, что все
его углы прямые. Параллелограмм относится к роду че-
тырехугольников, а видовое отличие заключается здесь
в параллельности противоположных сторон.
Когда математик вводит в свое рассуждение новый
объект и называет его видовое отличие, то он тем самым
формулирует некоторое утверждение, используемое при
выводе новых теорем. Например, построив некоторый
в с
A D
параллелограмм ABCD, он получает для дальнейших
умозаключений сразу два утверждения: «АВ параллель-
но CD» и «ВС параллельно AD» — два новых «кирпичи-
ка» для математической «кладки». А с точки зрения уме-
лого каменщика, это не так уж мало!
Судите сами: начиная изучать геометрию на плоско-
сти и познакомившись с фигурирующими в ее аксиомах
основными понятиями — точкой и прямой, школьник до-
бавляет к ним совсем немного новых — угол, треуголь-
ник, параллелограмм, окружность... Но какое богатое со-
оружение вырастает на этой основе на протяжении
школьного курса математики!
Блез Паскаль, французский математик, получил не-
школьное, а домашнее образование. Его учителем был
15
отец, Этьен Паскаль, один из просвещеннейших людей
своего времени.
Согласно учебному плану Паскаля-старшего матема-
тику предполагалось проходить с пятнадцати-шестнад-
цати лет. Но ребенок поломал все планы своего учителя.
Услышав от отца про геометрию, узнав от него несколь-
ко аксиом из «Начал» Эвклида, Блез стал интересовать-
ся дальнейшим.
Отец, считая, что время для этого еще не настало, от
разговоров о геометрии уклонялся. Каково же было его
удивление, когда однажды, зайдя в детскую, он застал
двенадцатилетнего сына за доказательством теоремы о
сумме углов треугольника.
Удивительно рано проявилась математическая ода-
ренность будущего прославленного ученого. Однако в
этой истории не менее удивительно другое.
Дело в том, что свои геометрические построения
Блез проводил с помощью «палочек» и «колечек» — так
он называл прямые и окружности. По всей вероятно-
сти, он представлял их себе имеющими вполне ощу-
тимую толщину. Точками ему, вероятно, служили эта-
кие бусинки, шарики определенного и постоянного ра-
диуса.
То, что столь необычные средства не помешали Пас-
калю прийти к успеху в его геометрических доказатель-
ствах, объяснимо лишь одним: для бусинок и палочек
справедливы все те аксиомы, что и для точек без
частей и прямых без ширины, как их определял Эв-
клид.
Через две точки можно провести прямую, и притом
только одну, говорим мы. Две бусинки можно соединить
палочкой, и притом только одной—так, вероятно, это
утверждение представлял себе маленький Блез.
Он представлял это так потому, что так ему было
удобнее, понятнее. Он, как сказали бы ученые, модели-
ровал своими палочками абстрактное понятие прямой.
Точно так же моделируем его мы, проводя карандашом
на бумаге ровные тонкие линии. Так же моделировал его
древний землемер, натягивая веревку между колышка-
ми, так же моделирует его сегодня геодезист лучом
лазера.
Подобных моделей может быть сколько угодно. И ес-
ли в них воплощены одни и те же геометрические аксио-
мы, все они подчиняются следствиям из аксиом.
16
Нечто похожее мы наблюдаем во всех точных науках.
Одно и то же уравнение описывает распространение
тепла, просачивание нефти через земные слои, проник-
новение электромагнитного поля в плазму. Одно и то
же уравнение описывает течение жидкости, прогиб мем-
браны, напряжения в брусе, подвергнутом кручению.
Само уравнение служит, как говорят, математиче-
ской моделью явления или процесса. Одна и та же мо-
дель бывает пригодна для нескольких процессов и яв-
лений, совсем непохожих друг на друга внешне, но под-
чиняющихся одним и тем же математическим закономер-
ностям. Если общее для них уравнение оказывается
слишком сложным и пока не поддается решению, можно,
следя за одним процессом, безошибочно судить о его
математическом двойнике.
Не заглянешь в толщу стального бруса, не увидишь
картину напряжений внутри него. И тогда эксперимента-
тор натягивает гибкую мембрану на жесткий контур,
повторяющий своей формой профиль бруса. Под равно-
мерной нагрузкой мембрана вспучивается. Ее изгибы
точь-в-точь соответствуют распределению напряжений
по сечению бруса. Почему это так? Потому что матема-
тическая задача формулируется одинаково и там и тут.
Мембрану и брус породнила математика.
В каждом таком примере выразительно проявляет-
ся мощь математики. Она умеет разобраться в разнооб-
разнейших вопросах, исходя из немногих взаимосвязан-
ных основных понятий и утверждений.
Наблюдая различные процессы и явления, ученый
старается разглядеть самые существенные их черты, са-
мые глубокие их закономерности. Часто они оказывают-
ся общими для широчайшего круга наблюдаемых собы-
тий. Общей оказывается и математическая модель, по-
строенная на основе этих закономерностей.
Впрочем, когда мы хвалим математику, мы должны
соблюдать осторожность.
Математические понятия — понятия отвлеченные, аб-
страктные. Это лишь слепок с реального мира, лишь его
бледный силуэт. И поэтому та же приближенность свой-
ственна результатам любой математической теории, ка-
17
кими бы строгими и логичными путями они ни были по-
лучены: выводы не могут быть точнее предпосылок.
Выделяя абстрактные понятия в чистом виде, отсе-
кая второстепенные детали, математик всегда обедняет
жизнь. В математических рассуждениях, логичных и пос-
ледовательных, нет места ни шутке, ни неожиданному
сравнению. Математическая мысль не исчерпывает всех
проявлений человеческого разума.
Рассказывая про то, откуда в математике берутся
аксиомы, теоремы, определения, мы ради наглядности
обращались за примерами к геометрии. Наш рассказ
нетрудно перефразировать на любую математическую
теорию. В ее основе — некоторый свод аксиом. Они со-
держат определения основных объектов теории. Новые
объекты определяются через род и видовое отличие. Из
аксиом по правилам логического вывода получаются
теоремы. Из них складывается математическая теория.
МНОЖЕСТВА
~ Буренка! Зорька! Пеструшка! — покрикивает пастух,
выгоняя коров из леса на опушку. Неровен час потеря-
ются. Особенно эта Зорька: чуть зазеваешься — ищи-
свищи! Пеструшка — та ничего: пока кнутом не хлоп-
нешь, с места не сдвинется. С Буренкой — своя беда: уж
больно бодлива, не подцепила бы кого на рога...
Для пастуха каждая корова — на особицу: у каждой
свой характер, свои привычки. Это вон для дачника все
коровы на опушке — просто стадо и только.
Вот ведь что значит точка зрения! Для одного—не-
повторимые индивидуальности. Для другого — совокуп-
ность, мыслимая как единое целое.
Вообще человеческому мышлению свойственно трак-
товать то или иное собрание предметов, родственных по
какому-либо признаку, как самостоятельный объект.
Первая скрипка, вторая скрипка, альт, виолончель,
контрабас, флейта, гобой, фагот, валторна, труба, литав-
ры. Про все, взятое вместе, мы говорим: оркестр.
Кофейник, молочник, сахарница, несколько чашек,
столько же блюдец. А все вместе —сервиз.
А, Б, В, Г, Д... Все вместе же — алфавит.
1, 2, 3, 4, 5... А вместе — так называемый натуральный
ряд чисел.
Не случайно каждую из этих совокупностей мы назы-
ваем существительным в единственном числе: оркестр,
сервиз, алфавит, ряд — идея объединения проглядывает
даже в такой мелочи.
Подобное объединение необходимо, когда прихо-
дится сравнивать какие-либо совокупности между со-
бой.
Представьте: вы — новосел. Вы приходите в мебель-
ный магазин, чтобы выбрать мебель для своей новой
квартиры — и убеждаетесь, что сделать это не так-то
просто. Какому гарнитуру отдать предпочтение? То ли
этому — светлому, неполированному? Или тому, что под
19
карельскую березу? А может быть, вон тому — с плюше-
вой обивкой в полосочку?
Каждый гарнитур, оставаясь набором отдельных пред-
метов, в вашем воображении фигурирует как единое це-
лое.
Так оно происходит и на выставке филателистических
коллекций, и на конкурсе эстрадных ансамблей... Всякая
процедура сравнения тех или иных совокупностей за-
ставляет осмысливать их как одно целое.
Так дело обстояло и тогда, когда в семидесятых го-
дах прошлого века немецкий математик Георг Кантор,
исследуя тригонометрические ряды и числовые последо-
вательности, встал перед необходимостью сравнивать
между собой бесконечные совокупности чисел.
Для решения возникших при этом проблем Кантор и
выдвинул понятие множества, суть которого вполне пе-
редается словами «совокупность», «собрание», «набор»,
«ансамбль» и т. д.
Это понятие, введенное в довольно узкой области ма-
тематики для довольно специальных целей, вскоре стало
с успехом применяться в других ее областях. Посвящен-
ные ему исследования приобрели самостоятельный инте-
рес и выделились в особый раздел математики — теорию
множеств.
В современной математике понятие множества счита-
ется одним из основных. Так или иначе с него начинается
изложение традиционных математических дисциплин и
построение новых математических теорий, возникающих
по мере того, как расширяется сфера применений мате-
матики.
Универсальность этого понятия в том, что под него
можно подвести любую совокупность предметов. Здесь
годится все: марки, числа, люди, точки, звезды, векторы,
коровы, функции... Даже сами множества могут объеди-
няться во множества: например, математики говорят про
множество фигур на плоскости, про множество тел в
пространстве, но каждую фигуру, каждое тело они мыс-
лят как множество точек.
Плодотворность теоретико-множественной концепции
в том, что она породила весьма богатый и мощный арсе-
нал широких понятий и универсальных методов. Оттого
теория множеств и служит прочным фундаментом мате-
матизации разнообразнейших наук: экономики, биологии,
лингвистики...
20
Что же такое множество? Что это за термин, в кото-
ром, как в ящике фокусника, скрываются и марки, и
числа, и звезды? Как в математике определяется это по-
нятие?
Если честно — то никак. Здесь мы не можем употре-
бить столь привычный для математиков способ опреде-
ления через род и видовое отличие. Согласно такому
способу всякое новое понятие вводится как разновид-
ность некоторого более общего, определенного ранее по-
нятия (скажем, параллелограмм есть разновидность че-
тырехугольника, прямоугольник есть разновидность па-
раллелограмма и т. п.). Но для понятия «множество» не
известно ничего более общего по отношению к нему.
Его удел такой же, как у всех основополагающих поня-
тий математики, которые выступают в аксиомах, не ого-
воренные никакими предварительными определениями.
Когда мы говорили, что слово «множество» имеет тот
же смысл, что слова «совокупность», «собрание», «на-
бор», «ансамбль», мы лишь сопоставляли с ним его сино-
нимы, которые, быть может, помогали сделать новый тер-
мин более ясным, но отнюдь не составляли его строгого
определения.
Нам кажется, что после сказанного у читателя появи-
лось некоторое недоумение: как же так — множество оп-
ределить нельзя, но выше мы говорили и про множество
натуральных чисел, и про множество букв русского алфа-
вита, и про множество фигур на плоскости...
Неувязка?
Никак нет. Как абстрактное математическое понятие
множество действительно неопределимо. Но определить
какое-либо конкретное множество — задача не из труд-
ных. Например, можно с полной определенностью гово-
а
/
элемент
множества
множество
принадлежности
€
\
21
рить о множестве архитектурных памятников Ленингра-
да: чтобы его задать, достаточно пройти по улицам горо-
да и указать дома, на которых висят чугунные доски с
надписью «Охраняется государством».
Так и со всяким множеством. Определить его —зна-
чит относительно любого предмета уметь ответить на во-
прос: принадлежит он данному множеству или не при-
надлежит?
Поэтому и говорят, что всякое множество однознач-
но и полностью определяется его элементами.
Так что пусть читатель не сетует, что термин «мно-
жество» остался неопределенным. В свете сказанного ос-
новное понятие теории множеств видится не за этим тер-
мином, а скорее за словом «принадлежать».
Для него введен особый символ, приведенный на ри-
сунке выше. Там показано, как ib символической записи
обозначается, что некоторый элемент а принадлежит не-
которому множеству А.
•
Говорят, что над входом в сад «Академия», где Пла-
тон любил беседовать со своими учениками, было напи-
сано: «Да не войдет сюда тот, кто не знает геометрии».
Беседуя со своими читателями о математике, мы не
гонимся за академизмом и не требуем от них особых
предварительных познаний. Тем не менее нам хочется
верить, что нашему читателю известны простейшие гео-
метрические фигуры — треугольник и окружность, па-
раллелограмм и прямоугольник, квадрат и ромб, а воз
можно, и некоторые свойства этих фигур. Все это приго-
дится нам в разговоре о множествах.
Мы также предполагаем в читателе некоторые на-
чальные познания из арифметики, надеемся, в частности,
что он имеет понятие о десятичных дробях, знает о суще-
ствовании бесконечных десятичных дробей — например,
представляет, что если попытаться выразить дробь 3/22
в десятичной записи, деля уголком 3 на 22, то в результа-
те получится 0,1363636... а дальше будет периодически
повторяться без конца одна и та же группа цифр (36).
Числа, которые выражаются конечными или бесконеч-
ными десятичными дробями, называются вещественными
(также действительными). К их множеству мы не раз бу-
дем обращаться за примерами. Не удивительно: ведь
среди них содержатся все натуральные (то есть целые
22
положительные) числа, все целые числа вообще (и поло-
жительные, и отрицательные; те и другие можно тракто-
вать как конечные десятичные дроби, не имеющие ни од-
ного знака после запятой). Во множестве вещественных
чисел заключаются также все рациональные числа, или,
другими словами, дроби, отношения целых чисел — ока-
зывается, всякое такое отношение можно представить ко-
нечной или бесконечной периодической десятичной
дробью (как мы только что сделали это с отношением
3/22). Если же бесконечная десятичная дробь неперио-
дична, то такое вещественное число называется иррацио-
нальным.
Математика знает также мнимые числа, комплексные
числа, но мы в нашей книге касаться их не будем.
•
Русское слово «множество» способно ввести в заблу-
ждение: оно неявно подразумевает некоторое изобилие.
Тем более что наши примеры множеств давали тому по-
вод. Однако математический термин «множество» этого
оттенка совсем не имеет.
Множество может состоять всего из двух элементов
(таково, например, множество естественных спутников
Марса — Фобос и Деймос). Может состоять из одного
(тогда его называют единичным множеством; пример —
множество естественных спутников Земли, в котором
единственный элемент —Луна). Наконец, математики
говорят про так называемое пустое множество, не содер-
жащее ни одного элемента. Это, например, множество ес-
тественных спутников Венеры или, если угодно что-ни-
будь повеселее, множество владельцев действующих веч-
ных двигателей, множество квадратных колес, множе-
ство острых шаров, множество кривых прямых...
Понятие пустого множества в математике не расцени-
вается как нечто маловажное. Для него даже придуман
специальный символ: 0.
Это может показаться мнительностью, но мы, право,
не без основания опасаемся, что некоторые типичные
примеры множеств могут подтолкнуть читателя к невер-
ному толкованию этого понятия.
Мы говорим, например, о множестве букв русского ал-
фавита (А, Б, В, Г...), о множестве натуральных чисел
23
(1, 2, 3, 4...). Элементы того и другого принято распола-
гать в определенном порядке. Но никакого определяюще-
го значения тот или иной порядок не имеет ни для этих
1--2 z6--7 15-
/ / /' /
' / / S
3 z5 z8 14
•/Z / /
4 9 13
/ /
10 12
। /
1 1
двух, ни для какого угодно множества. Как ни тасуй ко-
лоду, это будет одно и то же множество карт. И точно
так же алфавит можно привести в любом порядке — на-
пример, в том, который принят для клавиатуры пишущих
машинок. А натуральный ряд можно записать, скажем,
так, как ’показано на этой странице (в дальнейшем нам
еще пригодится такая его запись).
Здесь стоит отметить (позже мы поговорим об этом
подробнее), что существуют бесконечные множества,
элементы которых принципиально невозможно располо-
жить в виде какой-либо последовательности, как числа
натурального ряда. Таково, например, множество всех
вещественных чисел между нулем и единицей (включи-
тельно) .
Напоследок еще одно замечание по поводу тех мно-
жеств, которые поддаются перечислению. Если, скажем,
перечисляя русский алфавит, мы повторим какую-то бук-
ву два раза, множество останется тем же самым — рус-
ским алфавитом. Чтобы в таких случаях исключить воз-
можные недоразумения, говорят, что ни один элемент
множества не может содержаться в нем несколько раз.
Адам и Ева. Таково, согласно библейской легенде,
множество первых людей на Земле.
Меркурий, Венера, Земля, Марс, Юпитер, Сатурн,
Уран, Нептун, Плутон. Это множество планет Солнечной
системы.
И то и другое множество конечно, так что каждое
можно определить, указав все его элементы. (И если
желательно подчеркнуть, что указанные предметы рас-
сматриваются в совокупности как некоторое множество,
24
их перечисляют через запятую и ограждают эту строчку
с обеих сторон фигурными скобками.)
{$,9,д,СГД1гДб,Е} р,2,3,4Д. }
Андрей Болконский, Пьер Безухов, Наташа Ростова,
Николай Ростов, Анатоль Курагин и так далее— множе-
ство персонажей романа Толстого «Война и мир».
Один, два, три, четыре, пять, шесть и так далее —
уже знакомый нам натуральный ряд, множество положи-
тельных целых чисел.
Способы задания множеств в последних двух приме-
рах уже другие, нежели в первых.
Что касается множества персонажей романа «Война
и мир», то его в принципе можно было бы определить и
прежним приемом — перечислением. Для этого, правда,
потребовалось бы несколько страниц нашей книги. А вот
для натуральных чисел такой прием не годится даже в
принципе, поскольку их множество бесконечно.
Как быть? В некоторых подобных случаях из затруд-
нительного положения удается выйти, назвав лишь не-
сколько элементов множества. Троеточие или оборот «и
так далее», которыми принято обрывать такой список,
подчеркивают, что названное не исчерпывает всего мно-
жества. Однако если из этого незавершенного «перечня
становится понятно, как далее его продолжать, какие
предметы можно поставить в один ряд с названными,—
это значит, что есть критерий проверки, принадлежит
тот или иной предмет данному множеству или не при-
надлежит. Мы уже знаем: если такой критерий есть, то
множество задано совершенно определенно.
Впрочем, на способы задания множеств можно
взглянуть с другой стороны, с которой становится неза-
метным различие между конечными и бесконечными со-
вокупностями.
Присмотримся к описаниям упомянутых множеств:
«первые люди на Земле», «планеты Солнечной системы»,
«натуральные числа», «персонажи романа «Война и мир».
Такого описания вполне достаточно для того, чтобы
определить каждое из этих множеств. В подобных случа-
ях говорят, что множество задано с помощью характери-
стического (или определяющего) свойства, такого, что
им обладает каждый элемент этого множества и не об-
25
ладает ни один предмет, который этому множеству не
принадлежит. Принадлежность предмета данному мно-
жеству тогда можно выразить, сказав, что он обладает
данным свойством.
Поистине незаменим этот способ, когда элементы мно-
жества просто невозможно перечислить каким-либо
списком, даже оборванным словами «и так далее».
Взять хотя бы уже упоминавшееся по этому поводу
множество всех вещественных чисел между нулем и еди-
ницей (включительно). Написав эту фразу, мы, собствен-
но, и указали характеристическое свойство элементов
этого числового множества: каждое принадлежащее ему
число неотрицательно и в то же время не превосходит
единицы. Можно было бы заменить словесное описание
формульным (О^л'^1), но суть дела осталась бы преж-
ней.
Другой пример — окружность. Про нее говорят так:
множество точек, удаленных от центра на расстояние,
равное радиусу. И в этом выражается определяющее
свойство элементов этого точечного множества.
Делу время — потехе час.
Дел у нас с вами, читатель, еще много, а вот для раз-
влечений может не выкроиться ни минутки. Поэтому от-
ведем забавам хотя бы эту страничку.
Давайте сыграем в слова. Правила игры предельно
просты: берется какое-то слово, и из его букв образуют-
ся новые слова.
Не будем лазить за исходным словом в карман: нам
вполне подойдет заголовок этой главы.
МНОЖЕСТВА
нож
нос
сон
стон
жена
манеж
жетон
монета
жеманство
А теперь, читатель, забавы в сторону — займемся де-
лом.
26
Каждое из выписанных в столбик слов будем рассмат-
ривать как множество букв. По правилам игры буквы
каждого новообразованного слова в этом столбике чер-
пались из исходного слова. Иначе говоря, любой элемент
каждого нового множества букв принадлежит исходному
буквенному множеству.
Говорят, что некоторое множество включается в дру-
гое, если каждый элемент первого множества является
также элементом другого. При этом первое множество на-
зывается подмножеством (или частью) второго.
Согласно сказанному, множество букв слова «жетон»
является подмножеством (или частью) множества букв
(н, о, ж} £= (м, Н, О, Ж, Е, с, т, в, а)
символ включения
{ж, Е, Т, О, Н, О, Ж, Е, С, Т, В, А}
{Н, О, Ж}^{Ж, Е, Т, О, Н}
слова «множества», множество букв слова «нож» включа-
ется во множество букв слова «жетон» и т. п.
Нетрудно подобрать и математические примеры вклю-
чения множеств. Совсем недавно мы говорили, что вся-
кое натуральное число есть число вещественное, принад-
лежит их множеству. А это и означает, что множество на-
туральных чисел включено во множество вещественных.
С другой стороны, множество натуральных чисел вклю-
чает в себя множество нечетных чисел, а оно включает в
себя множество простых (напомним, что натуральное чис-
ло называется простым, если делится лишь на себя и на
единицу, иными словами, не разложимо на множители).
Множество прямоугольников включается во множество
параллелограммов, а оно, в свою очередь, является
частью множества четырехугольников.
То, что одно какое-то множество является частью дру-
гого, иногда совершенно очевидно. Так, например, дело
обстоит в случае с прямоугольниками и параллелограм-
мами. Определяющее свойство параллелограмма — па-
раллельность противоположных сторон. Всякий прямо-
угольник обладает таким свойством и, стало быть, при-
надлежит множеству параллелограммов.
Но иногда включение одного множества в другое при-
ходится доказывать. Не всякому, быть может, очевидно,
27
что любое простое число (кроме двойки) нечетно. А ме-
жду тем обосновать это просто. Ведь если бы оно было
четным, то оно делилось бы на два, то есть на число, не
равное ни ему самому, ни единице, и, стало быть, не было
бы простым.
Просмотрим теперь еще раз список слов, извлеченных
нами из слова «множества». Наша самая большая уда-
ча— это, несомненно, слово «жеманство». Будучи обра-
{ж, Е, М, А, Н, С, Т, В, 0} — {м, Н, О, Ж, Е, С, Т, В, А}
{М, Н, О, Ж, Е, С, Т, В, А}^ {Ж, Е, М, А, Н, С, Т, В, 0}
{Ж, Е, М, А, Н, С, Т, В, О} = {М, Н, О, Ж, Е, С, Т, В, А}
зовано по всем правилам нашей игры, оно как множество
букв включается в исходное слово «множества». Гор-
димся же мы им потому, что оно также и включает в се-
бя исходное слово. Действительно, каждая буква слова
«множества» принадлежит множеству букв слова «же-
манство».
Иными словами, каждое из этих двух множеств явля-
ется подмножеством другого. Причина такой взаимности
понятна: оба буквенных множества состоят из одних и
тех же элементов. Про такие множества говорят, что они
равны друг другу. А выражаясь строго, два множества
называются равными, если одно включается в другое, и
наоборот, то есть если оба состоят из одних и тех же эле-
ментов.
Попробуем и на этот счет подобрать пример из мате-
матики. Давайте рассмотрим два множества геометриче-
ских фигур: множество равносторонних треугольников и
множество равноугольных треугольников. Есть такая те-
орема: в треугольнике против равных сторон лежат рав-
ные углы. Следовательно, каждый равносторонний тре-
угольник является равноугольным, то есть наше первое
множество фигур (равносторонние треугольники) вклю-
чается 'во второе (равноугольные треугольники). Но
есть и такая теорема: в треугольнике против равных уг-
лов лежат равные стороны. Следовательно, каждый рав-
ноугольный треугольник — равносторонний, то есть и вто-
рое множество фигур включается в первое. Итак, оба
множества равны друг другу.
28
Общеизвестно: всякая селедка — рыба, но не всякая
рыба — селедка.
Ясно, что в этой поговорке речь идет о двух множест-
вах — множестве рыб вообще и множестве селедок в част-
ности.
Поскольку всякая селедка — рыба, множество селе-
док включено во множество рыб.
Но не всякая рыба — селедка. Иными словами, во
множестве рыб существует хотя бы один элемент, не при-
надлежащий множеству селедок, ну, скажем, лещ или
щука. В подобных случаях говорят не просто о включе-
нии, а о строгом включении.
Точно так же множество пешек строго включено во
множество шахматных фигур, множество простых чисел—
во множество натуральных чисел, множество квадра-
тов— во множество прямоугольников.
Некоторое множество, строго включенное в другое,
называется его истинным, или собственным, подмножест-
вом (а не просто подмножеством, как говорили мы в слу-
чае нестрогого включения).
Итак, множество селедок есть истинное подмножество
Символ строгого включения
множества рыб, множество простых чисел — истинное
подмножество натурального ряда и т. д.
Помните загадку-шутку: два отца и два сына, а всего
трое — как такое может быть?
По-видимому, вы знаете ответ: это мальчик, его отец
и его дед. Но даже если это известно, остается пораз-
мышлять вот над чем: в чем, собственно, парадоксаль-
ность загадки?
Да в том, что речь тут идет совсем не о числах (иначе
загадка не имела бы решения: два плюс два никак не
равно трем). Суть дела относится к теории множеств.
Два множества фигурируют здесь: множество отцов
(отец и дед мальчика) и множество сыновей (мальчик и
29
Отцы
S 1 "
Сыновья
его отец, доводящийся сыном деду). Решить загадку —
значит составить из них третье множество, которое на-
считывало бы три элемента.
Определяющий признак этого третьего множества в
том, что состоит оно из всех тех и только тех элементов,
которые принадлежат либо первому, либо второму мно-
жеству, то есть хотя бы одному из них — множеству от-
цов или множеству сыновей.
Когда новое множество строится из исходных по та-
кому правилу, то оно называется объединением исходных
множеств.
Итак, множество, состоящее из мальчика, его отца и
его деда, есть объединение множества отцов и множе-
ства сыновей.
Отец мальчика принадлежит обоим. Но в их объеди-
нение он входит только один раз, иначе это противоречи-
ло бы понятию «множества»: ни один элемент не может
содержаться в нем несколько раз. Так и объясняется па-
радокс, которым озадачивает шутка про двух отцов и
сыновей.
Чтобы получше рассмотреть смысл нового понятия —
объединения множеств, — возьмем бинокль.
Поглядите в левый окуляр и запомните все, что вид-
но в него. Потом в правый окуляр. А теперь глядите в
оба — что видите вы на этот раз? Все то, что попадает в
поле зрения либо левого, либо правого окуляра.
Применяя уже знакомый нам термин, можно сказать,
что множество точек характерной фигуры, напоминаю-
щей поваленную на бок восьмерку, есть объединение двух
точечных множеств — двух накладывающихся друг на
друга кругов.
Идею объединения множеств можно усмотреть во
зо
в
А
ди в
ДО В читается* объединение множества А и множества В
многих математических формулировках. Новый при-
мер будет связан с понятием абсолютной величины
действительного числа. Как она определяется? Если
число неотрицательное, то его абсолютная величина сов-
падает с ним самим. Скажем, абсолютная величина де-
сяти равна десяти. Абсолютная величина нуля равна ну-
лю. А чтобы получить абсолютную величину отрицатель-
ного числа, надо взять его с обратным знаком. Скажем,
абсолютная величина минус семи равна семи. (Заметим
попутно, что абсолютная величина любого числа в силу
данного определения не может быть отрицательной).
Зная это, разберемся теперь, что означает выражение:
«Множество чисел по абсолютной величине, большей еди-
ницы». Очевидно, все элементы этого числового множе-
ства— это либо положительные числа, большие едини-
цы, либо отрицательные числа, меньшие минус единицы.
Налицо объединение двух числовых множеств.
•
Поглядите еще раз в -наш бинокль, читатель.
Замечаете ли вы, что отнюдь не все предметы, кото-
рые видны в него, выглядят выпуклыми, объемными?
Дело в том, что объемность появляется у них лишь
тогда, когда человек глядит на них обоими глазами. Не-
даром физиологи называют объемное зрение бинокуляр-
ным (так сказать, «зрением в два глаза»).
дне
Д п В читается, пересечение множества А и множества В
В поле зрения бинокля попробуем очертить тот уча-
сток, где предметы смотрятся выпуклыми. Очевидно, это
будет та луночка, по которой перекрываются круговые
поля зрения левого и правого окуляра.
32
Придадим нашему выводу теоретико-множественное
звучание. Мы взяли два множества (поля зрения двух
окуляров) и образовали из них третье. Определяющий
признак этого третьего множества в том, что состоит оно
из всех тех и только тех элементов (в данном случае то-
чек), которые принадлежат и первому и второму мно-
жеству.
Когда новое множество строится из исходных по та-
кому правилу, то оно называется пересечением исходных
множеств.
После этого интересно вновь рассмотреть поставлен-
ную в предыдущем разделе проблему отцов и детей. Мы
уже отмечали, что отец мальчика принадлежит и множе-
ству отцов, и множеству сыновей. Теперь мы можем вы-
разиться более научно: единичное множество «отец ре-
бенка» есть пересечение множества отцов и множества
сыновей.
О множестве вещественных чисел, больших нуля и
меньших единицы, можно сказать, что это пересечение
множества вещественных чисел, больших нуля, и множе-
ства вещественных чисел, меньших единицы. О множе-
стве квадратов — что это пересечение множества прямо-
угольников и множества ромбов (если читателю это не
кажется очевидным, пусть он попытается доказать это
строго).
Руководитель школьного хора составляет расписание
репетиций.
«Так... Четвертые классы... Их три: А, Б, В. Из чет-
вертого А восемь человек. Не густо, но зато два солиста.
Четвертый Б. О, эти все певуны — всем классом записа-
лись. Четвертый В. Ни одного человека! Чем они там за-
нимаются? Ах да, все они в кукольном театре, только из
них он и состоит».
Руководителю хора еще предстоит согласовывать и
увязывать сроки спевок и репетиций, а для наших целей
наговоренного им вполне достаточно. Он описал всевоз-
можные отношения, какие могут существовать между
двумя множествами.
На помещенном здесь рисунке прямоугольник симво-
лически обозначает множество всех учеников школы.
2 Заказ 8651
33
А(]Х В^К К^В В = К 5ПХ - О
Заштрихованный овал в центре, помеченный буквой X,—
это множество учеников, поющих в хоре. Ну а теперь схе-
матически изобразим здесь же четвертые классы. Будем
отмечать соответствующие овалы теми же буквами, ко-
торыми эти классы обозначены в школьном расписа-
нии,— А, Б, В. (Кстати, и во вполне строгих математи-
ческих рассуждениях множества тоже обозначаются про-
писными буквами, правда, латинскими).
Итак, четвертый А. Восемь его учеников поют в хоре.
У множеств А и X есть общие элементы, эти множества
пересекаются, что и показано на рисунке.
Четвертый Б. Это множество тоже пересекается со
множеством X. Но ситуация здесь иная, нежели с пересе-
чением множеств А и X. Там множество А содержало
элементы, не входящие в X (всего лишь восемь учени-
ков— хористы). Там можно было говорить только о пе-
ресечении. А здесь наблюдается нечто большее: каждый
элемент множества Б есть элемент множества X. Иными
словами, множество Б включено во множество X.
Это включение строгое: ведь в хоре поют не только
ученики четвертого Б.
Четвертый В. Хористов тут нет. Множества В и X не-
пересекающиеся. (Говорят еще так: их пересечение пу-
сто.) А еще известно, что множество В и множество К
(кукольный театр) состоят из одних и тех же элементов.
Иначе говоря, множества В и К равны.
Вот мы и перебрали все отношения, какие могут су-
ществовать между двумя множествами. Два множества
могут не пересекаться (как множества В и X из нашего
примера), а могут и пересекаться (как А и X, Б и X, В и
К). В последнем случае возможны три варианта. Множе-
ства могут быть равны (как В и К). Могут строго вклю-
чаться одно в другое (как Б включается в X; о включе-
нии можно говорить и в случае двух равных множеств:
34
любое из них включено в другое, но тут уж речь идет о
нестрогом включении). Наконец, два множества могут
пересекаться так, что каждое имеет элементы, не принад-
лежащие другому (как А и X). Тогда говорят, что два
множества находятся в общем положении.
Круги и овалы, которые мы начали рисовать, экспе-
риментируя с биноклем, сослужили нам неплохую служ-
бу. С их помощью потом оказалось возможным проил-
люстрировать все отношения между множествами и опе-
рации над ними.
Подобные незамысловатые картинки называют диа-
граммами Венна, хотя еще раньше их применял извест-
А U В = А(\В
АПВ=АС1В
2*
' 35
ный математик Эйлер в своих знаменитых «Письмах к
немецкой принцессе».
Мы еще раз убедимся в пользе этих диаграмм, знако-
мясь с закономерностями, которым подчиняются опера-
ции над множествами.
Вот два примера — и совсем не рядовых: они носят
громкое название законов де Моргана (по имени иссле-
довавшего их шотландского математика)
Первый: дополнение объединения двух множеств рав-
но пересечению дополнений этих множеств.
Второй: дополнение пересечения двух множеств рав-
но объединению дополнений этих множеств.
Звучит сложновато, как трудно произносимая скоро-
говорка, — в переменчивых сочетаниях повторяющихся
терминов путается язык.
А теперь то же самое на диаграммах Венна. Двумя
перекрывающимися кругами обозначим на них два пе-
ресекающихся множества. Внешность каждого круга
представит собой дополнение соответствующего множе-
ства до универсального, обозначенного традиционным
прямоугольником (см. с. 00).
Верхняя картинка: внешность этой лежащей на боку
восьмерки из двух кругов можно было бы получить, обра-
зуя пересечение внешностей того и другого круга. Это
первый закон де Моргана в наглядном представлении.
Нижняя картинка: внешность луночки, по которой пе-
рекрываются круги, можно представить как результат
объединения внешностей того и другого круга. Таков в
наглядном представлении второй закон де Моргана.
Читатель, подробно разбиравший нарисованные на
предыдущих страницах диаграммы Венна, конечно, об-
ратил внимание на строчки символов, которыми сопро-
вождался каждый рисунок.
Большие латинские буквы повторяют в этих строчках
обозначения множеств, изображенных на картинках, а
значки, соединяющие буквы, обозначают операции над
множествами, проиллюстрированные картинками.
Эти цепочки символов навевают воспоминания о фор-
мулах школьной алгебры, где маленькие латинские бук-
вы, обозначавшие вещественные числа, соединялись зна-
ками арифметических операций.
36
Такая аналогия совершенно справедлива.
Ведь что собой представляют законы алгебры? Вы-
сказывания типа: от перемены мест слагаемых сумма не
меняется (переместительный закон); умножить сумму
на число — это все равно, что умножить на число каждое
слагаемое в отдельности и результаты сложить (распре-
делительный закон умножения относительно сложения).
Здесь нет никаких оговорок относительно чисел, к ко-
торым можно применять эти высказывания. Следователь-
но, выражаемые ими равенства выполняются всегда, ка-
кие конкретные числа в них ни подставишь. (Заметим,
что равенство двух алгебраических выражений, выполня-
ющееся при подстановке в него любых элементов неко-
торого числового множества, называется тождеством, оп-
ределенным на этом множестве.)
Освоив свод таких законов, можно с успехом зани-
маться тем, что называется алгебраическими преобразо-
ваниями: упрощать громоздкие выражения, придавать
им вид, удобный для тех или иных вычислений, и т. д.
Подобный свод законов — алгебра множеств — суще-
ствует и для операций, при помощи которых из одних
множеств образуются другие, — для объединения, пере-
сечения, дополнения.
В чем-то оба этих свода законов, эти две алгебры (чи-
сел и множеств) похожи. Иными словами, все эти фор-
мулы носят характер тождеств. Подобно формулам
школьной алгебры, они используются для того, чтобы пре-
образовывать выражения, содержащие символические
обозначения множеств, — упрощать их, придавать им оп-
ределенный вид и т. д.
Взгляните на левый рисунок на следующей странице.
Такая позиция сложилась на 26-м ходу в 21-й партии
титанического матча между Капабланкой и Алехиным,
состоявшегося осенью 1927 года.
Далее последовало:
26................ Cf6 — Ь2!
27. Лс1 — el Лс8— d8
27. а4:Ь5 аб : Ь5
29. h2 — h3 еб — е5
37
30. «Ле! — Ы е5 — е4
СЬ2 : d4
31. Kf3 — d4
32. ЛЫ — dl Кс4 : еЗ!
Белые сдались.
Мы надеемся, что любитель шахмат получил некото-
рое удовольствие, разбирая фрагмент знаменитой пар-
тии. Но, право, мы были бы бестактны, если бы привели
пример, понятный лишь шахматистам. Есть в нем нечто,
что имеет непосредственное отношение к теме нашего
разговора о теории множеств.
Присмотритесь к записи, не вникая в ее смысл. Всю-
ду в ней встречаются характерные пары, образованные
из строчной латинской буквы и натурального числа: f6,
Ь2, cl...
а Ь с d е f g h
На прописные латинские буквы обращать внимание
не будем — это сокращенные обозначения фигур. Чтобы
они не составили нам помехи, уберем фигуры с доски.
Что останется на ней тогда? Только лишь разметоч-
ные знаки.
Внизу — горизонтальный ряд букв, от а до h. Слева—
вертикальный столбик чисел, от 1 до 8.
Каждая буквенно-числовая пара, о которой говори-
лось выше, образуется так: сначала берется элемент из
первого, буквенного, множества и за ним ставится эле-
мент, выбранный из второго, числового, множества.
Кстати, само слово «пара» — термин теории множеств.
Так называются два элемента, расположенных в опреде-
ленном порядке (поэтому часто говорят не «пара», а
«упорядоченная пара»).
Не довольствуясь несколькими вышеприведенными
38
примерами, образуем всевозможные пары описанного
вида. Их множество мы назовем декартовым произведе-
нием двух исходных множеств — буквенного и числового
(читатель, вероятно, уже заметил про себя, что новообра-
зованное множество насчитывает 64 элемента, ровно по
числу клеток шахматной доски — ведь каждой клетке
соответствует своя пара и, наоборот, каждая пара коди-
рует свою клетку).
Понятие, с которым мы только что познакомились, на-
столько важно, что мы приведем особо его строгое опре-
деление: декартовым (или прямым) произведением од-
ного множества на другое называется множество всевоз-
можных пар, первые элементы которых принадлежат од-
ному множеству, а вторые — другому.
Теперь давайте разберем еще одну партию
1. 2е —4е
2. 2d —4d
3. 4е — 5е
4. 4d : 5с
7е — бе
7d — 5d
7с — 5с
К8Ь — 6с
Читатель, даже не очень сведущий в шахматах, веро-
ятно, сразу заметил: здесь что-то не так. Действительно,
мы сделали некоторую перестановку: в наших буквенно-
числовых парах (2е, 4d, 7с) на сей раз сначала идут
цифры, а потом уже буквы. А ведь в данном выше опре-
делении пары подчеркивалось, что порядок элементов в
ней существен. И потому мы не можем назвать равными,
скажем, две такие пары: е2 и 2е. Стало быть, множество
буквенно-числовых пар, о которых говорилось в преды-
дущем разделе (f6, е2, cl, d4 и т. п.), не равно множест-
ву пар, появившихся в нашем рассказе сейчас (2е, 6f,4d,
1с и т. п.), — ведь эти множества состоят не из одних и
тех же элементов.
Вывод? Он очевиден: произведение двух различных
множеств меняется от перемены мест сомножителей — в
противоположность произведению чисел, для которого
справедлив переместительный закон. Для множеств та-
кого закона нет.
Перестановка сомножителей ничего не изменит лишь
в том случае, когда перемножаемые множества равны.
Впрочем, и здесь все не так просто.
Возьмем только что применявшееся нами множество
39
целых чисел от 1 до 8. Умножим его на себя. В произве-
дении получится множество всевозможных пар вида:
(1,1), (1,2), (1,3), (2,1), (2,3), (3,4)...
Не кажется ли вам повторением наличие в этой строч-
ке пар (1,2) и (2,1)?
Мы сочтем свой рассказ не напрасным, если вы отве-
тите: нет, эти пары не равны, хотя и образованы одина-
ковыми элементами, потому что расположены эти эле*
менты в разном порядке.
Совокупность упорядоченных пар, на первом месте в
которых стоит элемент одного множества, а на втором—
элемент другого, мы назвали декартовым произведением
первого множества на второе.
Можно говорить не только о парах, но и, скажем, о
тройках — разумеется, даже упорядоченных. Например,
все обеды из трех блюд — это тройки, первый элемент ко-
торых принадлежит множеству первых блюд, второй —
множеству вторых, третий — множетву третьих. (Упоря-
доченность таких троек подчеркивается названиями
блюд: первое, второе, третье.) Такие обеды, составлен-
ные во всевозможных сочетаниях по естественному по-
рядку блюд, очевидно, образуют декартово произведение
трех множеств, где первый сомножитель—это множест-
во первых блюд, второй и третий—множества вторых и
третьих блюд соответственно.
Три блюда, конечно, не предел для тренированного
едока. Помните те обеды, которыми турецкий султан уго-
щал достославного барона Мюнгаузена? Согласно уве-
рениям барона, о честности которого ходят легенды, чис-
ло блюд в этих обедах было умопомрачительно большим,
так что для математического описания тех знамени-
тых трапез потребовалось бы понятие упорядоченной
п~ки.
(Читатель, вероятно, знает, что в математике буква п
применяется для обозначения натуральных чисел и пре-
имущественно в тех случаях, когда под нею можно подра-
зумевать произвольное натуральное число.)
Таким понятием располагает теория множеств. Упо-
рядоченной и-кой называется набор из п элементов, где
на первом месте стоит элемент первого множества, на вто-
ром— второго и так далее — до n-ного. Всевозможные
такие и-ки образуют декартово произведение тех п мно-
40
жеств, из которых берутся элементы для образования
упорядоченных и-ок.
Сомножители в произведениях множеств могут быть
и одинаковыми. Попробуйте-ка представить, например,
что получится, если множество букв русского алфавита
трижды умножить на себя. Очевидно, в результате полу-
чится множество упорядоченных троек букв, иными сло-
вами, множество всех трехбуквенных слов русского язы-
ка, осмысленных и не имеющих смысла: бал, лоб, мул,
дыр, бул, щыл...,
Заметим, что упорядоченные n-ки из элементов неко-
торого множества называют еще n-мерными векторами,
определенными на этом множестве. (Наряду с термином
«вектор» иногда в таких случаях употребляется равно-
значный ему термин «кортеж».)
Элементы, составляющие ту или иную n-ку, называ-
ются ее компонентами, или координатами, и различают-
ся по порядку: первая компонента, вторая и так далее.
ОТОБРАЖЕНИЯ
Без знания языка в чужой стране трудно.
Представьте: в каком-то чужедальнем аэропорту вы
спустились с трапа самолета, прошли таможенный до-
смотр и решили, скажем, известить домашних о благо-
получном прибытии. Надо бы спросить у кого-то, где
здесь можно телеграммку отбить, а вы по-ихнему, как го-
ворится, ни бум-бум. Как быть?
Вот для таких безъязыких и придуманы средства ви-
зуальной информации: красный крест — медпункт, нож-
ницы и расческа — парикмахерская, чемодан — камера
хранения, конверт — о! это как раз то, что вам нужно,—
почта.
Основное достоинство этих легко узнаваемых карти-
нок в том, что каждая строго соответствует определенно-
му виду услуг.
Медпункт
Почта
Парикмахерская
Итак, с одной стороны, множество разновидностей
сервиса, с другой — множество транспарантов. Соответ-
42
ствие между элементами этих двух множеств помогает
ориентироваться в незнакомой обстановке.
Вот еще один пример соответствия. «Если плотву ло-
вить собираешься — бери мотыля, а на язя бери кузне-
чика. Для окуня выползок хорош или ручейник; кстати,
на ручейника и плотва неплохо идет. Ну, а для леща ни-
чего лучше пшенной каши не придумаешь. Стерлядь, го-
воришь? Нет, она на все наши наживки — нуль внима-
ния, ее только неводом и возьмешь. С щукой — та же ис-
тория: ее либо неводом брать надо, либо блеснить». Так
поучает опытный рыбак начинающего, объясняя отточен-
ное многолетним опытом соответствие между множеством
рыб и множеством наживок, для этих рыб рекомендуе-
мых.
В холле гостиницы за спиной портье рядами висят
ключи. Каждый из них открывает дверь того номера, ко-
торому он соответствует.
Идет экзамен, и каждому экзаменующемуся ставится
соответствующая оценка — элемент множества {двойка,
тройка, четверка, пятерка}.
Заселяется новый дом. Опять соответствие: между
жильцами и номерами квартир.
Если в каждой из описанных ситуаций отвлечься от
конкретных деталей, то сухой остаток будет таков: есть
некоторое множество Л, и каждому его элементу ставит-
ся в соответствие определенный элемент некоторого мно-
жества В: трафарету — услуга, гостиничному номеру —
ключ, сдающему экзамен — оценка, жильцу — номер
квартиры. Причем с каждым элементом первого мно-
жества сопоставляется в точности один элемент вто-
рого.
Всякое такое соответствие в теории множеств назы-
вается отображением множества Л во множество В или
функцией с областью определения Л, принимающей зна-
чения из В.
В каждой паре из элемента множества Л и соответст-
вующего ему в данном отображении элемента множества
В первый называется прообразом (или значением аргу-
мента), второй — образом (или значением функции).
Все элементы множества В, выступающие в данном
отображении в роли образов, в совокупности называются
образом множества Л в этом отображении. (Ясно, что
при этом образ множества Л включен во множество В,
читатель легко докажет это.)
43
— Алло! Это справочная вокзала? Скажите, сколько
стоит билет до Амвросиевки?
— Докуда? До Аросевки?
— До Амвросиевки!
— До Абросимовки? Вас очень плохо слышно. Пожа-
луйста, по буквам.
— Анна, Михаил, Владимир, Родион, Ольга...
Итак, еще одно отображение. Множество букв рус-
ского алфавита отображается во множество русских
имен. И прежде невнятное сообщение становится отчет-
ливым и понятным.
Отображения и в науке часто применяются благо-
даря именно этому своему достоинству: они позволяют
заменить предмет исследования некоторым его образом,
по которому изучать предмет становится проще.
Возьмите схему любого прибора — хотя бы того же
телефона. Не правда ли, гораздо удобнее изучать не ре-
альный прибор, а его схему, где каждой детали постав-
лен в соответствие определенный значок?
Впрочем, понятие «отображение» важно не только
этим.
Возьмите любую деталь какого-либо прибора и заду-
майтесь над принципом ее действия. Как, например, ра-
ботает катушка индуктивности, заметная на схеме теле-
фона? По закону самоиндукции: если текущий по ней
ток непостоянен, то в ней возникает электродвижущая
сила, пропорциональная скорости изменения тока.
Опять отображение! Каждому значению скорости из-
менения тока ставится в соответствие значение элек-
тродвижущей силы.
44
Возьмите другие законы естествознания, владение
которыми дало человеку столь уверенную власть над
природой. Очень многие из них носят характер отобра-
жения, функции. Каждому значению силы, действующей
на тело, ставится в соответствие значение ускорения, при-
обретаемого телом (второй закон Ньютона). Каждому
значению давления в газе при постоянной температуре
ставится в соответствие значение плотности газа (закон
Бойля — Мариотта). Каждому значению расстояния ме-
жду двумя электрическими зарядами ставится в соответ-
ствие значение силы взаимодействия зарядов (закон
Кулона) и так далее.
Мы надеемся, что после сказанного читателю стала
ясна важность этого понятия — отображение, функция.
Если читатель проглядит еще раз примеры, через ко-
торые мы подводили его к понятию отображения, то он,
конечно, заметит что-то неладное в примере с рыбаком.
Во-первых, для некоторых рыб рекомендуется сразу
несколько наживок (окуню ставится в соответствие вы-
ползок и ручейник, плотве — ручейник и мотыль). А оп-
ределение отображения требует, чтобы каждому элемен-
ту множества прообразов соответствовал точно один
образ.
Во-вторых, некоторым рыбам (стерлядь, щука) не
соответствует никакая наживка. А определение отобра-
жения требует, чтобы образ был у каждого элемента мно-
жества прообразов.
Стало быть, сопоставление наживок с рыбами, изло-
женное устами старого рыбака, — не отображение.
Призванный к бдительности примером с рыбаком
читатель, вероятно, повнимательнее приглядится к дру-
гим примерам и остановит критический взор на описании
экзамена, трактуемого как отображение множества эк-
заменующихся во множество оценок (двойка, тройка,
четверка, пятерка). В этом числовом множестве — всего
четыре элемента. И если экзаменующихся больше, то
просто невозможно, чтобы у всех были различные оцен-
ки.
Допустимо ли, может спросить читатель, чтобы при
каком-то отображении нескольким прообразам соответ-
ствовал один и тот же образ?
45
Да, допустимо, поскольку в определении отображения
нет никаких оговорок на этот счет.
А как смотреть на то, возможно, не оставит своих со-
мнений читатель, если на экзамене никто не получит пя-
терку? Или на такой счастливый случай, когда никто не
получил двойку? Допустимо ли, чтобы при каком-то ото-
бражении какой-то элемент множества, из которого бе-
рутся образы, не был сопоставлен ни с одним элементом
из множества прообразов?
Да, допустимо, следует ответить и на сей раз, потому
что и на это мы не накладывали никаких запретов, ког-
да определяли отображение множества А во множество
В. Выделенный нами предлог в словно подчеркивает,
что некоторые элементы множества В вправе уклониться
от участия в отображении.
Если же роль образа падает на каждый элемент это-
го множества, то про такой поголовный охват говорят,
что множество А отображается на множество В.
Знаете ли вы, откуда в нашей речи взялось присловье
«жив курилка»? Оно пошло от старинной народной иг-
ры. Ее участники становятся в круг, а по нему пускается
зажженная лучинка. Каждый играющий передает ее со-
седу со словами: «Жив, жив курилка!» У кого в руках
лучинка погаснет, тот должен исполнить какое-то жела-
ние играющих.
Передача лучинки от одного участника игры к соседу
ставит в соответствие каждому элементу множества иг-
рающих элемент, принадлежащий тому же множеству.
Про такое соответствие говорят, что оно отображает мно-
жество в себя.
46
В каждом из наших прежних примеров, иллюстриро-
вавших понятие отображения, прообразы и образы при-
надлежали различным множествам. Однако определение
отображения на таком различии вовсе не настаивает. Ста-
ло быть, допустимы случаи, аналогичные игре с лучин-
кой, — отображения множеств в себя.
Нетрудно придумать и чисто математический пример
подобного отображения. Пусть каждому вещественному
числу х ставится в соответствие его квадрат: х2. И про-
образы и образы принадлежат здесь одному и тому же
множеству вещественных чисел. Оно отображается в се-
бя описанным соответствием.
Вот еще один математический пример такого рода, на
сей раз не алгебраического, а геометрического толка.
Каждой точке плоскости ставится в соответствие другая
точка той же плоскости, причем так, что направленные
отрезки, проводимые из какой-либо точки-прообраза в
соответствующую ей точку-образ, одинаковы по дли-
не и направлению. Описанным соответствием множество
всех точек плоскости отображается в себя.
Наши последние примеры — с числами, с точками
плоскости — вновь отличаются особенностью, которой не
было у прежних примеров. До сих пор участниками каж-
дого отображения были конечные множества. Но ведь
этого вовсе не требует определение отображения. В нем
вообще нет никаких ограничений на природу множеств,
которые могут участвовать в отображениях. Стало быть,
эти множества могут быть и бесконечными.
Разберем еще один пример такого сорта. Это отобра-
жение замечательно тем, что в нем математика черпает
львиную долю средств для наглядного изображения сво-
их понятий.
Начертим прямую, одну из ее точек отметим числом
47
2 2,7
---1----Г--- ♦ -I i—। 1 1__|-1----
-3-2-1 0 1-2-3 4
О, другую, лежащую правее, — числом 1. Отрезок между
этими точками назовем единичным, а всю прямую—чис-
ловой осью. Будем теперь последовательно откладывать
на ней единичный отрезок вправо от точки 1 и обозначать
получающиеся засечки числами 2, 3, 4 и так далее. От-
кладывая единичный отрезок влево от точки 0, будем от-
мечать новые последовательные засечки числами —1,
—2, —3 и так далее. На числовой оси можно изображать
и нецелые числа. Например, число представится на ней
серединой отрезка между точками 0 и 1, а чтобы изобра-
зить на числовой оси, скажем, число 2,7, нужно отложить
семь раз вправо от точки 2 десятую долю единичного от-
резка. Подобным образом на числовой оси отмечается
любое вещественное число, иными словами, так строится
отображение множества вещественных чисел на множе-
ство точек числовой оси.
А теперь скрестим на плоскости две числовые оси.
Возьмем какую-нибудь пару чисел, например (2,4).Пер-
вое число пары отложим на горизонтальной оси, второе—
на вертикальной. Через полученные засечки проведем
прямые, параллельные осям. Их пересечение обозначит
некоторую точку плоскости. Так, каждой паре веществен-
48
них чисел можно поставить в соответствие определенную
точку.
Сведущий читатель, конечно, распознал в этом пост-
роении идею декартовых координат. Рассказ о ней нам
остается лишь дополнить терминологическими пояснени-
ями: скрещенные числовые оси называются осями коор-
динат, обозначаются они латинскими буквами х (гори-
зонтальная) и у (вертикальная), точка их пересечения
называется началом координат, а пара чисел, определя-
ющая положение той или иной точки, называется коорди-
натами этой точки: первое число, откладываемое по гори-
зонтальной оси, — абсциссой, второе, откладываемое по
вертикальной, — ординатой.
Ради примера-на нашем рисунке в декартовой системе
координат отмечены точки плоскости, соответствующие
парам (1; 1), (—2; 4), (3; 9); (0,5; 0,25), (—1,5; 2,25).
Поскольку декартова система координат на плоско-
сти задается пересечением лишь двух числовых осей и по-
ложение точки в ней отмечается лишь двумя числами, ее
называют двумерной. Помещенный здесь же рисунок
трехмерной системы координат позволяет понять, как
множество всевозможных троек вещественных чисел ото-
бражается на множество точек пространства. Необходи-
мая для этого дополнительная ось отмечается буквой z,
а откладываемая по ней координата точки пространства
называется аппликатой.
Есть города, основатели которых словно отдавали
дань точным наукам. Математическая строгость с само-
го начала вносилась в планы таких городов.
Вот карта одного из старейших районов Ленингра-
да — Васильевского острова. Его линии и проспекты, пе-
ресекаясь под прямым углом, образуют геометрически
правильную сетку.
По такому же принципу застроен остров Манхеттен —
центральная часть Нью-Йорка. Математическая стро-
гость застройки подчеркнута тем, что улицам Манхетте-
на — продольным авеню и поперечным стрит — присвое-
ны не названия, а номера. В такой сетке улиц не запута-
ешься: два числа — номер стрит и номер авеню — одно-
значно указывают положение каждого перекрестка, а
добравшись до него, уже нетрудно отыскать нужный дом.
3 Зака 4 8631
49
Впрочем, прямоугольная сетка стрит и авеню, если
внимательней приглядеться к карте Манхеттена, не столь
уж математически безукоризненна. По самому краю
острова, почти вплотную к берегу, проходит первая аве-
ню. Но капризная природа сотворила берег не идеаль-
но ровным на всем его протяжении. В одном месте, укло-
няясь от направления первой авеню, он выдается значи-
тельным мысом. Мыс застроен, причем градостроители
выдержали строгий принцип планировки: авеню здесь
проложены параллельно остальным. Однако градострои-
тели не выдержали принцип в обозначении улиц: вместо
цифр в ход пошли буквы — авеню А, авеню В, авеню С
и Д.
А если сохранить верность номерным обозначениям?
Приближаясь к мысу и перебирая номера авеню —
третья, вторая, первая, какой номер естественно увидеть
на следующей авеню? Очевидно, нулевой. А дальше, ра-
зумеется, должны идти минут первая, минус вторая...
50
Г удзон
DC
□С
8
П2§сИС
д
Айрата
ПП^мОППСБДЬг^^'с1ии1|........ UUULJl_
УУиИопш(=)П^Ис=|ай955Ь^энс^;яАНЯЯ8Я^
ппПППИ© с:
\_J( II 1г~Т^г^ПГ II □ 1ПППГ ЮООООГПГЛексингтон-авеню ЕЮ d
____□□oom ’
ппппппппшпк
згасаХш
опаиодлпл
шошпс'гш
ЗЧЯРГТЖЭ^г>
□□□□
л ° и г • А й л е н д
Теперь переведите взгляд в район четвертой и пятой
авеню. Между ними пролегает Мэдисон-авеню не нуме-
рованная, как все, а именованная. Что если и ее переиме-
новать на числовой манер? Какой номер получила бы она
тогда? Четыре с половиной, не так ли?
Если проводить такой подход последовательно, то
любую точку карты можно определить как перекресток
двух «улиц» — двух прямых, идущих в направлении стрит
и авеню. Номер каждой «улицы» определяется тем, ка-
кой отрезок отсекает она на нулевой стрит или на нуле-
вой авеню. В ходе рассуждений 'план города с прямо-
угольной сеткой улиц превратился в прямоугольную де-
картову систему координат.
•
Примеры двумерных координатных систем мы поды-
скивали, изучая планировку Ленинграда и Нью-Йорка.
з
51
За примерами трехмерных координатных систем, по-
жалуй, нужно отправиться в пространство, подняться
над землей.
Но почему подняться? В третье измерение можно вый-
ти и в противоположном направлении. Человек сделал
это задолго до эры авиации и космонавтики — копая
шахты, добираясь до угольных пластов и рудных жил.
Взгляните на чертеж, изображающий горную выработ-
ку. Чтобы добраться до своего рабочего места, шахтер
должен спуститься до нужного квершлага, затем прое-
хать до нужного штрека, а затем до нужного участка.
Номер квершлага, номер штрека, номер участка — вот
три числа, которые записаны в наряде у шахтера, когда
он отправляется под землю, три числа, определяющих
пункт его назначения в подземном пространстве.
52
В строгой структуре горной выработки четко просмат-
ривается образ трехмерной декартовой системы коорди-
нат.
Отображение и функция.
В своих рассуждениях мы употребляли эти слова впе-
ремежку, и читатель мог посчитать их синонимами.
Это не совсем так. Чтобы показать тонкую разницу
между ними, обратимся к нашим испытанным примерам
отображений.
Пример с гостиницей. Каждому номеру ставится в
соответствие ключ. В роли прообразов здесь выступают
числа (номера). Всякое такое отображение называется
функцией числового аргумента.
Примеры с экзаменом и с новосельем. Здесь числа
выступают в роли образов (каждому экзаменующемуся
ставится в соответствие оценка, каждому новоселу — но-
мер его квартиры). Всякое такое отображение называет-
ся числовой функцией.
А теперь представьте, что в новом доме, куда недавно
вселились жильцы, устанавливают телефоны. Номеру
каждой квартиры ставится в соответствие номер телефо-
на. Как назвать такое отображение? Числовая функция
числового аргумента, не правда ли?
Наш недавний пример, где каждому вещественному
числу ставился в соответствие его квадрат, — тоже чис-
ловая функция числового аргумента.
На подобные примеры, когда и образы и прообра-
зы— числа, стоит обратить особое внимание. Именно в
таких случаях обычно говорят не «отображение», а
«функция», не «прообраз», а «значение аргумента», не
«образ», а «значение функции», не «множество прообра-
зов», а «область определения функции» (ее составляют
вещественные числа, как правило, из некоторого ограни-
ченного или неограниченного промежутка). Часто в таких
случаях употребляют термин «область значений функ-
ции»— это тот самый образ множества прообразов, о ко-
тором говорилось в конце раздела, где определялось по-
нятие отображения.
Свои особенные наименования есть у многих отобра-
жений специального вида.
Отображения, сопоставляющие числовые функции
числового аргумента друг с другом, именуются операто-
53
рами, функции с числами — функционалами. Отображая
какое-либо пространство на себя, говорят о преобразова-
нии этого пространства. (Скажем, когда недавно каждой
точке плоскости мы ставили в соответствие другую точ-
ку, отнесенную от первой на отрезок определенной дли-
ны и направления, это было так называемое преобразо-
вание параллельного переноса.)
Взгляните на такое выражение: 1+3 = 4. Примером
чего оно служит? Математик сказал бы, что оно иллюст-
рирует операцию сложения. А про выражение 2-5=10
он сказал бы, что здесь произведена операция умно-
жения.
Но ведь про первый пример можно сказать и так:
двум числам, 1 и 3, поставлено в соответствие число 4,
называемое их суммой. А про второй так: двум числам,
2 и 5, поставлено в соответствие число 10, называемое
их произведением.
И там и тут парам чисел ставятся в соответствие чис-
ла. Стало быть, мы опять имеем дело с отображением
(или, как можно еще сказать, с числовой функцией двух
числовых переменных).
Можно вообразить наиболее общий случай такого
рода, когда упорядоченным парам, составленным из эле-
ментов некоторых двух множеств, ставится в соответствие
элемент третьего множества. Всякое такое отображение
в математике принято именовать бинарной, или двумест-
ной, операцией («бис» по-латыни «дважды»), определен-
ной на произведении первого множества на второе (на-
помним, что совокупность упорядоченных пар из элемен-
тов двух множеств называется произведением этих мно-
жеств) со значениями из третьего множества.
Значит, и сложение и умножение чисел — это дейст-
вительно отображения, но того специфического вида, ко-
торые именуются бинарными операциями. Определены
обе эти операции на произведении множества веществен-
ных чисел на себя, и значения принимают опять-таки из
множества вещественных чисел.
Можно говорить вообще об л-местных операциях,
когда л-кам элементов ставятся в соответствие элементы
еще какого-то множества. (Правда, в таких случаях
обычно говорят о функциях л переменных.) «Обыкновен-
ные» отображения, когда с элементами одного множества
сопоставляются элементы другого (или того же самого),
тоже иногда трактуются как операции — их называют
54
унарными, или одноместными («унус» по-латыни один).
Когда, например, положительным числам ставятся в со-
ответствие их квадратные корни, говоря; об операции
извлечения квадратного корня.
Как все-таки многолико это понятие «отображение»!
Как широко оно применяется! Недаром во многих кур-
сах математики о нем говорится как об одном из основ-
ных понятий этой науки, не менее фундаментальном, чем
понятие множества.
Когда мы знакомились с пересечением и объединени-
ем множеств, с включением одного множества в другое,
на память о каждой операции над множествами или отно-
шении между ними нам оставалась выразительная сим-
волическая картинка — диаграмма Венна.
Вероятно, читателю хочется получить подобный суве-
нир, который давал бы наглядное представление о по-
нятии отображения.
Характерная картинка, приводимая для этой цели во
многих учебных пособиях по теории множеств, воспроиз-
ведена на странице 00. Овалы — это множества, точки —
их элементы, стрелки — соответствия. Из каждой точ-
ки левого овала, символизирующего множество прообра-
зов, исходит одна и только одна стрелка. В некоторые
точки правого овала (он изображает множество, элемен-
ты которого в данном отображении играют роль обра-
зов) упирается несколько стрелок, в некоторые—ни од-
ной. Все вполне соответствует определению отображе-
ния. Но выразительные возможности таких картинок яв-
но не настолько широки, чтобы показать существенные
черты того или иного конкретного отображения.
Более богатые изобразительные средства стоят за
термином «график отображения», который встречается в
работах по теории множеств. Поинтересуемся, что он оз-
начает. Оказывается, так именуется множество пар, по-
55
строенных из элементов двух множеств, участвующих в
отображении, причем первые элементы всех таких пар
в совокупности представляют собой все множество про-
образов, а второй элемент каждой пары является обра-
зом первого в данном отображении.
Скажем, если рассматривать экзамен как отображе-
ние, то его графиком будет экзаменационная ведомость,
полный перечень пар «фамилия — оценка».
Опять не очень живописно. И не очень понятно: поче-
му это называется графиком? Это слово обычно ассоци-
ируется с кривой, вычерченной в координатных осях.
Дело в том, что такие кривые тоже представляют со-
бой графики отображений, но весьма частного вида. Это
графики числовых функций числового аргумента. Ведь в
таких отображениях каждая пара «прообраз — образ»—
это пара чисел. (Напомним, что в подобных случаях
принято говорить не «прообраз», а «значение аргумен-
та», не «образ», а «значение функции».)
Всякую пару чисел можно изобразить точкой на ко-
ординатной плоскости. Перебрав все значения аргумен-
та из области определения функции, придав каждому со-
ответствующее значение функции и изобразив каждую
такую пару точкой плоскости, мы и получим график функ-
ции.
Когда, знакомясь с декартовой системой координат,
мы отметили на координатной плоскости несколько то-
чек, соответствующих приведенным в тексте числовым
парам, внимательный читатель наверняка подметил ха-
рактерное свойство этих пар: второй элемент каждой из
них есть квадрат перврго. Иными словами, эта россыпь
точек не что иное, как фрагмент графика отображения,
которое каждому вещественному числу ставит в соответ-
ствие его 'квадрат.
Изобразим на координатной плоскости все пары та-
кого рода. Они сольются в привычную параболу.
Рядом — график другого отображения, которое каж-
дому вещественному числу х ставит в соответствие
число х2+%+1. Глядя на формулу, не так-то легко отве-
тить на вопрос: какова область значений этой функции,
создаваемый ею образ множества всех вещественных
чисел? Но когда перед нами ее график, ответ почти оче-
виден: это множество тех вещественных чисел, которые
больше или равны 3/4.
Как видим, графикам числовых функций числового ар^
56
гумента присуща та наглядность, которая помогает бы-
стро и несложно исследовать свойства этих функций.
«Занимайте места согласно купленным билетам» —
это неписаное правило коротко и ясно определяет ото-
бражение множества зрителей на множество кресел. Зри-
тели — прообразы, кресла — образы.
Быть может, этот пример вызывает у нас неприятные
воспоминания. Вероятно, с вами случались такие казу-
сы, когда, придя в кинотеатр, вы обнаруживали, что ва-
ше место уже занято: растяпа-кассир продал на него два
билета. Вам ничего не остается, как искать свободное
кресло, билет на которое остался непроданным.
Какие же требования следует наложить на отобра-
жение, чтобы исключить подобные вещи — и накладки,
и пропуски? Этих требований два, и они совершенно
очевидны.
Во-первых, разным прообразам должны соответство-
вать разные образы (тогда не будет накладок: каждый
зритель получит свое кресло).
Во-вторых, каждый элемент множества, которому
принадлежат образы, должен иметь прообраз (тогда не
будет пропусков: каждое кресло получит своего зри-
теля).
Всякое такое отображение называется взаимно одно-
значным соответствием.
Смысл этого термина станет совершенно понятным,
если два требования, которым должно удовлетворять
любое отображение без накладок и пропусков, мы попы-
таемся сформулировать одной фразой. Тогда определя-
ющее свойство такого отображения выразится так: каж-
дый элемент множества, которому принадлежат образы,
имеет прообраз, и притом только один.
«Постойте!—вероятно, уже напрягает память чита-
57
тель. — Где-то раньше мне уже встречалась очень похо-
жая фраза!»
Спешим с подсказкой — давая определение понятию
бтображения, мы подчеркивали: каждый элемент мно-
жества прообразов имеет образ, и притом только один.
(Если не выполнено хотя бы одно из этих двух условий,
соответствие не получит звание отображения — вспом-
ните пример с рыбаком!)
Сравним теперь две фразы, обращающие на себя вни-
мание своим сходством:
каждый элемент множества, которому принадлежат
образы, имеет прообраз, и притом только один;
каждый элемент множества прообразов имеет образ,
и притом только один.
Эти фазы взаимозаменяемы, не правда ли? Стоит
лишь поменять местами слова «прообраз» и «образ». От-
сюда и термин «взаимно однозначное соответствие».
Такое переименование можно произвести с любой па-
рой «прообраз — образ». И тогда множество образов
взаимно отобразится на множество прообразов.
В нашем кинопримере для этого достаточно каждому
креслу поставить в соответствие сидящего в нем зрителя.
Это отображение называется обратным по отношению к
тому, которое каждому зрителю ставило в соответствие
его кресло.
Два множества, между которыми можно уетановить
взаимнооднозначное соответствие, называются эквива-
лентными.
Множество месяцев в году, например, эквивалентно
множеству зодиакальных созвездий. (Оттого-то древний
Водолей Рыбы Овен Телец Близнецы Рак Лев .Дева Весы Скорпион Стрелец Козерог
«= И Y б
Январь Февраль Март Апрель Май Июнь Июль АвгустСентябрьОктябрьНоябрь Декабрь
красный оранжевый желтый зеленый голубой синий фиолетовый
58
астролог, составляя гороскоп для очередного клиента, не
указывал, в каком месяце тот родился, а витиевато пи-
сал: «Появился на свет под таким-то знаком зодиака».)
Множество цветов в спектре эквивалентно множеству
нот в гамме. (Недаром иные незатейливые проекты цвето-
музыки предполагают, что на экране вспыхивают цвета,
соответствующие нотам мелодии.)
Если, прочтя наши примеры, вы начали подыскивать
свой собственный, а дело не клеится, не отчаивайтесь. У
вас всегда в запасе предельно простой вариант: возьмите
любое множество и с каждым его элементом сопоставь-
те тот же самый элемент. Такое отображение множества
на себя называется тождественным.
Не смущайтесь незатейливостью этого примера. У
него есть свои достоинства. Он иллюстрирует одно из
трех свойств, которыми обладает эквивалентность мно-
жеств. Именуется это свойство рефлексивностью, и за-
ключается оно в том, что любое множество эквивалент-
но самому себе.
А остальные свойства?
Довольно очевидно, что если мы подыскали для не-
которого множества другое, ему эквивалентное, то вто-
рое множество будет эквивалентно первому. В этом вы-
ражается второе свойство эквивалентности множеств,
именуемое симметричностью.
Доказать его просто. Ведь эквивалентность множеств
заключается в том, что между ними можно установить
некоторое взаимно однозначное соответствие. А оно+как
мы видели в предыдущем разделе, работает в обе сторо-
ны. С его помощью можно отобразить первое множество
на второе, но также можно, взяв обратное к этому ото-
бражению, отобразить второе множество на первое.
Еще пример, где множество месяцев в году отобража-
ется на множество знаков зодиака. Вспомним циферблат
больших часов Казанского вокзала в Москве: знаки зо-
диака сопоставлены там с цифрами, обозначающими ча-
сы дня. Опустив промежуточные звенья, можно сопоста-
вить напрямую месяцы и часы. В самом деле, если январь
соответствует Водолею, а Водолей на часовом цифербла-
те ставится рядом с цифрой 1, то это означает, что ян-
варь соответствует первому часу дня. Аналогичным об-
разом февралю можно поставить в соответствие второй
час, марту — третий и так далее до декабря, который
окажется сопоставленным с двенадцатым часом.
59
Отображение множества месяцев на множество часов
возникает при этом как результат определенной комби-
нации трех отображений, первое из которых сопоставля-
ет месяцы со знаками зодиака, второе — знаки зодиака
с цифрами от 1 до 12, третье — цифры с часами дня. Та-
кая комбинация называется произведением, или супер-
позицией, отображений.
Итак, если в цепочке множеств любые два соседа эк-
вивалентны друг другу, то эквивалентны и множества,
стоящие по краям цепочки. В этом выражается третье
свойство эквивалентности множеств, именуемое транзи-
тивностью.
У Марины Цветаевой в очерке «Мать и музыка»
есть такие строки:
«До явно белое, пустое, до — всего, ре — голубое,
ми — желтое (может быть, midi?), фа — коричневое (мо-
жет быть, фаевое выходное платье матери, а ре — голу-
бое — река?)».
Можно удивляться продемонстрированному здесь бо-
гатству поэтической фантазии. /Можно не соглашаться с
этими цветомузыкальными соответствиями (написавшая
процитированные строки и сама говорит далее, что у
каждого свои резоны на звуки и краски). Но бесспорно
одно: есть нечто общее между семью нотами гаммы и
семью цветами радуги. Это «нечто» роднит оба назван-
ных множества и с семью днями недели, и с семью стру-
нами гитары, и с семью чудесами света, и с семью хол-
мами, на которых стоит Рим, и с семью гномами из сказ-
ки о Белоснежке...
Это нечто общее выражается словом «семь». Все пе-
речисленные множества попарно эквивалентны, и в каж-
дом из них — по семь элементов.
Обратите внимание: именно так в математике и воз-
никает понятие натурального числа.
Натуральное число — это общее свойство попарно эк-
вивалентных множеств.
Так, число пять — это выражение той общности, ко-
торая связывает попарно эквивалентные множества пя-
ти олимпийских колец, пяти материков, пяти лучей мор-
ской звезды, пяти пальцев на руке.
60
У читателя, прочитавшего предыдущий отрывок, мог-
ло создаться впечатление: чтобы установить эквивалент-
ность двух множеств, сначала надо пересчитать одно,
потом другое и затем, сравнив их численности, убедить-
ся, одинаково ли количество элементов в них.
Но ведь, говоря так, мы оказываемся в порочном кру-
гу. В самом деле, понятие натурального числа мы строи-
ли на основе понятия эквивалентности множеств, а теперь
пытаемся устанавливать эту эквивалентность, основыва-
ясь на понятии натурального числа.
Порочного круга избежать можно. Эквивалентность
множеств можно устанавливать без всякого пересчета.
В партии перчаток, поступивших в магазин, множе-
ство левых перчаток эквивалентно множеству правых —
утверждать это можно, не заглядывая в накладную.
«На каждый прилив — по отливу», — сказал поэт, про-
возгласив тем самым, что множество приливов эквива-
лентно множеству отливов, хотя их никто не считал и во-
обще не может пересчитать: приливные волны набегали
на берега материков, когда на них и не пахло жизнью. И
будут набегать еще века и века...
Этот образ навевает мысль о бесконечности. В на-
шем рассказе об эквивалентности множеств она не пред-
ставляется чужеродной. Примеры с перчатками и при-
ливами явно подсказывают, что можно установить эк-
вивалентность не только конечных, но и бесконечных
множеств.
Но стоп! Бесконечность — вещь непростая, и прежде
чем рассуждать об эквивалентности бесконечных мно-
жеств, разберем несколько наводящих примеров.
«Мест нет».
Туристам и командированным, вероятно, хорошо
знакомо это традиционное «приветствие», которым их
встречала не одна гостиница.
А вот немецкий математик Давид Гильберт спроекти-
ровал такую гостиницу, в которой не возникает никаких
проблем с размещением гостей.
Администратор такой гостиницы спокоен даже тогда,
когда все номера заполнены. Даже в такой ситуации он
никогда не откажет вновь прибывшему.
61
— Вы желаете одноместный номер? Милости просим.
Только придется немного подождать. Сейчас мы пере-
селим жильца из первого номера во второй, жильца из
второго — в третий, жильца из третьего — в четвертый
и так далее. И пожалуйста — номер первый к вашим ус-
лугам.
Разумеется, то, что проделал администратор гостини-
цы Гильберта, невыполнимо ни в одной реальной гости-
нице. Будь в ней даже миллион номеров, жилец послед-
него номера в результате вышеописанного переселения
окажется выселенным. Такого не случится лишь в гости-
нице, где за каждым номером, к какому ни подойди,
есть дверь следующего.
Очевидно, количество номеров в этой гостинице бес-
конечно. Мы произносим это слово уже вполне созна-
тельно и без всякой опаски, ибо рассказ о гостинице
Гильберта позволяет строго определить понятие беско-
нечного множества.
Но прежде чем формулировать это определение, по-
говорим еще о достоинствах замечательной гостиницы.
Оказывается, она способна принять даже такую ту-
ристскую группу, число участников которой бесконечно.
Что в таком случае делает администратор? Например,
переселяет жильцов из первого номера во второй, из вто-
рого— в четвертый, из третьего - в шестой... Короче го-
воря, у каждого жильца в ордере на поселение прежний
номер заменяется номером вдвое большим. Таким обра-
зом, заселяются лишь четные номера, а первый, третий,
пятый и все остальные нечетные оказываются свободны-
ми. В них и поселяют одного за другим туристов из беско-
нечно большой группы.
Обратимся к схемам переселения, которое провел ад-
министратор гостиницы Гильберта в первый и во второй
раз. Первая строка каждой таблицы показывает разме-
щение жильцов до переселения, вторая — после. Жирные
цифры обозначают занятые номера, светлые — свобод-
ные. Стрелки указывают порядок переселения. Одновре-
62
менно они позволяют установить взаимно однозначное
соответствие между множествами номеров, занятых до
и после переселения.
Но ведь до переселения (и первого, и второго) были
заняты все номера гостиницы, все их множество, а пос-
ле— лишь часть этого множества, лишь его истинное
подмножество (то есть включенное во множество, но не
равное ему, вспомните поговорку: «Всякая селедка рыба,
но не всякая рыба — селедка»).
Итак, оба раза мы установили взаимно однозначное
соответствие между всем множеством и его истинным
подмножеством.
Часть множества эквивалентна целому. Ну не дико-
винка ли?
Для конечных множеств — диковинка. Для бесконеч-
ных— естественное явление, фундаментальное свойство,
которое можно принять за их определение.
Бесконечным называется множество, из которого
можно выделить эквивалентное ему истинное подмноже-
ство.
Диковинный мир, в котором Гильберт построил свою
гостиницу, — это, конечно, математическая фантазия.
Сейчас мы продемонстрируем еще одно явление того
же рода, вполне реальное, но еще более удивительное.
Займемся геометрическими построениями. Начертим
63
на листе бумаги отрезок, а над ним параллельно ему про-
ведем другой, вдвое меньший по длине. Серией парал-
лельных прямых соединим точки малого отрезка с точ-
ками одной из половинок большого. Так между множе-
ствами точек малого отрезка и половины большого уста-
навливается взаимно однозначное соответствие. Иными
словами, два эти множества эквивалентны.
А теперь возьмем те же самые отрезки, но построения
сделаем несколько иначе. Лучи, проведенные на этот
раз, устанавливают взаимно однозначное соответствие
между точками малого и большого отрезков. Стало быть,
оба множества точек эквивалентны.
Сопоставим два полученных нами вывода. Множество
точек половины большого отрезка эквивалентно множе-
ству точек малого, а оно, в свою очередь, эквивалентно
множеству точек всего большого отрезка. Но ведь по
свойству транзитивности, которым обладает эквивалент-
ность множеств (это свойство было объяснено тремя
разделами прежде), сказанное означает, что множество
точек половины большого отрезка эквивалентно множе-
ству точек всего отрезка в целом.
Разумеется, так оно получилось потому, что множе-
ство точек нашего (да и любого) отрезка бесконечно.
Этим примером мы еще раз продемонстрировали тео-
ретико-множественную истину: из бесконечного множе-
ства можно выделить эквивалентное ему истинное под-
множество.
Если читателю понравился фокус с отрезками, то мы
готовы предложить ему нечто еще более диковинное.
В чем заключается новый трюк, поясняет рисунок.
64
Ну не поразительно ли — множество точек отрезка
эквивалентно множеству точек полупрямой! Грубо гово-
ря, в отрезке столько же точек, сколько их в луче.
Числовая разметка рисунка показывает, что оба эти
точечные множества эквивалентны множеству всех веще-
ственных чисел между нулем и единицей включительно.
У последнего множества есть особое название, кото-
рое стоит запомнить на дальнейшее: континуум. Всякое
эквивалентное ему множество называется континуаль-
ным (а иногда и точно так же — континуум).
Тот же рисунок показывает, что множество всех по-
ложительных вещественных чисел континуально. Не-
большим усложнением схемы нетрудно обосновать, что
таково же и множество всех вещественных чисел вообще.
Можно доказать, что континуальным является и множе-
ство всех точек квадрата, и множество всех окружностей
на плоскости...
Кстати, свое название есть и у множеств, подобных
множеству номеров в гостинице Гильберта. Отличитель-
ное их свойство о том, что их элементы можно пронуме-
ровать, поставить во взаимно однозначное соответствие с
числами натурального ряда. Всякое такое множество на-
зывается счетным.
1 £ 1 1
1 /2 /3 z4 z5
Z / s /
2zz 2_/ 2
| z2 /3 z4 5
, / / /
3z 3ZZ 3ZZ 3 3
1 z1 2 * 4 z3 4 5
/ /
*_/ $_/ 4 4 4
1 z2 3 4 5
! /
5'5 5 5 5
1 2 3 4 5
4 Заказ 8651
65
Нетрудно показать, что счетным является, например,
множество всех дробей. Для этого их достаточно распо-
ложить в таблицу так, чтобы числитель каждой дроби
совпадал с номером ряда, в котором она находится, а
знаменатель — с номером столбца. А потом остается про-
нумеровать все дроби по схеме, приведенной на стр. 24.
Континуум (множество всех вещественных чисел ме-
жду нулем и единицей включительно) и натуральный ряд
(множество всех положительных целых чисел) в подоб-
ных сопоставлениях играют роль эталонов.
У дотошного читателя может возникнуть вопрос: а
как эти два эталона соотносятся между собой?
Оказывается, хотя оба множества и бесконечны, но
бесконечности эти разные. Множества эти неэквива-
лентны.
На числовой оси нетрудно показать, как из множества
положительных вещественных чисел, не превосходящих
единицы, можно выделить подмножество, эквивалент-
ное натуральному ряду: пусть единице соответствует
единица, двойке — одна вторая, тройке — одна третья и
так далее.
1111 1
6 5 4 3 2
I ... HI----1-----1----------------1
О 1
Но перенумеровать все точки единичного отрезка не-
возможно.
Соотношение между этими бесконечными множест-
вами — натуральным рядом и континуумом — примерно
такое же, как между двумя конечными множествами, на-
пример с пятью и десятью элементами. Из десятка всег-
да можно выделить пяток, из пятка десяток — никогда.
Когда некоторому конечному множеству можно поста-
вить во взаимно однозначное соответствие часть другого
конечного множества (или, выражаясь строго, истинное
подмножество другого конечного множества), говорят,
что численность первого множества меньше численности
второго. Скажем, если в первом пять, а во втором десять
элементов, то на языке чисел сказанное выразится так:
5<10 (пять меньше десяти).
Когда же два конечных множества эквивалентны, то
есть между ними можно установить взаимно однознач-
66
ное соответствие, говорят, что они равночисленны. Ска-
жем, если в каждом по пять элементов, то факт их рав-
ночисленное™ выражается равенством: 5=5 (пять рав-
но пяти).
В мире бесконечных множеств при подобных сравне-
ниях применяется иная терминология. Здесь не говорят
численность, а говорят мощность.
Если два бесконечных множества эквивалентны, то
есть между их элементами можно установить взаимно
однозначное соответствие, то их называют равномощны-
ми, или имеющими одинаковую мощность. Если же одно
бесконечное множество эквивалентно истинному подмно-
жеству другого, а в обратную сторону такой эквивалент-
ности установить уже нельзя, говорят, что мощность пер-
вого множества меньше мощности второго.
Таким образом, понятие мощности бесконечного мно-
жества представляет собой обобщение понятия числен-
ности, применимого лишь к конечным множествам.
Используя новое понятие, мы можем теперь придать
строгую форму сказанному прежде о натуральных чис-
лах и вещественных числах между нулем и единицей:
мощность счетного множества меньше мощности конти-
нуального.
4*
ОТНОШЕНИЯ
Брат моей жены — кто он мне? Деверь? Шурин? А кто
такая золовка? А свояченица?
Непросто разобраться в тонкостях родственных отно-
шений. Хорошо бы подвергнуть их математическому
анализу, но таких исследований, насколько нам известно,
еще никто не предпринимал. Поэтому мы изложим здесь
самые простые соображения на этот счет.
Большую семью, представленную замысловатой схе-
мой, будем рассматривать как некоторое множество.
Исследуем для начала какое-то одно отношение,
способное связать лишь два элемента нашего множества
(такое отношение называется бинарным). Например, та-
кое: «х есть брат у».
Прослеживая горизонтальные линии схемы, отберем
все те пары представителей исследуемой нами семьи, для
которых употребимо слово «брат». Например, Иван Пет-
рович есть брат Петра Петровича, Владимир Василье-
вич— брат Зинаиды Васильевны, Миша—брат Маши.
Очевидно, подобные высказывания могут утратить
смысл от перестановки имен. Миша — брат Маши, но не-
верно, что Маша — брат Миши.
Итак, речь идет о парах упорядоченных.
Разговор о таких парах у нас заходит уже не в пер-
вый раз. Множество всевозможных упорядоченных пар,
составленных из элементов некоторого множества, мы
привыкли называть произведением этого множества на
себя. В данном случае на себя умножается множество
родственников.
Отбирая среди всех возможных пар лишь те, для ко-
торых употребимо слово «брат», мы тем самым выдели-
ли из произведения множества родственников на себя не-
которое его подмножество. Перечень отобранных пар со-
ставил исчерпывающий рассказ об отношении «х есть
брат у» среди членов исследумой нами семьи.
Оказывается, таким образом можно полностью оха-
рактеризовать любое бинарное отношение, определенное
68
Дядя
на любом множестве: надо лишь перечислить все такие
пары элементов множств, в каждой из которых первый
элемент находится в данном отношении ко второму. По-
этому и говорят: всякое бинарное отношение, определен-
ное на том или ином множестве, есть некоторое подмно-
жество произведения этого множества на себя.
Среди всевозможных отношений, которыми можно
связать элементы того или иного множества, могут быть
и такие, которые охватывают не два, а больше элемен-
тов. Скажем, три — их называют тернарными. Это, на-
пример, отношение между родителями и ребенком. В
большой семье, представленной нашей схемой, это отно-
шение связывает Ивана Петровича, Ольгу Николаевну
и Машу, Мишу, Люсю и Андрейку. Чтобы описать отно-
шение между свояками, мы уже должны упоминать сра-
зу по четыре элемента множества родственников (сами
свояки и их жены, доводящиеся друг другу сестрами).
Ясно, что бинарные отношения проще тернарных и
прочих. Ими и занимаются больше. Их, как правило, и
имеют в виду, употребляя термин «отношение». Для не-
которых наиболее важных бинарных отношений введены
специальные обозначения: х<у (х меньше у), х = у (х
равно у), х^.у (х меньше или равно у), х~у (х эквива-
лентно у) и т. д.
•
Любой, даже малосведущий в медицине читатель
знает: кровь каждого человека относится к одной из че-
тырех групп.
Это существенно осложняет переливание крови от од-
ного человека другому: надо быть уверенным, что кровь
первого подойдет второму.
Отношения совместимости между группами крови не-
просты. Кровь первой группы можно переливать любому.
Люди с кровью второй группы могут быть донорами
лишь для обладателей такой же крови и для людей с
кровью четвертой группы. То же можно сказать и про
кровь третьей группы: она совместима лишь с собой и с
кровью четвертой группы. Наконец, обладатели крови
четвертой группы могут давать свою кровь лишь таким
же, как они.
Перед нами — еще один пример бинарного отношения.
Оно определено на множестве, элементы которого —
группы крови.
70
Если сказанное словами перевести на язык чисел, то
получится, что число 1 находится в описанном отноше-
нии к числам 1, 2, 3, 4; число 2 — к числам 2 и 4; число
3—к числам 3 и 4; число 4 — лишь к самому себе. Мож-
но выразиться еще короче: описанное отношение пол-
ностью характеризуется числовыми парами (1,1), (1,2),
(1,3), (1,4), (2,2), (2,4), (3,3), (3,4), (4,4).
занному выше дает приведенная рядом картинка, где в
числовой сетке жирными точками отмечены все только
что перечисленные пары чисел. (Первое число каждой
пары откладывается но нижнему горизонтальному обре-
зу сетки, второе — по левому вертикальному).
Кстати, перечень всех пар элементов множества, на-
ходящихся между собой в некотором отношении, назы-
вается графиком этого отношения. Мы намеренно прибе-
регли этот термин до разговора об отношениях между
числами, поскольку именно в этом случае графики отно-
шений выражаются сообразными этому слову наглядны-
ми картинками.
В той сетке, на которой мы изобразили отношение
совместимости между группами крови, нетрудно разгля-
деть фрагмент двухмерной системы координат. Возьмем
ее целиком. Пары чисел, находящихся в каком-либо от-
ношении, будем изображать точками плоскости. Первое
число пары будем откладывать по оси х (обозначая той
же буквой), второе — по оси у (обозначая соответствен-
но).
Для примера рассмотрим на множестве веществен-
ных чисел бинарное отношение «х равно у». Его гра-
фик— прямая линия, биссектриса угла между коорди-
натными осями.
Теперь рассмотрим на множестве всех вещественных
чисел бинарное отношение «х меньше у». Графиком для
него служит часть координатной плоскости, лежащая
кверху от только что построенной биссектрисы.
71
Собственно говоря, на координатной плоскости таким
способом можно изобразить любое бинарное отношение
между числами. Возникший при этом график будет пред-
ставлять собой некоторую фигуру, более или менее за-
мысловатую. И наоборот, всякую фигуру на координат-
ной плоскости можно трактовать как график некоторо-
го бинарного отношения между числами. Если точка
плоскости принадлежит этой фигуре, то первый элемент
пары чисел, выражающей координаты точки, находится
в данном отношении ко второму элементу.
Так перекидывается своеобразный мост между алге-
брой и геометрией: числовые отношения становятся гео-
метрическими фигурами, фигуры же можно описывать
на языке чисел. Желающих поупражняться в этом мы
отсылаем к рисункам, где графиками числовых отноше-
ний выступают круг и квадрат.
Сходство между словосочетаниями «график отноше-
ния» и «график функции» довольно глубокое, как выясни-
лось в предыдущем разделе. Но есть между ними и раз-
личия.
72
Иллюстрируя понятие функции, обычно рисуют кри-
вую в координатных осях. Причем такую, что любая пе-
ресекающая ее вертикаль имеет с ней лишь одну общую
точку.
Графиком отношения между числами может быть лю-
бая фигура на плоскости.(
Различие понять нетрудно. Вспомним определение
функции: каждому значению аргумента ставится в соот-
ветствие только одно ее значение. Поэтому среди пар
«значение аргумента — значение функции» (полный на-
бор которых и есть график функции) нет таких, у кото-
рых одинаковы первые элементы и различны вторые.
Для графиков отношений таких ограничений нет.
Потому и говорят: функция есть частный случай би-
нарного отношения.
Вспоминая ’понятию отображения, операции и т. п.,
родственные понятия функции, можно сказать, что и они
включаются как частности в понятие отношения.
Взять хотя бы операцию сложения. На уроках ариф-
метики нам давали такое ее определение: сложить два
числа х и.1/ означает поставить им в соответствие третье
число z, называемое их суммой.
Исходя из этого определения, бинарную операцию
сложения нетрудно представить как тернарное отноше-
ние: «х, будучи сложено с у, дает в сумме z>.
Среди математических символов, кажется, нет более
понятного и бесхитростного, чем знак равенства. Однако
эта простота обманчива. У бинарного отношения равен-
ства есть свои свойства, и о них стоит поговорить.
С отношением равенства мы чаще всего сталкиваемся
73
в мире чисел. Возьмем число 6. Вряд ли кому придет в
голову отрицать, что 6=6. Да и вообще каждое число
равно самому себе. Какой бы банальностью ни казалось
это свойство равенства, мы все-таки отметим его специ-
альным термином: рефлексивность.
Другие свойства равенства нам будет легче объяснить,
напомнив, что одно и то же число можно представить по-
разному. Например, 6 — это и 3+3, и 4+2, и 5+1. Так
вот, если 3+3 = 4+2, то 4 + 2 = 3+3. Подобную переста-
новку допускает равенство любых двух чисел. Называ-
ется это свойство равенства симметричностью.
Если 3+3 = 4+2, а 4+2 = 5+1, то, очевидно, 3+
+3=5+1, И какую бы тройку чисел ни взять, если
крайние порознь равны среднему, то они равны и между
собой. В этом выражается еще одно свойство равенства—
транзитивность.
Итак, рефлексивность, симметричность, транзитив-
ность. Три эти свойства составляют самую суть равен-
ства. Но, оказывается, они присущи не одному ему.
Вспомним: эти же три сакраментальных слова мы
произносили, говоря про эквивалентность множеств. Би-
нарное отношение эквивалентности между множества-
ми — ближайший родственник отношения равенства ме-
жду числами. (У этого родства глубокие корни: ведь
понятие натурального числа основано как раз на эквива-
лентности множеств.)
Возьмем отношение подобия фигур на плоскости. Оче-
видно, каждая фигура подобна самой себе. Если одна
фигура подобна другой, то вторая подобна первой. Если
же одна фигура подобна второй, а вторая — третьей, то
первая и третья также связаны отношением подобия.
Этими очевидными утверждениями мы выразили тот
факт, что отношение подобия фигур отличается свойства-
ми рефлексивности, симметричности, транзитивности.
Но отвлечемся от сугубо математических объектов —
чисел, фигур. Закроем книгу по математике и раскроем,
например, книгу телефонную.
74
Сколько здесь фамилий - множество! В прямом и
математическом смысле слова. Есть здесь и уникальные
экземпляры: Амемошкин, Балухатый, Винтайкин, Голо-
хвостиков... А есть и такие фамилии, которые встреча
ются часто: Кузнецов, Петров, Смирнов.
Отношение «быть однофамильцем» мы и рассмотрим
на множестве, перечень которого дан в телефонном
справочнике.
Нетрудно проверить, что и это отношение подчинено
триумвирату все тех же трех свойств: рефлексивности,
симметричности, транзитивности.
Количество примеров можно было бы приумножить—
в этом нам помогла бы и живая жизнь, и абстрактная
математика: отношение «быть на одном курсе» среди сту-
дентов вуза, отношение «иметь одинаковый остаток при
делении на три (или любое другое целое число)» среди
натуральных чисел, отношение параллельности среди
прямых линий на плоскости...
Несмотря на глубокое несходство этих бинарных от-
ношений, каждому из них присущи все те же три свой-
ства: рефлексивность, симметричность, транзитивность.
Всякое обладающее этими тремя свойствами бинар-
ное отношение принято называть отношением эквива-
лентности.
Говоря о важности этих отношений, достаточно ска-
зать: на том или ином из них основана любая классифи-
кация, любая систематика, любой каталог.
•
В театре—паника. До начала спектакля — два часа,
а исполнитель главной партии, любимец публики тенор
Самоцветов, откушавши чего-то прохладительного, вне-
запно потерял голос. Надо заменить его, но кем?!
Проблема^ неожиданно вставшая перед администра-
цией театра, поддается математическому толкованию. От-
носится она к теории множеств. Ведь вся оперная труп-
па— это множество людей. Возможность замены одного
исполнителя другим — это отношение между элемента-
ми рассматриваемого множества, причем бинарное. Лю-
битель математической четкости без труда придаст ему
строгую форму: «х может заменить у». Свойства этого
отношения легко выяснить, прислушавшись к разговору
в дирекции театра, где лихорадочно подыскивается вы-
ход из создавшегося катастрофического положения.
75
«Отоларинголога вызывали? Нет? Так вызывайте не-
медленно! Чем черт не шутит: укол, массаж—и Само-
цветов, возможно, заменит сам себя. (В этой шутке есть
доля истины: отношение заменяемости рефлексивно.) По-
том надо срочно выяснить, кого в последнее время заме-
нял Самоцветов. Аркадина? Прекрасно! Значит, Арка-
дин сможет заменить Самоцветова! (Заметим по поводу
только что сказанного: отношение заменяемости симмет-
рично.) Что?! Аркадин в гастрольной поездке? Тогда ско-
рее наведите справки, кто когда-нибудь заменял Арка-
дина. Не Петров ли?..» (Логика подавшего эту мысль
ясна: если Самоцветова может заменить Аркадин, а Ар-
кадина— Петров, то Петров может заменить и Самоцве-
това. Иными словами, отношение заменяемости транзи-
тивно.)
Итак, рефлексивность, симметричность, транзитив-
ность. Бинарное отношение заменяемости певцов пред-
ставляет собой отношение эквивалентности.
Следя за дальнейшим разговором в дирекции, мы бы
познакомились со всеми тенорами труппы. В других слу-
чаях, если бы речь шла о замене баса или сопрано, перед
нами предстали бы все обладатели этих голосов.
Так через отношение заменяемости мы пришли к су-
ществующему в любой оперной труппе разбиению певцов
по диапазонам голосов.
Случаен ли такой переход? Нет, глубоко закономе-
рен. Оказывается, всякое отношение эквивалентности,
определенное на любом множестве, задает некоторое раз-
биение этого множества на подмножества. Причем эти
подмножества попарно не пересекаются. (Иными слова-
ми, ни один элемент множества не принадлежит сразу
двум подмножествам. В то же время каждый элемент
принадлежит хотя бы одному подмножеству. Эти два по-
ложения и составляют суть термина «разбиение», про-
сторечивыми синонимами которого служат слова «клас-
сификация», «каталог» и т. д.)
•
Появившееся в нашем рассказе понятие разбиения не-
трудно пояснить новыми примерами.
Отношение «иметь одинаковый остаток при делении
на три» разбивает все множество натуральных чисел на
три подмножества: 3, 6, 9, 12... (они делятся на три без
остатка); 1, 4, 7, 10... (при делении на три они дают в ос-
76
татке единицу); 2, 5, 8, 11... (эти при делении натри да-
ют в остатке двойку). Отношение параллельности разби-
вает все множество прямых на плоскости на бесконечное
число подмножеств, каждому из которых принадлежит
совокупность всех попарно параллельных прямых.
Для подмножеств, на которые некоторое множество
разбивается тем или иным отношением эквивалентности,
есть особое название: классы эквивалентности. Звучит
оно, быть может, мудрено, но для его пояснения нетруд-
но подыскать и более наглядные слова.
Что такое, например, та или иная форма геометриче-
ских фигур? Один из классов эквивалентности, на кото-
рые множество фигур на плоскости разбивается отноше-
нием подобия, не. правда ли? Другой пример: направле-
ние. Это, если разобраться, — один из классов эквива-
лентности, на которые множество прямых на плоскости
разбивается отношением параллельности.
В этом рассуждении перед нами предстает еще одно
практическое достоинство отношений эквивалентности.
Рассматривая различные классы, на которые какое-то
множество разбито отношением эквивалентности, можно
задаться вопросом: а чем же именно эквивалентны друг
другу предметы одного класса? Путь обобщения, нача-
тый с такого вопроса, в итоге приводит к абстрактному
понятию свойства, общего для всех предметов класса. В
подобных случаях говорят, что понятию дано определе-
ние через абстракцию. Именно таким образом возникают
понятия направления, формы и т. д.
77
Эквивалентность — весьма обобщенная форма ра-
венства. Когда говорят об эквивалентности предметов,
подразумевают их сходство лишь в каком-то одном от-
ношении (именно в том, которое дало повод сопостав-
лять предметы между собой). А поскольку сопоставление
предметов некоторого множества можно провести по раз-
личным признакам, то различным получится в результа-
те и разбиение множества на классы эквивалентности.
Ярый болельщик «Спартака» делит все человечество
на приверженцев своей любимой команды и на тех, кто
не разделяет его симпатий.
Регулировщик уличного движения подразделяет всех
людей на тех, кто соблюдает, и на тех, кто нарушает.
А чеховская Каштанка делила мир на хозяев и заказ-
чиков; «между теми и другими была существенная раз-
ница: первые имели право бить ее, а вторых она сама
имела право хватать за икры».
И разумеется, каждое из этих разбиений человече-
ства не совпадает с другими, поскольку предметы, све-
денные в классы эквивалентности по какому-то одному
признаку, отнюдь не должны совпадать всеми другими
свойствами. (Полное совпадение всех свойств — это весь-
ма частное отношение эквивалентности. Оно называется
тождеством и задает предельно мелкое разбиение всяко-
го множества: каждый класс эквивалентности при этом
состоит из одного-единственного элемента.)
Однако, коль скоро предметы какого-то множества в
каком-то отношении объединены в один класс эквива-
лентности, с точки зрения этого отношения они неразли-
чимы, и каждый из них может быть заменен другим там,
где речь идет об этом отношении, выступая полноправ-
ным представителем своего класса эквивалентности.
Когда в вычислениях нам встречаются дроби вида
3/б или 4/i2 мы, не задумываясь, сокращаем их — за-
меняем 3/6 на Уг, 4/i2 на !/3 и т. п. На каком же основа-
нии мы делаем это? На том, что результат любого ариф-
метического вычисления не изменится, если всякую вхо-
дящую в него дробь заменить пропорциональной (умно-
жив или разделив ее числитель и знаменатель на одно и
то же число). Нетрудно показать, что отношение пропор-
циональности среди дробей — это отношение эквивалент-
ности. А поскольку, как только что говорилось, такая
78
эквивалентность равнозначна заменяемости в арифмети-
ческих вычислениях, то это и позволяет упрощать их, бе-
ря вместо любой сократимой дроби наиболее простого и
удобного представителя того класса дробей, к которому
она принадлежит, вместо 3/6, 4/в, 5/ю брать */2, вместо
4/i2, 7/2i, 4О/12о брать Уз и так далее.
Но повторим, подобное отождествление возможно
лишь с точки зрения арифметических действий. Не прав
будет тот, кто вместо адреса «Новослободская 4/j2» за-
пишет «Новослободская Уз». На множестве адресных
дробей нет других отношений эквивалентности, кроме
тождества.
Мы так долго говорили об отношениях эквивалентно-
сти, что читатель, вероятно, станет искать их свйства в
любом бинарном отношении.
Разумеется, такой поиск не всегда будет удачен.
Чеховская Каштанка, вероятно, напомнит читателю о
том, как ее хозяин, столяр Лука Александрович, проти-
вопоставлял друг другу профессии («Ты, Каштанка,—
недоумение. Супротив человека ты все равно, что плот-
ник супротив столяра»). Определенное таким противопо-
ставлением отношение между профессиями нерефлексив-
но (бессмысленно противопоставлять какую-то профес-
сию себе же), несимметрично (раз столяр поставлен
над плотником, то тем самым плотник не поставлен над
столяром)...
Подобные примеры подтверждают очевидное сужде-
ние: отнюдь не всякое бинарное отношение — эквивалент-
ность.
Однако проницательному читателю два последних
примера подскажут нечто большее. Несимметричность
рассмотренного там и тут отношения весьма строга: если
один элемент находится в данном отношении к другому,
не одинаковому с ним элементу, то отсюда следует, что
второй к первому в данном отношении отнюдь не нахо-
дится.
Подобное свойство называется антисимметрич-
ностью.
Звучание у термина замысловатое, а смысл простой:
этим свойством обладает всякое отношение, с помощью
которого в том или ином множестве устанавливается не-
который порядок.
79
Младенец, впервые увидевший матрешек, быстро по-
нимает: если одну из них можно вложить в другую, то
вторая в первую никак не войдет. Так выясняется тот
порядок, в котором составляются матрешки.
Ребенок, даже еще не обученный правилам вежли-
вости, но внимательный к происходящему вокруг, подме-
чает: вот из этих двух человек один при встрече с дру-
гим всегда здоровается первым; точно так же поступают
и эти двое, и вот эти тоже... (Правда, замечает внима-
тельный ребенок, есть люди, которые здороваются то так,
то сяк, не обращая внимания, кто должен делать это пер-
вым.)
Школьник, изучающий правила вычитания на счетных
палочках, видит: если из одного их количества можно
вычесть другое, не получая в остатке пустое место, то,
наоборот, вычитание уже не произведешь. Так постига-
ется порядок, в котором целые положительные числа вы-
страиваются в так называемый натуральный ряд: один,
два, три, четыре, пять...
Итак, все перечисленные отношения, каждое из ко-
торых наводит порядок в своем множестве, обладают
антисимметричностью: и отношение «х входит в у» ме-
жду матрешками, и отношение «х здоровается первым с
у» между людьми, и отношение «х меньше t/> (х<у) ме-
жду числами.
Но продолжим их рассмотрение далее. Если в одну
матрешку входит другая, а в эту другую — третья, то
третья войдет и в первую. Если одно число меньше дру-
гого, а это другое уступает по величине третьему, то пер-
вое также меньше третьего. То же самое можно сказать
про любое отношение старшинства, которое устанавлива-
ется между людьми.
Во всем этом мы узнаем хорошо знакомое нам свой-
ство транзитивности. Оно также весьма закономерно свя-
зывается с представлением о каком бы то ни было по-
рядке, старшинстве, подчинении, иерархии. (Что получит-
ся, если при установлении порядка забыть про транзитив-
ность, легко вообразить, вспомнив принцип средневеко-
вых феодалов: «Вассал моего вассала — не мой вассал».
Эта нетранзитивная формула так и отдает беспорядками
и распрями, которыми знамениты средние века.)
После сказаного естественно поинтересоваться: ну а
80
рефлексивность? Обладают ли ею анализируемые нами
отношения?
Взяв две одинаковые матрешки, мы не сможем вло-
жить одну в другую. Ни про одно число нельзя сказать,
что оно меньше самого себя. Стало быть, ни отношение
«х входит в у» между матрешками, ни отношение «х
меньше у» между числами рефлексивностью не обладают.
А вот в отношениях между людьми бывает и по-ино-
му. Глазами вышеописанного ребенка мы уже подмети-
ли: есть люди, которые при встрече не следят за тем, кто
должен здороваться первым: порой тот опережает это-
го, порой наоборот. Причина подобного безразличия по-
нятна: такие люди в каком-то смысле равны — по возра-
сту, по должности и т. п. Значит, отношение «х первым
здоровается с у» рефлексивно.
Кстати, в мире чисел тоже есть подобное отношение,
Выражается оно словами «меньше или равно». Это от-
ношение рефлексивное. Например, шесть меньше или
равно шести (в формульной записи: 6^6). И так можно
сказать про всякое число.
Мы приходим к выводу, что отношения, при помощи
которых устанавливается порядок в том или ином мно-
жестве, бывают двух видов.
Если бинарное отношение нерефлексивно, антисим-
метрично, транзитивно, то оно называется отношением
строгого порядка. Его типичный пример — отношение
«Х<1/».
Если бинарное отношение рефлексивно, антисиммет-
рично, транзитивно, то оно называется отношением не-
строгого порядка. Его типичный пример — отношение
«Х^1/>.
И вот какую еще деталь хотелось бы отметить: в каж-
дом из двух отношений порядка, строгого и нестрогого,
свойства антисимметричности проявляются по-своему.
При строгом порядке так: если один элемент находит-
ся в упорядочивающем отношении к другому, то отсюда
вытекает, что второй к первому в этом отношении не на-
ходится. Скажем, если пять меньше семи, то отсюда сле-
дует, что семь не меньше пяти.
При нестрогом же порядке могут найтись два элемен-
та, каждый из которых находится в упорядочивающем
отношении к другому. Но отсюда уже следует, что эти
два элемента эквиваленты (в частности, равны) друг
другу.
5 Заказ 8651
81
Так было, как мы уже видели, с отношением «х пер-
вым здоровается с у» между людьми: равенство по воз-
расту или по должности, как легко доказать, представ-
ляет собой отношение эквивалентности.
Еще отчетливее проявляется это в мире вещественных
чисел, если рассмотреть в нем отношение «х меньше или
равно у». Всгда можно подыскать два таких числа, что
х^у и у^х. Вдумчивый читатель, конечно, догадывает-
ся, что такие два числа обязательно равны друг другу.
«Каждый Охотник Желает Знать, Где Сидят Фазаны».
Эту фразу, вероятно, помнит всякий, кто когда-ни-
будь имел дело с красками и цветными карандашами.
Она позволяет запомнить последовательность цветов в
спектре. Их названия зашифрованы первыми буквами
слов мнемонической фразы: К — красный, О — оранже-
вый, Ж — желтый и так далее.
0,4 0,5 0,6 0,7 мкм
-1 .....
фиолетовый — синий—голубой—з е л е н ы й—желтый -оранжевый- красный
- За словом «последовательность» нетрудно разгля-
деть отношение строгого порядка. Действительно, отно-
шение предшествования цветов в их спектральной после-
довательности нерефлексивно (ни один цвет не предше-
ствует самому себе), антисимметрично (если один цвет
предшествует другому, то второй не предшествует перво-
му), транзитивно (если один цвет предшествует другому,
а тот — третьему, то первый предшествует третьему).
Читатель, знакомый с оптикой, понимает, что в осно-
ве упорядоченности цветов лежит глубокая физическая
закономерность. Дело в том, что природа света волновая.
Свет каждого цвета имеет определенную длину волны:
красный — наиболее длинную для всех спектральных
цветов, фиолетовый — наиболее короткую.
Длину световой волны можно выразить числом. Так
от оптики, от отношения «х предшествует у» на множе-
стве спектральных цветов можно перейти к математике, к
отношению «х меньше у» на множестве вещественных
чисел, выражающих длины световых волн.
Разговор о цветах и числах мы завели отнюдь не за-
тем, чтобы пояснить понятие порядка новыми иллюстра-
циями. Есть у этих примеров особенность, которую встре-
82
тишь не каждый раз, когда на каком-то множестве уста-
навливается отношение порядка, строгого или нестро-
гого.
Какие бы два различных спектральных цвета мы ни
взяли, относительно них мы всегда можем сказать, что
один предшествует другому. Какие бы два различных
числа нам ни встретились, относительно них мы всегда
можем утверждать, что одно обязательно меньше дру-
гого.
Говорят, что некоторое множество упорядочено неко-
торым отношением порядка, если любые два различных
элемента этого множества обязательно находятся в дан-
ном отношении друг к другу: либо первый ко второму,
либо второй к первому.
Итак, множество спектральных цветов упорядочено
отношением «х предшествует у». Множество веществен-
ных чисел упорядочено отношением «х меньше у»-9 это
же отношение упорядочивает и множество рациональных,
и множество целых, и множество натуральных чисел.
Начиная разговор про упорядоченность множеств, мы
отмечали, что ее встретишь не каждый раз, когда на том
или ином множестве устанавливается отношение поряд-
ка. Читателю могло показаться, что это зависит от при-
роды множеств: какому-то из них никак не придашь упо-
рядоченности, а иному она свойственна в силу самого его
характера; например, «упорядоченным от природы» в
представлении многих выглядит множество чисел.
Подобное мнение неверно. Когда какое-то множество
упорядочено, то дело тут прежде всего в характере отно-
шения порядка, которое на нем устанавливается. На од-
ном и том же множестве можно ввести и такой порядок,
которым оно будет упорядочено, и такой, который его не
упорядочивает.
Возьмем хотя бы множество натуральных чисел. Как
уже говорилось, его упорядочивает отношение «х мень-
ше у». Рассмотрим теперь на нем другое знакомое нам
отношение порядка: «х делит у», или, что то же самое,
«у делится на х». Результат рассмотрения может пока-
заться странным: новым отношением порядка множество
натуральных чисел отнюдь не упорядочено — нетрудно
найти в нем такие два числа, что ни одно из них не де-
лится на другое (5 и 7, 9 и 13 и т. д.).
Может быть, такая странность наблюдается только в
мире чисел?
5
83
Что ж, обратимся к миру фигур. Рассмотрим на нем
отношение вложения (такого, что контур вложенной фи-
гуры нигде не касается контура объемлющей). Это от-
ношение нерефлексивно (ни одну фигуру не вложишь в
себя), антисимметрично (если одна фигура вкладывает-
ся в другую, то обратное невозможно — ситуация такая
же, как с матрешками), транзитивно (здесь дело обсто-
ит опять-таки как с матрешками).
Как видим, все свойства строгого порядка присущи
отношению вложения. Но оно не упорядочивает множе-
ство фигур на плоскости: две различные фигуры, как по-
казано на правом рисунке, могут оказаться такими, что
первая не «ходит во вторую, а вторая не входит в пер-
вую.
А теперь станем сравнивать фигуры по площади. Мы
обнаружим, что этим отношением их множество упоря-
дочено: про любые две фигуры, не равные по площади,
можно сказать, что площадь одной из них больше пло-
щади другой. В частности, из двух фигур на нашем ри-
сунке, которые мы никак не смогли связать отношением
вложения, правая явно уступает по площади левой (это
можно и доказать: из всех ромбов с одинаковыми сторо-
нами наибольшая площадь у квадрата).
Итак, если на каком-то множестве введено некоторое
отношение порядка, это еще не гарантирует, что множе-
ство упорядочено этим отношением.
Если подобное наблюдается в строгой математике, то
тем более это вероятно в тех жизненных ситуациях, ког-
да речь заходит о каком-либо отношении типа порядка.
Например, говоря о картинах и спектаклях, литератур-
ных и музыкальных произведениях, употребляют слова
«лучше», «талантливее» и т. п. Если даже отношениям,
выраженным этими словами, свойственны все признаки
отношения порядка, остается открытым вопрос: упоря-
дочивают ли они упомянутые множества произведений
искусства? Всегда ли о любых двух постановках и книгах
84
можно сказать, что одна лучше или талантливее дру-
гой — подобно тому, как о двух цветах на картине мы с
уверенностью можем утверждать, что один предшествует
другому в спектре?
•
Бинарные отношения, которым мы посвятили немало
примеров, — это всего лишь частная разновидность от-
ношений, которые могут связывать элементы некоторого
множества.
Мы уже говорили, что существуют также отношения,
охватывающие сразу три, четыре, пять и вообще п эле-
ментов (n-арные отношения, как говорят математики).
Мы остановимся здесь на тернарных. Поясняя их, мы
приводили в качестве примера отношение между роди-
телями и ребенком. Нетрудно подыскать пример тернар-
ного отношения и в элементарной математике.
Рассмотрим множество всех отрезков. Возьмем какие-
либо три из них и спросим: можно ли составить из них
треугольник? Определяющее правило на этот счет фор-
мулируется так: сумма любых двух отрезков из всякой
троицы должна превосходить третий. Все тройки отрез-
ков, находящихся в таком тернарном отношении, при-
годны для того, чтобы строить из них треугольники.
Когда исследуется какое-либо бинарное отношение,
заданное на множестве вещественных чисел, то при этом
очень помогает его график — фигура на плоскости.
Очевидно, чтобы описать графиком некоторое тернар-
ное отношение между вещественными числами, нам по-
требуется уже трехмерное пространство с системой ко-
85
ординат в нем: каждую точку этого пространства можно
трактовать как тройку вещественных чисел.
Пусть элементы всякой такой тройки выражают со-
бой длины трех отрезков, из которых мы хотим составить
треугольник. Как мы уже установили, для желаемого
построения годится не всякая тройка, а лишь такая, эле-
менты которой находятся в вышеописанном тернарном
отношении.
Отберем все подходящие тройки и посмотрим: что за
точки соответствуют им в трехмерном пространстве? В
какую область пространства сложатся эти точки?
У нас получится пирамида, упершаяся вершиной в
начало координат, касающаяся ребрами координатных
плоскостей и не имеющая основания, — она простирается
неограниченно. Это и будет график того тернарного от-
ношения, о котором мы завели разговор.
•
Он был титулярный советник,
Она — генеральская дочь,
Он робко в любви ей признался —-
Она прогнала его прочь.
По всей вероятности, причиной трагедии послужило
какое-то несоответствие чинов и званий. Сейчас нам труд-
но это понять, но когда-то табель о рангах многое значи-
ла во взаимоотношениях людей (Табл. 1).
Армейские чины Гражданские чины
Г енерал-фельдмаршал Генерал от инфантерии, кавалерии, артиллерии Г енерал-лейтенант Генерал-майор Бригадир* Полковник Подполковник Майор Капитан (ротмистр) **) Штабс-капитан **) (штабс-ротмистр) ** Поручик Подпоручик Прапорщик (корнет **) Фендрик Канцлер Действительный тайный советник Тайный советник Действительный статский советник Статский советник Коллежский советник Надворный советник Коллежский асессор Титулярный советник Коллежский секретарь Корабельный секретарь Губернский секретарь Провинциальный секретарь Коллежский регистратор
* Чин существовал в XVIII ** Кавалерийский чин. ; веке, впоследствии был упразднен.
86
На соседней странице приведены армейская и граж-
данская колонки табели о рангах — в том ее варианте,
который относится ко времени создания процитирован-
ного романса. (Составленная Петром Первым, она впо-
следствии претерпевала некоторые изменения.)
Прослеживая взаимно однозначное соответствие ме-
жду множествами гражданских и военных чинов, мы ви-
дим: титулярный советник действительно не ровня гене-
ралу, поскольку в пересчете на военные чины соответ-
ствует всего лишь капитану. Не улыбается бедняге и
сравнение по гражданской шкале: здесь даже самому не-
знатному из генералов, генерал-майору, соответствует
действительный статский советник, что опять-таки гораз-
до выше титулярного советника.
Итак, несчастный уступает своему несостоявшемуся
тестю и по военной, и по гражданской линии. Потому что
взаимно однозначное соответствие, связывающее воен-
ную и гражданскую колонки табели о рангах, сохраняет
отношение старшинства, которое установлено в том и
другом множестве чинов.
Подобные случаи взаимно однозначного соответствия,
когда элементам одного множества, находящимся в не-
котором отношении, соответствуют элементы другого
множества, находящиеся в том же отношении, называ-
ются изоморфизмом.
Изоморфизмом было, например, взаимно однозначное
соответствие между множеством спектральных цветов и
множеством слов фразы: «Каждый охотник желает
знать, где сидят фазаны». Это соответствие сохраняло
отношение предшествования, которое можно ввести в обо-
их множествах.
Следует сразу же отметить, что наши примеры со сва-
товством титулярного советника и с фразой про охотни-
ка и фазанов дают еще не совсем полное, а сказать вер-
нее— предельно узкое представление об изоморфизме.
Когда он устанавливается между двумя множествами, то
не обязательно, чтобы элементы того и другого подчиня-
лись одному и тому же отношению, как было в примерах.
Об изоморфизме говорят и тогда, когда в каждом из
эквивалентных множеств действует свое отношение.
Важно лишь вот что: если несколько элементов из одного
множества связаны некоторым действующим там отноше-
нием, то соответствующие им элементы другого множе-
ства связаны господствующим там отношением.
87
В таких случаях говорят, что изоморфизм, установ-
ленный между этими множествами, переводит одно от-
ношение в другое.
Из этого примечания, которое подчеркивает широту
понятия изоморфизма, нетрудно понять, что им можно
связывать не только упорядоченные множества — в них
могут рассматриваться отношения весьма разнообразные,
как станет ясно из дальнейших примеров.
Ради эффекта возьмем для начала такой, где изомор-
физм устанавливается между множествами чисел и то-
чек, причем отношение, существующее в одном, на пер-
вый взгляд не имеет ничего общего с отношением, дейст-
вующим в другом множестве.
Множество чисел здесь составлено из всех делителей
числа тридцать: 1, 2, 3, 5, 6, 10, 15, 30. Множество то-
чек— это вершина куба, расположенного так, как пока-
зано на рисунке.
Введем в нашем числовом множестве бинарное отно-
шение кратности: «х делит у». (Мы уже рассматривали
его когда-то на множестве всех натуральных чисел и от-
метили, что оно этого множества не упорядочивает. Не-
сложно проверить, что не упорядочивает оно и наше чис-
ловое множество: в нем без труда можно подыскать та-
кие пары чисел, что ни одно из двух не делится на дру-
гое — 2 и 3, 5 и 6, 10 и 15.)
Во множестве вершин куба введем бинарное отноше-
ние следования: две вершины считаются связанными этим
отношением, если из одной в другую можно пройти по
ребрам куба снизу вверх.
Взаимно однозначное соответствие между обоими
множествами установлено самым простым образом: каж-
дой вершине приписан один из делителей тридцатки (см.
88
рисунок). Легко видеть, что это изоморфизм: если в на-
шем множестве чисел какое-то одно делится на другое,
то соответствующие им вершины куба связаны восходя-
щим путем по ребрам куба. Например, путь из точки 30
через точку 10 в точку 5 — это путь наверх. Остальные
пути читатель может проследить самостоятельно.
В примерах изоморфизма, подобранных нами, про-
стоты ради фигурировали такие множества, в которых
вводилось лишь одно-единственное отношение. Можно
рассмотреть случаи, когда в том и другом множестве, ме-
жду которыми устанавливается взаимно однозначное со-
ответствие, введено несколько отношений и каждое из
них, действующее в одном множестве, переводится в
свое, действующее в другом множестве. Таково наиболее
общее понятие изоморфизма.
и
правой колонки.
/V !д N
1,0 0,0000
1,1 0,0414
1,2 0,0792
1,3 0,1139
1,4 0,1461
1,5 0,1761
1,6 0,2041
1,7 0,2304
1,8 0,2553
1,9 0,2788
2,0 0,3010
два
в
Перед вами фрагмент таблицы десятичных лога-
рифмов. Слева — положительные числа, справа от каж-
дого из них в той же строчке поставлен его логарифм.
Так установлено взаимно однозначное соответствие ме-
жду множествами чисел левой
Возьмем в левой колонке
три числа, связанных тем
отношением, что произведе-
ние первых двух равно треть-
ему. (Напомним, что это
отношение тернарное, пос-
кольку связывает три чис-
ла.)
Возьмем теперь в правой
колонке числа, соответству-
ющие тем трем, что выбра-
ны нами в левой колонке,
иными словами, возьмем ло-
гарифмы чисел левой колон-
ки. Сложим два первых ло-
гарифма — у нас получится
третий.
И так будет всегда, какую
бы тройку вещественных
чисел мы ни взяли, лишь бы
давали третье.
первые
произведении
89
Итак, множество чисел правой колонки с тернарным
отношением «сумма» между ними связано изоморфизмом
со множеством чисел левой колонки, где действует тер-
нарное отношение «произведение».
Операция сложения гораздо проще и выполняется
легче, чем операция умножения. Таблица логарифмов
для того и существует, чтобы заменять умножение сло-
жением, а деление — вычитанием. Чтобы перемножить
два числа, следует отыскать в таблице их логарифмы,
затем сложить оба логарифма и таким образом полу-
чить в результате логарифм произведения, а напосле-
док по нему найти все <в той же таблице само искомое
произведение. Деля одно число на другое, из логарифма
первого следует вычесть логарифм второго.
Особенно эффективна эта процедура, когда требуется
перемножать и делить многозначные числа. С такими
числами, например, приходится иметь дело в астроно-
мии — оттого их и называют астрономическими.
Недаром французский естествоиспытатель Лаплас го-
ворил, что изобретение логарифмов удлинило жизнь аст-
рономов.
Тот, кто бывал в Москве, конечно, провел немало вре-
мени в московском метро и видел схемы его линий, выве-
шенные в каждом вагоне подземных поездов. Когда-то
эти схемы выполнялись в реалистической манере, изви-
листые линии были тесно привязаны к плану города. Но
впоследствии географическая точность была принесена
в жертву геометрической четкости: радиальные линии
стали прямыми, кольцевая превратилась в строгую ок-
ружность.
При всей своей географической недостоверности вто-
рой план не менее удобен, чем первый. Оба изоморфны
друг другу. Взаимно однозначное соответствие между
точками-станциями на них очевидно: и там и тут они от-
мечены одинаковыми названиями. Это соответствие со-
храняет отношение следования: и там и тут путь от «Кур-
ской-радиальной» ведет нас через «Бауманскую» к
«Электрозаводской», а пройдя от «Красносельской» к
«Сокольникам», мы оказываемся далее на «Преображен-
ской площади». И там и тут путь от «Беляева» до «Но-
вых Черемушек» проходит через «Калужскую», а чтобы
90
проехать от «Юго-Западной» до «Университета», соглас-
но тому и другому плану, надо проследовать через «Про-
спект Вернадского».
Если же судить с точки зрения ориентации, то второй
план даже предпочтительнее первого: он проще, нагляд-
нее.
Эта незатейливая иллюстрация вновь напоминает нам
о достоинствах изоморфизма. Он позволяет спрямлять
пути науки, заменяя один объект исследования другим,
более простым, но сохранившим (быть может, в преобра-
зованном виде) все связи между своими элементами, су-
щественные для исследования, свою структуру (кстати, в
дословном переводе слово «изоморфизм» и означает
«одинаковая структура»).
Примеров тому немало: от моделирования физиче-
ских процессов до наблюдавшихся порой попыток пере-
фразировать целые науки, перевести одну <на язык другой.
Раскройте вторую книгу «Начал» Эвклида и прочтите
первое предложение:
«Если одна из двух линий разделена на произвольное
число частей, то прямоугольник между этими двумя ли-
ниями равен вместе взятым прямоугольникам, содержа-
щимся между неразделенной линией и отдельными час-
тями другой».
Разобравшись в чертеже, вы, конечно, догадаетесь,
что Эвклид излагает на геометрическом языке распреде-
лительный закон умножения относительно сложения. И
возможно, вас удивит эта нарочитая наглядность: не про-
ще ли было написать алгебраическую формулу?
Все дело в том, что древнегреческие математики не
владели понятием вещественного числа в той мере, в ка-
кой оно известно нам. Греки пользовались целыми и ра-
циональными числами, но не знали иррациональных. В
этом смысле и нужно понимать, например, их вывод о
том, что диагональ квадрата не соизмерима с его сторо-
ной: отношение этих двух отрезков выражается числом
У2, числом иррациональным, неизвестным древним гре-
кам и, стало быть, несуществующим для них.
Не имея, с их точки зрения, общей меры, эти два от-
резка тем не менее существовали для греков как геомет-
рические объекты. И это подсказывало выход из затруд-
нительного положения: заменить исследование чисел ис-
следованием фигур.
91
Основой такой замены, как догадывается читатель,
послужил изоморфизм между множеством положитель-
ных вещественных чисел и множеством отрезков. Отно-
шение равенства чисел он переводит в отношение кон-
груэнтности отрезкою (это мудреное слово означает по-
просту совпадение или наложение), числовое отношение
«меньше» — в линейное отношение «короче», операция
сложения чисел заменяется при этом составлением отрез-
ков, операция умножения — построением прямоугольни-
ков и т. д.
Так и возникла «геометрическая алгебра», излагаемая
во второй книге «Начал». Чтобы придать ей общеприня-
тый вид, требуется лишь перевести ее предложения с
геометрического языка на буквенный. (Кстати, многие
термины «геометрической» алгебры внедрились в «бук-
венную» в непереведенном виде: мы говорим о квадрате
числа, о среднем геометрическом двух чисел.)
Вспомните, читатель, как на одной из предыдущих
страниц мы показали вам схему телефона. Мы иллю-
стрировали ею важность понятия отображения. Мы гово-
рили, что реальный прибор удобно изучать по его схеме,
где каждой детали поставлен в соответствие определен-
ный значок.
Но ведь телефон — это не просто скопление деталей:
трубка, диск, звонок... Лишь соединенные системой про-
водов они образуют телефон.
Так и схема телефона немыслима без соединительных
линий, показывающих, как связаны между собой отдель-
ные детали этого устройства.
Так и отображение одного какого-либо множества в
другое особенно ценно тогда, когда оно так или иначе
передает отношения, существующие между элементами
отображаемого множества, переводит их в отношения, ус-
тановленные между элементами множества-образа.
Всякое такое отображение называется изоморфизмом.
Надеемся, что после сказанного читатель убедился в
огромной важности и проистекающей отсюда широкой
применимости этого понятия.
ПОСЛЕДОВАТЕЛЬНОСТИ,
РЯДЫ
Мы в тире. С огневого рубежа стрелки посылают пулю
за пулей — каждый в свою мишень.
Следя за тем, как мишени покрываются пробоинами,
нетрудно отличить меткого стрелка от неопытного. Ма-
стера заметишь сразу, даже если ему досталась непри-
стрелянная винтовка. Пусть несколько первых выстрелов
будут неудачными. Начиная с некоторой, пробоины уже
не выйдут за границы белого круга мишени. Следите
дальше, и вы дождетесь выстрела, после которого пробо-
ины не выйдут и за границы яблочка. Вот уже все без ис-
ключения они ложатся внутрь шестерки... внутрь семер-
ки... восьми... девяти... (рис. слева).
А как успехи у соседнего стрелка? Там все наоборот.
Сколько ни наблюдай, он то и дело посылает пули в мо-
локо (рис. справа). Ясно — оружие в неопытных руках.
Если бы соревнования по стрельбе комментировал ма-
тематик, то он, пожалуй, нашел бы здесь удачные обра-
зы для разговора о последовательностях, пределах, схо-
димости.
Каждую пробоину он, разумеется, мыслил бы не как
рваное пятно, а как точку. Сужающиеся круги мишени в
его представлении не закончились бы на десятке: изу-
93
чая ход соревнований, он располагал бы внутри нее еще
меньшие, неограниченно сужающиеся круги. Математик
повел бы строгий счет выстрелам, и каждую пробоину от-
мечал бы своим номером. Перенумерованные элементы
множества пробоин математик назвал бы членами по-
следовательности. Впрочем, этот термин математик упо-
требил бы лишь после того, как убедился, что соревнова-
ния будут продолжаться неограниченно долго. Последо-
вательностью, подчеркнул бы математик, называется
бесконечное множество перенумерованных элементов.
Последовательность считается заданной, если известен
закон ее образования, то есть правило, согласно кото-
рому по любому названному номеру можно указать член
последовательности с таким номером.
Удовлетворив таким образом профессиональную тя-
гу к строгости, математик приступил бы к наблюдениям
за ходом соревнований.
Наблюдая за опытным стрелком, математик отметил
бы: какой малый круг ни возьми, начиная с некоторого
выстрела, все последующие пробоины ложатся внутрь
этого круга. Это значит, сказал бы математик, что после-
довательность пробоин стремится или сходится к центру
мишени, что центр мишени есть предел последователь-
ности пробоин.
Наблюдая за неопытным стрелком, математик очер-
тил бы вокруг центра мишени круг некоторого радиуса,
такой, что какой номер ни загадай, найдется пробоина с
большим номером, лежащая за пределами этого роково-
го круга. Это значит, сказал бы математик, что последо-
вательность пробоин не стремится, не сходится к центру
круга.
•
Снова тир.
Мишени сняты со щитов и положены на стол. Но по-
ложены обратной стороною вверх. Каждая пробоина ак-
куратно отмечена своим номером. Можно ли теперь от-
личить мишень опытного стрелка от мишени неопытно-
го? Можно ли определить, сходится ли последователь-
ность пробоин к некоторому пределу или, напротив, не
сходится ни к какому, иначе говоря, расходится? Суще-
ствует ли безошибочный критерий сходимости?
Да, существует. Он называется критерием Коши, по
имени математика, указавшего его впервые. И это дейст-
94
21
101 •
58 • 1
• •
2 5
• 3 4 •
6 9
10
12
• 7
8 И
вительно безошибочный критерий. Он выполняется, ес-
ли последовательность сходится. Он не выполняется, ес-
ли последовательность расходится.
Критерий Коши прост. Загадайте любое расстояние.
Теперь постарайтесь подыскать такой номер, чтобы рас-
стояние между любыми двумя пробоинами с большими
номерами было бы меньше загаданного. Если вам это бу-
дет удаваться всегда, какое малое расстояние вы ни за-
гадаете, "это и означает, что последовательность удовле-
творяет критерию Коши. А раз удовлетворяет, то, стало
быть, сходится к некоторому пределу.
Но каков же он, этот предел? Спрашивать так — зна-
чит требовать от критерия Коши больше, чем он может
дать. Он безошибочно подтверждает существование пре-
дела — и только. Что это за предел, надо еще поискать.
Однако уверенность, что искомое существует, часто об-
легчает поиск.
Заметим, что последовательность, удовлетворяющая
критерию Коши, называется фундаментальной.
А можно ли с помощью замечательного критерия опо-
знать расходящуюся последовательность?
Да, можно.
Внимательный читатель наверняка уже заметил
сходство между формулировкой критерия Коши и опре-
делением предела. По сходству, по аналогии с отрицани-
ем сходимости можно построить предписание, которое
позволило бы безошибочно уличить в расходимости рас-
ходящуюся последовательность.
Здесь тоже нужно подыскать некоторое контрольное
расстояние, такое, что какой номер ни загадывай, всегда
найдутся две пробоины с большими номерами, удален-
95
ные друг от друга на расстояние больше контрольного.
Такая последовательность не фундаментальна, стало
быть, она не сходится ни к какому пределу, иначе гово-
ря, расходится.
Заряд электрона, постоянная Планка, число Авогад-
ро... Есть несколько физических величин, за которыми
наука закрепила звание мировых констант. Это коэффи-
циенты, входящие в формулы важнейших физических за-
конов.
Постоянная Планка, например, служит коэффициен-
том пропорциональности между энергией кванта излуче-
ния и частотой соответствующей ему волны. Число Аво-
гадро необходимо, чтобы количественно выразить связь
между температурой, давлением и объемом идеального
газа.
Чтобы пользоваться физическими законами, чтобы
рассчитывать описываемые ими явления, нужно поточ-
нее знать мировые константы. А определить их можно
только из опыта, путем измерения.
Одна из таких мировых констант — скорость света.
Впервые ее попытался измерить в 1675 году датский аст-
роном Ремер. Наблюдая затмения самого яркого из спут-
ников Юпитера, Ио, он заметил, что когда Земля и Юпи-
тер находятся по разные стороны от Солнца, затмение
наступает позже по сравнению с тем случаем, когда
Земля и Юпитер находятся по одну сторону от светила.
Опоздание, решил Ремер, обусловлено большим рассто-
янием, которое в первом случае свет проходит от Юпи-
тера до Земли. Несложный расчет дал первую в истории
науки оценку для скорости света: 226 000 км/с.
96
Последующие исследователи усточняли оценку. В
1849 году Физо, пропуская луч между зубцами быстро
вращающейся шестерни, получил цифру 313 274,
304 км/с. Спустя четверть века Корню, используя тот же
метод, дал новую цифру: 298 400± 1000 км/с.
Напрашивается недоуменный вопрос: метод тот же, а
результат грубее — стоит ли упоминать о нем?
В результате Корню внимания заслуживают не циф-
ры, а знак «плюс-минус». Он напоминает, что каждый из-
мерительный метод имеет свою погрешность. (Физо яв-
но не учитывал этого, выписывая один знак своего резуль-
тата за другим.) Истинное значение измеряемой величи-
ны лежит в пределах этой погрешности. Истинное значе-
ние скорости света отличается от результата Корню не
более чем на 1000 км/с. А сказать вернее — результат
Корню отклоняется от истины не более чем на 1000 км/с.
Последующие исследователи старались гарантиро-
вать все меньшее отклонение. Добавка «плюс-минус» со-
кратилась до сотен, десятков, до нескольких километров
в секунду, а там счет пошел уже на метры в секунду...
(Попутно выяснилось, что Корню, правильно поста-
вив вопрос об ошибках измерений, переоценил возмож-
ности использованного им метода и в своем результате
указал погрешность, примерно в 1,5 раза меньшую ис-
тиной.)
— Майкельсон, 1926: 299796±4 км/сек • Мак-Ниш, 1962 ,, 299792.610.25 км/сек ’®6,7' . । 299792,5 ± 0,1 км/сек
о +1. | ±2000 км/сек]
Щ _ о
см _ о п км/
। Корню, 18/3: 298400±1000 км/сек
— +1 —
- -
Перефразируя эту физическую историю на математи-
ческий лад, можно сказать, что для любой малой погреш-
ности находился исследователь, начиная с которого все
последующие результаты отклонялись от истинного зна-
чения скорости света не более чем на эту погрешность.
6 Заказ 8651 97
Исследования продолжаются, растет точность изме-
рений. Последовательность результатов стремится, схо-
дится к величине скорости света.
•
Как по-честному разделить конфету между приятеля-
ми-мальчишками? Конечно, как в песне: тебе половина —
и мне половина.
И обладатель конфеты делит ее ровно на две части,
чтобы поделиться с товарищем. Полученную долю тот
тоже делит ровно пополам, чтобы поделиться со своим
приятелем. Тот — со своим. Тот — со своим... Все по-
честному: тебе половина — и мне половина.
Без кропотливых измерений и расчетов таким спосо-
бом можно разделить конфету на сколько угодно частей.
Нехорошо только, что доли получаются неравные. Вели-
чина очередной порции при таком делении неуклонно
уменьшается до нуля: полконфеты, четверть конфеты,
восьмая часть, шестнадцатая... И какую величину ни за-
гадай, начиная с некоторой порции, все последующие бу-
дут меньше загаданной величины.
Одна восьмая, одна шестнадцатая, одна тридцать вто-
рая, одна шестьдесят четвертая... От долей конфеты мы
незаметно перешли к числам. Это нам на руку. Последо-
вательное деление конфеты пополам неизбежно постави-
ло бы нас когда-нибудь (и очень даже скоро, где-то на
сороковом шагу) перед проблемой расщепления атомного
ядра. А число можно делить без конца, благо принцип
известен: начиная с первого числа, равного половине,
каждое последующее получается из предыдущего деле-
нием на два. Сказанное дает нам право назвать образу-
ющуюся при этом цепочку чисел последовательностью.
Ценитель наглядности, вероятно, посетует, что с пе-
реходом от конфет к абстрактным числам наши постро-
ения перестали быть осязаемыми. Что ж, их легко сде-
лать зримыми. Для этого надо взять числовую прямую
и отложить на ней члены нашей последовательности: од-
ну вторую, одну четверть и так далее.
|.
I I
-1 | О I 1
I..I I |нп I L J II I
ап а3 а2 fl1
98
И тогда воочию станет ясно, что, подобно своему кон-
дитерскому прообразу, наша последовательность схо-
дится к нулю, имеет нуль своим пределом.
Любитель строгости, пожалуй, потребует выразить
этот факт в математической формулировке. Мы сделаем
это, не порывая с графическим образом нашей последо-
вательности.
Ее стремление к нулю означает (следите за числовой
прямой!), что для любой сколь угодно узкой окрестности
нуля (ее полуширина обозначена традиционной в таких
случаях греческой буквой «эпсилон») найдется такой
номер, что все члены последовательности с большими
номерами будут находиться в этой окрестности.
В каком порядке они будут там располагаться, суще-
ственной роли не играет. Все они могут лежать по одну
сторону от предельной точки (в нашем примере — от ну-
ля), могут не совпадать с нею (как в нашем примере).
Могут и совпадать. Могут лежать и справа и слева от
предельной точки. Иногда какой-то член последователь-
ности может оказаться дальше от предельной точки, не-
жели предыдущий. Определение сходимости оставляет
без внимания эти детали. Ни одна из них сама по себе
не угрожает сходимости и недостаточна для того, чтобы
обвинять последовательность в расходимости.
По подозрению в том, что последовательность не схо-
дится к какой-то точке, лучше всего обращаться к стро-
гой формулировке этого факта. Вот она: последователь-
ность не сходится к данной точке, если существует не-
которая ее окрестность, такая, что для любого номера
найдется член последовательности с большим номером,
находящийся вне этой окрестности.
Существует ли предел спортивных возможностей че-
ловека?
Оспаривать их ограниченность не станет никто. Но
вместе с тем мы знаем, что вечных рекордов не бывает.
Еще недавно мечтой спринтеров было пробежать сто мет-
ров за десять секунд — и вот заветный рубеж уже пре-
одолен. И в то же время нельзя всерьез утверждать, что
какой-нибудь будущий рекордсмен пробежит стомет-
ровку за время, меньшее двух или одной секунды...
Разобраться в этом запутанном вопросе на первый
6
99
взгляд нелегко. А между тем, ставя его, мы употребили
несколько слов, которые помогут нам внести в каверзную
проблему поистине математическую ясность.
Это прежде всего слово «предел». Надежным основа-
нием наших дальнейших рассуждений послужит теория
последовательностей. Мы будем рассматривать рекорд-
ные результаты в беге на сто метров как члены некото-
рой последовательности.
Это, во-вторых, слово «меньше». Члены нашей после-
довательности— числа, их можно сравнивать по вели-
чине.
Это, в-третьих, слово «ограниченность». Утверждая,
что никто не сможет пробежать стометровку быстрее,
чем, скажем, за две секунды, мы заявили, что члены на-
шей числовой последовательности ограничены снизу, что
существует число, меньшее любого члена нашей после-
довательности.
Это, в-четвертых, слово «рекорд». Рекорд считается
таковым лишь в том случае, когда он превосходит преды-
дущее достижение. Очередной рекордный результат в бе-
ге на сто метров должен быть меньше прежнего. В этом
выражается существенная особенность нашей последо-
вательности: математик назвал бы ее монотонно убыва-
ющей, имея под этим в виду, что каждый последующий
ее член меньше предыдущего.
Вот теперь все готово для решающего утверждения.
В теории последовательностей есть теорема: всякая мо-
нотонно убывающая и ограниченная снизу числовая по-
следовательность имеет предел.
Это значит, что на шкале результатов в беге на сто
метров есть отметка, к которой стремится последователь-
ность рекордных достижений. Какую малую окрестность
этой отметки ни взять, все члены последовательности, на-
чиная с некоторого, будут лежать в этой окрестности. За-
метим, что это вовсе не противоречит утверждению о том,
что вечных рекордов не бывает. Ведь последователь-
ность рекордов может стремиться к своему пределу, не
достигая его, наподобие «конфетной» последовательно-
сти из предыдущего раздела. Если нынешний рекорд от-
Символ предела Член последовательности
Пт ап = А
л-*<» \
/ Предел
Индекс последовательности
(номер члена
последовательности)
too
личается от предела на десятую долю секунды, то следу
ющий может отличаться на пять сотых, следующий за
ним — на одну сотую, следующий — на пять тысячных...
и каждый очередной результат будет рекордом, посколь*
ку он меньше предыдущего. Нужно только замерять вре-
мя с точностью до все более мелких долей секунды.
В заключение напомним, что в своих рассуждениях
мы основывались на теореме о существовании предела
для всякой монотонно убывающей и ограниченной снизу
числовой последовательности. Есть также теорема о том,
что предел имеет всякая монотонно возрастающая и ог-
раниченная сверху последовательность. Эту теорему мы
применили бы, если бы подвергли математическому раз-
бору, например, рекорды штангистов.
«Теперь сходитесь».
Хладнокровно,
Еще не целя, два врага
Походкой твердой, тихо, ровно
Четыре перешли шага,
Четыре смертные ступени.
Свой пистолет тогда Евгений,
Не преставая наступать,
Стал первый тихо подымать.
Вот пять шагов еще ступили,
И Ленский, жмуря левый глаз,
Стал тоже целить...
Не пугайтесь, ради бога, не пугайтесь, читатель! Ро-
ковой выстрел, сразивший Ленского, не прозвучит на
этой странице. Эти пушкинские строки, этот отрывок из
«Евгения Онегина» мы привели исключительно как по-
вод для разговора о том, какое важное значение для ма-
тематики имеет понятие предела.
Перед вами несколько окружностей. Как граненый
ствол старинного дуэльного пистолета охватывает чер-
ный кружок дула, так каждую из этих окружностей охва-
тывает описанный правильный многоугольник. Внутри
каждой окружности — правильный вписанный много-
угольник с тем же числом сторон.
Прослеживая этот ряд слева направо, вы видите, что
число сторон у многоугольников растет: три, четыре,
пять, шесть...
Посмотрим, что происходит при этом с периметрами
101
вписанных и описанных фигур. Если отложить их на чис-
ловой прямой, засечки будут сходиться, как дуэлянты.
Но можно ли понимать эту сходимость в том же стро-
гом смысле, в каком мы говорим о сходимости последо-
вательностей? Существует ли предел, к которому стре-
мится последовательность периметров, скажем, вписан-
ных многоугольников? А описанных?
Оказывается, и тот и другой предел существует. Возь-
мем периметры описанных фигур. Их последовательность
монотонно убывает. К тому же она ограничена снизу —
например, периметром любого из вписанных многоуголь-
ников, хотя бы квадрата. Значит, эта последовательность
имеет предел. Сходится и последовательность вписанных
фигур: ведь она монотонно возрастает и ограничена
сверху — хотя бы периметром описанного квадрата.
Но что это? Последовательности, разговор о которых
мы начали с описания дуэли на пистолетах, сходятся,
словно противники, решившие схватиться врукопашную.
Похоже, что они сходятся к одному пределу.
Мельчась в изломах своих сторон, описанные много-
угольники все плотнее облегают окружность, все теснее
прижимаются к ней вписанные. Периметры тех и дру-
гих можно рассматривать как все более точные прибли-
жения длины окружности, а общий предел периметров -
как точное значение этой длины.
Р3 Р4 Р6Р8 О8°6 °4 °3
---------- »• • • ............♦ 1 1-- |-----• |
5/?------6/? 7/?...8R 9/? 10/?--11R
?п — периметр вписанного л-угольника — периметр описанного л-угольника
102
Замечательно, что с помощью той же процедуры оп-
ределяется длина других кривых: с этой целью исследу-
ется, как ведут себя длины ломаных, вписанных в кри-
вую, звенья которых укорачиваются неограниченно,
стремятся к нулю.
Уже этот пример показывает, какое важное значение
для математики имеет понятие предела.
Когда требуется определить некоторую величину, сна-
чала можно оценить ее приближенно, затем рассмотреть
еще ряд приближений все более точных, а потом, иссле-
дуя уже сам процесс приближения, найти искомую вели-
чину как предел последовательности ее приближенных,
все более уточняющихся оценок.
Определить искомую величину другим из известных
способов часто оказывается делом значительно более
трудным или попросту невозможным. Например, не из-
вестен другой способ определить длину кривой линии,
кроме только что изложенного.
Во многих семьях есть обычай, своего рода ритуал: в
день рождения сына отец подводит ребенка к дверному
косяку и торжественно отмечает на нем рост именинника.
Ребенок растет, и на косяке с годами возникает целая
лесенка отметок.
Отец и сын с любопытством рассматривают ее. «В
этом году я вырос всего на два сантиметра», — вздыхает
сын. «Мало каши ел! Ну, ничего, зато в прошлом году—
на пять,— утешает его отец.— Да и в позапрошлом ниче-
го— целых три прибавил».
Три, пять, два... Такова последовательность приростов
от года к году. Но есть и другая последовательность, и
юз
именно ее члены аккуратно выписываются рядом с засеч-
ками. Это — последовательность значений роста.
Две последовательности связаны друг с другом. Вто-
рая получается из первой сложением. Рост — это сумма
приростов за все предыдущие годы.
Чтобы отличить вторую последовательность от пер-
вой, необходимо ввести новые термины. Когда члены по-
следовательности предполагается суммировать, их назы-
вают членами ряда. Сумма нескольких первых членов
ряда называется его частичной суммой. Кстати, все чле-
ны нашего ряда — числа (три, пять, два...). Такие ряды
называются числовыми.
С годами мальчик становится юношей, юноша — муж-
чиной. Отметки на дверном косяке сближаются, и с неко-
торого времени их перестают ставить. Не потому, что
обычай забыт, а потому, что пропадает интерес: отметки
сливаются, ложась во все более тесную окрестность пре-
дельного роста.
Математик сказал бы, что последовательность значе-
ний роста, отмеченных на дверном косяке, имеет предел.
Или сказал бы так: ряд сходится. А поскольку значения
роста представляют собой частичные суммы ряда, мате-
матик мог бы попутно высказать такое определение: ряд
называется сходящимся, если последовательность его ча-
стичных сумм имеет предел; этот предел и называется
суммой ряда. Если же у последовательности частичных
сумм нет предела, то ряд называется расходящимся.
Итак, последовательность значений роста сходится. А
что можно сказать про последовательность приростов от
года к году?
Понятно, что члены этой последовательности убыва-
ют, стремясь к нулю. Будь иначе, человек рос бы неогра-
ниченно. Убывание членов ряда необходимо для его схо-
димости. Необходимо, но недостаточно.
Как вы думаете, что было бы, если бы ребенок за пер-
вый год вырос на дециметр, за второй — на полдецимет-
ра, за третий — на треть, за четвертый — на четверть и
так далее? До какого роста вырос бы сын?
Опираясь на утверждения соответствующего раздела
математики, мы со всей ответственностью заявляем, что
такой ребенок, живи он вечно, со временем перерос бы
любую наперед заданную гору.
Убывания слагаемых еще недостаточно для сходимо-
сти ряда. Они должны убывать достаточно быстро.
104
Насколько быстро — об этом говорят признаки сходи*
мости рядов.
•
Свои незаурядные математические способности Гаусс
обнаружил в раннем детстве.
Ученикам класса, в котором он учился, учитель одна-
жды задал вопрос: «Сколько будет, если сложить все це-
лые числа от одного до двадцати?»
Не прошло и несколько минут, как Гаусс крикнул:
«Нашел — двести десять!»
«Как тебе это удалось?» — спросил изумленный учи-
тель. И Гаусс рассказал о своей догадке: если сложить
первый член заданного ряда чисел с последним, получит-
ся столько же, если сложить второй с предпоследним
или третий с третьим от конца... Иными словами, члены
ряда, равноотстоящие от его концов, в сумме всегда да-
ют одно и то же число — двадцать один. Всего таких
сумм — десять. Ответ на поставленную задачу теперь по-
лучается перемножением двух этих чисел.
Мы поведали эту историю исключительно для того,
чтобы сказать, что ни о чем подобном мы больше гово-
рить не будем.
В школьной математике изучаются арифметические
прогрессии (то есть такие последовательности чисел, в
которых разность двух соседних равна постоянному чис-
лу) и прогрессии геометрические (то есть такие последо-
вательности чисел, в которых отношение двух соседних
равно постоянному числу). Даются формулы, позволяю-
щие вычислить сумму конечного числа членов той и дру-
гой прогрессии. Ничем подобным мы заниматься не бу-
дем. В нашем рассказе не встретятся больше слова «по-
следний член», «конец ряда». Нас будут интересовать бес-
конечные ряды.
Нельзя сказать, что наш рассказ при этом целиком
будет лежать за пределами школьной математики. Ведь
в ней тоже однажды встречается бесконечный ряд. Мы
имеем в виду бесконечно убывающую геометрическую
прогрессию.
О ней-то мы и поговорим сейчас. Как повелось, объяс-
няться мы будем не на языке формул, а на языке рисун-
ков.
В равнобедренный треугольник вписан круг. В про-
странство над ним —второй круг, касающийся первого и
105
боковых сторон треугольни-
ка. В пространство над вто-
рым кругом — третий. Так
весь угол при вершине тре-
угольника заполняется по-
следовательностью кружков
все меньшего радиуса. Их
число неограниченно.
Если провести горизон-
таль между первыми двумя
кругами, она отсечет от треугольника ему (подобный. За-
коны подобия подсказывают: диаметр второго кружка
так относится к диаметру первого, как диаметр третьего
к диаметру второго и так далее. Это постоянное отноше-
ние меньше единицы. Диаметры кружков образуют бес-
конечно убывающую геометрическую прогрессию.
А теперь вопрос: что будет, если последовательно скла-
дывать диаметры кругов? Чему равна сумма такого бес-
конечного ряда?
Если вы забыли школьную формулу для суммы бес-
конечно убывающей геометрической прогрессии, не огор-
чайтесь. В этом примере можно обойтись без формул.
Нужно лишь повернуть все круги так, чтобы их диамет-
ры стали вертикальными. Бесконечная сумма оказывает-
ся равной вполне конечной величине — высоте треуголь-
ника.
И вы снова убедитесь в том, что бесконечная сумма
членов некоторой последовательности может составлять
вполне конечную величину.
Нам показалось необходимым подчеркнуть это после
разговора о предельном росте человека. Тогда у читате-
ля, чего доброго, могло сложиться впечатление, будто
предел роста существует лишь потому, что с некоторого
возраста рост прекращается, приросты становятся рав-
ными нулю. Теперь в истории со вписанными кругами ни
один из суммируемых диаметров не равен нулю, и тем
не менее частичные суммы их ряда стремятся к пределу.
Все дело в том, что члены ряда стремятся к нулю доста-
точно быстро.
Ряды, рассматриваемые в математике, — это не про-
сто наборы наудачу взятых чисел. Члены ряда строятся
по определенному закону.
106
1 + - + - + - +
2 3 4 п
Вот так называемый гармонический ряд, описанный
нами на словах в истории с мальчиком-великаном:
Мы уже знаем, что суммирование этого ряда не ведет
к конечному результату. Гармонический ряд расходится,
его частичные суммы нарастают безгранично.
А вот другой ряд, уже сходящийся. Его суммирование
дает знаменитое число е, столь же популярное в матема-
тике, как и число л:
, 111 1
1 + - + - + - +
2! 3! 4! п\
В той и другой строчке чисел обратите внимание на
слагаемое, огражденное отточиями. Это так называемый
общий член ряда. Он-то и служит выражением законо-
мерности, по которой строится ряд. Подставив вместо п
конкретное число, мы получим величину слагаемого с
таким номером. В первом случае для этого нужно разде-
лить единицу на номер слагаемого, во втором единица
делится на произведение всех целых чисел от единицы до
п (такое произведение и обозначается символом /г!).
Закономерность, по которой строится ряд, — залог ла-
коничной его записи. Вместо длинной цепочки чисел ма-
тематик пишет выражение для общего члена ряда и пе-
ред ним ставит заглавную греческую букву «сигма», обо-
значающую суммирование.
Если сверху и снизу к этой красивой букве приписа-
ны числа, это значит, что речь идет о частичной сумме
ряда. Приписки — это номера первого и последнего сла-
гаемого частичной суммы, так называемые пределы сум-
мирования — нижний и верхний.
Член ряда
Символ суммирования
n-ная частичная
сумма ряда
Индекс
суммирования
Сумма бесконечного
ряда
5,
1 ак = hm Sf
Но если над знаком суммирования вы увидите зна-
чок оо, не принимайте его за поваленную набок восьмер-
ку. Бесконечность — вот как читается этот условный
107
знак. Это не цифра, а символ, подразумевающий предель-
ный переход. Заменяя им верхний предел суммирования,
обозначают предел частичных сумм, к которому они стре-
мятся при неограниченном возрастании числа слагаемых.
Этот предел частичных сумм, как мы уже знаем, и назы-
вают суммой ряда.
Наблюдательный читатель, конечно, припоминает, что
знак бесконечности уже встречался ему на предыдущих
страницах—в обозначении предела последовательности.
Там этот знак выражал неограниченное возрастание ин-
декса.
Это воспоминание дает нам повод еще раз подчерк-
нуть: бесконечность — не число, ее знак—не цифра, а
символ, подразумевающий предельный переход. Об этом
следует помнить ввиду многочисленных злоупотреблений
словечком «бесконечность», чем нередко грешат люди,
знакомые с математикой лишь понаслышке.
Видали ли вы, как молодой неопытный продавец взве-
шивает— ну, например, полкилограмма сахарного пес-
ку?
Два взмаха совком—и пакет с песком на весах. Пе-
ребор. Стрелка ушла за семьсот граммов. Приходится
отсыпать. Совок вычерпывает из пакета добрую полови-
ну содержимого, и пакет вновь на весах. На сей раз
меньше, чем нужно. Еще одно движение совком. Изли-
шек всего пятьдесят граммов. Снова песок сыплется из
пакета в ящик...
Порции песка, которые продавец досыпает и отсыпа-
ет перед очередным взвешиванием, образуют последова-
тельность. Члены этой последовательности как положи-
тельны (когда продавец добавляет песок), так и отри-
цательны (когда отсыпает). Своими действиями прода-
вец суммирует члены этой последовательности, и пото-
му они заслуживают звания членов ряда. А поскольку
постоянством знака они не отличаются, ряд называется
знакопеременным. Частичные суммы этого ряда находят-
ся в пакете. Мало-помалу они стремятся к пределу, на-
званному покупателем.
Всегда ли существует такой предел? Ясно, что нет.
Смотрите, как продавец, свесив песок, принялся отве-
шивать пряники. Стрелка весов зашла за нужную отмет-
108
ку. Один пряник долой. Стрелка весов остановилась, не
доходя до нужной отметки. Пряник добавлен. Снова пе-
ребор. Пряник снова снят. Опять недобор...
Взвешивание зашло в тупик. Пряник добавить, пря-
ник убавить... Поскольку члены ряда одинаковы по аб-
солютной величине, частичные суммы колеблются от од-
ного постоянного значения к другому и ни к какому пре-
делу не стремятся.
Ряд не сойдется никогда, если не принять специаль-
ных мер — не начать уменьшать его члены, не ломать
пряники на части.
Можно ломать, например, так: добавить половину
пряника, убавить одну треть, прибавить четверть, отнять
одну пятую...
Вы думаете, что произойдет та же история, что с
мальчиком-великаном? Нет, такой ряд будет сходиться.
На этот счет есть даже особая теорема. Но прежде чем
ее формулировать, отметим две важные особенности на-
шего ряда.
Во-первых, обратите внимание, как меняются знаки
его членов: — плюс — минус — плюс — минус... Такие ря-
ды называются знакочередующимися.
Во-вторых, заметьте, что по абсолютной величине
члены ряда монотонно убывают: половина, треть, чет-
верть...
После сказанного можно сформулировать теорему,
подходящую к случаю: знакочередующийся ряд, члены
которого монотонно убывают по абсолютной величине,
всегда сходится.
Конечно, не всякий знакопеременный ряд обладает
теми особенностями, которыми отличается описанное на-
ми взвешивание пряников. Сходимость знакопеременных
рядов — вопрос посложнее, нежели сходимость знакопо-
стоянных.
Один на три делится?
Первоклассник ответит на этот вопрос растерянным
<нет>. Десятиклассник с важностью заявит, что делится
и частное представляет бесконечную десятичную дробь-
ноль целых и три в периоде. Если же с этим вопросом вы
обратитесь к человеку, который привык смотреть на чис-
ла не с теоретической, а с практической стороны, то он,
109
пожалуй, поинтересуется: с какой точностью нужен от-
вет? Если достаточно двух знаков после запятой, ответом
будет 0,33. Если нужны три знака — 0,333. Четыре —
0,3333. И так далее.
Видно, что с увеличением точности на один знак к от-
вету приписывается очередная тройка. Эти приписки в
сущности представляют собой слагаемые ряда.
Частичные суммы этого ряда и называет практик в
ответ на заданную точность.
Стремятся ли к какому-нибудь пределу эти частич-
ные суммы? Сходится ли ряд?
Приглядитесь к его членам, и вы признаете в них бес-
конечно убывающую геометрическую прогрессию. А она
принадлежит к категории сходящихся числовых ря-
дов.
Но даже и без этого замечания поставленные вопро-
сы имеют чисто риторический (а точнее, учебно-методи-
ческий) характер. Ибо хорошо известно, что результат
деления единицы на три есть одна треть: !/3.
К рациональным числам относятся и конечные
десятичные дроби. Назовите любую из них, и вы тем
самым уже представите ее в виде отношения целых чи-
сел: три десятых —это 3/ю, двадцать пять сотых — это
25/100.
Ну а как быть с бесконечными непериодическими де-
сятичными дробями? Такой дробью выражается, напри-
мер, отношение диагонали квадрата к его стороне. Еще
Пифагору было известно, что выразить его рациональ-
ным числом, отношением двух целых чисел невоз-
можно.
Это открытие, сильно огорчившее Пифагора, дало
первый в истории математики пример иррационального
числа, то есть числа, не выразимого отношением двух
целых. О том, что всякое иррациональное число можно
представить бесконечной непериодической десятичной
дробью, Пифагор не знал.
Впрочем, тому же Пифагору было известно, что гипо-
тенуза прямоугольного треугольника равна корню квад-
ратному из суммы квадратов его катетов. На два рав-
нобедренных прямоугольных треугольника разрезается
квадрат своей диагональю, и для каждого она служит
гипотенузой. И если принять сторону квадрата за едини-
цу, длина гипотенузы выразится квадратным корнем из
двойки. Извлечь его можно с точностью до любого знака
110
после запятой — соответствующий метод несложен и из-
лагается даже в школьном курсе алгебры.
Каждый новый знак после запятой, который возника-
ет при все более точном извлечении корня, можно рас-
сматривать как очередной член ряда, а все удлиняющи-
еся десятичные дроби — как частичные суммы этого ря-
да. Несложными рассуждениями можно доказать, что
всякий такой ряд сходится, что последовательность его
частичных сумм всегда имеет предел (во-первых, эта
последовательность возрастает, во-вторых, она ограни-
чена сверху — например, числом, которое получается, ес-
ли заменить хотя бы первую из уже выписанных цифр
большей).
Но коль скоро предел существует, почему бы не на-
звать его искомым корнем квадратным из двух, тем чис-
лом, которое выражает отношение диагонали квадрата
к его стороне? Пусть мы не можем выразить его отноше-
нием двух целых чисел. Зато мы можем назвать его с лю-
бой требуемой точностью. Почему бы подобный процесс
последовательных приближений не счесть определением
любого иррационального числа?
Математики так и поступили. Считается, что ирраци-
ональное число определено, если его с любой точностью
можно приблизить последовательностью конечных деся-
тичных дробей.
Трисекция угла, удвоение куба, квадратура круга —
вот три каверзные задачи, выдвинутые античными мате-
матиками и впоследствии ставшие синонимом неразре-
шимости.
Но так ли уж они неразрешимы? Вот, скажем, квадра-
тура круга: мы выполним ее сейчас с помощью довольно
несложного приема.
Итак, пусть дан круг радиуса R, Требуется, пользуясь
лишь циркулем и линейкой, построить равновеликий ему
квадрат или прямоугольник.
Площадь круга радиуса R дается выражением л/?2.
Если бы нам удалось построить прямоугольник со сторо-
нами R и л/?, квадратура круга была бы выполнена.
Но вот загвоздка — как построить отрезок длиной
л/?? Как увеличить в л раз данный нам условиями зада-
чи радиус круга?
111
Если бы число л было рациональным, если бы выра-
жалось отношением двух целых чисел, то все было бы
просто. Радиус круга мы увеличили бы во столько раз,
каков числитель, а затем уменьшили бы результат во
столько раз, каков знаменатель, — и получили бы иско-
мое. Школьная геометрия знает, как увеличить или
уменьшить отрезок в любое число раз.
Увы! Число л иррационально...
И тут на помощь приходит числовой ряд, похожий на
тот, с которым мы познакомились за взвешиванием
пряников.
Я = 1 _ 1_ 1 1
4 3 5 7 9 Й’
Воспримем эту строчку чисел как руководство к дей-
ствию. Из отрезка, равного радиусу нашего круга, выч-
тем его третью часть, к результату прибавим пятую, из
полученного вычтем седьмую и так далее. Работы много,
но рано или поздно мы с любой заранее выбранной точ-
ностью построим отрезок длиной х/< л/?. Увеличим его в
4 раза, затем построим на нем как на основании прямо-
угольник с высотой R — его площадь и будет равна пло-
щади нашего круга.
Квадратура круга выполнена!
Так что же, проблема, о которой так долго говорили
математики, все-таки разрешима, и притом так просто?
Сознаемся, мы допустили небольшой подлог. Класси-
ческая формулировка задачи о квадратуре круга подра-
зумевает, что задача должна быть решена с помощью
циркуля и линейки за конечное число операций, и притом
точно. Наш же способ приближенный. Но он позволяет
112
приблизиться к поставленной цели с любой заранее уста-
новленной точностью путем несложных действий.
В этом и заключается основное достоинство рядов.
Недаром их теория занимает столь важное место в ма-
тематике. Недаром обозначение ряда — заглавная грече-
ская буква «сигма» — как символ математики имеет
столь же широкое хождение, что и интеграл.
«Московское время четыреста девяносто пять минут».
Есл'и бы с некоторых пор время по радио стали объ-
являть таким образом, то радиослушатели вскоре, веро-
ятно, разучились бы ориентироваться во времени.
То ли дело:
«Московское время восемь часов пятнадцать минут».
В тех случаях, когда требуются более точные данные
о времени, после минут указываются секунды. Можно
указать и доли секунды: десятые, сотые, тысячные, сколь
угодно малые — какие требуются заранее выбранной точ-
ностью.
В этом проявляется все та же особенность человече-
ского сознания, которая лежит и в основе приближений
с помощью последовательностей и рядов: всякое измере-
ние начинается с грубой оценки, а затем продолжается
все более мелкими уточнениями.
7 Заказ 8651
ФУНКЦИИ
Почему не бывает животных какой угодно величины? По-
чему, например, нет слонов в три раза большего роста,
чем существуют, но тех же пропорций?
Не правда ли, любопытными вопросами задавались
персонажи знаменитого трактата Галилея «Беседы и ма-
тематические доказательства, касающиеся двух новых от-
раслей науки».
Ответ, к которому пришли собеседники, таков: стань
слон в три раза больше, вес его тогда увеличился бы в
двадцать семь раз, как куб размера, а площадь сечения
костей и, следовательно, их прочность—только в девять
раз, как квадрат размера. Прочности костей уже не
хватило бы, чтобы выдержать непомерно увеличившийся
вес. Такой слон был бы раздавлен собственной тя-
жестью.
Рассуждение вполне четкое и ясное. Что же придало
ему такую наглядность и убедительность? То, что в осно-
ву вывода положены две строгие математические зависи-
мости. Первая устанавливает соответствие между разме-
рами подобных тел и их объемами: объем изменяется,
как куб размера. Вторая связывает размеры подобных
фигур и их площади: площадь изменяется, как квадрат
размера.
Не знай этого собеседники, сколько пришлось бы до-
искиваться до истины?
Этим выразительным примером мы хотим начать обе-
щанный в одной из предыдущих глав обстоятельный
разговор о числовых функциях числового аргумента.
Функции, о которых шла речь до сих пор, как прави-
ло, описывались словами. Словесное описание — один из
способов задания функции, и притом не лучший.
Можно задавать функцию табличным способом. Вы-
писать в ряд или в столбик несколько значений аргумен-
114
та, а ниже или рядом поместить соответствующие зна-
чения функции. Так составляют таблицы логарифмов и
синусов. Шкалы логарифмической линейки, расположен-
ные одна под другой, тоже представляют собой разновид-
ность таблицы.
Логарифмами и синусами мы еще успеем заняться.
За первым примером табличного задания функции обра-
тимся к «Энциклопедии домашнего хозяйства». Откроем
ее на той странице, где указаны максимальные, длительно
допустимые токи для проводов в зависимости от сечения.
По этим данным можно построить график. Пусть зна-
чения аргумента, приведенные в верхней строчке, послу-
жат абсциссами, а значения функции, приведенные в
нижней, — ординатами тех точек, которые мы станем на-
носить на координатную плоскость.
Точки соединим непрерывной плавной кривой. Гра-
фический способ делает информацию о функции зримой
и наглядной. Выразительная картинка вмиг расскажет о
характерных особенностях и поведении функции.
Если ваша цель — смонтировать проводку в своей
квартире, то вам достаточно для работы этого графика
или даже одной таблицы. Ведь провода, поступающие в
продажу, согласно ГОСТу имеют лишь определенные
стандартные сечения.
Но если вы интересуетесь существом дела, причинами
тех ограничений для тока, которые обусловлены сечением
применяемых проводов, то вы наверняка захотите понять:
каковы физические законы, которые определяют функци-
ональную зависимость, выраженную таблицей и отражен-
ную графиком?
Существо дела состоит здесь в том, что провода разо-
греваются, когда по ним течет ток. Нагрев прямо пропор-
ционален квадрату тока и обратно пропорционален сече-
нию провода. Предельно допустимый нагрев и определя-
ет критическое отношение квадрата тока к сечению про-
вода.
Увеличив ток в цепи, скажем, в два раза, мы должны
в четыре раза увеличить сечение проводов во избежание
их перегрева. Увеличив ток в три раза — в девять раз
увеличить сечение проводов.
Так мы приходим к формульному заданию интересу-
ющей нас функции — ток изменяется как корень квад-
ратный из сечения проводов: I=k^s.
Коэффициент пропорциональности k в этой формуле
7*
115
равен 16,3, если ток / измеряется в амперах, а сечение
жилы s — в квадратных миллиметрах.
Вместо таблицы в «Энциклопедии домашнего хозяй-
ства» можно было бы поместить лишь эту короткую фор-
мулу: она, как легко убедиться, неплохо соответствует
табличным данным, а незначительные расхождения мож-
но устранить ценой некоторого ее усложнения.
Мы (понимаем, что домашний мастер вряд ли принял
бы такую замену. Таблица дает готовые рекомендации
на все случаи житейской практики, а формула еще тре-
бует вычислений. Да к тому же в ней нет той наглядно-
сти, которая присуща графику. А особая точность цифр
домашнему мастеру не нужна.
Но математик в поисках сути явлений для своей ра-
боты предпочтет, конечно, формулы. В формульном
представлении функции легче поддаются исследованию
математическими методами: формулу можно подверг-
нуть различным математическим преобразованиям, чего
не сделаешь ни с таблицей, ни с графиком.
Разумеется, если формула чересчур сложна или по-
просту не существует (скажем, когда функциональная
зависимость получена из опыта), математик прибегает к
таблице. А за наглядным представлением о функции об-
ращается скорее к графику, чем к формуле.
Стоит заметить, что отнюдь не всякую функциональ-
ную зависимость, полученную из опыта, удается выра-
зить краткой формулой. Попробуйте сделать это, вооб-
разив графиком некоторой функции профиль ключа от
вашей квартиры или абрис горной цепи на журнальной
фотографии, — и вы убедитесь в невыполнимости заду-
манного.
116
В этом месте нам хотелось бы на краткое время пре-
рвать плавный ход изложения и поразмыслить над
только что построенным графиком.
Почему мы так непринужденно и решительно соеди-
нили непрерывной линией точки, нанесенные на коорди-
натную плоскость по данным таблицы? Почему не оста-
вили их редкой россыпью?
В этом, как нам кажется, проявилось представление,
давно и глубоко укоренившееся в нашем миропонимании.
По созвучию с крылатым «природа не терпит пустоты»
его можно выразить так: «природа не терпит разрывов».
Нельзя всерьез говорить о том, что поезд, идущий,
скажем, из Москвы во Владивосток, после остановки в
Омске незамедлительно очутился в Новосибирске, не по-
бывав при этом ни на одной промежуточной станции. Не-
прерывность времени и пространства — один из крае-
угольных тезисов механики. Непрерывным представляет-
ся нам чуть ли не всякое изменение, происходящее в при-
роде: все значения высоты от начального до конечного
принимает уровень воды в наполняемой ванне, все значе-
ния размера — длина горящей свечи и ширина ножа, сти-
рающегося от частой заточки. В рамках механических
моделей непрерывным считается не только пространство,
но и любая среда: металл, жидкость, даже газ — недаром
и аэродинамика, и гидродинамика, и теория упругости
объединяются названием «механика сплошных сред».
А ведь согласно современным представлениям мате-
рия состоит из отдельных частиц—атомов, молекул,
между которыми пустота, и все физические величины из-
меняются порциями -г- квантами. Но квантовая природа
материи проявляется в масштабах столь малых, столь
труднодоступных непосредственному восприятию, что мы
пренебрегаем ею, отнюдь не считая это изменой обще-
признанной Демокритовой концепции о зернистости все-
го сущего.
Строя график в координатах «сечение провода — ток»,
проводя непрерывную линию над всеми без исключения
точками некоторого промежутка оси абсцисс, мы заявля-
ем тем самым, что сечение провода может равняться лю-
бой величине из этого промежутка.
Что ж говорить о тех временах, когда квантовая тео-
рия еще не была создана, а концепция Демокрита небы-
117
ла признана основой научных представлений о материи?
Непрерывность математических образов была естествен-
ным и непременным требованием употребительных си-
стем мира — от Аристотеля («В отношении сущего при
отвлечении математик сохраняет только количественную
определенность и непрерывность») до Ньютона («Я рас-
сматриваю... математические количества не как состоя-
щие из очень малых постоянных частей, а как произво-
димые непрерывным движением»).
Отвечая этому требованию, математика разработала
систему вещественных чисел (под таким названием объе-
диняются числа целые, дробные и иррациональные). Ве-
щественные числа — совокупность непрерывная, и пото-
му оказалось возможным изображать их точками пря-
мой линии. С легкой руки Декарта функциональные за-
висимости стали изображать графиками на координат-
ной плоскости. Так математика привыкла дополнять по-
нятие функции неявным предположеним о непрерывно-
сти аргумента.
А между тем математическое определение функции
вовсе не требует этого. И потому оно общезначимо для
всей математики, потому им пользуются и в дискретной
математике, бурно развивающейся в последнее время,
находящей все больший спрос у экономистов, биологов,
лингвистов.
Собственно говоря, в определении функциональной
зависимости не требуется и того, что ею должны связы-
ваться только количества. Но традиция сильна и тут:
если соответствие устанавливается не между числами,
математик предпочитает слову «функция» слово «ото-
бражение».
У этой традиции тоже есть свои корни. Математика
исстари обслуживает науки, которые выражают свои ре-
зультаты в числах: механику, физику, химию. «Измерить
все измеримое и сделать измеримым все, что пока не под-
дается измерению», — эти слова Галилея сделало своим
девизом все точное естествознание.
Не удивительно, что учение о функциях развивалось
по преимуществу как учение о функциях непрерывной
числовой переменной. Именно на этом пути оно пришло
к одному из наиболее значительных своих достижений —
дифференциальному и интегральному исчислению.
Не удивительно и то, что все наши дальнейшие при-
меры будут приводить лишь к функциям подобного ро-
118
да и на них будут поясняться существенные особенности
понятия функциональной зависимости.
График, построенный по данным «Энциклопедии до-
машнего хозяйства», побуждает нас обратиться к читате-
лю еще с одним призывом к бдительности. В разговоре
о проводах и протекающих по ним токах отчетливо ощу-
щается то, что философы зовут причинно-следственной
связью. Ток, величина которого рассматривалась нами
как аргумент, есть причина нагрева проводов, степень ко-
торого рассматривалась как функция. Подобное харак-
терно для большинства расхожих примеров функцио
нальной зависимости: функция является выражением не-
которого следствия, причину которого выражает аргу-
мент. И тем не менее не следовало бы возводить такое
представление в абсолют. Такая трактовка сужает поня-
тие функции. Функциональная зависимость — не обяза-
тельно зависимость причинно-следственная.
В большом многоквартирном доме номеру каждой
квартиры можно поставить в соответствие число людей,
в ней проживающих. И это будет функциональная зави-
симость, вполне отвечающая ее каноническому определе-
нию, хотя ни о каких причинах и следствиях здесь гово-
рить не приходится. Номер квартиры никоим образом не
определяет численность проживающей в ней семьи.
•
Карл-Филипп-Теодор, курфюрст пфальцский, был не
чужд математики. Однажды, вспоминая прожитое, он
сказал: «Мне было X лет в году X2».
Жозеф-Луи Лагранж, французский математик, од-
нажды беседовал с Симоном Пуассоном, только начинав-
шим свой путь в науке, и, между прочим, сказал: «Я
стар; во время бессонных ночей я развлекаюсь числовы-
ми сравнениями. Гюйгенс был тринадцатью годами стар-
ше Ньютона, я тринадцатью годами старше Лапласа. А
Лаплас тридцатью годами старше вас».
В какой из этих исторических зарисовок больше мате-
матического колорита?
По-видимому, ответ не вызывает сомнений: в первой.
Хотя курфюрст и не задал вопроса, его высказывание вос-
принимается как формулировка задачи. Учтя, что родил-
119
ся он в 1722 году, можно составить квадратное уравнение
для X и определить из него неизвестное: речь идет о 1764
годе, когда курфюрсту было 42. В самом деле, 422= 1764.
Ну, а второе высказывание? Хотя это и слова матема-
тика, никакого математического содержания в них не
видится.
Действительно, что из того, что Гюйгенс тринадцатью
годами старше Ньютона? Возраст человека — величина
переменная. Если второе высказывание рассматривать
на манер первого, как уравнение, то у этого уравнения
будет не одно решение, а много: 33 и 20, 34 и 21, 40 и 27,
55 и 42...
И все-таки на слова Лагранжа можно взглянуть с та-
кой точки зрения, с которой они покажутся гораздо вы-
игрышнее.
Свяжем функциональной зависимостью возраст Нью-
тона и возраст Гюйгенса, обозначив их соответственно
через X и У, запишем эту связь в привычном для матема-
тиков виде: У=Х+13.
И тогда задавшись произвольным числом X из мно-
жества лет, прожитых Ньютоном в одно время с Гюйген-
сом, мы тотчас сможем выяснить, как велико соответ-
ствующее У, то есть сколько лет в тот момент было Гюй-
генсу.
Уже этот нехитрый пример демонстрирует важное до-
стоинство понятия функциональной зависимости: на язы-
ке функций можно формулировать утверждения, охваты-
вающие собой целые множества, а не только относящие-
ся к отдельным элементам этих множеств.
Математики в своих построениях пользуются функ-
циями весьма многочисленными и разнообразными. В
этой книге мы упомянем, естественно, лишь немногие из
них, наиболее употребительные.
•
С функцией «корень квадратный» мы познакомились
благодаря электротехнике. Но свести знакомство с нею
мы могли бы, например, в часовом ателье, приглядыва-
ясь к тому, как мастер выверяет ход маятниковых ча-
сов. Оказывается, их ходом управляет все та же функция
«корень квадратный»: именно такова зависимость перио-
да колебаний маятника от его длины.
120
Не откладывая на дальнейшее, поясним графиками
те функциональные зависимости, которые в своих рассу-
ждениях о размерах животных использовал Галилей,—
квадратичную и кубичную.
График, соответствующий первой из них, называется
параболой второй степени, или просто параболой. Соот-
ветствующий другой — параболой третьей степени. Ука-
зание степени считается обязательным, если она не рав-
на двум, — так о линиях, приведенных на следующих
графиках, говорят, что это параболы четвертой и пятой
степени.
Заметим, что функции такого рода называются сте-
пенными: каждому числу из области определения функ-
ции ставится в соответствие некоторая его степень — вто-
рая, третья, четвертая и т. д.
Когда в Москве Кремлевские куранты отбивают шесть
часов утра, в Якутске уже полдень. Расположенный по
долготе восточнее столицы, город раньше встречает солн-
це. Приезжие москвичи в Якутске переставляют свои ча-
сы на шесть часов вперед.
Перенесемся теперь на три века вспять. Парусник в
открытом море. Как определить долготу места, в кото-
ром он находится? Очень просто, если на корабле есть
часы, поставленные в порту отправления. Нужно изме-
рить местное время по солнцу и сравнить с показаниями
часов. Расхождение пропорционально разнице по долго-
те между тем пунктом, где находится корабль, и тем, в
котором были поставлены часы.
Точный закон этой пропорциональности позволяет
121
вывести простое соотноше-
ние: тремстам шестидесяти
градусам земной окружнос-
ти соответствуют двадцать
четыре часа, за которые Зем-
ля совершает полный оборот
вокруг своей оси. Поэтому ес-
ли часы отстают по сравне-
нию с местным временем на
шесть часов, корабль нахо-
дится на 90° восточнее того
места, где были поставлены
часы. Спешат на четыре ча-
са — на 60° западнее.
Разумеется, для подобного определения долготы нуж-
ны очень точные часы. А как можно требовать точности
от маятниковых часов, которыми снабжен парусник? Их
ход зависит от длины маятника, а она то и дело меняется:
теплый день сменяется прохладной ночью, и во время пла-
вания парусник приближается то к голубым полярным
льдам, то к пальмам тропиков. Тепло удлиняет маятник,
холод укорачивает. Такова неумолимая реальность.
И все-таки нашелся способ избежать неизбежного
зла. Чудо совершил в 1726 году английский часовой ма-
стер Джон Гаррисон. Это удалось ему потому, что он
знал функциональную зависимость длины металличе-
ского стержня от температуры, до которой стержень
нагрет.
Эту функцию (см. график сле-
ва) описывает прямая линия
Такая зависимость называется ли-
нейной. Суть ее в том, что одинако-
вым приращениям аргумента всегда
соответствует одно и то же прираще-
ние функции. Иначе говоря, функция
изменяется равномерно при равно-
мерном росте аргумента.
В нашем примере равномерному
нарастанию температуры соответст-
вует равномерное удлинение стержня. Полное его удли-
нение пропорционально начальной длине. Но что особен-
но важно — стержни из разных металлов удлиняются по-
разному от одного и того же прироста температуры. Ска-
жем, цинк расширяется примерно в три раза сильнее,
122
чем сталь. Этим и воспользовался Гарри-
сон: он собрал маятник из цинковых и
стальных стержней так, как показано на
рисунке. Общая длина стальных стерж-
ней в три раза превышала длину цинко-
вых. Расширяясь при нагревании и со-
кращаясь при охлаждении, стержни вза-
имно компенсировали изменения своей
длины, и груз маятника оставался на од-
ном и том же расстоянии от точки под-
веса.
Так что же, собственно, изобрел Гаррисон? Какова
математическая формула его изобретения? Как об этом
сказать в двух математических словах?
Читатель, видимо, заметил, что левый график внизу
отличается от предыдущего дополнительной линией.
Она показывает, как ведет себя при нагревании изобре-
тенный Гаррисоном маятник с компенсацией. Его дли-
на не зависит от температуры. Рассматриваемая как фун-
кция температуры, она постоянна при всех значениях ар-
гумента. Такая функция называется постоянной, или
константой (вот откуда на графике появилось латинское
сокращенное const). Она тоже относится к классу линей-
ных— изображается все той же прямой линией. Подоб-
ная независимость от значений аргумента — простейший
случай линейной зависимости. Здесь значение функции
можно назвать, не спрашивая об аргументе.
Из непостоянных линейных функций простейшая, по-
жалуй, та, значение которой всегда равно значению ар-
123
гумента. График этой функции — биссектриса прямого
угла, стороны которого — оси координат.
Любая другая прямая, исходящая из начала коорди-
нат, иллюстрирует случай, когда функция прямо пропор-
циональна аргументу. Чтобы вычислить значение такой
функции, аргумент умножают на коэффициент пропор-
циональности. (Эту величину называют еще констан-
той пропорциональности, или угловым коэффициентом:
он может служить мерой наклона соответствующей пря-
мой на графике. Чем больше угловой коэффициент, тем
круче нарастает функция по мере роста аргумента. А ес-
ли уголовой коэффициент меньше нуля — функция спа-
дает.)
Линейной функцией такого вида пользуются, когда
определяют стоимость товара по весу или путь, пройден-
ный в равномерном движении, по времени: коэффициен-
том пропорциональности в первом случае служит цена,
во втором — скорость.
На одной из предыдущих страниц, отметив, что не
всякую функциональную зависимость удается выразить
краткой формулой, мы не случайно в качестве примера
предоставили вам, читатель, ключ от дверного замка: сей-
час он в буквальном смысле слова послужит ключом к
124
небольшой математической проблеме, к которой нас под-
водит беседа о функциях.
Знаете ли вы, как таким ключом открывается двер-
ной замок? Что происходит внутри этого слесарно-меха-
нического устройства, когда вы вставляете ключ в замоч-
ную скважину и делаете положенное число оборотов?
Чтобы замок открылся, нужно провернуть барабан, в
котором сделана скважина. Но этому препятствуют шти-
фты, стоящие тесным строем внутри скважины, скользя-
щие вверх-вниз. Каждый из штифтов нужно поднять на
такую высоту, чтобы их верхние торцы оказались вровень
с поверхностью барабана. Если они выступят за нее, то
войдут в прорезь обоймы, расположенную точно над за-
мочной скважиной; если не достигнут поверхности бара-
бана, то из прорези обоймы находящиеся там штифты
вдвинутся в замочную скважину. И в том и в другом слу-
чае вращение барабана будет застопорено.
Штифты в замочной скважине поднимает ключ, вдви-
гаемый в нее. При этом высота каждого штифта, будучи
сложена с высотой профиля ключа в соответствующей
точке, должна дать в сумме диаметр барабана. Только
тогда он провернется.
Ну а причем здесь функция? Да притом, что, с точки
зрения математика, вся эта механика есть не что иное,
как операция сложения двух функций. Одна из них —
это профиль ключа. Другая — линия, очерчивающая
верхние торцы штифтов, когда замок заперт. Операция
сложения функций состоит в том, что в каждой точке из
общей области их определения к значению одной функ-
ции прибавляется значение другой. Тем самым опреде-
ляется, какое значение в данной точке имеет функция,
называемая суммой двух исходных.
Секрет дверного замка в том, что в результате сло-
жения двух функций, выраженных профилем ключа и
строем штифтов, получается функция-константа, посто-
125
значения одной функции вычитается значение другой. Та-
ким же образом происходит и перемножение функций: в
каждой точке значение одной умножается на значение
другой. Заметим: если одна из перемножаемых функций
представляет собой постоянную, то про другую в таком
случае говорят, что ее умножили на постоянный коэффи-
циент. Например, про функцию, выражающую прямую
пропорциональность, можно сказать, что она получается
в результате перемножения двух простейших линейных
функций—той, которая равна своему аргументу, и по-
стоянной, равной коэффициенту пропорциональности.
Наконец, подобным образом можно определить част-
ное двух функций. Заметим: функция-делитель не долж-
на обращаться в нуль ни при одном значении аргумента
из ее области определения.
Итак, мы умеем теперь применять к функциям все че-
тыре арифметических действия. В этом и состояла про-
блема, решить которую нам было необходимо для про-
должения разговора о функциях.
Пора опробовать в деле только что освоенные нами
действия над функциями. Возьмем линейную функ-
цию, выражающую 'прямую пропорциональность, и при-
бавим к ней функцию-константу. В итоге получится
линейная функция самого общего вида, примеры которой
нам дали измерения длины нагреваемого металлическо-
го стержня и определение долготы по часам. Постоянной
126
начальной температуре, во втором—долгота того места,
в котором были поставлены часы. Функция такой же
структуры определяет и стоимость проезда в такси: она
складывается из начального взноса и оплаты пройденных
километров.
Если линейную функцию самого общего вида умно-
жить на постоянную, она сохранит свой линейный вид.
Если сложить две прбизвольные линейные функции, по-
лучится опять-таки линейная функция.
А если к произвольной линейной функции прибавить
параболу второй степени, умноженную на некоторый
произвольный коэффициент? В итоге возникнет опять-
таки парабола второй степени; правда, ее вершина при
этом сместится, если первое из слагаемых, линейная
функция, не константа. Формулой 'для такой «смещен-
ной» параболы служит квадратный трехчлен самого об-
щего вида.
Если складывать постоянную и линейную функции,
параболы второй и более высоких степеней, то будут по-
лучаться функции, называемые полиномами.
В разговоре о конкретном полиноме принято указы-
вать его степень. Она равна наивысшей из степеней па-
рабол, которые были слагаемыми при образовании дан-
ного полинома. Поэтому, например, о квадратном трех-
члене говорят как о полиноме второй степени, о линей-
ной функции — как о полиноме первой, о постоянной —
как о полиноме нулевой степени.
Такая терминология не случайна. На предыдущих
примерах мы могли убедиться, что график полинома сво-
ей формой обязан параболе наивысшей степени, участво-
вавшей в его образовании. Так наклон графика линей-
ной функции, полинома первой степени сохраняется, ес-
ли к ней прибавить постоянную, полином нулевой степе-
ни. А если к ней прибавить полином второй степени, гра-
фик станет параболой.
127
Вся богатейшая семья механизмов, окружающих со-
временного человека, начиналась когда-то с семи про-
стых машин. Древние знали рычаг, блок, клин, ворот,
винт, наклонную плоскость и зубчатые колеса. Эти не-
хитрые по теперешним представлениям устройства умно-
жали силу человека.
Но... во сколько раз выиграешь в силе — во столько
же раз проиграешь в расстоянии. Так гласит золотое
правило механики, заключающее в себе теорию семи
простых машин.
График, приведенный на этой странице, есть нагляд-
ное выражение знаменитого правила. По горизонтальной
оси отложена сила, с которой, например, нужно давить
на плечо рычага, чтобы поднять заданный груз на задан-
ную высоту, по вертикальной — расстояние, которое прой-
дет при этом точка приложения силы.
Линия, выражающая такую функциональную зависи-
мость, называется гиперболой.
Если отвлечься от механической сущности графика,
то в чистом виде останется выражение обратной пропор-
циональности. Именно в соответствии с ней хозяйка де-
лит пирог между гостями. Чем больше гостей — тем
меньше порции.
Закон обратной пропорциональности глядит на нас и
со шкалы радиоприемника. Вы крутите ручку настрой-
ки, и стрелка движется вдоль шкалы, на которой два ря-
да чисел — метры и мегагерцы, длина волн и их частота.
Длина волн растет, частота падает. Но присмотритесь:
при любом сдвиге стрелки во сколько раз увеличилась
длина волны, во столько же раз упала частота.
График гиперболы можно увидеть на лабораторном
столе физика, демонстрирующего явления капиллярно-
сти. В штативе несколько тонких стеклянных трубочек,
расположенных в порядке возрастания диаметров. Из-
128
вестно, что в тонком канале смачивающая жидкость под-
нимается тем выше, чем меньше его диаметр. Поэтому в
самом узком канале жидкость поднялась выше всего, в
другом, диаметр которого в два раза больше, — в два ра-
за ниже, в третьем, что толще первого в три раза, — в
три раза ниже и так далее.
А теперь опустим в эту же жидкость этакий клин, об-
разованный двумя стеклянными пластинками, сомкнуты-
ми по вертикальному ребру. В узкую щель между стек-
лами жидкость устремится, как в капилляр. Высота ее
подъема определится шириной зазора. А он увеличива-
ется равномерно по мере удаления от острия клина.
Поэтому свободная поверхность жидкости четко вырисо-
вывает гиперболу — график обратной пропорционально-
сти.
Так как же все-таки возникла гипербола в стеклян-
ном клине?
В учебнике физики можно отыскать формулу h=k]d:
высота поднятия жидкости Л получается делением неко-
торого коэффициента k на ширину капиллярного зазора
d. Зазор в стеклянном клине пропорционален расстоянию
от острия клина, иными словами, выражается линейной
функцией от этого расстояния, а коэффициент определя-
ется свойствами жидкости (поверхностным натяжением,
удельным весом) и с расстоянием от острия клина не ме-
няется, остается постоянным. Итак, наша гипербола по-
лучилась в результате деления простейшей линейной
функции, константы на чуть более сложную линейную
функцию, выражающую прямую пропорциональную за-
висимость.
Обе эти функции, как мы знаем, простираются и в об-
ласть отрицательных значений аргумента. Учтя это, до-
строим график гиперболы до полного вида. (На нуль,
3 2 1 У у^к
-3 -2 -1 0 -1 -2 1 2 х
8 Заказ 8651
129
правда, делить нельзя, так что в нуле гипербола не оп-
ределена, в ее область определения эта точка не входит.)
Факт обратной пропорциональной зависимости мож-
но выразить и иначе, сказав, что связанные ею величины
в произведении дают постоянную.
Вспомним примеры из предыдущего раздела — ска-
жем, пример с тортом. Когда число гостей росло, вес пор-
ции уменьшался; произведение же этих двух величин ос-
тавалось равным постоянному весу торта. А пример с ра-
диоприемником? Произведение длины -радиоволны на ее
частоту всегда равно скорости света.
Заметим: объединяя в произведении зависимую и не-
зависимую переменные, мы получаем примеры так на-
зываемого неявного задания функции. Этот термин упо-
требляют во всех тех случаях, когда зависимая перемен-
ная не выражена через независимую, а вперемешку с
ней, в различных сочетаниях входит в некоторое матема-
тическое выражение, приравненное постоянной, а чаще—
нулю. Подставив в такое равенство значение независи-
мой переменной, соответствующее значение зависимой
подыскивают так, чтобы равенство удовлетворилось. В
этом и состоит закон соответствия, который определяет
функцию, заданную неявным образом'.
Сейчас много говорят об. информационном буме. По-
ток информации захлестывает: утверждают, что ее коли-
чество удваивается каждые десять лет.
Изобразим этот процесс наглядно, в виде графика не-
которой функции.
Примем объем информации в некоторый год за еди-
ницу. Поскольку эта величина послужит нам началом
дальнейших построений, отложим ее над началом коор-
динат, в которых будет строиться график, по вертикаль-
ной оси. Отрезок, вдвое больший, восставим над единич-
ной отметкой горизонтальной оси, считая, что эта от-
метка соответствует первому десятку лет. Еще вдвое
больший отрезок восставим над точкой <два>, соответ-
ствующей второму десятку, еще вдвое больший — над
точкой <три>... Декада за декадой — избранные нами
значения аргумента выстроятся по горизонтальной оси в
порядке равномерного нарастания, по закону арифмети-
ческой прогрессии: один, два, *ри, четыре... Значения
130
функции отложатся над ними, возрастая каждый раз
вдвое,— по закону геометрической прогрессии: два, четы-
ре, восемь, шестнадцать... (Нетрудно заметить, что эти
числа представляют собой последовательные степени
двойки — первую, вторую, третью, четвертую и так далее.)
А что если посмотреть, как нарастал поток информа-
ции до того года, который принят за начальный? Столь
же равномерно, откладывая единицу за единицей, прой-
демся по оси абсцисс влево от начала координат и над
отложенными значениями аргумента будем наносить на
график значения функции уже в порядке убывания —
вдвое с каждым шагом.
Теперь соединим все нанесенные точки непрерывной
гладкой линией — ведь количество информации нараста-
ет от десятилетия к десятилетию плавно, а не скачками.
Перед нами график так называемой показательной
функции.
Как же определяется эта функциональная зависи-
мость, обрисованная покуда лишь легким росчерком
пера?
По пути к строгой ее формулировке мы предлагаем
вам, читатель, поразмышлять над вопросом: во сколько
раз нарастает объем информации за пятнадцать лет, ес-
ли за декаду он увеличивается вдвое? Пятнадцать лет—
это полторы декады. Стало быть, ответ на поставлен-
ный вопрос дает высота построенной нами кривой в точ-
ке с абсциссой «полтора»: примерно в 2,83 раза. А теперь,
обратите внимание: абсциссе «один» на графике соот-
8:
131
ветствует первая степень двойки, абсциссе «два» — вто-
рая степень, абсциссе «три» — третья... Логично заклю-
чить отсюда, что число 2,83 есть двойка в степени пол-
тора.
Точно таким же образом график укажет нам любую
другую степень двойки —целую или дробную, положи-
тельную или отрицательную. Для этого стоит лишь отло-
жить показатель степени на оси абсцисс и измерить в
этой точке высоту кривой.
Итак, каждое значение нашей функции есть двойка в
степени, равной соответствующему значению аргумента.
Так и определяется показательная функция, описанная
нами. Число, возводимое в степень (в нашем примере им
служила двойка), называется ее основанием.
И еще один термин: график показательной функции
именуется показательной кривой. Иногда эту линию на-
зывают экспонентой (от латинского «ехропеге» — «вы-
ставлять напоказ»). Многим этот термин знаком по рас-
хожему словосочетанию «экспоненциальный рост», выра-
жающему наиболее броскую черту (показательной кри-
вой, — ее безудержно крутой взлет.
Примеры подобного роста подыскать нетрудно. Пока-
зательная функция непременно встречается при матема-
тическом описании таких процессов, в которых скорость
изменения некоторого количества в каждый момент про-
порциональна самому количеству.
По такому правилу размножается все живое: приплод
пропорционален достигнутой численности. По закону
все более крутого, экспоненциального роста увеличива-
ется колония микробов в чашке Петри. По такому же за-
кону плодились кролики, за короткий срок заполнившие
Австралию.
Природа знает и примеры экспоненциального спада,
когда скорость убывания некоторого количества в каж-
дый момент пропорциональна остатку (а стало быть,
уменьшается вместе с ним; в этом — характерная черта
экспоненциального спада).
Скорость химической реакции сохраняет пропорцио-
нальность количеству реагирующих веществ по мере то-
го, как они расходуются с течением времени. (В этой про-
порциональности заключается один из важнейших зако-
нов химии — так называемый закон действующих масс.)
Скорость радиоактивного распада точно так же сораз-
мерна с количеством еще нераспавшихся атомов. И тер-
132
мин «период полураспада» прекрасно отражает экспо-
ненциальный характер процесса: по прошествии этого пе-
риода число нераспавшихся атомов сокращается вдвое,
еще период спустя — вчетверо и так далее. Если процесс
изобразить графиком, то ординаты л^обых двух точек
кривой всегда будут отличаться ровно в два раза, если их
абсциссы разнятся на величину периода полураспада.
Иными словами, когда аргумент изменяется по закону
арифметической прогрессии, функция изменяется по за-
кону геометрической прогрессии (на сей раз убывающей).
А в этом — определяющая особенность показательной
функции.
•
Проницательный читатель отметил некоторую непол-
ноту, узость нашего описания показательной функции.
Строя ее график за разговором об информационном
буме или радиоактивном распаде, мы каждый раз разби-
вали горизонтальную ось координат на отрезки равной
длины и над засечками расставляли точки так, чтобы
каждая последующая располагалась вдвое выше или
вдвое ниже предыдущей.
Ну а если бы количество информации возрастало с
каждым десятилетием не в два, а, скажем, в два с поло-
виной раза? И соответственно по такому же закону изме-
нялась бы высота точек, наносимых на координатную
плоскость. Что, в результате получился бы график уже
не показательной функции?
Показательной. Но только с другим основанием, рав-
ным двум с половиной. Новый график, в общих чертах
напоминая прежний, устремлялся бы ввысь уже с не-
сколько иной скоростью
3 X
133
Всмотритесь в него: высота кривой над делениями го-
ризонтальной оси равна последовательным степеням чис-
ла два с половиной: минус первая его степень равна че-
тырем десятым, нулевая — единице, первая — двум с по-
ловиной, вторая — шести с четвертью и т. д.
Беря в качестве основания все новые положительные
числа, мы получали бы все новые показательные функ-
ции. Не стоило бы только назначать на роль основания
единицу — ведь она остается собой при возведении в лю-
бую степень, так что показательная кривая выродилась
бы в горизонтальную прямую. Но есть среди всех чисел
такое, которое чаще всех прочих служит основанием по-
казательной функции. О нем как-то раз у нас уже захо-
дила речь: это — число е, равное 2,71828... Выбор пал на
него в силу важных его достоинств, распространяться о
которых мы пока не имеем возможности.
Так что если в разговоре о показательной функции ее
основание не указывается, знайте, что им служит число е.
•
Сколько звезд на небе?
Одним из первых, кто попытался точно ответить на
этот вопрос, был древнегреческий астроном Гиппарх. При
его жизни в созвездии Скорпиона вспыхнула новая звез-
да. Гиппарх был потрясен: звезды смертны, они, как лю-
ди, рождаются и умирают. И чтобы будущие исследова-
тели могли следить за возникновением и угасанием звезд,
Гиппарх составил свой звездный каталог. Он насчитал
около тысячи звезд и разбил их по видимому блеску на
шесть групп. Самые яркие Гиппарх назвал звездами пер-
вой величины, заметно менее яркие — второй, еще столь
же менее яркие — третьей и так далее в порядке равно-
мерного убывания видимого блеска —до звезд, едва ви-
димых невооруженным глазом, которым была присвоена
шестая величина.
Когда ученые получили в свое распоряжение чувстви-
тельные приборы для световых измерений, стало возмож-
ным точно определять блеск звезд. Стало возможным
сравнить, насколько соответствует данным таких измере-
ний традиционное распределение звезд по видимому бле-
ску, произведенное на глаз.
Оценки того и другого рода сведем на одном графике.
От каждой из шести групп, на которые звезды распреде-
лил Гиппарх, возьмем по одному типичному представи-
134
телю. По вертикальной оси будем откладывать блеск
звезды в единицах Гиппарха, то есть ее звездную величи-
ну, по горизонтальной — показания приборов. За масш-
табную единицу горизонтальной оси примем блеск звезды
«б Тельца», стоящей посредине в ряду представителей
звездного сонма.
Сразу же бросается в глаза: отметки на горизонталь-
ной оси располагаются неравномерно. Объективные (при-
бор) и субъективные (глаз) характеристики блеска не
пропорциональны друг другу.
С каждым шагом по шкале звездных величин прибор
регистрирует возрастание блеска не на одну и ту же ве-
личину, как могло бы показаться, а примерно в два с по-
ловиной раза. Образно говоря, глаз сравнивает источни-
ки света по блеску, задаваясь вопросом «во сколько
раз?», а не вопросом «на сколько?». Мы отмечаем не аб-
солютный, а относительный прирост блеска. И когда нам
кажется, что он возрастает или убывает равномерно, в
действительности мы шагаем по его шкале все более раз-
машистыми шагами, покрывая при этом поистине ги-
гантский диапазон: в миллион миллионов раз различа-
ются по блеску источники света, самый слабый и самый
мощный, воспринимаемые человеческим глазом.
По тому же закону мудрая природа проградуировала
и наш слуховой аппарат. И оттого диапазон звуков, внят-
ных человеческому уху — от шелеста листвы до раска-
тов грома над головой, — почти столь же широк.
Кстати сказать, именно в силу описанной физиологи-
ческой особенности звезды, ярко горящие на ночном не-
бе, не видны днем, тонут в ослепительном блеске солн-
ца, рассеянном по небосводу. И таЫ и здесь сияние звезд
дает одну и ту же добавку к свету фона. Однако в пер-
вом случае (ночью) эта добавка велика по сравнению с
мерцанием неба, во втором же (днем) составляет весьма
135
незначительную долю от солнечного блеска (менее чем
миллиардную даже для самых ярких звезд). Оттого и
гаснут звезды в лучах утренней зари.
Оттого же и голос солиста, когда его пение подхваты-
вает хор, тонет в многоголосом звучании.
Суть функциональной зависимости, описанной нами
на примере зрения и слуха, в том, что возрастанию аргу-
мента в одно и то же число раз всегда соответствует од-
но и то же приращение функции. Когда аргумент меня-
ется по закону геометрической прогрессии, функция ме-
няется по закону арифметической.
Как же называется функция, с которой мы познако-
мились по звездному графику?
Прежде чем отвечать на этот вопрос, мы предложим
вам, читатель, несколько других. Вы без труда ответите
на них, обратившись к первому из графиков, приведен-
ных на стр. 135.
В какую степень нужно возвысить два с половиной,
чтобы получить шесть с четвертью? Во вторую, отвечает
упомянутый график. А в какую степень нужно возвысить
два с половиной, чтобы получить четыре десятых? В ми-
нус первую. А чтобы получить два с половиной? В первую.
А единицу? В нулевую.
Число, которое нужно употребить показателем степе-
ни при указанном основании для того, чтобы получить за-
данное число, называется логарифмом заданного числа
по указанному основанию.
Минус один, нуль, один, два — это логарифмы по ос-
нованию 2,5 для чисел 0,4; 1; 2,5; 6,25.
А теперь, не выпуская из памяти всю эту информацию,
вернемся к нашему звездному графику. Вот точка с по-
меткой «v Дракона А»: абсцисса — около четырех деся-
тых, ордината — примерно минус один. Вот точка «б Тель-
ца»: абсцисса — один, ордината — нуль. Точка «у Пер-
сея»: абсцисса —два с половиной, ордината — один. Точ-
ка «Кастор»: абсцисса — шесть с четвертью, ордината —
два.
Итак, ординаты выделенных точек графика являются
логарифмами абсцисс, взятыми по основанию два с по-
ловиной. Выраженная графиком функциональная зави-
136
симость заключается в том, что положительным числам
ставятся в соответствие их логарифмы. Такую функцию
естественно назвать логарифмической. А ее график име-
нуют логарифмикой.
В роли основания логарифмов встречаются различные
положительные числа. На практике весьма употребитель-
ны десятичные логарифмы, основание которых равно де-
сяти. В теоретических исследованиях популярнее так
называемые натуральные логарифмы, основанием кото-
рых служит уже знакомое нам число е.
Теперь становится понятным общепринятое и, быть
может, уже слышанное вами название этого числа: «ос-
нование натуральных логарифмов».
Кривая натурального логарифма, так называемая на-
туральная логарифмика, приведена в предыдущем раз-
деле рядом со звездным графиком.
•
Почему летом теплее, чем зимой?
Иногда в ответ на этот вопрос слышишь: потому что
Земля, двигаясь по своей орбите, зимой находится от
Солнца дальше, чем летом.
Но это совершенно неверно! Ведь орбита Земли — это
почти круг, в центре которого находится Солнце. Рас-
стояние нашей планеты от светила меняется слишком не-
значительно от месяца к месяцу, чтобы это было причи-
ной смены времен года.
Все дело в наклоне земной оси по отношению к пло-
скости земной орбиты.
Взгляните на рисунок: зимой в умеренных широтах
солнце невысоко поднимается над горизонтом, его лучи
137
лишь скользят по земле. Летом в моменты наивысшего
подъема над горизонтом солнце приближается к зениту,
его лучи падают почти отвесно на те же участки земного
шара.
Поток энергии, идущей от Солнца, одинаков во все
времена года. Но в зависимости от наклона солнечных
лучей она по-разному распределяется по земной поверх-
ности. Больше всего ее приходится на заданный участок
поверхности при отвесном падении света. Чем меньше
угол, который образуют лучи с поверхностью, тем мень-
ше их приходится на тот же участок.
Именно эту зависимость применяет (быть может, не
думая об этом) курортник, загорающий под солнцем юга,
когда он поворачивает свой топчан так, чтобы солнечные
лучи как можно менее отклонялись от перпендикуляра
к плоскости топчана.
Попытаемся определить точно: какая доля солнечной
.энергии, приходящейся на некоторый участок плоскости
при отвесном падении лучей, приходится на него при на-
клонном падении лучей под тем или иным углом?
На поставленный вопрос можно ответить, проследив
эволюцию жирно очерченного прямоугольного треуголь-
ника на приведенных чертежах. Гипотенуза, на которую
падают солнечные лучи, всюду одна и та же. Катет, через
который входят падающие на нее лучи, меняется подли-
не, уменьшаясь вместе с углом, который образуют с ги-
потенузой падающие на нее лучи.
Очевидно, интересующая нас доля солнечной энергии
равна отношению указанного катета к гипотенузе.
Как меняется эта доля в зависимости от угла падения,
удобнее судить, если все жирно очерченные прямоуголь-
ные треугольники собрать в одну связку, где их катеты
расположены параллельно друг другу, а гипотенуза ста-
ла радиусом некоторой окружности. И если задан угол,
под которым солнечные лучи встречаются с освещаемой
138
поверхностью, нужно отложить его на этой круговой диа-
грамме, из точки пересечения его наклонной стороны с
окружностью опустить перпендикулялр на горизонталь-
ный диаметр и взять отношение этого перпендикуляра к
радиусу окружности. Иными словами, в прямоугольном
треугольнике с заданным углом нужно взять отношение
противолежащего катета к гипотенузе. Полученное чис-
ло и укажет интересующую нас долю солнечной энергии.
Число, определенное таким образом и поставленное в
соответствие углу, для которого оно определялось, назы-
вается синусом этого угла. (См. выше график описанной
функциональной зависимости.)
Читатель, конечно, узнает не раз виденную синусоиду.
Если что-то и кажется здесь непривычным, так это неес-
тественно малая протяженность кривой. Обычно ее ри-
суют безгранично разбегающейся вдоль оси абсцисс,
волна за волной.
Продолжим синусоиду, переведя разговор о ней на те-
мы электротехники.
Почему трамвай работает на постоянном токе? Сту-
денческий фольклор отвечает на этот вопрос так: если бы
он работал на переменном, рельсы пришлось бы уклады-
вать по синусоиде.
Шутка напоминает о том, что переменный ток изменя-
ется во времени по закону синуса.
Откуда же здесь берется синусоида? Обратимся к уп-
рощенной схеме динамомашины — источника перемен-
ного тока. Ток возникает в рамке, которая равномерно
вращается в однородном магнитном поле. Величина то-
139
ка определяется скоростью изменения магнитного пото-
ка, пронизывающего рамку.
Рисунки показывают последовательные стадии этого
изменения. На них мы обнаруживаем все тот же прямо-
угольный треугольник, да еще и в том же удобном распо-
ложении, к которому мы пришли, определяя функцию
синуса. Гипотенуза этого треугольника вновь постоянна,
а катет, удвоенной длиной которого можно измерить ве-
личину магнитного потока, пронизывающего рамку (от-
мечено фигурной скобкой), меняется то закону синуса в
зависимости от yraa поворота рамки. Поскольку рамка
вращается равномерно, угол ее поворота может служить
мерой времени. Все сказанное позволяет заключить: маг-
нитный поток, пронизывающий рамку, меняется во вре-
мени по закону синуса.
По мере вращения рамки магнитный поток пронизы-
вает ее то с одной, то с другой стороны, и это выражает-
ся в сменах его знака — в тол ном соответствии с течени-
ем синусоиды. Оборот за оборотом — нарастания и спа-
ды потока в точности повторяются снова и снова. Так
вдоль оси абсцисс одна за другой выстраиваются волны
синусоиды, похожие друг на друга, как две капли воды.
Но это лишь график магнитного потока. Теперь нуж-
но оценить, какова в каждый момент времени скорость
его изменения - она-то и определяет ток в рамке.
140
О том, как это делается, мы поговорим позже, когда
речь пойдет о производных. А пока приведем без поясне-
ний соответствующий график.
Он имеет вид синусоиды, сдвинутой на четверть вол-
ны влево. Точное название этой кривой — косинусоида.
Однако очень часто из-за сходства с синусоидой ее оши-
бочно называют так же. В этом нет ошибки лишь в том
случае, если начало отсчета аргумента не указано.
Стоит отметить, что косинусоида, если рассматривать
ее как функцию угла, имеет столь же тесное отношение
к прямоугольным треугольникам, что и синусоида. Если
построить прямоугольный треугольник с заданным уг-
лом и измерить отношение катета, прилежащего к этому
углу, к гипотенузе, то получится величина, называемая
косинусом. Ее зависимость от угла и описывает косину-
соида.
Наконец, для каждого значения угла, при котором
строится прямоугольный треугольник, можно измерить
отношение катетов — скажем, противолежащего к при-
лежащему. Эту величину называют тангенсом. Любитель
математических выкладок без труда убедится в том, что
тангенс угла равен отношению синуса этого угла к ко-
синусу.
Определенные формулы связывают описанные функ-
ции и попарно: синус с косинусом, синус с тангенсом,
тангенс с косинусом. Эти связи проистекают из того, что
все три функции породнены прямоугольным треугольни-
ком, через который они определяются. От греческого
имени треугольника — «тригонон» — произошло собира-
тельное название «тригонометрические функции». К ним,
кроме синуса, косинуса и тангенса, относятся еще косе-
канс, секанс и котангенс, соответственно получаемые из
перечисленных по правилу обратной пропорционально-
сти.
141
В коллекции математических шуток есть такой во-
прос: каким по величине покажется угол в пять градусов,
если его разглядывать в лупу с десятикратным увеличе-
нием?
Угол, конечно же, не изменится. Ответ как будто оче-
виден. И все-таки давайте обсудим этот оптико-геомет-
рический феномен пообстоятельнее.
На рисунках одна и та же фигура, но выполненная
в разных масштабах, словно рассматривается через лу-
пы со все большим увеличением. Все сильнее удлиняют-
ся стороны треугольников, радиус окружности. Но при-
смотритесь: они увеличиваются всегда в одно и то же
число раз. Отношения их длин не изменяются.
Эта неизменность естественным образом связана с
постоянством углов на наших разномасштабных рисун-
ках: ведь рисунки подобны друг другу. Такая связь не-
когда и подсказала математикам мысль: мерить углы не
традиционными градусами, а числами — отношениями
линейных элементов тех фигур, которым принадлежат
углы.
Элементы, которые наиболее удобно использовать
для этой цели, мы вычертили пожирнее. Они образуют
сектор. Можно разделить длину дуги сектора на его ра-
диус и частное назвать величиной секториального угла
(на рисунках он отмечен дужкой).
Хороша ли такая мера? Однозначна ли? Не приведет
ли к недоразумениям? Давайте разберемся.
Представьте, что на каждом рисунке исчезло все,
кроме сторон угла, о котором идет речь. Проведем дугу
142
с центром в вершине этого угла, от одной его стороны до
другой. Каким бы ни был радиус дуги, огромным ли, кро-
хотным ли, возникший сектор будет подобен тем секто-
рам, что выделены на прежних рисунках. Точно таким
же будет отношение длины дуги, стягивающей угол, к
ее радиусу. А это значит, что предложенный метод опре-
деляет величину угла совершенно однозначно.
Описанный способ измерять углы называется радиан-
ной мерой.
Освоить ее нетрудно. Известно, что длина окружности
радиуса R равна 2л/?. Следовательно, полный угол, кото-
рый она охватывает, будет равен 2л, если его измерять
только что описанным способом. Прямой угол, вчетверо
меньший полного, тогда выразится числом л/2, угол в
45° — числом л/4, в 30°—числом л/6 и так далее.
Если радианную меру вам захочется обратить в гра-
дусную и наоборот, учтите, что они пропорциональны
друг другу и закон пропорциональности таков: угол в 1°
выражается ® радианной мере числом 0,017453..., а угол,
равный единице в радианной мере, в градусной составля-
ет 57° 17'44,8"... (дуга окружности, стягивающая такой
угол, по длине равна своему радиусу).
И пусть вас не удивляет, если в дальнейшем мы будем
говорить «синус двойки», «тангенс половины». Зная, как
соразмерены градусная и радианная меры, вы можете
прикинуть в уме: двойка — это примерно сто четырнад-
цать градусов, половина — чуть меньше двадцати девяти.
Такой пересчет удобен на первых порах знакомства
143
с радианной мерой. Надеемся, что впоследствии вы убе-
дитесь, что она гораздо удобнее градусной.
Вы увидите, например, что тригонометрические функ-
ции встречаются не только в задачах, связанных с угла-
ми, поворотами, вращением. Если аккуратно снять шкур-
ку с пластика колбасы, порезанной наискосок, то эта гиб-
кая полоска, расправленная на столе, превратится в вол-
ну синусоиды. А вот пример посерьезнее. По синусоиде
изгибается линейка, сжатая с концов, упругая балка под
непомерной нагрузкой.
Как поточнее перенести форму прогнувшейся линей-
ки на график? Какие единицы откладывать по горизон-
тальной его оси? Аргумент синуса мы привыкли выра-
жать в градусах. Но как измерить в них расстояние ме-
жду концами прогнувшейся линейки?
Вот тут и обнаруживает свои преимущества радиан-
ная мера. Выберем единицу измерения так, чтобы рассто-
яние между концами линейки выражалось числом л.
Отрезок такой длины отложим на оси абсцисс и постро-
им на нем график синуса.
Несколько характерных точек можно нанести на гра-
фик сразу. Синус прямого угла, как известно, равен еди-
нице, а радианная мера прямого угла — л/2. Это число
соответствует середине отрезка, отложенного на оси абс-
цисс,— значит над ней следует поставить точку с орди-
натой, равной единице. Синус 30° равен половине, а ра-
дианная мера этого угла — л/6. На графике появляется
еще одна точка с координатами л/6 и 1/2.
Так, точка за точкой на координатной плоскости воз-
никает аккуратная синусоида.
...А за окном то Bteepx взлетали, то вниз ныряли про-
вода, — вот непременный штрих картины, которую видит
из вагонного окошка пассажир поезда дальнего следо-
вания.
Впрочем, чтобы увидеть эти красивые взлеты и спады,
не нужно отправляться в дальнюю дорогу. Ведь точно
по такому же закону провисает и цепочка ходиков, и ве-
ревка, на которую хозяйка собирается вешать белье.
Оказывается, этот изящный прогиб математически
описывается полусуммой двух экспонент — одна с плю-
144
сом, другая с минусом перед аргументом. Называется та-
кая функция цепной линией.
Есть у нее и другое название — гиперболический ко-
синус. Оно связано с чисто математическими свойства-
ми функции и, казалось бы, затеняет ее связи с физиче-
ской реальностью. Это не так: абстрактность второго на-
звания при желании можно понять как указание на то,
что цепная линия пригодна не только для математическо-
го описания провисающих проводов и веревок.
Эта красивая функция задает, например, форму
мыльной пленки, натянутой между двумя проволочными
кольцами: если посмотреть на эту прозрачную трубку
сбоку, ее абрис будет представлять собой цепную линию.
Коль скоро речь пошла о гиперболическом косинусе,
нельзя не упомянуть о гиперболическом синусе — полу-
разности экспонент, одна с плюсом, другая с минусом пе-
ред аргументом.
Существует в математике и гиперболический тангенс,
который, как и в тригонометрии, конструируется в виде
отношения синуса и косинуса, разумеется, гиперболиче-
ских.
Определение тангенса—не единственная аналогия
между функциями гиперболическими и тригонометриче-
скими. Формулы, связывающие между собой гиперболи-
ческие функции, весьма похожи на формулы для триго-
нометрических функций.
Функции, о которых мы рассказывали до сих пор, на-
зывают элементарными. То же звание носят их всевоз-
можные комбинации с помощью знаков сложения, вычи-
тания, умножения, деления, извлечения корня. Употреб-
ляя понятия, речь о которых еще впереди, скажем ради
полноты, что обратные и сложные функции, полученные
из перечисленных, также называются элементарными.
Не нужно думать, что в математике есть принцип от-
бора, по которому функции зачисляются в разряд эле-
ментарных. Так распорядилась история. Функции, на-
званные элементарными, раньше, чем прочие, появились
в математике и сыграли важную роль в ее развитии и ее
приложениях. Опыт их использования богат, их символы
привычны.
9 Заказ Mb.Si
145
Функция Хевисайда
Если быть строгим, то на-
до признать, что функция,
изображенная на рисунке (ее
называют «абсолютная ве-
личина X», или «модуль X»),
почти столь же проста,
столь же элементарна, как
и линейная функция.
А функция Хевисайда,
изображение которой при-
ведено следующим? Состоя-
щая из двух горизонталей,
она-то уж совсем элементарна. Но появившаяся в мате-
матике на рубеже прошлого и нашего веков, она уже не
получила звание элементарной.
...«Бросая в воду камешки, смотри на круги, ими об-
разуемые, иначе такое бросание будет пустою забавою».
Последуем совету мудрого Козьмы Пруткова и понаблю-
даем за кругами на воде. Вот что мы увидим, если оста-
новим мгновение и рассечем пополам водную толщу.
Просматривая атлас функций — не найдется ли там
146
чего похожего? — мы бы крикнули «эврика!» на страни
це, где изображены так называемые функции Бесселя.
Функции Бесселя рождены для того, чтобы описывать
процессы в цилиндрических системах координат. Коле-
бания жидкости в топливном баке взлетающей ракеты,
поведение плазменного шнура в магнитном поле, распро-
странение тепла вокруг тепловыделяющего стержня в
ядерном реакторе — в любом из этих случаев найдется
применение функциям Бесселя.
Для этих функций введен особый символ, для них, как
для синусов и логарифмов, составляются таблицы, од-
нако в разряд элементарных они не занесены.
9
СВОЙСТВА ФУНКЦИЙ
Современная математика знает множество функций, и у
каждой свой неповторимый облик, как неповторим об-
лик каждого из миллиардов людей, живущих на Земле.
Однако при всей непохожести одного человека на дру-
гого у каждого есть руки и голова, уши и рот.
Точно так же облик каждой функции можно предста-
вить сложенным из набора характерных деталей. В них
проявляются основные свойства функций.
Функции — это математические портреты устойчивых
закономерностей, познаваемых человеком. Чтобы про-
иллюстрировать характерные свойства функций, нам по-
казалось естественным обратиться к пословицам. Ведь
пословицы — это тоже отражение устойчивых закономер-
ностей, выверенное многовековым опытом народа.
«Чем дальше в лес, тем больше дров»,гласит по-
словица. Изобразим графиком, как нарастает количество
дров по мере продвижения в глубь леса — от опушек, где
все давным-давно собрано, до чащоб, куда еще не ступа-
ла нога заготовителя.
Горизонтальная ось графика — это лесная дорога. По
вертикали будем откладывать (допустим, в кубометрах)
количество топлива на данном километре дороги.
График представит количество дров как функцию пу-
ти.
Согласно пословице эта функция неизменно возраста-
Продвижение в лес
Расстояние до кумы
148
ет. Какие две точки на оси абсцисс ни взять, для более
дальней (чем дальше в лес...) значение функции будет
больше (...тем больше дров). Такое свойство функции
называется монотонным возрастанием.
Сходное свойство иллюстрирует и пословица «Каши
маслом не испортишь». Качество каши можно рассматри-
вать как функцию количества масла в ней. Согласно по-
словице эта функция не уменьшится с добавкой масла.
Она, возможно, увеличится, но может оставаться и на
прежнем уровне. Подобного рода функции называются
монотонно неубывающими.
Чувствуете ли вы, читатель, разницу между дровами
и кашей? То бишь между монотонным возрастанием и
монотонным неубыванием?
Возрастание — это только вверх. Неубывание — это
либо вверх, либо ни вверх, ни вниз. Возрастание — част-
ный случай неубывания. Например, всюду постоянная
функция (константа) принадлежит к числу неубываю-
щих, хотя она ни на одном участке своей области опре-
деления не возрастает.
«Дальше кумы — меньше греха».
Функция, которая показывает, как изменяется мера
греха по мере удаления от кумы, монотонно убывающая.
«Выше меры конь не скачет». Если изобразить траек-
торию скачущего коня, то высота скачков в полном соот-
ветствии с пословицей будет ограничена сверху некото-
рой «мерой».
Вот знакомый график синуса. И здесь есть своя мера,
выше которой не вздымаются волны синусоиды. Такой
149
мерой, такой непреступаемой верхней гранью может по-
служить и десятка, и семерка, и тройка, и единица.
Единица среди всех перечисленных величин на особом
положении: это точная верхняя грань для значений си-
нуса.
В каком же смысле она точна? В том, очевидно, что
понизить ее уже нельзя. Для любого уровня, что ниже
точной верхней грани, найдутся значения функции, его
превосходящие. В этом одно из двух отличительных
свойств точной верхней грани. А другое и совсем очевид-
но: ее не превосходит ни одно значение функции.
Обратите внимание на это выражение: «не превосхо-
дит». Это значит «меньше или равно». Синус и в самом
деле кое-где равен единице — в точках, соответствующих
макушкам волн. Во всех остальных он меньше единицы.
Есть у значений синуса и точная нижняя грань— ми-
нус единица.
Есть точная нижняя грань и у значений показатель-
ной функции — нуль. Правда, в отличие от синуса, кото-
рый в некоторых точках равен по величине своей точной
нижней грани, у показательной функции нет ни одной
точки, где она обратилась бы в нуль. Как говорят, пока-
зательная функция своей точной нижней грани не дости-
гает.
(Это, разумеется, не мешает нулю служить точной
нижней гранью для показательной функции. Во-первых,
для любого уровня, даже чуть выше нуля, найдутся точ-
ки кривой, лежащие под этим уровнем. Во-вторых, ни
одна точка кривой не лежит ниже нуля. Нуль обладает,
таким образом, обоими отличительными свойствами точ-
ной нижней грани.)
Сверху же никаких ограничений для показательной
функции не существует. Какой уровень ни назначь, как
бы ни был он высок, найдется значение функции еще
150
большее. (Отметьте про себя эту фразу: в ней — опреде-
ление функции, неограниченной сверху.)
Однако показательная функция способна и на боль-
шее: превзойти любой назначенный уровень не только в
одной, но сразу во всех лежащих правее, более далеких
от нуля, точках. А это уже не простая неограниченность.
Про такую функцию говорят, что она стремится к беско-
нечности при бесконечном возрастании аргумента.
Чувствуете ли вы, читатель, тонкую разницу между
неограниченностью и стремлением к бесконечности? Ес-
ли нет, то специально для вас мы выведем на эту стра-
ницу, как на цирковую арену, своего математического
коня, который способен скакать выше любой меры. Мы
заставим его допрыгивать до все больших значений по-
казательной функции.
Если представить траекторию коня как график неко-
торой функции, то это будет функция неограниченная:
любую высоту наш конь возьмет в каком-то из прыжков.
Но выше превзойденного уровня он не останется навсег-
да. Такую функцию, хотя она и неограниченная, нельзя
назвать стремящейся к бесконечности.
Просматривая графики функций, о которых говори-
лось раньше, мы не раз найдем приложения только что
сформулированным понятиям.
Вот, например, логарифм. Он неограничен снизу: ка-
кой уровень ни назначь — каждый раз, как бы ни был
низок этот уровень, найдется значение логарифма еще
ниже.
Нельзя не заметить: рекорды глубины логарифм бьет
один за другим при значениях аргумента, все более близ-
ких к нулю. Говорят, что логарифм неограничен снизу в
окрестности нуля.
Про логарифм можно сказать и больше: его кривая
способна опуститься ниже любого назначенного уровня
не только в одной какой-то точке, близкой к нулю, но сра-
зу во всех точках некоторой окрестности нуля (ширина
окрестности, разумеется, зависит от того, какова назна-
ченная глубина). Это означает, что логарифм стремится
к минус бесконечности при стремлении аргумента к ну-
лю.
«При стремлении аргумента к нулю слева», — уточ-
151
нит нас, пожалуй, дотошный читатель. И тем самым
даст нам повод к рассказу о том, как и зачем математи-
ки иногда не обращают внимания на знаки чисел.
Плюс десять и минус десять — это, конечно, числа
разные. Но математик скажет, что они одинаковы по
абсолютной величине. Этот обобщающий термин позво-
ляет математику говорить, что гипербола стремится к
бесконечности при стремлении аргумента к нулю, что па-
рабола и линейная функция бесконечно возрастают при
бесконечном возрастании аргумента. Без упоминания
знаков плюс и минус бесконечное возрастание понимает-
ся как возрастание по абсолютной величине. И когда го-
ворят о стремлении аргумента к какой-то точке, считает-
ся, что он может стремиться к ней с любой стороны.
«Пересев хуже недосева», — издавна говорили зем-
ледельцы. Вековой опыт свидетельствовал: урожай лишь
до некоторой поры растет вместе с плотностью посева,
дальше он снижается, потому что при чрезмерной густо-
те ростки начинают глушить друг друга.
Эта закономерность ста-
нет особенно наглядной, если
изобразить ее графиком,
где урожай представлен как
функция плотности посева.
Урожай максимален, когда
поле засеяно в меру. Макси-
мум— это наибольшее зна-
чение функции по сравнению
с ее значениями во всех со-
вершина горы, с которой все
седних точках. Это как бы
дороги ведут только вниз, куда ни шагни.
В примере с урожаем дело обстоит точно так же, как
в той застольной ситуации, которую описывает послови-
ца «Недосол на столе — пересол на спине». Качество пи-
щи зависит, является функцией от количества соли в ней.
Мало соли — невкусно, много — тоже в рот не возьмешь.
А где-то в промежутке, в золотой середине, когда соли в
самый раз, кушанье становится особенно лакомым. В
этой точке кулинарная функция достигает максимума.
Малейшей щепотью соли больше или меньше — и дегу-
статор с утонченным вкусом скажет, что качество пищи
снизилось.
152
Есть у максимума антипод — минимум. Минимум —
это как бы дно впадины, из которой, куда ни шагни, все
дороги ведут только вверх.
Правда, если шагать все дальше, возрастание где-то
может смениться и спадом. Про минимум говорят тогда,
что он локальный. Звание абсолютного минимум получа-
ет лишь тогда, когда это наименьшее значение функции
для всей области определения. Если на всем ее протяже-
нии локальных минимумов несколько, то абсолютный
нужно еще поискать. Может, кстати, оказаться, что функ-
ция принимает наименьшее значение в граничной точке
области определения. (Все сказанное легко перефрази-
руется по отношению к наибольшему значению, абсолют-
ному и локальным максимумам.)
В семье элементарных функций, которая поставляла
примеры для наших предыдущих рассуждений, большин-
ство составляют функции, либо всюду возрастающие, ли-
бо всюду убывающие. Такое преобладание отнюдь не ха-
рактерно для всего огромного мира функциональных за-
висимостей. На практике гораздо чаще приходится иметь
дело с такими представителями этого мира, которые на-
делены обоими качествами: местами они возрастают, ме-
стами убывают. Участки убывания и возрастания стыку-
ются в точках максимумов и минимумов. Подобное мож-
но увидеть у параболы или синусоиды. Проследите эти
графики слева направо, от меньших аргументов к боль-
шим: в точке минимума спад сменяется ростом, в точке
максимума — наоборот. Общая стыкующая роль макси-
мумов и минимумов подчеркивается их обобщающим на-
званием «экстремум». Как под словом «ребенок» подра-
зумевается либо мальчик, либо девочка, так понятие
«экстремум» распадается на «максимум» и «минимум».
153
«Не круто начинай, круто кончай». Эта пословица
заслуживает того, чтобы быть включенной в правила
НОТ. Тем более что за ней так и видится графическое вы-
ражение, к чему так склонны теоретики научной органи-
зации труда.
Повелительное звучание пословицы явно рассчитано
на борьбу с противоположной, весьма распространенной
манерой работы. На нее тоже есть своя пословица: «Го-
ряч на почине, да скоро остыл».
Обе функции, представленные на графиках зависящи-
ми от времени, возрастающие. Но, как свидетельствуют
кривые, расти можно по-разному.
Наклон одной кривой постоянно увеличивается. Рост
функции усиливается с ростом аргумента. Такое свойство
функции называется вогнутостью.
Наклон другой кривой неизменно уменьшается. Рост
функции слабеет с ростом аргумента. Такое свойство
функции называется выпуклостью.
Если вам хочется получше уяснить различие между
выпуклостью и вогнутостью, сравните график роста че-
ловека с графиком роста населения Земли. Здесь опять-
таки и та и другая функции возрастающие. Но рост че-
ловека со временем замедляется: достигнув зрелого воз-
раста, человек уже не растет. Население земного шара,
напротив, с течением времени растет в,се быстрее и бы-
стрее. В первом случае мы говорим о выпуклости, во вто-
ром — о вогнутости.
Нетрудно найти иллюстрации этим понятиям и среди
элементарных функций. Показательная функция — во-
гнутая. Логарифм, корень квадратный — выпуклые. Вы-
пуклую параболу выписывает и снаряд, выпущенный из
пушки под углом к горизонту. Но присмотритесь подоль-
ше к его полету: достигнув максимальной высоты, он
начинает падать; однако искривление его траектории со-
храняет прежний характер, и это подсказывает, как рас-
154
пространить понятие вогнутости и выпуклости на случай
убывающих функций. Все усиливающийся спад — это
выпуклость, все замедляющийся — вогнутость.
Парабола вершиной вниз представляет собой вогну-
тую функцию: сначала она спадаетчвсе замедляющимися
темпами, потом нарастает все ускоряющимися. Вогнутой
функцией является и гипербола, построенная для поло-
жительных значений аргумента. Другая ветвь гипербо-
лы выпуклая.
Напоследок стоит отметить, что одна и та же функция
может иметь как участки выпуклости, так и участки во-
гнутости — поглядите на ту же синусоиду. Точки, в кото-
рых выпуклость сменяется вогнутостью или наоборот, на-
зываются точками перегиба.
•
«Это сказка про белого бычка». Так говорят, когда
какое-то дело безнадежно затягивается, когда раз за ра-
зом попытки уладить его приводят к пустому или бес-
смысленному результату.
Поговорку знают все, но не каждый знает, как расска-
зывается сказка. Важная деталь рассказа — реакция слу-
шателя. Сказка представляет собой диалог:
— Рассказать тебе сказку про белого бычка?
— Расскажи.
— Ты расскажи, я расскажи. Рассказать тебе сказку
про белого бычка?
— Так давай же!
— Ты так давай же, я так давай же. Рассказать тебе
сказку про белого бычка?
— Ну хватит!
— Ты ну хватит... и так далее.
Ссылку на сказку про белого бычка часто заменяют
цитированием первых слов песни «У попа была собака».
Ради полноты приведем и ее.
«У попа была собака. Он ее любил. Она съела кусок
мяса. Он ее убил. И в землю закопал. И надпись напи-
сал: «У попа была собака. Он ее любил...» и так далее.
Белый бычок и поповская собака нужны нам для раз-
говора о периодических функциях, для уяснения матема-
тического понятия периода и тех искажений, которые
привносятся в него обыденной речью.
Периодичностью в обыденной речи называют чуть ли
не всякую повторяемость. Но повторяемость может быть
155
160
более или менее строгой. Достаточно сравнить между со-
бой приведенные тексты: во втором, какую букву ни возь-
ми, она обязательно повторится через 89 букв. Про пер-
вый текст такого не скажешь.
В обыденной речи утвердилось выражение «период
солнечной активности». Если бы все явления на Солнце
подчинялись строгой «периодичности, их можно было бы
предсказывать на сколь угодно долгий срок. Стала бы не
нужна всемирная служба Солнца с ее круглосуточными
наблюдениями за дневным светилом, потеряли бы свой
хлеб астрономы, гадающие, как в ближайшее время из-
менятся количество солнечных пятен, интенсивность сол-
нечных вспышек и т. п.
Вся эта огромная армия может быть спокойна за свое
будущее. Максимумы и минимумы солнечной активности
сменяют друг друга через неодинаковые промежутки
времени и не совпадают по величине. Можно говорить об
их чередовании, о периодичности же в строгом смысле не
может быть и речи.
Большей строгостью проникнуто выражение «периоди-
ческая печать». Газеты выходят день за днем, а если по-
недельник и пропускается, то можно говорить о недель-
ном периоде. Журналы печатаются из месяца в месяц или
из декады в декаду, из недели в неделю. Однако абсолют-
ной строгости понятие периода не достигает и тут. Она
была бы здесь, если бы время выхода соблюдалось с
абсолютной точностью, а тексты полностью совпадали.
По-видимому, безупречные примеры периодичности
способна дать только математика. Здесь периодической
называется всякая такая функция, любое значение ко-
торой в точности повторяется каждый раз, когда аргу-
мент увеличивается на определенную величину, называ-
емую периодом.
(Стоит заметить, что для периодической функции нет
меньшей по сравнению с периодом величины того же
156
свойства. Большие могут быть: значения функции будут
повторяться и через два периода, и через три, и так да-
лее. Вот почему иногда говорят о наименьшем периоде
периодической функции.)
Прекрасные примеры периодических функций дает
тригонометрия: синус, косинус, тангенс... Вспомните наш
рассказ про динамомашину, вспомните, как вращающа-
яся рамка размеренно и точно раз за разом занимала
каждое из своих положений, вспомните пояснявшие рас-
сказ чертежи: цикличность процесса естественным обра-
зом обусловливает периодичность описывающих его
функций в их зависимости от угла и времени.
Для синуса и косинуса период составляет 360°, для
тангенса — 180°.
Психологи советуют: если вам нужно запомнить боль-
шой объем информации (скажем, большой текст), вооб-
разите себя прогуливающимся по хорошо знакомой ули-
це и мысленно привязывайте отдельные куски текста к
подъездам домов, афишным тумбам, киоскам... Когда по-
требуется воспроизвести заложенное в память, нужно
вновь мысленно отправиться на прогулку по той же ули-
це и считывать фразу за фразой с подъездов, заборов,
киосков...
Немало информации о свойствах функций было пред-
ложено вашему вниманию на предыдущих страницах.
Чтобы понадежнее уложить в память эту информацию,
давайте воспользуемся советом психологов.
Отправимся в путь на автомобиле по шоссе из пунк-
та А в пункт Б. Будем внимательно приглядываться к
рельефу дороги, связывая с его особенностями матема-
157
тические термины. Мысленно представим высоту в каж-
дой точке пути над некоторым воображаемым горизон-
тальным уровнем как функцию расстояния, пройденного
вдоль этой горизонтали. Промежуток от А до Б — об-
ласть определения описанной функции.
Ровный участок дороги, естественно, ассоциируется с
термином «константа». Дорога идет под уклон — это мо-
нотонное убывание. Кончился спуск — и водитель вклю-
чает газ, отмечая тем самым точку минимума. Дорож-
ный знак указывает подъем, а у математика наготове
свой термин — монотонное возрастание. Перевалили за
гребень холма — пройдена точка максимума. И снова
началось монотонное убывание, то есть спуск. На холмах
дорога выпукла, в ложбинах вогнута. Не отмеченные до-
рожными знаками стыки таких участков математик от-
метит про себя как точки перегиба.
Математические категории, о которых шла речь в
этом описании, естественным образом делятся на две
группы. Одни описывают поведение функции в окрестно-
сти некоторых характерных точек (максимум, минимум,
перегиб), другие — в некоторых промежутках (выпук-
лость, вогнутость, убывание, возрастание).
Чтобы в общих чертах воспроизвести профиль доро-
ги, на графике достаточно наметить его сначала в ок-
рестностях характерных точек, а затем, воспроизводя
его поведение в промежутках, заполнить пробелы.
По таким правилам можно восстановить облик любой
функции. Так удобнее рисовать даже те функции, кото-
рые выражены формулами — как говорят, заданы анали-
тически.
Но как по формуле функции определить ее характер-
ные точки?
Об этом мы еще поговорим, когда речь пойдет о про-
изводных.
Обкатанные в автомобильных прогулках, отточенные
на оселке народной мудрости, наши навыки обращения
с функциями мы применим сейчас во вполне серьезном
деле.
Физикам важно знать, как ведут себя газы при раз-
личных температурах и давлениях. Поведение газа оп-
ределяется взаимодействием между его молекулами.
158
Предположим для простоты, как это часто делается в
физике, что молекулы — это маленькие упругие шарики.
Рассмотрим две такие молекулы и будем изучать, какому
закону подчиняется сила их взаимодействия.
Известно, что на больших расстояниях молекулы вза-
имно притягиваются, причем с роётом расстояния сила
притяжения убывает, стремясь к нулю. При сближении
молекул она, напротив, возрастает. Когда шарики сбли-
жаются до соприкосновения, в игру вступает еще одна,
противоположно направленная сила —сила упругого от-
талкивания. Она тем больше, чем сильнее прижаты ша-
рики друг к другу, чем меньше расстояние между их цен-
трами. Гипотетически можно представить центры моле-
кул сближающимися на сколь угодно малое расстояние,
отчего сила их взаимного отталкивания возросла бы не-
ограниченно.
Располагая такой не слишком обширной информаци-
ей, можно приступать к графику. График должен изо-
бразить силу взаимодействия между молекулами как
функцию расстояния между их центрами.
Расстояние между центрами не может выражаться
отрицательным числом, не может и обратиться в нуль.
График рисуется над положительной полуосью абсцисс.
Это — область определения исследуемой функции.
Над дальним концом положительной полуоси абсцисс
проведем прилегающий к ней вогнутый штришок. Своей
близостью к горизонтальной оси он покажет, что с удале-
нием молекул друг от друга сила их взаимодействия убы-
вает до нуля, а вогнутой формой — что при сближении
молекул сила их взаимного притяжения возрастает все
круче. В точке с абсциссой, равной удвоенному радиусу
молекулы, на условной высоте отметим точку перегиба;
в этой точке силы упругого отталкивания, вступив в иг-
ру, заставляют кривую графика сменить свое прежнее,
все более крутое возрастание на возрастание все более
замедляющееся. В точке с абсциссой, еще меньшей, на
159
чуть большей высоте проведем дужку выпуклостью квер-
ху. Она означает, что сила взаимодействия достигла
максимума: с дальнейшим уменьшением аргумента силы
упругого отталкивания преобладают над силами притя-
жения, кривая устремляется вниз. Выпуклый отвесный
штрих проведем у нижнего конца оси ординат, чуть пра-
вее от него. Эта деталь показывает, что сила отталкива-
ния между молекулами неограниченно возрастает, когда
их центры неограниченно сближаются.
Поскольку сила взаимодействия между молекулами
определена для любого расстояния между их центрами,
график должен быть непрерывной линией. Соединим на-
меченные штрихи гладкой кривой.
Такую картину часто можно увидеть в книгах по фи-
зике, правда, в перевернутом виде; у физиков сложилась
традиция трактовать силы притяжения как отрицатель-
ные величины, силы отталкивания — как положительные.
Кривые такого сорта послужили для построения тео-
рии реальных газов, сформулированной Ван-дер-Вааль-
сом.
Оси координат играют для ветвей нашего графика
особую роль. Бесконечно удаляясь от начала координат,
ветви графика как бы притягиваются к этим своеобраз-
ным прямолинейным направляющим, неограниченно
сближаются с ними. Такие прямые называются асимпто-
тами.
Так случилось, что в нашем примере асимптотами
служат горизонтальная и вертикальные прямые. Более
характерно употребление этого термина по отношению к
наклонным прямым, когда к ним неограниченно прибли-
жаются ветки графика, уходящие в бесконечность.
Что нынче в моде? Этот вопрос встает перед каждым,
кто задумал шить костюм или хотя бы брюки. Что зака-
зывать— клеш или дудочки? Какую ширину предписы-
вают брюкам модные журналы в этом сезоне?
Ревностный поклонник моды тем и отличается, что он
всегда знает ответ на такой вопрос. Ему известна зави-
симость ширины брюк от сезона. Известна мода как
функция времени.
Ну а если клиент — невежда в вопросах моды?
Что ответить закройщику на его роковой вопрос:
160
«Брючки понизу сколько сантиметров делаем?»
Клиент в замешательстве. И не дай ему бог ляпнуть
наугад первую пришедшую на ум цифру. В ответ он рис-
кует услышать презрительное: «Э, батенька! Такое но-
сили лет пять назад, да перед самой войной, да еще при
царе Горохе...».
Оставим на этом вконец сконфуженного заказчика.
Проанализируем слова закройщика, ибо в них нам ви-
дится подлинно математическое содержание.
Что же он сказал? По ширине брюк он указал годы,
когда носили такие брюки. По значению функции моды
он установил значение аргумента. То есть значение
функции закройщик рассматривает как аргумент, а преж-
ний аргумент стал при этом функцией.
Ясно, что тем самым закройщик сконструировал не-
кую функциональную зависимость, тесно связанную с
первой. Говорят, что по отношению к первой такая зави-
симость является обратной.
Из ателье перенесемся в поликлинику. Врач велит
пациенту измерить температуру. В стеклянной трубочке,
которую пациент сует под мышку, заключен столбик рту-
ти. Он удлиняется от тепла человеческого тела. Вспоми-
нается часовая мастерская Гаррисона и опыты, в кото-
рых мастер определял длину металлических стержней как
функцию их температуры. Здесь врач проделывает нечто
обратное: по длине жидкого ртутного «стерженька» он
определяет температуру пациента. Он строит обратную
функцию по отношению к той, которую изучал Гаррисон.
Разумеется, к вопросу можно подойти с другой сторо-
ны и назвать прямой функцию, с которой имеет дело
врач, и обратной ту, значение которой прославило Гарри-
сона. А если быть справедливым до конца, то обе функ-
ции нужно назвать взаимно обратными. Противопостав-
лять их имеет не больше смысла, чем решать, кто из двух
близнецов старше.
Ю Заказ 8651
161
Правда, порой одна из двух взаимно обратных функ-
ций более употребительна, более привычна, ее символ
примелькался больше, и подобная неравноценность иг-
рает свою роль при распределении званий «прямая» и
«обратная». Арксинус, арктангенс называют обратными
тригонометрическими функциями, молчаливо отдавая
звание прямых синусу и тангенсу.
Из поликлиники — на космодром. Ракета, летящая в
космическом пространстве, наращивает скорость по за-
кону логарифма: именно эта функция позволяет по мас-
се израсходованного топлива указать скорость ракеты.
Скорость — функция, масса топлива — аргумент. Но ча-
сто возникает обратная задача, когда исходным иунктом
расчета является скорость ракеты. Чтобы вывести спут-
ник на орбиту, ракета должна развить первую космиче-
скую скорость. Какое количество топлива потребуется
ракете, чтобы достичь назначенной скорости? Масса топ-
лива в этом вопросе уже мыслится как функция, ско-
рость — как аргумент. Задачу решает функция, обратная
к логарифмической, — показательная.
Функция логарифмиче-
ская и функция показатель-
ная. Сведем их на одном гра-
фике. Бросается в глаза: они
расположены симметрично
относительно биссектрисы
угла, стороны которого —
оси координат. Это не удиви-
тельно — ведь переход от
прямой функции к обратной
заключается в 'переименова-
нии: функция становится ар-
гументом, аргумент — функ-
цией.
162
Заметим, что функция, обратная линейной, — это
опять-таки линейная функция. Простейшая из линейных
функций та, что равна аргументу, — обратна по отноше-
нию к самой себе, что, впрочем, очевидно: ее график
совпадает с биссектрисой угла между координатными
осям*и. 4
Корень квадратный и парабола тоже являются взаим-
но обратными функциями, и графики их тоже симметрич-
ны относительно той же биссектрисы.
А теперь — снова в ателье. Анализируя слова закрой-
щика с математической точки зрения, мы поначалу не
обратили внимания на то, что он назвал сразу несколько
значений функции, обратной к функции моды («...пять
лет назад, да перед самой войной, да еще при царе Горо-
хе»). Задумаемся над этим сейчас.
Мода повторяется, и это делает неоднозначной функ-
цию, значения которой называет закройщик. Та же при-
чина делает неоднозначной и арксинус — функцию, об-
ратную синусу.
В математике, как мы уже отмеча-
ли, принято рассматривать лишь одно-
значные функции. Именно поэтому ма-
тематик, отразив относительно биссект-
рисы координатного угла график сину-
са, оставляет от него лишь небольшой
участок и называет его главной ветвью
арксинуса (см. рисунок слева).
Резонно полюбопытствовать: какие
же свойства функции гарантируют то,
что обратная к ней окажется однознач
ной? Эти свойства — непрерывность и
монотонность.
О первом из двух понятий речь впе-
реди, а второе нам уже знакомо.
Беря в качестве примера взаимно
обратных функций параболу и корень
квадратный, мы не случайно взяли от
параболы лишь одну половину. Если
параболу не урезать до монотонного
вида, то в результате ее отражения
относительно биссектрисы координатного угла получи i-
ся такой график, с которого значения корня квадратного
можно брать и со знаком плюс, и со знаком минус. А это
10
163
тот самый случай, по поводу которого мы говорили ког-
да-то о нежелательности многозначных функций в мате-
матике.
Не было гвоздя —
Подкова пропала.
Не было подковы —
Лошадь захромала.
Ограничимся пока этим, ибо дальше в стихотворении
идут совсем уж страшные вещи — гибель командира, раз-
гром армии и так далее, и тому подобное.
Итак, лошадь. С чего начались ее неприятности? С то-
го, что непрочно державшаяся подкова отвалилась. А от-
чего подкова держалась непрочно? Оттого, что кузница
не обеспечила штатного количества гвоздей.
Боевое состояние лошади зависит от прочности кре-
пления подковы. Состояние лошади — функция, проч-
ность крепления — аргумент. Но эта прочность, в свою
очередь, обусловлена количеством гвоздей. Прочность —
функция, количество гвоздей — аргумент.
Так что же получается? Прочность крепления подко-
вы — это одновременно и функция и аргумент. Нет ли
здесь противоречия? Не ведет ли это к путанице?
Напротив! Описанная конструкция из функциональ-
ных зависимостей ведет к прояснению многих важных
вопросов.
Бывает, что изучить зависимость какого-то явления от
первопричины оказывается делом сложным. Чувствуется,
что взаимообусловленность между ними есть, но пере-
кинуть прочный мост четкой функциональной зависимо-
сти от одной к другой не удается. Дело облегчается, если
между чрезмерно далекими берегами посчастливится оты-
скать остров — некоторый фактор, который является
следствием первопричины и причиной окончательного, ис-
следуемого следствия. Иными словами, когда удается по-
строить некоторую промежуточную функцию, для кото-
рой независимая переменная служит аргументом, в то
время как сама промежуточная функция служит аргу-
ментом для исследуемой функции. И безнадежно разоб-
щенные прежде берега оказываются связанными этаким
двухарочным мостом.
164
И неясная прежде связь между комплектностью куз-
нечного оборудования и боеспособностью конницы про-
ясняется введением промежуточного звена — прочностью
крепления подков на копытах лошадей.
Подобная конструкция из двух функций называется
их суперпозицией, или сложной функцией.
В ходе пристального анализа цепочка функциональ-
ных зависимостей может удлиняться: былая первопричи-
на обнаруживает обусловленность более глубокими фак-
торами, а от явления, на котором прежде останавливал-
ся взгляд исследователя, тянется вереница далеко иду-
щих следствий. Двухарочный мост становится подобным
акведуку.
Взять хотя бы наше стихотворение:
Лошадь захромала —
Командир убит.
Конница разбита —
Армия бежит.
Враг вступает в город,
Пленных не щадя.
Оттого, что в кузнице
Не было гвоздя.
Поэт видит корень зла в гвозде и умалчивает о при-
чинах недостачи. Расследование можно продолжить. Мо-
жет быть, администрация кузницы халатно относится к
своим обязаностям? А может быть, ее подвели снабжен-
цы? А может быть, завод-изготовитель не выполнил
план? Или подкачали смежники?
Шутки шутками, а между тем подобные цепочки функ-
циональных зависимостей возникают при анализе одной
из серьезнейших проблем нашего времени. Эта пробле-
ма— «Человек и окружающая среда».
Ученые утверждают, что в наше время ледники тают
быстрее, чем, скажем, века два назад. И одну из причин
этого явления усматривают в развитии промышленности.
В чем дело? Может быть, в том, что топки заводов и
• фабрик греют атмосферу и это вызывает таяние льдов?
Нет, на столь непосредственное воздействие вряд ли хва-
тит тепловой энергии, выделяемой заводами и фабрика-
ми. Дело здесь в другом.
Замечали ли вы, как быстро тает весной грязный снег
при дорогах и как долго лежит он чистый на полях?
Пыль, копоть и прочие им подобные плоды цивилиза-
ции загрязняют атмосферу, переносятся ветрами на ог-
ромные расстояния, оседают на ледниках, и загрязнен-
165
ныи лед интенсивнее поглощает солнечные лучи, тает
быстрее.
Налицо сложная функция, или суперпозиция. Количе-
ству топлива, потребляемому заводами и фабриками
планеты, соответствует определенное количество пыли и
копоти, выбрасываемое в атмосферу, а этому количеству
соответствует определенное количество солнечной энер-
гии, поглощенное ледниками.
Зная эту сложную функцию, можно приступать к
анализу загадочного прежде таяния ледников.
Эта кривая, напоминающая головной убор времен
Наполеона, — своеобразный фирменный знак теории ве-
роятностей. Там она называется кривой нормального за-
кона распределения ошибок, или кривой Гаусса. ,
Казалось бы, этой функции, как и функции Бесселя,
можно посочувствовать: такая известная, такая распро-
страненная, а звания элементарной не удостоена.
Ч Не надо спешить с собо-
лезнованиями. Ведь элемен-
тарными функциями, как мы
уже говорили, считаются не
только полиномы и корни,
логарифмическая и показа-
тельная, тригонометрические
и гиперболические функ-
ции, не только все те, что по-
лучаются из них с помощью
сложения и вычитания, ум-
ножения и деления, но так-
же обратные к ним (напри-
мер, арксинус или арктан-
генс) и их суперпозиции.
Функция нормального распределения ошибок как раз
и представляет собой суперпозицию двух элементарных
функций, показательной и параболы, взятой со знаком
минус перед ней, а потому по праву принадлежит к чис-
лу элементарных.
Беря различные функции, можно создавать разнооб-
разнейшие их суперпозиции. Но будьте осторожны! Пом-
ните определение суперпозиции двух функций: одна слу-
166
жит аргументом для другой. Значит, область значений
первой функции должна попадать в область определения
второй. Забвение этой важной детали может привести к
курьезам. За примерами ходить недалеко.
Мы только что говорили про суперпозицию показа-
тельной функции и параболы со знаком минус перед ней.
Замените в этом сочетании показательную функцию
функцией «корень квадратный», и вы увидите, что полу-
чившаяся при этом сложная функция имеет смысл лишь
при нулевом значении независимой переменной. Ведь ко-
рень квадратный нельзя извлекать из отрицательных
чисел!
Смешная картинка, не правда ли? А почему она
смешна? Потому что в ней есть подвох. Ваш взгляд
скользит по ногам человечка, затем, как вы думаете,
вдоль туловища, скрытого газетой, затем подходит к краю
газеты, ожидая встретить там голову... ан нет! Голова
оказывается совсем в другом месте. Фигура нарисован-
ного человечка оказывается разорванной.
Сравните теперь эти графики — какая из двух функ-
ций более похожа на человека с газетой?
Конечно, вторая! Прослеживая взглядом ход линии,
при подходе к значению аргумента а мы обнаруживаем,
что значение функции в этой точке, указанное жирным
кружком, совсем не то, что ожидалось, — как на приве-
денном рисунке.
Первая из функций, представленных графиками, на-
зывается непрерывной в точке а, вторая — разрывной в
этой точке.
167
Непрерывность и разрывность — одни из важнейших
понятий, применяемых для анализа функций.
Судя по элементарным функциям, непрерывность —
явление весьма распространенное в мире функциональ-
ных зависимостей, разрывность же, напротив, экзотиче-
ское, так что наглядные примеры разрывных функций
подберешь не вдруг. Но мы все-таки попробуем их поис-
кать.
Замечали ли вы, читатель, как гасят свет в кинотеат-
рах перед началом сеанса? Осветитель медленно повора-
чивает рычажок реостата, и свет едва заметно и непре-
рывно гаснет, превращаясь в тьму.
Попробуйте воспроизвести это медленное и непрерыв-
ное угасание дома, попытайтесь так же загасить люстру,
поворачивая рычажок тумблера. У вас ничего не получит-
ся, даже если вы крепко будете держать рычажок, не да-
вая ему срываться. По мере его поворота свет до поры
до времени ничуть не убудет в яркости — и вдруг мгно-
венно погаснет, так что тьма останется неизменной при
дальнейшем движении рычажка. Подобный переход от
света к тьме описывается разрывной функцией.
Конечно, не следует придавать чрезмерного значения
тому, что тумблеры чаще служат выключателями, чем
реостаты. И все-таки приведенный пример позволяет ут-
верждать, что разрывные функции необходимы для спи-
сания совсем не таких уж редкостных явлений и уст-
ройств.
168
Как же определить понятия непрерывности и разры-
ва?
Не мудрствуя лукаво, можно сказать, что непрерыв-
ная функция — это такая, график которой можно нари-
совать, не отрывая карандаша от бумаги. А разрывная—
такая, которую так не нарисуешь. к
К сожалению, математиков такое определение не удо-
влетворит, ибо фигурирующие в нем карандаш и бума-
га — понятия нематематические. В строгом математиче-
ском определении должны содержаться лишь логические
и количественные понятия.
Однако, поставив вне закона карандаш и бумагу, мы
вовсе не отказываемся от наглядности. Определение не-
прерывности мы дадим с помощью картинки — той са-
мой, с которой начинался этот отрывок, а точнее, с по-
мощью газеты, которую держит в руках человек.
Возьмем у человечка его газету и наложим ее на пер-
вый из вышеприведенных графиков, причем так, чтобы
ее центр совпал с той точкой на линии графика, где функ-
ция исследуется на непрерывность. (Собственно, от сло-
ва «газета» уже можно отказаться и говорить о прямо-
угольнике с центром в интересующей нас точке.)
Мы можем так обрезать газету с краев, что график
функции на всей ширине газеты не вылезет за ее верхний
и нижний края. Суть определения непрерывности заклю-
чается в том, что такое можно сделать с газетой любого
размера, с тетрадным листом, с почтовой открыткой, с
трамвайным билетом, с прямоугольником любой высо-
ты: задавшись этой высотой, прямоугольник можно за-
тем так сузить с боков, что в столь узком промежутке
отклонения функции от ее значения в исследуемой точ-
ке будут меньше, чем высота прямоугольника. Такая
функция и называется непрерывной в данной точке.
169
Функция называется разрывной в данной точке, если
описанная процедура оказывается невыполнимой. Гово-
ря точнее, если найдется прямоугольник такой высоты,
что, как ни сужай его с боков, на любом зауженном про-
межутке найдется точка, по крайней мере одна, в кото-
рой значение функции будет выступать либо за верхний,
либо за нижний край прямоугольника.
•
Если предыдущий раздел начинался со смешной кар-
тинки, то этот начнется с загадочной.
Часть графика функции,
расположенная правее неко-
торой точки а, закрыта. Не
видно также, какоое значе-
ние функция принимает в
самой точке а. Чтобы под-
черкнуть это обстоятельство,
видимая часть графика за-
кончена стрелочкой в той
точке, в которой обрывается
кривая.
Попробуйте угадать — каков дальнейший ход графи-
ка? Как 'ведет себя та его ветвь, что скрыта от глаз?
Возможны варианты.
Возможны варианты.
Читатель, конечно, догадывается, что стрелка справа
несет ту же смысловую нагрузку, что и стрелка слева.
Как и раньше, значение функции в исследуемой точке от-
мечено жирным кружком. Функция может оказаться и
не определенной в точке а, тогда жирного кружка на гра-
фике нет.
Если стрелка упирается в жирный кружок, то она
становится излишней, и ее можно убрать. Если поступить
так с первым графиком, то после исправления мы узна-
ем в нем обычную непрерывную функцию. Функцию,
170
представленную вторым графиком, естественно назвать
непрерывной справа, представленную третьим — непре-
рывной слева. Но непрерывной в точке а — повторяем!—
можно назвать лишь функцию, изображенную на первом
графике, все остальные, как принято говорить, испыты-
вают разрыв в точке а. к
Теперь приглядимся внимательнее к неисправленным
вариантам и подумаем: что у них общего, несмотря на
все их различия? Нет, не только левая ветвь, но и орди-
ната точки, в которую указывает стрелка левой ветви
(на графике она отмечена буквой А). Это число именуют
особым названием—левым пределом функции (или пре-
делом слева) в точке а. По симметрии число В называ-
ют правым пределом функции (или пределом справа) в
точке а.
Функцию естественно назвать непрерывной в точке
а, если у нее в этой точке предел слева совпадает с пре-
делом справа и оба предела совпадают со значением
функции в этой точке.
Как же определить понятие предела функции?
В строгом определении, очевидно, не годятся описа-
ния типа: «Ордината точки, к которой подходит взгляд,
следя за ходом графика». «Следить взглядом» — поня-
тие не математическое. Однако из него нетрудно извлечь
вполне математическую идею: ведь в нем слышится от-
звук уже знакомого нам термина «последовательность».
Что будет, если к значению а устремить слева неко-
торую последовательность аргументов, не совпадающих
с а? (Говорим «не совпадающих», потому что функция
может быть и не определена в точке а). К какой вели-
чине устремится последовательность значений функции?
К значению А — подсказывает график. Так вот, если та-
кое будет происходить при любом выборе последователь-
ности аргументов, сходящейся к слева, то число А на-
зывается левым пределом функции ( или пределом слева)
в точке а. Точно так же определяется и предел справа.
Годится для определения и «метод газеты». Размес-
тим «газету» так, чтобы ее центр очутился в точке гра-
фика, соответствующей предполагаемому пределу — ска-
жем, пределу слева. Если при любой высоте «газеты» ее
левую половину удается обрезать сбоку настолько, что
171
ветвь графика, идущая налево, на урезанном промежут-
ке не выступает ни за верхний, ни за нижний край газе-
ты, то предполагаемый предел действительно является
левым пределом функции в точке а. (Напомним, что зна-
чение функции в самой точке а в рассуждениях о преде-
ле не принимается во внимание.) Точно так же по «мето-
ду газеты» определяется и предел справа.
В обоих определениях можно рассматривать сразу
обе половинки окрестности точки а. Так, в правом опре-
делении можно строить такие сходящиеся к а последова-
тельности, члены которых могут быть как меньше, так и
больше а (но не совпадать с а). И если полученные при
этом последовательности значений функции всегда бу-
дут сходиться к некоторому пределу, то он будет назы-
ваться просто пределом функции в точке а. Во втором
определении можно рассматривать значения функции на
всем протяжении «газеты» как вправо, так и влево от
точки а. И если знакомая нам процедура урезания каж-
дый раз позволяет заключать линию графика в рамки
«газеты», то ее центр будет называться пределом функ-
ции в точке а.
Напоследок — одно замечание. На картинке, с кото-
рой начался предыдущий раздел, можно было закрыть
не правую, а левую половину. Домысливание графика,
согласно уже перечисленным вариантам, не даст нам ни-
чего принципиально нового, разве что в последнем слу-
чае. Здесь в результате дополнения может получиться
нечто вот такое:
Оба графика соответству-
ют разрывным функциям:
ведь ни та, ни другая не име-
ют конечного предела в точ-
ке а. Иногда в таких случа-
ях говорят, что функция в
этой точке стремится к бесконечному пределу, обраща-
ется в бесконечность, имеет бесконечный разрыв и т. п.
Линейная и показательная функции, парабола и ко-
рень квадратный — каждая из них непрерывна в любой
точке своей области существования. Неразрывна всюду,
как говорят в таких случаях.
Прекрасные примеры всюду непрерывных функций
172
дают процессы движения. Причина в том, что простран-
ство и время непрерывны.
Недаром мы так охотно прибегали к образам движе-
ния, начиная рассказ о непрерывности. Но заметим: ког-
да дело дошло до строгих определений, мы перешли к
статическим изображениям прямоугольников, обрезаемых
то с боков, то сверху и снизу.
Если угодно, в этом переходе отразился знаменатель-
ный перелом в развитии математики.
Создавая учение о функциях, математики поначалу
охотно доверялись наглядным кинематическим аналоги-
ям, памятью о которых в математической терминологии
до сих пор остались слова «стремится», «возрастает» и
т. п. Аналогии часто были весьма плодотворными, но не-
редко заводили в тупики парадоксов. Решение парадок-
сов стало возможным лишь после того, как французский
математик Коши выбросил из уже созданного учения о
функциях ненужные остатки динамических образов и за-
менил их статическими.
Так возник тот «язык эпсилон-дельта», на котором
ныне трактуются понятия непрерывности и разрывов,
предела и производной (название языку дали применяе-
мые в нем обозначения для разброса функции и аргу-
мента).
И любопытно: нарочито статичный язык позволил
объяснить многие запутанные феномены движения вро-
де пресловутых парадоксов Зенона, позволил подвести
логическую базу под те представления о движении, на
почве которых развивались первые идеи учения о функ-
циях.
Что ж, это нередкое явление в развитии науки: уче-
ный охотно доверяется подсказывающей силе нагляд-
ных образов, но затем логическим анализом проверяет
подсказки и все достигнутое благодаря им.
ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ
ИСЧИСЛЕНИЕ
Знаете ли вы, что такое ралли?
Это автомобильные гонки, успех в которых определя-
ется соблюдением программы соревнований. Скажем, со-
блюдением сроков, отведенных на отдельные этапы мар-
шрута: штрафные очки назначаются и за опоздание, и за
опережение.
...Двое сидящих за столом завтра займут свои места
в автомобиле. Водитель и штурман, сегодня они обсу-
ждают тактику движения на предстоящем этапе ралли.
Лучший вариант, казалось бы, прост: по известному
расстоянию до пункта назначения и отведенному време-
ни рассчитать среднюю скорость движения и стараться
придерживаться ее на всем пути. На графике зависимо-
сти пройденного пути от времени такой идеальный режим
изобразится прямой с угловым коэффициентом, равным
скорости.
Длина предстоящего этапа — 300 км, отпущенное на
него время — 3 ч. Средняя скорость движения получается
отсюда простым делением: 100 км/ч.
Однако постоянная скорость — идеал едва ли дости-
жимый. Выдерживать ее во все время пути затрудни-
тельно. Да и неразумно: трудные участки лучше просле-
довать помедленнее, а на ровных и прямых, напротив,
поднажать. Вот и рекомендуемый график движения, роз-
данный участникам ралли, заметно уклоняется от иде-
альной прямой: судя по графику, стартовать предлагает-
ся не спеша и наверстать упущенное к концу этапа.
Но как определить поточнее режим скорости, верность
которому обеспечит рекомендуемую зависимость пути от
времени? Иными словами, как, зная зависимость пути
от времени, вычислить скорость в каждый момент, мгно-
венную скорость? Чему, судя по приведенному графику,
она равна, например, через час с момента старта?
Средняя скорость на всем этапе в целом способна
дать лишь грубый оценочный ответ па такие вопросы:
174
отклонения от нее за все время пути могли быть весьма
велики.
А если ограничиться отрезком времени покороче? Не
станет ли от этого средняя скорость более точной оценкой
скорости мгновенной?
Измерим среднюю скорость автомобиля за час, начи-
ная с интересующего нас момента. Как свидетельствует
график, на этом отрезке времени она составляет 95 км/ч.
Повторим измерения на получасовом интервале от
выбранного мгновения. Средняя скорость упала до
86 км/ч.
Можно надеяться, что эта цифра уже точнее оценива-
ет мгновенную скорость в интересующий нас момент:
дуга графика, которой мы ограничились на сей раз, едва
заметно отклоняется от отрезка прямой, стягивающего
ее концы.
Это побуждает брать для измерений средней скоро-
сти все меньшие промежутки времени: пятнадцать минут,
десять, пять, три, две, одну, половину, четверть...
Вот результаты этих последовательных замеров: 83;
82; 81; 80,6; 80,2; 80,1, 80,05 км/ч...
Полученная последовательность явно обнаруживает
стремление к пределу. Избранный нами путь ведет к ка-
кой-то цели.
Сделаем решающий шаг к ней: устремим к нулю про-
должительность интервала, на котором измеряется
средняя скорость.
Измерения при этом будут становиться все труднее.
В самом деле, как вести их на протяжении десяти- или
стотысячных долей секунды, за которые автомобиль про-
ходит лишь доли миллиметра? На пути к пределу мы
где-то перейдем грань между автомобильным спортом и
чистой математикой. Но это не должно нас пугать, к это-
му мы и стремились и автомобилем воспользовались
лишь для того, чтобы удобнее и быстрее добраться до
цели.
Предел, к которому стремится средняя скорость на
уменьшающихся до нуля, стягивающихся к данному мо-
менту отрезках времени (если этот предел существует!),
и называется мгновенной скоростью в данный момент.
Посмотрим еще раз на построенные графики. Мы ви-
дим на них последовательность секущих. Каждая прохо-
дит через две точки кривой. Одна из этих точек общая
для всех секущих и неподвижна. Другая стремится к
176
ней, так что расстояние между ними последовательно
уменьшается до нуля, до слияния обеих точек в одну.
Предельное положение секущих есть касательная —
таково определение этой прямой.
Итак, исследуя вопрос о мгновенной скорости, мы
нашли способ построения касательной. Мы видим, что
она проходит через заданную точку графика пути с угло-
вым коэффициентом, равным мгновенной скорости в со-
ответствующий момент времени.
Так, камень, сорвавшийся с пращи, свободно летит по
касательной к прежней траектории, указывая направле-
ние своей скорости в момент отрыва.
Касательная к графику пу-
ти меняет наклон от точки к
точке. Каждому моменту вре-
мени соответствует свое значе-
ние мгновенной скорости. И
для каждого момента рассчи-
тать ее можно с помощью та-
кой же процедуры, с которой
мы только что познакомились.
Вот итог таких расчетов. Точно придерживаясь тако-
го графика скорости, наши автомобилисты в своем дви-
жении в точности воспроизведут рекомендуемый график
пути.
У водителя и штурмана, которые на предыдущих
страницах так тщательно готовились к ралли, неприят-
ности. Расчеты мгновенной скорости, точный ее график —
все насмарку. Стало известно, что сильные дожди размы-
ли дорогу на последних километрах предстоящего этапа.
Финишировать придется на пониженной скорости, а гро-
зящее отставание компенси- |
ровать прибавкой темпа на
среднем участке. Во всяком
случае график скорости при-
дется перестроить — напри-
мер, вот так.
Но вот вопрос: удастся
ли уложиться в заданный
срок, двигаясь в соответст-
вии с новым графиком скоро-
1 1 Заказ 8651
177
сти? Не сулит ли он в итоге штрафных очков за опозда-
ние или опережение? Как рассчитать пройденный путь
по графику скорости, которая столь резко изменяется за
время движения?
Если бы скорость была неизменна, расчет не пред-
ставлял бы трудностей: пройденный путь был бы равен
произведению скорости на время. Та же формула позво-
лила бы довольно точно оценить пройденный путь, ес-
ли бы скорость за время движения менялась бы не слиш-
ком сильно. Время в пути следовало бы умножить на не-
которое среднее значение скорости, лежащее где-то ме-
жду максимальным и минимальным, — подобно тому,
как на прежнем графике скорости тонкая горизонтальная
прямая лежала между наивысшей и наинизшей точками
жирной кривой.
С новым графиком скорости, казалось бы, так уже не
поступишь. Слишком резко колеблется кривая. Лишь на
среднем участке ее можно без большой ошибки заменить
горизонтальной прямой, то есть счесть движение равно-
мерным, скорость — постоянной и путь, пройденный за
это время, рассчитать по той самой формуле: «скорость на
время». График движения на этом промежутке времени
изобразится прямолинейным отрезком.
На крайних участках скорость меняется сильнее, и ес-
ли применить такой же прием, погрешность будет поболь-
ше. Но все-таки это лучше, чем ничего.
Так получается первый приближенный вариант гра-
178
фика движения — трехзвенная ломаная. Наклон каждо-
го звена равен прикинутой нами средней скорости дви-
жения на каждом из интервалов разбиения.
Кажется, этап будет пройден не в срок, а с опереже-
нием в добрую четверть часа. Но с уверенностью это ут-
верждать еще нельзя — больно уж неточен расчет. Боль-
шие сомнения вызывает выбор средней скорости, в осо-
бенности на крайних интервалах разбиения. График ско-
рости там слишком сильно отклоняется от идеализиро-
ванного среднего.
Будь интервалы поуже, эти отклонения были бы на-
верняка поменьше, а результаты расчета — поточнее.
И действительно, разделив интервалы пополам и по-
вторив на каждом из шести новых интервалов ту же про-
цедуру, мы вычертим ломаную более гладкую. Еще раз
измельчим интервалы. Новый график отличается от пре-
дыдущего уже слабее.
Проведем такие построения еще и еще раз, разбивая
отрезок времени на все более мелкие части. Можно за-
метить, что новые графики все меньше отличаются друг
от друга. Сам собой напрашивается предельный пере-
ход: устремить к нулю длину интервалов разбиения.
Ломаная превратится в гладкую кривую. Это и будет
график движения, для которого задана зависимость ско-
рости от времени.
График оказался удачным: придерживаясь намечен-
ного режима скорости, наши автомобилисты пройдут
предстоящий этап в назначенный срок.
Посмотрим еще раз на графики скорости, по которым
готовились к ралли знакомые нам водитель и штурман.
Расчет показал, что пути, пройденные в согласии с
тем и другим графиком, одинаковы.
11
179
Можно ли было заранее
по какому-то внешнему при-
знаку предсказать столь за-
мечательное совпадение?
Такой признак на рисун-
ках отмечен штриховкой.
Это площадь под той и дру-
гой кривой, точнее, площадь
той и другой заштрихован-
ной фигуры, называемой
криволинейной трапецией.
Чтобы убедиться в спра-
ведливости признака, посмо-
трим еще раз, как мы строи-
ли график пути по графику
скорости. Возьмем один из
первых приближенных вари-
антов графика — ломаную.
Каждое из ее звеньев
мыслилось нами как график
некоторого равномерного
движения. Путь, пройденный
в таком движении — подъем
звена, — равен произведе-
нию времени на скорость.
От маленького звенышка на графике пути перейдем
взглядом к соответствующему интервалу времени на гра-
фике скорости. Только что вычисленное произведение
приобретает здесь смысл площади — площади прямо-
угольного столбика, имеющего этот интервал времени ос-
нованием, а отмеченную горизонтальной ступенькой
среднюю скорость — высотой.
Звено за звеном — столбик к столбику. Последователь-
ное их сложение дает величину, с одной стороны, почти
равную пройденному пути, с другой — почти равную пло-
щади под кривой скорости. Говорим «почти», потому что
замена графика скорости лесенкой горизонтальных сту-
пенек чревата погрешностями.
В результате предельного перехода это «почти» про-
падет, и остается точный вывод: площадь под кривой ско-
рости на некотором отрезке времени численно равна пу-
ти, пройденному за это время в таком режиме скоро-
сти.
Заметим: если скорость отрицательна, отрицателен и
180
путь, поскольку он пройден вспять. Иными словами, ес-
ли кривая скорости проходит под осью абсцисс, очерчен-
ная ею площадь получается отрицательной. По этому по-
воду говорят, что описанным способом площадь опреде-
ляется в алгебраическом смысле.
И вот что еще стоило бы заметить напоследок. Поня-
тие площади кажется весьма простым и не нуждающим-
ся в комментариях. А между тем если разобраться, мы
умеем определять площадь лишь для прямоугольников
(как произведение сторон) да для тех простых фигур,
которые удается перекроить в прямоугольник, например
для треугольников.
Читатель, вероятно, захочет добавить сюда и круг,
площадь которого выражается общеизвестной формулой
л/?2. Но мы воздержимся от добавки: ведь эта формула
получается отнюдь не перекройкой круга в прямоуголь-
ник (иначе квадратура круга не была бы проблемой!), а
с помощью процедуры, весьма похожей на описанную
выше: сначала круг разрезается на сектора, затем секто-
ра заменяются треугольниками, треугольники неограни-
ченно утоньшаются... Суть приема та же: криволиней-
ная фигура заменяется мозаикой из кусочков с прямыми
краями, площади которых определяются по классической
формуле, затем в процессе предельного перехода мозаи-
ка дробится так, чтобы площадь отдельного кусочка стре-
милась к нулю.
Так через предельный переход классическая формула
прямоугольника обобщается на криволинейные фигуры.
Настало время назвать своими именами вещи, о ко-
торых только что шла речь. Тем более что имена эти
громкие, широко распространенные, пользующиеся заслу-
женным уважением и почетом.
Процедура, позволяющая находить мгновенную ско-
рость движения, используя зависимость пути от време-
ни, называется дифференцированием, а число, которое
получается в результате дифференцирования, — произ-
водной. Итак, мгновенная скорость тела в данный момент
есть производная пути по времени в данный момент.
Каждому моменту времени соответствует свое значе-
ние производной. Определенная таким образом функция
называется производной по отношению к исходной, опи-
сывающей зависимость пути от времени.
181
Обратная процедура, позволяющая определять прой-
денный путь, используя зависимость скорости от време-
ни, называется интегрированием, а число, которое полу-
чается в результате интегрирования, — определенным ин-
тегралом. Итак, путь, пройденный телом от одного за-
данного момента времени до другого, есть определенный
интеграл от скорости по времени, взятый от начального
момента (он именуется нижним пределом интегрирова-
ния) до конечного (верхнего предела интегрирования).
За верхний предел интегрирования можно принимать
различные моменты времени, и каждому будет соответ-
ствовать свое значение пройденного пути, свое значение
определенного интеграла. Заданная таким образом функ-
ция называется первообразной по отношению к исходной,
описывающей зависимость скорости от времени.
...<Вы знаете, Зося, — убеждал Остап Бендер ЗосюСи-
ницкую, — на каждого человека, даже партийного, давит
атмосферный столб весом 214 кило».
Остап с его незнанием точных наук слишком занизил
цифру. Названная им величина была бы справедлива
для весьма большой высоты над уровнем моря. Ведь ат-
мосферное давление спадает с подъемом вверх, притом
со все убывающей скоростью. Любопытно, что этот спад
связан с другим характерным признаком больших вы-
сот, разреженностью воздуха, и связан самым непосред-
ственным образом: скорость, с которой на той или иной
высоте атмосферное давление убывает по мере подъема,
в точности равна удельному весу воздуха на этой высоте.
И если бы вам захотелось определить эту величину, зная
зависимость давления от высоты, к вашим услугам опе-
рация дифференцирования.
К дифференцированию прибегают всякий раз, когда
встает вопрос о скорости изменения какой-либо функции
по мере изменения аргумента, когда эта скорость оказы-
вается непостоянной, а определять ее требуется точно
для любого значения аргумента.
Заряд батареи, питающий электрическую цепь, убы-
вает со временем. Скорость убывания есть ток. Он может
оказаться различным в разные моменту и потому дол-
жен определяться как производная заряда по времени.
Тепло, содержащееся в нагреваемом теле, нарастает
с ростом температуры. Интенсивность нарастания есть
182
теплоемкость —своя для каждой температуры. И здесь
не обойдешься без дифференцирования — теплоемкость
есть производная количества тепла по температуре.
Не забудем, что дифференцирование служит еще и
средством для проведения касательных к кривой. Угло-
вой коэффициент касательной — эток производная функ-
ции, графиком которой служит кривая; производная бе-
рется при том значении аргумента, который соответству-
ет точке касания.
Подобно тому как дифференцирование оказывается
полезным не только при определении мгновенной скоро-
сти движения, так и интегрирование применяется не толь-
ко тогда, когда требуется рассчитывать пройденный путь
по времени и скорости.
Операция, обратная дифференцированию, интегриро-
вание позволяют определять, как зависит от времени за-
ряд, если в каждый момент известно значение тока, как
растет с температурой количество тепла в теле, если для
каждой температуры известна его теплоемкость.
Короче говоря, интегрирование позволяет рассчиты-
вать суммарный итог непостоянного изменения.
Не забудем, что интегрирование служит еще и средст-
вом для вычисления площадей. Площадь под кривой —
это определенный интеграл от функции, графиком кото-
рой служит кривая, взятая в пределах, между которыми
задана функция.
Несколькими страницами ранее, когда мы развешива-
ли ярлычки в витрине математических операций, мы сде-
лали вынужденный перерыв. И по-видимому, кое-кто из
читателей это почувствовал.
В самом деле, зачем говорить «определенный инте-
грал», если не существовал бы термин «неопределенный
интеграл»?
Е'|Сли такой вопрос возник у читателя, наш ответ не
заставит себя ждать.
Возьмем два графика, на одном из которых как функ-
ция времени изображена скорость движения некоторого
тела, а на другом — путь, пройденный телом.
Мы уже знаем, как во всеоружии терминологии опи-
сать родственные отношения между обеими функциями.
183
100 200 км/ч о 100 200 300 км
По отношению к скорости
путь есть первообразная по
времени. По отношению к
пути скорость есть производ-
ная по времени. Угловой ко-
эффициент касательной, по-
строенной в любой точке гра-
фика пути, равен высоте кри-
вой скорости над той же точ-
кой оси абсцисс.
А теперь возьмем график
пути и аккуратно, строго по
вертикали, без искажений
сдвинем нарисованную на
нем кривую вверх или вниз.
В любой точке кривой угло-
вой коэффициент касатель-
ной при этом останется
прежним. «Сдвинутая» функ-
ция по-прежнему останется
первообразной по отноше-
нию к скорости.
Сдвинуть функцию вверх или вниз — это значит при-
бавить к ней или отнять от нее функцию-константу.
Итак, первообразная плюс любая константа есть снова
первообразная.
Первообразных для одной и той же функции оказы-
вается бесконечно много. Все их семейство называется
неопределенным интегралом.
Это кажущееся излишество—не роскошь, а отраже-
ние природы вещей.
Когда вы отправляетесь в дальний путь на автомоби-
ле, на счетчике километров может стоять любая строчка
цифр. От этого, разумеется, не зависит пройденный путь.
Чтобы определить его, нужно из показаний счетчика в
момент финиша вычесть то, что показывал он в момент
старта.
Когда вы направляетесь в магазин за сметаной, вы
можете взять банку любого веса. От этого не зависит сто-
имость покупки. Вес отпущенной вам сметаны продавец
определяет как разность весов банки наполненной и
банки порожней.
В физике подобные примеры встречаются на каждом
шагу. Взять хотя бы выражение «разность потенциалов».
184
Ток в электрической цепи определяется именно ею, но
отнюдь не абсолютным значением потенциала на том или
другом конце цепи. Сходную особенность можно подме-
тить, когда речь идет об энергии или энтропии. Говорят,
например, что в термодинамически замкнутой системе
энтропия при любом реальном процессе либо возрастает,
либо (если процесс обратимый) остается неизменной.
Здесь опять-таки нет речи об абсолютном значении эн-
тропии, а говорится лишь о ее приращениях.
Попытавшись разобраться в причинах таких особен-
ностей, вы обнаружите, что все упомянутые физические
величины определяются с помощью интегрирования. На-
чало отсчета каждой из них можно «сдвигать» по про-
изволу.
Все будет происходить при этом точно так же, как
при расчетах пути по скорости. Путь — первообразная
для скорости. Его можно отсчитывать от любой началь-
ной точки. Но приращение пути от одного момента вре-
мени к другому при этом всегда будет оставаться рав-
ным одному и тому же числу — определенному интегра-
лу от скорости, взятому от одного из указанных момен-
тов времени до другого.
И это общий принцип: определенный интеграл, взя-
тый от некоторой функции в указанных пределах, есть
разность между значениями первообразной в указанных
предельных точках, на какой высоте над осью абсцисс
ни пролегал бы график первообразной.
Последнее замечание содержит в себе важный рецепт
для вычисления определенных интегралов. Он носит на-
звание формулы Ньютона — Лейбница.
Формула Ньютона - Лейбница... Люди, чьи имена
пишутся через черточку в названии открытия, невольно
кажутся сотрудниками. Однако с Ньютоном и Лейбни-
цем дело обстоит как раз наоборот. В свое время меж-
ду ними шли яростные споры о приоритете в создании
дифференциального и интегрального исчисления.
Сейчас их конфликту не придают большого значения:
считается, что к своим открытиям они пришли независи-
мо друг от друга и честь первооткрывателей делят по-
ровну. Оттого и пишутся через примирительную черточку
их фамилии в названии знаменитой формулы.
185
Впрочем, в чем Лейбницу повезло больше, так это
в системе обозначений. Здесь время решительно встало
на его сторону. Кто помнит сейчас о прямоугольной
рамке вокруг символа функции, с помощью которой
Ньютон предлагал обозначать интеграл? А точка над
символом функции, у Ньютона обозначавшая производ-
ную, ныне применяется лишь в механике — видимо, из
уважения к тому, кто впервые сформулировал ее законы.
Обозначения Лейбница между тем завоевали всеоб-
щее признание. Вот они на рисунке слева внизу.
Общих слов о дифференцировании и интегрировании
было сказано довольно. Настало время примеров.
Что будет, если продифференцировать логарифм?
Что станет с косинусом после интегрирования?
186
т
187
На эти вопросы отвечают графики. Их оси не разме-
чены масштабными засечками — это не так уж важно.
Важно лишь отметить, что аргумент тригонометриче-
ских функций (синуса и косинуса) в приведенных соот-
ношениях выражается в радианной мере.
Тому, кто желает поглубже вникнуть в закономерно-
сти приведенных соотношений, мы предлагаем повни-
мательнее разобрать какую-либо строчку этих таблиц —
скажем, последнюю.
Производная синуса есть косинус, гласит пара графи-
ков, соединенных равенством. Выражаясь графическим
языком, высота косинусоиды в каждой точке равна угло-
вому коэффициенту касательной к синусоиде в той же
точке.
По мере отхода от начала координат косинусоида
идет на убыль, и в соответствии с этим угловой коэффи-
циент касательной, построенной к синусоиде, становит-
ся все меньше. В той точке, где косинус обратился в
нуль, касательная к синусоиде горизонтальна, ее угло-
вой коэффициент тоже нуль. В дальнейших точках ее
угловой коэффициент отрицателен, и в соответствии с
этим косинусоида ушла под ось абсцисс.
Поскольку косинус по отношению к синусу есть про-
изводная, синус по отношению к косинусу служит пер-
вообразной. Геометрический образ первообразной — это
площадь. По последней строчке второго столбика ра-
венств проследим за тем, как изменяется площадь под
графиком косинуса, если ее вычислять интегрировани-
ем от начала
него предела.
координат до некоторого подвижного верх-
Эти изменения сравним с поворотами си-
нусоиды.
Покуда косинусоида про-
ходит над осью абсцисс, пло-
щадь под ней положительна
и нарастает, и в соответст-
вии с этим синусоида, вый-
дя из начала координат,
идет вверх. Высота косину-
соиды уменьшается, все
меньшие добавки к площади
дает увеличение верхнего
предела интегрирования, и
рост синусоиды замедляется.
Косинусоида ушла под ось
188
абсцисс, добавки к площади стали отрицательными, и си-
нусоида пошла на спад.
И вот в некоторой точке она обратилась в нуль. При-
смотритесь теперь к графику косинусоиды: вертикаль,
соответствующая верхнему пределу интегрирования, ог-
раничивает справа фигуру, распадающуюся на две ча-
сти; они равны друг другу, но лежат по разные стороны
от оси абсцисс, так что их площади имеют разные сто-
от оси абсцисс, так что их площади имеют разные знаки,
поэтому суммарная площадь этой двухлепестковой фи-
гуры в алгебраическом смысле равна нулю.
Читателю, который чувствует себя вполне освоив-
шимся с приведенными таблицами, мы хотели бы пред-
ложить несложную задачу: из функций, встречающихся
в первой таблице, выбрать такие три, чтобы первая бы-
ла производной от второй, а вторая —- производной от
третьей.
Готово? Убедитесь в правильности своего выбора.
А теперь смотрите внимательнее: мы превратим эту
тройку в пару.
Понятен ли вам смысл
этой записи? Не правда ли,
ее расшифровка очевидна:
операция дифференцирова-
ния, дважды примененная к
параболе, дает в результате
константу.
В подобной очевидно
сти — огромное достоинство
символического языка, ко
торый Лейбниц разработал
для дифференциального и
интегрального исчисления.
Итог этого небольшого
раздела подведем определе-
нием: результат двукратного
дифференцирования функ-
ции называется второй производной. Сходным образом
определяются третья производная, четвертая и т. д.
Воспользуемся еще раз автомобилем, на котором мы
так стремительно ворвались в область дифференциаль-
189
ного и интегрального исчисления. По графику зависимо-
сти пройденного пути от времени мы построили тогда
другой график, который показывал, как зависит от вре-
мени мгновенная скорость движения. Он получался из
первого дифференцированием — скорость есть производ-
ная пути по времени.
Взяв этот график, произведем над ним те же опера-
ции: определим скорость 'изменения скорости, найдем
'производную от производной, вторую производную шути
по времени. Короче говоря, найдем ускорение. Вот он —
результат дифференцирования скорости.
Ускорение... Честь введения этого понятия в механи-
ку (принадлежит Галилею. Великому физику посчастли-
вилось— он шел к своим выводам от изучения движений,
которые ускоряются простейшим образом. Он исследовал
падение тел и нашел, что все они падают на Землю с од-
ним и тем же ускорением, неизменным по ходу падения.
Факт замечательный! Располагая им, мы сможем поч-
ти автоматически повторить открытия Галилея — устано-
вить законы падения тел, то есть определить, по какому
графику нарастает со временем путь, пройденный падаю-
щим телом, — пусть это будет, к примеру, камень.
Сконструируем формулировку задачи из уже приме-
нявшихся картинок и символов. Искомый график заме-
ним картинкой со знаком вопроса, приписав к нему слева
знак второй производной. Отметим, что речь идет об ус-
корении: поставив справа знак равенства и график функ-
ции-константы, покажем, что это ускорение известно
нам — оно постоянно, не зависит от времени (рис.
внизу).
Такая комбинация уже попадалась нам на одной из
предыдущих страниц. Там она не содержала неясностей:
на месте вопроса была вычерчена парабола. Стало быть,
путь, пройденный «падающим камнем, растет со временем
по закону параболы.
190
Касательная, проведенная к нашей параболе в нача-
ле координат, горизонтальна, ее угловой коэффициент
равен нулю. Это значит, что камень начинает падать с
нулевой начальной скоростью, без толчка. Именно тако-
му случаю соответствует найденное нами решение.
Найденному решению можно подыскать наглядное
подтверждение. Падающий камень нужно толкнуть вбок.
Приданное ему горизонтальное движение сохранится —
смещение камня по горизонтали будет нарастать пропор-
ционально времени. А вертикальное, как мы уже знаем,
пропорционально квадрату времени. Траектория камня
будет параболой.
•
Особенность только что решенного нами уравнения
заключалась в том, что неизвестная функция стояла под
знаком производной. Уравнения подобного сорта называ-
ются дифференциальными. Порядок наивысшей произ-
водной, входящей в дифференциальное уравнение, назы-
вается его порядком. Например, уравнение, решенное на-
ми, — второго порядка.
Найти неизвестную функцию из дифференциального
уравнения — значит, как принято говорить, проинтегри-
ровать его, и если искомая функция найдена, ее называ-
ют решением дифференциального уравнения, а ее гра-
фик — интегральной кривой.
Наконец, еще один термин. Для его пояснения вернем-
ся вновь к задаче Галилея. Она решена нами не пол-
ностью. Пока что мы умеем рассчитывать лишь такое
падение камня, когда оно начинается без начальной ско-
рости, говоря попросту, когда камень выпущен из рук. А
если его подбросить вверх или толкнуть вниз?
В поисках ответа вспомним, как когда-то, найдя пер-
вообразную для заданной функции, мы сдвигали постро-
енную кривую вверх и вниз. От таких сдвигов первооб-
191
разна не переставала быть первообразной все для той
же исходной функции. И еще подумаем о том, что мыс-
лимы также сдвиги первообразной вшраво и влево —
это все равно, что изменить начало отсчета аргумента (в
нашей задаче — времени падения).
После этого возьмем интегральную кривую, постро-
енную нами для падения камня без начальной скорости,
возьмем эту параболу и, не поворачивая, передвинем ее
по координатной плоскости так, чтобы она проходила че-
рез начальную точку с должным угловым коэффициен-
том, равным начальной скорости, которая придана кам-
ню толчком вниз или броском вверх. Оказывается, это и
будет решением поставленной задачи.
Сохраняя свою форму, парабола свидетельствует, что
законы движения остаются прежними: это все то же рав-
ноускоренное падение. Сдвигаясь по координатной плос-
кости, парабола указывает, что начальные условия дви-
жения были иными.
Такое можно сказать про любой процесс: не изменяя
ни на миг законам своего течения, он будет все же течь
каждый раз по-особому в зависимости от того, каково со-
стояние в начальный момент.
Стало быть, решая дифференциальное уравнение,
описывающее процесс, необходимо учитывать начальные
условия.
Изменение начальных условий, как правило, приводит
к перестройке интегральной кривой. В задаче Галилея
все обошлось простым сдвигом параболы, но это скорее
редкое исключение, объясняемое простотой дифференци-
ального уравнения.
Если вы думаете, что дифференциальные уравнения—
это вещи, встреча с которыми в обыденной жизни исклю-
чена, то отложите на время эту книгу в сторону, возьми-
те свой транзистор, включите его и настройтесь на вол-
ну, разносящую по эфиру звуки легкой музыки.
А пока вы вращаете рычажок настройки, разрешите
коротко, в двух словах, прокомментировать ваши дейст-
вия на языке радиотехники и математики.
Если бы вы заглянули во внутренности своего радио-
ящика, то обнаружили, что рычажок настройки соединен
с конденсатором, а тот в свою очередь связан в замкну-
192
тую цепь с катушкой и другими деталями, важными сей-
час для нас лишь тем сопротивлением, которое они ока-
зывают электрическому току.
Конденсатор, катушка, сопротивление — вот радио-
техническая троица, образующая сердце каждого прием-
ника, колебательный контур. Частоту биений этого серд-
ца, частоту пульсаций заряда на конденсаторе регулирует
настроечный рычажок; когда она совпадает с частотой
передающей станции, приемник по законам резонанса
воспроизводит звуки, рассылаемые по эфиру антеннами
передатчика. Как же рассчитать частоту «пульсаций за-
ряда?
Всякая замкнутая электрическая цепь живет и рабо-
тает по закону Кирхгофа: если в цепи нет источников то-
ка, сумма падений напряжения на всех ее участках рав-
на нулю. В нашем контуре таких участков три — конден-
сатор, сопротивление, катушка. Напряжение на конден-
саторе пропорционально заряду, на сопротивлении — то-
ку, производной заряда по времени, на катушке — произ-
водной тока по времени, то есть второй производной за-
ряда. Коэффициентами пропорциональности между чле-
нами перечисленных пар служат соответственно емкость
конденсатора, величина сопротивления, индуктивность
катушки.
Определив падение напряжения на каждом из участ-
ков цепи, просуммируем их и «приравняем к нулю — «и вот
оно, уравнение заряда!
Заряд входит в него под знаком первой и второй про-
изводной. Уравнение получилось дифференциальное.
Вот так нежданно-негаданно на волнах легкой музы-
ки выплыло нечто, что в обыденной жизни, казалось бы,
встречаться не может — дифференциальное уравнение.
Мы не хотим утомлять вас перечнем других приборов
и явлений. Можете поверить нам на слово: там, где тре-
буется рассчитывать не только некоторые состояния, но и
изменения состояний, процессы, движения в самом ши-
роком смысле слова, — там всюду математик приходит к
дифференциальным уравнениям.
«Лишь дифференциальное * исчисление дает естество-
знанию возможность изображать математически не толь-
ко состояния, но и процессы: движение», — писал Эн-
гельс.
12 Заказ 8651
193
Картина мира, которую нарисовала классическая фи-
зика, выполнена в технике дифференциальных уравне-
ний.
Завоевывая для математики все более широкие сфе-
ры приложения, дифференциальное и интегральное ис-
числение одновременно наводило порядок и в тылах этой
древней науки. Оно давало универсальные и эффектив-
ные методы для решения многих задач, которые по своей
статической сути принадлежат к прежней, элементарной
математике, но с которыми та не могла совладать.
Элементарная математика знает формулы для объе-
ма пирамиды, конуса, шара. Каждая из этих формул да-
лась первооткрывателям приемом оригинальным и непо-
вторимым. Это скорее драгоценные камни, нежели строи-
тельный материал, из которого можно «смонтировать»
общую формулу для объема любого тела.
Как, например, вычислить объем лимона? Задача ка-
жется неразрешимой.
А между тем каждый из нас делает первый шаг к ее
решению, готовя лимон к употреблению, нарезая его на
дольки. С того же начал бы и знаток интегрального ис-
числения, готовясь вычислить объем этого эллипсоида
вращения из рода цитрусовых. Объем лимона равен сум-
ме объемов долек; для каждого из них он приближенно
выражается произведением высоты на площадь основа-
ния — либо верхнего, либо нижнего, а можно взять и
любую промежуточную величину.
В этом нетрудно усмотреть ту же схему интегрирова-
ния, по которой мы вычисляли площади криволинейных
фигур. Под таким углом зрения теперь видна вся дорога
до поставленной цели: сначала определить функцию, по
которой сечение лимона меняется вдоль его оси, для этой
функции найти первообразную и наконец воспользовать-
ся формулой Ньютона — Лейбница.
194
Так, в чисто статические на первый взгляд задачи
входят движение, переменные величины, а вместе с ни-
ми — методы дифференциального и интегрального исчис-
ления. И задачи, не разрешимые в рамках элементарной
математики, элементарно решаются благодаря новому
подходу, суть которого составляют йеременные величины.
Недаром вся созданная на их основе математика, обес-
печившая становление и развитие классической физики,
называется высшей в отличие от прежней, элементарной.
В популярной книге английского математика Литлву-
да «Математическая смесь» есть страничка, где приведе-
на забавная классификация углов из старого справочни-
ка по альпинизму:
перпендикулярно — 60°;
абсолютно перпендикулярно — 65°;
нависающе — 70°.
Смешно? Смешно. Но этот пример мы привели не
только ради смеха. Тут есть над чем поразмышлять со
всей серьезностью.
65°, 70°... Градусами измеряются углы. А углы обра-
зуются двумя прямыми. Но скажите, читатель: видели ли
вы когда-нибудь горы с прямыми склонами, словно у
египетских пирамид? Нет? Так что же тогда имеют в ви-
ду, когда говорят о наклоне непрямой поверхности или
линии?
Оставим пока поверхности в стороне, ограничимся
для начала линиями. На какой-нибудь гладкой линии от-
метим точку и спросим: каков в этой точке наклон ли-
нии?
Даже если вы не альпинист, ответ у вас, надеемся,
готов. Его подсказывает интуиция и содержание преды-
12'
195
дущих страниц. В отмеченной точке нужно построить ка-
сательную к кривой. И вот они — две прямые: касатель-
ная и горизонталь. Теперь уже можно говорить про угол.
А к углу можно приложить транспортир.
Но лучше в качестве меры угла использовать угловой
коэффициент касательной, то есть производную. И гово-
рить: наклон кривой в точке А равен плюс двум, наклон
в точке В — минус половине.
Мы описали этими словами изображенное на графи-
ке. Заметим попутно, что для опытного математика ссыл-
ка на график после таких слов становится излишней. Он
и без картинок представляет, что минус половина — это
пологий спуск, а плюс два — крутой подъем кривой, если
прослеживать ее слева направо.
В таких случаях математик часто обращает внимание
не столько на величину чисел, сколько на их знаки. Знак
без числа — это, конечно, потеря точности. Но зато при-
быль в общности. Ведь если наклон меняется плавно, то
рост остается ростом на некотором промежутке, а не
только в той его точке, где положительная производная
зарегистрировала рост. Положительный знак производ-
ной в промежутке — свидетельство возрастания функции
в этом промежутке, отрицательный — свидетельство спа-
да. Производная сменила знак в некоторой точке — зна-
чит в этой точке соседствуют участки роста и спада.
Значит, это точка экстремума — максимума или миниму-
ма. Спад сменился ростом — минимум. Рост сменился
спадом — максимум. (Заметим: если производная суще-
ствует в точке экстремума, то там она обязательно рав-
на нулю. Это облегчает поиск экстремумов).
Но расти и снижаться можно по-разному. Рост может
становиться все быстрее, а может, наоборот, замедлять-
ся и даже смениться спадом. Спад тоже может либо уси-
ливаться, либо тормозиться и даже перейти в рост. Осо-
бенности такого рода мы характеризовали словами «вы-
пуклость» и «вогнутость».
Выпуклость — это замедляющийся рост и нарастаю-
щий спад. Проследите взглядом ход нашей выпуклой
кривой слева направо, в направлении, указанном стрел-
кой оси абсцисс: наклон кривой уменьшается, уменьша-
ется производная.
А теперь немножко поиграем словами. Выпуклость —
это уменьшение производной. Уменьшение — это отрица-
тельная производная. Уменьшение производной — это от-
196
рицательная производная производной. Это отрицатель-
ная вторая производная. Итак, выпуклость — это отрица-
тельная вторая производная.
Вдумчивый читатель, конечно, разглядит точный
смысл за этой словесной игрой и согласится с ее резуль-
татом: отрицательный знак второй^ производной — свиде-
тельство выпуклости. Точно так же положительный знак
второй производной — свидетельство вогнутости.
Естественно предположить далее, что абсолютная ве-
личина второй производной может служить мерой кри-
визны— той скорости, с которой изменяется наклон каса-
тельной по мере роста аргумента. Предположение вер-
ное, однако точная формула кривизны содержит, кроме
второй, еще И первую производную и слишком сложна,
чтобы выводить ее здесь.
Точки, в которых выпуклость сменяется вогнутостью
или наоборот, — это точки перегиба. В них вторая про-
изводная меняет знак, обращается в нуль. Касательная в
таких точках пересекает кривую.
Наконец, еще об одной роли второй производной. Она
позволяет рассортировать экстремумы на максимумы и
минимумы. Ведь когда их ищут по нулям первой произ-
водной, они становятся неразличимы — первая производ-
ная обращается в нуль и там и тут. Вторая производная
все ставит на свои места. Вот, скажем, максимум. Это
макушка выпуклой кривой, а выпуклость — это отрица-
тельный знак второй производной. Стало быть, нуль пер-
вой шроизводной в сочетании с отрицательным значением
второй — безошибочное свидетельство максимума. Точно
так же нуль первой производной в сочетании с положи-
тельным значением второй — свидетельство мини-
мума.
И снова в путь! В путь по той дороге, которую мы ос-
воили незадолго до знакомства с производными.
Мы ехали по ней из пункта А в пункт Б и отмечали:
рост... максимум... спад... минимум... опять рост... выпук-
лость... перегиб... вогнутость... После разговора о диффе-
ренцировании мы можем разметить знакомый путь до-
рожными знаками. Ими послужат первая и вторая про-
изводные.
И тогда рассказ о рельефе дороги сократится до ком-
пактной таблицы из четырех строк чисел и символов.
197
X 0 4 7 11 14 17 20 23 27
У 3 3 2 1 1,5 2 3 4 3
У' 0 0 0 — -0,5 - 0 + 0,4 + 0 + 0,4 + 0 - -0,5
У" 0 0 0 — 0 + + + 0 — 0 + + + + 4- +
Вас озадачивает эта шифровка? Мы поможем вам про-
честь ее и восстановить по ней картину рельефа.
Числа первых двух строк таблицы — это координаты
характерных точек — экстремумов и перегибов, отмечен-
ных нулями в третьей и четвертой строке соответственно.
Их определяют, отыскивая нули первой и второй произ-
водных.
Нанесем эти точки на график. В точках перегиба от-
метим наклон, указанный в соответствующих клетках
третьей строки, в точках экстремумов расставим дуж-
ки— выпуклые в точках максимума и вогнутые в точках
минимума; отличать их друг от друга можно по данным
все той же таблицы — либо по знаку второй производ-
ной, либо по тому, с какого на какой меняет в этих точ-
ках свой знак первая производная.
Теперь остается соединить все эти элементы плавной
кривой — и схематический набросок рельефа дороги го-
тов.
Стоит присмотреться к той точке, где нуль первой
производной совпал с нулем второй. Это не экстремум, а
горизонтальная точка перегиба. В точках экстремума
нуль первой производной сочетается с ненулевым зна-
чением второй.
198
Всякий раз, когда мы вели разговор о дифференциро-
вании какой-либо функции, на ее графике неизменно
присутствовала касательная — наглядный образ произ-
водной. s
Прослеживая график функции на
подходе к точке касания, мы видим,
что он все теснее сближается с ка-
сательной, а на некотором проме-
жутке совсем не отличим от нее.
хотя общая точка у обеих линий
лишь одна: точка касния.
И мы понимаем, что дело здесь
не просто в грубости наших чертеж-
ных инструментов. Ведь стоит про-
вести через ту же точку другую пря-
мую, с другим угловым коэффициен-
том— и ощущение слитности пропадает, хотя и на этот
раз расхождение между кривой и прямой в окрестности
их общей точки уменьшается, стремясь к нулю, когда к
нулю стремится ширина окрестности.
В чем же здесь дело? Как выразить его суть строгим
математическим определением? Чем выделяется каса-
тельная среди всех прямых, проходящих через одну и ту
же точку кривой?
Тем, что расхождение ме*жду ней и кривой в окрестно-
сти точки касания стремится к нулю быстрее, чем шири-
на окрестности, когда та сужается. С другой прямой —
иначе: расхождение между ней и кривой стремится к
нулю почти пропорционально ширине окрестности.
Подойдем к делу с другой стороны. Возьмем график
какой-нибудь функции, выберем на нем какую-нибудь
точку, оградим ее некоторой окрестностью и попытаемся
провести через эту точку такую прямую, чтобы расхожде-
» ние между ней и графиком функции по мере сужения ок-
рестности стремилось к нулю быстрее, чем ширина окре-
стности. Если это удается сделать, функция называется
дифференцируемой в данной точке. При этом прямая на-
илучшего приближения неизбежно оказывается касатель-
ной: ее угловой коэффициент равен производной от
функции в выбранной точке.
К сожалению, нет правил без исключений. За любую
наугад взятую функцию нельзя поручиться в том, что она
199
будет дифференцируемой во всякой точке
из своей области определения.
Вот несколько экспонатов из музея
исключений.
Как ни прикладывай прямую к уголку,
изображенному на первом графике, рас-
хождение между ней и линией графика в
окрестности острия не будет вести себя
так, как этого требует определение диф-
ференцируемости. Стало быть, изобра-
женная здесь функция не дифференци-
руема в точке излома.
Неудача обязательно постигнет нас и
в той точке, где функция терпит разрыв
(второй график). Обратите внимание на
этот пример: чтобы быть дифференцируе-
мой в некоторой точке, функции необхо-
димо быть непрерывной в этой точке.
Необходимо, но недостаточно — об
этом свидетельствует третий график.
К счастью, элементарные функции, которые служили
нам примерами ранее, не доставят нам подобных разоча-
рований. Каждая из них дифференцируема в каждой
точке своей области определения.
Стоит отметить, что производная любой элементар-
ной функции есть функция элементарная: производная
логарифма — это гипербола, производная синуса — коси-
нус и так далее.
После разговора о дифференцируемости естественно
поговорить об интегрируемости.
С интегрированием мы познакомились при расчете
пройденного пути по переменной скорости. Мы оставили
тогда неосвещенной одну неясность. Разделив на несколь-
ко промежутков отрезок времени, на котором был задан
график мгновенной скорости, мы затем заменили кривую
лесенкой горизонтальных ступенек. Каждая ступенька
располагалась где-то между максимальным и минималь-
ным для своего промежутка значением мгновенной ско-
рости.
Но где именно? Как выбирать ее высоту?
Этот вопрос решается так: если независимо от выбо-
ра (как высоты ступенек, так и точек, которыми интервал
200
делится на промежутки) описанная процедура интегри-
рования всегда приводит к результату и притом к од-
ному и тому же, то такая функция называется интегриру-
емой.
Интегрирование — операция, гораздо менее прихотли-
вая, нежели дифференцирование.Юна применима ко всем
непрерывным функциям и даже к тем разрывным, кото-
рые испытывают конечный разрыв в конечном числе то-
чек.
Однако если дифференцирование элементарных функ-
ций всегда приводит опять-таки к элементарным, то для
операции, обратной к дифференцированию, то есть для
отыскания первообразной функции — такой результат
редкость.
Здесь можно привести аналогию из алгебры: возводя
в квадрат целое число, мы всегда получаем целое, однако
про обратную операцию — извлечение квадратного кор-
ня— такое скажешь не всегда.
ВМЕСТО ЗАКЛЮЧЕНИЯ —
ДИАЛОГ
АВТОРОВ
— Ну вот и окончилось наше путешествие по некоторым
интересным уголкам математики.
— И поскольку мы исполняли обязанности гидов,
уместно поинтересоваться: не осталось ли у кого-то ка-
ких-либо вопросов?
— Позволь мне спросить первому: как ты думаешь,
кто вместе с нами дошел до конца? Кому оказалось по-
лезным знакомство с математикой, лишенной формул и
строгих доказательств, место коих заняли шутки и поба-
сенки? Кто заинтересован в подобных книгах?
— Во-первых, мне кажется, преподаватели. Элемен-
ты высшей математики сейчас проникают даже в школь-
ный курс. Школьникам надо излагать ее иначе, чем сту-
дентам. Как говорил Паскаль, «предмет математики на-
столько серьезен, что полезно не упускать случая сде-
лать его немного занимательным».
— А можно воздействовать такими книгами непо-
средственно и на самих учеников, особенно если матема-
тика подавалась им в изрядно пересушенном виде и пото-
му казалась скучноватой. Привлеченные яркой оболоч-
кой занимательности, эти читатели попутно станут усва-
ивать и математическое содержание, которое до сих пор
казалось им горьким.
— Я вспомнил бы еще про тех, которым математика
сейчас нужна в гораздо большем объеме, чем излагалось
в школе и вузах, где они учились. Это биологи, лингви-
сты, социологи — короче, все те, кто пытается перевести
свою специальность на математические рельсы. Где
брать этим людям первые уроки математики? Из серьез-
ных учебников? Не слишком ли высока эта ступенька для
первого шага? Должны существовать книги, играющие
роль промежуточной ступеньки.
— И их должно быть тем больше, чем интенсивнее
происходит математизация знания. А ведь она ширится
и ускоряется на наших глазах. Уже давно замечено, что
202
из всех наук наиболее быстро развиваются точные. Вот
почему прочие науки стремятся перейти в разряд точных.
— Мне вспомнилось по этому поводу высказывание
Дарвина: «У людей, усвоивших великие принципы мате-
матики, одним органом чувств бодьше, чем у простых
смертных».
— А я хотел бы привести слова другого биолога,
хотя и менее известного, чем Дарвин. Это Фабр, автор
книг о жизни насекомых. Про математику он говорил,
что это «удивительная учительница в искусстве направ-
лять мысли, приводить в порядок неупорядоченное, вы-
корчевывать глупости, фильтровать грязное и давать яс-
ность. Но она, — продолжал далее ученый, — тот дели-
катный цветок, который произрастает не на всякой поч-
ве и распускается так, что никто не знает как».
— Имеется в виду, что никто не знает, каким обра-
зом некоторая область знания становится точной? К со-
жалению, исчерпывающих рекомендаций на этот счет,
действительно, не существует. И если мы с тобой про-
должим разговор на эту тему, мы сможем повторить лишь
самые общие соображения.
— Согласен. Но если мы не сумеем порекомендовать
представителю любой специальности, что именно следу-
ет делать ради математизации его науки, давай хотя бы
предостережем его от того, чего не следует делать.
— По крайней мере разберем некоторые хронические
заблуждения, касающиеся математики. Ну, например,
многим кажется, будто развитие каждой математической
дисциплины начинается с формулировки аксиом, невесть
откуда взявшихся. А потом на них выстраивается все
дальнейшее. Напротив! Четкая формулировка аксиом
той или иной математической дисциплины завершает це-
лькй этап ее развития, оформляет достигнутые резуль-
таты. Как говорил Энгельс, «принципы — не исходный
пункт исследования, а его конечный результат».
— Некоторые считают, что вся геометрия началась с
«Начал» Эвклида. А ведь до этой книги были открытия
Фалеса, Пифагора, Гиппократа, систематизированные
Эвклидом. Причем его систематизация была кое в чем
несовершенной, как выяснилось в прошлом веке. К исхо-
ду девятнадцатого столетия и была создана аксиоматика
геометрии, в основном приемлемая по тогдашним кано-
нам строгости. Она завершила, таким образом, двадцати-
пятивековой этап в развитии элементарной геометрии.
203
— Но логично спросить: если точная наука начинает-
ся не с аксиом, то с чего же?
— Об этом могла бы рассказать история таких клас-
сических точных наук, как механика, термодинамика, оп-
тика, электродинамика. Все начинается с накопления
экспериментальных фактов, установления устойчивых
связей между явлениями, обычно называемых законами.
Возьми хотя бы ту же электродинамику. Закон Ампера,
закон Фарадея, закон Био-Савара — сколько их было от-
крыто, покуда не появились уравнения Максвелла, свое-
образные аксиомы электродинамики, из которых вытека-
ли открытые до тех пор законы электромагнитного поля.
— Но, очевидно, ценность уравнений Максвелла этим
не исчерпывается. В самом деле, хороша ли та теория,
которая лишь по-новому излагает уже известное?
— Разумеется, нет! Теория и строится и развивается
ради получения новых знаний о природе. Аксиомы цен-
ны тем, что из них логическим путем выводятся утвер-
ждения, предсказывающие неизвестные ранее явления.
Так было и в электродинамике: тот же Максвелл, анали-
зируя свои знаменитые уравнения, пришел к заключе-
нию, что существуют электромагнитные волны, что свет
имеет электромагнитную природу... Его гипотезы потом
блестяще подтвердились экспериментами. Великий
принцип математики, заключенный в ее дедуктивном ме-
тоде, в способности вывести все свои утверждения из не-
многих аксиом, поистине вооружил физиков как бы новым
органом чувств, который позволяет им предвидеть и по-
стигать то, что они не могут увидеть и вообразить.
— Да, по-видимому, это хороший образец для любой
науки, желающей стать точной. Хотелось бы выделить
принципиальные моменты этого становления. По мере
того как экспериментаторы накапливают опытные фак-
ты, теоретики вырабатывают элементарные основопола-
гающие понятия, немногочисленные, но очень емкие в
том смысле, что наблюдаемые факты могут быть интер-
претированы как конкретные проявления этих понятий,
В механике к их числу принадлежит понятие материаль-
ной точки, в электродинамике—понятие напряженности
электрического или магнитного поля...
— И еще один принципиальный момент: анализ спо-
собов рассуждения, которые применяются в данной нау-
ке. Из них вырабатываются те принципы вывода, по ко-
торым из аксиом будут получаться следствия.
204
— Здесь, по-моему, дело обстоит намного легче. Ло-
гика у каждой науки одна. Очень хорошо, если найден-
ные в той или иной науке законы допускают количествен-
ную формулировку. Тогда для их выражения нужно
лишь выбрать подходящий математический аппарат, а
все дальнейшее идет по соответствующим правилам пре-
образования формул.
— Я не согласен со словом «выбрать». Это значит —
взять готовое. Такой путь, конечно, возможен и разумен.
Математика создала богатый арсенал методов, доказав-
ших свою эффективность и в механике, и в термодинами-
ке, и в оптике...
— И часто случается, что одно и то же уравнение по-
зволяет описать очень далекие по своему физическому
смыслу явления. Одна и та же формула, например, вы-
ражает и закон взаимодействия двух электрических за-
рядов, и закон притяжения двух масс. Вполне может
оказаться, что математический аппарат термодинамики
пригодится <в какой-то лингвистической теории.
— Но может случиться и так, что готового аппарата
для новой развивающейся науки на математических скла-
дах не найдется. Тогда его придется строить с нуля. Кста-
ти, это пойдет на пользу самой математике, пополнит ее
арсенал. Необходимость творчества может выявиться в
самых непредвиденных местах. Вот, скажем, ты уверен,
что во всех науках логика одна и та же — с ее извечным
«да — нет», «истина — ложь». Но вспомни, как ты голо-
суешь на собраниях. У тебя не две, а три возможности:
«за», «против», «воздержался». И недаром разрабатыва-
ются многозначная логика и еще более диковинные ло-
гические теории. Вполне возможно, что какая-то наука,
становясь точной, примет на вооружение такую логиче-
скую систему, которая точным наукам до сих пор была
неизвестна. Ведь закономерности в каждой области зна-
ния свои.
— Иными словами, превращение той или иной науки
в точную — это процесс, идущий из самой ее глубины, а
не бездумное заимствование уже известного математиче-
ского аппарата и отработанной терминологии.
— Такое, к сожалению, встречается нередко. В иных
книгах, написанных под девизом математизации науки,
по существу, нет ничего, кроме нагромождения формул
да жонглирования эффектными словечками: инвари-
ант, многомерность, изоморфизм...
205
— Искривленное пространство, векторное поле и
прочая и прочая.
— Математизация не в этом. Не боясь повториться, я
бы вновь попытался подчеркнуть два существеннейших
ее положения. Первое — это обобщение уже достигнуто-
го той или иной наукой и выделение нескольких основных
утверждений, если угодно, аксиом, содержащих точное и
полное описание взаимосвязей между элементарными
понятиями данной науки и одновременно служащих оп-
ределениями этих понятий. Второе — это закрепление
принципов вывода, согласно которым всякое утвержде-
ние данной науки логически вытекало бы из ее аксиом.
— Все это, конечно, очень просто порекомендовать,
но очень трудно выполнить. Проблем тут возникает не-
мало. Располагает ли данная наука необходимыми для
описанной процедуры основополагающими понятиями?
Если располагает и на их основе удалось сформулировать
некоторую систему аксиом, то полна ли эта система, то
есть можно ли исходя из нее вывести любое утверждение
данной науки, хотя бы любое из уже известных? Если же
система неполна, то как ее пополнить? Такое пополнение
рано или поздно окажется неизбежным с открытием но-
вых фактов... Вот что должно заботить специалиста, же-
лающего видеть свою дисциплину в ряду точных наук.
— А что касается формул, это уж как получится.
СОДЕРЖАНИЕ
Предисловие ............................................... 3
Вместо введения — диалог авторов ........................ 4
Теоремы, аксиомы, определения ........................... 8
Множества ................................................. 19
Отображения ............................................. 42
Отношения ............................................... 68
Последовательности, ряды................................. 93
Функции................................................... 114
Свойства функций........................................ 148
Дифференциальное и интегральное исчисление.............. 174
Вместо заключения — диалог авторов.......................202
Редактор Н. ФЕОКТИСТОВА
Юрий Петрович ПОПОВ
Юрий Васильевич ПУХНАЧЕВ
МАТЕМАТИКА В ОБРАЗАХ
Главный отраслевой редактор А. Нелюбов
Мл. редактор Н, Карячкина
Художник А. Григорьев
Худ. редактор М. Бабичева
Техн, редактор А. М. Красавина
Корректор В. Коночкина
ИБ № 10028
Сдано в набор 04.08.88. Подписано к печати 30.01.89. А08559.
Формат бумаги 84Х108’/з2. Бумага офсетная. Гарнитура литературная.
Печать офсетная. Усл. печ. л. 10,92. Усл. кр.-отт. 22,26.
Уч.-изд. л. 10,49. Тираж 80000 экз. Заказ 8651.
Цена 65 коп. Издательство «Знание». 101835, ГСП, Москва, Центр,
проезд Серова, д. 4. Индекс заказа 896703.
Типография издательства «Коммунист», 410002, г. Саратов, ул. Волжская, 28.