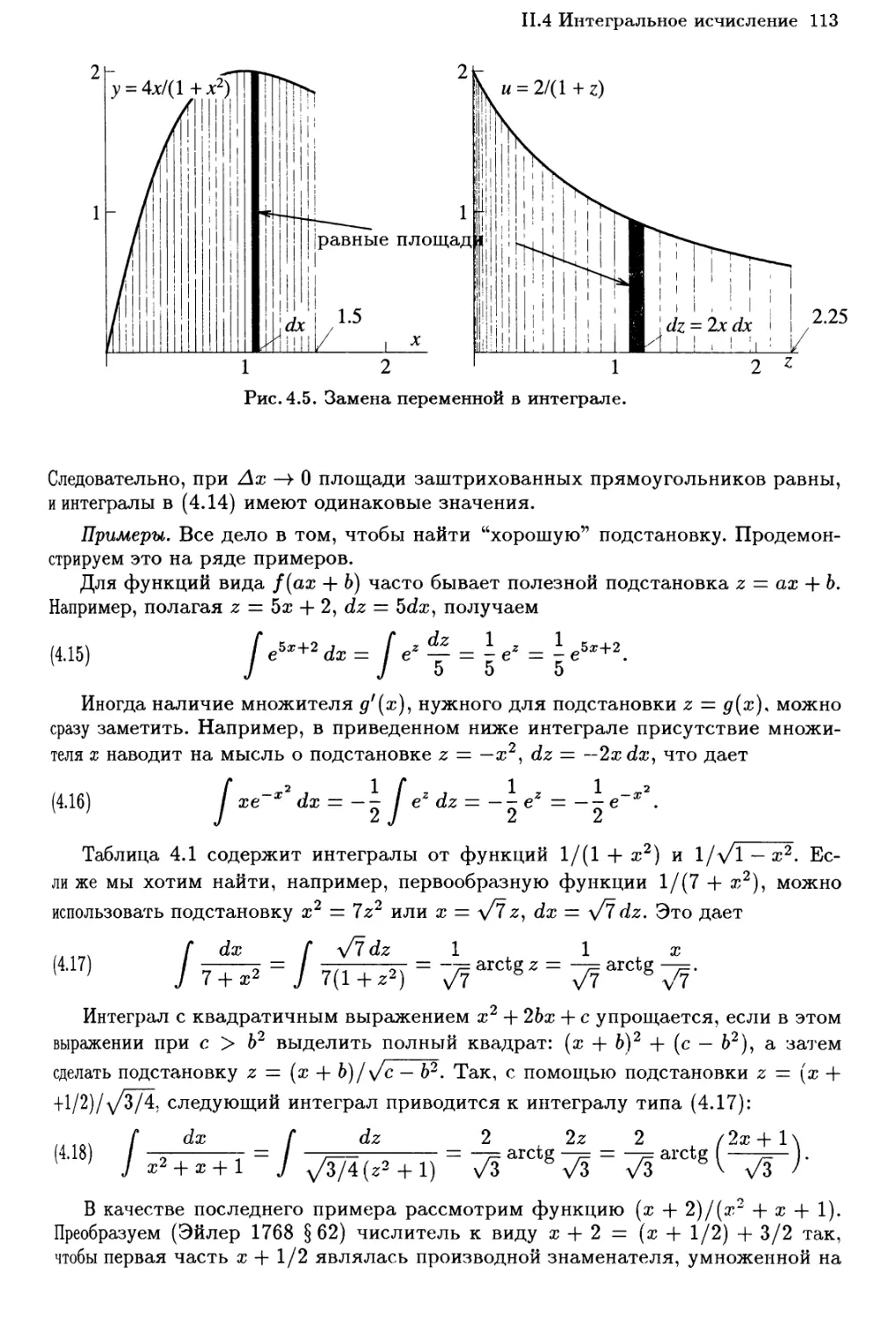
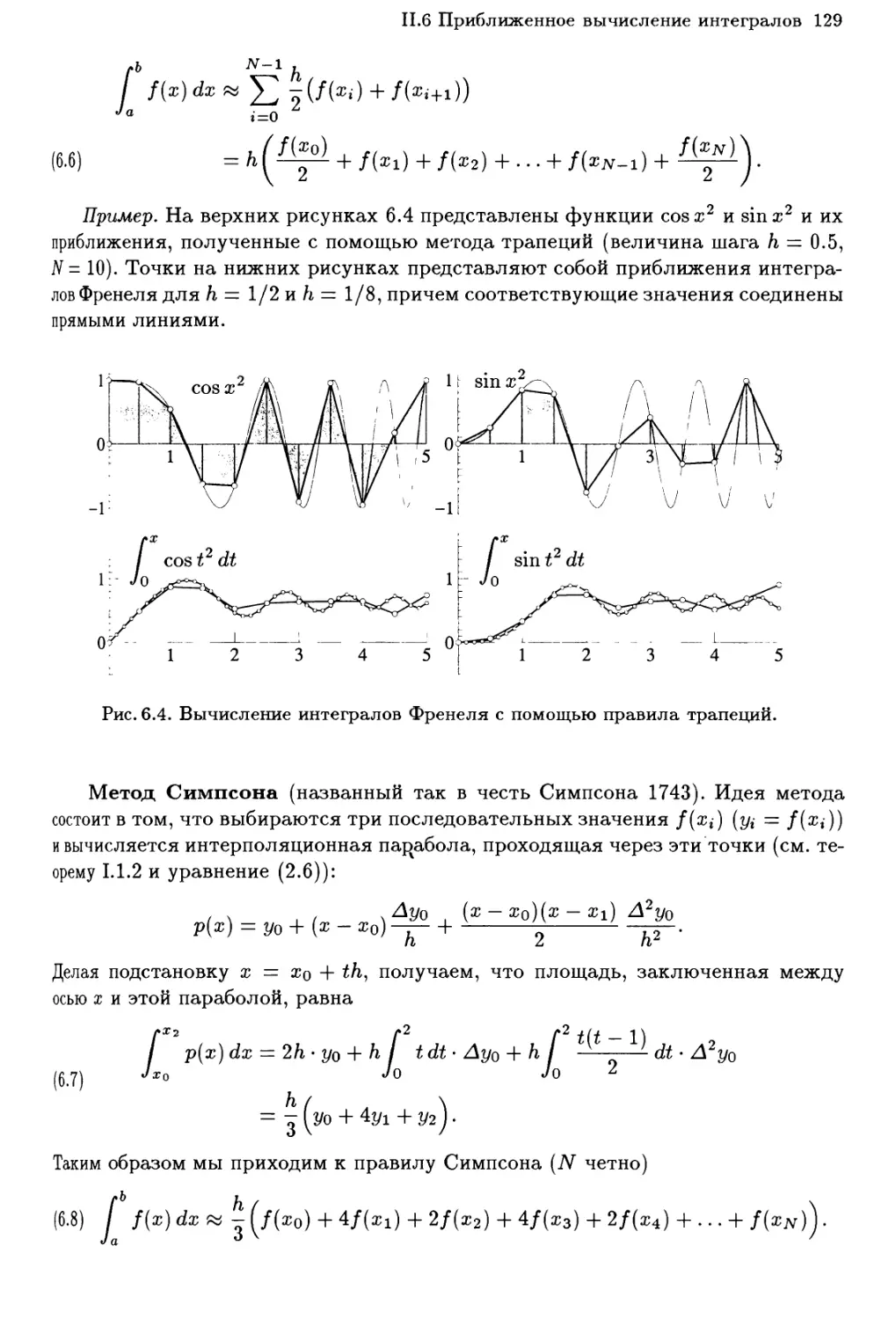
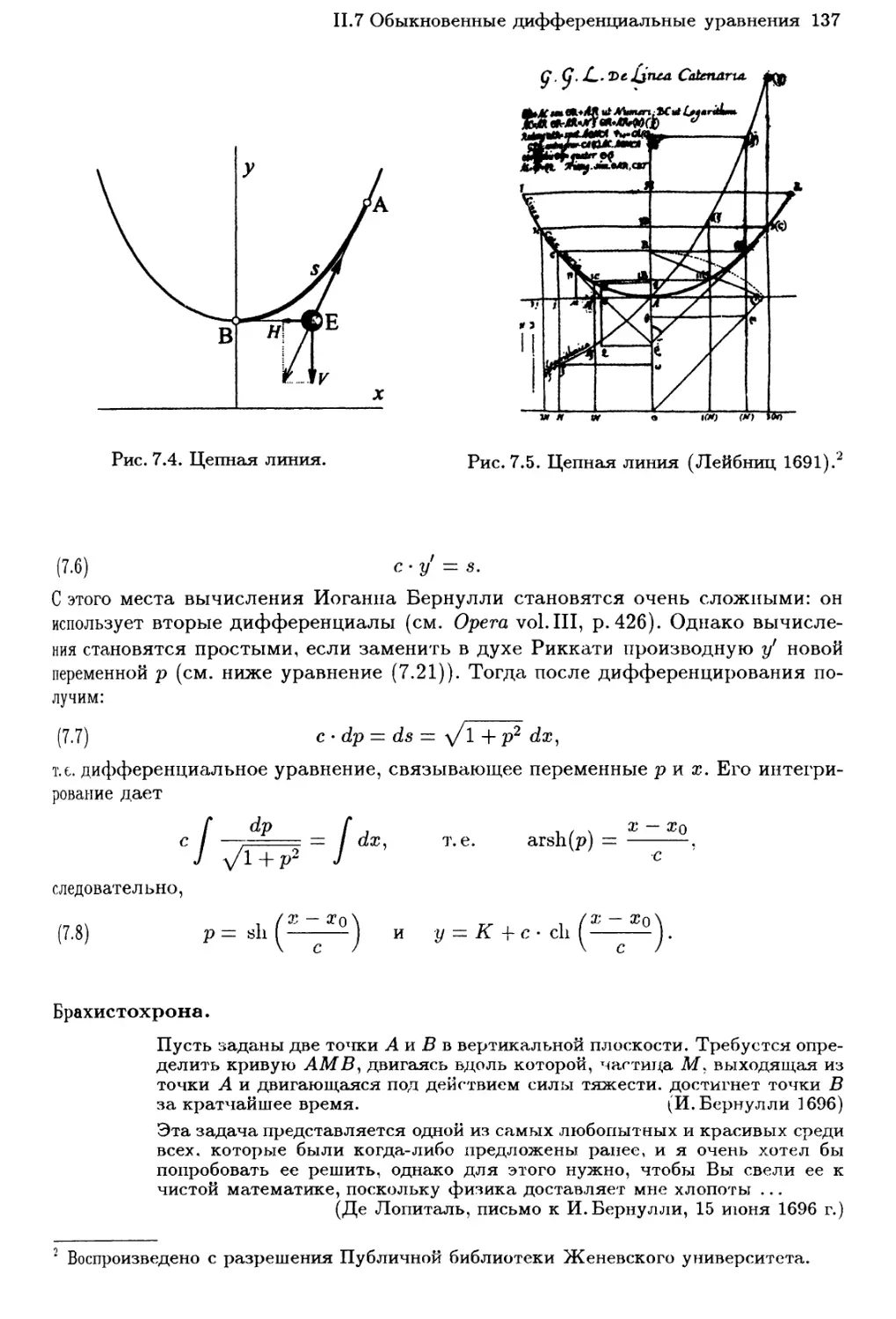
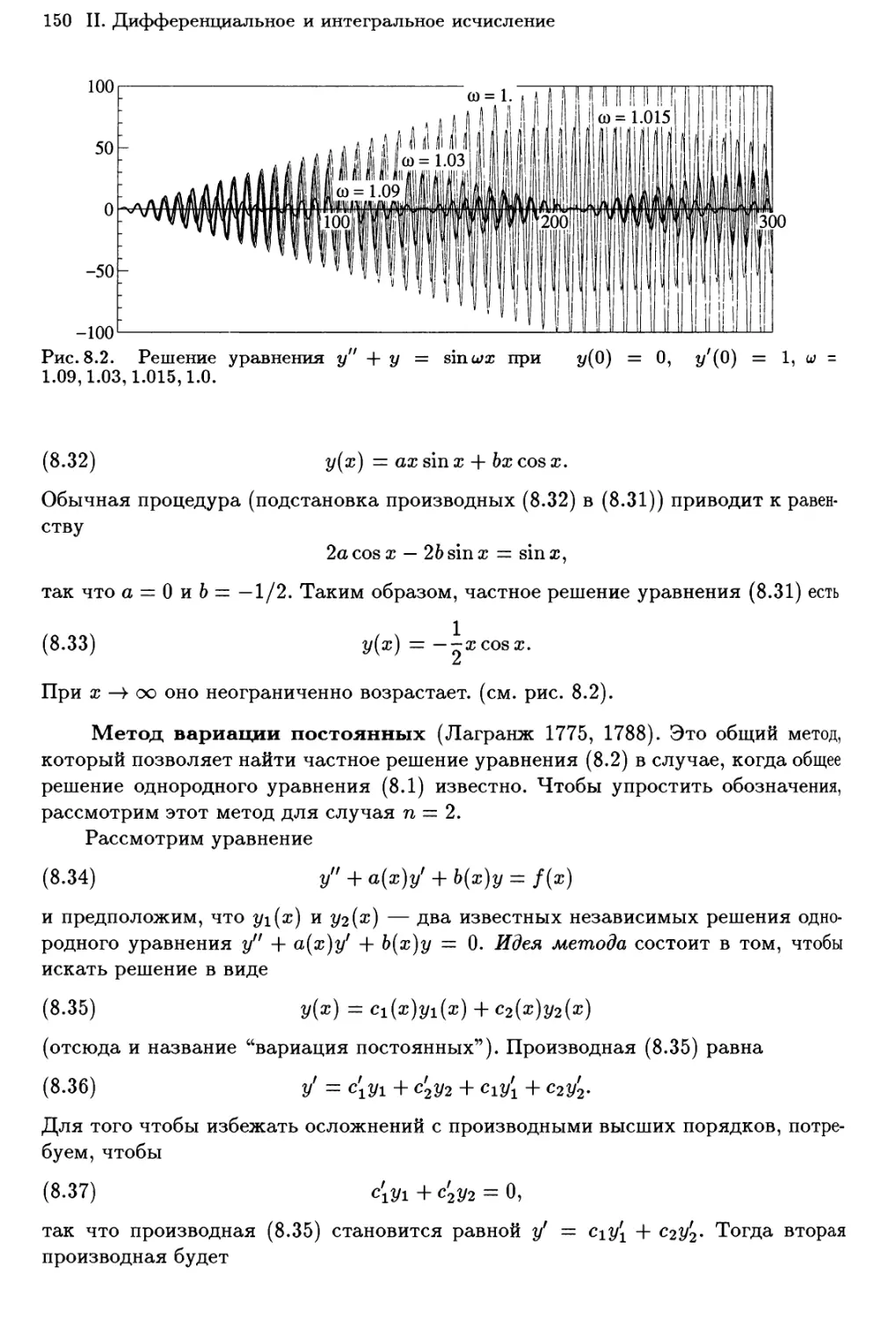
Математический анализ в свете его истории - Хайрер Э., Ваннер Г.

Автор: Хайрер Э. Ваннер Г.
Теги: анализ математический анализ функциональный анализ математика
ISBN: 978-5-89176-485-9
Год: 2008
Похожие
Специальные функции
Решение обыкновенных дифференциальных уравнений с использованием Matlab
Математика XIX века. Книга 3. Чебышевское направление в теории функций. Обыкновенные дифференциальные уравнения. Вариационное исчисление. Теория конечных разностей
Конкретная математика. Основание информатики
Текст
                    Undergraduate Texts in Mathematics
Readings in Mathematics
E. Hairer
G. Wanner
Analysis by
Its History
With 173 Illustrations
Corrected third printing 2000
Springer
New York
Berlin
Heidelberg
Barcelona
Hong Kong
London
Milan
Paris
Singapore
Tokyo

Э. Хайрер
Г Ваннер
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
в свете его истории
Перевод с третьего английского издания
под редакцией С. С. Филиппова
МОСКВА
Научный мир
2008

УДК 517
ББК 22.161
Х12
X 12 Хайрер Э., Ваннер Г.
Математический анализ в свете его истории. Пер. с англ. — М.: Научный
мир, 2008. — 396 с.
В книге излагаются основы математического анализа приблизительно
в той последовательности, в какой они создавались и совершенствовались
великими математиками прошлого. В первых двух главах показано, как
вычисления, связанные с решением практических задач, привели к
открытию бесконечных рядов, дифференциального и интегрального исчисления
и дифференциальных уравнений. Становлению математически строгой
теории в этих областях анализа функций одной и нескольких переменных в
19-м столетии посвящены главы III и IV.
Книга содержит большое число примеров, расчетов и иллюстраций,
что позволяет лучше понять побудительные причины многих
математических открытий и дать им глубокие объяснения. Прочесть эту книгу будет
интересно и приятно как студентам, так и преподавателям.
УДК 517
ББК 22.161
ISBN 978-5-89176-485-9 (русск.)
ISBN 0-387-94551-2 (англ.)
Originally published in English under
the title: "Analysis by Its History"
by E. Hairer and G. Wanner
© 1996 Springer-Verlag New York, Inc.
All Rights Reserved
© Научный мир, 2008,
перевод на русский язык.

Предисловие
... который отличался от традиционного сухого учебника математики.
(М. Клайн, из предисловия к изданию книги Клайна в мягкой обложке,
1972)
Также по этой причине я взял на себя труд сделать большое число
рисунков. (Брискорн и Кнёррер, Плоские алгебраические кривые, p.ii)
... Я хотел бы еще раз подчеркнуть ... пункты, в которых мое изложение
существенно отличается от обычного изложения в учебниках:
1. Иллюстрирование абстрактных рассуждений с помощью чертежей.
2. Акцентирование их связи со смежными областями, такими как
исчисление конечных разностей и интерполяция ...
3. Упор на историческое развитие.
Мне представляется крайне важным, чтобы именно будущий учитель
принимал во внимание все это. (Ф.Клейн 1908, англ. издание, р. 236)
Традиционно строгое изложение начального курса анализа дается
приблизительно в следующем порядке:
пределы,
множества,
^ => непрерывные => производные => интегрирование,
отображения ,
функции
С другой стороны, историческое развитие этих понятий происходило в обратном
порядке:
Кантор 1875 Коши 1821 Ньютон 1665 Кепл^Шб
Дедекинд Вейерштрасс Лейбниц 1675 _ iaqq
В этой книге, содержащей четыре главы
Глава I. Введение в анализ бесконечных
Глава П. Дифференциальное и интегральное исчисление
Глава III. Основания классического анализа
Глава IV. Функции нескольких переменных,
мы попытались восстановить исторический порядок. В главе I мы начинаем с
Кардано, Декарта, Ньютона и знаменитого Introductio Эйлера. Затем в главе II
дается интегральное и дифференциальное исчисление 17-го и 18-го столетий,
"исполненное на инструментах той эпохи", как сказал бы музыкант. Строгое
математическое обоснование анализа в 19-м веке для одного и нескольких
переменных, связанное с именами Коши, Вейерштрасса и Пеано, является темой глав
III и IV.
Эта книга — плод многолетней практики преподавания анализа обоими
авторами. В 1968 году второй из авторов впервые читал лекции по анализу в
университете Иннсбрука, где первый автор был студентом-первокурсником. С тех
пор мы оба читали эти лекции в нескольких унивеситетах на немецком и
французском языке, испытывая влияние многих книг и многих манер изложения.
Настоящий текст был в конце концов записан для наших студентов в Женеве на
французском языке. Он пересматривался и исправлялся каждый год, затем был
переведен на английский и снова пересмотрен и исправлен с неоценимой
помощью нашего коллеги Джона Штейнига. Он исправил так много ошибок, что мы
едва можем представить себе, что бы мы без него делали.

vi Предисловие
Нумерация. Каждая глава разбита на разделы. Формулы, теоремы, рисунки
и упражнения в каждом разделе нумеруются последовательно, при этом
указывается также номер раздела. Так. например, 7-я формула в разд. И.6 занумерована
"(6.7)" Ссылки на эту формулу в других главах даются в виде "(11.6.7)"
Библиографические ссылки. Когда мы пишем, скажем, "Эйлер (1737)" или
"(Эйлер 1737)", мы ссылаемся на работу Эйлера, опубликованную в 1737 г.,
полная ссылка на которую дана в разделе "Библиография" в конце книги. Иногда
мы даем более точные указания, как, например, "(Эйлер 1737, р. 25)" —
страница 25 в оригинале, чтобы помочь читателю, который пожелает взглянуть на
оригинальные источники и оценить нередко изящные и вдохновенные тексты
первооткрывателей. Если в списке библиографии нет соответствующей ссылки, мы
либо опускаем скобки, либо пишем, например, "(в 1580 г.)"
Цитаты. Мы вкючили много цитат из литературы. Те, которые появляются
в тексте, обычно переведены. Чтобы читатель мог ощутить дух математики как
интернациональной науки с долгой историей, иногда чтобы позабавить, а также
для тех, у кого нет легкого доступа к библиотеке со старыми книгами, в разделе
Приложение приводятся цитаты на языках оригиналов. Если источник
цитирования не включен в список библиографии, его название указывается в тексте,
как для приведенной выше цитаты из книги Брискорна и Кнёррера.
Благодарности. Текст был подготовлен в Женевском университете на нашей
рабочей станции Sun в редакторе plain Т^Х с использованием макросов
издательства Шпрингер, Нью-Йорк. Мы признательны за помощь, которую оказал нам
Ж.М.Наеф ("Mr. Sun" из "Службы информатики" нашего университета).
Рисунки либо копировались из старых книг (фотографировали Ж.М.Мейлан из
библиотеки Женевского университета и А. Перрюшу), либо были рассчитаны по
нашим программам на фортране и включены как постскрипт-файлы. Завершающая
печать выполнена на лазерном принтере с разрешением 1200dpi на факультете
психологии в Женеве. Мы также благодарны сотрудникам библиотеки
математического факультета и многим коллегам; ценные замечания и советы дали, в
частности, Р. Булирш, П.Дойфлхард, К.Любих, Р. Мерц, А. Остерманн, Ж.-К.
Понт и Х.М.Санс-Серна. Большую благодарность, наконец, мы хотим выразить
д-ру Инне Линдеманн и ее "команде" из издательства Шпрингер, Нью-Йорк за
всю ее помощь, компетентные замечания и доброжелательное сотрудничество.
Март 1995 Э.Хайрер и Г. Ваннер
Предисловие ко второму и третьему исправленным изданиям. Эти новые
издания позволили нам исправить несколько опечаток и улучшить текст во многих
местах. В частности, мы привели геометрически более наглядное представление
решения кубического уравнения, которое нашел Тарталья, улучшили
трактовку огибающих и дали более полное доказательство формулы преобразования
кратных интегралов. Мы благодарны многим студентам и коллегам; в часнос-
ти, Р.Б.Буркель, Х.Фишер, Ж.-Л.Годен и Х.-М.Мэр помогли нам обнаружить
ошибки и предложили возможные исправления. Особую благодарность мы хотим
выразить И. Кани, переводчику японского издания.
Март 1997, апрель 2000
Э. Хайрер и Г. Ваннер

Оглавление
Глава I Введение в анализ бесконечных. Перевод С, С. Филиппова
1.1 Декартовы координаты и полиномиальные функции 2
Алгебра 2
"Algebra Nova" 6
"Геометрия" Декарта 8
Полиномиальные функции 10
Упражнения 14
1.2 Показательные функции и биномиальная теорема 17
Биномиальная теорема 18
Показательная функция 24
Упражнения 27
1.3 Логарифмы и площади 29
Вычисление логарифмов 31
Вычисление площадей 33
Площадь под гиперболой и натуральные логарифмы 35
Упражнения 39
1.4 Тригонометрические функции 40
Основные соотношения и их следствия 43
Разложения в ряды 46
Обратные тригонометрические функции 49
Вычисление числа 7г 52
Упражнения 54
1.5 Комплексные числа и функции 57
Формула Эйлера и следствия из нее 58
Новый взгляд на тригонометрические функции 61
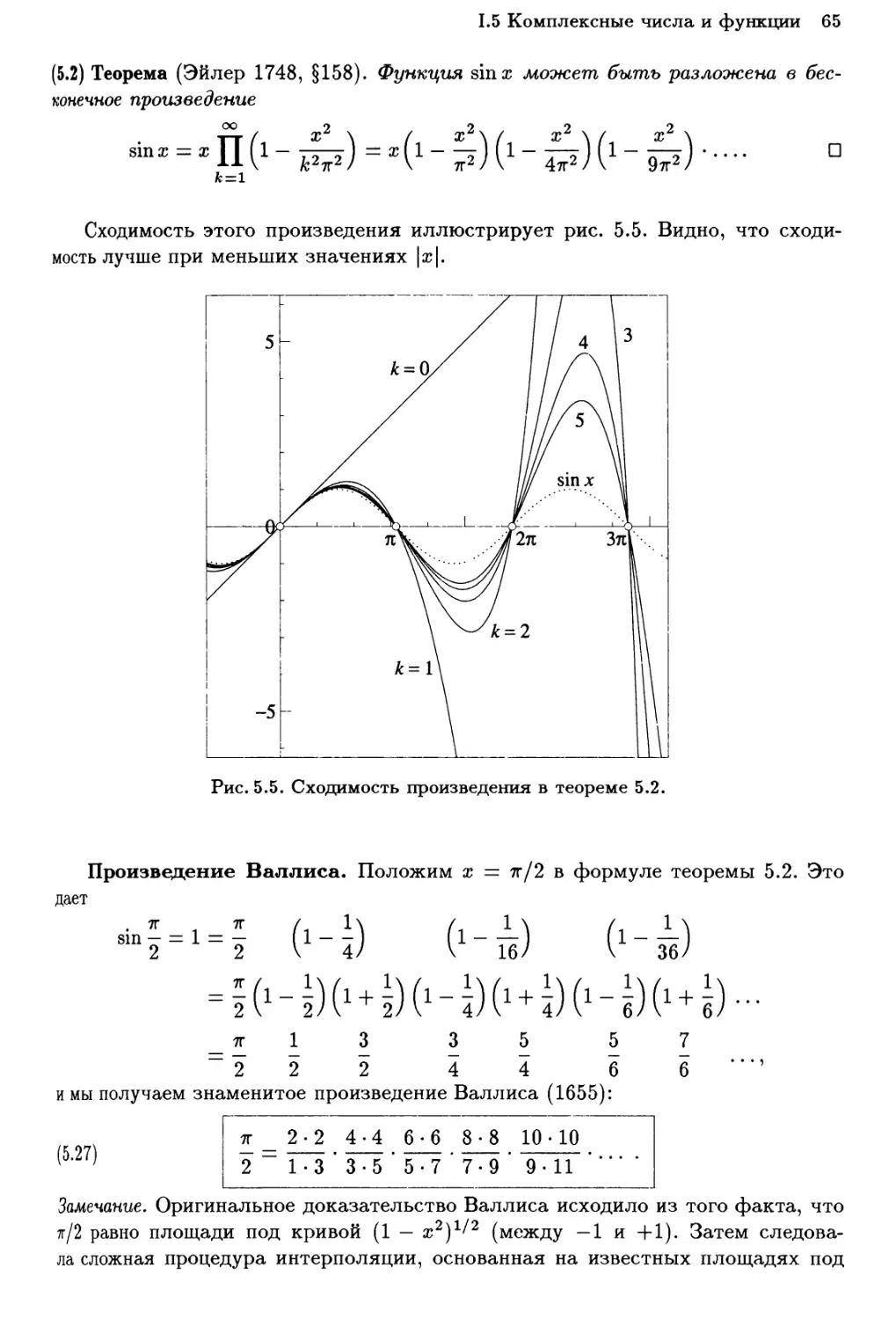
Эйлерово произведение для синуса 62
Упражнения 66
1.6 Непрерывные дроби 68
Источники 68
Подходящие дроби 71
Иррациональность 76
Упражнения 78
Глава II Дифференциальное и интегральное исчисление. Перевод О.Б. Москалева
П.1 Производная 81
Производная 81
Правила дифференцирования 84
Параметрическое представление и неявные уравнения 88
Упражнения 89
П.2 Высшие производные и ряд Тейлора 91
Вторая производная 91
De Conversione Punctionum in Series 94
Упражнения 97
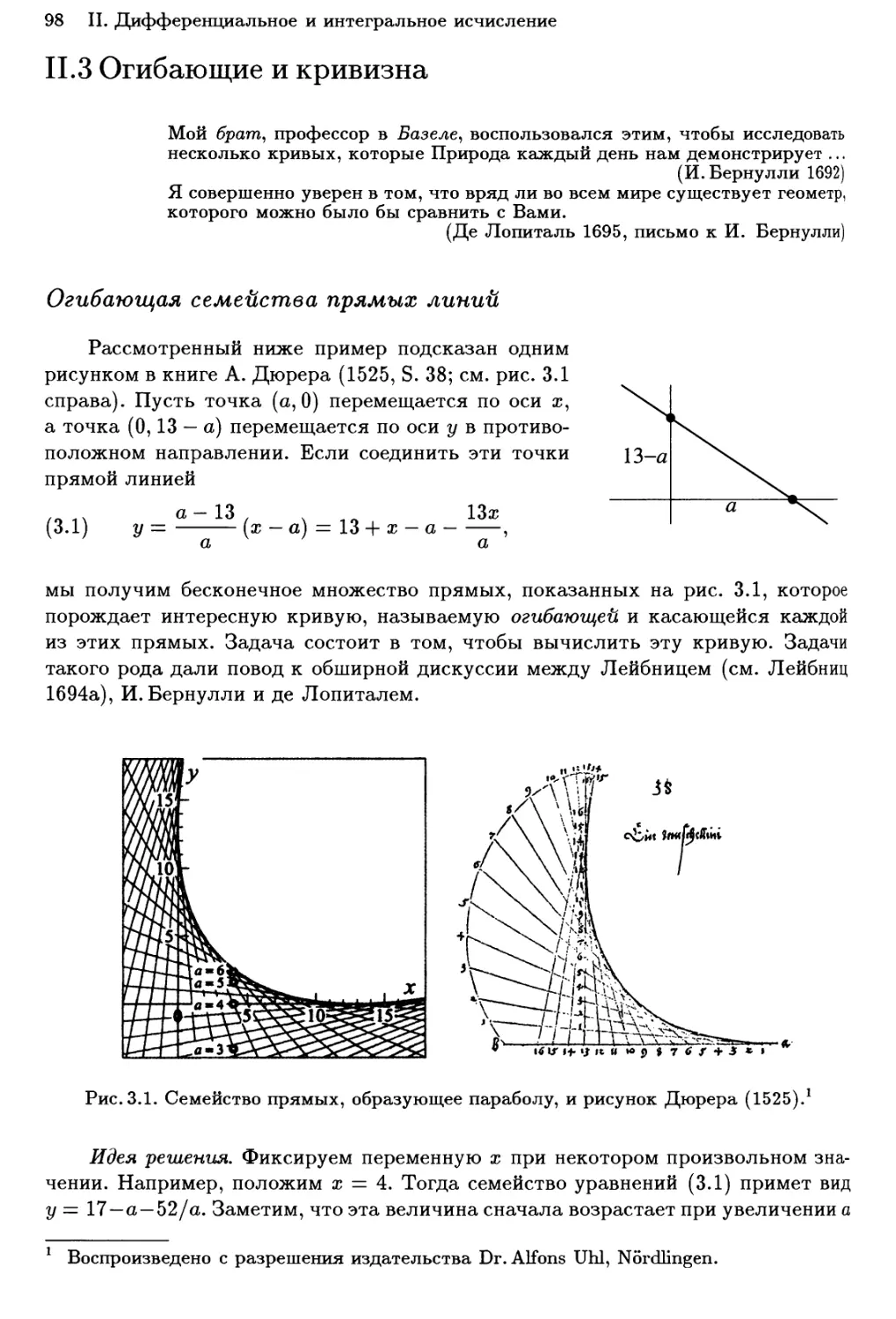
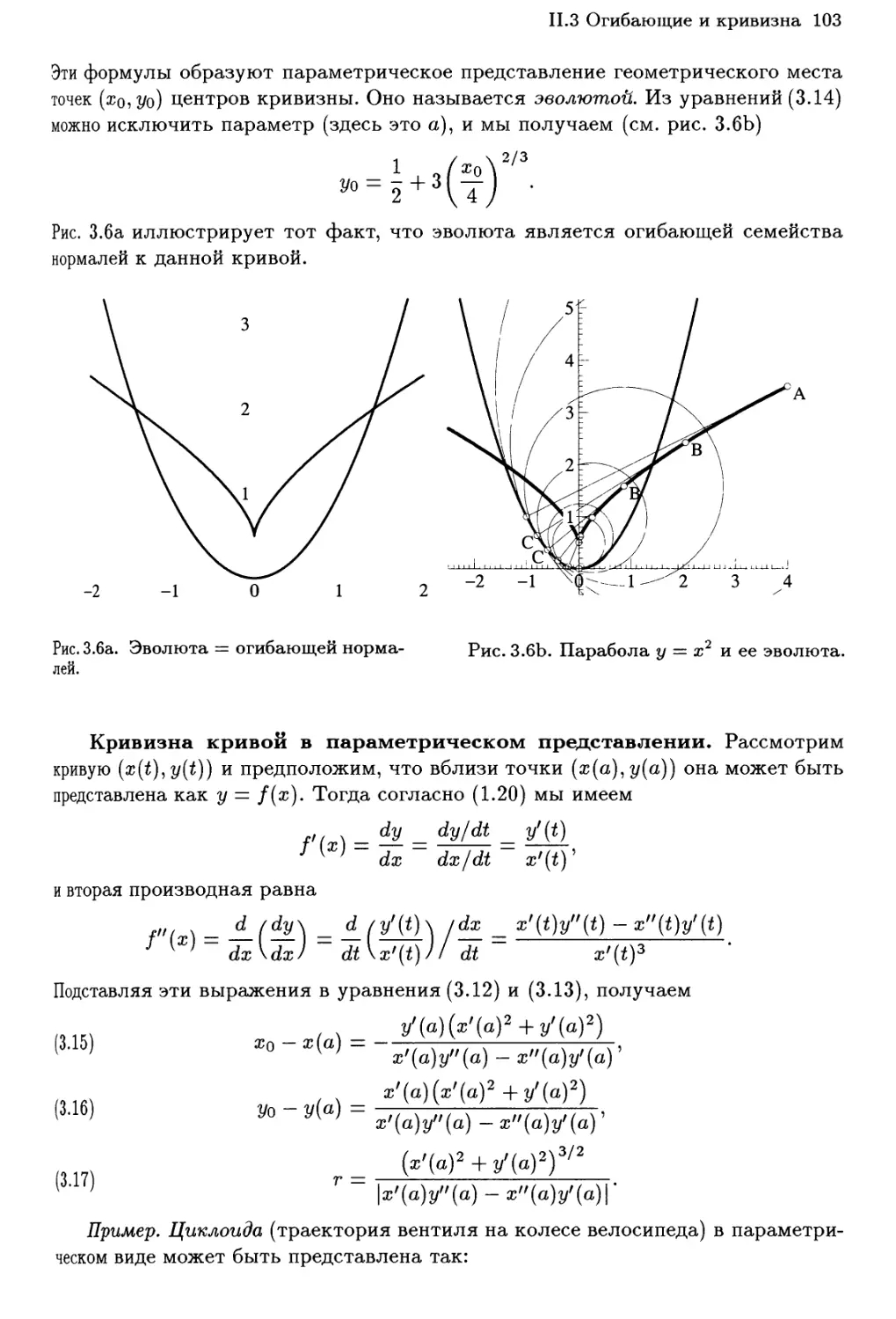
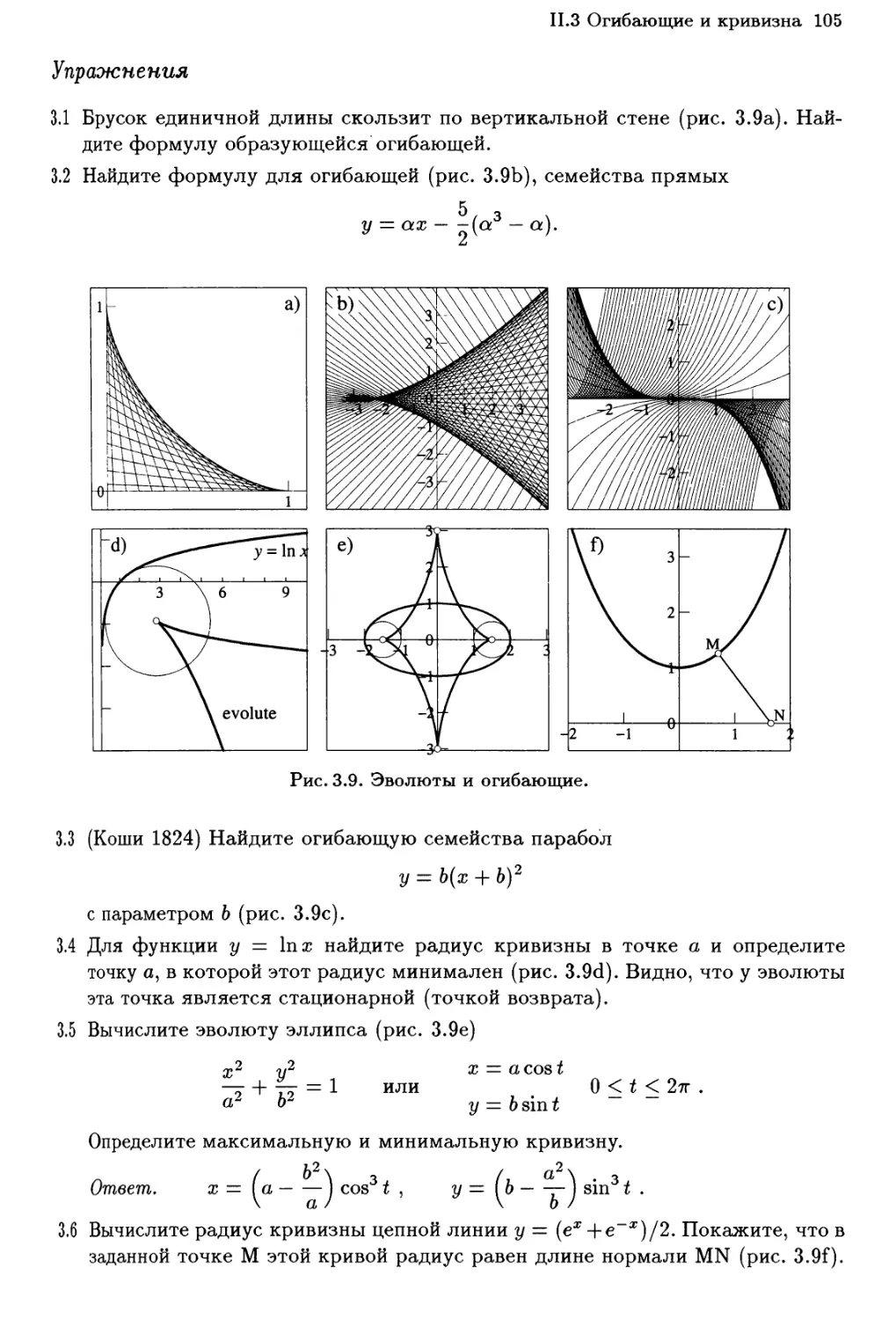
11.3 Огибающие и кривизна 98
Огибающая семейства прямых линий 98
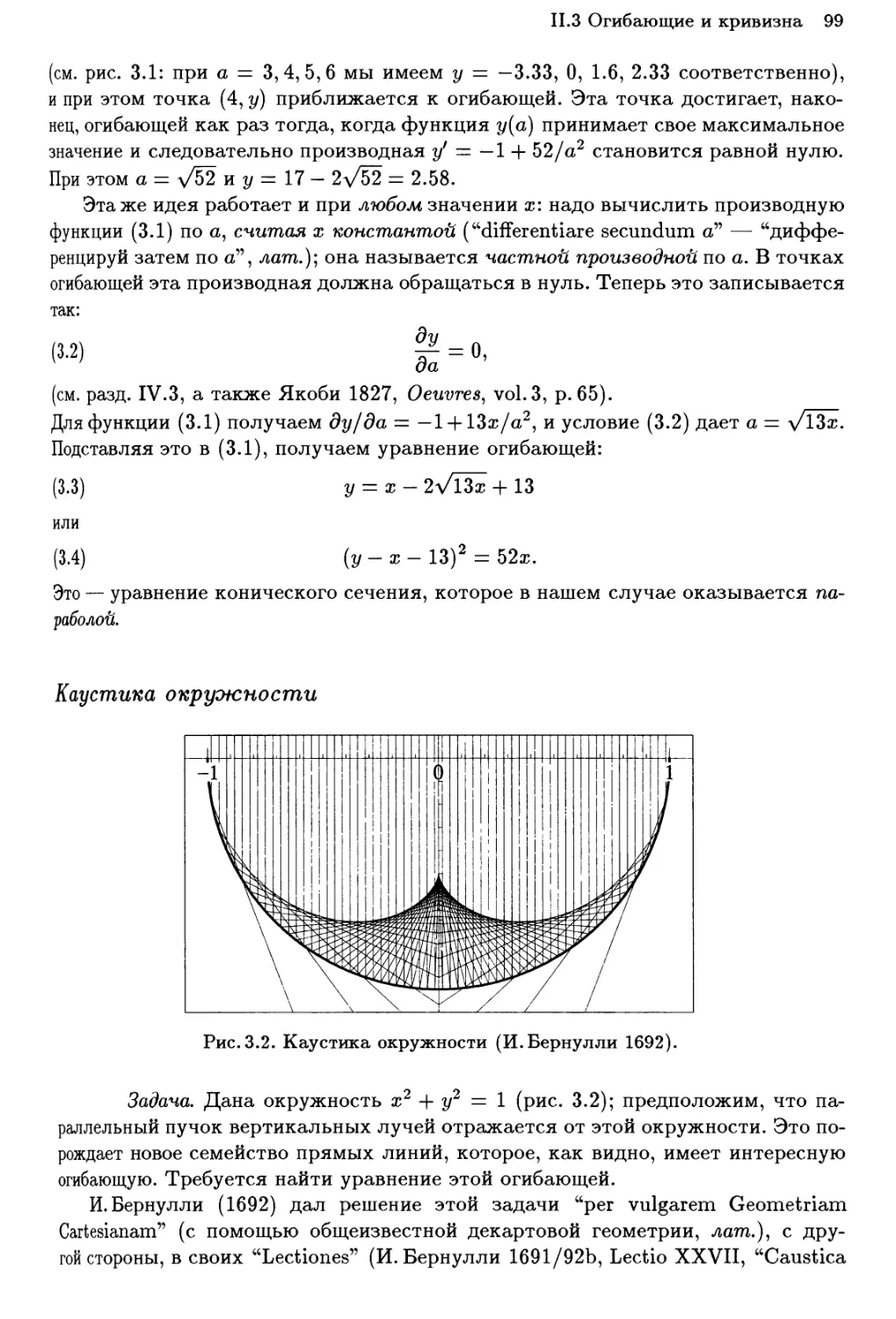
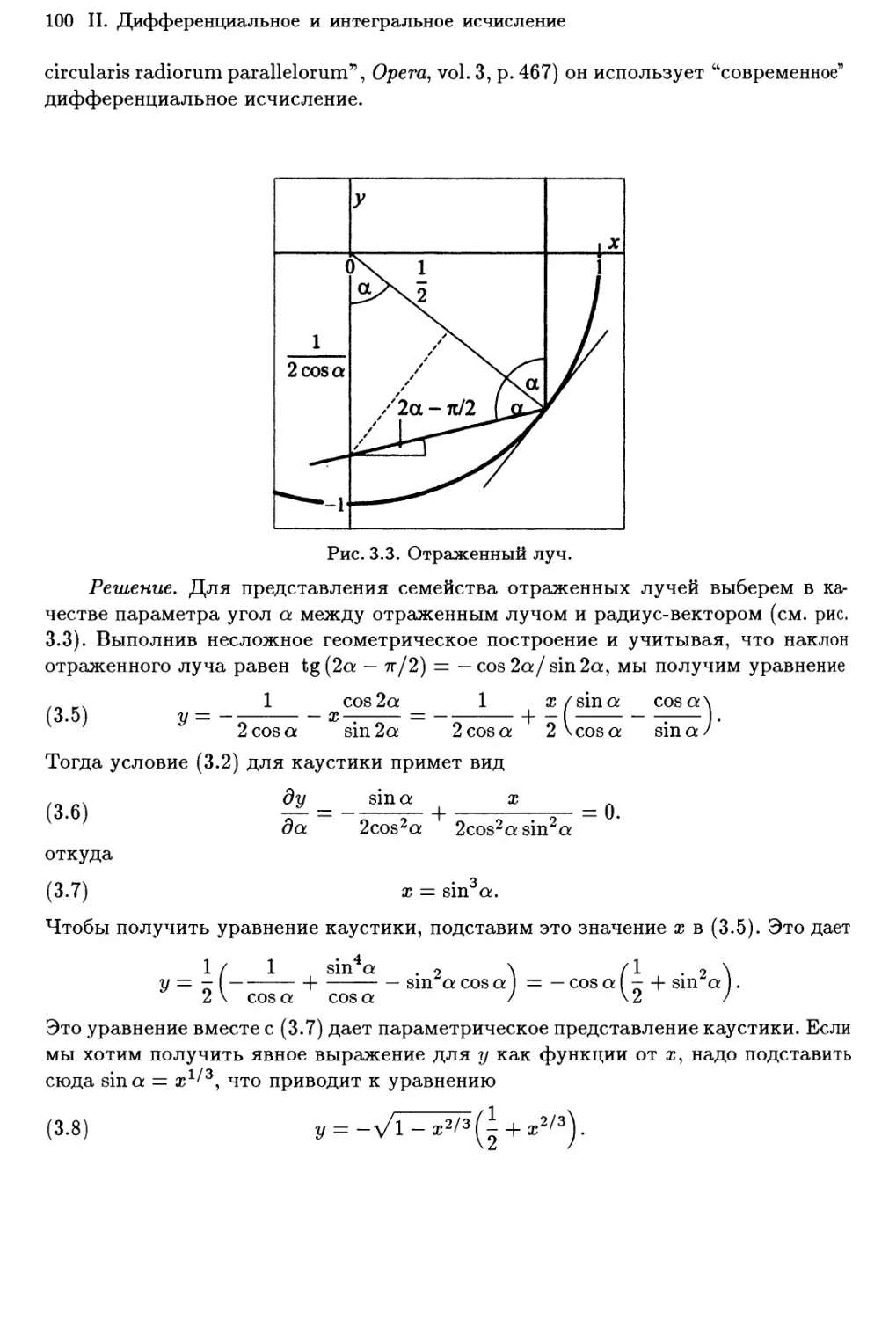
Каустика окружности 99
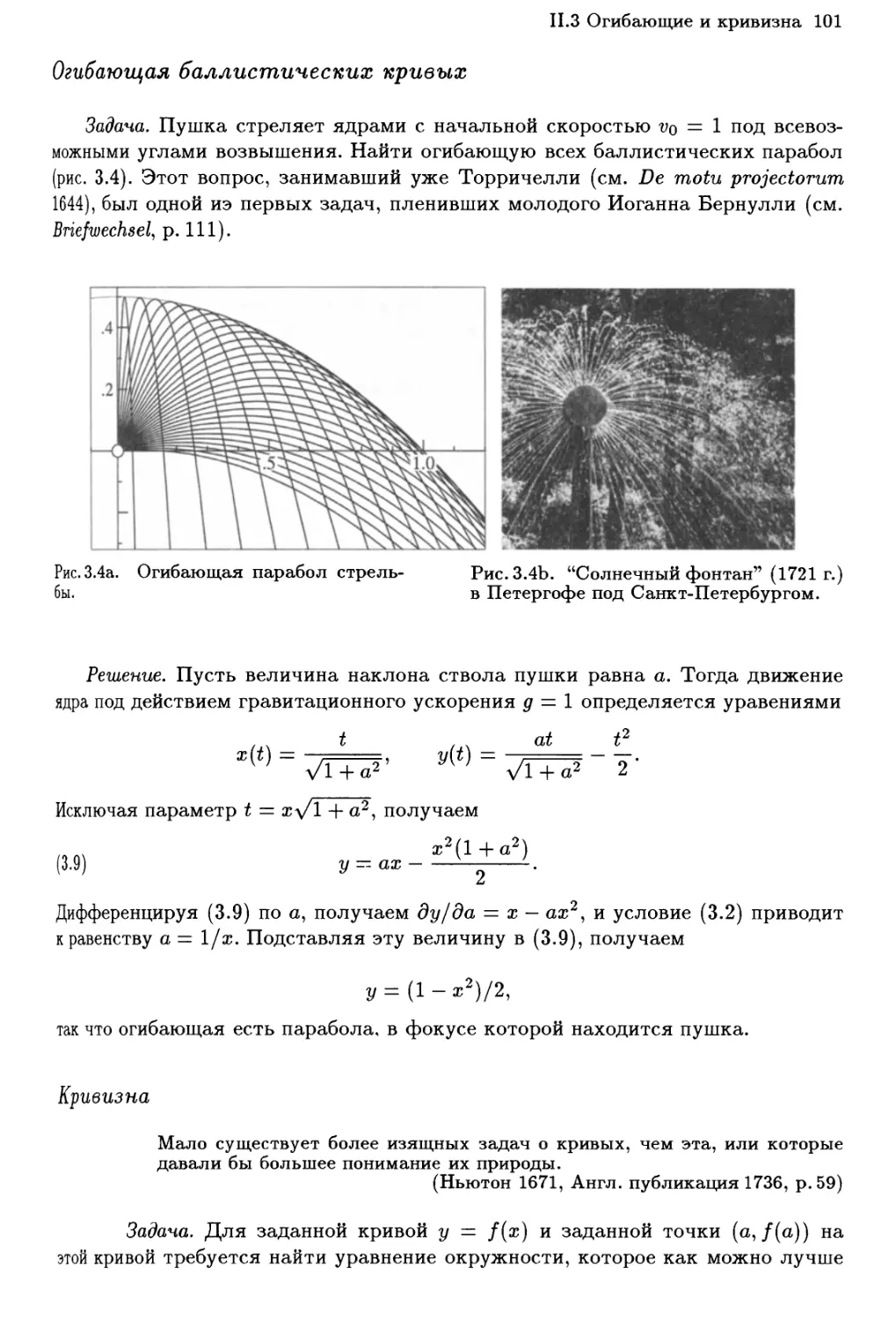
Огибающая баллистических кривых 101
Кривизна 101
Упражнения 105
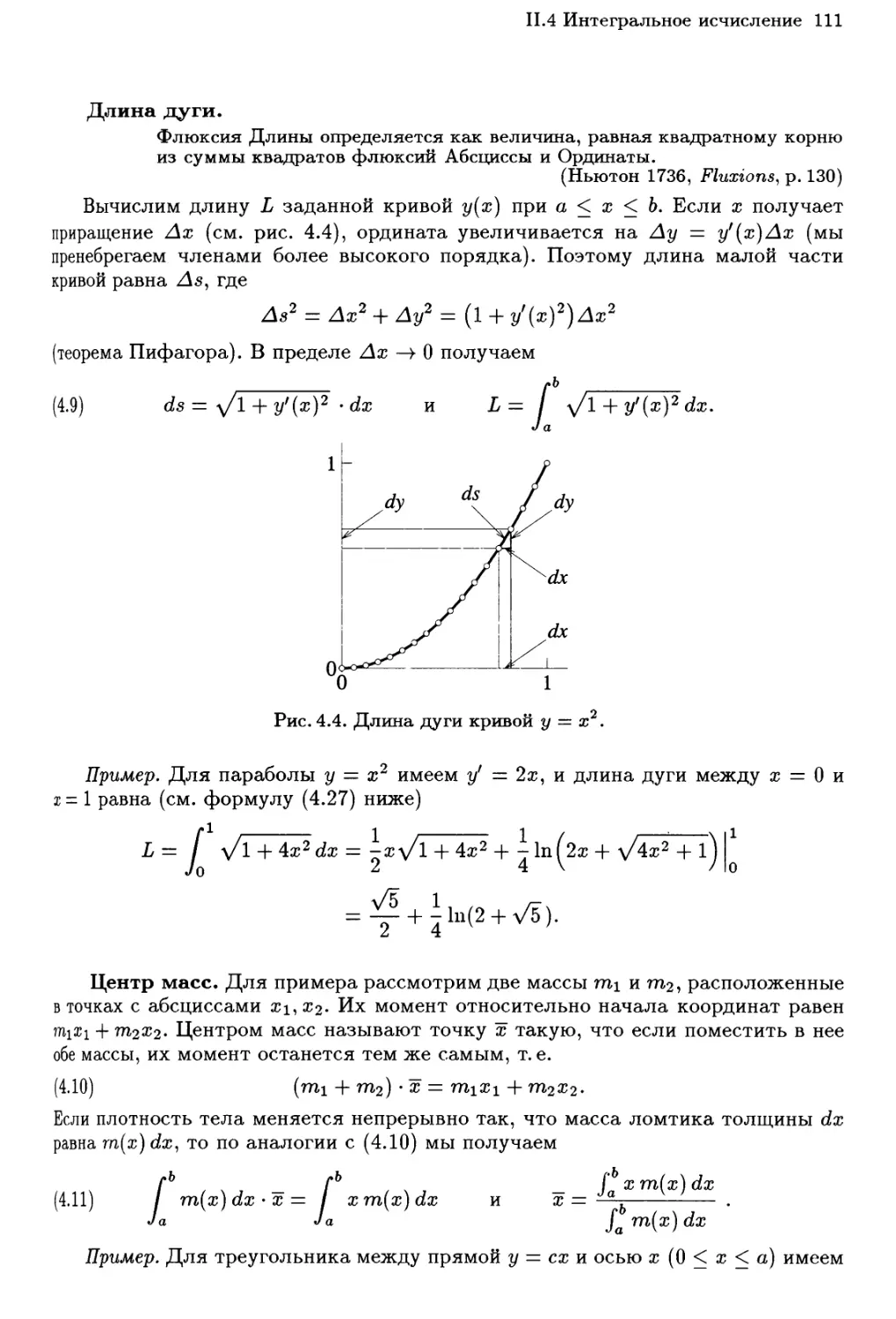
11.4 Интегральное исчисление 107
Первообразные 107
Приложения 109

Vlll
Оглавление
Техника интегрирования 112
Формула Тейлора с остаточным членом 116
Упражнения 117
11.5 Функции, имеющие элементарные интегралы 118
Интегрирование рациональных функций 118
Полезные подстановки 123
Упражнения 125
11.6 Приближенное вычисление интегралов 126
Разложения в ряды 126
Численные методы 128
Асимптотические разложения 131
Упражнения 132
11.7 Обыкновенные дифференциальные уравнения 134
Некоторые типы интегрируемых уравнений 139
Дифференциальные уравнения второго порядка 140
Упражнения 142
11.8 Линейные дифференциальные уравнения 144
Однородное уравнение с постоянными коэффициентами 145
Неоднородные линейные уравнения 148
Уравнение Коши 151
Упражнения 152
П.9 Численное решение дифференциальных уравнений 154
Метод Эйлера 154
Метод рядов Тейлора 156
Уравнения второго порядка 158
Упражнения 159
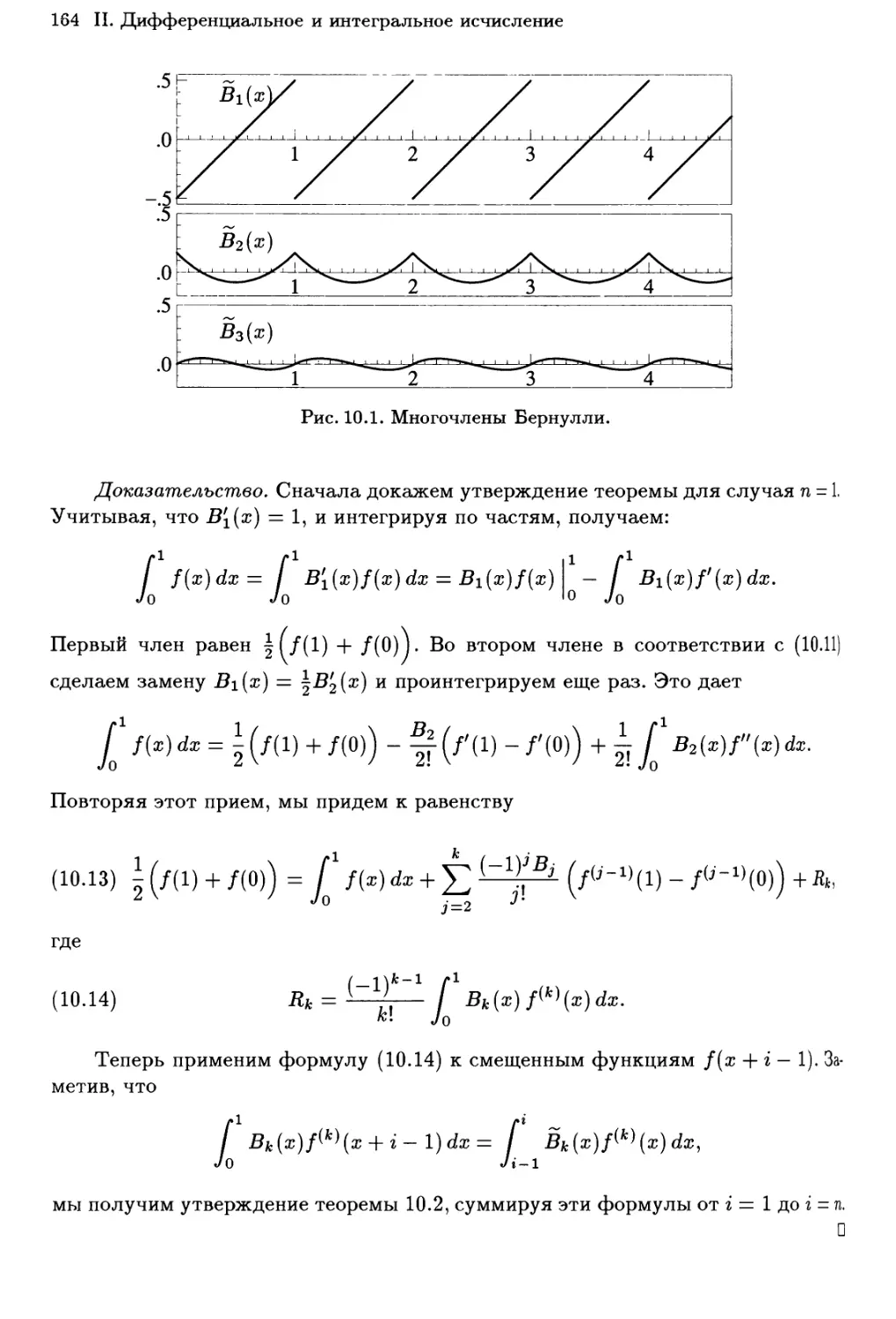
11.10 Формула суммирования Эйлера—Маклорена 160
Вывод формулы по Эйлеру 160
De Usu Legifcimo Formulae Summatoriae Maclaurinianae 163
Формула Стирлинга 165
Гармонический ряд и постоянная Эйлера 167
Упражнения 169
Глава III Основания классического анализа. Перевод О. Б. Москалева
111.1 Бесконечные последовательности и действительные числа 172
Сходимость последовательности 172
Понятие действительного числа 177
Монотонные последовательности и наименьшая верхняя грань 181
Точки накопления 183
Упражнения 185
111.2 Бесконечные ряды 188
Критерии сходимости 189
Абсолютная сходимость 192
Двойные ряды 195
Произведение Коши двух рядов 197
Изменение порядка суммирования и предельных переходов
в бесконечных рядах 199
Упражнения 200
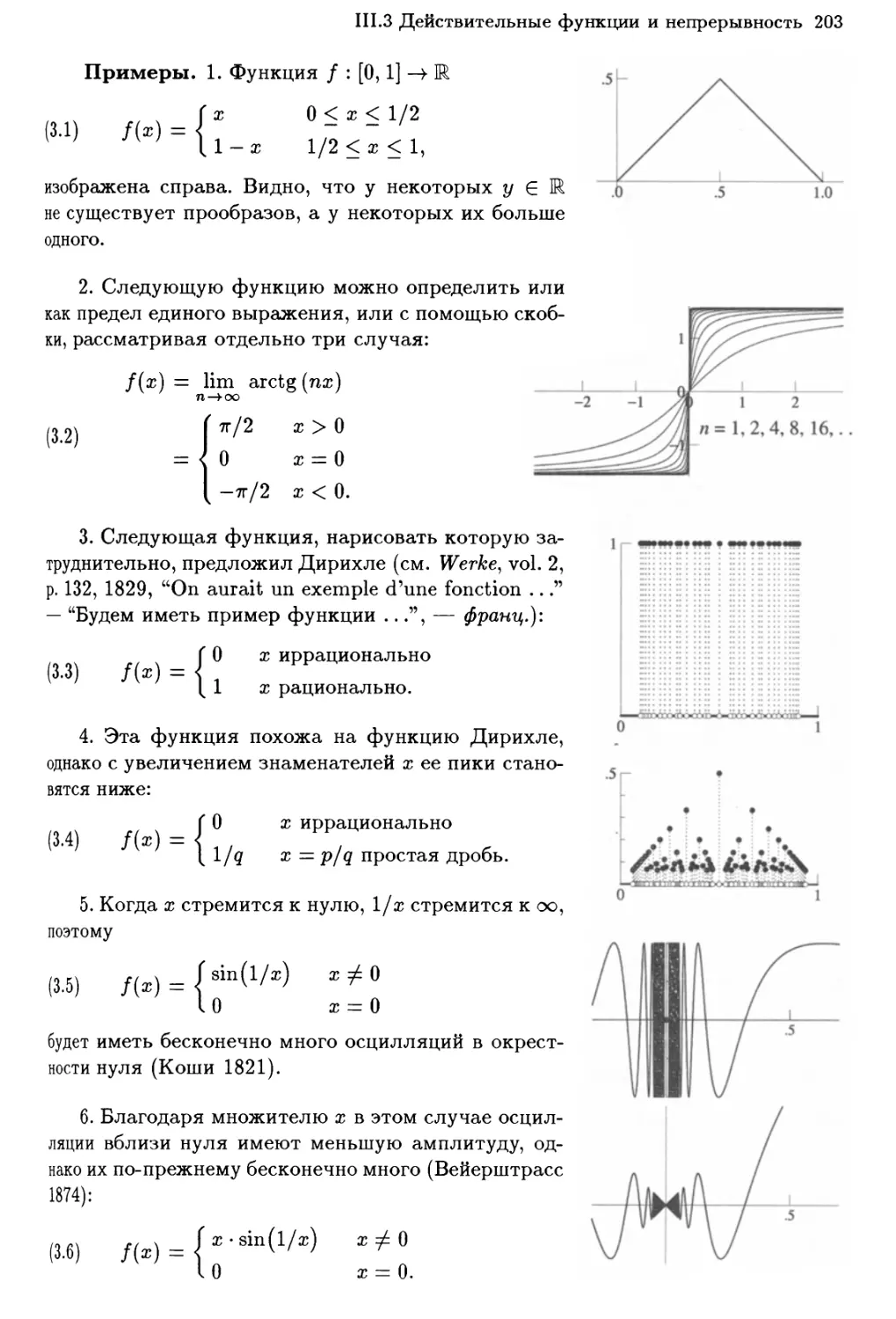
111.3 Действительные функции и непрерывность 202
Непрерывные функции 204
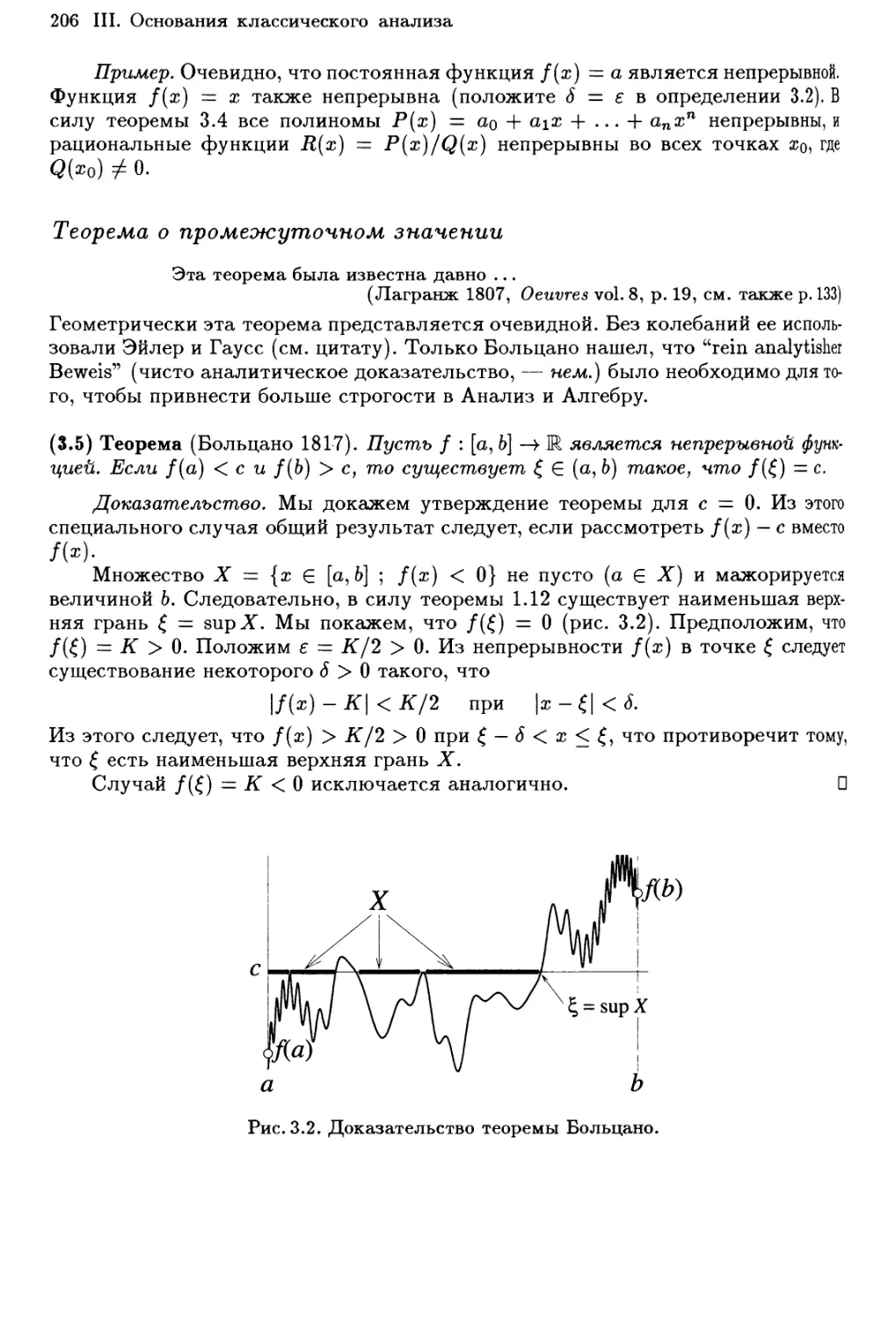
Теорема о промежуточном значении 206
Теорема о максимуме 207
Монотонные и обратные функции 208
Предел функции 209
Упражнения 211
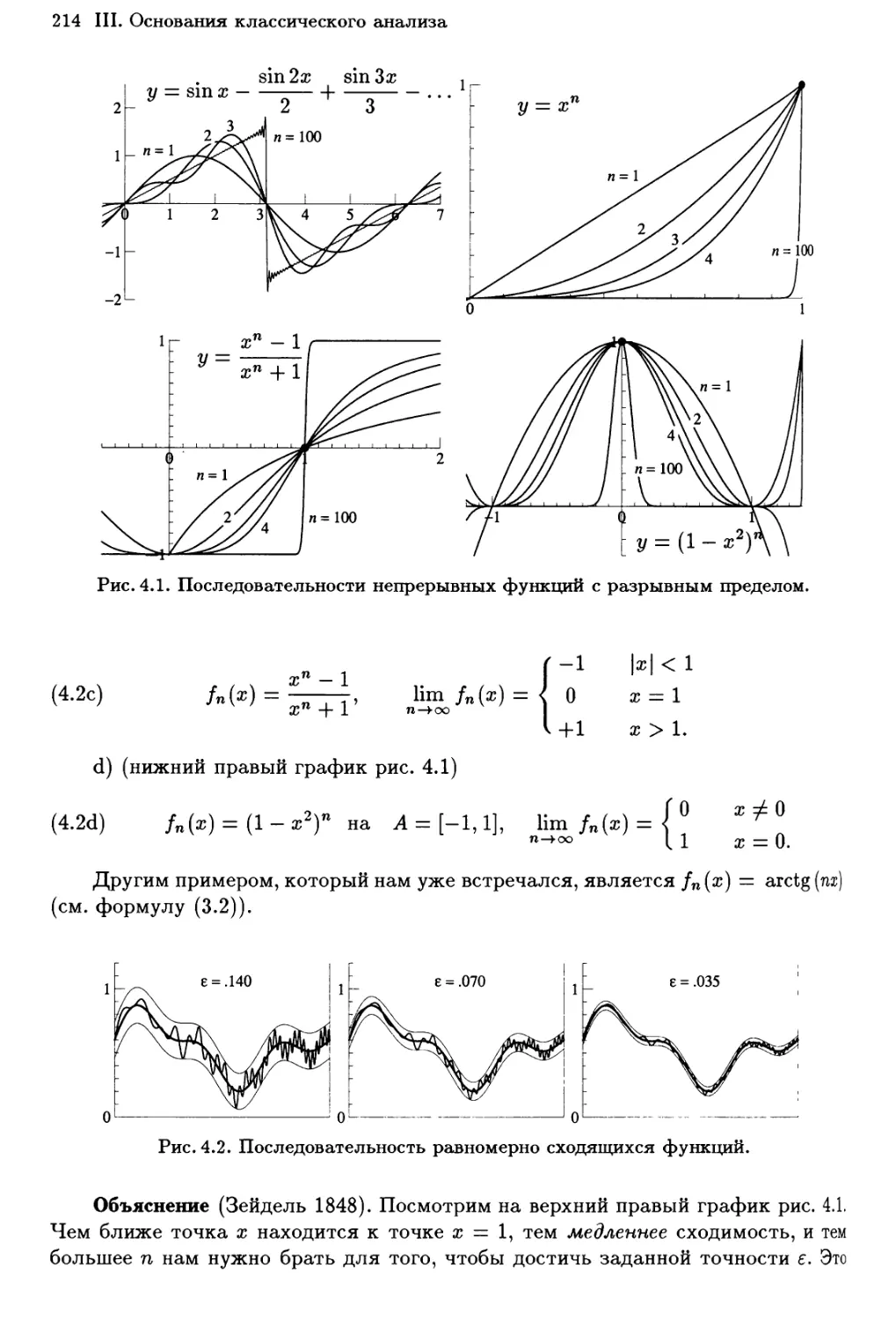
III.4 Равномерная сходимость и равномерная непрерывность
Предел последовательности функций
213
213

Оглавление ix
Критерий Вейерштрасса равномерной сходимости 216
Равномерная непрерывность 217
Упражнения 220
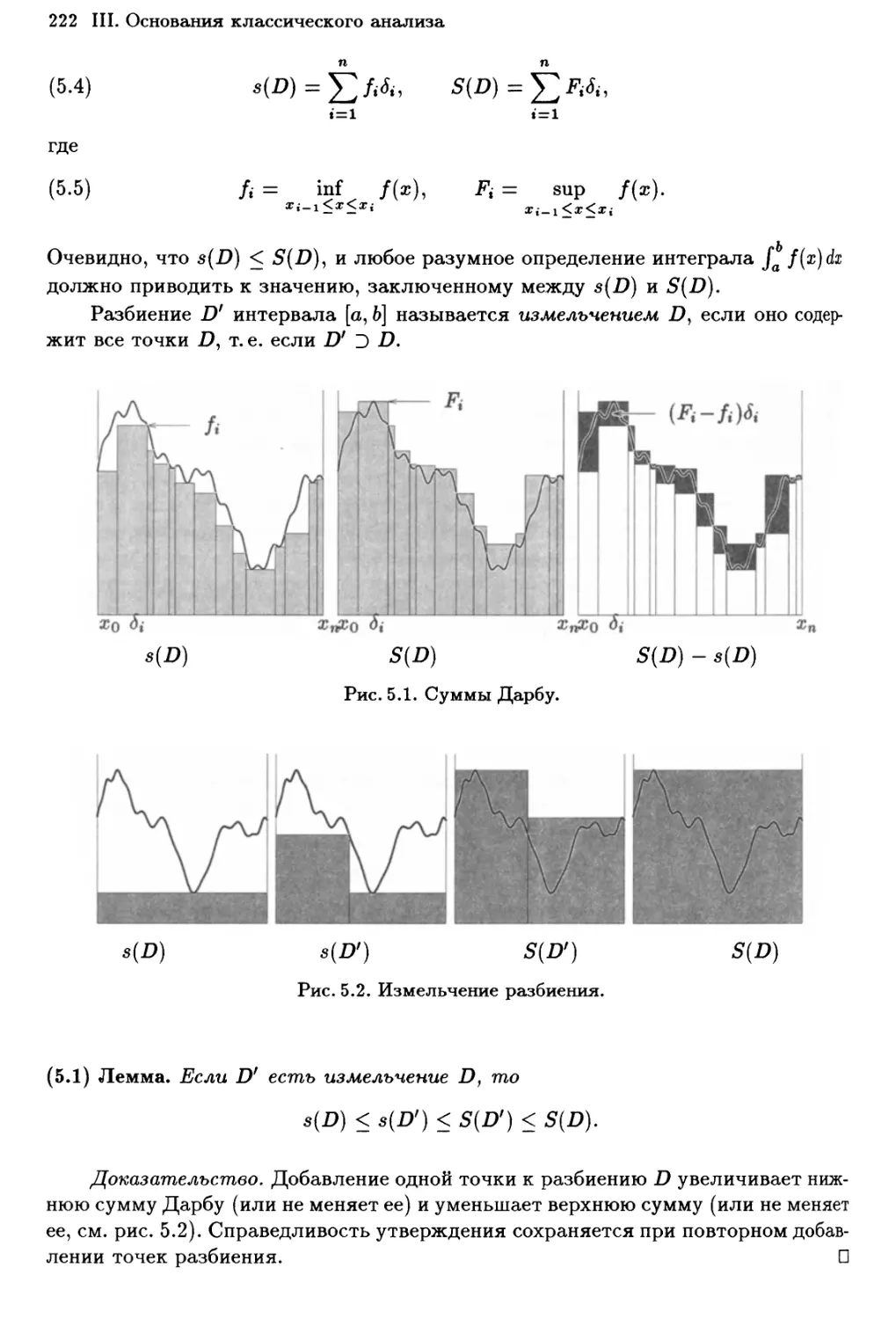
111.5 Интеграл Римана 221
Определения и критерии интегрируемости 221
Интегрируемые функции 226
Неравенства и теорема о среднем значении 228
Интегрирование бесконечных рядов 230
Упражнения 232
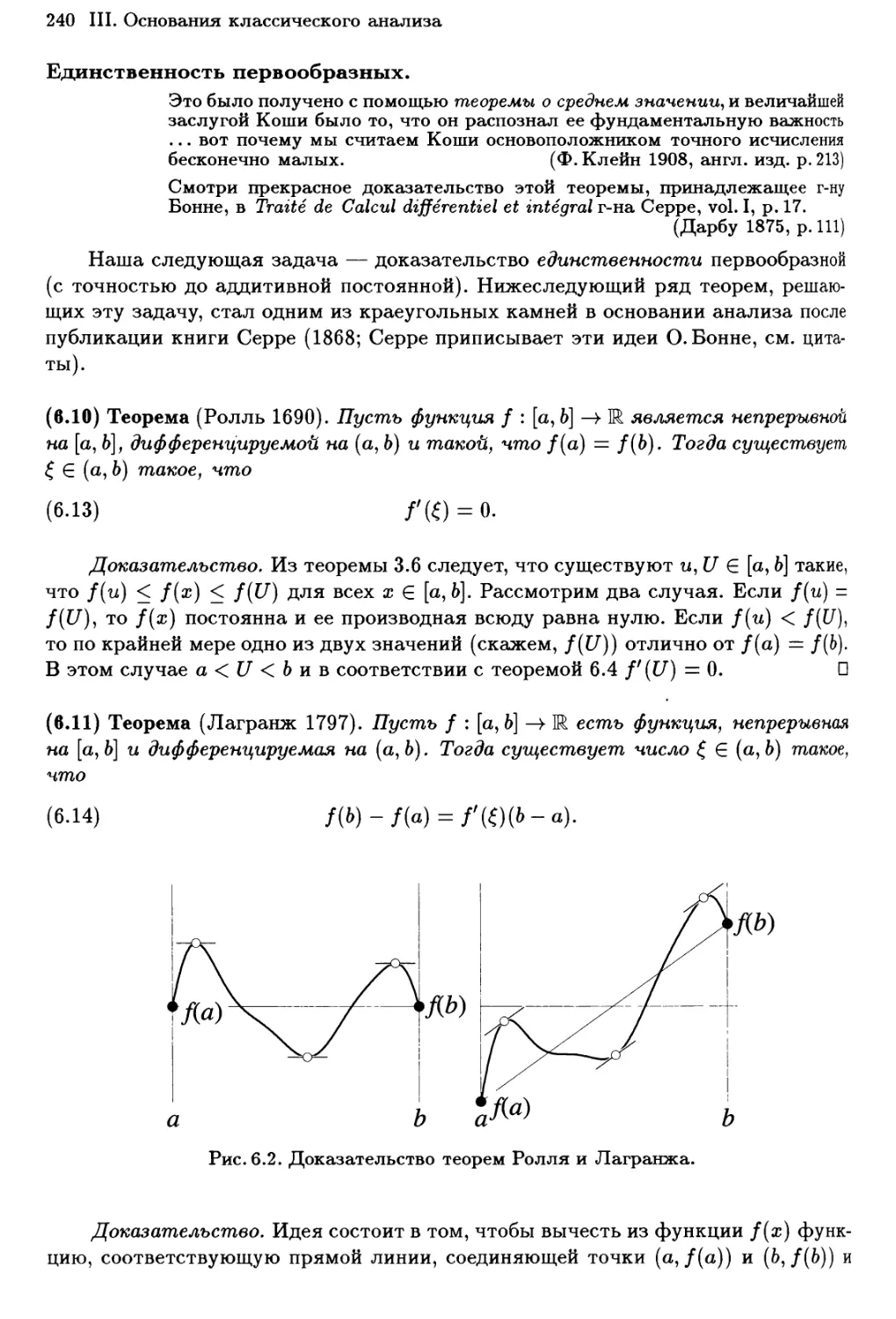
111.6 Дифференцируемые функщш 235
Фундаментальная теорема дифференциального исчисления 239
Правила Лопиталя 242
Производные бесконечных рядов 245
Упражнения 246
111.7 Степенные ряды и ряды Тейлора 248
Определение радиуса сходимости 249
Непрерывность 250
Дифференцирование и интегрирование 251
Ряд Тейлора 252
Упражнения 255
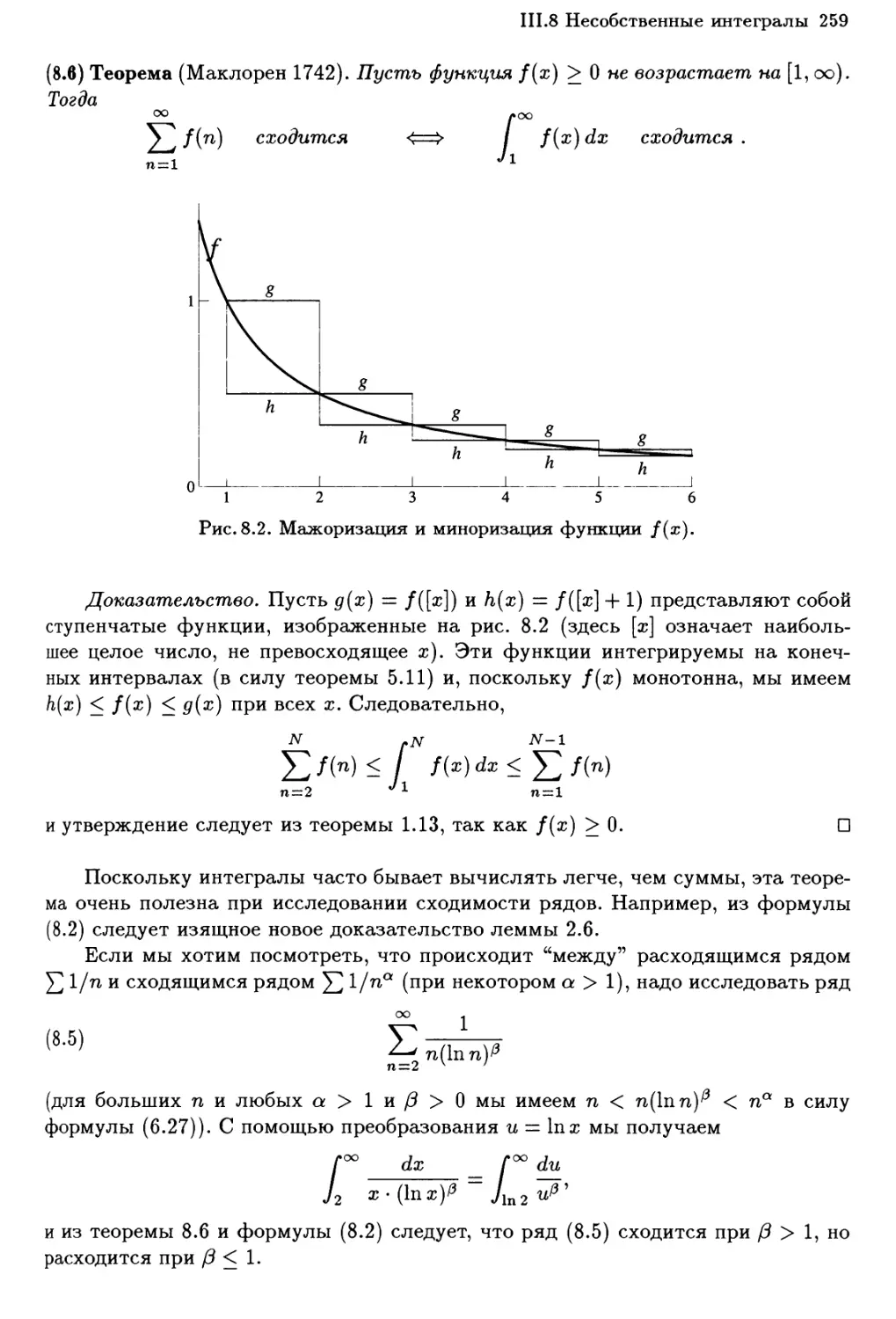
111.8 Несобственные интегралы 257
Ограниченные функции на бесконечном интервале 257
Неограниченные функции на конечном интервале 260
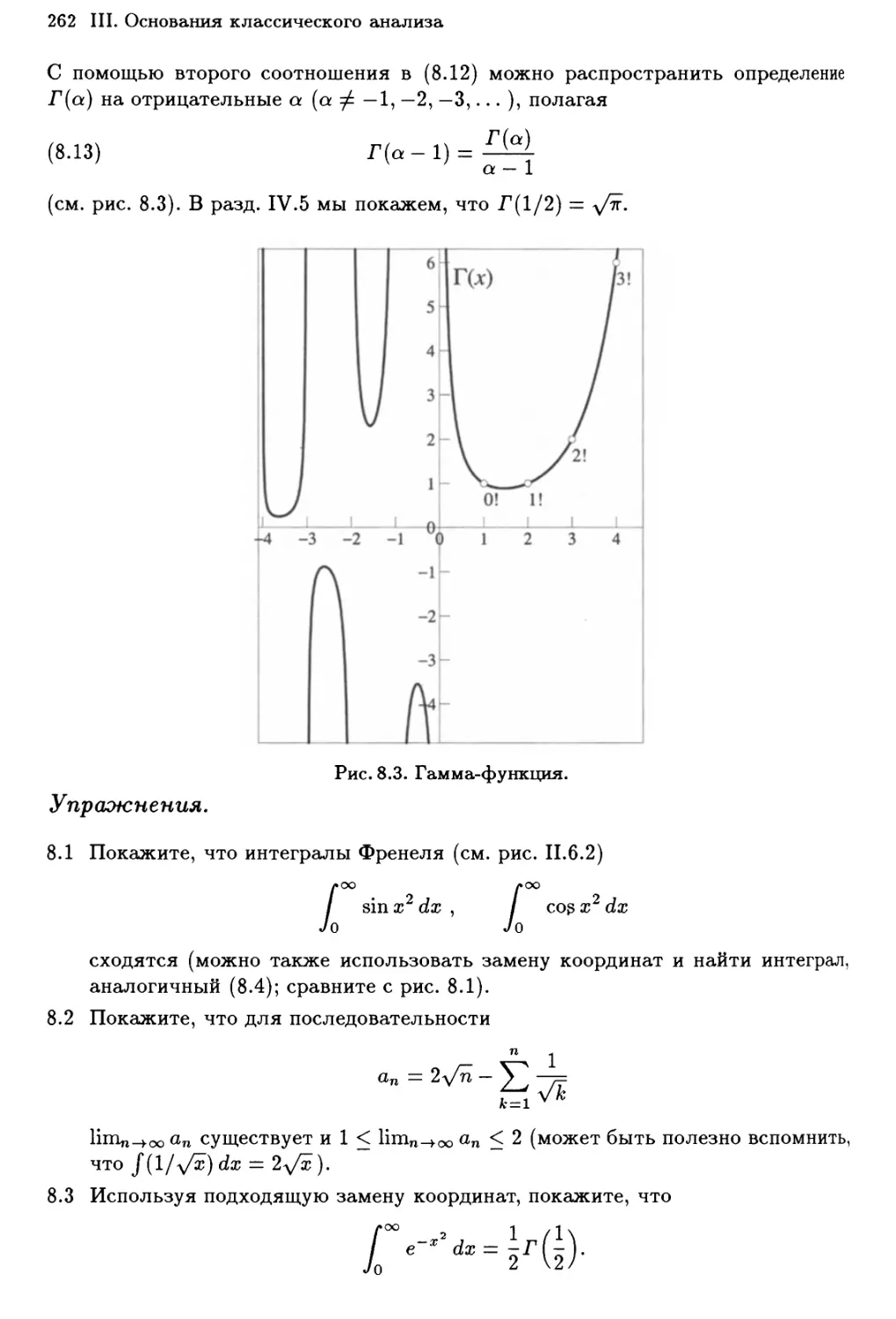
Гамма-функция Эйлера 261
Упражнения 262
111.9 Две теоремы о непрерывных функциях 263
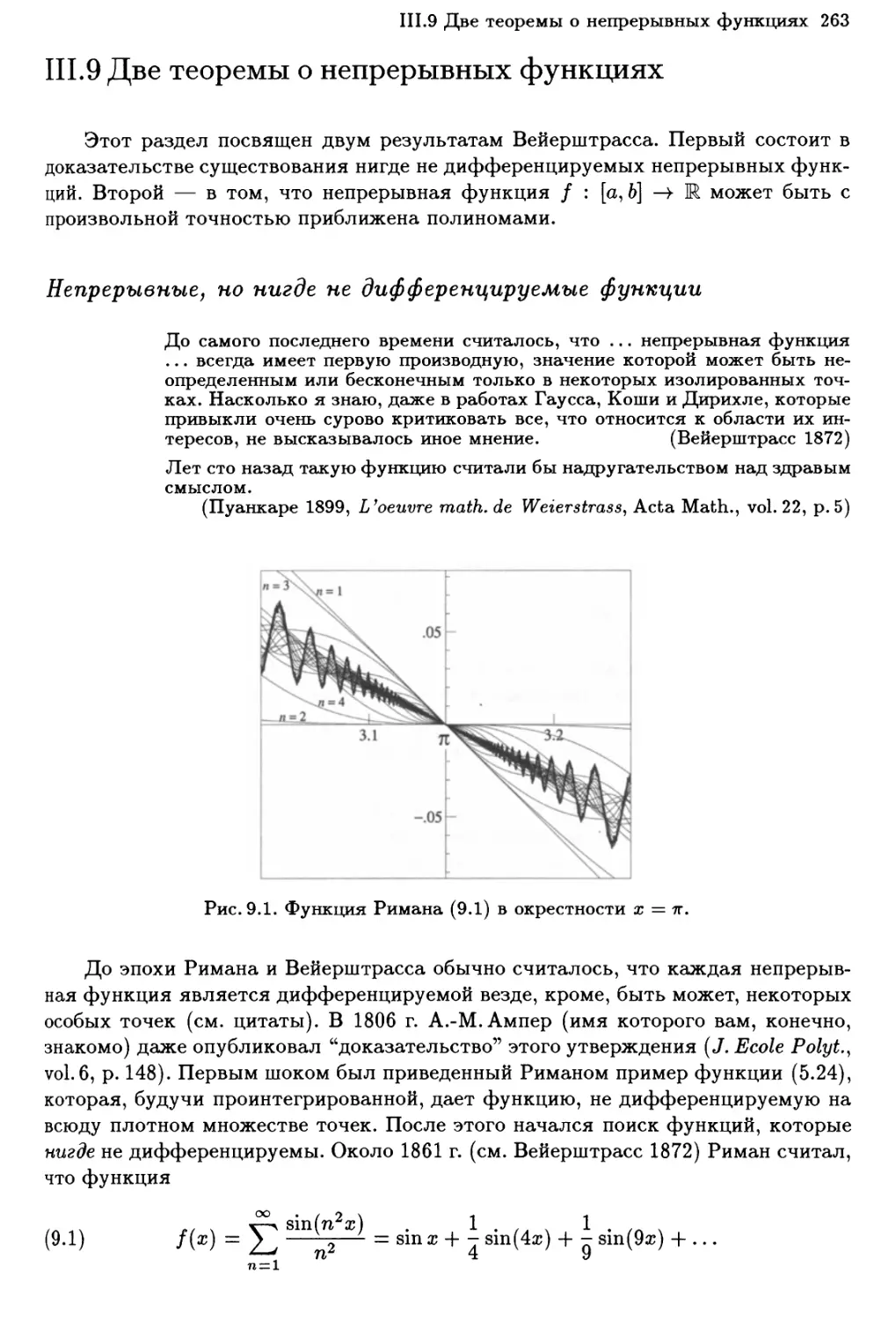
Непрерывные, но нигде не дифференцируемые функции 263
Аппроксимационная теорема Вейерштрасса 265
Упражнения 270
Глава IV Функщш нескольких переменных. Перевод В.В. Новиковой и В.М. Суслика
IV.1 Топология n-мерного пространства 273
Расстояния и нормы 273
Сходимость последовательностей векторов 275
Окрестности, открытые и замкнутые множества 278
Компактные множества 283
Упражнения 285
IV.2 Непрерывные функции 287
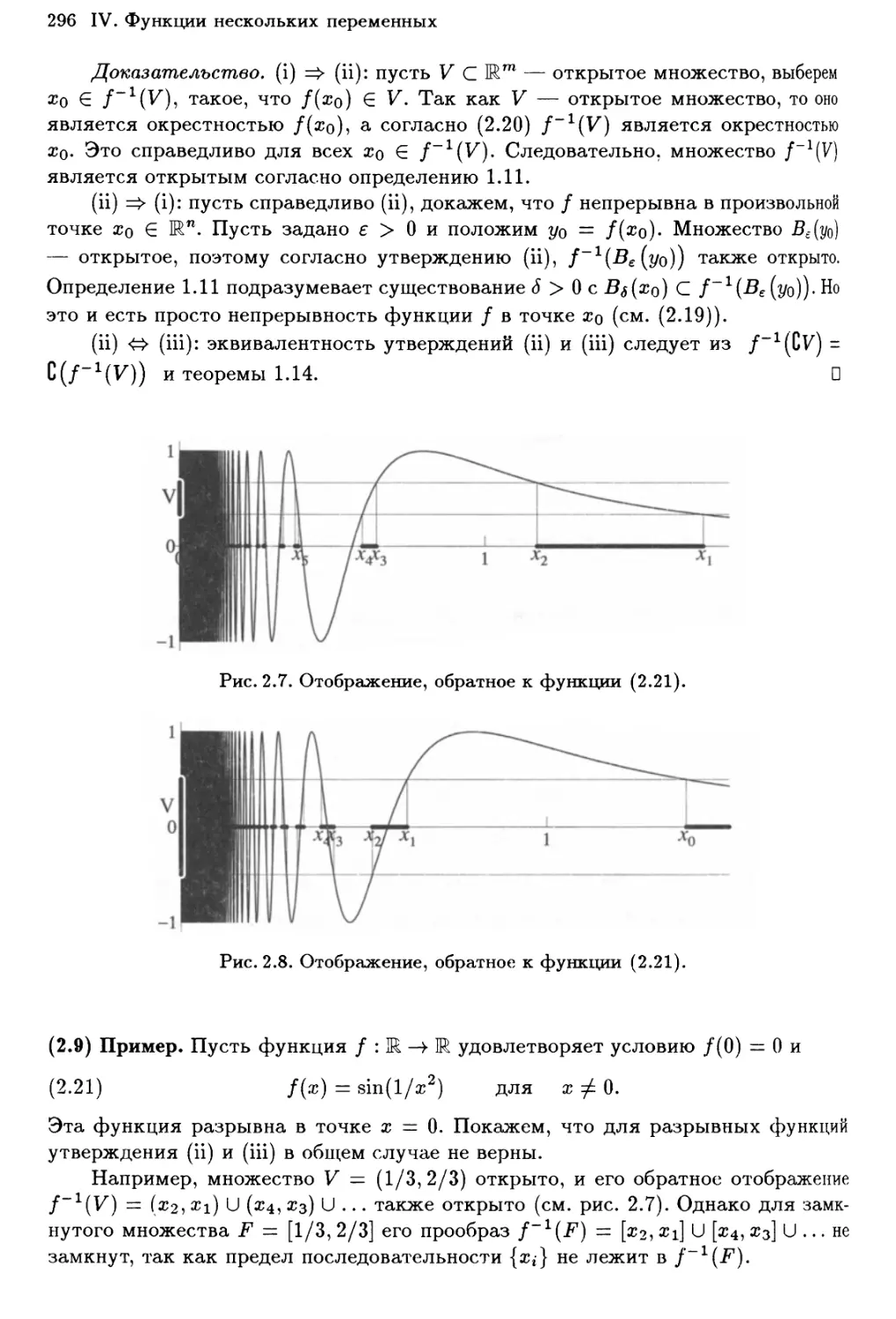
Непрерывные функции и компактность 289
Равномерная непрерывность и равномерная сходимость 290
Линейные отображения 293
Хаусдорфово описание непрерывных функций 294
Интегралы с параметрами 297
Упражнения 298
IV.3 Дифференцируемые функщш нескольких переменных 300
Дифференцируемость 302
Контрпримеры 304
Геометрическая интерпретация градиента 305
Теорема о среднем значении 308
Теорема о неявной функции 309
Дифференцирование интегралов по параметру 311
Упражнения 313
IV.4 Производные высших порядков и ряд Тейлора 316
Ряд Тейлора двух переменных 319
Ряд Тейлора для случая п переменных 320
Задачи на максимум и минимум 323
Условный минимум (множитель Лагранжа) 325
Упражнения 327

х Оглавление
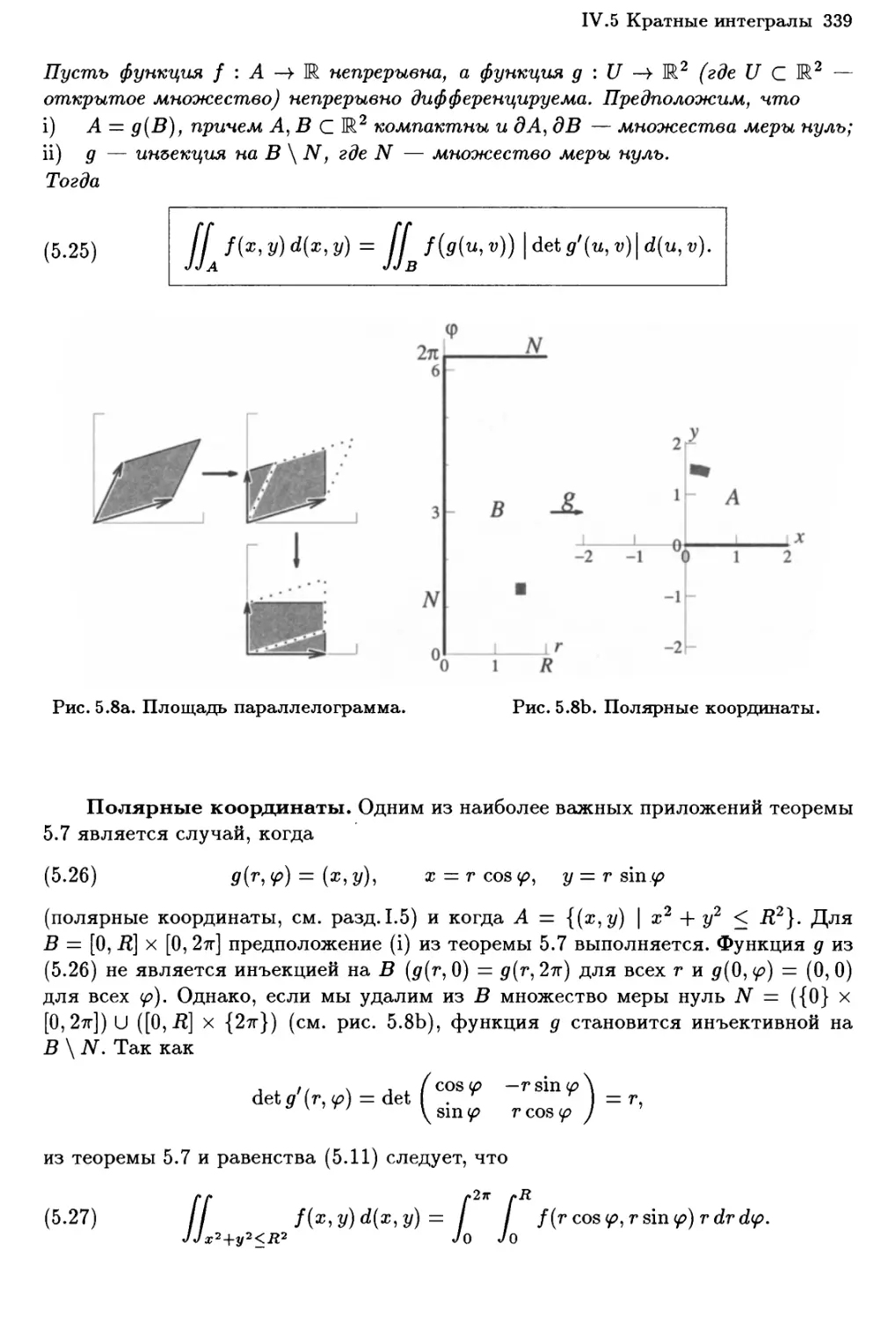
IV.5 Кратные интегралы 330
Двойные интегралы по прямоугольной области 330
Множества меры нуль и разрывные функции 334
Произвольные ограниченные области 336
Формула замены переменных в двойных интегралах 338
Интегралы по неограниченной области 345
Упражнения 347
Приложение: Цитаты на языках оригиналов 351
Библиография 358
Указатель обозначений 374
Алфавитный указатель
376

I
Введение в анализ бесконечных
... наши студенты-математики получили бы гораздо больше пользы от
изучения Introductio in Analysin Infinitorum Эйлера, чем от чтения
доступных современных учебников.
(Андре Вейль 1979, цитируется по книге: Дж.Д. Блантон 1988, p.xii)
так как учитель был достаточно здравомыслящим, чтобы позволить
своему необычному ученику (Якоби) заниматься Introductio Эйлера, в то
время как другие ученики с большим трудом . (Дирихле 1852,
речь, посвященная памяти Якоби и приведенная в Jacobi, Pverfce, vol. I, p. 4)
Эта глава объясняет, как возникли элементарные функции и какое влияние
на их вычисление оказала " Геометрия" Декарта. От интерполяционного
многочлена — к биномиальной теореме Ньютона и к бесконечным рядам для
показательных, логарифмических и тригонометрических функций. Глава
заканчивается обсуждением комплексных чисел, бесконечных произведений и непрерывных
дробей. Изложение следует историческому развитию этой темы на том уровне
математической строгости, который был тогда принят. Обоснование заключений,
которые могут показаться сомнительными, дает еще один повод для строгого
рассмотрения сходимости в главе III.
Книга Introductio in Analysin Infinitorum (Эйлер 1748) оказала большое
влияние на написание значительной части материала этой главы и дала ей название.

2 I. Введение в анализ бесконечных
1.1 Декартовы координаты и полиномиальные функции
Пока Алгебра и Геометрия были разделены, их прогресс был медленным,
а приложения ограничены. Но когда эти науки объединились, они оказали
друг другу взаимную поддержку и вместе двинулись вперед к
совершенству. Приложением Алгебры к Геометрии мы обязаны Декарту, это стало
ключом к величайшим открытиям во всех областях математики.
(Лагранж 1795, Oeuvres, vol. 7, p. 271)
Греческая цивилизация привела к первому большому расцвету
математических талантов. Начиная с эры Евклида (ок. 300 г. до Р.Х.), Александрия
становится мировым научным центром. Город был опустошен трижды (в 47 г. до Р.Х.
римлянами, в 392 г. христианами и, наконец, в 640 г. мусульманами), что привело
к закату этой цивилизации. После усовершенствования арабской письменности
(для нужд Корана), арабские писатели с рвением взялись переводить уцелевшие
фрагменты трудов греков (Евклида, Аристотеля, Платона, Архимеда,
Аполлония, Птолемея), а также индийских арифметиков, и сами начали новые
исследования в области математики. Наконец, во время крестовых походов (1100-1300
гг.) европейцы открыли для себя эту цивилизацию; Герхард Кремона (1114-1187),
Роберт из Честера (XII век), Леонардо из Пизы — "Фибоначчи" (ок. 1200 г.) и
Региомонтан (ок. 1460 г.) были основными переводчиками и первыми учеными
Западной Европы. В то время математика четко разделялась на алгебру, с одной
стороны, и геометрию — с другой.
Алгебра
Диофанта можно считать изобретателем Алгебры; ...
(Лагранж 1795, Oeuvres, vol. 7, p. 219)
Алгебра является наследием Древней Греции и Востока. В своей знаменитой
книге Китаб мухтасар ал-джебр ва-л-мукабала (Краткая книга восполнений и
противопоставлений, ок. 830 г.) Мохаммед бен Муса аль-Хорезми 1 положил
начало изучению квадратных уравнений. Наиболее старый из известных списков
этого сочинения датируется 1342 годом и начинается так: 2
Слова "алгебра" и "алгоритм" происходят от "аль-джебр" и "аль-Хорезми".
2 Воспроизводится (как и рисунки 1.1 и 1.2) с разрешения Бодлеевской библиотеки
Оксфордского университета (Bodleian Library, University of Oxford, Ms. Huntington 214,
folios 1R, 4R and 4V). Английский перевод см. Ф.Розен (1831).

1.1 Декартовы координаты и полиномиальные функции 3
Примеры аль-Хорезми. Рассмотрим квадратное уравнение
(1.1) ж2 + 10ж = 39.
Неизвестное решение х такого уравнения арабы называли dshidr (корень). Это
слово первоначально означало сторону квадрата заданной площади. ("Корень —
некоторая величина, которую надо умножить на себя", см. Ф. Розен 1831, с. 6).
Рукопись 1342 г. Современный чертеж
Рис. 1.1. Решение уравнения х2 + 10ж = 39.
Решение. Аль-Хорезми нарисовал квадрат со стороной ж, чтобы изобразить ж2, и
два прямоугольника со сторонами 5 и ж, изображающими член 10ж (см. рис. 1.1).
Уравнение (1.1) показывает, что площадь области, заштрихованной на рис. 1.1,
равна 39. Следовательно, площадь полного квадрата равна 39 + 25 = 64 = 8 • 8,
так что 5 + ж = 8иж = 3.
Рукопись 1342 г. Современный чертеж
Рис. 1.2. Решение х2 + 21 = Юж.
Второй пример из трактата аль-Хорезми — уравнение
(1.2) ж2 + 21 = 10ж,
которое в оригинале записано так: "Substancia vero et 21 dragmata 10 rebus
equiparantur" (перевод с арабского языка на латинский Роберта из Честера).
Этим примером мы хотим показать, что другие знаки членов требуют другого
чертежа. Чтобы получить решение ж, начертим квадрат для х2 и прибавим к
нему прямоугольник ширины х и неизвестной длины, который должен изображать
число 21 (рис. 1.2). Но согласно уравнению (1.2) полная длина всей полученной

4 I. Введение в анализ бесконечных
фигуры равна 10. Разделим фигуру вертикальной линией пополам и малый
прямоугольник (А), содержащийся между линией деления и квадратом ж2,
переместим наверх (В). Получится фигура (серая) высоиы 5, имеющая площадь, равную
21. Площадь же полного квадрата (серый и черный цвет) будет 5-5 = 25.
Следовательно, малый черный квадрат должен иметь площадь 25 — 21 =4 = 2-2, и
мы получаем х = 3. С помощью аналогичного чертежа (попробуйте это сделать!)
аль-Хорезми нашел и второе решение х = 7. Вот как описал свое решение сам
Мохаммед бен Муса аль-Хорезми (см. Розен 1831, с. 11):
... например, "некоторый квадрат и двадцать один равны в числах десяти корням того
квадрата." Иначе говоря, какова должна быть величина такого квадрата, который,
если добавить к нему двадцать один диргем, станет равным по величине десяти корням
этого квадрата? Решение: Раздели пополам число корней; половина есть пять. Умножь
это на себя; произведение будет двадцать пять. Вычти из этого двадцать один, что
было прибавлено к квадрату, останется четыре. Извлеки из этого корень, он равен двум.
Вычти это из половины корней, которая равна пяти, останется три. Это есть корень того
квадрата, величину которого надо найти, а сам квадрат равен девяти. Или можешь
прибавить корень к половине корней; сумма будет семь, это корень того квадрата, который
ты ищешь, а сам квадрат есть сорок девять.
В качестве примера аль-Хорезми дает решение следующей «загадки»: "Я
разбил число 10 на две части и, умножив одну часть на другую, получил в
результате 21. Чему равны эти части?" Полагая одну часть равной ж, а другую
10 — х и перемножив их, мы получим
(1.3) ж-(10-ж) = 21,
что эквивалентно уравнению (1.2). Следовательно, решение дается двумя
корнями уравнения (1.2), т.е. 3 и 7 или наоборот.
Решение уравнений третьей степени
Тарталья представил свое решение в плохих итальянских стихах ...
(Лагранж 1795, Oeuvres, vol. 7, p. 22)
... Я открыл общее правило, но пока я хочу сохранить его в секрете по
нескольким причинам.
(Тарталья 1530, см. М. Кантор 1891, vol. II, р. 485)
Попробуем решить, например, уравнение
(1.4) х3 + 6ж = 20,
или, выражаясь «плохими» итальянскими стихами, "Quando che'l cubo con le cose
appresso, Se agguaglia a qualche numero discreto ..." ("Когда какой-то куб с каким-
либо добавком Приравнен некому разумному числу ...", — ит.) (см. М. Кантор
1891, vol. II, р. 488). Николо Тарталья (1499-1557) и Сципионе даль Ферро (1465-
1526) нашли метод решения задачи, но они сохраняли его в тайне, чтобы победить
на состязаниях. Под давлением и соблазненный ложными обещаниями, Тарталья
раскрыл секрет Джероламо Кардано (1501-1576), зашифрованный в стихах и без
вывода ("suppressa demonstratione" — опустив доказательство, ит.). Кардано
восстановил вывод с большим трудом ("quod difficillimum fuit") и опубликовал
его в своей книге "Ars Magna" — "Великое искусство" в 1545 г. (см. ди Паскуале
1957, а также Стройк 1969, р. 63-67). Постараемся восстановить этот

1.1 Декартовы координаты и полиномиальные функции 5
Вывод. Представим х3 кубом с ребрами длины х (а как же иначе?), он
закрашен серым на рис. 1.3а; член 6х добавляется к кубу в виде трех призм с
квадратным основанием объема x2v и еще трех объема xv2 (белые на рис. 1.3а). Согласно
(1.4), мы получили тело объема 20, который является разностью объемов кубов
и3 и v3 (см. рис. 1.3а), т.е.
где
(1.5)
и3 - v3 = 20,
и = X + V.
Расположив шесть добавленных призм как показано на рис. 1.3Ь, мы видим, что
их общий объем будет равен вх (что и требуется), если
(1.6)
Suvx — 6ж
или
uv = 2.
Рис. 1.3а. Кубическое уравнение (1.4).
Рис. 1.3Ь. Обоснование формул (1.6).
ia*№matto.Excmplufii.cubiis &СброГ\*
oonrs^quantur^dutito^tmiam par*
ton&ad cubum,fit 8'duc ю dimidium nu
idinf^fitioo^ungf ioo&8jfitio8,acci
pr radiccm quf eft J* io89& cam gcmtaina
bis, altcri addr a i о, dimidium numtri, a b
ikcrominues tantundcm ,habcbis Bino*
wMi*io8p:!0,&Apotomcn!*io8 m:
jojiorum accip* ntw cub* & minue illam
cub'p:6reb9gcjlf* 26
t 26
8 io
i«8
fet6ftp:td
nnoBm.tb
te?:ai.teio8p:fo
m:i*v:ai.f*io8m:f
Рис. 1.3c. Из книги Кардано "Ars Magna" 1545, ed.Basilea 1570.3
Теперь мы знаем сумму (= 20) и произведение (= —8) двух чисел и3 и — v3 и
можем, следовательно, восстановить эти два числа, как в «загадке» аль-Хорезми
(1.3), в виде
и3 = 10 + л/Ш, -v3 = 10 - v/108.
3 Публикуется с разрешения Публичной библиотеки Женевского университета.

6 I. Введение в анализ бесконечных
Извлекая затем кубические корни и используя соотношение х — и — v, мы
получаем
(1.7)
(см. факсимиле из книги Кардано на рис. 1.3с).
Спустя несколько лет был найден метод решения уравнений четвертой
степени (Лодовико Феррари, см. Стройк 1969, р. 69 и далее, а также упражнения 1.1
и 1.2 в конце раздела). Но уравнение пятой степени оставалось непостижимой
тайной еще в течение столетий, пока, наконец, в 1826 г. Абель не доказал
невозможность его решения в радикалах.
"Algebra Nova"
Численная логистика — то, что раскрывается и исследуется с помощью
чисел; специфика раскрывается родом и формой вещей, как буквами
алфавита. (Виет 1600, Algebra nova, французское издание 1630 г.)
АЛГЕБРА - это общий метод вычислений с помощью определенных знаков
и символов, которые были придуманы и найдены удобными.
(Маклорен 1748, Трактат по алгебре, с. 1)
В старинных текстах рассматривались только частные примеры, и их авторы
выполняли "арифметические" вычисления, используя только числа.
Фундаментальная идея Франсуа Виета (Francois Viete 1540-1603: 1591 In artem analyticam
isagoge, 1600 Algebra nova) состояла в том, чтобы писать буквы А,В,С,Х,...
вместо неизвестных величин задачи (нередко геометрической) и использовать эти
буквы в алгебраических вычислениях (см. факсимиле на рис. 1.4а). Поскольку
оказалось, что ни одна задача древнегреческой эры не сопротивляется
применению метода
Геометрическая
задача
введи буквы
Алгебраическая
задача
вычисления
-»■
Решение
то Виет написал большими буквами: "NVLLVM NON PROBLEMA SOLVERE"
(т.е. "ДАЮЩИЙ РЕШЕНИЕ ЛЮБОЙ ЗАДАЧИ"). Эта великолепная идея
привела к появлению "Геометрии" Декарта.
Пример (трисекция угла). Знаменитая
классическая задача "Datum angulum in tres partes aequales
secare" (заданный угол раздели на три равные части
— лат.) с помощью соотношения
(1.8)
sin(3a) = 3 sin a cos" a
sin3 a
(см. ниже формулу (4.14)) и несложных вычислений
приводится к алгебраическому уравнению
(1.9) -4Х3 + ЪХ = В
(см. Виет 1593, Opera, р. 290). Его решение получается по формуле (1.14).

1.1 Декартовы координаты и полиномиальные функции 7
Формула для уравнения второй степени. В обозначениях Виета
сложный текст аль-Хорезми (см. с. 4) становится "формулой":
(1.10) х2+ах + Ь = 0 => хъ х2 = -а/2 ± у/а2 /4 - 6.
Excmple.
Qp'il faille a4)oufter A+D,auec ■+ t D,U
famae few A + В + j D# obfenunc ce qui а с(Ы
4it.
В +iD.
A + D.
A+B + jD.
Рис. 1.4a. Факсимиле из французского издания (1630) книги Виета(1600).4
Ci A quad. •+ В г in A, atquerar Zpiano. А •+ В cfto Е, Igitur Е quad.,
^xquabitur Z piano -+ В quad.
Confc&arium.
Icaquc/^pUm-rB^uaa. — В fit A, dc quaprimumquxrebatur.
Iraqac fi A cubus-— В piano $ in A, xquetur Z folido z.
^w>w£b^ »,u^,u»>w i" ^c-zfobdi^^^asr^, ^^..iJ, Eft A
dc qua quxneur.
Рис. 1.4b. Из книги Виета (1591a) (Operapp. 129, 150): решение уравнений A2-\-2BA = Z
и A3 - SB A = 2Z. Здесь неизвестная переменная обозначена А. Только Декарт ввел в
употребление выбор x,y,z для обозначения неизвестных.5
Формула Щ1Я уравнения третьей степени
о о у + а/3 — х о
(1.11) У +ayz + 6у + с = 0 => хй +px + q = 0.
Положим х — и -{- v (что соответствует (1.5), но с заменой "—г?" на CV), тогда
уравнение (1.11) примет вид
(1.12) и3 + v3 + (3uv + p)(w + v) + q - 0.
Полагая uv = — p/3 (что соответствует (1.6)), мы получим
(1.13) и3 + v3 = -q, u3v3 = -р3/27.
4 Воспроизводится с разрешения Публичной библиотеки Женевского университета.
5 Воспроизводится с разрешения Публичной библиотеки Женевского университета.

8 I. Введение в анализ бесконечных
С помощью «загадки» аль-Хорезми (1.3) и формул (1.10) мы получаем (см.
факсимиле на рис. 1.4Ь)
(1.14) х = \/-«/2+^/4 + р3/27+ y/-q/2-y/tf/4 + p>/27.
"Геометрия" Декарта
Здесь я прошу вас обратить внимание, между прочим, на то, что сомнения,
мешавшие старинным писателям использовать арифметическую
терминологию в геометрии, которые могли быть лишь следствием их
неспособности ясно осознать связь между этими двумя дисциплинами, внесли много
неясностей и путаницы в их объяснения. (Декарт 1637)
Геометрия, это гигантское наследие Древней Греции, была принесена в
Европу благодаря арабским переводам.
Например, Начала Эвклида (ок. 300 г. до н.э.) состоят из 13 "Книг",
содержащих "Определения", "Постулаты"и строго доказанные "Предложения" (всего
их 465). Столь же важное значение имеют Коники Аполлония (200 г. до н.э.).
Тем не менее, оставался нерешенным ряд задач, не поддававшихся усилиям
этих ученых: трисекция угла, квадратура круга, а также задача, упомянутая
Паппом в 350 г., которая вдохновила исследования Декарта.
Рис. 1.5а. Задача Паппа, чертеж Декарта.6
Задача Паппа. "Вопрос, решение которого было начато Эвклидом и
продолжено Аполлонием, но не было ими закончено, таков": Пусть даны три прямых
а, 6, с и три угла а, /9,7- Пусть для произвольно выбранной точки С точки В, D, F
на прямых а, 6, с таковы, что отрезки СВ, CD, CF образуют с прямыми а, 6, с
углы а,/3,7 соответственно (см. рисунки 1.5а и 1.5Ь). Найти геометрическое место
точек С, для которых
(1.15) CBCD = (CF)2.
6 Воспроизводится с разрешения Публичной библиотеки Женевского университета.

1.1 Декартовы координаты и полиномиальные функции 9
Рис. 1.5Ь. Задача Паппа. Рис. 1.5с. Уравнение прямой.
Декарт решил эту задачу, пользуясь "новой" и получившей признание
алгеброй Виета. Точка С определяется расстояниями АВ и ВС. Эти две "неизвестные
величины" обозначены буквами "ж" и "у" ("Que le segment de la ligne AB, qui est
entre les points A & B, soit nomme x. & que ВС soit nomme у" — фр-)- Рассмотрим
сначала только две из этих прямых (рис. 1.5с) ("& pour me demesler de la cofusion
de toutes ces lignes ..." — фр)- Проведем параллель к EF, проходящую через С.
Если углы заданы, то существуют такие постоянные К± и^2, что
и = Кг • CF, v = K2-y.
Так как АЕ = x + u + v = К$, получаем
(1.16) CF = d + £х + ky, d, £, к постоянные.
Аналогично,
(1.17) CD = тх + пу, га, п постоянные.
"Таким образом, вы видите, что ... длина каждой такой линии ... всегда может быть
выражена как сумма трех членов, один из которых есть неизвестная величина у,
умноженная или деленная на некоторую известную величину, другой есть неизвестная
величина х умноженная или деленная на некоторую другую известную величину, а
третий является известной величиной. Исключение должно быть сделано для случая,
когда заданные прямые параллельны ..." (Декарт 1637, р. 312, цитируется по
английскому переводу: Д.Е.Смит и М.Л. Латам 1925).
Таким образом, условие (1.15) примет вид
у • (тх + пу) - (d + £x + ку)2,
что является уравнением вида
(1.18) Ах2 + Вху + Су2 + Dx + Еу + F = 0.
При любом фиксированном значении у уравнение (1.18) становится квадратным
уравнением, которое решается алгебраически, см. (1.10). Преобразования
координат показывают, что (1.18) всегда представляет коническое сечение.

10 I. Введение в анализ бесконечных
Полиномиальные функции
Не только алгебра помогает геометрии, но и геометрия тоже помогает
алгебре, потому что декартовы координаты представляют алгебру в новом свете.
Действительно, если вместо (1.1) и (1.4) мы рассмотрим
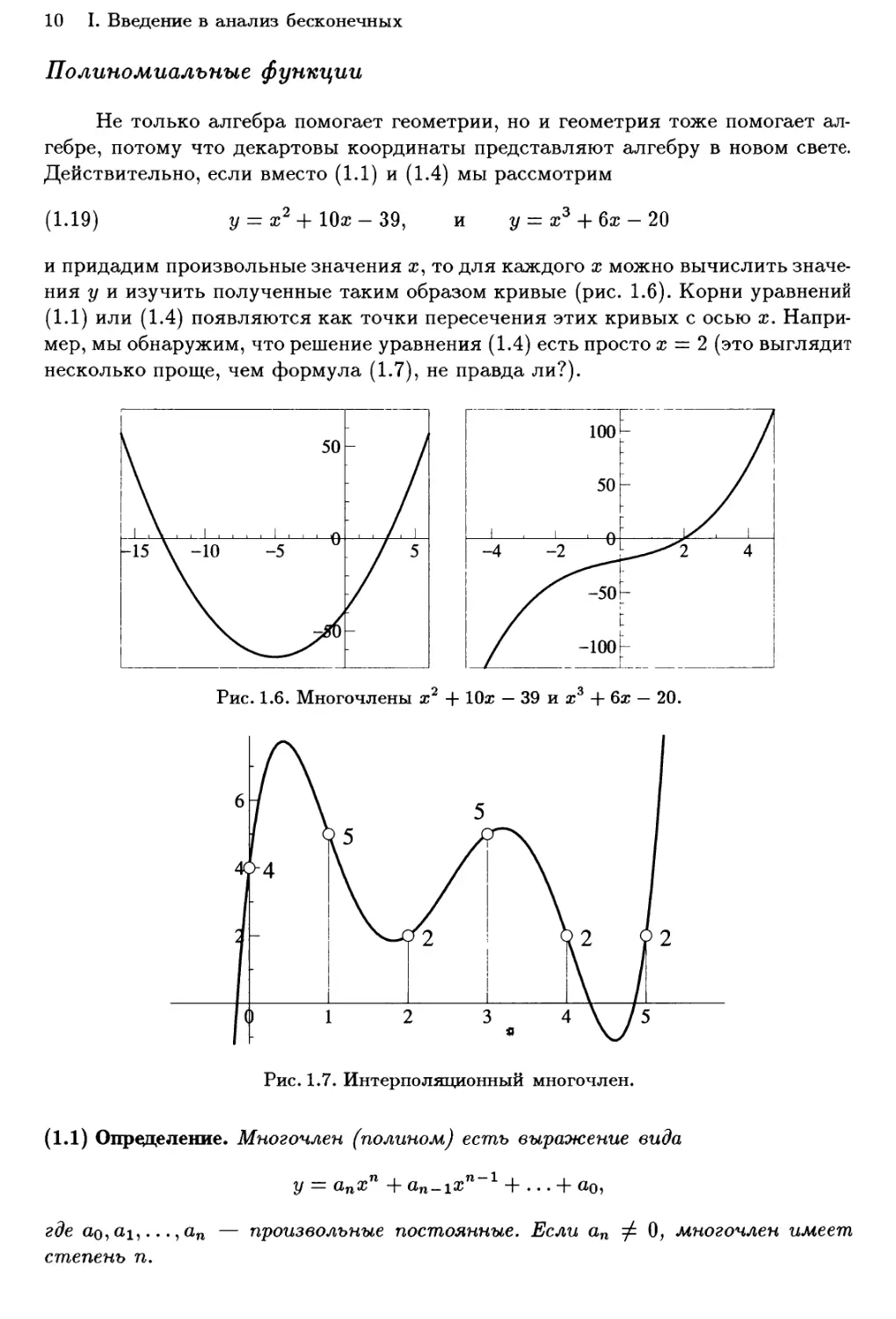
(1.19) у = х2 + 10ж - 39, и у = х3 + 6х-20
и придадим произвольные значения ж, то для каждого х можно вычислить
значения у и изучить полученные таким образом кривые (рис. 1.6). Корни уравнений
(1.1) или (1.4) появляются как точки пересечения этих кривых с осью х.
Например, мы обнаружим, что решение уравнения (1.4) есть просто х — 2 (это выглядит
несколько проще, чем формула (1.7), не правда ли?).
Рис. 1.6. Многочлены х2 + 10ж - 39 и х3 + 6х - 20.
Рис. 1.7. Интерполяционный многочлен.
(1.1) Определение, Многочлен (полином) есть выражение вида
у = апхп + ап-\хп~ + ... + ао,
где ao,ai,...,an — произвольные постоянные. Если ап ф 0, многочлен имеет
степень п.

1.1 Декартовы координаты и полиномиальные функции 11
Задача интерполяции. Пусть заданы п + 1 точек ж,-,2/,- ( рис. 1.7). Требуется
найти многочлен степени п, проходящий через все эти точки. Нас интересует
главным образом ситуация, когда все Х{ расположены на равных расстояниях и,
в частности, когда
xq — О, $1 = 1, Х2 = 2, жз = 3, ... .
Решение этой задачи, которое оказалось очень полезным при вычислении
логарифмов и в морской навигации, появилось в начале XVII века в работе Бриг-
гса и сэра Томаса Харриота (см. Голдстайн 1977, p. 23f). Ньютон (1676) подошел
к этой задаче с позиций "новой алгебры" Виета (см. рис. 1.8): напишем буквы
вместо неизвестных коэффициентов нашего многочлена, например,
(1.20)
у = А + Вх + Сх2 + Dx3.
1 AMciffit j
pivifct.DUF.Ord.
q—r) $—y
My-'
f J>-0 <-•
g—,) .—f
r_t) •—»
b-o f~«
Ordinate I
Л+*1+С1»+-ll» + f#«=/
Quoti per divifionem prodeuntes. ■ I
*+cXg+r + <fxgg + grH-rr+<*g*-ffl>r-f-gr« + r»-B J
*+ cxr+1 + <fxjr^-r*-f и + exr» + r'j -f n» + *»» di
J 4 cx,+> + «Jx и + it + ft + ex л 4- ''* -I- Л* + ti s «j
c 4 Jxg+ r-v #. + **gq+ V + rr -t-gi + w -f « = i*
tf + ixr + * + f + fxrr+м + ii+if-|-jf-H* =r
U+fX/'-H-f r + jef.
*+ех9-*-г-Н + г-*.
* = #. . I
1 - '
Рис. 1.8. Задача интерполяции у Ньютона (1676, Methodus Differentialis)7
Если величины Уо,У1,У2)Уз заданы, то "задача" преобразуется в
"алгебраические уравнения":
Абсциссы
х = 0
х = 1
х = 2
х- 3
Ординаты
Л
Л+Б+С+Я
Л + 2Б + 4С+8Я
Л + ЗБ + 9С + 27Z)
= 2/о
= Уг
= У2
= Уз
7 Воспроизведено с разрешения Публичной библиотеки Женевского университета.

12 I. Введение в анализ бесконечных
Здесь мы заметим, что величина А исчезнет, если вычесть уравнения первое из
второго, второе из третьего, третье из четвертого:
В + С + D = 1/1 - г/о =: Лу0
(1.21) В + ЗС + ID = j/2 - yi -. ЛУ1
B + 5C+l9D = y3- г/г =: Лу2,
В исчезнет, если снова произвести вычитания:
1С + 6£> = АУ1 - Ау0 =: А2уо
2C+12D = Ау2 - АУ1 =: А2У1,
и таким же способом исключается С:
(1.23) 6D = Л2У1 - А2у0 =: Д3уо.
Из этого уравнения находим D. Затем С из первого уравнения (1.22), а первое
уравнение (1.21) даст значение В. И мы придем к решению
(1.24) у = г/о + Луо ■ х + ^ • (х2 -х) + ^ ■ (х3 - Zx2 + 2х),
2 о
которое можно переписать в таком виде:
/ч Л./ч £ л х(х — 1) л9 х(х — 1)(х — 2) А*
(1.24') у = 2/о + Т Лу0 + \2} Л2уо + V t > ^ д L А3у0.
Используя треугольник Паскаля (см. разд. 1.2), можно показать, что формула
(1.24') — частный случай общей формулы для многочленов любой степени.
Справедлива следующая
(1.2) Теорема. Многочлен степени п, принимающий значения
Уо (для х = 0), т/1 (для х = 1),..., уп (для х = п)
задается формулой
х . х(х — 1) « х(х — 1)...(х — п+1) лп
у = у0+ -Лу0 + \ 0 }Л2у0 + ... + -* -^ }- Апу0.
1 1 • 2 1 • 2 •... • п
(1.3) Замечание. Обычай располагать разности в виде такой схемы:
Уо л где
Луо л2 л
2/1 А'уо Ау{ = yi+1 - у{
/1 огх ^ л2 Л У° л4 л2
(1.25) 2/2 Л ^22/1 ^ 4 2Л) ДУг = Ayi + 1 - Ayi
Ау2 Д*У1 3 л2 л2
УЗ л А2У2 A3yi = Д2Уг + 1 - A2Vi ,
Ау3
2/4 И Т.Д.
пошел от Ньютона (см. рис. 1.9).
Пример. Для значений из нашей задачи (рис. 1.7), мы получаем
4
5 -4 2/= 4+ - -х- —— -х(х- 1) + ...
-3 — 10 11-2
2 Q 6 ^22 613х ос 2 473я3
3 -12 43, => =4+ —— -35ж2 + —-—
5-6 21 — 30 24
2 ~3 3 9 9ж* 43ж*
0 ~~2~ + Т20"'

1.1 Декартовы координаты и полиномиальные функции 13
Л
ъ
с Ал
С С2 kJ
f ъ h ¥•
09 rS A^L.
§ €2 сЗ А#
Sic pergendum eft ad ultimam difierenriam. 'o
Рис. 1.9. Схема разностей у Ньютона (Ньютон 1676, Methodus Differentialis).'
-■В
Другие примеры, а) Рассмотрим многочлен, для которого решение уже
известно, а именно, у = ж3. Схема разностей дает:
ж = 0
ж=1
ж = 2
х — 3
О
" 1
1 ~ 6
7 " 6
8 12 "
19
27
2/ = 0 + 1-ж + б
ж(ж — 1)
+ 6-
ж(ж- 1){х- 2)
ж + Зж — Зж -h ж — Зж + 2х
Ь) В этом примере значениями многочлена при х — п будут суммы 13+23 + .. .-fn3,
ж = 0
х= 1
ж = 2
ж = 3
ж = 4
и мы получим формулу
о
I3
13 + 23
13 + 2з + Зз
I3 + 23 + З3 + 43
1
23 " 12
, 19 — б
З3 18 " О
,37 б ~ 0 ,
43 24 0 "
ж(ж-1) ж(ж-1)(ж-2) ж(ж - 1)(ж - 2)(ж - 3)
У - х + ' —о ь12 * ь6
24
ж4 ж3 ж2
Аналогично получаются формулы
8 Воспроизведено с разрешения Публичной библиотеки Женевского университета.

14 I. Введение в анализ бесконечных
п п
^ о _.о г\ ть ть ть
1+2+- + п=Т + У+б
(1.26) 13 + 2з+... + пз = ^+!^ + ^ + о
4 2 4
л А Л4 4 ™5 п4 п3 Л П
1 +2+- + п =У + У + Т + °-зо
15 + 25 + ... + п5 = _ + _ + _ + 0--.
Якоб Бернулли (1705) нашел общую формулу:
1Я + У + ... + п* = ^ + ^+ |Ап«-* + g(9 ; У - 2)Вп«-»+
Я + 1 z z 2 • о • 4
g(g-l)(g-2)(g-3)(g-4) 5
2-3-4-5-6 '
где
(1.27) А=-, B = -3Q, С=-, D = --, Е=-, F=-—, ...
так называемые числа Бернулли. Элегантное объяснение приведено в конце
следующей главы, в разд. 11.10.
Упражнения
1.1 Следующую задачу (мы запишем ее в обозначениях Виета)
х + у + z = 20
х : у- у: z
ху-Ъ
Зуан де Тонини да Кои (Zuanne de Tonini da Coi (Colla)) предложил 15
декабря 1536 г. Тарталье, который не смог решить ее (см. Нотари 1924).
Исключите переменные х и z и сообразите, почему. Кардано позже передал
задачу Феррари, который нашел решение (см. следующее упражнение). Не
удивительно, что позже Феррари и Тарталья обменялись нелицеприятными
письмами с жаркой полемикой по математическим вопросам.
1.2 Восстановите решение Феррари биквадратного уравнения
(1.28) х* + ах2 = Ьх + с.
Указание, а) Прибавьте а2/4 к обеим частям уравнения; это дает
v V 4
b) Рассматривая у как параметр, прибавьте у2 + ау + 2х2у к обеим частям
уравнения; это дает
2
(ж2 + °z + у)2 = 2х2у + Ьх + у2 + ау + с + °-.

1.1 Декартовы координаты и полиномиальные функции 15
c) Выражение в правой части, записанное как Ах2 -\-Bx-\-C, будет иметь вид
(ах + (З)2, если В2 = 4АС. Это дает кубическое уравнение для у.
d) Найдя у по формуле Кардано (1.14), вы получите два уравнения
О*2+ 7^+ 2/) =±(ая + /3),
каждое из которых имеет два корня.
Замечание. Любое уравнение z4 + az3 + bz2 -f cz + d — О можно привести к
виду (1.28) преобразованием х — z + a/4.
1.3 (Эйлер 1749, Opera Omnia, vol. VI, p. 78-147). Решите уравнение 4-й степени
ж4 + Вх2 + Сх + D = 0 ,
для этого сравните коэффициенты в обеих частях равенства
ж4 + Вх2 + Сх + D = (х2 +их + а)(х2 - их +/3)
и найдите уравнение третьей степени для и2. Решите это уравнение и
вычислите решения двух квадратных уравнений.
1.4 (Л.Эйлер 1770, Vollst. Anleitung zur Algebra, Opera Omnia, St. Petersburg —
Полное руководство no алгебре. Собрание сочинений, т. I.) Дано уравнение
4-й степени с симметричными коэффициентами, например,
(1.29) ж4 + Ьх3 + 8ж2 + Ъх + 1 = 0.
Разложите многочлен на множители (х2 + гх + 1)(х2 + sx + 1) и найдите
четыре решения (1.29).
Замечание. Другая возможность решить (1.29) — разделить уравнение на х2
и использовать новую переменную и = х + ж-1.
1.5 (Задача, предложенная Арменией и Австралией для 35-й Международной
математической олимпиады, проходившей в Гонконге 12-19 июля 1994 г.)
Пусть ABC — равнобедренный треугольник, где АВ = АС. Предположим, что: (i)
точка М — середина отрезка ВС, & точка О расположена на прямой AM так, что
ОБ перпендикулярно к АВ; (ii) Q — произвольная точка на отрезке ВС, отличная
от В и С; и (iii) точка Е лежит на прямой АВ, а F — на прямой АС, причем точки
Е, Q и F различны и лежат на одной прямой. Докажите, используя метод Виета,
что OQ перпендикулярно к EF тогда и только тогда, когда QE = QF.

16 I. Введение в анализ бесконечных
Р.Декарт (1596-1650)9 И.Ньютон (1642-1727)9
Summ* P$ttft4tum,
fa 00 inn +f я.
fan да f»> +iяя + in.
fai 00 £»4 +f»* + in».
/.♦ 00 £»' +*»♦ + bJ *—£я.
/я' 00 *"« +i»' +/»•**—Л яя.
/»< 00 К +i»6 + *»' *—±я»* +&■•
У 00 J»8 +i»r+/ji»**—i\»4 5|e+ /!««.
/•• 00 i«9 +*»» + b**-TW * + $«» *-^".
/я? X^^^+i"' + W *-/o"6 * + i*4 *—Л»»'
/»,e»Jr»,,+i«,0+ }П9 *_ ! я' * + I»1 *—i»' *+/?».
Quin imb quikgem progre/Tionieinibi attentius infpexerit, eundem
eriam condnuare poterit ab% Jus radociniorum ambagibut: Sumta
enim ( pro poteftatis cujusltbet exponente, fit fumma omnium *'£u
f* » rJrl»«+« + i* + iA.'-' + ^^fr Л,С"",+
cc-i.c-i.c-3.c-4 qC — S i c.c— l.c— i.c— j.c«-4.c.-S-*-*
* a . i . 4 . 5 . 6 a. 1.4.5.6. 7. *
D»<-7 . • . . &
Якоб Бернулли, Ars conj. 1705.9
9 Воспроизводятся с разрешения Публичной библиотеки Женевского университета.

1.2 Показательные функции и биномиальная теорема 17
1.2 Показательные функции и биномиальная теорема
Здесь уместно заметить, что я использую ж-1, ж-2, я-3, х~4 и т.д. вместо
7» 75"> 7»> ^4 и т.д., 12, х2, Ж2, ж» ,ж» и т.д. вместо у/х, л/ж3, \Za-s, ^х,
у/х^ и т.д., ж~2, ж~а ж~4 и т.д. вместо Д=, -зт=? "17= и Т*Д» Здесь правило
подсказано аналогией, которую можно усмотреть из таких геометрических
прогрессии, как эта: ж ,ж2,ж ,а;2,а;, ж2 , ж (или 1), х 2 5 х , х 2 ? х ,
и т.д. (Ньютон 1671, Fluxiones, р.З в англ.публ. 1736 г.)
Для заданного числа а мы пишем
(2.1) а-а = а2, а -а-а = а3, а-а-а-а = а4, ....
Эти обозначения входили в употребление медленно, главным образом благодаря
работам Бомбелли в 1572, Симона Стевина в 1585, Декарта и Ньютона (см. цитату
выше). Умножая, например,
а2 • а3 = (а • а) • (а • а • а) — а- а- а- а- а — а5,
легко заметить правило:
(2.2) ап -ат =ап+т.
В геометрической прогрессии (2.1), каждый член равен предыдущему,
умноженному на а. Можно продолжить эту последовательность и влево путем деления ее
членов на а. Это дает
Л-2 1 -1 _ 1 „О _ 1 1 Л 2 Л Л
а = , а = —, а = 1, а = а, а = а • а, ... ,
а • а а
где использовано обозначение
(2.3) а"т = 4г-
Таким образом, формула (2.2) остается справедливой и для отрицательных
показателей степени. Далее, повторно умножая 1 на у/а (где а должно быть
положительным числом), мы получим геометрическую прогрессию
1, у/а, у/а- у/а — а, у/а • у/а • у/а — va?, у/а* = а2, ... ,
которая подсказывает обозначение
(2.4) ат/п = v^.
Теперь формула (2.2) остается справедливой и для рациональных показателей
степени. Берутся только положительные значения корней, так что а5/2 лежит
между а2 и а3. Последний шаг, сделанный человечеством — иррациональные
показатели степеней. По словам Эйлера, они "труднее для понимания", но "Sic
о/1 erit valor determinatus intra limites a2 et a3 comprehensus" (лат.), т.е. "Так,
оУ есть величина, заключенная между а2 и а3", а также между а26/10 и а27/10,
между а264/100 и а265/100, между а2645/1000 и а2646/1000, и так далее.

18 I. Введение в анализ бесконечных
Биномиальная теорема
Хотя это предложение содержит бесконечное число случаев, я дам совсем
короткое его доказательство, приняв две леммы. Первая, самоочевидная,
состоит в том, что эта пропорция появляется во втором основании, потому
что совершенно ясно, что ср относится к а как 1 к 1. Вторая утверждает,
что если эта пропорция появляется в некотором основании, она с
необходимостью будет выполняться и в следующем основании.
(Паскаль 1654. Это одно из первых доказательств методом индукции.)
Развернем выражение (а + Ь)п. Умножая каждый результат снова на (а-Ь 6),
мы получим
(а + Ъ)° = 1
(а + 6)1 = а + Ь
(2.5) (а + 6)2 = а2 + 2аЪ+Ъ2
(а + б)3 = а3 + За26 + ЪаЬ2 + Ь3
(а + б)4 = а4 + 4а36 + ба262 + 4а63 + б4,
и т.д. При этом получается интересный треугольник ''биномиальных
коэффициентов" (Омар Алхайджама в 1080 г., Чу-ши Ки в 1303 г., М. Штифель в 1544 г.,
Кардано в 1545 г., Паскаль в 1654 г., см. рис. 2.1):
1
1 1
2 1
3 3 1
6 4 1
10 10 5 1
20 15 6 1
35 35 21 7 1
В нем каждое число является суммой двух стоящих выше. Попробуем найти
общий закон, определяющий эти коэффициенты. Легко заметить, что первая
диагональ треугольника состоит из "1", а вторая (1, 2, 3,...) — из "п". Для третьей
диагонали (1,3,6,10,...) угадывается " п'^~ ' ", для следующей " п х.2 з ~ "' и
т. д. Эти наблюдения подсказывают следующую теорему.
(2.1) Теорема (Паскаль 1654). Для всех п — 0,1, 2,... справедлива формула
(а + Ы = а" + \ а-Ч + ^^ а^Ч* + ^-^~2) a»-3fe3 + ... .
Это конечная сумма, содержащая п + 1 член.
Доказательство. Вычислим отношение каждого числа в (2.6) к соседнему
слева (Паскаль 1654, р. 7, "Следствие двенадцатое"):
(2.6)
1
1 4
1 5
1 б 15
1 7 21

1.2 Показательные функции и биномиальная теорема 19
Я
U JtrwimeiiatLl
Рис. 2.1. Оригинал публикации треугольника Паскаля (Паскаль 1654).1
(2.7)
7
1
б
1
5
1
6
2
4
1
Ь
?,
3
1
4
2
5
3
2
1
3
?,
4
3
1
1
2
2
3
3
4
4
1
?
2
3
3
4
1
3
2
4
3
5
1
4
2
5
1
5
2
6
1
6
1
7
Здесь уже нетрудно угадать общий закон. Мы докажем этот закон с помощью
"индукции по номерам строк" (см. цитату выше). Пусть
ABC
(2.8) D = A + B, Е = В + С
представляет фрагмент треугольника Паскаля, "индукционная гипотеза" имеет
вид:
В
А
!-!'
Тогда
(2.9)
С _ к-1
В~ I '
к-1
Е__ В + С _ 1 + g- _ l + *f* _ Ы+к2-к _ к
D
+ В л + 1 ф + 1 fi-t + kl
Воспроизводится с разрешения Публичной библиотеки Женевского университета.

20 I. Введение в анализ бесконечных
а это означает, что такая же структура обнаруживается и в следующей строке.
Из того, что отношения в n-й строке имеют вид п/1, (п—1)/2, (п—2)/3,... следует,
что коэффициенты (2.6) являются произведениями таких отношений. Например,
"20" в 7-й строке есть произведение
20 15 6 (2J) 4 5 6 _ 6-5-4
— 15 * б * 1 ~ з'2*1~3-2-1'
Мы видим, что теорема 2.1 справедлива в общем случае. □
Эти коэффициенты
п(п- l)...(n- j + 1) _п(п - 1)... (п - j + 1) (п - j)... 1
(2.10) J \ J)
п\ /n\
называют биномиальными коэффициентами, a n! = 1 • 2 •... • n — факториалом
числа п.
Приложение к интерполяционному многочлену. Разложим
выражения в схеме разностей (1.25):
2/о
2/1 ~Уо
2/1 У2 ~ 2^/1 + 2/о
2/2 - 2/1 Уз- 32/2 + 32/1 - 2/о •
2/2 2/з - 22/2 4- 2/1
2/з - 2/2
2/з
Появление треугольника Паскаля здесь не случайно, потому что каждый
элемент схемы является разностью двух элементов, стоящих слева от него. Далее,
каждый элемент схемы (1.25) есть сумма элемента, стоящего над ним, и
элемента, стоящего справа. Следовательно, схему можно переписать еще так:
2/о
Дуо
2/о + Лу0 Л2у0
Лу0 + Л2у0 Л3у0 .
уо + 2Лу0 + Д2Уо Л2Уо + Л3у0
Лу0 + 2Л2у0 + Л3у0
уо + ЪАу0 + ЗЛ2т/о + Л3у0
Здесь опять появился треугольник Паскаля. Таким образом, формула (2.10) дает
п л п(п — 1) л9 п(п — 1)(п — 2) о
уп = уо + у^2/о + V 2, М2з/0 + — ^ ^^32/о + • • • ,
что и доказывает теорему 1.2.
Отрицательные степени. Рассмотрим выражение
а-\- о
Если предположить, что |6| < |а|, то первым приближением к этому отношению
будет 1/а. Попробуем улучшить это значение, добавив неизвестную величину 8:

1.2 Показательные функции и биномиальная теорема 21
1 1
а + Ь а
1 = 1 + - + аб + Ъ8.
а
Пренебрежем членом 6rf, поскольку |6| < \а\. Тогда получим S — —Ь/а2. Повторяя
эту процедуру снова и снова (или, точнее, продолжая по индукции), мы получим
(2.11)
(а + Ь)-1^
1 _Ь_ ь^_Р
а а2 а3 а4
Тот же результат дает и теорема 2.1 при п = —1, но на этот раз ряд
оказывается бесконечным. Если умножить (2.11) на а и положить х = 6/а, мы получим
знаменитый геометрический ряд (Виет 1593):
(2.12)
1
1 + х
- 1 - х + х2 - х3 + ж4 - ж5 + ■
Ы<1.
Квадратные корни. Рассмотрим теперь (а + Ь)1'2 = Va + 6. Предположим
опять, что Ь мало, так что у/а + 6 га у^а, и будем искать такое 8 в выражении
л/a + b = у/а + <£,
чтобы оно давало лучшее приближение. Тогда
а + Ь= (у/а + 6)2 = а + 2у/а6 + 62.
Так как S мало, мы пренебрежем членом S2 и получим S = Ь/(2у/а).
Следовательно,
(2.13)
Va + 6 га л/^-Ь
2^/5
\Ь\<^а.
Пример: вычисление лД. Мы начнем с приближенного значения v = 1.4 и
положим a — v2^ Ь — 2 — а = 2 — v2. Тогда (2.13) дает новое приближение
2-v2
v +
2v
1/2 \
Повторно применяя полученную формулу, находим:
1.4
1.414285
1.4142135642
1.4142135623730950499
1.4142135623730950488016887242096980790
1.41421356237309504880168872420969807856967187537694807317667973799 .
Если те же вычисления выполнить в системе счисления с основанием 60, взяв
в качестве начального приближения число 1, 25, то получится 1, 24, 51,10 (здесь
запятые отделяют "цифры" шестидесятеричной системы). Это число найдено на
табличке из Вавилона, сделанной за 1900 лет до Р.Х. (см. рис. 2.2, а также ван
дер Варден 1954, гл. II, табл. 8Ь). Эта находка указывает, что формула (2.13)
использовалась уже во времена Вавилона и Древней Греции.
Следующий шаг сделали Алькаласади (около 1450 г.) и Бриггс (1624). Чтобы
улучшить (2.13), положим
Va + b = у/а + —— + S,
2у/а

22 I. Введение в анализ бесконечных
&
4t
Я, 10
25,35
Рис. 2.2. Клинописная табличка из Вавилона YBC 7289 (1900 лет до н.э.). На ней
изображен квадрат со стороной 30, указана длина диагонали 42,25,35 и отношение ее
к длине стороны 1, 24,51,10.2
возведем в квадрат обе части этого равенства:
4а
пренебрежем двумя последними членами и получим
l2 ц
a + b = a + b+ Ь 2>/аS + —F + <$2,
4а у/а
(2.14)
л/аТЬъ у/а+ —= -
ly/a
ь2
Пример. На этот раз для л/2 мы получим
2-у2 _ 4 - 4у2 + v4 _ 3<u 3 1
V+~2v' 8V ~ ~8~ + 2у~~ 2^'
Повторное применение этой формулы с начальным значением v = 1.4 дает
быструю сходимость:
1.4
1.4142128
1.41421356237309504870
1.41421356237309504880168872420969807856967187537694807317643 .
Равенства (2.13) и (2.14) примут более изящный вид, если в них разделить
обе части на у/а и заменить Ь/а на х:
2
(1 + х)* Ъ 1 + |, (1 + »)* « 1 + | - у.
Чтобы получить еще более точное приближение, можно продолжать повторение
описанных выше вычислений. В результате получится ряд вида
Воспроизводится с разрешения Йельской Вавилонской коллекции.

1.2 Показательные функции и биномиальная теорема 23
(1 + х) 2 = 1 + ^ + Ьх2 + сх3 + dx* + ... ,
коэффициенты 6, с, d,... которого надо определить. Для этого подставим этот
ряд в соотношение (1 + х)^(1 + ж)з = 1 + ж. Вычисление членов с
одинаковыми степенями х дает Ь = —1/8, с = 1/16, d = —5/128,... . Таким образом, мы
получаем лучшее приближение (Ньютон 1665)
128
х* + ...
ы 1(1-1)
(2.15) I (1 + х)* = 1 + ^х-±х2 + ±х3
Заметим, что
_1
~8
5_ _ _
~128 " 2.4-6-8 ~ 1-2-3-4
Это позволяет предположить, что теорема 2.1 справедлива и при п — 1/2.
Представленная на рис. 2.3 последовательность 1+ж/2, 1+ж/2—ж2/8,... иллюстрирует
сходимость (2.15) к л/1 -f х при — 1 < х < 1.
3-5 Ш-1)(§
1
16
1
2 "
_ 1-1
~ 2-4
-2)(§-
•3 _
•б ~
-з)
2 V 2
-1)(|-
1-2-3
-2)
л/ГТж
Рис. 2.3. Сходимость ряда (1 + х) а = 1 + |ж - |х2 + ^ж3 - yfg
Произвольные рациональные показатели степени
Все это происходило в те чертовские два года, 1665 и 1666, потому что
в те дни я был во цвете лет для изобретений и занимался математикой
и философией более, чем когда-либо с тех пор.
(Ньютон, цитируется по книге Клайн 1972, р. 357)
Одна из идей Ньютона из этих "anni mirabiles" (чудесных лет, — лат.),
подсказанная работой Валлиса (см. Замечание после уравнения (5.27)), —
попытаться интерполировать многочлены (1 + ж)°, (1 + ж)1, (1 + ж)2,..., чтобы получить
ряд для (1 + ж)а, где а некоторое рациональное число. Это значит, что надо
интерполировать коэффициенты в теореме 2.1 (см. рис. 2.4). Так как последние

24 I. Введение в анализ бесконечных
являются многочленами от п, ясно, что в результате получится то же самое
выражение, в котором п заменено на а. Таким образом мы приходим к следующей
общей теореме.
Рис. 2.4. Интерполяция треугольника Паскаля (автограф Ньютона, 1665 г.).3
(2.2) Теорема (обобщенная биномиальная теорема Ньютона). Для любого
рационального а при \х\ < 1
(1 + x) =l + jX+^-^x + j-^ x +... .
Даже Ньютон находил, что его основанная на интерполяции аргументация
была рискованной. Эйлер в своем Introductio (1748, §71) дает формулировку
общей теоремы ("ex hoc theoremate universali" — "отсюда общая теорема", лат.)
без всякого доказательства или комментария. И только Абель спустя столетие
почувствовал необходимость строгого доказательства (см. разд. III.7).
Замечание. Именно эта формула была выгравирована на надгробном памятнике
Ньютону в 1727 г. в Вестминстерском аббатстве. Не тратьте бесполезных усилий,
— в течение последующих ста лет формула оставалась неясной.
Показательная функция
... ubi е denotat numerum, cuius logarithmus hyperbolicus est 1 ("... пусть e
обозначает число, гиперболический логарифм которого есть 1", лат.).
(Первое определение числа е: Эйлер 1736b, Mechanica, p. 60)
Источники происхождения.
1. Ф.Дебон (1601-1652) был первым, кто прочел "Геометрию" Декарта,
вышедшую в 1637 г. Годом позже он предложил Декарту следующую
геометрическую задачу: найти такую кривую г/(ж), чтобы для каждой ее точки Р расстояние
3 Воспроизводится с разрешения издательства Cambridge University Press.

1.2 Показательные функции и биномиальная теорема 25
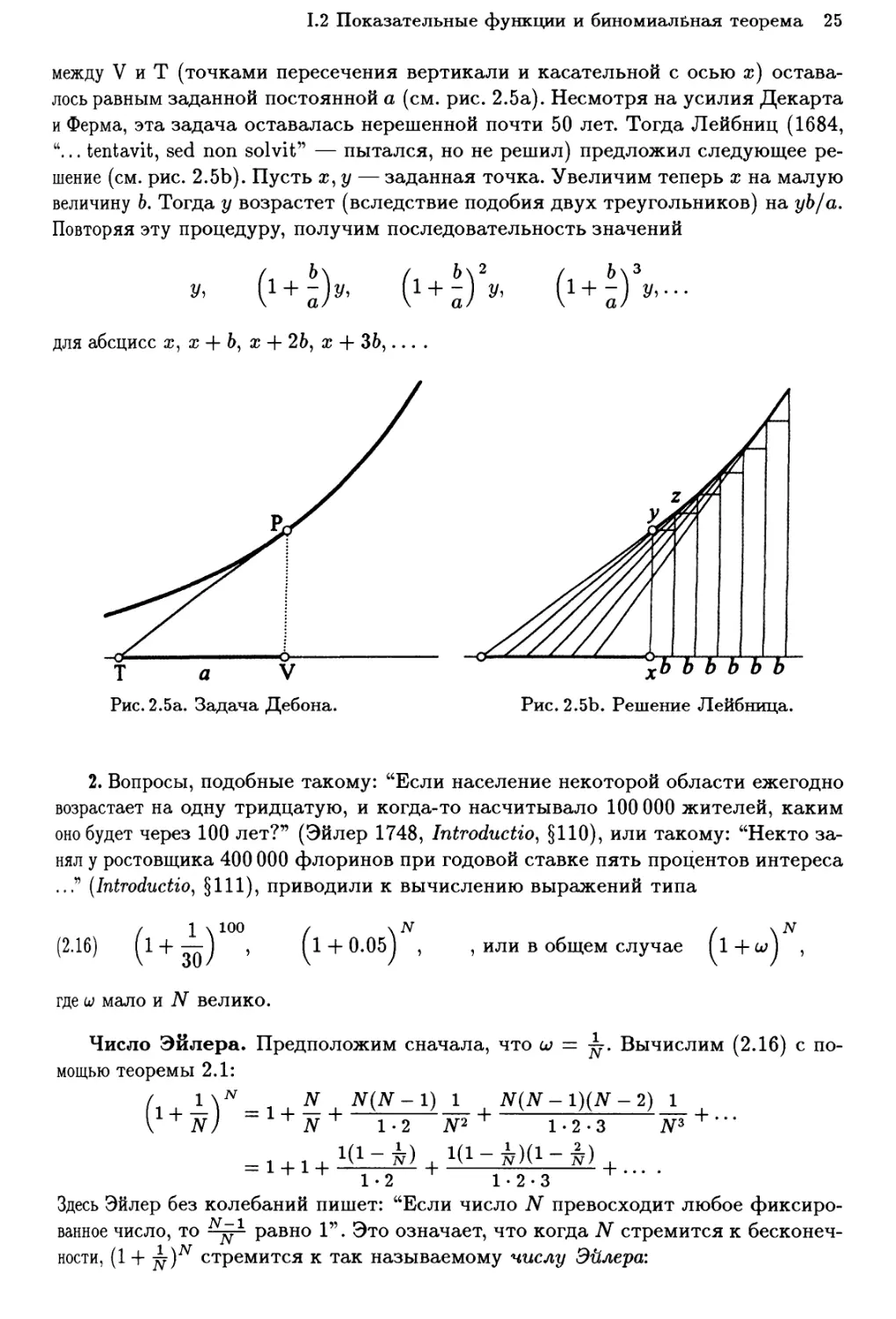
между V и Т (точками пересечения вертикали и касательной с осью х)
оставалось равным заданной постоянной а (см. рис. 2.5а). Несмотря на усилия Декарта
и Ферма, эта задача оставалась нерешенной почти 50 лет. Тогда Лейбниц (1684,
"... tentavit, sed поп solvit" — пытался, но не решил) предложил следующее
решение (см. рис. 2.5Ь). Пусть ж, у — заданная точка. Увеличим теперь х на малую
величину Ь. Тогда у возрастет (вследствие подобия двух треугольников) на уЬ/а.
Повторяя эту процедуру, получим последовательность значений
для абсцисс ж, х + 6, х + 26, х + 36,... .
Рис. 2.5а. Задача Дебона. Рис. 2.5Ь. Решение Лейбница.
2. Вопросы, подобные такому: "Если население некоторой области ежегодно
возрастает на одну тридцатую, и когда-то насчитывало 100 000 жителей, каким
оно будет через 100 лет?" (Эйлер 1748, Introduction §110), или такому: "Некто
занял у ростовщика 400 000 флоринов при годовой ставке пять процентов интереса
..." (Introduction §111), приводили к вычислению выражений типа
/ 1 \ 100 / ^N /чАГ
(2.16) (1 + ^л) ' (1 + 0.05) , , или в общем случае (1+ам ,
где ш мало и N велико.
Число Эйлера. Предположим сначала, что и; — -^. Вычислим (2.16) с
помощью теоремы 2.1:
/ 1\" N N(N-1) 1 N(N-l)(N-2) 1
V W/ ^ЛГ"1" 1-2 ЛГ2 1.2-3 N3^'"
= 1111 1(1"^} I ^-тП1-^) ,
1-2 1-2-3 '
Здесь Эйлер без колебаний пишет: "Если число N превосходит любое
фиксированное число, то ^^ равно 1". Это означает, что когда N стремится к
бесконечности, (1 + jf)N стремится к так называемому числу Эйлера:

26 I. Введение в анализ бесконечных
(2.17)
ТАБЛИЦА 2.1. Вычисление числа е
N (1 + &)"
1 + -J- +J-4- +J-
' 1! '2! ' * * * i _/V!
2.0
2.5
2.66
2.708
2.7166
2.71805
2.718253
2.7182787
2.71828152
2.718281801
2.7182818261
2.71828182828
2.718281828446
2.7182818284582
2.71828182845899
2.7182818284590422
2.71828182845904507
2.718281828459045226
2.7182818284590452349
2.718281828459045235339
2.7182818284590452353593
2.718281828459045235360247
2.7182818284590452353602857
2.718281828459045235360287404
2.7182818284590452353602874687
2.71828182845904523536028747125
2.718281828459045235360287471349
2.71828182845904523536028747135254
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2.000
2.250
2.370
2.441
2.488
2.522
2.546
2.566
2.581
2.594
2.604
2.613
2.621
2.627
2.633
2.638
2.642
2.646
2.650
2.653
2.656
2.659
2.661
2.664
2.666
2.668
2.670
2.671
Необходимо отметить, что аргумент Эйлера рискованный, потому что он
применяется бесконечное число раз. Применяя аналогичное "доказательство",
можно, например, получить, что
1=!+Ы+1+Ь£+£+-+£=о+о+о+-=о-
Мы вернемся к этому вопросу в разд. III.2. В табл. 2.1 сравниваются скорости
сходимости ряда (2.17) и последовательности (1 + -h)N-
Степени числа е. Положим теперь в (2.16) и — x/N, где х
фиксированное, скажем, рациональное число. Иначе говоря, мы одновременно устремляем
N к бесконечности и w к нулю так, чтобы их произведение оставалось равным
постоянной величине х. Та же манипуляция, что и выше, приводит к результату
(2.18)
:^)
N
^1 + Х + Т~2 + —3
+
1-2-3-4
+ ..

1.2 Показательные функции и биномиальная теорема 27
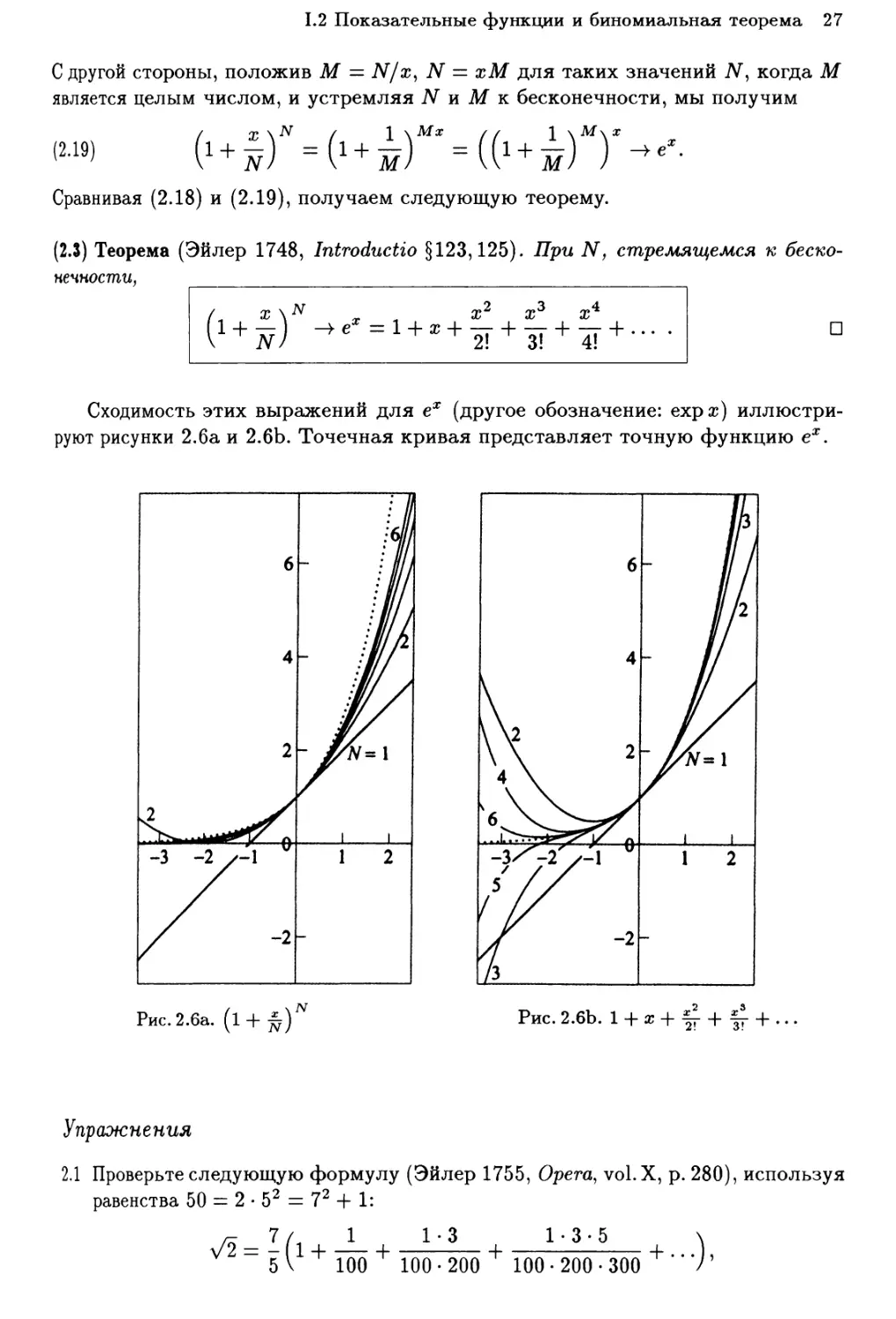
С другой стороны, положив М — N/x, N — хМ для таких значений ЛГ, когда М
является целым числом, и устремляя N и М к бесконечности, мы получим
Сравнивая (2.18) и (2.19), получаем следующую теорему.
(2.5) Теорема (Эйлер 1748, Introductio §123,125). При N, стремящемся к
бесконечности,
( х \N „ х2 х3 ж4
(1 + T7J -+ех = 1 + х + — + — + — + ...
2! 3! 4!
п
Сходимость этих выражений для ех (другое обозначение: ехр х)
иллюстрируют рисунки 2.6а и 2.6Ь. Точечная кривая представляет точную функцию ех.
6
4
2
s2 ^У
11 --^Wl-,-^ll**^J' Л
-3 -2/-1 °,
/ ~2
1 1
1 2 1
Рис. 2.6а. (l + f)^
Рис. 2.6Ь. 1 + х + §г + §г + -
2.1 Проверьте следующую формулу (Эйлер 1755, Opera, vol.X, p. 280), используя
равенства 50 = 2 • 52 = 72 + 1:
^=10-^-
1-3 1-3-5
+ «„„ „ +
100 100 • 200 100 • 200 • 300
...),

28 I. Введение в анализ бесконечных
"quae ad computum in fractionibus decimalibus instituendum est optissima"
(которая, как установлено при вычислении в десятичных дробях, является
оптимальной, — лат.). Сложите численно первые пять членов этого ряда.
Указание. Воспользуйтесь рядом для (1 — ж)-1/2.
2.2 Покажите, что записанное в шестидесятеричной системе число 1, 25,
является хорошим приближением к л/2. Покажите, что одна итерация
"вавилонского алгоритма" для квадратного корня, выведенная из формулы (2.13), дает
1, 24, 51,10,... , — значение, приведенное на рис. 2.2.
2.3 Умножая на себя дважды ряд
(1 + х)1/3 = 1 + ах + Ьх2 + сх3 + ... ,
определите коэффициенты а, 6, с,... . Должно получиться
Используя равенство 2 • 43 — 53 = 3, получите формулу
2
^=i(1 + r^5-iry:
(125)
2
2-5 2-5-8
+ 1 • 2 • 3 • (125)3 " 1 • 2 • 3 • 4 • (125)4 +
•)■
Замечание. Определение \/2 было одной из великих проблем
древнегреческой математики (удвоение куба).
2.4 Неравенства Бернулли (Якоб Бернулли 1689, см. 1744, Opera, р. 380; Барроу
1670, см. 1860, Works, Lectio VII, §ХШ, р. 224). Индукцией по п докажите,
что
(1 + а)п>1 + тш для а > -1, п — 0,1,2,...
1 — па < (1 — а)п < для 0 < а < 1, п = 2, 3,... .
1 + па
2.5 Чтобы исследовать сходимость (l + £) к е, рассмотрите последовательности
/ 1\п / 1\^+1
ап = [1 + -J и Ьп = (1 + -J .
Покажите, что
аг < а2 < а3 < ... < е < ... < Ь3 < Ь2 < Ьх
и что Ьп — ап < 4/п.
Указание. Используйте второе неравенство из упр. 2.4 при а = 1/п2.

1.3 Логарифмы и площади 29
L3 Логарифмы и площади
Tabularum autem logarithmicarum amplissimus est usus ... (но таблицы
логарифмов являются наиболее употребительными, — лат.)
(Эйлер 1748, Introduction §110)
Студенты обычно находят понятие логарифма очень трудным для
понимания. (Б.Л.Ван дер Варден 1957, р. 1)
М.Штифель (1544) выделил два ряда чисел (см. факсимиле на рис. 3.1):
-3
1
8
-2
1
4
-1
1
2
0
1
1
2
2
4
3
8
4
16
5
32
6
64
7
128
8
256
Amthubticae Libbk, пь aj7
| #d*dBon& «с pkneoftenctt ИЬ, i ♦ capftc degcoqtet.prognE
Vide ergo,
o* i» *• !• * i"» 6* 7. «•
i* *• 4* *• l6< **• *4» ив* if**
Stem ex additionc«n (upcrforc ordfoc) j ad у Aunt 8 .flc«n to-
ferioreordfoe)ex multiplication* 8 Jn 31 fiunt i?6.Eft autem
3 exponent fpftus odonarij э & j eft exponent mimed 31 ♦ & 8
eft exponent numcrl ij-tf. Item (Ion to prdtoe ibpcriorl,ex
lubcractocie 3 de7»Kminent4Uttto toferiori ordine ex Ши1-
Oone i*8 per 8 ,flimt i ^*
Scd oftendenda eft rfta fpeoilatto per cxcmplunu
\~Ъ\-*Ы о I il »l >l4lfl<l
1 il il Ц ll *1 4) 8|i6|3xK4l
Рис. 3.1. Из книги Штифеля (p. 237, p. 250).*
Мы видим, что переход от нижней строки к верхней преобразует произведения в
суммы. Например, вместо умножения 8 на 32 "in inferiore ordine" (в нижнем
порядке, — лат.), берем соответствующие "логарифмы" 3 и 5 "in superiore ordine"
(в верхнем порядке), вычисляем их сумму, которая равна 8, возвращаемся "in
inferiore ordine" и находим произведение 8 • 32 = 256. Более подробная таблица
такого типа была бы очень полезной, потому что складывать легче, чем
умножать. Такие "логарифмические" таблицы вычислили впервые Джон Непер (1614,
1619), Генри Бриггс (1624) и Йост Бюрги (1620). (\6yoq (логос) по-гречески
означает ''слово, связь", agiOuos (арифмос) — "число", поэтому "логарифмы" —
полезные связи между числами.)
(3.1) Определение. Функция £(х), определенная для положительных значений х,
называется логарифмической функцией, если для всех х,у > 0
(3.1)
t{x-y)=i(x)+l{y).
Воспроизведено с разрешения Публичной библиотеки Женевского университета.

30 I. Введение в анализ бесконечных
Если в (3.1) положить у = z/x, мы получим
(3.2) t(z/x)=l(z)-l(x),
а при х — у — 1 получим
(3.3) /(1) = 0.
Применяя (3.1) дважды к равенству х • у • z = (х • у) • я, найдем, что
(3.4) l(z.y.z) = l(x)+l(y)+l(z),
и аналогично для произведений четырех или более сомножителей. Далее,
применяя (3.4) к равенству у/х • у/х • %/х = ж, получим, что t(\/x) = \t(x)-> или в
общем случае
(3.5) 1(х%) = —1(х), где х^ = Ух™.
п
Основания логарифмов. Пусть задана некоторая фиксированная
логарифмическая функция 1(х). Предположим, что существует число а такое, что
£(а) = 1. Тогда (3.5) примет вид
(3.6) /(а?) = ^,
т.е. эта логарифмическая функция является обратной функцией для
показательной функции ах. Ее называют логарифмом при основании а и пишут
(3.7) у — loga ж, если х — ау.
Логарифмы при основании 10 (логарифмы Бриггса) особенно удобны для
вычислений, потому что сдвиг десятичной точки в числе приводит просто к
прибавлению целого числа к его логарифму. Но для теоретической работы наилучшим
основанием, как мы скоро увидим, является число Эйлера е (натуральные, или
неперовы, или гиперболические логарифмы). Эти логарифмы обозначают обычно
In ж или log ж.
"Золотое правило" Эйлера. Если логарифмы при одном основании
известны, то логарифмы при всех других основаниях получаются при помощи
простого деления. Чтобы в этом убедиться, возьмем логарифм числа х — ау при
основании Ь и применим формулы (3.7) и (3.5). Это дает
/л л\ 11 1 1°&Ь Х
(3.8) \ogbx = y\ogba => y = \ogax=- .

1.3 Логарифмы и площади 31
Вычисление логарифмов
Вычисляя корень квадратный из основания а, затем корень квадратный из этого
квадратного корня и т. д. и перемножая все эти величины, мы получим с помощью
(3.6) и (3.1) логарифмы многих чисел. Это иллюстрирует рис. 3.2 для а — 10.
1.00ь ..•
Числа
10.0000
7.4989
5.6234
4.2170
3.1623
2.3714
1.7783
1.3335
1.0000
Логарифмы
1.
0.875
0.75
0.625
0.5
0.375
0.25
0.125
0.
1101/4 101/2 103/4 10
Рис. 3.2. Последовательные корни из 10 и их произведения.
Однако мы предпочли бы знать логарифмы таких чисел, как 2,3,4,...ане4.2170
или 2.3714.
Метод Бриггса. Вычислим корень из 10, затем корень из этого корня и
будем продолжать так 54 раза (см. факсимиле на рис. 3.3). Это дает при с — 1/254
(3.9а) 10е = 1.00000 00000 00000 1278191493 20032 35 = 1 + а.
Затем таким же образом вычислим последовательные корни из 2 и получим
(3.9Ь) 2е = 1.00000 00000 00000 03847 73979 65583 10 = 1 + Ь.
Значение х = log102, которое мы ищем, удовлетворяет равенству 2 = 10х.
Следовательно,
ul (3.9b) (3.9а) (по теореме 2.2)
1-1-6 = 2 = (10 ) = (1 + а) « 1 + ах
и мы получаем
6 3847739796558310
(3.10) log10(2) = х « - = 127819149320032з5 * 0.3010299956638812.
Вычислено одно число. Объем работы, необходимой для целой таблицы, трудно
даже представить себе.
Интерполяция. В старые времена интерполяция была важным
инструментом для ускорения вычисления логарифмов. Пусть, например, были вычислены
четыре значения log10. Рассчитаем по ним разностную схему

32 I. Введение в анализ бесконечных
Arithmetic*
Numeri f*tim*t Mtfy inter Demarm & V*ituU.
i о
51612,77660,16837,93 3*9,08893,54
17781,79410,03892,28611,97?04,' 3
13 3и>»1431»16и*»4ог5б,6^з89,Зс8
11547.8198468945,81796,61918,113
10746^7828,3113i,7497^48|7.^ 38
I0366,3i9i8,43769»7997*>906i7,3i3i
10181,51711,71818,18414,7371318144
10090,3 y044,84i44»74377»59«>J»491
10045 >°73<Ч>И44*,Ч 156,64670,6113
10011,51148.19г9М9И4,б5*П,73б7
ioon>i494«>39937,93758,85395i5i8o5
1000 j1,61311,60120.86366,18495,91839
10001,81116,78778,01313,99*49,643*5
10001,40548,51694,71581,6176731717
iooGO;7ot7i,7894i,143 55,38811,70845
io«oo,3$i35,~2774*>l8*<^>o858i,37077
юооо,175б7,4844*,1б738.3 3846,78174
10000,08783,70363,46111,46574,07431
iooooo439*>84H7,31672,36281,88083
10000,01195,91867,55541.033*71077! °
10000,01097,95873,50104,09754,7294°
I0000j005 48,979 21 68211.14616,60150,4
ioooo,ooi74,48957>°738i,95°Pb15449>9
10000,00137,14477,595 * 0,83181,69571,5
;oooo»ooo68,6i138,56110,15737^18748,1
0000,00034,31119,11118,83911,75010,8
0000,00017,15559,59637,84719,93879,1
oooo,oooo8,57779>7945bo305bi7588,8
0000,00004,18889,8963 3,54198,41901,3
0000,00001, i4444>94793.77767t4»97Q>4 L
oooo,ooooi,07in,4739i,l4«>50>769i6,&
0000,00000, 53611,13694,13317,1483^4
0000,00000,16 805,61 M>7<>7 3 * ,5«$08,7
0000,00000,13401,809*3,1*383,99*77.7
ooootooooo,o 6 701 >4°4°l >°e 94*Л Г %' 9>*.
0000,00000,03 3SO>7°*3°>799i l,9t73o,o
0000,00000,01675,3^ 4,39815,61857,6
0000,00 ооо,оо8з7,б7557»*987*,7*4**,9
0000,00000,00418,83778.84917,^9087,9
oooo,coooo,ooi Q9,4i 8 89,41^61,60161,5
0000^00000,00104,70944,7 Ii30;*53l J>o
oooo,oocoo,o 0052,35471,3 5$14,>3°50,4
0000,00000,00026,17736,17807,460^8,9
ocoo,ooooo,ooo 13,08 868,0890 3,71167,3
0000,00000,00006,544 \ 4,04451,8 5 869,75
0000,00000,0000 3,17217,0212 5,91881,3 37
3000,00000,00001,63608,51111,96417,183
3000,00000,00000,81804,15556,48110,295
3000,00000,00000,40901,11778,14104,311
хюо,ооооо,ооооо,10451,06389,11051,946
>ооо,ооооэ,ооооо, 102 25,53194,56025,921!,!
юоо,ооооэ,ооооо,05111,76597,28012,947м
1000,00000,00000,02556,3 8198,64006,470 ЛЛ
fooo,ooooo,cooOv),o 1178,19149,3 *003>*3 5 ^
1,000
L*i*rithm mUwtlif,
0,50
o,*5
0,115
0,0615
0,03 **f
0^01561,5
0,00781,15
0,00390,625
0,00195,311*
0^00097^65615
0,00048,82811,5
0,00024,41406,25
0,00011,20703,115
0,00006,10351,5615
0,00003,05175,78115
0,00001,51587,89061,5
10,00000,76193,94531,15
0,00000,38146,97265,625
'0,00000,19073,48632,8125
0,00000,095 3 6,74 316,40615
0,00000,04768,37158,20311,5
0,00000,01384,18579,10156,15
0,00000,01191,09189,5 5078,115
0,00000,00596,04644,775 39,0615
[0,60000,00198,01311,38769,5 3 u s_
10,00000,00149,01161,193 84,76561,5
№,00000,00074,50580,59691,38181,* 5
^,00000,60037,1511^,19846,19140,6*5
10,00000,00018,61645,14913,09570,311^
,0,0,0000,00009,31 з*1,574*Ь^478Ыуб!5.
^00000,00004,65661,18730,77392,57811,5
o,ooooo,~****. 7Л%1Ъ£ы6*2 *8б9б(>289о6,15
0,00000,00001,16415,5^^^8, t44j3,i25
0,00000,00000,58107,66691,34674,07116,5615
O,ooo0tf,oooob,i9i03,83045,6>j37,03tf1?,igii5
10,00000,00000,14551,91521,83668,51806,6406*1,5
6,ooooo,ooooo,o7i75,9576t^taj4,i5903#3*o3«,*f
0*00000,00000,03 6 37,97880,70917,11951,66015,615
0,00000,00000,01818,98940,3 5458,56475,83007,8115
O,ooooo,ooooo,o0909>49470>'77>9>*8i37>9'y03>9o6i5
^,00000,00000,00454,74735,08864,64118,95751,9531*
^,00000,00000,00127,3^367,54431,31059,47875,976561
0,00000,00000,00113,68683,77*16,16019,73937,99818
Io,ooooo,ooooo,oo056,84341,88608,08014,86968,99414
^0,00000,00000,00018,41170,94304,^400^^^84^0^
b,ooooo,ooooo,oooi4,uo85,47^i,o'*ooj,7i74i,*4855
koo 000,00000,000 07,10541,73576,01001,85871,12416
O,oopc?o,ooooo,oooo3,55i7i,36788,oo500!,9i935,56iij
0,00000,00000,0000 1,776 3 5,683 94,00150,46467,78106
0^00000,00^^^^000,88817,84197,00115,1313 3,89051
;o,ooooo,ooooo, ooooo,444°8,9*098,5oo6i?6i6i6,945itf
0,00000,00000,00000,11104,46049,15031,30808,47163
|o,ooooo,ooooo,oooO*M *101,13014,61515,65404,33631
0,00000,00000,000*0,0) ^411511,31157,817^1,11115
Рис. 3.3. Вычисления Бриггса последовательных корней из 10 (Бриггс 1624).
Воспроизводится с разрешения Публичной библиотеки Женевского университета.

1.3 Логарифмы и площади 33
log(44) = 1.6434526765
0.0097598373
log(45) = 1.6532125138 -0.0002145194
0.0095453179 0.0000092277.
log(46) = 1.6627578317 -0.0002052917
0.0093400262
log(47) = 1.6720978579
Она дает интерполяционный многочлен (теорема 1.1, со сдвигом)
р{х) =1.6434526765 + {х - 44) (0.0097598373 +
ж — 45/ ж — 46 \\
+ —— (-0.0002145194 + —— • 0.0000092277J J,
Полученные с его помощью для нескольких выбранных значений х результаты
вместе с величиной ошибки (err) приведены в табл. 3.1. Несмотря на легкость
их вычисления, результаты оказались вполне хорошими. При желании точность
можно увеличить, добавив в разностную схему дополнительные точки.
ТАБЛИЦА 3.1. Ошибки интерполяционного многочлена
р(х) logio(jc)
44.25 1.645913252
44.50 1.648359987
44.75 1.650793026
1.645913275
1.648360011
1.650793040
2.34
2.42
1.35
•ИГ8
•1(Г8
■ИГ8
45.25 1.655618594 1.655618584 -1.05 • 10_й
45.50 1.658011411 1.658011397 -1.43 • 10"8
45.75 1.660391109 1.660391098 -1.04 • 10~8
46.25 1.665111724 1.665111737 1.32 • Ю-8
46.50 1.667452930 1.667452953 2.34 • Ю-8
46.75 1.669781593 1.669781615 2.24 • Ю-8
Прежде чем вернуться к вычислению логарифмов, совершим небольшой экскурс
в геометрию.
Вычисление площадей
Еще со времен Древней Греции задачи о вычислении площадей и объемов
возбуждали любознательность математиков. Вычисление площадей параболы и круга
были двумя из величайших достижений Архимеда (283-212 гг. до Р.Х.).
Начало XVII столетия ознаменовалось вычислением площадей под кривыми у = ха
как при целых, так и при произвольных значениях а (Бонавентура Кавальери,
Роберваль, Ферма).
Задача. При заданном а найти площадь под кривой у — ха между границами
х = 0 и х — В.

34 I. Введение в анализ бесконечных
Л, _ у1/3
У -X Ва
QaBa
Q2aBa
&В
ев
Рис. 3.4а. Ферма (1601-1665).3 Рис. 3.4b. Как Ферма вычислил площадь
под кривой ха.
Решение (Ферма 1636). Выберем О < 1, но близкое к 1, и рассмотрим
прямоугольники, образуемые геометрической прогрессией 1?, 6В, 02В, 03В,..., высоты Ба,
0аВа, 62аВа, 03аВа,... (рис. 3.4Ь). Тогда искомую площадь можно
аппроксимировать с помощью геометрического ряда:
1-й прямоугольник + 2-й прямоугольник + 3-й прямоугольник + ...
= В(1 - 0)Ва + В(0 - 92)6аВа + В{02 - 03)62аВа + ...
(3.12) 10
= Ва+1{1 - 0) (1 + Г+1 + 92а+2 + ...)= в°+\ J+1,
геометрический ряд
при условии, что а-\-1 > 0, т.е. а > — 1 (см. уравнение (2.12)). Пусть 0 — 1-е, где
£ мало. Тогда 1 — 0 = £, 0а+1 = 1 — (а + 1)£ -f •.. по теореме 2.2. Следовательно,
1-0 е 1
при е —>• 0.
1_0«+1 (а + 1)£ а+1
Сумма площадей прямоугольников (3.12) аппроксимирует (при а > —1)
площадь 5 сверху. Если высоты прямоугольников заменить на 0аВа, 02аВа,..., мы
получим приближение к 5 снизу. В такой ситуации величина (3.12) просто
умножается на 0а, а этот множитель стремится к единице при 0 —>■ 1. Поэтому оба
приближения стремятся к одной и той же величине, и мы приходим к
следующему результату:
(3.2) Теорема (Ферма 1636). Площадь под кривой у = ха между х = 0 и х = В
равна
Ва+1
S — -, если а > —1. □
а+1
3 Портрет Ферма воспроизводится с разрешения Математической библ. Женевского
университета.

1.3 Логарифмы и площади 35
Площадь под гиперболой и натуральные логарифмы
В сентябре месяце 1668 г. Меркатор опубликовал свою Логарифмотехнию,
которая содержит пример применения этого метода (т. е. бесконечных
рядов) для одного случая, а именно, для квадратуры гиперболы.
(Письмо Коллинза, 26 июля 1672 года)
Метод Ферма неприменим в случае гиперболы у — 1/х. Действительно,
геометрическая последовательность абсцисс Б, вВ, б2В, О3В,... дает для площадей
ряд (1-0)(1 + 1 + 1 + ...), частичные суммы которого образуют арифметическую
прогрессию. Это обстоятельство послужило отправной точкой для следующего
открытия, которое сделали Грегори из Сент-Винсента в 1647 г. и Альфонс Антон
де Сараса в 1649 г. (см. Клайн 1972, р. 354): площадь под гиперболой у = 1/х
является некоторым логарифмом (см. рис. 3.5).
= 1/х
равные площади
= 1/х
Рис. 3.5. Площадь под гиперболой есть логарифм.
Сжимая координаты х и растягивая координаты у, нетрудно заметить, что,
например, Площадь (3 -> 6) = Площадь (1 —У 2). Поэтому
Площадь (1 —> 3) + Площадь (1 -» 2) = Площадь (1 —> 6).
Это означает, что функция 1п(а) = Площадь (1 —>■ а) удовлетворяет тождеству
1п(о)+1п(Ь) = 1п(а.Ь)
и поэтому является логарифмом (logarithmus naturalis).
Ряд Меркатора. Сдвинув начало координат на 1, мы найдем, что 1п(1 + а)
есть площадь, заключенная под кривой 1/(1 + х) между 0 и а. Сделаем теперь
замену 1/(1 + х) — 1 — х + х2 — х3 + ... по формуле (2.12) и вместо площадей
под кривыми 1,ж,ж2,..., заключенными между 0 и а, подставим в соответствии
с теоремой 3.2 выражения
«, 2, 3, 4,
(см. рис. З.б). Заменив а на ж, мы найдем в результате, что
(3.13)
1п(1 +
х) =
х -
X2
2
+
X3
3
X4
4
+
X5
5
- + •••

36 I. Введение в анализ бесконечных
^
г—1
l/
площади
^
Рис. 3.6. Почленное интегрирование геометрического ряда.
(Н. Меркатор 1668). Сходимость этого ряда при различных значениях х юказана
на рис. 3.7. При значении х — 1 этот ряд принимает вид
(3.13а)
1 о , 1 1 1 1 1
Ь2=1-2+3-4+5-6+
Эта красивая формула имеет лишь ограниченное практическое применение (см.
табл. 3.2). При еще больших значениях х ряд вообще не сходится.
1п(1+ х)
Рис.3.7. Сходимость ряда х — ^- + ^ ^- + ...± jq- к 1п(1 + х).

1.3 Логарифмы и площади 37
Ряд Грегори. Заменим в (3.13) х на —х\
(3.14)
1п(1 — х) — —х
XXX X
и затем вычтем это равенство из (3.13). Это дает (Грегори 1668)
(3.15)
Примеры. Положив х — 1/2 в (3.14) и х = 1/3 в (3.15), мы получим
следующие два ряда для In 2:
(3.14а)
(3.15а)
ln2"2 + 2-22 ' 3-23
1 1 1
4-24
+ ..
1п2 = 2(-
V3
1 1 1
...).
.3 ' З-З3 5-35 7-37
В табл. 3.2 сравнивается поведение трех рядов (3.13а), (3.14а) и (3.15а) для In 2.
Сразу видно, какой из них наилучший.
ТАБЛИЦА3.2. Сходимость рядов для In 2
п
1
2
3
4
5
6
7
8
9
10
11
12
(3.13а)
1.000
0.500
0.833
0.583
0.783
0.617
0.760
0.635
0.746
0.646
0.737
0.653
(3.14а)
0.500
0.625
0.667
0.6823
0.6885
0.6911
0.69226
0.69275
0.69297
0.693065
0.693109
0.693130
(3.15а)
0.667
0.6914
0.69300
0.693135
0.6931460
0.69314707
0.693147170
0.6931471795
0.693147180559
0.6931471805498
0.6931471805589
0.69314718055984
Вычисления 1пр для простых чисел > 3. Благодаря формуле (3.1)
достаточно вычислить логарифмы простых чисел. Тогда логарифмы составных
целых, а также рациональных чисел могут быть получены с помощью сложения и
вычитания. Идея вычисления состоит в том, что надо разделить р на близкое к
нему число, логарифм которого уже известен, тогда можно применить ряд (3.15)
с малым значением х и получить быструю сходимость. Например, для р — 3
запишем
о 3 0 3 1+х 1
3=Г2' 2 = 1^ * *=5<
так что
(3.16)
1пЗ = 1п-
+ In 2 = In —Ц-
+ 1п2.
Другая возможность: 3 — (3/4) • 4, что приводит к равенству

38 I. Введение в анализ бесконечных
1 + 1
(3.17) 1пЗ = 21п2-1п \.
*■ ~~ 7
Но еще лучше использовать среднее геометрическое предыдущих выражений
=> 1пЗ = -1п2+-1пг-^
(3.18) 5= W^->/24 =» Ь5= ^1п2+^1пЗ+^1п-^-
V ^4 2 2 ^ — 49
7= а/^-л/48 => 1п7 = 21п2+^1пЗ+^1п-±^,
и так далее. Чем больше р, тем лучше сходится ряд (3.15). Приведем значения
логарифмов целых чисел от 1 до 10, полученные таким способом:
1п(1) = 0.000000000000000000000000000000
1п(2) = 0.693147180559945309417232121458
1п(3) = 1.098612288668109691395245236923
1п(4) = 1.386294361119890618834464242916
1п(5) = 1.609437912434100374600759333226
1п(6) = 1.791759469228055000812477358381
1п(7) = 1.945910149055313305105352743443
1п(8) = 2.079441541679835928251696364375
1п(9) = 2.197224577336219382790490473845
1п(10) = 2.302585092994045684017991454684 .
Усовершенствование этих вычислений по сравнению с вычислениями Бриггса,
произошедшее за считанные десятилетия (с 1620 до 1670), поистине
впечатляющее. Оно лишний раз демонстрирует громадный прогресс в математике,
начавшийся после появления "Геометрии" Декарта.
Связь с числом Эйлера. Связь между натуральными логарифмами и
числом е устанавливает следующая теорема.
(3.3) Теорема. Натуральный логарифм In ж есть логарифм при основании е.
Доказательство. Применим натуральный логарифм к формуле теоремы 2.3.
С использованием (3.5) и (3.13) это дает
b(l+i)"'=N.ln(l + i)=N.(i-^ + ...)-.,
так что lne^ = х. П
Итак, получена геометрическая интерпретация числа е: площадь под
гиперболой у = 1/х между 1 и е равна единице (см. рис. 3.8).
Произвольные степени. Логарифмы позволяют дать определение
произвольной степени любого числа а > 0 и вычислить ее (И. Бернулли 1697, Principia
Calculi Exponentialium, Opera, vol.1, p. 179). С учетом равенства a = elna имеем:
(3.19)
„b /\na\b ^61na
a = (e ) = e

1.3 Логарифмы и площади 39
Графики этих функций, рассматриваемых либо как функции а, либо как
функции 6, приведены на рисунках 3.9а и 3.9Ь.
I
г у=1/х
1Ь
е = 2.71828...
Рис. 3.8. Геометрический смысл е.
Рис. 3.9а. Функция у = ж°. Рис. 3.9Ь. Функция у = ах.
Упражнения
3.1 (Ньютон 1671, Метод флюксий; Эйлер 1748, Introduction §123). Покажите, что
2 = (4/3) • (3/2) приводит к
что позволяет одновременно вычислить In 2 и 1пЗ с помощью двух быстро
сходящихся рядов (3.15).
3.2 (Ньютон 1669, "Inventio Basis ex Area data"). Предположим, что площадь z
под гиперболой определяется формулой
1 2 1 3 1 4 1 5
z = х — -х + гж — -х + -х — . . . .
2 3 4 5
Найдите для х = ez — 1 ряд вида
х = z + Q>2Z2 + CL3Z3 + сц24 -f ... .
Вы откроете (заново) ряд для показательной функции.

40 I. Введение в анализ бесконечных
L4 Тригонометрические функции
Сивилла: это восходит к заре цивилизации.
(Дж.Клиз & Ч.Бут 1979, Fawlty Towers, The Psychiatrists)
Измерение углов. Одна из старейших задач в геометрии — измерение
углов, главным образом, в целях астрономии. В древнем Вавилоне окружность
делили на 360°, вероятно потому, что это число приблизительно равно числу дней
в году. Тогда половина окружности составляет 180°, прямой угол 90°, а
равносторонний треугольник имеет углы по 60° (см. рис. 4.1а). Птолемей1, в своем
Альмагесте (150 г. н.э.) добавил еще две "цифры" шестидесятеричной системы,
ставшие известными как partes minutae primae (первые малые доли, — лат,) и
partes minutae secondae (вторые малые доли). Они-то и стали нашими
"минутами" и "секундами". Но 360° не единственная возможность. Можно использовать
множество других единиц, например, в некоторых технических приложениях
используются грады; прямой угол равняется 100 град. Однако, как и для
логарифмов, существует естественная мера, основанная на длине дуги окружности
единичного радиуса, — радиан (см. рис. 4.lb). Приведем здесь длину дуги
половины окружности с той точностью, с которой ее вычислил Т. Ф.де Ланьи в 1719
году и воспроизвел Эйлер (с ошибкой в 113-м десятичном знаке, который здесь
исправлен):
3.14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
821480865132823066470938446... .
Для этого довольно необозримого выражения У.Джонс (1706, р. 243) ввел
сокращенное обозначение 7г ("periphery" — окружность). Тогда угол в 54°,
изображенный на рис. 4.1, составляет 547г/180 = 0.9425 радиан.
100 90 80 ™ 2тг/3 тг/2 71/3
4 4
110iuu - ои 70
120 60
130 50
140
150
160
170 0
71/6
3.
180 0 я 0
-1 0 1-1 0 1
Рис. 4.1а. Вавилонские градусы. Рис. 4.lb. Измерение угла длиной дуги.
Определение тригонометрических функций. Как можно измерить угол
линейкой? Мы можем измерить только хорду (см. рис. 4.2), а затем с помощью
таблиц попытаться найти угол, или наоборот. Такие таблицы возникли в
Древней Греции (Гиппарх, 150 г. до н.э. (утрачены) и Птолемей, 150 г.). Функция
"синус", связанная с функцией "хорда" соотношением sin а = (l/2)chord(2a),
возникла в индийской (Брахмагупта, около 630 г.) и средневековой европейской
Ptolemaios, Ptolemeus, Ptolemy, Ptolemaus, Ptolemee, Tolomeo, ....

1.4 Тригонометрические функции 41
науке (Региомонтан, 1464 г.). Эта функция, первоначально называвшаяся sinus
rectus (т.е. вертикальный синус), гораздо лучше приспособлена к вычислению
треугольников, чем функция "хорда".
chord а
О 1
Рис. 4.2. Функция "хорда" Птолемея.
tgcc
Рис. 4.3. Определения sin, cos, tg и ctg.
(4.1) Определение. Рассмотрим прямоугольный треугольник, расположенный в
круге радиуса единица, как показано на рис. J^.S. Длину катета,
противолежащего углу а, обозначают sin а, длину прилежащего катета — cos а. Их
отношения, которые являются длинами вертикальной и горизонтальной касательных
к окружности, обозначают
tga =
cos а
ctg а
Эти определения непосредственно приложимы к произвольному
прямоугольному треугольнику с гипотенузой с и сторонами а, Ь (где а — катет,
противолежащий углу а):
(4.1)
a = c-sina, 6 = c-cosa,
b- tga.
По традиции в геометрии углы обозначают малыми греческими буквами,
но когда мы переходим к радианам и к рассмотрению функций вещественной
переменной (см. графики на рис. 4.4), предпочтительнее малые латинские буквы
(например, х) для обозначения аргумента. Из приведенных чертежей могут быть
выведены многие формулы, такие как
sinO = 0, cosO = l, sin7r/2=l, cos7r/2 = 0, sin7r = 0, cos7r = — 1,
(4.2a)
(4.2b)
(4.2c)
(4.2d)
sin(—x) — — sin ж,
sin(z 4- 7r) = — sin ж,
sin(z + 7r/2) = cos ж,
sin2 x + cos2 x ■
cos(—x) = cos ж
COs(# + 7Г) = — COS X
cos(z + 7r/2) = — sin x
1.
Функции sin x и cos x являются периодическими с периодом 27Г, a tg ж
дическая функция с периодом 7Г.
перио-

42 I. Введение в анализ бесконечных
Рис. 4.4. Тригонометрические функции sinx, cos а; и tgx.
На рис. 4.5 воспроизведен чертеж кривой синуса (А.Дюрер 1525, Under-
weysung der Messung, S. 17). Дюрер называет эту кривую "eynn schraufen lini"
(винтовая линия, — старонем.) и считает, что она может быть полезна
каменщикам, строящим винтовые лестницы.
Рис.4.5. Кривая синуса в книге Дюрера (1525).2
Рис. 4.6. Значения sin 1, sin 2, sin3, ... (для п использована логарифмическая шкала).
Любопытный геометрический узор возникает, если построить график sinn
только для целых значений п (рис. 4.6, см. Стрэнг 1991, Ричерт 1992).
" Воспроизводится с разрешения издательства Dr. Alfons Uhl Verlag, Nordlingen.

1.4 Тригонометрические функции 43
Основные соотношения и их следствия
Эти уравнения имеют почтенный возраст. Уже Птолемей выводит ...
(Л.Виеторис, J.reine ang. Math., vol.186 (1949), p. 1)
Пусть а и /3 — два угла, соответствующие дугам х и у.
(4.2) Теорема (Птолемей 150 г. н.э., Региомонтан 1464).
(4.3)
(4.4)
sin(x + у)
= sin х cos у + cos х sin у.
cos(z + у)
= cos х cos у — sin x sin у.
Доказательство. При 0 < х, у < 7г/2 эти соотношения получаются
непосредственно из рассмотрения трех прямоугольных треугольников на рис. 4.7. Все
другие конфигурации х и у можно привести к этому интервалу с помощью
формул (4.2Ь) и (4.2с). □
sin р cos а
(4.5)
О \ cos (3 cos а 1
Рис. 4.7. Доказательство формул (4.3) и (4.4).
Разделив уравнение (4.3) на уравнение (4.4), получим
sin х cos у -f cos х sin у tg x + tg у
tg (x + y) =
cos x cos у — sin x sin у 1 — tg x tg у
Дальнейшие формулы. Заменив в (4.3) и (4.4) у на —у, получим
(4.3'j sin(z — у) — sin ж cos у — cos ж sin у,
(4.4') cos (ж — у) — cos ж cos ?/ + sin х sin у.

44 I. Введение в анализ бесконечных
Если сложить (4.3) и (4.3'), мы получим sin(z -f у) 4- sin(x — у) — 2 • sin ж cos у.
Введя новые переменные для х -\- у и х — у:
х-\-у = и, х = (u + v)/2,
что равносильно
x-y-v, y=(u-v)/2,
мы получим первую из трех следующих формул:
/ л п\ • • Л /tA + V\ {U — V\
(4.6) sin u H- sin v = 2 • sin ( —-— J • cos ( —-— J,
(4.7)
(4.8)
COS
. (U + V N
2~
U + COS V — 2 • cos I —-— 1 • cos ( —-— J,
u + vy
COS v — COS u
2.sin^__j.sin^__J,
а две другие получаются аналогичным образом.
Положив в (4.3) и (4.4) х — у, получаем
(4.9)
(4.10)
sin(2z) = 2 sin ж cos ж,
cos(2z) = cos2 х — sin2 x — 1 — 2 sin2 x — 2 cos2 x — 1.
А заменив в (4.10) x на ж/2, получим
(4.11) sin
(fW
1 — COS X
cos(|)=±
1 + COS ж
Некоторые значения синусов и косинусов.
Пропорции равностороннего треугольника и квадрата
дают значения синусов и косинусов для углов 30°, 60°
и 45°. Случай правильного пятиугольника (см.
чертеж) рассмотрел Гиппий (450 г. до н.э.). Из подобия р
треугольников АСЕ и AEF следует, что 1 + 1/х = ж,
откуда ж = (1 + \/5)/2, т.е. точка F делит диагональ
СА в золотом сечении (Эвклид, 13-я книга "Начал",
§8), поэтому sin 18° = 1/(2ж). Найденные таким
образом значения приведены в табл. 4.1. Полный список
значений sin а для а — 3°, 6°, 9°, 12°... приводит
Ламберт (1770с).
Формулы де Муавра. Путем замены в (4.3) и (4.4) у на пж, получаются
рекуррентные соотношения
(4.12) sin(n + 1)# = sin ж cos пх + cos ж sin пж,
(4.13) cos(n 4- 1)ж = cos жсовпж — sin ж sin пж.
Отправляясь от (4.9) и (4.10) и повторно применяя соотношения (4.12) и (4.13),
мы найдем, что

1.4 Тригонометрические функции 45
ТАБЛИЦА4.1. Некоторые значения синусов, косинусов и тангенсов
а
0°
15°
18°
30°
36°
45°
60°
75°
90°
радианы
0
тг/12
тг/10
7г/6
тг/5
тг/4
7Г/3
5тг/12
тг/2
since
0
^(л/3-1)
\/5-1
4
1
2
2 V 2
^2
2
^3
2
^(л/5+i)
1
cos а
1
^(л/3 + 1)
2 V 2
^3
2
4
^2
2
1
2
^(V3-i)
0
tga
0
2-л/З
(3\/5-5)л/5+\/5
10\/2
^3
3
y/s-VE(y/E-i)
2yf2
1
v^
2 + V3
ос
сов(Зж) = cos3 ж —3 sin2 ж cos ж
sin(3cc) = 3 sin ж cos2 ж — sin3 ж
сов(4ж) = cos4 x — 6 sin2 x cos2 x + sin4 x
sin(4z) = 4 sin ж cos3 ж —4 sin3 x cos x
cos(5z) = cos5 x — 10 sin2 x cos3 x +5 sin4 x cos ж
sin(5a?) = 5 sin x cos4 x — 10 sin3 ж cos2 x + sin5 ж.
Как видим, здесь опять появляется треугольник Паскаля; вычисления в
точности такие, как в разд. 1.2 (теорема 2.1). Таким образом, можно записать
следующие общие формулы, которые нашел де Муавр (1730) (см. Эйлер 1748, Introductio
§133):
П{П ~ !) • 2 п-2
cos пх = cos х —-— sin X COS X
1-2
п(п - l)(n- 2)(n- 3) . 4 n_4
H '\ л \ sin x cos" ^x - ...
1-2-3-4
n-i n(n-l)(n-2) . о n_3
sin nx — n sin ж cos ж sin ж COS ж
1-2-3
n(n - l)(n - 2)(n - 3)(n - 4) 5 5
+ 1.2-3-4-5 Sm XC°S Ж~--- '
(4.14)

46 I. Введение в анализ бесконечных
Разложения в ряды
Пусть дуга z бесконечно мала; тогда sin z = z и cos z = 1;...
(Эйлер 1748, Introduction §134)
Все предыдущие формулы (4.5)-(4.14) были выведены только с помощью
(4.3) и (4.4) с учетом (4.2а). Но теперь надо привлечь новую идею: когда х
стремится к нулю, то "синус вертикальный" сливается с дугой. Если угол измеряется
в радианах, то чем ближе х к нулю, тем лучшим приближением служит х для
sin х. Запишем это так:
(4.15)
ДЛЯ X
0.
COS X
sin ж
1-
X —
X2
2!
X3
3!
+
+
X4
4! "
хь
5! "
X6
' 6!
х7
7!
+
+
Xs
8! '" '
X9
9! '" '
А теперь применим идею, использованную при доказательстве равенств (2.14)
и (2.15), к формулам де Муавра (4.14). Положим х = y/N, п — ЛГ, где у —
фиксированная величина, а N стремится к бесконечности и ж к нулю. Заменим
теперь в соответствии с (4.15) sin ж на ж и cos ж на 1. Поскольку N —> ос, все члены
(1 — k/N) тоже заменятся единицей. Это приводит к следующим формулам, в
которых мы переменную у обозначим снова ж (Ньютон 1669, Лейбниц 1691, Якоб
Бернулли 1702):
(4.16)
(4.17)
Данное Ньютоном доказательство этих рядов указано в упр. 4.1, а приведенное
выше принадлежит Якобу Бернулли (см. также Эйлер Introduction §134).
Рис. 4.8 иллюстрирует сходимость рядов (4.16) и (4.17). Очевидно,
сходимость имеет место при всех ж (см. разд. III.7). Можно заметить, что после ж = 15
возникают проблемы с точностью вычислений, вызванные ошибками округления
(вычисления намеренно производились с одинарной точностью).
Замечание. При замене cos(y/N) единицей при больших значениях N
необходима осторожность, потому что это выражение возводится в АГ-ю степень.
Например, l + y/N стремится к единице при N —>■ ос, но это не так для (l-\-y/N)N
(см. теорему 2.3). В нашем случае спасительным является тот факт, что cos(y/N)
стремится к единице быстрее, чем 1 + y/N. Действительно,
cosN(y/N) = (l - sin2(y/N)) N'2 « 1 - 1 t. _* l
в силу (4.2d), теоремы 2.2 и (4.15).
Ряд для tg аз. Положим
sin ж
о in ju 3 5 Y
у — tg ж = = а±х + азх + а$х + а^х +
cos ж

1.4 Тригонометрические функции 47
—3 =
у - sinjc
Рис. 4.8. Сходимость рядов sin ж = я — §г + fi— .-.и cos х = 1 — fr + fr —
Чтобы найти czi, аз, as,..., помножим эту формулу на cos х и воспользуемся уже
известными рядами (4.16) и (4.17):
х3 хъ
х Ь
б 120
...=(.
aix + а3х3 + а5ж5 + ... И1
ж2 х4
У + 24
...о.
Сравнивая коэффициенты при ж, ж3 и ж5, получим
1 = аи
«1
+ «з,
«1 аз
откуда
и, продолжая, получим ряд
аз-"б + 2 - 3'
120 24
1
+ <*5,
1_ 1 _ _2_
0,5 ~ 120 " 24 + б " 15
(4.18)
х3 2х5 17 ж7 62 х9 1382 ж11 21844 ж13
6 3 15 315 2835 155925 6081075
Хотя общего правила не видно, оно все же существует, его основу составляют
числа Бернулли (1.29) (см. упр. 10.2 в разд. 11.10).
Старинные вычисления таблид. Из значений, приведенных в табл. 4.1,
которые были известны уже в древности, с помощью формул (4.3') и (4.4') можно
найти значения sin3°, cos3°, или, как было тогда принято, хорду chord 6°.
Далее, формулы половинного угла (4.11) позволяют вычислить chord 3°, chord l| ,
chord I , но не chord 1°. Птолемей заметил, что chord | приблизительно равна
половине chord 11 . Поэтому нетрудно догадаться, что chord 1° = | • chord l| ,
что в шестидесятеричной системе счисления дает (см. Або 1964, р. 121)
(4.19)
chord 1° = 0; 1, 2, 50 (точное значение 0; 1, 2, 49, 51, 48, 0, 25, 27, 22,...).

48 I. Введение в анализ бесконечных
Тогда значения sin и cos всех углов 2°, 3°, 4°, и т. д. получаются с помощью (4.14).
Около 1464 г. Региомонтан вычислил таблицу, в которой синусы всех углов даны
с интервалом в угловую минуту с пятью десятичными знаками ("SEQVITVR
NVNC EIVSDEM IOANNIS Regiomontani tabula sinuum, per singula minuta extensa
..."). На рис. 4.9 показана написанная его рукой таблица tgz (как правило, с
четырьмя верными десятичными знаками).
Рис. 4.9. Автограф таблицы tga Региомонтана (см. Каунцнер 1980).3
Вычисление sin 1° с очень высокой точностью было сделано Аль-Каши
(Самарканд, 1429 г.) посредством численного решения уравнения
(4.20) -4ж3 + Зж = sin 3°
(см. уравнение (1.9)) с помощью итерационного метода, и решение дано в шес-
тидесятеричной системе ("Мы извлекли его благодаря вдохновляющей силе от
присутствия Всевышнего ...", см. А. Аабе 1954):
sinl° = 0; 1, 2, 49, 43, 11, 14, 44, 16, 19, 16... .
А вот точное решение в шестидесятеричной системе, вычисленное на
современном компьютере:
sinl0 =0; 1, 2, 49, 43, 11, 14, 44, 16, 26, 18, 28, 49, 20, 26, 50, 41,... .
И еще раз отметим, каким громадным прогрессом было появление метода рядов
(4.17), который дает для sinl0 = sin(7r/180) = sin(0.0174532925...) при учете
всего лишь трех членов значение
sinl0 к 0.0174532925199-0.0000008860962+0.000000000013496
» 0.0174524064373 .
Воспроизводится с разрешения Nurnberger Stadtbibliothek, Cent V, 63, f. 30г.

1.4 Тригонометрические функции 49
Обратные тригонометрические функции
Тригонометрические функции определяют sin ж, cos ж, tg х для заданной
дуги х. Обратные тригонометрические функции определяют дугу х как функцию
sin ж, cos х или tg ж.
(4.3) Определение. Рассмотрим прямоугольный треугольник с гипотенузой
единичной длины. Если х обозначает длину противолежащего углу катета, то
arcsinz есть длина соответствующей этому углу дуги (см. рис, ^ЛОа).
Аналогично определяются величины arccosж и arctg ж (рис. 4-10Ь и 4-Юс),
1 1 1
arcsin х arccos х
О 1 0*1 0 1
Рис. 4.10. Определение arcsin ж, arccos я и arctg я.
Вследствие периодичности тригонометрических функций обратные
тригонометрические функции многозначны. Так называемые главные ветви их
удовлетворяют следующим неравенствам:
у = arcsin ж <$ х — sin?/ при — 1 < х < 1, —7г/2 < у < 7г/2,
у = arccos х О* х — cos у при — 1 < ж < 1, 0 < у < 7г,
у = arctg ж <=> х — tgy при — ос < х < сю, —7г/2 < у < 7г/2.
Ряд для arctg ж. Ряд для arctg х открыл Грегори в 1671г. В 1674 г. Лейбниц
переоткрыл его, а в 1682 г. опубликовал формулу в "Acta Eruditorum", выразив
восторг по поводу милости Господней, но не раскрыв пути, который привел его
к результату. Метод был найден лишь при исследовании его личных бумаг (см.
М. Кантор 1880-1908, vol. III, р. 80). Пусть b — заданная величина и у — arctg 6
(см. рис. 4.11а, где дуги AD и DC имеют одинаковую длину). Еще Архимеду, а
позже Кеплеру (см. рис. 4.12) было известно, что площадь G сектора OADCO
равна половине длины дуги:
(4.21) G = y.
Площадь F четырехугольника ОАВСО, составленного из двух одинаковых
треугольников, равна
(4.22) F = 6.
Задача состоит в вычислении площади L фигуры ABCDA. Лейбниц разбивает ее
на малые треугольники (один из которых показан на рис. 4.lib) с площадями

50 I. Введение в анализ бесконечных
Рис. 4.11. Вывод ряда для у = arctgx.
е с
Рис. 4.12. Площадь круга по Кеплеру, 1615 г.4
ибо
. „ /ft ч (4.10) л . 2 2 sin2 a 2tg2a 2х2
h=l-cos(2a) v = 2sin2а- 6 -
sin2 а + cos2 a tg2a-fl х2 + Г
Поэтому искомая площадь L есть площадь под графиком функции
*2 (2.12)
х"
ж2 + 1
™2 4 , ^6 ^,8 | ,„10 ,
X — X -\- X — X -\- X \- . .
(см. рис. 4.11с), т.е. по теореме 3.2 (Ферма)
Наконец, в силу (4.21) и (4.22)
Ь3 Ь5 Ь7 Ъ9 Ь11
^у-у + у-у+тг-+--
„ „ г L ь3 ь5 ь7 ь9 б11
В результате получается формула
(4.24)
справедливая щ
arctg х — х -
ж \х\ < 1.
х3 хъ
-у + у-
7 9
х' X*
-у + у-
х11
4 Воспроизводится с разрешения Публичной библиотеки Женевского университета.

1.4 Тригонометрические функции 51
Ряд для arcsin х
Один мой друг, весьма одаренный в отношении этих вещей, принес мне на
другой день кое-какие записки, в которых он описал методы вычисления
размеров величин, подобные методу г-на Меркатора, относящемуся к
гиперболе, но очень общие ... Его зовут г-н Ньютон; он член нашего Колледжа и
очень молод ... но необычайно способен и искусен в этих вещах.
(Письмо Барроу Коллинзу, 1669 г., цит. по Уэстфол 1980, р. 202)
После публикации книги Меркатора в конце 1668 г., в которой был
опубликован ряд для 1п(1 + ж), Ньютон поспешил показать свою рукопись "Об анализе"
(Ньютон 1669) некоторым из своих друзей, но не разрешил ее опубликовать. В
конце концов она была включена в первую главу "Analysis per quantitation"
(Ньютон 1711), опубликованного У. Джонсом. Ньютон не только нашел ряд Меркатора
много раньше, но и первым открыл ряд
(4.25)
1 ж3 1 • 3 хь 1 • 3 • 5 х7
а также ряды для sin х и cos х (см. упр. 4.1). Ньютон дал следующее
доказательство формулы (4.25).
Доказательство. Предположим, что х задано и мы хотим вычислить дугу у,
для которой х — siny (см. рис. 4.13). Если х увеличивается на Ах, то у возрастает
на величину Ау, которая, как легко видеть, равна
Ах
(4.26) Ауъ
VI - ж
потому что два заштрихованных треугольника на рис. 4.13 подобны. Эта
величина является площадью прямоугольника ширины Ах и высоты 1/\/1 — ж2.
Поэтому, как и на рис. 4.11с, полная длина дуги у равна площади под графиком
функции 1/Vl — х2 между 0 и ж. Разлагая эту функцию в ряд по биномиальной
теореме 2.2 при а = —1/2, получаем
(4.27)
VT^
1+гЯ!2 +
1-3
2-4
х* +
1-3-5
2-4-6
«о i
у/Т^Х*
-1 0 х 1 т АКБ С Е
Рис.4.13. Доказательство формулы (4.25) и иллюстрация из Ньютона (1669).5
Формулу (4.25) получим, заменяя функции 1, ж2, ж4,... соответствующими
им площадями (по теореме 3.2) ж, ж3/3, ж5/5,.... □
Правая часть рис. 4.13 печатается с разрешения Публ. библ. Женевского ун-та.

52 I. Введение в анализ бесконечных
Вычисление числа Пи
... Вы не будете отрицать, что Вы открыли совершенно замечательное
свойство окружности, которое навсегда станет знаменитым среди
геометров. (Письмо Гюйгенса Лейбницу, 7 ноября 1674 г.)
Поэтому отношение диаметра к окружности как 1,000,&с. к 3.141592653
.5897932384.6264338327.9502884197.1693993751.0582097494.4592307816
.4062862089.9862803482.5342117067.9+, верное до более чем ста
десятичных знаков, вычисленное тщательным и быстрым пером поистине
изобретательного г-на Джона Маккина, всего лишь как пример тех огромных
преимуществ, которые арифметические вычисления получают от
современного анализа, относится к предмету, который так тесно связан с
Природой, что привлекал умы самых замечательных математиков всех
времен к его рассмотрению ... Но метод рядов (который усовершенствовали
г-н Ньютон и г-н Галлей) выполняет это с большой легкостью в сравнении
с запутанными и многословными способами Архимеда, Виета, Ван Кой-
лена, Метьюса, Снеллиуса, Лансбергиуса и др. (У. Джонс, 1706)
Вычисляя периметры правильных многоугольников с п — б, 12, 24, 48, 96
сторонами и повторно применяя формулы (4.11), Архимед (283-212 до н.э.) получил
оценку
(4.28) 3 Щ < тг < 3 i.
Все попытки улучшить эти значения, делавшиеся в средние века, оказались
бесплодными. Наконец, Адриен ван Роомен (в 1580 г.), применяя метод Архимеда и
потратив годы на вычисления, преуспел в получении 20 десятичных знаков. Лу-
дольф ван Цейлен (van Ceulen = "из Кельна") в 1596-1616 гг. вычислил 35
десятичных знаков, которые в течение долгого времени красовались на надгробном
камне Лудольфа в соборе Святого Петра в Лейдене (Голландия). Чтобы достичь
этой точности, Лудольфу понадобилось продолжить вычисления до п — 6 • 260.
Ряд Лейбница. Мы знаем, что tg (7г/4) = 1 (см. табл. 4.1) и, следовательно,
arctg(l) = 7г/4. Положив в формуле (4.24) х = 1, мы получим знаменитый ряд
Лейбница (1682)
7Г
— -
4
= 1 -
1
—
3
+
1
— -
5
1
- —
У
+
1
— _
9
1
- —
11
+
1
—
13
- +... .
Мпвего DEOS
I
unparcgaudcft
Рис. 4.14. Иллюстрация Лейбница к ряду (4.29).'
Воспроизведено с разрешения Публичной библиотеки Женевского университета.

1.4 Тригонометрические функции 53
Хотя мы и согласны с Лейбницем относительно несомненной красоты его
формулы ("Господь любит нечетные числа", см. рис. 4.14), мы видим также, что она
совершенно неэффективна для практических вычислений, ибо, чтобы получить
50 десятичных знаков, пришлось бы сложить Ю50 членов, "labor fere in aeternum"
(затратив труд вечности, — лат.) (Эйлер 1737). Гораздо более эффективно
использование tg (7г/6) = 1/\/3 (см. табл. 4.1), что приводит к формуле
(4.30)
^^-sVsVtV^--)-
С ее помощью Т. Ф. де Ланьи в 1729 г., "exhibitus incredibili labore" (совершив
невероятный труд, — лат.), просуммировал 210 членов ряда и получил то значение
тг, которое приведено в начале этого подраздела. Можно использовать также ряд
(4.25) для arcsincc. Например, так как sin(7r/6) = 1/2, мы получим
тг 1 1 1 1-3 1 1-3-5 1
б 2 23-232-45-252-4-67.27
Составные формулы. Подставив в (4.5) и = tgx и v — tgy, мы получим
(при условии, что | arctg u-f arctgv| < 7г/2) формулу
(4.32)
/ и + V \
arctg и + arctg v = arctg ( )
V1 — uv /
Если положить и = 1/2 и v = 1/3, то дробь в правой части (4.32) равна единице.
Это приводит к формуле Эйлера (1737)
тг 1 1
(4.33) - = arctg -+ arctg-,
для которой ряд (4.24) сходится уже много лучше. Особенно привлекателен
подход Джона Маккина, опубликованный без подробностей в книге У. Джонса (1706,
р. 243). Положив и = v = 1/5, получаем
1 / 2/5 \ 5
2. arctg-= arctg (I-T7^j = arctg-.
Положив и - v = 5/12, получаем
5 / 2-5/12 \ 120
2 • arctg - = arctg (^^J = ^ Й9 *
Наконец, положим и = 120/119 и подыщем такое г?, чтобы
и + v 1-й 1
= 1, откуда v —
1-uv 1 + и 239

54 I. Введение в анализ бесконечных
ТАБЛИЦА4.2. Вычисление 7г по формуле Маккина
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
0.
-0.
0.
-0.
0.
-0.
0.
-0.
0.
-0.
0.
-0.
0.
-0.
0.
-0.
0.
-0.
200000000000000000000000000
2666666666666666666666667
64000000000000000000000
1828571428571428571429
56888888888888888889
1861818181818181818
63015384615384615
2184533333333333
77101176470588
2759410526316
99864380952
3647220870
134217728
4971027
185128
6927
260
10
1 0. 004184100418410041841004184
3 -0. 24416591787083803627
5 0. 256472314424647
7 -0. 3207130658
9 0. 43669
11 -0. 1_
"^ 0. 004184076002074723864538214
= 0. 197395559849880758370049763 тг = 3. 141592653589793238462643352
Все вместе эти формулы дают выражение
(4.34)
\ = 4 • arctg I - arctg ^,
для которого ряд (4.24) особенно привлекателен при вычислениях в десятичной
системе (см. табл. 4.2). "Тщательное и быстрое перо" Маккина нашло таким
способом 100 десятичных знаков.
Поиск других формул такого типа становится задачей теории чисел. Гаусс,
составив таблицу разложения на множители на 20 страницах, в качестве
побочного результата нашел, что
тг 1 1
— = 12 arctg — + 8 arctg — — 5 arctg ;
7Г
4
12 arctg —+ 20 arctg
239'
+ 7 arctg —— + 24 arctg
239
1
268
(см. Гаусс, Werke, vol.2, p. 477-502). На сегодняшний день рассчитано уже
несколько миллионов десятичных знаков числа 7г. Первые 100 000 цифр
(последняя из них 6) опубликовали Шенкс и Ренч мл. (1962). Более подробно старую и
современную историю вычисления 7Г описал Миел (1983).
Упражнения
4.1 (Ньютон 1669, "Inventio Basis ex data Longitudine Curvae".) Имея ряд z
6^ "•" 40 '
= x + \x3 + ^ж5 + у12ж? + ... Для arcsin (см. (4.25)), выведите ряд для
х = sin z в виде х — z + a^z3 -f a^z5 + a-jz1 + ... (по аналогии с упр. 3.2) и ряд
для w = cos2;, разложив сначала в ряд w = у/1 — х2 (см. рис. 4.15).

1.4 Тригонометрические функции 55
Si ex dato arcu Д) Sinus AB defideratur у aqua-
tionis %=* + 4xs + ^xJ +ttt*7> &c. fupra in-
ventac, (pofito nempe AB = x, *D = z, 8c A* = ij n
radix extrafta erit x = z — 4х* + 717** —т^*7
Et practerea fi Cofinum Aff ex ifto arcu dato cu-
3628800* > ^
1 40320
Рис. 4.15. Из Ньютона (1669), p. 17.7
4.2 Разберитесь в оригинальном доказательстве Птолемея теорем сложения
(4.3) и (4.4) для функции хорды (см. рис. 4.16).
jbiopotftio ш)\
jpiDriecboiiliemcqiwlfamareuumin fcmidmito:
J йкт quo maioa minoic fnperat <bo:da nota fict»
BlfViin frrmtroito. 3.b.d.(hp:j tumccru.j.d.iwfcrmtcboj
* dc.a.b.a.g.tMco nciam fieri cbo:djm.b.<viump;r a>::da
3 riutn pnmebtnao note ctum fttttf <bot<1<\b.cU.&& £Sim
in фм dril.ifero.n.b .gAiw.iincm.a.g.c.b.d.i ior<\fcnr f lite
i.a.b.f .g.d.oppofif л tttf.Ugf r><f p:m»ifljm quad fir cjr.ji.iiin.Ktf.rwfu
f et.SftU.d.rft iwffl.-qm j ылпкГсг arniU л&о.Ъ&шз fict; 4 qimrfof.
•рет blc phtrimo? arenfl сЫтЫ «чтоб?*. TVpieeetildwd* лгоютю
^tepiwcircflftrcntic ftiti fojttt.ndwdi or«e.u.er<iAiu^ fif^|u^
Рис.4.16. Доказательство Птолемея для chord(a -f /3); из Альмагеста в переводе
Региомонтана, напечатано в 1496 г.7
Указание. Используйте (и докажите)
"лемму Птолемея", которая утверждает, что
стороны и диагонали вписанного в круг
четырехугольника удовлетворяют равенству ас +
-\-bd = S182. Для доказательства леммы
надо провести прямую DE такую, чтобы углы
EDA и CDB были равны. Тогда получаются
подобные треугольники:
EDA £ CDB =» Ь/8г = u/d,
DCE = DBA => a/Sx = v/c,
откуда bd + ас — (и + v)Si = £1^2-
4.3 Гиперболические функции (Фонсене 1759, Ламберт 1770b). При заданном х
пусть Р — такая точка на гиперболе и
„2 _
= 1, что заштрихованная
площадь на рис. 4.17 (левом) равна ж/2. Тогда координаты этой точки
обозначают (chz, shz).
' Воспроизводится с разрешения Публичной библиотеки Женевского университета.

56 I. Введение в анализ бесконечных
a) Докажите, что
1а Лкч 1 е* +е~х _ ех - е~х
(4.35) chx = , sh# = .
Указание. Площади треугольников АСВ и PCQ равны. Следовательно,
равны и площади фигур АСРА и ABQPA, причем они равны (1па)/2, если через
а/у/2 обозначить расстояние от С до Q (рис. 4.17 правый).
b) Проверьте соотношения
sh (х + у) = sh х ch у + ch х sh у
(4.36) v -1-у; у -г у
сЪ.{х + у) — ch х ch у + sh ж sh t/.
c) Функции, обратные к (4.35), т.е. обратные гиперболические функции, или
"ареафункции", определяются так:
у — arsh х О х = sh у для — оо < х < ос, —оо < у < оо,
2/ = arch ж <£> х = chy для 0 < ж < оо, 1 < у < оо.
Докажите, что arsh х — 1п(ж + у/х2 + 1), arch ж = 1п(ж + л/#2 — 1 )•
1
Ч = 1/(20
sh jc
Рис. 4.17. Определение гиперболических функций.
4.4 Проверьте (и используйте) совет Ньютона (Ньютон 1671, РгоЫ. IX, §ХЫХ)
для вычисления 7г: вычисляя площадь а под дугой окружности у = ж1'2(1 -
—ж)1/2 между ж = 0иж = 1/4 с помощью разложения в биномиальный ряд,
покажите, что
тг = 24а + 3\/3/4
'2 1 12 1 1-12 1 1-1-321 \ Зч/З
24
/2 1 121 1-12 1 1-1-321 \
\3^~ 1Г 5 2* ~ 2~^4 " 7 2* ~ 2-4-6 ' 9 29 -•••; +

1.5 Комплексные числа и функции 57
1.5 Комплексные числа и функции
Ни истинные, ни ложные корни не являются всегда действительными,
иногда они являются мнимыми; иначе говоря, хотя мы всегда можем
представлять себе для каждого уравнения столько корней, сколько я назначил,
но не всегда каждому воображаемому нами корню соответствует
определенная величина. (Декарт 1637)
Первым, кто столкнулся с комплексными числами, был Кардано (1545). В
своей книге Ars Magna ("Великое искусство" — лат.) он задался таким вопросом:
как разделить заданный отрезок а&, имеющий длину, скажем, 10, "in duas partes"
(на две части — лат.) так, чтобы прямоугольник со сторонами, равными этим
двум частям, имел площадь 40. Каждому ясно (см. рис. 5.1), что площадь такого
прямоугольника не может быть больше 25, так что задача не имеет
действительного решения. Однако алгебра дает нам решение, так как соответствующее
уравнение (см. уравнение (1.3)) х2 — 10ж + 40 = 0 приводит ("ideo imaginaberis
(вообразив себе) у/—15") к результату
Ь + V^lE
5-V=15.
Хотя эти формулы совершенно бесполезны и софистичны ("quae uere est sophisti-
ca"), но в них должна содержаться доля истины, потому что произведение
(5 + v/r15)(5 - V^lE) = 25 - (-15) = 40
дает как раз то, чего мы хотим (см. рис. 5.1).
25 m:m:i5cjd.eft4°
Рис. 5.1. Из книги Кардано Ars Magna.1
В течение следующих столетий такие "невозможные" или "мнимые"
(Декарт; см. цитату выше) решения алгебраических уравнений встречались снова и
снова, породили множество диспутов, но постепенно все больше выяснялась их
полезность. Полной зрелости в обращении с ними достиг в своей работе Эйлер,
который позже ввел обозначение г для у/^1. Приведенные выше решения теперь
пишутся так: 5 ± гд/15, а комплексные числа общего вида
с = а + гб,
где а = Re (с) называется действительной (или вещественной), а Ь = Im (с) —
мнимой частью с. Интерпретацией комплексного числа а + гЬ как точки (а, Ь) на
Воспроизведено с разрешения Публичной библиотеки Женевского университета.

58 I. Введение в анализ бесконечных
двумерной комплексной плоскости мы обязаны диссертации Гаусса (1799) (см,
рис. 5.2), а также Аргану (1806, см. Клайн 1972, р. 630).
Рис. 5.2а. Комплексная плоскость и Рис. 5.2Ь. Комплексная плоскость
кубические корни. у Гаусса (1799).2
Действия над комплексными числами. При арифметических
действиях с комплексными числами применяются обычные правила арифметики
рациональных или действительных чисел с учетом соотношения г2 = —1. Поэтому
сумма (или разность) двух комплексных чисел
с = а -\- ib, w = и + iv
есть комплексное число, полученное сложением (или вычитанием)
действительных и мнимых частей. Произведение их примет вид (ср. с рис. 5.1)
(5.1) с • w = аи — bv + i{av + bu).
Чтобы вычислить частное w/c, заметим, что произведение с на комплексно
сопряженное с ним число
(5.2) с — a — ib
есть действительное неотрицательное число: с -с — а2 + Ь2. Умножая числитель
и знаменатель в w/c на с, видим, что при с ф 0 частное w/c принимает вид
w w-c au + bv .av — bu
Формула Эйлера и следствия из нее
... как показательные функции с мнимым показателем степени
выражаются через синусы и косинусы действительных дуг.
(Эйлер, 1748, Introduction §138)
Эта формула, открытая Эйлером в 1740 г. при изучении дифференциальных
уравнений вида у" + у — 0 (см. разд. П.8), является ключевой для понимания
арифметических операций с комплексными числами.
Воспроизводится с разрешения издательства Georg Olms Verlag.

1.5 Комплексные числа и функции 59
Определим егх с помощью ряда из теоремы 2.3 (с заменой х на ix). Используя
соотношения г2 = —1, г3 = —г, г4 = 1, г5 = г, ... и отделив действительную часть
от мнимой, получим
,., л . {ix)2 {ix)3 {ix)4 {ix)5
x2 .x3 x4 ,x5
= 1 + М-2!-гЗ! + 4!+г5!_---
(X X \ / X X \
1" ¥ + ¥ " + * • 7 +ЧЖ " з^ + 5Г" + • * -J = cosx + is[nx-
v :—^ / ^ :—VJ '
COS X gjn x
Результатом является знаменитая формула Эйлера (1743, Opera Omnia, vol.14,
p. 142)
(5.4) I tar , • -
v > \ e — cos ж 4- г sin ж.
В качестве первого ее приложения подставим в нее ж = 7г/2иж = 7г. Это дает две
элементарные формулы
eiK/2=i и ef> = -l,
в которых замечательные математические константы 7г, е и i связаны в
поразительно простых выражениях.
Полярные координаты. Формула (5.4) показывает, что точка ег<р имеет
действительную часть cos <р и мнимую часть sin <р, т.е. это та точка на
окружности единичного радиуса, у которой радиус составляет угол <р с действительной
осью (см. рисунки 5.2а и 4.3). Следовательно, каждое комплексное число можно
записать в виде
(5.5) с = а + ib = г • ег<р,
где
(5.6) г = у а2 + Ь2 = у/сТъ и <р = arctg ( -).
Величины г = \с\ и <р = arg(c) называют абсолютной величиной и аргументом
числа с. Пусть
с — г - ег<р и w — s - егв
— два комплексных числа, представленные в полярных координатах. Из (4.2а)
следует, что с = г-е"^, аиз теоремы 4.2 вытекает, что
elif • егв — (cos (р + г sin (р) - (cos 0 + г sin 0)
(5.7) = (cos <р cos 0 — sin ip sin 0) + i(cos <p sin 0 + sin ip cos 0) = e1^^6'.
Поэтому для произведения и частного мы получаем формулы
(5.8) с-ю = г8-е^+в\ Н = £.е<(*-«).
С г
Для этих действий представление комплексных чисел в полярных координатах
особенно удобно; при умножении радиусы перемножаем, а угли складываем, при
делении радиусы делим, а углы вычитаем.

60 I. Введение в анализ бесконечных
Корни. Допустим, что мы хотим найти у/с. И в этом случае полярные
координаты оказываются чудесным средством, потому что корни из произведем!
равны произведениям корней. Однако здесь нужна внимательность, потому что
е2гк = 1 и е4г7Г = 1 имеют кубические корни е2г7Г/3 и е4г7Г/3, отличные от 1. Таким
образом, имеются три кубических корня из с:
(5.9) Щ = ^г • ег>/3, ^ • е^/3*2*/3), ^ . e^W3^),
w = z3
z = wm
0 2
Рис. 5.3. Функция гу = zz и обратная к ней z — w1'3.
Для с = 3 + 2г эти корни показаны на рис. 5.2а. Следующий кандидат,
е6гк = 1, просто воспроизводит первый корень и не дает ничего нового.
Полученные таким образом корни образуют при п = 3 правильную звезду типа
той, что украшает автомобили марки "Мерседес", а при п > 3 —
многолучевые звезды, напоминающие "музыку огней". На рис. 5.3 представлено
отображение z ь-»- w = z3 для меняющихся значений z и обратная к нему функция
w ь-> z = w1/3 = y/w. Животное, морда которого при этом подвергается
ужасным деформациям, известно под именем "кот Арнольда". Обратное отображение
производит трех "котов" из одного.
Показательная функция и логарифм. Показательную функцию можно
распространить на комплексные аргументы следующим образом:
(5.10) ес = еа -eih = еа (cos 6 + г sin 6) при c = a + ib.
Это определение сохраняет основное свойство показательной функции: ec+w -
= ес • ew, которое следует из равенства (5.7). Природа логарифмов
отрицательных чисел дала повод к длительным и жарким диспутам между Лейбницем и
Иоганном Бернулли. Эйлер (1751) дал изумительный обзор этих дискуссий,
которые по возможности сохранялись в секрете, ибо подобные диспуты могли
повредить престижу чистой математики как точной и строгой науки. Истинная

1.5 Комплексные числа и функции 61
природа логарифмов отрицательных и комплексных чисел была тогда раскрыта
Эйлером ("Denouement des difficultes precedentes" — Развязка прежних
затруднений, — фр.) опять-таки с помощью формулы (5.4). Многие из противоречий
прежних диспутов снимались тем обстоятельством, что логарифм комплексного
числа представляет не одно число, а бесконечное число значений. Запишем с в
полярных координатах, т. е. в виде произведения
с = г-е^+2кк\ к = 0,±1,±2,... .
Чтобы сохранить свойства (3.1) и (3.7) у логарифмов с комплексными
аргументами, определим их так:
(5.11) ln(c) = ln(r) + i{<p + 2Ьг), к = О, ±1, ±2,... .
z = \nw w = ez
Рис. 5.4. Функция w — ez и обратная к ней z = In го.
На рис. 5.4 представлено отображение w = е2 и обратное к нему. Поскольку
мнимая часть логарифма — просто (р = arg(c), ясно, что после каждого оборота
<р^(р-\-2ж значения логарифмов повторяются снова и снова.
Новый взгляд на тригонометрические функции
Кратчайший путь между двумя истинами в действительной
области проходит через комплексную область.
(Жак Адамар, цит. по Клайн 1972, р. 626)
Заменив х в (5.4) на —ж, мы получим е~гх = cos ж — г sin ж; складывая и
вычитая эти формулы, получим

62 I. Введение в анализ бесконечных
е
(5.12) sin ж = —
(5.13) cos ж =
1 ег
(5.14) tgz = T
2г
г егх + е~*х
Таким образом, в комплексной области тригонометрические функции тесно
связаны с показательной функцией. Многие формулы из разд. 1.4 оказываются
связанными с формулами для ех. Например, формулы де Муавра (4.14) просто
констатируют, что егпх — (егх)п. Однако это не является новым доказательством,
поскольку этот вывод основан на равенстве (5.4), выведенном из формул (4.16]
и (4.17) для рядов, которые, в свою очередь, были доказаны с помощью формул
де Муавра.
Обратные тригонометрические функции. Если в формулы (5.12), (5.131
или (5.14) подставить переменные и вместо егх и v вместо sin ж, cos х или tgx,
получатся алгебраические соотношения, которые можно разрешить относительно
и. В результате обратные тригонометрические функции выразятся через
комплексные логарифмы следующим образом:
(5.15)_ arcsinx = — iln(j,x + у 1 — ж2),
(5.16) arccos х = — iln(x + гу 1 — ж2),
(5.17) arctgz= т1п(- 1.
2 \г — х/
Так как логарифмическая функция — функция многозначная, необходимо
обратить внимание на выбор правильной ветви этой функции, которую надо
использовать, т.е. на выбор значения к в формуле (5.11). Формула (5.17) объясняет
поразительное сходство между рядом (4.24) для у = arctgz и рядом Грегори
(3.15) для 1п((1 + х)/(1 — х)). Кроме того, формула Маккина (4.34) становится
эквивалентной следующей факторизации комплексного числа г-1 :
(5 18) - = t±l= (**±1\* /239г+1\-1
[ ' } г г-1 \5г- 1/ \239t-l/ '
Эйлерово произведение для синуса
... и я уже вижу способ найти сумму ряда f+5'+|+lV^~••• •
(И. Бернулли, из письма к его брату 22 мая 1691 г.)
Одной из великих задач, бросавших вызов математикам начала XVIII
столетия, было найти выражение для суммы обратных квадратов
(5.19) 1 + J_ + J_ + jL + J_ + ...=?
Иоганн Бернулли в течение многих десятилетий усердно искал это выражение,
Позже Эйлер (1740) нашел следующее элегантное решение. Из алгебры известно,
что, например,
(5.20) 1 - Ах + Вх2 - Сх3 = {1- ах)(1 - /Зх)(1 - <ух),

1.5 Комплексные числа и функции 63
где 1/а, 1//3, 1/7 — корни многочлена 1 — Ах + Вх2 — Сх3. Далее, первое из так
называемых "тождеств Виета" имеет вид:
(5.21) Л = а + /3 + 7.
Бесстрашно применив теперь тот же принцип к бесконечному ряду
sin ж
(5.22)
rf х*_
6 + 120
сего бесконечным числом корней ±7г, ±27г, ±37г,..., в качестве аналога равенства
(5.20) Эйлер взял
^-('-SX'^K'-sX'+sX'-sX'+s)-
= ('-Й(1-£Х'-£)--
Сравнивая это соотношение с (5.22), в качестве аналога тождества (5.21) получим
(заменив х на х2 )
(5.23) 1.1.1.1.1. 1
1
^2 + 4^2 + 9^ + 1б7Г2
+ ■
+ ■
г2 4тг2 9тг2 16тг2 25тг2
и сумма (5.19) оказывается равной 7г2/6. Нельзя не признать смелость этого
рассуждения, давшего такой красивый результат, но математическая строгость его
была недостаточной даже по меркам восемнадцатого столетия. Поэтому позже
Эйлер нашел лучшее доказательство (1748, Introduction §156). Начнем с
разложения на множители многочлена zn — 1.
Корни из единицы» Многочлен zn — 1 имеет
корни z = ^Г = e2ik«ln, к = 0, ±1, ±2,... . Так как
е2,7Г = 1, то только первые п последовательных
значений к порождают различные корни. Например,
для п—1 эти значения таковы:
, 4/Я/7
1,
р2гтг/7
-2*тг/7
, 6/71/7
, -6/л/'
•2/71/7
е4/тг/7 е-4гтг/7 ^гп/7 €~^к/7^
Факторизация, аналогичная (5.20), имеет место и
для многочленов с комплексными корнями.
Действительно, разделив многочлен p(z) на (z — с), мы
получим
p(z) = (z-c)q(z) +d,
где d = р(с). Если с является корнем p{z), то мы получим факторизацию
p(z) = (z — с)д(г). Применяя ту же процедуру к q(z) и повторно к
получающимся многочленам, мы получим разложение p(z) на линейные множители (z — с).
Таким образом, для нашего полинома z7 — 1 мы получим
1 = (z - 1) • (Z
„2i>/7
(*'
„4«>/7
)•(*■
-4гтг/7
-2гтг/7
)•(*■
»б»>/
7)Ф
э-6/тг/7
)•
Для общего случая справедлива

64 I. Введение в анализ бесконечных
(5.1) Теорема (Эйлер 1748, Introductio, Chap. IX). Для нечетных п имеет место
разложение
(п-1)/2
zn-l = (z-l) Д {z-e2ib''n)(z-e-2ik''n)
(5.24) fc=1
(n-l)/2
= (z-l) TT (z2-2zcos — + 1).
*=i n
Доказательство. Первое равенство есть разложение на множители, о
котором шла речь. Второе равенство получается с помощью (5.13). П
Посредством замены z —у z/a в (5.24) и умножения на ап можно получить
несколько более общий результат:
(п"1)/2 9Ьг
(5.25) zn-an = {z-a) TT {z2 - 2azcos — + а2).
k = l
Подставим теперь в (5.25) z = (1 + x/N), а = (1 — x/N) и положим п = N. Это
дает
>N / r.\N
= 17- П (2+^-2(l-^)coe—)
'п>-~£ь£о+~£))
fc=i х 7
2ж
(ЛГ-1)/2
-tN.x. JLJL ^ + ]^2 "1-сов(2*тг/^)А
Так как коэффициент при ж в многочлене (1 -f x/N)N — (1 — x/N)N равен 2
(см. теорему 2.1), то Сдг = 2 для всех N. При больших N левая часть нашего
равенства приближается к ех —е~х (теорема 2.3), а в правой части к-й множитель
стремится к
(1 + Й)'
потому что cosy « 1 — у /2 при малых у. В результате получается
Поскольку множителей бесконечно много, при предельном переходе здесь
требуется осторожность (обоснование см. в упр. III.2.5). Мы получим в левой части
sin ж, заменив х на ix. Итак, знаменитая формула выведена теперь способом,
который заслуживает больше доверия.

1.5 Комплексные числа и функции 65
(5.2) Теорема (Эйлер 1748, §158). Функция sin ж может быть разложена в
бесконечное произведение
-"Щ'-^Н^Х'-^Х1-^)'----
fc=l
Сходимость этого произведения иллюстрирует рис. 5.5. Видно, что
сходимость лучше при меньших значениях |х|.
Рис. 5.5. Сходимость произведения в теореме 5.2.
Произведение Валлиса. Положим х = ж/2 в формуле теоремы 5.2. Это
дает
•Ч-=? И) ('-п) 0-s)
_ тг 1 3 35 5Z
~2 2 2 4 4 6 6
и мы получаем знаменитое произведение Валлиса (1655):
Гтг_212 4-4 6J5 8j_8 10-10
1 ' 2~1-3'3-5'5-7'7-9'9-11-'""
Замечание. Оригинальное доказательство Валлиса исходило из того факта, что
7г/2 равно площади под кривой (1 — ж2)1/2 (между —1 и +1). Затем
следовала сложная процедура интерполяции, основанная на известных площадях под

66 I. Введение в анализ бесконечных
кривыми (1 — ж2)0, (1 — ж2)1, (1 — ж2)2, Как раз этой идеей
руководствовался Ньютон, когда он открыл общую биномиальную теорему, обсуждавшуюся в
разд. 1.2.
Упражнения
5.1 (Эйлер 1748, §185.) Положите х — 7г/6 в формуле теоремы 5.2 и получите с
помощью равенства sin(7r/6) = 1/2 другое произведение для 7г/2:
7г_3 И 12-12 18-18 24-24
1 " ' 2 " 2 ' 5-7 ' 11-13 ' 17-19 ' 23-25 '"' '
А теперь положите х = 7г/4, умножьте полученное произведение на
произведение Валлиса, и получится следующая интересная формула:
(5.29) ^^2,2 6,6 10^ 14.И 18^8
v ; 1-3 5-7 9-11 13-15 17-19
5.2 (Эйлер, Introductio §166,168.) Обобщите формулы (5.19) и (5.21) следующим
образом. Пусть
1 + AlZ + A2z2 + A3z3 + ... = (1 + axz){l + a2z)(l + a3z)
(здесь z стоит вместо x2 в теореме 5.2). Суммы степеней коэффициентов
обозначим так:
Si = а1 + а2 + а3 + ...
52 = а? + а\ + а§ + ...
£з = а1 + а2 + а3 + • • • »
и так далее. А теперь постройте "demonstratio gemina theorematis Neutoniani''
— конструктивное доказательство ньютоновских теорем (лат.)
Si=i4i
52 = AxSi - 2А2
(5.30)
53 = AiS2 - A2Si + ЗЛз
54 = AiSs - A2S2 + A3S! - 4Л4
и выведите из этих формул и теоремы 5.2 следующие суммы:
— — —
22 + З2 + 42 + "
— — —
1 + 94 + Q4 + И4 + ' '
(5.31) ^ J 4
J_ i_ _I_
26 + З6 + 4^ + "
— — —
28 + З8 + 48 + "
7Г2 _
6
7Г4
90 ~
7Г6 _
945 =
7Г8
9450
227Г2 1
2-2! ' 6
24тг4 1
2 • 4! ' 30
_ 267Г6 1
= 2^6!'42
28тг8 1
2-8! 30

1.5 Комплексные числа и функции 67
Замечание, На самом деле Эйлер написал эти выражения немного иначе, и
связь с "числами Бернулли" (см. разд. 11.10) стала ему ясна только через
несколько лет (1755, Institutiones Calculi Differentialis, Caput V, §§124,125,151,
"ingrediuntur in expressiones summarum..." — входят в выражения для сумм,
лат.).
5.3 (Эйлер 1748, §169.) Покажите по аналогии с предыдущим доказательством,
отправляясь от корней уравнения zn + 1 = 0, что
/ 4ж \ / А.х \ / 4ж \ / 4ж \
к = 1 v '
С помощью этого произведения получите такие выражения, как
i_ _I i_ - ![!
(5'32) i 1 1 1 =*
+ 34 + 54 + 74 + * " 96"
Покажите, что (5.32) можно получить также непосредственно из (5.31).
5.4 (Эйлер 1748, §§189-198.) Прологарифмируйте формулу из теоремы 5.2. При
этом произведение преобразуется в сумму. Найдите остроумные способы
вычисления
In (sin(ж))
с использованием выражений (5.31).
5.5 С помощью формулы Кардано (1.14) вычислите все корни уравнения
(5.33) х3 - Ъх + 2 = 0.
Несмотря на то, что все эти корни действительные, приходится вычислять
кубические корни из комплексного числа.
5.6 Упростите вычисления корней уравнения (5.33), используя следующую идею
(Виет 1591а). Положите х = ficosa и замените cos а на x/fi в тождестве
cos За = 4 cos3 а — 3cosa, чтобы получить
з Зи2 и?
х — х — cos За = 0.
4 4
Сравнивая это уравнение с (5.33), найдите //, а и х.

68 I. Введение в анализ бесконечных
L6 Непрерывные дроби
Теория непрерывных дробей — одна из наиболее полезных теорий в
арифметике ... Поскольку она отсутствует в большинстве работ по арифметике
и алгебре, она не может быть широко известной среди геометров. Я буду
удовлетворен, если смогу способствовать тому, чтобы сделать ее чуть
более привычной. (Лагранж 1793, Oeuvres, vol. 7, p. 6-7)
Мы скажем поэтому, что площадь круга относится к квадрату диаметра
как lKlxf-xirxIfxI^x^m. д. до бесконечности, или как 1 к
о 24 48 80 '
1 + ^
л 25
2+ —
о 49
2+ —
л 81
2 +
2 + и т. д. до бесконечности
Как эти приближения были получены ... объяснять здесь было бы
слишком долго, но это смогут узнать те, кому будет угодно заглянуть в этот
трактат. (Дж.Валлис 1685, A Treatise of Algebra, p. 318)
Мы уже видели, сколь полезны в анализе бесконечные суммы и бесконечные
произведения. Обсудим теперь третью возможность "infinitorum" (бесконечных,
— лат.) процессов — бесконечное деление, т. е. непрерывные (или цепные) дроби.
Источники
Алгоритм Евклида. Этот алгоритм для вычисления общего наибольшего
делителя двух целых чисел известен уже более 2000 лет (Евклид, прибл. 300 г. до
н.э., Начала, книга VII, предложения 1 и 2). Пусть заданы два положительных
целых числа, например, 105 и 24. Разделив большее число на меньшее, получим
частное 4 и 9 в остатке, т. е.
105/24 = 4 + 9/24.
Продолжим теперь этот процесс с делителем и остатком:
24/9 = 2 + 6/9, 9/6=1 + 3/6, 6/3 = 2.
Алгоритм должен закончиться, потому что делители образуют строго
убывающую последовательность положительных целых чисел. Последний ненулевой
остаток (здесь 3) и есть наибольший общий делитель, а скомбинировав
последовательные шаги, мы получим
24 1
2+-
1
1+2
Иррациональные числа. Если эту форму алгоритма Евклида
(последовательное вычитание целой части и обращение остатка) применить к
иррациональному числу, то алгоритм не может закончиться, потому что конечное выражение,
как в (6.1), должно быть рациональным. Например, для а — у/2 мы получим

1.6 Непрерывные дроби 69
1.4142 ... = 1 + 0.4142 = 1 + ——— = 1 +
2.4142... 2 + 0.4142...
Появление в последнем знаменателе вновь десятичных знаков л/2 неудивительно,
потому что л/2 удовлетворяет как раз уравнению а — 1 + 1/(1 + а) (чтобы
убедиться в этом, умножьте обе части уравнения на 1 + а). Продолжая, мы получим
следующую формулу Бомбелли (1572):
лД=1+1—1 .
(6.2) 2 + j
2 +
2 + ...
Простейшая из всех подобных последовательностей получается для "золотого
сечения":
1 + ^5
1.61803 = 1 +
(6.3)
1
1.61803
_! , 1
•♦Ьт=
1 + ...
Приведем еще несколько примеров:
г I 1
V3 = l + е = 2+ —
1+1—. 1+1
2 + ±
1 + ...
(6-4) 1+1
4 + i
1+i
1+1
6+...
1^1 = 1 . = 3+*
6 + 1 2+^
(6.5) " ' - . 1 -- . 1
6 + 15 +
10+1^— 1+1
14 + • • • ллл 1
292 +
1 + ...
Частные 1, 1, 2, 1, 2, 1, 2, 1,..., которые появляются для \/3? повторяются
периодически. Частные для еи(е — 1)/(е + 1) тоже проявляют регулярное
поведение. Ниже мы объясним это для (е — 1)/(е+ 1), т.е. для th (1/2) (см. равенство
(6.31) ниже). Однако в случае е регулярность сложнее (см. Гурвиц, Werke vol.2,
p. 130), а в случае 7Г она отсутствует вовсе, даже если сравнивать тысячи
частных: Ламберт (1770а) сравнил 27 частных, Лохе (1963) сравнил 968 частных.
Дробь лорда Броункера для 7г/4. Через год после открытия Вал лисом
бесконечного произведения для 7г лорду Броункеру удалось преобразовать его в
интересную цепную дробь (см. цитату в начале раздела и уравнение (6.23)
ниже). Этот результат побудил Валлиса включить теорию непрерывных дробей на
последних двух страницах его "Арифметики бесконечностей" (1655, см. Opera,
vol. I, р. 474-475).

70 I. Введение в анализ бесконечных
Непрерывная дробь Ламберта для tg ж
Но побудительный мотив к отысканию этих формул пришел из Анализа
бесконечных Эйлера, где выражение ... появляется в форме примера.
(Ламберт 1770а)
Как мы видели в разд. 1.4, функция tg х = sin х/ cos х имеет не очень простое
разложение в бесконечный ряд. Мы будем отправляться от формулы
tgs =
sin ж _ х - ж3/б + ж5/120
cos х ~ 1 - х2/2 + ж4/24 - ...
1 - х2/2 + ж4/24
При х
1-х2/6 + х*/120- ...
О знаменатель стремится к единице. Поэтому вычтем 1 и получим
х х
tgz = —
s2/3 - g4/30 + ...
1-ж2/6 + ж4/120-.
1
1-а>76+.
Здесь при х
1/3-ж2/30 + ...
0 последний знаменатель стремится к 3. Вычтя 3, получим
х
1
х
Продолжая в том же духе, мы найдем, что следующий знаменатель равен 5, затем
7, и т.д. Для человека восемнадцатого века (Ламберт 1768) далее не оставалось
сомнений, что следующая формула верна вообще:
tgz =
X
1-
х2
3-
х2
5-
х2
7-
„2
X
9-...
_ 1
1
X
1
3
X
1
5
X
1
7
X
(6.6)
Через пару десятилетий Лежандр (1794) дал полное доказательство этой
формулы (см. упр. б.б).
Выражение типа
(6.7)
4о +
Pi
01 + '
V2
42 +
Рз
9з + ..
называется непрерывной (или цепной) дробью. Дроби Pi/<?i, Р2/221 Рз/яз, • • •
называют звеньями цепной дроби. Если рк = 1, непрерывная дробь называется
регулярной (или обыкновенной).

1.6 Непрерывные дроби 71
Подходящие дроби
Если непрерывную дробь (6.7) оборвать на к-м звене, получается
рациональное число (когда все рк и qk — целые числа)
Pi
(6.8) q0 +
qi+
q2 + • • • + —
Як
которое называют к-й подходящей дробью непрерывной дроби. Мы хотим
записать эти рациональные числа в виде отношений двух целых чисел. Первые шаги
сделать легко:
та\ 1 Pl q°qi +Pl
(6.9а) qo + — =
(6.9b) q0 +
яг qi
Pl _ g0glg2 + Я0Р2 + Piq2
P2 qiq2 + V2
qi + —
q2
Обозначим Ak числители и Вк знаменатели при вычислении выражения (6.8)
таким способом. Из (6.9) мы получаем
Aq = qo, Во = 1,
М = qoqi+Pi, Вг = gi,
М = 000102 + 0ОР2 + Pl02, #2 = qiq2 + Р2-
Посмотрим теперь на эти формулы, как сказал Эйлер, "tamen attendenti statim
patebit" (чуть повнимательнее — лат.), и мы обнаружим следующую красивую
структуру:
(6.10) А2 = q2A1 + р2А0, В2 = g2£i + Р2В0.
Для вычисления Лз иВз, отношение которых должно быть равно
Pi
qo +
Р2
01 +
02+Рз/03
мы могли бы по образцу (6.9Ь) взять формулы для А2 и В2 и заменить всюду 02
на величину 02+Рз/0з- Но получаемые таким образом выражения в общем случае
не будут целыми числами. Поэтому умножим оба числа на 0з, что не изменит их
отношения, и из (6.10) получим
Аз = [{q2 + Рз/яз)Аг + рг А0 J • Яз, &з = ((02 + РзЫз)Вг +Р2В0) • 03.
После упрощения эти два выражения примут вид
А3 = q3A2 + рзАг, Я3 = 0з#2 + Рз#1.
Эта структура будет теперь повторяться снова и снова, и мы приходим к
следующей теореме.

72 I. Введение в анализ бесконечных
(6.1) Теорема (Валлис 1655, Эйлер 1737b). Числители и знаменатели
подходящих дробей (6.8) определяются рекурсивно формулами
(6.11)
причем
(6.12)
Ак = ЯкЛк-i +ркАк-2,
Вк - qkBk-i + РкВк-2,
А_1 = 1
S_i = 0
А) = qo
В0 = 1
М - QiQo + Pi
Вг = qt.
(6.2) Примеры. Уравнения (6.11) и (6.12), будучи применены к рассмотренным
выше примерам, порождают последовательности рациональных чисел:
1 + л/5 _ 1 2 3 5 8 13 21 34 55 89 144
2 ~ 1' Т' 2 ' 3' 5 ' ~8~' 13 ' 21 ' 34' 55 ' 89 '#'*
л/2~1 3 7 17 41 99 239 577 1393 3363
~ 1 ' 2 ' 5 ' 12 ' 29 ' 70 ' 169 ' 408 ' 985 ' 2378 ''"
Vs>,
125719267197265362989 1351
Т ' Т ' 3 ' 4 ' 11 ' 15 ' 41 ' 56 ' 153 ' 209 ' 571 ' 780 '" '
238111987106193 1264 1457 2721
Т'Т'З'Т'Т'зг' 39 ' 71 ' 465 ' 536 ' 1001
3 22 333 355 103993 104348
Г 7 ' 106 ' 113 7 33102 7 33215 7
которые быстро приближаются к исходным иррациональным числам (см. рис.
ел).
Рис. 6.1. Поведение ошибок подходящих дробей Ак/Вк (в логарифмической шкале)

1.6 Непрерывные дроби 73
Приближения для у/2 и \/3 были известны уже в древности. Архимед
использовал неравенства 265/153 < \/3 < 1351/780 без объяснений. Две
подходящие дроби 22/7 (Архимед) и 355/113 (Цу Чан-ши около 480 г. в Китае, Адриан
Метиус (1571-1635) в Европе) для числа 7г имеют качество выше среднего.
Объясняется это тем, что первый отбрасываемый знаменатель qu+\ велик (15 и 292
соответственно). Два другие очень точные приближения для 7г, которые
являются 11-й и 26-й подходящими дробями соответственно, вычислил И. Арима в 1766 г.
в Японии: 5419351/1725033 и 428224593349304/136308121570117 (см. Хаяси 1902).
С другой стороны, для золотого сечения все ^ = 1 и сходимость получается
медленной. В этом случае (6.11) становится рекуррентной формулой для чисел
Фибоначчи (Леонардо из Пизы, 1170-1250 гг., называемый также Фибоначчи).
Некоторые подходящие дроби непрерывной дроби (6.6) для tgx
(6.13)
Зж
15ж - х3
105ж - 10ж3
945ж - 105ж3 + ж5
1
с2 ' 15 - 6ж2 ' 105 - 45ж2 + ж4 ' 945 - 420z2 + 15ж4
показаны на рис. 6.2, они хорошо приближают функцию tgcc даже при переходе
через точки разрыва х = 7г/2, Зтг/2,....
у. 1. Jf:\ . Г.
п \( Щ
• . 1
: /1£
Рис. 6.2. Подходящие дроби непрерывной дроби для tgx.
Бесконечные ряды из непрерывных дробей. Для разности двух
последовательных подходящих дробей справедливы тождества
(6.14)
Лк+1
А*
Вк
Ak+iBk — АкВк+i
= (-1)
к PlP2 ' • • • * Pfc + 1
Bk+i Вк BkBk+i BkBk+i
В справедливости последнего равенства можно убедиться так: из (6.11) следует,
что
Ак+1Вк - АкВк+1 = {qk+iAk +pfc+iAfc_i)5fc - Ak(qk+1Bk + рк+1Вк_1)
= -рк+1(АкВк-г - Ak-iBk) = ...
= р2 •... • pfc+^-l)*^!^ - АоВг),
а из (6.12) вытекает равенство (AiBo — AoBi) -■ р±. Запишем подходящую дробь
Ак/Вк в таком виде:
вк
\вк Bk.J V
А,-
вк.
Ак-2
Вк-2
) + -+(%-%) +
Во'

74 I. Введение в анализ бесконечных
*+£-
PlP2 Р1Р2РЗ
В1В2 В2В3
_ Р\Р2РЪР\
В3В4
Тогда из (6.14) видно, что
(6 15) — = Pi Р1Р2 Р1Р2Р3 / ^fe-i Р1Р2 ' -"'Рк
Вк В\ В\В2 В2В3 Bk-iBk
и, таким образом, справедлива
(6.3) Теорема. Подходящие дроби (6.7) являются частичными суммами ряда
(еле)
I -—"I ■^J.-'-'Z ■-'L^'O -«-"O-^t I
D
Для регулярных цепных дробей, у которых все pk = 1, этот ряд имеет вид
J 1__ 1 1
В\ В\В2 В2В3 В3В4
Так как \/(Вк-\Вк) есть наименьшее возможное расстояние между двумя ра-
ционалными числами, имеющими знаменатели Bk-i и Вк, то интервал между
Ак-i/Bk-i и Ак/Вк не может содержать рационального числа со знаменателем,
не превышающим Вк-
Непрерывные дроби из бесконечных рядов. Пусть дан ряд
/*^ч 11111
(6.17) + + + ... ,
С\ С2 Сз С4 С5
где с, целые числа. Решим такую задачу: найти такие целые числа р», #t, чтобы
ряд (6.17) почленно совпадал с рядом (6.16) (при qo — 0).
Решение. Положим р\ — 1 и q\ — В\ — с\. Далее, разделим друг на друга
два последовательных члена ряда (6.16), чтобы упростить произведения р,, что
даст
(6.18) Ск-iBk = СкРкВк-2-
Это напоминает уравнение (6.11), если отвлечься от множителей Ск-i и Ск.
Поэтому вычтем из (6.18) уравнение (6.11), сначала умноженное на Cfc_i, а затем на
cjt, и получим
Ск-1ЯкВк-1 = {Ск - Ск-{)РкВк-2,
(ск-1 - ск)Вк - -ckqkBk-i.
В первой формуле мы заменим к на к + 1 и затем разделим два этих выражения.
Это исключает Вк и дает
/g 1дч СкЯк+i _ {ск+1 -ск)рк+\
Ск-Ск-i ckqk
Разумеется, p%,q% определяются неоднозначно. Поскольку мы хотим, чтобы это
были целые числа, то естественным выбором, который удовлетворяет равенству
(6.19), будет

1.6 Непрерывные дроби 75
(6.20)
Pk+i = ск, qk+i — Cfc+i - Ск
при к > 1. Итак, мы получили следующую формулу Эйлера (1748, §369):
(6.21)
Ci С2 Сз С4
С1 +
С2 - Cl +
4
сз - с2 +
С4 - с3 +
Применение этой формулы к двум известным рядам (см. разделы 1.3 и 1.4) дает
1 Л , 1 1 1 1
Ь2 = 1-2 + 3-4 + -=Г^
1 +
(6.22)
1 +
1 +
1 +
16
1 + ...
7Г л 1 1 1 1
4=1-3 + 5-7 + -=—Г
1 +
2 +
(6.23)
2 +
25
2 +
49
2 + ...
Вторая непрерывная дробь была найдена лордом Броункером, а здесь мы ее
получили из ряда Лейбница. Аналогично доказывается формула (Эйлер 1748,
§370)
(6.24)
1 1 1
+
С\ С\С2 С1С2С3
С1 +
Cl
С2-1 +
С2
сз- 1 +
сз
с4 - 1 + ...
из которой следует, например, что
i-i = i-J_ + ^_
е 1-2 1-2-3
1 +
(6.25)
1 +
2 +
3 +
4 + ...

76 I. Введение в анализ бесконечных
Иррациональность
У меня есть серьезные основания сомневаться, что настоящая статья будет
прочитана или даже понята теми, кто мог бы извлечь из нее наибольшую
пользу, а именно, теми, кто тратит много времени и усилий на попытки
решить задачу квадратуры круга. Всегда будет достаточно таких лиц ...,
которые очень мало понимают в геометрии ... (Ламберт 1770а)
Одной из нерешенных великих задач классического анализа была
квадратура круга (т.е. построение числа 7г) с помощью линейки и циркуля. Ламберт
был одним из первых, кто стал думать, что эта задача, бросавшая вызов
математикам на протяжении двух тысячелетий, неразрешима. Первым указанием
на такой результат могло бы быть то обстоятельство, что 7г — иррациональное
число. Поэтому была бы интересна теорема, утверждающая, что бесконечная
непрерывная дробь представляет иррациональное число.
Первая трудность. Может случиться, что непрерывная дробь не
представляет вообще никакого числа. Чтобы в этом убедиться, возьмем ряд
/л ft,.N 2 3 4 5 6 7
(6-26) ___ + ___ + ___ + ....
Понятно, что он не сходится, потому что его члены стремятся к ±1. Чтобы
получить соответствующую непрерывную дробь, положим в (6.17) с& = к/(к + 1) и
из (6.19) после упрощения получим
_P*±^=jfe3(fc + 2)e
Як+1 • Як
Возьмем целые Pk+i = к3(к -\- 2) и qu — 1. Легко убедиться, что у непрерывной
дроби
(6.27)
i + i
i + H
1+135
1 + ...
ее подходящие дроби не стремятся ни к какому действительному числу.
Вторая трудность. Существуют бесконечные непрерывные дроби,
представляющие рациональные числа. Например, для рационального числа 2 = 1 + 2/2,
подставляя повторно это представление 2 в знаменатели, мы получим
(6.28) 2=1 + ^ •
1 +
i + 2
1 +
(6.4) Теорема. Если pj и qj — целые числа, и существует такой индекс jo, что
для всех j > jo
(6.29) 0<Pj<Qj,
то непрерывная дробь (6.7) сходится к некоторому числу а, которое является
иррациональным.

1.6 Непрерывные дроби 77
Доказательство, Без потери общности можно принять, что условия 0 <
•pj < qj выполняются для всех j. В противном случае рассмотрим непрерывную
дробь, начинающуюся с Pj0/qj0- Сходимость этой непрерывной дроби и ее
иррациональность равносильны сходимости и иррациональности исходной
непрерывной дроби. Предположение 0 < р3< qj гарантирует, что подходящие дроби
нашей непрерывной дроби стремятся к некоторому действительному числу. Это
следует из "критерия Лейбница", который обсуждается в разд. III.2. Следуя идее
Лежандра (1794, Elements de Geometrie, Note IV), запишем непрерывную дробь
(6.7) без до в таком виде:
(6.30) а=_!* Где р=?* .
qi + р рз
?2 +
03 + • • •
Так как q\ > р\ и /3 > 0, то а < 1. Предположим теперь, что а = В/А, где
О < В < А, является рациональным числом. Тогда из (6.30) мы получим
pi - gia _ Арг - Вд1
а В
так что (3 выражается как рациональное число, у которого знаменатель меньше,
чем у а. Повторяя то же рассуждение для /3 — ргДяг + 7) и продолжая в том
же духе, мы будем получать все меньшие и меньшие знаменатели, которые все
являются целыми числами. Но это не может повторяться бесконечное число раз.
□
Отрицательные pj. Заключение теоремы 6.4 также верно, если (6.29)
заменить на
(6.29') 2\pj\ <qj-l.
В этом можно убедиться, повторно применяя тождество (верное при pj < 0)
<?i-i + ^r^ = fe-i-1) + -
ъ+Р J 1 \П
Чз ~ \Pj\+P
что при выполнении условия (6.29') преобразует непрерывную дробь в другую,
удовлетворяющую условию (6.29).
(6.5) Теорема (Ламберт 1768, 1770а; Лежандр 1794). Для любого рационального
х (х ф {)) значение tg х иррационально.
Доказательство. Предположим, что х = т/п — рациональное число, и
подставим его в формулу (6.6):
(6.31) tg-
га т/п га
п т/п т
1 - ■
2/2 2
т /п га
3 тг~,—^- Зп
2 / 2 2
т/п га
5 — Ъп —
In- ...

78 I. Введение в анализ бесконечных
Справа мы получили непрерывную дробь, в которой все члены — целые числа.
Поскольку множители 1,3,5,7,9,... растут неограниченно, условие (6.29')
выполняется для любых тип, начиная с некоторого индекса го- □
Такой же результат справедлив и для функции arctg . Действительно, если у
рационально, то х = arctg у должно быть иррациональным числом, ибо в
противном случае у — tg ж было бы иррациональным числом в силу теоремы 6.5. В
частности, 7Г = 4 arctg 1 должно быть иррациональным числом. Доказать
аналогичный результат для гиперболического тангенса thz = (ех — е~х)/(ех -\-е~х) = (е2х-
— 1)/(е2х + 1) даже легче, поскольку все знаки "минус" в (6.31) перейдут в знаки
"плюс". Обращая последнюю формулу, мы имеем ех = (th (ж/2) —1)/( th (ж/2)-|-1),
и еще получаем иррациональность значений ех и In ж при рациональных ж ф 0 и
ж ф 1 соответственно.
Упраэюнения
6.1 Покажите, что при использовании матричных обозначений числители Ak
и знаменатели Вк подходящих дробей (6.8) можно выразить в следующей
форме:
(Ак АкЛ fqo l\(qi Л(Ч2 1\ (Як-i Л(Як Л
\Вк Вк-г) \1 0)\pi 0)\Р2 0)'"\Рк-1 0J\Pk о)'
6.2 Рассчитайте численно регулярные непрерывные дроби для следующих
чисел:
л/2, л/3, л/5, л/6, л/7, л/2, #3, #4, у/Ь, л/б, Vl
и найдите существенное различие между квадратными и кубическими
корнями.
6.3 Покажите, что
1 1
1 1
а Н а +
1 . 1
а+ Ь +
1 1
а Н а +
а + ... ь+1
а + ...
являются решениями уравнения второй степени. Вычислите их значения.
6.4 Длительность астрономического года равна (Эйлер 1748, §382)
365 суток 5 часов 48/55//.
Вычислите разложение 5 часов 48'55" (выраженных в сутках) в регулярную
непрерывную дробь, а также соответствующие подходящие дроби. Не
забудьте дать ваш ценный совет папе Григорию XIII относительно его реформы
календаря.
6.5 Дайте подробное доказательство формулы (6.24).

1.6 Непрерывные дроби 79
i.6 Докажите формулу (6.6).
Указание (Лежандр 1794). Определите функцию
1 я
а а а
<p(z) _ i + __ + _______ + _______________ + ...
а
и покажите, что <p(z) — <p(z + 1) _ — — (p(z + 2) . Затем определите
z(z + 1)
функцию
(6.33) ф(г) = ____ + !! так что ф(г) = £ -
У z-(p(z) w z + ф(г + 1)
Итерации (6.33) приводят к непрерывной дроби. Наконец, положите а =
ж2/4, так что <р(1/2) = сЬж и ж<р(3/2) = shcc, и замените х на ix. Заметим,
что эти формулы связаны с непрерывными дробями для
гипергеометрических функций (Гаусс, Гейне; см. Перрен 1913, р. 313,353).
Л. Эйлер 1707-1783 К.Ф. Гаусс 1777-1855
С любезного разрешения Национального банка Швейцарии
и Федерального банка Германии.
Дж. Валлис 1616-1703 И.Г. Ламберт 1728-1777
С разрешения издательства Georg Olms Verlag Hildesheim
и университетской библиотеки в Базеле.

II
Дифференциальное и интегральное
исчисление
Область применимости этого исчисления громадна: оно приложимо как к
механическим, так и к геометрическим кривым; знаки радикалов не
представляют для него никаких трудностей, а часто даже удобны; оно легко
распространяется на любое желаемое число переменных, и сравнение
бесконечно малых любых видов становится простым. Кроме того, как мы
увидим в этой работе, оно приводит к бесчисленному количеству
открытий удивительных свойств кривых или прямых касательных, максимумов
и минимумов, точкек перегиба и возврата, огибающих, каустик
отраженных или преломленных лучей и т. д.
(Маркиз де Л опита ль 1696, введение к "Анализу бесконечно малых")
Эта глава посвящена знакомству с дифференциальным и интегральным
исчислением — величайшим математическим открытием всех времен. Мы
объясняем идеи Лейбница, Бернулли и Эйлера. Строгая их трактовка в духе XIX
столетия будет содержанием разделов III.5 и III.6.
Приведенный выше рисунок иллюстрирует тот факт, что это исчисление
высветило ярким светом темные, скрытые механизмы научных поисков.

II. 1 Производная 81
II. 1 Производная
Смею сказать, что это не только наиболее полезная и наиболее общая
известная мне геометрическая задача, но далее такая, о которой я мечтал
узнать. (Декарт 1637, р. 342, в англ. переводе р. 95)
Исаак Ньютон не был приятным человеком. Известно, что его
отношения с другими учеными были плохими, и в течение большей части своей
дальнейшей жизни он с ними ссорился и горячо спорил... Серьезный спор
возник у него с немецким философом Готтфридом Лейбницем. Лейбниц и
Ньютон независимо разработали раздел математики, называющийся
анализом, на котором основана большая часть современной физики ...
Говорят, что после смерти Лейбница Ньютон заявил, что он глубоко
удовлетворен тем, что он "разбил сердце Лейбница".
(Hawking 1988, A brief history of time, Bantam Editors, New York)
Какое презрение к не англичанам! Мы открыли эти методы безо всякой
помощи от англичан. (И. Бернулли 1735, Opera, vol. IV, p. 170)
То, что Вы сообщаете о Бернарде Нивентейте — просто пустяки. Кто
удержится от смеха по поводу его смехотворной ерунды, сказанной о нашем
исчислении, как будто он слеп к его преимуществам.
(Письмо И. Бернулли, цитируется по Пармантье 1989, р. 316).
Мы будем называть функцию fx первообразной функцией для функций
f'x, f"x, и т.д., которые производятся из нее, а эти последние мы будем
называть производными функциями от первообразной.
(Лагранж 1797)
Задача. Пусть задана кривая у = f(x). Требуется в каждой точке х найти
наклон этой кривой и касательную или нормаль к ней.
Откуда возникла эта задача
- вычисление углов, под которыми пересекаются две кривые (Декарт);
-конструирование телескопов (Галилей) и часов (Гюйгенс 1673);
-нахождение максимума и минимума функции (Ферма 1638);
-скорость и ускорение движения (Галилей 1638, Ньютон 1686);
-астрономия, проверка Закона Всемирного Тяготения (Кеплер, Ньютон).
Производная
Линейная функция у = ах + Ъ. Кроме
фиксированного значения ж, рассмотрим возмущенное
значение х + Ах. Соответствующие значения у
суть у = ах + Ьиу + Лу = а(х + Ах) + 6,
следовательно, А у — а Ах. Наклон прямой,
который определяется как ^, равен а. На рис. 1.1
представлены функции у = ах + 1 при
различных значениях а.
у - ах + Ъ
Ау = а Ах
0 х Ах
а = 2 а=1 а =1/2 а = 0 а = -1/2 а ■
Рис. 1.1. Наклон в зависимости от а.
а = -2

82 II. Дифференциальное и интегральное исчисление
Парабола у = ж2. Если х увеличить на Ах, то у увеличится на у + ^2/ =
(ж -f Ах)2 = х2 + 2хЛх + (Лж)2, так что (см. рис. 1.2а)
(1.1) Ау = 2хАх+(Ах)2.
Таким образом, наклон линии, соединяющей точку (ж, у) с точкой (х + Ах, у+Ау)
равен 2х + Ах. Если Z\z стремится к нулю, этот наклон будет стремиться к
наклону касательной к параболе.
2х Ах + Ах2
Рис. 1.2а. Касательная к параболе.
Рис. 1.2Ь. Касательная к параболе
(чертеж И.Бернулли 1691/92).1
Лейбниц (1684) представлял себе, что Ах и Ау становятся "бесконечно
малыми" ("tangentem invenire, esse rectam ducere, quae duo curvae puncta distantiam
infinite parvam habentia, jungat, ..." — "построить касательную означает провести
прямую, соединяющую две точки кривой, расстояние между которыми
бесконечно мало ..." — лат.) и обозначал их dx и dy. Далее, пренебрежем членом (dx)2,
который "бесконечно меньше" чем 2xdx, и вместо (1.1) получим
(1.10
dy = 2х dx или
dy о*
— — LX.
dx
Ньютон (1671, опубл. в 1736 г., р. 20) рассматривает свои переменные v, ж,
у, z "как постепенно и неограниченно возрастающие ... А скорости, с которыми
каждая флюента возрастает при своем общем движении (которые я могу назвать
флюксиями, ...), я буду обозначать теми же буквами с точками: v, ж, у, i". Их
значения получаются путем "отбрасывания членов ..., не равных ничему".
Ньютон категорически отказывался от публикации ("Прошу не публиковать ни одну
из моих математических статей без моего специального разрешения").
Якоб и Иоганн Бернулли переоткрыли дифференциальное исчисление в
третий раз, основываясь на невразумительной публикации Лейбница 1684 г.
("une enigme plutot qu'une explication" — скорее загадка, чем объяснение, фр.).
Воспроизводится с разрешения библиотеки Базельского университета.

II. 1 Производная 83
И.Бернулли в то время (1691/92) давал частные уроки по новому исчислению
самому маркизу де Лопиталю. С его точки зрения бесконечно малые величины
— это величины, которые можео прибавлять к конечным величинам, не изменяя
значений последних, а кривые — это многоугольники с бесконечно короткими
сторонами. Этот величайший из учителей (кроме своих многочисленных сыновей
и племянников, а также де Лопиталя он познакомил с математикой Эйлера)
придерживался того мнения, что слишком много разъяснений о бесконечно малых
скорее затруднит понимание для тех, кто не привык к длинным объяснениям.
В 1694 г. Б.Нивентейт впервые опубликовал критику бесконечно малых
(см. письмо И. Бернулли, процитированное выше), а в 1695 году появился
"Responsio" ("Ответ") Лейбница в июльском номере журнала Acta Eruditorum.
Маркиз де Лопиталь (1696) написал знаменитую книгу Analyse des infiniment
petits (Анализ бесконечно малых, — фр.) (см. рис. 1.3), которая привела к
явному прорыву в новом исчислении даже во Франции, где на протяжении многих
десятилетий наукой правили "картезианцы" (аббат Кателан, Папен, Ролль, и
ДР-)-
Рис. 1.3. Чертеж из книги Лопиталя Analyse des infiniment petits (1696).2
Епископ Беркли в 1734 г. опубликовал полемическую статью The Analyst
против бесконечно малых (см. цитату в разделе II.2, а также Стройк 1969, р. 333).
Маклорен (1742, Treatise of Fluxions, vol. И, p. 420): "... исследуйте отношение,
которое есть предел ..."
Эйлер в начале труда (1755, Institutiones Calculi Differentialis) поместил две
длинные главы De differentiis finitis (О конечных разностях, — лат.) и De usu
difjerentiarum in doctrina serierum (О применении дифференцирования в учении
о рядах), за которыми следуют шесть страниц на латыни о бесконечно малых,
прежде чем он рискнул написать "denotet dx quantitatem infinite parvam"
(обозначим через dx бесконечно малую величину), dx = 0 и adx = 0), но он требует,
чтобы "ratio geometrica 9l^- — \ erit finita" (геометрическое отношение 9l^l = f
было конечным). Он предпочитает обозначения Лейбница, а не Ньютона, и
пишет, что "... incommode hoc modo у repraesantur, cum nostro signandi modo d10y
facillime comprehendatur" (... такой способ представления неудобен, наш способ
dl0y легче для восприятия).
Даламбер (1754, Encyclopedic) вводит четкое понятие предела ("Этот предел
2 Воспроизводится с разрешения Публичной библиотеки Женевского университета.

84 II. Дифференциальное и интегральное исчисление
есть та величина, к которой отношение z/n приближается все ближе и ближе ...
Ничто не может быть яснее этого соображения; ...").
Лагранж (1797) сразу отвергает понятие бесконечно малых и пытается
основать анализ на степенных рядах ("Известны трудности, к которым приводит
предположение о существовании бесконечно малых, на которых Лейбниц
основывает свое Исчисление"). Он ввел термин производная и использовал для нее
вместо dy/dx обозначение (см. цитату)
(1.2) у' или f{x).
Коти (1823) отвергает ряд Тейлора (контрпример: у — е-1/* , см. разд. III.7)
и снова вводит бесконечно малые как предел.
Болъцано (1817) и Вейерштрасс (1861) доводят понятие предела до
совершенства с помощью е и S (см. главу III).
Ф.Клейн (1908) защищает ценность бесконечно малых для преподавания
("Разумеется, ценность употребления столь наивного понятия различна для
разных людей. Многие, и я принадлежу к ним, находят их весьма
удовлетворительными. Однако другие, которые одарены лишь чисто логическими способностями,
находят их совершенно бессмысленными ... В связи с этим я хочу рекомендовать
обозначения Лейбница ...")
Правила дифференцирования
His positis calculi regulae erunt tales (изложим здесь правила
вычисления следующим образом, — лат.):
(Лейбниц 1684)
Суммы и постоянные множители. Пусть у(х) = а • и(х) + b • v(x), где а и
Ь постоянные множители. Полагая у + Ау — у(х + Ах), и + Аи = и(х + Ас),
v + Av = v(x + Ах), мы получаем
Ау = а • Аи -+- Ь • Av
откуда следует правило дифференцирования
У =
аи + bv
=»
dy
dx
= а
du
dx
+ b-
dv
dx
или
у'--
= аи
+ bv'.
Произведения. Для произведения двух функций у(х) = и(х) • v(x) мы имеем
у + Ау — и(х + Ах) • v(x -f Ах)
= (и 4- Аи) • (v + Av) — uv + и Av + v Аи + Аи Av,
что приводит к dу = и dv + v du, "потому что du dv является бесконечно малой
величиной по сравнению с членами udv fe v du" (Де Лопиталь 1696, p. 4), или
У =
и
V
=J>
dy
dx
dv
dx
+
du
dx
или
у'
— UV
+
uv .
Примеры, x3 можно записать как произведение у = х3 = х2 -х, и из
вышеприведенной формулы следует, что у' — х2 • 1 + х • 2х — Зж2. Аналогичным образом

II. 1 Производная 85
для произведения у — х4 = х3 • х имеем у' = х3 • 1 + х • Зж2 = 4ж3. По индукции
получаем, что для любого положительного целого п
(1.5) У = хп => j/=n-ajn_1.
Частное. Для отошения у(х) = u(x)/v(x) двух функций имеем
и + Ли
у + Лу = ——г--
v + Л v
Вычитая у из левой и правой части этого равенства и используя геометрическую
прогрессию для выражения (1 + Лу/у)~х при v ф О, получаем
и -Ь Ли и у Ли — иЛу у Ли — иЛу
Лу =
у + Лу у у2 + и Лг>
V- г»
4v (Av)2
•)•
Таким образом, при условии, что у ф О, мы имеем
(1.6)
У= ~
у
dy v%-u%-
Пример. Функция у — х п — 1/хп есть частное от деления и — 1 на v = жп.
Используя (1.6), мы получаем
cfa/ —пжп_1
с/ж
У
1
1
п2п
—П
-п-1
хи ах х*и хп+1
В сущности, это есть уравнение (1.5) для отрицательных п
slope = 1/2 1
slope = 2
Рис. 1.4. Обратная функция.
Обратные функции. Пусть у — f(x) — некоторая функция, а, х = д(у) —
обратная к ней функция. Поскольку их графики являются отражениями друг
друга относительно прямой, проведенной под углом 45° (рис. 1.4), мы имеем
(1.7)
Лу
Лх
1
Лх
Лу
dy
dx
1
dx
dy
dx
при -#0.
Пример: у = ж1/2 является функцией, обратной к функции х — у2. Поэтому

86 II. Дифференциальное и интегральное исчисление
1/2 . dy _ 1 _ 1 1 _1 г-1/2
У ~ * ^ <*ж ~ 4| ~ 2</ ~ 2^ ~ 2
и уравнение (1.5) оказывается справедливым для рациональных п.
Экспоненциальная функция. Для экспоненциальной функции у = ех (см.
разд. 1.2) мы имеем
у + Ау = ех+Лх = ех • еАх и Ау = е*(еЛх - 1).
Используя разложение в ряд еЛх = 1 + Лж + (Ах)2/2\ + ... (теорема 1.2.3), мы
получаем
(1.8) у = е* => у' = ех.
Производной экспоненциальной функции является она сама.
Логарифмы. Есть несколько способов вычисления производной функции для
у = In ж.
a) Логарифмическая функция является является обратной к х = еу.
Согласно формуле (1.7),
/, лч , dy 1 1 1
b) Можно вычислить Ау из соотношения у + Ay = 1п(ж -f Ах) и получить
х -4- ^ж / /\у \
Лу = 1п(ж + Ах) - 1п(ж) - In L = In (1 + ).
X \ X /
(^ж\ ^ж 1 / /Ад^\ ^
1 Н ) = ( ) + ... (см. (1.3.13)) мы опять полу-
х / х 2 V х /
чаем формулу (1.9).
Тригонометрические функции. Сначала рассмотрим функцию у — sin х.
Используя уравнение (1.4.3), получаем
у + Ay = sin (ж + Лж) = sin х cos Лж + cos х sin Лж.
Используя разложение в ряд функций sin Ах и cos Ах (см. (1.4.16) и (1.4.17)), мы
получаем
/ (Ах)2 \ / (^ж)3 \
Лу = sinst- у + ...) + cos ж (Ас- ; +...)
и, следовательно,
(1.10) у — sin ж => y' = cosx.
Аналогично получаем
(1.11) у = cos ж ==> у' — — sin ж.
Для функции у = tgz = sin ж/cos ж мы используем формулу (1.6) и получаем
/„ .лч с?2/ cos2 ж + sin2 ж н 9 1
1.12 /= -2 = l+tg2x=-^-.
ах cosz ж cosz ж
Обратные тригонометрические функции. Из формулы (1.7) и
вышеприведенных формул для производных тригонометрических функций мы получаем

(1.13) у — arctgz
(1.14) у — arcsinz
(1.15) у — arccosx
II. 1 Производная 87
dy _ 1 _ 1 _ 1
dx dx/dy l+tg2y 1 + x2'
dy 1 1 1
dx cosy y/i _ sin2 y y/l-x2'
dy 1 -1 -1
dx -sinу у/1 - cos2 у лЛ - z2
Сложные функции. Рассмотрим функцию у = h(x) = f(g{x)) и пусть z =
д(х). Придавая аргументам функций приращения, получаем z + Az = д(х + Ах)
и у + Ay = h(x + Ах) — f(z + Лг). Из тривиального тождества
Ay _ Ay Az
Ах ~ Az Ах
следует, что
(Мб)
S = S-E """ "'M = /'W*))VM.
Для того, чтобы продифференцировать сложную функцию, следует перемножить
производные функций /ид.
Рис. 1.5. Сложная функция
Пример. Функция у = sin(2z) составлена из функций у — sinz и z = 2х (см.
рис. 1.5). Если мы используем формулу (1.16), то получим, что ее производная
равна у' — cos z -2 — 2 cos(2cc).
Согласно этим правилам вычисление производной любой функции,
составленной из элементарных функций (великая мечта Декарта, см. цитату в начале
этого раздела) становится банальностью. Например,
(z = x-\na) dv dy dz „л„„
у — а — е => —— = —— • —— — е • In а = m а • а ,
dx dz dx
аЛпх {z = a-\nx) dy dy dz a a a_1
y — x — e => — = — • — = x • — = a • x .
dx dz dx x
Итак, уравнение (1.5) справедливо для любого вещественного числа п.

88 II. Дифференциальное и интегральное исчисление
Параметрическое представление и неявные уравнения
В качестве примера возьмем кривую почтенного возраста: конхоиду Никомеда
(200 лет до Р.Х.). Если заданы два числа а и 6, конхоида определяется
следующим образом: на каждом луче, исходящем из начала координат G, расстояние
между точкой А на конхоиде и точкой F на горизонтальной прямой, проведенной
на высоте а, равно постоянной величине b (см. рис. 1.6).
Рис. 1.6. Конхоида Никомеда.
Из подобия треугольников FAB и FGL следует, что
у-а _ Ь
а ^Jx2 + у2 - &'
или
(1.17) (у-а)2(х2 + у2) = Ь2у2.
Если бы мы захотели выразить из этого уравнения у как функцию ж, нам
пришлось бы решать уравнение четвертого порядка для каждого значения х. Вместо
этого можно попытаться рассматривать само неявное уравнение (1.17) как
определяющее неявную функцию у от х.
Возможен и другой подход. Обозначив угол LGF как <р, мы получим
х = a te ш + Ь sin (р
(1.18)
у = а + bcostp.
Когда <р изменяется от —7г/2 до 7г/2, выражения (1.18) образуют
параметрическое представление нашей кривой. Такие параметрические представления не
являются единственными. Например, мы можем в качестве параметра t взять
расстояние GF (см. рис. 1.6). В этом случае мы получаем
х = (b/t + l)Vt2-a2
(1.19) W ;
у = (b/t + 1)а.
Эти выражения представляют правую часть кривой, когда t меняется от а до ос.
Теперь рассмотрим задачу вычисления касательной к конхоиде в данной
точке А (это задача И.Бернулли 1691/92).

II.1 Производная 89
Дифференцирование параметрического уравнения. Рассмотрим у во втором
уравнении (1.18) или (1.19) как функцию параметра, а параметр будем
интерпретировать как функцию, обратную к ж из первого уравнения. Тогда, используя
(1.16) и (1.7), получаем
dy dy dip dy /dx dy dy/dx
1.20) — = -r~ ' ~r~ — i- / T" или ~r — -r ~r-
dx dip dx dip I d(p dx dt / dt
Еще раз поблагодарим Лейбница за его обозначения. Дифференцируя уравнения
(1.19) и взяв отношения производных, для конхоиды мы получаем
dy —aby/t2 — а2
(1.21)
dx t3 + a2b
У этой формулы существует красивая интерпретация (И. Бернулли 1691/92):
обозначим через М такую точку, для которой треугольники LGF и GMA подобны.
Тогда касательная в точке А параллельна прямой, соединяющей М и F (см. рис.
1.6).
Дифференцирование неявной функции. Этот метод, который использовал
еще Лейбниц (1684), состоит в том, что вышеприведенные правила используются
для того, чтобы дифференцировать неявное уравнение, определяющее функцию
у(х) (в нашем примере уравнение (1.17)). Это приводит к формуле
2(у - a) dy (ж2 + у2) + (у- а)2{2х dx + 2ydy) = 2b2ydy
и после деления на 2с£ж,мы получаем
/122\ *У = -х(у-а)2 ^
dx (у-а)(х2+ у2) +(y-a)2y-b2y'
Более строго это неявное дифференцирование будет рассмотрено в разд. IV.3.
Упражнения
1.1 Обобщите правило дифференцирования (1.4) на три сомножителя:
у = и • v • w -> у' = и' • V • w + и • v1 • w + и • v • wf.
1.2 Вычислите производную dy/dx функции

90 II. Дифференциальное и интегральное исчисление
1.3 (Пример Эйлера 1755, §192.) Покажите, что если
у — е то у — е • е • е
1.4 Вычислите производную циссоиды
Диоклеса (около 180 г. до Р.Х.). Эта
кривая, которую Диоклес
использовал для решения трудной задачи
удвоения куба, получается с
помощью круга МСК как множество
точек пересечения прямых DM и BF,
где дуги ВС и CD равны.
Покажите, что касательная в точке А
параллельна прямой КН, где Н
такова, что EF и GH параллельны.
1.5 Вычислите производную окружности, определенной уравнением х2-\-у2 = г2,
с помощью дифференцирования неявной функции, а также посредством
разрешения уранения относительно у и последующего явного
дифференцирования.
1.6 (Лейбниц 1684.) Вычислите производную неявной функции у (ж),
определяемой уравнением
х (а + Ьх) • (с — хх)
+
+ axy/gg + уу +
УУ
= 0,
у (ex + fxx)2 ' У** y/hh + £х + тхх
где а, 6, с, е, /, #, fe, £ и т — постоянные. Это уравнение не представляет
какую-либо знаменитую древнюю вавилонскую или египетскую кривую и
вообще не представляет какого-либо особого интереса. Лейбниц выбрал его
в качестве ужасно сложного выражения, чтобы продемонстрировать мощь
своего исчисления.

11.2 Высшие производные и ряд Тейлора 91
IL2 Высшие производные и ряд Тейлора
Но понятия скорости скоростей, вторая, третья, четвертая и пятая
скорости и т.д., если я не ошибаюсь, превосходят все возможности человеческого
понимания. Чем дальше рассудок пытается следовать этим ускользающим
идеям и анализировать их, тем больше он теряется и смущается; ...
(Епископ Беркли 1734, The Analyst, см. Стройк 1969, Source Book, p. 335)
... нашим современным специалистам по анализу недостаточно
рассматривать только разности конечных величин: они также рассматривают
разности этих разностей и разности разностей первых разностей. И так далее
до бесконечности. Таким образом они рассматривают величины, которые
бесконечно меньше, чем наименьшая различимая величина; и другие,
которые бесконечно меньше, чем те бесконечно малые; и даже другие, которые
бесконечно меньше, чем предшествующие бесконечно малые, и так далее
без конца и предела ... Я признаю, что понимание того, что такое
бесконечно малая величина ... превосходит мои возможности. И я подозреваю,
что понимание того, что часть такой бесконечно малой величины, которая
бесконечно меньше ее, и, следовательно, будучи умножена в бесконечное
число раз, никогда не сравняется с малейшей конечной величиной,
представляет собой бесконечную трудность для любого человека; ...
(Епископ Беркли 1734, The Analyst)
Вторая производная
В разд. П. 1 мы видели, что для данной функции у = f(x) ее производная
f'(x) является наклоном касательной к кривой у — f{x). Следовательно, если
f'(x) > 0 на интервале а < х < 6, то функция возрастает на этом интервале, а
если f(x) < 0 на интервале а < х < 6, то она убывает на нем. Точки, в которых
f'(x) = 0, называются стационарными точками.
Рис. 2.1а. Геометрический смысл второй
производной.
Рис. 2.lb. Рис. И.Бернулли (1691/92).1
Ньютон (1665) и И.Бернулли (1691/92) были первыми, кто исследовал
геометрический смысл второй производной /. Чтобы получить у" — /"(ж), нужно
продифференцировать у' — ff(x). Если f"(x) > 0 на интервале а < х < 6, то ff{x)
возрастает, т.е. для двух точек хо < х\ справедливо f(xo) < f(xi). Это значит,
что величина наклона кривой в точке х\ больше, чем в точке хо и, следовательно,
кривая более изогнута кверху (см. рис. 2.1а, левый). В этом случае мы говорим,
что функция f(x) is выпукла книзу.
Аналогично, если f"{x) < 0 на интервале а < х < 6, то функция f(x)
называется выпуклой кверху (см. рис. 2.1а, справа). Точки, где /"(жо) = 0 и в которых
1 Воспроизведено с разрешения университетской библиотеки Базеля.

92 П. Дифференциальное и интегральное исчисление
вторая производная меняет знак, называются точками перегиба. На рис. 2.lb
представлен рисунок И. Бернулли, объясняющий это.
Задачи "de maximis &; minimis".
Я хочу только, чтобы он знал, что наши вопросы о de maximis et minimis
и de tangentibus linearum curvarum (о максимумах и минимумах и о
касательных к кривым линиям) были решены восемь или десять лет тому
назад и несколько человек, которые знали про это в последние пять или
шесть лет, могут это засвидетельствовать.
(Письмо Ферма Декарту, июнь 1638; Oeuvres, tome 2, p. 154-162)
Когда Величина является самой большой или самой маленькой, какой
она может быть, в этот момент она не уменьшается и не увеличивается.
Потому что если она увеличивается, то это значит, что ранее она была
меньше, и сейчас начинает увеличиваться ... С помощью Задачи 1 следует
искать Флюксию и предположить, что она равна нулю.
(Ньютон 1671, публикация на английском 1736, р. 44)
Задача нахождения максимальных и минимальных значений была одним из
самых первых побудительных мотивов к созданию дифференциального
исчисления (Ферма 1638), ее разрабатывал Лагранж на протяжении всей своей жизни
(см. Лагранж 1759).
В точке жо, где функция f(x) достигает своего максимального или
минимального значения, она не возрастает и не убывает. Поэтому мы получаем f'(xo) = О
(стационарную точку). Это будет (локальный) максимум, если знак ff(x)
меняется от + к — (это тот случай, когда f"(xo) < 0), и (локальный) минимум, если
знак f'{x) меняется от — к + (так бывает когда /"(жо) > 0). Итак,
f'(xo) = 0 и f"(xo) > О => хо — это локальный минимум,
f'(xo) = О и /"(жо) < 0 => хо — это локальный максимум.
Эти факты "sequentibus exemplis illustrabimus" — иллюстрируются следующими
примерами (лат.):
Пример 1. Рассмотрим функцию
(2.1)
3 2
у — X — X
(2.2)
Зж,
у' = Зж2 - 2х - 3,
у" = 6ж - 2.
Функция возрастает там, где у' > 0, т.е. при
х < (1 - у/Щ/Ъ и при х > (1 + у/Щ/Ъ. Она
выпукла книзу при х > 1/3 и выпукла кверху
при х < 1/3. Точка х = 1/3 является
точкой перегиба. Точка х = (1 — \/10)/3 является
точкой локального (но не глобального)
максимума, а точка х — (1 + vl0)/3 есть точка
локального минимума.
Пример 2. Рассмотрим функцию (см. Эйлер 1755, Pars Posterior, §265)
(2.3)
1
1 + ж
2'
(1 + z2)
2\2'
„ -6ж + 2х
У -
(1 + я2)
2^3 '

11.2 Высшие производные и ряд Тейлора 93
Рис. 2.2. Максимумы, минимумы и точки перегиба примера Эйлера.
которая изображена на рис. 2.2 вместе со своими первой и второй производными.
Функция у(х) имеет (глобальный) минимум при х = — 1, (глобальный) максимум
при х = 1, и точки перегиба при х = 0 и х = ±\/3. Она выпукла книзу на
интервалах — л/3 < х < О и \/3 < х < оо и выпукла кверху везде, кроме этих
интервалов.
Принцип Ферма.
Рис. 2.3. Рисунок И. Бернулли 1691/92.2
Рис. 2.4. Принцип Ферма.
Ферма хотел объяснить закон Снеллиуса преломления света на границе двух
сред, скорость распространения света в которых равны vi и V2 соответственно.
Пусть заданы точки А и В (рис. 2.4). Требуется найти углы ai и«2 такие, что
свет распространяется из А в В за минимальное время или с минимальным
сопротивлением. Это значит, что нужно найти такое значение ж, что
(2.4)
Т =
v^nn
Vl
■ +
yjb2 + (t-xy
V2
— mm!
Воспроизводится с разрешения библиотеки Базельского университета.

94 II. Дифференциальное и интегральное исчисление
Сам Ферма считал, что аналитическое решение этой задачи слишком трудно ("я
полагаю, что эта задача не из самых легких"). Соответствующие вычисления с
гордостью представил Лейбниц (1684) "in tribus lineis" (в семействе линий, —
лат.). Производная Т как функции от х равна
Т' =
1
2х
+
-2(1-
1
vi 2Va2 + х2 2y/b2 + {t-x)2 v2m
Замечая, что sinai = х/у/а2 -f х2 и sina2 = (£ — x)j \Ja2 + (£ — х)2, мы получаем,
что производная обращается в нуль при условии
sinai sina2
(2.5) =
Vi V2
(закон Снеллиуса). Если вычислить Г":
rplt _
+
Vl{a2 + x2)3/2 ' v2(a2 + {£-x)2)3/2
то отсюда следует, что это действительно минимум.
>0,
De Conversione Functionum in Series
(О превращении функции в ряд, — лат.)
Подход Тейлора.
Здесь мы фактически имеем беспримерно смелый переход к пределу.
(Ф.Клейн 1908, англ. изд., р. 233)
Рассмотрим (Тейлор 1715) точки х$, яi = #о + ^х-> ж2 = #o + 2Ах,... и
функцию /(ж), которая имеет значения у0 = /(жо), yi — f{xi), Уг — /(ж2),... в
этих точках.
Xq Х\
%2 Xq Х\ Х2 х0 хЪ
Рис. 2.5. Построение многочлена Тейлора.
Теперь вычислим интерполяционный многочлен, проходящий через эти
точки (см. рис. 2.5 и теорему 1.1.2, в которой положим х — xq + tAx, t = rc~^Q)
(2.6)
х-х0Луо (х- х0){х- хг) Л2у0
р{х)=уо + —; г~ +
1 Ах ' 1-2 Ах2 '
или многочлен более высокого порядка с большим числом членов. Если
положить Ах —>■ 0, #1 —>• а?о, #2 ""*" жо (или, как мы говорили, если взять бесконечно
малое Ах), то частное Ауо/Ах во втором члене стремится к f'(xo). Далее,
произведение (х — xq)(x — х\), стоящее в третьем члене, будет стремиться к (х — xq)2.

11.2 Высшие производные и ряд Тейлора 95
Тейлор постулировал, что вторая разность (деленная на Ах2) стремится ко
второй производной (см. упр. 2.5 и упр. III.6.4), а в общем случае
ДкУо dky |
(2.7)
Лхк dxk
= f(k)(
хо
Если мы будем брать все большее и большее число членов в интерполяционном
многочлене (2.6) и в то же самое время перейдем к пределу Ах —> 0, мы получим
знаменитую формулу
(2.8) f{x) = f(xo) + (x-x0)f'(x0) +
(х - Хо)
-/"Ы +
(х - хо)2
Г'Ы + ... .
2! ' v "' 3!
Все ряды, приведенные в первой главе, являются частными случаями этого
"series universalissima" (самого универсального ряда, — лат.). Например,
функция f(x) = 1п(1 + х) имеет производные
/(0) = 0, /'(0) = 1, /<fc>(0) = (-l)fc-1(fe-l)!
и мы получаем
1п(1 + х)
Х~Т +
-Т±"
Замечания. Более столетия формула (2.8) считалась справедливой в общем
случае. Потом Коши нашел пример функции, для которой ряд (2.8) сходится,
однако не к функции f(x) (см. разд. III.7). Кроме того, существуют примеры
функций, для которых ряд (2.8) не сходится, если х ф хо (см. упр. III.7.6). Более
удовлетворительное доказательство (2.8) (принадлежащее И. Бернулли), которое
использует интегральное исчисление, будет приведено в разд. П.4.
Подход Маклорена (Маклорен 1742, р. 223-224, art. 255). Для функции у =
((х) и заданной точки xq мы ищем ряд (или многочлен)
(2.9) р(х) = ро + (х - x0)q0 + (х - х0)2г0 + (х - x0)3s0 + ...,
для которого
(2.10) Р(0Ы = /(0Ы % = 0,1,2,...,
т.е. обе функции в точке х = хо имеют одинаковые производные вплоть до
некоторого порядка. Если в формуле (2.9) положить х = #о, то в силу (2.10) мы
получаем ро — р(хо) = f(xo). Теперь мы дифференцируем (2.9), снова полагаем
х = xq и получаем до = р'{хо) — /'(жо)- Последовательные дифференцирования
приводят к 2!r0 = f"(x0), 3!s0 = /'"(^о), и т.д. Итак, ряд (2.9) совпадает с (2.8).
Частичные суммы ряда (2.8) называются
многочленами Тейлора.
Пример. Выберем точку хо = 1 и
рассмотрим функцию, заданную с помощью (2.2).
Имеем f(x0) = -3, f'(x0) = -2, f"(z0) = 4 и
f"(xo) = б. Таким образом, многочлены
Тейлора первой, второй и третьей степени равны
Р1(х) = -3 - 2(х - 1) = -2х - 1,
Ф) = Мх) + Нх ~ !)2 = 2х2 " 6ж + 1,
Ф) = Р2{х) + |(ж - I)3 = х3 - х2 - Ъх.
/ Pi-
1 -2
/=Рз
-4
- \
, L_/ U
[ 2/ /3
/ /
/ /
/ /
/ /
/ /

96 П. Дифференциальное и интегральное исчисление
Метод Ньютона нахождения корней уравнений.
JfJ — 2J— 5=с
2+P=J
оГ»+д=р
1 —0,0054 + ' = if
1^0,00004854 +•* = »'
+J1
—5
Summa
+ i"
+ 6p»
+ юр
— i
Summa
+ *Мг
+ ",23?
-+-o,o6i
Summa
+ 2,10000000 1
—0,00^485?
•+2,09455147= J
+ 8 + I2p+-6p» + P»
— 4 —2p
— *
— 1 -Hop + 6p» +pi 1
+ 0,001 + 0,033 +• 0,39» + g» I
+ 0,06 +- 1,2 + 6,0 J
+ 1, + »°э I
г,%
|+ 0,061 + 11,23$ + ^,39* + 4* 1
+ 0,000183708—о,о68о4г+6,згЧ
h— 0,060642 +11,23
+ 0,061
1+0,000541708+11,1619бг+6,зг»|
negle&o, tc prodit ©\$r»+- n,i6io6r+- 0,000541708= о fere, five
(rejeCto 6\;rO r= "ЭДУ* e — °»о00О48И feft» ЭДф faibo io
oegativa parte Qpotientis. Deoique negativam partem Quotieotis ab
Affirmative fubducens babeo 2,09455147 Quotientem quciicam.
Рис. 2.6. Вычисления Ньютона корня уравнения ж3 — 2х — 5 = О.3
Многочлены Тейлора оказываются чрезвычайно полезным средством для
приближенного вычисления корней уравнений. Рассмотрим пример, приведенный
Ньютоном (1671):
(2.11) х3 -2ж-5 = 0.
Вычислим несколько значений функции f(x) — х3 — 2х — 5: /(0) = —5, /(1) ==
—6, /(2) = — 1, /(3) = 16. Отсюда следует, что существует корень, близкий к
хо — 2. Идея метода состоит в том, чтобы заменить кривую f(x) ее касательной
в точке хо: pi(x) = — 1 + 10(ж — 2). Корень pi(x) = 0, который равен х = 2.1,
является улучшенным приближением к корню уравнения (2.11). Далее возьмем
хо = 2.1 и повторим вычисление. Получаем рг(х) = 0.061 + 11.23(ж — 2.1) и новое
приближение для корня уравнения (2.11): х = 2.0945681. Следующий шаг дает
х = 2.0945515, где все приведенные цифры правильны (рис. 2.6 представляет
факсимиле вычислений, проведенных Ньютоном).
Использование многочлена второй степени (Э. Галлей 1694). В примере,
приведенном выше, выберем точку хо — 2.1 и используем два члена многочлена
Тейлора. Получаем
0.061 + 11.23(ж - 2.1) + 6.3(ж - 2.1)2 = О,
квадратное уравнение относительно z = ж—2.1, которое имеет два корня. Возьмем
корень меньший по абсолютной величине (т. е. тот, для которого х более близко
к 2.1) и получим
Воспроизводится с разрешения библиотеки Женевского университета.

11.2 Высшие производные и ряд Тейлора 97
Л „ -11.23 + VH.232 - 4 • 0.061 • 6.3
z — х — 2.1 = ——
12.6
и, следовательно, х — 2.0945515. Опять-таки все приведенные цифры правильны,
причем получены за одну итерацию.
Упражнения
2.1 (Эйлер 1755, §261). Исследуйте функции
у = х4 - 8ж3 + 22ж2 - 24ж +12, у = хъ - 5ж4 + 5ж3 + 1.
Найдите максимумы, минимумы, области выпуклости книзу, точки перегиба.
2.2 (Эйлер 1755, §272). Последовательность чисел
л/1=1, #2 = 1.4142, #3=1.4422, #4=1.4142, #5 = 1.3797,...
наводит на мысль, что функция у = у/х = хг'х имеет максимум, близкий
к х — 3. Где точно он находится? В каком отношении находится величина
этого максимума к минимуму функции у = хх?
2.3 (И.Бернулли 1691/92). Найдите х такое,
что прямоугольник, образованный
абсциссой и ординатой точки, находящейся
на окружности у = у/х — х2, имеет
максимальную площадь. Проверьте
максимальность путем вычисления второй
производной.
2.4 (Эйлер 1755, §272). Найдите такое ж, при котором ж sin ж имеет (локальный)
максимум (вы получите уравнение, которое лучше всего решать методом
Ньютона или Галлея; Эйлер приводит ответ (х = 116о14'21"20'"35""47'"";
правильные значения последних цифр суть 32""38""/).
2.5 Для функции у = х3 вычислите вторую разность
Л2у = (х + 2Лх)3 - 2(ж + Ах)3 - ж3.
Покажите, что эта разность, деленная на Лж2, при Лх —у 0 стремится к 6ж,
т.е. ко второй производной.
2.6 Пусть /(ж) = sin(a;2). Вычислите /'(ж), /"(ж), /'"(ж), /""(ж), ... и получите
ряд Тейлора
/(*) = /(0) + /'(О)* + /"(0)^ + /'"(0)^ + /""(0)^ +....
Существует ли гораздо лучший способ получения этого результата?
2.7 Покажите, что метод Ньютона в приложении к уравнению ж2 —2 = 0
тождественен (1.2.13), т.е. вавилонскому способу вычисления у/2. Однако формула
(1.2.13) отлична от метода Галлея. Почему?
2.8 (Лейбниц 1710). Обобщая (1.4), покажите, что для функции у(х) = и(х) -v(x)
у" = u"v + 2uV + ш;", у"' = u'"v + 3txV + 3uV + uv'".
Найдите общую формулу для у(пК

98 П. Дифференциальное и интегральное исчисление
IL3 Огибающие и кривизна
Мой брат, профессор в Базеле, воспользовался этим, чтобы исследовать
несколько кривых, которые Природа каждый день нам демонстрирует ...
(И. Бернулли 1692)
Я совершенно уверен в том, что вряд ли во всем мире существует геометр,
которого можно было бы сравнить с Вами.
(Де Лопиталь 1695, письмо к И. Бернулли)
Огибающая семейства прямых линий
Рассмотренный ниже пример подсказан одним
рисунком в книге А. Дюрера (1525, S. 38; см. рис. 3.1
справа). Пусть точка (а, 0) перемещается по оси ж,
а точка (0,13 — а) перемещается по оси у в
противоположном направлении. Если соединить эти точки
прямой линией
/0i4 а -13. х in 13ж
(3.1) у — (х — а) — 13 + х — а ,
а а
мы получим бесконечное множество прямых, показанных на рис. 3.1, которое
порождает интересную кривую, называемую огибающей и касающейся каждой
из этих прямых. Задача состоит в том, чтобы вычислить эту кривую. Задачи
такого рода дали повод к обширной дискуссии между Лейбницем (см. Лейбниц
1694а), И. Бернулли и де Лопиталем.
Рис. 3.1. Семейство прямых, образующее параболу, и рисунок Дюрера (1525).*
Идея решения. Фиксируем переменную х при некотором произвольном
значении. Например, положим х = 4. Тогда семейство уравнений (3.1) примет вид
у = 17 — а—52/а. Заметим, что эта величина сначала возрастает при увеличении а
1 Воспроизведено с разрешения издательства Dr. Alfons Uhl, Nordlingen.

11.3 Огибающие и кривизна 99
(см. рис. 3.1: при а — 3,4,5,6 мы имеем у — —3.33, 0, 1.6, 2.33 соответственно),
и при этом точка (4, у) приближается к огибающей. Эта точка достигает,
наконец, огибающей как раз тогда, когда функция у(а) принимает свое максимальное
значение и следовательно производная у' — — 1 + 52/а2 становится равной нулю.
При этом а = л/52 и у = 17 - 2 л/52 = 2.58.
Этаже идея работает и при любом значении х: надо вычислить производную
функции (3.1) по а, считая х константой ("differentiare secundum а" —
"дифференцируй затем по а", лат.); она называется частной производной по а. В точках
огибающей эта производная должна обращаться в нуль. Теперь это записывается
так:
(3.2) ду
да
о,
(см. разд. IV.3, а также Якоби 1827, Oeuvres, vol.3, p. 65).
Для функции (3.1) получаем ду/да = — 1 + 13ж/а2, и условие (3.2) дает а
Подставляя это в (3.1), получаем уравнение огибающей:
(3.3) у- ж-2л/13ж + 13
или
(3.4) {У-х- 13)2 = 52ж.
Это — уравнение конического сечения, которое в нашем случае оказывается
параболой.
Каустика окружности
II , J N , \\
-111111111111111
\[| 1 ill
\
11' Li i i LUlilUJ JJLLIJ1IJJ LJ
'1
M; hi! 11 i | i I! i
Wmm
\ ^\
lliliSP
/ /
I'll lil 111 1111'! !!i
i
1 1 и \\JSf
?1
Рис.3.2. Каустика окружности (И.Бернулли 1692).
Задача. Дана окружность х2 + у2 = 1 (рис. 3.2); предположим, что
параллельный пучок вертикальных лучей отражается от этой окружности. Это
порождает новое семейство прямых линий, которое, как видно, имеет интересную
огибающую. Требуется найти уравнение этой огибающей.
И.Бернулли (1692) дал решение этой задачи "per vulgarem Geometriam
Cartesianam" (с помощью общеизвестной декартовой геометрии, лат.), с
другой стороны, в своих "Lectiones" (И.Бернулли 1691/92b, Lectio XXVII, "Caustica

100 П. Дифференциальное и интегральное исчисление
circularis radiorum parallelorum", Opera, vol. 3, p. 467) он использует "современное"
дифференциальное исчисление.
У
tf4 l
1
2 cos а
-1
5>\3
/ \
/ \
/ х^
/
/2а - я/2 1
К,а
Iх
1
Рис. 3.3. Отраженный луч.
Решение. Для представления семейства отраженных лучей выберем в
качестве параметра угол а между отраженным лучом и радиус-вектором (см. рис.
3.3). Выполнив несложное геометрическое построение и учитывая, что наклон
отраженного луча равен tg (2а — 7г/2) = — cos 2а/sin 2а, мы получим уравнение
1
cos 2а
(3-5) У= 0 - . 0
2 cos а sin 2а
Тогда условие (3.2) для каустики примет вид
1 х
2 cos а 2
/ sin а cos а \
V cos а sin а /
(3.6)
ду
да
+
= 0.
2cos2a 2cos2asin2a
откуда
(3.7) х = sin a.
Чтобы получить уравнение каустики, подставим это значение х в (3.5). Это дает
1 / 1 sin4a .2 \ /1 • 2 \
у — 1 sin a cos a = — cos a - + sin a .
2 V cos a cos a / \ 2 /
Это уравнение вместе с (3.7) дает параметрическое представление каустики. Если
мы хотим получить явное выражение для у как функции от ж, надо подставить
Z1/3-
сюда sin a
(3.8)
, что приводит к уравнению
у = -у/1-Х2/з(1 + х2/зу

11.3 Огибающие и кривизна 101
Огибающая баллистических кривых
Задача, Пушка стреляет ядрами с начальной скоростью ^о = 1 под
всевозможными углами возвышения. Найти огибающую всех баллистических парабол
(рис. 3.4). Этот вопрос, занимавший уже Торричелли (см. De motu projectorum
1644), был одной иэ первых задач, пленивших молодого Иоганна Вернул л и (см.
Briefwechsel, p. 111).
Рис. 3.4а. Огибающая парабол стрель- Рис.3.4Ь. "Солнечный фонтан" (1721 г.^
бы. в Петергофе под Санкт-Петербургом.
Решение. Пусть величина наклона ствола пушки равна а. Тогда движение
ядра под действием гравитационного ускорения g — 1 определяется уравениями
X{t) = —L=, y{t) at t2
уТТ^"' VT+a2 2
Исключая параметр t — ху/1 + а2, получаем
(3.9) у = ах- у '
2
Дифференцируя (3.9) по а, получаем ду/да = х — ах2, и условие (3.2) приводит
к равенству а = l/х. Подставляя эту величину в (3.9), получаем
у = (1 - х2)/2,
так что огибающая есть парабола, в фокусе которой находится пушка.
Кривизна
Мало существует более изящных задач о кривых, чем эта, или которые
давали бы большее понимание их природы.
(Ньютон 1671, Англ. публикация 1736, р. 59)
Задача, Для заданной кривой у = f(x) и заданной точки (a,f(a)) на
этой кривой требуется найти уравнение окружности, которое как можно лучше

102 II. Дифференциальное и интегральное исчисление
аппроксимирует функцию f(x) в окрестности точки а. Эта окружность
называется окружностью кривизны, а ее центр — центром кривизны. Обратная величина
ее радиуса называется кривизной кривой в точке (a,/(a)).
Идея решения (Ньютон 1671). Уравнение
(3.10)
y = f{a)-f(a){x-a)
задает нормаль к кривой у = f(x) в точке х — а. Если увеличить а ("представьте,
что точка D сдвинулась по кривой на бесконечно малое расстояние"), получим
вторую нормаль, которая пересекает первую в центре кривизны (рис. 3.5).
Ситуация здесь та же, что и с огибающими (см. рис.3.lb). Поэтому вычислим
(3.11)
ду ,,, N /'» , ч 1
и из условия (3.2) найдем центр кривизны:
/Ч19л т „ (1 + (/'Ы)2)/» ., , хо-а (! + (/'(а))2)
(ЗЛ2) Х°-а = />) ' y°-f{a) = -TW= Па) ■
Для радиуса кривизны г = ^/(жо — а)2 + (у0 — /(а))2 и для кривизны /с получаем
_ (1 + (/'(а))2)3/2
(3.13)
!/"(«)
and к, —
(i + (/'W)2)
3/2 '
(Vo)
я + Дд
Рис. 3.5. Кривизна; рисунки Ньютона 1671, (Meth. Fluxionum- французский
перевод 1740).2
Пример. Для параболы у = х2 мы имеем г = (1 + 4а2)3/2/2, и центр кривизны
задается формулами
(3.14)
(1 + 4а2)2а и 3 2 (1+4а2) 1 „ ,
г0 = а - ^ yJ— = "4а ' Уо = а2+ g—- = - + За2.
Воспроизведено с разрешения издательства Albert Blanchard, Париж.

11.3 Огибающие и кривизна 103
Эти формулы образуют параметрическое представление геометрического места
точек (жо,2/о) центров кривизны. Оно называется эволютой. Из уравнений (3.14)
можно исключить параметр (здесь это а), и мы получаем (см. рис. 3.6b)
» = Ит)
2/3
Рис. З.ба иллюстрирует тот факт, что эволюта является огибающей семейства
нормалей к данной кривой.
Рис. 3.6а. Эволюта = огибающей
нормалей.
Рис. 3.6b. Парабола у = х2 и ее эволюта.
Кривизна кривой в параметрическом представлении. Рассмотрим
кривую (ж (£),?/(£)) и предположим, что вблизи точки (ж(а),у(а)) она может быть
представлена как у = f(x). Тогда согласно (1.20) мы имеем
f(x\ = !*У = dy/dt = t^l
1 [ } dx dx/dt x'(ty
и вторая производная равна
d_(dy\ =±(1/Щ /dx x'(t)y"(t)-x"(t)y'(t)
1 [Х> dx\dx) dt\x'{t))l dt x'{tf
Подставляя эти выражения в уравнения (3.12) и (3.13), получаем
у'(а)(х'(а)2+у'(а)2)
(3.15)
(3.16)
(3.17)
xq — х(а) =
х'(а)у"(а)-х"{а)у'(аУ
_ х'(а){х'(а)*+у'(а)2)
У° У[<1) х'{а)у"{а)-х"{а)у'{а)
{х'(а)2 + г/(а)2)3/2
\х,{а)уп{а)-хп(а)у,{а)\'
Пример. Циклоида (траектория вентиля на колесе велосипеда) в
параметрическом виде может быть представлена так:

104 П. Дифференциальное и интегральное исчисление
(3.18) x = t — sint, у = 1 — cost.
Вычисляя производные и используя уравнения (3.15) —(3.17), получаем, что
эволюта циклоиды задается выражениями
(3.19) xo = a + sma, у0 = — 1 + cosa.
Это опять циклоида, но в другом положении.
Рис. 3.7. Циклоида и ее эволюта.
mais aussy dans les
la roulette premiere
done la roulette A
le diametre AE = -
grandeur de AD, t
Рис. 3.8. Циклоида, рисунок И. Бернулли (1955, р. 254, письмо от 12 января 1695 г.
Л опита л ю).3
Эвольвенты, Возьмем заданную эволюту ABB (см. рис. 3.6b) и построим
новую кривую СС, определенную тем свойством, что длина дуги ABC постоянна
(вообразите себе нить, разматывающуюся с эволюты). Эти новые кривые
называются эвольвентами. Если одна точка эвольвенты совпадает с первоначальной
функцией /(ж), обе кривые будут иметь одинаковую кривизну. Отсюда следует
(что будет строго доказано с помощью идей, развитых в разд. III.6), что обе
кривые идентичны. Следовательно, не только эволюта, но также и эвольвента
циклоиды (при правильном выборе длины дуги) будет опять циклоидой (Ньютон 1671,
Prob. V, Nr. 34). Гюйгенс (1673) использовал это свойство для конструирования
лучших в его время маятниковых часов, основанных на том, что движущийся по
циклоиде маятник, является изохронным (см. рис. 7.8 в разд.II.7).
v^)
3 Воспроизведено с разрешения издательства Birkhaeuser, Basel.

П.З Огибающие и кривизна 105
Упражнения
3.1 Брусок единичной длины скользит по вертикальной стене (рис. 3.9а).
Найдите формулу образующейся огибающей.
3.2 Найдите формулу для огибающей (рис. 3.9Ь), семейства прямых
5/ 3 ч
у-ах- -(а - а).
Т) 1
1 f^X п
з \5ч
#
]0\ i
/s^Jz 2
V з
\ 2
1 п
2 -1 °
1 \n
1 :
Рис. 3.9. Эволюты и огибающие.
3.3 (Коши 1824) Найдите огибающую семейства парабол
у = Ь{х + б)2
с параметром b (рис. 3.9с).
3.4 Для функции у = In ж найдите радиус кривизны в точке а и определите
точку а, в которой этот радиус минимален (рис. 3.9d). Видно, что у эволюты
эта точка является стационарной (точкой возврата).
3.5 Вычислите эволюту эллипса (рис. 3.9е)
х — a cos t
х2 у2
Т + ТТ = 1 ИЛИ
О < t < 2тг
&2 у = bsint
Определите максимальную и минимальную кривизну.
Ответ. х = (а ] cos31 , у = ( b г- J sin31 .
3.6 Вычислите радиус кривизны цепной линии у = (ех +е~х)/2. Покажите, что в
заданной точке М этой кривой радиус равен длине нормали MN (рис. 3.9f).

106 П. Дифференциальное и интегральное исчисление
3.7 Из рис. 3.7 видно, что спица катящегося колеса порождает огибающую,
которая похожа на половинку малой циклоиды. Это становится более очевидным,
если нарисовать полные диаметры (рис. 3.10). Вычислите огибающую этого
семейства прямых линий
ч cost
у=1 + (x-t • —-.
sin t
12 3 4 5 6
Рис. 3.10. Малая циклоида как огибающая.
Гийом Франсуа Антуан де Лопиталь (1661-1704)
Иоганн Бернулли (1667-1748)4 Маркиз Сент-Месма и Монтелье,
граф Антремонтский, сеньор Дукский и прочих мест
Воспроизведено с разрешения издательства Georg Olms, Hildesheim.
Воспроизведено с разрешения издательства Birkhaeuser, Basel.

II.4 Интегральное исчисление 107
П.4 Интегральное исчисление
... notam J pro summis, ut adhibetur nota d pro differentiis ... (... обозначим
J суммирование, и пусть d употребляется для обозначения разностей ...,
лат.) (Письмо Лейбница к И. Бернулли, 8/18 марта 1696 г.)
... quod autem ... vocabulum integralis etiamnum usurpaverim ... (...
кстати ... слово "интеграл" до сих пор употребляется ..., лат.)
(Письмо И. Бернулли к Лейбницу, 7 апреля 1696 г.)
И в то время как г-н Лейбниц пишет символ J перед ординатой кривой
для того, чтобы обозначить сумму ординат или площадь [под] кривой, я
несколькими годами ранее обозначил ту же величину, написав ординату
в квадратике ... Таким образом, мои символы ... были самыми первыми
в своем роде. (Ньютон, письмо к Кейллу, 20 апреля 1714 г.)
Интегральное исчисление фактически гораздо старше дифференциального,
поскольку вычисление площадей, поверхностей и объемов занимало
величайших математиков, начиная с античных времен. Среди них были Архимед,
Кеплер, Кавальери, Вивиани, Ферма (см. теорему 1.3.2), Грегори СентВинсент, Гул-
дин, Грегори, Барроу. Решающий прорыв наступил, когда Ньютон, Лейбниц и
И. Бернулли независимо открыли, что интегрирование является операцией,
обратной дифференцированию, и, следовательно, все достижения
вышеупомянутых исследователей можно свести к нескольким правилам дифференцирования.
Знак интеграла ввел Лейбниц (1686), а термин "интеграл" ввел И. Бернулли и
опубликовал его брат Я. Бернулли (1690).
Первообразные
■■№
а х I ах\Х2--- хп = Ь
Рис. 4.1а. Идея Ньютона. Рис. 4.lb. Идея Лейбница. Рис. 4.1с. Рисунок Ньютона.1
Пусть нужно вычислить площадь между осью х и графиком заданной
функции у — f(x). Выберем на оси х точку а и обозначим z = F(x) площадь под
кривой /(ж), заключенную между а и х (рис. 4.1а). Тот факт, что
Воспроизведено с разрешения издательства Albert Blanchard, Париж.

108 П. Дифференциальное и интегральное исчисление
(4.1) функция f(x) является производное от F(x)}
является при этом решающим. Функцию F{x) называют первообразной для f(x).
Обоснование. В рассуждениях Ньютона отрезок BD движется по
рассматриваемой области ("И представим себе, что эти Площади ... порождаются
прямыми BE и BD, при их движении вдоль ...", рис. 4.1а, 4.1с); следовательно, если
х возрастает на Ах, то площадь возрастает на величину Az — F(x + Ах) - F(x),
которая, если пренебречь членами высшего порядка по Ах, равна f(x)Ax
(темный прямоугольник на рис. 4.1а). В пределе Ах —> 0 мы получаем
(4.2) dz = f(x)-dx и *L = f(x).
ах
Лейбниц рассматривает площадь как сумму (позднее как "интеграл")
маленьких прямоугольников (рис. 4.lb):
(4.3) zn = f{x1) Ахг + f(x2) Ах2 + ... 4- f{xn) Ахп.
Отсюда следует, что zn — zn_i = f(xn) Axn, и мы опять получаем (4.2), когда
Axi —>• 0. Следовательно, вычисление производной есть операция, обратная по
отношению к вычислению интеграла, подобно тому как вычисление разности
есть операция, обратная к вычислению суммы.
Перебрав много вариантов, Лейбниц остановился на таком обозначении
суммы (4.3) (в пределе Ах{ —> 0):
(4.4) Jf(x)
dx
(см. рис. 4.2). Теперь эта площадь в границах от а до 6 обозначается так:
(4.5) / f(x)dx
J а
(Фурье 1822), а "неопределенный интеграл" (4.4) обозначает любую
первообразную F(x) функции f(x).
Scd cxiis quae in
ffltfhodotangenttumcxjpofui, patct cflc d,£xx=xdx; ergo contra |
ixdxd* (uc enim potentates & radices in vulgaribus calculi», (ic no*
bis fumm* & differentiae feu f&d, reciprocal funt.)
Рис. 4.2. Первая публикация знака интеграла, старомодное "s" (Лейбниц 1686).2
Первообразные не единственны: к каждой первообразной F(x) можно
прибавить произвольную постоянную С и F(x) + С также будет первообразной той
же самой функции. Если положить С = —F(a), то мы получим такую
первообразную F(x) — F(a), которая обращается в нуль при х — а (вместе с площадью
z). Таким образом, площадь между а и Ъ равна
(4.6)
f f{x)dx = F(b)-F(a)
J а
2 Воспроизведено с разрешения Публичной библиотеки Женевского университета.

11.4 Интегральное исчисление 109
(см. "Основную теорему дифференциального исчисления" в разд. III.6).
Обращая формулы дифференцирования, мы получаем формулы для
первообразных. Например, производной функции f(x) = xn+1 является
функция f(x) = (п + 1)хп. Поэтому первообразной функции хп является функция
in+1/(n+ !)• Эта и другие формулы, являющиеся обращениями формул
раздела II. 1, собраны в табл. 4.1.
ТАБЛИЦА 4.1. Краткая таблица первообразных
/хп+1 Г 1
xndx= - + С Ыф-1) -dx = \nx + C
п+ 1 J х
I
ех dx = ех -f С
I sin х dx — — cos х + С I cos x dx — sin x + С
f 1 f 1
/ r- dx = arctg x + С I , dx — arcsin x + С
J 1 + x2 J y/l -x2
Большие таблицы первообразных могут занимать несколько сотен страниц.
Упомянем таблицы Грёбнера и Хофрейтера (1949), а также Градштейна и
Рыжика (1980). За последние годы эти сведения были введены во многие компьютерные
символьные системы.
Приложения
Площадь парабол. Согласно (4.6) и табл. 4.1, площадь под параболой п-го
порядка у — хп между х — а и х — Ь равна
Г5 ^п+1 ,ъ ьп+1 _ ап+1
(4.7)
J а П+1
71+ 1
где мы использовали обозначение .F(e)|£ = F(b) — F(a). При а = 0 эта формула
представляет собой теорему Ферма 1.3.2.
Площадь круга. Для того, чтобы вычислить площадь одной четвертой
части круга, рассмотрим функцию f(x) = л/1 — х2 при 0 < х < 1. Первообразной
этой функции является
х / 1
(4.8) F(x) = -yl - х2 + - arcsin ж.
Это можно проверить путем дифференцирования (4.8). В дальнейшем мы
увидим, как такие формулы получаются в действительности. Таким образом,
используя (4.6), мы приходим к соотношению
Площадь единичного круга = 4 / у 1 — х2 dx = 4(F(1) — F(0)) = 7г,
./о
поскольку sin(7r/2) = 1.

110 II. Дифференциальное и интегральное исчисление
Существует и другой изящный способ вычисления площади круга. Совсем
не обязательно предполагать, что f(x) dx являются маленькими вертикальными
прямоугольниками. Давайте разрежем круг (радиуса а) на бесконечно тонкие
треугольники (Кеплер 1615, см. также идею Лейбница, рис. 1.4.11). Площадь
такого треугольника равна
где d(p есть бесконечно малое приращение угла.
Полная площадь (сумма всех этих треугольников)
равна
/*2tt л2 л,„ ~2 /*2п
<р
2тг
= а27г.
Объем шара. Рассмотрим шар радиуса а (рис. 4.3) и разрежем его на
тонкие ломтики (диски толщиной dx и радиуса г = л/а2 — х2 ). Объем такого ломтика
равен dV = г2тг dx = (а2 — х2)тг dx, а для полного объема шара мы получаем
г+« , „зч|+а 4a3?r
(а2 — ж2)7г dx = 7г ( ха2 —— )
х = -а
(а2-х2)ш
х = а
Рис. 4.3. Объем шара.
Работа в силовом поле. Пусть сила f(s) действует вдоль прямой линии,
параметризованной величиной s. Работа, производимая при перемещении тела
из s в s + Л5, равна f(s)As (сила х путь). Таким образом, полная работа равна
Пример. На тело с массой 1 кг действует сила земного тяготения f(s) -
9.81 • R2/s2 [Н] , где R — радиус Земли и s — расстояние от тела до центра
Земли. Следовательно, для перемещения 1 кг с поверхности Земли в бесконечность
требуется энергия, равная
?2 Z?2|00
= 9.81Д=62.106 [Дж].
Г°° R В
Е= 9.81—d* =-9.81 —
Jr s2 s
R

11.4 Интегральное исчисление 111
Длина дуги.
Флюксия Длины определяется как величина, равная квадратному корню
из суммы квадратов флюксий Абсциссы и Ординаты.
(Ньютон 1736, Fluxions, р. 130)
Вычислим длину L заданной кривой у(х) при а < х < Ь. Если х получает
приращение Ах (см. рис. 4.4), ордината увеличивается на Лу — у'(х)Ах (мы
пренебрегаем членами более высокого порядка). Поэтому длина малой части
кривой равна Аs, где
As2 = Ах2 + Ау2 = (1 + у'{х)2)Ах2
(теорема Пифагора). В пределе Ах —У О получаем
Гь
и L= yjl + yf(x)2dx.
J а
(4.9)
ds = >/l + 2/'(z)2 • dx
dy ds
^ 4
t
dx
# 1
°0 1
Рис. 4.4. Длина дуги кривой у = х2.
Пример. Для параболы у — х2 имеем у1 — 2х, и длина дуги между х = 0 и
х-1 равна (см. формулу (4.27) ниже)
L= [ \Л + 4ж2dx = ^жл/l + 4ж2 + ^In(2z + \J\x2 + l)
^ + Iln(2 + V5).
Центр масс. Для примера рассмотрим две массы т\ и гаг, расположенные
в точках с абсциссами х\,Х2- Их момент относительно начала координат равен
•щъ\ + ^2^2. Центром масс называют точку х такую, что если поместить в нее
обе массы, их момент останется тем же самым, т.е.
(4.10) (mi + m2) • х — miXi + т2ж2.
Если плотность тела меняется непрерывно так, что масса ломтика толщины dx
равна гп(х) dx, то по аналогии с (4.10) мы получаем
(4.11)
/*6 /»6
/ гп(х) dx • х = / xm(x)dx и
J a J а
_ ja х m(x) dx
la Ш(Х) dx
Пример. Для треугольника между прямой у = сх и осью х (0 < х < а) имеем

112 II. Дифференциальное и интегральное исчисление
Nin, , ч С ex2 dx а3/3 2а
(4.12) m(x)=cz, x=J-fa -=-/- = -
J0 сжаж а-/2 6
Замечание. Для случайной переменной X с "функцией плотности" /(ж)
(удовлетворяющей условию f_ f(x)dx = I) величина х = J_ х f(x)dx называется
средним значением или математическим ожиданием переменной X.
Техника интегрирования
Рассмотрим теперь некоторые общие способы нахождения первообразной.
Систематический подход для некоторых важных классов функций будет изложен
в разд. И.5.
Прежде всего, заметим, что интегрирование является линейной операцией,
т.е.
(4.13) / (ci/i(ж) + с2/2(ж)) dx-cxj /i(z) dx + с2 / f2{x) dx.
Это сразу следует из того, что дифференцирование является линейной операцией
(см. формулу (1.3)).
Замена переменной (подстановка). Предположим, что
F(z) является первообразной функции f(z),
т.е. F'{z) — /(z), и рассмотрим подстановку z = g(x), которая преобразует
переменную z в х. Из формулы (1.16) следует, что
F(g(x)) является первообразной функции f(g(x))g'(x).
Следовательно,
лЬ Л0(Ь)
/ f(g(x))g'(x)dx= / f(z)dz,
Ja Jg(a)
(4.14)
потому что вследствие (4.6) обе части равны F(g(b)) — F(g(a)). Выражение в
левой части получается подстановкой z — д(х) в функции f(z) и dz — g'{x)dx.
Геометрическая интерпретация. Вычислим интеграл
I
15 4х
■ dx,
/о 1 + *2
используя подстановку z — х2. Поскольку dz = 2xdx, из формулы (4.14) получа-
/•l.O еу pZ.ZD су
/ --2xdx = ск = 2-1п(1 + г)
JQ 1 + х2 J0 1 + z
2.25
= 2-ln(l + z2)| ' =21n(3.25).
Рис. 4.5 иллюстрирует замену переменных z = х2 и функции 4ж/(1 + х2) на
2/(1 + z). Точки х и х + Ах преобразуются в z — х2 и z + Az — х2 -\- 2хАх -f Ах2.

11.4 Интегральное исчисление 113
1
| равные площади
I
Hi!
! I
1
Рис. 4.5. Замена переменной в интеграле.
i ! i !
! i I i ! I
j dz = 2xdx
2.25
Следовательно, при Ax —>• 0 площади заштрихованных прямоугольников равны,
и интегралы в (4.14) имеют одинаковые значения.
Примеры. Все дело в том, чтобы найти "хорошую" подстановку.
Продемонстрируем это на ряде примеров.
Для функций вида f(ax + b) часто бывает полезной подстановка z — ах + Ь.
Например, полагая z = Ъх + 2, dz = bdx, получаем
(4.15)
fe5x+2dx = fez
dz
Г
5х+2
Иногда наличие множителя д'(х), нужного для подстановки z = д(х)< можно
сразу заметить. Например, в приведенном ниже интеграле присутствие
множителя х наводит на мысль о подстановке z = —х2, dz = —2xdx, что дает
(4.16)
/же х dx = — - / <
2J
dZ=-\e>
1
Таблица 4.1 содержит интегралы от функций 1/(1 + х2) и 1/у/Т^2.
Если же мы хотим найти, например, первообразную функции 1/(7 + ж2), можно
использовать подстановку х2 = lz2 или х = у/7 z, dx = у/7 dz. Это дает
dx [ у/7 dz
(4.17)
Г dx Г V
J 7 + х2 ~ J 7(1
--= arete z
V7
1 x
7 + x2 J 7(1 + z*
Интегр>ал с квадратичным выражением х2 + 2bx + с упрощается, если в этом
выражении при с > Ь2 выделить полный квадрат: (х + Ь)2 + (с — Ь2), а затем
сделать подстановку z = (х + Ь)/л/с — Ь2. Так, с помощью подстановки z — (х +
+1/2)/уЗ/4, следующий интеграл приводится к интегралу типа (4.17):
(4.18)
Г dx Г
J х2 + х + 1 ~ J
dz
T/4(z2 + l) УЗ
arct
_2
7з
2x+V
Zz 2 rZx-\-L\
tg^ = 73ai'ctg(-17r)-
л/3
В качестве последнего примера рассмотрим функцию (х -\- 2)/(х2 + х + 1).
Преобразуем (Эйлер 1768 § 62) числитель к виду х + 2 = (ж + 1/2) + 3/2 так,
чтобы первая часть х + 1/2 являлась производной знаменателя, умноженной на

114 II. Дифференциальное и интегральное исчисление
постоянную. Теперь эту часть интеграла можно вычислить с помощью
подстановки z — х2 -\-x-\-l. Вторая часть интеграла равна умноженному на постоянную
выражению (4.18), и мы получаем
Интегрирование по частям. Второй способ интегрирования основан на
правиле дифференцирования произведения (1.4). Если проинтегрировать
формулу (uv)' = u'v + +ш/, мы получим u(x)v(x) — f(uf(x)v(x) + u(x)vf(x)) dx, или
/ uf(x)v(x) dx — u(x)v(x) — / u(x)v'(x) dx.
(4.20)
В этой формуле один интеграл заменяется другим. Если при этом множители и1
и v выбрать должным образом, вычисление второго интеграла может оказаться
более простым, чем первого.
Примеры. Вычислим интеграл j xsinxdx. Нет смысла в выборе и'(х) - х
(и(х) = х2/2) и v(x) = sin ж, потому что в этом случае вычислить второй интеграл
будет еще труднее, чем первый. Поэтому пусть и'(х) = sin ж (и(х) = —cos х) и
v(x) — х. Теперь по формуле (4.20) получаем
(4.21) / х sin х dx — —х cos х + / 1 • cos х dx — —х cos х + sin х.
Иногда интегрирование по частям приходится повторять. В следующем
примере мы сначала полагаем v(x) = х2, и'(х) — ех, а при втором интегрировании
по частям берем v(x) = х, и'(х) — ех:
(4.22) f х2 ех dx = х2ех -2 / хех dx = ех{х2 - 2х + 2).
Функции In х или arctg х имеют простые производные. Они часто
используются в качестве v(x):
(4.23)
/ In х dx — / 1 • In x dx = x In x — I — dx — ж (In x — 1),
/ arctg xdx — x arctg x — I —
dx
(4.24) " y + x
— x arctg x — - ln(l -f x2).
Последний интеграл в (4.24) вычисляется с помощью подстановки z — 1 Н- ж2,
dz — 2х dx.
Теперь вычислим интеграл f у/1 + Ах2 dx, который мы использовали при
вычислении длины дуги параболы. Полагая и'(х) — l,v(x) = л/1 + 4ж2 и интегрируя
по частям, получаем
4х2
: dx.
(4.25) j а/1 + 4ж2 dx = ж\/1 + 4ж2 - j
Второй интеграл выглядит не лучше, чем первый. Однако числитель можно
представить в виде 4х2 = (1+4ж2) — 1. Теперь интеграл можно разделить на две части,

11.4 Интегральное исчисление 115
одну из которых,
- / л/1 + 4ж2 dx (т.е. интеграл, который мы хотим вычислить)
можно перенести в левую часть. Вторая же напоминает последний интеграл
таблицы 4.1: производная функции arsh z есть l/\/l + z2 и, делая подстановку z — 2х
(см. упр. 1.4.3), мы получаем
(4.26) j ^==f = \ "* {2х) = \ In {lx + y/^x2 + l) •
Таким образом, интеграл (4.25) вычислен:
(4.27) f y/l + 4x*dx= |ж\Л + 4ж2 + j \ъЫх + \Аж2 + l).
Рекуррентные соотношения. Предположим, что нам нужно вычислить
интеграл
(4.28) /„ = /*sinn
х dx.
Положим и'(х) = sin ж, v(x) = sinn гх и произведем интегрирование по частям.
При этом получаем
/ sinn х dx = — cos х sinn_1 x + (n — 1) / cos2 ж sinn~2 x dx.
С учетом того, что cos2 х — 1 — sin2 ж, правый интеграл можно представить в виде
двух интегралов, 1п-2 и 1п- Перенося 1п в левую часть, мы получаем (1+п— 1)/п =
-cos£sinn-1x + (п — 1)/п_2, или
1 га — 1
(4.29) /„ = coszsin71-1^ /п_2.
п га
Это рекуррентное соотношение позволяет свести вычисление 1п к вычислению
интеграла 7i = J sin х dx = — cos x (если га нечетно), или 10 — J dx — х (если га
четно).
В качестве следующего примера рассмотрим интеграл
(4.30)
Jn~ J (! + **)»•
За неимением лучшей идеи воспользуемся интегрированием по частям, полагая
u'(x) = lnv(x) = l/(l + x2)n:
_ [ 1 _ х [ 2х2
Jn = J 1'(l + a,2)»<fa= (1 + а;2)п+пу (l+a^n+l^-
Используя такой же прием, как при вычислении (4.25), напишем в последнем
интеграле 2х2 = 2(1 +ж2) — 2и получим
х
J™ — И~>—2\^Г + %nJn ~ 2raJn+i.
(1 + х )
Нам не повезло, поскольку индекс га стал больше, а не меньше. Но это не важно,
из этого соотношения мы можем найти интеграл с большим индексом:
1 х 2га - 1
(4-31) J^ = ^jiT^ + ^rJn-
Это соотношение сводит вычисление (4.30) к вычислению J\ — arctgx.

116 II. Дифференциальное и интегральное исчисление
Формула Тейлора с остаточным членом
И. Бернулли (1694b, "Effectiones omnium quadraturam ..."), вычисляя
интегралы с помощью повторного интегрирования по частям, получил "generalissimam"
(самые общие, — лат.) ряды, подобные тем, которые позже получил Тейлор.
Впоследствии Коши (1821) нашел, что при разумной модификации этот метод
приводит в точности к ряду Тейлора для функции / с остаточным членом,
выраженным в виде интеграла.
Идея состоит в том, чтобы в соответствии с (4.6) написать
f(x) = /(а) + Г 1 • /'(*)
J а
dt
и использовать интегрирование по частям, положив uf(t) = 1 и v(t) = ff{t). Далее,
положим u(t) = — (х — t) (где х — постоянная) вместо u(t) = t (это ключевой
момент), и тогда мы получаем
f(x) = f(a) - (х -t)f(t)\X + Г(х - t)f'{t)dt
= f(a) + (х- a)f'(a) + Г (х - t)f"{t) dt.
J а
На следующем шаге мы полагаем u(t) — — (х — t)2/2! и v(t) = fff(t) и получаем
/(*) = /(а) + (a - a)f(a) + {^L- f"(a) + jf ^^ /'"(*) dt.
Действуя дальше аналогичным образом, приходим к следующему результату:
(4.32)
f{x) = £ Ц^ /О (а) + Г i^ f^ (t) dt.
i=o l' Ja к'
Пример. Если f(x) = ех, f^(x) — ех и а = 0, то формула (4.32) примет такой
вид:
(„3) е. = 1 + х + |! + ... + ^ + £(£^11е.л.
Вас может удивить, что остаточный член (величина ошибки от отбрывания ряда)
представлен в виде интеграла, хотя при вычислении подобного рода интегралов
могут возникнуть, как мы видели, немалые трудности. Конечно, если вычислить
интеграл в (4.33) с помощью рассмотренных выше искусных приемов, получится
просто ех — Y^i=o х%!&•> т-е- совершенно бесполезный результат. Основная идея
состоит в том, что можно оценить остаточный член, заменив подынтегральное
выражение в (4.33) какое-либо более простым. Например, для 0 < х < 1 будет и
О < t < 1, тогда значение е* лежит между числами 1 иЗ. Поэтому представляется
очевидным (и в дальнейшем будет обосновано теоремой III.5.14), что величина
соответствующей площади также заключена между величинами
fx{x-t)k Л3 xk+1 fX{x-t)k oJ 3xfc+1
/ V . t ; -ldt= — и / v ; . 3 dt = —.
Отсюда следует, например, что при к = 10 остаточный член меньше, чем Ю-7.

11.4 Интегральное исчисление 117
Упражнения
4.1 Пусть задана кривая с параметрическим представлением x(t), y(t).
Покажите, что длина ее дуги при a <t < b равна
L= y/x'{t)2+y'{t)2dt.
J а
Вычислите длину дуги циклоиды (3.18) при О < t < 2-к.
4.2 Вычислите интегралы
/х dx Г dx Г
VCT' б) /Тст' в) Jx2™xdx>
г) 1-п = I -r-zi—, д) / х3е~х dx. е) / агссоэжс/ж,
J sinnz J J
ж) / eax cos (3xdx, з) / eax sin/3xdx, и) /
ж2-6ж + 13*
Указания. В случае г) обратите уравнение (4.29), в случае д) напишите ж3 =
х-ж2, в случаях ж) и з) примените интегрирование по частям или разложите
j e(a+t/3)x ^ж на вещественную и мнимую части.
4.3 С помощью повторного интегрирования по частям покажите, что для целых
значений тип справедливо соотношение
/
J а
ъ (Ь-х)т{х-а)п _(6-a)m+n+1
(4-34) / " Г""" r~dx- .
v ' ' т\ п\ (m + n+1)!
и, в частности,
(1 - х2)п dx = ; -.
!V ; 1-3-б--- (2п+1)
/

118 II. Дифференциальное и интегральное исчисление
II.5 Функции, имеющие элементарные интегралы
Приведенная выше величина
ppads
qqss — ppaa
немедленно приводится безо всяких изменений к двум логарифмическим
дробям, если разбить ее на две части вот так:
ppads _ 2^5 2^s
qqss — ppaa qs —pa qs + pa
(Приложение к письму И.Бернулли 1699, см. Briefwechsel, vol. 1, p. 212)
Задача 3: Пусть X обозначает произвольную рациональную функцию от х.
Опишите способ, с помощью которого можно проинтегрировать выражение
Xdx. (Эйлер 1768, Opera Omnia, vol. XI, p. 28)
В предыдущем разделе мы изучили некоторые способы интегрирования. В
этом разделе мы будем систематически использовать эти способы для того,
чтобы показать, что интегралы от функций некоторых классов являются
элементарными. Элементарными называются функции, составленные из полиномов,
рациональных, показательных, логарифмических, тригонометрических и
обратных тригонометрических функций.
Интегрирование рациональных функций
Пусть R(x) — P(x)/Q(x) есть рациональная функция (Р(х) и Q(x) —
полиномы). Приведем конструктивное доказательство того, что функция J R(x)dx
является элементарной. Построение первообразной мы проведем в три этапа:
- приведение к случаю degP < deg Q (degP означает степень Р(ж));
- факторизация Q(x) и разложение R(х) на дроби;
- интегрирование дробей.
Сведение к случаю degP < degQ. Первое упрощение функции R(x)
возможно в случае deg Р > deg Q. В этом случае следует разделить Р на Q с
тем, чтобы получить
где S(x) и Р(х) являются полиномами (частное и остаток), причем degP < degQ.
В качестве примера рассмотрим
Р(х) _ 2х6 - Зж5 - 9ж4 + 23ж3 + х2 - 44ж + 39
^ ' ^ Q(x) ~ х5 + ж4 - Ьх3 - х2 + Sx - 4 *
Сначала избавимся от члена 2ж6, вычитая 2xQ(x) из Р(х), потом прибавим 5Q(x)
к Р(х), после чего получим
(5.3) Щ = 2х-Ь+ ^-20x^ + 4,+ 19
Q(x) ж5 + ж4 - 5ж3 - х2 + Sx - 4
Многочлен S(x) сразу интегрируется, так что только второй член выражения
(5.1) требует дополнительного исследования.

П.5 Функции, имеющие элементарные интегралы 119
Разложение на элементарные дроби. Предположим, что известно
разложение Q(x) на линейные множители:
к
(5.4) Q(x) = (х- ai)Wl {х - a2)W2 • ... • {х - ак)тк = Ц{х - a4)Wf.
*=1
Здесь ai,..., а* являются различными (возможно комплексными) корнями Q(x),
auii — их кратности. Следующая лемма показывает, как наша рациональная
функция может быть представлена в виде линейной комбинации простых дробей,
так называемых элементарных дробей. Этот способ был описан еще в переписке
между И. Бернулли и Лейбницем (около 1700 г.) и систематически использовался
И. Бернулли (1702), Лейбницем (1702), Эйлером (1768, Caput I, Problema 3) и
Эрмитом (1873).
(5.1) Лемма* Пусть Q(x) задается выражением (5.4) и пусть Р(х) является
многочленом, удовлетворяющим условию deg Р < deg Q. Тогда существуют
постоянные Cij такие, что
р/ \ _ _ _т*_ /"*.
Доказательство. Будем последовательно исключать из Q(x) множители
следующим образом: запишем Q(x) — (х — а)тд(ж), где а является корнем Q(x)
и д(а) ф 0. Покажем, что существуют постоянная С и многочлен р(х) степени
< deg Q — 1 такие, что
и , п:],,=, с, + р{х)
(х — a)mq(x) (х — a)m (х — a)m~1q(x)
или, (после умножения на общий знаменатель)
(5.7) Р(х) = С • q(x) + р(х) • {х - а).
Положив здесь х = а, получим
(5.8) С = P(a)/q(a).
Многочлен р(х) получается делением Р(х) — С • q(x) на (х — а). Применяя
рекурсивно эту процедуру к правой части соотношения (5.6), получим разложение
(5.5). □
Пример. Многочлен Q(x) из примера (5.2) имеет разложение
(5.9) Q(x) = хъ + х4 - Ьх3 - х2 + 8х - 4 = (х - 1)3(х + 2)2.
Применяя (5.7) и (5.8) при а = — 2 и m = 2, в качестве выражения (5.6) получим:
6ж4 - 20ж2 + 4ж + 19 _ -1 6ж3- 11ж2-ж + 9
(г-1)3(ж + 2)2 ~ (я + 2)2 + (х-1)3(я + 2) *

120 II. Дифференциальное и интегральное исчисление
Положив теперь а = — 2 и га = 1, получаем
6х4 - 20ж2 + 4ж + 19 _ -1 3 Зж2 - $х + 6
( } (ж - 1)3{х + 2)2 " (я + 2)2 + ~х~+2 + (ж - I)3 '
Заменим в последнем члене х на (х — 1) + 1, так что Зж2 — &х + б = 3(ж — I)2 ■
2(ж — 1) + 1, и вместо (5.10) получим окончательно
/Ciix 6ж4-20ж2 + 4ж + 19 1 -2 3-13
(5Л1) -7Г-^17^^^- = 7^^Тз+7^^? + ^-Г + 7ГТ^ +
(ж-1)3(ж + 2)2 (х-1)3 {х-1)2 х-1 (ж + 2)2 х + 2*
Вторая возможность. Из леммы 5.1 известно, что
(5Л2) —71 -пал- , «^2 = 71 Тчз + 71 ТТ? + I Г + 7ГТ"^2 +
(ж-1)3(ж + 2)2 (ж-1)3 (ж-1)2 х-1 (ж + 2)2 ж + 2'
Коэффициенты А{ и Д- можно вычислить следующим образом. Умножим
уравнение (5.12) на (х — I)3, так что
6z4-20z2 + 4z+19
(z + 2)2
= А0 + j4i(s - 1) + Л2(х - I)2 + (я? - l)3<7(z),
где функция д(х) определена в окрестности точки х = 1. Следовательно А{
являются первыми коэффициентами ряда Тейлора функции Р(х)/(х + 2)2 (см.
разд. П.2) и удовлетворяют соотношениям
1 d»" /6z4-20z2 + 4z + 19>
ild^V (z + 2)2 ,
х=-2
откуда Ао = 1, Ai = —2, Л2 = 3. Аналогично получаем
_ 1 (Р /6х4-20ж2 + 4ж + 19\
{ ~ ilS^V (ж-1)3 /
откуда Я0 = -1, Bi = 3.
Интегрирование элементарных дробей. Отдельные члены в
разложении (5.5) легко проинтегрировать, используя формулы разд. П.4 (см. табл. 4.1):
Г -1 -
/dx -г. тт^ ^—г, если ? > 1
- = \ ;-1х-аИ'
^ 1п(ж — а), если j = 1-
Используя уравнения (5.3), (5.9) и (5.11), получаем для нашего примера
/
^\ dx = x2-5x- 1 + -*- + 31п(ж - 1) + -J- + 3 \п(х + 2) + С.
Q(z) 2(ж — 1)^ ж —1 ж+ 2
Если все корни Q(x) действительны (т.е. а,- из (5.4) действительны), то C,j
в (5.5) также действительны, и мы выразили интеграл в виде линейной
комбинации действительных функций. Такой же процесс преобразования может быть
применен и в случае, когда Q(x) имеет комплексные корни.

II.5 Функции, имеющие элементарные интегралы 121
Пример с комплексными корнями. Предположим, что нам нужно
вычислить J(l + x4)~1dx. Поскольку корнями уравнения х4 + 1 = 0 являются
ai = (1 + г)/л/2, а2 = (1 - г)/л/2, с*з = (-1 + г)/л/2, «4 = (-1 - *)/>/2,
разложение леммы 5.1 дает
+
(5.14)
1 + ж4 ж-(1 + г)/х/2 ж-(1-г)/>/2
С D
+
+
я+(1-г)Д/2 ж + (1 + г)/^'
Согласно (5.8) мы получаем
1
А =
= ^(-1-.г
(5.15)
(ai-a2)(ai-a3)(ai-a4) п/2 • V2 • (л/2 + гуД) 8
ианалогично В = (—1 + г)л/2/8, С = (1 —г)\/2/8, D = (1 + г)\/2/8. Следовательно,
/л»
j = ^1п(Ж - (1 + г)/у/2) + В Щх - (1 - г)/у/2)
1 + х*
+ С1п(ж + (1 - г)/л/2) + Л Ь(ж + (1 + г)/л/2).
Используя (1.5.11) и соотношение
arctgu-h arctg(l/w) = < /Л Л
6 s v / ; | „^/2 для и < О,
которое следует из (1.4.5) или из (1.4.32), мы получаем
г-(а + Щ = Ь(Ж " « " *) = * Ч(* " ")8 + ^) + * arct^ —'
и правая часть выражения (5.15) может быть представлена в виде
(5.:
„, t dx V2 , хг + у/2х + 1 V2 / , /- чч , ^ ч\
d6)/^TT = T1%2_V2a;+rbx(arctg^+1)+arctg^-1))-
Как избежать комплексной арифметики. Если мы не хотим
использовать комплексную арифметику, то можно поступить следующим образом.
Предположим, что многочлен Q(x) имеет I различных комплексно-сопряженных пар
корней ai ± i/3i,.. .,а/ ± ify и к различных действительных корней 7ъ • • -?7ь
Тогда мы получаем действительное разложение
(5.17)
Q(x) = Ц((х- а,)2 + A2)mi П(* - -У.')"'.
г' = 1
• = 1
где Ш{ и п,- означают кратности корней. Теперь действительный вариант
леммы 5.1 выглядит следующим образом:

122 II. Дифференциальное и интегральное исчисление
(5.2) Лемма. Пусть Q(x) задан выражением (5.17), а Р(х) — многочлен с
действительными коэффициентами, удовлетворяющий условию degP < degQ. Тогда
существуют действительные постоянные Aij, Bij и dj такие, что
I гп{ . _ к Гц
/5 is) Р(ж) _y^vA Ajj+BjjX У^У" ^ij
Q(*) &&((«-«,-)»+#)' кгЫ^-Ъ
Доказательство. Действительные корни можно рассмотреть так же, как в
доказательстве леммы 5.1. Далее, напишем Q(x) — ({х — а)2+/32) q(x), где а+г/3
— корень Q(x) и q(a ± г/3) ^ 0. Тогда существуют действительные постоянные
А, В и многочлен р(х) степени < deg Q — 1 такие, что
Р(х) _ А-\-Вх р(х)
((я; _ а)2 +/32)тд(ж) ((Х - а)2 +/32)т ((ж _ а)* + /Р)таЛ(*)'
Чтобы доказать это, рассмотрим эквивалентное равенство
Р(ж) = {А + Бес) • ф) + р(х) • ((ж - а)2 + /?2).
Полагая х = а ± г/3, из этой формулы можно найти А и Б, а многочлен р(ж)
можно получить делением Р(ж) — (А + 5ж) • д(ж) на множитель ((ж — а)2 +/32).
Формула (5.18) теперь получается как при доказательстве леммы 5.1 индукцией
по степени Q(x). □
Для интегрирования общего члена выражения (5.18) преобразуем его
следующим образом:
А + Вх _ В(х-а) А + Ва
I
({х - а)2 + (З2)3 ({х - а)2 + (32У ((ж - а)2 + Р2)3
Первый член этой суммы можно сразу проинтегрировать с помощью подстановки
z — (х — а)2 + /З2, dz = 2(х — a)dx. Во втором члене нужно сделать подстановку
z — (х — а)//3, после чего получим интеграл, рассмотренный в последнем примере
разд. П.4. Следовательно, для j — 1 мы получаем
А-\-Вх , В , ,, ч9 л9Ч А + Ва /х — а\
(s-a)»+/P dX = J Ь((Ж - а) + ^ + -Ц- arCtg {—)
И для j > 1
Л + Вж , -В А + Ва т /х-а\
W/p — -I- Т ■ I )
((х-а)*+/РУ 2(j-l)((x-a)*+p)i-1 ^~' 'V /3 У
где Ji(z) = arctgz и
(5-19) 7>+1(ж) = _^_ + ?Ь1^М.
Пример. С помощью леммы 5.2 для функции (5.14) получаем разложение
1 1 Л + Бж C + Dz
/
1 + z4 (ж2 + лДх + 1)(ж2 - >/2s +1) х2 + \/2ж +1 ж2 - \/2z + 1'

П.5 Функции, имеющие элементарные интегралы 123
Если умножить это равенство на (х2 + л/2х -f 1) и положить х — (—1 ± г)/\/2, мы
найдем, что
1 1 =Ь г А (-1±ъ)
2=f2i 4 у/2 '
а сравнивая действительные и мнимые части, получаем, что А = 1/2, В — л/2/4.
Постоянные С = 1/2 и D = —у/2/А получаются аналогичным образом. Используя
приведенные выше формулы, мы опять получаем результат (5.16).
Замечание. Разложение на элементарные дроби вновь пробудило интерес
математиков XVIII столетия к корням многочленов и к алгебре.
Полезные подстановки
Теперь мы хотим использовать полученный выше результат и привести
несколько подстановок, расширяющих класс функций, неопределенные интегралы
от которых являются элементарными функциями. Далее в этом разделе R
обозначает рациональную функцию одного, двух или трех аргументов.
Интегралы вида JR( у/ах + 6, x)dx. Очевидной подстановкой является
(5.20) у/ах + b = щ х = - , dx---un~1-du,
а а
с помощью которой мы получаем
/ Ry \/ах + 6, х) dx = — / Ryu, \ип~х du — I R(u) du,
где R(u) есть рациональная функция. Последний интеграл можно вычислить с
помощью приемов, описанных выше.
Интегралы вида fR(e*x)dx. Очевидной подстановкой является и — еЛх,
что дает du — XeXxdx и dx — du/(Xu). В результате получается интеграл от
рациональной функции.
Пример.
/dx f dx —of
2+ shz ~ J 2 + (e* -e-*)/2 " J
du
u2 + 4u — 1
du 1 , u + 2 - л/5 11е* + 2-л/5
= —= In ■= — —= In
, +2)2-5 y/b tx + 2 + л/б y/E e* + 2 + x/b'
Здесь мы использовали формулу из упр. 5.1, приведенного ниже.
Интегралы вида fR(smx, cos ж, tg x)dx. Со времен античности
(Пифагор 570-501 до Р.Х.; см. также Р.К.Бук 1980, Sherlock Holmes in Babylon,
Am.Math. Monthly vol. 87, Nr. 5, p. 335-345) мы знаем, что тройки чисел (3,4,5),
(5,12,13), (7, 24, 25), ... удовлетворяют соотношению а2 + Ь2 = с2 и имеют общий
вид (и, (и2 — 1)/2, (и2 + 1)/2). Этот факт подсказал идею подстановки (Эйлер
1768, Caput V, §261)

124 II. Дифференциальное и интегральное исчисление
(5.21)
2и
since =
1 + и2
COS X —
1 + и2
tgж =
2и
1-й2
(Эйлер 1768, Caput V, §261). Легко проверить, что
sin ж = и{1 -Ь cos ж), так что точка (cos ж, sin ж)
является точкой пересечения прямой 7) = и(1 + £) с
единичной окружностью (см. рисунок).
Следовательно, мы получаем и = tg (ж/2), ж = 2arctgu
и
2
dx —
■du.
1 + и2
Если все эти подстановки произвести в интеграле
/Я(зтж,созж, tgж)dж, мы придем к интегралу от
рациональной функции.
Пример.
/dx _ Г 2du _ Г du
2 +sins = J (l + u2)(2+Ig7)" = J ti2 + ti+l'
Последний интеграл мы знаем из формулы (4.18). Таким образом,
dx 2
I
2 -f sin ж д/з
ctg(^(u+^)) = ^arctg(^(tgI + 5))-
Интегралы вида JR^y/ax2 + 2Ъх + с, х) dx. Идея (Эйлер 1768, §88)
состоит в том, чтобы с помощью соотношения ах2 + 2Ьх + с — а(х — z)2 определить
новую переменную z. Это приводит к подстановке
az — с
2{b + azY
dx
a(az2 + 2bz + с)
2(6 + az)2
dz,
(5.22)
у ax2 + 26ж + с = ±y/a (z — x) = ±y/a
z = ж ± у ax2 -f 26ж + с/ у/а,
az2 + 2bz + c
2(b + az) '
и мы опять получаем интеграл от рациональной функции. При а < 0 мы
приходим к комплексной арифметике, чего можно избежать, если использовать
преобразование из упр. 5.3.
Иногда бывает более удобно преобразовать выражение \/ах2 + 26ж + с с
помощью подходящей линейной подстановки z = ах + /3 к одному из следующих
видов:
yjz2 + 1, yjz2 - 1, \Д - *2-
После этого можно применить подстановки
(5.23) z=shu, 2=chu, z = sinu
соответственно, чтобы избавиться от квадратного корня под знаком интеграла.

П.5 Функции, имеющие элементарные интегралы 125
Пример. Рассмотрим опять интеграл (4.27). Полагая х — shu, получаем
s\i2u
/ \/х2 + \dx = / c\i2udu- / (- + —у—) du=^
+
u shuchu 1 , / r^ Tx xyjx2 + 1
= , + —5—= 2 ln(* + V^Tl) + —_.
Что касается функции, обратной к х — shu, см. упр. 1.4.3.
Упражнения
5.1 (И. Бернулли, см. цитату в начале этого раздела). Докажите, что
/:
dx 1 , х — а „
= — In + С.
х2 — а2 2а х + а
/f „[ах + b \
R[ а -, х dx является элементарной функцией.
V уех + / /
5.3 (Эйлер 1768, Caput II, §88). Пусть многочлен ах2 + 2Ьх + с имеет различные
действительные корни а,/3. Покажите, что подстановка z2 = (ж — /3)/(х — а)
преобразует интеграл
I R[ у ах2 + 2Ьх + с, ж j dx
(где # есть рациональная функция двух аргументов) в интеграл J R(z) dz,
где R — рациональная функция.
5.4 Некто С.L. Ever упростил соотношение (5.16) с помощью формулы (1.4.32),
сведя его к виду
/
dx лД . х2 + V2x + 1 лД хлД
1п ~о 7к 7 + ~Г arctg '
Ж4_|_1 8 х2->Дх+1 4 ь1-х2'
В результате получаем, например,
V In 5 + ^Г arctS (~2) = -0.1069250677,
./о
/о ж4 + 1 8 4
т.е. отрицательную величину для интеграла от положительной функции. Где
он ошибся и чему равно правильное значение?
5.5 Вычислите
/dx
Vi~2Ti
дважды, один раз с помощью подстановки (5.22), а второй — с помощью
подстановки (5.23). Это приведет к формуле arshx = \п(х + л/х2 + 1) (см.
упр. 1.4.3).
5.6 Докажите, что J #(sin2 ж, cos2 ж, tg х) dx можно проинтегрировать с помощью
подстановки
• 2 и2 2 1
sin х — - -, cos х — - -, tga? = и.
1 + uz 1 4- и1

126 II. Дифференциальное и интегральное исчисление
II.6 Приближенное вычисление интегралов
... потому что после всех этих попыток аналитики в конце концов пришли
к выводу, что следует оставить всякую надежду выразить эллиптические
дуги, используя алгебраические формулы, логарифмы и дуги окружности.
(Ламбер 1772, Rectification elliptischer Водеп ..., Opera vol. I, p. 312)
Хотя задаче численной квадратуры уже около двух столетий и она
изучалась многими геометрами: Ньютоном, Котесом, Гауссом, Якоби, Эрмитом.
Чебышевым, Кристоффелем, Гейне, Радо [sic], А. Марковым, Т. Стилтье-
сом [зге], К. Поссе, К. Андреевым, Н. Сониным и другими, тем не менее ее
нельзя считать в достаточной степени исчерпанной. (Стеклов 1918)
С помощью нашего метода легко убедиться в том, что интеграл j i-^£,
которым очень интересовались геометры, невозможно вычислить в
конечной форме ... (Лиувилль 1835, р. 113)
Несмотря на чрезвычайно интересные результаты предыдущих разделов и
на изобретательность Бернулли, Эйлера, Лагранжа и многих других, многие
интегралы не поддавались вычислению. Укажем несколько таких интегралов:
ех dx f dx
/•-*• /" It
/:, / vl — к2 cos2 xdx, I
л/4ж3 - <72x - (7з J J
dx С i С dx
. =, / \/l — k2 cos2 xdx, I — =.
y/lx*-g2x-gz J J ,/(l-x2)(l-k2x2)
Последние три называются "эллиптическими интегралами". Изучению этих
интегралов отдали много времени и труда Лежандр, Абель, Якоби и Вейерштрасс.
Интегралы, приведенные выше, не могут быть выражены через конечное число
элементарных функций (Лиувилль 1835, см. цитату). Здесь мы встречаемся с
новыми функциями, которые нужно вычислять новыми методами.
Мы рассмотрим три подхода: (1) разложение в ряд, (2) аппроксимация
многочленами (численное интегрирование) и (3) асимптотическое разложение.
Разложения в ряды
Идея этого метода состоит в том, чтобы разложить подинтегральную
функцию в ряд (либо по степеням ж, либо в терминах других выражений), после
чего провести почленное интегрирование. Обоснование этого метода будет дано в
разд. III.5.
Исторические примеры. Самым старым примером является вычисление
Меркатора (см. формулу (1.3.13))
1п(1 + х) = / dx- I (1 - х + х2 - ...)
dx — х 1 ... .
2 3
Далее, вычисление длины дуги окружности у — у/1 — х2 (см. формулу (4.9) и
теорему 1.2.2) — это ньютоновский подход к формуле (1.4.25):
dt
2 1 • 3 ,4 \.А 1 X3 1 • 3 X5

П.6 Приближенное вычисление интегралов 127
Рис. 6.1. Сходимость ряда (6.4)
(периметр эллипса).
t 1
х — I cos u2du
Рис. 6.2. Интегралы Френеля.
Периметр эллипса. Вычислим периметр эллипса с полуосями 1 и Ь:
2 У2
х + — = 1 или ж = cos 2, у = 6 sin 2.
Ь1
Поскольку dx = — sin tdt и dy = b cos tdt, периметр равен
г2тг рк/2
(Ы)
f™ /**/* ,
= / л/dx2 + dy2 = 4 / Vsin2 t + 62 cos2 * dt
Jo Jo
Г12 >
= 4 / VI- (l-b2)cos2<ctt.
a
Это "эллиптический интеграл" (отсюда и название), который не является
элементарным. Вычислим его следующим образом: предположим, что 1 > b > 0, и,
следовательно, 0 < а < 1. Идея вычисления состоит в том, чтобы использовать
ряд Ньютона для л/1 — х (теорема 1.2.2):
х 1-1
(6.2)
что приводит к
(6.3)
у/Г^= 1
Г7г/2
2 1-1-3 з
2Г X -
2 2-4 2.4-6
Гп'л а 1-1
[ / (1-77cos2 1 ~ ;гт q2 cos4 t ~ • • •) А-
Jo
2 2-4
Используя приемы из разд. П.4 (см. формулу (4.28) и далее), получаем
лтг/2
/о '
s2ntdt
тг 1-3-5'
2 "
(2п-
/о * 2-4-6-...-(2п) '
и(б.З) приводится к виду (см. Эйлер 1750, Opera, vol. XX, p. 49)
(6.4)
= 2ir(l-a
1 1
1-1 1-3
2*2 a 2-4 ' 2-4
1-1-3 1-3-5
....).
2-4-6 2-4-6
Сходимость этой формулы иллюстрирует рис. 6.1. При a = 0 (т.е. при 6=1) мы
имеем окружность, и Р = 27г. При а = 1 (т. е. b = 0) ряд очень медленно сходится
к точному значению 4.

128 II. Дифференциальное и интегральное исчисление
Интегралы Френеля. Интегралы Френеля (Френель 1818)
(6.5) x(t) = / cos(u2)du, y(t) = / sin(u2)du
Jo Jo
обладают интересными свойствами (упр. 6.4) и в плоскости (ж, у) образуют
красивую спираль (рис. 6.2). Они не являются элементарными. Однако функции
sin(ti2) и cos (и2) допускают разложение в простые бесконечные ряды (ряды для
sin г и cosz, где z — и2; см. (1.4.16) и (1.4.17)), с помощью которых можно почленно
вычислить интегралы следующим образом:
jQSm(u)du = jQ(u -зГ+^г-. • 0 dtt = Т " 7ТЗ! + ТГ75!
/ cos(n^) chx = / 1 \- ...)du — t 1
Jo ЛЛ 2! ^ / 5 • 2Г 9 • 4!
13
t
13-6!
+ ,
Сходимость этих рядов иллюстрирует рис. 6.3. Результаты превосходны для
малых значений t. Когда значение \t\ увеличивается, следует учитывать все большее
число членов.
Рис. 6.3. Вычисление интегралов Френеля с помощью степенных рядов; числа 5,9,13 в
7,11,15 означают наивысшую учитываемую степень t.
Численные методы
Предположим, что нам нужно вычислить интеграл fa f(x)dx, где интервал
интегрирования задан. Идея состоит в следующем: зафиксируем iV, разобьем
интервал [а, Ь] на N подинтервалов длины ft = (6 — a)/N",
xq — a, Xi = а -Ь ft, ж, = а + zft, xjv — &?
и локально заменим функцию f(x) на многочлены, которые можно легко
проинтегрировать.
Правило трапеций. Функция f(x) на интервале [ж,-,ж,-+1] заменяется
прямой линией, проходящей через точки (ж,-,/(я,)) и (z,+i,/(z,+i)). Интеграл на
интервале между ж,- и zt+i аппроксимируется площадью трапеции ft • (/(я,) +
/(xt+i))/2, и мы получаем

II.6 Приближенное вычисление интегралов 129
ГЬ ЛГ~1 h
/ /(x)ds «£-(/(*,■)+ /(*H-i))
J* i=o 1
(6.6)
м'^ + /Ы + /(*2) +... + /(**-!) + ^
Пример. На верхних рисунках 6.4 представлены функции cos ж2 и sin ж2 и их
приближения, полученные с помощью метода трапеций (величина шага h — 0.5,
N= 10). Точки на нижних рисунках представляют собой приближения
интегралов Френеля для h = 1/2 и /г = 1/8, причем соответствующие значения соединены
прямыми линиями.
-1
^ cos ж
2 Л
; 1 \ 1
\У
/ V
Л Jjj
V 1 //1
V ' (/ /
У
\/\ .5
cos t2 dt
<£-
11 sin x2
Рис. 6.4. Вычисление интегралов Френеля с помощью правила трапеций.
Метод Симпсона (названный так в честь Симпсона 1743). Идея метода
состоит в том, что выбираются три последовательных значения f(x{) (yi — f{x{))
и вычисляется интерполяционная падабола, проходящая через эти точки (см.
теорему 1.1.2 и уравнение (2.6)):
/ ч . / ч лУо . {х - х0){х - хг) Л2у0
р(х) = Уо + (х-х0)— + ^2".
Делая подстановку х = хо + th, получаем, что площадь, заключенная между
осью х и этой параболой, равна
(6.7)
fX2 f2 f2 t(t — 1)
/ p(x) dx = 2h • уо + h tdt-Ayo + h -Ц-—- dt • A2y0
Jx0 Jo Jo ^
= j (yo + 4yi+2/2).
Таким образом мы приходим к правилу Симпсона (N четно)
(6.8) J f(x) dxv^ (/(aj0) + 4/(3!) + 2f(x2) + 4/(х3) + 2/(я4) + • • • + f(xN)) •

130 II. Дифференциальное и интегральное исчисление
Методы Ньютона-Котеса. Если взять интерполяционные многочлены
высших порядков, аналогичным способом можно получить следующие
соотношения:
х4
f{x) dxv— (/(ж0) + 3/(a;i) + 3/(z2) + f{x3)),
f(x) dxv^ (jf(x0) + 32/(яя) + 12f(x2) + 32/(z3) + 7/(я4)),
и так далее. Первый метод, предложенный Ньютоном (1671), носит название
"правило 3/8". В 1711 г. Котес получил эти формулы для всех степеней до 10
(см. Голдстайн 1977, р. 77).
Численные примеры. Вычислим приближения к J± ^- = In(10) по разным
квадратурным формулам при N = 12, 24,48,... . Результаты приведены в табл.
6.1. Видно, что при каждом N результат существенно улучшается только
начиная со второго столбца (чтобы понять это см. упр. 6.5).
ТАБЛИЦА 6.1. Вычисление Г ^ по разным квадратурным формулам
N
12
24
48
96
192
384
768
1536
3072
6144
правило трапеций
2.34
2.31
2.305
2.303
2.3027
2.3026
2.3025
2.302587
2.3025858
2.3025852
метод Симпсона
2.307
2.303
2.3026
2.302587
2.3025852
2.3025851
2.302585093
2.3025850930
2.302585092996
2.3025850929941
метод Ньютона
2.31
2.303
2.3026
2.30259
2.3025854
2.3025851
2.302585094
2.3025850930
2.302585092999
2.3025850929943
метод Котеса
2.305
2.3027
2.30259
2.3025852
2.302585095
2.3025850930
2.3025850929947
2.30258509299405
2.3025850929940458
2.302585092994045686
Интересное явление наблюдается, если использовать правило трапеций для
вычисления эллиптического интеграла Р — JQ к л/1 — a cos21 dt (при b = 0.2,
а — 0.96, см. табл. 6.2). Сходимость здесь гораздо лучше, чем можно было бы
ожидать. Дело в том, что функция f(t) является периодической,
"сверхсходимость" объясняется формулой Эйлера-Маклорена разд. 11.10.
ТАБЛИЦА6.2. Вычисление эллиптического интеграла по правилу трапеций
N
12
24
48
96
192
384
правило трапеций
4.1
4.201
4.2020080
4.20200890792
4.20200890793780018891
4.2020089079378001889398329176947477824

II.6 Приближенное вычисление интегралов 131
Асимптотические разлоэюения
Этот метод применил Лаплас (1812) для вычисления интеграла J0 е~г dt
(см. Oeuvres, tome VII, p. 104 и упр. 6.7) и Коши в 1842 г. для вычисления
интегралов Френеля (см. Клайн 1972, р. 1100). В то время как разложение в ряд и
численные методы полезны при малых и умеренных значениях ж, метод
асимптотических разложений особенно подходит для больших ж.
Рассмотрим этот метод на примере интегралов Френеля. В предельном
случае х ->■ ос точное значение интеграла известно (упр. IV.5.14):
(6.9) / cost2dt = smt2dt=-J-.
Основная идея: надо представить интеграл в виде J0 = J0 — Jx , т. е.
(6.10) / cos t2 dt = - J - - / cos t2 dt.
Добавим под интегралом в правой части множители 2t и 1/(22) и применим
интегрирование по частям, полагая u(t) — 1/2, v(t) — sintf2, что дает
[°° 2 , 1 Г° 1 л 2 , 1 1 • 2 1 Г°° 1 • 2
- / cos t dt — / - • 2t cos t dt — sin x / — sin t
Jx 2jxt 2x 2jxt*
dt.
Мы получили интеграл, вычислить который на первый взгляд ничуть не
проще, чем первый. Однако если х велико, то интеграл в правой части, который
содержит дополнительный множитель 1/£2, по величине гораздо меньше, чем
первоначальный. Следовательно, для интеграла — J cost2 dt хорошим
приближением будет (2a?)_1sincc2. Если точность недостаточна, мы повторяем ту же
самую процедуру (теперь полагая u(t) = 1/t3 и v(t) = —cost2):
1 f°° 1 11 1-3 f°° 1
(6.11) -Ц _ebt»A = -—^co.^ + ^2^ ?co.*aA.
Продолжая далее, из (6.10) мы получаем
Г 2 , 1 /тГ 1 1
/ cost2dt= -W-+ --
Jo 2\j2 2х
1-3-5 1 2 1-3-5-7 1 . 2
(6.12) + ^ л ^ А ^ cos ж -|- „ ^ ^ ^— sina; — ...
1 ; 2•2•2•2 ж7 2 -2-2-2-2 х9
Аналогичная формула справедлива для второго интеграла Френеля:
•2 11 2 1-3 1.2
sin ж — ——- — cos ж — —— г- sin ж
2 - 2 х3 2 • 2 - 2 ж5
Г • 2 , 1 /тГ 1 1 2 11.2
/ sin £ dt — -л cosх sinX -f
Jo 2 V 2 2 ж 2-2 х3
1-3 1 2
COS ж
2-2-2 ж5
1-3-5 1 . 2 1-3-5-7 1 2
(6.13) + ^ ^ „ ^ — sin ж - ^ ^ ^ ^ ^ -г cosa; — ... .
1 ; 2-2-2-2 ж7 2-2-2-2-2 ж9
Необычайная точность этих приближений при больших ж проиллюстрирована на
рис. 6.5. Числа 1, 2, 3,... указывают число членов, учитываемых в разложениях
(6.12) и (6.13).

132 II. Дифференциальное и интегральное исчисление
Г
\А
//\
/г
г
Jo
10/
/2
sin*2 Л
20/ 30/
/ ' /
J 3 1
Рис. 6.5. Асимптотические разложения (6.12) и (6.13) с 1, 2, 3, 10, 20 и 30 членами.
(6.1) Замечание. Ошибка, вносимая обрыванием ряда (6.12), может быть
легко оценена. Например, если мы обрываем ряд после члена (2x)_1sinaj2,
приведенный выше вывод показывает, что ошибка определяется величиной интеграла
в (6.11), взятого по промежутку х < t < ос. С учетом того, что | cost2\ < 1, отсюда
получаем оценку (2х3)-1, что при х > 2 будет меньше чем 0.0625.
(6.2) Замечание. Бесконечные ряды (6.12) и (6.13) не сходятся при
фиксированном х. Дело в том, что общий член содержит множитель 1-3-5-7-9-...В
числителе, который превосходит все другие множители. Пуанкаре называл такие
ряды асимптотическими разложениями.
Упражнения
6.1 (И.Бернулли 1697). Выведите "series mirabili" (удивительный ряд, — лат.)
I
1 1111
хх dx = 1 - — + — - -г + -г &с.
22 З3 44 55
функции и вычислите fxn(\nx)ndx с помощью интегрирования по частям.
Указание. В представлении хх — ех1пх используйте ряд для показательной
6.2 Интеграл J x2dx/\/l - х4 встретился Я.Бернулли в его вычислениях,
связанных с упругой нитью, Лейбницу при изучении Isochrona Paracentrica
(парацентрической изохроны). Проверьте справедливость формулы (Лейбниц
1694b)
/
х2 dx _ 1 з 1
V/T^?" 3* + 7-2-1
*' +
1-3
11-4-1-2
zn +
1-3-5
15-8-1-2-3
-z15&c.
6.3 Так же, как в (6.7), выведите формулы Ньютона и Котеса с помощью
интегрирования интерполяционных многочленов степеней 3 и 4 на интервалах
[жо, яз] и [жо, х±] соответственно.
6.4 Для кривой, определенной соотношениями (6.5) (см. рис. 6.2), докажите, что
a) длина дуги между началом координат и точкой (x(t),y(t)) равна £,
b) радиус кривизны в точке (x(t),y(t)) равен 1/(2£).

II.6 Приближенное вычисление интегралов 133
6.5 Докажите, что метод Симпсона является точным для всех многочленов
степени 3.
6.6 Вычислите
/ —7—-—^Ldx
Jo
l + x2
методом Симпсона. Изучите уменьшение ошибки при увеличении N.
Ответ. Правильное значение интеграла равно (7г/8) In 2 = 0.2721982613 .
5.7 Используя равенство JQ e~f dt = д/5г/2 (см. формулу (IV.5.41)), получите
асимптотическое разложение для функции ошибок Ф(х) = -^ J* е~г dt ,
которое справедливо при больших значениях х (Лаплас 1812, Livre premier,
No. 44).
е-*2 (\ 1 1-3 1-3-5
6.8 Получите численное значение интеграла
^^ , е~х (1 * 1-3 1-3-5 \
Ответ. Ф{х) = 1 — - - + — - — Т+ ...).
л/7Г \х 2-х* 2Z • хь 2* • х( /
Г 1 cosx2dx = ^"{^f « 1.674813394 .
Jo yfi 4 - Г(3/4)
Возьмите два числа Л^1/10и£^10и вычислите этот интеграл
a) на интервале (0, А] с помощью разложения в ряд;
b) на интервале [А, В] методом Симпсона;
c) на интервале [В, ос) с помощью асимптотического разложения.

134 II. Дифференциальное и интегральное исчисление
II.7 Обыкновенные дифференциальные уравнения
Ergo &: horum integralia aequantur (Следовательно, и интегралы
всегда равны, — лат.). (Я. Бернулли 16901
В разделах II.4 и II.5 мы рассматривали задачу об отыскании
первообразной от заданной функции /(я), т-е- мы искали функцию у(х), удовлетворяющую
условию у'{х) — f(x). Теперь мы рассмотрим более трудную задачу, где функция
/ может зависеть также от неизвестной функции у(х). Обыкновенное
дифференциальное уравнение есть соотношение вида
(7.1) y' = f(x,y).
Мы хотим найти функцию у(х) такую, что у'{х) — /(ж, у(х)) при всех ж,
принадлежащих определенному интервалу. Рассмотрим сначала несколько исторических
примеров (более детальное изложение см. Ваннер 1988).
Изохрона Лейбница. Галилей открыл, что скорость тела, падающего из
начала координат вдоль оси у, увеличивается по закону v = y/—2gy, где g -
ускорение силы тяжести. Лейбниц в дискуссии с картезианцами о механике (в
сентябрьском выпуске журнала Nouvelles de la Republique des lettres от 1687 г.)
поставил следующую задачу: найти кривую у(х) (см. рис. 7.1) такую, что, если
тело скользит вдоль этой кривой, его вертикальная скорость dy/dt везде равна
заданной постоянной —Ъ.
-1
1г
Si
Kdx
Рис. 7.1. Изохрона Лейбница.
Через месяц "Vir Celeberrimus Christianus Hugenius" (знаменитейший муж
Христиан Гюйгенс) дал решение этой задачи, "sed suppressa demonstratione k
explicatione" (однако опустив доказательство и объяснение, — лат.).
Опубликованное Лейбницем (1689) "demonstrate" было неудовлетворительным, поскольку
решение было им сначала угадано, а затем доказано, что оно обладает желаемым
свойством. Вскоре общий метод нахождения решения с помощью "современного"
дифференциального исчисления был опубликован Я. Бернулли (1690). С этой
работы начался период замечательных открытий, сделанных Якобом и Иоганном
Бернулли, а впоследствии Эйлером и Даниилом Бернулли, что на несколько
десятилетий превратило Базель в мировой центр математических исследований.
Запишем формулу Галилея в виде

11.7 Обыкновенные дифференциальные уравнения 135
, . /ds\2 dx2+dy2 Л . ч
' ' \dt) = Ж2 = 9У ^ = длине дуги),
разделим ее на (dy/dt)2 — -f b2 (что является требуемым условием) и получим
/dx\2 л —2ду dy — 1
(7.3) ( —1+1- "— ~
\dyJ b2 dx y/-i-2gy/b2'
т.е. дифференциальное уравнение вида (7.1). Для того чтобы понять идею Бер-
нулли, перепишем (7.3) в виде
(7.4) dx = -^-l-^dy,
что выражает тот факт, что два узких полосатых прямоугольника всегда имеют
равные площади (см. рис. 7.1). И Якоб Вернул ли пишет "Ergo & horum Integralia
aequantur" (следовательно, и интегралы всегда равны, — см. цитату), имея в
виду, что площади Si и 5г также должны быть равны. Здесь впервые в математике
появилось слово "интеграл". Вычислив интеграл, мы находим решение:
Ь2 (
- *_7 1 _^ЕУ\3/2
~ 3 а\ Ь2 ) '
3<7
и "Solutio sit linea paraboloeides quadrato cubica ..." (Лейбниц: "решение —
полукубическая парабола").
Трактриса.
Выдающийся парижский медик Клод Перро, столь же знаменитый своими
работами по механике и архитектуре, хорошо известный своим изданием
Витрувия, бывший при жизни важным членом Королевской Французской
Академии Наук, предложил мне эту задачу, а до меня он предлагал ее
многим другим, не скрывая, что он не смог ее решить ...
(Лейбниц 1693)
Когда Лейбниц был в Париже (1672-1676), где брал
у Гюйгенса уроки математики, знаменитый анатом и
архитектор Клод Перро сформулировал следующую задачу:
для какой кривой касательная в каждой точке Р имеет
постоянную длину а между Р и осью х (рис. 7.2)? Для
иллюстрации этого вопроса он вынул "horologio portabili suae
thecae argenteae" (свои карманные часы в серебряном
футляре, — лат.) и потянул их по столу вдоль края. Он сказал, ""
что ни один математик из Парижа или Тулузы (Ферма) не
смог найти для нее формулу.
Лейбниц опубликовал свое решение (см. Лейбниц 1693) в виде
dy _ у \А2 -
2
, т.е. — dy — dx^
dx у/а2 -у2 У
утверждая, что он знал его довольно давно. Отсюда решение получается с
помощью квадратуры ("ergo & horum ..." — следовательно, и всегда ..., см. рис. 7.2
или 7.3). По утверждению Лейбница, было "хорошо известно", что эта площадь
может быть выражена через логарифм. Действительно, выполнив подстановки
sjdr - у2 — и, а2 — у2 = v2, —ydy = vdv, мы получаем

136 II. Дифференциальное и интегральное исчисление
-2 -1
-1
Рис. 7.2. Трактриса.
т к\ Г Va2 -у2 j /1—о 1 а- Va2 - у2
(7.5) х— \ — ay = —\/az — у1 — a log
Jy У У
(см. также упр. 7.1). Заметим, что интерес Лейбница к этой теории был связан
также с идеей использовать часы Перро в качестве механической машины
интегрирования для вычисления интеграла (7.5) (и, таким образом, логарифмов),
а также сконструировать другие механические устройства для вычисления
аналогичных интегралов.
Цепная линия (катеноида).
Однако, чтобы лучше судить о качестве Вашего алгоритма, я с нетерпением
жду Ваших результатов о форме провисающего каната или цепи, которую
предложил Вам исследовать г-н Бернулли, за что я ему очень благодарен,
потому что эта кривая обладает замечательными свойствами. Давно, во
времена моей молодости, когда мне было только 15 лет, я рассматривал
эту задачу, и доказал отцу Мерсенну, что это не парабола ...
(Письмо Гюйгенса Лейбницу от 9 октября 1690 г.)
Усилия моего брата не привели к успеху, мне повезло больше, поскольку
мне удалось найти способ ... Правда, это потребовало размышлений,
которые лишили меня сна на целую ночь ...
(И. Бернулли, см. Briefwechsel, vol. 1, p.98)
Галилей (1638) утверждал, что цепь, висящая на двух гвоздях, образуете
unguem" (в совершенстве) параболу. Приблизительно через 20 лет
шестнадцатилетний голландский мальчик (Христиан Гюйгенс) открыл, что это не так. В
конце концов задача о форме висящей гибкой нити ("Linea Catenaria vel Funicularis"
— линии цепи или каната) была решена Лейбницем (1691b) и И. Бернулли (1691).
Это было громадным успехом "нового" исчисления. Приведем здесь ход
рассуждений Иоганна Бернулли (Opera vol. Ill, p. 384, 426).
Пусть В — низшая точка и А — произвольная точка на кривой (рис. 7.4).
Проведем теперь касательные АЕ и BE и представим себе, что масса участка
цепи длиной s между точками А и В сосредоточена в точке Е, подвешенной на
"duorum filiorum nullius gravitatis" (двух невесомых нитях). Так как масса в точке
Е пропорциональна s, то параллелограм сил в точке Е показывает, что наклон
касательной в точке А пропорционален длине дуги s, т. е.
Воспроизводится с разрешения Публичной библиотеки Женевского университета.
ьишиип
dx
Рис. 7.3. Рисунок Лейбница (1693).1

11.7 Обыкновенные дифференциальные уравнения 137
С. Q. JL- T>t jjrua Catenarta.
Яяу.лв.вдя,с
Рис. 7.4. Цепная линия.
Рис. 7.5. Цепная линия (Лейбниц 1691).2
(7.6) с • у' = s.
С этого места вычисления Иоганна Вернул л и становятся очень сложными: он
использует вторые дифференциалы (см. Opera vol. Ill, p. 426). Однако
вычисления становятся простыми, если заменить в духе Риккати производную у' новой
переменной р (см. ниже уравнение (7.21)). Тогда после дифференцирования
получим:
(7.7) с-dp- ds = y/l +р2 dx,
т.е. дифференциальное уравнение, связывающее переменные р и х. Его
интегрирование дает
dp f f 1 / ч х — xq
J л/ГТ^ У
dec,
arsh(p)
следовательно,
(7.8)
Р=Л(^) и у = Х+с.сь(^).
Брахистохрона.
Пусть заданы две точки А и В в вертикальной плоскости. Требуется
определить кривую AM В, двигаясь вдоль которой, частица М, выходящая из
точки А и двигающаяся под действием силы тяжести, достигнет точки В
за кратчайшее время. (И.Бернулли 1696)
Эта задача представляется одной из самых любопытных и красивых среди
всех, которые были когда-либо предложены ранее, и я очень хотел бы
попробовать ее решить, однако для этого нужно, чтобы Вы свели ее к
чистой математике, поскольку физика доставляет мне хлопоты ...
(Де Лопиталь, письмо к И.Бернулли, 15 июня 1696 г.)
2 Воспроизведено с разрешения Публичной библиотеки Женевского университета.

138 П. Дифференциальное и интегральное исчисление
В 1638 г. Галилей доказал, что тело, скользящее из точки А в точку С (рис.
7.7), двигаясь вдоль кривой ADC, быстрее достигает конечной точки, чем
двигаясь по кратчайшему пути (за счет большей начальной скорости). После этого
он доказал, что движение вдоль ADEC, ADEFC и ADEFGC совершается
быстрее, и пришел к выводу, что быстрее всего движение происходит по окружности.
Иоганн Бернулли (1696), услышав, что его брат Якоб сделал ту же ошибку,
воспользовался этим поводом, чтобы устроить публичный конкурс, для того чтобы
найти брахистохрону (/3gaxv^ — короткий, XQ^vo^ — время). К его сожалению,
все представленные решения, включая решение Якоба, оказались правильными;
тем не менее решение Иоганна было наиболее элегантным: он исходил из
аналогии с "принципом Ферма" (см. уравнение (2.5)).
А
X
\. CL
У
•—•с
Рис. 7.6. Брахистохрона.
Рис. 7.7. Неправильная брахистохрона,
предложенная Галилеем.
Он рассматривает много слоев, где "скорость света" равна v = у/2ду (см.
уравнение (7.2) и рис. 7.6). Наиболее быстрый путь — это тот, который везде
удовлетворяет закону преломления (принцип Ферма)
Следовательно, в силу соотношения sin а = dx/ds, мы получаем
(7.9)
dy2
'1 + d?'
К
dx =
У
с-у
dy.
Опять-таки в соответствии с "ergo & horum integralia aequantur" (следовательно,
и интегралы всегда равны) подстановка
(7.10)
приводит к формуле
(7.11)
. 2 С С
у = с • sin и — cos 2и
У 2 2
хо — с и — - sin 2и
"ex qua concludo Curvam Brachystochronam esse Cycloidem vulgarem" (из чего
заключаем, что кривая наискорейшего спуска — обыкновенная циклоида, — лат.).

11.7 Обыкновенные дифференциальные уравнения 139
Некоторые типы интегрируемых уравнений
Теперь мы обсудим некоторые простейшие типы дифференциальных
уравнений, которые можно решить с помощью вычисления интегралов.
Уравнение с разделяющимися переменными.
(7.12) y' = f(x)g(y).
Все предыдущие примеры, а именно, (7.3), (7.5), (7.7) и (7.9), принадлежат к
этому типу. Их можно решить, если написать у1 — dy/dx, затем "разделить
переменные" и интегрировать ("ergo & ..."), т.е.
|Ш) ^ = /М* ■ f± = fn-)* + c.
Если G(y) и F(x) являются первообразными функций 1/д(у) и f(x)
соответственно, решение получается как G(y) = F(x) + С.
Однородное линейное уравнение.
(7.14) у' = f(x)y.
Это уравнение является частным случаем уравнения (7.12). Его решение имеет
вид
(7.15) In у = J f(x)dx + C, или у = С • ехр [J f{x)dx).
Неоднородное линейное уравнение.
(7.16) y' = f(x)y + g(x).
И.Бернулли предложил записать его решение в виде произведения двух
функций: у(х) = и(х) - v(x) (подобно идее Тартальи, см. уравнение (1.1.5)). Тогда мы
получим
du dv .. . . ч
— -v + — -и = t(x) • и • v + д(х).
ах ах
Если приравнять оба члена отдельно, получим
du
(7.17а) — = fix) • и для нахождения и,
dx
dv д(х)
(7.176) — = —т—г для нахождения v.
dx и(х)
Уравнение (7.17а) является однородным линейным уравнением относительно и
него решение дается выражением (7.15). После этого функция v(x) получается
с помощью интегрирования уравнения (7.176). Следовательно, решением
уравнения (7.16) является
(7.18)
у(х) = С • и(х) + и(х) J Ц-^dt, и(х)=ехр( f(t)dt).
Jo u(t) \J0 /
Это соотношение выражает тот факт, что решение (7.16) есть сумма общего
решения однородного уравнения и частного решения неоднородного уравнения.

140 II. Дифференциальное и интегральное исчисление
Дифференциальное уравнение Бернулли.
Правду говоря, нет ничего более остроумного, чем предложенное Вами
решение уравнения, написанного Вашим братом; и это решение столь
просто, что просто удивительно, насколько трудной казалась задача. Это
безусловно можно назвать элегантным решением.
(П.Вариньон, письмо к И. Бернулли от 6 августа 1697г.)
В 1695 г. Якоб Бернулли несколько месяцев бился над решением уравнения
(7.19) y' = f(x)-y + g(x)-yn.
Для Якоба это был хороший повод устроить официальный конкурс. Но у его
брата Иоганна возникли сразу две элегантных идеи (см. И. Бернулли 16796). Первая
из них рассмотрена в упр. 7.2, а вторая — изложенная выше: представить
решение в виде у(х) = и(х) -v(x). Для дифференциального уравнения (7.19) это опять
приводит к уравнению (7.17а) для и и к дифференциальному уравнению
(id
(7.20) —=g{x)u»-1(x)v»,
которое можно решить разделением переменных. Это приводит к решению
y{x)=u(x)(c+{l-n)[ fl^K"1^)*)1 1_П,
где и(х) — такое же, как в (7.18).
Дифференциальные уравнения второго порядка
Для того, чтобы убрать из вышеприведенной формулы вторые разности.
..., мы обозначим поднормаль BF как р. (Риккати 1712)
Дифференциальное уравнение второго порядка имеет вид
У" = /(я, 2/, г/)-
Аналитическое решение такого уравнения можно получить очень редко. Однако
существует несколько исключений.
Уравнения, не зависящие от у. Естественно, что следует сделать
подстановку р — у', после чего дифференциальное уравнение у" — f(x,yf) становится
уравнением первого порядка р' — /(ж,р). Заметим, что дифференциальное
уравнение (7.7) цепной линии является уравнением этого типа.
Уравнения, не зависящие от аз.
(7.21) У" = НУ,У')-
Идея (Риккати 1712) состоит в том, чтобы рассматривать у как независимую
переменную и искать функцию р(у) такую, что у' — р(у). Цепное правило приводит
к
„ _ dp _ dp dy _ , ^
dx dy dx
и уравнение (7.21) становится уравнением первого порядка
(7.22) Р'-Р=НУ,Р)-

П.7 Обыкновенные дифференциальные уравнения 141
Если функцию р(у) найти из (7.22), остается только проинтегрировать уравнение
t/ = р(у), которое является уравнением типа (7.12).
Пример. Движение маятника (см.
рисунок Леонардо да Винчи) описывается
уравнением
(7.23) */" +sin ?/ = О
(у описывает отклонение от положения
равновесия). Поскольку уравнение (7.23) не зависит
от£ (мы пишем t вместо ж, потому что эта
неременная в данном примере означает время), мы
можем использовать приведенное выше
преобразование и получить
©Bibl. National, Codex Madrid I 147r
9
P
p-dp— — sin у • dy и — = cos у + C.
Если обозначить амплитуду колебаний как А (для этой величины р — у' = 0) мы
получаем С — — cos А и
(7.24) р = -j- - у/2 cos у - 2 cos Л,
что является дифференциальным уравнением для у. После разделения
переменных мы получаем решение, выраженное в неявной форме через эллиптический
интеграл
(7.25) Г л, d\ л = *
J0 \J2 cos 7} — 2 cos A
(постоянная интегрирования получена в предположении, что у = 0 при t = 0).
Если Т— это период колебаний, то максимальное отклонение А достигается
при t — Т/4. Поэтому для периода мы получаем
(7.26)
щА dy 0 [А dy
= 4f * 2/
J0 V2 cos j/ - 2 cos A J0
^o8y-2coeA J0 ^sin2{A/2)-sin2(y/2)'
Мы видим, что он зависит от амплитуды А и близок к 27г в том случае, когда А
мало (упр. 7.5).
Изохронный маятник. Задача состоит в том, чтобы изменить обычный
маятник таким образом, чтобы его период перестал зависеть от амплитуды. Идея
Гюйгенса (1673, Horologium Оsdilatoriurn) состояла в следующем: надо изменить
круговую траекторию обыкновенного маятника так, чтобы ускоряющая сила
стала пропорциональной длине дуги з. В этом случае движение маятника будет
описываться уравнением
(7.27) а" Л- Ks = 0,
у которого колебания не зависят от амплитуды.

142 П. Дифференциальное и интегральное исчисление
Рис. 7.8. Изохронный маятник Гюйгенса.
Решение. Из подобия двух треугольников на рис. 7.8 (справа) мы видим,
что ускоряющая сила / = —dy/ds, так что наше требование, чтобы / = -Ks
принимает вид
(7.28) dy = K- sds.
Если 5 = 0 при у — 0 (т. е. начало координат помещено в самую нижнюю точку),
то интегрирование дает
(7.29)
У
К 2 /2у
У' т-е- 5 = Vir
Таким образом, у нашей кривой высота пропорциональна квадрату длины дуги
(И. Бернулли 1691/92Ь, р.489-490). Подстановка s из (7.29) в (7.28) дает
dy
Vv
= V2K л/dx2 + dy2
или, после возведения в квадрат,
(7.30) (- - l) dy2 = dx2
У
dy = dx,
где с — 1/{2К). С точностью до сдвига по оси у это уравнение совпадает с
уравнением брахистохроны (7.9), и мы видим, что траектория изохронного маятника —
циклоида. Как сказал И. Бернулли (1697с): "animo revolvens inexpectatam illam
identitatem Tautochronae Hugeniae nostrae que Brachystochronae" (неожиданное
совпадение этой таутохроны Гюйгенса и нашей брахистохроны знаменательно,
— лат.) (см. рис. 7.8).
Упражнения
7.1 Вычислите интеграл (7.5) для трактрисы с помощью подстановки у — a cost,
подставьте sin t = 1 — cos2t и выполните замену (5.21).
7.2 (И. Бернулли 16976). Решите дифференциальное уравнение "de mon Frere"
(моего брата, — франц.)

11.7 Обыкновенные дифференциальные уравнения 143
(7.31) y'=9(x)-y + f(x)-yn,
используя подстановку у — v^. Определите постоянную /3 так, чтобы
уравнение (7.31) стало линейным дифференциальным уравнением относительно
V.
7.3 Логистический закон роста народонаселения описывается
дифференциальным уравнением (Ферхюльст 1845)
у' = Ьу(а-у),
где а и Ь — постоянные. Выберите а = 5и& = 2и найдите решение,
удовлетворяющее условию у(0) =0.1.
7.4 Покажите, что дифференциальное уравнение вида
>•=<)
можно решить подстановкой v(x) = у(х)/х. Примените этот метод для
решения уравнения
,_ 9ж + 2у
У ~ 2х + у
7.5 Решение уравнения маятника
у" + ш2 sin t/ = 0,
соответствующее начальным значениям у(0) = А, у'(0) = 0, имеет период
Т=^[ (sm2(A/2)-sm2(y/2)y1/2dy
(см. уравнение (7.26)). Положите к — sin(A/2), используйте подстановку
sin(y/2) = к • sin а, найдите первые члены разложения Т по степеням к.
7.6 Решите дифференциальное уравнение
4 + у2
У =
4 +ж2
7.7 Движение тела в поле тяготения Земли описывается дифференциальным
уравнением
У2
где д = 9.81 м/с2, R = 6.36 • 106 м и у есть расстояние от тела до центра
Земли. Определите постоянные в решении так, чтобы у(0) — R и у'(0) = v.
Теперь найдите наименьшую скорость v такую, чтобы тело не возвратилось
на Землю (вторая космическая скорость).

144 И. Дифференциальное и интегральное исчисление
IL8 Линейные дифференциальные уравнения
... сегодня совершенно невозможно прочесть хотя бы одну строчку Да-
ламбера, в то время как большинство работ Эйлера можно читать с
восхищением. (Якоби, см. Шписс 1929, р. 139)
Пусть ао{х), ах(ж),..., an_i(x) — заданные функции. Мы называем
уравнение
(8.1) у(») + an.ifcjj/"-1) + ... + ai(x)y' + а0(х)у = О
линейным однородным дифференциальным уравнением порядка п и
(8.2) у<"> + an_1(x)j/("-1> + ... + ai(x)y' + а0(х)у = f(x)
линейным неоднородным дифференциальным уравнением. Введем следующее
обозначение для левых частей этих уравнений:
(8.3) С(у) : = y^+an-1(x)y(n-V + ... + a0(x)y,
так что (8.1) и (8.2) можно переписать в виде
(8.4) С(у)=0 и C(y) = f
соответственно. Назовем С дифференциальным оператором. Он действует на
функции у (ж), и результатом С(у) является также функция, заданная
формулой (8.3). Основное свойство этого оператора состоит в том, что он линеен, т.е.
(8.5) С{с1у1 + с2у2) = ci£(2/i) + с2С(у2).
Очевидным следствием этой линейности является следующий результат.
(8.1) Лемма. Если заданы п решений t/i(ж), у2(х),... ,уп(х) однородного уравнения
(8.1), то функция
(8.6) ci?/i(z) + с2у2(х) + ... + спуп(х),
где ci,..., сп — произвольные постоянные, также является решением того же
уравнения. D
Замечание. В решения уравнений первого порядка входит одна постоянная
(см. разд. П.7), а уравнения второго порядка содержат две произвольных
постоянных (см., например, уравнение (7.23)). Рассуждая по аналогии, можно
предположить (Эйлер), что решение уравнения порядка п содержит п постоянных, и что
(8.6) является общим решением уравнения (8.1), если у\{х),..., уп(х) — линейно
независимые функции. Функции у\{х),..., уп(х) называются линейно
независимыми функциями, если линейная комбинация (8.6) тождественно равна нулю
только в том случае, когда все с4 равны нулю. Например, 1,ж,ж2,ж3 являются
линейно независимыми функциями.

11.8 Линейные дифференциальные уравнения 145
(8.2) Лемма.
Общее решение однородного уравнения (8.1)
+
одно одно частное решение неоднородного уравнения (8.2)
общему решению неоднородного уравнения (8.2).
Доказательство. Пусть у есть частное решение уравнения (8.2), т.е. С(у) =
/. Тогда для произвольного решения у уравнения (8.1) (т.е. С(у) — 0) согласно
(8.5) мы имеем С(у + у) = /, поэтому у + у есть решение уравнения (8.2).
С другой стороны, если у есть другое решение уравнения (8.2) (т. е. С(у) = /),
тогда вследствие (8.5) мы опять имеем С(у — у) = 0,иу = у+(у — у) есть сумма
у и решения однородного уравнения (8.1). □
Вывод. Для того, чтобы решить дифференциальные уравнения (8.1) и (8.2),
надо - найти п различных (линейно независимых) решений уравнения (8.1), и
-найти одно решение уравнения (8.2).
Однородное уравнение с постоянными коэффициентами
Очень редко можно получить полное решение уравнения (8.1). Однако
существует несколько исключений. Наиболее важное из них -- то, когда
коэффициенты ai(x) не зависят от ж, т.е. когда
(8.7) уМ + оп-!^""1) + ... + ац/ + а0у = 0.
Другое исключение - когда а,-(ж) = а,-ж*"~п (это "уравнение Коши"). Этот случай
будет рассмотрен в конце настоящего раздела.
Основной идеей решения уравнения (8.7) является поиск решения в виде
(8.8) У(х)=ехх,
где А - постоянная, которую нужно определить (Эйлер написал об этом 15
сентября 1739 г. в письме к И. Бернулли и опубликовал в 1743 г.). Вычисляя
производные
у'{х) = \еХх, у"(х) = \2еХх, , yW(x) = \пеХх
и подставляя их в уравнение (8.7), мы получим
(8.9) (An + an-iA*1"1 + ... + aiA + а0)еХх = 0.
Следовательно, функция (8.8) является решением уравнения (8.7) тогда и только
тогда, когда А является корнем так называемого характеристического уравнения
(8.10) х(А) = 0, х(А) := An + «„-iA*"1 + ... + агХ + а0.

146 II. Дифференциальное и интегральное исчисление
Случай простых корней. Если уравнение (8.10) имеет п различных корней
Аь ... , Лп, то eAlX,..., еХпХ являются п линейно независимыми решениями
уравнения (8.7) (см. упр. 8.1). Таким образом, общее решение есть
(8.11) у(х) = CleAlX + с2еА2Х + ... + спеА»*.
Случай кратных корней. Рассмотрим простое дифференциальное
уравнение
(8.12) у(»> = 0,
где характеристическое уравнение Лп = 0 имеет нулевой корень кратности п.
Очевидно, что общим решением уравнения (8.12) является функция с\ + с^г \
сзх2 + ... + спжп-1, т.е. многочлен степени п — 1.
Далее, рассмотрим уравнение
(8.13) у'" _ Зщ/" + 3<А/- а3у = 0,
у которого характеристическое уравнение (Л—а)3 = 0 имеет корень а кратности 3.
Введем новую неизвестную функцию и(х) с помощью соотношения (Эйлер 17436)
(8.14) у(х) = еах -и{х).
Теперь, трижды дифференцируя это соотношение и подставляя результаты в
(8.13), мы получаем для и уравнение (8.12), где п — 3. Таким образом, общее
решение уравнения (8.13) равно
(8.15) у(х) = еах • (ci + с2х + с3х2).
Дифференциальные операторы. Приведенные выше вычисления
становятся особенно элегантными, если при заданной постоянной а мы введем
дифференциальный оператор Da с помощью соотношения
(8.16) Day = y' -а-у.
Композиция двух таких операторов Da и Db дает
(8.17) DbDay = (у1 - ау)' - Ь{у' - ау) = у" - {а + Ъ)у' + aby = DaDby.
Мы видим, что Da и Db коммутируют, и что DaDbDc .. .у = 0 есть
дифференциальное уравнение (8.7), коэффициентами которого являются коэффициенты
характеристического многочлена (Л — а) (Л — Ь) (Л — с)... . Таким образом,
уравнение (8.13) может быть записано в виде
(8.13') D3ay = 0.
Действуя оператором Da на (8.14), мы получаем
Day = ае -и-\-е • и — ае -и — е -п,
В\у — еах • и" и, наконец, D\y — еах • и^3\ Это доказывает тот факт, что (8.15)
есть общее решение уравнения (8.13).

II.8 Линейные дифференциальные уравнения 147
(8.3) Теорема (Эйлер 1743b). Предположим, что характеристическое уравнение
(8.10) представлено в виде
Х(А) = (А - Ai)mi (А - А2)т= •.... (А - Afc)m"
(с различными Xi), Тогда общее решение уравнения (8.7) дается формулой
(8.18) у(х) = Pl(x)eXlX+p2(x)ex*x + ... + Pk(x)ex"x,
ddepi(x) являются произвольными многочленами степени гп{ — 1 (это решение
включает в себя ровно Yli=i mt- = п постоянных).
Доказательство. Проиллюстрируем доказательство на примере двух
кратных корней: xW — (А —а)3(А —fr)4. В силу перестановочности Da и Db мы можем
записать дифференциальное уравнение в одном из двух видов:
(8.19) DtD3ay = 0, либо D3aDty = 0.
Решение у = еах • (ci+c2x-\-C3X2) уравнения D*y = 0 обращает в нуль левую часть
первого уравнения (8.19), а решение у = еЬх • (с± + с$х + сех2 + С7Х3) уравнения
D*y — 0 обращает в нуль левую часть второго уравнения (8.19). Таким образом,
обе эти функции являются решениями и имеют в совокупности семь свободных
постоянных. Идея доказательства линейной независимости этих функций
содержится в упр. 8.2. □
Как избежать комплексной арифметики. Результат теоремы 8.3
справедлив также и для комплексных Аг. Однако, если коэффициенты а, уравнения
(8.7) действительны, мы главным образом заинтересованы в функциях с
действительными значениями. Тот факт, что комплексные корни действительных
многочленов всегда появляются в виде сопряженных пар, позволяет нам упростить
(8.18). Пусть Ai = а + г(3 и А 2 = a — i/З есть пара таких корней. Соответствующая
часть решения (8.18) является многочленом, умноженным на
(8.20) еах{С1е^х + с2е~^х).
Используя формулу Эйлера (1.5.4), можно преобразовать это выражение к виду
(8.21) еах (di cos fix + d2 sin/Зж),
где d\ — c\ + c2 и d2 = i(c\ — c2) являются новыми постоянными. Это
выражение может быть упрощено, если написать d2 + id\ = Сег(р — Ccos<p -f гС sin <р.
Используя уравнение (1.4.3), мы получаем (см. рис. 8.1)
Сеах (sin (р cos /Зх + cos (р sin fix J = Ceax sin (fix + <p).
Пример. Уравнение маятника (7.23) для случая малых колебаний может
быть упрощено заменой sin у на у, так что оно примет вид
(8.22)
у" + аЛ/ = 0, u2=g/l,

148 II. Дифференциальное и интегральное исчисление
■ Л"/
<х>0
\'А
Щ
Рис. 8.1. Устойчивые и неустойчивые колебания.
где д — 9.$1м/с2 и £ — длина подвеса. Корнями характеристического уравнения
Л2 -\-и2 = О являются ±iu. Следовательно, общее решение уравнения (8.22) есть
y[i) - Csin(ut -f у?),
а период малых колебаний равен
Т = 2тг/а> = Iv^/Ify.
Неоднородные линейные уравнения
Задача состоит в нахождении одного частного решения уравнения С(у) - f.
т.е.
(8.23) у^ + ап-цЛ"1) + ... + а1У' + а0у = f{x).
Вследствие линейности уравнения (8.5) мы получаем следующий результат.
(8.4) Лемма (Принцип суперпозиции). Пусть у\{х) и У2{х) — решения уравнений
C(yi) = Д и С{у2) — /г- Тогда ciyi(x) + С2Уз(^) есть решение уравнения С (у) -
ci/i+c2/2. □
В тех случаях, когда неоднородность f(x) в уравнении (8.23) может быть
представлена в виде суммы простых членов, эти члены можно рассматривать по
отдельности.
Быстрый метод (Эйлер 1750b). Этот подход можно использовать, если
f(x) есть линейная комбинация функций zJ, еах, еах sin(a>z),..., точнее, если
функция /(ж) сама является есть решением некоторого линейного однородного
уравнения с постоянными коэффициентами. Идея состоит в том, чтобы искать
решение с аналогичной структурой.
Пример. Рассмотрим случай, когда / есть многочлен степени 2, например,
(8.24) у"' + by" + 2у' + у = 2х2 + х.
Будем искать решение в виде
(8.25) у(х) = а + Ьх + сх2.

11.8 Линейные дифференциальные уравнения 149
Если вычислить производные (8.25) и подставить их в (8.24), мы получим
сх2 + (6 + 4с)ж + (а + 26 + Юс) = 2х2 + х.
Сравнивая коэффициенты, получаем с = 2, 6 = — 7 и а = — 6, так что частное
решение уравнения (8.24) равно
у(х) = 2х" — 7х — 6.
Пример, Предположим, что функция f(x) есть синус
(8.26) у" -у +у = sin2x.
Недостаточно выбрать у(х) = а • sin2cc, потому что у' дает cos2#. Поэтому
напишем
(8.27) у(х) — а • sin 2х -f 6 • cos 2ж,
вычислим производные и подставим их в (8.26). Это приводит к условию
(а + 2Ь — 4а) sin 2х + (6 — 2а — 4b) cos 2х = sin 2ж.
Мы получаем линейную систему —За+26 = 1, —2а —36 = 0 с решением а = —3/13,
Ь= 2/13. Следовательно, частное решение есть
3 2
(8.28) у(х) = -— sin2x + — cos2z.
По-другому решить уравнение (8.26) можно следующим образом.
Рассмотрим уравнение
(8.29) у" - у' + у = e2i*
и будем искать его решение в виде у(х) = Ае2гх. Вычисляя производные,
получаем -4Л — 2iA + А — 1 и А — (—3 + 2г)/13. Поэтому решением уравнения (8.29)
будет
-3 + 2г^
(8.30) У(х) 13
Поскольку (8.26) является просто мнимой частью (8.29), мы получаем решение
(8.26) в виде мнимой части (8.30).
Обоснование этого подхода. По определению, f(x) удовлетворяет уравнению
Ci(f) — 0, где С\ = D™L>%... есть некоторый дифференциальный оператор с
постоянными коэффициентами. Действуя этим оператором на уравнение (8.23),
т.е. на уравнение вида С(у) = /, мы получаем (С\С){у) — 0 и видим, что
решение уравнения (8.23) удовлетворяет линейному дифференциальному уравнению
(С\С)(у) = 0. Общее решение этого уравнения известно из теоремы 8.3.
Случай резонанса. Рассмотрим, например, уравнение
(8.31) у" + у = sin х.
В этом случае мы не можем положить, у(х) = a sin ж + 6 cos ж, потому что эта
функция сама является решением однородного уравнения. По аналогии с
обсуждавшимся выше случаем двойных корней (см. также рис. 8.2) попробуем
положить

150 II. Дифференциальное и интегральное исчисление
Рис. 8.2. Решение уравнения у" + у = sinu;2; при у(0) = 0, у'(0) = 1, о; =
1.09,1.03,1.015,1.0.
(8.32) у(х) = ах sin х + bx cos х.
Обычная процедура (подстановка производных (8.32) в (8.31)) приводит к
равенству
2а cos х — 2b sin х = sin ж,
так что а = 0 и b = —1/2. Таким образом, частное решение уравнения (8.31) есть
(8.33) у(х) = — -х cos ж.
При х —>■ ос оно неограниченно возрастает, (см. рис. 8.2).
Метод вариации постоянных (Лагранж 1775, 1788). Это общий метод,
который позволяет найти частное решение уравнения (8.2) в случае, когда общее
решение однородного уравнения (8.1) известно. Чтобы упростить обозначения,
рассмотрим этот метод для случая п = 2.
Рассмотрим уравнение
(8.34) у" + а{х)у' + Ь(х)у = f(x)
и предположим, что у\(х) и У2{х) — два известных независимых решения
однородного уравнения у" + а{х)у' + Ь(х)у = 0. Идея метода состоит в том, чтобы
искать решение в виде
(8.35) у(х) = ci(x)yi(x) + с2(х)у2{х)
(отсюда и название "вариация постоянных"). Производная (8.35) равна
(8.36) у' = c[yi + с'2у2 + ciyi + С2У2-
Для того чтобы избежать осложнений с производными высших порядков,
потребуем, чтобы
(8.37) ^1+42/2 = 0,
так что производная (8.35) становится равной у' = ciy[ + С2У2- Тогда вторая
производная будет

11.8 Линейные дифференциальные уравнения 151
(8.38) у" = сг1У[ + с'2у'2 + с1У'1 + с2!/2;.
Если все эти формулы подставить в (8.34), то члены, содержащие с\ и с2,
исчезают, потому что мы предположили, что у\{х) и У2{х) являются решениями
однородного уравнения. Остается только
(8.39) ci^+c^ = /(*).
Если к этому присовокупить (8.37), мы получим линейную систему
W» с» F(s)
Матрица W(a:) называется матрицей Вронского. Вычисляя с'(х) из (8.40) и
интегрируя, мы получаем
с(х)= j W^tyFtydt,
Jo
и решение уравнения (8.34) дается выражением
(8.41) у(х) = (У1(х), у2(х)) (^g) = j\yi(x), y2(x))W-1(t)F(t)dt.
Пример. Рассмотрим уравнение с постоянными коэффициентами
(8.42) l/' + 2at/ + by = f{x),
где а2 < 6. Однородное уравнение имеет решения у\ (х) = e(a+^)*, у2{х) =
е(а-»/з)а^ где а _ _а и р _ у^_ а2 Матрица Вронского и обратная к ней матрица
имеют вид:
W(X) = *"" {(а + ф)е^ (а - ф)е-»'
Следовательно, из (8.41) мы получаем
(8.43) f3Jo V 2г '
±J"(eal-*Bm/3(z-t))f(t)dt.
/3,
Эта формула справедлива для любой функции f(t).
Уравнение Коши
Уравнение вида
(8.44) „<"> + fi-zlyt-D + ... + -^у' + ^у = 0

152 II. Дифференциальное и интегральное исчисление
обычно называется "уравнением Коши". Его аналитическое решение в деталях
было обсуждено Эйлером (1769, "Sectio Secunda, Caput V"). В этом случае вместо
решения вида еХх следует искать решения в виде
(8.45) у(х)=хг.
Пример. Рассмотрим задачу
(8.46) у" + V " \у = О-
х х1
Подстановка (8.45) приводит к
(г(г-1) + г- \)хг-2 = 0.
Корнями этого уравнения являются числа г — 1 и г = —1. Следовательно, общее
решение уравнения (8.46) есть
(8.47) у(а) =<**+-.
х
По-другому решить уравнение (8.44) можно с помощью подстановки
(8.48) х = е\ y(x) = z(t).
Поскольку
(8.49) г' = % = %■ ■ % = ху', z" = ... = xy' + х2у",
at ах at
уравнение (8.46) переходит в уравнение с постоянными коэффициентами z" -z-
0, к которому мы можем применить вышеизложенную теорию (теорема 8.3). Это
приводит к z(t) = с\ех -fC2e-t, что после обратной подстановки опять дает (8.47).
Упражнения
8.1 Если Ai,..., Лп являются различными комплексными числами, то
(8.50) cieAl*T + с2еА2Х + ... + спех»х = 0
для всех х тогда и только тогда, когда С\ — с2 = ... = сп = 0.
Указание. Из дифференцирования уравнения (8.50) в точке х = 0 следует,
что Yl7=i с«'^? = 0 для к — 0, 1,... . Рассмотрите выражение $^"=1 ctp(At), где
р(х) есть многочлен, обращающийся в нуль в точках Ai,..., \j-i, Ay+i,..., An,
но не в \j.
8.2 Если значения величин Ai,..., Ап различны, то
я
5^ (с,- +diX + eiX2)eXiX = 0
г = 1
для всех х тогда и только тогда, когда все коэффициенты с,-,dt-,e; равны
нулю.

П.8 Линейные дифференциальные уравнения 153
Указание. Докажите, что для произвольного многочлена справедливо
равенство
Х)(с,-р(А,-) + diP'(\i) + eiP"{\i)) = 0.
г = 1
1.3 Другой подход к случаю кратных характеристических значений (Даламбер
1748). Предположим, что А есть двойной корень уравнения (8.10). Расщепим
этот корень на два близких корня А и А + е (где е бесконечно мало). В этом
случае еАх,е^л+е^, а также их линейная комбинация
у(х) =
€(Х+е)х _ е\х
являются решениями задачи. Покажите, что в пределе е —> 0 последнее
выражение переходит в решение хеХх.
i.4 Найдите частное решение уравнения у" + 0.2?/ + у = sin(u>cc) и изучите его
амплитуду как функцию и. Какое явление вы заметили?
5.5 Вычислите частное решение уравнения у" — 2у' + у — ех cos х
a) путем подстановки у — Аех sin х + Вех cos х;
b) методом вариации постоянных;
c) с помощью решения уравнения у" — 2у + у — е^1+%'х.
8.6 Решите следующие однородные и неоднородные уравнения Коши:
х2у" - ху1 - Зу = 0,
ж V ~ 3j/ - Зу = ж4,
ж V - Ъху' + 4у = 0.
Последнее уравнение приведет к задаче о двойных корнях. Исследуйте
проблему их определения (Лорел и Харди 1933, Дети пустыни).
8.7 Пусть ух (х) и у2 (х) — два решения уравнения у"+а(х)у' + Ъ{х)у — 0.
Покажите, что вронскиан (определитель матрицы Вронского (8.40)) удовлетворяет
соотношению
det(w(a;)) =det(wr(»0)) -ехр(- f a{t) dt).
J Xo
Указание. Найдите дифференциальное уравнение для z(x) = det(W(x)).

154 II. Дифференциальное и интегральное исчисление
II.9 Численное решение дифференциальных уравнений
Я всегда замечал, что математики и физики с высшим образованием очень
хорошо знакомы с теоретическими результатами, но совершенно не знают
простейших приближенных методов. (Л.Коллатц, Численное
решение дифференциальных уравнений, Springer 1951, русский перевод 1960)
Часто бывает невозможно решить дифференциальное уравнение
(9Л) y' = f(x,y)
аналитически (например, у' = х2 + у2). Если же это возможно, может
оказаться, что получающиеся интегралы не элементарны (например, у11 + sin?/ = О,
см. (7.23)). Даже в том случае, когда все интегралы элементарны, полученные
формулы могут быть бесполезны. Например, решение уравнения у' — у4 +1
определяется следующим равенством (см. формулу (5.16))
которое трудно использовать, особенно если нам нужна у как функция х.
Поэтому представляют интерес численные методы, с помощью которых можно было
бы прямо решать уравнение (9.1).
Метод Эйлера
Задача 85: Получить хорошее приближение для интеграла произвольного
дифференциального уравнения. (Эйлер 1768, §650)
В каждой точке (ж, у) уравнение (9.1) определяет величину /(ж, у), т.е.
наклон кривой решения. Следовательно, можно представить себе поле направлений
(И. Бернулли 1694). Кривые, которые в каждой точке следуют этим
направлениям, являются решениями уравнения (9.1). На рис. 9.1 в качестве "Exemplores
patebit" (широко известного примера, — лат.) показано поле направлений для
уравнения Риккати
(9.2) у' = х2 + у2,
которое не имеет элементарного решения (Лиувилль 1841, "J'ai done pense qu'il
pouvait etre bon de soumettre la question a une analyse exacte ..." — Поэтому я
подумал, что возможно стоит более тщательно проанализировать этот вопрос,
— франц.). Очевидно, что решение не является единственным. Поэтому зададим
начальное значение
(9.3) у(х0) = у0.
Идея Эйлера (Эйлер 1768, Sectio Secunda, Caput VII). Выберем h > 0 и
заменим решение при хо < х < xq + h его касательной:
£(х) =уо + (х- хо) • /(.то, уо).
В точке х\ — хо + h получаем у\ — уо + hf(xo, Уо)- В этой точке мы опять
вычисляем новое направление и повторяем процесс для того, чтобы получить "valores
successive' (последовательные значения, — лат.):

11.9 Численное решение дифференциальных уравнений 155
ФМ/У//А
У/ШМ',
'ЛП'ЛРЛ'.
Рис. 9.1. Поле направлений для уравнения у = х2 + у2 и четыре решения.
9.4)
хп+1 = хп + А, уп+1 = уп + hf(xn,yn).
Это и есть метод Эйлера. Кривая, образованная соединением всех касательных,
называется ломаной Эйлера. В пределе h —> 0 эти ломаные все более точно
приближаются к решению (см. рис. 9.2).
Численный эксперимент. Рассмотрим дифференциальное уравнение (9.2),
выберем начальные значения хо = —1.5, уо = —1.4 и возьмем размер шага h
равным 1/4, 1/8, 1/16, 1/32. Получающиеся ломаные Эйлера приведены на рис.
9.2. Численное приближение и ошибки при х = 0 приведены в табл. 9.1. Видно,
что ошибка убывает вдвое, когда шаг уменьшается вдвое ("quot"означает
отношение ошибок при двух последовательных значениях длины шага). Объяснение
этого факта можно найти в любом учебнике по численному анализу (например,
в книге Хайрер, Нёрсетт, Ваннер 1990, разд. П.З, стр. 166).
Таблица 9.1. Метод Эйлера
Таблица 9.2. Метод (9.5)
l/h
4
8
16
32
64
128
256
512
У(0)
0.7246051
0.2968225
0.1577289
0.0999576
0.0734660
0.0607632
0.0545412
0.0514618
ошибка
-0.6762019
-0.2484192
-0.1093256
-0.0515543
-0.0250628
-0.0123599
-0.0061380
-0.0030586
quot
2.722
2.272
2.121
2.057
2.028
2.014
2.007
l/h
2
4
8
16
32
64
128
256
2/(0)
-0.7330279
-0.1063739
0.0153874
0.0409854
0.0466509
0.0479776
0.0482984
0.0483772
ошибка
0.7814312
0.1547771
0.0330159
0.0074179
0.0017523
0.0004257
0.0001049
0.0000260
quot
5.049
4.688
4.451
4.233
4.116
4.058
4.029

156 II. Дифференциальное и интегральное исчисление
Рис. 9.2. Ломаные Эйлера для уравне- Рис. 9.3. Параболы второго порядка.
ния у' = х2 + у2.
Метод рядов Тейлора
Задача 86: Значительно улучшить предыдущий метод приближенного
интегрирования дифференциальных уравнений, чтобы результат был ближе
к истине. (Эйлер 1768, §656)
Заметим, что (9.4) представляет собой два первых члена разложения в ряд
Тейлора. Чтобы улучшить точность, давайте введем третий член, так что
h2
(9-5) Уп+i = Уп + hy'n + —у';.
Поскольку у'п — /(жп, уп), для вычисления у'^ следует просто
продифференцировать дифференциальное уравнение по х. Для уравнения у' — х2 + у2 это дает
(9.6) у" = 2х + 2уу' = 2х + 2х2у + 2у3.
Численные результаты, полученные с помощью (9.5) при h = 1/2, 1/4, 1/8 и 1/16.
приведены на рис. 9.3. Здесь ломаные метода Эйлера заменены
"полипараболами", составленными из отрезков парабол усеченного ряда Тейлора. Ошибки в
точке х — 0 приведены в табл. 9.2. При малых h результаты значительно лучше,
чем при применении метода Эйлера: при уменьшении длины шага вдвое ошибка
уменьшается в четыре раза.
Замечание. Разумеется, можно принять во внимание дальнейшие члены ряда
Тейлора, например,
h2 h3
(9-7) Уп+i = yn + hyn + — Уп + -у
Завысите производные получаются повторным дифференцированием
дифференциального уравнения. Для нашего уравнения Риккати мы получаем из (9.6)

11.9 Численное решение дифференциальных уравнений 157
Рис. 9.4. Векторное поле уравнения маятника (9.8').
Рис. 9.5. Решения уравнения маятника (9.8').
Рис. 9.6. Численные решения уравнения маятника (9.8').

158 II. Дифференциальное и интегральное исчисление
у'" = 2 + 2уУ + 2уу" = 2 + 4ху + 2х4 + 8яУ + 6у4,
у"" = 4у + 12ж3 + 20zy2 + 1бж4у + 40zV -f 24у5, и т.д.
Уравнения второго порядка
В качестве примера рассмотрим уравнение маятника (7.23)
(9.8) |/" = -вту.
Введем новую переменную для производной у'. Теперь (9.8) выглядит так:
у' = v
v — — sin у.
Эту систему можно интерпретировать как векторное поле, которое в каждой
точке (t/, v) задает скорость точки (у(ж), ^(ж)), двигающейся вместе с изменением
параметра х (рис. 9.4). Точки решений (у(х), v(x)) везде движутся с предписанной
скоростью. Они представлены на рис. 9.5. Овалы соответствуют колебаниям, а
синусоиды соответствуют вращениям маятника с переворотами.
Метод Эйлера. Идея Коши (1824) состоит в том, чтобы приложить метод
Эйлера (9.4) к обеим функциям у(х) и v(x). Если заданы начальные значения
у(хо) = уо, v(xo) = vo и длина шага h > 0, то аналог метода (9.4) в применении к
системе (9.8') выглядит так
(9.9) жя+1 = жп+А, уп+i - уп + h-vn, vn+1 = vn -h-sin(yn).
На рис. 9.6 представлена ломаная Эйлера для начальных значений у(0) = 1.2,
v(0) = 0 при h — 0.15. Мы с ужасом видим, что вопреки физической реальности
наш метод предсказывает нарастание амплитуды колебаний, оканчивающееся
опрокидыванием маятника.
Метод рядов Тейлора. Дифференцируя (9.8') по ж, получаем
(9.10) у" — v — — sin у, vn — — cos у - у — — cos у • v,
что позволяет нам использовать дополнительный член ряда Тейлора. Аналогом
уравнения (9.5) является
Уп+i = Уп + п>уп + —уп=уп + hvn - — sin уп,
(9-11) о
h2 h2
vn+i = vn + hv'n + — v'n =vn- hsm(yn) - — cosyn • vn.
Результаты гораздо лучше (см. рис. 9.6 справа), даже если h в два раза больше.

11.9 Численное решение дифференциальных уравнений 159
Упражнения
9.1 Примените метод Эйлера при h = 1/N к уравнению
у' = Aj/, у(0) = 1
с тем, чтобы получить приближение величины у(1) — ех. Результатом будет
хорошо известная формула из главы I.
9.2 (Функция, обратная к функции ошибок). Определим функцию у(х) с
помощью соотношения
2 у -е
vWo
dt.
Продифференцируйте эту формулу и покажите, что у(х) удовлетворяет
дифференциальному уравнению
0F
2/(0) = 0.
Вычислите первые четыре члена ряда Тейлора для у(х) (записанного в точке
х = 0).
9.3 (Уравнение Ван-дер-Поля). Вычислите у(г) и
у(%) для г — 1,2,3 для решений дифференци-
ального уравнения
у' = v,
v1 -e(l-y2)v -у,
и найдите численно решение, используя метод
рядов Тейлора третьего порядка при е = 0.3,
начальных значениях у(0) = 2.00092238555422,
v(0) = 0, и при 0 < х < 6.31844320345412.
Правильное решение на этом интервале при этих
начальных условиях периодично.

160 II. Дифференциальное и интегральное исчисление
11.10 Формула суммирования Эйлера—Маклорена
Король называет меня "мой профессор", и я — счастливейший в мире
человек! (Эйлер гордится своей службой у Фридриха II в Берлине)
У меня здесь есть один геометр, он — большой циклоп ... у него остался
только один глаз, а новая кривая, которую он сейчас вычисляет, может
сделать его совсем слепым. (Фридрих II; см. Шписс 1929, р. 165-166.)
Эта формула была получена независимо Эйлером (1736) и Маклореном
(1742). Она является мощным средством для вычисления с помощью
дифференциального исчисления таких сумм, как гармоническая сумма 1+§ + § + --- + ;->
сумма логарифмов In2 + 1пЗ + In4 + ... -f Inn = Inn!, сумма степеней lk + 2к +
3fc + ... + nfc, или сумма обратных степеней 1 + ^4-^- + ... + ^.
Задача. При заданной функции /(ж), найти формулу для суммы
п
(10.1) 5 = /(1) + /(2) + /(3) + ... + /(») = Е /(J)
1 = 1
("investigatio summae serierum ex termino generali" — отыскание сумм рядов из
конечных общих границ, лат.).
Вывод формулы по Эйлеру
Первая идея (см. Эйлер 1755, pars posterior, § 105, Маклорен 1742, Book II,
Chap. IV, p. 663f) состоит в том, чтобы рассматреть еще сумму со сдвинутыми
аргументами:
(10.2) s = /(0) + /(1) + /(2) + ... + /(„- 1).
Вычислим разность S — s. Воспользуемся формулой Тейлора (2.8), положив в
ней х — хо = — 1, так что
га п tu\ /'W,/"W /'"(0,
В результате получится
/(») - /(о) = Е т - ± Е f(i) + ± Е /"'и - ± Е'""« + • • • •
i = l i = l i = l i = l
Эта формула содержит 5^/'(i), но если записать ее для первообразной от / и
затем выразить эту первообразную через /, мы получим формулу для X)/W:
(ю.з) £яо= [nf(*)** + hilf'w-Tiflf'W
i=l J° z- i=l 6- i=l 4- ,-=1
Вторая идея состоит в том, чтобы исключить суммы J2 Г -> Y1 /"? Yl f" ^ • • • в
правой части (10.3) с помощью этой же формулы, в которой / последовательно
заменяется на /', /", /'" и т.д. Это приведет нас к формуле вида

11.10 Формула суммирования Эйлера—Маклорена 161
£/(*) = Г /(*) dx - a(f(n) - /(0)) +/3{f(n) - /'(0))
(10.4) ti Jo
-l(f"(n) - f"(0)) +6(f'"(n) - f'"(0)) - ... .
Для того чтобы вычислить коэффициенты а,/3,7> • • • » последовательно заменим
/ в (10.4) на /', /",... и получим
E/W =/o"/(*)d* -а(/(п) -/(0)) +/3(/'(п)-/'(0)) -... ,
-££)/'(*) =-^(/(п)-/(0))+§(/'(п)-/'(0))-... ,
JjEAO =+i(/'(n)-/'(0))-... ,
Согласно (10.3) сумма всех этих выражений должна быть равна f0 f(x)dx.
Следовательно, мы получаем
(Ю.5) «+^,=°, ^ + | + ^0' T+i + S + iT0'-'
откуда следует, что а = -|, /3=^,7 = 0, <5 = -755, • • • и
(10.6)
~(Г(п)-Г(0)) + з^(^(п)-/<')(0))+..
(10.1) Пример. Если применить эту формулу для вычисления суммы почти
миллиона членов
+ I^0-Tk10"4+2k10"6 + -Ri11-463758469'
то она дает прекрасное приближение точного значения с помощью всего лишь
нескольких членов. Однако эта формула бесполезна для вычисления суммы первых
членов 1 + | Н- ... + jq .
Числа Бернулли. Обычно заменяют коэффициенты а, /3, 7? • • • на Д'Л'
(Bq = 1, а = i?i/l!. /3 = Б2/2!,...), так что формула (10.5) запишется в виде
(10.5') 2В1 + Во = 0, ЗБ2 + ЗВг + В0 = 0, ..., Х)(.)В,- = 0.
,-=о W
Вот числа Бенулли, вычисленные Эйлером:

162 II. Дифференциальное и интегральное исчисление
В0 — 1, В\ — —-, В2 — -, 54 — — —, В6 — — > #8 — -»jji
30'
42'
1
30
43867
D _ 5 „ _ 691 D_7 D_ 3617
Bl°-66' Б12~"2730' Bl4-6' Bl6-~W Bl8~"W
'20 — —
>26
174611
330 '
8553103
#22 —
#28 —
854513
138 '
23749461029
#24 —
236364091
#30 —
2730 '
8615841276005
6 ' ~'° 870 ' ""~ 14322
и Вз = B$ = ... = 0. В этих обозначениях формула (10.6) принимает вид
(10.6')
J2f(i)= Г f(x)dx+Uf(n)-f(0))
+ £||(/(2*-1)w-/(2'!-1,(°))-
Пример. Если f(x) = ж9, то ряд (10.6') конечен и представляет собой хорошо
известные формулы Я.Бернулли (1.1.26), (1.1.27).
Производящая функдия. Для того чтобы лучше понять, что такое числа
Бернулли, рассмотрим одну из великих идей Эйлера: возьмем функцию V(u),
коэффициентами ряда Тейлора которой являются рассматриваемые числа, т.е.
определим ее как
(10.7)
V(u) = 1 + аи + /Зи2 + <уи3 + <^4 + • • •
Теперь формулы (10.5) или (10.5') просто означают, что
__, ч /, и и2 и3 \
т.е.
(10.8)
V(u)
еи - 1
Таким образом, бесконечное число алгебраических уравнений выражается одной
аналитической формулой. Из того факта, что функция
(10.9)
и _ и и _и еи/2 + е-«/2
(U> +2~ ^ГГТ + 2 ~ 2 ' е«/2 _ е-«/2
является четной функцией, следует, что 1?з = #5 = #7

11.10 Формула суммирования Эйлера—Маклорена 163
Be Hsu Legitimo Formulae Summatoriae Maclaurinianae
(О травильном использовании формулы Маклорена)
Подставим теперь функцию f(x) — cos(27rx), для которой /(г) = 1 при всех
I. в формулу (10.6'). В левой части мы получим 1 + 1 + ... + 1, ав правой 0 +
0+ 0 + ..., потому что функция сов(27тж) вместе со всеми своими производными
периодична с периодом 1. Мы видим, что написанная формула неверна\ Другая
неприятность сотоит в том, что для большинства функций / бесконечный ряд в
(10.6') расходится.
Поэтому необходимо оборвать ряд после конечного числа членов и
получить выражение для остатка. Это сделал и изложил на прекрасном латинском
языке (см. заголовок выше) Якоби (1834), Он переделал доказательство Эйлера,
везде используя остаточный член Бернулли—Коши (4.32). Позже было
установлено (Виртингер 1902), что доказательство может быть проведено просто путем
повторного интегрирования по частям, подобно доказательству формулы (4.32).
Основную роль в доказательстве играют так называемые многочлены Бернулли.
Многочлены Бернулли. Многочлены
Вг{х) = Box + Bi =х~\
В2(х) = В0х2 + 2Вхх + В2 = х2 - х + |
В3{х) = В0х3 + Wxx2 + W2x + В3 = х3 - \х2 + \х
В4(з) = В0х4 + АВхх3 + 6Б2ж2 + 4Б3ж + В4 = х4 - 2х3 + х2 - ^ ,
или в общем случае
к
(10.10) Вк(х)=^2(.)ВгХк-\
i=o ^г'
удовлетворяют соотношениям
(10.11) В'к{х) = *Bfc-i(s), Bfc(0) = B*(l) = Вк.
В самом деле, первая формула — это свойство биномиальных коэффициентов
(см. теорему 1.2.1), а вторая следует из определения и из формул (10.5').
(10.2) Теорема. Мы имеем
£f(i) = [f{x )dx + К/(п) -т]
+Ет(/(Н)(")-/(Ь1)(°))+^
(10.12) Rk =
(-I)*"1
Г Bk(x)fW(x)dx.
Jo
ЗдесьBk{x) является функцией, которая получена из многочлена Вь{х) при О <
г< 1 путем его периодического продолжения с периодом 1 (см. рис. 10.1).

164 II. Дифференциальное и интегральное исчисление
Рис. 10.1. Многочлены Вернул ли.
Доказательство. Сначала докажем утверждение теоремы для случая п = 1.
Учитывая, что В[(х) = 1, и интегрируя по частям, получаем:
[ f(x)dx= [ B,1{x)f{x)dx = B1(x)f(x)\1- f B1(x)f{x)dx.
Jo Jo 1° Jo
Первый член равен |(/(1) + /(0) J. Во втором члене в соответствии с (10.11)
сделаем замену Bi(x) = ^В'2(х) и проинтегрируем еще раз. Это дает
£ f(x) dx = \ (/(1) + /(0)) - Щ (/'(1) - /'(0)) +±£B2(x)f"(x) dx.
Повторяя этот прием, мы придем к равенству
к
Z
3=2
1 к
(юла) \(m + m) = l f(x)dx+j2{-:^Pl(f(i-14i)-f{i-1)(Q))+Rb
где
(10.14)
Rk = ( 1}ы J В* (*)/<*>(*) <Ь.
Теперь применим формулу (10.14) к смещенным функциям f(x + г — 1).
Заметив, что
[ Bk{x)fW{x + i-l)dx= [ Bk(x)fW(x)dx,
Jo Ji-1
мы получим утверждение теоремы 10.2, суммируя эти формулы от г = 1 до ъ - п.
U

11.10 Формула суммирования Эйлера—Маклорена 165
Оценка остаточного члена. Из оценок (для 0 < х < 1)
Ш*)\<\, |^2(*)| < |, |Вз(*)|<!|, 1Д4(*)|<Щ,
которые легко проверить, а также из того факта, что | /0 д(х) dx\ < J0 \д(х)\ dx,
видно, что
(10.15)
№ <\[ \f'(*)\dx, \R2\ <^£ \f'{x)\dx,
Это и есть те строгие оценки остаточного члена формулы суммирования Эйлера—
Маклорена, которые мы хотели получить. Дальнешие максимальные и
минимальные значения многочленов Бернулли вычислил Лемер (1940); см. упр. 10.3.
(10.3) Замечание. Если мы применим формулу теоремы 10.2 к функции
/(£) = hg(a + th), где h = (b — а)/га, и перенесем член (/(га) — /(0))/2 в левую
часть, то получим (положив zt- = а + ih)
-g{x0) + h^29(^i)-\-^9{xn)= g{x)dx
к
(10.16) +^Bj(g^Hb)-g^\a))
i=2 J*
Lfe + l /•« _
+ (-l)fc-1^-y Bfc(^(fc)(a + ^)(i<,
где в левой части узнается правило трапеций. Из уравнения (10.16) видно, что
главный член ошибки есть {h2/\2){д'(Ъ) — д'{а)). Однако если д — периодическая
функция, то все члены в ряде Эйлера—Маклорена исчезают, и ошибка
становится равной Rk при произвольном к; это объясняет удивительно хорошие
результаты в табл. 6.2 из разд. И.6.
Формула Стирлинга
Положим f(x) = In ж в формуле Эйлера—Маклорена. Поскольку
п
J2 /(*) = h 2 + In 3 + 1п4 + In 5 + ... + lnra = In (n!),
i=2
мы получаем приближенное выражение для факториалов га! = 1 • 2 •... • п.
(10.4) Теорема. (Стирлинг 1730). Справедлива формула
,iAi^ , уДтгп гап / 1 1 1 1 ~ \
(Ш7) П' = — ^^т^\1^-Ж* + Ш*-т* + ^
где \Rq\ < 0.0006605/га8. Поэтому, когда га —> ос, справедливо приближение

166 И. Дифференциальное и интегральное исчисление
(10.18)
Замечание. Эта знаменитая формула особенно полезна в комбинаторном
анализе, статистике и теории вероятностей. Уравнение (10.17) оборвано после
четвертого члена просто потому, что следующий член не умещался на этой строке.
Численные значения, полученные из формул (10.18) и (10.17) (с одним,
двумя и тремя членами) для п=10ип=100, приведены в сравнении с п! в табл.
10.1.
ТАБЛИЦА 10.1. Факториал и его приближение формулой Стирлинга
п = 10 : Стирлинг 0 = 0.35|9869561874103592162317593283
Стирлинг 1 = 0.36288|1005142693352994116531675
Стирлинг 2 = 0.36287999f7141301292538591223941
Стирлинг 3 = 0.3628800000(21301281279077612862
п! = 0.362880000000000000000000000000
п = 100 : Стирлинг 0 = 0.93)2484762526934324776475612718
Стирлинг 1 = 0.93326215|7031762340989619195146
Стирлинг 2 = 0.933262154439(367463946383356624
Стирлинг 3 = 0.9332621544394415(32371338864918
п! = 0.933262154439441526816992388563
•107
• ю7
•107
•107
• ю7
• 10158
. Ю158
. ю158
• ю158
• 10158
Доказательство. Выше мы видели (пример 10.1), что формула Эйлера—
Маклорена становится неэффективной, когда высшие производные функции f(x)
на рассматриваемом интервале становятся большими. Поэтому мы используем
формулу с f(x) — In х для суммы от г = п + 1 до г — га. Поскольку
/■
6?
~dx~J
(1пЖ) = (-1Г1^-^,
hixdx — ж In ж — ж,
из теоремы 10.2 мы получаем, что
т 1
у] /(г) = In га! — In n! = га In m — m — (n In n — n) + - (in m — In n)
i=n + l
(10-19) +^(1-1)-4(^-4)+^
12 \m n/ 360 VmJ n6J
где |Л5| < 0.00123/n4 для всех m > п. Эта оценка получена из формул (10.12)
и (10.15) и из того факта, что |.Z?5(e)| < 0.02446 при 0 < х < 1. В выражении
(10.19) каждый из членов Inn!, nlnn, п, и (1/2) Inn по отдельности расходится
при п —> оо. Поэтому соберем их вместе и положим
(10.20)
7п = Ьп! + п - (п + -) Inn,

11.10 Формула суммирования Эйлера—Маклорена 167
после чего выражение (10.19) приводится к виду
(10.21) 7п = 1т + ^ (- - -) - -^ (\ - -U - Л5.
12 \п т/ 360 Уп-5 тг/
При достаточно больших п и га 7п и 7т становятся сколь угодно близкими.
Поэтому можно предположить, что значения 7ш при т —>■ оо сходятся к величине,
которую мы обозначим как 7 (строгое доказательство будет приведено в теореме
Ш.1.8, принадлежащей Коши). Теперь в уравнении (10.21) перейдем к пределу
т -> ос, после чего получим
lnn! + n_(n+i)lnn = 7 + _i.__L_ + £5,
где |Й5| < 0.00123/п4. Если теперь вычислить экспоненциальную функцию от
этого выражения, мы получим
V^ П" _ П _„7 „„( 1 1
+ R5
(10.22) »! = Д.^. где Dn = * • ехр^ ^
Это равенство будет доказательством формулы (10.18), а также (10.17), если мы
установим, что предел Dn (т.е. D — е7) равен л/2ж. С этой целью вычислим с
помощью (10.22) выражение
Рп • Д, _ п! • п! - (2п)2п • в-2пу^ _ 2 • 4•6 • 8 •... • 2п л/2
£>2п ~ п2п • е~2п • п • (2п)\ ~ 1.3-5-7-...-(2п-1) ' v^'
которое также стремится к D. Эта формула напоминает нам произведение Вал-
лиса (уравнение (1.5.27)). Действительно, квадрат этой величины
'Рп-Рп\*_ 2-2-4-4-6-6 ••• (2п)(2п) 2(2п+1)
, D2n ' "" 1-3-3-5-5-7 ••• (2n-l)(2n+l) n
-»• тг/2 ->•4
стремится к 27Г, так что .D = л/27Г- Приведенная в теореме оценка Rg следует из
(10.12) и неравенства \В9(х)\ < 0.04756. П
Гармонический ряд и постоянная Эйлера
Попробуем вычислить сумму ряда
1 111 1
1+2 + 3 + 4 + -+п'
полагая f(x) = 1/х в теореме 10.2. Поскольку /У)(ж) = (-1)^'! х 3х, мы вместо
(10.19), получаем
,ллоЧ 2-f ;~/ х X+2\rn n) 12Vra2 n2/
(10.23) »'=»+i n
_W_1 4__W_J M J_(J: M Б
+ 120Vm4 n4/ 252 Vm6 n6/ + 240Vm8 ^/ + 9'

168 II. Дифференциальное и интегральное исчисление
где, в связи с тем, что |£э(я)| < 0.04756, мы имеем |Д9| < 0.00529/п9. В отличие
от (10.20), при собирании расходящихся членов мы получаем выражение
п 1
Уп = ^2~ -Inn,
которое можно исследовать в точности так же, как и выше, и показать, что это
выражение сходится. При этом мы получаем постоянную
(10.24) i + I + i + ...+ I_inn_>7 = 0.57721566490153286....
2 3 п
Рис. 10.2. Автограф Эйлера (письмо к Я.Бернулли 1740, см. Фельман 1983, с.96.)1
Эта новая математическая постоянная называется "постоянной Эйлера" (см. рис.
10.2, где приведен автограф Эйлера с его постоянной и ее использование для
вычисления суммы примера 10.1). Полагая в (10.23), как и выше, т -> ос, получаем
(10-25) i\=^+lnn+i-ib+ii^-2^ + 2^+^
г = 1
где \Rg\ < 0.00529/п9. Чтобы вычислить постоянную 7> положим, например,
п = 10 в уравнении (10.25) (как это сделал Эйлер) и получим значение (10.24).
Эту постоянную вычислил с большой точностью Д. Кнут (1962), но до сих пор
неизвестно, является ли она рациональным или иррациональным числом.
1 Воспроизведено с разрешения издательства Birkhaeuser Verlag, Basel.

11.10 Формула суммирования Эйлера—Маклорена 169
Упражнения
10.1 Спираль Феодора состоит из прямоугольных треугольников со сторонами
длиной 1, у/п и у/п + 1. Она делает полный оборот после построения 17
треугольников (по-видимому, именно поэтому Феодор не рассматривал корни
большие у17). Сейчас нам нет нужды беспокоиться о таких мелочах.
Давайте узнаем, скольким оборотам соответствует миллиард таких треугольников.
Для этого нужно вычислить величину
1 юоооооооо л
27Г £U V*
(см. рис. 10.3) с ошибкой меньшей чем 1. Это упражнение не только
позволяет еще раз оценить мощь формулы Эйлера—Маклорена, но также приводит
нас к необходимости вычисления интересного интеграла.
Рис. 10.3. Спираль Феодора Киренейского, 470-390 гг. до Р.Х.
10.2 (Формула ряда Тейлора для tgz). Если положить ctgz = 1/ tg ж и сШж =
1/th ж, то можно видеть, что уравнение (10.9) является рядом Тейлора
функции (ж/2) cth (ж/2). Отсюда можно получить ряд для ж • cth ж и, полагая
х И- гж, ряд для ж • ^ж. Наконец, используйте формулу
2 • ^2ж = ^ж — tgж
и получите коэффициенты разложения tg ж. Сравните их с формулой (1.4.18).
10.3 Проверьте численно оценки (Лемер 1940)
|Б3(ж)| < 0.04812, \В5(х)\ < 0.02446, \В7(х)\ < 0.02607,
\В9(х)\ < 0.04756, \Вц{х)\ < 0.13250, \В13(х)\ < 0.52357
при 0 < ж < 1.

Ill
Основания классического анализа
... Я не уверен в том, что буду заниматься геометрией через десять лет. Я
также думаю, что может быть рудник уже слишком глубок, и раньше или
позже его следует забросить. В настоящее время в физике и химии
делаются более блестящие открытия, которые вдобавок легче использовать ...
(Лагранж, 21 сентября 1781 г., письмо к Даламберу, Oeuvres, vol. 13, p. 368)
После смерти Эйлера в 1783 г. в математике наступил период застоя. Чего
только не сделал Эйлер: создал непревзойденное изложение исчисления
бесконечно малых и дифференциального исчисления (Эйлер 1748, 1755), взял
берущиеся интегралы, решил решаемые дифференциальные уравнения (Эйлер 1768.
1769), раскрыл загадки жидкостей (Эйлер 1755b), механики (Эйлер 1736b,
Лагранж 1788), вариационного исчисления (Эйлер 1744), алгебры (Эйлер 1770).
Казалось, что единственное, что следует делать — это изучать 30000 страниц работ
Эйлера.
"Теория аналитических функций" Лагранжа (1797), "свободная от всех
рассмотрений бесконечно малых величин, исчезающих величин, пределов и
флюксий", тезис Гаусса (1799) об "Основной теореме алгебры" и изучение сходимости
гипергеометрических рядов (Гаусс 1812) ознаменовали начало новой эры.
Больцано заметил, что первое доказательство Гаусса недостаточно строго:
в 1817 г. он приводит "чисто аналитическое доказательство теоремы о том, что
между двумя числами, которые соответствуют противоположным знакам
значений функции, существует по крайней мере один корень уравнения" (теорема
III.3.5 ниже). В 1821 г. Коши вводит новые требования к строгости в своем
знаменитом "Курсе анализа". Он ставит следующие вопросы и отвечает на них.
- Что такое производная? Ответ: предел.
- Что такое интеграл? Ответ: предел.
- Что такое бесконечный ряд а\ + аг + «з + • • •? Ответ: предел.
Отсюда следует вопрос:

171
Что такое предел? Ответ: число.
И. наконец, последний вопрос:
- Что такое число?
Около 1870-1872 гг. Вейерштрасс и его соратники (Гейне, Кантор), а
также Мере, ответили на этот вопрос. Они также исправили много неточностей в
доказательстве Коши, прояснив понятия равномерной сходимости (см. рисунок
ниже), равномерной непрерывности, а также почленного интегрирования и
дифференцирования бесконечных рядов.
Основная часть этой главы — это разделы III.5, III.б и III.7, которые
посвящены соответственно интегральному исчислению, дифференциальному
исчислению и бесконечным степенным рядам. Подготовительные разделы от III. 1 до
III.4 являются основой для построения нашей теории. Раздел III.8 завершает
интегральное исчисление, а раздел III.9 содержит два результата Вейерштрасса о
непрерывных функциях, которые представляли собой значительные достижения
той эпохи.
Вейерштрасс объясняет Коши равномерную сходимость,
а тот размышляет над контрпримером Абеля
(рисунок К.Ваннер)

172 III. Основания классического анализа
III.1 Бесконечные последовательности и
действительные числа
Если для каждого положительного целого п задано число sn, то говорят, что
задана (бесконечная) последовательность, и мы пишут
(1.1) {sn} = {su s2, s3, 54, 55,...}.
Число sn называют n-м членом или общим членом последовательности. В
качестве первого примера приведем последовательность
(1.2) {1,2,3,4,5,6,...},
которая является арифметической прогрессией. Этот термин означает, что
разность между ее двумя последовательными членами постоянна.
Последовательность
(1-3) {q°,q\q2,q\q\q\...}
называется геометрической прогрессией (это значит, что частное от деления ее
двух последовательных членов постоянно).
Сходимость последовательности
Говорят, что некоторая величина есть предел другой величины, если
последняя приближается к первой ближе, чем на любую сколь угодно малую
величину ...
(Даламбер 1765, Encyclopedic, tome neuvieme, a Neufchastel.)
Когда переменная величина сходится к некоторому пределу, часто бывает
полезно указать этот предел с помощью специального обозначения, что мы
будем делать, ставя аббревиатуру
lim
перед рассматриваемой переменной ... (Коши 1821, Cours d'Analyse)
Если члены sn последовательности (1.1) для достаточно больших п сколь
угодно близко приближаются к некоторому числу s, мы называем это число
пределом последовательности (1.1). Это понятие чрезвычайно важно и нужно
определить его более точно:
- "сколь угодно близко" означает "на расстоянии меньшем, чем любое
положительное число £", т. е. \sn — s\ < е. Здесь | • | есть абсолютное значение и поэтому
sn обязано быть близко к s как в положительном, так и в отрицательном
направлении;
- "для достаточно больших п" значит, что должно существовать такое N, что
вышеприведенная оценка справедлива для всех п > N.
Используя символы V ("для всех") и 3 ("существует"), мы можем
представить изложенное выше в следующей компактной форме:
(1.1) Определение (Даламбер 1765, Коши 1821). Мы говорим, что
последовательность (1Л) сходится, если существует число s такое, что
(1.4)
Ve>0 ЗАГ>1 Vn>N \sn-s\<e.
В этом случае мы пишем
(1.5) s = lim sn или

III.1 Бесконечные последовательности и действительные числа 173
Если утверждение (1.4) не справедливо ни при каком s, то говорят, что
последовательность (1.1) расходится.
Рис. 1.1. Сходимость последовательности (1.6).
(1.2) Примеры, Рассмотрим последовательность
г 1 2 3 4 5 1
12' 3' 4' 5' 6' '"/' ГД6
Эта последовательность сходится к 1, поскольку
п+ 1
\Sn ~ 1|
- 1
71+ 1
< е
\п + 1
при п > 1/е—1. Таким образом, при данном е > 0 в качестве N мы можем выбрать
любое целое число, большее чем 1/е — 1, и условие (1.4) будет выполнено.
В качестве следующего примера возьмем последовательность
1
S3
(1.6)
5i = 1,
54 = 1 +
1
2
$2 =
1
3
1 + г
1
4'
'4
3'
,„ = £(-1)[(«-1>/*]
«=1
(здесь [г/2] обозначает наибольшее целое /г, не превосходящее г/2; т.е. [г/2] = Aj,
если г = 2к или г = 2к + 1). Эта последовательность несколько менее тривиальна
и изображена на рис. 1.1. Видно, что она сходится к числу, близкому к 1.13
(которое, как видно из результатов главы I, равно 7г/4 + In 2/2). Видно, что для
данного е (здесь е — 0.058) существует последнее sn (здесь 51б), для которого не
выполняется неравенство |sn — s\ < е. Следовательно, (1.4) справедливо для N =
17. То, что несколько предшествующих членов ($з, $5, • • •) также удовлетворяют
оценке, не противоречит требованиям (1.4).
(1.3) Теорема. Если последовательность {sn} сходится, она ограничена, т.е.
(1.7) ЗВ Vn>l |*П|<Я.
Доказательство. Положим е = 1. По определению сходимости мы можем
выбрать такое целое число 7V, что \sn — s\ < 1 для всех п > N. Используя

174 III. Основания классического анализа
неравенство треугольника (см. упр. 1.1), мы получаем |sn| = \sn — s + s\ <
\sn — 5I + N < 1 + N Для n > N, н утверждение доказано, причем В -
max{|si|, |s2|,..., |stv-i|, \s\ + 1}. С
Ограниченность последовательности не является необходимым условием ее
сходимости. Например, последовательность
(1.8) К} = {1, 0> 1, 0, 1, 0, 1, О,...}
ограничена (при В = 1), но не сходится. Последовательность (1.2) не сходится и I
не является ограниченной. Общая арифметическая прогрессия
(1.9) {sn} = {d, 2d, 3d, 4d, 5d, ...}
тоже не ограничена (при d ф 0). При d > 0 эта последовательность удовлетворяет
следующему требованию:
(1.10) VM>0 3iV>l Vn>iV sn>M.
Для того чтобы убедиться в этом, возьмем целое число N, удовлетворяющее
условию N > M/d. Если (1.10) справедливо, мы говорим, что последовательность
{sn} стремится к бесконечности и пишем
lim sn — оо or sn —У ос.
п—»-оо
Аналогичным образом можно определить linin-^oo sn — — сю.
Исследуем теперь сходимость последовательности (1.3).
(1.4) Лемма. Для геометрической прогрессии (1-3) имеем
{0 при \q\ < 1,
1 при q — 1, |
оо при q > 1.
Последовательность (1.3) расходится при q < — 1.
Доказательство. Начнем со случая q > 1. Положим д = 1 + г(г>0)и
применим теорему 1.2.1, после чего получим
qn = (1 + г)п = 1 + пг + П^П ~ ^ г2 + ... > 1 + пг.
Таким образом, члены qn стремятся к бесконечности (при заданном М следует
выбрать N > М/r в соотношении (1.10)). При q — 1 утверждение тривиально.
В случае, когда \q\ < 1, рассмотрим последовательность sn — (1/|^|)п,
которая в силу вышеизложенного стремится к бесконечности. При заданном е > О
положим М = 1/е и приложим (1.10) к последовательности {sn}. Это доказывает
существование такого целого числа 7V, что для всех п > N мы получаем sn > М,
или, что то же самое, |^п| < е. Это доказывает, что ^п —У 0. При ^ = — 1
последовательность осциллирует между —1 и 1, а когда q < — 1, она не ограничена и
осциллирует. D
Следующая теорема упрощает вычисление пределов.
(1.5) Теорема. Рассмотрим две сходящихся последовательности, sn —>• s и
vn —> v. Тогда последовательности, составленные из вычисленных почленно
сумм, произведений и частных их членов также сходятся, и мы имеем

III.1 Бесконечные последовательности и действительные числа 175
(1.11) lim (sn + vn) = s + v
n-юо
(1.12) lim (sn -vn) = S'V
n—»oo
(1.13) lim ( — J = —, если vn ф О и v ф 0.
п-юс\уп/ V
Доказательство. Начнем с доказательства соотношения (1.11). Из
неравенства треугольника получаем
\{sn + vn) - {s + v)\ = \sn - s + vn - v\ < \sn - s\ + \vn - v\ < 2e - ef
<e <e
Для того, чтобы доказательство было логичным, эту последовательность формул
следует читать справа налево: при заданном произвольно малом е' > 0 выберем
е > 0 таким, что 2е = е'. Согласно предположению, две последовательности {sn}
и {vn} сходятся к s и v. Это означает, что существуют числа Ni и 7V2 такие, что
\зп - з\ < е при п > Ni и \vn — v\ < е при п> N2. Выбирая N = max(JVi, iV2), мы
получаем, что утверждение (1.4) справедливо для последовательности {sn +vn}.
В дальнейшем мы не будем повторять эти рассуждения.
Для доказательства (1.12) мы должны оценить величину snvn — sv.
Прибавляя и вычитая "смешанные произведения" — svn + svn, получаем
\snvn - sv\ — \snvn - svn + svn - sv\
<\Vn\' К ~ S\ + \s\ • \vn - V\ < (B + \s\) € = €f.
Здесь мы использовали теорему 1.3 для последовательности {vn}.
Достаточно доказать (1.13) для случая, когда sn = 1 при всех п, и,
следовательно, s = l. Тогда результат для общего случая будет следовать из
соотношения (1.12), потому что sn/vn есть произведение (l/vn) и sn. Сначала заметим,
что значения \vn\ не могут стать сколь угодно малыми. Действительно, полагая
е- \v\/2 в определении сходимости, мы получаем \vn — v\ < \v\/2 (и
следовательно также \vn\ > \v\/2) при достаточно большом п. С помощью этой оценки мы
получаем
\v-Vn\ к 2\vn - v\ 2е _ ,
Uj^ I . IijI U>|2 Iij|2
Vn V
(1.6) Теорема. Предположим, что последовательность {sn} сходится к s и что
sn <В для всех достаточно больших п. Тогда предел этой последовательности
также удовлетворяет неравенству s < В.
Доказательство. Мы покажем, что s > В приводит к противоречию. Для
этого мы положим е = s — В >0и используем соотношение (1.4), откуда следует,
что для достаточно больших п мы имеем
s - sn < \sn - s\ < е = s - В,
так что sn > 5, что противоречит предположению теоремы. □
Замечание. Аналогичное утверждение для строгих неравенств (из sn < В
для всех п следует s < В) не справедливо. Это следует из контрпримера sn =
п/[п+ 1) < 1, для которого НгПп-юо sn = 1.

176 III. Основания классического анализа
Последовательности Коши. Теперь давайте разберемся в одном важном
вопросе. Определение сходимости (1.4) приводит нас к необходимости оценить
\sn — s\; предел s должен быть известен. Но что нам делать, если предел $
неизвестен, или, как в примере (1.6), мы знаем его недостаточно точно? В этом
случае строгая оценка \з — зп\ < е невозможна при произвольном е > 0. Чтобы
преодолеть это препятствие, Коши предложил заменить \sn — s\ < е в (1.4) на
\sn — 5n+fc| < е для всех членов sn+fc, следующих за членом зп.
(1.7) Определение. Последовательность {sn} называется последовательностью
Коши или фундаментальной последовательностью, если
(1.14)
Ve>0 3N>1 Vn>N Vfc > 1 |sn-sn+fc|<e.
1.4 h
1.2 H
4!l *
1.4
i
U 1-2
1.0
млч
Рис. 1.2. Последовательность (1.6) как последовательность Коши,
Пример. Рис. 1.2 иллюстрирует условие (1.14) для последовательности (1.6).
Видно, что, например, для е — 0.11, условие (1.14) справедливо при п > 17.
Более того, (1.14) справедливо для любого е > 0, потому что 1/(п + 2) + 1/(п + 3)
стремится к нулю.
(1.8) Теорема (Коши 1821). Последовательность {sn} действительных чисел
сходится (к действительному числу в качестве предела) тогда и только тогда,
когда она является последовательностью Коши.
То, что сходящиеся последовательности должны быть последовательностями
Коши, следует непосредственно из неравенства \зп — sn+k\ < |sn — s| + |s — s„+*| <
2e. Отдавая должное интуиции Коши, отметим здесь, что строгое
доказательство обратного утверждения возможно только в том случае, если мы поймем, что
такое иррациональные и действительные числа. В отличие от ранее полученных
результатов (теоремы 1.3, 1.5и 1.6), теорема 1.8 не справедлива, если мы
рассматриваем только рациональные числа. Например, рассмотрим последовательность
(1.15)
{1 , 1.4, 1.41, 1.414, 1.4142, 1.41421,...}.
Разумеется, это последовательность Коши (|sn — sn+fc| < 10 n+1), но ее предел
\[2 не является рациональным числом.

III.1 Бесконечные последовательности и действительные числа 177
Понятие действительного числа
Чем больше я думаю об основах теории функций, а думаю я об этом
беспрестанно, тем больше я убеждаюсь в том, что фундамент, на котором они
должны быть построены, это истины из алгебры ...
(Вейерштрасс 1875, Werke, vol. 2, p. 235)
Пожалуйста, забудьте все, что вы учили в школе, потому что вы этому
не научились — Мои дочери изучают (химию) уже несколько семестров.
Они думают, что выучили дифференциальное и интегральное исчисление
еще в школе, но даже сейчас они не знают, почему справедливо равенство
х • у = у • х. (Ландау 1930, англ. перевод 1945)
Итак, л/3 — только символ для числа, которое еще нужно найти, но
не определение этого числа. Однако это определение удовлетворительно
дается с помощью моего метода как, скажем,
(1.7,1.73,1.732,....)
(Г. Кантор 1889)
... определение иррациональных чисел, геометрическое представление
которых часто приводило к путанице В моем определении я исхожу из
чисто формальной точки зрения, называя определенные символы числами,
так что существование этих чисел не вызывает сомнения. (Гейне 1872)
И тогда мое чувство неудовлетворенности стало столь сильным, что, в
конце концов, я решил начать думать, пока не найду чисто
арифметического и абсолютно строгого обоснования принципов анализа бесконечно
малых. ... Я достиг этой цели 24 ноября 1858 г., ... но я никак не мог
решить вопрос о форме публикации, потому что, во-первых, предмет не
легок для изложения, и, во-вторых, материал не очень плодотворный.
(Дедекинд 1872)
Принижение анализа до простой игры с символами ...
(Дюбуа-Реймон, Allgemeine Funktionentheorie, Tubingen 1882)
В течение многих десятилетий никто не знал, как следует строго вводить
иррациональные числа, как правильно понять, что должно быть "предельным
членом" последовательности Коши, такой как (1.15). Этот "гордиев узел" был в
конце концов разрублен независимо Кантором (1872), Гейне (1872), Мере (1872)
(и аналогичным образом Дедекиндом 1872) с помощью следующей смелой идеи:
объявляется, что вся последовательность Коши — "это и есть" искомое
действительное число (см. цитаты). Это значит, что мы связываем
последовательность Коши, состоящую из рациональных чисел sn (впредь называемую
рациональной последовательностью Коти) с действительным числом.
По-видимому найден изящный способ разрешить трудности с теоремой 1.8.
Однако нужно сделать еще многое: надо найти способ отождествлять различные
рациональные последовательности Коши, представляющие одно и то же
действительное число, определить алгебраические отношения и отношения порядка для
этих новых объектов. Тогда станет ясно, что доказательство теоремы 1.8 будет
более сложным, чем мы могли себе представить, потому что члены sn в (1.14)
сами могут быть действительными числами, т. е. рациональными
последовательностями Коши. Все эти детали были подробно проработаны Ландау (1930) в его
знаменитой книге, где он сам замечает, что многие ее части — "eine langweilige
Miihe" (способны наводить скуку, — нем.).
Отношение эквивалентности. Предположим, что
V2 соотнесено с {1.4 ; 1.41 ; 1.414 ;...}
л/3 соотнесено с {1.7 ; 1.73 ; 1.732 ;...},

178 III. Основания классического анализа
тогда л/2 • \/3 должно быть соотнесено с последовательностью произведений
{2.38 ; 2.4393; 2.449048,...}.
С другой стороны, \/б может быть также соотнесено с {2.4 ; 2.44 ; 2.449 ;...}.
Поэтому нам следует отождествить две эти последовательности.
Две рациональные последовательности Коши {sn} и {vn} называются
эквивалентными, если limn^.00(sn — vn) = 0, т.е. если
(1.16) Ve>0 ЗЛГ>1 Vn>N \sn-vn\<e.
В этом случае мы пишем {sn} ~ {vn}. Нетрудно проверить, что (1.16) определяет
отношение эквивалентности на множестве всех рациональных
последовательностей Коши. Это значит, что выполнены условия
{sn} ~ {sn} (рефлексивность)
{sn} ~ {vn} => {vn} ~ {sn} (симметричность)
{sn} ~ {vn}, {vn} ~ {wn} => {sn} ~ {wn} (транзитивность).
Таким образом, становится возможным разделить множество рациональных
последовательностей Коши на классы эквивалентности,
vn} {vn} — рациональная последовательность Коши и {vn} ~ {sn}\.
Элементы классов эквивалентности называются их представителями.
(1.9) Определение. Действительными числами называются классы
эквивалентности рациональных последовательностей Коши, т. е.
М = < {sn} {sn} — рациональная последовательность Коши >.
Множество Q рациональных чисел можно рассматривать как подмножество
множества Ш следующим образом: если г есть элемент множества Q
(сокращенно г Е Q), то стационарная (постоянная) последовательность {г, г, г,...} есть
рациональная последовательность Коши. Следовательно, мы отождествляем
рациональное число г с действительным числом {г, г,...}.
Сложение и умножение. Чтобы работать в М, мы должны определить
обычные действия. Пусть s — {sn} и v — {vn} — два действительных числа.
Тогда мы определяем их сумму (разность) и произведение (частное) как
(1.17) s + v := {sn + vn}, s-v := {sn-vn}.
Здесь нужна некоторая осторожность. Прежде всего, мы должны убедиться в
том, что последовательности {sn+ vn} и {sn-vn} являются рациональными
последовательностями Коши (это следует из соотношения \(sn + vn) — (sn+k + ^n+fe)l <
\sn — sn+k \-\-\vn —Vn+k | Для суммы, а для произведения получается так же, как при
доказательстве теоремы 1.5). Теперь мы должны показать, что (1.17) правильно
определены. Если мы выберем другие представители классов эквивалентности s
и v, например, {s'n} и {vfn}, результат s + v должен быть тем же самым. Чтобы
это показать, нам нужно доказать, что из sn — sfn —У 0 и vn — vfn —>• 0 следует
(sn +vn) — (sfn -\-vfn) —У 0 и (sn -vn) — (s'n -vrn) —У 0. Это можно получить совершенно
так же, как при доказательстве теоремы 1.5.

III.1 Бесконечные последовательности и действительные числа 179
На следующем шаге нам нужно проверить известные правила вычислений
с действительными числами (коммутативность, ассоциативность,
дистрибутивность). Здесь и начинается "langweilige Muhe" Ландау. Эти детали мы опускаем
и отсылаем читателя или к прекрасной книге Ландау, или к любому учебнику
алгебры.
Упорядоченность. Пусть s = {sn} и v = {vn} — два действительных
числа. Введем определение
s < v :<=> 3е'>0 ЗМ>1 \/т>М sm < vm - е',
(1.18) "
s < v :<=> s < v или s = v
(здесь число е' должно быть рациональным для того, чтобы избежать
двусмысленности в определении). Довольно сложное определение s < v означает, что для
достаточно больших т элементы sm и vm должны отчетливо отделяться друг от
друга. Это обеспечивает также непротиворечивость определения. Очевидно, что
недостаточно потребовать, чтобы sm < vm (в качестве контрпримера приведем
две последовательности {1,1/2,1/3,1/4,...} и {0, 0, 0,...}, они обе представляют
действительное число 0).
Соотношение s < v формулы (1.18) определяет соотношение
упорядоченности. Это значит, что
s < s (рефлексивность)
s < v, v < w => s < w (транзитивность)
s < v, v < s =$> s = v (антисимметричность).
Приведем здесь только доказательство антисимметричности. Предположим, что
s <v и v < s, по s ф v. Тогда существуют положительные рациональные числа
е[ и е!2 такие, что sm < vm — е^ при т > М± и vm < sm — е'2 при т > М2.
Следовательно, при т > max(Mi, М2) имеем е2 < sm — vm < —efly т.е. мы пришли
к противоречию.
(1.10) Лемма. Упорядочение < в (1.18) является всеобщим, т. е. либо s < v, либо
v < s для любых двух действительных чисел s и v при s ф v.
Замечание. Соотношение s ф v является отрицанием соотношения s = v,
которое выражается формулой (1.16). Для того, чтобы сформулировать
отрицание утверждения, подобного (1.16), нам потребуется несколько формул логики.
Пусть S(x) есть утверждение, зависящее от х Е А (А — некоторое множество) и
-iS(e) его отрицание. Тогда г
Vx£A S(x) является отрицанием 3х Е А ->5(ж),
ЗхЕА S(x) является отрицанием \/х Е A -*S(x).
Чтобы получить отрицание длинного утверждения, следует обратить все
кванторы (V Н 3) и заменить окончательное утверждение на его отрицание. Таким
образом, для s ф v из (1.16) получается следующая формула:
(1.19) 3е>0 \/N>l 3n>N \sn-vn\>e.
Утверждение "все (V) полярные медведи белые" несправедливо, если существует (3)
по меньшей мере один окрашенный (не белый) полярный медведь, и наоборот.

180 III. Основания классического анализа
Доказательство леммы 1.10. Пусть s = {sn} и v = {vn} — два различных
действительных числа, так что для них (1.19) справедливо. Положим теперь б' =
е/Ъ. Поскольку {sn} и {vn} являются последовательностями Коши, существует
Ni такое, что \sn — sn+*| < е' при п > N\ и к > 1, и существует N2 такое, что
\vn — vn+k I < ef при n > N2 и к > 1. Если положить N = max(iVi, iV2), то из (1.19)
следует, что существует целое число п > N такое, что \sn — vn\ > е. Есть две
возможности:
(1.20) sn - vn > е или vn - sn > е.
Рис. 1.3. Иллюстрация двух возможностей в (1.20).
При к > 1 числа sn+fc и vn+k остаются в кругах радиуса е' — е/3 (см. рис. 1.3).
Следовательно, (1.18) справедливо при М = А^", и мы имеем s > v в первом случае
и v > s во втором. D
Абсолютная величина. Поскольку мы показали, что упорядочение
является всеобщим (лемма 1.10), становится возможным определить абсолютную
величину числа s как s для s > 0 и — s для s < 0. Непосредственным следствием
этого определения является формула
(1.21) M=TW} для s = КГ-
Для действительных чисел справедливы неравенство треугольника \s-\-v\ < \s\-\-
\v\ и все его следствия.
Замечание. В определениях и теоремах 1.1-1.7 мы были недостаточно
точны при использовании понятия "число". Чтобы быть логически корректными, все
утверждения должны были использовать только понятие рационального числа.
Теперь, когда мы не без труда установили понятие действительного числа,
можно распространить эти определения на действительные числа и проверить, что
утверждения теорем остаются справедливыми и в более широком контексте.
Доказательство теоремы 1.8.
... до сих пор эти предложения рассматривались как аксиомы.
(Мере 1869, см. Дюга 1978, р. 82)
Пусть {si} является последовательностью Коши действительных чисел
такой, что каждое Si само является классом эквивалентности рациональных
последовательностей Коши, т.е. Si = {5in}n>i- Идея доказательства состоит в том,
чтобы выбрать для каждого i число, которое становится все меньше и меньше
(например, 1/2г) и использовать определение рациональной последовательности
Коши, что приводит к формуле
3Ni>l \/n>Ni Vfc>l |*n-*,»+*I < -•
Li
После этого мы полагаем V{ := S{^{ и рассматриваем рациональную
последовательность {vi} (см. рис. 1.4).

III.1 Бесконечные последовательности и действительные числа 181
Рис. 1.4. Сходимость последовательности Коши.
a) Сначала мы покажем, что |v,- — s,-| < 1/г. Согласно (1.21), действительное
число \vi — Si\ представляется рациональной последовательностью Коши {|v,- —
Stm|}m>l- ПОСКОЛЬКУ При ГП > N{
l-l I 1-1 1
\Щ ~~ sim\ — |5»,ЛГ{ sim\ ^ л • — • ~~ о'
zz г 1г
то из (1.18) при е1 = 1/2г следует, что |г>,- — S{\ < 1/г.
b) Далее мы покажем, что {vi} является рациональной последовательностью
Коши. Замечая, что величина \v{ — ^t+fcl не меняется от того, что мы
рассматриваем ее как рациональное или действительное число, мы имеем
\Vi - Vi + k\ = \vi - Si + Si - si+k -f si + k - vi+k\
(1.22) < \у{ -8{\+ \si - Si+kI + \si+k - vi+kI < T + e + —— < 2e
г г + к
для достаточно больших i и для к > 1. В качестве кандидата на предел {vn}
рассмотрим класс эквивалентности s := {vn}, обозначаемый как {st}. Из (1.22)
следует, что |v,- — s| < Зе (для достаточно больших г), так что Vi -> s.
c) Наконец, мы докажем, что 5г- —>• s. Из частей а) и б) этого доказательства
и из неравенства треугольника имеем
\si - s\ < \si —Vi\ + \vi - s\ < -7 + 3£ < 4e
г
для достаточно больших г. Следовательно, 5г- —>■ s, и теорема 1.8 доказана. □
Монотонные последовательности и наименьшая верхняя грань
Наша следующая задача — строго доказать, что ограниченная монотонно
возрастающая последовательность сходится к действительному пределу. Этот
результат много раз использовался в гл. II, особенно в разд. 11.10. Для нашей
цели полезно следующее определение.
(1.11) Определение. Пусть X является подмножеством Ш. Действительное
число £ называется наименьшей верхней гранью (или точной верхней гранью)
множества X, если

182 III. Основания классического анализа
1) М х £ X х < £, и
2) \/е>0 ЗхеХ х>£-е.
В этом случае мы пишем £ = supX.
Условие 1) выражает тот факт, что £ является верхней гранью X, в то время
как условие 2) означает, что £ — е уже не является верхней гранью, так что £
действительно есть наименьшая из всех верхних граней. Наш следующий результат
касается существования такой точной верхней грани: "Эта Теорема... ", как
писал Больцано в 1817 г., "... чрезвычайно валена (см. Штольц 1881, р. 257). Она
основана на теореме 1.8 и не справедлива в Q (множество X — {х Е Q | х2 < 2}
не имеет точной верхней грани в Q).
Рис. 1.5. Существование наименьшей верхней грани монотонной последовательности.
(1.12) Теорема. Пусть X — не пустое и ограниченое сверху подмножество 1
(т.е. ЗВ Vx GX х < В). Тогда существует действительное число £ такое,
что £ = sup X.
Доказательство. Следуя Больцано (а также Евклиду, Начала, Книга X),
проведем доказательство с помощью метода деления пополам. Построим
вложенные отрезки [ап,/Зп] с длинами, стремящимися к нулю как геометрическая
прогрессия, такие, что ап не является верхней гранью X, а /Зп является.
Поскольку X не пусто, можно найти такое число с*о, которое не является верхней
гранью (выберем элемент х множества X и возьмем а0 слева от х). Из нашего
второго предположения (X ограничено сверху) следует существование верхней
грани. Выберем одну из них и обозначим ее как Д). Идея доказательства в том,
чтобы рассмотреть среднюю точку 7 = (<*о + Д))/2 (см. рис. 1.5). Существуют две
возможности: или 7 есть верхняя грань X (в этом случае мы полагаем а\ :— ао
и fii := 7)? или это не так (тогда мы полагаем а\ := 7 и Pi '•— А))-
Повторяя эту процедуру, мы получаем последовательность отрезков [ап,/Зп] с длинами
/?„-ап = (А,-а0)/2п.
Из построения видно, что все левые и правые границы последующих
отрезков принадлежат отрезку [ап,/Зп]. Следовательно, мы получаем оценки
i i / а Ро-а0 Po-ct0
|a„ -a1l+k\ <(jn-an = ———, \pn -pn+*l < Pn ~ <*„ = ———.
Из этого следует, что {an} и {/Зп} являются последовательностями Коши. В силу

III.1 Бесконечные последовательности и действительные числа 183
теоремы 1.8 они сходятся, и поскольку (Зп — ап = (Д) — ао)/2п —У О, они имеют
один и тот же предел £ (теорема 1.5). Из теоремы 1.6 следует, что £ есть верхняя
грань X (из х < (Зп следует х < £). Далее, при заданном е > О существует а„,
удовлетворяющее неравенству ап > £ — е. Поскольку ап не является верхней
гранью X, £ — е также не может ей быть. □
(1.13) Теорема. Рассмотрим последовательность {sn}, которая монотонно
возрастает (sn < sn+i) и ограничена сверху (sn < В для всех п). Тогда она сходится
к действительному пределу.
Доказательство. По предположению множество X — {s±, 52,53,...} не пусто
и ограничено (см. рис. 1.5). Поэтому в силу теоремы 1.12 существует £ = supX.
По определению sup X значение £ — е при заданном е > 0 не является верхней
гранью X. Следовательно, существует такое JV, что sjy > £ — е. Поскольку X
ограничено величиной £, мы имеем
£ - € < 8N < Sn+1 < Sn+2 < SN+3 <•••<£>
так что £ — е < sn < £ (и следовательно \sn — £| < е) для всех п > N. Это
доказывает сходимость {sn} к £. □
(1.14) Следствие. Рассмотрим две последовательности, {sn} и {vn}.
Предположим, что {sn} монотонно возрастает (sn < sn+i) и что sn < vn для всех
(достаточно больших) п. Тогда
{vn} сходится => {sn} сходится,
{sn} расходится => {vn} расходится.
Доказательство. Если последовательность {vn} сходится, то согласно
теореме 1.3 она ограничена. Следовательно, {sn} также ограничена и согласно теореме
1.13 сходится. Вторая строка является логическим обращением первой. □
Замечание. Аналогичным образом мы определяем нижнюю грань
множества, а также ограниченные снизу и монотонно убывающие последовательности, и
используем обозначение
(1.23) С = ЫХ
для наибольшей нижней грани или точной нижней грани X (т. е. х > f для всех
х£ X и Ve > О Зх G X такое, что х < £ + е). При этом можно сформулировать
теоремы, аналогичные теоремам 1.12 и 1.13.
Точки накопления
Я нахожу поистине удивительным, что лекции г-на Вейерштрасса и г-на
Кронекера, которые так трудны и читаются на таком высоком уровне,
могут привлечь так много студентов — от 15 до 20.
(письмо Миттаг-Леффлера 1875, см. Дюга 1978, р. 68)
Последовательность
1213141516
3> 3' 4> 4' 5' 5' 6' 6> 7> 7'
(1.24) — — — — — -+0
^ ^ ^ ^ ^ _>1

184 III. Основания классического анализа
не сходится, однако если из нее удалить члены через один, она сходится к О
или к 1. Последовательность, из которой удалены некоторые члены, называется
"подпоследовательностью". Точнее,
(1.15) Определение. Последовательность {s'n} называется
подпоследовательностью последовательности {sn}, если существует возрастающее отображение
а : N -> N с s'n = s^n) ("возрастающее" означает, что а(п) < сг(т), если
п < т).
(1.16) Определение. Точка s называется точкой накопления (или предельной
точкой) последовательности {sn}, если существует подпоследовательность,
сходящаяся к s.
Примеры. Точки 0 и 1 являются точками накопления последовательности
(1.24). Интересным примером является последовательность
/II?I?31234123451234561 1
( } 12'3'3'4'4'4'5'5'5'5'6'6'6'6'6'7'7'7'7'7'7'8''"Г
у которой все числа, расположенные между 0 и 1 (включая 0 и 1) являются
точками накопления. Например, для того чтобы показать, что In 2 является точкой
накопления последовательности (1.25), рассмотрим последовательность
г_6_ _69_ №_ 6931 69314 693147 1
llO' 100' 1000' 10000' 100000' 1000000' '"У
Без сомнения, она содержится в (1.25) и сходится к In 2.
Неограниченные последовательности {1, 2, 3, 4, 5,...}, { — 1, —2, —3, —4, —5,...}
и {1, —1, 2, —2, 3, —3, 4, —4,...} не имеют точек накопления.
(1.17) Теорема Больпано-Веиерштрасса (лекция Вейерштрасса 1874 г.).
Ограниченная последовательность {sn} имеет по меньшей мере одну точку
накопления.
Доказательство. В своем первоначальном доказательстве Вейерштрасс
использовал метод деления пополам, так же, как в доказательстве теоремы 1.12.
Располагая этой теоремой, рассмотрим множество
(1.26) X — {х | sn > х для бесконечно многих п}
и просто положим £ = supX, это и будет точка накопления (см. рис. 1.6). Такое
число существует, потому что X не пусто и ограничено сверху
(последовательность {sn} ограничена). По определению точной верхней грани только конечное
число sn может удовлетворять условию sn > £ + £, и существует бесконечное
число членов 8П, которые превосходят £ — е (е является произвольным
положительным числом). Следовательно, бесконечное число членов sn лежит в интервале
Теперь давайте произвольно выберем элемент последовательности, лежащий
в промежутке [£ — 1,£ + 1] и обозначим его как s^ = s^i). Выберем элемент в
промежутке [£ — 1/2,£ + 1/2], номер которого отличен от а(1) (это возможно,
поскольку их бесконечно много), и обозначим его как sf2 = s<r(2)- На п-м шаге
в качестве s'n = s<7(n) выберем элемент последовательности, который лежит в
промежутке [£ — 1/п,£ + 1/п] и номер которого отличен от <т(1),..., <т(п — 1).

III.1 Бесконечные последовательности и действительные числа 185
Подпоследовательность, полученная таким образом, сходится к £, потому что
К-*|<1/п. □
%-\1п
£+1/л
£ = sup X
Рис. 1.6. Доказательство теоремы Больцано-Вейерштрасса.
Замечание. В доказательстве мы получили не просто точку накопления, а
наибольшую точку накопления. Мы называем ее "верхним пределом"
последовательности и обозначаем ее как
(1.27) £ = limsupsn = sup{z G Ш | sn > х для бесконечно многих п}
п—юо
(см. также упр. 1.12). Наименьшая точка накопления определяется как
(1.28) £ = liminf sn — infix G Ш I sn < x для бесконечно многих п\.
n-юо k ' J
Пример. Для последовательности
/5 _1 4 __1 5 __1 6 _1 7 __1 1
12,"2'3,"3,4'~4,5,"5,6,~6,**J
имеем limsupn_).00 sn = 1, liminfn_,.oo sn — 0, sup{sn} = 3/2, inf{sn} = -1/2.
Упражнения
1.1 (Неравенство треугольника). Рассматривая все возможные комбинации
знаков, покажите, что для любых двух действительных чисел uav справедливо
неравенство
(1.29) |и + г;|< \u\ + \v\.
Теперь покажите, что для любых трех действительных чисел и, v и w
справедливо неравенство
(1.29') \u-w\<\u-v\ + \v- w\.
1.2 Покажите, что последовательность {s„}, где
_ 2п- 1
Sn ~ „ A Q '
П + О
сходится к s = 2. Для заданного е > 0, скажем, для е = 10"5, найдите такое
число iV, что \sn — s\ < е при п > N.
1.3 Покажите, что последовательности
1111 1
1-5 3-7 5-9 7-11 (2п-1)(2п + 3)

186 III. Основания классического анализа
1 1 1
8п = л л „ + л п л + л л „ + • • • +
1-2-3 2-3-4 3-4-5 '" n(n+l)(n + 2)
являются последовательностями Коши, и найдите их пределы.
Указание. Разложите на элементарные дроби рациональные функции
1 1
(2i-l)(2j + 3) (j-l)j(j + l)
1.4 Пострюйте примеры последовательностей sn и vn, обладающих свойствами
lim sn — оо и lim vn = О, чтобы проиллюстрировать следующие возмож-
п—юо п-»оо
ности:
a) lim (sn -vn) = оо;
n-юо
b) lim (sn • vn) — с, где с является произвольной постоянной;
п—юо
c) последовательность 5n • vn ограничена, но не сходится.
1.5 Рассмотрите три последовательности
sn - yjn -f 1000 - yfn, vn = y/n + y/n- y/n, un = Jn+ —— - y/n.
Покажите, что sn > vn > un при n < 106, и вычислите lim sn, lim vn
n->oo n-^oo
и lim un, если они существуют. Расставьте эти пределы в возрастающем
п—юо
порядке.
1.6 С помощью оценок из упр. 1.2.5 покажите, что последовательность
1\п
-=ю
является последовательностью Коши. При е — 10 5 найдите такое целое JV,
что \vn — vn+k | < € при n > N и к > 1.
1.7 Для двух рациональных последовательностей Коши {ап} и {Ьп} обозначим
через {ап • Ьп } последовательность, полученную из почленных произведений
их членов. Покажите, что
a) последовательность {ап • &„} является последовательностью Коши; и
b) если {ап} ~ {sn} и {6n} ^ {vn} согласно определению (1.16), то имеет
место {ап • 6n} ^ {sn • vn}. Это доказывает, что произведение двух
действительных чисел, определенное соотношением (1.17), не зависит от выбора
представителей.
1.8 Докажите следующее: если s является единственной точкой накопления
ограниченной последовательности {sn}, то последовательность сходится и
limn-^oo sn — s. С помощью контрпримера покажите, что это свойство не
имеет места для неограниченных последовательностей.
1.9 (Коши 1821, р. 59; называется также "суммированием по Чезаро"). Пусть
Ишп-юо ап - а и
1 п
Покажите, что Ншп-юо Ьп — а.
а*.
п ^—'
к=1

III. 1 Бесконечные последовательности и действительные числа 187
1.10Пусть а является иррациональным числом (например, а = у/2).
Рассмотрите последовательность {sn}, определенную как
sn = (па) mod 1,
т.е. sn 6 (0,1) есть па с удаленной целой частью. Вычислите si, S2, 53,
54,... и изобразите эти значения. Покажите, что каждая точка отрезка [0,1]
является точкой накопления этой последовательности.
Указание. Для £>0ип> 1/е по меньшей мере две точки из si, 52,..., sn+i
(назовем их Sk и Sk+t) находятся на расстоянии, меньшем чем е. Тогда точки
Sfc, Sk+i, Sk+21, • • • образуют сетку с шагом < е.
Замечание.. В начале компьютерной эры эта процедура была стандартным
методом получения псевдослучайных чисел.
1.11 Пусть {sn} и {vn} являются двумя ограниченными последовательностями.
Покажите, что
limsup (sn +vn) <limsupsn +limsupt;n
n—ЮО n—)-oo n—*-oo
liminf (sn + vn) > liminf sn + liminf t;n.
n—too n—ЮО n—too
С помощью примеров покажите, что неравенство может быть строгим.
1.12Докажите, что для последовательности {sn}
limsupsn = lim vn, где vn = sup{sn, sn+1, sn+2, • •-}•
п-юо П-+ОО
1.13 Вычислите все точки накопления последовательности
* 1
{Sn} = {pu, Р2Ь Р22, Р31, Р32, РЗЗ, Р41, Р42, • • •}, Pife/ = ]Р "^•
Покажите, что limsup5П = 7г2/б (см. формулу (1.5.23)) и что liminf sn — 0
(см. рис. 1.7).
Рис. 1.7. Последовательность со счетным числом точек накопления.

188 III. Основания классического анализа
III.2 Бесконечные ряды
Я приложу все усилия, чтобы внести ясность в ту ужасную невразум!
тельность, которая сейчас царит в Анализе. В нем настолько отсутствуй
какой-либо план или система, что поистине удивительно, как много людей
им занимаются. И что еще хуже — в нем абсолютно отсутствует строгость.
(Абель 1826, Oeuvres, vol.2, p.263)
Коши сумасшедший и с ним невозможно поддерживать хорошие
отношения, хотя в настоящее время он является единственным человеком,
который знает, как нужно излагать математику. То, что он делает,
великолепно, но очень путано ... (Абель 1826, Oeuvres, vol. 2, p. 259)
Со времен Ньютона и Лейбница бесконечные ряды
(2.1) а0 + сц + а2 + а3 + ...
являлись универсальным средством для всех вычислений (см. главу I). Сейчас
мы точно сформулируем, что именно представляет собой ряд (2.1). Идея состоит
в том, чтобы рассмотреть последовательность {sn} частичных сумм
п
(2.2) so = а0, si = ao + ai, ..., sn = } ^at
•=o
и использовать определения и результаты предыдущего раздела.
Классический справочник по бесконечным рядам — книга Кноппа (1922).
(2.1) Определение. Мы говорим, что бесконечный ряд (2.1) сходится, если
последовательность {sn}, определенная соотношением (2.2), сходится. В этом
случае мы пишем
оо
Ещ = lim sn или V^ai = lim sn.
П—¥00 *-~* П—УОО
г=0 »>0
1
1
1-q
Рис. 2.1. "Геометрическое" изображение геометрической прогрессии.
(2.2) Пример. Рассмотрим геометрическую прогрессию, п-я частичная сумма
которой дается выражением sn = 1 + q + q2 + ... + qn (см. рис. 2.1). Если умножить
это выражение на 1 — q, большинство членов уничтожаются, и (если q ф 1)
1 — qn+1
sn = 1 + q + q2 + ... + qn = —-^ .
1-q
Тогда с помощью леммы 1.4 и теоремы 1.5 мы получаем

III.2 Бесконечные ряды 189
если \q\ < 1,
1 + Ч + Ч2 + Q3 + Q4 + ЧЪ + • • • :
1-q
расходится —> сю если q > 1,
расходится если g < — 1.
Критерии сходимости
Найти простое выражение для sn обычно бывает невозможно, а явным
образом вычислить предел последовательности {sn} трудно. В этом случае
естественным будет приложить критерий Коши (теорему 1.8) к последовательности
частичных сумм. Поскольку sn+k — Sn = o>n+i + а>п+2 + ... + «n+ь мы получаем
(2.3) Лемма. Бесконечный ряд (2.1) сходится к действительному числу в том
и только том случае, если
\/е>0 3N>Q Vn>N Vfc > 1 \ап+1 + ап+2 + ... + ап+к\ < е. П
Полагая в этом критерии к — 1, мы получаем, что
(2.3) lim аг = О
г'-юо
является необходимым условием сходимости (2.1). Однако (2.3) не является
достаточным условием сходимости (2.1). Это следует из контрпримера:
Л 1111111111
1+2 + 2 + 3 + 3 + 3 + 4 + 4 + 4 + 4 + 5 + -^°°-
Ниже мы обсудим некоторые достаточные условия сходимости (2.1).
Критерий Лейбница. Рассмотрим бесконечный ряд, в котором знаки
членов чередуются:
(2.4) а0 - ах + а2 - а3 + сц - • • • = У^(-1)гаг-.
г>0
(2.4) Теорема (Лейбниц 1682). Пусть члены знакопеременного ряда (2.4) при всех
г удовлетворяют условиям
а% > 0, аг-+1 < аг-, lim аг- = 0;
г—юо
тогда ряд (2.4) сходится к действительной величине s и справедлива оценка
(2.5) \з — зп\ < а.
п + 1?
т. е. величина ошибки п-й частичной суммы не больше, чем первый
отброшенный член.

190 III. Основания классического анализа
Рис. 2.2. Доказательство критерия Лейбница.
Доказательство. Обозначим через sn п-ю частичную сумму ряда (2.4).
Тогда из предположения монотонности следует, что S2k+i = S2fc-i + «2* — G2fc+i >
s2k-i и что 82k+2 = S2k — a>2k+i + a>2k+2 < *2k- Из положительности a2*+i следует,
что S2k+i < 82к, так что, комбинируя эти неравенства, мы получаем
S\ < 8$ < S$ < $7 < . . . < Sq < S± < S2 < SQ
(см. рис. 2.2). Следовательно, sn+k при всех к находится между sn и sn+i, и
(2.6) \sn+k - 8п\ < \зп+1 - зп\ = an+i.
Отсюда вследствие теоремы 1.8 следует сходимость {sn}, поскольку an+i
стремится к 0 при п —>■ оо. Наконец, оценка (2.5) получается путем рассмотрения
предела к —>• ос в (2.6) (с использованием теоремы 1.6). D
Примеры. Итак, мы установили сходимость рядов (1.4.29) и (1.3.13а):
i 1 1 1
i ! ! !
Однако мы не доказали строго, что первая сумма равна 7г/4, а вторая In 2 (см.
пример 7.11 ниже). Если превратить цепную дробь (1.6.7) в бесконечный ряд, мы
получим (см. формулу (1.6.16))
Pi_ _ Р1Р2 Р1Р2РЗ _ Р1Р2РЗР4
В\ В\В2 -02-Вз В3В4
Если предположить, что целые числа р, и дг положительны, то это ряд с
перемежающимися знаками (от второго члена и далее). Далее, мы имеем Вк -
qkBk-i + ркВк-2 > РкВк-2, из чего следует, что члены ряда монотонно убывают
по абсолютной величине. При дополнительном предположении, что 0 < рг < д,
для всех г > 1, (см. теорему 1.6.4), мы имеем
ВкВк-1 = ЧкВ1_х -\-pkBk-iBk-2 > 2pkBk-iBk-2
и, следовательно, также BkBk-i > 2k~1pkPk-i' •. • 'Pi- Это доказывает, что члены
ряда стремятся к нулю, и, согласно теореме 2.4, рассматриваемый ряд сходится.

111.2 Бесконечные ряды 191
Мажорирование и минорирование рядов. Следующий критерий
чрезвычайно полезен при исследовании бесконечных рядов с неотрицательными
членами.
(2.5) Теорема. Предположим, что 0 < аг < Ь{ для всех (достаточно больших) г.
Тогда ^ ж
^2i=o k сходится => 2г=о аг сходится,
Y^hzoа* расходится => YmLo ^« расходится.
Доказательство. Этот результат немедленно следует из следствия 1.14, если
ПОЛОЖИТЬ Sn — Y17=0 ai И Vn — Х)Г=0 &• * П
В качестве первого приложения этой теоремы приведем простое
доказательство расходимости гармонического ряда Yli>i J (Н- Оресме, ок. 1350 г.; см. Стройк
1969, р. 320). Заминорируем этот ряд следующим образом:
Ebi= 1 + 1+5 + 5 +1 + 1 + 7 + 5 +1+^ + ---+^ + £ + •••
Е<*.= 1 +1 + ; + \ +1 + \ +1 +1 + д + h + • • • + h+h + • • • •
1/2 1/2 1/2
Поскольку ^2 а{ расходится, из неравенства 0 < аг < 6г- следует, что
гармонический ряд ^2 hi также расходится.
В качестве другого примера рассмотрим ряд (1.2.18) для ех (например, при
jb=10):
, m 1Q2 ю3 1о4 ю5
Опустим первые 10 членов (это не влияет на сходимость), и сравним полученный
ряд с геометрической прогрессией (пример 2.2 при q = 10/11 < 1):
Ю10 1011 Ю12 Ю10/, 10 10-10 10-10-10
1U" 1U" _ iU Л iU 1U-1U 1U-1U-1U \
+ TIT + ~12!~ + ToTV + И + Tbl2 + 11-12-13 + " 7
Ю10/ 10 102 103 \
Из сходимости геометрической прогрессии следует сходимость ряда (2.7).
Аналогично можно доказать, что ряд (1.2.18) сходится при любых х. Такое сравнение
с геометрической прогрессией мы будем использовать в нескольких случаях (см.
критерии 2.10 и 2.11, лемму 7.1, теоремы 7.5 и 7.7).
(2.6) Лемма. Ряд
— — — — —
' " > ia ' 2а За 4а 5а
сходится при всех а > 1. Он расходится при а < 1.
Доказательство. Расходимость ряда при а = 1 (гармонический ряд) была
установлена выше. При а < 1 члены ряда становятся еще больше, так что ряд

192 III. Основания классического анализа
расходится в силу теоремы 2.5. Далее мы покажем, что ряд (2.8) сходится при
а = (к + l)/fc, где к > 1 есть целое число. Идея доказательства состоит в том,
что рассматривается ряд
1--L + -L-J- + J-- -У(-1).-н±
V2 № Щ Уь " £? ' W
который сходится в силу критерия Лейбница. Сумму двух его последовательных
членов можно заминорировать следующим образом:
/ллч 1 1 у/2г- fy2i^l „ 1
где Ск — 1/(к-2(к+1)/к) есть постоянная, не зависящая от г. Последнее
неравенство в (2.9) получается из тождества ак—Ък = (а—Ь)(ак~1+ак~2Ь+ак~3Ь2+...-\-Ьк~1)
при а = yli и Ь — y/2i — 1 следующим образом:
V2i-ty2i=l= ,..WI. 1W, , L____> 1
(2i)(*-i)/* + ... + (2г - 1)(к~1)/к ~ к • (2i)(k~1)/k'
Таким образом, согласно теореме 2.5, ряд (2.8) сходится при а = (к + 1)/к.
Наконец, при произвольном а > 1 существует целое число к такое, что а > (к + l)/fc.
Если еще раз применить теорему 2.5, мы получим сходимость при всех а > 1. D
Абсолютная сходимость
Пример. Согласно критерию Лейбница, ряд
/Л1М l l l l I
(2Л0) !__ + ___ + __. + ...
сходится (к In 2). Если мы перегруппируем ряд следующим образом:
iIAIIIIJLJLI J L
~2~4 + 3~6~8 + 5~ 10 ~12 + 7 " 14 ~ 16 + "' '
1/2 1/6 1/10 1/14
мы получим ряд
1 1 1 1 _1__ --(г -- --- -- \
2 ~ 4 + 6 ~ 8 + 10 ~ 2V ~2 + 3~4 + 5~"7'
сумма которого вдвое меньше, чем у первоначального. Это показывает, что
значение суммы бесконечного ряда может зависеть от порядка суммирования.
(2.7) Определение. Ряд ^°10 а'% называется перегруппировкой ряда Y^7Loai> если
каждый член Yll^oа* появляется в Yll^Lo ai Ровно один раз, и наоборот (это
значит, что существует биекция а : No —>■ No такая, что а\ — аа^у, здесь
No ={0,1,2,3,4,.-.}Л

111.2 Бесконечные ряды 193
Объяснение. Элегантное объяснение приведенного явления было дано Ри-
маном (1854, Werke, р. 235, "... ein Umstand, welcher von den Mathematikern des
vorigen Jahrhunderts ubersehen wurde ..." — "... одно обстоятельство, не
замеченное математиками прошлого столетия ...", нем.). В действительности Риман
показал гораздо больше: при любом заданном действительном числе А возможно
так переставить члены ряда (2.10), что полученный таким образом ряд будет
сходиться к А. Причина этого в том, что ряд, составленный из положительных
членов ряда (2.10) и ряд, составленный из его отрицательных членов,
л 1111
1+3+5+7+9+-
1
То
расходятся (или, что эквивалентно, ряд (2.10), у которого все члены заменены
на их абсолютные величины, расходится).
Идея доказательства состоит в том, чтобы взять несколько первых
положительных членов 1 + 1/3 + ... , пока сумма их не превзойдет А (это обязательно
произойдет, поскольку ряд из положительных членов расходится). Потом мы
прибавляем отрицательные члены до тех пор, пока сумма не станет меньше А
(это обязательно произойдет, потому что —1/2 — 1/4—... расходится). После этого
мы опять продолжаем прибавлять положительные члены, пока А не будет снова
превзойдено, и так далее. Продолжая далее этот процесс, мы получаем ряд с
перегруппированными членами, который сходится к А (ср. примеры на рис. 2.3).
VVvv
"v^v^V** "v** М
l.Z— l-h3 2 + 5+7 + 9 4+11+-*
I , I , L
20
40
60
1.5
1.4
1.3
1.2
1.1
1.0
\^\.~**\*~**4
i.5 = i + § + !-! + f + i + £ + .
^ч
20 40
Рис. 2.3. Перегруппировки ряда (2.10).
60
(2.8) Определение. Ряд (2.1) называется абсолютно сходящимся, если сходится
ряд
|ао| + |ai| + \а2\ + \а3\ + ... .
(2.9) Теорема (Дирихле 1837b). Если ряд ^^0а* абсолютно сходится, то все
его перегруппировки сходятся к тому же пределу.
Доказательство. По критерию Коши абсолютная сходимость означает, что

194 III. Основания классического анализа
Ve>0 ЗЛГ>0 Vn>7V VЛ: > 1 |an+i| + |an+2| + ... + |an+fc| < е.
Для заданного е > О и соответствующего N > О выберем целое число М таким
образом, что все члены ао, сц,..., адг имеются в М-й частной сумме s^- = X)t=oa«
перегруппировки. Таким образом, в разности sm — sfm, все члены ao, сц,.. .,ад-
исчезают (при га > М), и мы видим, что
\sm ~~ sm I < |адг+1| + |ajv+2|-h ...+ \aN+k\ < е,
где к является достаточно большим целым числом. Тем самым мы показали,
что sm — s'm -) 0 и что перегруппировка сходится к тому же пределу, что и
первоначальный ряд. D
Теперь мы сформулируем два критерия абсолютной сходимости
бесконечных рядов.
(2.10) Критерий частных (Коши 1821). Если члены ап ряда (2.1)
удовлетворяют условию
(2.11) limsup^±il < 1?
то ряд абсолютно сходится. Если Итт£п_юо |an+i|/|an| > 1, то он расходится.
Доказательство. Выберем число q такое, что limsup,^^ |an+i|/|a„| < q < 1.
В этом случае только конечное число частных |an+i|/|an| превосходит q, и мы
имеем
3N>0 Vn>N l-^-<q.
\Q>n\
Из этого, в свою очередь, следует, что |ajv+i| < (?laiv|> |алг+2| £ 92|алг|? |адг+з| <
д3|адг| и т.д. Поскольку геометрическая прогрессия сходится (у нас 0 < q < 1),
ряд X]»>ola*'l также сходится. Если liminfn-^oo |an+i|/|an| > 1,
последовательность {|an|} монотонно возрастает при п > АГ, и необходимое условие сходимости
(2.3) не удовлетворяется. D
Примеры. Общим членом ряда для функции ех является ап — хп /п\. В этом
случае |an+i|/|an| — \х\/(п-\-1) —>■ 0, так что ряд (1.2.18) абсолютно сходится при
всех действительных х. Аналогично, ряды для since и cos ж абсолютно сходятся
при всех х.
Для ряда (2.8) этот критерий не применим, потому что |an+i|/|an| = (п/{п-\-
1))«-Я.
(2.11) Критерий корня (Коши 1821). Если
(2.12) limsup Vki] < !»
п—юо
то ря# ^../^ абсолютно сходится. Если limsupn_>00 y|a^~| > 1, он расходится.
Доказательство. Как и в предыдущем доказательстве, выберем число q < 1,
строго большее limsupn_).00 \/|an|. Следовательно,

III.2 Бесконечные ряды 195
3N>0 Vn>N y\an\<q.
Отсюда вытекает, что \ап\ < qn при п > ЛГ, и из сравнения с геометрической
прогрессией следует абсолютная сходимость ряда Х1«-=о а»'- Если ^m suPn-»oc \/1а™1 >
1, условие (2.3) не удовлетворяется, и ряд не может сходиться. □
Двойные ряды
Рассмотрим двумерный массив действительных чисел
«00 + «01 + а02 + «03 + -
so
+ + + + +
«10 + «11 + «12 + «13 + • • . = Si
+ + + + +
= 52
«20 + «21 + «22 + «23 +
(2.13) + + + + +
«30 + «31 + «32 + «33 +
= s3
+ + + + +
V0 + vl + ^ 2 + t>3 + • •
???
и предположим, что мы хотим просуммировать их все. Существует много
естественных способов для этого. Можно сложить элементы г-й строки, обозна-
Еоо
г_0 s«> можно сложить элементы j-ro
столбца, обозначить результат как Vj, а потом вычислить YITLo vj- Можно также
выписать все элементы в некотором линейном размещении этой
последовательности. Например, мы можем начать с аоо, потом прибавить элементы a,j, для
которых г + j — 1, потом те, для которых г -f j — 2, и т. д. Это дает
(2.14) а0о + («ю + «oi) + («20 + «и + «02) + («зо + ...) + ••• •
Обозначим здесь пары индексов (0,0), (1,0), (0,1), (2,0),... как <т(0), сг(1),
<т(2), (т(3),... , так что а является отображением а : No —>• No х No, где
No х N0 = {{i,j) \i G No, J G N0} — так называемое декартово произведение
No на No- Для общего случая мы введем определение
(2.12) Определение. Ряд YlT=o ^к называется линейным размещением двойного
ряда (2.13) если существует биекция <т : No —>■ No х No такая, что 6* = «<т(*)-
Теперь зададим себе вопрос: приводят ли различные методы суммирования
к одному и тому же результату? Будут ли выполняться равенства
оо оо оо оо
(2.15) 50 + 5i 4- ... = ^2 \^2 ач) = ^2 [Y1 ач) = *>0 + Vi + . . . ,
i=0 j=0 j=0 i=0
и сходятся ли разные линейные размещения двойного ряда к одной и той же
величине?

196 III. Основания классического анализа
М
1 - 1 + 0 + 0 +..
+ + + +
0 + 1 - 1 + о +.
+ + + +
0 + 0 + 1 - 1 +..
+ + + +
0 + 0 + 0 + 1 -..
+ + + +
.= 0
+
.= 0
+
. = 0
+
.= 0
+
1 + 0 + 0 + 0 +... =1^0
м
Рис. 2.4а. Контрпример. Рис. 2.4Ь. Двойные ряды.
Контрпример, изображенный на рис. 2.4а показывает, что это не так, если
не ввести некоторые дополнительные предположения.
(2.13) Теорема. (Коши 1821, "Note VII"). Рассмотрим двойной ряд (2.13) и
предположим, что
т т
(2.16) 3B>0 Vm>0 ^]Г|а0-|<Я.
Тогда все ряды в (2.15) сходятся, и выполняются все равенства (2.15). Более
того, каждое линейное размещение двойного ряда сходится к одной и той же
величине.
Доказательство. Пусть &о + &i + &2 4- • • • есть линейное размещение
двойного ряда (2.13). Последовательность {^Г=о 1^*1) монотонно возрастает и
является ограниченной (по предположению (2.16)), так что ^2°10 \Ь{\ и Yl^o ^«' также
сходится. Аналогично мы можем установить сходимость рядов Si = X^Loau и
t=o a*i*
По примеру доказательства теоремы 2.9, приложим критерий Коши к ряду
X^oN и получим
V£>0 37V>0 \fn>N Vfc>l |6n+i| + |bn+2| + ...+ |bn+fc|<e.
Для заданного ООи соответствующего N > 0 выберем целое число М такое,
что все элементы &о, &ь • • •» ^n находятся в ящике 0 < г < М, 0 < j < М (см.
Рис. 2.46). При таком выборе 6о, 6i,..., бдг присутствуют как в сумме Х^_0 6» (для
/ > ЛГ), так и в YlT=o Si=oau (ПРИ m ^ М и п > М). Следовательно, при / > iV,
т> М и п > М мы имеем
(2.17)
>=0 7=0 »=0
< \bN+1\ + ...+ \bN+k\<e

III.2 Бесконечные ряды 197
при достаточно большом к. Положим s = Х^ъю ^* и пеРейдем к пределам I —у оо и
п -> ос в (2.17). Теперь поменяем порядок конечных суммирований YaLo Sj=o **
Ej=o2^Lo и перейдем к пределам / —> ос и га —>• ос. В силу теоремы 1.6 это
приводит нас к
I га | | п
'i=o
£*-*
t'=0
< е and
<е.
Следовательно, Х)|Ъю 8* и SJLo Ч? сходятся к одному и тому же пределу s. □
Произведение Коши двух рядов
Если нам нужно вычислить произведение двух бесконечных рядов X)i^o а* и
Ej^o fy' то слеДУет сложить все элементы двумерного массива
ао&о «о^1 ао&2 а>оЬз
aibo а\Ъ\ сцЬ2 сцЬз
(2.18) агбо о>2^1 ^2^2 ^2^з
«3^0 «3^1 «3^2 «3^3 • • • •
Если мы расположим элементы так, как это сделано в (2.14), то получим так
называемое произведение Коши двух рядов.
(2.14) Определение. Произведение Коши двух рядов Y^Lo а* и YITLo ^з ОПредеАЯ-
/ v ( 2^ ап-з 'bj\ = a0b0 + («о&1 4- «1^0) + (ао&2 + «1^>1 + «2^>о) + ... .
n=0^j=0 '
ется как
ОО / п
Вопрос в том, является ли произведение Коши сходящимся рядом и
представляет ли оно в действительности произведение рядов Yi>oa* и Yj>o^J-
(2.15) Контрпример (Коши 1821). Согласно критерию Лейбница, ряд
V^4" л/3 л/4 + v^
сходится. Рассмотрим произведение Коши этого ряда на самого себя. Поскольку
/ ,, an-j ' Oj
i=o
= £
1
>
2n + 2
Vn + 1 - j • y/JTl - n + 2
(это неравенство является следствием неравенства (п + 1 — х)(х + 1) < (1 + ™/2)2
при 0 < х < п), необходимое условие (2.3) сходимости произведения Коши не
удовлетворяется (см. рис. 2.5). Этот пример иллюстрирует тот факт, что
произведение Коши двух сходящихся рядов не обязательно сходится.

198 III. Основания классического анализа
Рис. 2.5. Расходимость произведения Коши в контрпримере 2.15.
(2.16) Теорема (Коши 1821). Если два ряда Y^TLo а* и YlTLo^j абсолютно
сходятся, их произведение Коши также сходится, и мы имеем
(2.19)
(ОО ч • ОО ч ОО / П ч
г=0 ' ^ j=0 ' п=0 ^ j=0 '
Доказательство. По предположению мы имеем £}£10 1а*1 — ^ и Sj^Lo Ifyl -
5з. Таким образом, для двумерного массива (2.18) для всех т > О
яг тп
г=0 j=0
и мы можем применить теорему 2.13. Сумма г-й строки равна Si — аг • Ylj=o^J и
J2°l0 Si = (Х1|Ъ:0 a«')(]C^Lo fy)* Согласно теореме 2.13 произведение Коши, которое
является линейным размещением (2.18), также сходится к этому значению. D
Примеры. Рассмотрим два ряда при \q\ < 1:
1 + я + q2 + q3 + • • • =
Их произведение Коши
1-9
l-q + q2-q3 +
1+9
i + q2 + q4 + q6 + • • •
действительно является произведением (1 — q) 1и(1+д) 1.
Произведение Коши абсолютно сходящихся рядов
X2 ж3
1 + Х+2! + 3!+'--
1 + У+Уй+Уй + -
дает ряд для ех+у (используйте биномиальное тождество теоремы 1.2.1).

III.2 Бесконечные ряды 199
Замечание. Утверждение теоремы 2.16 остается справедливым, если только один
из рядов сходится абсолютно, а второй сходится (Ф. Мертенс 1875, см. упр. 2.3).
В предположении, что ряды ^,аг, ^ bj, а также их произведение Коши
(определение 2.14) сходятся, тождество (2.19) справедливо (Абель 1826, см. упр.
7.9).
Изменение порядка суммирования и предельных переходов в
бесконечных рядах
В нескольких местах в главе I мы сталкивались с проблемой перемены
порядка суммирования бесконечного ряда и предельного перехода (например, при,
получении ряда для ех в разд. 1.2 и рядов для sin ж и cos ж в разд. 1.4). Мы
рассматривали ряд dn — YlT=oSnJi зависящий от целочисленного параметра п, и
использовали тот факт, что Ит^^оо dn = Y^TLo^111™^™ s^j- Уже в разд. 1.2
(после формулы (1.2.17)) мы говорили, что это не всегда справедливо и что при этом
необходима некоторая осторожность. В следующей теореме сформулированы
достаточные условия справедливости такой перемены.
(2.17) Теорема. Пусть все элементы последовательности {sqj, sij, S2j, • • •}
имеют одинаковый знак и \sn+ij\ > |snj| для всех п и j. Если существует грань В
такая, что Yll=o \snj\ < & ^ля всех ™ > О, то
оо со
(2.20) lim > snj => lim sn7.
j=0 j=o
Доказательство. Идея доказательства состоит в том, чтобы
переформулировать предположения так, чтобы можно было бы непосредственно использовать
теорему 2.13. В начале этого раздела мы видели, что каждый ряд можно
превратить в бесконечную последовательность, если рассмотреть частичные суммы
(2.2). И обратно, если заданы частичные суммы so, si? 82,..., мы можем
однозначно определить элементы а,- такие, что Х)Г=оа* ~ Sn* Для этого нужно положить
а0 = 5q и а,- = Si — 5t_i при i > 1. Применяя это рассуждение к
последовательности {soj, sij, 52j,...}, мы определяем
п
clqj := Sqj, Qij •= $ij — Si-ij, так ЧТО /.aij = snj-
i=0
Заменяя snj этим выражением, приведем (2.20) к виду
оо п
<2-21) А™ Е Еа" = Е Д™ Еа'г
j=0 г=0 j=0 i=0
Меняя порядок суммирования в выражении в левой части (2.21) (это можно
делать в силу теоремы 1.5), мы видим, что (2.21) эквивалентно (2.15). Таким
образом, нам остается только проверить условие (2.16). Из предположений,
относящихся к {soj, sij,...} следует, что все элементы aoj, а^,... имеют одинаковый
знак. Следовательно, мы имеем

200 III. Основания классического анализа
1=0 t=0 j=0 j=0
В силу теоремы 2.13 из этого следует (2.21), и следовательно также (2.20). D
(2.18) Пример. Сейчас мы дадим строгое доказательство теоремы 1.2.3. Из
биномиальной теоремы следует, что
/ у\п У2(1--) У3(1- 1)(1-1)
(2.22) (l + i) =1 + у+У-\^>+У[ 1"2М3 »>+...,
что представляет собой ряд, зависящий от параметра п. Положим
_, _ 2/2(W) у3(1-^)(1-^)
$п0 — J-? ^nl — У? $п2 — : ~ , 5пз — - - - ,
Для фиксированного у все элементы последовательности {so./, sij,...} имеют
одинаковый знак, и {Isojl, l5ij'l? • • •} монотонно возрастает. Более того, мы имеем
j=0 j=0 */*
потому что по критерию частных ряд YlT=o \у\Ч 3* сходится. Следовательно,
можно применить теорему 2.17, и мы получаем,
lim
п—юо
(1+ynY = 1+y+1i + yi + yi+--
Упражнения
2.1 Вычислите произведение Коши двух рядов
X X у у
f(x)=X- —+ --... И д(у)=1-- + --...
и найдите ряд для f(x)g(y) + g{x)f(y). Обоснуйте свои вычисления. Не
кажется ли вам результат знакомым?
2.2 Покажите, что произведение Коши двух расходящихся рядов
(2 + 2 + 22 + 23 + 24 + ...) (-1 + 1 + 1 + 1 + 1 + 1 + ...)
сходится абсолютно.

111.2 Бесконечные ряды 201
t
yyyWWWWWWWWWWWVww^
£(-ir«»
ЕнгЕ0''0»-'
t=0
Рис. 2.6. Расходимость произведения Коши из упр. 2.4.
2.3 (Мертенс 1875). Предположим, что ряд
Y^zO a* СХ°ДИТСЯ и что YlT=o bj
сходится абсолютно. Докажите, что
произведение Коши, соответствующее
определению 2.14, сходится, и что
соотношение (2.19) справедливо.
Указание.
Положите сп = ^j=oan-jbj и
примените неравенство треугольника (только к
первым суммам) в тождестве
а0ьо
ахЬ0
а2Ь0
аъЬ0
а<р\
а\ъ\
а2Ьх
аъъ\
\алЬх
а<Рг
ахЪ2
а2Ь2
аъЪ2
ш
а0Ьъ\
а\Ь-\
а2Ьъ\
аъЪъ
аФЛйф*3£Ф(\
w£h
шшт
EZ
2п
п 2n-j
2п 2n-j
XIе'- (Ha«){Y^bi) = Y.bj S ai + Yl bi XI a>-
*=0 *=0 j=0 j=0 i=n + l j=n + l *=0
2.4 Определите постоянные ai, аг, аз, сц,... так, чтобы произведение Коши двух
рядов
(l - аг + а2 - а3 + ...) (l - сц + а2 - а3 + ...) = (l - 1 + 1 - 1 + ...)
стало расходящимся рядом 1 —1+1 —... . Покажите, что ряд 1—ai+a2— аз+...
сходится (рис. 2.6). Может ли он сходится абсолютно?
Указание. Использование производящей функции для чисел 1, — ai, a2,
—03,... сводит это упражнение к известной формуле главыI и к
произведению Валлиса.
2.5 Обоснуйте формулу (1.5.26). Для этого возьмите логарифм и используйте
идеи примера 2.18.

202 III. Основания классического анализа
Ш.З Действительные функции и непрерывность
Здесь мы называем Функцией переменной величины такую величину,
которая любым образом составлена из этой переменной величины и
постоянных. (И.Бернулли 1718, Opera, vol. 2, p. 241)
Следовательно, если /(f + с) обозначает некоторую произвольную
функцию ... (Эйлер 1734, Opera, vol. XXII, p. 59)
Если теперь любому х соответствует единственное конечное у, ... то у
называется функцией х на этом интервале ... Это определение не требует
существования общего правила для разных частей кривой; можно
представить себе, что кривая составлена из весьма разнородных компонент,
или что она нарисована и не следует никакому закону.
(Дирихле 1837)
Со времен Декарта действительные функции у — f(x) действительной
переменной х являются универсальным средством изучения геометрических кривых
и, со времен Галилея и Ньютона, средством для механических и астрономических
вычислений. Слово "functio" было предложено Лейбницем и И. Бернулли,
обозначение у = f(x) было введено Эйлером(1734) (см. цитаты). В эпоху Лейбница,
Бернулли и Эйлера действительные функции обычно представляли себе
составленными из элементарных функций ("expressio analytica quomodocunque .... Sic
a -f 3z, az — Az2, az + by/a2 — z2, cz etc. sunt functiones ipsius z" — "каким бы ни
было аналитическое выражение .... Так, a + Zz, az — Az2, az-\-h\Ja2 — z2, cz и т.п.
суть функции от z" — лат., Эйлер 1748). При этом допускались разные формулы
для разных областей ("curvas discontinuas seu mixtas et irregulares appellamus" —
"кривые, называемые не непрерывными либо составными и нерегулярными" —
лат.). 19 век, в основном под влиянием уравнения распространения тепла Фурье
и исследований рядов Фурье, проведенных Дирихле, принес более широкое
определение: "любая нарисованная кривая" или "любые значения у, определенные в
зависимости от значений я" (см. цитату выше).
(3.1) Определение (Дирихле 1837). Функция f : А —>• В состоит из двух
множеств — области определения А и области значений В, и из правила, которое
сопоставляет каждому х Е А единственный элемент у Е В. Это соответствие
обозначается как
у — f[x) или х у-ь fix).
Мы говорим, что у является образом х и что х является прообразом у.
На протяжении этого раздела областью значений будет Ш (или некоторый
интервал в!),а областью определения — интервал или объединение интервалов,
имеющих вид
(а, Ь) = {х £ М | а < х < Ь}, или [а, Ь] = {х е Ш \ а < х < Ь}, или
(а, Ь] = {х G М | а < х < Ь}, или [а, оо) = {х£Ш\а<х< ос}, или ....
Интервал (а, Ь) называется открытым, а [а, Ь] — замкнутым интервалом или
отрезком.
При описании функций, которые заданы разными выражениями на
различных частях А, мы будем обычно использовать фигурную скобку, как в
нижеследующих примерах.

III.3 Действительные функции и непрерывность 203
Примеры. 1. Функция / : [0,1] ->■ М
Г х 0< х< 1/2
I 1 — х 1/2 < ж < 1,
изображена справа. Видно, что у некоторых у Е Ш
не существует прообразов, а у некоторых их больше
одного.
2. Следующую функцию можно определить или
как предел единого выражения, или с помощью
скобки, рассматривая отдельно три случая:
f(x) = lim arctg (пх)
п—юо
(3.2)
= <
( тг/2 х > О
О х = 0
-тг/2 х < 0.
3. Следующая функция, нарисовать которую
затруднительно, предложил Дирихле (см. Werke, vol. 2,
p. 132, 1829, "On aurait un exemple d'une fonction ..."
— "Будем иметь пример функции ...", — франц.):
( 0 х иррационально
(3.3) /(* = .
{1 х рационально.
4. Эта функция похожа на функцию Дирихле,
однако с увеличением знаменателей х ее пики
становятся ниже:
0 х иррационально
\/q х — p/q простая дробь.
(3.4) /(*) = { '
5. Когда х стремится к нулю, 1/х стремится к ос,
поэтому
(3.5) f(x) = [s[n^X>> Х^°
10 х = 0
будет иметь бесконечно много осцилляции в
окрестности нуля (Коши 1821).
6. Благодаря множителю х в этом случае
осцилляции вблизи нуля имеют меньшую амплитуду,
однако их по-прежнему бесконечно много (Вейерштрасс
1874):
(з.б) /(*) = (ж*81п(1/ж) хф0
10 ж = 0.

204 III. Основания классического анализа
7. Согласно Вейерштрассу (1872), наш последний
пример принадлежит Риману (см. разд. III.9). Здесь
функция определена бесконечным сходящимся
рядом
(3.7, /(,,-f*^!.
п = 1
Непрерывные функции
... f(x) назовем непрерывной функцией, если ... численные значения
разности
f(x + a)-f(x)
неограниченно убывают вместе с а ...
(Коши 1821, Cours d 'Analyst, p.43)
Здесь мы называем величину у непрерывной функцией ж, если, задаваясь
величиной е, мы можем доказать, что существует величина 6 такая, что
для любой величины, лежащей между хо — 5 ... хо + 6 соответствующая
величина у лежит между уо — е .. .уо + е. (Вейрштрасс 1874)
Коши (1821) ввел понятие непрерывной функции, требуя, чтобы
неопределенно малые изменения х приводили бы к неопределенно малым изменениям у
(см. цитату). Больцано (1817) и Вейерштрасс (1874) были более точны (вторая
цитата): разность f(x) — f(xo) должна быть сколь угодно мала, если разность
х — хо достаточно мала.
(3.2) Определение. Пусть А есть подмножество Ш и хо £ А. Функция f : А -> I
является непрерывной в точке хо, если для каждого е > О существует S > О
такое, что для всех х Е А, удовлетворяющих условию \х — хо\ < 8, мы имеем
\f(x) - f{x0)\ < е, или
I Ve>0 36 > 0 Ухе А : \x-x0\<S \f(x)-f{x0)\<e.\
Функцию f(x) называют непрерывной, если эта функция непрерывна во всех
точках х$ £ А.
На рис. 3.1а представлена непрерывная функция, а а на рис. 3.1b-3.1f —
функции с разрывами.
Обсуждение примеров (3.1)-(3.7). Функция (3.1) непрерывна везде,
даже при хо — 1/2; функция (3.2) разрывна в 0; (3.3) разрывна везде; (3.4)
непрерывна при иррациональных хо и разрывна при рациональных xq (см. упр. 3.1);
(3.5) разрывна при хо = 0; (3.6) непрерывна везде, даже при х — 0; (3.7), у
которой, как кажется, имеются громадные колебания, тем не менее везде непрерывна,
как будет далее показано в теореме 4.2.
(3.3) Теорема. Функция f : А —У Ш непрерывна в точке xq Е А тогда и только
тогда, когда для каждой последовательности {жп}п>1 с хп Е А
(3.8) lim f(xn) = f(xo), если lim хп = х$.
n-юо п-юо

III.3 Действительные функции и непрерывность 205
Рис. 3.1. Непрерывные и разрывные функции.
Доказательство, При заданном е > О выберем 8 > О, как в определении
3.2. Поскольку хп —> хо, существует N такое, что \хп — хо\ < 8 при п > N. В
силу непрерывности в точке жо мы имеем \f(xn) — f(xo)\ < s при п > AT, и (3.8)
справедливо.
Теперь предположим, что условие (3.8) выполнено, но f(x) разрывна в точке
xq. Отрицание непрерывности в точке xq формулируется как
3е>0 VJ>0 ЗхеА : \х-х0\<8 \f{x)-f(x0)\>e.
Идея доказательства состоит в том, чтобы взять 8 = 1/п и приписать величине х
(которая зависит от 8) индекс п. Это дает последовательность {хп} с элементами
из А такими, что \хп — Xq\ < 1/п (следовательно, хп —>• жо), и в то же время
\f{xn) — fixo)\ > ^? что противоречит (3.8). □
(3.4) Теорема. Пусть /:А-+Шид:А-*Ш являются непрерывными в точке
xq Е А функциями, и пусть Л — действительное число. Тогда функции
f + 9, А-/, /•#, //# {если д(хо)фО)
также являются непрерывными в точке xq функциями.
Доказательство. Возьмем последовательность {хп} с элементами,
содержащимися в А и сходящуюся к хо- Из непрерывности функций / и д следует, что
}(хп) —>■ fixo) и д(хп) —> ^(жо) при п —>• ос. Тогда согласно теореме 1.5
/(ж„) + flf(a;„) ->• f(x0) + flf(aJo),
так что /+gf является непрерывной в точке хо в силу теоремы 3.3. Непрерывность
остальных функций можно доказать аналогичным образом. D

206 III. Основания классического анализа
Пример. Очевидно, что постоянная функция f(x) — а является непрерывной.
Функция f(x) = х также непрерывна (положите S — е в определении 3.2). В
силу теоремы 3.4 все полиномы Р(х) = ао + сцх + ... + опжп непрерывны, и
рациональные функции R(x) = P(x)/Q(x) непрерывны во всех точках жо, где
ЯЫ ф о.
Теорема о промежуточном значении
Эта теорема была известна давно ...
(Лагранж 1807, Oeuvres vol. 8, p. 19, см. также р. 133)
Геометрически эта теорема представляется очевидной. Без колебаний ее
использовали Эйлер и Гаусс (см. цитату). Только Больцано нашел, что "rein analytisher
Beweis" (чисто аналитическое доказательство, — нем.) было необходимо для
того, чтобы привнести больше строгости в Анализ и Алгебру.
(3.5) Теорема (Больцано 1817). Пусть f : [а, Ь] —»■ М является непрерывной
функцией. Если /(а) < с и f(b) > с, то существует £ Е (а, Ь) такое, что /(£) = с.
Доказательство. Мы докажем утверждение теоремы для с — 0. Из этого
специального случая общий результат следует, если рассмотреть f(x) — с вместо
я*)-
Множество X = {х Е [a, b] ; f(x) < 0} не пусто (а Е X) и мажорируется
величиной 6. Следовательно, в силу теоремы 1.12 существует наименьшая
верхняя грань £ = supX. Мы покажем, что /(£) = 0 (рис. 3.2). Предположим, что
/(£) = К > 0. Положим е — К/2 > 0. Из непрерывности f(x) в точке £ следует
существование некоторого S > 0 такого, что
\f{x)-K\<K/2 при \х-£\<6.
Из этого следует, что f(x) > ИГ/2 > 0 при £ — S < х < £, что противоречит тому,
что £ есть наименьшая верхняя грань X.
Случай /(£) = К < 0 исключается аналогично. D
Рис. 3.2. Доказательство теоремы Больцано.

111.3 Действительные функции и непрерывность 207
Теорема о максимуме
Этой теоремой, которая утверждает, что непрерывная функция
действительной переменной достигает своих точных верхней и нижней граней, т. е.
обязательно имеет максимум и минимум, Вейерштрасс создал инструмент,
незаменимый в настоящее время для математиков, занимающихся
тонкими аналитическими или арифметическими исследованиями.
(Гильберт 1897, Gesammelte Abh., vol. 3, p. 333)
В лекциях Вейрштрасса 1861 г. следующая теорема названа "Hauptlehrsatz"
(главной теоремой, — нем.). Она была опубликована Кантором в 1870 г.
(3.6) Теорема. Если f : [а, Ь] —>• Ш является непрерывной функцией, то она
ограничена на [а, Ь] и достигает своих максимума и минимума, т.е. существуют
и G [а, Ь] и U Е [а, Ь] такие, что
(3.9) f(u) < f(x) < f{U) для всех х Е [а, Ь].
Обсуждение предположений. Функция / : (0,1] —»• М, определенная как
/(ж) = 1/ж, не ограничена на А = (0,1]. Следовательно, предположение о том,
что область А замкнута, является важным.
Пример функции / : [0, оо) —> М, заданной как f(x) = ж2, показывает, что
ограниченность области определения функции f(x) является важным
предположением.
Функция / : [0,1] —>■ М, определенная как /(1/2) = 0 и
f(x) = {х-1/2)-2 при хф1/2,
является разрывной в точке х — 1/2 и неограниченной. Таким образом, важно
предположить, что функция является всюду непрерывной".
Наш последний пример — это функция / : [0.1] —>■ М,
которая ограничена, но не имеет максимума:
Г —Зж + sin(l/x) при х ф 0
"х> = 1 п п
L 0 при х — 0 .
Наименьшая верхняя грань множества {f(x) \ х Е [0,1]}
равна 1, однако не существует U G [0, 1] такого, что
f(U) = 1.
Доказательство теоремы 3.6. Сначала докажем, что f(x) ограничена на
[а, 6]. Предположим противное:
(3.10) Vn>l Зхп£[а,Ъ] |/(zn)|>n.
Согласно теореме Больцано-Вейерштрасса (теорема 1.17), в последовательности
£i,£2, £3, • • • содержится сходящаяся подпоследовательность. Чтобы не вводить
для нее новых символов, обозначим ее члены опять через #i, жг, жз,... и скажем
"выделив подпоследовательность, предположим, что" linin
—юо хп — £. Поскольку
/непрерывна в точке £, из теоремы 3.3 следует, что lin^^oo f(xn) = /(£). Это
противоречит предположению (3.10) и доказывает ограниченность f(x).
Чтобы доказать существование U £ [а, 6], удовлетворяющего соотношению
(3.9), рассмотрим множество Y = {у ; у — f(x), а < х < b}. Это множество
не пусто и ограничено (в чем мы только что убедились). Следовательно точная
верхняя грань М = sup У существует. По определению 1.11 точной верхней грани

208 III. Основания классического анализа
величина М—е (при произвольном е > 0) не является верхней гранью У. Выбирая
е — 1/п, мы найдем последовательность элементов хп Е [а, 6], удовлетворяющих
соотношению
(3.11) М -1/п< f(xn) < М.
Применяя теорему Больцано-Вейерштрасса и выделяя сходящуюся
подпоследовательность {хп}, обозначим ее предел через U — Нп^-юо хп. В силу
непрерывности f(x) в точке U из (3.11) мы получаем /(17) = М.
Существование минимума доказывается аналогично. D
Монотонные и обратные функции
(3.7) Определение. Пусть А и В являются подмножествами Ш. Функцию } :
А —>- В называют
• инъективной, если f{xi) Ф f{x2) Щи х1 ф х2 ,
• сюръективной, если V у Е В Зх Е A f(x) = у ,
• биективной, если она является инъективной и сюръективной,
• возрастающей, если f{xi) < /(жг) nvu xi < х2 >
• убывающей, если f{xi) > /(жг) при х\ < ж 2 ,
• неубывающей, если f{xi) < /(^2) яри #1 < ж2 ,
• невозрастающей, если f{xi) > /(жг) ™PW ж1 < #2 ,
• монотонной, если она является невозрастающей или неубывающей, и
• строго монотонной, если она является возрастающей или убывающей.
Строго монотонные функции являются инъективными. Интересно, что
обратное утверждение для действительных непрерывных функций, определенных
на интервале, является также справедливым.
(3.8) Лемма. Если функция f : [а, Ь] —>• Ш непрерывна и инъективна, она является
строго монотонной.
Доказательство. Надо доказать, что для любых i
трех точек и < v < w справедливо соотношение ^v) t
(3.12) f(v) лежит между f(u) и f{w) .
В самом деле, допустим, что величина f(v) лежит вне Т
этого интервала, причем она ближе, скажем, к f(u).
Тогда существует такое £, лежащее между v и ги, что Л^)г
f(u) — /(£) (теорема 3.5), а это противоречит инъектив-
ности /. Следовательно, если а < с < d < 6, единственно
возможными являются неравенства и v £ w
/(о) < f(c) < f(d) < f(b) или f(a) > /(с) > /(d) > f(b);
все другие конфигурации неравенств противоречат (3.12). D
Из сюръективности функции / : А —>■ В следует, что каждое значение у £ В
имеет по меньшей мере один прообраз. Поэтому из инъективности следует
единственность этого обратного образа. Следовательно, биективная функция имеет
обратную функцию /_1 : В —> Л, определенную как
(3.13) Г\у)=х ^ f(x)=y.

III.3 Действительные функции и непрерывность 209
(3.9) Теорема. Пусть функция f : [а, Ь] —У [с, d\ является непрерывной и
биективной. Тогда обратная функция /-1 : В —У А также является непрерывной.
Доказательство. Пусть последовательность {уп}^ где уп Е В, такова, что
Ншп-юо уп = уо. Используя теорему 3.3, надо показать, что НгПп-юо f~1{yn) =
- /_1(Уо)- Рассмотрим последовательность {хп} = {/_1(Уп)}- Пусть {х'п} есть
сходящаяся подпоследовательность (которая существует в силу теоремы Боль-
цано-Вейерштрасса). Обозначим ее предел как хо- Из непрерывности f(x) в точке
xq следует, что
f(x0) = lim f(x'n) = lim y'n = y0
n—too n—too
и, следовательно, xq — f~1{yo)- Таким образом, каждая сходящаяся
подпоследовательность последовательности {хп} = {/_1(Уп)} сходится к f~1(yo)- Эта
точка является единственной точкой сгущения последовательности {f~1{yn)} и мы
имеем /-1(уп) —> /_1(2/о) (см. также упр. 1.8). □
Пример. Каждая из функций ж2, ж3,... является строго монотонной на [0, оо)
и имеет там обратную функцию: у/х, у/х, .... Согласно теореме 3.9 эти функции
непрерывны.
Предел функции
Возможно, что понятие предела функции впервые с достаточной
строгостью определил Вейерштрасс.
(Принсгейм 1899, Enzyclopddie der Math. Wiss., Band II.1, p. 13)
Предположим, что f(x) в точке xq не является непрерывной или даже не
определена в ней. В этом случае интересно выяснить, существует ли, по
крайней мере, предел функции f(x) при ж, приближающемся к xq. Очевидно, что xq
должно быть тесно связано с областью определения /. Мы будем говорить, что
xq является точкой накопления множества Л, если
(3.14) V£>0 ЗхеА Ъ<\х-хо\<8.
Для ограниченного интервала множество точкек накопления состоит из
интервала и двух его конечных точек.
(ЗЛО) Определение. Рассмотрим функцию f : А —>■ 1R, и пусть xq является
точкой накопления А. Мы говорим, что предел f(x) в точке хо существует и
равен уо, т. е.
(3.15) lim f(x) = уо,
X—УХо
если
(3.16) Уе > 0 36 > О \/х G А : 0 < \х - х0\ < S \f(x) - у0\ < е.
Это определение можно изменить так, чтобы включить в него такие
ситуации, когда Xq = ±ос и/или уо = ±ос (см., например, формулу (1.10)). Из

210 III. Основания классического анализа
предположения, что хо — точка накопления, следует, что множество х Е Д
О < \х — хо\ < S не пустое.
На основе определения ЗЛО условие непрерывности f(x) в точке хо можно
сформулировать следующим образом (см. определение 3.2):
(3.17) lim f(x) существует и lim f(x) = f{xo).
X—YXq X—¥Xq
Примеры. Функция, изображенная на рис. 3.1Ь, имеет предел Y\mx^Xof{x))
отличный от f(xo). Для функции (3.4) предел lim^-^xo f(x) существует для всех
хо (см. упр. 3.1; имейте в виду, что точка хо явно исключена в определении 3.10)
и lim*-^ f(x) = 0.
Более слабым свойством является существование односторонних пределов.
(3.11) Определение. Мы говорим, что существует предел функции f(x) в точке
хо слева (соответственно справа), если (3.16) справедливо при условии х < xq
(соответственно хо < х). Эти пределы обозначаются
(3.18) lim f(x) = уо и соответственно lim fix) = уо-
x-txo- x-tx0 +
Функции, изображенные на рис. 3.1Ь, 3.1с и 3.1d обладают левосторонними и
правосторонними пределами (часто равными /(жо)). У функций, изображенных
на рис. 3.1е и 3.1f, эти пределы не существуют. Следующая теорема является
аналогом критерия Коши (теоремы 1.8).
(3.12) Теорема (Дедекинд 1872). Для существования предела lim^-^ f(x)
необходимо и достаточно, чтобы
(3.19) Ve>0 Э5>0 Vx,x Е А : °< |* " Х°\ <\ \f(x) - f{x)\ < е.
и < \х — Хо\ < д
Доказательство. Необходимость следует из неравенств
I/O") - /(*)1 < 1/(*) ~Уо\ + \уо- /(2)| < 2е.
Для доказательства достаточности выберем какую-нибудь сходящуюся к хо
последовательность {х{} с xi Е А. Из (3.19) следует, что последовательность
{Уг} с yi — f(xi) является последовательностью Коши и, согласно теореме 1.8,
сходится к некоторому пределу уо- Для любого ж, удовлетворяющего условию
0 < \х — хо\ < J, мы теперь получим (опять же с помощью (3.19)), что
1/(*) - Stol < \f(x) - Г(х{)\ + \f{xi) - y0\ < 2e
при достаточно больших г. D
Аналогичные результаты имеют место и в случае хо — ±ос или когда
пределы односторонние.

111.3 Действительные функции и непрерывность 211
Упражнения
3.1 Покажите, что функция (3.4) непрерывна во всех иррациональных хо и,
разумеется, разрывна в рациональных х$.
Указание. Если у вас возникли затруднения, возьмите хо = уД-\ке= 1/10
и определите, при каких значениях х будет f(x) > е. Отсюда определяется
то £, для которого утверждение определения 3.2 справедливо.
3.2 (Прингсгейм 1899, р. 7). Покажите, что функция Дирихле (3.3) может быть
представлена в виде
f(x) = lim lim (cos(n!7ra?)) .
n-»oo m-юо x
3.3 Вычислите пределы
ж2 + Зж + 2 ,. л/4 + х - л/4 - х
lim - —, lim .
х-¥-1 х* — 1 х-+0 2х
Не забудьте, что (у/а — vb)(y/a + л/b) = а — Ь.
3.4 Покажите, что если / : [а, 6] —У [с, d\ непрерывна в точке xq и д : [с, d\ —>
[щу] непрерывна в точке уо = /(#о)> сложная функция (д о f)(x) — g{f(x))
непрерывна в точке жо-
3.5 Вот несколько функций / : А —> М:
1) f(x)=x-8in(l/x)-2x А =[0,0.2]
2) f{x) = х/{х2 + 1) А = [-4, +4]
3) та же функция А = (—ос, +оо)
4) /(ж) = (1/л/йпж) - 1 А = (0,тг)
5) та же функция А = [0,7г]
6) f(x) = ^ж~-8т(ж2) Л = [0, 7]
7) та же функция А — [0, ос)
8) f{x) = arctg {(х - 0.5)/(ж2 - 0.1ж - 0.7)) А = [-1.5,1.5]
9) /(ж)=зт(ж2) А = [-5,5]
10) та же функция А = (—ос, оо)
11) /(ж) = ^ж~ i4 = [-l,l]
12) та же функция А = (—ос, ос)
13) f(x) = cos х + 0.1 sin(40z) Л = [-1.6,1.6]
14) f{x) = ж - [ж] А= [0,3]
15) f(x)=y/x-sm(l/x)-2y/x А = [0,0.1]
16) f(x)=3-l/y/x{l-x) Л = (0,1)
17) fix) = sin(5/s) - х А = [0, 0.4]
Здесь [ж] обозначает наибольшее целое число, не превосходящее ж. В тех
случаях, когда вышеприведенные определения /(ж) не имеют смысла (например,

212 III. Основания классического анализа
когда некоторый знаменатель равен нулю), положите f(x) = 0. Определите,
какие из этих функций изображены на рис. 3.3.
Рис. 3.3. Графики 12 функций из упр. 3.5.
3.6 Какие из функций упр. 3.5 непрерывны на А? В каких точках они разрывны?
3.7 Какие из функций упр. 3.5. обладают максимальным значением на А? Какие
достигают минимального значения на А?

111.4 Равномерная сходимость и равномерная непрерывность 213
III.4 Равномерная сходимость и равномерная
непрерывность
В работе г-на Коши можно найти следующую теорему: "Если члены ряда
ио + и\ + U2 + ... — непрерывные функции, ... то сумма s ряда — тоже
непрерывная функция ж." Однако мне кажется, что существуют исключения
из этой теоремы. Например, ряд
sin х — \ sin 2х + | sin Зх ...
разрывен при каждом значении (2га + 1)7г величины ж, ...
(Абель 1826, Oeuvres, vol. 1, p. 224-225)
После эпохи Коши—Больцано (первая половина 19-го столетия) в анализе
оставались два важных пробела. Во-первых, понятие равномерной сходимости,
которое проясняет что такое предел последовательности непрерывных функций
и интеграл от этого предела. Во-вторых, понятие равномерной непрерывности,
обеспечивающей интегрируемость непрерывных функций. Оба эти пробела были
восполнены Вейерштрассом и его школой (вторая половина 19-го столетия).
Предел последовательности функций
Рассмотрим последовательность функций Д, Д, /з,... : А —» Ш. При
заданном х £ А значения Д(ж), /2(ж), /з(я)>.. • составляют последовательность чисел.
Если предел
(4.1) lim fn(x) = f{x)
п—юо
существует для всех х Е А мы говорим, что {/п(я)} поточечно сходится на А
к f(x). Коши утверждал в своем Курсе анализа (1821, Cours d'analyse algebrique,
p. 131; OeuvresII.3, p. 120), что если (4.1) сходится при всех х из Аи если все fn(x)
являются непрерывными, то f(x) также непрерывна. Приведем четыре
контрпримера к этому утверждению; первый принадлежит Абелю (1826, см.
вышеприведенную цитату).
Примеры.
a) (Абель 1826, см. верхний левый график на рис. 4.1)
1Л л . г / \ • sin2z sin3z sin4z sinnx
(4.2a) fn(x) =sinz h — — + ...± .
Z 6 4 n
На рис. 4.1 представлены Д(ж), Д(ж),/з(сс) и Доо(#)- По-видимому, что {/п(я)}
сходится к прямой у = ж/2 при —7г < х < 7г (это можно доказать с помощью
теории рядов Фурье), но /п(7г) = 0 и при 7Г < х < 37Г пределом является у —
х/2 - 7Г. Таким образом, предельная функция разрывна.
b) (правый верхний график рис. 4.1)
(4.2Ь) fn{x) = xn на Л = [0,1], limfn{x) = l° M<1
п—юо
Х=1.
с) (нижний левый график на рис. 4.1)

214 III. Основания классического анализа
sin 2х sin Зж
у = sin х (-
п = 100
Рис. 4.1. Последовательности непрерывных функций с разрывным пределом.
(4.2с)
х--1 f"1 |X|<1
•Мж) ~ п , л, lim/n(s)=< 0 х = 1
Хп -\- 1 п-юо I
1+1 ж>1.
d) (нижний правый график рис. 4.1)
(4.2d) fn(x) = (l-x2)n пъ А = [-1,1], lim/„(x) = (°
0 ж^О
Другим примером, который нам уже встречался, является /п(ж) = arctg(nx)
(см. формулу (3.2)).
е = .035
Рис. 4.2. Последовательность равномерно сходящихся функций.
Объяснение (Зейдель 1848). Посмотрим на верхний правый график рис. 4.1.
Чем ближе точка х находится к точке х = 1, тем медленнее сходимость, и тем
большее п нам нужно брать для того, чтобы достичь заданной точности е. Это

111.4 Равномерная сходимость и равномерная непрерывность 215
и позволяет зародиться разрыву. Поэтому мы должны потребовать, чтобы при
заданном е > О разность fn{x) — f(x) была бы меньше, чем е при всех х Е Л,
если, конечно, п > N (см. рис. 4.2).
(4.1) Определение (Вейерштрасс 1841). Последовательность fn : А
мерно сходится на А к f : А —>• М если
равно-
(4.3)
Ve>0 3JV > 1 Vn>N ЧхеА
\f»(x) - f(x)\ < е.
В этом определении важно, что N зависит только от е и не зависит от х Е А.
Именно поэтому в определении (4.3) "Уж Е Л" стоит после "3N > 1".
Как и в разд. III. 1 (определение 1.7), мы можем заменить f(x) в (4.3) на
элементы последовательности, следующие за fn(x). При этом мы получим критерий
Коти равномерной сходимости:
(4.4) Ve>0 3N>1 Mn>N Vfc > 1 Ухе A \fn{x) - fn+k{x)\ < е.
(4.2) Теорема (лекции Вейерштрасса 1861 г.). Если fn : А —У Ш являются
непрерывными функциями и если fn{x) равномерно сходится на А к f(x), то f : А-+Ж
является непрерывной функцией.
/„(*о)
Рис. 4.3. Непрерывность f(x)
Доказательство. Идея доказательства состоит в том, чтобы разложить
{(х) - f(xo) "in drei Theile (на три части, — нем.) е\ 62 £3", после чего
использовать оценку для fn{x) — fn{xo) и дважды оценку (4.3) (см. рис.4.3). При
заданном е > 0 выберем N такое, что условие (4.3) будет выполнено. Поскольку
функция /n{x) непрерывна, существует S > 0 такое, что |/лг(ж) — /лг(жо)| < е
при \х — хо\ < S. С помощью неравенства треугольника мы получаем, что если
\х- х0\ < S, то
\f(x)-f(x0)\ < \f(x)-fN{x)\ + \fN(x)-fN{z0)\ + \fN{zo)-f{x0)\ < 35,
< е <е
что может быть сделано произвольно малым.
< е
П

216 III. Основания классического анализа
Вопрос. Существует ли последовательность непрерывных функций /п(я).
сходящаяся к непрерывной фу*чкции /(ж), такая, что сходимость /п(я) -> /(ж)
we равномерная? Как мы видели выше, в теореме 4.2 равномерная сходимость
является достаточным условием непрерывности /(ж), однако в каких-то
частных случаях она может оказаться не необходимой. История этой задачи, которой
занимались многие математики в 1850-1880-х годах, многократные попытки ее
решения и ложное "доказательство" изложены у Г.Кантора (1880).
Первый пример (аналогичный примеру Кантора):
Легко видеть, что Нтп-юо /п(ж) = 0 при любом заданном х ф 0. Функции /п(х)
имеют максимум высоты у = 1 при х — 1/п (см. левый график на рис. 4.4),
поэтому сходимость не является равномерной. Дело, однако, в том, что при х = О все
функции /п (х) равны нулю. Поэтому здесь последовательность также сходится,
и предельная функция является непрерывной.
Второй пример аналогичен первому, причем понять его еще проще (правый
график на рис. 4.4):
(4.6) /„(*)
их
2 — пх
0
0 < х < 1/п
1/п<х< 2/п
2/п < х.
Третий пример приведен в упр. 4.1.
,л=50 л=3л=2
А 1 2 "| 1
Рис. 4.4. Неравномерная сходимость к непрерывному пределу.
Критерий Вейергитрасса равномерной сходимости
Рассмотрим теперь важный случай, когда функции являются частичными
суммами
(4.7)
где fi : А -»
Sn{x) = ^Л(з),
i=0
действительные функции. Назовем ряд

III.4 Равномерная сходимость и равномерная непрерывность 217
оо
(4-8) £/<(*)
• =0
равномерно сходящимся на А, если последовательность {sn(x)} соотношения
(4.7) равномерно сходится на А.
(4.3) Теорема (критерий Вейрштрасса). Пусть
(4.9) 1/п(я)| < сп для всех х Е А
и пусть Y^nLocn является сходящимся рядом чисел. Тогда ряд Ц.8) равномерно
сходится на А.
Доказательство. Из (4.9) ясно, что сп > 0. Далее, имеем
\sn+k(x) - sn(x)\ = \fn+k(x) + ... + fn+i{x)\
< |/n+fc(x)| + ...+ \fn+i{x)\ < cn+k + ... + cn+i < e.
Последняя оценка справедлива при п > N и всех к > 1, потому что по условию
теоремы ряд ^сп сходится. Заключение теоремы следует из критерия Коши
(4.4). □
Примеры, а) Поскольку |sin(rax)| < 1 и J^ 1/п2 сходится, ряд (3.7)
равномерно сходится на Ш и представляет непрерывную функцию. С другой стороны,
в примере Абеля (4.2а) требуется расходимость ряда 1-f 1/2 +1/3+1/4+1/5-К ..
для того, чтобы предельная функция была разрывной.
Ь) Ряд для показательной функции
2 3
(4.Ю) е1=1+ж+!г+!г+---
сходится при всех х £ М, но не сходится равномерно на R (см. рис. 1.2.6b). Чтобы
все-таки применить нашу теорему, выберем фиксированное и и рассмотрим А =
[-u,u]. Мы знаем, что числовой ряд YlT=oun/n]- сходится, и так как |жп/п!| <
ип/п\ для \х\ < и, из теоремы 4.3 следует, что ряд (4.10) равномерно сходится
на каждом замкнутом интервале [—щи]. Поскольку и было произвольным, мы
получаем, что ех непрерывна при всех х £ Ж.
Равномерная непрерывность
Кажется, до сих пор не отмечалось, что ... непрерывность в любой
отдельной точке ... не является непрерывностью ... , которую можно назвать
равномерной непрерывностью, потому что последняя равномерно
распространяется на все точки и во всех направлениях. (Гейне 1870, р. 361)
Общие идеи доказательства нескольких теорем в §3 соответствуют
принципам г-на Вейерштрасса, которые стали мне известны из личных бесед с
ним, а также с г-ном Шварцем и г-ном Кантором, так что ...
(Гейне 1872, р. 182)
Определение 3.2 непрерывности функции / : А —> Ш говорит, что для каждого
xq £ А и каждого е > 0 существует 8 > 0 такое, что разность \f(x) — f{xo)\

218 III. Основания классического анализа
ограничена величиной £, если \х — хо\ ограничена величиной 8. Проблема в том,
что эта величина 8 не обязательно одна и та же для всех xq Е А.
Рис. 4.5. Функции (а) и (Ь) неравномерно непрерывные, (с) — равномерно непрерывная,
Примеры. На рис. 4.5а,Ь представлены графики функций у — 1/х на
А — (О,1] и у = х2 на А = [0, оо). В обоих случаях видно, что величина J,
обеспечивающая выполнение неравенства \f(x) — f(xo)\ < е при заданном £, стремится
к нулю, в первом случае при хо —> 0, а во втором — при хо —¥ оо. Напротив, для
функции у — у/х на А = [0,1] (рис. 4.5с), несмотря на то, что наклон ее графика
в нуле бесконечен, существует наименьшее 8т^п = е2, которое положительно.
Э^о <Jmin, хотя и является обычно излишне малым, может быть использовано на
вс^м интервале А = [О,1]. Мы называем это свойство равномерной непрерывное-
тгю. Это понятие постепенно было формировалось в лекциях Дирихле в 1854г.
и оейерштрасса в 1861г.; первая публикация принадлежит Гейне (1870, р. 353).
(4.4) Определение. Функция f : А —>• М равномерно непрерывна на А, если
Ve>0 38 > 0 \/х0еА \/х е А : \х - х0\ < 8 \f(x)-f(x0)\<e.
Замечание. Равномерная непрерывность заданной функции часто может
быть установлена с помощью теоремы Лагранжа о среднем значении (см.
теорему III.6.11)
(4.11) /(*)-/(*о) = ЛО(*-*о).
Если А является интервалом и / дифференцируема на* А, причем
(4.12) M = sup|/,(OI<oo,
ил
то при заданном е мы можем удовлетворить требованию определения 4.4,
положив 8 — е/М (см. также упр, 4.3 ниже). Однако дифференцируемость отнюдь не
является необходимой, и имеет место следующая удивительная теорема.

III.4 Равномерная сходимость и равномерная непрерывность 219
(4.5) Теорема (Гейне 1872). Пусть А является замкнутым интервалом [а, 6] и
функция f : А —> М непрерывна на А; тогда f равномерно непрерывна на А.
Первое доказательство (по Гейне 1872, р. 188). Предположим, что условие в
определении 4.4 не выполнено, и выберем 8 = 1/га для п = 1,2,.... Это приводит
нас к
(4.13а) 3е>0 Vl/n>0 Зх0п€А Зхп £ А : \хп - х0п\ < 1/п
(4.13Ь) такие, что \f{xn) — f(xon)\ > е.
Выбирая сходящуюся подпоследовательность из {хп} (которую мы опять
обозначим через {хп}; см. теорему 1Л7), имеем Нп^-юо хп = х, а \хп — хоп\ < 1/п> мы
имеем также Нп^-юо хоп = х. Так как / непрерывна, мы имеем (см. теорему 3.3)
lim f{xn) = f(x) = lim f{x0n),
n—юо n—too
что противоречит (4.13b). □
Второе доказательство (Люрот 1873). Выберем е > 0. Пусть для каждого
х Е [а, Ь] 6(х) > 0 есть длина наибольшего открытого интервала / с центром в х
такого, что |/(у) — f{z)\ < е для y,z £ /. Более точно,
(4.14) 8(х) = supjcJ > 0 | Vy, z £ [х - 8/2, х + 8/2] \f(y) - f(z)\ < е}
(где, разумеется, величины ж, у, и z должны лежать в А). В силу непрерывности
f(x) в точке х множество {8 > 0 | ...} в (4.14) не пусто, поэтому 8(х) > 0 для
всех х £ А. Если ($(ж) = ос при некотором ж £ Л, оценка \f{y) — f{z)\ < е
справедлива без всяких ограничений, и любое 8 > 0 будет удовлетворять условиям
определения 4.4.
х jc+ti 2т]
Рис. 4.6. Доказательство Люрота теоремы 4.5.
Если 8(х) < ос для всех х £ Л, мы переходим от х к х ± п. Новый интервал /'
не может быть больше, чем 8(х) + 2\rj\, потому что в противном случае I будет
целиком содержаться в Г и может быть расширен; он не может быть также
меньше, чем 8(х) — 2\г)\. Таким образом, 8(х) является непрерывной функцией.
Из теоремы максимума Вейерштрасса (теорема 3.6) в ее "минимум"-варианте
следует, что существует такое значение жо, что 8(хо) < 8(х) при всех х £ А. Это
значение 8(хо) по определению положительно и может быть использовано для
того, чтобы удовлетворить условию в определении 4.4. □
Замечание. Если вас не удовлетворили два приведенных доказательства, вы
можете ознакомиться с третьим, опубликованным Дарбу (1875, р. 73-74),
основанным на последовательном делении интервалов.

220 III. Основания классического анализа
Упражнения
4.1 Покажите, что функции
/„(*) = (п + 1)хп(1-х), х £А =[0,1]
сходятся к нулю при всех жЕД однако имеют максимум при х = п/(п +1)
асимптотической высоты 1/е. Следовательно, в этом примере нет
равномерной сходимости, несмотря на то, что предельная функция непрерывна.
4.2 (Прингсгейм 1899, р. 34). Покажите, что ряд
00 2 1
п = 1
a) абсолютно сходится при всех х Е Ш и
b) не сходится равномерно на [—1,1].
c) Вычислите f(x). Является ли эта функция непрерывной?
4.3 Функция / : [0,1] —>• М, определенная как
f(x) = { ^' (Sb * + 2) ПРИ ° < Х ~ *'
I 0 при х — 0,
непрерывна на [0,1] и, следовательно, должна быть равномерно непрерывной.
Для заданного е > 0, скажем, е — 0.01, найдите в явном виде 8 > 0 такое,
для которого
Ужьжг €[0,1] : \Xl-x2\<8 \f{x1)-f{x2)\<e.
Указание. Используйте теорему о среднем значении в стороне от начала
координат и прямую оценку для значений, близких к 0.
4.4 Какие из функций, изображенных на рис. 3.3 (см. упр. 3.5) равномерно
непрерывны на А ?

111.5 Интеграл Римана 221
III.5 Интеграл Римана
Таким образом, наш первый вопрос состоит в следующем: какой смысл
мы придаем / f(x) dx ? (Риман 1854, Werke, p. 239)
Благодаря озарению, на которое способны лишь величайшие умы,
знаменитый геометр [Риман] обобщает понятие определенного интеграла, ...
(Дарбу 1875)
Обсуждение понятия интеграла в разделах П.5 и П.6 было основано на
формуле
(5.1) [ f(x)dx = F(b)-F(a),
J а
где F(x) есть первообразная функции f(x). Мы неявно предполагали, что
такая первообразная всегда существует и является единственной (с точностью до
аддитивной постоянной). Теперь мы дадим точное определение J f(x) dx, не
зависящее от дифференциального исчисления. Это позволит нам ввести J f(x) dx
для более широкого класса функций, включающего разрывные функции и
функции, для которых первообразная неизвестна. Строгое доказательство формулы
(5.1)для непрерывных / будет дано в разд. III.6.
Коши (1823) ввел с доступной в то время строгостью понятие интеграла
непрерывной функции как предела суммы. Риман (1854), просто как попутное
замечание в своей диссертации, посвященной тригонометрическим рядам,
определил интеграл для более общего класса функций. В этом разделе мы изложим
теорию Римана и ее обобщения, принадлежащие Дюбуа-Реймону и Дарбу. Еще
более общие теории, которые мы здесь не рассматриваем, принадлежат Лебегу
(1902 г.) и Курцвайлю (1957 г.).
Общие предположения. На протяжении этого раздела мы будем
рассматривать функции / : [а, Ь] —>• М, где [а, 6] = {х \ а < х < 6} — ограниченный
интервал и f(x) — ограниченная функция, т.е.
(5.2) ЭМ>0 VzG[a,6] \f(x)\ < М.
В противном случае определение сумм Дарбу (см. ниже) будет невозможно.
Ситуации, в которых не выполняется одно из этих предположений, будут обсуждены
в разд. III.8.
Определения и критерии интегрируемости
Мы хотим определить интеграл как площадь, заключенную между графиком
функции и горизонтальной осью. Идея состоит в том, чтобы разделить интервал
[а, Ь] на меньшие подынтервалы и аппроксимировать площадь суммой площадей
малых прямоугольников. Разбиение на подинтервалы обозначается
(5.3) D - {ж0,Ж1,ж2,...,жп},
где а — хо < Х\ < ... < хп = 6, а длина подинтервала равна Si — Х{ — Х{-\. Теперь
мы определим нижнюю и верхнюю суммы Дарбу (см. рис. 5.1):

222 III. Основания классического анализа
п п
(5.4) a(D) = J2 М, S(D) = £ ^Л,
1=1 t=l
где
(5.5) Л= inf /(*), F,= sup /(*).
Xi-i<X<Xi Xi-i<X<Xi
Очевидно, что s(D) < S(D), и любое разумное определение интеграла Ja f(x)dx
должно приводить к значению, заключенному между s(D) и S(D).
Разбиение D' интервала [а, Ь] называется измельчением £>, если оно
содержит все точки £>, т. е. если D' Э D.
8(D) S(D) S(D) - s{D)
Рис. 5.1. Суммы Дарбу.
8(D) s(D') S{D') S{D)
Рис. 5.2. Измельчение разбиения.
(5.1) Лемма. Если D' есть измельчение D, то
s{D) < s(D') < S(D') < S{D).
Доказательство, Добавление одной точки к разбиению D увеличивает
нижнюю сумму Дарбу (или не меняет ее) и уменьшает верхнюю сумму (или не меняет
ее, см. рис. 5.2). Справедливость утверждения сохраняется при повторном
добавлении точек разбиения. D

111.5 Интеграл Римана 223
(5.2) Лемма. Если D\ и D2 являются двумя произвольными разбиениями, то
s(D1)<S(D2).
Доказательство. Возьмем D' = Di U D2, т.е. разбиение, содержащее все
точки обоих разбиений (при этом точки, которые появляются дважды,
считаются только один раз). Поскольку D' является измельчением как Di, так и D2,
утверждение нашей леммы следует из леммы 5.1. □
Из леммы 5.2 следует, что если задана функция / : [а, Ь] —у М, множество
нижних сумм Дарбу мажорируется любой верхней суммой Дарбу (и наоборот):
8(D) S(D)
(И IIII1I1
Таким образом (теорема 1.12), имеет смысл рассмотреть наименьшую верхнюю
грань нижних сумм и наибольшую нижнюю грань верхних сумм. Следуя Дарбу
(1875), введем обозначения
(5.7) / f(x)dx = inf S(D) (верхний интеграл),
J а
(5.8) / f(x)dx = sups(D) (нижний интеграл).
Ja D
(5.3) Определение. Функция f : [a, b] —>• Ш, удовлетворяющая условию (5.2),
называется интегрируемой (в смысле Римана), если нижний и верхний интегралы
(5.7) и (5.8) равны. В этом случае мы убираем черточки в формулах (5.7) и
(5.8) и получаем иинтеграл Римана^.
(5.4) Теорема. Функция f : [а, Ь] —> Ш интегрируема тогда и только тогда, когда
(5.9) \/е>0 3D S{D)-s{D)<e.
Доказательство. По определению функция f(x) интегрируема в том и
только том случае, если два множества в соотношении (5.6) сколь угодно близки. Это
значит, что при заданном е > 0 существуют два разбиения D\ и D2 такие, что
S{D2) — s(Di) < е. Полагая D = £>i U D2 и применяя лемму 5.1, мы доказываем
справедливость утверждения. □
(5.5) Пример. Рассмотрим функцию f(x) — х на интервале [а, 6]. При
эквидистантном разбиении Dn = {жг- = а + ih | г — 0,1,..., n, h — (Ь — а)/п) из (1.1.28)
мы получаем

224 III. Основания классического анализа
/„ х V- / , Ъ2 а2 (Ь-а)
1=1
2
2п "
о/г, ч V- / ч Ь2 а2 (Ь~а)2
S{Dn) = l^Xi • (Xi - Ж.--.1) = у- у + —^—,
1=1
так что S(Dn) — s(Dn) = (b—a)2/п. Для достаточно больших п эта величина
меньше, чем любое е > 0. Таким образом, эта функция интегрируема и ее интеграл
равен б2/2 - а2/2.
(5.6) Пример. Функция Дирихле / : [0,1] —>■ М, определенная с помощью
соотношения (см. (3.3))
(1 х рационально
f(x) = i n
(\) x иррационально,
не интегрируема в смысле Римана, потому что на каждом подинтервале
присутствуют рациональные и иррациональные числа, так что /,- = 0 и F{ = 1 для
каждого г. Следовательно, s(D) = 0, S(D) = 1 для всех разбиений.
Г!
(5.7) Пример. Функция / : [0,1] -»• М
0 х иррационально или х = 0
1/q х — p/q (несократимая дробь)
(см. (3.4)) разрывна при всех положительных рациональных х. Однако при
фиксированном е > 0 только конечное число (скажем, к) значений х таковы, что
f(x) > е. Теперь мы выберем разбиение D с max,-J,- < е/к такое, что значения
ж, для которых f(x) > £, лежат внутри подинтервалов. Так как /(ж) < 1, то из
этого следует
S(D) < e + bmaxJ,- < 2е.
г
Но 5(D) = 0, и мы видим, что наша функция интегрируема и что /0 f(x) dx - 0.
Теорема Дюбуа-Реймона и Дарбу
Однако я чувствую, что способ формулировки критерия интегрируемости
должен быть улучшен. ( Дюбуа-Реймон 1875, р. 259)
(5.8) Теорема (Дюбуа-Реймон 1875, Дарбу 1875). Функция f(x), удовлетворяющая
условию (5.2), интегрируема в том и только том случае, если
\/е>0 38 > 0 VDeVs S{D)-s{D)<e.
Здесь T>s обозначает множество всех разбиений, удовлетворяющих условию
max; S( < 8.
Доказательство. Достаточность (часть "в том случае") является простым
следствием теоремы 5.4. Трудность доказательства необходимости (части
"только в том случае") состоит в том, что разбиение D, о котором мы знаем лишь, что
шах; 8{ < £, может быть совершенно иным, чем разбиение D теоремы 5.4.

111.5 Интеграл Римана 225
DUD xo xi x2 ... xu
Рис. 5.3. Доказательство Дюбуа-Реймона и Дарбу.
Зафиксируем е > О и пусть D есть разбиение, удовлетворяющее условию
(5.9), т.е. площадь заштрихованной области на рис. 5.3а Л = S(D) — s(D) меньше,
чем е. Важно, что D = {жо, х±,..., хц] состоит из конечного числа точек. Теперь
возьмем произвольное разбиение D £ T>s (см. рис. 5.3Ь) и положим Л = S(D) —
s(D). Нам надо доказать, что Л становится произвольно малым, когда S —>■ 0.
Рассмотрим объединение D' = DUD двух разбиений и положим Л! — S(D') —
s(D') (см. рис. 5.3с). Суммы Дарбу для D' и D везде одинаковы, за исключением
интервалов, содержащих точки из D (рис. 5.3d). Поскольку таких интервалов не
больше, чем п — 1, их длина < J, а так как — М < f(x) < М, мы имеем
(5.10) Л < Л' + 2(п - 1)<Ш.
Учитывая, что Л' < Л < б (заметим, что £)' есть измельчение D), из этой оценки
мы видим, что Л < 2е при условии, что £ < е/(2(п — 1)М). □

226 III. Основания классического анализа
Суммы Римана. Рассмотрим разбиение (5.3), и пусть £i, £г? • • • ? £п
является таким множеством точек, что хо < £1 < xi < £2 < я 2 < £з < • • • • Назовем
сумму
п
(5.П) * = £/&)•*
суммой Римана. В силу (5.5) мы имеем /г- < /(£») < i^'» так что 5(-^) < °" < 5(D).
Из теоремы 5.8 следует, что
(5.12)
$^/(&)*й -* / f{x)dx при maxJj -> О,
t=i Ja
при условии, что / : [а.Ь] —> Ш является интегрируемой функцией. Римановы
суммы весьма удобны для доказательств свойств интеграла. Например, переходя
к пределу max; J, —>• 0 в тривиальном тождестве
п п п
5>i/i(fc) + С2/2&)) • Si = Cl £ /i(fc) • Si + С2 X) Л(6) • *>
t = l t = l i = l
получаем формулу (II.4.13) при условии, что обе функции интегрируемы.
Интегрируемые функции
Посмотрим теперь, какие классы функций являются интегрируемыми.
(5.9) Теорема. Пусть fug — две интегрируемые на [а, Ь] функции и пусть X —
действительное число. Тогда функции
f + 9, А-/, /•<,, l/l, f/g (if \g(x)\> 00 )
также интегрируемы.
Доказательство. Ha протяжении всего доказательства мы будем
использовать тот факт, что Fi — fi является наименьшей верхней гранью вариаций f(x)
на [жг_1,жг], т.е.
(5.13) sup \f(z)-f(y)\ = Fi-fi.
xyye[xi-i,xi]
В самом деле, предположим, что е > О задано. По определению Fi и /,-
существуют £,7) G [ж,-_1,ж,-] такие, что /(£) > Fi — е, f(r}) < /,- + £, и, следовательно,
/(£) — f(r}) > Fi — fi — 2e. Поэтому Fi — fi является не только верхней гранью
величины \f(x) — f(y)\, но также наименьшей верхней гранью.
а) Пусть h(x) = f(x) + g(x); обозначим Ft-, Gj, Hi их точные верхние грани и
соответственно /«, #;, hi точные нижние грани на [ж,-_1,ж,-] (см. (5.5)). Используя
неравенство треугольника и (5.13), при х,у Е [жг_1,жг] получим
\h(x) - h(y)\ < \f(x) - f(y)\ + \g(x) - g(y)\
(5.14) <(Fi-fi) + (Gi-gi).

111.5 Интеграл Римана 227
Применяя (5.13) к функции Л, мы получим (Hi — hi) < (Fi — /») + (Gi — #»), и
разность верхней и нижней сумм Дарбу удовлетворяет неравенству
(5.15) £(#,- - hi)Si < "£№ ~ fi)b + E(G«' ~ ^Mi-
При заданном e > О выберем разбиение D (теорема 5.4) такое, чтобы каждый
член в сумме в правой части неравенства (5.15) был меньше, чем е (в
действительности мы имеем два различных разбиения для / и #, но если взять их
объединение, то можно считать, что они совпадают). Следовательно, ^Д#» — hi)8i < 2е
и функция h(x) = f(x) + д(х) является интегрируемой в силу теоремы 5.4.
Ь) Доказательство остальных утверждений проводится аналогично.
Например, для h(x) = А • f(x) вместо (5.14) мы используем
|Л(*)-лЫ1 = |ан/(*)-/М1,
заключаем, что (Hi — hi) < |А| • (F,- — /,-), и получаем интегрируемость так же,
как выше. Для произведения h(x) = f(x) • д(х) мы используем
14*) - h(y)\ < \f(x)\ ■ \д(х) - д(у)\ + \д(у)\ ■ \f(x) - f(y)\
<M-\g(x)-g(y)\+N.\f(x)-f(y)\
(обе функции f(x) и д(х) ограничены в силу предположения (5.2)). Наконец, для
доказательства последнего утверждения достаточно показать, что 1/д(х)
интегрируема (потому что f(x)/g(x) = f(x) • (1/д(х)). Положим h(x) — 1/д(х) и
заменим (5.14) на
\hM hUA\ №(у)-з(х)\ / \9{х)-д(у)\
Щя)-НШ=Ыу)Ш*)\- с> ■
п
Поскольку постоянная функция и f(x) = х интегрируемы (пример 5.5), из
вышеприведенной теоремы следует, что полиномы и рациональные функции (вне
сингулярностей) интегрируемы. Следующая теорема принадлежит Коши (1823),
но строго доказана она была приблизительно 50 лет спустя с использованием
понятия равномерной непрерывности.
(5.10) Теорема. Если функция f : [а, Ь] —>• Ш непрерывна, то она интегрируема.
Доказательство. Существенным является то обстоятельство, что /
равномерно непрерывна (теорема 4.5). Это значит, что для данного е > 0 существует
такое 8 > 0, что
\х-у\<8 => \f{x)-f{y)\<e.
Возьмем разбиение D такое, что max,-£,- < 8. Если х,у £ [жг_1,жг], то \f(x) —
f(y)\ <еи (вследствие (5.13)) Fi-fi < е. Отсюда S(D)-s(D) = £"=i(^ -fi)8i <
sY^=18i = е(Ь — а), и интегрируемость f(x) следует из теоремы 5.4. D

228 III. Основания классического анализа
(5.11) Теорема. Если функция f : [а, Ь] —у Ш является неубывающей (или невоз-
растающей), то она интегрируема.
Доказательство. Неубывающая функция принимает свое наименьшее
значение в левой крайней точке интервала [жг_1,жг], а наибольшее — в его правой
крайней точке. Следовательно, /»• = /(z,_i), Fi = /(ж;), так что /t+i = Fi для
г — 1,..., п — 1. Дальнейшая идея состоит в том, чтобы рассмотреть
эквидистантные разбиения, где длина подинтервалов равна S. В этом случае мы имеем
J2(Fi - fi)S = Ftf - hS + F2S - f2S + F3S-f3S + ...= (f(xn) - f(x0)) -6<e,
если величина S достаточно мала. Это доказывает интегрируемость f(x). D
(5.12) Замечание. Если мы изменим значения интегрируемой функции в
конечном числе точек, функция останется интегрируемой и значение интеграла не
изменится. Это видно из рассуждения, подобного приведенному в примере 5.7.
(5.13) Замечание. Пусть а < 6 < с и / : [а, с] —> Ш — функция, сужения которой
на [а, Ь] и на [6, с] интегрируемы. Тогда / интегрируема на [а, с], и
лс лЬ у»с
(5.16) / f(x)dx= f{x)dx+ f(x)dx.
Действительно, складывая суммы Дарбу сужений / на интервалы [а, 6] и [6, с],
мы получаем сумму Дарбу на интервале [а, с].
Для а > Ь или а — Ъ определим
(5.17) / f(x)dx = - f{x)dx и / f(x)dx = 0,
Ja Jb Ja
так что равенство (5.16) справедливо для любой тройки чисел (а,Ь,с).
Неравенства и теорема о среднем значении
Следующие неравенства часто бывают полезны при оценке интегралов. Мы
уже использовали их в разд. 11.10 для получения оценок (П. 10.15).
(5.14) Теорема. Если функции f(x) и д(х) интегрируемы на интервале [а,Ь]
(здесь а <Ь) и f(x) < g(x) при всех х Е [а, 6], то
/»0 /»0
/ f(x)dx< I g(x)dx.
J a J а
Доказательство. Для сумм Римана имеем Х^Г=1/(^«)^* ^ 2Г=10(&)й> и^°
6{ > 0. При maxiSi -> 0 мы получаем вышеприведенное неравенство (см. (5.12) и
теорему 1.6). □

III.5 Интеграл Римана 229
(5.15) Следствие. Для интегрируемых функций справедливо соотношение
I / f{x)dx\ < f \f{x)\dx.
Доказательство. Надо применить теорему 5.14 к очевидным неравенствам
Применяя следствие 5.15 к произведению f(x) • g(x) двух интегрируемых
функций и используя соотношение \f(x)-g(x)\ < M-\g(x)\, где М = s\ipxe^a Ь] |/(ж)|,
мы получаем следующую полезную оценку:
(5.18) / f{x)-g(x)dx\< sup \f(x)\- \g(x)\dx.
' J a ' x£[a,b] Ja
Следующее неравенство аналогично (5.18), однако функции / и g
рассматриваются в нем симметричным образом.
(5.16) Неравенство Коши—Шварца (Коши 1821 в Мп, Буняковский 1859 для
интегралов, Шварц 1885, §15 для двойных интегралов). Следующее неравенство
справедливо для интегрируемых функций f(x) и g(х):
(5.19) \j f{x)g{x)dx\ < J f P(x)dx-J f g2(x)dx-
Доказательство. Из теоремы 5.9 известно, что функции /•#, /2, и д2
интегрируемы. Используя теорему 5.14 и линейность интеграла, мы имеем
0<У (f{x)-19(x))2 dx
лЬ /*b лб
= / f2{x)dx-2j f{x)g{x)dx+j2 I g2(x)dx.
J a J a J a
Обозначив A — ja f2(x) dx, В — ja f(x)g(x) dx и С = ja g2(x) dx, мы видим, что
А- 27Б + 72C > 0 для всех действительных j. При С = 0 из этого следует,
что Б = 0. При С / 0 дискриминант квадратного уравнения не может быть
положительным (см. (1.1.12)). Поэтому В2 < АС, но это и есть неравенство (5.19).
□
(5.17) Теорема о среднем значении (Коши 1821). Если f : [а, 6] —У Ш является
непрерывной функцией, то существует £ Е [а, Ь] такое, что
(5.20) / f(x)dx = f(t).(b-a).
Ja
Доказательство. Пусть т и М являются минимальным и максимальным
значениями функции f(x) на [а, 6] (см. теорему 3.6), так что т < f(x) < М для
всех х £ [а, Ь]. Используя теорему 5.14 и деля обе части (5.20) на (6 — а), получаем

230 III. Основания классического анализа
1 Г
т < / f{x) dx < М.
о-a Ja
Величина Ja f(x) dx/(b — а) лежит между т = f(u) и М = f(U). Следовательно,
согласно теореме Больцано 3.5, существует такое £ Е [а, Ь], что эта величина
равна /(£)• Это доказывает справедливость равенства (5.20). D
(5.18) Теорема (Коши 1821). Пусть функция f : [а, Ь] —> Ш непрерывна и функция
д : [а, Ь] —> Ш интегрируема и всюду неотрицательна (или всюду
неположительна). Тогда существует такое £ Е [а, Ь], что
(5.21) / f{x)g{x)dx = f{Z) [ g(x)dx.
J a J а
Доказательство. Предположим, что д(х) > 0 при всех х (в противном случае
заменим д на — д). Тогда
т-д(х) < f(x)g(x) < М • д(х) при х £ [а, 6],
где га и М — минимальное и максимальное значения функции f(x). Остальная
часть доказательства аналогична доказательству теоремы о среднем значении.
D
Интегрирование бесконечных рядов
До самого последнего времени считалось, что интеграл от сходящегося
ряда ... равен сумме интегралов от отдельных членов, и г-н Вейерштрасс
был первым, кто заметил, что ...
(Гейне 1870, Ueber trig. Reihen, J. f. Math., vol. 70, p. 353)
В нескольких случаях (например, при выводе ряда Меркатора (1.3.13), а
также в примерах из разд. П.6) мы почленно интегрировали бесконечные ряды.
Это означает, что мы меняли порядок интегрирования и перехода к пределу для
функций. Теперь мы обсудим, при каких условиях это допустимо.
Первый пример. Пусть ri, Г2, гз, Г4,... — последовательность,
содержащая все рациональные числа в промежутке между 0 и 1, например,
112 12 3 12 3 4 1
2' 3' 3' 4' 4' 4' 5' 5' 5' 5' б' '" '
Определим функции
(5.22) /»(*)= Г ПРИ *G^>r-2,r3,...,rn}
[О в противном случае.
По замечанию 5.12, каждая из функций /п : [0,1] —> Ш интегрируема, и их
интегралы равены нулю. Однако предельная функция /(ж), которая является
функцией Дирихле из примера 5.6, не интегрируема. (От этой трудности поможет
избавиться интеграл Лебега).

111.5 Интеграл Римана 231
Второй пример. Графиками функций
(5.23) fn(x):
п=4
п2х
О < х < 1/п
2п - п2х 1/п < х < 2/п
О 2/п < х < 2
являются треугольники с уменьшающимися
основаниями и увеличивающимися высотами, причем
./о
/п(ж) dx = 1 для всех п.
Однако предельная функция есть f(x) = 0 при всех
х Е [0,1]. Здесь f(x) интегрируема, но
lim / fn(x)dx^ / lim fn(x)dx.
n^ocj0 JQ n-+oo
(5.19) Теорема. Рассмотрим последовательность fn(x) интегрируемых функций
и предположим, что она равномерно сходится на [а, 6] к функции f(x). Тогда
функция f : [а, Ь] —> Ш интегрируема и
lim / fn(x)dx— I f(x)dx.
n-+°° J a J a
Доказательство. Равномерная сходимость означает, что для каждого е > О,
существует целое число N такое, что для всех п > N и всех х Е [а, Ь] выполняется
неравенство |/п(я) — /(я)| < е. Следовательно, для всех ж, у Е [а, &]
1/(з)-/М1<1Ы*)-/лгМ1 + 2е.
Применив равенство (5.13), мы найдем, что
№-fi) <{FNi-fm) + 2e,
где, так же как в (5.5), мы использовали обозначения i*V,- = supx._i<x<a.t. /дг(ж) и
fNi = infa^^x^. /лг(ж). Функция /лг(ж) интегрируема, так что для некоторого
разбиения интервала [а, 6] величина разности между верхней и нижней
суммами Дарбу, т.е. ^2i{FNi — /л/ч)й5 меньше чем е (теорема 5.4). Из этого следует,
что ЕД^' — /»')й < £{^ + 2(Ь — а))> и функция /(ж) оказывается интегрируемой.
Поскольку интегрируемость предельной функции f(x) установлена, из
следствия 5.15 вытекает, что для п > N
/ fn{x)dx- f(x)dx\< \fn(x)-f(x)\dx<e{b-a).
1 J a J a J a
Отсюда следует утверждение теоремы.
□

232 III. Основания классического анализа
(5.20) Следствие* Рассмотрим последовательность fn{x) интегрируемых
функций и предположим, что ряд Х^°_0 /п(ж) равномерно сходится на [а, Ь]. Тогда
XI/ fn{x)dx= Y^fn(x)dx-
«—п^а J а „_п
Рис. 5.4. Пример Римана интегрируемой функции.
Пример Римана.
Поскольку эти функции ранее не рассматривались, будет полезно начать
с частного примера. (Риман 1854, Werke, р. 228)
Для того, чтобы продемонстрировать мощь своей теории интегрирования,
Риман (1854) предложил следующий пример функции, являющейся разрывной
на каждом интервале (см. рис. 5.4):
,5.24) /(.) = £*£>. где *,,)={;-« ZllU'l
п = 1
и (х) означает ближайшее к х целое число. Эта функция разрывна в точках
х — 1/2, 1/4, 3/4, 1/6, 3/6, 5/6,... , но тем не менее в силу теоремы 4.3 ряд
(5.24) равномерно сходится, и в силу замечания 5.13 функции /п(ж) являются
интегрируемыми. Следовательно, / интегрируема.
Упражнения
5.1 Для функции
/(ж)= J1 при я = 0, §,§,|,§,...
\х в противном случае
и заданного е > 0, например е = 0.01, явно постройте разбиение, для которого
S(D) — s(D) < е. Из этого будет ясно, что / интегрируема в смысле Римана.

111.5 Интеграл Римана 233
5.2 Рассмотрите функцию f(x) = х2 на интервале [0,1]. Вычислите нижнюю и
верхнюю суммы Дарбу для эквидистантного разбиения Х{ — i/n, где i =
О,1,..., п. Из полученных результатов сделайте вывод, что / интегрируема.
5.3 Покажите, что численные приближения, полученные по правилу трапеций
(см. разд. II.6)
[h = (b — a)/N и & = a + г/i), а так же по правилу Симпсона (N четно)
J f(x) dx*^ (/(&) + 4/(6) + 2/(6) + 4/(6) + • • • + /(6v)),
являются суммами Римана для некоторого разбиения D. Следовательно,
сходимость этих методов обеспечена при N —>• оо для всех функций,
интегрируемых по Риману.
5.4 (Дини 1878, Chap. 13). Покажите, что
/ ln(l — 2а cos ж + а2) dx — О для а2 < 1,
Jo
ln(l — 2а cos х + а2) dx — 7г In а2 для а2 > 1,
I
/о
вычислив суммы Римана для эквидистантного разбиения Х{ — т/п, где £г на
каждом подинтервале является левой крайней точкой жг_1. Суммы Римана
окажутся логарифмом произведения, с которым мы уже встречались (см.
разд. 1.5).
5.5 Пусть функция / : [а, Ь] —у Ш удовлетворяет следующим условиям:
i) / непрерывна, ii) Vx G [а, 6] мы имеем f(x) > 0 и iii) Зжо G (а, Ь) такое,
что f(xo) > 0. Покажите, что в этом случае
(5.25) / f(x)dx>0.
J а
Постройте контрпримеры, показывающие что для доказательства (5.25)
необходимо соблюдение каждого из трех предположений i), ii) и iii).
5.6 Вычислите интегралы
к/2 . 2п j * 1-3-5-...-(2п-1)
sm2nxdx= - v ;
У0 2 2-4-6-...-2п
Г/2 • 2n+i ^ 2.4-6....-2n
/ sm2n+1xdx= ——— —.
Jo 3-5-7-....(2n+l)
Используя тот факт, что 0 < since < 1 при 0 < х < 7г/2, и теорему 5.14,
покажите, что
/»7г/2 рп/2 рп/2
/ sin2n xdx> sin2n+1 xdx> sin2n+2 x dx.
Jo Jo Jo

234 III. Основания классического анализа
Если вышеприведенные значения подставить в эти неравенства, мы придем
к доказательству произведения Валлиса (1.5.27) с точной оценкой ошибки.
5.7 Покажите, что
i / х4(1-х)Чх< [ Ж*(1 ~ Х/ dx < [ х*(1-х)Чх.
2 Jo Jo ! +х Jo
Вычисление этих интегралов приведет к удивительному результату
(вспомните разд. 1.6).
Указание. Чтобы вычислить /0 ж4(1 — ж)4 dec, см. упр. II.4.3.
5.8 Покажите, что ряд
1
1 2,4 6,8
= 1 — X + X — X + X
1 + Ж2
равномерно сходится на А = [—6,6] при любом 6 таком, что 0 < b < 1.
Следовательно, этот ряд можно почленно интегрировать на А = [0, 6] (или
на А = [—6, 0]), что приводит к хорошо известному ряду для arctgfr.
о 10 1
Рис. 5.5. Перемена порядка перехода к пределу и интегрирования.
5.9 Для последовательностей функций /п : [0,1] —>•
пх , ч „ , ч п2х
а) ■/»(*) -(1+„23,2)2' Ь) МХ)~ (1 + п2а.2)2
(см. рис. 5.5) вычислите ишп-юо /п(ж) при х — 0 и х ф 0. Найдите точки
максимумов /п(ж) и определите, является ли сходимость равномерной. Наконец,
докажите справедливость равенства
lim / fn(x)dx— I lim fn(x)dx.
n^°°Jo Jo n_>0°

111.6 Дифференцируемые функции 235
III.6 Дифференцируемые функции
... строгость, которой я хотел достигнуть в моем Cours d'analyse, ...
(Коши 1829, Legons)
Полная вариация f(x + h) — f(x)... в общем случае может быть
представлена ... в виде суммы двух членов ... (Вейерштрасс 1861)
Производная от функции была введена и обсуждалась в разд. П.1. Теперь,
когда мы располагаем понятием предела, можно дать ее строгое определение.
(6.1) Определение (Коши 1821). Пусть I — интервал ихо £ I. Функция f : I —> Ш
называется дифференцируемой в точке хо, если предел
(6.1) f\X0) = lim /(Ж) ~ /(Жо)
x^hx0 X — Хо
существует. Значение этого предела называется производной f в точке х$ и
обозначается f'(xo). Если функция f дифференцируема во всех точках I и если
/':/-> М непрерывна, f называется непрерывно дифференцируемой.
Иногда удобно писать х = ж о + /ь, так что
(к о\ *ч„ \ - i;™ /fop + К) - f{x0)
(6.2) / (хо) - hm .
При заданном хо можно также рассмотреть функцию г : / —>• М, определенную
как г(хо) — 0 и
(6.3) r(x) = f(x) ~ /(Жо) - /'(хо) при X ф х0.
X — Хо
Теперь равенство (6.1) эквивалентно lim^-^ г(х) — 0 и мы приходим к
следующему критерию.
(6.2) Формулировка Вейерштрасса (Вейерштрасс 1861, см. вышеприведенную
цитату). Функция f(x) является дифференцируемой в точке хо тогда и только
тогда, когда существуют число f'(xo) и непрерывная в точке xq функция г(х)
такая, что г(хо) — 0 и
(6.4) f{x) = f(x0) + f{x0){x - х0) + r(x)(x - хо). □
У формулы (6.4) есть то преимущество, что она не содержит предела
(вместо этого в ней используется непрерывность г(х)) и включает в себя уравнение
касательной у — f(xo) + f(xo)(x — хо) к f(x) при х — жо- Кроме того, это будет
послужит основой для теории дифференцируемости функций нескольких
переменных.
Еще более простые формулы и доказательства можно получить, если два
члена в формуле (6.4) объединить, полагая
(6.5) <p{x) = f'(x0)+r(x).

236 III. Основания классического анализа
(6.3) Формулировка Каратеодори (Каратеодори 1950, с. 121). Функция f(x)
дифференцируема в точке хо тогда и только тогда, когда существует непрерывная
в хо функция <р(х) такая, что
(6.6) f(x) = f(x0) + <р{х)(х - х0).
Величина <р(хо) является производной f'(xo) функции f в точке хо- □
Из (6.6) видно, что если / дифференцируема в точке жо, то она непрерывна
в этой точке. Далее, из (6.5) и (6.3) (или прямо из (6.6)) видно, что функция
(6.7) (р(х) — —^ —- при х ф хо
X — Хо
определена единственным образом при х ф хо, т.е. производная f{xo) определена
единственным образом (если она существует).
Замечания и примеры.
1. Очевидно, что функции f(x) = 1 и f(x) = х дифференцируемы. Диффе-
ренцируемость функции f(x) = х2 следует, например, из (6.6), если
воспользоваться тождеством х2 — х$ = (х + хо)(х — хо) (см. также разд. П.1).
2. Подчеркнем, что дифференцируемость в точке хо является локальным
свойством. Если мы изменим значения функции вне интервала (хо — £, хо + е)
при некотором е > 0, свойство ее дифференцируемости в точке хо и значение
производной f'(xo) не изменятся.
3. Если / = [а, Ь] является замкнутым интервалом и хо — а, то (6.1) следует
заменить правосторонним пределом.
4. Рассмотрим функцию f(x) — \х\ (абсолютная величина х). Если хо > О,
она дифференцируема и f'(xo) = 1; при хо < 0 она также дифференцируема, но
ее производная равна f'(xo) = — 1. Эта функция не дифференцируема в точке
хо = 0, потому что f(x)/x — \х\/х не имеет предела при х —> 0.
5. Функция
0 если х иррациональное или целое i
1/q2 если х = p/q (несократимая дробь)
разрывна при каждом иррациональном жо- Однако она
дифференцируема в точке х0 = 0, ибо функция ip(x) L^,^^1;|4^;Д1^
из (6.6) равна <р(х) = f(x)/x. Поскольку \f(x)\ < |ж|2, °
\imx-+o<p{x) = 0 и f'{x0) = 0.
(6.4) Теорема. Если функция f : (а, Ь) —>• М дифференцируема в точке хо G (а, Ь)
и Пхо) > 0, то существует такое S > 0, что
f(x) > f(xo) для всех х, удовлетворяющих неравенствам хо < х < xo + S,
f(x) < f(xo) для всех х, удовлетворяющих неравенствам хо — 6 < х < xq.
Если функция достигает в точке хо максимума (или минимума), то f'(xo) = 0.
Доказательство. Неравенство /'(жо) > 0 означает, что <р(хо) > 0 (см.
(6.6)). По непрерывности <р(х) > 0 в окрестности точки хо- Теперь
доказываемые неравенства следуют из (6.7). Если функция имеет максимум в точке ж о, то
/(*) = { 1 /.2

111.6 Дифференцируемые функции 237
f(x) < f(xo) по обе стороны от точки xq. Это возможно только если f'(xo) = 0.
□
(6.5) Замечание. Из теоремы 6.4 не следует, что функция, удовлетворяющая
условию f'(xo) > 0, монотонно возрастает в некоторой окрестности точки xq. В
качестве контрпримера рассмотрим функцию f(x) (см. рис. 6.1), заданную как
/(0) = 0 и
/(ж) = х + £2sin(l/x2) при X ф 0.
Она всюду дифференцируема и удовлетворяет условию /'(0) = 1 (потому что
f(x) — х + г(х) • х, где \г(х)\ < \х\). При х ф 0 производная
/'(*) = l + 2*sin(l)-^cos(l)
сильно осциллирует вблизи начала координат. Поэтому, хотя /(ж) заключена
между двумя параболами, существуют точки с отрицательными производными,
находящиеся сколь угодно близко к началу координат. Согласно теореме 6.4
существуют точки £i < £2, близкие к 0, для которых /(£i) > /(£2)- Ниже мы
покажем (следствие 6.12), что если f(x) > 0 для всех х Е (а, 6), функция
является монотонно возрастающей. Таким образом, построение этого контрпримера
оказалось возможным только потому, что / не является непрерывно
дифференцируемой функцией.
Рис. 6.1. Графики функции у = х + х2 sin(l/x2) и ее производной.
(6.6) Теорема. Если функции fug дифференцируемы в точке х$} то функции
/ + ^, f'9, f/g {если д(хо)фО)
тоже дифференцируемы в этой точке, и справедливы формулы разд. II. 1 для
производных этих функций.
Доказательство. Мы приведем два различных доказательства для
произведения / • д. Для / + д и f/g доказательства аналогичны.

238 III. Основания классического анализа
Первое доказательство основано на тождестве
f{x)g{x) - f(xo)g{x0) д(^)-д{хо) . , J{x) - f{x0)
X — Xq X — Xo X — Xq
которое получается путем прибавления и вычитания члена f(x)g(xo). Используя
непрерывность функции / в точке хо (формула (6.4)), а также дифференциру-
емость /иди теорему 1.5, мы получаем, что при х —>• хо выражение в правой
части равенства имеет конечный предел f{xo)gr(xo)+g(xo)fr(xo). Следовательно,
произведение / • д дифференцируемо в точке xq.
Второе доказательство основано на формулировке Каратеодори 6.3. По
предположению,
f{x) = f(x0) + <р{х)(х - хо), <р{х0) = f'{xo),
(о.о)
д(х) = д{х0) + ф{х)(х - ж0), Ф(х0) = д'(х0).
Перемножив два равенства (6.8), мы получаем
f{x)g(x) = f(x0)g(x0) + \J{x0)il>(x) + д(х0)<р(х) + <р • ф • (х - x0)J {х - х0).
Очевидно, что функция в больших скобках является непрерывной в точке яо и
ее значение при х = хо равно f(xo)gf(xo) + g{xo)f'(xo). □
(6.7) Теорема (цепное правило для сложных функций). Если у — f(x)
дифференцируема в точке хо и если z = g(y) дифференцируема в точке уо — f{xo), ™>о
сложная функция (д о f)(x) = g[f(x)) дифференцируема в точке хо и
(6.9) (9ofY(x0)=g'(yo)-f(xo).
Многие наши студенты оценят краткость и изящество этого
доказательства. (Кун 1991)
Доказательство. Используя формулу (6.6), перепишем условие теоремы в
виде
f(x) - f(x0) = (р(х)(х - х0), <р{х0) = /;(зо),
9(у) - 9{уо) = Ф{у){у ~ Уо), Ф{уо) = д'{уо)-
Подставляя у — уо — f(x) — f(xo) из первого уравнения во второе, получаем
9{f{x)) - g{f{xo)) = Ф(1{х)) <р(х){х - х0).
Функция ф(/{х)) <р(х) непрерывна в точке хо, и ее значение при х — хо равно
g'(f(xo))-f'(x0). □
(6.8) Теорема (обратные функции). Пусть функция /:/—>■ J является
биективной и дифференцируемой в точке zo G/, и предположим, что f'(xo) ф 0. Тогда
обратная функция /-1 : J —> I дифференцируема в точке уо = f(xo), и
(6.10) (/-1)'Ы= !
ГЫ'

111.6 Дифференцируемые функции 239
Доказательство. По тереме 3.9 функция /_1(у) непрерывна. В
формулировке Каратеодори (6.6)
f(x) - /(ж0) = <р(х)(х - ж0), <р{х0) = f'{x0)
заменим х и хо на /~г(у) и /_1(уо)> а /(ж) и /(жо) на у и уо> после чего получим
у-уо = <р(ГЧу))(Г1(у)-Г1(уо)).
Из условия теоремы видно, что <p(f~1{yo)) ф О, и это неравенство остается
справедливым (по непрерывности) в некоторой окрестности уо, поэтому деление
допустимо, и мы получаем
/~1(у)-Г1Ы = у(/_11(у))(у-»ь)-
Это завершает доказательство, так как по теореме 3.9 функция l/(p(f~1(y)) тоже
непрерывна. □
Фундаментальная теорема дифференциального исчисления
Формула (П.4.6) является основным результатом всех вычислений разд. П.4.
Сейчас мы изложим строгое доказательство этого результата. В частности, мы
покажем, что у каждой непрерывной функции /(ж) есть первообразная,
единственная с точностью до аддитивной постоянной.
(6.9) Теорема (существование первообразной). Пусть f : [а, Ь] —>• Ш есть
непрерывная функция. Тогда функция
F(x)= Г /(«),
J а
(6.11) F(*)= / f{t)dt
J а
(которая существует в силу теоремы 5.10) дифференцируема на (а, Ъ) и
удовлетворяет соотношению F'(x) — /(ж). Следовательно, она является
первообразной функции /(ж).
Доказательство. Из формулы (5.16) мы имеем
(6.12) F(x)-F(x0)= / f{t)dt.
J Xq
Применяя теорему 5.17 о среднем значении, мы получаем
F(x)-F(x0) = №)(x-xo),
где £ = £(ж, жо) лежит между ж и жо- При ж —> жо значение £(ж, жо) стремится к
жо, и в силу непрерывности функции / в точке жо мы имеем limrr_).;ro /(£) = /(жо).
Это доказывает (см. (6.6)) дифференцируемость ^(ж), причем F'(xq) = /(жо). □

240 III. Основания классического анализа
Единственность первообразных.
Это было получено с помощью теоремы о среднем значении, и величайшей
заслугой Коши было то, что он распознал ее фундаментальную важность
... вот почему мы считаем Коши основоположником точного исчисления
бесконечно малых. (Ф.Клейн 1908, англ. изд. р. 213)
Смотри прекрасное доказательство этой теоремы, принадлежащее г-ну
Бонне, в Traite de Calcul differentiel et integral г-на Ceppe, vol. I, p. 17.
(Дарбу 1875, p. Ill)
Наша следующая задача — доказательство единственности первообразной
(с точностью до аддитивной постоянной). Нижеследующий ряд теорем,
решающих эту задачу, стал одним из краеугольных камней в основании анализа после
публикации книги Серре (1868; Серре приписывает эти идеи О.Бонне, см.
цитаты).
(6.10) Теорема (Ролль 1690). Пусть функция f : [а, Ь] -
на [а, Ь], дифференцируемой на (а, Ь) и такой, что f(a)
£ Е (а, Ь) такое, что
(6.13)
/'(О = о.
К является непрерывной
f(b). Тогда существует
Доказательство. Из теоремы З.б следует, что существуют и, U Е [а, Ь] такие,
что f(u) < f(x) < f{U) для всех х Е [а, Ь]. Рассмотрим два случая. Если f(u) -
/(С/), то f(x) постоянна и ее производная всюду равна нулю. Если f(u) < f(U),
то по крайней мере одно из двух значений (скажем, f{U)) отлично от f(a) = f(b).
В этом случае а < U < Ь и в соответствии с теоремой 6.4 f'(U) = 0. □
(6.11) Теорема (Лагранж 1797). Пусть f : [а, Ь] —>• Ш есть функция, непрерывная
на [а, Ь] и дифференцируемая на (а, 6). Тогда существует число £ Е (а, Ь) такое,
(6.14)
f(b) -/(о) = f(Z)(b-а)
|
а Ъ а^и> Ъ
Рис. 6.2. Доказательство теорем Ролля и Лагранжа.
W
Доказательство. Идея состоит в том, чтобы вычесть из функции f(x)
функцию, соответствующую прямой линии, соединяющей точки (a,f(a)) и (6, f(b)) и

III.6 Дифференцируемые функции 241
имеющей наклон (f{b) — /(a))/(6 — а), а затем применить теорему Ролля (рис.
6.2). Определим функцию
(6.15) h(x) = f{x) - (/(a) + (х - а) /(^~^(а)).
В силу соотношений h(a) = h(b) — 0 и
о — а
Равенство (6.14) следует из h'(£) = 0 (теорема 6.10). П
(6.12) Следствие. Пусть функции f,g : [a, 6] —> Ш непрерывны на [a, Ь] и
дифференцируемы на (а, Ь). В этом случае
a) если /'(£) = 0 при всех £ Е (a, Ь), то f(x) = С (постоянная);
b) если /'(£) = gf{£) при всех £ Е (а, Ь), то f(x) — g(x) + С;
c) если /'(£) > 0 при всех £ Е (а, 6), то /(ж) монотонно возрастает, т.е.,
f{xi) < /(#2) rcpu всеж а < xi < Ж2 < 6; гх
d) если |/'(£)| < М при всех £ Е (а, 6), то |/(#i) — /(^2)! < M\xi — Жг| при
^1,ж2 Е [а, &].
Доказательство. Используя формулу (6.14) на интервале [а, х] получаем
утверждение (а) при С = f{a). Утверждение (Ь) следует из (а). Два остающихся
утверждения получаются из теоремы 6.11, примененной на интервале [xi, х2]. □
(6.13) Фундаментальная теорема дифференциального исчисления1. Пусть
функция f(x) непрерывна на [а, 6]. Тогда существует первообразная F(x) функции
f(x), единственная с точностью до аддитивной постоянной, и
(6.16) [ f{x)dx = F{b)-F{a).
J а
Доказательство. Существование F(x) очевидно из теоремы 6.9.
Единственность (с точностью до постоянной) очевидна из следствия 6.12Ь. Если F(x)
является произвольной первообразной функции /(ж), мы имеем F(x) = J f(t) dt + C.
Полагая x = a, имеем С = F(a), и формула (6.16) получается, если мы положим
х - 6. □
На рис. 6.3 представлено впечатляющее генеалогическое дерево теорем,
необходимых для строгого доказательства Фундаментальной теоремы. Если бы
Лейбниц увидел эту схему, у него могло бы не хватить смелости для того, чтобы
сформулировать и использовать эту теорему.
"Фундаментальная теорема дифференциального исчисления" позволяет нам
формулировать теоремы Дифференциального исчисления раздела III.6 как
теоремы Интегрального исчисления (разд. III.5) и наоборот. В нескольких случаях
1 В отечественной литературе эту теорему и формулу (6.16) обычно называют
"основная формула интегрального исчисления". — Прим. ред.

242 III. Основания классического анализа
Фундаментальная теорема дифференциального исчисления
L
теорема 6.11
Лагранж
теорема 5.10
существование J
j-
теорема 6.10
Ролль
замечание 5.13
J а = J а """ il
-J-
теорема 6.4
/' > 0 => ...
теорема 5.17
о ср. значении
теорема 1.5
Ит(+, -, /)
теорема 4.5 i
равном, непрер. I
теорема 3.3
непрер. ф-ция
опред. вещ. чисел, опред. предела; логика
Рис. 6.3. Генеалогическое дерево Фундаментальной теоремы.
мы использовали этот факт в разд. II.4. "Интегрирование с помощью
подстановки" (формула (II.4.14)) и "Интегрирование по частям" (формула (II.4.20)) теперь
получают солидную теоретическую основу. Надо только потребовать, чтобы
рассматриваемые функции были бы непрерывными с тем, чтобы интегралы
существовали.
Правила Лопиталя
... совершенно чужд суетной славы, которую так жадно ищет большинство
ученых ... (мнение Фонтенеля
о Гийоме Франсуа Антуане де Лопитале, маркизе Сент-Месма и Монтелье,
графе Антремонтском, сеньоре Дукском, 1661-1704)
Кроме того, я признаю, что я очень многим обязан светлым умам братьев
Бернулли, особенно младшего, который ныне профессор в Гронингене. Я
без ограничений пользовался их открытиями ... (де Лопиталь 1696)
Начнем со следующего обобщения теоремы Лагранжа 6.11.
(6.14) Теорема (Коши 1821). Пусть функции f : [а, Ь] -* М и д : [а, Ь] —> Ш непре-

111.6 Дифференцируемые функции 243
рывны на [а, 6] и дифференцируемы на (а, Ь). Если д'(х) ф О при а < х < Ь, то
д(Ь) ф д(а) и существует £ £ (а, Ь) такое, что
f(b)-f(a) _/'(0
(6.17)
д(Ь)-д(а) 9>(0'
Доказательство. Прежде всего отметим, что из теоремы Рол ля следует, что
д(Ь) ф д(а), поскольку д'(£) ф О при всех £ £ (а, Ь). Теперь заметим, что при
д(х) — х равенство (6.17) сводится к теореме 6.11. Действуя по аналогии с
доказательством этой теоремы, вместо (6.15) возьмем
(6.18) Цх) = f{x) - (/(а) + (д(х) - д(а)) Щ^щ) ■
Условия теоремы Ролля 6.10 для этой функции удовлетворены, и, следовательно,
существует £ £ (а, 6) такое, что h'(£) = 0. Это эквивалентно (6.17). □
Задача. Предположим, что мы хотим вычислить предел частного f(x)/g(x).
Если обе функции /(ж)и д(х) стремятся к 0 или ос при х —У 6, мы приходим к
неопределенным выражениям вида
0 оо
- или —.
0 ос
Следующие теоремы и примеры показывают, как действовать в таких случаях.
(6.15) Теорема (И.Бернулли 1691/92, Лопиталь 1696). Пусть f : (а,Ь) -> Ш и
д : (а,Ь) —>Ш дифференцируемы на (а, Ь) и пусть д'{х) ф 0 при а < х < Ь. Если
(6.19) lim f{x) = 0 и lim д(х) = 0
x-+b— x—tb—
и существует lim f'(x)/g,{x) = А, то
Х-¥Ь —
(6.20) lim 44 = Km 4т4-
х-+ь- дух) х^ь- д'(х)
Доказательство. Существование предела ff(x)/gf(x) при х —>■ Ь— означает,
что при заданном е > 0 существует такое S > 0, что
(6.21)
т А
< е при 6 — S < £ < Ь.
Из теоремы 6.14 для и, г; Е (6 — 5, 6) следует, что
(6.22)
/(«)-/(*) j |/'К)
-А
0M-0M I 1^(0
-А
< е.
В этой формуле мы полагаем v —>• 6—, используем (6.19) и получаем, что
|/(и)/#(и) — А| < е при 6 — 6 < и < Ъ. Это доказывает равенство (6.20). □
(6.16) Замечание. Слегка изменяя доказательство, можно видеть, что

244 III. Основания классического анализа
- теорема справедлива при b = +00;
- теорема справедлива при Л = -foo или Л = —ос; и
- теорема справедлива в пределе х —>■ а+.
(6.17) Теорема. В предположениях теоремы 6.15, где (6.19) заменено на
(6.23) lim f(x) = 00 и lira g(x) — ос,
х—уЪ— ~ ' *■
формула (6.20) также справедлива.
Доказательство. Умножим (6.22) на
х-*Ъ-
g(v) -g{u)
9{v)
Л 9(и)
1 j—t » что дает
9{v)
(6.24)
Ф)
А
V q(v)J
< е
1
я{и)
9{v)
В выражении в левой части выделим и оценим \f(v)/g(v) — А|. Используя
"обратное" неравенство треугольника |Л| — \В\ < \А — В\ (или \А\ < \А — В\ + \В\),
получаем
т
9{v)
-А
< е
1-
9(у)\ , |/М - Aflf(w)
0ОО
+
$М
Теперь при фиксированном гх устремим -у —>■ Ь—. В силу (6.23) выражение в правой
части стремится к е. Следовательно, при v достаточно близком к 6, справедливо
неравенство \f(v)/g(v) — Л| < 2е. Это и доказывает утверждение теоремы. D
Примеры. Отношение функций f(x) = sin ж и д(х) = ж при ж —>■ 0 приводит к
неопределенному выражению 0/0. Используя теорему 6.15, мы получаем
(6.25)
sin ж COS ж
lim = lim —-— = 1.
х-ч-0 х
>о 1
Очевидно, что эти равенства следует читать справа налево. Так как существует
lmxp-^ocosz = 1, то lim^-^o sin х/х также существует и равен 1.
Рассмотрим теперь функции f(x) = еах (а > 0) и д(х) = хп, которые обе
стремятся к оо при х —>- оо. Повторное применение теоремы 6.17 (и замечания
6.16) дает
е осе
(6.26) lim = lim =—- — lim
Л 2 Лагг
a e
ат-юо £n х4оопЖп_1 аг-)-oo n(n — 1)жп_2
anea;r
lim :— = 00.
x—>-oo 77,!
Это показывает, что экспоненциальная функция еах при ж —>■ оо возрастает
быстрее, чем любой полином.
При а > 0 из теоремы 6.17 и замечания 6.16 мы получаем
(6.27)
\пх _. 1/х .. 1
lim = lim г = lim —
х—юо СС
гг—)-оо ах
а-1
0.
Следовательно, любой полином возрастает быстрее, чем логарифм.
Неопределенные выражения вида
0-ос
или
0°
или
оо

III.6 Дифференцируемые функции 245
можно рассматривать так же, как в следующих примерах:
(6.28) lim (ж • In ж) = lim -^ = lim /f . = lim (-ж) = О,
v ' x-)-0+v ' x->-0+ 1/X rr->0+ —1/X2 x-+0K '
(6.29) lim xx — lim ехр(ж1пж) = exp[ lim ж In ж) = exp(O) = 1,
V ' x-»0+ x->0+ ч 7 *\ *_>()+ / V У
(6.30) lim tyx = lim ж1/* = expf lim —\ = exp(0) = 1.
X —юо #—юо \ x—юо ж /
В последних двух примерах мы использовали непрерывность экспоненциальной
функции.
Производные бесконечных рядов
Где доказано, что можно получить производную бесконечного ряда
почленным его дифференцированием?
(Абель, 16 января 1826 г., Oeuvres, vol. 2, p. 258)
Следующая теорема дает обоснование почленного дифференцирования
бесконечных рядов.
(6.18) Теорема. Пусть fn : (а, Ь) —> Ш — последовательность непрерывно
дифференцируемых функций. Если
г) lim /п(ж) = /(ж) на (а, Ь), и
п—>оо
ii) lim fn(x) = р(х) и сходимость равномерная на (а, Ь),
п—юо
то /(ж) непрерывно дифференцируема на (а, 6), и для всех ж Е (а, 6)
(6.31) lim /;(*) = /».
П—ЮО
Доказательство. Нетрудно догадаться, что существенным "ингредиентом"
этого доказательства (кроме фундаментальной теоремы дифференциального
исчисления) является теорема 5.19 о перемене порядка перехода к пределу и
интегрирования. Зафиксируем точку жо Е (а, о). Так как {fn(x)} сходится равномерно
на (а, 6), то
fX fX
/ p(t) dt = lim / f'n{t) dt = lim (fn(x) - /„(a*)) = /(*) - /(so).
«'.To «/.To
Из теоремы 6.9 следует, что р(х) — /'(ж) и что равенство (6.31) справедливо.
Непрерывность /'(ж) следует из теоремы 4.2. □
(6.19) Контрпримеры. Примеры функций (см. рис. 6.4)
ж 1
(6.32) fn (ж) = 1 + п2ж2 и fn (ж) = - sin(naj)
показывают, что одного условия г) (даже при наличии равномерной сходимости)
недостаточно для того, чтобы доказать равенство (6.31).

246 III. Основания классического анализа
Рис. 6.4. Равномерная сходимость, при которой lim f'n ф (lim fn)'-
Упражнения
6.1 Зададим положительное число п и определим функцию /п : Ш —> Ш как
fznsin(l/z3) при х ф О,
L О при ж = 0 .
Сколько раз fn дифференцируема и какие производные fn непрерывны?
6.2 С помощью двух различных методов (используя (6.1), а также формулировку
Каратеодори (^-6)) покажите, что если д(х) дифференцируема в точке хо и
д(хо) ф О, то 1/д(х) также дифференцируема в точке х$.
6.3 Покажите, что следующая функция является возрастающей на [0,1]:
г, ч Г х • (2 — cos(lnx) — sin(lnx)) 0 < х < 1
L 0 х = О,
но существует бесконечное количество точек, где /'(£) = 0. Противоречит
ли это формуле (6.14)? Является ли f(x) дифференцируемой при х — 0?
6.4 а) Пусть функция h : [а, Ь] —у Ш непрерывна на [а, Ь] и п раз дифференцируема
на (а, 6). Покажите, что если h(x) имеет п + 1 нулей на [а, 6], то существует
такая точка £ £ (а, 6), что Мп)(£) = 0.
Указание. Повторно применяйте теорему Ролля.
Ь) Положим h(x) — f(x) — р(ж), где р(х) есть интерполяционный полином на
равноотстоящих точках сетки (см. формулу (Н.2.6)). Покажите, что для п
раз дифференцируемой функции f(x) (см. формулу (II.2.7))
(6.33) ^ = /(»>(£).
6.5 Функция, изображенная на рис. 6.5, которую часто называют "чертовой
лестницей", показывает, что теорема Лагранжа (см. следствие 6.12а) не столь
тривиальна, как это может показаться. Если х в системе с основанием 3
имеет, например, представление х = 0.20220002101220... , то f(x) в системе
с основанием 2 получается посредством замены единицами всех двоек,
предшествующих первой единице, и отбрасыванием всех следующих за ней цифр,
(в нашем примере f(x) = 0.101100011). В частности,

III.6 Дифференцируемые функции 247
/(*) = § при ЖЕ [§,§], /(ж) = £ при sG [§,§], /И = | при же [|,§].
Покажите, что эта функция непрерывная и неубывающая. Она
дифференцируема, ее производная f'(x) = 0 на множестве меры 1/3 + 2/9 + 4/27 + 8/81 +
+ ... = 1, т. е., как принято говорить, почти всюду. Тем не менее /(0) ф /(1).
1.00 г
.75
.50
.25 Ь
0 1/3 2/3 1
Рис.6.5. "Чертова лестница".
6.6 Используя правило Лопиталя (и логарифмы), вычислите lim
иг-
6.7 (Приближенное спрямление дуги окружности). Пусть задана окружность
радиуса 1. При заданной точке М на окружности пусть N будет точкой на
касательной в точке О такой, что N0 — дуге МО. Вычислите точку Р,
находящуюся на прямой ОС и на одной прямой с N и М (см. рис. б.6). Каково
предельное положение Р, если а стремится к нулю?
Рис. 6.6. Приближенное спрямление дуги окружности.
Замечание. Ответ равен 3. Поэтому, если Р поместить точно в точке х — 3,
N0 будет отличным приближением для дуги МО.
6.8 Рассмотрим последовательность
/n(z) = y^ + *2 п=1,2,3,4,... .
Покажите, что fn{x) равномерно сходится на [—1,1] к некоторой
функции f(x). Является ли f(x) дифференцируемой? Для каких значений х
Итп_юо Д'г(ж) = f'(x) ?

248 III. Основания классического анализа
III.7 Степенные ряды и ряды Тейлора
После научной конференции, на которой Коши изложил свою теорию
сходимости рядов, Лаплас поспешил домой и оставался там в уединении до
тех пор, пока не окончил исследование рядов в своей Mecanique celeste.H
счастью, все они оказались сходящимися. (М.Клайн 1972, р. 972)
Пусть со, ci, С2, сз,... — последовательность действительных коэффициентов
их — независимая переменная. Тогда ряд вида
оо
£
п=0
(7.1) S^ спхп = с0 + с^х + с2х2 + с3х3 4- • -
называют степенным рядом. В этом разделе мы исследуем, на каком множестве
значений х некоторый ряд вида (7.1) сходится. Мы изучим также свойства
функций (непрерывность, производные, первообразные), представляемых степенными
рядами (7.1).
(7.1) Лемма. Предположим, что ряд (7.1) сходится при некотором х. Тогда он
сходится также при всех х таких, что \х\ < \х\. Более того, для каждого г\
такого, что О < г] < \х\, ряд (7.1) сходится абсолютно и равномерно на интервале
[-v,v\-
Доказательство. Из сходимости ряда ^2спхп следует, что
последовательность {спхп}п>о ограничена (см. формулу (2.3) и теорему 1.3), т.е. существует
такое, что |спжп| < В при всех п > 0. Значит, при \х\ < Т] мы имеем
V
х
V
спхп\<\сп\т]п^\сп2п\'\Ц <Bqn, где q = -^ < 1.
х
Из теоремы 2.5 следует, что сходимость и абсолютная сходимость ^спжп имеет
место. Равномерная сходимость следует из теоремы 4.3. D
(7.2) Определение. Введем определение
(7.2) £ = sup{|#| таких, что Х^п°=ос«жП сходится }
и назовем g радиусом сходимости ряда (7.1). Положим g = оо, если (7.1)
сходится при всех действительных х.
(7.3) Теорема. Ряд (7.1) сходится при всех х, для которых \х\ < д, он
расходится при всех х, для которых \х\ > д, и мы имеем равномерную сходимость на
интервале [—rj, п], где 0 < г\ < д.
Доказательство. Пусть х удовлетворяет условию |ж| < д. Тогда существует
такое £, что \х\ < \х\ < д, причем ряд (7.1) сходится при х (в определении 1.11
положите е = (д — \х\)/2). Таким образом, согласно лемме 7.1, мы имеем
сходимость в точке х. Равномерная сходимость на интервале [—77, rj\ доказывается
аналогично. □
Эта теорема ничего не говорит о сходимости ряда при х — д и х = — д. Ив
самом деле, в этих точках могут возникать различные ситуации, как показывает
следующий пример.

111.7 Степенные ряды и ряды Тейлора 249
(7.4) Пример. Ряд
(7.3)
Ехп X ЯГ Х° X*
п = 1
2а За 4а
+ ...
при а = О является геометрической прогрессией (пример 2.2, не считая
первого члена), при а — 1 он сводится к —1п(1 — х) (формула (1.3.14)), а при а = 2
это "дилогарифм Эйлера" (Эйлер 1768, Inst. С ale. Int., Sectio Prima, Caput IV,
Exemplum2). Радиус сходимости ряда (7.3) g = 1 и не зависит от значения а (см.
пример 7.6 ниже). При а — О ряд расходится на обоих концах интервала
сходимости. При а — 1 он расходится при х — +1 (гармонический ряд), но сходится
при х — — 1 (по критерию Лейбница). При а — 2 ряд сходится и при х — +1, и
при ж = — 1 (см. лемму 2.6).
Определение радиуса сходимости
Следующие теоремы дают полезные формулы для определения радиуса
сходимости.
(7.5) Теорема (Коши 1821). Если lim |cn/cn+i| существует (или равен оо), то
п—ь-оо
Сп
(7.4)
g — lim
сп+1
Доказательство. Применим критерий 2.10 к ряду ^2пап с ап = спхп. Так
как
lim
П—ЮО
Яп + 1
= lim
п—юо
СП + 1Ж
п + 1
СтаЖ7'
= |ж| lim
сп+1
= |х|/
lim
п—юо
Сп + 1
ряд (7.1) сходится, если |ж| < lim |cn/c„+i|. Он расходится, если |ж| > lim |cn/cn+i|.
Из этого следует формула (7.4). □
(7.6) Примеры. Для ряда (7.3), где сп — 1/тга, |cn/cn_j_i| — (1 + 1/тг)а —> 1 при
п -^ оо. Следовательно, его радиус сходимости g = 1. Аналогично для
биномиального ряда, который представляет функцию (1 + х)а (теорема 1.2.2), имеем
\сп/сп+1\ = (п + 1)/|а - п\ -> 1 и ^ = 1.
В разд. III.2 было доказано, что разложение в ряд функции ех (см. теорему
1.2.3), а также функций sin ж и cos ж (см. формулы (1.4.16) и (1.4.17)), сходится
при всех действительных ж. Следовательно, радиус их сходимости есть g = ос.
Примером ряда с радиусом сходимости g = 0 является ряд
1 + ж + 2!ж2 + 3!ж3 + 4!ж4 + ... .
В этом случае сп = п! и |cn/cn+i| = 1/(п + 1) —)• 0.
К ряду
(7.5)
ж3 ж5 ж7
arctg ж = ж-у + у-у + ---
формула теоремы 7.5 непосредственно не приложима,

250 III. Основания классического анализа
потому что |cn/cn+i| попеременно равно 0 и ос. Если мы поделим члены ряда
на ж и заменим х2 на новую переменную z, ряд (7.5) будет представлен в виде
Sn cnZn, где сп = 1/(2п + 1). В силу теоремы 7.5 для этого ряда мы имеем д - 1.
Следовательно, ряд (7.5) сходится при \х2\ < 1 (т.е. при \х\ < 1), и д — 1.
В то время как в формуле (7.4) требуется существование предела,
следующий результат справедлив без такого рода ограничения (см. также упр. 7.1
(7.7) Теорема (Адамар 1892). Радиус сходимости ряда (7.1) равен
1
(7.6) е =
limsup \/|сп|
Доказательство. Применим критерий 2.11 к ряду J2nan^ где ап ~ СпХП'
Поскольку
limsup \/|ап| = |ж| • limsup ^/|сп|,
п—юо га —юо
видно, что ряд (7.1) сходится при \х\ < l/lim^-j.oo sup ^/|сп|. Он расходится, если
\х\ > 1/ limn_юо sup ij/|cn|. D
Непрерывность
Пусть D есть область сходимости ряда (7.1):
(7.7) D = [х | где ряд (7.1) сходится },
т.е. ряд (7.1) определяет функцию / : D —у М, заданную формулой
оо
(7.8) f(x) = ^2 спхП ПРИ x£D.
71=0
Из равномерной сходимости на [—7?, rj] при 0 < r\ < g следует (см. теоремы 7.3
и 4.2), что f(x) является непрерывной функцией в открытом интервале (—g,q).
Следующая знаменитая теорема Абеля рассматривает вопрос о непрерывности в
конечных точках интервала сходимости.
(7.8) Теорема (Абель 1826). Предположим, что ряд (7.8) сходится в точке xq = g
(или в точке хо = — д). Тогда функи,ия f(x) непрерывна в точке xq — g (или
zo = -Q)-
Доказательство. Предположим для простоты, что g = 1 а хо — -\-1. Если
это не так, растянем и/или обратим интервал сходимости, сделав замену xq на
±хо/д. Поскольку согласно предположению сходимость при xq — 1 имеет место,
из леммы 2.3 следует, что для п > N и к > 1
(7.9) \сп+1 + сп+2 + ... 4- сп+к | < е.
Выберем теперь произвольное х из [0,1]. Для fn{x) = Y^=oCiX% мы имеем

111.7 Степенные ряды и ряды Тейлора 251
(7.10) /»+*(*) - /»(*) = c„+ia;n+1 + сп+2хп+2 + ... + сп+кхп+к.
Если все с,- > 0, то из формулы (7.9) видно, что \fn+k(x) — fn(x)\ < е. В противном
случае представим члены суммы (7.10) несколько более сложным способом (здесь
мы записали это для случая к — 4):
СП+1ЖП+4 + сп+2хп+* + сп+3хп+4 + сп+4хп+4 +
+ сп+1(жп+3-ж"+4) + cn+2(xn+3-xn+i) + сп+3(хп+3-хп+4) +
+ сп+1(хп+2-хп+3) + сп+2(х"+2-х"+3) +
+ сп+1{хп+1-хп+2)
(этот процесс называется суммированием по частям (Абель 1826, см. упр. 7.2)).
В каждой строке мы можем выделить общий (положительный) множитель хп+к,
хп+к~1 — хп+к, ... и с помощью (7.9) и неравенства треугольника получить, что
!/»+*(*) -fn(x)\<e- (хп+к + a;"+fc-1-a;"+fc + ... + х»+1-х»+2) < е
равномерно на [0,1]. А тогда непрерывность функции f(x) в точке хо = 1 следует
из теоремы 4.2. D
Дифференцирование и интегрирование
Поскольку у/п —у 1 при п —у оо (см. формулу (6.30)), из теоремы 7.7 следует,
что почленно продифференцированный или проинтегрированный степенной ряд
имеет такой же радиус сходимости, что и первоначальный ряд. При этом имеет
место следующая теорема.
(7.9) Теорема. Функция f(x) = Y^=oc^xn дифференцируема при \х\ < q, где g —
радиус сходимости и g > 0, причем
оо
(7.11) f'(x) = J2ncnxn-1.
п = 1
Функция f(x) имеет также первообразную на (—g,g), которая равна
(7.12) / /(*)А = 5>—у.
J° п=0 П + V
Доказательство. При 0 < п < g сходимость этих рядов равномерна на [—rj, rj]
(конечно, также и на (—7?, г/)). Теперь из теоремы 6.18 следует, что функция f(x)
дифференцируема на (—77, ту) и что ее производная равна (7.11). Аналогично,
формула (7.12) следует из следствия 5.20. □
(7.10) Замечание. Если ряд (7.1) сходится, скажем, в точке х = д, то
продифференцированный ряд (7.11) вовсе не обязан сходиться в этой точке. Так обстоит
дело, например, для ряда (7.3) при а = 2. Однако из сходимости (7.1) в
точке х = д следует сходимость (7.12) в этой точке (см. упр. 7.3). Таким образом,
используя теорему 7.8, мы видим, что тождество (7.12) справедливо при всех
xeD.

252 III. Основания классического анализа
(7.11) Пример. Радиус сходимости геометрической прогрессии (пример 2.2) д = 1.
Интегрируя ее почленно, используя теорему 7.9 и определение логарифмической
функции In (разд. 1.3), мы получаем, что при х Е (-1,1)
(7.13)
Г dt х2 х3 х4 х5
Щ1+х) = 1 ш = ж-у + у-т + у
Более того, ряд в (7.13) сходится при х = 1, и, в силу теоремы 7.8, мы получаем,
что In 2 = 1 — 1/2 + 1/3 — 1/4 + ... (на этот раз строго!).
Ряд Тейлора
... чтобы оценить величину остаточного члена этого ряда. Эта задача,
одна из наиболее важных в теории рядов, до сих пор не решена ...
(Лагранж 1797, р.42-43; Oeuvres, vol.9, p.71)
В 1797 г. (второе издание вышло в 1813 г.) Лагранж написал целый трактат,
в котором в основу анализа было положено разложение функции в ряд Тейлора
ОО / \(
(7.14) /(я) = ^1^1/(0^)
(см. формулу (П.2.8)), что, как он считал, позволило ему изгнать из анализа
бесконечно малые величины, пределы и флюксии ("degages de toute consideration
d'infiniment petits, d'evanouissans, de limites ou de fluxions", — франц.). Но эта
мечта продержалась только около 25 лет.
Если рассматривать х — а как новую переменную, наш ряд примет вид (7.1),
и полученные выше результаты, относящиеся к сходимости рядов, будут
применимы. Первая трудность состоит в том, что существуют бесконечно
дифференцируемые функции, для которых ряд (7.14) не сходится ни в какой точке х ф а
(см. упр. 7.6 ниже). Однако даже из сходимости ряда в (7.14) не обязательно
следует тождество (7.14), как видно из следующего контрпримера.
(7.12) Контрпример.
... формула Тейлора, которую уже нельзя принимать в общем случае ...
(Коши 1823, Resume, р. 1)
Коши (1823) рассмотрел функцию
(7.15) /(*)
при х ф О
при х — О,
которая везде непрерывна. Эта функция является настолько "плоской" в начале
координат (см. рис. 7.1), что /^(0) = 0 при всех г. Действительно, согласно
правилам дифференцирования мы получаем (при х ф 0)
л.) = $■ .-«•■. л» = (4 + ?)■«-"-
и видим, что f^(x) является полиномом от переменной 1/ж, умноженным на
e-i/x ^ Поскольку для всех п функции х~пе~1/х стремятся к нулю, когда х -4- О
(см. примеры после теоремы 6.17), мы имеем f^(x) —> 0 при х —> 0. Из того

HI.7 Степенные ряды и ряды Тейлора 253
Рис. 7.1. Графики функции е 1'х и ее производных.
факта, что f^(x)/x -» 0 при х —>• 0, следует, что /(*+1)(0) = lim/^o f^%\h)/h = 0.
Таким образом, рядом Тейлора для функции f(x) (7.15) является 0 + 0 + 0 + ...,
который, очевидно, сходится при всех ж. Однако формула (7.14) неверна при
хфО.
Чтобы установить справедливость равенства (7.14) для конкретных
функций, надо рассмотреть частичные суммы их рядов Тейлора и оценить их
остаточные члены. Полезная в этом контексте формула (И.4.32) была выведена в
конце разд. П.4. Этот результат подытожен в следующей теореме.
(7.13) Теорема. Пусть f(x) является к +1 раз непрерывно дифференцируемой на
[а, х] (или на [ж, а], если х < а). Тогда
/(») = Е Ц^ /(0 («) + Г Т^ /(fc+1) W А- П
Биномиальный ряд
... но больше всего удовольствия мне доставляет статья ... о простом ряде
т(тп — 1) о
1+тх+ —^— ^ X + . . .
Я полагаю, что это первое строгое доказательство биномиальной формулы ...
(Абель, письмо к Холмбо 1826, Oeuvres, vol. 2, p. 261)
Строгое доказательство биномиального тождества
/71Гч /1 . \« 1 , , Q(a~ *) 2 , а(а~ l)(g-2) з ,
(7.16) (1 + х) = 1 + м Н ^ ж + — ^j х + • • •
при |ж| < 1 и произвольном а было впервые получено Абелем в 1826 г.
Доказательство, основанное на ряде Тейлора, можно найти в лекции Вейерштрасса (см.
Вейерштрасс 1861).
Если положить f(x) = (1 + х)а и вычислить производные этой функции
f'(x) = а{\ + z)a_1, f"\x) = а(а - 1)(1 + ж)а~2,... , то мы увидим, что ряд (7.16)

254 III. Основания классического анализа
является просто рядом Тейлора функции f(x) = (1 + ж)а. Его радиус сходимости
д = 1 был вычислен в примере 7.6. Чтобы доказать справедливость тождества
(7.16) при \х\ < 1, надо доказать, что остаточный член (см. теорему 7.13)
а — к — 1
dt
(7.17) Rk(x) = ^ {±-^- а{а - 1) ..... (а - fc)(l + t)
сходится к нулю при к —> ОС.
Используя теорему 5.17 и полагая £ = OkX при 0 < 0* < 1, мы получаем
Rk(x) = (Ж~^Ж) а(а - 1) • • • (а - Jfe)(l + внх)-*-1 • х
Ja-l)(a-2)...(g-t) t /^у ,
Множитель аж постоянен; величина (1 + Окх)а г лежит между (1 + х)а 1 и 1 и
ограничена; из того, что 0< 1 — Ok < 1 + OkX для всех \х\ < 1, следует, что
множитель ((1 — 0k)/{l + 0kx)) ограничен единицей. Поскольку остающийся множитель
(a-l)(a-2)---(a-fc) к
к\ Х
при всех \х\ < 1 можно рассматривать как общий член сходящегося ряда, он
стремится к нулю согласно (2.3). Следовательно, мы имеем Rk{x) -> 0 при к ->• ос,
и тождество (7.16) установлено при \х\ < 1.
Если ряд (7.16) сходится при х = +1 или х = —1, он представляет
непрерывную функцию (теорема 7.8). Следовательно, он равен (1 -\-х)а также и в этих
точках.
Оценка остаточного члена без использования интегрального
исчисления. Попытки Лагранжа (1797) вычислить остаточный член в формуле
Тейлора увенчались получением следующих изящных формул ("се theoreme nouveau
et remarquable par sa simplicite et sa generalite ..." — "эта новая теорема
замечательна своей простотой и своей общностью ...", — франц.):
f(x)=f(a) + (x-a)f(t)
(7.18) Я*) = /(«) + (*-*)/'(«) + {jL^~ ПО
f{x) = /(о) + (*-«)/» + ^=p£ /"(«) + (-^ Г«),
и т.д., где £ — неизвестная величина, заключенная между а и х.
(7.14) Теорема (Лагранж 1797). Пусть f(x) — функция, непрерывная на [а, х] и
к + 1 раз дифференцируемая на (а, ж). Тогда существует £ Е (а, х) такое, что

HI.7 Степенные ряды и ряды Тейлора 255
Доказательство. Следуя элегантной идее Коши (1823), запишем остаточный
член как
к
(7.19) Rk{x) = f{x)-ST{-^1 f{i)(a)
i=0
и сравним его с функцией Sk{x) — (х — a)fc+1 /(к + 1)!. Имеем
Я(а)=0, Д» = 0, , Д(*)(а) = 0
и аналогично S^l'(a) = 0 для г — О,1,..., к. Последовательно применяя теорему
6.14, получаем
Rk(x) Rk(x) - Rk(a) j%(&) R'k(^) - R'k(a)
Sk(x) Sk(x)-Sk(a) S£(6) %(&) - S>k(a)
l7m ^(6) Щ(Ь)-Щ(а) Д<*+1)(6+1)
1 ) 5?«2) 5»(6)-^'(«) ••' 5ifc+1)(6+i)'
где £i лежит между x и a, £2 — между £i и a, и т.д. Поскольку S^ '(ж) = 1 и
R{*+1){x) = /(*+1)(я), из (7.20) мы получаем, что
Д*(х) = 5*(х)-/(*+1)(0,
где £ = £jfc+i- Теорема доказана. □
Замечание. Соотношение между остаточными членами теорем 7.13 и 7.14
дается теоремой 5.18. Доказательство, принадлежащее Лагранжу, см. в упр. 7.8.
Упражнения
7.1 Определите радиус сходимости ряда
f(x) = 1 + 2х + х2 + 2х3 + х4 + 2ж5 + ...
и покажите, что теорема 7.5 здесь неприложима, а теорема 7.7 приложима.
7.2 (Суммирование по частям, Абель 1826). Пусть {ап} и {Ьп} — две
последовательности. Докажите, что
N N
/I а>пЪп — 22 Ап^п - bn+i) + ANbN+1 - Л_1&0,
п=0 п=0
где А-1 — а — произвольная постоянная, аЛп = а + ао + о>\ + • • • + ап.
Указание. Воспользуйтесь тождеством
апЪп — (Ап - An-i)bn — An(bn - 6n+i) - An-ibn + Anbn+1.
7.3 Рассмотрим ряды
oo 00
Cn и Lt-
П
n=l n=l

256 III. Основания классического анализа
Докажите, что из сходимости первого ряда следует сходимость второго.
Доказательство содержит трудность, аналогичную той, которая была в
доказательстве теоремы 7.8 и которую можно преодолеть с помощью аналогичной
идеи (суммирование по частям, см. предыдущее упражнение).
7.4 Исследуйте сходимость ряда Ньютона—Грегори
. , ч 1 х3 1-3 хъ 1-3-5 х7
агсвш(х) = х + - т + — у + ^4^у + -"
при X = 1 И X = —1.
Указание. Для понимания асимптотического поведения коэффициентов
полезно вспомнить о произведении Валлиса.
7.5 Пусть D' — область сходимости ряда (7.11).
Докажите, что равенство в формуле (7.11)
имеет место при всех х Е D'.
7.6 Пример бесконечно дифференцируемой
функции, ряд Тейлора которой не сходится (см.
Лерх 1888, Прингсгейм 1888). Покажите, что
ряд
/(*)
cos 2х cos Ах cos 8х cos16ж
+ ^^— + ^— + 7^ + ■
1! 2! 3! 4!
и все его производные равномерно сходятся на
Ш. Покажите, что его ряд Тейлора в начале
координат имеет вид
/(0) + /'(0)* + ..
= (е-1)--
-1
2!
-х< +
- 1
064
4!
6!
-zD +
и расходится при всех х ф 0.
Тем не менее, для того, чтобы вычислить, например, /(0.01) (правильное
значение /(0.01) = 1.71572953), полезны два первых члена этого ряда.
Почему?
7.7 Исследуйте сходимость ряда (7.16) при ж = 1иж = —1.
7.8 Следуя Лагранжу, выведите формулы (7.18), используя, как бы мы сказали
в настоящее время, соображения "гомотопии".
Указание. Положите
(7.21)
f[x) = f(x — zx) + zxf (х — zx) +
2!
■/'V
zx">+ зГл^'
где z — переменная, заключенная между 0 и 1, и где х рассматривается как
фиксированная постоянная. Положите z = 0, и получите R(0) = 0. Если
2 = 1, мы видим, что (#3/3!)jR(1) есть искомый остаточный член. Теперь
продифференцируйте (7.21) по z, что дает Rf(z) — 3z2f"(x — zx) . Наконец,
проинтегрируйте от 0 до 1 и примените теорему 5.18.
7.9 (Абель 1826). Докажите, что тождество (2.19) справедливо, если ряды ]Г\ сц,
^2 ■ bj и их произведение Коши сходятся.
Указание. Примените теорему Абеля 7.8 к функции f(x) • д(х), где f(x) =
J2i агх% и 9{х) - Yjj bjxJ-

III.8 Несобственные интегралы 257
III.8 Несобственные интегралы
Теория интеграла Римана Ja f(x) dx в разд. III.5 основана на
предположениях, что [а, Ь] — конечный интервал и что функция f(x) на нем ограничена.
Теперь мы продемонстрируем, как эти ограничения можно преодолеть. Если хотя
бы одно из этих двух предположений не выполнено, то говорят о несобственном
интеграле.
Ограниченные функции на бесконечном интервале
(8.1) Определение. Пусть f : [а, ос) —>■ Ш интегрируема на каждом интервале
[а,Ь], где Ь> а. Если предел
ь
лОО лО
/ f(x)dx:— lim / f(x)dx
J a *-+~Л
существует, то мы говорим, что f(x) интегрируема на [а, оо) и что /а°° f(x)dx
является сходящимся интегралом.
Только зануды излагают общий случай. Настоящие учителя разбирают
примеры. (Парлетт, см. Math. Intelligencer, vol. 14, No. 1, p. 35)
(8.2) Примеры. Рассмотрим сначала экспоненциальную функцию на интервале
[0,оо). По определению 8.1 мы имеем
/ e~xdx = lim / e~xdx = lim (-е"Н )= lim (1 - е"ь) = 1.
Jo Ъ-+оо Jq Ь—юо \ 10 / Ь—юо
Привыкнув к этому определениею, мы просто напишем
= 1.
л ОС
(8.1) / e~xdx = -e-x
Jo
о
(8.2)
Далее, рассмотрим функцию х а на интервале [1,оо):
1-а ,оо ^расходится при а < 1
при а > 1 .
[°° dx _ f°° _а ж1_а I» Грасходит
Л ^ = Л Х dX = r^\i =\(а-1)-1
При а = 1 первообразная равна In х и несобственный интеграл расходится. Но
как мы можем проверить интегрируемость на интервале [а, ос) в случае, когда
нам не известна первообразная в явном виде?
(8.3) Лемма. Пусть f : [а, оо) —> Ш интегрируема на каждом интервале [а, Ь].
a) Если |/(ж)| < д(х) при всех х > а и J g(x)dx сходится, то J f(x)dx
также сходится.
b) Если 0 < g(x) < f(x) при всех х > а и J^° д(х) dx расходится, то J°° f(x) dx
также расходится.

258 III. Основания классического анализа
Доказательство. Часть (а) следует из критерия Коши (теорема 3.12) и
теоремы 5.14, так как \ fb f(x)dx\ < Jb \f(x)\dx < Jb g(x)dx < e при достаточно
больших b < b. Часть (b) очевидна. D
(8.4) Пример. При a > 0 рассмотрим функцию (1 + жа)-1 на интервале [0,оо).
Разделим интеграл на две части, а именно,
г°° dx г1 dx Г°°
dx
+ ха
Первый интеграл является "собственным". Для оценки второго учтем, что
111
-— < < — при ж > 1.
2жа - 1 + жа - жа -
Таким образом, из леммы 8.3 и формулы (8.2) следует, что интеграл (8.3)
сходится при а > 1 и расходится при а < 1.
sin ж
2л Зя .^-— 4тс
Рис. 8.1. График функции sin х/х.
(8.5) Пример. Рассмотрим существование интеграла
ЛОО
Ж
— dx.
Функция /(ж) = sin ж/ж непрерывна в точке ж = 0, причем /(0) = 1, так что в этой
точке не создает трудностей. Использование оценки | sin ж| < 1 ничего не дает,
поскольку интеграл $1 ж-1 dx расходится. Однако из графика функции /(ж) (см.
рис. 8.1) видно, что интеграл может быть представлен как знакопеременный ряд
вида а0 - а1 + а2 - а3 + ... , где
/,7rsinжJ r27rsinжJ r^sii
/ аж, а\ = — I аж, а2 =■ I —
JO х Jn х J2n a
Этот ряд сходится в силу критерия Лейбница (теорема 2.4). Условие a,-+i < а,
можно проверить путем подстановки жн->ж — 7г,аа;—>>0 следует из простой
оценки 0 < аг- < 1/г.

111.8 Несобственные интегралы 259
(8.6) Теорема (Маклорен 1742). Пусть функция f(x) > 0 не возрастает на [1, оо).
Тогда
У j f(n) сходится
п = 1
/оо
f(x)dx сходится .
8
h
8
h
8
"
h
8
h
I _ I
8
h
I
12 3 4 5 6
Рис. 8.2. Мажоризация и миноризация функции f(x).
Доказательство. Пусть g(x) = f([x]) и h(x) = f([x] + 1) представляют собой
ступенчатые функции, изображенные на рис. 8.2 (здесь [х] означает
наибольшее целое число, не превосходящее х). Эти функции интегрируемы на
конечных интервалах (в силу теоремы 5.11) и, поскольку f(x) монотонна, мы имеем
Кх) < f(x) < я{х) ПРИ всех х- Следовательно,
N rN N-1
п-2 Jl п=1
и утверждение следует из теоремы 1.13, так как f(x) > 0. □
Поскольку интегралы часто бывает вычислять легче, чем суммы, эта
теорема очень полезна при исследовании сходимости рядов. Например, из формулы
(8.2) следует изящное новое доказательство леммы 2.6.
Если мы хотим посмотреть, что происходит "между" расходящимся рядом
^2 1/п и сходящимся рядом ^2 1/па (при некотором а > 1), надо исследовать ряд
(8.5)
оо 1
-^ n(lnn)^
п=2
(для больших п и любых а > 1 и /3 > 0 мы имеем п < п(\пп)Р < па в силу
формулы (6.27)). С помощью преобразования и = In ж мы получаем
Г°° dx Г°° du
J2 х • (1пхУ ~ Jln2u^
и из теоремы 8.6 и формулы (8.2) следует, что ряд (8.5) сходится при /3 > 1, но
расходится при j3 < 1.

260 III. Основания классического анализа
Интегралы в пределах от —ос до +оо.
Было бы неблагоразумно вводить следующее определение:
(8.6)
/ОО лГ
f(x) dx — lim / f(x) dx
-oo r-*°°J-r
(если этот предел существует). Такое определение приводит к бессмыслице, если.
например, использовать формулу преобразования (П.4.14) при z — х-\-\ (dz — dx).
Согласно вышеприведенному определению мы получили бы
/+оо Л+ОО
zdz = 0 и / (х + 1) dx = ос.
-oo J — оо
(8.7) Определение. Пусть f : Ш —>• Ш — функция, интегрируемая на каждом
ограниченном интервале [а, Ь]. В этом случае мы говорим, что интеграл
/ОО лО лОО
f(x)dx:= / f(x) dx + / f(x)dx
-oo J — oo JO
существует, если оба несобственные интегралы в правой части существуют.
Два интеграла
AcoiT^ и Le dx
сходятся в смысле определения 8.7. Первый стремится к 7г (первообразной
является arctg х). Сходимость второго интеграла видна из леммы 8.3, если
использовать неравенство е~х < е~х при х > 1.
Неограниченные функции на конечном интервале
(8.8) Определение (Гаусс 1812, §36). Если функция f : (а, Ь] —>• IR интегрируема
на каждом интервале вида [а + £, Ь], то мы вводим определение
/ f(x) dx := lim / f(x) dx
если этот предел существует.
Это определение включает и случаи, когда \f(x)\ —>■ ос при х —> а.
Аналогичное определение можно ввести, если \f(x)\ —> ос при х —У Ь. Для проверки
интегрируемости такой функции нетрудно приспособить лемму 8.3, сделав
очевидные изменения.
(8.9) Примеры. Для функции х~а на интервале (0,1] имеем
расходится при а > 1
(8
Г1 dx .. Г1 dx _. ж1_а Г расходит.
7) / — = lim / — = lim = < 1л ч -
Jo xQ £^°+Je х<* ^-^о+1-а|е [(l-a)-1
при а < 1.

III.8 Несобственные интегралы 261
В случае а — 1 интеграл также расходится. Следовательно, гипербола у — 1/х
(а — 1) является предельным случаем с бесконечной площадью слева (0 < х < 1)
и справа (х > 1). Если а уменьшается, площадь слева становится конечной, а
если а увеличивается, становится конечной площадь справа.
Интеграл
f1 since f1 since 1
/ dx — I • ax
Jo X J0 X X
сходится в том и только том случае, когда a — 1 < 1, т.е. а < 2. Это связано с
тем фактом, что функция f(x) — sin х/х непрерывна в нуле и /(0) = 1.
Гамма-функция Эйлера
В течение всей своей жизни Эйлер интересовался "интерполяцией"
факториалов 0! = 1, 1! = 1, 2! = 2, 3! = 6, 4! = 24,... на, нецелые значения. Эту величину
он обозначал 1-2-3-4-...-Ж ("De Differentiatione Functionum Inexplicabilium",
см. 1755, Caput XVI of Inst. Calc. Diff., Opera, vol.X). В конце концов в 1781 г.
он нашел определение (полностью "explicabilium" — явное, лат.),
используемое и ныне: интегрирование по частям следующего интеграла (где и(х) — ж11,
v'(x) — е~х) приводит к
Г00 loo Г°°
(8.8) / xne~xdx = -хпе~х\ +n/ хп-1е~х dx.
Член хпе~х обращается в нуль при х — 0 (п > 0) и при х —» ос, поэтому
лоо
(8.9) / xne-*dx = nl
Jo
Заменим здесь п нецелым действительным числом.
(8.10) Определение. Для а > 0 введем определение
/•ОО
(8.10) Г{а):= / хос-1е~х dx.
Jo
Теперь надо показать, что интеграл (8.10) сходится. Здесь имеются две
трудности: подынтегральная функция неограниченна при х —>■ 0 (если а < 1), и
интервал интегрирования бесконечен. Поэтому разобьем интеграл на два:
(8.11)
/»1 лОО
/ xa-1e~xdx+ / ха~1е~х dx.
Из оценки ха~1е~х < жа-1, из леммы 8.3 и из формулы (8.7) следует, что первый
интеграл в (8.11) сходится при а > 0. Для второго интеграла в (8.11) используем
оценку ха~1е~х = ха~1е~х/2 -е~х/2 < Ме~х/2 (см. примеры после теоремы 6.17)
и опять лемму 8.3.
Из формулы (8.9) и вычислений в (8.8) следует, что
(8.12) Г(п+1)=п!, Г(а+1) = аГ(а) при а > 0.

262 III. Основания классического анализа
С помощью второго соотношения в (8.12) можно распространить определение
Г (а) на отрицательные а (а ф — 1,— 2,— 3,...), полагая
(8.13) Г(а-1) = ^Щ
а — 1
(см. рис. 8.3). В разд. IV.5 мы покажем, что Г(1/2) = у/тт.
Рис. 8.3. Гамма-функция.
Упражнения.
8.1 Покажите, что интегралы Френеля (см. рис. П.6.2)
/ sin х2 dx , / cos х2 dx
Jo Jo
сходятся (можно также использовать замену координат и найти интеграл,
аналогичный (8.4); сравните с рис. 8.1).
8.2 Покажите, что для последовательности
п 1
ап = 2л/п -У_\—7=
Нтп-юо ап существует и 1 < Пшп-юо ап < 2 (может быть полезно вспомнить,
что J(l/y/x) dx — 2у/х ).
8.3 Используя подходящую замену координат, покажите, что
Г
Jo
'-Ч'Й)-

III.9 Две теоремы о непрерывных функциях 263
III.9 Две теоремы о непрерывных функциях
Этот раздел посвящен двум результатам Вейерштрасса. Первый состоит в
доказательстве существования нигде не дифференцируемых непрерывных
функций. Второй — в том, что непрерывная функция / : [а, Ь] —> Ш может быть с
произвольной точностью приближена полиномами.
Непрерывные, но нигде не дифференцируемые функции
До самого последнего времени считалось, что ... непрерывная функция
... всегда имеет первую производную, значение которой может быть
неопределенным или бесконечным только в некоторых изолированных
точках. Насколько я знаю, даже в работах Гаусса, Коши и Дирихле, которые
привыкли очень сурово критиковать все, что относится к области их
интересов, не высказывалось иное мнение. (Вейерштрасс 1872)
Лет сто назад такую функцию считали бы надругательством над здравым
смыслом.
(Пуанкаре 1899, L'oeuvre math, de Weierstrass, Acta Math., vol. 22, p. 5)
Рис. 9.1. Функция Римана (9.1) в окрестности х = тг.
До эпохи Римана и Вейерштрасса обычно считалось, что каждая
непрерывная функция является дифференцируемой везде, кроме, быть может, некоторых
особых точек (см. цитаты). В 1806 г. А.-М. Ампер (имя которого вам, конечно,
знакомо) даже опубликовал "доказательство" этого утверждения (J. Ecole Polyt.,
vol. 6, p. 148). Первым шоком был приведенный Риманом пример функции (5.24),
которая, будучи проинтегрированной, дает функцию, не дифференцируемую на
всюду плотном множестве точек. После этого начался поиск функций, которые
нигде не дифференцируемы. Около 1861 г. (см. Вейерштрасс 1872) Риман считал,
что функция
/л .4 л/ ч v^ sm(n2x) . 1 . 1А ч 1 . /л v
(9.1) f(x) = 2^ —K-j-^ = sin x + - 8ш(4ж) + - sin(9s) + ...
71 = 1

264 III. Основания классического анализа
(см. формулу (3.7)), которая непрерывна, поскольку ее ряд равномерно сходится
(см. теоремы 4.3 и 4.2), нигде не дифференцируема. Вейерштрасс признал, что
ему не удалось доказать это утверждение, и действительно, Жерве (1970) нашел,
что в некоторых точках функция (9.1) дифференцируема, например, в точке х -
7г (см. рис. 9.1).
(9.1) Теорема (Вейерштрасс 1872). Существуют непрерывные функции, которые
нигде не дифференцируемы.
Доказательство. В результате вычислений объемом в две страницы
Вейерштрасс показал, что ряд
оо
(9.2) f(x) = ]TVcos(an:c),
71 = 1
равномерно сходящийся при b < 1, нигде не дифференцируем при аЪ > 1 + 37г/2.
В дальнейшем многие исследователи, заинтригованные этим явлением, изобрели
новые примеры. Среди них были, в частности, Дини (1878, Chap. 10), фон Кох
(1906, см. рис. IV.5.6 ниже), Гильберт (1891, см. рис. IV.2.3 ниже) и Такаги (1903).
Функцию Такаги вновь открыл Толл (1982) и назвал ее функцией "бланманже".
Эта функция определяется следующим образом. Рассмотрим функцию
, х , ч Гх 0 < ж < 1/2
(9-3) ВД= 1 Л7,~'Л
У 1 — х 1/2 < х < 1
и продолжим ее периодически (т.е. К(х + 1) = К(х) при всех ж), что дает
непрерывную зигзагообразную функцию. Теперь определим (см. рис. 9.2) функцию
°° 1 111
(9.4) f(x) = £ -# (2"х) = К(х) + - К(2х) + - К(Ах) + - К(8х) + ... .
п=0
Поскольку |if (я)| < 1/2 и 1+ 1/2+1/4+1/8 +... сходится, ряд (9.4) сходится
равномерно (теорема 4.3) и представляет непрерывную функцию f(x) (теорема
4.2). У функции f(x) есть замечательное "фрактальное" свойство: разность
между f(x) и усеченными рядами в (9.4) опять является функцией "бланманже",
однако масштабированной с помощью множителя 2_п, т.е.
f(x)-Y^jjK(Vx) = ±;f(2nx).
3=0
Чтобы показать, что функция (9.4) нигде не дифференцируема,
воспользуемся изящным рассуждением, которое предложил де Рам (1957). Его идея состоит
в том, чтобы для заданной точки х0 взять числа ап = г/2п и /Зп — (i + 1)/2п (где
г — целое число, такое, что ап < хо < /Зп) и рассмотреть отношение
(М) Т. = /W.WK),
Так как при значениях ж, равных ап и /Зп, сумма в (9.4) оказывается конечной,
то тп определяет наклон функции, заданной усеченным рядом Х1?=о ojK№x)

III.9 Две теоремы о непрерывных функциях 265
2/3
1/3
Рис. 9.2. Функция "бланманже".
на интервале (ап,/5п) (см. рис. 9.2, где видно, что при xq = 1/3 эти наклоны
попеременно равны 0,1, 0,1,...).
При увеличении п всегда rn+i = rn ± 1, так что последовательность {гп} не
может сходиться.
С другой стороны, гп есть среднее взвешенное двух наклонов:
г у f(Pn)-f(*0) , п у ,/Ы-/К)
гп = Ап з h (1 - \п) ,
Рп — жо ж0 — ап
где Лп = ((Зп — хо)/(/Зп — an) G (0,1] (если ап = х$, то Лп = 1 и второе слагаемое
отсутствует). Поэтому из дифференцируемости (9.4) в точке xq вытекало бы, что
при достаточно больших п
|гп-/'|< \пе + {I - \п)е = е.
Мы пришли к противоречию. □
Аппроксимационная теорема Вейерштрасса
Это фундаментальное предложение установил Вейерштрасс.
(Борель 1905, р. 50)
Мы только что переварили первый сюрприз Вейерштрасса — существование
непрерывных функций, не имеющих производной. Теперь займемся вторым: мы
можем сделать такие функции дифференцируемыми столько раз, сколько
пожелаем, даже полиномами, если только мы согласны примириться с произвольно
малой ошибкой е.

266 III. Основания классического анализа
(9.2) Теорема (Вейерштрасс 1885). Пусть f : [а, Ь] —> Ш — непрерывная функция.
При каждом е > 0 существует полином р(х) такой, что
(9.6) \р{х) — f{x)\ <е для всех х £ [а)Ь]-
Другими словами, f(x)—e < р(х) < f{x) + e, т.е. полином р(х) заключен межЩ
f(x) —ей f(x) + е на всем интервале [а, Ь].
Приведем компиляцию составленных Борелем (1905, р. 50) и Мейнардусом
(1964, р. 7) списков математиков, представивших доказательства этой теоремы
(что показывает, насколько оба были очарованы красотой этого результата):
Вейерштрасс (1885), Пикар (1890, р. 259), Лерх 1892, Вольтерра 1897, Лебег
1898, Миттаг-Лёфлер 1900, Ландау (1908), Д.Джексон 1911, С.Бернштейн 1912,
П. Монтель 1918, Маршан 1927, В. Гончаров 1934. Эта теорема, связанная и с
аппроксимацией тригонометрическими полиномами, обобщалась различными
способами (см. Мейнардус 1964, §2). Приведенное далее доказательство основано на
идее, которую сегодня мы назвали бы идеей "последовательностей Дирака".
Последовательности Дирака. Следуя Ландау (1908, см. рис. 9.3а),
положим
х2)п если -1 < х < 1,
в противном случае,
1 • 3 • 5 • 7 •... • (2п + 1)
2•2•4 • 6 •... • 2п
(9.7) ipn{x
где множитель
(9.8) it*
выбран так, чтобы
/+оо
<pn(x)dx = l
-ОО
(см. упр. П.4.3). При возрастании п эти функции все более концентрируют свою
"массу" вблизи начала координат.
(9.3) Лемма. Пусть функции <рп{х) определены формулой (9.7). Для каждого
е > 0 и каждого S > 0 (0 < S < 1) существует целое число N такое, что для
всех п > N (см. рис. 9.3Ь)
(9.10) 1-е < J <pn{x)dx < 1,
(9.11) / <pn(x)dx+ (pn(x)dx<e.
Доказательство. Начнем с доказательства (9.11). Так как 1-х2 > 1-х при
0< х < 1, то f*(l-x2)ndx > f*(l-x)ndx= 1/(п+1), и поэтому ип < |(п + 1).
Следовательно, при S < \х\ < 1 мы имеем
0 < <рп(х) < <рп{&) < 2{п +!)•(!- S2)n.

III.9 Две теоремы о непрерывных функциях 267
Положим q:— 1 — S2 < 1, тогда (1 — 82)п — qn убывает по степенному закону, так
что (п+ 1) • (1 — 82)п —> 0 (см. (6.26)). При достаточно больших п из этого следует,
что 0 < <Рп(%) < £/% если 6 < \х\ < 1, и неравенство (9.11) вытекает из теоремы
5.14. Оценка (9.10) получается вычитанием (9.11) из (9.9). □
Рис. 9.3а. Последовательность Дирака.
Рис. 9.3Ь. Концентрация массы.
Доказательство аппроксимадионной теоремы Вейерштрасса.
Предположим, что 0 < а < 6 < 1 (общий случай приводится к этому путем
преобразования вида х i-> а + /?ж с подходящим образом выбранными постоянными а и
(3). Теперь продолжим f(x) до непрерывной функции на [0,1], например, полагая
f[x) — f(a) при 0 < х < а и f(x) = f(b) при Ь < х < 1, и для £ Е [а, Ь] положим
(9.12)
Р«(0 := / f{x)<pn(x-£)dx = цп / /(ж)(1 - (z-£)2)ndz.
,70 ./О
Если мы разложим множитель (1 — (х — £)2)п с помощью биномиальной
теоремы, мы получим полином от £ степени 2п, коэффициенты которого являются
функциями х. Подставляя его в (9.12), мы видим, что рп(£) является полиномом
степени 2п.
Мотивация. При фиксированном £ Е [а, Ь] пик функции у>п(я — 0 будет
сдвинут к точке £ (рис. 9.5). Следовательно, произведение f(x)-<pn (х—£) умножает
величину пика на приблизительно /(£). Поэтому, учитывая (9.9), можно ожидать,
что интеграл (9.12) будет близок к /(£).

268 III. Основания классического анализа
О а $-6 % £+5 Ъ 1
Рис. 9.4. Доказательство Ландау.
Оценка ошибки аппроксимации. Для оценки величины разности между рп{(]
и /(£) воспользуемся неравенством треугольника следующим образом:
i Г1 f*+s
М0-/(01< / /(*)Ы*-0<**- / /(х)^„(х-0^
1 JO J£-6
(9.13) + / /(«)^„(ж-0^- / f(Z)<Pn(x-t)dx
]j£-6 J£-6
I Г*+6 I
+ /(0 / M*-0^- ДО •
Зафиксируем некоторое e > 0. Поскольку / непрерывна на [0,1], она является
там равномерно непрерывной (теорема 4.5). Следовательно, существует S > О, не
зависящее от £ и такое, что
(9.14) |/(*)-/(01<* при \x-t\<6.
Если это необходимо, значения S можно уменьшить так, чтобы выполнялись
неравенства S < а и S < 1 — 6. Следовательно, всегда будет [£ — £,£ + £] С [0,1]. Кроме
того, функция f(x) ограничена, т.е. удовлетворяет неравенству \f(x)\ < М при
х £ [0,1] (теорема 3.6).
Мы можем теперь оценить три члена в правой части неравенства (9.13)
следующим образом. Для первого из них используем ограниченность функции f(x)
и неравенство (9.11) и найдем, что он ограничен величиной Me. Аналогично из
неравенства (9.10) следует, что третий член ограничен величиной Me. Наконец,

111.9 Две теоремы о непрерывных функциях 269
из (9.14) и (9.9) следует, что второй член ограничен величиной е. Таким образом,
при достаточно больших п мы получаем
Ы0-/(01<(2М+1)£.
Поскольку эта оценка справедлива равномерно на [а, 6], теорема доказана. □
1.0
.8
.6
.4
.2
.25 .50 .75 1.00
Рис. 9.5. Сходимость полиномов (9.12) к функции f(x) из (9.15).
(9.4) Пример. Рассмотрим функцию / : [1/8, 7/8] —> М, определенную как
1/8 < х < 1/4 ,
1/4 < х < 1/2 ,
1/2 < х < 3/4 ,
3/4 < х < 7/8 .
Как и в предыдущем доказательстве, мы продолжим ее до непрерывной функции
на [0,1]. Полиномы рп{(,) (9.12) изображены на рис. 9.5 для п — 10, 100 и 1000.
Видно, что равномерная сходимость имеет место на [1/8, 7/8], но не на [0,1]. Это
связано с тем, что при £ — 0 или £ = 1 половина пика функции <рп(х) в (9.12)
срезана. Поэтому предположение 0<а<6<1в вышеприведенном доказательстве
не может быть отброшено.
Графики на рис. 9.5 были получены с помощью вычисления интеграла в
(9.12) для 400 значений £ методом, аналогичным описанным в разд. II.6.
Вычислять 2000 коэффициентов полинома смысла не имело.
(9.15)
/(*) = {
-3.2ж + 0.8
3/8)2
^1/64 - {х
7 • 0/64 -(х- 5/8)2
17.6s-5.7
при
при
при
при

270 III. Основания классического анализа
Упражнения
9.1 Используя произведение Валлиса, покажите, что множители /лп в (9.8) при
п —>■ ос ведут себя асимптотически как у/п/7г, и что оценка в доказательстве
леммы 9.3 немного грубовата.
9.2 Покажите, что
(9.16) <pn(x) = J^e-nx\ п= 1,2,3,...
является последовательностью Дирака, т.е. удовлетворяет условиям (9.9),
(9.10) и (9.11) (в разд. IV.5 мы увидим, что J™ е~х dx — л/ъ ). Это та
последовательность, на которой Вейерштрасс основывал свое доказательство.
9.3 Найдите постоянные сп такие, что последовательность функций
сп ( cos(—) 1 при — 1 < х < 1,
(9.17) <рп(х) =
^ 0 в противном случае
будет последовательностью Дирака (см. упр. 5.6).
Эта последовательность, с помощью тригонометрических формул типа
(1.4.4'), приводит к аппроксимациям непрерывных на [—7Г, 7г] функций
тригонометрическими полиномами.
9.4 Пусть
. (п при \х\ < 1/(2п),
L 0 в противном случае.
Покажите, что для каждой непрерывной функции f(x)
lim / <рп(х — £)f{x) dx = /(£) при всех а < £ < 6.
п->°° Ja
9.5 Разложите (1 — (х — С)2)3 по степеням £ и покажите, что
/■4 + coB(s4 + v^-sin(3s)/ 2чЗ
Уо 721п(* + 1) + *. 11-^-*) J ^
является полиномом от £.

IV
Функции нескольких переменных
Рисунок К.Ваннер
Следует отметить стимулирующее влияние физики на рождение таких
математических сущностей, как кватернионы, гиперчисла Грассмана и
векторы. Эти творения стали частью математики. (М. Клайн 1972, р. 791)
Функции нескольких переменных берут свое начало из геометрии (например,
кривые, зависящие от параметров (Лейбниц 1694а)) и из физики. Одной из
наиболее известных задач в 18-м веке был расчет движения колеблющейся струны
(Даламбер 1748, см. рис. 0.1). Положение струны u(x,t) является функцией
пространственной координаты х и времени t. Важным прорывом в систематическом
изучении исчисления нескольких переменных, который произошел около
середины 19-го столетия, была идея обозначать пары (а затем и n-мерные наборы)
(х1,х2) = :
\xlt x2i • • • ? хп) — '-
одной буквой и рассматривать их как новые математические объекты.

272 IV. Функции нескольких переменных
Их называли "экстенсивными величинами" — Грассман (1844, 1862),
"комплексами" — Пеано (1888) и "векторами" — Гамильтон (1853).
Рис. 0.1. Движение колеблющейся струны (клавесин).
В разд. IV. 1 будут определены нормы в n-мерном пространстве, что позволит
нам довольно просто обобщить определения и теоремы о сходимости и
непрерывности (разд. IV.2). Однако дифференциальное (разделы IV.3 и IV.4), так же как и
интегральное (разд. IV.5) исчисление в случае нескольких переменных приводят
к новым сложностям (перестановка частных производных, изменение порядка
интегрирования, перестановка операций интегрирования и дифференцирования).

IV. 1 Топология n-мерного пространства 273
IVЛ Топология n-мерного пространства
Замечательно, что эта идея, которая настолько проста и в своей основе
заключается в рассмотрении совокупности нескольких различных величин
(таких, как рассматриваемые далее "экстенсивные величины") как новой
независимой величины, развилась фактически в новую науку; ...
(Грассман 1862г., Ausdehnungslehre, р. 5)
... весьма полезно рассмотреть "комплексы" из чисел или числа,
составленные из нескольких величин, ...
(Пеано 1888г., Мат. Анн., vol.32, р. 450)
Введем пары действительных чисел (cci, х2), наборы п упорядоченных
действительных чисел (#1, х2) • • •? Хп) и будем называть их векторами. Совокупность
всех таких пар обозначается
(1.1) М2 = 1хМ= {{хих2) ; хих2 Gl},
а совокупность всех n-мерных наборов
(1.2) 1п = Мх1х...х1= {(si,32,...,3n) ; ж*бМ,Ы,...,п}.
Векторы можно складывать (покомпонентно) и умножать на действительные
числа. С добавлением этих операций мы назовем Шп n-мерным действительным
векторным пространством.
Расстояния и нормы
Двумерное пространство Ш2 можно представлять себе как плоскость, где
компоненты Xi и Х2 являются декартовыми координатами. Расстояние между
двумя точками х = (xi,x2) и у — (2/1,2/2) находится по теореме Пифагора (рис.
1.1):
(1.3) d{x, у) = ^/Ы-х1у + {у2-х2)2.
Это расстояние зависит только от разности у — х и обозначается также \\у — х\\2,
где ||z||2 = a/zi + z2 если z ~ (*i? ^г)-
Рис. 1.1. Расстояние в!2. Рис. 1.2. Расстояние в!3.
В трехмерном пространстве расстояние между точками х — {х\,х2, х$) и у =
(2/1,2/2? уз) находится путем двукратного применения теоремы Пифагора (первый
раз для треугольника DEF, затем для треугольника ABC, рис. 1.2). В этом случае
мы получим d(x, у) = \\у — ж||2, где \\z\\2 = yjz\ -\- z\ + z\.

274 IV. Функции нескольких переменных
Аналогично, в n-мерном пространстве Rn мы определим
(1.4)
|2=)/*?+*2 + ... + *2
и назовем это евклидовой нормой z = (zi, 22,..., zn). Расстояние между х Е 1п и
у G Мп определяется как d(x, у) — \\у — ж||г.
(1.1) Теорема. Евклидова норма (1-4) обладает следующими свойствами:
(N1) ||ж||>0 и ||я;|| = 0«»ж = 0,
(N2) ||Аж|| = |А|-||ж|| Зая ХЕШ,
(N3) ||ж + 2/|| < ||ж|| +1|2/|| (неравенство треугольника).
Доказательство. Свойство (N1) тривиально. Так как Хх — (A#i,..., Ххп),
мы имеем ЦАжЩ = (Axi)2 + ... + (Ажп)2 — |А|2 • ||ж||2, что и доказывает свойство
(N2). Доказательство свойства (N3) следует из цепочки выкладок
I*+y\\i = Е>*+^)2 = Еж*+2 Е xkw<+Е ^
fe=i fc=i fc=i fc=i
<INIi + 2|Nl2||y||2 + lMli = (Nl2 + lMl2)2.
Замечание. В этом доказательстве мы использовали оценку
(1.5)
Е
fc=i
ж* 2/*
<
Е
^ fc=i ^ fe=i
Е%2'
которая называется неравенством Коши—Шварца. Оно выводится из
неравенства Х)£=1(ж& ~~ 1Ук)2 > 0 аналогично (III.5.19). Вводя обозначение
(1.6)
(ж, у) :=^zfe2/fc
fc=i
для скалярного произведения двух векторов ж и у, неравенство (1.5) можно
записать короче:
(1.5;)
IMI<INI
2 -112/112.
В дальнейшем равенством (1.4) в явном виде мы будем пользоваться редко.
Обычно мы будем просто использовать свойства (N1), (N2) и (N3).
(1.2) Определение. Отображение \\ • \\ : Шп —>■ Ш, удовлетворяющее свойствам
(N1), (N2) и (N3), называется нормой в Шп. Пространство Шп с введенной в
нем нормой называется нормированным векторным пространством.

IV. 1 Топология n-мерного пространства 275
Примеры (Жордан 1882, Cours d'Analyse, vol.1, p. 18; Пеано 1890b, p. 186,
сноска; Фреше 1906). Кроме евклидовой нормы (1.4) существуют и другие нормы:
п
(1.7) Iklli = $^1Ж*1 4-норма,
к = 1
(1.8) INloo = max \xk\ максимум-норма,
fc = l,...,n
i/p
(1.9) \\x\\p = ( V] \xk\p ) ^р-норма, p > 1.
(х>гУ
Проверка свойств (N1) и (N2) для этих норм и проверка свойства (N3) для норм
(1.7) и (1.8) тривиальна. Далее, мы увидим, что неравенство треугольника
(свойство (N3)) справедливо и для (1.9) при любых р > 1 ("неравенство Гёльдера",
см. формулу (4.42)).
(1.8) Теорема. Для любых х Е Шп справедливы неравенства
(1.10) Halloo < ||»||2 < ||»||l < л - Н^Поо.
Доказательство. Мы докажем только второе неравенство (для остальных
доказательство тривиально и поэтому опускается). Возведя в квадрат \\х\Ц
равенство (1.7) и выполнив умножение в правой части, мы получим сумму квадратов
Yjx\ (которая равна \\х\\\) и смешанных произведений |ж*| • |ж/|, которые не
отрицательны. Из этого следует, что ПжЦ^ > П^Щ- □
Каждая из этих норм может быть мажорантой и минорантой для каждой
из остальных (при умножении на положительное число). Это показывает, что
нормы ||z||i, \\х\\2 и ||ж||оо эквивалентны в смысле следующего определения.
(1.4) Определение. Две нормы || • \\р и
существуют положительные константы С\ и С2 такие, что
(1.11) Ci • \\х\\р < \\x\\q < С2 • \\х\\р при любых хеШп.
Сходимость последовательностей векторов
Нашей следующей целью является распространение определений и
результатов разде. III. 1 на бесконечные последовательности векторов. Мы рассмотрим
последовательность {ж,-},->1, где каждый Х{ является вектором, т.е.
(l.lzj Х{ = (Хц, Х2ъч • • • •) хпг)ч 2 = 1, Z, О, . . . .

276 IV. Функции нескольких переменных
(1.5) Определение. Будем говорить, что последовательность {жг}г>ъ задаем-
мая (1.12), сходится к вектору а — (ai, a2,..., ап) 6 Мп, если
V£>0 ЗАГ>1 \/i>N \\xi-a\\<e.
Как и в одномерном случае, будем писать lira Х{ — а.
Рис. 1.3. Сходящаяся последовательность в!2.
Это определение в точности совладает с (III. 1.4), только "абсолютные
величины" заменены "нормами".
(1.6) Замечание. Чтобы быть точным, следует указать норму, используемую в
определении 1.5, например, евклидову норму. Но если норма || • \\р эквивалентна
норме, || • ||д, то справедливо утверждение
(1.13) сходимость по норме || • \\р <=> сходимость по норме || • \\q.
Действительно, из \\х{ — а\\р < е и (1.11) следует, что ||ж,- — a\\q < С2С. Так как
б > 0 в определении (1.5) произвольно, мы можем заменить его на е' — Сгб, и мы
увидим, что из сходимости по норме || • \\р следует сходимость по норме || • \\q.
Теорема 1.3 показывает, что нормы || • ||i, || • ||г и || • ||оо эквивалентны.
Далее мы увидим, что все нормы в Шп эквивалентны (теорема 2,4). Следовательно,
мы могли использовать любую норму в определении 1.5 и сходимость
последовательности векторов {xi} не зависит от выбора нормы.
(1.7) Теорема. Для последовательности векторов (1Л2) мы имеем
lira xi — а <£=> lira xj-i — а* для k — 1, 2,..., n,
г—>-oo
т.е. сходимость вЖп означает покомпонентную сходимость.
Доказательство. Для нормы (1.8) имеем
(1.14) ||жг-а||оо<б «=> \xki-a>k\<£ Для к = 1, 2,..., гг.

IV.1 Топология n-мерного пространства 277
Выбирая норму || • ||оо в определении 1.5, мы и получаем требуемое утверждение.
□
После этой подготовки легко переписать и другие определения и результаты
разд. III. 1 для случая большей размерности. Например, мы назовем
последовательность {#«}«> 1 векторов ограниченной, если существует число В > О такое,
что ||жг|| < В для всех г > 1. Опять-таки, ограниченность не зависит от
выбора нормы. Так же, как в теореме III. 1.3, мы видим, что сходящиеся векторные
последовательности ограничены.
Последовательность {£«}«> i называется последовательностью Коти, если
(1.15) Ve>0 3N>1 \/i>N V£>1 \\Xi - xi+i\\ < е.
Используя максимум-норму в (1.15), видим, что для к — 1,..., п действительные
последовательности {жь}*>1 являются последовательностями Коши. В
результате, мы непосредственно получаем следующее обобщение теоремы III. 1.8.
(1.8) Теорема. Последовательность векторов в Шп сходится тогда и только
тогда, когда она является последовательностью Коши. □
Обобщение теоремы Больцано—Вейерштрасса несколько сложнее.
(1.9) Теорема (Больцано—Вейерштрасса). Любая ограниченная
последовательность векторов в Мп содержит в себе сходящуюся подпоследовательность.
Доказательство. Пусть последовательность {#;}«>i ограничена. Сначала
рассмотрим последовательность {£ь}г>1 первых компонент. Эта
последовательность также ограничена, и по теореме III. 1.17 мы можем выделить из нее
сходящуюся подпоследовательность, скажем,
(1.16) £l,l, £l,5, £l,9, ж1,22, Zi,37, #1,58, ж1,238, £l,576, •" '
Затем мы рассмотрим вторые компоненты. Однако основная идея состоит в учете
только тех членов последовательности вторых компонент, которые
соответствуют членам, присутствующим в (1.16), а не всем членам первоначальной
последовательности. Полученная последовательность ограничена, и мы вновь можем
применить теорему III. 1.17 для нахождения сходящейся подпоследовательности,
скажем,
(1.17) £2,1, ж2,9, ^2,58, £2,576, ••• •
Теперь подпоследовательность х\, хд, #58, £576, • • • сходится и по первой, и по
второй компоненте. Для случая п — 2 доказательство закончено. Если же п > 2,
рассмотрим третьи компоненты, соответствующие (1.17), и т.д. После выборки
n-й подпоследовательности число ее членов все еще бесконечно, и мы имеем
подпоследовательность, сходящуюся по всем компонентам. □

278 IV. Функции нескольких переменных
Окрестности, открытые и замкнутые множества
Под "множеством" мы подразумеваем сущность М, образованную из
собранных воедино по нашей интуиции или нашему замыслу неких
определенных и различимых объектов т. Эти объекты мы называем
"элементами" множества М. (Г. Кантор 1895, Werke, р. 282)
Никто не сможет изгнать нас из рая, который Кантор создал для нас.
(Гильберт, Math. Ann., vol.95, p. 170)
Новая эпоха в математике началась, когда Дедекинд (около 1871 г.) и Кантор
(около 1875 г.) стали рассматривать множества точек как новые математические
объекты.
Для множеств А,ВвШп мы будем использовать следующие символы:
(1.18) А С В если все элементы А принадлежат также 5,
(1.19) А П В = {х G Шп ; х G А и х G В},
(1.20) AUB = {х£Шп ; х еА или я G #},
(1.21) А \ В = {х G Шп ; х G А но х £ 5},
(1.22) £А = {хеШп ; х£А).
В Жп роль открытого интервала играет множество
(1.23) В£(а) = {х G Мп ; \\х - а\\ < е},
которое мы назовем кругом (шаром) радиуса е с центром в точке а (см. рис. 1.4).
р=\. /7=1.5 р = 2. р = 3. р=100.
Рис. 1.4. Круги радиусов е = 1,1/2,1/4 для ||ж||Р, р = 1, 1.5, 2, 3, 100.
(1.10) Определение (Хаусдорф 1914, Chap. VII, §1; см. также р. 456). Пусть а Е
Шп. Множество V С Шп называют окрестностью точки а, если существует
в > 0 такое, что В£ (а) С V.
Круги (или шары) В£(а) зависят от нормы (|| -||i, ||- ||г, или || • ||оо,...);
определение "окрестности", однако, не зависит от используемой нормы (при условии
эквивалентности норм). Каждый шар В£(а), соответствующий некоторой норме,
всегда содержит в себе шар Бе/(а), соответствующий какой-нибудь другой норме
(рис. 1.5).
(1.11) Определение (Вейерштрасс, Хаусдорф 1914, р. 215). Множество U С Мп
открыто (в оригинале "ein Gebiet" — область, нем.), если U является
окрестностью каждой своей точки, т. е.
U открыто <=> Vx G U 3е>0 B£(x)cU.

IV. 1 Топология n-мерного пространства 279
Рис. 1.5. Окрестности.
(1.12) Определение (Г. Кантор 1884, р. 470; см. Ges. Abhandlungen, p. 226).
Множество F С Мп называется замкнутым, если каждая сходящаяся
последовательность {ж,-},->1 с Xi £ F имеет своим пределом точку, принадлежащую F,
т. е.
F замкнуто <J=> а — lim ж,- и Х{ Е F влечет а Е F.
i—too
Примеры в Ш. Так называемый "открытый интервал" (а, Ь) — {х Е Ш ; а <
х < 6} является открытым множеством. Действительно, для каждого x Е (а, &)
число е — гаш(ж-а, 6—ж) является строго положительным, так что В£ (х) С (а, &).
С другой стороны, последовательность {а+1/г} (где г > 1) сходится, её элементы
принадлежат (а, 6) для достаточно больших г, но ее предел не принадлежит (а, 6).
Поэтому множество (а, 6) не замкнуто.
Множество [а, 6] = {х Е М ; а < х < Ь} замкнуто (см. теорему III. 1.6). Однако
ни а, ни Ъ не имеют окрестности, полностью принадлежащей [а, Ь]. Следовательно,
[а, Ь] не является открытым множеством.
Интервал А = [а, Ь) не является, ни открытым ни замкнутым, так как а не
имеет окрестности, полностью принадлежащей [а, 6), а предел
последовательности {6 — 1/г} не лежит в [а, 6).
В заключение отметим, что множество Ш = (—оо, +оо) является
одновременно открытым и замкнутым, и таким же свойством обладает пустое множество 0.
(1.13) Лемма.
a) Множество А
b) Множество А
Доказательство, а) Для а Е ^4 возьмем е — 1 — ||а||, которое является
положительным. При таком выборе Ве(а) С А (см. рис. 1.6), так как, используя
неравенство треугольника, для х Е Ве (а) имеем
||х|| = ||ж — а + а\\ < ||ж — а|| + ||а|| < £ + ||а|| = 1.
Следовательно, А является открытым множеством.
{х Е Шп ; ||ж|| < 1} открыто,
{х Е Шп ; ||ж|| < 1} замкнуто.

280 IV. Функции нескольких переменных
р=\. р=\.5 р = 2. р = Ъ. /7=100.
Рис. 1.6. Открытые множества (х £ М2 ; \\х\\р < l}.
/?=1. /7=1.5 Р = 2. р = 3. /? = 1
Рис. 1.7. Закрытые множества |ж Е М2; ||я;||р < l}.
b) Рассмотрим последовательность {жг}г>1, элементы которой
удовлетворяют условию Х{ Е А (для любых г) и lim^oo жг- = а. Покажем, что а £ А. Допустим
обратное: а £ А (т.е. ||а|| > 1, см. рис. 1.7), и возьмем е = \\а\\ — 1. Для этого е
существует N > 1 такое, что ||ж,- — а\\ < е при г > N. Используя неравенство
треугольника (или, лучше, упр. 1.1), мы получаем
||а5,-|| = \\xi — а + а\\ > ||а|| — ||ж,- — а\\ > ||а|| — е — 1
для достаточно больших г. Это противоречит сделанному предположению, что
Х( Е ^4 для всех г. Поэтому i = {ж G Мп ; IMI < 1} является замкнутым
множеством. D
Дальнейшие примеры. Множество А = {х Е М2 ; £i,£2 Е Q, ||я|| < 1} не
является ни открытым, ни замкнутым. Действительно, каждый круг содержит
иррациональные точки, а предел рациональных точек может быть
иррациональным.
Рис. 1.8. Канторово множество.
Знаменитое канторово множество (Г. Кантор 1883, Werke, р. 207, Example 11;
см. рис. 1.8) задается следующим образом:
(1.24)
А = [0,1] \ {(1/3,2/3) U (1/9,2/9) U (7/9,8/9) U ...}
оо
г = 1
Оно не является открытым (например, точка х — 1/3 не имеет окрестности в А),
но является замкнутым (см. замечание 1.16 ниже).

IV. 1 Топология rt-мерного пространства 281
"Треугольник Серпиньского" (рис. 1.9) и "ковер Серпиньского" (рис. 1.10)
(Серпиньский 1915, 1916) — двумерные обобщения канторова множества.
Изображения на рисунках 1.9 и 1.10 не только очаровательны из-за их эстетической
привлекательности, они еще напоминают нам, что множества могут быть весьма
сложными объектами.
Рис. 1.9. Треугольник Серпиньского. Рис. 1.10. Ковер Серпиньского.
(1.14) Теорема. Справедливы утверждения:
i) F замкнуто => ZF открыто ,
ii) U открыто => ZU замкнуто .
Доказательство, i) Пусть F замкнуто; допустим, что ZF не открыто. Тогда
существует такая точка а Е ZF (т.е. а £ F), что для всех е > 0 имеем Ве(а) $_
CF. Выбирая е = 1/г, видим, что существует последовательность {жв-}г->1, члены
которой удовлетворяют условиям Х{ Е F и ||а^: — а\\ < 1/г. Так как F — замкнутое
множество, то а Е F, и мы пришли к противоречию.
ii) Допустим теперь, что СС/ не замкнуто. Это означает, что существует
последовательность с элементами xt Е СС/ (т.е. жг- ^ СС/), которая сходится к
некоторому а £ ZlJ (т.е. а Е /7). Поскольку С/ —- открытое множество, существует
такое е > 0, что В£(а) С U. Значит. хг (£ В£(а) при любом г. Мы пришли к
противоречию.
П
(1.15) Теорема (Хаусдорф 1914, р. 216). Для конечного набора множеств
справедливы, утверждения:
i) C/i, С/г,..., ^™ открытые => U\ П С/г П ... П С/т открыто.
ii) Fi, F2. . .., i*1™ замкнутые => i*\ U .Рг U . .. U Fm замкнутое.

282 IV. Функции нескольких переменных
Для произвольного семейства множеств (с индексами из множества Л)
справедливы утверждения:
iii) U\ открытые множества УАеЛ => Uag^ ^ = {жЕМп; ЗАЕЛ, x£U\)
является открытым множеством,
iv) F\ замкнутые множества УАеЛ => (~)ХеЛ F\ = {х£Шп ; УАеЛ, x£F\}
является замкнутым множеством.
Доказательство. Начнем с доказательства утверждения (i). Предположим,
что х Е U\ П ... П Umt т. е. х Е £/& для всех к = 1,..., га. Так как Щ являются
открытыми множествами, то существуют бк > 0 такие, что В£к{х) С £/*. Полагая
£ = min(£i,..., £m), получаем положительное £ такое, что Ве(х) С E/i П ... П С/т.
Доказательство утверждения (iii) еще проще и поэтому опускается.
Эквивалентности утверждений (i) <=> (ii) и (iii) <=> (iv) следуют из "правил де Моргана"
C(c/1nc/2) = (C^1)u(Ct/2),
C(tfiUtf2) = (Cl7i) П (С172)
и теоремы 1.14. D
Рис. 1.11. Открытые множества Рис. 1.12. Закрытые множества
с замкнутым пересечением. с открытым объединением.
(1.16) Замечание. Из этой теоремы видно, что канторово множество в равенстве
(1.24) является замкнутым. Действительно, его дополнение
СЛ = (-ос, 0) U (1, ос) U (1/3, 2/3) U (1/9, 2/9) U (7/9, 8/9) U ...
является объединением бесконечного числа открытых интервалов и будет
открытым множеством согласно теореме 1.15.
(1.17) Замечание. Утверждения (i) и (ii) теоремы 1.15 для бесконечного числа
множеств в общем случае не справедливы.
Рассмотрим, например, семейство открытых множеств
(1.26) 11г = {хеШ2; \\х\\< 1 + 1/*},

IV. 1 Топология n-мерного пространства 283
однако их пересечение £7*2 П £7"з П [7*4 П ... = {х Е М2 ; ||ж|| < 1} не является
открытым (рис. 1.11).
Аналогично, семейство замкнутых множеств (рис. 1.12)
(1.27) Fi = {ж G М2 ; \\х\\ < 1 - 1/г}
имеет объединение F2U F3U F±U ... = {х Gl2 ; ||ж|| < l}, которое не является
замкнутым множеством.
Компактные множества
Мы уже обращали на это внимание и далее во всей книге будем
убеждаться в важности понятия компактных множеств. Все, кто занимался общим
анализом, понимают, что невозможно обойтись без этого понятия.
(Фреше 1928, Espaces abstraits, p. 66)
(1.18) Определение (Фреше 1906). Множество К С Мп называется компактным,
если для каждой последовательности {ж;};>1 с элементами из К существует
подпоследовательность, сходящаяся к некоторому элементу а £ К.
(1.19) Теорема. Для множества К С Жп справедливо утверждение
К компактно <£=> К ограничено и замкнуто.
Доказательство. Пусть К ограничено ( т.е. ||ж|| < В для всех х Е К) и
замкнуто. Возьмем последовательность {ж«}г>1 с элементами из К. Эта
последовательность ограничена и имеет согласно теореме 1.9 сходящуюся
подпоследовательность. Предел этой подпоследовательности принадлежит множеству if, так
как К замкнуто. Следовательно, К — компактное множество.
Пусть теперь К — компактное множество. Из этого следует, что К
замкнуто, так как каждая подпоследовательность сходящейся последовательности
сходится к тому же пределу. Чтобы показать, что множество К ограничено, мы
предположим обратное, т.е. существование последовательности {жг}?
удовлетворяющей условию: xi G К для всех г и ||жг-|| -> оо. Очевидно, что из нее невозможно
выделить сходящуюся подпоследовательность, так что К не может быть в этом
случае компактным множеством. □
(1.20) Замечание. Компактные множества являются, по определению 1.18,
именно теми множествами, к которым применима теорема Больцано—Вейерштрасса.
Так как эта теорема является базовой для всех основных результатов о
равномерной сходимости, равномерной непрерывности, о максимуме и минимуме,
утверждение Фреше не было преувеличением (см. цитату).
(1.21) Теорема (Гейне 1872, Борель 1895). Пусть К — компактное множество,
a {U\}\£A — семейство открытых множеств U\, удовлетворяющее условию
(1.28) \\ U\ D К (открытое покрытие).
хел
Тогда, существует конечное число индексов Ai, А2,..., Am таких, что
UXlUUx2U...UUXTn DK.

284 IV. Функции нескольких переменных
Контрпримеры. Прежде чем перейти к доказательству этой теоремы,
покажем, что ни одно из предположений не может быть опущено.
В примере
К = {х ; ||z|| < 1}, Ui = [х ; ||z|| < 1 - 1/i}, г = 1, 2,...
невозможно найти конечное покрытие К. Это обусловлено тем, что К не
замкнуто.
Если
К = Mn, Ui = {х ; ||х|| < i}, * = 1, 2,... ,
множество К не ограничено. И в этом случае невозможно найти конечное
покрытие К. Следовательно, ограниченность К является существенной.
В последнем примере рассмотрим компактное множество К = {ж ; ||ж|| < l},
но не открытые множества £/,-, задаваемые формулой
{1 <р 1 "|
(г cos (р, г sin <р) ; 0 < г < 1, —— < — < — >.
Ни одно из С/,- не является лишним в покрытии {Ui}i>o (рис. 1.13).
Рис. 1.13. Неоткрытое покрытие К. Рис. 1.14. Доказательство Гейне.
Доказательство. Следуя Гейне (1872), мы вкладываем компактное
множество К в n-мерный куб / (квадрат для п = 2; см. рис. 1.14). Допустим, что нам
необходимо бесконечное число множеств U\ для покрытия множества К.
Разделим куб 7" на 2П маленьких кубов путем деления его ребер пополам (здесь
Л? ^2> -Tj» А)- Одно из множеств К П Ij (j = 1,..., 2П) требует бесконечного числа
множеств U\ для покрытия. Допустим, что этим множеством является К П It и
обозначим его К\. Далее разделим куб Ii на 2П маленьких кубов и т.д. Таким
образом получаем последовательность множеств
KDKiD^DKsD ... ,
каждое из которых требует бесконечного числа открытых множеств U\ для
своего покрытия.
В каждом К{ мы выберем Х{ £ К{. Последовательность {#;} является
последовательностью Коши, так как диаметр К{ стремится к нулю. Следовательно

IV. 1 Топология n-мерного пространства 285
(теорема 1.8), она сходится, и мы обозначим ее предел а. Так как К —
компактное (следовательно, замкнутое) множество, то а Е К. Из (1.28) следует
существование Л такого, что а Е U\. Так как U\ — открытое множество, то существует
е > О такое, что В£(а) С U\. Используя тот факт, что диаметр Ki стремится к
нулю, заключаем, что для достаточно больших т мы имеем Кт С Ве (а) С U\.
Следовательно, Кт покрывается одним U\. Это противоречит предположению,
что К не может быть покрыто конечным числом U\. □
Упражнения
1.1 Пусть || • || — норма в Шп. Докажите, что
|1М1-1М1|<11*-»1|.
Указание. Применить неравенство треугольника к \\х\\ = \\х — у + у\\.
1.2 Покажите, что
1И|2<|И|1<л/НИ1з Vaj€ffin.
Покажите, что эти оценки "оптимальны", т.е. если
HMl2<IM|i<C4Wl2 VzEffT,
то с < 1 и С > л/п .
1.3 У г-на К.Л.Эвера была идея ввести "норму" вида
1И|1/2 = (Х>г/2)2.
i=l
Покажите, что эта "норма" не удовлетворяет неравенству треугольника.
Исследуйте также множество В — {х Е М2 ; ||ж||1/2 < 1} и покажите, что
оно не выпукло.
о
1.4 Для каждого множества А из Шп определяется множество А внутренних
точек множества А как
о .
А— {х | А является окрестностью х}
и замыкание А множества А как
А = {х | А пересекается с любой окрестностью х}.
Покажите, что А является замкнутым множеством (в действительности наи-
о
меньшим замкнутым множеством, содержащим в себе А) и что А — открытое
множество (наибольшее открытое множество, содержащееся в А).
1.5 Покажите, что для двух множеств А и В из Мп
о
о
AUB = AUB, АГ\ В =АПВ .
Найдите два множества А и В из JR, для которых справедливо
о о
АПВфАПВ AUB фАи В

286 IV. Функции нескольких переменных
1.6 (Треугольник Серпиньского 1915). Пусть а,Ь,с три точки в М2, образующие
равносторонний треугольник. Рассмотрите множество
оо > оо оо
Т={Ха + ,Ь+,с; А = £ * , „ = £ £ , * = £ £ },
1 = 1 1 = 1 1 = 1
где Л,, /х,-, i/t- равны 0 либо 1, причем справедливо равенство А, + /х, + v%\ - 1
для всех г. Определите вид Т. Является ли оно открытым? Замкнутым?
Компактным?
1.7 Покажите, что
\\*\\ = з (l^il + Ы) + з шах{l*1''I*2'}
является нормой в!2. Определите для этой нормы вид "единичного круга"
J3i(0) = {хеШ2 ; ||я?||< 1}.
1.8 Покажите, что отображение N : Ш2 —> М, определенное как
N(zi, х2) — \jo,x\ + 2Ьх\Х2 + сх\,
является нормой вМ2 тогда и только тогда, когда а > 0, ас — Ь2 > 0.
1.9 Выведите теорему Больцано—Вейерштрасса из теоремы Гейне—Бореля.
Указание. Предположим, что {хп} является последовательностью, у которой
все ||жп|| < М, но нет точек накопления. Тогда для каждого ас \\а\\ < М
существует е > 0 такое, что В£ (а) содержит только конечное число членов
последовательности {хп}.
1.10 Докажите, что Шп и 0 являются единственными подмножествами Мп,
одновременно замкнутыми и открытыми.

IV.2 Непрерывные функции 287
IV.2 Непрерывные функции
... согласно мнению всех математиков, трудности, которые испытывали
читатели этой работы, связаны с тем, что ее текст написан скорее в
философской, чем математической манере Преодоление этих трудностей
было существенной задачей для меня, так как я хотел, чтобы эта книга
была читаема и понятна не только для меня, но также и для остальных.
(Грассман 1862, "Professor am Gymnasium zu Stettin")
Пусть А подмножество Rn. Функция
(2.1) /:A->Mm
отображает вектор x = (ei, ..., xn) G А в вектор у = (yi,..., ym) G Mm. Каждая
компонента у является функцией п независимых переменных. Таким образом,
запишем
У\ = Л(Ж1,...,ЖП)
(2.2) у = f{x) или :
Ут = Jm (ж1? • • • ч хп)-
1
Рис. 2.1а. Функция у = х\ + х\. Рис. 2.lb. yi = cos 10х, y2 = sin 10i, 0 <
x < 3.
Примеры, а) Скалярная функция (га = 1) двух переменных (п = 2) может
быть интерпретирована как поверхность в М3. Например, функция у = х\ + х\
представляет параболоид (рис. 2.1а).
Ь) Двумерная вектор-функция (га = 2) одной переменной (п = 1)
представляет кривую в М3. Например, спираль на рис. 2.lb задается соотношениями
ух = cos Юж, у2 = sin 10х. Если мы спроецируем кривую на плоскость (yi, уо), то
получим ее "параметрическое пpeдcтaвлeниe,, в!2(в нашем примере —
окружность).
(2.1) Определение. Функция f : А —> Мш, А С 1" непрерывна в точке х0 G А,
если
V£ > О 3S > 0 Уж G А : ||z - z0|| < S \\f(x) - f(x0)\\ < e.

288 IV. Функции нескольких переменных
Это в точности соответствует определению III.3.2 с заменой абсолютных
величин на нормы. Наше определение не зависит от конкретного выбора норм, коль
скоро нормы эквивалентны (по тем же соображениям, что и в замечании 1.6).
Если мы используем максимум-норму в Мт, то получим, по аналогии с теоремой
1.7, следующий результат.
(2.2) Теорема. Функция f : А —>• IRm, А С Шп, задаваемая формулами (2.2),
непрерывна в точке хо Е А тогда и только тогда, когда функции fj : А —>• 1
непрерывны в точке хо для всех j = 1,..., га. □
Как следствие этой теоремы, для изучения непрерывности достаточно
рассматривать только случай га = 1. Постоянная функция f(x) = с, очевидно,
всюду непрерывна. Проекция вектора х — (zi,..., хп) на k-ю координатную ось, т.е.
р(х) = Хк является, тоже непрерывной в каждой точке хо = (жю,...,хпо), так
как \xk — Xko\ < ||z — £о|| (в определении 2.1 выбирается S = е).
Почти тривиально обобщение определения III.3.10 предела функции и
теорем III.3.3 и III.3.4 на случай нескольких переменных, если, конечно,
произведение и отношение имеют смысл (простой заменой абсолютных величин на
норму). Следовательно, полиномы нескольких переменных, например, /(asi, а?2, хз) -
х\х\ — x\x\xz + ^.x\ — 1, являются непрерывными всюду, и рациональные функции
непрерывны во всех точках, где знаменатель не равен нулю.
Рис. 2.2. Стереограмма разрывной функции /(ж^жг) формулы (2.3) (держите рисунок
на расстоянии около 20 см и пристально смотрите как бы сквозь бумагу на некий объект
на расстоянии 20 см за ней, тогда две картинки сольются в одну трехмерную).
Пример. Рассмотрим функцию / : Ш2 —> 1R, задаваемую выражением
—« о при х\ + х% > 0
х\ + х\
О При Xi = Х2 = О
(см. рис. 2.2). Она непрерывна в точках удовлетворяющих условию х\ + х\ > 0.
Для выяснения её поведения в окрестности начала координат используем
полярные координаты х\ — rcos<£>, Х2 — rsin<p, так что (при г > 0)
г2 cos <р sin <р 1 .
У = о = о smV
rz 2

IV.2 Непрерывные функции 289
Следовательно, функция постоянна на прямых, проходящих через начало
координат, величина этой постоянной зависит от угла <р. В каждой окрестности точки
(О, 0) функция (2.3) принимает все значения между -1-1/2 и —1/2. Поэтому она не
может быть непрерывной в точке (0,0).
Этот пример интересен тем, что соответствующие функции одной переменной
х\ i-> /(xi, 0) ИХ2И /(0, х2) непрерывны в начале координат. Поэтому у теоремы
2.2 для независимых переменных х нет аналога, как думал Коши (1821, р. 37).
Его ошибку исправил Пеано (1884, "Annotazione N.99"), указав контрпример,
приведенный выше.
Непрерывные функции и компактность
Мы продолжим обобщение результатов разд. III.3 на функции нескольких
переменных. Многие из них обобщаются буквально. Например, аналогом
теоремы III.3.6 является следующая
(2.3) Теорема. Пусть К С Мп — компактное множество и функция f : К —>• Ж
непрерывна на К. Тогда f ограничена на К и достигает на нем максимума и
минимума, т. е. существуют и Е К и U £ К такие, что
f(u) < f(x) < f(U) для всех х G К. □
Эта теорема приводит к следующему результату, который мы анонсировали
ранее в замечании 1.6.
(2.4) Теорема. Все нормы в Шп эквивалентны. Это означает, что если N : Шп —>■
Ш является отображением, удовлетворяющим условиям (N1) - (N3) теоремы
1.1, т. е. если
(N1) N(x)>0 и N{x) = Q<$x = Q,
(N2) N{Xx) = |А| N(x) для ХеШ,
(N3) N(x -f у) < N(x) -f N(y) (неравенство треугольника),
то существуют числа С\ > 0 и Сг > 0 такие, что
(2.4) Ci||z||2 < N(x) < C2INI2 для всех х Е Мп.
Доказательство. Покажем сначала, что N(x) непрерывна. Запишем вектор
х в виде х = ziei + х2е2 + ... + хпеп, где ех = (1,0,.. .,0), е2 = (0,1, 0,..., 0) и
т.д. Тогда из (N3), (N2) и неравенства Коши—Шварца(1.5) следует, что
N(x) = N{x1e1 + ... + xnen)<N(x1e1) + ... + N(xnen)
< \Xl\ • Щег) + .. - + \хп\ • N(en) < \\х\\2 • С2,
где с С2 = \/N{ei)2 + ... + N(en)2. Это доказывает правое неравенство в (2.4).
Непрерывность N(x) доказывается теперь следующим образом:
N(x) - N(x0) = N(x -х0 + хо) - N(x0)
< N{x - х0) + N(x0) - N{x0) < C2\\x - Ж0Ц2,

290 IV. Функции нескольких переменных
и аналогично N(xo) — N(x) = ... < Сг||жо _ я||2» так что
(2.6) \Щх)-Щхо)\<С2\\х-хо\\2.
Рассмотрим теперь функцию N(x) на компактном множестве
К = {хеШп; IN|2 = i}.
Из теоремы 2.3 следует, что минимум нашей функции достигается в некоторой
точке и £ К, т.е.
(2.7) N(z) > N(u) для всех z Е К.
Полагая С\ — N(u) (согласно свойству (N1) это положительно число) и
учитывая, что для произвольного х Е Шп (х ф 0) будет аз/ЦжЦг Е К, мы получим
c,<-<w)-ikN(x)-
Это доказывает левое неравенство в (2.4). D
Равномерная непрерывность и равномерная сходимость
Как и в разд. III.4, назовем функцию / : А —>■ Шт, А С Шп равномерно
непрерывной, если она непрерывна на А, и 8 из определения 2.1 можно выбрать
не зависящим от точки хо Е А. Мы получим следующее обобщение теоремы
Ш.4.5.
(2.5) Теорема (Гейне 1872). Пусть f : К -> Rm непрерывна на К и К С Шп -
компактное множество. Тогда f равномерно непрерывна на К.
Доказательство. Два доказательства теоремы Ш.4.5 могут быть легко
перенесены на случай нескольких переменных. Приведем здесь третье доказательство
этой теоремы, основанное на теореме 1.21 Гейне—Бореля.
Из условия теоремы мы знаем, что
(2.8) Ух0еК Уб>0 36 > 0 Ухе К : \\х-х0\\<6 \\f(x) - f{x0\\<e.
Простейшей идеей было бы рассмотреть множество шаров {В$(хо)}Хоек как
открытое покрытие К и выделить из него конечное покрытие. Но мы быстро
поймем, что эта идея не эффективна. Выберем более осторожный путь.
Зафиксируем оОи для каждого а £ К определим открытое множество
Ua = {х ; \\х — а\\ < 8/2, где 6 зависит от хо = а и определено в (2.8) }.
Эти множества образуют открытое покрытие К. Так как К — компактное
множество, то уже конечный набор множеств Uai, • • •, UaN покрывает множество К.
Используя соответствующие этому набору числа Si,..., Sjy, определим
S = mm{S1/2,S2/2,...,SN/2}.
Теперь, пусть х £ К и у £ К — произвольные точки, удовлетворяющие
условию \\х — у\\ < 8. Покажем, что \\f(x) — f(y)\\ < 2е. Так как х Е К, то

IV.2 Непрерывные функции 291
существует индекс г такой, что х £ Uai, т.е. ||ж — а,-|| < Si/2. Тогда из условия
\\х~ у\\ < ^ < <^/2 и неравенства треугольника следует, что ||у — а4|| < Si. Из (2.8)
мы, таким образом, получаем
№) " /МП < Н/(*) - /ЮН + И/К) - /МП < е + е = 2е,
что и доказывает утверждение. □
Все определения и результаты разд. III.4, относящиеся к равномерной
сходимости последовательности функций, переносятся непосредственно на случай
нескольких измерений. Поэтому, если последовательность непрерывных функций
fk : А —> Мт, Л С Мп равномерно сходится на Л к функции /(ж), эта
предельная функция будет непрерывной (прямое обобщение теоремы III.4.2). Рассмотрим
интересный пример.
Рис. 2.3. Кривая Пеано—Гильберта.
Кривая Пеано—Гильберта.
Непрерывная кривая может заполнять некоторую часть пространства: это
один из наиболее замечательных фактов теории множеств, открытием
которого мы обязаны Г. Пеано. (Хаусдорф 1914, р. 369)
Кантор(1878) открыл сенсационный факт: существует взаимно-однозначное
соответствие между точками интервала и точками квадрата. Но отображение
Кантора не было непрерывным. Затем Пеано (1890) нашел, искусно
манипулируя координатами, представленными в системе счисления с основанием 3,
непрерывную кривую, полностью заполняющую квадрат. Вскоре после этого Гильберт
(1891) обнаружил такие кривые с помощью красивого "geometrische Anschauung"

292 IV. Функции нескольких переменных
(геометрически наглядного приема, — нем.): он повторно делил квадраты на
четыре подквадрата и соединял их центры кривой так, чтобы выдерживалось
направление аналогичной кривой с предыдущего шага (см. рис. 2.3).
А ВА ВА В
Рис. 2.4. Построение кривых Гильберта.
Другое построение. Пусть ip(t) = (x(t),y(t)), 0 < t < 1 произвольная
непрерывная кривая, соединяющая точки А = (0, 0) для < = 0иВ= (1,0) для t = 1
(см. рис. 2.4). Определим новую кривую Ф(р посредством соотношения
(*¥>)(*) = {
(§(y(4i),x(4i)) при 0<*<!
§(*(4t-l),l + y(4t-l)) при \<t<\
|(1 + х(4А - 2), 1 + y(4t - 2)) при | < t < *
4
[§(2-y(4i-3),l-z(4t-3)) при f <t<l.
Это соотношение опять задает непрерывную кривую, соединяющую А = (0,0) для
^ = 0иБ = (1,0) для t — 1 (см. вторую картинку на рис. 2.4) так, что процедура
может быть повторена (см. третью картинку на рис. 2.4). Эта процедура приводит
к последовательности функций <ро = <р, <Р\ — $<Ро, <Р2 — Ф<Р\ и так далее. Когда
же мы стартуем с другой кривой i/i(t) с \\<p(t) — Ф{1)\\ос < К для t Е [0,1], то
||Фу>(£) — Фч/'МИ^ < К/2 (см. рис. 2.4). Отсюда следует, что
(2.9) |Ы<)-У'*(*)||<-К-2-*,
и взяв ф{Ь) — <Prn(t) и К = 1, получим
(2.10) 1М*)-¥>*+т(*)Н<2-'.
Из (2.10) видим, что последовательность функций <Pk(t) сходится равномерно
(по критерию Коши (Ш.4.4)) и, следовательно, имеет непрерывный предел (poc(t)
(теорема III.4.2). Далее, из (2.9) видим, что предельная функция не зависит от
начальной функции <fo(t). Кривая Гильберта на рис.2.3 по сравнению с кривыми
на рис.2.4 имеет незначительное отклонение вблизи конечных точек интервалов
[г/4*, (г + l)/4fc], которое исчезает при к —У оо.
Интересно, что обе координаты x(t) и y(t) являются новыми примерами
непрерывных функций, которые нигде не дифференцируемы (ср. с разд. III.9).

IV.2 Непрерывные функции 293
Линейные отображения
Линейные отображения являются важными примерами равномерно
непрерывных функций. Пусть А — матрица
/ an «12
I «21 022
(2.11) А= .
Рассмотрим отображение х •-)• у = Ах, где
«In \
а>2п
G"mn '
(2.12)
У* - ^2ачхэ-> 0 = 1, 2,..., m
(при работе с матрицами удобно записывать векторы как векторы-столбцы, так
что (2.12) — просто обычное произведение двух матриц).
(2.6) Теорема (Пеано 1888а, р. 454). В евклидовой норме для всех х Е Жп
(2.13)
\\Ах\\2 < М.||ж||2
М
У1 i=ij=i
Доказательство. Применяя неравенство Коши—Шварца (1.5) к сумме в
формуле (2.12):
»?< (IX) (£»*)•
;=1
3 = 1
и суммируя последнее неравенство по г от 1 до га, получаем желаемый результат.
D
Как следствие линейности Ах получим
\\Ах — Ах0\\ < М • \\х — хо\\
с М из теоремы 2.6. Это показывает, что отображение х »-» Ах является
равномерно непрерывным на Шп (возьмите S = е/М, не зависящее от хо).
Пример. Рассмотрим двумерную матрицу
А= /л/2 + 1 1_\ M=v/6 + 2^= 2.9713.
На рис. 2.5 построены множества {х ; ЦжЦг < 1} и {у = Ах ; ЦжЦг < 1}. Мы видим,
что второе множество лежит в круге радиуса М, что подтверждает оценку (2.13).
Более того, мы видим, что величена М не является оптимальной.

294 IV. Функции нескольких переменных
Рис. 2.5. Мажорирование линейной функции.
Матричная норма. Наименьшее число М, удовлетворяющее неравенству
(2.13) называется нормой А (матричной нормой). Обозначим
(2.14) |И|2:=8ир{||УЬ||2; ||г||2 < 1}.
Очевидно, что Ц-АЦг < М с М из (2.13), и что
(2.15) ||Лх||2<||Л||2||г||2
для всех векторов х. Точное вычисление величины ЦАЦг использует
собственные значения матрицы Ат А. В частности, для предыдущего примера она равна
||А\\2 = у 3 + у/2 + \/б + 2\/2 = 2.6855 (см. рис. 2.5 и упр. 4.9).
Хаусдорфово описание непрерывных функций
Рассмотрим теперь новое описание непрерывности, более изящное, чем в
определении 2.1. Вместо работы с нормами мы будем использовать
окрестности и открытые множества.
Для заданной функции / : Rn —> Rm и множеств U С Мп, V С Ш™ определим
(2.16) /(17) = {f(x) Elm; xeU} (образ U),
(2.17) ГЧУ) = {xEln; f(x) E V} (прообраз V).
(2.7) Пример. Рассмотрим функцию / : Ш2 —>■ М2, отображающую (х,у) на (u,v)
по формуле
(2.18) w = ж + |, v = {x + 2)у3 - Ъ-{х + 1)у + |.
Эта функция изображена на рис. 2.6 для —1.1 < х<у < 1.1. Для подмножества [/
(светло-серое животное из породы кошачьих1) нарисуем множество /(С/), а для
V (темно-серое животное из породы кошачьих) множество /~1(Vr). Видно, что
1 Кот Арнольда (ср. рис. 1.5.3 и 1.5.4 — Прим. ред.).

IV.2 Непрерывные функции 295
обратное отображение связного множества не обязательно связно. Это
обусловлено тем обстоятельством, что в нашем примере функция / не является взаимно
однозначной.
У
/
-1
Рис. 2.6. Прямое и обратное отображение для функции (2.18).
Описание непрерывности на языке окрестностей. Множество,
состоящее из таких х G Мп, которые удовлетворяют условию \\х — хо\\ < S, есть Bs(xo)
(см. формулу (1.23)). Множество тех х Е Мп, для которых \\f(x) — уо\\ < £, есть
f~1(<Be(yo))- Поэтому, если уо = /(#о) и А = Мп, условие определения 2.1 может
быть записано как
(2.19) Ve>0 3S>0 В6{х0) С /^(ftfob)).
Так как окрестность V точки уо характеризуется существованием е > 0 такого,
что В£(уо) С V, мы видим, что (2.19) эквивалентно следующему утверждению:
(2.20)
для победой окрестности V точки уо /-1(V) — окрестность точки хо-
Эта интерпретация непрерывности в точке хо более изящна и остается верной в
более общих "топологических пространствах". Характеристика всюду
непрерывной функции / : Шп —> Шт в терминах открытых и замкнутых множеств дается
следующей теоремой.
(2.8) Теорема (см. Хаусдорф 1914, р. 361). Для функции f : Шп —>• IRm следующие
три утверждения эквивалентны:
\) f непрерывна наШп;
ii) для каждого открытого множества V С Шт множество /~1(Vr) является
открытым б!п ;
iii) для каждого замкнутого множества F С Мт множество /_1(F) является
замкнутым вШп.

296 IV. Функции нескольких переменных
Доказательство, (i) => (ii): пусть V С Шт — открытое множество, выберем
хо £ /_1(^), такое, что /(жо) G V. Так как V — открытое множество, то оно
является окрестностью /(жо), а согласно (2.20) /~1(Vr) является окрестностью
хо. Это справедливо для всех хо £ /_1(V). Следовательно, множество /_1(V)
является открытым согласно определению 1.11.
(ii) => (i): пусть справедливо (ii), докажем, что / непрерывна в произвольной
точке хо G Шп. Пусть задано е > 0 и положим уо = f{xo)- Множество В£(уо)
— открытое, поэтому согласно утверждению (ii), f~1(Be{yo)) также открыто.
Определение 1.11 подразумевает существование S > 0 с Bs(xq) С f~1(B£(yo)). Но
это и есть просто непрерывность функции / в точке хо (см. (2.19)).
(ii) О* (iii): эквивалентность утверждений (ii) и (iii) следует из /_1(CV) =
С(/_1(^)) и теоремы 1.14. D
Рис. 2.7. Отображение, обратное к функции (2.21).
Рис. 2.8. Отображение, обратное к функции (2.21).
(2.9) Пример. Пусть функция / : М —> М удовлетворяет условию /(0) = 0 и
(2.21) f(x) = sin(l/z2) для х ф 0.
Эта функция разрывна в точке х — 0. Покажем, что для разрывных функций
утверждения (ii) и (iii) в обы!,ем случае не верны.
Например, множество V = (1/3,2/3) открыто, и его обратное отображение
/-1(У) = (#2, xi) U (ж4, хз) U ... также открыто (см. рис. 2.7). Однако для
замкнутого множества F — [1/3, 2/3] его прообраз f~1(F) — [#2, #i] U [х±, жз] U ... не
замкнут, так как предел последовательности {х{} не лежит в f~1(F).

IV.2 Непрерывные функции 297
Рассмотрим открытое множество V = ( — 1/2,1/2); его обратное
отображение /-1(V) = (жо,ос) U (^2,xi) U ... U {0} не является открытым, так как
оно не является окрестностью нуля (см. рис. 2.8). С другой стороны,
обратное отображение замкнутого множества F — [—1/2,1/2], которое есть f~1(F) =
[хо, сю) U [кг, Ei] U ... U {0}, является замкнутым.
(2.10) Пример. Наш последний пример иллюстрирует тот факт, что теорема 2.8
не имеет аналога для прямых отображений. Рассмотрим непрерывную функцию
/ : Ш -> М (см. рис. 2.9)
(2.22) /(,) = Ii^.
Отображение открытого множества U = (3/4,2) есть множество f(U) = (4/5,1],
которое не является открытым; отображение замкнутого множества F = [3, сю)
есть множество f(F) = (0,3/5], которое не является замкнутым.
Рис. 2.9. Прямые отображения для функции (2.22).
Интегралы с параметрами
Допустим, что мы имеем функцию двух переменных /(ж,р), определенную
для х Е [а, Ь] и р Е [с, с?]. Если мы проинтегрируем эту функцию по ж,
(2.23)
F(p)= f f(x,p)dx,
J а
мы получим функцию от р. Возникает вопрос, можем ли мы гарантировать, что
функция F(p) будет непрерывной.
(2.11) Контрпримеры. В формуле (Ь) из упр. III.5.9 заменим п2 один раз на 1/р,
а другой раз — на р:
(2-24) f(x,p) = *1\ р > 0, 0 < х < 1,
(1 + х2/р)2
(2.25) f(x,p) = ?Х р > 0, 0 < х < оо,
(1 +pxzy

298 IV. Функции нескольких переменных
и в обоих случаях положим /(ж,р) = 0 при р = 0.
В первом случае р —> 0 соответствует п —у ос на рис. III.5.5.Ь,
следовательно, F(p) = J0 f(x,p)dx будет стремиться к неравной нулю константе, тогда как
F(0) = 0. Заметим, что f(x,p) непрерывна везде, кроме точки х — р — 0.
Во втором случае при р —>• 0 функция f(x,p) имеет вид все более низкого и
расплывающегося к бесконечности горба, причем площадь под кривой
сохраняется. И в этом случае F(p) не является непрерывной в точке р = 0. В то же время
функция f(x,p) непрерывна всюду, но область интегрирования не ограничена.
В случае, когда f(x,p) непрерывна всюду и область интегрирования
является компактным множеством, мы знаем, что функция f(x,p) равномерно
непрерывна (теорема 2.5), и доказательство следующего утверждения будет легким
упражнением (см. также доказательство теоремы 3.11 ниже).
(2.12) Теорема. Если f(x,p) — непрерывная функция на [a, b] х [c,d\, то
F(p)= f f{x,p)dx
J а
является непрерывной функцией на [с, d]. U
Упражнения
2.1 Покажите, что существуют три различных значения переменной t, для
которых координаты кривой Гильберта ^оо(^) равны (1/2,1/2).
2.2 Докажите, что "матричная норма" (2.14) является нормой в En'm.
Рис. 2.10. Кривые Пеано.
2.3 а) Рис. 2.10 показывает кривые Пеано, построенные на основе
оригинальных формул (см. Пеано 1890). Дайте объяснение их структуры, аналогичное
приведенному для рис. 2.4 (вам понадобится рассмотреть животное, которое
связывает противоположные углы квадрата).
Ь) В самом последнем предложении своей статьи Пеано утверждает без
каких-либо дальнейших разъяснений, что х и у как функции t нигде не
имеют производных ("Ces х et у, fonctions continues de la variable t, manquent
toujours de derivee" — "У этих x и у, непрерывных функций переменной L
всегда отсутствует производная", — франц.). Докажите это утверждение.

IV.2 Непрерывные функции 299
Указание. Модифицируйте доказательство теоремы Ш.9.1, которое
предложил де Рам. Положите ап = г/971, /Зп = (г + 1)/9п. При этих значениях
аргументов точки кривой Пеано окажутся в противоположных углах квадрата
со стороной 3~п, так что гп = Зп.
Покажите, что если К С Мп является компактным множеством и функция
/ : К —> Шт непрерывна, то f(K) С Мт тоже компактное множество.
Функция / : М2 —> М, определяемая формулой
Яхг,хг)=\цТЦ ПРИ *? + *3>0'
I 0 При Х\ = Х2 = О,
разрывна в точке (0,0) (почему?). Найдите открытое множество U С Ш и
замкнутое множество F С М такие, что /_1(С7) не будет открытым и f~1(F)
не будет замкнутым.
Определим отображение Р : IR2 —>• М2 (которое назовем проекцией) так:
P(zi,z2) = (жь0).
a) Покажите, что отображение Р является непрерывным.
b) Найдите открытое множество С/СМ2, для которого P(U) не будет
открытым.
c) Найдите замкнутое множество Fcl2, для которого P(F) не будет
замкнутым.
Замечание. Пункт (Ь) очень прост, но пункт (с) сложнее. Как видно из упр.
2.4, вам придется искать неограниченное множество F.
Рис. 2.11. График функции (cosх — cosy)/(x — у).
Один наивный пользователь компьютерного пакета математических
программ (такого, как "Maple") захотел построить трехмерный график функции
cos х — cos у Л Л
д{х, у) = -, -8 < х < 8, -8 < у < 8
х-у ~ ~ ~ ~
и получил результат вроде показанного на рис. 2.11. Как надо определить д
при х — ?/, чтобы получить непрерывную функцию? Для полученной
функции проверьте условия определения 2.1 непрерывности функций двух
переменных.

300 IV. Функции нескольких переменных
IV.3 Дифференцируемые функции нескольких
переменных
Мы, немцы, следуя Якоби, вместо этого употребляем круглое д для
обозначения частных производных. (Вейерштрасс 1874)
Нашей следующей целью является введение понятия дифференцируемости
для функций более чем одной переменной. Так как деление на вектор х - xq
смысла не имеет, прямого пути для обобщения определения III.6.1 нет.
Частные производные. Если в рассматриваемой функции / : U ->• М,
U С Шп зафиксировать все переменные кроме одной и рассмотреть ее теперь как
функцию этой переменной, мы сможем применить определение III.6.1.
Рассмотрим, например, функцию у = /(ж1,Ж2) ДВУХ переменных в окрестности точки
(хю, Его)- Введем для ее производных обозначения
г /(ею + h,x2o) - f(x10,x2o) Of , х
bm - = : -г— {x10,X2o)
/i-ю h dxx
,. f{xi0>X2Q+h)- f(xio,X2o) df f v
h^-0 h ox2
и назовем их частными производными / по х\ и по Х2 соответственно.
Используются также другие обозначения частных производных: fXi(xw, #20)? А'/(жю> ж2о)-
dif(xw,X2o) или сходные с ними.
Геометрически частные производные можно интерпретировать следующим
образом. Функция у = /(ж1,Жг) определяет поверхность в М3 (с координатами
»1, ж2 и у), пересечение которой с плоскостью ж2 = Ж20 представляет собой
кривую xi ь-> /(ж1,Ж2о)- Поэтому частная производная df/dxi определяет наклон
этой кривой, а уравнение
ft Р
У — f(xio, ж2о) + д— (жю? ж2о) {х± - Хю)
ОХ\
является уравнением касательной к этой кривой в точке (жю,Ж2о)-
Аналогично, уравнение касательной к кривой Х2 »-> /(#ю?Я2) есть У = f(xWix2o) +
df/dx2(xw,X2o)(x2 — Х20)? а плоскость, проходящая через две касательные,
задается уравнением
ftp ft-F
(3.2) у = /(жю, ж20) + g— (жю, ^2о) («1 - жю) + g— (жю, ж20) (ж2 - ж20).
Функцию /(Ж1.Ж2) называют дифференцируемой в точке (жиьжзо)? если
плоскость (3.2) является "хорошей" аппроксимацией для f(x±, Х2) в некоторой
окрестности ТОЧКИ (жю, Ж2о), Причем Не ТОЛЬКО ВДОЛЬ ПрЯМЫХ Х\ = Жцэ И Ж2 = Ж20-
(3.1) Пример. Поверхность, определенная выражением у = e~Xl~X2, построена на
рис. 3.1. Частными производными этой функции будут
-^-(хи х2) = -2zie-*?-x', -J-(xu х2) = -2х2е-**-х2*.
ОХ\ ОХ2

IV.3 Дифференцируемые функции нескольких переменных 301
Вычислив значения этих производных в точке (жю, х2о) = (0.8,1.0), можно
построить касательную плоскость в этой точке с помощью уравннения (3.2). Она
тоже показана на рис. 3.1.
Рис. 3.1. Касательная плоскость к поверхности у — е *i х2 (стереограмма).
Случай двух зависимых переменных. В случае двух функций двух
переменных
(3.3) 2/i = A(zi, ж2), у2 = /г(ж1, х2)
запишем уравнение (3.2) для каждой из этих функций:
У\ - fi{xio,x2o) + д—(ею,ж2о)(я1 - а?ю) + -z—(хю,Х2о){х2 - ж2о),
(3-4) £; ^
2/2 = /2(3510,^20) + о—(^io,^2o)(^i - азю) + tj—(жю,ж2о)(ж2 ~~ Ж2°)*
Эти уравнения удобнее записывать в векторной форме:
(3.4') y = f{x0) + f'{xo){x-x0),
где f'(xo) теперь матрица, называемая матрицей Якоби (см. Якоби 1841):
(3'5) /(о)1|ы йы
Эти обозначения позволят нам перенести большинство формул разд. III.6 на
случай нескольких переменных.
(3.2) Пример. Рассмотрим функцию / : Ш2 —>• М2, определенную выражением
(о *\ f/T\ _ /7i(zi, ж2) \ _ / л/2^1 + sin(»i + х2) \
{6'Ь) ПХ)- \/2(хиХ2)) - [V^X.+COS^-X,))'
Эта функция переводит начало координат (#i, х2) — (0, 0) в точку (тд, у2) = (0,1),
прямые линии в кривые и малые квадраты в множества, похожие на паралле-
лограмы (см. рис. 3.2). Матрица Якоби для (3.6) имеет вид:
( v ,, . _ /\/2 + cos(xi + ж2) cos(cci + x2) \
1 j J V j "" V -8Ш(ЯЯ-Ж2) ^/2 + 8ш(Ж1-Х2)У '
и уравнение (3.4) при xq = (0,0)т, уо = f{xo) преобразуется в уравнение

302 IV. Функции нескольких переменных
/о ох (У1-Уы\ _ {у/2 + 1 1\{х1-х10\
[6'Ь) \У2-У2о)-{ 0 V2j{x2-x20)'
Линейное отображение, задаваемое формулой (3.8), в точности то же самое, что и
на рис.2.5. Сравнивая рис. 3.2 с рис. 2.5, можно заметить, что нелинейное
отображение (3.6) в малой окрестности хо аппроксимируется линейным отображением,
определяемым матрицей Якоби. Можно заметить, что для малых величин x-xq
точки оси х\ (для которых Х2 — а?2о = 0) отображаются в векторы, кратные
(л/2 + 1, 0)т, а точки оси х2 — в векторы, кратные (1, л/2)Т (см. стрелки на рис.
3.2). Следовательно, столбцы матрицы Якоби являются образами "инфинитези-
мальных единичных векторов".
Рис. 3.2. График отображения (3.6).
Дифферепцируемостпь
... что непосредственное обучение у Вейерштрасса приводило студентов в
уныние и было вполне понятно только тем, кто уже познакомился с
предметом где-нибудь еще. Наиболее важные учебники были написаны
иностранцами ... Вероятно, первым из них был учебник моего друга Штольца
(Иннсбрук): "Vorlesungen iiber allgemeine Arithmetik" ("Лекции по общей
арифметике", — нем.) ....
(Ф.Клейн 1926, Entwicklung der Math., p. 291)
Рассмотрим функцию
(3.9) /:£/->Мт, UcRn,
и пусть хо G U — внутренняя точка U (U является окрестностью xq).
(3.3) Определение (Штольц 1887, Фреше 1906). Функция (3.9) называется
дифференцируемой в точке хо, если существуют линейное отображение f'(xo) : ]Rn ->
Mm и непрерывная в точке хо функция г : U —»• Шт такие, что г(хо) = 0 и
(3.10) f{x) = /(х0) + f{x0){x - хо) + r{x)\\x - х0\\.

IV.3 Дифференцируемые функции нескольких переменных 303
(3.4) Замечание, Если функция является дифференцируемой в точке хо, то она
непрерывна в этой точке. Более того, все ее частные производные существуют в
точке хо. Это следует из того, что для х — хо — hej (где еу = (0,..., 0,1, 0,..., 0)т
с j-R компонентой, равной 1) равенство (3.10) обращается в
f(*o + he,)-f{zo) = fl{xo) + r{xo + Ж
а а
Так как г(х) непрерывна в точке хо, предел этого выражения существует при
h —>■ 0 и равен
т— (ж0) = f(xo)ej, откуда ^"Ч^о) = fi{xo)€j
OXj OXj
(здесь f(x) = (/i(x),..., /m(#)))- Следовательно, линейное отображение
единственно.
Аналог формулировки Каратеодори (равенство (6.6) из разд. III.6) дает
следующая лемма.
(3.5) Лемма. Функция f(x) из (3.9) является дифференцируемой в точке хо тогда
и только тогда, когда существует матричнозначная функция <р(х), зависящая
от хо и непрерывная в точке хо, такая, что
(3.12) f(x) = f(x0) + <p(z)(x-zo).
Производная функции f(x) в точке хо равна /'(жо) = ф{хо).
Доказательство. Для заданной функции <р(х) положим
f(x0) := <р(х0), г(х) := ((р(х) - <р(жо))тр—^
\\х — Хо\\
и заметим , что равенство (3.10) выполняется. Так как норма вектора (х—хо)/\\х—
яо|| равна единице, то из непрерывности функции <р(х) в точке хо следует, что
г(х) —> 0 при х —)• Хо.
С другой стороны, предположим, что имеет место (3.10). Определим теперь
<р(хо) := fixo), а при х ф х0
(3.13) <р(х) := f'(x0) + r(x){*~Xo)l
\\х — Хо\\
(произведение вектора-столбца г(х) на вектор-строку (х — хо)Т является
матрицей). Тогда <р(х)(х — хо) = f'(xo)(x — xo)-\-r(x)\\x — xo\\. Функция <р(х) непрерывна
в точке жо, так как по теореме 2.6 \\<р(х) — f'(xo)\\ < \\г(х)\\ и ||г(е)|| -» 0 при
х —>- xq. П
Следующий результат дает достаточное условие дифференцируемости,
которое может быть проверено рассмотрением только частных производных.

304 IV. Функции нескольких переменных
(3.6) Теорема. Пусть f : U —>• Ш и хо Е U (внутренняя точка). Если все частные
производные df/dxi существуют в окрестности точки хо и непрерывны в xq,
то функция f дифференцируема в этой точке.
Доказательство. Рассмотрим доказательство для случая п = 2. Обобщение
на случай произвольных п проводится непосредственно. Идея доказательства
заключается в записи разности f(x) — f(xo) в виде
/(si, х2) - /(жю, ж20) = (/(Ж1, х2) - /(жю, х2)) + (/(жю, х2) - /(жю, х20))
и применении теоремы Лагранжа III.6.11 к каждой из разностей. Это дает
f{xUX2) - f{x10,X2o) = ~z (£l,£2)(zi _ хю) + Т (^Ю,Ь)(Ж2 - Ж2о)-
(73?! ОХ2
Полагая <p(xi, х2) = ( -—(£i, х2), tj—(жю,^) , приходим к равенству (3.12).
Непрерывность <р(х) в. точке хо следует из условия теоремы. D
Согласно определению 3.3 вектор-функция f(x) = (Д(ж),..., fm{%))
Дифференцируема в точке хо тогда и только тогда, когда функции fi(x)
дифференцируемы в точке хо для всех г — 1,..., га. Из теоремы 3.6 следует, что функции,
компоненты которых являются полиномами от #i,..., жп, рациональными
функциями или элементарными функциями, дифференцируемы в всех точках, где они
определены.
Контрпримеры
Разрывная функция, у которой частные производные существуют
всюду. Рассмотрим функцию / : М2 —>■ М, заданную выражением
{Х\Х2 0 0
-2—2 ПРИ Х1 + Х2 > О
О при £i = х2 = О
(см. рис. 2.2). Частные производные в начале координат равны нулю, так как
/(#1,0) = 0 для всех х\ и f(0,x2) = 0 Для всех х2. А в любой точке вне
начала координат существование частных производных очевидно. Тем не менее,
функция (3.14) является разрывной в начале координат (см. разд. IV.2).
Разрывная функция, у которой производные по направлению
существуют всюду. Частные производные являются специальным случаем так
называемых производных по направлению. Рассмотрим функцию / : IR2 —>■ М и
вектор v единичной длины {\\v\\2 = 1). Тогда функция g(t) := f(xo-\-tv)
представляет кривую, образуемую пересечением поверхности у = /(zi, х2) с вертикальной
плоскостью {(ж, у) | х — хо + tv,t G М}. Её производная обозначается как
/oira df ( ч г f(xo + hv)-f{x0)
3.15) — ж0 := hm
ov ft-^o h
и называется производной функции f по направлению (вектора v ). Частные
производные получаются из нее при v — (1, 0)т и v = (0,1)т.

IV.3 Дифференцируемые функции нескольких переменных 305
Рассмотрим функцию
(3.16) f(xux2)-~
Для v = (cos#, sin#)T получим
при х\ + х\ > О
при х± = х2 = 0.
„, ч *cos20sin0
g(t) = f(tv) =
t2 cos4 в + sin2 0*
Эта функция дифференцируема при t = 0 и любом значении в (заметим, что
для sin0 = 0 имеем g(t) — 0 при любых t). Следовательно, все производные
по направлению существуют. Однако на параболах х2 = ах\ функция является
константой, а именно, f{xi,ax\) = а/(1 + а2), и все значения между — 1/2 и
1/2 реализуются в каждой окрестности начала координат (см. рис. 3.3) Таким
образом, она не является здесь непрерывной.
Рис. 3.3. Функции (3.16) (стереограмма).
Геометрическая интерпретация градиента
Для функции / : U —> М, т. е. для случая т — 1 и произвольного п, матрица
f(xo) в (3.5) является вектором-строкой. Его обычно обозначают
(3.17) rad/= (А ^-,...,Щ = (A, A,..., l)/=v/
Здесь формальный вектор (оператор)
5 5
V3xi ' дх2 ' ' *' <Эжп/
(Гамильтон 1853, art. 620) называется набла "из-за того, что этот знак
удивительно напоминает ассирийскую арфу" (Дж.У. Гиббс 1907, р. 138). Формула (3.10)
тогда приводится к виду
(3.18) f(x) - f(xo) +grad/(z0) * {х - х0) + г(х)\\х - ж0||,
а уравнение (3.2) касательной плоскости к поверхности у — f(x) примет вид
У- f{xo) + grad/(z0) • (х-хо).

306 IV. Функции нескольких переменных
Чтобы исследовать функцию f(x) в окрестности точки яо, возьмем х = xo+tv
и пренебрежем последним членом в (3.18). Получим
(3.19) f(xo+tv)=f{x0)+tgiadf(x0)-v + ... .
Пусть v — вектор единичной длины. Легко вывести следующие свойства:
• Вектор grad/(#o) ортогонален линии уровня {х ; f(x) = f(xo)}- Это следует
из (3.19), если мы устремим t —> О, так как из равенства f(xo + tv) = f(xo)
следует grad/(xo) • v = 0.
• Функция возрастает при grad/(zo) • v > 0. Из неравенства Коши—Шварца
(1.5) следует, что v = grad/(xo)/|| grad/(zo)|| есть направление, в котором
f(x) растет быстрее всего. Напротив, направление наиболее крутого спуска
функции задает вектор v = — grad/(a?o)/|| grad/(жо)||.
• Если функция f(x) имеет максимум (или минимум) в точке хо, то
необходимым условием этого является равенство grad/(zo) = 0.
Рис. 3.4. Линии уровня и градиенты функции (3.20).
Рис. 3.4 показывает линии уровня f(x) = С (где С = г/20; г — 1,..., 30) для
функции
(3.20) /(si, х2) = х\- 4жхж2 + Ъх\.
Её градиент grad/(zi, жг) = (2zi — 4^2, —4жх 4- Южг) показан стрелками. Мы
видим, что градиент ортогонален линии уровня и что длина grad/(zo) показывает
крутизну поверхности у — f(x).
Цепное правило. Рассмотрим две функции
/ 9
Шп у Шт у Шр
X i—у у I—> Z
и исследуем дифференцируемость сложной функции (д о f)(x) = g(f(x)). Как и
в разд. III.6, мы используем описание Каратеодори (здесь это лемма 3.5).
Предполагая, что функция / дифференцируема в точке жо, а функция д — в точке
у0 = /(жо), мы имеем

IV.3 Дифференцируемые функции нескольких переменных 307
f(x) = f(x0) + <р{х)(х - ж0), д(у) = д{уо) + Ф(у){у ~ 2/о)•
Взяв t/ = /(ж), уо = /(яо) и подставив первое равенство во второе, получим
(3.21) g(f(x)) = g(f{x0)) + ^(/(z)M*)(* - хо).
Так как произведение if>{f{x))<p(x) непрерывно в точке жо, производная сложной
функции д о / равна этому выражению, вычисленному в точке х$, т-е.
(3.22) (<7°/)'Ы = </Ы-/'Ы.
Записанное в координатном представлении, призведение (3.22) примет вид
(3.23)
который обобщает формулу Лейбница (П. 1.16).
10
/
А.
1 ,
-.8
I ,
-.6
1 ,
-.4
1 , |
-.2 /
/ 2
А
.6
.8
1.0
\ 12
IX
1.6
^ ,
X
i
.2
1
.4
<
, 1
.6
1
У
Рис. 3.5. Движение эластичного маятника.
Пример. Предположим, что движение эластичного маятника задано в
полярных координатах: f(t) = (r(t),<p(t)) , см. рис. 3.5.г Если мы хотим найти
скорость маятника в декартовых координатах
(3.24)
С)
9{г,<р)
_ ( г cos <р
rsin<p
надо продифференцировать х и у по t. Так как матрица Якоби преобразования
(3.24) задается выражением
(3.25)
,, ч /cos<z> — rsm<p\
д (г,(р) = . г
v 7 у sin if Г COS <f J
1 Кривые на этом рисунке являются решениями дифференциальных уравнений и
были получены с помощью численных методов (см. разд. П.9).

308 IV. Функции нескольких переменных
мы получим из (3.22), что
х = cos <р • г — г sin (р • ф, у — sin (р • г + г cos (р • ф
(производная по времени t обозначается точкой сверху). Это позволяет,
например, вычислить кинетическую энергию
T(t)
т
2 ,х2+у2) = ^(г2 + г2ф2).
Теорема о среднем значении
Мы хотим обобщить формулу f(b) — f(a) = /'(£)(& —а) из теоремы Лагранжа
(разд. III.6) на случай нескольких переменных.
Случай га = 1. Рассмотрим функцию / : Шп —>■ М, и пусть заданы две
точки a Е Мп и b Е Шп. Соединим эти точки прямой линией
x = a + (b-a)t, 0 < * < 1
и положим
g{t):=f(a+(b-a)t).
Если f(x) является дифференцируемой во всех
точках интервала {а + (6 — a)t ; t Е (0,1)}, то g(t)
тоже дифференцируема, и из (3.22) следует, что
g'{t) = f{a+{b-a)t){b-a).
Так как #(0) = /(а), #(1) = /(b), теорема III.6.11, примененная к функции #(<),
дает д(1) — g(0) = gf(r)(l — 0) и, следовательно, также
(3.26) f(b)-f(a) = f(t)(b-a),
где точка £ лежит на отрезке, соединяющем точки а и Ь. Уравнение (3.26)
выглядит подобно (III.6.14), но здесь f'(£)(b — а) — скалярное произведение двух
векторов.
Общий случай. Для функции / :
для каждой компоненты f(x). Это дает
мы можем применить (3.26)
(3.27)
/ fi(b)-fi(a) \
\/т(Ь)-/т(а)/
\ dfm (С
£№\ /Ьх
дхп
сц
(U)/
*ьп
где все £,- Е Шп принадлежат отрезку прямой, соединяющей точки а и Ь.
Недостаток этой формулы в том, что аргумент £г- различен для каждой строки.
Мы не можем надеяться, что равенство (3.26) будет справедливо для всех
компонент функции / : Шп —> Шт. Контрпримером является: fi{x) — cos ж,
/2(ж) = since, а — 0, b — 27г. Если мы удовлетворимся неравенством, то
ситуация здесь такова:

IV.3 Дифференцируемые функции нескольких переменных 309
(3.7) Теорема. Пусть функция f : U —> Шт, С/ С Мп дифференцируема во всех
точках "открытого" сегмента (а, 6) := {х = а + (6 — а)£ ; 0 < t < 1}
(предполагается, что эти точки являются внутренними точками U) и в норме (2.14)
\\f'{x)\\ < М для всех х Е (а, Ь).
Тогда
(3.28) 11/(Ь)-/(а)Н<М-||Ь-а||.
Доказательство. Рассмотрим функцию
m
(3.29) g(t) := ^ с,- /,■ (а + (6 - а)*) = ст/(а + (6 - a)t),
г = 1
где ci,..., cm — произвольные пока коэффициенты. Производная функции g(t)
равна
771 П л /.
»'(*) = ^c,XT^(a+(6-a)<)(&i-ai)=cT/'(«+(fe-«)*)(fe-a)-
i=l j=l ^
Применение теоремы III.6.11 дает
(3.30) cT(f(b) - /(a)) = 0(1) - g(0) = ff'(r) = ст/'(0(& - «),
где £ = а+(6—а)т принадлежит сегменту (а, 6). Разумно положить с = /(6) —/(a),
чтобы сделать выражение в левой части (3.30) по возможности большим. Тогда,
применяя неравенство Коши—Шварца к правой части (3.30), получим с учетом
(2.15):
\\f(b)-f(a)\f<\\f(b)-f(a)\\.M.\\b-a\\.
Отсюда получим (3.28) после деления на ||/(b) —/(a) II (заметим, что утверждение
(3.28) очевидно при ||/(6) - f(a)\\ = 0). □
Теорема о неявной функции
Неявные уравнения f(x,y) = С были центральной темой "Геометрии"
Декарта 1637 года (см., напр., уравнение (1.1.18)). Никто не сомневался, что
такие уравнения определяют геометрические кривые у — у(х). а Лейбниц
даже знал, как дифференцировать такие функции. Однако в эпоху Вейерштрас-
са (см. Дженокки—Пеано 1884, р. 149-151) математики почувствовали
необходимость более строгого доказательства, которое гарантировало бы, что уравнение
f(x,y) = С эквивалентно уравнению у = у(х) в некоторой окрестности точки
(яо>2/о)} удовлетворяющей условию /(жо>2/о) — ^- Мы будем говорить, что
неявное уравнение /(ж, у) — С может быть разрешено относительно у.
Рассмотрим, например, окружность х2 + у2 = С и фиксируем точку (а?о, Уо),
причем Xq + Уо = С- Если уо > 0, мы получим у(х) — л/С — х2, а для уо < 0
имеем у(х) = — л/С — ж2, но если уо = 0, то невозможно найти функцию у(ж),

310 IV. Функции нескольких переменных
удовлетворяющую условию х2 + у(х)2 — С для всех х в некоторой окрестности
точки Хо.
В дальнейшем мы положим F(x, у) = /(ж, у) — С и заменим условие /(ж, у) -
Сна F(x,y) = 0.
(3.8) Теорема о неявной функции. Рассмотрим функцию F : Ш2 —>• Ш и точку
(жо, Уо) Gl2u предположим, что частные производные dF/dx и dF/dy
существуют и непрерывны в окрестности (жо,2/о)« Если
dF
(3.31) F{xo,yo) = 0 и (Жо,уо)^о,
ду
то существуют окрестности U у точки хо и V у точки уо, а также
единственная функция у : U —)• V такие, что у(хо) = уо и
(3.32) F(x,y{x))=0 для
всех х £ U.
Функция у(х) дифференцируема в U, и ее производная равна
dF/дх (х,у(х))
(3.33) у'(х)
dF/dy {х,у(х))
Доказательство. Предположим, что dF/dy(xo,yo) > 0 (в противном случае
мы будем работать с — F вместо F). Из непрерывности dF/dy следует
существование S > 0 и /3 > 0 таких, что
OF
(3.34) -g-(x,y) >/3>0 при |ж-ж0|<<* и \у-уо\<8.
Отсюда следует, что F(xo,y) является монотонной возрастающей функцией у, и,
так как ^(жо, уо) = 0, мы имеем F(xo, Уо—S) < 0 < ^(жо, Уо+S). Из непрерывности
F следует существование <$х > 0 (Si < S) такого, что (см. рис. 3.6)
F(x, yo~S)<0< F(x, уо + S) при |ж - ж0| < Si.
Теперь положим U = (xo — Si, жо + ^i), V = (yo — S,yo-\-S) и применим для каждого
фиксированного ж £ U теорему Больцано III.3.5 к ,Р(ж,у), рассматриваемой как
функция от у. Это доказывает существование функции у : U —У У,
удовлетворяющей условию (3.32). Единственность функции у(х) в V следует из монотонности
F(x,y) как функции у.
Нам еще надо доказать, что функция у(х) дифференцируема в произвольной
точке Ж1 £ U. Как и в доказательстве теоремы 3.6, мы воспользуемся
соотношением
dF dF
F(ж, у(х)) = F(xu yi) + -^ (£, у{х)) (ж - жх) + — (жь rj) (у(х) - уг),
где yi = 2/(ei), £ лежит между ж и жх, а 77 — между у(х) и ух. Используя (3.22) и
(3.34), мы получим
<т\ ( \ ( \( \ (Л dF/dx((,y(x))
(3.35) у(ж) - ух = <р{х)(х - жх), (р(х) = — , ч-.
dF/dy(xi,rj)

IV.3 Дифференцируемые функции нескольких переменных 311
Si
• фу(4
С*о. Уо)
1—ёееееебвеееее—'
Рис. 3.6. Доказательство теремы о неявной функции.
Функция dF/dx непрерывна и, следовательно, ограничена при \х — xq\ < Si и
\у — уо\ < S некоторой величиной М. Отсюда, учитывая неравенство (3.34), мы
заключаем, что |<р(ж)| < М//3 и непрерывность у(х) является следствием (3.35).
После того как непрерывность у(х) доказана, становится очевидной и
непрерывность (р(х) в asi, вследствие чего у(х) является дифференцируемой в х\. Формула
(3.33) получается вычислением предела Yun<E^.Xl <р(х). П
Замечание. Если дифференцируемость функции у(х) установлена, формула
(3.33) получается посредством дифференцирования тождества F(x,y(x)) = 0.
Эта процедура называется дифференцированием неявной функции и уже была
использована в конце разд. П.1.
Дифференцирование интегралов по параметру
Теперь мы хотим выяснить, является ли интеграл, содержащий параметр р
(см. формулу 2.23), дифференцируемой функцией р, и если является, то может
ли быть вычислена его производная путем перемены порядка интегрирования и
дифференцирования по параметру, т. е. интегрированием df /др.
(3.9) Пример. Интеграл
(3.36)
I
г/2
еах cos х dx
з°*/2 - (
а2 + 1
легко вычисляется, если взять действительную часть интеграла Jl e(a+i)rr ^х
Если мы продифференцируем обе части (3.36) несколько раз по параметру а, то
получим формулу
(3.37)
I
г/2 _ / а7 у /еа*/2 -а\
~ \da) V а2 + 1 /'
которую получить другими методами было бы гораздо сложнее.

312 IV. Функции нескольких переменных
(3.10) Контрпример. Рассматривая рис. III.5.5а, мы видим, что интеграл от fn(x)
при п —>■ ос ведет себя подобно С /п. Это наводит на мысль заменить в формуле
(а) упр. III.5.9 целое п действительной переменной \/р и определить функцию
(3-38) /^p) = (i//vp2)2 = (^F при р2 + х2>0
и /(0,0) = 0. Тогда,
(3-39) F(p) = jf f(x, р) dx = 2(р2Р+ 1}
имеет производную в нуле F'(0) — 1/2. С другой стороны, интеграл от функции
dfi \ ) —/2| 2П при хф 0
fy(x>p) = \ (р2 + я2)3
t 0 при х = 0
при р = 0 равен нулю. Так как производная df/dp в начале координат разрывна,
этот контрпример не противоречит следующей теореме.
(3.11) Теорема. Рассмотрим функцию f : [а, Ь] х [с, d] —> Ш и предположим, что
частная производная -gf-(x,p) существует и непрерывна на [а, b] х [с, а1]. Если
интеграл
(3.40) F(p):= [ f(x,p)dx
J а
существует для всех р Е [с, d], mo функция F(p) дифференцируема и ее
производная равна
(3.41) F'(P) = L %^P^dx-
Доказательство. Рассмотрим очевидное тождество
F(p)-F(Po) fbff(x,p)-f(x,p0)^
-sy
J a
dx.
P-PO J a Ч P-PO /
К подынтегральному выражению правой части применим теорему Лагранжа
III.6.11, которая дает частную производную -?f-(x,r)) (с 77, зависящим от х).
Вычтем Ja ^Чж,ро) dx из обеих частей тождества. Используя неравенство из
следствия III.5.15, получим, что
(3.42)
F(p) - F(Po)
Р-Ро
- / -K-{x,po)dx\< / —-(x,rj)-—-(x,po)
Ja dp I J a \dp Op
dx.
<€
Так как df/др непрерывна на компактном множестве [a, b] х [с, d], то она
равномерно непрерывна на нем (теорема 2.5), так что для достаточно малых р — ро

IV.3 Дифференцируемые функции нескольких переменных 313
разность в правой части (3.42) может быть ограничена сверху для всех х сколь
угодно малым е. Это показывает, что левая часть (3.42) сколь угодно близка к
нулю и, следовательно, F дифференцируема, а ее производная имеет вид (3.41).
□
Упражнения
3.1 Рассмотрим функцию / :'.
(см. рис. 3.7а),
г.3 . „,з
I 0 При Х\ — Х2 — 0.
Является ли функция / непрерывной? Имеет ли она производные по
направлению в начале координат? Являются ли частные производные df/dxi
и df/dx2 непрерывными? И является ли / дифференцируемой?
Рис. 3.7. Стереограммы к упражнениям 3.1, 3.2 и 3.3.
3.2 Рассмотрите те же вопросы для функции f(xi, Х2) = yl^i^T? показанной на
рис. 3.7с (Оперный театр города Сидней).
3.3 Покажите, что / : Ж2 -
f(xux2) =
1, определенная как
#1 Х2 Sinl
о
при Х\ — Х2 = 0
(см. рис. 3.7Ь) всюду дифференцируема, но ее частные производные не
непрерывны в начале координат. Эта функция — двумерный аналог функции,
изображенной на рис. Ш.6.1.

314 IV. Функции нескольких переменных
3.4 Для заданной константы а определим функцию / : Ш2 —у Ш формулой
f(x1,x2) = {^a прнх1ха#0
[ 0 при xix2 = 0.
Определите значения параметра а, при которых (а) / непрерывна и (Ь) /
дифференцируема.
3.5 Пусть функция / : Шп —У Ш задана выражением f(x) = хтАх, где А
постоянная п х п матрица. Покажите, что ее производная имеет вид f{x) -
хт (А + Ат) (в случае затруднения выпишите явно все члены / при п — 2).
3.6 Пусть V(x,y) — дифференцируемая функция и
W(r,(p) := V(rcos (р, rsin^>).
Примените цепное правило и покажите, что
(dV_\2 /dV\2 _ /dW\2 1 /dW\2
\дх) +\ду) ~ V дг ) + г2\д<р ) '
3.7 Дифференцируемую функцию / : Жп —> Ш называют однородной порядка р,
если
(3.43) f(ax) = apf(x) при а > 0, х <Е Мп.
Покажите, что функции tg^i/a^)* у/2х\ + Ъх\ + 4ж§ и х\—Ьх\х\+х\х\
являются однородными (какого порядка?) и покажите, что однородные функции
удовлетворяют тождеству Эйлера:
х1-—(х) + ... + хп-—(х) =pf(x).
ОХ\ охп
Указания. Продифференцируйте (3.43) по а.
Рис. 3.8. Леминиската Бернулли и овалы Кассини.
3.8 Исследуйте функции у (ж), неявно определяемые уравнением
(3.44) (ж2 + у2)2 - 2ж2 + 2у2 = С.
При С = 0 это уравнение описывает знаменитую "лемнискату" Якоба
Бернулли (1694), см. рис. 3.8. Найдите положения точек, в которых dF/dy — О,

IV.3 Дифференцируемые функции нескольких переменных 315
т.е. точек, в которых теорема о неявной функции не применима.
Найдите также положения максимумов решений (3.44), т.е. точек, в которых
у'(х) = 0, и покажите, что они лежат на окружности.
3.9 Рассмотрите те же вопросы для "декартова листа"
х3 + у3 - Зху
(см. рис. 4.2 ниже).
3.10 Найдите точки х El2, где столбцы матрицы f(x) в (3.7) являются
векторами одинакового направления (т.е. det/'(cc) = 0). Эти точки помечены,
соответственно, "о" и "х" на рис. 3.2.
Ответ, ((к + I + 3/4)тг, (к - I + 1/4)тг) и ((к + / + 3/4)тг, (к - I - 3/4)тг) для
kjez.
3.11 Как вы думаете, какой из следующих двух интегралов проще вычислить:
/ (in ж) dx или / ха(\пх) dx ?
Jo Jo
Видно, что второй интеграл можно продифференцировать по параметру а.
Сделайте это, дав обоснование, и вычислите оба интеграла.
3.12 Используя тот факт, что
dx 7Г
/
./о
при а > 1,
/0 а - cos х у/а2 - 1
проверьте, что
dx 5л/бтг fK dx Wy/b-K
Г dx _ 5л/бтг Г
J0 (5-cosж)2 ~ 288 И Уо (6^
4 cos х)3 1000
3.13 Покажите, что при а > 0
- rvr\ j_
dx— - arctg (a) • log.(l + a ).
I
a\og(l + ax) ^_ 1^ ,_л ,__/n , __3
/o x2 + l 2
Указание. Продифференцируйте интеграл по а и обоснуйте это действие.
3.14 Покажите, что
/
./о
SinCC 7Г
х Х~ 2*
Указание. Используя определение III.8.1, теоремы 3.11 и III.б. 18, а также
упр. II.4.2.h, покажите, что при а > 0
»=/ е~ах dx => F'{a) = - e-axsmxdx = —
Jo х Jo 1 +
2*
l + a:
Наконец, видоизменив доказательство из примера III.8.5, покажите, что
функция F(a) непрерывна справа при а = 0+.

316 IV. Функции нескольких переменных
IV.4 Производные высших порядков и ряд Тейлора
Теперь легко видеть, что дифференциалы этого рода сохраняют свою
величину, если изменить порядок дифференцирования по переменным.
(Коши 1823, Resume, р. 76)
Рассмотрим сначала функции /(ж, у) двух переменных. Частные
производные, такие, как df /дх, тоже являются функциями двух переменных, и мы можем
для них тоже вычислять частные производные, как показано на следующей
схеме:
дх
/(я, У)
д_
дх
д_
дх
дх2
д_
ду
д_1
ду
_д_
ду
d2f
ду2
д_
ду
д_
дх
d2f ? d2f
д_
дх
дхду дудх
д_
ду
д_
дх
d3f ? d3f
д_
дх
дхду2 ду2дх
Возникает вопрос: зависят ли эти производные от порядка дифференцирования?
(4.1) Пример. Следуя Эйлеру (1734, Coram. Acad. Petrop., vol. VII, p. 177),
рассмотрим функцию /(ж, у) — yfx2 + пу2 и вычислим частные производные (при
х2 + пу2 > 0):
ox yjx2 + пу2
w-(x,y) =
пу
d2f
дудх
d2f
(х,у) =
(ж, 2/) =
-пху
{х2 + пу2)3/2'
—пху
дух",У' у/х* + пу*' дхду"""" (г2 + ш/2)3/2'
Эйлер затем объявил (см. также Эйлер 1755, §226), что вообще
(4.1)
d2f d2f
дудх дхду
Однако это не верно без некоторых дополнительных предположений, как мы
можем увидеть из следующего контрпримера.
(4.2) Контрпример. Г.А.Шварц (1873) привел первый, довольно сложный
контрпример для (4.1) (см. упр. 4.1). Более простой контрпример позже
получил Пеано (1884, "Annotazione N. 103"), рассмотрев функцию
(4.2)
f(x,y) = xyg(x,y),

IV.4 Производные высших порядков и ряд Тейлора 317
где д(х,у) ограничена (но необязательно непрерывна) в окрестности начала
координат. Для этой функции имеем
— (0,2/ = hm = ктуд(х,у).
ах х-*о х х-+о
Производная этого выражения по у
o2f
-(0,0) = limf lim^y))
дудх у-
при условии, что этот предел существует. Аналогично имеем
d2f
(4.4)
dxdy
(0,0)=lim( \im д(х,у)).
x-+0 \ y-+0 /
Остается только выбрать функцию д(х,у) такую, чтобы пределы (4.3) и (4.4)
были различными. Такой функцией будет, например,
(4.5)
д{х,у)
х2-у2
х2 + у2
при х +у > 0,
для которой Мтх->од(х, у) = — 1 для всех у ф 0, a \imy->og(x,y) = +1 для всех
х ф 0. Следовательно, смешанные частные производные
d2f
(0,0) = -1
а2/
(0,0)
дудх "' "у ~ " дхдуУ
различны для функции, определенной соотношениями (4.2) и (4.5).
(4.3) Теорема. Рассмотрим функцию f : Ш2 —)■ Ш, для которой частные
производные Q~f qj ддх сУЩествУюш в некоторой окрестности точки (хо,уо), причем
о+ непрерывна в точке (жо, Уо)- Тогда существует ^j- в точке (жо, Уо) и верно
равенство
d2f d2f
~{х0,уо) = ^ТБ~(жО'2/о)-
дудх
дхду
Доказательство. Рассмотрим маленький
прямоугольник со сторонами h и к. Значения , >^
/ в его вершинах обозначим /оо, /оъ /ю и ^° ~y
/ц. Тогда частные производные
приблизительно равны
(4.6)
(4.7)
df ( ч /ю - /оо
тг-(ж0,2/о) « г ,
-о- (же 2/о + «) « т ,
д2/ ^ ff(^o,2/o + fe) - ff(^o,t/o) ^ /и - /oi - /ю + /(
5у5ж fc h - к

318 IV. Функции нескольких переменных
и аналогично
Too
(4 8) 92f ~U(x° + h'y^-U(Xo'yo} ^fii-ho-foi + fo
дхду h к • h
Выражение для правых частей в (4.7) и (4.8) одинаковы (Эйлер: "... huius
theorematis veritatem exercitati facile perspiciant ..." — показать справедливость
такой теоремы представляется легким упражнением, — лат.), и утверждение
теоремы представляется правдоподобным.
Чтобы сделать доказательство строгим, мы заменим разности в (4.6) по
теореме Лагранжа III.6.11. Однако здесь возникает некоторое затруднение из-за
того, что промежуточные точки £ для двух разностей будут различными. Чтобы
обойти эту трудность, рассмотрим функцию
(4.9) g{x):=f(x,yo + k)-f{x,y0)
и применим к ней теорему Лагранжа: д(хо + К) — д(хо) = hg'(£). Это дает
где £ лежит между xq ижо + Zi. Далее применим теорему Лагранжа к производной
ах(£>2/)> Рассматривая её при этом как функцию у, и получим
(77 лежит между у0 и у0 + к).
Благодаря непрерывности д-^ в точке (хо,уо) из (4.10) следует, что для
любого е > 0 существует S > 0 такое, что при h2 + к2 < S2
I /и - /ю - /oi + /оо d2f
/11 -Л0-/01 + /00 = Н~9^(£>2/° + *0~ -j^ (£>2/о))>
h • к dydx
{хо,Уо)
< е.
При к -> 0 разности (/ц - /ю)/& и (/0i - foo)/k стремятся к |^(ж0 + h,y0) и
§^(#о,Уо) соответственно. Следовательно, при |fe| < S
\1{^(*о + Гь,уо)-^(хо,Уо))--^(хо,Уо)\<е.
Это как раз и означает, что
1То Л 1^(Ж0 + Л'Уо) ~ ду-(хо'Уо)) = dyte{Xo'^
и утверждение теоремы, таким образом, доказано. D
Эта теорема, примененная несколько раз, позволяет нам изменять порядок
дифференцирования и в производных более высокого порядка. Например,
_д_д__д__д_д_г_ д__д_ д_д_ д_ ААААА/-
дх ду дх дх ду дх дх ду дх ду дх дх дх ду ду

IV.4 Производные высших порядков и ряд Тейлора 319
Теорема применима также для функций более чем двух переменных.
Действительно, мы всегда можем за один раз переставить две частные производные,
считая остальные переменные константами.
Ряд Тейлора двух переменных
Нашей следующей целью является обобщение ряда Тейлора на функции
двух переменных. Идея такого обобщения (Коши 1829, р. 244) заключается в
сведении проблемы к задаче с одной переменной путем соединения точек (х0,у0) и
(хо + h, уо + к) прямой линией. Рассмотрим, таким образом, функцию
(4.11) g{t) :=f{x0 + th,y0 + tk)
и применим к ней формулу (III.7.18) (ряд Тейлора для функции одной
переменой). Для этого вычислим производные от g(t). Если функция /(ж, у)
дифференцируема достаточное число раз, цепное правило нам дает
(4.12) g'(t) = -J-(x0 + th, у0 + tk)h + -/-(х0 + th, у0 + tk) к,
ох оу
затем
(4.13) 9»«) = д^(.щ + £L(.)kh + *f_{.)kk + 0(.)«,
где опущенный аргумент частных производных / есть (х0 + th, уо + tk). Два
центральных члена в (4.13) равны согласно теореме 4.3 (дальнейшее
дифференцирование будет давать биномиальные коэффициенты). Подстановка найденных
выше производных #(£), например, в
g(l)=g(0)+g'(0) + ±g>'(0) + ±g»'(6)
(где О < 0 < 1) приводит к следующему результату:
О Л О £
f(x0 + h, уо + к) = f(x0> уо) + Q~(xo, Vo)h + ^-(жо, Уо)к
if^f, ,и2 ,J2/, „, , d2f,
+ 2 (w(X0>y°)h2 + 2dxfrj{X0'y°)hk + ду*ЫУ0)к2)
(4Л4) +l(U^h3 + ZMy-^h2k
d3f lf ,Lta , d3f,
+ 3^'">Л*2 + ^К'">*Э)'
дхду2 ду
где £ = xo+Oh иг} = уо+6к — промежуточные точки. Можно, конечно, применить
и теорему III.7.13 с остаточным членом в интегральной форме.

320 IV. Функции нескольких переменных
(4.4) Пример. Рассмотрим функцию f(x,y) = е~х ~у (см. также пример 3.1). Ее
частные производные равны
<¥-(х,у) = -2хе-**-»\
д21
дх
d2f
^(х,у) = (4х2-2)е-х'-У2
— (ж, у) = -2уе х у ,
*/,_.л _,„.».. ,*.-.»-,»
9_
ду
2{х,у) = (4у'-2)е-
дхдУ{Х>У)=1№{Х>У) = 4ХУе~Х2~у2-
Если мы пренебрежем остаточным членом в (4.14) и положим хо = 0.9, уо = 1-2,
то получим квадратичную аппроксимацию
/(0.9 + Л, 1.2 + к) « е"2'25(1 - 1.8Л - 2Лк + 0.62/i2 + 2.16/i& + 1.88Л2).
На рис 4.1 сравниваются эта аппроксимация и рассматриваемая функция f(x,y).
Область изменения переменных на графике — 1<ж<2, —1<у<2.
Рис. 4.1. Аппроксимация Тейлора второго порядка для функции f(x,y) = е~
Ряд Тейлора для случая п переменных
Теперь мы распространим наши формулы на функции вида
/ : Шп -> Мт,
где f(x) = (Д(ж),..., /т(ж)) состоит из га действительных функций от х Е Шп.
Зафиксируем хо Е Mn, h Е Шп и применим результаты разд. III.7 к функции
g{t) := fi(xo + th). Получаем
fi{x0 + h)= fi(x0) + Y, q£: Mhj + у J2 E дхдх (ж°) hihk
j = l J ' j = l k = l 3
nun
(4.15)
d*fi(xo + 9ih)
&JH£~',i~i dxjdxkdxt
j=ifc=it=\ j
^ IV IV fC
+ ^тЕЕЕ
hjhkht.
Мы можем пойти даже дальше и записать (формально, без рассмотрения
сходимости ряда)

IV.4 Производные высших порядков и ряд Тейлора 321
g=i Я' ii=iia=i i,=i ^^ ' ' *^
Эти формулы довольно громоздки и "взывают" о более компактной записи,
которая, говоря словами Дьёдонне, "изгнала бы орды индексов". Линейный член в
(4.15) является как раз г-м элементом произведения f'(xo)h (матрицы Якоби на
вектор h). Чтобы упростить квадратичный член, рассмотрим билинейное
отображение f"(x) : Шп х Жп —>■ Мт, чья г-я компонента при действии на пару векторов
и и v определяется как
(4.16) (/"(*)(«, ф=££^(*)^-
j=lk=l J
Следовательно, квадратичный член в (4.15) есть г-й элемент вектора f"(xo)(h, К).
Мы можем продолжить интерпретацию высших производных как полилинейных
отображений. Например, f'"(x) :Шп хМп хШп —>► Rm определяется выражением
п п п
d3fi
(4.17) (г («к», v,„)\ ■= ЕЕЕ^^и w.
В этих обозначениях формулу (4.15) можно переписать как
(4.18) /(а* + К) = /(я*) + f'(x0)h + i f"(x0)(h, h) + R3.
Для остаточного члена R$ нельзя написать R^ = (1/3!)/;//(жо + Oh)(h,h,h), так
как промежуточные точки жо + Oih in (4.15) в (4.15) могут быть различны для
каждой компоненты. Однако мы можем использовать интегральное
представление (теорема III.7.13) для получения формулы
(4.19)
Д3= Г (1 ^ f'"{x0 + th){h,h,h)dt.
(4.5) Замечание. Для вектор-функции g(t) = {gi{t),.. .,gm(t)) мы используем
запись
(4.20) J g{t)dt:=([ gi(t) dt,..., / gm{t)dt) .
Вид этой записи наводит на мысль об использовании оценки
(4.21) II / g(t)dt\\< [ \\g(t)\\dt,
11 JO " Jo
которая получается как результат рассмотрения римановых сумм и применения
к ним неравенства треугольника, записанного в виде || J2i #(&)й|| < Yli 11#(&)11й-

322 IV. Функции нескольких переменных
Оценка остаточного члена. Допустим, мы хотим оценить остаточный
член #з (4.19). Принимая во внимание (4.21), нам надо оценить выражение
||//"(ж)(Л, Л, Л)||. Для евклидовой нормы эта оценка может быть получена
повторным применением неравенства Коши—Шварца. Обозначив выражение (4.17)
через аг-, имеем
п п
a>i := ]Г bijUj, а2 < ( ^ b^J \\и\\2,
j=i i=i
n
k=l k = l
n n
Cijk := Yl diJUw*> сЬк ^{J2 dbkt) IH|2>
1=1 1=1
где dijki — дхдхдх * Подстановка c2jk из последнего неравенства в предыдущее,
а затем 6?- в первое дает
«.2<(EEE4^)ihi2ihi2ini2.
j=ik=n=i
Вычислив Yli я2 и квадратный корень из этой суммы, мы получим
(4.22) \\f"'(x){u, v, w)\\ < М(х) \\и\\ \\v\\ \\w\\,
где
\ т п п п «о г
(4.6) Лемма. Пусть функция f : Шп —» Шт трижды непрерывно
дифференцируема. Тогда остаточный член R^ в формуле (^Л8) удовлетворяет неравенству
ЦДз||<^- sup M(x0 + th),
где М(х) определена формулой Ц.23).
Доказательство. Применение оценки (4.21) к (4.19) дает
1|Дз|| < f ^^ \\f"(x0 + th)(h, h, A)|| eft.
Из неравенства (4.22) следует, что выражение \\f"(xo + th)(h, Л, h)\\ не
превосходит supt6r01i М(xo+th)\\h\\3, и утверждение леммы теперь следует из неравенства
(III.5.18). ' D

IV.4 Производные высших порядков и ряд Тейлора 323
Задачи на максимум и минимум
Наша следующая цель — обобщить результаты разд. П.2 относительно
необходимых и достаточных условий локального максимума(или минимума) на
случай функций z = f(x,y) двух переменных. Мы уже видели в разд. IV.3
(геометрическая интерпретация градиента), что grad/(xo, Уо) = О, т.е.
(4.24) ^(zo,2/o) = 0, ^(zo,yo) = 0
— необходимое условие максимума (или минимума). Точки, удовлетворяющие
условию (4.24), называются стационарными точками функции f(x,y).
В достаточно малой окрестности стационарной точки (жо, Уо) (если \х — хо\ и
12/ — 2/о | малы) остаточным членом в (4.14) можем пренебречь, и условие
д2 f d2f d2f
(4.25) д^(х°'y^h2 + 25^"(Ж°'Уо)Нк + а~^(ж°'Уо)к2 > °
гарантирует, что f(xo + ft, Уо + к) > /(жо?2/о) (если функция только дважды
непрерывно дифференцируема, то берем меньшее число членов ряда Тейлора и
используем непрерывность вторых частных производных). Поэтому, мы имеем
локальный минимум, если (4.25) выполняется для всех (ft, к) ф (0,0). Если
выражение в (4.25) отрицательно для всех (ft, fc) ф (0,0), мы имеем локальный
максимум. В случае, когда (4.25) принимает и положительные, и отрицательные
значения в зависимости от выбора (ft, /г), точка (хо, уо) называется седловой
точкой функции, т.е. существуют направления, в которых функция возрастает, и
другие, в которых она убывает.
Для того чтобы проверить, является ли положительной квадратичная
форма Ah2 + 2Bhk + С к2 для всех (ft, к) ф (0,0), возьмем Л = h/k и рассмотрим
квадратный трехчлен А\2 + 2ВХ + С. Этот полином принимает только
положительные значения, если А > 0 и АС — В2 > 0, и только отрицательные значения,
если А < 0 и АС — В2 > 0. Мы, таким образом, доказали следующий результат,
который был опубликован в самой первой работе молодого Лагранжа.
(4.7) Теорема (Лагранжа 1759). Пусть функция f : Ш2 —У Ш дважды непрерывно
дифференцируема, и условие (4-24) удовлетворяется. Тогда
a) точка (жо, Уо) есть точка локального минимума, если в этой точке
d2f d2f d2f ( d2f \2
b) точка (жо, Уо) является точкой локального максимума, если в точке (жо, Уо)
d2f d2f d2f / а2/ \2
дх2 дх2 ду2 \дхду/
c) в случае, когда в точке (жсь Уо) выполняется неравенство
d2f d2f ( d2f \2
эта точка является седловой точкой. □

324 IV. Функции нескольких переменных
(4.8) Пример. Функция
(4.29)
/(ж, у) = х3 + у3 - Ъху
порождает знаменитый "декартов лист" (письмо Декарта к Мерсенну 23 августа
1638 г.). Линии уровня этой функции построены на рис. 4.2. Вычисляя частные
производные
£(,„) = а.'-*. |
(ж, у) = Ъу2 -Зж,
мы видим, что функция (4.29) имеет две стационарные точки, а именно, (0,0) и
(1,1). Проверка достаточных условий теоремы 4.7 показывает, что точка (0,0) —
седловая точка, а точка (1,1) — точка локального минимума (см. рис. 4.2).
Рис. 4.2. Линии уровня декартова листа (4.29).
Обобщение на случай п переменных. Рассмотрим действительную
функцию z — /(xi,..., хп) более чем двух переменных. Мы видели в разд. IV.3, что
необходимым условием локального экстремума (максимума или минимума) в
точке xq G Шп является
(4.30)
grad/(z0) = 0.
Для получения достаточных условий надо исследовать квадратичный член в
(4.15). Если положить h = (/ii,..., /in)T, этот член может быть записан как
(hTН(жо)/ь)/2, гДе матрица
/ а*?(
э2/
дх\дхп
(Ху
(4.31)
Н(х) =
а2/
дхпдхi
(х)
&(*)

IV.4 Производные высших порядков и ряд Тейлора 325
называется матрицей Гессе, или гессианом (Гессе 1857, Crelle J. f. Math., vol.54,
p. 251). Если условия теоремы 4.3 выполняются, то эта матрица симметрична.
Если в дополнение к (4.30) матрица (4.31) является "положительно
определенной" в точке жо, т.е. hTH(xo)h > 0 для всех h ф 0, то точка жо является точкой
локального минимума. Стационарная точка хо будет точкой локального
максимума, если Н(хо) является "отрицательно определенной", т.е. hTH(xo)h < 0
для всех h ф 0. По вопросам о способах проверки условий положительной
(отрицательной) определенности матрицы размерности > 3 мы отсылаем читателя к
любому стандартному курсу линейной алгебры (см., напр., Халмош 1958, р. 141,
153).
Условный минимум (мноэюителъ Лагранжа)
Задача. Требуется найти локальный максимум (или минимум) функции
/(ж, у) при дополнительном условии (связи) д(х, у) = 0. Если мы обозначим
множество точек линии уровня функции д как А — {(ж, у) \ д(х, у) = 0}, то нам надо
найти точку (ж0,2/о) € А такую, что /(ж, у) < f{x0,y0) для всех (ж, у) G А.
При прямом подходе мы должны были бы разрешить неявное уравнение
д(х, у) — 0 относительно у для получения явной функции у — G(x) (см. теорему о
неявной функции 3.8) и отыскания экстремума функции F(x) = /(ж,(3(ж)). При
более общем подходе мы можем попытаться найти параметризацию (ж(£),у(£))
линии уровня А и рассмотреть функцию F(t) = /(ж(£), y(t)). Необходимым
условием для экстремума в точке (жо,?/о) = {x{to),y{to)) будет Ff(to) = 0, т.е.
(4.32) Дяо,2/о)я'(*о) + -/(зо,2А>)2/М = 0.
ох оу
Это уравнение служит для определения to и отбора возможных кандидатов на
решение. Однако этот подход часто является бесполезным, так как трудно
получить подходящую параметризацию.
Идея Лагранжа (1788, premiere partie, Sect. IV, §1, Oeuvres, vol.11, p..78). Из
(4.32) видно, что grad/(a?o,'!/o) ортогонален вектору (ж'(£0), У*{to)) касательной к
линии уровня А. Следовательно (см. разд. IV.3), в точке локального экстремума
векторы grad/(^o, уо) и &&dg(xo, уо) имеют одинаковое направление (см. рис.
4.3). и мы получили необходимое условие экстремума
(4.33) grad/(x-0,yo) = Agrad</(z0, Уо), д{хо,Уо) = 0
(если grad/(xo,yo) ф 0). Параметр А называется множителем Лагранжа.
Уравнения (4.33) представляют собой три условия для трех параметров жо, Уо, А. Введя
функцию Лагранжа
(4.34) £(ж, у, А) := /(ж, у) - \д(х, у),
мы можем представить условие (4.33) в более изящном виде:
(4.35) grad£(so,2/b,A) = 0.

326 IV. Функции нескольких переменных
gradg
grad/ and grad g
grad/
grad g
lines ax+by=const
grad g grad g
Рис. 4.3. Условный максимум функции /(я, у) = х + 2у, р = 3.
(4.9) Пример. Пусть даны положительные числа а, 6 и р > 1. Вычислим максимум
функции
(4.36) /(ж, у) =az + ty
в области х > 0, у > 0 при наличии связи у(ж, у) = 2^ + 2^ — 1 = 0 (см. рис. 4.3).
Следуя идее Лагранжа, пишем функцию £(ж,у, Л) = ах + by — \(хр + у^ — 1);
необходимое условие (4.35) примет вид
(4.37) a - pAzg"1 = 0, b - pAyg"1 = 0, «g + yg = 1.
Первые два соотношения дают
/ а xi/(p-i) / 6 \i/(p-i)
*°=U ' У0=\тР)
и подставляя результат в оставшееся соотношение, получим
(4.38)
(4.39)
где
(4.40)
(s)
а\я ( Ь \я
+ (—) =1.
Ар/ чАр;
Р
р-1
i + i = l.
Р 5
Равенство (4.39) позволяет нам вычислить Л. Подставляя результат в (4.38),
получаем искомое решение
ая/р Ья/р
(4.41)
(см. рис. 4.3).
XQ —
(а* + Ь*)
i/p'
Уо =
{а* + &*)
1/р'

IV.4 Производные высших порядков и ряд Тейлора 327
Неравенство Гёльдера (Гёльдер 1889). Пусть £, г\ и р > 1 — положительные
числа. Тогда
У
{Р + тГ)1*' (& + ГГ)1"
удовлетворяют равенству хр + у? = 1, и из примера (4.9) следует, что
— ax + by < ах0 + by0 ~
(^+7?p)i/p-—--—--(a9 + 69)i/P-
Таким образом, мы получаем
гдеpnq связаны соотношением (4.40). С помощью индукции по п это неравенство
может быть обобщено:
(«2) ± *,,<( ± «Г) '"(Ё »?)"'•
t = l » = 1 t = l
где Жг и уг положительны. Это и есть так называемое неравенство Гёльдера. При
р— q — 2 оно сводится к неравенству Коши—Шварца (1.5).
Используя (4.42), мы можем доказать неравенство треугольника для нормы
||ж||р, определяемой равенством (1.9). Действительно, для двух векторов ж, у Е Шп
имеем
п п п
\\х+у\\р = Е \xi + ы\р ^ Е м • I*--+^ip_1 + Е iwi • !*•+иг-1-
•=i i=i i=i
Применим (4.42) к обеим суммам в правой части этого неравенства и получим
г = 1 *= 1 г = 1
= 1И1р-1к + 2/|1Г1-
Отсюда получаем ||ж + у||£ < (||ж||р + ||у||р)-Цж-f у||^-1 и как следствие неравенство
треугольника ||ж + у\\р < \\х\\р + \\у\\р.
Упражнения
4.1 (Г.А. Шварц 1873). Покажите, что для функции
п2 arctg % — у2 arctg - при ху ф 0
/(*,¥) = {f
вторые частные производные в начале координат различны:
при жт/ = 0
52/ , 52/
дхду дудх

328 IV. Функции нескольких переменных
4.2 Покажите, что формула Тейлора (4.14) справедлива только в случае,
когда все частные производные, входящие в нее, непрерывны. Это
отличается от случая одной переменной (см., напр., теорему III.6.11). Пеано (1884,
"Annotazione N. 109") привел следующий контрпример: пусть
( ХУ при х2 + у2 ф 0
f(x,y) = I л/х2 + у2
(0 в противном случае
и хо = уо = —a, h = к = а + Ь. Он показывает, что равенство (4.14) может
нарушиться, если его записать с остаточным членом первого порядка
Я -Р Я -Р
f(x0 + h, уо + к) = /(я?о, Уо) + ^;(£, v)h + ^-(£, tj)*,
где £ = хо + Oh и 7? = т/о 4- 0к — промежуточные точки. Этот контрпример
исправил ошибку в книге Серре.
4.3 Проанализируйте в примере 4.4 пересечения графика функции /(ж, у) с
графиком ее тейлоровской аппроксимации второго порядка в окрестности точки
(#о> Уо) и объясните звездообразную форму кривых (см. рис. 4.1). Как вы
думаете, почему авторы выбрали именно точку (0.9,1.2) для этого рисунка, а
не точку (0.8,1.0), как для рис. 3.1?
Указание. Используйте поправочный член в формуле (4.14).
4.4 Пусть / : Ш2 —)■ Ш дифференцируемая функция, удовлетворяющая условию
grad/(z) =д(х) • жт,
где д : Ш2 —>- Ш. Покажите, что / — постоянная на окружности {х Е
Ж2; \\х\\=г).
4.5 Покажите, что U = (ж2 + у2 + г2)-1/2 удовлетворяет дифференциальному
уравнению Лапласа
d2U d2U d2U п 2 2 2 п
w+W + ^ = 0 при x+y+z >0-
4.6 Найдите стационарные точки функции
f{x,y) = (х2 + у2) - $ху
и исследуйте линии уровня /(ж, у) — Const в окрестностях этих точек
(сходство этих кривых с уже рассмотренными — преднамеренно).
4.7 Найдите максимум функции ^Jxyz при условии (х + у + г)/3 = 1. Какой
вывод можно сделать из этого результата? (Мы видели в примере 4.9, что
вычисление условного максимума является превосходным способом получения
интересных неравенств.)
4.8 Найдите максимумы или минимумы функции х2-\-у2 -\-z2 при наличии связей
х2 у2 z2

IV.4 Производные высших порядков и ряд Тейлора 329
Замечание. Если требуется удовлетворить двум условиям, надо ввести два
множителя Лагранжа.
4.9 Пусть
— матрица из примера в разд. IV.2. Найдите максимум функции f(x) =
ЦЛжЦз при наличии связи ||а?||| — 1 = 0. Результатом будет величина ЦЛЦг,
определяемая равенством (2.14).
4.10 Покажите, что функция / : Ж2 —>■ М, задаваемая формулой
f(x,y) = (y-x2)(y-2x2),
имеет в начале координат стационарную точку, но не локальный минимум.
Тем не менее, на всех прямых, проходящих через начало координат, функция
имеет локальный минимум. Этим контрпримером Пеано (1884, "Annotazioni
N. 133-136") исправил другую ошибку в книге Серре. Такая непочтительная
критика работы крупнейшего французского математика никому
неизвестным 25-летним итальянцем никого не привела в восторг (см., напр., Пеано,
Ореге, р. 40-46).

330 IV. Функции нескольких переменных
IV.5 Кратные интегралы
Известно, что вычисление или даже только редукция кратных интегралов
обычно представляет весьма значительные трудности ...
(Дирихле 1839, Werke, vol. I, p. 377)
Риманов интеграл от функции одной переменной (разд. III.5) представляет
собой геометрически площадь между графиком функции и осью х. Мы обобщим
это понятие на функции двух переменных / : А —> М (где А С М2) таким образом,
что интеграл будет представлять объем между поверхностью z = f(x,y) и
плоскостью (ж, у). Многие определения и результаты разд. III.5 могут быть
перенесены непосредственно. Однако возникают дополнительные технические трудности,
так как области интегрирования в!2 часто оказываются более сложными, чем в
Ш (см. рис. 5.1). После этого обобщение на функции более чем двух переменных
будет более или менее простым.
d
с
а '
прямоугольная невыпуклая несвязная
Рис. 5.1. Возможные области в Ш2.
Двойные интегралы по прямоугольной области
Мы начнем с рассмотрения функций / : / —>■ R, область определения
которых I = [а, Ь] х [с, d] — {(х,у) | а < х < 6, с < у < d} является замкнутым и
ограниченным прямоугольником в!2, и предположим, что функция ограничена,
т.е.
(5.1) 3M>0 \/{x,y)eI \f{x,y)\<M.
Рассмотрим разбиения
Dx = {x0,xi,...,xn} для [а, 6],
(5.2)
Яу = {Уо,Уи--">Ут} Для [c,d],
где а = хо < х\ < ... < хп = Ь и с = у0 < у± < ... < ут — d. Обозначим
Iij — [ж,_1, Xi] х [j/j__i, yj] маленький прямоугольник, показанный на рис.5.2, а его
площадь как
(5.3) fjt(Iij) = (xi - Xi-^fa - yj-i).

IV.5 Кратные интегралы 331
Рис. 5.2. Разбиение прямоугольника на элементы Uj.
Используя обозначения
(5.4) Л/ = bf /(ж, J/), Fij = sup /(ж, у),
(*»»)€/у (*,у)€/у
определим теперь верхнюю и нижнюю суммы:
п т n m
(5.5) s(Dx х Ду) = X)Z)/^№i)» £(£>* х А,) = EE^(J»i)-
t=ii=i *=ij=i
Если добавлять точки к разбиению Dx (или к Dy), то нижняя сумма не убывает
и верхняя сумма не возрастает (ср. с леммой Ш.5.1). Более того, нижняя сумма
не может стать больше чем верхняя сумма (лемма III.5.2). Поэтому имеет смысл
следующее определение.
(5.1) Определение. Пусть функция f : I —>• Ш удовлетворяет условию (5.1). Если
(5.6) sup s(Dx х Dy) = inf S(DX x Dy),
(Dx,Dy) {Dx,Dy)
то функция f(x,y) интегрируема на I, а величина (5.6) обозначается как
(5.7) f(x,y)d(x,y) или f(x,y)d(x,y).
Из этого определения и вышеупомянутых свойств, следует, что функция / :
I —У Ш является интегрируемой тогда и только тогда, когда
(5.8) Ve > 0 3 (Дг, Dy) S(DX х Dy) - s{Dx х Dy) < е
(см. теорему III.5.4). Теорема Дюбуа-Реймона (теорема III.5.8) также имеет свой
аналог.

332 IV. Функции нескольких переменных
(5.2) Теорема. Пусть T>s — множество всех пар разбиений (Dx, Dy) таких, что
maxi(xt- — £;_i) < S и ma,Xj(yj — yj-i) < S. Функция f : I —>Ш, удовлетворяющая
условию (5.1), является интегрируемой тогда и только тогда, когда
Ve>0 3J>0 4(Dx,Dy) eV6 S{DX x Dy) - s{Dx x Dy) < e.
Доказательство. Пусть для некоторого е > О задано разбиение (Dx/Dy))
удовлетворяющее условию (5.8). Это индуцирует сетку, длина которой (внутри
прямоугольника [а, Ь] х [с, а1]) равна L — (п — l)(d — с) + (га — 1)(Ь — а) (см. левый
рис. 5.3). Возьмем теперь произвольное разбиение (Dx, Dy) G D<j, обозначим Л —
S(DX х Dy) - s(Dx x Dy) и положим D'x - Dx U Dx, Dy = Dy U Dy и Л' =
S(D'X x Dy) - s(D'x x D'y). Тогда получим, как и в (Ш.5.10),
Л < Л' + L • S • 2М
(см. правый рис. 5.3). Дальнейшее умозаключение такое же, как в доказательстве
теоремы III.5.8. □
Рис. 5.3. Разбиение Dx х Dy (слева); разбиение D'x х D'y и его элементы J,j, пересекающие
Dx х Dy (справа).
ПуСТЬ £i,...,£n И 7/1,..., 77т ТаКОВЫ, ЧТО Ж,_1 < £i < Xi И 2/j_i < ?7i < Уз-
Тогда из теоремы 5.2 следует:
(5.9)
п т л«
У^У^Д&^Хя*" -жг-1)(%- — 2/j-i) - // f{x,y)d(x,y)
.■=1 i=l ^
< г
при условии, что тахг(жг- — жг_х) < (S и тах^(% — 2/j-i) < £. Это неравенство
справедливо, потому что и сумма, и интеграл в (5.9) заключены между s(Dx xDy)
и S{DX х Dy).
Повторные интегралы. Внутренняя сумма в (5.9), т.е. YlT=i /(&» Vj){yj ~
г/7_ 1), является суммой Римана для функции /(&, у). Предполагая эту функцию
интегрируемой (в смысле определения III.5.3) для всех г, мы получим из (5.9),
что

IV.5 Кратные интегралы 333
(5.10) \^1 /(&>»)<*» (*<-*<-i) - JJif(x,y)d(x,y)\<e.
Здесь мы снова сталкиваемся с римановой суммой, на этот раз для функции
х н->. Jc f(x,y) dy. Оценка (5.10) отражает тот факт, что суммы Римана сходятся
к JJj /(ж, у) d(x, у), если тахДже — x,-_i) —>• 0. Следовательно,
(5.11) J У f(x, у) dy^j dx = JJ /(*, у) d(x, у)
(см. упр. 5.1), и доказан следующий результат.
(5.3) Теорема (Штольц 1886, р. 93). Пусть /:/—>• Ш интегрируема, и
предположим, что для каждого х Е [а, 6] функция у \-+ /(ж, у) является интегрируемой
на [с, d]. Тогда функция х н->> J f(x,y)dy интегрируема на [а, 6] и имеет место
тождество (5.11). □
Следовательно, вычисление двойного интеграла сводится к вычислению
двух более простых (повторных) интегралов, и может быть использована
техника, развитая в разделах П.4, II.5 и III.5. По симметрии мы имеем также формулу
(5.12) j Qf f(x,y)dx^dy = jjf(z,y)d{z,y)
при условии, что / : / —>■ Ж интегрируема и функция х »->■ /(ж, у) является
интегрируемой на [а, Ь] для каждого у Е [с, d]. Два тождества (5.11) и (5.12) вместе
показывают, что повторные интегралы независимы от порядка интегрирования
(при выполнении указанных предположений).
Контрпримеры. Покажем, что существование одного из интегралов в (5.11)
необязательно влечет за собой существования другого.
Рис. 5.4а. Неинтегрируемая функция.
Рис. 5.4b. Интегрируемая функция.
1) Пусть функция / : [0,1] х [0,1] —» Ш (рис.5.4а) определена выражением
(5.13)
f(x
■-С:
если (х,у) = (Щ^,Ц^
противном случае.
, где п,
кЛ
целые,

334 IV. Функции нескольких переменных
Для любого фиксированного х Е [0,1] существует только конечное число точек, в
которых f(x,y) ф 0. Следовательно, JQ f(x,y)dy = 0n повторный интеграл в
левой части (5.11) существует. Однако каждый прямоугольник [ж,-_1,ж,-] х [%-i,%]
содержит точки, в которых /(ж, у) = 1, и точки, в которых /(ж, у) = 0.
Следовательно, s(Dx х Dy) = 0 и S(DX х Dy) = 1 для всех разбиений, и интеграл в правой
части (5.11) не существует.
2) Функция (рис. 5.4Ь)
(5.14)
/(ж, у) =
при (х = 0 или х = 1) и у Е '
при (у = 0 или у = 1) и х Е <
в противном случае
интегрируема, так как точки, в которых /(ж, у) ф 0, составляют множество,
которым можно пренебречь (см. ниже). Но при х = 0 или х = 1, функция у н-» /(ж, t/)
является функцией Дирихле из примера III.5.6, которая не интегрируема.
Множества меры нуль и разрывные функции
Непрерывные функции / : I —> Ж являются равномерно непрерывными (I —
компактное множество, теорема 2.5) и, следовательно, интегрируемыми.
Доказательство этого факта аналогично доказательству теоремы III.5.10. В дальнейшем
мы докажем интегрируемость функций, у которых множество точек разрыва не
слишком велико.
(5.4) Определение. Говорят, что множество X С / С М2 есть множество меры
нуль, если для каждого е > 0 существует конечное множество прямоугольников
Ik — [a*, bk] х [с*, dk], (к = 1,..., п) таких, что
(5.15)
xc{Jh
!>№)<£•
*=i
fc=i
О 1 2 0 1 2 0
S=±, Ец = 0.880 * = 55. Ep = 0.475
Рис. 5.5. Множество меры нуль.
S = &, 2р
2
0.263

IV.5 Кратные интегралы 335
Типичными множествами меры нуль являются границы "регулярных"
множеств, например, треугольников, кругов, многоугольников (см. пример на рис.
5.51). Это вытекает из следующего результата.
(5.5) Лемма. Пусть <р : [0,1] —У Ш2 представляет кривую на плоскости и
допустим, что
(5.16) \\<p{s) ~ <p{t)\\oo < M-\s-t\ для всех М Е [0,1].
Тогда образ у?([0,1]) есть множество меры нуль.
Доказательство. Разделим [0,1] на п интервалов Ji, J2, •.., Jn одинаковой
длины 1/n. Для s,t £ Jk имеем \\<p{s) — ^>(£)||oo < M/n, т.е. <p(Jk) содержится в
квадрате I* со стороной < 2М/п. Следовательно, вся кривая целиком
содержится в области, состоящей из п квадратов Д,..., /п, площадь которой ограничена
величиной
А ,Т ч ^А/2М\2 4М2
£м'*)<£(—) = — <*>
k=i k=i
если п достаточно велико. Это и доказывает выполнение условия (5.15). D
Рис. 5.6. Множество меры нуль, кривая фон Коха.
Условие (5.16) является достаточным, но не необходимым для того, чтобы
кривая являлась множеством меры нуль. Например, кривая фон Коха (1906)
1 Множество имеет меру нуль, конечно, только в строго математическом смысле!

336 IV. Функции нескольких переменных
на рис. 5.6 является множеством меры нуль (см. упр. 5.5), хотя имеет
бесконечную длину (следовательно, условие (5.16) выполняться не может). Кривая
Пеано—Гильберта (рис. 2.3), конечно, не является множеством меры нуль.
Однако треугольник и ковер Серпиньского (рис. 1.9 и рис. 1.10) являются другими
интересными примерами множеств меры нуль.
(5.6) Теорема. Пусть / : J —» IR — ограниченная функция (удовлетворяет
условию (5.1)) и определено множество
X = {(ж, у) G / ; / разрывна в точке (ж, у) }.
Если X является множеством меры нуль, то функция /(ж, у) интегрируема.
Доказательство. Пусть дано О 0 и Ufc=i ^ является конечным
покрытием множества X, удовлетворяющим условию (5.15). Слегка расширим 7* и
рассмотрим открытые прямоугольники Ji,..., Jn такие, что Jk D h для всех к
и X^fc=i n{Jk) < 2е. Множество Н :— I \ \J^=1 Jk является тогда замкнутым
(теоремы 1.15 и 1.14) и, следовательно, компактным (теорема 1.19). Сужение на Я
функции /(ж, у) является равномерно непрерывным (теорема 2.5), что означает
существование S > 0 такого, что |/(ж, у) — /(£, т/)| < е всякий раз, когда |ж — £\ < S
И\у-7]\<6.
Стартуем теперь с сетки DxxDy, содержащей все вершины прямоугольников
Ль • • -•> Jn, и измельчаем ее до тех пор, пока расстояния жг- — cc^-i и yj — yj-i не
станут меньшими, чем S. Затем разобьем разности S(DX х Dy) — s(Dx х Dy) в
соответствии с
Y, (Fij-fij)№j)+ Е (^-/и)м^)-
IijCH 1ц<£Н
Левая сумма < ец(1) вследствие равномерной непрерывности /(ж, у) на Н;
правая сумма < 4Ме из-за того, что объединение прямоугольников I{j (которые не
содержатся в Н) содержится в Ufc=i Jk с площадью меньшей, чем 2е. Обе оценки
вместе показывают, что разность S(DX х Dy) — s(Dx х Dy) может быть сколь
угодно малой. D
Произвольные ограниченные области
Этот метод заключается просто в умножении подлежащего
интегрированию выражения на коэффициент, равный единице в области
интегрирования и нулю вне нее. (Дирихле 1839, Werke, vol. I, p. 377)
Пусть А С M2 — ограниченная область, содержащаяся в прямоугольнике
I (т. е А С /), и / : А —у Ш — ограниченная функция. Мы хотим найти объем
цилиндрического тела, ограниченного сверху поверхностью z = /(ж, у), а снизу
частью плоскости (ж, у), а именно, А.
Идея Дирихле (1839) состоит в рассмотрении функции F : / —у М,
определяемой как
/(ж, у) если (ж, у) Е А,
0 в противном случае.
(5.17)
Р{*,У)
-

IV.5 Кратные интегралы 337
Если F интегрируема в смысле определения 5.1, то мы определим
(5.18)
/У f(x,y)d{x,y) = /У F{x,y)d{x,y).
Обычная ситуация — когда / : А —у Ш непрерывна на Л и граница Л, т.е.
множество
(5.19)
дА
:={(*,
у)еш2
каждая окрестность точки
содержит элементы из А
и (ж, у) 1
и из СЛ J
является множеством меры нуль. В этом случае все точки разрыва функции F
лежат на границе ЗЛ, и из теоремы 5.6 следует интегрируемость F.
Повторные интегралы. Множество А часто может быть описано одним из
следующих способов:
(5.20) А = {{х, у) | а < х < 6, ^(х) <у< <р2{х) },
(5.21) А = {(х, y)\c<y<d, фг(у)<х< ф2{у) },
где (pi(x) и i>j(y) — известные функции (см. рис. 5.7). В этом случае формулы
(5.11) и (5.12) вместе с (5.18) дают
ГЬ / /*<г?2(а?)
(5.22)
(5.23)
/у [*> / ГУЛ*) \
// f{x,y)d{x,y)= / / f(x,y)dy)dx,
JJA Ja \J(pi{x) /
// f{x,y)d{x,y)= / / f(x,y)dx)dy.
JJA Jc XJipxiy) /
v2(y)
типа (5.20)
типа (5.21)
Рис. 5.7. Области в М2.
не типа (5.20)
Примеры. 1) Для множества А = {(ж, у) \ — а < х < а, х2 < у < а2}
хотим вычислить центр тяжести:
__ 1АУ<1{Х,У) _ За2
У~ JAd(x,y) ~ 5 '
С помощью формул (5.22) и (5.23) находим:

338 IV. Функции нескольких переменных
///*.»)(^/". (£*»*)*=х-
jL^^ao^--
а4/2 - х4/2
dx) dy =
-а
2л/У
О
2) Вычислим момент инерции круга А = {(ж, у) \ х2-\-у2 < а2}, вращающегося
вокруг одного из своих диаметров:
(5.24)
1~ \\ 2/2^(я,у)= / / y2dydx.
J J A J — a J — y/a^ — x2
pa ру/а2 — х2
1A J — a J — \fa? — x7
Величина внутреннего интеграла равна |(а2 — ж2)3'2, а для внешнего интеграла
мы используем замену х = asintf, dx = a cos tdt, у/а2 — х2 = a cost. Это дает
гтг/2
1=1 -a4 cos4 tdt = а4 —.
J-K/2 3 4
-тг/2
Следующая фундаментальная теорема о замене переменных существенно
упрощает вычисление таких интегралов, как (5.24) (см. пример 5.8 ниже).
Формула замены переменных в двойных интегралах
... это работает для любой другой формулы jj Zdxdy, так как она может
быть преобразована в JJ Z(VR — ST) dtdu теми же самыми подстановками
(Эйлер 1769b)
Интегрирование с помощью подстановки (формула (П.4.14))
гя(Ь)
/ f(x)dx= / f(g(u))gf(u)du
Jg{a) Ja
— важный инструмент для вычисления интегралов. Если g : [а, Ь] —>- [с, cf| —
взаимно однозначное (и непрерывно дифференцируемое) отображение, то эта
формула может быть переписана как
/ f(x)dx= [ f(g(u))\g'(u)\du,
J с J а
где абсолютная величина корректирует знак в случае, когда д'(и) < 0 (и,
следовательно, д(Ь) < д(а)). Следующая теорема является аналогом этого для случая
двойных интегралов.
(5.7) Теорема (Эйлер 1769b, Opera, vol.XVII, p.303 (для n = 2); Лагранж 1773,
Oeuvres, vol. 3, p. 624 (для n = 3); Якоби 1841, Werke, vol. 3, p. 436 (для любых n)).

IV.5 Кратные интегралы 339
Пусть функция f : А —>• Ш непрерывна, а функция д : U —>■ Ш2 (где U С М2 —
открытое множество) непрерывно дифференцируема. Предположим, что
i) А — д(В), причем i,Bcl2 компактны и 5Л, ЗБ — множества меры нуль;
ii) # — инъекция на B\N, где N — множество меры нуль.
Тогда
(5.25)
// f{x,y)d(x,y) = f(g{u,v)) \detg'(u,v)\d(u,v).
Рис. 5.8a. Площадь параллелограмма.
Рис. 5.8b. Полярные координаты.
Полярные координаты. Одним из наиболее важных приложений теоремы
5.7 является случай, когда
(5.26)
g(r, <р) = (ж, у), х = г cos <р, у — т sin (f
(полярные координаты, см. разд. 1.5) и когда А = {(ж, у) \ х2 + у2 < Л2}. Для
Б = [О, Л] х [0, 27г] предположение (i) из теоремы 5.7 выполняется. Функция g из
(5.26) не является инъекцией на В (g(r, 0) = #(r, 2ir) для всех г и #(0, <р) = (0, 0)
для всех (р). Однако, если мы удалим из В множество меры нуль N = ({0} х
[0,27г]) U ([0, R] х {27г}) (см. рис. 5.8Ь), функция g становится инъективной на
B\N. Так как
deter'(г, (р) = det ( . ) = г,
* v ^} \s\wip г cos (р J '
из теоремы 5.7 и равенства (5.11) следует, что
г2тг лД
(5.27) // f(x,y)d(x,y)= / / f (г cos (р, г simp) г drd<p.
JJxi+yiKR2 Jo Jo

340 IV. Функции нескольких переменных
2rv
Рис. 5.9. Преобразование сетки.
Доказательство теоремы 5.7
Основная идея. Покроем В сеткой из замкнутых квадратов Зр со стороной
длины S (см. левый рис. 5.9), определим множество В = {/3 | Зр ПВ ф 0}, и пусть
(up,vp) координаты левой нижней вершины квадрата J'р. Мы предполагаем, что
S достаточно мало, так что все Зр {(3 Е В) лежат в U. Образ g(Jp) множества
Jp является приблизительно параллелограмом со сторонами (рис. 5.9, правая
картинка)
(5.28)
<*= ^(^/з^/з)^
b=fo(uP>vrfS
(см. пример 3.2). Далее, из элементарной геометрии известно, что площадь этого
параллелограмма равна определителю 2
det
\а>2 Ь2)
\(цЬ2 - a2bi\
I
(5.29) площадь параллелограма = | det(a 6)|
и, имея в виду неравенство (5.9), мы получаем, что
f(x,y)d(x,y) « ^2ff{g{up,vp)) • (площадь g{Jp))
/зев
w 1^/(^(^,^)) \detg'(up,vp)\fi(Jp)
рев
* f{g{u,v)) \detg'(u,v)\d(u,v).
Эти выкладки показывают, что равенство (5.25), по-видимому, имеет место.
2 Оба выражения в (5.29) являются
i) инвариантными относительно преобразования Ь и-)- Ъ + Ха (принцип Кавальери),
п) и равными для прямоугольников со сторонами, параллельными осям, для таких
прямоугольников матрицы диагональны, см. рис. 5.8а.
Более подробно об этом см. Стрэнг (1976, р. 164).

IV.5 Кратные интегралы 341
Строгие оценки. Подынтегральные выражения в равенстве (5.25)
непрерывны на А и В соответственно. Так как А и В — компактные множества, то эти
функции ограничены. Кроме того, дА и дВ — множества меры нуль, так что
из (5.18) следует, что оба интеграла в (5.25) существуют. Далее мы расширим
область определения / на всё IR2, положив /(ж, у) = 0 вне А.
Чтобы описать точный смысл левого интеграла в (5.25), кроме описанного
выше разбиения В мы введем разбиение А на квадраты /а, определим множество
А — {а | 1а П А ф 0} и выберем точки (жа, уа) Е 1а П А ("рыбьи глаза" на рис.
5.10). Равенство (5.25) будет доказано, если показать, что разность сумм Римана
для обоих интегралов
(5.30) ^Г f(xa,ya)iA(Ia) - ^2,f(g(up,vp)) \detgf(up,vp)\fj,(Jp)
аеЛ /3GB
может быть сделана меньше любого заданного е > 0 (см. теорему 5.2 и
формулу (5.9)). Оказывается, что длина стороны у квадратов 1а должна быть много
меньше, чем 8 (длины стороны у Jp). Мы возьмем ее < е • S.
Рис. 5.10. Квадраты /а, для которых а принадлежат Vp.
Разложение множества Л. Левая сумма в (5.30) содержит гораздо больше
членов, чем правая. Чтобы сравнивать соответствующие члены в этой разности,
представим множество Л как
Л = М Vp (объединение непересекающихся множеств),
(зев
причем
(5.31а) {ха,Уа) <Eg{Jp) если a<EVp,
(5.31b) aeVp если Ia С g(Jp) и JpCB\N

342 IV. Функции нескольких переменных
(см. рис. 5.10). Поскольку (жа, уа) Е А — д(В) С Цзев 9(Jp)> всегДа можно для
заданного а £ А найти такое /3, которое удовлетворяло бы условию (5.31а). Чтобы
иметь возможность удовлетворить условию (5.31Ь), надо показать, что
существует не более одного (3 Е В такого, что Jp С B\N, причем 1а С g{Jp)- Предположим,
что 1а С g(Jp) П g{Jj3') Для некоторых (3 ф /3'. Так как функция д инъективна
на В \ iV, мы имеем g(Jp) П g{Jp') С g{Jp П <//з')> так что и -f а С #(«//з Л *//з')- Но
J'р П J/з' является либо пустым множеством, либо одной точкой, либо сегментом
некоторой линии, и поэтому g(Jp П J/з') — множество меры нуль согласно лемме
5.3. Следовательно, при /3 ф /3' включение 1а С g(Jp П J/з') невозможно.
Теперь множества Vp определены, и мы, воспользовавшись тем, что YlaeA =
Ylpes IljcczVb ' запишем выражение (5.30) в виде YlpeB Dp, где
(5.32) Dp = ^2 fixa,ya)^(Ia) -f(g{up,vp)) \ detg'(up, vp)\ [i(Jp),
и займемся оценкой этих членов. Рассмотрим пока только так называемые
"внутренние" Jp, т.е. предположим, что Jp С В \N. Запишем Dp в виде
(5.33а) D(,= J2 (/( •^a? Уа
(5.33b) + /(<7(и/3,^))( J^ l*{Ia)-\detg'(up,vp)\n{Jp)}
aeVp
и оценим оба выражения отдельно.
Оценка (5.33а), Так как g(u,v) непрерывно дифференцируема, gf(u,v)
ограничена на компактном множестве В (теорема 2.3), т.е.
(5.34) \\д'(и, v)\\ < Мг для {и, v) Е В.
Отсюда по теореме о среднем значении 3.7 следует, что
||(ха,Уа)Т -g{up,vp)\\ < Мг-б-л/2 для aeVp
(действительно, точка (xa,yQ) лежит в g(Jp), а элементы Jp отстоят от (up,vp)
на расстояние, не большее чем S • л/2 ). Тогда из равномерной непрерывности
/ на А (/ непрерывна на компактном множестве А) следует, что \f(xa,ya) -
f(g(up, vp)) | < e для достаточно малых 8 (напомним, что g(Jp) С А, ибо Jp —
"внутренние"). Поэтому
(5.35)
XI [f(Xa,ya) ~ f(g(up,Vp))j fl(Ia)\ <6 ]Г M^a).
a€Vp ' ос€Т/з
Оценка (5.33Ь). Теперь надо более внимательно рассмотреть вопрос,
насколько точно множество g(Jp) можно приблизить параллелограммом,
натянутым на векторы а и 6 из формулы (5.28). Это последнее множество обозначим
через
Rp = {g(up,vp) + —(up,vp)s+ — (u^vp)t I s E [0,6], t E [0,J]|.

IV.5 Кратные интегралы 343
Вычислим расстояние между соответствующими точками g(up+s, vp+t) в g(Jp) и
д(ир, vp)-\-Q^(up, vp) s+ foiup, vp)t в Щ следующим образом. Формула (III.6.16),
записанная для F(r) — д(ир + rs, vp + rtf), означает, что
flf(w/3 + s,vp+t) - g(up, vp) = / g'(up + re, ^ + rt) • f * J dr.
Вычитая dg/du(up,vp) • s + dg/dv(up,vp) • t из обеих частей этого равенства,
получим
р(ир + s,vp+t) - (g{up,vp) + -^(up,vp)s+ — (up,vp)t)^
- I / (g'{up + re, vp + rt) - g'{up, vp)) • f M dr < y/2eS
при 0 < s,t < J. Последняя оценка следует из равномерной непрерывности д' на
компактном множестве В (напомним, что Jp — "внутреннее").
Теперь включим Rp между двумя множествами:
Rp С Rp С Rp ,
где (см. рис. 5.10)
Л+ = {множество точек с расстояниями < 2y/2eS от ближайшей точки вД^}
Л~ = {множество точек ъ Rp с расстояниями > 2\/2е8 от границы}.
Так как расстояние 2\/2е8, выбранное в этих определениях, вдвое больше
величины л/2е6, которая, с одной стороны, является максимальным расстоянием
между соответственными точками в g(Jp) и Rp, а с другой — максимальным
диаметром квадратов 1а, между множествами RZ и Rt в силу (5.31а) и (5.31Ь)
включено также объединение 1а для a^Vp (см. опять рис. 5.10):
Rp С \J 1а СЯ+.
осетр
Поскольку Rt\Rp является "кольцом" длины < 4Mi<$ (см. (5.34)) и "толщины"
указанные включения приводят к следующей оценке:
| £ №<*) ~ 1*{Щ)\ < ^{Щ \ Rp) < (4Mi*)(V2*J).
aeVe
Следовательно, мы получили, что
(5.36) \f(g{up,vp))( Y, М'а) -\^9f{up,vp)\yi(Jp))\< CeS2 = Cefi(Jp),
aeVp
где С = М • 4Afi • 4лД
Финал. Если Jp <f_ B\N (так что Jp пересекает множество меры нуль dBUN),
мы оценим Dp из (5.32) так: \Dp\ < M2fJ>(Jp), где Мг — константа, зависящая от

344 IV. Функции нескольких переменных
ограничений на / и д'. Если 8 достаточно мало, то из (5.15) следует, что сумма
этих \Dp\ будет < Мге. Для остальных же 3$ мы используем (5.35) и (5.36)
совместно с (5.33) и получим оценку
aeV/з
В итоге разность (5.30) римановых сумм, т.е. Ylpes-Dp, является сколь угодно
малой (< Const • е). О
(5.8) Пример. Пусть А = {(ж, у) | х2 + у2 < R2} — круг радиуса R. Его площадь
может быть вычислена как
ff f2n f^ R2
// l-d(x,y)= / rdrdip = — -2тг = Д2тг.
Момент инерции в случае вращения вокруг диаметра равен
ff 2 м ч f^ Г 2 • 2 л л #*
II уг й{х,у) — I / г sin (р -rdrdip = ——.
Момент инерции в случае вращения относительно оси, проходящей через центр
и перпендикулярной плоскости круга, равен
ff f2n f^ Л^тг
11 (х2+ y2)d(x,y) = / / г2 -rdrdip- ——.
sinG d(p
Рис. 5.11. Сферические координаты.
Сферические координаты. Перенос результатов этого раздела на случаи
большего числа измерений возможен без особых затруднений. Приведем
интересное приложение формулы (5.25) в трехмерном случае.
Введем сферические координаты g(r,(p,0) = (ж, у, z), определяемые
соотношениями

IV.5 Кратные интегралы 345
(5.37) х = г cos <р sin 0, у — г sin <р sin 0, z = rcos0
(рис. 5.11). Они весьма удобны для вычисления тройных интегралов по сфере
А = {(ж, у, z) | ж2 + у2 + z2 < R2}. Для В = [О, Л] х [0, 2тг] х [0, тг] и АГ = ЗБ все
предположения теоремы 5.7 удовлетворяются. Вычисляя матрицу Якоби для #,
(cos (р sin 0 —г sin <р sin 0 г cos (р cos 0 \
sin (р sin 0 г cosy? sin 0 г sin (р cos О I ,
cos0 0 —rsin0 )
получим для нее детерминант, равный det #'(г, у>, 0) = r2sin0, откуда (Лагранж
1773)
(5.38) jj^ f(x,y,z)d(x,y,z) = HI f(r,<p,0)r2smOd(r,<p,e),
где f(r,<p,6) = f (r cos <p sin 0, r sin <p sin 0, r cos 0). Глядя на рис 5.11, мы можем
лучше понять эту формулу "directement sans aucun calcul" (прямо, без всяких
вычислений, — фр.) как сказал Лагранж.
Объем сферы получим, полагая f(x,y,z) — 1:
2тг /»Д
/»/»/» /»7Г flZTT flit
l-d(x,y,z)= / / r2sin0drd<pd9
JJJ A JO Jo Jo
4Д3тг
3
Момент инерции относительно оси, проходящей через начало координат, равен
^ f 9.9* 9.^,, ,л SR ТГ
(х2+ V2)d{x,y,z)= / / r2sin20.r2sin<9drcfy>d0 =
JJJ A Jo Jo Jo
15
Интегралы no неограниченной области
В некоторых случаях приходится вычислять интегралы по неограниченной
области. Так же, как в разд. III.8 (несобственные интегралы), это может быть
сделано переходом к пределу. Проиллюстрируем это утверждение некоторыми
интересными примерами.
Интеграл Гаусса. Мы хотим вычислить интеграл I = J е~х dx. Идея
заключается в возведении I в квадрат и преобразовании в двойной интеграл:
(5.39) /2= lim ( f e~x2dx^ f е~у2 dy} = lim ff e'**-** d{x, y),
где Ar = [0, R] x [0, R]. Вид функции в двойном интеграле подсказывает перейти
к полярным координатам. Полагая Dr = {(ж, у) | х2 -\- у2 < R2, х > 0, у > 0},
получим
(5.40) lim ff e-x2-y2d(x,y)= lim / / e^rdrdip =?-.

346 IV. Функции нескольких переменных
Здесь дополнительное "г", возникающее из формулы (5.27), оказалось весьма
кстати: оно позволяет взять внутренний интеграл с помощью простой
подстановки. Вопрос в том, равны ли пределы в (5.39) и (5.40). Если f(x,y) > 0 (как в
нашем случае), то мы имеем
// f{x,y)d{x,y) < f(x,y)d(x,y) < f(x,y)d(x,y)
JJdr JJar JJdvir
как следствие вложения Dr С Ar С D^r (cm.
маленький рисунок справа). Таким образом,
существование Птд-юо JJD f(x,y)d(x,y)
влечет существование Итя-юо JJAr /(ж, у) d(x, у),
и оба предела равны. Соответственно / = у/7г/2.
Существует также интересная связь с гамма-
функцией:
О 1
/»ОО /»ОО Л л.
(5.41) лД = 27 = 2 / е~х2 dx = / е~* —, = Г(1/2)
Jo Jo Vt
(см. определение III.8.10).
1234567^ т 1234567*
Рис. 5.12. Исследование преобразования (5.43).
Формула произведения для гамма-функции. Из определения III.8.10,
имеем
/»СЮ /»оо
Г{а) = / е-хха~Чх, Г(/3) = / e^y^dy,
Jo Jo
так что (см. Якоби 1834, Werke, vol. VI, p. 62)
(5.42) Г(а)Г{Р)= lim ff е"*-^*-Y"1 d(x,y),
д->°° JJar
где, как и выше, Ar = [0, R] х [0, R]. На этот раз мы используем преобразование
х + у = и,
(5.43)
т.е.
= s(u,v)=[UvV)

IV.5 Кратные интегралы 347
(см. рис. 5.12), для матрицы Якоби которого det gf(u, v) = det I J = 1. Если
положить теперь Br = {(ж, у) |ж>0,2/>0,ж + у<#}, мы найдем, что
lim [[ e-x-*xa-1yf*-1d(x,y)= lim / е~и ( [ (и - ^""V"1 dv)du
я-+оо JJBr я-юо J0 \ Jo /
(5.44) = lim f e-VyT+^du- f (1 - *)a" V"1 <ft,
где мы использовали подстановку v = u-t(0<t<l). Рассуждение, аналогичное
использованному для интеграла Гаусса, гарантирует равенство пределов (5.42)
и (5.44). В (5.44) фигурирует так называемая бета-функция:
(5.45) В(а,р) := / (1 - J)0"1^"1 ctt,
Jo
и мы получили формулу
которая обобщает равенство (П.4.34) на произвольные показатели степени.
Контрпример, Функция /(ж, у) = (ж —у)/(х+у)3 непрерывна на А = [1, ос] х
[1,оо]. Тем не менее, имеет место следующий, результат:
(5.47) / [ *~\-dxdy ф [ [ (X~\„dydx
V v ' V v '
+ 1/2 -1/2
(см. также упр. 5.3), нарушающий равенства (5.11) и (5.12). Это возможно только
для неограниченной области А и функции /, которая меняет знак на А.
Упражнения
5.1 Пусть д : [а, Ь] —>• М ограниченная функция, предположим, что все ее римано-
вы суммы сходятся к фиксированному значению а, если тахг(жг- — e,-_i) —>■ 0.
Докажите, что д(х) интегрируема (по Риману) и J д(х) dx = а.
5.2 На / := [0, 7г] х [0,1] определим функцию / : / —> R как
cos ж при у EQ
0 в противном случае.
г/ ч Г cos ж при v Е
Какой из интегралов
/ (/ f{x,y)dx)dy и / (/ f(x,y)dy)dx
существует? Является ли функция / : I —>• М интегрируемой?

348 IV. Функции нескольких переменных
5.3 Покажите, что
1 л1
II
Jo Jo
х-у
(х + у)2
dxdy
Jo Jo (* +
У)
3 dydx
-1/2
+1/2
(см. рис. 5.13). Противоречит ли это соотношение равенствам (5.11) и (5.12)?
д ( —х \ х — у
Указание, Используйте равенство -^-[ г^- = г^-.
дх\(х + у)2/ (х + у)3
Рис. 5.13. Функция .* К9 с не коммутирующими повторными интегралами (стерео-
грамма).
5.4 Попробуйте вычислить
/
-1Ж-,
—2 cos <р Н- 2г
dr
)d(p,
0<R<1 .
2r cos (p + r2
Существует лучший способ вычисления этого интеграла, в котором полезна
формула
d<p
I
Jo
а> \Ъ\
/0 a + bcos(p у/а2 - Ь2
(см. аналогичный пример после формулы (П.5.21)).
Результат: 7 = 0; см. также упр. III.5.4.
5.5 Докажите, что кривая фон Коха на рис. 5.6, несмотря на бесконечную длину,
является множеством меры нуль.
Указание. Возьмите расстояние между двумя конечными точками равным 1.
Рассматривая верхнюю кривую рис. 5.6, можно видеть, что она содержится
в прямоугольнике со сторонами 1 и 1/3. Следующая кривая содержится в
объединении четырех прямоугольников со сторонами 1/3 и 1/9, и т.д.
5.6 Покажите, что "треугольник Серпиньского" (рис. 1.9) является множеством
меры нуль в!2.
5.7 Множество ^>([0,1]), где
<p(t)
-(*)•
является множеством меры нуль вопреки тому, что функция (р не
удовлетворяет условию

IV.5 Кратные интегралы 349
\\<p(t) - <р{з)\\ < M\t - s\ для всех t, s G [0,1].
5.8 Вычислите площадь поверхности, заключенной внутри петли декартова
листа (4.29). Испытайте два способа: а) полярные координаты; Ь) замену
переменных
и — х Н- у , v — х — у ,
5.9 Вычислите площадь поверхности, заключенной внутри петель лемнискаты
(х2 + у2)2-2(х2-у2)=0.
Попробуйте два способа: а) полярные координаты; Ь) повторные интегралы.
5.10 Пусть
Вп(г) = {(ял, ..,хге)Е1п;ж| + ... + ^<г2}
— шар радиуса г в Шп. Покажите, что его объем равен
Г 7Г 2 ГП
Тп{г) = / d(aji,...,x„) = .
JBn{r) ^(2+1)
Указание. Воспользуйтесь методом индукции по п > 1. Вам будет полезна
формула, выведенная выше для бета-функции.
5.11 Вычислите объем симплекса
Ап{с) = {(xi,...,xn) е Шп ; Xi > 0 и a^i + ж2 + ... + жп < с}.
Ответ: сп /п\.
5.12 Вычислите
xyz(l — х — у — z) dxdydz,
/т
где Т — тетраэдр, определяемый условиями
Т= {(s,y,z) ; ж>0, ?/>0, z > 0, ж + у + z < l}.
Используйте подстановку
х + у + z = щ у -\- z = и + V, Z — UVW.
Ответ: 1/7!.
5.13 Пусть Ar = [0, R] х [0, Л] и DR = {(ж, у) | х2+у2 < R2}. Рассмотрите пределы
lim // sin(x +у )d(x,y) и lim // sin(ec + у2) d(x, у).
д->°° УУля к^°° JJdr
Докажите, что первый предел существует, а второй не существует.
Указание. Используя формулу sin(x2 + у2) — sin х2 cos у2 + cos х2 sin у2 в
первом интеграле, докажите, что /0 sin ж2 dec сходится к пределу при R —у ос.
Для второго интеграла используйте полярные координаты.

350 IV. Функции нескольких переменных
5.14 Докажите, что
/к .«ч f°° cos ж , рк f°° sinx , Гк
Затем, выведите из этих соотношений формулу (П.6.9).
Указание. Подстановка х = Uy/z (z — положительный параметр) в равенство
(5.41) дает
-| су /»СЮ
(5.49) -7= = -= / e~zu2 du.
лД л/тт J0
Умножьте это равенство на etz и проинтегрируйте от А > 0 до 5, измените
порядок интегрирования в повторных интегралах и рассмотрите пределы
В —у оо и А —> 0. Обоснуйте все шаги.
Замечание. При использовании более глубоких результатов комплексного
анализа это упражнение становится совсем легким.

Приложение. Цитаты на языках оригиналов
стр. 1: da der Lehrer einsichtig genug war den ungewohnlichen Schuler (Jacobi)
gewahren zu lassen und es zu gestatten, dafi dieser sich mit Eulers Introductio
beschaftigte, wahrend die iibrigen Schuler muhsam ....
(Dirichlet 1852, Gedachtnisrede auf Jacobi, in Jacobi's Werke, vol.1, p. 4)
стр. 2: Tant que l'Algebre et la Geometrie ont ete separees, leurs progres ont ete lents
et leurs usages bornes; mais lorsque ces deux sciences se sont reunies, elles se
sont prete des forces mutuelles et ont marche ensemble d'un pas rapide vers la
perfection. С'est a Descartes qu'on doit l'application de l'Algebre a la Geometrie,
application qui est devenue la clef des plus grandes decouvertes dans toutes les
branches des Mathematiques. (Lagrange 1795, Oeuvres, vol. 7, p. 271)
Diophante peut etre regarde comme l'inventeur de l'Algebre;
(Lagrange 1795, Oeuvres, vol.7, p. 219)
стр. 4: Tartalea exposa sa solution en mauvais vers italiens ...
(Lagrange 1795, Oeuvres, vol.7, p. 22)
... trovato la sua regola generale, ma per al presente la voglio tacere per piu
rispetti. (Tartaglia 1530, see M. Cantor 1891, vol. II, p. 485)
стр. 6: Le Logistique Numerique est celuy qui est exhibe & traitё par les nombres, le
Specifique par especes ou formes des choses: comme par les lettres de Г Alphabet.
(Viete 1600, Algebra nova, French ed. 1630)
стр. 8: Ou ie vous prie de remarquer en passant, que le scrupule, que faisoient les anciens
d'vser des termes de l'Arithmetique en la Geometrie, qui ne pouuoit proceder,
que de ce qu'ils ne voyoient pas asses clairement leur rapport, causoit beaucoup
d'obscurite, Sz d'embaras, en la fagon dont ils s'expliquoient. (Descartes 1637)
стр. 18: Quoy que cette proposition ait vne infinite de cas, i'en donneray vne demonstration
bien courte, en supposant 2 lemmes.
Le 1. qui est evident de soy-mesme, que cette proportion se rencontre dans la
seconde base; car il est bien visible que cp est a a comme 1, al.
Le 2. que si cette proportion se trouue dans vne base quelconque, elle se trouuera
necessairement dans la base suivante.
(Pascal 1654, one of the first induction proofs)
стр. 29: Der Begriff des Logarithmus wird von den Schulern im allgemeinen nur sehr schwer
verstanden. (van der Waerden 1957, p. 1)
стр. 34: Mense Septembri 1668, Mercator Logarithmotechniam edidit suam, quae specimen
hujus Methodi (i.e., Serierum Infinitarum) in unica tantum Figura, nempe, Quad-
ratura Hyperbolae continet. (Letter of Collins, Julii 26, 1672)
стр. 43: Die Gleichungen haben ein ehrwurdiges Alter. Schon Ptolemaus leitet ...
(L. Vietoris 1949, J.reine ang. Math., vol. 186, p. 1)
стр. 52: vous ne laisserez pas d'avoir trouve une propriete du cercle tres remarquable,
ce qui sera celebre a jamais parmi les geometres.
(Letter of Huygens to Leibniz, Nov. 7, 1674)
стр. 57: Au reste tant les vrayes racines que les fausses ne sont pas tousiours reelles;
mais quelquefois seulement imaginaires; c'est a dire qu'on peut bien tousiours en
imaginer autant que iay dit en chasque Equation; mais qu'il n'y a quelquefois
aucune quantite, qui corresponde a celles qu'on imagine.
(Descartes 1637, p. 380)
стр. 58: ... quomodo quantitates exponentiales imaginariae ad sinus et cosinus arcuum
realium reducantur. (Euler 1748, Introductio, §138)
стр. 62: ... et ie voy deja la route de trouver la somme de cette rangee f + ^ + | + 1^е^с-
(Joh. Bernoulli, May 22, 1691, letter to his brother)

352 Приложение. Цитаты на языках оригиналов
стр. 68: La Theorie des fractions continues est une des plus utiles de l'Arithmetique
comme elle manque dans les principaux Ouvrages d'Artihmetique et d'Algebre,
elle doit etre peu connue des geometres ... je serai satisfait si je puis contribuer a
la leur rendre un peu plus familiere. (Lagrange 1793, Oeuvres, vol. 7, p. 6-7)
стр. 70: Die Veranlassung aber, diese Formeln zu suchen, gab mir des Herrn Eulers Analysis
infinitorum, wo der Ausdruck ... in Form eines Beyspieles vorkommt.
(Lambert 1770a)
стр. 76: Ich kann mit einigem Grunde zweifeln, ob gegenwartige Abhandlung von denjenigen
werde gelesen, oder auch verstanden werden die den meisten Antheil davon nehmen
sollten, ich meyne von denen, die Zeit und Muhe aufwenden, die Quadratur des
Circuls zu suchen. Es wird sicher genug immer solche geben ... die von der
Geometrie wenig verstehen (Lambert 1770a)
стр. 80: L'etendue de ce calcul est immense: il convient aux Courbes mecaniques, comme
aux geometriques; les signes radicaux luy sont indifFerens, & meme sou vent
commodes; il s'etend a tant d'indeterminees qu'on voudra; la comparaison des
infiniment petits de tous les genres luy est egalement facile. Et de la naissent
une infinite de decouvertes surprenantes par rapport aux Tangentes tant courbes
que droit es, aux questions De maximis & minimis, aux points d'inflexion & de
rebroussement des courbes, aux Developees, aux Caustiques par reflexion ou par
refraction, &c. comme on le verra dans cet ouvrage.
(Marquis de L'Hospital 1696, Analyse des infiniment petits)
стр. 81: Et j'ose dire que c'est cecy le problesme le plus utile, &; le plus general non
seulement que ie sgache, mais mesme que i'aye iamais desire de sgauoir en
Geometrie (Descartes 1637, p. 342)
Quel mepris pour les non-Anglois! Nous les avons trouve ces methodes, sans aucun
secours des Anglois. (Joh. Bernoulli 1735, Opera, vol. IV, p. 170)
Ce que tu me rapport es a propos de Bernard Niewentijt n'est que quincaillerie.
Qui pourrait s'empecher de rire devant les ratiocinations si ridicules qu'il batit sur
notre calcul, comme s'il etait aveugle a ses avantages.
(Letter of J oh. Bernoulli, quoted from Parmentier 1989, p. 316).
Nous appellerons la fonction fx, fonction primitive, par rapport aux fonctions
f'x, f"x, &c. qui en derivent, et nous appellerons celles-ci, fonctions derivees, par
rapport a celle-la. (Lagrange 1797)
стр. 92: Je desire seulement qu'il sache que nos questions de maximis et minimis et
de tangentibus linearum curvarum sont parfaites depuis huit ou dix ans et que
plusieurs personnes qui les ont vues depuis cinq ou six ans le peuvent temoigner.
(Letter from Fermat to Descartes, June 1638, Oeuvres, tome 2, p. 154-162)
стр. 98: Mon Frere, Professeur a Bale, a pris de la occasion de rechercher plusieurs courbes
que la Nature nous met tous les jours devant les yeux ... (Joh. Bernoulli 1692)
Je suis tres persuade qu'il n'y a gueres de geometre au monde qui vous puisse etre
compare. (de L'Hospital 1695, letter to Joh. Bernoulli)
стр. 118: La quantite cy dessus
ppads
qqss — ppaa
se reduit immediatement, sans autre changement, a deux fractions logarithmicales,
en la partageant ainsi
ppads _ \pds \pds
qqss — ppaa qs —pa qs -f pa
(Annex to a letter of Joh. Bernoulli, 1699, see Briefwechsel, vol. 1, p. 212)
Problema 3: Si X denotet functionum quamcunque rationalem fractam ipsius x,
methodum describere, cuius ope formulae Xdx integrale investigari conveniat.
(Euler 1768, Opera Omnia, vol. XI, p. 28)
стр. 126: ... weil die Analysten nach alien Versuchen endlich geschlossen haben, dafi man die
Hoffnung aufgeben musse, elliptische Bogen durch algebraische Formeln, Logarith-
men und Circulbogen auszudrucken. (J.H.Lambert 1772, Opera, vol.1, p. 312)

Приложение. Цитаты на языках оригиналов 353
Bien que le probleme (des quadratures) ait une duree de deux cents ans a peu
pres, bien qu'il etait l'objet de nombreuses recherches de plusieurs geometres :
Newton, Cotes, Gauss, Jacobi, Hermite, Tchebychef, Christoffel, Heine, Radeau
[sic], A.Markov, T. Stitjes [sic], C.Posse, C.Andreev, N.Sonin et d'autres, il ne
peut etre considere, cependant, comme suffisamment epuise. (Steklov 1918)
On s'assurera aisement par notre methode que 1'integrate j e fx , dont les
Geometres se sont beaucoup occupes, est impossible sous forme finie ...
(Liouville 1835, p. 113)
стр. 135: Claudius Perraltus Medicus Parisinus insignis, turn &; Mechanicis at que Architect o-
nicis studiis egregius, & Vitruvii editione notus, idemque in Regia scientiarum
Societate Gallica, dum viveret, non postremus, mihi & aliis ante me multis
proposuit hoc problema, cujus nondum sibi occurrisse solutionem ingenue fatebatur
(Leibniz 1693)
стр. 136: Mais pour juger mieux de l'excellence de vostre Algorithme j'attens avec impatience
de voir les choses que vous aurez trouvees touchant la ligne de la corde ou chaine
pendante, que Mr. Bernouilly vous a propose a trouver, dont je luy scay bon gre,
parce que cette ligne renferme des proprietez singulieres et remarquables. Je l'avois
consideree autre fois dans ma jeunesse, n'ayant que 15 ans, et j'avois demontre au
P. Mersenne, que ce n'estoit pas une Parabole ...
(Letter of Huygens to Leibniz, Oct. 9, 1690)
Les efforts de mon frere furent sans succes, pour moi, je fus plus heureux, car je
trouvai l'adresse ... И est vrai que cela me couta des meditations qui me deroberent
le repos d'une nuit entiere (Joh. Bernoulli, see Briefwechsel, vol. 1, p. 98)
стр. 137: Datis in piano verticali duobus punctis A et В assignare mobili M, viam AM В per
quam gravitate sua descendens et moveri incipiens a puncto A, brevissimo tempore
perveniat ad alterum punctum B. (Joh. Bernoulli 1696)
Ce probleme me paroist des plus curieux et des plus jolis que Ton ait encore propose,
et je serois bien aise de m'y appliquer, mais pour cela il seroit necessaire que vous
me l'envoyassiez reduit a la mathematique pure, car le phisique m'embarasse ...
(de L'Hospital, letter to Joh. Bernoulli, June 15, 1696)
стр. 140: En verite rien n'est plus ingenieux que la solution que vous donnez de l'egalite de
Mr. votre frere; &; cette solution est si simple qu'on est surpris que ce probleme ait
paru si difficile: с'est la ce qu'on appelle une elegante solution.
(P. Varignon, letter to Joh. Bernoulli "6 Aoust 1697")
Per liberare la premessa formula dalle seconde differenze, , chiamo p la
sunnormale BF. (Riccati 1712)
стр. 144: ... es ist ganz unmoglich, heute noch eine Zeile von d'Alembert hinunterzuwurgen,
wahrend man die meisten Eulerschen Sachen noch mit Entzucken liest.
(Jacobi, see Spiess 1929, p. 139)
стр. 154: Ich habe immer wieder beobachtet, dafi Mathematiker und Physiker mit ab-
geschlossenem Examen uber theoretische Ergebnisse sehr gut, aber uber die
einfachsten Naherungsverfahren nicht Bescheid wufiten.
(L.Collatz 1951, Num.Beh. Diffgl, Springer-Verlag)
PROBLEMA 85: Proposita aequatione differentiali quacunque eius integrale com-
pletum vero proxime assignare. (Euler 1768, §650)
стр. 156: PROBLEMA 86: Methodum praecedentem aequationes differentiales proxime
integrandi magis perficere, ut minus a veritate aberret. (Euler 1768, §656)
стр. 160: Der Konig nennt mich lmeinen Professor', und ich bin der glucklichste Mensch auf
der Welt! (Euler is proud to serve Frederick II in Berlin)
J'ai ici un gros cyclope de geometre ... il ne reste plus qu'un oeil a notre homme,
et une courbe nouvelle, qu'il calcule a present, pourrait le rendre aveugle tout a
fait. (Frederick II, see Spiess 1929, p. 165-166.)
стр. 170: et je ne reponds pas que je fasse encore de la geometrie dans dix ans d'ici. II
me semble aussi que la mine est presque deja trop profonde et ... il faudra tot ou
tard l'abandonner. La physique et la chimie offrent maintenant des richesses plus

354 Приложение. Цитаты на языках оригиналов
brillantes et d'une exploitation plus facile ...
(Lagrange, Sept. 21, 1781, Letter to d'Alembert, Oeuvres, vol. 13, p. 368)
стр. 172: On dit qu'une grandeur est la limite d'une autre grandeur, quand la seconde peut
approcher de la premiere plus pres que d'une grandeur donnee, si petite qu'on la
puisse supposer, ...
(D'Alembert 1765, Encyclopedic, tome neuvieme, a Neufchastel)
Lorsqu'une quantite variable converge vers une limite fixe, il est sou vent utile
d'indiquer cette limite par une notation particuliere, c'est ce que nous ferons, en
plagant l'abreviation
lim
devant la quantite variable dont il s'agit (Cauchy 1821, Cours d1 Analyse)
стр. 177: ... Je mehr ich ueber die Principien der Punctionentheorie nachdenke — und ich
thue dies unablassig —, um so fester wird meine Ueberzeugung, dass diese auf dem
Fundamente algebraischer Wahrheiten aufgebaut werden muss ...
(Weierstrass 1875, Werke, vol.2, p. 235)
Bitte vergifi alles, was Du auf der Schule gelernt hast: denn Du hast es nicht gelernt.
... indem meine Tochter bekanntlich schon mehrere Semester studieren (Chemie),
schon auf der Schule Differential- und Integralrechnung gelernt zu haben glauben
und heute noch nicht wissen, warum x • у = у • x ist. (Landau 1930)
л/3 ist also nur ein Zeichen fur eine Zahl, welche erst noch gefunden werden soil,
nicht aber deren Definition. Letztere wird jedoch in meiner Weise, etwa durch
(1.7,1.73,1.732,...)
befriedigend gegeben. (G. Cantor 1889)
Definition der irrationalen Zahlen, bei welcher Vorstellungen der Geometrie
... oft verwirrend eingewirkt haben. ... Ich stelle mich bei der Definition auf den
rein formalen Standpunkt, indem ich gewisse greifbare Zeichen Zahlen nenne, so
dass die Existenz dieser Zahlen also nicht in Prage steht. (Heine 1872)
Fur mich war damals das Gefuhl der Unbefriedigung ein so uberwaltigendes,
dass ich den festen Entschluss fasste, so lange nachzudenken, bis ich eine rein
arithmetische und vollig strenge Begrundung der Principien der Infinitesimalanaly-
sis gefunden haben wiirde. ... Dies gelang mir am 24. November 1858, ... aber zu
einer eigentlichen Publication konnte ich mich nicht recht entschliessen, weil erstens
die Darstellung nicht ganz leicht, und weil ausserdem die Sache so wenig fruchtbar
ist. (Dedekind 1872)
Die Analysis zu einem blossen Zeichenspiele herabwurdigend ...
(Du Bois-Reymond 1882, Allgemeine Funktionentheorie, Tubingen)
стр. 180: ... jusqu'a present on a regarde ces propositions comme des axiomes.
(Meray 1869, see Dugac 1978, p. 82)
стр. 184: "Qne chose etonnante, je trouve, c'est que Monsieur Weierstrass et Monsieur
Kronecker peuvent trouver tant d'auditeurs — entre 15 et 20 — pour des cours si
difficiles et si eleves. (letter of Mittag-LefRer 1875, see Dugac 1978, p. 68)
стр. 188: Je consacrerai toutes mes forces a repandre de la lumiere sur I'immense obscurite
qui regne aujourd'hui dans l'Analyse. Elle est tenement depourvue de tout plan et
de tout systeme, qu'on s'etonne seulement qu'il у ait tant de gens qui s'y livrent
— et ce qui pis est, elle manque absolument de rigueur.
(Abel 1826, Oeuvres, vol. 2, p. 263)
Cauchy est fou, et avec lui il n'y a pas moyen de s'entendre, bien que pour le
moment il soit celui qui sait comment les mathematiques doivent etre traitees. Ce
qu'il fait est excellent, mais tres brouille (Abel 1826, Oeuvres, vol. 2, p. 259)

Приложение. Цитаты на языках оригиналов 355
стр. 202: On appelle ici Fonction d'une grandeur variable, une quantite composee de quelque
maniere que ce soit de cette grandeur variable &; de constantes.
(Joh. Bernoulli 1718, Opera, vol. 2, p. 241)
Quocirca, si /(^ + c) denotet functionem quamcimque
(Euler 1734, Opera, vol. XXII, p. 59)
Entspricht nun jedem x ein einziges, endliches y, ... so heisst у eine ... Function von
x fur dieses Interval!. ... Diese Definition schreibt den einzelnen Theilen der Curve
kein gemeinsames Gesetz vor; man kann sich dieselbe aus den verschiedenartigsten
Theilen zusammengesetzt oder ganz gesetzlos gezeichnet denken.
(Dirichlet 1837)
стр. 204: f(x) sera fonction continue, si ... la valeur numerique de la difference
f(x + a)-f(x)
decroit indefiniment avec celle de a ... (Cauchy 1821, Cours d 'Analyse, p. 43)
Wir nennen dabei eine Grosse у eine stetige Function von x, wenn man nach
Annahme einer Grosse e die Existenz von 6 beweisen kann, sodass zu jedem Wert
zwischen xq — 6 ... xq + 8 der zugehorige Wert von у zwischen yo — e ... yo + £
liegt. (Weierstrass 1874)
стр. 206: Ce theoreme est connu depuis longtemps ...
(Lagrange 1807, Oeuvres, vol. 8, p. 19, see also p. 133)
In seinem Satze, dem zufolge eine stetige Funktion einer reellen Veranderlichen
ihre obere und untere Grenze stets wirklich erreicht, d.h.ein Maximum und
Minimum notwendig besitzt, schuf WEIERSTRASS ein Hilfsmittel, dass heute
kein Mathematiker bei feineren analytischen oder arithmetischen Untersuchungen
entbehren kann. (Hilbert 1897, Gesammelte Abh., vol. 3, p. 333)
стр. 209: Der Begriff des Grenzwertes einer Funktion ist wohl zuerst von Weierstrass mit
genugender Scharfe definiert worden.
(Pringsheim 1899, Enzyclopadie der Math. Wiss., Band II.1, p. 13)
стр. 213: Dans l'ouvrage de M. Cauchy on trouve le theoreme suivant: "Lorsque les differens
termes de la serie uq + u\ + uo + . • • sont des fonctions ... continues, ... la somme s
de la serie est aussi ... fonction continue de re." Mais il me semble que ce theoreme
admet des exceptions. Par exemple la serie
sin x — \ sin 2x + | sin 3x ...
est discontinue pour toute valeur (2m + l)7r de x, ...
(Abel 1826, Oeuvres, vol. 1, p. 224-225)
стр. 217: Es scheint aber noch nicht bemerkt zu sein, dass ... diese Continuitat in jedem
einzelnen Punkte ... nicht diejenige Continuitat ist ... die man gleichmassige
Continuitat nennen kann, weil sie sich gleichmassig uber alle Punkte und alle
Richtungen erstreckt. (Heine 1870, p. 361)
Den allgemeinen Gang des Beweises einiger Satze im §. 3 nach den Principien des
Herrn Weierstrass kenne ich durch mundliche Mittheilungen von ihm selbst, von
Herrn Schwarz und Cantor, so dass (Heine 1872, p. 182)
стр. 221: Also zuerst: Was hat man unter J f(x)dx zu verstehen?
(Riemann 1854, Werke, p. 239)
L'illustre geometre [Riemann] ... generalise, par une de ces vues qui n'appar-
tiennent qu'aux esprits de premier ordre, la notion de Pintegrale definie,
(Darboux 1875)
стр. 224: Ich fuhle indessen, dass die Art, wie das Criterium der Integrirbarkeit formulirt
wurde, etwas zu wunschen ubrig lasst. (Du Bois-Reymond 1875, p. 259)
стр. 230: Bis in die neueste Zeit glaubte man, es sei das Integral einer convergenten Reihe
... gleich der Summe aus den Integralen der einzelnen Glieder, und erst Herr
Weierstrass hat bemerkt ...
(Heine 1870, Ueber trig.Reihen, J. f. Math., vol.70, p. 353)
стр. 232: Da diese Functionen noch nirgends betrachtet sind, wird es gut sein, von einem
bestimmten Beispiele auszugehen. (Riemann 1854, Werke, p. 228)

356 Приложение. Цитаты на языках оригиналов
стр. 235: ... la rigueur, dont je m'etais fait une loi dans mon С ours d'analyse, ...
(Cauchy 1829, Legons)
Die vollstandige Veranderung f(x + h) — f(x)... lasst sich im allgemeinen in zwei
Teile zerlegen (Weierstrass 1861)
стр. 240: Voir la belle demonstration de ce theoreme, donnee par M. O. Bonnet, dans le Traite
de Calcul differentiel et integral de M. Serret, 1.1, p. 17. (Darboux 1875, p. Ill)
стр. 242: tout a fait au-dessus de la vaine gloire, que la plupart des Sgavans recherchent
avec tant d'avidite ... (Fontenelle's
opinion concerning Guillaume-Frangois-Antoine de Lhospital, Marquis de Sainte—
Mesme et du Montellier, Comte d'Antremonts, Seigneur d'Ouques, 1661-1704)
Au reste je reconnois devoir beaucoup aux lumieres de Mrs Bernoulli, sur tout a
celles du jeune presentement Professeur a Groningue. Je me suis servi sans fagon
de leurs decouvertes (de L'Hospital 1696)
стр. 245: Ou est-il demontre qu'on obtient la difFerentielle d'une serie infinie en prenant la
difFerentielle de chaque terme? (Abel, Janv. 16, 1826, Oeuvres, vol.2, p. 258)
стр. 252: ... et de juger de la valeur du reste de la serie. Ce probleme, l'un des plus importants
de la theorie des series, n'a pas encore ete resolu ...
(Lagrange 1797, Oeuvres, vol.9, p. 42-43, 71)
... la formule de TAYLOR, cette formule ne pouvant plus etre admise comme
generale (Cauchy 1823, Resume, p. 1)
стр. 253: ... mais celui qui me fait le plus de plaisir с'est un memoire ... sur la simple serie
m(m — 1) о
1 + mx + —^— '- xz + ...
J'ose dire que с'est la premiere demonstration rigoureuse de la formule binome ...
(Abel, letter to Holmboe 1826, Oeuvres, vol. 2, p. 261)
стр. 263: Bis auf die neueste Zeit hat man allgemein angenommen, dass eine ... continuirliche
Function ... audi stets eine erste Ableitung habe, deren Werth nur an einzelnen
Stellen unbestimmt oder unendlich gross werden konne. Selbst in den Schriften
von Gauss, Cauchy, Dirichlet findet sich meines Wissens keine Ausserung, aus der
unzweifelhaft hervor ginge, dass diese Mathematiker, welche in ihrer Wissenschaft
die strengste Kritik uberallzu iiben gewohnt waren, anderer Ansicht gewesen seien.
(Weierstrass 1872)
И у a cent ans, une pareille fonction eut ete regardee comme un outrage au sens
commun.
(Poincare 1899, L'oeuvre math, de Weierstrass, Acta Math., vol.22, p.5)
стр. 266: Telle est la proposition fondamentale qui a ete etablie par Weierstrass.
(Borel 1905, p. 50)
стр. 273: Es mag auffallend erscheinen, dass diese so einfache Idee, welche im Grunde
genommen in weiter nichts besteht, als dass eine Vielfachsumme verschiedener
Grossen (als welche hiernach die extensive Grosse erscheint) als selbststandige
Grosse behandelt wird, in der That zu einer neuen Wissenschaft sich entfalten
soil; (Grassmann 1862, Ausdehnungslehre, p. 5)
... il est tres utile d'introduire la consideration des nombres complexes, ou nombres
formes avec plusieurs unites, (Peano 1888a, Math. Ann., vol.32, p. 450)
стр. 278: Unter einer "Menge" verstehen wir jede Zusammenfassung M von bestimmten
wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens
(welche die "Elemente" von M genannt werden) zu einem Ganzen.
(G. Cantor 1895, Werke, p. 282)
Aus dem Paradies, das Cantor uns geschafFen, soil uns niemand vertreiben konnen.
(Hilbert, Math. Ann., vol.95, p. 170)
стр. 283: Nous avons deja signale et nous reconnaitrons dans tout le cours de ce Livre
l'importance des ensembles compacts. Tous ceux qui ont eu a s'occuper
d'Analyse generale ont vu qu'il etait impossible de s Jen passer.
(Prechet 1928, Espaces abstraits, p. 66)

Приложение. Цитаты на языках оригиналов 357
стр. 287: ... ist die Schwierigkeit, welche nach dem Urtheile aller Mathematiker ... das
Studium jenes Werkes wegen seiner ... mehr philosophischen als mathematischen
Form dem Leser bereitet Jene Schwierigkeit nun zu beheben, war daher eine
wesentliche Aufgabe fur mich, wenn ich woflte, dass das Buch nicht nur von mir,
sondern audi von anderen gelesen und verstanden werde.
(Grassmann 1862, "Professor am Gymnasium zu Stettin")
стр. 291: Eine stetige Kurve kann Flachenstucke enthalten: das ist eine der merkwurdigsten
Tatsachen der Mengenlehre, deren Entdeckung wir G. Peano verdanken.
(HausdorfF 1914, p. 369)
стр. 300: Wir Deutsche gebrauchen statt dessen nach Jacobi's Vorgange fur partielle Ableit-
ungen das runde д. (Weierstrass 1874)
стр. 302: ... daft Weierstrafl' unmittelbarer Unterricht die Spontanitat der Horer zu sehr
unterdruckte und in der Tat nur fur den voll verstandlich war, der schon anderweitig
mit dem Stoff sich vertraut gemacht hatte. Die grofteren Werke sind von Auslandern
geschrieben ... Wohl das erste stammt von meinem Preunde Stolz (Innsbruck):
"Vorlesungen uber allgemeine Arithmetik"
(F.Klein 1926, Entwicklung der Math., p. 291)
стр. 316: Or il est facile de voir que les difFerentielles de cette espece conservent les memes
valeurs quand on intervertit l'ordre suivant lequel les differentiations relatives aux
diverses variables doivent etre effectuees. (Cauchy 1823, Resume, p. 76)
стр. 330: On sait que 1'evaluation ou meme la reduction des integrates multiples presente
generalement de tres grandes difficultes
(Dirichlet 1839, Werke, vol. I, p. 377)
стр. 336: Cette methode consiste simplement a multiplier I'expression qu'il s'agit d'integrer
par un facteur dont la valeur est egale a l'unite dans l'etendue que les integrations
doivent embrasser, et qui s'evanouit en dehors de cette etendue.
(Dirichlet 1839, Werke, vol. I, p. 377)
стр. 338: locum habet pro quacunque aha formula J J Zdxdy, quippe quae per easdem
substitutiones transformatur in hac J J Z(VR - ST) dtdu... (Euler 1769b)

Библиография
References
Курсивом в квадратных скобках после ссылки указаны разделы, в которых
цитируется данная работа.
Абель (N.H.Abel 1826):
Recherches sur la serie 1 + f x + т(^2"^ж2 + ™(™~Жт~2) xs + ... , Oeuvres 1,
p. 219-250; German transl. Journal reine u. angew.Math. (Crelle), 1 (1826), p. 311-
339. [111.2], [III.4], [III.7]
Абель (N.H.Abel 1881):
Oeuvres completes, ed.by L. Sylow ad S.Lie, 2 volumes, Christiania,
MDCCCLXXXI. [III.2], [III.4]. [III.6]
Або (A.Aaboe 1954):
Al-Kasht's iteration method for the determination o/sin 1°, Scripta math. 20 (1954),
p. 24-29. [1.4]
Або (A.Aaboe 1964):
Episodes from the early history of mathematics, Random House, New Math. Library,
Yale Univ. 1964. [1.4]
Адамар (J.Hadamard 1892):
Essai sur Vetude des fonctions donnees par leur developpement de Taylor. J.de
Math.(4), 8 (1892), p. 101-186. [III.7]
Архимед (Archimedes, ~ 240 B.C.):
On the measurement of the circle, (Адх^^'П^щ, KvkXov fj,ergrjaк;), many editions,
in particular: J.L.Heiberg, Leipzig 1880; T.L.Heath, The works of Archimedes,
Cambridge University Press, 1897. [Имеется перевод: Архимед. Сочинения. —
М.: Физматгиз, 1962. — Измерение круга, с. 266-271.] [1.4], [L6]
Барроу (I.Barrow 1860):
The mathematical works, Ed. W. Whewell, xx+320 pp. + 220 Figs. Cambridge 1860,
reprinted G. Olms Verlag, 1973. [1.2]
Бернулли Иоганн (Joh.Bernoulli 1691):
Solutio problematis funicularii, exhibita a Joh. Bernoulli, Basil. Med. Cand., Acta
Eruditorum 10, MDCXCVI, p. 274-276; Opera I, p.48-51. [II.7]
Бернулли Иоганн (Joh.Bernoulli 1691/92):
Die Differentialrechnung von Johann Bernoulli, Nach der in der Basler Universitats-
bibliothek befindlichen Handschrift ubersetzt von Paul Schafheitlin, Akademische
VerlagsgeseUschaft Leipzig, 1924. [Ill], [II.2], [III.6]
Бернулли Иоганн (Joh. Bernoulli 1691/92b):
Lectiones Mathematics, de methodo integralium, aliisque, consrciptce in usum
III. Marchionis Hospitalii, published 1742 in Opera 3, p. 385-558. [II.3]
Бернулли Иоганн (Joh. Bernoulli 1692):
Solutio curvcE caustics per vulgarem geometriam Cartesianam; aliaque, Acta Erud.
Lips. 11 (1692), p. 30; Opera I, p. 52-59. [II.3]
Бернулли Иоганн (Joh. Bernoulli 1694):
Modus generalis construendi dsquationes differentiales primi gradus, Acta Erud.
Lips. 13 (1694), p.435; Opera I, p. 123-125. [II.9]
Бернулли Иоганн (Joh. Bernoulli 1694b):
Effectionis omnium quadraturam & rectificationum curvarum per seriem quandam
generalissimam, Acta Erud. Lips. 13 (1694); "Additamentum" to the paper Joh.
Bernoulli (1694). [II.4]
Бернулли Иоганн (Joh. Bernoulli 1696):
Problema novum ad cuius solutionem Mathematici invitantur, Acta Eruditorum
15, MDCXCVI, p. 264-269. Opera I, p. 155-161. [Имеется перевод: Бернулли И.
Избранные сочинения по механике. — М.-Л.: ГТТИ, 1937. — Новая задача, к
разрешению которой приглашаются математики, с. 19-20.] [II.7]

Библиография 359
Бернулли Иоганн (Joh. Bernoulli 1697):
Principia calculi exponentialium, seu percurrentium, Acta Erud. Lips. 16 (1697),
p. 125; Opera I, p. 179-187; see also Opera III, p. 376. [1.3], [11.6]
Бернулли Иоганн (Joh. Bernoulli 1697b):
De Conoidibus et Sphaeroidibus quaedam. Solutio analytica Aequationis in Actis
A. 1695, рад. 553 propositae (A Fratre Jac.Bernoullio), Acta Eruditorum 16,
MDCXCVII, p. 113-118. Opera I, p. 174-179. [IL7]
Бернулли Иоганн (Joh. Bernoulli 1697c):
Solutioque Problematis a se in Actis 1696, p. 269, proposit, de invenienda Linea
Brachystochrona, Acta Eruditorum 16, MDCXCVII, p. 206; Opera I, p. 187-193.
[Имеется перевод: Бернулли И. Избранные сочинения по механике. — М.-Л.:
ГТТИ, 1937. — Решение задачи, предложенной мною в "ACTA" за 1696 г.,
с. 269, о нахождении "брахистохронной линии", с. 26-39.] [П.7]
Бернулли Иоганн (Joh. Bernoulli 1702):
Solution d'un probleme concernant le calcul integral, avec quelques abreges par
raport a ce calcul, Histoire de l'Acad. Royale des Sciences a Paris, Annee MDCCII,
Memoire, p. 289-297; (1697), p. 125. Opera I, p. 393-400. [II.5]
Бернулли Иоганн (Joh.Bernoulli 1742):
Opera Omnia, 4 volumes, Lausannae & Genevae 1742; facsimile reprint (Curavit
J.E.Hofmann) 1968, Georg Olms Verlag Hildesheim. [III.3]
Бернулли Иоганн (Joh. Bernoulli 1955,1988):
Der Briefwechsel von Johann Bernoulli, 2 volumes, Birkhauser Verlag Basel. [II.3],
[II. 5], [I1.7]
Бернулли Якоб (Jac. Bernoulli 1689):
Positiones arithmeticae de seriebus infinitas, earumque summa finita, Basileae,
1689, Opera 1, p. 375-402. [1.2]
Бернулли Якоб (Jac. Bernoulli 1690):
Analysis problematis ante hac propositi, de inventione linece descensus a corpore
gravi percurrendce uniformiter, sic ut temporibus dequalibus <£quales altitudines
emetiatur: & alterius cujusdam Problematis Propositio, Acta Eruditorum 9,
MDCLXXXX, p.217-219. [1Щ [II.7]
Бернулли Якоб (Jac. Bernoulli 1694):
Constructio curvae accessus & recessus aequabilis, ope rectificationis curvae
cujusdam algebraicae, Acta Eruditorum 13 (1694), p. 336-338, Opera 2 p. 608-612. [IV.3]
Бернулли Якоб (Jac. Bernoulli 1702):
Section indefinie des arcs circulaires, en telle raison qu'on voudra; Avec la maniere
d'en deduire les Sinus, &c, Hist. Acad. Sciences de Paris (1702), p. 281; Opera,
p. 921. [1.4]
Бернулли Якоб (Jac. Bernoulli 1705):
Ars conjectandi, opus posthumum, published posthumously Basileae MDCCXIII:
Werke 3, p. 107-286, Basel, 1975. [Имеется перевод: Бернулли Я. Искусство
предположений, ч. 1-3. — Берлин: NG, 2006; Бернулли Я. О законе больших
чисел. — М.: Наука, Физматлит, 1986.] [1.1]
Бернулли Якоб (Jac.Bernoulli 1744):
Opera, 2 volumes, VIII+484-1139 pp., Ed. G.Cramer, Genevae 1744.
Блантон (J.D.Blanton 1988):
Introduction to analysis of the infinite. English translation of Euler (1748), Springer-
Verlag New York, 1988. [I.l]
Больцано (B.Bolzano 1817):
Rein analytischer Beweis des Lehrsatzes, dass zwischen je zwei Werthen, die ein
entgegengesetztes Resultat gexvdhren, wenigstens eine reelle Wurzel der Gleichung
liege, Prag 1817; Ostwald's Klassiker #153, 1905 (see also Stolz 1881). [III.0], [III.3]
Борель (E.Borel 1895):
Sur quelques points de la theorie des fonctions, These, parue aux Ann.Ecole
normale sup. 3e serie, 12 (1895), p. 9-55; Oeuvres 1, p. 239-285. The "Theorem of
Heine-Borel" is in a "Note" at the end of the thesis. Paris, 1905. [IV. 1]
Борель (E.Borel 1905):
Lecons sur les fonctions de variables reelles et les developpements en series de
polynomes, redigees par M.Frechet, Gauthier-Villars, Paris 1905. [III.9]
Бриггс (H.Briggs 1624):
Arithmetica Logarithmica, Londini, Excudebat Gulielmus Iones, 1624. [1.2], [1.3]

360 Библиография
Бук (R.C.Buck 1980):
Sherlock Holmes in Babylon, Am. Math. Monthly 87,Nr.5 (1980), p. 335-345. [II.5]
Буняковский (V.Buniakowsky 1859):
Sur quelques inegalites concernant les integrales ordinaires et les integrales aux
differences finies, Memoires de Г Acad, de St-Petersbourg (VII), 1 (1859), Nr.9.
[III.5]
Бюрги (J.Burgi 1620):
Arthmetische und geometrische Progress- Tabulen, Prag, 1620. [1.3]
Валлис (J.Wallis 1655):
Arithmetica infinitorum, sive nova methodus inquirendi in curvilineorum quadratur-
am, aliaque difficiliora matheseos problemata, Anno 1655 typis edita; Opera mathe-
matica I (1695), p. 355-478; reprinted Georg Olms Verlag, 1972. [1.5], [1.6]
Ваннер (G. Wanner 1988):
Les equations differentielles ont 350 ans, L'Enseignement Mathematique 34 (1988),
p. 365-385. [II.7]
Варден, ван дер (B.L.van der Waerden 1954):
Science awakening I, Egyptian, Babylonian, and Greek Mathematics, Kluwer Acad.
Publ. Dordrecht, The Netherlands; English editions 1961, 1969, 1975, 1988.
[Имеется перевод: ван дер Варден Б.Л. Пробуждающаяся наука: Математика
Древнего Египта, Вавилона и Греции. — М.: URSS (КомКнига), 2006.] [1.2]
Варден, ван дер (B.L.van der Waerden 1957):
Uber die Einfuhrung des Logarithmus im Schulunterricht, Elemente der Math. 12
(1957), p. 1-8. [1.3]
Вейерштрасс (К. Weierstrass 1841):
Zur Theorie der Potenzreihen, manuscript 1841, published 1894 in Werke 1, p. 67-
74. [III.4] .
Вейерштрасс (К. Weierstrass 1861):
Differential Rechnung, Vorlesung an dem Koniglichen Gewerbeinstitute, manuscript
1861, typewritten by H.A. Schwarz, Math. Bibl. Humboldt Universitat Berlin. [III.3],
[IlUh [Ш.6], [III.7]
Вейерштрасс (К. Weierstrass 1872):
Uber continuirliche Functionen eines reellen Arguments, die fur keinen Werth
des letzteren einen bestimmten Differentialquotienten besitzen, Konigl. Akad. der
Wiss. Berlin, Werke 2, p. 71-74. [III.3], [III.9]
Вейерштрасс (К. Weierstrass 1874):
Theorie der analytischen Funktionen, Vorlesung an der Univ. Berlin 1874,
manuscript (ausgearbeitet von G.Valentin), Math. Bibl. Humboldt Universitat Berlin.
[III.l], [III.3], [IV.3]
Вейерштрасс (К. Weierstrass 1885):
Uber die analytische Darstellbarkeit sogenannter willkurlicher Functionen reeller
Argumente, Konigl. Akad. der Wiss. Berlin, Werke 3, p. 1-37. [HI.9]
Вейерштрасс (К. Weierstrass 1894-1927):
Mathematische Werke, 7 volumes, Berlin and Leipzig, 1894-1927. [III.l]
Виет (F.Viete 1591):
In artem analyticam isagoge, Tours 1591, Opera, Ed. Pranciscus van Schooten, 1646,
p. 1-12. [Ll]
Виет (F.Viete 1591a):
De aequationem recognitione et emendatione, publ. posth. 1615, Opera, Ed.
Pranciscus van Schooten, 1646, p.84-158. [Ll], [1.5]
Виет (F.Viete 1593):
Ad angulares sectiones theoremata KA0OAIKQTEPA, publ. posthumously 1615,
Opera, Ed. Franciscus van Schooten, 1646, p. 287-304. [Ll], [1.2]
Виет (F.Viete 1600):
Algebra nova, French transl. with commentaries: Introduction en Гart analytique
ov novvelle Algebra, oeuvre dans lequel sont veus les plus miraculeux effects des
sciences Mathematiques, pour l'inuention & solution, tant des Problemes, que
Theoremes, 1630. [Ll]
Виртингер (W.Wirtinger 1902):
Einige Anwendungen der Euler-Maclaurin'schen Summenformel, insbesondere auf
eine Aufgabe von Abel, Acta Mathematica 26 (1902), p. 255-271. [11.10]

360 Библиография
Бук (R.C.Buck 1980):
Sherlock Holmes in Babylon, Am. Math. Monthly 87,Nr.5 (1980), p. 335-345. [lib]
Буняковский (V.Buniakowsky 1859):
Sur quelques inegalites concernant les integrales ordinaires et les integrales am
differences finies, Memoires de Г Acad, de St-Petersbourg (VII), 1 (1859), Nr.9.
[III.5]
Бюрги (J.Burgi 1620):
Arthmetische und geometrische Progress-Tabulen, Prag, 1620. [1.3]
Валлис (J.Wallis 1655):
Arithmetica infinitorum, sive nova rnethodus inquirendi in curvilineorum quadratur-
am, aliaque difficiliora matheseos problemata, Anno 1655 typis edita; Opera mathe-
rnatica I (1695), p. 355-478; reprinted Georg Olms Verlag, 1972. [1.5], [1.6]
Ваннер (G. Wanner 1988):
Les equations differentielles ont 350 ans, L'Enseignement Mathematique 34 (1988),
p. 365-385. /27.7/
Варден, ван дер (B.L.van der Waerden 1954):
Science awakening I, Egyptian, Babylonian, and Greek Mathematics, Kluwer Acad.
Publ. Dordrecht, The Netherlands; English editions 1961, 1969, 1975, 1988.
[Имеется перевод: ван дер Варден Б.Л. Пробуждающаяся наука: Математика
Древнего Египта* Вавилона и Греции. — М.: URSS (КомКнига), 2006.] [1.2]
Варден, ван дер (B.L.van der Waerden 1957):
Uber die Einfuhrung des Logarithmus im Schulunterricht, Elemente der Math. 12
(1957), p. 1-8. [1.3]
Вейерштрасс (К. Weierstrass 1841):
Zur Theorie der Potenzreihen, manuscript 1841, published 1894 in Werke 1, p. 67-
74. [Ш.4] .
Вейерштрасс (К. Weierstrass 1861):
Differential Rechnung, Vorlesung an dem Koniglichen Gewerbeinstitute, manuscript
1861, typewritten by H.A. Schwarz, Math. Bibl. Humboldt Universitat Berlin. [III.3],
[III.4], [Ш.6], [III.7]
Вейерштрасс (К. Weierstrass 1872):
Uber continuirliche Functionen eines reellen Arguments, die fur keinen Werth
des letzteren einen bestimmten Differentialquotienten besitzen, Konigl. Akad. der
Wiss. Berlin, Werke 2, p. 71-74. [III.3], [III.9]
Вейерштрасс (К. Weierstrass 1874):
Theorie der analytischen Funktionen, Vorlesung an der Univ. Berlin 1874,
manuscript (ausgearbeitet von G.Valentin), Math. Bibl. Humboldt Universitat Berlin.
[III.l], [III.3], [IV.3]
Вейерштрасс (К. Weierstrass 1885):
Uber die analytische Darstellbarkeit sogenannter willkurlicher Functionen reeller
Argumente, Konigl. Akad. der Wiss. Berlin, Werke 3, p. 1-37. [HI. 9]
Вейерштрасс (К. Weierstrass 1894-1927):
Mathematische Werke, 7 volumes, Berlin and Leipzig, 1894-1927. /7/7.i/
Виет (F.Viete 1591):
In artem analyticam isagoge, Tours 1591, Opera, Ed. Pranciscus van Schooten, 1646,
p. 1-12. [1.1]
Виет (F.Viete 1591a):
De aequationem recognitione et emendatione, publ. posth. 1615, Opera, Ed.
Pranciscus van Schooten, 1646, p.84-158. [1.1], [1.5]
Виет (F.Viete 1593):
Ad angulares sectiones theoremata KA0OAIKQTEPA, publ. posthumously 1615,
Opera, Ed. Franciscus van Schooten, 1646, p. 287-304. [1.1], [1.2]
Виет (F.Viete 1600):
Algebra nova, French transl. with commentaries: Introduction en Vart analytique
ov novvelle Algebra, oeuvre dans lequel sont veus les plus miraculeux effects des
sciences Mathematiques, pour l'inuention & solution, tant des Problemes, que
Theoremes, 1630. [1.1]
Виртингер (W.Wirtinger 1902):
Einige Anwendungen der Euler-Maclaurin'schen Summenformel, insbesondere auf
eine Aufgabe von Abel, Acta Mathematica 26 (1902), p. 255-271. [11.10]

362 Библиография
Bikinis Graftmanns in Holzschnitt"); revised edition Die Ausdehnungslehre, 1862,
reprinted Teubner, 1896. [IV.0], [IV.1], [IV.2]
Грёбнер и Хофрейтер (W. Grobner & N.Hofreiter 1949):
Integraltafel, erster Teil: unbestimmte Integrale, 166 pp.. Springer-Verlag, Wien und
Innsbruck, 1949. [1Ц]
Грегори (J.Gregory 1668):
Exercitationes geometricae. Appendicula ad veram circuli et hyperbolae quadratur-
am, London, 1668. [1.3]
Гурвиц (A.Hurwitz 1962, 1963):
Mathematische Werke, ed. Abtlg. Math. Phys. ETH Zurich, 2 volumes, Birkhauser
Verlag Basel und Stuttgart, 1962, 1963. [1.6]
Гюйгенс (C.Huyghens 1673):
(Christiani Hugenii Zulichemii) Horologium oscillatorium, sive de motu pendulorum
ad horologia aptato demonstrationes geometricae, Paris, 1673. [II. 1], [II.3], [III]
Даламбер (J.le Rond d'Alembert 1748):
Suite des recherches sur le calcul integral, quatrieme partie: Methodes pour integrer
quelques equations differentielles, Hist. Acad. Berlin, tome IV, p. 275-291. [II.8],
[IV.O]
Даламбер (J.le Rond d'Alembert 1754):
Calcul differentiel, article under "D" of the famous Encyclopedic ou Dictionnaire
raisonne des sciences, des arts et des metiers, mis en ordre et publie par M. Diderot
& par M. D'Alembert, tome quatrieme, p.985, a Paris, MDCCLIV. [II.1]
Даламбер (J.le Rond d'Alembert (1765):
Limite, article under "L" of the Encyclopedic, tome neuvieme, p. 542, a Neufchastel,
MDCCLXV. [III.l]
Дарбу (G.Darboux 1875):
Memoire sur les fonctions discontinues, Annales. Ecole norm. sup. Ser. 2, 4 (1875),
p. 57-112. [ПЦ], [111.5], [III.6]
Дедекинд (R. Dedekind 1872):
Stetigkeit und irrationale Zahlen, first edition 1872, forth edition 1912, English
translation Continuity and irrational numbers in Essays on the theory of numbers,
Dover, 1963; Werke 3, p. 314-343. [Имеется перевод: Дедекинд P. Непрерывность
и иррациональные числа, изд. 4-е, испр. — Одесса: Mathesis, 1923.] [IllЛ]
Декарт (R.Descartes 1637):
La Geometrie, Appendix to the Discours de la methode, Paris 1637, English
translation, with a facsimile of the first edition, D.E.Smith & M.L. Latham, The
Oper Court Publishing Сотр., 1925, reprinted 1954 by Dover. [Имеется перевод:
Декарт P. Геометрия: с приложением избранных работ П. Ферма и переписки
Декарта. — М.-Л.: ОНТИ, 1938. Декарт Р. Рассуждение о методе. С
приложением: Диоптрика, Метеоры, Геометрия. — Л.: Изд-во АН СССР, 1953.] [И],
[1.2], [1.5], [11.1], [IV.3]
Дженокки и Пеано (A. Genocchi & G. Реапо 1884):
Calcolo differenziale е principii di calcolo integrale, "pubblicato con aggiunte dal
Dr. Giuseppe Peano" Torino, 1884; German edition (G.Bohlmann & A.Schepp),
1899. [Имеется перевод: Дженокки А. Дифференциальное исчисление и начала
интегрального исчисления. — Петербург: Akademia, 1922.] [IV.3]
Джервер (J.Gerver 1970):
The differentiability of the Riemann function at certain rational multiples of тг,
Amer.J.of Math. 92 (1970), p. 33-55. [III.9]
Джонс У. (W.Jones 1706):
Synopsis palmariorum matheseos: or, New introduction to the mathematics:
containing principles of arithmetic & geometry, demonstrated, in a short and easie method
..., London, 1706. [1.4]
Дини (U.Dini 1878):
Fondamenti per la teoria delle funzioni di variabili reali, Pisa, 1878, german
translation by Luroth and Schepp, Teubner Leipzig, 1892. [III. 5/, [III. 9]
Дирихле (G.L.Dirichlet 1837):
Uber die Darstellung ganz willkurlicher Functionen durch Sinus- und Cosinusreihen,
Rep.der Physik, 1837; also: Ostwald's Klassiker Nr. 116, Leipzig, 1900; Werke 1,
p. 133-160. [III.3]

Библиография 363
Дирихле (G.L. Dirichlet 1837b):
Beweis des Satzes, dass jede unbegrenzte arithmetische Progression, deren erstes
Glied und Differenz ganze Zahlen ohne gemeinschaftlichen Factor sind, unendlich
viele Primzahlen enthdlt, Abh. der Konigl. Preussischen Acad, der Wiss. Berlin, 1837,
Werke 1, p. 313-342. [Имеется перевод: Дирихле Л. Лекции по теории чисел.
— М.: Изд-во ЛКИ, 2007. — Доказательство теоремы, что всякая
бесконечная арифметическая прогрессия, первый член и разность которой суть целые
числа, не имеющие общего множителя, содержит бесконечно много простых
чисел, с. 296-309.] [III.2]
Дирихле (G.L. Dirichlet 1839):
Uber eine neue Methode zur Bestimmung vielfacher Integrale, Ber. uber die Verh. der
Konigl. Preussischen Acad, der Wiss. Berlin, 1839, p. 18-25; Werke 1, p. 381-390.
[IV.5]
Дюбуа-Реймон (P.Du Bois-Reymond 1875):
Ueber eine verdnderte Form der Bedingung fur die Integrirbarkeit der Functionen,
Journal reine u. angew.Math. (Crelle), 79 (1875), p. 259-262. [III.5]
Дюга (P.Dugac 1978):
Sur les fonaements de Vanalyse, These, Paris 1978; see also Fondements de Vanalyse,
Chapter VI of Abrege d'histoire des mathematiques 1700-1900sous, la direction de
Jean Dieudonnee, Hermann editeurs, Paris, 1978. [III.l]
Дюрер (A.Durer 1525):
Underweysung der messung, mit dem zirckel un richtscheyt, in Linien ebnen unnd
gantzen corporen, durch Albrecht Durer zu samen getzoge, und zu nutz alle
kunstlieb habenden mit zu gehorigen figuren, in truck gebracht, im jar. M.D.XXV.
Facsimile reprint Verlag Dr.Alfons Uhl, Nordlingen, 1983. [I.4], [II.3]
Евклид (Euclid, (~ 300 B.C.):
The elements, (ЕУКЛЕ1ЛОУ, ZTOIXEIA); many translations and editions, first
mathematical book ever printed (Venice 1482); the today's definite text is due
to J.L.Heiberg 1883-1888; English translation with commentaries: Sir Thomas
L. Heath 1908 and 1925; reprinted 1956 by Dover Publications in three volumes.
[Имеется перевод: Евклид. Начала, кн. 1-6, 7-10, 11-15, т. 1-3. — М.-Л.: Гос-
техиздат, 1948-1950.] [1.1], [1.4], [1.6], [III. 1]
Жордан К. (C.Jordan 1882):
Cours d'analyse de VE cole ploy technique, Paris, 1882-1887 (3 volumes). [IV.1]
Зейдель, фон (L.Seidel (Philipp Ludwig von) 1848):
Note uber eine Eigenschaft der Reihen, welche discontinuirliche Functionen darstel-
len, Denkschriften der Munchener Akademie, Jahrgang 1848. [III.4]
Кантор (G. Cantor 1870):
Beweis, dass fur jeden Werth von x durch eine trigonometrische Reihe gegebene
Function f(x) sich nur auf eine einzige Weise in dieser Form darstellen lasst,
Journal reine u.angew. Math. (Crelle), 72 (1870), p. 139-142; см., в частности,
сноску на с. 141. Gesammelte Abhandlungen, p. 80-83. [III.3]
Кантор (G. Cantor 1872):
Uber die Ausdehnung eines Satzes aus der Theorie der trigonometrischen Reihen,
Math. Annalen 5 (1872), p. 123-132. Gesammelte Abhandlungen, p. 92-102.
[Имеется перевод: Кантор Г. Труды по теории множеств. — М.: Наука, 1985. —
Обобщение одной теоремы из теории тригонометрических рядов, с. 9-18.] [III.1]
Кантор (G. Cantor 1878):
Ein Beitrag zur Mannigfaltigkeitslehre, Journal reine u. angew.Math. (Crelle), 84
(1878), p. 242-258. Gesammelte Abhandlungen, p. 119-133. [Имеется перевод:
Кантор Г. Труды по теории множеств. — М.: Наука, 1985. — К учению о
многообразиях, с. 22-35.] [IV.2]
Кантор (G. Cantor 1880):
Fernere Bemerkung uber trigonometrische Reihen, Math. Annalen 16 (1880), p. 267-
269. Gesammelte Abhandlungen, p. 104-106. [III.4]
Кантор (G. Cantor 1883):
Ueber unendliche, lineare Punktmannichfaltigkeiten, N5, Math. Annalen 21 (1883),
p. 545-591. Gesammelte Abhandlungen, p. 165-209. [Имеется перевод: Кантор Г.
Труды по теории множеств. — М.: Наука, 1985. — Основы общего учения
о многообразиях. Математически-философский опыт учения о бесконечном,

364 Библиография
с. 63-106.] [IVЛ]
Кантор (G. Cantor 1884):
Ueber unendliche, lineare Punktmannichfaltigkeiten, N6, Math. Annalen 23 (1884),
p. 453-488. ("Fortsetzung folgt"); Gesammelte Abhandlungen, p. 210-246.
[Имеется перевод: Кантор Г. Труды по теории множеств. — М.: Наука, 1985. — О
бесконечных линейных точечных многообразиях, с. 106-141.] [IV. 1]
Кантор (G. Cantor 1889):
Bemerkung mit Bezug auf den Aufsatz: Zur Weierstrafi Cantorschen Theorie
der Irrationalzahlen, Math. Annalen 33 (1889), p. 476, Gesammelte Abhandlungen,
p. 114. [III.l]
Кантор (G. Cantor 1932):
Gesammelte Abhandlungen, ed. E.Zermelo, Springer-Verlag, Berlin, 1932. [Имеется
перевод: Кантор Г. Труды по теории множеств. — М.: Наука, 1985.] [IV. 1]
Кантор (М. Cantor 1880-1908):
Vorlesungen fiber Geschichte der Mathematik, vol. I 1880, vol. II 1891, vol. Ill 1898,
vol. IV 1908; many later editions and printings, Teubner Verlag, Leipzig. [Ll], [1-4]
Каратеодори (С. Caratheodory 1950):
Funktionentheorie, Erster Band, Verlag Birkhauser Basel, 1950, 288 pp. [III.6]
Кардано (H. Cardano 1545):
Ars magna de rebus algebraicis, Nurnberg, 1545. [I.l], [1.2], [1.5]
Каунцнер (W.Kaunzner 1980):
Uber Regiomontanus als Mathematiker, p. 125-145 in: Regiomontanus-Studien,hrsg.
G.Hamann, Osterr. Akad. der Wiss. , Wien, 1980. [Ц]
Кеплер (J.Kepler 1615):
Nova stereometria doliorum vinariorum, in primis Austriaci, figures omnium aptiss-
im<£, Authore Ioanne Kepplero, imp. Caes. Matthiae I. ejusq; fidd. Ordd. Austriae
supra Anasum Mathematico, Lincii, Anno M.DC.XV. [Имеется перевод: Кеплер
И. Новая стереометрия винных бочек. — М.-Л.: Гостехиздат, 1935.] [II.4]
Клайн (M.Kline 1972):
Mathematical thought from ancient to modern times, New York, Oxford Univ. Press,
1238 pp. [1.2], [1.3], [1.5], [II.6], [III.7], [IV.0]
Клейн (F.Klein 1908):
Elementarmathematik vom hoheren Standpunkte aus, third edition 1924, Grundlehr-
en, Band XIV, Springer-Verlag Berlin; Engl, transl. Dover. [Имеется перевод:
Клейн Ф. Элементарная математика с точки зрения высшей. Лекции,
читанные в Геттингенском университете, т. 1 (изд. 4-е), т. 2 (изд. 2-е). — М.: Наука,
1987.] [IIЛ], [11.21 [III.6]
Клейн (F.Klein 1926, 1927):
Vorlesungen fiber die Entwicklung der Mathematik im 19. Jahrhundert, 2 volumes,
Springer-Verlag Berlin 1926, 1927, reprinted in one volume Chelsea New York 1967,
Springer-Verlag 1979. [Имеется перевод: Клейн Ф. Лекции о развитии
математики в XIX столетии, т. 1. — М.: Наука, 1989. Клейн Ф. Лекции о развитии
математики в XIX столетии, т. 2. — М.-Ижевск: Ин-т компьют. исслед., 2003.]
[IV.3]
Кнопп (К.Кпорр 1922):
Theorie und Anwendung der unendlichen Reihen, Grundlagen, Bd. 2, Springer-
Verlag, Berlin, 1922, second ed. 1924, third ed. 1931, fourth ed. 1947. [III.2]
Кнут (D.E.Knuth 1962):
Euler's constant to 1271 places, Math, of Comput. 16 (1962), p. 275-281. [11.10]
Кох, фон (H.von Koch 1906):
Une methode geometrique elementaire pour Гetude de certaines questions de la
theorie des courbes planes, Acta Mathematica 30, (1906), p. 145-174. [IIL9], [IV.5]
Коши (A.L.Cauchy 1821):
Cours dfanalyse algebrique, Oeuvres serie 2, vol. III. [Имеется перевод: Коши А.Л.
Алгебраический анализ. — Лейпциг, 1864.] [II.4], [IIIЛ], [IIL2], [III.3], [III.4]
[III.5], [Ш.6], [III.7], [IV.2]
Коши (A.L.Cauchy 1823):
Resume des legons sur le calcul infinitesimal, Oeuvres serie 2, vol. IV, p. 1-261.
[Имеется перевод: Коши А.Л. Краткое изложение уроков о
дифференциальном и интегральном исчислении. — СПб: Императорская Академия Наук,
1831.] [II.1], [III.5], [III.7], [IV.4J

Библиография 365
Коши (A.L.Cauchy 1824):
Resume des Lecons donnees a I'Ecole Royale Poly technique. Suite du Calcul
Infinitesimal; published: Equations difterentielles ordinaires, Ed. Chr. Gilain, Johnson,
1981. [11.3], [11.9]
Коши (A.L.Cauchy 1829):
Legons sur le calcul differentiel, Oeuvres serie 2, vol. IV, p. 265-572. [HI.6], [IV.4]
Кун (S.Kuhn 1991):
The derivative a la Caratheodory, Math. Monthly 98, Nr. 1 (1991), p. 40-44. [III.6]
Лагранж (J.L.de Lagrange 1759):
Recherches sur la methode de maximis et minimis, Misc. Taurinensia, Torino 1
(1759), Oeuvres I, p.3-20. [II.2], [IV4]
Лагранж (J.L.de Lagrange 1773):
Sur Vattraction des spherotdes elliptiques, Nouv. Mem. Acad, royale Berlin annee
1773, Oeuvres 3, p. 619-649. [IV.5]
Лагранж (J.L.de Lagrange 1775):
Recherche sur les Suites Recurrentes, Nouveaux Mem. de l'Acad. royale des Sciences
et Belles-Lettres, Berlin. Oeuvres 4, p.159. [II.8]
Лагранж (J.L.de Lagrange 1788):
Mechanique analitique, Par M. de la Grange, Paris, MDCC.LXXXVIII, Oeuvres 11
and 12. [Имеется перевод: Лагранж Ж. Аналитическая механика, т. 1 (изд.
2-е), т. 2. — М.-Л.: Гостехиздат, 1950.] [П.8], [III.0], [IV.4]
Лагранж (J.L.de Lagrange 1797, 1813):
Theorie des fonctions analytiques, contenant les principes du calcul differentiel,
degages de toute consideration dHnfiniment petits, d} evanouissans, de limites ou
de fluxions, et reduits a Vanalyse algebrique des quantites finies, A Paris, de
l'imprimerie de la republique, Prairial an V (1797), deuxieme edition: Gauthier-
Villars, 1813. [II. 1], [III.O], [111.6], [III.7]
Лагранж (J.L.de Lagrange 1867-1882):
Oeuvres, 14 volumes, ed. by J.-A.Serret et G.Darboux, Paris 1867-1882, reprinted
1973, Georg Olms Verlag Hildesheim. [1.1], [III. 7]
Ламберт (J.H.Lambert 1768):
Memoire sur quelques proprietes remarquables des quantites transcendantes circulai-
res et logarithmiques, Mem. Acad. sc. Berlin 17 (1768), p. 265-322, Opera II, p. 112-
159. [1.6]
Ламберт (J.H.Lambert 1770a):
Vorldufige Kenntnisse fur die, so die Quadratur und Rectification des Circuls
suchen, Berlin 1770, Opera I, p. 194-212. [Имеется перевод: Архимед, Гюйгенс,
Лежандр, Ламберт. О квадратуре круга. — М.: УРСС, 2003. — Ламберт И.Г.
Предварительные сведения для ищущих квадратуру и спрямление круга, с.
121-143.] [1.6]
Ламберт (J.H.Lambert 1770b):
Observations trigonometriques, Mem. Acad. sc. Berlin 24 (1770), p. 327-357, Opera
II, p. 245-269. [1.4]
Ламберт (J.H.Lambert 1770c):
Algebraische Formeln fur die Sinus von drey zu drey Graden, Berlin, 1770, Opera
I, p. 189-193. [1.4]
Ламберт (J.H.Lambert 1946, 1948):
Opera Mathematica, 2 volumes, Orell Fussli Verlag Zurich.
Ландау (E. Landau 1908):
Uber die Approximation einer stetigen Funktion durch eine ganze rationale Funkti-
on, Rendiconti di Palermo 25 (1908), p. 337-346; Collected Works 3, p. 402-410.
[III.9]
Ландау (E. Landau 1930):
Grundlagen der Analysis, Akad. Verlagsges. Leipzig (1930), 134 pp. American
editions with translated prefaces 1945, 1947, Chelsea Pub. Сотр. [Имеется перевод:
Ландау Э. Основы анализа. — М.: ИЛ, 1947.] [III. 1]
Лаплас (P.-S.de Laplace 1812):
Theorie analytique des probabilites, Paris, 1812, second edition 1814, third edition
1820. [Имеется перевод введения к последним изданиям: Лаплас П.С. Опыт
философии теории вероятностей. Популярное изложение основ теории
вероятностей и ее приложений. — М.: 1908.] [II.6]

366 Библиография
Лежандр (А.-М.Legendre 1794):
Elements de geometrie, first edition 1794, fouth edition 1806, many later editions.
[Имеется перевод: Лежандр A.M. Основания геометрии и тригонометрии. —
СПб: 1837.] [1.6]
Лейбниц (G.W. Leibniz1 1682):
De vera proportione circuli ad quadraturn circumscriptum in numeris rationalibus
expressa, Acta Eruditorum 1, 1682, p. 41-46. [14], [HI.2]
Лейбниц (G.W.Leibniz 1684):
Nova methodus pro maximis et minimis, itemque tangentibus, qu<E nee fractas,
nee irrationales quantitates moratur, & singulare pro illis calculi genus, Acta
Eruditorum 3, 1684, p. 467. [Имеется перевод: Избранные отрывки из
математических сочинений Лейбница. Успехи матем. наук, 1948, т. 3, вып. 1. — Новый
метод максимумов и минимумов, а также касательных, для которого не
служат препятствием ни дробные, ни иррациональные величины, и особый для
этого род исчислений, с. 166-173.] [1.2% [IIЛ], [II.2]
Лейбниц (G.W.Leibniz 1686):
De geometria recondita et analysi indivisibilium atque infinitorum, Acta Eruditorum
5, June 1686, p. 292-300. [Имеется перевод: Избранные отрывки из
математических сочинений Лейбница. Успехи матем. наук, 1948, т. 3, вып. 1. — О глубокой
геометрии и анализе неделимых, а также бесконечных, с. 175-177.] [1Ц]
Лейбниц (G.W.Leibniz 1689):
De linea isochrona in qua grave sine acceleratione descendit et de controversia cum
DN. Abbate D. C, Acta Eruditorum 8, 1689, p. 195. [IIЛ]
Лейбниц (G.W.Leibniz 1691):
Quadratura arithmetica communis sectionum conicarum quae centrumhabet, indeque
ducta trigonometria canonica ad quantamcunque in numeris exactis exactitudinem
a tabularum necessitate liberata, cum usu speciali ad lineam rhomborum nauticam,
aptatumque illi planisphaerium, Acta Eruditorum 10, April 1691, p. 178-182. [Ц]
Лейбниц (G.W.Leibniz 1691b):
De linea in quam flexile se pondere proprio curvat, ejusque usu insigni adinveniendas
quotcunque medias proportionales & logarithmos, Acta Eruditorum 10, 1691, p. 277-
281 and 435-439. [IIЛ]
Лейбниц (G.W.Leibniz 1693):
Supplementum geometrids dimensorice, seu generalissima omnium tetragonismorum
effectio per motum: similiterque multiplex constructio linea ex data tangentium
conditione, Acta Eruditorum 12, 1693, p. 385-392. [II.7]
Лейбниц (G.W. Leibniz 1694a):
Nova calculi differentialis applicatio et usus ad multiplicem linearum constructionem
ex data tangentium conditione, Acta Eruditorum 13, July 1694. [Имеется перевод:
Избранные отрывки из математических сочинений Лейбница. Успехи матем.
наук, 1948, т. 3, вып. 1. — Новое приложение и употребление
дифференциального исчисления к многообразному построению линий по данному свойству
касательных, с. 186-187.] [П.З], [IV.0]
Лейбниц (G.W.Leibniz 1694b):
Constructio propria problematis de curva isochrona paracentrica, ubi et generaliora
quaedam de natura et calculo differentiali osculorum, et de constructione linearum
transcendentium, una maxime geometrica, altera mechanica quidem, sed
generalissima. Accessit modus reddendi inventiones trans cendentium linearum universales, ut
quemvis casum comprehendant, et transeant per punctum datum, Acta Eruditorum
13, August 1694. [II.6]
Лейбниц (G.W.Leibniz 1702):
Specimen novum analyseos pro scientia infinita circa summas et quadraturas, Acta
Eruditorum 21, May 1702. [Имеется перевод: Избранные отрывки из
математических сочинений Лейбница. Успехи матем. наук, 1948, т. 3, вып. 1. — Новый
пример анализа для науки о бесконечном, относящийся к суммам и
квадратурам, с. 182-184.] [П.5]
Лейбниц обычно подписывал свои работы на латинском языке G. G. L. (Gothofredo
Gulielmo Leibnitio).

Библиография 367
Лейбниц (G.W.Leibniz 1710):
Symbolismus memorabilis calculi algebraici et infinitesimalis in comparatione potent-
iarum et differentiarum, et de lege homogeneorum transcendantali, Miscellanea
Berolinensia ad incrementum scientiarum, 1710. [IL2]
Лемер (D.H.Lehmer 1940):
On the maxima and minima of Bernoulli polynomials, Amer. Math. Monthly 47
(1940), p. 533-538. [11.10]
Лерх (M.Lerch 1888):
Uber die Nichtdifferentiirbarkeit gewisser Functionen, J. Reine und Angew. Math.
(Crelle) 103 (1888), p. 126-138. [III.7]
Лиувилль (J.Liouville 1835):
Memoire sur Vintegration d'une classe de fonctions transcendantes, J.Reine und
Angew. Math. (Crelle) 13 (1835), p. 93-118. [11.6]
Лиувилль (J.Liouville 1841):
Remarques nouvelles sur I'equation de Riccati, J.de Math, pures et appl. (Liouville)
6 (1841), p. 1-13. [II.9]
Лохе (G. Lochs 1963):
Die ersten 968 Kettenbruchnenner von n, Monatsh. f. Math. 67 (1963) p. 311-316.
[i.6]
Лопиталь, де (G.de L'Hospital 1696):
Analyse des infiniment petits, pour Pintelligence des lignes courbes, A Paris, de
PImprimerie Royale. M.DC.XCVI. [Имеется перевод: Лопиталь Г.Ф. де. Анализ
бесконечно малых. — М.-Л.: ГТТИ, 1935.] [Ill], [III.6]
Люрот (J.Luroth 1873):
Bemerkung uber gleichmassige Stetigkeit, Math. Ann. 6 (1873) p. 319-320. [III.4]
Маклорен (C.Maclaurin 1742):
A treatise of fluxions, in two books, Edinburgh, MDCCXLII. [II.1], [П.2], [11.10],
[IIL8]
Мейнардус (G.Meinardus 1964):
Approximation von Funktionen und ihre numerische Behandlung, Springer Tracts
in Nat. Phil., 180 pp., Springer, 1964, English transl., Springer, 1967. [III.9]
Мере (Ch.Meray 1872):
Nouveau precis d'analyse infinitesimale, Paris, 1872. [III.l]
Меркатор (N.Mercator (= Kaufmann) 1668):
Logarithmo-technica; sive methodus construendi logarithmos nova, accurata, et
facilis; written 1667, published London, 1668. [1.3]
Мертенс (F.Mertens 1875):
Ueber die Multiplicationsregel fur zwei unendliche Reihen, J. Reine und Angew.
Math. (Crelle) 79 (1875), p. 182-184. [III.2]
Миел (G.Miel 1983):
Of calculations past and present: the Archimedean algorithm, Amer. Math. Monthly
90 (1983), p. 17-35. [1.4]
Муавр, де (A.de Moivre 1730):
Miscellania analytica de seriebus et quadraturis, Londini, 1730. [1.4]
Henep (J.Napier 1614):
Mirifici logarithmorum canonis descriptio, Edinburgi, 1614. [1.3]
Henep (J.Napier 1619):
Mirifici logarithmorum canonis constructio, Edinburgi 1619, Engl, translation: The
construction of the wonderful canon of logarithms, by William Rae MacDonald,
1888. [1.3]
Нотари (V.Notari 1924):
L'equazione ai quarto grado, Periodico di Matematiche, Ser. 4, vol.4 (Bologna
1924), p. 327-334. [1.1]
Ньютон (I.Newton 1665):
Annotations from Wallis, manuscript of 1665, published in The mathematical papers
of Isaac Newton 1, Cambridge University Press, 1967. [Имеется перевод: Ньютон
И. Математические работы. — М.-Л.: ОНТИ, 1937. — Извлечение из двух
писем Ньютона к Дж. Валлису, с. 256-264.] [1.2], [П.2]

368 Библиография
Ньютон (I.Newton 1669):
De analyst per dsquationes numero terminorum infinitas, manuscript of 1669,
published in Newton (1711) by W.Jones, p. 1-21; Works 2, p. 165-173. [Имеется
перевод: Ньютон И. Математические работы. — М.-Л.: ОНТИ, 1937. — Анализ
с помощью уравнений с бесконечным числом членов, с. 3-24.] [1.3], [1.4]
Ньютон (I.Newton 1671):
Methodus Fluxionum et Serierum Infinitarum, manuscript of 1671, published
"translated from the author's Latin original not yet made publick, London 1736";
Opuscula mathematica, vol. I; French translat. "par M.de Buffon, Paris MDCCXL";
facsimile reprint Ed. Albert Blanchard, Paris, 1966. [Имеется перевод: Ньютон И.
Математические работы. — М.-Л.: ОНТИ, 1937. — Метод флюксий и
бесконечных рядов, с. 25-166.] [1.2], [1.3], [1.4], [П.1], [11.2], [П.З], [II.6]
Ньютон (I.Newton 1676):
Methodus differentialis, manuscript mentioned in a letter of Oct. 1676 to Oldenburg,
published in Newton (1711) by W.Jones, p. 93-101. [Имеется перевод: Ньютон И.
Математические работы. — М.-Л.: ОНТИ, 1937. — Метод разностей, с. 210-
217.] [1.1]
Ньютон (I.Newton 1686):
Philosophic naturalis principia mathematica, Autore IS. NEWTON, Londini, 1686,
second edition 1713, third edition 1726, English transl. 1803, French transl. "par feue
Madame la Marquise du Chastellet" a Paris, 1756. [Имеется перевод: Ньютон И.
Математические начала натуральной философии. — М.: Наука, 1989.] [II. 1]
Ньютон (I.Newton 1711):
Analysis per quantitatum series, fluxiones, ac differentias, published by W.Jones,
London 1711. [1.4]
Ньютон (I.Newton (1736): см. Ньютон (1671).
Пармантье (M. Parmentier 1989):
G. W. Leibniz, la naissance du calcul differentiel, 26 articles des Acta Eruditorurn,
Mathesis, Paris, Librairie Philosophique J.Vrin, 1989. [II.1]
Паскаль (B.Pascal 1654):
Traite du triangle arithmetique, avec quelques autres petits traitez sur la mesme
matiere, written 1654, published posthumously, Paris, 1665. [1.2]
Паскуале, ди (L.di Pasquale 1957):
Le equazioni di terzo grado nei "Questi et inventioni diversev di Nicolo Tartaglia,
Periodico di Matematiche, Ser. 4, vol.35 (Bologna 1957), p. 79-93. [1.1]
Пеано (G.Peano 1884):
"Annotazioni" al trattato di calcolo del 1884, (see Genocchi & Peano 1884), Opere
scelte I, p. 47-73. [IV.2], [IV.4]
Пеано (G.Peano 1888):
Calcolo geometrico, secondo VAusdehnungslehre di H. Grassmann, Torino 1888;
German edition: Die Grundzuege des geometrischen Calculs, Teubner Leipzig, 1891;
see also: Math. Annalen 32 (1888), p. 451. [IV.0]
Пеано (G.Peano 1888a):
Integration par series des equations differentielles lineaires, Math. Annalen 32
(1888), p. 450-456. [IV.1], [IV.2]
Пеано (G.Peano 1890):
Sur une courbe, qui remplit toute une aire plane, Math. Annalen 36 (1890), p. 157-
160. [IV.2]
Пеано (G.Peano 1890b):
Demonstration de Vintegrabilite des equations differentielles ordtnaires, Math.
Annalen 37 (1890), p. 182-228. [IV.1]
Пеано (G.Peano 1957-1959):
Opere scelte, 3 volumes, Edizioni Cremonese, Roma 1957-1959. [IV.4]
Перрон (О.Perron 1913):
Die Lehre von den Kettenbruchen, Teubner Leipzig und Berlin, 520 pp., many later
editions. [1.6]
Пикар (E.Picard 1890):
Traite d'Analyse, tome I, Gauthier-Villars, Paris 1890, 2eme edition 1901. [III.9]
Прингсгейм (A.Pringsheim 1893):
Zur Theorie der Taylor'schen Reihe und der analytischen Functionen mit beschrdnk-
tem Existenzbereich, Math. Annalen 42 (1893), p. 153-184. [Ш.7]

Библиография 369
Прингсгейм (A. Pringsheim 1899):
Grundlagen der allgemeinen Funktionenlehre, in: Encyklopddie der math. Wiss.
II.1.1, (1899), p. 1-53. [III.3], [III.4]
Птолемей (CI. Ptolemy ~ 150):
це^аХт] ovvtol^i^ (— Great Collection = Almagest = Al ^е^ьстт]), latin translation
G.Peurbach & Regiomontanus (Epitoma almagesti per Magistrum Georgium de
Peurbach et eius Discipulum Magistrum Jo.de Kunigsperg ...), completed 1462,
printed 1496. [Имеется перевод: Птолемей Клавдий. Альмагест или
математическое сочинение в тринадцати книгах. — М.: Наука. Физматлит, 1998.] [1.4]
Рам, де (G.de Rham 1957):
Sur ип exemple de fonction continue sans derivee, L'Enseignement Mathematique
3, (1957), p. 71-72; Oeuvres, p. 714-715. [111.9]
Региомонтан (J. Regiomontanus = Johannes Muller from Konigsberg 1464):
De triangulis omnimodis libri quinque, written 1464, printed 1533. [1.4]
Риккати (J.Riccati 1712):
Soluzione generale del Problema inverso intorno a raggi osculatori,.., determinar la
curva, a cui convenga una taVespressione, Giornale de'Letterati d'ltalia, 11 (1712),
p.204-220. [II.7]
Риман (B.Riemann 1854):
Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe, Habilit-
ation thesis, Gottingen, 1854, Werke, p. 227-271. [Имеется перевод: Риман Б.
Сочинения. — М.-Л.: Гостехиздат, 1948. — О возможности представления
функции посредством тригонометрического ряда, с. 225-261.] [III.2/, [III.5]
Ричерт (N.Richert 1992):
Strang's strange figures, Amer. Math. Monthly 99, Nr. 2, p. 101-107. [1.4]
Роберт из Честера (Robert of Chester 1145):
Liber algebre et almuchabolae de questionibus arithmeticis et geometricis, first latin
translation of Al-Khowarizmi's Al-jabr, new critical edition: B.B.Hughes, Steiner
Verlag Wiesbaden, Stuttgart, 1989. [1.1]
Розен (F.Rosen 1831):
The Algebra of Mohammed ben Musa, Edited and translated by Frederic Rosen,
London 1831, reprinted Georg Olms Verlag, 1986. [1.1]
Рол ль (M.Rolle 1690):
Traite d Algebre, ovprincipes generaux pour resoudre les questions de Mathematique,
Livre second, Chap. VI, p. 124f. (1690). [III.6]
Серпиньский (W. Sierpinski 1915):
Sur une courbe dont tout point est un point de ramification, published in Polish in
Prace Mat.-Fiz.27 (1916), p. 77-86; French summary: C.R. 160 (1915), p. 302-305;
French transl. Oeuvres choisies, vol.11, p. 99-106. [IV. 1]
Серпиньский (W. Sierpinski 1916):
Sur une courbe cantorienne qui contient une image biunivoque et continue de toute
courbe donnee, French summary: C.R. 162 (1916), p. 629-632. French transl. Oeuvres
choisies, vol. II, p. 107-119. [Имеется оригинал: Серпиньский В.К. О кривой,
содержащей в себе образ всякой кривой. Математический сборник, 1916, т. 30,
вып. 2, с. 267-287. — М.: Изд. Моск. матем. общ-ва.] [IV.1]
Серре (J.A.Serret 1868):
Cours de calcul differentiel et integral, Paris, 1868 (see in particular p. 17-19),
German transl. Teubner, 1884. [Имеется перевод: Серре И.А. Курс
дифференциального и интегрального исчислений. — СПб: Типография Товарищества
М.О.Вольф, 1903.] [III.6], [IV.4]
Симпсон (T.Simpson 1743):
Math, dissertations on a variety of physical and analytical subjects London,
1743. [II.6]
Стеклов (V.Steklov 1918):
Remarques sur les quadratures, Bull.de l'Acad. des Sciences de Russie (6), vol. 12,
(1918), p. 99-118 (Петроград, Изв. Акад. наук, серия 6, 1918, т. 12, с. 99-118).
[II.6]
Стирлинг (J.Stirling 1730):
Methodus differentialis: sive tractatus de summatione et interpolatione serierum
infinitarum, Londini, MDCCXXX. [11.10]

370 Библиография
Стройк (D.J.Struik 1969):
A source book in mathematics 1200-1800, Harvard University Press, Cambridge,
Mass., 1969. [Имеется перевод: Стройк Д.Я. Краткий очерк истории
математики, изд. 5-е, испр. — М.: Наука, Физматлит, 1990.] [II. 1], [112], [III.2]
Стрэнг (G.Strang 1976):
Linear algebra and its applications, Academic Press, New York, 1976, 374 pp.
[Имеется перевод: Стрэнг Г. Линейная алгебра и ее применения. — М.: Мир, 1980.]
[IV.5]
Стрэнг (G.Strang 19911:
Calculus, Wellesley-Cambridge Press, Wellesley, Mass., 1991. [1.4]
Такаги (T.Takagi 1903):
A simple example of the continuous function without derivative, Tokio math. soc. 1
(1903), p. 176-177. [III.9]
Тейлор (B.Taylor 1715):
Methodus incrementorum directa & inversa, Auctore Brook Taylor, LL.D. & Regiae
Societatis Secretario, Londini, MDCCXV. [II.2]
Толл (D.Tall 1982):
The blancmange function, continuous everywhere but differentiable nowhere, Math.
Gazette 66, Nr.435 (1982), p. 11-22. [III. 9]
Уэстфол (R.S.Westfall 1980):
Never at rest; a biography of Isaac Newton, Cambridge Univ. Press, 908 pp. [1.4]
Фельман (E.A. Fellmann 1983):
Leonhard Euler, ein Essay uber Leben und Werk, in: Leonhard Euler 1707-1783,
Gedenkband des Kantons Basel-Stadt, Birkhauser Verlag Basel, 1983. [11.10]
Ферма (P.Fermat 1636):
De Aequationum localium transmutatione et emendatione ad multimodam curviline-
orum inter se vel cum rectilineis comparationem, cui annectiturproportionis geomet-
ricae in quadrandis infinitis parabolis et hyperbolis usus, Oeuvres, vol. 1, p. 255-288;
french transl. Oeuvres, vol.3, p. 216. [1.3]
Ферма (P.Fermat 1638):
Methodus ad disquirendam maximam et minimam, Oeuvres vol. 1, p. 133-179; french
translation Oeuvres, vol.3, p. 121-156. [Имеется перевод: Декарт P. Геометрия:
с приложением избранных работ П. Ферма и переписки Декарта. — М.-Л.:
ОНТИ, 1938. — Ферма П. Метод отыскания наибольших и наименьших
значений, с. 154-157.] [II.2]
Ферма (P.Fermat 1891, 1894, 1896):
Oeuvres, 3 volumes, Gauthier-Villars Paris.
Ферхюльст (P.F. Verhulst 1845):
Recherches mathematiques sur la loi d'accroissement de la population, Nuov. Mem.
Acad. Roy. BruxeUes, 18 (1845), p.3-38. [II.7]
Фонсене, де (D.de Foncenex 1759):
Reft exions sur les quantites imaginaires, Miscellanea Phil.-Math. Soc. Taurinensis,
1 Torino, 1759, p. 113-146. [1.4]
Френель (A.Fresnel 1818):
Memoire sur la diffraction de la lumiere, Mem. Acad. sc. 5, Paris, 1818, p. 339. [116]
Френель (A.Fresnel 1818):
Memoire sur la diffraction de la lumiere, Mem. Acad. sc. 5, Paris, 1818, p. 339. [II.6]
Фреше (M.Frechet 1906):
Sur quelques points du calcul fonctionnel, Palermo Rend. 22, p. 1-74, These Paris,
1906. [IV. 1], [IV.3]
Фурье (J.B.J.Fourier 1822):
La theorie analytique de la chaleur, Paris, 1822; a manuscript of 1807 entitled Sur
la propagation de la chaleur was not published due to objections of Lagrange. [1Ц]
Хайрер, Нёрсетт, Ваннер (E. Hairer, S.P. N0rsett, G. Wanner 1993):
Solving ordinary differential equations I. Nonstiff problems, Springer-Verlag Berlin
Heidelberg, 1987, Second edition 1993, 528 pp. [Имеется перевод: Хайрер Э.,
Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений.
Нежесткие задачи. — М.: Мир, 1990.] [II.9]
Халмош (P.R. Halmos 1958):
Finite-dimensional vector spaces, Second edition, Van Nostrand, 1958, Springer

Библиография 371
UTM, 1974, 200 pp. [Имеется перевод: Халмош П. Конечномерные векторные
пространства. — М.: Физматгиз, 1963.] [IV.4]
Хаусдорф (F.Hausdorff 1914):
Grundzuge der Mengenlehre, dem Schopfer der Mengenlehre HERRN GEORG
CANTOR in dankbarer Verehrung gewidmet, Leipzig, 1914; English translation:
Chelsea, 1957. [Имеется перевод: Хаусдорф Ф. Теория множеств, изд. 2-е, испр.
— М.: УРСС, 2004.] [IVЛ], [IV.2]
Хаяси (T.Hayashi 1902):
The values of тг used by the Japanese mathematicians of the 17th and 18th centuries,
Bibliotheca mathematica, ser. 3, 3 (1902), p. 273-275. [1.6]
Хорезми, аль- (Al-Khowarizmi 830):
Al-jabr w'al muqdbala, see: Robert of Chester (1145) and F.Rosen (1831).
[Имеется перевод: Хорезми Мухаммад аль-. Математические трактаты. — Ташкент:
Наука, 1964. — Об исчислении алгебры и альмукабалы, с. 25-93.] [1.1]
Цейлен, ван (L.van Ceulen 1596, 1616):
Van de Circkel, daarin geleert wird te finden de naeste proportie des Circkels
diameter tegen synen Omloop, Delft. [1.4]
Шварц (H.A.Schwarz 1873):
Ueber ein vollstdndiges System von einander unabhangiger Voraussetzungen zum
Beweise des Satzes -$- ( q^ ) = -§^ ( q )> Verhandlungen der Schweizerischen
Naturf. Ges. (1873), p. 259-270; Werke 2, p. 275-284. [IV.4]
Шварц (H.A.Schwarz 1885):
Ueber ein die Fldchen kleinsten Fldcheninhaltes betreffendes Problem der Variations-
rechnung, Acta soc.scient. Fenn. 15 (1885), p. 315-362; Werke 1, p. 223-269. [III.5]
Шенкс и Ренч (D. Shanks & J.W. Wrench Jr. 1962):
Calculation of ж to 100000 decimals, Math.Comp. 16 (1962), p. 76-99. [1.4]
Шписс (O.Spiess 1929):
Leonhard Euler, Ein Beitrag zur Geistesgeschichte des XVIII. Jahrhunderts, Verlag
von Huber, Prauenfeld, Leipzig, 1929. [II.8], [11.10]
Штифель (M.Stifel 1544):
Arithmetica integra, Nurnberg, 1544. [1.2], [1.3]
Штольц (O.Stolz 1879):
Ueber die Grenzwerthe der Quotienten, Math. Ann. 14 (1879), p. 231-240.
Штольц (O.Stolz 1881):
B. Bolzano's Bedeutung in der Geschichte der Infinitesimalrechnung, Math. Ann. 18
(1881), p. 255-279. [III.l]
Штольц (O.Stolz 1886):
Die gleichmassige Convergenz von Functionen mehrerer Verdnderlichen zu den
dadurch sich ergebenden Grenzwerthen, dass einige derselben constanten Werthen
sich nahern, Math. Ann. 26 (1886), p. 83-96. [IV. 5]
Штольц (O.Stolz 1887):
Bemerkungen zur Theorie der Functionen von mehreren unabhangigen
Verdnderlichen, Innsbrucker Berichte; see also O. Stolz, Grundzuge der Differential- und Integral-
rechnung, Teubner Leipzig, 1893. [IV.3]
Эйлер (L. Euler 1734):
Additamentum ad dissertationem de infinitis curvis eiusdem generis, Comm. acad.
scient. Petrop.7 (1734/5), 1740, p. 184-200; Opera 22, p. 57-75. [III.3]
Эйлер (L. Euler 1736):
Methodus universalis series summandiulteriuspromota, Comm. acad. scient. Petrop.,
vol. 8, p. 147-158; Opera Omnia, vol. XXIV, p. 124-137. [11.10]
Эйлер (L.Euler 1736b):
Mechanica, sivemotus scientia analytice exposita: instar supplementi ad comrnentar,
Acad, scient. Petrop. 1736; Opera Omnia, Ser. 2, vol. I-II. [1.2] [III.0]
Эйлер (L. Euler 1737):
De variis modis circuli quadraturam numeris proxime exprimendi, Comm. acad.
scient. Petrop. 9 (1737), p. 222-236; Opera 14, p. 245-259. [1.4]
Эйлер (L. Euler 1737b):
De fractionibus continuis dissertatio, Comm.acad.se. Petrop. 9 (1737), p. 98-137;
Opera 14, p. 187-215. [Имеется перевод: Эйлер Л. Введение в анализ бесконеч-

372 Библиография
ных, т. 1 (изд. 2-е). — М.: Физматгиз, 1961. — О непрерывных дробях, с. 269-
286.] [1.6]
Эйлер (L.Euler 1740):
De summis serierum reciprocarum, Comm. ас. sc. Petrop. 7 (1734/5), 1740, p. 123-
134; Opera 14, p. 73-86. [1.5]
Эйлер (L.Euler 1743):
De summis serierum reciprocarum ex potestatibus numerorum naturalium ortarum
dissertatio altera in qua eaedem summationes ex fonte maxime diverso derivantur,
Miscellanea Berolinensia 7 (1743), p. 172-192; Opera 14, p. 138-155. [1.5]
Эйлер (L.Euler 1743b):
De integratione aequationum differentialium altiorurn graduum, Miscellanea
Berolinensia, vol. 7, p. 193-242; Opera Omnia, vol. XXII, p. 108-149. See also: Letter from
Euler to Joh. Bernoulli, 15. Sept. 1739. [II.8]
Эйлер (L.Euler 1744):
Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive
solutio problematis isoperimetrici latissimo sensu accepti, Lausannae & Genevae,
Opera Omnia (intr. by Caratheodory), vol. XXIV, p. 1-308. [Имеется перевод:
Эйлер Л. Метод нахождения кривых линий, обладающих свойством максимума
или минимума, или решение изопериметрической задачи, взятой в самом
широком смысле. — М.: ГТТИ, 1934] [III.0]
Эйлер (L.Euler 1748):
Introductio in analysin infinitorum, Tomus primus, Lausannae MDCCXLVIII, Opera
8. French transl. 1785, 1796; German transl. 1788, 1885 (reprinted Springer 1983);
English transl. Blanton (1988). [Имеется перевод: Эйлер Л. Введение в анализ
бесконечных, т. 1-2. — М.: Физматгиз, 1961.] [1.0], [1.2], [1.3], [1.4], [1.5], [1.6],
[II 1.0], [II 1.3]
Эйлер (L.Euler 1750):
Animadversiones in rectificationem ellipsis, Opuscula varii argumenti 2 (1750),
p. 121-166; Opera 20, p. 21-55. [II.6]
Эйлер (L.Euler 1750b):
Methodus aequationes differentials altiorum graduum integrandi ulterius promota,
Novi Comment, acad. scient. Petrop., vol. 3, p. 3-35; Opera Omnia, vol. XXII, p. 181-
213. [II. 8]
Эйлер (L.Euler 1751):
De la controverse entre Mrs. Leibniz et Bernoulli sur les logarithmes des nombres
negatifs et imaginaires, Mem.ac.sc.Berlin 5 (1751), p. 139-179; Opera 17, p. 195-
232. [1.5]
Эйлер (L.Euler 1755):
Institutiones calculi differentialis cum eius vsu in analysi finitorum ac doctrina
serierum, Imp. Acad. Imper. Scient. Petropolitanae, Opera 10. [Имеется перевод:
Эйлер Л. Дифференциальное исчисление. — М.-Л.: Гостехиздат, 1949.] [1.2],
[1.5], [ИЛ], [П.2Ъ [H-10L [Ш.0], [Ш.8], [IV.4]
Эйлер (L.Euler 1755b):
Principes generaux du mouvement des fluides, Mem. ac. sc. Berlin 11 (1755), p. 274-
315; Opera Ser. II, 12, p. 54-91. [Имеется перевод: Эйлер Л. Общие законы
движения жидкостей. Известия РАН. Механика жидкости и газа. 1999, 6, с. 26-54.1
[III.0]
Эйлер (L.Euler 1768):
Institutiones Calculi Integralis, Volumen Primum, Opera 11. [Имеется перевод:
Эйлер Л. Интегральное исчисление, т. 1. — М.: Гостехиздат, 1956.] [II.4], [II.5],
[II. 9], [II 1.0], [II 1.7]
Эйлер (L.Euler 1769):
Institutiones Calculi Integralis, Volumen Secundum, Opera 12. [Имеется перевод:
Эйлер Л. Интегральное исчисление, т. 2. — М.: Гостехиздат, 1957.] [II.8], [II 1.0]
Эйлер (L.Euler 1769b):
De formulis integralibus duplicatis, Novi comm. acad. scient. Petrop. 14 (1769): I,
1770, p. 72-103; Opera 17, p. 289-315. [IV.5]
Эйлер (L.Euler 1770):
Vollstandige Anleitung zur Algebra, von Hrn. L. Euler, St. Petersburg, gedruckt bey
der Kays. Acad, der Wissenschaften, 1770; Opera 1. [1.1], [III.0]

Библиография 373
Эйлер (L.Euler 1911-):
Opera Omnia, more than 80 volumes in 4 series, series I contains the mathematical
works, Teubner Leipzig und Berlin, later Fussli, Zurich. [1.1], [III.O], [III.8]
Эрмит (Ch.Hermite 1873):
Cours d'Analyse de VEcole Poly technique, Paris, Gauthier-Villars, 1873; Oeuvres
3, p. 35-54. [Имеется перевод: Эрмит Ш. Курс анализа. — Л.-М.: ОНТИ, 1936.1
[II.5]
Якоби (C.G.J.Jacobi 1827):
De singulari quadam duplicis integralis transformatione, J. Reine und Angew. Math.
(Crelle) 2 (1827), p. 234-242; Werke 3, p.57-66. [ILS]
Якоби (C.G.J.Jacobi 1834):
De usu legitimo formulae surnmatoriae Maclaurinianae, J. Reine und Angew. Math.
(CreUe) 12 (1834), p. 263-272; Werke 6, p. 64-75. [11.10]
Якоби (C.G.J.Jacobi 1841):
De determinantibus functionalibus, J. Reine und Ang. Math. (Crelle) 22 (1841),
p. 319-359; Werke 3, p. 393-438. [IV.5/, [IV.5]
Якоби (C.G.J.Jacobi 1881-1891):
Gesammelte Werke, 8 volumes, ed. by C.W. В orchard t, Berlin, 1881-1891, new
edition Chelsea New York, 1969. [1.1], [IV. 5]

Указатель обозначений
о
А множество внутренних точек А 285
А замыкание А 285
ao + «i + a2+ бесконечный ряд 188
(а, 6) открытый интервал 202
[а, Ь] замкнутый интервал (отрезок) 202
а + ib комплексное число 57
arccos х функция арккосинус 49
arcsin х функция арксинус 49
arctg х функция арктангенс 49
arch х функция, обратная гиперболическому косинусу 56
arsh х функция, обратная гиперболическому синусу 56
В(а,/3) бета-функция 347
В£ (а) круг (или шар) радиуса е с центром а 278
Bk число Вернул л и 161
Bk{x) полином Бернулли 163
cos ж функция косинус 41
ch х функция гиперболический косинус 56
ctgx функция котангенс 41
D разбиение интервала 221
det определитель 340
dx, dy бесконечно малые величины 82
d(x,y) расстояние между х и у 273
dy/dx производная от у 82
е число Эйлера 26
ех показательная функция 27
ехр х показательная функция 27
/(17) образ множества U 294
/_1(V) прообраз множества V 294
Г{х) производная функции f(x) 84
f"(x) вторая производная от /(ж) 91
рк>(х) к-я производная от f(x) 94
grad/ градиент / 305
inf X наибольшая нижняя граница (точная нижняя грань)
С(у) дифференциальный оператор 144
limn->оо $п предел последовательности 173
linLr-^o /(ж) предел функции 209
limmfn-j-oo sn наименьшая точка накопления, или нижний предел
limsupyj^^ sn наибольшая точка накопления, или верхний предел
In х натуральный логарифм (logarithmus naturalis) 35
loga х логарифм по основанию а 30
п! факториал п 20
(п.) биномиальные коэффициенты 20
Q множество рациональных чисел 178

Указатель обозначений 375
Шп множество всех n-мерных векторов 273
|з| абсолютная величина действительного числа 180
s(D) нижняя сумма Дарбу 222
S(D) верхняя сумма Дарбу 222
sin ж функция синус 41
sh х функция синус гиперболический 56
{sn} (бесконечная) последовательность 172
supX наименьшая верхняя граница (точная верхняя грань) 182
tg х функция тангенс 41
th х функция гиперболический тангенс 78
х G А х является элементом множества А 204
(ei, ..., хп) вектор (п-мерный) 273
у' производная у 84
уп вторая производная у 91
Ауо, ^2Уо> • • • конечные разности 12
<рп(х) последовательность Дирака 266
Ф(х) интеграл ошибок 133
7 постоянная Эйлера 168
Г (а) гамма-функция Эйлера 261
к, кривизна 102
/i(7) мера прямоугольника / 330
7г длина единичной полуокружности 40
д радиус сходимости 248
ЭА граница множесива А 336
df/dxi частная производная 300
V/ градиент / (набла) 305
\\А\\2 норма матрицы 294
||z||i ^i-норма z 275
||z||2 евклидова норма z 21А
\\z\\p ^р-норма z 275
\\zWoq максимум-норма z 21Ъ
Yy^oai Yli>oai бесконечный ряд 188
/ f(x) dx первообразная f(x) или неопределенный интеграл 108
Ja f(x) dx интеграл f(x) 108
Jj /(ж? У) ^(ж? У) двойной интеграл 331
А С В А является подмножеством В 278
А П В пересечение множеств А и В 278
A U В объединение множеств А и В 278
А\В разность множеств 278
ZA дополнение множества А 278
V квантор "для всех" 172
3 квантор "существует" 172
<, < отношение порядка 179

Алфавитный указатель
Абель Н.Х. (Abel, N.H.) 126, 171, 188,
199, 213, 245, 355, 358
Абеля теорема (Abel's theorem) 250 и д.
Або A. (Aaboe, А.) 47, 358
Абсолютная величина (absolute value)
172, 180
комплексного числа (~~ of complex
~) 59
— сходимость (~ convergence) 192
Адамар Ж. (Hadamard, J.) 61, 250, 358
Алгебра (Algebra) 2
"Алгебра Нова" (Algebra Nova) 6 и д.
Александрия (Alexandria) 2
"Аль-джебр ва-л-мукабала" (Al-jabr w'al
muqabala) 2
Аль-Каласади (Alkalsadi) 22
Аль-Каши (Al-Kashl) 48
"Альмагест" (Almagest) 40
Аль-Хорезми — см. Хорезми
Ампер А.-М. (Ampere, А.-М.) 263
Антисимметричность (antisymmetry) 179
Аполлоний (Apollonius) 2, 8
Архимед (Archimedes) 2, 33, 49, 52, 73,
107, 358
Арган (Argand) 58
Аргумент комплексного числа (argument
of complex number) 59
Ареафункции (area functions) 56
Арима И. (Arima, Y.) 73
Аристотель (Aristotle) 2
Арифметическая прогрессия (arithmetic
progression) 34, 172
Арнольд В.И. (Arnold, V.I.) 60 и д.
"Ars Magna" 4 и д., 57
Асимптотические разложения
интегралов (asymptotic expansions of integrals)
130 и д.
Баллистические кривые (ballistic curves)
101
Барроу (Barrow) 28, 51, 358
Беркли, епископ (Berkeley (Bishop)} 83, 91
Бернулли Даниил (Bernoulli, Daniel) 134
Бернулли Иоганн (Bernoulli, Johann)
38, 60, 62 и д., 81 и д., 89, 91, 93,
97 и д., 104, 106, 116, 118 и д., 125, 132,
134 и д., 140, 142 и д., 145, 154, 163,
168, 202, 243, 351 и д., 355, 358 и д.
Бернулли Якоб (Bernoulli, Jacob) 28, 46,
82, 107, 133 и д. 140, 162, 314, 359
Бернулли многочлены (Bernoulli's
polynomials) 163
— числа (~ numbers) 14, 47, 161 и д.
Бесконечная последовательность (infinite
sequence) 172
Бесконечный ряд (~ series) 188, 245
Бета-функция (beta function) 347
Биективная функция (bijective ~) 208
Билинейное отображение (bilinear
mapping) 321
Биномиальная теорема (binomial
theorem) 18 и д., 23 и д., 253
Биномиальный коэффициент
(~ coefficient) 20
Бисекция (bisection) 182
"Бланманже" функция (blancmange
function) 264 и д.
Блантон Дон:.Д. (Blanton, J.D.) 1, 359
Бодлеевская библиотека (Bodleian
Library) 2
Больцано Б. (Bolzano, В.) 84, 170, 182,
204, 206, 213, 359
Бомбелли (Bombelli) 17, 69
Бонне О. (Bonnet, О.) 240
Борель Э. (Borel, Е.) 265 и д., 283, 357,
359
Брахистохрона (brachistochrone) 137 и д.,
142
Брахмагупта (Brahmagupta) 40
Бриггс Г. (Briggs, Н.) 22, 29 и д., 38, 359
Брункер, лорд [Lord Brouncker) 69, 75
Бук Р.К. (Buck, R.C.) 123, 360
Буняковский В. (Bunyakovski, V.) 229, 360
Бюрги И. (Burgi, J.) 29, 360
Вавилон (Babylon) 22, 28, 40, 123
Валлис Дон:. (Wallis, J.) 23. 66, 68 и д., 72,
79, 360
Валлиса произведение (Wallis's product)
65 и д., 167, 233 и д.

Алфавитный указатель 377
Ван-дер-Поль Б. (Van der Pol, В.) 159
Ваннер Г (Wanner, G.) 134, 155, 360, 370
Варден, ван дер (Waerden, van der)
21 и д., 29, 351, 360
Вариация постоянных (variation of
constants) 150 и д.
Вейерштрасс К. (Weierstrass, К.) 84, 126,
171, 177, 184, 203 и д., 206 и д., 213,
215 и д., 218, 230, 235, 253, 263 и д.,
278, 300, 302, 309, 354 и д., 360
Вейерштрасса аппроксимационная
теорема (Weierstrass's approximation theorem)
265 и д.
— критерий (~ criterion) 216 ид.
Вейль Андре (Weil, Andre) 1
Вектор (vector) 272 и д.
Векторное пространство (~ space) 273
Верхний интеграл (upper integral) 223
Виет Ф. (Viete, F.) 6 и д., 10, 21, 52, 63,
67, 351, 360
Виеторис Л. (Vietoris, L.) 43, 351
Виртингер В. (Wirtinger, W.) 163, 360
Внутренность множества (interior of а
set) 285
Возрастающая функция (increasing
function) 91, 184, 208
Вычисление логарифмов (computation of
logarithms)
, Бриггс (~~, Briggs) 31 и д.
, Грегори (~~, Gregory) 36 и д.
, Ньютон (~~, Newton) 39
Галилей Г. (Galilei, G.) 81, 134, 136 и д. ,
202, 361
Галлей Э. (Halley, Е.) 52, 96, 361
Гамильтон У.Р. (Hamilton, W.R.) 272,
305, 361
Гамма-функция (gamma function)
261 и д., 346
Гандель Г.Ф. (Handel, G.F.) 60
Гармонический ряд (harmonic series) 167,
191
Гаусс К.Ф. (Gauss, C.F.) 54, 58 и д., 79,
170, 206, 263, 361
Гаусса интеграл (Gaussian integral)
345 и д.
Гейне Э. (Heine, Е.) 79, 171, 177, 217, 219,
230, 283 и д., 290, 354 и д., 361
Гёльдер О. (Holder, О.) 361
Гёльдера неравенство (Holder's inequality)
275, 327
Генеалогическое дерево
фундаментальной теоремы (genealogical tree of
fundamental theorem) 242
Геометрическая последовательность
(geometric sequence) 34, 172, 174
— прогрессия, геометрический ряд
(geometric series) 21, 33, 188 и д.
Геометрия (geometry) 8
Герхард Кремона (Gerhard Cremona) 2
Гессе О. (Hesse, О.) 361
Гессиан, матрица (Hessian matrix) 325
Гиббс Дою.У. (Gibbs, J.W.) 305, 361
Гильберт Д. (Hilbert, D.) 206, 264, 278,
291, 355, 357, 361
Гиперболические логарифмы (hyperbolic
logarithms) 30
— функции (~ functions) 56
Гиппарх (Hipparchus) 40
Гиппий (Hippasus) 44
Главные ветви (principal branches) 49
Голдстайн ГГ. (Goldstine, Н.Н.) 10, 361
Градиент (gradient) 305 и д.
Градгигпейн И.С. (Gradshteyn, I.S.) 109,
361
Граница наибольшая нижняя (greatest
lower bound) 184
— наименьшая верхняя (least upper ~)
182
Грассман Г (Grassmann, Н.) 271 и д.,
287, 357, 361 и д.
Грёбнер В. (Grobner, W.) 109, 362
Грегори Дэн:. (Gregory, J.) 37 и д., 49, 62,
107, 362
Грегори из Сент-Винсента (Gregory of
St. Vincent) 35, 107
Григорий XIII, папа (Gregory (Pope
G.XIII)) 78
Гурвиц A. (Hurwitz, A.) 69, 362
Гюйгенс X. (Huyghens, C.) 52, 81, 104,
134, 136, 142, 351, 353, 362
Даламбер Ж. Лерон (Alembert, J. le
Rond d') 83, 144, 170, 172. 271, 354, 362
Дарбу Г. (Darboux, G.) 221, 221 и д..
224 и д., 240, 356, 362
— суммы (~ sums) 221, 331
Двойной интеграл (double integral)
330 и д., 338
— ряд (~ series) 195 и д.
Дебон (Debeaune, F.) 24
Дедекинд P. (Dedekind, R.) 177, 210, 278,
354, 362
Действительная часть (real part) 57
Действительные числа (~ numbers)
177 и д.
, сложение и умножение (~~,
addition and multiplication) 179
, упорядочение (~~, order) 179
Декарт P. (Descartes, R.) 1, 16, 57, 81,
202, 309, 324, 351, 362

378 Алфавитный указатель
Декарта геометрия (~ geometry) 8 и д.,
25, 38
Декартов лист (folium cartesii) 315, 324
Декартово произведение (Cartesian
product) 195
Де Моргана правила (de Morgan rules)
282
Детерминант (determinant) 340
Дэюенокки A. (Genocchi, А.) 309, 362
Доюервер Ж. (Gerver, J.) 264, 362
Джонс У. (Jones, W.) 40, 51, 53, 362
Дини У. mini, U.) 233, 264, 362
Диоклес (Diodes) 90
Диофант (Diophantus) 2
Дирака последовательность (Dirac
sequence) 266, 270
Дирихле Г.Л. (Dirichlet, G.L.) 1, 193,
202 и д., 218, 224, 230, 263, 330, 336,
351, 355 и д., 362 и д.
Дифференциальное уравнение
обыкновенное — см. Обыкновенное
дифференциальное уравнение
второго порядка (second-order
differential equation) 140 ид., 158
Дифференциальный оператор (differential
operator) 144, 146
Дифференцирование логарифма
(differentiation of logarithm) 86
— обратной функции (~~ inverse
function) 85, 238
— показательной функции (~~
exponential) 86
— произведения (product ~) 84
— ряда (series ~) 27, 200, 217, 245
— тригонометрической функции (~~
trigonometric functions) 86
— частного (quotients ~) 85
Дифференцирования правила (~ rules)
84 и д., 237 и д.
Дифференцируемая функция (differen-
tiable function) 235 и д.
нескольких переменных (~~ of
several variables) 300 и д.
Длина дуги (arc length) 111
, параметрическое представление
(~~, parametric representation) 117
Дробь непрерывная (continued fraction)
68 и д.
— подходящая (convergent of ~~) 71
— элементарная (partial fraction) 119
Дюбуа-Реймон П. (Du Bois-Reymond, P.)
177, 221, 224 и д., 331, 354 и д., 363
Дюга П. (Dugac, Р.) 181, 184, 354, 363
Дюрер A. (Diirer, А.) 42, 98, 363
Евклид (Euclid) 2, 8, 44, 182, 363
Евклида алгоритм (Euclidean algorithm)
68
Евклидова норма (~ norm) 274
Жордан К. (Jordan, С.) 275, 363
Задача (problem)
— Дебона (~ of Debeaune) 24
— интерполяции (interpolation ~) 10, 20
— Паппа (^ by Pappus") 8 и д.
Замкнутое множество (closed set) 279
Замыкание множества (closure of a set)
285
Звено непрерывной дроби (partial
quotient) 70
Зейдель Л. (Seidel, L.) 214, 363
Золотое правило (golden rule) 30
— сечение (~ mean) 44, 69, 72
Измельчение разбиения (refinement of а
division) 222
Изохрона Лейбница (isochrone of Leibniz)
134 и д.
Изохронный маятник (isochronous
pendulum) 141
Индукция, метод доказательства
(induction proof) 18, 351
Интеграл (integral)
— верхний (upper ~) 223
— Гаусса (Gaussian ~) 345 и д.
— двойной (double ~) 330 и д., 338
— зависящий от параметров (~ with
parameters) 297, 311 ид.
— кратный (multiple ~) 330 и д.
— неопределенный (indefinite ~) 108
— несобственный (improper ~) 257, 345
— нижний (lower ~) 223
—, определение (~, definition) 221 и д.
— повторный (iterated ~) 332 и д., 337,
347 ид.
— эллиптический (elliptic ~) 126,
130 и д., 141
Интегральное исчисление (integral
calculus) 107 и д.
Интегрирование (integration)
— бесконечного ряда (~ of infinite series)
230
— по частям (~ by parts) 114
— приближенное (approximate ~)
126 и д.
— с помощью асимптотического
разложения (~ by asymptotic expansion)
131 ид.
подстановки (~ by substitution)
112, 123 ид.
ряда (~ by series) 126 ид.

Алфавитный указатель 379
— степенного ряда (~ of power series) 251
— рациональных функций (~~ rational
functions) 118
— тригонометрических функций (~~
trigonometric functions) 123 и д.
— численное (numerical ~) 128 и д.
Интегрируемая функция (integrable
function) 223, 226 и д., 331, 336
Интервал (interval) 202, 279
— замкнутый (closed ~) 202, 279
Интерполяция (interpolation) 10 и д., 20
— логарифмов (~ of logarithms) 31 и д.
— многочлена (~~ polynomial) 10 и д.,
20
Инфимум (infimum) 184
Инъективное отображение (injective
mapping) 208
Кавальери Б. (Cavalieri, В.) 33
Кантор Г. (Cantor, G.) 171, 177, 206,
215 и д., 278 и д., 291, 354, 357, 363 и д.
Кантор М. (Cantor, М.) 4, 49, 351, 364
Кантора множество (Cantor set) 280, 282
Каратеодори К. (Caratheodory, С.) 236,
238, 303, 364
Кардано Док. (Cardano, G.) 4 и д., 18, 57,
67, 364
Касательная (tangent) 82 и д.
— плоскость (~ plane) 300
Кассини овалы (Cassinian ovals) 314
Катеноида (catenary) 136 и д.
Каунцнер В. (Kaunzner, W.) 48, 364
Каустика (caustic) 99 и д.
Кеплер И. (Kepler, J.) 49 и д., 81, 107,
110, 364
Клайн М. (Kline, М.) 23, 35, 58, 61, 248,
271, 364
Клеён Ф. (Klein, F.) 84, 94, 240, 302, 357,
364
Клиз Дою. и Ч. Бут (Cleese, J. &
С. Booth) 40
Кнопп К. (Кпорр, К.) 188, 364
Кнут Д. (Knuth, D.) 168, 364
Колеблющаяся струна (vibrating string)
272
Коллац Л. (Collatz, L.) 154, 353
Коллинз (Collins) 35, 51, 351
Компактное множество (compact set) 283
Комплексная плоскость (complex plane)
57 и д.
Комплексное число (~ number) 57
Комплексные операции (~ operations) 58
Конхоида Никомеда (conchoid of
Nicomedes) 88
Корень (root) 3, 21
— из комплексного числа (~ of complex
number) 60
— из единицы (~ of unity) 63
— квадратный (square ~) 21
, л/2 21 и д., 28, 69, 72, 177
, л/3 177
— кратный (multiple root) 146
Косинус (cosine function) 41 ид., 59, 62
—, ряд (~ series) 46
— гиперболический (hyperbolic ~) 56
Котангенс (cotangent function) 41
Кох Г., фон (Koch, Н. von) 264, 335, 348,
364
Коти О.Л. (Cauchy, A.L.) 84, 105, 116,
131, 158, 163, 170 и д., 176 и д., 188 и д.,
194, 197 и д., 204, 213, 221 и д., 229 и д.,
235, 242, 249, 252, 255, 263, 289, 316,
319, 354 и д., 364 и д.
— критерий сходимости (Cauchy's
criterion for convergence) 176, 210, 215
— последовательность (Cauchy sequence)
176, 181, 277
— произведение рядов (~ product of
series) 197 и д., 200 и д.
— уравнение (Cauchy's equation) 145,
152 и д.
Коти—Шварца неравенство (Cauchy-
Schwarz inequality) 229, 274
Кратные корни (multiple roots) 146
Кривая Пеано—Гильберта (curve of
Peano-Hilbert) 291 и д., 335
— фон Коха (von Koch's ~) 335, 348
Кривизна (curvature) 101 и д.
Кривизны окружность (circle of ~)
101 и д.
— центр (center of ~) 101
Критерий корня (root test) 194
— Лейбница (Leibniz's criterion) 189, 258
— частных (ratio test) 194
Круг (disc) 278 и д.
Кун С. (Kuhn, S.) 238, 365
Лагранж Ж.Л. (Lagrange, J.L. de) 2, 4,
68, 83, 92, 150, 170, 206, 218, 240, 252,
254, 256, 308, 318, 323, 325, 338, 345,
351 и д., 355 и д., 365
Лаграноюа множитель (~ multiplier)
325 и д.
Ламберт И. Г. (Lambert, J.H.) 44, 55,
69 и д., 76 и д., 79, 126, 352 и д., 365
Ландау Э. (Landau, Е.) 177 и д., 266, 354,
365
Ланьи Ф., де (Lagny, F. de) 40, 53
Лаплас П.С. (Laplace, P.S.) 131, 133, 365
Лебег A. (Lebesgue, Н.) 221, 230, 266

380 Алфавитный указатель
Лежандр A.M. (Legendre, A.M.) 70, 77,
79, 126, 366
Лейбниц Г.В. (Leibniz, G.W.) 46, 49 и д.,
52 и д., 60, 75, 80, 82 и д., 89 и д., 93,
97 и д., 107 и д., 110, 119, 133 и д.,
188 и д., 202, 271, 307, 309, 351, 353,
366 и д.
Лемер Д.Г. (Lehmer, D.H.) 165, 169, 367
Лемниската (lemniscate) 314
Леонардо да Винчи (Leonardo da Vinci)
141
Леонардо Пизанский (Leonardo da Pisa) 2,
73
Лерх M. (Lerch, М.) 256, 266, 367
Линейное дифференциальное уравнение
(linear differential equation) 144
с постоянными коэффициентами
(~~~ with constant coefficients) 145 и д.
, вариация постоянных (~~~,
variation of constants) 150 и д.
Линейное отображение (~ mapping)
293 и д.
Линия уровня (level curve) 306
Лиувилль Ж. (Liouville, J.) 126, 154, 353,
367
Логарифм (logarithm) 29 ид., 78, 95
— Бриггса (Briggs's ~) 30 и д.
—, вычисление (computation of ~) 31 и д.
— гиперболический (hyperbolic ~) 30
—, дифференцирование (~,
differentiation) 86
— комплексный (complex ~) 61
— натуральный (natural ~) 30, 35 ид.
— Непера (Napenan ~) 30
—, In 2 36 и д., 38 и д., 75, 190, 192, 252
Логистический рост (logistic growth) 143
Лохе Г. (Lochs, G.) 69, 367
Лопиталъ, де, маркиз (L'Hospital,
Marquis de) 80, 82 и д., 98, 106, 137, 242,
352 и д., 356, 367
Лопиталя правила (L'Hospital's rules)
242 и д.
Люрот И. (Luroth, J.) 219, 367
Мажорирование ряда (majorizing of а
series) 191 и д.
Маккин Дж. (Machin, J.) 52 и д., 62
Маклорен К. (Maclaurin, С.) 6, 83, 95,
160, 259, 367
Максимум (maximum) 92 ид., 206 и д.,
289, 306, 323 и д.
— условный (conditional ~) 325 ид.
Максимум-норма (~ norm) 275
Матрица (matrix) 293
Маятник (pendulum) 141 и д., 157 и д.,
307
— изохронный (isochronous ~) 142
Мейнардус Г. (Meinardus, G.) 266, 367
Мере Ш. (Мёгау, Ch.) 171, 177, 180, 354,
367
Меркатор Н. (Mercator, N.) 35 ид., 51,
126, 351, 367
Мерседес (Mercedes) 60
Мертенс Ф. (Mertens, F.) 199, 201, 367
Метиус A. (Metius, А.) 52, 73
Метод рядов Тейлора для
дифференциальных уравнений (Teylor series method
for differential equations) 156 и д.
Миел Г. (Miel, G.) 54, 367
Минимум (minimum) 92 ид., 306, 323 и д.
— условный (conditional ~) 325 и д.
Минорирование ряда (minorizing of а
series) 191 и д.
Минута (minute) 40
Миттаг-Леффлер Г. (Mittag-Leffler, G.)
184, 266, 355
Мнимая часть (imaginary part) 57
Множество (set)
— замкнутое (closed ~) 279
— компактное (compact ~) 283
— меры нуль (null ~) 33 ид.
— открытое (open ~) 278
Момент инерции (moment of inertia) 338,
344
Монотонная последовательность
(monotone sequence) 182
— функция (monotone function) 208
Муавр A., de (Moivre, A. de) 44, 62, 367
Набла (nabla operator) 305
Наибольшая нижняя граница (greatest
lower bound) 184
Наименьшая верхняя граница (least
upper bound) 182
Наискорейший спуск (steepest descent)
306
Наклон линии (slope of line) 81 и д.
Невозрастающая функция (nonincreasing
function) 208
Непер Дж. (Napier, J.) 29, 367
Непрерывная дробь (continued fraction)
68 и д.
, иррациональность (~~,
irrationality) 68, 76
как бесконечный ряд (~~ as
infinite series) 73 и д.
регулярная (regular ~~) 70, 74
, сходимость (convergence of ~~) 190
— функция (~ function) 204
нескольких переменных (~~ of
several variables) 287 и д.
Неравенство (inequality)

Алфавитный указатель 381
— Бернулли (Bernoulli's ~) 28
— Гёльдера (Holder's ~) 275, 327
— для интегралов (~ of integrals)
228 и д.
— Коши—Шварца (Cauchy-Schwarz ~)
229, 274
— треугольника (triangle ~) 180, 185,
251, 274, 285, 327
Нёрсетпт СП. (N0rsett, S.P.) 155, 370
Неубывающая функция (nondecreasing
function) 208
Неявное дифференцирование (implicit
differentiation) 89, 311
— уравнение (~ equation) 88
Нивентейт Б. (Nieventijt, В.) 83
Никомед (Nicomedes) 88
Норма (norm) 274 и д.
— евклидова (Euclidean ~) 274
— £р (^р-погт) 275
— матрицы (matrix ~) 293 ид.
Ньютон И. (Newton, I.) 16, 17, 39, 46, 51,
54 и д.. 81 и д., 91, 101 и д., 107 и д.,
111, 126, 130, 188, 202, 367 и д.
Ньютона биномиальная теорема
(Newton's binomial theorem) 23 и д.
— вычисление логарифмов (~
computation of logarithms) 39
— интерполяция (~ interpolation) 10 и д.
— метод решения уравнений (~ method
for equations) 96
— тождества (~ identities) 66
Ньютона—Котеса методы (Newton-
Cotes methods) 130
Образ множества (direct image of a set)
294 и д.
Обратное отображение множества
(inverse image of a set) 294 и д.
Обратные тригонометрические функции
(inverse trigonometric functions) 49 и д.
--, дифференцирование (~~~,
differentiation) 87
Общий член бесконечной
последовательности (general term of infinite sequence)
172
Объем (volume)
— как интеграл (~ by inegration) 110
— шара (~ of ball) 349
Обыкновенное дифференциальное
уравнение (ordinary differential equation) 134
— — Бернулли (Bernoulli's ~~~) 140
—, вариация постоянных (~~~,
variation of constants) 150 и д.
— второго порядка (~~~ of second
order) 140 и д., 158
линейное неоднородное (linear
inhomogeneous ~~~) 139, 144 и д.,
148 и д.
линейное однородное (Бпеаг
homogeneous ~~~) 139, 144 и д.
, разделение переменных (~^^?
separation of variablesj 139
, ряд Тейлора (<~~~, Taylor
series) 156 и д.
с постоянными коэффициентами
(-^^^ with constant coefficients) 145 и д.
, численное интегрирование
(^,~^? numerical integration) 154 и д.
Огибающая (envelope) 98 и д.
Ограниченная последовательность
(bounded sequence) 174, 277
Окрестность (neighborhood) 278 и д.
Омар Хайям (Omar Alkhaijama) 18
Определитель (determinant) 340
Орем Н. (Oresme, N.) 191
Основная формула интегрального
исчисления 241
Остаточный член формулы Тейлора
(remainder of Taylor's formula) 116, 319,
321 и д.
— — Эйлера—Маклорена (~ of Euler-
Maclaurin ~) 163 ид.
Открытое мнежество (open set) 278
— покрытие (~ covering) 283
Открытый интервал (~ interval) 202, 279
Отношение порядка (order relation) 179
Отображение (mapping)
— билинейное (bilinear ~) 321
— линейное (linear ~) 293
— полилинейное (multilinear ~) 321
Отрицание (negation) 180
Отрицательно определенный (negative
definite) 325
Отрицательные показатели (~ exponents)
17, 20
Папп (Pappus) 8
Параметрическое представление
(parametric representation) 88 и д.
— кривизны (~~~ of curvature) 103
Пармантье М. (Parmentier, М.) 81, 352,
368
Паскаль Б. (Pascal, В.) 12, 18 и д.. 351,
368
Паскаля треугольник (Pascal's triangle)
18, 45
Паскуале Л., ди (Pasquale, L. di) 4, 368
Пеано Д-яс. (Peano, G.) 272 и д.. 275, 289,
291 и д.. 293, 309. 316, 328 и д., 357,
362, 368
Пеано кривая (Peano's curve) 298

382 Алфавитный указатель
Первообразная (primitive) 107 и д., 239
Перестановка суммирования ряда и
предельного перехода (exchange of series
and limits) 199 и д.
— членов ряда (rearrangement of a series)
192 и д.
Периметр эллипса (perimeter of ellipse)
127
Периферия (periphery) 40
Перро К. (Perrault, С.) 135
Перрон О. (Perron, О.) 79, 368
Петергоф (Peterhof) 101
Пи, число (pi, 7г) 40 и д., 52 и д., 59,
68 и д., 72, 75 и д., 190
Пикар Э. (Picard, Е.) 266, 368
Пифагор (rythagoras) 111, 123
Платон (Plato) 2
Площадь (area)
— как интеграл (~ by integration)
109 и д.
функция (~ as function) 56
— под гиперболой (~ of hyperbola)
35 и д.
полиномиальной функцией (~ of
polynomial functions) 33 и д.
Подпоследовательность (subsequence) 184
Подходящая дробь (convergent of
continued fraction) 71
Пойрбах R (Peurbach, G.) 369
Показательная функция (exponential
function) 24 и д., 39, 59, 78, 117
комплексная (complex ~) 60
Полином (polynomial) 10
—, интерполяция (interpolation of ~)
10 и д., 94
Полное упорядочение (total order) 179
Положительно определенный (positive
definite) 325
Полярные координаты (polar coordinates)
59, 339
Последовательность (sequence) 172
— векторов (vector ~) 275
— монотонная (monotone ~) 182
— ограниченная (bounded ~) 174, 277
— функций (~ of functions) 213
Поточечная сходимость (pointwise
convergence) 213
Предел (limit)
— верхний (~ superior) 185, 187
— левый, правый (left-sided, right-sided
~) 210
— нижний (~ inferior) 185, 187
— последовательности (~ of sequence)
172
функций (~~~ of functions) 213
— функции (~ of function) 209
Представительный (representative) 178
Прингсхейм A. (Pringsheim, А.) 209, 211,
220, 256, 355, 368 и д.
Проекция (projection) 299
Производная (derivative) 81
—, см. также Дифференцирование
— бесконечного ряда (~ of infinite series)
245
— вторая (second ~) 91
— параболы (~ of parabola) 82
— по направлению (directional ~) 304
— степенного ряда (~ of power series) 245
— частная (partial ~) 99, 300
высшего порядка (higher ~~)
316 и д.
Производящая функция (generating
function) 162
Птолемей (Ptolemy) 2, 40, 43, 47 и д., 55,
351, 369
Птолемея лемма (Ptolemy's lemma) 55
Пуанкаре A. (Poincare, Н.) 263, 356
Пятиугольник (pentagon) 44
Работа в силовом поле (work in force
field) 110
Равномерная непрерывность (uniform
continuity) 217 и д., 290
— сходимость (~ convergence) 215, 291
Радиан (radian) 40
Радиус кривизны (radius of curvature) 102
— сходимости (~~ convergence) 248 и д.
Разбиение интервала (division of interval)
221
Разделение переменных (separation of
variables) 139
Разностная схема (difference scheme) 12
Рам Г., де (Rham, G. de) 264, 369
Расстояние (distance) 273
Региомонтан (Regiomontanus) 2, 41, 43,
47, 54, 369
Резонанс (resonance) 150
Рекуррентное соотношение (recurrence
relation) 115
Ренч Дэю.У., мл. (Wrench, J.W.Jr.) 54,
371
Рефлексивность (reflexivity) 178 ид.
Риккати Я. (Riccati, J.) 140, 353, 369
— уравнение (Riccati's equation) 154
Риман Б. (Riemann, В.) 193, 203, 221,
232, 263, 356, 369
Римана интеграл (~ integral) 221 и д.,
330
— суммы (~ sums) 226
Ричерт Н. (Richert, N.) 42, 369
Роберваль (Roberval) 33

Алфавитный указатель 383
Роберт из Честера (Robert of Chester)
2 и д., 369
Розен Ф. (Rosen, F.) 2, 4, 369
Ролль М. (Rolle, М.) 83, 240, 369
Ромен А., ван (Roomen, A. van) 52
Рыжик ИМ. (Ryzhik, LM.) 109, 361
Ряд (series) 188 и д.
— гармонический (harmonic ~) 167, 191
— геометрический (geometric ~) 21, 33,
188 и д.
— Грегори для In (~ for In, Gregory) 37
— для арксинуса (~~ arcsin) 51, 256
— для арктангенса (~~ arctan) 49 и д.,
249
— для косинуса (~~ cosine) 46
— для показательной функции (~~
exponential function) 27, 200, 217
— для синуса (~~ sine) 46
— для тангенса (~ tangent) 46 ид., 169
— Меркатора для In (~ In, Mercator)
35, 252
— степенной (power series) 248
— Тейлора (Taylor ~) 94 и д.
Сараса А.А., де (Sarasa, A.A. de) 35
Секунда (second) 40
Серпинъский В. (Sierpinski, W.) 281, 369
Серпиньского ковер (Sierpinski's carpet)
281, 335
— треугольник (~ triangle) 281, 286, 335,
348
Серре Ж.A. (Serret, J.A.) 240, 328 и д.,
369
Симметрия (symmetry) 178
Симпсон Т. (Simpson, Т.) 129, 369
Симпсона метод (Simpson's method)
129 и д.
Синус гиперболический (hyperbolic sine)
56
—, ряд (series for ~) 46
—, функция (~ function) 41 и д., 59, 62
—, sinl0 48 и д.
Скалярное произведение (scalar product)
274
Сложная функция (composite function) 87
Снеллиус В. (Snellius, W.) 52, 94
Солнечный фонтан (Sun Fountain) 101
Стационарная точка (stationary point) 91,
323
Стеклов В. (Steklov, V.) 126, 353, 369
Степенной ряд (power series) 248
Стереограммы (stereograms) 288, 301, 305.
313, 320, 348
Стирлинг Дон:. (Stirling, J.) 165, 369
Стирлинга формула (Stirling's formula)
165
Строго монотонная функция (strictly
monotone function) 208
Стройк Д.Я. (Struik, D.J.) 4, 91, 191, 370
Стрэнг Дж.. (Strang, G.) 42, 340, 370
Сумма пч (sum of nq) 13 и д., 16, 160
— обратных степеней (~ of reciprocal
powers) 62, 67, 160, 191, 259
— частичная (partial ~) 188
Суммирование по частям (partial
summation) 251, 255
Суперпозиции принцип (superposition
principle) 148
Супремум (supremum) 182
Сферические координаты (spherical
coordinates) 344
Сходимость (convergence)
— абсолютная (absolute ~) 192
интегралов (~ of integrals) 257 и д.
— покомпонентная (componentwise ~)
276
— последовательности (~ of sequence)
172
векторов (~~ vector sequence)
275 и д.
— поточечная (pointwise ~\ 213
— равномерная (uniform ~) 215, 291
— ряда (~ of a series) 188
— степенного ряда (~~ power series)
248 и д.
Сципионе даль Ферро (Scipione dal Ferro)
4
Сюръективная функция (surjective
function) 208
Такаги Т. (Takagi, Т.) 264, 370
Тангенс гиперболический, th (tanh) 69,
78
—, непрерывная дробь (tangent, continued
fraction) 70
—, ряд (series for ~) 46 и д.
—■, функция (~ function) 41 и д., 62, 73,
77
Тарталъя Н. (Tartaglia, N.) 4, 351
Тейлор В. (Taylor, В.) 91, 116, 370
Тейлора многочлен (Taylor polynomial) 95
— ряд (~ series) 94 и д., 160, 252 и д.
для двух переменных (~~ for two
variables) 319 и д.
— п переменных (~~~ п variables)
320 и д.
, остаточный член (remainder of ~~)
116, 319, 321 ид.
Теорема (theorem)
— Абеля (Abel's ~) 250 и д.
— биномиальная (binomial ~) 18 и д.,
23 и д., 253

384 Алфавитный указатель
— Больцано (~ of Bolzano) 206
— Больцано—Вейерштрасса (Bolzano-
Weierstrass ~) 184, 277, 283, 286
— Вейерштрасса аппроксимационная
(Weierstrass's approximation~ ) 265
— Гейне—Бореля (~ of Heine-Borel) 283,
286
— Дюбуа-Реймона и Дарбу (~~ Du Bois-
Reymond and Darboux) 224, 332
— Лагранжа (~ of Lagrange) 240
— максимума (~ of maximum) 206 и д.,
289
— о неявной функции (implicit function
~) 309 и д.
промежуточном значении
(intermediate value ~) 206
среднем значении (mean value ~)
229 и д., 308 и д.
— Ролля (~ of Rolle) 240
— сложения (addition theorem)
для арктангенсов (~~ for arctan)
53
гиперболических функций (~~
for hyperbolic functions) 56
синусов и косинусов (~~ for sine
and cosine) 43
тангенсов (~~ for tangent) 43
Толл Д. (Tall, DO 264, 370
Торричелли Э. (Torricelli EO 101
Точка накопления (accumulation point)
множества (~~ of set) 209
последовательности (~~ of
sequence) 184
— перегиба (inflection point) 91
Трактриса (tractrix) 135 и д.
Транзитивность (transitivity) 178 и д.
Трапеции правило (trapezoidal rule) 129
Тригонометрические функции
(trigonometric functions') 40 и д.
Трисекция угла (trisection of an angle) 6
Угол (angle) 40
Уравнение (equation)
— биквадратное (quartic ~) 6, 14
— квадратное (quadratic ~) 2 ид., 7
— Коши (Cauchy's ~) 145, 152 и д.
— кубическое (cubic ~) 4 и д., 7, 48, 67,
96
— Лапласа (Laplace ~) 328
— пятой степени (~ of fifth degree) 6
— Риккатпи (Riccati's ~) 154
— характеристическое (characteristic ~)
145
Условный минимум (conditional minimum)
325 и д.
Уэстфол (WestfaU) 51, 370
Факториал (factorial) 20
Фельман Э.А. (Fellmann, EJL) 168, 370
Феодор Киренеиский (Theodorus of
Cyrene) 169
Ферма П. (Fermat, R) 25, 34 и д., 50, 81,
92 и д., 107, 135, 352, 370
— принцип (Fermat's principle) 93, 138
Феррари Л. (Ferrari, LO 6, 14
Ферхюльст П.Ф. (Verhulst, RFO 143, 370
Фибоначчи (Fibonacci) 2, 73
Фонсене Д. (Foncenex, DO 55, 370
Формула подстановки (substitution
formula) 112, 123 и д.
— преобразования для двойных
интегралов (transformation ~ for double
integrals) 338
— Стирлинга (Stirling's ~) 165
— суммирования Эйлера—Маклорена
(Euler-Maclaurin summation ~) 130,
160 и д.
— Эйлера (Euler's ~) 58 ид.
Формулы де Myaepa (de Moivre's
formulas) 44 и д.
Френель A. (Fresnel АО 370
Френеля интегралы (Fresnel's integrals)
127 и д., 131 и д., 262
Фреше М. (Frechet, МО 275, 283, 302, 357,
370
Фридрих //, король (Frederick II) 160, 354
Фундаментальная теорема
дифференциального исчисления (fundamental
theorem of differential calculus) 109, 239,
241
Функция (function)
— "бланманже" (blancmange ~) 264 и д.
— возрастающая (increasing ~) 91, 184,
208
— выпуклая (convex ~) 91
— гиперболическая (hyperbolic ~) 56
— дифференцируемая (differentiable ~)
235 и д. , 300 и д.
— интегрируемая (integrable ~) 223,
226 и д. , 331, 336
— логарифмическая (logarithmic ~)
29 и д.
— монотонная (monotone ~) 208
— невозрастающая (nonincreasing ~) 208
— непрерывная (continuous ~) 204, 287
, нигде не дифференцируемая
(continuous, nowhere differentiable ~)
263 и д.
— нескольких переменных (~ of several
variables) 287
— неубывающая (nondecreasing ~) 208
— обратная (inverse ~) 208

Алфавитный указатель 385
тригонометрическая (inverse
trigonometric ~) 49 и д.
— однородная (homogeneous ~) 314
—, определение (definition of ~) 202
— ошибок обратная (inverse error ~) 159
— показательная (exponential ~) 17,
24 и д.
— полиномиальная (polynomial ~) 10
— сложная (composite ~) 87
— тригонометрическая (trigonometric ~)
40 и д.
— убывающая (decreasing ~) 91, 208
Фурье Ж.Б.Ж. (Fourier, J.B.J.) 108, 370
Хаирер Э. (Hairer, Е.) 155, 370
Халмош П.P. (Halmos, P.R.) 325, 370 и д.
Характеристическое уравнение
(characteristic equation) 145
Харриот, сэр Томас (Harriot, Sir Thomas)
10
Хаусдорф Ф. (HausdorfT, F.) 278, 281,
294 и д., 357, 371
Хаяси Т. (Hayashi, Т.) 73, 371
Хокинг Ст..У. (Hawking, St.W.) 81
Хорда (функция) (chord function) 40 и д.
— 1° (chord 1°) 48
Хорезми, Мухаммед бен Муса аль-
Хорезми (Mohammed ben Musa Al-
Khowarizmi) 2 и д., 7, 371
Хофрейтер Я. (Hofreiter, N.) 109, 362
Цейлен Лудольф, ван (Ceulen, L. van) 52,
371
Центр кривизны (center of curvature) 101
— масс (~ of mass) 111
— тяжести (~ of gravity) 337
Цепная дробь — см. Непрерывная дробь
— линия — см. Катеноида
Цепное правило (chain rule) 87, 239, 306
Циклоида (cycloid) 104, 138, 142
Циссоида Диоклеса (cissoid of Diocles) 90
Частичная сумма (partial sum) 188
Частная производная (~ derivative) 99,
300
Чезаро суммирование (Cesaro summation)
187
Чертова лестница (devil's staircase)
246 и д.
Численное интегрирование (numerical
integration) 128 ид.
дифференциальных уравнений (~~
of differential equations) 154 и д.
Число (number)
— действительное (real ~) 177 и д.
— комплексное (complex ~) 57
— Эйлера (Euler's ~) 25, 38
Чу Ши Ки (Tshu shi Kih) 18
Шар (ball) 278 и д., 349
Шварц Г.А. (Schwarz, Н.А.) 229, 316, 327
371
Шенкс Д. (Shanks, D.) 54, 371
Шписс О. (Spiess, О.) 144, 160, 353, 371
Шгпифель М. (Stifel, М.) 17, 29, 371
Штольц О. (Stolz, О.) 182, 302, 333, 357,
371
Эвольвента (involute) 104
Эволюта (evolute) 103
Эйлер Л. (Euler, L.) 39, 46, 53, 57 и д.,
60 и д., 72, 79, 83, 92, 97, 118 и д.,
123 и д., 127, 144 и д., 154 и д., 160,
162 и д., 170, 202, 206, 249, 316, 318,
338, 351 и д., 355, 357, 371 и д.
Эйлера биквадратное уравнение (Euler's
quartic equation) 6, 14
— быстрый метод (~ quick method) 148
— гамма-функция (~ gamma function)
261 и д., 346
— золотое правило (~ golden rule) 30
— Introductio 1, 17, 24, 25, 27, 29, 39, 40,
44, 46, 58, 63 и д., 66 и д., 75, 78
— ломаная (Euler's polygon) 155
— метод для дифференциальных
уравнений (~ method for differential equations)
154 и д.
— показательная функция (~ exponential
function) 17, 24 и д.
— постоянная (~ constant) 167 и д.
— произведение для синуса (~ product
for sine) 62 и д.
— формула (~ formula) 58 и д.
— число (~ number) 25, 30, 38, 59, 69, 72
Эйлера—Маклорена формула
суммирования (Euler-Maclaurin summation
formula) 130, 160 и д.
Эквивалентности классы (equivalence
classes) 178
— отношение (~ relation) 178
Эквивалентные нормы (equivalent norms)
275, 285, 289
Экспонента (exponential) 17 и д.
Элементарная дробь (partial fraction) 119
Эллиптический интеграл (elliptic
integral) 126, 130 и д., 141
Эрмит Ш. (Hermite, Ch.) 119, 373
Якоби К.Г.Я. (Jacobi, C.G.J.) 99, 126,
144, 163, 300, 338, 346, 351, 353, 373
Якобиан (Jacobian) 301

Научное издание
Эрнст Хайрер, Герхард Ваннер
МАТЕМАТИЧЕСКИЙ АНАЛИЗ В СВЕТЕ ЕГО ИСТОРИИ
Ведущий редактор А.В. Тыглиян
Компьютерный набор Г.П. Чуркиной
Художник обложки Ф.И. Садилов
Издательство "Научный мир"
Тел./факс (007)(495)291-28-47 E-mail: naumir@benran.ru
Internet: http:// bookish.iring.ru
Подписано к печати 30.04.08. Формат 70x100 1/i6-
Печать офсетная. Печ. л. 24,5. Усл. печ. л. 31,85
Тираж 800 экз. Заказ 50
Издание отпечатано с готовых диапозитивов в типографии 000 "Галлея-Принт"
Москва, 5-я Кабельная, 26