БИБЛИОТЕЧКА
ФИЗИК О-М АТЕМАТИЧЕСКОЙ
ШКОЛЫ
МАТЕМАТИКА
А. В. КУЖЕЛЬ
МАТЕМАТИЧЕСКИЕ
ИМПРОВИЗАЦИИ
КИЕВ
ГОЛОВНОЕ ИЗДАТЕЛЬСТВО
ИЗДАТЕЛЬСКОГО ОБЪЕДИНЕНИЯ
«ВИЩА ШКОЛА» ч
1983
22.1
К 88
УДК 51 (075.3)
Математические импровизации. К у ж е л ь А. В.—
К.: Вища школа. Головное изд-во, 1983*—96 с.—(Б-чка
физ.-мат. школы. Математика).
На доступных примерах показана импровизация в ма-
тематике, способствующая развитию математических на-
клонностей учащихся, углублению их интереса к мате-
матике, укреплению уверен г. ости в своих силах. Материал
книги может быть использован как в процессе самостоя-
тельной работы, так и на различных внеклассных меро-
приятиях.
Для учащихся физико-математических школ и стар-
ших классов общеобразовательной школы.
Табл. 5. Ил. 8.
Редакционная коллегия: член-корреспон-
дент АН УССР А. В, Скороход (отв. редактор), профес-
сор Л. Л. Калужнин, профессор Н. Я. Кованцов, доцент
В. И. Коба, доцент Я. Я. Лященко, доцент /О. /И. Ры-
жов, профессор Л4. Я. Ядренко (зам. отв. редактора),
кандидат педагогических наук Л. В, Кованцова
Реценаенты: доктор физико-математических
наук, профессор М. Я, Ядренко (Киевский государ-
ственный университет), старший научный сотрудник
М. Я. Кратко (Институт математики АН УССР)
Редакция литературы по математике и физике
Зав. редакцией В. Л* Корженевич
1702000000-140
К ^211(04)^83" 397а~83
Cj Издательское объеди-
нение «Вища школа»,
1983
ПРЕДИСЛОВИЕ
Трудно представить себе человека, который назвал бы
музыку скучной и неинтересной, мотивируя это изоби-
лием в ней нот. Однако мнение о математике, как о науке
скучной и неинтересной, где одни только формулы или
иксы и игреки, можно услышать довольно часто. В дей-
ствительности для специалистов-математиков формулы
являются своеобразным языком, который дает возможность
анализировать, выявлять закономерности, делать новые
открытия и записывать их строгим и четким математи-
ческим языком. А для непосвященных формулы — это свое-
образная стена, завеса, за которой укрылась математика.
Так ли непроницаема эта стена? Может быть, эту
стену можно пробить, приподнять завесу «таинственности»
математики, увлечь этой наукой молодых людей и любо-
знательных школьников, заставить их волноваться перед
встречей с неизвестными разделами математики, почув-
ствовать себя участниками открытий в некогда скучной
и неинтересной для них науке. Такую трудную задачу
ставит автор перед собой. И если предлагаемая книга
заинтересует читателя, это будет высшей оценкой усилий
автора.
В книге на конкретных и доступных для учащихся
средней общеобразовательной школы примерах автор по-
казал, что в математике, как и в музыке, можно «импро-
визировать», т. е. устанавливать новые факты, свойства,
закономерности, другими словами, делать открытия и в
такой области знаний, как математика. Надо только найти
и рассмотреть более общий случай, порассуждать об ана-
логии, каким-то образом изменить метод доказательства
или вместо конкретных чисел ввести определенные пара-
метры.
Многие из приведенных в предлагаемой книге фактов
публикуются впервые, а именно: условие несократимости
дроби вида ; второе обобщение теоремы Вильсона;
достаточное условие существования невещественных кор-
.3
ней многочлена; условие периодичности функции; связь
между tgna и многочленами Чебышева, а также фор-
мула для n-й степени квадратной матрицы; формулы для
sin a, cos а и е* для кватернионов, а также общий вид
функции на множестве кватернионов.
Отзывы и пожелания просим направлять по адресу:
252054, Киев-54, ул. Гоголевская, 7, Головное издатель-
ство издательского объединения «Вища школа», редак-
ция литературы, по математике и физике.
ГЛАВА I
ДЕЛИМОСТЬ ВЫРАЖЕНИЯ
abn + сп + d НА т
§ 1. Делимость чисел
(основные понятия)
Говорят, что целое число а делится на целое число Ь,
если существует такое целое число с, что а = Ьс. Если
а делится на Ь, то кратко это записывают так> а • Ь (или
Ь\а — читается: b делит в). При этом а называют дели-
мым, а b — делителем числа а.
Например, 52 > 13, 52-52, 52 •(—26) и т. д. Знак • за-
меняет слово «делится» и является отношением, а не опе-
рацией (подобно отношениям параллельности (||), перпен-
дикулярности (_L), меньше (<) и др.). Поэтому записи
(а 4- Ь) • с и а 4- b • с означают одно и то же: сумма а 4- b
делится на с, тогда как записи (а 4- b) tc и а 4- Ъ :с имеют,
очевидно, различный смысл. В связи с этим будем поль-
зоваться более простой записью: а 4- Ь • с. Точно так же
из двух равносильных записей: (а -\-Ь) <с и а 4- Ь < с
пользуемся второй, более простой, записью.
Запись 0 :0 не имеет смысла (делить на нуль нельзя), тогда как
запись 0*0 является правильным утверждением. Объясняется это
тем, что деление чисел — это операция в множестве действительных
чисел (подобно операции сложения, вычитания или умножения чисел)
и результат применения этой операции должен быть однозначным.
Что касается делимости чисел, то, как уже отмечалось, это отно-
шение в множестве целых чисел (подобно отношениям <, _L, [|, ~
и др.). И здесь уже, в отличие от предыдущего случая, однознач-
ность элемента с, для которого а = Ь«, не требуется. Поэтому, так
как существует такое число в, что 0 = 0 • с (например, 0 = 0-7),
то на основании определения понятия делимости чисел приходим
к заключению, что 0 делится на 0 (т. е. 0 • 0).
Запись а • b означает, что а не делится на Ь. Так,
10;7, 2:3, 1:0 и т. д.
Непосредственно из определения делимости чисел вы-
текают следующие свойства.
1.	Если а;Ь, а Ь\с, то а-с.
2.	Если а [о и b • с, то а + b-о и а — Ь\о.
3.	Если a • о или b • о, то ab • в.
4.	Если а\Ь и а=^0, то |а|>|Ь|.
5.	Если а • b и | а | < Ь, то а = 0.
5
Замечание 1. Если а + b • ct то это не означает, что а\0
и b : с. Так, 17 + 18 ; 7, тогда как 17 : 7 и 18 2 7, Однако, если из-
вестно, что сумма а + b делится на с и одно слагаемое делится
на с, то и второе слагаемое делится на с.
Замечание 2. Из того что ab • с, также не вытекает, что
а: с или b t с. Так, 6 • 8 : 12, тогда как 6 : 12 и 8: 12. Однако, если
кроме условия ab • с дополнительно известно, что один из множите-
лей (а или Ь) взаимно прост с с, то тогда второй множитель делится
на с (см. гл. 2, теорема 2.3).
§ 2.	Конкретные примеры
На различных олимпиадах, в сборниках конкурсных
задач часто встречаются задачи типа: доказать, что при
любом целом неотрицательном т
1)	4"+15/г—1-9;	4) 38п+? —26/г —27: 169;
2)	10" + 18п — 1:27;	5) 2л+23л + 5п — 4 :25;
3)	32"+» + 40п _ 27:64;	6) 4 • 32л+2 + 32/г — 36; 64.
Подобного типа задачи легко решаются с помощью прин-
ципа математической индукции. Покажем это на послед-
нем примере.
Положим
Тп = 4 • 32Л+24- 32п — 36.
При п = 0 Т9 = 0 • 64. Пусть
Тк = 4 • 32А+2 + 326 — 36 = 64.	(1.1)
Тогда
Tk+i = 9 • 4 • 32*+2 + 326 — 4.	(1.2)
Исключая из (1.1) и (1.2) 4  32А+2, находим
Тк+1 = 9Т* — 2566 + 320.
А так как 7\ : 64, 256 • 64, 320 • 64, то Tk+i • 64 и, следо-
вательно, на основании принципа математической индук-
ции при любом целом неотрицательном п Тп • 64.
§ 3.	Общий случай
Каждое из соотношений 1) — 6) можно представить
в виде
abn + сп 4- d • tn,	(1.3)
где здесь и в дальнейшем а, Ь, с и d — некоторые целые
числа, a tn — натуральное число (tn > 1). Например,
в случае предпоследнего выражения а = 4, b = 6, с = 5,
d = —4, m = 25.
6
В связи с этим возникает вопрос: нельзя ли исследо-
вать рассматриваемую задачу в общем виде и сформули-
ровать условия, которым должны удовлетворять числа
а, Ь, с и d, чтобы выражение abn + сп + d при любом
целом неотрицательном п делилось на заданное натураль-
ное число /п?
Оказывается, такие условия выполняются.
Теорема 1.1. При любом целом неотрицательном п
выраокение abn + сп + d делится на т тогда и только
тогда, когда
a + d'-m, (b—1)с[т, < (Ь—1)4-с-/п.	(1.4)
Например, в случае примера 5
а 4- d = 0:25, (b — 1) о = 25 : 25, a (b — 1) + с = 25 : 25,
и, следовательно, выражение 2'1+2Зл + 5п — 4 делится на 25
(для любого n£N0, где Af0 = ЛГ(_1 {0} — множество целых
неотрицательных чисел).
□ Обозначим
Тп = abn + сп -J- d.
Пусть известно, что при любом n£N9 Тп\т. Тогда,
в частности, при п = 0 получим То = а + d\m.
Используя теперь равенство
Тх = а (Ь — 1) + с + (а + d),
а также то, что 7\ и a-j-d делятся на т, приходит к за-
ключению, что а(Ь—l) + cjm (см. замечание 1, § 1).
Аналогично, учитывая, что
Т2 — Л = ab (&—!) + с, Т3 — Т2 = ab* (b — 1) + с
делятся на т, получаем, что
6(Т2-Т1)-(Т3-Т2) = с(6-1)
также делится на т.
Таким образом, если при любом п £N0 выполняется
(1.3) (или, что то же самое, Тц'-т), то справедливы и со-
отношения (1.4).
Пусть теперь наоборот: выполняются соотношения (1.4).
Покажем, что при таком условии Тп\т при любом n^N3.
Действительно,
Tq = о d; /л,	~ a(b —	т.
Предположим, что при некотором k£N Тк-т, и покажем,
что TkJf\\tn. Для этого рассмотрим разность
Tk+i-Tl = bTk-k(b-\)c-b(a + d).	(1.5)
7
Так как (Ь—а + d\m и, на основании предпо-
ложения, Tk\m. то правая часть (1.5) делится на т.
Следовательно, и левая часть этого равенства делится
на т:
ТЛ+1— 7\\т.	(1.6)
А так как Тг\т, то, учитывая (1.6), 7\+1 также делится
на т. Но тогда, на основании принципа математической
индукции, приходим к заключению, что при любом п Q
выражение abn + сп + d делится на т. g
§ 4. Об одном свойстве
коэффициента с
Рассмотрим примеры 1) — 6) из § 1. В каждом из этих
примеров квадрат коэффициента при п делится на mi
152;9, 182-27, 4О2:64, 262; 169, 322:64.
В связи с этим возникает вопрос: случайное ли это со-
впадение или общее свойство? Оказывается, что отмечен-
ное свойство носит общий характер.
Теорема 1.2. Если при любом п из NQ выражение
abn + сп + d делится на /и, то с2 • т.
□ При условии теоремы выполняются соотношения
(1.4). А так как в2 = сА — аВ, где A =a(b— 1) + о\т9
В = (Ь — 1)с\т, то и с2 • т. g
УПРАЖНЕНИЯ
1.	Известно, что при любом л £ ;V0 4П + 15л + d • 9, Каким ус-
ловиям удовлетворяет d?
2.	Известно, что при любом л С АГ® 4Л + сп — 1| 9. Каким усло-
виям удовлетворяет с?
3.	Известно, что при любом «С Nt bn + 15л — 1 • 9. Каким ус.
ловиям удовлетворяет Ь?
4.	Подберите а, b, с и d так, чтобы при любом л £ ДГ0 выраже-
ние abn + сп + d делилось на 1980.
ГЛАВА 2
УСЛОВИЕ НЕСОКРАТИМОСТИ ДРОБИ
ВИДА
ал + Ь
сп + d
§	1. Наибольший общий делитель
Если целые числа а и b делятся на некоторое цело,
число d, то d называют общим делителем этих чисел*
Наибольший из общих делителей заданных чисел а и Ь
3
навивают наибольшим общим делителем этих чисел (со-
кращенно НОД). В литературе употребляются различные
обозначения!
НОД (а, Ь), Д(а, Ь), (а, Ь).
Мы будем пользоваться последним обозначением для
НОД чисел а и Ь.
Точно так же можно определить НОД произвольной
конечной совокупности целых чисел. Однако в дальней-
шем нам понадобится лишь понятие НОД двух чисел.
Нетрудно видеть, что если хотя бы одно из чиеел
а или b отлично от нуля, то их НОД существует и яв-
ляется натуральным числом. Так, (28, 49) = (—28, 49) = 7.
Аналогично, на основании определения, (18, 0) = 18.
В то же время НОД (0, 0) не существует, так как нет
наибольшего числа, на которое делились бы числа 0 и 0.
Непосредственно из определения НОД вытекают сле-
дующие его свойства;
1)	(a, b) = (|a|, |6/)(f *; = ]/~х2 — модуль числа х).
2)	Если а\Ь (Ь^О), то (a, b) = | b |.
Числа а и b называются взаимно простыми, если
(a, b) = 1. Так, числа 25 и 12 взаимно простые. Числа
1 и —1 и только эти числа являются взаимно проетыми
с любым целым числом (в том числе и сами с собой).
Теорема 2.1 (о делении с остатком). Пусть
а — целое, b— натуральное число. Тогда существуют
и при том единственные целые числа q и г такие, что
a = bq + r (0<г<6).	(2.1)
□ Пусть1 q = jyj. Тогда q^ -у < q -f- 1, откуда
bq^.a <bq + b.	(2.2)
Пусть r = a — bq. Тогда a = bq -|- г и, на основании (2.2),
0^r<&. Таким образом, возможность представления
числа а в виде (2.1) доказана. Остается доказать един-
ственность такого представления.
Предположим, что наряду с (2.1) имеет меето также
а = bqt + Г! (0 < гх < Ь).	(2.3)
Вычитая из (2.1) (2.3), получим 0 = b (q — qi) + г — г{, т. е.
b(q — qi)=r1 — r.	(2.4)
1 [я] означает «целая часть числа х». По определению, [х] есть
наибольшее целое число, не превосходящее х.
9
Следовательно, r\ — r\b. А так как 0и —Ь<
< —г 0, то —b < г, — г <Ь, т. е. | гх — г | < Ь. Поэтому,
с учетом свойства 5 (гл. 1, § 1), rt — г —О, т. е. ri = r.
После этого (2.4) запишем в виде b(q — ft) = 0, откуда
вытекает, что ft — q (так как Ь=#=0). Этим доказана
и единственность (2.1). 
Числа q и г из (2.1) называют соответственно непол-
ным частным и остатком от деления а на Ь.
Теорема 2.2. Пусть at b — произвольные, не рав-
ные одновременно нулю целые числа. Тогда найдутся
такие целые числа и и о, что
(a, b) = au + bv.	(2.5)
□ Рассмотрим целые числа вида ах + by, где {х, y}c:Z
(т. е. x£Z и y£Z). Среди таких чисел имеются как от-
рицательные, так и положительные числа. Пусть А —
множество всех натуральных чисел вида ах + byi
Л = (ах+6z/|{x, y)<=.Z, ах + by£N}.
Обозначим через т наименьшее число1 в множестве А.
Таким образом, при некоторых и и v из Z т = аи -f- bv.
Применяя к числам а и т теорему о делении с остатком,
получим
а = mq + г (0 г < т),
откуда
г = а — mq = а — (аи 4- bv) q = as + bt,
где s = 1 —uq£Z и t = —vq£Z.
Предположим, что г 0. Тогда г = as + bt G А и r<m,
что противоречит выбору числа т. Следовательно, г — 0,
т. е. а\т (так как a=mq).
Точно так же, применяя теорему о делении с остатком
к числам Ь и т, устанавливаем, что Ь\т. Следовательно,
т — общий делитель чисел а и Ь. Но тогда =
= (a, b). С другой стороны, так как т = аи + bv и а • d,
b\d, то m\d и, таким образом, tn^d. В результате при-
ходим к заключению, что т = d, т. е. имеет место равен-
ство (2.5). g
Следствие 2.1. Наибольший общий делитель (а, Ь)
чисел а и b делится на любой общий делитель этих
чисел.
1 Неявно мы пользуемся так называемым принципом наимень-
шего числа, который формулируется так: в каждом непустом мно-
жестве натуральных чисел содержится наименьшее число. Заметим,
что на практике этим принципом часто пользуются как очевидным
фактом.
10
□	Если а\т и Ь\т, то, на основании равенства (2.5),
(а, Ь) также делится на m.g
Следствие 2.2. Пусть числа а, b— взаимно простые.
Тогда найдутся такие целые числа и и V, что
аи + bv = 1.	(2.6)
□	Так как числа а и Ь взаимно простые, т. е. (а, b) = \t
то равенство (2.6) непосредственно следует из равен-
ства (2.5). 
Теорема 2.3. Пусть произведение ab делится на о
и (а, с) = 1. Тогда b-с..
□	Так как (а, с) = 1, то, на основании следствия 2.2,
au + cv= 1, где и и v — некоторые целые числа. Умно-
жая обе части последнего равенства на Ь, получим
abu + cbv = b.	(2.7)
А так как по условию ab • с, то левая часть равенства
(2.7) делится на с. Следовательно, b также делится
на с. 
Числа и и v в теореме 2.2 определяются неодно-
значно. Действительно, пусть ик = и 4- kb, vk = v — ka, где
k£Z. Тогда
аик + bvk = аи + bv = (a, b).
Теорема 2.4. Пусть а, b — целые числа, т — нашу-
ральное число и (а, т) = 1. Тогда существует и при том
единственное число г и такое, что
аг -}-Ь\т (0	< /п).
□	На основании следствия 2.2 найдутся такие целые
числа и и и, что au-{-mv = l. Умножая это равенство
на —Ь, получим
а (—Ьи) —mbv — —b.	(2.8)
Применим теперь к числам —Ьи и т теорему о делении
с остатком:
—bu = mq + г (0 г < т).	(2.9)
На основании (2.8) и (2.9) ar + b=m(bv— aq), откуда
следует, что ar 4- Ь • т.
Предположим, что при некотором целом k (0^.k<m)
ak -\-b\m. Тогда
(ar 4-6) — (ak 4- b) — a (r — k)\ m.
А так как (a, m) = l, то, в силу теоремы 2.3, г — k-m.
Но |г — k\ <т. Следовательно, k = г. g
п
§ 2. Конкретный пример
Довольно распространенными являются задачи типа:
доказать, что при любом целом n(n£Z) дробь
несократима.
Решение. Предположим, что при некотором n$Z
рассматриваемая дробь сократима. Тогда существует такое
натуральное число d > 1, что
14n4-3;d, 21n + 4;d.
Но тогда при любых целых Ли/
(14п 4- 3)Л + (21л + 4) ltd.
В частности, при Л = 3 и 1 = —2 получаем, что 1 • d.
А это невозможно, так как, на основании предположе-
ния, d > 1.
Таким образом, предположение о том, что дробь
^-2^4 сократима, неверно. Следовательно, при любом
целом п рассматриваемая дробь несократима.
§ 3.	Общий случай.
Регулярные дроби
Рассмотрим теперь дробь
где а, Ь, с, d — фиксированные целые числа (параметры),
а п может быть любым целым числом. Выясним, каким
условиям должны удовлетворять параметры дроби (2.10),
чтобы эта дробь была несократимой при любом целом п.
Преджде всего ясно, что числа b и d должны быть
взаимно простыми, так как в противном случае при п =
= Л • (b, d), и, в частности, при п = 0 дробь (2.10) будет
сократимой.
Итак, в дальнейшем предполагаем, что
(/>,</)=!.	(2.11)
Кроме того, предполагаем, что каждое из чисел а, Ь, в
и d отлично от нуля.
Лемма 2.1. Если числитель и знаменатель дроби
(2.10) делятся на т, то числа п и т, а также и=*
= (а, с) и т взаимно простые.
12
□	Пусть an + bim и (п, т) = s. Тогда an4-ft*s
(так как /п-s) и njs. Следовательно, b-s. Аналогично
устанавливаем, что и d • s (если сп 4- d • /п). Следовательно,
1<з<(&, d)= 1,
т. е. s = 1.
Аналогично, если (и, т) = k, где и = (а, с), то а • А
(так как а\и, а и-А) и an+b\k (так как ап 4- Ь'-т,
a tn\k). Но тогда b\k. Точно так же устанавливаем, что
d • А. А так как (6, d) = 1, то А = 1. 
Теорема 2.5. Пусть при некотором n£Z числитель
и знаменатель дроби (2.10) делятся на натуральное
число т. Тогда т есть делитель целого числа Q, опре-
деляемого равенством
□	Пусть и = (а, с). Тогда а = uai, о = «Cj, где а1(
<?i — некоторые целые числа. Если при этом числитель
и знаменатель дроби (2.10) делятся на т (m$N), то,
очевидно,
01 {сп 4-d) — {an 4- b) • m.	(2.13)
А так как aiC = Cia, то (2.13) запишем так! a\d— bci\m.
Теперь остается заметить, что
aid-bci = ^d-b^ = a-^ = Q.m (2.14)
Следствие 2,3. Если
\ad— bc\ = {а, с),	(2.15)
то дробь (2.10) несократима.
□	При условии (2.15) Q— 1 или Q = —1. Но тогда,
на основании теоремы 2.5, при любом n£Z общий дели-
тель т числителя и знаменателя дроби (2.10) равен 1
(так как Q\m). 
Определение. Дробь (2.10) будем называть регуляр-
ной, если ее параметры удовлетворяют условию (2.15).
Так, рассмотренная в § 2 дробь является регулярной!
114.4 — 21 .3| = (14,21).
Таким образом, на основании предыдущего, произволь-
ная регулярная дробь является несократимой.
13
§ 4. Нерегулярные дроби
Рассмотрим теперь тот случай, когда дробь (2.10)
не является регулярной. Это означает, что число Q, опре-
деляемое равенством (2.12), отлично от 1 и —1. Если
при этом Q = 0, то ad = be. Следовательно, ad • b и be • d.
А так как (ft, d) = 1, то (теорема 2.3) a* b и c\dt т. e.
a = balr c = de!» Но тогда bard = bdclt откуда a1=c1.
Таким образом, в рассматриваемом случае
ап + b __ b (kn 4- 1)
сп d ““ d (kn + 1) *
где k=a1 = cx. Следовательно, при Q = 0 дробь (2.10)
2
является несократимой лишь при п = 0 или при п = — у,
если 2 • k.
Пусть теперь —1, 0, 1], т. е. |Q| > 1.
Теорема 2.6. Если у числа Q имеется такой дели-
тель т > 1, что (at т) = 1 или (с, /и) = 1, то при неко-
тором n£Z числитель и знаменатель дроби (2.10) де-
лятся на т.
□ Пусть, например, Q-m, т> 1 и (а, т) = 1. Тогда
(теорема 2.4) найдется такое целое число r(0^r<zn)
что аг-\-Ь\т. А так как, на основании (2.13) и (2.14)»
*
й, (сг 4- d) — Ci (ar -I- b) = Q j tn,
то и в! (сг 4- d) • tn. Но (alt т) = 1, так как аг— делитель
числа а и (a, tn) = 1. Поэтому (теорема 2.3) сг 4- d • т.
Таким образом, в рассматриваемом случае числитель
и знаменатель дроби (2.10) при п = г делятся на т, т. е.
дробь (2.10) не является несократимой при всех целых п. g
Например, рассмотрим дробь + *. Для этой дроби
14.3 — 21-4	—42 с v	л
Q = —(П-2ij— = ~т~ ~ ~числа Q имеются дели-
тели 2 и 3 взаимно простые соответственно с числами
21 и 14. Поэтому при некоторых значениях п числитель
и знаменатель рассматриваемой дроби делятся на 2 (или
на 3). Действительно, числа 14п + 4 и 21/14-3 при п =
— 1 4- 2& делятся одновременно на 2, а при п = 1 4- 3k —
на 3.
В связи с предыдущим возникает вопрос: может ли
нерегулярная дробь быть несократимой? Оказывается, мо-
жет. Действительно, рассмотрим следующую дробь;
14
12л +1 г»	ч	л 36 — 20	» «-у
2бд.|_з • ДЛЯ этой дроби Q = —— = 4. Предположим,
что при некотором n£Z
12/? + 1 • m, 20n + 3 $ tn (m> 1).
А так как, на основании теоремы 2.5, число т должно
быть делителем числа Q, то т = 2 или m == 4. Однако
очевидно, что ни при каком целом п числа 12п + 1 и 20/?+3
не могут делиться ни на 2, ни на 4. Следовательно рас-
сматриваемая дробь является несократимой.
Нетрудно видеть, что и в общем случае выражения
ап + b и сп + d ни при каком целом п не могут делиться
на заданное число tn, если число b не делился на (а, т)
или число d не делится на (с, tn).
УПРАЖНЕНИЯ
1.	Что можно сказать о сократимости (или несократимости)
дробей
Юл+ 9	1бл + 10	8л+ 15	9л + 8
15л+ 8’	8л+ 9 ’ 9л + 10 ’ 10л + 15 ?
2.	Каким условиям должны удовлетворять числа а, Ь, си d,
чтобы дроби
ап + 9 Юл+ 6 Юл+9 Юл+9
15л+ 8 ’ 15л + 8 ’ сп + 8 ’ 15л + d
были регулярными?
ГЛАВА 3
ТЕОРЕМА ВИЛЬСОНА
§ 1. Простые числа
Натуральное число р > 1 называется простым, если
у него нет других натуральных делителей, кроме единицы
и самого числа р. Если же р = pip2, где Pi и ра — отлич-
ные от единицы натуральные числа, то р называется
составным числом. Число 1 не относится ни к простым,
ни к составным числам.
Так, первыми простыми числами являются следующие
числа:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...
Свойство 1. Если простое число р делится на неко-
торое натуральное число а > 1, то а = р.
15
Действительно, если бы а-=^р, то у простого числа/,
было бы три делителя: 1, а и р(1 < а < р), что невоз-
можно.
Свойство 2. Произвольное целое число а либо делится
на простое число р, либо взаимно простое с р.
В самом деле, если (a, p) = d, то d=l или d = p.
В первом случае числа а и р взаимно простые, а во вто-
ром — а • р.
Свойство 3. Если произведение двух (или нескольких)
целых чисел делится на простое число р, то хотя бы
один из множителей делится на р.
Действительно, пусть ab • р и а не делится на р. Тогда
(свойство 2) (а, р) = 1 и, следовательно, b • р (теорема 2).
Аналогично рассматривается случай большего числа мно-
жителей.
Свойство 4. Наименьший не равный единице нату-
ральный делитель целого числа а есть простое число.
Действительно, пусть а • q, где q > 1 — наименьший
натуральный делитель числа и и q составное. Тогда q —
= be, где 1 < b < q, 1 < с < q и {Ь, с] с N. Но тогда
а • Ь, что противоречит выбору числа q. Следовательно,
q — простое число.
Свойство 5. Наименьший простой делитель состав-
ного натурального числа а не превосходит Vа.
В самом деле, пусть р — наименьший простой дели-
тель числа а. Тогда a = pb, где р^-Ь. Но тогда р*^
pb — а, т. е. р С Ка.
Таким образом, если у натурального числа а нет про-
стых делителей, не превосходящих )/а, то число а про-
стое. Этот факт часто используют на практике при уста-
новлении простоты числа а.
Теорема 3.1 (основная теорема арифме-
тики). Произвольное натуральное число а>1 можно
представить в виде произведения простых чисел и при
том единственным способом (если не учитывать порядок
расположения множителей).
Доказательство этой теоремы несколько громоздкое,
и мы не будем его приводить (см. (2], с. 9).
Теорема 3.2. (Евклида). Множество простых
чисел бесконечно.
□ Пусть множество простых чисел конечное и рх,
ра, .... рп — все такие простые числа. Рассмотрим нату-
ральное число Q = pipa ... рп4-1. На основании тео-
ремы 3.1 число Q можно представить в виде произведения
16
некоторых простых чисел qlt qit ...» q* (среди которых
могут быть и равные). Таким образом,
PtPt • • • Рп + 1 = <71*7» • • • *7®	(3-1)
Правая часть равенства (3.1) делится на простое число ft.
При этом ft не может совпадать ни с одним из чисел
р19 Р& • • • • Рп* Следовательно, предположение о том,
что множество простых чисел конечное и совокупность
А» Ра» •••» Рп содержит все простые числа — неверное.
А это означает, что множество простых чисел бесконеч-
ное. 
Замечание. Довольно распространенным является следующее
«определение» простого числа: натуральное число р > 1 называется
простым, если оно делится только на себя и единицу. Однако среди
натуральных чисел нет таких, которые делятся «только на себя
и единицу». Действительно, число 5, например, делится не только
на 5 и 1, но и на —5 и —1. А среди целых чисел имеется лишь
одно число, которое делится только на себя и единицу—это
число —1.
Таким образом, если строго логически пользоваться сформулиро-
ванным определением, то мы должны сделать заключение, что про-
стых чисел попросту не существует.
Правильная формулировка предыдущего определения такая: на
туральное число р>1 называется простым, если натуральными
делителями этого числа есть лишь само число р и 1.
§ 2. Теорема Вильсона
Теорема 3. 3. Натуральное число р > 1 является
простым тогда и только тогда, когда1
(р—1)1 + 1;р.
(3.2)
□ Пусть р — простое число. Если р = 2, то (р— 1)1+
+ 1 = 2 \р. Точно так же легко проверяется, что (р—1)1 + 1
делится на р при р = 3 и р = 5. Поэтому в дальнейшем
будем предполагать, что р > 5.
Рассмотрим множество А = (2, 3, ..., р — 2}, и пусть
а£А. Тогда (а, р) = 1 и, следовательно, на основании
теоремы 2.1, существует и при том единственное число
га такое, что
0<ги<р, ага—\\р.
1 Произведение первых п натуральных чисел кратко обозначают
л! (читается: эн-факториал). Так, 5! = 1 • 2.3 • 4 • 5 = 120. Кроме
того, по определению, 0! = 1.
17
При этом га=/=0 и га=И=1. Следовательно, г„>2. Кроме
того, га^р — 1. Действительно, предположим, что га =
= р — 1. Тогда
ara — 1 — ар — (а+ 1): р,
что невозможно, так как а + 1 ^р— 1, и, следовательно,
число а + 1 не может делиться на р. Таким образом,
га=£р — 1. Но тогда 2^г0<р —2, т. е. га£А.
Покажем, что га^'а. Действительно, пусть га = а,
т. е. а2 — 1 \р. Тогда (а— 1)(а 4- 1) -р, и, следовательно,
а — 1: р или а + 1: р. Однако это невозможно, так как
—1<р —3, 3^а+1<р— 1.
Итак, для произвольного числа а из множества А
в этом множестве существует и при том единственное
число га такое, что ага — 1: р, причем га =/= а. Обозначим
Oj = а, а2 = га, А4 = {а4, а2},
и пусть а3—некоторое число из А, отличное от а4 и а2
(т. е. а3£А, Ogg/li). Рассуждая как и раньше, приходим
к заключению, что в множестве А имеется такое число
а4 (а4 Ф а3), что а3а4 — 1 • р. При этом число а4 опреде-
ляется однозначно и отлично от а4 и а2. Действительно,
предположим, что а4 = аг. Тогда ала2 — 1 • р и а4аг — 1 • р,
и, следовательно,
(а3а2 — 1) — (а4а2 — 1) = а2 (а3 — а4): р.
А так как (а2, р) = 1, то а3 — а^\р, где |а3 — а4\<р.
Но тогда (см. гл. 1, § 1, свойство 5) а3=а4, что про-
тиворечит выбору числа а3(а3^ А4). Таким образом, а4£ Ар
Рассмотрим множество Ла={а1, а2, а3, а4}. Пусть А2=#А
и а3 — некоторое число из А, не принадлежащее А2. Для
этого числа в А найдется и при том единственное число
а3 и такое, что
а„а9 — 1: р, а3 £ А2, а3 #= аъ.
Если множество А3 = (а4, а2, а3, а4, аъ, а3}^А, то рас-
суждая как и раньше, найдем числа а7 и а8 из А, не при-
надлежащие множеству А3, и такие, что а7а3 — 1-р.
Продолжая этот процесс, через конечное число шагов
получим
А = (о4, а2, а3, ...,
где п = р — 1 — четное число и при k — 2, 4, ... , п
ak_1ak — 1: Р или, что то же самое,
= 1 + W* (* = 2, 4, ..., п).
18
Перемножая эти равенства, получим
оха2 ... ап = 1 + pq.
А так как числа а1( а2........ап совпадают с числами
2, 3.....р — 2 (но расположены, вообще говоря, в дру-
гом порядке), то
аха2 ... ап = 2 • 3 ... (р — 2) = (р — 2)!
Таким образом,
(р — 2)! = 1 + pq.
Умножая обе части этого равенства на р—1, получим
(р-1)1 = -1+р(<?+ 1).
Следовательно, (р— 1)1 + 1 \р.
Обратное утверждение доказывается совсем просто.
Действительно, пусть (р—1)1+1 делится на р. Предпо-
ложим, что р — составное число. Тогда р делится на
некоторое число т такое, что 1 < т < р. Но тогда
(р— 1)! \т. и, следовательно, 1 */п, что невозможно. Таким
образом, предположение о том, что число р — составное,
неверное, fl
Замечание. Прежде чем приступить к доказательству тео-
ремы Вильсона, идею доказательства первой части этой теоремы
можно проиллюстрировать на конкретном примере. Пусть, например,
р=11. Тогда Л = {2, 3, 4, 5, 6, 7, 8, 9). Пусть = 2. Тогда
а2 = 6, так как — 1 = 12 — 1 • 11, и Aj = {2, 6}. Пусть теперь
а3 = 3, Тогда а4 = 4 (а3а4—1 = 11’1!). Следовательно, Ла={2,3»
4, 6}. Рассматриваем следующее число а6 = 5. Тогда а9 = 9, Л3 =
= {2, 3, 4, 5, 6, 9). Аналогично а7 = 7, а8 = 8, после чего Л4 =
= {2, 3, 4, 5, 6, 7, 8, 9} = Л. Но тогда
ДаазЯ4Я5ава7а8 — 1=2*6’3‘4‘5«9*7«8—1=91 — 1;Н-
Следовательно, 10! + 1 • 11.
§ 3. Первое обобщение
теоремы Вильсона
Теорема 3.4. Пусть р — простое число. Тогда для лю-
бого целого числа п (О^и^р—1)
nl(p-(n+ 1))! + (—1Г :р.	(3.3)
Наоборот, если р> 1 и (3.3) имеет место хотя бы для
одного целого числа п, удовлетворяющего условию 0
<>i^p — 1, то р — простое число.
19
□ Пусть р— простое число и
0„ =
Тогда, как легко проверить,
ап + fln+i = п\ (р — (п 4- 2))! р.
Следовательно, ап + ап+1 • р. А так как а0 = (р — 1)! +
+ 1 • р, то и 01 • р. Но тогда at • р и т. д.
Таким образом, числа а0, аг....ар_г делятся на р,
что и доказывает 3.3. Наоборот, пусть при некотором п
ап\р (0 п < р — 1). Тогда ап+1; р (так как ап + ап+1 • р).
Продолжая эти рассуждения, получим, что о» х = (р—1)! +
+ 1»р. Но тогда, на основании теоремы Вильсона, р —
простое число.в
Следствие 3.1. Натуральное число р>2 является
простым тогда и только тогда, когда
\!п i\ 1*
[(Ч2)1] +*-1)2 ’-р-	<3-4)
□ Достаточно в предыдущей теореме взять п = В
Следствие 3.2. Пусть р — простое число вида 4й + 3.
Тогда
(т) ! + 1:Р иЛи (т) 1 ~ 1 :Р-	(3.5)
□	При р =s 4А + 3 соотношение (3.4) запишем в виде
откуда и следует (3.5). в
Теорема 3.5. Пусть р —простое число. Тогда
С;_1 + (-1)л+1:р (0<п<р-1),	(3.6)
где Ст — биномиальный коэффициент.
□	Воспользовавшись формулой Ст = лГ(^_П)1» полу-
чим, что
пЦр-(п+ 1)Ц (С;_1 + (-1)',+') =
= (р - 1)! + 1 + (-1)л+1 (п! [р - (п + 1)]! + (-1)"). (3.7)
А так как правая часть в (3.7) делится на р, то и левая
часть в этом равенстве делится на р. Однако п\ [р —
— (n-f-l)]! не может делиться на р. Следовательно,
Спв^ + (-1)"-*-1 :р. в
20
Следствие 3.3. Для любого ££{0, 1, 2, р — 2)
С*_> ч- с*±1 Sp.
Пример. Пусть р = 11. Тогда
с}0 + 1 = ю + 1: п, с?в — 1 = 45 — 1; п, с’10 + 1 = 120 + 1: п,
cj,—1 = 210—1-11, с‘о + 1 =252+ 1 ; п.
При этом
с!» + С10= П: 11. С|о + Схо = 55;11. ...
Теорема 3.6. (Ферма). Пусть (а, р) = 1. Тогда
ар~1 — 1 • р.
□ Применяя к числам аир теорему о делении с ос-
татком (гл. 2, § 1), получим a —pay-[-г (0<г<р).
Но тогда
ар~1 — 1 = (pai + г)р~' — 1 = pN + rp~l — 1.
Следовательно,
ap-i _ 1: р ~ гр-\ _ J: р.	(з,8)
На основании (3.8) приходим к заключению, что при г = I
утверждение справедливо! ар~х — 1 делится на р.
Пусть г = 2. Тогда
г-1_1=(1 + 1)'’-1-1=С“_1 + С;_,+ C2p-t + ... CgZ?. (3.9)
А так как, с учетом следствия 3.3, в правой части ра-
венства (3.9) сумма двух рядом расположенных слагаемых
делится на р, то и 2"-1 — 1 • р.
Предположим, что при некотором Л£{1, 2, ..., р—1)
Л"-1 — 1 • р. Если при этом k + 1 < р, то
(k + 1)₽_| _ 1 = Л"-1+ Ср_1^"2+	+ • • • + Cftk,
(3.10)
где, на основании теоремы 3.5,
Cftp_. = W* + (-l/.	(З.Н)
Но тогда, с учетом равенств (3.10) и (3.11),
(k + l)p~1 — 1 = pq + k (kp~2 — k°~3 4---h k — 1).
Умножая обе части последнего равенства на k + 1, получим
(k + 1) ((Л + I)""1 - 1] = pq(k + 1) + k(kp^- 1). (3.12)
А так как на основании предположения Л₽-1 — 1: р, то
правая часть в (3.12) делится на р. Учитывая теперь, что
21
k + 1 не делится на р (так как k + 1 < р), приходим
к заключению, что (k +	— 1 • р.
Следовательно, для любого г£{1, 2, ...» р — 1}
гр~г — 1 j р, что, на основании (3.8), и доказывает тео-
рему. |
§ 4. Второе обобщение
теоремы Вильсона
Пусть т > 1—фиксированное натуральное число.
Рассмотрим совокупность
аъ а2, ..., as (ах = 1, as = т — 1)	(3.13)
всех натуральных чисел, меньших т и взаимно простых
с tn. Число а из совокупности (3.13) назовем согласован-
ным с /и, если а2— 1 \т. В противном случае (т. е. если
а2—1 не делится на т) число а из совокупности (3.13)
будем называть несогласованным с т.
В таблице, которая здесь приведена, выписаны сово-
купности вида (3.13) для натуральных чисел 15. При
этом числа, согласованные с mt выделены жирным
шрифтом.
т	Совокупность (3.13)	т	Совокупность (3.13)
2 3	1, 1, 2	9 10	1, 2, 4, 5, 7, 8 1, 3, 7, 9
4	1, 3	11	1, 2, 3	9,	10
5	1, 2, 3, 4	12	1, 5, 7, 11
6	1, 5	13	1, 2, 3	И,	12
7	1, 2, 3, 4, 5, 6	14	1, 3, 5, 9, И, 13
8	1, 3, 5, 7	15	1, 2, 4, 7, 8, И, 13, 14
Отметим некоторые свойства согласованных и несогласо-
ванных чисел.
Свойство 1. У простого числа р>2 имеются лишь
два согласованных числа: 1 и р — 1.
□ Действительно, если 1 < а < р — 1, то, как уже
отмечалось в § 2 (при доказательстве теоремы Вильсона),
разность а2 — 1 не может делиться на р. Следовательно,
а не является согласованным с р числом, g
Свойство 2. Если число а согласованное с т, то число
т — а также согласованное с т.
22
□ Действительно, пусть а2—1 \т. Тогда (т— а)*—
— I — in* — 2am + (а* — 1) • т, причем 1 т — а^т — 1
и (т —а, т) = 1.
Следовательно, т— а — согласованное с т число, в
Следствие 3.4. Если а — несогласованное с т число,
то т — а—также несогласованное с т.
Свойство 3. Пусть а — согласованное с т число. Тогда
а(т — а) + 1 • т.
□ Действительно, так как а*—1-т, то
а(т — а) 4- 1 = ат — (а* — 1) • т. g
Теорема 3.7. Пусть т>2 и а^, а2, ... , as (а, = 1,
as == т — 1) —все натуральные числа, меньше т и взаим-
но простые с т. Тогда
аха2... а, — (—1) 2 jm,	(3.14)
где 6 (т) — количество согласованных с т чисел.
Заметим, что если т = р — простое число, то flxa2...at=
= (р — 1)1, и, на основании свойства 1, б(р) = 2. Сле-
довательно, в этом случае (3.14) запишем в виде (р —
— 1)! + 1 • р, что согласуется с теоремой Вильсона.
□ Пусть bi, b2........Ьг(г = б(т)) — все согласован-
ные с т числа, В = {бх, b2, ... , br], х, = blt х2 = in —
— bv На основании свойства 2, х2 £ В, причем х2 xt.
Действительно, если бы х2 = хх, то имело бы место ра-
венство т = 2Ь1. А так как (т, bj) = 1, то указанное
равенство возможно лишь при бх = 1. Но тогда т = 2,
что противоречит условию теоремы.
Пусть В2 = {хх, х2}. Если В2=£В, то обозначим через
х3 некоторое число из В, не принадлежащее В2, и пусть
х4=т — х3. Тогда х4=/*х3 и, кроме того, х4=/=хх, х4^
Ф х2. Действительно, предположим, что х4=хх, т. е.
т — х3 = хх. Тогда х3 = т — хх = х2, что противоречит
выбору числа х3. Аналогично, если х4 = х2, то т — х., =
= т — хх, и, следовательно, х3 = хх, что также невоз-
можно. Продолжая эти рассуждения и учитывая, что при
т > 2 число б (т) — четное, получим
В = (хх, Х2, Х8, .... Хг},
причем, на основании предыдущего,
х2=т — хх, xt=m — х3, .... хг=т— xf_i.
га
Но тогда, с учетом свойства 3,
*1*2 + 1 : т> *з*4 + 1:	• • • > *г-1*г 4- 1 • т,
или, что то же самое,
ХхХ2 = — 1 + tnqi, х»х4= —1 4- mqv ...»xr_txr= —1 +mqn,
(3.15)
где ft = y = ~2^- Перемножая равенства (3.15), получим
Цт)
ххх2... х, = (—1) 2 +m(f-	(3.16)
При этом числа х1( хг......хг совпадают с числами
61( Ьг, ..., Ьг, расположенными, может быть, в другом
порядке. Поэтому равенство (3.16) можно записать в виде
Цт)
ЬгЬ2... Ь, = (—1) 2 + '”?•	(3.17)
Если г = s, то теорема доказана (так как в таком
случае (3.14) легко следует из (3.17)).
Предположим, что г < з и
С = {сх, с4, ...»	•
совокупность всех несогласованных с т чисел. Обозна-
чим у! = сх. Тогда, рассуждая так же, как и при дока-
зательстве теоремы Вильсона (§ 2), приходим к заключению,
что в С найдется такое число yt, что У1Уг— 1-/п. При
этом у.2 =£ у!, так как yi — несогласованное с т число.
Пус~ь Сг — {«/1( уг}. Если Са^С, то обозначим через
Уз некоторое число из С, не принадлежащее Са. Для
числа уз в С найдется такое число у4, что уау4 — 1 • т,
причем у4 £ С2 (последнее обосновывается так же, как
и при доказательстве теоремы Вильсона).
Продолжая этот процесс, получим
£ = {Уъ У г* • • • • Уз-/•}»
причем, на основании предыдущего,
У1Уг — 1: ydi — 1: tn.........ys-'-iys-t — 1: т.
Но тогда
У1Уг = 1 + tntu уау4 = 1 + mt.......Уз-гЛк-, = 1 + mtt.
Таким образом,
У1Уа - </.-/= 1 + tnt.
24
При этом числа ylt у2, ... , ys_r совпадают с числами
Ci, сг, .... с,_г, записанными, возможно, в другом по-
рядке. А это означает, что равенство (3.13) можно запи-
сать в виде
qc, ... e,_r = 1 + mt.	(3.19)
Перемножая теперь почленно равенства (3.17) и (3.19)
и учитывая, что
(biba... br) (cict... c,_r) = OjOj ... a„
получим равенство
8<"») . .
o1aJ ... а, = (— 1) 2 + nid>
откуда следует (3.14) g
УПРАЖНЕНИЯ
1.	Имеются ли среди чисел 1983, 1987, 1991, 1993, 1997, 1999
простые числа?
2.	Докажите следствие 3.3 беэ использования теоремы Вильсо-
на и теоремы 3.5.
Указание. Используйте свойство суммы 4-
3.	Докажите теорему 3.5, воспользовавшись следствием 3.3.
ГЛАВА 4
ИССЛЕДОВАНИЕ УРАВНЕНИЯ
хп + рж* + fl = 0
§ 1. Комплексные числа
Комплексные числа часто определяют как выражения
вида а 4- Ы, где а, b — действительные числа, a i — не-
который символ, который называют мнимой единицей.
При этом предполагается, что комплексные числа удо-
влетворяют следующим условиям (аксиомам).
Аксиома 1.
а + Ы = с + di *» а = с, b = d,
Аксиома 2.
(а + Ы) + (с + Л) = (а + с) + (b + d)i.
Аксиома 3.
(а + bi) (с + di) = (ас — bd) + (ad + be) i.
25
Таким образом, аксиомой 1 характеризуется равенство
комплексных чисел, а аксиомами 2 и 3 — операции сло-
жения и умножения таких чисел.
Опираясь на аксиомы 1—3, нетрудно уже чисто логи-
ческим путем установить, что операции сложения и ум-
ножения комплексных чисел коммутативны, ассоциативны
и операция умножения связана с операцией сложения
дистрибутивным законом. Другими словами, если
г = а + Ы, к = с + Л’, и = k + И
есть произвольные комплексные числа, то
z + X = X + z, (z + к) + и = z + (X + и),
zK = Xz, (zX) и = z (Xu),
(z + X) и = zu + Xu.
Кроме того, операции сложения и умножения комп-
лексных чисел оказываются обратимыми. Это дает воз-
можность ввести операции вычитания и деления рассмат-
риваемых чисел:
(а + Ы) — (с + di) = (а — с) + (b — d) ц
а + Ы________ас + b(l , Ьс — ad .
— c» + d2 + с* + d* 1‘
При этом последнее равенство имеет место лишь при
условии, что c24-d2=#0, или, что то же самое, если
с 4~ di О 4“ Oi.
Отождествляя комплексное число а 4- Oi с действи-
тельным числом а, получим «включение» множества дей-
ствительных чисел /? в множество комплексных чисел,
которое обычно обозначается буквой С (Z?czC). При
этом, применяя к действительным числам а и Ь, которые
рассматриваются как комплексные числа (а = а 4- Oi, b =
= Ь + Oi), операции сложения, умножения, вычитания и
деления, которые были определены для комплексных чи-
сел, мы получим те же результаты, которые получили
бы, применяя к указанным числам соответствующие опе-
рации, определенные для действительных чисел. Например,
(а + Oi) (Ь 4- 00 — iab — 0 • 0) 4- (а0 4- 0b) i = ab 4- 0i = ab.
Таким образом, действительные числа можно рассмат-
ривать как частный случай комплексных чисел. В связи
с этим комплексное число а 4- Ы называют невеществен-
ным, если b Ф 0.
На основании предыдущего, осуществляя арифмети-
ческие операции над действительными числами, мы не
можем получить невещественное число. Однако обратное
26
не всегда верно: в результате применения арифметических
операций к невещественным комплексным числам мы мо-
жем получить как невещественные, так и вещественные
числа. Прежде чем проиллюстрировать это, условимся
относительно следующих естественных обозначений:
0 4-6/ = Ы, 1 • i = /, i2 = ii.
Тогда /а = (0 4- 1 • 0 (0 4- 1 • 0 = (0 • 0 — 1 . 1) 4- (0 . 1 4-
4-1*0)/ = —1, т. е. /а = —1.
Учитывая последнее равенство, часто пишут: / = К — L
Однако при этом следует помнить, что равенство / =
= И—1 можно получить (при соответствующем расшире-
нии понятия корня), но нельзя использовать его в ка-
честве определения числа /.
В связи с этим, например, в «Пособии для поступающих в ву-
зы» (Наука, 1973, с. 87) Г. В. Дорофеев, М. К. Потапов и Н. X. Ро-
зов пишут: «И все же поступающий не должен допускать при из-
ложении теории комплексных чисел явных нелепостей. Например,,
часто «определяют» комплексные числа так: «комплексным числом,
называют числа вида а 4- bit где а и b — действительные числа,,
a i = У/—1». На самом деле это определение просто непонятно. Ведь
внак радикала употребляется (см. гл. 1, § 2) для обозначения ариф-
метического квадратного корня из положительного действительного’
числа, а что означает —1 — неизвестно!».
Число z = a — Ы называют комплексно сопряженным^
(или просто сопряженным) с комплексным числом г =
= а 4- bi. Как легко проверить,
z 4- 5 = 2а, zz = а2 4- Ь2,
т. е. сумма и произведение числа z и сопряженного чис-
ла z есть вещественные числа. При этом вещественное
число \z\ = ]/‘zz называют модулем комплексного числа г.
Впервые о комплексных числах упоминается в книге итальян-
ского математика Кардано (1501—1576) в связи с исследованием
уравнения третьей степени (см. § 4). Однако долгое время комплекс-
ные числа считали нереальными; их называли «абсурдными», «мни-
мыми», «невозможными», «фиктивными» и т. п. Объясняется это тем,
что вёе наявные числа можно было как-то связать с реальным»
объектами (счет, измерение и т. п.), тогда как в случае комплекс-
ных чисел сделать это долгое время не удавалось.
Однако все это не мешало ученым пользоваться комплексными
числами как некоторыми вспомогательными величинами, что часто
упрощало математические преобразования.
Постепенное выяснение свойств комплексных чисел привело
к осознанию того, что эти числа не менее реальны и важны для
математики и различных приложений, чем более привычные нату-
ральные, рациональные или иррациональные числа.
2?
Окончательное признание комплексные числа получили после
того, как было найдено геометрическое истолкование их в работах
датского математика Каспера Вессел я (1745—1818) и швейцарского
математика Аргана (1768—1822).
§ 2. Квадратные уравнения
В школьном курсе математики подчеркивается, что
квадратное уравнение, т. е. уравнение вида
ах1 + Ьх 4- с = 0 (а 0)	(4.1)
может либо иметь корни, либо их не иметь. Например,
уравнение
х2 + 10х + 26 = 0,	(4.2)
которое может быть преобразовано к виду
(х + 5)2+1=0,	(4.3)
не имеет корней, так как «выражение (х + 5)2 4- 1 при
любом значении переменной х положительно, следова-
тельно, уравнение (4.3) не имеет корней». Все это верно,
если корни квадратного уравнения искать среди действи-
тельных чисел. Однако ситуация существенно изменится,
если мы будем искать корни уже в более широком мно-
жестве— в множестве комплексных чисел. Так нетрудно
проверить, что комплексные числа хх = — 5 4- i и ха —
= —5 — i есть корни уравнения (4.3), или, что то же
самое, уравнения (4.2).
Оказывается, что не только указанное конкретное
уравнение, но и любое квадратное уравнение имеет кор-
ни в множестве комплексных чисел. В дальнейшем мы
покажем это в случае квадратного уравнения с действи-
тельными коэффициентами. Но предварительно рассмот-
рим уравнение вида
г2 = а (а < 0).	(4.4)
Найдем z в виде г = х + yi. Подставляя это значение
в (4 4) и возводя з квадрат, получим
х* _ yt 4. 2x.yi = а,
откуда
х2 — у2 = а, 2ху = 0.
Так как а<0, то, очевидно, у=#=0. Но тогда х = 0 и,
следовательно, у* = —а больше нуля. Корни этого урав-
28
нения	= К—а и г/2 =— У—а- А это означает, что
корни уравнения (4.4) имеют вид
zt =У — ai, z2 = — У — al	(4.5)
(или, что то же самое, zt =У1а}1, z2 ®—J^|a|i).
Учитывая равенство z? = а, условимся (по аналогии
со случаем а>0) писать z1 = Vra. Тогда, на основании
(4.6),	_
Уа =V—ai (а < 0)	(4.6)
и, в частности, при а = —1 V—1 =1.
На основании (4.5) также получаем г2 = —У а.
Рассмотрим теперь общее квадратное уравнение
az2 + bz + c^0	(4.7)
с действительными коэффициентами а, b и с. Поступая
так же, как и в случае обычного квадратного уравнения
(относительно вещественного неизвестного), преобразуем
это уравнение к виду
где D — b2— 4ас, или, что то же самое,
Но тогда, учитывая предыдущие рассуждения, можем
найти корни zx и г2 уравнения (4.7):
. __± ,	__	ft , /б	ft	/5
1 2а	V 4а* ~	2а ‘1" 2| а |	’ г* “ 2а	2| а |	’
При а > 0 последние выражения запишем так:
_6+ /й»_4ас	,	_&_/м-4ас	,. д.
Z1 ------23------’	= ------2а--------‘	(4-8>
Если же а < 0, то |а| = — а, и мы получим равенства
(4.8), в которых, однако, zx и z2 поменяются местами.
Таким образом, корни zx и z2 квадратного уравнения
(4.7) с действительными коэффициентами всегда сущест-
вуют и находятся по тем же формулам, что и корни урав-
нения ах2 + Ьх 4- с = 0 при Ь2 — 4ас 0. Следует только
помнить, что в случае Ь2 — 4ас < о У Ь2 — 4ао вычисля-
29
ется по формуле (4.6). Для иллюстрации рассмотрим сно-
ва уравнение (4.2). На основании (4.8) устанавливаем, что
— 10 + /100— 104 _ — 10 +	4 _ — ю + /4(
21 —	2	2	2	’
т. е. 21 = — 5 4-1. Аналогично г2 = —5 — I.
В общем случае, как и в случае вещественных кор-
ней, также справедлива теорема Виета: сумма корней
квадратного уравнения (4.7) равна — , а произведение
корней равно ~ , т. е.
Zl+Zt = —^) ZiZ2 = ~.	(4.9)
Равенства (4.9) легко установить, используя равенства
(4.8).
§ 3. Тригонометрическая форма
комплексных чисел
Пусть на плоскости задана прямоугольная система ко-
ординат. Поставим в соответствие комплексному числу
а + Ы точку плоскости с координатами (а, Ь). В резуль-
тате получим взаимно однозначное соответствие между
множеством комплексных чисел и точек плоскости. В свя-
зи с этим на практике комплексные числа часто отож-
дествляют с точками плоскости и вместо «комплексное
число z = а + bi» говорят «точка z = а + Ы».
С другой стороны, учитывая, что каждой точке пло-
скости с координатами (а, Ь) соответствует единственный
вектор с началом в точке (0, 0) и концом в точке (а, Ь),
комплексное число а + Ы часто отождествляют с таким
вектором (что более удобно при иллюстрации действий
над комплексными числами). В связи с этим вместо «комп-
лексное число z =а .+ Ы» говорят также «вектор г=а+Ы».
Угол а между осью абсцисс и вектором г=/=0, отсчи-
тываемый от положительного направления оси абсцисс,
называют аргументом комплексного числа г. Из рис. 1
видно, что
& = rsinq>, a=rcosq>,	(4.10)
где г = j/a2 +	—длина вектора z (или, что то же са-
мое, модуль комплексного числа z).
14спользуя (4.10), убеждаемся, что
а + Ы = г (cos ф + i sin ф).	(4.11)
30
Правую часть в (4.11) называют тригонометрической фор-
мой комплексного числа г. Тригонометрическая форма
комплексных чисел особенно удобна для записи операций
умножения и деления комплексных чисел. Например, если
г = г (cos ф + i sin ф), А, = s (cos а 4- i sin а),
то, как легко проверить (используя теоремы сложения
тригонометрических функций),
гХ = rs [cos (ф + а) 4- i sin (ф 4- a)J, (4.12)
4 = 4 (соз(ф— а) 4- i sin (ф — а)[.	(4.13)
Л S
В частности, на основании (4.12),
z2 = г2 (cos 2ф 4* i sin 2ф).
Воспользовавшись принципом математи-
ческой индукции, нетрудно проверить,
что
zn = rn (cos пф 4- t sin Пф). (4.14)
В частности, при г = 1 получаем так
называемую формулу Муавра
(cos ф 4- i sin ф)" = eos пф 4- i sin пф.
(4.15)
Рис. 1.
При этом формулы (4.14) и (4.15) справедливы не только
при натуральных п, но и при любых целых п.
Тригонометрическая форма комплексного числа дает
возможность довольно просто решать уравнения вида
zn = 0, где n£N, а 0 — фиксированное комплексное чис-
ло. Действительно, записывая 0 в тригонометрической
форме
0 = г (cos ф 4- i sin ф),
простой проверкой (с использованием формулы (4.14)),
убеждаемся, что рассматриваемое уравнение имеет п раз-
личных корней, которые определяются формулой
п/—(	ф4-2^л , . .	+ 2kJx\
h = V (cos 4-1 sin — j,
(4.16)
где k£{0, 1, .... n— 1}. Все эти корни расположены
через равные промежутки на окружности радиуса R =
= >/7 с центром в начале координат.
31
§ 4. Уравнение х8 4- рх 4- q = О
Произвольное кубическое уравнение
у3 + ay2 4- by 4- с = О
с помощью подстановки у = х — -у можно привести к виду
х3 4- рх 4- q = 0.
(4.17)
Поэтому, не ограничивая общность, можем рассматривать
лишь кубические уравнения вида (4.17). В дальнейшем
условимся, что р и q — вещественные числа.
В отличие от квадратного уравнения корни кубиче-
ского уравнения находятся уже не так просто. Если спо-
соб решения квадратного уравнения знали еще за 2000
лет до нашей эры (Вавилон), то общий способ решения
кубического уравнения был предложен лишь в XVI веке.
Если р = 0, то корни уравнения (4.17) могут быть
найдены способом, рассмотренным в предыдущем пара-
графе, или простым разложением на множители
х8 4- q = (х 4- а) (х1 — ха 4- а2) (<х = y^q).
Откуда следует, что Xj =—y^q, а остальные два корня
ха и х8 уравнения х8 4- q = 0 находим как корни урав-
нения х2 — ах 4- а2 = 0.
Теорема 4.1. Пусть р=^0. Тогда корни уравнения
(4.17) могут быть найдены по формуле
2, 3}),	(4.18)
где ак — корни уравнения.
а8 = -|4-ГО (*> = т+4)«	(4-19)
□ Действительно, пусть а — корень уравнения (4.19)
и х == а — £ (индекс k для удобства не пишем). Тогда
иСС
х» 4- рх 4- q = а3 - За2 £ 4- За <£» -	4- ра -
-3-а + ^=а*-2^ + ^
32
А так как1 * = Т + то
a8~2w + ?=-H?=0. Ц
Замечание. Обозначим р* = —^. Тогда, как легко про-
верить, Р* есть корень уравнения
рз = _А_/о.	(4.20)
удовлетворяющий условию сц0* = — -у. Поэтому формулы для
корней уравнения (4.17) часто записывают в следующем виде (фор-
мулы Кардано): = а* + Ра» где а* и Ра — корни соответственно
Р
уравнений (4.19) и (4.20), удовлетворяющие условию аара =-.
Иногда корни уравнений (4.19) и (4.20) записывают также в виде
а=	Р=	(4.21)
FA	FA
Тогда формулу для корней уравнения (4.17) записывают так:
х =	(4.22)
где D определяется равенством (4.19). Однако при этом следует
помнить, что корни (4.21) определяются неоднозначно и что в фор-
муле (4.22) следует брать такие значения аир, произведение которых
р
равно-----,
о
§ 5. Исследование корней уравнения
х3 + рх + q = 0
Установленные в предыдущем параграфе формулы Кар-
дано для решений кубического уравнения (4.17) дают
возможность выяснить, какие корни этого уравнения
вещественные, а какие — нет. При этом оказывается, что
все зависит от знака числа D —	4- ~. А именно, име-
ют место следующие утверждения.
1.	Если D>0, то уравнение (4.17) имеет один ве-
щественный корень и два невещественных корня.
1 Действительно, на основании (4.19)
откуда и следует рассматриваемое равенство.
2 3-60
33
2.	Если D < 0, то все три корня уравнения (4.17) —
вещественные.
3.	Если D =0, то все ко/.ни уравнении (4.17) — ве-
щественные, причем два из них, совпадают (кратный корень).
Доказательство этих утверждений существенно опи-
рается на формулы Кардано, и, следовательно, такие до-
казательства применимы лишь в случае кубического урав-
нения (4.17). Однако, оказывается, сформулированные
утверждения можно обосновать совершенно иным методом,
который при этом приме-
ним и в случае других
классов уравнений (см.
§ 6).
Итак, с целью иссле-
дования корней уравне-
ния (4.17) рассмотрим
функцию f, которую за-
дано формулой
f (х) = х3 + рх + q.
Так как lim = 1, то
*3
при достаточно больших
по модулю отрицатель-
ных значениях х f (х) <
<0, а при достаточно
больших положитель-
ных значениях х [ (х) >0.
Кроме того, функция/непрерывна. Поэтому ее график дол-
жен^хотя бы один раз пересечь ось абсцисс. А это означает, что
уравнение (4.17) имеет хотя бы один вещественный корень.
Чтобы выяснить вопрос о наличии или отсутствии
других вещественных корней, рассмотрим производную
функции f: f* (х) = Зх2 4- р. Если р > 0, то f (х) > 0
(x£R). Следовательно, f — возрастающая функция. Поэто-
му график этой функции пересекает ось абсцисс лишь
в одной точке. А это означает, что при р > 0 функция
f имеет лишь один вещественный корень.
К такому же заключению приходим и в случае р = 0.
Пусть р < 0. Тогда, как легко убедиться, точки
являются соответственно точкой максимума и точкой ми-
нимума рассматриваемой функции f. Все возможные слу-
чаи размещения эк трепальных значений функции f пока-
34
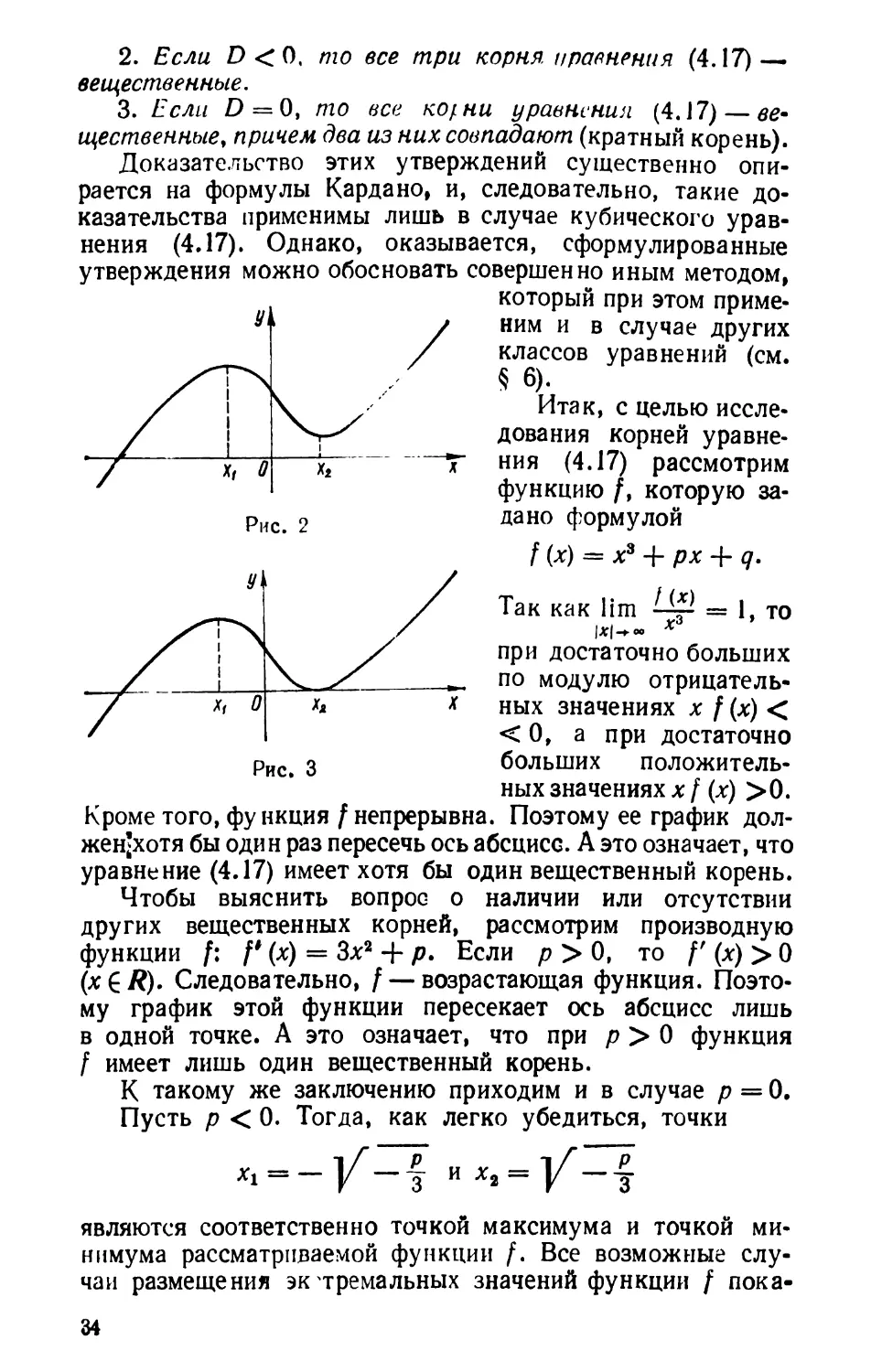
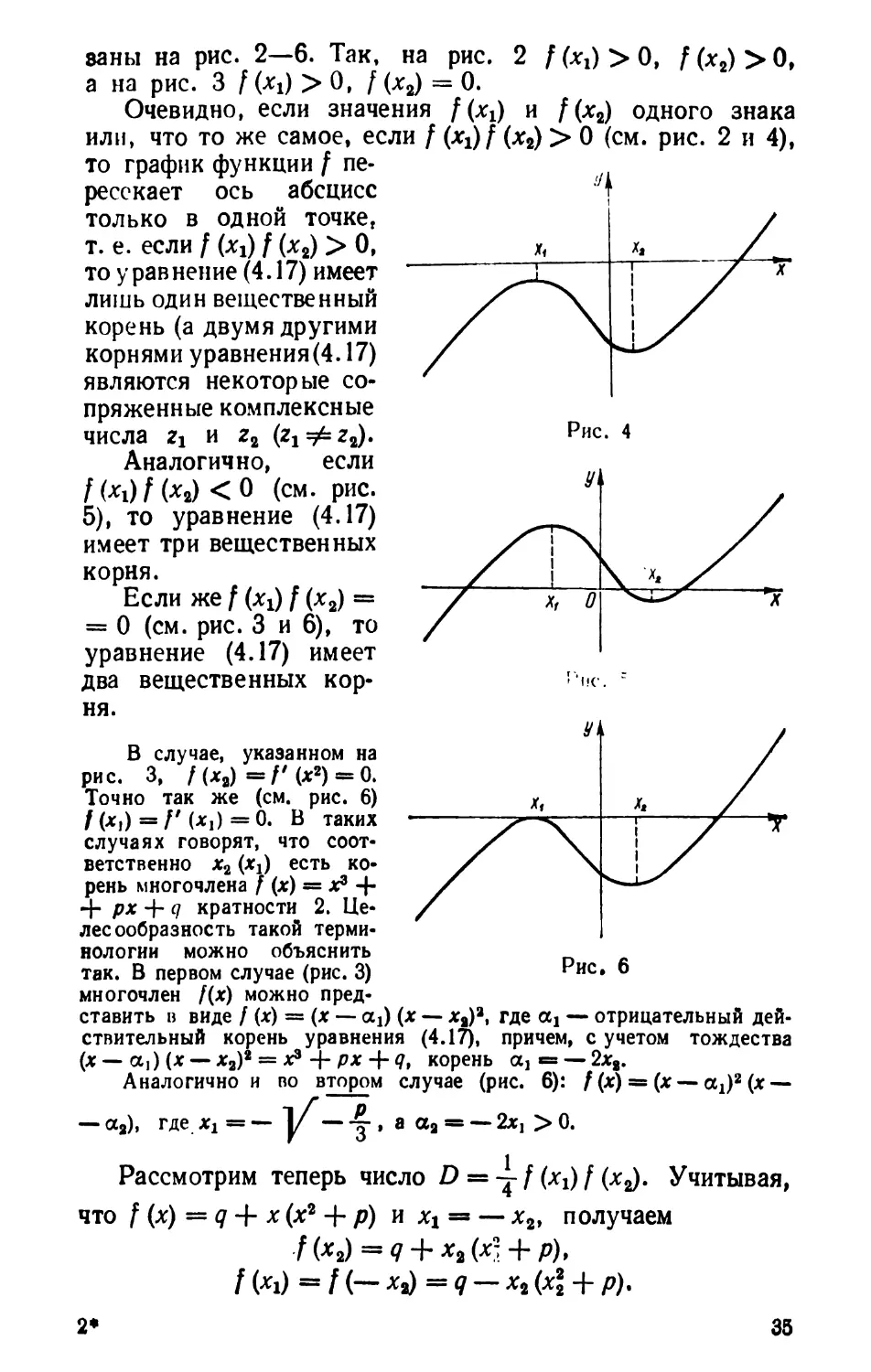
ваны на рис. 2—6. Так, на рис. 2 f (xj > 0, f (х2) > 0,
а на рис. 3 f (xj > 0, f (х2) = 0.
Очевидно, если значения f(xi) и /(х2) одного знака
или, что то же самое, если / (хх) f (х2) > 0 (см. рис. 2 и 4),
то график функции f пе-
ресекает ось абсцисс
только в одной точке,
т. е. если f (хх) f (xt) > О,
то уравнение (4.17) имеет
лишь один вещественный
корень (а двумя другими
корнями уравнения(4.17)
являются некоторые со-
пряженные комплексные
числа 21 и z2
Аналогично, если
f (xv)f (х2) <0 (см. рис.
5), то уравнение (4.17)
имеет три вещественных
корня.
Если же f (Xi) f (х2) =
= 0 (см. рис. 3 и 6), то
уравнение (4.17) имеет
два вещественных кор-
ня.
В случае, указанном на
рис. 3, / (х2) = /'(х2) = 0.
Точно так же (см. рис. 6)
f (*i) =/'(*]) ==0. В таких
случаях говорят, что соот-
ветственно х2 (xj есть ко-
рень многочлена / (х) = х3 +
+ рх + q кратности 2. Це-
лесообразность такой терми-
нологии можно объяснить
так. В первом случае (рис. 3)
многочлен /(х) можно пред-
ставить в виде / (х) = (х — cq) (х — ха)2, где а2 — отрицательный дей-
ствительный корень уравнения (4.17), причем, с учетом тождества
(х— а,) (х — ха)2 = х3 + рх + qt корень «]= — 2ха.
Аналогичной во втором случае (рис. 6): f (х) = (х — aj2 (х —
— аа), где Xi = — 1/ — -тг , a aa = — 2xj > 0.
Рассмотрим теперь число D = ~ f (xi) f (х^. Учитывая,
что f (х) = q + х (х2 + р) и х, = — х2, получаем
f (*а) = <7 + х2 (х; + р),
f(xi)=f(—xj=q — x2(xl + p).
2*
35
Поэтому
4D = 72 — х2 (х2 + р)2,
(4.23)
где
х? = - f , (х2 + р)2 = (^)2 =	.	(4.24)
Используя теперь (4.23) и (4.24), получим
При этом, на основании равенства D = f (xv) f (х2) и пре-
дыдущих рассуждений, приходим к заключению, что если
D>0, то уравнение (4.17) имеет один вещественный
корень и два невещественных корня, а при D^O урав-
нение (4.17) имеет три вещественных корня, причем в слу-
чае D = 0 два из них совпадают (кратный корень).
Таким образом, сформулированные в начале параграфа
утверждения мы установили без использования формул
Кардано. В следующем параграфе этот метод будет ис-
пользован в более общем случае.
§ 6. Исследование корней уравнения
х" + рх'г + 7 = 0
Рассмотрим уравнение
хп + pxk + q = 0,	(4.25)
где п и k (п > k) — нечетные натуральные числа, а р и
7— некоторые вещественные числа, и попробуем методами
предыдущего параграфа выяснить вопрос о количестве ве-
щественных (невещественных) корней уравнения (4.25). С
этой целью рассмотрим функцию
/ (х) = хп + pxk + q.
Так как п — нечетное, то, как и в предыдущем случае,
при достаточно больших по модулю отрицательных зна-
чениях xf(x)<0, а при достаточно больших положи-
тельных значениях х / (х) > 0. Кроме того, функция f
непрерывна и, следовательно, ее график должен хотя бы
один раз пересечь ось абсцис. А это означает, что урав-
нение (4.25) также имеет хотя бы один вещественный
корень.
36
Чтобы установить природу других корней уравнения
(4.25), рассмотрим производную функции fj
f (х) = хк~1 (пхп~к + pk).	(4.26)
Так как числа k — 1 и п — k четные, то, как следует из
(4.26), при /'(х)>0 для любого x£R (х^= 0). А
это означает, что f — возрастающая функция на числовых
промежутках ]— оо, 0[ и ]0, оо[. Но тогда функция f
возрастает и на всей числовой прямой1. Поэтому в рас-
сматриваемом случае уравнение (4.25) имеет лишь один
вещественный корень (а остальные корни — невеществен-
ные).
Рассмотрим теперь случай р <0. Тогда, с учетом (4.26),
критическими точками функции f являются точки: Xt =
= —"'у/'__—> х2 = 0 (при k > 1), х3 ="	__£*.Для ис-
следования функции f строим соответствующую таблицу
X	1—*11	*1	Ixtixj	*2	1*2:хз[	*3	1*з; 1
/'(»	+	0	—	0	—	0	+
/ (X)	/	1 (*|)		/(х2)		/(Хз)	/
		max				min	
Таким образом, Хх есть точка максимума, а х3 — точка
минимума функции f. Поэтому, как и в случае (4.17),
приходим к заключению:
1.	Если f(xj) f(x3)>0, то уравнение (4.25) имеет
лишь один вещественный корень.
2.	Если f (х3) /(х3) = 0, то уравнение (4.25) имеет
два вещественных корня.
3.	Если f(Xi) / (х3) < 0, то уравнение (4.25) имееет
три вещественных корня.
1 Заметим, что если на промежутках ]— оо, 0[ и ]0, оо| функ-
ция f убывает (или возрастает), то из этого не следует, что f убы-
вает (или возрастает) на всем множестве определения. Примером
тому является функция /, определяемая формулой f (х) = — . Однако
в нашем случае такое заключение (о возрастании функции /) спра-
ведливо в силу того, что зта функция непрерывна в точке х = 0.
37
Остальные корни в каждом из предыдущих случаев —
невещественные1.
Рассмотрим выражение
р =	f(x9).	(4.27)
Воспользовавшись тем, что х3 = — xlt f (х) = xk (xn~h +
4- р) Ч- q и х"“* = х,**’* = —	, приходим, после неслож-
ных преобразований, к равенству
2»	2п
f (Xi) f (•»») = ^ - Л	(п - к)«.
Но тогда
. Ч.	2*	,	. 2л
О= М_У-k—	М9ох
\п — kJ	\ п /	(4.28)
Учитывая теперь равенство (4.27) и сформулированные
ранее утверждения 1 — 3, убеждаемся в справедливости
следующей теоремы.
Теорема 4. Пусть число D определяется равенст-
вом (4.28).Тогда npuD>0 уравнение (4.26) имеет лишь
один вещественный корень, при D = 0 — два вещест-
венных корня, а при D < 0 — три вещественных корня.
Остальные корни уравнения (4.25) —невещественные.
Замечание. Введем функцию sign* („знак числа х“)> кото*
рая определяется так:
( 1 (* > 0),
sign х = { О (х = 0),
I- 1 (х < 0).
Тогда общее количество вещественных корней уравнения (4.25)
определяется формулой 2 — signD.
УПРАЖНЕНИЯ
1.	Докажите, что корни уравнения za=a+^	опреде*
ляются формулами
a2 + b* — a z
2
где 0 = si gn b — знак числа b.
1 Относительно возможного количества невещественных корней
38
2.	Докажите формулы (4.12), (4.13) и (4.14).
3.	Воспользовавшись формулой Муавра (формула 4.15), докажи-
те, что при любом натуральном п.
si пл (р = Сд cos”-1 ф sin ф — C’cos”-Зф sin9 ф + С& cos”-5 ф 51п6ф—...»
cos «ф = cosn ф — С’ cos”-2 ф sina ф + С4 с s”—4 ф sin4 ф —	.
4.	При каком р уравнение х9 + Р& + 12 = О имеет только один
вещественный корень? два вещественных корня? три вещественных
корня?
5.	При каких q уравнение х9—18x3 + (/ = 0 имеет только один
вещественный корень? два вещественных корня? три вещественных
корня?
6.	Исследуйте уравнение хг + рхк + q = 0, где п > k — нату-
ральные числа при условии, что а) п — четное, k — нечетное; б) п —
нечетное, k — четное; в) п. и k — четные числа.
ГЛАВА 5
ОБ ОДНОМ ДОСТАТОЧНОМ УСЛОВИИ
СУЩЕСТВОВАНИЯ
НЕВЕЩЕСТВЕННЫХ КОРНЕЙ МНОГОЧЛЕНА
§ 1. Корни многочлена
В гл. 4 было показано, что в случае многочленов
второй или третьей степени корни таких многочленов
существуют и могут быть вычислены непосредственно.
Существуют также формулы для вычисления корней
многочлена четвертой степени. Однако в общем случае
нет формул для вычисления корней многочленов степе-
ни п > 4. Поэтому для таких многочленов возникает,
прежде всего, вопрос о существовании корней. Ответ
на этот вопрос дает теорема Гаусса: у произвольного
многочлена степени п^ 1 имеется хотя бы один ком-
плексный корень. Заметим, что в настоящее время су-
ществует много различных доказательств теоремы Гаус-
са, однако все они чрезвычайно сложные и громозд-
кие или устанавливаются с помощью неэлементарных
предложений, на обоснование которых также затрачи-
ваются значительные усилия.
Пример многочлена
f (х) = (х — а)3 = х3 — Зах2 + Заах — а3 (5.1)
показывает, что многочлен может иметь один и только
один корень.
39
Пусть f (х) — многочлен степени п п xt — корень это-
го многочлена. Разделив f (х) на х — хь получим тож-
дество
f (х) = (х — xj Л (х) + г,	(5.2)
где г — некоторое число, а (х) — многочлен степени
п—1. Подставляя в (5.2) х = хъ получим г = 0, и, сле-
довательно,
f{x) = {x — x1)fl(x).	(5.3)
Если при этом п—1 > 1, то, на основании теоремы
Гаусса, у многочлена fi(x) имеется некоторый корень
х2. Но тогда, по аналогии с (5.3),
fi (х) = (х — х2)/2(х),	(5.4)
где /2(х)— многочлен степени п — 2. Подставим (5.4) в
(5.3). В результате получим
f (х) = (X — Xi) (х — х2) /2 (х). 
Продолжая этот процесс, получим тождество
f (х) = а0 (х — Х1) (х — х2)... (х — х„),	(5.5)
где a0 = fn(x) — многочлен степени п — п=0, т. е. чис-
ло. Очевидно, а0 — старший коэффициент многочлена
f (х), т. е.
f (х) = ай хп + 4z1xn-1 + а2х'1-2 + • • • + ап, (5.6)
где а0, а1г..., ап — некоторые другие числа — коэффи-
циенты многочлена f (х). Подставляя (5.6) в (5.5), раскры-
вая скобки в правой части тождества (5.5), получим (при-
равнивая соответствующие коэффициенты прих'1*’1, хп~-,...)
Х1 4- х2 + • • • + хп — — ,
«о
Xi х2 + Хх Х3 + ... + х„_| Хп = ~
x1x2...xn = (— l)”g.
“О
Формулы (5.7) являются обобщением формул Виета,
о которых шла речь в четвертой главе.
На основании (5.5) числа
хь х2,..., хп	(5.8)
являются корнями многочлена f (х). При этом среди чи-
сел xlt х2,..., хп могут быть и равные (так, в случае
40
многочлена (5.1) хх = х2 = х3 = а). Если некоторый ко-
рень хт встречается в (5.8) ровно k раз (k > 1), то го-
ворят, что хт есть кратный корень А-кратности. Так, в
случае многочлена (5.1) а есть кратный корень крат-
ности 3.
На основе предыдущих рассуждений приходим к за-
ключению, что с учетом кратности у произвольного мно-
гочлена f (х) степени п имеется ровно п корней. Так,
у многочлена (5.1) без учета кратности — один корень,
а с учетом кратности — три корня.
Отметим, что существует простой способ проверки кратности
корня. Так, корень х0 многочлена f (х) является кратным корнем
этого многочлена тогда и только тогда, когда f (х0) = 0, т. е. если
х0 является также корнем производной многочлена f (х). При этом,
если /' (х0) = Г (*о) = • • • =	(х0) = 0, тогда как /(ft) (х0) О,
то х0 есть корень многочлена f (х) кратности k.
§ 2.	Случай квадратного уравнения
Известное из школьного курса математики условие
отсутствия вещественных корней (или, что то же самое,
наличия невещественных корней) уравнения х2 4- рх 4-
4-<?= 0, где р и q— вещественные числа, состоит в том,
что
р2 —4<7<О.	(5.10)
При q <0 неравенство (5.10) невозможно и, таким обра-
зом, в этом случае уравнение (5.9) не может иметь не-
вещественных корней.
Неравенство (5.10) устанавливается в процессе реше-
ния уравнения (5.9), причем соответствующий метод об-
основания неприменим в случае многочленов более высо-
кого порядка.
Однако неравенство (5.10) может быть установлено
и другим способом. Действительно, если хх и х2— ве-
щественные корни уравнения (5.9), то
А так как Xj 4- хг = — р, ххх2 = q и х* 4-	= (*i 4-
4-х2)2 — 2х! х2 = р2— 2q, то неравенство (5.11) запишем
так: р2—2q 21 q |. Таким образом, если справедливо
неравенство
р2 < 2 («у 4-1 <71),	(5.12)
то корни уравнения (5.9) не могут быть вещественными.
41
Следовательно, неравенство (5.12) является достаточ-
ным условием существования невещественных корней
уравнения (5.9). При ?<0 неравенство (5.12) невозмож-
но. Если же q>0, то неравенство (5.12) запишем в ви-
де (5.10).
Таким образом, условие существования невеществен-
ных корней уравнения (5.9) (т. е. неравенство (5.10))
можно установить другим способом, который, как ока-
зывается, применим и в случае многочленов произволь-
ной степени (см. § 3).
§ 3.	Общий случай
Рассмотрим теперь уравнение
хп + а’1хп~1 + • • • 4- an_i х + ап = 0,	(5.13)
где alt аг,..., ап— вещественные числа, и пусть xlt х2,
..., хп — вещественные корни уравнения (5.13) (выписа-
ны с учетом кратности). Воспользовавшись известным
неравенством1
г>1 + г>8-1-р	,
которое справедливо для любых неотрицательных чисел
bi, b2,..., bn, получим
**+*’+•••+хгп	^/х*х*..х*.
--------П------1 2 п	(5.14)
При этом (см. формулы Виета в § 1)
х2 + х2 +---------h Хп = — 01, Х1Х2 ...Хп = (— 1)" ап,
Х1Х2 + *i*8 + • • • + хп-\ Хп = а2.
Но тогда, очевидно,
*1 + *г + • * • + Хп = (*i + *з + • • • + */i)2 —
— 2 (х2х2 + Х1Х3 +-----1- *п_1 Хп) = 0* — 2аг.
Следовательно, неравенство (5.14) можем записать так:
я — 2at n /“»“
——	°" •	(5.15)
На основании предыдущего, неравенство (5.15) выпол-
няется при условии, что все корни уравнения (5.13) ве-
1 Доказательство этого неравенства можно найти в [8J.
4’
шественные. Следовательно, если для некоторого урав-
нения вида (5.13) справедливо неравенство
at — 2a2<nyan,	(5.16)
то корни такого уравнения не могут быть все вещест-
венными.
Таким образом, неравенство (5.16) является достаточ-
ным условием существования невещественных корней
уравнения (5.13).
На основании предыдущего, если ап =/= 0 и а* 2ап
(в частности, если = а2 = 0), то независимо от значе-
ний других коэффициентов уравнения (5.13) среди кор-
ней этого уравнения имеются и невещественные корни.
Рассмотрим теперь уравнение
апуп + ап-.1уп-'+ ••• +а^+ 1 =0,	(5.17)
которое получается из уравнения (5.13) в результате за-
мены х=±-. Если хи х2, ..., хп — корни уравнения
У
(5.13), то, очевидно, —,	----корни уравнения
(5.17) (предполагаем, что ап^=0, и, следовательно,
#=0)«
Рассуждая теперь так же, как и при обосновании
условия (5.16), получим другое достаточное условие су-
ществования невещественных корней уравнения (5.13)
(или, что то же самое, уравнения (5.17)) в виде следую-
щего неравенства:
ап—1 — 2an_2 ап < п yf а%'~2.	(5.18)
(Это неравенство можно получить, непосредственно ис-
пользуя неравенство (5.16)).
На основании (5.18) приходим, в частности к заклю-
чению, что если оба предпоследних коэффициента урав-
нения (5.13) равны нулю (или a’_i 2ап—2 ап) и оп=#=0,
то некоторые из корней уравнения (5.13) невещественные.
Замечание. Условие существования невещественных корней
уравнения (6.13) (т. е. неравенства (5.16) или (5.18)) в общем слу-
чае является достаточным, но не является необходимым. Действи-
тельно, рассмотрим уравнение
я» — Пл2 4-36* —26 = 0.	(5.19)
Корни этого уравнения:
*1 = 1, *а — 5 -f- i, *8 = 5 — 1.
43
При этом
а* — 2а2 = 11* — 2 -36 = 49, nY^ = 3 ^2б\
2	3 Г~2
Таким образом, а1 — 2а2 > 3 у/ ап (так как, очевидно, 493 > 27 X
X 26*). Следовательно, не все корни уравнения (5.19) вещественны
и в то же время неравенство (5.16) не выполняется. В случае квад-
ратного уравнения рассматриваемые условия являются не только
Достаточными, но и необходимыми.
Применим полученные результаты к решению такой
задачи.
Задача. Найти все многочлены, коэффициенты ко-
торых равны 1 или — 1, имеющие только вещественные
корни.
Решение. При п — 1 такими являются многочлены
х — 1 и х + 1 (старший коэффициент, очевидно, можем
считать равным 1). Поэтому в дальнейшем предполагаем,
что 2.
Если корни многочлена f (х) = хп + ajX”-1 + • • • +
+ an-ix + an вещественны и 1, 1}, то неравенст-
во (5.15) в таком случае запишем в виде 1—2а2^п.
Это неравенство, очевидно, может выполняться лишь при
а2 = — 1 и п 3. Таким образом, остается рассмотреть
два возможных случая: п = 2 и п — 3.
а)	Пусть п = 2. Тогда f (х) = х2 + агх — 1, где аг £
€{—1, 1}. Искомые многочлены х2 + х—1 их2 — х—1.
б)	Пусть /г = 3. Тогда f (х) = х3 + агх2 — х + а3. За-
менив х на — и рассуждая' точно так же относительно
многочлена <р (у) = а3у3 — у2 + аху + 1 (или воспользо-
вавшись неравенством (5.15)), убеждаемся, что аг и а3
должны быть числами разных знаков. Следовательно,
возможные многочлены такие:
X3 + X2 — X — 1, X3 — X2 — X + 1.
Каждый из этих многочленов удовлетворяет условию за-
дачи (корни этих многочленов соответственно —1, —1,
1 и —1, 1, 1)
Таким образом, существует всего лишь шесть много-
членов, удовлетворяющих условию задачи: х+1, х—1,
X2 + X — 1, X2 — X — 1, X3 + X2 — X — 1, X3 — X2 — X + 1 .
Заметим, что ответ в этой задаче не изменится, если
потребовать, чтобы только первые три коэффициента
и свободные члены рассматриваемых уравнений равнялись
1 или — 1.
44
УПРАЖНЕНИЯ
1.	Запишите формулы Виета для корней уравнений:
а)	х3 + рх + q = О,
б)	х* + х3 + 9х» _ 8Х + 3 = 0.
2.	Подберите р так, чтобы уравнения
а)	хЬ + рх4 + 6х3 + ха + 8х + 32 = 0,
б)	х* + бх4 + рх3 + х3 + 8х + 32 = О
имели невещественные корни.
3.	На V республиканской олимпиаде юных математиков предла-
галось найти положительные корни уравнения
_ (л + 1) xn + 1 = о (п с N).	(5.20)
Оказывается, это уравнение имеет единственный положительный
корень х = 1 (см. [7], с, 86). Докажите, что:
а)	х = 1 —кратный корень уравнения (5.20) (кратности 2);
б)	при п > 3 не все корни уравнения (5.20) вещественные;
в)	при нечетном п уравнение (5.20) не имеет отрицательных
корней, а при четном — имеет один отрицательный корень первой
кратности, содержащийся в интервале ]—1, 0[,
ГЛАВА 6
ПЕРИОДИЧНОСТЬ ФУНКЦИИ,
УДОВЛЕТВОРЯЮЩЕЙ УСЛОВИЮ
f (х + а) = aff ,(*j (а =£ 0)
' '	*	7 Y/ (х) + о v /
§ 1. Конкретный пример
Рассмотрим известную задачу: доказать, что функция /,
удовлетворяющая условию
/(* + *) = Щ)Т1’	(М
где а =/* 0 — некоторое фиксированное число, периодиче-
ская.
Обосновывается это уравнение следующим образом.
Используя тождество (6.1), находим
+ (6'2>
Учитывая теперь (6.2) и (6.1), получаем
/(х + За)- f(x + a}-
Но тогда, на основании (6.3) и (6.2),
Следовательно, функция f, удовлетворяющая условию
(6.1), является периодической с периодом Т = 4а.
Может возникнуть вопрос: существуют ли функции,
удовлетворяющие условию (6.1)? Покажем, что таких
функций можно построить бесконечное множество. Пусть
например, а = 1 и f(x) = 3 при х£ [0, 1[. Тогда, на осно-
вании (6.1), при х+ 1 €[1»2[
f(r  П	3~*- 1
1	' - /(х)+1 _3+1 “ 2 •
Аналогично, на основании (6.2), при х 4- 2 g [2, 3[
тй—I-
Точно так же, на основании (6.3), при *4-36(3, 4[
/(х-ЬЗ)--------------2.
Если же х4-4£[4, 5[, то f(x + 4) = 3 и значения функ-
ции f начинают повторяться.
График рассматриваемой функции изображен на рис. 7.
Аналогично, выбирая f(x) — с, гдес£(—1, 0, 1), можем
построить новую периодическую функцию с периодом
Т = 4 При этом, разумеется, на промежутке [0, 1( функ-
ция f не обязательно должна быть постоянной (см. упр. 1).
4Ь
В связи с рассмотренным примером возникает следую-
щая задача. Предположим, что функция /удовлетворяет
условию
+ =	(6.4)
где а, р, у, 6 и а=^=0— некоторые фиксированные дей-
ствительные числа (параметры). Всегда ли будет такая
функция периодической? В § 3 будет показано, что нет,
не всегда. Но тогда возникают следующие естественные
вопросы:
1) какими должны быть параметры а, р, у и 6, чтобы
функция /, удовлетворяющая условию (6.4), была перио-
дической?
2) пусть п — фиксированное натуральное число. Мож-
но ли подобрать параметры а, 0, у и 6 так, чтобы число
па было периодом рассматриваемой функции /, тогда как
числа та при т < п (т С N) уже не являлись бы периодом
функции /?
Предварительно рассмотрим некоторые вспомогательные
понятия, которые представляют и самостоятельный интерес.
§ 2. Квадратные матрицы и действия над ними
В различных теоретических построениях, а также при
решении многих задач, имеющих важное прикладное зна-
чение, используются таблицы чисел вида
1	9\	/3	7\	(х	у\
fi	3/,	1,0	2J,	\Z	t),	...
Такие таблицы называют квадратными матрицами (вто-
рого порядка1). Числа (или величины), из которых со-
ставлена матрица, называют элементами этой матрицы.
При этом две матрицы считаются равными тогда и только
тогда, когда их соответствующие элементы равны:
/а b\ Ik l\ a = k, b = l,
d)~\m n)"’*'o=mt d = n.
1 При решении многих вопросов часто возникает необходимость
использовать квадратные матрицы, у которых три строки и три стол-
бика — матрицы третьего порядка, а также матрицы 4-го и вообще
произвольного п-го порядка, или прямоугольные матрицы типа
(о 7 в)* Олнако в дальнейшем нам понадобятся только квадратные
матрицы второго порядка.
47
В множестве таких матриц определяют следующие
операции:
а)	Операция умножения на число. Эта опера-
ция определяется равенством
(х у\ (сх
су\
CZ)
Таким образом, чтобы умножить матрицу на число,
необходимо на это число умножить все элементы рас-
сматриваемой матрицы.
б)	Операция сложения матриц. Сумма двух
матриц определяется равенством
/а Ь\ (х у\(а + х b + у\	_
Матрица Iq qI называется нулевой и выполняет роль нуля
в множестве матриц:
(а Ь\ , /0 0\ (а Ь\
\с d) + (J) 0/ = \с d) •
Операция сложения матриц коммутативна, ассоциатив-
на и обратима. Это означает следующее. Если мы для
удобства условимся обозначать матрицы большими бук-
вами: А, В, С, ... X, Y и т. д., то, с учетом определе-
ния операции сложения матриц, без труда убеждаемся
в справедливости следующих предложений.
1) Для любых матриц А, В и С
А + В = В + А, (А + В) + С = А + (В + С).
2) Для любых матриц А и В существует такая матри-
ца X, что А + X = В.
в) Операция умножения матриц. Эта опера-
ция, представляющая для нас особый интерес, опреде-
ляется так:
(а Ь\ (х у\ lax + bz ay + bt\	/(t R
d) \2 t]~ \cx 4- dz cy -j- dt) •
Операция умножения матриц уже некоммутативна (т. е.,
вообще говоря, АВу=ВА), однако ассоциативна: (АВ)С =
= А (ВС) и связана с операцией сложения дистрибутив-
ным законом!
(А + В) С = АС + ВС, А(В + С) = АВ + АС.
Наряду о нулевой матрицей особую роль в множестве
матриц играет единичная матрица Е, которая опреде-
48
ляется равенством: Е =	. Используя (6.6), нетрудно
проверить, что для любой матрицы А справедливо
АЕ = ЕА = А.
Операция умножения матриц дает возможность также
рассматривать степени произвольной матрицы А:
А2 = АА, А3 = А2А, . ..,	=
При этом, по определению, А° = Е.
§ 3. Условие периодичности в общем случае
Пусть функция f удовлетворяет условию (6.4). По-
ставим в соответствие указанному тождеству матрицу
л /а В\
Д = gj, т. е. матрицу, элементами которой являются
параметры а, 0, у и 6, входящие в тождество (6.4). Ис-
пользуя (6.4) и рассуждая так же, как и в § 1, получим
f (х + 2а) = ст/<*+.аШ = tt«Z,(*;+A,	(6.7)
' '	’	У/ (х + а) + 6	у2/ (х) + б2	' '
где соответствующая матрица
а2 р2\ /а2 + ру
^2 М \уа + 6у
ар + рб\ _ /а р\ /а р\
ур + S2 / — \У	6/ \у 6/ —
Таким образом, если тождеству (6.4) отвечает матрица
А, то (6.7) отвечает матрица А2. Точно так же убежда-
емся, что тождеству
f(x + За) =
«з/ (*) + %
Уз/ (х) + ^з
отвечает матрица Д3. Используя принцип математической
индукции, приходим к заключению, что при любом нату-
ральном п 2 f (х + па) можно представить в виде
f (х + па) = j-jr-,	(6.8)
' V 1	’ Inf (X) 4-	v ’
где я") = Л". Другими словами, тождеству (6.8)
отвечает матрица Ап.
Теорема 6.1. Пусть при некотором натуральном
п Ап = sE, где А =	— матрица, отвечающая тож-
деству (6.4), Е = (’ 0) — единичная матрица и s#=0 —
49
некоторое число. Тогда функция f, удовлетворяющая
условию (6.4), является периодической с периодом Т =
— па.
Если при этом функция f принимает не менее трех
разных значений, то наименьшее натуральное число п,
при котором па есть период функции f, определяется
условиями: Ап = sE и ни при каком s Ak=£ sE, если
k < п.
□ Пусть при некотором n£N Ап = sE, т. е.
6j=sl0 U~kO sj
Тогда
ocn = дп = s, pn = Yn = 0.
Следовательно, на основании (6.8),
/(x4-па) = o/{x)+s ~ I
t. e. / — периодическая функция и T = па — ее период.
Пусть теперь функция f, удовлетворяющая условию
(6.4), принимает не менее трех различных значений и при
некотором натуральном п Ап = sE. Предположим, кроме
того, что при любом натуральном k < п Ак=£ сЕ, каким
бы ни было число с. Тогда, на основании предыдущего,
па — период функции f. Пусть при некотором натураль-
ном т < п та также является периодом функции /, т. е.
<6-9’
где	= Ат. Запишем (6.9) в виде
Ym^2 + (6т — “т) У + Рт = 0.	(6- Ю)
где у = f (х). Если хотя бы один из коэффициентов в
(6.10) отличен от нуля, то уравнение (6.10) не может
иметь более двух решений. С другой стороны, по усло-
вию, функция f, а значит, и переменная у в (6.10) прини-
мают не менее трех различных значений. Другими слова-
ми, уравнение (6.10) имеет три (и более) различных корня.
Это возможно только при условии, что все коэффициенты
уравнения (6.10) равны нулю, т. е. ут = 6т—ат = рп=0.
Но тогда
Л'п = (от бт) = с£ (с = а- = 6т),
что противоречит условию (Ат^с£).
60
Таким образом, предположение о том, что та (т < п)
есть период функции f, приводит в рассматриваемом
случае к противоречию.
Пример, Пусть функция f удовлетворяет условию
f (х + а) =
/ (х) cos ф — sin ф / _______
f (х) sin ср + cos ф v п
(6.П)
где п — фиксированное натуральное число. Соответству-
ющая тождеству (6.11) матрица
д __ /cos<p —sin <р\
л \sin <р cos <р/ ’
При этом, как нетрудно убедиться,
/созЛф —sinA<p\
Я \sin k(f СОвАф/
А так как <p = ~ , то cos n<p = —1, sin n<p = 0. Следова-
лп /—1	0\	'	~
тельно, A = I q  j I = —E. Это означает, на основа-
нии предыдущей теоремы, что па является периодом рас-
сматриваемой функции f. С другой стороны, если т < п
(m£N), то 0 < т<р < л. Тогда вт/пф=/=0, и, следова-
тельно, Ат^=сЕ (для любого числа с). Таким образом,
та (при т < и) не может быть периодом функции f (если
множество значений этой функции состоит более чем из
трех различных значений).
УПРАЖНЕНИЯ
I.	Постройте график функции /, когирая удовлетворяет условию
(6.1), если:
а)	а=1, /(*) = * (х€ [О, 1[);
б)	о= 1, /(х) = ха (ж€ [О, Ц);
в)	а = ~ . f (х) = sin х (х € |\	.
2.	Можно ли подобрать параметр р так, чтобы функция /, удов-
летворяющая условию:
a) № +	«) /<«+“>-8/М+’з’
была периодической с периодом 2а? За?
51
3.	Пусть функция f удовлетворяет условию
'('+о,-тат1	<6Л2>
Докажите, что эта же функция удовлетворяет условию
Z( )- Y/W-a *	(6J3)
4.	Пусть Л=(“	, В= ®	— матрицы, отвечающие
соответственно тождествам (6.12) и (6.13). Чему равны произведения
АВ и ВЛ?
5.	Пусть функция f удовлетворяет условию:
f (х + а) = cos ~ sin
f (х) sin У 2л + cos У 2л
Докажите, что при любом натуральном п f (х + па) =£ f (х).
ГЛАВА 7
ВОЗВРАТНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
ВТОРОГО ПОРЯДКА
§ 1. Числа Фибоначчи
Рассмотрим последовательность вида
Wl, и2, ... , ип, ... ,
(7.1)
где и[ = и2 = 1, ип^\ = ип + ип^\ (п > 1). Таким образом,
каждый член последовательности (7.1), начиная с треть-
его, равен сумме двух предыдущих и эта последователь-
ность содержит такие числа: 1, 1, 2, 3, 5, 8, 13, 21,
34, 55, ... Рассматриваемые числа принято называть числа-
ми Фибоначчи (более подробно о таких числах см. [3]).
Для нахождения n-го числа Фибоначчи ип нет необхо-
димости знать все предыдущие числа Фибоначчи. Оказы-
вается, что для ип имеет место следующая формула, ко-
торую принято называть формулой Бине:
1 //1 + /5V2	/1-/5\п\
2 / \ 2 ))'
(7.2)
Действительно, непосредственной проверкой убеждаем-
ся, что если числа ип определяются формулой (7.2), то
«1 = u2 = 1, Кроме того, как легко проверить,
62
А так как
3+/5Л + /5? 3-/5	/1-/5?
2	\	2	/ ’	2	~= \	2	/ ’
то, на основании (7.3) и (7.2),
ип + Ы„_1 = U„+i.
Это и означает, что произвольный член последовательности
(7.1) определяется формулой (7.2). Другое обоснование
(7.2) можно найти в [3].
§ 2.	Возвратные последовательности
По аналогии с предыдущим рассмотрим последователь-
ность
fi, v2........................ (7.4)
где
Vi = a, v2 = b и un+i = 2ау„ + py„_i (7.5)
(а, b, а, (J — некоторые параметры). В частности, при
а = Ь = 2а = р = 1 последовательность (7.4) совпадает
с последовательностью чисел Фибоначчи.
Как для чисел Фибоначчи, так и для более общих
последовательностей вида (7.4) характерной особенностью
является то, что каждый член такой последовательности,
начиная с третьего, определяется через предшествующие
два члена. Такие последовательности называют возврат-
ными (или рекуррентными) последовательностями второ-
го порядка1.
В дальнейшем предполагаем, что а2 + р У=0. Покажем,
что при таком условии для элементов (7.4) имеет место
следующий аналог формулы Бине:
vn = 4- Ка + V) (а + /а2 + р)п~‘+ (а—у) (а — /а'-’+Р)'1-'],
(7.6)
где у =	• Действительно» если vn определяется
формулой (7.6), то, как нетрудно проверить, ui = а, v2= b.
Кроме того, при п > 1
2ау,1 + рщ,-! = 11(а + ?) (« + /^Тр)"-2 (2а2 +
+ 2а И^+Р + Р) + (а - у) (а - /^+Р)П-2 (2а2 -
- 2а /а2 + р + р)],	(7.7)
1 Рассматривают также возвратные последовательности 3-го,
4-го и вообще л-го порядка — см. [6].
53
где
2а2 + 2a / c^TP + P = (a + Ka^+P)’»	(7.8)
2a2 —2aKa2 + p4-P = (a —/a2 + p)2.	(7.9)
Подставляя (7.8) и (7.9) в (7.7), получим, на основании
(7.6), что 2ai>n -|- Pvn-i = Vn+i. Следовательно, элементы
последовательности (7.4) определяются формулой (7.6).
В частности, если о = 6 = 2а = р = 1, то формула (7.6),
как легко проверить, совпадает с (7.2).
§ 3.	Многочлены Чебышева
При доказательстве формулы (7.6) нигде не использо-
вался тот факт, что a, b, а и р — числа. Это означает,
что формула (7.6) справедлива также и в том случае,
если (7.4) есть последовательность значений функции или
некоторых многочленов, которые удовлетворяют условию
(7.5).
Например, если а = х, b = 2х2—1, a = х, р = —1,
то соответствующая последовательность (7.4) состоит из
многочленов, которые называют многочленами Чебышева
первого рода и обозначают Тп(х). Первые пять многочле-
нов Чебышева первого рода такие:
Л (х) = х,
Тг (х) = 2х2 — 1,
7’3(х) = 22х8 —Зх,
Т4(х) = 23х4 — 8х2 + 1,
Ть (х) = 24х5 — 20.x3 4- 5х.
В случае многочленов Чебышева (при указанных зна-
чениях а, Ь, а и Р) у = V х2 — 1, и, следовательно, на
основании (7.6), соответствующую формулу для много-
членов Тп(х) запишем в виде
т. (,) =	.	(7.10)
(В записанном виде формула (7.10) определяет многочле-
ны Чебышева при |х|^1. Однако после возведения в
степень выражений, входящих в (7.10), корни исчезают
и мы получаем формулу для многочленов Чебышева на
всей числовой прямой).
Из (7.10) также следует, что при любом натуральном п
Тп(1) = 1, Т„(-1) = (-1)".
54
Аналогично, если а = 2х, b = 4х2 — I, а = х, р = —1,
то соответствующая последовательность (7.4) является
последовательностью многочленов Чебышева второго рода,
которые обычно обозначают ип(х). В этом случае
2х» -1	.	(х+/х*^П|	(х —/х» —1)а
° + 1'- V..-t 
Следовательно, соответствующая формула для много-
членов Чебышева второго рода имеет вид
(7.11)
Воспользовавшись формулами (7.10) и (7.11), нетруд-
но проверить, что многочлены Чебышева первого и второ-
го рода связаны между собой соотношениями:
Tn+i (х) = (n + l)un(x),
м« W = Йт Т "+1 ~	Un<^‘
§ 4.	Формула для tgna
Формулу для tgna можно получить, используя выра-
жения для sin па и cos па (см. гл. 4, упр. 3). В даль-
нейшем будут получены другие формулы для tg па. При этом
существенно используется формула 7.6 (аналог формулы
Бине для общего члена возвратной последовательности).
Так как
ТО
tg2a=-r^r (x=tga),	(7.13)
tg 3a = tg (2a 4- a) = 773^75•	(7-14)
и вообще, при любом натуральном п,
tgna = иМ?! = tga)’ <7-15)
Чл \л/
где Рп(х) и Qn (х) — некоторые многочлены. При этом
Pi(х) — х, Р2(х) = 2х, Рь( ) — Зх — Xs, ... j
QiW-Ъ Qa(x)=l-x2, Qj(x) = 1 — Зх2, ...
55
Воспользовавшись формулами (7.12) и (7.15), получим
Рп(х)
te (п 4- 1) а — tfi (па 4- а)_ Qn(*) Рп (х) 4- xQn (х)
tg(«+ l)a-tg(na + a)-.	=Qn(x)_xPn(x) ,
Qn(x)
и, следовательно,
Pn+I (х) = Рп (х) + xQn (х),	(7.16)
Qn+i(x) = Qn(x) — хРп(х).	(7.17)
На основании (7.16) и (7.17)
Pn+i (х) — Рп (х) = Рп (х) — Рп-1 (х) + х (Qn (х) — Qn_i (х)),
(7.18)
Qn (X) — Qn-i (х) = —хР„_, (х).	(7.19)
Подставляя (7.19) в (7.18), получим
Рп+1 (х) — Рп (х) = Рп (х) — Pn-t (х) — Х2Р„_1 (х).
Следовательно, Рп+\ (х) = 2Рп (х) — (1 + х2) Pn-i (х). Точно
так же устанавливаем, что
Q„+I (х) = 2Qn (х) - (1 + х2) Qn_, (х).
Таким образом, многочлены Рп (х) и Q,, (х) удовлетворяют
одному и тому же рекуррентному соотношению: нп+1 =
= 2аип + Р«и-1» где a = 1, £ = — (1 + х)2. При этом в
случае многочленов Рп (х) их = х, ы2 (х) = 2х, тогда как
в случае многочленов Qn (х) их = 1, иг = 1 —х2. Но тогда
для нахождения многочленов Рп (х) и Qn (х) мы можем
воспользоваться общей формулой (7.6). Так, в случае
многочленов Рп (х) а = 1, £ = — (1 + х2), а = х, b = 2х.
Тогда у = —:~х —	. Следовательно,
У — х* Iх 11
а + т = Т7Г7(1+|Х|°. «-V = -|7j7(l-W0.
а + j/a2 + £ = 1 + |х| i, a — К«2 + £ = 1 — | х| I,
после чего
Рп W = 2ТТП 1(1 +1 X! 0я-(1 -I х|<)"].
Рассматривая случаи х > 0 и х < 0, убеждаемся, что не-
зависимо от знака х Рп (х) определяется формулой
Рп W = 4 К1 - х/)п - О + Х4)п].	(7.20)
56
Аналогично в случае многочленов Qn (х)
а=1, р = — (1 + х2), <2=1, Ь=\— х2,
и, следовательно,
___________________________ у2
а +У = 1 + Л1<> о — у = 1 — jx|t,
а + ]Лх2 + р = 1 +1 I, а — У а2 + р = 1—|xj/.
Но тогда, независимо от знака х,
Qn (х) = 1 [(1 - xif + (1 + х0"].	(7.21)
Используя (7.20) и (7.21), получим следующую общую
формулу для tg/ia:
Формулу (7.22) можно, очевидно, записать в виде
.	(cos a — i sin a)" — (cos a + t sin a)" .
8 (cos a — i sin a)« + (cos a + i sin a)" v '
Заметим, что в справедливости (7.23) можно убедиться и
непосредственно, воспользовавшись формулой Муавра.
Обозначим теперь t = cos а, и пусть sin a = У" 1 — t1.
Тогда формулу (7.23) запишем в виде
„„ - (/-</i-<8)"-G + t|/i-/2)n,
или, что то же самое,
tg na =
(/-	+ У/2-!)" •
G - V /2 - 1)" + (/ + V i1 - 1)" '
(7.24)
(7.25)
С другой стороны, на основании (7.10) и (7.11),
(/ _ /FZH)"— (I +	-----2/F^1u„_i (Г). (7.26)
(/_ /Т2ТГ1)" + (/+= 2Т„ (/).	(7.27)
Но тогда, с учетом (7.25), (7.26) и (7.27),
tgna = _ZiE^iW t-.	(7>28)
А так как Z2— 1^0, то
= i = i sin a. (7.29)
57
Подставляя (7.29) в (7.28), получим следующую формулу
для tgna:
tg па = sin а,	(7.30)
где t = cos а, а ип^.\ (/) и Тп (/) — многочлены Чебышева
соответственно второго и первого рода. Отметим, что
формула (7.30) справедлива и в том случае, если sina =
= _ /ттг?.
Таким образом, формула (7.30) устанавливает инте-
ресную связь между tgna и многочленами Чебышева.
§ 5. Формула Мечина для числа л
и ее аналоги
Формулой Мечина называют формулу
Т = 4 arctg | - arctg ,	(7.31)
которую установил английский астроном и математик
Джон Мечин (1680—1751) и использовал ее для вычисле-
ния числа л. Позже были получены различные аналоги
формулы Мечина:
1.	Формула Гаусса:
~= 12 arctg ^ + 8 arctg — 5 arctg
2.	Формула Стирлинга:
~ = 4 arctg у — arctg ~ + arctg ± •
3.	Формула Штермера:
J = 6 arctg у 4- 2 arctg + arctg .
4.	Формула Шульца:
у = arctg ~ + arctg -1 + arctg -g-.
Существуют разные способы доказательства указанных
формул (см. доказательство формулы Штермера в [1],
с. 374, 450). Здесь мы покажем, как рассматриваемые
формулы могут быть обоснованы с помощью результатов,
ба
установленных в предыдущем параграфе. Действительно,
пусть
а = arctg у, p = arctg55g.
Тогда
1
tc (4а - В) = tg4a-^- =
g( Р) i+tg4atg|5 Р4(Х) J_’
+ <?4 (х) * 239
т. е.
te (4a R) —	/7 32)
Tg (ча	р; — 239	(х) + (х),	( / .JZ)
где х = tga = -i-. А так как, на основании (7.20) и (7.21),
р4 (х) = — 4г3 + 4х, Q4(X) =х« —6х2+1,
то
р.^-ЦР. <)=^75+1- р-м>
Но тогда, на основании (7.32) и (7.33),
,.	R. 239 • 480 — 476	239  240 — 238
Tg (4a	р) — 239 476 + 48() — 239.238 + 240 —
239 (239 + 1) — 238 = 239а + 1 _ ,
239 (239 — 1) + 240 — 239» + 1 ~ 1 '
Таким образом, tg(4a — P) = tg-£ А так как | (4a — Р)—
я I
— 4‘1<л;» то, на основании предыдущего равенства, при-
ходим к заключению, что 4a—Р =. А это и есть ра-
венство (4.31).
Аналогично могут быть обоснованы и остальные фор-
мулы (т. е. формулы Гаусса, Стирлинга, Штермера и
Шульца).
Рассмотрим теперь некоторые аналоги предыдущих
формул. А именно, предположим, что при некоторых
целых т, п, р и q справедливо равенство
/и arctg4-n arctg=	(7.34)
Запишем эту формулу в виде;
Y = та + пр ^а = arctg у, р = arctg .	(7.35)
59
Тогда, на основании (7.12) и (7.15),
tg 4 = tg(/na + /ф) =	+	=
s 4 ь' r/ 1 — tg/na tgnfi
Рт(х) Рп(У)
Qm(x}^Qn(y) Pm(x)Qn(y) + Pn(y)Qm(x)
1 _Рт <*> Рп^ (*>	~Рт W Рп (У) ’
Qm(x)Qn(y)
где х = tg а = у, у = tg р = у. Учитывая, кроме того,
что tgy = 1, запишем равенство (7.36) в виде
или, что то же самое,
(7.37)
Таким образом, если выполняется (7.34), то справед-
ливо также и равенство (7.37). Наоборот, если выполня-
ется равенство (7.37), то, на основании (7.36),
tg(ma + np)= 1 = tg
откуда следует, что
та 4- пр = ~ + /гя.	(7.38)
Если при этом окаж тся, что
та + пр — ~ < я,
то в (7.38) k = 0 и, следовательно, выполняется равенство
(7.35) (или, что то же самое, равенство (7.34)).
Используя равенство (7.37), можно подбирать т, п, р
и q так, чтобы выполнялось равенство (7.34). Например,
имеют место равенства)
у-= arctg у 4-arctg-у,
~ = 2arctgу — arctgу,
•J-= 2 arctg-у 4-arctg у.
60
Точно так же можно рассмотреть, например, различ-
ные аналоги формулы Шульца, т. е. формулы вида
у = arctg + arctg у + arctg у .	(7.39)
Если выполняется равенство (7.39), то, как легко прове-
рить (вычисляя тангенс от обеих частей равенства (7.39)),
имеет место равенство
। _ pg + pr + gr — I
pqr — р — д — г
Исключая из последнего равенства г, найдем
_ РР Н~ Р 4- ? — 1 _ । ,_2 (р -f- р)
pq — р — д — 1 "Г pq — р — q— 1 *
В частности, при р = 2
г-|х2(’ + 2)_о , Ю
Следовательно, в этом случае (р = 2) необходимо прове-
рять все значения q, для которых 10 делится на q— 3.
Приведем соответствующие значения q и г.
Остается проверить значения q и г, отмеченные знаком +
(остальные значения симметричны).
Точно так же можно проанализировать случаи р = 3,
р = 4 и т. д.
§ 6.	Формула для n-й степени
квадратной матрицы
В главе 6 было показано, что функция /, удовлетво-
ряющая условию (6.4), является периодической, если при
некотором натуральном п Ап = sE, где А =	— мат-
рица, отвечающая тождеству (6.4), Е = । j — единичная
матрица и s 0 — некоторое число (теорема 6.1). Однако
исследовать соотношение Ап = sE непосредственным воз-
61
ведением в п-ю степень — довольно громоздкая и утоми-
тельная работа. Здесь мы покажем, как эту задачу можно
значительно облегчить, если воспользоваться изложенными
выше результатами.	/
Теорема 7.1. Пусть А = Тогда
А2 + рА + qE = 0,	(7.40}
где р = —(а + d), q = ad — bc, а 0 =	— нулевая
матрица.
□ Действительно, так как
А + оЕ ~(а (a + d 0	b\
A + Pb-\cd) \ 0 а + d/ \ c — al’
TO
A' + pA Л (A + pE) -	bcad] =
что и доказывает равенство (7.40). 
Запишем теперь равенство (7.40) так:
А2-----рА — qE.	(1А\>
Тогда, на основании (7.40) и (7.41),
А3 = —рА2 — qA = —р (—рА — qE) — qA =
= (/>’ —+ pqE.
Продолжая этот процесс, убеждаемся, что при любом
натуральном п
Ап = и„А + vnE,	(7.42
где ип и ип— некоторые величины, зависящие от р, q
и п. При этом, очевидно, «1 = 1, ы1 = —р, «3 = р2— р;
«1 = 0, и2 = —q, v3 = pq. Воспользовавшись теперь равен-
ствами (7.41) (7.42), получим	'
Лп+1 = АпА = ипА2 + vnA =» (—рип + ил) А — qunE,
и, таким образом, ип+1 = —рип + vn, vn+1 = —qun. Но
тогда при п > 1 vn = —qun_i, и, следовательно,
«л+1 = — рип — qun_x.	(7.43)
Это означает, что {ип\—возвратная последовательность
второго порядка. Но тогда ее члены могут быть найдены
с помощью обобщенной формулы Бине (формулы (7.6)).
62
В рассматриваемом случае и1 = а = \, иг = Ь = —р,
а = — Р = —q. Поэтому, если а2+р=^(р2—4<?) =#0,
то __	______
Z-аа _ -р g  Ур*-4д-р
/а» + |5	/р»-4<7	/р«-4?
V р2 — 4<?	2
Но тогда, как нетрудно убедиться,
„	(р-V р1- W>n - (д + /	/7 44v
иП----9Л	, /  -	,=	• V 'п>
1	V р2 — 4<?
Теорема 7.2. Пусть А = Q, где b Ф 0 или с=#0.
Тогда равенство Ап = sE выполняется в том и только
том случае, если в (7.42) ип = 0.
□ Пусть un = Q. Тогда, на основании (7.42), An=sE,
где s = vn.
Наоборот, пусть известно, что при некотором нату-
ральном п Ап = sE. Тогда равенство (7.42) запишем так:
sE = ипА + vnE, т. е. ипА = гЕ, где г = vn — s. Или,
что то же самое,
Если при этом Ь#=0, то из равенства ипЬ = 0 имеем, что
ип=0. Если же Ь = 0, то, по условию, с#=0. Но тогда
из равенства ипо — 0 получаем ип = 0. 
Таким образом, на основании результатов, установлен-
ных в предыдущей главе и настоящем параграфе, вопрос
о периодичности функции f, удовлетворяющей условию
(6.4), сводится к вопросу о нахождении таких значений п,
при которых Ап = sE. А этот вопрос, в свою очередь,
сводится к задаче нахождения таких натуральных п, для
которых ип = 0.
Рассмотрим в связи с этим следующие возможные
случаи.
1. р2— 4<?У=0 (<?=/= 0). Предположим, что при некото-
ром n£N ип — 0. Тогда, на основании предыдущей
теоремы, Ап = sE, где s = vn = —Покажем, что в
этом случае u„_i#=0, и, следовательно, з#=0. Действи-
тельно, пусть ып_1 = 0, т. е.
(р — И)п~1 = (р + h)n~l (h=Vp2 — \q).	(1А5)
63
С другой стороны, так как ип = 0, то
(р — h)n = (p + h)n.	(1AQ)
Но тогда, на основании (7.45) и (7.46),
(р — Л)"-1 (Р + Л) — (Р — Л)п = 2й (р — h)n~1 = 0.
А так как, по предположению, Л=#0, то p — h, т. е.
р2 = р2— 4q, что невозможно, так как q^O. Пришли к
противоречию. Следовательно, s=#0.
В рассматриваемом случае ип определяетоя формулой
(7.44). Укажем в связи с этим один довольно простой
способ нахождения таких натуральных чисел п, что
ип = 0. Действительно, если н„=0, то, на основании
(7.44), (р — Ир2 — 4q)n = (р + Ир2 — 4<7)'1 или, что то же
самое,
0п = 1
р — / р» —
р+
(7.47)
6 =
Ясно, что и наоборот: если имеет место равенство (7.47),
то ип = 0. Таким образом, задача нахождения периода
функции f, удовлетворяющей условию (6.4), сводится к
нахождению таких натуральных чисел п, для которых
справедливо равенство (7.47).
Пример. Пусть A = (j т. е. А есть матрица,
отвечающая уравнению (6.1). Тогда р = —2, q = 2, р2—
— 4q = —4. Следовательно,
fl - 2~2‘ =	- с1-О2 _
2 + 2/	1 + /~	2
Но тогда О4 = 1, и функция/, удовлетворяющая усло-
вию (6.1), является периодической о периодом Г = 4а.
2. Пусть р2 = 4<7(7=jA0). Тогда соотношение (7.43)
запишем так! иЛ+1 = —рип — у ип^ц причем, как и раньше,
«1=1, н2 = —р. Нетрудно проверить, что в таком случае
Следовательно, ни при каком натуральном п ип=£0.
А это означает, что при или с#=0 An^=sE.
В предыдущих двух случаях предполагалось, что
q =+ 0. Объясняется это тем, что если q = ad — be = 0
64
и одно из чисел Ь или с отлично от нуля, то функция f9
удовлетворяющая условию
является постоянной (периодической с любым периодом
Т=/=0).
Действительно, пусть, например, с=/=0. Тогда
of (х) + h __ acf (х) + bc __ acf (х) + ad ___ а
cf(x) + d~~c(cf(x) + d)~c(cf(x) + d)~ с ’
УПРАЖНЕНИЯ
1.	Докажите формулы Гаусса, Стирлинга и Штермера (§ б).
2.	Проанализируйте формулу (7.39) при р = 3.
3.	Пусть z = а + Ы — комплексное число. Тогда
2а + pz + q = 0 (р = — (z + 2), q = | z | *).
Рассуждая так же, как и в § 6, найдем, что zn — unz + vn. Устано-
вите формулы1 для ип и vn.
ГЛАВА 8
КВАТЕРНИОНЫ
§	1. Современная теория комплексных чисел
В гл. 4 отмечалось, что комплексные числа часто
определяют как выражение вида а + Ы, где а, b — дей-
ствительные числа, a i— «некоторый символ, который
называют мнимой единицей». При этом, естественно, воз-
никают вопросы: что это за символ? существует ли он?
а если существует, то сколько их? и т. п.
Здесь мы рассмотрим современный подход при постро-
ении теории комплексных чисел, а затем изложенные
идеи используем для построения новых, важных для реше-
ния многих прикладных задач, объектов — кватернионов.
При этом использование результатов гл. 6 дает возмож-
ность рассмотреть свойства функций, определенных на
множестве кватернионов, и, в частности, изучить свойства
sina, cosa и еа (а — кватернион).
1 Многочлены ип и vn имеют ряд важных свойств. В частности,
они дают возможность построить одну последовательность ортого-
нальных на всей числовой прямой функций (см.: Кужель О. В. Про
один клас многочлен!в та ортогональних на oci (—оо, оо) функщй.—
ДоповМ АН УРСР, 1967, сер. A, Ns 12).
з-бо 3
65
Приступая к построению комплексных чисел, напомним,
что еще в шестом классе рассматриваются пары действи-
тельных чисел (а, Ь). Каждая такая пара есть, по сути,
множество, состоящее из двух действительных чисел а и b
с указанием, какое из этих чисел должно стоять на пер-
вом месте, а какое—на втором. В связи с этим такие
пары называют также упорядоченными парами.
Так, на основании сказанного, множества {5, 7} и
{7,5} равны, тогда как пары (5,7) и (7, 5) — различны.
И действительно, если мы рассматриваем на плоскости
точку А с координатами (5, 7) и точку В с координатами
(7, 5), то это, очевидно, различные точки плоскости.
В связи с этим две пары (а, Ь) и (с, d) считаются рав-
ными тогда и только тогда, когда а = с, b = d. Таким
образом, по определению,
(а, b) = (с, d) ** а = с9 b = d.
Введенное так отношение равенства в множестве пар
удовлетворяет обычным условиям. А именно: z = z; если
z = X, то X = г; если z = X, X = и, то z = и, где г, X
и и — рассматриваемые пары.
Обозначим через С совокупность всех упорядоченных
пар вида (а, Ь), где а, b — действительные числа, и опре-
делим в множестве С операции сложения (4-) и умноже-
ния (•) следующим образом:
(a, b) + (с, d) = (а + с9 b + d)9
(а, Ь) • (с, d) = (ас — bd9 ad + be).
Непосредственной проверкой убеждаемся, что опреде-
ленные так операции сложения и умножения коммута-
тивны, ассоциативны и операция умножения связана с опе-
рацией сложения дистрибутивным законом. Другими сло-
вами, если z, X и и — упорядоченные пары, то
z 4- X = X 4* z, (z 4- X) 4- w = z 4- (X 4- w),
гХ = Xz, (zX) и = z (Xu), г (X + и) = zX 4- га.
Множество упорядоченных пар С будем называть мно-
жеством комплексных чисел, а элементы множества С —
комплексными числами.
Последующие две теоремы характеризуют то, что опе-
рации сложения и умножения комплексных чисел обратимы.
Теорема 8.1. Для любых комплексных чисел z = (а, Ь)
и К= (с9 d) найдется такое комплексное число и = (х, у)9
что z 4- а = X.
66
□	Пусть х = с — a, y=d — b. Тогда, как легко прове-
рить, z + и = X. 
Комплексное число и, определяемое предыдущей тео-
ремой, называют разностью комплексных чисел Хиг
и обозначают так: и —г— X.
Таким образом, в множестве комплексных чисел С
определена операция вычитания чисел.
Теорема 8.2. Пусть г = (а, Ь) =/=(0,0) и X = (с, d)—
произвольные комплексные числа. Тогда найдется такое
комплексное число и, что zu — X.
□	Так как а=/=0 или Ьу=0, то а2 + 62=£0. Рассмот-
рим комплексное число
« = (-ГГм>	• (с, d).	(8.1)
Тогда, как нетрудно проверить, zu = (1, 0) (f, d) = (с, d). 
Комплексное число и, определяемое равенством (8.1),
называют частным комплексных чисел Хиги обозна-
X
чают: и = — .
z
Следовательно, в множестве комплексных чисел С
определена также и операция деления чисел.
Отождествим теперь комплексное число (а, 0) с дей-
ствительным числом at
(а, 0) = а.	(8.2)
Тогда множество действительных чисел R будет подмно-
жеством множества комплексных чисел C(/?czC). При
этом, как нетрудно убедиться, для любого комплексного
числа (с, d.)
а (с, d) = (а, 0) (с, d) = (ас, ad).	(8.3)
Рассмотрим, кроме того, комплексное число (0, 1),
которое называют мнимой единицей и обозначают бук-
вой it
I = (0, 1).	(8.4)
Тогда, на основании определения операции умножения
и равенства (8.2), i2 = (0, 1)(0, 1) = (—1, 0) = — 1, т. е.
i2 = —1. Таким образом, при таком способе построения
множества комплексных чисел мнимой единицей является
вполне реальный объект — упорядоченная пара (0, 1).
Теорема 8.3. Произвольное комплексное число (а, Ь)
можно представить в виде
(а, Ь) =а + Ы.	(8.5)
з*
67
□ Воспользовавшись соотношениями (8.2), (8.3) и (8.4),
получим (а, Ь) = (а, 0) + (0, Ь) = а 4- Ь (0, 1) = а 4- bi. 
Так же, как и в гл. 4, определяются сопряженное
число г = а — Ы и модуль |г| комплексного числа zt
| г | = V z - г = Ка2 + Ь2.
§ 2. Определение и основные свойства
кватернионов
Таким образом, рассмотрение упорядоченных пар дей-
ствительных чисел дает возможность построить новое,
более широкое, числовое множество — множество ком-
плексных чисел С. В связи с этим возникает естествен-
ный вопрос: а нельзя ли построить новое «числовое>
множество, рассматривая упорядоченные пары комплек-
сных чисел? Оказывается, можно, и к решению этой за-
дачи мы сейчас приступаем.
Итак, рассматриваем упорядоченные пары в виде
(гД), где z и X — комплексные числа. Как и раньше,
считаем, что
(z.X) = (и,о) ** г = и, X = V,	(8.6)
Совокупность всех таких пар обозначим через Н и
введем в Н операции сложения и умножения следующим
образом:
(z,X) 4- («,ц) = (z 4- и, X 4- v),
(г,к) (u,v) >= (zu — kv, zv 4- ku).	(8-7)
Множество И о такими операциями называем мно-
жеством кватернионов, а элементы множества Н — ква-
тернионами.
Как и в случае комплексных чисел, убеждаемся, что
перация сложения кватернионов коммутативна, ассоци-
ативна и обратима. Что же касается операции умноже-
ния кватернионов, то она уже не является коммутатив-
ной. Действительно, (0,1) (0,0 = (t,0), (0,0 (0,1) = (—i,0),
и, таким образом, (0,1) (0,0 =#=(0,0 (0,1).
В остальном свойства операции умножения кватерни-
онов такие же, как и в случае комплексных чисел; опе-
рация умножения в Н ассоциативна, дистрибутивна от-
носительно операции сложения и обратима. Первые два
из указанных свойств доказываются непосредственным
умножением кватернионов. Поэтому более детально рас-
смотрим лишь свойство обратимости операции умноже-
ния кватернионов.
68
Действительно, пусть (г,X) Ф (0,0) и (и, и) — некоторые
кватернионы. Покажем, что существует такой кватернион
(е,0), что
(zA)(e,O) = («,0.	(8.8)
На основании (8.7) уравнение (8.8) можно записать так:
(ze — Х0, Z0 + Хе) = (и,о), откуда, с учетом (8.6),
fze — Х0 = и,
(z0 + Хе = V.
Записывая последнюю систему в виде
(ze— Х0 = и,
(Хе z'0 = v,
находим е и 0:
___ ги 4- Хр л _ w — Ха
8~ |?|«+|Х|« ’ ° - |г|« + |Х|» ’
Таким образом, искомый кватернион
lp rn _ / Й<+ Xti zt> — Ха )
|Z|»+|X|» ’ |2|« + I Х|« ) ’
что и доказывает обратимость операции умножения в Н.
Отождествим кватернион (z,0) с комплексным числом z:
(2,0) = z.	(8.9)
Тогда множество комплексных чисел С будет подмно-
жеством множества кватернионов Н (СаН). При этом,
как нетрудно убедиться, для любого кватерниона (и,о)
z(u,v) = (zu, zv), (u,v)z=(uz, vz). (8.10)
Следовательно, в общем случае z(«,v)=# (u,v)z.
§ 3. Базисные кватернионы
На основании (8.9), (1,0) =1, (1,0) = i. Введем еще
следующие обозначения: /=(0,1) k = (0,i), Тогда, как
легко проверить, учитывая равенства (8.7) и (8.9),
р = /« = ^ = —1, ij = k, ik = —j,
(8.И)
ji = — k, jk = i, kl = /, kj = — i.
Например, kj =s (0,1) (0,1) = (— i,0) = —i.
69
Соотношения (8.11) удобно записать в виде следую-
щей таблицы:
X	1	i	/	k
1	1	i	/	k
i	i	— 1	k	-f
i	i	— k	— 1	i
k	k	i	— i	— 1
Из (8.11) имеем
i2 = /2 = ^ = 1/7. = —1.	(8.12)
Можно показать, что и наоборот: из (8.12) вытекают все
соотношения (8.11).
Теорема 8.4. Произвольный кватернион а = (гД)
единственным способом представим в виде
а = а0 + «it + а2/ + а3Л,	(8.13)
где а0, а1( а2, а3— некоторые действительные числа.
□ Пусть z = а0 + ах{, X = а2 + а3(. Тогда а = (z,0) 4-
+ (ОД) = (а0 + cqi.O) 4- (0,а2 4- a3i) = а0 + а,: + (0,а2) +
4- (О,а30 = а0 4- aji 4- а2/ 4- а3Л.
Таким образом, возможность представления (8.13) обо-
снована. Докажем теперь его единственность. Предполо-
жим, что имеет место также равенство: a = 0О 4- Pi* +
4- Ре/ + М- Вычитая из этого равенства (8.13), получим
с0 4-	4- c2j 4- c3k = 0,	(8.14)
где сг=Рг — аг — действительные числа. При этом (8.14)
можно записать в виде (с0 4- cvi, с2 4- c3i) = (0,0), откуда
вытекает, что с0 4- Ы = с2 4- c3i = 0. Но тогда с0 = сг =
= с2 = с3=0, т. е. Ро = ао> Pi = “i. Р8 = а2> 0з = аз>
что и доказывает единственность представления (8.13). 
В связи с доказанной теоремой кватернионы 1, », / и
k называют базисными кватернионами.
§ 4. Векторная часть кватерниона
На основании теоремы 8.4, произвольный кватернион a
можно представить в виде
a = a0 + a (a = ail + аз/ + ааЛ). (8.15)
70
При этом а0 называют действительной частью, а а—
векторной частью кватерниона а.
Величину (т. е. кватернион) [аф] = afJ— ра назы-
вают коммутатором кватернионов а и р. Очевидно,
коммутатор [осф] = 0 тогда и только тогда, когда ар =
= Ра. В таком случае говорят, что кватернионы аир
коммутируют.
Нетрудно также проверить, что [а,р] = [а,р], т. е.
коммутатор кватернионов а и ₽ совпадает с коммутато-
ром их векторных частей.
Учитывая правило умножения базисных кватернионов,
убеждаемся, что
СТ = — (а?р) + а х К	(8.16)
где
(СТ = “iPi + агРз + азРз» (8.17)
а х Р*= (а2р3 — а3₽2)» + (“зР1 — «1Рз)/ + («1Р2 — a2Pi) k.
(8.18)
При этом действительное число (а,Р) называют ска-
лярным произведением кватернионов а и р, а кватернион
а х Р — векторным произведением кватернионов аир.
Приведем основные свойства скалярного произведе-
ния векторных частей кватернионов.
—> —>•	—>•
1.	(a,a)^0, причем (а,а) = 0 ♦♦ a = 0.
2.	СТ = (рСТ_^
3.	(aa,P) = a(a,P) a£R.
4.	(a +K.V) = СТ) + (P.V)-
Далее нас будут больше интересовать свойства век-
торного произведения a х р. В частности, имеют место
следующие свойства:
I.	а х Р = — рха.
II.	(аа) х Р = а (а х р) («€/?).
III.	а X а = 0.
IV.	а х Р = 0 тогда и только тогда, когда кватерни-
—>	—
оны аир линейно зависимы.
71
При этом аир называют линейно зависимыми, если
—>	—>	—*-
а = ср (или 0 = са), где с — некоторое действительное
число.
Обоснование первых трех свойств векторного произ-
ведения не представляет труда. Поэтому рассмотрим
лишь последнее свойство.
П.\ сть секторные части аир кватернионов а и р ли-
нейно зависимы. Если, например, а = ср, то aj = срп
а2 = ср2, аз = сРз- Но тогда, на основании (8.17), ах
хТ=о.
Наоборот, предположим, что а х р = 0. Если при этом
—>-	—
a = 0, то a = ср (с = 0) и, таким образом, сформулиро-
ванное свойство имеет место. Поэтому в дальнейшем
—>	—>
считаем, что а Ф 0 и Р =#= 0. Это, в частности, означает,
что среди чисел pi, р2 и р3 хотя бы одно отлично от
нуля. Пусть, например, рх =# 0. Так как, по предполо-
—>
жению, а х Р = 0, то, на основании (8.18),
агРз = азРз> азР1 = а1Рз> а1Рз = агР1* (8.19)
Пусть с =	. Тогда аг = срх. Кроме того, на осно-
Pi
—>	~>
вании (8.19), аа = сР2, а3 = ср3, т. е. a = ср.
Аналогично рассматриваются и другие случаи (Р2=#=
0, р85^0, а также а1=^0, а2=/=0 или а3у= 0). Этим
рассматриваемое свойство (свойство IV) обосновано.
Теорема 8.5. Кватернионы аир коммутируют
—>•
тогда и только тогда, когда их векторные части а и
Р линейно зависимы.
□ Учитывая (8.16), а также равенства (а,р) =(Р,а),
а X Р = — Р Ха, находим
[а,PJ = [а,К1 ="aF— ра = 2а х"р.	(8.20)
Пусть кватернионы аир коммутируют (т. е. ар = ра).
Тогда [а,Р] = 0 и, на основании (8.20), ахР=0. Но
тогда (свойство IV) а и 0 линейно зависимы.
Наоборот, пусть аир линейно зависимы. Тогда а х
X Р = 0 и, на основании (8.20), [а,р] = 0. 
72
§ 5.	Сопряженные кватернионы
Кватернион а = (г,—X) будем называть сопряженным.
относительно кватерниона а = (z,X). Непосредственно из
определения сопряженного кватерниона следует, что
1.	1 = 1, i = —i, / = — /, k = — k.
2.	Если а = а0 + ocji 4-а2/+ а3£, то а=а0— ati —
— а2/— a3k. Или, что то же самое, если а = а0 + а, то
а = а0— а.
3.	а = а.
4.	а + р = а + р.
5.	ар = р а.
Первые четыре свойства очевидны. Докажем послед-
нее. Пусть а = (z,X), р = (u,v). Тогда ар =(zu — Xu,
zv + Хи), ар = (г и — Хи, —zv— Хи), ра = (и, —и) (г,
— К) = (йг— оХ, —и X — vz). Следовательно, ар = ра.
Заметим также, что кватернионы а и а всегда комму,
тируют. Действительно, если а = а0 + а, то а = а0 — а.
Следовательно, векторные части (а и —а) кватернионов
а и а линейно зависимы. Но тогда, на основании теоре-
мы 8.5, [а,а]=0, что и доказывает рассматриваемое предпо-
ложение.
§ 6.	Норма кватерниона
Пусть а = (z,X). Тогда аа = (z,X) (z, — X) = (. z- +
+ jX|2, 0) = |z|’ + l Х|*>0. Или, что то же самое, если
а = аи + а21 + а2/ + a3k, то аа = а„ + а’ + а’ + а’.
Определение. Число N(a)=]/~aa называется нормой1
кватерниона а.
Таким образом, на основании предыдущего, если
а = (z,X) = а0 -J- а^' +	+ а3Л,
то
N (а) = Г№+|Х|2 = /а’ + а* + а‘ + а92.
1 Часто нормой кватерниона а называют число аа. Но при та*
ком определении свойство 6 уже не выполняется.
73
Приведем следующие свойства нормы кватерниона.
1. N (1) = N (i) = W (/) = У (k) = 1.
□ Доказательство очевидно. 
2.	ЛЦа) = ЛГ(а).	_	_
□ Действительно, N (а) = Vа а = ]/"аа = N (а). |
3.	Пусть г— комплексное число, а а— кватернион.
Тогда
N (za) = N (az) = | z| N (а).
□ Действительно, N (га) = l^za za — Yга а г =
= У | г |2 N* (a) — \z\N (а). 
4.	а + а 2W (а).	_____________
□ Действительно, а + а = 2а0 2V а’ + а?+	+
+ а‘ = 2N (а). 
5.	N (ар) = N(a) N (0).	_____
□ Действительно, X (ар) = j/"ap р а = V № (Р) а а =
= N (р)Каа = N (р) W (а). 
6.	ЛЦа + Р)СЛГ(а) + ЛГ(Р).
□ Действительно, воспользовавшись свойствами 4 и 5,
получим № (а + Р) = (a + Р) (а + р) = a a + р р + а р 4-
+ ра = №(а) + № (Р) 4- а р 4-	< № (а) 4- №(р) 4-
+ 2Af(ар) = ;V2(a) + №(р) + 2N (a) N (Р) = [У (а) 4-
+ AW- 
Теорема 8.6. Пусть а=/=0. Тогда решение урав-
нения ах = Р (ха = Р) определяется формулой
____ аР / ______ Р<х\
Х ~ № (а) И — № (а) / *
□ Умножая обе части равенства ах = р слева на а,
получим (аа)х = ар, или, что то же самое, № (а) х =
= ар. Но тогда х =	. Аналогично рассматривается
сличай уравнения ха = р. |
§ 7.	Функция ё1
Пусть 2 = х 4- yi. Определим ег равенством ег = ех х
X (cosy + /sin у).	(8.21)
Основные свойства определенной так функции е*
следующие.
74
1.	Если z — х + yt, то | ег | = ех.
□ На основании (8.21) 1ег1 = У'(ех cosy)2 4-(е* siny)2 =
= е*. 
2.	Для любого комплексного г ехФЪ.
□ Так как для любого действительного х е* #= О и
(в21 = ех, то ег 0. |
3.	Для любых комплексных г и К ег еу = ег+х. (8.22)
□ Пусть г — х + yi, X = а 4- fM- Тогда ег е* = е*е“х
X (cosy + isiny)(cos0 4- rsinp) = ех+а [(cosy cos0 — siny x
X sin0) + i (cosy sin0 4- siny cos0)] = e*+“ [cos(y + p) +
+ fsin (y + 0)] = ex+\ 
4.	Функция e1 периодическая с периодом 2nl.
□ На основании (8.21) ег+2п‘ = ех+^+2л>1 = ех х
X (cos (у + 2л) 4- isin (у 4- 2л)) = ех (cosy 4- isiny) = t*.
Следовательно, если f(z) = ex, то для любого комплекс-
ного числа z f (г 4- 2л«) = f (z). g
5.	Для любого целого числа т
(ег)т = етг.	(8.23)
 При т = 0 и т = 1 равенство (8.23) очевидно. Если т = 2,
то, на основании (8.22), (е2)2 = ег ez = е22.
Предположим, что равенство (8.23) справедливо для всех нату-
ральных т <k. Тогда (е2)л+! = (ez)k ez = ekz ez ~ ekz+z = e(*+I)2.
Таким образом, на основании принципа математической индукции,
равенство (8.23) справедливо для всех натуральных tn.
Пусть т —целое отрицательное число. Тогда т =* — л, где
п £ N. При этом
(е2)"1 (ег)п = (е?)т+п = (?)° = е0,2 = emz+nz = emz enz. (8-24)
А так как для натуральных п равенство (8.23) обосновано, то, учи-
тывая (8.24), имеем (ez)m епг = етг епг. Следовательно, (ez)m =emz.g
§ 8.	Функции sinz и cos г
На основании равенства (8.21), el“ = cosy + isiny,
e*^s=cosi/ — fsiny, откуда следует (формулы Эйлера):
eiy — е~{у
cosy = —, siny =-----------gj— .	(8 25)
Равенства (8.25) справедливы для любого действительно-
го числа у. Однако правые части этих равенств, на ос-
новании предыдущего, имеют смысл и в случае комп-
75
лексных значений у. Учитывая это, мы можем опреде-
лить с помощью равенств
cosz =
еи + е~и
2
sinz =
е‘г - е~1г
И
(8.26)
функции cosz и sin z для любого комплексного числа z.
Рассмотрим основные свойства определенных так
функций sinz и cosz.
1.	sinz и cosz — периодические функции с периодом 2л.
□	На основании равенств (8.26) и свойства 4 (§ 7),
sin(z 4- 2л)
gZ/4-2nr _ е—/г—2л/	е/г е—/г
--------21-------------- —2Г— = Sin2‘
Аналогично доказывается, что cos (г 4- 2л) = cos г. 
2. Функция cosz — четная, a sinz — нечетная, т. е.
cos (—г) = cos г, sin (—z) = —sin z.
□	Доказательство вытекает непосредственно из ра-
венств (8.26). 
3. Имеют место следующие формулы сложения:
sin (г 4* X) — sin z cos X 4- cos z sin X, (8.27)
cos (z 4- X) = cos z cos X — sin z sin X. (8.28)
□ Вычисляя, с учетом равенств (8.26), правую часть
в (8.27), получим
sin г cos X 4- cos г sin X =
_ (etz — е~1г) (e^ 4-	4~ (е<г 4-	(e‘K —	_
4i	””
2eizeiK — 2e~ize~iK /U+М _	.
=---------T.--------------------------= sin (z 4- X),
что и доказывает равенство (8.27). Аналогично обосновы-
вается и равенство (8.28). 
Заметим, что на основании равенств (8.27) и (8.28)
можем записать обычные формулы двойного угла!
sin 2г = 2 sin z cos z, cos 2z = cos2 z — sin2 z.
Кроме того, положив в (8.28) X = —z, получим тожде-
ство cos2 z 4- sin2 z = 1.
4. Равенство sinz — 0 имеет место тогда и только
тогда, когда г = kn; равенство cos z = 0 имеет место
тогда и только тогда, когда г =-^-+/гл (k£Z).
□ Так как, на основании равенств (8.25) и (8.26), при
вещественных г sin г является обычной тригонометрической
функцией, то sin /гл = 0.
76
Пусть теперь наоборот: известно, что для некоторого
z Ь а + pi sinz = 0. Тогда, на основании (8.26),	= е~,я
и, следовательно, | е1г | = | е~и |. А так как iz = ia — р,
то, с учетом свойства 1 (§ 7), |е‘г| = £—0. Аналогично
| е~‘г | = «Р. Следовательно, = е~&, т. е. е2₽ = 1. Это
возможно только при условии, что р = 0. Но тогда
sin z = sin a = 0 (a G R), откуда z = a = 2kn.
Аналогично устанавливается, что если cosz = 0, то
zQR и z = у + 2kn. 
Таким образом, на основании предыдущего, нули (или
корни) функций sinz и cosz расположены на веществен-
ной прямой и совпадают о нулями тригонометрических
функций sin х и cosx.
Рассмотренные свойства функций sinz и cosz такие
же, как и соответствующие свойства рассматриваемых
в школьном курсе математики тригонометрических функ-
ций sin х и cos х. Однако, оказывается, не все свойства
тригонометрических функций сохраняются при переходе
в комплексную область. Так, на множестве комплексных
чисел С функции sinz и cosz не являются ограниченными
по модулю, тогда как в случае действительных х
| sin х 1 и (cos х |	1.
Например, при z = yi, на основании (8.26),
cos yl =
е~У + еу
2
. е-У _ еУ
sin yi =---------
°	2i
Таким образом, cos yi — положительное вещественное
число, тогда как sin yi — чисто мнимое число. При этом,
если ^#=0, то е-у^еУ. Но тогда, на основании нера-
венства а + - >prab (а^О, Ь^О, a=£b), приходим к за-
ключению, что cos yi > Уе~УеУ = 1 («/=/= 0). Кроме того,
очевидно lim cos yi = оо, lim| sin yi | = оо.
§ 9. Кватернион еа
Пусть a — кватернион. Тогда (§ 4) a = a0 + a, где
a = aii 4- а2/ 4- a3k — векторная часть кватерниона а.
Рассмотрим кватернион J (а), который определяется равен-
ством
J(a) =
а (а =/= 0),
-V (а)
0 (а = 0).
(8.29)
77
Основные свойства величины J (а) такие)
1)	J (а) = —J (а);
3)J2(a) = —1 (а#=0);
4)N(7(a))=l (а=/=0).
Первое свойство непосредственно вытекает из равенства
a = —a.
Для обоснования второго свойства достаточно заме-
тить, что если a = i, то a = i и N (a) = N (z) = 1.
На основании равенства (8.16) и определения нормы
N (a) (§ 6) при a #= О
/2(а) = = _1,
№ (а)	«1 + а2 + а3
что и доказывает третье свойство «/(a).
Для доказательства последнего свойства воспользуемся
равенством N (za) = |z | N (а) (г £ С). Тогда при а О
N (J (а)) ——\^-N(a) = l. Определим теперь равен-
fl (а)
ством
“ — [cos Л/ (а) 4- <7 (a) sin N (а)],	(8.30)
где а0 — действительная часть кватерниона a (§ 4).
В частности, если a = a£/?, то a0=a, a=0,
A7(a) = 0, J(a)=0. На основании (8.30), е“ = е°.
А нелогично, если a = г = а 4- bi (b Ф 0) — комплекс-
►
ное число, то «„ = а, а = Ы, N (a) = | b |, J (а) = 07, где
( 1 (Ь>0),
ibi “1—1 (ft<0).
Но тогда, с учетом (8.30),
е“ = е* [cos |6| + Z0sin| Ь|],
где cos | b | = cos b, 0 sin | b | в sin 91 b | = sin b.
Следовательно, 6°+“ = еа (cos Ь 4- i sin b).
Аналогично устанавливаются следующие «частные» фор-
мулы)
ea+bi = еа (cos b 4- / sin b),	(8.31)
ga+ЬЛ _ ga (cos ft 4- sin b).	(8.32)
Таким образом, с учетом предыдущего, в лучае дей-
ствительных или комплексных а определение е“ по фор-
78
муле (8.30) не противоречит определению еа (а 6 /?) и ег (г =
= a + bi — формула (8.21)).
Рассмотрим теперь свойства кватерниона еа.
1.	Пусть е“ = 0. Тогда
0о = е“» cos N (а), 0 =а J (a) e®»sin N (а).	(8.33)
□ Доказательство непосредственно вытекает из фор-
мулы (8.30). 
2.	N (е“) = е“..
□ Пусть е“ = 0. Так как №(0) = 0? + № (0), то,
с учетом равенств (8.33) и У (га) = | г | N (a) (zQC), по-
лучим № (е“) = е2®» cos2 N (а) + е2®» sin2 Af (а) № (J (а)) =
— е2“« (cos2 N (а) + sin2 W (а)) = е2“». 
3.	Для любого кватерниона а е“=/=0.
□ Так как N (е®) = е®« =#0, то е®у=0. 
4.	е®»+“ = е«оё®.
□ Так как J (а) = J (а), то сформулированное свой-
ство непосредственно вытекает из равенства (8.30). 
5.	Равенства
е®е₽ = е®+₽, е№ = е«*+“	(8.34)
выполняются тогда и только тогда, когда векторные
части кватернионов а и 0 линейно зависимы.
□ На основании (8.29) и (8.30) кватернионы е® и
—
можно представить в виде еа = А + Ba, = С + D0,
где А, В, С и D — вещественные числа. Предположим,
что выполняются равенства (8.34). Тогда е^е^ = е₽е®. Сле-
—>	—>•
довательно, векторные части Ва и D0 кватернионов е®
и е? линейно зависимы. Но тогда, очевидно, линейно
зависимы и векторные части аир кватернионов аир.
——>
Наоборот, пусть кватернионы а и 0 линейно зависимы.
Пусть, для определенности, 0 = га, где г — некоторое
вещественное число. Если при этом г = 0, то 0 = 0. Сле-
довательно,
_ ^a.+p.+a = ^а+Р.
Поэтому в дальнейшем предполагаем, что г=#=0. Пусть,
например, г <0. Тогда
—>
JV(0j = |r|jV(o5----rN&), J(0) = -^r = -J (a).
N (0)
79
Следовательно,
..-0 = е0> [cos rN (а) 4- J (a) sin rN (а)].	(8.35)
Но тогда, на основании (8.30) и (8.35),
е“еР = е^+Зо [(cos N (a) cos rN (а) — sin W (a) sin rN (а)) 4-
—>	—►
4* Да) (cos N (a) sin rN (a) + sin N (a) cos rN (a))].=
e ga,+₽, [cos (1 4- r) N (a) 4- J (a) sin (1 4- r) N (cT)].	(8.36)
С другой стороны, a 4-p =s (1 4-Иа- Но тогда N(a +
4-P) = |l+r|tf(a), Да4-Р) = 8Да), где 0=^^..
Поэтому
e®+₽ = t«.+3. [cos (14-г) У (a) 4- Да 4- P) sin | 1 4- r I N (a)]=<
= ea»-h% [cos (1 4- r) N (a) 4- J (a) sin 01 1 4- r | N (a)] —
= <?“«+&> [cos (1 4- Г) N (a) 4- J (a) sin (1 4- r) N (a)].	(8.37)
В равенствах (8.36) и (8.37) правые части равны. Следо-
вательно, е“еЗ = е“+3. Аналогично рассматривается случай
г > 0. Этим первое равенство из (8.34) доказано. Второе
равенство вытекает из того, что в рассматриваемом случае
еве? = еРе“. 
6.	Функция не является периодической. Однако
имеет место периодичность в следующем смысле (перио-
дичность «по направлению»):
а)	Для любого а вида a = a 4- bi
еа+2тМ = еа (mQZ).
б)	Для любого а вида a — a + bj
в)	Для любого а вида a = а 4- bk
ga+imnli^ga (m^Z).
§ 10. Кватернионы sin а и cos a
Пусть a = a0 4- a — кватернион. Определим sin a
и cos a следующими равенствами)
sin a = sin a0 cos IN (a) — i7(a) cos a0 sin IN (a), (8.38)
cos a = cos a0 cos IN (a) 4- iJ (a) sin a0 sin iN (a). (8.39)
80
При а = а0 равенства (8.38) и (8.39) запишем так:
sina = sina0, cosa = cosa0.
Аналогично, если a = г = а0 +	(ах=#=0), то N (а) =
e 1а11»
j(a) = et (е = -г^-={_1
Следовательно, sin а = sin а0 cos i | ах | — i2 cos а0 sin X
X «О' ах j = sin а0 cos iai 4- cos а0 sin zaj = sin (a0 4- iai) =
= sinz.
Аналогично устанавливается, что в случае a = z cos a,
определенный по формуле (8.39), совпадает с cosz, кото-
рый был определен для комплексных z в § 8.
Таким образом, принятое здесь определение sin a
и cos а в’случае, когда a — кватернион, не противоречит
принятому ранее определению sinz и cosz для г^С-
Рассмотрим некоторые свойства функций sin a
и cos a.
1.	sin а и cos a — периодические функции с периодом 2л.
□ Доказательство непосредственно вытекает из (8.38)
и (8.39). 
2.	sin (—a) = —sin a, cos (—a) = cos a.
□ Доказательство вытекает из равенств (8.38) и (8.39)
——>•
с учетом равенств J (—а) =—J (a), N (—а) = Af(a). 
3.	Для любого кватерниона а
sin2 а + cos2 а = 1.	(8.40)
□	Равенство (8.40) проверяется непосредственным воз-
ведением в квадрат правых частей равенств (8.38) и (8.39). И
4. sina = 0 тогда и только тогда, когда a =/пл;
cosa = 0, тогда и только тогда, когда а = " 4- тл.
□	Пусть а = тл. Тогда а = 0. На основании (8.38),
sin a = 0.
Наоборот, пусть sin a = 0. Если a = 0, то, на основа-
нии (8.38), sinao = O, откуда а = а0 = тл.
Предположим, что a =/= 0. Тогда J (а) =£ 0, N (а) > 0.
Следовательно, sinzW(a)^=0, cos IN (a) #=0 (см. §8).
Кроме того, так как число sin iN (а) чисто мнимое, то
число i sin iN (a) — вещественное. Но тогда действитель-
ная и векторная части кватерниона 0 = sin а определяются
равенствами 0О = sin a0 cos iN (a), 0 = — iJ (a) cos a0 sin x
81
X IN (а). Если при этом 0 = sin a = 0, то 0О = 0 и 0 = 0,
что возможно только при условии: sinao = O, cosa0 = 0.
—>
Полученное противоречие указывает на то, что при a =/= О
sin a =5^ 0. Таким образом, из равенства sin a = 0 следует,
что a£R. Но тогда, на основании предыдущего, a = тп
(m£Z).
Аналогично устанавливается, что cosa = 0 тогда
и только тогда, когда а =	+ тл (т £ Z). 
5. Пусть кватернионы а и 0 линейно зависимы. Тогда
sin (a + 0) = sin a cos 0 + cos a sin 0,	(8.41)
cos (a + 0) = cos a cos 0 — sin a sin 0.	(8.42)
□ Действительно, учитывая равенства (8.38) и (8.39),
получим (приводя после перемножения подобные)!
sin a cos 0 + cos a sin 0 =
= sin (a0 + 0O) cos iN (a) cos iN (0) =
—	iJ (0) cos (a0 + 0O) cos iN (a) sin iN (0) —
—	iJ (a) cos (a0 + 0O) sin IN (a) cos iN (0) +
+ J (a) J (0) sin (a0 + 0O) sin iN (a) sin iN (0). (8.43)
—►	—►
Если при этом1 0 = ra, где г £ Rt то N (0) = | г | N (а),
J (0) = QJ (а) (в « дтр) » и таким образом, с учетом ра-
венства </2(а) = —1, можем записать (8.43) так!
sin a cos 0 + cos a sin 0 =
= sin (a0 + 0O) [cos iN (a) cos irN (a) —
— sin iN (a) sin if) | r | N (a)] — iJ (a) cos (a0 + Po) X
X [cos iN (a) sin i01 r | N (a) -f- sin iN (a) cos irN (a)] =
= sin (a0 + 0O) cos i (1 + r) N (a) —
— iJ (a) cos (a0 + 0O) sin i (1 + r) N (a).	(8.44)
—>
С другой стороны, sin (a + 0) = sin (a0 + 0O + (1 + r) a) =
= sin(a0 + 0o)cosi| 1 + r|AT(a) — iJ (a + 0) cos (a0 4- 0O) X
1 Случай r = 0 тривиальный. Поэтому рассматривается случай
r^O.
82
X sin i 11 4- r | N (а), где J (a 4-0) =—= eJ (a)
i 1 Ч-r |ЛГ (a)
{-1- И)-
Но тогда
sin (a + P) = sin (a0 4- p0) i (1 + r) W (a) —
— iJ (a) cos (a0 + po) sin ie, 11 + r | N (a).	(8.45)
А так как e (1 4- r | = 1 4- г, то правые части в (8.44)
и (8.45) совпадают. Этим равенство (8.44) доказано. Точно
так же обосновывается и равенство (8.42). 
В заключение заметим, что из равенств (8.41) и (8.42)
обычным способом получаем формулы «двойного угла»!
sin 2a = 2 sin a cos a, cos 2a = cos2 a — sin2 a.
§ 11. Функции от кватернионов
Може возникнуть, естественно, вопрос: почему ква-
тернионы е®, sin а и cos а определялись именно форму-
лами (8.30), (8.38) и (8.39), а не какими-то другими?
Чтобы ответить на этот вопрос, рассмотрим некоторые
предварительные понятия (ряды и их свойства, а также
представление функций ех, sinx и cos х в виде рядов).
Пусть оь а2, а3, ... , ап, ... есть произвольная по-
следовательность чисел (которые, вообще говоря, могут
быть комплексными). Выражение
°i 4- й-г 4~ а3 + • • • + ап • • •	(8.46
называют рядом, а числа оь а2, а3, ... , ап, ... членами
ряда. Этот ряд называют сходящимся, если сходится
числовая последовательность
Sj, Ss, S3, ... , Sn, •.. >	(8.47)
где Si = Oi, S2 = Oi 4* Oj, S3 = щ 4* a4 4* a3, ...» Sn =
= Oi 4- o2 4- os 4- • • • 4- on. При этом числа Sn называют
частичными суммами ряда (8.46).
Если S — предел последовательности (8.47), то S на-
зывают суммой ряда (8.46) и пишут
S == О! + о2 4~ о3 4~ • • • 4* о„ 4* • ”
или
s- V
Л=1
При этом говорят, что ряд (8.46) сходится к сумме S.
83
В том же случае, когда последовательность частич-
ных сумм (8.47) не имеет предела, ряд (8.46) называют
расходящимся.
Простейшим примером ряда является так называемый
геометрический ряд
а + aq + aq2 + • • • + aqn + • • •,	(8.48)
членами которого являются элементы бесконечной гео-
метрической прогрессии a, aq, aq2, ... , aqn, .... При
этом, как известно из школьного курса математики,
если 1<71 < 1, то ряд (8.48) сходится и его сумма 5 =	•
Ясно также, что при а = 0 ряд (8.48) сходится независимо
от значения q и его сумма 5 = 0. Если же а 0 и | q |	1,
то ряд (8.48) расходится (расходящийся ряд). Заметим,
что условие сходимости или расходимости ряда (8.48)
справедливо не только в случае вещественных а и q, но
также и в том случае, когда а и q — комплексные числа.
Необходимым условием сходимости ряда (8.46) является
стремление к нулю его n-го члена при п-+<х> (т. е. усло-
вие ап->0 при п-»-оо). Это вытекает из того, что ап =
= 5Л— S„_i. Следовательно, lima„ = lim5n— lim5n_! =
И->оо	П-*> оо	П-*>оо
= s —5 = 0.
Однако это условие не является достаточным. Так,
ряд 1+4 + т + т + 4'+----------!" 7Г + ‘ ’ КОТОРЫЙ на*
эывают гармоническим рядом, расходится, хотя его п-й
член а„ = -^—>-0 при п-*-оо (см., например, [4], с. 22).
Существуют различные признаки сходимости рядов.
Здесь мы сформулируем (без доказательства) некоторые
из наиболее употребляемых на практике достаточных
признаков сходимости рядов.
1.	(Признак сравнения рядов). Пусть |а„|^Ьп,
где Ьп — члены сходящегося ряда bx + b2 + b3 + • • • +
+ Ьп + • • • • Тогда ряд (8.46) сходится.
2.	(Признак д’Аламбера). Если существует
такое число q < 1, что, начиная с некоторого номера т,
-^-^q (п>т),
I ап I
то ряд (8.46) сходится. Если же при п~^т выполняется
неравенство	> 1, то рассматриваемый ряд рас-
ходится.
84
3.	(Признак Коши). Если существует такое
число q < 1, что
то ряд (8.46) сходится. Если же при п^т	ап|> 1,
то рассматриваемый ряд расходится.
Обоснование этих признаков в случае рядов с веще-
ственными (положительными) членами можно найти в [4].
В общем случае сформулированные признаки могут быть
обоснованы методами, сходными с теми, которые рас-
сматриваются в [4].
Воспользовавшись признаком д’Аламбера или призна-
ком Коши, нетрудно убедиться, что при любом комп-
лексном г сходятся следующие ряды:
2	2а
1 + тг + ^ + зг+--- + тг + -”«	<8-49)
2®	2&	9*1
г--Зг+-!Г-7Г+"-.	<8-«»
2а	т4	26
т+тг- 1г + •	<8-5|>
При этом, оказывается, существуют следующие важные
и интересные соотношения (х£/?):
е ~ 1 + П + 2! + "ЗГ + ’ ‘ ’’
уЗ	у7
sin х = х	др +	-5|	+
,	Ха ,	X*	Xе	,
COSX — 1	21	+	4!	61	+	*’ '*
Обоснование этих равенств можно найти, например, в [4J
(гл. 5, § 3, 8).
Учитывая последние три равенства, а также сходи-
мость при любом комплексном г рядов (8.49), (8.50)
и (8.51), определяют ег, sin г и cosz (z£C) следующим
образом:
= 1 + —+ — +— + ...
е 1	1!	21	3!
Z®	Z1
sinz = г	др + -gp	рр -Ь • • •,
cos г = 1	2Г + 77	ёГ + • • • •
Тогда, как легко проверить, е'г = cosz + isin z, е~‘г =
= cosz — »sinz.
85
Таким образом, sinz и cosz можно записать в виде (8.26).
А это означает, что принятое здесь определение sin z,
cosz (а также и ег) эквивалентно определению, которое
было дано в § 7 и 8.
Точно также можем поступить и в случае кватернио-
нов. А именно, нетрудно показать, что для любого ква-
терниона а ряд
1 ± а ± а2 ± а3 х ..
сходится1 к некоторому кватерниону 0. Этот кватернион,
по аналогии с предыдущим, обозначим через еа:
*“=‘ + тг + <+ £ + ••••	<8-52>
Точно так же определим sin а и cos а:
а3	.а5 а7	,	/о
sina =	a-3r	+ -gr--7r	+	...»	(8.53)
.	а2	. а4 а6	.	/О сл\
C0Sa=	1	_ —	+__ —	+	....	(8.54)
Оказывается, что такое определение кватернионов еа,
sin а и cos а эквивалентно прежнему. Чтобы не повторять
рассуждения отдельно для е“, sin а и cos а, рассмотрим
общий случай.
Пусть в некотором круге |z| </? (/? оо)
f (г) = а0 + «12 + а2г2 Ч--------F «„г" Ч---.
Определим f (a) (a-кватернион) равенством
f (a) = а0 + «!« Ч- «2«2 +-----------И апаП + • • ’•
Так как a — корень квадратного уравнения с действи
тельными коэффициентами а2 — ра Ч- q = 0, где р = а Ч-
Ч- а = 2а0, q = № (а) = аа, то, рассуждая так же, как
и в гл. 7 (§ 6), убеждаемся, что ап — ипа Ч- vn, где = 1,
и2 — Р\ «1 = 0, ц2 = —Q- При этом an+1 = (ипа Ч- vn) а =
= «„ (ра — 7) + Vna = (ипр + vn) а — qun = ип+1а + v„+1.
Следовательно, v„+1 = — qun, un+l = рип+ vn = рип—qun^.
Таким образом, чиола ип образуют возвратную последо-
1 Определение сходимости ряда, членами которого являются
кватернионы, такое же, как и в случае обычных числовых рядов.
При этом последовательность кватер ионов ai, a«, ..., an, . .. на*
зывается сходящейся к кватерниону а, если /v(art —а)->0 при
оо.
86
вательность второго порядка. Используя обобщенную
формулу Бине для таких чисел, находим
ип = —U- (Г - г”) (z = а0 + iN (а)),	(8.55)
2Л/(а)
Vn = i^a) (2n^a _	(8,56)
2ЛЦа)
Тогда
/ (a) = S anan = ( S an«n)a + £	(8-57>
n=Q	n=0	n=0
где, на основании (8.55),
SanUn=ajn“ S°n2n}’
n=0	k ' nr=0	n=0
или, что то же самое,
У апип = —4-	— f (*))•
2"(a).
Аналогично находим
, . . If И /(*)
П 2АГ (a) I 2
Или, так как zz = a0 4- N2 (а) = № (а), то
У = —4^ (zf (z) — zf (z)),
2JV(a)
—>-
что, в свою очередь, учитывая равенство z =s a0 + iN (a),
можно преобразовать к виду
Sn Tl _ ta. (f (г) - f (i) ,/(*) + / (i)
unVn-----------------------1	9---- .
2^ (a)	1
n=o	' '
Но тогда, на основании (8.57), (8.58) и (8.59),
f (a) - ia~^ (f (z) - f +
2N (a)	2
где
ta —ia0	,. a	i ...	)
----=>— = »--------- (a) = — -97 J (a).
2Л^ (a)	2tf(a)	J	24
(8.59)
(8.60)
(8.61)
87
Подставляя (8.61) в (8.60), получим следующее оконча-
тельное выражение для / (а):
f (а) = МШ +	J(а).	(8.62)
При этом формула (8.62) справедлива для всех а, для
которых |z|</?. А так как |z| = Af(oc), то, таким обра-
зом, указанная формула имеет место для всех кватернио-
нов а, норма которых N (а) < R. В частности, соответст-
вующие формулы для е“, sin а и cos а справедливы для
любого кватерниона а.
Пусть [(г)=е*. Тогда, на основании (8.62),
ea„eW(a) , eaCe-ZW(a) ea„gZ\(a) _ ea,e-lN(O)
=---------%----------+-----------21--------J (а) =
= е“" [cos iN (а) + J (a) sin iN (а)|,
что согласуется с формулой (8.30). Аналогично, если
/ (z) = sin z или / (z) = cos z, то получаем соответствующие
формулы для sin а и cos а (т. е. формулы (8.38), (8.39)).
В заключение отметим, что так как aJ (а) = J (a) a
« J2 (а) — — 1, то
(J(a)a)n=;n(a)an=
а"
J (а) ап
—а"
—J (а) а"
(п — 4k),
(п = 4k + 1),
(п = 4k + 2),
(n=4k + 3).
(8.63)
Поэтому, как легко проверить, на основании (8.52), (8.53),
(8.54) и (8.63),
сЛахх _ cos а 4- J (a) sin a.	(8.64)
Таким образом, мы получили аналог формулы Эйлера для
кватернионов. Воспользовавшись (8.64), нетрудно также
получить следующие аналоги формул Эйлера в случае
кватернионов:
еУ(а)а . g—J«x)a	вУ(аух _ е—/<а)а
cos а  ------21------1 sin ос  ---------------.
УПРАЖНЕНИЯ
1. Докажите, что при zC С
ег = е*, sinz = sinz, cos г = cosz.
2. Так же, как и при построении кватернионов, можем рассмат-
ривать упорядоченные пары кватернионов. В результате построим
множество так называемых чисел Кели (см. [5]). Какими формулами
следует определить е*, sins, coss в случае чисел Кели?
£8
ДОПОЛНЕНИЕ
Метод математической индукции
I.	Индукция в математике. Индукция (лат. inductio— на веде*
ние) означает переход от частного к общему. Другими словами, под
индукцией понимают своеобразный метод рассуждений, в результате
которого от некоторых частных фактов (примеров, утверждений,
результатов наблюдений и т. п.) переходят к общим выводам,
утверждениям, положениям.
Индукцией широко пользуются как в быту, так и в науке. Так.
в физике многие ваконы формулируются на основе некоторой сово-
купности наблюдений, экспериментов. В математике индукцией также
пользуются довольно широко и плодотворно. Например, уже в млад*
ших классах ученики приходят к общим правилам:
а + b s= b + a, ah = Ьа,
неоднократно сталкиваются с конкретными примерами типа: 5 + 7 =
-7 + 6, 5 • 7 = 7 • 5 и т. д.
Во многих случаях индукция дает возможность получить новые
формулы, установить те или иные закономерности. В то же время
применение индукции может привести и к ошибочным выводам.
Приведем в связи с этим некоторые примеры.
Пример 1. Пусть при некотором действительном а число S =
— а + ~ — цел е. Тогда S2 = а2 + 2 + ~, откуда следует, что»
число а2 + “й = £а—2 также является целым.
Точно также S3 = а3 + 3 (а +	~ .
Таким образом, д8 + ”з— снова целое число. Это наталкивает
на мысль (индуктивный переход!), что при любом натуральном п
число
Sn = а" +1 (Sx = S)	(1)
является целым, В п. 3 показано, что это действительно так.
Пример 2. Пусть Тл = 2зЛ+1, Тогда Т0 = 3 13, 7\ = 23 +
+ 1=9! 9, Та = 513:27.
Таким образом, То 1 3, 7\ : З2, Т2 t З8. Поэтому естественно пред-
положить, что Тп : 3rt+x. В п. 2 это предположение будет подтверж-
дено.
Пример 3. Рассмотрим числа вида Fn = 22” + 1. При п = 0.
1, 2, 3, 4 эти числа простые: = 3, Fj = 5, Fa = 17, F3= 257,
F4 = 66537.
В связи с этим французский математик П. Ферма (XVII в.) вы-
сказал предположение, что при любом натуральном п число Fn —
простое. Однако в данном случае индуктивный переход оказался
89
ошибочным. Как позже показал Л. Эйлер (XVIII в.), при п=5 это
число составное: F6 = 641 • 6700417.
Некоторые другие поучительные примеры ошибочных утвержде-
ний, которые были сформулированы в результате индуктивного пере-
хода от частных примеров к общим выводам, можно найти в [8].
Таким образом, переход от частного к общему не всегда приво-
дит к правильным утверждениям. В связи с этим возникает важный
вопрос: когда такой переход закономерен? Во многих случаях ответ
на этот вопрос можно получить с помощью так называемого принципа
математической индукции.
2.	Принцип математической индукции. Этот принцип заключается
в следующем.
Если некоторое утверждение S справедливо для п = 1 и из
предположения, что оно справедливо для n = k, следует его спра-
ведливость для	то это утверждение справедливо для
любого натурального п.
Заметим, что принцип математической индукции иногда называют
принципом полной математической индукции, тогда как индукцию,
о которой шла речь раньше, называют неполной индукцией.
Таким образом, применение принципа математической индукции
состоит из двух этапов:
1)	проверка или обоснование справедливости рассматриваемого
утверждения S для п = 1;
2)	на основании предположения о справедливости утверждения
S для п = k доказывается его справедливость для п = & + 1.
Только после завершения указанных этапов можно делать вывод
о справедливости утверждения S для любого натурального п.
Проиллюстрируем применение принципа математической индукции
в случае примера 1 (п. 1).
Если Тп = 2зЛ + L то число 7\==9 делится на За и, таким
образом, утверждение S (т. е. сформулированное ранее предположе-
ние о том, что Тп : Зп+1 (для ли 1) справедливо.
Предположим, что рассматриваемое утверждение справедливо для
л = k, т. е. Tk 3*+1. Тогда, очевидно, Т^+1 = 23^>a + 1 = (23*)3 +
+ 1 = (23* + 1) [(2а*)а — 23*+ 1] или, учитывая очевидное тождество
ха-х+1 =(х+ 1)(х- 1) - (х+ 1) + 3, Tk+1 = Tk[Tk(x^ 1)-
— Tk + 3] (х = 2 ). В правой части последнего равенства Зл+1
(на основании предположения), а выражение в скобках делится, оче-
видно, на 3. Следовательно, Т$+1 делится на Зл+1 • 3 = Зл+а, т. е.
рассматриваемое утверждение справедливо и при л = k + 1. Но тогда,
на основании принципа математической индукции, Тп 3^+J при любом
натуральном л.
3.	Другие формы принципа математической индукции. Пусть
требуется вычислить сторону а2л правильного 2л-угольника, вписан-
ного в окружность единичного радиуса. При л =2 правильный 2п-
угольник есть квадрат, сторона которого а4 = ]/2 . Воспользовавшись
формулой удвоения	___________________
aan+l = j/"2 — 2 j/" 1 —	.
находим а8, а10, а32 (л = 3, 4, б) и выдвигаем гипотезу, что
а3п= ]/" 2 — J/ 2 + V2+...+ У'2 •	(2)
п-—2 двойки
90
Формула (2) справедлива для п = 2, и из предположения, что
она справедлива для п = k (k > 2), вытекает, как нетрудно проверить,
что эта формула справедлива и для п =	1. На основании сказан-
ного приходим к заключению, что (2) справедлива при любом нату-
ральном п > 2.
Таким образом, обоснование (2) состоит из обоснования следующих
двух предложений: 1) формула (2) справедлива для п = 2 и 2), если (2)
справедлива для n = k (k > 2), то она справедлива и при п = &+ !•
Характерной особенностью в этих рассуждениях есть то, что
справедливость формулы (2) проверяется не при п = 1 (в связи с тем
что 2-угольника не существует), а при п = 2. Закономерность ука-
занного подхода вытекает из следующей теоремы.
Теорема /. Пусть утверждение S удовлетворяет условиям:
1)	Утверждение S справедливо для т=а, где а — фиксирован-
ное целое число.
2)	Если утверждение S справедливо для т = k (k > а), то оно
справедливо и при т = k-\- 1.
Тогда это утверждение справедливо для любого целого числа
т"> а.
О Теорема легко доказывается с помощью принципа математи-
ческой индукции. Действительно, так нак для т = а утверждение
справедливо, то достаточно доказать для т> а. При этом т> а
тогда и только тогда, когда т = а 4- п, где п 6 /V. Поэтому справед-
ливость утверждения S достаточно доказать для всех т вида т =
= а + п (п £ N). С учетом условия утверждение S справедливо для
т » а + 1 (так как оно справедливо для т = а), и, таким образом,
это утверждение справедливо для п = 1.
Предположим, что оно справедливо для п = k. т. е. для т =
=• а 4- /е. Тогда оно справедливо и для т + 1 = (а 4- k) 4- 1 = и +
+ (&4-1), т. е. для п = k + 1. Но тогда, на основании принципа
математической индукции, рассматриваемое утверждение справедливо
для всех натуральных чисел п, или, что то же самое, для всех целых
чисел т = а 4- п (п € N), т. е. для т > а. 
Отметим, что, на основании доказанной теоремы, в случае при-
мера 2 мы могли бы проверять справедливость соответствующего
утверждения не при п = 1, а при п = 0.
Теорема 2. Если утверждение S справедливо для п = 1 и иэ
предположения о его справедливости для всех натуральных п <fe
(k б N) следует его справедливость для п =	1, то это утвер-
ждение справедливо для всех натуральных п.
Теорема 3. Пусть М —множество натуральных чисел. удов-
летворяющее следующим условиям: 1 Q М. и если k £ М. то и k-\-
4- 1 G М. Тогда M = N.
Совсем просто показать, что и наоборот: из предположения о
справедливости теоремы 2 или теоремы 3 следует справедливость
принципа математической индукции. Таким образом, принцип матема-
тической индукции эквивалентен утверждениям теорем 2 и 3. В связи
с этим довольно часто теоремы 2 и 3 (и особенно теорему 2) форму-
лируют как принцип математической индукции.
Нетрудно также теоремы 2 и 3 сформулировать в несколько
более общем виде (аналогично теореме 1).
Воспользуемся теперь теоремой 2 для обоснования равенства (1).
При п= 1 Si = а + у есть, по условию, целое число. Целым так-
же является и число 50 = а0 4-	— 2, Предположим, что при всех
91
натуральных л <А? Sn £ Z. Как легко проверить, S1S^ = S^_1—
— 5л+1, и, следовательно, число $*+1 ~	целое (как раз-
ность двух целых чисел). Таким образом, на основании теоремы 2,
число Sn целое при любом натуральном п.
4.	Принцип наименьшего числа. Принцип математической индук-
ции эквивалентен также так называемому принципу наименьшего
числа: о произвольном непустом множестве натуральных чисел со-
держится наименьшее число.
Действительно, пусть Т — непустое множество натуральных чисел
(т. е. TczN, Т 0). Если 1 С Л то число 1 и будет наименьшим
в Т. Поэтому рассмотрим случай, когда 1 С Т. Тогда для любого а
из Т 1 < а (т. е. число 1 меньше любого числа а из Г). Обозначим
через М множество всех натуральных чисел, каждое их которых
меньше любого числа а из Г. Так как 1 С Л1, то М 0. Если мы
предположим, что для любого k из М k 4- 1 С М, то, по принципу
математической индукции (или теоремы 3), М = N. Но тогда Т = 0
(так как Т и Л4 не имеют общих элементов). Следовательно, наше
предположение неверно. Это означает, что в М найдется такое число
kt для которого k + 1 С Л1. Но это возможно только при а= £4-
4-1^7’. Покажем, что а — наименьшее в Т число. Действительно,
предположим, что b С Т и b < а. Тогда b <.а~ 1, т. е. b Сле-
довательно, b £ М (так как при любом х из Т (b < х). Но тогда
(при х = Ь) имеем b < Ь, т. е. получим противоречие. Следовательно,
для любого х из Т а < х и a т. е. а — наименьшее в Т число.
Покажем теперь, что и наоборот: принцип математической ин-
дукции может быть обоснован с помощью принципа наименьшего
числа. Действительно, пусть утверждение S справедливо для п = 1,
из предположения о его справедливости для п = k вытекает спра-
ведливость этого утверждения для л = £-|-1. Обозначим через Т
множество натуральных чисел и, для которых утверждение S не
имеет места. Предположим, что Т =£ 0. Тогда, на основании прин-
ципа наименьшего числа, в Т содержится наименьшее число а. При
этом, очевидно, а> 1 (так как 1 Рассмотрим число k~ а— 1.
Так как k С Tt то для числа п = k утверждение S справедливо. Но
тогда, на основании условия, утверждение S справедливо и для
п = k 4- 1, т. е. для п = а. А так как а С Л то для п = а утвержде-
ние S не должно иметь места. Получили противоречие. Следовательно,
предположение о том, что Т 0, неверное. Таким образом, Т — 0.
А это означает, что утверждение S справедливо для всех натураль-
ных л. Этим доказательство эквивалентности принципа математической
индукции и принципа наименьшего числа завершено,
5.	Биномиальные коэффициенты. Пусть п — натуральное число.
Произведение всех натуральных чисел от 1 до л обозначается л!
(читается: эн-факториал). Кроме того, по определению, 0! = L Таким
образом,
О! = 1, л! = 1 • 2 • 3 •• л (л С ЛГ).
Если л б N, то числа С*, определяемые равенствами
««<»>........."»• я
называют биномиальными коэффициентами,
92
Нетрудно убедиться, что эти числа можно записать также в виде
k л (п — 1) (п — 2)... [л — (£-f- 1)]
п	1 • 2 • . .. • k
Основные свойства биномиальных коэффициентов такие:
п гН-! _ п рь. о\ гН-1 _ п "b.J pk.
°	~*+1Ч>	Сп+1-д,+ 1Ч>
3) с* = ст*; 4) скп + с*+* = сЭД.
Свойства 1, 2 и 3 непосредственно вытекают из (3). Для доказа
тельства свойства 4 воспользуемся свойствами 1 и 2:
pk । ✓>АН-1 _pk । pk________~~F I pk___ ✓'•АН-!
I G/l “ “Г £ j bZI — £	|
Теорема 4. Пусть n — натуральное число и а, b — произволь-
ные (действительные или комплексные) числа, Тогда
(а + fe)n = ап + С\ап-Ч> + С’а'1-’*2 4- ... 4- CJJ-1 ahn~1 + &п.	(4)
О При п — 1 левая и правая части в (4) равны: а b = а + Ь.
Предположим, что формула (4) справедлива при n = kt т. е. (а +
-f. b)k = ak + C^a^b + C2kak~2b2 + . .. + bk. Умножая обе части
этого равенства на а^Ь и перемножая почленно выражения в пра
вой части полученного равенства, найдем
(а 4- fr)*+l = <?+’ 4- (1 4- ci) akb 4- (Ci 4- ci) a*-'d2 4-
4-(Ci4-C|)aA-2&24-...4-b*+1.	(5)
Воспользовавшись теперь свойством (4)$ запишем (5) в виде (4) (при-
Л = k 1).
Таким образом, формула (4) справедлива при п = 1 и из предпо-
ложения, что она справедлива при п = kt вытекает, что эта формула
справедлива и при л = &+ 1. Но тогда, на основании принципа мате-
матической индукции, эта формула справедлива при любом натураль-
ном п. Ц
ОТВЕТЫ
Глава 1. 1. d 9k — 1 (k 6 Z); 2. с --= 9k — 3 (k £Z); 3. b =
as 9k — 5 (k C Z); 4. Один из возможных наборов: а = 25, b = 67,
с = 330, d= 1955.
Глава 2. 1. Каждая из заданных дробей сократима (например:
первая — при п — —2; вторая — при п = 2; третья — при п = 0; чет-
вертая— при п = 3. 2. а С {15; 17}, b = б, с С {9; 10), d£{13; 14}.
Глава 3. 1. Простые числа: 1987, 1993, 1997, 1999.
(Глава 4. 1. Пусть z = * + yL Тогда уравнение z2 = а + bi экви-
валентно системе
{х2 — у2= а
\2ху = Ь.
Задача может быть решена и непосредственной проверкой.
4. р > — 3	— один вещественный корень; р = —3 у^Зб — два
вещественных корня (один из них — кратный); р <—Зу/36— три
з^щественных корня.
б* I ЯI > 8 V 6 — один вещественный корень; | q | = 8^]/6 — два
вещественных • орня (один из них кратный); |^|<8р<6 — три ве-
щественных корня.
93
Глава 5. 1. а) + ха + х3_= О, ххха + х^г, + хах3 = р, *зв
= —q. 2. а) Если | р | < 4 }/2 , то заданное уравнение имеет неве-
щественные корни, б) Если р > 8, то заданное уравнение имеет не-
вещественные корни.
Глава 6. 1. а) См, рис. 8. 2. а) (р = —3)=>Т = 2а; б) (р =
= -у)=>Г=За; в) (р = --^)=>Г = За; г) (р = -1)=>7’*=
3. Достаточно из (6.12) найти f (х) и в полученном тождестве
заменить х на х — а.
5. Пусть при некотором п(п Q N) f (х + па) = f (х). Тогда
flr -L пп\ -	f W C0S rtf₽ - Sin П(Р - 1	M
f (X + Па) “	/ (x)sin/zq> + cosn<p “ '	W’
где	(p =	2 л. Но тогда	(/2 (х) -f- 1) sin ф = О, что невозможно, так
как	sin пер =£ 0 и /а (х) + 1	0.
Глава 7. 2. При р = 3 возможные следующие значения для q
и г:
q -3
1	3
г
1—373
3. Un = 1 [(а-ЫГ - (а +	; vn = - (а2 + *2)
Глава 8. 1. Использовать формулы для е2, sin г, cosz.
ОГЛАВЛЕНИЕ
3
Предисловие
Глава 1. Делимость выражения abn + сп + d на т , . . .	5
§ 1.	Делимость чисел (основные понятия)....... 5
§ 2.	Конкретные примеры....................... 6
§ 3.	Общий случай............................. 6
§ 4.	Об одном свойстве	коэффициента с.......	8
Упражнения.................................... 8
..	ап + b
Глава 2. Условие несократимости дроби вида-------.
сп Н- а
§ 1.	Наибольший общий делитель................ 8
§ 2.	Конкретный пример....................... 12
§ 3.	Общий случай. Регулярные	дроби.......... 12
§ 4,	Нерегулярные дроби...................... 14
Упражнения................................... 15
Глава 3. Теорема Вильсона................................ 15
§ 1.	Простые числа........................... 15
§ 2.	Теорема Вильсона........................ 17
§ 3.	Первое обобщение теоремы Вильсона ....	19
§ 4.	Второе обобщение теоремы Вильсона......	22
Упражнения................................... 25
Глава 4. Исследование уравнения хп + pxk + q » 0 . . . . 25
§ 1.	Комплексные числа....................... 25
§ 2.	Квадратные уравнения.................... 28
§ 3.	Триюнометрическая форма комплексных чисел 309
| 4.	Уравнение х3 + рх + q = 0................ о
§ 5.	Исследование корней уравнения х3 + px-[-q=0	33
§ 6.	Исследование корней уравнения xn+pxk-{-q=0 36
Упражнения................................... 38
Глава 5« Об одном достаточном условии существования
невещественных корней многочлена...................... 39
§ 1,	Корни многочлена........................ 39
§ 2.	Случай квадратного уравнения............ 41
§ 3.	Общий случай............................ 42
Упражнения................................... 45
Глава 6. Периодичность функции, удовлетворяющей уело-
вию /(х + а) =	0).............. 45
§ 1.	Конкретный пример....................... 45
§ 2.	Квадратные матрицы и действия над ними . .	47
95
§ 3.	Условие периодичности в общем случае ... ч
Упражнения......................................I
Глава 7. Возвратные последовательности второго порядка . I»
§ 1.	Числа Фибоначчи........• . .............
§ 2.	Возвратные последовательности............ ь
§ 3.	Многочлены Чебышева...................... 5
§ 4	Формула для tg па......................... 5
§ 5.	Формула Мечпна для числа л и ее аналоги . .
§ 6.	Формула для n-й степени квадратной матрицы 6
Упражнения...................................
Глава 8. Кватернионы...................................... *
§ 1.	Современная теория комплексных чисел . . .
§ 2.	Определение и основные свойства кватернионов
§ 3.	Базисные кватернионы....................
§ 4.	Векторная часть кватерниона............. 7(
§ 5.	Сопряженные кватернионы................. 7'
§ 6.	Норма кватерниона........................7и
§ 7.	Функция ег.............................. 7<
§ 8.	Функции sin г и cos г................... 7*
§ 9.	Кватернион еа............................. 7
§ 10.	Кватернионы sin а и cos а............... 8
§11.	Функции от кватернионов................ 8,
Упражнения................................... 81
Дополнение. Метод метематичеокой индукции................ 8?
1.	Индукция в математике..................... 81
2.	Принцип математической индукции........... 9i
3.	Другие формы принципа математической ин-
дукции ....................................... 9(
4.	Принцип наименьшего числа................. 9.
5.	Биномиальные коэффициенты................. 9*
Ответы...................................................
БИБЛИОТЕЧКА
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ШКОЛЫ
МАТЕМАТИКА
Александр Васильевич Кужель
МАТЕМАТИЧЕСКИЕ
ИМПРОВИЗАЦИИ
Редактор О. С. Дзюба
Литредактор А. П. Ковальчук
Художественный редактор Е. В. Чурнй
Технический редактор Л. Ф. Курышева
Корректор И. П. Бойко
Информ, бланк К? 75Г4
Сдано в набор 29. 12. 82. Подп. в печать 02.06.83. БФ 02675.
Формат 84x108/32. Бумага типогр № 2. Лит. гарн. Выс.
печать. 6,04. уол. печ. л. 5,36. усл кр.-отт. 4,93 уч.-изд. л.
Тираж 10000 экз. Изд. № 6194 Зак 3-6Г Цена 15 ч.
Головное издательство издательского объединение <Вища
школа». 252054, Киев-54. Гоголевская. 7
Отпечатано с матриц Харьковской книжной фабрики
им. М. В. Фрунзе в Харьковской городской типографии
№ 16, г. Харьков-3, ул. Университетская, 16. Зак. jQgg
15 IL
АВ.КУЖЕЛЬ
МАТЕМАТИЧЕСКИЕ
I ИМПРОВИЗАЦИИ