Автор: Воднев В.Т. Наумович Н.Ф. Наумович А.Ф.
Теги: математика справочник издательство высшая школа формулы по математике математические формулы
ISBN: 5-339-00083-4
Год: 1988
Текст
В.Т. ВОДНЕВ
А.Ф НАУМОВИЧ
Н.Ф НАУМОВИЧ
ОСНОВНЫЕ
МАТЕМАТИЧЕСКИЕ
ФОРМУЛЫ
Справочник
Под редакцией Ю. С. Богданова
Издание второе,
переработанное и дополненное
Минск «Вышэйшая школа» 1988
ВЕК 22.1я2
В 62
УДК 51(035.5)
1702010000—104
В----------------91—88
М304(03)—88
ISBN 5-339-00083-4
© Издательство «Вышэйшая школа»,
1980
© Издательство «Вышэйшая школа»,
1988
i
ПРЕДИСЛОВИЕ
В настоящее время все большее значение приобретает под-
готовка специалистов по фундаментальным научным дисципли-
нам, в том числе по математике. В связи с этим на разных
уровнях расширяется и углубляется содержание занятий по ма-
тематике, что требует привлечения новых методических средств.
В частности, оказывается целесообразным широкое применение
различных подручных пособий.
Одним из таких пособий призван служить справочник «Ос-
новные математические формулы», составленный на основе разра-
боток, которые велись в Белорусском государственном
университете на кафедре высшей глатематики факультета приклад-
ной математики. Эти разработки предназначены в первую
очередь для использования при работе над учебным мате-
риалом, а также на занятиях различных типов. Вместе с тем
необходимо подчеркнуть, что книги такого рода должны способ-
ствовать усвоению содержательного математического материала,
по никак не заменять его.
Справочник рассчитан на читателей, закончивших какой-то
цикл обучения, которые, помня о существовании нужных формул,
могут быстро найти их для практического использования.
Книга состоит из четырнадцати глав. Включая в каждую
главу соответствующий материал, авторы не заботились ни о де-
лении его на школьный и вузовский, ни о логической связи
между главами.
Внутри каждой главы вводятся необходимые обозначения
и приводятся основные формулы, зачастую без исчерпывающего
объяснения условий их применения. Как правило, не указываются
и естественные ограничения на переменные.
В тексте используется прямоугольная декартова система
координат (если не оговорено противное). Для упрощения
формулировок используются символы: V («любой»), Я («су-
ществует»), => («следует»), о- («равносильно», «тогда и только
тогда»), | (отрицание) и некоторые другие.
Во втором издании значительно расширена глава «Высшая
алгебра», в которую включены основные вопросы линейной
алгебры (линейные пространства и их линейные преобразова-
ния, квадратичные формы, однородные системы линейных уравне-
ний). Добавлена новая глава «Тензорное исчисление». Те или
иные изменения внесены практически во все главы, изменена
структура некоторых из них. Для удобства читателей составлен
предметный указатель.
Мы будем очень благодарны всем, кто пришлет свои заме-
чания и пожелания. Наш адрес: 220080, Минск, Ленинский
проспект, 4, БГУ им. В. И. Ленина, кафедра высшей математики.
Авторы
3
НЕКОТОРЫЕ ПОСТОЯННЫЕ
(с точностью до 0,0001)
л = 3,1416 2л = 6,2832 л/2 = 1,5708 л/3 = 1,0472 л/4 = 0,7854 1/л = 0,3183 л2 = 9,8696 л3 =31,0063 л' =97,4091 -7^ = 1,7725 л/180 = 0,0175 (л/180)2 = 0,0003
е =2,7183 е2 = 7,3891 М = 1g е = 0,4343 л/ё= 1,6487 1/е = 0,3679 1/M = In 10 = 2,3026
In 2 = 0,6931 In 3= 1,0986 In 4= 1,3863 In 5= 1,6094 In 6= 1,7918 In 7= 1,9459 In 8 = 2,0794 In 9 = 2,1972
-72 = 1,4142 73= 1,7321 -75 = 2,2361 -/6 = 2,4495 •7T = 2,6458 -7^0 = 3,1623
1 = 0,3333 1 =0,1429
4- =0,1667 О 7-o.iiu
A = 2. = o,5ooo 1-Аг=о.°оЮ
l=4=0,1667 i-7o -<w"4
1=1 = 0,0417 7l = 5040 = °’0002
4
I. ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ
1.1. ПЛАНИМЕТРИЯ
Некоторые обозначения
[АВ] — отрезок с концами А и В,
I АВ |, АВ — длина отрезка [АВ],
Л АВС, ЛИ — угол с вершиной в точке В.
Л (а, Ь) — угол со сторонами (лучами) а и Ь,
АВС, ЛАВС — величина угла,
1° — один градус, 1/180 часть развернутого угла,
Г — одна минута, Г=(1/60)°,
I" — одна секунда, 1" =(1/60)',
1 рад — один радиан, 1 рад = (180/л)° « 57° 17'45",
Iе — один град, 1/100 прямого угла, Iе = 0,9°.
Связь между различными мерами угла
л / 10 V
— рад = ^—aj.
Треугольник (рис. 1.1)
Сумма внутренних углов: а + (3 +
А- у = л.
Теорема косинусов:
а2 = 62 + с2 — 2bc cos а.
Ь2 = а2 + с2 — 2ас cos р.
с2 = а2 А- b2 — 2ab cos у.
_ а b
Теорема синусов: —:--- = ------=
sin а sin р
= 5^п у = 2R (R — радиус описанной
окружности).
Величина внешнего угла: щ = р А-
А- У- Р, = а А- У, У> = а А- р.
Периметр: 2р = а А- & + с (р — полупериметр)
Свойства средней линии: [ЕТ] ||[AC], EF = -^-AC (рис. 1.2).
Свойства медиан: OF = у AF, ОЕ = у СЕ, ОН = у ВН (рис. 1.3).
5
Свойства высот: ha : Иь : hc = —.
а о с
AD АВ . . ..
Свойства биссектрис:(рис. 1.4).
Длина медианы, высоты и биссектрисы, проведенных из вершины В-.
1 /о 2 ", --~i и 2->/7(р-а)(р-д)(р-с)
ть = + 2с — b , Ль = —--------,
2д]аср(р — Ь)
1ь = -----;----•
а + с
Площадь:
S = у аЛ0 = у bhb = -у chc,
S = 4- ab sin у = ~ ас sin (5 — be sin а,
2 2 2
S =-у/р(р — а) (р — Л) (р — с) (формула Герона),
Прямоугольный треугольник (рис. 1.5)
Если Р — л/2, то а + у = л/2.
Теорема Пифагора: а2 + с2 = Ь2 (а, с — длины катетов; b — длина
гипотенузы).
6
c~ = cbb, а2 = аьЬ, h'l = ahcb.
b b
"'• = y ₽ = y-
a 4- c — b c ac
2 ’ 5 2~ ~
blit,
~2~
a — b sin a — b cos y,
c = b sin у = b cos a.
a — c tg a = c cig у,
c = a tg у = a cig a.
Равнобедренный треугольник (рис. 1.6)
mb = hb — 1ь — ya2 — b2/4,
л — p c _ bhb ______ a2 sin p
2 ’ 5 ~ ~2~ “ 2
P и c. 1.6 P и c. 1.7
Равносторонний треугольник (рис. 1.7)
m = h = I = ад/з/2, R = а\/з/3, r = ад/з/G, R = 2r, S = a2-fi/4.
Параллелограмм (рис. 1.8)
Свойства сторон и углов: [ДВ]||[СР], АВ = CD, [Д£>] || [Z?C], AD =
= ВС, ABAD= ABCD, ААВС= /LADC, а + р = л.
Свойства диагоналей: АО — ОС, ВО = OD, АС2 + BD2 = 2(а2 + Ь2).
Ромб (рис. 1.9)
Свойства сторон и диагоналей: |ДВ|||[£)С|, [5С] || [ЛО], АВ = ВС =
^CD = AD, [ДС| ± [В£>|, АС2 + BD2 = 4а2.
Площадь: S — ah, S — a2 sin a, S = — ЛС BD.
7
Прямоугольник (рис. 1.10)
Свойства сторон и углов: АВ = CD, AD = ВС, L4 В] l| [CD], Г A D\ II [ВС]
Z BAD = А АВС = ABCD = A ADC = л/2.
Свойства диагоналей: AC = BD, d = у/a2 + b'2.
Площадь: S — ab.
Квадрат (рис. 1.11)
Свойства сторон и углов: АВ
= Л BCD = A CD А = л/2.
Длина диагонали: d = а~\/2.
Площадь: S = а2 = d2/2.
ВС = CD = DA, ABAD = ААВС =
Трапеция (рис. 1.12)
Свойства сторон: [Л £>] || [ВС],
|ЛВ]Х1СД].
Свойства средней линии: [EF]||
II [AD], EF = (а + 6)/2.
Площадь: S = (а + b)h/2, S —
=^EF-h.
Многоугольники
Выпуклый п-угольник
Сумма внутренних углов: (н — 2)л.
Сумма внешних углов: 2л.
Число диагоналей: и(н — 3)/2.
Вписанный и описанный многоугольники
(R — радиус описанной окружности; г — радиус вписанной окружности;
р — полупериметр многоугольника; S — его площадь).
Треугольник
£
Р
abc .
8
Четырехугольник
Если четырехугольник ABCD вписан в окружность, то Z-BADA-
+ ^.BCD = ;i, ZLABC + AADC = л.
Если четырехугольник ABCD описан около окружности, то АВ4-
+ CD = AD + ВС.
Подобные многоугольники
Если Ф| и Ф2 — подобные многоугольники с коэффициентом по-
добия k, a Pi и Р2, 5, и S2 — соответственно их периметры и площади,
то Pi : Р2 = k, 5i : S2 = k2.
П равильные п-угольники
Величина внутреннего угла: а„ — л(п — 2)/п.
Сторона: an = 2R sin (л/л), an — 2r tg (л/л) (/? — радиус описанной
окружности; г — радиус вписанной окружности, апофема). В частности,
а3 = Яд/з = 2г^3, сц = R^2 = 2r, а6 — R = 2г/д/з, aa = R~\j2 — ^2 =
= 2r(-V2-l).
nR2 . 2л Pnr na„r PnR л
Площадь: S„ = —— sin------, S„ = ——- = —_—, S„ = __ cos —
2 л 2 2 2 л
(Pn—периметр л-угольника).
Окружность и круг
(г — радиус; а — 2г — диаметр)
Углы, вписанные в окружность: zLABC = zLAOC, Z.ADC =
= л------А.АОС (рис. 1.13).
Рис. 1.15
Рис. 1.14
Свойства хорд: АК-КВ — СКX
X KD, а = 2r sin (а/2) (рис. 1.14).
Свойства секущих: АСAD =
= AF • АЕ = АВ'2 (рис. 1.15).
Длина окружности: С = 2лг = лс/.
Длина дуги в а радиан: I = аг.
Длина дуги в р? / = лг(3/18О.
Площадь круга: 5 = лг2 = лс/2/4.
Площадь сектора в а радиан:
SceK = аг2/2.
9
Площадь
11лещадь
сектора в (3°: £ССк — лг2р/360.
кругового сегмента, содержащего дугу в р°:
5сеги = (-f^- - sin Р°)-
1.2. СТЕРЕОМЕТРИЯ
Призма
Площадь поверхности: Slip = 2SOCH + S6oK, где S0CI, — площадь осно-
вания призмы; 5бок — площадь боковой поверхности призмы; S6oK==
= Pl', Р — периметр перпендикулярного сечения; / — длина бокового
ребра.
Объем: V = QH, V = QJ, где Q — площадь основания; И — высота
призмы, Qi — площадь перпендикулярного сечения.
Прямоугольный параллелепипед (рис. 1.16)
Свойства диагоналей: ACi — BDi = СА । — DB\ = d, d2 = a2 4~
4- b2 + с2. Все диагонали параллелепипеда пересекаются в одной точке
и делятся сю пополам.
Площадь поверхности: S = 2{аЬ 4- Ьс 4- ас).
Объем: V — abc.
В частности, для куба а = b = с, d = а~\]3, S — 6a2, V — a3.
Пирамида (рис. 1.17)
Площадь поверхности: S„„p — S6oK 4- SOCII, где S6oK — площадь бо-
ковой поверхности пирамиды; Soc„ — площадь основания.
Объем: V = у QH, где Q — площадь основания; И — высота пи-
рамиды.
Правильная пирамида
•$бок = у Р^бок, где Р — периметр основания; /г6ок — высота боко-
вой грани.
Q = 5б0К cos а, где a — угол между боковой гранью и плоскостью
основания.
10
Усеченная пирамида
Объем: V — -у (Q> л/Q i Q2 + Q2\ где — высота; Qi, Q> — пло-
щади оснований.
Для правильной усеченной пирамиды 56ок =-у (pi 4~ где
р\, Pi — периметры оснований; /^ок — высота боковой грани.
Рис. 1.18
Рис. 1.19
Цилиндр (рис. 1.18)
Площадь боковой поверхности: S6m = 2nRH.
ПлоЩадь полной поверхности: 5ЦИЛ = 2л/?// 4* 2л/?2.
Объем: V = jiR2H.
Конус (рис. 1.19)
Площадь боковой поверхности: SCoK = nRL.
Площадь полной поверхности: SK0H = nRL + л/?2.
Объем: V — л/?2//,
и
Усеченный конус (рис. 1.20)
•$бок = л(/? + г)/, SKOI, = Л/?- лг2 4" л(/? 4- г)/,
V = у л/7(/?2 4- Rr 4- г2).
11
Шар (рис. 1.21)
Площадь поверхности: S = 4л/?2.
4
Объем: V — — л/?3.
Площадь сферического сегмента: 3 = 2л/?// (Н — высота сегмента).
Объем шарового сегмента: V = — nH2(3R — Н~).
2
Объем шарового сектора: V = — л/?“//.
1.3. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Поворот плоскости вокруг центра О на угол а
Обозначение: R° или R'1.
Свойство поворотов: /?* + 360°п = /?“ (ц — целое).
Композиция поворотов: R^o Rq = Rao° Rq< Rq° Rao = /?o+fi, Ro°^oa =
= E (тождественное преобразование).
Координатные формулы поворота на угол а
Если /?o(P) = /’i и Р — (х; у), = (хр, уф, то при повороте вокруг
точки 0(0; 0):
Xi = х cos а — у sin а;
yi = х sin а ф- у cos а;
при повороте вокруг точки О(х0; у0):
Xi = (х — хо) cos а — (у — уо) sin а,
у, = (х — хо) sin а + (у - уо) cos а.
Центральная симметрия (симметрия относительно точки О) на плоскости
Определение: Zo = R'J0.
Композиция центральных симметрий:
1) с общим центром: Zo° Zo = Е\ _________
2) с различными центрами: ZOj° ZOi = 2О|О2.
Координатные формулы центральной симметрии относительно на-
чала координат: Х\ = —х, yt — —у.
Осевая симметрия (симметрия относительно прямой /) на плоскости
Обозначение: S/ (/ — ось симметрии).
Композиция осевых симметрий:
1) если /1 _1_ /2, О — точка пересечения осей, то Si,° Sl2 = Sll°Sl[ —
= Zn (центральная симметрия);
2) если /ill/2, то SZ1oS/2 = S/2oSZl = Г (параллельный перенос).
Координатные формулы осевой симметрии:
относительно оси OY: Xi = —х, у\ = у,
относительно оси ОХ: Х| = х, у, — —у,
относительно прямой у — х: Xi = у, у\ = х.
12
Подобие
Определение преобразования подобия F* с коэффициентом подобия
k(k> 0): если X, = F*(x), Г( =F*(r), то X,У, = kXY.
Композиция преобразований подобия: Fk2° Fk' — Fk'ki.
Подобные фигуры
k
Обозначение: Ф1С0Ф (фигура Ф1 подобна фигуре Ф с коэффи-
циентом k).
Свойства подобных фигур:
1
1) Ф со ф (рефлексивность);
k i/k
2) (Ф1 со Ф) о (Ф соф,) (симметричность);
3) (Ф| со Ф, ф2 со ф,) => (ф2 со Ф) (транзитивность);
k
4) (Ф1 со Ф) => (Si : S = k2) (отношение площадей подобных
фигур).
Гомотетия
Обозначение: Н1г0 (гомотетия с центром О и коэффициентом k,
Л=#0).
Свойства гомотетии:
1) Н'о= Е; 2) Hq'=Zo; ____ ______
3) если Х.^У/^Х), У, = /^(У), то XtYi=kXY, Х,У| = \k\XY,
Н'0/к(Х^ = Х.
Координатные формулы гомотетии с центром 0(0; 0; 0):
xi—kx, y\ = ky, Z\ = kZ.
Параллельный перенос
Координатные формулы: х\ = ха, у\ = у -ф b (на плоскости);
Х1=%4- a, y\=y-\-b, Z\ = z + с (в пространстве); а, Ь, с — по-
стоянные.
Векторы
Обозначения: АВ, АВ, а, а, а.
Длина вектора, модуль
lai, |а|, а.
(абсолютная величина):
МВ|, |ЛВ|,
Рис. 1.23
13
Рис. 1.24
Сумма векторов:
АВ А-ВС = АС (правило треугольника)
(рис. 1.22)]_ ___
ОА + ОВ = ОС (правило параллелограм-
ма) (рис. 1.23);
АА । -f- А1А2 4-... + А„_ \Ап = ААп (прави-
ло многоугольника);
ОА 4 ОВ + ОС = OS (правило паралле-
лепипеда, [OS] — диагональ).
Разность векторов: а-Ь=аА(— Ь).
Формула вычитания векторов: ОВ — ОА—АВ (рис. 1.24).
Признак коллинеарности векторов: а = а&(&4=0).
Законы векторной алгебры
Для любых векторов а, Ь, с и любых чисел а, р справедливы
равенства: а 4- b= b 4 а, а 4 (о 4 с) = (а 4- й) 4- с, а 4-0 = а, (ар)а —
— а(Ра), аа + ра = (а 4 р)а, аа4 «6 — а(а 4* b\Q-a = а>0 = 0.
Координатные формулы
Пусть I, /, k — взаимно ортогональные единичные векторы, име-
ющие направления координатных осей; Xi, у\, z\ — координаты век-
тора а\ х2, у2, г> — координаты вектора b; а = хи А-Уд 4* Z\k, b =
= x2i 4- y>j 4- z2k или a=(%i; yc, zt), b=(x>\ y2\ z2). Тогда:
a 4- b =(xi 4-хз ; y1 4 y2; z\ 4- z2), a — & = (xi — x2; y\ — y2\ Z\ — z->),
aa = (axr, ayi; az,), |a| = д/х| 4- yf 4- zt
Если 4(ai; a2; a3) — начало вектора, B(bc, b2\ bz)— его конец, то
AB=(bi— ai; b2— a>\ b2 — аз),
\AB\ =-\l(bt - atf 4- (b2 -aAj1 4- (63 - atf.
Скалярное произведение
Скалярное произведение векторов а и Ь:
а • b = |a| |fe| cos ср,
где <р — угол между векторами а и Ь\ если a — Q либо b = б, то
а • b — 0.
Из определения скалярного произведения следует, что а • b =
= |a| праЬ = l&lnpsn, где, например, прйЬ есть величина проекции век-
тора b на направление вектора а.
Скалярный квадрат вектора: а • а — а'.
14
Свойства скалярного произведения: а • b — b • а, (аа) • b — <х(а • Ь),
(а + Ь) • с = а • с + 6 • с, а • а О, а - а — Ооа = О, а • b = 0 -о а ± Ь,
Скалярное произведение в координатах
Если а = x\i + y\j + zifc, 6 = хге + c/2j + z2/c, то а • 6 = Х|Х2 + c/ic/2 +
+ ZK2, а2 = х2 + у] + z?.
Угол между векторами
cos (а, Ь) = —i—72—,
|а| 161
Х|Х2 + У\У2 + Z1Z2
cos (а, 6) =
д/xf + c/f + z2 "д/хг + I/2 + z2
Векторное произвеоение
Векторное произведение векторов а и b — вектор, обозначаемый
[а6], [а, Ь] или а X 6, для которого:
1) Ца6]1 == |а| |6| sin ср (ср — угол между векторами а и Ь,
О + ф + л);
2) [аб] _1_ а, [а6] _!_ 6;
3) тройка а, Ь, [а 6]—правая.
Свойства векторного произведения: [6а]=—[ай], [(аа)6] =
= [а(а6)] = а[а6], [(а + 6) с] = [а с] + [6 с], [с(а + 6)] =[са] + [сб], [аа] =
= 0, [аЬ] = 0оа||6; если аЦб, то |[а6]| равен площади паралле-
лограмма, построенного на приведенных к общему началу векто-
рах а и Ь.
Векторное произведение в координатах
Если а = хй + {/!/ + Z\k, b =xzi + y2j + z2k, то
[ай] = {y\z2 — zxy2)i + (zix2 — xiz2) / + (x!«/2 — y\x2)k,
i j k
[a6]= xi z/i zi
x2 C/2 z2
В частности,
[' «'] = [/ /] = [* Л]= 0, [с /[=*, [М]= с,
№ И = /. [ / i ] = — 6, [k /] = - с, [/£]=—/.
15
Некоторые соотношения
[[а Ь] с] = (а • с)Ь — (Ь • с)а (двойное векторное произведение),
[[а 6]с] + [[6 с]а + [[с а]&] = О (тождество Якоби),
[а Ь] • [с d] = (а • с) (6 • d) — (а • d) (Ь • с), [а 6]2 = агЬ2 — (а • 6)2.
Смешанное произведение трех векторов
Определение: а b с = [а Ь] • с — а ’ [Ь с].
Свойства смешанного произведения: a b с = b с а = с а b —
= — b а с — — с b а = - ас b, (аа) b с — a (a b) с — а b (а с), (а 4~
A~b)cd = acd-}~bcd, а b с — Оо а, Ь, с — компланарны.
Если V — объем параллелепипеда, построенного на приведенных
к общему началу векторах а, b и с, то V = а b с, если тройка а, Ь, с
правая, и V = —а b с, если тройка левая.
Смешанное произведение в координатах
Если а = x\i + у\j + z\k, b — x2i + y2j + z2k,
c = x3i + y3i +
4- Z3k, TO
= X\y2Z3 + Z1X2J/3 + y\Z2X3 — Z\y2X3 — XiZ2y3 — IJ\X2Z3.
Проекции вектора на ось
Обозначения: npza — проекция вектора а на ось /; npza — величина
проекции вектора а на ось I.
Свойства проекций: np,(a + b) = npza + npz6, npz(a + 6) = npza +
+ пpib, npz(aa) — anpza, npz(aa) = anpza.
Составляющие (компоненты) вектора г (рис. 1.25):
г = ОМ = О A -j- О В 4“ ОС = х I 4“ у j 4“ zk,
О А = xi — пргг, ОВ — у j = пр; г, ОС = zk — пр*г.
Координаты вектора г: х = пргг =
= |r|cosa,y= пр;г = klcosp, z = nptr =
= |r| cos у (a, P, у — углы, образуемые
вектором г с положительными направле-
ниями осей координат Ох, Оу, Oz прямо-
угольной декартовой системы координат),
cos a, cos р, cos у называются направ-
ляющими косинусами вектора г = xi 4-
4-у/ + 2^; cosa = x/|r|, cos р = у/\г\,
cosy = z/\r\, где |rl — д/х2 4- у2 4" 22;
cos2 a 4- cos2 р 4- cos2 у = 1. Если е = r/\r\ —
единичный вектор в направлении г, то
е = cos at 4- cos Р/ 4~ cos yk.
16
2. НАЧАЛА АНАЛИЗА И АЛГЕБРЫ
2.1. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Законы действий над числами
Переместительный закон сложения: а + b — b 4- а.
Сочетательный закон сложения: (а 4- Ь) + с = а 4- (Ь + с).
Переместительный закон умножения: ab = Ьа.
Сочетательный закон умножения: (ab)c — а(Ьс\
Распределительный закон умножения относительно сложения:
(а 4- Ь)с — ас 4- Ьс.
Распределительный закон умножения относительно вычитания:
(а — Ь)с = ас — Ьс.
Дробные выражения
Действия с дробями (предполагается, что знаменатели дробей от-
личны от нуля):
а Ь _ а 4- Ь
с с ~ с
ас ас
b d bd ’
а с ad
b ' d be ’
~b + -d
a —a
b ~ b
= an
b) ~ bn'
bd
-b’
Проценты
Процент — одна сотая часть числа.
II П/ л II А Р
Нахождение р % числа А: В=
и л п/ г, л В • 100
Нахождение числа А, если р % его равны В: А = -------
Р
Пропорциональность
Пропорция — равенство двух отношений:
— “т, b #= 0, d 0
d
17
(a, d—крайние члены пропорции; b, с—средние члены пропорции).
Основное свойство пропорции: ad — be.
Выражение члена пропорции через остальные:
be , ad ad , be
—г, b —----, с = d —-------
а с
Если истинна пропорция — = —
то истинны и следующие про-
а b b d d
порции: — — —-, — = —, —
с da с Ь
с — d а + b _____ с + d а — b
d ’ а с ’ а
с а + b _ с 4- d а — b
a' b ~ d Ь
с — d а + b с + d
с 'а — Ь с — d ‘
Прямая пропорциональность — функция, заданная формулой
у kx, k =/= О,
где k — коэффициент пропорциональности; у, х — пропорциональные
переменные.
Свойство прямой пропорциональности: Х1/ха = У\1ут. '
Обратная пропорциональность — функция, заданная формулой
y — k/x, k О, X 0.
Свойство обратной пропорциональности: Xi/хг — yi/y\-
Степени и корни
Степень с целым показателем
ап = а-а-а (и раз, п £ N, п #= 1),
а'— а, а° = 1 (а =Д 0), а~п=\/ап (а 0).
Свойства:
aman = am+n, am/an = am-n, (am)n = amn,
(ab)n = anbn, (a/b)n = an/bn.
Корень п-й степени
\a— арифметический корень п-й степени из числа а, а 0,
д/a 0, п g N, п > 1.
Свойства:
(jja') = a, xfab =\fax[b,
д/a/b =!у/а/\[b (Ь > 0), = д/ц.
В частности, д/а — арифметический квадратный корень: (д/a)2 =
= а, д/a2 = | а |.
Степень с дробным (рациональным) показателем
ат^п = д/Z™, т 6 Z, п 6 N, п > 2, а > 0.
Свойства степени с действительным показателем
(а > 0, b > 0, х Е R, У Е R).
18
аха* = ax+\ (аху = ах“, (aby = axbx,
(a/by — ax/bx, ax = bxl°e‘,a,
ax — ex,na — exp (x In a), ax=10x,ga.
Прогрессии
Арифметическая прогрессия
Арифметическая прогрессия — числовая последовательность (ая),
определяемая условиями: 1) а\ = а; 2) an+i = ап + d, п — 1, 2, ... (d —
разность арифметической прогрессии).
Свойства арифметической прогрессии:
ап + ап+2
Gn-f-i === ^« + 2 Яп-Н — rj •
Формула /i-го члена: ап — ai + d(n — 1).
Формулы суммы п первых членов:
с (ai4-an)n с 2a14-d(n—1)
•Jn — Г> ,Ол Q
Геометрическая прогрессия
Геометрическая прогрессия — числовая последовательность (Ья),
определяемая условиями: 1) Ь\ — b (Ь =# 0); 2) bn+i = bnq (q 0), п = 1,
2, ... (q — знаменатель геометрической прогрессии).
Свойства геометрической прогрессии:
b+ i/bп = bn~\-'2/bn-^it bц-^~\ == bпЬп+2*
Формула /г-го члена: bn — btqn~'.
Формулы суммы п первых членов (<? =# 1):
с bnq — bi с bi(qn— 1)
q-\ ’ n~ q-l ’
Сумма бесконечной геометрической прогрессии:
b + bq + bq~ + ...= b/(l — q), \q\
Некоторые тождества
|+24-3+„.+ л= "(,12+l>,
+ У+ 3!+...+ «’= "('+1)(2" + 0
Illi ь
134-23 + 33+-+п3= ”2(« + 0L,
1 +3 4-5+... + (2п- 1) = п2,
12 + 32 + 52 +... + (2п - I)2 =
I3 + З3 + 53 + ... + (2/1 — 1)3 = /г2(2п2 — 1),
19
1 • 2 + 2 • 3 ++ л(п + 1) = -П-П + 'j (” + 2) ,
1 • 4 + 2 • 7 +... +/г(3/г + 1) = /2(,г + I)2,
1 • 2 • 3 + 2 • 3.4+...+п(п + l)(n + 2)= 2_rt(n +1)(п + 2)(п + 3),
I2 — 22 + З2 — 42 +.„+(— 1)л-’п2 = (— 1)"-' + D. t
_L_ + 1 i . 1 e n
1-2 2-3 n(n + 1) n + 1 ’
1 । 1 । । ______________1__________ n
1 -3 3-5 (2n- l)(2n+ 1) 2/г + 1 ‘
Формулы сокращенного умножения
а2 — Ь2 — (а — 6) (а + Ь),
а3 — Ь3 = (а — b) (а2 + ab + Ь2),
а3 + Ь3 = (а + 6) (а2 - ab + Ь2\
a4 -b4 = (a-b') (а3 + a2b + ab2 + 63) = (а - 6) (а + Ь) (а2 + Ь2),
а3 — b5 = (а — b) {а4 + a3b + a2b2 + ab3 + Ь4),
а5 + Ь5 = (а + Ь) (а4 — a3b + a2b2 — ab3 + Ь4\
ап - Ьп = (а-Ь) (ап~' + ап~2Ь +... + abn~2 + Ьп~'),
+« + Ь2п+' ={а + Ь}(а2п - а2п~'Ь ± а2п~2Ь2 -...+ а2Ь2п~2 --
- ab2n~' + Ь2п\
(а + 6)2 = а2 + 2аЬ + Ь\ (а — Ь)2 = а2 - 2аЬ + Ь2,
(а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3,
(а — 6)3 — а3 — За2Ь + ЗаЬ2 — Ь3.
Свойства числовых неравенств
1. Если а <_ Ь, то при любом с: а + с < b + с.
2. Если а < b и с > 0, то ас < Ьс.
3. Если а <; b и с < 0, то ас > Ьс.
4. Если а < Ь, а и Ь одного знака, то \/а > 1/6.
5. Если а<6 и c<.d, то а + с <. Ь d, a — d <Ь — с.
6. Если a<b, c<d, а > О, Ь > 0, с > 0, d > 0, то ac<bd.
7. Если а < Ь, а>0, Ь > 0, то а2 < b2, a" <bn (n £ N).
8. Если |а| < |6|, то а2 < Ь2.
Некоторые неравенства
1. Сравнение среднего геометрического и среднего арифметиче-
ского неотрицательных чисел:
~\[ab^ (а + 6)/2 (равенство лишь при а = Ь).
\/aia2...a« — (й! + а2 +... + а,,) (равенство
лишь при О] =
= а2 = ... = ап).
2
а2 + Ь2
1, а, Ь > 0 (равенство лишь при а = 6).
20
3. a -f- 1 /а 2, _a > О (равенство лишь при а = 1).
4. д/а 4- b д/а + д[ь, а, b > 0 (равенство лишь при ab = 0).
5. Неравенство Буняковского:
{a\bi 4~ Й2&2 И- ••• 4~ йпЬп)2 (а? 4~ <12 4*... 4- а?,) (й? 4“ ^2 4~ 4~ Ь„).
6. Неравенство Бернулли:
(1 4-/гГ> 1 +nh, h> -1, n€N,
(1 4~ h 1) (1 4- /12)••• (1 4" h,t) 1 4~ h\ 4~ h<i 4-... 4~ hn
(/zi. h-2, .... hn — числа одного знака, большие —1).
7 1 3 2n — 1 1
2 4 2п д/2ч + 1
8. 1 4—— 4—7= 4~ ••• 4—~\[n, n > 1.
д/2 д/з д/м
9. Неравенства с модулем:
\а + Ь\ < |а| 4-\Ь\, \а-Ь\^ |а| + \Ь\,
\а-Ь\^\а\ - \Ь\, \а-Ь\> ||а| - IMI,
|а| ^bo-b^a^b.
Логарифмы
loga b (а > 0, а =# 1, Ь > 0) — логарифм числа b по основанию а.
Основное логарифмическое тождество: а10^6 = 6.
Ig b— десятичный логарифм (логарифм по основанию 10):
10'^ = Ь.
In b — натуральный логарифм (логарифм по основанию е):
e'nb = b.
Переход от одного основания к другому:
loga b =
logr ь
logc а ’
г> 1 > I lg b In b lg b lg b
В частности, loga Ь = ------- = —г~ — -------, In b — -4---- — ——
ь log/, a lg a Ina Ig a M
(Л4 = lg e — [ 1 « 0,4343 — модуль перехода от натуральных лога-
рифмов к десятичным).
Свойства логарифмов (a, v > 0):
loga а = 1, loga 1 = 0, loga {uv) = loga U ф- loga V,
loga -y = — loga v, loga ~ = loga U — loga V,
П r- I
loga Ma — a loga u, loga д/и = — loga а, M £ N, n. =£ I.
2.2. ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
Тригонометрические функции
sin a, cos а,
tg а — sin а/cos а, а ф n/2 4- nn, n
21
ctg a = cos a/sin a, a лп, Z,
seca=l/cosa, а^л/2 + лл, nfZ,
cosec a = 1 /sin a, a лп, n^Z.
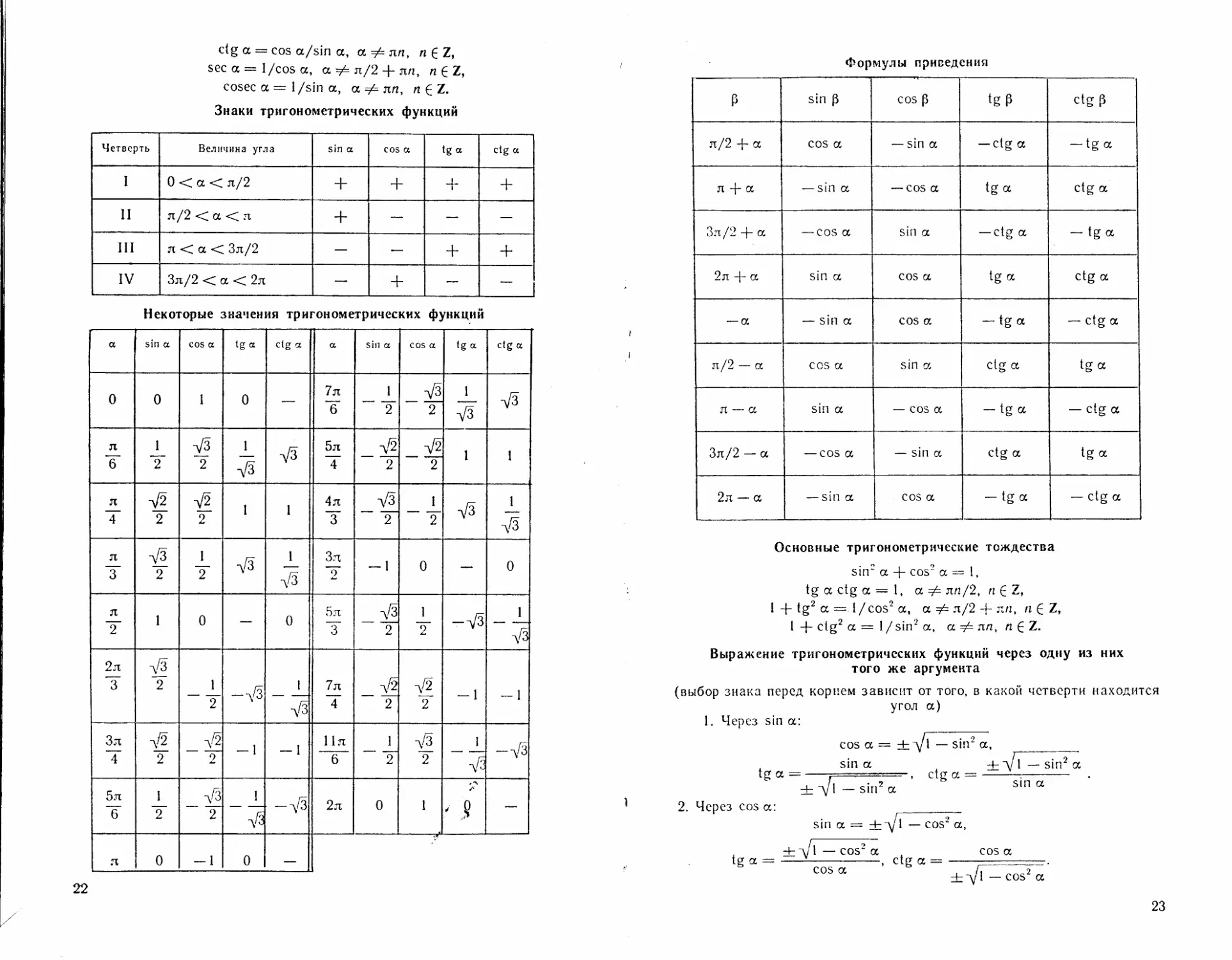
Знаки тригонометрических функций
Четверть Величина угла sin a cos a tg a ctg a
I 0 < a < л/2 + + + +
11 л/2 < a < л + — — —
III л < a < Зл/2 — — + +
IV Зл/2 < a < 2л — + — —
Некоторые значения тригонометрических функций
a sin a cos a tg a ctg a a sin a cos a tg a Ctg a
0 0 1 0 — 7л У 1_ у 2 1 д/3 д/3
л T 1 У V3 2 1 д/з 5л ~T 2 _л/2 2 1 1
Л T д/2 2 2 1 i 4 л У 2 1_ У д/3 1 д/3
Л T 2 1 2 д/3 i д/з Зл ~2 — 1 0 — 0
Л У 1 0 — 0 5 л у _ У? 2 1 У — д/3 1 1 'bi 1
2л У Vf 2 _ 1 У -д/3 1 с511 ~ 7л У 2 2 -1 -1
3л т -\/2 2 2 -1 -1 11л 6 _ 1 ~ У д/3 2 -|> 1 — д/3
5л У 1 2 2 1 л/3 — д/з 2л 0 1 ' .9 —
л 0 -1 0 —
22
Формулы приведения
р sin р COS Р tg Р ctg Р
л/2 4- а cos а — sin а — ctg а — tg а
л 4- а — sin а — cos а tg а ctg а
Зл/2 4- а — cos а sin а -ctg а — tg а
2л 4- а sin а cos а tg а ctg а
— а — sin а cos а — tg а — ctg а
л/2 — се cos а sin а ctg а tg а
л — а sin а — cos а - tg а — ctg а
Зл/2 — а — cos а — sin а ctg а tg а
2л — а — sin а cos а — tg а — ctg а
Основные тригонометрические тождества
sin2 а + cos2 а = 1,
tg а ctg а = 1, а =/= лп/2, п С Z,
I + tg2 а — 1/cos2 а, а #= л/2 + лл, п Е Z,
1 ctg2 а = 1 /sin2 а, а =/= лл, п £ Z.
Выражение тригонометрических функций через одну из них
того же аргумента
(выбор знака перед корнем зависит от того, в какой четверти находится
угол а)
1. Через sin а:
cos а — ±у \ — sin2 а,
, sin а ±
tg а =------ . т.--:-, ctg а = —
± 1 — sin2 а
sin а
2. Через cos а:
sin а — ± д/1 — cos2 а,
± д/1 — cos2 а
cos а
ctg а =
cos а
±д/1 — cos2 а
23
3. Через tg а:
l 1
ctg а = ---,
tg а
tg а 1
sin ос = -- —. cos а — ------------- —.
±V 1 + tg2 а ± V1 + tg2 а
4. Через ctg а;
L 1
tg а = —---,
ctg а
1 ctg а
sin а = ------ -..., cos а= ---- fe -.
± VF + ctg2 a ±з/l + ctg2 а
Формулы сложения
sin (а + P) = sin a cos p -P cos a sin p,
sin (a — p) = sin a cos p — cos a sin p,
cos (a + p) = cos a cos p — sin a sin p,
cos (a — p) = cos a cos p + sin a sin p,
♦ „r QA _ tga + tgp tg a — tg p
tg(a + ft)_ —tg(<»-₽)= TTt^TtTp-
(в последних двух формулах a л/2 + лп, p =/= л/2 + лп и соответст-
венно а + р #= л/2 -р лп, а — р =/= л/2 ~Р лп, п £ Z);
ctg (а + р) = ~ 1 , clg (а _ р) = A«_C£g Р + 1
ctg а + ctg р ctg р — ctg а
(в последних двух формулах а лп, р лп и соответственно а -р р =#
=/= лп, а — р пп, п £ Z).
Преобразование суммы тригонометрических функций
I - о о - ОС -р р ос — Р
sin a + sin р = 2 sin —^-t— cos —у-!—t
о a a + P . a — P
sin a — sin p = 2 cos sin -—^-t—,
cos a + cos p = 2 cos — " cos a ,
cos a — cos p = —2 sin a sin — ~ ,
. , 1 n sin (a + P) „ л
tg “ ~P tg p —--------------— a, p =/= ——p лп, n e L,
cos a cos p 2
. , i a sin la 4- P)
ctg a -P ctg p = 7 , a, p лп, n^Z,
sin a sin p
. 1 n sin (a — P)
ctg a — ctg p =-------7 . -7 , a, p лп, n£ Z,
sin a sin p
24
A sin x + В cos x =yA2 + В2 sin (x + cp0),
где cpo — угол, для которого cos cp0 = Л/д/Л2 + В2, sin cp0 = В/д/л2 + В
в частности, sin х + cos х = д/2~sin (х + л/4),
tl -f" 1 . /2
п sin—2—*sin—X
2 si"^=---------sinU/2)
6=1 ' '
х
—, х Ф 2л/г, k С Z,
cos —----cos
2 sin (x/2)
n
, sin (n + 1 /2) x _ , , „
7, cos kx = ——— z 7 , x Ф k£Z.
2 sin (x/2)
Преобразование произведения тригонометрических функций в сумму
sin a sin р = — (cos (а — р) — cos (а + р)),
sin а cos р = — (sin (а — р) + sin (а + Р)),
cos а cos р = (cos (а — р) -f- cos (а + Р)).
Тригонометрические функции двойного и тройного аргумента
sin 2a — 2 sin a cos a,
cos 2a = cos2 a — sin2 a — 1 — 2 sin2 a = 2 cos2 a — 1,
sin 3a — 3 sin a — 4 sin3 a, cos 3a = 4 cos3 a — 3 cos a,
2 tg a 3 tg a — tg3 a
tg 2a = ------3a = • , о г 2------------------•
1 — tg2 a 1 — 3fg2 a
Тригонометрические функции половинного аргумента
(выбор знака зависит от того, в какой четверти находится угол а/2)
а
5111 7 =
— cos a
2
а
7
cos a
2
2
1 — cos a , a sin a
---------- tg — =----------------
1 4- cos a 2 1 + cos a
Выражение тригонометрических функций через
половинного аргумента
1 — cos а
sin а
тангенс
tg « =
_ 2 tg (а/2) 1 - tg2 (aj/2)
1 + tg2 (a/2) 1 + tg2 (a/2)
2 tg (a/2) _ 1 — tg2 (a/2)
-tg2(a/2)’ 2 tg (a/2)
25
Преобразование степеней синуса и косинуса
sm2a = -|-(1 - cos 2a), cos2 a = 4-cos 2a),
3 l 1
sin a — — (3 sin a — sin 3a), cos3 a = — (3 cos a 4- cos 3a),
sin1 a — -|-(3 — 4 cos 2a 4- cos 4a),
О
cos1 a — -(3 4-4 cos 2a 4~ cos 4a).
2.3. ОСНОВНЫЕ ФОРМУЛЫ
ДЛЯ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
Определение гиперболических функций
Гиперболический синус: sh х =---------.
ох 4- с х
Гиперболический косинус: ch х = ---—--.
Гиперболический тангенс:
,, sh х е“ — е~*
th х = ----= ----------.
ch х ех е-*
Гиперболический котангенс:
, ch х ех4-с-х п
cth х =----= —---------х Ф 0.
sh х е — е
Основные тождества
ch2 х — sh2 х — I; th х cth х = I, x 0;
I — th2 x = -4—i cth2 x — I = —4—. x =/= 0.
ch2 x sir x
Выражение гиперболических функций через одну из них
I.
2.
Через sh х:
ch х = yl 4~ sh2 х;
и sh х Vi 4- sh2 х
th x = —: cth x = —-------1,
VI 4- sh2 V x
Через ch x:
sh x = sgn x д/ch2 x — 1;
ch x
X 7^ 0.
cth x =----------------- x =# 0.
sgn хд/ch2 x — I
26
3. Через th х:
sh х = Х —; ch х = ________—,
-\/1 — th2 х д/1 — th2 х
cth х = -гг—, х О.
th х
Формулы сложения
sh (х + у) = sh х ch у + ch х sh у, ch (х + у) = ch х ch у + sh х sh у,
sh (х — у) — sh х ch у — ch х sh у, ch (х — у) — ch х ch у — sh х sh у,
,, , . th х — th у
th (х — у) = ------г—77^—.
v ' 1 — th X th у
th (*+,,)=
v 1 + th х th у
Сумма и разность одноименных гиперболических функций
, I L П UX + У , Х ~ У
sh х + sh у = 2 sh —ch —-—,
2 2
, . О . X — у , Х + у
sh х — sh у = 2 sh ——— ch —-—,
у 2 2
, . п . x + у , x — у
ch х + ch у = 2 ch —
i l о t. x + у , x — у
ch x — ch у = 2 sh ——sh ———,
2 2
Преобразование произведения
гиперболических функций в сумму
sh х ch у — у (sh (х + у) + sh (х — у)),
ch х ch у = ~ (ch (х + у) + ch (х — у)),
sh х sh у = у (ch (х + у) — ch (х — у)).
Гиперболические функции двойного аргумента
ch 2х = sh2 х 4- ch2 х = 1 + 2 sh2 х = 2 ch2 х — 1,
2 th х
sh 2х — 2 sh х ch х, th 2х —-------------.
1 + th х
Гиперболические функции половинного аргумента
, х / ch х — 1 .х / ch х + 1
sh у = sgn x-yj----------- ch У = V-----2---'
27
Выражение гиперболических функций
через тангенс половинного аргумента
u 2 th (х/2) , I + th2 (х/2)
sh х = -----V——, ch х —-----!,
1 - th2 (х/2) 1 - th2 (х/2)
lhx= _2_11Цх/2)
1 4- th2 (x/2)
Преобразование степеней
sh2 x = -у (ch 2x — 1), ch2 x = -y(ch 2x + I),
th2 x = -C<77—, , (sh x + ch x)" = sh tix + ch nx.
ch 2x + 1 7
2.4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. ФОРМУЛА НЬЮТОНА
Перестановки. Размещения. Сочетания
Число перестановок из п элементов:
Рп = 1 • 2 • 3 — п = п\.
Число размещений из и по m(/i т):
ду = пЛ_ (0! = 1, 1! = 1),
(п — т)\ '
Ап — п(п — 1)-(п — т + 1), А°п = 1,
Л"'+1 =(/г - tri) А™,
Апп = Рп = п\, А"~' = Апп — п\.
Число сочетаний из п по т (и т):
ш!(п — /и)! ’
Ст = П(п — 1)-(п — Щ 4- 1) _ П(П — 1)...(П — Щ 4- |)
т\ ~ 1 • 2 • 3 --т
Свойства числа сочетаний:
С? = Спп~т, О^т^п, С°п = Спп = 1,
(Л 4- С'п 4-... + Спп = 2п.
Рекуррентная формула для числа сочетаний:
С? 4- С” +1 = CnVi'. О ш < д.
Формула бинома Ньютона
(а 4- Ь)' — а 4- Ь,
(а 4- Ь)2 = а2 4- 2аЬ 4- Ь2,
(а 4- Ь)3 = а3 4- За2д 4- Зад2 4- Ь3,
(а 4- д)4 = а4 4- 4а3д 4- 6а2й2 4- 4ад3 4- д4,
28
(a + bf = a5 + 5a4 b + 10a362 + 10a2fc3 + 5ab* + b\
(a + b)n = C°an + C'nan- 'b + C2an~2b2 + ... +
+ C,’,an-",bn‘ + ... + Cnnbn, n 6 N.
Если /г-й член ((&-|-l)-e слагаемое) разложения степени бинома
обозначить через Г*, то
Tk = C*an~kbk.
Треугольник Паскаля
О 1
1 1 1
2 12 1
3 13 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
8 1 8 28 56 70 56 28 8 1
9 1 9 36 84 126 126 84 36 9 1
10 1 10 45 120 210 252 210 120 45 10 1
(n-я строка состоит из чисел С°п, Ch, ..., С").
Возведение многочлена в степень
(а + b + с)2 = а2 + Ь2 + с2 + ‘lab + 2ас + 2Ьс,
(а + Ь — с)2 = а2 + Ь2 + с2 + 2аб — 2ас — 2Ьс.
(а — b — с}2 = а2 + Ь2 с2 — 2аЬ — 2ас 4- 2Ьс,
(а 4- b 4- с)3 = <з3 4- Ь3 4- с3 4- 3(а2б 4- а2с 4- Ь2а 4- Ь2с +
+ с2а 4- с2б) 4* бабе,
(а 4- 6 4- с)4 = а4 4- 4- с4 4- 4(а36 4- а3с 4- Ь3а +
4- Ь3с 4- с3а 4- с3Ь) 4- 6(а2б2 4- а2с2 4- Ь2с2) +
4- \2{а2Ьс 4- Ь2ас 4- с2аб),
(а14-а24-... + аР)',= 2
&1 ki~\- kp = П
(суммирование ведется по всем целым неотрицательным k\, k?, ..., kp, та-
ким, что k\ 4~ k-2 4-... 4- — n).
2.5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА И ЧИСЛОВЫЕ МНОЖЕСТВА
Множества
Натуральных чисел: N = (1, 2, 3, ...}.
Целых чисел: Z = {..., —2, —1, 0, 1, 2, ...}.
f I
Рациональных чисел: Q — т € Z, п Е N
V п I
29
Действительных (вещественных) чисел:
R = [а0, «(Яг--- ao€Z, ак € (О, 1, 2, .... 9}).
Числовые промежутки
Отрезок (замкнутый промежуток, сегмент):
[я; Z>] = {х Е RI й. -С х Ь].
Интервал (открытый промежуток):
]я; Ь[ = (х Е RI а < х < Ь].
Полуинтервалы:
[я; b[ = [х Е RI а -С х < Ь\-
]я; b] = {х Е RI а < х 'С Ь].
Бесконечные числовые промежутки (лучи, полупрямые):
[я; + оо[ = [х Е Rix я}, ]я; + оо[} — {х Е Rix > я},
] — оо; я] = {х Е RI х -'Д я), ] — оо; а [ = (х Е RI х < я).
Числовая прямая: R=|— оо; -ф оо[.
Замечание. Наряду с приведенными используются н обозначения (а; Ь) — для
ин сервала; |а; Ь), (а; Ь] — для полуинтервалов; [и; + оо), (а; + оо), (— оо; а], (— оо; а) —
для лучей; (— оо ; 4- оо) — для числовой прямой.
2.6. ЧИСЛОВЫЕ ФУНКЦИИ
Основные понятия
Область определения (множество задания) функции f: А-> R:
А = £(/)
Множество значений функции /:
£(/) = {f(x)lxEX} = f(X).
График функции:
Г/ = [(х. </)ER2Ia-EX, у = /(х)}.
Четная функция:
VxEA=> — х Е А' и Д — х) — Дх).
Нечетная функция:
VxEA'=>— хЕА и /( — х) =—Дх).
Периодическая функция (периода о>):
Vх Е А=> х + w Е А, х — (о Е А и I'(х 4~ to) — f (х).
Монотонные функции
Функция f строго возрастает (возрастает) на множестве А:
Vх„ х2 Е A, Xi < x2=>f(xi) < f (х2).
Функция f возрастает (не убывает) на множестве А:
V X;, х2 Е A, Xi <. х2=^[(xi) I (^2).
Функция f строго убывает (убывает) на множестве А:
Vxi, х2 Е A, xi < Х2=>/(Х|) > f(x2).
Функция f убывает (не возрастает) на множестве А:
Vxi, Х2 Е A, Xi < X2=>f(x>) > f(x2).
Основные функции
Линейная функция
у = ах + b, я, b Е R,
0(f) = R, £(D = R (я 0), E(f) = {6) (я = 0).
Функция строго возрастает при а > 0, строго убывает при а < 0.
График функции— прямая линия.
Квадратичная функция
у = ах2 + Ьх + с, а=£ 0, £>(/) = R.
1. При я > 0
£(/) =
' 4яс — Ь2 .
--------— • 4- оо .
I 4я L
Функция строго убывает
и строго возрастает
"а Г 2? +“1
вершиной в точке
2. При я < 0
График функции — парабола с осью х— —Ь/(2а\
b 4ас — Ь2 \
— —; ----------1 и ветвями, направленными вверх.
2я 4я /
4яс — Ь2
4я
Функция строго возрастает на — — 2я '* СТРОГО Убывает
b
2а
вершиной в точке
на
График функции — парабола с осью х— —Ь/(2я),
b 4ас — Ь2
2а' 4я
и ветвями, направленными вниз.
Степенная функция у = х“, а Е R
1. а — 2п, п Е N:
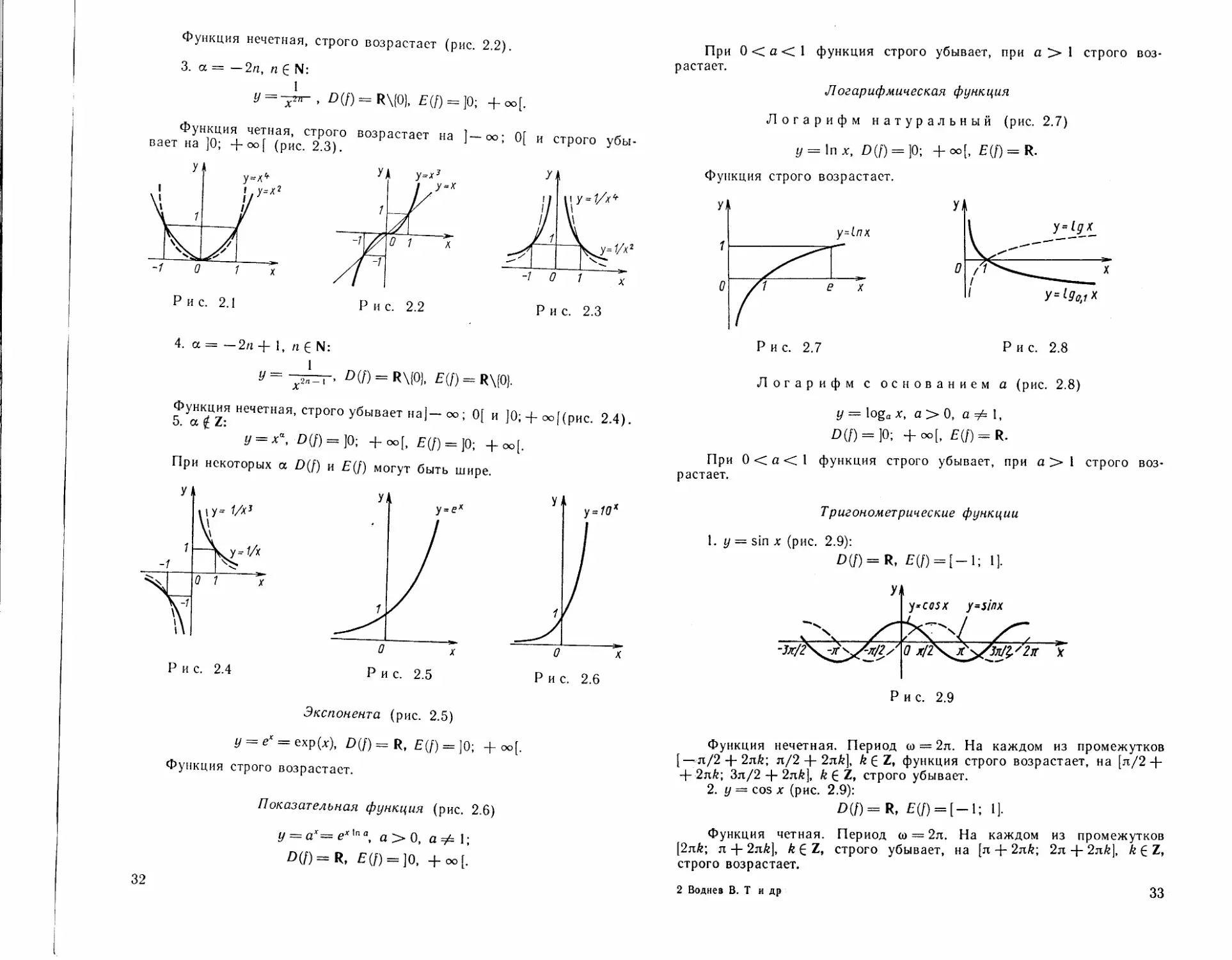
у = х2п, £(f) = R, £(D = [0; +~[.
Функция четная, строго убывает на ]— оо; 0] и строго возрастает
на [0; + оо[ (рис. 2.1).
2. а — 2п — 1, п Е N:
у = х2"-', /)(/)= R, E(f) = R.
31
30
Функция нечетная, строго возрастает (рис. 2.2).
3. а = — 2n, п g N:
, £>(/) = R\{0), £(f) = ]0; +оо[.
Функция четная, строго
на
4. а = — 2п + 1, п £ N:
я ~ -jir- £>(/) = R\W. £(/) = R\(0).
Функция нечетная, строго убывает на]—оо; 0[ и ]0; + оо](рис. 2.4).
5. a £ Z:
у = ха, D(f) = ]0; +оо[, £(/) = ]0; +«>[.
При некоторых а £)(/) и £(/) могут быть шире.
Экспонента (рис. 2.5)
у = е* = ехр(х), E(f) = ]O-, + оо{.
Функция строго возрастает.
Показательная функция (рис. 2.6)
у = ах— е*'па, а > 0, а 1;
D(f)=R, £(/) = ]0, +оо[.
32
При 0 < а < 1 функция строго убывает, при а > 1 строго воз-
растает.
Л огарифмическая функция
Логарифм натуральный (рис. 2.7)
У = 1пх, £»(/) = ]0; +оо[, E(p) = R.
Функция строго возрастает.
Логарифм с основанием а (рис. 2.8)
У = loga х, а > 0, а #= 1,
D(f) = ]O; + оо[. E(D=R-
При 0 < а < 1 функция строго убывает, при а > 1 строго воз-
растает.
Тригонометрические функции
1. у = sin х (рис. 2.9):
£>(/) = R, £(/) = [-!; 1].
Рис. 2.9
Функция нечетная. Период со — 2л. На каждом из промежутков
[ — л/22л6; л/2 -f- 2л&], k С Z, функция строго возрастает, на [л/2+
+ 2nfe; Зл/2 + 2л/г], /г £ Z, строго убывает.
2. у — cos х (рис. 2.9):
D(f)=R, E(f) = [ —1; 1].
Функция четная. Период со = 2л. На каждом из промежутков
[2лЛ; л + 2лй], k 6 Z, строго убывает, на [л 4- 2л£; 2л + 2л/г], k £ Z,
строго возрастает.
2 Воднез В. Т и др
33
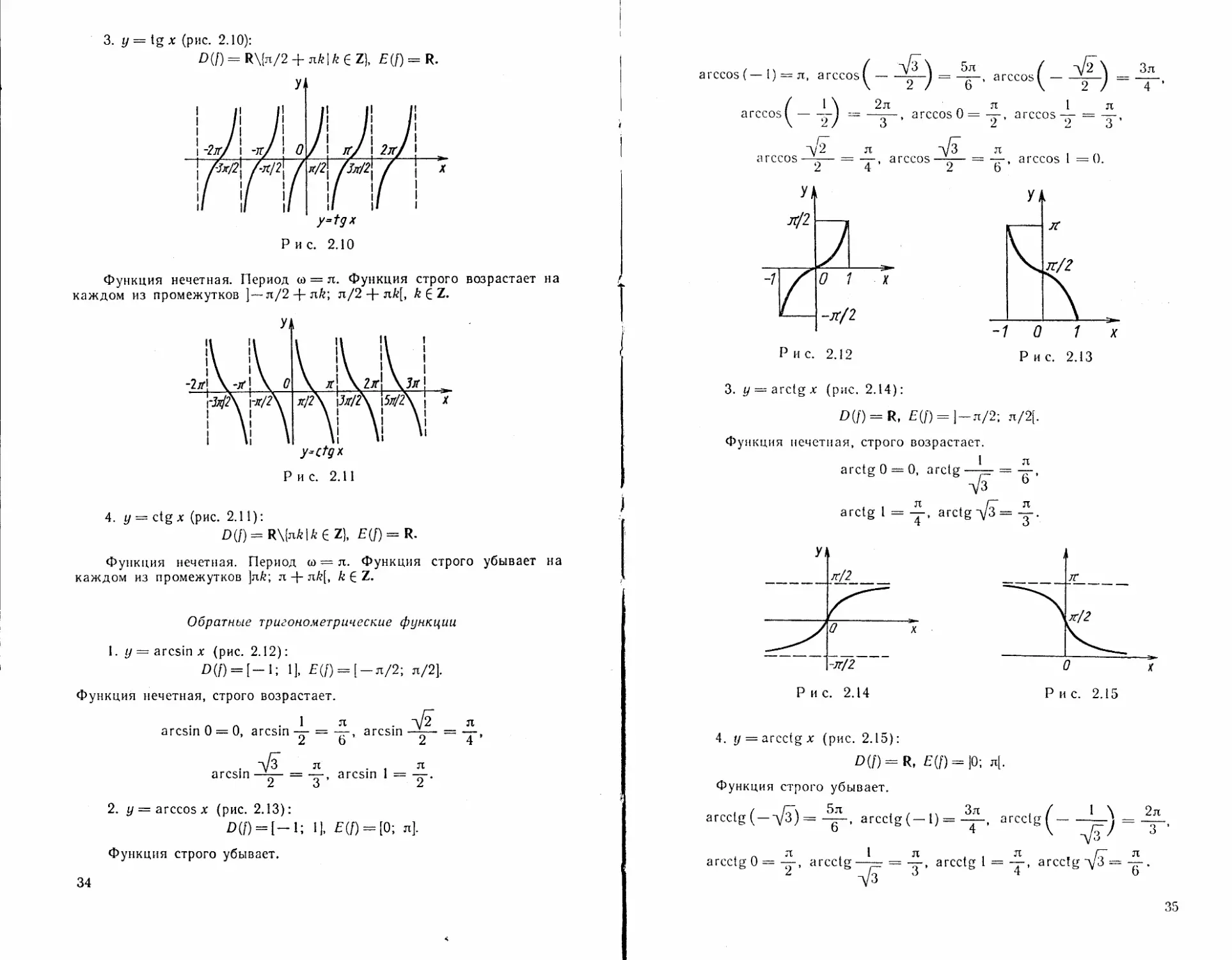
3. У — tg X (рис. 2.10):
£>(/) = R\[n/2 4-jtA-I/г С Z), E(f)=R.
Функция нечетная. Период « = л. Функция строго возрастает на
каждом из промежутков ] — л/2 + л&; л/2 + л/е[, k £ Z.
4. у = ctg х (рис. 2.11):
£>(/) = € Z), E(f) = R.
Функция нечетная. Период ы — л. Функция строго убывает на
каждом из промежутков ]л/г; л + л/г[, k С Z.
Обратные тригонометрические функции
1. z/ = arcsin х (рис. 2.12):
£>(/) = [—!; 1], Е(/) = [ —л/2; л/2].
Функция нечетная, строго возрастает.
• Л а • 1 я • V2 я
arcsin 0 = 0, arcsin — = —, arcsin ——- = —,
2 b 2 4
. ~у/з л . л
arcsin = —, arcsin 1 —
2. t/ = arccosx (рис. 2.13):
£>(/) = [—!; 1], f(/) = [0; л].
Функция строго убывает.
34
3. y = arctgx (рис, 2.14):
D(f) = R, £(/) = ] —л/2; л/2[.
Функция нечетная, строго возрастает.
arctgO = O, arctg—
л/з b
4. y = arcctgx (рис. 2.15):
£>(/) = R, £(/)== |0; л[.
Функция строго убывает.
arccig (-д/?) = arcctg(-l)= arcctg^ — —
arcctg 0 = arcctg —= -у, arcctg 1 = arcctg д/з" — .
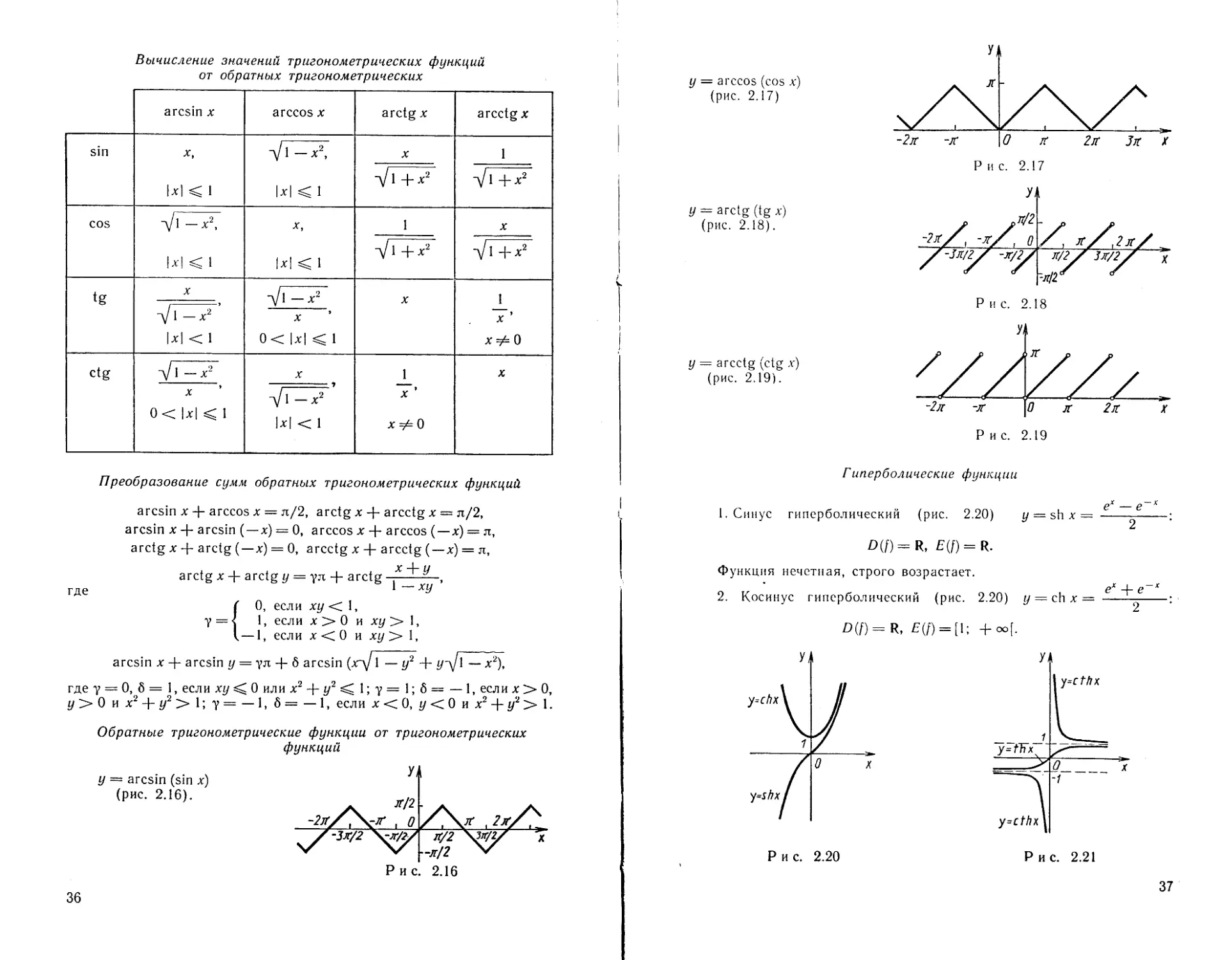
Вычисление значений тригонометрических функций
от обратных тригонометрических
arcsin x arccos x arctg x arcctg x
sin x, Ix| < 1 л/1 —x2, Ix| C 1 X V1 +*2 1 V1 +*2
cos д/i —x2, |x| < 1 x, |x| C 1 1 V1 +x2 X V1 +*2
tg X "V 1 — x2 Ixl < 1 ~\/l —x2 X 0< |x| C 1 X 1 x ’ x =# 0
ctg д/1 — x2 X О < |x| < 1 X V I — X2 |x| < 1 1 X ’ x #= 0 X
Преобразование сумм обратных тригонометрических функций
arcsin х + arccos х — л/2, arctg х + arcctg х — л/2,
arcsin х + arcsin ( — х) = 0, arccos х + arccos ( —х) = л,
arctg х + arctg (—х) = 0, arcctg х + arcctg ( —х) = л,
где
arctg х + arctg у = ул + arctg
х + у
1 — ху ’
{О, если
1, если
— 1, если
ху<\,
х > 0 и ху > 1,
х < 0 и ху > 1,
arcsin х + arcsin у = ул + 6 arcsin (х^/1 — у2 + У~ф — х2),
где у = 0, 6 = 1, если ху 0 или х2 у2 1; у = 1; 6 = 1, если х> О,
у > О и х2 + У2 > 1; У = — 1 > 6 = — 1, если х < 0, у < О и х2 + у2 > 1.
Обратные тригонометрические функции от тригонометрических
функций
у — arcsin (sin х)
(рис. 2.16).
Рис. 2.16
36
у = arccos (cos x)
(рис. 2.17)
у = arctg (tg x)
(рис. 2.18).
у = arcctg (ctg л-)
(рис. 2.19).
Рис. 2.19
Гиперболические функции
1. Синус гиперболический (рис. 2.20) у = sh х =-----------------
£>(/)-R, E(f) = R.
Функция нечетная, строго возрастает.
ех -I- с ~ х
2. Косинус гиперболический (рис. 2.20) у — ch х — -------------
37
Функция четная, строго убывает на ]—оо; 0[ и строго возрастает
на [0; + оо [.
s h X € 'Х — сх
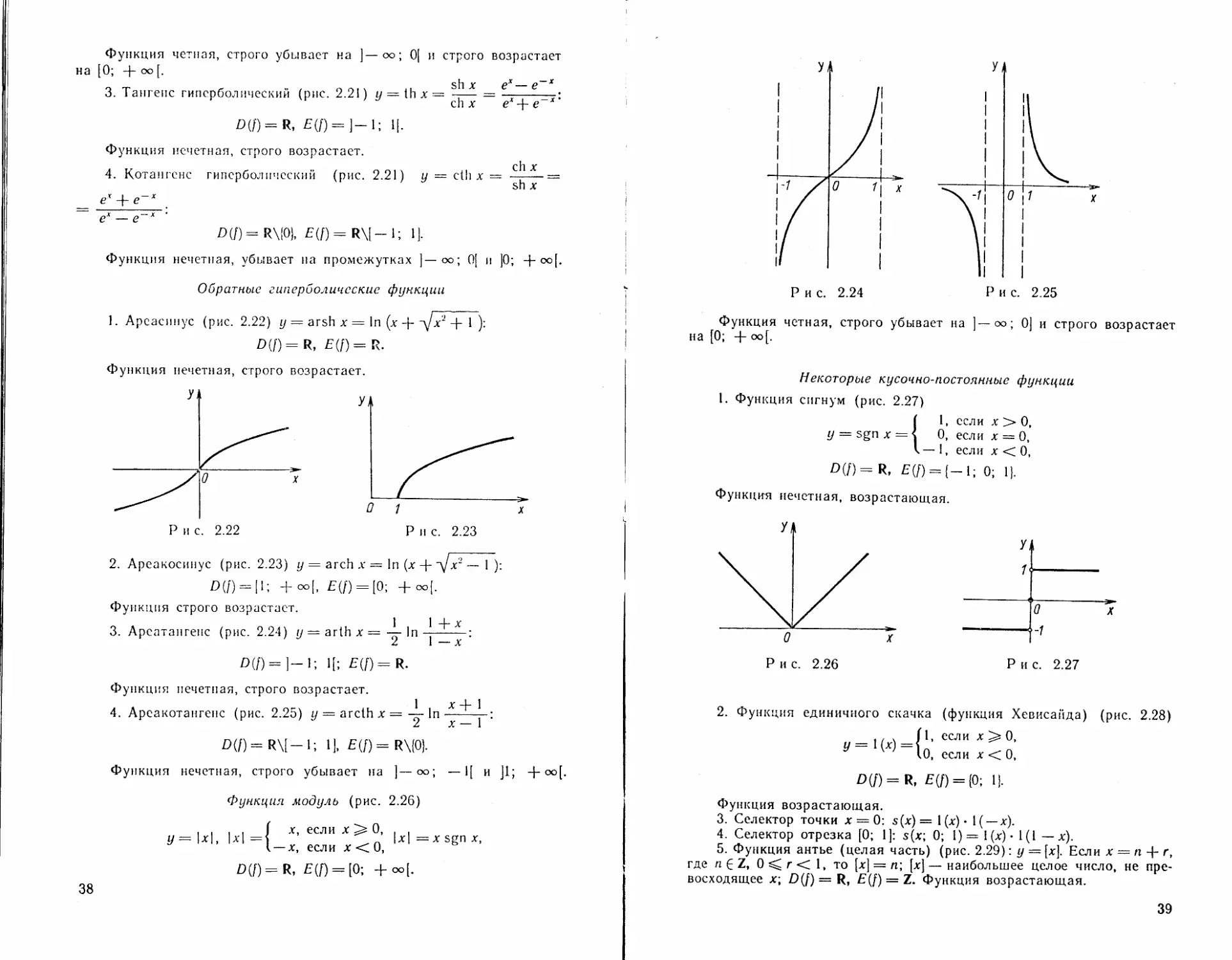
3. Тангенс гиперболический (рис. 2.21) у = th х = -— = —------7:
r ch х е~*
W) = R. £(/') = ]—!; 1|.
Функция нечетная, строго возрастает.
ch х
4. Котангенс гиперболический (рис. 2.21) у = cth х — —-— —
е* е~х
€Х — в~~ Х
£>(/)= R\{0), £(f)=R\[—1; 1].
Функция нечетная, убывает на промежутках ]—оо; 0[ и ]0; + °°[-
Обратные гиперболические функции
1. Арсасинус (рис. 2.22) у = arsh х = In (х + + 1 )
D(D = R, £(f) = R.
Функция нечетная, строго возрастает.
2. Ареакосинус (рис. 2.23) у = arch х — In (х Ц- д/х2 — 1 );
W) = |1; + «>[. £(/) = [□; +оо[.
Функция строго возрастает.
1 1 + х
3. Арсатангенс (рис. 2.24) у = arth х = — In —----:
W) = ]-1; И; £'(D=R-
Функция нечетная, строго возрастает.
1 х -4- 1
4. Ареакотангенс (рис. 2.25) у = arcth х — — In —-j-:
£>(/)= R\[—l; 1], £(f)=R\{0}.
Функция нечетная, строго убывает на ]—оо; —1[ и J1; 4-оо[.
Функция модуль (рис. 2.26)
{х, если х 5s 0,
|х| =х sgn х,
— х, если х < 0,
D(f)=R, £(f) = [0; +оо[.
38
Функция четная, строго убывает на ]— оо; 0) и строго возрастает
на [0; + оо[.
Некоторые кусочно-постоянные функции
1. Функция сигнум (рис. 2.27)
{1, если х > 0,
0, если х = 0,
— 1, если х < 0,
£>(/)= R, £(/) = {-!; 0; 1).
Функция нечетная, возрастающая.
2. Функция единичного скачка (функция Хевисайда) (рис. 2.28)
У = 1W={q
если х > 0,
если х < 0,
D(f) = R, E(f) = {0; 1).
Функция возрастающая.
3. Селектор точки х = 0: s(x) = 1 (х) • 1( — х).
4. Селектор отрезка [0; 1]: $(х; 0; 1)= 1(х)- 1(1 — х).
5. Функция антье (целая часть) (рис. 2.29): у — [х]. Если х — п + г,
где п £ Z, 0 г < 1, то [х] = п; [х] — наибольшее целое число, не пре-
восходящее х; £)(/) = R, £(f) = Z. Функция возрастающая.
39
Функция Дирихле
1, если
О, если
х рациональное,
х иррациональное.
3. УРАВНЕНИЯ И НЕРАВЕНСТВА*
3.1. ЛИНЕЙНЫЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
Линейное уравнение
ах + Ь = 0.
а ь М
0 Любое — Ь/а
= 0 = 0 R
= 0 ^0 0
Линейные неравенства
1. ах + Ь > 0.
а ь М
> 0 Любое ] — Ь/а; 4-оо[
<0 То же ] — оо ; — Ь /и[
= 0 > 0 R
= 0 <0 0
2. ах 4-6^0.
а ь М
> 0 Любое [ — Ь/а; 4-оо [
< 0 То же ]— оо ; — Ь/а]
= 0 > 0 R
= 0 <0 0
Неравенства ах + Ь < 0 и ах 4~ Ь < 0 сводятся к рассмотренным
умножением на —1.
* Всюду в этой главе через М обозначено множество решений соответствующего урав-
нения (неравенства), 0 —пустое множество (отсутствие решений)
41
3.2. КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Квадратное уравнение
ах2 -ф Ьх + с = 0, а =# 0.
Дискриминант: D = Ь — 4ас.
Если D > 0, то квадратное уравнение имеет два различных корня:
х\, х'2, которые могут быть вычислены по формулам:
х _ — Ь — ~\[b2 — 4ас ___ — b 4- д/б2 — 4ас
1 2а . х2 — 2а
или
. _ -6/2-д/(6/2)2-ас _ -6/2 + д/(^/2)2 — ас
Xi — --------------------- Х2 — ----------------------.
а а
Если D = 0, то квадратное уравнение' имеет единственный корень
xi = —Ь/(2а). Если D < 0, то действительных корней нет. (О комплекс-
ных корнях квадратного уравнения см. в § 5.2.)
Частные случаи
1- х2 4~ рх 4~ <7 = 0 (приведенное квадратное уравнение), D —
= p2-4q;
при D > 0
при D = 0
х1 = — р/2.
2. ах2 4~ 2&х 4- с = 0, D — 4 (62 — ас);
при D > 0
— k — л/k2 — ас — k 4- д/fe2 — ас
Х| = ---------------, Хг — --------------,
а а
при D — О
Xi — — k/a.
3. ах2 4* Ьх — 0, 6 ф= 0: Xi = 0, х2 — — b/а. ч
4. ах2 4- с — 0, ас < 0: Х| -- —с/а, х2 — у—с/а.
5. ах2 — 0: Х| = 0.
Связь между коэффициентами и корнями
квадратного уравнения (формулы Виета)
Если Х|, х2— корни квадратного уравнения ах2 4* Ьх -ф с = 0, то
xt 4* х2 — — b/а, х\х2 — с/а.
Для уравнения х2 4~ рх 4" Q = 0
Xi 4- х2 — — р, xix2 — q.
Разложение квадратного трехчлена на множители
Если D > 0, то ах2 4- Ьх 4- с — а(х — х>) (х — х2).
Если D = 0, то ах2 4~ Ьх -ф с = а(х — х\)2.
42
Квадратичные неравенства
D — дискриминант, Xi, х2 (xi < х2)— корни квадратного уравне-
ния ах2 4- Ьх + с — 0.
1. ах2 + Ьх + с > 0.
D а м
> о > 0 ]— оо; Х|[ и ]х2; 4- °°[
> о < 0 >1! х2[
= 0 > о R\{x>)
= 0 < 0 0
< о > о R
<0 < 0 0
2. ах2 + Ьх 4- с 0.
D а Л1
> 0 > 0 ]— ОО ; Х|] и [*2; 4- °°[
> 0 < 0 [xi! х2]
= 0 > о R
= 0 < 0 )Х|)
< 0 > о R
< о < 0 0
Неравенства ах2 4~ Ьх 4~ с < 0 и ах2 4- Ьх 4- с 0 сводятся к рас-
смотренным умножением на —1.
Частные случаи
Биквадратное уравнение
ах4 4~ Ьх2 4- с = 0.
Сводится к квадратному уравнению заменой х2 = у.
43
3.3. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Показательное уравнение
ах = Ь, а > 0, а ф 1.
1. b > 0. Единственный корень x=logub.
2. b 0. Уравнение корней не имеет.
Показательные неравенства
1. а* < Ь.
b a M
IK\J\I ООО > 1 0 < a < 1 ]— oo; loga b[ Jloga b; 4-oo[ 0
b a M
> 0 > о <0 > 1 0<a< 1 ]loga b; 4-oo[ ]— oo; loga R
3.4. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
Логарифмическое уравнение
loga х — Ь, а > 0, а #= I.
Единственный корень х = аь.
Логарифмические неравенства
1. iOga X < Ь.
= ]а6; 4-оо[.
2. loga х > b.
М = ]0; <?[.
Если а > 1, то М = ]0; afr[. Если 0 < а <2 1, то М —
Если а > 1, то М = ~]аь; 4- оо[. Если 0 < а < 1, то
3.5. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
Тригонометрические уравнения
1. sin х = а (|а| < 1)=>х = (— 1)А arcsin а 4- nk, k С Z.
Частные случаи
sinx = O =$~x — nk, k£1,
44
sin x — 1 =>x — л/2 + 2л/г, k ё Z,
sin x = — 1 =>x — —л/2 + 2л/?, k ё Z.
2. cos x = a (|a| l)=>x = ± arccos a 4~ 2 л/г, k £Z.
Частные случаи
cos x = 0 =>x = л/2 + nk, k £ Z,
cos x = 1 =>x — 2nk, k £ Z,
cos x = — 1 =>x — л 2nk, Л ё Z.
3. tg x = a=>x = arctg a + nk, k £ Z.
Частные случаи
tgx = O =^х = л£, k ё Z,
tg x = 1 =>x —л/4 4-л^, k ё Z,
tg x = — 1 =>x = —л/4 4~ nk, k ё Z.
4. ctg x = <2=>x = arcctg a + nk, k £ Z.
Частные случаи
ctg x = 0
ctg x = 1
==r^ x — л/2 4" л/:,
=>x — л/4 4- л/г,
ctg x = — I =>x = Зл/4 4- Ttk,
/cez,
Z,
/гё Z.
Тригонометрические неравенства
1. sin x < a.
a M
— 1 < a 1 a > 1 a C — 1 — л — arcsin a 4- 2л/: < x < arcsin a 4- 2/гл, k ё Z R 0
2. sin x > a.
a M
— 1 sC a < 1 arcsin a -|- 2л/г < x < л — arcsin a 4- 2л/г, k ё Z
a < — 1 R
a 1 0
3. cos x < a.
a M
— 1 < а 1 a > 1 a — 1 arccos a 4- 2nk < x < 2л — arccos a 4- 2л/>, k Z R 0
45
4. cos x > a.
— arccos a 4~ 2л/г < x < arccos a 2л/г, k £ Z
R
0
5. tg x < a =>—л/2 + л/г < x < arctg a -f- л/г, k g Z.
6. tg x > a => arctg a + nk < x <Z л/2 -f- л/г, /г £ Z.
7. ctg x a =>arcctg a Ц- л/г < x <. л + nk, k £ Z.
8. ctg x > o=> л/г < x <Z arcctg a + л/г, k £ L.
3.6. ПРОСТЕЙШИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА,
СОДЕРЖАЩИЕ МОДУЛЬ
Уравнения
I х — а\ — Ь.
ь м
> 0 (а — Ь; а + Ь\
= 0 {а}
<0 0
Неравенства
ь м
/AV о о \а — Ь\ а 4- Ь[ 0
ь м
> 0 = 0 <0 |—оо; а — b[U]a4“b; + оо[ R\(a} R
3.7. МЕТОДЫ ПРИБЛИЖЕННОГО РЕШЕНИЯ
УРАВНЕНИЙ ВИДА f(x) = O (f непрерывна)
Метод половинного деления
Если Хо и Х| таковы, что f(x0) f(xi) < 0, то полагаем Хг — (х«+
+ xj)/2 и вычисляем /(ха). Если /(ха) = 0, то корень найден. В противном
случае из отрезков [хо; хц] и [хг; х,] выбираем тот, на концах которого
46
f принимает значения разных знаков, и проделываем аналогичную
операцию. Процесс продолжаем до получения требуемой точности.
Метод простых итераций
Уравнение f(x) — 0 преобразуем к виду х = <р(х). Выбираем некоторое
приближение Хо искомого корня, последующие приближения вычисляем
по формуле
Xn+i = <р(хя), п = 0, 1, 2, ...
При выполнении определенных условий последовательность (хя) схо-
дится к х* — корню уравнения f(x) — 0.
Метод Ньютона (метод касательных)
Если хо — начальное приближение корня уравнения f(x) = O, то
последовательные приближения находят по формуле
хп+1=х„-----п—0, 1, 2, ...
f М
Если f' и f" непрерывны и сохраняют определенные знаки на
отрезке [a; b\, а f(a)f(b)<0, то, исходя из начального приближения
Хо € [а; &], удовлетворяющего условию f(x0) f"(x0) > 0, можно вычислить
с любой точностью единственный корень уравнения f(х) — 0.
Метод секущих (метод хорд)
Если Хо, Х| — приближенные значения корня уравнения f(x) = O,
a I(*о) f (xi) < 0, то последующие приближения находят по формуле
fM ( X — 1 О
ХЛ+' Х,‘ КХп)~/(Х„_О П ’ 2’ -
Методом хорд называют также метод, при котором один из концов
отрезка [а; 6] закреплен, т. е. вычисление приближения корня урав-
нения f(x) = O производят по формулам:
х° = Ь, х.+, = х„ - (х. - а)
либо
КО /д х
Хо - а, хя +! - х„ (6 х„).
При этом предполагается, что корень уравнения находится на отрезке
[а; Ь], a f"(x) сохраняет знак на [а; д].
47
4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
4.1. СИСТЕМЫ КООРДИНАТ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
Системы координат на плоскости
Декартовы прямоугольные координаты (рис. 4.1)
О — начало координат, Ох — ось абсцисс. Оу — ось ординат,
i, j (1'1 = 1/1 = 1, I _L /)— базисные векторы, х — ОМХ— абсцисса
точки М(МХ — проекция точки М на ось Ох параллельно оси Оу), у —
= ОМу — ордината точки М(МУ — проекция точки М на ось Оу парал-
лельно оси Ох).
Декартовы косоугольные (афинные) координаты (рис. 4.2)
О — начало координат, Ох\, 0x2 — оси координат, х\ = OMXl, х2 =
— ОМХ1—координаты точки M(MXl— проекция точки М на ось Oxi
параллельно оси Ох2, аналогично МХг), et, е2 — базисные векторы.
Полярные координаты (рис. 4.3)
О — полюс, Ох — полярная ось, р =
= | ОМ| — полярный радиус, ф — полярный
угол.
Главные значения р и <р: 0^р<оо,
— л<ф<л (иногда 0Ср<оо, 0<ю<
< 2л).
Выражение декартовых
прямоугольных координат
через полярные
X = Р COS ф,
У = р sin ф.
48
Выражение полярных координат
через декартовы прямоугольные
a
ГТ~, J х У
р = + У , COS ф = 1 , Sin ф = :
Vx2 + у2 л/*2 + у2
Системы координат в пространстве
Декартовы прямоугольные координаты (рис. 4.4)
О — начало координат, Ох — ось абсцисс, Оу — ось ординат, Oz —
ось аппликат, i, j, k (I i | = | j | = \~k\ — 1, i JL /, i ± k, j -L k) — базис-
ные векторы. Oxy, Oxz, Oyz — координатные плоскости, x — OMX —
абсцисса точки M(MX — проекция точки М на ось Ох параллельно
плоскости Oyz), у — ОМу — ордината точки М(МУ — проекция точки М
на ось Оу параллельно плоскости Oxz), z — OMx—аппликата точки
М(Л4г — проекция точки М на ось Oz параллельно плоскости Оху).
Декартовы косоугольные (афинные) координаты (рис. 4.5)
О —начало координат, Ох\, 0x2, Ох3—-оси координат, Oxix2, ОХ[Х3,
Охгх3 — координатные плоскости, xi = OMXi, i=l, 2, 3,— коорди-
наты точки Л4(МЛ| — проекция точки М на ось Ох\ параллельно плоскости
Ох3х3, аналогично МХ2, МХз), е\, е2, е3 (е^гвз =# 0)— базисные векторы.
Цилиндрические координаты (рис. 4.6)
Главные значения р, <р, z: 0^р<+оо, — лСф^л, — оо <
< Z < + оо.
Связь между декартовыми прямоугольными и цилиндрическими
координатами:
х — р cos ф, у = р sin ф, z — z.
Сферические координаты (рис. 4.7)
Главные значения р, ф, 0: 0^р<4-оо, — л < ф л, О^О^л.
Иногда вместо 0 рассматривают ф: — л/2 ф л/2.
49
Связь между декартовыми прямоугольными
и сферическими координатами
х = р sin 0 cos (р, х — р cos ф cos <р,
У = р sin 0 sin <р, или у — р cos ф sin ф,
z = р cos 0 z = p sin ф.
4.2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ
ПРЯМОУГОЛЬНЫХ КООРДИНАТ НА плоскости
Параллельный сдвиг координатных осей (рис. 4.8)
х = х' + а,
У = У' + Ь,
Поворот координатных осей (рис. 4.9)
rx — х’ cos а — у' sin а,
\у = х' sin а + у' cos а,
х' = х cos а + у sin а,
у' — —х sin а + У cos а.
50
Параллельный сдвиг и поворот
координатных осей (рис. 4.10)
х = х' cos а — у' sin а + а,
у = х' sin а 4- у' cos а + Ь,
х' =(х — a} cos а 4~ G/ — 6) sin а,
у’ = — (х — a) sin а + (у — 6) cos а.
4.3. ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Расстояние между двумя точками
d = д/(г2 — 7[f ,
где ri и г2— радиусы-векторы точек Л1| и М2.
В координатах:
на прямой d — д/(х2 — xi)2 = |х2 — х11;
на плоскости d — ^/(х2 — х,)2 4~ (у2 — у,)2;
в пространстве d = д/(х2 — xi)2 4- (у2 — yt)2 + (г2 — 2i)2.
Деление отрезка в данном отношении X
В координатах:
на прямой х । х 1 + X ’ xi -j- Хх2 у, 4" Ху2
на плоскости х 14-Х 14-Х = Х| 4" Хх2 yi 4~ Ху2 Z\ 4“ Xz2
в пространстве 1 4- X 1 4" X 1 4" X
Середина отрезка (X = 1)
Г\-\-Г2
г = — 2 ‘
координатах: на прямой на плоскости Х| 4- х2 х~ 2 xi 4“ х2 Х 2 4- У 2 'У= 2 ’
в пространстве Х| 4- х> х~ 2 У1 4- У2 Z1 4- Z2 2 2
5!
Координаты центра масс
системы материальных точек
Если в точках Mt (с радиусами-векторами г() сосредоточены массы
m, (/= 1, 2, ...» k\ то радиус-вектор центра масс
miri 4- т2г2 + — + rnkrk
mi + т2 + ...+ тк
В координатах:
/П|Х| 4- т2х2 4-...4- rnkXk
х — —----------------------,
mi 4- т2 4---+ тк
__ m\t/i 4- т2у2 4~•••4* ткук
т\ 4- т2 4~ .-.4“
_ ffliZi 4- m2z2 4- —4- rnkzk
mi 4- m24---4- mk
Площадь треугольника по трем точкам
_Если £i, г2, гз — радиусы-векторы вершин треугольника, а = г2 —
— ri, b = Гз — Г|, то
S = ~ |[а Ь]| = у Цг2 — ri, гз — Г|]|.
В координатах:
в общем случае
5 = I У2 ~ У* 22 — 2‘ I 2 t I ^2 — Z1 Х2 — Х1
2 \ I Уз — tji z3 — Zi I I z3 — Zi Хз — X|
+ I X2 —X| y2 — tjl I 2\l/2_
I X3 — X| Уз — у I I / ’
для треугольника, лежащего в плоскости
S = 4-mod|X2 Xi У‘2 У'
2 I Хз — X! Уз — yi
Оху (moda=|a|),
xi yi 1
X2 y2 1
хз уз 1
= — mod
Объем параллелепипеда
Если_параллелепипед_ построен на приведенных к общему началу
векторах a, b,_c, aj-|,_r2, гз, г4— радиусы-векторы его соответствующих
вершин (а — г4 — r\, b = гз — г,, с — г2 — г,), то объем параллелепипеда
V = mod (а b с) = mod ((г4 — ri) (гз — п) (г2 — 7|))-
В координатах
V = mod
Х4 — X)
Хз — Х|
Х2 — Х|
yi—yi
Уз — У1
У2 — У\
— Zl
— Zi
Z2 — Zi
= mod
X| yi Zl 1
X2 У'2 Z2 1
Хз Уз Z3 1
x4 У\ Z3 1
52
Объем тетраэдра
Если а, Ь, с — исходящие из одной вершины ребра тетраэдра,
a ri, Г2, гз, Гз — радиусы-векторы соответствующих вершин тетраэдра,
то его объем
V = 4- mod (а & с) = 4- mod ((г4 — г() (гз — ri) (г2 — и)),
о о
4.4. ПРЯМАЯ НА ПЛОСКОСТИ
Способы задания прямой
Общее уравнение прямой
Ах + By + С = 0 (А2 + В2 > 0).
Вектор п = (Л; В) — нормальный вектор прямой.
В векторном виде: п • г С — 0, где г — радиус-вектор произвольной
точки на прямой (рис. 4.11).
Частные случаи:
1) By + С — 0 — прямая
раллельна оси Ох;
2) Ах С — 0 — прямая
раллельна оси Оу;
3) Ах + By — 0 — прямая
ходит через начало координат;
4) у — 0 — ось Ох;
5) х — 0 — ось Оу.
Уравнение прямой в отрезках
па-
па-
про-
х_ , У_
а "г b
где а, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
х cos а + у sin а — р = 0,
где а — угол, образуемый нормалью к прямой и осью Ох; р — рас-
стояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Ах By С
±-^А2 + В2
Здесь ---- — нормирующий множитель прямой; знак выбира-
-4-уЛ2 -f- В2
ется противоположным знаку С, если С #= 0, и произвольно, если С — 0.
Векторно-параметрическое уравнение прямой
г = го 4- at,
53
где Л1о(го) = Af0(x0; Уо) — фиксированная точка, лежащая на прямой; а =
— (!', т)—направляющий вектор (см. рис. 4.11).
В координатах (параметрические уравнения):
X = Xg 4“ It,
У = Уо 4“ rnt.
Каноническое уравнение прямой
ил и
Д — До у — Уо
I т '
Уравнение прямой по двум точкам (рис. 4.12)
Л Хо И — tjg
х I — До у I — у 0 ’
Х — Хо У — уо
Д| — До у> — Уо
= о,
ил и
х у 1
До уо 1
Д| у, 1
= 0.
Уравнение прямой по точке и угловому коэффициенту '(рис. 4.12)
У — Уо = /г(д — До) или у = kx ф- Ь,
Vi — Уо
где k = tg а =--------; b — величина от-
Д| — До
резка, отсекаемого прямой на оси Оу.
Отклонение точки от прямой
6 = До cos а + уо sin а — р
с ЯДо 4~ Вуо 4~.С
или о =-------
±л[а2 + в-
где знак перед корнем противоположен зна-
ку С, если С 0, и выбран произвольно,
если С = 0.
Расстояние от точки до прямой
d — | До cos а ф- уо sin а — р |, d =
1Ддо4-Вуо4- Cl
д/л2 4- В2
Взаимное расположение двух прямых
Прямые /г, • г 4- С| = 0 и п2 • г + Со = 0:
пересекаются о
параллельны (но не совпадают) о п \ = Хп2 (п> || пф, С\
совпадают -о п\ = Хп2, С, = ХС2.
54
Прямые А |Л- Д- В\у 4- С( = 0 и Л2х Д- В2у Д- С2 = О:
А । В\
пересекаются о —— ~в~''
, А, В< Ct
параллельны (но не совпадают) о —— —------- Д= ----;
А2 В2 С2
A i В\ Ci
совпадают о —г— = —— = ——.
А 2 В 2 С 2
Прямые у = k\x Д- bt и у = k2x Д- b2:
пересекаются о kt fe2;
параллельны (но не совпадают) о /г1 — k2, bt b2;
совпадают о /г, = k2, bt — Ь2.
Угол между двумя прямыми
- - ГЦ • П2 А1А2А-В1В2
COS ф = COS (/?!, П2) — —Г----=---- — ------- ------------
|П,| |л2| д/д? Д-В? -у/Al Д- В2
k2— k\ А । В2— A'iBt
1 Д- k[k2 Д1Д2 Д- B\B2
Необходимое и достаточное условие
перпендикулярности двух прямых
П\ • п2 = 0, или А 1А2 + В1В2 = 0, или kik2 = — 1.
Расстояние между параллельными прямыми
Если прямые заданы уравнениями Ах + By -J- Ci — 0 и Ах -f- By 4-
-j- С2 — 0, то
, IC2-C1I
а = — ,
V^2 + B2
а если уравнениями г = Го + at и г = п + at, то
J I\а, Г1 — го]1
а — ------------.
I а |
Пучок прямых
Если S(xo! Уо)— центр пучка, то уравнение пучка
А (х - хо) + В(у - уо) = О (Д2 + В2 > 0).
Если центр задан пересечением двух прямых
Д ix Д- Bty Д- Ci =0,
.Д 2х Д- В2у Д- С2 = 0
А, В,)
то уравнение пучка
а(Д |Х Д- В\у Д- С|) Д- р(Д2х Д- В2у Д* С2) — 0 (а2 Д- р2 > 0).
55
4.5. ПРЯМАЯ В ПРОСТРАНСТВЕ
Способы задания прямой
Векторно-параметрическое уравнение
Г — Го + а/,
где Мо(го) = М0(х0; у0; z0) — фиксированная точка, лежащая на прямой;
а = (/; ш; п)— направляющий вектор.
В координатах (параметрические уравнения):
X = Хо -ф //,
У = Уо + mt,
z = zo + nt.
Канонические уравнения прямой
X — Л'о у — у о Z — Zq
I tn п '
Уравнения прямой по двум точкам
х — л-о __ у — у0 z — Zo
Х| — Х() у\ — Уо Z\ — Zo
Прямая как линия пересечения двух плоскостей
(Aix -ф- В}у ф- C\Z ф— D\ = О,
1/12х ф- В2у ф- C>z ф- D2 — О
при условии, что не имеют места равенства
Л _ В, _ С,
А> В> С2
Направляющий вектор такой прямой
где
7,= (А,; В,; С,); /72 = (А2; В2; С2).
Взаимное расположение двух прямых
Если прямые заданы уравнениями г = г\ ф- a\t и г — г2 ф- а2/, то они:
1) параллельны (но не совпадают) о а, || а2Цг2 — гр
2) совпадают о й| || а21| г2 — гг,
3) пересекаются о а} Ц а2, (г2 — Г|) а, а2 — 0;
4) скрещиваются о он\а2, (г2 — г,) а,а2 0.
Если а, —_(/,; /и,, л,), г, = (х<; у,; z,), i— 1, 2, то случаи 1—4 имеют
место, когда ( | — знак отрицания условия):
56
т\ П\
Х| У2 — У\ Z-2 — Z\
%2 — %! У'2 — У1 Z2 — Z}
/1 mi п\ = 0;
1'2 m2 п2
х2 — Л-| У'2 — У1 Z-2 — Z\
/! т\ П\ =7^ 0.
1'2 т2 П-2
Расстояние между двумя параллельными прямыми
d = ^Г2 ~ — 1^2 - Г|)а2]1
l<2il |а2|
В координатах
Расстояние между двумя скрещивающимися прямыми
|(г2 — ri)ai а2|
В координатах
mod
х2 — Xi у2 — у\ Zi — Z\
11 mi ni
1'2 tTl'2 tl2
Угол между двумя прямыми
- _ а\ • а2
cos ср — cos (а.\, а-2) — =------------—
lail |а2|
/1/2 И- mim2 H|/z2
д/7т ту Ц- и2 д/7 2 4~ т2 + п~2
Необходимое и достаточное условие
перпендикулярности двух прямых
ai>a2 = 0 или l\l-z + т,т2 + «т2 — 0.
Взаимное расположение прямой и плоскости
Плоскость п • г + D = 0 и прямая г — г0 + at:
1) пересекаются о п • а 0;
2) прямая лежит в плоскости -о п • а — 0, п • r0 + D — 0;
3) параллельны о п • а = 0, п • г0 + D #= 0.
57
Если го = (хо', уо', Zo), а = (1; т; п), п=(А; В; С), то случаи 1—3
имеют место, когда:
1) At + Вт + Сп V— 0;
2) At + Вт + Сп = 0, Ах0 + Ву0 + Cz0 + 0 = 0;
3) А1 + Вт + Сп = 0, Дл'о + Вуо + Czo + D 0.
Необходимое и достаточное услозие
перпендикулярности прямой и плоскости
- А В С
а || п или —- = — = —
/ т п
Угол между прямой и плоскостью
sin q> = |cos (а, п)| = =
|а|1л|
= \А1 + Вт + Сп|___________
-Ja2 + в2 А- с2 -yjl2 + т2 + п2
Точка пересечения прямой с плоскостью
- - п • го + D
г = го — а —— -------.
п • а
В координатах:
X = ха + //|, у = Уо + mt[, z = Zo + nil,
где
Лхр + Вуо + Czo + D
1 Al + Вт + Сп
Уравнения прямой, проходящей через точку М0(г0)
перпендикулярно к плоскости п • г + D — О
г = Го + nt.
В координатах:
х — хо + At,
У = Уо + Bt,
z = zo + Ct.
4.6. ПЛОСКОСТЬ
Способы задания плоскости
Общее уравнение плоскости (рис. 4.13)
Ах + By + Cz + D = О,
где Л2 + В2 + С2 > 0; п = (Л; В; С) — нормальный вектор плоскости.
В векторном виде п • г + D — 0.
58
Частные случаи общего уравнения
плоскости:
1) By + Cz + D = 0 — параллель-
на оси Ох;
2) Ах + Cz + D — 0 — параллель-
на оси Оу;
3) Ах + By + D — 0 — параллель-
на оси Oz;
4) Cz + D = 0—параллельна пло-
скости Оху;
5) By -f- D — 0—параллельна пло-
скости Oxz;
6) Ах + D — 0— параллельна пло-
скости Oyz;
7) Ах + By + Cz = 0 — проходит
через начало координат;
8) By + Cz = 0 — проходит через ось Ох;
9) Ах + Cz — 0 — проходит через ось Оу;
10) Ах + By = 0 — проходит через ось Oz;
11) z = 0 — плоскость Оху;
12) у = 0 — плоскость Oxz;
13) х = 0—плоскость Oyz.
Уравнение плоскости в отрезках
где а, Ь, с -- величины отрезков, отсекаемых плоскостью на осях ко-
ординат.
Нормальное уравнение плоскости
х cos а + у cos р -}- z cos у — р = 0,
где а, р, у — углы, образуемые нормальным вектором плоскости с
осями координат; р — расстояние от начала координат до плоскости.
Приведение общего уравнения плоскости к нормальному виду:
/1х-| By A- Cz А-О _ q
±д/^2+ Я2+ С2
Здесь —— ........... -—нормирующий множитель плоскости, знак
±д/а2 4- В2 + С
которого выбирается противоположным знаку D, если D =4= 0, и про-
извольно, если D — 0.
Уравнение плоскости по точке и нормальному вектору
В векторном виде
п • (г — Го) = 0.
В координатах
А (х — Хо) + В (у — уо) А~ C(z — Zo) = 0.
59
Уравнение плоскости по точке
и двум неколлинеарным векторам
В векторном виде
В координатах
(г — го) а b — 0.
х — х0 у — у о z — г0
11 ГП\ П\
/г т2 п2
Уравнение плоскости по трем точкам
В векторном виде
(г — Го) (Г| — Го) (г2 — Го) = 0.
В координатах
х — Хо
Х| — Хо
Х-2 — Хо
У — У о
У1 — Уо
У2 — Уо
г — г0
2\ — 2о
22 — 2о
= 0
или
Хо
Х2
У
Уо
У\
У2
2
2о
2l
22
= 0.
Параметрические
уравнения плоскости
В векторном виде
В координатах:
га + и а v Ь, а\ь.
X — Xq 4" l\U -f- l2V,
У = Уо 4- тщ 4- m2v,
г = z0 + п\и 4- n2v.
Уравнение плоскости, проходящей через две параллельные
прямые г = Г| 4- at и 7 = г2 4- ah
(г —п)(г2 —п)а = 0.
Если прямые заданы соответственно уравнениями:
x = X\-\-lt, x = x2-\-lt,
y = y\+mt, и у = у2 4- mt,
2 = Z\ 4- nt Z = Z2 + nt,
то уравнение плоскости есть
х —Х| у —у\ г — 21
Х2 — Х1 У2 — У1 Z2 — Z\
I m п
= 0.
60
Уравнение плоскости, проходящей через две пересекающиеся
прямые г = г\ + ад и г = r2 + a2t‘
(г — ri) ац а2 — 0 или (г — г2) сц а2 = О.
Если ai=(Zi; тг, гц), a2 — {lp, тА п2>, fi=(xi; f/i; Zi), то уравнение
плоскости есть
X — Х|
/.
/2
У — Z/i
пц
т2
z — z
П\
П2
= 0.
Отклонение точки от плоскости
6 — Хи cos а + у0 cos р + Zo cos у — р
или
Лхо + Byo -j- Czo + D
±д/л2 + в2 + с2
где знак перед корнем противоположен знаку D, если D -Ф 0, и выбран
произвольно, если 0 = 0.
Расстояние от точки до плоскости
d = I хо cos а + г/о cos р + z0 cos у — р |,
I Ахо + Byo -j- Czo + О |
d =----------------------—...—----.
д/л2 + В2 + С2
Взаимное расположение двух плоскостей
Если плоскости заданы уравнениями П\ • г + D\ = 0, п2 • г + О2 = О,
то они:
1) пересекаются <=> /21X «г;
2) параллельны (но не совпадают) о щ — k п2 (гц|| /г2), D\ W2',
3) совпадают о п । = X п2, Di — ХО2.
Если плоскости заданы уравнениями A i% + Вщ + C\Z D\ = 0 и
А2х + В2у + C2z + О2 = 0, то случаи 1—3 имеют место, когда:
А, _ Bt _ Ci
2) ~а7 ~ ~В7 ~ ~С7 ~D7’
А[ Bi _ Ci _ Г».
3) "Л? - ~В7 ~ ~С7 ~ Di'
Угол между плоскостями
-/ ГЦ • П2
COS <Р = COS (П|, п2) = —=------------=—
|«11 lr?2l
61
/41/12 “Ь В, В 2 4~ С\С\
д/д? 4~ В2 + С? 7^2 + Bl + cl
Необходимое и достаточное условие
перпендикулярности двух плоскостей
ni-/i2 = 0 пли A |Д2 В\В2 + С\С> = 0.
Расстояние между параллельными плоскостями
Если плоскости заданы уравнениями Ах 4- By + Cz 4* О| = 0 и Ах 4~
4- By 4- Cz + О2 = 0, то
d_ \D-2-DA
~\/Д2 4- В2 4- С2 ’
а если уравнениями п(г — г\) = 0 и п (г — г2) = 0, то •
, |[Г2 — Г|, rt|l
а —-------=------.
|п|
Пучок плоскостей
Если
р4|х4*В|у4'С|~4~В| = 0, — / А ।
кД2х 4- В2у 4* C2z 4- D2 — 0 у А 2
В.
в2
С, )
есть ось пучка, то уравнение пучка
а(Л!Х 4-Bi//4-C.Z 4-D() 4-Р (Д2Х 4-в2у 4-C2Z 4-Г)2) = 0 (а2 4- р2 > 0).
Связка плоскостей
Если S(x0; уо', Zo) — центр связки, то уравнение связки имеет вид
А(х- х0) 4- В(у - уо) 4- C(z - zo) = 0 (Д2 4- В2 4- С2 > 0).
Если центр задан пересечением трех плоскостей:
Hix4-Biy4-Ciz4-Z?i = 0,
А2х 4~ В2у 4- C2z 4- D2 = 0,
Азх 4- Взу 4" C3Z 4~ D3 — 0,
А । Bi С|
а2 в2 С2
Д3 Вз Сз
=# о,
то уравнение связки имеет вид
а(Д|Х 4- В\у 4- Ciz 4- Di) 4- Р(Д2х 4- В2у 4- C2z 4- D2) 4- у(Дзх 4-
4* Взу 4~ C2z 4- Оз) — 0 (а- 4- Р‘ 4* Y" > 0).
62
4.7. ЛИНИИ ВТОРОЙ СТЕПЕНИ
Канонические уравнения
Окружность
Окружность радиуса R с центром в начале координат:
х2 + у2 = R2.
Уравнение касательной к окружности в произвольной точке
Мо(хо; уо): ххо + УУо = Л2.
Параметрические уравнения: х = R cos t, у = R sin t.
Окружность радиуса R с центром в точке С(а; Ь):
(х — а)2 + (У — bf = R2.
Эллипс (рис. 4.14)
Пусть на плоскости заданы две точ-
ки F\ и Ft (|F1F2I = 2с) и дано число
а (а > с). Эллипс — множество точек М
плоскости, для каждойдаз которых сум-
ма расстояний от точек F\ и F2 равна
2а. Точки F\ и F2 называются фокусами
эллипса; [Л\А2], |Л 21 = 2а — большая
ось; [В1В2], |BiB2| —2Ь — малая ось;
О — центр; /?1( —с; 0), 0) — левый
и правый фокусы; А ь Д2> В\, В2 — вер-
шины; Г\ — IF1A4I, Гг = I/^2-А41 —фо-
кальные радиусы;
а2 - с2 = Ь2.
Каноническое уравнение:
Эксцентриситет:
а а
Фокальные радиусы: г\ — а + ех, Г2 = а — ех.
Фокальный параметр: р = Ь2/а.
Уравнения директрис: х= —а/е, х = а/е.
Основное свойство директрис: r/d = е, где г — фокальный радиус
любой точки эллипса; d — расстояние от нее до соответствующей (одно-
сторонней) директрисы.
Уравнение касательной в точке М(хо; уо):
ххо ( ууо
а
Свойство касательной к эллипсу: F2ML = LMK.
Уравнение нормали в точке М(х0; уо):
а У° , \
У - У о = -5— (х - х0).
b хо
63
Уравнение диаметра
ентом k):
(сопряженного хордам с угловым коэффици-
Параметрические уравнения эллипса: х —a cost, y = b sin t.
Полярное уравнение: р = р/ (1 — е cos ср).
Площадь, ограниченная эллипсом: S — лаЬ.
Гипербола (рис. 4.15)
Пусть на плоскости заданы две
точки F\ и F2 (|/?|/?2| = 2с) и дано
число a (Q<.a<.c). Гипербола —
множество точек М плоскости, для
каждой из которых модуль разности
расстояний от точек F\ и F2 равен
2а. Точки F\ и F2 называются фо-
кусами гиперболы; [Л 1Д2], |Д1Д2| =
— 2а— действительная ось; [В162],
IBiB2\ = 26 — мнимая ось; О —
центр; Fi( —с; 0), F2(c-, 0) — левый
и правый фокусы; Д|, А2 — вер-
шины; ri = |F|M|, r2—\F2M\—
фокальные радиусы: с1 — а2 — Ь2
Каноническое уравнение: ——
Эксцентриситет; е — —
Фокальные радиусы:
для правой ветви г। = ex -J— а, г2 = ех — а~,
для левой ветви г\ — —(ех + а), г2 = — (ех — а).
Фокальный параметр: р = Ь> /а.
Уравнения директрис: х= — а/е, х — а/е.
Основное свойство директрис: r/d = е, где г — фокальный радиус
любой точки гиперболы; d — расстояние от нее до соответствующей
(односторонней) директрисы.
Уравнение касательной в точке М(хо; уо):
ХХо ууп
а2 Ь2
Свойство касательной к гиперболе: F\ML = F2ML.
Уравнение нормали в точке Л4(х0; уо):
а Уо .
у — уо ~ — —2— (х - Хо).
6 Хо
b b
Уравнения асимптот: у = — х, у—-----— х.
х2
Уравнение гиперболы, сопряженной данной: —5-
У2
Ь2
-1.
Уравнение равносторонней гиперболы:
64
каноническое х~ — у2 = а1",
отнесенное к осям как к асимптотам: ху = Ь, у = Ь/х (\Ь\ = а‘/2).
Уравнение диаметра (сопряженного хордам с угловым коэффици-
ентом k):
Ь2
a2k
Параметрические уравнения гиперболы:
11олярное уравнение: р = р/(1 — е cos ф).
х = a ch t, у — b sh /.
Парабола (рис. 4.16)
Пусть на плоскости заданы точка F и пря-
мая А, не проходящая через F. Парабола —
множество всех тех точек М плоскости, каж-
дая из которых равноудалена от точки F и
прямой А. Точка F называется фокусом,
прямая А — директрисой параболы; (О/7) —
ось, О — вершина, \CF\ = р — параметр,
Т(р/2; 0) — фокус, г = | FM | — фокальный
радиус.
Каноническое уравнение: у2 = 2рх.
Эксцентриситет: е = , ,, - = 1.
IA1/CI
Фокальный радиус: г = х: ф- р/2.
Уравнение директрисы: х= —р/2.
Уравнение касательной в точке /И(х(); у(>):
= Р(х + хо).
Свойство касательной к параболе: FMN = FNM (М — точка ка-
сания; А— точка пересечения касательной с осью Ох).
Уравнение нормали в точке М(хо; уо):
у — у» =
Уравнение диаметра, сопряженного хордам с угловым коэффици-
ентом k: у = p/k.
Параметрические уравнения параболы: х = /2/(2р), y — t.
Полярное уравнение: р — р/(1 — cos ф).
У =
3 Воднсв В. Т. и др
65
Другие формы канонического уравнения (рис. 4.17):
У2 = — 2рх, х2 = 2qy, х2 = — 2qy (р > О, q > 0).
Общие уравнения линий второй степени
Общее уравнение
анх2 + 2ai2xy ф- а22у2 + 2а,х ф- 2а2у ф- а = 0 (а2| ф- а22 ф- а22 > 0)
определяет одну из следующих линий:
1) X2 У2 а2 Ь2 = 1 — эллипс,
2) £ 1 = - 1 — 0 (мнимый эллипс),
ь 3) ф = 0 — точка (две мнимые прямые), пересекающиеся
4) X2 У2 а2 Ь2 = 1 — гипербола,
J) 1 = 0 — две пересекающиеся прямые;
II {6) У2 = 2рХ — парабола;
<7) X2 = а2 (а ^0) — две параллельные прямые,
ш1 8) X2 =—а2 (а^0) — 0 (две мнимые параллельные
прямые),
9) X2 = 0 —две совпадающие прямые.
Инварианты общего уравнения линий второй степени
Инварианты по отношению к преобразованию одной декартовой
прямоугольной системы в другую:
/i = ац ф-а22, /2 = I °" °'21 ,
' 9 099 *
ап 6Z12 а.
/з = Ц|2 а22 а2
ai а2 а
Характеристическое уравнение линии второй степени
А,2 -/Д ф- /2 = 0,2
его корни Xi, А2 € R-
Классификация линий второй степени по числу центров
I группа — имеющие единственный центр симметрии,
II группа — не имеющие центра симметрии,
66
Ill группа — имеющие прямую центров симметрии.
I 1-2 Ф о,
Пч>/2 = 0, /з#=0;
Шо/2 = 0, /3 = 0.
Канонический вид линий второй степени
I группа: Л|А'2 Ч~ А2У2 + hjji = 0;
II группа: ЦК2 ± 2д/— /з/Л У = 0;
III группа: ЛА2 + К/К = О,
где
„ I 01| О|I . I O22 02I
К = I Т
1 ai а 1 1 02 о 1
Необходимые и достаточные признаки линий второй степени
' 1 <- ф- /2 > о. /1/з<0,
2< > /2 > о, /1/з>0,
1 3< > о, /з = 0,
4< > к < о, /з ¥= 0,
, 5< > /2 < о, /з-О,
II < 6 -ф > /2 = 0, /з#=0;
Г 7 < > /2 = о, /з = 0, К <0,
III < 8< > /2 = 0, /з = 0, к > о,
< 9< >/2 = о, /з = 0, к = 0.
Расположение эллипса и гиперболы относительно исходной
системы координат
Координаты нового начала (центра) — решение системы
oil [X Ц- О12У + 0| = 0,
012% + 0221/ + 02 = 0.
Угловой коэффициент новой осн О'Х (в случае ai2 0)
k = (А, — aj 1) /012.
Расположение параболы относительно
исходной системы координат
Координаты вершины — решение системы, определяемой уравне-
нием параболы и уравнением ее оси:
Она, -К O12O2
О] |Х а 12у Ч--------:------ = О
О|| + 022
ИЛИ
O22O2 Ч" О12О1
O12-V + О22У Ч---------;-------- = О-
Он Ч- 022
Параметр параболы: р = ~\J — /з/Л.
67
Направляющий вектор оси (в сторону ее вогнутости):
<212 <222
а\ а2
аи
а\
<212
а2
4.8. ПОВЕРХНОСТИ ВТОРОЙ СТЕПЕНИ
Канонические уравнения
Ccbepa
Сфера радиуса R с центром в начале координат:
Параметрические уравнения:
х — R cos и cos и,
у = R cos и sin v,
у — R sin и.
Сфера радиуса R с центром в точке S(a; b; с):
(х — а)2 + (у — Ь)2 + (г — с)2 = R2.
Эллипсоид (рис. 4.18)
Каноническое уравнение:
Дг + Эл + = 1 (-а > °’ b > °- с > °)-
и" Ь~ с-
х~ ф-tr -J- 2“ — R .
а=^= b с — трехосный
а — b =/= с — эллипсоид
а = с b — эллипсоид
b — с а — эллипсоид
а = b = с — сфера.
эллипсоид;
вращения вокруг оси Oz;
вращения вокруг оси Оу;
вращения вокруг оси Ох;
68
Конус второй степени (рис. 4.19)
Каноническое уравнение:
+ -4 - -4=° > °-ь > °-с > °)
а b с
а = Ь — конус вращения (прямой круговой).
Сечения конуса плоскостями: в плоскости, пересекающей все прямо-
линейные образующие,— эллипс; в плоскости, параллельной одной
прямолинейной образующей,— парабола; в плоскости, параллельной
двум прямолинейным образующим,— гипербола; в плоскости, проходя-
щей через вершину конуса,— пара пересекающихся прямых или точка
(вершина).
Однополостный гиперболоид (рис. 4.20)
Каноническое уравнение:
= 1 (а > 0, b > 0, с > 0).
а = b — однополостный гиперболоид враще-
ния вокруг оси Oz.
{уК {К
—- + ~ = 1
а2 Ь2
z = 0.
9 9 9
л х~ I -'С 2 о
Асимптотический конус: —- Н--------- = 0.
J а2 b с2
Сечения однополостного гиперболоида плос-
костями — либо эллипс, либо парабола, либо
гипербола, либо пара прямых (прямолинейных
образующих).
Прямолинейные образующие
Через произвольную точку Мо(хо; у0-, Zo) проходят две прямолиней-
ные образующие с направляющими векторами (Л; my, П\) и (/2; гну п?), где:
A-()2o/(tzc) — уй/Ь yoZo/(bc) + Хо/а
1\ = а —-—5----т——, m\ = b —5— --------5——, п\ = с;
хо/а + yo/b2 xl/a + уо/Ь
xozo/(ac) + уи/b Уо?о/(Ьс) — х0/а
!•> = а —-— ---т—т—-, т^ — Ь —7.———, п-> — с.
x-Ja + у»/Ь2 хо/а2 + уо/Ь2
В частности, если точку Л1и выбирать на горловом эллипсе
(A4o(A|); у(); 0)), то уравнениями прямолинейных образующих будут:
— ауа/Ь
у — у<>
Ьхо/а
Z X — Л'О
с ’ ау-}/Ь
У — У»
— Ьхп/а
z
с
69
Двуполостный гиперболоид (рис. 4.21)
Каноническое уравнение:
9 9 9
Х~ U" 2“
—2—I—--------— — — 1 (а > О, b > 0, с 0).
а b с~
а = Ь — двуполостный гиперболоид вращения вокруг оси Oz.
Асимптотический конус:
Сечения двуполостного гиперболоида плоскостями: либо эллипс, ли-
бо гипербола, либо парабола, либо точка, либо 0.
Рис. 4.21
Р и с. 4.22
Эллиптический параболоид (рис. 4.22)
Каноническое уравнение:
— + = 2z (р > 0, р > 0).
р — q — параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями — либо эллипс,
либо парабола, либо точка, либо 0.
Гиперболический параболоид (рис. 4.23)
Каноническое уравнение:
— - — = 2z (р > 0, q > 0).
Р Ч
Сечения гиперболического параболоида плоскостями — либо гипер-
бола, либо парабола, либо пара прямых (прямолинейных образующих).
70
Прямолинейные образующие
Через каждую точку Mo(*o; уо; £о) проходят две прямолинейные
образующие:
х — Хо у — Уо z — Zo
л/р Xohjp — yo/^q
X — Хо У — Уо z — 2о
~^Р Хо/-\[р + Уо/^Jq
Р и с. 4.24
Эллиптический цилиндр (рис. 4.24)
Каноническое уравнение:
х^ tn
-—+У= 1 (а > о, ь > 0);
а b
при а = Ь — круговой цилиндр.
Гиперболический цилиндр (рис. 4.25)
Каноническое уравнение:
А- - 4г = 1 (« > 0, ь > 0).
а- b
71
Параболический цилиндр (рис. 4.26)
Каноническое уравнение:
х2 = 2ру (р > 0).
Общие уравнения поверхностей второй степени
Общее уравнение
<2i ix2 + а-22у2 + a33z2 + 2а\2ху 4- 2ai3xz + 2а2Луг + 2а{х +
2а2у 4~ 2(i3.z 4~ а = 0 (ат । а22 4~ Озз 4~ оТз 4~ <25з 4“ о2г > 0)
определяет одну из
следующих поверхностей:
Z X2 . У2 Z2
1) ~ 4 — а~ Ь~ с X2 , У2 , Z2 = 1 — эллипсоид,
2) —~ 4 — а- Ь с- X2 , У2 , Z2 = — — 0 (мнимый эллипсоид),
3) —— 4" —Г Н ~ а- Ь~ с~ X'2 Y2 Z2 = 0 — точка (мнимый конус),
4) —— + “77 ~ а~ Ь~ с~ X2 Y2 Z2 - 1 — одиополостный гиперболоид,
5) —— + “77 ~ а Ь' с X2 Y2 Z2 = — — двуполостный гиперболоид,
Л) а'2 Ь'2 с2 = 0 конус второй степени;
/ II t 7) - 8) - X'2 Y'2 Р + й X2 Y'2 Р Q --2Z — --2Z — эллиптический параболоид, гиперболический параболоид;
9) + = 1 — эллиптический цилиндр,
III Ю) И) X2 Y2 а2 Ь2 X'2 Y'2 а2 Ь2 = - 1 = 0 — 0 (мнимый эллиптический цилиндр), — прямая,
12) X2 X2 а2 Ь'2 = 1 — гиперболический цилиндр,
13) X2 У^ Ь2 = 0 — пара пересекающихся плоскостей;
IV { 14) X2 = 2pY — параболический цилиндр;
{15) X2 = а2 —пара параллельных плоскостей,
16) X2 = — а2 — 0 (пара мнимых параллельных плоскостей),
17) X'2 = 0 —пара совпадающих плоскостей.
72
Инварианты общего уравнения поверхности второй степени
Инварианты по отношению к группе ортогональных преобразований
/1 = о, । а-22 + Озз,
, I О| 1 сц 2 1 . I <21 1 <213 I . I 022 ^23 1
/2 = + + „ ’
1 О|о 022 1 1 О|3 0)3 1 1 023 «33 1
fill О|2 013
/3 = 0,2 U‘2‘> a^s ,
013 023 Озз
011 012 013 о 1
О|2 а-22 а-23 а-2
К —
О|3 023 Озз Оз
Oi а-s аз а
Характеристическое уравнение поверхности
второй степени
Л3 —/Д2 +/2Х —/з = О,
его корни — Xi, к-2, Х3 £ R.
Классификация поверхностей
второй степени по числу центров
I группа — имеющие единственный центр симметрии,
II группа — ранга 2 и не имеющие центра симметрии,
III группа - имеющие прямую центров симметрии,
IV группа — ранга 1 и не имеющие центра симметрии,
группа — имеющие плоскость центров симметрии
1 < > /з #= 0;
II < > /з = 0, Л ¥= 0;
III < > /з = 0, К = 0, Is =У= 0;
IV < > /з = 0, /. -0, /> = 0, К-2 0;
V < > /з = 0, /. = 0, /2 = 0, К-2 = 0.
Канонический вид поверхностей второй степени
I группа — Х|Х2 + УоУ2 + XsZ2 + /1//3 — 0;
II группа — Х|Х2 + Хо}'2 ± 2xj — I1/I2Z = 0;
III группа — Х|А'2 + Хо}'2 + K-i/I-2 — 0;
IV группа - Х|Х2 ± 2д/ — К->/1\ У = 0;
V группа — Х;Л"2 -|- К\/1\ — 0,
где
К-1 = а 11 0)2 о । 012 О22 Оо + Он 013 013 Озз О| Оз + Ооо а-23 а2з озз а-2 Оз
О) Оо О 0| а3 0 02 Оз о
73
Необходимые и достаточные признаки
поверхностей второй степени
1 о /2 > 0, Ц1з >0, h < 0,
IV { 14 О /з = 0, /4 = 0, /2 = 0, К2 #= 0;
{15 о К\ <0,
16 о К\ > 0,
17 <=> /G =0.
Координаты центра поверхности второй степени — решение системы
СИ ix -|- а^у -f- CI13Z -f- Oi = 0,
012-Х 4~ а^у -К G23Z 02 = О,
013* + С1-23У + азз2 4- Оз = 0.
5. ВЫСШАЯ АЛГЕБРА
5.1. КОМПЛЕКСНЫЕ ЧИСЛА
Алгебраическая форма комплексных чисел (рис. 5.1)
Обозначения, терминология
z = а + bi, i2 — — 1,
где i — мнимая единица; а — действи-
тельная часть: а — Re г; bi — мнимая
часть: b = Im z; числа вида Ы — чисто
мнимые; плоскость Оху — комплексная
плоскость; ось Ох — действительная
ось; ось Оу — мнимая ось;
z = а — Ы — число, сопряженное
числу z — а + Ы\
г = |г| — xja2 + b2 — модуль комплексного числа;
Ф = arg г, — л < ф л либо 0 ф < 2л,— аргумент комплексного
числа z (главное значение аргумента);
cos ф = zz/^/a2 + b2, sin ф = Ь/ -\1а~ + b2, 1g ф — b/а (а =/= 0),
Args — множество аргументов числа z:
Arg z — arg z + 2л£, k C Z.
Действия над комплексными числами
Если zi = a -R bi, z2 = с + di, то:
Z, + z2 = (а + Ы) + (с + di) = (а + с) + (6 + d)i,
Z\ — z2 — (а + bi) — (с + di) — (a~c)-{-(b — d)i,
Z\ = z2oa = c, b = d,
z\z2 = (a + bi) (c + di) = (ac — bd) + (ad + bc)i,
Z\ a + bi ac + bd be — ad .
z2 c di c~ d~ c2 -j- d?
i4k 1, ?*+' = Z, iik + '2 = — 1, Z^ + 3 = —k E N.
Тригонометрическая форма комплексных чисел (рис. 5.1)
z — г (cos ф + i sin ф),
где г — модуль; ф — аргумент комплексного числа.
Если zi — r\(cos ф| 4-1 sin ф|), z-2 ~ r2(cos фг + i sin ф2), то:
75
Z\Z-2 = rir2(cos (qi + q2) + i sin (q, + q2)),
Z| rt
— = — (cos (qn — q2) + i sin (q, — q2)),
? = r (cos q — i sin q) = r (cos (— q) + z sin (— q)),
Z\ = Z2<>r\ = Г2, qi = q2 + 2л/?, k £ Z.
Формула Myaepa
(r(cos q + i sin q)/! = r"(cos nq + i sin nq).
Извлечение корней из комплексных чисел
-\jr (cos q + i sin q) = д/7^ COS ‘ sin -- — ,
k = 0, 1, n — 1.
Корни из единицы
nr- 2nk , . . 2л/г
Л/ 1 = cos ---— + I sin ----, k = 0, 1, /1 — 1.
V II n
В частности,
Свойства сопряженных чисел
2| + — Z\ + Z-2, Z\ — Z2 = Z\ — 22, Z|Z2 = 21 Z2,
/ Z| \ 2| ----- - -
( —) = —. (2") = (2)", zz = a- 4- b- = |z|2.
X 22 / Z2
Свойства модуля
\z\ = |z|, | 2122 | = I 21 | | 22 I, | z" | = \z\'\ I — I =
1 Z-2 । I Z21
I г, | — | Z-2 I < ,2| + Z2| < |Z[| + | 22 I ,
\Z\| — I Z2 | < | 21 — 22 I < I 21 | + | 22 | .
Свойства аргумента
Arg (Z|Z2) = Arg 21 + Arg 22, Arg — = Arg 2| — Arg z-2,
Z2
Arg z" — /? Arg 2, Arg 2 = — Arg 2.
76
Показательная (экспоненциальная) форма
комплексных чисел
г = rei,f,
где г — модуль; <р — аргумент; e"f = cos ф + i sin ф.
z = re!' — r (cos ф — i sin ф),
Z-2 Г-2
пГ~ "Г / • ф 4“ 2 Л k \
yz = д/г exp I i —----—I, k — 0, 1, n — I
p''l _1_ e-‘4' p'4_p-‘'P
COS Ф =--------------, sin ф =-----------.
5.2. МНОГОЧЛЕНЫ
Многочлен степени n
f(x) = Go + G1X +.„ + «,,-ix'1-1 + anx\
c-.fR или ai; g C, k = 0, 1, .... ц,—коэффициенты; a„ — старший коэф-
фициент; an #= 0.
Равенство многочленов
= g^oak = bk, k = 0, 1, .... n,
где bk — коэффициенты многочлена g(x) (bn— старший коэффициент).
Сложение многочленов
Если g(х) = bo b \Х bm — tx"' 1 -j- bmx"‘, b,n =4= 0, n 4? tn, to
/(x) -j- g(x) — co 4~ 4-... 4- cn- ix” 1 4- cnxn,
где с, = a, 4- bi, i = 0, 1, ..., m; c, — ah j = tn 4- 1, tn 4- 2, n.
Умножение многочленов
f (x) g (x) = do 4" d\X 4* ... 4" + щХ ‘^n,
k
где dk — S ciibk—i, k — 0, 1, ..., n 4- m. В частности, do = aobo, d\ =
/=0
= a<)b\ 4" &\bo, d'2 = ctob-2 4~ &\b\ 4“ Oobo, ..., dn-^m — anbin.
Алгоритм деления с остатком
Для любых /(х), g(x) существуют q(x) (частное) и г(х) (остаток),
такие, что Дх) — g(x)g(x) + Д*), причем степень г(х)< степени g(x) или
г(х) = 0. Многочлены ^(х) и г(х) определены однозначно.
Частное и остаток находят с помощью так называемого правила
деления «уголком».
77
Пример.
7 (л) = 2х5 + х* - 5л-1 + 12х: + Юл- - 2, д(х) = х1 - 2х + 7.
_2х5 + л4 - 5л-1 + 12л’ + Юл- - 2 | х3 — 2х + 7
2х5 -4х3 + Их* 12х2 + х - 1 = q (х)
_х4- х1- 2х'+10х-2
х4 - 2х;+ 7х
__— х' -j- *^л' — 2
— л"'_____4- 2х — 7
х + 5 = Дх)
Делители многочлена
Делитель многочлена f(x) — многочлен g(x), такой, что
f(x) = g(x)?(x).
Наибольший общий делитель двух многочленов
Наибольший общий делитель многочленов f(x) и g(x) — такой их
общий делитель d(x), который делится на любой другой их общий
делитель.
Алгоритм Евклида
(алгоритм последовательного деления)
нахождения наибольшего общего делителя
многочленов f(x) и g(x)
К*) = gW <71W + п(х),
g(x) = гДх) q2(x) + г2(х),
т\(х) = гДх) q3(x) + г3(х),
r*_3(x) = rft_2(x)<7/(_,(x) + rfc-i(x),
г к _ 2 (х) = rk -1 (х) qk (х) + гк (х),
— i (х) = гДх)?*+1(х).
Тогда гДх) — наибольший общий делитель /(х) и g(x).
Схема Горнера
Если Дх) = ciox''+ aix" 1 + ... + ап-ix + an, g(x) = x — с, то при де-
лении f(x) на g(x) частное q(x) имеет вид
q (-'•') — ь oxn 1 -|- btxr~ ~ ь,।—2x -|- bn-1,
где bu = a0, bk = cbk-tak, k 1, 2, ..., n— 1. Остаток г находится
по формуле r — cb,t-\ + an.
a0 di a2 d/J — 1 an
c b0 = = do bt = — cbo + a । b2 = — cb i 4- d2 bn-\ = = cbn-2 + d„-i r = f(c) = = cbn-i + an
78
Корни многочлена
Корень многочлена /(х)— число а, такое, что /(а) — 0.
/'(«) = Oof(x) -= (х — а) q(x).
Число а — /г-кратный корень многочлена /(х), если
f (х) = (х — а)* ср(х), <р(а) =# 0.
Если число а является fe-кратным корнем многочлена f(x), то при
k > 1 оно будет (k — 1)-кратным корнем первой производной этого
многочлена; при k — 1 число а не является корнем производной.
Разложение многочлена степени п на множители
Многочлен f(x) с комплексными коэффициентами
f(x) = ап(х — ai)*’(x — a2)4’-• (х — as)4
Здесь oci, a2, .... as — различные корни многочлена кратностей kt, k>, ks
соответственно (kt k? +... + ks — ri).
Многочлен f(x) с действительными коэффициентами
/(x) = a„(x — ai)';'(x — аг)*2-- - (x — a.,)*'(x2 + p\X -f- qt)1'---
•• -(x2 + pmx +
Здесь ai, a2, ..., as — различные действительные корни многочлена,
кратностей соответственно /г,, /г2, .... ks; pt, q\, .... pm, qm — различные
пары действительных чисел, удовлетворяющих неравенствам pi — 4q\ <
< 0, ..., pm — 4qm < 0 (каждый множитель х2 + Pi* + qt можно пред-
ставить в виде (х — ₽<) (х — j},), где 0„ (Е — пара ‘сопряженных комплекс-
ных корней кратности /,).
Интерполяционная формула Лагранжа
«4-1
/и = S
i= 1
сфх— Ь\)---(х — 6,— |) (х — 6i+i)-..(x— &п+|)
(6, ~ bt)- -ibi - - bi+tY \bi - bn + t) ’
Эта формула позволяет найти многочлен степени п по известным его
значениям с, в п + 1 точках bt, i — 1, 2, ..., п -ф- I.
Пример.
bl bt = 1 62 = 3 63 = 4
Ci = Z(6i) Ct = 2 c2 = — 2 Сз = — 1
(х-3)(х-4) (х— 1)(Х —4)
(1-3)(1-4) (3-1)(3-4)
1>- 1) (-V — 3)
(4 - 1)(4 - 3)
х- — 6л + 7.
Формулы Виета
Если ((х) = хп + а\хп^' 4- а2хл-2 +... + ап-\Х + ап и a)t a2, .... a;1 —
корни многочлена (каждый кратный корень взят здесь столько раз,
какова его кратность), то:
79
а। = — (a। + a2 +... -j- a,i),
a2 = aia2 -ф ai«3 + + aia« + а2аз -ф... + a„_ ia,„
аз — — (aia2a3 -ф aia2a4 -ф + «л-гЯл- ia„),
a«-i = ( — I)™-1 (aia2 • • - a„_ । -ф aia2 • • • arl-2a.n -ф... -ф a2a3... arl),
a„ = (— l)"aia2- • a„.
В частности, при n = 2=>ai = — (ai -ф a2), a2 = а^г; при и = 3=>
=>Я| = — (ai + a2 -ф a3), a2 — aia2 -ф aia3 + a2a3, a3 = — aia2a3.
Вычисление корней многочленов
Уравнения второй степени (квадратные)
Для общего уравнения ах2 -ф Ьх -ф с = О
• — ~ — д/^2 ~~ ^ас
2а
Для приведенного уравнения х2 -ф рх -ф q — О
(Формулы верны при любых коэффициентах, действительных или ком-
плексных.)
Уравнения третьей степени (кубические)
Уравнение у3 4 -ф ау2 -ф by -ф с — 0 заменой у = х — а/‘3 сводится к
уравнению х3 + рх + q = 0, где р = — a2/3 b, q = 2a3/27 — ab/‘3 -ф с.
Корни последнего уравнения находятся по формуле Кардано:
А' = ^-д/2 + ^/4 + р3/27 + ^-q/2-^/4 + p3/21,
при этом, беря последовательно по одному из трех значений кубического
корня a — д/—q/2 -ф ~\Jq2/4 -ф р3/27, следует из трех возможных зна-
чений корня р = д — q/2 — д/<ф/4 -ф р3/27 выбрать то, для которого
аР = — р/3.
Границы корней
Для многочлена f(x) = аох'г -ф а1х"~ 1 -ф... -ф ап_\х -ф а„:
1) верхняя граница модулей корней — число 1 -ф-Л/1а()|, где А =
= max {|ai |, |a2|, ....
2) верхняя граница положительных корней — число 1-фд/б/а0,
где <2о > 0; В — наибольшее число из модулей отрицательных коэф-
фициентов; k — помер первого из отрицательных коэффициентов;
3) нижняя граница положительных корней — число l/^^, где —
верхняя граница положительных корней многочлена ф|(х) = х"/(1/х);
4) верхняя граница отрицательных корней — число — 1 /N>,
где N> — верхняя граница положительных корней многочлена ффх) —
= х'7(-1/х);
80
5) нижняя граница отрицательных корней — число —/Уз, где Л\3 —
верхняя граница положительных корней многочлена <рз(х) — — х).
Метод Ньютона разыскания верхней границы
положительных корней
Если для многочлена
старшим коэффициентом
f'(c)>0, ..., Г(с)>0, то
корней.
f(x) с действительными коэффициентами и
«о > 0 выполняются условия f(c) > О,
с служит верхней границей положительных
Приближенные вычисления корней
Метод линейной интерполяции
Если простой корень а отделен границами а и b (а < а < Ь), то
в качестве приближенного значения а берется число
- af(b)
Метод Ньютона
Если а — простой корень многочлена [(х) и ]а; Ь[ —- промежуток,
не содержащий, помимо а, других корней этого многочлена, а также
ни одного из корней многочленов ['(х) и f"(x), то приближенное зна-
чение корня находят по формуле
с = а, —
где а, - - то из чисел а и Ь, для которого знак )\х) совпадает со зна-
ком ?"(х).
Общие корни двух многочленов.
Результант. Дискриминант
Общие корни
Общие корни многочленов /(х) и g(x) — в точности все корни
их наибольшего общего делителя d(x).
Результант
Результант многочленов f(x) = аохп ф- а\Хг ф- a„ _ i a" -f- a „ и
Й'(х) — box'1 ф- Ь\ у’’ 1 -ф... ф- bs_ i.r ф- bs — определитель
Qo ai а„ 0 ... 0
0 а0 a«-i а„ ... 0 J1 s строк
R(f, g) = 0 0 ... an
bo b\ ... bs 0 ... 0
0 bo ... b„-i bs ... 0 n строк
0 0 ... bS
81
Этот определитель в первых $ строках содержит коэффициенты много-
члена /(х), в последних п строках-—коэффициенты многочлена g(x),
а на свободных местах — нули.
Многочлены fug имеют хотя бы один общий кореньо/?(/, g) — 0.
Другие выражения для результанта:
п S
R(f, g} = asM П II
i=l/=1
где а./, р/ — корни многочленов Дх) и g(x) соответственно;
II
R(f< g) — ао П Я (а.),
1=1
/?а, g)=(-irw П/(₽/).
/=1
Дискриминант
Формула
Dtf} = alT2 П (а, -а;)2.
1 ^/<1^/1
Ш /') = (-!) 2 a0D(j)
позволяет выразить дискриминант многочлена через его коэффициенты.
Гурвициан многочлена
Для многочлена /(х) = х" ф- а{хп~' +... + ап_ ,х + ап гурвициан —
определитель
О1 1 0 0 . . 0
Оз О2 О| 1 . 0
<25 О1 Оз О2 . .. 0
«7 Об «5 а4 . .. 0
0 0 0 0 . . о„
(если / < 0 или j > п, то считается а, = 0).
Критерий Гурвица
Действительные части всех корней многочлена /(х) отрицательны
тогда и только тогда, когда все главные миноры гурвициана положи-
тельны.
Для п = 2: di > 0, а> > 0.
Для п = 3: Qi > О, 0Щ2 — а-з > 0, а3 > 0.
82
5.3. ОПРЕДЕЛИТЕЛИ
Определения
В перестановке сц, а2, ..., ап чисел 1, 2, п два числа а, и а; со-
ставляют инверсию, если I <_ j, но а, > а,. Число всех возможных ин-
версий данной перестановки обозначают /(а,, а2, ..., ап). Перестановку
называют четной, если / — четное число, и нечетной, если I — нечет-
ное число.
Определитель (детерминант) квадратной матрицы А = (^ац)— число
(обозначение А = det (а,,) = det А = |а,;|)
Д= 2 (—*’••••• к
(/,. к>, .... к„)
где 2 означает, что суммирование производится по всем пере-
(*,, k2.... k„)
становкам k\, k>, ..., kn чисел 1, 2, ..., n.
В частности, при п = 2
А = |а" °121 =(-1)'и.21аиа22 + (_1)Л2. 1)й12а21 =
I Я21 022 I
= (— 1 )°atia22 + (— 1)‘°|2«21 = 011022 — Oi2o2i;
при п — 3
Оц О|о 013
о2| 022 О23
О31 Озг Озз
А =
= (_ 1)/о. 2, з)а11а22азз
+ (— 1)/(2’ 3' '’0,2023031 + (— 1)/(3' ' 2'а1за2|Оз2 +
+ (— 1/ ' 3‘ -'О! (023032 + (— 1)/Л 2' ‘’013022031 +
4- (— 1)/ 2- ' 3О12О21азз = 0| 1022033 + 012023031 +
+ O13O21O32 — О12О2|Озз — 0,1O23O32 — О|зО22Оз|.
На рис. 5.2 проиллюстрирован закон, по которому составляется
определитель матрицы третьего порядка: слева дано правило вычисле-
ния положительных членов определителя, справа — отрицательных.
Миноры определителя
Минор Mi, элемента о(/ определителя А порядка п — определитель
порядка п — 1, полученный из А вычеркиванием t-й строки и /-го столбца.
83
Главные миноры определителя
Для det А —
й| 1
«21
«12
Й22
й 1 п — 1 й I п
«2 л — I «2/1
главные миноры есть
а,
a„i
ап2
Опп
определители
«II
«21
Й 12
«22
й| | I
«21
... а। п_।
... й2п-1
А2 =
ai>
а22
, А„ — det А.
А1 — I й 111 — й 11,
«л - 1 1 й(1_ I 2
Алгебраические дополнения
Алгебраическое дополнение элемента a,j определителя А — опреде-
литель /),/ = (—1)' + /Л4,/, где М,/ — минор элемента ар.
Разложение определителя
По элементам Z-й строки:
п
А = «11/4,1 -(- й,2/4,2 + OiaAin = й,*А,/г.
А' 1
По элементам /-го столбца:
/1
А й 1 jA ij -f- aiojA 2j “f-... -j- й;1//1 nj —- X cikjA ki-
ll = i
Например, при n — 4
разложение по первой
строке
А ==
йп
«21
«31
«41
«I 2
«22
«32
«42
«13
#23
«33
«43
а н
«21
«34
«4 4
й[ ।
^22
«32
«42
«23
«33
«43
«24
«34
«4 1
+ (------ 1)' «12
Й21
Й31
Й41
«23
«33
«43
Й24
«34
«4 1
+ (-1)'+3«13
«21
Й.31
Й4 I
«22 «24
«32 «34
й 4 2 «44
«н
«2 1
«31
«41
«22
«32
«12
«23
«33
«43
Свойства определителей
1. det А = det А г.
2. Если все элементы какой-нибудь строки (столбца) определителя
равны нулю, то определитель равен нулю.
84
3. Если матрица В получена из матрицы А перестановкой двух
каких-либо ее строк (столбцов), то det В = — det А.
4. Общий множитель всех элементов произвольной строки (столбца)
определителя можно вынести за знак определителя.
5. Определитель, содержащий две пропорциональные строки (столб-
ца), равен нулю.
6. Пусть А = (а,Д— квадратная матрица порядка n; k — фикси-
рованное натуральное число: 1 k п; В, С, D — матрицы, которые
получаются из А заменой ее k-й строки (столбца) соответственно
строками (столбцами) ои, а2, ..., ап; р,, р2, ..., рп; cti Д-а3 Д- р2, ...,
а„ Д- Рп- Тогда det D = det В Д- det С.
7. Определитель не меняется от прибавления к какой-либо его
строке (столбцу) другой его строки (столбца), умноженной на произ-
вольное число.
8. Если какая-либо строка (столбец) определителя есть линейная
комбинация других его строк (столбцов), то определитель равен нулю.
9. det (АВ) = det А • det В.
5.4. МАТРИЧНОЕ ИСЧИСЛЕНИЕ
Обозначения, терминология
/Матрица размеров т X п — система тп чисел (элементов матрицы),
расположенных в прямоугольной таблице из т строк и п столбцов.
Если т — п, матрицу называют квадратной матрицей порядка п. Обо-
значения:
кратко
а и й pi ... a in
0'21 й32 С1‘2п
- ... dm,i _
или более
Две матрицы А
если ач — bij V i, j.
A=(a(/)m„, А = (ан), соответственно [а,[ач].
и В одинаковых размеров равны (запись А = В),
85
#11
021
— матрица-столбец,
— верхняя треугольная матрица,
— нижняя треугольная матрица,
“ И|| 012
О а>->
_ О О
~ CL | | О
«21 Й22
L а,и аП2 ... О-пп
“ Ц| 1 0 ... 0
0 Я22 ... 0
— О 0 ... Пдп —
— диагональная матрица,
а 0 ... О
О а ... О
О 0 ... а
— скалярная матрица,
1 0 ... О
О 1 ... О
— единичная матрица
О 0 ... 1
, с /в \ s (1.если 1 — Л
(кратко: Е — (о,,), где .— символ Кронекера).
(О, если i =# I, г '
Если все а1; действительны, то матрица А называется действитель-
ной; если хотя бы одно из чисел at, комплексное, то матрица называется
комплексной.
Сложение матриц
Суммой матриц A — (aij) и В одинаковых размеров называется
матрица С — (сч) тех же размеров, у которой VОбо-
значение: С = А-\-В.
Свойства сложения матриц: Л+В = В + Л, (Л + б) + С = Л-|-
+ (5 + С), А + О = А, А + (-Л) = О VA, В, С.
Вычитание матриц
А —В=А +(-В).
86
Умножение матрицы на число
Произведением матрицы Д=(а,7) на число а называется матрица
С = (ctj) тех же размеров, у которой с,7 — оса,-,-V i, j. Обозначение: С —
= а. А.
Свойства: 1-А=А, а(0Л) = (а0)Л, а(А Д- В) — аА Д- аВ, (а Д
Д-р)4 =аЛ Д УД,В и V а, PER.
Умножение матриц
Произведением матрицы А = (aik} размеров т X п на матрицу В —
= (bkj} размеров п X р называется матрица С = (СчУ размеров m X р, у
п
которой с,, = anbij A- ctrib-ii Jrainbnj = S aikbk, V i, j. Обозначение:
C = AB.
Свойства: AE = EA = Д, AO = OA =0, (AB)D =A(BD\ a(AB) =
= (aA)B = Д(аВ), (Д Д- B)D = AD Д- BD, D(A Д- B) = DA Д- DB (при
условии, что указанные операции имеют смысл).
Для квадратных матриц А и В, вообще говоря, АВ ВА.
Транспонирование матриц
— —
| й|2 . • [ п dll Й21 • 1
А = 0'21 Й22 • ^2п =>АТ = О|2 а-2'2
$ m 1 m 2 &гпп Otn а-2П . а,,,,.
Свойства: (.4 Т)г = А, (аА)г = аА Т, (4 Д В)т = А т Д- Вт, (АВ)Т =
= ВТАТ.
Специальные классы квадратных матриц
Симметрические матрицы: А=АГ,
А — (а,,) — симметрическая о а,/ = а/,- V /,/.
Кососимметрические матрицы: А = —А1,
А = (aij) — кососимметрическая -о а,7 = —ац V i,j,
Ортогональные матрицы: АА т = Е,
п
А — (ац) —• ортогональная о 2 ача/к — 6,Л..
Невырожденные (неособенные) матрицы: det А 0.
Вырожденные (особенные) матрицы: det А = 0.
Обратная матрица
Матрица Д-1 — обратная для матрицы А, если
АА~' =А~'А =Е.
87
Для квадратной матрицы А
тогда, когда det А 0.
обратная существует тогда и только
____1
det А
Ли А21 ... Л,,,
Л 12 Л 22 ... Л ,;2
пп
где А,/ — алгебраические дополнения элементов матрицы Л.
Свойства: (Л ')- 1 ==Л, (АВ) ~ 1 = В ~ 'А ~ ', det Л ' 1 = 1/det Л.
Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называют:
1) умножение какой-нибудь строки (столбца) на отличное от нуля
число;
2) прибавление к какой-нибудь строке (столбцу) другой се строки
(столбца), умноженной на произвольное число;
3) перестановку местами любых двух строк (столбцов).
Вычисление обратной матрицы
с помощью элементарных преобразований
Если с помощью элементарных преобразований строк квадратную
матрицу Л можно привести к единичной матрице £, то при таких же
элементарных преобразованиях над матрицей Е получим Л-1.
При м е р. Л =
Л|£)=Г 1 -3 I 1 о] Г> -3 I 1 о!
L —2 4 I О L0 —2 I 2 1J
Ко второй строке
прибавляем пер-
вую, умноженную
на 2.
Вторую строку
умножаем
на —1/2.
Г 1 -3 I 1 о 1 Г 1 0 I -2 -3/2
L О I I - 1 - I /2J [ О I I - I - I /2.
К первой строке при-
бавляем вторую, ум-
ноженную на 3.
-3/21
-1/2J-
Ранг матрицы
Ранг матрицы — наивысший порядок отличных от нуля ее миноров.
Обозначение: rank Л.
Базисный минор матрицы — любой отличный от нуля минор порядка
г = rank Л.
88
5.5. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Общий вид системы
й] |Х| 4“ Я|2Х2 4" ••• 4~ ^tr.-Vn — bi,
021-^1 "1“ ^22^2 4“ •4“ 0. >,iXn = Ь-2,
a„,tX\ 4- а„|2-^2 4- 4" ciinnXn — bm,
a- i= 1, 2, ..., tn; j= 1, 2, n, — коэффициенты системы; bi--
свободные члены; xi, x2, xn — переменные; tn, n 6 N.
Если все b, = 0, система называется однородной.
Матрицу
называют расширенной матрицей системы, а матрицу С — |fi с>
для которой АС — В,— вектор-решением системы.
Критерий совместности линейных уравнений
Система совместна тогда и только тогда, когда rank А — rank D.
Правило Крамера
Если m = п и det А #= 0, то система совместна и имеет единствен-
ное решение Х = А~'В или, что то же самое, х,= det .4,/det А, где
det А, — определитель, полученный из det/1 заменой Его столбца столб-
цом свободных членов.
Общее решение
системы линейных уравнений
Если система линейных
например, R —
<2| I Ц)2
<221 в 22
уравнений АХ — В
.. 0|г
— базисный
совместна, rank А = г
минор матрицы систе-
а,\ а,2 ... агг
89
мы, то она равносильна системе
оj ।х 1 ai2<<2 4"••• 4- a\rXr — b\ — ai* r_j_ । л'г_|-1 —... — Qiltxlt,
Й2|А'| 4~ 022*2 4* 4" a2rXr = Ь > — Cli r-|- I A'r + I — ... — а->пХ„,
Ori*'i 4- йт'1Х2 4- 4- cirrXr — br — a, f_|..i A'r-|. 1 — ... — arnxn.
Придавая переменным xr+i, xr+2, ..., xn (свободным переменным)
произвольные значения xr + i = ar + i, xr + 2 = ar + 2, ..., xn — a,,, получаем
однозначно (например, по правилу Крамера) Xi = ai, х2 = a-2, ....
х, = аг. Тогда (а,, а>, ..., ап) — решение исходной системы.
Метод Гаусса
Метод Гаусса — метод последовательного исключения переменных.
С помощью элементарных преобразований строк расширенной матри-
цы I) системы матр
нцу А системы приводят к
Си С\2 ... С|Г • • • С1 п d\
0 Сц ... С2г • •• Cin di
0 0 ... Сгг • • Сгп dr
0 0 ... 0 ... 0 dr + \
0 0 ... 0 ... 0 dm
ступенчатому виду:
(с„ #= О, z= 1, 2. г). Если среди чисел dr + i, dr + 2, .... dm есть отлич-
ные от нуля, система несовместна.
Если r/, + i — dr\ 2 = ...— dm — 0,то:
1) при г — п исходная система равносильна системе
с, ।А| 4- ci2х2 4-... 4" с\пхп — dI,
С'22х2 4~ 4~ С2пХц = di,
имеющей единственное решение (сначала находим из последнего урав-
нения х,„ из предпоследнего х„_| и т. д.);
2) при г <п исходная система равносильна системе
С| |А'| 4“ С12%2 4" 4~ ClrXr — d\ — Cl r_|- I АО + I — ... — C|
C22X2 4- 4- C2<A'r — di — C2 r + l xf 4-1 — ... — C2„Xn,
CrrXr — dr — Cr ,+ 1 A'r+ I — ... — CrnXn,
имеющей бесчисленное множество решений (ao + i, ау + 2, .... х„— свобод-
ные переменные).
Однородные системы линейных уравнений
Однородная система линейных уравнений АХ — О всегда совместна.
Она имеет нетривиальные (ненулевые) решения, если г = гапк/1<п.
Для однородных систем базисные переменные (коэффициенты при
которых образуют базисный минор) выражаются через свободные пере-
менные соотношениями вида:
90
Х\ = d\ |Xr+ 1 + d\2Xr-j-2 + ... + t/| ri- rXn,
X'2 = d2lXr + 1 -(- d:22Xr + ‘2 4~ d2 n — rXn,
Xr = drlXr+1 dr2Xr + ‘2 + ••• + dr n — rXn.
Тогда n — г линейно независимыми вектор-решениями будут:
dw
du
d\2
d22
d2
dr\
dr2
0
Cn^r =
dr n
0
0
, C2 =
а любое другое решение является их линейной комбинацией. Вектор-
решения (ci, с2, .... ся_г) образуют нормированную фундаментальную
систему.
В линейном пространстве Vn множество решений однородной систе-
мы линейных уравнений образует подпространство размерности п — г;
(Ci, со. .... с„~г)— базис этого подпространства.
5.6. «ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Определение линейного пространства
Пусть V — непустое множество (его элементы будем называть век-
торами и обозначать х, у, z, ...), в котором установлены правила:
1) любым двум элементам х, у 6 V соответствует третий элемент
х + у Е V, называемый суммой элементов х, у (внутренняя операция);
2) каждому х С V и каждому а £ R отвечает определенный эле-
мент ах (внешняя операция).
Множество V называется действительным линейным (векторным)
пространством, если выполняются аксиомы:
1. х + у — у + х V х, ytV.
II. (х + у) + z = X + (у + z) V х, у, z t V.
III. 3 б Е V (нулевой элемент, такой, что х + 0 — х, Vx£V).
IV. V х Е V 3 ( —х)Е V (элемент, противоположный элементу х),
такой, что х + ( —х) = б.
V. 1 • х = х V х Е V.
VI. a(0x) = (a0)x V х Е V, V а, |3 Е R-
VII. а(х -ф у) = ах + ау Vx, у Е V, V а Е R-
VIII. (а + fi)x — ах + рх V х Е V, V а, р Е R-
Аналогично определяется комплексное линейное пространство (вме-
сто R рассматривается С).
91
Подпространство линейного пространства
Множество V Е V называется подпространством линейного про-
странства V, если:
1) V х, y^V'=>x + ye Е';
2) V х£ V', Va 6 R(C)=>ax€ Е'.
Линейная комбинация векторов
Линейной комбинацией векторов х,, х2, хг называют вектор
г
У — <Х[Х\ 0,2X2 <XrXr = X OLkXh,
k = l
где ai, a2) a,ER(C) — коэффициенты линейной комбинации. Если
at = а2 =... = аГ — о, комбинация называется тривиальной, если Ла,
=# 0,— нетривиальной.
Линейная зависимость и независимость векторов
Система хц, х2, ..., х, Е |/ линейно зависима о Л аь а2, .... a, Е R(C),
£ аг > 0, что aiXi + а2х2 +... + a,xr = S а^х/, = 0.
<=1 k=1
Система xt, х2, .... х, Е Е линейно независима о ( S а^х* = 0
\ Х/г=>
=> а, - а_> —... = а, =01.
Критерий линейной зависимости векторов
Для того чтобы векторы хц, х2, ..., xf (г > 1) были линейно зависимы,
необходимо и достаточно, чтобы хотя бы один из этих векторов являлся
линейной комбинацией остальных.
Размерность линейного пространства
Линейное пространство V называется ц-мерпым (имеет размер-
ность п), если в нем:
1) существует п линейно независимых векторов;
2) любая система п + 1 векторов линейно зависима.
Обозначения: п — dim Е; Е„.
Базис пространства Е„. Координаты вектора
Базис — любая упорядоченная система <?|, е2, ..., е„ из п линейно
независимых векторов пространства Vn-
Обозначение: (е) = (щ, е>, еП).
Для каждого вектора хЕ Е„ существуют числа х,, х2, ..., х„ Е R(C),
такие, что
92
Числа Xj, х2, ..., хп называются координатами вектора х в базисе
(ei, в2, ..., еп) (определяются однозначно), Х = (х)— координатный стол-
бец вектора х в этом базисе. Употребляется запись: x = (xi; х2; х„).
Справедливы формулы:
п п II
X = 2 xkek, у = 2 ykek => X + у — 2 (xfe 4- ук) ек,
k = 1 /;= 1 k= 1
х = у о хк — ук, k=\, 2, п,
п п
Х= 2 хкек=> Хх — 2 (XXk)ek.
k=\ k=\
Матрица системы векторов
Для векторов Xi = (<2ц; a2i; ...; aHi), x2 = (ai2', <222; оп2),
х,,, = (ai,„; a2m; a„m) в базисе (ef, е2, .... еп) — матрица
<2| 1 Ц|2 ... dim
. <221 <222 О2т
<2п1 <2п2 ... Опт
т векторов пространства Vn линейно независимы тогда и только тогда,
когда rank А = т.
Матрица S перехода от базиса (e) = (ei, е2, ..., еп) к базису (е') =
= (e'i, е2, .... е'п)— матрица системы векторов (е') в базисе (е).
S11 S12 Sin
Sn2 Snn
= s 11 e 1 s2ie2 4-... 4- sn\d„,
e'2 — si2<?i 4- s22<?2 4- 4- s,i2t\,
d’i —Sln^i 4-S2„e2 4-..-4-SnnCi,
или кратко:
е- — S SjtCj, i — 1, 2, .... n; (e') = (e)S.
Если, det S 0, to (e) — (e')S ', t. e. S 1 — матрица перехода от
базиса (?') к базису (е).
Преобразование координат вектора
Если х = (е)Х — (е')Х', то X = SX'. В развернутой записи:
Л'1 — S, 1 Л' ( — S| 2-V2 4~ 4" S 1пХ«,
Л"2 = S21X1 4“ S22X2 4" ... 4“ S2nXn,
Хп — $л|Х| 4* Sn2*2 + ... + SnnX'-.
Очевидно, что X' = S~lX.
5.7. ЕВКЛИДОВЫ ПРОСТРАНСТВА
Определение
Действительное линейное пространство Е называется евклидовым,
если каждой паре векторов ~х, ~у £ Е сопоставляется число х • у Е R так,
что у х, у, z £ V и € R выполняются аксиомы:
I. х • у = у • х.
II. (х + у) • z = л- • z + у • г.
III. (Хх)-у = 1(х-у).
IV. х • х 43 0, х • х = Qox — 0.
Число х • у называют скалярным произведением векторов х и у,
х • х — скалярным квадратом вектора х (пишут х2). Введенная опе-
рация называется скалярным умножением векторов х и у.
Длина вектора
Длина вектора х £ Е — число |х| — д/ х2.
Свойства:
1) |х| = Оох = ();
2) |Хх|_= |X|Jx| V х£Е V ХЕ R;
3) |х-у|_<|хНу| V X, у е Е (неравенство Коши — Буняковского);
4) |х + у| < |а'| -|- |у| V х, у е Е (неравенство треугольника).
Угол между векторами
Углом между векторами х е Е и у С Е называют угол ср, для которого
х • у
cos ф = ———, 0 $4 ф < 2л.
|х| |у|
94
Ортогональные векторы
Векторы х, у £ Е ортогональны, если х • у = 0.
Нормированные векторы
Вектор х С Е называется нормированным или единичным, ес-
ли |х| = 1.
Если х =# 0, то соответствующими этому вектору нормированными
векторами будут хо = х/|х|, хб = — х/|х|.
Ортонормированный базис
Система векторов X], Хг, .... х„, п 2, для которой
называется ортонормированной.
Во всяком пространстве Еп, п > 2, существует ортонормированный
базис. Из произвольного базиса (gi, g2, g,t) пространства Еп ортого-
нальный базис может быть построен с помощью процесса ортогона-
лизации:
Л = gi,
h = + M2)7i» где M2) = — ,
/Т
Гз = Ъ + М’Т, + где М” - - ~
fl П
fk — gk + Ak)f । + Л.'з'Уг +... + X^2_ tfk-1, где Ef'1 =-———, j — 1,
fl
2, k - 1.
Пронормировав каждый вектор f*, k = 1, 2, ..., n, получим орто-
нормированный базис. В ортонормированном базисе (ei, е2, е„) для
векторов х = Х|<?1 + х2е2 4-... + хпеп, у = у\в\ 4- у2е2 +... + упеп имеем:
х • у = Xiy। Х2У2 Ч-•• • Ч- x,tyn = хkyh — YrX = Хт Y,
= I
Iх I = д/х~1 4- Х2 + ••• 4“ х1-
5.8. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
ЛИНЕЙНОГО ПРОСТРАНСТВА
Определение линейного оператора
Преобразование (оператор, отображение) f линейного пространства
в себя (запись /: Е-э-V) называется линейным, если:
95
1) /(л’1 + х2) — Кхд Ч~ V •*'1, л'2 Е V;
2) дй) = л/(7; v х е v, v х е R(C).
Условия 1 и 2 равносильны соотношению
f(ax, + f}x2) = af(xi) 4- р/(л-2) V х,, х2 Е V, V а, р Е R(C).
Матрица линейного оператора
Матрица линейного оператора f: V,,-+Vn в базисе (<?,, е2, ..., е,,') —
матрица
А =
«II О|9
«21 Й22
С1 I п
G 2п
оп\ а.п2
Chin
столбцами которой являются столбцы образов базисных векторов
f^e^ — e' оператора f, т. е. e,' = f(e,) = S а^е,.
i = 1
Линейный оператор называется невырожденным, если det Д =4= 0.
Связь между координатами вектора и его образа
Если х Е Еп в базисе (<?,, е2, е„) имеет координатный столбец
X = (Х| х2 ... х„)г, / — линейный оператор с матрицей А в данном базисе,
У = (t/i у2 ... у,У — координатный столбец вектора у — fix), то У = АХ
(употребляется также запись у — Ах). Более подробно:
yi — Оц-^i 4~ а 12X2 Д-... + ainXn,
У‘2 = а2|Х| 4~ CI22X2 4- ••• Ч- ci2nxn,
Уп — Ch, । X [ 4” С1ц 2Х 2 4- ... 4- Q ,1цХц.
Связь между матрицами одного и того же
линейного оператора в разных базисах
Если в базисе (<?|, ..., еп) линейный оператор f: Vn-^Vn имеет
матрицу А, в базисе (ef, е2, ..., е„) — матрицу В, a S — матрица
перехода от первого базиса ко второму, то
В =S~'AS.
Произведение и сумма линейных операторов
Если fug — линейные операторы пространства Vn с матрицами
А и В в базисе (с,, е2, .... е„), то операторы произведения ((g°f')(x) =
— и суммы f 4- g ((f Ч~ g) (*) = fW + &W) — линейные и имеют
в том же базисе матрицы ВА и А 4- В соответственно.
96
Оператор, обратный данному линейному оператору
Линейный оператор ср: Vn~^Vn называется обратным линейному
оператору f: Vn-+Vn, если (f ° <р) (х) = (ф°/) (х) = х V х £ К„.
Обозначение: =
Для существования f~' необходимо и достаточно, чтобы f был
невырожденным оператором. Если А — матрица оператора f в некотором
базисе, то оператор в том же базисе имеет матрицу Л-1.
Ядро и область значений линейного оператора
Ядро оператора f: V-+V—множество, обозначаемое Ker f:
Kerf = {х€ Vlf(x) = 0}.
Область значений (образ) оператора [: К-*- V — множество, обо-
значаемое Im f:
Im f = {y£ V\y = f(x), x£ I/}.
Множества Ker / и Im f являются подпространствами простран-
ства К.
Ранг оператора f: Кл-> Vn (обозначение: dim Im /') — ранг мат-
рицы А линейного оператора f,
dim Im f — rank A.
Дефектом оператора f: Vn~+Vn называют dim Ker f,
dim Im f -ф dim Ker f = n.
Собственные векторы и собственные значения
линейного оператора
Ненулевой вектор х £ Vn называется собственным вектором линей-
ного оператора f: Vn~^Vn, если 3A£R (А^С для комплексного Vn),
такое, что Дх) = Ах. Число А называется собственным числом (собст-
венным значением) оператора /, соответствующим этому собственному
вектору.
Если в некотором базисе оператор f имеет матрицу Лив том же
базисе вектор х имеет координатный столбец X, то АХ = АХ или
(Л - АЕ)Х = О.
Собственные числа А линейного оператора f: Vn-+Vn— корни
характеристического уравнения det |а,/ — А6(/| = 0, где (а,j) — матрица
оператора f, 6,7 — символ Кронекера.
Для каждого собственного значения Ао соответствующие собст-
венные векторы могут быть найдены из матричного уравнения (Л —
— Ао£)Х = О или соответствующей ему системы линейных уравнений
(ан — Aq)xi Я- а12X2 -ф... -ф ai«x;i = О,
^2|Х| -ф (tl-22 — А())Хг -ф ... ф СЦцХп = О,
Пп|Х| -ф а„2х2 -ф ••• -ф (апп — Ао)х„ — 0.
Линейный оператор называется оператором простой структуры,
если существует базис, состоящий из собственных векторов этого опе-
ратора. Матрица линейного оператора в этом базисе имеет вид
4 Воднев В. Т. п’ао.
97
Zi о ... о
о z2... о
о о ... z„
где Z/ — соответствующие собственные значения.
5.9. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
ЕВКЛИДОВА ПРОСТРАНСТВА
Ортогональные операторы
Линейный оператор f: Еп-+Еп называется ортогональным, если
х-у = f(x) • f(y) V х, у £ Еп.
Для того чтобы оператор ft Еп~+Еп был ортогональным, необхо-
димо и достаточно, чтобы его матрица в ортонормированном базисе
была ортогональной.
Ортогональные операторы и только они сохраняют длину век-
тора, т. е.
|/(х)| = |х| Vx^E„.
Сопряженные операторы
Оператор /*: Еп-+Еп называется сопряженным линейному опера-
тору Еп-+Еп, если
f(x)-t/ = x-f*(y' Vx, у£Е„.
Оператор /* также является линейным оператором. Если / в не-
котором ортогональном базисе имеет матрицу А, то в этом базисе
оператор /* имеет матрицу Ат.
Свойства сопряженных операторов: (/*)* = f, (fg)* = g*j*, (j + g)* =
= i* + g*, (af)* = a/* V a 6 R, (/*)“1 = (/-')* (/ — невырожденный).
Самосопряженные операторы
Линейный оператор /: Еп^Еп называется самосопряженным (сим-
метрическим), если
f(x)-y = x -f(y) Vx, УЕД-
Для самосопряженного оператора /* = f.
Оператор ft Еп-*-Еп является самосопряженным тогда и только
тогда, когда его матрица в некотором ортонормированном базисе сим-
метрическая.
Свойства самосопряженных операторов: 1) самосопряженный опе-
ратор имеет только действительные собственные числа; 2) всякий само-
сопряженный оператор является оператором простой структуры;
3) для всякого самосопряженного оператора существует ортонормиро-
ванный базис, состоящий из собственных векторов этого оператора.
98
5.10. КВАДРАТИЧНЫЕ ФОРМЫ
Определение квадратичной формы
Квадратичная форма переменных Xi, Х2, .... х„ — функция
п п
f(xi, х2, ..., х„) = S 2 а,/Л-,л-у = ЦцХ1 + ai2X|X2 4-...+
/=1 / = 1
Ф й|„л'|Л',| ф- a^iXiXt 4- а22х2 ф-... ф- о2,1Х2х„ ф-... 4- а„|Х,|Х| ф-
4“ О-п2ХпХ‘1 ф ... 4- ОллФн
а,,- — коэффициенты квадратичной формы. Без ограничения общности
считают а,, = a.ji, тогда
/(х,, х2, .... х„) = Он? 4- 2a)2X|X2 ф.-ф 2а|„Х1Х„ ф
4“ <222Х2 ф 2а >лХ ’Хз ф 4" 2a2nX2X„ ф ... 4- ClnnXn.
Если переменные хд, х2, .... хп принимают действительные значения
и а1; С R, квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица
называется матрицей квадратичной формы, ее ранг — рангом квадра-
тичной формы. Квадратичная форма называется невырожденной, если
det Л Ф 0.
Главные миноры матрицы А называются главными минорами квад-
ратичной формы.
В пространстве Vn квадратичную форму можно записать в виде
Хт АХ, где X — координатный столбец вектора х = (хд х2; ...; х„).
В пространстве Еп квадратичную форму можно представить в виде
/(х) • х, где /— линейный самосопряженный оператор, матрица кото-
рого в некотором ортонормированном базисе равна А.
Канонический вид квадратичной формы
Квадратичная форма называется канонической, если все а,, — О,
। ф /, т. е.
п
f(xh х2, ..., х„) = Z а„х; = |Х| ф а22х2 ф-... 4- аппх„.
i = 1
Всякую квадратичную форму можно привести к каноническому
виду с помощью линейных преобразований. На практике обычно при-
меняют следующие способы.
1. Ортогональное преобразование пространства
f(xi, х2, ..., хф — XrAX = Xii/i ф л2у2 ф-ф- Хпу*п,
99
где Xi, Х2, — собственные значения матрицы А.
2. Метод Лагранжа — последовательное выделение полных квадра-
тов. Например, если а}] 4=0:
/(%!, х2, .... хл) = (ацхг +2ai2XiX2+ .+2ab!xix„) + f1(x2, х„) =
2 1
= 011 (х? -----Х| (012X2 -ф 013X3 -|- ... -|- О1МХП) -)-— (о 12X0 -|-
аИ Ql!
+ о 13X3 + ... 4- О|„х„)“-— (О|2х2 + О 13X3 + ... + 01„Х„)2 ф-
Оп
+ /2(х2, ..., X„)=—i--~+f2(.X2, ..., Х„).
Zu 11 OX 1
Затем подобную процедуру проделывают с квадратичной формой f2(x2,
..., х„) и т. д. Если в квадратичной форме все о„ = 0, но есть а,у 4= О,
i 4= /, то после предварительного преобразования дело сводится к рас-
смотренной процедуре. Так, если, например, ai2=#0, то полагаем Xi =
= У\ — Z/2, х2 = У\ 4- у2, Ху = (/у, / — 3, ..., П.
3. Метод Якоби (в случае, когда все главные миноры А,, Д2, ..., А«
квадратичной формы отличны от нуля):
/(xi, х2, ..., х„) = Хт АХ = Aiyi -)—-—У2-\~----\—г-У»-
А1 Ап-1
Нормальный вид квадратичной формы
Для действительной квадратичной формы
Дх1, х2, ..., хл) — X r АX = е\уу -|- е2у2 4~ Ч- £гУг,
где е, = ± 1; г — rank А.
Для комплексной квадратичной формы
f(xj, х2, ..., х„) = X1АХ — у\ 4- у2 ••• 4_ Уг, г — rank 4.
Для действительных квадратичных форм имеет место закон инер-
ции квадратичных форм: число положительных и число отрицательных
квадратов в нормальном виде квадратичной формы не зависит от
способа приведения квадратичной формы к нормальному виду с помощью
невырожденных линейных преобразований.
Классификация действительных квадратичных форм
Положительно-определенные
Квадратичные формы, для которых /(х,, х2, ..., х„) > 0 Vx,, х2, ...,
хл>таких, что X) + х2 4-... +хл > 0. Нормальный вид: у, + yl 4-...4- у’п.
Квадратичная форма является положительно-определенной тогда и
только тогда, когда все се главные миноры положительны: ДА > О,
k= 1, 2, ..., п, (критерий Сильвестра).
Отрицательно-определенные
Квадратичные формы, для которых /(Х|, х2, ..., хл) <0 Vxi, х2, ..., хл,
таких, что Х| 4-х2 +... + х^ > 0. Нормальный вид: — у\ — у'ъ —... — ул.
Квадратичная форма является отрицательно-определенной тогда и толь-
ко тогда, когда (—1)ЛА* > 0, k= 1, 2, .... п.
100
П оложительно-полуопределенные
Квадратичные формы, для которых f(xi, х2, хп) О VXi, х2, ...х„,
таких, что х? + х2 +>• 0. Нормальный вид: у2 -ф yl +... {- у2,
г <n, г — rank А.
Отрицательно-полуопределенные
Квадратичные формы, для которых f(X|, х2) ..., х„)^0 VХ|, х2, ..., х„,
таких, что xf + х2-ф ••• + х„ > 0. Нормальный вид: — y'i — у2 — ...— у2,
г < п, г — rank А.
Неопределенные
Квадратичные формы, которые принимают как положительные, так
и отрицательные значения. Нормальный вид: у i ф У% + ... + yl —
— у* + 1 — ... — у2, I ^.k<r ^п, r= rank А.
6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
6.1. ПРЕДЕЛЫ И ЧИСЛОВЫЕ РЯДЫ
Свойства пределов
1. Если последовательности (а,,) и (+) сходятся, то
lim (а„ + Ьп~) = lim ап + lim bn, lim anbn = lim an lim b>„
Г1-+- OO fl—► OO fl—> oo n—> oo n—> oo oo
lim (a„ — bn) = lim an — lim bn, lim can — c lim an,
n—^OO /г—>-OO n—> oo n—> oo n—> OO
n lim an
. . rt->-OO
lim — = —-----------— ( Inn bn + 0).
Il—> oo bn 11171 bn n-^oo
n-> oo
2. Если lim an = a, \im bn — b и an + bn V n, to a < b.
tt~+CG П->0О
3. Если an < cn + b V n и lim an — lim b„ = a, to lim cn — a.
n—>~ OO n—^oo n-> OO
4. Если lima,, — a, to lim |a„| = |a|.
П->оо M->oo
Некоторые пределы
lim qn = 0 (|</| < 1), lim tiqn — 0 (|g| < 1),
n—>OO oo
lim (1 + \/ri)n — e, lim (n“/aM) — 0 (|a| > 1),
n—>OO 72->OO
lim (a"/n!) = 0, lim (In n/n) = 0,
П->оо /I—>oo
lim (ln'?n/na) — 0 (a > 0), lim -’{/a = 1 (a > 0),
П—► oo /7—^00
lim fin = 1, lim (1/^1) = 0, lim (n/ffn\) = e,
fl—^OQ H->OO V H->- OO V
aonk aaik -|-... -|- an ao
lim ——----------— -------= — (b0 ¥= 0),
bon + b>n +..•+&„ b0 1
lp + 2Pnp 1
lim---------—------—-----------,
n-»oo np+ p 1
lim (----!--1----!-----1_ _L J_\ । 2
n->oo\a+l 1 /г + 2 2n)~ 2'
lim ( 2'4 -2a V I
n->-oo \ 1 • 3--(2/i — 1)/ 2n + 1
я
= “2“ (формула Валлиса),
•c-^0 x ’ x-<-0 x~
1 .. tg x
, Inn = i
2 x
102
lim (1 + *)l/x —
lim (1 + l/x)x — e,
X-+- oo
In (1 + x) l°ga(l + x) 1
lim-------------= 1, lim--------:---------= —--------,
x->0 x x->o x In a
i- e ~ 1 । i- a ~
lim----------= 1, lim----------------
x-»-0 x x->-0 x
sh x , ch x — 1
lim----------= 1, lim----------------
x->0 x л-^о x1
= In a,
.. th x .
lim------= 1,
|jm ,Q. ~1.7.-J-----L — a [im xa In x = 0 (a > 0),
x x^ + o '
lim -П --- — 0 (a > 0), lim = 0, lim Xх = 1.
л'~*- + oo xa x~* + oo ex >->- + о
Сравнение функций
f 00
f(x) = o(g(x)) при x^-a, если lim—— = 0.
x->a g(x)
f(x) = O(g(x)) при x->a, если существуют интервал ]a; 0[, содер-
жащий точку а, и постоянная М, такие, что |f(x)| ^M|g-(x)|, x£]a; 0[,
х =# а.
Локально эквивалентные функции: f(x) ~ g(x) при х->а, если
Некоторые эквивалентности (при х->-0): sin х ~ х, tg х ~ х, 1 —
— cos х ~ х2/2, arcsin х — х, arctg х ~ х, ех—1 ~ х, sh х ~ х, ch х —
X2 I-----
— 1 ~ , ах — 1 ~ х In a. In (1 + х) ~ х, In (х 4- д/х2+ 1) ~ х, (1 {-
4- х)а - 1 ~ ах.
Формула Стирлинга: п!-----^2шГ(п/е)п при ц->оо.
Числовые ряды
ОО
Hi я-? ... 4~ ak -j-... ~ 2 а*.
£ = 1
Частная (частичная) сумма ряда: Sn = ai + аг +... + ап.
Сумма ряда: S= lim Sn (если предел существует).
оо
00
Ряд сходится, если S конечно; тогда 2 ak = S.
k=i
Необходимое условие сходимости ряда: lim а* — 0.
А-*-оо
оо
Остаток ряда: г„ — 2 an + k.
k= I
°° 1
Гармонический ряд S — расходится; его частная сумма
fe = i k
Sri — 1 4—g—।—з" —n" ='n n + + 6,1
(C — постоянная Эйлера: С = 0,5772...; en->0, n->-oo).
103
Обобщенный гармонический ряд
оо
сходится при а >
Л = 1
1, рас-
ходится при а 1.
Признаки сходимости для положительных рядов
Признак сравнения
ОО
Если 0 а/; < bk V k, то из сходимости ряда S bk следует схо-
k = 1
оо оо
димость ряда 2 ак, а из расходимости ряда аь — расходимость
ft = 1 k = 1
ОО
ряда 2 bk.
ft = 1
Предельный признак сравнения
Ok оо оо
Если lim —— — I, то при 0 < / <-]-оо ряды а* и S bk или
ft->-oo bk k— 1 ft = i
оба сходятся, или оба расходятся; при / — 0 из сходимости ряда
оо оо
bk следует сходимость ряда 2 при I = + оо из расходимости
k = 1 k — I
оо оо
ряда S Ьк следует расходимость ряда S а*. В частности, если а* ~
fe=l ' k=\
оо оо
~ bk при k-+<x>, то ряды 2 а* и S bk или оба сходятся, или оба
ft = i k=\
расходятся.
Степенной признак
Если ak с/kA при k-+ оо, 0 < с < + оо, то при а > 1 ряд схо-
дится, при а 1 расходится.
Признак Д’Аламбера
1 °°
Если lim--------— q, то при 0 q < 1 ряд S а* сходится, при
fe->oo Ok k=l
q > 1 расходится.
Признак Коши
Если lim \[ak = q (или lim \/ak = q\ то при 0 < q < 1 ряд
со k^-CO
со
S ak сходится, при q > 1 расходится.
104
Признак Раабе
(d \ 00
--------1 ) = /•, то при r> 1 ряд S ak сходится,
Яд ц. I / k — 1
при г < 1 расходится.
Признак Гаусса
йь ц / 1 \
Если -----= Х4---------Е О ( , , ), е > 0, то при X > 1 ряд
Яд+ 1 п \ k + /
ОО
S Од сходится; при X < 1 расходится; при X—1, ц > 1 сходится:
й= 1
при Х= 1, р. I расходится.
Интегральный признак
Если f убывает на [1; + оо[ и неотрицательна, то ряд S f(k) схо-
k= I
+ оо
дится или расходится вместе с интегралом $ f(x)dx.
1
Признаки сходимости для знакопеременных рядов
Признак Лейбница
Ряд 2 (— 1/ 1 Од, Од > 0, сходится, если (од) монотонно стремится
k= 1
к нулю. При этом
оо fl
S (-1)4-'ад- 2 (-1/-’ад
ft== 1 /г=1
ап + |.
Если (од) монотонна
ОО
дится ряд S akbk-
k=\
Признак Абеля
оо
и ограничена, а ряд S bk сходится, то схо-
И= 1
Признак Дирихле
Если (од) монотонно стремится к нулю,
оо ОО
S bk ограничены, то ряд X akbk сходится.
k = l k=l
а частные суммы ряда
Некоторые ряды
а + aq + aq2 +... + aqk^' +••.= , 1<?1 < h
1 ч
105
q sin a + q2 sin 2a 4-... 4- qk sin ka +... =-g..b.in.”-
1 — 2q cos a 4 q2
q cos a 4- q2 cos 2a + -.. + d'cos ka + ... =-cos a — у—
1 — 2q cos a 4- q2 ’
1 + —+ —+ 4-— 4- =e
1! 2! k\ ’
l-± + l-... + ^- + .,.= ln2,
I <71 < 1,
Id < i.
6.2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
Определение производной
Г(*о) = lim
Ах—О
/ (х0 4~ Ах) — / (х0)
Ах
f,z . .. fW-fW
/ (Хо) - lim-------,
x-hVo X %о
f,z \ f f(x + h) — f(x)
/ (x) — lim ——-—/-
/<—o n
Односторонние производные
, x .. ^(xo + Ax) - f(x-o)
f+(xo)= lim ------------------
Ax—4-0 Дх
f, ( . .. /'(xo + Ax)-f(xo)
/'_(xo)— lim
Ax—-o
Дх
Функция, дифференцируемая в точке хо
f(xo + Ах) — f(xo) 4 ДДх 4~ о(Дх) при Дх—>0,
— f' (л'о)-
Дифференциал
dp = f(x)dx, f'(x) =
106
Дифференцирование арифметических комбинаций
(и, v, w — дифференцируемые функции, а, р— постоянные)
(аа + Ру)' = аи' + ри', d(au + р^) — adu + fidv,
(uv)' = u'v + uv', d(uv) = udv + vdu,
(uvw)' = u'vw + uv'w + uvw',
d(uvw) = vwdu + uwdv + uvdw,-
u\' u'v — uv' . , u\ vdu —udv
— I =------5---- (у ¥= 0), d[ — I =-------,
V / V2 \ V / y2
dv
v1
Производная композиции (сложной функции)
= wrw.
Производная обратной функции
(rw^.
Логарифмическая производная функции f
<ln/w)' = -W'/w>0-
Производные основных элементарных функций
Г(*)
с 0 ах ax In a
X 1 In X 1/x
ах*”1 In |х| 1/X
х2 2х logs X 1 x In a
~\/х ——- , х>0 sin х cos X
2^/х
1 /х -1/х2 COS X — sin x
ех ех tg X
COS X
107
Окончание
(и1")' = (ev |п— uuv 'и' + uv In и • v'.
Производные высших порядков некоторых функций
fU)
с х* In X ех ах sin х cos X sh х chx у = arctg x 0 a(a — l)-(a —n + l)xa~" (-l)"-‘(n _ i)!x-o (0! = 1) ex ax In" a sin (x + лп/2) cos (x + лп/2) fsh x при n — 2k, Ich x при n = 2k — 1 (ch x при n = 2k, Ish x при n - = 2k — 1 = {n— 1)! cos" у sin n(y + n/2)
Производная линейной комбинации
(аи + ри)(п) — аи(п) 4- ри(п).
Формула Лейбница
(uv/”) = X CWn~k)vw
k = 0
108
(С*— биномиальные коэффициенты; и(0)= и, у(0) — у).
Дифференциалы высших порядков
d"y = f^xjdx'1 (х—независимая переменная),
dn(au + (Зу) = ad” и + pd"y,
d“(uu) = S Ckldn-kudkv.
k = 0
Производные функции, заданной параметрически
, у\ ,, Ю y't^'t — х'ёу\
>X = У;г- =~ --------— = -----------7~7^--------
Xt x'l (x[)
, (n) (Ул-''’)/'
=----------— > Ух- = ----------------;----
Xt xt
Формула конечных приращений
f(b) — /(а) = Г(а + — а)) (Ь — а), 0 < 0 < 1,
\f = f(xQ + Ах) — / (хо) = f'(x0 + ОАх) Ах, 0 < 0 < I.
Формула отношения конечных приращений
f(fe)-f(g) r(a + e(Z,_Q))
g(b) — g{a) g\a + e(b -a))’
Раскрытие неопределенностей
О оо
вида — и — по правилу Лопиталя
О оо
lim ——— =
х-^а g(x)
lim
х-^-а
Г(х)
g'W
f' (х)
(если lim v существует).
g'(x)
Локальный экстремум дифференцируемой функции
Необходимое условие локального экстремума
Если Хо — точка локального экстремума функции f, то /'(хо) = О.
109
Достаточные условия локального экстремума
I правило. Пусть f'(xo) = 0.
Если f' при переходе через точку Хо меняет знак с «-(-» на « —»,
то Хо — точка локального максимума.
Если f' при переходе через точку хо меняет знак с «—» на « + »,
то хо — точка локального минимума.
Если f' при переходе через точку х0 не меняет знака, то точка Хо
не является точкой локального экстремума.
II правило. Пусть f дважды дифференцируема в точке х0, ['(х0) =
= 0, f"(xo)=#O.
Если f"(xo)<O, то Хо — точка локального максимума.
Если f"(х0)> 0, то Хо — точка локального минимума.
III правило. Пусть f п раз непрерывно дифференцируема в
точке хо и f'(x0) = f"(x0) =... = f(rt-1)(x0) = 0, ^")(хо)#=О.
Если n-—четное и (х0) < О, то х0 — точка локального мак-
симума.
Если п — четное и fw(x0) > 0, то х0 — точка локального ми-
нимума.
Если п — нечетное, то Хо не является точкой локального эк-
стремума.
Выпуклые функции
Функция f на интервале ]а; Ь[:
1) выпукла (выпукла вниз), если
f((l — а)х, + ах2) < (1 — а)/(Х|) + а/(х2)
V Xi, х2 Е ]а; b[, V а € [0; 1];
2) строго выпукла (строго выпукла вниз), если
f((l — a)xi + ах2) < (1 — a)f(xi) + а/(х2)
V Xi, x2g]a; xi =/= х2, 7 а Е ]0; 1[;
3) выпукла вверх, если
f((l — а)Х| + ах2) >(1 — a)f(xi) + а/(х2)
V xi, х2 Е ]«; b[, V а Е [0; 1]
4) строго выпукла вверх, если
f((l — a)xi 4- ах2) > (1 — a)f(xi) + af(x2)
V xi, х2 Е ]а; b[, xi #= х2, V а Е ]0; 1[.
Признаки выпуклости дифференцируемых функций
1. Если f' возрастает на ]а; 6[, то f выпукла на ]а; (если f'
строго возрастает, то f строго выпукла).
2. Если f”(x)^O Vx Е ]а; Ь[, то f выпукла на ]а; Ь[ (если
обращаясь в нуль, возможно, лишь в конечном числе точек, то f
строго выпукла).
3. Функция f выпукла тогда и только тогда, когда график функ-
ции лежит не ниже касательной, проведенной к нему в любой его
точке.
110
Свойства выпуклых функций
(« \ п п
2 a.kxk ) с S akf{xk) \xk Е ]а; 6[, ° С ak С 1, S at = 1.
k=\ / k=\ k=\
В частности: f(atXi + a2x2) С aif(xi) + a2f(x2) Vxi, x2 € ]a; fe[, 0 < a, < 1,
0 a2 < 1, a । + a2 = 1.
f(x) — f(x,) f(x2) —f(x,)
2. --------------------у x,, X2< x £ a; w x < % <; x2.
X — X1 Х-2 — X|
3. Точки любой дуги графика лежат под хордой, стягивающей
эту дугу.
4. Функция f непрерывна на интервале ]а; Ь[ и имеет в каждой его
точке конечные односторонние производные.
5. Функция f имеет на ]а; Ь[ не более одного локального минимума и
не имеет локальных максимумов.
Точки перегиба
Пусть функция f определена в некоторой окрестности точки х0,
непрерывна в точке Хо и имеет в этой точке конечную или бесконечную
производную. Если при переходе через точку хо функция f меняет
направление выпуклости, то х0 называют точкой перегиба функции f,
а точку (х0; f(xoj)— точкой перегиба графика функции f. График функ-
ции переходит с одной стороны касательной, проведенной в точке
(хо; f(x0)), на другую сторону. Точки перегиба f — точки экстремума
ДЛЯ f'.
Необходимые условия наличия перегиба
/"(хо) —0 либо /"(хо) не существует.
Достаточные условия наличия перегиба
1. Если /"(х) меняет знак при переходе через точку хо, то хо —
точка перегиба.
2. Если )"(х0) =/'"(х0) = ...==/('1~')(хо) = О, /(л)(х0) #= О, то при п
четном Хо — точка перегиба, при п нечетном Хо не является точкой
перегиба.
6.3. ФОРМУЛА ТЕЙЛОРА. СТЕПЕННЫЕ РЯДЫ
Формула Тейлора
/(х) = f(a) + -IM (х - a) + (x - a)’ +... +
+ -4^(х-д)л + /?л(х)
(/?n(x)— остаточный член формулы Тейлора).
Остаточный член формулы Тейлора
В форме Лагранжа:
R„(x)= '(',+11(а + (>(-п» (Х^Г'. 0<е<!.
(п + 1)!
111
В форме Коши:
/(" + ')(а + 01(х-а))
/?„(х) =-----------------L(i — 0|)"(х — а)" +*, 0 < 0, < 1.
В форме Пеано:
Rn(x) = о((х — а)п) при х-+а.
В интегральной форме:
Rn(x)= -L j +
Ш"н
ir.WI<4A_;
(!+,)=! + a, + ++...+ ;<“-" +) +
+ Rn(x), x£]—1; 1[,
R„(x) = ~ ~ (1 + 0x)a-n 1 (1 - 0)''x'' + 1, 0 < 0 < 1,
Многочлен Тейлора порядка п
|x|n +1 | 1 + 0x|
1)
2)
Тп(х) — /(«) + ) (х — а)+ — (х — а)2 +... ф-
Формула Тейлора
для некоторых элементарных функций
Ox
Rn (x) = -Л.
(« + 1)!
X , X5 , r2"'-1
D , . sin(2"i+°(0x) ?m, .
'MX>=~ (2,0+1)! j + - °<0<
ID / \ I I Л I
!^2'"WI ^72^+1)! ;
х2 х4 Y~"‘
cos х = I - — + _ - ... + (_ 1Г-р^- + Яг,. + | W,
„ , . COS(2", + 2)(0x) 2 J 2
^ + 'W=-(2,n + 2)! X • O<0< I.
1п(1+х) = х-Д1 + ^_...+
*£[0; I]:
п
/?„(х) =---------------------- 0 < 0 < 1
(« + 1)(1 +0х)п+' ’ *•
4~ I
|Л.(х)| < -±—
х € ]— 1; 0[:
arctg x — x —
3
+ __...+(_ If _+R!_.)!w
x€[ —1; 1|.
I rI2m + 3
|/?2m + 2«| < 4-LrT.
2m + 3
Ряд Тейлора
1(a) + -a)+ (* - «У2 + - + f - a)n +... =
Основные разложения в ряд Тейлора
г хп
£=1 + -ir + ^- + -+5o-+-xeR-
±д=х - 4+4—+<- (44v+ х е *
1 - 4+4 -+<-1>"-44 +••••хе R’
In (1+х) = х-^ + ^ - + (-1)"-'4+- х£|-|; '!
(I + х)а = 1 + ах -|-—-- х* +... +
+ a(a - *)••.•(« ~п + .4 хп + х е ]- 1; Ц,
V5 Х^т '
arctgX = X- _ + -^ -... + (-|f-'^-—j- +.... ieH; 1].
Некоторые другие разложения
х3 X5 X2"1'1
sh х = X + — + -gj- + - + (2,„_ 1}! +••- х 6 R,
112
X~ Y1 Y-"'
ch X = 1 J------L —---1_ _|__x I .. Г p
-r 2! -r 4! + - + (2m)! +..., A(ER,
1 4- X Y3 1-5 r2in — I
Т^т=2(.1 + -г + Л.+...+ ^__ц>
1
T+7 = 1 ~x + x' -••• + (- *6]-1; If,
1
T—x = 1 + x + *’+••• + Xn +..., x€]-l; If,
1
-j——г — 1 + 2x + 3x- +- + (n + l)x" +..., X c ]— 1;
vr+x = l + lx- > >+ I
о lb
+ (-!)'
(2n — 3)!! ,
(2л)!! X
l 1 - 3
Ух+-8
€1-1; i],-
16
+ (-!)'
(2л — 1)!!
x +-’ ^J-1; 1],
arcsin x = x 4-!— x3 4-----1 ‘ r5 -4-
2-3 + 2-4-5 X +-“
, (2/1 — 1)!! x2"+l
+ “ (2n)!! 2T+T %€[-l; 1],
4- л/Пк V2\ — v _ 1 „3 , 1-3
2-3 2-4-5 ~-
+ (— 1Г - — 1)!! 2n+ ,
+ ( } (2л)!!(2л + 1) +"’’ x€I“,; 4-
Степенные ряды
ОО
2 сп(х — а)п.
п = 0
Радиус сходимости
(формула Коши — Адамара),
R ~ lim I -—-— I , /? -------------
/1->оо I С„+| I п[
hm Л/|c,J
П—> оо
Интервал сходимости
\a-R-, а +/?[.
114
Действия над степенными рядами
Если Rt — радиус сходимости ряда 2 апхп, R2 — радиус сходи-
п = 0
ОО
мости ряда 2 Ьпхп, а, |3 — числа, то
« = о
а 2 апхп + р 2 Ьпхп — 2 (аа„ + pbn)xn, |х| < min {/?i, R2[,
п = 0 п = 0 п = 0
У ОО X Z ОО к ОО , П \
( 2 апхп)( 2 Ьпхп) = 2(2
IхI < min (/?i, R2};
( 2 ant^dt— 2 antndt, | а I < R\, |x| <ZRe,
a 'л =0 ' (i =0 а
( 2 апх"') — 2 nanxn~\ |x| </?i.
\ л = 0 / (1=1
6.4. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Функции двух переменных
Приращение функции
bf = Д*о + Ах, уо + Ay) — f(x0, Уо).
Функция, дифференцируемая в точке (хо; уо)
А/ — А Ах + ВАу + о(р) при р->0 (р = "\/Ах2 + Ау2).
В этом случае дифференциал функции в точке (х0; уо):
df = ЛАх + ВАу, df = ~^-dx + -^-dy,
df df , ,
' , —----частные производные, вычисленные в точке (х0; уо).
дх ду
Дифференцирование композиции
1. Если z = f(x, у), х = x(t), y—:y{t), то
dz _ __, df dy
dt ~~ dx dl dy dt
2. Если z~ [(x, у), x = x(/, s), y = y(t, s), to:
dz _ df dx df dy
dt dx dt dy dt
115
dz _ df dx df ду
ds dx ds ду ds ’
. dz , , dz , dz , dz
dz = + -^“4 =-dTdt + ~Wds
Однородная функция степени k
f(tx, ty) = tkf(x, y)Vx, у, t.
Тождество Эйлера для однородной функции степени k
Формула конечных приращений
f (x0 + Ax, у о + Ay) — / (хо, уо) = Щх0 + 0Дх, у0 + 0 Ду) Ах +
+ f'y(xo + 9Ах, уо + 0Ау)Ду, О < 0 < I.
Градиент функции f
, f df - df -
grad + "X~/-
dx dy
npoueeodnan no направлению, onpedeляeмoмy
вектором I = cos a • z + sin a • j
df dj df . df
« “ d?cos“+*7slna- -gr=sr^i-i.
Частные npoueeodiibie высших порядков
Равенство смешанных производных
d2f __ d2f
дхду дудх ’
если указанные производные непрерывны.
116
Дифференциалы высших порядков
(х, у — независимые переменные)
d2f = -^-^2 + 2
d2f
дхду
. . , d2f , 2
dxdy + —— dy ,
dy2
m
dmf — У cz yv . =
L-j dx dy
k = o
( д d \m
dmf = (-^-dx + -г-dy) f,
1 \ dx dy )
. d , . d , ,,
где d = -y- dx —— dy — оператор дифференцирования.
Формула Тейлора
f(x< У) = Кхо> У») + у (фдфХ ~+ "ду”^ У°)+-" +
+ “ %о) + 1^У " Уо)) /(х°’ Уо) + R'”'
у 1 1 dkf(x0, уф
L k\ и охк
f(x, у) —
k-\- / < т
d'f(xu, уф
X --------—7----- (Х — Л'О) (У — У-Ф + R,;,-
ду'
Формула Тейлора в дифференциалах
dj , d2f ' , d'nf ( dm + 1/(xo + OAx, i/o + ОЛу)
Л/ ТГ + ~2Г + "• + ml (т + 1)!
о<е < 1.
Производные функций, заданных неявно
Если у = (р(х) определяется уравнением Е(х, у) = 0, то
F'x(x, ф(х))
<Р W = ~ “F77---77Г’
Е,(х, ср (%))
Fx
кратко: у' =-----;
Су
ч>"«- - ттк-(С'-т;2- +
(фу)
Локальный экстремум функции двух переменных
Необходимое условие локального экстремума
дифференцируемой функции
Если (х0; уо) — точка экстремума функции f, то
117
-^-(х0, Уо) = О и -^-(х0; Уо) = О, или df(x0, уф = О.
Достаточные условия локального экстремума
дважды дифференцируемой функции
d~f d2f d~f
Обозначим А = —'-(х0, уф, В = (х0> Уо), С = --'—(х0, уф,
дх дхду ду
Если D > О, А > 0, то (х0; уо) — точка минимума.
Если D > О, А < 0, то (хо; уф — точка максимума.
Если D < О, экстремума в точке (хо; уф нет.
Если D = 0, необходимы дополнительные исследования.
Функции п переменных
u = f(xi, х2, хф.
Приращение функции в точке (х?, х2; ...; х°)
Af = f(x? + Axl> .... х“ + Ах„) - Дх?; х°).
Функция, дифференцируемая в точке (х?; х2; ...; х°)
А/ — А । Ах, Л2Дх2 +... 4- АпАхп + о(р) при р->0
/ Г~п \
\р = \XAxIJ. в этом случае дифференциал функции f в точке
(4; х2; ...; х2):
df = AlAxi 4- А2Дх2 4-... 4- АпАхп,
df — I dx\ 4—dxz 4~ ••• 4—dxn,
dxt дх2 дхп
df f' df f'
~дхф =,х‘’ частные производные первого порядка функ-
ции f.
Дифференцирование композиции
Если U = f(X|, Х2) ..., хф, Xk = <fk(tl, t2, .... /т), А=1, 2, ..., п, то
ди _ df dtfi df дц)2 ( ( df dqn . , n
dtj ~ dxt dtj + dx2 dti +-+~д7ф ~dt~'
n m
, У ди . V du
du= J -3—dxk = / -r— dt;.
l—j dxk L—t dt, ‘
t=i /=1
Дифференциалы высших порядков
(xi, x2, ..., xn — независимые переменные)
,2 д2и Q д2и 2 д2и 2
du — -—у- dx~i 4- -j- dx2 4-... 4- —-у dx2 4-
dxf dxi дх2п
118
-^2 -j2
+ 2 ——— dxidxi + 2 — dxidx3 4-... 4-
дх idx2 ОХ|ОХ3
д^и д'и
4~ 2 ———— dx2dxz +... -j- 2 —j------ч - dxn— [dxn,
дх2дхз dxn_idxn
,2 / д д д \2
d и — (—-— dxi 4—ч— ах2 4- 4—з— dxn I и,
\ дх\ дх2 дхп /
d и — I —— dxi 4- —— dx2 4" ••• 4- ~— ахп I и,
\ dxi дх2 дхп /
где d — dx\ 4—Д- dx2 4- ... 4—Д- dxn — оператор дифференци-
дх\ дх2 дхп
рования.
Формула Тейлора
V 4-^4- , ,
‘f-"iT + ‘2r+-+“Sr +
(х° 4- 9Axi, .... хй 4- №хп)
, 0 < 0
(т+ 1)!
Локальный экстремум функции п переменных
Необходимое условие экстремума
дифференцируемой функции
Если (х?; х§; ...; х„) — точка экстремума функции f, то
-Д-(х?, х°, ..., х°) = 0, k=\, 2, ..., п, или й[(х(1, х", ..., х°) = 0.
дхк
Достаточное условие экстремума
дважды дифференцируемой функции
Если S IdxJ^O, df(xi, ..., хЙ) = 0 и d2f(x?....... хЙ) < 0, то
fe = i
(х?; х”; ...; хй) — точка максимума.
Если S |dxJ=#0, df(xl хЙ....... хЙ) = 0 и d2f(x°i, хЙ, .... хЙ) > О,
fc=i
то (х°; хй; хй) — точка минимума.
Условный экстремум
Постановка задачи
В области D найти экстремумы функции u = f(xi, х2, ..., х„) при
условии, что переменные Xi, х2, .... хп в Ь удовлетворяют m (m < п) усло-
виям (связям):
Ф! (Х|, Х2, Хп) — О,
Ф2(Х1, Х2, ..., Хп) = 0, , .
Фт(Х1, Х2, ..., Х„) — О,
119
причем функции Ф|, Фг, Ф,я независимы в D.
Необходимые условия локального
условия экстремума
Функция Лагранжа
L — I + А,|Ф1 + Х2Ф2 + ... + А.„|ФШ.
Если (х°; х°; ...; х”) — точка локального условного экстремума, то
в этой точке
—-—— 0, 6=1, 2, ..., л; Ф, — 0, i—1, 2, ..., пг.
dxk
(2)
Каждой точке экстремума сопутствует единственный набор чисел
Достаточные условия локального
условного экстремума
Пусть (х?, хг, ..., х„; X?, Хг, .... Х„) — решение системы (2), d2L —
второй дифференциал функции Лагранжа, вычисленный в этой точке,
а часть переменных dxi, dx?, dxn в d2L исключена с помощью
соотношений £/Ф| = 0, </Фэ — О, ..., (/Фт = 0, полученных дифференци-
рованием условий (1).
Если получившаяся квадратичная форма d2L есть положительно
определенная квадратичная форма п — m переменных, то (х°; х"; ...;
х°) — точка условного локального минимума, если же d2L — отрица-
тельно определенная квадратичная форма, то (х?; х°; ...; х°)—точка
условного локального максимума.
Выпуклые функции п переменных
Выпуклое множество
Множество D с R" называется выпуклым, если вместе с точками
X, Y оно содержит отрезок [ХЕ]: XX, Y £ £>=>(!— а)Х -ф аУ Е D Va£
е 10; 1J.
Выпуклые функции
Функция и = f(X), заданная на выпуклом множестве D, называется
выпуклой, если
/((1 _ а)Х + аУ) < (1 - a)f (X) -ф а/(У)
VX, У Е D, VaE[0; 1],
и строго выпуклой, если
/((1 - а)Х + а У) < (1 - а)/(Х) -ф а/(У)
XX, Y£D, Х#= У, V а Е ]0; 1[.
120
Признак строгой выпуклости
Если в каждой точке X области D второй дифференциал d2f(X)
есть положительно-определенная квадратичная форма от дифферен-
циалов независимых переменных, то f строго выпукла в D.
Свойства строго выпуклых функций
Строго выпуклая функция имеет не более одной точки локального
минимума в D и ни одной точки локального максимума. Точки гло-
бального максимума строго выпуклой функции, определенной на вы-
пуклом компакте, лежат на границе этого компакта.
Если f дифференцируема, строго выпукла на выпуклой области D
и имеет стационарную точку Хо £ D, то Хо является точкой глобаль-
ного минимума f, притом единственной.
7. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
7.1. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНЫХ АРГУМЕНТОВ
Определение
На множестве U задана вектор-функция, если с каждой его точкой
М сопоставлен вектор г(М). Если U — множество точек на прямой и
на ней введена декартова координата t, то вектор-функция на U
является вектор-функцией одного скалярного аргумента: /-(/); если U —
множество точек на плоскости и на ней введена декартова система
координат Оии, то имеем вектор-функцию r(u, и) двух скалярных ар-
гументов.
Предел вектор-функции
а — предел г(М) в точке Л1о, если V е > 0 26(e) > О, ХМ, 0<
< IММ01 <^6(f)=> |r (М) — а | е. Запись: lim г (Л4) = а.
М^М0
Если lim г,(Л4) = а,- (7=1, 2, 3), lim f(M) = а, то:
М->-Мо Л1-»-Л1о
lim (ri (Л1) ± r2(M)) = at ± а2,
lim (/(М)Г1(М)) = аа1( lim (гЦМ) • г2(М)) = а, • а2,
М->-Мо М-ьЛ70
lim [r1(M)r2(M)| = [ак32], lim (rl(M)r2(M)r3(M)) — ata«a3.
Непрерывность вектор-функции
г (М) непрерывна в точке Мо, если lim г (М) — г (Мо). Вектоо-
М—Мо
функция г (Л1), непрерывная в каждой точке множества U, называется
непрерывной на множестве U.
Дифференцирование вектор-функции
Производные вектор-функции г (/)
-,/л dr г (I + ft) — г (/)
dt h-^0 II
= (r"(/))z, ..., ?"’(/)-(/'’-’’(О/.
122
Если г, (/) и f(f) дифференцируемы, то:
(ri ± r2y = r{ ±r{, (fr)' = f'r + fr',
(ri • Г2у = r{ • r2 4- Г1 • r2', [Г1Г2]' = [rib] + [Г1Г2],
(г1Г2гз)/ = + Г\Г2гз 4“ Г\Г2Гз.
Дифференциал вектор-функции r(t): dr — г ’ (t)dt.
Дифференцирование вектор-функции двух скалярных аргументов
dr - г(и 4- h, v) — r(u, v)
---— ru = lim-----------------------’
du h^-o h
<0-=?.= lim 7("' ° +
du ft-*o h
dr — rudu 4- rvdv,
d2r - d . d2r - d ,
2" — Гиа — Д (r“)> j 2 — Гии —
du du dv dv
d2r _ d (-, d2r _ - _ d -
dudv du dvdu dv
Если rUu и rJU непрерывны, то гии = г^и и
d2r — rUudu2 + 2ruududv + rVJdv2.
Формула Тейлора
Для вектор-функции одного скалярного аргумента
7(/о4- ДО = Г(М+ Д^'(/о)4- - g)— /•"(/о)4~ —4-
+ -^гг“г7(л)(/о)+?(/о’ Д/))’
где lim е (to, А/) — 0.
д/->о
Для вектор-функции двух скалярных аргументов
г(«4- Au, v + Ду) = г (и, v)~ydr(u, у) -ф d2r (и, у)4-.-4-
4- dnr (и, у) 4- (Д«2 4- Ду2)л/2е (и, у, Дм, Ду),
где du = Ди; dv — Ду; lim е(ы, у, Ди, Ду) = 0.
\и- + Ди2->-0
7.2. ПЛОСКИЕ ЛИНИИ
Способы аналитического задания
1. г — r^f — x^fi 4- у(Т) / — векторно-параметрическое уравнение.
123
Jx = x(/),
х. । _ , — параметрические уравнения.
mJ У \Ч
3. у — f(x) — явное уравнение.
4. F(x, у) = 0—неявное уравнение.
Уравнение касательной к линии.
Для линий, заданных уравнениями 1—4, уравнения касательных
будут соответственно:
1) p(X) = 7+V'; =
х' у'
3) У-у = f'(x)(X-x); 4) (Х-х)/Л+ (Е-у)Е' = 0,
где X, Y — текущие координаты точки на касательной; р — радиус-
вектор этой точки; х, у — координаты точки касания; X — параметр.
Уравнение нормали к линии
Для линий, заданных уравнениями 1—4, уравнения нормалей будут
соответственно:
1) (р-7(/))т'(/) = 0; 2) (Х-х)х' + (Г-у)у' = 0;
3) Х-х + (У-у)Д(х)=0;4) 2L=A = 22=А.
Fy
Соприкосновение k-ro порядка
1. Линии г = rt(s) и г — r2(s) имеют при s = so соприкосновение /г-го
порядка, если р = r2, dr\/ds = dr2/ds, ..., dkri/dsk = dk72/dsk,
dk+'r\/dsk + ' =# dk+'r2/dsk+'.
2. Если одна из линий задана уравнениями х = х(/), у = y(t\
а другая — уравнением /Дх, у) — 0, то в точке соприкосновения /г-го
порядка: F(x(t), y(tj) — 0, dF/dt = О, ..., dkF/dtk = 0, dk + lF/dtk +1 0.
Асимптоты линии
Вертикальные асимптоты
1. Линия задана уравнением у = Дх). Если limf(x)=oo, то
х-+а
х — а— вертикальная асимптота. В частности, если lim Дх) = оо,
x->a-(-0
то х = а — вертикальная правосторонняя асимптота; если же
lim f(x)=oo, то х — а — вертикальная левосторонняя асимптота.
2. Линия задана уравнениями х — х(Г), у = y(f). Если lim х(/) = а,
/—►/о
lim «/(/)== оо, то х = а — вертикальная асимптота. В частности, если
limx(/) = a + 0, lim y(t)= оо, то х — а—вертикальная правосторон-
t-+t0
няя асимптота; если же lim x(t) = а — 0, lim y(t)= оо, то х = а —
вертикальная левосторонняя асимптота.
124
Наклонные асимптоты
1. Линия задана уравнением y = f(x).
Если lim(f(x) — kx— b) = 0, то прямая у — kx + b — наклонная
Х~> ОО
f (х)
асимптота. При этом k = lim ------, b— lim (f(x) — kx).
x—>oo X X—>oo
Если lim (f(x) — kx — b) = 0, то прямая у — kxb — наклонная
X-* -J- oo
f (-^)
асимптота вправо, k — lim --------, b— lim (f(x) — kx).
x->+oo X x-*- + 0
Если lim (f(x) — kx — b) = 0, то у — kx + b — наклонная асимп-
— оо
f (-^)
тота влево, k = lim -------, b= lim (f(x) — kx).
X—> — оо X x—> — oo
2. Линия задана уравнениями x — x(/), y — y(t).
Если limx(/)=oo, lirny(f) —a (a —конечное число либо один
из символов —оо, со) и линия обладает асимптотой y = kx-\-b,
то /г = lim , b— lim (y(t) — kx(t)).
x(t) t^ta
Длина дуги (натуральный параметр) линии
б
г = r(t)=>s = \r'(t)\dt,
h
X = X(t)\ ? / ,2 ,2 ,.
(=>s= д/х + у' (it,
у = у(Х)> /,
У = IW=>s = \ V1 +f'2(x)dx,
<₽2 ______
r = r(<p)=^s= 5 д/г2 + r,2d(p.
<₽i
Дифференциал длины дуги
В декартовых координатах:
ds — \dr\ = д/dx2 + dy2 — д/х'2 + У'2 dt.
В полярных координатах:
ds = x[dr2 Ц- r2dq2 = xjr2 + r,2dq.
Кривизна линии
г ~ r(t) =>k — ^Г_/ -, г — r{s)^k = | г |,
IrT
X = x(/),l _ \x'y" -x"y'\
У ~ y(J) ' (x'2 + y' )i/2
125
y = f(x)=>k
\у"\
(1 + y'2)3/2 ’
F(x, y)=O=>k =
r = r(cp)=> & —
Радиус кривизны: R = \/k.
Натуральные уравнения линии
* = ад, F(k, s)=o.
Формулы Френе
dr - dv
—— — «V, —— = — kx,
ds ds
где т — единичный вектор касательной; v — единичный вектор нормали;
k — кривизна.
Семейство линий. Огибающая
Особые точки линии F(x, у) = 0 — точки, для которых F(x, у) = О,
К(х, у) = 0, F'y(x, у) = 0.
Уравнение семейства линий: F(x, у, С) — 0, где С—параметр.
Дискриминантная линия семейства F(x, у, С) = 0.’
F(x, у, С) — 0, F'c(x, у, С) = 0.
Если в точках дискриминантной линии F'x2 + F'2 > 0, то она явля-
ется огибающей. Случай F'x = Fy = 0 требует дополнительного исследо-
вания.
7.3. ПРОСТРАНСТВЕННЫЕ ЛИНИИ
Способы аналитического задания линий
1. г — r(t) — x(t)i + y(t)j -f- z(/)&— векторно-параметрическое урав-
нение.
{х — x{t),
у = y{t), — параметрические уравнения.
z = z(/)
у = фМ,
z —
— явное задание.
[F(x, у, а)-=0,
4. — неявное задание.
1Ф(х, у, а) = 0
126
Элементы сопровождающего трехгранника (рис. 7.1)
Уравнение касательной прямей
(X, У, Z — текущие координаты точ-
ки на касательной; р — радиус-век-
тор этой точки; х, у, z — координаты
точки касания)
1. р(А) = г + кг'.
, Х — х Y-y
2. -----— =---
X у
F'y Ft
Ф£ Фг
‘ У-у
F' F'x
Ф' ф;
ГлаВная
нормаль
F'x F'y
ф; ф;
Уравнение нормальной плоскости
1. (р — г) • г' — 0.
2. (X - х)х' + (У - у)у' + (Z - ф' = 0.
Х-х У-У Z — z
F’x F'y Ft
ф( Ф^ ф:
Уравнение главной нормали
1. р = г-|-
Уравнение бинормали
1. р = Г + к г'г"].
X — х У — у Z — z
I у' z I I z' х' I I х' у' 1
I у" z" I I z" х" I I х" у" I
Уравнение соприкасающейся плоскости
1. (р — г)г'г" = 0
X - X у-у Z — z
2. х' у' z' = 0
х" у" z"
127
Уравнение спрямляющей плоскости
*' у'
к" у"
Единичные векторы осей
сопровождающего трехгранника
Касательной: т = г'/|г'| = г.
г » ~ [[/-'г"]/-'] Г
I лавнои нормали: и — —------------—-— = ——.
1[г'г"]| |г'| И
Г о [г’г"\ [гг]
Бинормали: р = _ = .. .
1[г'г"]| |г|
Длина дуги (натуральный параметр) линии
7=7(t)=>s = 5 \7'(t)\dt,
ti
( х = х(/), t,__________________
) У = y(0. => S = j Vх'2 + у'2 + z'2dt,
I z = z(/) У
IУ = У W. ? л--------------7i-------Г
I / \ 5 — ] у 1 -I- у z' dx.
1г = г(х) v
Дифференциал длины дуги
В декартовых координатах:
ds = \ dr \ = д/dx2 4- dy2 + dz2 = д/х'2 + у'2 + z'2dt.
В цилиндрических координатах:
ds — xjdr2 4- r2d<p2 + dz2.
В сферических координатах:
ds — д4/р2 4- p2dO2 4- р2 sin2 0dq>2.
Кривизна линии
г — г (/) k =
г = г (s) => /г = I г |,
128
X — x(s),
V z = z(s)
Радиус кривизны; R = \/k.
Кручение линии
X = x(/),
у = y(J\
Z = 2(/)
У 2
Z
Натуральные уравнения линии
X = A'(s),
y = y(s), =>
2 = 2(S)
k = k (s),
.X —
Формулы Френе
— — kv, v = H + xp,
ds ds
p = —— = —xv.
ds
7.4. ПОВЕРХНОСТИ
Способы аналитического задания
1. Г = r(u, a) = x(u, v)i + y(u, v)j + z(u, v)k — векторно-параметри-
ческое уравнение.
5 Воднев В. T. и др
129
j X = x(u, v),
2. \ У — y(u, v),—параметрические уравнения.
\ z = z(«, v)
3. z = f(x, y) — явное уравнение.
4. F(x, у, z) = 0 — неявное уравнение.
Касательная плоскость к поверхности
(X, Y, Z — текущие координаты точки на касательной плоскости;
р — радиус-вектор этой точки; х, у, z — координаты точки касания
, . - д г - дг
(соответственно для нормали); г„ = ——, ги = —-------касательные век-
ди ди
торы к координатным линиям соответственно v — const, и = const; хи —
дх дх
= -ч—, ха = ——, ...)
ди до
I. (р —- г) гиг и = 0.
Х — х у-у Z — z
2. хи Уч Zu = 0.
X и У V Zv
4. (X - x)F'x + (Y - y)F' + (Z - z)F' = 0.
Нормаль к поверхности
1. Р = г + Х[гиг„].
2.
3.
4.
Х — х _ Y — y _ Z — z
Уи Zu Zu Хц Хц Уи |
Уи Zu Zu Хи Хи Уи
X — х Y — у _ Z — z
fl = ~fl~ = -1
Y — у __ Z — z
~~fT~ ~ ~fT~
Единичный вектор нормали к поверхности
при этом [г;1г„] =
У и
У»
Zu
Zv
У“ k.
У«
Точки, в которых [гцгр] = 0, называются особыми.
130
Первая основная квадратичная форма поверхности
ф, = ds2 — dr2 — Edu2 + 2Fdudv Д- Gdv2,
где
dr = rudu + rvdv,
E = E(u, v) = ru • ru = r2u = x2u + y2 + z2u,
F — F (u, I/) — Г и • ru —XuXv Д- уиУv I Z„ZV,
G = G(u, u) = rv • r„ = r~ — X2 + Уи + zi,
в неособых точках E > 0, G > 0, EG — F2 > 0.
Угол между двумя линиями на поверхности
Косинус угла между двумя линиями r = ri(f) (или и = и\(1), и —
= ui(/)) и г = r2(f) (или и — u2(t), о — 02(C). проходящими через точ-
ку («; f). _ _
dri dr2
cos ф = ——-------—— =
И/'ll \dr2\
Eduidu2 + F(du\dv2 + du2dvd) + Gdvidv2
-\jEdu2 + 2Fdu\dv\ 4- Gdv2 -y^Edu2 + 2Fdu2dv2 + Gdv%
Если t — s, to
dui du2 / du[ dv2 du2 dv\ \ dv\ dv2
cos ip — E — --------[- El —----j----1-------3— ) + G —------— .
ds ds \ ds ds ds ds / ds ds
Для угла между координатными линиями:
F . -JEG- F2
COS ф = ——7 ИЛИ Sin ф = --------=—.
д/eg -\Ieg
Плошадь замкнутой области на поверхности
S = \\^\\rur„.\\2diidv = д/EG — F2dudv.
D D
Вторая основная квадратичная форма поверхности
ф2 — — dr • dti == п • d2r = Ldu2 + 2Mdudv + ^dc|3,
где n — единичный вектор нормали к поверхности;
— — — — и и F и Г v
L = L(u, V) = П • Гии = —Пи Ги = —
_ - - - - - ruvrur-j
М = Л1(и, и) = —Пи • rv — —tlv • Г и — п • ruv = —-----—;
д/EG - F2
- - - - ГииГиГи
N = ^(U, и) = tl • rvv — —nv • rv = —
-\EG - F'2
131
Кривизна нормального сечения (нормальная кривизна)
линии на поверхности
dr • dn
ds2
= L
. n.. du du , / du V
+ 2Л1 —----------h ЛЧ----) =
ds ds \ ds /
LduI 2 + 2Mdudv + Ndu2 tp2
Edu2 + 2Fdudv + Gdv2 <p.
Главные кривизны
Находятся как корни k\ и ki уравнения
(EG - F2}k2 -(JEN + LG- 2FM)k + LN - M2 = 0.
Формула Эйлера
kn = ki COS2 ф + k-2 sin2 tp,
где <p — угол между направлениями, соответствующими нормальным
кривизнам k\ и kn.
Средняя (эйлерова) кривизна поверхности
kx + k2 EN — 2FM + GL
2 2 (EG — E2)
Полная (гауссова) кривизна поверхности
К=Ы2 =
LN — М2
EG — F2 '
Типы точек поверхности
Эллиптическая точка — К > 0; гиперболическая — К < 0; парабо-
лическая — К — 0.
Главные направления. Линии кривизны
Направления du : du, для которых
I Ldu -j- Mdu
I Edu + Fdu
Mdu -j- Ndu I
Fdu + Gdv I
= 0,
называются главными, а линии, удовлетворяющие этому уравнению,—
линиями кривизны.
Сопряженные направления
Сопряженными называют направления, для которых
Lduidui + M{diixdv2 + du2du\) + Ndv\dv2 — 0.
132
Асимптотические направления и линии
Направления du : dv, для которых
Ldu2 + ZMdudv + Ndv2 — О,
называются асимптотическими направлениями, а линии, удовлетво-
ряющие этому уравнению,— асимптотическими линиями.
Геодезические линии
Геодезическими называются линии, удовлетворяющие условию
ndrd2r = О,
где п — вектор нормали к поверхности.
Если координатная сеть ортогональна, то дифференциальными
уравнениями геодезических линий будут:
или
Специальные классы координатных линий
Ортогональные о F = 0; сопряженные о- М — 0; линии кривиз-
ны о F — 0, М = 0; асимптотические о L = 0, N = 0.
7.5. СПЕЦИАЛЬНЫЕ КЛАССЫ ЛИНИЙ
И ПОВЕРХНОСТЕЙ
Линии на плоскости
Астроида (рис. 7.2)
(см. также гипоциклоиду модуля tn = 1/4).
Уравнение в декартовых координатах:
х2/3 + у2/3 _ ^2/3
Параметрические уравнения:
X — R cos3(//4), у = R sin3 (//4).
3
Площадь, ограниченная астроидой: S = — л/?2.
О
Длина дуги от точки А до произвольной точки М(/):
S/ = у R sin2 у ,
133
Длина всей астроиды: s = 6R.
Радиус кривизны в произвольной точке: Rk — — R sin
t
~2
Гипоциклоида (рис. 7.3)
Гипоциклоиду —линия, описываемая точкой окружности радиуса г,
катящейся без скольжения по другой окружности радиуса R внутри
нее (m = r/R— модуль гипоциклоиды)
Параметрические уравнения:
х = (R — mR) cos mt + mR cos (/ — mt),
у = (R — mR) sin mt — mR sin (/ — mt),
где mR = r.
Частные случаи см. на рис. 7.4.
Р и с. 7.4
134
Длина дуги от точки А до произвольной точки M(t):
st — 8mR(\ + tn) sin2 (//4).
Дтина одной ветви гипоциклоиды: s — 8mR(\ + m).
Площадь сектора, ограниченного одной ветвью линии:
S = тл(/? + mR) (R + 2т/?).
Радиус кривизны в произвольной точке:
4/?m(l-|-m) . /
/?/. =-------------------о -------sin —.
2m + 1 2
Декартов лист (рис. 7.5)
Декартов лист — линия, заданная уравнением
х3 + у3 — Заху = 0.
Параметрические уравнения:
За sin <р cos ф
Полярное уравнение: р =------z------г——.
sin3 ф +COS' ф
Асимптота: у — —х — а.
Площадь, ограниченная петлей декартова листа: S = За2/2.
Кардиоида (рис. 7.6)
(см. также эпициклоиду с модулем m = I)
Уравнение в декартовых координатах:
(х2 + у2 + 2гх)2 = 4г2 (х2 + у2).
Параметрические уравнения:
х — 2r cos t — г cos 2/, у — 2r sin t — г sin 2t.
Полярное уравнение (с полюсом в точке А):
р — 2г(1 — cos ф).
135
Длина дуги от точки А до произвольной точки М:
s9 — 16г sin2 (ф/4).
Длина всей кардиоиды: $ = 16г.
Площадь, ограниченная кардиоидой: S = блг2.
Радиус кривизны в произвольной точке:
„ 8 . ф
/д = -у г sin —.
Конхоида Никомеда (рис. 7.7)
Конхоида Никомеда — линия, полученная при увеличении или
уменьшении каждого радиуса-вектора точек данной прямой у = а на
одну и ту же величину /, т. е. ОЛ41 == ОК + /, ОМ2 = ОК — / Y К.
Уравнение в декартовых координатах:
+ у2) (У — а)2 — 12у2 = 0.
Полярное уравнение: р =—:-------± /.
sin ф
Асимптота: у = а.
Лемниската Бернулли (рис. 7.8)
(см. овалы Кассини при а = с).
Р и с. 7.8
Уравнение в декартовых коорди-
натах:
(х2 + у2)2 — 2а2 (х2 — у2) = 0.
Полярное уравнение: р2 = 2агсоз2ф.
Длина дуги лемнискаты между
точками, для которых ф| = 0 и ф2 = ф:
136
ч>
С dw
% = а \ ——Т
q у 1 — 2 sin2 <р
(эллиптический интеграл первого рода).
Площадь сектора между осью и радиусом-вектором, соответству-
„ °2 • о
ющим углу ф: = — sm 2ф.
Площадь, ограниченная лемнискатой: S = а2/2.
Радиус кривизны: R = р/(3 cos 2ф).
Локон (верзиера) Аньези (рис. 7.9)
Пусть имеется круг диаметром |ОС| = а. Локон Аньези — мно-
жество точек М, для каждой из которых OB : BD — ОС : ВМ.
Уравнение в декартовых координатах:
У = а3/(х2 + а2).
Асимптота: у — 0.
Площадь между верзиерой и ее асимптотой: S = ла2.
Рис. 7.10
Овалы Кассини (рис. 7.10)
Овалы Кассини — множество точек плоскости, произведение рас-
стояний от каждой из которых до двух данных точек (фокусов) постоянно.
Уравнение в декартовых координатах:
{х2 + у2)2 — 2с2(х2 — у2) = а4 — с4,
где Fi( — с; 0), F2(g 0)— фокусы; |MFi| |AfF2| — а2.
При а сд/Г линия выпуклая, при с <Z а <. cxj2 имеет вид овала
с двумя утолщениями, при а = с — лемниската Бернулли, при с > а
состоит из двух замкнутых линии.
137
Розы
р = a sin /гср, a, k > 0; a, k — const.
Уравнение, название График
р — a sin 3(р, трехлепестковая роза
р = a sin 2ф, четырехлепестковая роза
р — a sin (5ф/3)
р — a sin(4q/3)
138
Окончание
Общие свойства
1. Если k— нечетное число, роза состоит из k лепестков.
2. Если k — четное число, роза состоит из 2k лепестков.
3. Если k — m/n, п > 1,— рациональное число, роза состоит из
т лепестков при тип нечетных и из 2т лепестков, если одно из
этих чисел четное (при этом каждый следующий лепесток частично
покрывает предыдущий).
4. Если k — иррациональное число, роза состоит из бесчисленного
множества лепестков, частично накладывающихся друг на друга.
Спирали
139
Продолжение
Уравнение, название
График
Р =
спираль гиперболическая
р = ад/ср,
спираль «жезл»
о
спираль Корию
(клофоида)
cos —du.
= а
у = а
у — а
спираль параболическая
sin —— du,
р = ал, а
спираль логарифмическая
140
Окончание
Дополнительные сведения о некоторых спиралях
Гиперболическая спираль (р = а/<р)
Асимптота: у = а.
Площадь сектора, ограниченного дугой гиперболической спирали
и двумя радиусами-векторами pi и р2 с углами "ф| и фг:
$ — y(pi — рг)-
Длина дуги между точками Л41(рь cpi) и Мг(р2; фг):
s = аГ— 4- In (<р + д/1 +Ф2 )] •
L Ф J <Р!
Логарифмическая спираль (р = а4)
Длина дуги между точками М\(pt; ф1) и A42(p2'> фг):
Радиус кривизны: R = рд/1 + In2 а.
Спираль Архимеда (р — аф)
Длина дуги между точками М\(рь ф|) и М2(рг; фг):
s = у [фа/1 + Ф2 + In (ф + V1 + Ф2)]^-
Площадь сектора, ограниченного дугой спирали Архимеда и двумя
радиусами-векторами pi и рг, соответствующими углам ф1 и фг:
141
5 = (р2 — Pl)/(6а).
Площадь, ограниченная полярной осью и п-м витком спирали:
3„ = л3а2(п3 — (п — I)3).
Строфоида (рис. 7.11)
Даны точка О и прямая, находящаяся от точки О на расстоянии
ОА == а. Вокруг точки О вращается луч, пересекающий прямую в пе-
ременной точке В. Строфоида — множество точек Mit i — 1, 2, таких, что
ВМ\ = BMt = AB.
Уравнение в декартовых координатах:
(х2 -ф у2) (х — а)2 — а~у2 — 0.
Уравнение в полярных координатах:
р = a /cos <р ± a tg <р.
Параметрические уравнения:
Площадь, ограниченная петлей строфоиды:
3 = 2а2 — ла2/2.
Трактриса (рис. 7.12)
Трактриса —линия, у которой длина касательной является постоян-
ной величиной а.
Уравнение в декартовых координатах:
х = а In -У\ + _ уг
Параметрические уравнения:
х = a^ln tg-^- + cos tj, y = asint.
142
Длина дуги, отсчитываемая от точки
точки: st — —a In sin t.
Площадь, ограниченная трактрисой и
Радиус кривизны: R = a ctg t.
Д(0; а) до произвольной
ее асимптотой: S = ла2/2.
Улитка Паскаля (рис. 7.13)
Рис. 7.13
На произвольном луче ОА от точки А пересечения его с окруж-
ностью р = 2а cos ф по обе стороны откладываются отрезки AMi =
= AAfa = I — 2Ь. Улитка Паскаля — множество точек Mi.
Уравнение в декартовых координатах:
(х2 + у2 — 2ах)2 — /2(х2 + у2) = 0.
Уравнение в полярных координатах:
р = 2а cos ф ± /•
Площадь, ограниченная улиткой (для случая I > 2а):
S = л (2а2 + /2).
При I = 2а получается кардиоида.
Цепная линия (рис. 7.14)
Цепная линия — линия, форму кото-
рой принимает гибкая однородная, не-
растяжимая тяжелая нить с закрепленны-
ми концами.
Уравнение в декартовых координатах:
у = у (ех/а + е~х/а) = a ch -у.
Длина дуги от вершины до произволь-
ной точки Л1(х; у):
s = a sh — = у/у2 - а-. Рис. 7.14
а
Площадь, ограниченная цепной линией, двумя ее ординатами и
осью абсцисс:
S = a2 (sh - sh = a (xjyl - а2 - -y/rf-a2).
143
Радиус кривизны: R = a ch2 — — .
Циклоида—линия, которую описывает точка М, расположенная
на расстоянии d от центра круга радиуса а, катящегося без сколь-
жения по прямой. Если d — а, циклоида называется обыкновенной,
d > а,— удлиненной, d < а,— укороченной.
Обыкновенная циклоида
Параметрические уравнения:
х — a(t — sin /), у = а(1 — cos t).
Уравнение в декартовых координатах:
а — у г у
х = a arccos —-----~\2ау — у .
Длина дуги циклоиды от исходной точки (/ — 0) до произвольной
точки Л1(/):
s( — 8а sin2 (//4).
Длина одной арки циклоиды: s = 8а.
Площадь, ограниченная одной аркой циклоиды и ее базисом: S —
= Зла2.
Радиус кривизны в произвольной точке: R = 4а sin (//2).
Удлиненная (укороченная) циклоида
Параметрические уравнения:
х = at — d sin t, у = a — d cos t.
Циссоида Диоклеса (рис. 7.16)
Пусть даны окружность диаметром ОА = 2а и касательная к ней
в точке А и пусть ОВ — произвольный луч. Циссоида Диоклеса —
множество точек М, для которых ОМ — СВ.
144
Уравнение в декартовых координатах:
у2 — х3 /(2а — х).
Полярное уравнение:
Параметрические уравнения:
а _ а
Х = t2 + 1 ’ У ~ t(t2+ 1) ‘
Длина дуги циссоиды от ее вершины до
точки с абсциссой
Рис. 7.16
s = а(г — 2) +
(г-л/з)(2 + Уз) ,
(г + Уз)(2-У5) ’
где z — д/(4а — Зх)/(а — х).
Площадь, ограниченная циссоидой и ее асимптотой: S — Зла2.
Эвольвента (развертка) окружности (рис. 7.17)
Эвольвента окружности — траектория конца туго натянутой нити,
сматываемой с неподвижной круглой плоской катушки.
Параметрические уравнения:
х = a(cos t 4- t sin t), у = a(sin t — t cos t).
Длина дуги: s( = a/2/2.
Площадь сектора, ограниченного дугой эвольвенты, осью абсцисс
и радиусом-вектором ОМ: S=a2t3/6.
Радиус кривизны в произвольной точке: R—at.
Эпициклоида — линия, описываемая точкой окружности радиуса г,
145
катящейся без скольжения по другой окружности радиуса R вне ее
(m = r/R — модуль эпициклоиды).
Параметрические уравнения:
(х = (R + mR) cos mt — mR cos (/ 4- mt),
lz/ = (R + mR) sin mt — mR sin (/ + mt).
Формулы длины дуги,
такой же вид, как и для гипоциклоиды.
площади сектора, радиуса кривизны имеют
Линии в пространстве
Винтовая линия (рис. 7.20)
Рис. 7.20
Винтовая линия — линия, описываемая
точкой М, которая вращается с постоянной
угловой скоростью го вокруг неподвижной оси
(Ог) и одновременно перемещается поступа-
тельно с постоянной скоростью и вдоль
этой оси.
Параметрические уравнения:
х — a cos со/, у — a sin cof, z — vt
или
x = a cos ср, у = a sin ср, z = 6cp,
где a — радиус цилиндра, на котором располо-
жена линия; ср = cd/; b — v/ш = /г/2л; h —
шаг винтовой линии.
Проекции винтовой линии на координат-
ные плоскости:
на плоскость хОу:
х + у — а — окружность;
на плоскость yOz:
у = a sin(z/&) — синусоида;
на плоскость xOz:
х — a cos (z/b)— синусоида.
Длина винтовой линии от точки пересечения с плоскостью хОу до
произвольной точки Л1: s — ^\]а2 -f- b21.
Параметрические уравнения винтовой линии, где за параметр при-
нята длина дуги:
146
s . s bs
x = a cos —— у = a sin — z = — .........
да2 + b~ Дх*2 + b- -\ja2 + b2
Кривизна: k = c?/(a2 -|- b2).
Кручение: x = b/(a2 + ft2).
Линия Вивиани (рис. 7.21)
Линия Вивиани — линия пересечения сферы радиуса а круглой
цилиндрической поверхностью, диаметр которой равен радиусу сферы
и одна из образующих проходит через центр сферы.
Неявные уравнения:
х2 + у2 + z2 = а2,
,х2 -фу2 — ах — 0.
Параметрические уравнения:
х — a cos2 и, у = a cos и sin и, z= sin и,
Коническая спираль (рис. 7.22)
Коническая спираль — линия, описываемая точкой М, которая дви-
жется по прямой OL со скоростью, пропорциональной расстоянию
ОМ, а прямая OL, не перпендикулярная к оси Oz, равномерно враща-
ется вокруг нее с постоянной угловой скоростью со.
Параметрические уравнения:
х = аекч cos ср, у = aeh'f sin ср, z = beklf,
где /г = /п/со.
Коническая винтовая линия
Коническая винтовая линия —линия, описываемая точкой М, кото-
рая движется по прямой OL с постоянной скоростью, а прямая OL, не
147
перпендикулярная к оси Oz, равномерно вращается вокруг нее с посто-
янной угловой скоростью (см. рис. 7.22)
Параметрические уравнения:
х ~ at cos t, у — at sin t, z = bt.
Поверхности
Поверхность вращения
(от вращения линии х = /(м), z — ср(и) в плоскости xOz
вокруг оси Oz).
Параметрические уравнения:
{х — f (и) cos v,
у — f(u) sin v,
Z = 4>(u).
Первая квадратичная форма:
ds2 = (f'~ + (p'2)du2 + f2dv2.
Вторая квадратичная форма:
Ф2 = ------- ((Гф" — ф7")^и2 + fv'dv2).
V/' +ф'
Гауссова кривизна:
к _ ч>'(Кч>" — f"y')
КГ2 + ф'2)
Сфера (рис. 7.23)
Параметрические уравнения:
{х = R cos и cos v,
у — R cos и sin и,
z — R sin и.
Первая квадратичная форма:
ds2 = R2(du2 + cos2 udv2).
Вторая квадратичная форма:
ф2 = R(du2 cos2 udv2).
Гауссова кривизна: К — 1 /R2.
Тор (рис. 7.24)
Тор поверхность, которая получается при вращении окружности
х = а + b cos и, у = 0, z — b sin и, b С а вокруг оси Oz.
Параметрические уравнения:
148
х = (a + b cos u) cos v,
у = (a + b cos u) sin v,
z = b sin u.
Первая квадратичная форма:
ds2 = b2du2 + (a + b cos u)2dv2.
Вторая квадратичная форма:
(p2 — bdu2 + cos и (a + b cos u)dv2.
г cos u
Гауссова кривизна: К = -г-,—;—---------г"
b(a + b cos и)
Р И С. 7.24 Р II С. 7.25
Катеноид (рис. 7.25)
Катеноид— поверхность, которая получается при вращении цепной
линии x = ach(u/a), у — 0, z — и вокруг оси Oz.
Параметрические уравнения:
. и , и
х — а сп — cos V, у = а ch — sin v, z — и.
а а
Первая квадратичная форма:
ds2 — ch2 — du2 + a2 ch2 — dv2.
a a
Вторая квадратичная форма:
<рг = adv2-----du2,
a
Гауссова кривизна: К —----------------
J a2 ch1(u/a)
Псевдосфера (рис. 7.26)
Псевдосфера — поверхность, которая получается при вращении
149
трактрисы х = a sin и, у = 0, z = a(\nig ——f-cos вокруг оси Oz.
Параметрические уравнения:
{х = a sin и cos v,
у = a sin и sin v,
г = a(ln tg (ы/2) + cos и).
Первая квадратичная форма:
ds2 = a2 ctg2 и du2 + a2 sin2 и dv2.
Вторая квадратичная форма:
<р2 = a ( — ctg и du2 + sin и cos и dv2).
Гауссова кривизна: /< =—1 /а2.
Прямой геликоид (рис. 7.27)
Прямой геликоид— поверхность, образованная движением прямой,
вращающейся вокруг оси и перпендикулярной к ней и одновременно
поступательно движущейся в направлении этой оси, причем скорости
этих движений пропорциональны.
Параметрические уравнения:
х — и cos v, у = и sin v, z = av.
Первая квадратичная форма:
ds2 = du2 + (и2 + a2) dv2.
Вторая квадратичная форма:
2adudv
Ф2 = — —г—---- »
-уи2 4- а2
Гауссова кривизна: /< = — а2/(а2 + и2)2.
150
8. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
8.1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первообразная
Первообразной функции f на промежутке / называется функ-
ция F, такая, что F'(x) = f(x) Ух£/.
Неопределенный интеграл
\f(x)dx = F(x) + C,
где F — первообразная функции /' (на промежутке); С — произвольная
постоянная.
Основные свойства
1. (\[(x)dx)' = f(x), d\[(x)dx = f (x)dx.
2. \F'(x)dx = F(x) -ф C, \dF(x) — F(x) -ф C.
3. Если $ f(x)dx = F(x) -ф С, to
j f(ax -ф b)dx — ~F(ax + b) ф- C, a=^= 0.
4. \(a,f(x)-±-fig(x))dx — a \ f(x)dx + \ g(x)dx, a2-ф (32 0.
Замена переменных в неопределенном интеграле
1. f (и(хУ) и' (х) d х = $ f(u)du = F(u) -ф С — F(u(x\) -ф С.
2. Если х = <р(/), q/(/)#=0, F — первообразная для (g°(p)q/, то
5 g(x)dx = 5 g(<p(O)<P'(O^ = (О + С = F(cp~1 (х)) + С.
Формула интегрирования по частям
$ udv = uv — vdu,
(и, и—дифференцируемые функции).
Простейшие интегралы
0 • dx — С, I • dx = dx = х + С,
\ xdxz,~ -ф С, \ x‘2dx = -ф С,
J Л J о
151
\ " = arcsin х + С,
{ dx . х , л
\ - — arcsin-----р С,
х/а'2 — х2 а
— dx = In (х + д/х2 + 1) + С,
J Vx2 + 1
-7^-. = In |х + д/х2 — 1 I + С,
J д/Х2-1
J х/а2^2 dx = у х/а2 - х2 -f- ± arcsin ~ + С,
xjx2 + a dx= у xjx2 + а + ~ In |х + х]х2 + а | + С,
\ exdx = ех + С, \ axdx — ----р С,
J I п а
$ In xdx = X In X — X + С, $ sin xdx = — cos x + C,
152
J cos xdx = sin x + C,
I dx , _ f dx
\ ;— = —ctgx + C, \----------— = tgx4-C,
J sin X J COS* X
tg xdx — — In |cos x| + C, 5 ctg xdx — In ] sin x| + C,
5 sli xdx = ch x + C, J ch xdx = sh x + C,
( —— = — cth x + C, — th x + C,
J sh2 x J ch2x
th xdx = In ch x + C, J cth xdx = In J sh x| + C.
Интегрирование рациональных функций
Интегрирование простейших рациональных функций
( д
1. \ Axkdx = , , хк+ 1 + С, k #= — 1.
J /г + 1
I д
2. \ ------------dx = A In |х — а| 4- С.
J х — а
С Л Д
3. \ —----— dx —----—————-------—— -|~ С, k =/= 1.
J (х - а/ (1 _ ^) (х _ а/"1
С Мх Л- И о р
4- 1 ~2~;--—ах, р — 4(? < 0, заменой х + 4~=/ сводится
J х2 + рх + q 2
к линейной комбинации интегралов
—г—~т = — In (t2 + а2) + С и
J /*4~а2 2 '
I Мх + / v ,, п
о. \ - dx, р~ — 4q < 0, /г > 1, заменой х -4-= t сво-
J (Г + рх + q)k 2
- •< Г { tdt 1
дится к линеинои комбинации интегралов \ :— =----------- X
J (t2 + a2)A 2(1 -й)
dt
-—— (последний можно вычислить по ре-
4- а )
куррентной формуле (см. § 8.2)).
Разложение правильной дробно-рациональной функции
на элементарные дроби
Если Р(х), Q(x)—многочлены, степень Р(х) меньше степени Q(x)
и Q(x) = (х— «,)*'(х — а2)А’:---(х2 + р|Х + <7i)z'(х2 + Р2Х + ^2)/2 ..., где
р2 — 4<?, < 0, то
Р(х) Л| А2 Akt
—— =--------------1------------ + ... 4------—- 4- +
Q(x) х — oci (х—ct|)2 (х — oci)*1
М i х -|- N । М2х А~ N 2
------------1_ -------— 4~--4-
х~ + piX + qi (х* 4- р,х + qty
153
М/,х ч- м,
(х2 4-Р1Х + ?i)Zi
После умножения на Q(x) искомые коэффициенты разложения на-
ходятся из условия тождественного равенства двух многочленов.
Если корпи многочлена Q(x) простые, Q(x) = (х — ai) (х — аг)...
••(х — ая), то
РИ Вп
Q(x) х — ai х — аг х — а,,’
где В* = P(a.k)/Q'(а-ь). В этом случае коэффициенты могут быть найдены
и методом домножения:
О Г Р(х} . 1
в,=Еж(
Интегрирование рациональной функции в общем случае
Любую рациональную функцию можно представить в виде S(x) +
Р(х)
-|- /тг-у, где S, Р, Q — многочлены, степень Р< степени Q.
\Х)
После разложения P(x)/Q(x) на элементарные дроби интегриро-
вание рациональной функции сводится к интегрированию простейших
рациональных функций.
Метод Остроградского выделения рациональной части интеграла
от рациональной функции
Если P(x)/Q(x)— правильная дробь, то
Q(x) Qi(x) + J Q2(x)
где Qi(x) = НОД (Q(x), Q'(x)), Qz(x) = Q(x)/Qi(x), Pi(x), P2(x) — много-
ч !ены, степень Pi (x) степени Qi(x)— 1; степень P2(x)^ степени
Q>(x) — 1.
Если Q(x) = (x — a,)*1 (x — a2)*2---(x2 + p{x -ф qi}1' (x2 -ф p2x -ф q2}12...,
to Qi (x) = (x — ai)*"-1 (x — a2)A2“‘(x2 + pix + pi)'1-1 (x2 + p2x+
+ (/г)'2-1.-, Q2(x) = (x — ai)(x — a2)---(x2 + pix + (x2 + P2X + <72) -
Метод рационализации
(/? — рациональная функция двух переменных)
Интегрирование иррациональностей от дробно-линейной функции
дГх G N» > 1, I °° л I 0
J \ V ух -j- б / I у 6 I
рационализует подстановка
ах -ф р
ух+ 6
154
¥
3
И нтегрирование биномиальных дифференциалов
xm (а + bxnydx, т, п, р С Q, ab =Ф0
рационализуется лишь в трех случаях:
1) р Е Z; подстановка x = tk, где k — общий знаменатель т и п;
2) пг g Z; подстановка а + bxn = tk, где k — знаменатель р;
п
3) _'11 .~tJ—(_ р £ Z; подстановка ах~п + b — 1к, где /г — знамепа-
п
тель р.
Интегрирование рационально-тригонометрических функций
5 R (sin х, cos x)dx
всегда рационализует универсальная подстановка
2/
1 + ’
1 -I2 Л
cos х —---т-, dx =
1 +/2
2dt \
1 + t2 /
tg (х/2) = t
^sin X —
Специальные подстановки
I
ж
Й'
Г
1. Если R( — sin х, cos x) = — R(sinx, cos x), то рационализует под-
становка cos x = t.
2. Если R (sin x, —cos x) =—R (sin x, cos x), то рационализует
подстановка sinx=/.
3. Если R (— sin x, —cos x) = R (sin x, cos x), то рационализует
подстановка tgx=/.
Интегрирование рационально-гиперболических функций
R (sh x, ch x) dx
x f 2t 1 -4* t2
рационализует подстановка th — —t ^shx = —-------ch x = —----------
1. При R( —sh x, ch x) = — R(sh x, ch x) рационализует подстановка
ch x = t.
2. При R(shx, — ch x) = —R(sh x, ch x) — подстановка sh x = t.
3. При R( — sh x, —-chx) =R(shx, ch x) — подстановка th x = t.
Вычисление интегралов вида \R(x, ~\Jax2 + fex + c )dx.
Подстановки Эйлера:
1) a > 0; рационализуют подстановки ~\jax2 ф- bx с = ± ~\/ax -f- /;
2) c 0; рационализуют подстановки “\/пх2 + bx + с = tx ± д/с;
3) b2 — 4qc > 0, ax2 + bx + c = q(x — x,) (x — x2); рационализуют
подстановки ax2 ф- bx c = t(x — x(), где i = 1 либо i = 2.
В частных случаях бывают целесообразны следующие подстановки:
\R(x, -\/а2 — x2)dx, x==qsin/ или х = a cos t,
155
n. I > , а а
R(x, -ух — a )dx, x = acht, х=-------- или х =——-,
cos t sin t
R(x, -ylx2 + a~)dx, x = a sh t или x = a tg t.
Интегрирование некоторых трансцендентных функций
1. j P(x)eaxdx, P(x)— многочлен.
Интеграл можно вычислять интегрированием по частям или мето-
дом неопределенных коэффициентов, отыскивая результат в виде
P(x)eaxdx = Q(x)<?av -f- С, а О,
где Q(x) —- многочлен той же степени, что и Р(х).
Имеет место результат
t P(x)eaxdx = епх + + а^О.
J \ а а ап /
2. P(x)cos axdx, $ Р(х) sin axdx, Р(х) — многочлен.
Кроме интегрирования по частям, можно пользоваться формулами:
{ d( \ л sin ах (г,/ \ . Р(4)(х) \ ,
\ Р(х) cos axdx —-------( Р(х)------------1----—------... 1 -ф
J а \ а2 а4 /
+ ДфД ф-w_ + ГфД \ + с, а +0.
а- \ а- а' /
С с- \ • I cosax / Р"(х) , Р(4)(х) \ ,
\ Р(х) sin axdx =---------I Р(х)-----------------х_-----... ) -ф
J а \ а" а4 /
sin ах / . Р"'(х) , Р(3)(х) \
+----— Р *--------------- +--------г2" -•••)+ С, а 0.
а~ \ а~ а' )
8.2. ТАБЛИЦЫ НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
(произвольная постоянная С в правых частях опущена)
Интегралы от рациональных функций
Хп 4 1 Г Л >-
x,ldx =------—-, п е Z, п =/= - 1. 2. \ — = 1п |х|.
н 1 J х
(ax + b)ndx = , а 6 Z, п - 1, а 0.
а {п + 1)
г/х 1 ,
-------—- — —In | ах + Ь |, а ФО.
ах -ф b а
dx 1 !
---------— = —--------------, а 0.
(ах -ф ЬУ а ах -ф b
xdx
ах -ф b
x2dx
ах + b
х b ,
----------- In |ах + Ь\, а 0.
а а~
х2 Ьх , Ь2 ,
—----------— 4----г In |ах 4- b\, а =^0.
2а а~ а
156
8. ’ n - 1 Г xndx V {-\)kbkxn-k , (-1W , , \ , , “ / , м fe+1 + n+i In|ax4-6|, a=4=0. J ax 4- b L_i {n — k)a + a + fc = O Г xdx b 1
9. \ r- — —5 F —n In | ax 4- b 1, a =4= 0. j {ax 4- b)2 a2 {ax 4- b)
io. 1 Г x2dx x b2 2b \ / , ,v> = 2 3/ , 3 In ]ax 4- 6|, a =4= 0. J {ax 4- b)~ a a {ax 4- 6) a
11. Г x”dx xn । n Г x,l~'dx q J (ax 4~ 6)2 a(ax + 6) a J ax 4- b
12. f x3dx x3 bx2 , b'2x b3 . n j ax 4- b 3a 2a2 a3 a4
13. ’ xndx £ ( (ax 4- 6)"‘ {in — l)a(ax 4~ 6)m_1 n f xn ~1 dx 4 \ r, a, b^O, m > 1. (m — l)a } (ax 4- b)"‘
14. 1 dx 1 , 1 x I i / 1 M Ь 1 1 r 1 > ) x(ax + b) b 1 ax + b 1
Sdx 1 , 1 , I x
--------— —------------j- —— In I----
x{axb)~ b{ax-\-b) b~ ' ax 4- b
f dx 1 1
J x{ax 4- b)3 2 b {ax + b)2 b2{ax 4- b)
ax 4~ b
, b^O.
dx V 1 , 1 ,
x(ax+b)n Li kbn-k{ax + b)k b"
k= i
dx a 1
x2{ax 4- b~)2 b'2(ax 4- 6) b2x
2a , I x
—-In---------
b 1 ax 4- b
dx 1 a , x ,
—---------=---------------- In ------ , b =4
x2 {ax 4-6) bx b~ । ax 4- b ।
dx _ a 2a
х2{ах + Ь)л 2b2 {ax 4- 6)2 Ь3{ах + Ь)
1 За I x I
----r--------— I n ----- , b =4= 0.
b x b । ax 4- b *
dx a 1 a2 । I x
x\ax 4- b) b2x 2bx2 b3 ' ax 4- b
dx 1
xn{ax 4- 6)"‘ ~ ~ {n - \}Ьхп~{ {axb)m~' ~
- (" + "‘-2)a 1-------4^--------, Ь 0, n >
b{n — I) J хг,-'{ах + ЬУ‘
157
23. С ах + b , ах ар — ab , , 2 In |ах + р|, а=4=0. J ах + р а а
24. f (ах4-д)2 а2х2 , а / ар — ab \ \ rrr-i-R dx~ \Ь )* + J ах 4- р 2а а \ а / (ар — ад)2 in |ах + ₽ 1, а =+ 0. а
25. С ах + b a$ — ab . а , . , о1 \ / 1 д\2 " 2/ । о\ Р 2 1П аХ Р » а + 0. J (ах + р)2 а2(ах+Р) а2
26. ( ^ах 4~ dx _ fi2x («Р —- ad)2 J (ах + р)2 a2 aJ(ax-Lp) 2а(ар — ab} , , _——| п | ах + Р1, а 0. а
27. ( dx = + ьу J (ах + Р)'п (т — 1)а(ах 4- р)'Г!-1 . па С (ax4-d)"_| J 4~ . ,. \ ; г- dx, а #= 0, т > 1. (т — 1)а J (ах + 3/'
28. С dx — 1 | ах 4" Р 1 j {ах 4- Ь) (ах + р) ар-ад П 1 ах + b 1 ’ аЬ °'
29. С dx 1 J (ах 4- Ь) (ах 4- Р)2 (ар — ад) (ах 4- Р) а , I ах 4- b I + . п , „ In , ар — ад =4= 0. (ар — ад)“ 1 ах 4- Р 1
30. Г xdx = —д j (ах 4~ Ь) (ах 4~ Р) а (ар — ад) П йХ О + z д , . 1 п 1 ах + р 1, ар ад =4= 0, а =4= 0, а =4= 0. а (ар — да)
31. С xdx а । । , । J (х + а)(х4-д) а-д " |х + а| In |х 4- д |, а =4= д. а — д
32. f xdx _ Ь J (x 4- a) (x 4- d)2 (a — d) (x 4- d)
a , 1
— In , a + b.
(a - by ! ‘ b 4- x '
1/1 1 \
33 \ । 1 I ।
J (x 4- a')\x 4- d)2 у z — д)2 V x 4- a ' x 4- d /
, 2 , | x 4- a |
4“ — г In , a y= d.
(a - d)- । 1 x + b '
f xdx 1 / a b \
34 \ ( 1 \
J (x 4-a)2(x 4-d)2 (a - by \ x 4" a x 4~ b J
a 4- b j ! x 4- a |
1 , a =4= d.
(a - d)3 1 x4-d ।
x2rfx 1 / a2 d2 \
3b. ' J (x + a)2(x 4-d)2 (a —d)2 \x4-a x + b) , 2ad , I x 4- a 1 , , 4 - In 1 , a + b. (a — b) ' x 4- b ।
36. C dx 1 ln|x4-al J X(X + <1)(X + S) ab 111 1 a(6-a) - "1У + Ь' .^o,b^o,a^b. b<b — a)
37. C dX 1 < X , A \ 1 ’ = А аГС1£ П ’ a^0- J x 4- a a a
38. C dx 1 , dx , \ ,2 . , о = , arctg , a + o, b + o. J b~x~ 4* a~ ab a
39. f Xdx 1 . . 2 , 24 » — = — In (x2 4- a2). J x2 + a2 2 V '
40. f xdx 1 J (x2 4-a2)2 2(x2 + a2)’
41. t x lx J (x2 + a2)2 2a2(x24-a2) + 2a3 a ' “ °’
42. C dx _ X 3x J (x24-a2)3 4a2(x24-a2)2 8a4(x24-a2) + -^arctBV
43. C dx x J (2a —2)a2 2(n - l)a2(x2 4-a2)"-1 + 2n — 3 Г dx n , + (2,<-2)^ Г(? + а2)’-" ' П>
44. f xdx 1 J (x2 4- a2)n 2(n — 1) (x2 4-a2)"-1 ' n> '
45. f x2dx , x \ = x — a arctg —, a =4= 0. J x“ 4- a~ a
46. 5 (x24-a2)2 2(x2 + a2) + 2a ard^’^°- J ~т~ U ) Z —|— a ) Au, u-
47. C x3cfx _ a2 1 2 , 24 J (x24-a2)2 2(x2 + a2) + 2 n(% +a)>
48. C x~dx x J (x2 4- a2)n 2 (a — 1) (x2 + a2)"~1 , 1 C dx „ . ~r i > . , a =4= 0, a > 1. 2(n— 1) J (x2 + a2)''-'
49. (* dx 1 . x2 \ -> 5— — —— in — a 4= 0. j x(x“ 4- a2) 2a‘ x~ 4~ a1
50. C dx 1 1 x \ ... 2 , 24 = ’ i alTtS ’ a#=0. j x (x 4-a) a^x a a
158
159
191
di/ и i g eanvog 9
b -f- xd -f- Г Л — b^
xp } Z
(b + xd + 7x) (,</ — b^) _ 7(b + xd + zx)
d + xz ~ xp
bf — ^d^+d + xz b$ — zd^'
0<^~ -d b^_ d + j ul j
7d - b^ 7d - b^ ~
0 > Ьъ — xl '——---SpjB-------
u 7 6 d 4- xz Z )
b + xd + 7x f
=-------\ '08
xp J
(>p =f /V c
xp J У
’0^0 *
------------1 ’ZZ
Q^V ‘
V — X
X
.v^
xp
V — .X
xpx
91
'0^° 3pjB-^-— =
zx I
I £Щ? П rvz
1'1 X 1—
xpx J
D — . X C
xp
v
'0 ¥= о ‘--»—Зрлв-----
о — zp^x I
v
Зрлв
frZ
V
(fV + x) V£
£L
'ZL
1Z
OZ
xp,x
Vv
3pjB ^:—
n —xz I
+ xd — x og
------UI-----------
z(x + 0) I
xpx
69
091
xp
; x xp
£p>
•n =z= о '-31Э.1В-
p —1
?p + ,W - ?y u zf9_ = £P +
_(o + x) I xp
'89
79
Z 7x— v C
•|г-г°1 U1 ~T ~ \ ’9S
l ЛГЛ J
<, . i -4y-?A) C - »z) ,
xp J 8 —
!-4%- ^)z°(l - u)3 ^X-Zu) f
-------------------- ---------- t ’Qp
x xp J
'0 7»
’0 ¥= <7 ‘o =7= V ‘
xq — v
xq + v
WK _
I ~ xp
83.
~2~ In I*2 + Px 4“ </l —
xdx
x2 + p.r + q
P x 2x —|- p 9
---7=--arctg ~7~p~-4qc 0,
-\*q~P2 -yliq-p2
— In | x2 -)- px 4- q | —
_ p in I 2x + p
2л/р2— 4P 2x 4- p 4- д/р2 — 4<?
' P~ — 4q > 0.
2p I x2 4- px 4- q I
p 2x 4- p
---------- arctg---------,
<n/4<7 — p2 -^4q — p2
p2 — 4q < 0,
dx
x(x2 + px 4- q)
2<? I x2 4- px 4- q I
- — P In I 2^ + р-д/р2-4у
2^n/p2-4p 2x 4- p 4- д/р2-47
p2 — 4q > 0.
Интегралы от иррациональных функций
162
163
164
38. [ —X ll— — = 4" 11 + — °2 Vх*' + °’'-
JVx!+“2 _____
С dx 1 . I <2 Ц- д/х2 + о" 1
39. \ —— - — = — — 1п| ------------ р а =4= 0.
\ Г 9 । •> О. I л* I
J Хд/Х" + СГ I >
40. f___‘'х = - dZ+^1 . а о.
J /Д.< + а1
4 [ С dx = _ Л/*2 + °2 1 |П I ° + V-у2 + а2 I
’ j хзу? w 2а'1х1 2аЛ I х I
а =/= 0.
42. д/х2 4-a2dx = уд/х2 + а2 4- In | х + д/х2 4-о2).
43. I (х2 + a2)3/2dx == У л!х2 + а2 (2х3 4- 5п2х) 4-
1 О V
4 - у a4 In (х + д/х2 4-а2).
44. х д/х2 4- a2 dx.= у (х2 4- а2)3/2.
45. х(х2 4-а2)3/2^х = у (х2 4-а2)5/2.
46. ( х2д/х2 4- а2 dx = 4~ ° Х д/-^2 4~ «2 —
] v o'
- In (х 4-д/х2 4-а2).
. _ С д/х~ 4“ °' , Г~Г^7 9 । I Q 4- д' х" -4 <2" I
47. \ -*-----dx = д/х 4- а~ — a In ------------1 .
48 г (4+Д1 Т? -
J X <> ’
11 I о 4* д/х" 4~ fl 2 I
— а In ----Y---------- .
1 X |
.г, С д/^х2-^- а~ , д/х" 4~ °2 . । / । гд i ~2\
49. \ --у----dx =---------------Н In (х 4- д/х 4- а ).
J X X
50. t зЯ+7 ^4°/.-
J xJ 2х2
16з
166
167
, a . x
+ — arcsin —.
о a
Интегралы, содержащие экспоненту
f Г ах
1. \exdx = ex. 2.\axdx=--------, а > 0, а^1.
J j In а
3. ( eaxdx = — еах, а 0. 4. f xexxdx = —-Т* еах, а О
J а J а
с С 2 а2х2 — 2ах + 2 пг
5. \ х еа dx -----------1— е , а О
J а
R f з ах j а3*3 ~ За2х2 + бах — 6
6. \ x^eaxdx = ----------а о.
168
7. xex\ix = у ех\ 8. х3ех'dx = у (х2 — 1) е*’
9. $ х[х e^dx = 2(х - 2д/7 + 2) еЛ
10. f е'Гх г С dx . ех \ —— dx = 2еЛ 11. \ — = In -. J -д/х ' е + 1 +е
12. ( — = — — In |а 4- beax\, а^О, a=H=0. J а 4- Ьеах а аа Г dx 1 j I еах 1 . 1
13. J (а 4-Ьеах)2 аа2 | а 4- Ьеах | аа(а 4- Ьеах) ’ a 0, а =/= 0.
14. [ e"dx = _1_ In |а + ^ол|, а =# 0, 6=^0.
j а + beax <xb
15. С — = 2 arctg -\/ех — 1.
J ”\/ ех — 1
( ах • с . а sin Рх — р COS Рх ах „2 ft2 , л
16. \ е sin рхах =----------=——5---------е > а ' Р и-
J а 4~ Р
,, С ах ОХ а COS рх + Р sin рх „2|_о2 ,л
17. \ е cos Rxdx —----------,-----5------е , а + р =^= О.
J а2 + р2
f еах / 2 \
18. \ еах sin2 xdx = —5-----( а sin х — sin 2х 4---), а =# 0.
J а2 4- 4 \ а /
С еах / 2 \
19. \ еах cos2 xdx = —,-----( а cos2 х 4- sin 2х 4-), а =^= 0.
J а2 4- 4 \ а /
Интегралы, содержащие логарифм
И । In xdx = х In х — х. 2. loga xdx — [n a (x In x — x), a =H= 1.
3. ’ In (ax 4~ b)dx — — {ax 4- b) In (ax 4~ b) — x, a 0. Г x2 , x2
4. \ x In xdx = -7— In x —. J 2 4
5. ' Г a2x2 — b2 , , . ,, ax2 — 2bx n \ x In (ax 4- b) dx = ^2 'n (ax + 4a > a 0-
6. f x3 x3 \ X2 1П Xdx — -g-'11 X g--
7. f x“^' Xa+I \ xa In xdx — —T-Inx , , n2’a=?M- J a 4-1 (a 4-1)
8. f In x , (In x)2 \^TdX- 2 •
9. {hldx= ln* Г. «#=1.
10. f In (ax 4-^). = A ln x _ In (ax + b\ b Ф 0. J x2 b bx
169
20. \ in |x2 — a2| dx = xln |x2 —a2| —2x4-a In
11. 5 In2 xdx — x In2 x — 2x In x 4- 2x.
f x%
12. \ x In2 xdx = — In2 x-— In x 4——.
C In2X , 113
13. \------dx = — In x.
J x 3
, f ln2x In2 x 2 In x 2
J x x xx
C clx
15. \ —~---= In Un x|.
J X In X
1C C dx 1
16. \ ----- = ----------------г-> CC 1.
j x(ln x)“ (1 — a) (In x)“~ 1
17. j In (x2 + a2) dx — x In (x2 + a2) — 2x 4~ 2a arctg (x/a).
18. x In (x2 + a2) dx — — a - In (x2 + a2)-у.
t a C 2 1 / 2 । 2\ j i / 2 i 2\ 2x2 2a2X
19. \ x- In (x2 + a2) dx = — In (x2 + a2)-— 4--------
J 3 УЗ
I * + Q I
I x — а Г
21. x In |x2 — a2| dx = - - 2 a In |x2 — a2|-
22. In (x + д/х2 -|- a2) dx — x In (x 4- д/х2 4- a2) — д/х2 4- a2.
23. J In (x 4- д/х2 — d2)dx = x In (x + д/х2 — a2) — д/х2 — a2.
24. x In (x + д/х2 + a2) dx — ——— In (x + дД2 + a2) —
4
25. x In (x + д/х2 — a2) dx — —- - -°- In (x + д/х2 — a2) —
хд/х2 — a2
Интегралы, содержащие тригонометрические функции
1. sin xdx = —cos x. 2. $ cos xdx = sin x.
3. sin (ax 4- b) dx —--cos (ax 4-6), a =# 0.
4. cos (ax 4- 6) dx = у sin (ax 4-6), a 0.
5. J x sin xdx — sin x — x cos x. 6. $ x cos xdx = cos x 4- x sin x.
170
7. \ х sin axdx — — sin ax-------x cos ax, a=/=Q.
J a a
8. \ x cos axdx = — cos ax -]---x sin ax, a#=0.
J a a
9. j x2 sin xdx — 2x sin x — (x2 — 2) cos x.
10. J x2 cos xdx = 2x cos x + (x2 — 2) sin x.
C 2 / x2 2 \
11. \ x2 sin axdx = — x sin ax — (------- Jcos ax, a #= 0.
J a \a a /
C 9 2 / x2 2 \
12. \ x2 cos axdx = —— x cos ax + (--------— ) sin ax, a 0.
J a \ a a /
13. J x3 sin xdx — (3x2 — 6) sin x — (x3 — 6x) cos x.
14. $ x3 cos xdx — (3x2 — 6) cos x -f- (x3 — 6x) sin x.
15. J x" sin xdx = — x" cos x + n $ xn~1 cos xdx.
16. xm cos xdx - xm sin x — m J xm~1 sin xdx. f , x sin 2x , „ f n x , sin 2x
17. \ sin2 xdx — ~2 4—• 18. \ cos2 xdx — — H -—
19. f . , x2 x sin 2x cos 2x \ X sin* xdx — — s . J 4 4 8
20. f 9 , x2 , x sin 2x , cos 2x \ x cos" xdx = — 1 - 1 5 . J 4 4 о
21. C 9 . a , x3 (x2 1 \ _ x cos 2x \ x sin xdx — I — — I sin 2x . J 6\48/ 4
22. C 9 9 , X3 / X2 1 \ , x cos 2x \ x cos* xdx = ——( — — 1 sin 2x . J 6 \ 4 о / 4
23. ’ i sin3 xdx — cos3 x — cos x.
24. | i cos3 xdx = у sin3 x + sin x.
25. 1 . . 3x sin 2x , sin 4x p.n xdX= 8 4 1 32 .
26. ' . , 3x , sin 2x , sin 4x Jcos xdx= 8 + 4 32 .
27. ‘ ' R 2,1. 1 sin& xdx — — cos x + — cos x — cos x. ) 3 5
28. ’ 2 1 1 cos5 xdx = sin x — sin3 x + — sin5 x. J 3 b
29. ' 1 • 6 л 5 15 . _ . 3 . . 1 1 sin0 xdx — x sin 2x -4- —- sin 4x ---r- sin 6x. ) 16 64 64 192
30. ’ 5 15 3 1 l cos6 xdx = -77- x + -7ГГ sin 2x + sin 4x + yat s'n 6x. J 16 64 64 192 Г dx .1 x 1 „„ f dx , 1 , (x , л \ |
31. ’ —= In I tg-p~—I— 32. \ =ln tg(—+ —) J sin x 1 b 2 1 j cos x 1 \ 2 4/1
171
33. C dx f ол C dx ) sin2x ~ CtgX 34’ \~ =tgx. J stn x J cos x
35. C dx — C0S X i 1 t I X X I J sin3 X 2 sin2 X 2 n 1 g7 г
36. ( dx — sin x _i_ 1 i L (x , \ 1 J cos3 x 2 cos2 x 2 П 1 g \ 2 4 / Г
37. 1 Г dx 1 \ . 4 — ~ctg x Ctg3 X. J sin x 3 &
38. 1 Г dx 1 1 4 3 \ 4 — tg X H tg3 X. J cos4 x 3 b
39. ' ? xdx J sin2x ~ xctgx + lnlsmxl.
40. C xdx \ — X tg X 4- In |cos x|. J COS”X
41. ’ C dx / x л \ J 1 4” sin x g \ 2 ~4 )'
42. 1 [ dx — x j 1 4- cos x g 2
dx
(1 + sin x)2
dx
(1 4- cos x)2
dx
(1 — sin x)2
dx
(I — cos x)2
dx
_ 1 . X 1 , 3 X
— ----t ---- —I— -f P" --
2 S 2 6 ё 2
1 . X 1 . 3 х
~=~TctgT-Tctg У
= -Uarctg (V2tgx).
Л/2
-4 C dx 1 tgx
54. \ -————— = —— arctg .
J 1 + cos x 2
172
сс С . . а . sin (а — р)х sin(a + p)x . . ,
55. ах sin Мх = 2(а_р)---------2(g + p) , | a M I PI.
f o , sin (a — p)x sin (a + p) x .
56. \ cos ax cos fixdx = —----------rr----1----, |a| |p|.
J 2 (a — p) 2 (a + p)
dx
a + sin x
58. -----
J a + cos x
( 2 . atg(x/2) + 1 . . .
.., arctg ..-, |a| > 1,
~\/a2 — 1.........-\/a2— 1
1 in a tg (x/2) + 1 - л/l-a2
„ -д/l —a2 a tg (x/2) -f- 1 + -д/l —a2
( 2 (a— l)tg(x/2)
— ....- arctg---------|a| > 1,
•д/а2 — 1 ~yJa2 — \
1 ln (1 - a) tg (x/2) + д/l— a2 ।
w -д/l —a2 (1 — a) tg (x/2) + -\/l —a2
61.
dx
a2 + sin2 x
dx
a2 -|- cos2 x
a=£0.
dx
2 ' 9
a — sin x
1 , a tg x , _
--- • arctg— & , а ф 0.
a-yjl -}-a2 "\/l +a2
f 1 i "ya2 — 1 tg x
.... ..— arctg— , |a| > 1,
ад/a2 — 1 a
y/1 —a2 tg x a
yi — a2 tg x — a
lai < 1.
1 a tgx
---- ----- arctg — . , I a | >
ад/а2 — 1 "ya2 — 1
1 , a tgx — Vl— a2
2a~\J 1 — a2 a tg x + -yl — °2
„„ 1' . , sin2 X _ . f . 2 j
63. \ sin x cos xdx = —-—. 64. \ sin x cos xdx = —
f . 2 , sin3 x rc f • з j
65. \ sin2 x cos xdx = —-—. 66. \ sin x cosJ xdx = —
, la| < 1.
COS3 X
3 ’
cos4 X
4 ’
67. \ sin x cos xdx — —-—
Г „ , cos x , ,
68. \ sin x cos xdx =--------—:—, n =/= — 1.
J n + 1
f . „ , sin"+lx , ,
69. \ sin x cos xdx —----——, n =/= — 1.
J n + 1
70. \ sin2 x cos2 xdx = (4x — sin 4x).
173
76.
sin3 x cos3 xdx = - -L cos 2x 4- J- cos3 2x.
lb 48
dx
“7“-------- = In tg X .
sin X COS X s
dx
sin x cos2 x
dx
sin2 x cos x
dx
sin x cos3 x
dx
COS X
sin x
--------j------Ь In I tg X'|.
2 cos x
----F In |tgx|.
2 sin x
sin3 x cos x
77 I d*
J Items’x =‘8*-с‘8'-
78. (4V-dx=-l-. 79.
J cos x cos x J sin2 x sin x
„ C sin x 1
89. \ ----dx = -----------— n
J cos" x (n — 1) cos"”1 x ’
cosx I
81. \ -------dx —----------------------
J sin"x (n — l)sin"~‘x
f sin2x
82. \--------dx — — sin x 4
j cos x
oo f cos2 x ,
—:----dx = COS X 4- In
sin X 1
sin2 X
----5— dx — tg x — x.
COS X
sin2 x sin x
-----— dx = —-------—
cos x 2 cos“ x
84.
86.
C cos2 x
°5- \ ——— dx = — ctg x — x.
J sin x
4Ч<1+т)Ь
87.
COS X
88.
cos X ,
“- dx~ —
sin x 2 sin2 x
sin2 x , 1 .
dx = — tg3 x. 89.
- — In
2
90.
COS X
sin3 X
cos2 x . 1 .
~;— dx —-----------ctg3 x.
sin’x 3
COS X
d* =---_sin2x — In |cos xj.
f. i cos X
J sin x
92. LSX x
J cos2 X
dx = ~ cos2 x 4- In |sin x|.
dx — cos x 4-----------
cos x
1
93. \ --°-, X
J sin2 X
„. f sin3 x , i „
94. \----j—dx ~ — tg" x 4- In I cos x|.
J cos x 2
dx = — sin x —
sin x
174
95. ( — dx —-------— ctg2 x — In |sin x|.
J sin3 x 2
C sin x j 1 /1 t \
96. \ -т-r----dx — — In (1 + cos x).
J 1 + COS X
— C COS X .
97. \ ——;—:---dx = In (1 + sin x).
J 1 + Sin X
no [ sin x , . x
98. \ -7------dx = In (1 — cos x).
J 1 — COS X
C cos x , ... . 4
99. \ —---г---dx = — In (1 — sin x).
J 1 — sin x
100 ( _______dx__________ 1_______1 . It Al
j sin x (1 + cos x) 2(1 -|- cos x) 2 П I g 2 I
l01 (_________dx_______=__________1_______1 I ( x. jrr
J cos x(l + sin x) 2(1 +sin x) 2 П I g\2 4
102’ J sin x(l - cos x) = “ 2(1 - cos x) + T ln Itg ~2 I '
ioq( dx — 1 _i_ 1 i It (x _i_ n
J cos x(l - sin x) - 2(1 - sin x) + 2 I g \ 2 + 4,
dx
sin x + cos x
105. \ dx 1 - I , (x л \ I sin x — cos x ft 1 \ 2 8/1
106. \ sin xdx x 1 . . . . . —; = -7Г FT 1П 1 Sin X + COS X|. sin x + cos x 2 2
107. j cos xdx x , 1 . . . , , — : = — + -ft In | SIH X + COS X|. sin x + cos x 2 2
108. \ sin xdx x , 1 , , . — — — + -FT In 1 Sin X — COS X . 1 sin x — cos x 2 2
109. I cos xdx x , 1 , . . . 1 — = ft + -FT In 1 sin X — cos X . ) sin x — cos x 2 2
110. 1 Г dx 1 . ( n \ l — tg 1 x 1. J (sin x + cos x) 2 & \ 4 /
111. ‘ Г dx 1 . ( . л \ L • t2 = о tg Iх + A )• J (sin x — cos x) 2 \ 4 /
112. ’ ’ dx 1 , b tg x , , л 1 a‘cos»x + Z,Wx = 0(,arClg a a^°-
113. ’ [_ — = —L_ln Ii,tgx + a. 1, J a2 cos2 x — b2 sin2 x 2ab 1 fttgx — a 1
175
115.
116.
118.
120.
121.
122.
123.
— In | д/a2 — 62cosx4-
b2
Ssin xdx
-r-r.-:-.-- —
д/a2cos2 x 4- ft2sin2x
cos xdx
cos2x 4- &2sin2x
4- д/а2 cos2 х4~ ft2 sin2x |, | a I > | b |,
~7=1= arcsin -^T~^cosx
д/б2 — a2 । ft I
— in 1 ylb2 — a2 sin x 4~
д/ft2 - a2
4- д/a2 cos2x 4-b2 sin2x |, | b\ > | a |,
$tgxdx = — In |cosx|.
J tg2 xdx = tg x — x.
tg3 xdx = -1- tg2 x 4- In |cos x|.
I 1 . ya2 — b2 sin x
I —— - . arcsin — ------;—;------
I д/a2 — b2
LlftKIal.
117. J ctg xdx = In I sin x|.
119. j ctg2 xdx — — ctg x — x.
ctg3 xdx =----ctg2 x — In | sin x|.
dx * , 1 . । •
T+ tg x = У + У l«nx + cosx|.
l +ctgx ° У ~У1п lsi"* + c°s*l-
dx x 1 , , .
। _ tgx = у — -j ln I sin x — cos x|.
l-ctgx = y + yln lsi"X-COSX|.
dx
a 4- b tg x
a2 4- b2 =/= 0.
dx
a2 4- b2 In |a cos x 4- b sin x|),
----------= —v——у (ax — b In | a sin x 4- cos x |),
a 4- b ctg x a2 4- b2
a2 4- ft2 ¥= 0.
Интегралы, содержащие обратные тригонометрические
функции (a > 0)
1. \ arcsin — dx = х arcsin — 4~л/а2 — х2.
J а а ’
с f X , х -----------7
2. \ arccos — dx = х arccos-----~уа —х .
J a a v
176
е
3. ^arcsin dx = x^arcsin — 2x4-
4-2 д/о2""— x2 arcsin -^-.
(.C x 2x2 — a2 xx гт~—7
6. \ x arccos — dx =------arccos-------л/а2 — x2
J a 4 a 4 v
7 C 2 x . x3 x , x2 4- 2а2 i~T--7
7. \ x arcsin — dx=—-arcsin---------Ц-л/а — x .
J а 3 a 9 v
о C 2 x , x3 x x2 4- 2a2 гт------------------7
8. \ x arccos — dx — arccos--------—---da- — x2
J a 3 a 9 v
9- arctg dx = x arctg ~---In (x2 + a2).
10. arcctg dx — x arcctg 4- In (*2 + a2)-
11. t x arctgdx = X ta arctg— -
J a z az
12. J x arcctg dx = arcctg
13. ( x2 arctg — dx — arctg —-~ In (x2 + a2),
j а з а b о
14. [ x2 arcctg — dx — arcctg — 4~ ---In (x2 + a2).
J a 3 abb
Интегралы, содержащие гиперболические функции
П
1. $shxdx = chx. 2. Jchxdx = shx.
3. х sh xdx = x ch x — sh x. 4. J x ch xdx — x sh x — ch x.
5. J x2 sh xdx = (x2 4- 2) ch x — 2x sh x.
6. x2 ch xdx = (x2 + 2) sh x — 2x ch x.
7 C . 2 j sh 2x x C 2 sh 2x , x
J 4 2 J 4 2
„ C , 2 , x sh 2x ch 2x x2
j 4 8 4
f ,2 . x sh 2x ch 2x , x2
10. ^xch2xdx=---------------— + v.
С cv
11. \sh3xdx=——----ch x. 12.
,„ f dx 1 . | ch x + 1 |
13. \--- —---In ------!-
J sh x 2 I ch x — 1 I
ch3 xdx = X 4- sh x.
177
14.
15.
17.
18.
19.
20.
22.
23.
24.
25.
27.
dx
= arctg (sh x) = 2 arctg ex + Ct.
dx
sh2 x
xdx
sh2 x
xdx
— —cth x.
dx
j— = th x.
ch x
— — x cth x + In | sh x\.
—ъ— — x th x — In ch x.
ch x
dx ___ 1
1 + sh x П
dx ,, x
.—-— =th-5-.
h ch x 2
dx
1 - th (x/2)
C dx
21. \ = Ithxl.
J sh x ch x
J sh x ch2 x ch x 1 2 1
C dx 1
\ —------— =-------------arctg (sh x).
J sh x ch x sh x
f dx
\ T-----ГТ— = -2 eth 2x.
J sh x ch x
$ th xdx — In ch x.
5 th2 xdx = x — th x.
26. J cth xdx = In | sh x|.
28. J cth2 xdx = x — cth x.
Некоторые рекуррентные формулы
dx _ x 2n — 3 f dx
(х2+1)" (2n-2)(x2+I)"-' + 2n-2 J (x2+ l)"-' ’
t/x , „
-2 - T- = arctg x + C.
x2 4- 1
C dx _________________X_________2n — 3
J (x2 + a2)" (2n — 2) a2 (x2 + a2)n“1 + (2n — 2) a2
f dx [ dx 1 x
x \ 7TT—7ТГ’ \ “T—г = ~ arctS--------h c-
J (x2 + ay J x2 + a2 a a
X t - —-2 dx, m > I, (= - д/l - x2 + C,
J -д/1 — x2 J д/Т — x2
dx д/l —x2
хтд/1 -x2 (m-l)xm-‘
178
= In I '-V^l +C, t —
x ' J-
C- f . V u sin' + 1 X COS1*-1 X ,
5. \ sin x cos' xdx —----------k
J v + (l
sinv x cos'1 2 xdx, \ sinv x cos'1 xdx =
v, ц C R, v + ц =^= 0.
6. xnexdx — xnex — n J xn~'exdx.
7. xn sin xdx — ~xn cos x + n J xn~' cos xdx.
8. J xn cos xdx = xn sin x — n J x"-1 sin xdx.
Q f dx _ x
J (a2 - b2x2)n ~ (2n — 2) a2 (a2 - b2x2)n~l
2n — 3 f dx
(2/i — 2) a2 J (a2 — b2x2)n~l ' n>
dx _ cos x ii — 2 f dx
sin" x (/i — 1) sin"“‘x n — 1 J sin"~2x ’ n>
dx sin x , n — 2 f dx
———— — —— — —I— 1 \ * 1
cos"x (n —i)cos"~'x n — 1 J cos"“2x
xdx x cos x 1
------ =---------------------------------------------|_
sin"x (/i — l)sin" x (/t — 1) (n — 2) sin" 2x
Г xdx xsin x 1
13. \ ------ —------------------------------------------L
J cos" x (a — l)cos" *x (a — 1) (a — 2) cos" 2X
, /г-2 Г xdx
H--------\ -------Z75~ ’ n > 2.
n — 1 J cos" X
C t СГЛ 1 X Г
14. \ tg” xdx = —— -------\ tg"-2xdx, n > 1.
J n — i j
15. ctg"xdx =----------------ctgn-2xdx, /i > 1.
C i 1 n x п C
16. \ xp In’xrfx = ------------4-~ \ xp In’-1 xdx, p, - 1.
J P + 1 P + 1 J
[ In (ax+ 6) In (ax + b)
I / . \ --------u X = — -----------— Ч-
J xp (p-l)xp-‘
. C adx
—\ ----------------—— p 1 ,
J (P — 0 (ax + b) xp~'
,n{dx ch x n — 2 C dx
18. \ ------------------------\---------, n. > i.
J sh" x (a—1) sh" x a —1 J sh" 2x
179
19 f dx = sh x _ , tl — 2 C dx
J ch” x (n — 1) ch”-*x n — 1 J ch”_2x ’
20. ( th” xdx = - 1‘-.2А + f th”"2 xdx, n > 1.
J и — 1 J
Г ci hn 1 x Г
21. cth” xdx = - + \ cth”"2 xdx, n > 1.
1.
4.
7.
9.
11.
12.
13.
14.
15.
18.
21.
24.
27.
30.
33.
35.
37.
39.
Некоторые неберущиеся интегралы
(неопределенные интегралы, являющиеся
неэлементарными функциями)
dx, j ех' dx.
sin х .
-----dx.
sin x2dx.
cos X .
------dx.
3. J cos x2dx.
dx
6.
— dx.
sin x ,
------dx, n £ N.
dx
1 ex
8- \ , n € N.
1 vn
1 cos x
10. \----------dx,
1 v'1
д/(1 — x2)(l — k2x2)
x2dx
-\/(l — X2) (1 — k2X2)
dx
5 V' — &2 s>n2 x
f xdx
J sin x
Г sin2 x ,
\---------dx.
x2dx
sin x
1 COS X
19. \--------dx.
n
6N.
17.
J sin x
20. ( - xdx
J cos X
xdx
cos x
$ x ctg xdx.
arccos x .
---------dx.
e .
—5- dx.
x2
dx
x2 In x
22. J x tg xdx.
25. (-SlKirfx.
arctg x ,
-----—dx.
xdx
dx.
f arcsin x ,
26. \-----------dx.
29.
32. (
J In X
o. C In (ax + b) ,
34. \1--------------------------------------------------!—Ldx, a^O.
36. $ In sin xdx.
$ In cos xdx.
j ex In xdx.
38. In tg xdx.
( sh x ,
40. \-------dx.
J x
180
C ch2 A'
45. \--------dx.
J x
xdx
sh x
xdx
ch x
8.3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Формула Ньютона — Лейбница (формула двойной подстановки)
ь
f(x) dx = F(b) - F(d)=F(x)\ha =
a
([ непрерывна; F — первообразная для f).
Теорема Барроу
Если f непрерывна, то \ f(J)dt^ —f(x).
Свойства интеграла
Линейность
ь ь ь
5 (а/(х) + $g(x))dx = а 5 f(x)dx + 0 5 g(x")dx.
а а а
Аддитивность
Ь с b
\f(x)dx = \f(x)dx-\- \f(x)dx,
а а с
\f(x)dx =— \f(x)dx, \f(x')dx = 0.
a ba
Монотонность
b b
Если f(x] g(x) и a<b, to \f(x)dx^. g(x)dx. В частности, если
a a
b
f(x)^0, a<b, to ^ftx'jdx^O.
a
Теоремы о среднем
Первая теорема о среднем
ь
$ f(x)dx = p(b — а)
а
181
(|л — среднее значение функции).
Если / непрерывна, то
ь
\Kx)dx==f®(b-a), a^^b.
а
Вторая теорема о среднем
Если f, g непрерывны, a g не меняет знак, то
ь ь
$ fW g(x)dx = J g(x)dx, a^l^b.
a a
Формула Бонне
f 1 b
5 f W gWdx = g(a) j f(x)dx + g(b) J f(x)dx
a a g
(g монотонна).
Оценки интегралов
1. Если А < f(x) < В, а < Ь, то
ь
A(b — d)^ \f(xjdx^B(b — a).
а
Ь Ь
2. $ f(x)dx < j lf(x)|dx, а < b.
1 а ’а
b
3. Если |/(х)| < Af, то I j f(x)dx I < Mlb — а|.
। a *
Преобразование интегралов
Замена переменных
ь ₽
\l{x)dx^ 5/(ф(0)ф'(С^
a a
(ф строго монотонна, непрерывно дифференцируема; ф(а) = а; <р(Р) = Ь).
Интегрирование по частям
ь ь
$ u(x) v'(x)dx = [и(х)у(х)]* - j u(x)u'(x)dx
а а
(и, и непрерывно дифференцируемы).
182
\ Приближенное вычисление интегралов
Формула средних прямоугольников
Ь
5 f(x)dx — h(y42 + Узп + ••• + //n-1/2) + R,
а
h _ -----Е , Xk — а _|_ рщ о '-С k п,
п
xk-l/2 = -~2~ (Xk-l + xk), £/Лг — 1/2 ~ f(xk-i/‘2)-
(b — df _
R = f (U а С ё < 6.
24м“
Формула трапеций
f(x)dx = h -----------h У\ + У2 + ••• + + R>
h = —----—, xk = a + kh, 0 sC k < n, yk = Kxk),
11
: 12n
Формула Симпсона
J f(x)dx = — ((t/0 + l/2n) + 2(y2 + У< + ••• + У2/1-2)-}-
a
+ 4(У1 + Уз +•• + ysri-i)) + R,
Ih = , xk = a + hk, tjk = f(xk\ 0 < k 2n,
2м
R = —-------- f(4)(n)> a 'С л C b.
180«
Некоторые приложения интеграла
Площадь криволинейной трапеции
ь
S = f(x)dx
а
’ (f непрерывна и неотрицательна).
Площадь фигуры, ограниченной линиями y = f(x), у — g(x),
< х — а, х = Ь,
ь
S = $ IfW — g(.x)\dx.
183
Площадь криволинейного сектора в полярных координатах
1 ?
5== “оЧ r2(<PW
z а
Объем фигуры через площади поперечных сечений
ь
V = j S(x)dx.
а
Объем фигуры, полученной вращением
криволинейной трапеции
ь
Вокруг оси Ox; V = л $ f2(x)dx,
а
b
Вокруг оси Оу; V = 2л \xf(x)dx.
а
Длина кривой
1. Заданной уравнением у = [(х'), а^х^Ь;
ь
s = $ V1 +(f'W)2dx.
а
2. Заданной параметрически:
а) на плоскости (х — х(/), у = у(Г), а «С t < 0):
Э ______________
s= Wx'2(0+ у/2(/МЛ
а
б) в пространстве (х = х(/), у = y(f), z = z(t\ а < t < 0):
₽ _______________________________________
s = 5 лД/2(0 + У/2(0 + Z'\t}dt.
а
3. Заданной полярным уравнением г — г(ср), а si ср 0:
Р ___________
5 = J -д/г2(ф) + Г/2(ф) d((>.
а
Площадь поверхности фигуры вращения
1. Полученной вращением кривой у — f (х), а х Ь, вокруг оси Ох,
ь
S = 2njf(x)-Vl +(Г(< dx.
а
2. Полученной вращением кривой х = х(/), у — у({), а 0,
вокруг оси Ох,
₽ ___________________
5 = 2л $ + dt.
а
184
Центр масс кривой у = fix'), a^x^b
(р — р(х) — плотность кривой).
ь
Масса: пг = $ р(х)*\/1 + (f (х))2 dx.
а
Статические моменты относительно координатных осей:
ь
Мх = $ р(х) /Мл/1 +(f'W)2 dx,
а
b
Му = $ р (х)X д/l 4- (/'(х))2 dx.
а
Координаты центра масс: Хо = My/m, уо = Мх/т.
Центр масс криволинейной трапеции
(плотность р постоянная)
ь
Масса: m — р $ f(x)dx.
а
Статические моменты относительно координатных осей:
ь ь
Мх — -у f2(x)dx, Му = р xfixfdx.
а а
Координаты центра масс: х0 = My/m, уо —Мх/т.
8.4. ИНТЕГРАЛЫ ОТ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Двойной интеграл
Сведение к повторному
ь
\\f(x, у) dxdy = \dx $ f(x, y)dy
D a <p(x)
(область D ограничена кривыми x = a, x — b, у = <p(x), у = ф(х),
ф(х)<ф(х)).
Замена переменных
\\f(x, y)dxdy = \\f(x(u, vf, y(u, v))\J(u, v)\dudv,
D G
отображение х = х(ы, и), y = y{u, v) — диффеоморфизм множества G
на D, 1 (и, о)—якобиан отображения:
.. . D(x, у)
J(u, —j—=
D(u, v)
дх дх
ди dv
ду ду
ди dv
185
В частности, переход к полярным координатам х = г cos ф, у =
= г sin ф (якобиан J(ф, г) — г)
ЭД f(x, y)dxdy = \\f(r cos ф, r sin ф) rdydr.
D G
Некоторые приложения двойного интеграла
Площадь плоской фигуры
S = ЭД dxdy.
D
Объем цилиндроида
v = у)dxdy.
D
Площадь поверхности
1. Заданной уравнением z = f(x, у):
HW+S)'
D
2. Заданной параметрически (х = х(и, и), у — у(и, и), z = z(u, о)):
S= ЭД д/eG — F2 dudv,
u
где
ч>у+(М+(>у- ч#у+(>у+(>у
Р _ дх дх ду ду dz dz
ди dv ди dv ди dv ’
либо
S — ЭД д//Г + В2 + С2 dudv,
й
где А —
D(y, z) = D(z, х) . = Р(х, у)
D(u, v) ’ D(u, v) ’ D(u, v) '
Масса плоской фигуры
m ~ ЭД P(x> y}dxdy
D
(p(x, y) — плотность).
Статические моменты отно"ительно координатных осей
Мх= ЭДур(х, y)dxdy, Му= ЭДхр(х, y)dxdy.
О D
186
Координаты центра масс
Хо = Му/m, уо = Мх/пг.
Моменты инерции
Относительно оси Ох:
h = 5$ У2р(*. U)dxdy.
D
Относительно оси Оу:
]у=\\ *2Р(*> У)dxdy.
D
Относительно начала координат:
/о = ^(х2 + у2)р(х, у)dxdy.
D
Тройной интеграл
Сведение к повторному
b i|>(x) h(x, у)
\\\f(x, у, zjdxdydz = dx $ dy J f(x, у, z) dz.
E a <p(x) g\x,y)
Замена переменных
555 f (x, y, zjdxdydz — 555 f(x(u, v, w\ y(u, v, w), z(u, v, w]) X
E E'
X |/(u, u, w)\dudvdw,
отображение х = х(«, и, w), у — у(и, v, w). z = z(u, v, ь у) — диффео-
морфизм множества Е' на Е; J(u, и, w) ,, ч D(x, у, z) J {и, V, W)= г = D(u, v, w) — якобиан отобра) дх дх дх ди dv dw ду ду ду ди ди дш dz dz dz du dv dw кения:
В частности, в цилиндрических координатах х = г cos ср, у — г sin ср,
z = z, |J(ср, г, z)| — г:
555 К*. У> 2}dxdydz= \\\^г cos ср , г sin ср, z) rdqdrdz\
Е Е'
в сферических координатах х — г cos ср cos ф, у = г sin ср cos ф, г —
= г sin ф, |/(<р, ф, г)| — г2 cos ф:
555 f (х, У> 2) dxdydz — 555 Кг cos Ф cos Ф> r s*n Ф cos Я7» r s*n Ф) X
Е Е’
X г2 cos фс/срс/фс/г.
187
Приложения тройного интеграла
Объем тела
V = dxdydz.
Е
Масса тела
>п = )$$р(*> У, z) dxdydz
Е
(Р = р(*, у, г) — плотность тела).
Координаты центра масс
Хо = ~ Ш *Р(*. У< 2) dxdydz,
Е
= ~ УР(*. У’ z) dxdydz,
Е
2° = ~ Ш гР(х> У, z) dxdydz.
1 Е
Моменты инерции
Относительно координатных плоскостей:
hy = $^г2р(х- У, z) dxdydz,
Е
Л/? — W*2p(x, у, z) dxdydz,
Е
$^У2Р(Х> У’ z) dxdydz.
Е
Относительно координатных осей:
1х = (у2 + 22)р(л-, у, z) dxdydz,
Е
jy= Ш(х2 + 22)р(*. У, z) dxdydz,
Е
$55 (*2 + У2)р(*. У, z)dxdydz.
Е
Относительно начала координат:
/о = $^(х2 + у2 + z2) р(х, у, z)dxdydz.
Е
188
Криволинейные интегралы
Криволинейный интеграл 1-го рода (Кри-1)
\f(x, у) ds.
I
Сведение Кри-1 к определенному интегралу
Если кривая / задана уравнением у — g(x), a^x^.b, то
ь
\f(x, у) ds — \f(x, g(x))-yj\ + (g'(x))2 dx.
I a
Если кривая / задана параметрически (х = x(t), y — y(t)),
а С t р), то
Jf(x, у) ds — \f(x(t), у(/)Ы*'(0)2 + (У'(0)2 dt.
I а
Криволинейный интеграл 2-го рода (Кри-2)
\Р(х, y)dx + Q(x, y)dy.
i
Изменение направления обхода по кривой
Р(х, у) dx + Q(x, y)dy= — $ Р(х, у) dx + Q(x, у) dy.
АВ BA
Сведение Кри-2 к определенному интегралу
1. Кривая / задана уравнением у = [(х), х изменяется от а до Р:
₽
\Р(х, y)dx + Q(x, y)dy = \ (Р(х, f(x))+Q(x, f(x))f'(x))dx.
I а.
2. Кривая I задана параметрически: x = x(t\ у = y(f), t изме-
няется от а до Р:
Р
\р(х, y)dx+Q(x, у) dy = \(P(x(t), y(t)) х'(t) + Q(x(t), y(t))y'(/)) dt.
I a
Сведение Кри-2 к Кри-1
$ Р(х, у) dx + Q(x, у) dy = $ (Р(х, у) cos а(х, у) + Q(x, у) sin а(х, y))ds,
i 1
где а(х, у) — угол между направлением касательной к кривой /, согла-
сованным с направлением обхода на кривой, и положительным
направлением оси Ох.
189
Формула Грина
J /ЭСГ- y)^ + Q(jf. = —
dD D
^)dxd,J-
Если D—односвязная область, то dD (граница области D} —
простая замкнутая кривая, обход по которой совершается против часовой
стрелки. Если D — неодносвязна, то dD — совокупность замкнутых
кривых, обход по которым совершается так, что D остается слева.
Первообразная дифференциального выражения
Если в односвязной области D для функций Р и Q выполняется
о- dQ дР
условие Эйлера = > т0 дифференциальное выражение
Р(х, y)dx + Q(x, y)dy является полным дифференциалом, т. е. существует
функция и = и(х, у} (первообразная), такая, что du = Р(х, y)dx
+ Q(x, y)dy всюду в области D. Первообразная может быть вы-
числена по одной из формул:
х у
и = 5 y)dx + $ Q(x0, y)dy + С,
Хо Уо
У X
и= 5 Q(x, у)Уу + 5 Р(х, y0)dx + C.
Уо Хо
Кри-2 от выражения, являющегося полным дифференциалом, не
зависит от формы пути, соединяющего точки (х,; у(), (х2; y2), и может
быть вычислен с помощью формулы двойной подстановки:
(*2. Уг) .
5 Р(х, у)Ух 4-Q(x, y)dy = u(x2, y2) — u(xt, yi) = u(x, у) (Х2:^г).
(Xt.!/|) 'ОшуО
Некоторые приложения криволинейных интегралов
Длина кривой
s — J ds.
I
Масса кривой
т = J р(х, у, z)ds
I
(р = р(х, у, z) — плотность кривой).
Координаты центра масс
Хо = — \ хр(х, у, z) ds,
m J
/
190
У"= —\ УР^Х' У' Z^ds’
i
If,
Zo = — \гр(х, у, z) ds.
i
Работа
Работа силы /? = (Р(х, у, z)\ Q(x, у, z); R(x, у, z)) вдоль кривой /:
А — \ Р(х, у, z) dx + Q(x, у, z)dyR(x, у, z)dz.
i
Поверхностные интегралы
Поверхностный интеграл 1-го рода (Пови-1)
\\f^x, у, z)dS.
s
Сведение к двойному
1. Поверхность S задана уравнением z — z(x, у), (х; у) £ D:
^Дх, у, z)dS= \\f(x, у, z(x, y))V> +(2i)z + (z;)2 dxdy,
S D
y. z)dS = y. z(x, y)) |cos^ y)| ,
S D
где y(x, y) — величина угла между нормалью к поверхности и положи-
тельным направлением оси Oz.
2. Поверхность S задана параметрически: x = x(u, а), у = у(н, v),
z = z(u, и), (u; а) £ Q:
Ц Дх, у, z) dS — \\f(x(u, v), y(u, v), z(u, i>)) ~\JeG — F2 dudv,
S Й
dx dx , du dy , dz dz
=------------— —-—------------, или
du du du dv du dv
\\f(x, y, z~)dS — \\f(x(u, v\ y(u, v), z(u, a))-\M2 -f- B2 4- C2 dudv,
S Q
dy dz dz dx dx dy
du du du du du du
где A — dy dz ; в = dz dx ; c — dx dy
dv dv dv ~dv dv dv
191
Поверхностный интеграл 2-го рода (Пови-2)
55 Р(х, у, z) dydz + Q(x, у, z) dzdx 4- R (х, у, z) dxdy
по фиксированной стороне двусторонней поверхности S.
Пови-2 по разным сторонам S+ и S- одной
и той же поверхности S
55 Р(х, у, z) dydz-\-Q(x, у, z) dzdx + R(x, у, z) dxdy—
S +
— — 55p(x, y, z) dydz 4- Q(x, y, z) dzdx + R(x, y, z)dxdy.
s~
Сведение Пови-2 к Пови-1
55 Р(х, у, z) dydz + Q(x, у, z) dzdx + R(x, у, z) dxdy =
s
= 55 (P(x, У, z)cos a + Q(x, y, z) cos £ + R(x, y, z) cos y) dS,
s
где cosa(x, y, z), cos p(x, y, z), cos y(x, y, z)—направляющие коси-
нусы нормали, соответствующей выбранной стороне поверхности.
Сведение Пови-2 к двойному интегралу
1. Поверхность S задана параметрически: х = х(и, и), у — у(и, v),
z — z(u, u), (w; и) £ й:
55 Р(х, у, z) dydz + Q(x, у, z) dzdx 4- R(x, У, z) dxdy =
s
= ± 55 (M + QB + RQdudv
Q
(Д, В, C — CM. c. 191), выбор знака перед интегралом согласуют
со стороной поверхности, по которой ведется интегрирование.
2. Поверхность S задана уравнением z = z(x, у), (х; у) £ D;
55/?(х, у, z) dxdy = 55 /?(х, у, z(x, уУ) dxdy,
S D
если Пови-2 вычисляется по верхней стороне поверхности S;
55 /?(Х, у, z)dxdy= — 55/?(х, у, z(x, у)) dxdy
s D
для нижней стороны поверхности S.
Формула Стокса
5 Р(х, у, z) dx Q(x, у, z) dy 4- /?(х, у, z) dz =
ds
Cf fdR dQ \ , , , /дР dR\., . (dQ dP\ . .
s
192
обход контура dS (границы поверхности S) согласован с выбором
оооны поверхности S.
Формула Стокса в символической форме
Р(х, у, z)dx + Q(.v, у, z)dy + R(x, у, z) dz —
dS
dydz dzdx dxdy
_ СГ _d_ д d
J J dx dy dz '
s P Q R
5 P(x, y, z)dx + Q(x, y, z) dy + R(x, y, z) dz =
dS
cos a cos p cos у
— И д — — dS
J J dx dy dz
s P Q R
(cos a, cos p, cos у — направляющие косинусы нормали, соответствую-
щей выбранной стороне поверхности).
Формула Остроградского
Р(х< z)dydz + Q(x, у, z)dzdx + R(x, у, z)dxdy—
дЕ
Е
(дЕ — внешняя сторона поверхности тела £);
55 (Р cos a + Q cos PH-/? cos y) dS —
dE
= 555 (^-+^+^’)“!";г
£
(cos a, cos p, cos у — направляющие косинусы внешней нормали к по-
верхности dE).
8.5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
Несобственный интеграл
по неограниченному промежутку (НИ-1)
Определение НИ-1
4-оо ' А
5 f(x)dx= 1чп 5 f(x)dx.
а А->- + оо а
7 Воднев В. Т и др.
193
Формула двойной подстановки
Если F— непрерывная первообразная функции f на [а; + оо[, то
+ 0°
$ f(x)dx = F(+oo)-F(a) = F(x)lf°°,
а
гдеЕ(4-оо)= lim F(x).
Х—> 4" ОО
Линейность
4* оо 4“ °° 4- °°
S (af(x) + pg(x))Jx = а 5 f(x)rfx + p $ g(x)dx,
а а а
если интегралы в правой части сходятся.
Аддитивность
4~ оо ь 4~00
$ f(x)dx = \f(x)dx + $ f(x)dx,
a a b
+ °0
если сходится $ f(x)dx, где с — min (а; Ь}.
С
Замена переменных
4-оо р
j f(xjdx= S/(ф(О)ф'(О^.
а а
ф монотонна и непрерывно дифференцируема и отображает промежуток
с концами се и р на [a; -j-oo[.
Формула интегрирования по частям
-{- оо 4- °°
5 а(х) ц'(х) dx = [u(x) а(х)]7°° — j u(x) и'(х) dx.
а а
Признаки сходимости НИ-1 от положительных функций
Первая теорема сравнения
+ 0°
Если 0<f(x)<g(x) на [а; + °°[. то из сходимости $ g{x)dx сле-
а
+ 00 4- 00
дует сходимость $ f(x)dx, а из оасходимости $ f(x)dx— расходимость
а а
4- 00
5 g(x)(Zx.
а
194
Вторая теорема сравнения
fM +(°°
Если lim —т— = с, то при 0 < с < 4~ оо интегралы \ f(x)dx
+ оо ё W а
-}- оо
и 5 g(x)dx или оба сходятся, или оба расходятся. При с = 0
а
4- 00 4- 00
из сходимости J g(x)dx следует сходимость j f(x)dx (из расходи-
а а
4~оо 4-оо
мости $ f(x)dx—расходимость $ g(x)dx). При с — 4- оо из сходи-
мости К*) dx следует сходимость $ g(x)dx (из расходимости
а а
4“ оо 4- оо
$ g(x)dx — расходимость J f(x')dx).
а а
Степенной признак
Если f(x) ~ с/х’1 при х-> + оо, 0 < с < +°°>то при а > 1 интеграл
4- ОО
J f(x)dx сходится, при 1 — расходится.
а
Признак А беля
+ оо
Если $ f(x)dx сходится, a g монотонна и ограничена на [а; +°°[.
а
+ 0°
то 5 сходится.
а
Признак Дирихле
Если [ имеет ограниченную первообразную на [а; + оо[, a g
4~ оо
монотонно стремится к нулю при х-> + °°> то J f(x) g(x)dx сходится.
а
Несобственный интеграл
от неограниченной функции (НИ-2)
Определение НИ-2 (Ь—особая точка)
b b —1|
\ f(x) dx = lim \ f(x) dx.
J n-* + 0 J
a a
195
Формула двойной подстановки
Если F — непрерывная первообразная функции f на
ь
$ f(x) dx = F(b — 0) — F(a) = F(x) 1Г °,
[а; Ь[, то
где F(b — 0) = lim F(x).
Степенной признак сравнения
для положительных функций
Если /(х)~ ———- при
- ху
О
$ f(x)dx сходится, при
b — 0, то при
интеграл
a 1 — расходится.
Эйлеровы интегралы
^-функция
в (а, ₽) =
$ ха '(1—х)₽ 'dx, а > 0, Р > 0,
о
В (а, р) =
I ха“'
J (1 +x)a+|i
о
Выражение
В-функции через Г-функци
С и м м е т р и я В-ф у н к ц и й
В(а, ₽) = В(р, а).
Формулы понижения
В(а,
В (а,
для
Р) = а р _ 1 В <а ~ 1 > Р)’ « > •, Р > 0,
Р)= V+р'— 1 В(-а’ Р “ а > °- Р>1-
Вычисление В-ф у н к ц и и
некоторых значений аргумента
(п - I)’
В (a, /г) = -------J------_______________ nfN
(a + и — 1) (a + n — 2)---(a + l)a ’ ’
D \ — ')! (rt — •)!
В (m, n) = —---—-A———, m, n £ N,
(in -f- и — 1)!
В (a, 1) = B(l, a) = 1/a.
Формула дополнения
ю
196
Г-функция
-|- ОО
Г(а) = xa~'e~xdx, а > 0.
о
Формула понижения
Г(а + 1) = аГ(а), а > 0.
Формула дополнения
Г (а) Г(1 — а) — л/sin ал, 0 < а < I.
Формула Эйлера — Гаусса
________________па(п — 1)!_______
ггДГ'Х (а + п — 1) (а + п — 2)--(а + 1)а
Формула Лежандра
Г(а)г(а + 1')=-^тГ(2«).
Вычисление некоторых значений Г-функции
Г(1) = 1, Г(2) = 1, Г(п) = (zi — 1)!, ngN,
Поведение Г-функции
lim Г(а) =4-оо, lim Г(а)=4-°°,
а-> 0 а-> оо
Tmin — 0,886... при а =1,462...
Выражение некоторых интегралов через эйлеровы
197
Некоторые именные интегралы
Интеграл Дирихле
+ °°
sin ах , л
—х— dx="~2 Sgn “•
Интеграл Пуассона
о
Интегралы Лапласа
I cos ах Л ... ,
J VT7dx = -?We6
О
х sin ах ,
Л . , ।
sgn а •
Интегралы Френеля
Интеграл Эйлера
-|- оо
С у®— I „
1 X t Л
\ ТП-----.
J 1 + х sin ал
о
О < а < 1.
Формулы Фруллани
Если / непрерывна на [0; 4-оо[, 3/(4-oo)CR, то
f(ax)-f(6x) ь
-------------dx = (/(0) - f (+ оо)) In —-
Л и
а, b > 0.
+ оо
С f fx)
Если f непрерывна на [0; +оо[, \ ^-—dx сходится V А > 0, то
А
+r rfx=f(0)lnA. а, 6>0.
J X CL
0
198
Некоторые интегралы
+ оо
f dx
J "х^
оо
С dx _ 2л
' !+*3 3^3 ’
1
С dx л
J v ’
dx
(а2 4-х2) (Ь2 + х2)
л
2аЬ(а 4- Ь) ’
1 1
\ In xdx = — 1, \ х In xdx —----------i-,
J J 4
0 0
л/2 л/2
In sin xdx =------у In 2, In cos xdx =-----------у In 2,
о о
f(2k — 1)!! л _
— ----при n = 2k, k — 1,2, ...,
(2kY^
(2ГИ)Й ПРИ " = 2*4- 1,^0, 1,2,...;
199
ь
f(x) §(x)dx = f(0), f — непрерывна,
л/2
dx
л
J a2 sin2 x 4- b2 cos2 x 2\ab\ ’ a
о
2л
f dx
2л
-yjl — a2
0
л/2
Sdx л
1 — a2 cos2 x —
&
г
9. КОМПЛЕКСНЫЙ АНАЛИЗ
9.1. КОМПЛЕКСНОЗНАЧНЫЕ ФУНКЦИИ
ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
Определение
Отображение о: Х->-С, X cz R, называется комплекснозначной функ-
цией действительной переменной. Задать функцию о(/) можно в виде
о(/) = £(/) +/п(0. * X, где Е=(0, п(0 — действительные функции.
Предел
lim о(/) = lim g(/) + i lim r|(f),
lim (aoi(t) + bo2(C) = a lim Oi (/) + 6 lim a2(0,
lim (oi(Z) o2(0) = Hm °i(0 •
/->-/() t^-to
lim o\(f)
.. oi(Z) t^tB
lim---------= —------------—
t^t0 lim o2(/)
lim o2(0<
t-f-to
( lim o2(/) 0).
Производная
o'(0=
Д/->0
о(/ + Xt) — o(/)
bi
(aoi (/) + fro2(/))' = ao( (/) + &a2(0,
(ai(0 a2(0)' = of(0 02 W + Oi(0 o2(/).
/Qi(0 \
\o2(0 )
02(0
Интеграл
₽ P ₽
Jo(Od/= dt + i\x\(t)dt,
a a a.
₽ в в
$(aoi(0 + &o2(0) dt = a $ oi(/) dt -j- b J o2(/) dt,
a a a
p a ₽ Y ₽
5 o(0 dt= - J o(Z) dt, J o(/) dt = $ 0(0 dt + J o(/) dt,
a P a a Y
201
0
d/ = F(₽)-F(a) = F(/)|§,
a
где F — первообразная для a.
Формулы Эйлера
elt = cos t + i sin t, e~lt — cos t — i sin t.
Уравнение окружности
1. Центр в точке zo, радиус R:
z = Zo + Re“, О С t < 2л.
2. Центр в точке zo — 0, радиус R-.
z = Re‘‘, О t < 2л.
3. Центр в точке z0 = О, радиус R— 1:
z = е‘‘, О t < 2л.
9.2. КОМПЛЕКСНЫЕ ФУНКЦИИ
Функция комплексной переменной (ФКП)
w — f(z), z С D, D cz С,
W = и(х, y)4-iu(x, у), z = x + iy.
Экспонента
w = е2 = ex(cos у i sin у),
z z2 zn
е* = 1 4- —- + — 4-... + _ + .... z € С.
Свойства:
e2l + ?2 = е2' е2\ ег+2ш — е (периодичность),
|ег|=ех, Arg е2 — у 4- 2nk, k £ Z,
e2k2i = 1, k е Z, ея‘= - 1, e-11' = — 1, ел,/2 = i, e~ni/2 = -i.
Тригонометрические функции
ei2 + e-i2 . ei2 — e^‘2
cos z —----------, sin Z =----X----,
2 2j
sin z e‘2 — е-1г
tg z —------—---------——,
cos z i(e‘2 + e u)
, cos z i(e‘2 4- e~‘2)
ctg z =------= —--------—
sin z e‘2 — e 12
Z^ Z^ Z^n
«Sz=i-^ + --... + (_irw + ..., 2ec,
73 5 ~2n+l
™г = г- зГ + -5Г-- + (-1>"(2^+1)!+--геС’
cos2 z 4- sin2 г = 1, cos (z 4- 2л) = cos z, sin(z 4- 2л) = sin z,
202
Im cos z — — sin x sh y,
Im sin z — cos x sh y,
sin z = — i sh (z.
cos2 z — sin2 z = cos 2z, 2 sin z cos z — sin 2z,
sin (Z| + Z2) — sin Zi COS Z2 + COS Zi sin Z2, COS (Z1 4- Z2)
= cos z\ cos Z2 — sin zi sin Z2,
Re cos z = cos x ch y,
Re sin z — sin x ch y,
cos z = ch iz,
tg z = —i th iz, ctg z = i cth iz.
Гиперболические функции
sh z =-------------------
chz=—_
,, sh z e'— e
th z —-=-----
ch z e* + e
cth z
z“
4!
z5
z
ch z = 1 4* у
sh z — z + у + -51—h ••• +
ch z = cos iz,
sh z = —i sin iz,
Re ch z — ch x cos y,
Re sh z — sh x cos y,
2
_ ch z
sh z
z2" ,
(2n)!
z2"+l
ег — e г
z£C,
(2n + l)!
th z = — t tg iz,
cth z — i ctg iz,
Im ch z = — sh x sin y,
Im sh z = ch x sin y.
zee,
Логарифм
Ln z = In z + 2 tiki, In z — In |z| 4~ i arg z,
Ln (Z1Z2) = Ln zt + Ln Z2, Ln (Z1/Z2) = Ln zi — Ln z-i,
Lnz" = nLnz, ReLnz = ln|z|, Im Ln z —Arg z.
Обратные тригонометрические
и обратные гиперболические функции
Arcsin z = — i Ln (iz + v 1 — z2 ),
Arccos z = —i Ln (z 4- yz2 — 1 ),
. . t, i 4- z
Arctg z= у Ln y—y,
Arsh z = Ln (z 4- ~^z2 4- 1),
Arth z = 4” Ln *2 ,
2 1 — z
Arcctg z = Ln
z — i
z + i'
Arch z = Ln (z 4~ \z2 — 1
* ,, 1 , z 4~ 1
Arcth x = — Ln----------—
2 z — 1
Определение:
Производная ФКП
f,z ч f(z 4- Az) — f(z)
f'(z)= hm ---------t4—'---.
Az
Условия Коши — Римана существования производной
f(z) = u(x, y) + iv(x, у)-.
ди dv dv ди
дх ду ’ дх ду '
функции
203
В этом случае
< ди ди ди . ди
I = "3------Ь1 ~л~ = -S-----1 -г- •
дх дх ду ду
Условия Коши — Римана в полярных координатах (z = reL,f w —
= u(r, <p)-f- iv(r, (p)):
du ___ 1 dv du dv
dr r d(p ’ dq> ~~ Г dr '
Интеграл ФКП
J /(2) dz.
v
Связь интеграла ФКП и Кри-2
5 /(2) dz = \и(х, у) dx - и(х, у) dy + i\ v(x, у) dx + и(х, у) dy
TV т
(/(z) = u(x, y) + iv(x, у)).
CeedeHue интеграла ФКП к интегралу
от комплекснозначной функции
действительной переменной
Если у: z = o(/), /£[а; 0], то
0
\f(z)dz =
V а
Формула Ньютона — Лейбница
Если /' аналитическая в области D, F — первообразная для f,
21, 22 € D, то
5/'(2) </г = Е(22)-Е(г1) = Е(2)|^.
г.
Свойства интеграла
I. \(af(z) +bg(z))dz = a\f(z)dz +b \g(z)dz, а, b £ С.
V Y Y
2. f(z)dz = \f(z)dz+ \f(z)dz, у = Vi U y2, Yi Пу2= 0.
V Yi Yz
3. j /(г) dz = — $ f(z) dz.
V
4. | 1/(2) Ids Ml, M = max |f(z) |, / = дд.у.
v Y г e Y
Если f(z) аналитическая в области D и непрерывная в D U dD,
где dD — граница области D, то имеют место:
1) интегральная теорема Коши:
U(s) ds = O;
dD
2) интегральная формула Коши:
~2iti j s-z = Vz€Z>;
dD
204
3) интегральное представление для производных:
n! f f(s)
2nt J (g —?)n+1
dD
= f^z)
V z£D.
Степенные ряды
S Сь (z — z0)*, Ck, Zo, z E C.
fe = 0
Радиус сходимости степенного ряда
Круг сходимости: (z| |z —zol</?).
Ряд Тейлора
Если /(z) аналитическая в области D и Zo Е D, то
/(z) = £^L(z-Zo)*, |z-z0|</?,
* = о
R равно расстоянию от точки Zo до границы области D.
Нули аналитической функции
Для того чтобы точка zo была нулем кратности k функции /, не-
обходимо и достаточно выполнение одного из следующих условий:
1) f(z0) = r(z0)=... = ffc-,)(z0) = 0, Rzo)=#O;
2) f(z) = (z — z0)*<p(z), <p(zo)=/=O;
3) f(z) = c*(z — Zo)* + c* + i(z — Zo)* + I^=#0.
Если Zo — oo — нуль порядка k функции f(z), то f(z) = z-*<p(z),
<p(°o) =# 0.
Ряд Лорана
Если функция f(z)—аналитическая в кольце r< |z — ZoI < R, то
+ °°
f(z)= S Ck(z — z0)*,
k — — oo
J_ C He) dz
2л/ J Ig — Zo)*+1
|г —Zol =p
k E Z, Г < p < R.
Изолированные особые точки
однозначного характера
Тип особой точки zo функции определяется видом разложения f(z)
в ряд Лорана в окрестности точки zo:
ОО
1) f(z)= S ck(z — Zo)*, 0 < |z — Zol </?, тогда z0 — устранимая
k = 0
205
особая точка;
ОО
2) Кг) = ck(z — z0)\ 0 < |z — Zo| </?, c_m^0, тогда z0 —
k = — m
полюс порядка m;
-|- oo
3) f(z)= S Ck(z — zo)\ 0<|z — Zol </?, и бесконечное число
k = — oo
коэффициентов c_*, k g N, отлично от нуля, тогда Zo — существенно
особая точка.
Если Zo — полюс порядка т, то f(z) — <p(z)/(z — z0)m, <p(z) — ана-
литическая, (p(zo)=7^O.
Вычеты и их применение
res f(z) — вычет функции f(z) относительно изолированной особой
2 = г»
точки zq:
res/W=-l-
z = za ZJll J
|г — г0|=р
(в круге |z —zol р нет других особых точек).
+ °о
Если f(z) = 2 ck(z — z0)\ 0 < |z — z0| < R, то
k = — 00
res f(z) = c-i.
z = z0
Вычисление вычетов
1. Zo — устранимая особая точка:
res f(z) — 0.
z = z0
2. zo — полюс:
a) Zo — простой полюс:
res f(z) = lim ((z — z0) f(z)).
Z = Zq Z—^Zq
В частности, если f(z) = <р(г)/ф(г), ф(г0) = О, ф'(го)=#0, q>(z0) =# О, то
res = ф^о) -
г = гоф(г) Ip'(Zo)’
б) го — полюс порядка т:
1 сГ~'
res = 7т—ЙГ lim /У,— ' ~ z°ynf^
г = га [т — 1)! г-*г0 az
(формула также верна, если Zo — полюс порядка не выше т).
3. Zo — существенно особая точка. Вычет находится по разложению
в ряд Лорана.
Вычет относительно бесконечно удаленной точки
|г| —р
206
(f(z)— аналитическая в области р^|г|<-4-оо; обход контура — по
часовой стрелке).
res f(z) = —C-i,
Z = OO
C-i —коэффициент при z-1 в разложении f(z) в ряд Лорана в окрест-
ности точки Zo = оо.
Вычисление вычета в бесконечно удаленной точке
1. z = оо — правильная точка:
res К2) — 2(К°°)~К2))>
2= оо 2-> оо
z = оо — нуль:
res f(z) = — lim zf(z).
Z — oo 2—> oo
В частности, если )(z) —Л/z"1 при z-* оо, то
r, , f —А, если m = 1,
resf(z) = ’
z= оо [0, если m > 1.
2. z = оо — полюс порядка не выше т:
3. Если f(z) представима в виде f(z) = tp где ф(е)— аналити-
ческая в точке g = 0, то
res f(z)= — <р'(0).
Z= ОО
Если f(z) имеет конечное число особых точек Zk, k — 1, 2, п, в ко-
нечной части плоскости, то
res f(z) — — S res f(z).
2= oo k=l Z = Zt
Основная теорема о вычетах
Если f(z)—аналитическая на границе dD области D и внутри
области, за исключением конечного числа особых точек Zi, Z2, z„,
лежащих в D, то
5 /(z) dz = 2ni S res /(z)
dD * = 1 * = z‘
(обход контура положительный).
Вычисление интегралов от функций
действительной переменной
2 л
г 1 С /z2-l- I г2 — 1 \ dz
1. \ R(cos t, sin Z) dt — — \ /?(—x----, ——I—- (R — pa-
0 lz| = l
циональная функция двух переменных).
+ °°
2. Если /?(х) — рациональная функция, а $ R(x) dx сходится, то
— оо
207
oo n
5 R(x)dx = 2m S res /?(z),
— oo k = 1 Z = Zk
где Zk — все особые точки функции 7?(z), лежащие в верхней полу-
плоскости (Im Zk > 0).
Если gi, g2, .... Чт — особые точки функции R(z), лежащие в ниж-
ней полуплоскости, то
+ оо т
5 R(x) dx = —2л1 S res /?(z).
— ОО =
3. Если R(x) — рациональная функция, не обращающаяся в нуль на
действительной оси, R(x) ~ c/xk(x-+ оо, с =# 0, k 1), то
$ e‘axR(x) dx — 2т S res (?az/?(z)), a>0
— oo I Z== Zk
(Zk — все особые точки, лежащие в верхней полуплоскости);
j e~,fiJC/?(x)dx=-2ш S res (е~‘₽г/?(z)), ₽>0
— оо = 1 Z =
— все особые точки, лежащие в нижней полуплоскости).
4-оо 4-00 + 00
Замечание. $ R(x) sin ctxdx = Im R(x) e,axdxt R(x)cos txxdx —
— oo — OO —- oo
+ o°
= Re $ R(x)eia*dx.
4. Если R(x) — рациональная функция, аналитическая в верхней
полуплоскости, за исключением конечного числа изолированных особых
точек zi, аг, .... zn (Im zk > 0), имеет на действительной оси простые
полюса Xi, х2..... хт и |R(z)|-*O, z-+oo (Im z > 0), то
v. p. eiaxR(x) dx = 2m S res (e'a27? (z)) + ni S res (e‘az/?(z)).
_ oo —-1 Z ~~ Zk k —— 1 Z — X ft
Конформные отображения некоторых областей
на единичный круг |иу| < 1
1. Верхней полуплоскости Im z > 0:
w = е‘а ——a С R, Im Zo > 0.
z — Zo
2. Единичного круга |z| <1:
Z — Zo
w = e'a----——, a 6 R, | zo I < 1.
1 — ZoZ
3. Полосы 0<Rez<n, —oo<Imz<+°°:
(щ — 1)/(щ + 1) —
4. Полукруга |z| < R, Re z > 0:
z2 + 2Rz - R2
w = i —y---—------rr-
208
9.3. РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
Ряд Фурье
Тригонометрическая система
1. cos х, sin х, .... cos kx, sin kx, ...
Коэффициенты Фурье функции f периода 2л
Л
at, = — \ f(t) cos ktdt, k=0, 1, 2, ....
Л J
— л
Л
bk = — \ f(t) sin ktdt, fe=l, 2, ...
JI J
— л
либо
a 4- 2л
ak — — \ f(t) cos ktdt, k—0, 1, 2.........
л J
a
a 4- 2л
bk — — \ /(/) sin ktdt, k = 1, 2, ...
JI J
a
Ряд Фурье функции f
OO
——|- > (ak cos kx + bk sin kx).
k = \
л
2 C
Если f четная, то bk = 0, ak = — \ f(t) cos ktdt, ряд Фурье
л j
о
oo
a° i V a/
— + > ak cos kt.
k = i
Л
2 C
Если f нечетная, то ak = 0, bk = — \ f(t) sin ktdt, ряд Фурье
л J
о
oo
S bk sin kx.
k = i
Если функция f кусочно-непрерывна и кусочно-дифференцируема, то
ОО
(ак cos kx + bk sin kx) = -у ([(« — 0) + f(x + °))-
8 Воднев В. T. и др.
209
Неравенство Бесселя
2 ” П
~2—ь у (°* + bl) у J f2(-0 dx.
k = 1 — л
Равенство Парсеваля
2 00 я
-у + (а* + Ы) = у /2(х) dx.
/г = I — л
Ряд Фурье в комплексной форме
"4"д.
ckeikx, = A- j /(/) e~ikldt, k е Z.
fe= — оо
Ряд Фурье функции периода 21 по системе
do у* / ktix knx \
-у + > ( ak cos —-------h bk sin —-—L
k= i
где
/
ak = -j- /(/) cos dt, 1г — 0, 1,2,...;
-i
i
= у f (0 sin-y-^0 £ = 1,2,...
-l
(коэффициенты Фурье).
Ряд Фурье функции f по ортогональной системе функций
(Рь ф2?“., фа, ... на отрезке [a; Z>]
ОО
2 Ck(fk(x),
k=\
b
где Ck = ~т~;,2 \ dt' k = !> 2> -
IlTdl J
a
Равенство Парсеваля (условие полноты)
24 || ф4 ||2 — \[2(х) dx.
ка1 а
210
Интеграл Фурье
Интеграл Фурье для кусочно-непрерывной и абсолютно интегри-
руемой на ]— оо; + оо[ функции f:
4- оо
$ (а(Х) cos кх + b(k) sin лл-)(/Х,
о
4-00 + оо
где а(Х.) = — \ f (/) cos ktdt\ b(k)=— i f(t') sin ktdt.
П J л J
— oo — co
-j- oo
2 f
Если f четная, то b(X) = 0, a(X) =— \ f(f)cos>ddt, интеграл Фурье
л J
4“ oo 0
5 a (к) cos kxdk.
о
4“ OO
2 C
Если f нечетная, то a(X) = 0, b(k)=~ V [(/) sin ’/.tdt, интеграл
JI J
0
4~ oo
Фурье $ b(k) sin kxdk
о
Интеграл Фурье в комплексной форме
4-оо -Е оо
c^e-^dk c(k) = -^~ f(f)eiUdt
Zn J
— oo — 00
или
4~ oo 4- °°
_L ( dX ( fWe^'^dt.
2л J J
— oo — oo
Преобразование Фурье функции f
4“ oo
F(X) = ( f(0 e-^dt.
"\/2л
* — oo
Обратное преобразование Фурье
1 +r°°
f(x) = —— I F(X) el)'xdk
"\/2п
— oo
Косинус-преобразование функции f
о
211
Синус-преобразование функции f
i— + 00
/2 f
Л(А) = -\/— \ f(t) sin Mdt.
V л J
0
Некоторые разложения в ряды Фурье
Л — X
~2~
ОО
Zsin нх
--------, 0 < х < 2л,
п
п=1
л — 2х Y* sin 2пх
4 “ / , 2п
п= 1
О < х < л,
4
sgn X = —
л
sin (2п — 1) х
2n — 1
, —л < х <. л,
212
i— V I 1
In Г(х) = In д/2л + > —— cos2anx3-(С + In 2лл) sin 2лпх,
О < х < 1,
(С — постоянная Эйлера: С — 0,5772...)
9.4. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Преобразование Лапласа
/7(р) = +
о
([ — оригинал; F — изображение).
Запись: f = F, f(f) = F(p).
Условия на оригинал
1. £)(/) = R, f(t) = O V / <0.
2. f — кусочно-непрерывна на R.
3. ЗМ, За, такие, что lf(/)l Меа1.
Линейность
fir=Fi, {2 ?= F2=>afi + Р/г v* aFi aFz.
Теорема подобия
Если f(/) = F(p), л > 0, то f(M) = — F 0^.
Теорема запаздывания
Если /(/) = F(p), a > 0, то f(t — a) = e~paF(p).
Теорема смещения
Если F(p) = f(O- “€C, то F(p — a) = ^'Ко-
дифференцирование оригинала
Если f(/) = F(р), /'(/) —оригинал, то
Г(/)#рР(р)_/( + 0).
Если f(n>(/) — оригинал, то
fW(/) = pn F(p) - рп-1 к+0) - РП-2Г (+0) -... -
-pf(n-2)( + 0)-f(n-|)( + 0).
213
Интегрирование оригинала
t
Если / == Л то Цт) dx = F(p)/p
о
Дифференцирование изображения
Если F = f, то ^"’(р) (- 1)П/ЛД/).
Интегрирование изображения
Р Г • F f Г1 \ 7
Если г = I, —-----оригинал, то —-— == \ г (s) ds.
Р
Изображение свертки (теорема умножения)
Если ft = Fi, f2 = F2, to
f,(T)f2(/-T) dx = F,(p) F2(p).
о
Интеграл Дюамеля
Если f непрерывна на [0; 4- оо[, ф непрерывно дифференцируема
на [0; + a / F, ф = Ф, то
/
/(/) ф( + 0) + 5 /(т) ф'(/ - т) dx = pF(p) Ф(р)
о
(формула Дюамеля).
Формула Меллина обращения преобразования Лапласа
eplF(p)dp, х>а.
X —<оо
Первая теорема разложения
Если F(p) = У —
La Р'
П а=0
ряд Лорана, сходящийся при |р| > R, то
/(/) =
о, ко.
214
Вторая теорема разложения
п г/ \ Fl^ г
Пусть г(р) = р -----правильная рациональная дробь и
г2(р) = (р _ P1)m' (р — р2)тг-(р - piYn:.
Тогда
I тк
Z
k=1/=1
где
1 dl~'
Ак‘ = 71--юГ Ит -утгг((Р - Р*Г W
(/ — 1)! p-+pt dp1
В частности, если все корни знаменателя простые и
РАр) = (р — pi) (р — Рг)-(р — рД
ТО
у
L '
k= I
Некоторые применения операционного исчисления
1. Решение задачи Коши для линейного дифференциального урав-
нения с постоянными коэффициентами
х(,,) + On-t/"-0 +-+ айх = /(/),
xW(0) = ^, /г = О, 1, .... п- 1.
Применяя преобразование Лапласа и используя теорему о диф-
ференцировании оригинала, приходим к уравнению
(р"ВД - рп-'^ - рП~% -...-Pln-1 - |„-|) +
+ a„_t(pn~ 'X(p) — рп-2£о —... — Вл-г) +••• + ai(P^(p) — Во) +
+ а0Х(р) = К(р),
где х(0 Х(р); f(t) F(p).
Преобразуя, получаем уравнение вида Т(р) Х(р) — Т(р) — F(p), от-
у, . T(p) + F(p)
куДаХ(р)=------—--------
Из последнего соотношения получаем возможность найти оригинал
%(/) по его изображению Х(р).
Начальная задача х(л)(/0) = В*. k = 0, 1, ..., п — 1, сводится за-
меной т = t — to к описанной.
2. Решение задачи Коши для систем линейных дифференциальных
уравнений с постоянными коэффициентами. Схема применения преобра-
зования Лаплшл такая же, как в п. 1.
fr-n + p-.-S,
Ч У — X — 2у = — 1 4- /,
Применяя преобразование Лапласа, приходим к алгебраической системе:
Г рХ(р)_ 1 -4Х(Р)+Г(р)=у-^,
| рУ(р) - I - Х(р) - 2Г(р) = - 1 + 4.
215
откуда Х(р)= ' 4- 1 , У(р) = _ ' +х(/) = / + е3', y(0=-Z + e3'
Р Р — ° р р — О
3. Решение интегральных уравнений Вольтерра типа свертки
t
*(/) — f(0 + 5 W ~т) х(т) ^т-
о
Применяя преобразование Лапласа, получаем
X(p) = F(p) + K(p)X(p),
где x(J) = Х(р); /(/) = F(p); k(f) = К(р\
Из последнего уравнения выразим Х(р) и по Х(р' найдем оригинал
х(/) — решение интегрального уравнения.
4. Вычисление несобственных интегралов.
Если f = F, g = G, то
5 f(/)G(/)d/=+$ F(t)g(t)dt
о о
(формула Парсеваля).
Таблица основных преобразований Лапласа
Оригинал Изображение Оригинал Изображение
1 1 i sin ы( 2pco
Р (p2 + co2)2
1 t cos со/ p2 — co2
Р2 (P2 + <o2)2
/2 2 sh со/ co
р3 p2 - co2
t\ п е N п! ch со/ p
р»+1 p2 — co2
Г(а> -1) Г(а+1) elt sin со/ co
ра+! (p-X)2 + co2
г' 1 e1' cos со/ p — X
р — X (p-X)2 + co2
teKI 1 sin / arcctg p
(р - X)2 /
Геи, п 6 N, и! ln(l + 7)
(р-хг+*
tae", а > — 1 Г(а+1) (р-Х)а + 1 6(/) 1
sin со/ <0 6(/ - a), a > 0 0—op
р2 + ш2
cos to/ Р
р2 + ш2
10. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
10.1. СКАЛЯРНОЕ ПОЛЕ
Определения
Скалярное поле определяется скалярной функцией точки и — и(М) =
= и(х, у, z) — u(r), где М(х; у, z) — точка пространства, г = (х; у; г) —
ее радиус-вектор.
Поверхности уровня
и(х, у, z) — С, С — const.
Линии уровня плоского скалярного поля
и(х, у) = С, С — const.
Оператор Гамильтона (линейный дифференциальный оператор
\7 (набла)):
Градиент
Градиент скалярного поля — вектор
Свойства градиента
grad с = 0, с — const,
grad (u + п) = grad и + grad v,
grad (см) — c grad u, c — const,
grad (uv) = 'J grad и + и grad и,
, / м \ v grad м — м grad v
grad (— ) = --------5-------—
grad f(u) = f'(u) grad u, grad un = nun 1 grad u.
grad Ir| = r/\r\.
217
Градиент скалярного ноля в цилиндрических координатах
. ди - , 1 ди - , ди -
grad и = —— ер 4------—- е^ 4- —— е:
др р с*ф dz
Градиент скалярного поля в сферических координатах
ди -
gra<lu=—г,+
1 ди - ( 1
р дй е° 1 р sin О
ди -
Оф
Производная скалярного поля и по направлению
I = (cos ос; cos (3; cos у)
ди _ и (х + t cos а, у -f- t cos р, z + t cos у) — u(x, у, z)
dl /-+o t
du
~dl
du , du n , du
—— cos cz -4—-— cos 3 -—-— cos y,
dx dy dz ‘
= (grad и • I) = \ grad и I cos (grad и, I).
du I । , i
-37- ==lgrad«|,
1 max
если / имеет
направление grad и.
10.2. ВЕКТОРНОЕ ПОЛЕ
Определение
Векторное поле определяется векторной функцией точки
F = F(M) = F(r) = Р(х, у, z)i + Q(x, у, z) j ф- R(x, у, z) k,
где М(х; у, г)— точка пространства; г = (х; у, z)— ее радиус-вектор.
Векторная линия
Векторная линия (силовая линия, линия тока) поля — решение
системы
dx _ dy ____ dz
~P~ = ~Q= ~R~'
Дивергенция (расходимость) векторного поля
дР . dQ . dR -
div F = —---h —-----h —- = V F.
dx dy dz
Свойства дивергенции
div c = 0, c — const, div r — 3.
div (F| ф- F2) = div Ft 4- div F2, div (cF) — c div F, c — const,
div (u F) = и div F -f- F - grad u, div (n • с) = c • grad и, c — const.
218
Дивергенция векторного поля в цилиндрических координатах
- 1 / д dF<f dF, \
div F = — (~ч—(Р/7р)+ -кг~ +р-з—)•
р \dp dtp dz )
Дивергенция векторного поЛя в сферических координатах
- 1 / д д dF,,, \
div F = —5-------- (—— (Ff,p~ sin 0) + р —- (Fa sin 0) + p —--),
p" sin 0 \ dp dO d<p /
Ротор (вихрь) векторного поля
д
дх
Р
или в символическом виде
i k
д д
ду dz
Q R
Свойства ротора
rot F = [ V, F] =
rote — 0, с — const, rot г — О,
rot (Fl + F2) = rot Fl + rot F2, rot (» F) = и rot F + [grad u, F],
div [Fi, F‘>] = Fi • rot F, — Fi • rot F2.
Поток векторного поля
Поток векторного поля F(M) через поверхность S в сторону, опре-
деляемую единичным вектором нормали п — (cos a; cos Р; cos у),
П= \\(F-n)dS= \\FndS =
s s
= 55 (P cos a + Q cos ₽ + ^ cos Y) dS =
S
= Pdydz 4- Qdxdz + Rdxdy,
s _
где Fn—величина проекции вектора F на направление вектора п.
Если поверхность S задана уравнением z = f(x, у), (х; у) g D, поток
через верхнюю сторону поверхности ме чно вычислить по формуле
П = 55 д^дхУ- р(х’ У’ f (х’ У)) - Q(-X’ lJ' КХ' +
+ Я(Х, у, f(x, y))^dxdy.
Если уравнение поверхности S есть г = г (и, v), (и; v)^G, то
Г Г _ Г dr dr 1
п= У(и’ z(u’ ^[dt7’ ~dv\dudv'
G
219
Линейный интеграл
Линейный интеграл от вектора F по линии I
$ F . dr = J Fsds = 5 Pdx + Qdy + Rdz,
i i i
где Fs — проекция вектора F на касательную к /. Линейный интеграл
выражает работу векторного поля F вдоль линии /.
Циркуляция
Циркуляция векторного поля F вдоль контура I — линейный инте-
грал вдоль замкнутой линии /: ф F-dr.
I
Формула Стокса
(^Pdx + Qdy + Rdz =
dS S
,/dP dR\,, , / dQ
+ -----)dzdx + I
\ dz dx f \ dx
- ^r)dxdy
или в векторной форме
j F • dr = $$ (n • rot F) dS,
os s
где n — единичный вектор нормали к поверхности S, направление ко-
торого таково, что при обходе контура I — dS поверхность S остает-
ся слева.
Формула Остроградского
+ R cos у) dS = 5$ Pdydz ф- Qdzdx ф- Rdxdy
dV
или в векторной форме
\\\ div FdV = $$ FndS,
V dV
где dV — S — внешняя сторона поверхности, ограничивающей тело V;
п — единичный вектор внешней нормали к ней.
Потенциальное векторное поле
Векторное поле F — потенциальное, если F = grad и. Функция и
называется потенциалом векторного поля F. Поле F — (P, Q, R) по-
тенциально в односвязной области тогда и только тогда, когда rot F — Q
220
dR dQ dP dR dQ dP n
или —— = ——, —— = ——, —— = ——. Потенциал в этом случае
dy dz dz dx dx dy
можно найти, например, по формуле
X у 2
и(х, у, г) = \ Р(х, у, z}dx-\- $ Q(xo, У, z) dy -f- $ R(x0, y0, z)dz-]-C.
Хц ya 2a
Соленоидальное векторное поле
Векторное поле F называется соленоидальным, если divF = 0.
Оператор Лапласа
* 2 d2, d2, d2
А — V — —— + 2" + л 2 •
dx~ dy dz
Оператор Лапласа в yuAundpunecKux KoopduHarax
1 d / du \ 1 d2u d2u
о ( P ”Z / ~T~ 2~ *”Z 2~ ' 2~"
p dp \ dp / p dtp dz
Оператор Лапласа в сферических KOopdimaTax
1 d / 2 du \ 1 d
p2 dp \ dp / p2 sin 9 d0
1 d2u
p2 sin2 9 d<p2
• a
sin 9-----
dO
Уравнение Лапласа
—
d2u d2u d2u
dx2 dy2 dz2
Функции, удовлетворяющие уравнению Лапласа, называются гар-
моническими.
Операции второго порядка
rot grad и = [ V, V и] — 0, div rot F V • [V, F] = О,
div grad и = V • V и — V2u =»- \u,
grad divF=V(V.f)=(^ + ^+^-V +
\ dx dxdy dxdz /
+ ( Q2P 4-^-4- d*R ^4- ( d2p + °2Q + °2R \k
\ dxdy dy2 dydz / \ dxdz dydz dz2)
rot rot F = [V, [V, F]]= V -(V -F)-(V • V)F =
= grad div F — Д F,
где AF = AP i + AQ j + &Rk.
11. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
11.1. ТЕНЗОРЫ. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
Индексные обозначения,
предварительные сведения
В тензорном исчислении принято соглашение: если в некотором
одночленном выражении имеется индекс, написанный один раз внизу,
другой раз вверху, то подразумевают, что по этому индексу произво-
дится суммирование от 1 до и (если только не сделано специальной
оговорки).
Примеры
1 Разложение вектора х £ Va по базису (<?|, е2.е„):
п
х = 2 XkCt => х = xkeii
k = \
(номера координат условимся писать теперь вверху)
2. Линейная форма а И„:
)(х)= 2 a,x,=>f(x) = a,x'.
/ = 1
3. Квадратичная форма в
п п
f(x, х)= 2 2 a:jxiXj=> f(x, x) = aljx‘xl
i — I j = 1
4. Действие линейного оператора f: Уя-* Vn с матрицей А =(«//] на векторы базиса:
п
f(ei) = el= 2 а/(е/=>)(е()= а/ё/.
/=1
(в элементах матрицы А теперь верхний индекс указывает номер строки, нижний —
п
номер столбца) При этом формула у‘ — 2 a--xi для вычисления координат вектора
у = Ах по координатам вектора х может быть записана так: у' = а'рс1.
5. Преобразование базисных векторов пространства Кл:
п _____________________________ _
ё; = ^2| syej => е! = s\ej.
Здесь S = [$*) — матрица перехода от базиса (е) к базису (е'). При этом <?, = /{<?/. где
г = 161 — S_J — матрица перехода от базиса (е') к базису (е). Если в V„ задан вектор х =
= х‘е* = х'‘е!, то х’1 = х‘ = sfx'1.
Контравариантные векторы
Контравариантный вектор — совокупность упорядоченных систем
п чисел, сопоставленных каждому базису данного пространства таким об-
222
разом, что переход от системы, сопоставленной одному базису, к си-
стеме, сопоставленной другому базису, происходит по закону а'1 =
— 4а* или ak — s'?а''.
С этой точки зрения координаты вектора х Е Vn образуют контрава-
риантный вектор. Слово «контравариантный» означает «изменяющийся
в обратном направлении» (здесь учтено, что при переходе от одного ба-
зиса к другому векторы и их координаты соответственно преобразу-
ются с помощью обратных матриц).
Ковариантные векторы
Ковариантный вектор — совокупность упорядоченных систем п чи-
сел, сопоставленных каждому базису данного пространства таким обра-
зом, что переход от системы, сопоставленной одному базису, к системе,
сопоставленной другому базису, происходит по закону al — slaa или
ak = tkO.'. Слово «ковариантный» означает «изменяющийся так же»
(здесь учтено, что законы преобразования рассматриваемых систем
чисел совпадают с законами преобразования базисных векторов). При-
мером ковариантного вектора служат коэффициенты линейной формы:
если f(x) = а'х'1 — akXk, то а' = а* = t‘kal.
Законы преобразования чисел,
являющихся произведениями компонент векторов
Если а и b — контравариантные векторы, то:
a'1 b'! = t'kt\akbl, a‘b’ — s'ks\a’kb'1.
Если а и b — ковариантные векторы, то:
a'bj — sls'flkbi, ciibj — tlt’jalbl.
Если a — контравариантный, a b — ковариантный вектор, то:
a'‘bj — llks\akbt, a‘bj — s‘kilja'kbl.
Если a1', .... a'" — компоненты p контравариантных векторов,
bjp+l, • ••, 'bjr—компоненты q ковариантных векторов (p + q — r), to
совокупность nr чисел, являющихся произведениями компонент этих
векторов, при переходе от одного базиса к другому преобразуется
по закону
a'i'-a'» b'b+-b'h = bip+i - b,,
ah-ab bip+l-bb = sb-si; a'1’ 6< + 1- ,.
Определение тензора
Тензором ранга г, р раз контравариантным и q раз ковариантным
(р -|- q = г), называется совокупность упорядоченных систем пг чисел,
сопоставленных каждому базису некоторого линейного пространства
Vn таким образом, что переход от системы, сопоставленной одному
базису, происходит по закону, действующему для произведений коорди
нат (компонент) р контравариантных и q ковариантных векторов, т. е.
। Л 1 Л II q k\...kp
<2/.../« ~ t ki’" t kpS jt " S jt Cl ,
223
Тензор, р раз контравариантный и q раз ковариантный, сокращенно
называют тензором типа Верхние индексы в обозначениях назы-
вают контравариантными, нижние — ковариантными. Ранг тензора часто
называют его валентностью.
Примеры
1. Контравариантпые и ковариантные векторы есть тензоры типа q у и । у Их
часто называют соответственно векторами и ковекторами.
2. Коэффициенты квадратичной формы /(х, х) образуют симметрический тензор типа
/ ° \
I I, т. е. симметрический ковариантный тензор ранга два.
3. Элементы матрицы А линейного оператора f: Vn—f-V„ образуют тензор типа
( I, т. е. смешанный тензор ранга два.
4. Если всем базисам пространства Vn сопоставлено одно и то же число, то оно
определяет тензор нулевого ранга ^типа 0^’ ^ако" тен30Р имеет только одну компо-
ненту. Его называют главным инвариантом.
Тензорам ранга два любого типа соответствует квадратная матрица порядка п,
равного размерности пространства.
11.2. ДЕЙСТВИЯ НАД ТЕНЗОРАМИ
Сложение тензоров
Если а/.'.'.Х и компоненты двух тензоров одного и того же
типа относительно произвольного базиса (е), то +
+ — компоненты тензора также типа называемого суммой
двух данных тензоров.
Умножение тензоров
пов
Если a'jH'j, и Ьц''^'—компоненты двух тензоров соответственно ти-
(^ ) и ( Г / относительно произвольного базиса (е), то —
— — компоненты тензора типа
называемого произ-
ведением двух данных тензоров.
Транспонирование тензоров
Транспонирование тензора по двум ковариантным или двум контра-
вариантным индексам — преобразование тензора аТ;;'' в тензор Ь'-^
того же типа, компоненты которого отличаются от компонент исходного
тензора только порядком транспонируемых индексов.
Например, при транспонировании по индексам и и имеем
224
Свертывание тензоров
Свертывание тензора по одному верхнему и одному нижнему ин-
дексу — операция, заключающаяся в приравнивании какого-либо верх-
него и какого-либо нижнего индексов тензора и последующем суммиро-
вании по этому совпадающему индексу.
Например, операция свертывания тензора по индексам й и /| состоит в
следующем:
/И»-/. — aaj2:.\, 1 U•• i, + а 2+ - + anj2.../,'
При свертывании ранг тензора всегда понижается на 2, и тензор
/р\ (Р—
типа \z?/ пеРеходит в тензор типа ]. Тензор, получающийся
в результате свертывания данного тензора, называют сверткой.
Один из способов получения численных инвариантов состоит в р-
кратном свертывании р раз ковариантного и р раз контравариантного
тензора.
Примеры
1. Перемножив тензор с компонентами а,, и два контравариантных вектора с компо-
нентами xk и х1, получим тензор ранга четыре Ь?/ с компонентами а^хкх‘. Дважды
свернув этот тензор, получим инвариант aijX'x’, представляющий квадратичную форму
f(x. х).
2. Пусть А = [а,] и В = [&?] — матрицы линейных операторов пространства Vn.
В результате перемножения смешанных тензоров а\ и Ьк получится смешанный тензор
d‘k ранга четыре с компонентами Свертка по индексам /, k есть смешанный тензор
ранга два с компонентами с\ = а'„Ьк = а‘> 6,- + -ф ...-f- a‘„b*. Матрица С — [cjj пред-
ставляет произведение матриц А и В.
Симметрирование тензора
Симметрирование тензора по группе s ковариантных или контра-
вариантных индексов — операция, состоящая в следующем: транспони-
руем тензор, совершая всевозможные перестановки индексов выбранной
группы; складываем полученные так s! тензоров и делим эту сумму на si.
Полученный тензор обозначается заключением выбранной группы ин-
дексов в круглые скобки.
Примеры
I. а(,,) = — (а1' + °' )- 2- а(;ц) = "g" + а‘чк + + а‘к1‘ + а'*( + a'itk).
Альтернирование тензора
Альтернирование тензора по группе s ковариантных или контра-
вариантных индексов — операция, состоящая в следующем: транспони-
руем тензор, совершая всевозможные перестановки индексов выбранной
группы; складываем тензоры, полученные четными перестановками
индексов, и вычитаем тензоры, полученные нечетными перестановками
индексов; результат делим на si. Полученный тензор обозначается
заключением выбранной группы индексов в квадратные скобки.
Примеры
1 •а1"’ = 4 (“" - 2- “L,, = 4- + а»'< ~ — — “/«)
2 О
225
11.3. ТЕНЗОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Метрический тензор пространства
Из аксиом евклидова пространства следует, что оно может быть
определено как такое линейное пространство, в котором задана поло-
жительно-определенная квадратичная форма. Другими словами, евкли-
дово пространство — это такое линейное пространство, в котором задан
симметрический тензор g,j типа ^2)’ такоя> что ёУ^х‘> О Для всех
ненулевых векторов.
Тензор gq называется фундаментальным метрическим тензором про-
странства. Если (e) = (ei, вг, .... еп)— базис пространства Еп, то gtj =
= (ег, е,). Числа х, = gikXk (свертка метрического тензора с вектором
х = (х'; х2; ...; х") называются ковариантными координатами вектора х
в отличие от его контравариантных координат х‘. Ковариантные коор-
динаты— это проекции вектора х на базисные векторы, ибо х, =
= gikxk — (еь ek) хк — (eit екхк~) — (е,-, х). В ортонормированном базисе
Х( — х‘.
Компоненты матрицы g‘‘, обратной матрице gtj, образуют дважды
контравариантный тензор, называемый контравариантным метрическим
тензором. Справедливы формулы х' = gl,Xi.
Поднятие и опускание индекса
Переход от контравариантных координат вектора к его ковариан-
ным координатам по формулам х, = gikxk называют опусканием индекса,
а переход от ковариантных координат к контравариантным по форму-
лам х' = g‘'Xi — поднятием индекса.
Операцию опускания или поднятия индекса в евклидовом простран-
стве применяют к тензорам любого строения. Например, gihak' = bk,
g^a'J — ck‘k
Длина вектора.
Угол между векторами
х • у gii^y1
cos ср = •_ - = ——=—=
1*1 lyl ygyx'x1 ygijijy1
— Х‘У‘ — gi'X'yi
~^yi -xlg^XiXj -\^gyj
Примеры из физики и механики
1 Тензор деформаций — тензор, определяющий положение точек тела после дефор-
мации по отношению к их положению до деформации. Компоненты этого тензора:
— 1 ( ди‘ 4- дик 4- dU‘ dU‘
+ дх, + дх, дх, )’
где х, — декартовы прямоугольные координаты точки тела до деформации; и, — коорди-
наты вектора перемещения и.
В случае малой деформации пренебрегают величинами второго порядка, и тогда
226
Матрица этого тензора
<?U|
<?Л'|
I / ди2 ди\
2 VdAj + дхг )
1 ( ди3 дт \
2 \dxi + дхз /
I / dui ди2 \
2 \ дхз dxi /
ди2
дх2
1 ( диз ди2 \
~2 + 7ДГ /
и 2. Тензор напряжений — тензор, определяющий распределение внутренних напряже-
нии в деформируемом теле. Его матрица
симметрическая. Компонента а,* — i-я компонента силы, действующей на единицу по-
верхности, перпендикулярную к оси xi:. Так, на единичную площадку, перпендикулярную
к оси Ох, действуют нормальная к ней (направленная вдоль оси Ох) сила а,х и танген-
циальные (направленные по осям Оу и Ог) силы и а„.
3. Тензор инерции определяется компонентами /,/, i, / = 1, 2, 3, где Л,— осевые
моменты инерции твердого тела относительно оси Oxi, a /1(, i =# / — центробежные мо-
менты инерции, взятые с обратным знаком: 1
11.4. ТЕНЗОРНЫЙ АНАЛИЗ
Тензорное поле
Говорят, что в области V cz Еп задано тензорное поле, если каждой
точке М С V поставлен в соответствие тензор одного и того же типа.
При переходе от одной системы координат (х1, х2, ..., х") к другой
(х'1, х'2, ..., х'п) локальная система координат в каждой точке меняется,
Г Л л “ “
причем базисные векторы преобразуются по формулам в/ —------------г е2.
дх'1
Таким образом,
а.
дх 1 дх'" дх'1' дх'"
, /ki • f^p дх дх
dx dx ихь uxi<
Абсолютный дифференциал.
Ковариантные производные
Для тензорных полей компоненты приращения тензора не равны
приращениям его компонент. Для контравариантного векторного поля
и1 приращение равно выражению
Du1 = du‘ + rkiukdx‘,
гч' 1 im ( дёкт dglm dgkl \ v ,,
где Ги — — glm (---;—|---------------) — символы Кристоффеля.
\ дх‘ дх dxm /
Слагаемое du‘ учитывает зависимость компонент приращения тензора
от приращения его компонент, а слагаемое r‘kiukdxl — зависимость ком-
понент приращения тензора от изменения системы координат при пере-
ходе от точки к точке.
Вектор Du‘ называют ковариантным (абсолютным) дифференциа-
лом контравариантного векторного поля, а совокупность величин V/«z =
227
= + flyu* — ковариантной (абсолютной) производной этого поля.
Ковариантная производная ковариантного векторного поля
\jU, = ——.-FijUk-
дх1
Для тензорного поля ковариантная производная определяется
формулой
. ди1: . .
'ViUj — -1- + — rfu‘k
дх
В общем случае
+ Й uj'.tx + ...+ n - Го, -
-г^«И-...-г^и/»
Абсолютный дифференциал DT тензорного поля Т любого типа
связан с ковариантными производными этого поля формулой
£)?’= VjTdx’.
Ковариантная производная тензорного поля образует тензорное по-
ле, имеющее на одну ковариантную валентность больше, чем исходное
поле.
В прямоугольных системах координат Г)4 = 0, и поэтому ковари-
антное дифференцирование тензорных полей переходит в обычное.
Правила ковариантного дифференцирования (для суммы и произве-
дения тензоров) совпадают с правилами обычного дифференциро-
вания. Ковариантное дифференцирование перестановочно со сверты-
ванием.
12. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
12.1. ЛИНЕЙНЫЕ ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
Линейное однородное уравнение первого порядка
У' + р(х)у = 0.
Общее решение: у = Се ^^pMdx.
Решение задачи Коши, у(хо) = у0:
— Jp(/)dr
у = уое
Линейное неоднородное уравнение первого порядка
У' + P(x)y = q(x).
Общее решение:
y = e-^dx(C+ \q(x)e^Mdxdx).
Решение задачи Коши, у(хо) = у0:
-\py')dt f ?р(т)Л д
у = е л-» (,уо + yq(t)exo at).
Хо
Линейное однородное уравнение второго порядка
с постоянными коэффициентами
у" + ау' + Ьу = о.
Характеристическое уравнение
X2 + аХ + 6 = 0.
Характеристические числа
Общее решение
1. В случае Х< =/= Хг
у(х) — C\eUx + CietiX.
Если Xi — а — ip, Хг = а + ф, то общее решение можно записать
и в форме
229
у{х) = (Л cos Рх 4- В sin рх) еах.
2. В случае Xi = Х2
у(х) = (С, + С2х)+'Х.
Линейное неоднородное уравнение второго порядка
с постоянными коэффициентами
у" + ау' + Ьу = [(х).
Общее решение неоднородного уравнения есть сумма общего ре-
шения однородного уравнения у" ау' + 6 = 0 и некоторого частного
решения у* неоднородного.
Вид частного решения у* неоднородного уравнения
в некоторых конкретных случаях
I. /(х) = Рт(х), Р,„(х) — многочлен степени ш:
а) число 0 не является корнем характеристического уравнения
X2 + йХ + 6 = 0, т. е. 6 + 0, тогда
У* = Qm(x),
где Q,„(x)— многочлен порядка т;
б) число 0 — корень характеристического уравнения, т, е. 6 = 0,
тогда
у* = xQ,„(x),
если 0 — простой корень, т. е. а + 0;
y* = x2Q„,(x),
если 0 — кратный корень, т. е. а = 0.
2. f(x) = eaxP„,(x):
а) число а, не является корнем характеристического уравнения,
тогда
У* = eaxQm(x);
б) а — корень характеристического уравнения:
у* = xeaxQ„,(x),
если a — простой корень;
У* = x2eax Qm(x),
если a — кратный корень. ~
3. f (х) = /э„1(х) cos рх + Pz(x) sin рх, р + 0:
а) число t’P не является корнем характеристического уравнения,
тогда ~
у* = Qa(x) cos рх + Q*(x) sin рх, k = max {m; /];
6) z’P — корень характеристического уравнения:
у* = x(Q+x) cos рх + Qk(x) sin p.v), k = max [m; I}.
4. f(x) = e“x(Pm(x) cos Рх + Л(х) sin px), p += 0:
а) число a +/р не является корнем характеристического урав-
нения, тогда
у* = eax(Q+x) cos рх + Qa(x) sin рх), k — max [tn; /};
230
б) а + ip— корень характеристического уравнения:
у* = xeax(Qk(x) cos рх + Q/((x) sin рх), k — max {/n; /}.
Линейное однородное дифференциальное уравнение
/г-го порядка с постоянными коэффициентами
yw + ап-1у(',~''> + ...+ а\1)' + аоу = 0.
Характеристическое уравнение
X’ -|- д,-|Г_| + ... + аД + Яо — О,
Xi, Х2, .... — корни характеристического уравнения.
Общее решение
1. Все корни характеристического уравнения различные, тогда
у = Cic>,x + С2еКгХ +•••+ СпеКх.
Если среди корней есть пары комплексно-сопряженных корней,
например 7.| = а -{- ip, л2 = а — ip, решение можно записать и в виде
у — Cteax cos рх + С2еах sin рх -f- С3е’-зХ + ••• + Спе1"х.
2. Среди корней характеристического уравнения есть кратные, на-
пример, Х| имеет кратность k (остальные — простые), тогда
у = CieK'x 4- С2хе}-'Х + •• + Ckxk~'ek,x +
+ Cft + Ie’“+,x +...+
Если среди корней есть пары сопряженных корней кратности k,
например Xi — a -f- ip, Х2 — а— ip, решение можно записать в виде
у = erix(C\ cos рх + С2 sin рх) 4-хеах(С3 cos рх + С4 sin рх) + ...+
+ xk~'eax(C2k-i cos рх + C2ft sin рх) -f-...
Линейное неоднородное уравнение
с постоянными коэффициентами
У™ + ап-° +... + О| У' + аоу = /(4
Общее решение неоднородного уравнения есть сумма общего реше-
ния однородного уравнения и некоторого частного решения у* неоднород-
ного уравнения.
Вид частного решения у* неоднородного уравнения
в некоторых конкретных случаях
(Рm(x), Pz(x) — заданные многочлены степени m, I;
Qm(x), Qk(x) — искомые многочлены степени не выше т, k)
1. f(x) = Pm(x):
а) число 0 не является корнем характеристического уравне-
ния, тогда
231
у* = Qm(x);
б) число 0 — корень кратности s характеристического уравнения:
у* = xsQm(x')-
2. f(x) = eaxPm(x~):
а) число а не является корнем характеристического уравне-
ния, тогда
у* = eaxQm(x);
б) число а — корень кратности s характеристического уравнения:
z/* = xseajrQm(x).
3. f (х) = Рт(х) cos рх + Р;(х) sin 0х:
а) числа ±z0 не являются корнями характеристического уравне-
ния, тогда
У* = Qa(x) cos ₽х + Qk(x) sin рх, /г = max {m; I}',
б) числа ±ip — корни кратности s:
у* = xs(Q*(x) cos px + Q*(x) sin px), k — max {m; I}.
4. f (x) — eax{Pm(x) cos px + Pi(x) sin px):
а) числа a ± zp не являются корнями характеристического урав-
нения, тогда
у* = eax(Qft(x) cos px + Qk(x) sin Px), k — max {m; /};
б) числа a ± zp — корни кратности s:
у* = xseax(Q*(x) cos Px + Qft(x) sin Px), k — max [rn\ /}.
Принцип суперпозиции
Если z/i(x)— решение линейного уравнения
y(,i) + prt_i(x)y(n-l) +... + р\(х}у' + po(x) у = fk(x), k = \, 2, .... m,
m
то у — S z/ft(x) — решение уравнения
= ' m
y('1) + pn_i(x)y(',-|)+-.+ pi(x)z/' + po(x) y= s fk(x}.
A = 1
Метод Лагранжа вариации произвольных постоянных
при нахождении общего решения линейного
неоднородного уравнения
Если известно общее решение
У — С\У\(х) + C2z/2(x) + ...+ Спуп(х)
(Ci, С2, ..., Сп — произвольные постоянные) однородного уравнения
y(n) + Pn-iWy(n-l)...pi(x)z/' + р0(х)у = О,
то общее решение неоднородного уравнения
У(л) + Рп-1 (х) у(п-° +... + pi (х) у' + р0(х) у = /(х)
можно искать в виде
у = Ci(x)z/j(x) + C2(x)z/2(x) + ...+ Cn(x) у„(х).
232
Cfc(x) определяются из системы
S G(x)yV’(x) = 0, / = 0, 1, .... п-2, S С1(х)1/л-')(х) = /(4
ft=i k=\
Уравнение Эйлера
хпум 4- an_ix"_|y(n-l) + ...+ щху' + аоу = f(x)
(аП_\, ап-2, .... ао — постоянные) заменой независимой переменной
х = е‘ сводится к линейному уравнению с постоянными коэффициен-
тами вида
+ Ьп-\у?‘ +... + biy't + boy = /(е^-
Линейная однородная система дифференциальных уравнений
с постоянными коэффициентами
У\ — й\\У\ + «12</2 4*...+ й.\пУп,
У2 = С12\У\ + «22</2 + ... + U2nyn,
Уп = Пп\У\ + ап2У2 + ••• + аппУп-
В векторной форме:
dY/dx = AY,
где
«11 <312 ... «1л
«21 «22 ... П2п
Пп\ Пп2 “• Ппп
yiW
у2(х) . dY_
• 1 dx
Уп{х)
Характеристическое уравнение
или det (Л — Х£) = 0.
Нахождение общего решения системы по методу Эйлера
1. Если Xk — простой корень характеристического уравнения, то
ему соответствует решение
Уl—y^ex‘x, y2 = y2eKtX, .... уп = упе^х;
числа yi, уг, •••> Уп находятся из системы
(<Z11 — X*)yi й[2У2 + + Я1л?п == О,
<321УI + («22 — А,*) 72 + + «2n?rt = О,
а!„уi + an2Y2 + — + (апп — X*) уп = 0.
233
2, Если X* — корень кратности т характеристического уравнения,
то ему соответствует решение вида
!Л = Pt(x) е’1Х, </2 = Рг(х) е1,х, .... уп = Р„(х) eltX,
где Pi(x), Р2(х), Рп(х) — многочлены степени не выше т — I,
имеющие в совокупности т произвольных постоянных.
Коэффициенты многочленов можно определить, подставив выраже-
ния для yi, у2, ..., уп в исходную систему.
Найдя решения, соответствующие каждому корню характеристи-
ческого уравнения, общее решение системы получим как линейную
комбинацию этих решений.
Например, если все корни характеристического уравнения про-
стые, а решениями, соответствующими этим корням 2,*, будут:
У\ = Yai<?w, у2 = ук2еЪх, ..., (/,, = у/;,/г = I, 2, ..., и,
то общее решение этой системы имеет вид:
У\ = С\Ч\\е'К'х + СгТг!^’2* + ••+ С„уП1в,-'’х
г/2 = С|у12е’|Х ф- 4-...Ч- Спу„2ем,
Уп = Ci у! „е Х,х 4- С2у2пе,-2Х +... + Спуппе1-Х.
Линейная неоднородная система дифференциальных уравнений
с постоянными коэффициентами
-IL = A У + F,
ах
где
f>W
F=
Общее решение неоднородной системы есть сумма общего решения
однородной системы и некоторого частного решения неоднородной
системы.
Для нахождения общего решения неоднородной системы можно
применить метод Лагранжа вариации произвольных постоянных.
12.2. НЕЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнения с разделенными переменными
Р(х) dx + Q(y) dy = 0.
Общий интеграл
5 Р(х) dx + $ Q(y) dy = С.
Уравнение с разделяющимися переменными
Pi W Q । (у) dx 4- Р2(х) <2г(у) dy = 0.
234
Общий интеграл
Qdu)
<Ыу)
dy = С.
Уравнение в полных дифференциалах
Р(х, у) dx 4- Q(a-, у) dy = О,
dQ _ дР
дх ду
Существует такая функция и(х, у), что
du = Р(х, у) dx + Q(x, у) dy.
Общий интеграл уравнения в полных дифференциалах
и\х, у) = С.
Функция и может быть представлена в виде
х у
п(х, у) = 5 р(х> У)^ + 5 <Ж> У^У-
Хо £/о
Интегрирующий множитель
Функция ц(х, у) называется интегрирующим множителем для
уравнения
Р(х, у) dx + Q(x, у) dy = О,
если уравнение
|i(x, у) Р(х, у) dx + у (х, у) Q (х, ij)dy = О
ес-ть уравнение в полных дифференциалах.
Интегрирующий множитель удовлетворяет уравнению
д 1п у, ? д In ц дР dQ
дх ду ду дх
Если -------/ Q = ф(х) (не зависит от У), то ц —
— ехр ф(х) dx).
Аналогично, если ------—'Ф(у) (не зависит от х), то
ц =ехр( — $ф(у) dy).
Однородное уравнение
Р(х, у) dx + Q(x, у) dy = О,
где Р(х, у), Q(x, у) — однородные функции одной и той же степени а:
P(tx, ty) = РР(х, у), Q(tx, ty) = taQ(x, у).
Подстановка у = их, dy = xdu -j- udx переводит однородное уравне-
ние в линейное относительно функции и:
(P(l, u) + «Q(l, и)) dxxQ(\, u)du—().
235
dy / aix + biy + Ci \
Уравнение вида —— — /I--------—:--------I
dx \ ax + by + c J
1. Если прямые a\x + bay + Ci = 0 и ax + by Ц- с = 0 пересекаются
в точке (x0; yn), то замена £ = х — хо, Л = У — Уо приводит его к однород-
ному уравнению
di] _ / Qis + M \
d'i ~ + )'
2. Если прямые а{х + ftjy + щ — О и ах by с — Q параллельны,
то замена z — a\x-\-b\iy приводит к уравнению с разделяющимися
переменными
dz . / a\z + aiCi \
—j— — b i H----:-----) + a ।.
dx \ az + G|C /
Обобщенное однородное уравнение
P(x, у) dx + Q(x, y)dy — 0.
Существуют постоянные а и p, такие, что имеют место тождества:
Р(/х, Гу) = /рР(х, у),
Q(/x, /ау) =/fl-a+1Q(x, у), a=#l.
Сводится к уравнению с разделяющимися переменными введением
новой функции z по формуле y — zxa.
Уравнение Бернулли
у' + р(х)у = q(x)ym, т=£0, т^\.
Подстановкой и—у'~"‘ сводится к линейному
и’ + (1 — т) р(х) и — (1 — ni) q(x).
Уравнение Риккати
у'= р(х)у2 + у(х)у + г(х).
Если известно какое-либо из решений у — ф(х), то уравнение сво-
дится к линейному подстановкой ы = 1/(у — ф(х)).
Уравнение Лагранжа
у = Хф(у') + ф(у').
Дифференцируя по х и полагая у' — р, приходим к линейному
уравнению относительно х как функции р:
d х
(ф(р) — р) + Хф'(р) + Ф'(р) = 0.
Уравнение Клеро
у = ху'ф(у') — частный случай уравнения Лагранжа.
236
Дифференциальные уравнения,
допускающие понижения порядка
Уравнение, не содержащее
явно независимой переменной
F(y, У', у”...... г/(л)) = 0-
Подстановка у'— р понижает порядок уравнения на единицу,
п // dp ,,, ч d2P । (dp\2
При этом у" = р—t-, у"' = р+ PI-7-) и т. д.
dy dyz \dy /
Уравнение, не содержащее искомой функции
F(x, у', у"..у(п)) = 0.
Подстановка у' — р понижает порядок на единицу.
В общем случае
F(x, у^, y{k+'\ .... у(л)) = 0.
Подстановка yw = p понижает порядок на k единиц.
Уравнение, однородное относительно переменных у, у', ..., у(л)
F{x, у, у', ..., у(л)) = 0,
где F(x, ty, ty'. /у(л)) = taF(x, у, у', .... у(л)).
Подстановка z = y'/y понижает порядок уравнения на единицу.
Обобщенное однородное уравнение
F(x, у, у', .... у(л)) = 0,
где F(tx, tay, ta~'y'. ta-nyW)= FF(x, у, у', .... у(л)).
Вводя новые переменные t и z по формулам х = е‘, у = zea‘, при-
ходим к уравнению, не содержащему явно t и, следовательно, допуска-
ющему понижение порядка.
12.3. УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Однородное линейное уравнение с частными производными
первого порядка
t / \ ди .. . .ди
fl{Xi, Х2, .... Хп)—--Fh(Xl, *2, .... хп)~-+
ох\ 0x2
+ fn(Xt, х2, .... Хп)-^—=0.
дхп
Если ф|(Х1, Х2, .... Хп), ф2(Х1, Х2, .... Хл), ..., фя_|(Х1, Х2. Хл)
суть первые интегралы системы
dxt dx2 dxn
b(xi. x2... x„) “ f2(xi, x2, .... xn) — fn(xi, x2, ..., x«) ’
то общее решение однородного линейного уравнения с частными про-
изводными имеет вид
и = Ф(фь ф2, ..., фл-1),
237
где Ф — любая функция, имеющая непрерывные частные производные
ПО ф|, ф2, •••, Фп-1.
Решение задачи Коши для однородного
линейного уравнения
Задача Коши: найти решение и, удовлетворяющее условию
и |X1=t = ф(л-2.. хп).
Составляем систему функциональных уравнений:
Ipj (g, Л'2, Хп) = С\,
фг(£, х2, .... хп) = С2,
Ф п — I (ъ, Хг, ..., Хп) — Сп — I,
из которой выражаем х2, хп через %, Ci, С2..... Сп-г.
x1 = o)|(g, Ci, С2, ..., Cn-i), i = 2, ..., п.
Функция
и = ф(о)2(^, ф|, ф2, •••, фп-i), Юз(£, ф1, Фг, •••, фп-1).
фь фг, .... Ф«-|))
и есть решение задачи Коши.
Неоднородное линейное уравнение
с частными производными первого порядка (квазилинейное)
, , .ди .ди
f\ (xi, х2, .... х„, и)—--|-/2(Х|, Хг, ..., Хп, и)—---Н--4-
ОХ\ 0X2
, . . , ди , .
+ fn(xi, х2, .... хп и)-д~ = £f(xi, х2, .... хп, и).
ОХп
Если искать решение этого уравнения в неявном виде о(м, х\,
хг, хп) — 0, то для определения функции v приходим к однородному
линейному уравнению
fl(X|, Х2,
dv
dxt
dv
дх2
dv dv
+ Mxi, х2, ..., хп, и)—------Ь g(xi, х2..... хп, и) —— =0.
аХп du
Линейное относительно старших производных
уравнение второго порядка
Л(х, у)-^-+2В(х, у)
дх
д~и
дхду
4- С(х, у)
д2и
ду2
ди ди
х, у, и, -т—, ——
дх ду
(Л2 + В2 + С2 #= 0).
Классификация уравнений второго порядка
1. Если В2 —ДС>0 в области G, то уравнение гиперболиче-
ского типа.
238
2. Если В2 — АС = 0 — параболического типа.
3. Если В2 — АС < 0 — эллиптического типа.
Канонический вид уравнений второго порядка
1. Каноническое уравнение гиперболического типа:
д2и „ / ди ди \
-—г— = Fix, у, и, -т—, -3— I
дхду \ дх ду /
или
д2и д2и ди ди \
---о-------7Г — В х, у, и, —т—, ——- I.
дх2 ду2 \ дх ду /
2. Каноническое уравнение параболического типа:
3. Каноническое уравнение эллиптического типа:
д2и
дх2
Дифференциальное уравнение характеристик уравнения
. / \ д2и , nD . . д2и . . д2и
А (*> + 2В + С(х’ = F
дх дхду ду
есть
А (х, у) dy2 — 2В(х, у) dxdy + С(х, у) dx2 = 0.
Задача Коши для неограниченной струны
д2и , д2и
---Т- = а'---т*
dt2 дх2
I / ч ди I ,..
при начальных условиях ы — <р(х), -37- = ф(х).
I г=о dt I /=0
Решение:
x-j-at
. *4“ ^0 фС^ — ^0 । 1 С / \ ,
и(х, /)=. -------+-^ J
х — at
(формула Д’Аламбера).
Колебание полуограниченной струны
д2и 2 д2и л
0,
-< X < + О°, t >
Решение:
и I — 0, и I = ф(х), ------------I = ф(х).
Iх=о I/=о dt I/=о
239
x + at
= + + + 1 f ч,(т)
4 ' 2 2a J
x — at
где
Ф(х) =
ф(х), x > О,
— ф( — х), х < О;
•ф(х), х > О,
— ф( — х), X
<0.
Метод Фурье для уравнения колебаний
ограниченной струны
I.
Начальные условия: и = ср(х), — гр(х).
1 / = о dt 1 /=о
Граничные условия: н|Л==о = О, «L- = / = 0.
Решение:
ОО
V-' / knat , , , knat \ . knx
и(х, t)= / («feCOS—-------1- bk sin—-—I sin——,
k = i
где
/ i
2 C ... knx , . 2 C , . . . knx
ak= -r- \ q>W sin —-— dx; bk = -r— \ i|’W sin —j— dx-
I 1 I KTtCl I L
о 0
Уравнение теплопроводности для нестационарного случая
ди 9
---= а
dt
д2и д2и д2и \
дх2 ду2 dz2 )
Распределение температуры в неограниченном стержне
Начальное условие: и |/=о — Кх)-
Решение:
+ °° 2
и (х, 0 =------ S f(£) exp f
2ax^t J V 4aZ f
v — oo
(интеграл Пуассона).
Распределение температуры в стержне,
ограниченном с одной стороны
ди 9 д2и
---= 0
dt дх2
240
Начальное условие: и |/ = о — f(x).
Краевое условие: и |х = 0 = ф(/).
Решение:
и (х, /) =
(£-
4а2(
— ехр
ср(п)ехр
х2
4а2 (Z — г|)
О
^ +
О
х (t — n) 3/2rfn-
Распределение температуры в ограниченном стержне
ди , d2u
--= а ——,
dt дх2
Начальное условие: и(х, /)|/=о = f(x)-
Граничные условия: и|х = о=Л, u\x = i = В.
Решение:
В —А V1 , / а2л2п2 ,\ . плх
и(х, /) = А Н------х 4- exp - t\ sin ,
п = I
I
Л = и<fWsin "Тdx- ~^,л + н |)“+'В)-
о
Уравнение Лапласа
Л. + Л +£±=0 нлн Д« = 0,
дх2 ду2 dz2
д2 д2 д2
гпр А -------1-------1--т — оператор Лапласа.
ГДе dx2 dy2 dz2
В плоском случае уравнение Лапласа имеет вид
d2u д2и =
dx2 + ду2
Задача Дирихле для круга
d2u d2u
дх2 dy2
u\r=R== f(cp)
(ф, г — полярные координаты).
Решение:
1 С R2 — г2 ______
U^' J /?2 — 2/?г cos (/- ф)
— л
(интеграл Пуассона).
9 Воднев В. Т. и др.
13. МАТЕМАТИЧЕСКАЯ ЛОГИКА
13.1. МНОЖЕСТВА И ОТОБРАЖЕНИЯ
Множества
Множество А, состоящее из элементов х, у, ...:
А = {х, у, ...}, х£А, у^А, ...
Множество А, состоящее из элементов х, удовлетворяющих усло-
вию Р;
Л = (х|х удовлетворяет условию Р].
1 U У II
-Т.
- пустое множество.
В — А является подмножеством В.
В — А не является подмножеством В.
В — множества А и В совпадают,
4=Во((ЛсВ)А(Вс/1)).
Объединение множеств
л и в = ui (* е/*) V (-<€£))
A U В = В U А (коммутативность),
A U А — А (идемпотентность),
(Л (J S) и С = A U (В (J С) (ассоциативность),
A U 0 = А, А cz (Л U В), В <= (Л U В)-
Пересечение множеств
л п В = {х| (х е л) л (х g В')}.
А П В — В П А (коммутативность),
А П А — А (идемпотентность),
(Л П В) П С = А П (5 П С) (ассоциативность),
(Л U В) П С = (Л П С) U (В П С),
(Л П В) и с - (Л и С) л (в и С)
(дистрибутивность),
ЛП0 = 0, (ЛПВ)с=Л, (ЛЛВ)<=В.
Разность множеств
Л\В = {х|(хбЛ)Д(х^ В)}.
Л\Л = 0, л\0 = А,
(Л\В) л с = (Л п С)\в - (Л Л Q\(B л С),
Л\В = Л\(ЛПВ), А =(Л Л В)иИ\В).
242
Дополнение множества до основного множества U
Обозначение: CA(CVA, А и, А').
СА = U\A (Л cz U), С (СА) = Д,
A U СА = U, А(]СА = 0, (Лет. В)о(СВ cz СД).
Законы двойственности (законы де Моргана)
с (А п В) = СА и св, С(Д и б) = сд п се.
Декартово (прямое) произведение множеств
д X в = {(х; у)| х 6 А, у е В}.
(Д X В = В X Д)о(Д = В).
А X Д — А2 — декартов квадрат множества Д,
А X Д Х...Х Д = Дл.
п раз
Отображения множеств
f: Х->У, Xi/, f: х->у (х £ X, у € V), х4у (х£Х, у £ Y).
X (или D(f)) — множество задания (область определения) отобра-
жения f.
Множество значений (образ множества X) отображения f:
{y\ytY, y = f(x), х£Х}.
Обозначения: f(X), E(f).
Простейшая классификация отображений
Отображение f: X-+Y:
1) инъективно (инъекция), если
Vxi, х2 Е X' xi #= x2^f(xi) =# f(x2);
2) сюръективно (сюръекция, отображение X на Y), если
K*) = Y;
3) биективно (биекция, взаимно однозначное отображение), если
оно инъективно и сюръективно.
Обратное отображение
f~l; Y-^X — определяемое для биекции f: X->V следующим обра-
зом: если f(x) = у, то f~‘(y) = x.
= x v хех, f(f-'(y)) = yv yeY
Композиция отображений
Если f: X->F, g: Y-+Z, то их композицией (произведением) назы-
вают отображение g°f: X-^Z, определяемое формулой (g°f)(x) =
= g(f(x)), хех.
243
Счетные и несчетные множества
Множества А и В эквивалентны, если существует биекция А на В.
Запись: А — В.
А ~ В=>В ~ А (симметрия),
А ~ А (рефлексивность),
(Л ~ В) Д (В ~ С)=> А ~ С (транзитивность),
А конечно, если существует п, такое, что А~{1, 2.... п},
А счетно, если А ~ N,
А несчетно, если А бесконечно, но не счетно.
Если А — В, то говорят, что А и В имеют одинаковую мощность.
Множество Q счетно, множество R несчетно.
Множество А называют множеством мощности континуума, если
13.2. АЛГЕБРА ВЫСКАЗЫВАНИЙ
Обозначения высказываний
х, р, q, г, ...— высказывания,
р = 1 — р — истинное высказывание,
р = 0 — р — ложное высказывание,
р — отрицание высказывания р.
Обозначения логических операций
Операция Обозначение Другие обозначения
Дизъюнкция («или» нераздели- тельное) Конъюнкция («и одновременно») Отрицание Импликация («влечет» или «если..., то...») Эквивалекция («равносильно») V А t III
Определения логических операций
р р
0 1 1 0
р <7 Р V <7 р Л q Р=><7 Р*><7
0 0 0 0 1 1
0 1 1 0 1 0
1 1 0 1 1 1 0 1 0 1 0 1
244
Основные равносильности
Закон двойного отрицания
р = р.
Идемпотентность
рУ р\/...\/р = р, р/\Р /\-/\Р = Р-
Коммутативность
ру q = qy р, p/\q = q/\p-
Ассоциативность
рУ (? V r) = (p\y q) v г, р /\(q Л г) = (р Д <?) Д г.
Дистрибутивность
р V (7 Л 0 = (р V q) Л (р V г)=(рУ q)y г
P Л (Р V Г) = (р Л q)V (Р Л г) = pq v рг.
Законы де Моргана
рУ q = р f\q, р f\q = рУ q-
Формулы с константами
р\/р={, рх/О = р, pVl = l,
рДр = 0, р Д 0 = О, р/\\=р.
Дополнительные равносильности
p^q=py q,
pop = (p=>q') д^р} = p q V pq,
pq\/pq = p©q (сумма по модулю 2),
P © 1 = p, p V q = p © q © pq,
p\/q — p\q (стрелка Пирса),
p/\q — p\q (штрих Шеффера),
_+p^p, plp = p,
pq V pq == p (закон склеивания),
p\/pq — p (закон поглощения),
pq \/ pr = pq V P'' V qr (закон обобщенного склеивания).
245
Формулы представления булевых функций
Литерал
км' °' = '-.v,elO; И.
если О/ = О,
Элементарное произведение
= Лх-А...А<; = х-х-..х-.
Элементарная сумма
Dt = xf," V х,? V - V х£
Дизъюнктивное представление булевой функции
F(xi, х2, х„) —
— V X?' xa2—x'k F(O|, 02, .... СТ*. Х*+|, Х„).
01, 02, .. , О»)
Совершенная дизъюнктивная нормальная форма
F(xlt х2, ... х„) = V х^хГ'-'х’” = V k,.
F(a\, о2, , о„) = I i = 1
Конъюнктивное представление булевой функции
F(x,. х2, ... х„)- Л (х? V хГ V-- V-CV
(0|, 02, ... Оц)
VF(o1, оА, хА+|, ..., х„)).
Совершенная конъюнктивная нормальная форма
F(xi, л-.,, х„) =
F О|, о,, ., о,,) =0 1 = 1
Полином Жегалкина
F(X|, х2, ..., х„) = ® Ki,
i= ।
где /<( = x,i Xi2---xim(rn < п) или К, 6 (0; 1),
Формулы представления в неклассических базисах
F(xit х2, ..., х„) — ((х,|х,)|Л(х|, .... х,_|, 0, .. х„))|
l(xi|F(x....... Х,_|, 1, х, + 1, х,,)),
F(xi, х2, ..., х„) = ((|х,) | А(хь Х,_|, 1, Х,+ |, хп) |
|(x,|F(xi, .... x,_i, 0, х, + |, Хп)),
246
F(xi, x2..... xn) — (Xi® l)F(xi, Xz-i, 0, x, + i, хп)ф
............. х<_|, 1, x/+i, .... x„).
13.3. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
Аксиомы
I
1 p=>(q=>p). 2. (p=>(p=>r))=>((p=>p)=>(p=>r).
II
i p A q=>p- 2. p л q=>q-
3. (p=>?) =>((/?=>/) =>(?=> <? A r)).
Ill
1 p=>p v q- 2. q^p v q-
3. (p=>r)=>((p=>r)=>-(p V P=>r)).
IV
1 (p=>p)=>(p=>p). 2. p=>p. 3. p=>p.
Правила вывода
(|-----знак выводимости)
Правило подстановки
I— Р I— ^?(р),
где S?(p) — формула, полученная из р путем подстановки формулы
q вместо переменной х.
Правило заключения
(I— р л 1— (р=>ч))=^ I— q-
Некоторые выводимые формулы
1- [-(q=>s). 2. p(s=^p). 3. \-р=>р.
(s в формулах 1, 2 — произвольная выводимая формула.)
4. )-(р=>р)=>((7=>Н=>(Р=>П)-
5. \-(p^(q=>ry)=>(q=>(p=>rA
6. Нр=>(р=>р А ?)•
7- [~(p=>(q=^A)=^(p a q=>r).
8. н (р А? =>г)=>(р=> ('?=>'•))•
247
13.4. ПРЕДИКАТЫ
Обозначения
F(x), F(xi, х-2, ..., х„)— предикаты,
V—квантор всеобщности (общности),
3—квантор существования.
Связь кванторов с операциями
алгебры высказываний
Если а2, .... ап}, то
3 xF(x) = F(a>) V F(a2) V ... V Е(аД
VxF(x) = F(Q|) д F(a2) Л ... Л F(a„).
Основные равносильности
1 Vx F\'x) = 3 х Fix'). 2. Эх F(x) = Vх F(x).
3. Vx Ft(x) AV x F^x) =\x (F'\xj Д F2(x)).
4. 3 x Fi (x) V 3x F2(x) = 3x (Fi(x) V F2(x)).
5. VxiVx2 F(xi, x2) = Vx2VXi F(xi, x2).
6. 3xi3x2 F(xi, х2)=Зх2Эх| F(xi, x2).
Некоторые формулы, выводимые
в исчислении предикатов
1 Vx F(x)=>F(x). 2. F(x)^»3x F(x).
3. V x F(x)=>3x F(x). 4. V x (F(x) V EWj-
5. Vx2 (F1(x1)=>(F2(x2)=>F1(xi))).
6. V xhVx2 (Fi(xi)=>(F2(x2)=^Fi(xi))).
7 Эх, Vx2 F(xr, x2)=>Vx23xi F(xi, x2).
14. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
14.1. СЛУЧАЙНЫЕ СОБЫТИЯ
Определение, основные формулы
Классическое определение вероятности
Р(А) — т/п
(т — число благоприятных исходов опыта; п — число всех его исходов).
Теорема сложения вероятностей несовместных событий
Р(А +В)=Р(Л) + Р(В).
Теорема сложения вероятностей совместных событий
Р(А В) — Р(А) А- Р(В) - Р(АВ).
Теорема умножения вероятностей независимых событий
Р(АВ) = Р(А) Р(В).
Теорема умножения вероятностей зависимых событий
Р(АВ) = Р(А) Р(В/А) = Р(В) Р(А/В\
где Р(В/А)—вероятность события В при условии, что произошло
событие А.
Формула полной вероятности
Р{А) = S P{Bk')P{A/Bk\
k — 1
где В\, В?, .... Вп — полная группа гипотез, т. е.
BiB, = 0, i=£j, U Bi = Й
i— 1
(й — достоверное событие).
Формула Бейеса
n/п /ла P(Bm) Р(А/Вт)
Р(Вт/А)=—-----------------, т=1, 2, ..., п,
£ Р(Вк)Р(А/Вк)
где Bi, В2, ..., Вп — полная группа гипотез.
249
Повторение испытаний
Формула Бернулли
Рп^ = С^р^\ _ру-^= _ру-\
К\\11 ““ к н
где Path) — вероятность появления события А ровно k раз при п неза-
висимых испытаниях; р — вероятность появления события А при каждом
испытании.
Вероятность того, что при этом событие А:
1) наступит п раз: Рп{п) = рп\
2) не наступит ни разу: Рп(0) = (1 —/?)";
3) наступит хотя бы один раз: Р— 1 —(1 —р)п;
4) наступит не более k раз: Р = Рп(О) + /’«(I) +•••+ Pn(k)-,
5) наступит нс менее /г раз: Р = P„(k) 4- Pn(k 4* 1) + ••• + Рп(и).
Локальная теорема Лапласа
Р^)~-Т==^^-е-гЛ
~\2лпр(\ — р)
где Pn(k) — вероятность появления события А ровно k раз при п незави-
симых испытаниях; р — вероятность появления события А при каждом
k — пр
испытании; / = — -—.
— Р)
Интегральная теорема Лапласа
P(k{ k k2) Ж Ф(х2) - Ф(х>),
где — вероятность того, что в п независимых испыта-
ниях событие А появится не менее k\ и не более k2 раз; Ф(х) =
1 С — пр
— ——= \ е ' dt — функция Лапласа; ал = —-=====-; х2 =
Л/2л J -\Jnp(\— р)
k2 — пр
лМр(1 —р)
Оценка отклонения относительной частоты
от постоянной вероятности
Наивероятнейшее число ko появления события А при п независи-
мых испытаниях
250
пр — (1 — р)< ko < пр + р
(п — число испытаний; р — вероятность появления события пои одном
испытании).
14.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Дискретные случайные величины
Xi — значения величины X,
Pi = P(X = Xi\ i=\, 2, .... п; S Pi=\.
i = 1
Математическое ожидание
М(Х) = S Xipi.
i= 1
Свойства:
1) М(С)=С, С—постоянная; 2) М(СХ) = СМ(Х\
3) A4(Xi + Х2) = Af(Xi) + Х1(Х2), где Xi, Х2—независимые случай-
ные величины;
4) M(X,X2) = Л1(Х>) М(Х2).
Дисперсия
D(X) — M ((X - М (X))2), D (X) = М (X2) - (M (X))'2
Свойства:
1) £>(С)-0; 2) D(CX) — С2£>(Х);
3) £)(Xi + Х2) = £>(Х|) + £>(Х2), где Х(, Х2 — независимые случайные
величины.
Среднее квадратическое отклонение случайной величины X
o(x)-VwT
Начальный момент порядка k случайной величины X
МХ) = Х!(Х*)= 2 x’!lPi.
i= i
Центральный момент порядка k случайной величины X
МХ) = А1((Х-Л1(Х)П
Биномиальный закон распределения
Р(х - k)= С^р\\ - рУ1-\ k^Q, 1, .... п,
М(Х) = пр, £>(Х)-пр(1-р).
251
Закон Пуассона
a.ke~k
P(X = k)=—^—, tx > 0, k = O, 1, .... n,
M(X) = a, D(X) = a.
Закон больших чисел
Неравенство Чебышева
Р(\Х- Л1(А')| < е) > 1 - £>(х)/е2.
Теорема Чебышева
п п
lim р( I — У X,- — У Л1(Х,) I <Б^ = 1,
П-> оо \ I П / , П / , I /
( = 1 1=1
Xi—попарно независимые случайные величины; £)(%<) С; С
стоянная.
Непрерывные случайные величины
ПО-
Интегральная функция (функция распределения)
F(x) = P(X< х).
Свойства:
1) 0< F(x)< 1;
3) lim F(x) = 0,
х—>---оо
2) л-| < x2^F(xi) < F(x2);
lim F(x) = 1;
X—► оо
4) Р(а 'С х < b) = F(b) — F(a).
Дифференциальная функция распределения
(плотность вероятности)
f(x) = F'(x),
где F(x) — интегральная функция.
Свойства:
+ оо
1) f(x)^Q- 2) $ f(x)dx= 1;
— оо
b
4) Р(а < X < b)= $ f(x)dx.
а
3) F(x)= $ f(p)dt-,
— оо
Числовые характеристики непрерывной случайной величины
Математическое ожидание
оо
М(Х)= $ xf(x)dx.
— оо
252
Дисперсия
D(X) = M{(X-M(X))2),
оо
D(X) = $ (х — M(Xf)2 fix') dx,
— оо
4-00 -j- оо
D(X) = $ x2f(x)dx — ( j xf(x)dx)2.
— оо — оо
Некоторые законы распределения
непрерывных случайных величин
Равномерное распределение
f 0, если х < а,
f(x) — < 1 /{b — а), если а «С х «С Ь,
(О, если х > Ь,
{О, если х < а,
(х — сг)/(ft — а), если а s/ х Ь,
1, если х > Ь.
Нормальное распределение (распределение Гаусса)
/(х) =-----'—е 2°2
о у2л
М(Х) = a, D(X) = a2,
Р(<х < X < Р) = of _ ф|
где Ф(х)= —-= \ е ?/2dt — функция Лапласа;
Л/2л J
Р(|Х - а| <б) = 2Ф(6/о).
14.3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Эмпирическая функция распределения
F*(x) — пх/п,
где пх — число выборочных значений, меньших х; п — объем выборки.
Выборочное среднее
(несмещенная, состоятельная оценка математического ожидания)
где Xi — выборочные значения; п — объем выборки.
253
Выборочная дисперсия
(смещенная, состоятельная оценка дисперсии)
Исправленная выборочная дисперсия
(несмещенная, состоятельная оценка дисперсии)
п
i= 1
Функция правдоподобия для оценки
неизвестного параметра а
распределения случайной величины X
В дискретном случае
£(%[, х2, ..., хп, a) = p(xi, а)р(х2, а)---р(хп, а),
где р(хк, а) — Р(Х — Xk), Xi, .... х„ — выборочные значения.
В абсолютно непрерывном случае
L(x\, х2... х„, a) = /(xi, a)f(x2, a,)--f(xn, а),
где f(x, а) — плотность распределения X.
Доверительные интервалы с коэффициентом доверия р
в случае нормально распределенной
генеральной совокупности
1. Для математического ожидания при известной дисперсии о2
где tp — корень уравнения Ф(/) = р/2; Ф — функция Лапласа.
2. Для математического ожидания при неизвестной дисперсии
— S — S
х — /р — - ; х + tp —т- —
уп — 1 уп — 1
s2 — выборочная дисперсия; tp удовлетворяет условию
</р) = р; tn-1 — случайная величина, распределенная
Стьюдента с п — 1 степенями свободы.
3. Для дисперсии
]ns2//2; ns2/tl[,
где Z2, tl находятся из условий:
/Ж-11 <
по закону
1 + р
2
Р(Х2_,</?) =
Р(Х2_.<^) =
254
Xn-i — случайная величина, распределенная по закону %2 с п — 1 степе-
нями свободы.
Выборочный корреляционный момент величин X и У
п
Кху = “ (у‘ ~
i = 1
х, у—выборочные средние величин X и У соответственно.
Выборочный коэффициент корреляции
Г ху == Kxy/SxSy,
где $?, s2 — выборочные дисперсии величин X и У.
Выборочный коэффициент регрессии У по X
Sy Кху
lo — Гху = й •
Sx SJ
Выборочное уравнение регрессии
У — У = — х}.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Абсолютная величина вектора 13
Аддитивность интеграла 181, 194
Алгебра векторная 14
— высказываний 244
— высшая 75
Алгебраическая форма комплекс-
ного числа 75
Алгоритм деления с остатком 77
— Евклида 78
— последовательного деления 78
Альтернирование тензоров 225
Анализ комплексный 201
— тензорный 227
Аргумент комплексного числа 75,
76
Асимптота 124
— вертикальная 124
• — гиперболы 64
— наклонная 125
Астроида 133
Б
Базис линейного пространства 92
— ортогональный 95
— ортонормированный 95
Бета-функция 196
Бинормаль линии 127
Биссектриса треугольника 6
В
Валентность тензора 224
Вектор 13
— единичный 95
— — бинормали 128
— — главной нормали 128
— — касательной 128
— — нормали к поверхности 130
— ковариантный 223
— контравариантный 222
— нормированный 95
Вектор-решение системы 89
Вектор-функция скалярного ар-
гумента 122
Векторное произведение 15
— — двойное 16
Векторы ортогональные 95
Вероятность 249
Вершина гиперболы 64
— параболы 65
— эллипса 63
Взаимное расположение плоско-
стей 61
— — прямой и плоскости 57
— — прямых 54, 56
Вихрь векторного поля 219
Выборочное среднее 253
Выпуклость функции НО, 120
Высота треугольника 6
Вычет функции 206
Г
Гамма-функция 197
Геликоид прямой 150
Геометрия аналитическая 48
— дифференциальная 122
— - элементарная 5
Гипербола 64
— равносторонняя 64
Гиперболоид двуполостный 70
— однополостный 69
Гипоциклоида 134
Гомотетия 13
Градиент скалярного поля 217
— функции 116
Границы корней 80
256
График функции 30
Гурвициан многочлена 82
Д
Действительная часть комплекс-
ного числа 75
ось комплексной плоскости 75
Действия над степенными ряда-
ми 115
Декартов лист 135
Деление отрезка в данном отно-
шении 51
Делитель многочлена 78
— многочленов (общий наиболь-
ший) 78
Детерминант 83
Дефект линейного оператора 97
Диагональ квадрата 8
— параллелограмма 7
— прямоугольника 8
— прямоугольного параллелепи-
педа 10
— ромба 5
Диаметр гиперболы 65
— параболы 65
— эллипса 64
Дивергенция векторного поля
218
Директриса гиперболы 64
— параболы 65
— эллипса 63
Дискриминант многочленов 82
Дискриминантная линия семей-
ства 126
Дисперсия 251, 253
— выборочная 254
— — исправленная 254
Дифференциал 106
— абсолютный 227
— вектор-функции 123
— длины дуги 125, 128
— • ковариантный 227
Дифференциалы высших поряд-
ков 109, 117, 118
Дифференцирование алгебраи-
ческих операций 107
— вектор-функции 122, 123
— изображения 214
— композиции 115, 118
— оригинала 213
— функции 106
Длина вектора 13, 94, 226
— дуги линии 9, 125, 128
— кривой 184, 190
— окружности 9
Дополнение алгебраическое 84
— множества 243
Дробь 17
— элементарная 153
3
Задача Дирихле 241
— Коши 238, 239
Закон больших чисел 252
— двойного отрицания 245
— Пуассона 252
— распределения (бинормаль-
ный) 251
Законы векторной алгебры 14
— двойственности 243
— де Моргана 243, 245
Замена переменных в двойном
интеграле 185
— — — неопределенном инте-
грале 151
— — — несобственном инте-
грале 194
— — — определенном интегра-
ле 182
— — — тройном интеграле 187
Знаки тригонометрических функ-
ций 22
И
Измерение углов градусное 5
— — радианное 5
Изображение свертки 214
Инвариант линии второй степе-
ни 66
— поверхности второй степе-
ни 73
Интеграл 151
— двойной 185
— Дирихле 198
— Дюамеля 214
— комплекснозначной функции
201
— линейный 220
— неопределенный 151
— несобственный 193
— определенный 181
— Пуассона 198
— тройной 187
— функции комплексной пере-
менной 204
— Фурье 209, 211
— Эйлера 198
257
Интегралы, зависящие от пара-
метра 193
— криволинейные 189
— Лапласа 198
— неберущиеся 180
— от иррациональных функций
162
— — рациональных функций
166
— — функций нескольких пере-
менных 185
— поверхностные 191
— простейшие 151
— содержащие гиперболические
функции 177
— — логарифмы 169
— — обратные тригонометриче-
ские функции 176
— — тригонометрические функ-
ции 170
— — экспоненту 168
— Френеля 198
— эйлеровы 196
Интегрирование биномиальных
дифференциалов 155
— изображения 214
— иррациональностей 154
— оригинала 214
— по частям 182
— рационально-гиперболи-
ческих функций 155
— рационально-тригонометри-
ческих функций 155
— рациональных функций 153,
154
— трансцендентных функций
156
Интервал 30
— доверительный 254
— сходимости степенного ря-
да 114
Исчисление высказываний 247
— дифференциальное 102
— интегральное 151
— матричное 85
— операционное 213
— тензорное 222
К
Канонические уравнения линий
второй степени 63
— — поверхностей второй сте-
пени 68
— — прямой 53, 56
258
Канонический вид квадратичной
формы 99
— — линий второй степени 67
— — поверхностей второй сте-
пени 73
Каноническое уравнение гипер-
болического параболоида 70
— — — цилиндра 71
— — гиперболы 64
— — двуполостного гиперболо-
ида 70
— — конуса второй степени 68
— — однополостного гипербо-
лоида 69
— — параболического цилинд-
ра 72
— — параболы 65
— — эллипса 63
— — эллипсоида 68
— — эллиптического параболо-
ида 70
— — — цилиндра 71
Кардиоида 135
Касательная к гиперболе 64
— — линии 124, 127
— — окружности 63
— — параболе 65
— — эллипсу 63
— плоскость 130
Катеноид 149
Квадрат 8
Квадратичная форма 99
— — неопределенная 101
— — отрицательно-определен-
ная 100
— — отрицателыю-полуопреде-
ленная 101
— — поверхности (вторая) 131
— — — (первая) 131
— -— положительно-определен-
ная 100
— — положительно-полу-
определенная 101
Квантор всеобщности 248
— существования 248
Ковектор 224
Комбинаторика 28
Композиция отображений 243
Компоненты вектора 16
Конус 11
— асимптотический 69
— второй степени 68
— усеченный 11
Конхоида Никомеда 136
Координаты аффинные 48, 49
— вектора 16, 92
— — ковариантные 226
— —- контравариантные 226
— декартовы косоугольные 48,
49
— — прямоугольные 48, 49
— полярные 48
— сферические 49
— цилиндрические 49
Корень из числа (арифметиче-
ский) 18
— — комплексного числа 76
— многочлена 79, 80
— — кратный 79
Косеканс 22
Косинус гиперболический 26
Косинус-преобразование функ-
ции 211
Котангенс 22
— гиперболический 26
Коэффициент корреляции (выбо-
рочный) 255
— пропорциональности 18
— регрессии (выборочный) 255
Коэффициенты Фурье функции
209
Кривизна главная 132
— линии 125, 128
— — нормальная 132
— нормального сечения 132
— поверхности гауссова 132
— — полная 132
— — средняя 132
— — эйлерова 132
Критерий Гурвица 82
— линейной зависимости векто-
ров 92
— совместности системы линей-
ных уравнений 89
Круг 9
— сходимости степенного ряда
205
Кручение линии 129
Л
Лемниската Бернулли 136
Линейная зависимость векторов
92
— комбинация векторов 92
— независимость векторов 92
— форма 222
Линейность интеграла 181, 194
Линии координатные асимптоти-
ческие 133
— — кривизны 133
— — ортогональные 133
— — сопряженные 133
Линия асимптотическая 133
— векторная 218
— Вивиани 147
— винтовая 146
— — коническая 147
— второй степени 63
— геодезическая 133
— кривизны 132
— плоская 123
— пространственная 126
— уровня 217
— цепная 143
Логарифм 21
— десятичный 21
— натуральный 21
— комплексного числа 203
Логика математическая 242
Логические операции 244
Локон Аньези 137
М
Масса кривой 190
— плоской фигуры 186
— тела 188
Матрица 85
— верхняя треугольная 86
— вырожденная 87
— действительная 86
— диагональная 86
— единичная 86
— квадратная 85
— квадратичной формы 99
— комплексная 86
— кососимметрическая 87
— линейного оператора 96
— невырожденная 87
— неособенная 87
— нижняя треугольная 86
— нулевая 85
— обратная 87
— ортогональная 87
— особенная 87
— перехода от базиса к базису
93
— противоположная 85
— симметрическая 87
— системы векторов 93
— — линейных уравнений 89
— — — — расширенная 89
— скалярная 86
— ступенчатая 85
— транспонированная 87
259
- — трапециевидная 85
Матрица-столбец 86
Матрица-строка 85
Медиана треугольника 5
Метод Гаусса 90
— касательных 47
— Лагранжа 100, 232
— линейной интерполяции 81
— Ньютона 47, 81
— Остроградского 154
— половинного деления 46
— последовательного исключе-
ния переменных 90
— простых итераций 47
— рационализации 154
— секущих 47
— Фурье 240
— хорд 47
— Эйлера 233
— Якоби 100
Минор матрицы базисный 88
— определителя 83
— — главный 84
Мнимая единица 75
— ось комплексной плоскос-
ти 75
— часть комплексного чис-
ла 75
Многоугольник 8
— вписанный 8
— выпуклый 8
— описанный 8
— правильный 9
Многоугольники подобные 9
Многочлен 77
— Тейлора 112
Множества эквивалентные 244
— одинаковой мощности 244
Множество 242
— выпуклое 120
— задания отображения 243
— — функции 30
— значений отображения 243
— — функции 30
— мощности континуума 244
— несчетное 244
— счетное 244
— числовое 29
Множитель интегрирующий 235
Модуль вектора 13
— комплексного числа 75, 76
Момент инерции 187, 188
— корреляционный (выбороч-
ный) 255
— статический 185, 186
Монотонность интеграла 181
Н
Направления асимптотические
133
— главные 132
— сопряженные 132
Направляющие косинусы 16
Непрерывность вектор-функции
122
Неравенства 20, 42
— квадратичные 43
— линейные 41
— логарифмические 44
— показательные 44
— содержащие модуль 21, 46
— тригонометрические 45
— числовые 20
Неравенство Бернулли 21
— Бесселя 210
— Буняковского 21
— Коши — Буняковского 94
— треугольника 94
— Чебышева 252
Нормаль к гиперболе 64
— —• линии 124
— — параболе 65
— — поверхности 130
— — эллипсу 63
— линии главная 127
Нормальный вид квадратичной
формы 100
Нормирующий множитель плос-
кости 59
— — прямой 53
Нули аналитической функции 205
О
Область значений линейного опе-
ратора 97
— определения отображения 243
— — функции 30
Образ множества 243
— оператора 97
Объединение множеств 242
Объем конуса 11
— — усеченного 11
— куба 10
— параллелепипеда 10, 16, 52
— пирамиды 10
— — правильной 10
— — усеченной 11
— призмы 10
— тела 188
— тетраэдра 53
260
— усеченного конуса 11
— усеченной пирамиды 11
— фигуры 184
— цилиндра 11
— цилиндроида 186
— шара 12
— шарового сегмента 12
— — сектора 12
Овалы Кассини 136, 137
Огибающая семейства линий
126
Ожидание математическое 251,
252
Окружность 9, 63, 202
Оператор Гамильтона 217
— Лапласа 221
— линейный 96
— — Дифференциальный 116
— — невырожденный 96
— — простой структуры 97
— — самосопряженный 98
— обратный 97
— ортогональный 98
Операторы линейные сопряжен-
ные 98
Операции второго порядка век-
торного поля 221
Определитель 83
— произведения матриц 85
Опускание индекса 266
Осевая симметрия на плоскости
12
Основное свойство дроби 17
. Основные свойства определенно-
го интеграла 181
Ось гиперболы 64
— параболы 65
— эллипса 63
Остаток ряда 103
Остаточный член формулы Тей-
лора 111
— — — — в форме интеграль-
ной 112
— — — — — — Коши 112
— — — — — — Лагранжа
111
— — — — — — Пеано 112
Отклонение точки от прямой 54
— — — плоскости 61
Отображение множеств 243
— биективное 243
— взаимно-однозначное 243
— инъективное 243
— конформное 208
— линейного пространства 95
— обратное 243
— сюрьективное 243
Оценки интегралов 182
П
Парабола 65
Параболоид гиперболический 70
— эллиптический 70
Параллелепипед 10
Параллелограмм 7
Параллельный сдвиг координат-
ных осей 50
— перенос 13
Параметр линии натуральный
125, 128
— гиперболы 64
— параболы 65
— эллипса 63
Первообразная дифференциаль-
ного выражения 190
— функция 151
Пересечение множеств 242
Перестановки 28
Пирамида 10
— правильная 10
— усеченная 11
Планиметрия 5
Плоскость 58
— комплексная 75
— нормальная 127
— соприкасающаяся 127
— спрямляющая 128
Плотность вероятности 252
Площадь боковой поверхности
конуса 11
— — — правильной пирамиды
10
— — — — усеченной пирами-
ды 11
— — — призмы 6
— — — усеченного конуса 11
— — — цилиндра 11
— замкнутой области поверх-
ности 131
— квадрата 8
— криволинейного сектора 183
— криволинейной трапеции 183
— круга 9
— кругового сегмента 10
— параллелограмма 7, 15
— плоской фигуры 186
— поверхности 186
— — вращения 184
--- пирамиды 10
— — призмы 10
— — прямоугольного паралле-
261
лепипеда 10
— — сферического сегмента 12
— — шара 12
— полной поверхности конуса 11
— — — усеченного конуса 11
— — — цилиндра 11
— правильного многоугольни-
ка 9
— прямоугольника 8
— ромба 7
— сектора 9
— трапеции 8
— треугольника 6, 52
Поверхность 129
— вращения 148
— второй степени 68
— уровня 217
Поворот координатных осей 50
— плоскости вокруг центра 12
Поднятие индекса 226
Подобие 13
Подпространство линейного про-
странства 92
Показательная форма комплекс-
ного числа 77
Поле векторное 218
— — солсноидальное 221
— — потенциальное 220
— скалярное 217
— тензорное 227
Постоянная Эйлера 103
Поток векторного поля 219
Правило деления уголком 78
— Крамера 89
— Лопиталя 109
— многоугольника 14
— параллелограмма 14
— параллелепипеда 14
— треугольника 14
Предел 102
— вектор-функции 122
— комплекснозначной функции
201
Предикат 248
Преобразование Лапласа 213
— линейного пространства 95
— Фурье 211
— — обратное 211
Преобразования алгебраические
17
— декартовых координат 50
— интегралов 182
— координат вектора 94
— линейные евклидова прост-
ранства 98
— — линейного пространст-
ва 95
— . матрицы (элементарные) 88
— плоскости (геометрические)
12
Приближенное вычисление инте-
гралов 182
— — корней 81
— решение уравнений 46
Призма 10
Признак сходимости числового
ряда 104
— — — — Абеля 105
— — — — Гаусса 105
— — _ — Д’Аламбера 104
— — — — Дирихле 105
— — — — интегральный 105
— — — _ Коши 104
— — — — Лейбница 105
— — — — Раабе 105
— - - — сравнения 104
— _ — — — предельный 104
— — — — степенной 104
Признаки сходимости несобст-
венных интегралов 194
Приращение функции 115, 118
Прогрессия арифметическая 19
— геометрическая 19
— — бесконечная 19
Проекции вектора 16
Произведение векторов вектор-
ное 15
— - скалярное 14, 94
— — смешанное 16
— комплексных чисел 75, 76
— линейных операторов 96
— матриц 87
— множеств декартово 243
— — прямое 243
— тензоров 224
Производная 106
— вектор-функции 122
— линейной комбинации 108
— ковариантная 227
— комплекснозначной функции
201, 203
— композиции 107
— логарифмическая 107
— обратной функции 107
— односторонняя 106
— по направлению 116
— скалярного поля 218
— сложной функции 107
— степенно-показательной
функции 108
262
Производные высших порядков
108
— функций, заданных неявно
117
— — — параметрически 109
— частные 116
— элементарных функций 107
Промежутки числовые 30
Пропорциональность обратная
18
— прямая 18
Пространство евклидово 94
— векторное 91
— линейное 91
Процент 17
Процесс ортогонализации систе-
мы векторов 95
Прямая в пространстве 56
— на плоскости 53
Прямолинейные образующие 69,
71
Прямоугольник 8
Псевдосфера 149
Пучок плоскостей 62
— прямых 55
Р
Работа силы вдоль кривой 191
Равенство Парсеваля 210
Радиус кривизны 126
— сходимости степенного ряда
114, 205
— (фокальный) гиперболы 64
— — параболы 65
— — эллипса 63
Развертка окружности 145
Размерность линейного прост-
ранства 92
Размещения 28
Разность векторов 14
— матриц 86
— множеств 242
Ранг матрицы 88
— линейного оператора 97
— тензора 224
Раскрытие неопределенностей
109
Распределение Гаусса 253
— нормальное 253
— равномерное 253
Расстояние между параллельны-
ми плоскостями 62
— — — прямыми 55, 57
— — скрещивающимися пря-
мыми 57
• — —• точками 51
- — от точки до плоскости 61
— — — — прямой 54
Расходимость векторного поля
218
Результант многочленов 81
Розы 138
Ромб 7
Ротор векторного поля 219
Ряд гармонический 103
— — обобщенный 104
— Лорана 205
— степенной 114, 205
— Тейлора 113, 205
— Фурье 209, 210
— числовой 103
С
Сведение поверхностных инте-
гралов к двойным 192
Свертывание тензоров 225
Связка плоскостей 62
Связь между координатами век-
тора и его образа 96
— — матрицами линейного опе-
ратора в разных базисах 96
Секанс 22
Секущая окружности 9
Селектор отрезка 39
— точки 39
Семейство линий 126
Середина отрезка 51
Символ Кристоффеля 227
— Кронекера 86
Симметрирование тензоров 225
Синус гиперболический 26
Синус-преобразование 212
Система векторов ортонормиро-
ванная 95
— линейных дифференциальных
уравнений 233, 234
— — уравнений 89
— ---- однородных 90
Системы координат 48, 49
Скалярный квадрат вектора 14,
94
Сложение векторов 14
— матриц 86
— многочленов 77
— тензоров 224
Случайная величина 250
Случайное событие 251
Собственное значение линейного
оператора 97
263
— число линейного оператора 97
Собственный вектор линейного
оператора 97
Соприкосновение линий 124
Сопровождающий трехгранник
линии 127
Составляющие вектора 16
Сочетания 28
Спирали 139
Спираль Архимеда 139, 141
— Галилея 139
— гиперболическая 140, 141
— «жезл» 140
— коническая 147
— Корню 140
— логарифмическая 140, 141
— параболическая 140
— Ферми 141
Способы задания линии 123, 126
— — плоскости 58
— — поверхности 129
— — прямой 53, 56
Сравнение функций 103
Среднее арифметическое чисел
20
— геометрическое чисел 20
Среднее квадратическое отклоне-
ние 251
Средняя линия трапеции 8
— — треугольника 5
Статистика математическая 253
Степень многочлена 29
— числа 18
Стереометрия 10
Строфоида 142
Сумма векторов 14
— комплексных чисел 75
— линейных операторов 96
— матриц 86
— ряда 103
— — частичная (частная) 103
— тензоров 224
Сфера 68, 148
Схема Горнера 78
Сходимость ряда 103, 104
Т
Таблица основных преобразова-
ний Лапласа 216
Таблицы неопределенных инте-
гралов 156
Тангенс 21
— гиперболический 26
Тензор 223
— деформаций 226
264
— инерции 227
— метрический 226
— напряжений 227
Теорема Барроу 181
— запаздывания 213
— косинусов 5
— Коши интегральная 204
— Лапласа интегральная 250
— — локальная 250
— о вычетах 207
— Пифагора 6
— подобия (в операционном ис-
числении) 213
— синусов 5
— смещения 213
— Чебышева 252
Теоремы о среднем 181
— разложения 214, 215
Теория вероятностей 249
Тождества 19
— гиперболические 26
— тригонометрические 23
Тождество основное логарифми-
ческое 21
— Эйлера 116
— Якоби 16
Тор 148
Точка перегиба 111
— поверхности гиперболическая
132
— — особая 130
— — параболическая 132
— — эллиптическая 132
— особая изолированная 205
— — устранимая 205
— — полюс 205
— — существенно 206
Трактриса 142
Транспонирование матриц 87
— тензоров 224
Трапеция 8
Треугольник 5, 8
— Паскаля 29
— прямоугольный 6
— равнобедренный 7
— равносторонний 7
Тригонометрическая система
функций 209
— форма комплексного числа 75
У
Угол между векторами 15, 94, 226
— — линиями на поверхности
131
— — плоскостями 61
— — прямой и плоскостью 58
— — прямыми 55, 57
— треугольника внешний 5
Улитка Паскаля 143
Умножение векторов (скаляр-
ное) 94
— матриц 87
— многочленов 77
— тензоров 224
Уравнение Бернулли 236
— биквадратное 43
— дифференциальное 229
— — в полных дифференциалах
235
— — линейное 229
— — нелинейное 234
— — неоднородное 229, 230, 231
— — однородное 229, 231, 235
— — — обобщенное 236
— — с разделенными перемен-
ными 234
— — с разделяющимися пере-
менными 234
— квадратное 42
— Клеро 236
— кубическое 80
— Лагранжа 236
— Лапласа 221, 241
— линейное 41
— логарифмическое 44
— показательное 44
— регрессии 255
— Риккати 236 ,
— теплопроводности 240
— характеристическое 229, 231,
233
— — линейного оператора 97
— — линии второй степени 66
— — поверхности второй степе-
ни 73
— Эйлера 233
Уравнения в частных производ-
ных 237
— линии натуральные 126, 129
— — векторно-параметрические
124, 126
— — неявные 124, 126
— — параметрические 124, 126
— — явные 12, 126
— плоскости 58
— поверхности векторно-пара-
метрические 129
— — неявные 130
— — параметрические 130
— — явные 130
— прямой 53
— содержащие модуль 46
— тригонометрические 44
Условия Коши — Римана 203, 204
Ф
Фигуры подобные 13
Фокус гиперболы 64
— параболы 65
— эллипса 63
Формула Бейеса 249
— Бернулли 250
— бинома Ньютона 28
— Бонне 182
— Валлиса 102
— Герона 6
— Грина 190
— двойной подстановки 181, 194,
196
— дополнения 196, 197
— интегрирования по частям
151, 194
— Кардано 80
— конечныхприращений 109,116
— Коши интегральная 204
— Коши — Адамара 114, 205
— Лагранжа интерполяцион-
ная 79
— Лежандра 197
— Лейбница 108
— Меллина 214
— Муавра 76
— Ньютона — Лейбница 181,
204
— Остроградского 193, 220
— Парсеваля 216
— полной вероятности 249
— Симпсона 183
— средних прямоугольников 182
— Стирлинга 103
— Стокса 192, 220
— Тейлора 111, 112, 117, 119,
123
— трапеций 183
— Эйлера 132
— Эйлера — Гаусса 197
Формулы Виета 42, 79
— приведения 23
— рекуррентные 178
— сложения (в тригонометрии)
24
— — гиперболических функций
27
— сокращенного умножения 20
— тригонометрические 21
— Френе 126, 129
— Фруллани 198
— Эйлера 202
265
Функции булевы 246
— гиперболические 26, 37
— — двойного аргумента 27
— — половинного аргумента 27
— двух переменных 115
— комплекснозначные 201
— комплексной переменной 203
— комплексные 202
— кусочно-постоянные 39
— монотонные 30
— нескольких переменных 115
— обратные гиперболические 38,
203
— — тригонометрические 34,
203
— тригонометрические 21, 33
— — двойного аргумента 25
— — комплексного переменного
202
— — половинного аргумента 25
— — тройного аргумента 25
— числовые 30
— эквивалентные 103
Функция антье 39
— возрастающая 30
— выпуклая НО, 120
— гармоническая 221
— Дирихле 40
— дробно-рациональная 153
— единичного скачка 39
— квадратичная 31
— косинус 33
— — гиперболический 26, 38
— котангенс 34
— — гиперболический 26, 38
— Лагранжа 120
— Лапласа 250, 253
— линейная 31
— логарифмическая 33
— модуль 38
— нечетная 30
— однородная 116
— периодическая 30
— показательная 32
— правдоподобия 254
— правильная дробно-линейная
153
— распределения 252
— — эмпирическая 253
— сигнум 39
— синус 33
— — гиперболический 26, 37
— степенная 31
— тангенс 34
— — гиперболический 26, 38
— убывающая 31
— Хевисайда 39
— четная 30
— экспонента 32, 202
Ц
Центр масс 184—186, 188, 190
— — системы материальных то-
чек 52
— линий второй степени 67
— поверхностей второй степени
74
Центральная симметрия (на пло-
скости) 12
Циклоида 144
— обыкновенная 144
— укороченная 144
Цилиндр 11
— гиперболический 71
— параболический 72
— эллиптический'71
Циркуляция векторного поля 220
Циссоида Диоклеса 144
Ч
Четырехугольник 9
Числа вещественные 30
— действительные 30
— комплексные 75
— — сопряженные 75, 76
— натуральные 29
— рациональные 29
— характеристические 229
— целые 29
Ш
Шар 12
Э
Эвольвента окружности 145
Экспонента 32, 202
Экспоненциальная форма комп-
лексного числа 77
Экстремум функции локальный
109, 117, 119
— — условный 119
Эксцентриситет гиперболы 64
— параболы 65
— эллипса 63
Эллипс 63
Эллипсоид 68
Эпициклоида 75
Я
Ядро линейного оператора 97
ОГЛАВЛЕНИЕ
Предисловие ................... .. 3
Некоторые постоянные. . , 4
1. Элементарная геометрия ... 5
1.1 Планиметрия . . 5
1.2. Стереометрия . . 10
1.3. Геометрические преобразования 12
2. Начала анализа и алгебры ... 17
2.1 Алгебраические преобразования . . 17
2.2. Тригонометрические формулы .... 21
2.3. Основные формулы для гиперболических функций . 26
2.4. Элементы комбинаторики. Формула Ньютона . 28
2.5. Действительные числа и числовые множества 29
2.6. Числовые функции................................... 30
3. Уравнения и неравенства................................. 41
3.1. Линейные уравнения и неравенства................... 41
3.2. Квадратные уравнения и неравенства ... 42
3.3. Показательные уравнения и неравенства . . 44
3.4. Логарифмические уравнения и неравенства . . .44
3:5. Тригонометрические уравнения и неравенства .... 44
3.6. Простейшие уравнения и неравенства, содержащие мо-
дуль .................................................. 46
3.7. Методы приближенного решения уравнений вида f(x) = 0
(f непрерывна) ................................. 46
4. Аналитическая геометрия . . 48
4.1. Системы координат на плоскости и в пространстве 48
4.2. Преобразование декартовых прямоугольных координат
на плоскости........................................... 50
4.3. Простейшие задачи аналитической геометрии . 51
4.4. Прямая на плоскости................................ 53
1.5. Прямая в пространстве ...... 56
4.6. Плоскость ......................................... 58
267
4.7. Линии второй степени................................ 63
4.8. Поверхности второй степени.......................... 68
5. Высшая алгебра........................................... 75
5.1. Комплексные числа................................... 75
5.2. Многочлены.......................................... 77
5.3. Определители........................................ 83
5.4. Матричное исчисление................................ 85
5.5. Системы линейных уравнений.......................... 89
5.6. Линейные пространства............................... 91
5.7. Евклидовы пространства.............................. 94
5.8. Линейные преобразования линейного пространства . . . 95
5.9. Линейные преобразования евклидова пространства . . . 98
5.10. Квадратичные формы................................. 99
6. Дифференциальное исчисление............................. 102
6.1. Пределы и числовые ряды.............................102
6.2. Производные и дифференциалы....................... 106
6.3. Формула Тейлора. Степенные ряды.....................111
6.4. Функции нескольких переменных.......................115
7. Дифференциальная геометрия...............................122
7.1. Вектор-функция скалярных аргументов................ 122
7.2. Плоские линии............................... .... 123
7.3. Пространственные линии............................. 126
7.4. Поверхности........................................ 129
7.5. Специальные классы линий и поверхностей.............133
8. Интегральное исчисление..................................151
8.1. Неопределенный интеграл.............................151
8.2. Таблицы неопределенных интегралов...................156
8.3. Определенный интеграл.............................. 181
8.4. Интегралы от функций нескольких переменных .... 185
8.5. Несобственные интегралы и интегралы, зависящие от па-
раметра ............................................... 193
9. Комплексный анализ.......................................201
9.1. Комплекснозначные функции действительной переменной 201
9.2. Комплексные функции.................................202
9.3. Ряд Фурье. Интеграл Фурье...........................209
9.4. Операционное исчисление.............................213
10. Элементы теории поля.....................................217
10.1. Скалярное поле.....................................217
10.2. Векторное поле.....................................218
268
11. Тензорное исчисление<................................222
11.1. Тензоры. Определения и примеры.................222
11.2. Действия над тензорами.........................224
11.3. Тензоры в евклидовом пространстве..............226
11.4. Тензорный анализ......................... . . 227
12. Дифференциальные уравнения...........................229
12.1. Линейные обыкновенные дифференциальные уравнения
и системы............................................229
12.2. Нелинейные дифференциальные уравнения . . . 234
12.3. Уравнения в частных производных.......... . . 237
13. Математическая логика............................... 242
13.1. Множества и отображения.................. . . 242
13.2. Алгебра высказываний..................... . . 244
13.3. Исчисление высказываний..................... . 247
13.4. Предикаты................................ . . 248
14. Теория вероятностей и математическая статистика . . 249
14.1. Случайные события..............................249
14.2. Случайные величины....................... . . 251
14.3. Математическая статистика......................253
Предметный указатель.....................................256