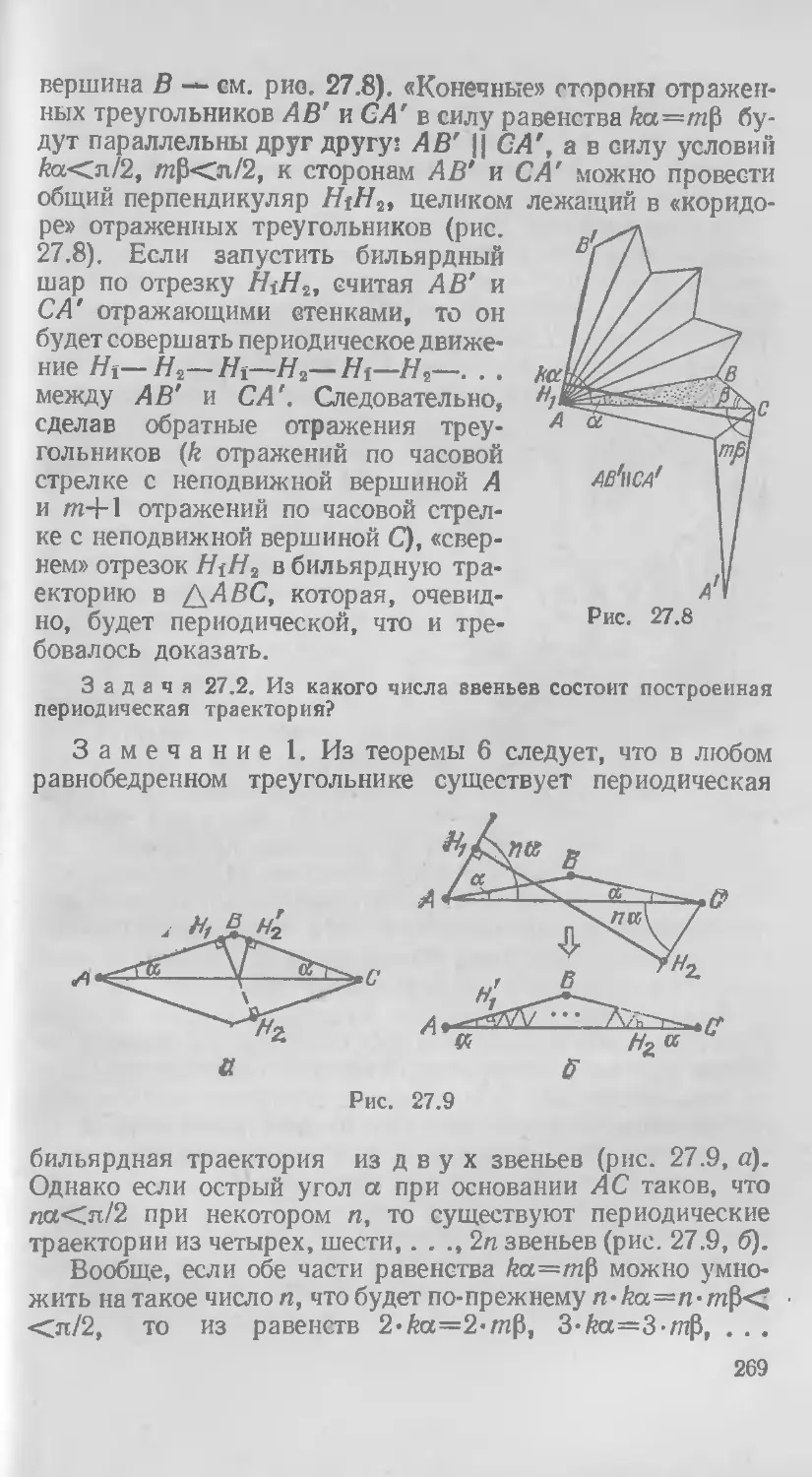
Автор: Гальперин Г.А. Земляков А.Н.
Теги: теория игр математика задачи по математике математические бильярды
ISBN: 5-02-014080-5
Год: 1990
Текст
\ БИБЛИОТЕЧКА -КВАНТ-
выпуск 77
ш
ГА. ГАЛЬПЕРИН
А.Н. ЗЕМЛЯКОВ
ТЕМ Т Ч С
Р Ы
ББК 22.18 Серия «Библиотечка «Квант»
П7 основана в 1980 г.
УДК 519.83@23)
РЕДАКЦИОННАЯ КОЛЛЕГИЯ
Академик Ю. А. Осипьян (председатель), доктор физико-
математических наук А. И. Буздин (ученый секретарь), ака-
академик А. А. Абрикосов, академик А. С. Боровик-Романов,
академик Б. К. Вайнштейи, заслуженный учитель РСФСР
Б. В. Воздвиженский, академик В. Л. Гинзбург, академик
Ю. В. Гуляев, академик |А. П. Ершов |, профессор С. П. Ка-
Капица, академик А. Б. Мигдал, академик С. П. Новиков, ака-
академик АПН СССР В. Г. Разумовский, академик Р. 3. Сагдеев,
профессор Я. А. Смородинский, академик | С. Л. Соболев |,
член-корреспондент АН СССР |Д. К. Фаддеев]
Реце нее нт
доктор физико-математических наук Л. А. Бднимович
Гальперин Г. А., Земляков А. Н.
Г17 Математические бильярды (бильярдные задачи и
смежные вопросы математики и механики).— М.:
Наука. Гл. ред. физ.-мат. лит., 1990.— 288 с.—
(Б-чка «Квант». Вып. 77)
ISBN 5-02-014080-5
Рассказывается о поведении бильярдного шара на столе
произвольной формы без луз. Описание этого поведения
приводит к решению разнообразных вопросов математики
и механики: задач о переливании жидкости, об освещении
веркальных комнат, об осциллографе и фигурах Лиссажу и
др. На доступном школьникам языке вводятся понятия
конфигурационного и фазового пространства, понятия геоде-
геодевических на простейших двумерных поверхностях, предла-
предлагаются (с решениями) многочисленные интересные задачи.
Для школьников 9—10-х классов.
1604010000—012
Г ЪЯ№*> 162'89 ББК 22.18
ISBN 5-02-014080-5
математической литературы,
1990
ОГЛАВЛЕНИЕ
Предисловие 5
Введение 7
Часть I. БИЛЬЯРДЫ В ВЫПУКЛЫХ ОБЛАСТЯХ С
КРИВОЛИНЕЙНОЙ ГРАНИЦЕЙ 24
Глава 1. Бильярд в круге 24
§ 1. Шар в круглом бильярде без луз 24
§2. Теорема Якобн. Применение к теории чисел 31
§ 3. Теорема Пуанкаре о возвращении. Конфи-
Конфигурационное и фазовое пространства. Па-
радоко Цермело и модель Эренфестов 42
Глава 2. Бильярд в эллипсе 60
§ 4. Эллипс и его бильярдные свойства. Каус-
Каустики 60
§ 5*.Задача об освещении невыпуклой области 78
§ 6. Экстремальные свойства бильярдных тра-
траекторий. Принцип Ферма и теорема Бнрк-
гофа 89
Часть II. ГЕОМЕТРИЯ И ФИЗИКА ПРЯМОУГОЛЬ-
НОГО БИЛЬЯРДА 100
Глава 3. Геометрия прямоугольного бильярда 100
§ 7. Бильярдный шар на прямоугольном стола
без луз 100
§ 8. Тор и его обмотки 108
§ 9. Бильярд в прямоугольнике и тор 117
Глава 4. Физика прямоугольного бильярда 122
§ 10. Фигуры Лиссажу 122
§11. Бильярд в прямоугольнике н осциллограф 129
§ 12. Задача о пеленге 133
Часть III. ГЕОМЕТРИЯ И АРИФМЕТИКА СТОЛКНО-
СТОЛКНОВЕНИЙ 137
Глава 5. Одномерный «газ» из двух молекул 139
§ 13. Два упруго сталкивающихся шара на от-
отрезке 139
§ 14. Два шара на отрезке: сведение к бильярду
в треугольника 147
3
§ 15. Два шара на полупрямой: сведение к би-
бильярду в угле 153
Глава 6. Одномерный «газ» из большого числа молекул 159
§ 16. Три упругих шара на прямой 159
§ 17. п упругих шаров на прямой 165
§ 18*. Число столкновений между молекулами
одномерного «rasa» 178
Глава 7**. Многомерный «газ» 187
§ 19. Конфигурационное пространство «rasa» из
п молекул в пространстве и сосуде 190
§ 20. Сведение «газа» в пространстве и сосуде
, к бильярду 193
§21. Рост числа столкновений между молеку-
молекулами «газа» 197
Ч а сть IV. БИЛЬЯРДЫ В МНОГОУГОЛЬНИКАХ И
МНОГОГРАННИКАХ 206
Глава 8. Геометрия многоугольного бильярда 207
§22. Бильярды в «торических» многоугольниках 207
§ 23. Склейка поверхностей из многоугольников 216
§ 24. Бильярды в «рациональных» многоуголь-
многоугольниках и поверхности 226
Глава 9. Поведение бильярдных траекторий в многоуголь-
многоугольниках 235
§ 25. Траектории в рациональных многоуголь-
многоугольниках и обмотки кренделей 236
§ 26. Может ли непериодическая траектория в
выпуклом многоугольнике не быть всюду
плотной в нем? 246
§ 27. Перяодические траектории в многоуголь-
многоугольниках и многогранниках 255
Заключение 282
Список литературы 287
Посвящается
нашим Учителям
ПРЕДИСЛОВИЕ
В данной книге изучаются так называемые бильярд-
бильярдные системы. К простейшим из них относятся «бильярд в плоской
области» (точечный шар, движущийся внутри круга, прямоугольни-
прямоугольника, эллипса, многоугольника и т. д.) и «одномерный бильярд» (ко-
(конечное число точечных шаров, движущихся по отрезку, лучу или
по всей бесконечной прямой). Общим свойством бильярдных систем
является закон абсолютно упругого отражения. О геометрических,
«арифметических», физических следствиях этого закона и расска-
рассказывается в книге.
Методы исследования бильярдных систем (например, анализ
поведения бильярдных траекторий), с одной стороны, примыкают
к традиционной геометрии, а с другой — лежат на стыке отраслей
современной математики — теории чисел, топологии, эргодической
теории и теоретической механики. Будучи, как правило, вполне
-¦ яементарными, эти методы позволяют получить далеко не элемен-
элементарные выводы.
Многие из излагаемых в книге результатов являются класси-
классическими и восходят к Кориолису, Больцману, Пуанкаре, Киркгофу.
Современная теория бильярдов является одним из актуальных на-
направлений математической физики. Ее основы были заложены со-
советским математиком Я. Г. Синаем и его школой. Проблемы этой
теории непосредственно близки к переднему краю сегодняшней ма-
математики. Поэтому книга, возможно, будет интересна не только
школьникам, ио и студентам, и специалистам — математикам, ме-
механикам, физикам. В ней сформулировано немало вопросов, ос-
остающихся открытыми, и мы надеемся, что кому-нибудь из читателей
книги удастся продвинуться в их исследовании. Учитывая элемен-
элементарность методов (при неэлементарности результатов) и плодотвор-
плодотворность свежего взгляда иа рассматриваемые вопросы и проблемы, мы
особенно рассчитываем на читателей-старшеклассников.
Многие из решаемых в книге задач разбирались на занятиях
кружков в физико-математической школе-интернате при МГУ, в
летнем лагере Малой академии наук Крыма «Искатель». Часть ма-
материала публиковалась в журнале «Квант» (см. список литературы
в конце книги). Некоторые идеи и результаты, приводимые в кни-
книге, неоднократно обсуждались с участниками семинара МГУ по тео-
теории динамических систем и с его руководителем Я. Г. Синаем *).
*) В течение долгого времени и до последних дней своей жизни
этим семинаром вместе с Я. Г. Синаем руководил также замечатель-
замечательный математик и популяризатор науки В. М. Алексеев A932—1980).
Этот семинар является одним из наиболее известных мировых
центров по теории динамических систем и, в частности, по теории
бильярдов; часть приводимых нами результатов принадлежит его
участникам. Многолетнее участие авторов в работе этого семинара
в значительной мере способствовало написанию этой книги.
Читателю не следует рассчитывать на легкое чтение — через
некоторые параграфы, наверное, придется буквально продираться,
вооружившись карандашом и бумагой, иногда — ножницами и
клеем, а может быть, микрокалькулятором или компьютером. Кни-
Книгу не обязательно читать подряд — напротив, проскочив (как
бильярдный шар) через параграф или главу, читатель может найти
интересующий его (и доступный ему) материал — потом можно и
возвратиться.
В книге много отступлений от чисто бильярдной тематики,
вызванных тем, что бильярды имеют отношение к большому числу
интересных и, иа наш взгляд, красивых задач, и поэтому мы наде-
надеемся, что читатель сможет разнообразить свои впечатления, узнать
что-то новое и даже не совсем обычное.
Но стоит сразу предупредить любителей игры в бильярд —
в нашей книге нет не только соответствующих полезных советов,
но даже и правил этой древней игры. Эта книга — по матема-
математике, а любителям обычного бильярда мы можем порекомендовать
публикации журнала «Наука и жизнь» (см. [1] в списке литературы)
н книгу Г. Г. Кориолиса «Математическая теория явлений бильярд-
бильярдной игры» (М.: Гостехиздат, 1956), а также посетить возродившие-
возродившиеся чемпионаты страны по бильярду.
Как известно, «нестрого» не означает «неверно», равно как и
«строго» не означает «уместно» или «интересно» (это высказываение
принадлежит современному американскому физику Дж. Лебови-
uy — одному из ведущих специалистов по статистической механике).
Поэтому в большинстве важных математических вопросов (при изло-
изложении методов) мы старались придерживаться полной (насколько
это возможно при принятом элементарном подходе) строгости, од-
однако в ряде вопросов более общего (физического) характера (когда
касались общих принципов или идей) ограничились интуитивным
> ровней описания. Это следует иметь в виду и читателю-ригористу,
и читателю-«физику», привыкшему больше доверять своей интуиции.
Представление о структуре книги можно получить не только
из оглавления — в конце Введения, в котором сформулирована
основная часть рассматриваемых далее вопросов и проблем, коротко
рассказано и о последовательности изложения.
Читатель, заинтересовавшийся дальнейшими деталями «мате-
«математики бильярдов» или другими подходами к излагаемым вопро-
вопросам, может обратиться к списку литературы в конце книги.
Мы благодарны Я. Г. Синаю, внимательно прочитавшему всю
рукопись и сделавшему много замечаний и предложений по улучше-
улучшению ее текста, а также Л. А. Бунимовичу, Я. Б. Песину, А. М. Сте-
пину и Ю. П. Соловьеву, своими замечаниями способствовавшими
улучшению отдельных мест книги.
ВВЕДЕНИЕ
Читатель, конечно, имеет представление об
игре в бильярд на прямоугольном столе с лузами (рис. В. J).
Появившись до нашей эры в Индии и Китае, бильярд через
много веков перекочевал в европейские страны — упоми-
упоминание о нем имеется в
английских летописях
VI века. Более поздние
сведения о появлении
бильярда в Европе от-
относятся к XVI веку.
Так, французский ко-
король Карл IX в Варфо-
Варфоломеевскую ночь *) иг-
играл в бильярд, когда раз- Рис. В. 1
дался условный звон ко-
колоколов парижского собора Сен-ЖерменД'Акселеруа. Затем
В. Шекспир в «Антонии и Клеопатре»**) заставляет еги-
египетскую царицу Клеопатру играть в бильярд со своей фрей-
фрейлиной (акт II, сцена 5; см. эпиграф к части III). В 1760 г.
английский король Георг II издал указ, запрещающий
игру в бильярд в общественных местах под страхом
штрафа в 10 фунтов. В России бильярд стал известен и
распространился при Петре I. Как правило, в бильярд
играли на прямоугольном столе с шестью лузами, из кото-
которых четыре располагались в углах стола, а две — в сере-
серединах более длинных сторон; отличались эти игры лишь
количеством шаров — иногда довольствовались тремя ша-
шарами (как, например, английский король Генрих VIII), а
иногда — пятнадцатью или двадцатью.
*) Варфоломеевская ночь (известная также под названием
«парижская кровавая баня»)— историческое событие, происшедшее
в ночь на 24 августа 1572 г., когда католики учинилн избиение гуге-
гугенотов (французских протестантов).
**) Ш е к с п и р В. Полное собрание сочинений: В 8 т.
Т.7.— М.: Искусство, 1960. Трагедия написана в 1616 г.
Подобно тому как азартная игра в кости вызвала к жиз-
жизни «исчисление» вероятностей, игра в бильярд послужила
предметом серьезных научных исследований по механике
и математике. Описанию движения бильярдного шара
(с учетом трения) на прямоугольном столе с лузами посвя-
посвящена книга известного французского физика Г. Г. Корио-
лиса, написанная им в 1835 г. за год до избрания его ака-
академиком Парижской академии наук.
Известны различные варианты игры на бильярде. На-
Например, так называемый французский бильярд вообще не
имеет луз (при игре во французский бильярд нужно по-
попасть в заданный шар после нескольких столкновений
с другими шарами — см. литографию известного худож-
художника XIX века А. Оберландера на второй странице об-
обложки). Французский бильярд и послужил прообразом
математического бильярда, которому посвящена эта книга.
Представьте себе горизонтальный бильярдный стол
произвольной формы, но без луз. По этому столу без тре-
трения движется точечный шар, абсолютно упруго отражаясь
от бортов (рис. В. 2). Спрашивается, какой может быть
траектория этого шарика!
Математическая проблема бильярда, или проблема
траекторий, состоит в том, чтобы найти ответ на этот воп-
вопрос. Описанная механическая система — точечный шар
в бильярдной области Q, ограниченной бортом Г (границей
области Q),— и называется математическим бильярдом.
Траектория бильярда в области Q определяется начальным
положением точки q (q ? Q) и начальным вектором ее ско-
скорости v. Пренебрежение трением означает, что абсолютную
величину скорости v при движении точки мы считаем неиз-
неизменной во времени, поэтому задаваемый в начальный мо-
момент времени /=0 вектор v можно считать единичным,
характеризующимся лишь своим направлением. Направле-
Направление вектора v(f), т. е. направление движения шара, ме-
меняется только при его ударе о борт. Это происходит по зако-
закону абсолютно упругого отражения: после удара шара
(точки q{t)) о борт Г в точке Р шар движется так, что
его «угол падения равен углу отражения». Если борт Г
в окрестности точки Р криволинейный, то углы падения
и отражения — это углы, составленные «падающим» и «от-
«отраженным» отрезками траектории с касательной MN к кри-
кривой Г, проведенной в точке Р (рис. В. 2) *). Таким образом,
*) В физике обычно принято отсчитывать углы падения и от-
отражения от нормали к кривой Г в точке Р. Нам удобнее отсчитывать
углы от касательной.
8
траектория бильярда — это вписанная в кривую Г ло-
ломаная, которая может быть однозначно построена по сво-
своему начальному звену.
Борт Г бильярда может иметь и точки излома — типа
точек А%, А2, ... на рис. В.2. Касательная к кривой Г
в такой точке не определена. Поэтому бильярдную траек-
траекторию, попадающую в такую точку, мы будем считать окан-
оканчивающейся в ней. Такие «тупиковые» траектории в опре-
определенном смысле исключительны, и мы их, как правило,
N
Рис. В.2
Рис. В.З
рассматривать не будем. Сформулированная выше проб-
проблема траекторий относится к поведению неособых, беско-
бесконечных во времени траекторий.
Общая математическая проблема бильярда заключается
в том, чтобы описать возможные типы бильярдных траек-
траекторий в данной области Q. Простейший принцип такого
о шсания — разделение траекторий на периодические, или
замкнутые, и остальные — непериодические. На рис. В.З
изображены некоторые периодические траектории бильяр-
бильярдов в прямоугольнике, в правильном треугольнике, в
круге.
Траектория с «начальным условием» (q, v) будет перио-
периодической (или замкнутой), если через некоторое время
(через период) точка возвращается в свое начальное поло-
положение q с первоначальной скоростью v. Периодические дви-
движения воспринимаются как наиболее «правильные» —
такими мы привыкли представлять, например, движения
планет около Солнца и качания маятника. Рассматривае-
Рассматриваемая проблема в отношении периодических траекторий сво-
сводится, в частности, к вопросу о существовании: в любой ли
области Q существуют периодические (замкнутые) траек-
траектории? Другой вопрос — о критерии периодичности: как
по данным начальным условиям (q, v) узнать, будет ли соот-
соответствующая траектория периодической?
В первых двух частях книги мы найдем критерии перио-
периодичности для бильярдов в круге и в прямоугольнике. Во
второй главе будет решен и вопрос о существовании перио-
периодических траекторий бильярда в произвольной выпуклой
области с гладкой (без изломов) границей. А вот этот же
вопрос для бильярдов в многоугольниках (даже в тупо-
тупоугольных треугольниках!) до настоящего времени остается
открытым. Иначе говоря, неизвестно, в любом ли много-
многоугольнике (или тупоугольном треугольнике) существуют
периодические траектории. А ведь этот вопрос, по сути,
относится к элементарной геометрии. Известные нам све-
сведения по данному поводу приведены в гл. 9.
Интерес представляют и такие вопросы: Какое число
звеньев может иметь периодическая траектория? Какие
периоды имеют периодические траектории в данной об-
области (если принять минимальный период периодической
траектории, скажем, за единицу)?
Оказывается, это далеко не праздные вопросы — на-
например, они имеют прямое отношение к исследованию спе-
специальных систем квантовой механики. Однако объяснение
этого выходит далеко за рамки наших возможностей в дан-
данной книге.
Взамен рассмотрим элементарную задачу совсем из
другой области, изящно решаемую с помощью бильярдов.
Речь пойдет о «переливаниях», которые, казалось бы, не
имеют уж ничего общего с бильярдами. Начнем с класси-
классической головоломки.
Имеются два сосуда вместимостью 7 и 11 литров и
большая бочка, наполненная водой. Как с помощью этих
двух сосудов отмерить ровно 2 литра воды? Всякие уловки
запрещены, т. е. на сосудах нельзя делать никаких отме-
отметок, их нельзя наклонять, чтобы отмерять доли литра,
и т. д.
Предложенная задача решается либо алгебраическим
методом, либо методом проб и ошибок. При чем же здесь
бильярдные шары?
Как ни странно, но головоломки на переливание жид-
жидкостей можно очень легко решать, вычерчивая бильярдную
траекторию шара, отражающегося от бортов ромбического
стола! Границы таких столов удобнее всего рисовать на бу-
бумаге, на которую нанесена сетка из одинаковых равносто-
равносторонних треугольников. В рассматриваемой задаче стороны
стола должны иметь длины 7 и 11 единиц (рис. В.4). По
10
*
5 0
0 5
5" ¦<? 7 В 910 ft
0ff88f t
0
о**7
о i i 7
ft 9
5 7
Рис- в-4
0 7
горизонтали отложено количество воды в 11-литровом со-
сосуде в любой момент времени, а по вертикали — та же ве-
величина для 7-литрового сосуда.
Как же пользоваться диаграммой? Представьте себе,
что шар находится в левой нижней вершине в точке 0.
Он будет перемещаться вдоль нижнего основания ромба до
тех пор, пока не достигнет правой боковой стороны в точ-
точке 11. Это означает, что
11-литровый сосуд на-
полнен до краев, а 7-
литровый пуст. Отразив-
Отразившись упруго от правого
борта, шар покатится
вверх и влево и ударит- Л^Д
ся о верхний борт в точ- 0у / 2 3
ке с координатами 4 по #.<4-
горизонтали и 7 по вер-
тикали. Это означает,
что в 11-литровом сосу-
де осталось всего 4 лит-
ра воды, а 7 литров из
него перелили в меньший
сосуд.
Прослеживая дальнейший путь шара и записывая все
этапы его движения до тех пор, пока он не попадет в точку 2
верхнего борта, вы получите ответ и узнаете, в какой по-
последовательности необходимо производить переливания,
чтобы отмерить 2 литра воды. Все 18 переливаний изобра-
изображены схематически на рис. В.4. Наклонные стрелки гово-
говорят о том, что вода переливается из одного сосуда в другой,
а вертикальные означают, что либо вода целиком выли-
выливается из меньшего сосуда обратно в бочку, либо больший
сосуд надо наполнить водой до краев.
Является ли это решение самым коротким? Нет, су-
существует второй путь, когда воду сначала наливают в
7-литровый сосуд. На диаграмме (рис. В.4) это соответствует
тому, что шар из точки 0 катится вверх вдоль левого борта
до тех пор, пока не ударится в верхний борт. Нарисовав
траекторию бильярдного шара, читатель убедится в том,
что точка 2 достигается на этот раз за 14 отражений от
борта. Полученное решение с 14 переливаниями уже яв-
является самым коротким.
Требуется немного сообразительности, чтобы применить
метод бильярдного шара к любой задаче о переливании
жидкости с помощью не более чем трех сосудов. Поскольку
И
кроме как во введении об эткх задачах мы говорить больше
не будем, поговорим об этом методе здесь более подробно.
Рассмотрим старую головоломку с тремя сосудами, вос-
восходящую еще к Никола Фонтана, итальянскому матема-
математику XVI века, которого друзья называли Тартальей *).
Восьмилитровый сосуд до краев наполнен водой. С помощью
двух пустых сосудов объемом 3 и 5 литров воду надо по-
поровну разлить в два больших сосуда. Диаграмма для этой
задачи — ромбический стол размером 3X5 — изображена
на рис. В.5. Главная диаго-
*? ."? ?*~ наль Ромба, поделенная нак-
наклонными прямыми на 8 частей,
относится к 8-литровому со-
сосуду.
Как и в предыдущей зада-
задаче, бильярдный шар начинает
свое движение из точки 0.
Нарисовать его траекторию
совсем несложно. С ее помо-
помощью вы получите решение в минимальным числом перели-
переливаний, равным 7.
Если объемы двух меньших сосудов не имеют общего
делителя (т. е. взаимно просты), а объем третьего сосуда
больше или равен сумме объемов двух меньших, то с по-
помощью этих трех сосудов можно отмерить любое целое
число литров, начиная с 1 литра и кончая объемом среднего
сосуда
Имея, например, сосуды вместимостью 15, 16 и 31 литр,
вы сумеете отмерить любое количество воды от 1 до 16
литров. Такая процедура невозможна, если объемы двух
меньших сосудов имеют общий делитель (подумайте сами,
почему). Когда объем большего сосуда меньше суммы
объемов двух других, возникают новые ограничения. Если,
например, объемы сосудов равны 7, 9 и 12 литрам, то у ром-
ромбического стола надо отсечь нижний правый угол (рис.
В.6). Тогда шар сможет попасть в любую точку от 1 до 9,
за исключением точки 6. Несмотря на то, что 7 и 9 взаимно
просты, отмерить 6 литров воды оказывается невозможным
из-за того, что самый большой сосуд имеет слишком ма-
маленький объем.
*) Тарталья по-итальянски означает «заика». Он родился в
1500 г. в итальянском городе Брекчия. В 1512 г. во время взятия го-
города французами Тарталья был ранен в нижнюю часть лица, что
отразилось на его речи; товарищи прозвали его заикой.
12
,0723
Исследование различных возможностей, возникающих
при использовании сосудов разных объемов, с помощью
метода «бильярдного шара» чрезвычайно увлекательно.
Однако заниматься этими вопросами мы в этой книге не
будем, оставив их на рассмотрение читателя. Отметим
только, что обобщение указанного метода на случай четы-
четырех сосудов сводится к дви-
движению бильярдного шара в
объемной (тетраэдрической)
области.
Предлагаем читателю еще
одну задачу на переливания.
Задача. Имеется 10-лит- Су-
Суровое ведро, доверху заполнен-
заполненное водой, и два пустых бидона
объемом 3 и 5 литров. Требуется
часть воды (целое число литров)
вылить, а оставшуюся воду раз-
разделить иа три равные части.
Рассмотрим другой тип
элементарных геометрических
задач, относящихся к бильяр-
бильярдам. В них либо требуется
найти замкнутую траекторию бильярдного шара в данном
многоугольнике, либо найти путь бильярдного шара, по-
попадающего через заданное число ударов из одной фиксиро-
фиксированной точки внутри многоугольника в другую.
Для решения таких задач существует очень удобный и
кажный метод «зеркального отражения», или «выпрям-
л >ния» бильярдной траектории, принадлежащий немецкому
математику Г. А. Шварцу *) (о применении этого метода
см. части II и IV). Метод этот является основным техни-
техническим приемом при решении бильярдных задач в много-
многоугольных областях Q и послужит нам в дальнейшем клю-
ключом при нахождении и исследовании разнообразных биль-
бильярдных траекторий. Опишем его.
Сложное, вообще говоря, поведение бильярдной тра-
траектории в многоугольной области Q можно существенно
упростить, представив его иначе. А именно, сядем на
бильярдный шар О, как барон Карл Фридрих Иероним фон
Мюнхгаузен на пушечное ядро, и вооружимся системой
\ \ \ \ \ \ \ \ V
\\ \ \ \ \ \ "
\\ \ \ \
Рис. В.6
*) Герман А пандус Шварц A843—1921) — известный немецкий
математик, специалист по математическому анализу и теории функ-
функций; имеет также крупные заслуги в областях, связанных с так ва-
вываемой «изопериметрической проблемой».
13
-ВЧ.Б'Г'
Яг
б'
координат, направив ось Оу по направлению движения,
а ось Ох — вправо перпендикулярно оси Оу. В этой сис-
системе координат наша бильярдная траектория изобразится
осью Оу (т. е. прямой линией), а область Q будет представ-
представляться нам как последовательность копий Qu Qs, Qs, . . .
этой области, «нанизанных» на ось Оу таким образом, что
соседние копии Qt и Qi+1 зеркально симметричны относи-
относительно их общей стороны. В этом построении, связанном
с переходом к новой системе координат, и заключается
метод выпрямления бильярдной траектории.
Совокупность копий {Qt}, как бы нанизанных на «ко-
«копье» Оу, образует «коридор» QQiQsQ3 . . . Возвращению из
системы координат Мюнхгаузе-
Мюнхгаузена в исходную, прикрепленную
к фигуре Q, соответствует на-
наложению «гармошкой» коридо-
коридора QQiQzQs. . (который полез-
полезно считать прозрачным) на ис-
исходную фигуру Q; при этом ось
Оу переходит в рассматривае-
рассматриваемую бильярдную траекторию.
Продемонстрируем метод
выпрямления на следующих
примерах.
А. Пусть на прямоугольном бильярдном столе нахо-
находится один шар; под каким углом его следует направить
из точки А, чтобы он после заданного числа отражений от
бортов попал в точку В (например, в лузу)?
Для решения отразим прямоугольник (исходный би-
бильярд) симметрично относительно всех его сторон; все
полученные таким образом прямоугольники вновь отразим
относительно всех их сторон, и так далее до бесконечности
(на рис. В.7 показаны также образы точки В при этих сим-
метриях). В результате всех сделанных отражений траек-
траектория шарика «распрямляется» (например, на рис. В.7
траектория AdC2CsB последовательно переходит в
A&DDB' AC^E" '
Рис. В.7
, &ii).
Если полученная «выпрямленная траектория» прохо-
проходит через образ точки В в одном из прямоугольников, то,
очевидно, траектория шара в исходном прямоугольнике
пройдет через В. Поэтому, для того чтобы пустить шар из
точки А так, чтобы он после заданного числа отражений
о стенки прямоугольного бильярда попал в точку В, нужно
провести такой отрезок с началом в точке А и концом в од-
одном из образов точки В, чтобы он пересек это же самое
14
в
Iff
/\Варенье/
Рис. В.8
число раз линии сетки «клетчатой плоскости». Проделав
обратную процедуру «свертывания» проведенного отрезка,
превратим его в искомую траекторию в исходном бильярде
(рис. В.7). Общая «теория прямоугольного бильярда» из-
изложена в части II книги.
Б. Рассмотрим бильярд в равностороннем треугольнике.
Поскольку одинаковыми равносторонними треугольниками
можно без щелей и перекрытий замостить всю плоскость,
и здесь применима проце-
процедура «выпрямления биль-
бильярдной траектории».
Оказывается, траекто-
траектория бильярдного шара ре-
решает следующую известную
задачу: найти кратчайший
путь, по которому должна
ползти пчела из точки А
f точку В внутри равно-
равностороннего треугольника,
чтобы сначала насладиться
медом на одной стороне
треугольника, потом сахаром — на другой стороне, и,
наконец, вареньем — на третьей. (Предполагается, что
каждая сторона полностью вымазана соответствующим
сладким веществом.)
Ответ приведен на рис. В.8. Нетрудно видеть, что любой
другой путь, ведущий требуемым образом от Л к В, после
зеркальных отражений превращается в путь из точки А
в точку В"', длина которого больше длины отрезка А В"',
и поэтому не является кратчайшим.
В. Сразу же возникают два интересных вопроса, свя-
связанные с обобщением плоского бильярда на случай прост-
пространства: существуют ли замкнутые бильярдные траекто-
траектории внутри куба, являющегося пространственным аналогом
квадрата, и тетраэдра — пространственного аналога рав-
равностороннего треугольника?
Как и раньше, бильярдный шар считается идеальной
упругой невесомой частицей, отражающейся от стенок по
закону «угол падения равен углу отражения». Вместо шара
можно рассматривать луч света, отражающийся от зер-
зеркальных стенок внутренней поверхности многогранника и
не попадающий ни на ребра, ни в его вершины (в противном
случае ответом на поставленный вопрос следовало бы счи-
считать любую из диагоналей, по которой из конца в конец
двигался бы шар).
15
В одной из многочисленных статей о Льюисе Кэрролле *)
есть упоминание о бильярде внутри куба. Это одна из тех
задач, которые не могли не привлечь внимания изобрета-
изобретателя круглого бильярдного стола. Идея об игре в бильярд
внутри кубического «стола» далеко не столь надуманна,
как это может показаться на первый взгляд. Дело в том,
что реальные молекулы воздуха в кубической комнате
как раз и представляют собой «бильярдные шары», сталки-
сталкивающиеся друг с другом и со стенками комнаты по закону уп-
упругого удара. Правда, они находятся в поле тяжести и ис-
испытывают сопротивление воздуха. Если отбросить эти огра-
ограничения, то получим настоящий бильярд с огромным чис-
числом (порядка 102S) шаров. Этому бильярду мы посвятим
в нашей книге достаточно много места — практически всю
часть III; с ним, кроме метода выпрямления бильярдной
траектории, связано много разнообразных физических,
геометрических и алгебраических идей, часть которых бу-
будет освещена ниже.
Но вернемся к движению одного шара в кубе и приме-
применим к кубу тот же метод «выпрямления траектории», что
Рис. В.9
и для квадрата. Произведя 5 отражений от граней куба,
мы получим искомую замкнутую траекторию, изображен-
изображенную на рис. В.9 жирной штриховой линией со стрелкой и
представляющую собой одну из четырех возможных тра-
*) Льюис Кэрролл (псевдоним Чарлза Доджсона) A832—1898),
автор знаменитых книг про Алису, математик по профессии, пре-
преподаватель Оксфордского университета (Англия), увлекался и би-
бильярдом. Он придумал круглый бильярдный стол и сочинил пра-
правила игры на этом столе A890). О некоторых изобретениях Кэр-
Кэрролла рассказывает Мартин Гарднер в своих популярных киигах
«Математические досуги», «Математические головоломки и развле-
развлечения», «Математические новеллы» и др.
16
екторий, каждая из которых является решением задачи.
Если «свернуть» кубы, проделав обратные отражения, по-
получим замкнутую бильярдную траекторию из б звеньев
равной длины в исходном кубе. Представив себе куб разме-
размером 1X 1X 1, состоящим из 27 маленьких кубиков с ребром
Vs каждый, несложно понять, что каждое звено этой траек-
траектории является диагональю такого кубика (рис. В.Ю),
так что его длина равна Кз/3_== l/КЗ, а длина всей траекто-
траектории составляет 6/КЗ = 2 1^3.
Эта траектория известна химикам-органикам как «шес-
«шестиугольник в форме кресла». Она часто встречается в угле-
углеродных соединениях, например в циклогексане, где шесть
углеродных атомов соединены одновалентными связями
в кольцо, а атомы водорода располагаются вне этого кольца.
Интересно отметить также, что если эту бильярдную траек-
траекторию спроектировать на любую грань куба, то в проекции
получится прямоугольник размером VSX2/S, а если ее
спроектировать на три плоскости, параллельные трем диа-
диагоналям, то получаются ромбы; еще в одной проекции (ка-
(какой?) получается правильный шестиугольник.
Обращаясь теперь ко второму вопросу — о замкнутой
бильярдной траектории в тетраэдре,— поступим точно
Рис. В. 11
так же, как и в случае куба: отразив тетраэдр симметрично
относительно трех его граней (рис. В.11), мы получим замк-
замкнутую траекторию из четырех звеньев, которая по одному
разу касается каждой грани. Существенно сложнее ре-
решается задача о замкнутой бильярдной траектории, кото-
которая имеет все звенья равной длины. Одна такая траектория
изображена на рис. В. 11 штриховой линией, а всего их
существует три, причем совершенно одинаковой формы.
17
Каждая из них имеет точки излома на гранях тетраэдра
в одной из вершин маленького равностороннего треуголь-
треугольника, расположенного в центре грани. Стороны этого ма-
маленького треугольника равны' 1/10 ребра исходного тет-
тетраэдра, а каждое звено траектории имеет длину l/KlO»
«г 0,3162777..., так что весь путь бильярдного шара внутри
тетраэдра составляет в этом случае 4-l/Kl0« 1,2649... .
Метод зеркальных отражений, который мы продемонст-
продемонстрировали на примерах А — В, дает возможность не
только строить разнообразные периодические бильярдные
траектории в «хороших» многоугольниках (или многогран-
многогранниках), но и отыскать критерий периодичности траекторий
в таких областях, как прямоугольник или правильный
треугольник. Скажем, для бильярда в квадрате неособая
траектория, направленная под углом а к стороне квадрата,
окажется периодической в том и только в том случае, когда
число ft=tga является рациональным, т.е. представимо
в виде обыкновенной дроби т/п (т — целое, п — нату-
натуральное). А как же будут себя вести траектории, для ко-
которых число ft=tga иррационально"? Например, если
Примитивный ответ: эти траектории будут непериоди-
непериодическими,— говорит нам только о том, что движение будет
каким-то «неправильным». Но «насколько неправильным»?
Это очень интересный вопрос, но лишь в том случае, если
на него дается содержательный ответ! А таких ответов мо-
может быть и несколько.
Во-первых, непериодическое движение может оказаться
«почти периодическим», или квазипериодическим, как при-
принято говорить в классической механике. Грубо говоря,
квазипериодичность движения означает, что хотя его тра-
траектория и не замкнута, но через некоторое время (через
квазипериод) она идет близко к предыдущему отрезку
траектории. Характерные квазипериодические траектории
бильярдов в квадрате и круге показаны на рис. В. 12.
Вопрос: обязана ли непериодическая траектория
быть квазипериодическоШ Оказывается, для бильярда в
круге, в прямоугольнике, в правильном треугольнике и во
многих других многоугольниках действительно обязана.
А вот в эллипсе существуют траектории, которые неперио-
непериодичны и не квазипериодичны, но их, по сути, немного!
(См. ниже § 4.) И опять-таки, в общем случае (для областей
произвольного вида и даже для многоугольников) ответ
на поставленный вопрос неизвестен.
18
Далее, если внимательно рассмотреть квазипериодиче-
квазипериодические траектории на рис. В. 12, становится понятным, что они
«стараются» все более плотно заполнить целую область:
их близкие отрезки все сдвигаются и сдвигаются, так что
траектория на рис. В. 12, а заполняет «территорию» квад-
квадрата, а на рис. В. 12, б—круговое кольцо. На сериях
рис. В. 13, а, б (полученных с помощью компьютера) пока-
показан процесс постепенного распределения траекторий по
своим областям.
Рис. В.12
Возникает следующий вопрос: не будут ли эти траекто-
траектории всюду плотными — в квадрате, в кольце? Иначе го-
говоря, оставит ли такая траектория хотя бы какое-нибудь
«пустое местечко» в области — например, кружок (хотя бы
очень маленький), который она никогда не пересечет?
Оказывается, в данных случаях не оставит! Указан-
Указанные непериодические траектории всюду плотно заполнят
соответствующую область: какой бы (сколь угодно малый)
кружок мы ни взяли (в квадрате или в кольце), рано или
поздно траектория пересечет этот кружок. Если считать,
что бильярдный шар «чернильный» и оставляет после себя
след, то он со временем обязательно закрасит всю область
(квадрат или кольцо) целиком, каким бы тонким не был чер-
чернильный след (но имеющим все-таки ненулевую толщину).
Ясно, что периодическая траектория свойством всюду
плотности обладать не может — она может заполнить об-
область «очень плотно», но не всюду плотно. Обязана ли про-
произвольная непериодическая ^траектория в области Q быть
всюду плотной во всей этой области? Это будет верно (что
мы дальше докажем с помощью вполне элементарных рас-
рассуждений) для бильярда в прямоугольнике, в правильном
треугольнике и некоторых других областях. Это не так для
бильярда в круге и эллипсе и даже в некоторых многоуголь-
19
никак, что тоже будет нами показано (см. § 26). Наконец,
для многоугольников (и просто для треугольников) общего
вида вопрос остается открытым. Неизвестен пока ответ
даже на более простой (казалось бы!) вопрос: в любом ли
Рис. В. 13
многоугольнике Q существует всюду плотная (в Q) траек-
траектория?
(Устройство всюду плотных множеств даже на числовой
прямой К может быть довольно сложным. Простейшие
примеры таких множеств — множество всех рациональных
20
чисел Q, или всех конечных десятичных дробей Q1Of или
множество всех иррациональных чисел Q. Их всюду плот-
плотность почти очевидна: если взять на числовой прямой лю-
любой интервал Л сколь угодно малой длины е>0, то на нем
найдутся числа всех трех указанных типов. Действительно,
если взять число d положительное, но меньшее е/2, то хотя
бы одна из точек ±d, ±2d, ±3d, . . . попадет в интервал А.
Осталось выбрать число d в виде соответствующей дроби:
UN, либо 10"^, либо V2/N, где N— натуральное.)
Дальнейшим усилением свойства всюду плотности
бильярдных траекторий является свойство их равномерной
распределенности в соответствующей области и более об-
общее свойство эргодичности, играющее важную роль в ма-
математике, механике, в статистической физике. Объясним,
в чем заключается общее свойство эргодичности бильярда
в области Q.
Если бильярдная траектория всюду плотна в области Q,
т. е. бильярдный шар рано или поздно обязательно попа-
попадает в любую заданную фигуру Ф, лежащую в Q, то можно
заняться вопросом: какую долю времени шар проводит
в фигуре Ф? Имеется в виду, что сначала мы вычисляем
долю времени за фиксированный промежуток Т (т. е. вы-
вычисляем отношение k(T)=t/T, где t — время, в течение
которого за промежуток Т шарик побывал в области Ф),
а затем устремляем Т к бесконечности и берем предел
fc= iim %(T).
Если окажется, что указанная доля времени, которую
проводит шарик в фигуре Ф, пропорциональна площади
фигуры. Ф (или, что то же самое, пропорциональна отноше-
отношению площади фигуры Ф к площади области Q), и это верно
для «типичной» траектории, то говорят, что данная бильярд-
бильярдная система эргодична *). Отношение tIT (вернее, его
предел при Т-*- со) называется «временным средним»,
а отношение площади фигуры Ф к площади области Q —
«пространственным средним». Поэтому эргодичность сис-
системы формулируется еще и как возможность заменять вре-
*) Строго говоря, эргодичность означает, что почти каждая
фазовая кривая проводит в измеримой области фазового пространства
(см. § 3) время, пропорциональное объему этой области. Свойство,
о котором говорится в тексте, можно называть «слабой зргодично-
стью». Термин «типичная траектория» здесь не обсуждается, его
следует понимать в интуитивном смысле. (Для сравнения: «типич-
«типичные» числа на отрезке [0, 1] иррациональные, а рациональные
числа —«исключительные».)
21
менные средние пространственными средними. Траектория
в эргодической системе заполняет область всюду плотно и
равномерно, т. е. «размазана» по области с равной «плот-
«плотностью». Свойство эргодичности сильнее свойства всюду
плотности, поскольку подразумевает его выполнение;
таким образом, из эргодичности системы следует всюду
плотность типичной траектории, но не наоборот, хотя очень
часто оказывается, что если какая-то траектория всюду
плотна, то и вся система эргодична.
Изучению эргодических свойств динамических систем
посвящен целый раздел современной математики — так
называемая эргодическая теория, изучающая «хаотические»
свойства динамических систем, в которую теория бильярдов
входит в качестве подраздела. Предмет настоящей книги
также относится к этой теории.
Структура книги. Изложение материала в кни-
книге ведется последовательными переходами от простых би-
бильярдных систем к более сложным. Трудные места в книге
(иногда это касается целых параграфов и глав) отмечены
одной или двумя (это зависит от сложности) звездочками;
при желании их можно пропустить.
В части I книги изучаются выпуклые бильярды,
границы которых не содержат прямолинейных участков:
круглый, эллиптический и произвольный бильярд с криво-
криволинейной границей. Наряду с их исследованием демонст-
демонстрируются общие математические методы, позволяющие при-
применять бильярд в этих областях к решению некоторых тео-
теоретико-числовых, геометрических и физических задач.
В части II проведено полное исследование бильярда
в прямоугольнике, сводящееся к исследованию траекторий
равномерно движущейся по тору (поверхности бублика)
точки, и показана связь между бильярдными траекториями
в прямоугольнике и фигурами Лиссажу на осциллографе
Исследованию «газа шаров» — упруго сталкивающихся
твердых шаров в пространстве и сосуде — посвящена
часть III. Интересными здесь являются геометрические
методы решения задач о росте числа столкновений молекул,
расположенных на прямой, плоскости, в пространстве и
в ограниченных областях («сосудах»), сводящие рассмотре-
рассмотрение системы шаров к бильярдам специального вида.
Следующая часть книги — часть IV — рассказывает
о бильярдах в многоугольниках с произвольным числом
сторон. Оказывается, что, как и в случае прямоугольника,
бильярды в многоугольниках специального вида (в «ра-
«рациональных» многоугольниках, все углы которых соизме-
22
римы с я) сводятся к изучению непрерывных траекторий
на замкну-шх ограниченных поверхностях — так называе-
называемых «кренделях» или «сферах с ручками» (см. рисунок на
третьей странице обложки). Отдельно изучаются некото-
некоторые классы периодических траекторий в тупоугольных
треугольниках.
Наконец, в заключении читатель сможет «с высоты
птичьего полета» обозрегь целые классы бильярдов, кото
рые в зависимости от области, в которой движется бильярд-
бильярдный шар, носят названия рассеивающих (бильярдов Синая),
фокусирующих и осциллирующих. В каждом классе бильяр-
бильярдов наблюдается свой тип поведения траекторий, но все
эти бильярды являются моделями реальных физических
систем, в которых движение неотличимо от случайного,
т. е. является хотя и однозначно определенным (детерми-
(детерминированным), но крайне нерегулярным и непредсказуемым.
Модели, демонстрирующие подобное поведение, обнаружены
практически во всех разделах физики и число их непре-
непрерывно растет. Изложение этого материала книги ведется
на обзорном уровне.
ЧАСТЬ I
БИЛЬЯРДЫ В ВЫПУКЛЫХ ОБЛАСТЯХ
С КРИВОЛИНЕЙНОЙ ГРАНИЦЕЙ
Глава 1
БИЛЬЯРД В КРУГЕ
Простейшая ограниченная выпуклая область
с криволинейной границей на плоскости — круг. С иссле-
исследования траекторий шара в круглом бильярде мы и начнем
наш рассказ о бильярдах в выпуклых областях с криволи-
криволинейной границей.
Во введении ставилась общая проблема бильярда в
произвольной области Q. Естественно ожидать, что для
простейшей области Q — круга — точных ответов на по-
поставленные во введении вопросы должно быть больше, чем
для более сложных областей, а сами ответы должны быть
более простыми и окончательными, чем в других случаях.
Иными словами, естественно ожидать, что проблема биль-
бильярда в круге поддается полному исследованию. Так оно и
оказывается. Более того, приводимые в этой главе рассуж-
рассуждения и теоремы являются фундаментом для всех последую-
последующих рассуждений и результатов.
§ 1. Шар в круглом бильярде без луз
Рассмотрим шар в круге Q, ограниченном
окружностью Г. Его траекториями являются вписанные
в Г ломаные PnPiPzPsPt ¦ . ., обладающие свойством ра-
равенства в точках Pi, Pit Ря, . . . углов падения и отраже-
отражения, отсчитываемых от касательных или от радиусов ОРи
0Pit . . . (рис. 1.1, а). Отметим, что из этого свойства сле-
следует, во-первых, что все звенья траектории равны между
собой:
Рр р р р р р р
0*1 — * 1* 8 — '2*3 — * 8* 4 — • • ч
и во-вторых, что равны опирающиеся на них центральные
углы:
24
плотности бильярдной траектории. Поэтому
бильярдная траектория в круге не всюду плотна в нем.
Tl.i не менее мы можем выяснить не только указанные
факты отрицательного, так сказать, свойства, но и пол-
полностью решить проблему бильярда в круге: дать критерий,
позволяющий выделять периодические траектории и изу
чить характер поведения непериодических траекторий.
Для этого обозначим через а радианную меру углов
/_Р<РРи /_Р\ОРг, . . .. Ясно, что каждая вершина Ph
траектории P0PiPsP3 . . . получается из предыдущей вер-
вершины Pk~i поворотом на угол а относительно центра О
окружности Г, откуда следует, что вершина Рп получается
из начальной вершины Рв поворотом на угол па. Докажем,
что вид бильярдной траектории в круге полностью опреде-
определяется числом а. А именно:
(а) если число а соизмеримо с п, т. е. дробь а/я является
рациональным числом (равным некоторой дроби т/п с це-
целыми т и п), то бильярдная траектория периодична;
(б) если аил несоизмеримы, т. е. число а/л иррациональ-
иррационально, то отвечающая углу а траектория непериодична.
Доказательство, (а) Если а соизмеримо с л,
то его можно представить в виде ос = -^--2я, где т и п —
целые числа. Тогда па=2пт, и поэтому при повороте на
угол па каждая точка окружности Г переходит в себя.
В частности, все вершины рассматриваемой бильярдной
траектории P0PiP2P8... обладают тем свойством, что
т. е. вершины, начиная с и-й, повторяются. Это и означает,
что бильярдная траектория периодична, и утверждение
пункта (а) доказано.
Сколько же звеньев будет содержать рассматриваемая
траектория PBPiP 2. . .? Если — =s—— несократи-
несократимая дробь, то отвечающая а периодическая траектория —
это траектория P0Pi. . .Pn-iP0, где п — знаменатель ука-
указанной дроби, и состоит она ровно из п звеньев. При т= 1
это будет правильный и-угольник, вписанный в окруж-
окружность Г (рис. 1.2, а), а при т^2 бильярдная траектория
представляет собой правильную самопересекающуюся замк-
замкнутую (звездчатую) ломаную, вписанную в Г (рис. 1.2, б).
Иными словами, бильярдный шар после п отражений от
борта Г оказывается в исходной точке Рй, сделав т оборо-
26
тов вокруг центра О (т. е. повернувшись вокруг центра
на угол 2пт).
(б) Предположим, что бильярдная траектория и в этом
случае периодична. Докажем тогда, что аил соизмеримы,
что противоречит условию пункта (б) и тем самым доказыва-
доказывает его утверждение.
Из периодичности траектории вытекает, что, начиная с
некоторого номера п, еершины траектории повторяются:
РП=Я„, Рп+1=Ри Pn+i~Pi, и т. д. Но это означает, что
при повороте на па радиан точка Ро переходит сама в себя;
а _ 3
2П 7
следовательно, па есть целое кратное полного угла: па—
—2пт. Отсюда — = рациональное число.
Искомое противоречи получено.
Про периодические траектории в круге мы уже выясни-
выяснили все досконально в пункте (а) приведенного доказатель-
доказательства. Доказательство же пункта (б) велось от противного и
поэтому качественное поведение непериодических траекто-
траекторий нам пока неизвестно. Однако интуитивно ясно, что не-
непериодическая бильярдная траектория должна вести себя,
в отличие от периодической, неким «нерегулярным» спо-
способом.
Эту «нерегулярность» можно себе представить, например,
так. Будем считать, что бильярдный шар при движении ос-
оставляет «чернильный след» ненулевой «толщины». Если шар
описывает периодическую траекторию, то, хотя она может
быть очень «звездчатой» (см. п. (а)), и заполнять кольцо К
между внешней и внутренней окружностями Г и у «очень
плотно», но все-таки не «всюду плотно» — на кольце обяза-
обязательно останутся такие участки (например, маленькие
27
Рис. 1.3
кружки), которые периодическая траектория никогда не
пересечет (рис. 1.3).
Задача. Укажите неточность на рис. 1.3.
Указание. Траектория бильярдного шара не может пе-
пересекать маленький кружок так, как на рис. 1.3,— показанное
стрелкой звено не касается внутренней окружности кольца.
Иное дело, когда шарик описывает непериоди-
непериодическую траекторию. В этом случае он рано или поздно
побывает в любом кусочке кольца К. Другими слова-
словами, каким бы тонким ни был чернильный
след, оставляемый бильярдным шаром (но
имеющим все-таки ненулевую толщину), он
i со временем обязательно закрасит все коль-
| цо К целиком (рис. 1.4). Это и означает
нерегулярность, а на математическом язы-
языке — «всюду плотность» бильярдной тра-
траектории в кольце К. (Вспомним, что в нача-
начале параграфа мы выяснили, что никакая
бильярдная траектория в круге Q не всюду
плотна в нем, т. е. чернильный след шара не может закра-
закрасить всего круга; однако для кольца К такая возможность
логически ничему не противоречит.)
Оказывается, непериодическая траектория в круге Q
действительно всюду плотна в кольце К с границей Гит'
Это утверждение мы еще раз сформули-
сформулируем уже в виде математической теоремы
в § 2 и там же полностью докажем.
А пока отметим, что утверждение о всю-
всюду плотности бильярдной траектории в
кольце будет вытекать из того факта, что
точки отражения шара от борта Яо, Pi,
Я2, . . . расположены на окружности Г
всюду плотно, т. е. внутри лю-
любой дуги А окружности Г имеется хотя
бы одна точка Pk. Это последнее утверж-
утверждение носит название «теоремы Якоби» *).
Оно также будет доказано в § 2. Отметим
здесь только, что теорема Я коби явля-
является основным инструментом при дока-
доказательстве почти всех дальнейших тео-
теорем, связанных с «всюду плотностью»
бильярдных траекторий.
*) К. Г. Я. Я коби A804—1851) — крупнейший немецкий ма-
математик, известный своими исследованиями в теории чисел, в меха-
механике и в других областях науки.
28
Рис. 1.4
После всего сказанного бильярд в круге можно считать
полностью исследованным. Резюмируем полученные резуль-
результаты в виде теоремы.
Теорема 1. Траектория бильярда в круге является
либо периодической, если число а/я рационально, либо всюду
плотной в кольце К между бортом Г и концентрической с Г
окружностью у, если число а/п иррационально.
Задача 1.1. Бильярдный шар находится на круглом столе
радиуса R=l на расстоянии / от его центра. Установите характер
бильярдной траектории (периодическая она или иет, какую об-
область всюду плотно заметает), если шарик выпущен под углом <р
к диаметру, на котором он находится (рис. 1.5).
Ответ. Периодична, если число —arccos(fsin ф) рацио-
рационально, и всюду плотно заполняет кольцо с внутренним радиусом
I sin ф в противном случае.
Задача 1.2. Исследуйте бильярд а) в полукруге (рис. 1.6);
б) в четвертькруге (рис. 1.7). Указание. Попробуйте свести
эти бильярды к" бильярду в круге.
Рис. 1.5
Рис. 1.7
Задача 1.3. Исследуйте бильярд а) в круговом концен-
концентрическом кольце; б) в круговом секторе угловой величины а;
в) * в криволинейном четырехугольнике, который высекается из
кольца сектором угловой величины а.
Задача 1.4. а) Докажите, что никакая непериодическая
бильярдная траектория в круге не содержит двух параллельных
звеньев.
б) Может ли у периодической бильярдной траектории в круге,
какие-то два звена которой параллельны друг другу, быть 1717
звеньев? 1718 звеньев? А если она самопересекающаяся? Если
может, укажите способ построения всех периодических траекторий
г таким числом звеньев и найдите максимальную длину траекторнн
из этого класса (принимая радиус круга за 1).
в) Обобщите вопрос пункта б) на произвольное число звеньев
п (см. также задачу 6.6 из § 6).
Р е ш е н и е. а) Если какие-то два звена А В и CD траектории
параллельны, то они центрально-симметричны относительно центра
круга О. Поэтому и вся траектория центрально-симметрична от-
относительно О (рис. 1.8). Значит, если шар перешел со звеиа АВ
на звено CD после и отражений, то еще через п отражений он вер-
вернется на звено А В, и вся траектория замкнется — траектория
окажется периодической.
Поэтому, если заранее выбрать радиус г внутренней окруж-
окружности у кольца К (радиус внешней равен 1) и провести к у две
29
параллельные касательные^ то они заведомо не будут звень-
звеньями одной траектории, если только число arccos r несоизмеримо с л.,
б), в). Если бильярдная траектория периодическая н содер
жит два параллельных звена, то все звенья разбиваются на пары
параллельных (рис. 1.8), так что число звеньев п в этом случае
обязательно четно. Итак, 1717 звеньев бьпь не может. 1718
звеньев у траектории быть может — например, у правильного
вписанного 1718-угольника Р. Остальные бильярдные траектории
с изломами в вершинах многоугольника Р получатся, если соедя
нять эти вершины через одну, через две, через три и т. д. Однако
1718=2-859 (859 — простое число), поэтому, соединяя вершины
через одну, получим два 859-угольника без общих вершин. Ана
логична ситуация, когда соединяются вершины через 3 (на чет
вертую), через 5 (на 6-ю) и т. д.— получается несколько замкнутых
Рис. 1.8
Рис. 1.9
Рис. 1.10
ломаных. Если же соединять вершины через k—1 на k-ю, где k
взаимно просто с 1718 (т. е. вершину 1 соединить с (й+1)-й, 2-ю —
с (й+2)-й и т. д.), то полученные замкнутые бильярдные ломаные
будут содержать ровно 1718 звеньев, причем все звенья будут раз-
разбиты на 859 пар попарно параллельных (см. рис. 1.9, иа котором
изображена траектория из 14=2-7 звеньев). Наибольшей длины
звенья будут у траектории, соединяющей вершины 1 и 858, 2 и 859,
3 и 860 и т.д. Из треугольника Д1М0 на рис. 1.10 следует, что
длина звена A; 858) равна
/=2 sin (а/2) = 2 sin (857п/3436).
Поскольку угол, стоящий под знаком синуса, равек примерно
п/4, имеем /^t 2 sin (п/4)= ^2, поэтому максимальная длина биль-
бильярдной траектории из 1718 звеньев равна
/,= 1718/ = 3436sin (857П/3436) и 3446/Ти 4851,632.
Шар при ее обходе сделает 857 оборотов.
Задача 1.5. В круглом бильярде в некотором месте сде-
сделана луза — кружок радиуса е, не содержащий центра круга
Доказать, что точечный бильярдный шар можно расположить
в такой точке круга и запустить в таком направлении с единичной
скоростью, что он а) не попадет в лузу никогда; б) попадет в лузу,
пройдя до попадания путь длины, большей заданной величины L
Останется ли верным это утверждение, если шарик расположен
в заранее заданной точке круга? А если точку его расположения
можно выбирать, а направление вектора скорости фиксированно?
30
Задача 1.6. В круглом бильярде в заданных п точках
расположены точечные бильярдные шары. Доказать, что их можно
эапустить в таких направлениях, что а) никакие два нз них никогда
не столкнутся, б) любые деэ из них столкнутся (сталкивающиеся
шарики проходят друг сквозь друга без отклонений).
Задача 1.7. Доказать, что два заданных шара радиуса
0,0001 можно запустить в круглом бильярде радиуса 1 е таких
направлениях, что онн обязательно столкнутся друг с другом,
но не раньше, чем каждый из них пройдет путь заданной длины L.
Задача 1.8. Можно ли запустить два шара радиуса 10~"
в круглом бильярде радиуса 1 так, чтобы они никогда не столкну-
столкнулись?
Задача 1.9. Предположим, что бильярдная траектория
в круге всюду плотно заполняет кольцо К. Верно лн, что любой
фиксированный кружок внутри кольца пересекают бесконечно
много звеньев этой бильярдной траектории? А Еерно ли, что через
какую-то точку этого кружка не проходит нн одно звено траек-
траектории?
Задача 1.10*. Верно ли, что доля времени, проводимая
бильярдным шаром в кружке нз задачи 1.9, равна (в пределе)
отношению площади этого кружка к площади кольца j<?
§ 2. Теорема Якоби.
Применение к теории чисел
В этом параграфе мы докажем теорему, сфор-
сформулированную в конце § 1. Сформулируем ее здесь еще раз
(мы приводим более трудную часть теоремы).
Теорема 1. Если а и п несоизмеримы (т. е. число
а/я иррационально), то любая траектория бильярда в кру-
круге, отвечающая углу а (т. е. каждое звено которой видно из
центра круга под углом а; рис. 1.1, б), всюду плотно запол-
заполняет кольцо К.
Доказательство теоремы 1 опирается на следующую ос-
основную теорему этого параграфа, в дальнейшем применяе-
применяемую в качестве основного рабочего инструмента при доказа-
доказательстве утверждений, иногда имеющих мало общего с
бильярдными задачами, например утверждений из теории
чисел (об этом см. ниже).
Теорема Якоби. Пусть а — несоизмеримое с к
число, {Ро, Pi, P2, .. .}—{Ph} —бесконечная последова-
последовательность точек окружности Г татя, что каждая следу-
югцая точка последовательности Pk+t получается из преды-
предыдущей точки Ph поворотом около центра на а радиан.
Тогда для любой дуги А окружности Г хотя бы одна точка
последовательности {Ph} лежит на этой дуге.
Задача. Докажите, что иа дуге Д находится бесконечно
много точек последовательности {Р/,}.
31
Решение. Если бы на дуге Д располагалось только к о-
нечное чнсло точек (например, как крайний случай, только
одна точка), то нашлась бы некоторая дуга А', лежащая внутри
дуги Д и не содержащая ни одной точки последовательности
{Pit}- Это противоречит теореме Якоби: по этой теореме на дуге Д'
имеется хотя бы одна точка последовательности.
Прежде чем доказывать аеоремы Якоби, выведем из нее
теорему 1.
Доказательство теоремы 1. Пусть а ~
несоизмеримое g л число, у — окружность, которой каса-
касаются все звенья каждой отвечающей углу а бильярдной
траектории внутри окружности Г. Пусть К — кольцо
между у и Г, a D — произвольный кружок внутри кольца
К. Проведем через центр кружка D хорду MN окружности
Г, касающуюся окружности у (рис. 2.1). Если провести
касательные к кружку D, касающиеся окружности у, то
они высекут на окружности Г некоторую дугу Л, в которой
расположена точка М. Очевидно, что для любой другой
точки М' дуги Л касательная, проведенная из нее к окруж-
окружности у по ту же сторону, что и хорда MN, пересечет
кружок D.
Рассмотрим теперь любую бильярдную непериоди-
непериодическую траекторию РпРхРг. . . , отвечающую углу а.
Требуется доказать, что хотя бы одно из ее звеньев пересе-
пересекает кружок D.
Согласно теореме Якоби, точки Ро, Р±, Рг, . . всюду
плотно заполняют окружность Г. Следовательно, хотя бы
одна из них, скажем Рп, лежит на пост-
построенной выше дуге Л. В силу выбора этой
ДУГИ одно из ДВУХ звеньев траектории,
выходящей из точки Рп (а, тем самым, ка-
касательных к окружности у), пересекает
кружок D (в качестве точки М' на
рис. 2.1 следует взять точку Рп). Тем
самым теорема 1 доказана.
Доказательство теоре-
Рис. 2.1 м ы Я к о б и. Двигаясь от точки Ро
последовательными дуговыми шагами
величиной а каждый (рис. 2.2) и попадая в точки Ри Р2,
Р3, ., остановимся в точке Рп, как только впервые
перескочим точку Ро (дуга PnPn-i меньше 2л, а дуга Р0Рп
больше 2л). Обозначим точку Р„ буквой А, а ближайшую
к ней из точек Рп-\ (до перескока) и Рп (после перескока) —
буквой В. Тогда Р — длина дуги АВ — не больше а/2:
Р<а/2.
32
Начав двигаться от точки В прыжками величиной а,
мы через некоторое число шагов попадем в точку, отстоя-
отстоящую от точки В на 6, затем на 2В, потом на 36 и т д
(рис. 2.2).
Можно считать, что у нас сжался масштаб длины и мы
движемся по окружности Г дуговыми шагами уже величи-
величиной 6, по крайней мере вдвое мень-
шими, чем величина шага а при на-
чальном движении от точки А.
После определенного числа шагов
величиной р каждый, мы впервые
перескочим точку В и выберем пос-
после этого ближайшую к ней (из двух
точек — до перескока и после него)
точку С. Пусть длина дуги ВС рав-
равна <р, тогда ф<р/2^а/4. Как и выше, Рис. 2.2
получим, что можно опять изменить
масштаб длины и считать теперь величину прыжка рав-
равной ф.
Повторяя описанный процесс k раз, получим величину
прыжка, не большую чем а/2*. Но при больших k величи-
величина а/2* стремится к нулю, т. е. становится меньшей про-
произвольного числа е> О, так что мы попадем в любую, сколь
угодно малую дугу Д, произвольно выбранную на окруж-
окружности Г. Теорема Якоби доказана.
Для любителей формальных доказательств описанное рассуж-
рассуждение проведем более техническим способом.
Пусть Д—произвольная дуга на окружности Г, е—ее радиан-
ная мера. Выберем такое натуральное число N, что jr- < e. Ра-
Разобьем окружность Г на N равных подлине дуг Д^, Д2, .... Д/v;
радианная мера каждой из них равна 2n/N и меньше е.
Рассмотрим теперь Л/+1 первых точек последовательности
Cft}. т. е. точки Ро, Ри ..., P/v. Согласно принципу Дирихле*),
хотя бы на одной из N дуг Д*, .... Дд лежит по крайней мере две
из этих точек; допустим, точки Рп и Рт лежат иа дуге А/ (счи-
(считаем m=rt+/> n). Пусть длина дуги РпРщ (в радианах) равна б,
тогда 6<|Д,|=^<е.
Рассмотрим далее точки последовательности {P/J о номерами
«, т=п+/, п+2/, п+31, .... т. е. точки Р„, Pn+t, Рп+ы ••¦•
каждая из которых получается из предыдущей поворвтом.на угол
fa—точно так же, как точка Р„+[ получается из точки Р„. Таким
*) Принцип Дирихле состоит в следующем: если в k ящиках
лежит fe-J-1 предмет, то хотя бы в одном ящике больше одного
предмета.
Г. А. Гальперин, А. Н. Земляков
83
образом, соседние точки выделенной последовательности отстоят
друг от друга на дугу радианной меры 6. Так как 6 < е, то хотя
бы одна из точек Р„, Pn+i, Pn+2tt ¦•• обязана попасть на дугу Д.
Тем самым теорема Яксби доказана.
Задача. Где в доказательстве теоремы Якоби использо-
использовалась несоизмеримость чисел аил? (Если аил соизмеримы,
то теорема, очевидно, неЕерна).
Ответ. Из несоизмеримости следует утверждение, что точки
А, В, С, ... различны (в доказательстве петитом — различны
точки Рп и Pn+t).
Кроме теоремы 1, теорема Якоби имеет и много других
интересных следствий.
Одной из важных проблем теории чисел является зада-
задача о распределении дробных долей разных функций, в
частности многочленов. Задача о распределении дробных
долей многочленов связана с оценками числа решений дио-
фантовых уравнений (уравнений с целыми коэффициента-
коэффициентами, для которых ищутся целочисленные решения) в алгеб-
алгебраической теории чисел.
Рассмотрим многочлен у = аол:"+а:1л:п~Ч-. . .-г-а„_1л: +
+ап. При каждом конкретном значении х можно вычислить
число у; при нецелых коэффициентах многочлена оно, как
правило, будет нецелым. Вычтя из него его целую часть,
т. е. наибольшее целое число [у], не превосходящее у,
получим дробную часть числа у, которая обозначается фи-
фигурными скобками: {у} —у — [у]. Ясно, что всегда 0 <{#}<1,
так что при каждом х число {у} принадлежит полуинтер-
полуинтервалу [0, 1).
Как распределены числа {yh} на полуинтервале [0, 1),
когда х пробегает все целые числа k =. . ., —2, —1, 0, 1,
2, . . . ?
Это и есть задача о распределении дробных долей мно-
многочленов. Теорема Якоби позволяет частично решить эту
задачу для линейных многочленов, т. е. многочленов
первой степени.
Утверждение 1. Дробные части чисел yh = ak-\-b,
когда k пробегает все целые значения от —то до +оо, либо
образуют конечное множество точек на полуинтер-
полуинтервале [0, 1), либо всюду плотное множество точек
на этом интервале. Первый случай реализуется при рацио-
рациональном, а второй — при иррациональном числе а (число b
при этом может быть произвольным).
Доказательство. Искривим полуинтервал [0, l)i
на котором расположены дробные части {уъ}, так, чтобы
его концы совпали, и, склеив их, получим окружность еди-
единичной длины S1 (рис. 2.3). Затем сделаем второй шаг: на-
34
мотаем всю числовую ось R на полученную окружность
так, чтобы точка Ъ оси R совпала со склееншши точками
О и 1 окружности (рис. 2.4).
Тогда все точки ak+b отпечатаются на окружности S1;
«выпрямив» эту окружность в исходный полуинтервал
[О, 1), мы получим на нем все дробные час-
части чисел yh=ak+b. ау \
Однако на окружности S1 отпечатки всех тт
точек уп получаются из отпечатка точки 41
уо=Ь поворотом на углы ka радиан, где
й 2 1 0 1 2 П
р у р, /\д
. . ., —2, —1, 0, 1, 2, .... Поэтому, \_/1
если число а рационально, то отпечатков на
S1 будет конечное число; если же а ирраци- Рис# 2-3
опально, то их будет бесконечно много и
располагаться они на окружности будут, по теореме Яко-
би, всюду плотно, а это и требовалось доказать. Утверж-
Утверждение 1 доказано.
Для многочленов больших степеней, чем 1, решение
задачи о распределении дробных долей существенно услож-
усложняется, хотя с наглядно-геометрических позиций все дело
фактически также сводится к применению теоремы Якоби,
+0О
только не для окружности, а для тора (см. § 8). Но об этом
мы поговорим чуть позже — в гл. 3, когда речь пойдет
о бильярде в прямоугольнике. Отметим пока только, на-
насколько тесно взаимосвязаны разные разделы математики:
от геометрических задач — бильярдов в круге — мы пере-
Щли к задаче из совсем другого раздела математики — тео-
теории чисел, а позже перейдем к бильярдам в других обла-
областях, исследование которых поможет при решении совсем
Новых задач из других областей математики. Собственно
говоря, одной из целей нашей книги является попытка на
*• 35
конкретном наглядном геометрическом материале дать
почувствовать читателю многообразие математики и ее
единство.
Вернемся, однако, к вопросу о распределении дробных
долей многочленов. Полный ответ на него был получен в
виде теоремы выдающимся математиком XX века Германом
Вейлем. Прежде чем сформулировать эту теорему, приведем
одно важное определение.
Определение. Произвольная бесконечная пос-
последовательность точек {Рп} на единичной окружности S1
(или на отрезке [0, 1]) называется равномерно распределен-
распределенной на S1 (на [0, 1]), если для любой ее дуги (интервала)
Л «доля» попавших на нее точек равна длине этой дуги (ин-
(интервала) /(Д).
Иными словами, если ограничиться лишь конечным
числом п точек Ро, Pi, . . . , Рп-и то отношение числа k(n)
точек, попавших в дугу Л, к общему числу точек п, т. е.
их доля k(n)/n на окружности длины 1, будет мало отли-
отличаться от длины дуги /(Л). Это отличие будет тем меньше,
чем большее число точек мы рассматриваем, и в пределе при
п-9-оо величины k(n)/n и /(Л) совпадут. Сказанное можно
выразить формулой
lim *JS = /(A). A)
Свойство равномерной распределенное™ — асимптотиче-
асимптотическое.
Можно доказать следующее утверждение.
Теорема о равномерном распреде-
распределении точек на окружности. Последователь-
Последовательность точек Ро, Ри Р2, Р3, Р4, . . . на окружности S1, по-
полученных каждая из предыдущей поворотом на иррацио-
иррациональный (несоизмеримый с 2я) угол а, равномерно распреде-
распределена на S1.
Формально строгого доказательства этой теоремы мы
здесь не будем приводить; опишем лишь правдоподобные
рассуждения, которые при желании можно довести до стро-
строгого доказательства. При доказательстве теоремы Якоби
мы пользовались тем обстоятельством, что сначала произво-
производились прыжки одинаковой величины а, затем (после из-
изменения масштаба длины) — прыжки одной и той же
величины р^а/2, затем все прыжки становились равными
Т^ а/4, и т. д. Итак, при каждой замене масштаба прыжки
имеют одну и ту же величину, которая меньше
величины прыжка рри предыдущей замене масштаба в 2 или
36
большее число раз. Равенство длин этих прыжков и их
экспоненциальное убывание *) при каждой замене масштаба
означает, что число точек, попавших в данный интервал А,
пропорционально его длине — это выполнено тем точнее,
чем больше сделано замен масштабов длины. Но это и
означает равномерность распределения.
Задача. Доказать, что из равномерной распределенное™
последовательности точек {Я*} на окружности S* вытекает всюду
плотность нх расположения на S1.
Решение. Действительно, на любой дуге Д имеетси хотя
бы одна точка Р/,.
Теорема Г. Вейля о дробных долях многочленов форму-
формулируется так.
Теорема Вейля. Если среди коэффициентов а»,
аи а2, . . ., ап-х многочлена у =aoxn+a1xlt-l+. . .4-а„_,* +
+ ап хотя бы один — число иррациональное, то последова-
последовательность {yk},edeyh=ci<>kn+a1kn-l+. . .+ а„_1Л+ап. рав-
равномерно распределена на полуинтервале [О, 1).
Теория равномерного распределения была создана
Г. Вейлем в 1916 году. Она появилась на стыке нескольких
математических дисциплин (действительный и комплекс-
комплексный анализ, теория чисел, теория вероятностей и др.)
и долгое время ее приложения ограничивались различными
вопросами «чистой» математики и механики. Вычислитель-
Вычислительная математика заинтересовалась равномерно распределен-
распределенными последовательностями- в 50-х годах, после возникно-
возникновения методов Монте-Карло, когда оказалось, что точки
таких последовательностей могут в некоторых случаях иг-
играть роль квазислучайных чисел.
Классическое направление теории равномерного распре-
распределения связано с изучением дробных долей различных
функций (например, многочленов; см. выше), оценками
тригонометрических сумм и следующим известным крите-
критерием Вейля, связанным с эргодичностью.
Критерий Вейля. Для того чтобы последовательность
*о. *i, хг хп, . . . была равномерно распределена на отрезке
[0, 1], необходимо и достаточно, чтобы для любой интегрируемой
(по Риману) функции f(x) выполнялось соотношение: «среднее
временнбе равно среднему пространственному», т. е.
71- 1 1
lim 1
п - « п
а) = С /(*) dx. B)
*) Члены геометрической прогрессии а^=ск,Яь со знаменателем
Ч, по модулю меньшим 1, образуют экспоненциально стремящуюся
к 0 последовательность.
37
На первый езгляд требования A) и B) кажутся различными.
Чтобы показать сеяэь между ними, Еыберем произвольный интер-
интервал Д= (о, Ь) на отрезке [0, 1] и рассмотрим функцию /д(х), назы-
называемую обычно характеристической функцией, или индикатором
интервала Д: она тождественно равна 1 на интервале Д и тождест-
тождественно равна 0 вне его (рис. 2.5). Тогда
п-1
2
k=0
¦ • ¦ + fА
есть число точек, попавших в интервал Д, т. е. число k(n) нз фор-
формулы A), a
i а ь i ь
J fд (х) dx= J /д (х) dx+ J f& (x) dx+ J f& (x) dx = J dx = b-a = l
0 0 a b a
поэтому при / —f& (x) соотношения B) н A) совпадают.
a b 1
Phc. 2.5
Совпадение временного среднего и пространственного
среднего для простейшего случая равномерно распределен-
распределенной последовательности точек обобщается в теории дина-
динамических систем на случай так называемых эргодических
систем. В эргодической системе действует преобразование Т,
не переводящее в себя никакого подмножества системы с
мерой, отличной от 0 или 1, т. е. из равенства Т(А)=А,
где А — подмножество системы, следует, что мера множест-
множества А (длина, площадь, объем А в одно-, двух- и трехмерном
случаях) равна либо 0, либо 1. Примером эргодической си-
системы может служить окружность S1, на которой действует
преобразование поворота Т на иррациональный угол а
(рис. 2.6). Для этой системы выполнено равенство B), по-
поэтому последовательность точек
(так называемая «орбита преобразования Г») равномерно
распределена на окружности, а стало быть, всюду плотно
ее заполняет.
Именно равенство B) и утверждает, что доля времени,
которую частица (скачущая по окружности точка) прово-
дит в заданной обласги (дуге А), равно мере (длине) этой
области.
Обсуждение вопросов, связанных с эргодичностью, рав-
равномерной распределенностью и всюду плотностью, закон-
закончим в этом параграфе следующей замечательной арифмети-
арифметической задачей, решаемой бильярдным шаром в круге.
Задача. Рассмотрим последовательные степени двой-
двойки: 1, 2, 4, 8, 16, 32, 64, 128, 256, ... и выпишем подряд
первые цифры полученных чисел:
1,2,4,8,1,3,6,1,2,5,1,2,4,...
а) Встретится ли в этой последовательности цифра 7?
б) Какая цифра встречается в последовательности чаще:
7 или 8? Во сколько раз?
в) Вообще, с любого ли набора цифр может начинаться
степень двойки? С какой частотой появляется заданный на-
набор ЦИфр GiG2. . Мг?
Решение. Начнем решать задачу «с конца», т. е.
ответим сначала на вопрос в), который естественным обра-
образом обобщает вопросы а) и б).
Пусть A=aid2. . мг—г-значное число. Если 2" на-
начинается с набора А, то 2п=А. . . , а так как число А
не меньше А• 10* и строго меньше (А + 1)-Юк, где k — чис-
число цифр, приписанных справа к А, то
Логарифмируя по основанию 10, получаем
Отметим на числовой оси все промежутки между числами k и
k-\- lg M -|—— V т. е. окружим все целые точки k числовой
оси полуинтервалами одинаковой длины lg ( I +-«-)•
Возьмем теперь круглый бильярд, длина окружности
которого равна I (т. е. радиус бильярдного круга равен
l/Bjt)), и, как при доказательстве утверждения 1, намота-
намотаем числовую ось на границу этого бильярда — окруж-
окружность S1 (рис. 2.7). Тогда все целые точки 0, 1, 2,... , k,. . .
сольются в одну точку на окружности, а все промежутки
\k, k-\-\g(\ +-4-) 1— в одну дугу Л (g концомО, который
39
ей принадлежит) длины / (Д) = lg A + -j- J. Обозначим Р„
точку на окружности, в которую попадает при этой намотке
число (—lg A).
А теперь задача сводится к моделированию первых цифр
последовательности 2" следующим движением бильярдного
шара в круге: запускаем шар из точки Ро в точку Pi на ок-
окружности такую, что ^PiP2=lg2, и рассматриваем всю
последовательность Ро, Р(,
Р2, Р3, . . . точек отраже-
отражения шарика от борта; те п,
для которых точки Р„ при-
принадлежат дуге Д, являются
искомыми показателями
двойки — для них числа
2" начинаются с набора
GiGs. . .аг.
Но число a=lg 2 —
иррациональное *), поэто-
поэтому последовательность точек Ро, Pi, Р2, . . . , получающихся
друг из друга поворотом на угол а, по теореме Якоби за-
заполняет окружность всюду плотно. Следовательно, степень
двойки может начинаться с произвольного набора цифр
А=агаг. . .ат. Более того, поскольку последовательность
точек Ро, Pi, P2, ...равномерно распределена на
окружности, доля тех чисел п, для которых 2" начинаете!
с набора А, в пределе равна длине интервала Д, т. е. равна
lg f 1 + "г) • Это и есть частота появления набора aiG2. . мг
в качестве первых цифр чисел 2".
После сказанного ответить на вопросы а) и б) не пред-
представляет труда. Цифра 7 в последовательности первых цифр
чисел 2" обязательно встретится. Встречается она с часто-
частотой, равной lg A + l/7)=lg 8—lg 7. Цифра 8 в этой последо-
последовательности встречается с частотой Ig(l + l/8)=lg9—lg 8.
Так как 8/7>9/8, то (как это ни странно на первый взгляд —
особенно после рассмотрения начала последовательности,
указанной в условии задачи), семерки встречаются чаще
восьмерок, причем в Л9~|ё8~ 1,14 раз. А то, что вначале
восьмерки встречаются все же чаще семерок, связано со
*) Если lg 2—mln, где тип — целые числа, то 2= 10я1 /", и тог
да 2"= 10я», чего Сыть не может, так как 2" не может оканчиваться
нулем (п>0).
40
следующим обстоятельством: иррациональное число lg 2
примерно равно рациональному числу 3/10. Действительно,
сделав на окружности 10 прыжков длины lg 2, мы сдвинем-
сдвинемся на дугу 10 lg 2«;3, т. е. окажемся примерно в начальной
точке. Среди первых 10 степеней двойки нет ни одной, на-
начинающейся с 7 (это экспериментальный факт), а начинаю-
начинающиеся с 8 — есть, поэтому и среди следующих 10 степеней
двойки опять нет ни одной, начинающейся с 7 (а с 8 — есть)
и т. д.; это будет происходить до тех пор, пока Юп • lg 2
не станет уже существенно отличаться от целого числа —
тогда и появляется семерка.
В заключение отметим, что числа 3", 4"=2г", 5", 6",
7", 8", 9", 11", 12", 13" и т. д. (пропускаются степени, ос-
основания которых кратны 10) также чаще начинается с 7,
чем с 8, причем, как и для 2", чаще в % =рт!щ раз. Это
объясняется равномерностью распределения точек на ок-
окружности длины 1 при отражении бильярдного шара с уг-
углами поворота a=lg3, lg 4, lg 5, lg 6, . . ., являющимися
иррациональными числами.
3 а д а ч а 2.1. Промоделируйте бильярдом в круге все степени
числа 3, начинающиеся с набора цифр 1989.
Задача 2.2. Докажите, что если число р ие является сте-
степенью 10, то среди чисел р, рг, р3, р*, . . . найдутся такие, десятич-
десятичная запись которых начинается с любой наперед заданной комби-
комбинации цифр. С какой цифры чаще начинаются эти числа — с 7
или 8 и во сколько раз? Сравните полученный ответ с ответом
для р=2 и объясните полученный резуль-
результат.
Задача 2.3. Существует ли такое
натуральное п. что sin п<10~100;>
юор
sin/
A Y w-10O
Рнс. 2.8
Рис. 2.9
Ответ. Существует. У к а 8 а н и е. Промоделируйте по-
последовательность sin 0, sin I,- sin 2, sin 3, ... бильярдом в круге
Радиуса I и учтите, что числа I и 2я несоизмеримы (рис. 2.8).
Задача 2.4. При качении одной окружности по другой
любая точка катящейся окружности описывает кривую с «острия-
«остриями» _ эпициклоиду (рис. 2.9). Докажите, что если радиусы этих
окружностей несоизмеримы, то «острия» эпициклоиды заполняют
неподвижную окружность всюду плотно,
41
Задача 2.5. По окружности Sx длины Y 2 катитси снаружи
окружность Sg длины I (без проскальзывания). На окружности
52 красным цветом отмечена точка А касания двух окружностей.
При качении окружности S2 no Sx точка А делает на Sx в точках
касания красные отпечатки Аи \, А8, .... В свою очередь, полу-
получающиеся красные точки на окружности Sx делают отпечатки на
окружности S2i которые, в свою очереди делают отпечатки на ок-
окружности Sj и т. д. Сколько красных то
чек будет на окружности Si, когда ок
ружность S2 сделает п оборотов около
Sj? Иными словами, с какой скоростью
растет число отпечатков на окружнос-
окружности Si?
Ответ. На неподвижной окружнос-
окружности будет п точек. Указание. После
первого оборота иа Si, кроме точки А, бу-
будет только один красный отпечаток Ах иа
расстоянии 1 (по дуге окружности Sx) от
А (рис. 2.10), а на S2—два отпечатка:
А' — это бывшая точка А — и отпечаток
от точки А. Точка А на St уже не даст но-
новых отпечатков на Si, а точка А' даст пос-
после одного оборота один новый отпечаток
А%. Вообще, с каждым оборотом все, кро-
кроме одной, красные точки на S2 пройдут
по своим старым следам на неподвижной
окружности и потому не дадут новых отпечатков, и лишь одна
новая точка будет давать отпечатки — один за оборот. Таким
образом, хотя красные отпечатки заполнят неподвижную окруж-
окружность всюду плотно, скорость их появления всего лишь линейная.
Задача 2.6. Числа о и Р несоизмеримы между собой и с
числом п. Докажите, что ни при каком целом п сумма s=sin па+
+sin пР не равна 2, но существует бесконечно много таких п, что
s отличается от 2 меньше чем иа 0,000001, С какой частотой встре-
встречаются такие числа п?
Рис. 2.10
V
§ 3. Теорема Пуанкаре о возвращении.
Конфигурационное и фазовое пространства.
Парадокс Цермело и модель Эренфестов
1. В математике часто случается, что некото-
некоторые утверждения или их следствия удается удачно обобщить
и получить при этом ряд новых, неизвестных ранее следст-
следствий, иногда далеко выходящих за рамки рассматриваемого
вопроса. Таким интересным во многих отношениях обобще-
обобщением следствия теоремы Якоби о попадании любой точки х
окружности S1 в любую свою окрестность является теорема
Пуанкаре о возвращении, возникшая, впрочем, впервые из
потребностей механики. Мы позже расскажем, в связи с
чем величайший математик нашего века Анри Пуанкаре
сформулировал эту теорему для механики, вначале же по-
42
говорим о том, как естественным образом обобщается ука-
указанное следствие теоремы Якоби.
В этой теореме фигурирует окружность S1 и преобразо-
преобразование Т — поворот окружности на некоторый угол а.
Далее рассматривается произвольная точка х на S1 и ее
образы при поворотах на углы а, 2а, За, ... — точки
х, Т(х), Т*(х)=Т(Т(х)), ТЦх)=Т(ТЦх)) и т. д. (они в фор-
формулировке теоремы Якоби обозначались Ро, Pi, Я2, . . .).
Все образы точки — ее положения на окружности в пос-
последовательные моменты времени — в совокупности назы-
называются орбитой преобразования Т. Про эту орбиту и ут-
утверждается, что при иррациональном а она всюду плотно
заполняет окружность, в частности некоторый образ точ-
точки х попадает в любую наперед заданную окрестность точ-
точки х (а при рациональном а орбита замкнется, т. е. для не-
некоторого п будет выполнено равенство Тп(х)=х).
Окружность S1 будем считать расположенной на плос-
плоскости, а ее поворот представлять себе как преобразование
(поворот) всей плоскости, не меняющее площадей фигур,
при котором окружность S1 переходит в себя: T(Sl)=S1.
Анри Пуанкаре заметил, что если плоскость — двумерное
пространство — заменить на пространство любого числа
измерений (трехмерное, четырехмерное и т. д.), окруж-
окружность — на произвольную ограниченную область *) D
в этом пространстве, а преобразование Т считать взаимно
однозначным (не «склеивающим» никакие две точки в одну),
сохраняющим объемы и при этом переводящим область D
в себя, то указанное следствие из теоремы Якоби сразу же
обобщается, а ее доказательство упрощается. Приведем
формулировку теоремы Пуанкаре и ее доказательство.
Теорема Пуанкаре о возвращении.
Пусть Т — сохраняющее объемы взаимно однозначное, пре-
преобразование пространства, переводящее ограниченную об-
область D пространства в себя: T{D)—D. Тогда в любой сколь
угодно малой окрестности U внутри D найдется точка х,
которая после нескольких применений к ней преобразования
Т снова возвращается в область U: точка Т" (х) принадле-
принадлежит области Uпри некотором п>0 (рис. 3.1). Более того,
почти все точки области U возвращаются снова в U — объем
^возвращающихся в U точек равен нулю **).
*) Областью в пространстве называется такая его часть, кото-
которая вместе с каждой точкой содержит целиком и некоторый шарик
с Центром в ней.
**) Мы предполагаем, что множество невоэвращающихся точек
имеет объем.
43
Замечание. Усилением теоремы Пуанкаре служит ут-
утверждение, что почти все точки области U возвращаются в U бес-
бесконечно много раз. На доказательстве этого усиления мы останав-
останавливаться не будем.
Рис. 3.1
Рис. 3.2
Доказательство теоремы Пуанкаре.
Рассмотрим области U=T°(U), T(U), T*(U), T3(U)
Их бесконечно много, все они имеют одинаковый ненулевой
(по условию) объем и все содержатся внутри D.
Если бы никакие две из них не пересекались, то суммар-
суммарный объем равнялся бы бесконечности, и тогда область D
не имела бы конечного объема. Однако область D ограниче-
ограничена, и поэтому какие-то две (по крайней мере) области Тк „С)
и Т1 (U) (&>/^0) пересекаются, т. е. имеют общие точки.
Но тогда пересекаются и области Т~1 G* (U))—Tk~l (U) и
T-l(Tl(U))=T°(U)=U (рис. 3.2). Пусть # —произволь-
—произвольная точка пересечения областей Тп (V) и U, где n=k—/.
Так как каждая точка области Т" (U) получается из неко-
некоторой точки области U в результате действия преобразова-
преобразования Тп (по определению записи Т" (?/)), то и точка у, ле-
лежащая в Т" ((/), получается из некоторой точки х области U
таким же способом: у=Тп (х). Но точка у одновременно ле-
лежит и в области U. Следовательно, точка х через п шагов
вернулась опять в область U. Первая часть теоремы дока-
доказана.
Докажем вторую часть. Пусть V — множество невоз-
вращающихся в U точек. Тогда множества V, T(V), T2 (V),
T3(V), . . . попарно не пересекаются. Действительно, если
T*(V) и Т1 (V) пересекаются, то множество Tk~l(V) пе-
пересекается g V, а значит, некоторые точки из V вернулись
снова в V, а тем самым и в область V — противоречие. По-
Поскольку полученных множеств бесконечно много и все они
имеют одинаковый объем v, то, в силу ограниченности объе-
объема области D, число v не может быть отличным от нуля.
Значит, объем множества V равен 0. Доказательство теоре-
теоремы завершено.
44
Из теоремы Пуанкаре о возвращении мы получим ниже
несколько интересных следствий. А пока что отметим, что
из нее очень просто получается утверждение теоремы Яко-
би. Действительно, если Т — поворот окружности S1 на
угол а, то при а = 2л — (пг и п целые) преобразование Тп —
тождественное и любая точка х ? S1 через п шагов возвраща-
возвращается в точности на свое место: Т" (х)=х. Если же аФЧп —
ни при каких целых m и п, то по теореме о возвращении
Рис. 3.3
для любого е>0 существует такое натуральное п, что
\Тп (х)~x\<z (рис. 3.3) —следствие теоремы Якоби по-
получено. Теперь остается лишь заметить, что все точки ок-
окружности равноправны, и если у — любая точка из окрест-
окрестности U точки х, то она снова вернется в эту же окрест-
окрестность. Теорема Пуанкаре предсказывает также возвраще-
возвращение в окрестность исходного положения шарика, движуще-
движущегося без трения в несимметричной чашке (рис. 3.4).
Появление теоремы Пуанкаре о возвращении было сти-
стимулировано развитием классической механики, которая
на рубеже XX века приобрела практически завершенный ха-
характер благодаря многочисленным выдающимся математи-
математическим работам как самого Анри Пуанкаре, так и других
математиков (Лагранжа, Гамильтона, Лиувилля, Якоби
и др.). Одним из освежающих моментов, внесенных этими
работами в классическую механику, было понятие конфи-
конфигурационного и фазового пространств механической систе-
системы. Коснемся коротко этих понятий — они нам пригодят-
пригодятся и при изучении бильярдов (см. часть IV).
2. Конфигурационное пространст-
пространство — это пространство конфигураций, т. е. возможных
Положений заданных объектов. Например, две точки xt и
Х2, движущиеся по прямой К1, можно задать одной
45
изображающей или конфигурационной точкой х, но уже рас-
расположенной на плоскости IR2; при этом первая координата
точки х определяет положение на прямой (R1 первой точки
Xi, а вторая координата — положение второй точки хг
(рис. 3.5, а). Три точки хи х2, хя на прямой к1 заменяются
одной точкой х=(х1г х2, х3) трехмерного конфигурационного
пространства R3 (рис. 3.5, б); четыре точки лп, х2, х3, xt
на прямой R1 — одной точкой х= (xi, x2, xs, xt) четырехмер-
четырехмерного конфигурационного пространства R* и т. д. (Много-
(Многомерное пространство можно представлять себе как обычное
л2
I
w*
/
Рис. 3.5
трехмерное, но со многими независимыми осями коорди-
координат *); точка х={хи ¦ ¦ ., л:п) в нем имеет п координат, т. е.
столько, сколько имеется независимых осей.) Увеличение
числа объектов увеличивает и число измерений конфигур а-
ционного пространства, так называемую размерность про-
пространства (число независимых координат), или иначе, число
степеней свобоЗы'системы. Размерность конфигурационного
пространства может быть увеличена и за счет увеличения
размерности исходного пространства, в котором распола-
располагаются сами объекты. Например, две точки х= (xt, xt),
у= {tjt, y2) на плоскости R2 задают одну точку г=\х, у)=
= (xj, х2, уи у2) в четырехмерном конфигурационном
•) См. в журнале «Квант» № 6 за 1986 г. статью С. В. Дужина и
В. Н. Рубцова «Четырехмерный куб», в которой рассказывается о
четырехмерном пространстве, гиперплоскостях и других многомер-
нык объектах.
пространстве R4 (рис. 3.5, в), а две точки * = (*!, хг, xs)
и У= (f/i. Уа. Уз) в трехмерном пространстве R3 задаются од-
одной конфигурационной точкой г= (х, у) = (лгь х2, х3, уи
ift, Уъ) в ^-мерном пространстве R6 (рис. 3.5, г).
Часто на конфигурацию объектов накладываются какие-
либо ограничения. Тогда совокупность конфигураций бу-
будет заполнять не все многомерное пространство, а лишь
его часть, и именно эта часть будет в этом случае называть-
называться конфигурационным пространством. Например, если точ-
точка #i на прямой R1 не может обгонять точку хг, т. е. если
Рис. 3.6
всегда Xi^x2, то конфигурационным пространством будет
множество точек плоскости {(хи х2)}, удовлетворяющих
условию JCi^#2, т.е. полуплоскость в плоскости R8
(рис. 3.6, а). Если же две точки xi и х2, двигаясь свободно
на отрезке [0, 1], не могут покинуть его пределов, т. е.
0^*1^1 и 0^лг2^1, то конфигурационным пространством
будет множество точек {(xi, x2)}, заполняющих квадрат со
стороной 1 (рис. 3.6, б).
Еще пример: предположим, что две точки х% и хг дви-
движутся по прямой (R1 так, что всегда Xi =^jcg, но расстояние
между точками не превосходит 1 — точки связаны нерастя-
нерастяжимой (но гибкой) нитью длины 1. Тогда координаты кон-
конфигурационной точки (хи xt) удовлетворяют условиям
*i ^ x2 ^ xt-\-1 и поэтому конфигурационное пространство
этой системы — наклоненная под углом 45° полоса шири-
шириной 1/К2.
Чтобы показать разнообразие конфигурационных про-
пространств, приведем более экзотические примеры. Конфи-
Конфигурационное пространство системы, состоящей из движу-
движущихся по двум окружностям S\ и S\ точек xt и х2 — это мно-
множество точек x~(xt, jc2) на двумерном торе — поверхно-
поверхности «бублика». Тором является и конфигурационное про-
пространство «двойного маятника» — механической системы
из двух связанных вращающихся стержней, изображенной
на рив. 8.10 (см. §8). Каждое положение двойного маят-
чика задается парой углов ipi, ty2, меняющихся независимо
47
друг от друга от 0 до 2зт. Более подробно о торе рассказы-
рассказывается в § 8.
Множество С упорядоченных пар точек (а, Ь), первая
из которых принадлежит множеству Л, а вторая — множест-
множеству В, называется прямым произведением множеств А и В:
С=АХВ. Прямое произведение пространств (не являю-
являющихся нульмерными—точками)—это пространство большей
размерности: RxXlR2=IR3, R2XlR2=[R4 и т. д. Прямые
произведения других множеств устроены более сложно:
квадрат — прямое произведение двух отрезков, тор —
прямое произведение двух окружностей; бесконечный ци-
цилиндр — прямое произведение прямой на окружность
и т. д. *).
Иногда только одно введение конфигурационного про-
пространства позволяет решить довольно трудную задачу (эта
популярная сейчас олимпиадная задача впервые была опуб-
опубликована в 6-м выпуске серии «Математическое просвеще-
просвещение», 1961 г.).
Задача (Н. Н. Константинов). Из города А в город В
ведут две дороги (рис. 3.7, а). Два велосипедиста, связанные
веревкой длины, меньшей 2а, могут проехать из города А
в город В по разным дорогам, не разорвав веревки. Смогут
ли разминуться, не столкнувшись друг с другом, два тол-
толстяка радиуса а каждый, идя один из города А в город В,
а другой из города В в город Л?
Решение. Введем вдоль первой дороги координату
хи а вдоль второй дороги — координату х2 и рассмотрим
конфигурационную плоскость Oxtx2. Одновременное поло-
положение велосипедистов или толстяков изображается конфи-
конфигурационной точкой .7= (хи х2) этой плоскости. Одновремен-
Одновременному движению по обеим дорогам соответствует движение
конфигурационной точки х. Если длина первой дороги рав-
равна ht а второй — 12, то координата Xi меняется от 0 до U,
а л:2 — от 0 до 1г\ следовательно, конфигурационная точка
обязана находиться в прямоугольнике OKLM (рис. 3.7, б),
который и является конфигурационным пространством.
Велосипедисты начинают двигаться из города А (точка О
в конфигурационном пространстве), а заканчивают движе-
движение в городе В (вершина прямоугольника L). Значит, в
конфигурационном пространстве движению велосипедистов
соответствует траектория (кривая) а, идущая из О в L.
*) Не следует думать, что конфигурационное пространство —
всегда прямое произведение. Топологически оно может быть уст-
устроено сложнее: множество пар точек, находящихся на фиксиро-
фиксированном расстоянии на сфере S?,— это трехмерная сфера S9.
48
Аналогично, движению толстяков будет соответствовать
траектория Р, идущая из вершины М прямоугольника в
вершину К. Очевидно, кривые аир, находясь внутри пря
моугольника OKLM, пересекутся в какой-то точке х—
= (xi, лг2) внутри него. В этой точке координаты велосипе
дистов и толстяков одинаковы. Но это означает, что рас
стояние между толстяками меньше 2а (ведь велосипедисты
К х,
Рнс. 3.7
проехали это место, не разорвав веревки!), а следователь
но, толстяки обязательно столкнутся. Задача решена.
Другие, более естественные примеры конфигурацион-
конфигурационных пространств появятся в следующих частях этой книги.
При движении конфигурационной точки х возникает ее
траектория х (t), называемая конфигурационной траекто-
траекторией или орбитой.
Задача. Что является конфигурационным пространством
а) круглого бильярда? б) трех точек прямой R1, из которых первые
две не обгоняют третьей? в) трех точек прямой R1, нз которых
первая всегда левее второй, а вторая левее третьей? г) двух точеч-
точечных планет, движущихся вокруг Солнца по окружностям? д) Ка-
Какова размерность конфигурационного пространства девяти планет
Солнечной системы (планеты считать точками)?
Ответы, а) Круг, в котором движется бильярдный шарик.
б) Пересечение полупространств Xx<xs и ж2<х3. в) Пересечение
полупространств *1<жа и Х2<*8. г) Двумерный тор Ti=S1XS1.
Д) 1+1 + . . .+ 1=9.
3. Фазовое пространство. Рассмотрим движение неко-
некоторой системы объектов — частиц, тел и т. п. Добавим к
пространству конфигураций {х} этих объектов простран-
пространство их скоростей {v} (векторов), т. е. будем рассматривать
всевозможные пары {(лг, v)}. Полученное множество пар
(х — положение, v — скорость) называется фазовым прост-
пространством системы, а изображающая систему точка (дг, v) —
Фазовой точкой системы. Иными словами, фазовым прост-
пространством называется множество всевозможных состояний
Движения системы. Например, если точка х на прямой К1
Может двигаться по ней с произвольной скоростью v, то
Фазовым пространством будет плоскость №={(х, v))
49
(рис. 3.8, а); фазовым пространством двух точек на
прямой К1 будет четырехмерное пространство R*
(рис. 3.8, б), а двух точек на плоскости — 8-мер-
8-мерное пространство R8 (поскольку у каждой точки по две коор-
координаты положения и по две координаты скорости, итого
4+4=8 координат; рис. 3.8, в).
Рис. 3.8
Процесс называется детерминированным, если весь его
будущий ход и все его прошлое однозначно определя-
определяются состоянием в настоящий момент. Такими процессами
являются, например, процессы радиоактивного распада
и размножения бактерий. Бывают и недетерминированные
процессы: таково движение частиц в квантовой механике
(ни прошлое, ни будущее не определены настоящим одно-
однозначно) или же распространения тепла (будущее определе-
определено настоящим, а прошлое — нет).
Классическая механика рассматривает движение систем,
будущее и прошлое которых однозначно определяются
начальными положениями и начальными скоростями всех
точек системы, т. е. рассматривает детерминированные про-
процессы. В каждый момент времени tB механическая система 5
находится в положении x(t0) и имеет конкретный вектор ско-
скорости v(t0); фазовая точка этой системы (лг(<0). *>D)) п0Л"
ностью и однозначно (детерминированно) характеризует
эволюцию системы как в прошлом, при всех f<?Oi так я в
будущем, при всех t>te. Зная одно-единственное состоя-
состояние движения системы S@)—(x(t(,), v(to)) в момент U,
можно однозначно определить состояния движения этой
системы сразу во все моменты времени: {S (/)}= {(х (I), v @)»
—°o<f<oo}. Множество состояний движения {SOO)"
50
это множество всех фазовых точек {x(t), v(t)}, которое
носит название фазовой траектории. Таким образом, одна
точка фазовой траектории однозначно определяет всю фа-
фазовую траекторию (рис. 3.9). Если в
момент времени U задать другое на-
начальное состояние движения системы
S, т. е. взять другую начальную фа-
фазовую точку (х1 (t0), v' {t0)), то и вся
фазовая траектория {S'{t)}={xl (t),
v'(t)} будет другой. Никакие две раз-
различные фазовые траектории не могут
пересекаться, так как в противном Рис. 3.9
случае по фазовой точке их пересече-
пересечения (x(ti), v(ti)) нельзя было бы однозначно восстано-
восстановить две р а з н ы е фазовые точки (x(te), v(t0)) и (х'(t0).
Задача. Может ли фазовая траектория механической си-
системы пересекать саму себя? Быть замкнутой?
Ответ. Не может. Может.
Важно отличать состояние системы от состояния двиэюе-
ния: первое задается координатами, второе — координа-
координатами и скоростями. Зная одни лишь координаты {х}, мы
не можем предсказать дальнейшее движение системы, но
зная координаты {л:} и скорости {©} — можем. Предполо-
Предположение о том, что замкнутую систему можно описать хоть
каким-то фазовым пространством и системой кривых в нем
(иногда все вместе называют фазовым портретом) — это ма-
математическое содержание классического принципа детер-
детерминизма *).
Рассмотрим теперь механическую систему S в момент
'=0. Она может находиться в этот момент в различных со-
состояниях Si@), S2@), Ss@), . . ., которые задаются раз-
различными фазовыми точками (Хг @), z»i@)), (ж2@), г»2@)),
(#8@), va@)), . . . Каждое начальное состояние системы
Sj @), т. е. каждая начальная фазовая точка (хс@), г»г@)),
в силу детерминированности, однозначно определяет всю
*) Известен знаменитый парадокс Зенона: летящая стрела и не
подвижная стрела находятся в одном и том же месте пространства;
чем же отличается полет от неподвижности? Ответ состоит в том,
что видимое место стрелы — это всего лишь проекция х на прост-
пространство положений ее «истинного места» в пространстве пар (х, v):
01 фазового пространства остается только конфигурационное. Па
Радокс Зеиона можно истолковать как первую догадку о роли фа-
фагового пространства,
51
фазовую траекторию {S|@} в фазовом пространстве, так
что для указанных начальных состояний системы S опреде-
определено сразу бесконечно много фазовых траекторий {Si@},
{5г@}. {5в@}. ••• (Рис- 3.10). Преобразование, переводя-
переводящее любую начальную фазовую точку (лг(О), г»@)) в точку
(л: (t), v (t)), называется фазовым преобразованием за время t,
Т', а множество всех преобразований {Г'} — фазовым по-
потоком: каждая фазовая точка движется по своей фазовой
кривой.
В фазовом пространстве начальные состояния системы S
могут занимать некоторую область U—U@). В момент t
V
\U@)
х
(t+f)
X
Рис. 3.10
Рис. 3.11
все точки области U, двигаясь каждая по своей фазовой
траектории, оказываются в новых точках фазового прост-
пространства и образуют новую область U(t) (рис. 3.11). Как свя-
связаны между собой области U@) и U(t)? Оказывается, на
этот счет для многих механических систем (в частности, для
так называемых еамильтоновых систем) справедлива сле-
следующая замечательная теорема.
Теорема Лиувилля. Объемы областей t/@)
и U (f) одинаковы.
В дальнейшем будут рассматриваться системы, для ко-
которых утверждение теоремы Лиувилля будет выполняться.
Исходя из этой теоремы, все фазовое пространство можно
представлять себе заполненной несжимаемой жидкостью,
которая движется в фазовом пространстве (несжимаемость
и означает сохранение объемов). Разберем два примера
движения такой «фазовой жидкости».
Пример 1. Исследуем, как меняются состояния де-
вяти планет Солнечной системы. Для простоты будем счи-
считать, что каждая из них представляет собой точку массы '
и движется вокруг Солнца по своей окружности, не влияя
на остальные планеты. Тогда фазовым пространством это''
52
системы является 54-мерное пространство К§4, поскольку
у каждой планеты три пространственные координаты (они
выделяют Зх9=27-мерное конфигурационное пространство
R") и три координаты вектора скорости (они выделяют ЗХ
Х9=27-мерное пространство скоростей). Однако поскольку
каждая планета с номером k (планеты нумеруются в порядке
удаления от Солнца) движется по окружности, то ее про-
пространственные координаты (хи k, xit к, x3i k) удовлетворяют
условию *1 И-*!, fc+4. k=Rh где Rk—радиус орбиты k-й
планеты, и поэтому конфигурационная точка х, изображаю-
изображающая положение всех девяти планет, движется не по всему
27-мерному пространству, а лишь по его ограниченной час-
части—так называемому 9-мерному тору T' = S1xS1x ... xS1
9 раз
(о торе см. далее главы 3 и 8). Кроме того, абсолютная ве-
величина (модуль) скорости каждой планеты постоянна:
|г»*| = Vvk.i + Vk.2 + Vk.» — const, k = 1, 2, ..., 9. Каждое
из этих девяти равенств задает двумерную сферу, а все ра-
равенства вместе выделяют в 27-мерном пространстве скоро-
скоростей ограниченную часть — 18-мерное «многообразие»
...xS*.
9 раз
В итоге в фазовом пространстве К64 выделяется некото-
некоторое ограниченное 9+18=27-мерное множество D=TVX
*М18. переходящее под действием фазового потока Т в
себя: T(D)=D. Если (лг(О); v @)) 6 D — фазовая точка
для обозначения состояния Солнечной системы в момент
t~0 и U — ее произвольная окрестность, т. е. множество
всех близких по координатам и скоростям положений пла-
планет Солнечной системы, то U — область в D, объем которой
под действием преобразования Т не меняется: объем
Т{11)=объем U по теореме Лиувилля. Мы пришли к услови-
условиям теоремы Пуанкаре о возвращении и можем заключить
из нее, что через некоторое время все планеты окажутся
вблизи своих начальных положений и будут иметь прибли-
зительно начальные скорости: при некотором п точка
^"(л:@), v@)) будет лежать в той же окрестности U, что и
чачальная фазовая точка (х@), v@)).
^Другим замечательным примером движения несжимае-
несжимаемой фазовой жидкости, обсуждением которого мы и заклю-
заключим этот параграф, служит следующая динамическая систе-
^a. имеющая уже некоторое отношение к бильярдам.
Пример 2*. Возьмем два сосуда, один (А), напол-
НеНный газом, другой (В) пустой. Что произойдет, если эти
БЗ
Рис. 3.12
сосуды соединить трубкой и открыть клапан соединитель-
соединительной трубки?
В соответствии со вторым началом термодинамики газ
устремится из сосуда А в сосуд В и будет перетекать из А
в В, пока давление в обоих сосудах не сравняется. Однако
мы сейчас рассмотрим эту же ситуацию совершенно с дру-
другой точки зрения, при этом привлечем теорему Пуанкаре
о возвращении и получим совершенно неожиданный ре-
результат!
В статистической механике считается, что газ в сосуде
состоит из большого числа молекул, взаимодействующих
по законам классической механики. Такой газ является
замкнутой (гамильтоновой) системой с большим числом
степеней свободы, и поэтому фа-
фазовое пространство этой системы
имеет очень большую размерность
(как известно, в кубическом санти-
сантиметре при нормальных условиях
содержится приблизительно 10м
молекул). Фазовый поток, опреде-
определяемый уравнениями движения мо-
молекул газа, по теореме Лиувилля
не меняет объемов областей фазо-
фазового пространства. А тогда при-
применима теорема Пуанкаре: фазовая точка подходит с тече-
течением времени сколь угодно близко к своему начальному
состоянию, такому, при котором все молекулы газа пе-
перейдут опять в сосуд А (рис. 3.12).
Итак, через некоторое время газ снова соберется в сосу-
сосуде Л, а в сосуде В вновь будет вакуум. Возникает явное
противоречие со вторым началом термодинамики: из него
следует, что газ соберется снова в сосуде А с вероятностью
О, а теорема Пуанкаре утверждает, что — с вероятностью И
Это противоречие носит название парадокса Цержло,
по имени математика, придумавшего его в связи с дискус-
дискуссией между физиками по обоснованию термодинамики с по-
позиций молекул яр но-кинетической теории. Разгадка пара-
парадокса состоит в том, что «некоторое время», через которое
повторится исходное (вернее, почти исходное) положение
молекул газа, больше времени существования Солнечной
системы.
Указанную разгадку наглядно интерпретировали в
1907 году известные физики Пауль и Татьяна ЭренфестЫ
на простой и красивой вероятностной модели. Сосуд А со-
содержит большое количество пронумерованных шаров (м°"
54
лекул газа»), а сосуд В пуст. Из третьего сосуда, наполнен-
наполненного пронумерованными билетиками, вынимается наугад
один (скажем 17-й), и тогда шар, отмеченный этим номером,
перекладывается из А в В. Билетик возвращается обратно
и возобновляется вынимание билетиков и перекладывание
шаров из сосуда в сосуд. Каждый раз, вынимая наугад
какой-то номер от 1 до N (N — общее первоначальное чис-
число шаров в сосуде А), шар с этим номером перекладывают
из того сосуда, в котором он находится в этот момент, в дру-
другой (рис. 3.13).
Рис. 3.13
Интуиция подсказывает нам, что до тех пор, пока в со-
сосуде А шаров намного больше, чем в сосуде В, вероятность
того, что мы вынем номер, принадлежащий шару из сосуда
А, будет заметно больше вероятности того, что мы вынем но-
номер, принадлежащий шару из сосуда В. Таким образом,
вначале будет наблюдаться сильный «переток» шаров из
сосуда А в сосуд В. Продолжая вынимать билетики, мы за-
заметим, что вероятность вытягивания номера шара из сосу-
сосуда А будет меняться в зависимости от предыдущих вынима-
выниманий билетиков. (Эта форма зависимости вероятности от
предшествующих событий носит название цепи Маркова,
и в модели, которую мы рассматриваем, все имеющие к
этому отношение факты могут быть строго и точно выведе-
выведены.) Оказывается, что в среднем число шаров в сосуде А
будет в действительности убывать с той скоростью, которую
и предсказывает термодинамическая теория, пока пример-
примерно половина шаров не окажется в сосуде В. Но вы-
вычисления показывают также, что если игру продолжать
Достаточно долго, то с вероятностью 1 все шары попадут на-
назад в сосуд А, как и утверждает теорема Пуанкаре!
Сколько же выниманий в среднем требуется, чтобы вер-
нУться снова к этому исходному положению? Ответ гла-
гласит — 2Nt а это исключительно большое число, даже если
65
количество шаров N не превосходит 100. Этим и объясня-
объясняется, почему наблюдения, которые мы производим, дают нам
движение шаров только в одном направлении без каких-
либо осцилляции — мы слишком недолго ждали!
Для экспериментальной проверки теоретических под-
подсчетов игру Эренфестов провели на ЭВМ. Начали с 16 384
шаров в сосуде Л, и каждый «прогон» состоял из 200 000 вы-
выниманий. Была вычерчена кривая, даюшая число шаров в
сосуде А по результатам каждой тысячи выниманий
Экспоненциальное уоывание числа шаров
Рис. 3.14
(рис. 3.14). Как и ожидалось, убывание числа шаров в со-
сосуде А сначала происходило по экспоненциальной кривой.
Но, начиная со значения, близкого к положению равнове-
равновесия (т. е. к 8192 — половине общего числа шаров), кривая
стала неровной, произвольно отклоняясь то вверх, то вниз.
Прокомментируем парадокс Цермело еще и с бильярд-
бильярдных позиций. Рассмотрим для этого прямоугольный би-
бильярдный стол без луз, на котором находятся 16 бильярд-
бильярдных шаров. Предположим, что эти шары, как и молекулы
газа в сосуде, движутся без трения по поверхности бильярд-
бильярдного стола, сталкиваясь упруго друг с другом и с его бор-
бортом. Мысленно разделим весь стол на две равные части --
левую (А) и правую (В). Введем понятие состояний.
Бильярд находится в состоянии 0, если в пределах левой
половины нет ни одного шара; в состоянии 1, если в преде-
пределах левой половины находится 1 шар- в состоянии 2, если
в пределах левой половины находятся 2 шара, и т. д.; Б
состоянии 16, если в половине А собрались все 16 шаров-
Заметим теперь, что состояния 0 и 16 могут быть реали-
реализованы единственным способом: когда все шары
находятся справа или когда все они находятся слева. Со-
Состояния 1 и 15 могут быть реализованы 16-ю различными
способами: первый шар находится слева, остальные — прЗ"
56
ва; второй шар находится слева, остальные — справа и
т. Д. Для подсчета числа способов, которыми могут быть реа-
реализованы состояний 2 и 14, будем рассуждать так. Имеется
15 способов, в которых участвует шар номер 1, а именно:
слева (справа) находятся шары 1 и 2, 1 и 3, . ., 1 и 16;
14 способов, в которых участвует шар номер 2: это шары
2иЗ, 2и4, ..., 2 и 16 (способ «2 и 1» уже учтен в предыду-
предыдущем случае); 13 способов с участием шара номер 3: это шары
3 и 4, 3 и 5,. . ., 3 и 16; и так далее. Всего получаем 15+14+
+. . .+2+1 = 120 способов. Количество способов, которы-
которыми может быть реализовано каждое состояние, назовем
его «весом». Сведем «веса» в таблицу.
Состояния
0 и 16
0 и 15
2 и 14
3 и 13
4 и 12
5 и 11
6 и 10
7 и 9
8
Количество способов
реализации («вес»)
1
16
120
560
1S20
4368
8008
11440
12 870
Из таблицы видно, что наибольшим числом способов
могут быть реализованы состояния 7, 8 и 9, т. е. состояния,
когда примерно половина шаров расположена на левой
половине бильярда, а другая половина — на правой. Для
каждого отдельного шара нет никаких оснований выделять
преимущественную область его пребывания. С тем же ус-
успехом мы можем утверждать, что нет никаких оснований
предпочесть одну какую-либо конфигурацию расположения
Другой. А тогда, какова бы ни была эта конфигурация,
Рано или поздно она реализуется, а средний промежуток
времени, в течение которого на бильярдном столе имеет
место данная конфигурация, одинаков для всех конфигура
ций. Каждый из рассмотренных выше способов представля-
^ частный случай конфигурации. Следовательно, средний
промежуток времени, в течение которого бильярд находит-
находится в данном состоянии, пропорционален количеству спо-
способов, которыми реализуется данное состояние. Поэтому
большую часть времени бильярдный стол проводит в сос-
Б7
стоях 7, 8, 9 (примерно в 12 тысяч раз большую, чем в со-
состояниях 0 и 16).
Можно рассуждать и иначе. Если, бросив взгляд на
бильярдный стол, мы застали его в состоянии 0 или 1 A5
или 16), у нас есть все основания ожидать, что в скором вре-
времени на смену этому состоянию придет какое-нибудь более
часто встречающееся (аналог выравнивания давления в при-
примере с сосудами А и В с газом). Наоборот, если мы застаем
стол в состоянии 7, 8 или 9, у нас есть все основания считать,
что еще в течение достаточно долгого времени он будет пре-
пребывать в этом состоянии. Можно сказать, что «состояние
бильярда стремится к состояниям 7, 8 или 9». Это верно в
том смысле, что действительно на смену редко встречаю-
встречающимся состояниям быстро приходят часто встречающиеся
состояния.
Состояния, введенные выше, имеют и определенный фи-
физический смысл. Заметим, что общая масса шаров, распо-
расположенных, скажем, в левой половине бильярда, равна массе
одного шара, умноженной на номер состояния. С этих по-
позиций можно сказать, что большую часть времени бильярд-
бильярдная система проводит в таком состоянии, когда масса ша-
шаров, расположенных слева, примерно равна массе шаров
справа.
Мы специально потратили так много времени, чтобы чи-
читатель смог до конца понять и как следует прочувствовать
следующее обстоятельство. Единственно реально наблю-
наблюдаемое на поверхности стола физическое явление — это то,
что шары двигаются, сталкиваются друг с другом и с бортом
стола, и вследствие этого описывают весьма сложные траек-
траектории. Все остальное есть лишь различные способы описа-
описания этого обстоятельства и, возможно, различные его след-
следствия. Обнаруженные нами закономерности выполняются
тем точнее, чем больше имеется шаров (или молекул газа в
сосуде). Например, для 16 шаров средний промежуток
времени, в течение которого стол будет находиться в одном
из «средних» состояний, составляет примерно 0,328 от пол-
полного времени наблюдения, для 50 шаров — уже 0,8, для
100 шаров — 0,94, ну а для 1028 молекул газа в сосуде оно
неотличимо от 1 (вспомним, что для газа из такого числа
молекул фазовое пространство 6-10аз-мерно1).
Тем самым решение парадокса Цермело становится пол-
полностью прозрачным: система молекул стремится к состоя-
состоянию с наибольшим «весом», а состояние с наименьшим воз-
возможным «весом», хотя обязательно и реализуется — п°
теореме Пуанкаре,— но в среднем это происходит ничтожно
58
редко. Как остроумно ответил великий физик Л. Больцман
на возражения Цермело, связанные с теоремой Пуанкаре:
«Долго же Вам придется ждать!»
Задача*. Доказать, что если между бильярдными шарами
на прямоугольном столе произошел хотя бы один Удар, то за бес-
бесконечное время их произойдет бесконечно много. Указание.
Достаточно доказать, что в системе произойдет еще хотя бы один
удар (не обязательно между теми же шарами). Если состояние
системы «типичное», то по теореме Пуанкаре система вернется в
близкое к исходному состояние, и нужный нам удар произойдет.
Но даже и в «исключительном» состоянии системы произойдет
второй удар, так как рассматриваемую задачу можно свести к
движению точки на торе (см. части II—IV), траектория которой —
либо периодическая (и тогда система возвращается в точности в
исходное состояние), либо всюду плотна (и тогда система прихо-
приходит в близкое состояние).
Глава 2
БИЛЬЯРД В ЭЛЛИПСЕ
Нельзя отрицать, что буквально с первого взгляда круг при-
привлекает пас своей простотой, однако даже самому консерва-
консервативному астроному достаточно лишь мимолетного знакомства
с эллипсом, чтобы убедиться в том, что идеальная простота
круга сродни бессмысленной улыбке идиота. По сравнению
со сведениями, которые несет эллипс, круг ие дает ничего.
Возможно, рассчитывая иа физическую простоту Вселенной,
мы тоже мыслим окружностями, проецируя свое элементар-
элементарное мышление на бесконечно запутанный окружающий мнр...
Э. Беля.
Математика—царнца и служанка науки
Стол не выстлан сукном,
Кий изогнут крюком,
И шары все на эллипс похожи!
Поэма «Микадо»
§ 4. Эллипс и его бильярдные
свойства. Каустики
Хорошо известна задача о нахождении на за-
заданной прямой / такой точки М, для которой сумма расстоя-
расстояний до двух заданных точек Л и В, лежащих по одну сторо-
сторону от прямой /,— наименьшая.
Искомой будет точка М пересече-
пересечения отрезка АХВ с прямой /, где
Ау — точка, симметричная точке А
относительно прямой / (рис. 4.1)-
^ Действительно, AM+MB=AiM+
+MB=AiB, тогда как для любой
другой точки М' на прямой *
имеем
ЛМ' + М'В = АгМ' + М'В > AtB,
что вытекает из неравенства треугольника (для Д AiM'B)
Следовательно, АМ'+М'В>АМ+МВ.
60
И хотя эта задача настолько популярна, что без нее прак-
практически не обходится ни одно обсуждение задач на макси-
максимум и минимум *), мы привели ее здесь потому, что она
послужит нам необходимым трамплином при нахождении
аналогичной точки М на произвольной кривой; при исследо-
исследовании этой общей задачи мы сра-
сразу же столкнемся с необходи-
необходимостью использовать понятие
эллипса и его бильярдные свой-
свойства.
Какое же отношение рассмот-
рассмотренная задача имеет к эллипсу,
гиперболе или же другой кри-
рой? И при чем здесь бильярд?
Впрочем, на последний вопрос ответить просто. Взгля-
Взглянем еще раз на рис. 4.1: ^1=^/3, а так как, кроме того,
^/2=^/3 (как вертикальные углы, ведь AiMB — прямая!),
имеем /У=/Ъ. Следовательно, точка М на прямой I об-
обладает тем свойством, что AM и ВМ являются звеньями
одной бильярдной траектории: эти звенья образуют равные
углы с «зеркалом» I (угол падения равен углу отражения).
Вот теперь мы достаточно «вооружены» для рассмотрения
первого бильярдного, или оптического, свойства эллипса.
Но прежде чем обсуждать его, поговорим о самом эллипсе
и его простейших геометрических свойствах.
Определение. Эллипсом называется множество
точек М на плоскости, для которых сумма расстояний до
двух фиксированных точек Ft и /"а этой плоскости — вели-
величина постоянная (рис. 4.2):
FtM + F2M = const.
3 а д а ч а 4.1. Можно ли в эллипс вписать правильный много-
многоугольник? Если можно, то сколько сторон он может иметь?
Ответ. Можно вписать только правильный треугольник и
квадрат, поскольку вписанный правильный многоугольник впи-
вписан одновременно и в окружность, пересекающуюся с эллипсом не
более чем в четырех точках — вершинах многоугольника.
На рис. 4.3 показано, как можно начертить эллипс на
е. Положим лист бумаги на чертежную доску и прико-
прикорм к нему две кнопки или булавки. Напросив на них ни-
нитяное кольцо, длина которого должна быть больше удвоен-
удвоенного расстояния между кнопками, натянем нить острием
*) См., например, недавно вышедшую в серии «Библиотечка
*Квант» книгу В, М. Тихомирова «Рассказы о максимумах и миниму-
минимумах» (м., 1986), а также книгу Н. Б. Васильева и В. Л. Гутенма-
*<фа «Прямые и кривые» (М., 1978).
61
ось.
карандаша, чтобы получился треугольник FiMF2. Если
вести карандаш по бумаге так, чтобы нить все время оста-
оставалась натянутой, то треугольник будет деформироваться
но его периметр будет оставаться постоянным. Постоян-
Постоянной будет и длина стороны FiFt; следовательно /yW+/VW=
=const и карандаш опишет эллипс. (Этот способ вычерчи
вания эллипса используют садовники при изготовлении цве-
цветочных эллиптических клумб, только они вместо кнопок
втыкают в землю два колышка, натягивают кольцо из ве-
веревки, а сам эллипс вычерчивают на земле не карандашом,
а палкой с острым кон-
концом. Аналогичным спо-
способом действовали древ-
древние этруски, рисуя слож-
сложные овалы — разгадку
способа рисования пред-
\Больщая ложил великий физик
Максвелл, и с тех пор
они называются «овала-
«овалами Максвелла».)
Точки Fi и Ft носят
Рис. 4.3 названия фокусов эллип-
эллипса (от латинского fo-
focus — очаг *)); середина О отрезка FiFt (линии фоку-
фокусов) — центр эллипса; отрезки CD и ЕН, первый из
которых — продолжение линии фокусов, а второй перпен-
перпендикулярен ему и проходит через центр О эллипса (рис. 4.2),
называются осями эллипса, и если СГУЩЕН, то CD — боль-
большая ось, а ЕН — малая; половины этих осей, т. е. отрез-
отрезки OD,OCu OE, ОН называются полуосями, соответственно.
большой и малой; отношение расстояния от фокуса до цент-
центра к большой полуоси, т. е. число OFi/OC (или OFJOD),
равное также отношению FXF2 к большой оси CD, характе-
характеризует «сплюснутость» эллипса и называется его эксцентри-
эксцентриситетом При совпадении фокусов эксцентриситет равен
нулю и эллипс превращается в окружность.
Обозначив большую полуось буквой a (OC—OD=a)>
малую — буквой Ь (ОЕ=ОН=Ъ), половину длины отрезка
фокусов FtFt — буквой о (O/7i=OF2=1/s/;'tF2=c) и эксцент-
эксцентриситет—буквой е {OFi/OC~OFJOD=e), найдем связь
между этими величинами. Соединив для этого точку Е L
фокусами, получим равнобедренный треугольник FiE?*
(рис. 4.2). Найдем его стороны.
*) По причине, которая будет иена дальше.
62
Поскольку для любой точки М эллипса FiM+F2M—
=const, то, взяв в качестве М точку D — правый конец
большой полуоси эллипса, получим
FtC = F2D, FtD + F2D = const, Ffl^Ffi + a,
поэтому
FtD + F2D = a + (Ffi + F,C) = a + a = 2a
Итак, const=2a. Тогда для Д/ч/?/^ имеем FiE+EFs=2a, а
поскольку FiE=EFt, то FiE=EFt=a. А теперь рассмотрим
прямоугольный треугольник FiOE с катетами EO=b, OFi—c
и гипотенузой ?/7i=a. Из него с = Уаа—Ьа, Ъ = Va2—с\
а эксцентриситет эллипса равен
отсюда с = ае и b — Va*—(aey = aV\—ё2.
Задача 4.2. В эллипсе с большой полуосью 10 см и эксцент-
эксцентриситетом 0,1 вычислить, во сколько раз расстояние между фокусом
и центром превосходит разность полуосей.
Ответ. В 20 раз (=1 см : 0,5 мм).
Замечание. Эллипс с нулевым эксцентриситетом —
это окружность, а с малым (е«0) — очень похож на окруж-
окружность. Если расстояние фокуса от центра — первого поряд-
порядка малости, то различие полуосей — второго порядка:
br=aV\ —е2» а A —V2 e°) *)• Известно, что орбиты планет
Солнечной системы являются эллипсами с очень малыми
эксцентриситетами (порядка 0,001),
в фокусе которых находится Солнце.
Вернемся к первому бильярдному
(оптическому) свойству эллипса. Возь-
Возьмем на эллипсе с фокусами Ft и F^
произвольную точку М (рис. 4.4).
Для любой точки N на эллипсе спра-
ведливо равенство
FtN + F2N = FtM + F2M, Рис> 4>4
a Для точки Af, лежащей внутри эллипса, сумма t2
Меньше, чем FiM+FzM. Построим прямую /, проходящую
через точку М и образующую равные углы с отрезками
FiM и F2M: Zy—/2- Если теперь М' — произвольная
т°чка прямой /, отличная от М, то
FfM' + F2M' > Ft
*) Пря малых х У1 +х да 1 + х/я *.
63
как это было выяснено в начале параграфа. Следовательно
точка М' лежит вне эллипса. '
Мы получили, что прямая / имеет только одну
общую точку с эллипсом — точку М; все же остальные точ-
точки прямой I расположены вне эллипса. Такую прямую
называют касательной. Таким образом, справедливо
Утверждение 1 (первое бильярдное свойство
эллипса). Касательная к эллипсу, проведенная в его произ-
произвольной точке М, образует равные углы с отрезками FfM
и F2M, соединяющими оба фокуса с этой точкой.
Из первого бильярдного свойства эллипса вытекает сра-
сразу, что как бы мы ни выпустили бильярдный шар из одно-
одного фокуса, он после одного отражения от эллипса (от борта
стола) пройдет через второй фокус, после второго отраже-
отражения — опять через первый фокус и так далее.
Знаменитый Льюис Кэрролл написал небольшую книж-
книжку и об эллиптическом бильярдном столе. В одиннадцатом
издании Британской энциклопедии в примечании к статье
о бильярде написано: «В 1907 г. в Англии для разнообразия
введен овальный стол». Однако ни у этого, ни у бильярдного
стола Льюиса Кэрролла луз не было. Только в 1964 г
Эдвин Э. Робинсон получил патент на круглый бильярдный
стол с четырьмя лузами. Тогда же в США появилась при-
придуманная Артуром Фриго игра «Эллиптипул», в которой
луза располагалась в одном из фокусов эллиптического
стола. На таком столе, ударяя шары о борт, можно все вре-
время выигрывать.
Теперь мы можем дать иную интерпретацию решения за-
задачи о нахождении точки М на прямой I, реализующей мини-
минимум суммы АМ+ВМ для заданных
точек А а В (рис. 4.1): та точка М
на прямой I является искомой, в кото-
которой один из эллипсов с фокусами А и В
касается этой прямой (все такие эл-
эллипсы называющая софокусными).
В точности то же решение полу-
получится, если прямую I заменить про-
Рис. 4.5 извольной кривой «у- Сформулируем
точный вопрос.
Вопрос. Дана кривая у и две точки АиВпо одну сто-
сторону от нее (рис. 4.5). Как найти на кривой у точку М тп'
кую, чтобы сумма расстояний АМ+ВМ была (среди всех воз-
возможных) минимальной. . . или максимальной?
Мы оставляем читателю возможность самому поразмыШ-
64
лять над этим вопросом, полный ответ на который отложим
до §6.
Остановимся немного на некоторых оптических интер-
интерпретациях первого бильярдного свойства эллипса. Предпо-
Предположим, что эллипс представляет собой «зеркальную» кри-
кривую, от которой луч света отражается по закону «угол па-
падения равен углу отражения». Если в одном из фокусов
такого зеркального эллипса помещен точечный источник
света, то после отражения от стенок эллипса все лучи
пройдут через второй фокус. Описанное явление можно
'.Солнце
Земля
Рис. 4.6
наблюдать реально, в трехмерном пространстве. Для это-
этого нужно взять поверхность, получающуюся вращением эл-
эллипса вокруг прямой FlFt, соединяющей его фокусы,—
она называется эллипсоидом вртирния,— покрыть ее из-
изнутри зеркальным слоем, а в одном из фокусов поместить
точечный источник света («солнце»). Тогда наблюдатель,
находящийся внутри эллипсоида, увидит два «солнца».
В салом деле, обратив взгляд к первому фокусу, наблюда-
наблюдатель непосредственно увидит размещенное там «солнце».
Но к, посмотрев в направлении второго фокуса (где в дей-
действительности ничего нег), он также увидит «солнце»
(рис 4.6, а). И как бы ни перемещался наблюдатель внут-
внутри зеркального эллипсоида, на него почти везде будут све-
светить два «солнца».
Но вот наблюдатель, находящийся внутри зеркального
эллипсоида, решил принять меры, которые избавят его от
«мнимого солнца», и поместил во втором фокусе небольшое
Непрозрачное тело («экран»), преграждающее путь отра-
отраженным лучам. Результат оказывается несколько неожи-
неожиданным: теперь все лучи, исходящие от «солнца» Л, после
отражения от стенок зеркального эллипсоида собираются
(«фокусируются») на экране F2, и это может вызвать ин-
интенсивный его разогрев. Например, поместив в фокус Ft
г°рящую свечу, можно зажечь бумажку, находящуюся во
Бтором фокусе. Заметьте, что для фокусировки не обяза-
Г- А. Гальперин, А. Н. Земляков &5
телыю иметь целый зеркальный эллипсоид, достаточно ис-
использовать лишь часть его поверхности *).
А что увидит «несгораемый» наблюдатель, оказавшийся
во втором фокусе Ft эллипсоида, если в первый его фокус F^
поместить источник света? Все лучи, выходящие из F,
и отражающиеся от эллипсоида, попадают в точку F2; та-
таким образом, для наблюдателя в F2 весь эллипсоид будет све-
светиться.
Если изготовить зеркальный эллиптический отража-
отражатель, в одном из фокусов которого находится Солнце (нас-
(настоящее!), а в другом — котел с водой, то можно добиться
кипения воды в котле за счет сфокусированного отража-
отражателем излучения Солнца. Удивительного в этом ничего
нет: ведь отражатель имеет большую площадь и со всей его
поверхности солнечная энергия направляется на обогрев
котла. Такие солнечные установки уже сейчас имеют не-
некоторое применение. А в будущем может быть удастся,
построив огромный зеркальный отражатель (в форме час-
части эллипсоида, рис. 4.6, б), использовать энергию тех лу-
лучей, которые проходят мимо Земли?
Отметим еще, что фокальное свойство эллипса использу-
используется для аттракционов. В США имеются знаменитые «шеп-
«шепчущие галереи», которые представляют собой помещения с
эллипсоидальными потолками. Наиболее известна шепчу-
шепчущая галерея в Скульптурном зале Капитолия, без посеще-
посещения которой не обходится ни одна экскурсия. Прекрасная
комната шепотов, правда меньшего размера, имеется у
входа в бар в нижнем этаже Центрального вокзала в Нью-
Йорке. Двое людей, стоящих там лицом к стене в диаго-
диагонально противоположных углах квадратной площадки,
хорошо слышат друг друга, даже когда на площадке тол-
толпятся люди **). Аналогичный эффект наблюдается в Доме
композиторов в Дилижане (СССР). Впервые теория эффекта
«шепчущих галерей» была предложена известным физиком
лордом О. Н. Рэлеем в его статье 1910 г. «Проблема шеп-
шепчущей галереи» и в его классической книге «Теория звука».
Задача 4.3. Возьмем вырезанный из бумаги круг, поставим
ва нем точку А в любом месте, отличном от центра, и сложим крУ
так, чтобы точка А совпала с какой-либо точкой окружности. Ра"
зогнем листок и снова согнем, совместив точку А уже с друг0"
точкой окружности. Докажите, что если этот бумажный круг
*) Поэтому фокус и называется фокусом — по-латыни focus-'
это очаг.
**) Отметим, что эффект «шепчущих галерей» был известен еШ*
в древнем Китае (свидетельством чему являются остатки стен, гД
этот эффект хорошо проявляется).
66
перегибать так, чтобы его край все время проходил через точку А,
то огибающая линия сгиба будет эллипсом (рис. 4.7).
Решение. Обозначим буквой О центр круга. Пусть круг
сгибается по прямой XY; на точку А попадает точка В края круга,
при этом ЛВХЛТ и прямая AT делит отрезок АВ пополам. Обо-
Обозначим буквой С точку пересечения прямых XY и ОВ (рис. 4.7, б).
Тогда АС=ВС, поэтому OC-\-AC=OC+CB=R, где R — радиус
окружности. Следовательно, при любом сгибе круга сумма ОС-\-АС
Рис. 4.7
постоянна и равна его радиусу. Следовательно, геометрическое
место точек С, движущихся при перемещении точки В по окруж-
окружности, является эллипсом Э с фокусами в точках А и О. Из биль-
бильярдного свойства эллипса следует, что все линии сгиба касательны
к эллипсу Э, поэтому он является огибающей бесконечного множе-
множества линий сгиба XY.
Задача 4.4. а) Докажите, что тень на столе, отбрасываемая
лежащим на нем круглым мячом при его освещении точечным
источником света S, является эллипсом. Где находится фокус
этого эллипса?
б) Наклоните круглый цилиндрический стакан с водой под
некоторым углом. Докажите, что поверхность воды примет форму
эллипса.
Решение. Оба пункта задачи решаются одним приемом и
используют свойство равенства всех общих касательных к двум
заданным сферам. Приводимое доказательство предложено бель-
бельгийским математиком XIX века Ж. Данделеиом в 1822 г
а) Мяч вписан в конус с вершиной S, который пересекается с
плоскостью я (столом) по некоторой кривой у; А — точка касания
мяча с плоскостью п. Впишем в конус еще один шар, касающийся
плоскости я, но с другой стороны (рис. 4.8, а) в точке В. Пусть
М — произвольная точка кривой у. Через точку М и вершину
конуса S проведем прямую, касающуюся обоих шаров в точках
X и Y. Соединим точку М с точками А к В.
Отрезки МА и MX — касательные к мячу, проведенные из
одной точки, значит, МА—МХ. По той же причине MB=MY.
Следовательно,
причем длина отрезка XY не зависит от положения точки М на
Ча кривой у—XY и есть общая касательная к двум шарам! Итак,
^¦^-T-MB=const, поэтому у — эллипс, что и требовалось доказать.
Фокусами эллипса у являются точки А к В. в частности мяч ка-
касается cmo/ia e фокусе отбрасываемой им тени.
3*
67
б) Решение этой задачи почти дословно копирует решение
задачи а. Действительно, если граница поверхности воды есть
кривая у (рис. 4.8, б), то два вписанных в цилиндрический стакан
шара, касающиеся поверхности воды в точках А к В, облад--от
тем свойством, что для любой точки М?у справедливо равенство
MA + MB = MX + MY =» XY,
где XY — общая касательная к этим шарам* длина которой пе
вависит от выбора точки М иа у. Следовательно« поверхность воды
Рис. 4.8
в стакане дейстеительно имеет форму вллипса с фокусами в течках
А и В.
Используемые при доказательстве сфере называются сферами
Дснделена.
Теперь мы, основываясь на имеющихся знаниях геомет-
геометрических свойств эллипса, получим некоторые другие
бильярдные свойства эллипса.
Утверждение 2 (второе бильярдное свойство эл-
эллипса). Звенья траектории бильярдного шара, выпущенного
из произвольного фокуса эллипса,
асимптотически (в пределе) стремят-
стремятся к большой оси эллипса, т. е. после
некоторого числа ударов о борт движе-
движение шара будет происходить в сколь
угодно малой полосе, содержащей боль-
большую ось эллипса (рис. 4.9).
Доказательство можно
проводить по-разному, например вы-
вычислить, как меняется расстояние от точек ударов ша-
шара об эллипс до его большой оси и доказать затем, что
оно уменьшается быстрее, чем некоторая убывающая гео-
геометрическая прогрессия; или же доказать аналогичное
68
Рис. 4.9
утверждение для углов, образуемых звеньями траекто-
траектории с большой осью эллипса. Эти доказатетьства весьма
громоздки и желающие погут попробовать свои силы на их
самостоятельном поиске. В качестве «подсказки» может
служить указание к задаче 4.5.
Мы же поступим по-другому, не используя при доказа-
доказательстве никаких формул, а используя только достаточно
простые, но одновременно изящные рассуждения.
Пусть Ai, Bi и А 2 — три последовательные точки уда-
ударов шара о борт, причем Аг и А2 лежат на верхней полови-
половине эллипса, a Bi — на нижней (рис. 4.10). Тогда, как легко
Рис. 4.10
Ркс. 4.11
видеть, точка А2 лежит ниже точки Ai, т. е. ближе к боль-
большой оси, поскольку /_А\ВъА% целиком содержится в
/_AiBiM (M —левый конец большой оси эллипса).
Дальнейшие точки ударов об эллипс будем обозначать
BiyA3, Bs,Ait. . ., причем все точки Вп располагаются ниже
большой оси эллипса, а все Ah — выше нее. При этом каж-
каждая с^дугощая точка Ak будет находиться ниже предыду-
предыдущей Ai^ (поскольку Ak лежит на дуге эллипса Ak-iM),
но выше точки М — левого конца большой оси. Докажем,
что при /е->-оо точка Аи стремится к точке М,— это и будет
Доказывать утверждение 2.
Предположим, однако, что предельной точкой для пос-
последовательности Ль Л2, . . ., Ah, ... является не точка
М, а некоторая другая точка, которую обозначим Л^;
тогда А„ лежит выше большой оси (рис. 4.11). Это означа-
означает, чго все звенья траектории Bk-iAn с достаточно больши-
большими номерами k сколь угодно близко подходят к отрезку
В„Ак, где точка В^ лежит на нижней половине эллипса
и является пересечением прямой Л^ fi с эллипсом.
Что же произойдет, если бильярдный шар будет еыпу-
Щ°н из точки ?„ в точку AJ
Очевидно, если вся рассматриваемая нами траектория
сколь угодно близко подходила к отрезку А^В^, то теперь,
С9
двигаясь из В„ в Ат, шар должен отразиться от эллипса
в точке А„ и пойти в точности по тому же
отрезку АкВт, но в обратном направлении —
от Л„ к BJ Однако при этом шар непременно должен прой-
пройти опять через фокус Fi, поскольку он лежит на отрезке
А^В^, хотя по первому бильярдному свойству эллипса
шар "после отражения в точке Л„ пойдет по прямой A^F^ —
через второй фокус. Полученное противоречие дока
зывает, что А„ и М должны совпадать: предельное движение
шара должно происходить в сколь угодно малой окрест-
окрестности большой оси.
Замечание. В математических рассуждениях часто ис-
используется приведенный выше прием: для некоторого множества
{Ап} состояний произвольной системы, имеющего предельное
состояние Асе, рассматривается это предельное состояние системы
/4TC и затем исследуются его свойства, которые во многих случаях
Слизки к свойствам допредельных состояний системы Ап, А„+1, . ..
Зная эти свойства, можно делать соответствующие выводы о пове-
поведении системы в целом.
Вопрос. Обратим движение шара, выпущенного из
фокуса: звенья его траектории, близкие к большой оси эл-
эллипса, начнут удаляться от большой
оси. Не противоречит ли это утверж-
утверждению 2?
Задача 4.5. На горизонтальном
диаметре окружности с центром О выб-
выбраиы точки Ьг и О2, равноудаленные от О
(рис. 4.12). Для произвольной выбранной
точки Pj на окружности строятся точки
Р%, Ps. pi, • • •> такие, что хорды Р^,
Рис. 4.12 РгРз, РзРц • • • попеременно проходят
через точки Ог и О2. Доказать, что поло-
положение хорды PnPn+l при л-»-оо стре-
стремится к горизонтальному диаметру.
Указание. Можно провести рассуждения^ аналогич-
аналогичные проводимым при доказательстве утверждения 2. Но можно*
введя обозначения ^ Р,ОО1=<р1, ^ Р20О2=фг, доказать, что
iS-if = JT7tg ~|r> ^№?=0^11?, R — радиус окружности. Анало-
Аналогично вводятся углы фя=^ря001, (ft=Z. P*OO2 и т. д,| для ко-
которых выполнены те же соотношения
Таким образом, последовательность tg^, tg^, tg^ , .,, образует
?i ti it
бесконечную геометрическую прогрессию со знаменателем
70
я потому ее общий член стремится к 0. Следовательно,- Фп->-0 при
я->|», т. е. траектория стремится к горизонтальному отрезку.
Прежде чем перейти к третьему бильярдному свойству
эллипса, введем в рассмотрение еще одну кривую, тесно
связанную с эллипсом. Эта кривая называется гиперболой.
Определение. Гиперболой
называется множество точек М на
плоскости, для которых модуль раз-
разности расстояний до двух фиксиро-
фиксированных точек Ft и F2 — фокусов ги-
гиперболы— величина постоянная (рис.
4.13):
Рис. 4.13
Гипербола состоит из двух «кус-
«кусков», называемых ее ветвями. Как и для эллипса, для ги-
гиперболы имеет место
Оптическое свойство. Касательная I в про-
произвольной точке М гиперболы является биссектрисой угла
^FMF /\=/2 (рис. 4.13).
\MFl — MFS| = const.
Задача 4.6. Докажите справедливость оптического свой-
свойства гиперболы.
Указание. Решите задачу о нахождении на прямой /
такой точки, для которой разность расстояний от двух за-
заданных точек А. В наибольшая.
Мы приведем еще один способ доказательства оптиче-
оптического свойства гиперболы. Возьмем на гиперболе две очень
Рис. 4.14
Рис. 4.15
близкие точки М и Mi (рис. 4.14), и пусть Р — точка пере-
пересечения прямых FtMi и F2M, a Q — точка пересечения пря-
прямых F^Mi и FtM. Посмотрим теперь «через лупу» на че-
четырехугольник MiPMQ (рис. 4.15). Мы можем считать (при-
(приблизительно), что PMi\\MQ и РМ\\MiQ, так как точки Ft
и Л. находятся очень далеко — сравнительно с размерами
чегырехугольника MtPMQ. Итак, будем считать (прибли-
71
j. снно), что MiPMQ — параллелограмм. Проведем теперь
с кружности с центрами Fi и Fit проходящие через
точку Мъ Вблизи рассматриваемого параллелограмма
(см. рис. 4.15) дуги этих окружностей будут представлять-
представляться прямыми MiL и МгК, перпендикулярными сторонам
параллелограмма и поэтому
^(F1M1+LM)—{FtMl+KM)=(F1M1—FiM1)+(LM—KM).
Но так как F%M—F2M—FiMi—F^Mt (M и Mi лежат на
одной ветви гиперболы), то LM—KM. А тогда прямоуголь-
прямоугольные треугольники Д/(Л| Mi и /\ЬММЛ равны (по гипотену-
гипотенузе и катету) и, следовательно, ^/1=^/2. Это и завершает до-
доказательство оптического свойства гиперболы (для того
чтобы это «приближенное» рассуждение сделать точным,
нужно еще перейти к пределу при Mi-*-M).
Замечание. Для гиперболы оптическое свойство
можно сформулировать еще и так: лучи, выходящие из од-
одного фокуса, отражаясь от гиперболы, будут расходиться
Рис. 4.16
таким образом, что кажутся выходящими из второго фо-
фокуса.
Утверждение 3 (третье бильярдное свойство эл-
эллипса). Любая бильярдная траектория в эллипсе касается
либо эллипса, либо гиперболы, софокусных (т. е. с теми otce
фокусами) с данным эллипсом. Первый случай реализуется,
когда первое (а тем самым и произвольное) звено траектории
не пересекает отрезка фокусов, а второй случай — когда
первое (а тем самым и произвольное) звено траектории от-
отрезок фокусов пересекает. При этом во втором случае ссот-
ветствующие точки касания могут лежать не на сами*
звеньях ломаной, а на их продолжениях (рис. 4.16).
Доказательство. Пусть ЛИ и ААг — два пос-
последовательных звена бильярдной траектории в эллипсе,
причем отрезок АгА не пересекает отрезка фокусов Fv*
72
(рис. 4.17). Из первого бильярдного свойства эллипса следу-
следует, что /_AXAFX=/_A*AFi, поэтому отрезок АА^ также не
пересекает отрезка фокусов FiF2.
Возьмем точку Би симметричную Ft относительно AtA
ii проведем отрезок BiF2. Он пересечет АХА в точке Сх;
при этом u1=F1C1+CiFi=BiC1+CiFi=B1Fi, а для всякой
точки D ка отрезке АХА, отличной от d, выполнено нера-
неравенство ul=FlCi+C}Fz<:FlD-\-DFi.
Отсюда следует,' что эллипс, софокусный с исходным,
для которого сумма расстояний до А и F2 равна щ, к а-
с а е т с я АХА и притом в точке Си Аналогичное построе-
построение проделаем с отрезком АА2 (рис. 4.17), найдем точку
С2 и величину u2—FiC2-\-CzF2. Таким образом, точка Cs
лежит на софокусном эллипсе с const=
= w., касающемся отрезка ЛА2.
Рис. 4.17
Рис. 4.18
Докажем, что точки d и С2 лежат на одном и том
ж е эллипсе, т. е. докажем, что«1=и2. Для этого заметим,
что ABiAF^ABsAFt (по двум сторонам и углу между
ними — с вершиной А), откуда BtF^B.Fi, т.е. ih=u2,
что н требовалось. Игак, отрезки AtA и А~А2 касаются о д-
ного софокусного эллипса с константой u=BiF2=B2Fi.
Случай гиперболы рассматривается аналогично (раз-
(разберите его самостоятельно) — он возникает, когда отрезок
AiA пересекается, с отрезком FtF2 и j/_AtAA2 лежит в н у т-
Р и /JFiAF2. Утверждение 3 доказано.
Третье бильярдное свойство эллипса позволяет ввести
понятие каустической кривой, сокращенно каустики.
Определение. Пусть Q — произвольная выпук-
дая область на плоскости, ограниченная кривой Г, в которой
бильярдный шар описывает траекторию . . .P-tP0Pi. . .
Кривая у, лежащая внутри области Q, называется каусти-
*°й, если выполнено следующее условие: из того, что хотя
"Чодно звено PftPft+i траектории бильярда . . .P-iPnPi. . .
касается у, следует, что все остальные звенья этой тра-
екЮрии также касаются кривой у (рис. 4.18). Иными сло-
73
вами, траектория бильярдного шара после каждого отра-
отражения касается кривой у — каустики бильярда Q.
Простейшим примером каустики может служить ок-
окружность, которой касается траектория бильярдного шара
в круге. В круглом бильярде имеется только одно се-
семейство каустик — концентрические окружности.
Третье бильярдное свойство эллипса состоит в том, что
у эллиптического бильярда Q существует два семей-
семейства каустик: это эллипсы Гс и гиперболы Нс, софокусные
с Г — границей Q.
Оказывается, что все выпуклые области Q с достаточно
гладкой границей Г (т. е. такой, в каждой точке которой
можно провести касательную, причем в близких точках
Рис. 4.19
границы Г эти касательные образуют друг с другом малый
угол) имеют бесконечно много каустик, накапливающихся
к границе Г (этот сложный результат установлен В. Ф. Ла-
Лазуткиным). Отсюда вытекает, что бильярд в области Q на
плоскости, ограниченной гладкой выпуклой кривой Г,
не эргодичен (напомним, что в случае эргодичности шар про-
проводит в каждом кружочке внутри области Q время, пропор-
пропорциональное его площади- в нашем же случае есть участки
области Q, куда шар вообще не попадает). Например, би-
бильярдная траектория шара в эллипсе, не пересекающая
отрезка фокусов, может, самое большее, заполнить всюду
плотно кольцо между софокусными эллипсами Г (внешняя
граница кольца) и Гс (внутренняя граница кольца), но
никогда не попадет внутрь области, ограниченной эллип-
эллипсом (рис. 4.19, а). Более того, если Q — произвольная об-
область (а не только эллипс), Г — его граница, а Гс — какая-
то каустика в Q, то почти любая непериодическая бильярдной
74
траектория, касающаяся каустики Гс, всюду плотно за-
заполняет область между бортом бильярда Г и этой каусти-
каустикой («кривое кольцо»; рис. 4.19, б) *).
Более прост такой факт, замеченный В. Б. Минасяном.
Оказывается, если задана выпуклая кривая у и тре-
требуется найти все кривые Г, для которых у является каусти-
каустикой, то их можно получить следующим образом. Обозна-
Обозначим /(v) длину кривой у и зафиксируем число s, превосходя-
1 щее / (у). Тогда Г=ГК состоит из следующего множества то-
1 чек А: если из А провести ка-
касательные отрезки к у, найти
сумму длин этих отрезков и
части кривой у, заключенной
между их концами, то эта
сумма будет постоянной и
| равной s (рис. 4.20). Указан-
ный факт объясняется следую-
щим образом. a+b+y+z>*c+d+z+a)=a
' Если мы накинем на кри- Рис. 4.20
вую у веревочную петлю дли-
длины s, s>l(y), и натянем ее в точке А, то две касательные
| АХ и A Y из точки А к кривой у вместе с оставшейся частью
веревки между точками касания X и Y, плотно обтягиваю-
обтягивающей у, в сумме дадут s. Проведя через точку А прямую /,
образующую равные углы с отрезками ХА и YA, видим, что,
в силу выпуклости кривой у, при малом перемещении вле-
влево или вправо веревочной петли в натянутом состоянии точ-
точка А сходит с прямой / и оказывается в той же полуплоско-
полуплоскости относительно прямой /, в которой расположена вся кри-
кривая у. Это и означает, что точка А перемещается также по
выпуклой кривой Г, а поэтому прямая / является ка-
касательной к Г в точке А. Следовательно, ХА и AY — два
I последовательных звена бильярдной траектории
внутри кривой Г, касающиеся кривой у. Таким образом.
*) Доказательство этого факта довольно просто, но не совсем
элементарно. Достаточно доказать, что множество точек отражений
типичной бильярдной траектории всюду плотно иа внешней грани*
Че Г, а дальше действовать, как и в случае круглого бильярда. Ока-
Оказывается, кривую Г можно отобразить взаимно однозначно и взаимно
непрерывно на окружность так, что последовательные точки отрач
Жения бильярдной траектории перейдут в равноотстоящие точки на
0кРужности (это утверждение носит в математике, в более общей
Формулировке, название «теорема Данжуа»). Если множество то*
Чек на окружности всюду плотно ее заполняет, то и множество
Прообразов — точек излома рассматриваемой бильярдной траектории
Ьа кривой Г — заполняет кривую Г также всюду плотно.
73-
у действительно каустика для бильярда внутри области
ограниченной полученной кривой Г.
Подведем итог полученным сведениям о траекториях
эллиптического бильярда (правда, не все факты нами дока-
доказаны). Бильярдная траектория в эллипсе либо периодиче-
периодическая (замкнутая — к этим траекториям относятся и дв
оси эллипса), либо непериодическая. Во втором случае
выделяются траектории, звенья которых поочередно про-
проходят через фокусы — их поведение описывается вторым
бильярдным свойством. Остальные не-
непериодические траектории всюду плот-
плотно заполняют либо кольцо между эл-
эллипсами Г и Гс, либо область между
двумя ветвями софокусной гиперболы
Нс (именно всюду плотность мы и не
доказали).
В заключение параграфа укажем на
интересную связь между бильярдом в
эллипсе и свободным движением мате
риальной точки на поверхности элли-
эллипсоида. Движение частицы на эллипсои-
эллипсоиде происходит по кратчайшей кривой —
так называемой геодезической. Будем уст-
устремлять малую ось эллипсоида к нулю;
тогда эллипсоид в пределе превратится в эллипс, а тра-
траектория частицы по геодезической на эллипсоиде — в
бильярдную траекторию в этом эллипсе (рис. 4.21). При
этом разумно считать, что эллипс двусторонний и при каж-
каждом отражении бильярдная траектория переходит с однон
стороны эллипса на другую, двигаясь прямолинейно (по
геодезической).
Эта идея сведения бильярдной задачи к задаче про гео-
геодезические на «раздутом» бильярде, и обратно — задачи
про геодезические к бильярдной — играет большую роль
при исследовании динамики бильярда для областей, от-
отличных от внутренности эллипса, и является мостиком,
связывающим теорию динамических систем с дифференци-
дифференциальной геометрией.
Читателям, которым нравятся физико-математические
парадоксы, предлагаем в завершение «эллиптической» темы
подумать над следующим парадоксом, на первый взгляд
опровергающим второе начало термодинамики: в теплоизо-
теплоизолированной системе тел не может происходить пере-
передачи тепла от тела более холодного (или той же температу-
температуры) к телу более горячему.
76
Рис. 4.21
К пярадоксу приводит построение такой теплотолиро-
рэнной системы, в которой, напротив, одно из тел с перво-
первоначально одинаковой температурой начинает остывать, а
второе — нагреваться. Рассмотрим конструкцию, показан-
показанную на рис. 4.22 н состоящую из двух зеркальных половин
(ВС и AD) двух софокусных эллипсов и соединяющих их
прямолинейных зеркальных перегородок АВ и CD (Л и
D — концы малой полуоси внешнего эллипса, В и С —
внутреннего). В фокусах Fit Fz помещены два точечных ис-
источника тепла, первоначально имеющие равные тем-
температуры; зеркальные стенки конструк-
конструкции отражают все лучи (без какого-
либо поглощения). Согласно первому
бильярдному свойству эллипса, все теп-
тепловые лучи, выходящие из источника Fu
частью отразившись от стенки ВС, час-
частью — от стенки AD, попадают в точку
F2. Если бы все тепловые лучи, исхо-
исходящие из второго источника Fit попа-
попадали бы в точку Fi, то тогда оба источ-
источника не меняли бы со временем свою
температуру.
Однако н е в с е лучи из Fz попада-
попадают в Fi. На рис. 4.22 изображена одна из
траекторий луча F2MNFZ, который пос-
после отражения в точке М внешнего эллипса попадает в пе-
перегородку DC (двигаясь при этом в направлении фокуса
Ft), отражается от нее в точке N и ... попадает снова в
F2\ To же самое происходит и с лучами, попадающими сна-
сначала в перегородку, отражающимися от нее и после второго
отражения от внешнего эллипса снова попадающими в
F2 (на рис. 4.22 изображена одна из траекторий, отражаю-
отражающаяся от перегородки АВ).
В результате тело F2 получает, кроме лучей от тела Fu
часть своих собственных лучей, и поэтому начинает нагре-
нагреваться; тело же F% остывает. Налицо явное нарушение вто-
второго начала термодинамики. В чем же дело? (В качестве
Указания к разгадке парадокса предлагаем читателю 'за-
'заменить точечные источники Fi и F2 маленькими кружками
и посмотреть, как проходят отраженные лучи вблизи фо-
фокусов).
Рис. 4.22
77
§ 5*. Задача об освещении
невыпуклой области
Простые геометрические свойства эллипса,
описанные в предыдущем параграфе, могут быть использо-
использованы при исследовании следующего вопроса: каким наи-
наименьшим количеством точечных источников света (лампа-
чек) можно осветить внутренность ограниченной области Q
на плоскости? Граница dQ области Q представляет собой
Рис. 5.1
Рис. 5.2
замкнутую несамопересекающуюся кривую L на плоскости;
таким образом, двигаясь по кривой L, мы будем оставлять
область й все время по одну сторону от L.
Конечно же, если область Q является выпуклой (т. е.
с каждыми двумя ее точками А, В весь отрезок А В принад-
принадлежит области), то достаточно одной лампочки, которую
можно поместить в произвольном месте (рис. 5.1). Действи-
Действительно, если О — лампочка, а А—произвольная точка об-
области Q, то луч О А освещает точку Л; таким образом, все
точки области Q освещены лампочкой О.
А если область Q невыпукла? Тогда одной лампоч-
лампочки для освещения области может уже не хватить: на рис. 5.2
, Рис. 5.3
Рис. 5.4
лампочка О не освещает ни одной точки Л, лежащей в за-
заштрихованной области. Впрочем, на рис. 5.2 мы просто не-
неудачно выбрали местоположение для лампочки: точка на
рис. 5.3 уже выбрана более удачно, и лампочка О освещает
всю область Q.
Если область Q содержит такую точку О, из которой
«видны» все остальные ее точки (как, например, области
78
на рис. 5.3 и 5.4), то область Q называют звездчатой, а
точку О — «точкой видимости». К звездчатым областям
относятся, в частности, все выпуклые фигуры. Ясно, что
любую звездчатую область можно осветить одной лам-
лампочкой (где ее следует поместить?).
Предположим теперь, что Q — не звездчатая область:
никакая ее точка О не является «точкой видимости». Тогда
одна лампочка, в какое бы место области мы ее не помести-
поместили, полностью ее не осветит; для освещения Q нужно
больше одной лампочки. Можно предположить, что для
освещения хватит конечного числа лампочек, как
бы сложно ни была устроена область Я, лишь бы только ее
граница L—dQ не имела точек излома, или, как говорят,
была достаточно гладкой. Это подтверждается строгой тео-
теоремой, которую мы приведем в конце этого параграфа; в
ней даются необходимые и достаточные условия на струк-
структуру границы. Эти условия в математике коротко называ-
называются условиями гладкости гранту.
Пока что нами ничего не было сказано о бильярдных
свойствах области Quo связи сформулированного вопроса
об освещении с бильярдами.
Мы уже знаем, что движение луча света при отражении
от границы области,осуществляется по бильярдному закону
«углы падения и отражения равны». Поэтому, чтобы пос-
поставленный вопрос об освещении приобрел новое звучание,
будем считать, что граница области fi — зеркальная, и лю-
любой луч света при попадании на границу отражается от нее
по бильярдному закону. При такой постановке рассматри-
рассматриваемая задача, с одной стороны, должна, по-видимому, уп-
упроститься, поскольку многие невыпуклые области, грани-
границы которых раньше «поглощали» свет и которые не могли
быть освещены одной лампочкой, теперь, обладая зеркаль-
зеркальной границей, позволяют лучам проникать в «запретные»
зоны и освещать их; а, с другой стороны, задача должна
Усложниться, так как теперь мы вынуждены следить за всем
бесконечным ходом каждого луча, исходящего нз точечного
источника.
Итак, считая с этого момента и до конца, параграфа об-
область Q зеркальной, попробуем дать предварительный, ги-
гипотетический ответ на исходный вопрос.
Ответ 1. Для освещения любой ограниченной области Q
достаточно одной лампочки.
Обсудим этот ответ. Мы дали его в надежде на то, что
некоторый луч, выпущенный из лампочки, рано или позд-
поздно после многократных отражений от границы, попадет
79
б наперед заданную точку области. Напр:; '.ер, еслл Q
невыпуклый многоугольник (рис. 5.5), то лучи, выпущен-
выпущенные из произвольного точечного источника О внутри него,
полностью осветят этот многоугольник, как бы «хитро»
ни была устроена его граница. Это утверждение про много-
многоугольник все специалисты-математики, занимающиеся
бильярдными проблемами, считают справедливым, хотя
строго оно до сих лор не доказано. (Некоторые вопросы,
связанные с бильярдами в многоугольниках, приводят
порой к неожиданным результатам — об
этом подробнее рассказано в четвертой
части книги.)
Мы же будем считать теперь, что
граница дО, не имеет изломов, т. е. в
каждой точке границы можно провести
касательную. Казалось бы, если для ос-
освещения невыпуклого многоугольника,
как было сказано (но не доказано), хва-
хватит одной лампочки, то для области Q,
получающейся из многоугольника
«скруглением» его вершин, одной лампочки хватит тем бо-
более.
Однако гипотетический ответ 1, являясь (с большой веро
ятностью) верным для многоугольников, неверен в общем слу
чае — для областей с гладкой границей. В замечательней
Рис. 5.5
Рис. 5.6
примере области, для освещения которой нужно много лам-
лампочек, используется только знание того, что выпущенньЛ
из одного фокуса эллипса луч света после отражения прой-
пройдет через второй его фокус, а луч, выпущенный не из фо-
фокуса, никогда не пройдет ни через один фокус (рис. 5.6, а, 6).
Сформулируем существование такой области в виде утверь
дения.
Утверждение 1 Для любого натурального я
существует область с гладкой границей, для освещения ко-
которой необходимо более п точечных источников (лампо-
чек).
Построим явно эту обль^гь п и докаже- для нее ут рж-
1. Построение производится в несколько этапов *).
Зтап 1. Рассмотрим верхнюю половину эллипса с боль-
большой осью АВ, дополненную двумя «мочками», ограниченны-
ограниченными полуокружностями, соединяющими фокусы Fi и /¦"., с
точками А и В (рис. 5.7). Полу-
Полученной области fii дадим назва-
название «телефон».
Лемма 1. Никакой луч,
выходящий из левой мочки те-
телефона fii, никогда не попадет
на отрезок FiFs.
Доказательство.
Действительно, рассмотрим пер-
первое отражение луча, выпущенного из левой мочки (рис.
5.8, а). Как падающий, так и отраженный лучи лежат
вне Д FiXF2, поэтому отраженный луч не пересечет
отрезок FiFs. Если Y — вторая точка отражения
Левая
мочка
Правая
мочка
Рис. 5.7
Рис. 5.8
(рис. 5.8, б), то падающий и отраженный лучи в точке У
лежат вне Д/^УТ^ и опять-таки не пересекают отрезок
фокусов FiFss. Вообще, если первоначально выпущенный
из мочки луч отражается от точки Z границы ойь лежащей
на эллипсе (т. е. выше прямой FiFt), то он и отраженный
луч обязательно расположены вне /\FiZF?. Следовательно,
выпущенный из левой мочки луч в конце концов попадет в
правую мочку, ни разу не пересекая отрезка фокусов FxF^,
после одного или нескольких отражений в правой мочке
луч до вторичного попадания в левую мочку также ни разу
не пересечет отрезка Р^Рг, что следует из приведенного
выше рассуждения и полной равноправности обеих мочек.
Это и доказывает лемму 1.
Приведем еще одно столь же простое, но более изящное, до-
доказательство леммы 1. Отбросим мысленно нижнюю границу эб-
*) На каждом этапе строится область, граница которой в мес-
Тах соединения криволинейных и прямолинейных частей затем
•сглаживается» (это особо не оговаривается в дальнейшем).
ласти fit (обе полуокружности мочек и отрезок фокусов)* и допол-
дополним телефон нижней половиной эллипса. Мы не знаем, как луч
света ведет себя в мочке, ио как только он выходит из нее в верх-
верхнюю половину эллипса, будем считать, что он отразился от нижней
(фиктивной) половины эллипса в соответствующей точке С (рис. 5.9).
Но, как мы знаем из § 4, любая бильярдная траектория в эллипсе,
одно звено которой не пересекает FlF2, обладает тем свойством,
что и в с е ее звенья не пересекают отрезка фокусов FjF2 (поскольку
все звеиьи касаются софокусного эллипса, содержащего отрезок
/^Fa внутри себя). В частности, этим свойством обладают звенья
в верхней части эллипса, которые в действительности являются
звеньями траектории луча света, выпущенного из левой мочки;
этим доказательство леммы 1 и завершается.
Левая
мочка
Правая
ночка
Рис. 5.9
Рис. б. 10
Этап 2. От телефона Qi легко перейти к зеркальной об-
области Q2, которая не может быть освещена одной лампочкой.
Построим сначала область Qi, изображенную на
рис. 5.10; она отличается от области Qi тем, что середина
отрезка FiFt заменена неглубокой «ямкой» в виде полуок-
полуокружности.
Лемма 2. Если лампочка находится в одной из мочек
или же в ямке, то она не освещает область Q[ полностью.
Доказательство. Если лампочка расположена
в одной из мочек, то ни один луч, исходящий из нее, не пе-
пересекает отрезка F\Fa по лемме 1 и тем самым не попадает
в ямку. Следовательно, в этом случае ямка вообще не ос-
освещена.
Пусть теперь лампочка О находится в ямке. Предполо-
Предположим, что какой-то луч у, исходящий из лампочки, после
некоторого числа отражений от границы dQ't попал в мочку,
для определенности в левую. Если точка Р мочки освещена
этим лучом, то перенесем лампочку О из ямки в точку Р-
Тогда один из лучей, выходящих из лампочки Р, геометри-
геометрическая траектория которого совпадает с траекторией луча У
(изменено только направление движения), попадет в
ямку,—и осветит точку О в ней. Это противоречит лемме
1 — никакой луч, исходящий из точки Р, не может попасть
в ямку. Лемма 2 доказана.
82
Задача Б.1. Можно ли область fij осветить тремя лампоч-
лампочками?
Ответ. Можно, и даже напрямую (т.'е. без отражений от
границы) — поскольку ili можно представить в виде объединения
трех звездчатых областей (каких?).
Задача 5.2. Можно ли область fii осветить одной лам-
лампочкой?
Ответ. Можно. Указание. Поместите лампочку в
точку М —середину дуги эллипса (рис, Б.П.а).
Рис. б. И
Решение. Для доказательства того, что лампочка, поме-
помещенная в середину М дуги эллипса, осветит всю область Qi, до-
достаточно доказать, что полностью будут освещены обе мочки те-
телефона (вся остальная часть области Q[ освещается лампочкой
напрямую).
Рассмотрим для доказательства набор специально выбран-
выбранных лучей, выходящих из М. Первый луч выберем выходящим из
М в сторону центра Ох левой мочки (рис. 5.11, б). Проходя через
центр полуокружности О1( луч MOt отражается от нее в точке Ki
и движется в противоположном направлении К\М, попадает в
точку М, отражается от дуги эллипса в этой точке, проходит затем
через центр О2 правой мочки (полуокружности) и, отразившись
от правой полуокружности в точке /fs, движется опять в обратном
направлении К^М, чтобы после отражения в точке М начать снова
двигаться по МКу. Таким образом, MKiMK^M — периодическая
бильярдная траектория.
В качестве второго луча, выпущенного из лампочки М, вы-
выберем такой, который после отражения в точке Л^ левой мочки
пройдет через левый фокус эллипса F1# Такой луч у найдется,
поскольку луч, идущий из М в А — левый конец большой оси
(рис. 5.11), после отражения попадет в некоторую точку левой
мочки, а луч, идущий из М в Ki, отражается в Ki в обратном на-
направлении; таким образом, некоторый луч y=MNlt лежащий
между лучами МА и MKlt после отражения пройдет через Fj.
Далее, луч v отразится от дуги эллипса (в точке N2) и попадет
во второй фокус эллипса F2.
Наконец, рассмотрим все лучи, расположенные между
лучом Y=AfiV! и лучом MKi. Поскольку лучи у и МКг определяют
на правой мочке точки F2 и К2, то все лучи между ними заполняют
Целиком всю дугу F2/B полуокружности. Соединив F2 и /С2 отрез-
отрезам, находим, что все рассмотренные лучи освещают полностью
сегмент круга Fa/B (он заштрихован на рис, 5,11, б),
вз
Следовательно, вся правая ночка области Qt' полностью ос-
освещена лампочкой М. Из симметрии следует, что по гем же сооб-
соображениям освещена и вся левая мочка. Итак, область fii полностью
г свешена одной лампочкой, помещенной в точку М. Задача решена.
Переходим к построению области Q2. Область fi2 стро-
строится из двух экземпляров области Q\ следующим образом.
В первом экземпляре — обозначим его Q] — вытягиваем
ямку в «трубу» (рис. 5.12, а), а во втором экземпляре Q[ —
обозначим его Q\ — вытягиваем в «трубу» одну из мочек
Труба
5.12
(рис. 5.12, б). Область ?22 получается «склеиванием» об
ластей Q\ и Q\ по общим отрезкам XY их труб (рис. 5.12, в).
Эта область содержит три мочки, одну трубу и одну ямку.
Лемма 3. Область Q2 не может быть освещена одной
лампочкой.
Доказательство. Так как йг—ЗД U ?2i. то лам-
лампочка может располагаться либо в области Q), либо в облас-
области Q\ (отрезок XY считаем общим для обеих этих областей).
Разберем отдельно указанные два случая.
Если лампочка находится в области Q{ и, быть может,
даже ее освещает (см. задачу 5.2), то она никак не может
осветить целиком область Q^. Действительно, область fii
может освещаться исключительно лучами, идущими от лам-
лампочки через трубу — все эти лучи пересекают отрезок XV
и попадают в О.\. Однако из леммы 2 следует, что ни один из
этих лучен не попадает в ямку области Qi\. Итак, в первом
случае в области Q\ неосвещенным местом является ямка.
Если же лампочка находится в области Q\, то лучи, про-
проникающие в область п\, опять-таки все проходят через тру-
трубу, т. е. выходят из бывшей ямки области Q\. И снова, по
лемме 2 получаем, что все эти лучи не попадут в мочки об-
области Q}. Итак, во втором случае неосвещенным местом об-
области Q2 оказываются обе мочки области Q}. Лемма 3 дока-
доказана.
Зтап 3. Сейчас мы модернизируем область Q2 и постро-
построим область ?2, о которой говорится в утверждении 1.
Для этого не будем ограничивать количество областей
Й,', из которых будет построена область Q. Не будем такясе
подробно описывать построение области Q, а отошлем чита-
читателя сразу к рис. 5.13, на котором изображена структура
области п.
Область Q содержит большое число мочек и труб, а так.
же одну ямку. Она состоит из объединения областей fi{,
Область ¦
Рис. 5.13
в ка>к„\ю из которых включается часть трубы, ограничен-
ограниченная сбрезком XY с соответствующими индексами. Поэтому
если лампочка О находится в области Q[, то она не может
ответить целиком ни область fij (при />1), ни область Ql\l
(при i<2N), так как лучи, проникающие в эти области из
п\ через соединяющие их трубы, либо не осветят мочек, либо
не осветят ямки. (Подробное доказательство аналогично
приведенному в лемме 3.)
Следовательно, на каждую область Q[, i=l, 2, . . ., 2N,
нужно для ее освещения не менее одной лампочки,
которая должна располагаться в этой области. Значит, для
полного освещения всей области Q нужно не менее 2N лам-
лампочек. Поэтому, если 2N>n, то область Q не может быть ос-
освещена п лампочками. Утверждение 1, таким образом, пол-
Hi стыо доказано.
После сказанного мы можем дать второй гипотетический
ответ на поставленный вопрос о числе лампочек.
Ответ 2. Для освещения любой ограниченной области Q
всегда достаточно конечного числа лампочек.
Построенный пример показывает, что это конечное число
лампочек может оказаться сколь угодно большим.
Однако и ответ 2 оказывается неверным! В действитель-
действительности справедливо
Утверждение 2. Существует такая ограничен-
ограниченная область Q*, для освещения которой необходимо беско-
бесконечно много лампочек.
85
Докажем это утверждение. Рассмотрим рис. 5.13 и от-
отбросим в нем всю правую часть, идущую после многоточия.
Многоточие на возникшей картинке будет означать теперь,
что «телефоны» Q\, fi'j, О,, . . . продолжаются одинаковым
образом вправо до бесконечности. Как следует из утверж-
утверждения 1, полученную бесконечную — неограниченную —
область нельзя осветить конечным числом лампочек.
Однако в утверждении 2 говорится об ограниченной области
Q*.
Получить ее из построенной неограниченной области
несложно, если применить известный в математике прием
Рис. 5.14
«сжатия»: он состоит в том, что вместо одинаковых (кон-
(конгруэнтных) областей п[ рассматриваются области, убываю-
убывающие в своих размерах по геометрической прогрессии, на-
например, со знаменателем 2. Итак, считаем область г12&\
вдвое меньшей области Q\, область l/tQl — вдвое меньшей
области 1/iQ\ и так далее (рис. 5.14).
Полученная в результате область Q* имеет конечные раз-
размеры (по горизонтали размер примерно вдвое больший, чем
горизонтальный размер области Q\) и обладает тем свой-
свойством, что для ее освещения нужно бесконечно много лам-
лампочек. Утверждение 2 доказано.
Отметим, что область Q* имеет на границе особую
точку Р; в ней, как говорят математики, нарушается глад-
гладкость границы. Нетрудно видеть, что никакой луч, выпущен-
выпущенный из произвольной точки области й*, не достигает точки
Р (объясните, почему).
Для каких ограниченных областей Q ответ 2 все оке
справедлив?
Здесь мы вынуждены вернуться к началу этого параграфа
и дать ответ на поставленный вопрос об устройстве границы
dQ области Q, которую можно осветить конечным числом
лампочек напрямую (т. е. без отражений от границы)-
Ясно, что ответ на этот вопрос будет одновременно ответом
и на поставленный вопрос про зеркальную область, посколь-
поскольку если зеркальную область нельзя осветить конечным чис-
86
лом лампочек (как, например, область О* на рис. 5.14),
то и напрямую ее осветить нельзя; если же область Q мож-
можно осветить конечным числом лампочек напрямую, то и
зеркальная область Q освещается тем же (конечным) на-
набором лампочек (а может быть, и меньшим набором).
Выше мы отмечали, что звездчатая область освещается
одной лампочкой, помещенной веточку видимости». Любая
область, которая может быть разбита на конечное число
звездчатых областей, освещается конечным числом лампочек
напрямую — по числу звездчатых областей разбиения.
Отсюда следует, что область Q* на рис. 5.14 не может быть
разбита на конечное число звездчатых областей
(объясните, почему). Все дело в том, что граница dQ*
имеет особую точку Р — в ней нарушается гладкость гра-
границы. Оказывается, что если все точки границы области
Q — неособые (точное определение см. ниже), то Q может
быть покрыта конечным числом звездчатых областей,
и тем самым, освещена конечным числом лампочек.
Дадим точное определение неособой точки и приведем
формулировку утверждения о разбиении области на звезд-
звездчатые множества.
Определение. Точка Р границы дп называется
неособой, если, во-первых, через Р можно провести
касательную 1Р (прямую, имеющую g границей dQ только
одну общую точку — Р), во-вторых, через близкие к Р точ-
точки границы Q также можно провести касательные lQ, и,
^-третьих, угол a=lQ lp между касательными lQ и 1Р яв-
является непрерывной функцией длины дуги ^QP,
проходящей от точки Q к точке Р по границе дп (рис.
^•15, а). Если все точки границы неособые, то говорят, что
граница дп имеет гладкость С1 и называют ее ^-гладкой
границей.
Геометрический смысл О-гладкой границы dQ состоит
в том, что на малой дуге ^АВ границы все касательные ма-
л° отличаются друг от друга, т. е. все попарные углы меж-
ДУ ними малы и тем меньше, чем ближе друг к другу точки
87
А и В (рнс. 5.15, б). Это означает, что пересечение круга Dp
с центром Р ? dfi с областью Q мало отличается от пересече
ния круга Dp с полуплоскостью, ограниченной касательно
в точке Р (рис. 5.15, е).
Утверждение 3. Любая ограниченная область Q
с О-гладкой границей дп является объединением конечного
числа звездчатых множеств.
Доказательство. Для каждой точки Р области
Q выберем открытый круг *) Dp с центром Р, це-
л и к о м лежащий в области Q, если Р — ее внутренняя
точка, и пересекающий Q по звездчатому множест-
множеству, если Р лежит на границе. Последнее можно сделать,
поскольку Р — неособая точка границы и пересече-
пересечение D^(\Q мало отличается от пересечения круга D,, с по-
полуплоскостью, ограниченной касательной в точке Р
(рис. 5.15, е).
Таким образом, вся область Q оказывается покрытой
бесконечным числом открытых кругов Dp, центры которых
лежат в й или на границе <ЭО. Из математического анализа
известно, что из этого покрытия можно выбрать конечное чис-
число элементов (кругов), также полностью покрывающих всю
область Q (поскольку Q — замкнутое**) и ограниченное
множество на плоскости). Рассматривая пересечения этих
кругов с областью Q, мы видим, что они являются звезд-
звездчатыми множествами. Таким образом, получаем покры-
покрытие области Q конечным числом звездчатых множеств, что и
требовалось доказать.
Сформулируем окончательный результат в виде тео-
теоремы.
Теорема. Зеркальная область Q, ограниченная зам-
замкнутой кривой L без изломов (т. е. такой, в каждой точке
которой можно провести единственную касательную), мо-
может быть освещена (и даже напрямую) конечным набором
лампочек, если L является кривой гладкости С1. Если же хо-
хотя бы одна точка кривой L является особой, конечного на-
набора лампочек для освещения области Q может не хва-
хватить.
*) То есть круг без границы.
**) Множество называется замкнутым, если все его предельные
точки принадлежат самому множеству. Таким множеством являет-
является, в частности, область с границей. (Напомним, что предельная
точка множества S — это такая точка, в любой окрестности которой
расположено бесконечно много точек множества S.)
88
§ 6. Экстремальные свойства
бильярдных траекторий.
Принцип Ферма и теорема Биркгсфа
Начнем параграф с ответа на следующий воп-
вопрос, уже поставленный в § 4.
Вопрос. Если у — произвольная кривая на плоско-
плоскости, А и В — mwxu, лежащие по одну сторону от у, то
где следует выбрать точку М на кривой у, чтобы сумма
АМ+ВМ длин отрезков AM и ВМ была минимальной . . .
или максимальной?
Поясним предварительно, почему в вопросе фигурирует
как минимум суммы АМ+ВМ, так и ее максимум.
1
-У
в
'А
Рис. 6.2
Если кривая у обращена своей выпуклостью в сторону
точек А и В (рис. 6.1), то для траектории АМВ нетрудно
опять вывести «принцип наименьшего пути» (справедливый
в случае, когда у — прямая): путь АМВ.кратчайший, если
отрезки AM и ВМ образуют с касательной к кривой у
в точке М равные углы. Действительно, вся кривая у ле-
лежит по одну сторону от своей касательной I, а точки А и
В — по другую, стало быть, для произвольной точки М' € У,
отличной от М, имеем ^
АМ' + М'В> АМ + МВ.
Однако, если у обращена к точкам Л и В не выпуклостью,
а вогнутостью (рис. 6.2), то приведенное рассуждение не
проходит: кривая у вместе с точками А и В лежит по одну
сторону от касательной / и выписанное выше неравенство
становится неверным. Сейчас вы увидите, что от суммы
АМ+МВ нельзя требовать только ее минимальности, а
правильно говорить об экстремальности, подразумевая так-
*е другой крайний случай —максимальность суммы АМ+
+МВ.
Итак, мы ищем на кривой у такую точку (или точки) М,
Чтобы сумма расстояний от двух заданных точек Л и В,
"ежащих по одну сторону от у, была экстремаль-
н°й (минимальной или максимальной).
89
Если у — эллипс с фокусами А и В, то в качестве точки Af
можно взять любую точку эллипса: сумма АМ+МВ здесь
всегда одна и та же. Если же у — не эллипс с фокусами А
и В, то рассмотрим для каждого числа s, большего длины
отрезка АВ, множество Г8 таких точек М, для которых
AM+MB=s. Тогда Г8 — эллипс с фокусами А и В, а
множество всех таких эллипсов {Г8} образует семейство
софокусных эллипсов: чем больше s, тем больше
размеры этих эллипсов и меньше их эксцентриситеты.
В прямоугольной системе координат Оху софокусные эллипсы
с центром О записываются единой формулой, зависящей от одного
параметра t:
-?- + -?- = 1.
где а и b — фиксированные числа. То, что для разных t эти эл-
эллипсы имеют одинаковые фокусы, следует из рис, 4.2 и из постоян-
постоянства разностей квадратов полуосей:
поскольку все эти разности равны с2 — квадрату расстояния от
центра до фокуса эллипса (докажите это); при <=0 получаем эллипс
с полуосями а и b и эксцентриситетом е= с/а. У эллипса, внутри кото-
которого расположен софокусный эллипс, эксцентриситет меньше, так
как величина с у них одинакова, а у внутреннего эллипса большая
полуось меньше {e2 = c/Va2 + f2 > et = c/Ya2-\-ti при t2 < <i)-
Докажем, что искомой экстремальной точкой М (еслг
она существует) на у является такая точка, в которой один
1\
из эллипсов 1\о указанного семейства касается кривой у.
а
6
В самом деле, если кривая у по обе стороны от точки
касания М лежит вне касающегося ее эллипса *л
(рис. 6.3, а), то сумма АМ+ВМ минимальна, поскольку лю-
любая другая точка М' на у лежит одновременно на co^oi^/r"
ном эллипсе Г,, са >s0, т. е. St^AM' +M'B>sB=AM +m^
Если же кривая у вблизи точки М лежит в н у т Р
касающегося ее в М эллипса TSo (рис. 6.3, б), то длина л
90
маной АМВ, равная s0, больше чем длина любой другой ло-
ломаной АМ'В, так как точка ЛГ лежит на софокусном эл-
эллипсе ГЯ) с Si<So-
«Смешанный случай», изображенный на рис. 6.3, в,
не дает ни минимума, ни максимума. Экстремум следует
понимать, как сказано выше — по сравнению с б л и з к и-
м и к М точками (такой экстремум называют локальным).
Если предположить, что мы умеем строить семейство
софокусных эллипсов и находить точки касания эллипсов
этого семейства с кривой у, то утверждение можно считать
доказанным.
Для наших целей вполне достаточно такого (принци-
(принципиально возможного, но с трудом осуществимого на прак-
практике) способа отыскания локальных минимумов и максиму-
максимумов длины ломаной АМВ, и мы сейчас извлечем из этого
способа замечательные следствия.
Из первого бильярдного свойства эллипса следует
Общий принцип экстремальности
бильярдной траектории. Если ломаная АМВ
с данными концами А и В и точкой излома М, принадлежа-
принадлежащей данной кривой у, имеет наименьшую или наибольшую
(т. е. экстремальную) длину среди всех близких к
ней двузвенных ломаных с точками излома на кривой у
и т е м и же концами А и В, то эта ломаная является тра-
траекторией бильярдного шара (бильярдной траекторией),
ведущей из точки А в точку В после отражения от борта,
имеющего форму кривой у.
Доказательство. Кривая у в точке М касается
какого-то эллипса Г,о с фокусами А и В. Следовательно, ка-
касательная / к кривой"? в точке М является одновременно и
касательной к эллипсу Г5е. Но углы, образованные звенья-
звеньями AM и ВМ ломаной АМВ о. касательной / к эллипсу, рав-
равны между совой. Это и означает, что АМВ — бильярдная
траектория с бортом у, что и требовалось доказать.
Задача 6.1. Привести пример кривой Yi показывающий,
что обращение принципа экстремальности бильярдной траектории
неверно: может случиться так, что бильярдная траектория
АМВ не является ии локально минимальной, ни локально мак-
максимальной.
Задача 6.2. Доказать, что если кривая у выпукла,
т.е. целиком лежит по одну сторону от своей касательной, то об-
Ращенне принципа экстремальности бильярдной траектории спра-
Ведливо: любая бильярдная траектория АМВ в этом случае имеет
"Ли локально минимальную, или локально максимальную длину.
Приведем пример, показывающий, что для выпук-
выпуклой кривой у могут реализовываться одновремен-
91
н о и минимальные, и максимальные бильярдные двухзвен-
н^е чочаные АМВ Пусть у — окружность, АиВ — фикси-
фиксированные точки в'нутри этой окружности. Тогда из семей-
<чва {Ts} софокусных эллипсов с фокусами Л и Б выделя-
выделяются четыре эллипса VSi , Г5>, Т$з, TS)y два из которых
касаются окружности у внутренним образом — пусть это
эт1ип ы Vs и Ts, а два — эллипсы TSa и Ts —внеш-
—внешни.! образом. Возникшие четыре точки касания4 Ми М2,
MSi Alt (рис. 6.4) являются точками столкновения с бортог
у бильярдного шара, который из точки А после одного удара
° б°РТ П0ПаДает в «««У В,
и доставляющие: точки Mi и
M2 — локальный минимум
длины ломаной АМВ, точки
Ма и Mi — локальный мак-
максимум этой длины.
Принцип экстремальности
бильярдной траектории яв-
- , . ляется частным (и простей-
4(maE; шим) случаем одного из основ-
Рис. 6.4 иых принципов классической
механики и оптики— принци-
принципа наш гньшего действия, или экстремального принципа Фер-
Ферма {ъ оптике он носит название принципа Мопертюи). В оп-
оптике принцип Ферма (Мопертюи) состоит в том, что свет вы-
выбирает из всех возможных путей, соединяющих две дани:-
точки, тот путь, который требует наименьшего вр
мепн для его прохождения. Применительно к бильяр
этот принцип можно сформулировать так: бильярдный и1
«умный» и выбирает самый короткий из всех возможнч
путей (мы считаем раз и навсегда скорость бильярдного ша-
шара постоянной, поэтому минимальность длины его тра-
траектории эквивалентна минимальности времени его движ.
ния но этой траектории). Фактически этот принцип для
бильярдного шара нами обоснован выше чисто математи-
математически Оказывается, всю классическую механику можно
строиib как геометрическую оптику многомерного прост-
пространства, основываясь именно на принципе Ферма, носяще-
носящего в механике название «принцип Гамильтона» (подробнее
об этом см., например, книгу В. W. Арнольда «Математи-
«Математические методы классической механики» (М.: Наука, 19'у>
с. 217 и далее)). Но эта аналогия оптики и механики не-
неэлем нтарна (она требует развитой техники дифферент1'
ального исчисления) и останавливаться на ней мы не буДеМ>
а обратимся к более простой и наглядной аналогии.
92
Задача 6.3. Докажите принцип обратимости', если биль-
бильярдный шар попал из точки А в точку В после нескольких отра-
отражений от борта y бильярдного стола, то при его движении из точки
В (^противоположной начальной скоростью шар попадет в точку А,
двигаясь точно по тому же пути, но в обратном направлении.
Принцип обратимости мы уже использовали в рассуждениях § Б.
Принцип Ферма позволяет чнсто математически доказать
закон Снеллиуса — Декарта о преломлении луча света на
границе двух оптических сред с разной плотностью («си-
(«синус угла падения луча света в первой среде и синус угла
преломления во второй среде относятся как оптические
плотности этих сред»; рис. 6.5), а также доказать, что от-
отношение оптических плотностей I
двух сред равно отношению скорое- Ч5
тен движения света в них. На этих
доказательствах мы также не будем :
здесь останавливаться, они увели '.
бы нас далеко от бильярдной темы. .'; .
Отметим лишь, что принцип Фер '•
ма, в отличие от принципа причин- •
ности в физике (суть которого сое- ?^
тоит в том, что свет последователь- sin 0Z "г vz
но идет из одной точки простран- Рис. 6.5
ства в другую, затем в следующую и
т. д.) совсем иначе объясняет причину явлений в природе.
Вместо причинной обусловленности, когда из одного на-
нашего действия вытекает другое, из того — третье и т. д.,
этот принцип говорит следующее: в данной ситуации сеет
выбирает путь g наименьшим, или, правильнее, с экстре-
экстремальным временем прохождения. Но как удается свету
выбирать такой путь? Разведывает он что ли сосед-
соседние пути и сравнивает их потом друг с другом? В некотором
смысле так и происходит. Эта способность света
связана с понятием длины волны и поэтому ее нельзя по-
понять в рамках геометрической оптики; длина волны, грубо
говоря, есть тот отрезок впереди лежащего пути, который
свет может «почувствовать» и сравнить с соседними путя-
путями *). Бильярдный шар является как бы математической
*) Ответ на поставленный вопрос о свете дает квантовая меха-
"нка, а ответ на вопрос, почему при отражении луча света от зерка-
"а время его движения от источника А до детектора В также экстре-
экстремально (иными словами, почему при отражении от зеркала угол
прения равен углу отражения) дает КЭД — квантовая электродина-
электродинамика (см. недавно вышедшую в «Библиотечке «Квант» книгу извест-
известно американского физика Ричарда Фейнмана «КЭД. Странная те-
Рия света и вещества» (вып. 66. М.: Наука, 1988)).
93
абстракцией светового луча, во внутреннее состояние кото-
которой заложена «длина волны», позволяющая шару выбирать
кратчайший (экстремальный) путь среди всех близких
(«виртуальных», т. е. возможных) путей.
Принцип Ферма приводит также к так называемому
принципу Гюйгенса, который, в свою очередь, объясняет,
почему кратчайшими путями распространения света явля-
являются лучи. Обсудим немного этот момент с математиче-
математических позиций.
Пусть в точке А расположен источник света. Рассмот-
Рассмотрим множество всех точек X, до которых свет из точки А
Рис. 6.6
может дойти за время, не большее заданного U Граница
ФА (() этого множества называется волновым фронтом точ-
точки А через время t и состоит из точек, до которых свет может
дойти за время t и не может дойти быстрее. Мы не предпо-
предполагаем, что среда, в которой распространяется свет, одно-
однородная, поэтому волновой фронт ФЛ @ не обязательно яв-
является окружностью. Между волновыми фронтами, соот-
соответствующими разным значениям t, имеется замечательное
соотношение, открытое Гюйгенсом, которое и носит назва-
название принципа Гюйгенса. Этот принцип мы сформулируем
в виде теоремы.
Теорема Гюйгенса. Рассмотрим волновой
фронт ФА (/) точки А через время t. Построим для каждой
точки X этого фронта, считая их источниками света, вол-
волновой фронт Фх(т) через время т. Тогда волновой фронт
Ф л(^+ т) точки А через время t+t будет огибать все построен-
построенные фронты Фх(т) (X?OA{t); рис. 6.6, а).
Доказательство. Рассмотрим точку У на фрон-
теФ А (t+r) точки А через время t+r. Тогда существует путь
из Л в У, по которому время распространения света РавН°
/+т, и нет более короткого пути. Рассмотрим на этом пут
точку X, до которой свет идет время t. Никакого боле
короткого пути из Л в X не может быть, так каК
противном случае путь из Л в У не был бы кратчайшим (е
94
можно было бы укоротить). Значит, точка X лежит на фронте
фА (t). Точно так же, путь XY свет проходит за время т,
и из точки X в точку У нет более короткого пути. Следова-
Следовательно, точка У лежит на фронте Фх(т) точки X за
время т.
Докажем, что фронты ФА (t+r) и Фх(т) касаются
друг друга в точке У, а не пересекаются. Если бы они пере-
пересекались (рис. 6.6, в), то в некоторые точки фронта ФА(И-т)
луч мог бы из точки X добраться за время, меньшее т, а
значит, из точки А — за время, меньшее И-т. Это проти-
противоречит определению фронта Ф.д(И-т). Итак, фронты
фх(т) и ФА(Н-т) касаются друг друга в точке У,
что и требовалось доказать.
Принцип Гюйгенса приводит к двум описаниям процесса
распространения света. Во-первых, из него следует, что дос-
достаточно следить за лучами, т. е. кратчайшими путями рас-
распространения света. В этом случае локальный характер
распространения света задается его вектором скорости. Ес-
Если направление луча известно, то величина вектора ско-
скорости задается свойствами среды. А с другой стороны, мож-
можно следить за волновым фронтом и исследовать его пове-
поведение.
Бильярдный шар как бы сочетает в себе оба принципа
геометрической оптики — прямолинейность движения луча
света в однородной среде и осуществление выбора среди
всех возможных близких друг к другу траекторий экстре-
экстремальной, определяемой касанием волнового фронта — в
данном случае это один из софокусных эллипсов — с бор-
бортом бильярда.
Это сочетание двух принципов геометрической оптики
позволяет доказать одну важную и сложную теорему о пе-
периодических бильярдных траекториях в выпуклых
областях с достаточно гладкой границей (см. с. 97).
К ее обсуждению мы и перейдем.
Рассмотрим бильярдный стол в виде выпуклой
области Q с гладкой границей Г. Диаметр этого стола, т. е.
отрезок с концами на границе Г наибольшей воз-
возможной длины обладает следующим замечательным свойст-
вом: он перпендикулярен границе Г в своих концах.
Действительно, если наибольшая хорда MN не перпен-
перпендикулярна к касательной / к границе Г в точке М, то сдви-
нУв немного точку М по кривой Г в точку М' так, чтобы
Угол M'MN был тупым (рие. 6.7), получим треугольник
WM'N, в котором сторона M'N больше стороны MN (как
Лежащая против тупого угла). Следовательно, хорда MN
95
имеет не максимальную длину, что противоречит предпп
ложен ию.
Отсюда вытекает, что если запустить бильярдный шао
по диаметру стола Q, то он будет сталкиваться с бортом Г
под прямым углом и отражаясь, двигаться по диаметру
Итак, длиннейшая хорда бильярдного выпуклого стола,
пройденная шаром в обоих направлениях, дает одно из
простейших периодических движе-
движений — движение периода 2, т. е. по
двузвенной траектории (звенья кото-
которой отличаются направлениями). Ес-
Если мы начнем теперь непрерывно вра-
вращать эту хорду, уменьшая ее длину
настолько мало, насколько это возмож-
возможно, так, чтобы в конце этого преобра-
преобразования оба ее конца поменялись местами, мы будем иметь
промежуточное положение наименьшей длины, которое бу-
будет хордой, пересекающей Г в месте наименьшей ширины
стола Q (см. задачу 6.4). Эта хорда дает второе периодиче-
периодическое движение, также периода 2.
Задача 6.4. Докажите, что эта вторая хорда имеет длину,
равную наименьшей ширине полосы, ограниченной двумя парал-
параллельными прямыми, в которую полностью помещается вся обчасть Q.
Детальное изучение небольших возмущений обоих этих
периодических движений показывает, что движение вдоль
наибольшей хорды неустойчиво (т. е. малое отклонение
вектора скорости приводит к большим изменениям траек-
траектории шара), в то время как второе движение может быть
устойчивым или неустойчивым.
Далее, будем искать периодическое движение бильярд-
бильярдного шара периода 3, т. е. «гармонический» треугольник
с вершинами на кривой Г, являющийся бильярдной тра-
траекторией. Его, как и периодическую траекторию перио-
периода 2, следует искать среди всевозможных вписанных в Q
треугольников, и выбрать среди них треугольник макси-
максимального параметра. Строгое доказательство этого (и более
общего) факта мы приведем чуть позже, а сейчас обратим
внимание на два обстоятельства: во-первых, гармониче-
гармоническому треугольнику отвечают два периодических дви-
движения — по и против часовой стрелки; во-вторых, при
непрерывном изменении этого треугольника, не меняя
порядка его вершин и стараясь уменьшать его периметр
настолько мало, насколько это возможно, так, чтобы в
конце этого преобразования получить тот же треугольник,
96
но с циклически переставленными вершинами, мы прой-
пройдем через треугольник наименьшего периметра, который
также будет гармоническим и также будет соответствовать
двум (по и против часовой стрелки) периодическим дви-
движениям периода 3,
Таким же путем может быть установлено существование
двух гармонических п-угольников, делающих k<.n!2 обо-
оборотов вдоль кривой Г, где k — число, взаимно простое с п
(точное утверждение содержится в формулировке зада-
задачи 6.6). Два периодических движения, соответствующих
n-угольнику типа максимума, будут неустойчивы, в то вре-
время как два периодических движения, соответствующих
n-угольнику типа минимакса, могут быть устойчивыми
или неустойчивыми.
Поняв принципиально картину поведения указанных
периодических бильярдных траекторий в выпуклых об-
областях, сформулируем и докажем точную математическую
теорему о периодических движениях бильярдного шара в
выпуклой области Q. Теорема и ее доказательство, которое
мы здесь приведем, принадлежит известному американ-
американскому математику Дж. Биркгофу A884—1944).
Теорема Биркгофа. У бильярда в любой вы-
выпуклой области Q на плоскости, ограниченной замкнутой
гладкой кривой Г, существуют периодические бильярдные
траектории с любым числом звеньев nZ^3.
Доказательство. Пусть число п фиксировано.
Построим конкретную периодическую бильярдную тра-
траекторию из п звеньев.
Рассмотрим всевозможные вписанные в Q замкнутые
ломаные у, число сторон у которых не превосходит п (в
рассмотрение входят вписанные трехзвенные, четырех-
звенные, . ., л-звенные ломаные). Выберем среди них
ту ломаную Yd У которой периметр максимален.
(Мы не будем вдаваться здесь в подробности, связанные
с доказательством существования такой ломаной.)
Мы утверждаем, что тогда ломаная Yo имеет ровно п
звеньев.
Действительно, если бы число звеньев у нее было мень-
меньше п, то ее периметр можно было бы увеличить, заменив
произвольное ее звено Р%Рг на ломаную PiPaP* с верши-
н°й Ро на дуге между Pi и Я2.
Докажем теперь, что Yo — бильярдная траектория в
власти Q, т. е. при всех k последовательные звенья ло-
ложной Ph-iPft и PfcPft+i образуют равные углы с каса-
т&льной к Г в точке Ph (рис. 6.8).
г- А. Гальперин* А. Н. Земляков Ч*
Из максимальности периметра ломаной ув следует, что
сумма Ph-iP+PPh+i для всех точек Рна jnyrePh-iPhPh+1
кривой Г максимальна именно при Р=Ри, иначе периметр
ломаной Yo можно было бы увеличить.
Рассматривая семейство эллипсов Г8 с фокусами в
точках Рй_1 и Ph+i, найдем тот эллипс tSci, который к а-
с а е т с я кривой Г в некоторой точ-
точке Я — такой эллипс обязательно най-
найдется, так как наша кривая гладкая
и выпуклая. Но тогда ясно, что
сумма Ph-iP+PPk+i максимальна по
всем точкам Р, лежащим на дуге Г
между Рй_1 и Pti+i- Для любой дру-
другой точки М 6 Г соответствующий ей
эллипс из семейства Г8 пересе-
пересекает кривую Г и лежит строго
внутри эллипса TSd, поэтому Ph-iM+
+MPh+l<Ph-iP+PPь+i. Отсюда вы-
вытекает, что касание эллипса Г5о с кривой Г происходит
именно в точке Р=Ри- А тогда из первого бильярдного
свойства эллипса следует, что звенья Pfc_iPft и PhPh^
образуют равные углы с прямой /, являющейся одно-
одновременно касательной как к эллипсу Г5о, так и к кривой
Г в точке Ph и поэтому Ph-tP j, и PhPh+t — Два звена биль-
бильярдной ломаной в области Q. Теорема полностью доказана.
Задача 6.5. Какой из вписанных в окружность п-уголь-
ников имеет наибольший периметр?
Решение. Правильный п-угольник. Действительно, замк-
замкнутая бильярдная траектория из п звеньев в окружности является
ломаной максимальной длины (по теореме Биркгофа), а с другой
стороны,— это обязательно правильный п-угольник (если только
шар делает один оборот вокруг центра; см. § 1).
Задача 6.6. Пусть фиксировано натуральное число г(зЗ>-
Обозначим через q>(n) количество чисел k, меньших л и взаимно
простых с п *). Докажите, что существует не менее (р(п)/2 перио-
периодических п-звениых бильярдных ломаных на плоскости, вписанных
в данную выпуклую область Q с гладкой границей Г (рис. 6.9).
Решение. При доказательстве теоремы Биркгофа можно
было ограничиться доказательством существования бильярдной
*) Функция ф (п) называется функцией Эйлера и вычисляется
по формуле
гдеn=Pj1pj*. . ,prk — каноническое разложение п на простые мно
жители.
98
траектории, при движении по которой бильярдный шар обойдет
кривую Г ровно один раз; то же доказательство остается
справедливым в классе всех ломаных, обходящих кривую Г ровно
2 р а з а, ровно 3 р а з а и так далее. При этом следует заметить,
что 1) число обходов k достаточно брать только взаимно простым
ел, и что 2) обходу шарика вдоль ломаной, делающей k оборотов
Рис. 6.9
по часовой стрелке, отвечает та же ломаная, но делающая k обо-
оборотов против часовой стрелки. Поэтому геометрически различных
ломаных лишь <р(п)/2, что и требовалось доказать.
Задача 6.7. (Задача Фаньяно.) Докажите, что в области Q.
имеющей форму остроугольного треугольника, существует замк-
замкнутая бильярдная траектория из трех звеньев. Указание.
Точки излома этой траектории — основания высот треугольника
(см. § 27).
Задача 6.8. Верно ли, что в любом треугольном бильярде
существует периодическая бильярдная траектория из а) 6 звеньев?
б) из меньшего, чем ваданное п, числа звеньев?
Ответ, а) В остроугольном существует всегда; в тупоуголь-
тупоугольном, как правило, не существует; б) в тупоугольном треугольнике
с очень тупым углом число звеньев у любой периодической траек-
траектории может быть сколь угодно большим (т. е. для заданного я
число звеньев может превосходить п). Это связано с тем, что если
бильярдный шар попал в острый угол, то вылететь из этого угла
он сможет только после очень большого числа отражений (под-
(подробнее об этом см. гл. 6 и § 27 гл. 8).
Зддача 6.8 показывает, что теорема Биркгофа для многоуголь-
многоугольников неверна. Причина этого будет прояснена в § 27,
ЧАСТЬ II
ГЕОМЕТРИЯ И ФИЗИКА
ПРЯМОУГОЛЬНОГО БИЛЬЯРДА
Глава 3
ГЕОМЕТРИЯ ПРЯМОУГОЛЬНОГО БИЛЬЯРДА
В этой главе сформулированная во введении
общая проблема бильярдных траекторий исследуется для
бильярда в прямоугольнике. Прямоугольник, как и круг,
имеет во всех своих граничных точках (кроме вершин)
постоянную кривизну — только не положитель-
положительную, как у круга, а нулевую. Кроме того, одинаковыми
прямоугольниками можно замостить всю плоскость, как
это было объяснено во введении. Именно поэтому для биль-
бильярда в прямоугольнике, так же как и для бильярда в
круге, естественно ожидать полного решения проблемы
поведения бильярдных траекторий. Оказывается, методы,
использованные в гл. 1, работают и в случае прямоуголь-
прямоугольника, позволяя не только провести полное исследование
рассматриваемого прямоугольного бильярда, но и свести
его, в некотором смысле, к уже изученному бильярду в
круге.
§ 7. Бильярдный шар на прямоугольном
столе без луз
Напомним, что бильярдом в прямоугольнике
называется такая система: один точечный бильярдный
шар на прямоугольном бильярдном столе ABCD без луз,
движущийся по нему без трения и отражающийся от его
сторон («бортов») по бильярдному закону «угол падения
равен углу отражения».
Простейшие бильярдные траектории в прямоуголь
нике — периодические. Они могут быть нескольких типов:
состоять из дважды проходимых отрезков между протнвс-
положными сторонами (рис. 7.1, а); образовывать семей-
семейства параллелограммов со сторонами, параллельными
диагоналям прямоугольника (рис. 7.1,6); образовывать
100
самопересекающиеся замкнутые ломаные (рис. 7.1, в)
и т. д.
Бывают и такие траектории, которые попадают в вер-
вершины прямоугольника (рис. 7.1, г). В таком случае не-
непонятно, как шару следует двигаться после выхода «из
угла»: закон упругого отражения на этот счет никаких
указаний не дает. Все такие траектории мы будем назы-
называть особыми и, как правило, рассматривать не будем.
С D
С D
В
с ю
й?
В А
В
т. е. если траектория попала в вершину, оборвем ее, и от
траектории останется только ее часть (полутраектория).
(Впрочем, из дальнейших рассмотрений будет понятно,
что в случае прямоугольного бильярда шар можно считать
вылетающим после попадания в вершину в точности в
противоположном направлении; такого
вывода нельзя делать для бильярда в .
произвольном многоугольнике. Объясне- Q г
ние этому вы сможете найти, решив г
задачу 7.3, или же обратившись к а\
гл. 8). а3.
«Сходу» нарисовать хотя бы одну не- р I
периодическую траекторию бильярда в
прямоугольнике уже значительно слож-1
нее. Задачу о распознавании периоди- рис_ 7 2
ческих и непериодических траекторий
бильярда мы сейчас решим с помощью
Упоминавшейся во введении процедуры «выпрямления тра-
траекторий». Опишем ее в общем случае — для бильярда
в произвольном многоугольнике.
Пусть PiP2Ps. . . — произвольная не особая (т. е. не
попадающая в углы) траектория бильярда в многоуголь-
многоугольнике Q=AiAiAs. . .Ап (рис. 7.2). Построим по этой ло-
Маной специальную прямую. А именно, отразим наш мно-
многоугольник Q вместе с ломаной Р2РзР^- . • относительно
той стороны многоугольника, на которой лежит точка Рг
(первое звено ломаной РгР2 мы не трогаем). Согласно
Закону отражения, отрезок РгР'л, симметричный отрезку
101
Р2Ра, является продолжением отрезка PiP8, и первый
кусок ломаной PiPjjPsP4. . . — PiP2Ps — нами выпрям-
выпрямлен. Теперь отразим второй (полученный из Q при первом
отражении) многоугольник Qi относительно той его сто-
стороны, на которой лежит следующая точка излома pj.
Получим следующий многоугольник Q2, и образ звена PsPl
при новом отражении будет, опять-таки, продолжением
отрезка PiP2P'. Продолжая так и далее, мы можем любой
А
Л
в
О
в''/
с
/
i
А
•
•
>
с
В
г
а
Рис. 7.3
кусок ломаной Р\Р^РЪР^ . . «выпрямить», т. е. последо-
последовательными отражениями превратить в отрезок прямой
PiPtP'J>l
Конечно, для разных траекторий придется делать раз-
различные последовательности выпрямляющих отражений.
Однако если мы рассматриваем бильярд в прямоуголь-
прямоугольнике, мы можем с самого начала с помощью отражений
замостить всю плоскость прямоугольниками, рав-
равными данному, получив решетку из прямоугольников.
Нарисовав на этой плоскости произвольный луч, не про-
проходящий ни через одну из вершин получившихся прямо-
прямоугольников, мы можем с помощью процедуры, обратнс»
описанной, «сложить» этот луч в траекторию бильярда
в исходном прямоугольнике ABCD (рис. 7.3, а). Заметим,
что при таком «складывании» решетки прямоугольниког-
в исходный прямоугольник ABCD в каждую точку М
прямоугольника ABCD попадает бесконечно много точек
М,ПъП плоскости — именно, все те точки, которые полу-
получаются из М описанными выше отражениями (рис. 7.3, о)-
Если траектория, выходящая из точки М под углом я
к стороне АВ, периодична, то это означает, что после вы-
выпрямления из этой траектории получится прямая, np°v '"
дящая через М и через одну из точек Мт<По. Если ну-
ровать точки М,^п индексами тип, как указано на р1^
7.3, б, то точка МтсгПе должна быть такой, что то » По ~~
J02
четные числа. Именно (и только) в этом случае бильярд-
бильярдный шар проходит через ту же точку М под прежним
углом а: номера т0 и пв показывают, сколько нужно сде-
сделать отражений относительно вертикальных и горизон-
горизонтальных сторон прямоугольников, чтобы получить из
точки МтоуПо точку М; при этом нечетное число отра-
отражений меняет направление, четное же — не меняет (см.
рис. 7.3, в).
Докажем, что неособая траектория, выходящая из точки
М прямоугольника ABCD под углом а к стороне АВ, пе-
периодична в том и только в том случае, когда тангенс ее
угла наклона ft=tga соизмерим с отношением сторон
ajai прямоугольника ABCD.
Действительно, только что было выяснено, что перио-
периодичны те и только те траектории, которые (после выпрям-
выпрямления) соответствуют прямым, идущим из точки М в одну
•
•
п
К
С
Рис. 7.4
из точек вида М2тЛп. Заметим теперь, что точка МШЛп
получается из М сдвигом на вектор 2m-AB+2n-AD (до-
(докажите это: рис. 7.4, а), так что АММ2т>2пК имеет ка-
катеты с длинами MK=2mat и М2т>2пК—2па2. Таким
образом,
т. е. k соизмеримо с a Jut. Обратно, если число k соизме-
соизмеримо с ajat, т. е. k— — —, то любая прямая, выходящая
из точки М с тангенсом угла наклона k, проходит через
точку, получающуюся из М сдвигом на вектор 2т-АВ+
"\-2n-AD, т. е. через точку М2и,г„ (проверьте!). Если эта
пРямая не проходит через вершины прямоугольников,
то ей соответствует неособая периодическая траектория,
что и требовалось доказать.
103
Заметим, что в рассматриваемом случае мы все-таки
можем продолжить и любую особую, т. е. заканчиваю-
заканчивающуюся в одной из вершин прямоугольника, траекторию
за эту вершину: ничто не мешает на плоскости, замощенной
нашими прямоугольниками, продолжить, например, МС
за вершину С (рис. 7.4, б), и считать тем самым, что,
попав в вершину С, бильярдный шар вылетает из нее по
тому же пути, по какому он туда залетел — после соот-
ьетствующих отражений луч СМ' совмещается с лучом
СМ. Таким образом, в случае бильярда в прямоугольнике
можно считать, что движение по любой траектории про-
продолжается неограниченно во времени (например, дважды
проходимая диагональ АС прямоугольника — это перио-
периодическая траектория).
Из доказанного утверждения следует
Теорема 1. Если тангенс угла наклона k траек-
траектории соизмерим с числом ко=а2/а!, то независимо от на-
начального положения бильярдного шара его движение будет
периодическим; в противном случае траектория неперио-
непериодична.
Итак, с помощью теоремы 1 мы научились по началь-
начальному звену траектории шара определять, является ли эта
траектория периодической или непериодической. Для этого
надо найти отношение длин сторон прямоугольника или,
что то же самое, тангенс угла наклона диагонали прямо-
прямоугольника и тангенс угла, под которым запущен шарик,
и поделить первое число на второе: если в результате
получится рациональное число, то траектория периодична,
если же — иррациональное, то иепериодична. Кстати,
отсюда сразу следует также и то обстоятельство, что для
фиксированного начального вектора скорости шара тра-
траектория будет периодической или непериодической н е-
завиеимо от его начального положения на прямо-
прямоугольном столе. Поэтому, если запустить параллельно
друг другу сразу несколько бильярдных шаров, они либо
одновременно опишут периодические траектории, либо
никогда не пройдут по своему старому следу. Последова-
Последовательность отражений этих шаров от бортов бильярда будет
различной, если они находятся достаточно далеко дрУг
от друга. Если же шары находятся достаточно близко, то
последовательность бортов, от которых они отражаюи-Я,
будет одной и той же (рис. 7.5, а). Если первое звено тра-
траектории одного бильярдного шара окружить параллель-
параллельными звеньями целого семейства траекторий другил шаров,
т< полученные траектории, в случае, когда они период»1'
104
ческие, заполнят самопересекающнйся «коридор» (рис.
7.5, б). Таким образом, зная одну периодическую траек-
траекторию, мы параллельным сдвигом ее звеньев получаем
другую периодическую траекторию.
а б
Рис. 7.5
Задача 7.1. а) Доказать, что у всех несссбых «параллель-
«параллельных» периодических траекторий в прямоугольнике равнее число
звеньев и равные длины, б)* Доказать, что в прямоугольнике
существуют сколь угодно длинные периодические траектории.
Решение. Это следует из рассмотрения выпрямленных
траекторий, изображающихся на решетке прямоугольников рав-
равными параллельными отрезками.
Задача 7.2. У края бильярда, имеющего форму правильного
2п-угольника, стоит шар. Как надо запустить шар от борта, чтобы онй
отразившись по разу от всех бортов, вернулся в ту же точку? До-
Доказать, что при этом длина пути шара не зависит от выбора началь-
начальной точки.
Как же ведет себя на прямоугольном столе непе-
непериодическая бильярдная траектория? В круге и
эллипсе, как мы помним, непериодическая траектория ке
заходила в некоторые участки — в концентрический круг
и, соответственно, в софокусный эллипс (или в криволи-
криволинейные сегменты софокусной гиперболы), однако запол-
заполняла всюду плотно кольцо между их границами. В прямо-
прямоугольнике она уже заходит во все его участки и заполняет
его всюду плотно. В этом и состоит основной результат
о непериодических траекториях в прямоугольном бильярде.
Теорема 2. Если k/k0 — иррациональное число, то
любая траектория с угловым коэффициентом k всюду плотно
заполняет весь прямоугольник, т. е. пересекает любой
{сколь угодно малый) круг, лежащий внутри него.
Таким образом, если точечный бильярдный шар за-
запустить из любого положения М в любом направлении а
таком, что число tg a/tg <р иррационально, где ф — угол
наклона диагонали к горизонтальной стороне, то он рано
или поздно столкнется с другим, уже неточечным бильярд-
бильярдным шаром (диском) N, куда бы мы его ни поставили и
сколь бы мал он ни был! Следовательно, игрокам (в случае
отсутствия трения) ие нужно особенно стараться, чтобы
попасть в другой шар (или лузу!), надо лишь иметь терпе-
терпение и время, чтобы дождаться нужного столкновения.
105
Доказательство теоремы 2 будет дано в § 9 и будет
опираться, как и в случае круга, на теорему Якоби.
Наметим здесь лишь краткую схему ее доказательства.
По прямоугольнику ABCD будет построен «фундаменталь-
«фундаментальный» прямоугольник вчетверо больших размеров, в ко-
котором исходная бильярдная траектория превратится в
«скачущую» со стороны на сторону траекторию; для из-
избавления от этих «скачков» граница фундаментального
прямоугольника будет специальным образом склеена, и в
результате склейки получится замечательная поверх-
поверхность — тор («бублик»), на котором «скачущая» траек-
траектория превратится уже в непрерывную кривую. Иссле-
Исследование этой кривой и приведет к доказательству теоремы 2.
Примечательно, что для прямоугольного бильярда спра-
справедлива следующая альтернатива: либо траек-
траектория бильярда периодична, либо всюду плотно заполняет
прямоугольник. В гл. 9 выяснится, что это верно не для
всякого выпуклого многоугольника (при выяснении опять
будет использована теорема Якоби!).
Задача 7.3*. Найдите критерий периодичности бильярдных
траекторий в равностороннем треугольнике.
Задача 7.4*. Укажите все многоугольники Q, которыми
с помощью описанных выше последовательных отражений можно
замостить плоскость без перекрытий и так, чтобы любая цепочка
последовательных отражений, при которой из Q получается какой-то
многоугольник Q', давала один и тот же результат. (Например,
правильными шестиугольниками можно замостить плоскость, од-
однако последнее требование здесь не выполнено — от шестиуголь-
шестиугольника Q к соседней ячейке Q' можно прийти двумя способами —
с помощью одного отражения относительно AF и с помощью ком-
композиции двух отражений — относительно АВ и затем относительно
вм I
Рис. 7.7
AF' (рис. 7.6). Результаты будут разные — скажем, в вершину,
обозначенную буквой X, в первом случае переходит вершина Е,
во втором — вершина С.
Замечание. Задача 7.4 н другие близкие вопросы обсуЖ"
даются в статье А. Н. Виленкина «Калейдоскопы» (Квант. 1972.
№ 8. С. 41—49), правда в другой связи.
Задача 7.5. Пусть бильярдная траектория МА попадает
в вершину А угла ВАС величины а. С помощью последователь-
106
ных отражений замостим часть плоскости углами той же величины
(рис. 7.7), продолжим МА за вершину А и обратными отражениями
построим луч AM". Казалось бы, тем самым мы можем определить,
как выходит бильярдный шар из вершины угла (под направлением
AM"). Однако здесь может возникнуть неоднозначность, ибо после-
последовательные отражения исходного угла можно начать со стороны
АВ или со стороны АС, и может оказаться, что от этого зависит
направление AM". Рассмотрите случай угла а=2л/3. Выясните,
для каких углов а упомянутая неоднозначность не возникает.
Задача 7.6. В прямоугольном бильярде из точки А посы-
посылается шар параллельно диагонали. Найти множество таких точек
М в бильярде, что второй шар, посланный из точки М одновре-
одновременно с первым и с той же скоростью (как по величине, так и по
направлению), столкнется с ним.
Задача 7.7. В точечное отверстие границы прямоугольного
бильярда влетает бильярдный шар. Может ли шар с некоторого
момента начать двигаться внутри бильярда по замкнутой траек-
траектории? А если бильярд не прямоугольный? (Указание: поменяйте
скорость шара на противоположную.)
Задача 7.8. В прямоугольном бильярде шар движется по
замкнутой траектории. Угол между какими-то двумя соседними
авеньями равен 90°. а) Может ли у траектории быть 4 звена? Если
да, то при каком соотношении сторон? б) А может ли быть 5 звеньев?
6 звеньев? 17 звеньев? 18 звеньев?
Задача 7.9. В прямоугольном бильярде произвольным
образом запущены два неточечных шара под углами а и Р к одному
борту, причем tg а и tg P иррациональны. Обязательно ли они
когда-либо столкнутся?
Задача 7.10. Из вершины прямоугольного бильярда раз-
размером mX2n, где тип — целые нечетные числа, под углом 45°
к стороне послан шар. Попадет ли он после нескольких отражений
от бортов: а) в противоположную вершину; б) в соседнюю верши ну
(рассмотреть два случая соседней вершины); в) в середину какой-
либо стороны? г) Сможет ли шар побывать в середине двух про-
противоположных сторон?
Задача 7.11. Как будет вести себя шар в прямоугольном
бильярде из задачи 7.10, если его выпустить из вершины под углом
30°? 60°?
Задача 7.12. а) Занумеруем стороны прямоугольного биль-
бильярда числами 1, 2, 3, 4. Пусть в нем движется шар, траектория
которого непериодическая. Выпишем подряд номера всех сторон,
о которые отражался шар: nlt n2, «js . . . . Может ли полученная
последовательность оказаться периодической?
б)* Решите ту же задачу для непериодической траектории у
в произвольном выпуклом fe-угольнике, стороны которого зануме-
занумерованы числами от 1 до ft.
Решение. Докажем, что последовательность nlt п^, ,., —
непериодическая, от противного.
Пусть период последовательности п^, п2, . . . равен Т, причем
Т четно (в противном, случае рассмотрим удвоенный период). Вы-
Выпрямим траекторию у шарика, сделав последовательные отражения
многоугольника относительно сторон %, n2, n3i ... , Получим
коридор из одинаковых многоугольников Mi, М2, Мя, . . ., содер-
содержащий прямую / — выпрямленную траекторию у.
Рассмотрим в этом коридоре многоугольники Mt и MT+i.
Многоугольник Mj+i можег быть получен из Mt либо параллель-
107
яым переносом на некоторый вектор а, либо параллельным перено-
переносом и поворотом. Во втором случае Mf+i получается из Mt одним
поворотом с центром в некоторой точке О на некоторый угол а.
А тогда в цепочке многоугольников Mt, Mf+i, M2T+i, • . . каж-
каждый из ннх получается из предыдущего либо параллельным пере-
переносом на одни н тот же вектор а, либо поворотом на один н тот же
угол а с центром О. Во втором случае весь коридор располагался
бы в ограниченной части плоскости и поэтому не мог бы содержать
прямую I. Следовательно, возможен только первый случай: много-
многоугольники в указанной цепочке получаются последовательно друг
из друга параллельным переносом на вектор а. А тогда все звенья
траектории у с номерами 1, T+l, 2T+1, ... в исходном много-
многоугольнике Mt параллельны друг другу. Если они начинаются в
различных точках А1г А2, А3, А$, . . . одной и той же сто-
стороны многоугольника Мх, то нетрудно видеть, что А1А2=А2А3=
= A8At=. . . . Это противоречит тому, что все эти точки лежГат на
одной стороне многоугольника, поскольку сумма AtA2-\-A2A3-\-
+А3Ал-{-. . . бесконечна. Таким образом, все точки Alt А2, . . ,
совпадают, а потому совпадают и звенья траектории у с номерами 1,
Г+1, 2Т+1, ЗТ+1, . . ., т.е. у — периодическая траектория,
что противоречит условию задачи.
Замечание. В пространственном многограннике после-
последовательность nlt n2, na, . . . номеров граней, от которых отража-
отражается бильярдный шар, может быть периодической, несмотря на
то, что траектория шара у непериодическая. Это связано с тем, что
в пространстве кроме параллельных переносов и поворотов вокруг
осей имеются еще н винтовые движения: повороты вокруг осей
со сдвигами вдоль них. В этом случае множество точек отражения
шара от любой из граней п^ заполняет всюду плотно некоторый
эллипс на этой грани.
§ 8. Тор и его обмотки
Временно оставим бильярды в прямоуголь-
прямоугольнике и обратимся к весьма важным поверхностям, часто
встречающимся в механике — к торам. Тором называется по-
поверхность, получающаяся при вращении окружности S1 от-
относительно непересекающей эту окружность прямой MN,
в- '"
Меридианы Параллели
Рис. 8.2
лежащей в плоскости окружности (рив. 8.1). Форму"
тора имеют надувной спасательный круг, автомобильная
камера, поверхность бублика. На торе, как и на сфере,
108
можно провести меридианы — линии пересечения тора со
всевозможными плоскостями, проходящими через ось вра-
вращения MN, и параллели — окружности, получающиеся
из точек исходной окружности при вращении относительно
MN (рис. 8.2). Выбрав на торе «гринвичский меридиан»
и «экватор», т. е. зафиксировав меридиан и параллель,
«Гринвичский»
меридиан
1Ш
6
Рис.
1
8.3
Г2/2Я
i
а
Ъ
0* a
в
ь
можно ввести на нем долготу %, отсчитываемую по парал-
параллелям от выбранного меридиана, и широту ip2, отсчитыва-
отсчитываемую по меридианам от экватора (рис. 8.3, а). Более точно,
точка А тора Т имеет координаты (ifr, -ф2), если она полу-
получается из точки О пересечения выбранных линий поворо-
поворотом на угол -ф2 вдоль меридиана и последующим поворотом
на угол i[)i относительно оси MN (оба поворота осуществ-
осуществляются в выбранных направлениях; рис. 8.3, б). Углм
fi и ifa будем измерять в радианах; плоская (как в геог-
географии) карта тора представляет собой квадрат на плоскости
-J
Рис. 8.4
Chl:ji)j2: 0 <:i)Ji <2л, 0 <% <:2л. Точки экватора (-фа=0 или 2я)
и «гринвичского меридиана» (ipi=0 или 2л) представ-
представлены на этой карте дважды — точки нижней и верхней
стороны квадрата, лежащие на одной вертикали (т. е.
точки вида (\]н, 0) и (ipi, 2л)) изображают одну и ту же точку
на торе; аналогично, точки левой и правой сторон квад-
квадрата, лежащие на одной горизонтали, изображают также
одну и ту же точку. Будем считать карту резиновой и
склеим упомянутые точки; на рис. 8.4 склеиваемые гтороны
сбозначены одинаковыми буквами (о, Ъ) со стрелками, пока-
показывающими, как нужно склеивать эти стороны (стрелку
109
со стрелкой — в том же направлении). Как и сле-
следовало ожидать, в результате получим тор, а сетка гори-
горизонталей и вертикалей на карте превратится в сетку па-
параллелей и меридианов на торе. Иногда тор и определяют,
как поверхность, получающуюся из «резинового» квад-
квадрата указанной склейкой.
Рассмотрим теперь простейшее движение точки по тору:
пусть точка А движется так, что ее широта и долгота ме-
меняются равномерно — с постоянными скоростями ац и (о2.
ft
гп
о
Itt
Рис. 8.5
В этом случае можно написать формулы для зависимости
tyi и "фв от времени t:
Здесь имеется в виду, что, как и в тригонометрии, мы по-
позволяем координатам % и % принимать произвольные
(большие 2и и отрицательные) значения, однако не забы-
забываем, что для любых целых тип точка с координатами
(tyi+2nm, ty2+2nn) совпадает с точкой с координатами
№'» ^Ы- На всей плоскости Офхфг написанные уравнения
задают прямую tJj2 = — ^ -\- у. Учтем теперь, что в дейст-
действительности мы должны считать, что *ф? и ip2 меняются
лишь от 0 до 2я, так что как только точка, движущаяся
по этой прямой, доходит до одной из сторон квадрата,
являющегося картой тора, эта точка «перескакивает» в
соответствующую точку противоположной стороны квад-
квадрата и продолжает двигаться по квадрату в том же направ-
направлении, что и раньше — до следующего перескакивания
(рис. 8.5). Таким образом, на карте соответствующий «марш-
«маршрут» — траектория движения — состоит из отрезков, па-
параллельных друг другу; после склейки квадрата в тор эти
отрезки склеиваются к непрерывную кривую на торе —
она обматывает тор с «угловыми» скоростями (Oi по эква-
экватору и (оа по меридиану (на промежуточном этапе склейки
мы получаем движение по винтовой линии на цилиндре с
соответствующим перескакиванием о одного его основания
ПО
Тип C.1)
Рис. 8.6
Тип C.2}
на другое). Эта кривая называется траекторией обмотки
тора с частотами (coiF со2).
Выясним, когда траектория обмотки тора с частотами
(coi, со2) является замкнутой (периодичес-
к о й).
Если сй,=О, то траектория—это меридиан, и движе-
движение по нему периодично с периодом Т2=2л/ы2. Если со2=»
=0, то происходит периодическое движение по параллели.
Пусть обе частоты coi и со2 отличны от 0. Тогда через
промежутки времени, кратные Т1=2п/ац, движущаяся
точка оказывается на одном и том же меридиане, а через
промежутки времени, кратные Т2=2л/со2, точка оказы-
оказывается на одной и той же параллели. Движение перио-
периодично тогда и только тог-
тогда, когда через некоторое
время Т точка окажется в
своем первоначальном мес-
месте, т. е. на тех же парал-
параллели и меридиане. Для
этого нужно, чтобы эгот
промежуток времени Тбыл
кратен как 7\, так и Т2,
т. е. T—mTi и Т=иТ2 с целыми m и п. Таким образом,
необходимое и достаточное условие
периодичности движения — это существование на-
натуральных тип таких, что tnTi=nTt, т. е. m-2jt/coi=s
=п-2л/со5; последнее означает, что число ю2/«1 рацио-
рационально (co2/o>i=m/n).
Итак, если «i и со2, скажем, положительны и соизме-
соизмеримы друг с другом, то любая траектория обмотки с ча-
частотами coi, (о, периодична. На торе это будет замкнутая
кривая, причем если co2/«i — несократимая дробь, то эта
кривая п раз обходит тор вдоль параллели и m раз — вдоль
меридиана. Такая кривая называется циклом типа {т, п).
На рис. 8.6, а изображен цикл типа C,1), а на рис.
8.6, б — цикл типа C,2).
Из полученных рассуждений вытекает, что в случае
несоизмеримых частот оц и ©s траектория об-
обмотки будет непериодической.
Как же она будет обматывать тор? Ответ на этот вопрос
Дает
Теорема. Если число co=co2/cof иррационально, то
любая траектория соответствуюи^й обмотки тора всюду
плотна на торе, т. е. проходит черьз любую (сколь угодно
Щю) область на торе.
Ш
Доказательство. Пусть U—произвольная область
на торе; проведем меридиан S тора, пересекающий область
U по дуге А (рис. 8.7), и рассмотрим последовательные
точки пересечения траектории обмотки тора с этим мери-
меридианом — Ро, Pi, Р8, . . . . Точка, двигаясь вдоль траек-
траектории, возвращается на меридиан S через промежутки
времени, равные Ti=2jt/coi. За каждый такой промежуток
времени долгота точки г|)г меняется на одну и ту же вели-
величину ср = со27\= —-2л = со-2л. Это означает, что точка Рп
пересечения траектории с меридианом S получается из
предыдущей точки пе-
Ч//Ч ресечения Pn-i поворо-
"Tv i том на угол ф=со-2л
вдоль этого меридиана.
В случае и р р а ц и о-
нальности со из
рис g 7 теоремы Якоби вытека-
вытекает, что хотя бы одна
из точек Р„ попадет на
дугу А. Следовательно, траектория пересечет область U,
чго и требовалось доказать.
Отметим также, что, поскольку последовательность
точек Рп на меридиане S не только всюду плотна, а еще
и равномерно распределена (т. е. точка Р„ попадает
в произвольную дугу А меридиана 5 с вероятностью, равной
отношению ее длины к длине меридиана) и аналогичное
утверждение имеет место и для произвольной параллели
на торе, траектория обмотки тора с иррациональным со
заполняет тор равномерно, т. е. движущаяся рав-
равномерно вдоль этой траектории точка проводит в наперед
заданной области U тора время, пропорциональное ее
площади.
Зафиксировав частоты обмотки coi и (ог, мы можем
через каждую точку тора провести траекторию этой
обмотки и рассмотреть все эти траектории сразу. Они
образуют так называемый поток траекторий, или инячр,
обмотку тора (до сих пор речь шла только о тра-
траекториях обмотки). Если число а)=сог/(О1 рационально,
го обмотка называется рациональной, в противном случа-
говорят об иррациональной обмотке тора. Все траектории
рациональной обмотки тора периодж.м (с одним и тем *<-
периодом), а любая траектория иррациональной сбч*.гК|1
:сюду плотно заполняет тор.
112
Можно интерпретировать упомянутые потоки так: на
торической планете Тог дует ветер — так, что на квад-
квадрате (карте тора) направление ветра одинаково во всех
точках — под углом а к оси ОЦ\ (рис. 8.8, а). Сев на воз-
воздушный шар, мы полетим по ветру Если нам повезет с
погодой — tg а окажется иррациональным,— то наше пу-
путешествие будет весьма познавательным, ибо мы побываем
(благодаря только ветру, который, по предположению,
не меняется) над всеми уголками топической танеты\
2п
а
Ввтвр Ветер
на планете Тог на Звмлг
а &
Рис. 8.8
Если же tg а будет рациональным, мы совершим «а/>-:ч;и>е
кругосветное путешествие», вернувшись в ту же точку.
(На сферической Земле такого ветра не бывает — это
весьма сложная теорема. Более простой, но нетривиальный
факт заключается в том, что в любой момент времени на
Земле найдется хотя бы одна точка, в которой нег ветра!
(рис. 8.8, б). Существование таких «ветров» на торе и
является причиной того, что эта поверхность часто появ-
появляется в задачах механики. Объяснение же такой исклю
чительности тора состоит в том, что его так называемая
эйлерова характеристика равна нулю. Об эйлеровой ха-
характеристике поверхностей см. § 23; более подробно об
этом и о связи эйлеровой характеристики со свойствами
«ветров» на поверхности — теоремой Пуанкаре о сумм
индексов векторного поля — можно прочитать в кнше
В Г. Болтянского и В. А. Ефремовича «Наглядная топо-
топология» («Библиотечка «Квант», 1982. Вып. 21).
Замечание об обмотках тора. Кроме
конкретного представления тора в виде поверхности буб-
бублика, его можно представить и абстрактно, как множе-
множество пар точек (фх, ф.г), где tyi и ip4 независимо друг от друга
принимают произвольные значения от 0 до 2л, г. е. можно
считать, что точки фх и ij>2 движутся каждая равномерно
по своей окружности, а тор {(ipi, i|>4)} — это конфигурацион-
113
ное пространство этих точек. Именно поэтому говорят,
что «тор есть прямое произведение окружностей» и запи-
записывают это в виде T2=S1XS1. Если при этом отношение
угловых скоростей co2/coi движущихся по окружностям
точек иррационально, то это означает, что конфигурацион-
конфигурационная траектория точки г]э= (ifa, ч]J) на торе всюду плотно
его заполняет, и следовательно, точки i]>i и 1]э2 на своих
окружностях в некоторый момент времени будут нахо-
находиться почти в первоначальном (т. е. в сколь^угодно близ-
близком к нему) положении. Аналогично, если имеется п>2
окружностей, по которым равномерно движутся точки Pit
Р2, ¦ -, Рп, то их конфигурационным пространством будет
поверхность и-мерного тора T"=S1XS1X. . .XS1 (« раз),
расположенного в 2и-мерном пространстве R2n=IR!x
X. . . X [Ra (n раз) (абстрактный двумерный тор Т2 можно
считать вложенным в 4-мерное пространство IR4), по ко-
которому движется одна конфигурационная точка ty— (ф,,
^2, • • •, 'Фп), где 0<iJj(<:2jt, t=l, .... п. Если «i, «2, . .
... ,юп — угловые скорости движения точек Pi, . . ., Рп по
окружностям, т. е. il)i=coiH-(pi, . . .,'Фп=«п^+Фп, гдеф!,...
• • м 4>п — фазы (начальные положения точек на окруж-
окружностях), то точка ¦ф@=(<й1<+ф1, . . ., «пИ-фп) описывает
на торе Т" траекторию обмотки. Оказывается, эта траек-
траектория, как и в случае двумерного тора, либо замкнута,
либо всюду плотно заполняет некоторый тор ~Р, k<n.
(В механике торы Т" называются лиувиллевскими то-
торами, а равномерное движение точки по тору — «условно-
периодическим» движением.) Замкнутой траектория будет,
если &1СоН-. . .+&пюп=0 при некоторых целых klt ...
... ,kn, а всюду плотной — если таких целых чисел нет.
Это замечание дает возможность быстро решить не-
непростые задачи 8.7—8.10.
Задача 8.1. Какая поверхность получится, если у прямо-
прямоугольника (рис. 8.4) склеить сначала стороны Ь, а потом стороны о?
Задача 8.2. Рассмотрим «резиновый»
шестиугольник и склеим попарно его проти-
противоположные стороны. Какая поверхность при
этом получится?
Задача 8.3. Какая поверхность полу-
получится после попарной склейки противополо-
противоположных сторон правильного восьмиугольника!1
Задача 8.4. Какая поверхность по-
получится, если склеить стороны восьмиуголь-
восьмиугольника так, как указано на рис. 8.9?
Задача 8.5. Резиновый мяч (или гл
бус) можно вывернуть наизнанку, проделав в нем дырку. М°
ли подобным образом вывернуть наизнанку тор? Что в это» -*
чае произойдет с параллелями и меридианами?
114
Задача 8.6. Нарисуем на торе цикл типа (т, п), затем по-
положим веревочку на эту кривую и свяжем ее концы, и, наконец,
уберем (уничтожим) тор, оставив веревочку. В каких случаях
иа веревочке после распутывания не будет узлов? (Рассмотрите
для начала цикл типа C,2) — см. рис. 8.6,6.)
Задача 8.7*. а) Доказать, что существует такое натураль-
натуральное п, что числа 2" и 3" начинаются с цифры 7 одновременно,
б) Верно ли то же самое для чисел 2" и 5я?
Решение, а) Мы должны найти такие натуральные числа п и
klt ft2, чтобаодновременно выполнялись равенства7.10fti*s2"<8-10*i
и 7-10fta<3rt < 8-10*а, или, иначе,
fti<nlg2—Ig7
fea<nlg3-lg7
Если вспомнить решение задачи про первые цифры чисел 2" в
конце § 2, то мы приходим к следующей ситуации: на одной и
той же окружности S1 длины 1 отмечена дуга Д длина lg(8/7) и
точка Ро—-отпечаток числа (—lg 7) при иамотке числовой оси R*
на эту окружность; точка Ро «раздваивается» на две Ро и Ро (обе
они сливаются с Ро) и каждая из иих начинает «прыгать» по ок-
окружности в одну сторону прыжками величиной Ig2 и Ig3 соот-
соответственно; в результате возникают их «следы» Р[, Р'2, Р'з ... и
Ри P'L Par ••• Надо доказать, что через некоторое равное число
п прыжков обе эти точки окажутся на указанном интервале Д—это
п и будет искомым.
Рассматривая конфигурационное пространство пар точек (Р'п,
Рп), получаем двумерный тор "Г*н"^1х51« причем угловая скорость
движения конфигурационной точки Р=(Р'п, Рп) по меридиану тора
(по первому экземпляру окружности S1) равна G>i = lg2, а угловая
скорость движения по параллели тора (второму экземпляру S1)
равна co2 = lg3. Если бы движение конфигурационной точки Р по
Т0РУ Т* было непрерывным, то ее траектория заполнила бы этот
тор всюду плотно. Однако движение точки Р дискретно—она
«скачет», меняя свое положение на торе только в целочисленные
моменты времени t=\, 2, 3 п и поэтому теорему об
обмотках тора применить здесь нельзя. Доказать, что множество
«следов» точки Р всюду плотно на торе Хг» можно, еели каким-
то образом удастся дискретное движение точки Р превратить в
непрерывное так. чтобы получилась некоторая обмотка тора, но,
разумеется, уже ие двумерного.
Можно поступить следующим образом. Введем формально еще
одну окружность, по которой запустим третью точку, Ро", кото-
которая будет двигаться непрерывно с постоянной угловой скоростью
Шз=1. Рассмотрим конфигурационное пространство трех точек
(Р', р\ Р"'), каждая из которых движется по своей окружности
длин.: 1 — первые две движутся равномерно е угловыми скорос-
скоростями Wj и (Hi, а третья движется равномерно с угловой ско-
скоростью со8. Им является трехмерный тор T3 = S1xSlxS1 и по нему
конфигурационная точка Р = (Р\ Р", Р1") движется уже непре-
непрерывно, задавай обмотку тора Xs. Исходный тор Тг можно пред-
представлять себе расположенным в трехмерном торе У3 так же, как
окружность S1 в торе fг — в виде параллели (рис. 8.2); тогда
Рассматриваемая обмотка тора f3 пересекает тор Хг через рав-
равные (единичные) промежутки времени и оставляет на этой «дву-
115
мерной параллели» следы—точки пересечения Рп=(Р'п, Рп), ко-
торые являются конфигурационными точками на торе "J2- Полу-
Полученная обмотка тора ~|f3i по сделанному в конце § 8 замечанию,
будет всюду плотной в ~§3, если Х^^о^-г-йгШг-Ь&зИз ?= О при
всех целых kl3 k2, k3. В нашем случае выражение для 'к имеет
вид X = ki Ig2 + fe2 Ig3+fe3. и если бы оно принимало Еначение О
при некоторых целых ku fe2, k3, то 10^ = 2fti3ftal0*s= 1, откуда
?1 = fr2 = fc3 = 0 в силу взаимной простоты чисел 2, 3, 5. Значит,
Я. Ф 0 при всех целых k±, k^, k3, поэтому обмотка всюду плотна
па X3 и, следовательно, точки ее пересечения с X2 заполняют
тор X2 всюду плотно, что и требовалось доказать.
б) Если первая цифра у чисел 2" и 5" равна х, то, представив
эти числа в виде 2"=а-10", 5" = Р-10" @ < а, Р < 1), видим, что
при х < 3 «Р < 1 и поэтому произведение самих чисел меньше
10" —противоречие; при д: > 3 оф > 1 и тогда произведение самих
чисел больше 10"—опять противоречие. Поэтому остается только
возможность # = 3: при перемножении а на Р «в столбик» проис-
происходит перенос единицы в разряд единиц, т. е. @,3.. .)-@,3...)
превращается в 1,000...0-
Итак, одновременно числа 2" и 5" вогут начинаться только с
тройки (например, при п = 5). И это несмотря на то, что каждое
из этих чисел может начинаться с произвольной цифры!
Геометрически возникшее явление объясняется тем, что по-
построенная в пункте а*) обмотка трехмерного тора уже не будет
всюду плотной в нем; в силу равенства 2-5= 10 число Ji = fcilg2+
+ ki lg 5 + k3 может стать равным нулю при некоторых целых ku
k2, k3 (каких?); поэтому эта обмотка будет пересекать двумерный
тор "|"а по множеству точек, не всюду плотному на X2 (так как
сама обмотка тора X3 в рассматриваемом случае всюду плотно
заполняет лишь некоторый двумерный тор, расположенный в ~fl»
но не совпадающий с X2)-
Задача пункта б) предлагалась первым из авторов для реше-
решения в журнале «Квант» A988, № 4). Предлагаем решить анало-
аналогичную задачу для троек чисел 2", 3",
7" и 2", 3", 5".
Задача 8.8. Вокруг Солнца вра-
вращается планета с радиусом орбиты R,
а вокруг нее в той же плоскости —
спутник с радиусом орбиты г, причем
угловые скорости их вращения несо-
несоизмеримы. Доказать, что спутник за-
заполнит всюду плотно кольцо с центром
в Солнце, внутренний радиус которого
равен {R—г), а внешний — (/?+')•
Замечание. Указанная систе-
система «Солнце — планета — спутник* но-
носит еще название «двойной маятник»;
его конфигурационное пространство-
Рис 8.10 тор -р (рис> 8.10).
Задача 8.9. Рассмотрим систе-
систему, состоящую из двух планет одинакового радиуса е>0, враша-
ющихся по окружностям различных радиусов с общим центром
О и расположенных в различных плоскостях (более близкая к ^
планет А видна под большим углом из точки О, чем планета Dh
Доказать, что если отношение угловых скоростей вращения пла-
116
Тог
нет иррационально, то затмение более далекой планеты близкой
планетой (с точки зрения наблюдателя, находящегося в центре О
системы) будет происходить бесконечное число раз.
Решение. Затмение происходит, если в данный момент
времени / планеты А и В ©называются близко к одному из двух
лучей, на которые точка О разбивает прямую пересечения пло-
плоскостей орбит (рис. 8.11). Если (ф0, i]H) — точка тора, соответству-
соответствующая положению планет на таком луче AM, то затмение произой-
произойдет, если точка тора (tp, 1M), соответствующая положению планет в
момент времени t, удовлетворяет условию | tp—ср0 |+ | ip—v|>0 | <
<7i—Тг. гДе Yi и Y2 — углы, под которыми видны планеты из
точки О. Такие точки (ф, \|э) образуют квадрат с центром в точке
(фо! 'Фо) и диагональю 2(yt—у2). Если в момент времени t=Q поло-
положения центров планет А, В характеризуются углами а и Р, то в
произвольный момент t соответствующие им углы будут равны
Ф=ш1Н-а, ty=(o2f+P, откуда — =^_ и ^ — ^ф^.^ где
Я = —— а + Р. Координаты ф, i}> связаны, таким образом, линей-
линейным соотношением, задающим на плоскости Офф прямую с угловым
коэффициентом щ/а^. В силу иррацио-
иррациональности со2/(й1 на торе возникает и р-
рациональная обмотка, и поэтому
конфигурационная точка (ф, ip) рано или
поздно подойдет к точке (фо,^о), что и до-
доказывает требуемое: найдется бесконечное
множество точек (ф, 'ф), для которых бу-
будет происходить затмение. Задача ре-
решена.
Задача 8.10. Из некоторой точки
сферической планеты одновременно отпра-
отправились в бесконечное путешествие два
путешественника, каждый по своему большому кругу и со своей
постоянной скоростью. Доказать, что путешественники вновь Bcipe-
тятся, т. е. расстояние между ними в некоторый момент станет
меньше 1 м.
Задача 8.11. Двое .часов со стрелками идут равномерно,
но одни из них немного отстают, а) Доказать, что в какой-ю мо-
момент показания часов будут отличаться менее чем на 1 с. б)* Ре-
Решить ту же задачу для п равномерно идущих часов со стрелками:
доказать, что найдется момент времени, когда показания любой
пары часов будут отличаться менее чем на 1 с,
§ 9. Бильярд в прямоугольнике и тор
Напомним, что в § 7 для изучения траекторий
бильярда в прямоугольнике Q=ABCD была предложена
бедующая конструкция.
Прежде всего с помощью отражений относительно
сторон прямоугольника ABCD, а также относительно
Сторон уже отраженных прямоугольников замостим всю
Носкость прямоугольниками Qm,n, равными ABCD=
117
=Qo, о- Прямоугольник Qm> n получается из прямоуголь-
прямоугольника ABCD с помощью т последовательных отражений
относительно вертикальных сторон и п последовательных
отражений относительно горизонтальных осей (рис. 9.1,о).
Проведя на замощенной описанным образом плоскости
прямую M.N, мы можем с помощью обратных отражений
ее куски, лежащие в прямоугольниках Qm< „, перевести
в исходный прямоугольник QOi 0. Тем самым из прямой
с
Qm,n
Q11
Qio
'N
В
a
M
5
Рис. 9.1
MN мы получим траекторию бильярда в прямоугольнике
QOiO (рис. 9.1,6).
Удобно изучать не одну бильярдную траекторию от-
отдельно, а целый пучок траекторий. Для этого на замощен-
замощенной плоскости проведем семейство параллельных друг
другу прямых с углом наклона а к оси АВ. Теперь заме-
заметим, что нет необходимости рассматривать этот пучок пря-
прямых на всей плоскости, а достаточно ограничиться
четырьмя прямоугольниками — QOiO, Qli0, QOil и Q1?1,
образующими один большой прямоугольник Г^ЛЛИ^Л1
(рис. 9.1, в). Допустим, траектория MN нашего пучка в
точке Mi покидает прямоугольник П. Двумя отражениями
относительно прямых А1А\ и DDt мы возвращаем луч MiN
внутри прямоугольника П. Композиция упомянутых от-
отражений есть параллельный перенос на вектор А1 А, и
луч MiN при этом переносе переходит в луч M[N'. В свою
очередь, когда луч M\N' в точке М2 выходит опять из
прямоугольника П, мы с помощью параллельного пере-
переноса, задаваемого вектором ЛИ, переносим луч М2#
внутрь П, и так далее. Вместо того, чтобы рассматривать
движение шара по прямой MN, мы можем (и, как мы ай-
4aG увидим, это более удобно) считать, что доходя до гра-
границы прямоугольника П, шар перескакивает в соответ-
соответствующую точку противоположной стороны и двия' гСЙ
в том же направлении до следующего перескакива!
таким образом, траектория шара состоит из послед»- d'
118
тельности параллельных отрезков на прямоугольнике П.
Чтобы получить из этой траектории траекторию бильярда,
достаточно перегнуть прямоугольник П по средним ли-
линиям (рис. 9.2). Прямоугольник П назовем «фундамен-
«фундаментальным прямоугольником» для исходного прямоуголь-
прямоугольного бильярда.
Конечно, более удобно рассматривать движение по
непрерывным траекториям. Для этого достаточно склеить
соответствующие точки противоположных сторон: склеить
/:/
f'A
ЛАЛЛ
о
КХХ)
Рис. 9.2
Рис. 9.3
верхнюю и нижнюю стороны а в прямоугольнике П, по-
получив цилиндр, а затем боковые стороны b (рис. 9.3).
Ясно, что после склейки оснований цилиндра получится
тор, а рассмотренные выше траектории станут непрерыв-
непрерывными — это и будут траектории обмотки тора\
Найдем частоты этой обмотки. Если считать,
что бильярдный шар движется со скоростью 1, то при
движении под углом а к стороне АВ прямоугольника
ABCD проекции скорости на горизонтальную и верти-
вертикальную оси равны Ui=cos а и u2=sin а. В терминах
координат на торе щ и иг — это скорости движения кон-
конфигурационной точки вдоль параллелей и вдоль меридиа-
меридианов. В нашем случае тор склеен из прямоугольника П со
сторонами 2«1 и 2о2 (здесь а±—АВ, a2=AD — стороны исход-
исходного прямоугольника ABCD) и периоды движения по эква-
2fli 2flf m 2а« 2fl9
тору и по меридиану равны Тг =—-———, Г2=—=——.
Согласно определению, соответствующие частоты равны
_ 2л _ cos a _ sin»
119
Вспомнив результаты § 8, получаем:
A) если число ш=—=—i-tga рационально, то опи-
санная обмотка тора рациональна, и все ее траектории
периодичны;
B) случаю иррациональности со = — tg а соответствует
иррациональная обмотка тора, и тогда любая траектория
обмотки всюду плотно заполняет тор.
Поскольку бильярдный поток на прямоугольнике <2=
—ABCD получается из обмотки тора (или, что то же самое,
«потока с перескакиванием» на прямоугольнике П) скла-
складыванием тора вчетверо, соответствующим складыванию
прямоугольника П по средним линиям, мы получаем из
рациональных обмоток тора пучки перио-
периодических бильярдных траекторий на прямоуголь-
прямоугольнике Q, а из иррациональных обмоток — пучки
непериодических и всюду плотных на
прямоугольнике Q траекторий бильярда. Тем самым тео-
теорема 2 из § 7 о всюду плотности бильярдных траекторий
доказана.
Резюмируем проделанное в § 7 — 9.
Бильярд в прямоугольнике удается свести к обмоткам
тора, при этом траектории бильярда оказываются либо
периодическими, либо всюду плотными в прямоугольнике;
периодичность (или всюду плотность) траектории опреде-
определяется только начальным направлением движения, но не
зависит от начального положения шара.
К изучению бильярдов в многоугольниках мы вернемся
позже, в гл. 8 и 9, а сейчас в виде задач затронем несколько
интересных вопросов, связанных с обмотками тора.
Задача 9.1 (см. § 22). Доказать, что для бильярда в равно-
равнобедренном прямоугольном треугольнике любая неособая траек-
траектория либо периодична, либо всюду плотно заполняет треуголь-
треугольник. Показать, что особые траектории этого бильярда (т. е. те тра-
траектории, которые попадают в вершины) можно естественным об-
образом продолжить за вершины (см. Задачу 7.5) так, что они оказы-
оказываются опять либо периодическими, либо всюду плотными.
Задача 9.2 (см. § 22). Доказать утверждение задачи 9.1^ для
бильярда в равностороннем треугольнике. (Для этого попытайтесь
обобщить рассмотрения этого параграфа на случай плоскости,
замощенной равносторонними треугольниками — попробуйте ог-
ограничиться несколькими треугольниками, как выше мы ограни-
ограничились четырьмя прямоугольниками; постройте затем «поток с
перескакиванием».)
Задача 9.3 (см. § 15 и гл. 7). При изучении бильярдов в
многоугольниках (например в треугольниках) возникает следую"
щий вопрос — ие может ли бильярдная траектория «застрять»
120
Рис. 9.4
в угле (не попасть точно в вершину угла, а «запутаться» около
вершины — конечно, если так бывает, то эти траектории не могут
быть всюду плотными!)? Ответьте на этот вопрос. Сформулируем
задачу более точно.
Дан угол А раднанной величины а. Бильярдный шарик за-
залетает внутрь этого угла. Сколько может произойти столкновений
шара со сторонами угла, прежде чем шар вы-
вылетит из угла и полетит без столкновений?
(Стороны угла — бесконечные лучи; рис. 9.4).
Может ли быть бесконечно много столкно-
столкновений? (Рассмотрите сначала случаи а=
=я/2, я/4, я/3, 2я/5.) Докажите, что шар вы-
вылетит из угла в направлении, параллельном А
направлению влета, тогда и только тогда,
когда а=я/л, где я — натуральное число.
Прн доказательстве теоремы 2 из § 7
можно было воспользоваться следующей лем-
леммой.
Задача 9.4 (лемма о зайцах). В не-
некотором узле О квадратной решетки на>
днтся охотник, а в остальных узлах сидят
одинаковые и одинаково расположенные зай-
зайцы — кружки радиуса е с центрами в этих узлах. Охотник нау-
наугад стреляет (траектория пули — луч /, выходящий из точки О).
Вернется ли он домой с добычей?
Решение. Если траектория пули проходит через узел, от-
отличный от точки О, то заяц, сидящий в этом узле, будет убит «в
самое сердце» (в центр кружка).
Поэтому интересен только тот слу-
случай, когда узел О — единственный
на траектории пули, т. е. тангенс
угла наклона луча / к оси Ох и р-
рационален. Оказывается, что
и в этом случае какой-нибудь заяц
будет убит. Обозначим точки пере-
пересечения луча /с вертикальными пря-
прямыми сетки через А0=0, Alt A2,
А3, .... Ап, . . . (рис. 9.5). Сов-
Совместим все квадраты решетки, кото-
которые пересекает луч /, с кпадратом
OMNK, тогда каждая точка Ап пе-
перейдет в некоторую точку А п на сто-
стороне MN. Найдутся такие точки
Am и Ат+к, расстояние между кото-
которыми будет меньше е (почему?).
Докажите самостоятельно, что тогда
расстояние от точки Af, до одного
из узлов решетки меньше в (в частности, если А'т и A'm+k сов-
совпадают, то Ак буде1 узлом решетки).
Решение этой задачи почти воспроизводит доказательство
теоремы Якоби, и то обстоятельство, что если из точек прямой,
ваполняющих ее всюду плотно, выпустить пучок параллельных
ПРЯМЫХ, ТО ОНИ ЗаПОЛНЯЮТ ВСЮДУ ПЛОТНО ВСЮ ПЛОСКОС1Ь.
Рис. 9.5
Глава 4
ФИЗИКА ПРЯМОУГОЛЬНОГО БИЛЬЯРДА
Эта глава посвящена как фигурам Лиссажу,
так и их изображениям на экране осциллографа, хорошо
известным физикам-электронщикам. Мы приведем мате-
математическое определение этих понятий и свяжем их (с
помощью осциллографа) с бильярдом в прямоугольнике
и обмотками тора, а также решим с помощью обмоток тора
одну геометрическую задачу об обнаружении неподвиж-
неподвижного объекта на плоскости.
Основной материал этой главы мы будем «разбавлять»
задачами, решения которых (иногда приводимые в тексте)
используются для получения последующих результатов,
поэтому желательно, чтобы читатель принял активное
участие в решении этих задач.
§ 10. Фигуры Лиссажу *)
Фигурами Лиссажу называются кривые на
плоскости Оху, описываемые во времени t точкой с коор-
координатами x(t), y(t), где
= a2 cos ((
когда t меняется от—оо до +°о. Здесь ак>0, а2
постоянные, называемые амплитудами фигуры Лисса-
Лиссажу; <щ>0, @2>0 — постоянные, называемые частотами
фигуры Лиссажу- цч и сра — постоянные, называемые
начальными фазами. Другими словами, фигурой Лиссаясу
называется траектория точки, которая движется «°
*) Лиссажу Жюль Антуан A822—1880) — французский физию
Фигуры, названные его именем, он применил для оптического и ¦
следования сложения колебаний.
122
плоскости Оху так, что ее координаты х и у совершают
гармонические колебания, т. е. меняются по гармониче-
гармоническому закону A). Фигуры Лиссажу можно наблюдать на
экране осциллографа, подавая соответствующие напряжения
на горизонтальную и вертикальную оси.
Поскольку при любом / выполнены неравенства
\y(t)\<a2,
фигура Лиссажу целиком лежит в прямоугольнике Q
размерами 2oi на 2с2 с центром в начале координат. Да-
Далее, если cos(wi/+(pi)=±l, то при этих значениях t фи-
фигура Лиссажу соприкасается с вертикальными
сторонами прямоугольника Q, а при t таких, что cos («>2Н-
+фг)—±1. фигура Лиссажу касается горизонталь-
горизонтальных сторон Q.
Заметим, что координата x(t) меняется периодически
с периодом Ti=2it/(Oi и координата y(t)— тоже периоди-
периодически, но с другим периодом — Т2=2яЛо2. Движение
точки {х(t), у(t)) будет периодическим в том и
только том случае, когда для некоторых целых тип mTi—
=пТ2, т. е. когда 7\ и Т2 соизмеримы (продумайте это).
,-, 7\ со»
Поскольку -jr- — —» условие периодичности состоит в
рациональности числа ю = —.
Сейчас мы укажем удобный способ изображения фи-
фигур Лиссажу, а заодно получим информацию о поведении
непериодических фигур Лиссажу. Прежде всего, введем
вместо t новую переменную
когда / меняется от —оо до Ч-оо, и тоже меняется от —оо
до +оо, и наоборот. Выразим t через и:
и подставим полученное выражение в формулу для y(t);
в результате возникнет следующая зависимость у от и:
у(и) = а2 cos (ом + Р) = fl2 cos ю (и—а),
где (D=(D2/a>i, a=—fVw, P=q>2—(ocpi. Наконец, выберем
за единицу масштаба аи т. е. заменим сц на 1, а2 на а—
=o2/oi. Теперь формулы, задающие фигуру Лиссажу,
принимают совсем простой вид:
у (и) = a cos (ы (и—а)).
123
Рис. 10.1
На рис. 10.1 нарисованы вырожденные фигуры Лиссажу
с фазой ос=0, со=1 (рис. 10.1, с) и со=2 (рис. 10.1,6):
при (о=1 и ос=0 у=а cos u=ax и мы получаем дважды
проходимый отрезок прямой; если со=2 и ос=0, то у=
=acos2u=a{2cos2u—\)=2ах2—а и
соответствующая фигура Лиссажу —
дважды проходимая дуга параболы.
Задача 10.1. Докажите, что при
а=0 и а=п (п — натуральное число) фи-
фигура Лиссажу представляет собою часть
графика многочлена степени п: у=Тп(х),
(Многочлены, получающиеся таким обра-
образом, называются многочленами Чебыше-
ва *).)
' В общем случае (при а^=0)у нель-
нельзя разумным образом выразить через
х, и мы поступим иначе. Чтобы нари-
нарисовать на плоскости Оху заданную
уравнениями B) фигуру Лиссажу,
которую мы обозначим L(co, ос), нарисуем сначала на
вспомогательной плоскости Оиу график функции
у = О COS СОИ,
который обозначим Гш. Чтобы получить график Гш, а
функции у=а cos со (и—ос), достаточно перенести график
Гш на ос вдоль оси Ои (рис. 10.2). „.
Рассмотрим бесконечный прямой *
круговой цилиндр радиуса 1, на кото-
котором выделена одна образующая — ось
Оу — и одна направляющая — окруж-
окружность S. Приложим плоскость Оиу к
цилиндру, совместив оси Оу на плоскости у
и на цилиндре так, чтобы ось Ои каса-
касалась окружности S. Теперь намотаем
всю плоскость Оиу на цилиндр (рис.
10.3). Конечно, процедура намотки лишь
воображаемая; плоскость считается «бес-
«бесконечно тонкой», прозрачной — на ней
лишь отмечена кривая ГИ1„ (указанная
намотка аналогична намотке прямой
IR1 на окружность при решении числовой задачи в § 2).
Эта кривая, намотанная на цилиндр, дает пространст-
*) П. Л. Чебыше A821—1894)— крупнейший русский мате-
математик, основоположник петербургской математической школы»
Многочлены, названные его именем, являются многочленами,<наш-
124
венную кривую, которую обозначим Г (о, а). Заметим,
что переносу на а по оси Ои, при котором из графика
Гш получается график Гш, а, соответствует (после намотки
плоскости на цилиндр) поворот около оси цилиндра
на угол а радиан. Отсюда сле-
следует, что для получения кри-
кривой Г (о), а) можно поступить
так: намотать на цилиндр
график Г(„ функции у—
-acos(cou) и полученную кри-
кривую Г(ю) повернуть на угол
а около оси Oif/! (рис. 10.4).
Итак, мы получили прост-
пространственную кривую Г (о, а),
лежащую на цилиндре. Вооб-
Вообще говоря, эта кривая будет
иметь точки самопересечения.
Она целиком лежит в куске
цилиндра \у \^а около окружности
оольцо» получается после намотки
плоскости Оиу); точкам касания
Рис. 10.3
10.4
S на цилиндре (это
на цилиндр полосы
графика ГШ1(Х
Рис. 10.5
с прямыми у—±а соответствуют точки касания кривой
Г (со, а) с верхней и нижней окружностями S(+) н S(_,,
ограничивающими упомянутый кусок цилиндра (рис. 10.4).
Наконец, приложим к цилиндру с изображенной на нем
кривой Г (о, а) плоскость Оху так, чтобы своей осью Оу
°на касалась цилиндра по образующей О2у2. получающейся
из образующей цилиндра Оу поворотом на л/2 около оси
®луг. После этого спроектируем кривую Г(о), а) с цилиндра
Менее уклоняющимися от нуля» (см. научно-популярную книгу:
Данилов Ю. А. Многочлены Чебышева.— Минск: Вышэйшая
^к 1984)
1984).
125
на плоскость Оху — так сказать, посмотрим на кривую
Г («и, а) сбоку — так, чтобы ось цилиндра Oit/i слилась с
образующей 0гу2 цилиндра и осью Оу на плоскости, а
образующая цилиндра Оу спроектировалась в прямую
х=1 (рис. 10.5).
Задача 10.2. Доказать, что проекция кривой Г (со, а) на
плоскость Оху есть фигура Лиссажу L(w, a).
Решение. Точка (u, a cos ю(м—а)) графика Ги_ а после
намотки плоскости Оиу на цилиндр перейдет в точку цилиндра (J,
высота которой над окружностью S по нап-
направляющей цилиндра равна /i=acosco(u—a),
и при проекции иа плоскость Оху точка U
перейдет в точку V с ординатой y=h=
=cos ш(ы—а). Чтобы иайти абсциссу точки (/',
рассмотрим точку М, в которой проходящая
через U направляющая цилиндра пересекает
окружность S (рис. 10.6). Угол ^.О^М,
согласно определению намотки, равен ы, и
координата по оси Ох проекции М на Ох
'0.6 равна O2M'=cos и. Таким образом, проек-
проекция точки U иа плоскость Оку имеет коор-
координаты (х, у) = (cos и, cos ш (и—а)), что и требовалось доказать.
Итак,*, для построения фигур Лиссажу Z,(w, a) доста-
достаточно намотать косинусоиду у=а cos ъш на цилиндр
и затем спроектировать ее на соответствующую плоскость
(повернув перед этим на угол ос кривую или плоскость
Оху\). Таким образом, чтобы нарисовать семейство
фигур Лиссажу /-(ю, а) с фиксированным ю и разными а,
достаточно построить всего лишь одну кривую — ци«
линдрическую косинусоиду Г (о). Рассмотрим несколько
частных случаев.
Случай со=1. При намотке косинусоиды y=acosu
на единичный цилиндр один период @<:ы<2я) косину-
косинусоиды наложится на цилиндр ровно один раз, и ГA) будет
замкнутой кривой с одним минимумом и одним максимумом
(самой высокой и самой низкой точкой, если высоту из-
измерять по образующим цилиндра).
Задача 10.3. Доказать, что кривая ГA) — плоская,
г. е. целиком лежит в одной плоскости. (Эта кривая есть сечение
цилиндра плоскостью.)
Задача 10.4. Доказать, что сечение цилиндра плоскостью,
наклонной к его оси, есть эллипс (определение эллипса см. в § *••
(Решение эгой вадачи с помощью сфер Данделеиа приведено в
§ 4 — см. еадачу 4.4.)
«Рассматривая» полученную кривую с разных сторон>
нетрудно изобразить семейство фигур Лиссажу с 0)=
(т. е. с cui=(D.>). Поскольку перпендикулярная проекция
эллипса есть либо круг, либо опять эллипс, фигуры Ли '
126
сажу с @=1 суть эллипсы, вписанные в прямоугольник П
(рис. 10.7).
Случай @=2. Два периода косинусоиды у=а cos 2м
дадут при намотке на единичный цилиндр только один
х
Рис. 10.7
Рис. 10.8
слой на цилиндре, и кривая Г B) имеет 2 минимума и 2
максимума. Полученная кривая уже не плоская (она
похожа на проволочное седло). Ее «рас-
«рассмотрение» дает семейство фигур Лиссажу
с (о=2 (рис. 10.8).
Случай @=3/2. Кривая Г C/2) на
Цилиндре замкнется, когда мы намотаем на
него два слоя — три периода косинусоиды
У— асов у и. Эта кривая будет иметь само-
самопересечение уже на цилиндре. Изобразите
какую-нибудь из соответствующих фигур
Лиссажу (рис. 10.9).
При рассмотрении фигур Лиссажу с
ы=1 и (о=2 бросается в глаза их сход-
сходство с семействами периодических траек- Рис. 10.9
торий бильярда в прямоугольнике (см.
Рис. 7.1), только у траекторий бильярда вместо точек
касания со сторонами прямоугольника — точки излома.
127
Это сходство отнюдь не случайно, и мы его обсудим в сле-
следующем параграфе (подумайте над этим вопросом само-
самостоятельно).
Займемся теперь непериодическими фигурами Лиссажу.
Теорема. Любая непериодическая фигура Лиссажу
всюду плотно заполняет прямоугольник П={|я;|^1,
\у\<а).
Доказательство. Поскольку фигура Лиссажу
L(co, а) получается в результате проекции цилиндриче-
цилиндрической косинусоиды Г (со, а) на плоскость Оку, причем про-
проекция части цилиндра Ц={\у\^а), лежащего между
окружностями S(+) и S(_, (см. выше) есть в точности
прямоугольник П, достаточно доказать, что при иррацио-
иррациональном со кривая Г (о, а) всюду плотно заполняет ци-
цилиндр Ц. Для этого рассмотрим точки касания кривой
Г (о, а) с верхней окружностью S(+). Они получаются
при намотке на окружность S(+) из точек касания графика
у=а cos со (и—а) с прямой у—а, т. е. из таких точек ип,
что со(ып—а)=2лп. Отсюда находим:
После намотки эти точки дадут последовательность точек
Мп на окружности S(+), причем, поскольку ип — ариф-
арифметическая прогрессия с разностью ср=2л/со, точки Мп
получаются каждая из предыдущей поворотом по окруж-
окружности S(+) на угол ср. Согласно теореме Якоби (§ 2),
если числа ср и л несоизмеримы, точки Мп
всюду плотно заполняют окружность S(+). Несоизмери-
Несоизмеримость ср с я означает иррациональность отношения ср/я=
=2/со, т. е. иррациональность со. Из всюду плотности
множества точек Мп по окружности S(+) уже несложно
вывести всюду плотность кривой Г (со, а) на цилиндре (про-
(проведите подробный вывод сами). Теорема доказана.
Эта теорема тоже весьма напоминает соответствующие
свойства бильярдных траекторий. Из нее следует, что
самый лучший способ нарисовать фигуру Лиссажу с ир-
иррациональным со — зарисовать сплошь весь прямоуголь-
прямоугольник П ! Если наблюдать такую фигуру Лиссажу на эк-
экране осциллографа, то можно заметить, что она плывет —
за экраном как бы поворачивается невидимый цилиндр
с нарисованной на нем цилиндрической косинусоидой.
На самом деле это не плывущая, аодна и та же Фи"
гура Лиссажу (если только не меняются фазы cpi и фг).
но ранее начерченная ее часть потухла на экране. Если
128
бы не было такого затухания, то мы увидели бы всюду
плотную на экране фигуру Лиссажу, если только отно-
отношение (o=(o2/o)i «подобрать иррациональным». («Всюду
плотность» на экране соответствовала бы тому, что весь
экран светился бы; более того, экран светился бы все
равномернее и равномернее,— но это довольно сложное
утверждение.) Заметим, что «иррациональных чисел боль-
больше, чем рациональных»: рациональные числа можно за-
занумеровать, а иррациональные нельзя. В теории вероят-
вероятностей часто используется следующий факт: «если наугад
ткнуть пальцем (точечным!) в какую-либо точку на чис-
числовой прямой, то с вероятностью 1 мы попадем в точку с
иррациональной координатой». Поэтому подобрать ю ир-
иррациональным можно, выбрав его «наугад».
Задачи физики, в которых появляются фигуры Лиссажу,
довольно подробно рассмотрены в ряде статей из «Кванта»: Минц
И. А. Странный маятник A971. № 6. С. 30—32); Кошкин Г. Л.
Опыты с маятниками A972. № 1. С. 26—31); Сипаева Н. А. Фигуры
Лиссажу A972. № 7. С. 23—28). Там же описаны соответствующие
опыты.
Задача 10.5. Придумать способ рисования кривых на пло-
плоскости Оху, задаваемых уравнениями: a) x=sin t, y=f(t); б) «=/(/),
f/=cos /. (Здесь f(t) — заданная функция; мы имеем в виду способ,
аналогичный описанному способу построения фигур Лиссажу.)
Задача 10.6. Докажите, что фигуры Лиссажу L(l/co, a)
с амплитудами а!=а2=1 равны соответствующим фигурам Лис-
Лиссажу L(co, P) с тем же со и каким-то Р. (Рассмотрите сначала случаи
ю= 2 (—=— 1 ; со=п (—=—1, где п — натуральное.)
Задача 10.7. Какое наибольшее число точек самопересе-
самопересечения может иметь фигура Лиссажу, если а) со=и, б) ш=1/я,
в) co=m/n (тип — натуральные)?
§11. Бильярд в прямоугольнике
и осциллограф
В § 9 было показано, что траектории биль-
бильярда в прямоугольнике получаются из траекторий обмоток
тора Т «складыванием тора вчетверо». Рисунок 11.1 на-
напоминает, в чем состоит это складывание. С точки зрения
математики с помощью этого складывания мы каждой
точке М тора Т ставим в соответствие некоторую вполне
определенную точку М' прямоугольника Q. Такое соот-
соответствие, как хорошо известно (см., например, раздел II
книги А. Н. Колмогорова «Математика — наука и профес-
профессия», «Библиотечка «Квант», 1988. Вып. 64), называется
отображением тора Т на прямоугольник Q. Обозначим*
* Г. А. Гальперин. А. Н. Земляков 129
его /б:
ft- T-
Для точки N внутри Q имеется ровно 4 прообраза — точки
Mit Afa, Ms, Мц тора, для которых /б (Mk)=N (рис. П.2).
Если на торе рассмотреть кривую Г, являющуюся траек-
траекторией обмотки тора (см. § 8), то образ этой кривой при
отображении f6 — кривая ^6(Г)
и в прямоугольнике, являющаяся
траекторией бильярда.
В § 10 мы обратили внима-
внимание на сходство между траекто-
траекториями бильярда и фигурами
Лиссажу (рис. 11.3). Оказывает-
Оказывается, причины этого сходства сос-
состоят в том, что фигуры Лисса-
Лиссажу также являются образами
траекторий обмоток тора при
некотором отображении /0 тора
Т в прямоугольник П, в который вписаны фигуры Лисса-
Лиссажу — П={(х, у): | х Koi, | у | <ог}, если фигуры Лис-
Лиссажу задаются формулами
х @ = ох cos (©!* + <Pi), у (t) = о2 cos (a2t + ф2).
Отображение fB: T -*-П мы сейчас опишем. Оно оказы-
оказывается весьма похожим на отображение f6; если отобра-
ТТ
.
/и
•/v
» ¦
Рис. 11.2
Рис. 11.3
жение ^б назвать «бильярдом», то отображение /0 естест-
естественно назвать «свободным осциллографом» (осциллографом,
показывающим фигуры Лиссажу).
Итак, в целом ситуация такова. Имеются два «почти
одинаковых» отображения f6 и /о тора Т в прямоугольник.
При этом траектория Г обмотки тора при отображении
«бильярд» переходит в траекторию бильярда f6(Г), при
отображении «осциллограф» переходит в фигуру Лиссажу
130
/0(Г). В этом смысле «бильярд» и «осциллограф» устроены
одинаково, или, как часто говорят в таких случаях, изо-
изоморфны.
Опишем теперь отображение «свободный осциллограф»
/0. Рассмотрим тор Т с координатами (ifc, %) на нем (дол-
(долготой и широтой — см. § 8). Точке тора М с координатами
№f. Фг) поставим в соответствие точку М' плоскости Оху
с координатами #=aicos ifr, у=агсо&^ и положим М'=>
=/0(М). Тем самым отображение /0 полностью определе-
определено — оно задается формулой
G2COSiJJ).
Траектория Г обмотки тора g частотами (coj, cos) зада-
задается формулами
Образ траектории Г этой обмотки при отображении /0
на плоскости есть кривая
Подставляя сюда выражения для %(/) и %(t), получим,
как и ожидалось, формулы фигуры Лиссажу:
a2cos(c
Таким образом, действительно, фигуры Лиссажу являются
образами траекторий обмоток тора при отображении /0.
Посмотрим теперь, как «устроено»
это отображение. Разобьем тор на *2
четыре квадрата, как указано на рис. -Zft
11.4. Пусть M=t$i, ip2) — точка
внутри квадрата Qoo, т. е. 0<%<п, rt
рассмотрим еще три точки
) M (
Bn—qlt ijJ), Moi= (%-, 2n—
( 2) Н
м,
'01
М
^10
Io Bnqlt j2), Moi (%, 2j2),
M,i= Bn—ipi, 2n—1]J). Нетрудно ви- ft» rt Q,02Tf %
деть, что эти точки получаются из М рис. ц_4
симметриями относительно средних
линий квадрата; с другой стороны, согласно известным
формулам тригонометрии
/о (Л*,„) = /о (ЛГв1) = f0 (Мя) = /0 (М)
(проверьте!), т. е. эти четыре точки при отображении /0
переходят в одну — точно так же, как и при соответст-
соответствующем отображении /б. Наконец, поскольку функция
z=cosi|j осуществляет взаимно однозначное отображение
5* 131
отрезка 0 <if <:n на отрезок —1 <2<1, отображение (х, у)=*
— (flicosipi, a2cosip2) отображает взаимно однозначно квад-
квадрат Qoo на прямоугольник П={—Ci<x<Ci, —а2«:г/«22}
(проверьте!).
' Итак, отображение «осциллограф» /0 действует так:
сначала тор Т «складывается», как и при отображении
«бильярд» }6, вчетверо — соответствующий квадрат пере-
перегибается по средним линиям и превращается в свою чет-
четверть Qoo. При этом траектории обмотки превращаются
в траектории бильярда в квадрате QOo- После этого к квад-
квадрату Q применяется взаимно однозначное отображение /^
его на прямоугольник П, при котором траектории биль-
бильярда «сглаживаются» и превращаются в фигуры Лиссажу!
(Последнее отображение при ai=a2=l есть сжатие, но не
равномерное; благодаря неравномерности и сглаживаются
углы.) Приведенное описание показывает, что «бильярд»
и «осциллограф» действительно «изоморфны» — «отлича-
«отличаются на взаимно однозначное преобразование». Изоморфизм
между фигурами Лиссажу и траекториями бильярда можно
пояснить довольно просто и по-другому. При движении
точки {x(t), y{t)), описываемом уравнениями фигуры Лис-
Лиссажу
х @ = «! cos (со±/ + <pi), у (/) = а.г cos (<oa/ + <р2),
координаты хну (или проекции точки (х, у) на оси Ох
и бу) совершают гармонические колебания. При движении
же бильярдного шара (х, у) по прямоугольнику {0<x<at,
0«:г/«:а2} координаты хну также совершают колебания,
только не гармонические, а соответствующие закону уп-
упругого отражения. Можно написать формулы, по которым
меняются х и у в этом случае:
Здесь {и} — обозначение для дробной части числа и. Гра-
График зависимости х от t, задаваемой выписанной формулой,
схематически изображен на рис.
11.5. Таким образом, траектории
А
V
v
\ /\t бильярда задаются формулами,
аналогичными формулам для фн*
гур Лиссажу — с той разницей,
что вместо функции cos и в этих
Рис. 11.5 формулах фигурирует функция
с(и) = |2{и}-1|.
Задача 11.1. Полученное описание фигур Лиссажу каК
образов траекторий обмотки тора при указанном отображении
132
дает возможность сразу доказать всюду плотность фигур Лиссажу
с иррациональным отношением шг/а>,. Проведите точное рассуж-
рассуждение.
Задача 11.2. Отображение /0 есть композиция проекций
тора — убедитесь в этом, показав, что при описанном ниже по-
построении (по шагам) получаются фигуры Лиссажу.
1 шаг. На плоскости Oif^t]^ рисуем прямую и наматываем
эту плоскость на горизонтальный цилиндр радиуса 1.
2 ш а г. Проектируем полученную на цилиндре кривую на
плоскость О^у.
3 ш а г. Наматываем плоскость С%^ на вертикальный цилиндр
радиуса 1.
4 ш а г. Проектируем полученную на цилиндре кривую на
плоскость Оху — должны получиться фигуры Лиссажу с ампли-
амплитудами 0^ = 02=1.
§ 12. Задача о пеленге
Пусть на плоскости даны две различные точки
Ai и Л2. Около этих точек вращаются прямые U и /2 с
постоянными угловыми скоростями (Oi и ю2. Пусть M(t) —
точка пересечения прямых /± и /2 в мо-
момент времени t. Задача о пеленге заклю-
заключается в описании «кривой пеленга» —
траектории движения точки МA) (рис.
12.1). В некоторые моменты времени
прямые U и /2 параллельны — тогда мы
считаем (как и происходит на самом
деле), что точка М «отлучилась на бес-
бесконечность».
Если периоды вращения 7\=2:п;/| coi | и Г2=2я/| со2 |
соизмеримы, то, очевидно, движение точки М (t)
будет периодическим — повторяющимся через некоторый
промежуток времени. Однако нарисовать соответствующие
кривые не так уж просто, и мы, в качестве разминки, ог-
ограничимся рассмотрением случая сй1=юг.
Если ti)i=(o2=(o, т. е. движение прямых h и /2 про-
происходит с одинаковыми угловыми скоростями и в одном
направлении, то из рис. 12.2 видно, что углы cti и ос2 равны
(оба эти угла равны a-At) и поэтому углы /_AiMAi и
^.А^М'Аг равны. Следовательно, в этом случае точка
M(f) движется по дуге окружности, проходящей через
точки Ai и Л2 *). Какая именно это дуга, зависит от на-
начальных положений прямых h и /2 (если в начальный
Момент /i и /2 параллельны, то они будут такими и всегда).
*) Как известно, множество точек М, лежащих по одну сторону
•эт^прямой А±А% и таких, что ^i4,Mi42=a= const, представляет со-
собой дугу окружности с хордой i41i42.
133
Нетрудно показать, что после перехода прямой U через
положение А2А3 точка М продолжает двигаться по дуге
той же окружности, что и раньше. Таким образом, «пе-
«пеленг» с частотами t0i==co2 происходит по окружностям,
проходящим через точки At и Аг.
В случае coi——со2 кривые пеленга будут гиперболами,
проходящими через точки Ах и Л2 (рис. 12.3), доказатель-
M=M(jr+At)
M(t)
Рис. 12.2
Рис. 12.3
ство чего мы не приводим. Попробуйте нарисовать какие-
нибудь кривые пеленга с о>1=±2со2-
Теорема. Если coj и со2 несоизмеримы, то любая
кривая пеленга всюду плотно заполняет всю плоскость,
т. е. пересекает любой круг на плос~
кости (где бы он ни лежал и сколь
бы мал он ни был).
Нетрудно вывести эту теорему из
теоремы Якоби. Мы поступим, одна-
однако, чуть изящнее — построим отобра-
отображение /п тора Т в плоскость R2, при
котором траектории обмотки тора о
частотами ац, со2 перейдут в соответст-
соответствующие кривые пеленга.
Это отображение fa: T-*- R2 (еС*
тественно его назвать «пеленгом») чрезвычайно просто —
точке тора М с координатами i|>i, % мы ставим в соот-
соответствие точку М' пересечения прямых h и 1г, проходящих
через наши две точки At и А% и образующих с прямой
ЛИг углы % и vj32 соответственно (рис. 12.4). Таким об-
образом, тор Т — конфигурационное пространство точек М.
При этом мы считаем, что на каждой из прямых h и '«
выбраны направления, и углы ipi, -ф2 отсчитываются от
направления луча АгА? до этих выбранных направлении.
Если оказывается, что прямые /i(ipi) и М1!^) параллель-
параллельны, то соответствующая точка тора переходит «в бесконе
ность» (так будет на «диагонали» тора •ф1="фв и на парзл
134
лельной «кривой» гр2==%±л). Отображение fn выбрано имен-
именно так, чтобы при движении конфигурационной точки
тора по траектории обмотки:
образ этой точки на плоскости двигался по кривой пеленга!
(Обдумайте это' утверждение.) Отображение /„ будет ото-
отображением тора на всю плоскость, причем даже четы-
четырехкратным— точки (ifr, ip2), (т^+я, ty2), (ipi,
Рис. 12.4
Рис. 12.6
, гра+л) при \р!ф% и 0<il3i<n, 0<1р2<л переходят
в одну и ту же точку плоскости. Сетка параллелей и ме-
Ридианов на торе при таком отображении переходит в сет-
КУ, образованную пересечениями прямых, проходящих
через точки Ai и Ла (рис. 12.5).
135
Если coi и ю2 несоизмеримы, то на торе траектория Г
его обмотки всюду плотна, и отсюда немедленно следует
всюду плотность кривой пеленга /П(Г). Действи-
Действительно, чтобы показать, что кривая пеленга заденет
кружок К. (рис. 12.6), рассмотрим прямоугольник (или
квадрат) U на торе Т, переходящий при отображении
/п внутрь круга К. Поскольку траектория Г пересекает U
(что следует из всюду плотности Г на торе), кривая пе-
пеленга /П(Г) пересекает К!
На этом мы закончим рассмотрение вопросов, связан,
ных с обмотками торов, и вновь возвратимся к бильярдам
ЧАСТЬ III
ГЕОМЕТРИЯ И АРИФМЕТИКА
СТОЛКНОВЕНИЙ
Придворный!
Эй, мувыканты!
Входит Марлиан.
Клеопатра;
Нет, ие надо их,—
Давай, в шары сыграем, Хармиана.
В. Шекспир. «Антоний и Клеопатра»
В этой части книги будет исследована ме-
механическая система «газ абсолютно упругих шаров» —
система шаров, упруго сталкивающихся друг с другом,
а также со стенками сосуда, в который эта система поме-
помещена. В физике часто пользуются такой моделью при опи-
описании поведения реального газа, т. е. считают молекулы
газа твердыми шарами, а столкновения между ними —
упругими. В дальнейшем мы часто для удобства шары
будем называть молекулами. В нормальных условиях
число содержащихся в 1 см3 молекул воздуха очень ве-
велико — их порядка 1023, и от многократных столкнове-
столкновений молекул друг с другом возникает «хаос» — равно-
равномерное распределение молекул.
Изучение движения молекул газа относится к области
физики, называемой статистической механикой. Основы
этой науки были заложены в трудах Максвелла, Больц-
мана, Гиббса. Людвиг Больцман *) выдвинул так назы-
называемую «эргодическую гипотезу», в настоящее время но-
носящую его имя и состоящую в том, что система «газ шаров»
эргодична **). На этой гипотезе основан вывод известных
из школьного курса физики законов Бойля — Мариотта,
Гей-Люссака, уравнения Клапейрона — Менделеева и дру-
других уравнений молекулярно-кинетической теории газа.
Однако сама гипотеза Больцмана до сих пор доказана
только для частных случаев.
*) Людвиг Больцман A844—1906) — выдающийся австрийские
Ученый, работы которого оказали огромное влияние на развитие
Фундаментальной физики в силу нх принципиальной новизны и глу-
бииы. Относящаяся к статистической механике эргодическая гипо-
гипотеза отражает лишь небольшую часть чрезвычайно разносторонней
научной деятельности Л. Больцмана.
**) О понятии эргодичности см. конец введения.
137
Выдающийся вклад в решение этой проблемы и в обо-
обоснование статистической механики внесли советские уче-
ученые Н. С. Крылов и Я. Г. Синай. Важной идеей в их ис-
исследованиях явилось то, что газ можно заменить бильяр-
бильярдом, правда, в очень многомерной и криволинейной об-
области специального вида. Возникновение многомерного
пространства говорит о сложности рассматриваемой задачи.
Сведение системы абсолютно упругих шаров к системе
бильярдного типа впервые появилось в книге Н. С. Крыло-
Крылова «Работы по обоснованию статистической физики»
(М.: Изд-во АН СССР, 1950), а последовательная матема-
математическая теория была развита Я. Г. Синаем, который в
1970 г. в работе «Динамические системы с упругими от-
отражениями» (см. [17]) доказал, что уже система из двух
твердых дисков в прямоугольнике является эргодичной.
В этой части мы остановимся только на простейших
геометрических н «арифметических» свойствах «газа ша-
шаров». Геометрию столкновений отражает описание конфи-
конфигурационного пространства системы, сведение ее к биль-
бильярду и описание поведения полученной бильярдной ча-
частицы; а арифметику — подсчет числа столкновений между
шарами.
Изучение геометрии и арифметики столкновений в си-
системе двумерных дисков или трехмерных (а
тем более многомерных) шаров довольно сложно для на-
начинающего читателя. Поэтому эту центральную тему мы
поставили в конец части III и отметили ее двумя звездоч-
звездочками — гл. 7 при первом чтении можно пропустить. Вза-
Взамен этого в гл. 5 и 6 мы подробно рассматриваем модель
одном ер ного «газа» — систему упруго сталкиваю-
сталкивающихся частиц на прямой или ее части (полупрямой или
отрезке). Эта модель существенно проще и вполне до-
доступна школьникам. При ее изучении сначала возникает
рассматривавшийся ранее бильярд в прямоугольнике, и
мы можем применять уже известные из части II резуль-
результаты. Попутно обнаружатся и новые эффекты, которые
частично будут исследованы сразу же, а частично сведутся
к изучению бильярдов в многоугольниках — эти биль-
бильярды рассматриваются в части IV.
В гл. 5 разобран простейший случай одномерного «га-
«газа» — системы двух частиц на прямой. Для него про-
проводится относительно полное исследование.
Уже для одномерного «газа» из т р е х молекул полное
исследование системы может быть осуществлено до конца,
лишь когда молекулы не заключены в какой-либо «сосуд» ~~
138
отрезок, а свободно движутся по бесконечной прямой,
сталкиваясь только друг с другом. Изучение поведения
системы из трех молекул на отрезке сразу приводит к
системе из большого числа молекул на прямой, и оно
может быть исследовано только качественно (т. е. могут
быть получены лишь некоторые оценки на различные
параметры системы — число столкновений между моле-
молекулами и т. п.). Некоторые результаты этого исследования
приведены в гл. 6. Трудным в этой главе является § 18,
который отмечен одной звездочкой.
Глава 5
ОДНОМЕРНЫЙ «ГАЗ» ИЗ ДВУХ МОЛЕКУЛ
В этой главе исследуется одномерный «газ»
из двух молекул — двух шаров на отрезке, упруго
сталкивающихся друг с другом и упруго отражающихся
от концов этого отрезка. Доказывается, что указанная
система эквивалентна бильярду в прямоугольном треуголь-
треугольнике; исследование возможных бильярдных траекторий
дает возможность предсказывать поведение шаров на
отрезке.
§ 13. Два упруго сталкивающихся шара
на отрезке
Пусть на отрезке ОА длины а движутся без
трения два точечных шара, имеющих массы Ш\ и т2 (рис.
13.1). Считается, что шары сталкиваются между собой
абсолютно упруго, т. е. если до соу-
соударения их скорости были равны Vi m v v m
и vt, то их скорости после соударе- ^' 7^_ш
ния «! и м2 вычисляются из закона Щ т
сохранения импульса О\ ¦¦-р |Д
2 (I) 0t
и закона сохранения энергии Рис. 13.1
S- B)
Формулы A) и B) составляют систему уравнений, из ко-
которой, зная vt и v2, можно найти т и ы2 (рис. 13.1).
Задача 13.1. а) Найти из системы A), B) Uj и ыя, б) Найти
изменения импульсов Дрх и &рг шаров после удара.
139
Ответ.
. пц—гпг , 2m2
mi+m2 '---•- ~-
6) Api «= miu?—miVi
Импульс каждого шара меняется на положительную величину
Ар вс "У*2 | и2—ох |- У левого шара он уменьшается на
Ар, у правого — на Ар увеличивается*).
Явные формулы для щ и ы2 нам не потребуются, важно
лишь знать, что законы сохранения A) и B) позволяют
однозначно определить щ и ы2 по vy и у2. Далее, мы счи-
считаем, что шары абсолютно упруго
VU-!*' ,Л отскакивают от границ отрезка — то-
~ п=~1 чек О и Л. Это означает, что при coy-
n\*-*I ' \j\ дарении, скажем, первого шара с точ-
точкой О, шар отскакивает от О и дви-
Рис 13.2 жется с первоначальной скоростью,
но в противоположном направле-
направлении: «i=— Vy (рис. 13.2).
Физическим прототипом этой математической модели
служит система двух жестких (упругих) маленьких шаров
масс пц и т2, катающихся без трения в тяжелом желобе
О А со стенками О и Л. Иногда эту систему мы будем на-
вывать «одномерным газом двух молекул».
Сформулируем интересующие нас вопросы.
1. При каких начальных скоростях и положениях шаров
движение системы двух шаров периодично?
2. Какие бывают непериодические режимы движения
шаров?
Введем на отрезке О А систему координат Ох, выбрав
точку О за начало отсчета, и обозначим Xi и xz координаты
шаров. В промежутке времени между соударениями (ша-
(шаров друг с другом или одного из них с соответствующей
стенкой) скорости шаров Vi и vt не меняются, а координа-
*) Заметим, что при столкновении скорость правого шара
может только увеличиться (хотя ее модуль может и уменьшиться,
если, например, шар двигался влево и его скорость была отри-
отрицательной).
140
ты xt и х2 меняются равномерно;
xi = Vft + ait хъ = v2t + аа. C)
После соударения скорости v± и у2 заменяются на скорости
и\ и «s, и движения опять равномерны:
Xi = Uit + bu x2 = utt + ba. D)
В принципе, по начальным положениям и скоростям шаров
можно последовательно вычислять моменты соударений,
пересчитывать скорости (с помощью формул из задачи 13.1
при соударении шаров, и по формулам щ=—у*, ыа=уг
или Wi=fj, ы2=—уг при соударении первого или второго
шара со стенкой); после этого можно изобразить на пло-
плоскости Otx графики движения шаров x=Xi(t) и х—х2((),
что, однако, нетрудно сделать лишь в случае /ni=m2.
Задача 13.2. Доказать, что после столкновения шары рав-
равной массы обмениваются скоростями: «1=f2, «2=t^.
Решение. При m,=m2 система A), B) принимает вид
Подстановкой и2 из первого уравнения во второе убеждаемся,
что эта система имеет не более двух решений (так как получается
квадратное уравнение относительно щ). Решения этой системы
очевидны — это (щ, «2)='(f1, ч2) и (ult ы2)= (ч2, чх). Первое из них
лишено физического смысла (если ui=v1, ы2=и2, то это соответствует
тому, что шарики проходят друг через друга, не меняя скоростей!).
Действительности соответствует решение «i=a2, u2=vlt т. е. шары
обмениваются скоростями.
Теперь можно проследить, что происходит с графиками
x=Xi(t)=Vit+cti и x=xi(t)=v,t+ai после того, как шары
А.
равных масс сталкиваются — соответствующие прямые,
пересекаясь, «обмениваются» угловыми коэффициентами,
и графики движения шаров на плоскости Gtx —- это
141
симметричные друг к другу ломаные МИМ; и МгАМ'2
(рис. 13.3,а).
Задача 13.3. На оси Ох движутся п шаров одинаковой массы.
Как выглядят графики движения всех этих шаров на плоскости
Otx, если шары сталкиваются между собой абсолютно упруго и
только попарно (тройные столкновения исключаются)? (Рассмот-
(Рассмотрите сначала случаи п=3 и 4.) Каково максимальное число столк-
столкновений этих шаров (после которого шары разлетаются без столк-
столкновений)? Может ли произойти бесконечное число соударений?
(Напомним, что в этой задаче на оси Ох нет никаких «стенок».)
Решение. Совокупность графиков движения п шаров рав-
равных масс представляет собой объединение я лучей иа плоскости
Otx, проведенных из начальных положений шаров х=а,- (при t=0)
с угловыми коэффициентами с; (рис. 13.3,6); по такой картивке
легко проследить график движения je=Jti(O. (Из рисунка видно,
что первый шар после разлета имеет скорость v3, второй —1>6,
третий — ?i2, четвертый — с, и пятый — t^.) Видно, что макси-
максимальное число Л'тах соударений п шаров равных масс равно макси-
максимальному числу точек попарных пересечений п лучей на плоскости.
Поскольку каждые два луча могут пересекаться только в одной
точке, Nmax равно числу пар из п лу-tefl, т. е. Nmax =C%=n(n—1)/2.
Физически Wmax достигается, например, так: шары движутся
слева направо, причем начальная скорость каждого шара больше
скорости его правого соседа.
Чтобы уяснить, как ведут себя графики движения
системы двух шаров на отрезке, осталось рассмот-
рассмотреть, что происходит, например, с графиком х=хг({)—
~vtt+a2 после того, как второй шар сталкивается со
Of,
Рис. 13.4
стенкой А. Этот график заменяется на х=хг^)=
где ыг=—аг; таким образом, угловой коэффициент графика
меняет знак, как только x=x2(t) становится равным о,
(т. е. второй шар налетает на стенку), и график как бы
«отражается» от прямой х=а. Аналогично, график x—Xi (О
при столкновении первого шара со стенкой О отражается
от прямой лг=О (рис. 13.4,а). .
Сейчас мы уже можем нарисовать графики х—хЛч
и x=Xt (t) движения двух шаров равной массы на
отрезке (см. рис. 13.4,6). Для этого достаточно знать
142
лишь начальные полбжТМя и начальные скорости ша-
шаров.
Задача 13.4. Доказать с помощью описанных графиков,
что движение двух шаров равиой массы иа отрезке ОА периодично
тогда и только тогда, когда начальные скорости шаров v1 и и, со-
соизмеримы.
Замечание, Мы не обсуждаем здесь вопроса о том, что
происходит, когда оба шара одновременно налетают на одну и
ту же стеику. Эти особые движения анализируются ниже.
В общем случае тгфтг рисовать графики x=xt{t)
и х=х2 @ — довольно трудоемкое занятие, ибо закон из-
изменения скоростей при столкновении не есть просто обмен
скоростями. Налетая на тяжелый шар, легкий отскаки-
отскакивает, чуть изменяя его скорость (рис.
13.5; для наглядности мы рисуем шары
толстыми, по предположению же они то-
точечные). Как же быть? Выход из положе-
положения таков.
Будем следить за движением шаров
одновременно, т. е. рассмотрим
конфигурационное пространство, опреде- .¦ \ -..
ленное в общем виде в §3. Именно, если
шары находятся в точках x=Xi и х=хг, Рис- 13-5
этому положению системы поставим в
соответствие точку М на плоскости OxiXit имеющую
координаты (xi, xt). Плоскость Охххг — конфигураци-
конфигурационное пространство нашей системы. При движении ша-
шаров на отрезке их координаты х± и Хг меняются во
времени; таким образом, изменяются во времени и
координаты (xi, хг) точки М плоскости OxiXt, т. е. эта
(одна!) точка движется по плоскости OxiXq. Напомним,
что точка М называется изображающей или конфигураци-
конфигурационной точкой (отметим, что это не есть реальная — мате-
материальная — точка; это лишь «абстрактная», вспомогатель-
вспомогательная точка!). Таким образом, одновременному движению
двух шаров соответствует движение конфигурационной
точки М на плоскости ОхгХ2. Поскольку в промежутках
времени между столкновениями Xi и х2 меняются по ли-
линейному закону (Xi—Vit+ai, #2=и2И-а2), от столкно-
столкновения до столкновения точка М движется по прямой на
плоскости OxiX2, причем с постоянной скоростью v= (vt, у2)!
Эта «воображаемая» скорость изображающей точки назы-
называется конфигурационной скоростью точки М.
При движении шаров по отрезку ОА координаты шаров
подчиняются неравенствам 0 <jci <sx2 «а. Эти неравенства
задают на плоскости OxiXa равнобедренный прямоуголь-
143
ный треугольник Q, ограниченный прямыми Xi—О, Хг=хг
и хъ=а, и конфигурационная точка движется в пределах
этого треугольника (рис. 13.6,а). Если точка М попадает
на его гипотенузу OB (Xi=x2), то это соответствует столк-
столкновению шаров между собой. Соударению же шаров со
стенками О и Л соответствует «столкновение» конфигу-
конфигурационной точки М с катетами ОА {хг=0) и АВ {х2=а)
треугольника Q.
а
Итак, от столкновения до столкновения (т. е. при дви-
движении внутри треугольника Q) конфигурационная точка
движется по прямой со скоростью v== (fi, v2). После «со-
«соударения» точки М с границей треугольника скорости vi
и v2 заменяются на «i и ыг, точка М «отскакивает» от гра-
границы и снова движется, но уже по новой прямой с новой
скоростью и= (ии иг). Посмотрим теперь, как точка М
отскакивает от границ. (Еще раз отметим, что точка М,
ее движение по треугольнику и отскакивание от границы —
воображаемые, однако они описывают реальное движение
двух шаров по отрезку О А.)
При соударении точки М с катетом ОА (*i=0) конфи-
конфигурационная скорость v= (vi, v2) заменяется на и= («ь
«2)= (—Vi, v2), т. е. меняется ее компонента по оси Oxi.
Очевидно, это соответствует тому, что М отражается от ОА
по закону упругого удара (угол падения равен углу отра-
э'сения). При столкновении М с катетом АВ (х2—а) ско-
скорость v~ (vu у2) заменяется на и= (щ, ы2)= (if, —°г)»
т. е. меняется ее компонента по оси Ох2] это соответствует
упругому отражению точки М от катета АВ (рис. 13.6,0).
К сожалению, «закон отскакивания» точки М от гипоте-
гипотенузы АВ, определяемый из законов сохранения A) и B).
швее не совпадает с законом упругого отражения, если
1щфтЛ. Проще всего в этом убедиться, изобразив траек-
144
торию точки М для соударения легкого и тяжелого шаров
(см. рис. 13.6,е). Поэтому при тхфт2 траектории точки М
в треугольнике Q рисовать не так уж просто. Однако
положение можно исправить, и это мы сделаем в следующем
параграфе.
Задача 13.5. Доказать, что при т1=тг закон отскаки-
отскакивания конфигурационной точки М от гипотенузы есть закон уп-
упругого отражения.
Решение. В случае тх—т^ при столкновении шаров про-
происходит обмен скоростями: us=v1, ut=v2 (см. задачу 13.2). Следо-
Следовательно, при соударении конфигурационной
точки М с гипотенузой ОВ происходит замена
«= (vu "г) на «= («и «a)'= fe. ^l). т- е- нектор
и конфигурационной скорости после соударения
получается из вектора V перестанов-
перестановкой координат. Отсюда очевидно (рис.
13.7), что вектор в симметричен вектору v от-
относительно биссектрисы 0L координатного угла
^102 (если отложить v и и от одной точки О).
Но это и означает, что углы, образуемые тра-
траекторией точки М до и после отскакивания от
гипотенузы, равны.
Из задачи 13.5 вытекает много заме- Рис. 13.7
чательных следствий. Например, нетруд-
нетрудно видеть, что траектории бильярда в треугольнике Q по-
получаются из траекторий бильярда в квадрате ОАВС (рис.
А в 13.8) «складыванием» квадрата по диа-
"""" ' "* гонали ОВ. Отсюда следует, что движе-
движение двух шаров равной массы на отрезке
ОА периодично тогда и только тогда,
когда тангенс угла наклона, соответ-
соответствующий бильярдной траектории,
т. е. vjvt,— рациональное число. Если
же число vjvi иррационально, то соот-
соответствующая траектория бильярда в
квадрате ОАВС всюду плотно заполняет квадрат (см.
§ 9). Отсюда следует, что получающаяся из этой траек-
траектории складыванием вдоль ОВ траектория бильярда в
треугольнике Q тоже всюду плотно заполняет треугольник
(проверьте!). Для системы двух шаров на отрезке полу-
получаем такое следствие.
Теорема. Если два шара равной массы тг=тг
движутся по отрезку ОА так, что их начальные скорости
vi и уг несоизмеримы, то для любых двух сколь угодно малых
интервалов отрезка ОА в некоторый момент времени t
первый шар будет находиться в первом интервале, а вто-
второй — во втором.
145
Рис. 13.8
Действительно, таким положениям шаров соответст-
соответствует прямоугольник П со сторонами Д#{ и Д#г в треуголь-
треугольнике ОАВ (рис. 13.9), а всюду плотная траектория обяза-
обязательно пересекает П!
Траектории шаров, обладающих описанным в теореме
свойством, являются, таким образом, всюду плотными.
Можно сказать поэтому, что для шаров равной массы
движение на отрезке либо перио-
периодично, либо всюду плотно. Такие
свойства движений уже обсужда-
обсуждались нами ранее. К ним мы еще
вернемся в части IV.
Подведем итоги этого парагра-
параграфа. Вместо того, чтобы следить
за движением двух шаров на
отрезке, можно следить за движе-
движением одной изображающей точ-
точки М в треугольнике Q. Точки
Рис. 13.9 этого треугольника изображают
положение обоих шаров системы;
этот треугольник Q является конфигурационным простран-
пространством системы двух шаров на отрезке. Траектории точки М
на Q (так называемые конфигурационные траектории сис-
системы) суть ломаные внутри Q. Дальнейший анализ «газа»
из двух молекул проводится в следующем параграфе.
Конечно, конфигурационное пространство можно оп-
определить и для нескольких шаров на прямой. Например,
для трех шаров на прямой нужно взять три оси Охг, Охг,
Оха в пространстве, и по этим осям откладывать коорди-
координаты первого, второго и третьего шаров. Тем самым по-
положение трех шаров на прямой задается одной точкой в
трехмерном пространстве Охгхгха, и конфигурационное
пространство Q такой системы будет уже подмножеством
трехмерного пространства R3.
Задача 13.6. Указать в трехмерном пространстве Rs кон-
конфигурационное пространство системы трех шаров на прямой Ох.
Задача 13.7. Нарисовать на плоскости R2 конфигурацион-
конфигурационное пространство системы двух шаров на полупрямой х>0 (в точке
О прямой поставлена упруго отражающая стенка).
Задача 13.8. Найти конфигурационное пространство си-
системы трех шаров на отрезке 0«х<:а. Как ведут себя конфигу-
конфигурационные траектории этой системы, если массы шаров одина-
одинаковы (и шары сталкиваются абсолютно упруго друг с другом я
со стенками х=0 и х=а)?
При рассмотрении системы четырех шаров на пря-
прямой конфигурационное пространство будет уже ч е т ы-
146
рехмерным — положение всех четырех шаров зада-
задается четырьмя числами {хи хг, х9, хл). Если рассматривать
систему двух шаров на плоскости Оху, то для описания
их положения нужно тоже четыре числа — координаты пер-
первого шара {хг, уг) и координаты второго шара (д;2, уг),—
и конфигурационное пространство снова четырехмерно.
Таким образом, при анализе задач механики возникает
необходимость рассматривать пространство четырех и более
измерений. Но об этом мы подробно говорили уже в § 3.
В § 14 будет произведено специальное линейное преоб-
преобразование конфигурационного пространства системы двух
шаров на отрезке, в результате чего задача о поведении этой
системы сведется к бильярдной задаче в треугольнике.
§ 14. Два шара на отрезке: сведение
к бильярду в треугольнике
Прежде чем сводить систему двух шаров на
отрезке к бильярдной системе *), напомним необходимые
сведения из геометрии, касающиеся векторов. Для опреде-
определенности будем говорить о векторах в пространстве.
Скалярным произведением (А, х) ненулевых векторов ft и х на-
называется число, равное произведению длин этих векторов |А|и
|дс| на косинус угла между ними:
(ft, дс) = I A: I -1 -к | • cos ф.
Из этого определения следует, что для любого числа К
(kk, x) = K{k, х)
и
(ft, х) = <х, ft).
Кроме того, поскольку |ft|cos<p есть численная величина проек-
а -* *
Рис. 14.1
ции вектора ft на направление вектора х, которую мы обозначим
Px(k), то (рис. 14.1,а)
~(k,x) = \x\-Px(k),
Нетрудно видеть, что для любых двух векторов Аи/ проекция
их суммы на направление вектора х равна сумме проекций век-
*) В изложении способа сведения рассматриваемой механиче-
механической системы к бильярду мы придерживаемся лекции 10 кни-
книги [10].
147
торов ft и / на это направление (рис. 14.1,6):]
Подставив эту формулу в предыдущую, получим основное свой-
свойство скалярного произведения —л иней н ость:
(ft+/, x) = (k, *) + (/, х).
Пусть теперь в пространстве выбрана ортогональная система
ксюрдинат Ох\Хгх3, и в\, е^, е3—единичные векторы, направленные
по осям координат; пусть координаты
векторов ft и х в этой системе равны
(кг, k2, ka) и (*!, хг, ж3). Это означает,
ЧТО ft= ^1+^2^2+^3*3 И Х = Х1в1 +
+*г^2 + *з*з (рис. 14.2). Подставим
эти выражения вместо ft и х в ска-
скалярное произведение (ft, x); восполь-
воспользовавшись выписанными выше фор-
формулами, а также тем, что (ег, ei)—
= (ег, ег) = (ея, ea)=l, a («?,, ег) =
=(«i. ea) = (e2, es) = 0 (так как
cos 0=1, a cos (я/2) = 0), получим
формулу для скалярного произведения в координатах:
(ft, *) =
В случае плоскости соответствеиио получим
(ft, x) =
Вернемся теперь к результатам § 13, касающимся си-
системы двух шаров масс тг и тг на отрезке 0<.х<а. Напом-
Напомним эти результаты. Пусть xt и хг — координаты шаров;
тогда 0<Х1<?Х2<а. Эти неравенства задают на плоскости
OxiXz треугольник Q, и положение обоих шаров определяет
конфигурационную точку М= (хи хг) в этом треугольнике.
При движении шаров по отрезку координаты Xi и хг меня-
меняются, а конфигурационная точка М движется по треуголь-
треугольнику Q. Между двумя столкновениями скорости гь и fs
шаров и конфигурационная скорость v= (vit у2) изобра-
изображающей точки не меняются, и конфигурационная точка М
движется по отрезку внутри треугольника. «Соударению»
точки М с катетами треугольника ОА и ОБ соответствует
столкновение первого или второго шара на отрезке ОА
с соответствующей стенкой (О или А), и после столкновения
конфигурационная скорость становится равной и= (—vit
ч2) или и=A»1, —у2), что соответствует упругому отражению
точки М от катетов. Если пг^фт^, тотоударение точки М
с гипотенузой, соответствующее столкновению шаров ДРУГ
с другом, ведет к замене конфигурационной скорости
©=(уьи2) на скорость а=(ии щ), вычисляемую из законов
сохранения импульса и энергии (см. формулы A), B) § 13),
148
и точка М отскакивает от гипотенузы вовсе н е п о закону
упругого отражения. Задача, которую мы сейчас решим,
заключается в том, чтобы изменить координаты xt и х2
так, чтобы и последнее из описанных соударений точки М
происходило как в бильярде — «угол падения равен углу
отражения».
Законы сохранения импульса и энергии нам удобнее
записать в виде
г = const, A)
| = const. B)
Введем вместо xt и х2 координаты Xi и х2 по формулам
т. е. «растянем» плоскость Охххг по осям Oxi и Ох2 в V tnl
и Vm2 раз соответственно. Положение первого шара будет
определять теперь координата *,, а второго — координата
х2; положению шаров сопоставим изоб- а
ражающую точку М с координатами
ку
и хг) на плоскости OxiXt. Посколь-
Посколь'В
l^ini ' г Ni Рис. 14.3
хг удовлетворяют неравенствам 0 <Xi<x2<a, числа j^i
и д:2 удовлетворяют неравенствам 0 ^ xx\V тл ^хг1Утг ^
и изображающие точки М заполняют на плоскости
треугольник Q—OAB, ограниченный прямыми
г л 1Г)Ъ\ v 1/й~ п (A r\ v 1%/"ггГ v П/"ггГ /nii\
(рио. 14.3). Нетрудно вычислить координаты точки В:
Ъл = а Virtu Ь2 — а Vm2, откуда следует, что ОВ=а ¦ т, где
(u Q
Движению шаров по отрезку ОА соответствует движение
изображающей точки М в треугольнике Q, причем, как
и раньше, конфигурационная скорость дане меняется
в течение промежутка времени между столкновениями,
т. е. при движении точки М внутри треугольника Q. Новая
конфигурационная скорость v есть
149
Действительно, так как "xk=Vmkxkt
ik = %-=V-m-hd-? = Vm-kvk, *-I, 2.
Докажем, что изображающая точка М при соударении
с любой из сторон треугольника Q отражается по закону
упругого соударения.
Действительно, легко видеть, что при соударении М с
катетами ОА и ОВ конфигурационная скорость v= fa,
vt), как и раньше, становится равной и= (—у, у2) или и=
= (Vi, —tij), что соответствует упругому соударению с ка-
катетами. Соударение М с гипотенузой ОБ подчиняется
законам сохранения A) и B). Перепишем их в новых обоз-
обозначениях vi — Vm1v1, vt = Vrtn2vi. Закон сохранения
энергии B) примет вид
vi + vI = const,
т. е. при соударении с гипотенузой квадрат длины вектора
v не меняется, откуда
| v | = const. C)
Закон сохранения импульса A) дает
V тг vx + Vm2 y2 = const,
или (см. выше формулу для скалярного произведения)
(v, m) = const,
где tn = {Vnii, V т2). Поскольку т — постоянный вектор,
a (v, т)= | v | • | т \ • cos q>, где q> — угол между векто-
векторами v и т, то из того, что | z» | не меняется (см. C)), сле-
следует, что косинус угла между v и т при соударении изобра-
изображающей точки с гипотенузой ОВ также не меняется. Вспом-
Вспомнив, что ОВ=а-т, т. е. гипотенуза имеет то же направле-
направление, что и вектор т, мы получаем, что при этом соударении
не меняется косинус угла между конфигурационной ско-
скоростью v и гипотенузой. Таким образом, если ф1 — угол
падения конфигурационной точки М, ф2—угол ее отраже-
отражения, то cos q>i=cos фг, откуда следует, что ф!=фг, чТ0 и
требовалось доказать! (Возможность фг=л—ф1 исключается
из физических соображений — почему?)
150
Итак, доказана
Теорема 1. Замена координат xk=*Vln~kxk(k=\t2)
сводит систему двух шаров массы mi и т2 на отрезке
длины а к бильярду в прямоугольном треугольнике Qa—
—ОАВ с катетами AB = aVmx и ОА=а]/гт2, т. е.
с острым углом /_АОВ, равным
Теперь естественно попытаться решить для системы ша-
шаров с массами ть т2 на отрезке [0, а], т. е. для бильярда
в треугольнике Qa, общую проблему бильярдных траекто-
траекторий. Эта проблема исследована нами для бильярда в пря-
прямоугольнике сведением к обмоткам тора. К сожалению,
Ромбоид
Рис. 14.4
роме
геометрическое сведение бильярда в Qa при а^п/4 к биль-
бильярду в прямоугольнике невозможно: отражениями относи-
относительно сторон треугольника можно получить бильярд
в ромбоиде или ромбе," но не в прямоугольнике
(рис. 14.4).
Конечно, можно попытаться свести этот бильярд н е-
посредственно к тору (мы так «стремимся» к тору
потому, что при удаче можно будет применить теорему Яко-
би). Это можно сделать, кроме а=я/4, увы, еще только в
случае а=зт/6 (или а=л/3). Справедливо следующее утвер-
утверждение, которое мы докажем позже, в § 22 гл. 8.
Теорема 2. Бильярд в прямоугольном треугольнике
Qa с острым углом а сводится к обмоткам тора тогда и
только тогда, когда <х=зт/4 и л/6 (или я/3), т. е. когда mt=
=тг и mi=Sm2 (или тг=Ътх).
Отметим, что не в любом прямоугольном треуголь-
треугольнике каждая бильярдная траектория либо периодична,
либо всюду плотна: при малых величинах острого угла а
бильярдная траектория в прямоугольном треугольнике
Qa может заполнять всюду плотно лишь некоторую подоб-
подобласть этого треугольника. Пример построения такой
151
траектории в многоугольниках с числом сторон н^4 бо-
более прост и единообразен, чем для треугольника Q«(n=3);
он приводится в § 25. На языке «газа» из двух моле-
молекул ситуация может быть сформулирована следующим об
разом:
Теорем а 3. Можно подобрать такое соотношение
масс между шарами и выбрать такие их начальные состоя-
состояния (координаты и скорости), что множество точек
столкновения этих шаров на отрезке [0, а] будет либо
а) конечным, либо б) всюду плотно заполнять весь отрезок
[О, а], либо в) всюду плотно заполнять конечное число
непересекающихся отрезков на отрезке [О, а].
Этой теоремой-резюме мы и закончим параграф о систе-
системе из двух молекул на отрезке.
Задача 14.1*. а) Доказать, что система трех шаров рав-
равной массы на отрезке сводится к бильярду в некотором тетра-
тетраэдре, б)* Доказать, что при подходящем выборе координат си-
система трех шаров разных масс mlf m2, ms также сводится к
бильярду в некотором тетраэдре.
Задача 14.2. Рассмотрим систему двух шаров масс т1 и «2
на полупрямой х>0, причем в точке *=0 на этой прямой постав-
поставлена упруго отражающая стенка. Пусть н момент времени /~0
правый шар движется по направлению к стенке. Всегда лн левый
шар после конеч ного числа соударений оттолкнет правый?
(Рассмотрите ситуацию, когда тг гораздо больше т^.) Верно ли,
что в этой системе произойдет лишь конечное число столк-
столкновений Ю Если верно, то может ли N быть сколь угодно большим
(при данных т1 и т2)? Можно ли написать, что N<cNe, где число
Ne зависит т о л ь к о от масс шаров?
Задача 14.3* (см. § 15). Рассмотрим систему трех шаров
масс /я,, тг, т3 на бесконечной прямой без стенок, и пусть в на-
начальный момент времени первый и третий шары движутся на-
навстречу друг другу. Сможет ли второй шар растолкать первый
и третий шары? (Представьте, что т2 — очень легкий пииг-понго-
вый шарик, a mt н ms — массивные стальные шары.) Ответь-
Ответьте также в этом случае на три последние вопроса предыдущей
задачи.
Задача 14.4. Луч света попал в зеркало, имеющее форму
бесконечного а) двугранного угла, б)* трехгранного (или много-
многогранного) угла. В случае б) будем считать, что луч никогда не
попадает точно в ребра двугранных углов. Мокет ли быть так,
что луч «запутывается» внутри зеркала и никогда ие вылетает
оттуда?
Задача 14.5. а) Дано зеркало, имеющее форму двугранного
угла величины а. Вы рассматриваете в нем изображение свечи.
Сколько всего изображений свечи можно увидеть? б)** Ответить
на тот же вопрос для зеркала, имеющего форму трехгранного
угла, двугранные углы которого равны А, В, С,
152
§ 15. Два шара на полупрямой}
сведение к бильярду в угле
В этом параграфе мы ответим на некоторые
важные для дальнейшего исследования системы одномер-
одномерного газа вопросы, связанные с двумя молекулами на пря-
прямой и полупрямой.
А. В качестве первого шага решим задачу из § 9: может
ли бильярдная траектория «запутаться» внутри угла и
остаться там навсегда?
Поставим задачу более точно. Рассмотрим бильярд в бес-
бесконечной области Qt, ограниченной двумя сторонами угла
AeAAi величины а. Траектории бильярда в такой области
Ад
"О А Рг Ао
Рис. 15.1 Рис. 15.2
определяются как обычно — это ломаные, по которым дви-
движется шар, упруго отражаясь от сторон угла. Отличие этого
бильярда от бильярда в ограниченной области состоит в том,
что в данном случае траектория может «уходить в бесконеч-
бесконечность», т. е. после одного из соударений шар будет двигать-
двигаться по лучу, никогда более не соударяясь go сторонами угла.
Так будет в том случае, когда направление движения шара
лежит между направлениями лучей АА0 и AAi (рис. 15.1).
Вопрос заключается в следующем: всякая ли траектория
бильярда внутри угла А0ААх после некоторого конечного
числа N отражений от сторон угла уходит на бесконеч-
бесконечность?
Ответ оказывается утвердительным. Для того чтобы это
Доказать, рассмотрим произвольную траекторию MPiP2. ..
и применим к ней процедуру выпрямления в помощью после-
последовательных отражений относительно сторон угла A0AAi
(Рис. 15.2).
Если первая точка соударения Pi лежит на луче ААи
то мы отражаем угол Qt = /_AaAA\ относительно луча АА\
и получаем угол Qs=/_АхААг. Затем мы отражаем угол Q2
относительно луча ААг и получаем угол Qa=/_АгААъ
и т. д. (рис. 15.3). Применяя к отрезку PiPs рассматривае-
рассматриваемой траектории MPtP^Ps... одно из упомянутых отраже-
153
ний, к следующему отрезку Р2Р6 — два отражения (отно-
(относительно AAi и AAS) и т. д., мы переместим эти отрезки в
углы Q2, Qs и т. д.; из закона «угол падения равен углу
отражения» следует, что отраженные отрезки составляют
луч — продолжение луча MPi за точку Pi на плоскости.
Обратно, мы можем замостить с помощью описанных
отражений часть плоскости углами Qu Q2,... Начертив произ-
произвольный луч МРи идущий из точки М внутри угла Q
в сторону точки Pi на луче ААи теми же отражениями,
Рис. 15.4
но проводимыми в противоположном порядке, мы можем
построить по лучу MPi бильярдную траекторию MPiP^...
внутри угла Qt. Из сказанного выше вытекает, что указан-
указанным образом получается любая бильярдная траектория
MPiP^..., первая точка излома которой лежит на луче
AAf. Точкам пересечения луча MPi с лучами ААи АА2>. . .,
делящими плоскость на углы Qt, Q2, . . ., при обратных
отражениях соответствуют точки соударения Pi, Рг, . .
траектории со сторонами угла Qt. Очевидно, всевозможные
лучи MPi (при различных положениях точек М внутри
Qi и точек Pi на луче AAi) заполняют заштрихованную
на рис. 15.4 область Q между лучом ААВ и лучом АА\ —
продолжением луча АА\ за точку А. В этой области Q с по-
помощью отражений можно поместить лишь конечное
число No рассматриваемых углов Qt, Qi3. . . — так как все
эти углы равны по величине а, а угол Q (больший развер-
развернутого) измеряется величиной зт+ct, то Noa <:я+а, откуда
NB<(n/a)+l. Иначе говоря, число углов Qu Qz.- • ••
помещающихся внутри Q, равно
[]
здесь [и] — обозначение для целой части числа и (наиболь-
(наибольшего целого числа, не превосходящего и). Если сторон
AAN^ последнего из этих углов Qt^v—ANtt^ AANri не сов
падает с лучом АА', то луч MPi может проходить еше п
154
одному углу — углу <2лг„+1. получающемуся из QN, отра-
отражением относительно луча AANti, однако луч MPi уже не
может пересечь луч AANn+l, ибо этот луч лежит вне обла-
области Q. В этом случае (ААКлФАА[) луч MPi может пере-
пересечь самое большее Nn лучей — AAt, AA2,. . ., AAN.
Это означает, что число N соударений бильярдной траекто-
траектории со сторонами угла не превосходит No:
Заметим, что N может принимать любое значение от 1 до
NB — это зависит от направления луча MPi.
В случае, когда луч AANo совпадает с лучом АА'и нет
необходимости рассматривать еще один угол QNri+i, ибо
луч MPi не может пересечь луча A A Nr. Этот случай (ААЫ =
=AAi) соответствует тому, что п есть целое кратное числа
а, и максимальное число соударений тогда равно NB—1
(луч MPi может пересекать лучи AAi, ААЪ,. . ., AANc^).
Подведем итоги. Для числа а, 0<а<Гзт, положим
Л/о = — -f 1, если — не целое,
NB—1=1—1, если —целое.
Теорема. При движении бильярдного шара внутри
угла величины а траектория шара имеет не более чем N (а)
точек соударения со сторонами угла, и после некоторого
числа N<N(a) соударений эта траектория уходит на
бесконечность.
Нетрудно видеть, что введенное выше число N (а) можно
при любых а записать одной формулой:
(проверьте это!).
Б. Доказанная в п. А теорема дает возможность найти
максимальное число столкновений шаров масс mi и тг, дви-
двигающихся по полупрямой х^О, в точке х=0 которой
поставлена отражающая стенка (задача 14.2). Координаты
*i и xs этих шаров удовлетворяют неравенствам 0<xi<:xa.
После введения координат Х\ = V т± xt и х2 = У тг х2, как в
§ '4, мьГможем свести систему этих шаров к движению кон-
конфигурационной точки М— (хи Хц) внутри угла Q на плоско-
155
сти 0*1*2, задаваемого неравенствами 0 <! ¦ *i_- <! 5?—.
V т, у тг •
точка М движется внутри этого угла (/_АОВ на рис. 15.5)
по бильярдной траектории, а точкам соударения траектории
со сторонами угла (ОВ или ОА) соответствуют столкнове-
столкновения исходных шаров (друг с другом или левого шара со
стенкой в точке х—0 соответственно). Прямая ОВ задается
уравнением г— = г^~~ ¦ и точка с координатами (КтГ
У mi У т2
V т2) лежит на ней. Отсюда следует, что величина а уг-
угла АОВ равна
Таким образом, максимальное число столкновений рас-
рассматриваемых шаров равно
arctg У~
J-
Тем самым решена задача 14.2: первый шар столкнется со
вторым шаром и со стенкой не более чем N (а) раз, после чего
\
и
Wa=arctg \
Рис. 15.5
ее
Щ
шары разлетятся и больше столкновений не будет. В част-
частности, получаем следующее.
1) Если т,=т2, то a=arctg 1=зт/4 и
ответ этот можно получить и из соображений обмена ско-
скоростями при упругих соударениях шаров масс пц=т*-
Картинка столкновений (рис. 15.6) на плоскости Otxi вы-
выглядит в данном случае, как на рис. 13.3,6 (столкновения
пронумерованы цифрами /, 2, 3, 4).
156
2) Если mj многоменьше тг, то 1/ ^1 и a=arctg 1/ ——
«довольно малые» числа. Из формулы для N(a) следует, что
число столкновений в этом случае «довольно велико», как
и следовало ожидать: легкий шарик mi «мечется» между
стенкой и тяжелым шариком т2 достаточно долго, прежде
чем «отпихнет» (но «отпихнет» обязательно!) шарик тг от
стенки.
В. Приложим теперь доказанную в п. А теорему к за-
задаче о числе отражений луча света в зеркале, имеющем
Рис. 15:7
форму бесконечного двугранного угла величины а (задача
14.4а). Прежде всего следует точно сформулировать за-
закон отражения луча света от плоского зеркала — или закон
отражения летающего в пространстве точечного бильярд-
бильярдного шара от плоскости 9* (уместнее было бы говорить о ша-
РИке для игры в пинг-понг). Пусть ломаная АРВ — это
траектория луча света (или шарика), отражающаяся от
плоскости 5s в точке Р. Известный из физики закон отра-
отражения гласит: лучи РА и РВ и перпендикуляр PN к пло-
плоскости 5s в точке Р лежат в одной плоскости <ЛР, причем
•"Учи РА и РВ образуют с лучом PN одинаковые углы
157
(рис. 15.7, а). Отсюда следует, что при отражении относи-
относительно плоскости 5s луч РВ переходит в луч РВ', являю-
являющийся продолжением луча АР за точку Р (рис. 15.7, б).
Таким образом, к траектории луча света внутри зеркала,
имеющего форму бесконечного двугранного угла Qi с гра-
гранями ?0 и ft и ребром АВ (рис. 15.7, в), можно применить
процедуру отражения в гранях этого угла, аналогичную
описанной в п. А; при этом последовательными отражения-
отражениями можно выпрямить траекторию MPiP2. . . — превра-
превратить ее в луч МРи который пересекает двугранные углы
Q2l Qs получающиеся из Qt последовательными отра-
отражениями в гранях угла. Точки пересечения луча MPt с
полуплоскостями 5il, ^2,. . . соответствуют точкам отра-
отражения луча света от граней 3*в и 3*i исходного угла. Если
рассмотреть плоскость 91, перпендикулярную общему реб-
ребру АВ всех двугранных углов Qu Qj,. . ., и луч MPi спроек-
спроектировать на эту плоскость в луч М'Р'и то, рассматривая
точки пересечения луча М'Р\ с лучами AAi, ААг,. . .,
получающимися в пересечении плоскости 91 с полуплоско-
полуплоскостями 5*0, 8*и- ¦ •» как и при доказательстве теоремы п. А,
получим: максимальное число отражений луча света в гра-
гранях зеркала, имеющего форму двугранного угла величины а,
равно N(a)=—[—п/а]. Задача решена. Другой путь к ее
решению вытекает из утверждения следующей задачи.
Задача. Доказать, что если угол АРВ в пространстве К3
спроектировать на плоскость 91> параллельную биссектрисе PL
этого угла, то проекция PL' биссектрисы на эту плоскость 91
является биссектрисой проекции А'Р'В' рассматриваемого угла.
Вывести отсюда, что проекция траектории луча света внутри
зеркала, имеющего форму двугранного угла Q с ребром АВ, на
плоскость 91, перпендикулярную АВ, является бильярдной траек-
траекторией внутри плоского угла A0AAi, получающегося в сечении
двугранного угла Q плоскостью 91.
Теперь мы полностью готовы к исследованию одномер-
одномерного «газа» из трех и большего числа молекул.
Глава 6
ОДНОМЕРНЫЙ «ГАЗ»
ИЗ БОЛЬШОГО ЧИСЛА МОЛЕКУЛ
В этой главе мы последовательно перейдем от
двух к трем и большему числу молекул одномерного «газа».
При этом мы исследуем сначала систему п шаров (упругих
частиц) произвольной массы на прямой. В § 16 мы получим
точную оценку числа столкновений грех шаров на
прямой, зависящую только от соотношений между их мас-
массами (но не зависящую от их начальных положений и ско-
скоростей); затем ответим на вопрос о том, может ли в системе
из п упругих шаров на прямой произойти бесконечно много
столкновений (в § 17 даются два разных подхода к ответу на
этот вопрос — аналитический и изящный геометрический);
наконец, в § 18 ответ § 17 подкрепляется равномер-
равномерной (т. е. не зависящей от начальных условий) оценкой
числа столкновений в системе из п упругих шаров на пря-
прямой и с ее помощью оценивается рост числа столкновений п
молекул «газа» в одномерном сосуде — на отрезке прямой.
§ 16. Три упругих шара на прямой
Рассмотрим систему трех шаров масс пц, тг,
Щ, движущихся по оси Ох. Предположим, что шары точеч-
точечные, сталкиваются друг с другом абсолютно упруго, причем
происходят только попарные столкновения: левого ша-
Рика (mi) со средним (т8) и среднего — с правым (т3).
Всегда ли в такой системе происходит конечное число
спюлкновений на всем бесконечном промежутке времени, или
** существуют такие начальные условия (положения, ско-
Росши и массы шаров в момент t=0), что число столкно-
столкновений бесконечно"?
Нетривиальность этого вопроса наглядно демонстриру-
на таком примере. Пусть два очень больших «сталь-
159
ных» шара движутся с очень малыми скоростями навстречу
друг другу, а между ними летает с очень большой ско-
скоростью очень легкий пинг-понговый шарик, отскакивая от
стальных шаров как от стенок со все возрастающей скоро-
скоростью по мере приближения этих шаров друг к другу.
Совершенно неясно, «растолкает» ли легкий пинг-понговый
шарик массивные шары, а если даже и растолкает, то не
может ли он до этого момента (заметьте, на конечном
промежутке времени!), увеличивая частоту своих колебаний
и скорость, уже столкнуться с ними бесконечно много
раз? Мы докажем в этом параграфе, что такого не происхо-
происходит: число столкновений между тремя шарами на прямой
всегда конечно и зависит только от соотношений их масс
(но не зависит от их начальных положений и скоростей).
Точная оценка этого числа приводится в формулируемой
в конце параграфа теореме.
Координаты трех шаров обозначим xlt хг, xs и будем
отмечать положение шаров конфигурационной точкой Л4=
—jfcci, х?, х3) трехмерного пространства R3 с системой коор-
х, < х-, « <?т динат OxtfzXs. Всевозможные по-
положения конфигурационной точки
М подчиняются неравенствам л:^
^дг2<л:9. Первое из них, хг<хг,
задает в пространстве Охгх?х3 полу-
полупространство, лежащее по одну
сторону от плоскости ^i,», задан-
заданной уравнением xt=xz; второе,
х2 <х3, задает полупространство,
ограниченное плоскостью 5\,,з с
уравнением xt=xa. Оба неравенства
вместе задают пересече-
пересечение этих полупространств — один из двугранных углов
Q, образованный плоскостями 5\i2 и 5%,.,, (рис. 16.1). Ребро
этого двугранного угла — прямая 0L, задаваемая равенст-
равенствами Xi—x2=xs. Положению конфигурационной точки
M—(xi, xit xs) на гранях Q — плоскостях ^i,* и 5*ц,ш~~
соответствуют попарные столкновения между шариками
Xi=Xi и x2=xs; если же М лежит на ребре угла 0L, то это
соответствует тройному столкновению шаров % =
=хг=х3, которое мы не будем рассматривать. При движе-
движении шаров по прямой Ох в течение промежутка времени от
столкновения до столкновения скорости шаров fli, ^г. v*
сохраняются; это означает, что при соответствующем дви"
женин точки M=(jtlt х.г, х3) в конфигурационном прост-
пространстве 0х1Хгх3 эта точка М движется с постоянной конф'1'
160
ш
Рис.
гурационной скоростью v= (vit v2, v3) по некоторой прямой.
После столкновения М отскакивает от соответствующей
грани угла Q с новой скоростью и= (ui, u2, и3); состав-
составляющие новой скорости ии «2, us вычисляются из соответ-
соответствующих законов сохранения. Например, при столкно-
столкновении шаров mi и тг (при отскакивании М от плоскости
^1.г) ua=vs, а скорости lit и и2 определяются законами
сохранения A), B) из § 13. Вообще говоря, этот закон отска-
отскакивания вовсе не есть закон упругого отражения точки М
от соответствующей плоскости. Напомним, что при у п-
р у г о м отражении точки М, налетающей со скоростью
v= (Vi, v2, v3) на плоскость 5\ скорость w= (wt, wit ws)
точки М после отражения определяется следующими усло-
условиями:
(A) длины векторов v и w равны: \ v | = | w |;
(Б) если п — вектор, перпендикулярный плоскости 5*,
то векторы v, w и п компланарны, т. е. лежат в одной
плоскости;
(B) углы, образуемые векторами v и we вектором п, равны
(но w=fcv); это условие удобно записать с помощью скаляр-
скалярного произведения:
(w, я) = — (V, п).
Замечание, относящееся к элементарной
геометрии. Если плоскость 5* в пространстве OxiK2k% задает-
задается уравнением
то это уравнение можно переписать с помощью скалярного произ-
произведении в виде
(о, х) = е,
где а — вектор с координатами (alt а2, ая), ах — вектор с началом
в начале координат 0= @, 0, 0) и концом в точке М с координа-
координатами (xlt x2, х3). Вспоминая геометрический смысл скалярного
произведения (см. начало § 14), запишем наше уравнение в виде
\а\-Ра(х) = с,
где Р„(х) — численная величина проекции .вектора х на направ-
направление вектора а. Таким образом, плоскость 5\ веданная уравне-
"ием (a, x)=c^alxi+aixi-\-asxB=c состоит из тех и только тех
точек М, для которых численная величина проекции вектора ОМ
"а пектор о равна данной величине,
P()
Отсюда ясно, что плоскость 5* перпендикулярна вектору о. Таким
°бразом, в качестве вектора я, перпендикулярного к плоскости 5*,
заданной уравнением ад+ааХг+азЯв—ci можно взять вектор
n=a={Ol, a2, о,).
' • А. Гальперин, А. Н. Земляков ИЯ
Введем вместо х\, xit xs другие координаты хи xit х„,
аналогичные рассмотренным в § 14, так, чтобы движение
новой изображающей точки М= (хи х%, х3) подчинялось
закону упругого отражения при соударениях с плоскостями
отражений #Ь2 и 5\,3 в пространстве 0xiX2xs. Именно,по-
Именно,положим
Движение точки М—(хи х2, xs) происходит в двугранном
угле Q, задаваемом неравенствами
Этот угол ограничен плоскостями столкновений 5*ii2 и
заданными соответственно уравнениями
Xi X2 ЛЕа Х3
ребро его — прямая 0L, заданная уравнением
*1 Xj Х3
Vтх Vint. Vms
Скорость v= (Vi, fa, vs) изображающей точки М по-преж-
по-прежнему не меняется в промежуток времени между столкнове-
столкновениями и связана со скоростью v— (vlt v2, v3) формулами
Докажем, что соударение изображающей точки М с пло-
плоскостями столкновений 5\, 2 и #2t s (отвечающее попарным
столкновениям шаров ти тг, ms) происходит по закону
упругого отражения, т. е. скорости да и м до и после соу-
ударения удовлетворяют условиям (А), (Б), (В), сформули-
сформулированным выше. Доказательство этого такое же, как и в
§14.
Рассмотрим, например, соударение точки УЙ с плоскостью
столкновения 5*1,2- В старых координатах Ох\, О*а, Oxs скорости
v и и до и после' столкновения связаны соотношевиями
miUi -f- т8ы2
Перейдем в этих уравнениях к величинам и^ =
162
=Y mft «*• Получим
U A)
B)
C)
Возводя обе части равенства A) в квадрат и складывая с равен-
равенством C), получим
«1 + «1+из = и? -[-
откуда следует, что |я| = | v\. Тем самым условие (А) проверено.
Чтобы проверить условие (Б), т. е. компланарность векторов
v*e(vi, vi, vs), и = (щ, н2. us) и вектора я, перпендикулярного
плоскости столкновения 5*1,2, достаточно представить я в виде
i (тогда я лежит в плоскости векторов ©, ю). Так как
уравнение плоскости 5*i,s имеет вид
*i Ж2 1 1 ~ . „ - „
-тт== ,/-—-. "лв -7=*! — -7=ж8+0-хя=0,
V mi V m2 V m, Km,
то согласно замечанию, сделанному выше, в качестве вектора я
можно взять вектор
VV mi Km,
Вычтем из вектора v вектор а; так как Vs = us, мы получим вектор
©—e = (»i—иь »s—и», 0).
Перепишем уравнение B) в виде
где %,— число, которому равны обе части этого равенства. Отеюда
- - к - - Ь
F mi F m2
Сравнивая теперь формулы для я и для v—ю, получаем
i—a=kn,
откуда я =-г-ф — -г-и. Таким образом, вектор я выражен через
я и а в явном виде, и условие (Б), таким образом, доказано.
Наконец, проверим, что и условие (В), т. е. соотношение
{п, n) = -{i, я) D)
тоже выполнено. Запишем обе части доказываемого соотношения
D) в координатах, учитывая, что П = 1 . • """-i/ • I
V^^U V^ml V YnTi Ym^J'
6* 163
т. е.
D')
V mi V т2
Чтобы доказать D'), перепишем B) и C) в виде
V mi {Vx — iii}— V т2 (u2 — v2),
~2 ~2 " ~2
V} —U( = a» — V2-
Разделив почленно последнее равенство на предпоследнее, получим
требуемое соотношение D'). Закон упругого столкновения вы-
выполнен.
Итак, система трех шаров масс ти т2, т3 на оси Ох
сводится к бильярду внутри двугранного угла Q. Чтобы
нчйти максимальное возможное
число столкновений между шарами до
их разлета, достаточно знать величину а
двугранного угла Q, выраженную через
массы ти т2, ms. Найдем ее.
Угол между гранями двугранного уг-
угла равен углу между векторами, перпен-
перпендикулярными граням этого угла и соот-
соответственно направленными (рнс. 16.2;
поясните это). В данном случае грани
угла— плоскости ^^иУ,,,, а нужным
образом направленные векторы, перпендикулярные к этим
плоскостям — это
= (-^=, — -Л=, О) и raf3 = @, — -4=, -Д=
Рис. 16.2
V
т2
-4
V
ms
(см. геометрическое замечание). Рассмотрим скалярное
произведение этих векторов; если а — угол между векто-
векторами, то мы имеем
Учитывая, что
находим
cos a =¦
1/т2
l/_L4—L 1/J-4—L
164
Итак,
а = arccos V m1m^\i<m1 + m2) (m2 + m3)] .
Учитывая результаты, полученные в § 15, получаем сле-
следующее утверждение.
Теорема. Каковы бы ни были начальные положения
искорости трех шаров масс ти tn2, tns на прямой, эти шары
разлетятся после не более чем N{mu m2, т3) попарных
столкновений (и будут затем двигаться уже без столкно-
столкновений); здесь
N (ти тг, т3) = - [ -arccos у
Заметьте, что из «чисто физических» соображений полу-
получить такую оценку было бы весьма трудно (напомним, что
оценка точная — может быть ровно N (ти т2, т3)
столкновений!). Более того, вовсе не очевидно, что
шары разлетятся после некоторого числа столкновений!
(Заметим, что при mi=m2==m3=m эта оценка дает
/V (т) = —[ — агссо"м/2) I = 3« чт0 Равно С%> как и Должно
быть для трех шаров равных масс.)
Только что решенную задачу о числе столкновений трех
шаров можно поставить и в случае п шаров на прямой с
массами mt, m2f. . ., тп. Однако уже при п=4 придется
рассматривать изображающую точку М—(хи хи х3, х4)
в четырехмерном конфигурационном пространстве R*.
Конечно, при определенных навыках и некоторой смелости
можно разобраться и с бильярдом в четырехмерном прост-
пространстве. Мы, прежде чем читатель перейдет к § 17, оставим
ему этот случай в качестве задачи; укажем только, что
задачу о числе столкновений четырех шаров различ-
различной массы можно свести к задаче о числе отражений луча
света, попавшего в зеркало, имеющее форму трехгранно-
трехгранного угла (в обычном трехмерном пространстве; см. задачу
Н.46)). Последняя задача и сама по себе весьма сложна;
°на будет решена также в § 17. Что касается п>4 шаров,
то можно пойти и по другому пути, указанному в § 17 и 18.
§ 17. п упругих шаров на примой
Для п>3 шаров с массами ти пг2,. . ., тп,
Движущихся по оси Ох, так же как и для трех шаров, мож-
ио ввести конфигурационное пространство — (п—1)-гран-
иый угол Q в n-мерном координатном пространстве Rn=
165
~Oxtx2xs ... xn, выделяемый неравенствами
(каждое неравенство xh^.xk+i задает полупространство в
R").
Все рассуждения предыдущего параграфа, сводящие
систему из п шаров к бильярду в (л—1)-гранном угле
\ \Гт1 ^ \Гт2 ^ ^ V
mn
где хи x2t. . ., хп — новые координаты в конфигурацион-
конфигурационном пространстве R", связанные со старыми координатами
Xi, х2,. . ., Хп равенствами
xt = Vm1 xlt х2 = Vm2 х2, ..., хп = V~т„ хп,
переносятся дословно и на этот общий случай, но посколь-
поскольку при п>3 число п— 1 больше 2, задача уже не сводится
к плоскому случаю — отражения бильярдной конфигураци-
конфигурационной точки М происходят не в двугранном угле,
т. е. происходят не от двух, а от большего числа стенок.
С многогранным (даже трехгранным) углом все становится
гораздо сложнее уже в трехмерном пространстве R3. По-
Поэтому мы временно отойдем от такого рассмотрения, сводя-
сводящего всю задачу к многомерной геометрии, и попробуем
применить аналитические методы при исследовании систе-
системы из п молекул на прямой. В конце параграфа мы вновь
вернемся к конфигурационному пространству и предложим
читателю красивое геометрическое решение.
Сформулируем еще раз задачу о «газе» молекул на пря-
прямой, решаемую в этом параграфе *).
Для п шаров на прямой с массами mt, . . ., тп, началь-
начальными положениями хи . ., хп и скоростями vlt . ., "п
выяснить, всегда ли конечно число столкновений между
ними на бесконечном промежутке времени, считая все проис-
происходящие столкновения парными и упругими (т. е. подчи-
подчиняющимися законам сохранения импульса и энергии; см.
формулы A) и B) § 13).
В случае шаров равных масс, mi=. . .=mn, ответ на
этот вопрос утвердительный: полное его решение приведено
в задаче 13.3. Максимальное число столкновений между
*) Впервые эту задачу (и даже более общую — о BbWieJH
бильярдной частицы из многогранного угла) чисто геометрическ
решил Я. Г. Синай (см. [7]); аналитическое решение предложил
независимо А. Авдеев и первый из авторов этой книги.
166
шарами в этом случае равно числу пар шаров Q—
=п(п—1)/2 и связано это, напомним, с тем, что при столк-
столкновении двух одинаковых шаров они просто обмениваются
скоростями, или, говоря иначе, один шар как бы проходит
сквозь другой, поменявшись с ним на ходу номерами (по-
(поэтому-то каждый шар может «пройти сквозь другой» лишь
не более п—1 раз).
Для п>3 шаров произвольных масс ответ на поставлен-
поставленный вопрос также утвердительный, хотя полу-
получить верхнюю оценку числа TV столкновений между ними
существенно труднее, чем для шаров равных масс или для
трех шаров разных масс. Эту оценку мы получим в § 18,
а сейчас приведем самое короткое из известных нам ана-
аналитических решений задачи.
А. Аналитическое решение.
Теорема 1. Число столкновений в системе из п упру-
упругих шаров на прямой конечно на бесконечном промежутке
времени.
Доказательство будем вести индукцией по чис-
числу шаров. В § 16 было доказано, что при п = 3 число
столкновений конечно.
Допустим (это будет предположением индукции),
что при любых начальных условиях в группе из любого числа
k<n шаров за время от 0 до Т (где Т может быть равно
+ оо) происходит только конечное число столкновений.
Докажем, что конечным будет и число столкновений в
системе из k=n шаров (шаг индукции,).
Доказательство поведем от противного. Предпо-
Предположим, что при каких-то начальных условиях п шаров за
время от 0 до Т сталкиваются бесконечно много
раз, и получим противоречие.
1Q. Перенумеруем шары в порядке их следования по
оси л:, но справа налево (рис. 17.1). В каждый
л к+г к ---3 2 1
•-в—о—*-•)-• * I*—•—•—•-
-*¦
Увеличение импульса рк
Рис. 17.1
момент времени будем рассматривать суммарный импульо k
правых шаров:
pk = tn1vi + m^ut+ ... +mkvfc,
гДе k принимает все значения от 1 до п. Докажем, что при
167
каждом парном столкновении импульс р\, может только
увеличиться.
Действительно, ph не меняется, если сталкиваются шары
левее (?+1)-го или правее /г-го — в первом случае шары
с номерами /г-4-2, . . ., п никак не влияют на сумму m&i +
+ . . .\-тъУъ, а во втором не меняется скорость t»h и суммар-
суммарный импульс ph-i=miVi+. . .+mk-iVb-i (рис. 17.1). Если
же k-i\ шар сталкивается с (&+1)-м, то рн увеличивается,
ибо (&+1)-й шар толкает k-i\ вправо, увеличивая скорость
Vb, а тем самым и сумму myUi+. . .-{-mhVh.
Занумеруем теперь подряд натуральными числами
1,2 s, ... все происходящие столкновения в системе
шаров. Пусть и(,в — скорость j-ro шара после s-ro по поряд-
порядку столкновения в системе (в котором t-й шар мог и не
участвовать), a /?jf — импульс ph после s-ro столкновения.
Из сказанного выше следует, что для каждого k = 1, 2,. ..
..., п последовательность {р^} неубывающая, т. е.
С другой стороны, при всех столкновениях суммарная кине-
кинетическая энергия всех п шаров сохраняется:
V2 {Щ$ + т%Щ + ... +т^) — Е — const
Отсюда следует, что скорость каждого шара i в каждый
момент времени ограничена сверху:
mtvi <2Е и \v,I < l/— < l/-^-,
где mmiB — наименьшая из масс mj, . . ., тп. А тогда для
любого k и любого s получаем
т. е. после каждого столкновения двух шаров исходной
системы суммарный импульс правой /г-точечной*снстемы
шаров с номерами 1, 2, . . ., k ограничен сверху числом
(т,+ ... +тк)У2Е/ттп.
Итак, при каждом k=\, 2, . . ., п последовательность
{pf}, s=l, 2, .... является монотонной и ограниченной.
Поэтому, согласно теореме Вейерштрасса *), все последо-
последовательности {/?'V}, {рЧ*}, . . ., {р™} имеют пределы при
*) Которая утверждает, что ограниченная монотонная (в03'
растающая или убывающая) последовательность {*„} имеет преДе'
при п-> оо.
168
s-»-oo. Ho piV=m1vif, следовательно, существует предел
lim v[s) = Wy.
s-
Далее, pf^m^+m2v4>, поэтому существует и предел
lim visi = w2 (объясните подробно, почему). Точно также,
из равенства p{f=tn1vil>+m2vf+mgV(^ и существования
пределов lim /?СД lim v[s> = wit lim vis> = w2 следует су-
S-* 00 S -¦ 00 S-* 00
шествование предела lim &^ = wB. Продолжая это рассуж-
S-* 00
дение, выводим существование пределов скоростей всех
шаров *):
lim Vks> = wk, fe = l, 2 п.
S -»¦ 00
2°. Теперь мы покажем, что все предельные скорости ьиц
равны между собой: Wi = w2 = . . . = wn — w.
Рассмотрим два соседних шара: k-u и (k-\-\)-i\. За вреыя
от 0 до У, в течение которого по нашему предположению в
системе из п шаров произошло бесконечное число
столкновений, k-i\ и (й+1)-й шары также должны были
столкнуться бесконечно много раз.
Действительно, если бы они столкнулись лишь конеч-
конечное число раз, то с некоторого момента t0, где O<ito<iT,
они перестали бы сталкиваться и тогда вся система из п
шаров с момента U разделилась бы на две: правую, в
которую входят шары с номерами от 1 до ft, и л е в у ю —
с номерами от k+l до п. В каждой из этих систем число
шаров строго меньше п, а тогда по предположению индук-
индукции число столкновений в каждой из них конечно как на
промежутке времени от 0 до t0, так и на промежутке времени
от ?0 до Т. В результате получаем, что и во всей системе из п
шаров число столкновений на промежутке времени (О, Т)
конечно, что противоречит нашему исходному пред-
предположению.
Рассмотрим некоторое столкновение между шарами k
и k + l; пусть оно имеет номер s в серии всех столкновений
системы из п шаров. Из закона сохранения импульса
имеем равенство
*) Л. Н. Васерштейи и F. А. Гальперин доказали общее ут-
утверждение о том, что в любой (даже многомерной) системе из конеч-
конечного числа центрально отталкивающихся частиц все частицы имеют
предельные скорости. Это утверждение используется при доказа-
доказательстве теоремы в гл. 7.
169
(при этом (s—1)-е столкновение может произойти и между
шарами, отличными от ft и &+1), а из закона сохранения
энергии — равенство
mk Ks>)? + mk+l WUY = mk (иГ'
Переносами слагаемых в разные части равенств получаем
и после почленного деления последнего равенства на пред-
предпоследнее (такое деление возможно: f'l'^ 4s' и fl/b+
поскольку s-й удар произошел именно между k-м и
шаром!) получаем соотношение
-» = !&-!» +oft,.
Оно справедливо для бесконечного числа столкно-
столкновений s между k-м и (&+1)-м шаром, поэтому в нем можно
перейти к пределу при s-»-oo. Для предельных скоростей
получим 2wh=2wk+1, откуда wfl=wk+i. Итак, все предель-
предельные скорости равны между собой:
что мы и хотели доказать в этом пункте.
3°. Пусть и'?, . . ., и(|?—начальные 'скорости шаров;
из закона сохранения импульса следует, что для каждого
столкновения s выполнено равенство
Поэтому, переходя к пределу при Sj-»-oo, находим
Щ< + • • • + "*„<' = {Щ + -..+ тп) w,
откуда
4rf
Но величина справа — скорость центра масс всей системы
из п шаров. Итак, скорость каждого шара стремится я
скорости центра масс всей системы (если число соударений
бесконечно).
Перейдем в связи с этим в систему центра масс, т. е. в
систему отсчета координат, которая движется относительно
исходной системы отсчета равномерно со скоростью в>-
В ней все предельные скорости равны 0; следовательно, и
предельная энергия в системе центра масС
170
равна 0. Однако в силу инерциальности системы отсчета,
связанной с центром масс, в ней, как и в исходной системе,
выполнен закон сохранения энергии; а раз предель-
предельная энергия равна 0, то и начальная энергия
шаров в системе центра масс также равна 0.
Это может быть лишь тогда, когда все начальные скорости
шаров в системе центра масс были равны 0, т. е. когда в ис-
исходной системе отсчета все начальные скорости шаров были
равны ш.
Но при одинаковых начальных скоростях шаров столк-
столкновений между ними вообще не может происходить! Это
противоречит исходному предположению о том, что в систе-
системе происходит бесконечно много столкновений,
Следовательно, исходное предположение неверно —
число столкновений может быть только конечным, что и
требовалось доказать.
Повторим кратко схему доказательства нашего утверж-
утверждения. Мы предположили, что в любой системе с меньшим
чем п числом шаров количество столкновений конечно (а
для п=3 это предположение мы доказали в § 16), и пред-
предположили затем, что внекоторой системе из п шаров
количество столкновений бесконечно. Отсюда мы
вывели, что любые два соседних шара должны сталкиваться
друг с другом также бесконечно много раз, а тогда их ско-
скорости должны стремиться к одному и тому же пре-
пределу, равному скорости центра масв системы. Но, поскольку
выполнен закон сохранения энергии, эти скорости уже с
начального момента равнялись скорости центра масс. Од-
Однако шары с равными скоростями вообще не могут сталки-
сталкиваться! Итак, если предположить бесконечность количества
ударов в «газе» из п молекул, то из этого выводится, что это
количество равно нулю — явный абсурд! Поэтому число
ударов и в системе из п шаров конечно на всем бесконеч-
бесконечном интервале времени. Это число мы оценим явно в § 18.
Б. Геометрическое решение *). К рассмотренному краси-
красивому аналитическому рассуждению добавим теперь геомет-
геометрическое, пожалуй еще более красивое и прозрачное рас-
рассуждение, использующее, как мы обещали в начале пара-
параграфа, конфигурационное пространство — многогранный
Угол Q. Заодно обобщим ситуацию и сформулируем сле-
следующую задачу.
*) Это решение существенно отличается от впервые предложен-
предложенного Я. F. Свнаем решения в статье [71. Оно было получено неза-
независимо А. М. Степиным и первым из авторов этой книги.
171
В многомерном пространстве расположен произвольный
п-гранный угол Q с вершиной в начале координат О. Внутри
этого многогранного угла движется бильярдная частица,
отражаясь упруго (по бильярдному закону) от его граней.
Перестанет ли когда-нибудь бильярдная частица сталки-
сталкиваться с гранями угла Q? Конечно или бесконечно число ее
отражений от граней за бесконечное время*
Для двугранного угла величиной а ответ мы знаем: иско-
искомое число отражений конечно и не превосходит N(a)=
——[—п/а] (см. § 15, п. В). Число N(a) было получено
с помощью выпрямления траектории — превращения ее в
прямую. Так же, но несколько хитрее, мы поступим и
сейчас.
Теорема 2. Бильярдная частица в многогранном
угле Q с некоторого момента движется по лучу, не пересе-
пересекающему его граней. До этого момента частица сделает не
более N (Q) отражений от граней Q, причем число N (Q) за-
зависит только от геометрических характеристик угла
Q, но не от начального положения и направления скорости
частицы.
Доказательство. Для наглядности докажем тео-
теорему 2 в случае многогранного угла в трехмерном
пространстве 1RS. Пусть а,, аг, . . ., ап —двугранные
углы многогранного угла Q. Опишем сферу S2 радиуса 1 с
центром в вершине О угла Q. Тогда п-гранный угол Q вы-
высечет на сфере S*сферический многоугольник А=АхАг. . .Ап,
вершины которого At—точки пересечения ребер угла Q
со сферой, а стороны АгАи АгАъ, . . ., АпАх —дуги боль-
больших окружностей, высекаемые на сфере его гранями
(рис. 17.2, а). Длины сторон Л (/4(+( многоугольника равны
плоским углам AiOAt+i (так как радиус сферы равен 1),
а углы Ai, . . ., Ап многоугольника А — двугранным
углам аь а8, . . ., а„ многогранного угла Q.
Рассмотрим теперь бильярдную траекторию внутри Q-
Она представляет собой многозвенную ломаную, не обяза-
обязательно лежащую в одной плоскости, число изломов которой
нам неизвестно — оно может быть как конечным, так и бес-
бесконечным (пока мы ничего не знаем), а также может либо
содержать бесконечный луч (тогда бильярдная частица,
летящая по нему, уже не сталкивается со стенками много-
многогранного угла Q), либо не содержать такого бесконечного
луча (в этом случае множество соударений со стенками
172
заведомо бесконечно; но и в первом случае число соударе-
соударений может быть априори бесконечным — только звенья
траектории в этом случае становятся сколь угодно малыми,
и частица как бы «застревает» в угле Q).
Применим к бильярдной траектории уже использовав-
использовавшуюся ранее процедуру «выпрямления», состоящую в том,
что мы каждый раз производим симметричное отражение
угла Q и бильярдной траектории относительно очередной
выпрямленная
траектории
Рис. 17.2
его грани, от которой отражается частица (подробнее о
процедуре выпрямления см. во введении и в пп. А и В
§ 15). В результате таких отражений (которых может быть
и бесконечно много, по неизвестному пока числу точек изло-
излома траектории) получим последовательность многогранных
углов Q, Qi, Q2, Qs, . . ., каждые два из которых симмет-
симметричны друг другу относительно общей грани, и прямую /,
пересекающую эти многогранные углы,— выпрямленную
бильярдную траекторию. Многогранные углы {Qt} высе-
высекают на сфере S2 р а в н ы е сферические многоугольники,
имеющие общие стороны,— все они получаются симмет-
симметричными отражениями на сфере из многоугольника Л=
~AtA2. . .Ап.
Рассмотрим центральную проекцию бильярдной тра-
траектории в угле Q на сферу с центром О. На сфере получится
многозвенная ломаная, расположенная в сферическом мно-
многоугольнике Л и состоящая из дуг больших окружностей
сферы S2. Звенья этой ломаной отражаются от сторон сфери-
сферического многоугольника А\ . . . Ап по закону «угол паде-
падения равен углу отражения». Действительно, пусть отра-
отражение происходит, например, от стороны AiA2, т. е. про-
проекция бильярдной частицы на сферу S2 движется по зве-
звеньям MiMz и M2MS, где точка М2 лежит на стороне ЛИ»
173
(рис. 17.3). Следовательно, сама частица отражается от
грани OAiAt многогранного угла Q. Отразив Q симметрич-
симметрично относительно этой грани (переведя его в многогранный
угол Qi) мы «выпрямим» два соседних звена бильярдной
траектории — проекция на сферу отрезка, симметричного
второму звену траектории, будет дугой M2M'S, являющейся
продолжением дуги МгМ2. Следовательно, /_А\М.гМх^
а так как ^/.А2М2М:,-=^/А3МгМа, то
— звенья МгМ2 и М2М3 на-
наклонены к стороне AiA2 под равными углами, что и требо-
требовалось.
Итак, проекция на сферу бильярдной траектории в
угле Q является бильярдной траекторией в сферическом
многоугольнике Л. После выпрямления бильярдной траек-
траектории в Q, что в проекции на сферу отвечает выпрямлению
бильярдной траектории в сфе-
сферическом многоугольнике Л, по-
получим, как уже говорилось, пря-
прямую / и ее центральную проек-
проекцию на сферу с центром О — ду-
дугу у. Но дуга у — этов точности
половина большой окружносгт\
Это хорошо видно из рис. П.2,6
17.3 (концы дуги у не включаются в
нее). Следовательно, длина дуги
V равна зх, и, тем самым, бильярдная кривая в угле Q
(имеющая бесконечную длину) превращается в ломаную
внутри многоугольника Л конечной длины зх (начало и
конец этой ломаной могут лежать строго внутри Л).
Еще раз внимательно исследуем звенья бильярдной ло-
ломаной в многоугольнике Л. Проекция М бильярдной
частицы движется по сферической ломаной внутри много-
многоугольника Л и проходит суммарный путь длины п. Если
точка М движется по тем звеньям сферической ломаной,
которые отражаются от двух соседних сторон много-
многоугольника Л, например от сторон At-tAt и AiAi+1, то она
отражается от этих сторон (не являющихся сторонами
угла At многоугольника Л) не более N(at)=—[—я/а*'
раз (таково число отражений бильярдной частицы от
двугранного угла с ребром OAt и гранями OAt-iAt и
OAtAi+i; см. также рис. 17.2, в). Но не может ли возник-
возникнуть такая ситуация: точка М попадает в угол At б е с к о-
нечно много раз, причем каждый раз все бли**
174
и ближе к вершине А(—это не будет противоречить
конечности суммарной длины всех проходимых ею звеньев
внутри Л\
Чтобы отвергнуть такую возможность, поступим сле-
следующим образом: окружим каждую вершину At кружком
Ki фиксированного радиуса так, чтобы кружки не пересе-
пересекались, а оставшуюся часть многоугольника Л (за исклю-
исключением всех этих кружков) обозначим S3 (рис. 17.4). Пусть
d — минимальное расстояние между точками сто-
сторон AiA^, A^Ag, . . ., AnAi, принадлежащих части S мно-
многоугольника (т. е. между точ-
точками сторон d, . . ., о„, не ле-
лежащими в кружках {Kt}). Тогда
точка М, выйдя из кружка Ki,
вновь попадет в этот кружок,
лишь пройдя расстояние, не
меньшее d. Сколько же раз точка
М может попасть в кружок Ki?
Вне этого кружка она прохо- Рис. 17.4
дит путь, меньший суммарного
пути по всем звеньям, т. е. меньший щ значит,
количество ее заходов в кружок Ki не может превос-
превосходить m~[n/d]+l. Внутри же каждого кружка Kt точка
М сталкивается только со сторонами угла At и испы-
испытывает, по сказанному выше, не более N{at) столкновений.
Всего столкновений точки М со сторонами многоугольника
Л внутри всех кружков поэтому не более mGV(<*!)+
+yV(a2)-K . ,+N(an)). К этому числу следует добавить
количество столкновений точки М g частями сторон аи . . .
..., ап многоугольника Л, лежащими вне кружков {К{\.
Но от одного такого столкновения до другого точка М
проходит путь, не меньший d, поэтому число этих столкно-
столкновений не больше указанного выше числа т. Следовательно,
общее число столкновений точки М со сторонами много-
многоугольника Л, равное числу столкновений бильярдной ча-
частицы с гранями угла Q, не превосходит
W <Л/ (Q) = m (N (tti) +N (a2) + ... + W («„) +1)=
йе at, . . ., вд — двугранные углы многогранного угла Q.
Мы, таким образом, не только доказали, что число JV
столкновений частицы о гранями угла Q в трехмерном про-
пространстве конечно, но и оценили его числом N(Q), завися-
175
1дим только от геометрии многогранного угла Q
от его плоских углов (они неявно входят в величину d) и
двугранных углов аь а2, . . ., ап.
Аналогичное рассуждение, по существу индукционное,
проводится и для многогранного угла Q в многомерном
пространстве (Rft(?>3). Случай трехмерного пространства
R8 мы свели к случаю двумерного, но уже сферического
пространства S2 (правда, с ограниченным многоугольни-
многоугольником, а не с бесконечным углом); точно так же, случай четы-
четырехмерного пространства Rk сводится к рассмотрению
«сферического» многогранника на трехмерной еди-
единичной сфере S3—{x\+x%+xl+xl*=l}, и т. д. В результате
получается равномерная (т. е. зависящая только от
геометрии угла Q) оценка числа ударов с гранями.
Остановимся коротко на доказательстве для общего
случая fe-мерного пространства [R4, в котором находится
Л-мерный n-гранный угол Q" с вершиной в начале коорди-
координат О, и сведем его к случаю размерности k—1. Опишем
единичную (k— 1)-мерную сферу S"'1 с центром в О; грани
угла Q" высекут на сфере Sk~l некоторый сферический
[k—1)-мерный многогранник
Л. Бильярдная траектория
вместе с бильярдной части-
частицей проектируется на сферу
S* в виде «сферической
бильярдной ломаной» в А, по
которой движется точка М.
После выпрямления бильярд-
бильярдной траектории получаем пря-
прямую /, центральная проекция
которой на сферу S* дает по-
половину дуги большой окруж-
окружности длины л (рис. 17.2, б). Следовательно, сумма длин
звеньев сферической бильярдной ломаной в сферическом
многограннике Л равна зх. Точки пересечения ребер мно-
многогранного угла Q со сферой S* — вершины А1г А2, • ¦ ¦
..., Ап—окружим непересекающимися шарами Ki, ..., Кп
размерности k—1; двумерные, трехмерные, . . ., (k—2)-
мерные грани многранника Л окружим попарно непересе-
непересекающимися окрестностями — (k—1)-мерными цилиндрами
(схематически это изображено на рис. 17.5). Внутри каж-
каждого шара Kt точка М отражается только от (k—2)-мерныХ
граней (k—1)-мерных многогранных углов Qf~\ Q§~\ • • •
176
К,
Рис. 17.5
.... Qn \" поэтому число столкновений точки М с этими
гранями не превосходит некоторой константы, зависящей,
по предположению индукции, только от геометрии углов
Qi Q*. Аналогичные равномерные оценки имеют
место и для отражений точки М от граней сферического
многогранника Л, находящихся внутри построенных ци-
цилиндров. Как и в случае пространства 1RS и сферы S2, в слу-
случае пространства Rft и сферы Sk~l мы должны учесть ко-
количество заходов точки М в построенные шары и цилиндры;
по аналогичным соображениям, они не превосходят неко-
некоторого числа m=[n/d]+l, где d — геометрическая харак-
характеристика оставшейся после выкидывания шаров и цилинд-
цилиндров из многогранника А части S3. В результате можно
получить верхнюю равномерную оценку числа стол-
столкновений точки М с гранями сферического многогранника
А, которая оценивает сверху также и число столкновений
исходной бильярдной частицы. Теорема 2, таким образом,
доказана.
Заодно получено второе решение задачи про п шаров на
прямой; для этого в качестве многогранного угла Q следует
брать (и— 1)-гранный угол Q = i(хи ...,х„)?R": ~ЛХ— <
^ ... ^ " у. В отличие от приведенного аналитичес-
V тп )
кого решения, где утверждается лишь, что число столкно-
столкновений между шарами не может быть бесконечным, в геоме-
геометрическом решении получен гораздо более сильный
результат, говорящий о наличии единой (равномер-
(равномерной) оценки числа столкновений для всех систем шаров
с данными массами.
Теорема 3. Число столкновений за бесконечный про-
промежуток времени между п шарами на прямой меньше неко-
некоторой константы N{tnlt .... тп), зависящей только от
соотношений масс этих шаров ти .... тп (эти соотно-
шения определяются геометрией многогранного угла
Q(tnu . . ., тп), т. е. плоскими, двугранными, трехгран-
трехгранными, .... углами Q) и не зависящей от начальных поло-
положений Xi, . . ., х„ и скоростей vu . . ., vn шаров.
Исходя из некоторых других, более физических сообра-
соображений, получим оценку константы N(m.i, . . ., тп) в § 18.
Задача*. В прямой круговой конус влетает бильярдная
частица, а) Перестанет ли она когда-нибудь сталкиваться с ним?
б) Конечно ли число ее столкновений с поверхностью конуса?
177
в) Если да, то зависит ли это число от начальных положения и
скорости частицы?
Ответ, а) Перестанет. 6) Конечно, в) Зависит. Указание
к решению. Рассмотрим центральную проекцию бильярдной
траектории у на сферу с центром в вершине конуса. Вся спроек-
спроектированная траектория у' будет располагаться в круглой «шапоч-
«шапочке», высекаемой на сфере конусом, причем ломаная у' будет вести
себя в «шапочке», как бильярд в обычном круге, т. е. будет распо-
располагаться полностью в круговом кольце и иметь равные звенья.
Рассуждая, как и раньше, нетрудно показать, что длина ломаной
у' равна я, поэтому число звеньев у у', а тем самым и у у конечно.
Но чем «касательнее» частица будет запущена в конус, тем звенья
ломаной у' будут меньше, и поэтому их количество будет зависеть
от начального состояния влетающей частицы.
§ 18*. Число столкновений между
молекулами одномерного «газа»
В этом параграфе мы сначала оценим число
столкновений между п молекулами «газа» на прямой, а за-
затем решим аналогичную задачу в «сосуде» — на отрезке
прямой. Геометрическое решение задачи о числе столкно-
столкновений между п шарами с массами ти . . ., т„, упруго
сталкивающимися на прямой, дает возможность получить
верхнюю оценку этого числа, но выписать ее явно на основе
соображений § 17 довольно затруднительно. Мы приведем
новые соображения, которые позволят получить искомую
оценку аналитически и выписать ее явно. Эта оценка будет
зависеть только от числа п шаров и от отношения макси-
максимальной массы тгаах в системе к минимальной массе mmin.
При ее выводе мы будем использовать полученные в § 17
знания о том, что число столкновений в рассматриваемой
системе конечно на бесконечном промежутке времени (и
некоторые следствия, например о том, что моменты столкно-
столкновений h, ts, ... не могут скапливаться на оси времени, и
т. д.). Будет доказана
Теорема 1. Число столкновений в системе из п
шаров на прямой с массами пц, . . ., тп не превосходит
2 [8п2 (п— 1) /"шах )" 2, где mmix и тт,п — максимальная и
минимальная масса шара.
Доказательство*). Перейдем к системе коор-
координат g началом в центре MaGG системы шаров. В этой
*) Прежде чем читать доказательство, читателю полезно озна-
ознакомиться с принципом Лагранжа, которому посвящен «Рассказ
двенадцатый» упоминавшейся в § 4 книги В. И. Тихомирова «Расска-
«Рассказы о максимумах и минимумах». Впрочем, кратко этот принцип из-
изложен нами иа с. 180.
178
системе отсчета
m1xi+ ... + т„х„ = 0, m1vi+ ..
Энергию всей системы молекул в рассматриваемой системе
отсчета обозначим Е:
Занумеруем подряд моменты столкновений частиц: t\<.
<.и<Лъ<.. . . Согласно закону сохранения импульса в мо-
момент th импульс каждой из столкнувшихся частиц изменя-
изменяется на одну и ту же положительную величину,
которую обозначим Ари (мы считаем скорость частицы поло-
положительной при ее движении вправо по прямой и отрица-
отрицательной при ее движении влево): импульс левой столкнув-
столкнувшейся частицы уменьшается на Aph~>0, а правой — уве-
увеличивается на Aph (см. задачу 13.1). Пусть рг=т,иг —
импульс частицы i, a N=N(tm, . . ., тп) — общее число
столкновений в рассматриваемой системе шаров за беско-
бесконечный промежуток времени. Оценку числа N проведем в
несколько этапов.
Этап 1. Оценим сумму Д^+Дрз-К . ,-\-ApN. Для этого
умножим импульс каждого шара на его номер и сложим по-
полученные величины, т. е. рассмотрим функцию времени t
Функция ^(t) постоянна между двумя столкновениями и
меняется только в момент столкновения tk на некоторую
величину A!Ph. Вычислим A!Ph, считая, что в момент th
столкнулись шары / и г+1:
i+ ... +п-р„,
Итак, 9*(t) в момент удара th меняется на Aph. Если мы
найдем верхнюю и нижнюю оценки !Ртах и !Ртш функ-
функции !P(t), то мы тем самым сможем получить и верхнюю
оценку для суммы ^Арк, поскольку
к
179
Как будет следовать из дальнейшего, достаточно получить
только верхнюю оценку 9*тах (мы увидим, что ^min =
Рассмотрим функцию *)
$ = X. (i-m-Oi + %-т-о, + ц-m,- -^-) — ц?,
1 = 1 ч '
где X и [х, — неопределенные коэффициенты. В искомой
экстремальной точке v=(vi, . . ., vn) все производные
этой функции по переменным vt, i~l, . . ., п, обращаются
в нуль:
•&'с( = (i + ^) mt + \mtvt = 0.
Отсюда получаем п равенств:
»| = —^. '=». 2 "•
п
Подставив найденное значение уг в равенство 2m(^i =0,
найдем
*¦ i "И
'i
где М =2 m(— суммарная масса всей системы шаров, а
Мх = 2 i'tnt — первый момент (этот термин взят из теории
i= i
вероятностей).
Подставив теперь »,- = — ^— в равенство
*) Функция X называется функцией Лагранжа (см. об этом
уже упоминавшуюся книгу В. М. Тихомирова «Рассказы о макси-
максимумах и минимумах»), а применяемый здесь метод носит название
«правило множителей Лагранжа» и состоит в том, что, добавляя
к оцениваемой функции540 все имеющиеся ограничения, умножен-
умноженные на неопределенные коэффициенты (в данном случае это
полу-
S"»!/) и И. ( У^ -Щг—EJ), дифференцированием
i=i / \i=i /
ченной функции X находят экстремальные точки.
180
найдем
п
или, введя обозначение М2 = 2 i%-tnt (второй момент)
и подставляя найденное значение К,
Зная "к и [г, можно вычислить экстремальные значения
функции $*у)
Отсюда следует, что
следовательно,
(--§-). A)
Замечание. Читатели, знакомые с теорией вероятно-
стеи, заметят, что число Dt, — —=—^-^—есть дисперсия случай-
случайной величины |, принимающей значение i с вероятностью т,/М.
Поэтому выполнено неравенство
—м
которое превращается в равенство, если положить крайние массы
т, и тп равными УИ/2, а все прочие массы — нулю (это неравен-
неравенство можно доказать и чисто алгебраически).
Этап 2. Всю ось времени t разобьем на «быстрые про-
промежутки», на каждом из которых какие-то два соседних
шара имеют большую относительную скорость и не сталки-
сталкиваются друг с другом. Напомним, что начало системы
координат находится в центре масс системы п шаров.
Промежуток времени [/f, tf2] (где t2 может, вообще гово-
говоря, принять значение +оо, тогда отрезок превратится в
161
венства (для определенности считаем, например, что /</):
к— О/К I V, — Vl
= r/_L _1_ч
\\m.i ' mi+i)~
\mi+imi+i) I" • • • -Г ^ m/2 -1-
m,- my J \ m,- ' ' my)
Так как начало координат находится в центре масс системы,
то в каждый момент для каждого шара i существует шар /
такой, что скорости vt и v} имеют противоположные на-
направления, а тогда, учитывая B),
Ы<^-^<2с\^\Г7^Тт/ш{^
для всех i=l, 2, . . ., п.
Оценим кинетическую энергию всей системы шаров
сверху:
2?
Z-i 2 ^Z- 2 М Z- '
1=1 1=1 1=1
Полученное противоречивое неравенство ?¦<? доказывает
неправомерность сделанного нами предположения. Утверж-
Утверждение доказано. 1
Этап 3. Оценим количество быстрых промежутков.
Каждому максимальному по длине быстрому промежутку
Itu t2] соответствует «сильный» удар некоторых шаров
i—1 и i, происходящий или в момент tit или в момент ts,
при этом для всех / G [tlt t2]
Изменение импульса при этом ударе равно (см. зада-
задачу 13.1)
, >C
С другой стороны, Ap(/_i. /> равно какому-то hph, где k —
Номер момента tu в последовательности всех моментов
183
АДЕ «I
ВКЛАДЕ «I
полуинтервал [tu +00)) будем называть быстрым, если
какие-то два соседних шара i—1 и i ни разу не сталкиваются
в течение этого промежутка, причем их относительная
скорость превышает некоторую положительную постоян-
постоянную сг>0: | vt{t)—Vi-tU) I >сг при всех t? [tu tt].
Конечно, любой промежуток времени, в течение
которого в системе не было вообще столкновений,— быст-
быстрый (поскольку положительную константу ct можно опре-
определить уже после выбора этого промежутка как модуль
разности скоростей ча^стиц i—I и г). Это верно, но только в
этом случае ct будет зависеть от положений и скоростей
шаров, а этого мы хотим избежать, чтобы получить оценку
числа столкновений. Наша цель — сначала подобрать
константы сг, не зависящие от положений и скоростей ша-
шаров, а затем уже получить соответствующие быстрые
промежутки. Заодно мы хотим, чтобы каждый момент вре-
времени t попадал хотя бы в один из таких быстрых проме-
промежутков.
Утверждение. Существует такой набор кон-
констант сг, с3, . . ., сп, зависящих только от масс частиц и
полной кинетической энергии Е, что объединение быстрых
промежутков времени повеем парам (i—1, i) покрывает всю
ось времени.
Доказательство. Введем число
с — -
B)
У —
Am mi
где М—ГП1 + . . .+тп. Положим теперь для каждого i=2,
3, 4, ...
Утверждается, что для каждого момента времени t су-
существует такое I, что | vt(t)—a,_i(/) | ^ct — это и озна-
означает, что все быстрые промежутки покрывают полностью
ось времени.
Предположим, однако, противное: пусть в некоторый
момент t для всех t=2, 3, .... п
С учетом этого предположения справедливы такие нера'
182
венства (для определенности считаем, например, что /</):
mi+1j
i+1 /)
! LI < 2c (-!+... +-LV
mi mj}^^ \mi ^ '§' ^ ntj )'
ntj
Так как начало координат находится в центре масс системы,
то в каждый момент для каждого шара i существует шар /
такой, что скорости vt и v} имеют противоположные на-
направления, а тогда, учитывая B),
\vl\<\vi-v/\<2c
У ш(Ит^
_i_\
м
для всех i=l, 2, . . ., п.
Оценим кинетическую энергию всей системы шаров
сверху:
2?
п т.
?2>«*
Полученное противоречивое неравенство Е<.Е доказывает
неправомерность сделанного нами предположения. Утверж-
Утверждение доказано. 1
Этап 3. Оценим количество быстрых промежутков.
Каждому максимальному по длине быстрому промежутку
[tt, t2] соответствует «сильный» удар некоторых шаров
1—1 и I, происходящий или в момент tu или в момент t2,
при этом для всех t?[tt, t2]
Изменение импульса при этом ударе равно (см. зада-
задачу 13.1)
С другой стороны, &Pa-i, d равно какому-то Дрй, где k —
номер момента tk в последовательности всех моментов
183
Сгционернь.
(открытое
именуемый
11 ВКЛАДЧИК вно
принимает денежнь
1.2. Срок вклада: 1 г
Дата окончания
Дата возврата в
'•j. Процентная ста
капмчкымк деньга
Г.Тс ПЯГТ
.астоящегс Договор
^. i. БАНК обязуется
начислять по вк/
'сачить тайну tii
р' ''врзтить по
процентами нзчисле
, UJ1 TBfi
_. ВКЛАДЧИК име
".оаершать, по вк
" повиями нас.ояи.
получать процент
'¦«аспоряжаты я в
независимо от
- процентами
9ШЗТ1 вклад
¦ рш ни
ть ющиали б БА
rff'JI.* ЕЧ"" - г-з
i '¦'
столкновений шаров, и поэтому изменение импульса при
каждом сильном ударе не меньше с: Аръ^с. Следова-
Следовательно, количество сильных ударов не больше чем
2 Ар* )\с. Оценим это число, учитывая формулы A) и
B):
тЛ
Осталось теперь заметить, что каждый момент сильного
удара — конец отрезка [/ь t2] — принадлежит не более
чем двум быстрым промежуткам, стало быть, число бы-
быстрых промежутков не больше удвоенного числа сильных
ударов, т. е. не превосходит величины
kf — M\. C)
J" "
Этап 4. Оценим число столкновений N (гщ, . . ., /ип).
Итак, существует разбиение оси времени, состоящее не
более чем из К отрезков, причем на каждом отрезке (бы-
(быстром промежутке) всю систему шаров можно считать раз-
разбитой на две невзаимодействующие системы. Поэтому мож-
можно воспользоваться индукцией и написать:
N (ти ..., тп) ^ К • max (N (ти ..., тг) +
1 < .' < П
4- N (/иг+,, ..., tnn)) + число сильных ударов,
где N (nil, ¦ • ., tnr) — число столкновений в системе г
шаров с массами mlt .... тг. Мы будем далее делать гру-
грубые оценки, заменяя, например. К/2 на К и т. п.— нас ин-
интересует лишь возможность получить явную форму-
л у для оценки.
Так как число сильных ударов не больше К (даже не
больше К/2), то
N(mt тп)^К- max (N(tnit ..., mr) +
+ N(mr+i, ...,mn) + l)-
Пусть Tr — максимальное из чисел N(mlt, . . ., ^(г)» Г|Де
mt, i • • •» tti[ —произвольные г масс из пц, . . ., tnn, т. е.
184
Tr равно максимальному числу столкновений в системе из
г шаров, выбранных из данных п шаров. Тогда
(мы опять выписали заведомо грубую оценку).
Наконец, введя Ur=Tr-\-l, получаем
Из этого неравенства уже легко получить оценку для Un
(между двумя шарами на прямой может произойти макси-
максимум один удар, так что T2=l, a U2—2).
Следовательно, учитывая равенство C), получаем
-Mi]
N(mu ..., тп) ^2^16 if^MVM.M-Mi] < D)
ТаккакУ — <— и VМ2М — М?<4"м(«— П<
<[^-n(n—1)ттах(см. замечание в конце первого этапа),
то окончательно получаем верхнюю оценку числа столкно-
столкновений в исходной системе п шаров:
N(mu ...,тп)^
V '«mill/ V '
Конечно, оценка E) грубее оценки D), но одновременно
нагляднее ее. Теорема 1 доказана.
Выведем теперь из теоремы 1 общий результат о росте
числа столкновений между молекулами газа в одномерном
«сосуде» — отрезке XY с упруго отражающими краями
X и Y (при столкновении шарика с краем — концом от-
отрезка — его скорость меняется на противоположную).
Теорема 2. Число столкновений в системе из п
шаров в одномерном «сосуде» XY растет не более чем с ли-
линейной скоростью по времени t. Иными словами, суищтвуют
Какие константы а и cs, не зависящие от начальных поло-
положений и скоростей шаров, а зависящие только от масс и
полной энергии системы, что число столкновений в сосуде
XY за время t не превосходит N (t) <Cit+Ct.
185
Доказательство. Отразим симметрично отре-
отрезок XY вместе со всей системой шаров (поменяв при этом
скорости всех шаров на противоположные) относительно
концов X и Y. Получим отрезок X'Y', на котором уже
движутся Зл шаров (рис. 18.1). Столкновению шара с кон-
концом отрезка XY отвечает в новой системе на отрезке Х'У
столкновение двух шаров равной массы (рассматриваемого
и симметричного ему), движущихся навстречу друг другу с
у' х ух'
Рис. 18.1
равными, но противоположными скоростями; после столк-
столкновения эти шары разлетятся, поменявшись скоростями.
Можно считать поэтому, что они просто прошли друг сквозь
друга. Положим длину отрезка XY равной 1. За время Д/=
__J__
Umax Vr2?/mmin
двигаться из точки X' или У, не может долететь до концов
отрезка XY. Поэтому за время At система шаров в «сосуде»
XY не чувствует краев X' и У «сосуда» Х'У. Следователь-
Следовательно, за время At число столкновений шаров в сосуде XY
между собой и об края X и Y не превосходит числа N3n
столкновений Зи шаров на всей бесконечной прямой (так,
будто концы X' и У отсутствуют все это время). По теоре-
теореме 1
у р
=-— 1/ *^Р ни один шарик, начавший
За промежуток времени t, который можно покрыть отрез-
отрезками At в количестве fe= 1 -ду I -Ь1 ([• ] — целая часть) про-
произойдет, следовательно, не более N(t)<.k-N3n столкнове-
столкновей
ний:
что и требовалось доказать.
Глава 7**
МНОГОМЕРНЫЙ «ГАЗ»
Уже исследование системы из п упругих ша-
шаров на прямой представляет собой весьма непростую
задачу, отчасти решенную нами в гл. 6. Исследование
двумерного и трехмерного «газа» молекул вносит новые
особенности: меняется характер столкновений и качествен-
качественно сложнее становится конфигурационное пространство
системы. Тем не менее систему из п молекул удается свести
к бильярдной (правда, многомерной) системе (т. е. к дви-
движению бильярдного шара в некоторой области) и доказать
утверждения, аналогичные теоремам § 17 и 18. Мы предпо-
предполагаем, что в системе происходят только двойные
столкновения.
Опишем, как происходит упругое столкновение двух
шаров. Отметим, что, в отличие от шаров на прямой из
гл. 6, которые мы считали точечными, в этой главе будут
рассматриваться шары ненулевого радиуса. Разложим
скорость каждого шара на
две составляющие — нап-
направленную вдоль линии
центров шаров и перпенди-
перпендикулярную к ней. В момент
столкновения шаров, когда
расстояние между их цент-
центрами равно сумме радиу-
радиусов и они имеют общую ка-
касательную плоскость 5\ происходит перераспределение
нормальных составляющих скоростей «при-
«прилета» v±, направленных по линии центров шаров (перпен-
(перпендикулярно плоскости 9*), согласно формулам A3.1) и
A3.2) — законам сохранения импульса и энергии (это дает
Два алгебраических уравнения с двумя однозначно опреде-
определяемыми неизвестными — новыми составляющими скоро-
187
отлето
прилета
Рис. А
стей вдоль линии их центров). Параллельные же плоскости
9* (тангенциальные) составляющие скоростей V\\ остаются
без изменения (рис. А). Сложив новые составляющие ско-
скоростей каждого шара, получим скорости их «отлета» (на
рис. А »отлета= Щ +«х)- Отметим, что в нашей модели
шары при ударе не закручиваются.
Уже одно знание правила обмена скоростей при столк-
столкновении двух шаров позволяет решать разнообразные зада-
задачи. Приведем две такие задачи.
Задача 1. Под каким углом могут разлетаться два одина-
одинаковых упругих шара, один из которых покоится?
Решение. Случай центра л ьн о г о удара исследо-
исследовался в задаче 13.2: налетающий шар после удара останавлива-
останавливается, а покоящийся приобретает скорость налетающего, как будто
налетевший шар прошел «сквозь» иего. Угол разлета здесь равен 0.
Если же удар нецентральный, то движущийся шар
полностью передает неподвижному свою центральную составляю-
составляющую, оставляя себе ортогональную составляющую. Следовательно,
угол разлета шаров в этом случае всегда равен 90°.
Задача 2. Плоскость разделена вертикальной прямой /
иа две полуплоскости. В левой полуплоскости расположен один
шар, в правой — я шаров, все шары одинаковы. Шар из левой
полуплоскости посылается с некоторой скоростью в правую и
между шарами начинают происходить упругие столкновения.
Какое наибольшее число шаров может оказаться в левой полупло-
полуплоскости в результате всех столкновений?
Решение. Слева от прямой /не могут оказаться все
п+1 шаров, так как полный импульс всей системы постоянен и
равен импульсу первоначально движущегося шара, т. е. направлен
вправо. Не могут слева оказаться и л шаров, так как в этом
случае справа от I двигался бы о д и н шар, и из закона сохранения
импульса его скорость превосходила бы скорость исходного шара
(чтобы скомпенсировать отрицательную вдоль горизонтальной
оси О* составляющую импульса п левых шаров), а тогда его ки-
кинетическая энергия превзошла бы исходную, что противоречит
закону сохранения энергии.
Докажем, что слева от прямой I могут окапаться п—1 шаров.
Утверждение 1. Можно так поставить неподвижный
шар на пути движущегося, что движущийся шар после удара от-
отклонится на произвольный наперед заданный малый угол. Это ясно
из того, что шар можно поставить так, что налетающий шар только
немного его коснется, а, значит, и отклонится несильно. При этом
угол разлета этих двух шаров будет равен 90° согласно решению
предыдущей задачи.
Утверждение 2. Неподвижный шар можно поставить
так, что если налетающий шар имеет отрицательную составляю-
составляющую скорости вдоль оси Ох, то после столкновения скорости обоих
шаров будут иметь отрицательные составляющие вдоль этой owe
оси. Это утверждение — следствие предыдущего: если скорость *
налетающего шара составляет угол а<90° с отрицательным направ-
направлением оси Ох, то неподвижный шар можно поставить так, ч1
скорость первого шара uv после столкновения будет составлять с^
угол P=ty2(90o—а), а с отрицательным направлением оси Ох —
188
угол а+Р=1/2(а+90о)<90о. Скорость второго шара и2. направ-
направленная под 90° к скорости и, первого шара, составит с отрнцатель-
ным,ьаправлением оси Ох угол 4^(90°—а)<90°, т. е. обе скорости
И, и щ имеют отрицательные составляющие вдоль оси Ох.
Перейдем к доказательству основного утверждения задачи.
Присвоим шару слева от прямой / номер 0, а шары справа от I
занумеруем числами 1, 2, 3 л. Шар I поставим на пути шара 0
так, чтобы шар 0 после столкнове-
столкновения отклонился на 10° (это можно
сделать согласно утверждению 1);
шар 1 полетит под углом 80°
к положительному направлению
оси Ох. На пути шара 1 поставим
шар 2 так, чтобы шар 1 откло-
отклонился на угол 10°, тогда шар 2 по-
полетит под углом 20° к отрицатель- "
ному направлению оси Ох (рис. Б). р
Шар 3 поставим так, чтобы после
столкновения с ним шара 2 оба
они полетели в отрицательном направлении оси Ох (утверждение 2).
На пути шаров 2 и 3 поставим шары 4 и 5 соответственно так, чтобы
все шары: 2, 3, 4 и 5 после столкновений продолжали двигаться
влево. Эта процедура продолжается до полного исчерпания запаса
шаров. Задача решена.
В этой главе будет последовательно приведено:
A. Описание конфигурационного пространства системы п
упруго сталкивающихся шаров в пространстве и в сосуде
специальной формы (к ним относятся (§ 19) многоугольни-
многоугольники и многогранники).
Б. Сведение рассматриваемой системы из п шаров к
бильярду в многомерной области сложной формы, описан-
описанной довольно просто в § 20.
B. Доказательство дискретности множества
моментов столкновений в системе п шаров (т. е. того, что
удары не накапливаются: число ударов между шарами и с@
стенками сосуда в любой конечный промежуток времени ко-
конечно; см. §21). Фактически это доказательство сводится к
решению такой задачи: может ли бильярдная частица, по-
попавшая в криволинейный угол, стороны которого направле-
направлены выпуклостями навстречу друг другу, «застрять» в нем?
Ответ на этот вопрос отрицателен; он решается здесь вполне
школьными методами.
Г. Доказательство того, что шары произвольных масс
на плоскости или в пространстве разлетаются после к о-
печного числа ударов, и оценка роста числа ударов в
«газе» из п молекул в сосуде (например, в параллелепипе-
параллелепипеде или любом другом многограннике, а также в сосудах с
выпуклыми внутрь стенками; см. конец § 21).
189
§ 19. Конфигурационное пространство
«газа» из п молекул в пространстве и сосуде
Пусть в пространстве К3 (случай плоскости
R2 аналогичен) расположены п «твердых» шаров с радиусами
fit i~2, ¦ ¦ ¦ i"n (об их массах речь пойдет позже). «Твердость»
означает здесь, что ни один шар не может зайти внутрь
другого, т. е. расстояние между центрами любых двух ша-
шаров i и / не меньше суммы их радиусов.
Каково конфигурационное пространство этих п шаров}
Конфигурационное пространство одного шара —.
то самое трехмерное пространство, в котором он находит-
находится, поскольку его центр может находиться в люб о й точ-
точке этого пространства (х, у, г).
Положения центров всех п шаров определяют, таким об-
образом, п трехмерных пространств, т. е. Зп-мерное изобра-
изображающее пространство R3", любая точка х которого имеет
3« координат — последовательно выписанных координат
центров п шаров: х= (хи уи Zi, х2у уг, zs; . . . хп, уп, гп).
Однако не любая точка пространства R3" задает
какое-то расположение твердых шаров, т. е. не любая точка
R3n является конфигурационной. Действительно, расстоя-
расстояние между центрами {xt, yt, zt), (xt, ys, Zj) шаров I и / долж-
должно быть больше или равно сумме их радиусов rt-\-rj\ поэто-
поэтому неравенство
задает невозможное расположение этих шаров
(когда один шар «залез» внутрь второго).
Для каждой пары (i, j) мы должны написать неравенство
A) — получим Cn=ll2n(n—1) неравенств, в совокупности
задающих то множество в изображающем пространстве Rsni
где конфигурационная точка располагаться не может.
Это множество назовем невозможным, а любую ее точку —
невозможной точкой. Дополнение к невозможному множест-
множеству в R3" — это и есть та область Q, где располагается кон-
конфигурационная точка, т. е. Q — конфигурационное про-
пространство системы п твердых шаров. Опишем его более де-
детально.
Возьмем шары с номерами 1 и 2 (радиусов п и г2) и за-
забудем на время об остальных п—2 шарах. Если центр_ fa»
Уи Zi) шара 1 зафиксировать, то неравенство A) для ^ '
/=2 задаст множество невозможных центров (х2, Уг> г"
шара 2. Им является шар IUi с центром (xt, yu Zi)
г1+г2 (рис. 19.1). Если же зафиксировать центр (xit У2,
190
шара 2, то неравенство A) задаст невозможные положения
центров (#i, уи 2Х) шара 1 — им является шар Ш2 с центром
(#2. Уг, z2) того же радиуса п-\-г2. Шары LUi и Ш2 мы долж-
должны рассматривать в различных экземплярах
трехмерного пространства R:i и R2, а невозможная точка
X={xi, yi, Zi,x2, у2, z2) принадлежит 3+3=6-мерному про-
пространству R". Точки (х1г yi, Zi), (х2, y2, z2) независимо друг
от друга пробегают полностью свои трехмерные простран-
пространства — К? и R? соответственно, и каждой из них отвечает
конкретный шар — Шх и Ш2 радиуса rx+r2 — в другом
мерный
'эллипсоид
Рис. 19.1
Рис. 19.2
трехмерном пространстве (Щ в пространстве R2, Ш2 —
в Rj). Следовательно, невозможное множество в
рассматриваемом случае двух шаров — внутренность бес-
бесконечного наклонного (под равными углами к осям 0хи
Оуи Ozu 0х2, 0у2, 0г2) цилиндра в б-мерном пространстве
R6 (условная картинка для этой ситуации приведена на
рис. 19.2). Граница этого цилиндра — 5-мерная вы-
выпуклая поверхность в б-мерном пространстве (сечения ко-
которой — 4-мерные эллипсоиды или 4-мерные сферы S4).
Фиксированному невозможному положению шаров 1 и 2
(когда они пересекаются) отвечает произвольное положение
шаров 3, 4, ...,«, и поэтому центры всех п шаров задают в
пространстве R3" невозможную точку (xt, уи zt\ . . .; хп,
Уп, г„), лежащую в произведении внутренности
полученного цилиндра на C«—6)-мерное пространство
R3n~e, т. е. внутри бесконечного цилиндра Ц«> в 3«-мерном
пространстве, у которого «образующая» — это C«—6)-
мерное пространство R3n~e, а перпендикулярное сечение —
4-мерный эллипсоид (рис 19.2).
Как было сказано выше, невозможное множество в
кЯп — это СЪ—ЧгП (п—1) внутренностей таких бесконеч-
191
ных цилиндров \\ij, а конфигурационное пространство Q
область вне этих цилиндров. Заметим, что все С2п цилинд-
цилиндров пересекаются по некоторой области в R3",— она соот-
соответствует одновременному пересечению всех п шаров в ис-
исходном трехмерном пространстве.
Из всего сказанного важно усвоить следующее: конфигу-
конфигурационное пространство п свободных упругих твердых трех-
трехмерных шаров Q — это многомерное (Зп-мерное) простран-
пространство, из которого выкинуто С'п выпуклых множеств 1\и
(читатель может представлять себе Ц(у в виде обычных
трехмерных цилиндров), так что само Q — невыпуклое
множество.
Иными словами, конфигурационным пространством Q
можно считать бесконечный сосуд с выпуклыми внутрь
стенками (границами цилиндров), внутри которого летает
конфигурационная точка х, как-то отражаясь от его стенок
(рис. 19.3) Если точка х попадает на цилиндр Ц,;, то это
.••:.:.•.¦¦•¦.¦¦•.-•••. значит, что в этот момент столк-
": нулись шары i и /, а остальные
:: шары не столкнулись.
Рис. 19.3
Сосуды с «.зазон»
Рис. 19.4
Перейдем к «газу» молекул в сосуде. Мы ограничимся
специальным, но широким классом сосудов, похожих на
конфигурационное пространство «газа» молекул. Сосуд —
это часть трехмерного пространства, ограниченная или не-
неограниченная, которая получается, если из пространства вы-
выкинуть конечное число выпуклых тел (как выше в Зп-мер-
ном пространстве были выкинуты выпуклые пересекающиеся
цилиндры 1Хи). Стенки сосуда, таким образом, считаются
выпуклыми внутрь сосуда (среди них могут встречаться н
плоские стенки) (рис. 19.4). Например, сосудом может быть
многогранный угол с плоскими или выпуклыми внутрь
стенками. Рассуждениями, аналогичными приведенным вы-
выше, можно показать, что справедливо
Утверждение. Конфигурационным пространст-
пространством системы п твердых упругих шаров в трехмерном сосуде
192
с выпуклыми внутрь стенками является сосуд Q в Зп-мерном
пространстве также с выпуклыми внутрь (Зп—1)-мерными
стенками.
В следующем параграфе мы сведем движение конфигу-
конфигурационной точки х в указанном сосуде Q к движению би-
бильярдной частицы в некотором другом сосуде Q, имеющем
также выпуклые внутрь стенки.
§ 20. Сведение «газа» в пространстве
и сосуде к бильярду
Итак, мы выяснили устройство конфигура-
конфигурационного пространства Q системы п твердых шаров в про-
пространстве и в сосуде с выпуклыми внутрь стенками: Q пред-
представляет собой сосуд в Зя-мерном пространстве R3n с вы-
выпуклыми внутрь (Зп—1)-мериыми стенками Wi, . . ., Wh.
В пространстве R3" имеется Зп осей: Охи Оу, Огх; Ох2,
0у2, 0г2; . . .; Охп, Оуп, Ozn, а конфигурационная точка
XGQ имеет Зп координат: x=(xit yit Zu . . .; хп, уп, гп).
Конфигурационная точка х движется в сосуде Q следующим
образом: между ее столкновениями со стенками {Wt} она
движется равномерно и прямолинейно (это соответствует"
тому, что в исходной системе трехмерных шаров в сосуде
также нет столкновений, т. е. шары движутся равномерно и
прямолинейно); столкновению шара с другим шаром или со
стенкой сосуда соответствует попадание конфигурационной
точки х на одну из стенок Wt сосуда Q (если точка х попала
на пересечение двух или нескольких стенок, то это соот-
соответствует тройному или многократному столкновению ша-
шаров, а такие столкновения мы исключили из рассмотрения).
Таким образом, конфигурационная траектория является
ломаной, состоящей из прямых звеньев.
Как и в гл. 5 и б, произведем преобразование простран-
пространства R3", выполнив следующие растяжения по осям:
При таком преобразовании область Q перейдет в область Q
также с выпуклыми внутрь стенками Wu . . ., Wh, а тра-
траектория конфигурационной точки х—в траекторию новой
' Г. А. Гальперин, А. Н. Земляков 193
точки
x~(xlt i/j, zlt ¦¦¦, хп, уп, zn),
которая также является ломаной. Будем обозначать пере-
переход от л: к л: символически равенством х = V~т х, где Y"in
символизирует указанные растяжения
по осям. Докажем следующее
Утверждение. Точка х яв-
является бильярдной частицей в сосуде
Q, т. е. модуль ее скорости равен 1 и
каждые два соседние звена ее траекто-
траектории образуют равные углы с внутрен-
внутренней нормалью п к стенке W в точке из-
излома траектории (рис. 20.1).
Рис. 20.1 _
Замечание. Прежде чем читать
дальше, советуем читателю вновь обра-
обратиться к § 16, где аналогичное утверждение для трех шаров на
прямой доказано с помощью понятия гкаляриого произведения
векторов.
Доказательство. Замене координат x = V~mx
соответствует точно такая же замена скорости точки х,
т. е. если v—(Vi, . . ., vn) —скорость конфигурационной
точки х, a v — скорость точки х, то v = Vmvi
v = (iit .... ij = (Vmiv1, V7n2v2, ..., Кт^ю„),
где г)г —трехмерная скорость t-ro шара в рассматриваемый
момент времени. Пусть Е — полная энергия всей системы п
шаров:
i= I «= 1
по закону сохранения энергии ?=const. Положим (выбо-
(выбором соответствующей единицы измерения энергии) 2?=1-
Тогда
|i|! = (e, ю)-2(К^-, Кт'/в/) = 21'п;(в/, *»,)==
ii ?1
Итак, проверено, что модуль скорости точки х в каждый
момент равен 1. Осталось проверить свойство «угол паде-
194
пня равен углу отражения». Для этого достаточно доказать
что вектор, равный разности скоростей отлета и прилета
е точке столкновения со стенкой, перпендикулярен к этой
стенке (точнее, к касательной к этой стенке плоскости).
Пусть vn— скорость прилета точки х, a v0 — скорость
ее отлета (рис. 20.1). Если точка х попала на стенку W со-
сосуда Q, то это означает, что либо какой-то шар в исходном
сосуде столкнулся с его стенкой — будем считать, что это
шар 1, либо столкнулись какие-то два шара в сосуде —
будем считать, что это шары 1 и 2. Тогда
v
a,
_
0; Ут3<о3,
v
it
где viu, vi0 — скорости прилета и отлета t-го шара в трех-
трехмерном сосуде, t=l, 2 (скорости шаров 3, 4, . . ., п, разу-
разумеется, не меняются в момент удара). В случае, когда шар 1
сталкивается со стенкой, v2n = ю20 = ю2.
Обозначим через Р (двумерную) плоскость касания столк-
столкнувшихся шаров 1 и 2 или шара 1 со стенкой в трехмерном
сосуде; ей отвечает (Зп—1)-мерная касательная плоскость
!Р к рассматриваемой стенке W сосуда Q (рис. 20.2).
Разберем сначала случай столкновения шаров. Напо [-
ним, что в момент упругого столкновения шаров их танген-
тангенциальные составляющие сохраняются, а нормальные пе-
перераспределяются по законам сохранения импульса и
енергии.
Пусть шары 1 и 2 столкнулись друг с другом и коснулись
Плоскости Р в точке, являющейся концом трехмерного
вектора а, а шары 3, 4, . . ., п в этот момент расположены
произвольным обр азом — их центрами являются произволь-
J* 1D5
ные (допустимые) векторы гя, rit . . м"г„ трехмерного про-
пространства. Тогда 3«-мерный вектор
г = (Кт>, V~m2a\ г6, г4, .... гп) € К8"
отвечает столкновению шаров 1 и 2 и лежит в плоскости
5", причем если вектор а пробегает все пространство IR3
(или всю^ область внутри сосуда в R3, если рассматривается
«газ» в сосуде), то плоскость S" состоит только из таких век-
векторов. Следовательно, нам надо доказать, что (v0—vn) J_ r;
этого достаточно, чтобы «угол падения» был равен «углу
отражения». Вычислим скалярное произведение этих век-
векторов и получим О, что и докажет их взаимную перпенди-
перпендикулярность. Напомним, что скалярное произведение двух
векторов одного евклидова пространства КЛ' (любой раз-
размерности N) равно сумме произведений их одноименных ко-
координат:
х2, ..., xN), (уи уг, ..., #„)> =
. . . + Х„уп.
Скалярное произведение в RSn, в отличие от скалярного
произведения (•, <) в R3, будем обозначать (•, •) .
Вычисляем:
0—*»2п);0;0;0; ...;0);
<vo—vn, /•>==
= <(Km1(©i0—©и); Vtn2(v2O—ю2п)^0; ...; 0),
(Vm[a; V7n2a; rs; ...; rn)>=(Km"i(ti1(,-©,„),
Vmx a) + (Ущ {v20—v2n), Vm% a)+0 + ... + 0 =
= mi (®io—©in, a) + m2 {v20 — v2n, a) =--
2, a)=0.
Здесь введены следующие обозначения:
=/>(t'—pB} — импульсы, приобретенные соответственно ша-
шарами 1 и 2 после удара. При этом по закону сохранения им-
импульса A/>i+A/>2=0; действительно, p'T'+p'F'^'i'+P'a'*
Мы доказали тем самым, что точка х отражается по
бильярдному закону, когда она попадает на стенку W, яв"
ляющуюся каким-то цилиндром Ц,-, 2, т. е. когда стенка W
отвечает за столкновение шаров 1 и 2.
196
Если же стенка W сосуда Q отвечает за столкновение
шара 1 с какой-то стенкой исходного трехмерного сосуда,
то надо доказать, что
(vo—vn)±k,
где
#€R3 — вектор, принадлежащий двумерной плоскости
касания шара 1 со стенкой исходного сосуда; г2, г„, ...
...,/•„€ К3—допустимые центры шаров 2, 3, .... л, а Ю2П=
= г»20=г»2. Опять вычисляем скалярное произведение и
получаем 0:
—ю1п); 0;
поскольку />(+)=р(~> при абсолютно упругом ударе шара
о стенку. Утверждение доказано.
§ 21. Рост числа столкновений между
молекулами «газа»
В предыдущих двух параграфах движение аб-
абсолютно упругих шаров в трехмерном пространстве или
сосуде с выпуклыми внутрь стенками было сведено к дви-
движению бильярдной частицы х в области Q Зп-мерного про-
пространства RSn, представляющей
собой сосуд с выпуклыми внутрь
стенками Wi, . . ., Wk. Сосуд Q
обобщает рассмотренные в гл. 6
многогранные углы с плоскими
стенками — Q может быть мно-
многогранным углом или ограни-
ограниченной областью с выпуклыми
внутрь стенками (рис. 21.1).
Возникает вопрос, аналогичный
5 и 6:
Могут ли точки столкновения частицы хсо стенками
сосуда Q бесконечно накапливаться? Например, может ли
бильярдная частица х «застрять» в угле с выпуклыми внутрь
стенками? (На плоскости легко нарисовать две касающиеся
197
Многогранный yso/i
с боднутыми стенками
Рис. 21.1
поставленному в гл.
кривые, образующие нулевой угол — вылетит ли из него
бильярдная частица или застрянет?) Более точно:
Конечно ли число столкновений бильярдной частицы х
е Q со стенками {Wt} за конечный промежуток времени
7<+оо?
Положительный ответ на этот вопрос дается теоремой 1
и означает дискретность (т. е. отсутствие точек
tttzts tk t tftz-too *
Дискретное и недискретйов
множества
Рис. 21.2
накопления) множества {^} моментов столкновений
(рис. 21.2).
Теорема 1. Множество моментов столкновений
бильярдной частицы х в сосуде Q с его стенками дискретно.
Следствие. Множество всех моментов столкнове-
столкновений в системе абсолютно упругих шаров, движущихся в
сосуде с выпуклыми внутрь стенками, дискретно: на любом
конечном интервале времени число столкновений шаров друг
с другом и со стенками конечно.
Доказательство теоремы проведем от про-
противного. Предположим, что существует точка накопления
fo=/=+oo моментов U, t2, ta, . . . столкновений частицы х о
стенки сосуда Q. Раз tk-*-t0 при &->оо, то в сосуде Q есть точ-
точка А, являющаяся геометрической точкой накопления то-
точек столкновения, т. е. лг(/ь)->Л при tk-+to- Точка А при-
принадлежит сразу нескольким стенкам Wlt,. . ., W!s сосуда Q,
образующим «кривой многогранный угол с выпуклыми на-
навстречу друг другу стенками». Мы будем считать, что рас-
рассматриваемые моменты столкновения находятся на таком
маленьком интервале вокруг точки U, что точка х сталки-
сталкивается только с указанными стенками сосуда Q, и уже
не сталкивается с остальными его стенками (с которыми
могла сталкиваться до этого). Кроме того, частица х ни-
никогда не попадает в Л — удар в А запрещен.
Пусть p(x(t), А) —расстояние от частицы л-до точки А
в момент/. Из того, что х(<)->¦ А, следует, что
p(x(t), Л)-*0 при /->/„. (D
Мы же докажем сейчас, что при всех t, сколь угодно близких
198
к t0, p(x(t), А) больше некоторой положительной констан-
константы, т. е. не стремится к О, и тем самым получим нужное
противоречие.
Для этого мы введем следующую функцию времени
r(t) — расстояние от точки А до луча у~ (t) с началом в
точке Л"@ и направленным в сторону движения частицы Л"
(рис. 21.3).
Ht)
a
Рис. 21.3
Лемма. Функция r(t) — «расстояние от точки А до
луча y~(t)» — положительная неубывающая функция пе-
переменной t.
Доказательство этой леммы разобьем на две
части: докажем ее сначала на промежутке {$ъ-и th) между
двумя ударами, а затем — в сам момент удара tk (вернее,
на маленьком промежутке (th—е, *ь+е), охватывающем мо-
момент удара).
1. Между двумя последовательными ударами частицы
о стенки сосуда луч у~ (t) передвигается по себе — перехо-
переходит в свою часть, т. е. y~(t) содержит луч y~(t') при t'>t,
поэтому расстояние от точки А до луча у~ (f) может толь-
только увеличиться (как на рис. 21.3, б, когда это расстояние
равно длине отрезка с концами Лил") либо остаться тем же
(как на рис. 21.3, а, когда расстояние от Л до луча равно
длине перпендикуляра, опущенного из Л на этот луч).
Итак, если t<t' — моменты времени между двумя после-
последовательными ударами, то r(t)<gr(t').
2. Пусть теперь th — момент столкновения частицы со
стенкой W, (tk—е, /ь+е) — маленький временной интер-
интервал вокруг этого момента.
Обозначим у^'^—у-(th—е) луч, по которому частица
подлетела к стенке W, a Y(+)=Yi (^ь) — ЛУЧ» по кото-
которому она отлетела от этой стенки. Пусть !Р — каса-
касательная плоскость к стенке W в точке удара x(th), причем
вся стенка лежит по одну сторону от нее, как ограничиваю-
ограничивающая выпуклое множество (рис. 21.4). Если отразить луч
199
•у(+) симметрично относительно плоскости 5s, то он перейдет
в луч Yjf4^ft) — продолжение луча yl~* (см. рис. 21.4), и
поэтому луч vJr'Cfh) с началом в точке x(th) € Улежит с
той же стороны от плоскости 5*, что и точка А, а луч y<+) —
с другой стороны от плоскости 5*. Следовательно, расстоя-
расстояние АВ до луча у'"' меньше рас-
расстояния АС до луча v(+>, что и
означает, что r(th—e)<r h{th+e).
Лемма доказана.
Из нее следует, что частица х
не может сколь угодно близко
приблизиться к точке А, т. е. не-
неверна формула A). Действитель-
Действительно, в противном случае сколь
угодно малым стало бы и рас-
расстояние r(t) при t-+t0, хотя в
лемме было доказано, что рас-
расстояние r(t) от точки А до луча,
по которому движется частица,
не меньше расстояния л@) от
точки А до первоначального луча у~ @), по которому летела
частица. Можно даже оценить, сколько времени частица х@)
будет приближаться к точке А—оно не больше (в предпо-
предположении, что модуль скорости частицы равен 1) расстояния
d@) отточки л: @) до точки В — основания перпендикуляра
Рис. 21.4
Рис. 21.5
АВ, опущенного из А на луч 7^@) (Рис- 21.5, а). Действи-
Действительно, если бы на пути частицы не было стенки W, она
приближалась бы к точке А по лучу у~ @) вплоть до совпа-
совпадения с точкой В, т. е. время d@), а потом стала бы удалять-
удаляться отточки А. Но из-за того, что в результате столкновений
со стенками расстояние r(t) от точки А до луча движения
200
частицы растет, расстояние d(l) от точки хA) до осно-
основания перпендикуляра В (t), опущенного из А на луч у~ (О,
уменьшается, и общее время приближения части-
частицы х к точке Л поэтому меньше d@) (график изменения d(t)
приведен на рис. 21.5, б).
Теорема 1, таким образом, доказана.
Сделаем простое, но очень важное замечание. Теорема 1
в некотором смысле обобщает геометрические теоремы § 15
о «незастреваемости» бильярдного шара в угле с прямоли-
прямолинейными сторонами на плоскости и в многогранном угле с
плоскими стенками в пространстве. Однако есть и сущест-
существенное отличие. В § 15 мы фактически во всех случаях ука-
указки число столкновений со стенками угла, больше которого
не может быть на всем бесконечном интервале времени.
В нашей же теореме 1 мы этого не только не утверждали,
ноине можем утверждать существования такой оцен-
оценки числа ударов.-
В самом деле, если взять на плоскости «нулевой» угол,
образованный двумя касающимися выпуклыми кривыми,
смотрящими друг навстречу другу (например, двумя пара-
параболами у=—100д;2 и г/=10~10°л:2),то чем ближе к их общей
касательной мы запустим бильярдную частицу, тем боль-
большее число столкновений произойдет, прежде чем она выле-
вылетит из этого угла, и это число может быть сделано больше
любого наперед заданного Ne. Однако если рассматриваемый
кривой угол «ненулевой», т. е. в него можно поместить обыч-
обычный многогранный угол с плоскими стенками так, что его
вершина принадлежит пересечению стенок кривого угла,
то верхняя оценка числа ударов, по-видимому (пока это
недоказанная гипотеза), существует. Сообщим без доказа-
доказательства, что для системы шаров в трехмерном пространст-
пространстве в отвечающем ей бильярде Q все кривые многогранные
углы между соседними стенками сосуда {Wt} ненуле-
в ы е. Это позволит нам доказать конечность числа столк-
столкновений между шарами в пространстве на всем бесконечном
интервале времени, а не только на любом конечном, праь-
да, уже не геометрическим, а аналитическим способом,
похожим на доказательство § 17. На основе этого будет
затем объяснено, почему число столкновений между моле-
молекулами «газа», помещенного в сосуд с плоскими и выпуклы-
выпуклыми внутрь стенками, растет линейно со временем.
Теорема 2. В системе из п упругих шаров с произ-
произвольными массами пц, . . ., тп, движущихся в трехмерном
201
пространстве, за бесконечный промежуток времени может
произойти лишь конечное число столкновений.
Доказательство. Разобьем сначала всю систе-
систему шаров на автономные группы, т. е. такие группы,
что никакие два шара из разных групп начиная с некото-
некоторого момента 70 уже никогда не сталкиваются друг с дру-
другом (таких групп может быть и одна — вся система шаров).
Мы хотим доказать, что таких групп будет ровно п, по од-
одному шару в группе — это и означает,
что шары с момента То не сталкиваются.
Если в какой-то группе больше одно-
,2 го шара, то в ней происходит бесконеч-
^,_ ное число столкновений (иначе группа
of\y распалась бы на более мелкие автоном-
АВшномная ные подгруппы), причем для любых двух
группа шаров шаров Л и В из этой группы найдутся
такие шары Си С2 Ch из той же
Рис. 21.6 группы, что А сталкивается с Сг беско-
бесконечно много раз, Ci и С2 сталкиваются
бесконечно много раз, . . ., Ch и В сталкиваются бесконеч-
бесконечно много раз: можно представлять себе связный граф g
конечным числом вершин, символизирующих шары в группе,
причем ребром соединены те вершины, для которых соот-
соответствующие шары сталкиваются бесконечно много раз
(рис. 21.6).
Предположим, что имеются автономные группы, в ко-
которых больше одного шара. Рассмотрим одну из них и обоз-
обозначим ее / (в качестве примера можно иметь в виду группу,
изображенную на рис. 21.6). Выберем в этой группе какие
то два шара, сталкивающихся между собой бесконечно
число раз. Выше уже доказано, что все эти столкновения
между ними не могут произойти на конечном проме-
промежутке времени (столкновения не скапливаются по теоре-
теореме 1), так что эти моменты столкновений стремятся к +о°-
Точно так же, как и в § 17 при аналитическом доказательст-
доказательстве конечности числа столкновений между п шарами н а
прямой (см. п. А § 17), можно доказать, что у этих
шаров существуют предельные скорости при t-^-oo, равные
между собой как векторы (мы не останавливаемся на под-
подробном доказательстве, полученном Л. Н. Васерштейном
и Г. А. Гальпериным и использующем существенную ма-
математическую технику, связанную с системами центрально
отталкивающихся частиц). А так как любые два шара из ав-
автономной группы / соединяются в графе некоторой цепочкой
шаров, сталкивающихся попарно бесконечно много
202
то и у всех шаров существуют предельные скорости при
/->оо, причем все они равны между собой (как векторы) и
равны векторной скорости центра масс рассматриваемой
автономной группы /.
Перейдем поэтому в инерциальную систему координат,
связанную с центром масс группы / — в ней центр масс
группы / имеет нулевую скорость. Тогда скорости всех ша-
шаров группы / в выбранной системе координат стремятся к
О при t-+co (к скорости центра масс группы), и, следова-
следовательно, полная кинетическая энергия Et(t) этой автоном-
автономной группы стремится к 0 при t-*-<x>.
Однако в силу автономности группы / при ?>Т0 (на-
(напомним, что в момент То произошел распад всей системы п
шаров на автономные группы — эти группы перестали
взаимодействовать друге другом) в ней выполнен закон сох-
сохранения полной энергии (в нашем случае он совпадает с
законом сохранения полной энергии поступательного дви-
движения): E,(t)=const при t>T0. Но поскольку ?/(/)-> О
при t-*-oo, имеем const=0; значит, с момента ТО все шары
группы / имеют тождественно нулевую скорость
в системе центра масс.
Поэтому с момента То в группе / не происходит н и
одного столкновения, что противоречит тому,
что их в группе / бесконечно много при t>Te.
Следовательно, предположение, что в автономной груп-
группе может быть больше одного шара, противоречи-
противоречиво, откуда вытекает, что автономных групп с момента То
ровно п — по одному шару в каждой. Это означает, что с
момента То все шары движутся равномерно и прямолиней-
прямолинейно. Теорема 2 доказана.
Итак, шары в пространстве после конечного числа уда-
ударов перестают сталкиваться.
Задача 21.1. Может ли система шаров в каком-либо сосуде
вести себя следующим образом: с некоторого момента шары пере-
перестают сталкиваться со стенками сосуда (а сталкиваются только
между собой)?
Имеется гипотеза (ее доказательство интенсивно раз-
разрабатывается математиками в последнее время), что это
число ударов меньше некоторой величины No, не зависящей
от начальных положений и скоростей шаров (при фиксиро-
фиксированной полной энергии системы), т. е. имеет место рав-
равномерная по начальным условиям оценка числа уда-
Ров. Более общая гипотеза: в многогранном «ненулевом»
Угле с выпуклыми внутрь стенками (т. е. во внешности к
выпуклым телам пространства, имеющим общее непустое
.203
рересечение) также имеет место равномерная оценка: би-
бильярдная частица испытывает от стенок угла отражения,
число которых не превышает числа No, не зависящего от
начального состояния частицы (из второй гипотезы не-
нетрудно вывести гипотезу о шарах).
Из этих гипотез можно получить, что если газ из п моле-
молекул (шаров) находится в сосуде, имеющем вид параллеле-
параллелепипеда или другого многогранника, или в сосуде с выпук-
выпуклыми внутрь стенками (среди которых могут быть и плос-
плоские стенки), то число столкновений молекул газа друг с
другом и со стенками за время t не превосходит t
Рис. 21.7
где а и с2 — некоторые постоянные, зависящие только от
кинетической энергии Е системы и геометрии сосуда.
Например, для параллелепипеда надо поступить точно
так же, как и при доказательстве теоремы 2 § 17: отразить
параллелепипед П симметрично относительно всех своих
граней, ребер и вершин вместе с содержащимся внутри
него «газом», получив новый параллелепипед ГГ с объемом
и числом молекул в 27 раз большим (рис. 21.7, а). За малый
промежуток времени At = УmmiJBE) влияние краев парал-
параллелепипеда П' не будет чувствоваться внутри П, и поэтому
число столкновений п молекул внутри П за этот промежу-
промежуток не будет превосходить константы Nnn, которой оце-
оценивается число столкновений 27/г молекул во всем про-
пространстве IR3. За время t число столкновений поэтому
не больше
что и требовалось доказать.
В общем же случае сосуда с выпуклыми внутрь стенка-
стенками (некоторые стенки могут быть и плоскими) следует по-
204
ступить так: в конфигурационном пространстве системы —
сосуде Q с выпуклыми внутрь стенками — окружить его
вершины, ребра и грани всех размерностей окрестностями
(рис. 21.7, б), внутри которых число столкновений меньше
фиксированных универсальных констант; перелет же из
одной окрестности в другую длится промежуток времени,
больший некоторого *0>0, и поэтому число ударов при этом
перелете не больше числа столкновений в системе свобод-
свободных шаров в пространстве, т. е. не больше некоторой дру-
другой константы. Поэтому число ударов здесь также не пре-
превосходит Cit+C2.
ЧАСТЬ IV
БИЛЬЯРДЫ В МНОГОУГОЛЬНИКАХ
И МНОГОГРАННИКАХ
Во второй части книги подробно рассматри-
рассматривался бильярд в прямоугольнике, и его исследование сво-
сводилось к изучению траекторий точки, движущейся по то-
тору,— двумерной замкнутой поверхности «с одной дыркой»
(поверхности бублика). Оказывается, во многих случаях
изучение бильярда в многоугольниках сводится к изучению
траекторий точки, движущейся по кренделю,— двумерной
замкнутой поверхности с двумя или большим числом «ды-
«дырок». Такие поверхности возникают в классической меха-
механике при рассмотрении вопросов, связанных с так назы-
называемыми интегрируемыми и почти интегрируемыми дина-
динамическими системами, и являются геометрическими след-
следствиями законов сохранения в системе (или, как говорят
механики, первых интегралов системы: на этих поверхно-
поверхностях некоторая функция принимает постоянное значение).
У нас они естественным образом возникнут при рассмотри
нии динамических систем «бильярд в многоугольнике» и «ш <•
ры на отрезке». Эти поверхности переходят в себя под дейст-
действием фазового потока (см. § 3) и поэтому называются и
вариантными (т. е. «сохраняющимися»).
Часть IV состоит из двух глав — 8 и 9. В гл. 8 дается
подробное описание поверхностей, отвечающих бильярдгм
в конкретных многоугольниках, объясняется, как так""
поверхности склеиваются из нескольких экземпляров
многоугольника, и решается вопрос о поведении типичных
бичьярдных траекторий в рассматриваемых многоуголь-
многоугольниках.
В гл. 9 изучаются бильярды в многоугольниках,
углы которых соизмеримы с п — в так называемых ра-
рациональных многоугольниках: исследуется поведение ти-
типичных и индивидуальных (выбранных специальным обра-
образом) бильярдных траекторий. В этой же главе изучаются
периодические траектории в многоугольниках и многогран-
многогранниках.
?06
Глава 8
ГЕОМЕТРИЯ МНОГОУГОЛЬНОГО БИЛЬЯРДА
В этой главе исследуются бильярды в так на-
называемых торических многоугольниках, отличных от пря-
прямоугольника, но сводящихся к изучению торических < б-
моток (§ 22), а также бильярды в многоугольниках, сводя-
сводящихся к обмоткам более сложных поверхностей (§ 24). Опи-
Описание и классификация этих поверхностей приводится в
§23.
§ 22. Бильярды в «торических»
многоугольниках
Пусть Q — многоугольник на плоскости. За-
Задача, которую мы решаем, —как можно более подробно
исследовать поведение траекторий бильярда в многоуголь-
многоугольнике Q. Траектории бильярда, рано или поздно попадающие
в одну из вершин многоугольника Q, мы называем особыми
и считаем закончившимися в со-
соответствующей вершине. В §7 была
указана процедура выпрямления г~1?*~\Уа1[~*/^7\р1
любого куска особой или неособой
траектории: превращение его с по-
помощью последовательных отраже-
отражений в отрезок прямой линии (см.
рис 7.2). В § 9 для исследования
траекторий бильярда в прямоу-
прямоугольнике было проведено изобра-
изображенное на рис. 22.1 построение,
которое состоит в частичном вы-
выпрямлении траектории с помощью
отражений. При этом мы ограни-
ограничиваемся четырьмя прямо-
прямоугольниками — исходным прямоугольником Q и тремя пря-
прямоугольниками Qie, Qoii Qa, получающимися из Q отраже-
отражениями относительно двух его сторон и их общей вершины.
Как только выпрямленный кусок траектории ММ' пере-
пересекает границу большого четырехугольника Q = AAiA2A3,
выходящий из Q луч РХМ' мы переносим параллельно —
так, чтобы сторона А±А2 совместилась со стороной АА3;
иначе говоря, из полученной (переносом из точки Pi) на
отрезке AAS точки Р[ мы проводим луч Р[Р2 в том же нап-
направлении, что и исходный луч ММ'. Далее, переносим
точку Р2 со стороны А3А2 в соответствующую точку Р2
207
PL
P'z
-rfl»
н ъ
1
Рис.
22.1
р ^^—
на стороне ААг и проводим через Р'г следующий отрезок
траектории — в том же направлении.
С одной стороны, если с помощью отражений наложить
прямоугольники Qlo, Qoi, Qu на прямоугольник Q, то от-
отрезки MPi, Р'гРг, P'iPs и т. д. дадут на Q траекторию
бильярда.
С другой стороны, чтобы траектория на большом пря-
прямоугольнике Q стала непрерывной, достаточно склеить со-
соответствующие точки сторон А3А2 и AAi, а затем — сторон
АхАг и AAS. После склейки отрезки МРг, Р[Рг, Р^Рз, . .
составят непрерывную кривую на торе, получающемся из
Q в результате склейки (см. § 8). Эта кривая является тра-
траекторией соответствующей обмотки тора.
Отступление. В дальнейшем нам придется
склеивать поверхности из разных многоугольников; всег-
всегда при этом склеиваемые сто-
стороны будем обозначать одина-
одинаковыми буквами со стрелка-
стрелками, показывающими, в каком
направлении приклеиваются
стороны друг к другу. В прин-
принципе, можно пару сторон с и
с приклеить друг к другу в
двух направлениях (рис.
22.2,а и 22.2,6): в первом
случае из прямоугольника
получается поверхность цилиндра, во втором — так назы-
называемый лист Мёбиуса. Это совсем разные поверхности: край
цилиндра состоит из двух замкнутых кривых — «верхней»
S(+) и «нижней» S'"'; край же листа Мёбиуса — одна кри-
кривая S.
Задача 22.1. Что получится из листа Мёбиуса, если его
разрезать вдоль средней линии (она помечена штриховой линией
на рис. 22.2, б)?
При склейке поверхности из многоугольника полезно
считать многоугольник эластичным, а траектории нари-
нарисованными на нем. Эластичность многоугольника нужна,
чтобы его сжимать или вытягивать для осуществления
склейки. При этом склеиваемые друге другом стрелки мож-
можно сжимать и вытягивать одновременно, но вытягивать со-
совершенно одинаково (чтобы обозначенные одной буквой точ-
точки на стрелках совпали после склейки).
Вернемся после сделанного отступления к обсуждению
бильярда в прямоугольнике. Вместо того чтобы рассматри-
208
й
Рис. 22.2
вать одну индивидуальную траекторию на большом пря-
прямоугольнике Q, состоящую из параллельных друг другу
отрезков, удобнее сразу рассмотреть все траектории од-
одного и того же направления — в § 9 они назывались пуч-
пучком параллельных траекторий. Разным исходным направле-
направлениям соответствуют разные пучки. После склейки прямо-
прямоугольника Q в тор указанным выше способом те отрезки
данного направления, которые лежат на одной траектории,
автоматически подклеятся друг к другу. В этом и состоит
некоторое преимущество рассмотрения целого пучка тра-%
екторий. После склейки разные пучки параллельных тра-
траекторий дадут разные обмотки тора (§ 9). Напомним
полученные в § 8 сведения об обмотках торов. Обмоткой
тора называется пучок траекторий — кривых на торе,—
по которым движется точка, если ее движение складывает-
складывается из равномерного вращения вдоль параллелей и равно-
равномерного вращения вдоль меридианов, характеризуемых
соответствующими периодами обмотки Тх и Т2 (Ti — вре-
время, за которое точка возвращается на те же меридианы,
Т2 — время возвращения на те же параллели). Если пе-
периоды Ti и Т2 обмотки соизмеримы, т. е. TtlTu=mln — ра-
рациональное число, то движение точки периодично с периодом
T~nTi=mTz и происходит по замкнутым кривым на торе.
В случае когда 7* и Тг несоизмеримы, движение неперио-
непериодично, и каждая траектория этой (иррациональной) об-
обмотки всюду плотно заполняет тор.
Найдем периоды обмоток, получающихся из соответст-
соответствующих потоков бильярдных траекторий в Q. Если Vi и
v2 — составляющие скорости движения бильярдного шара
по горизонтальному и вертикальному направлениям, at
и а2 — длины соответствующих сторон исходного прямо-
прямоугольника Q, то легко видеть, что соответствующие перио-
периоды равны
т __ 2ai т — 2°2
1 ¦% — ' % М. о — ^—-
1 V! ' 2 V2
Их отношение есть-^г-==—/— = — tg а, где а — угол
траекторий пучка с горизонтальным направлением AAi.
Если — tg а иррационально, то траектории бильярда
всюду плотно заполняют прямоугольник; в противном
случае траектории бильярда периодичны (это следует из
сформулированного свойства обмоток тора и из способа
получения бильярдных траекторий из траекторий на Q).
209
В § 13 было дано решение задачи о бильярде в прямо-
прямоугольном треугольнике с острым углом ф=я/4. Именно рас-
рассматривался пучок параллельных траекторий в квадрате Q,
составленном из восьми экземпляров треугольника Q —
из Q^Qe и Qi-r-Q7» получающихся из Q отражениями
(рис. $2.3). Если траектория МРх выходит из квадрата Q,
то ее продолжение РуМ', лежащее, например, в треуголь-
треугольнике Q'3 (см. рис. 22.3), следует пере-
перенести в треугольник Qe: треугольник
Qs получается из Qt параллельным
переносом, и нет необходимости рас-
рассматривать продолжение Рт_М' траек-
траектории бильярда в этот треугольник,
ибо из соответствующей точки Р{ уже
проведен кусок траектории Р\Р2 дан-
данного пучка, который при соответст-
соответствующих симметриях дает тот же кусок
траектории бильярда в треугольнике
Q, что и PtM'. Точно так же убеж-
убеждаемся, что и все прочие треуголь-
треугольники Q'b, полученные из Q& отражениями относительно
сторон квадрата Q, получаются из каких-то треуголь-
треугольников набора Qi, Q2, . . ., Q8 параллельным переносом
(например, Qi — из Q4, Q2 — из_ф7 и т. д.). Поэтому
при выходе траектории за пределы Q нет необходимости ри-
рисовать продолжение траектории в соответствующем тре-
треугольнике QI, — можно перенести точку выхода Р в соот-
соответствующую точку Р' противоположной стороны квадрата
Q и двигаться по уже нарисованной траектории пучка па-
параллельных траекторий. Таким образом, траектории биль-
бильярда в Q получаются из описанных траекторий потока с
перескакиванием с одной стороны на противоположную в
квадрате Q отражениями, при которых все треугольники
Qu ¦ • • Q? накладываются на Q; чтобы сделать траектории
непрерывными, нужно склеить противоположные стороны
квадрата, как указано на рис. 22.4. Отметим, что правило
склейки выбирается не произвольным образом, а в соот-
соответствии с естественной процедурой выпрямления траекто-
траектории бильярда. На торе получаем обмотку; если (иь v2) —
составляющие скорости бильярдного шара вдоль горизон-
горизонтального и вертикального катетов треугольника, а длины
катетов равны а, то периоды обмотки равны T1—2alvu
T2=2a/v2, Ti/T2=v2hi и из свойств обмотки тора получаем:
210
Если отношение vjvi рационально, то тпа^кпюрия
бильярда периодична в треугольнике Q, в противном случиг
траектория всюду плотно заполняет весь треугольник Q
Заметим, что, как и в случае бильярда в прямоугольни-
прямоугольнике, в рассмотренном случае особые траектории, попадаю-
попадающие в *^ршины треугольника, можно естественным обра-
ь
\
/
/
\
*
\
/
\
\
/
или
/
\
Рис.
>
/
22
4
a
W ?¦•¦':•¦'
•...:.':./.;,¦¦¦.
зом продолжить за вершины — на рис. 22.5 показано, как
продолжить траекторию, попадающую в точку А — вер-
вершину угла зт/4. Будучи таким образом продолжены, особые
траектории ничем не отличаются от неособых после склеи-
склеивания квадрата в тор.
Исследуем теперь бильярд в разностороннем треуголь-
треугольнике Q. Рассмотрим в нем пучок параллельных траекторий.
W
Ри 29.5
Рм 22 6
Построим с помощью отражений еще пять таких же тр^
угольников — Qi-r-Q6; они вместе с Q=Qe образуют пр
вильный шестиугольник Q (рис. 22.6). Распространим пу-
пучок параллельных траекторий на весь этот шестиугольник.
При выходе траектории из пределов Q продолжение тра-
траекторий следовало бы рисовать в симметричных треуголь-
треугольниках Qk, но, они получаются из Qi—Qe параллельными пе-
переносами (например, & — из Q5, Q's — из Qe и т. д.), и
поэтому вместо отрезка траектории РМ, выходящего из
Q, достаточно рассмотреть уже нарисованный отрезок Р'К
211
внутри Q, где точка Р' — соответствующая точке Р точ-
точка противоположной стороны шестиугольника Q. Таким
образом, если считать, что движущаяся точка, доходя до
стороны s шестиугольника Q, мгновенно перескакивает в
такую же точку на противоположной стороне s' шести-
а угольника и продолжает
с П^Ф /\~7\ двигаться в том же направ-
) К Ф лении, то получающиеся
траектории (последователь-
ности параллельных отрез-
Afft PiP Р^
при наложении g помощью
симметрии всех составляю-
Рис. 22.7 щих шестиугольник Q тре-
треугольников на треугольник
Q—Qe (рис. 22.7) в треугольнике Q дают траектории
бильярда. С другой стороны, «закон перескакивания»
дает правило попарной склейки сторон шестиугольника
Q; произведя эти склейки — см. рис. 22.8 — получим
тор (что не было очевидно с самого начала!). Для
Рис. 22.8
удобства на склеиваемом шестиугольнике нанесены гори-
горизонтальные линии, а склеиваемые друг с другом вер-
вершины помечены одинаковыми буквами А и В. При склей-
склейке получаемый «по дороге» цилиндр (рис. 22.8,в) прихо-
приходится «подкручивать», чтобы произвести склейку сто-
сторон Ъ и с. Горизонтальные линии в конце концов дадут на
торе не параллели, а линии обмотки типа B,1), т. е. замк-
замкнутые кривые, делающие два оборота вдоль параллелей и
один вдоль меридианов. Пучок параллельных траекторий
дает на торе семейство кривых, но получится ли обмотки
тора — еще вопрос!
Здесь помогает другой способ склейки тора из шести-
шестиугольника Q. Именно, склеим пары сторон а, Ь, с еще на
плоскости, отрезав от Q треугольники Af и А2 по отрезкам
212
л и tit, и, перенося их надлежащим образом, подклеим к
остатку Q и друг к другу (рис. 22.9, а, б). Получим ромб
/?=CiC2C3C4 с углом зт/3. В этом ромбе следует склеить
соответствующие точки противоположных сторон т и т.
a
Рис. 22.9
Рис. 22.10
пил, ибо мы разрезали по линиям тип. Но это почти стан-
стандартная «модель тора»,— продеформировав ромб в квадрат
(рис. 22.9, в, г), мы можем склеить из него тор обычным об-
образом. Траектории рассматриваемого пучка в ромбе уст-
устроены так же, как траектории бильярдного пучка в тре-
треугольнике, только перескакивание происходит парал-
параллельно сторонам ромба.
После деформации ром-
ромба в квадрат и после-
последующей склейки на торе
получится обмотка. Най-
Найдем ее периоды.
Период Ti вдоль па-
параллелей равен времени,
которое требуется биль-
бильярдному шару, чтобы пройти один раз вдоль меридиана
п, т. е. от одной стороны ромба т до другой стороны т.
Если модуль скорости шара равен v, а ее направление
образует угол а со стороной АВ исходного треугольника
Q=ABC (рис. 22.10), т. е. с диагональю ромба СгС9, то
проекция скорости на направление, перпендикулярное сто-
сторонам т — CiC2 и CsCt, равна v cos (я/3—а). Если расстоя-
расстояние между сторонами ромба равно а, то Ti=a/[v cos (л/3—
—а)]. Аналогично находим T3=a/[v cos(n/3+«)I.
Итак,
Tt _cos (я/З+с)
Т2 ~~cos (л/3—а)'
и мы видим, что опять траектории бильярда периодичны или
всюду плотны в зависимости только от направления тра-
213
ектории. Поскольку cos (-g- ± ом — у cos a -l g~ si" a,
1\ _ cos a— ^3" sin a _ 1 — V
cosa-f V'Tsina l-f/Ttga
tga
а это число рационально или иррационально в зависимости
от того, рационально или иррационально число k --= V3 tg a.
Подведем итоги. Если описанными выше построениями
бильярд в многоугольнике Q можно свести к обмоткам тора,
то многоугольник Q будем называть торическим. Для биль-
бильярда в торическом многоугольнике Q1 выполнена следую-
следующая альтернатива:
либо траектория периодична;
либо траектория всюду плотно заполняет весь много-
многоугольник Q.
В рассмотренных примерах тот факт, какая часть аль-
альтернативы имеет место, зависит лишь от направления движе-
движения бильярдного шара, но не от его начального положе-
положения.
Для любого торического многоугольника проблема
бильярда может быть разрешена (т. е. все траектории мо-
могут быть классифицированы в указанном смысле).
Какие еще многоугольники, кроме рассмотренных трех
типов, являются торическими? Оказывается, торическим
является лишь еще прямоугольный треугольник с остры-
острыми углами л/6 и зт/3 (половина равностороннего треуголь-
треугольника). Справедлива
Теорема 1. Бильярды в многоугольниках, отличных
от указанных четырех типов (прямоугольник и треугольни-
треугольники с углами л/2, л/4, л/4; л/3, л/3, л/3; л/2, л/6, л/3) нельзя
свести к обмоткам торов.
Мы приведем доказательство этой теоремы в конце сле-
следующего параграфа.
Задача 22.2. Свести бильярд в прямоугольном треуголь-
треугольнике с углами л/6 и л/3 к обмоткам торов (осуществив построения,
аналогичные проводившимся выше).
Задача 22.3 (см. § 24). Провести построения, аналогичные
проводившимся выше, для случая прямоугольного треугольника
с углами я/8 и Зя/8: свести бильярд к пучкам параллельных тра-
траекторий с перескакиваниями. Затем осуществить склейку сторон,
соответствующую получающимся перескакиваниям и убедиться,
что полученная поверхность не является тором, т. е. тре-
треугольник с углами л/2, л/8, Зл/8 — не торический.
214
В заключение рассмотрим еще одну занимательную
картинку, относящуюся к бильярду в равностороннем тре-
треугольнике Q=ABC. Именно рассмотрим в Q пучок траекто-
траекторий, параллельных стороне АВ. Чтобы нарисовать продол-
продолжение этих траекторий, не нужно производить отражения
относительно стороны АВ (ибо траектории ее не пересекают),
а достаточно продолжить траектории в два треугольника
Qi и Q2, образующих вместе с Q трапецию Q=ACA'C
(рис. 22.11). Траекторию МР,
выходящую из трапеции в точ-
точке Р, следовало бы продолжить
в треугольник Q*, но после пос-
последовательных отражений отре-
отрезок РМ' дает в исходном тре-
угольнике уже нарисованный там
отрезок P'N; согласно нашим
правилам мы будем считать, что
движущаяся по МР точка, дойдя до Р, перескакивает в точку
Р' и продолжает двигаться по трапеции в том же направле-
направлении. Иначе говоря, параллельный пучок на трапеции следует
интерпретировать как пучок с перескакиванием со стрелки а
в соответствующую точку стрелки а' (рис. 22.12). Чтобы
траектории стали непрерывными, стрелки нужно склеить
Рис. 22.11
Рис. 22.12
(в указанном направлении!). После склейки мы получим
лист Мёбиуса (!), а на нем — пучок траекторий, параллель-
параллельных средней линии листа Мёбиуса. На исходном треуголь-
треугольнике Q—ABC этот пучок дает траекторию KLM, составлен-
составленную из средних линий треугольника ABC (она соответствует
средней линии листа Мёбиуса), и семейство «двойных» тра-
траекторий, окружающих KLM. Оказывается, при анализе
задач механики могут появляться даже такие «странные»
поверхности, как лист Мёбиуса. Главные же «странности»
нас ждут в § 24.
Для понимания § 24 опишем предварительно (в § 23)
построение двумерных поверхностей с помощью склейки
многоугольников и докажем теорему классификации дву-
двумерных поверхностей.
215
§ 23. Склейка поверхностей
из многоугольников
Замкнутая многогранная поверхность опре-
определяется в школьном учебнике геометрии как множество
точек в пространстве, составленное из многоугольников и
удовлетворяющее некоторым условиям.
Основное свойство такой поверхности за-
заключается в том, что каждая ее точка М обладает окрест-
окрестностью, которая может быть непрерывно преобразована е
обычный круг с центром в точке М (рис. 23.1). Окрест-
Окрестностью точки М будем называть множество точек по-
поверхности, удаленных от М не более чем на некоторое рас-
расстояние е>0. При наших непрерывных преобразованиях
м
Окрестность точки М
Рис. 23.1
окрестность можно изгибать, местами сжимать или рас-
растягивать, но запрещается «склеивать» между собой ее точки
и «разрывать» окрестность. Если представить себе окрест-
окрестность точки М сделанной из резины, то нужное преобразо-
преобразование можно получить, если положить окрестность под
пресс и, медленно растягивая (так, чтобы не получилось
складок и разрывов), расплющить ее. Указанным основ-
основным свойством обладают не только замкнутые многогран-
многогранные, но и искривленные поверхности, например сфера или
тор. Если в сфере вырезать две дырки и заклеить их под-
подходящим образом изогнутой «ручкой» — боковой поверх-
поверхностью цилиндра, то получится сфера с ручкой (поверх-
(поверхность гири), которая может быть преобразована в тор сжа-
сжатиями и растяжениями (рис. 23.2, а). Приклеив к сфере
аналогичным образом две ручки, мы получим так назы-
называемый крендель, или сферу с двумя ручками; на рис 23.2, б
эта поверхность представлена в пяти видах. Можно тем
же способом построить сферу S(p) с любым числом прикле-
приклеенных ручек р^?0; число р называется родом поверхности
216
S{p), а саму поверхность называют иногда кренделем с р
дырками. Легко видеть, что все сферы с ручками обладают
основным свойством.
Сфера
t дырками ,
еры ' ' Л
С ВВиМЯ :¦¦ .
ручками -.¦;¦ :¦.•:..;¦?
Крендель
Полная поверхность цилиндра также обладает этим
свойством, а вот уже его боковая поверхность им не облада-
обладает: точки М на окружностях оснований имеют окрестности
в виде искривленного полукруга — их нельзя без разры-
разрывов и склеек деформировать в круг с центром в точке М
(рис. 23.3). Далее, поверхность двойного конуса и объеди-
объединение двух пересекающихся сфер
не обладают основным свой-
ством, а объединение двух непе-
ресекающихся сфер обладает
(рис. 23.4).
М
Рис. 23.4
Мы хотим исключить из рассмотрения также поверх-
поверхности, состоящие из нескольких отдельных кусков. По-
217
требуем поэтому, чтобы любые две точки поверхности можц ,
было соединить проходящей по поверхности непрерывной
линией. Это свойство называется связностью поверхности.
Итак, рассматриваемые в дальнейшем поверхности —.
связные.
Не будем мы рассматривать и бесконечно протяженные
поверхности — такие, как плоскость или бесконечная ци-
цилиндрическая поверхность, а также поверхности типа кру-
круга без границы (открытого круга). Поэтому наложим еще
условие конечности. Потребуем, чтобы поверхность мож-
можно было разбить (разрезать) на конечное число «кри-
«криволинейных многоугольников», каждый из которых без
разрывов и склеек можно преобразовать в плоский выпук-
выпуклый многоугольник (с границами). Например, сфера по
экватору и четырем меридианам разрезается на 8 криволи-
криволинейных треугольников, а плоскость на конечное число мно-
многоугольников разбить нельзя. Если поверхность разбита
на треугольники, любые два из которых либо имеют общую
сторону, либо общую вершину, либо вообще не пересе-
пересекаются, то это разбиение называется триангуляцией по-
поверхности.
Итак, далее мы рассматриваем только такие поверх-
поверхности (множества точек пространства), которые обладают
тремя перечисленными свойствами: основным свойством,
свойством конечности и связностью. Эти поверхности бу-
будем коротко называть двумерными компактными поверх-
поверхностями без края (иногда слова «без края» будем опускать).
Заметим, что любая рассматриваемая поверхность делит
пространство на две части — внешнюю (неограниченную)
и внутреннюю (ограниченную) и поэтому является двусто-
двусторонней, а также является ориентируемой: любую малень-
маленькую окружность с нанесенной на ней ориентацией (стрелкой)
нельзя так подвинуть по поверхности, чтобы она вер-
вернулась на старое место, но ориентация на ней изменилась.
Следует отметить, что имеются также неориентируемые.
поверхности, например лист Мёбиуса (см. рис. 22.12),
имеющий одну сторону (на нем ориентацию окружности
можно изменить специальным ее движением по листу -^
вдоль средней линии), но такие поверхности имеют к р а й
и здесь не рассматриваются.
Две компактные поверхности считаются эквивалентны-
эквивалентными (математики говорят — топологически эквивалентными).
если существует обратимое отображение одной из
них на другую, при котором нет ни разрывов, ни склеек,
но допускаются растяжения и сжатия, изгибания и разги-
218
бания (для таких отображений в математике также есть
специальное слово — гомеоморфизм). Например, поверх-
поверхность тетраэдра эквивалентна (гомеоморфна) сфере, две
последние поверхности на рис. 23.2, а эквивалентны тору,
а все пять поверхностей на рис. 23.2, б эквивалентны друг
ДРУГУ.
Задача 23.1. Покажите, что сфера, тор, крендель и вообще
сфера с любым числом ручек S (р) обладают свойством конечности,
т. е. укажите их разбиения на ко-
конечное число криволинейных много-
многоугольников.
Задача 23.2. Укажите, сфере
с каким числом ручек эквивалентна:
а) поверхность чашки (рис. 23.5, с);
б) поверхность стула (рис. 23.5, б);
в) поверхность оконного переплета
(рис. 23.5, е); г) поверхность «плас-
«пластилинового человечка», у которого
пальцы рук образуют два сцеплен-
сцепленных кольца (рис. 23.5, г).
Задача 23.3*. Покажите, что
тор и сфера ие эквивалентны.
Указание. Придумайте та-
такое свойство, которое сохраняется
при рассматриваемых преобразовани-
преобразованиях (гомеоморфизмах) и которым одна
из этих поверхностей обладает, а
другая — нет.
Пластилинобыи
человечек.
Рис. 23.5
Поверхность, обладающая свойством конечности, раз-
разрезается на многоугольники и поэтому может быть склеена
из многоугольников. Каким наименьшим числом много-
многоугольников можно при этом обойтись? Мы уже видели, что
тор может быть получен склейкой противоположных сто-
сторон квадрата (или прямоугольника), т. е. для тора доста-
достаточно иметь один многоугольник. Для кренделя SB)
(т. е. для сферы с двумя ручками) достаточно также о д-
н о г о многоугольника — 8-угольника (рис. 23.6). Ока-
Оказывается, любая компактная поверхность S может быть
склеена из одного многоугольника W, который называется
разверткой поверхности S. Собственно говоря, это почти
очевидно, и вот почему.
Триангулируем поверхность S и каждую сторону каж-
каждого треугольника отметим какой-либо буквой, причем раз-
разные отрезки отметим разными буквами. Кроме того, каж-
каждую сторону треугольника ориентируем, т. е. по-
поставим на ней произвольным образом стрелку. Разрежем
поверхность S вдоль всех полученных отрезков (сторон
•реугольников) — S рассыпется на конечное число «кри-
219
вых» треугольников. Мы считаем, что разрезая поверхность
вдоль какого-то отрезка, мы ставим на обоих «берегах» раз-
разреза ту букву, которая стояла на отрезке (рис. 23.7). В ре-
зультате на каждой стороне треугольника будет отмечена
ориентация: сторона снабжена стрелкой.
Наша цель: склеить обратно все это множество тре-
треугольников, но таким образом, чтобы получился один
плоский многоугольник. Начнем построение с того, что
выберем какой-то треу-
треугольник Дх; рассмотрим
его сторону — она снаб-
снабжена какой-то буквой а
и стрелкой. Так как каж-
каждая буква входит в об-
общий набор сторон в точ-
точности два раза (посколь-
ку поверхность S не имеет края, а каждый разрез
имеет два берега), то найдется еще один треугольник
Д2, на стороне которого стоит та же буква а. Склеим
эти треугольники по общей стороне а, совмещая направле-
направления стрелок — получится плоская фигура, разделенная на
два треугольника, на границе которой стоят новые буквы и
стрелки. Берем какую-то букву ft на этой границе и ищем
свободный треугольник Д3, на стороне которого имеется та
же буква ft — такой треугольник обязательно найдется,
причем ровно один; приклеиваем Д3 к этой фигуре по общей
стороне ft, совмещая стрелки, и т. д. Процесс закончится в
тот момент, когда все треугольники будут исчерпаны. Дей-
Действительно, мы приклеим в точности все тре-
треугольники — в противном случае (если никакая буква на
границе получающейся области не встречается среди букв
220
ца оставшихся еще неприсоединенных треугольниках),
склеив все попарные буквы, вернемся к исходной поверх-
поверхности S, и она окажется несвязной (состоящей больше чем из
одного куска) — противоречие со свойством связности.
Итак, при указанном склеивании мы исчерпаем все
треугольники и получим плоский многоугольник W с
буквами и стрелками на сторонах его границы, причем
каждая буква будет встречаться ровно два раза, так что
число сторон у W будет четным. Зафиксируем на много-
многоугольнике W ориентацию, а затем, начав с произвольной
вершины и совершая обход границы, последовательно вы-
выпишем все буквы на сторонах W, причем, если направление
обхода совпадает со стрелкой на стороне, будем пи-
писать букву в степени (+1); если же не совпадает —
пишем в показателе (—1). В результате получится слово W
вида W=--a%xaf*. . .af^ (рис. 23.8), однозначно задающее
многоугольник W (мы специально многоугольник и слово
обозначаем одной буквой W).
Мы сопоставили каждой поверхности S многоугольник
и слово W, правда, неоднозначно (слово зависит от триан-
триангуляции поверхности). Слово W
можно рассматривать как код
поверхности S, и это кодирова-
кодирование неоднозначно: одной и той
же поверхности отвечает беско-
бесконечное число кодов — по числу
триангуляции на S. Если про-
произвести требуемые склейки на
границе многоугольника W _7 _7 _г
(склеивая стороны с одинаковы- w-aiazaz a4a4 aiaz аз
ми буквами по стрелке), то по- Код многоугольника
лучим исходную поверхность. рис 23 8
Оказывается, однако, что
поверхность S может быть
склеена из такого многоугольника W, для которого совер-
совершенно ясно, что после склейки поверхность S будет пред-
представлять собой S (р) — сферу с р ручками. Этим многоуголь-
многоугольником является 4р-угольник с кодом W=a1b1a^1bi1a2b!l
ЩхЬгх. . .Opb-pup^bp1: слово а^а^Ьг1 отвечает тору — сфере
с одной ручкой S(l), слово аАаг^Г^Ьгаа^; дает склей-
склейку двух ручек, т. е. крендель SB); . . .; вообще, каждая
новая четверка букв а^ьа^Ь^отвечает приклейке одной
новой ручки к уже имеющейся сфере с ручками (геомет-
(геометрически это несложно представить, производя указанные
221-
вслове последовательные склейки). Слово Ш^
. . МрЬрп^Ьр1 называется каноническим, а отвечающий
ему многоугольник W — канонической разверткой поверх-
поверхности S. Сформулируем точную теорему.
Теорема I (теорема классификации двумерных ком-
компактных поверхностей без края). Любая компактная ориен-
ориентируемая поверхность S в трехмерном пространстве эк-
эквивалентна (гомеоморфна) сфере с ручками S(p).
Доказательство. Достаточно доказать, что у
поверхности S имеется канонический код &^Ь1
b'b1
. . .upbpdp'-bp1.
Мы уже знаем, что поверхность S имеет какой-то код
W, отвечающий некоторой триангуляции. Многоугольник
W представляет собой плоский четноугольник с числом сто-
сторон 2п (п не обязательно четно), все сторо-
ры которого разбиты на пары с одинаковыми
буквами, и каждая пара затем склеиваемся
так, чтобы стрелки на них совпали. При этом
склеиваются и вершины, которые разбива-
разбиваются на группы, внутри каждой из которых
они склеиваются в одну точку (например,
/Ifie группы на рис. 23.9 все вершины шестиугольника
вершин разбиваются на две группы — черные и
Рис. 23.9 белые).
Доказательство теоремы будет про о-
диться следующим образом: будем перестраивать много-
многоугольник W с помощью операций (разрезаний и приклеива-
приклеиваний), выполнение которых приводит к другому коду той ж"
поверхности S или эквивалентной (гомеоморфной) ей; про-
проделав все эти операции, придем в конце концов к иско-
искомому коду aiMf^r1. . .Opbpdp'-bp1, отвечающему сфере
с р ручками, откуда и сделаем вывод, что S гомеоморфна
S(p). Нужные нам перестройки таковы.
1 . Слово W можно перестроить так, чтобы все верши-
вершины многоугольника W склеились в одну точку.
Предположим, что количество групп склеивающихся
точек больше одной. Обозначим одну из этих групп {Р)<
другую группу — {Q}. Тогда имеется такое ребро а, что его
начало принадлежит группе {Р}, а конец — группе {<?}•
Выполним разрезание и последующую склейку многоуголь-
многоугольника W, указанные на рис. 23.10. Напомним, что каждая
буква на границе многоугольника встречается дважды;
нас сейчас интересуют две буквы с на рисунке, которые
склеим по стрелке. Результат перестройки (разрезания и
склейки) — многоугольник W, у которого вершин в мно-
222
жестве {Р} стало на одну меньше, а в множестве {Q} —
на одну больше. Взяв еще одну вершину из {Р}, мы тоже
южем уничтожить ее с помощью какой-нибудь группы (не
обязательно с помощью {Q}). Так будем уменьшать число
вершин в группе {Р}, пока
в {Р} не останется ровно
одна вершина. Последний
шаг: так как в {Р} одна,
вершина, соседние ребра име-
имеют вид а и а'1. Тогда делаем
перестройку, указанную на
рис. 23.11 (склеиваем ребра а
и а'1) и уничтожаем послед-
последнюю вершину В группе {Р}. Рис. 23.10
Такими операциями уничто-
уничтожаем постепенно все группы вершин, кроме одной, вер-
вершины которой составляют полный набор вершин возник-
возникшего многоугольника и склеивают поэтому в одну точку.
2°. Если W—Aaa'1!}, где А и В — слова, а — буква, то
W можно перестроить в слово W'=AB. Эта операция,
называемая свертыванием, показана на рис. 23.11.
«=>
Рис. 23.11
В дальнейшем считаем, что в слове W нет сочетаний ви-
вида аа'1. Заметим также, что в слове W нет и двух одинако-
одинаковых букв в одинаковых степенях, т. е. W=?. . . а. . .
¦ . .а . . . и №ф. . .а'1. . .а'1..., поскольку при склейке
таких двух противоположно ориентированных сторон по-
поверхность S становится неориентируемой — существует
путь, вдоль которого у окружности меняется ориентация
(эта склейка эквивалентна добавлению листа Мебиуса, ко-
который мы исключили из рассмотрения). Таким образом,
~сли в слове W встретилась буква а, то буква а встретится в
№ вновь лишь в степени (—1).
3°. Если буквы аи а'1 не стоят рядом в слове W (что мы
предположили выше), то найдутся буквы Ь и Ь'1 такие,
то пары а, а и Ь, Ь'1 разделяют друг друга (рис. 23.12, я).
Тогда эту четверку можно заменить на сочетание вида
"\)х~гу~г, сохраняя условия шагов Г и 2° (рис. 23.12, б и в).
223
Если при этом случайно возникнут сочетания сс~г, то они
устраняются свертыванием.
В результате применений конструкций шагов Г—3° мы
преобразовали исходное слово W к слову W, состоящему
только из сочетаний вида хух~1у~1, что и требовалось до-
доказать. Число таких сочетаний равно числу ручек у по-
поверхности S — ее роду р.
tf ^
Задача 23.4. Пусть поверхность S имеет код W—aia2. ..
...fl^arW1. . .an1, т. е. у 2и-угольника W попарно склеиваются
противоположные стороны. Определите канонический код поверх-
поверхности S и ее род.
Ответ. S=S(p), где р=[л/2].
После того как мы с помощью теоремы классификации
поняли, что поверхность S эквивалентна какой-то сфере с
ручками, у нас может возникнуть вопрос, нельзя ли получить
для поверхности S два различных канонических кода
W - аЖ-%-1... агЬХ-%-\
отвечающих сфере S(p)c p ручками и сфере S(r)cr ручками,
причем рфг> Если бы два таких канонических кода име-
имелись, то поверхности S(p) и S(r) были бы эквивалентны
(гомеоморфны).
Для ответа на этот вопрос введем понятие эйлеровой ха-
характеристики поверхности. Если поверхность S разбита
на многоугольники, и в этом разбиении имеется В вершин,
224
Р ребер и Г граней (многоугольников), то число
называется эйлеровой характеристикой поверхности S-Если
W — произвольная развертка поверхности S, то с помо-
помощью элементарных операций Г—3е она преобразуется в
каноническую развертку. Легко заметить, что эти элемен-
элементарные операции не меняют числа %(S). В самом деле, когда
мы в многоугольнике проводим диагональ, числа Р и Г
увеличиваются на 1, а В не меняется;
когда производим разрезание вдоль проведенной диагона-
диагонали с последующим склеиванием, числа РиГ уменьша-
уменьшаются на 1 при неизменном В; при свёртывании
(отбрасывании сочетания аа~1) числа ВиРуменьша-
ю т с я на 1, а Г не меняется. Поэтому величина В—Р+Г
во всех случаях не меняется.
Пусть теперь W — каноническая развертка
aibia^bi1. . Mpbpa^bp1. Для нее В=1 (все вершины склее-
склеены в одну; см. п. Г доказательства теоремы 1), Р=2р (та-
(таково число сторон у канонической развертки) и Г=1 (мно-
(многоугольник W — один). Получаем
)=1—2/7+1=2—2р.
Поэтому, если бы существовали два различных
канонических кода W и W, указанных выше, то мы полу-
получили бы
откуда р=г и, следовательно, слова W и W совпадают.
Следовательно, справедлива
Теорема 2. Никакие две сферы с разным числом ру-
ручек не эквивалентны (не гомеоморфны).
3 а д а ч а 23.5. а) Докажите, что у всякого выпуклого много-
многогранника сумма числа вершии н граней больше числа ребер на 2.
б) Вычислите эйлерову характеристику тора и кренделя SB).
в) Докажите, что для любой триангуляции любой поверхности
B-J-P-f-Г — четное число.
Другое доказательство теорем 1 и 2 приведено в книге:
Болтянский В. Г., Ефремович В. А. Нагляд-
Наглядная топология.— М.: Наука, 1982 («Библиотечка «Квант»,
вып. 21).
Теперь, зная, как двумерные поверхности склеиваются
Из многоугольника, вновь вернемся к бильярдам в много-
многоугольниках.
" Г. А. Гальперин, А. Н. Земляков 225
§ 24. Бильярды в «рациональных»
многоугольниках и поверхности
Рассмотрим бильярд в прямоугольном тре-
треугольнике Q с острыми углами п/8 и Зя/8. Пучок параллель-
параллельных траекторий в этом треугольнике продолжим до пучка
в правильном восьмиугольнике Q, составленном из 16
треугольников, равных Q и получающихся из Q последова-
последовательными отражениями относительно катета и гипотенузы,
угол межл] которыми равен я/8 (рис. 24.1, а). Как и в § 22^
'и 'ю
Рис. 24.1
нетрудно проверить, что траектории бильярда в исходном
треугольнике Q получаются при наложении всех упомяну-
упомянутых треугольников на треугольник Q из траекторий точки,
движущейся по нарисованным отрезкам и перескакивающей
с одной стороны восьмиугольника Q на соответствующую
точку противоположной (параллельной) стороны. Таким
образом, бильярд задает склейку сторон восьмиугольника
¦Q, указанную на рис. 24.1, б).
Осуществим эту склейку. Внимательно проследите за
ее этапами (рис. 23.6). В результате мы получим крендель —
описанную в § 23 поверхность, как бы склеенную из двух
торов. При склейке отрезки траектории указанного выше
пучка с перескакиванием подклеятся друг к другу и обра-
образуют непрерывную траекторию на кренделе. Все траекто-
траектории данного пучка параллельных траекторий после склей-
склейки дадут пучок траекторий на кренделе, который мы будем
называть обмоткой кренделя.
В отличие от обмоток тора, обмотки кренделя имеют
особые точки; в данном случае на кренделе будет ровно одна
особая точка А, к описанию которой мы и переходим. Гру-
Грубо говоря, если в окрестности точки М траектории ведут
себя «примерно параллельно», то такая точка М называется
226
цеособой (рис. 24.2, а). Поведение траекторий в окрестно-
окрестности особых точек не такое, как на рис. 24.2, а, а «особое».
Нетрудно понять, что при склейке из восьмиугольника Q
точки внутри Q будут неособыми. Если точка М на
кренделе получается склейкой двух соответственных точек,
Mi и М2, лежащих на параллельных сторонах Q, то онл
сакже не будет особой — при подклеивании окрестностей
точек Мх и М2 друг к другу мы получаем окрестность точки
М на кренделе, траектории в которой ведут себя как на
рис. 24.2, б. Таким образом, особая точка на кренделе
доожет получиться лишь при склейке вершин восьми-
восьмиугольника Q. Нетрудно проверить, что все восемь вершин Q
дают при склейке ровно одну точку А на кренделе (это
следует из п. 1° доказательства теоремы 1 § 23). Окрестность
этой точки склеивается из восьми секторов Ri—Re — ок-
окрестностей вершин восьмиугольника Q. Подклеим эти сек-
секторы величиной Зя/4 каждый друг к другу в соответствии с
законом склейки (рис. 24.3). Мы видим, что при такой под-
подклейке получатся три слоя (так как 8-Зя/4=3-2я), по-
поэтому все секторы величиной Зя/4 каждый придется сжать
в три раза, чтобы можно было осуществить склейку в о д и н
слой. При этом сжатии следует считать траектории потока
нарисованными на секторах — и после их склейки получит-
получится картина траекторий в окрестности точки А.
8* 227
Мы увидим после осуществления подклейки (соответст-
(соответствующие рассуждения приведены ниже), что в точку д
входят ровно три траектории, и выходят
ровно три траектории. Эти траектории соответствуют
особым траекториям бильярда в треугольнике Q, заканчива-
Зл
ющимся или выходящим из вершин углов величины — __
именно из э т и х вершин получаются восемь вершин вось-
восьмиугольника Q. В три вершины — Л3, Л4, Аъ — траектории
пучка параллельных линий входят, а из трех — Аи Лт,
Л „ — выходят. После склейки входящие и выходящие
траектории дают входящие в особую точку А и выходя-
выходящие из нее траектории; эти особые траектории, кончающие-
кончающиеся и начинающиеся в Л, называют сепаратрисами, т.е.
fit
«Обезьянье»
седло
с$ Мулыписед/
Рис. 24.4
«разделяющими». Сепаратрисы действительно как бы раз-
разделяют остальные траектории — две близкие к сепаратри-
сепаратрисе МА траектории Mj.Ni и M2N2, лежащие по разные сто-
стороны от МА после того, как сепаратриса заканчивается i
точке Л, уходят друг от друга.
Итак, бильярд в треугольнике Q с углами „
-§- сводится к обмоткам кренделя. Эти обмотки имеют
ровно одну особую точку А, поведение траекторий в окрест-
окрестности которой описано выше.
228
2L 2- и
В общем случае особые точки с таким поведением траек-
траекторий называются мультиседлами. Мультиседла могут
иметь любое четное число 2п сепаратрис — п входящих и
п выходящих; единственное ограничение состоит в том, что
я>2. Такое мультиседло будет называться мультиседлом
типа п. Мультиседло типа п=2 принято называть просто
седлом (рис. 24.4).
Оказывается, мультиседла появляются всякий раз при
исследовании поведения пучка параллельных траекторий
бильярда в многоугольнике Q, близких к особым траекто-
траекториям бильярда, заходящим в вершины углов многоуголь-
многоугольника Q. Прежде чем дать некоторую общую конструкцию,
приведем еще один способ построения мультиседла типа 3,
появляющегося на кренделе, склеенном из правильного
восьмиугольника.
Будем приклеивать друг к другу введенные выше секто-
„ Зп .
ры величиной -т-, не деформируя их при этом,
.. Зя
как делалось ранее. Углы секторов равны -^, и уже после
приклеивания сектора R2 к сектору Ri следующий подклеи-
подклеиваемый к R2 сектор R3 перекроется с Ri (рис. 24.5, а).
Мы будем считать, что перекрывающаяся с Ri часть сек-
сектора $з образует новый слой, или лист, идущий сверху
над Ri (рис. 24.5, б); секторы Rt и R6, приклеиваемые далее,
тоже лежат на втором листе — над первым листом
(рис. 24.5, в). Сектор /?„ дает уже тройное наложение (вмес-
(вместе с Ri и Rs), и мы будем считать, что секторы RR, R7, Rg
идут уже по третьему листу. Сделав полный (тройной)
оборот вокруг особой точки, мы вновь попадаем в сектор Ru
поэтому свободный край fts следовало бы приклеить к сво-
свободному краю Ru но для этого его нужно «продеть» через
два нижних листа (рис. 26.6, г); если сделать так, то полу-
получится поверхность с самопересечением, как на рис. 24.5, д.
Состоящую из трех листов окрестность точки А называют
трехлистной ветвящейся окрестностью А, а саму точку А —
точкой ветвления порядка 3. Чтобы получить из ветвящей-
ветвящейся окрестности точки А обычную окрестность точки А
на кренделе, нужно сжать ветвящуюся окрестность в три
раза так, чтобы каждый из трех листов превратился в кру-
круговой сектор с углом у, а после этого подклеить друг к
другу свободные края первого и последнего листов, прев-
превратившихся в секторы. Эта процедура была выполнена
выше.
229
Поскольку при склейке секторов Ri—Rt в ветвящуюся
поверхность бильярдные траектории подклеивались "друг
к другу м образовывали на каждом листе семейство парал-
параллельных линий одного и того же направления, то на каж-
каждом листе ровно одна траектория входит в точку ветв-
ветвления Ли ровно одна траектория выходит из А
причем траектории, лежащие по одну сторону от входящей
в Л сепаратрисы остаются на том же листе, а лежащие по
другую сторону — переходят на другой лист. При указан-
указанном трехкратном сжатии ветвящейся окрестности сепарат-
сепаратрисы останутся входящими в Л и выходящими из Л луча-
лучами, а остальные траектории превратятся в идущие вдоль
соответствующих сепаратрис кривые. Таким образом, пос-
после сжатия пучка параллельных траекторий на 3-листной
ветвящейся окрестности точки ветвления Л получится муль-
тиседло типа 3.
Сепаратрисы, входящие в особую точку Л, следует счи-
считать заканчивающимся в этой точке, ибо при выборе пути
выхода бильярдного шара, движущегося по сепаратрисе,
возникает несколько возможностей — каждая из выходя-
выходящих из Л сепаратрис ничем не хуже других. (Эту неодно-
неоднозначность мы и обходим, считая, что сепаратрисы закан-
заканчиваются в Л; образно говоря, бильярдный шар, попав в Л,
сидит там и думает, по какому же пути ему пойти, и ни-
никак не может найти ответа. Мы бессильны помочь «думаю-
«думающему» шару, ибо ни из каких разумных соображений вы-
выбрать один путь из трех нельзя, и поэтому мы считаем, что
шар останется в Л. Обдумайте и вы эту ситуацию.)
Рассмотрим теперь общую задачу о поведении пучка
параллельных траекторий бильярда в каком-то многоуголь-
многоугольнике Q, близких к траектории МА, заходящей в вершину
Л многоугольника Q. Пусть U=/_BAC — угол много-
многоугольника Q при вершине Л, а — величина этого угла.
Попробуем, как раньше, продолжить пучок параллельных
траекторий в угле U=Ui на углы U2, U3, Uit . . ., полу-
получающиеся из U последовательными отражениями (эти от-
отражения нужны для выпрямления бильярдной траектории
(рис. 24.6)). Строя углы] {Uk}, на каждом из них нарисуем
пучок параллельных траекторий в том же направлении, что
и в угле U. Последовательно «обкладывая» вершину Л уг-
углами Uk, мы видим, что, вообще говоря, после одного «обо-
«оборота» вокруг Л свободная сторона АС исходного угла Ц
вовсе не обязана совместиться с соответствующей стороной
АСг какого-то из углов Uh — возможно, поверх Ut, U2, ¦ ¦ ¦
придется наложить второй слой углов Uk; поверх второ-
230
го слоя может лечь третий и т. д. Рассмотрим тот случай,
когда после m-кратного обкладывания около вершины А
некоторая сторона АСп все-таки совместится с АС. Тогда
наша процедура обрывается, и мы получаем m-листную вет-
ветвящуюся окрестность точки А, а также пучок параллельных
Рис. 24.6
траекторий одного и того же направления на каждом из т
листов. При этом следует считать, что траектория со сто-
стороны АС исходного угла U переходит на сторону АСп пос-
последнего из углов Uh. После m-кратного сжатия ветвящейся
окрестности все т листов превратятся в т секторов вели-
величины 2п/т каждый; подклеив после сжатия АСп к АС, мы
получим обычную окрестность точки А. Пучок параллель-
параллельных траекторий на m-листной окрестности дает мультисед-
ло типа т на обычной окрестности. •
Заметим, что если АСп действительно совпадет с АС
и мы получим m-листную окрестность точки А, то последний
из углов Uk имеет четный номер, ибо при последова-
последовательных отражениях стороны ACh и ABt чередуются
(рис. 24.6). Следовательно, на т листах, составляющих
вместе угол величины 2лт, укладывается четное число 2я
углов {Uk} величины а. Отсюда 2па=2лт и а=( — т.
Обратно, если величина а исходного угла U представляет-
представляется в виде а= (— )я, где тип взаимно просты, то легко про-
проверить, что после 2/г последовательных отражений сторона
АСп впервые совпадет с AC, a углы Ult U2, . . ., Uin да-
дут m-листную ветвящуюся окрестность точки А. Таким
образом, конечнолистная ветвящаяся окрестность верши-
вершины А угла величины а может быть построена в том и толь-
только в том случае, когда а имеет вид (-^ ]я, т. е. а соизмери-
231
мо с п. В противном случае (когда отношение а/л иррацио-
иррационально) окрестность описанного выше типа построить не
¦удается, и случай несоизмеримых с п углов не дает таких
«простых» особых точек, как точки ветвления конечного
порядка.
Заметим, что если а имеет вид а= —, т. е. /и=1, опи-
описанное построение сразу дает однолистную окрестность, и
особая траектория, попадающая в точку А, может быть
естественным (и однозначным) образом продолжена за точ-
точку А. В этом случае точку А не имеет смысла считать осо-
особой. Сказанное позволяет доказать теорему 1 из § 22.
Предварительно предлагаем читателям решить неслож-
несложную задачу.
Задача 24.1. Найти все многоугольники Q, все углы ко-
которых имеют вид п/п (бильярд в таких многоугольниках не будет
иметь особых точек и особых траекторий).
Решение задачи 24.1 показывает, что к указанному виду
«неособых» многоугольников относятся торическне много-
многоугольники — четырех указанных в теореме 1 § 22 видов —
и только они. Значит, во всех остальных многоуголь-
многоугольниках бильярдные пучки либо имеют особые точки типа муль-
тиседел (когда все углы многоугольника соизмеримы с
л), либо, если хотя бы один угол многоугольника несоизме-
несоизмерим с л, более сложные особенности. Это и доказывает тео-
теорему 1 из § 22.
Пример 1. Пусть U — угол величины а=2я/3. Тог-
Тогда его вершина А имеет 2-листную окрестность, что дает
особую точку типа седла (т~2). Такими являются все углы
• правильного шестиугольника. Отсюда вытекает, что даже
бильярд в правильном шестиугольнике имеет особенности
(см. ниже задачу 24.3).
Вернемся теперь к построению обмоток кренделей, от-
отвечающих бильярдам и разберем несколько примеров их
построения.
Пример 2. Пусть Q — прямоугольный треугольник
с острыми углами «1=л/10 и а2=2л/5. Рассмотрим пучок
параллельных траекторий в правильном 10-угольнике Q,
составленном из 20 треугольников, равных Q, «обложенных»
с помощью последовательных отражений вокруг вершин
угла «1. Нетрудно проверить, что бильярд задает склейку
пар противоположных сторон Q (траектории бильярда по-
получаются из траекторий параллельного пучка именно с та-
такими перескакиваниями).
232
Задача 24.2. Произвести указанную склейку и выяснить,
к обмотке какой поверхности сводится этот бильярд. Выяснить,
сколько и каких особых точек будет иметь получающаяся обмотка.
Решение. После склейки получится такой же, как и рань-
раньше, крендель с двумя дырками (нарисуйте картинки самостоятель-
самостоятельно; см. также теорему § 23). Особые точки будут получаться из
вершины углов «2=2л/5 — это будут седла (мультиседла типа 2).
Всего таких углов столько же, сколько треугольников в 10-уголь-
нике, т. е. 20; так как 2-2st=10-2st/5, одно мультиседло получа-
получается склейкой 10 экземпляров угла величины а2. Следовательно,
иа кренделе будет ровно 20/10=2 седла. (Другой способ это уви-
увидеть — показать, что вершины 10-угольника Q при склейке дают
иа кренделе две точки — А и В- каждая из них будет особой с
двумя входящими и двумя выходящими сепаратрисами.)
Итак, бильярд в треугольнике с углами я/2, я/10, 2я/5
сводится к обмотке кренделя, имеющей две особые точки
типа седла.
Во всех разобранных примерах торы и крендели полу-
получались склейкой сторон некоторого многоугольника Q, по-
получающегося из исходного многоугольника Q его уклады-
укладыванием на плоскость с помощью симметрии. В многоуголь-
многоугольнике Q, который мы будем теперь называть фундаменталь-
фундаментальным многоугольником, рассматривался пучок параллельных
траекторий с перескакиванием с одной стороны Q на дру-
другую. Перескакивание определялось так, чтобы траектории
«скачущего» пучка, представляющие собой последователь-
последовательности параллельных отрезков на Q, после обратного «скла-
«складывания» Q на исходный многоугольник Q давалн бы траек-
траектории бильярда в Q. С другой стороны, закон перескакива-
перескакивания определял склейку фундаментального многоугольника
Q, после которой из Q получалась некоторая поверхность
Sq (тор или крендель). Траектории пучка с перескакива-
перескакиванием после склейки давали уже непрерывные траектории на
SQ. Движение по этим траекториям называется обмоткой
поверхности SQ. Эта обмотка может иметь некоторое число
N=NQ особых точек, типы мультиседел которых рав-
равны rrii, mit .... mN.
Задача 24.3. Исследовать бильярды в перечисленных ниже
ногоугольииках Q (построить для них фундаментальные много-
многоугольники Q; указать закон склейки сторон Q; выяснить (проделав
склейку), какой вид имеет поверхность Sq; найти число особых
точек N=Nq и их типы щ, .... т^):
A) Q — треугольник с углами я/2, л/12, 5я/12;
Б) Q — треугольник с углами я/2, л/5, Зя/10;
B) Q — параллелограмм с углами я/3 и 2я/3;
Г) Q — параллелограмм с углами я/4 и Зя/4;
Д) Q — правильный шестиугольник,
233
(A)
(Б)
(В)
С4)
Фундаментальньщ
многоугольник Q
Подерхность (крен-
(крендель родор) SQ=S(p)
Q^ZOQ
Типы
acoGbix точен
m=5
,
2,2,2
G седел
Ответ к этой задаче дадим в виде таблицы.
Читатель может самостоятельно продолжить эту таб-
таблицу, рассмотрев другие многоугольники.
Глава 9
ПОВЕДЕНИЕ БИЛЬЯРДНЫХ ТРАЕКТОРИЙ
В МНОГОУГОЛЬНИКАХ
Здесь рассматриваются, в основном, бильярды
в многоугольниках с соизмеримыми с я углами — рацио-
рациональных многоугольниках.
Бильярд в любом рациональном многоугольнике, как и
бильярд в прямоугольнике, сводится к обмоткам, но уже
не тора, а кренделя — сферы с ручками,— который полу-
получается в результате склеек нескольких экземпляров мно-
многоугольника. Однако обмотки кренделя, в отличие от об-
обмоток тора, имеют особенности — так называемые точки
ветвления, отвечающие, грубо говоря, склеиваемым вер-
вершинам многоугольника; бильярдные же траектории, ис-
искривившись после склеек, имеют в окрестностях точек вет-
ветвления вид гипербол (см. § 24).
Оказывается, что для обмоток кренделей справедлива
почти та же теорема, что и для обмоток тора: «типичная» об-
обмотка кренделя заполняет его всюду плотно. Эта теорема
формулируется в§ 25. Результаты § 25 получены Н. Н. Зем-
ляковым и А. Б. Катком (см. [19] в списке литературы).
В отличие от обмоток тора, делящихся в точности на два
класса: периодические и всюду плотные на всем торе, на
кренделе бывают непериодические траектории, получаю-
получающиеся после склеек из бильярдных траекторий и заполня-
заполняющие всюду плотно лишь часть кренделя. Построение
такой траектории приведено в § 26, а доказательство того,
что она заполняет часть кренделя, основано на теореме
Якоби. (В механике появление кренделей возникает в тех
случаях, когда функции, выражающие законы сохранения,
«не перестановочны», или, как говорят, «не находятся в ин-
инволюции».) Наконец, в § 27 доказывается, что в любом
рациональном многоугольнике существует периодическая
траектория и исследуются периодические траектории в не-
некоторых тупоугольных треугольниках.
235
§ 25. Траектории
в рациональных многоугольниках
и обмотки кренделей
В этом параграфе мы ответим на два вопроса,
которые, возможно, уже возникли и у читателя.
В любом ли многоугольнике Q бильярд можно свести к
обмотке некоторой поверхности Sq?
Что дает сведение бильярдов к обмоткам кренделей Sq?
Прежде всего опишем еще один подход к бильярдам,
дающий возможность строить пучки с перескакиванием.
Пусть Q — фиксированный многоуголь-
многоугольник. Выберем на плоскости направле-
направление отсчета углов — скажем, будем за-
задавать направление v на Q углом ф,
отсчитываемым от направления сторо-
стороны А В многоугольника Q против
А в часовой стрелки до направления v. Угол
Рис. 25.1 ф будем измерять в радианах, причем
так, что 0<ф<2я (рис. 25.1). •
Для каждого числа ф между 0 и 2я заготовим свой эк-
экземпляр многоугольника Q, на котором нарисуем пучок
параллельных траекторий с направлением ф. Этот много-
многоугольник Q с нарисованными на нем траекториями обозна-
обозначим ф(ф). Таким образом, мы «запасли» бесконечный набор
экземпляров Q(q>) многоугольника Q. Наложив их друг на
друга в порядке возрастания ф, получим призму высоты
2я, в основании которой лежит многоугольник Q.
¦ Рассмотрим шар, «скачущий» с одного многоугольника
на другие многоугольники по следующему правилу. Если
в начальный момент времени шар находился на многоуголь-
многоугольнике СКфО, то он движется по своей траектории до тех пор,
пока не попадет на одну из сторон, скажем CD. Если бы
шар был бильярдный, то он отскочил бы от стороны CD
по закону упругого отражения и стал бы двигаться под
новым направлением ф2. Наш же скачущий шарик переска-
перескакивает со стороны CD многоугольника Ф(фО в ту же точку
той же стороны CD другого многоугольника СКфа).
где ф2 было определено выше (из закона упругого отраже-
отражения), и движется по нарисованной на ф(ф2) траектории.
Дойдя до стороны KL многоугольника ф(ф2), шарик пере-
перескакивает в ту же точку на той же стороне KL с л е Д У"
ю щ е г о многоугольника ф(ф3), где ф3 — направление,
под которым движется бильярдный шар после соударения
со стороной KL, налетев на нее под направлением ф2- На
236
С(ф3) скачущий шарик движется по нарисованной на Q(<p3)
траектории, и так далее (рис. 25.2). Таким образом, скачу-
скачущий шарик перескакивает с одного многоугольника на
другой, и-его траектория, которую мы назовем скачущей,
состоит из отрезков траекторий, нарисованных на мно-
многоугольниках <2(ф1), Q(q>2), Q(<p3), . . .
Заметим, что если наложить все эти многоуголь-
многоугольники друг на друга, то отрезки скачущей траектории дадут
траекторию бильярда в многоугольнике Q. С другой сторо-
стороны, если приложить ф(ф2) к Q(<pi) по стороне CD,
Рис. 25.2
затем приложить ф(ф3) к ф(ф2) по стороне KL и т. д., то
отрезки скачущей траектории будут продолжать друг друга,
образуя прямую линию. (Тем самым установлена связь меж-
между только что введенным скачущим движением и обсуж-
обсуждавшимися ранее пучками с перескакиваниями.)
Скачущие траектории, начинающиеся на одном и том же
многоугольнике Q(q)i), могут перескочить на разные эк-
экземпляры многоугольников {@(ф)}, если они приходят на
разные стороны многоугольника СКфО: скажем, приходя
на CD, траектория с Q(<pi) перескакивает на ф(ф2), а при-
приходя на ED — на ф(ф2). Если к Q(<pi) по сторонам CD и DE
приложить, соответственно, экземпляры ф(ф2) и ф(ф2),
то при попытке «выпрямить» одновременно обе
траектории может оказаться, что ф(ф2) и Q((f-z) бу-
будут иметь наложения (рис. 25.3). Однако наложившиеся
траектории физически различны (они соответствуют разным
направлениям движения в исходном многоугольнике Q),
и поэтому мы обязаны либо рассматривать двуслойную (дву-
237
25.3
листную) поверхность, наложенную на плоскость (это при-
водит к точкам ветвления из § 24), либо считать, что экзем-
экземпляры Q (ф2) и Q (фг) «изготовлены из эластичного материа-
материала», и деформировать их так, чтобы при приложении (т, е.
при подклейке) их к Q(<pi) они не перекрывались. Дефор-
Деформацию экземпляров {СКф)} следует
делать (и это очень существенно!)
вместе с нарисованными на них
траекториями; вторая из указанных
точек зрения приводит к склейкам
из многоугольников {<2(ф)} различ-
ного рода вспомогательных поверх-
ностей, что и делалось нами ранее.
Заметим, что если Q — невыпуклый
многоугольник, то даже прикладыва-
прикладывание к Q(<pt) одного экземпляра приводит к перекрытиям
(и к рассмотрению многолистных поверхностей).
Задача 25.1. Для каких многоугольников Q ска-
скачущие траектории, начинающиеся в каком-то из экземпля-
экземпляров ф(ф1), после всевозможных перескакиваний побывают
только в конечном наборе многоугольников Q(цц),
СКфг). • ¦ •> СКфлО и не попадут ни на один из других экзем-
экземпляров ф(ф)? (Такие многоугольники для краткости будем
называть имеющими конечный тип. В этом и только в этом
случае можно надеяться, что после указанных выше склеек
получится какая-нибудь «конечная» поверхность, а скачу-
скачущий поток приведет к обмотке этой
поверхности.)
Чтобы решить сформулированную
задачу, напишем формулу для закона
перескакивания (или закона склей-
склейки).
Задача 25.2. Пусть скачущая
траектория из экземпляра Q(q>) пере-
перескакивает в экземпляр ф(ф') через
сторону KL, образующую с выбран-
выбранным направлением АВ (от которого
отсчитываются углы ф) угол а. Выразить ф' через Ф и а.
Решение. Согласно определению скачущих траек-
траекторий, задачу можно сформулировать так: бильярдный шар,
двигаясь под углом ф к направлению А В, ударяется о сто-
сторону KL, образующую с А В угол а; найти угол ф' ^^
направлением движения шара после удара и стороной
Из рис. 25.4 ясно, что у'+у=а, ф=р+а. Из закона уп-
упругого отражения Р=у, поэтому ф'=а—у=а—Р=а
238
Рис.
— (ф—а)=2а—ф. Нужная формула полученаг
ф' = 2а—ф. A)
Задача 25.3. Обозначим стороны многоугольника Q
буквами сц=АВ, я2, а3, . . ., ап; пусть ah — угол между
стороной flh и направлением А В (в частности, «1=0). До-
Допустим, что все числа а1г. . .,ап соизмеримы с п, т. е. имеют
вид ah= (tnh/nh)n. Доказать, что в этом случае многоуголь-
многоугольник Q имеет конечный тип (см. задачу 25.1).
Решение. Приведем дроби mk/nk к наименьшему
общему знаменателю N — запишем ah в виде ah= (rhIN)n.
Докажем, что скачущие траектории, начинающиеся в мно-
многоугольнике СКфо), после любого числа перескакива-
перескакиваний оказываются в одном из многоугольников Q(q), где
Ф имеет вид
Ф = Ф„1 = ±Ф0+-|-2п, /п = 0, 1, 2, .... N-L B)
Очевидно, ф=ф0 имеет такой "вид. Поэтому достаточно дока-
доказать, что если ф имеет указанный вид и из многоугольника
Q((f) траектория перескакивает в Ф(ф'), то и ф' имеет такой
же вид. Допустим, что перескакивание происходит через
сторону ah. Согласно формуле A)
ЕСЛИ ф = фт = ±фо + ~2я, ТО
т. е. ф' имеет опять такой же вид. Утверждение доказано.
Задача 25.4. Доказать, что предположение задачи 25.3
(все .углы а/, соизмеримы с я) выполнено тогда и только тогда,
когда все углы многоугольника Q соизмеримы с п.
Многоугольники Q, все углы которых соизмеримы с л,
для краткости мы называем рациональными. Эти много-
многоугольники, как доказано, относятся к конечному типу, и
только для них бильярд может быть сведен к обмотке соот-
соответствующей поверхности. Построение этой поверхности мы
сейчас и опишем.
Приведем все числа ah из задачи 25.3 к наименьшему об-
общему знаменателю N, как в решении этой задачи, и рас-
рассмотрим 2N экземпляров л-угольникаф=СКфт), где ф* оп-
определены формулами B). Согласно задаче 25.3, многоуголь-
239
ники этого набора при определенной бильярдом в много-
многоугольнике Q склейке приклеиваются друг к другу: n-2N
сторон этих многоугольников разбиваются на пары в соот-
соответствии с законом склейки, и эти пары сторон подклеи-
подклеиваются друг к другу. Конечно, частично склейку можно
произвести, прикладывая (без перекрытий) многоуголь-
многоугольники Q (ф±) друг к другу на плоскости — при этом получает-
получается большой многоугольник Q на плоскости, который мы
ранее называли фундаментальным. Для окончательной
склейки следует считать фундаментальный многоугольник
и многоугольники Q(<p*) эластичными.
Теорема 1. В результате описанной склейки много-
многоугольников {Q(<p*)} получится замкнутая ориентируемая
поверхность SQ, вид которой однозначно определяется на-
набором углов аи . . ., ап, или же набором углов многоуголь-
многоугольника Q.
На доказательстве этой теоремы мы останавливаться не
будем; оно вытекает из общей теоремы § 23 о склейке
поверхностей из многоугольников и рассуждений § 24.
Из определения склеек следует, что скачущие траекто-
траектории на поверхности Sq будут непрерывными, и поток этих
траекторий дает обмотку SQ (возможно, с особыми точками).
Поверхность Sq является кренделем S (р) некоторого рода р,
т. е. сферой с р ручками (см. § 23).
Можно показать, что поверхности Sq из теоремы 1 не могут
быть сферами (т. е. Sq=?*=S@)), а торами (Sq=SA)) они являются
лишь тогда, когда Q принадлежит к одному из перечисленных в тео-
теореме 1 из § 22 торических типов. (Это следует из упоминавшейся
в § 8 теоремы Пуанкаре «о ветрах» на поверхностях.) Отсюда вы-
вытекает, что для системы двух упругих шаров на отрезке (см. § 13)
их движение сводится к потокам на инвариантных торах только при
соотношениях масс m1=tni, т2=3т1 и т1=3т2, в случае же когда
угол а = arctg \rmi/m2 соизмерим с зт (см. § 14), система шаров
имеет две не меняющиеся со временем функции, два так называемых
первых интеграла: интеграл энергии H=ll2m1v\-\- ll2m2vl и ин-
интеграл f(<p)= I ф | mod Bл/АО (определенный в решении задачи
25.3), и сводится к потокам на инвариантных кренделях рода pSs2.
Итак, мы установили, что для рациональных много-
многоугольников изучение бильярда можно свести к изучению
обмоток кренделей.
Примеры. Проделаем описанную процедуру Для
некоторых рациональных многоугольников, частью уже
исследованных ранее.
A. Q — прямоугольник. Тогда а1=а3—0, а2=а4=^/2,
общий знаменатель дробей N=2, и для склейки SQ нужно
240
взять 2ЛГ=4 экземпляра Q(y)~ с ф=±ф0 и ф=я±ф0. «Но-
«Новая» склейка, конечно, дает то же, что и раньше, в § 9,—
тор.
Б. Q — Т-образный 6-угольник (рис. 25.5). Здесь c*i=
=а3«=а5=0, а2=а4=ав=я/2, N=2, и SQ получается из
2N—4 экземпляров Q(y) — с ф=±ф0 и ф=я±ф0. На плос-
плоскости сразу нарисуем фундаментальный многоугольник Q,
имеющий форму рамы; склеиваемые стороны обозначены
«•
ъ
Р
A
t
-
A
\
d
и
1
с
с
1
d
A1
i
-
A
Рис. 25.5
одинаковыми буквами. После склейки сторон внешнего кон-
контура получается тор с прямоугольным вырезом; «оттянув»
этот вырез, отрежем кусок тора по кривой т и склеим
пары стороне и d — получим тор с дыркой т, края которой
нужно приклеить к краям такой же дырки на исходном торе.
В итоге получим крендель S B). Соответствующая обмотка
имеет ровно одну особую точку — мулыписедло типа 3,
получающееся при склейке вер-
вершин внутреннего контура рам-
рамки Q.
Задача 25.5. Построите по-
поверхности Sq для многоугольников
Q, имеющих форму букв П, О, Т
(рис, 25.6).
В. Q — равносторонний треугольник. Для него ах=0,
а2=2я/3, а3=я/3; ЛГ=3 и SQ склеивается из 2ЛГ=6 эк-
экземпляров ф(ф) —Для ф=±Фо, 2я/3±Фв| 4л/3±Фо.
241
Рис. 25.6
Г. Q — правильный 6-угольник. Здесь ai=a4=O, a2=»
=а5=я/3, а3=ав=2я/3; N=3, SQ склеивается из 2N—Q
шестиугольников Q(<p), где <р=±ф0, 2я/3±ф0, 4л/3±ф0.
Д. Q — прямоугольный треугольник с углами я '8 и 3 л/8.
Для него ai=0, а2=я/2, a3=n:8; N—8 и SQ склеивается
из 2iV=16 треугольников <2(ф), с ф=±<ро+ (т/8Jя, где
т=0, 1,2, . .,7.
Е. Q — прямоугольный треугольник с углами л/5 и
Зя 10. Для него ах=0 а2=я/2; а3=я/5; N=10 и SQ склеи-
склеивается из 20 экземпляров ф(ф), с ф=±фо+(т/10Jп, где
т=0, 1, 2, . . ., 9.
Перейдем теперь к ответу на второй вопрос: какие
выводы позволяет сделать сведение бильярдов в рациональ-
рациональных многоугольниках к обмоткам кренделей? В отличие от
обмоток торов, обмотки кренделей — значительно более
сложный объект, и если обмотки тора были полностью ис-
исследованы в § 8 с помощью теоремы Якоби о поворотах ок-
окружности, то аналогичный анализ обмоток кренделей дале-
далеко не так прост. Мы лишь сформулируем теорему о бильяр-
бильярдах в рациональных многоугольниках, доказываемую с
помощью рассмотрения обмоток кренделей.
Направления траекторий бильярда в любом рациональ-
рациональном многоугольнике Q можно разделить на два класса, ко-
которые мы назовем «плохими» и «хорошими». (Определение
этих классов направлений приведено ниже.)
Теорема 2. Любая траектория, идущая в «хорошем»
направлении, всюду плотно заполняет многоугольник Q
(либо попадет в вершину Q, и тогда ее продолжение в обрат-
обратную сторону всюду плотно заполняет Q) — это свойство
не зависит от начального положения бильярдного шара. Сре-
Среди траекторий, идущих в «плохих» направлениях, могут
встречаться периодические траектории. Наконец, хороших
направлений «значительно больше», чем «плохих» (множество
«плохих» направлений можно занумеровать натуральными
числами).
Приведем построение, с помощью которого определяют-
определяются «плохие» направления.
Зафиксируем положение АгА2. . .Ап многоугольника Q
на плоскости, и разрешим «перекатывать» многоугольник Q
из своего первоначального положения последовательными
отражениями (переворачиваниями) относительно его сто-
сторон (в произвольной последовательности), и отметим на
плоскости все точки Вх, В2, . . ., в которые могут попасть
вершины многоугольника Q. (Множество этих точек S-—
= {Bi, В2, . . .}, разумеется, бесконечно, однако счетно.)
242
«Плохими» направлениями называются направления все-
всевозможных лучей вида AkBh, где A ft — любая вершина
многоугольника Q в исходном положении, Bt — произ-
произвольная точка множества 53. Остальные направления на-
называются «хорошими». В следующем параграфе будет при-
приведен пример бильярдной траектории, идущей в «плохом»
направлении, но не периодической.
Задача 25.6. Доказать, что для произвольного многоуголь-
многоугольника Q (даже иррационального) есть хотя бы одно «хорошее» на-
направление.
Задача 25.7. Построить множество <81 для торических мно-
многоугольников и проверить, что теорема 2 для них выполнена.
Задача 25.8. Построить множество <Э для правильного
E-угольиика; для ромба с углом я/3 (и для параллелограмма с та-
таким же углом).
Задача 25.9*. Доказать, что для правильных и-угольников
при пфЗ, 4 и 6 множество S) всюду плотно на плоскости, т. е. в
любом круге произвольного радиуса е найдется хотя бы одна точка
этого множества.
Решение. Достаточно доказать, что множество с/Я цент-
центров многоугольников всюду плотно. Если правильный и-уголь-
ник Q перекатить через свои стороны четное число раз, то
стороны полученного и-угольника Q' будут параллельны сторонам
исходного, так что Q' получается из Q параллельным переносом.
Докажем две леммы.
Лемма 1. Если три вершины А, В, С параллелограмма
принадлежат множеству сМ, то и четвертая его вершина D также
принадлежит множеству <$,.
Доказательство следует из того, что мы сможем
пройти из точки С в точку D, осуществляя те же параллельные
переносы многоугольника, что и при переходе из точки В в точку А.
Лемма 2. Множество оМ переходит в себя при повороте на
угол 2п1п вокруг любой из его точек.
Доказательство. Построим цепочку и-угольников, при-
примыкающих друг к другу по стороне и «соединяющих» наш и-уголь-
ник Q с центром в точке О с и-угольннком с центром в любой дру-
другой точке А множества сМ. При повороте на угол 2п1п вокруг точки
О эта цепочка многоугольников переходит в другую цепочку, сое-
соединяющую исходный многоугольник с многоугольником, центром
которого является точка А', полученная из А тем же поворотом.
Следовательно, точка А' также принадлежит множеству сМ и лемма 2
доказана.
Мы хотим доказать, что множество сМ всюду плотно ha
плоскости, в частности, что в нем найдутся сколь угодно близкие
точки.
Предположим, что это не так, т. е. предположим, что все рас
стояния между точками множества a/fl больше некоторого положи-
положительного числа d. Отсюда и из леммы 1 следует, что qS — решет-
к а, т. е. точки множества cS — это точки пересечения двух се-
семейств параллельных прямых, разрезающих плоскость на оди-
одинаковые параллелограммы (докажите это сами). Но из леммы 2
следует, что эта решетка переходит в себя при повороте на угол 2л/п.
Из этого немедленно следует, что существует правильный п-уголь-
243
ник с вершинами в ее узлах. Докажем, что тогда п может быть равно
только 3, 4 и 6 — это будет противоречить условию эадачи и тем
самым опровергать наше предположение, что множество q/Ц, ие всюду
плотно.
Числа п=3, 4 и 6 подходят. Если п=5, то, проведя в правиль-
правильном 5-угольнике с вершинами в узлах решетки cf все диаго-
диагонали, получим, что 5 их точек пересечения также принадлежат
решетке (как четвертые вершины параллелограммов, три из ко-
которых — узлы решетки). В полученном меньшем 5-угольиике,
подобном исходному, опять проведем все диагонали — получим
меньший подобный 5-угольник с вершинами в узлах и т. д. В конце
концов сторона пятиугольника станет меньше минимального рас-
расстояния между узлами решетки, и в этот момент возникнет про-
противоречие.
Если же nia7, то все отрезки, соединяющие центр О и-уголь-
ника с его вершинами, параллельно перенесем в узел решетку
чтобы точка О совпала с этим узлом. Вторые концы этих отрезков
будут также лежать в узлах решетки c/fl по лемме 1. Проделав это
построение нужное число раз, придем к тому, что возникнет п-
угольник с вершинами в узлах, все стороны которого меньше ми-
минимального расстояния между узлами решетки <М — противо-
противоречие. Задача 25.9 решена.
Оказывается, множество 93, построенное выше по мно-
многоугольнику Q, «почти для всех» многоугольников Q (на-
(например, для иррациональных многоугольников) всюду плот-
плотно на плоскости! Попробуйте это доказать.
Задача 25.10. Докажите, что для почти всех начальных
положений двух упругих точечных ?1аров на отрезке [0, а], массы
которых относятся как 1 : C+2^2), множество точек их столк-
столкновений друг с другом всюду плотно иа отрезке [0, а].
Решение. Движение шаров эквивалентно бильярду в
прямоугольном треугольнике Q с углом л/8, поскольку (см. § 14)
3—2V2=(V2— 1)* =
3 + 21/
__(l — cos(jt/4)\2/ 25нг»(л/8) X g я.
V sin (л/4) ) V2sin(n/8) cos (я/8) J g 8"
Выбрав для бильярдной частицы в треугольнике Q «хорошее»
направление, получим в нем, по теореме 2, всюду плотную биль-
бильярдную траекторию. Точки излома траектории, лежащие иа ги-
гипотенузе, всюду плотно ее заполняют. Но эти точки и отвечают
точкам столкновений шаров на отрезке [0, а], что и требовалось
доказать.
Теорема 2 для торических многоугольников была дока-
доказана в части II; для остальных рациональных многоуголь-
многоугольников (даже для правильного 6-угольника) элементарное
ее доказательство в настоящее время неизвестно.
Про бильярды в многоугольниках, хотя бы один угол
которых несоизмерим с я, известно совсем немного. Как фи-
244
зики, так и математики уверены в справедливости следую-
следующих утверждений.
Гипотеза I. Если хотя бы один угол многоуголь-
многоугольника Q несоизмерим с л, то «типичная» траектория би-
бильярда в Q всюду плотно заполняет многоугольник Q.
Гипотеза II. Более того, типичная траектория
бильярда проходит («рано или поздно») сколь угодно близ-
близко к любой наперед заданной точке многоугольника Q под
направлением, сколь угодно близким к любому наперед за-
заданному направлению в этой точке. (Как следует из задачи
Рис. 25.7
25.3, утверждение гипотезы II в случае рациональных мно-
многоугольников несправедливо. С другой стороны, теорема 2—
это утверждение гипотезы I для рациональных многоуголь-
многоугольников. Слова «типичная траектория» имеют смысл выбран-
выбранная наугад траектория).
Недавно математики С. Кирчкоф, Г. Мазур и Дж. Смай-
ли доказали, что для бесконечного множества «иррациональ-
«иррациональных» многоугольников гипотеза II справедлива *). Однако
для произвольного иррационального многоугольника Q она
пока не доказана. (Здесь уместно отметить, что гипотеза II
доказана для бильярда в так называемых «вогнутых» мно-
многоугольниках — в области Q, ограниченных дугами кри-
кривых, выпуклыми внутрь Q (эти бильярды носят названия
«бильярдов Синая»; см. Заключение); она также доказана
для бильярда в прямоугольнике с вырезанным из него кру-
кругом (рис. 25.7). Обе упомянутые теоремы очень сложны и не
элементарны.) Для бильярдов в иррациональных много-
*) Эти авторы доказали также, что для «почти всех» поверх-
поверхностей Sq, где Q — рациональный многоугольник, бильярдный по-
поток на них эргодичен. Используя их результат, А. М. Степин и
Ф. Эрдман доказали, что для «массивного» множества прямоуголь-
прямоугольных треугольников (так называемого «всюду плотного множества
второй категории») бильярд эргоднчен; тем самым для механической
системы «два упругих шара на отрезке» эргодичность является «ти-
«типичным» свойством,
245
угольниках пока что неизвестно доказательство даже тако-
такого «ослабления» гипотезы I:
Гипотеза 0. В произвольном многоугольнике Q су-
существует хотя бы одна траектория, всюду плотно запол-
заполняющая Q.
Доказано пока только следующее утверждение, при-
принадлежащее К. Болдригини, Ф. Маркетти и М. Кину: ти-
типичная бильярдная траектория в произвольном многоуголь-
многоугольнике сколь угодно близко подходит хотя бы к одной из его
вершин (причем это доказательство опять-таки не эле-
элементарно).
В пользу этих гипотез, выдвинутых на основе «общих
физических соображений», говорят только результаты чис-
численных экспериментов на ЭВМ. (В этих экспериментах для
простоты рассматриваются бильярды в прямоугольных тре-
треугольниках, отвечающих системе двух шаров на отрезке.)
В заключение отметим два весьма интересных и краси-
красивых направления, в которых можно развивать изложенные
здесь методы и идеи. Первое — это бильярды в многогран-
многогранниках, второе — бильярды в сферических многоугольни-
многоугольниках (т. е. в многоугольниках на сфере, ограниченных ду-
дугами больших кругов; бильярдный шар в этом случае дви-
движется по дугам больших кругов и отражается от сторон по
закону «угол падения равен углу отражения».— см. геомет-
геометрическое доказательство утверждения в § 17).
Задача 25.11*. Пусть Q — многогранник. Ввести (опре-
(определить) «скачущие траектории» и решить задачу 25.1 для этого
случая.
§ 26. Может ли непериодическая траектория
в выпуклом многоугольнике
не быть всюду плотной в нем?
Положительному ответу на выне-
вынесенный в заголовок вопрос будет посвящен весь настоящий
параграф. Более того, оказывается, что непериодические и
не всюду плотные траектории бывают уже в рациональных
многоугольниках. Из теоремы 2 § 25 немедленно следует,
что все такие траектории идут в «плохих» направлениях,
и поэтому не являются типичными. Однако сама возмож-
возможность существования этих траекторий говорит о гораздо
большей сложности структуры обмоток инвариантных
кренделей, чем обмоток торов, которые либо периодические,
либо всюду плотны.
Точный ответ на поставленный вопрос заключен в сле-
следующей теореме.
246
Теорема 1. Для любого п на плоскости существует
выпуклый п-угольник Q, в котором найдется непериодиче-
непериодическая и не всюду плотная бильярдная траектория у.
Докажем мы эту теорему конструктивно — для каждого
п предъявим n-угольник и бильярдную траекторию в нем,
которая будет обладать указанным свойством. Опишем план
доказательства. Мы рассмотрим только случай п^А, а
случай треугольника (л=3), как существенно более слож-
сложный, затронем в конце параграфа.
ч if'
А'
С Л=4
Рис. 26.1
Сначала будет построен специальный выпуклый шести-
шестиугольник АВСА'В'С, в котором мы укажем бильярдную
траекторию, всюду плотно его заполняющую, причем би-
бильярдный шар ни разу не отразится от сторон А В и
А'В'. Затем, продолжая пары сторон АС, ВС и В'С,
А'С до их пересечения в точках L и U, получим четырех-
четырехугольник LCL'C, в котором указанная бильярдная траек-
траектория ни разу не попадет в окрестности ABL и A'B'L' вер-
вершин LylU (рис. 26.1, а). Тем самым теорема будет доказана
для и=4. Для л=5, 6, 7, ....... доказательство получа-
получается просто из случая л=4: достаточно обрезать светлые
уголки у четырехугольника LCL'C, как мы получим мно-
многоугольник с нужным числом сторон, а бильярдная траек-
траектория в нем (например в 9-угольнике на рис. 25.1, б) по-
прежнему будет всюду плотно заполнять шестиугольник
АВСА'В'С и не будет заходить в обрезанные окрестности
вершин L и L'.
Приступим к построению искомого шестиугольника
АВСА'В'С и нужной нам бильярдной траектории. Шести-
Шестиугольник АВСА'В'С будет удовлетворять следующим ус-
условиям:
Г. Он центрально-симметричен: АВ\\А'В', АС'\\А'С и
ВС\\В'С (рис. 26.2; стороны АВ и А'В' считаем верти-
вертикальными);
2Э. Угол при вершине А равен я'2+а, угол при вершине
В равен jx/2+P, где 0<а, Р<п/2, причем
ctg2a>tgp, ctg2p>tga A)
247
(условия A) возникнут сами собой, когда мы в дальнейшем
станем исследовать бильярдную траекторию);
3°. Перпендикуляр к стороне АС в точке А является одно-
одновременно биссектрисой уела /ВАС, а перпендикуляр к сто-
стороне ВС является одновременно биссектрисой угла /_АВС
(рис. 26.2).
Приведем геометрическое построение шестиугольника с
такими свойствами. Зафиксируем острые углы аир.
а) Проведем через конец А отрезка А В прямую АС под
углом 2а, а через конец В — прямую ВС под углом 2р"
(рис. 26.2). Обе прямые АС и ВС пе-
пересекутся в некоторой точке, посколь-
ку 2а+2р<л.
б) Проведем биссектрисы углов
/ВАС и /_АВС.
в) К первой биссектрисе проведем
через точку А перпендикуляр АС и
ко второй биссектрисе — перпенди-
КУЛЯР ВС- Точки С' и С получаются
как точки пересечения проведенных
Рис. 26.2 перпендикуляров к биссектрисам с
прямыми ВС и АС. В результате по-
получится фигура, затемненная на рис. 26.2.
г) Осталось провести прямые С В' || ВС и С А' || АС
и отложить на них отрезки С'В'—ВС и СА'—АС, а затем
соединить отрезком точки А' и В'.
Нетрудно видеть, что построенный шестиугольник
АВСА'В'С' будет центрально-симметричным (требование Г)
и удовлетворять требованиям 2е и 3 .
Объясним «бильярдный» смысл условия 3°. Допустим,
что мы послали точечный бильярдный шар из точки В в
точку А вдоль стороны В А, забыв на время, что А и В —
вершины. Тогда шар отразится от прямой АС. и пойдет по
прямой АС в вершину С. Точно так же, если шар движется
из рершины А в вершину В, то он, отразившись от прямой
ВС, попадет в вершину С. Таким образом, ВАС и ABC —
двухзвенные «предельные» бильярдные траектории, вооб-
вообще-то исключаемые нами из рассмотрения (мы договорились
в прошлых параграфах считать попавший в вершину угла
шар застрявшим в ней), но играющие важную роль при до-
доказательстве. Тем же свойством обладают двухзвенные би-
бильярдные траектории А'В'С и В'А'С (рис. 26.3), когда шар
движется из вершины в вершину вдоль стороны А'В .
Пусть теперь бильярдный шар расположен в некоторой
точке X внутри шестиугольника АВСА'В'С. Запустим его
248
со скоростью, по модулю равной 1, параллельно стороне
АВ вверх. Докажем, что при некотором выборе углов а и Р
вся бильярдная траектория движения шара всюду плотно
заполнит шестиугольник АВСА'В'С.
Рассмотрим для доказательства пучок отрезков внутри
шестиугольника, параллельных стороне АВ, концы кото-
которых принадлежат границе шестиугольника. Наш шар дви-
движется вверх вдоль одного из этих отрезков MN. После пер-
первого отражения от стороны шестиугольника {АС на
рис. 26.3) NM'
гонали АС и, отразившись
М' от противоположной стороныСА',
.3) он движется по отрезку NM' параллельно диа-
АС и, отразившись в точке ,
° У
м
Пучок траекторий
Рис. 26.3
начинает двигаться вверх по другому fi 0*^ J V* --»0
отрезку из пучка параллельных:
M'N' || А В (это происходит вследст-
вследствие свойства 3° шестиугольника
АВСА'В'С). Следовательно, можно в
рассмотреть бильярдное преобразова-
преобразование пучка параллельных отрезков,
переводящее отрезок MN в отрезок
M'N', т. е. одно вертикальное звено
бильярдной траектории — в следующее вертикальное звено
этой же траектории, асам пучок — в себя (рис. 26.3). А как
ведут себя наклонные звенья траектории, параллельные
либо диагонали АС, либо диагонали ВС? Очень просто: если
шар отразился от одной из сторон АС или СА', то наклонное
звено будет идти параллельно диагонали АС; если же шар
отразился от стороны ВС или симметричной ей В'С —
то параллельно диагонали ВС.
Это дает -нам возможность по абсциссе х точки X, в ко-
которой находится шар, движущийся вертикально ВЕерх, оп-
определить абсциссу f(x) точки, в которой окажется шар, ког-
когда будет двигаться по следующему вертикальному звену
своей траектории. Поместим непосредственно под шести-
шестиугольником горизонтальный отрезок [0, 1], отметив его
концы числами 0 и 1 @ — это проекция стороны АВ, I —
проекция А'В' на отрезок), и спроектируем весь пучок вер-
тпкальных отрезков на этот отрезок. В результате проек-
проекции каждое звено пучка перейдет в о д н у точку, а весь
пучок — целиком в отрезок [0, 1]. Под действием бильярд-
бильярдного преобразования каждое вертикальное звено бильярд-
бильярдной траектории переходит в следующее вертикальное звено,
следовательно проекция х этого звена перейдет в проекцию
f(x) второго вертикального звена. Как по числу х вычислить
число f(x)?
249
Для ответа на этот вопрос естественно весь пучок парал-
параллельных отрезков разделить на два: левый — от стороны АВ
до вертикальной прямой /, проходящей через вершину С
шестиугольника, и правый — от прямой / до стороны А'В'
(рис. 26.4). Левый пучок спроектируется на отрезок [0, а],
а правый — на отрезок [а, 1].
Точка 0 — левый конец отрезка [0, 1] — под действием
/ переходит в точку /@), которая есть проекция на [0, 1]
вертикального звена, прохо-
проходящего через вершину С (в это
звено переходит сторона А В
под действием бильярдного
Рис. 26.4
Рис. 26.5
преобразования), а точка а — проекция вертикального
звена CD' (рис. 26.4) — в точку /(а)=1 (в проекцию сто-
стороны А'В' на отрезок [0, 1], т. е. в его правый конец). Не-
Нетрудно сообразить, используя равенство противоположных
сторон параллелограмма, что, поскольку точка а смести-
сместилась вправо на 1 — а, то и все точки отрезка [0, а] под дей-
действием преобразования / сместятся вправо на 1—а, т. е.
/@)=1 —а, и вообще f(x)—x + A —а) при 0 <х ^а.
Если же вертикальное звено принадлежит правому пуч-
пучку и проектируется в точку у на отрезке [а, 1], то аналогич-
аналогичные рассуждения показывают, что под действием бильярд-
бильярдного преобразования оно перейдет в звено, проектирую-
проектирующееся в точку у—а?[0, 1], т. е. f(y)= у — а при а<#^*-
Наглядно действие преобразования / отрезка [О, П со"
стоит в перемене местами отрезков 10, а] и [а, 1], или, по-
другому, в перекладывании этих отрезков (рис. 26.5). Вве-
Введем обозначение Ь=\—а. Мы получили, что
J х + Ь при х€[0, а]; A)
Пх>~\ х—а при Х?[а, 1].
Если свернуть отрезок [0, 1] в окружность S1 еднничнои
250
длины, то выписанная двойная формула для / превратится
в одинарную:
f(x) = x + b при x?S\ B)
Действительно, при 0^.х^.а эта формула совпадает с ис-
исходной, а при х^а точка f(x) — х— а = (х + Ь)— 1 на
окружности S1 совпадает с точкой х-\-Ь (так как длина
окружности равна 1).
Таким образом, перекладывание f двух отрезков эквива-
эквивалентно повороту окружности S1 на угол Ь=\—а. Поэтому
можно воспользоваться теоремой Якоби из § 2 и сформули-
сформулировать следующее
Утверждение. Перекладывание f двух отрезков
[О, а] и [а, II является либо периодическим — при рациональ-
рациональном а, либо всюду плотным — при иррациональном а: тра-
траектория любой точки #?[0, 1] (последовательность f(x),
/(/(*)),/(/(/(*))),...) либо пери-
периодическая, либо всюду плотно
заполняет отрезок [0, 1].
Из этого утверждения выте-
кает, что при рациональном а
бильярдная траектория в шес-
шестиугольнике АВСА'В'С перио-
периодическая (замкнутая), а при ир-
иррациональном а всюду плотно
заполняет весь шестиугольник.
Нам осталось поэтому лишь по-
подобрать такой шестиугольник,
чтобы для него число а было иррациональным. Зафикси-
Зафиксируем длину стороны АВ (с фиксирования отрезка АВ мы
начали построение шестиугольника АВСА'В'С') и выразим
числа а и Ь—\ —а через АВ и углы аир. Обратимся к
рис. 26.6.
Из прямоугольного ?\АМС получаем С'М=АМХ
Xtga=otga, а из прямоугольного ДВС'Ы — C'N=
=BN-tg(n/2—2|})=о ctg 2p\ Поскольку, с одной стороны,
MN=C'N—C'M=a(ctg 2p—tg a), а с другой — MN=AB,
находим А В=а (ctg 2р—tg a) и
АВ
G~ctg2p—tga* l°J
Аналогичным образом можно получить формулу для Ь:
, АВ ...
b D)
Положительность чисел а и Ь эквивалентна выполнению ус-
условия 2", накладываемому на шестиугольник.
251
Поскольку отрезок АВ фиксирован, а функции ctg 28
и tg а непрерывны, можно непрерывным изменением углов
а и Р добиться того, чтобы отношение А В/ (ctg 28 — tga)
стало иррациональным (это отношение иррационально
для почти всех а и |3 из интервала @, л/2)). Итак, для по-
почти всех шестиугольников число а = а(а, р) иррацио-
иррационально.
Следовательно, для почти всех шестиугольников, удов-
удовлетворяющих условиям Г, 2°, 3°, указанная бильярдная тра-
траектория всюду плотна в них, что и требовалось доказать.
Таким образом, для п = 4 и для п > 4 теорема доказана.
Для п = 3 теорему доказывать не будем; отметим только,
что существует равнобедренный треугольник с очень тупым
углом при вершине, в котором специальным образом (очень
хитрым!) построенная бильярдная траектория всюду плот-
плотно заполняет лишь некоторую его часть. Доказательство в
случае /2=3 опять сводится к рассмотрению перекладывания
двух отрезков, возникающего при специальных симметрич-
симметричных отражениях треугольника относительно его сторон.
Следствием теоремы 1 для п = 3 служит теорема 3 из
§ 14. Действительно, для «газа» из двух точечных молекул
на отрезке конфигурационным пространством является пря-
прямоугольный треугольник, а если отношение масс молекул
очень велико, то острый угол этого треугольника очень мал.
Отражая треугольник относительно катета, лежащего про-
против этого угла, получаем равнобедренный треугольник с
очень тупым углом (близким к л) при вершине. Неперио-
Непериодическая, но и не всюду плотная траектория в этом тре-
треугольнике заполняет всюду плотно конечное число отрезков
на гипотенузе исходного треугольника, что и доказывает
теорему 3 из § 14.
Формулы C) и D) для вычисления а позволяют постро-
построить конкретные n-угольники, в которых указанная
бильярдная траектория всюду плотно заполняет лишь не-
некоторую часть. Можно даже построить рациональ-
рациональные многоугольники с этим свойством. Построим сначала
шестиугольник АВСА'В'С, для которого а=лЛ2, Р=
=л/6 — углы при его вершинах А, В, С равны 7л/12, 2я/3
и Зя/4 соответственно. Заметим, что нам в действительности
достаточно проверить, что отношение Л (а, $)=а/Ь—а/ A —о)
иррационально (объясните сами, почему); число alb уже не
зависит от длины отрезка АВ. Вычисляем:
262
т. е. alb иррационально и, значит, указанная выше бильярд-
бильярдная траектория в таком шестиугольнике всюду плотна.
Продлевая его стороны до взаимных пересечений, как на
рис. 26.1, а, получаем параллелограмм с углами л/4 и
Зл/4, а обрезая специальным образом эти углы, как на
рис. 26.1,6, получаем другие многоугольники с углами,
соизмеримыми с л, т. е. рациональные многоугольники,
обладающие требуемой бильярдной траекторией.
Мы знаем (см. § 25), что бильярд в рациональных мно-
многоугольниках сводится к обмоткам кренделей. В случае
параллелограмма с углами л/4 и
Зя/4 бильярд в нем сводится к об-
обмоткам кренделя рода р=3 (сферы
с тремя ручками), имеющего два
мультиседла одинаковых типов
mi=m2=3 (см. таблицу к задаче
24.3). Проследим, как на этой по-
поверхности — сфере с тремя ручка-
ручками — ведет себя построенный пу-
пучок параллельных отрезков.
Мы знаем, что бильярдное пре-
преобразование пучка параллельных
отрезков, описанное выше, являет-
является перекладыванием двух отрезков,
что наглядно можно изобразить в
виде потока кривых на двойной
«ленте» (рис. 26.7).
Эта двойная лента топологически эквивалентна (гомео-
морфна) тору Тс дыркой, также показанному на рис. 26.7.
Бильярдная траектория в шестиугольнике на торе Т всюду
плотно заполняет его, омывая оба берега дырки (смыкаю-
(смыкающихся в особых точках А и В, причем из первой во вторую
идут две сепаратрисы): левый пучок параллельных отрез-
отрезков в шестиугольнике омывает дырку на торе слева, а пра-
правый — справа. К этой дырке подклеивается сфера с двумя
ручками, в которой также имеется дырка: обе поверхности
подклеиваются краями своих дырок по их границам. Итак,
построенная бильярдная траектория всюду плотно запол-
заполняет одну ручку поверхности S C) и не заходит на осталь-
остальные две ручки.
Такая же топологическая ситуация имеет место и в об-
общем случае для построенного рационального
п-угольника: бильярдная траектория заполняет всюду плот-
плотно одну из ручек поверхности S(p), отвечающей этому п-
угольнику (число ручек р зависит от типов мультиседел,
253
Рис. 26.7
т. е. от углов при вершинах п-угольника), и не заходит на
остальные ручки. Это следует опять-таки из того, что в
пучке параллельных отрезков происходит перекладыва-
перекладывание двух отрезков, т. е. имеет место картина, изображен-
изображенная на рис. 26.7.
Сформулируем в заключение две интересных, но труд,
но доказываемых теоремы о периодических бильярдных
траекториях в рассматриваемом л-угольнике Quo неперио-
непериодических, но и не всюду плотных траекториях в трехмерных
многогранниках.
Теорема 2. Пусть Q — п-угольник из теоремы 1.
Тогда для любой наперед заданной точки в шестиугольнике
ABC А'В'С внутри Q сколь угодно близко к этой точке про-
проходит периодическая бильярдная траектория, направле-
направление которой сколь угодно мало отличается от вертикаль-
вертикального (параллельного отрезку АВ).
Можно сказать и по-другому:
Пусть Q — п-угольник из теоремы 1, X — произволь-
произвольная точка в шестиугольнике АВСА'В'С внутри Q. Тогда
бильярдный шар можно поместить в точку М, сколь угод-
угодно близкую к точке X, и запустить его под таким малым уг-
углом к вертикали (т. е. почти параллельно стороне АВ),
что шарик опишет периодическую бильярдную траекторию.
Отметим, что при доказательстве теоремы 2 существен-
существенным сбразом используются свойства цепных дробей. И,
наконец.
Теорем а 3. Б пространстве существует выпуклый
многогранник, в котором найдется непериодическая бильяр-
бильярдная траектория, заполняющая всюду плотно трехмерную
область внутри него.
Таким многогранником является прямая призма О, в
основании которой лежит n-угольник Q из теоремы 1. Ока-
Оказывается, бильярдному шару можно придать такую началь-
начальную скорость v, что проекция шара на основании призмы
Q будет описывать всюду плотную траекторию в шести-
шестиугольнике АВСА'В'С внутри Q, а его проекция на образую-
образующую призмы заполняет ее всюду плотно; таким образом,
траектория шара всюду плотно заполнит призму О' с осно-
основанием АВСА'В'С и той же высотой, что и призма Q. Дока-
Доказательство этой теоремы также не элементарно.
Прямая треугольная призма служит конфигурационным
пространством «газа из двух молекул» — шаров масс trii и
т2 одинакового диаметра D, имеющих одинаковую верти-
вертикальную составляющую скорости,— расположенного в
квадрате размером 1X1 с упруго отражающими стенками.
254
1 \
1 ;
1 \
Я
'- 1
; Г
; i
Рис. 26.8
Точки столкновения этих шаров всюду плотно заполняют
несколько прямоугольников внутри этого квадрата
(рис. 26.8). Это утверждение вытекает из теоремы 3 § 14 и
теоремы 3 настоящего параграфа.
§ 27. Периодические траектории
в многоугольниках и многогранниках
1. Мы уже много узнали о свойствах бильяр-
бильярдов в разнообразных многоугольниках. Мы узнали,- что в
торических многоугольниках каждая бильярдная траекто-
траектория либо периодична, либо всюду плотна (§ 22); что дви-
движение бильярдного шара в рациональном многоугольнике
. квивалентно движению фазовой точки по некоторой по-
поверхности — обмотке сферы с ручками (§ 24); что типичные
траектории в рациональных многоугольниках заполняют
их всюду плотно (§ 25), но что не всякая траектория явля-
является либо периодической, либо всюду плотной (§ 26), как
это имеет место для торических многоугольников.
Однако мы еще не задавали такой «простейший» вопрос:
а в каждом ли многоугольнике существует периодическая
бильярдная траектория?
До сих пор полного ответа на него нет даже для тре-
треугольников. В этом параграфе будет дан ответ лишь для ра-
рациональных многоугольников и приведены известные в на-
настоящее время и просто описываемые конструкции периоди-
периодических траекторий в довольно большом классе треуголь-
треугольников.
Читателям, внимательно изучившим § 6 гл. 2, может
показаться, что теорема Биркгофа о наличии периодической
бильярдной траектории с любым числом звеньев в любой
выпуклой области с гладкой границей переносится и на слу-
случай выпуклых многоугольников. Однако это не так — чуть
позже мы докажем, что у периодических траекторий в неко-
некоторых треугольниках число звеньев не может быть мень-
меньшим заранее заданной величины, и укажем на то «препятст-
«препятствие», из-за которого доказательство теоремы Биркгофа для
255
многоугольников «не проходит» (см. в связи с этим задачу
6.8). '
Доказательство существования периодических бильяр-
бильярдных траекторий в рациональных многоугольниках, приве-
приведенное в этом параграфе, интересно тем, что в нем неожидан-
неожиданным образом используется абстрактная теорема Пуанкаре
о возвращении из § 3, которая будет применена к инвари-
инвариантной поверхности, описанной в § 24. Кроме того, теорема
Пуанкаре позволит сделать некоторые интересные выводы
и для случая произвольной (не обязательно многоуголь-
многоугольной) области, в которой движется бильярдный шар. При
написании этого параграфа нами частично использована
статья [14].
2. Прежде чем переходить к конкретным утверждениям
о периодических траекториях в многоугольниках и их до-
доказательствам, сформулируем справедливую, на наш взгляд,
гипотезу о периодических бильярдных траекториях в лю-
любой области на плоскости, до сих пор не доказанную и не
опровергнутую.
Гипотеза. В любой ограниченной области й на
плоскости с кусочно-гладкой границей существует перио-
периодическая бильярдная траектория.
(То же утверждение о периодических траекториях, по-
видимому, справедливо и в пространстве любого числа изме-
измерений. Аналогичная гипотеза о существовании в любой
ограниченной области хотя бы одной всюду плотной траек-
траектории уже неверно — например, всюду плотных траекто-
траекторий нет в круге и в «телефоне» fi2 из § 5 гл. 2.)
3. Начнем исследование периодических траекторий в
многоугольниках с решения задачи 6.7 — задачи Фаньяно.
Теорема 1. В любом остроугольном треугольнике
ABC существует периодическая траектория. А именно она
состоит из трех звеньев, образующих вписанный треуголь-
треугольник минимального периметра; вершины этого треугольника
являются основаниями высот исходного остроугольного
треугольника ABC *).
Доказательство. Мы докажем сначала, что сто-
стороны треугольника, вершины которого F, G, Е — осно-
*) Дадим механическую интерпретацию трехзвенной периоди-
периодической траектории в остроугольном треугольнике ABC. Пусть на
каждой из его сторон надето по колечку, которые свободно могут
скользить по сторонам. Колечки попарно соединим натянутыми ре-
резинками и отпустим. При этом колечки и резинки образуют верши-
вершины и стороны треугольника наименьшего периметра, вписанного
в ABC, который одновременно является периодической бильярдной
траекторией в нем,
256
АЕ BF и CG треугольника ЛБС, образуют
вукдадам «углам отражения»:
GE, /BEG=/CEF
=z/EFc (остальные
d «i. АЕ. BF
и СС пересекаются в точке W.
Построим на отрезках АН а
СН, как на диаметрах, две ок-
окружности (рис. 27.1).
Первая окружность пройдет
через точки G и F, поскольку
/AGH=Z.AFH=n/2' a втораЯ
т аналогичной причине — че-
через точки Е и F. По теореме
о вписанных углах имеем:
Рис. 27.1
ь доказать
екая бильярдная траектор™
Докажем теперь, что лисг
A V
Рис. 27.2
5i
А"В" (рис. 27.2, а).
9 Г А. Гальперин, А. Н. Земляков
Обратим прежде всего внимание на то, что конечное
положение А"В"С" может быть получено из начального
положения ABC простым параллельным переносом. Чтобы в
этом убедиться, посмотрим, что происходит с треугольни-
треугольником после двух первых отражений. Очевидно, что эти два
отражения эквивалентны одному повороту ?\АВС по ча-
часовой стрелке вокруг неподвижной вершины С на угол 1С
(буквами А, В, С обозначены и величины углов при вер-
вершинах А, В, С). Точно так же мы могли бы перевести его
из этого положения в пятое вращением по часовой стрелке
около неподвижной точки В' на угол 2В и, наконец, вра-
вращением на угол 2А вокруг неподвижной точки А" мы при-
привели бы его в положение седьмое, т. е. в конечное. В итоге
1\АВС повернулся по часовой стрелке на угол 2А+2В+
+2С=2(А+В+С)=2я. В результате /\АВС совершает
полный оборот и принимает то же положение, что и вначале,
оказываясь лишь передвинутым по плоскости параллельно
себе. В частности, АВ \\ А"В", АС \\ А"С" и ВС || В"С.
Нетрудно видеть, что /\GFE после всех указанных отра-
отражений перейдет в /\fi"F"E", причем длина отрезка ЕЕ" будет
равна удвоенному периметру ?fiFE—это следует из того,
что по доказанному GFEG — бильярдная траектория, и
поэтому она после указанных отражений «выпрямится»
именно в отрезок ЕЕ" (рис. 27.2, а). Стороны любого дру-
другого /\LJVW, вписанного в ?\АВС, после того же набора
отражений перейдут в ломаную U. . .U", причем, как нет-
нетрудно показать (докажите!), отрезок UU" будет параллелен
отрезку ЕЕ" и равен ему по длине (используйте то, что ВС ||
1В"С"). Значит, длина этой ломаной будет больше длины
отрезка UU"=EE", т. е. периметр ?JJVW будет больше
периметра /\J3EF. Значит, периметр /\fiEF минимально
возможный, что и требовалось доказать.
Замечание. Кроме периодической траектории
GFEG в остроугольном /\АВС существует бесконечно много
других периодических траекторий. Действительно, если
мы пошлем шар не по отрезку FE, а по близкому и парал-
параллельному ему отрезку F'E', который мы можем выбрать
бесконечным числом способов, то шар опишет «параллель-
«параллельную» GFEG периодическую траекторию F'E'G F"E"G"t
вдвое большей длины, чем GFEG (рис. 27.2, б). Докажите
это утверждение самостоятельно. Таким образом, траек-
траектория GFEG — это как бы «сдвоенная» траектория
F'E'G'F"E"G"F'.
Вообще, если Г — периодическая бильярдная траекто-
траектория в некотором многоугольнике Q, то любая близкая ей
5F8
«параллельная» (в указанном выше смысле) траектория Г'
также будет периодической, так как шар отражается от тех
же самых сторон и в той же последовательности. Значит,
построта одну периодическую траекторию, мы одновре-
одновременно получаем бесконечно много других периодических
траекторий той же длины. Это множество траекторий
носит название «пучок параллельных траекторий».
4. Для тупоугольного треугольника дело обстоит гораз-
гораздо сложней. Во-первых, в нем только основание одной из
высот попадает на сторону, а не на ее предложение; осталь-
остальные два основания лежат вне треугольника, поэтому дока-
доказательство теоремы 1 «не работает». Нельзя получить в
тупоугольном треугольнике периодическую траекторию из
трех звеньев еще и потому, что вписанный в него треуголь-
треугольник минимального периметра вырождается в высоту ВН,
опущенную на максимальную сторону АС. Более того, в
конкретном тупоугольном треугольнике периодическая
траектория из минимально возможного количества звеньев
может быть очень длинной. А именно справедлива
Теорем а 2. Для любого натурального числа п су-
существует тупоугольный треугольник ABC, в котором лю-
любая периодическая бильярдная траектория имеет больше
чем п звеньев.
Доказательство. Выберем такие малые числа
аир, чтобы число N(a, P)=min {—[—я/а], —[—л/рЧ}
превосходило заданное число п (N(a)=—[—л/a] — мак-
максимальное число отражений шара в угле величиной а).
Кроме того, потребуем, чтобы числа a, Р и jx были рацио-
рационально независимыми, т. е. чтобы если хотя бы одно из
целых чисел k, т, I отлично от 0, то сумма ka-\-mp+
-f ЫФО. Возьмем числа а и р в качестве острых углов ту-
тупоугольного Д ABC (выраженных в радианах). Если в
ДЛВС нет ни одной периодической бильярдной траектории
(мы считаем — см. гипотезу,— что такого никогда не
бывает), то теорема 2 доказана. (Это чисто логическое вы-
высказывание: если какого-то объекта не существует, то для
него выполнено любое свойство, в частности то, что
звеньев у несуществующей периодической траектории боль-
больше п.)
Пусть теперь Г — некоторая периодическая траектория
в /\АВС Докажем, что у нее имеется хотя бы одно звено
XY, концы которого лежат на боковых сторонах А В и ВС
(рис. 27.3, а).
Предположим противное: пусть бильярдный шар после
каждого удара от боковой стороны попадает на основание
9* 8S9
fi
AC, т. е. отражается от сторон треугольника так: боковая
сторона ¦-*¦ основание .-» боковая сторона *~* основание Л
Тогда из рис. 27.3, 6 можно определить, как связаны
углы ф и ф двух соседних отражений шара от основания-
либо ф'=ф—2а, либо ф'=ф+2р (см. по этому поводу зада-
чу 25.2, где для другого
угла приводится похожая
формула). Следовательно,
если ф0 — начальный угол|
под которым шар был запу-
запущен к основанию АС, то
после некоторого очередно-
очередного отражения он равен
Ф=фо+тр—ka, где т и
k — целые числа. Посколь-
Поскольку траектория Г периоди-
периодическая, при некоторых т
iTn t и k угол Ф должен отли-
отличаться от угла ф0 на полное число оборотов:
ф = Фо + 2ns =Ф ф0 + /и|3—ka = ф0 + 2ns =Ф
=И— k)u + m$ + {— sJjt = O.
Мы получили, что а, р и л рационально зависимы, а это
противоречит выбору углов аир. Следовательно, наше
предположение о том, что шар после каждого отражения от
боковой стороны попадает на основание АС, неверно т е
в последовательности его отражений от сторон треуголь-
треугольника обязательно встретится пара
... i-^.боковая сторона*-*боковая сторона*-* ...
Итак, периодическая траектория Г действительно содержит
такое звено XY, что Х^АВ, Y^BC.
Посмотрим, как движется шар после пролета по звену
XY (допустим, от X к У). В силу малости углов а и Р
отрезок А У либо параллелен основанию АС, либо наклонен
к АС под малым углом. «Выпрямляя» бильярдную траек-
траекторию, видим, что шар будет после пролета по отрезку XY
двигаться в /ВСА до тех пор, пока не столкнется с его
сторонами ВС и СА максимальное возможное число раз
Л'(Р) [—я/р] (см. § 15, п. Л); лишь после всех этих от-
отражений шар «вылетит» из /ВСА, т. е. начнет отражаться
только от сторон АВ и АС. Обратив движение шара во
вРем|™. аналогичным образом исследуем его движение
в /ВАС после пролета по звену XY от У к X. Шар будет
260
двигаться в /_ВАС до тех пор, пока не совершит в нем
максимальное возможное число отражений N(a)=—[—л/а].
Итак, траектория Г содержит не менее N (a, p)=min {N(a),
N (Р)} звеньев, что согласно выбору углов аир превосхо-
превосходит исходное число п. Теорема 2 доказана.
5. Теорема 2 показывает, что для многоугольника тео-
теорема Биркгофа «не работает». Это объясняется тем, что в
теореме Биркгофа рассматриваются строго выпуклые об-
области, границы которых являются гладкими кривыми, т. е.
не имеют изломов, как у многоугольников. Если начать
проводить доказательство этой теоремы для многоугольни-
многоугольников, то сразу видно «препятствие», не позволяющее ее дока-
доказать. Оно состоит в том, что нужная периодическая траек-
траектория из данного числа п звеньев имеет часть своих точек
излома ввершинах многоугольника, а такие траекто-
траектории нами не рассматриваются. Если границу многоуголь-
многоугольника у всех вершин «сгладить», то для полученной области
теорема Биркгофа уже будет верна, при этом все точки
излома у периодической n-звенной траектории (где «<С
<.N(a, P) из теоремы 2) будут сосредоточены на «сгла-
«сглаженных» участках, и только при ri>N (а, |3) шар начнет
отражаться от прямолинейных участков границы.
6*. Рассмотрим одно общее свойство бильярдных тра-
траекторий в произвольной области Q. Имеет место важная
Теорема 3. Почти любая бильярдная траектория
Г в области Q либо является периодической, либо проходит
сколь угодно близко и под сколь угодно малым углом к любой
своей точке.
Замечание. Теорема 3 отнюдь не утверждает, что
если бильярдная траектория в Q не периодична, то она всюду
плотна в Q. Напомним, что в конце § 26 указан пример об-
области Q, в которой построенная траектория не периодична
и не всюду плотна в Q. Другой пример Q-^круг.
Доказательство этой теоремы основывается на
рассмотрении фазового пространства системы. (Чи-
(Читателю мы рекомендуем здесь еще раз просмотреть § 3.)
А. Фазовое пространство. Множество на-
направлений, под которыми бильярдный шар может двигать-
двигаться с единичной скоростью, образует
а) окружность S1 в случае плоской области Q;
б) двумерную сферу S2 в случае пространственной об-
области Q (а если Q — и-мерная область, то (и—1)-мерную
сферу S").
Точками фазового пространства 12 являются пары
(<?, v), где q — положение шара в области Q (точка), а.
261
v — направление движения шара, когда он находится в
точке q; можно считать, что v — это точка (конец вектора)
на окружности S1 в двумерном случае, и точка на сфере
S" для больших размерностей.
Мы ограничимся здесь плоской областью Q; в общем
случае доказательство повторяется почти дословно, с за-
заменой «окружности» на «сферу». Окружность S1 можно
представлять себе в виде отрезка [0, 2л], у которого «скле-
«склеены» концы 0 и 2л. Фазовое пространство Q получается из
прямого произведения Q на S1, т. е. из множества пар (q, ч>),
где <?€Q, fCS1, некоторыми склейками. Его можно пред-
представить наглядно в виде призмы, в основании которой
Рис. 27.4
расположена область Q, а образующей является полуинтер-
полуинтервал [0, 2л). Надо помнить только, что многие точки грани-
границы этого цилиндра Q «склеены» — представляют совпадаю-
совпадающие точки (например склеены оба основания призмы —
нижнее и верхнее). Далее, вся призма «расслоена» на бес-
бесконечное число слоев — областей Q(v), причем Q(v) —
это исходная область Q, но снабженная пучком параллель-
параллельных отрезков в направлении v: шар на слое Q (v) движется в
направлении v, в какую бы точку его ни поместить. Можно
на плоскости, содержащей область Q, выбрать некоторую
ориентированную ось / и направление v заменить углом q>,
образованным этим направлением с осью /@<ф<2я).
Тогда шар после отражения от границы Q начнет двигаться
в направлении v', образующем некоторый новый угол ц.' с
осью / (рис. 27.4). В цилиндре п это будет отвечать тому,
что фазовая точка, двигаясь по слою Q(v)=QD>) и Дойдя до
его границы, «перескочит» на слой Q(z>')=Q(<p')> соответ-
соответствующие точки (А, ф) и (Л, ср') границ Q(q>) и Q(cp) при
этом склеятся друге другом. (Эта ситуация в точности соот-
соответствует описанию «скачущей» траектории из § 25, поэтому
советуем читателю еще раз перечитать начало § 25.)
262
Б. Фазовые траектории. Итак, фазовая тра-
траектория — это скачущие в цилиндре Q со слоя на слой от-
отрезки; если осуществить все склейки точек границы ци-
цилиндра типа (А, <р)~(Л, <р'), то получится непрерывная
кривая в трехмерном фазовом пространстве Q. В § 25 в ка-
качестве областей Q подробно рассматривались рациональ-
рациональные многоугольники, и в результате всех склеек возникала
непрерывная фазовая траектория, целиком расположенная
на некоторой двумерной поверхности — сфере с ручками
S(p). Этот важный факт нам пригодится позже. В общем
случае фазовая кривая не лежит ни на какой поверхности,
а каким-то сложным образом располагается в трехмерном
многообразии Q.
В. Теорема Лиувилля. Теорема состоит в
том, что бильярдный фазовый поток, т. е. совокупность
бильярдных преобразований St в фазовом пространстве Q,
сохраняет объем в Q. Это означает, что если в Q выделить
некоторую область 5?, то под действием бильярдного пре-
преобразования St эта область перейдет за время / в область
3l'—St{Ж) того же объема.
Докажем теорему Лиувилля в случае, когда выделение
области 5?ей — это одновременное выделение какой-то
площадки Р в бильярде Q и какого-то отрезка А на обра-
образующей цилиндра [0, 2л]. Затем одновременно из всех
точек {<?} площадки Р мы выпускаем с единичной скоростью
бесконечное число бильярдных шаров, каждый под своим
углом ф, отвечающим некоторой точке отрезка Д. Через
время t все шары займут новое положение {q'} и образуют
площадку Р'; при этом они будут двигаться под угла-
углами {ср'} из некоторого нового отрезка А' образующей ци-
цилиндра.
Пока шары движутся внутри бильярда Q, отрезок А на-
направлений их движения не меняется: А'=Д, при этом пло-
площадь Р' равна площади Р, а значит и объемы трехмерных
областей 5? и Э1' одинаковы (они равны произведению пло-
площади Р на длину отрезка А). Когда же происходит отраже-
отражение относительно границы Q, то, разбивая границу бильяр-
бильярда Q на мелкие дуги и заменяя каждую такую дугу малым
отрезком, получаем после процедуры «выпрямления» близ-
близких траекторий через этот малый отрезок, что площадь пло-
площадки Р' не изменилась и длина отрезка А' новых направ-
направлений движения шаров также не изменилось; стало быть,
не изменился и объем области Ж в цилиндре Q — он остал-
остался равным объему исходной области Л. Теорема Лиувилля
для бильярдов доказана.
263
Г. Теорема Пуанкаре о возвращении.
Таким образом, отображение St удовлетворяет условиям
теоремы Пуанкаре о возвращении: St(Q)=Q и 5, сохраняет
меру (объем) вй. А тогда из этой теоремы следует, что
почти все точки из любой окрестности U точки
(q, v)?Q снова возвращаются в ту же окрестность U. Это и
означает, что бильярдный шар вновь (притом бесконечное
число раз!) возвращается как в сколь угодно малую окрест-
окрестность своей исходной точки q бильярда Q, так и в сколь угод-
угодно малую окрестность исходного направления <р. Если би-
бильярдная траектория в Q периодична, то фазовая
точка приходит в точности в исходное положение (q, q>)
бесконечно много раз; если же бильярдная траектория в Q
непериодична, то можно показать, что в общем
случае она заполнит всюду плотно некоторую подобласть
фазового пространства Q.
Все сказанное выше верно в случае, когда число слоев
№(ф)} бесконечно. Для этого случая теорема 3 доказа-
доказана. Однако не всегда множество слоев {(?(ф)} бесконечно.
7*. Остановимся особо на случае, когда Q — рациональ-
рациональный многоугольник. Тогда множество {(?(ф)} состоит из
конечного числа слоев: бильярд-
бильярдный шар в многоугольнике, выпущен-
выпущенный ПОД ПРОИЗВОЛЬНЫМ УГЛОМ фо К
одной из своих сторон, после всевоз-
всевозможных отражений от границы много-
многоугольника может двигаться лишь в ко-
конечном количестве направлений ф0, Фь
Ф2|- • -I Ф^(РИС- 27.5). В § 24 было дока-
доказано, что после соответствующей склейки
слоев <2(ф0), Q{q>i), <3(ф2) Q(q>N)
возникает поверхность <М — сфера с
ручками, инвариантная (т. е. переходя-
переходящая в себя) относительно действия фазового (бильярдного)
гютока St. При этом фазовый поток St сохраняет, как было
уже сказано, фазовый объем, и опять применима теорема
Пуанкаре о возвращении. Из нее, в частности, следует, что
фазовая точка бесконечно много раз попадает в сколь угодно
малую окрестность точки (q, q>0), т. е. попадает в точки {q't
ф'), где \q—<?'|<е и |ф—ф' | <Z e (е — произвольное,
заранее выбранное малое положительное число). Но если
число е очень мало, т. е. меньше всех величин |фо—Фг1»
1ф~фу|, где i, /=!,. „N, \Ф1, то [ф„—ф'|<в при
т' € {фо! Ф1, • . ., ФаЛ будет выполняться лишь для ф'=
—-фо Следовательно, для рационального многоугольника Q
мы доказали более сильное утверждение.
Теорема 4. Любая бильярдная траектория Г в
рациональном многоугольнике пересекает любую окрест-
окрестность любой своей точки под одним и тем же направлением
(а не под сколь угодно близким).
Иными словами, бильярдный шар в рациональном мно-
многоугольнике Q может быть запущен под произвольным
фиксированным углом ф0 к выбранному направлению /
отсчета углов так, что он будет бесконечно много раз под-
подходить сколь угодно близко к своему начальному положе-
положению под тем же самым углом ф0 к прямой /.
Заметим, что о наличии периодической траектории в Q
теорема 4 ничего не говорит. Более того, § 26 дает примеры
траекторий, удовлетворяющих теореме 1, но не периоди-
периодических.
8. И тем не менее остается сделать еще один только ма-
маленький шаг, чтобы получить периодическую траекторию в
любом рациональном многоугольнике.
Теорема 5. В любом рациональном многоугольнике
Q существует периодическая траектория.
Доказательство*). Выберем в качестве оси /
из п. 6А произвольную сторону АВ многоугольника Q.
Положим в теореме 4 фо=я/2. Это означает, что шар послан
перпендикулярно стороне АВ.
Докажем, что в этом случае шар можно выпустить из
такой точки стороны АВ, что его движение будет периоди-
периодическим.
Действительно, согласно утверждению теоремы 4, шар
может быть запущен по прямой р\_АВ из точки С стороны
АВ так, что через некоторое время он снова будет двигаться
по некоторой прямой р', перпендикулярной АВ и проходя-
проходящей вблизи от р. Если прямая р' совпадает с р, то все дока-
доказано: шар отражается перпендикулярно от стороны АВ и
движется по первоначальной траектории. Не менее очевиден
*) Приводимое доказательство предложено А. М. Степиным.
Недавно американский математик Г. Мазур, используя мощные
современные аналитические методы, доказал, что множество на-
направлений звеньев периодических траекторий всюду плотно на
окружности S1 , т. е. звенья периодической траектории в рациональ-
рациональном многоугольнике могут образовывать сколь угодно малый угол
с любой наперед выбранной прямой. Таким образом, узких пучков
параллельных периодических траекторий в рациональном много-
многоугольнике в действительности бесконечно много. Преимущество
геометрического доказательства состоит в том, что оно обобщается
и на рациональные многогранники (см. п. 10).
265
и случай различных прямых р и р'\ если шар движется по
прямой р' от стороны АВ, то следовательно, перед
этим он двигался по прямой р' кстороне АВ. Значит,
после отражения от стороны Л б шар пойдет вточности
пи тому же пути, по которому он двигался до отражения, но
в обратном направлении. А это и означает, что траектория
его движения — периодическая. Теорема 5 доказана.
Следствие. В любом рациональном п-угольнике Q
существует не менее п/2 несовпадающих периодических тра-
траекторий, имеющих разные наборы сторон, с которыми
происходят столкновения шара.
Доказательство. По теореме 5 периодическую
траекторию можно направить перпендикулярно каждой
из п сторон многоугольника. Однако эти траектории могут
иметь один и тот же набор сторон. Поскольку никакая
траектория не может иметь звенья, перпендикулярные
более чем двум сторонам многоугольника, получаем,
что не менее п/2 из этих траекторий имеют разные наборы
отражений. Следствие доказано.
Нетрудно построить л-угольник, в котором ровно
п'2 различных периодических траекторий со звеньями,
перпендикулярными сторонам: это любой 2/г-угольник («=
=2k) с попарно параллельными сторонами (например,
правильный 2/г-угольник).
Из теоремы 5 получается очень красивая геометрическая
картина на той инвариантной поверхности, которая склеи-
склеивается из нескольких экземпляров данного многоугольника.
Эта поверхность в общем случае является сферой с р руч-
ручками S (/?) и некоторым количеством особых точек — муль-
тиседел разных типов (см. § 25). На этой поверхности
«перпендикулярная» периодическая" траектория Г, пост-
построенная в доказательстве теоремы 5, замкнута и, разумеется,
не попадает ни в одну особую точку. Начав двигать по сто-
стороне А В точку С, из которой перпендикулярно АВ запу-
запускается шар, видим, что траектория Г будет периодической
тогда и только тогда, когда она не попадает ни в одну особую
точку на поверхности S(p). Это соответствует тому, что
перпендикуляр р, восстановленный в точке С на основании
АВ, не проходит ни через одну из вершин многоугольников,
полученных отражениями из исходного многоугольника Q
при выпрямлении траектории Г (при этих отражениях
траектория Г переходит в перпендикуляр р; рис. 27.6).
Как только перпендикуляр р пройдет через какую-то вер-
вершину одного из отраженных многоугольников, так сразу
траектория Г попадет в особую точку на поверхности S(p).
866
Рис. 27.6
Из рис. 27.6 видно, чтодлявсех точек С, лежащих
на интервале dC2czAB, где Сь С2 — основания перпен-
перпендикуляров рх и р2 к прямой АВ, проходящих через две
вершины отраженных многоугольников, запущенный из
точки С шар опишет периодическую траекторию одной и
той же длины. Перпендикуляры
Pi и р2 задают «коридор» перио-
периодических траекторий равной
длины. Можно доказать (этого
мы делать здесь не будем), что
весь отрезок АВ разбивается на
конечное число отрезков,
каждый из которых задает се-
семейство периодических «перпен-
«перпендикулярных» траекторий одина-
одинаковой длины (траектории в воз-
возникающих «коридорах» имеют
одинаковую последовательность
отражений). Отсюда следует,
что длины «перпендикулярных»
траекторий ограничены.
9. Вернемся вновь к периодическим траекториям в тре-
треугольниках. Пусть аир — величины острых углов А и С
/\АВС: 0<а, P<Ot/2. Проведем на плоскости две взаимно
перпендикулярные оси и будем отмечать на горизонталь-
горизонтальной оси величину угла а, а на вертикальной — величину
угла р. Пара (а, C) характеризует (с точностью до подобия)
треугольник ABC, которому поставим в соответствие одну
точку М с координатами (а, р) на плоскости Оар. Напри-
Например, точке М=(л/3, л/3) соответствует равносторонний
треугольник, а точке М=(я/4, л/4) — равнобедренный
прямоугольный треугольник.
Задача 27.1. а) Какие треугольники соответствуют точкам
(л/6, л/3); (л/100, л/100); (а, р), где а+Р>л/2; а+р<л/2? б) Ка-
Каким треугольникам отвечают точки иа плоскости Осф, отстоящие
от начала координат @, 0) на расстояние, меньшее л/100?
Ответ, а) Прямоугольный; равнобедренный тупоугольный;
остроугольный; тупоугольный, б) Тупоугольные треугольники с
тупым углом y>A00—]/)л/100.
Множество точек (а, Р) на плоскости Оар заполняет
в первой четверти квадрат OXYZ без границы со стороной
л/2: 0<а<л/2, 0<Р<я/2. Этот квадрат назовем «диаграм-
«диаграммой треугольников» D.
Отметим на диаграмме D те точки (а, Р), для которых в
отвечающих им треугольниках с острыми углами аир
существует периодическая траектория.
267
Из теоремы 1, доказанной выше, следует, что на диаграм-
диаграмме отмечены все точки, идущие выше диагонали XZ квад-
квадрата OXYZ, соединяющей вершины Х= (О, л/2) и Z—
= (л/2, 0) (рис. 27.7, а). Действительно, верхний (закра-
(закрашенный) /\XYZ на рис. 27.7, а отвечает всем остроуголь-
остроугольным треугольникам, поскольку для этих точек а+р>
>д/2, а тогда третий угол треугольника у=п—(а+р)<
<я/2 — острый.
Всем точкам /\XOZ на диаграмме D под диагона-
диагональю XZ квадрата отвечают тупоугольные/\АВС, посколь-
поскольку при а+р<Ьт/2 тре-
третий угол треугольника
у=я—(а+Р)>д/2 — ту-
тупой (все прямоугольные
треугольники отмечены
точками самой диагона-
0@0)—7(krf\ о""'"'"""'"'Z ли xz)- Если каждый
' ^'" ¦"' из углов аир соизме-
соизмерим с п, т. е. если а—
= (p/q)n, р=(т/и)л, р,
q, m, n — целые числа,
то /\АВС — рациональный (третий угол у тоже соизмерим
с л); отсюда по теореме 5 в /\АВС существует периоди-
периодическая траектория. Следовательно, на диаграмме D отме-
отмечены все рациональные точки в треугольнике OXZ, запол-
заполняющие его всюду плотно (рис. 27.7, б). Множество таких
точек счетно, а его мера (площадь) равна 0.
Однако можно указать в /\0XZ более «массивное» мно-
множество отмеченных точек, имеющее ненулевую площадь.
Оно возникает при рассмотрении следующих трех конст-
конструкций, уже не связанных с соизмеримостью углов аир
с д.
Конструкция I.
Теорема 6. Пусть острые углы а и р /\АВС связаны
соотношением ka=m$<.n/2, где k и т — некоторые нату-
натуральные числа. Тогда в /\АВС существует периодическая
траектория.
Доказательство. Отразим /\АВС зеркально k—1
раз относительно своих сторон, начиная g отражения отно-
относительно стороны А В а двигаясь против часовой стрелки
(при каждом таком зеркальном отражении вершина А
неподвижна) и т раз относительно своих сторон, начиная о
отражения относительно стороны АС и двигаясь также
против часовой стрелки (при этих отражениях неподвижна
268
в'.
вершина В — см. рио. 27.8). «Конечные» стороны отражен-
отраженных треугольников АВ' и С А' в силу равенства ka—m§ бу-
будут параллельны друг другу: АВ' || СА', а в силу условий
ka<Lnl2, mP<3i/2, к сторонам АВ' и С А' можно провести
общий перпендикуляр #i#2, целиком лежащий в «коридо-
«коридоре» отраженных треугольников (рис.
27.8). Если запустить бильярдный
шар по отрезку Н±Н2, считая АВ' и
СА' отражающими стенками, то он
будет совершать периодическое движе-
движение Hi—H2—Hi—H2—Ht—Hs—. . .
между АВ' и СА'. Следовательно,
сделав обратные отражения треу-
треугольников (ft отражений по часовой
стрелке с неподвижной вершиной А
и т-\-\ отражений по часовой стрел-
стрелке с неподвижной вершиной С), «свер-
«свернем» отрезок HtH2 в бильярдную тра-
траекторию в /\АВС, которая, очевид-
очевидно, будет периодической, что и тре-
требовалось доказать.
Задача 27.2. Из какого числа ввеньев состоит построенная
периодическая траектория?
Замечание 1. Из теоремы 6 следует, что в любом
равнобедренном треугольнике существует периодическая
Рис. 27.8
Рис. 27.9
бильярдная траектория из д в у х звеньев (рис. 27.9, а).
Однако если острый угол а при основании АС таков, что
па<п/2 при некотором п, то существуют периодические
траектории из четырех, шести,. . ., 2« звеньев (рис. 27.9, о).
Вообще, если обе части равенства ka=mf> можно умно-
умножить на такое число п, чтобудет по-прежнему п»/га=п-тР<
<я/2, то из равенств 2-ka=2-mP, 3-/га=3-яф, . . .
269
p
. . ., n'ha=n-in$ и приведенных выше рассуждений сле-
следует, что в ДАВС существуют периодические траектории
из k+m, 2(k+m), 3(k+m), . . ., n(k+m) звеньев. «Парал-
«Параллельные» им периодические траектории состоят из того
же числа звеньев.
Замечание 2. В равнобедренном рациональном
треугольнике есть еще один замечательный тип периоди-
периодических траекторий: если у траектории Г одно звено у па-
параллельно основанию АС, то Г — периодическая траекто-
траектория. Это следует из теоремы 4.
Действительно, по теореме 4, сколь угодно близко к зве-
звену у проходит другое звено у' траектории Г, параллельное
<S> (быть может, у' и у сов-
совпадают). Запустим из точки
М пересечения высоты ВН
и звена у в противопо-
противоположных направлениях од-
одновременно два одинако-
одинаковых бильярдных шара с
равными скоростями. Через
некоторое время они одно-
к временно окажутся в точке
М' пересечения высоты ВН
и звена у', двигаясь на-
навстречу друг другу, от-
Рис. 27.10 толкнутся друг от друга и
начнут двигаться симмет-
симметрично в обратных направлениях по уже пройденному пу-
пути Следовательно, через какое-то время шары вновь ока-
окажутся в точке М на звене у, столкнутся, и процесс начнет
повторяться. Это и доказывает, что траектория Г — пе-
периодическая. (Более того, отсюда вытекает, что у Г имеется
но более двух звеньев, параллельных АС.)
Аналогичное утверждение справедливо для любого
ргшионального многоугольника Q, имеющего ось симметрии:
послав шар перпендикулярно этой оси, получаем периоди-
периодическую траекторию. Удовольствие повторить приведенное
рассуждение для этого случая мы предоставляем читателям.
Конструкция I (теорема 6) дает на треугольнике OXZ
диаграммы D «веер» отрезков, лежащих на прямых {р=
~(k/m)a}, начинающихся в начале координат (Q, 0) и кон-
кончающихся в точках {(л/ Bk), n/Bm))}, где k am — всевоз-
всевозможные натуральные числа (рие. 27.10). «Веер» состоит из
счетного множества отрезков и имеет нулевую плоскую
?70
Конструкция П.
Два других «веера» отрезков, выходящих на диаграмме D
из точек (я/2, 0) и @, л/2), дает следующая теорема.
Теорема 7. Если острые углы а и р ?\АВС связаны
равенством а+/ф=п/2, где k — натуральное число, причем
2а+р>я/2, то в ДА ВО существует периодическая траек-
траектория. То же имеет место для треугольников, у которых
Р+А:а=я/2, 2р+а>я/2.
Следствие. В любом прямоугольном треугольнике
существует периодическая траектория (для доказательст-
доказательства в теореме 7 достаточно п ,
положить k=l).
Доказательст-
в о. Сделав k симметрич-
симметричных отражений ДАВС по
и против часовой стрел-
стрелки, при которых вершина
С, отвечающая углу р, не-
неподвижна, получим симмет-
симметричный относительно пря-
прямой АС «веер» А В . . .
. РСР'. . .В'А треуголь-
треугольников на плоскости (рис. 27.11). Рассмотрим «ромбоид»
АВСВ' и в нем отрезок ММ', параллельный диагонали ром-
ромбоида ВВ' и близкий к ней (ММ'\_АС). Выпустим по от-
отрезку М'М бильярдный шар. В силу неравенства 2а+
+ Р>п/2 шар после отражения от стороны АВ пойдет
по прямой MN, пересекающей все стороны треуголь-
треугольников, лежащих в левой полуплоскости, ограниченной
прямой АС (проверьте это!). Затем он отразится по
бильярдному закону от стороны СР последнего треуголь-
треугольника в точке N, и, в силу равенства a+k$—n/2, пойдет по
отрезку NN', параллельному MM' (NN'_[_АС; проверьте
это). Оказавшись в правой полуплоскости, шар отразится
от стороны СР' соответствующего треугольника в точке W
и опишет симметричную полутраекторию в правой полупло-
полуплоскости.
В результате шар опишет периодическую, симметрич-
симметричную относительно прямой АС, четырехзвенную траекторию
M'MNN' в «веере» треугольников АВ. . .РСР'. . .В'А.
Сложив этот веер «гармошкой», свернем траекторию
M'MNN' в периодическую траекторию Г в исходном тре-
треугольнике ABC. Теорема 7 доказана.
«Веерная» конструкция из треугольников АВ. . .РСР'...
. ..В'А дает «веер» надиаграмме?>: он образован отрезками,
271
выходящими из точки Z диаграммы в направлении точек
(О, л/2), @, л/4), @, л/6), . . ., (О, nlBk)),. . .; вторые
концы этих отрезков лежат на прямой 2а+р=я/2, соеди-
соединяющей точку X диаграммы с
точкой (я/4, 0) (рис. 27.12).
Аналогичный «веер» выхо-
выходит из точки X. Отрезки пер-
первого «веера» лежат на прямых
in 1 , л)
¦sP = — ~ka'~2kh «сгущаю-
«сгущающихся» к оси Оа, а второго-
на прямых <|3 = —
«сгущающихся» к оси
Замечание. Приве-
Приведенная здесь конструкция в
точности повторяет идею тео-
теоремы 5, но не использует «ра-
«рациональности» углов треугольника. А именно, периодичес-
периодической является любая траектория в рассматриваемом треу-
треугольнике, два звена которой перпендикулярны основанию
/1С*.
Конструкция III(устойчивые траектории).
В этой конструкции будут фигурировать неравенства,
связывающие углы аир, которые дадут сразу целые о б-
ласти отмеченных на диаграмме D точек.
108 6 4
Рис. 27.12
Рис. 27.13
Рассмотрим для тупоугольного ?\АВС с острыми углами
аир такие натуральные числа k и т, что &сс<я/2 и /«р<
<л/2, но (&+1)сс>я/2 и (/?г+1)Р>я/2. Сделаем к— 1 зеркаль-
зеркальных отражений /_ВАС\\ т—1 зеркальных отражений /_АСВ
так, чтобы «крайние» лучи АА' и СС образовывали с пря-
мой АС углы ^Л'ЛС=А'а и /С'СА=т$, лежащие в
верхней полуплоскости (рис. 27.13, а). Эти крайние лучи
лежат в «коридоре» между перпендикулярами pt, p2 к отрез-
отрезку АС, восставленными в его концах Л и С. Следователь-
Следовательно, лучи АА' и СС пересекаются; точку их пересечения
обозначим В'.
Задача 27.3. Доказать, что ДЛВ'С — остроугольный.
В остроугольном ДЛВ'С построим, согласно теореме 1,
периодическую бильярдную траекторию НгН2Н%, точки
излома которой — основания высот СНи АН2 и В'Н3
(рис. 27.13, б). Если отрезок #i//2 будет пересекать исход-
исходный /\АВС, т. е. этот отрезок будет лежать ниже вер-
вершины В, то сделав (k—l)+(m—1) «обратных» зеркальных
отражений образов углов /_ВА Си /_ВСА вместе с кусками
траектории HiH2Hs, мы переведем бильярдную траекторию
HiH2Hsb /\^AB'C в периодическую бильярдную траекторию
в исходном тупоугольном /\АВС, содержащую 2(k—1)+
+2{т— 1)+3=2(/г+т)—1 звеньев.
Итак, необходимым и достаточным условием (крите-
(критерием) существования в тупоугольном ДЛВС периодической
траектории рассматриваемого вида является прохождение
отрезка Н\Нг ниже вершины тупого угла В. Очевидно, что
если острые углы а и р в /\АВС немного «пошевелить» произ
вольным образом, т. е. заменить {\АВС на /\AiBid с остры-
острыми углами cti и Pi, мало отличающимися от а и р соответст-
соответственно, то в нем также будет существовать периодическая
траектория рассматриваемого вида. Отсюда вытекает, что
на диаграмме D отмеченные точки для данных k и т
займут целую область. Следующее неравенство является
критерием того, что отрезок //i//2 пересекает ДА ВС.
Утверждение 1. Отрезок Н^Н, проходит ниже
вершины В (пересекает А А ВС) тогда и только тогда,
когда выполнено неравенство
tg (-g—fto) ctgp+ tg (f-mp) ctga <
)(i) A)
или эквивалентное ему неравенство
A — ctg ka• tg a) A —ctg mP• tg P) > 1 — tg a tg p. (Г)
Утверждение 1 мы предоставляем доказать читателю
самостоятельно, оставляя его в качестве не очень сложной,
но довольно громоздкой элементарной геометрической
задачи.
273
Неравенства A), (Г) задают бесконечное (счетное) число
областей на диаграмме D, которые нумеруются парами
натуральных чисел (к, т). Приведем несколько более удоб-
удобных последовательных ослаблений точного неравенства A),
которые также гарантируют прохождение отрезка ЯхЯа
ниже вершины В:
B)
C)
D)
п
tga
— mP
Р
*#
Эти неравенства задают все меньшие и меньшие области по
сравнению с областью, задаваемой неравенством A). На их
доказательстве останавливаться мы также не будем. Приве-
Приведем множество точек на диаграмме D, задающееся неравен-
неравенством A) (на рис. 27.14, а изображены последовательно
Ж.
2п
14 12 10 в
IL
&¦
к-т-2
Рис. 27.14
вложенные области A)зB)г)C)зD) для k=m—2y а на
рис. 27.14, б—ьб6льшая часть множества A)). Это множест-
множество состоит из объединения бесконечного числа серий ча-
частично пересекающихся криволинейных «равнобедренных»
«прямоугольных» треугольников, идущих вниз и влево от
«базового» треугольника с вершиной (у-, у-), где я=2,
3, 4, ... Кривые границы задаются выражением A), в
274
котором знак неравенства заменен знаком равенства, и
очень похожи на куски эллипсов (неравенство C), заменен-
замененное на равенство, дает в точности уравнение эллипса)
Таким образом, доказана
Теорема 8. Если в тупоугольном ДА ВС острые
углы а « р удовлетворяют неравенствам
с целыми киши одному из неравенств A), B), C) или
D), то в нем существует периодическая траектория из
2(k-\~m)—1 звеньев и пучок «параллельных» ей периодиче-
периодических траекторий из вдвое большего числа звеньев.
fi
X
1 , •<* V». IV
zv о s z<s
Рис. 27.15
Завершающий этап в исследовании периодических биль-
бильярдных траекторий в треугольниках состоит в одновремен-
одновременном изображении всех отмеченных ранее точек на диаграм-
диаграмме D. Это изображение получится, если мы наложим все
диаграммы рис. 27.7, 6, 27.10, 27.12 и 27.14, б друг на друга
с изображенными на них множествами точек. В результате
получим диаграмму D, которая изображена на рис. 27.15, а.
На рис. 27.15, б изображено гипотетическое множество
точек, отвечающих высказанной в начале этого параграфа
гипотезе,— полностью зачерненный квадрат OXYZ.
Вообще следует сказать, что периодические траектории
весьма чувствительны к форме треугольника. Причина
разрушения или рождения периодической траектории —
прохождение через угловую точку границы. Этим обстоя-
обстоятельством объясняется замысловатый характер фигуры
рис. 27.14,6, изображающей множество тупоугольных
треугольников с периодическими траекториями, построен-
построенными в конструкции III.
10*. Завершим этот параграф пространственным анало-
аналогом теоремы 5. Проведем через произвольную точку О
275
пространства плоскости, параллельные всем граням некото-
некоторого многогранника Q, и начнем совершать относительно
них зеркальные отражения. После каждого отражения будут
получаться, кроме исходных плоскостей, новые плоско-
плоскости, относительно которых также будем производить отра-
отражения.
Будем рассматривать многогранники Q со следующим
свойством: в результате всех возможных отражений отно-
относительно исходных и вновь возникающих плоскостей полу-
получится лишь конечное число направлений, перпендикуляр-
перпендикулярных этим плоскостям. Многоугольник Q на плоскости,
обладающий таким свойством, является рациональ-
рациональным — все его углы соизмеримы с п. По аналогии много-
многогранник Q мы будем также называть рациональным — все
двугранные углы между любыми двумя его гранями также
соизмеримы с я (докажите!). (Правда, в отличие от плоского
случая одной только рациональности углов нам будет не-
недостаточно.)
Все рациональные многогранники классифицированы
для всех размерностей пространства. Среди них имеются
многогранники, которые в научной литературе носят, в
честь знаменитого математика Германа Вейля, название
«камера Вейля» и появляются при изучении современного
алгебро-геометрического раздела математики — теории
групп и алгебр Ли. Из камер Вейля составляются рацио-
рациональные многогранники. (Камеры Вейля возникают и в
современных исследованиях по механике и физике.)
Как и для рациональных многоугольников, для рацио-
рациональных многогранников справедливо следующее утверж-
утверждение.
Утверждение 2. Б рациональном многограннике
при движении по бильярдным траекториям из данного
начального направления может получиться только конеч-
конечный набор направлений движения.
Доказательство. «Выпрямляя» бильярдную
траекторию, т. е. производя зеркальные отражения относи-
относительно тех граней многогранника, на которых расположены
точки излома траекторий, в силу рациональности многогран-
многогранника получаем, что в какой-то момент будет произведено
отражение относительно плоскости, параллельной уже
ранее рассмотренной грани. Это означает, что направление
движения бильярдного шара в этот момент совпадает g
одним из предыдущих его направлений движения. Следова-
Следовательно, общее количество направлений движения бильярд-
бильярдного шара конечно, что и требовалось доказать.
276
Из этого утверждения вытекает
Теорема 8. В людом рациональном многограннике Q
существует бесконечно много периодических бильярдных
траекторий.
Доказательство почти дословно повторяет дока-
доказательство теорем 3, 4 и 5. Действительно, фазовое прост-
пространство Q бильярдной системы в Q получается из прямого
произведения QxSn~l (S"'1—(и—1)-мерная сфера на-
направлений движения шара, если Q—л-мерный многогран-
многогранник) некоторыми склейками (отождествлениями точек), а в
силу рациональности многогранника Q и утверждения 2
фазовая траектория в & располагается лишь в конеч-
конечном числе «слоев» — в многогранниках Q(cp0), Q(<Pi), . . .
• • • t <2(фт): в них шар движется в направлениях ф„, фь. . .
..., фт. По теореме Пуанкаре о возвращении получаем, что
фазовая точка вернется в сколь угодно близкую к начальной
точку, причем под тем же направлением, под каким начала
двигаться (см. теорему 4).
Если исходный угол вылета шара равен фо=я/2, то шар
может быть выпущен из такой точки фиксированной грани
многогранника перпендикулярно ей (этих точек бесконечно
много), что через некоторое время он столкнется с этой же
гранью опять под прямым углом (см. теорему 5). После от-
отражения шар начнет двигаться в обратном направлении по
той же траектории. Следовательно, указанная траектория
движения является периодической. Если число граней у Q
равно N, то аналогичных «ортогональных» бильярдных
траекторий не менее Л72 — по одной для каждой грани
(с учетом того, что для каких-то двух граней может полу-
получиться та же самая траектория). Вокруг каждой периоди-
периодической траектории имеется целый пучок «параллельных»
ей периодических траекторий, поэтому множество периоди-
периодических траекторий в рациональном многограннике Q бес-
бесконечно. Теорема 8 доказана.
Доказательство существования периодической траек-
траектории в любом многограннике до сих пор не известно. На-
Напомним только, что почти любая бильярдная траектория Г
в любой области Q подходит к любой своей точке q ? Г
сколь угодно близко и под сколь угодно малым углом (теоре-
(теорема 3).
Задача 27.4. В правильном треугольнике, как и в любом
остроугольном, существуют периодические траектории из трех и
из шести ввеньев (рис. 27,2). Существуют ли в правильном тре-
треугольнике периодические траектории из ббльшего числа ввеньев?
Из сколь угодно большого числа ввеньев?
277
Задача 27.5. Бильярдный шар, отражаясь от сторон пра-
правильного треугольника, прошел через некоторую точку 7 раз.
Доказать, что он пройдет через эту же точку еще хотя бы один раз.'
Останется ли верным это утверждение, если заменить число 7 на 6?
Задача 27.6. Дай рациональный многоугольник Q. Дока-
Докажите, что существует число n—n(Q), обладающее следующим свой-
свойством: если бильярдный шар в Q прошел через некоторую точку л
раз, то он пройдет через нее еще хотя бы раз, а если шар прошел че-
через эту точку меньше л раз, то, вообще говоря, через нее он может
больше и ие пройти.
Задача 27.7. Докажите утверждение задачи 26.6 для ра-
рациональных многогранников (многогранников Вейля). Указа-
Указание. Воспользуйтесь утверждением 2 из п. 27.10.
Задача 27.8* (Г. А. Гальперин, А. М. Степин). а) Докажите,
что ни в каком треугольнике с попарно различными сторонами
иет четырехзвенной периодической траектории, б) Существует ли
остроугольный треугольник, имеющий периодическую траекторию
из 5 звеньев? Из 7? Ответьте на этот вопрос для любого нечетного
числа 2fe+l, fe>3. в)** Постройте периодическую траекторию из
16 звеньев в тупоугольном треугольнике с углами а и р4, удовле-
удовлетворяющими условиям
Т~"\Ш<а<Т- f<P<3«-
Решение, а) Предположим, что в некотором треугольнике
имеется четырехзвенная периодическая траектория. Тогда какие-то
д в е из четырех ее точек излома А, В, С, D находятся на одной
стороне треугольника, а две другие иа этой стороне не лежат.
Пусть, например, иа стороне MN треугольника лежат точки В
и D. Однако хорошо известно, что на прямой MN существует
только одна точка X, для которой ?АХМ= ?CXN (см.
рис. 4.1). Следовательно, точки В и D совпадают, и наша траек-
траектория оказывается двухзвенной, что противоречит сделанному
предположению.
б) Искомый треугольник существует в обоих случаях. Строится
он так, как об этом рассказано в конструкции III.
Если остроугольный /\АВС таков, что ^б<л/4, то, отразив его
симметрично относительно стороны ВС, продлим сторону ВА'
полученного ?\А' ВС до пересечения в точке С" с продолжением
vTopoHbi AC исходного треугольника. Легко видеть, что возникаю-
возникающий ?\АВС — остроугольный (?ABC'=2?B<nl2, C<?BCA<
<л/2) и поэтому в нем существует трехзвенная периодическая
траектория, точки излома Hlt Нг, Нй которой — основания высот
Д/4ВС. Заметим, что высота BHS является одновременно высотой
н в Д/46С, поэтому точка Hs лежит внутри отрезка АС, а не иа его
продолжении СС (как могло бы случайно оказаться). Кроме
того, Нг?ВА'. Отразив теперь симметрично относительно прямой
ВС часть трехзвенной траектории HiH2Hs, лежащей вне?\АВС,
получаем 5-звенную периодическую траекторию ъ/\,АВС. Другая
Б-звениая периодическая траектория получается тем же способом,
если сделать вначале зеркальное отражение ДЛВС относительно
стороны АС.
Аналогично строится остроугольный Д/46С, содержащий
7-звенную периодическую траекторию: если ^В<л/6, то надо
сделать два зеркальных отражения Д/46С вокруг вершины В
278
против чаговой стрелки, продлить сторону ВА" у получившейся
фигуры Ф=ВАА'А" до пересечения в точке С" с продолжением
стороны АС, и построить трехзвеиную периодическую траекторию
НхН%Нъ в остроугольномДЛбС", целиком расположенную в фигуре
Ф. (Принадлежность траектории НХН2Н3 фигуре Ф можно доказать
непосредственно — оставляем это читателю, а можно, проверив
выполнение неравенства (Г) из конструкции III, справедливое
для рассматриваемого треугольника.) Сворачивая затем фигуру Ф
в трехслойную «гармошку», т. е. делая последовательно обратные
отражения зеркально-симметричных треугольников вместе с рас-
расположенными в них частями траектории НхНгНа, получим 7-звен-
ную периодическую траекторию в Д46С. Другая 7-звенная тра-
траектория получится, если делать отражения ?\АВС вокруг вершины
В по часовой стрелке. Заметим, кстати, что вДЛбС одновременно
имеются и две Б-звенных периодических траектории (почему?).
Вообще, если ?B<.nl2k (при этом углы А и С превосходят
~2~~~2?< поскольку ?^АВС остроугольный), то вокруг вершины В
можно сделать k—1 зеркальных отражений Д46С, а затем, получив
«коридор» Ф для частично выпрямленной траектории, по указан-
указанному выше рецепту построить остроугольный ?\АВС и трехзвен-
ную (частично выпрямленную) траекторию в нем, которая при
сворачивании «коридора» Ф в гармошку даст 3+2(?—1)=2?+1-
звеннуго периодическую траекторию ъ/\,АВС. В этом же треуголь-
треугольнике имеются также н периодические траектории из 2k—1, 2k—3,. ..
. . ., 5 и 3 звеньев — это следует из того, что описанную проце-
процедуру отражений можно проделать k—2, k—3, . . . раз. Таких
траекторий довольно много — ведь кроме «большого» остроуголь-
остроугольного ДЛбС можно строить и другие остроугольные треугольники
с вершиной В, вмещающие в себя «коридор» Ф, а затем чертить в
них соответствующие периодические траектории.
в) Построим периодическую траекторию в/\АВС, углы кото-
которого а= ?_ВАС и Р= ?ВСА удовлетворяют неравенствам
Пусть точка А' симметрична точке А относительно прямой ВС,
В' — точке В относительно А 'С, С" — точке С относительно А'В'
F — точке С относительно А В, F' — точке С относительно AF
(рис. 27.16). Поскольку Р>зг/3, точка В' лежит ниже прямой АС:
//4Сб'=Зр>л. Пусть Е — точка пересечения отрезка А'В' с
прямой АС. Так как в ?\А'ЕС угол А'ЕС равен л—(а+(л—2Р))=
=2Р—а>2л/3—а>2л/3—я/8>л/2, точка С", как симметричная
точке С относительно А'В', лежит ниже прямой АС. Оказывается,
что прямая А'С наклонена влево, т.е. ?A'DC — острый:
?_A'DC=n— Bа+(л—2Р))=2(Р— се)<4а<4-л/8=л/2. Из усло-
условий на а и р следует, что ?F'AC и /_A'DA — острые.
Докажем, что в остроугольном ?sAND, образованном прямыми
AD, AF' и DA' основание высоты Ни опущенной иа AD, принад-
принадлежит отрезку АС. Действительно, /_A'DA=2fi—2a<Aa.= ?.F'AD
(здесь использовано неравенство Р<3а) и поэтому достаточно
ваметить, что CD<AC. Последнее неравенство выполнено, по-
поскольку сторона CD в Д/4'CD лежит против угла CA'D, равного 2а
и меньшего угла A'DC, противолежащего стороне А'С и равного
2Р—2а Bа<эт/4<эт/3<Р).
27Э
Пусть #2 и #э — основания высот, опущенных на боковые
стороны Д/4/VD. Каждый из углов ДЛ ND при вершинах А и D
отличается от л/2 меньше, чем на 0,004 (проверьте!), поэтому от-
отрезок НгНв пройдет ниже точки В. Фигуру Ф, составленную из
7 треугольников, равныхДЛйС (см. рис. 27.16), наложим «гармош-
Рис. 27.16
кой» на ДДВС. При этом периодическая траектория y^^i
в Ф перейдет в периодическую траекторию вДЛВС, состоящую
из 15 звеньев. Задача в) полностью решена.
Заметим, что построенная траектория у вДЛВСиз задачи
27.8 в) устойчива: это означает, что при небольшой
деформации ДЛiЗC (т. е. небольшими изменениями углов п.
и р при его основании) она переходит в близкую к у 15-
звенную периодическую траекторию.
Общий способ построения тупоугольных тре-
треугольников с устойчивыми периодическими траекториями
таков (частный случай изложен выше в конструкции III).
280
Пусть для треугольника До с вершинами А, В, С и
острыми углами а, р при основании АС построена цепочка
треугольников
A-2I» ••¦! Д-1> До» Al> •••» Д2*»
пересекающихся с горизонтальной прямой АС и верхней
полуплоскостью, причем соседние треугольники цепочки
имеют общую сторону и симметричны относительно нее.
Поскольку результат применения двух последовательных
отражений относительно непараллельных осей есть пово-
поворот, то треугольник Д_2г повернут относительно До на
некоторый угол nia+n2$+nsn; аналогично, треугольник
Дгь повернут относительно треугольника До на угол /^а-Ь
+m2p+msn. Предположим, что пары целых чисел {щ, л2)
и (mi, т2) непропорциональны, а треугольники Д_2, и
Дай имеют стороны, перпендикулярные прямой АС. Если к
тому же на прямой АС нет других вершин треугольников
цепочки, кроме А и С, то оказывается, что сколь угодно
малым изменением углов аир можно получить треуголь-
треугольники, имеющие устойчивые периодические траектории.
Остается только заметить, что построенная в решении
задачи в) 15-звенная периодическая траектория получается
применением этой общей конструкции к прямоугольному
треугольнику с углом л/8.
ЗАКЛЮЧЕНИЕ
Изложенные в книге результаты о поведении
бильярдных траекторий в специальных областях — круге,
эллипсе, прямоугольнике, «рациональных» многоуголь-
многоугольниках — дают лишь первые, начальные сведения о теории
бильярдов. Хотя эти результаты красивы и интересны,
но они, по сути дела, составляют лишь небольшой «остро-
«островок» в теории бильярдов.
Начало современной теории бильярдов было положено в
трудах Я. Г. Синая. В 1970 г. им была опубликована фун-
бильярд Синай
Рис. 3.1 Рис. 3.2
даментальная работа [17], в которой введен и изучен боль-
большой класс бильярдных систем — так называемых рассе-
рассеивающих бильярдов, которые впоследствии стали называть-
называться «бильярдами' Синая».
Бильярды Синая устроены так: их граница состоит из
кусков выпуклых кривых (в пространстве — кусков выпук-
выпуклых поверхностей), обращенных своими выпуклостями
внутрь бильярдной области (рис. 3.1). Эти бильярды явля-
являются рассеивающими: любой (не обязательно узкий) пучок
бильярдных частиц, летящих параллельно, после отраже-
отражения от выпуклой стенки разлетается расходящимся веером
(рис. 3.2) и остается расходящимся при всех последующих
отражениях от границы бильярдной области. Эта ситуация
кардинально отличается от той, которая имеет место, ска-
282
жем, для бильярда в многоугольнике, где параллельный
пучок после столкновения с прямолинейной стенкой оста-
остается по-прежнему параллельным, если только не попадает в
вершину. В бильярде Синая близкие вначале бильярдные
траектории с течением времени достаточно быстро расхо-
расходятся и угол между соседними траекториями первоначально
параллельного пучка возрастает после каждого отражения
от границы. Поскольку площадь области Q конечна, траек-
траектории бесконечной длины начинают со временем перепуты-
перепутываться, ,что приводит к хаосу.
На строгом математическом языке это обстоятельство
находит свое выражение в следующем важном свойстве
бильярдных траекторий (см. [17]): в рассеивающих бильяр-
бильярдах имеет место эргодичность, т. е. типичная траектория
бильярдного шара проходит сколь угодно близко от любой
точки q бильярда Q, причем во всевозможных направле-
направлениях, и приводит в любой окрестности точки q долю време-
времени, пропорциональную площади этой окрестности. Отметим
также, что бильярды Синая обладают сильной неустойчи-
неустойчивостью, которая характеризуется тем, что даже небольшое
изменение начального состояния (положения q или скорости
V) бильярдной частицы в области Q приводит к «сильным»
изменениям его траектории, которая очень быстро перестает
быть похожей на исходную.
Теория рассеивающих бильярдов применяется при ис-
исследовании многих важных моделей статистической физи-
физики — при доказательстве эргодичности газа твердых стал-
сталкивающихся молекул, исследовании газа Лоренца (см.
[18]) и других.
Впоследствии Л. А. Бунимович исследовал другой класс
бильярдов — так называемые фокусирующие бильярды
(или, как теперь принято их называть, бильярды Буни-
мовича), в которых, несмотря на отсутствие рассеива-
рассеивающих участков границы, также обнаруживается явление
рассеивания и, как следствие, хаотичность поведения
траекторий.
Наиболее известным и популярным примером такого
бильярда является «стадион», который получится, если
раздвинуть две половинки круглого бильярда и вставить
между ними одинаковые параллельные отрезки (т. е. гра-
граница «стадиона» состоит из двух дуг окружностей и двух
касательных к ним отрезков) — рис. 3.3, а. Несмотря на то,
что два прямолинейных участка границы «стадиона» могут
быть сколь угодно малыми, а сам стадион почти не отличать-
отличаться от круга, бильярд в «стадионе» будет уже хаотическим!
283
(Напомним, что бильярдная траектория в круге не всюду
плотна в нем.)
Хаотичность имеет место и для других примеров биль-
бильярдов Бунимовича, изображенных на рис. 3.3, б—з.
Бильярды на рис. 3.3, б, в являются модификациями
стандартного «стадиона», поскольку имеют только круглые
и прямолинейные куски границы, и поэтому их также можно
называть «стадионами» (нестандартными). Границы «цветоч-
нообразных» областей на рис. 3.3, г, д состоят только из
^Стадионы"»
^Гибриды»
Рис. 3.3
дуг окружностей. Наконец, из рассмотренных уже областей
можно вырезать разнообразные дыры (рис. 3.3, е, ж) или
же создавать «гибриды» — соединять специальным образом
куски рассеивающих и фокусирующих бильярдов, как на
рис. 3.3, з.
Отметим, что круглые куски границ стадионов и цветоч-
нообразных областей (дуги окружностей) обладают следую-
следующим важным свойством: дополнение к любой дуге до целой
окружности расположено внутри области — только в этом
случае бильярд в соответствующей области будет хаотич-
хаотичным. Например если рассмотреть бильярд, состоящий
из двух одинаковых круглых сегментов, то, в случае когда
сегмент вмещает в себя острый угол (т. е. содержит полу-
полукруг), бильярд будет хаотичным, а когда вписанный угол
прямой или тупой — хаотичности нет (рис. 3.4, а, б). Во
втором случае у бильярда имеется устойчивая пери-
одическая траектория АВ периода 2—если эту траекторию
немного «пошевелить», то возникшая новая траектория будет
по-прежнему располагаться вблизи отрезка АВ. В сегменте
же рис. 3.4, а смещенная траектория уйдет от исходного
положения и заполнит со временем всю область.
Весьма интересным является вопрос о числе геометри-
геометрически различных периодических траекторий в произвольном
ограниченном бильярде. Можно
доказать, что для строго выпукло-
выпуклого бильярда с гладкой границей на
плоскости число N(n) периодичес-
периодических траекторий, имеющих не более
чем п звеньев, при больших п не
меньше ЗпЧп2. Эта оценка была
фактически известна еще Биркго- Рис. 3.4
фу, который определял число k-
звенных траекторий для каждого k от 3 до п (см. § 6).
Совсем недавно И. К. Бабенко, используя средства
современной топологии, доказал, что для строго выпуклого
бильярда с гладкой границей в трехмерном пространстве
число N (п) при больших п не меньше п2/2 In п.
Вообще говоря, такая оценка является довольно грубой
и во многих случаях может быть улучшена. В случае рас-
рассеивающего бильярда Я. Г. Синаем, Н. И. Черновым и
Л. А. Бунимовичем недавно получена асимптотически точ-
точная оценка числа N(n): 2c*n<?N(n)<2c*n, где сг и с2 —
некоторые топологические характеристики рассматривае-
рассматриваемого бильярда. Таким образом, в бильярдах Синая число
периодических траекторий растет экспоненциальное ростом
числа звеньев п. Кроме того, можно показать, что периоди-
периодические траектории рассеивающего бильярда всюду плотны в
фазовом пространстве. Имеются также соображения в поль-
пользу того, что и в выпуклом бильярде с гладкой границей
общего вида число периодических траекторий растет экспо-
экспоненциально с ростом п.
Напоследок упомянем о так называемых осциллирую-
осциллирующих бильярдах на бесконечных бильярдных столах. Биль-
Бильярд называется осциллирующим, если у него существуют
осциллирующие траектории — временами уходящие сколь
угодно далеко, а временами возвращающиеся. Поведение
бильярдного шара на столе, уходящем в бесконечность,
является моделью движения частицы в электромагнитных
полях, определенных конфигурацией («ловушках»).
Следующий специальный класс осциллирующих биль-
бильярдов исследовал А. М. Леонтович A962 г.). Рассмотрим
285
Рис. 3.5
стол, ограниченный осью абсцисс и «колоколообразной»
кривой — графиком положительной непрерывной четной
гладкой функции f(x), стремящейся при |л:|-»-оо к некото-
некоторой прямой у=А^0 (рис. 3.5). Бильярдная траектория
будет неограниченной, если она не заключается -в
полосу Xi «лг<*:2 ни при каких xt и х2, и осциллирую-
осциллирующей, если она пересекает ось Оу бесконечно много раз.
А. М. Леонтович доказал, что при Л>0 существуют
осциллирующие траектории (но существует и бесконечно
много неосциллирующих, ухо-
уходящих на бесконечность без
возвращения к оси Оу), а при
А=0 любая траектория —
осциллирующая (среди них есть
' как ограниченные, так и неог-
неограниченные траектории).
При изучении бильярдов в
неограниченных областях ес-
естественно возникает постановка
задачи о рассеянии в области
параллельного пучка частиц
(или волнового фронта). Рас-
Рассматривая эту задачу, А. Ю. Плахов и А. М. Степин
описали области, для которых рассеянный (уходящий)
пучок параллелен исходному (входящему). Такое поведение
пучка является аналогом квантового эффекта аномального
рассеяния, впервые экспериментально обнаруженного в
1986 г. Б. Я. Зельдовичем и его коллегами по Физическому
институту АН СССР.
В действительности современная теория бильярдов не
ограничивается только упомянутыми выше системами:
имеется много других классов бильярдов, которые сейчас
исследуются математиками и физиками. Долгое время при
изучении таких бильярдов основное внимание уделялось
вопросам о хаотичности траекторий; в этом направлении в
последнее время были получены весьма общие результаты.
Однако наряду с этим никогда не ослабевал интерес и к
таким задачам, которые рассматривались в нашей книге.
Для их решения, по-видимому, нельзя предложить столь
же общие методы, и поэтому решение конкретных задач
всегда представляет известный интерес, тем более что, как
мы уже отмечали, оно иногда достигается применением эле-
элементарных приемов.
Тех читателей, которые захотят попробовать здесь свои
силы, ждет широкое поле деятельности.
СПИСОК ЛИТЕРАТУРЫ
1. Кориолис Г. Г. Математическая теория явлений бильярдной
шры.— М.: Гостехиздат, 1956.
2. БорахеостоеВ. Бильярд// Наука и жизнь. 1966. №№ 2—4, 6, 11.
3. Гальперин Г. А. Бильярд^ Кваит. 1981. №4.
4. Земляков А. Н. Математика бильярда // Квант. 1976. № 5.
5. Земляков А. Н. Арифметика и геометрия столкновений Ц Квант.
1978. №4.
6. Земляков А. Н. Бильярды и поверхности // Квант. 1979. № 9.
7. Синай Я. Г. Бильярдные траектории в многогранном угле // Ус-
Успехи математических наук. 1978. Т. 33, вып. 1.
8. Гальперин Г. А. Упругие столкновения частиц на прямой // Ус-
Успехи математических наук. 1978. Т. 33, вып. 1.
9. Гальперин Г. А. О системах абсолютно упругих шаров, движу-
движущихся в пространстве или сосуде // Доклады АН СССР. 1979.
Т. 245, № 2.
10. Синай Я. Г. Введение в эргодическую теорию (лекция 10).—
Ереван: Изд-во Ереванского университета, 1973.
11. Корнфельд И. П., Синай Я. Г., Фомин С. В. Эргодическая тео-
теория.— М.: Наука, 1980.—Гл. 6.
12. Биркгоф Г. Динамические системы.—М.; Л.: ОГИЗ, 1941.
13. Арнольд В. И. Математические методы классической механи-
механики.— М.: Наука, 1979.
14. Гальперин Г. А., Степин А. М. Периодические движения
бильярдного шара // Квант. 1989. № 3.
15. Тихомиров В. М. Рассказы о максимумах и минимумах.— М.:
Наука, 1986 (Библиотечка «Квант». Вып. 56).
16. Берже М. Геометрия: в 2-х томах.— М.: Мир, 1984.— Гл. 9 и
17. Синай Я- Г. Динамические системы с упругими отражениями.
Эргодические свойства рассеивающих бильярдов // Успехи ма-
математических наук. 1970. Т. 25, вып. 2.
18. Синай Я. Г. Эргодические свойства газа Лоренца // Функцио-
Функциональный анализ и его приложения. 1979. Т. 13, вып. 3.
19. Земляков А. Н., Каток А. Б. Топологическая транзитивность
бильярдов в многоугольниках // Математические заметки. 1975.
Т. 18, № 2.
Научно п пулярное издание
ГАЛЬПЕРИН Григорий Александрович
ЗЕМЛЯКОВ Александр Николаевич
МАТЕМАТИЧЕСКИЕ БИЛЬЯРДЫ
(бильярдные задачи и смежные вопросы матема-
математики и механики)
Библиотечка «Квант»; выпуск 77
Заведующий редакцией Г. С. Куликов
Редактор А. Г. Мордвинцсв
Художественный редактор Т. Н. Колъченко
Технический редактор Е. В. Морозова
Корректоры О. М. Карпова. Л. С, Сомова
ИБ № 32724
Сдано в набор 20.06.89. Подписано к печати 23.01.90. Т-06432. Формат
84X108/32. Бумага офс. Mi 2. Гарнитура литературная. Печать высокая.
Усл. печ. л. 15.12. Усл. кр.-отт. 16,96. Уч.-изд. л. 16,92. Тираж 130 000 экз.
Заказ № 9—325 Цена 65 Коп.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудового Красного Знамени
МПО «Первая Образцовая типография» Государственного комитета СССР
по печати. 113054 Москва, Валовая, 28
Отпечатано на полиграфкомбинате ЦК ЛКСМ Украины «Молодь» ордена Тру-
Трудового Красного Знамени издательско-полиграфического объединеиия ЦК ВЛКСМ
Лоподая гвардия»: 252119, г. Кнев-119, ул. Пархоменко, 38—44.
Р
а
а
к
2
звенная
траектория