Автор: Бесекерский В.А.
Теги: общее машиностроение технология машиностроения теория автоматического управления сборник задач
Год: 1972
Текст
ОГЛАВЛЕНИЕ
Предисловие...........•....................................9
Раздел I
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Глава 1. Дифференциальные уравнения и передаточные функ-
ций звеньев и автоматических систем................. 11
§ 1.1. Дифференциальные уравнения и передаточные функ-
ции звеньев..................................... 11
§ 1.2. Типовые динамические звенья.................... 32
§ 1.3. Дифференциальные уравнения и передаточные функ-
ции автоматических систем............................. 36
§ 1.4. Структурные схемы и их преобразование.......... 46
Глава 2. Частотные характеристики динамических звеньев
и систем автоматического регулировании ............ 51
§ 2.1. Характеристики динамических звеньев............ 51
§ 2.2. Амплитудно-фазовые характеристики разомкнутых си-
стем автоматического регулирования ................... 63
§ 2,3. Вещественные частотные характеристики замкнутых
систем автоматического регулирования.................. 73
§ 2.4. Логарифмические характеристики систем автомати-
ческого регулирования................................ 79
Глава 3. Устойчивость линейных систем.................... 89
§ 3.1. Алгебраические критерии устойчивости '......... 89
§ 3.2. Критерий устойчивости Михайлова........... 101
§ 3.3. Критерий устойчивости Найквиста................109
§ 3.4. Определение устойчивости по логарифмическим ча-
стотным характеристикам разомкнутой системы . . . 120
§ 3.5. Построение областей устойчивости......... . . 125
Глава 4. Построение переходных процессов в системах
автоматического регулирования........................130
• §4.1. Классический метод решения дифференциальных урав-
нений ............................................130
§ 4.2. Применение изображений Лапласа и Карсона—Хеви-
сайда ............................................... 140
4 ОГЛАВЛЕНИЕ
§ 4.3. Приближенные методы расчета переходных процессов 158
Л. Использование вещественных частотных характе-
ристик ..........J ........................ 158
Б. Использование сопрягающих частот л. а. х. ... 165
В. Использование нормированных кривых для мини-
малыю-фазовых систем с типовыми л. а. х. ... 167
Г. Построение кривой переходного процесса графи-
ческим методом..............................172
Глава 5. Оценка качества регулирования..................176
§ 5.1. Определение точности при наличии задающего воз-
действия .............................................176
§ 5.2. Определение точности при наличии возмущающего
воздействия...........................................191
§ 5-3. Корневые методы оценки динамических рвойств . . . 194
§ 5.4. Оценка по кривой переходного процесса ...... 198
§ 5.5. Интегральные оценки........................ . 201
§ 5.6. Частотные оценки динамических.свойств ........206
Глава 6. Синтез линейных систем . ।.....................211
§ 6.1 Выбор параметров САР по требуемой точности . . . 211
§ 6.2. Алгебраические методы выбора параметров САР . . 224
§ 6.3. Частотные методы выбора параметров САР. Расчет
последовательных корректирующих устройств .... 231
§ 6.4. Расчёт дополнительных обратных связей н прямых
параллельных корректирующих связей....................249
§ 6.5. Расчет систем комбинированного управления .... 263
§ 6.6. Расчет последовательных корректирующих контуров,
работающих на несущей частоте........................279
Глава 7. Случайные процессы в линейных системах .... 273
§ 7.1. Вычисление корреляционных функций и спектраль-
ных плотностей.........................\..............273
§ 7.2. Прохождение случайного стационарного сигнала че-
рез линейную систему..................................286
§ 7.3. Оптимальные системы .........................295
Глава 8. Системы с переменными параметрами..............302
§ 8.1. Построение переходных процессов . ........ 302
§ 8.2. Оценка устойчивости н качества регулирования . . . 309
Глава 9. Системы с запаздыванием . и с распределенными
параметрами .-........................................314
§ 9.1. Системы с временным запаздыванием.......... .314
. § 9.2. Системы с распределенными параметрами ........ 321
Глава 10. Импульсные системы.......................... 324
§ 10.1. Дискретные функции и уравнения импульсных систем 324
§ 10.2. Устойчивость к качество импульсных систем ...336
ОГЛАВЛЕНИЕ"
5
• ‘ у Раздел II
.-..НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Глава 11. Составление уравнений нелинейных систем . . . 343
§11.1 Уравнении нелинейных следящих систем............343
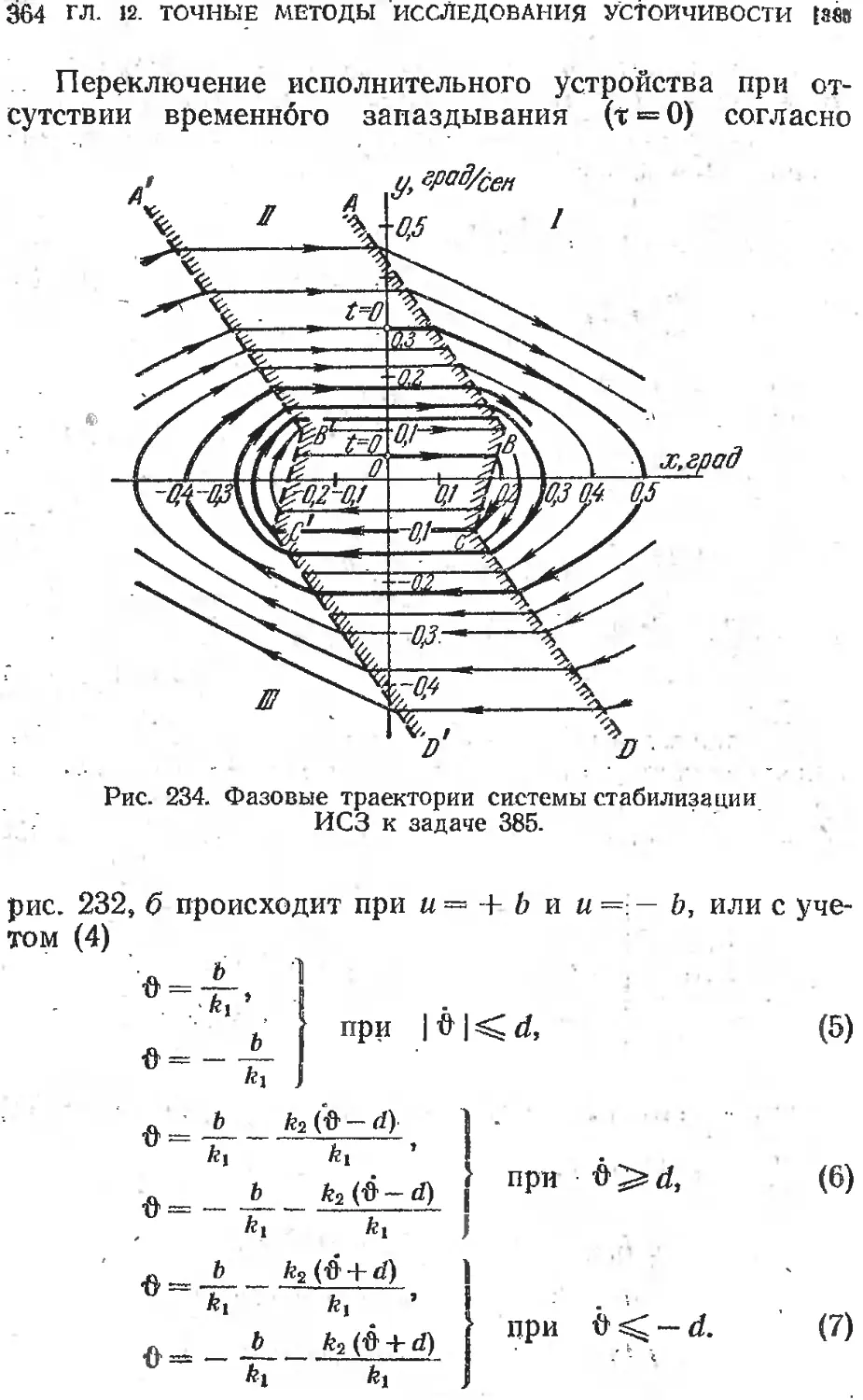
§ 11.2. Уравнения нелинейных систем стабилизации......350
Глава 12. Точные методы исследования устойчивости и ав-
токолебаний ....................................... 356
§ 12.1. Метод фазовых траекторий.......................356
§ 12.2. Метод А. М. Ляпунова — А. И. Лурье.........; . 369
§ 12.3. Частотный метод В. М. Попова . . ...........374
.§ 12.4. Метод припасовывапня..........................378
Глава 13. Приближенные методы исследования устойчиво-
сти и автоколебаний....................................383
§'13.1. Алгебраические способы определения устойчивости
и автоколебаний.................................383
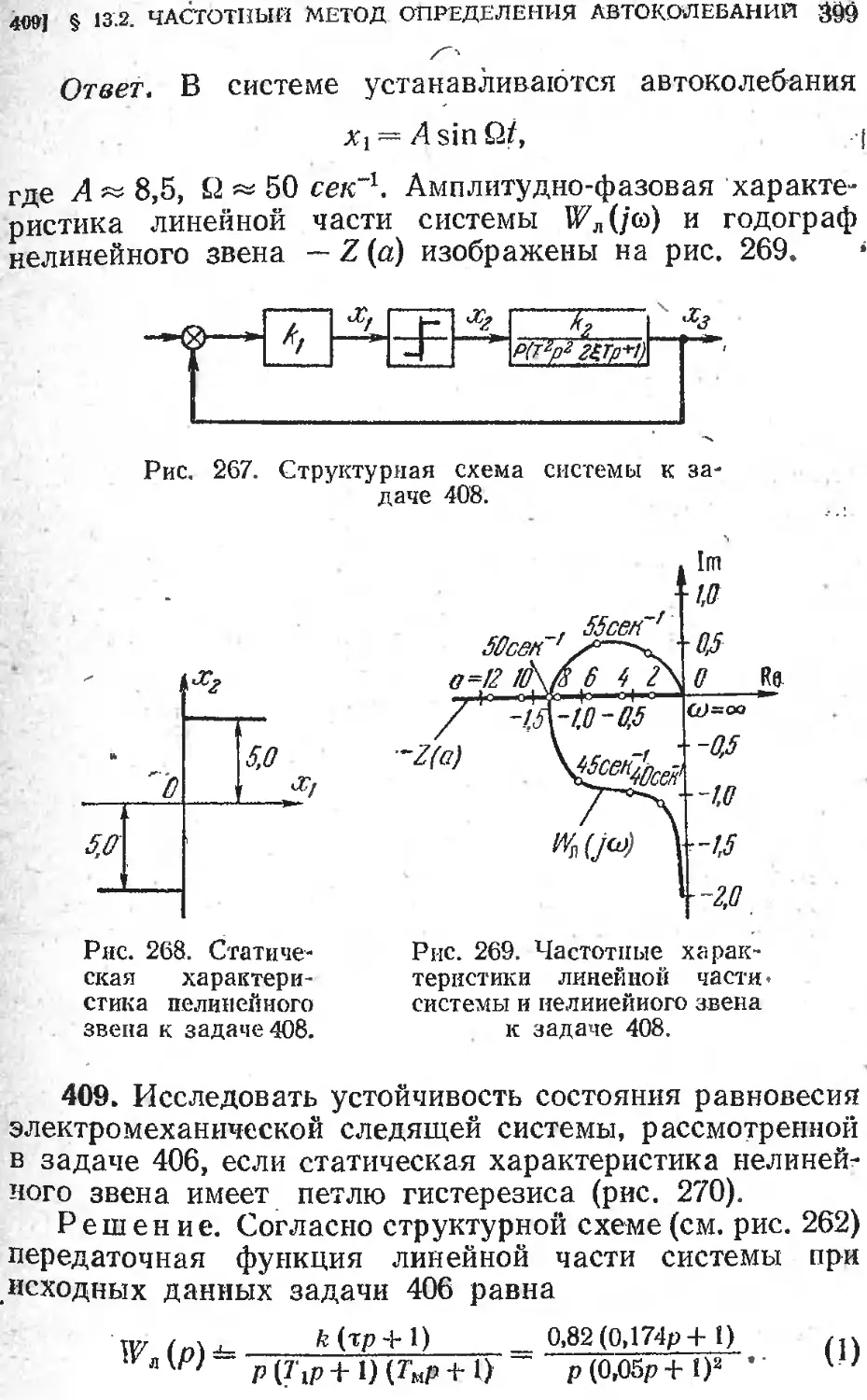
§. 13.2. Частотный метод определения автоколебаний .... 392
Глава 14. Оценка качества нелинейных систем..............402
:§ 14.1. Исследование колебательных переходных процессов
аналитическими методами................................402
i§ 14.2. Исследование колебательных переходных процессов
частотными методами.................................. 412
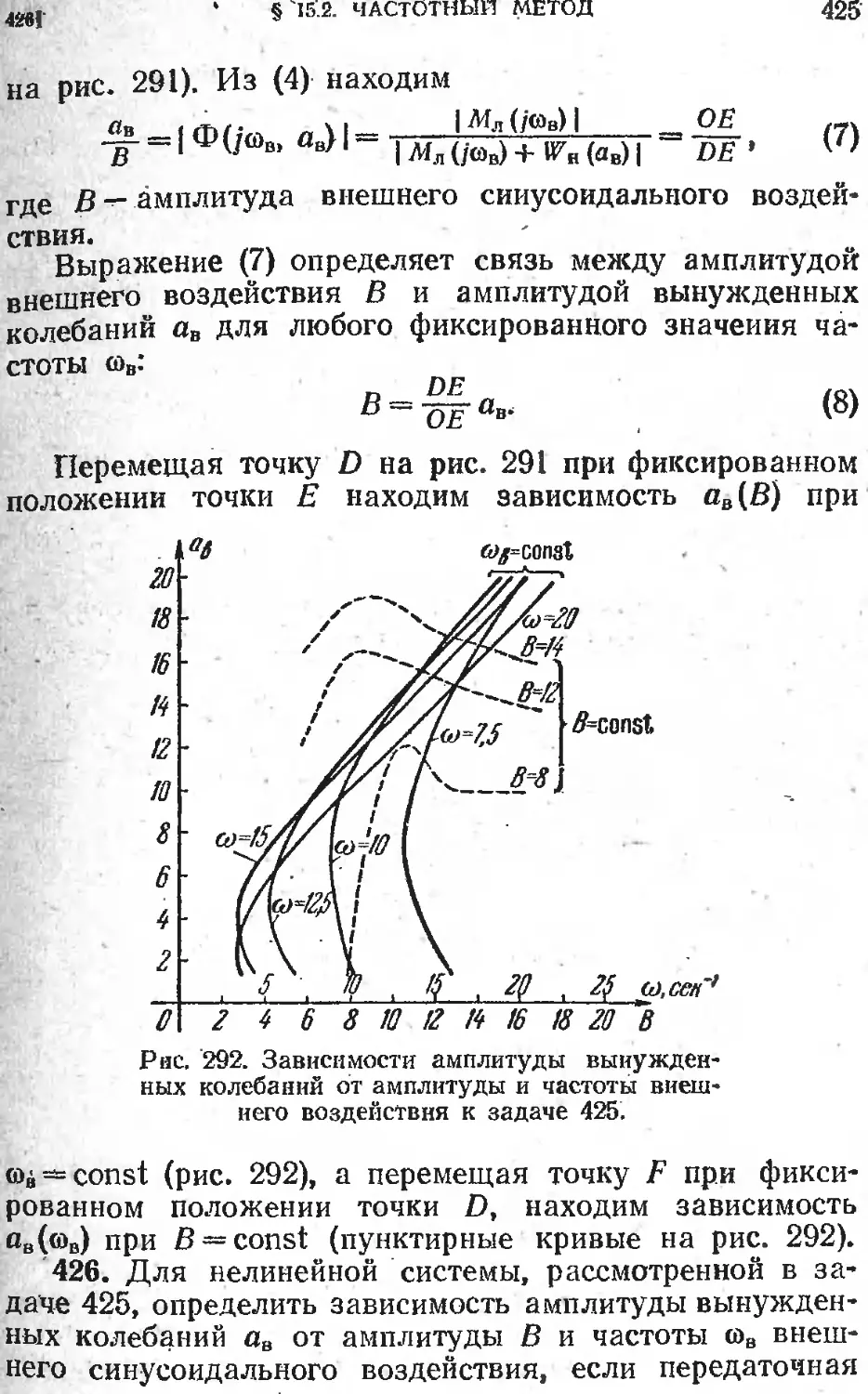
Глава 15. Вынужденные колебания в нелинейных системах 417
§ 15.1.' Отыскание симметричных одночастотных вынуж-
! денных колебаний графическим методом.................417
§ 15.2. Отыскание симметричных одночастотных вынуж-
денных колебаний частотным методом.....................423
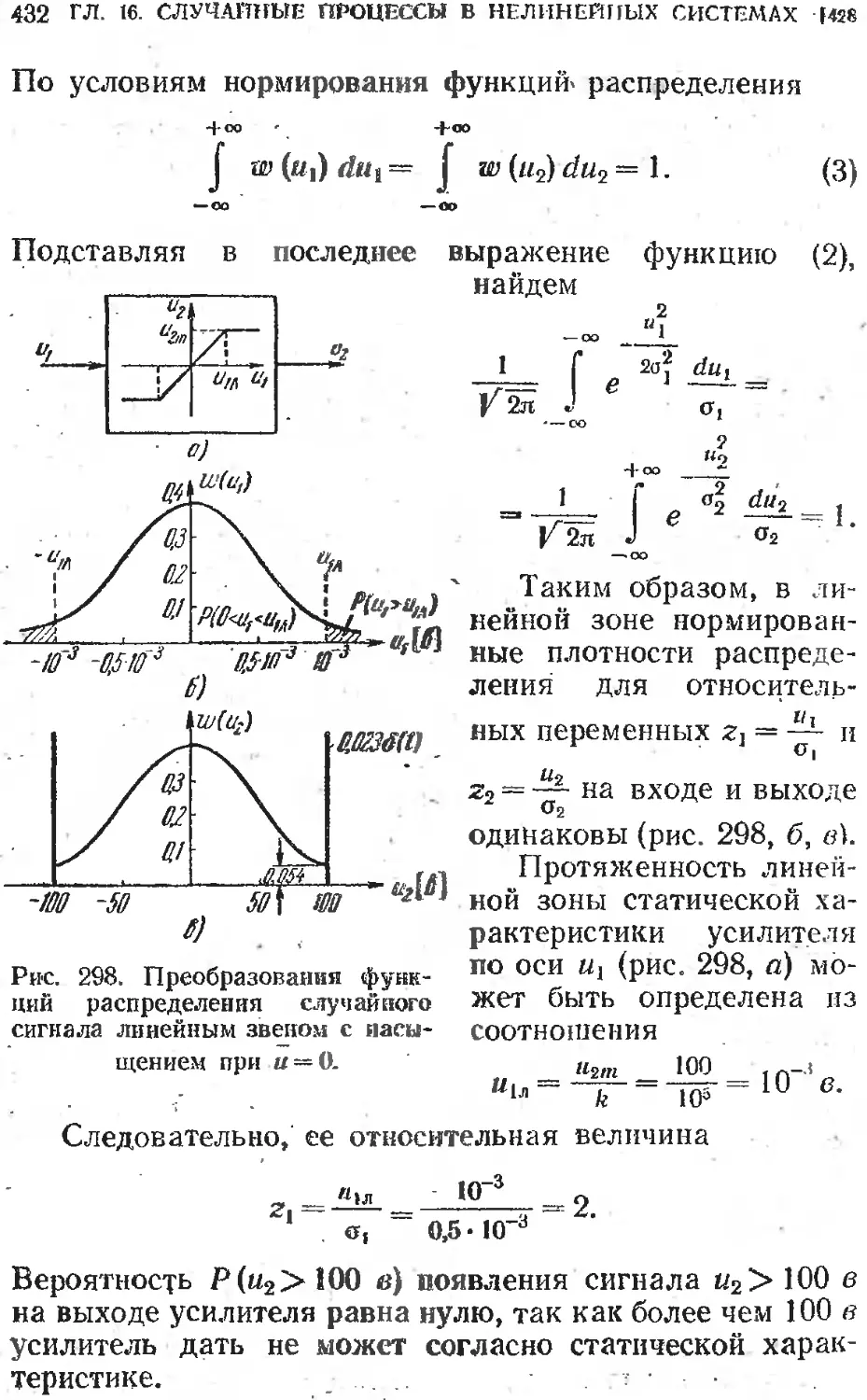
Г д ^ва 16; Прохождение случайных процессов через нелиней-
ные системы . ....................................... 431
. ,§16.1. Определение функций и моментов распределения
случайного процесса на выходе нелинейной системы 431
§ 16.2. Расчет нелинейных систем с помощью статистичес-
кой линеаризации-..................................... 438
... i
‘ Ра з де л III
ОПТИМАЛЬНЫЕ, ЦИФРОВЫЕ, САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ
И МОДЕЛИРОВАНИЕ
Гл'ава 17. Синтез оптимальных систем управления.........448
'§ 17.1. Синтез оптимальных систем с использованием прин-
ципа максимума....................................... 448
§ 17.2. Синтез оптимальных систем методом динамического
программирования и- классического вариационного.
исчисления .• '. 455
ОГЛАВЛЕНИЕ
Глава 18. Системы с цифровыми вычислительными машина-
ми (ЦВМ)..............................................460
§ 18.1. Передаточные функции систем с ЦВМ при учете'
квантования по времени............................4.60
§ 18.2. Устойчивость и оценка качества...............466
. § 18.3. Синтез систем- с ЦВМ.......................471
Глава 1-9. Экстремальные и самонастраивающиеся си-
стемы ............................................480
§ 19.1. Составление структурных схем экстремальных и са-
монастраивающихся систем и исследование их ус-
тойчивости ................................... ..... 480
§ 19.2. Качество систем экстремального управления .... 489
Г лава 20. Составление схем для моделирования автомати-
ческих систем на непрерывных вычислительных машинах 499
§ 20.1. Составление схем для моделирования элементов
автоматических систем на электронных вычислитель-
ных машинах . ..........................................499
§ 20.2.‘ Составление схем’ для моделирования дифференци-
альных уравнений и автоматических систем на элек-
тронных вычислительных машинах-.................513
Приложение..............................................522
' 1. Изображения по Лапласу и Карсону—Хевисайду-фун- .
кций времени . ...................................522
2. Z-преобразования функций времени.................524
3. Нормированная- логарифмическая частотная фазовая
характеристика апериодического звена первого порядка 525
4. Нормированные логарифмические амплитудная и фазо- .
вая характеристики колебательного звена ........... 525
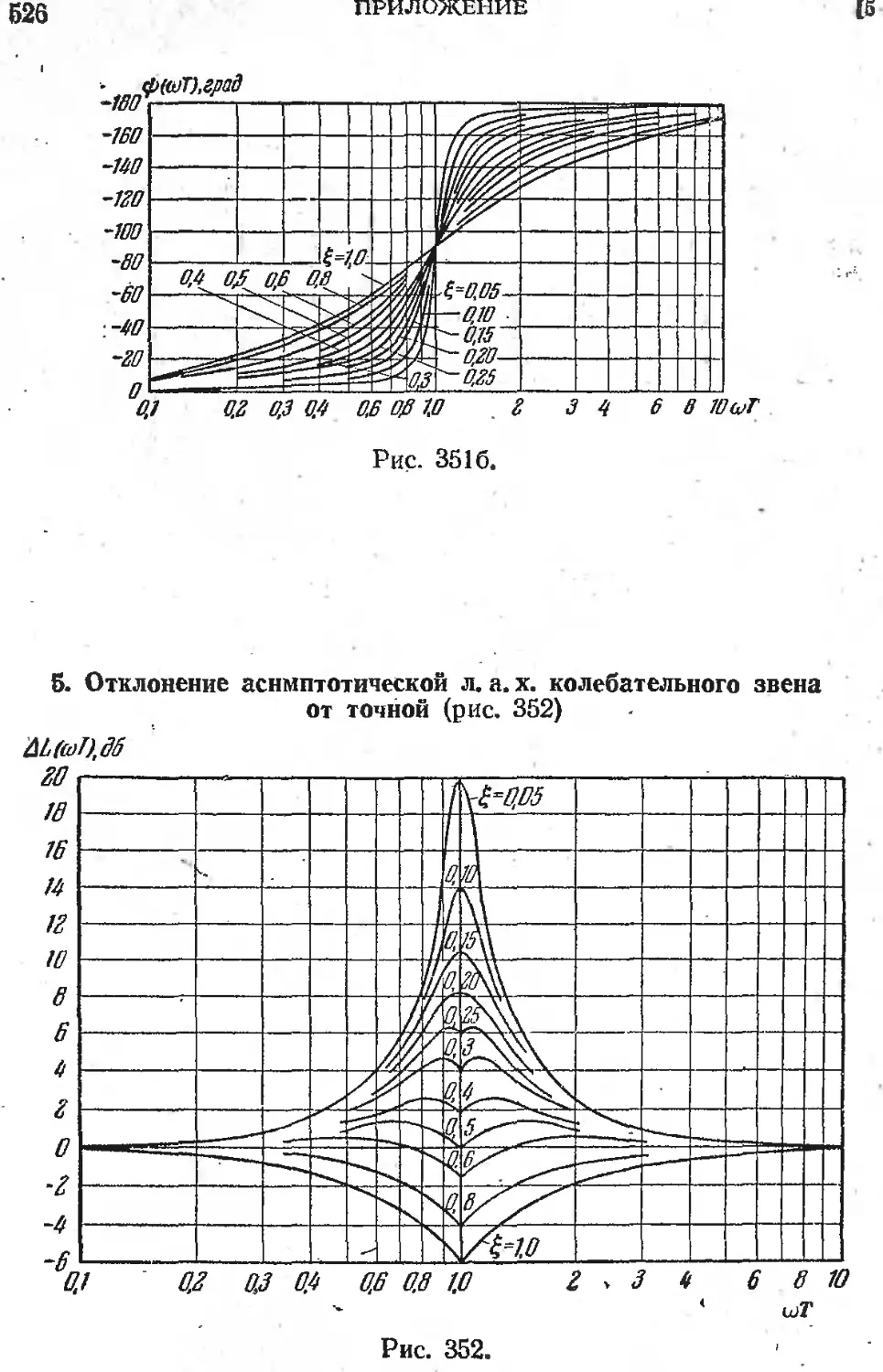
5. Отклонение асимптотической л. а. х. колебательного зве-
на от точной . . . . .............................526
6. Критерий устойчивости Гурвица....................527
7. Диаграмма Вышнеградского с линиями равного затуха-
ния в процентах за один период . . ................528
8. Диаграмма ВЬшшеградского с линиями равной норми-
рованной степени устойчивости h0 = h у ав/а3 ...... 529
9. Эквивалентные начальные условия в системе регулиро-
вания после воздействия на нее единичной ступенчатой
функции ...........................................529
10. Решения, однородных дифференциальных уравнений пер-
вого, второго и третьего порядков...................530
ОГЛАВЛЕНИЕ 7
11. Номограмма для построения вещественной частотной
характеристики замкнутой системы по амплитудно-фазо-
вой характеристике разомкнутой системы (вещественная
круговая диаграмма).................................. 531
12. Кривые для определения времени переходного процесса
и перерегулирования по коэффициенту наклона трапе-
цеидальной вещественной частотной характеристики . . 531
13. Кривые для определения времени переходного процесса
и перерегулирования для вещественной частотной ха-
, рактеристики, имеющей максимум......................532
14. Зависимость требуемого запаса по фазе' от модуля
в децибелах при различных показателях колебатель-
ности . . .......................................... 532
15. Номограмма для построения вещественной частотной
характеристики по заданным качественным и показа-
телям ......................................• . .'. . 533
16. Нахождение квадратичной интегральной оценки .... 534
17. Формулы для интегрирования спектральной плотности 535
18. Нормированные стандартные передаточные функции ра-
зомкнутой системы ....................................535
19. Типовые л. а. х., соответствующие заданному запасу
устойчивости ........................... > ...... 53S
20. Нормированные кривые переходных процессов для ти-
повых л. а. х.................................... . . . 541
21. Корректирующие звенья постоянного тока............542
22-Корректирующее звено переменного тока (двойное
Т-образное звено)................................. 544
23. Приведение дифференциальных уравнений к каноничес-
кой форме........................................... 547
24. Достаточные условия устойчивости нелинейных систем
второго, третьего и четвертого порядков . ............550
25. Переход от л. а. х. вида 20 lg| I + W (/со) | к л. а. х.
вида 20 1g | W (/<о) | ............................551
26. Типовые л. а. х. систем с ЦВМ при учете квантования
по времени............................................554
27. Типовые последовательные дискретные корректирующие
звенья................................................550
28. Коэффициенты гармонической линеаризации основных
нелинейных характеристик. ........................ . . 558
29. Нормированные амплитудно-фазовые частотные харак-
теристики релейных исполнительных механизмов. . . 562
8 ОГЛАВЛЕНИЕ
30. Коэффициенты статистической линеаризации некоторых
типовых нелинейностей.............................565
31. Нормированный интеграл плотности вероятности нор-
мального закона распределения .............. ..... 571
32. Нормированная плотность вероятности нормального за-
кона распределения ..............................573
33. Моделирование элементов структурных схем автомати-
ческих систем на операционных усилителях..........574
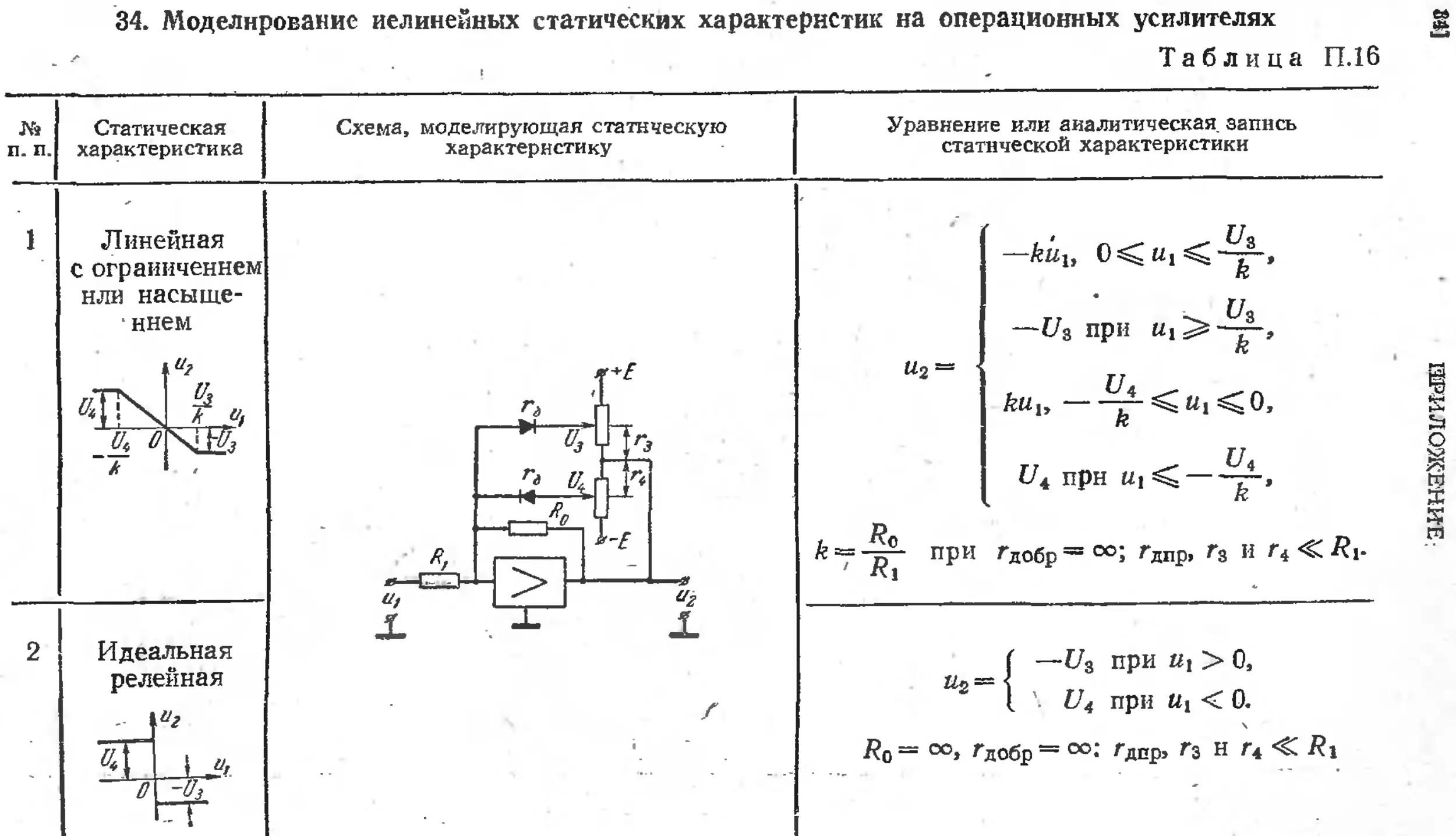
34. Моделирование нелинейных статических характеристик
. иа- операционных усилителях.....................579
85. Таблица функций h (<0)........................- 582
Литература...........................................586
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ
АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
И УПРАВЛЕНИЯ
Под редакцией
В. А. БЕСЕКЕРСКОГО
ИЗДАНИЕ ЧЕТВЕРТОЕ, СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования СССР
। в качестве учебного пособия
С ля студентов высших технических
учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1072
6Ф6.5
С 23
УДК 621.078(076.1)
Авторы:
В. А. БЕСЕКЕРСКИЙ, А. Н. ГЕРАСИМОВ,
Л. Ф. ПОРФИРЬЕВ, Е. А. ФАБРИКАНТ,
С. М. ФЕДОРОВ, В. И. ЦВЕТКОВ,
Сборник задач по теории автоматического регули-
ровании и управления, под редакцией В. А. Бесекер-
с к о г о, издание четвертое, стереотипное, издательство
«Наука», Главная редакция физико-математической ли-
тературы, М., 1972.
Сборник рассчитан на студентов, специализирую-
щихся в области теории автоматического регулирования
и следящих систем, а также на студентов других спе-
циальностей, изучающих теорию автоматического ре-
гулирования. и управления. Сборник, содержащий 491
задачу,-^ориентируется на ряд используемых в вузах
книг. В,- качестве основной принята книга В. А. Бесе-
керского| 'и Е. П. Попова «Теория систем автоматиче-
ского регулирования». Построение сборника, содержа-
ние, терминология и методика изложения в основном
соответствуем этой книге.
ТаблЯ32. Илл. 376. Библ. 43 назв.
3-3-14
154-72
ПРЕДИСЛОВИЕ
Настоящий сборник рассчитан на студентов, специа-
лизирующихся в области автоматического регулирова-
ния и управления, но может быть использован и сту-
дентами других специальностей при изучении ими тео-
рии автоматического регулирования.
Круг вопросов, охватываемых сборником, включает
в себя темы, входящие, как правило, в программы по
теории автоматического регулирования или теории авто-
матического управления многих вузов.
Сборник ориентируется на ряд используемых в вузах
книг, список которых приведен в конце сборника.
В качестве основной принята книга В. А. Бесекерского
и Е. П. Попова «Теория систем автоматического регу-
лирования», выходящая вторым изданием в 1972 г. По-
строение сборника, содержание, терминология и мето-
дика изложения в основном соответствуют этой книге.
Аналогично указанной книге в сборнике применяется
одинаковый символ для обозначения оператора диф-
ференцирования, используемого при операторной форме
записи дифференциальных уравнений, в которые входят
функции времени (оригиналы), й‘комплексной перемен-
ной в преобразованиях Лапласа и Карсона—Хевисайда.
При этом предполагается, что читатель самостоятельно
может разобраться в значении этого символа в зависи-
мости от того, используются ли в уравнениях функции
времени или их изображения, и знает правила.перехода
от оригиналов к изображениям с учетом начальных
условий.
10
ПРЕДИСЛОВИЕ
Сборник задач написан В. А. Бесекерским (главы
5, 7, 8 и 10), А. Н. Герасимовым (главы 3 и 9),
С. В. Лучко (главы 11—15), Л. Ф. Порфирьевым (гла-
вы 16, 17 и- 19), Е. А. Фабрикантом (главы 2 и 4),'
С. М. Федоровым (главы 6 и 18) и В. И. Цветковым
(главы 1 и 20).
Авторы приносят благодарность А. В. Нетушилу и
Б. П. Рязанову за полезные замечания, сделанные при
просмотре рукописи третьего издания.
В четвертом издании исправлены замеченные опе-
чатки и неточности.
Авторы
РАЗДЕЛ /
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
ГЛАВА 1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
ЗВЕНЬЕВ И АВТОМАТИЧЕСКИХ СИСТЕМ
/
§ 1.1. Дифференциальные уравнения
и передаточные функции звеньев
1. Составить в общем виде дифференциальное урав-
нение электромагнита с пружиной и демпфером
(рис. 1, а), если.за входную величину принять напря-
жение и, а за выходную — перемещение якоря х и
считать известными приведенные к точке А силы пру-
жины Fn, демпфера Fc< электромагнита гэ и инерцион-
ную силу F„. Влиянием сил сухого трения пренебречь.
Решение. Выберем начало отсчета, как показано
на рис. 1, а. Составим уравнение равновесия сил, при-
веденных к точке А,
тх + + с2х = Fa (z, х) ' (1)
и уравнение равновесия напряжений
u~iR + L(6, > (2)
где тх = F„ — инерционная сила, пропорциональная
ускорению х и приведенной массе подвижных частей
т; clx = FR — сила демпфера, пропорциональная ско-
рости х и коэффициенту демпфирования q; с2х = F,, —
сила пружины, пропорциональная перемещению х и
коэффициенту упругости или жесткости пружины с2;
12
ГЛ. 1, УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
[1
и, / — напряжение и ток обмотки электромагнита;
£ = 7,(6, I) — индуктивность обмотки электромагнита, за-
висящая в общем виде от рабочего зазора б и тока i
(при насыщении магнитопровода); R — активное сопро-
тивление обмотки электромагнита; F3 = F3(i, х) —си-
гис. 1. Электромагнит с пружи-
1ч. ной и демпфером.
ла электромагнита, являю-
щаяся функцией двух пере-
менных.
Предположим, что всегда
остается рабочий зазор бо=#О
й такой, что справедливо со-
отношение
£э (£. х) = С3/2Х 2 при б б0,
(3)
где с3 — постоянный коэф-
фициент. Наличие воздуш-
ного зазора (б>60) и ра-
бочих (ограниченных) зна-
чений тока i исключает
насыщение магнитопровода.
Поэтому индуктивность не
зависит от тока, а только
от перемещения L = L(x).
На основании гипотезы ма-
лых отклонений будем счи-
тать, что L = Lo — const в
окрестности выбранного постоянного значения х = х(1.
Тогда нелинейное уравнение (2) становится линейным:
U — IR + Lo .
(4)
Б уравнениях (1), (3) и (4) только член в правой части
уравнения (I) или его выражение (3) являются нелиней-
ными. Линеаризуем его, для чего запишем в виде
F(F3, i, jc) = F3-c3/2jT2 = 0. (5)
Тогда линеаризованное уравнение в малых отклонениях
относительно установившегося' статического значения
21 § 1.1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 13
переменных (i = io, а = х0, F3 = Fa0) примет .вид
/ dF \о . „ z dF л . , / dF \о . _
(dF, ) 3 + ( di ) Дг + ( дх ) ^Х~ °'
тт „ dF dF dF
Найдя частные производные -ттг, -тт-, -т— из (5) и
подставив в них установившиеся значения переменных,
получим ’
i\Fs — ki Аг + k2\x = 0 или AF3 = &! Дг — &2ЛЛ,. (?)
где &( = 2с3г0х“2, k2 = 2с3г|х“3. Знак минус в (7) означает,
что при увеличении Ах сила AFa уменьшается. Коэф-
фициенты передачи kt и k2 можно найти графически
из статических характеристик Рэ = с3х32 • г2 и Рэ=г?3г^ • х-2
нахождением тангенса угла наклона касательных, про-
веденных в точках (г0, F30) и (х0, F30) соответственно.
Выразив Аг из (7) и: подставив в (4), а полученный
результат, разрешенный .относительно. AFa, — в (1) и
сделав преобразования, получим
(ТэР + 1)(г1р2 + Т\р + 1) х (/) = ku (О,
где Тэ = — постоянная времени обмотки электромаг-
нита,
у. _ Г1 у. _ / tn * 1 ' k\ _ tl
*- c2 + k2 ’ 2 r c2 + k2’ Р(с2 + й2)’
— оператор или символ дифференцирования..
2. Найти передаточную функцию гидравлического
исполнительного устройства (рис. 2, а), применявшегося
совместно с центробежными, измерителями угловой ско-
рости ЦИС для регулирования скорости вращения теп-
ловых двигателей. За входную величину принять переме-
щение х муфты ЦИС 3, а: за выходную — перемещение у
заслонки или регулирующего органа (РО) теплового
двигателя (рис. 2,. б). ’ '
Решение. Гидравлический двигатель (золотник 2
с силовым поршнем 1) вместе с'изодромом (пружина 5
с демпфером 6) могут находиться в покое только при
Одном определенном положении рычага 4, когда пружина.-
14
ГЛ. 1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ .
находится в ненапряженном состоянии и золотник 2 —
в среднем положении (как показано на рис. 2). При
этом муфта 3 ЦИС занимает положение, соответствую-
щее заданной угловой скорости Q. При отклонении й
от заданной муфта 3 сдвинется, сместит золотник 2 и
вся система придет в движение, до тех пор, пока ско-
рость й вновь не станет заданной.
1. Уравнение гидравлического двигателя. Усилия',
развиваемые силовым поршнем, значительно превосходят
Рис. 2. Гидравлическое исполни-
тельное устройство.
силы сопротивления и.
инерционные силы, по-
этому их влиянием можно
пренебречь. Тогда, если
не учитывать сжимае-
мость жидкости и считать,
что площадь окна, откры-
ваемого золотником, про-
порциональна его пере-
мещению г, уравнение
гидродвигателя будет
^- = klz или py = kxz,
(D
где k{— коэффициент пе-
редачи.
2. Уравнение рычага,
связанного с муфтой, изо-
дромом и золотником.
Перемещение муфты х
вызывает перемещение золотника z и силового поршня,
который перемещает поршень демпфера хос в сторону,
обратную перемещению муфты. Следовательно, имеем
уравнение
z = k2(x- k3xm), (2)'
где — коэффициенты передачи; а, b —
длины плеч рычага, (см. рис. 2).
3. Уравнение цепи обратной связи. В цепь обратной
связи входит демпфер, пружина и рычаг 4.- Составим
3] § 1.1. УРАВНЕНИЯ И .ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 15
уравнение равновесия сил
С1*ОС + С2*ос = С3у, (3)
где с1Хос = ^’д — сила демпфера, пропорциональная ско-
рости перемещения поршня демпфера хОс‘> с2х0С — Fa —
сила пружины; . с3у = Fc — сила, развиваемая силовым
поршнем; с2, с3 — постоянные коэффициенты.
После 'преобразования уравнения (3) получим
(Тоср + 1) Хос = k4py. (4)
где Тос = — —постоянная времени цепи обратной связи,
с2
k4 = —— коэффициент передачи.
Найдя хос из (2) и подставив в его выражение z
из (1), получим
• <3 * 5)
Подставив (5) в (4),' найдем дифференциальное урав-
нение гидравлического исполнительного устройства
(Гр+1)ру(0 = 6(Госр+1)х(0, (6)
где
'Г ._ t? kjkz /у\
1 4~ 1 1 kik^k^ 1
откуда искомая передаточная функция
W{p) =
k (Трср + 1)
p(jp + l)
3. Найти передаточную функцию и дифференциаль-
ное уравнение пассивной электрической цепи (рис. 3)
относительно напряжений щ и и2.
Решение. Для нахождения передаточных функций
электрических цепей, подобных изображенной на рис. 3,
Удобно пользоваться операторной формой записи сопро-
тивлений: индуктивного — pL, емкостного — и актив-
ного — R, где р = — символ или оператор дифферен-
цирования.
16
ГЛ. 1,-УРАВНЕНИЯ ННЁРЕДАТОЧНЫЕ функции
[3
Преобразуем электрическую цепь рис. 3 в эквива-
лентную ей (рис. 4), где
рС,
7 ( }= I__1 _ ^г(^2Р +?зд,Р~И)
Z2W Р2 + £2р*С2р р(Г& +Пр) ’
T^VC^, TlL~±-, TiC = RlCl,
,_________ /. L
Tz—\^C2L2, T2L — -r^, T2C — R2C2.
Размерность всех постоянных-времен (3) [7'] = се/с.
Так как падение напряжения на последовательно
соединенных сопротивлениях пропорционально величине
Рис. 3. Схема к задаче 3.
Рис. 4. Эквивалентная
схема.
сопротивлений, то передаточная функция эквивалентной
цепочки (рис. 4) находится как отношение
1W („\ __ ^2 (р) _ -^ВЫХ (р) _ % 2 (р) /л\
-'Pi(P) ZBX(p) Z1(p) + Z2(p)’ у '
Подставив (1), (2) в (4), получим искомую переда-
точную функцию электрической цепи
iyz/„x________________/?г(6оР3 + 61Р2 + б2Р + Ьз) _______ /1-Х
K2<bllpi + bip2 + b2p + bs) + J:il(d0pi+dip3+d2p2+d3p}’
bo = Т2ТIC, . bl,==,T2 + T2L,TiC' b2 — T2L~^~TlC, 63=1,
^o = T27'2, di T2yl2C di = TцТ2c + T2, d^ — Tzc”
4] § 1.1. УРАВНЕНИЯ И’'ПЕРЕДАТОЧНЫЕ ' ФУНКЦИИ' ЗВЕНЬЕВ.. 17
Дифференциальное уравнение рассматриваемой элек-
трической цепи относительно напряжений имеете вид
[#2(ЬоР3+ ••• + b3) + Ri (d0p4 + ... + d3p)] и2 (t) =
= R2(b0ps+ + (6)
4. Составить дифференциальное уравнение и найти
передаточную функцию трансформатора (рис. 5) отно-
сительно напряжений щ и и2. Электрические параметры
трансформатора приведены на
рис. 5.
Решение. Дифференциаль-
ные уравнения равновесия напря-
жений цепей первичной и вто-
ричной обмоток трансформатора
имеют вид
U/t W?
Ui = rdi + Lipii + Mpi2, (1) Рис 5‘ Схема тР.ансФ°Р
1 11 1,1 r ' матора к задаче-4.
О = r2C + ^2pi2 + M pii + u2, (2)
где rb Lb ii — сопротивление, индуктивность и ток пер-
вичной обмотки; r2, L2, i2 — то же для вторичной обмотки;
7? — сопротивление нагрузки; /гь и2 — входное и выходное
напряжения трансформатора; М — коэффициент взаимо-
индукции обмоток.
Найдя выражение для тока £ из уравнения (1) и
подставив в (2), получим дифференциальное уравнение
трансформатора
Г LjL2 — М2 2 I L2r 1 + ^-i (R + Zs) . 11 /р,_
W + Р + п (R + rJ -P + 1 -
—7^5^. <3>
или.
- Т1)р2 + (Т1 + Т2) р + 1] и2 (/) = - кх^рщ (0, (4)
-Г £1 -Г _ М т -ъГ' М2
гдеЛ-—, Г2-)? + г2, т>- г, ’ Гз"У nW
Р + Г2 '
Размерность коэффициента и всех постоянных
времени [Т{] = сек (z = l, 2, 3). .Так как коэффициент свя-
зи Л4/|//.|£2в трансформаторе со.стальным сердечником
18 ГЛ. f. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ (S
близок к единице, то М» УLXL2, a LXL2 — Af2~0
или Т]Т2 — Гз 0. Тогда уравнение трансформатора (4)
упростится
[(7\ + Т2) р + 1] «2 (0 = ktipu^t). (5)
Для режима холостого хода (/? = оо, Г^О) имеем
(Ttp+ 1)м2(0 = — ЪРЩ (0-
На . основании дифференциального уравнения (5)
можно записать передаточную функцию-трансформатора
по напряжению,
tw Z „\ = U2 (р) ___fer~lP
W W U! (Р) (П + Т2) Р + 1 ’
из которой видно, что трансформатор является инер-
ционным дифференцирующим звеном. Знак минус в диф-
ференциальных уравнениях трансформатора означает,
что фаза выходного напряжения изменяется на 180°
относительно входного.
5. Составить дифференциальное уравнение трансфор-
матора (рис. 5), если входной величиной является ток ilt
а выходной — напряжение и2.
Решение. Запишем дифференциальное уравнени$(1)
задачи 4 в виде
Щ =П«1(1 + Tip) + Mp (1)
Подставив Ы] из (1) в уравнение (4) задачи 4 и сделав
преобразования, получим
(Т2р+ 1)«2(0 = - kMpidt), (2)
где коэффициенты Т2, k, М соответствуют обозначениям
задачи 4.
Для режима холостого хода (/? = оо, Т2 — 0, fe=l)
имеем
«2(0 = — Mpiiit), (3)
откуда видно, что в режиме холостого хода трансфор-
матор представляет собой идеальное дифференцирую-
щее звено, если входной величиной ^является ток,
а выходной — напряжение.
в] §1.1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ (9
6. Найти дифференциальное уравнение и передаточ-
ную функцию относительно напряжений и{ и и2 пассив-
ной электрической цепи RC в виде моста (рис. 6).
моста (см. решение зада-
Решение. Токи плеч
чи 3)
. _ щС^р . _ ufizp
h Г1Р+1 ’ 12 T2p+l ’
7\ = 7?iCi> T2 — R2C2t P = -£‘
Тогда
«2<0=-jjfe(0-Wi(0 =
uM},
Рис. 6. Мостовая схема к за-
даче 6.
откуда искомое дифференциальное уравнение имеет вид
(TlP-+ 1) (Т2р + 1)ц2(/) = (Г-тУ)щ(0 (1)
и передаточная функция равна
, 1-Т,Т9р2
W = (TiP +1) (Т2р +1) = (Г1Р + D (Т2р +1) ’
где:Т,=
7. Найти передаточную функцию электрического
моста (рис. 6), если сопротивление резисторов — R2
и емкость конденсаторов С] = С2.
Решение. При равенстве сопротивлений и емкостей
противоположных плеч моста (рис. 6) постоянная вре-
мени Т\ = Т2=Т и передаточная функция (2) задачи 6
принимает вид
кр> (1 + Тру \ + Тр--
8. Найти передаточную функцию гидравлического
демпфера (рис. 7), если пренебречь влиянием массы
подвижных частей и принять за входную величину
силу F, а за выходную — перемещение поршня х.
Решение. Приложенной силе F будет противостоять
демпфирующая сила Хд = ctx, где — коэф фициент
20.. , ГЛ. 1.. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ : [8
О)
L
демпфирования, пропорциональный вязкости жидкости
и площади поршня и обратно пропорциональный пло-
щади пропускного отверстия.
Тогда имеем рх — kF, где
k = с?1, и
Х(р) k
Р
Рис. 8. Схема и график
к задаче 10.
Рис. 7. Поршень с ци-
линдром (демпфер).
9. Найти передаточную функцию по условиям пре-
дыдущей задачи, если учесть массу подвижных частей.
Ответ.
"' F(p) р(Гр+ 1) ’ С] ’
т — масса подвижных частей.
10. Найти передаточную функцию, электрической
цепи (рис. 8, а) > по огибающей модулированного сиг-
нала с несущей частотой ®с = 2зт/с, где fc — частота сети.
Реш ение. На основании формулы (4) задачи. 3-
передаточная функция электрической цепи (см. рис. 8, а)
' T = RC,
^1(Р) ^р2+Гр+1
Амплитудная частотная характеристика (а. ч. х.) имеет
вид
. . Д(<о) = ЦТ(j<o)|= .. (2)
V(r-7^2)2+:rW
Tl = LC. (1)
ад.4 1.1; УРАВН Hl Я lb ПЕРЕДАТОЧНЫЕ ФУНКЦИИ; ЗВЕНЬЕВ 2
Анализ зависимости (2) показывает, что график а. ч. х.
электрической цепи рис. 8, а имеет вид, изображенный
на рис. 8, б, причем при резонансной частоте <й==<й0=-^-,
а. ч. х. принимает, максимальное значение А(®0)=1,
а при и ®0 < ® оо А (со) < 1.
•Амплитудная частотная характеристика на рис. 8, б
напоминает а. ч. х. апериодического звена первого по-
рядка, с коэффициентом передачи fe==l и со0 = 0. Най-
дем условие, при котором а. ч. х. с достаточным приб-
лижением является симметричной относительно резонан-
сной частоты соо, т. е. может рассматриваться как а. ч. х.
апериодического звена первого порядка относительно
резонансной частоты соо. Для этого найдем частоты Oj
и со2 из условия идентичности подавления боковых ча-
стот апериодическим звеном первого порядка и электри-
ческой цепью (см. рис. 8, б):
A(®) = ^ = -7L.
v /2 /2
Подставив (2) в (3), получим уравнение
_______Та ____1
решив которое, найдем выражения для боковых частот:
- т+ ]/т’2 + 47’^ т+ |/Л7'2 + 47'2
Чтобы а. ч. х., изображенная на рис. 8, б, была,
симметричной относительно резонансной частоты <оо=То1
необходимо, чтобы выполнялось условие
С0| <02 1 , т2 (р.\
.Условие (6) вы полняется при
т.е. Т <2Т0, или/?<2]/^- (7)
У0 с
Следовательно, электрическую цепь (рис. 8, а) можно
пред ставить в виде апериодического звена первого
22
JL, УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
ги
порядка по огибающей модулированного сигнала, если
выполняется условие (7) и если несущая частота или
частота сети ©с = <о0.
Для определения эквивалентной постоянной времени
апериодического звена первого порядка по огибающей
необходимо найти полосу пропускания рассматриваемой
электрической цепи
Л Т
Д(0п — ®2 ~ ~ т2 ~ .
7 0 Ь
Эквивалентная постоянная времени
<9>
Тогда при выполнении условия (7) и при подборе па-
раметров L, С так, чтобы ®0 = ®с, можно записать выра-
жение для передаточной функции электрической цепи на
рис. .8, а по огибающей модулированного сигнала в виде
"’'W-TSTT- (,0)
11. Найти передаточную функцию электрической
цепи (рис.'8, а) по огибающей модулированного сигнала
при Р = 1000 ом, С = 0,2 мкф,Ь = 0,8 гн и несущей
частоте входного сигнала fc = 400 гц.
Решение. Воспользуемся формулами предыдущей
задачи. ___ ________________
Постоянные времени TQ = VbC = Vo,8 - 0,2 IO-6 =
= 0,4 • 10’3 сек, T = RC= 1000 • 0,2 • 10~6 = 0,2 • IO’3 сек.
Условие (7) выполняется. Резонансная частота ®0=^- =
7 О
=------х-=2500 сек~\ -Частота входного сигнала ©с=
0,4-10-3
= 2nfc = 6,28 • 400 = 2512 сек"1, т. е. условие. <о0 = <ос
практически выполняется. Условие (7) можно уточнить
по формуле (6)
СО] +и2
(8)-
0,04 - 1(Г6
-к + ‘~ 2575 сек'
0,16-10 6 . 4 (0,16 10-6)2
Ы§ 1.1. V БИЕНИЯ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 23
откуда следует, что а. ч. х. симметрична относительно
.. И]4-и2
резонансной частоты, так как ---» <о0.
Эквивалентная постоянная времени Т9 = 2^ = 2 =
—1,6 • Ю'3 сек. Передаточная функция по огибающей
модулированного сигнала
№(р)---------------
1,6.103р + 1
массы под-
11
IIIIIIII11II
12. Найти передаточную функцию пружины и демп-
фера (рис. 9), если пренебречь влиянием
вижных частей и принять за входную
величину силу F, а за выходную — пе-
ремещение точки А (поршня) х.
-Решение. Составляем уравнение
равновесия сил F = Fn4- Fn = ctx4- с2х,
где Ci — коэффициент демпфирования,
а с2 — коэффициент упругости пру- ।
Жины. Тогда имеем (Tip 4- 1) х = kF, |
где Ti — — , k = с2\ откуда передаточ-
с2
ная функция
13. Найти передаточную функцию
по условиям предыдущей задачи, если
учесть приведенную к точке А (см. рис. 9) массу под-
вижных частей.
Ответ. Искомая передаточная функция
xi
Рис. 9. Поршень
с цилиндром и пру-
жиной.
(/?)--.>-. д------->
Т^р + 1 iP + 1
tn — масса подвижных частей.
14. Изменится ли тип динамического звена, к кото-
рому относится .демпфер, рассмотренный в задачах 8
и 9, если входную и выходную величины поменять
местами? Найти передаточные функции.
24 ГЛ. 1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ .ФУНКЦИИ
us
J. , >п
~ Cl
чах 8
15.
НИЯ и
Ответ. Да, изменится. Без учета массы передаточ-
ная функция ”
где k=; 'Ci. С учетом массы —
. Коэффициенты ш и с/, определены в зада-
и 9.
Составить дифференциальное уравнение движе-
передаточную функцию двигателя с независимым
возбуждением • (рис. 10, а)
относительно угловой скоро-
сти £2 при моменте нагрузки
М„-0. •
Ответ. Дифференциаль-
ное уравнение движения
(TaTup2 + Tup + \)Q(t)~
= kuBK (/).
Рис. 10. Схема и механические
характеристики к задаче 15.
Тя = о” / в” — электромаг-
Кя + Кв
нитная постоянная времени
цепи якоря; Ья, Ря — индук-
тивность и активное сопро-
тивление якоря; LB, /?в ~ ин*
дуктивность и внутреннее
сопротивление оконечного
каскада усилителя, питаю-
щего двигатель.
T^JTT = J^ = J^~
• . электромеханическая посто-
янная времени двигателя; / — приведенный к валу дви-
гателя момент инерции вращающихся частей; Мп — пу-
сковой момент двигателя при £2 = 0; ’£2Х х—угловая ско-
рость холостого хода при моменте двигателя М = 0;
<4 .
Се ~ й° ’
XX ।
и0
вх
с = -^- /°
IS] § 1.1. УРАВНЕНИЯ И ПЕРЕДАЖОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 25
—ток короткого замыкания цепи якоря двигателя при
£2 = 0, р = I I = — коэффициент, наклона механиче-
| CliVi | iVi
fixx 1
ских характеристик двигателя, £= —^- =---------коэффи-
6'вх се
циент передачи. Для двигателей постоянного тока
с независимым возбуждением |3 = const при ивх = var.
Передаточная функция двигателя
= ТЯТ^ + ТыР + 1 ‘
16. Найти дифференциальное уравнение движения и
передаточную функцию двигателя
Суждением (см. рис. 10, а) отно-
сительно угла поворота а.
Ответ:
{ТмТяр2+ Тмр + 1) ра (0 = kuBX (0,
ira (р) = 1Т т .
' р(ТяТыр2 + Тмр+1)
17; Найти передаточные функ-
ции двигателя постоянного тока
с независимым возбуждением,
пренебрегая влиянием электро-
магнитных переходных процессов
в цепи якоря (см. задачи 15 н-16).
Ответ,
с. независимым воз-
18. Найта передаточные функ-
ции двухфазного асинхронного
двигателя (рис. 11, а) при мо-
Рис. 11. Схема и механи-
ческие характеристики
к задаче 18.
менте нагрузки 7И„= 0. Механические характеристики
имеют вид рис. 11, б, а электромагнитными переход-
ными процессами в статоре и роторе можно пренебречь.
Решение. Аналогично предыдущей задаче, лере-
Цаточные ' функции асинхронного двигателя по угловой
26
ГЛ. 1. .^РАВНЕНИЯ .и ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
ив
скорости
й по углу
^а(р)= р(Тмр+1) ’
Электромеханическая постоянная времени Ты про-
порциональна коэффициенту наклона •механической ха-
рактеристики р (см. задачу 15):
й°
Тм==/₽о = Г^,
п
где / — приведенный к валу двигателя момент инерции
вращающихся частей; х. -Мп, Ро — соответственно угло-
вая скорость холостого хода, пусковой момент и коэф-
фициент наклона аппроксимированной прямой линией
механической характери-
стики, соответствующей
наиболее часто принимае-
мым значениям управляю-
щего напряжения иу = U°
в автоматической системе
й°- ’
(см. рис. 11, — —
коэффициент передачи
двигателя.
19. Для компенсации
индуктивного сопротивле-
ния обмотки управления
двухфазного асинхронно-
го двигателя в ее цепь
Рис. 12. Электрические и струк- включают конденсатор
турная схемы к задаче 19. емкостью С (рис. 12, а).
Требуется найти переда-
точную функцию двигателя с учетом динамических
свойств образовавшегося контура LCR в цеци обмотки
управления.
Решение. Динамические свойства, выражающиеся
инерционностью электромеханических процессов двига-
№] § 1.1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 27
теля, полностью определяются, передаточными ф нк.
ВИЯМИ Wq(p) и 1У«(р) (см. задачу 18).
Для определения передаточной функции контура LCR
обмотки управления составим эквивалентную схему цепи
обмотки управления рис. 12,. б, где L — индуктивность,
Pv
R = — приведенное активное сопротивление обмотки
7у
управления, /у — номинальный ток, Ру — номинальная
активная мощность обмотки управления, С — емкость
конденсатора, включаемого в цепь управления. Влия-
нием внутреннего сопротивления источника, питающего
обмотку управления, пренебрегаем.
Контур LCR подробно рассмотрен в задаче 10. Его
передаточная функция по огибающей модулированного
сигнала с несущей частотой, равной частоте сети fc или
круговой частоте сети ®с = 2л/с,
Передаточная функция (1) справедлива при выпол-
нении
При выполнении обоих условий передаточные функ-
ции двухфазного асинхронного двигателя
Ip'o (п) — № =--------Ь-------
Uy(p) (Гэр+1)(ГмР +I) ’
IF (п\ — а (р) ________________
оЛ" Uy(p) р(ТаР+1)^+1) •
Структурная схема двигателя принимает вид, изобра-
женный на рис. 12, в.
После незначительных преобразований можно полу-
чить новые выражения для определения эквивалентной
постоянной времени
L 2 х. 2 2 К1 — cos2 <р
7’а = 2 -тт- =--- = — tg <р -----------
s R в>с R ис ь т «Ос cos <р
где <йс » <й0 = , xL = ®CL—индуктивное сопротивле-
ние обмотки управления,cos <р —коэффициент мощности
(1)
~ 2л/<
Vlc
(2)
ГЛ. 1. УРАВНЕНИЯ и ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
обмотки управления при работе без конденсатора (в но-
минальном режиме).
20. Индуктивность обмотки управления двухфазного'
асинхронного двигателя L = 0,05 гн, а приведенное ак-
тивное сопротивление /? = 150 ом. Какой должна быть
емкость конденсатора, включаемого в цепь обмотки
управления, если частота сети /с — 400 гц? Можно ли
пользоваться передаточной функцией (1) из предыду-
щей задачи?
Ответ. 1) С = 3,2 мкф. 2) Можно, так как 7? = 150 ом
ом.
. 21. Найти передаточную
трической цепи LC в виде
рис. 13 (см. задачи 6 и
- Ответ. W (р) = l~T Р
т = уьс.
-22. Найти дифференциальное
уравнение движения поршня
функцию пассивной элек-
моста, изображенного на
7).
Рис. 14. Поршень
с цилиндром и пру-
жиной.
1 + Гр2 ’
Рис. 13. Мостовая схема
к задаче 21.
относительно корпуса х1 под действием силы F (рис. 14)
без учета массы подвижных частей.
Решение. Составим уравнение равновесия сил
F = Fa + Fn = ctx3 + с2х2, где xs = xt — х2 — перемещение
поршня относительно цилиндра, х2—перемещение точки А.
Подставив в уравнение сил вместо х3 его значение,
получим
pxi (/) = kxF (f) + -’0*2(0.
где k. = с;‘, fe„=? щсг1,. т. = с.с;1 (см. задачи 8 и 12).
I X X XI 1 к
§ 1.1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ -29
23. Найти дифференциальное уравнение движения
по условиям предыдущей задачи, учитывая массу по-
движных частей.
Ответ.
(ТХР + 1) px,i (0 = (0 + k2 (т2р2 + тхр — 1) х2 (О,
„ т, , / т, — т2
где Т\ ~ > т2 — у ———-, гги — масса поршня с ры-
чагом, т2 — приведенная масса пружины с цилиндром
(см. задачи 9 и 13).
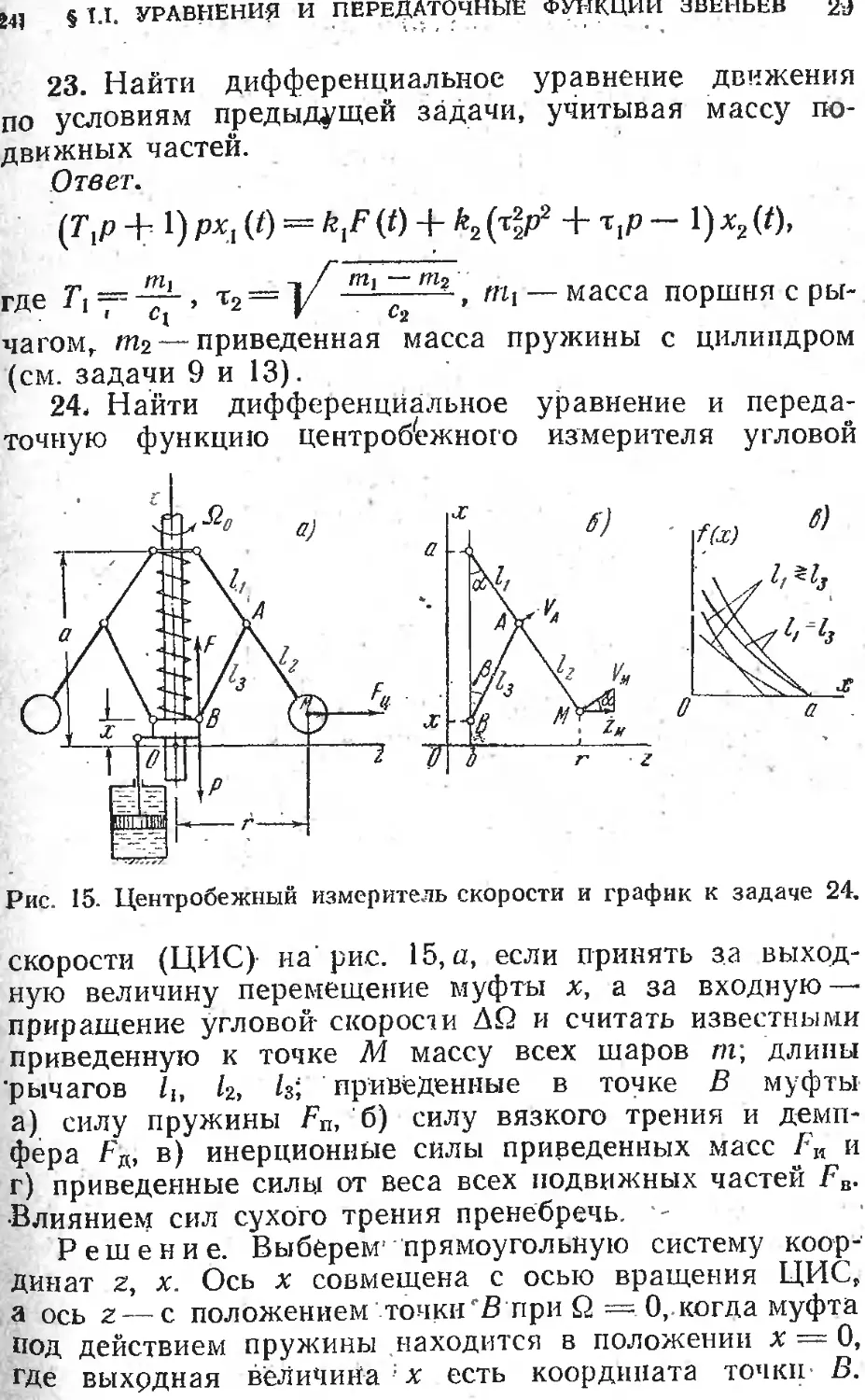
24. Найти дифференциальное уравнение и переда-
точную функцию центробежного измерителя угловой
Рис. 15. Центробежный измеритель скорости и график к задаче 24.
скорости (ЦИС) на рис. 15, а, если принять за выход-
ную величину перемещение муфты х, а за входную —
приращение угловой скорости ДО и считать известными
приведенную к точке М массу всех шаров т; длины
рычагов /ь /2, й; приведенные в точке В муфты
а) силу пружины Fn, б) силу вязкого трения и демп-
фера й'д, в) инерционные силы приведенных масс Fn и
г) приведенные силы от веса всех подвижных частей FB.
Влиянием сил сухого трения пренебречь. •-
Решение. Выберем прямоугольную систему коор-
динат z, х. Ось х совмещена с осью вращения ЦИС,
а ось z — с положением точки'В при Q = О, когда муфта
под действием пружины находится в положении х — 0,
где выходная величина : х есть координата точки В.
30
ГЛ. 1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
[24=
Движущей является центробежная сила шаров
Fa = mrll2, (1)
где г = zM — расстояние точки М от оси х.
На муфту действуют приведенные силы сопротивле-
ния Р и приведенная движущая сила F (см. рис. 15, а).
Приведем к точке В силу Fa на основании равенства
мощностей
FxB = FatM, F = FU^, (2)
Лв
где хв, zM — составляющие скорости перемещения точек В
и М по соответствующим координатным осям. Опре-
делим zM:
гм — VM cos а — VA cos а — хв tg а р-, . (3)
где Z = Z]+Z2, Va, Vm —линейные скорости точек А и М
При их вращательном движении относительно общего
центра с координатами (&, а), а, р — углы, показанные
на рис. 15, б.
Подставив (3) в (2) с учетом (1), получим
F = m-i--t—Й2 = ktfi {г, а, р) Й2, (4)
Zi tg а + tg р 1'1'
где Аг= m , А (г, а, р) = ^^^р.
Из рис. 15, б находим
г — b + Z sin а, х — а — Ц cos а — Z3 cos р, . (5)
где а = Zi + Z3, b — радиус муфты и фланца, к которому
крепятся рычаги-держатели шаров. Из соотношения (5)
видно, что переменные г, х, а и р связаны между собой
нелинейной функциональной зависимостью. Следова-
тельно, можно найти
fi (г, a, P) = f(x). ’ (6)
Например, при Z3=Zj (а = р, a = 2Zj) <
fi (г, а) = f(x) = (2Z, - х) Г --- - = + -М . (6, а)
[ 2 У 41^(2^ -х)2 4ZiJ
42] § 1.1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ 3]
Подставив (6) в ({I), получим
Р = ^(х)Й2. (7)
Линеаризуем- выражение (7) в окрестности малых
отклонений переменных х и Q относительно выбранного
установившегося режима Q = й0, х = х0:
ДТ = )° Дх + (ДЙ = ^iQoZ) Дх + 2^1Й0Б ДЙ, (8)
\ ОХ / \ С/Ьй /
где
В установившемся режиме приведенная сила сопро-
тивления Р — Fn + FB. При этом приведенная сила от
веса подвижных частей (в основном от веса шаров) FB
также зависит от перемещения муфты х; эта зависи-
мость также является нелинейной. Приближенно примем
FB = const. Тогда в динамическом режиме для малых
отклонений уравнение равновесия1 сил примет вид
kF„ + кРл + kFB = кР = kF,
ИЛИ
тв кх -Р с, Дх + с2 Дх = кх + 2fe1Q0E ДЙ, (9)
где та~ приведенная к точке В масса подвижных
частей, х, х — скорость и ускорение муфты, ct — коэф-
фициент демпфирования, с2 — коэффициент упругости
пружины. Преобразуем уравнение (9)' к виду
(т!р2 + Г]Р+1)Дх (0 =/г ДЙ(0. (1°)
где
У — 1 yi _______ Ci &2fejQp£
।
Для всех практически осуществимых ЦИС по схеме
рис. 15,а функция f(x) имеет падающий характер
(рис. 15, в), а коэффициент D = ~4X^ I имеет отрица-
аХ >Х=Хп
тельный знак, который необходимо учитывать при
82 1 ГЛ. 1. УРАВНЕНИЯ II ПЕРЕДАТОЧНЫЕ ФУНКЦИИ [®5
вычислении параметров k, Т\, Т2 и при записи уравне-
ний (9) и (10).
Передаточная функция ЦИС
, W(P)= k .---------
' Т2Р2+Т1Р+1
Г
§ 1.2. Типовые динамические звенья
25. Какое динамическое звено имеет функцию веса
w (/) = 50 (е-5< — е-1“) • !,(/)? Найти параметры этого звена
и записать выражение передаточной функции.
Решение. Способ 1. Приведенная функция веса
состоит из двух экспонент. Следовательно, это аперио-
дическое звено второго порядка с весовой функцией вида
. ( _2_\
w (/) = -7—(е Тз — е Tt) • 1 (/),
т 3 — / 4
откуда находим 7’3 = 0,2 сек> Т4 — 0,1 сек и k = (0,2 —0,1)Х
Х50 = 5,
W = (0,2р + 1) (0,1р+ 1) ’
Способ 2.
СО
(р) = J (Op р/ dt — (1 + 0j2p)(1+0ilp) »
о
откуда 7'3 = 0,2 сек, Т4 — 0,1 сек, k = 5.
26. Найти переходную функцию неустойчивого звена
5
с передаточной функцией W (р) — q lpL'j •
Ответ. 1г (/) = 5 ( — 1 + е10/) • 1 (t).
27. Найти параметры передаточной функции колеба-
тельного звена, если его переходная функция имеет вид,
изображенный на рис. 16. '
Решение. Способ 1. Переходная характеристика
колебательного звена записывается в виде
. /г (/) —" fe | l — e~'ilt ^cos M + у sin • ! .(/).
271
« 1.2. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
33
Затухание колебаний происходит по экспоненте с постоян-
ной времени 7^, = —- = 0,5 сек, откуда у = 2 сек"1. Период
колебаний 7\ = у = 0,628 сек, откуда Я, = 10 сек-1.
Рис. 16. Переходная функция.
Составляем систему уравнений
V = у = 2, ]
X = = 10, |
(1)
решив которую, находим Т = 0,1 сек, £ = 0,2. Из графика
рис. 16 определяем k = 20.
Способ 2. Определив амплитуды А1 и Л2 (см. рис., 16),
можно найти коэффициент затухания переходного про-
цесса у по формуле
।
. X , Al 10 . 10 о
у = — In—Л- = — In7, ~ 2.
' л А2 л 5,3
Подставляя значения частоты затухающих колебаний X
и коэффициента у в систему уравнений (1), находим
постоянную времени Т и параметр затухания £.
34 ГЛ. Т. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ 128
Передаточная функция
1W / \ k 20
\Р)~ Т2р2 + 21Тр+\ ~ 0,01р2 + 0,04р+1 *
.. 28. Устройство работает на переменном токе. Каким
типовым звеном определяются его динамические свойства
по огибающей, если переходная характеристика имеет
вид, изображенный на рис. 17? Колебания с частотой
Рис. 17. Переходная функция звена,
работающего на переменном токе.
сети на графике показаны без соблюдения масштаба
времени. Определить параметры передаточной функции
звена.
Ответ. Колебательное звено с передаточной функцией
= 0,0042р2 + 0,028р+ 1'
29. Известны следующие параметры центробежного
измерителя скорости (см. рис. 15): приведенная к
точке М масса шаров /п = 0,02 кг; I =-6 см, 1{ = 3 см;
стабилизируемая угловая скорость Qo= 150 сек-1; коэф-
31j § 1.2. ТИПОВ Е ДИНАМИЧЕСКИЕ ВЕЯ 35
фициент D = — 0,11 • 10~3; приведенная к точке В масса
подвижных частей тп = 0,09 кг; коэффициент упругости
пружины с2 = 0,7 н • лГ1.
Каким должен быть коэффициент демпфирования cit
чтобы центробежный измеритель скорости был аперио-
дическим звеном второго порядка?
Ответ.
' ct 0,54 н • сек • лГ1
Для решения этой задачи следует воспользоваться дан-
ными задачи 24.
30. По переходной функции, изображенной на рис. 18,
определить тип и передаточную функцию звена. Пере-
ходная функция представляет собой сумму линейного и
экспоненциального членов.
Ответ. Это — интегрирующее звено с замедлением.
Его переходная функция
Г ( * П
h(i) = klt — T\l — е • !(/)•
Уравнение асимптоты переходной функции Лд(/) = k (t — T)
позволяет определить параметры передаточной функции
Т-0,4 С№,
31. Функция! веса апериодического звена первого
порядка изображена на рис. 19. Определить параметры
пеРедаточной функции.
36
ГЛ. Т. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ Г*2
Рис. 20. Структурная схема
к задаче 32.
Ответ. Коэффициент передачи k = 2 и постоянная
времени Т = 0,2 сек.
32. Как изменятся постоянные времени, коэффициент
передачи, время и форма переходного процесса аперио-
дического второго порядка или колебательного звена
при охвате его жесткой отри-
цательной обратной связью
с коэффициентом передачи /г0
(рис. 20)?
Ответ. Время переход-
ного процесса уменьшится,
так как уменьшатся обе по-
стоянные времени Т2 и Tt\
форма переходного процесса
изменится (например, вме-
сто апериодической может стать колебательной), так как
постоянная времени Тх уменьшится в большей степени
(в 1 + kxk0 раз), чем Т2 (в + kyka раз). Коэффициент
передачи уменьшится в 1 + krk0 раз.
33. Как изменятся постоянная времени Г, и коэф-
фициент передачи kx апериодического звена первого
порядка, если его охватить идеальной гибкой отрица-
тельной обратной связью с передаточной функцией цепи
обратной связи Щ,с (р) = Рор?
Ответ. Постоянная времени возрастает (Г = + kxk^,
а коэффициент передачи останется тем же (k = /г().
§ 1.3. Дифференциальные уравнения и передаточные
Л функции автоматических систем
34. На рис. 21, а представлена принципиальная схема
автоматической системы регулирования (стабилизации)
скорости теплового двигателя. Чувствительным элемен-
том {ЧЭ) является центробежный измеритель скорости
(ЦИС). Исполнительным устройством (ЯУ) является
гидравлический двигатель, состоящий из золотника 2,
связанного с муфтой ЦИС 3, и силового поршня /,
связанного с заслонкой, или регулирующим органом (РО).
Составить структурную схему, найти передаточные
функции разомкнутой системы W (р), замкнутой системы
относительно регулируемой величины Ф (р), относительно
ОШИбКИ •[>,(/?) и ПО возмущению Ф( (р), если ЛII 110:1 pi! :о-
BJiiiiwe уравнения отдельных звеньев имеют такой в 1 ц
1) двигатель (объект)
’ (Гор + 1)£2='М-/?,Л1 ,
гщ £2 —угловая скорость, у — перемещение заслонки,
Л1„ — момент нагрузки;
Рис. 21. Принципиальная (а) и структурная (б)
схемы к за чаче 31.
2) центробежный измеритель скорости (см. задачу 24)
(Т2р9+ Т у) + l)x = fe2AQ,
где х — перемещение муфты и золотника, Т2, Tj —по-
стоянные времени ЦИС;
3) гидравлический двигатель
РУ = ^Зх,
А’о, k2 и k3 — коэффициенты передачи.
38 гл. t. уравнения и передаточные ФУНКЦИИ '135
Решение. Составим структурную схему (рис. 21,6),
где обозначены: йвс — приведенная или эквивалентная
угловая скорость настройки, задаваемая поджатием
пружиньРЦИС (см. рис. 21, а); — составляющая угло-
вой скорости от перемещения заслонки у, а й" —от
момента нагрузки М„, причем Q = Q' + Q", и- ошибка
или отклонение Ай = йвс — И. Тогда передаточная функ-
ция разомкнутой ^системы по задающему воздействию
К
w (D\ = . =_________________________________
ОНс(Р) Р{ТоР + \){Т^ + Т1Р+1У
= /г0/г2/г3 [сек ’],
и по возмущению (по нагрузке)
“7<М-та-"-^Лт-
Передаточная функция замкнутой системы относи-
тельно регулируемой величины
ф (р). .______________________________«____________
Йнс(р) l + IF(p) р(7’ор+1)(7’22р2+Г1р+1) + К ’
Передаточная функция замкнутой системы относи-
тельно ошибки
ф А^(Р) 1 р(Т0р+1)(Т2р+Т1Р+1)
х(Р’~ Йнс(р) ~ 1 + Г(р) р(7’0р + 1)(7’2р2+Г1р+1) + К
и по возмущению
ф О = Q[p} = Wf{p) = _ klP(T22pz+TlP+l)
f(P МВ(Р) l + IF(p) р(Гор + 1)(Т2р2 + Т\Р + 1) + К *
35. Найти передаточные функции системы стабилиза-
ции угловой скорости (см. предыдущую задачу), если
гидравлический двигатель охватить гибкой отрицатель-
ной , обратной связью в виде демпфера и пружины
(см. рис. 2).
Ответ.
пт (А) =_________(УосрТ 1)-----------
р(7’2р2+7’1р+1)(7’р+1)(Г0р+1) ’
= k^ska, Wf (р) = + j ,
.37] § 1-3. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ 39
.1 Ф (р) =----------------1)-----------------------
Ю 47 р (Т2р2 + TlP + 1) (Тр + 1) (ГОР + 1) + К (Тжр + 1) ’
" л z ч р(ф2+7’1Р+1)(7’р+1)(7’0р+1)
ф г (р) = 7—5------г----------------------------,
р (ту + г,р +1) (Тр + 1) (Гор +1) + к (Тжр + 1)
L ф ( ) = ^р(^р24-Г1Р+1)(Гр+1)___________
р(ф2+7’1р + 1)(Тр+1)(Т0р + 1) + К(?’оср + ])’
где коэффициенты Т^, Т nk'3 = k определены в задаче 2,
а остальные коэффициенты — в задаче 34.
36. Найти дифференциальные уравнения движения
автоматической системы стабилизации угловой скорости
(рис. 21) относительно регулируемой величины (Q) при
задающем воздействии (йкс) и при возмущении (Л4Н).
Дифференциальные уравнения отдельных звеньев системы
рис. 21 приведены в задаче 34.
Ответ.
а) [р(Тор + 1)(Т2р2 + TlP+l) + K]Q(О = №нс(О
или
( (а0р4 + aip3 + а2р2 + а3р + а4) Q (/) = b0Qm (/),
где а0 = Т0Т2, а{ = Т2 + TOTV а2 = То + Ту а3 = 1, а4 = £>0=/(j
б)
[р (Тор + 1) (Tip2 + 71Р + 1) + к] Q (0 =
^-к,р(т1р2 + т1Р + \}ма (О
или
(«оР4 + G1 р3 + а2р2 + а3р + а4) й (/) =
= - (J0p3 + dtp2 + d2p) Ма (О,
где
do — ktT2, d\ = k\T i, d2=Lki.
37. Найти дифференциальные уравнения движения
системы стабилизации угловой скорости (см. рис. 21)
относительно ошибки (AQ) до задающему воздействию
(Йнс) й по возмущению (Л4Н). Дифференциальные урав-
нения отдельных звеньев системы рис. 21 определены
в задаче 34. i
40 ГЛ. 1. УРАВНЕНИЯ И -ПЕРЕДАТОЧНЫЕ -ФУНКЦИИ - [3S
Ответ.
а) [р (Г.СР.+ 1) (^Р2 + Пр + 1). + 4 АЙ (0 =
= р (Тор + 1) (Tip2 + Tip + 1) Q„< (0;
б) [р(Гор4- 1)(Г22р2+Пр + 1) + 4ай(/) =
= kip(T22p2 + Tip+\)Ma(t).
38. Составить структурную схему и найти передаточ-
ные функции разомкнутой W(р), Wf(p) незамкнутой
Рис. 22. Принципиальная («) и структурная (б) схемы сле-
дящей системы.
Ф(р), Фх(р), Ф; (р) (см. задачу 34) следящей системы
(рис. 22, а), если звенья системы описываются следую-
щими уравнениями:
1) элемент сравнения & = Р', —
2) потенциометрический датчик и = РрЗ;
3) усилитель (Тур + l)uj = k2u, Ту — постоянная вре-
мени усилителя;
4) двигатель (Т„,р + 1) pa = k3u} — kAMt„ Ти— постоянная
времени двигателя;
.891 § 1-3. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ 4{
5) редуктор •0,2 = k5a, kb k2, k3, kt, k5 — коэффициенты
передачи.
Ответ. Структурная схема представлена на рис. 22, б;
W= р(Тур+ 1).(Гмр+ 1)’ К = kik,k3k5[ceK
Д'
Ф = Р(Л'Р+О(7’мр+1) + К *
й , ч___________ktk5[Typ+l) ___
Р ( ГуР + 1) (Т’мР + 1) + К
ф / 1 Р (ТуР + 1) (Л1Р + 1)
Л {Р) ~ Р (?уР + 1) (УмР + 1) + /<-
39. Составить структурную схему и найти передаточ-
ные функции следящей системы (см. рис. 22, а), если
Рис. 23. -Структурные схемы следящей системы.
непосредственно с валом двигателя соединить тахогенера-
тор,- а его напряжение подать на вход усилителя в проти-
вофазе с выходным напряжением потенциометрического
42 - ГЛ. f. УРАВНЕНИЯ И' ПЕРЕДАТОЧНЫЕ ФУНКЦИИ' (40
датчика угла рассогласования. Дифференциальное урав-
нение тахогенератора птг=7гсра. Уравнения остальных
звеньеи следящей системы приведены в условии пре-
дыдущей задачи.
Ответ. Структурная схема представлена на рис. 23, а.
Для вывода передаточных функций структурную схему-
рис. 23, а необходимо преобразовать: перенести сум-
матор 2 на вход сумматора 1 (рис. 23, б). Тогда
W = р[(Гур+1)(Гмр + 1) + МзМ ’ К =
W ( }- М5(Тур + 1)
р[(Гур+1)(Гмр+1) + Л2Ыв] ’
ф =- Р [(Тур + 1) (Д,Р + П + W.J + к ’
_ , . Р [(ГуР + 1) (Тмр + 1) + Р^з/гв]
'Р> = Р [(Гур + 1) (Гмр + 1) + М.з/г6] + к ’
. k4ks (Тур + 1)
Qf [р’~•
40. Найти дифференциальные уравнения движения
следящей системы (см. рис; 22) относительно ошибки (&)
по задающему воздействию (-Oj и по возмущению (А4Н).
Дифференциальные уравнения отдельных звеньев при-
ведены в условии задачи 38.
Ответ.
а) [р(ТуР+ 1)(Тмр + 1) + /С]^(0 =
= р(7’ур + 1)(7’мр + подо,
или
(«оРа +- «ip2 + а2р + а3) -0 (/) = (Ь0р3 4- bvp2 + b2p) (t),
v «о = bo = ТуТк, al — bi = Ty + TK, a2 = b2= 1,
\ d
v а3 = /<, р = -5Г.
6) [р (ТуР + 1),(тмр + I) + ДО (0 = ШТуР + 1) мн (0
или
(о0р3 + «1Р2 + а2Р + «з)(0 = (dop + di) M„(t),
do — k^k5Tу,. di ~ kqk5, P ~ ~dt ’
41]§ 1.3. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ 43
41. На рис. '24, а изображена принципиальная схема
дистанционной следящей системы с синусно-косинусными,
вращающимися трансформаторами (СКВТ), на которой
обозначены: -&и Аг— углы поворота командной и испол-
нительной осей, •0=0'1—•02 — ошибка, РМ — рабочий меха-
низм (объект), Р — редуктор,.Д— двигатель, ТГ—тахогене-
ратор. Параметры элементов следующие: йДв'рад-1] —
коэффициент передачи чувствительного элемента (СКВТ)
Рис. 24. Следящая система.
в линейной части характеристики, k2 и k3 — коэффициенты
усиления усилителей по напряжению, k4 [рад • в"1 сек-1] —
коэффициент передачи исполнительного двигателя, kr,~
= /г-1 — коэффициент передачи редуктора, п — передаточ-
ное отношение, k6 [в-сек -рад-1] — коэффициент передачи
тахогенератора, k7 [рад-н^-см"1-сек-1] — коэффициент на-
клона механической характеристики двигателя, 1\ и
Т2—постоянные времени усилителя и двигателя, Т = RC —
постоянная времени дифференцирующей цепи.
Требуется составить структурную схему и определить
передаточную функцию разомкнутой системы, переда-
точные функции замкнутой системы: а) относительно
Управляемой величины по. задающему воздействию,
б) относительно ошибки по задающему воздействию.
44
ГЛ. 1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
[42
в) относительно ошибки по возмущающему воздействию
и добротность следящей системы по моменту нагрузки Мл.
Ответ. Структурная схема изображена на рис. 24, б.
Передаточная функция разомкнутой системы
.,7, ч_____________/< (1 + Тр)_________
{р’ р [(1 + Ор) (1 + Т2р) (1 + Тр) + ШвТр] ’
где добротность по скорости (отношение постоянной
скорости слежения к установившейся ошибке)
К — kikik^k,^ [сек-1].
Передаточная функция замкнутой системы относи-
тельно управляемой величины по задающему воздействию
Ф (р)______________________________________________
'р> р ((1 + т>р} (1 + Лр) (1 + Гр) + k3kikeTp] + К (I + Тр)
Передаточная функция замкнутой системы относи-
тельно ошибки по задающему воздействию
Ф (п\= р К1 + Т'р^ + т^ + гр) + ЫЛ;7р]_____________
p[(l + Tip)(]+Tip)(l + Tp) + kikikBTp] + K(l + Tp) •
Передаточная функция замкнутой системы относи-
тельно ошибки по возмущающему воздействию (моменту
нагрузки Мк)
ф , ч ______________fe7feg(l + Г1Р)(1 + Гр)__________
и Р [(1 + Ttp) (1 + Т2р) (1 + Тр) + ksk4/г6Гр] + к (1 + Тр) •
Добротность по моменту (отношение момента на-
грузки М» на исполнительной оси системы к рассогла-
сованию в установившемся режиме)
к _ К Кп2 kyk^kin
k7k5 k7 k7
42. Для предыдущей задачи определить численные
значения коэффициентов, входящих в передаточную
функцию разомкнутой системы, при'- следующих исход-
ных данных: крутизна чувствительного элемента fej=
I в/град = 57,3 в/рад, коэффициенты усиления усили-
теля ^2 = 2,5 и /г3 = 80, номинальное значение напряже-
ния двигателя t7H=H0 в, скорость холостого хода
«хх = 9000 об/мин и пусковой момент Л4П = 55 Г-см =
W .§ 1.3. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ 4У
= 0,54 н • см, момент инерции двигателя с объектом
J = 0,098 г • см2—0,01 Г-см- сек2, передаточное отношение
редуктора п — 1000, коэффициент передачи тахогенера-
тора &6 = 0,001 в мин/об = 9,6 • 10'3 в сек/рад, постоян-
ная времени усилителя = 0,01 сек, постоянная вре-
мени-дифференцирующей цепи Т = 0,14 сек.
Решение. Коэффициент передачи двигателя
, Qx. у лп.х.х 3,14-9000 о„ т _>
~иТ~ ЗОР,, ~ 30-110 “8,6 Рад'в ' сек •
Коэффициент наклона механической характеристики
1 Рх.х лпх.х 3,14-9003 п _] _]
~ “мГ ~ 30М7 “ 30-55 ~ 17,2 рад ’ Г 'СМ 'СеК •
Постоянная времени двигателя
Т2 = J = Jk7 = 0,01 • 17,2 = 0,172 сек.
2 Л4„ 7
Добротность системы , по скорости
К = kik2k3k4k5=-----iodo"—~ 100 сек ‘
Передаточная функция разомкнутой системы
,г/ /пч =________100(1+.0,14р)______
W р (14- 1,18р + 0,027р2 + 0,00024р3) '
Раскладывая знаменатель последнего выражения на
множители, передаточную функцию разомкнутой системы
можно представить в следующем виде:
_________/<(1 + Гр)______
p(l + 7'3p)(l+2gr4p+r2p2)
где Т3— 1,16 сек, Т4 = 0,0145 сек и g = 0,8.
Добротность по моменту
/<п2 100-10002 - Q 1П6 „ д-1
AVI = —у— =-----— = 5,8 •. 10ь Г • см • рад =
/Су I «jZ
= 1700 Г • см (уел. мин)~1°
46
ГЛ. I; УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
[4Т
§ 1.4. Структурные схемы и их преобразование
43. Преобразовать динамическое звено, описываемое
дифференциальным уравнением
(7’2рЧ-7’1Р+1)^ = 4- (1)
во встречно-параллельное (с обратной связью) соедине-
ние консервативного и идеального дифференцирующего
звеньев.
Решение. Преобразуем дифференциальное урав-
нение (1) к виду
*2 = r2J+l Х' ~ грТТ *2’ (2)
По уравнению (2) составим структурную схему
(рис. 25, а), которая переносом сумматора, или элемента
Рис. 25. Структурные схемы к за-
даче 43.
сравнения, и объедине-
нием двух последов атель-
но соединенных звеньев
преобразуется в искомую
схему на рис. 25, б.
44. Найти передаточ-
ную функцию замкнутой
системы Ф(р) автоматиче-
ской системы, структур-
ная схема которой изо-
бражена на рис. 26, а.
Решение. Освобо-
димся от перекрестных
связей неструктурной схе-
ме на рис. 26, а, для чего
перенесем узел / через
сигнала (рис. 26, б).
находим искомую
звено !F3 по направлению действия
По полученной структурной схеме
передаточную функцию
Ф(р) =
.1 + Г,Г2+ Г2Г3+ Г,Г2Г3
45.\Найти дифференциальное уравнение автомати-
ческой бистемы, структурная схема которой изображена
на рис. 26, а, относительно управляемой величины //(/)
461
§ 1.4. СТРУКТУРНЫЕ' СХЕМЫ И ИХ ПРЕОБРАЗОВАНИЕ
47
по задающему воздействию g (t), если
У ’ Гз (Р) = k3.
Решение. Воспользовавшись решением предыдущей
задачи, найдем
Ф (р) = = —2?° ,
' . G (р) й0р2 + «1р + а2
где. Y(р), G (р) — изображения управляемой величины
Рис. 26. Структурные схемы к задаче 44.
и задающего воздействия, р = с + /со — комплексная пере-
менная, Ьс= klk3, «0 = Tiki, #1 = + k3T i,. Ct.2 — ki + &з+
+ k[k3. Тогда искомое дифференциальное уравнение
(а0р2 ч- щр + а2) у (0 = bog (/),
где р = — символ дифференцирования.
46. Найти дифференциальное уравнение автомати-
ческой системы, структурная схема которой изображена
на рис. 27, а, относительно управляемой величины y(t)
по возмущению f(t), если
= г2(р) = тр, r3(p) = fe3. <4(р) = тДт.
т2р + /Зр + 1
48
ГЛ. 1. УРАВНЕНИЯ и передаточные функции
Решение. Вначале получим передаточную функцию
автоматической системы по возмущению Of(p), для чего
преобразуем структурную схему рис. 27, а. Перенесем
сумматор 2 через звено и заменим Wi, W2 одним
Рис. 27. Структурные схемы к задаче 46.
звеном (рис. 27, б). Найдем передаточную функцию
разомкнутой системы по задающему воздействию
W = ЩрТ = ^5
и по возмущению
Wf(p) = ^=W5(p).
Тогда
Ф / \== Wf _ d°p+di
f Р Г (р) 1 + 117 (р) аор3 + щр2 + а2р + а3 ’
где У (р), Р(р)~ изображения управляемой величины
y(t) и возмущения f ((), р = с + /со — комплексная пере-
менная, d0 = £r7’., d, = kc. ап = Т.Т1, а. = Т1 + Т,Т...
^2 T^~l~ + h^k^TJ, = J -|-
47] § 1.4. СТРУКТУРНЫЕ СХЕМЫ И ИХ ПРЕОБРАЗОВАНИЕ 49
Отсюда искомое дифференциальное уравнение имеет
вид
(аорЗ + щр2 4- а2р + а3) у (t) = (dop + dt) f (/), p = .
47. Найти следующие передаточные функции авто-
матической системы, структурная схема которой
Р.ис; 28. Структурные схемы к задаче 47.
изображена на рис. 28, а: разомкнутой системы по за-
дающему воздействию W(p) и по -возмущению 'Wf(p)’,.
БО ~ ГЛ. (. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ (48
основную Ф(р), по возмущению Of(p) и относительно
ошибки по задающему воздействию Фх(р).
Решение. Преобразуем структурную схему рис.28, а
(см. рис. 28. 6, е и г). По структурной схеме рис. 28, г
найдем
W(p)= ^1Г2Г3)^4 + Г5, rf(p) = r3r4,
(Ы \ W^1WZb+(1 + W^1WZ2^3)^4+^5
tWJ-i + №I№2 + (l + №1№2№3) Г4+1Г6 ’
п. , , ________Г3Г4___________
\Р) ~ 1 + Wiw2 + (1 + WtW2W3} W4 + F6 ’
Фх = l + ^^ + tl + ^^rg) r4+r6' •
48. Найти дифференциальные уравнения автомати-
ческой системы, структурная схема которой изображена
на рис. 28, а, относительно управляемой величины y(t)
по задающему воздействию g(t) и по возмущению f(t),
а также относительно ошибки x(t) по задающему воз-
действию g(t) и по возмущению f(t), если W71(p) = /ji,
Ответ. ’
D (р) У (0 = (&оР2 + bip 4- b2) g (О,
О (р) У (0 = (d0p2 + dip + d2) f (t),
D (p) x (0 = (c0p3 + qp2 4- c2p) g (t),
' D (p) x (t) = - (dopz + d^ + d2) f (0,
где характеристический полином системы
D (р) = аор3 4- аур2 + а2р + а3- п0 = с0, ai = fc0 + ci>
й2 = Ь\ Ч- Сг, йз= b2", bo = kikak^Ti + TiTs,
bi — kikzki Ti-}• Tz-}• kikzkaTz-]-kskt Ti,
bz — 1 4- kikzks 4- k^kt *;
Co= k4lTiTz, Ci = (7’14-7’2), Сг = /г41;
do^ksTiTz, dt = /j3(7’i 4-7’2), d2 — k3, Р~~м'
ГЛАВА 2
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ДИНАМИЧЕСКИХ ЗВЕНЬЕВ И СИСТЕМ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
§ 2.1. Характеристики динамических звеньев
49. Построить амплитудно-фазовую характеристику
звена с передаточной функцией
Г(р)=-|-.
Ответ. Амплитудно-фазовая характеристика совпа-
дает с отрицательной полуосью мнимых чисел (рис. 29, а).
50. Построить амплитудно-фазовую характеристику
звена с передаточной функцией
Ответ. Амплитудно-фазовая характеристика совпа-
дает с отрицательной полуосью вещественных чисел
(рис. 29, б).
51. Построить амплитудно-фазовую характеристику
цепи RC, представленной на рис. 30, а\ Р = 1 ком,
С — 10 мкф.
Решение. Частотная передаточная функция цепи
равна
<0
где
T = RC= 103- 10~5= 10"2 сек.
Преобразуем выражение (1) таким образом, что-
бы оно представляло собой комплексное число в
52гл. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [бГ
алгебраической форме:
* (М=и М+iv М = + i =
___ tO (t>___i_ ; 10 ~e> (t)\
i + ioA2 7 i + io~V * * '
Задаваясь отдельными значениями co,. можно по
формуле (2) вычислить ряд пар значений U(со) и V(co)
6)
jVfa»
Р Ufa»
а>=оо
4,5-
-Z,0- -UPP,5K
Л
I
«2
Рис. 29. Амплитудно-фазовые характеристики интегри-
рующих звеньев первого порядка (а) и второго по-
рядка (б).
и построить по ним амплитудно-фазовую характеристи-
ку цепи.
Однако анализ выражения (2) показывает, что эта
характеристика определяется уравнением
V2 + (U - 0,5)2 = 0,52
и для положительных частот является полуокруж-
ностью, расположенной в верхней полуплоскости с цен-
тром в тучке (0,5; /0) и радиусом 0,5 (рис. 30,6).
Из выражения (2) видно, что при со = 0 U7(/w) =
.= 04- /0, а при (о~оо W(/со) —. 1 + /0. Точки, соответ-
53]
§ 2.1. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
53
ствующие этим, а также некоторым промежуточным
частотам, указаны на рис. 30, б; значения частоты на
этом и всех последующих рисунках даны в рад!сек.
Рис. 30. Амплитудно-фазовая характеристика дифферен-
\ пирующего звена (случай 1).
Рис. 31. Амплитудно-фазовая хд*
рактеристика апериодического зве-
на первого порядка.
Частоты, соответствующие промежуточным точкам кри-
вой, могут быть найдены следующим образом.
Аргумент комплексного числа (2) равен
Ф = arg W (» = arctg ~ = arctg , (3)
поэтому луч, проведенный из начала координат под
углом ф к оси абсцисс, пересекает амплитудно-фазовую
характеристику в точке,
в которой величина со
определяется через ф со-
гласно (3). Один такой луч
показан на рисунке.
52, Построить ампли-
тудно-фазовую характе-
ристику апериодического
звена с передаточной
функцией
W (р} = —-—, =-------
W \ + Тр l+O.lp-
Ответ. См. рис. 31 (а. ф. х. представляет собой полу-
окружность).
53. Найти уравнение кривой, представляющей собой
амплитудно-фазовую характеристику дифференцирую-^
54 гл. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ
щего звена, изображенного на рис. 32, а. Построить
амплитудно-фазовую характеристику звена для случая
/?1 = 40 ком, R2 — 10 ком, С = 2,5 мкф.
Рис. 32. Амплитудно-фазовая характеристика дифференцирующего
' звена (случай 2).
Рис. 33. Амплитудно-фазовая характе-
ристика апериодического звена второго
порядка.
Ответ. Уравнение кривой’ имеет вид
где
- Р /?| + /?2 '
(1)
Согласно (1) амплитудно-фазовая характеристика
является для положительных частот полуокружностью,
расположенной в верхней полуплоскости, с центром
B5J § 2.Г. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ 55
5 точке ( /О') и радиусом 1 2 р . Эта характери-
стика построена для указанных данных на рис. 32, б.
54. Построить амплитудно-фазовую характеристику
апериодического звена второго порядка с передаточной
функцией 1Г(р)=^г+ TlP)(i + T2p) если /< = 8’
У] = 80 мсек, Т2— 12 мсек.
Ответ. См. рис. 33.
Рис. 34. Амплитудно-фазовая характеристика колебатель-
ного звена.
55. Построить амплитудно-фазовую характеристику
колебательного звена с передаточной функцией
W = 1 + 2^р+Г2рг ’
при /г=1; g = 0,15, Г = 0,02 сек.
Ответ. См. рис. 34.
56 ГЛ 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ, ЗВЕНЬЕВ. И СИСТЕМ [56
56. Построить амплитудно-фазовую характеристику
зв_*на с передаточной функцией
W^(P)= ,, д г Ч,
' ’ Р (1 + Тр)
35. Ам ыитудно-
(1)
(2)
Рис.
фазоаая характеристика
последовательного соеди-
нения интегрирующего
звена и апериодического
звена первого порядка.
k — 10 сек-1, Т = 0,25 сек.
ртвет. См. рис. 35; штриховой линией показана
асимптота, к которой стремится, а. ф, х. при со—>0.
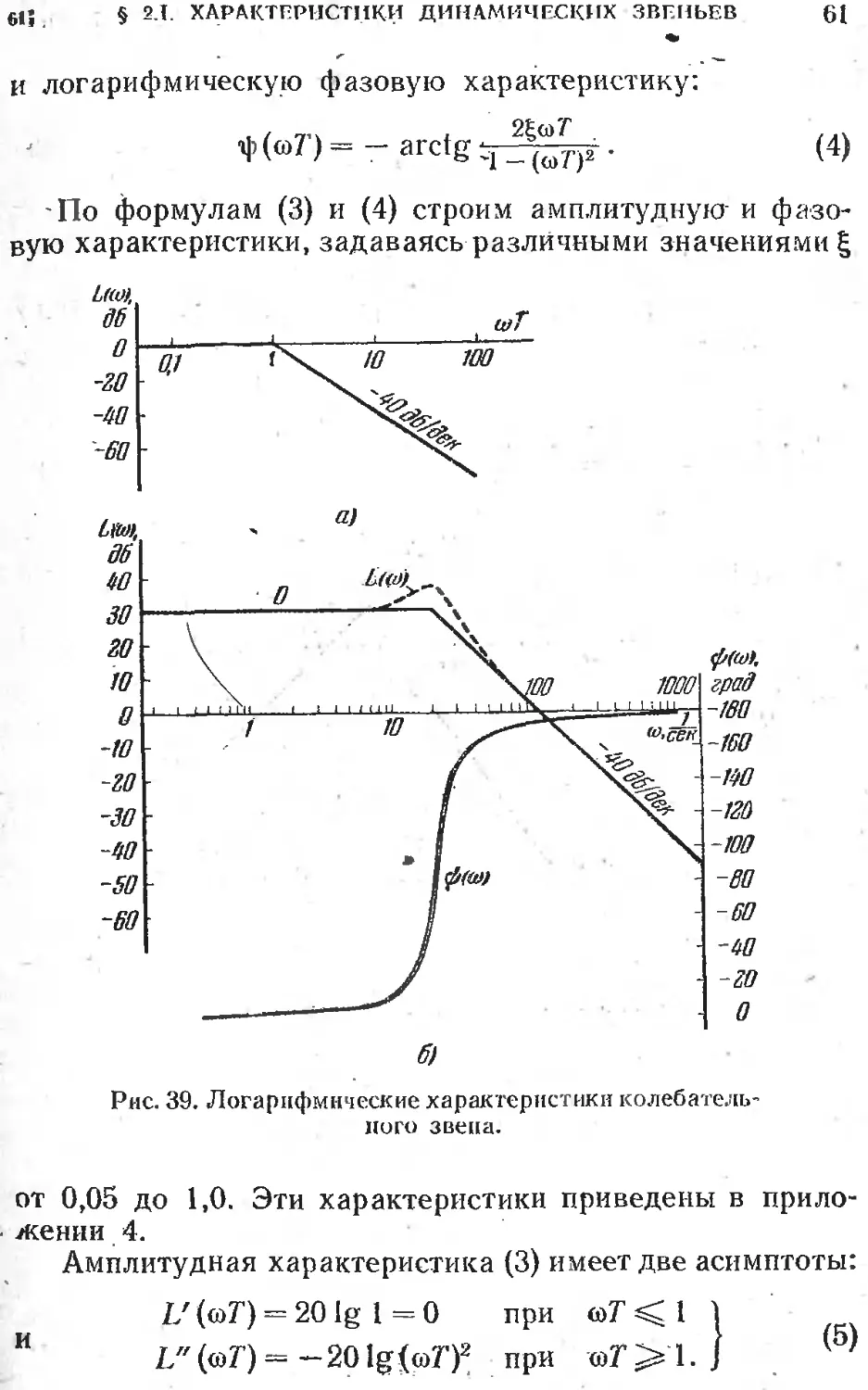
57. Построить логарифмические амплитудную L(co)=
= 20 lg| W (ja) | и фазовую ф(со) характеристики аперио-
дического звена с передаточной
функцией
'TW-TTzf
для двух случаев: а) в виде, при-
годном для любых k и Т; б) для
k = 100, Г = 50 мсек.
Решение. Логарифмическая
амплитудная характеристика, со-
бтветствующая выражению (1),
равна
L (со) = 20 1g | W (/со) 1 =
= 201g „ k .
& V 1 + (соГ)2
Асимптотическая логарифми-
ческая амплитудная характери-
стика, соответствующая (2), по-
строена на рис. 36, а; по оси
абсцисс отложена величина соУ
в логарифмическом масштабе, по
оси ординат — L (со) в децибелах,
л. а. х. имеет согласно (2) излом
Слева от излома она горизонтальна
Асимптотическая
в точке, где со Г =1.
и расположена на высоте 20 Ig k, справа от излома она
имеет наклон — 20 дб/дек. Точка пересечения характе-
ристики с осью частот, т. е. частота сос среза, опре-
деляется из условия
А Ь
.£ (сос) ~ 20 lg-^-y = 0 или сос = -у-.
§ 2.Т’. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ 57
Наибольшее ' о’тклбнениё асимптотической характе-
ристики от точной имеет место при соТ = 1 и составляет,
как можно найти из выражения (2), 3 дб. При со7' = О,5
Рис. 36. Логарифмические характеристики устойчивого и неустой-
чивого апериодических звепьео к задачам 57 и 58.
и <вГ = 2 отклонение асимптотической характеристики
от точной равнб примерно 1 Об, а за пределами участка
иТ = 1 ± 1 октава это .отклонение ничтожно мало.
Фазовая характеристика звена определяется согласно
(1) выражением
ф (®) = a-rg 17 (/о) = — arctg (3)
58 гл. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [КГ
В области низких частот >0, в области высоких
частот -ф(о)-> — 90°; при аТ = 1 ф(и)=—45°. Из вы-
ражения (3) следует также, что фазовая характеристика
симметрична относительно точки аТ = 1, -ф == —45°.
Фазовая характеристика апериодического звена
с передаточной функцией (1) построена согласно (2)
в виде ф (оУ) в приложении 3.
При построении использована следующая таблица:
соТ 0 0,05 0,1 0,2 0,5 1 2 5 10 20 ч со
Ф (®Т), град 0 —2°50' —5°40' —И°20' —26°30' —45 —63°30' —78°40' —84°2С/ —87° 10' —90°
Логарифмические амплитудная и фазовая характе-
ристики звена с передаточной функцией
построены на рис.. 36, б; штриховой линией показана
точная амплитудная характеристика в части, где она
не совпадает с асимптотической, построенной согласно
формуле (2). По оси абсцисс отложена частота <в
в логарифмическом масштабе, по оси ординат — деци-
белы и градусы.
58. Построить логарифмические амплитудную и фа-
зовую характеристики неустойчивого апериодического
звена с передаточной функцией
~ -1 + 0,05/) '
Ответ. Амплитудная характеристика L (<о) та же,
что и для устойчивого звена с передаточной функ-
цией (4) в предыдущей задаче (см. рис. 36, б).
Фазовая характеристика ф(<о) дана на рис. 36,6
пунктирной кривой.
59. Передаточная функция динамического звена равна
»<₽)-тот™-
611
§ 2.1.. ХАРАКТЕРИСТИКИ ДИНАМИЧЕ КИК ЗВЕНЬЕ
Построить логарифмические амплитудную £(<в) и фа-
зовую ф (со) характеристики звена при К = 400 сек-1 для-
трех случаев: 1) Т = 25 мсек, 2) Т=5 мсек, 3) Т = 2,5 мсек.
Указание. При построении фазовой характе-
ристики целесообразно использовать приложение 3.
Ответ. См. рис. 37; Индекс при L (®) иф(®) означает
номер случая. Для первого случая (Т = 25 мсек) пунк-
тиром показана точная амплитудцая характеристика.
Рис. 37. Логарифмические характеристики к задаче 59.
60. Построить логарифмические амплитудную и фа-
зовую характеристики системы с передаточной функцией
ivz / \ К 300
" \Р) - (1 + Тр)2 “ (1 + 0,025р)2 •
Ответ. См. рис. 38. Из рисунка видно, что при вы-
черчивании логарифмических характеристик не обяза-
тельно строить логарифмическую сетку частот, доста-
точно лишь сделать соответствующие отметки на оси
частот. - •
Для нанесения этих отметок обычно используется
шкала логарифмической линейки; удобный масштаб
имеет шкала кубов малой логарифмической линейки.
61. Построить логарифмические амплитудную и фа-
зовую характеристики колебательного звена с переда-
|6<3' Г.П 2 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ E6I
точной функцией
1 W(p) = 1+2^Тр+Т2р2 ‘
1 Рассмотреть случаи:
1) характеристики £ (е>7 ) и при k=l и g=0,£>5;
0,10; . 0,8; 1,0;
2) характеристики £(о) и ф(®) при k = 30, £=0,2,
Т = 50 мсек.
Рис. 38. Логарифмические характеристики к задаче 60.
'Решение. 1) Частотная передаточная функция,
соответствующая (1) при £=!., равна
- = (1 - rW) + j2£,Ta •
Из (2) находим логарифмическую амплитудную харак-
теристику
° ' L(“r)^201gW=WlbwF (3)
§ 2.1 ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ 61
*
и логарифмическую фазовую характеристику:
ф (а>Т) = - arctg ц ?^ЫГП2 (4)
По формулам (3) и (4) строим амплитудную- и фазо-
вую характеристики, задаваясь различными значениями g
Рис. 39. Логарифмические характеристики колебатель-
ного звена.
от 0,05 до 1,0. Эти характеристики приведены в прило-
жении 4.
Амплитудная характеристика (3) имеет две асимптоты:
L' (о>7) = 201g 1 = 0 при <лТ <1 1 1
L" (©/’)=-201g (со/')2 при <оГ>1./ (5)
62 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИС ЕМ [62
Асимптотическая амплитудная характеристика, опре-
деляемая выражениями (5), построена на рис. 39, а.
Для колебательного звена асимптотическая ампли-.
тудная характеристика может очень отличаться от точ-
ной, что следует из сравнения рис. 39, а с рисунком,
приведенным в приложении. 5. Поэтому для колебатель-
ного звена обычно строится точная амплитудная харак-
теристика. Это построение удобно проводить, суммируя
Рис. 40. Логарифмические амплитудные характеристики
к задаче 63,
ординаты асимптотической характеристики с ординатами
кривой отклонения AL(co) асимптотической характе-
ристики от точной; такая кривая дана в приложении 5.
2) Характеристики L (со) и -ф (со) для звена с пере-
даточной функцией
пу / , _ 30 30 гг..
w \Р>~ I + 2 • 0,2 • 0,05р + 0,0025р2 “ 1 + 0,02р + 0,0025р2 ’
построенные с использов анйем приложений 4. и 5, при-
ведены на рис.,39, б.
62. Построить логарифмические амплитудную и фа-
зовую характеристики неустойчивого колебательного
звена с передаточной функцией
= 1 - 2^ Гр + Т2р2’
при А = 30, 7 = 50 мсек, £ = 0,2.
М] §22 АМПЛИТУДНО-ФАЗОВЫЕ ХАРАКТЕРИСТИКИ 63
<
Ответ. Амплитудная характеристика совпадает с L (<о)
устойчивого колебательного звена в предыдущей задаче,
имеющего передаточную функцию (6) (см. рис. 39, б).
Фазовая характеристика отличается от -ф (со) для звена
с передаточной функцией (6) только знаком.
63. На рис. 40 изображены асимптотические лога-
рифмические амплитудное характеристики минимально-
фазовых звеньев. Найти передаточные функции этих
звеньев.
Ответ.
Wt (р)= /1 . т A t » & = 100, Л = 100 мсек, Т2=8 мсек-,
(I + тip) (I +1 2р) •
6 = 0,025 сек, 7 = 0,15 сек.
J 1 + Тр’
§ 2.2. Амплитудно-фазовые характеристики разомкнутых
систем автоматического регулирования
64. Система автоматического регулирования имеет
структурную схему, показанную на рис. 41; ЧЭ — чув-
ствительный элемент, Д —двигатель, Р—редуктор. Пере-
даточная функция разомкнутой системы равна
W = ’ р(1 + 7’1РГ(1 + 72р) '
Построить амплитудно-фазовую характеристику системы
при /( = 400 сек-1, 7г=80 мсек, 72=12 мсек.
Ответ. Амплитудно-фазовая характеристика может
быть построена по приведенным в таблице значениям
модуля А (со) и аргумента ф(со) частотной передаточной
функции W (jo) = А (со) е'*(е>).
(&,сек~1 0 2 5 10 20 50 100 300 ОО
А (о) оо 196 74 31 10,3 1,66 0,319 0,015 0
ф (о), град -90 -100 -115 -135 -162 -197 -223 -252 -270
64 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ
65. Система автоматического регулирования имеет
структурную схему, показанную на рис. 41. Передаточ-
ная функция разомкнутой системы имеет, вид
р(1+Г,р)(1 + г2р) •
Найти такой способ изображения амплитудно-фазовых
Рие. 41. Структурная схема к задачам 64 и 65.
характеристик, который позволил бы охватить случаи
различных сочетаний параметров А, Т\, ?У системы.
Решение. Представим выражение (1) в виде
“ ^pd+^pHl +aTlP) >
Частотная передаточная функция, соответствующая
выражению (2), имеет вид
117 «»> - тлгтгттздйттгзд “ -
• =KTtU0 + }КТгУ0 (Т^). .р)
Задавшись последовательностью близких друг к другу
значений a = T2/Ti от « = 0дой=1, можно построить
семейство амплитудно-фазовых характеристик, практи-
чески охватывающих все возможные варианты систем
с передаточной функцией (1). ,
II а рис. 42 построено семейство подобных ампли-
тудно-фазовых характеристик для а = 0; 0,2; 0,4; 0,6; 0,8.
Построение выполнено на основе выражения (3) по его
модулю и аргументу для различных значений частоты;
66] § 2.2. АМПЛИТУДНО-ФАЗОВЫЕ ХАРАКТЕРИСТИКИ 65
по осям координат отложены величины
Uo (<о) = (КТ^1 U (<4 и Vo (со) = (КТО’1 V (®).'
Переход к характеристике, соответствующей опреде-
ленному значению КТ\, осуществляется умножением
чисел, отложенных по осям координат, на величину КТр
Интерполирование позволяет легко получить ампли-
тудно-фазовые характеристики систем, для которых ве-
личины а — T^/Ti отличаются от приведенных на рис. 42.
66. Построить амплитудно-фазовые характеристики
двух' систем, . имеющих . в .разомкнутом состоянии
6S ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ ТОТ
передаточные функции:
а> ВД-
^г(₽) = р(Ц-0,05р)(1+0,02р) *
Указание. Возможно использование готовых кри-
вых из предыдущей задачи.
Ответ. См. рис. 43.
Рис. 43. Амплитудно-фазовые характеристики к задаче 66:
а) кривая для первой системы, б) для второй системы.
67. Построить амплитудно-фазовую характеристику
системы, блок-схема которой дана на рис. 44; ЧЭ — чув-
ствительный элемент, Д — двигатель, Р — редуктор. Пе-
редаточная функция разомкнутой1 системы имеет вид
/<(1 + Т2р) ' 500(1 4-0,ОЗр)
w w P(l4-TlP)(l + TsP) p.(l+0,lp)(l+0,00fip) ’
g 2.2. АМПЛИТУДНО-ФАЗОВЫЕ ХАРАКТЕРИСТИКИ 67
Ответ. См. рис. 45.
68. Найти уравнение кривой, представляющей собой
амплитудно-фазовую характеристику системы, имеющей
Рис. 44. Блок-схема к задаче 67.
Рис. 45. Амплитудно-фазовая характери-
стика к задаче 67.
следующую передаточную функцию:
Построить амплитудно-фазовую характеристику для
случая Д’ = 100 сек~2 и Т 0,2 сек.
Решение. Частотная передаточная функция равна
W (/со) = = U (со) + jV (со),
68 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ (69
где
= V(<o)=-^. (1)
Из (1) находим
= (2)
Согласно (1) н (2) амплитудно-фазовая характери-
стика представляет собой для положительных частот
ветйь параболы, лежащую в третьем квадранте ком-
плексной плоскости.
Точка амрлитудно-фазовой характеристики, соответ-
ствующая какому-либо значению частоты <о, легко опре-
деляется как точка пересечения параболы с лучом, про-
веденным из начала координат и составляющим с осью
вещественных чисел угол
- ф = arctg— — л + arctg соТ.
Амплитудно-фазовая характеристика для заданных
параметров построена на рис. 46.
69. Передаточная функция разомкнутой системы
равна
Построить ее амплитудно-фазовую характеристику при
К = 50 сек~2 а К.~ 200 сек-2.
Ответ. См. рис. 47. ..
>69]
$ 2;2. АМПЛИТУДНО-ФАЗОВЫЕ ХАРАКТЕРИСТИКИ
69
// /
Рис. 47. Амплитудно-фазовые характеристики к за-
даче 69. Шкала I—для А = 50, шкала 77—для
7<=200.
Рис. 48. Амплитудио-фазовые характеристики к задаче 70.
Шкала А — для К — 200 сект3, шкала Б — для /С = 100 сект3.
70 ГЛ. 2. ЧАСТОТНЫЕ. ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [70'
70. Построить амплитудно-фазовую характеристику
системы с передаточной функцией в разомкнутом со-
стоянии
К. (1 + 0,2р)2
р3 (1 +0,04р)
при К = 200 сек~3 и Д' = 100 сек~3.
Ответ. См, рис. 48.
71. На рис. 49 приведена цепь тахометрической обрат-
ной, связи с пассивными корректирующими контурами;
Рис; 49. Схема к задаче 71.
ТГ — тахогенератор. Построить амплитудно-фазовую
характеристику этой цепи, если ее передаточная
74J
§ .2.2. АМПЛИТУДНО-ФАЗОВЫЕ ХАРАК ЕРИСТИКИ
7Т
Функция равна
W = (1 + Г1Р/(1 + у2р) ’
/С = 4 в-сек2/град, Г] =0,5 сек, Т2 = 0,1 сек.
Ответ. См. рис. 50, где числа, отложенные вдоль
осей, имеют размерность
в)град.
72. Построить ампли-
тудно-фазовую характери-
стику цепи с передаточной
функцией
_ 100
Р (~1 +о,1р)
Ответ. См. рис. 51.
73. Построить ампли-
тудно-фазовые характери-
стики систем с передаточ-
ными функциями
(А) Г(р) =
______________к______________
( - 1 + 27-tp + 72р2) (1 + Т2р) '
(Б) W (р) =
______________К (1 + Т,р)___________
(-1 + 27- ,р + Т2р2)(| + Г2р) П + Г.р)
Рис. 51. А. ф. х. системы
с неустойчивым звеном.
для случая К = 5, Т{ = 0,1 сек,. Т2 = 0,05 сек, 73 = 0,03 сек,
Т4 = 0,006 сек.
Ответ. См. рис. 52.
74. Блок-схема системы гироскопической стабилиза-
ции, разомкнутой на входе датчика угла прецессии,
может быть представлена [4, 5] в виде, показанном
на рис. 53; ДУП — датчик угла прецессии, Д — двига-
тель, Р — редуктор, Г — гироскоп. Передаточная функция
разомкнутой системы может быть при безынерционном
72 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [74
Рис. 52. Амплитудно-фазовые характеристики к задаче 73.
прецессии
Рис. 53. Блок-схема системы гироскопической стабилиза-
ции к задачам 74 и 75.
Рис. 54. Амплитудно-фазовые характеристики гироскопиче-
ских систем.
------§ 2.3. ВЕЩЕСТВЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ 73
• \
усилителе записана в виде
* А*
W = р(1+2£,Тр+Т2р2}
Построить амплитудно-фазовую характеристику этой
системы при К. =20 сек-1; £ = 0,15, 7^ = 0,02 сек.
Ответ. См. кривую А на рис. 54.
75. Система гироскопической стабилизации, блок-
схема которой дана на рис. 53 (см. также задачу 74),
имеет при инерционном усилителе следующую переда-
точную функцию в разомкнутом состоянии:
p(\ + TlP)[l+2lT2p+Tlp2) '
Построить амплитудно-фазовую характеристику этой
системы при /< = 20 сек-1, 7\ = 0,2 сек, Г2 = 0»02 сек,
1 = 0,15.
Ответ. См. кривую Б на рис. 54.
§ 2.3. Вещественные частотные характеристики
замкнутых систем автоматического регулирования
76. Построить вещественную частотную характери-
стику Р(ю) замкнутой системы автоматического регули-
рования. Передаточная функция разомкнутой системы
(1>
К = 20 сек-1, 7'=0,1 сек.
Решение. Вещественная частотная характеристика
строится по точкам. Эти точки могут быть найдены раз-
личными способами.
а) Вещественная частотная характеристика Р (<о) мо-
жет быть построена по ее аналитическому выражению
Р (и) = Re [Ф (/©)], (2)
Ф(/©) —частотная передаточная функция замкнутой
системы, равная
♦(Ю-тЖг <3>
74ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ
Согласно (3) и (1) получаем
ф,. , К(К-Тео2) .
^0°>) (К-7(02)2+ (02 1 (X- 7'0>2)2 4-0)2 • W
Из (4) и (2) находим
о _ К (К—Та2) = 20 (20 — 0,1со2)
г (К - Та2)2 + со2 (20 - 0Дсо2)2 + (о2 * W
Подставляя в (5) различные значения о, получаем
табл. 1 для построения Р (со):
Таблица 1
сек”1 0 5 7 10 15 18 20 25 30 40 50 60 оо
Р (<й) 1,00 1.06 1,08 1,00 —0,23 —0,25 —0,50 —0,35 —0,24 —0,15 —0,08 —0,06 0
По данным табл. 1 на рис. 55, а построена веще-
ственная частотная характеристика.
б) Если для ряда значений частоты со имеются ко-
ординаты U (со) и V (со) точек амплитудно-фазовой
Таблица 2
<а. сек 1 0 5 7 10 20 40 СО
и (со) — оо -1,60 -1,34 -1,00 -0,41 -0,13 0-
V (со) — оо -3,18 -1,93 -1,00. -0,21 -0,02 0
характеристики разомкнутой системы (табл. 2), то соот-
ветствующие значения Р(со) можно найти по, формуле
р/,а_ l/2(co) + V2(<o) + (7(<o)
Р{(а> ~ -[l + VTa)Y+V2(a) • (6)
В случае, когда координаты точек амплитудно-фазо-
вой характеристики заданы в виде модуля Д(со) и ар-
гумента ф(<о) (табл. 3) частотной передаточной функции
W (/со), характеристика Р (со) может быть построена
по формуле
' Л2 (со) + 2Л (со) cos if (со)+ .1 ’ ' ’
7в]
§ 2.3.- ВЕЩЕСТВЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
75
Таблица 3
<л, сек
30 40 50 60
Я (о)
ip (со), град
оо 3,56 2,34
-90-116-125
1,41 0,448
-135 -154
0,211 0,121 0,078 0,054
—162 —166 —169 —170
0
—180
получаемой из формулы (6) при подстановке
U2 (о) + V2 (о) = А2 (о) и [/(«>) = A (to) cos ф (ю).
в) Если имеется амплитудно-фазовая характеристика
разомкнутой системы, то для построения Р(со) удобно
использовать формулу
Р — Аг + и (ц\
Р (°>) — В2 , С8)
получающуюся из (6) при подстановке Д2(«>)= f72(co)4-'
Е2(«)) и В2(а>) = [1 + t/(co)]2+ V2(«>). Величины Д(®)
Рис. 55. Вещественная частотная характеристика к задаче 76.
и В (ю) для каждой заданной частоты <о легко получить
из амплитудно-фазовой характеристики, так как Д(о>)
76 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [77
представляет собой модуль вектора 1Г(/со), т. е. рас-
стояние от начала координат до заданной точки k ха-
рактеристики, а В (со) — расстояние от точки (—1,/0)
до точки k (рис. 55).
Числа, входящие в .формулу (8) и необходимые для
построения вещественной частотной характеристики,
приведенной на рис. 55, а, можно получить из ампли-
тудно-фазовой характеристики системы с передаточной
функцией (1), изображенной на рис. 43, а. .
г)- Для построения вещественной частотной характе-
ристики системы по имеющейся амплитудно-фазовой
характеристике (рис. 43, а) можно
воспользоваться номограммой,
называемой вещественной круго-
вой диаграммой. Такая номо-
грамма дана в приложении 11.
Р(Ш)
1.2
1,0
0,8
0.6
0.4
0.2
0
_1____I t I ! I I |
50 100150\ 200 250 300 350 400 550 500
-QZ
Рис. 56. Вещественная частотная характеристика
к задаче 77.
77. Построить вещественную частотную характери-
стику Р(с>) замкнутой системы автоматического регули-
рования, если передаточная функция разомкнутой си-
. 500(1 +0,03р)
стемы W(p) p(i+о,1р)(1+о,ОО6р) ‘
Таблиц а 4
“1 со, сек 0 10 20 30 40 50 100 200 500 СО
А (о) со 36,8 13,0 6,85 4,6 3,38 1,35 0,488 0,095 0
ф (со), град -90 -122 -130 -130 -130 -130 -133 -136 -165 -180
7gj § 2.3. ВЕЩЕСТВЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ 77
* ч
- При построении Р(со) может быть использована ам-
плитудно-фазовая характеристика системы, приведенная
на рис. 45, либо табл. 4 величин модуля Л(<о) и аргу-
мента ф(<о) частотной1 передаточной функции системы.
Ответ. См. рис. 56 и задачу 76.
78. Построить вещественную частотную характери-
стику Р(<о) замкнутой системы. Амплитудно-фазовая
Рис. 57. Амплитудно-фазоваяи веществен-
ная частотная характеристики .к задаче 78.
характеристика разомкнутой системы-дана на рис. 57, а.
При построении могут быть использованы данные табл. 5.
Ответ. См. рис. 57, б и задачу 76.
Таблица 5
—1 со. сек 0 2 4 7 10 15 20 ОО
оо 10.32 2,80 1,05 0,58 0,28 0,16 0
ф (со), град —180 —175 —172 —172 —177 —188 -199 -180
78 гл, 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ J79
79. Построить вещественную частотную характери-
стику замкнутой статической системы. Амплитудно-
фазовая характеристика разомкнутой системы дана
в виде кривой Б на рис. 52.
Ответ. См, рис. 58 и задачу 76.
Рис. 59. Вещественная частотная характе-
ристика к задаче 80.
80. Построить вещественную частотную характери-
стику замкнутой статической системы. Амплитудно-
фазовая характеристика разомкнутой системы совпадает
С приведенной на рис. 33.
Ответ, См. рис. 59 и задачу 76.
В21 § 2.4. ЛОГАРИФМИЧЕСКИЕ ХАРАКТЕРИСТИКИ 79
81. Построить вещественную частотную характери-
стику замкнутой системы с астатизмом третьего порядка.
Рис. 60. Вещественная частотная
характеристика к задаче 81.
Амплитудно-фазовая характеристика разомкнутой си-
стемы дана на рис. 48 (шкалы с буквой А).
Ответ. См. рис. 60 и задачу 76.
§ 2.4. Логарифмические характеристики систем
автоматического регулирования
82. Построить логарифмические амплитудную и фа-
зовую характеристики системы с передаточной функцией
= 1 + 0,12р + 0,002р2 " (1)
Решение. Для построения логарифмических ха-
рактеристик следут разложить знаменатель (1) на два
сомножителя.
80 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ [82
Для этого определяем корни знаменателя, которые
оказываются равными —10 сек-1 и —50 сек-1, и пред-
ставляем (1) в виде
W = (1 + Лр) (1 + Г2р) = (1 +0,1р) (1 + 0,02р) •
Отсюда находим логарифмическую амплитудную харак-
теристику системы
L (о) — 201g | +д1<о) (1 + jO,O2<o) |
= 201g .......... 42___________. (3)
И1 + (0,1ю)2][1 + (0,02®)2] V ’
Из выражений (2) или (3) следует, что асимптоти-
Рис. 61. Логарифмические характеристики к задаче 82.
— 10 сек-1 и ®2= 1/Г2 = 50 сек~1 и состоит из трех участ-
ков: горизонтального, проведенного на высоте 201g 40 =
= 32 дб; участка с наклоном —20 дб]дек', участка с на-
84] § 2.4. ЛОГАРИФМИЧЕСКИЕ ХАРАКТЕРИСТИКИ 81
клоном —40 дб/дек. Эта асимптотическая характери-
стика представлена на рис. 61.
Так как отношение 7’i/712 = 5, т. е. превышает две
октавы, то из решения задачи 57 следует, что откло-
нение асимптотической амплитудной характеристики
от точной в районе каждого излома имеет такой же
вид, как й для апериодического звена и не превы-
шает 3 дб.
Фазовая характеристика имеет вид
•ф (<о) = — arctg 0,1 о — arctg 0,02®. (4)
Последнее выражение позволяет построить 'ф(м) по
точкам. Однако проще построить ф(®) как сумму орди-
нат фазовых характеристик -ф, (со) и фгС®) двух аперио-
дических звеньев с постоянными времени = 1 сек и
7*2 = 0,2 сек, так как каждая из этих характеристик
легко строится при помощи графиков приложения 3.
Фазовая характеристика ф(ю) системы дана на
рис. 61.
83. Построить логарифмические амплитудную и фазо-
вую характеристики системы с передаточной функцией
/ \ 12,5
W v3’ = р(1 +0,004р + 0,0004р2) *
Указание. Передаточную функцию следует при-
вести к виду, удобному для построения логарифмических
характеристик, т. е. найти, соответствует ли полином
второй степени в знаменателе двум апериодическим
звеньям или он соответствует колебательному звену, и
определить необходимые параметры этих звеньев.
Ответ. См. рис. 62.
84. Система автоматического регулирования, блок-
схема которой построена по образцу, представленному
на рис. 44, имеет в разомкнутом состоянии передаточ-
ную функцию >
W(n) =________- _______=
p(l + TlP)(l+T3p)O + TiP)
=___________K(1 +0,017p)________________ m
P (1 +0,05p) (1 + 0,0025p)(l +0,001p) ' ' '
82 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ 184
Построить логарифмические асимптотическую амплитуд-
ную и фазовую характеристики системы для двух зна-
чений коэффициента усиления: К = 500 сек""1 и /< =
= 2000 сект1.
Решение. Частотная передаточная функция, соот-
ветствующая (1), имеет вид
в/ (ко) =----------^<(1 +/0,017®)---------
w м ' ja (1 + /0,05®) (1 + /0,0025м) (1 + /0,001 ®) * v '
Из выражения (2) или из выражения (1) видно, что
асимптотическая амплитудная характеристика имеет вид
ломаной прямой с участками, имеющими отрицательный
наклон 20—40 — 20—40—60 дб)дек, и с изломами в точ-
ках о, = 1/71. — 20 сек"1, со2 = 1/72 = 59 сек"1, <о3 — 1/Т3 =
= 400 сек"1, ®4 — 1/Т4 = 1000 сек"1; первый участок
характеристики является частью прямой с наклоном
— 20 дб/дек, пересекающей ось частот в точке <о = /<.
Асимптотические амплитудные характеристики £j(<o)
для случая /<=500 сек"1 и £2(<о) для случая /<=2000 сек"1
изображены на рис. 63.
Фазовая характеристика для обоих случаев совпа-
дает и, согласно. (1) или (2), может быть найдена как
496)
§ i.4. ЛОГАРИФМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
83
сумма ординат фазовой характеристики фо(<о) идеального
интегрирующего звена, фазовых .характеристик ф, (о),
ф3(и) и ф4 (<о) апериодических звеньев с постоянными
времени Тъ Ts и Г4и ф2(<о)-дифференцирующего звена
с постоянной времени Т2-
. Указанные фазовые характеристики звеньев и резуль-
тирующая фазовая характеристика 4(со) всей системы
построены на рис. 63.
85. Построить логарифмическую асимптотическую
амплитудную характеристику L(<o) и логарифмическую
фазовую характеристику ф(<о) системы с передаточной
84 . ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ (88
функцией
П7 — К(1 + 1\р),
при К — 75 сек"2, 7\ = 200 мсек, Т2 — 25 мсек, Т3 — 6 мсек.
Ответ. См. рис. 64.
86. Построить логарифмическую амплитудную и фазо-
вую характеристики системы с передаточной функцией
• гс/лл /<(1 + Пр)2 _ 7<(1-Ю,25р)2
Р3 (I + Т2р) (I + Т3р) р3 (1 + О.ОЗр) (1 + 0,008р)
для трех случаев: 1) К = 250 сек"3; 2) К — 75 сек"3;
3) 1000 сек"3.
Ответ. На рис. 65 показаны асимптотические, ампли-
тудные характеристики LJco), £2(<й) и ^з((й)> причем
индекс соответствует номеру случая; для случая 1 пункти-
ром показана точная амплитудная характеристика. Фа-
зовая характеристика ф(®) для всех случаев одна и та же.
87. Построить логарифмические амплитудную й фазо-
вую характеристики системы со следующей передаточной
Рис. 65. Логарифмические характеристики к задаче 86.
86 ГЛ. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ 188
функцией:
= р (1 + 0,104р +0,0008р2 + 0,0004р3) ’
Указание. Знаменатель передаточной функции
следует разложить на множители, чтобы привести W(p)
к виду, удобному для построения логарифмических
характеристик.
Ответ. Амплитудная £(<о) и фазовая ф(<о) характе-
ристики построены на рис. 66.
88. Построить логарифмические амплитудную и фазо-
вую характеристики системы с передаточной функцией
W (р) = —---------------Л-5Г-
(И-т^О+г^р + ^р2)
при Д'= 0,0645 сек; 7, = 30 мсек; Т2 = 7 мсек; § = 0,2.
Ответ. См. рис. 67.
89j §2.4. ЛОГАРИФМИЧЕСКИЕ ХАРАКТЕРИСТИКИ 87
*
89. Построить логарифмические амплитудно-фазовые
характеристики системы с передаточной функцией
\т( ._____+
W W “ р (1 + TlP) (1 + Т3р) (1 + Лр)
_ К(1 + 0,017р)
р (1 + 0,05р) (1 + 0,0025р) (I + 0,001р)
для двух случаев: 1 = = 500 сек"1', 2)/С = 7<2 =
= 2000 сек"1.
Рис. 68. Логарифмические амплитудно-
фазовые характеристики к задаче 89.
Решение. Для построения логарифмической ампли-
тудно-фазовой характеристики 201g | W (/со) | = f [ф (/’со)]
предварительно строятся логарифмические амплитудная
и фазовая характеристики системы. Используя эти
83 гл. 2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ 1»0
(см. задачу 84),
скую амплитудно-
характеристики Lx (со) и ф((о), изображенные на рис. 63
строим по точкам логарифмиче-
фазовую характеристику для случая
K = = 500 сек-1? Эта
ф(а9, град
характеристика представ-
лена на рис. 68 (кривая /).
Числа возле отметок на
кривой указывают соот-
ветствующие значения ча-
стоты со в сек-1.
Высокочастотная часть
кривой, для которой
ф(со) < — 180°, заменена
ее зеркальным отображе-
нием в оси ординат. Для
этой части кривой, пока-
занной на рисунке пункти-
ром, на оси абсцисс преду-
смотрена дополнительная
шкала углов от —180 до
—280°. На рисунке име-
ется также шкала запаса
по фазе, равного т}(со) =
= ф(со)+ 180°.
Длд случая /< = /<0 =
= 2000 сек-1 аналогичная
кривая может быть по-
Рис. 69. Логарифмические ампли- строена переносом всех
тудно-фазовые характеристики точек кривой / на 12 дб
к задаче 90. вверх (201g K2IK1 = 12 дб),
см. рис. 68, кривая 2.
• 90. Построить логарифмические амплитудно-фазовые
характеристики системы с передаточной функцией
tvz (— К(14-Г1р) _______К (1 + 0,2р)
Р2 (1 + Т2р) (1 + ГзР) Р2 (1 + 0,025р) (1 + 0,006р)
для двух случаев: 1) /< = 75 сек-2; 2) /< = 400 сек~2.
Указание. Возможно использование решения за-
дачи 85.
Ответ. См. рис. 69, где кривая 1 относится к первому
случаю, а кривая 2 — ко второму.
ГЛАВА 3
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
§ 3.1. Алгебраические критерии устойчивости
91. Характеристическое уравнение системы имеет вид
р3 + р2 + 2р+ 1=0.
Определить устойчивость системы.
Ответ. Система устойчива.
92. Характеристическое уравнение системы имеет вид
5р3+2р2-3р+1 = 0.
Определить устойчивость системы.
Решение. Система неустойчива, так как не вы-
полняется необходимое условие устойчивости.
93. Передаточная функция разомкнутой системы
U4p) = -7FZt-v-
47 Р (1 + Тр)
Определить условия устойчивости замкнутой системы.
Ответ. /(>0, Т>0.
94. Передаточная функция разомкнутой системы
где Д' = 100 сек~2.
Определить устойчивость замкнутой системы.
Ответ. Замкнутая система находится на границе
устойчивости.
95. Определить устойчивость замкнутой системы, если
передаточная функция разомкнутой системы имеет вид
tF(p)= р2(1 + тр)»
90
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
где Д' — 20 сек"2 — добротность системы по ускорению,
Т = 0,01 сек — постоянная времени.
Ответ. Замкнутая система структурно неустойчива,
т. е. неустойчива при любых значениях Д и 7V 0.
96. Структурная схема системы приведена на рис. 70.
Коэффициент усиления разомкнутой системы Д > 0,
постоянная времени 7’>0.
Определить устойчивость
-/+Z/7
у разомкнутой системы и усло-
вие устойчивости замкнутой
системы.
Рис. 70. Структурная схема
системы к задаче 96.
Ответ. Разомкнутая си-
стема неустойчива. Замкну-
тая система устойчива при
Д>1.
97. Характеристическое уравнение системы имеет вид
(&1 г k2) р3 + щр2 + а2р + а3 = 0,
где kt = 25 сек3, k2 = 25 сек3, at = 10 сек2, а2 = 5 сек,
а3 = 25. Определить устойчивость системы.
Решение. Коэффициент при старшем члене харак-
теристического полинома aQ — ky — k2. При Aj — k2<0
система неустойчива, так как не выполняется необходи-
мое условие устойчивости. При aQ = k\ — k2 > 0 и при
выполнении условия а}а2 — а0а3>0 (см. приложение 6)
система устойчива. В данной задаче а0 = fej —£2 = 25 —
— 25 = 0. Система находится на границе устойчивости.
98. Характеристическое уравнение системы имеет вид
а0р4 + щр3 + а2р2 + а3р — 0,
где «0 =10 сек4, «, = 5 сек3, а2 = 2 сек2, а3=10 сек.
Определить устойчивость системы.
Решение. Характеристическое уравнение системы
запишем в следующем виде:
(«оР3 + а{р2 4- а2р + а:,)р^ 0.
(1)
Из (1) видно, что один из корней характеристического
уравнения равен нулю. Система будет находиться на
границе устойчивости, если все остальные корни харак-
теристического уравнения лежат в левой половине
1021
§ 3.I.- АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
91
плоскости корней. Для этого должны выполняться усло-
вия устойчивости для полинома
а0р3 + а{р2 + а2р + а3,
которые имеют вид
а0>0, а(>0, а2>0, а3>0, aia9>aoa3.
Для значений коэффициентов а0, ..., а3, принятых
в задаче, последнее неравенство не выполняется. По-
этому система неустойчива.
99. Решить предыдущую задачу для следующих зна-
чений коэффициентов:
а) ао=1О сек4, 0^ = 5 сек3, а2 = 2 сек2, а3 = 1 сек;
б) а0—10сек4, а(=5 сек3, а2 = 2 сек2, а3 = 0,5 сек.
Ответ, а) Система находится на границе устойчивости;
б) система находится на апериодической границе устой-
чивости.
100. Передаточная функция разомкнутой системы
имеет вид
д-
W “ р2 (1 + TlP) (1 + ТгР) ’
где /С = 50 сек"2 — общий коэффициент усиления разом-
кнутой системы; 7\=1 сек, Т2 — 0,05 сек — постоянные
времени. Определить устойчивость замкнутой системы.
Ответ. Система структурно неустойчива, т. е. не-
устойчива при любых значениях общего коэффициента
усиления разомкнутой системы К и постоянных времени
Т{ Ф 0 и Т2 0.
101. Передаточная функция замкнутой системы авто-
матического управления имеет вид
Д
ф = Tt Т1Р3 + (Г, + Г2) р2 + р + к ’
где К = 50 сек"1, 71 = 0,2 сек, Т2 = 0,2 сек.
Определить устойчивость системы.
Ответ. Система неустойчива.
102. Решить задачу 101, если К — 50 сек"1,1\ = 0,1 сек
й = 0,02 сек.
Ответ. Система устойчива.
92
ГЛ. 3. УСТОЙЧИВОСТЬ ДИНЕИНЫ ТЕМ
[103
103. Движение автоматической системы описывается
следующей системой дифференциальных уравнений:
ф-й(уо + т) = с2Уо+Д.
Уо + у + Й11’!= “ ClVo + ^2,
Y + йф = -kt <Yi - у„) + б3,
(О
где Yu— задающее воздействие; 6lt б3 — возмущаю-
щие воздействия; Yi> Yo> Ф ~~ координаты системы;
й = 1,16 • 10-3 сек-1, kt = 10 сек-1, сь с2— коэффициенты.
Определить условия устойчивости системы.
Решение. “Зэданпем систему дифференциальных
уравнений (1) в символической форме:
рф - й (yo + Y) = c2Yo + 61.
PYo + PY + йф = - CjYo + 62.
PY + &ф = — kt (y - Y4) + *з»
(2)
где p —символ дифференцирования.
Характеристический полином автоматической системы
равен определителю системы уравнений (2):
—й — (й + с2) р
Д(р) = Д(р) = Р Р + Q й p + ki 0 й
Характеристическое уравнение системы:
Р3 + (<Ч + &[) Р2 + (й2 + fejCj) р + й2(£( + С|) + ЙС2^[ =
= а0р3 + щр2 + а2Р + аз = 0>
где а0 =1, = с( -Ь^, а2 = й2-^ feicb а3 —
= й2 (ki + с,) + ЙС2^[.
Условие устойчивости получим, используя критерий
устойчивости Гурвица (приложение 6). В данной задаче
система будет устойчивой при выполнении следующих
неравенств:
«о>0, <3)>0, «2>0. а3>0, а^ — аоа^О. (3)
JOT! § I- АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ 93
Подставляя в неравенства (3) значения коэффициен-
тов системы, получим условие устойчивости
с? + /г.с.
с9 < 1 о 1 = 863с? + 8630с,.
104. Определить устойчивость автоматической си-
стемы управления, если ее движение описывается сле-
дующей системой дифференциальных' уравнений:
ф-й(у0 + у) = с3у0.
у0 + у + йф = — C1YO,
у + йф = — ki (у0 - уи) + J k2 (у0 - уи) dt,
где уи — задающее воздействие; у, у0, ф —координаты
системы; й = 1,16 • 10-3 сек-1, k2 — 3 • 10~s сек-2, kt = 1X
X 10 2 сек-1, с( = 10 1 сек-1, с2 = 2,5 • 10-2 сек-1 — коэффи-
циенты. Определить устойчивость системы.
Ответ. Система устойчива.
105. Передаточная функция разомкнутой системы
имеет вид
FW-
'' р?(1 + Т2р)
Определить условие устойчивости замкнутой системы.
Ответ. Ti > Т2.
106. Передаточная функция разомкнутой системы
имеет вид
W ^ = ДТ+тр)з '
где К = 5 — общий коэффициент усиления разомкнутой
системы, Т = 0,5 сек — постоянная времени. Определить
устойчивость замкнутой системы.
Ответ. Замкнутая система устойчива.
107. Передаточная функция разомкнутой системы
одноосной гироскопической стабилизации имеет вид
р(1+2^Ттр + ^)'
Общий коэффициент усиления разомкнутой системы
/С = 50 сек-1, постоянная времени Тг = 0,01 сек. Опреде-
94ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ систем ГОТ
лить: а) при каких значениях коэффициента демпфиро-
вания £ гироскопический стабилизатор устойчив; б) усло-
вие устойчивости.
Ответ, а) Гироскопический стабилизатор устойчив
при коэффициенте демпфирования g>0,25; б)
108. В одноосном гироскопическом стабилизаторе,
рассмотренном в задаче 107, для увеличения области
устойчивости введен сигнал, пропорциональный произ-
водной от угла прецессии. При этом передаточная функ-
ция разомкнутой системы будет следующей:
r(p)==
р(1+2£Тгр+Т^Р )
Определить: а) условие устойчивости гиростабилизатора;
б) устойчивость гиростабилизатора при общем коэффи-
циенте усиления разомкнутой системы /< = 50 сек-1; при
постоянных времени 7’г = 0,01 сек, т = 0,01 сек; коэффи-
циенте демпфирования £ = 0,1.
Ответ, а) К< гиростабилизатор устойчив.
109. Передаточная функция одноосного гиростабили-
затора имеет вид
где ki = 25 сек-1 — коэффициент усиления разомкнутой
системы; 77 = 0,01 сек — постоянная времени.
Для демпфирования системы последовательно в ка-
нал управления введено звено с бесконечной полосой
пропускания (рис. 71) и коэффициентом усиления ^2= 1-
Выбрать постоянную времени корректирующего звена Т
из условия устойчивости.
Решение. Передаточная функция разомкнутой
системы
W(p) = H'JrVvfUr
p(l+7X)(l + 7p)
где К — kik2 — общий коэффициент усиления разомкну-
той системы.
1И1 § 3.1. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ ®5
*
Характеристический полином замкнутой системы
равен сумме полиномов знаменателя и числителя пере-
даточной функции разомкнутой системы:
D (р) = Р (1 + Т'гр2) < 1 + Тр) + К (1 - Тр) =
= Гг/У + Тгр3 + Тр2 + (1 - КТ) р + К.
Используя критерий устойчивости Гурвица для авто-
матических систем, имеющих характеристический поли-
ном четвертого порядка (приложение 6), получаем усло-
вие устойчивости гиростабилизатора
1 г?
Гиростабилизатор устойчив, например, при
=0,015 сек.
Рис. 71. Структурная схема гиростабили-
затора к задаче 109.
Рис. 72. Структурная схема к задаче 110.
НО. Структурная схема автоматической системы
приведена на рис. 72. Постоянные времени звеньев
7’1 =0,01 сек, 7’2 = 0,5 сек, 7'3 = 0,05 сек. Определить
критическое значение общего коэффициента усиления
разомкнутой системы К = ПРИ котором автома-
тическая система находится на границе устойчивости.
Ответ. Критическое значение общего коэффициента
усиления разомкнутой системы Кк=16,8 сек-1.
111. Передаточная функция разомкнутой системы
имеет вид
pU + TipXI+TsP) ’
96
гл. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
[112
где К — добротность системы по скорости; 7\ = 0,2 .сек,
7'з = 0,02 сек — постоянные времени объекта управления
и усилителя; Т2 — постоянная времени корректирующего
устройства. Определить значения постоянной времени
корректирующего устройства Г2, при которых замкну-
тая- система устойчива при любых положительных зна-
чениях добротности системы по скорости.
Ответ. Т2 = 0,018 сек.
112. Структурная схема электромеханической следя-
щей системы приведена на рис. 73. Коэффициент пере-
дачи измерительного элемента kKt 8= 1 в/град ~ 57,3 в/рад,
Рис. 73. Структурная схема электромеханической следящей
системы.
коэффициент усиления усилителя ky = 1000, коэффициент
передачи двигателя kR = 50 рад/в сек коэффициент пере-
дачи редуктора fep= 10-3, постоянная времени двигателя
7М = 0,05 сек, постоянная времени усилителя Ту =
= 0,005 сек. Определить: а) устойчивость электромехани-
ческой следящей системы при отсутствии тахометриче-
ской обратной связи; б) значения коэффициента пере-
дачи тахогенератора kTT, при которых следящая система
устойчива.
Ответ, а) Следящая система неустойчива;
б)
-тг
^и. akykuky
J- + _L
- Гм Гу
- 1 0W1 = 2,4 • 10~3
в • сек!рад.
113. Схема электромеханической следящей системы
приведена на рис. 74, а. Коэффициент передачи измери-
тельного элемента, выполненного на СКВТ, kH.a = 1 efepad',
коэффициент усиления первого усилителя — коэффи-
циент усиления второго усилителя — k2, постоянная
времени второго усилителя — Т — 0,0у05 сек; коэффн-
113) § ЗЛ. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ 97
циент передачи двигателя &д = 50 padje • сек\ постоянная
времени двигателя 1\, = 0,05 сек-, коэффициент передачи
редуктора kp— 1 : 1000= 10-3. Для демпфирования си-
стемы первый усилитель охвачен отрицательной обрат-
ной связью. Общий коэффициент усиления разомкнутой
системы из,условия обеспечения точности работы сле-
дящей системы должен быть не менее 300 сек~1.
Рис. 74. Схемы электромеханической следящей системы к задаче 113-
Определить коэффициенты усиления усилителей и
параметры корректирующего контура из условий обе-
спечения устойчивости системы и заданного значения
общего коэффициента передачи разомкнутой системы.
Решение. Передаточная функция корректирующего
контура . 1
где kK = 1, Т = RC.
Структурная схема электромеханической следящей
системы, начерченная в соответствии со схемой 74, а,
приведена на рис. 74, б.
98
ГЛ 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
При отсутствии корректирующего контура переда-
точная функция разомкнутой системы равна
Wt = р (1 + Гур) (1 + тыР) ’
где К' = k„. sktkzkjip — общий коэффициент усиления
разомкнутой системы. Условие устойчивости замкнутой
системы имеет вид
К' <4- + 4" = 220 сек’1.
По условию задачи общий коэффициент усиления
разомкнутой системы должен быть больше 300 сек-1.
Для обеспечения устойчивости введем в систему кор-
ректирующее звено (пунктир на рис. 74).
Передаточная функция разомкнутой системы при
введении в систему корректирующего звена имеет вид
W(р) = —------т ^+Тр}-------------,
р v +1'4-fe," р) <1 + <1 + Г:'р)
т, э • klk^kjikp - .л.
где /< = ——-----------общий коэффициент усиления ра-
зомкнутой системы.
Постоянную времени корректирующего звена Т вы-
берем равной постоянной времени двигателя Тм. Это
всегда можно сделать выбором параметров Д и С.
Положим Д = 0,1 мом. Тогда С = = 0,5 мкф.
При Т = Та передаточная функция разомкнутой си-
стемы равна
Г(р) = ^-------------------,
р(1+таг₽)(1 + ГуР)
а характеристическое уравнение замкнутой системы
имеет вид
1181
§ 3.1. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
99
Условие устойчивости записывается в виде
К<4- +
1у
kl + 1
Ти
Из последнего неравенства получаем выражение для
определения ki>
Выбираем == 9.
Величину коэффициента усиления k2 выбираем из
условия обеспечения заданного значения общего коэф-
фициента усиления разомкнутой системы:
k = Kd + ki) _ 300(1 +9) = 174
2 *и. akikukp 57,3 • 9 50 • 10~3 ”
• 114. Передаточная функция разомкнутой системы
W (р) = р(1 + Т,р)(1 + Ггр) *
Общий коэффициент усиления разомкнутой системы
/( = 500 сек-1, постоянная времени 7’1 = 0,02 сек. Опре-
делить значение постоянной времени Т2, при котором
замкнутая система оказывается на границе устойчивости.
Ответ. Т2 = 2,22‘ 10~3 сек.
115. Структурная схема системы управления стати-
чески устойчивого летательного аппарата приведена на
Рис, 75. Структурная схема системы управления
статически устойчивого летательного аппарата
по углу тангажа.
рис. 75. Коэффициенты передачи kx = 1, k2 = &, постоян-
ные времени 7\ = 0,5 сек и Т2 = 2 сек. Определить:
а) устойчивость системы без корректирующего звена
100
'ГЛ. 3. УСТОЙЧИВОСТЬ линейных систем
(Пв
(1FK = хр на рис. 75); б) величину постоянной времени
корректирующего звена т из условия устойчивости.
Ответ: а) система неустойчива;
б) т > Ti = 0,5-сек.
116. На рис. 76 приведена структурная схема системы
управления жесткого статически неустойчивого лета-
тельного аппарата. Постоянная времени рулевого при-
вода Т\ — 0,5 с«к; постоянная времени объекта Тг—2 сек.
Рис. 76. Структурная схема системы управле-
ния статически неустойчивого летательного
аппарата.
Определить значения постоянной времени корректирую-
щего звена т и общего коэффициента усиления разо-
мкнутой системы К — kxkz из условия обеспечения
устойчивости системы.
Ответ. Условия устойчивости системы имеют сле-
дующий вид:
т> Ti, К> 1, К>
Система устойчива, например, при К = 5, т = 0,7 сек.
117. Структурная схема автоматической системы
приведена на рис. 77. Коэффициенты передачи звеньев
Рис. 77. Структурная схема системы к задаче 117.
fej = 2 • 103, k2 ~6, k3 = 0,25-10-3; постоянные времени
х — 0,7 10~3 сек, Т2 — 1,42 сек, Та = 2,2-10~2 сек; коэф-
1211
§12 КРИТЕРИИ УСТОЙЧИВОСТИ МИЛАН ОБА
ТОТ
фициент демпфирования g == 0,68 • 10’’. Определить
тойчивость системы.
Ответ. Система устойчива,
118. Определить устойчивость автоматической
стемы, характеристическое уравнение которой имеет
' Йор5 + Й,р4 + Й2р3 + «зР2 + Й4р + «5 == о
при следующих значениях коэффициентов:
а) й0 = 0,005 сек5, щ =0,15 сек4, «2=1,25 сек3,
а3 = 5 сек2, щ — 50 сек,
б) Со — 0,005 сек5, «1 = 0,1 сек4,
а3 = 20 сек2, ал = 50 сек,
Ответ, а) Система неустойчива; б) система устойчива.
, 119. Характеристическое уравнение замкнутой авто-
матической системы имеет вид
«оР® + «1Р5 + а2р4 + азР3 + «1Р2 + йзР + йб = 0,
где йо — 1 сек6, at = 2 сек5, а2 ='3 сек4, а3 = 4 сек3,
а4 = 5 сек2, «5 = 6 сек, а6=
= 100.
Определить устойчивость
системы.
Ответ. Система неустой-
чива.
ус-
си-
вид
й6 = 300;
а2 = 2,5 сек3,
а5 = 200.
10
У
20
ы=0
Рис. 78. Кривая Михайлова
к задаче 120.
Ю 20 *
-Ю
~0
-20 -Ю 0
§ 3.2. Критерий
устойчивости Михайлова
120. Система автомати-
ческого управления имеет
характеристическое уравне-
ние четвертого порядка.
Кривая Михайлова системы
приведена на рис. 78. Определить устойчивость автома-
тической системы.
Ответ. Система устойчива.
121. Используя критерий устойчивости Михайлова,
определить- устойчивость электромеханической следящей
системы, передаточная функция которой в разомкнутом
102
ГЛ. 3: УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
1121
состоянии равна
г (р)= р (1 + Тур) (1 + Тир) •
где Д' = 58 сек~х — общий коэффициент усиления разом-
кнутой системы, Ты — О',57 сек — постоянная времени
двигателя, Ту — 0,01 сек — постоянная времени усилителя.
Решение. Характеристический полином замкнутой
системы имеет вид
D (р) = р (I + Тур) (I + Тыр) + К =
= 7’у7’мр3 + (Гу + Гм)р2 + р + ^
Для построения кривой Михайлова определим веще-
ственную и мнимую части функции D (]&):
X (со) = Re D (/со) = К - (Ту + Тм) со2 = 58 - О,58со2,
Y (со) = Im D (/со) = со — ГуГмсо3 = со — 5,7 • 10"3co3-
Вычислим Х(со) и У (со) для ряда значений частоты со.
Результаты вычислений сведем в таблицу:
<0, сек”1 0 5 10 13 15 ОО
X (со) 58 44 0 -40 -70. — ОО
У (со) 0 4 4,5 0 -5 — оо-
Ш)
§ -3.2.. КРИТЕРИИ УСТОЙЧИВОСТИ МИХАЙЛОВА ЮЗ
По данным таблицы построим кривую .Михайлова
(рис. 79). Кривая Михайлова последовательно проходит
через три квадранта. Следовательно, система устой-
чива.
' 122. Передаточная функция разомкнутой системы
имеет вид
где К-общий коэффициент усиления разомкнутой си-
стемы, Т>0 — постоянная времени.
Используя критерий устойчивости Михайлова, полу-
чить условие устойчивости замкнутой системы.
Решение. Характеристический полином замкнутой
системы равен сумме полиномов числителя и знамена-
теля передаточной функции
разомкнутой системы:
D(p)~Tp + K — 1.
Вектор D (/со) получаем,
заменяя в характеристиче-
ском полиноме р на /со,
= /соГ + К. — 1 =
= Х(со) 4- /У (со),
гдеХ(со) = К- 1, У (со) = соУ.
Для устойчивости систе-
мы необходимо и достаточно,
чтобы вектор D (jo) при изменении частоты со от нуля
до то повернулся на угол <р = 4у- (рис. 80) .При Д< 1
кривая Михайлова расположена во втором квадранте
угол поворота вектора £)(/со) при изменении часто-
ты со от нуля до оо равен <р=—а при /С>1
равен = Итак, замкнутая система устойчива при
К>1.
123. Система автоматического управления имеет ха-
рактеристический полином шестого порядка. На рис. 81
приведены кривые Михайлова для различных значений
параметров системы. Определить устойчивость системы.
Рис. 80. Годограф вектора
D (у со) к задаче 122.
104
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
[124
Ответ. 1 — система находится на границе устойчи-
вости; 2 — система устойчива; 3 —система неустойчива.
Рис. 81. Кривые Михайлова к задаче 123.
124. Система автоматического управления имеет ха-
рактеристическое уравнение пятого порядка. На рис. 82
приведена кривая Михайлова системы. Определить
число корней характеристического уравнения с отрица-
тельной вещественной частью и число корней характе-
ристического уравнения с
положительной веществен-
ной частью.
Решение. Угол пово-
рота вектора D (ja) при из-
менении частоты со от О
до оо равен
ср = —/л, (1)
Рис. 82. Кривая Михайлова г^е 1г ПОРЯД°К характери-
к задаче 124. стического уравнения; I—чи-
сло корней характеристиче-
ского уравнения с положительной вещественной частью.
Из рис. 82 видно, что угол поворота вектора
при изменении частоты со от 0 до о° равен
<Р = Т
После подстановки в (1) значения угла ф = -^- и п = 5
12*1'-- § 3.2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА |05
получаем, что число корней характеристического урав-
нения с положительной вещественной частью
- л л
5"2~~2
> I =---f--±- = 2.
зх
Кривая Михайлова через начало координат не про-
ходит, поэтому число корней с отрицательной веще-
ственной частью равно п — / = 5 — 2 = 3.
Рис. 83. Кривая Михай-
лова к задаче 125.
Ps
Рл
Р/
'Рг
'P.t
Rep
Рис. 84. Расположение корней
характеристического уравнения
к задаче 125.
V
Рис. 85. Кривая Михай-
лова к задаче 126.
125. На рис. 83 приведена кривая Михайлова авто-
матической системы, имеющей характеристическое урав-
нение пятого порядка. Нари-
совать качественную картину
расположения корней характе-
ристического уравнения на пло-
скости корней.
Ответ. Картина располо-
жения корней приведена на
рис. 84.
126^ Автоматическая систе-
ма имеет характеристическое
уравнение четвертого порядка.
Кривая Михайлова системы
приведена на рис. 85. Опреде-
лить число корней характеристического уравнения с от-
рицательной вещественной частью.
Ответ. Характеристическое уравнение системы имеет
Два корня с отрицательной вещественной частью.
106
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
пэт
127. Передаточная функция замкнутой автоматиче-
ской системы имеет вид
.______________К__________
~ аор4 + atp3 + а2р2 + а3р +К ’
где /<=100 сек~\ а3— 1, «2=1 сек, «[ = 0,02 сек2,
Оо — 0,001 сек3.
Определить устойчивость системы с помощью кри-
терия устойчивости Михайлова.
Ответ. Система неустойчива.
128. Передаточная функция разомкнутой системы
имеет вид
р(1+Лр)(1 + Г2р)(1 + Г8р)’
где К — общий коэффициент усиления разомкнутой си-
стемы; 7’1 = 0,5 сек, Т2 = 0,1 сек, Т3 = 0,02 сек —постоян-
ные времени.
С помощью критерия устойчивости Михайлова опре-
делить значение общего коэффициента усиления ра-
зомкнутой системы /<к, при котором система оказывается
на границе устойчивости.
Решение. Характеристический многочлен замкнутой
системы равен
D (р) = р (1 + ЛР)(1 + Т2р) (1 + Т3р) + К =
= т\т2т3р* + (Т\Т2+Т\Т3+Т2Т3) р3 +
+ (Т1 + Т2 + Т3)р2 + р + К.
После подстановки вместо Tt, Т2, Т3 их числовых
значений получаем
£) (р) = 10-3р4 + 62 • KTV + 610 • Ю’У + р + К.
D (/со) получаем, заменяя в характеристическом поли-
номе р на /со,
£) (/со) = X (со) +/У (со),
где
X (®) = К - 610 10’V + 1О"3со4,
У (со) = со - 62 • 1О~3со3.
При нахождении системы на колебательной границе
устойчивости кривая Михайлова проходит через начало
(39] § 3.S. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА 107
координат при частоте ©=#=0. Поэтому при /С = /(к.
х(а) = — 6 ю • io~V + io’V=о, (О
, Y (0) = о - 62.10"3©3 = 0. (2)
Из второго уравнения находим значение квадрата
частоты, при котором кривая Михайлова проходит через
начало координат:
а2 = (62 • Ю-3)-' сек~2. (3)
Подставляя (3) в (1), после несложных преобразова-
ний получаем
„ 610-1(Г3‘ 10~3 с
Лк =-------з-----9---— 9,6.
62-10 3 622-10 ь
129. Передаточная функция разомкнутой системы
автоматического управления имеет вид
W(Р) ~ (I +2ГЛР-1- (1+М0 + гзР) ’
где К — общий коэффициент усиления разомкнутой си-
стемы; Ti = 0,05 сек, Т2 = 0,2 сек, Ts = 0,l сек —постоян-
ные времени: g = 0,5 — коэффициент демпфирования.
С помощью критерия устойчивости Михайлова опре-
делить значение общего коэффициента усиления ра-
зомкнутой системы /Ск, при котором замкнутая система
находится на границе устойчивости.
Ответ. Кк — 0,40.
130 Структурная схема автоматической системы при-
ведена на рис. 86.
Рис. 86. Структурная схема системы к задаче 130;
Общий коэффициент усиления разомкнутой системы
К == = 10; постоянные времени Т = 0,2 сек, То~
= 0,8 сек. Используя критерий устойчивости Михайлова,
определить величину постоянной времени корректирую-
108
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫ СИСТЕМ-
|131
щего устройства т = тк, при которой система находится
на границе устойчивости.
Ответ. тк = 0,2 сек.
131. Структурная схема системы автоматической
стабилизации статически неустойчивого объекта приве-
дена на рис. 87.
_Рнс. 87. Структурная схема системы автомати-
ческой стабилизации статически неустойчивого
объекта.
Постоянные времени привода Т\ = 0,5 сек, Т’2=0,1 сек.
Постоянная времени объекта Го = 2 сек. Коэффициент
передачи объекта k0 = 1. Коэффициент передачи привода
/гп = 0,5 град • в~1; Коэффициент передачи корректирую-
щего устройства &2 = 20 град • сек"1 в"1. Используя кри-
терий устойчивости Михайлова, определить значения
коэффициента передачи klt при котором система нахо-
дится на границе устойчивости.
Ответ. При = 2 в/град система находится на апе-
риодической границе устойчивости. При kY = 27 в/град
система находится на колебательной границе устойчи-
вости.
132. Характеристическое уравнение автоматической
системы имеет вид *
а0р5 + «]р4 + а2р3 + «Зр2 + а4р + а5 — 0,
где
а0 = 3 • 1СГ4 сек", ах = 5 • 10~3 сек, а2 = 0,1 сек,
а3 = 0,5 секг, «4 = 0,9 сек, «5=1.
Определить устойчивость системы.
Решение.
£)(/со) = Х(®) + 7Г(®),
где
X (со) = а5 — «3«»2 + й|(о4,
Y (со) = а4в> — «2®3 + «о®5.
(3S] § 3.3- КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА 109
После' подстановки в выражения для X(со) и Y (со)
числовых значений а0, . ..,,а5, получаем
X (со) = I - 0,5®2 + 5 • 10“3®4,
Y (to) = 0,9® - ОД ®3 + 3 • 10~4®5.
Неотрицательные корни уравнения Y (со) — 0:
И] — 0, й, = 3,2 сек"1, ®3 — 18 сек"1.
Положительные корни уравнения X(to) = 0:
со4= 1,41 сек~1г ®5 = 9,9 сек~1.
Неотрицательные корни уравнений X (со)=0 и У(со)=О
перемежаются. Это говорит о том, что кривая Михай-
лова последовательно проходит пять квадрантов. Сле-
довательно, система устойчива.
133. Используя критерий устойчивости Михайлова,
определить устойчивость автоматической системы, если
ее характеристическое уравнение имеет вид
«оР5 + «1Р4 + «2р3 + «зР2 + а4р + а5 = 0»
где
а0 = 0,15- 10~2 сек5, аг = 5 • 10~2 сек4, а2 = 0,6 сек3,
с?з = 4 сек2, = 20 сек, а5 — 500.
Ответ. Система неустойчива.
134. Характеристический многочлен автоматической
системы равен
D (р) = 2 • 10~4р6 + 80 • 10 V + 3 • 10"*р4 +
+ 1,24р3 + Юр2 + 40р + 34.
Определить устойчивость системы,
Ответ. Система устойчива.
§ 3.3. Критерий устойчивости Найквиста
135. Амплитудно-фазовые характеристики устойчи-
вых в разомкнутом состоянии систем приведены , на
рис. 88.
Определить устойчивость замкнутых систем.
no
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
ПЙ6
Ответ. 1 — замкнутая система устойчива; 2 — замкну»
тая система неустойчива; 3 — замкнутая система устой*
чива.
Рис. 88. А. ф. х. к задаче 135.
136. Передаточная функция электромеханической
следящей системы в разомкнутом состоянии имеет вид
F (р) = /, Гг ,
Р (1 + гмр) (1 + Гур)
где К = 100 сек-1 — добротность следящей системы по
скорости; Л. = 0,1 сек — постоянная времени двигателя;
/^ = 0,02 сек — постоянная времени усилителя.
Определить, устойчивость электромеханической еле*
дящей системы,’ используя критерий устойчивости Найк-
виста.
Решение. Для построения а. ф. х. разомкнутой
системы определим амплитудную частотную характери-
стику Л (со) , и фазовую частотную характеристику ф(со):
К J_________=_____________100___________
“ со/1 + (соГм)2/1 + (со7у)2 со /1 + (со • 0,1 )2 К1 + (со • 0,02Р’
ф (со) = arg W = arg ~ 90°+ф1+ф2,
где
ф1 (со) = — arctg (£>ТМ — — arctgO, 1со,
Фг{со) ~ - arctg соГу = —arctg0,02co.
§ S3. КРИТЕРИИ УСТОЙЧИВОСТИ НАЙКВИСТА _ Щ
Вычислим Л(ю), %(«>), ф2(®), Ф(®) Для ряда значе-
ний ю. Результаты вычислений сведем в таблицу:
—- 1 0), сек 0 5 10 15 25 50 100
А оо 18 6,9 3,56 1,32 0,28 0,045
ф1, град 0 -26 -45 -56 -68 -79 -84
ф2. град 0 -6 -11 -17 -26 -45 -64
ф, град -90 -122 -144 -153 -184 -214 -238
По данным таблицы построена а. ф. х. разомкнутой
системы (рис. 89).
Знаменатель передаточной функции разомкнутой си-
стемы имеет один нулевой корень. Поэтому ветвь а. ф. х.,
соответствующую частотам дополним дугой окруж-
ности бесконечно большого радиуса так, чтобы вектор
Рис. 89. А. ф. х. разомкнутой системы.
W(j<a) повернулся по часовой стрелке на угол, равный 90°
(рис. 89). Из рис. 89 видно, что а. ф. х. разомкнутой
системы охватывает точку (— 1, 0). Следовательно, зам-
кнутая система неустойчива.
137. Используя критерий устойчивости Найквистау
определить устойчивость электромеханической следяще,
системы, рассмотренной в задаче 136 при следующий
параметрах системы: а) /< = 50 сек~\ 7^ = 0,1 сек, Т = х
112
ГЛ. а. УСТОЙЧИВОСТЬ линейных систем
[138
•=.0,025 сек; б) Д — 200 сек"1, Ты = 0,02 сек, Ту — 0,002 сек;
в) Д = 50 сек-1, Та = 0,1 сек, Ту = 0,005 сек.
Ответ, а) Система находится на колебательной гра-
нице устойчивости; б) система устойчива; в) система
устойчива.
138. Передаточная функция электромеханической
следящей системы в разомкнутом состоянии имеет вид
/с
~ Р (1 + тмр) (1 + Гур)
На рис. 89 приведена а. ф. х. разомкнутой системы,
построенная для добротности системы по скорости
Д ~ 100 сек."'. *
Определить, при каких значениях Д замкнутая си-
стема устойчива.
Ответ. Замкнутая система устойчива при Д < 57 сек"1.
139. Передаточная функция одноосного гироскопи-
разомкнутом состоянии.имеет
вид
Г ~ р(1+2У>+ГУ7 ’
где Д = 40 сек~\ Тг = 0,02 сек,
6-0,15.
Используя критерий устой-
чивости Найквиста, определить
устойчивость гиростабилиза-
тора в замкнутом состоянии.
Ответ. А. ф. х. разомкнутой
системы приведена на рис. 90.
Гиростабилизатор неустойчив.
140. Передаточная функция
системы управления статиче-
ски устойчивым объектом в разомкнутом состоянии имеет
вид
П/ / . К (1 + тр)---
(i+MO + W
где Д — 1 — общий коэффициент усиления разомкнутой
системы; т — 0,1 сек — постоянная времени корректирую-
щей о устройства; Г! —0,2 сек — постоянная времени
Рис. 90. А. ф. х. разомкну-
той системы к задаче 139.
§ 3.3. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА «
исполнительного устройства; 7’0 = 0,5 сек — постоянная
времени объекта.
Используя критерий устойчивости Найквиста, опре-
делить устойчивость замкнутой системы.
Решение. Амплитудная частотная характеристика
разомкнутой системы
._______КК1 + (<вт)г ___________V1 + (о,1ю)г_____
А “ “ К1 + (®Л)2 - И - <«• Го)21 КГ+ (0,2га)2 • 11 - (0,5га)21 ‘
Фазовая частотная характеристика
[ arctg on — arctg гаГ, = arctg 0,1® — arctg 0,2®
! при ®<-2- = 2 сек~1,
I /o
•ф(®) = t arctg®t — arctgaTi — 180° =
I v — arctg 0,1®—arctg 0,2® — 180°
1 I
4 I при ® = 2 ceiC1.
* 0
Вычислим A (®) и ф(®) для ряда значений частоты ®.
Результаты вычислений сведем в таблицу:
<й, сек^ 0 1 1,5 ®->2—0 со >24-0 2‘4 3 5 Об
Л (<о) 1 1,33 2,2 оо оо 2,1 0,7 1,15 0
ф (га). град 0 -6 -9 -.11 -191 -192 -204 -198 -180
- По данным таблицы построена а. ф. х. разомкнутой
системы (рис. 91).
При частоте ® = = 2 сек"1 а. ф. х. имеет разрыв.
*0
Ветви а. ф. х., соответствующие частотам —0 и
* о
® -> — + 0, дополним полуокружностью бесконечно боль-
того радиуса. Полуокружность проводим по часовой
стрелке от ветви а. ф. х., соответствующей ®->-^~0,
К ветви, соответствующей га->-4-4-0 (рис. 91).
< ' 1 о
!(4 , ГЛ. з. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ систем
[Ui
Из рис. 91 видно, что а. ф. х. разомкнутой системы
охватывает точку (—1, 0). Следовательно, замкнутая
система неустойчива.
Определить устойчивость этой системы можно
и более простым способом.
Из выражения для фазовой характеристики следует^
Что при т>7'1 для всех частот ф(со)>—180°. Поэтому
Рис. 91. А. ф. х. разомкнутой сисге-
"мы к задаче Г40;
а. ф. х. при т > Т] не заходит в третий квадрант и
система устойчива при любых значениях /(>0 и Тй.
При т < Г1Ф (<о) < —180° для всех частот По-
* о
этому часть а. ф. х., соответствующих частотам <о>~,
лежит в третьем квадранте, причем ветвь а. ф. х.,
соответствующая <о—>-^ + 0, уходит в бесконечность.
1 о
Поэтому при т<7'1 система неустойчива при любых К
и То. В данной задаче т<7’1. Поэтому система не-
устойчива.
141. Передаточная функция разомкнутой системы
равна
Г (р) =-------KV + 'P)---- ,
(1 + Г1Р)(1+Г2р)(1 + ф2)
М31
§ 3.3. КРИТЕРИИ УС.ТОИЧНВОСТИ*НАЙКВИСТА
11S
где к == 1, т=0,4 сек, Т 1=^,2 сек, Т2 = 0,1 сек, То = 0,5 сек.
Используя критерий устойчивости Найквиста, опреде*
лить устойчивость замкнутой системы.
Ответ. Замкнутая система устойчива.
142. Передаточная функция разомкнутой системы
имеет вид
Г(р)-
А (р)
(1 + ТУ)В(р) ’
где В (р) — многочлен, все корни которого имеют отри-
цательные вещественные части.
На рис. 92 приведена а. ф. х. разомкнутой системы.
Определить устойчивость
замкнутой системы.
Ответ, Замкнутая систе-
ма устойчива.
Рис. 92. А. ф. х. разомкнутой
системы к задаче 142.
Рис. 93. А. ф. х. .к задаче 143.
•143. Передаточная функция разомкнутой системы
равна
№(р)- >
где К>0, Т>0, п>2.
Определить условие устойчивости замкнутой системы.
Решение. Вид а. ф. х. разомкнутой системы по-
казан на рис. 93.
(16 ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ (144
Фазовая частотная характеристика системы равна
ф (е>) = — п arctg <в7\
-Определим значение частоты ® = <в_я, при котором
ф (е>) — — п arctg аТ = — л, (I)
Из (1) находим, что
Для устойчивости данной системы необходимо и
достаточно, чтобы
<2>
Из (2) находим условие устойчивости
*<(]/ l+tg2v)"
1
Следует отметить, что устойчивость этой системы
не зависит от величины’ постоянной времени Т.
144. Определить устойчивость системы, передаточная
функция которой в разомкнутом состоянии имеет вид
p(l + Tp)tt •
где К>0, Т>0;
Ответ. При п=1 система устойчива при любых
значениях /<>0 и Г>0. При система устойчива
при
к<------------
145. Используя критерий устойчивости Найквиста,
определить устойчивость системы автоматической стаби-
лизации летательного аппарата, передаточная функция
*461
§ 3.3. КРИТЕРИИ УСТОЙЧИВОСТИ НАЙКВИСТА
117
которой в
разомкнутом состоянии имеет вид
W(p)
К(1+тр)
р(-1 + Тр) ’
где К = 4 сек-1, Т — 1 сек, т = 0,5 сек.
Решение. Амплитудная частотная характеристика
разомкнутой системы имеет вид
- л кл . К/» + (<^)2 2 1+(0,5<в)2
1 . ®К1 + (®П2 ® ’ ,+ е)2 ‘
фазовая частотная характеристика равна
ф(со) =? a rctg сот — 90° — (180° — arctgco/') =
= — 270° + arctg О,5со + arctg со.
На рис. 94 приведена а. ф. х. разомкнутой системы
. Знаменатель передаточной функции разомкнутой сн
стемы имеет один нулевой корень. Поэтому ветвь а. ф. х.
соответствующую ча-
стотам со —> 0, дополним
дугой окружности беско-
нечно большого радиуса
(см. рис. 94).
Многочлен знамена-
теля передаточной функ-
ции разомкнутой системы
содержит один положи-
тельный кЪрень.
Угол поворота векто-
ра, начало которого нахо-
дится в точке (— 1,0), а
Рис.. 94. Л. ф. х. к задаче 145.
конец на а. ф. х., при
изменении частоты со от + 0 до оо равен 180°. Следова-
тельно, замкнутая система устойчива.
146. Структурная схема автоматической системы
приведена на рис. 87. Постоянные времени т = 0,1 сек,
Т1 = 0,05 сек, Т'2==0,01 сек, Го = 2 сек. Коэффициенты
передачи ki = & в'град~х, Z?n = 0,5 град • в-1, fe() — L
k2 — 0,2 в • сек • град~1.
' Определить устойчивость системы, используя крите-
рий устойчивости Найквиста.
’ Ответ. Система неустойчива.
118
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
(147
147. На рис. 95 изображена структурная схема двух-
канальной следящей системы с антисимметричными
перекрестными связями.
Коэффициенты передачи звеньев k\ = I, kz = 2, k3 =
=5 сек~\ Постоянная времени Т — 1 сек. Коэффициент
перекрестной связи а = 2.
Определить устойчивость системы.
Рис. 95. Структурная схема двухканальной
следящей системы с антисимметричными
связями.-
Решение. Двухканальные автоматические системы
с идентичными каналами и антисимметричными связями
удобно рассчитывать путем введения комплексных коор-
динат.
Согласно структурной схеме рис. 95 напишем урав-
нения движения системы:
х1 = Т+Т^^1~ах^> ' <0
Л1==Т+7> fci + axi), (2)
(g, - тд), (3)
22 = ^l(g2-g2)» (4)
= (5)
£2 = y*2- (6)
<47j 5 3.3 КРИТЕРИЙ УСТОЙЧИВО ТИ НАЙКВИСТА . 41<f
Умножая уравнения (2), (4) и (6) на J и складывая
их соответственно с уравнениями (1), (3), (5), после
несложных преобразований получаем
2 = Й1(§“У), (8)
У = у-х, (9)
где х = X] + /х2, z - zt + jz2, g = gi + jg2, y = yi + jy2.
Рис. 96. А. ф. x. к задаче 147.
В результате решения системы уравнений (7) —(9)
имеем
W (р)
У 1 + Г (р)
где
117 (п\_____kik^ks_____ ______К_________
''У' р (Тр + 1 — jak2) р (Тр + 1 — jak2)
— передаточная функция разомкнутой системы.
Частотная характеристика разомкнутой системы равна
W (/®) = - Tf,—(®) + V (со),
w 7 у со (/(of + 1 — jak2) ' ’ ' 7
где
11 АА —__ К ~ ak^ — -10(®-4)
®[1 + (и7-сР2)2] со [1 4-(со—4)2] ’
v , ч__________К __________10
со [1 + (соГ —afe2)2] о[1+(<о —4)2] *
120
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
(148
Передаточная функция разомкнутой системы имеет
комплексные коэффициенты. Поэтому для определения
устойчивости необходимо построить а. ф. х. в диапазоне
частот — со ч- + оо.
А. ф. х. системы приведена на рис. 96. Из рис. 96
видно, что а. ф. х. разомкнутой системы не охватывает
точку (— 1, 0). Следовательно, двухканальная следящая
система устойчива. ,
148. Структурная схема системы приведена на рис. 97.
Параметры системы равны: К = 20 сек'1, Т — 1 сек, а — 2.
Определить устойчивость системы.
Рис. 97. Структурная схема двух-
канальной следящей системы к за-
даче 148.
Ответ. Система неустойчива. Следует отметить, что
при отсутствии перекрестных связей (при а = 0) система
устойчива при любых,7<>0 и Г>0.
§ 3.4. Определение устойчивости по логарифмическим
частотным характеристикам разомкнутой системы
149. Передаточная функция электромеханической сле-
дящей системы в разомкнутом состоянии имеет вид
Г = Р(1 + Гм5(1+Тур) ’
где К — 75 сек'1, Ты — 0,02 сек, Ту = 0,005 сек.
Определить устойчивость замкнутой системы по
логарифмическим частотным характеристикам разомкну-
той системы.
1491 § 3.4. ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕР’-' ’’КИ 123
Решение. Устойчивость системы будем определять
по асимптотической л. а. х. и л. ф. х. Частоты излома
асимптотической л. а. х. равны
= т\ = ода = 50 сек °2 = 77 = ода = 200 сек~х-
К Низкочастотная асимптота л. а. х. пересекает ось
чкЛ£тот при частоте
© = /< = 75 сек'1.
По этим'' данным строим асимптотическую л. а. х.
(рис. 98). разовая частотная характеристика равна
ф ~ (®) + Фа (®) + Фз (®)>
где ф|(©) = —90°, ф2(®) = — arctg©7M = — arctg0,02«,
ф3(®) = — arctg Гу© = =» arctg 0,005©.
V й’б
-40
Ш
135'
Рис. 98. Асимптотические л. а. х. и л. ф. х. к задачам
149 и 152.
Графики функции ф2(ю) и Фз(®) строим с помощью
шаблона.
Л. ф. х. получаем графическим сложением функций
^i(®)> ф2(©)> Фз(®) (см. рис. 98).
120
7л. 3. устойчивость линейных систем
I I SO
Л. ф. х. пересекает линию ф = —-180° при отрица-
тельных значениях асимптотической л. а. х. Следова-
тельно, замкнутая система устойчива.
В данной задаче л. ф. х. является монотонной функ-
цией от частоты со, поэтому задачу можно решить без
построения л. ф. х.
После построения асимптотической л. а. х. опреде-;
ляем частоту среза разомкнутой системы со — сос = 60 ce^-i
(см. рис. 98).
Значение фазы при частоте среза , - <
Ф (®с) = — 90° — arctg (0,02 • 60) — arctg (0,005 • 6,0) =
= — 157°> — 180°.
Следовательно, замкнутая система устойчива.
150. Определить устойчивость системы, рассмотрен-
ной в задаче 149 при Ту = O,OQ§r‘ сек, Тн = 0,02 сек,
К = 300 сек-1.
Ответ. Система неустойчива.
151. Передаточная функция разомкнутой системы
имеет вид
К(1 +тр)
Р (1 +7мр) (1 +Тур) ’
где /< = 300 сек"1, Гм = 0,02 сек, Гу = 0,005 сек,
1 = 0,0045 сек. Определить устойчивость системы.
Ответ. Система устойчива-.
152. Для электромеханической следящей системы,
рассмотренной в задаче 149, определить значение доб-
ротности системы, при котором система находится на
колебательной границе устойчивости.
Решение. Логарифмическая фазовая характери-
стика определяется выражением
Ф (®) = ф1 (со) + ф2 (со) + ф3 (®).
где ф) (со) = — 90°, ф2 (®) = —- arctg соГм, ф3 = — arctg соГу.
Графики функций ф2(со) и ф3(со) строим с помощью
шаблона. Л. ф. х. получаем графическим сложением
характеристик фДсо), ф2(<о) и ф3(со) (см. рис. 98).
Система находится на колебательной границе устой-
чивости, если л. а. х. пересекает ось частот при частоте
пересечения л. ф. х. линии ф = <—180°, со =100 сек-1.
isel § 3.4. ЛОГАРИФМИЧЕСКИЕ ЧКСТОТН.1 IE ХАРАКТЕРИСТИКИ (23
Асимптотическая л. а. х. системы в диапазоне частот
0 ч- — имеет наклон —20 дб/д^ек, в диапазоне частот
J- -4- v— —40 дб)дек, в диапазоне
Гм
I
частот
. 1 у
— 60 дб[дек. Зная наклоны асимптотической л. а. х.,
оо---
легко начертить асимптотическую л. а. х., пересекаю-
щую ось частот па частоте пересечения л. ф. х. линии
ф = —180° (см. рис. 98). Добротность системы по ско-
рости К — Кк определяем по точке пересечения низко-
частотной асимптоты л. а. х. с осью частот /<|( = 200 сек-1.
Точное значение /<к — 250 сек~\ Ошибка в определе-
нии Ак объясняется отличием асимптотической л. а. х.
от действительной.
153. Определить устойчивость замкнутой автомати-
ческой системы, если ее передаточная функция в ра-
зомкнутом состоянии имеет вид
P[l + TlP)(l + T2P)(l + TsP) ’
где А = 300 сек~\ Т[ = 0,2 сек, Т2 = 0,05 сек, Т3 = 0,02 сек.
Ответ. Система неустойчива.
154. Для системы, рассмотренной в задаче 153, опре-
делить значение общего коэффициента усиления разомк-
нутой системы /<1(, при котором система находится на
.колебательной границе устойчивости.
Ответ. /<к = 20 сек~х.
155. Структурная схема автоматической системы
приведена на рис. 76. Определить устойчивость системы,
если /< = й1^2=Ю, Гг = 2 сек, Г1 = 0,05 сек, т —0,1 сек.
Ответ. Система устойчива.
156. Передаточная функция одноосного гиростабили-
затора при коэффициенте демпфирования £ = 0 в ра-
зомкнутом состоянии имеет вид
1Г(р)=* , % ,
р Р[у+тУ)
где А = 40 сек~\ Тг = 6,5' 10-3 сек.
Для демпфирования системы последовательно в
Цепь управления введено . корректирующее звено с
124
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
[157
передаточной функцией
Определить величину постоянной времени Т, при
которой гиростабилизатор будет устойчив.
Решение. На рис. 99 приведены асимптотическая
л. а. х. и л. ф. х. нескорректированной системы (сплош-
ная линия). Для устойчивости системы необходимо,
Рис. 99. Асимптотическая л. а. х. и л. ф. х. к задаче 156.
чтобы л. ф. х. пересекала линию ф = —180° в диапазоне
частот /< -ь Поэтому постоянную времени корректи-
рующего звена необходимо выбирать из условия
Система устойчива, например, при Г = 0,01 сек.
157. Определить устойчивость одноосного гиростаби-
лизатора, передаточная функция которого в разомкну-
том состоянии имеет вид
Г (р) = -----£----—,
^(ц-г^р + т-у)
где К = 40 сек-1, Тт = 6,5- 10-3 сек, ^ = 0,2.
Ответ, Гиростабилизатор устойчив.
1801 § 3.5. ПОСТРОЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ 125
158. Определить устойчивость системы, структурная
схема которой приведена на рис. 87, если kt = 20 в/град,
/г2 = 40 в • сек • град-1, 7\ = 0,5 сек, Tz = 0,1 сек, То —
«г 2 сек, ka — 0,5 град • в-1, k0 — 1.
Ответ. Асимптотическая и точная л. а. х. системы
приведены на рис. 100. Система устойчива.
Рис. 100. Асимптотическая л. а. к. и л. ф. х. к задаче 158.
159. Решить предыдущую задачу при kt = 20 в/град,
fe2==100 в- сек-град, Т-—0,5 сек, Т'2 = 0,1 сек, То —
— 2 сек, kn 0,5 град)в, k0 — 1.
Ответ. Система неустойчива.
§ 3.5. Построение областей устойчивости
160. Передаточная функция статической системы
автоматического управления в разомкнутом состоянии
имеет вид
Г = (1 + 7\р)(1 +\р)(1 + ?зР) ’
где Т2 — 0,2 сек, Т3 = 0,1 сек.
Построить область устойчивости системы в плоско-
сти параметров 7\ и К.
126
ГЛ. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
[160
Решение. Характеристический многочлен замкну-
той системы имеет вид
D (р) = (1 + TiP) (1 + Т2р) (1 + Т3р) + К =
- Т^ТзР3 + (Т{Т2 + TtT3 + Т2Т3) р2 + (Г, + Т2 + Т3) Р + /<=
«= О.ОЗ^р3 + (0,02 + 0,37’1) р2 + (0,3 + Tt) р + к + 1.
Для построения областей устойчивости найдем выра-
жение для границ области устойчивости.
Для получения уравнений границы области устойчи-
вости, соответствующих наличию в характеристическом'
многочлене системы беско-
нечного и нулевого корня,
приравняем нулю коэф-
фициент при старшей сте-
пени характеристического
многочлена и свободный
член характеристического
многочлена.
В результате получим
следующие уравнения гра-
ниц области устойчивости:
^ = 0, (1)
Я=-1. (2)
Уравнение для грани-
Рис. 101. Область устойчивости цы области устойчивости,
к задаче' 159. соответствующей нахо-
ждению системы на ко-
лебательной границе устойчивости, найдем, приравнивая
нулю предпоследний определитель Гурвица An_] = 0.
В дайной задаче это условие принимает вид
(0,02 + 0,377) (0,3 + = 0,0277 (1 + К).
Отсюда получаем
(1 + 15Т,) (15 + 50Т,)
В соответствии с уравнениями (1), (2), (3), на рис. 101
построены границы области устойчивости. Линия, соот-
ветствующая уравнению К — — 1, практически сливается
с осью абсцисс.
163)
§35 ПОСТРОЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ
127
Областью устойчивости . является область А (см.
рис. 101), так 'как для любой из точек внутри этой
области выполняется условие устойчивости.
161. Передаточная функция разомкнутой системы
равна
= (i + rlP)(i+2g7p + ?V) > .
где Tt = 0,2 сек, Т = 1 сек — постоянные времени испол-
нительного устройства и объекта; /( — общий коэффи-
циент усиления разомкнутой
системы; £ — коэффициент
демпфирования.
.Построить область устой-
чивости замкнутой системы
в плоскости параметров К, g.
Ответ. Область устойчи-
вости системы приведена на
рис. 102.
162. Передаточная функ-
ция одноосного гиростабили-
затора в разомкнутом со-
Рис. 102. Область устойчивости
к задаче 160.
стоянии имеет вид
К"
где К. — общий коэффициент усиления разомкнутой си-
стемы, g—коэффициент демпфирования, Тг — постоян-
ная времени.
Построить область устойчивости одноосного гироста-
билизатора на плоскости параметров К, Тт для значений
коэффициента демпфирования g = 0,l, g = 0,2, g = 0,3.
Ответ. Область устойчивости системы приведена
на рис. ЮЗ.
163. На рис. 87 приведена структурная схема си-
стемы автоматической стабилизации летательного ап-
парата.
Постоянные времени привода исполнительного устрой-
ства 7'1 = 0,5 сек, 7’2 = 0,! сек. Постоянная времени
объекта 7’0 = 2 сек. Коэффициенты передачи привода
исполнительного устройства и объекта йп = 0,5 град [в,
Aq = 1.
128 гл. 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ П63
Построить область устойчивости системы на плос-
кости Kz-
Решение. Характеристическое уравнение замкну-
той системы
(1 + Tip)(1 + Т2р)(— 1 + То/?2) + knko(ki 4- k2p) =
= TiTzTlp* + (74 + T2) Top5 + (То - 7’17’2) р2 +
+ (kok^kz —Tt — Т^)р + — 1.
Найдем уравнения границ области устойчивости.
Уравнение апериодической границы устойчивости
Рис. 103. Область устойчивости одноосного
гидростабилизагора к задаче 161.
найдем, приравняв нулю свободный член характеристиче-
ского уравнения. Тогда
ft*=W=2e-^-1- (1)
Колебательной границе устойчивости соответствует
равенство нулю характеристического комплекса
D(/(o) = X((o) + /T((o) = 0,
или
X (со) = koknki - 1 - (То - TtT2) и2 4- Т1 Т2Т2о^ = 0, (2)
У((о) = (Мп^2-Т1-Т2)й-(Т14-7’2)То(о3 = 0. . (3)
§ 3.5. ПОСТРОЕНИЕ ОВЛАСТЕИ УСТО ЧИВО ТИ {29
Из уравнения (2) получаем
------------Kkn--------- (4>
В дальнейшем можно из (3) найти выражение для
, _ Г) + Т2 Л + г2 2 (5)
k‘~ М. + ()
Уравнения (4) и (5) — уравнение границы устойчиво-
сти, записанное в параметрической форме.
В данной задаче проще поступить следующим об-
разом.
А,
град
Рис. 104. Область устойчивости к задаче 162.
Из (3) найдем выражение для со2 и подставим его
в (2). В результате получим уравнение параболы
= J_ (Уо-УЛ)(^М2-^.7^) _
1 *0*п *0*о (Л + ^Т'о
_ Л.^ (*о*п*2- у1-.^)г = k (_ J 73 . 10-2k + J 7) (6)
*o*u(^i + ^)2^
По уравнениям (1) и (6) на рис. 104 построена гра-
ница области устойчивости. Областью устойчивости
является область А. Это можно проверить, применив
любой критерий устойчивости к одной из точек,- при-
надлежащих этой области.
ГЛАВА 4
ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В СИСТЕМАХ АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
§ 4.1. Классический метод решения дифференциальных
уравнений
164. Найти выходную величину y(t) системы, опи-
сываемой уравнением
для двух случаев.
1. На вход системы подается задающее воздействие,
изменяющееся по гармоническому закону
g(0 = GM.sinQZ;
начальное условие у(0) — уо-
2. При установившемся режиме, соответствующем
задающему воздействию g(/)~GMsinQ<, происходит
скачкообразный сдвиг фазы управляющего воздействия
на -}-90о; сдвиг происходит в момент, когда Qt = 2пп,
где п — целое число.
Ответ.
1. 0(0 = I'm sin (£2/ — Ф) + (1/о4-Ум8шф)в т,
УМ = -7=°М = , ф = ДГС1ёШ\
“ у 1 + (ЙГ)« s
__
2. y(t) = yMcos(QZ — ф) — Ум (sin ф + cos ф) е г.
^JSJ § 4.1. КЛАССИЧЕСКИЙ МЕТОД РЕШЕНИЯ УРАВНЕНИИ 131
165. Дана следящая система, представленная на
рис. 105. На -вход}силителя 1 подается разность между
задающим воздействием g и выходной величиной у.
Рис. 105. Блок-схема следящей системы
к задаче 165.
Кроме того, на усилитель подается первая производ-
ная g' задающего воздействия. 2 — двигатель, редуктор
и исполнительный механизм.
Система описывается уравнением
(Tp?+p + ®y(t) = (fap + K)g(i}. (1)
Постоянная времени Т — 5 мсек, коэффициент усиления
по задающему воздействию /< — 40 сек~1, коэффициент
усиления по производной задающего воздействия /<т »-
= 0,8. Найти закон изменения выходной величины g
для двух следующих случаев.
1. При отработке системой рассогласования у0 при
отсутствии задающего воздействия и нулевой’ началь-
ной скорости.
2. При задающем воздействии в виде единичной- сту-
пенчатой функции 1 (0 и нулевых начальных условиях
г/_о = гДо — 0.
Решение. 1. Дифференциальное уравнение си-
стемы для первого случая имеет вид
(Г^ + р + Юр^^О или (О,ОО5р* + р4-4О)0(О = О. (2)
Характеристическое уравнение
0,005/j2 4- р + 40 = 0
(3)
имеет два вещественных корня — Рх — —55,3 сек
р2 — —144,7 сек-1.
132
ГЛ. 4„ ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
[16S
Для
Иия (2)
случая вещественных корней решение уравне-
имеет вид
y(t)^Ale-a‘t + А2е~“К (4)
где а( и а2 — абсолютные значения корней характери-
стического уравнения.
Начальные условия:
при t =О
У = Уо, 1
/ = /о = О- J
Из (4) и (5) получаем
А + Л2 = у0, 1
— сцД — а2Л2 = 0. J
Из (G) находим
д = А2=-^-.
1 а2 —«1 щ — а2
(5)
(6)
(7)
Решение задачи для первого случая имеет вид
согласно (4) и (7):
У ® = а -а " (а2е"“‘' ~ а1^““2<) 1 (0
или
y(t) = Уо (1,619е~55-3/ - 0,619е-'«.7<) 1 (t). (8)
Выражение (8) можно также получить непосред-
ственно по данным задачи, если воспользоваться при-
ложением 10, где приведены решения однородных
уравнений первой, второй и третьей степеней как при
вещественных, так и при комплексных корнях.
2. Дифференциальное уравнение системы для вто-
рого случая может быть записано, согласно (1), в виде
(а0р2 + atp + а2) у (/) = (bap + i>i) g (t), (9)
где а0 — Т = 0,005 сек, aI = 1, а2 = К = 40 сек-1, Ьо — Кт —
= 0,8, bt = /< = 40 сек"1.
Прежде всего найдем начальные условия, имеющие
место непосредственно после воздействия на систему
единичной ступенчатой функции.
Для этого удобно воспользоваться приложением 9,
В соответствии с указанным приложением найдем из (9)'
Jfi5] - § 4.1. КЛАССИЧЕСКИЙ МЕТеД РЕШЕНИЯ УРАВНЕНИЙ 133
п == 2j tn — 1 и получим \
У+о ~ У-о ~ О’
4о'= Л + % НО = О + да 1«) = 160-1 (о сек-'. (10)
Решение уравнения (9) удобно свести к решению
однородного уравнения с теми же коэффициентами,
перейдя к новой переменной
Z (О У (О Ууеи (11)
где
^ = ^1(0 = -^ 1(0= КО (12)
ип и2
— частное решение уравнения (9), т. е. установившееся
значение выходной величины у. Таким образом, вместо
(9) получаем уравнение
(аор2 + щр + а2) Z (0 = 0 (13)
при начальных условиях
2+0 = ^+0 -- Уу^ z+o = y'+Q- (14>
Эти соотношения получены из уравнения (11).
; Решение (13) имеет вид
• z (t) — + A^~a2t, (15)
где, согласно первому случаю, щ = 55,3 сект1, а2 —
=*= 144,7 сек-1.
Для определения постоянных интегрирования Л1 и
А2 получаем из (15), согласно (10), (12) и (14), урав-
нения
А + А2 = z+0 у+0 уусг
Или
А + А = -1(0,
„ „ , (16)
а1 А а2^2 2+0 У+0
Или
— а1Д1 — а2/12 = 160 • 1 (0«
134 ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ [1«5
Из (16). получаем
А-~?2а1601(0 = 0,171-1(0,
(17)
А = -^.+J£0 1 (/) ,= - 1,171-1 (0.
Заметим, что решение уравнения (13) можно получить,
используя1 приложение 10.
О.О1 0,02 ЦОЗ О.О4 0.05 0.06 0,07t,СМ
1.0
0.8
0.8
0,4
0Z
О
001 0.02 ЦОЗ 0fl4 0,05 0,06 0,071,сея
Рис. 106. Кривые переходных процессов
к задаче 165;
1 — ненулевые начальные условия, 2 — реакция системы
* на ступенчатое воздействие.
Из (15) получим, согласно (11), (12) и (17),
f/(0 = z(0 + //уст = (о, 171е-55.з/_ l,171e-M4.7/) t (/) + j щ
Таким образом, при воздействии на систему единичной
ступенчатой функции 1 (0 выходная величина изменяется
по закону
г/(0 = [1 +0,171e-55>3f — 1,171е~144.^] 1(0- (18)
'e(t.n§ 4.1. КЛАССИЧЕСКИЙ-1 МЕТОД РЕШЕНИЯ УРАВНЕНИИ 135*
По уравнению (8) на рис. 106. построена, кривая 7,
а < пог. уравнению (18) т- кривая 2.
166. Решить задачу 165 при следующих' данных:
Т. = 0,005 сек, К = 200 сек'1, Кг = 0,8..
Ответ.
1. При согласовании- системы ее закон движения
y(t) = l,155i/oe’w sin (173/ + 60°)
(кривая.! на. рис. 107).
Рис. 107. Кривые переходных процессов к за-
- дане 166;
1 — ненулевые начальные условия, 2 — реакция системы
на ступенчатое воздействие.
2. При воздействии на систему единичной'ступен-
чатой функции.
y(t) = [1 + l,059e-looi sin (173/ - 70°50')] 1 (/).
(кривая 2 на рис. 107).
136
ВТК- 4, ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ [167
167. Найти функцию -веса w (i): 1) для-системы,
представленной в задаче 165; 2) для системы, предста-
вленной в задаче 166.
Указание. Возможно, использование переходных
функций этих систем, полученных в задачах 165 и 166.
Ответ.
1) w (/) = (169,2е-144’7/ - 9,45е~55>3/) 1 (/);
2) w (!) = 212e~I0Mcos(173/ - 40°50') 1 (!).
168. Найти переходную функцию h(i) и функцию
веса w(i) системы, описываемой уравнением
(аор2 + atp + а2) у (!) = bog (!).
Все коэффициенты уравнения положительны; Ьо — а2,
а2>4а0а2.
Ответ.
[ а — а р~а'^ \
Л(0 = U «.........а
где и а2 — абсолютные значения корней характеристи-
ческого уравнения системы.
,169. Дана статическая система автоматического ре-
гулирования, описываемая уравнением
(аор2 + щр + а2) у (!) = bog (!),
где а() = 0,002 сек2, •«) = 0,12 сек, а-2 = &, Ь0 = 4.
Найти реакцию- системы на ступенчатое воздействие
g(O = go-1 (t).
Ответ.
У (0 = go [0,8- e-w sin (40/ + 53°10')] 1 (!).
170. Система автоматического регулирования описы-
вается уравнением
(аоря + щр2 +. а2р + а3) у (!) = (Ьйр + bt) g (i), (1)
где а0 — 5 • 10 4 сек2, = 0,105 сек, а2“2,16, а3 = 61=’
= 65,3 сек~\ Ьо= 1,16,- . •
§ 4.1. КЛАССИЧЕСКИЙ МЕТОД РЕШЕНИЯ УРАВНЕНИИ
137
Найти переходный процесс для двух случаев: 1
1. При включении системы после ее предваритель-
ного рассогласования на величину х0.
. 2. При задающем воздействии в виде единичной
ступенчатой функции у (t) = 1 (/) и нулевых начальных
условиях у_0 — У_а = %о = 0.
1. Решение для случая 1. Характеристическое
уравнение, соответствующее (1), имеет при заданных
коэффициентах вид
0,0005р3 + 0,105р2 + 2,16р + 65,3 = 0.
Корни уравнения (2) могут быть найдены каким-либо
из известных методов. Эти корни равны
р{ = — а == — 180 сек~1, |
р2,3 = — у ± /А = — 10 ± /25 сек*1. ]
Выходная величина системы, характеристическое урав-
нение которой имеет один вещественный и пару ком-
плексных корней, имеет вид
у (t) = Ae~at + Ве~* sin (Kt + 6).
Начальные условия равны
(4)
4/(0) = %, /(0) = 0, /'(0) = 0. (5)
Из (4) находим
if (0 = — аЛе*а< + Be~yt [A. cos (Kt + 6) — у sin (Kt + 6)],
у" (/) = a2Ae~at + Ве~* [(у2 - A2) sin (Kt + 6) -
— 2уА cos (Kt + 6)].
(6)
Из выражений (4) —(6) получаем систему уравнений для
определения постоянных интегрирования А, В, 6:
А + В sin 6 = у»,
— а/1 + ВК cos б — уВ sin б = 0,
(7)
а2А + В (у2 — К2) sin & — 2уА cos 6 = 0.
После подстановки а, у, К согласно (3) найдем
4 = 0,0246%, B = l,13%, б = 59°50/. (8)
1.38
гл; 4! ПОСТРОЕНИЕ. ПЕРЕХОДНЫХ ПРОЦЕССОВ
1171
Подстановка. (8)- в (4). дает решение задачи:
У ('0 = Уч [0,0246е-18И + 1,13e-10fsin (252 + 59°5€И)].
Этот результат можно получить непосредственно из (2)
н (5); если воспользоваться приложением 10.
2. Указание к решению задачи для второго слу-
чая. Начальные условия, имеющие место непосредственно
после приложения ступенчатого воздействия, могут быть
определены при помощи приложения 9.
Ответ.
[1 + 0,0541e~18w - l,0541zrIM sin (25/ + 88° 15')] 1 (2).
171. Найти переходный процесс в системе, данной
в предыдущей задаче, при управляющем воздействии,
нарастающем по линейному закону
g (2) = «21 (2).
Укааание. Частное решение дифференциального
уравнения системы, т. е. вынужденную составляющую
переходного процесса, следует искать в виде
У в = b + с2.
Ответ.
y(t) = a[t~ 0,000302e~18w -
- 0,0392e~10i sin (252 - 23°30') - 0,01532] 1 (2).
172. Система автоматического регулирования описы-
вается уравнением
(aop + a1)y(2) = 6oPg(0. (О
Найти переходный процесс в системе при помощи
интеграла Дюамеля для двух видов управляющего воз-
действия:
1) ^(2) = «21(2); (2)
2) g (2) = & (е_<7< — e-rt) 1 (2) (3)
при нулевых начальных условиях.
Решение, для случая g(2) = all (/)•
172] § КЛАССИЧЕСКИЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ 139
Интеграл Дюамеля может -быть записан .в виде
р.(0 = g (0)А (0 + ,J g'fr) h(t - т) dr, (4)
о
где h (0 — переходная функция системы.
Для определения h(t) найдем .реакцию системы на
единичное ступенчатое воздействие, т. е. решим урав-
нение
(Оо'р + fli) f/(0 = ьор 1 (0 (5)
при .нулевых начальных условиях.
В соответствии с уравнением (5) найдем
У уст = 0. (6)
Используя приложение 9, найдем также
= = _ 47)
С учетом (6) и (7) решение уравнения (5) имеет вид
у (t) = Ае~^ + УуСТ = Ае~^ = 1 (0 А е~^, (8)
где 7’ = -^.
ai
Таким образом, переходная функция системы равна
л(0=А.бНч(/). (9)
Для линейного управляющего воздействия (2) имеем
gz(0=«- (Ю)
Подставим (9) и (10) в (4):
p(O=-J а~ е * dr. (Н)
о
Интегрируя уравнение (11), находим ответ для пер-
вого случая1 задачи:
,у.(/-)==аМ1 -е’ЯкО-
г .
140
ГЛ. 4.' ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
И 73
Ответ для случая апериодического управляющего
воздействия (3):
<r-qrT}e rt - (д~дгТ)е qT+ (q-r}e т
~<7
173. Найти переходный процесс в системе, описы-
ваемой уравнением
- (aoP + a^yUj^bogit),
при затухающем колебательном задающем воздей-
ствии
g (t) — ce~rt sin O.t
и нулевых начальных условиях.
Указание. Предлагается применить интеграл
Дюамеля.
Ответ.
1/(0 = с
-у- — rj e~ri sin fit — S2e rt cos fit + fie r
K"
-y- H +fi2]
KO,
rhe T =
Ol
§ 4.2. Применение изображений Лапласа
и Карсона — Хевисайда
174. Передаточная функция разомкнутой системы
автоматического регулирования равна
рЦ + Гр) = р(1 +0,1р) • '1)
Найти переходную h(i) и весовую ш (0 функции замк-
нутой системы.
Решение. Передаточная функция замкнутой си-
стемы, с учетом (1), равна
ф (ni = ________К —___________20 (2)
w 1 + №(р) Тр2 + р + К 0,1р2 + р + 20’ w
JMj § 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА - ХЕВИСАИДА J4J
Переходная функция h(f) представляет собой реакцию
системы на единичное ступенчатое воздействие 1 (/).
Изображение У(р) выходной величины y(t) замкнутой
системы при задающем воздействии g(t), изображе-
ние которого равно G (р), представляет собой при нуле-
вых начальных условиях произведение
У(р) = Ф(р)С(р).
Изображение единичной ступенчатой функции по Кар-
сону-Хевисайду равно 1, а по Лапласу у. Поэтому
переходная функция h(t) системы может быть получена
как результат обратного преобразования по Карсону —
Хевисайду передаточной функции . замкнутой системы,
т. е. выражения (2), либо как результат обратного пре-
образования по Лапласу произведения
7Ф(^ = 7(^7Т2бГ- (3)
Для перехода от изображения (2) или (3) к искомому
оригиналу h(t) необходимо знаменатель изображения
разложить на множители. Для этого приравняем зна-
менатель (2) нулю,
Тр2 + р + К=.О или 0,1/?2 + р + 20 = 0, (4)
и найдем корни полученного уравнения (4):
Pi= - у + /А = - 5+ /13,2 сек"1, 1
р2= — у — /А = — 5 — /13,2 сек-1. J
Далее можно записать знаменатель выражения (2) в виде
0,1р2 +р + 20 = 0,1 (р ~ Pi)(p- р2) =
. = 0,1 [р - (- у + /А)] [р - (- у - /А)] =
= 0,1 [(р + у)2 + А2] = 0,1 [(р + 5)2 + 13,221(6)
Теперь вместо (3) получим
1 ф , ,_________20______ 200 т
р 0,1р [(р + 5)2 + 13,22] р[(р + 5)2 + 13,2«] ’
142
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
.Ц74
Из таблиц изображений функций по Лапласу (см. при-
ложение 1) подбираем формулу, соответствующую вы-
ражению (7):
-------- --1—,/ e-v/ sin (Л/ — ф),
₽Кр + у)2 + *2]---------т2,+ л2 Л,/у24-Л2
ф== arctg-—-. (8)
При подборе формул следует иметь в виду, что в имею-
щихся справочниках эти формулы располагаются в по-
рядке возрастания степени полинома от р в знаменателе
изображения.
Для случая вещественных и для случая комплексных
корней всегда предусматриваются отдельные формулы.
Так, если бы корни знаменателя изображения (2) ока-
зались вещественными, следовало бы вместо формулы
(8) взять табличную формулу
Р (Р + а) (Р + ₽) ’ а₽ а — £ \ а £ ) ’
где а и Р — абсолютные значения корней.
Сопоставляя (7) и (8)., получаем оригинал выраже-
ния (7), т. е. переходную функцию системы,
й(/) = ф(р) =
= Г—200-----------^^-7- sin (13,2/ + 69° 15')] 1 (/),
|_52+13,22 1 3.2 У 52+ 13,22 J v ’
ИЛИ
h (t) = [1 - 1,068е-5< sin (13,2/ + 69° 15')] 1 (/). (9)
Замечание. Следует обратить внимание на вычи-
сление угла ф по формуле (8), так как знаки в форму-
лах для ф., типичных для подобных выражений, запи-
сываются своеобразно. Знак числителя в выражении
для тангенса ф является знаком синуса ф, а знак зна-
менателя является знаком косинуса ф. Таким образом,
формула для ф содержит указание на квадрант, в ко-
тором находится этот угол. Это позволяет освободиться
от двойственности в ответе для ф, обусловленной совпа-
дением тангенсов двух углов, отличающихсй на л.
13 2
В рассматриваемом примере, гдetgф=-----=—2,64,
из двух возможных значений ф, равных —69° 15 и
17BJ §4 2. ИЗОБРАЖЕНИЯ ЛАПЛАвА И КАРСОНА ХЕВИСАЙД [43
4-1Ю°45', следует взять второе число, так как выраже-
~ X 132
нце ф = arctg — == arctg указывает, что угол нахо*
дится во втором квадранте.
В результате из формулы (8) следует
sin (М - ф) = sin (13,2# - 110°45') = - sin (13,2# + 69°15'),
что и учтено при записи выражения (9).
Функция веса w (i) системы может быть найдена как
производная переходной функций (9) по времени.
Функция веса может быть найдена и непосредственно
по передаточной функции (2), как ее обратное преобра-
зование по Лапласу,
»(0-г'[Ф(р)1-г.-'[0Л||,^тж]-
= [(Р + 5)г+13,22 ]’
либо как обратное преобразование по Карсону — Хеви-
сайду произведения
пФ (р) = =_=____________260р--- (11)
р 0,1р2 + р + 20 (р + 5)2 +13,22 1 ' '
Подбираем из таблиц изображений функций по Лап-
ласу формулу; соответствующую (10):
В- (р + у)2 + X2 Т е~У( sin
Согласно (7), (10) и (12) получаем функцию веса системы
w(t)= 15,15е~а sin 13,2/ 1 (/). (13)
175. Для замкнутой системы автоматического регули-
рования, -данной в предыдущей задаче, найти закон изме-
нения выходной величины y(t) при отсутствии задаю-
щего воздействия, начальном рассогласовании //(О) = г/о
и нулевой начальной скорости.
Решение. Согласно уравнению (2) предыдущей
задачи, дифференциальное уравнение замкнутой системы
Имеет вид
(Гр2+р+Ю#(0.=К§(0, 0)
144 ГЛ. 4' ПОСТРОЕНИЕ. ПЕРЕХОДНЫХ ПРОЦЕССОВ {175
где g (t) — задающее воздействие. Для получения
из (1) изображения выходной величины y(t) необходимо
использовать операторные выражения для производных
с учетом начальных условий. Запишем эти выражения
по Лапласу,^ полагая, что Y(р) есть изображение функ-
ции y(t)
y'(t)^pY(p)~ y(Q), 1
Р2У (О = У" (0 = P~Y (р) - ру (0) - у' (0). J
Здесь у(0) и у' (0) — начальные значения выходной вели-
чины и ее производной. Из (1) и (2), учитывая, что
g (t) = 0, получаем
Tp2Y (р) - Тру (0) - Ту1 (0) + рУ (р) - у (0) + KY (р) = 0,
или
у см — (Гр + у(0) + ?У (0)
Г(р) Трг+р + К • w
Подставляя значения начальных условий у(О) = уо и
р'(0) = 0 и коэффициентов уравнения Т = 0,1 сек и
Л = 20 сек~1, получим
у (п\ _ ~Ь 1) Уо _(O.lp + 1) уо (р + 10) уо / .х
0,1р2 + р + 20. 0,1 [(р + 5)2+13.22] (р + 5)2+13,22 ’ { )
Подходящая табличная формула (по Лапласу)
- Т W-V)2 + ^ (М + ф), (5)
^arctgyj^.
Из изображения (4) на основании формулы (5)
получим
У (0 = Уо ~-1°-~1з^+ 13’22 sin (13,2/ + 69° 15')
или
у (/) = Pol,068е~5' sin (13,2/ + 69° 15').
Замечания. Применение табличных формул типа
формулы (5) не является единственным способом пере-
хода от изображения функции к ее оригиналу. Возможно,
например, использование теоремы разложения.
j7Bj. § 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА - ХЕВИСАЙДА ’ Мб
До перехода к оригиналу y(t) можно произвести
проверку правильности изображения У (р) по некоторым
признакам. Возможна, в частности, проверка изобра-
жения по его размерности. Изображение по Карсону-
Хевисайду какой-либо функции, например y(t),
оо
Y(p) = p f y(t) e~pfdt, (6)
о
имеет ту же размерность, что и оригинал y(t). Это
видно, например, из того, что изображение ступенчатой
функции по Карсону — Хевисайду равно самой функ-
ции, т. е. при f>0. Из выражения (6) слё*
дует, что аргумент р изображения имеет размерность
время'1. Размерность изображения функции по Лапласу
со
У(р) = Л[р(/)] = J y(t)e'pidt (7)
о
равна размерности оригинала, умноженной на время,
т. е. отличается от размерности изображения (6) по Кар-
сону — Хевисайду множителем время.
Применим эти. сведения о размерностях к проверке
изображения по Лапласу (3) координаты у исследуемой
системы. Правая часть выражения (3) должна иметь
размерность произведения координата X время. Учиты-
вая, что размерность р — это время'1, находим, что все
слагаемые числителя выражения (3) имеют размерность
координаты, а знаменателя — время'1. Следовательно,
проверка по размёрности дает положительный результат.
Перейдем к другим видам проверки изображения.
Непосредственно по выражению (3) можно найти
начальное значение оригинала
р (0) = lim рУ (р). (8)
Р -> со
Применяя (8) к (3), получаем у (0) = у- у (0).
По выражению (3) можно найти также предел ориги-
нала y(t) при /—>оо, если этот предел существует,
по формуле
lirri у (0 = lim рУ (р). (9)
/ -> со р->0
146
ГЛ'. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ - ЦИ
Признаком наличия указанного предела оригинала
является расположение всех полюсов изображения У (<р)
только в левой полуплоскости комплексного переменного
р, т. е. вещественные части всех корней знаменателя
функции Y (р) должны быть отрицательными. Для. выра-
жения (3) это условие выполняется. Применяя (9) к (3),
находим у(°о) = -^-=0, что заведомо правильно, так как
из физических соображений следует, что в рассматривае-
мой задаче установившаяся ошибка равна нулю.
Указанные виды проверки полученного изображения
дают лишь необходимые условия правильности резуль-
тата-, однако практически эти условия часто являются
и достаточными.
176. Передаточная функция разомкнутой системы
равна
W(p} =----------------=------------------
W (1 + Т1Р) (1 + Т,Р) (1+0,2р)(1+0.01р) ’
Найти переходную функцию замкнутой системы.
Ответ.
h (t) = (0,750 + 0,341е-80/ - 1,091 е"25*) 1 (t).
177. Для системы предыдущей задачи найти закон
движения при отсутствии , задающего воздействия
при начальных условиях у(0) = уо и у'(0) = у'о.
Указание- Решение является суммой двух сла-
гаемых, одно из которых пропорционально у0, а дру-
гое — у'о- эти слагаемые удобно найти отдельно и резуль-
таты сложить.
Ответ.
У (0 = Уо [1,455"2Ы - 0,455е~“] + 0,0182//'[е"25' - е*®“].
178. Для замкнутой следящей системы с переда-
точной функцией (см. задачу 174)
' Ф 0,1р2+р + 20
найти закон движения при задающем воздействии
в виде ступенчатой функции gjl (/) и при начальных
условиях у (0) = уй и у' (0) = 0. -
Jg0]§ 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА- ХЕВИСАЙДАП7
Ответ.
y(t) = go\\- 1.068е-« sin (13,2^ + 69° 15')] +
+ 0о1,О68е-5< sin (13,2/ + 69° 15').
179. Для следящей системы, которая в разомкнутом
состоянии имеет передаточную функцию
W (п) —----------— --------------
Р (1+ Тр) р (1 + 0,0067р) ’
найти выходную величину y(t) при задающем воздей-
ствии, в виде ступенчатой функции g(t) — gol (0 и при
начальных условиях у (0) — yQ и y'(ty — y'o.
Ответ.
у (1) = go 11 - 1 ДЗЗе-30* + 0,333а-120*] +
+ у0 [ 1,333е-3" — О,333е-12И] + 0,011 If/' [а-30* - е"120*].’
180. Найти закон изменения выходной величины y(t)
замкнутой следящей системы при ступенчатом задаю-
щем воздействии 1 (/) и нулевых начальных условиях.
Передаточная функция разомкнутой системы
'Ки+ТгР) _ 500 (1 + 0,03р) ,.ч
VP> P(l +Т,р)(1 +ТзР) р(1+0,1р)(1+0;006р) ’
Решение. Находим передаточную функцию замкнут
той системы
ф I п\ — ___________' К (\+Т2р)__________=
1 + г(р) ра + ЛрД! +Г3р) + /<(1 +Т2р)
___________15 р + 500_______
. 0,0006р3 + 0,106р2 + 16р + 500 ’ 1 1
Изображение по Карсону — Хевисайду искомой реакции
системы на ступенчатое воздействие имеет вид
Х(р) = Ф(р). (3)
Далее, независимо от предполагаемого способа пере-
хода от (3) к оригиналу, необходимо найти корни зна-
менателя изображения (2), т. е. корни уравнения
О.ОООбр3 + 0,106р2 + 16р + 500 = 0. (4)
148 ' ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ (180
В результате расчета, который здесь не приводится,
получаем следующие корни уравнения (4):
Pi = — 39,2 сек"1,
р2 =(—.68,8 + /128,5) сек"1,
р3 = (—68,8 —/128,5) сек"1.
(5)
Если теперь знаменатель изображения (2) предста-
вить, с учетом (5), в виде произведения
0,0006р3 + 0,106р2 + 16р + 500 =
= 0,0006 (р + 39,2) [(р + 68,8)2 + 128,52],
то перейти к оригиналу можно при помощи таблиц
изображений.
Здесь используем другой способ перехода к ориги-
налу — при помощи теоремы разложения. Пусть искомая
функция y(t) имеет следующее изображение по Кар-
сону — Хевисайду:
Y (р) = В _ bgpm + bipm * + ... +bm-ip + bm (gj
•D(p) aopn + atpn~l + ... + an-tp + an ’ -
(7)
причем m n и уравнение D (p) = 0 не имеет нулевых
и кратных корней. Тогда согласно теореме разложения
оригинал y(t) может быть найден по формуле
Р(0) + & PkD'(pk) е ’
k*= I
где pi, ..., pk, ..., рп — корни уравнения, a £)'(р)=
•=^-£)(р). В соответствии с (2) и (3), запишем
у (п) =_________15р + 500_______=
1 и ' О.ОООбр3 + О.Юбр2 + 16р + 500
_________25 000. (р + 33,3)__
р3 + 176,6р2 + 26 700р + 833 000 ’’
Сопоставляя (8) и (6), находим
В (р) = 25 000 (р + 33,3), В (0) = 833 000,
D (р) = р3 + 176,6р2 + 26 700р + 833 000,
D (0) = 833 000, £)'(р) = Зр2 + 353р + 26 700. .
(8)
(9)
1801 § 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА — ХЕВИСАЙДА 149
Согласно теореме- разложения (7) получим
-Л 25 000 (р. +33,3) ni
у (t) = 1 + У —т-2—Р------------—Г ер< (10)
Й Р/г (3₽а + 353^ + 26 700)
Вычислим отдельно слагаемые, находящиеся в (10)
под знаком суммы. При /?] = — 39,2 сек-1 получим
рР1« =___2J47500___ 39 2/ = П 91 ftp-39,2t ft 1 V
PtD'ipt) е -39,2-17430 ’ De .
Прйр2=(-68,8+/128,5) сек"1— 146еу118°!0' сек1 получим
g (Рз) epj _ 2,5 • Ю4 * * * В * .- 133,5e/105 25 e(-68,8+y 128.5) t _
paD' (р8) 146е,118°10' - 3,4 - 10V'166°53'
— 0,672е' (»54,>8')e-68,8/e/-128,5t = 0,672е' (128.Й+154’ 8') e-68,8t# ( J2)
При рз = ( —68,8 — /128,5) сея:-1= 146е/,18°10/ сек~х получим
-^з) . е^ = 0»672е-' (128^+154» 8') р-68,8/. . ( ) 3)
PiD (рз) ’ v ’
Выражение (13) записано без расчета, непосред-
ственно по виду выражения (12), так как корни р2 и
сопряженные, а коэффициенты в выражении (10) чисто
вещественные. При этих условиях комплексные выра-
жения (12) и (13) заведомо являются сопряженными.
Если бы все корни уравнения (4) были веществен-
ными, то выражения (И) —(13) не содержали бы ком-
плексных чисел и расчет можно было бы закончить
подстановкой этих выражений в формулу (10).
В данном случае выражения (12) и (13) являются
комплексными, поэтому их следует преобразовать. При-
меняя к сумме сопряженных выражений (12) и (13) фор-
мулу Эйлера
получаем
Д(Рз)
=
-в epj -]__________________
P2D' (р2) p3D' (рэ)
= 0,672е~68-8< [е/(128.И+1540 8') [ e~i (128,5<+154«8')J _
' = 1,345е-68-« cos (128,5/ + 154° 8Э =
= - 1,345е-68’й cos (128,5/— 25° 52'). (14)
150
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ' ПРОЦЕССОВ
[181
Подстановка функций (11) и (14) в формулу (10) дает
реакцию системы на ступенчатое воздействие 1 (t):
y(i) = [1 + 0,216е-39'-и - 1,345е"68,8/ cos (128,5^-25° 52')] 1 (/).
(15)
Отдельные слагаемые этого уравнения и кривая y(t)
построены на рис. 108.
Рис. 1Q8. Переходный процесс в следящей .системе с .астатизмом
первого порядка .при ступенчатом ' задающем воздействии.
181. Для замкнутой следящей системы, приведенной
в предыдущей задаче, найти в общем виде изображе-
ние У (р) по Лапласу и Карсону — Хевисайду выходной
величины y(t) через изображение G(p) задающего,
воздействия при ненулевых начальных условиях p(Q)=i/o,
/(0) = Ро и р"(0) = р"
Ответ. Изображение по Лапласу
У(р) = £[р(0] =
= [(15р + 500) G (р) + (6 • lOV + 0,106р + 16) у0 +
+ (6 • 10~4р 4- 0,106) уо + 6 • ГО-4ро] X
X [6 • 10~4р34- 0,106р2 + 16р + 500]"1.
jgjj §42. ИЗОБРАЖЕНИЯ ЛАПЛАСА: И КАРСОНА—ХЕВИСАЙДА151
Изображение по Карсону — Хевисайду
у (р) == [(15р + 500) G (р) + р (6- 10-у + &,Ю6р + 16)у04-
+ р (6 • 10"4р + 0,106) у'о + 6 • 10~Х] X
X [6 • 10"У 4- 0,106р2 4- 16р 4- 500]-1.
182. Найти закон движения системы, приведенной
в задачах 180 и 181, при отсутствии задающего воздей-
ствий’ и начальных условиях р(О) = уо, р.'(0) = 0 и
t/'(0)«=0.
Ответ.
y(t) = уоП.221е-39'2Л4-О,335е-68^ sin (128,5/ - 41° 45')].
183. Следящая система, приведенная в задаче 180,
имеет в разомкнутом состоянии передаточную функцию
w , х в /<(1 +Г2Р)______________500(1 + 0,03р)
W W р (1 + Г,р) (1 + Г3р) р (1 + 0,1р) (1 + О.ООбр) •
Найти выходную величину y(t) замкнутой следящей
системы при задающем воздействии в виде, импульс-*
ной’ функции Д6(/) при нулевых, начальных условиях;
6(0—единичная импульсная, функция. Найти функцию
веса w(fj системы.
Ответ.
y(t) = A [— 8,46е~39-2* 4- 196,4e-68-8Z sin (128,5/ 4- 2° ЗО')]р
184. Для замкнутой следящей системы, передаточная
функция которой в разомкнутом состоянии равна
17 (р\ —----К----—--------------
W р(Ц-Гр) р(1 +0,0067р)'*
найти, выходную величину y.(t) при линейном задающем
воздействии g(/) = o/l(/) и нулевых начальных усло-
виях.
Решение. Передаточная функция замкнутой си-
стемы равна
, ч W (р)____________3600_____ /1 ч
W 1 + Г (р) ~ р2 + 150р -ь 3600 • . . ' ’
152 ' ' ГЛ. 4. ПОСТРОЁНИЁ ПЕРЁХОДНЫХ ПРОЦЕССОВ
{184
Изображение задающего воздействия по Лапласу
= (2)
Согласно (1) и (2) изображение выходной величины по
Лапласу равно
<3>
Для отыскания оригинала выражения (3) можно
использовать теорему свертывания, согласно которой
У (О = J (т) х2 (t - т) dr, (4)
если
У(р) = Х1(р)Х2(р) (5)
(6)
х2(0 = Хг(р). (7|
В соответствии с (5) изображение (3) следует раз-
бить на два сомножителя с таким расчетом, чтобы
произведение их1 оригиналов легко интегрировалось.
Выберем эти сомножители следующий! образом;
У z ч , ' ' 3600 • а г
Г (Р) ~ р (р2 + 150р + 3600) ' р ’
т. е.
у / \ _ ______3600______ 3600_____________
р(р2+ 150р + 3600) р(р + 30)(р+120) ’
Х2(р) = ~. (9)
Знаменатель выражения (8) разложен на множители
обычным путем. Для выражений (8) и (9) подбираем под-
ходящие формулы из таблицы изображений по Лапласу
... . .. ±e-« ' -₽*
------*---—__________________Р____ (Ю)
р(р + а)(р + ₽) ’ «Р ' а —р ’ V '
7 = 1(0- СО
г
1851 § *.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА»!! КАРСОНА — ХЕВИСАЙДА 153
Теперь из (6) —(11) найдем
х, (/) = (1 - 1,333е~зм + 0,ЗЗЗе-120<) 1 (/), (12)
x2(0 = al(0- (13)
Подставим оригиналы (12) и (13) в формулу (4) теоремы
!/(/) = J [1 — l>333e-30t + 0,333e-I20r] • [«1 (Z — т)] (/т. (14)
о
Интегрируем (14):
y(t) = а [т + 0,0445e~30t - 0,00277e“’20t]'.
Отсюда искомое решение задачи:
y(t) = a (t + 0,0445е~зш - O,OO277<rI2of - 0,0417) 1 (/).
Задающее воздействие g (/) и выходная величина у (t)
троены на рис. 109.
Рис. 109. Переходный процесс в следящей
системе с астатизмом первого Порядка при
линейном '' задающем воздействии.
24
185. Передаточная функция разомкнутой следящей
темы равна
W = р(1 +Тр) р (1 + О.ООЬ/р) *
IE 4 ГЛ? 4. । ПОСТРОЕНИЕ ПЕРЕХОДНЫХ! ПРОЦЕССОВ! [184
Найти ошибку x(t) = g(t)^—y(t) замкнутой следя-
щей- системы, при:нулевых начальных условиях для за-
дающего воздействия двух видов:
1) при ступенчатом воздействии g(t)~gijl(ty,
2.) при задающем-.: воздействии, нарастающем по ли-
нейному закону g(t) = atl (if).
Указание. Передаточная функция следящей си-
стемы относительно ошибки равна ,
Ф* в 1 + 1Г (р) *
Ответ.
1) х(0 = gb(1.333e-30i —0,333erI20<) 1 (/),
2) х (t) = а (0,0417 - 0,0445е~30< — 0,00277е-'20/) 1 (/).
Ошибка-для. обоих:, случаев.-построена. на, рдс. НО.
Рис. НО. Графики ошибки следящей системы
с астатизмом первого порядка при. ступенча-
том (кривая 1) - и линейном (кривая.:- 2) зада-
ющих воздействиях. Правая шкала оси орди-
нат-относится к.; кривой левая шкала —
к; кривой-2.
186. Следящая система, схема которой дана на
рис; 111, имеет' в разомкнутом ’ состоянии - передаточную
функцию
Г (р)==Ж(р) ^(р^-у^у •
!8S] § 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА - ХЕВИСАЙДА 155
Система состоит из.двух звеньев, между которыми при-
кладывается возмущение f(t). Найти выходную вели-
чину У (О для ступенчатого возмущения = при
отсутствии задающего воздействия g(t) и нулевых
начальных условиях; К. = kik2 ~ 24 сек-1, Т = 6,7 мсек,
= 0,01 в^сек"1. Последний коэффициент записан
f(t)
ym
Рис. 111. Структурная схема следящей си-
стемы к задачам 186 и 188.
в предположении, что координаты у (Г) и g(/) безраз-
мерные, а входные величины второго звена, в том числе
возмущение /(/), имеют размерность напряжения.
Ответ.
у (/) == 1О"7о [4,17 - 4,45е"30/ + 0,278e’12Oi] 1 (t).
187. Следящая система состоит из двух звеньев,
показанных на рис. Ill;
(п) = -fe|fez-=______—------
р (1 + Тр) р(1 +0,025р)
На вход второго звена действует возмущение в виде
импульсной функции f (t) = Лб (/); , задающее воздей-
ствие g(t) отсутствует, начальные условия нулевые.
Найти выходную величину y(t) замкнутой следящей
системы.
Ответ.
у (О = Ml ,053e-2°*sin (60/ - 71° 34') 1 (/).
188. Передаточная функция разомкнутой следящей
системы равна
156
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
1183
где Д —400 сек'2^ Т = 0,01 сек. Найти выходную вели-
чину y(t) замкнутой системы при ступенчатом задаю-
щем воздействии g(O = gol(O и нулевых начальных
условиях.
Ответ.
У (0 = go [1 + l,053e-2W sin (60/ -71° 34')] 1 (/).
189. Даны две следящие системы, имеющие в разом-
кнутом состоянии передаточные функции:
*>
2) «ЭД =йД+Дй,
где Д1 = 100 сек'1, Г] = 25 мсек, /<2 = 4000 сек'2, =
= 10 мсек. Найти выходные величины y(t) и ошибки
Рис. 112. Ошибки при задающем воздействии g (/) =
= al • 1 (t) Для следящих систем с астатизмом первого
порядка Xi (/) и с астатизмом второго порядка хг (/)-
х (0 = g (0 ~ У (0 замкнутых следящих систем при линей-
ном управляющем воздействии, g (t) = atl (/), и нулевых
начальных условиях. Построить . на одном графике
кривые ошибок для этих систем.
1«2| § 4.2. ИЗОБРАЖЕНИЯ ЛАПЛАСА И КАРСОНА - ХЕВИСАЙДА (57
Ответ,
Ул (t) = а [/ — 0,01 — О,О167е~20< sin (60/ — 36° 50')] 1 (/),
Х1 (/) == а [0,01 + 0,0167е~2ад sin (60/ - 36° 50')] 1 (/),
у2 (/) ==«[/- 0,0167^ sin 60/] 1 (0,
x2(/)==«0,0167e-2Wsin60/ 1 (/).
Кривые Xi (/) и л'2(/) построены на рис. 112.
190. Замкнутая система автоматического регулиро-
вания описывается уравнением
(0.1479/?4 + 3,7р3 + 15,61/?'- + 17,9/? + 20) у (/) =
= (17,9/? + 20) g(/).
Найти выходную величину y(t) при ступенчатом задаю-
щем воздействии £(/) = gol (/) и нулевых начальных
условиях.
Ответ.
у (t) = g0 [ 1 + 1,456e-°'s* sin (1,2/- 72°) +
4- 0,398e-« — 0,019e-20q 1 (/).
191. Найти выходною величину y(t) системы, данной
в предыдущей задаче,' при отсутствии задающего воз-
действия и начальных условиях y(fi)~y0, —
ff"(0)==y" и у"'(0) = у'".
Ответ.
y(t) = yo[l,202e~°-5e(l,2t - 45°) + 0,155е-« - 0,005-20Z] ф-
-+-£/'[1,112e-°'5<sin(l,2/ — 4°50') ф- 0,099е“« — 0,005e~2WJ ф-
+у" [0,283e~0>5Z sin (1,2/ — 19° 30') + 0,096е~«—0,002е-20(] ф-
ф- f/'"[0,288e-°’3Zsin(l,2/—22° 15') + 0,114е« —0,004е-'20(].
192. Найти переходную h(() и весовую w(/) функ-
ции системы, передаточная функция которой равна
где п — целое положительное число.
Указан, и е. Следует воспользоваться теоремой
свертывания.
158 ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ Ц0Э
Ответ.
ап ** ап Rkl
k=0 J
«гл. гл К лП-1 -af
wW-(n-l)!/ е •
§ 4.3. Приближенные методы расчета
переходных процессов
А. Использование вещественных частотных
характеристик [31, 32]
193. По вещественной частотной характеристике Р (о)
системы регулирования (рис. 113, а) построить кривую
переходного процесса при единичном,ступенчатом воз-
действии и нулевых начальных условиях.
Решение. Кривая Р(<£>) приближенно заменяется
несколькими трапецеидальными кривыми с таким рас-
четом, чтобы сумма ординат трапеций равнялась орди-
нате вещественной частотной характеристики Р (со).
В данном случае можно взять четыре трапеции, пока-
занные на рис. ИЗ, б; одна из них положительная,
остальные отрицательные. Каждая трапеция должна
иметь типовой вид, показанный на рис. 113, в; тогда она
полностью определяется тремя числами: частотой среза сос,
коэффициентом наклона % = <Od/coc и высотой г. Трапеции
на рис. 113, б имеют параметры, указанные в табл. 1.
Таблица 1
№ трапеции 1 2 3 4
X II 0,62 0,31 0,46 0,70
©с, сек-1 16 5,5 >61,5 28,5
Г 1,62 -0,09 -0,24 -0,29
Далее следует воспользоваться таблицами функ-
ций h(t0).
Рис. 113. Приближенная замена вещественной частотной характеристики суммой трапецеидальных
функций частоты и получение кривой переходного процесса.
§ 43. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА
160 Г.л.,.4, ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Функция h(t0) представляет собой кривую переход-
ного процесса системы, вещественная частотная характе-
ристика которой — единичная трапеция, имеющая г = + 1
и сос= 1 cetC1. Табличные функции h (t0) приводятся для
различных коэффициентов наклона 0^%^1, причем
допускается интерполяция, если % лежит между двумя
табличными значениями. Сокращенная таблица таких
функций дана в приложении 35.
Возьмем таблицу h(t0) функций для х = 0,62 (коэф-
фициент наклона трапеции 1) и выпишем ряд значений
времени t0 и функции h(t0) (см. первые две строки
В табл. 2). Для получения точек кривой у (/) переход*
Кого процесса, соответствующего неединичной трапеции,
Каждое значение функции следует умножить на
высоту трапеции г, а время t0 разделить на частоту
среза од, т. е.
: y^=rhsd}-
В третьей и четвертой строках табл. 2 даны числа I
и y^t) для трапеции 1.
Аналогично получаем y2(t), Уз(() и г/4(0 для осталь-
ных трапеций (см. таблицы 3—5). По данным таблиц 2—5
на рис. 113, г построены графики yi(t), #2(0> У&У)
и y4(t). Складывая ординаты этих кривых с учетом их
знаков, получаем на рис. 113, г кривую’у(t) переход?
кого процесса в заданной системе при единичном сту-
пенчатом воздействии. На рисунке указана также вели-
чина уу„= lim y(t).
t-> со
В случае неединичного ступенчатого воздействия
g(t) = go\(t) ординаты кривой y{t) следует умножить
на g0.
194. По вещественной частотной характеристике си-
стемы регулирования (рис. 114, а) построить кривую
переходного процесса y(t) при задающем воздей-
ствии g(O = g'ol(O и нулевых начальных условиях.
Ответ. Кривую Р(со) можно заменить двумя трапе-
циями, показанными на рис. 114, а пунктиром. Данные
трапеции 1: % = 0,78, сос = 79 сек-1, г = 0,688; данные
трапеции 2: % = 0,84, сос = 95 сек-1, г = 0,2.
194]
§ 4,3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА
161
Таблица 2
Трапеция 1
То 0 0,2 0,4 0,8 1,0 1,6 2,6 3,0 4,0
л (10) 0 0,10 0,20 0,40 0,50 0,75 1,04 1,Н 1,16
/, сек 0 0,0125 0,025 0,050 0,0625 0,100 0,162 0,188 0,250
Ух (t) 0 0,17 0,33 0,65 0,81 1,21 1,68 1,80 1,88
^0 4,4 4,8 5,4 6,0 7,0 7,8 9,0 10
h (t0) 1,15 . 1,12 1,07 1,01 0,95 0,94 0,96 l;oo
t, сек 0,275 0,300 0,337 0,375 0,438 ' 0,488 0,562 0,625
Ух (0 ,1 86 1,82 1,73 1,64 1,54 1,52 1,56 * 1;62
Таблица 3
Трапеция 2
t, сек |o| О,юэ| 0,21в| 0,364, 0,54б| 0,72в| 0,822, 1,09 | 1,27 .
ViU) lol - 0,022, -0,043, - 0,067.1 - 0,086, - 0,09б| - 0,09в| - 0,09б| - 0,094
Таблица 4
Трапеция 3
t, сек 0 0,0065 0,0163 | 0,026 0,0325 | 0,0488
Уз(0 0 -0,043 -0,108 | -0.163 -0,194 | -0,25
t, сек 0,065 0,0813 0,0976 0,114 0,13
Уз(1) -0,271 -0,269 — 0,254 -0,242 -0,235
Таблица 5
Трапеция 4
if, сек 0 0,014 0,028, 0,042, 0,070 0,105 0,133 0,176
(0 0 -0,064 -0,122, -0,467, -0,267 -0,328 -0,339 — 0,314
t, сек 0,210 0,246 0,281 0,316 0,351 0,386 ) 0,456
У< (0 -0,284 -0,27 -0,27 -0,284 -0,296 -0,302, -0.29Q
162 гл. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ (19S
По этим трапециям построены кривые ^(0 и у2(0
на рис. 114, б; на этом же рисунке дана искомая функ-
ция y(t) для случая £0=1- При g0 #= 1 ординаты
кривой y(t) следует умножить на g0. '
Рис. 114. Вещественная частотная ха-
рактеристика Р (а) и кривые переход-
ного процесса х (/) к задаче 194.
195. Построить кривую y(f) переходного процесса
замкнутой системы при ' задающем воздействии
и нулевых начальных условиях. Передаточ-
ная функция разомкнутой системы
W (р) --------------------------------=
(-1 + 2TlP + + т2р) (1 + Г4р)
_________________5(1 + 0,03р)____________
(—1 + 0,2р + 0,01р2) (1 + 0,05р) (1 + 0,006р) *
Указание. Возможно использование результатов
решения задач 73 (Б) и 79.
4.3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА
Ли»
1.В
а)
б)
Рис. 115. Вещественная частотная характеристика и
кривая переходного процесса к задаче Шб.
164 ГЛ. 4. ПОСТРОЕНИЕ рЕРЕХОДНЫХ ПРОЦЕССОВ ПИ
Ответ. См. рис. 115,-б. Кривые г/1,2,з.4(0 построены
по четырем трапециям, показанным на рис. 115, а.
196. Построить кривую у (t) переходного процесса
замкнутой системы при задающем воздействии
gи нулевых начальных условиях.
рнстика и кривая переходного процесса к за-
даче 196.
Передаточная функция разомкнутой системы
, , К(1 + 7'2р) = 500(1 +0,03р)
р (I + Г,р) (1 + Т3р) р(1+0,1р)(1+0,006р) •
Указание... Возможно использование результатов
решения задач 67 и 77.
Ответ. См. рис. 116, б. Кривые Уцг, з(0 построены
по трем трапециям, показанным на рис. 116, а.
19?]
S 43. ПРИБЛИЖЕННЫЕ АЙИГОДЫ РАСЧЕТА
165
Ji. Использование сопрягающих частот л. а. х. [32]
19.7. Передаточная функция разомкнутой системы
|,а"“ ' V(p)=
"От р(1 + г,р)(1 + ад
(1)
где /( = 500 сек~1, Т[ = 0,1 сек, Т2 = 0,025 сек, Т3 =
_ 0,0025 сек. Построить приближенную кривую ошибки
х (/) = g (/) — у (/) системы при единичном ступенчатом
воздействии g (0=1(0 и нулевых начальных условиях.
Построение произвести по сопрягающим частотам лога-
рифмической амплитудной частотной характеристики.
Рис. 117. Л. а. х. и кривая переходного про-
цесса к задаче 197.
Р е ш е н и е. Л. а. х. системы построена на рис. 117, а.
Эта л. а. х. удовлетворяет условию, состоящему в том,
'чТо протяженность ее участка, пересекающего ось частот
с наклоном —20 дб/дек, должна составлять не менее
одной декады; поэтому построение искомой, кривой по
сопрягающим частотам л. а. х.. является возможным.
166
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
£187
по
из
Определяем частоту среза л. а. х. непосредственно
л. а. х. или по формуле сос = 7<-^-, следующей
рисунка; ©с = 125 сек-1.
В соответствии с методом использования сопрягаю-
щих частот л. а. х., отбрасываем в л. а. х. всю ее часть,
лежащую правее частоты среза, и заменяем ее горизон-
тальным участком, совпадающим с осью частот. Этой
новой преобразованной л. а. х. соответствует передаточ-
ная функция
Я(1 + Г2р)(1 + 4-р)
Г* (р) =----------’
Р(1 + Т\р)
(2)
или
+ р) («с + р)
где &>! = 1/Т ь
Формулам
передаточная
w*(p) =----
ТгР\тГ
= (р + о2) (р + Ос) (р-н40) (р 4-125)
p(p + Oi) р(р+10) ’ ' '
®2 = 1/Г2.
(2) и (2') соответствует преобразованная
функция системы относительно ошибки
Ф* (п\ - 1 =. Р_(Р +10) . zqx
47 W Г*(р) (р+40) (р +125) • w
Учитывая изображение Лапласа G(p) = ~ для воз-
действия g (0 = 1 (/), находим изображение Лапласа
для первого приближения х*(/) функции x(t)
Х(р) = Ф7р)С(р)=¥^±^. (4)
Из таблиц изображений по Лапласу находим подходя-
щую формулу:
р + 6 . (6-q)e~af-(6 -P)e~w
(p + a) (р + Р)' . ₽-a ‘ ' 7
Формулы (4) и (5) дают ответ для первого приближе-
ния ошибки системы:
х* (0 = 1,353е~1И - 0,353е-4М. (6)
Эта функция построена сплошной линией на рис. 1.17, б.
>§43 ТОИБЛИЖЕНП'ЫЕ -МЕТОДЫ РАСЧЕТА 167
Для получения второго приближения х*(/) искомого
решения следует ординаты кривой х*(0 умножить на
поправочный коэффициент р в диапазоне T^<t<T2,
т е. 0,0025 сек <t< 0,025 сек. Этот коэффициент опре-
деляется из формулы
I <Г*(р)-|
р |1 + ^(р)1р=/Юс
или, согласно (1) и (2),
(р + 40) (р + 125)
р(р + 10).
500(1 +0,025р)
1+ р(1+0,1р)(1 +0,0025р)
р=/125
(/125 + 40) (jl25 + 125) (/125 + 400)
50 000 (/125 4- 40) + /125 (/125 + 10) (/125 + 400)
Второе приближение решения построено на рис. 117, б
пунктиром. На этом же рисунке крестиками отмечены
точки, относящиеся к точному решению.
В. Использование нормированных кривых
для минимально-фазовых систем
с типовыми л. а. х. [2, 4, 5]
198. Передаточная функция разомкнутой следящей
системы равна
П7 (п) = Ки+Т2р) = 100(1 +0,160р)
{Р' р2 (I + Tsp) (1 + Лр) Р2 (1 + 0,024р) (1 + 0,004р)‘
Построить график выходной величины y(t) при ступен-
чатом " задающем воздействии g (/) = g01 (/), g0 = 10 град
и нулевых начальных условиях.
Решение. Строим логарифмическую амплитудную
характеристику заданной системы (рис. 118, а). Согласно
приложению 19 находим, что эта л. а. х. является ти-
повой_симметричной, тип 2-1-2-3. Базовая частота ©0“
а Й = Г100 = Ю сек~\
По приведенной в приложении 19 формуле находим
показатель колебательности системы
М = = -|£±1 ~1,4,
т—1 5,7—1 ’ 1
168
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
{198
где
Т2 _ Т2 0,16' с _
m п Т2 + Т. 0,024 + 0,004 ~ Л
2
i—3
При М ~ 1,4 искомая кривая y(t) переходного про-
цесса должна быть построена как промежуточная между
Рис. 118. Л. а. х. и кривая переходного процесса к за-
даче 198. '
нормированными кривыми,.приведенными для М = 1,3 и
Л1=1,5 в приложении 20, рис. П. 12. При переходе от
J0(j§ 4.3. ПРИБЛИЖЕКНЫВ» МЕТОДЫ РАСЧЕТА 169
нормированной кривой переходного процесса к
у (/) следует абсциссы нормированной кривой разделить
на ®о= Ю сек~\ а ординаты умножить на g0 = 10 град.
В результате получаем кривую y(t), построенную
на рис. 118, б.
199. Передаточная функция разомкнутой системы
равна
w ( } = ________250(1 +0,024р)_____
w (1 + 0,2р)2 (1 + 0,0024р) (1 + 0,0016р) 1
Построить кривую y(t) переходного процесса в замкну-
той системе при ' задающем воздействии g(t)=l (t)
и нулевых начальных условиях.
Ответ. Кривая y(t) переходного процесса может быть
получена приближенно из нормированной кривой пере-
ходного процесса для симметричной л. а. х. при М = 1,4;
базовая частота <в0 = 79 сек"1.
200. Передаточная функция разомкнутой системы
равна
Wln\= 400(1 +0,04р)
w W р (1 + о, 1 р) (1 + 0,003р) (1+ 0,0008р)2 '
Построить кривую переходного процесса y(f) в замкну-
той'системе при ступенчатом задающем воздействии
g(t) = gol (t), go = O,5 и нулевых начальных условиях.
Ответ. Кривая y(t) может быть приближенно по-
строена по нормированной кривой — (<в0/) для М = 1,3;
Йо
базовая частота <в0 = 63;2 сек-1.
201. К следящей системе, имеющей в разомкнутом
состоянии передаточную функцию
Г(р) =
/<(1 + Г2р)
Р2 (1 +7» ’
К = 400 сек"2, Т2 — 0,078 сек, 7’3 = 0,020 сек, приклады-
вается при нулевых начальных условиях задающее
воздействие g(t) = a-t-1 (/), а = 20 град /сек. Построить
график ошибки воспроизведения этого , задающего
воздействия.
IW
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
1201
Решение. Строим л. а. х. системы (см. Ьл(а) на
рис. 119, а). Л. а. х. относится к типу 2-1-2... (см.
б)
Рис. 119. Логарифмические амплитудные характеристики
и кривая ошибки воспроизведения лилейного задаю-
щего воздействия к задачам 201 и 202.
последнюю строку табл. 1 приложения 19). Базовая ча-
стота л. а. х. <о0 =]//<== (/400 =20 сек-1. Показатель
колебательности
Л1
т + 1 _ 4,9 _ . „
т-1 “ 2,9 “
§ 4.3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА
171
где
т —
• Искомая кривая ошибки системы определяется нор-
мированной кривой ошибки воспроизведения линейного
задающего воздействия, приложение 20, рис., П. 14
(часть Б, случай 1).
Искомая кривая ошибки x(t) (см., рис. 119,6) полу-
чается из нормированной кривой для М — 1,7 делением
абсцисс последней на величину ы0 — 20 сек-1 и умноже-
нием ординат на отношение а/а0 = 10/20 = 0,5 град.
Ошибка стремится к нулю, поскольку система обладает
астатизмом второго порядка.
202. К следящей системе, имеющей в разомкнутом
состоянии передаточную функцию
W (р)
К(1+Т2р)
р (1 + 71р)(1 + Т3р) ’
где К = 133 сект1, Т = 0,333 сек, Т2 = 0,078 сек,
Т3 = 0,020 сек, прикладывается при нулевых начальных
условиях задающее воздействие g(t) = а • t-1 (/), а —
— 20 град!сек. Построить график ошибки воспроизведе-
ния этого воздействия.
Ответ. Приближенное решение имеет вид графика
на рис. 119, б, полученного из нормированной кривой
приложения 20, соответствующей л. а. х: системы Ь2(а>),
изображенной на рис. 119, а. Установившаяся ошибка
равна
а
^уст
10
133
0,075 граб = 4,5 угл. мин.
203. Передаточная функция разомкнутой системы
равна
;,500 (1 + О.ОЗр)
W (Р) р (1. + 0,1 р) (1 + О.ООбр) ’
1. Использовать нормированные кривые переходных
процессов для построения графика выходной величины
y(t) замкнутой системы при единичном ступенчатом за-
дающем воздействии и нулевых начальных условиях.
172
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
2. Решить эту же задачу точно (классическим или
операторным методом), а также используя веществен-
ную частотную характеристику системы.
Построить все три решения на одном графике.
Указание. Во второй части задачи можно восполь-
зоваться решениями задач 180 и 196.
у(1>
1,2
'ум
О 0,01 0,03 0,03 0,04 0,05 0.06 t,CBK
Рис. 120. Кривые переходного процесса к задаче 203, полученные
тремя способами:
по нормированным кривым-^- (соо/)— сплошная линия, с помощью
точного решения — крестики и по вещественной частотной характе-
ристике — кружки.
Ответ. На рис. 120 построена кривая y{t), найден-
ная приближенно по нормированным кривым переход-
ных процессов, при ®о = 7О,7 сек-1 и М=1,5. 'Точки,
относящиеся к точному решению, отмечены крестиками,
а точки, полученные по вещественной частотной харак-
теристике, кружками.
Г. Построение кривой переходного процесса
графическим методом
204. Построить график выходной величины y(t) в
системе, описываемой уравнением.
й04т- + ад = М(0 или 2-^- + 20t/ = 5g(0, (1)
(Al III
где 'задающее воздействие g(t) задано графически
на рис. 121, а. Размерности y(t) и g{t) одинаковы.
Начальное условие у (0) = —2. Использовать графический
метод Д. А. Башкирова [3],
§ 4.3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РАСЧЕТА . 173
Решение. Запишем (1) в виде Т~ + у = g^[t), где
постоянная времени Т = aja{ = 2/20 = 0,1 сек, а возму-
щающее воздействие gt (t) = (Ь0/д() g (0 = 0,25g (t). По-
строим на рис. 121, б две системы координат: t, y(t)
Рис. 121. Построение кривой переходного процесса у (/) гра-
фическим методом.
и 0 £i(0> имеющие одинаковые масштабы, причем оси
времени обеих систем совмещены, но начало О! отсчета
gi(t) сдвинуто вправо относительно начала О отсчета
g(0 на величину Т. Построим согласно формуле для
£1(0 и рис.. 121, а функцию g\(0.
Выбираем шаг интегрирования М = Т1п, где « — це-
лое число. Возьмем А/= 0,020 сек и разделим, графики
174 ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ [205
на рис. 121,6 на участки но 0,02.0.. сек. На графике
функции gi (t) отметим точками d2, d3, ... значения
этой' функции, имеющие место в середине каждого
участка. Отложим на графике y(t} начальное значение
1/(0) =—2 и соединим прямой линией полученную точку
Ci с точкой di. Пересечение прямой c^i с абсциссой
конца первого участка дает вторую точку с2 искомой
кривой. Проводя прямую c2d2, получаем точку с3 на
пересечении этой прямой с абсциссой конца второго
участка и т. д. Искомая функция y(t) определяется как
плавная кривая, соединяющая точки сь с2, с3, ...
205. Построить график выходной величины y(t) в
системе, описываемой уравнением
«o^- + «iJ/ = M(O. «о=1 ^к, «1 = 20, &0 = 12
при i/(0) = 0,25 и задающем воздействии g(t), задан-
Рис. 122. Кривая переходного процесса к задаче 205.
ном в виде таблицы .задающее воздействие имеет
размерность выходной величины)
t, мсек 0 5 10 15 20 25 30 35 45 50
gift 0 —0,300 —0,466 —0 584 —0,640 —0,637 —0,559 -0,350 +0,300 +0,575
t, мсек 60 .65 75 85 ICO 115 125 140 160 CO
+0,900 +0,968 + 1,000 +0,950 +0,759 +0,564 +0,472 tb0,387 +0,350 +0,334
Ответ. См. рис. 122.
ГЛ. 4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
175
206. Построить график выходной величины в системе,
описываемой уравнением
«о + 4F + = b°s
а0 = 0,048 сек2, ai = 0,4 сек, . а2= 10, Ьо = 5
при у(0) = —1,5, г/(0) = 75 сек-1 и задающем воз-
действии g (0, показанном на рис, 123, а.
к виду
г-Л-5-+Л<+*-г,(0
Ответ. См. рис. 123, б.
ГЛАВА 5
ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
§ 5.1. Определение точности
при наличии задающего воздействия
207. Передаточная функция замкнутой следящей
системы имеет вид
ф (р) __ Ъврт + Ь1Рт 1 + + bm-ip + bm
аорп + aibn~l + ... + an-ip + ал
Каковы условия получения: 1) астатизма нулевого
порядка; 2) астатизма первого порядка; 3) астатизма
второго порядка?
Ответ. ,
1) &m¥=an;
2) bm — ап; bm.\^A=an.\, «
3) Ьт — Ctn, bm_y G-n—i, Ьвп-2.-
208. Передаточная функция разомкнутой следящей
системы рис. 124 имеет вид
Ц7 (п) = -AoPm + ^lpm 1 + • + Ani-tf) + Am
Ворп + в 1Рп 1 + ... + B„_lP + вп
Каковы условия получения: 1) астатизма нулевого
порядка; 2) астатизма первого порядка; 3) астатизма
второго порядка?
Ответ.
1) вп^о-,
2) В„ = 0; . .
3)B„ = 0hB„.1 = 0. .
~ § 5.1. ТОЧНОСТЬ ПРИ ЗАДАЮЩЕМ ВОЗДЕЙСТВИИ VTJ
209. Передаточная функция разомкнутой следящей
системы рис. 124 имеет вид
W = pd + HpHl + ^p) •
Определить первые три коэффициента ошибки, а
также добротность по скорости.
Решение. Находим передаточную функцию отно-
сительно ошибки:
ф*(р) = 1 + Г(р) =
р(1 + 7~ip) (1 + Т2р)
р(\ + Т\р)(\ + Т2р) + К'
Рис. 124. Следящая система.
Разлагаем это выражение в ряд делением числителя на
знаменатель
о + (т,+т2)р2 + т1т2р’
Т * 1 - • т, + т2 ,, г,гг
р+ к р + к р + к
К + р + (Г, + Гг) рг+ Г,Ггр«
4р+4 (т.+ъ—^рч-...
Л Л \ Л/
Далее можем написать тождество
с0 + с1р + ~р2 + ... = yP + -^(7’i + 7'2-^)p2+ ...
Отсюда получаем коэффициенты ошибок:
со=О, ^-^-[сек], = y (Л + У’г--^-) [сек2].
Добротность по скорости:
= у- = К [сек-’].
L 1
210. Для предыдущей задачи определить численные
значения коэффициентов ошибок, если /< — 100 сек~\
7\ = 0,01 сек и 7’2=0>005 сек.
Ответ. с, — 0,01 сек и -^- = 0,00005 сек2.
211. Определить величину установившейся ошибки
Для предыдущей задачи при движении следящей системы
со скоростью £2=12 град [сек.
178 гл. -8, ОЦЕНКА КАЧЕСТВА, РЕГУЛИРОВАНИЯ 1212
Ответ.
0Уст = -^ = qQ = 0,01 • 12 = 0°,12 = 7', 2.
212. Передаточная функция замкнутой системы
(см,, рис. 124)., имеет вид
гт» / + 200
u W ~ 0,001 р3 + 0,502р2 + 6р + 200 •
Найти установившееся значение ошибки (после затуха-
ния переходного процесса) при изменении входной ве-
личины по закону
g(/) = 5 + 20/+ К)*2.
Решение. Находим передаточную функцию-отно-
сительно ошибки:
_ , , . , 0,001р3 + 0,502р2 + р
Ф(Р)~ 0,001р3 + 0,502р2 + 6р + 200 *
Делением числителя на знаменатель (см. задачу 209)
находим коэффициенты ошибок:
с0 = 0, Cj = сек и ~% = 0,00236 сек2.
Далее находим производные
- £'(0 = 20 + 20/,
£"(0 = 20
Выражение для ошибки имеет вид
к (/) = Cog (0 + С1£' (0 + -у- g" (0 =
+ 20 °>00236 = °>1472 + °>lf-
213. Передаточная функция разомкнутой системы
(см. рис. 124)’ имеет вид
>17 / _ 50(1 + 0,15р)
w'p) р2(1 + 0,02р)’
Определить первые три коэффициента ошибки, а также
добротность по скорости и добротность, по ускорению.
SHJ ' § 5-h точиоеть ПРИ 'ЗАДАЮЩЕМ ВОЗДЕЙСТВИИ 179
Ответ.
с0 = О, С| = 0, — = 0,02 сек2;
добротность по скорости Ка->оо, добротность по уско-
рению /Се = 50 сек-2.
214. В статической системе регулирования (рис. 125, я)
передаточная функция разомкнутой системы имеет вид
w № = ’(1 + т1Р)(1 + ад •
Определить коэффициент передачи ф(р) = т неединич-
ной обратной связи, при котором система приобретает
Рис. 125. Статическая система с кеединичной обратной
связью.
астатизм первого порядка, и передаточную функцию
разомкнутой эквивалентной системы с единичной обрат-
ной связью (см. рис. 125, б).
Решение. Передаточная функция замкнутой си-
стемы равна [2]
ФЫ = .....У-(р)..=.............*___________ (1)
1 + тГ(р) Т1Т2р2 + (Т^ +Т2) р + 1 + mK
Условие отсутствия статической ошибки. Ф (0) = 1 или
К — 1 + тК, откуда
Тогда передаточная функция замкнутой системы при-
обретает вид
Ф = Т{Т2р2 + (Г, + Т2)р + К ’
180 .. ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ 1218
а эквивалентная передаточная функция разомкнутой
системы с единичной обратной связью равна
,F/ . . ф(р) = К Кд
Wa(P) 1-ф(р) + + Р^Л-Тзр)'
где добротность по скорости
__ К
Ка г, + т2
и эквивалентная постоянная времени
т
э 1\ + Т2’
215. Для предыдущей задачи определить первые два
коэффициента ошибки в двух случаях:
1) общий коэффициент усиления прямой цепи стаби-
лен (Д = const);
2) общий коэффициент, усиления прямой цепи неста-
билен (К =# const).
Решение. В случае Д'= const имеем из (2) пере-
даточную функцию по ошибке:
Ф (о) = 1 — Ф (р) =* .
лЛР) 1 TJip^ + iTr + T^p + K'
Разлагая ее в ряд делением числителя на знаменатель
(см. задачу 209), находим .коэффициенты ошибок:
А П + Т2
с0 = 0 и ct = - ‘-у .
В случае Д’ =/= const примем К.~Ко + ^К (будем пола-
А/С ,. ... . ,
гать, что -£—<1, а коэффициент передачи цепи обрат-
ной связи пг = 1 —j—J . Передаточная функция замкну-
той системы (1) в этом случае приобретает вид.
Ф (р) -------------------W •
+ (Г, + Г2) р + 7<0 + АД -
С 51 ТОЧНОСТЬ ПРИ ЗАДАЮЩЕМ ВОЗДЕЙСТВИИ {81
2161 ’ . I
Передаточная функция по ошибке.
Т^ + ^ + ТОр--^-
Фл(р). == 1 — Ф(р),=------------------------ др“ •
т\т2Р* + (г, + г2) р + к0 + ДК -
Оо
Разлагая ее в ряд, получаем
_________________________д/с___________м
С° Ко(Ко + ДК--~р) *о ’
\ Л о /
(Л + Т2) (Ко + МО „, т1 + т2
1 ( К + АК Г К° ’
216. Определить передаточную функцию неединичной
обратной связи ф(р), при которой в статической системе
регулирования устраняются статическая и скоростная
ошибки. Структурная схема системы регулирования
с неединичной обратной связью приведена на рис. 125, а.
Передаточная функция равна
Г (р) = >. ,г .
(1 +Р1р).(1 + Т2р)
Решение. Передаточная функция замкнутой си-
стемы с неединичной обратной связью в' общем случае
имеет вид
У _ Ampm + Am-1pm‘l + ...+A1p+A0
l + ^(p)W(p) ВпРп + Вп_1Р^+ ... + в iP + Bo •
Статическая ошибка обращается в нуль при
А> — Во-
При выполнении дополнительного условия
А, = ВХ
в .системе устраняется скоростная ошибка.
В рассматриваемой задаче ликвидация статической
и скоростной ошибок может быть достигнута при Biiet
Дении в цепь обратной связи фильтра с передаточной
функцией
182
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ [217
Тогда передаточная функция замкнутой, системы прини-
мает вид
Г = Ф(Р)==_______М________=
G 1+1|>(р)Г(р)
/С (1 + Т2р)
ЪТ&р* + (Г1Т2 + Г1Т2 + г2т2) р2 + (7\ + т2 + т2) р +1 + w •
При
1 +
k _
«ес —
и
К^2 ~ ТI + У2 + т2»
система будет обладать астатизмом второго порядка,
Статическая и скоростная ошибки обращаются при этом
в нуль.
217. Для статической системы (рис. 125, а) с пере^
даточной функцией разомкнутой системы
W (1 + т1Р)(1 + т2Р)
и передаточной функцией цепи обратной связи ф(р) = /п,
выбранной так, чтобы получить астатизм первого по-
рядка, определить два первых коэффициента ошибки,
если Т1 = 1 сек, 7'2 = 0,02 сек и /< = 1000 ±50.
Решение. На основании формул, полученных в за-
даче 215, имеем
- =-Чо^= 1>°2 • IO’3 сек.
Ад 1UUU
218. В статической системе регулирования (рис. 126)
передаточная функция разомкнутой системы имеет вид
Г (1 + ТоР) (1 + т1Р) (1 + т2Р) *
,ей] '§ g.1. ТОЧНОСТЬ ПРИ ЗАДАЮЩЕМ ВОЗДЕЙСТВИИ 183
Определить коэффициент передачи п масштабирующего
устройства в выходной или входной цепи, при котором
система приобретает астатизм первого порядка относи-
тельно управляющего воздействия.
Рис. .126. Статическая система с масштаби-
рованием.
Решение. Передаточная функция замкнутой си-
стемы с учетом масштабирующего устройства
ф = Т0ТгТ2Р° + (тот1 + тот\ + т^) р2 + (Tt + т2 + т8) р + /( •
Условие получения астатизма первого порядка
откуда &меем
219. Для предыдущей задачи определить передаточ-
ную функцию разомкнутой эквивалентной системы без
масштабирующего устройства.
Ответ.
„7 ф(₽) _ Ка -
wa{P) 1-ф(р) р (1 + ар + Ьр2) *
’где эквивалентная добротность по скорости
Tb + Ti + T2 ^сек
коэффициенты
ТрТ-! + Г0Га + ЛД;
Го + Л+Тг ’ .
l _ Т0ТjTz
Tc + Tt+Tz'
181
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
1220
220. Для системы комбинированного управления
(рис. 127) определить условия получения астатизма тре-
тьего порядка и коэффициент ошибки с3. На рис. 127
обозначено: ЧЭ — чувствительный элемент, состоящий из
Рис. 127. Система комбинированного управления.
двух потенциометров П1 и П2 задающей и принимаю-
щей осей, Д — исполнительный двигатель, и Р2 —ре-
дукторы, ТГ — тахогенератор, К.Д—корректирующий кон-
тур, 9] — угол поворота задающей оси, 02 — угол поворота
принимающей исполнительной оси, 0 = 0, — 02 — рассогла-
сование. Исходные данные: kt = 1 в!град = 57,3 в/рад —
крутизна чувствительного элемента; &2 = 25 — коэффи-
циент усиления по напряжению предварительного уси-
лителя основной цепи; &3 = 4 — коэффициент усиления по
напряжению оконечного усилителя; /?4 = 27,3 об/е мин =*
= 2,86 padje сек. — коэффициент передачи исполнитель-
г2й1§ 5.I.. ТОЧНОСТЬ ПРИ ЗАДАЮЩЕМ' ВОЗДЕЙСТВИИ 18g
ного двигателя; fc5 = ^=-^-коэффициент передачи
редуктора Pf, k6 = 0,055 в мин/об = 0,525 в сек/рад — коэф-
фициент передачи тахогенератора; k7 — коэффициент уси-
ления по напряжению предварительного усилителя
в цепи коррекции, kR = i2 — 500 — коэффициент передачи
редуктора Р2; Ту = 0,005 сек — постоянная времени уси-
лителя; 1\ = 0,1 сек — постоянная времени исполнитель-
ного двигателя; 7’1 = Р1С и jr2==-^^-С —постоян-
ные времени пассивного дифференцирующего контура.
Искомыми параметрами являются k7, Т\ и Т2.
Рис. 128. Преобразованная -струк-
турная схема системы комбиниро-
ванного управления.
Решение. Преобразованная структурная схема рас-
сматриваемой системы изображена на рис. 128. Пере-
даточные функции частей основной цепи:
IFi (p) = ktk2,
Передаточная функция цепи коррекции:
• (I)
Передаточная функция замкнутой системы:
<т> г „а _ (р) = нИр) + <р(р)Г2 (р)
1 0! (р) 1 + Г (р) ’ ™
где . передаточная функция исходной разомкнутой си-
стемы
ir,wir8(P)-p((+r^(l+.rtf). (3)
183 'ГЛ. Б. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ (220
Общий коэффициент усиления:
Л =^гМ^5=------------шбб---“ 16/4 сек •
Передаточная функция относительно ошибки равна
.© гм- е<Р) -л . (4\
Ф®(р)_ е,(Р)-1 1 + 1Г(р) * W
Подстановка (1) и (3) дает
ф /п\_ г>0р4 + г>1Р3 + ь2р2+.ЬзР ,/ф
Фе (р) (1 + Г2р) [ГуГдр3 + (Гу + 7-).р2 +,р+к] » W
где
Ьо = Т2Т уТ д,
bi = TyTR + TyTz + ТаТ2,
^2 = Ту + 7д + 'Т2 —
&3 = 1 k^kik^kgk-jkg -уЛ .
Условия получения астатизма третьего порядка
й3 = 0 и Ь2 = 0,.
Отсюда получаем два- уравнения:
ь = '•*'
7 Тх '
Т 2 (kzkikzkf,kyk& — 1) = Ту + Тл, (7)
В два уравнения (6) и (7.) входят три неизвестные: klt
Ti и Т2. Третье, недостающее уравнение может быть
получено на основании требований, накладываемых на
величину последующих коэффициентов ошибки после с0,
cd и с2, которые равны нулю, так как система имеет
астатизм третьего порядка. Если никаких ограничений
на последующие коэффициенты ошибки не наклады-
вается, то' расчет -можно сделать на -основании следую-
щих соображений.
Для дифференцирующих пассивных контуров отно-
г2
шен-ие постоянных времени у- обычно равно приблизи-
тельно 10. Положив в уравнении'(6) ~-= ГО, получаем
* 2
221]§ S.K ТОЧНОСТЬ- ПРИ ЗНАЮЩЕМ ВОЗДЕЙСТВИИ 187
требуемое значение коэффициента усиления усилителя
в цепи коррекции
А
L______7*2 _____Ю • 1000___ п од
'г1 ~ 4 • 2,86 • 0,525 • 500 ’ ’
Из (7)' находим’ требуемое значение постоянной временит
Гу + Гд 0,005 + 0,1
^2 = fe3fe4fe6/e6MS - I 4-2,86-0,5-0,525-3,34- 1 =
~То~-¥ = 0,°1 “ cett*
Кроме того, находим
= 1072 = 0,И7 сек.
При выполнении условий (6) и (7) передаточная функ-
ция по ошибке (5) приобретает вид
ff) (пх ________________^оД4 + bip3_______
0 W (1 + Т2р) [TyW + (Гу + Гд):ра + р +к] • W
Делением числителя на знаменатель (8) находим коэф-
фициент ошибки по третьей производной управляющего
воздействия:
с3 _ &1 Т’уТ’д + Т’уТ’я + Гд-^
3! к. К *
Подстановка численных значений дает
с3 0,005-0,1+0,005-0,0117 + 0,1 -0,0117 . „ 1п-4 3
------------------------------------------1,3« 10 сек.
.6 16,4
Уравнение (9) является тем недостающим уравнением,
которое может быть использовано для совместного ре-
шения с уравнениями (6) и (7).
221. В системе регулирования (рис. 129) для повы-
шения порядка астатизма введены два изодромных
устройства, ИМ1 и ИМ2. Определить первые пять коэф-
фициентов ошибки.
Ответ.
сх,—л г — г Л Сз Ct — +
Со-и, Cj-O,. С2.-О, 24---------------
К
188
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
1222
222. Передаточная функция разомкнутой следящей
системы имеет вид
W (р) = pd + r.pHl + T’^) •
Значения параметров К = 20 сек~\ = 0,02 сек и
Т2 = 0,03 сек. На вход системы поступает гармоническое
воздействие с амплитудой 0imax = 10° и периодом
Тк = 7 сек. Определить амплитуду Ошибки.
Рис. 129. Система с нзодромиыми устройствами.
Решение. 1) Для точного решения найдем пере-
даточную функцию относительно ошибки
(п\ - 1 . = р(1 + Нр)(1+Лр)
l + W(p) р(Д+Т1Р)(1+Т2Р) + К ’
После приведения подобных членов и подстановки
значений параметров имеем
Ф9(р)- 6-140>3+.^jgd.±P_.
. 6-10 4р3 + 5-10 р +р + 20
Амплитуда ошибки:
' , Ощах ~ I (/®) | 91 maxi
Находим модуль частотной передаточной функции
относительно ошибки при со = со1( = = 0,9 сек"1.
* К
। ,/ y-i , 6 10 4 (j<oK)3 + 5-10 2 (/<Дц)2 + /ц>к _
I е I - 6.10-4 (/{0к)3 + 5.10-2 (/{0к)2 + /{Ок 20
_ I- г- 0,004 + /0,9 I _ / 0,00+ + 0,92 _ п
“I 20+ /0,9 |“Г 202 + 0,92 U,U
223J § 5.1. ТОЧНОСТЬ ПРИ ЗАДАЮЩЕМ ВОЗДЕЙСТВИИ [89
Далее находим
Вшах = 0,045 • 10 = 0°,45 = 27'.
2) Для приближенного решения находим модуль ча-
стотной передаточной функции разомкнутой системы при
© = ®к:
20
Л (©к) — 1 W (/®к) I — 0,9 у J + од2.0'022 J/- J + 0>92.0>032 — 22,2.
Амплитуда ошибки:
e- = TS-2& = °°>45 = 27'-
223. Для. следящей системы дана л. а. х. разомкну-
той системы (рис. 130). Определить амплитуду ошибки,
Рис. 130. Л. а. х. следящей системы.
если входное воздействие изменяется по закону 0( =
в 61 max Sin ®|с/, где eimax=15°, а ®к = 0,2 сект1.
Решение. По л. а. х„ изображенной на рис. 130,
определяем значение модуля в децибелах при частоте
® == ©к = 0,2 сек~1. ,
L (юк) = 20 1g А (юк) = 45 дб.
Далее находим 1g А (®к) = 2,25. По логарифму опре-
деляем модуль:
А(юх)= Г0?-25 = 168.
190
ГЛ. 5. ОЦЕНКА КАЧЕСТВА- РЕГУЛИРОВАНИЯ
[•224
Амплитуда ошибки:
224. Решить предыдущую задачу, если:
О 01 max = 5°, ®к = 0,1 1/сетс;
2.) 01 max =10°, Юк = 0,8 1/сСк;
3) 01 max = 30°, ®к = 0,4 1/сек;
Ответ: 1) О',88; 2) 14',2; 3) 21',2. .
• 225. Передаточная функция разомкнутой следящей
системы имеет вид
Г(р) =
К(1+Тлр)
р(1 + Лр) in- ад ’
где /< = 200 сек"1, 71 = 0,5 сек, Г2 = 0,1 сек и Т3 = 0,01
сек. Определить фазовую ошибку при воспроизведе-
нии гармонического входного сигнала с амплитудой
Olmax = 20° и периодом Тк = 1 сек.
Решение. 1) Для точного решения находим час-
тотную передаточную функцию замкнутой системы при
<о = ®к = ~ = = 6,28 \[сек.
•* К
Д) / • \ W _______________________/С(1 4- _
1 + Г(/фк) jttK(l+/ttK7’1)(l + /ttK7’3)+A-(l+/<BK7’5l
________________(1 + /<Дк^г)_____________
К~ш2 (7, + Т3) + j [QK (1 + ЯГ2) _ Q3 Т-.Гз] *
Подстановка численных значений параметров дает
ф«“‘> = 15Т7ЭТ-1да-Л0325,
откуда
, '0,0325 4. Л ПО Ют
<р=-arctg-~-=-arctg0,03 ~ - Г,7.
2) Для приближенного решения примем, что в рай-
оне частоты входного воздействия частотная переда-
точная функция- разомкнутой системы имеет вид
’ j<o(1+ jco7i)
_, 52 ТОЧНОСТЬ ПРИ ВОЗМУЩАЮЩЕМ ВОЗДЕЙСТВИИ
2281 5
При значении й = ©к передаточная функция отно-
сительно ошибки может быть принята равной
_ ,. , ,1 /<ок (1+/<окГ1)
. Фе(/«М « г (/ок) К
ОТКуДИ 1 - К9Я
ф—I-- >= - = - 0.0314 =
= - Г,8:.
226. Определить фазовую ошибку для предыдущей
задачи, если:
1 ) Тк— 10 сек\ 2) Тк = 2 сек.
Ответ. 1) — 0°,18; 2) -0°,9.
§ 5.2. Определение точности при наличии
возмущающего воздействия
227. Для следящей системы, изображенной на рис. 24
(задачи 41 и 42), определить установившееся зна-
чение моментной ошибки, если момент нагрузки на ис-
полнительной оси составляет М =* 200 Г • см, а к. п. д.
редуктора равен 0,8.
Решение. Добротность по моменту рассматрива-
емой следящей системы (см. задачу 42) составляет
Км = 1700 Г'см
угл.мин
Отсюда находим моментную ошибку:
п _ Мп _ М _ 2000 _ .,
м Км чКм 0,8:1700
228. Решить предыдущую задачу, если задан мо-
мент нагрузки на оси двигателя Мнд = 5 Г-см.
Решение. Определяем добротность по моменту,
отнесенную к оси двигателя:
к _ _ 1700 _ . „ г -см
'Дмд i 1000 ’ угл.мин '
где t= ЮОО —передаточное отношение редуктора. Мо-
ментная ошибка:
192
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
1.22®
229. Определить моментные ошибки для следящих
систем с астатизмом первого порядка при следующих
исходных данных.
1) Добротность по скорости Ка = 200 сек-1, пере-
даточное отношение редуктора i = 500, скорость холо-
стого хода двигателя пхх = 6000 об!мин, пусковой мо-
мент Л1п=100 Г-см, момент нагрузки, приведенный к
оси двигателя, Л4нд = 30 Г-см.
2) /<£2 = 500 сек-1, i= 10000, пхх = 7500 об!мин, Ма~
= 300 Г • см, Мал =150 Г • см.
Ответ.
3440яп Мнд 3440 - 3,14 - 6000 30
1 \ а _ ______хх д ___________.__________= (V Ч
' ЗОгЛ^ Мп 30-500-200 . 100 ’
й 3440 • 3,14 • 7500 150 „ „„
30-10000-500 ' 300
230. На рис. 131 изображена структурная схема
системы регулирования. Значения параметров kt = 10,
Рис. 131. Структурная схема
к задаче 230.
/г2 = 2 сек *, 7\==0,1 сек, и Т2= 1 сек. Возмущающее
воздействие меняется по закону f = fmax sin a>Kt, где
fmax = 15 и сок=5 сек-1. Определить амплитуду ошиб-
ки Xniax-
Решение. Передаточная функция по возмущаю-
щему воздействию в замкнутой системе равна
W (р)
ф/(р) = Т+г (р)
,____&2
_______Р(1 + ТчР)_______ =
р,__________Мй__________
Р (1 + TlP) (1 + т2р)
__________Ml + Лр) .
р (I + Т\р) (I + Т2р) + kiki
2зг1
§ 5.2. ТОЧНОСТЬ ПРИ .BO3MSJJ1.WBWM ВМЗДИИе.1ВИИ
Амплитуда- ошибки:
Лщах == I Ф/ 0°’к) I fгаах =
^s/inax 1 + Т]
l^[/c1k1-(^(rI + T2)l2 + «%
Подстановка числовых значений дает
: 2- 15/1+ 58-О,I2
< Ли1а* /[10-2 - 5s? <Q,1 + 1)]2 4-52 (1 — 52 • 0,П)2 2’65, ;
231. Внешняя характеристика генератора (зависи-
мость йапряжения на его зажимах от тока нагрузки)
изображена на рис. 132. Наклон характеристики .со-
ставляет р = 0,1 в/a. Генератор имеет статическую си-
стему стабилизации напря-
жения с общим коэффици-
ентом усиления по разомкну-
той цепи К = 200. Опреде-
лить установившуюся ошиб-
ку при скачке нагрузки
А/п= 100 а.
Решение.
А[/ =
_ РА/н _ о,1 юо лп.
I + К 1 +200 },0° в-
U,в
120
60 -
4/7 -
о
Рис.
4/7 60 120 160 1, а
132. Внешняя характери-
стика генератора.
температуры печи в
232. В системе стабилизации
качестве чувствительного элемента используетря тер-
мопара. При отключенной системе регулирования внеш-
.нее возмущение вызывает отклонение температуры от
'заданного значения Ато = 2ОО° С. Определить устано-
вившееся отклонение те1Мперат'уры, если используется
п^тема регулирования с передаточной функцией ра-
зомкнутой системы
* ’ (р) = (1 + Т'Р) (] + Т1Р) ’
К
1где /< = 500.
X Решение.
«V
У Дт =
Ато ___ 200 ~ Л 4° С
1+Л' .1 + 500 °’4
194
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
1233
§ 5.3. Корневые методы оценки динамических
свойств ,
233. Даны характеристические уравнения систем
регулирования:
1) р3 + 14р2 + 53р+ 130 = 0,
2) р3 + 11р2 + 51р + 41 =0,
3) р3 + 2,5р2 + 27р+ 13 = 0,
4) р4 + 7р3 + 418р2 + 1220р + 808 = 0,
б) р4 + Зр3 + 5,5р2 + 6р + 2,5 = 0.
Определить корни уравнения, степень устойчивости
А, колебательность ц и затухание г] системы.
Указание; При вычислении корней целесообразно
воспользоваться методикой, изложенной в книге [23].
Ответ.
1) Pi — — Ю сек'1, р2,з = ( — 2 ± /3) сек'1,
о 2л
h = 2 сек'1, ii = -g = 1,5, г[=1—е ц = 98,5%;
2) Pi = ~ 1 сек'1, Р2;з = (—5 ± /4) Сек'1,
/г=1 сек'1, (Л = 0,8, т] = 99,96%;
3) р!= — 0,5 сек'1, Р2,з~ 1 ± /5) сек'1,
h = 0,5 сек'1, у. = 5, т] = 71,5%;
4) Pi = — 1 сек'1, р2 = —2 сек'1, Рз14 = (“-2 ± ]20)сек~1,
А = 1 сек'1, у. = 10, г) — 47 %;
5) р!= — 1 сек'1, р2 = — 1 сек'1, р3>4=(—0,5±/1,5) сек'1,
h= 0,5 сек'1, (Л = 3, т] = 88%.
234. Даны характеристические уравнения систем
регулирования:
1) р3 + 4р2 + 41р + 64 = 0, 1 (р
2) р3+ 14р2+ 144р+ 1000 = 0. )
Пользуясь диаграммой Вышнеградского, определить без
отыскания корней затухание и степень устойчивости.
§ 15.3. КОРНЕВЫЕ МЕТОДЫ 195
Решение. 1) Используем подстановку р =V.64 q =
= 4^. Тогда уравнение (1) после деления на 64 приоб
.ретает вид
<73 + <72 + т|-<7+ 1 =-0-
41
Параметры Вышнеградского А == 1 и B = jg--2,56. По
диаграмме Вышнеградского с- нанесенными линиями
равного затухания (приложение 7) находим т) = 70%.
По диаграмме Вышнеградского с нанесенными ли-
ниями равной степени устойчивости (приложение 8)
находим относительную степень устойчивости Ло = 0,25.
Далее определяем абсолютное значение степени устой*
чивости h — 4h0 = 1 сек"1.
2) Tj = 75 %, h-—2 сек"1.
235. Дана передаточная функция разомкнутой сис»
темы с астатизмом первого порядка'
W(p)~- . (1)
'' р(1 + Тр) ' ’
Определить соотношение между добротностью по скоро*
сти Кй и постоянной времени Т, при котором затухание
за один период будет не меньше заданного значения т)-
Решение. Находим характеристическое уравнение
системы
1 + Г(р) = 0
или, после подстановки (-1),
р2 + 4-р + ^ = 0. (2)
Корни этого уравнения
Pi.2 = --2F±(3)
где
И Р у р ^р2 •
196
ГЛ. 5. ОЦЕНКА КАЧЕСТВА УЛИРОВАНИЯ
128®
Колебательность связана с затуханием .за одни период,
зависимостью
Далее находим
|=f4KQr-l. (5)
Совместное решение (4) и (5) дает искомое условие. .
«
---Ц-^ + 0,25. (6)
(1пт^г)
236. В системе с передаточной функцией разомкнутой
системы
р(1 + 7р)
постоянная времени Т — 0,1 сек. Определить допустимое
значение добротности по скорости, соответствующее полу-
чению затухания за один период т] = 90%, t] = 95%,
т| = 98% и 11== 100% (см. предыдущую задачу).
Ответ. Ко = 31,1 сек~1, Ко = 13,6 сек-1, 1<с> = 8,7 сек-1,
Кй = 2,5 сек-1.
237. Передаточная функция разомкнутой системы
с астатизмом второго порядка имеет вид
w(p)=-Ke{lptTp}- • (1)
Определить соотношение между добротностью по уско-
рению Ке и постоянной времени Т, при котором затуха-
ние за один период будет не меньше заданного значе-
ния чу
Решение. Находим характеристическое уравнение
замкнутой системы
1 + Г(р) = 0
или
Р2 + ЛеГр + Ке = 0. . ,.(2)
. - S 5.3. КОРНЕВЫЕ МЕТОДЫ
197
Корни этого уравнения
КеТ - л/ ^т'2'
(3)
Колебательность
и = 4 = V ТгчГЁ ~ 1 •
(4)
Используя соотношение между колебательностью и
затуханием
2л
Р = —--j~
In т—~~
1 -п
(5)
находим окончательно
1
Лег2 '
т + 0,25,
(6)
1 — i]
2
или
Кг?2
T-V-+0,25
(7)
1 — Т]
238. В системе с передаточной функцией разомкну-
той системы
Г (р) = ffsU.+TP)
добротность по ускорению /Се=100 сек~2. Определить
минимальное значение постоянной времени' Т, соответ-
ствующее получению затухания за один период г] = 90%,
T| = 95%, г) = 98% н т]=100% (см. предыдущую задачу).
; Ответ. Т = 0,069 сек, 7 = 0,086 сек, Т = Ъ,\Ъ7 сек,
7 ~ 0,20 сек.
239. В статической системе регулирования передаточ-
на.я функция разомкнутой системы имеет вид
W= (I + адU + Т,Р) •
времени равны 7’0=1 сек и Г] = 0,5 сек.
допустимой значение общего коэффициента
Постоянные
Определить
ГЛ. 5. ОЦЕНКА КАЧЕСТВА НЕГУ ЛИР ВА - ИЯ
Т5Ж
усиления К, при котором затухание за один период
будет не меньше т) = 90%.
Ответ.
(То + Л)2 Г
п2
.1
I -Т]
(1+0.5)2
1 -0,-5
д- т т
т-1-0,25 -1 =
3,142
1
1-0,'
+- 0,25 - 1 = 8,5.
§ 5.4. Оценка по кривой переходного процесса
240. Замкнутая система регулирования описывается
дифференциальным уравнением
(aQp2 + a!p+ l)^ = (aip + l)g. (1)
Определить величину перерегулирования в предположе-
нии, что корни характеристического уравнения комплекс-
ные Р1,в —— а±/Р, для случая отсутствия задающего
Воздействия g — О. Начальные условия у = у$ и г/ = 0
Йри t = — 0.
Ответ. Переходный процесс определяется выражением
У = Уое~а1 (cos pf + sin р^ =
e~at sin
'=^0
При исследовании на экстремум можно получить
Первое значение
Ут=~Уое ^П = ~Уое 14
Отсюда искомое перерегулирование:
। > ° „
а _ Цт| е р = ехр
У0
(2)
его
(3)
(4)
4Т'
условие
241. Для предыдущей задачи определить
отсутствия перерегулирования.
Ответ. ₽ = 0, что соответствует выполнению условия
<0,254
—------i 54 ОЦЕНКА П КР1ВОИ ПЬРЬЛОДНиги UPUHEtCT |QJ
*44 1 з
242. Для задачи 240 определить соотношение коэф-
фициентов, при котором перерегулирование будет а =
₽ 10%, <г = 20%, а = 50%.
Ответ. ao = O,72tzf; a0=l,22tf; a0 = 5,25af.
243. Для системы регулирования, дифференциальное
уравнение (1) которой приведено в задаче 240, опреде*
лить перерегулирование при подаче на вход ступенчатой
функции gol (t), если до приложения входного воздей-
ствия система находилась в покое.
Ответ. Переходный процесс определяется выражением
11 = ГГ. Г 1 — (рпс Я/ — Д cin I
Исследование его на максимум дает
• Z/(n = £oLl+e 11 J
Отсюда определяется перерегулирование
где
= exp
So F
2fl
arctgT^?
u
-1 .
ц= P
. °
244. Для соотношения коэффициентов a0 и ait соот-
ветствующих получению перерегулирования <т= 0%,
о=10%, сг = 20% и о = 50%, при согласовании из не-
подвижного положения (см. задачи 241 и 242), опреде-
лить величину перерегулирования при подаче на вход
ступенчатого воздействия g(O = £o‘l(O и произвести
сравнение величин перерегулирования.
. Ответ. Значения перерегулирований сведены в таб-
лицу:
Вид движения о <Zq =* 0,25 а । 9 а0 = 0,72 Cj 9 д0= 1,22 а. а0 = 5,25а.
Согласование из неподвиж- ного положения .... 0% 10% 20% 50%
итР’аботка единичного сту- пенчатого воздействия 13,5% 2596 32% 55%
200
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
1245
245. Передаточная функция замкнутой системы регу-
лирования .имеет вид
. / ,_______счр+ 1_____
Р) ~ asp3 + а2рг + Clip + 1
На вход системы поступает воздействие типа единичной
ступенчатой функции 1 (/). Посредством построения пере-
ходного процесса определить перерегулирование и время
переходного процесса при следующих значениях коэф-
фициентов:
1) а( = 0,33 сек, «2,= 0,01 сек2, ал = 1,58 • Ю^1 сек1;
2) О] = 0,415 сек, п2 = 0,04 сек1, tz3 = 0,002 сек';
3) «1 = 0,087 сек, а2 = 0,0025сек2, а3 = 0,435 • 10-4сек'.
Ответ.
1) 0=13,8% 4 = 0,775сек;
2) о = 26,5 %, 4=1,17 сек;
3) 0 = 37,2%, 4 = 0,27 сек.
246. На рис. 133 изображена вещественная частоты-
пая характеристика замкнутой системы. Определить
ориентировочные значения перерегулирования и времени
переходного процесса.
Решение. Интервал существенных частот для ве-
щественной характеристики ®с = 20 сек"*. Это дает время
переходного процесса
л . 4?t
®е. “ , ©с ’
Р(ы)
Рис. 133. Вещественная частотная
ИЛИ
0,157 сек <tu< 0,628 сек.
Перерегулирование о<
< 18%.
характеристика. Для более точного
расчета необходимо об-
ратиться к кривым, данным в приложении 12. Коэф-
фициент наклона вещественной характеристики (см.
рис. 133) составляет и = 0,4. Это Дает о =10% и 4 =
у
= -,q = 0,35 сек.
~§ 5.5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ20Г
24» 1
247. Определить перерегулирование и время переход-
ного процесса для вещественной частотной характери-
стики, изображенной на рис. 134.
Рис. 134. Вещественная характеристика.
Решение. Высокочастотную часть характеристики,
соответствующую Р(®)<0, можно отбросить, так как
РП11п<0,2. Тогда перерегулирование в системе равно
g< 1,18Ршах-Р(0) _ 1,1g-1,2-1 а 41 = 41
uv. J и,41 41/0.
Время переходного процесса
^> — = -—=0,0628 сек.
п 05с 50 ’
Для более точного расчета необходимо обратиться
к кривым приложения J3. В результате их использова-
ния определяем
АОЛ, 1 3jX 3*3,14 А 1 О
о = 23% и /„=»— =—рх— = 0,18 се/с.
<ос зо
§ 5.5. Интегральные оценки
248. Передаточная функция разомкнутой следящей
системы с астатизмом первого порядка имеет вид
~ Р (1 + 1'ip) (1 + Tip) ’
V При значениях постоянных времени Тj = 0,02 сек п Тг~
=0,04 сек. определить значение добротности по скорости,
соответствующее. минимуму квадратичной интегральной
оценки, при отработке ступенчатого воздействия gr(^)==
&о-1(О
202
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ 1248
Решение. Передаточная функция замкнутой сис-
темы
ф (Р) = JEW =_______________________________
l + W(p) Яй + р + (Г1 + 7’2)р2 + 7’17’2рЗ •
Изображение по Лапласу выходной величины имеет вид
1
Л{Р)~ Ка + р + (Т1 + 7'2)р2 + 7'1Г2р3 р =
Ьо 1
CQ-ba^ + a^ + ajp3 р ",
В соответствии с приложением 16 находим значение
интегральной оценки
г В0Д0
где Во = Ь20 = К2а, я0 = . Значения опр а0 - «2 0 Д= 0 й] — а3 =я0(«1а 0 - а0 а2 я( — а2 0 Ао= а0 а, - я3 =afa2- 0 — Яд Я2 В результате имеем • , Г > 1 Г1 + г2)2 1 еделителег 2 — ОдОз)» Gi°oG3^aoai<
2Л Для получения к оценки приравняв di 1 'Q ‘ 2 Т1+Г2-Кй7’1Т2 J шнимального 'значения м нулю производную Г i < Лт2(у1 + т2)2 0- интегральной = 0j
dKa 2 L Kl ' {Тх + Т2-КаТхТ2у
откуда оптимальное значение добротности
7'17’2 + (7’1+7’2)р/7'17’2
249]
ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
208
Подстановка численных значений постоянных времени
дает
^->.w-4W-7^°24 сек"
249. Передаточная функция разомкнутой системы
имеет вид
{l} p(l+Tp)’
При фиксированных значениях Т — 0,1 сек и доброт-
ности по скорости Да = 20 сек~1 определить значение
коэффициента К\, определяющего уровень сигнала по
первой производной, соответствующее минимуму квад-
ратичной интегральной оценки при подаче на вход уп-
равляющего воздействия в виде единичной импульсной
функции Д (0 = 6(0-
Решение. Передаточная функция замкнутой систе-
мы равна
, ч ^(Р) KQ + KlP
1+Г(р) ка + (1+^)р + ^2 •
Изображение входного воздействия G(p)— 1. Изобра-
жение выходной величины
У(р) = Ф(р)G(р) = + .
Значение квадратичной интегральной оценки (см. при-
ложение 16)
/ — +52А2
Коэффициенты равны
Bi = ^ = K?2, =
а0 = Ка> «] = 1 + К] и а2 = Т.
264
ГЛ. 5. ОЦЕНКА КАЧЕСТВА-РЕГУЛИРОВАНИЯ
1250’
Значения определителей
«0 ~ «2 0
Д= 0 61.0 =a0a,a2 = /<'s(l + ^1)7’»
0 - " CIq @2
а0 at 0
Aj= 0 а0 0 = ф2 = К|Г,
0 0 02
а0 - 02 ал
А2= 0 «1 «о =°о = /<и-
0 —' а0 0
Далее находим
f K^qT + K2^ КаТ + К]
^KlKa(l+Ki)T 2(1 +К,) т '
Для нахождения минимума / приравняем нулю произ-
водную = 0. В результате имеем
'/C2 + 2^-V=0>
откуда
/с, = - I + У~1 + кат.
Подстановка численных значенийхдает
Ki = - 1 + V 1 +20-0,1 = 0,73.
250. Передаточная функция разомкнутой
имеет вид
системы
Г(р) =
/7(1 +Тр)
При фиксированном значении постоянной времени
Т = 0,2 сек определить оптимальное значение доброт-
ности по скорости, соответствующее минимуму интег-
ральной оценки вида-
/= J (х2 + т2х2)dx (1)
2501
Л 6;5.' ИНГЕ РАЛЬНЫЬ иЦЫ КН-
206
При подаче на вход единичного ступенчатого воздейст-
вия g(f)=l(f) Для значений постоянной времени экст-
ремали т = 0, т = 0,1 сек, т = 0,5 сек и т = 1 сек.
Решение. Разбиваем интеграл (1) на два интеграла
' ОО - . оо
z = f1 + /2= [ jfdt+i? J x*dt.
о о
Находим передаточную функцию замкнутой системы
, / ч
Ф Ка + р+ТР* •
Изображение выходной величины при G (р) = равно
Б- соответствии с приложением 16 находим
Г _ В0Д0
* 2ацД ’
Значения коэффициентов:
В0=602 = ^, «0 = /<й,
Значения определителей:
(2)
«1 = 1 и а2 = Т.
До —
«о
0
Ф
а0
— а->
— а.,
Ф
й0в1 ’
— + ctca2 — 1 + КиТ.
Д =
Подставляем найденные значения в (2); получим
Для нахождения 12 определяем изображение скорости
изменения выходной величины
рУ (р) = у 3 .
^а + р+ fp
206
ГЛ. 5. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
[251
В соответствии с приложением 1'6 находим
/ /2 == т2
ДА
2а2А ’
(3)
где В; = 62 = Лд, а определитель
Далее имеем
'2----‘
Результирующее значение интегральной- оценки равно
1+КдГ Кдт2
2Ка + 2
(4)
Для нахождения оптимального значения4!(<>. приравняем
нулю первую производную (4):
После дифференцирования имеем
-_L- + t2 = 0,
откуда оптимальное значение добротности по скорости
Лй = -~. Численные значения Ля~» со, Да =10 сек'1,
Кя = 2сек'1 и /<<2=1 сек'1.
§ 5.6. Частотные оценки динамических свойств
251. На рис. 135 изображена амплитудная частот-
ная характеристика замкнутой системы. Определить
показатель колебательности.
Ответ.
М IФ (/<й) I max 3,2 . г-
т~- |Ф(0Н “ 2 • ,0, \
252J § Б-6. ЧАСТОТНЫЕ ОЦЕНКИ ДИНАМИЧЕСКИХ СВОЙСТВ 207
252. На рис. 136 изображена амплитудно-фазовая
характеристика разомкнутой следящей системы. Она
может быть построена по.таблице
Re W (ja) -2 -1,75 -1,5 -1,25 -1 -0,75 -0,5 -0,25 0
Im W (ja) -4,95 -1,8 -1,75 -1,6 -1,4 -1,05 —0,85 -0,65 -0,55
Определить показатель колебательности замкнутой
" Решение. Для нахождения показателя колебатель-
ности необходимо определить параметры окружности,
которой касается амплитудно-фазовая характеристика.
Параметры окружности связаны с показателем колеба-
тельности формулами
п _ М М*
~ М2-1 И Ь ~ М2 - 1 ’
где 7? — радиус окружности, а С — сдвиг центра окруж-
ности влево от начала координат. В результате подбора
определяем, что касающаяся окружность соответствует
М = 2, = и С = 4-
о о
Построение сделано пунктиром на рис. 136.
208
ГЛ. 5: ОЦЕНКА КАЧЕСТВА РЕГ ЛИРОВАНИЯ
[25.3
253. Передаточная функция разомкнутой следящей
системы имеет вид
+ Гр) ’
Определить соотношение между добротностью по ско-
рости Ка и постоянной времени, при котором' система
будет иметь показатель колебательности не более задан-
ного значения М. .
Решение. Передаточная функция замкнутой системы
равна
1 {Р> 1 + Г (р) ка + р + Тр> •
Частотная передаточная функция замкнутой системы
запишется в виде
Ф = Ka + ja~a2T ’
Ее модуль равен
К,,
| Ф (/со) | = ------ .
/(Кп-<о2Г)2 + <о2
Исследование на максимум этого выражения дает зна-
чение показателя колебательности
I Ф (/со) |max = = М (при КаТ > 0,5).
у4КвГ-1
Из последнего выражения находим
„ .г ^ж + мУм2-1
i\al -ч;---9-----
254. Решить предыдущую задачу, если передаточная
функция разомкнутой системы имеет вид
1У(р)^Ке(^+1р1;
где КЁ — добротность по ускорению, а т— постоянная
времени корректирующего контура.
Ответ.
2 М2-М рАР-1
М2 — 1
SS#J
§ 5.6. ЧАСТОТНЫЕ. ОЦЕНКИ ДИНАМИЧЕСКИХ СВОЙСТВ 2Q9
• 255. На рис. 137 изображены логарифмические частот-
ные амплитудная и фазовые характеристики (л. а.х.
и л. ф. х.) разомкнутой системы. Определить показатель
колебательности замкнутой системы.
Рис. 137. Л. а. х. н л. ф. х. разомкнутой системы.
Решение. Для нахождения показателя колебатель-
ности необходимо таким образом построить запретную
зону для фазовой характеристики, чтобы фазовая харак-
теристика касалась этой зоны. Построение запретной
зоны делается в соответствии с приложением 14, где при-
ведены необходимые запасы по фазе в функции модуля
в децибелах для различных значений показателя коле-
бательности. В результате подбора определяем, что пока-
затель колебательности М — 1, 2. Построение запретной
зоны показано пунктиром на рис. 137.
256. Построить л. а. х. и л. ф. х. и определить по-
казатель колебательности, если передаточная функция
разомкнутой системы имеет вид
1)
2)
3)
4)
_ 100 (1 +0,173р) .
р2 (1 +0,035р) ’
1У7 {п\_ 25 (1 + 0t66p) w
р2(1 + 0,03р) ’
UZ (п\ = 400 (1 4~ 0Л р) .
W р(1 +р)(1+0,013р) ’
IV7 / \ 1000 (14* 0,05р)
~ р(1 +0,4р)(0,013р) •
10 Л 5 ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ [257
Ответ. 1) М = 1,5; 2) М = 1,1; 3) М = 1,3; 4) М = 1,7.
257. Передаточная функция разомкнутой системы
имеет вид
₽П(1 + Л-р)
[=1
Определить условие, при котором показатель колеба-
тельности замкнутой системы не будет превышать еди-
ницу, если число постоянных времени является произ-
вольным, т. е. п — произвольное целое число.
Ответ. <-
п
, i=i
258. Для амплитудной частотной характеристики
замкнутой системы (см. рйс. 135) определить полосу
пропускания системы.
Ответ. <вп = 30 сект1, fn = 4,8 гц.
. 259. Для л. а. х., изображенной на рис. 137, опре-
делить ориентировочное значение полосы пропускания.
Ответ. В первом приближении полосу пропускания
замкнутой системы можно принять равной частоте среза
л. а. х. разомкнутой системы. В результате имеем
®п ®ср = 13 сек'1 или fn = 2,1 сц.
ГЛАВА 6
СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
§6.1. Выбор параметров САР по требуемой точности
260. Для системы стабилизации углового положения
некоторого тела (рис. 138) выбрать такое значение коэф-
фициента передачи по углу k^, чтобы при внешнем
л
л
Регулируем,
объент
брр
'/силитель
' прообразов.
Рсполн.
орган
^упр
'Регулятор
Рис. 138. Блок-схема системы стабилизации углового положения тела.
возмущающем' моменте Л1(/) = т0 отклонение угла ф
не превышало допустимое значение фдоп.
Уравнение отдельных звеньев системы имеют вид:
1. Уравнение регулируемого объекта
J ' rff Ulytip + UIq,
где J — момент инерции тела, ф — угол поворота тела,
Ф —его угловая скорость, mynp — управляющий момент
со стороны исполнительного органа системы стабилиза-
ции, т0 — внешний возмущающий момент.
212
ГЛ. G. СИНТЕЗ -ЛИНЕЙНЫХ СИСТЕМ
(ген
2. У равнение исполнительного органа, совместно
с усилителем-преобразователем
ШуПр
где 0 — коэффициент передачи исполнительного органа
и усилителя-преобразователя..
3. Уравнение регулятора (принятый.закон управления)-
и = — (/г1?ф + /г-фф).
Решение. Уравнение замкнутой системы стабили-
зации может быть записано в виде
J 4^ + /г,'-о/г'ф Ди~ + = mo>
откуда
фициента усиления К
Рис. 139. Система регулиро-
вания температуры.
,b < . и ъ > w°
Д0П ^ii.o^ip ’l’ ^и. о Флоп
261. Определить требуемое значение общего коэф-
для системы регулирования тем-
. пературы (рис. 139) из усло-
вия обеспечения нужной
точности регулирования в'
установившемся режиме.
Отклонение регулируе-
мой величины Ф измеряется
с помощью термометра со-
противления, включенного
в мостовую схему. Напря-
жение- и с диагонали моста
поступает на балансный уси-
литель Ус, который управ-
ляет двигателем Дв. Через
редуктор Р двигатель при-
водит в движение регули-
рующий орган. Регулирующий орган воздействует на
объект за счет изменения величины регулирующего
воздействия у.
Уравнения звеньев имеют вид.
1. Уравнение регулируемого объекта,
(1 + Tip) О = — /?!У + kJ,
4 . е 61 ВЫБОР ПАРАМЕТРОВ ПО ТРЕБУЕМОЙ ТОЧНОСТИ 213
£Ь^Т Ь
где [сек] — постоянная времени объекта, kt и k6 —
коэффициенты передачи, f — возмущающее воздействие.
2. Уравнение чувствительного элемента — моста с тер-
мометром сопротивления
и = /г2'0,
где k2 [в!град] — коэффициент передачи.
3. Уравнение привода вместе с усилителем
(1 + Т2р) РУ == k3u,
где Т2 [сек] — электромеханическая постоянная времени,
k3 [ 1/сек] — коэффициент передачи.
Решение. Общий коэффициент усиления разомк-
нутой системы должен выбираться из условия
идоп.
где f — значение скорости возмущающего воздействия;
©лоп-Допустимое значение ошибки в установившемся
режиме.
262. Определить требуемое значение коэффициента
усиления для тахометрического привода постоянной
Рис. 140. Тахометрический привод постоянной .
скорости.
скорости (рис. 140). Допустимая ошибка скорости вра-
щения при моменте нагрузки по валу двигателя
Л4.п = 0,2ЛТкз не должна превышать 0,1% от скорости
холостого хода.
Решение. Ошибка регулирования AQ состоит из
Двух слагаемых4
Дй = 1+ 1Г(р)йз * 1 + Г Go) М'1’
214
ГЛ. 6 СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
12С2
где й3 — заданная скорость вращения привода, W (р)
передаточная функция разомкнутой системы, WM(p) —
передаточная функция разомкнутой системы по моменту
нагрузки. Первое слагаемое соответствует ошибке из-за
выбранного закона регулирования, второе слагаемое
определяет составляющую ошибки, вызванную действием
момента нагрузки Мк.
Если учитывать постоянную времени усилителя Ту
и электромеханическую постоянную времени двигателя
Ти, то
и
(1 + Тыр)(1 + Тур)
Ер
\ * “Г л МР/
где Мкз — момент короткого замыкания, развиваемый
двигателем, Пэ —скорость холостого хода двигателя, К.—
общий коэффициент, усиления разомкнутой системы.
Выражение для ошибки регулирования AQ принимает
вид
АО (Т’мТ'ур2 + (7м + Ту) р + 1] й3
“ ТиТур? + (Ти + Ту)р+1 + К ±
ТГ-£М1 + 7уР)
тытур2 + (ты + ту)р + 1+к • v ’
Обычно настройка системы осуществляется таким
образом, чтобы ошибка регулирования была наимень-
шей. Этому условию соответствует такая настройка,
при которой в статической системе устраняется стати-
ческая ошибка от закона регулирования. Для ликви-
дации статической ошибки коэффициент передачи глав-
ной обратной связи должен отличаться от единицы и
быть равным
Кос = -^, (3).
т. е. в системе регулирования должна иметь место
неединичная обратная связь.
263J § в k ВЫБОР' ПАРАМЕТРОВ ПО ТРЕБУЕМОЙ ТОЧНОСТИ 215
Чтобы обеспечить требуемую точность поддержания
скорости вращения при моменте нагрузки Л4н = 0,2Л4кз,
коэффициент усиления разомкнутой системы К должен
быть выбран из условия
откуда
Мк ДЙ
/г — Мкз _______0,2 ~ 0.001 __ inq /гл
Л ~ а8 ~ °’001 ~ w
й
263. Определить местоположение л. а. х. разомкнутой
следящей системы из условия, чтобы ошибка слежения
не превышала Отах =С Кб при изменении входного воз-
действия по гармоническому закону
01 = 61 тах Sill (0к/,
где 0] шах = 25°,
й>к = ^- = 6,28 Х/сек.
1 к
Структурная схема следящей системы показана на
рис. 141, а.
Решение. Ошибка слежения, вызванная измене-
нием входного воздействия, равна
Отах == | | _|_ ц?- (jey) | гаах ПрИ ® ®к> (0
где W\ja) — частотная передаточная функция разомк-
нутой системы. Так как обычно в современных следя-
щих системах 11Г(/сок)|^>1, то можно воспользоваться
приближенной зависимостью
А ~ в»П1ах
|№(уИк)Г
.Разрешая выражение (2) относительно 11Г(/сок)|, по-
лучим требуемое значение модуля частотной передаточ-
пой функции
(3)
216
ГЛ.-6. СИНТЕЗ ЛИНЕЙНЫХ систем
ISS1
или , '
LK = 20Ig IW(ja) I = 201g -fe-. (4)
Umax
По формуле (4) в логарифмической системе координат
Рис. 141. а) Структурная схема сле-
дящей системы; б) построение конт-
рольной точки йк.
(рис. 141, б) построена так называемая контрольная
точка Ак:
©к = 6,28 1/сек, 201g = 20 1g = 60 дб.
'и’шах Ь<>
Требуемая точность слежения будет достигнута, если
Л. а. х. системы будет лежать выше точки Лк, в пределе
пересекая ее (рис. 141, б.)
264. Определить запретную область для л. а. х.
разомкнутой следящей системы из условия, чтобы
ошибка слежения не превышала 0Г11ах^ Г,0 при изменении
j 81 ВЫБОР ПАРАМЕТРОВ НО АП'СВУ МОН И) 1НОСГИ 217
входного воздействия с максимальной скоростью
Ц^40град/сек и максимальным ускорением е=60 град1сек*.
Решение. В тех случаях, когда закон изменения
входного задающего воздействия неизвестен, расчет
мЪжно вести на эквивалентное синусоидальное воздей-
ствие [4].
Параметры эквивалентного режима определяются
по формулам
<ок = -jy = 1,5 се/Г1,
е1гаах=—= 4 = 7т = 26°>7- (О
WK WK 1,5
Здесь сок — угловая частота колебаний эквивалентного
Синусоидального воздействия, 0| тах — амплитуда коле-
баний эквивалентного синусоидального воздействия.
Координаты контрольной точки Дк (см. предыдущую
задачу) равны (рис. 142)
®к = -£- = 1,5 сек-1,
LK = 20 lg = 20 1g = 20 1g 1600 « 63 дбг"
“max evnjax
Для построения всей запретной области найдем геоме-
трическое место контрольных точек AKt, соответствующих
двум случаям: 1) когда Q максимально, а е убывает
до нуля, 2) когда е максимально, а Й убывает до
нуля. В первом случае геометрическим местом точек
будет являться прямая, проходящая с наклоном
— 40 дб/дек через точку Дк. Во втором случае — прямая
с наклоном —20 дб)дек (см. рис. 142).
Для обеспечения требуемой точности слежения л. а. х.
разомкнутой следящей системы не должна заходить
в запретную зону, ограниченную этими прямыми.
265. Для следящей системы, структурная схема ко-
торой показана на рис. 141, а, построить низкочастотную
Рис. 143. Построение низкочастотной части желаемой
л. а. х»
часть желаемой л. а. х. и определить требуемую вели-
чину общего коэффициента усиления из условия обес-
печения необходимой точности слежения. Система обла-
дает астатизмом первого порядка. Требования, предъ-
являемые к точности слежения, те же, что и в задаче 264.
Решение. Для облегчения задачи демпфирования
системы л. а. х. должна располагаться как можно левее.
Предельно допустимое смещение л. а. х. влево ограни-
чивается запретной зоной по точности. С этой точки
зрения целесообразно, чтобы низкочастотная ветвь
желаемой л. а. х., имеющая наклон —40 дб!дек, про-
ходила как можно ближе к линии запретной зоны
(рис. 143), т. е. чтобы ®0 = со0к и Г1 = 1/©к.
Однако первая асимптота.л. а. х., имеющая наклон
—20 дб[дек, должна проходить выше границы запрет-
ной области 3 дб (см. рис. 143),
267]§ 6.1. ВЫБОР ПАРАМЕТРОВ ПО ТРЕБУЕМОЙ ТОЧНОСТИ 219
Если эту асимптоту- продлить до пересечения с нуле-
вой осью, Фо точка пересечения даст значение общего
коэффициента усиления разомкнутой системы (доброт-
ности по скорости Ка).
Согласно рис. 143 имеем
-.гт; Я , . < 40-600 оллл -1
Ко = V 2 а--= 1,41----j--= 3400 сек \
vmax 1
Базовая частота
®й = 1/1,41 ^-=1,191/ -^- =
Г Vmax V vnlax
== 1,19/60-60 = 71,3 сек-1.
266. Определить требуемую величину общего коэф-
фициента усиления разомкнутой следящей системы.
Следящая система обладает астатизмом второго порядка.
Остальные данные те же, что* в задаче 143.
-Ответ. Общий коэффициент .усиления разомкнутой
системы добротность по ускорению КЕ’= 3600 сек-2.
267. Для следящей системы, обладающей астатиз-
мом первого порядка, определить параметры низко-
частотной части желаемой л. а. х. из условия обеспече-
ния требуемой точности слежения без учета и с учетом
.момента нагрузки. Максимальная скорость слежения
П = 24 град [сек, максимальное ускорение е=20 гр ад)сек1,
допустимая величина ошибки -&гаах = 0°,1. Момент на-
грузки, приведенный к валу двигателя, Л!„ = 2 Гем =
~ 19,6 • 10-5н • м. Жесткость механической характери-
п Qn 5000*6- ГГ» П 1 /Г' / ГА
стики Р = = 57Э 10 = 52,3 1/Г • см • сек. (где Qo =
— 5000 об1мин — скорость холостого хода, Мо = 10 Тсм==
= 9,81 • 10-4н • м — пусковой момент двигателя). Пере-
даточное отношение редуктора 1= 1000.
Решение. 1. Момент нагрузки отсутствует (см. за-
дачу 265). Тогда
Г, = — = — =1,2 сек, (1)
1 сок е ’ ’
1 / л Р 1,41 • 24 ооо —i
Ка = V 2 а— = — = 338 сек (2)
°тах ид
220' .....'ГЛ. 6. СИНТЕЗ Л1П1ИПНЫХ СИСТЕМ- [2S7
2. Двигатель нагружен моментом ЛД = 2 Гем. Демп-
фирование системы осуществляется- по первому ме--
тоду [4], т. е. введением обратных связей, охватывающих
двигатель, или производных от угла рассогласования.
Тогда
— = — = 1,2 сек., (3)
1 «к в ’
ь, 1/"о ® , РМ, 090 । 104,6 — 57,3
K,J==l2^+оД7“338 + 6,i.jooo -
= 338 + 60 = 398 сект1, (4)
где Onuxi — ошибка, приведенная к валу двигателя.
3. Двигатель нагружен, ЛД = 2 Гем. Демпфирование
системы осуществляется по второму методу [4], т. е.
введением инерционности в усилительный канал. Тогда
Г, <0,236 + , (5)
W е
где Д, = -т^г- — моментная ошибка, приведенная к испол-
л<?
нительной оси.
Если общий коэффициент усиления выбрать равным
1 & 24 о.п .
—=— = 240 сек ‘,
итах
ТО
а, = Р^н — 104>6 ~.57,3 _,,о „„р
л /<цг 240-1000 ’
И _________
т (\ OQ-н ^(0,1 4-0,025)3 ~ позе
/,<0,236—1— = 0,0935 сек.
0,025 V 20
Если величину общего коэффициента усиления увели-
чить, например, до
Да = 300 сек-1,
то
ч а, Р^,, _ 104,6 • 57,3 лО
м Kai 300 • 1000 и ,uz
и .________
Тл < 0,236 Х^0>| +02°2)3 = 0,1.1 сек.
0,02^20 ’
£в«3 § 6.1. ВЫБОР ПАРАМЕТРОВ ПО ТРЕБУЕМО}’! ТОЧНОСТИ 22,1
«п»
Для иллюстрации на рис. 144 построены л. а. х.
соответствующие трем рассмотренным случаям.
Рис. 144. Низкочастотные ветви желаемой л. а. х.:
1) без учета момента нагрузки; 2) с учетом момента
нагрузки при первом методе демпфирования; 3) с учетом
момента нагрузки при втором методе демпфирования.
268. Для системы регулирования построить низко-
частотную часть желаемой л. а. х., если известно, что
при изменении входного задающего воздействия по
закону &! = 0Iraax sin aKt, где
6}max = 30°,
®к = 12,56 сек~\
1 к
допустимая ошибка слежения не должна превышать по
фазе Д<р^1°, по амплитуде и---^1%. Система обла-
Хает астатизмом первого порядка. В области низких
частот передаточная функция разомкнутой системы
аппроксимируется выражением
К„
Решение. На рис. 145, а показана векторная диа-
грамма ошибок. Ошибка слежения
Л
#-TTwW=<?+'s)e‘“<,A+<’’’
222
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
126»
где Од —синфазная составляющая ошибки, ^ — квадра-
турная составляющая ошибки. Фазовая ошибка
* г II
A<P = arctgp,-OAj ,
относительная амплитудная ошибка
&& | 'fl'i | — | I
6tmax Olmax
Если считать, что при частоте <ок модуль | W (jcoK) | I,
то фазовую ошибку можно подсчитать по приближенной
формуле
1 т... 01тах _ 6*к
Дф~ в.тах 1 пч) :
а относительную амплитудную ошибку — по формуле
ДО ~ 1 р 61'гах _ ®кГ1 _ <°к
®lmax ~ ®lmax ~ 61тах W (К) *й ’
Задание величины фазовой и относительной ампли-
тудной ошибок определяет предельное левое положение
первой и второй асимптот л. а. х.:
.. йк 12,56-57,3 _оп
= Кя = -д^- — —j—— = 720 сек \
Вид низкочастотной части желаемой л. а. х. показан
на рис. 145, б.
269. Для замкнутой системы комбинированного упра-
вления определить уровни компенсирующих сигналов
§ 6.1. ВЫБОР ПАРАМЕТРОВ ПО ТРЕБУЕМОЙ ТОЧНОСТИ 223
по первой и второй производным от входного воздей-
ствия, при которых в системе, обладающей астатизмом
первого порядка, устраняются скоростная ошибка и
ошибка, зависящая от ускорения. Структурная схема
замкнутой системы комбинированного управления при-
ведена на рис. 146. Компенсирующие сигналы имеют
йид
_ЧР (Р) 01 = ("ПР +
где Ti — отношение крутизны сигнала по первой произ-
водной от 0] к крутизне сигнала по ошибке т2 — отно-
шение крутизны сигнала по второй производной к кру*
тизне сигнала по первой производной от Ot.
Рис. 146. Структурная схема следящей
системы комбинированного управления.
Решение. В системе комбинированного управле-
ния выходная величина О2 пропорциональна не только
ошибке Ф, но и компенсирующему сигналу т. е.
02= W (р) 1-й + <р (р) fy],
где W (р) = р(1+7',^(!"+г2р) ~ передаточная функция ра-
зомкнутой системы.
Ошибка в замкнутой системе равна
Л [1 - Г (р)Ф(р)]0,
1+1Г(р)
! Подставляя значения W (р) и <р(р), получим
_ [Г 1 Tgp3 + (Г) + Tg — KfiTq'tg) р2 + (1 — р] Ф1
71ГгрЗ + (Т1 + Т2)р2 + р + /Сй
224 ГЛ- '6- СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ [27С
При выполнении условия
1
т* “ Кц
в системе устраняется скоростная ошибка.• При допол-
нительном условии
7 1 + 7\ — /ChTjTj
или
т2 — Г1 + Т2
обращается также в пуль ошибка, зависящая от уско-
рения.
Эквивалентная передаточная функция разомкнутой
системы соответствует системе, имеющей астатизм треть-
его порядка:
\W (п\ (р) И + Ф (р)1 ...
1 - (р) <Р (р)
=___________Аа(1 + т|р + т1т2рг)
“ 7’1Т2р3 + (7’1 + Т2-Кйт1т2)р2 + (1-Ает|)р
А"й(1+т1р + т|т2р5)
W
§ 6.2. Алгебраические методы выбора параметров САР
270. Система регулирования напряжения с угольным
регулятором (рис. 147) описывается уравнением третьего
порядка
[(1 + Тор) (1 + Г lP) (.1 + Т2р) + МР] Ап =
= (TlP + l)(l+T2p)f(t),
где Гр = 0,02 сек — постоянная времени - генератора
(объекта регулирования), /г0 = 36 в/о,и — коэффициент
передачи генератора, Тi — постоянная времени чувстви-
тельного элемента (обмотки электромагнита), Т2 — по-
стоянная времени регулятора (угольного столба), £р =
= 0,405 ом/в — коэффициент передачи регулятора.
Выбрать варьируемые параметры системы регулиро-
вания 7'1, Т2 так, чтобы обеспечить степень устойчивости
Ло^О,4 при колебательной форме переходного процесса.
Решение. Обратимся к диаграмме Вышнеградского
(приложения 7 и 8). Характеристическое уравнение
270] § 6.2. АЛГЕБРАИЧЕСКИЕ МЕТОДЬк ВЫБОРА ПАРАМЕТРОВ 225
системы регулирования имеет вид
abpz + aip2 + а2р + а3 = 0, (1)
а0 = 1\Т\Т2, Д1 = Т0Г1 +/'[Т'г + ГоГг,
а2=Тр + Т{ + Т2, а3— 1 + kokp.
Приведем его к нормированному виду
q3 + Aq2 + Bq + 1 — О, (2)
Д — а' — 1 + ^0^2 + ^1^2
Л 3 _____ 3 ______________
/гЖ(1+мР)
и
В = = у- Г° + Г1 + 7'г- (3)
— параметры Вышнеградского.
Решить задачу можно было бы, задавшись предва-
рительно значениями А и В (например, А = 4 и В = 3),
Рис. 147. Система регулирования напряжения
с угольным регулятором.
Удовлетворяющими поставленным требованиям. Однако
такой путь определения Три Т2 связан с. решением
220
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
(270
системы двух кубических уравнений. Проще можно найти
значения Tt и Т2 методом последовательных приближе-
ний, задаваясь их численными значениями и наблюдая
траекторию точки с координатами Л и В на диаграмме
Вышнеградского.
Подставляя заданные значения параметров в (3),
получим расчетные формулы для вычисления А и В’.
д = + в = 0,02 +Г,+ Г2 . 0у
1,84/(7\Г2Н 1,7
2П] § 6 2. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ* ВЫБОРА ПАРАМЕТРОВ 227
Результаты вычислений Л и В по формулам (4) при
изменении Т2 и при Л = 0,01 сек приведены ниже.
Та, сек 0,1 ОД 0,5 0,9 1 2
А 1,8 2,1 2,8 3,3 3,5 3,8
в 0,8 1,1 1,9 2,4 2,8 4,4
На диаграмме Вышнеградского (рис. 148) построена
траектория точки G{A, В). Из построения следует,' что
для обеспечения поставленного требования Ло> 0,4 доста-
точно'при 3"i = 0,l сек выполнение условия
0,5<7’2<1,8. . (5)
Это условие может быть выполнено соответствующей
настройкой демпфера регулятора.
Если бы траектория G не попала в желаемую об-
ласть диаграммы Вышнеградского, то нам пришлось бы
изменить значение Т\ и' аналогичным образом найти
новую, смещенную траекторию, проходящую через нуж-
ный участок диаграммы.
Изменения параметров Т{ и Т2 следует вести, со-
гласуясь с технической возможностью обеспечения зада-
ваемых значений.
271. Для следящей системы, схема которой приве-
дена на рис. 149, определить требуемые значения коэф-
фициента усиления усилителя и коэффициента пере-
дачи по петле обратной связи k0 при заданных значениях
общего коэффициента усиления системы Да = 500 сек"1
и степени затухания переходного процесса т] = 98%.
Передаточная функция разомкнутой системы с учетом
тахометрической обратной связи имеет вид
К
l+kQ Z<Q
где TM — 0,03 сек — электромеханическая постоянная вре-
мени двигателя, Д = kikTpkyk№ — общий коэффициент
228
ГЛ. в. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
ten
усиления системы без учета влияния обратной связи,
= в/рад — крутизна чувствительного элемента,
/гдв= QTif рад!сек • в — коэффициент передачи двигателя,
ku = с, k[p 3— коэффициент трансформации вход-
ного трансформатора, ko с — коэффициент передачи цепи
обратной связи.
Рис. 149. Следящая система с тахомет-
: рической обратной связью.
Решение. Найдем передаточную функцию замкну-
той системы относительно ошибки
--^ = ^(Р) =
р+-£~ (1 + k0)
_______ * м ________
р2 + ~^~ (1 + ko) р+ £-
1 м 1 м
(1)
Характеристическое уравнение замкнутой системы
при этом равно
p' + Brf + B^Q, (2)
Где
В1 = 7~(1 + *о) и В2 = -£-.
1 м 1 м
При степени затухания т] = 98% должно выполняться
условие
m
В?
В2 =
(3)
или
§ 6 2. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ♦ВЫБОРА ПАРАМЕТРОВ 22S
откуда
fey = 7JTtA-t-l-(1 4-feo)2-
у 1р/М«1«дв«тр
Общий коэффициент усиления системы Ля связан с коэф-
фициентом усиления /( соотношением
1+/г0 16ТМ Г+М- (4)
Из этого равенства следует, что
(5)
Численные значения коэффициентов равны
^ = ^4^500-1 = 16,3,
К = Ка (1 + ko) = 500 (1 + 16,3) = 8700 сек'1,
К 870°-0,55 .
UiMrp 1-3 1 ’
1 ko с = т^г-.— —= 0,0057 в • сек/рад.
°" С Куйдв 1617 ’ '
272. Пользуясь методом стандартных переходных
характеристик [2,15] (см. приложение 18), выбрать пара-
метры системы регулирования так, чтобы время затуха-
ния переходного процесса было t 1,5 сек, а величина
перерегулирования а ^10%. Передаточная функция
разомкнутой системы имеет вид
W(p)
.. КеО.+ Пр)
р2(1 Ч-Г2р) ’
где Ке — общий коэффициент усиления разомкнутой си-
стемы по ускорению, Т t и Т2 — постоянные времени.
Решение. Соответствующая стандартная переда-
точная функция имеет вид (приложение 18)
Я7(Р) =
6,ЗсОоР +
р3 + 5,1соо
230
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1273
Приравнивая ее заданной передаточной функции, полу-
чим условия для выбора параметров:
<о2 6,3
•
Для того чтобы время затухания
не
величины,
чтобы
1
z 5,1а>о
Рис. 150. Корневой годограф -
к задаче 274.
переходного процесса
превышало заданной
необходимо,
т 9 „ _j
g>o = Y = 6 сек \
где т — время переходного
процесса. Тогда
Ле = # = 7,05 сек"2,
О,1
71 =-—=1,05 сек,
с J с = 0,032 сек.
чЛ • о
Таким образом, переда-
точная функция разом-
иметь вид
7,05 (1 + 1,05р)
р2 (1 + 0,0326р) •
Т2 =
кнутои системы должна
№(р)
273. Пользуясь методом стандартных переходных
характеристик (приложение 18), выбрать параметры сле-
дящей системы так, чтобы общий коэффициент усиления
разомкнутой системы по ускорению был бы 100 сек“2,
а величина перерегулирования а^10%. Общий вид пе-
редаточной функции разомкнутой системы тот же, что
в задаче 272.
Ответ.
vrw/„\ 100 (1 + 0,28р)
р2 (1 +0,0087р)
274. Для системы автоматического регулирования,
имеющей в разомкнутом состоянии передаточную
5 6.3. ЧАСТОТНЫЕ МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ 231
функцию' к _ k
~ Р(1 + Г1Р)(1 + ад “ ( JW П ’
р\р + tJV’+KV
где Т = 1 сек, ^2 — 0,25 сек, k = , построить корневой
годограф.
Ответ. Корневой годограф состоит из трех ветвей,
поскольку знаменатель функции W (р) имеет третью сте-
пень. Вид годографа показан на рис. 1'50.
§ 6.3. Частотные методы выбора параметров САР.
Расчёт последовательных корректирующих устройств
275. Построить желаемую л-. а. х. и произвести выбор
последовательного корректирующего устройства для си»
стемы автоматического регулирования, если передаточ*
ная функция разомкнутой системы при отсутствии кор-
ректирующего устройства имеет вид
2^"
W = Р(Р + Т1Р) (1 + т2р) (1 + Г3р) (1 + Г4р) ’
где 1\ = 0,1 сек, Т2 — 0,02 сек, Т3 = 0,01 сек, Т4 = 0,005 сек.
Система регулирования должна быть астатической
системой первого порядка и удовлетворять следующим
-показателям качества: а) коэффициент ошибки по ско-
рости = сек, б) коэффициент ошибки по ускоре-
нию С2 = 0,06 сек2, в) перерегулирование о при единич-
ном ступенчатом управляющем воздействии не должно
превышать 30%, г) время переходного процесса /п при
едйничном ступенчатом управляющем воздействии не
должно быть больше чем 0,8 сек при числе колебаний,
не превышающем двух.
Решение. В соответствии с методом [30, 32] на
рис. 151 построена исходная л. а. х. L нескорректиро-
ванной системы с коэффициентом усиления К. а, равным
требуемому
Ка = — 200 сек-1.
2 fj s пн f; линейных систем
да
Затем по заданным показателям качества построена
желаемая л. а. х. L>K. Первая сопрягающая частота же-
лаемой л. а. х.л согласно пункту б), определяется из сле-
дующего приближенного выражения: v
со, = a ng1 опл 0,08 сек~\
Для обеспечения условия пункта в) достаточно, чтобы
Рис. 151. Логарифмические амплитудные и фазовые частотные
характеристики к задаче 275.
желаемая л.- а. х. Лж имела запас устойчивости по мо-
дулю ±16 дб и по фазе 45° (рис. 152).
Найдем теперь значение частоты среза «с. 'Пользуясь
приложением 12,13, получим при ст —30%, что соответ-
ствует Ршях =1,3,
11,5.. , .
<йс ~ 14 сек,
Проведем через точку сос прямую с наклоном 20 дб на
декаду. Пересечение этой прям,ой со второй асимптотой
№1
§63 ЧАСТОТНЫ? МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ 233
желаемой л. а. х., имеющей наклон 40 дб на декаду,
даёт вторую сопрягающую частоту, <а2= 1,3 сек-1. В рас-
сматриваемом примере сос/(о2> 10, что вполне допустимо.
Таким образом, желаемый’ вид £ж при <о<®с найден
Таким образом, желаемый’
Перейдем к выбору фор-
мы при <о>(ое, обращая
особое внимание на то, что-
I,
вб
Л
граб
бы на каждом из участков
наклон желаемой л. а. х.
возможно меньше отличался
от наклона исходной л. а. х.
Попытаемся удовлетво-
рить заданным условиям ка-
чества, ограничившись раз-
ностью наклонов между £ж
Рис. 152. Кривые для выбора
запаса устойчивости по мо-
дулю I и яо фазе ц.
и L, не превышающей 20 дб
на декаду. Тогда £ж должна
иметь, как это ясно из
рис. 151, спрягающие ча-
стоты и3= 50 сек'1, м.;=100 сек'1, соответствующие со-
прягающим частотам исходной л. а. х. Начиная с частоты
®s = 200 сек'1, желаемая л. а. х. совпадает с исходной
л. а. х. Желаемая передаточная функция имеет вид
Запас устойчивости определяется видом логарифмиче-
ских характеристик в области средних частот, т. е
в интервале со2 со <о3. Проверим, имеет ли полученная
X а. х. £ж требуемый запас устойчивости по фазе при
L№= 16 дб (ю = (о2), 0 дб (ю = <ос) и 14 дб (<о = <о3).
Согласно рис. 151 при £ж = 16 дб со = 2 сек'1 и
ф(2)= - 90- arctg’ -Ла-+ arctg-Д- = - 121°.
Это соответствует запасу по фазе
• ц 180° + ф = 180° -121° = 59°.
234
ГЛ. 6: СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ'
[275
При Lx = — 14 дб, <0 = 50 сек *,
тр (56) = -90 - arctg- arctg — - 2 arctg = -190°
и соответственно р.= 180°— 190°— — 10°.
При £ж = 0, (о = (ос = 14 сек-1,
ф (14) = - 90° - arctg + arctg — - arctg ~ -
~ arctg “100 ~ 2 arctg 200 ~ ~ 108°’
и соответственно
p = 180°- 108° = 72°.
Из трех полученных значений ф(®) только второе не
укладывается в требуемые пределы. Это может привести
к незначительному увеличению абсо-
лютного значения | PmIn | по сравне-
нию с принятым (J Pmln | = Pmax - 1 =
=0,3), что, как известно [30, 32],
несущественно.
Поэтому найденная л. а. х. £ж
может использоваться для синтеза
корректирующих средств.
Вычитая ординаты L из орди-
нат желаемой л. а. х. £ж (рис. 151),
получим л. а. х. последовательного
корректирующего устройства, кото-
показана. В рассматриваемой задаче
С,
Д-
•0
сг
0------------i----0
Рис. 153. Пассивное
интегро-дифферен пи-
рующее звено.
рая на рис. I5l не
в качестве корректирующего устройства нужно исполь-
зовать пассивное интегро-дифференцирующее звено
(рис. 153), передаточная функция которого имеет вид
Ф
WK(p)
(1 + 0,77р) (1 +0,1р)
(1 + 12,5р) (1 +0,005/0-’
Для проверки полученных результатов построим фа--
зовую характеристику фж(ю) (рис. 151), а также, поль-
зуясь номограммой приложения 11, определим веще-
ственную частотную характеристику Р(а) замкнутой
системы (рис. 154, а). Применяя метод трапецеидальных
= $ 6.3. ЧАСТОТНЫЕ ME ОДЫ ВЫВ PA ПАРАМЕТРОВ 235“
характеристик, построим график переходного процесса
(рис. 154, б). Переходный процесс в системе удовлетво-
ряет заданным показателям качества.
Р(а»
Рис. 154. я) Вещественная частотная характеристика замкнутой си-
стемы; б) график переходного процесса.
• 276. Произвести выбор последовательного корректи-
рующего устройства для системы автоматического регу-
лирования. Передаточная функция разомкнутой системы
без коррекции имеет вид
W = (1 + т1Р) (1 + твР) (I + тзР) ’
где Ti =0,05 сек, Т2=.0,1 сек, Т3 —0,2 сёк. Скорректи-
рованная система должна обеспечивать следующие по-
казатели качества переходного процесса при ступенча-
том управляющем воздействии: а) перерегулирование
о^20%; б) время затухания переходного процесса
/п 0,6 сек при числе колебаний п 3; в) установив-
шаяся ошибка Д не должна превышать 3%.
Решение. Произведем выбор корректирующего
устройства при помощи амплитудно-фазовых характе-
ристик [1, 36]. Для получения установившейся ошибки
в 3% необходимо, чтобы коэффициент передачи системы
был не ниже
„ - 1 -А _ 1-0>03 _
Л Д 0,03
236
ГЛ в' СИНТЕЗ"ЛИЙЁЙНЫХ СИСТЕМ
а?в
Длй ' построения амплитудно-фазовой характеристики
ско,рректированной системы нужно выбрать соответствую-
щую форму вещественной частотной характеристики Р(со).
Рис. 155. я) Вещественная частотная характеристика; б) гра-
' фик = е) мнимая частотная характеристика.
\ <0о 7
Исходя из заданных показателей качества, а также
задаваясь коэффициентом наклона х = 0,7, найдем, поль-
зуясь номограммой (см. приложение 14), значения веще-
ственной частотной характеристики Р (со), обеспечиваю-
щей нужные качественные показатели скорректированной
системы. Для о = 20% и Ртах=1,0 находим-Рга1п = 0,3;
6 6 3 ЧАСТОТНЫЕ МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ 237
В761 У
запас устойчивости по модулю А/? = 55%, запас по фазе
д<р = 40°, а также = При заданном времени ре-
гулирования получим интервал положительности
3,8л; 3,8я ПГ1
(Оп = — = -тгтг ~ 20 сек. \
/и 0,6
На основании значения сои и параметров, положенных
в основу номограммы приложения .14, построена веще-
ственная частотная характеристика jP (со) (рис. 155, а).
К 32
Начальная ордината Р (0) = t = С*’97*
ad = х<опО,7 • 20 = 14 сек"1,
а,, = Х<о„0,5 • 20 = 10 сек"1,
' (Од = x„®60,5 -10 = 5 сек"1,
а2 = 25 сек"1, = =-~ = 42 сек"1,
z v z.j 0,6 ’
coj = jqcoo = 0,7 • 42 = 29 сек"1.
При помощи графика Q = f I—I, составленного для
\ р>о!
трапеции высотой, равной единице (рис. 155, б), Построена
мнимая частотная характеристика замкнутой системы
(рис. 155, в).
По характеристикам Р (со) и Q (со) легко построить
амплитудно-фазовую характеристику скорректированной
системы [36|. Эта характеристика построена на рис. 156, а
по данным табл. 1. На рис. 156, б пунктирной линией
изображена амплитудно-фазовая характеристика нескор-
ректированной системы (табл. 2).
Таблица 1
Амплитудно-фазовая характеристика скорректированной системы
<а, сек"1 20 25 30 40 60
' ' ~ ч Яс(<») 0,37 0,20 0,17 0,11 0,06
фс(й) -116° -130° -150° -160“ -181’
238
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1276
Таблица' 2
Амплитудно-фазовая характеристика
нескорректированной системы
<», сек"1 15 20 25 30 40 50
R (ш) 4,6 2,3 1,15 0,99 0,5 0,23
ф (о) -164° -185° — 230° -208° -220° -231°
Модуль и аргумент амплитудно-фазовой характери-
стики корректирующего устройства получатся из харак-
Рис. 156. Амплитудно-фазовые характеристики: а) скорректиро-
ванной системы; б) нескорректированной системы; е) корректиру-
ющего устройства.
теристик нескорректированной и скорректированной си-
стем
7?Г( (Ю) «Л (“> = ei [*с «*>-* <«»]
Данные вычислений сведены в табл. 3.
2771
§ 6.3. ЧАСТОТНЫЕ МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ
239
Таблица 3
Амплитудно-фазовая характеристика
корректирующего устройства
(0, — 1 сек 15 20 25 30 40 50
Як (<о) 0,23 0,16 0,174 0,17 0,22 0,26
Фк (<о) 33° 69° 70° 58° 60° 50°
По найденным значениям можно построить ампли*
тудно-фазовую характеристику корректирующего устрой*
ства.
Дальнейшее решение задачи состоит в том, чтобь(
выбрать такой тип корректирующего контура, амплй-
тудно-фазовая характеристика которого наиболее близко
совпадает с расчетной амплитудно-фазовой характери-
стикой корректирующего устройства.
Предположим, что в области низких и высоких частот
амплитудно-фазовые характеристики скорректированной
и нескорректированной систем должны совпадать. Тогда
в .качестве корректирующего контура следует выбрать
пассивное интегро-дифференцирующее звено с переда-
точной функцией
17/. _ (I + ГгкР) (1 + Т3кр)
w к w (1 + !Г1кР) (1 + ЛкР) •
Амплитудно-фазовая характеристика этого контура пред-
ставляет собой окружность с центром в точке Oi
(рис. 156, в). Взяв для любых четырех точек значений
модуля 7?к или фазы фк, найдем постоянные времени
7’1к=1,85 сек, ^=0,18 сек, 7’3к=0,08 сек, Т0,02 сек.
277. Определить передаточную функцию последова-
тельного корректирующего устройства для следящей
системы, передаточная функция которой имеет вид
W = р2(1 + Пр) (АЧрХИ-ЗД ’
где 7’1 = 0,04 сек, Т2 = 0,01 сек, 7’3 = 0,002 сек. Следя-
щая система должна иметь астатизм второго порядка
240
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
[278
и удовлетворять следующим показателям качества: а) об»
щпй коэффициент усиления по ускорению 100 сек"2;
б) перерегулирование о ^30%; в) время затухания пе-
реходного процесса 1П
0,45 сек.
Ответ.
Рис. 157. График переходного
процесса к задаче 277.
№к(р) =
_ (1+0,25р)(1+0,04р) -
(1 + 0,0029р) (1 + 0,00066р) ’
График переходного про-
цесса построен на рис. 157.
278. Произвести дина-
мический синтез следя-
щей системы по следую-
щим качественным пока-
зателям: ошибка хП1ЭХ «С 0,1 град при максимальной
скорости слежения- QImax = 20 град/сек и максимальном
ускорении eImax = 5 град/сек2', запас устойчивости оцени-
вается по показателю колебательности М 1,5.
Передаточная функция исходной нескорректирован-
ной системы имеет вид
W(p)
РО + ТР) ’
где Т' = 0,1 сек.
Решение. Определяем запретную область по точ-
ности (рис. 158):
= А = 0,25 сек-1, <0„ = Ата*. = 2° 200 се^1
I2|max 20 ’ я Хтах 0,1
Желаемую л. а. х. системы £ж в области низких частот
формируем из двух отрезков прямых, имеющих наклон
— 20 дб!дек и — 40 дб!дек с точкой излома на частоте
®к ~ ~ 0,25 сек-1.
Для обеспечения требуемой точности £ж приподни-
маем над запретной областью на 3 дб, т. е. необходи-
«6 3. ЧАСТОТНЫЕ МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ 241
27“ ’ s
мое значение общего коэффициента усиления опре-
деляется -из условия
Ко = 1,41 фй = 1,41 = 282 сек~1
82 w Лтях
(00= 1,19<00>К= 1,191/^5- =8,42 сек'. i
г #тах \
Определяем постоянные времени 7’2 и 7’3 (см. рис. 158):
У^ лг^г=ад2 У"У-1= 0,206 сеКг-
г-з-т-тйт1-0,042
Передаточная функция скорректированной системы, т. е.
соответствующая желаемой л. а. х., может быть запи-
сана в виде
Kq (1 + ^zP)
Гск = р (1 + Т1Р) (1 + Гзр) •
Для коррекции системы следует использовать пас-
сивное интегро-дифференцирующее звено с передаточной
функцией
if/ Л? . П + адСЧ-Ур)
а + ЛрИИ-’-ГэР)
242
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
[279
Схема этого звена и его частотные характеристики
показаны на рис. 159.
i Рис. 159. Интегро-дифференцирующее звено и’его ча-
стотные характеристики.
279. Определить последовательное корректирующее
устройство и рассчитать необходимый коэффициент уси-
ления усилителя k2 для следящей системы, структурная
Рис. 160. Схема следящей системы.
схема которой изображена на рис. 160. На схеме обо-
значено:
Д — двигатель, ДУ — корректирующее устройство,
Р — редуктор, ЧЭ — чувствительный элемент, определяю-
щий рассогласование, РМ — рабочий механизм, fyiify-*
углы поворота задающей и исполнительной осей.
Исходные данные:
1) крутизна чувствительного элемента
kl = 10 мв/угл • мин = 34,4 в!рад‘,
§63 ЧАСТОТНЫЕ МЕТОДЫ В БОРА ПА М ТРО
2) передаточное отношение редуктора г = 3500
3) максимальная скорость слежения £2 = Ь град {сек =
= 300 угл. мин!сек-,
4) максимальное ускорение
е = 2 град!сек2 — 120 угл. мин!сек2',
5) максимальная ошибка = Г;
6) максимальное напряжение выхода усилителя
Птах =110 е‘>
7) максимальная скорость • двигателя при полном
открытии усилителя £2дтах = 6000 об/лшц = 630 \/сек',
8) пусковой- момент Л40 = 100 Г • см = 9,81 • 10-3н • м\
механические характеристики двигателя совместно с
усилителем представляют собой параллельные прямые;
9) момент нагрузки на оси двигателя Л4„= 10 Г • см =
= 9,81 • Ю-4 н-м;
10) момент инерции, приведенный к оси двигателя,
J = 0,018 Г • см • сек2 = 17,6 • 10“8 кг • м2',
11) постоянная времени усилителя 7'у = 0,02 сек',
12) показатель колебательности М 1,5.
Решение. Передаточная функция разомкнутой си-
стемы при отсутствии корректирующих устройств равна
произведению передаточных функций звеньев:
ktk2k3 у
Г W = р (1 + Тлр) (1 + Тур) = р (1 + ТаР) (1 + Тур) ' W
Коэффициент передачи двигателя равен
, Рд max 630
«3 = -77-= "ТТгГ = 5>73 в 1 • сек
итах 1
Коэффициент наклона механических характеристик дви-
гателя вместе с редуктором
о__ Ро Рд max 630
Р ~~~Г = 1М0 = 3500 • 100 =
= 1,8 • 10~3 1/Г • см • сек = 6,3 угл • мин!Г • см • сек.
Постоянная времени двигателя
= M ’ 0.018 « 0,1 сек.
244
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
(879
Для определения необходимого значения общего
коэффициента усиления (добротности) по скорости Ка по-
строим запретную зону для низкочастотной части л. а. х.
(см. задачу 264). Контрольная частота
<*>.< = -g- = у = 0,4 сек-1.
Ордината контрольной точки
I ОЛ1 Й2 + РЛ4НЙ 3002 +6,3-10-300
L«=20 ig' =20's —i.12o ; =59 дб-
Предельное значение добротности по скорости
.. Q + fJA4H 300 + 6,3- 10 о/?о —1
Лй = —л-----=-----i-----= 363 сек .
“max *
По этим данным построена запретная область (рис. 161).
Проверим возможность работы следящей системы
без корректирующих звеньев. Так как первая сопрягаю-
щая частота л. а. х. передаточной функции (1), равная
<di = -4- = 10 сек~\ значительно больше контрольной
1 л
частоты <вк=.0,8 сек-1, то можно в качестве оконча-
тельного значения, добротности по скорости принять
279р* § 6.3. ЧАСТОТНЫЕ МЕТОДЫ ВЫБОРА ПАРАМЕТРОВ 245
значение, равное 363 сек"1. Соответствующая л. а. х.
тиПа i—2 — З показана на рис. 161.
Допустимая сумма постоянных времени
V 1 м2 + мУ7л^\
U'Ke 2
1 1,5=+1,5/1,5*-1
= _— ------------= 0,0054 сек.
В действительности сумма имеющихся постоянных вре-
мени
2 Т = 7\ + 7'у = 0,10 + 0,02 = 0,12 сек.
Таким образом, убеждаемся, что без корректирующих
устройств система не будет обладать требуемым пока-
зателем качества.
Рассмотрим возможный способ улучшения динами-
ческих свойств системы при помощи последовательных
звеньев [4].
При введении в прямой канал пассивного звена,
содержащего инерционную часть, необходимо так сфор-
мировать желаемую л. а. х., чтобы пик ошибки в районе
перемены знака скорости не превосходил заданного
максимального значения Отах. Найденному значению
добротности по. скорости Ка — 363 секУ соответствует
добротность по моменту
Л7> 363
Кы — — -gy ~ 57,5 Г• см/угл • мин.
Моментная ошибка
S’ = = 10 « 0 174'
Км 57,5
Допустимое значение большей постоянной времени
h = 0,236 = 0 236 = 0 1б сек^
ОмУе 0,174 У 120
По добротности ЛЬ = 363 сек-1 и постоянной времени
Л ==0,16 сек можно построить низкочастотную часть
246
ГЛ. в. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
л. а. х. (рис. 161). Базовая частота л. а. х.
/1Q _ ЛЗбЗ" .
17 = V олб =47>б сек ••
Сформируем теперь низкочастотную и высокочастотную
части желаемой л. а. х. типа 1—2—1—2. По.базовой
частоте определим требуемое значение второй постоян-
ной времени:
72w?]/"Ж-Т = 47£ ЦГЛ = 0,0365 сек‘
Третья постоянная времени равна
= _1_ /ЩЕП______L_ Vb5(l^-D _ 0 0073 срк
13 «о М +1. “ 47,5 1,5 +1 U,UUZ3 сек.
По этим данным построена вся желаемая л. а. х. £ж.
Л. а. х. корректирующих средств получается в результате
вычитания ординат располагаемой л. а. х. из ординат
желаемой л. а. х. Эта разностная' л. а. х. также изо-
бражена на рис. 161. Из вида этой л. а. X; следует, что
последовательно корректирующее устройство должно со-
стоять из:
. I) пассивного интегро-дифференцирующего звена
с передаточной функцией
П7 / \ _ (, + + ТгР^
(н-ада + ад •
где постоянная времени 1'в определяется из известного
свойства интегро-дифференцирующего звена
Тв =
тят2
Т1
0,05 • 0,0365
0Д6
0,0114 сек;
2) идеального дифференцирующего звена с переда-
точной функцией
1^к2(р)= 1 + ТУР,
3) комбинации пассивного дифференцирующего звена
и линейного усилителя с общей передаточной функцией
. , т О + ?вр)
. Гкз = 1 + ТзР = ky В1 + Т3р *
§ 6-3- частотные методы выбора параметров ~ 247
Идеальное дифференцирующее звено может при-
ближенно создаваться за счет использования тахогене-
паторов на задающей и исполнительной осях, включен-*
ных встреДно и вводящих производную от угла рас-
согласования.
В случае включения сигнала от тахогенератороз.
в том же месте, куда включен и сигнал от основного
Рис. 162. Схема с тахогенераторами для получении звена чистого
дифференцирования.
чувствительного элемента (рис. 162), требуемая крутизна
напряжения каждого тахогенератора равна
kTT = kiTy = 10 • 0,02 = 0,2 мв • сек/угл • мин =
= 0,37 в • сек/об = 0,06 в • сек.
Пассивные звенья должны вводиться в прямой канал
усиления и могут состоять из R С-цепей.
Коэффициент усиления усилителя с учетом дополни-
тельного усиления, необходимого для работы пассивного
т
Дифференцирующего звена равен
Т„ KQi 0,0114 363-3500
k<2 = = у-.— = n пп„о о. . V ~ = 9850.
z Г3 kik3 0,0073 34,4 • 5,73
В случае невозможности устящ””'и тахогенераторов
Ддя введения производной от угл., рассогласования
Можно изменить вид требуемых юрр^.тхрующих средств.
248
ГЛ 6 СИН ЕЗ ЛИНЕИНЬХ СИСТЕМ
тт
Как видно из рис. 161, идеальное дифференцирующее
звено получилось вследствие того, что высокочастотная
асимптота исходной л. а. х. имеет большой наклон По
сравнению с наклоном желаемой л. а. х. Для устранения
этого можно изменить вид желаемой л. а. х. в высоко-
частотной области, перейдя от л. а. х. типа 1—2 —1—2
К л. а. х. типа 1 —2—1 —3, но с тем же запасом устой-
чивости.
Высокочастотная часть последней л. а. х. показана
на рнс. 161 пунктиром. Ей соответствует передаточная
функция
{Р) p(t + r1P)(t + T5p)2 •
Постоянная времени Г5 определяется как
Т 1 "1 f — О п ллс с
= 2^ V -ii+г-=т ~ °’0036 сек-
Л. а. х. корректирующего устройства показана для
этого случая ца рис. 161 также пунктиром. Из рассмо-
трения этой л. а. х. видно, что корректирующее устрой-
ство последовательного типа должно состоять из трех
пассивных звеньев: интегро-диффереицирующего звена
и двух пассивных дифференцирующих звеньев в комби-
нации с линейным усилителем с общей передаточной
функцией
\¥/ ( 1 (1 + 14-Увр 1+Гур
ж К (Р) = (I+T’jpHI+T’bP) ’ 1 + г5р ‘ 1 + Т5р °"
_ (1+/’др)(1+Г2р)(1 + Гур)
(I + ^pHI+TspE
Коэффициент усиления /гу будет выше, чем в пре-
дыдущем случае,
ТуТв 0,02 • 0,0114
ky = -А- =-------г- = 17>5-
’ 0,00362
Общий коэффициент усиления усилителя оказывается
также значительно больше,
' ' Kni- - 363-3500 .
: ^^ = 17’5Ж75Ж==?10000- -
777.S 6 4 РАСЧЕТ ДОПОЛНИ Ельныл иы'лилял i.bmi.w2Щ
*91f s
Возможен и иной выбор высокочастотной части желае-
мой л.а. х., в частности, соответствующей передаточной
функции вида
т( .__________Ко (1 + 7*0
' W[P)~ р (1 + Tip} (1 + Ttp} (1 + Ггр) .
При этом Tt =/= Т5, но их сумма по-прежнему должна
быть равной
т . т _ 1
§ 6.-4. Расчет дополнительных обратных связей
и прямых параллельных корректирующих связей
280. Произвести расчет дополнительной обратной
связи для следящей системы задачи 278.
Решение. Найдем дополнительную обратную связь
Foc(p), эквивалентную пассивному интегро-дифферен-
цирующему звену lFnKy(/’X полученному при решении
задачи 278. Предположим, что дополнительная обратная
связь охватывает часть системы с передаточной функцией
где
Тогда
1 И^пку (р)
^пку(р)Гс(р) =
, (1+Т2р)(1 + Тр)
_ (1-ЬПрХИ-Гзр) = feocp*
(1 + 7~ар) (1/Ь Тр.)_fee 1 + Тгр *
(1 + T’lp) (1 + Т3р) p(i+Tp)
, _ П + Гз-Гг-Г
kc
Возможная схема осуществления этой обратной связи
показана на рис. 163.
281. Произвести выбор параметров жесткой тахо-
метрической обратной связи для следящей системы,
схема которой приведена на рис. 164. Исходные данные
те же, что и в задаче 279, кроме Тл = 0,05 сек.
250
ГЛ/6. СИНТЕЗ ЛИНЕЙНЫХ-СИСТЕМ
[281
Р е ш е.н и е. Передаточная функция разомкнутой си-
стемы с учетом действия тахометрической обратной
связи примет вид
где /Сна = -j ---новое значение общего коэффициента
усиления по скорости (добротности по скорости), а=>
Рис. 163. Схема допол-
нительной обратной свя-
зи к задаче 280.
Рис. 164. Схема следящей системы
с жесткой тахометрической об-
ратной связью.
звена второго порядка, Аос = &9&3А1Г “ коэффициент уси-
ления канала обратной связи, /гтг —крутизна тахогене-
ратора и масштабирующего устройства в цепи обратной
связи.
Для обеспечения необходимого запаса устойчивости,
оцениваемого величиной показателя колебательности,
следует соблюсти неравенство [2]
Гл + Гу 1 м^ + мУм^!
1+feoe 2 *
Нужно учесть также то обстоятельство, что введе-
ние жесткой тахометрической обратной связи изменяет
в (1 +&ос) раз наклон механических характеристик испол-
нительного двигателя. Требуемое значение добротности
по скорости при учете более жестких механических
§64 РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ ОБРАТНЫХ СВЯЗЕЙ ggl
характеристик равно
О ,
wmax 1 । ,
rr 1 "г Ко С
АнЯ — л
ишах
(3)
~ Решая два последних уравнения совместно, можно
определить требуемое значение коэффициента усиления
канала обратной связи.
^тах (Гд + Гу)
Ь°с 2р$тах
^ахГл + ^у)2 , РМв(Гд + Гу)
41х ^тах Н^тах
300 -0,7 . _ / 3002 • 0,072 6,3 • 10 0,07 . _
= 2 • 1,96 -1 1 ф V 4 • 1,9б2 • 1 Н ЩП = IU’
где __ ’ __________________
М2 + мУм2- 1 1,52+ 1,5/1,52- 1 , __
f |Х3=3 2 2 =я 1 ,Уо.
Требуемое значение добротности по скорости (3)
Кка =-------~^ = 306 сек-1.
Допустимая сумма постоянных времени (2)
V-T 1 1,52+1,5F1,52-1 nnnc.
2J = 306 --------2 .......= °’0064 СвК-
Имеющаяся эквивалентная постоянная времени
Гд+Гу 0,07 ’
а = ="< , ,п = 0,0064 сек.
1 + kox. 1 + 10
е
Таким образом, задачу выбора параметров цепи обрат-
ной связи можно считать решенной.
Передаточная функция разомкнутой демпфированной
системы примет вид
W (р) = .
р (1 + ар + Ьсг) р (1 + 6,4 • 10 Зр + 9,1 • 10 6р2)
2§2
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1282''
В заключение определим требуемый коэффициент
усиления усилителя и требуемую крутизну тахогенера-
тор?. Общий коэффициент усиления разомкнутой цепи,
следящей системы при отключенной обратной связи
должен быть равен
Кия = (1 + fc9c) = 306 • 11 ~ 3360 сек'1.
Коэффициент усиления усилителя
K'Qi 3360-3500 „ „
= kik3 = 34,4 • 5,73 = 59
Требуемое значение крутизны тахогенератора с учетом
масштабирующего устройства
____________ £ос 1^
ГЛ-----г-лелл-- -5- ~ 3 • 10 5 в • сек.
k2k3 t>9 500 • t>,73
Большое значение коэффициента усиления усилителя
является недостатком рассмотренного варианта введе-
ния обратной связи.
282. Произвести выбор параметров гибкой тахометри-
ческой обратной связи для следящей системы, схема
' Рис. 165. Схема следящей системы с гибкой
тахометрической обратной связью.
которой приведена на рис. 165. Исходные данные те же,
чтоб задаче 279. Крутизна тахогенератора /етг = 0,05 в-сек:
Решение. В связи с тем, что используется демпфи-
рование по первому способу [4] (см. § 6.1), желае-
мую л. а. х. LK можно так сформировать, чтобы ее
первый излом совпадал с контрольной частотой точки Ак
4821 S 5 4 РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ ОБРАТНЫХ СВЯЗЕН 253
(рис. 166). При этом л. а. х. должна быть поднята выше
запретной зоны на 3 дб. Требуемое значение добротности
по скорости будет Kia = V"2 /Cq = 1,41 • 363 = 512 сек-1.
Цдб
Рис. 166. Логарифмические амплитудные характер.(стики к задаче 282.
Это вызывает необходимость иметь коэффициент усиле-
ния усилителя
Базовая частота желаемой л. а. х.
®« = |//<ТГ= |' 0,4 • 512= 14,3 сект'.
Вторая постоянная времени желаемой л. а. х.
Г-~ «7 \ м- 1 = HJУ i,5-i = °’ 2 сек •
Допустимая сумма постоянных времени, соответствую-
щих сопрягающим частотам правее частоты среза [2, 4],
254
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1282
равна
У ' ГШЗ£11_0,024 сек.
44 (й0 М +1 14,3 1,5+ b ’
Сформулируем желаемую л. а. х. таким образом,
чтобы ее высокочастотная асимптота имела одинаковый
наклон с высокочастотной асимптотой располагаемой
л. а. х. L. В данном случае этот наклон составляет
60 дб/дек. Тогда в высокочастотной части желаемой
л. а. х. можно иметь двойной излом при частете со5 = ~.
Соответствующая постоянная времени должна быть равна
У т 0,024
7’5 = ^- = -2- = 0,012 сек.
Для упрощения корректирующих средств можно про-
должить участок с единичным наклоном желаемой л. а. х.
до совпадения высокочастотных- асимптот £ж и L, что
показано на рис. 166 пунктиром. Это даст некоторое
увеличение запаса устойчивости. Постоянная времени,
определяющая двойной излом желамой л. а. х., может
быть определена непосредственным измерением сопря-
гающей частоты. Она равна Т6 = 0,009 сек.
Построенной таким образом желаемой л. а. х. соот-
ветствует передаточная функция разомкнутой системы
w, , _ КтйО + М 512(1+0,12р)
W'P) p(l + TlP)(A + Tep)2 р (1 + 2,5р) (1 + 0,009)2 "
В дальнейшем мы будем ориентироваться на этот более
простой случай.
На рис. 166 построена л. а. х. корректирующих
устройств последовательного типа LK, полученная вычи-
танием ординат L из ординат Ьж. Она соответствует
последовательному включению интегро-дифференцирую-
щего и дифференцирующего звеньев с передаточной
функцией
w а+ади + адв + т-ур)
(1 + Tip) (1 + тйР)2
Полученная передаточная функция играет вспомога-
тельную роль, так как по условию задачи коррекция
282) § 6.4. РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ ОБРАТНЫХ СВЯЗЕЙ 255
системы должна осуществляться обратной связью, а не
последовательными звеньями. Поэтому, пользуясь ею,
необходимо вычислить эквивалентную обратную связь.
Передаточная функция корректирующего звена в цепи
тахогенератора может быть Определена по формуле
Гпэ(р)Гс(р)’
где Гс (р) = (1 +7т^)2ц + “ передаточная функция
части системы, охватываемой обратной связью.
В результате подстановки значений Wc(p) и Гпз(р)
имеем
Го. с (р)= [(^1 + 27б- Г2- Тд - Гу)р +
+(71+2Т17б-Т2ТД-Т2ТУ - ТлТу)р2 + (Л71- Т2ТЛТУ)р3] X
X [Мз(1 + ЗДГ1.
Такое звено является физически нереализуемым, так
как степень многочлена в числителе выше степени много-
члена знаменателя. Однако можно попытаться приме-
нить какое-либо физически реализуемое звено с переда-
точной функцией, близкой к желаемой. В качестве физи-
чески осуществимой передаточной функции можно взять,
как первое приближение, функцию
и/ (р\ =___Ъе.____— ь ТгР
W “ k2k3 (1 + Т2р) к°-с 1 + Т2р ’
где ‘-'W
Эта передатойная функция может быть реализована
при помощи тахогенератора постоянного тока, простого
делителя и дифференцирующей /?С-цепи с постоянной
времени Г2 = 0,12 сек.
Потребный коэффициент передачи в цепи обратной
связи
ko. С = kn • k№ = 0,12 - 9100 - 5,73 - 0,05' = 40’^ ’ *
Специальный делитель может и не устанавливаться,
но в этом случае место включения обратной связи
в усилители должно быть выбрано таким образом, чтобы
256
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
{282
от этого места до выхода усилителя коэффициент уси-
ления по напряжению составлял
^2 = 1гЖ0. с = 9100 • 40,5 10’3 = 3,6.
Таким образом, в первом приближении передаточная
функция корректирующего звена в цепи обратной связи
должна быть
W-„.I(P) = 40,5.10-sI^r.
Проверим теперь применимость этого звена для дости-
жения нужных динамических качеств для формирования
л. а. х. желаемого вида. Передаточная функция разом-
кнутой системы с учетом гибкой тахометрической обрат-
ной связи примет вид
Ц7 (р) =_____+М___________
H'ckW р (I + aiP + а2р2 + a3ps) ’
где
а 1 = Ту + Уд + Т2 "Т k2k^k0_ СУ2 = У у + Уд + Т2 + Т\ = 2,74 сек,
а2 = Ту Уд + Ту У2 + УДУ2 = 1,64 • 10"4 сек,
а3 = УуУдУ2 = 2,4 • 10’4 сек.
Раскладывая знаменатель полученной передаточной
функции на множители, получаем
, , ^Тй(! +Т2р)
И/ (М =-------—------—_____ =
WckW р(1 + 7»(1+ар + (>р2)
= 512(1 + 0,12р)______
р (1 + 2,74р) (1 + 0,6 • 10-2р + 0,88 • 10"У) ’
В низкочастотной части эта передаточная- функция
практически совпадает с передаточной функцией, соот-
ветствующей желаемой л. а. х. У>,(. Небольшое отличие
имеется только в величине постоянной времени
У1 = 2,74 сек, формирующей первый излом л, а. х.
В высокочастотной области условие ограничения суммы
постоянных времени выполнено, так как tz=0,6-10 2 сек,
а по условию допустимая сумма постоянных времени
составляет 2 У = 2,4 10~2 сек.
Проверка того, чтобы пик амплитудной характери-
стики колебательного звена не заходил в запретную
2831 § М- расчет дополнительных обратных, связей 257
область ДЛЯ высокочастотной части л. а. х., т. е. . .
mod | W (/ю) | < >
подтверждает допустимость подобной аппроксимации.
При желании можно получить более точное совпа-
дение полученной передаточной функции с желаемой
в низкочастотной области и устранить неравенство Т=ДТ}.
Для этого необходимо уточнить значение коэффи-
циента koc и выбрать его. равным
Аос = -р" ^ос = • 40’5 • 1 ° 5 = 37>4 10’5.
Тогда аналогичным образом можно получить скор-
ректированную передаточную функцию разомкнутой си-
стемы в виде
Г (П)==____________512U+0J2P)___________
р (1 + 2,5р) (1 + 0,65 • КГ2/; + 0,95 • 10-4р2) *
283.' Определить вид и параметры обратной связи
для электрогидравлической следящей системы, блок-
схема которой приведена на рис. 167, а. На рис. 167, а
обозначено: А и Б — части гидрорегулятора, ГУ — гидро-
усилитель, ПД — приводной двигатель, РМ — рабочий
механизм, УД — управляющий двигатель, ЧЭ -- чувстви-
тельный элемент (тахогенератор), Р — редуктор. Переда-
точная функция разомкнутой системы имеет вид
Г(р) = ^,хт-г,
Г Р<1 +7\р) (1 +/гмР)
где — добротность по ускорению, Та = 0,05 сек — элек-
тромеханическая постоянная времени управляющего дви-
гателя, 7™ = 0,02 сек — гидромеханическая постоянная
времени гидрорегулятора. Система должна иметь доброт-
ность по ускорению /QZ>25 сек~2 и показатель колеба-
тельности М^1,8. Обратная связь охватывает упра-
вляющий двигатель и усилитель.
Решение. На рис. 168 построена л. а. х. исходной
системы Ьи при значении Дв — 25 сек~2. Там же построена
желаемая л. а. х. . .Ьж, отвечающая всем требованиям
качества, предъявляемым к системе.
258
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
(283
Рассмотрим порядок определения вида и параметров
обратной связи.
С учетом дополнительной обратной связи передаточ-
ную функцию разомкнутой системы Wjk(p) можно за-
писать в виде
(р)--------w —-—
1 + Гх(р).Гос(р) .
где W'oc(p) — передаточная функция цепи дополнитель-
ной обратной связи, Wx(p)— передаточная функция
Рис. 167. Схемы электрогидравлической сле-
дящей системы.
части системы, замыкаемой обратной связью. Из при-
веденного выражения следует, что л. а. х. цепи обратной
связи Loc можно определить по известным л. а. х. и
L„ в следующей последовательности [4], [28]:
§ 6.4. РАСЧЕТ дополнительных ЕР TH !Х СВЯЗЕЙ 259
1) из л. а. х. исходной системы Ьи вычитается желае-
мая л. а. х. Ьж, т. е. определяется л. а. х. Lb соответ-
ствующая передаточной функции 1 + Wx (р) Woc (р);
2) по виду л, а. х. Lt строится л. а. х. L2, соответ-
ствующая передаточной функции Wx(p)Woc(p);
3) из л. а. х. L2 вычитается л. а. х. той части си-
стемы, которая замыкается обратной связью Lx, в резуль-
тате чего определяется л. а. х. цепи обратной связи Loc.
260
ГЛ.. 6.. СИНТЕЗ- ЛИНЕЙНЫХ СИСТЕМ
№4
В решаемой задаче разностная л, а. х. Ь.л. будет пол-
ностью располагаться под осью нуля децибел, что вызо-
вет нарушение условия минимальности фазы при пере-
ходе к л. а. х. £2 [4]. Поэтому прежде следует увели-
чить коэффициент усиления исходной системы настолько,
чтобы разностная л. а. х. L\ полностью лежала выше оси
нуля децибел.
На рис. 168 построена л. а. х. исходной системы с уве-
личенным коэффициентом усиления К'-=^ о>' =3600 сек'1,
которая обозначена Lp. Там же изображена разностная
л. а. х. Т|, полученная вычислением желаемой л. а. х. LIK
из располагаемой л. а. х. Lp. Для определения л. а. х, Z,2
обратимся к таблице преобразования л. а. х. (приложе-
ние 25, п. VII).
Поскольку обратная связь охватывает управляющий
двигатель я усилитель, то
Wx(p)~ иГт-х’
р(1 + 7др)
Соответствующая этому выражению л. а. х. Lx построена
на рис. 168.
ДЗычитая из ординат л. а. х. L2 ординаты л. а. х Lx,
строим искомую л. а. х. Loc, по виду которой может
быть записано выражение для передаточной функции
цепи обратной связи
в/ (п\_ Р (1 + Др)
W'ocW- 1 + 7-2р .
где
^ос „
—, т2 = —, д = —.
G>oc (£>з
Полученную передаточную функцию можно легко реа-
лизовать, включив в цепь обратной связи тахогенера-
тор и пассивное звено указанного типа (рис. 167, б).
284. Определить вид обратной связи для системы, рас-
смотренной в задаче 283, в предположении, что цепь об-
ратной связи охватывает часть усилителя, т. е. Wx (р) = kx.
Остальные данные те же,, что в предыдущей задаче.
Ответ. Передаточная функция цепи обратной связи
имеет вид >
IJ7 (п\_ ^ос (1 + Др)
OCV' . (1 + ггр)(1 + тмр)-
7^51 § 6.4. РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ. ОБРАТНЫХ СВЯЗЕЙ 261
.... 285. Произвести выбор параметров прямой парал-
лельной корректирующей связи для системы автомати-
ческого регулирования, структурная схема которой
Рис. 169. а) Структурная схема системы с введением прямой па-
раллельной корректирующей связи; б) л. а. х. к задаче 285. '
показана на рис. 169, о. Передаточная функция разомк-
нутой исходной системы имеет вид
= Р(1 + 7’у₽)(1 + 7'др) ’
262
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1285
где Ка = 900 сек"1, Уд = 0,08 сек, Ту —0,02 сек. После
введения прямой параллельной связи система должна
обладать астатизмом второго порядка, иметь доброт-
ность по ускорению Кв = 100 сек~2 и показатель коле-
бательности М 1,5.
Решение. Передаточную функцию разомкнутой
системы с учетом введения прямой параллельной связи
представим в виде
KE(l+-^p)
Гск = р2 (1 + 7» (1 + Тур) ’
где
Ke = Kaknc.
Реализация прямой связи, осуществляющей введе-
ние сигнала, пропорционального интегралу от ошибки
(рассогласования), возможна путем использования интег-
рирующего привода.
На рис. 169, б изображены л. а. х. исходной системы LK,
желаемая л. а. х. Ьж и л. а. х. прямой связи £пс.
Требуемое значение коэффициента передачи по цепи
прямой связи knc определяется из условия
или
, Де 100 л 1 1 —1
fenC~ 900 — 0,11 СеК '
Отношение целесообразно выбрать равным .
Отсюда
0,018.
1 <02 6
Для выполнения этого условия придется намеренно
уменьшать коэффициент передачи первого звена, охва-
тываемого прямой параллельной связью. Одновременно
во столько же раз увеличивается коэффициент передачи
другого звена, входящего в прямой тракт усиления,
чтобы сохранить постоянной величину Ко.
Введением интегрирующей связи удается приблизить
л. а. х. исходной системы £и к желаемому виду £ж
только в области низких и частично средних частот (£ж).
<sej § 6.5. СИСТЕМЫ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ 263
. Окончательное приближение л. а. х. системы к желае-
мому виду может быть достигнуто путем коррекции
л. а. х. системы в области средних и высших частот
применением последовательных корректирующих звеньев
либо с помощью эквивалентных им прямых или обрат-
ных связей,
§ 6.5. Расчет систем комбинированного управления
286. Определить требуемый уровень компенсирующего
сигнала по первой производной от входного воздействия,
при котором устраняется скоростная ошибка системы
Рис. 170. Структурная схема системы комбини-
рованного управления.
(рис. 170), звенья которой имеют следующие переда-
точные функции:
<р(р)=='т,р,
WAp)~ku
I
где fe, = 10 в[град, = 10 град!сек, T = 0,02 сек, т [сек] —
коэффициент, определяющий уровень компенсирующего
сигнала.
Решение. Передаточная функция замкнутой системы
относительно ошибки имеет вид
^Ар> 1 + W, (р) W2 (р) ’
откуда
«•w-KtStF- (2)
J р р т R-\R-2
264'
'ГЛ-.-6.' СИНТЕЗ ЛИНЕЙНЫХ. СИСТЕМ
(287
Условие устранения скоростной ошибки
k2t — 1.
Следовательно, требуемый уровень компенсирующего
сигнала равен
1 п . в сек
Т==-1—= 0,1 --г .
«2 граи
287. Определить требуемые уровни компенсирующих
сигналов по первой и второй производным от входного
воздействия для. следящей системы комбинированного
управления (см. рис. 170) с передаточными функциями;
W,(P)= 1,
= р(1 +Г1р)(1+Г2р) ’
где 7] = 0,05 сек, Т2.= 0,002 сек. Система должна обес-
печивать слежение с ошибкой хтах^0о.1 при макси-
мальной скорости слежения Qmax = 150° сёк~г. и макси-
мальном ускорении. е1пах = 750 град/сек2. Показатель
колебательности А1 1,5.
Решение. На рис. 171 построена контрольная
точка с координатами
! 'е _
®к = = 5 сек 1
и • • •
Q2 1502
L, = 20 1g= 20 I g « 50 дб.
лшах emax 1 /эи
...Если провести через эту контрольную точку низко-
частотную асимптоту л. а. х., соответствующей переда-
точной функции исходной системы, то требуемое значе-
ние добротности по скорости составит
/<П = Ртах. = 150 = 150() сек_^
Хщах 0,1
Однако известно, что при заданном значении показателя
колебательности М наименьшее допустимое значение
добротности по' скорости при отсутствии каких-либо
28ВГ
6 . СИСТЕМЫ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
265
корректирующих средств составит (4]
= 1,5^+1,5 И =
Ай = 2 (Г, + Г2) 2(0,05 + 0,02) tu •
Если ввести сигнал первой производной от управляю-
щего воздействия, следящая система приобретает свой-
ства системы с астатизмом второго порядка.
Рис. 171. Л. а. х. к задаче 287.
Требуемое значение добротности по ускорению равно
= ~ = = 7500 сек'*.
•*max 1
Требуемое значение добротности по скорости при этом
для исходной системы определяется по формуле
Хп = (Tj + Т2) /<е = 0,052 • 7500 = 390 сек~\
т. е. Дя получается уже значительно меньше, чем Ка.
При введении дополнительно второй производной тре-
буемая добротность по третьей производной
А = 5-750 = 37500
7 - Ашах 0,1
266 гл. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ [288
Требуемая добротность по скорости может быть опре-
делена по выражению
Кй" = [Г,Т2 + 'C3(Ti + T2)]Ky.
Приравняв К,'а добротности по скорости, которую можно
иметь без корректирующих средств (/<£2 = 40 сек"1), по-
лучим требуемое значение постоянной времени т3:
Ка-Т, TJC, 40 - 0,05 • 0,002 • 37500 _о
т — ы 1 2 у _________ i о к . 1 л о
3 (П + Г2) Ку (0,05 + 0,002) • 37500 °’
Постоянные времени, определяющие уровни вводимых
сигналов, находятся из условий компенсации
т = 4- = = 0,025 сек,
Щ2 40
т2 = Tj + Т2 + т8 = 0,05 + 0,002 + 0,018 = 0,070 сек.
Таким образом, передаточная функция компенсирующей
цепи должна иметь вид
, ч . 0,025 • 0,070р2
ф(р) 0,025р+ 1 +00018р •
/
Л. а. х. системы, соответствующая найденным пара-
метрам, показана на рис. 171 (нижняя л. а. х).
288. Определить требуемый уровень компенсирую-
щего сигнала, пропорционального первой производной
от входного воздействия,
<P(P) = TlP>
и произвести расчет других необходимых корректирующих
средств для следящей системы, передаточная функция
которой в разомкнутом состоянии имеет вид (см. рис. 170)
W = р (1 + Гдр) (1 + Тур) ’ (Р) = 1 •
где 7\ = 0,1 сек — электромеханическая постоянная вре-
мени двигателя, Ту = 0,05 сек— постоянная времени уси-
лителя. Система должна обладать астатизмом вто-
gSgJ § 6.5. СИСТЕМЫ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ 267
оого порядка и обеспечивать слежение с ошибкой
$ ^2 уел. мин при максимальной скорости слежения
^шах ^.3^ град]сек и максимальном ускорении етах =
=т30 град!сек2. Запас устойчивости определяется пока-
зателем колебательности 2И^1,5.
Решение. Определим вначале желаемую эквива-
лентную передаточную функцию разомкнутой системы.
Первая асимптота л. а. х. представляет собой прямую
с наклоном 40 дб[дек. Положение ее определяется базо-
вой частотой (рис. 172)
<»о = VX = = 30 сек"1.
Для получения запаса устойчивости, соответствую-
щего показателю колебательности М, передаточная
Функция для области средних частот должна иметь
вид [4]
^эж(р) =
Н (1 +Г2р) ’
268 ГЛ. в. СИНТЕЗ'ЛИНЕЙНЫХ СИСТЕМ
где
: = 900 сек~2,
Tt - — т/тг4 = 4г 1/ = 0,0575 сек,
1 «о г М — 1 30 Г 1 д -1 ’ ’
^2 = ^т^1 = г1^т 0,0575 = 0,0115 сек.
z М + 1 1,5+1
Желаемая передаточная функция замкнутой системы
равна
(Т> (М = ^эж (р) _______/Св (1 Ч- У (р)_
u ж 1 + Гэм (р) Ке + KBTiP + р2 + 72р3 •
При введении компенсирующего сигнала передаточную
функцию замкнутой системы можно представить в виде
Фж = Ф1 (р)+Фг {р}-
Сравнение приведенных выражений дает
Ч (p) = TiP = TiP,
или •
т, = Г, = 0,0575 сек,
что определяет требуемый уровень компенсирующего си-
гнала. Далее, имеем
Л) ( пV_ ______л«__________u ;_____KBTip_________
Ке + к.Г1р + р2+ТзР< . Кг + КеТ^ + рЧ-Тчр*
= <!>! (р) + Ф2(р).
Желаемая передаточная функция исходной следя-
щей системы равна
КеТ.р + Кг.
1
Г, _ 17,4__________
1 р(1+ар + Ьр2) р(1+0,0193р + 0,00022р2) '
Передаточная функция нескорректированной системы
имеет вид
W/ ( п) == —:-—________L_ =________________________
. .р.(1+7др)(Н-Гур). р [I + (Гд + 7’у) р + ГдГур2] •
— « 65. СИСТЕМЫ КОМБИНИРОВАННОГО УИР В ПЕННИ 269
Сравнение двух последних выражений показывает, что
для получения равенства (р) =₽ W (р) необходимо
выполнение следующих условий:
Ка = 17,4 сек21,
Тя + = 0,0193 сек,
ТДТУ = 0,00022 сек2. .....
Выполнение первого условия не представляет труд-
ностей, так как добротность по скорости К®,.предста-
вляющая собой общий коэффициент передачи разомк-
нутой системы, может быть принята любой. Выполнение
второго, и третьего условий требует введения корректи-
рующих звеньев, снижающих коэффициенты при р и р2
в квадратной скобке выражения для W(р), так как без
корректирующих звеньев
Т’д + Т'у = 0,15 сек и Уд Гу = 0,005 сек2.
Это может быть сделано введением жестких обратных
связей, охватывающих усилитель и усилитель совместно
Рис. 173. Структурная схема системы к задаче 288.
с двигателем (рис. 173). В этом случае передаточная
функция разомкнутой цепи вместе с обратными связями
будет равна
^С.с (Р) = . Ла,----------------7 .
270
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
1289
Сравнивая последнее выражение с выражением для
Ц/Ж(р), получаем
Гд + Т-у 4- ktTz
1 + fei + k2
= « = 0,0193 сек,
ТЛТУ
1 + ki + k2
= 0,00022 сек2,
откуда находим требуемые коэффициенты усиления по
первой и второй петлям обратных связей (см. рис. 173)
fej = l,9 /г2 = 22,5.
§ 6.6. Расчет последовательных корректирующих
контуров, работающих на несущей частоте
289. Выбрать схему и параметры звена переменного
тока, л. а. х. которого по огибающей соответствует
С
Рис. 174. а) Л. а, х. реального дифференцирующего звена; б) схема
резонансного РАС-звена.
дифференцирующему звену (рис. 174, а) с передаточной
функцией
T^l+Tzpy
где 7^ = 0,08 сек, Т2 = 0,01 сек. Несущая частота сои
равна 3140 сек-1.
Решение. Передаточную функцию реального диф-
ференцирующего звена переменного тока по отношению
к частоте огибающей Q можно для достаточно узкой
полосы частот Q записать в виде
2891 § б-6' ПОСЛЕДОВАТЕЛЬНЫЕ КОРРЕКТИРУЮЩИЕ КОНТУРЫ 271
о 72 0,01 л , г,,-» _ /Г'
По условию задачи и0 — v.izo и 1Л~
_ у, = 0,08 сек.
В настоящее время получили распространение сле-
дующие виды дифференцирующих звеньев: а) двойные
или параллельные Г-образные /?С-звенья; б) мостовые
Т-образные /?С-звенья; в) мостовые RC- и £С-звенья;
г) резонансные PLC-звенья.
Рассмотрим возможность применения резонансного
PLC-звена (рис. 174, б). Передаточная функция такого
звена по огибающей имеет вид
Г(/£2) = ^-^------1+»£__
*,+/?2 i+iQZ^C
Для нашего случая
2Р,С = Тд, 2RXC
R2
---------------i— = Go и
Таким образом, получаем
тырьмя неизвестными:
0,08 = 2/?iC,
0,125 = - ,
R.i + Rz
Т?2 -т- /-»
Я, + Rz ~ 1 дСг°’
1
®н= ---- •
VTL
четыре уравнения с че-
w'-w-g&r.
3140 = -yU-.
К LC
Величина сопротивления R2 обычно бывает задана
(равна входному сопротивлению последующего устрой-
ства). Пусть R2 равняется 100 ком. Определим Rt:
0,125/?!+ 0,125 • 100= 100,
„ 87,5 -пп
Р1 = qj25 = 700 КОМ-
Определим теперь емкость конденсатора С:
0,08 0,08 п .
С 2/?i 2-0,7 °»057 мкф.
В заключение найдем индуктивность L:
. 1 ю6 1 о
L — —5— -----5-----= 1,8 гн,
<в„С 31402 - 0,057
272
ГЛ. 6. СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
Гаев
290. Определить параметры двойного Т-образного
звена (рис. 175), работающего на несущей частоте
<ои = 2зт/„ = 314 сек~1. Остальные условия те же, что
в предыдущей задаче.
Решение. Для определения параметров звена обра-
тимся к таблице, приведенной в приложении 22.
По условию задачи произведение Гд®н = 25. Путем
интерполирования данных можно найти Go, соответ-
ствующее полученному произведению Тла>а. Коэффи-
циент Go, определенный таким образом, оказывается
равным 0,02. Таким образом,
полученное значение Go по
сравнению с его заданным зна-
чением можно уменьшить; Это
в свою очередь при сохранении
7’1.= 7’д=0,08 сек может приве-
сти к уменьшению постоянной
времени Т2 до значения
= 0,08-0,02 = 0,0016 сек-.
Рис. 175. Схема двойного
7-образного 7?С-звена. Обычно уменьшение по-
стоянной времени не свя-
аано с ухудшением динамических свойств корректируе-
мой системы.
Перейдем к определению параметров двойного
Г-образного звена. Пусть С1 = С2 = С3 = С = 0,5 мкф.
Тогда (см. приложение 22)
„ а 0,394-10е О!-пл
R\ = —Т Ъс 2о00 ом,
' <онС 314-0,5 . ’
1 I Пб
= 2<о„Са = 2-314-0,5-0,394 8000 ОМ’
К2 <о„С
10е
1,41 -314-0,5
4500 ом.
291. Определить параметры двойного Т-образного
звена. Постоянная времени 7\ = 0,0047 сек. Несущая
частота ®н = 2nf„ = 3140 сек~1, Ct = С2 = С = 1 мкф.
Ответ. Go = 0,034, Ri*= 134 ом, /?2г=380 ом, /?3=225сш.
ГЛАВА 7
СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ
СИСТЕМАХ
§ 7.1. Вычисление корреляционных функций
и спектральных плотностей
292. Определить корреляционную функцию 7?(т) и
спектральную плотность X (<о) для величины, изменяю-
щейся по гармоническому закону
х = A sin (р/ + ф).
Проверить, что интегрирование спектральной плотности
по всем частотам, а также значение /?(0) дают средний
квадрат (в данном случае он равен дисперсии) рассмат-
риваемой величины. Амплитуда' А =10 и угловая ча-
стота р = 2 сек"1.
Решение. Корреляционная функция
+ г
(т) — lim ~ ( х (/) х (/ + т) dt =
г.
= ~ j A2 sin (р/ + ф) sin (р/ + Рт + ф) dt == cos рт,
о
2зт
где То = -^~. Подстановка исходных данных дает
R (т)~= 50 cos 2т, а также /? (0) = 50.
274 ГЛ. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [283
Спектральная плотность может быть вычислена на
основе интеграла Фурье [2]:
оо оо
S (со) = / Я (т) = f 4г е’7“т COS Рт dx ==
— оо — оо
оо
А2 С
= -у- COS (ОТ COS рт dx —
— оо
оо
А2 Г
— -j- J [cos (со — р) т 4- cos (со 4- р) т] dx —
— оо
=[б (со-Р) 4-б (со 4-Р)],
где 6 (о — р) и б (со 4- Р) — единичные импульсные функции,
расположенные при частотах со = р и со = — р.
Интегрирование спектральной плотности по всем ча-
стотам дает
Ц-оо Ц-оз
~Г J S (со) с/со =j" [б(со - Р) + б (со + Р)] dco.
— оо —оо
Интегралы от единичных импульсных функций равны
единице,
4-оо 4-оо
[ б (со — р) dco = J б (со 4- Р) dco = 1.
—оо —оо
Поэтому в результате получаем
4-оо
i J swd—4-JF-50-
—оо
2S3. Для стационарного случайного процесса, имею-
щего постоянный спектр в полосе от — соп до 4- <оп
(рис. 176), вычислить среднее значение (математическое
ожидание), средний квадрат (момент второго порядка)
и дисперсию, а также найти аналитическое выражение
й построить график корреляционной функции.
§ 7.1. ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ 275
Решение. Среднее значение случайной величины
равно нулю х = 0, так как спектральная плотность не
содержит при о = 6 особенностей типа импульсной функ-
ции (дельта-функции). В результате дисперсия равна
среднему квадрату случайной величины
D = х2 — х2 = х2 = о2,
где о — среднеквадратичное отклонение. Далее находим
4-00 +“п
= i / S(o)do = ^- J 7Vdo = ^
— оо —(О
где До = 2оп — полоса частот (в радианах в секунду).
Последняя, формула может быть записана также в сле-
дующем виде:
^=D = N/\f,
N
. г Дсо
где А/ = — полоса ча-
стот (в герцах). Средне-
квадратичное значение
случайной величины
хск = ст = Yn /ДД
-а„
О
Аы
ы,сек
Рис. 176. Белый спектр в ограни-
ченной полосе частот.
. Корреляционная функция может быть определена на
основе интеграла Фурье [2]:
Ц-оо со
/?(т) = —- I \(о) do = — | S (o) cos от do
— оо О
или
“п
1 Г N
Я (т) = — | N cos от dto = — sin о„т.
о
График корреляционной функции изображен на
рис. 177. Значение корреляционной функции при т = 0
равно
/? (0) = lim — sin опт = —“и. = D.
. т->о лт п я
2 76 ГЛ. 7; СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ (2»S,
294. Для предыдущей задачи определить . нормиро-
ванное значение спектральной плотности и корреляцион-
ной функции.
Рис. 178. Корреляционнаифупк-
цня экспоненциального вида.
Ответ. Нормированная спектральная плотность при
ип «С © -С ®п равна
о((й) = А^.=г^Д = 1 .
' ' D А© А)
Нормированная корреляционная функция
л 1^\ — _ 5111 мпт
Р \Ч п гот"
LJ I
Значение р (т) при т = О
/гх\ 1 sin C0[jTj <
p (0) = li tn ——— = I.
' T_>0 (Ont
295. В результате обработки осциллограммы стацио-
нарного случайного процесса с математическим ожида-
нием (средним значением), равным нулю,, получено вы-
ражение для корреляционной функции
/? (т) = De-'1 1 т I,
где D = 100 — дисперсия и ц = 5 сек-1 — параметр зату-
хания. Корреляционная функция построена па рис. 178.
Определить спектральную плотность и построить ее
график.
Решение. Спектральная плотность может быть
найдена согласно интегралу Фурье [2]
4-OQ 4-00 , .
5 (©) = [ R (т) е-ког t/т = J De~111 х dx.
< 71 ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ 277
S*>vJ S'
Последний интеграл для удобства желательно разбить
на два:
5(®) = £>
О 00
J г dt + J 4Г«*+/®) * dt
-оо О
2pD
р.2 4- а2
2TD
1 4- ю2Г2 ’
где
Т = — = 0,2 сек.
в
Подстановка численных значений дает
О , ч 40
5 И - 14-0,04а2 •
Спектральная плотность построена на рис. 179.
Рис. 179. Спектральная плотность,
соответствующая корреляционной
функции на рис. 178.
2S6. Решить предыдущую задачу, если рассматри-
ваемый стационарный случайный процесс имеет среднее
значение (математическое ожидание) х — 5. Построить
графики корреляционной функции и спектральной плот-
ности.
Ответ. Средний квадрат случайной величины
JF=£) + x2= 100 + 52= 125.
Корреляционная функция
R (т) = De-в и । + х2 = 100с-5111 + 25.
278 ГЛ. Т. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [297
Спектральная плотность
' sW-WW+t^-WW+1+W.
где 6 (<о) —единичная импульсная функция. Графики
построены на рис. 180.
Рис. 180. Корреляционная функция
и спектральная плотность к за-
даче 296.
2S7. В результате обработки осцилограммы -случай-
ного стационарного процесса с математическим ожида-
нием, равным нулю, получено выражение для корреля-
ционной функции:
(т) = 1 т I cos 0т, (1)
где D = 40 — дисперсия, pi = 0,5 сек-1 — параметр затуха-
ния (коэффициент нерегулярности) и р = 2 сек-1 — резо-
нансная частота. Корреляционная функция изображена
на рис. 181. Найти аналитическое выражение и по-
строить график спектральной плотности.
Ответ. Спектральная плотность
S (со) = piD [ц2 + (р_ю)2 + ц2 + (р + ш)2 ] •
S98J § 7.1. ‘ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИИ 279
После подстановки численных значений
ч 20 20
3 (О) - 0 25 + (2 - <о)2 + 0,25 + (2 + <о)2 *
График спектральной плотности изображен на рис. 182.
Рис. 181. Корреляционная функция
нерегулярной качки.
3(а»
Рис. 182. Спектральная плотность нере-
гулярной качки.
2S8. Для аппроксимации формулы корреляционной
функции по исходным данным предыдущей задачи при-
нято более точное выражение
/?(т) = £)е-и 1 т 1 (cos 0т + у sinPI т | j.
Найти спектральную плотность для этого случая.
Ответ.
q i х ц г. Г 20 — <о , 2₽ + <о 1
0 U + (0 _ Ю)2 + + (р + Ю)2 J ~
= 1П Г 4~ю 4- 4 + -___1
L 0,25 + (2 - <о)2 0,25 + (2 + w)2 J*
280 ’"ТЛ. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ в ЛИНЕЙНЫХ СИСТЕМАХ [299
299. Стационарный случайный процесс на входе сле-
дящей системы имеет вид, представленный на рис. 183.
Среднеквадратичное значение рассматриваемой вели-
чины хск = 2. Средняя протяженность участка к = const
составляет Т = 10 сек. Определить корреляционную функ-
цию и спектральную плотность.
Рис. 183. Типовой входной сигнал
следящей системы.
Решение. Корреляционная функция может быть
найдена по выражению
R (т) = Fp1 + х2Р.2, (1)
где х2 —средний квадрат, а х2 —квадрат среднего зна-
чения случайной величины, Рt — вероятность нахожде-
ния перемножаемых ординат случайного процесса на
интервале х = const, т. е. вероятность отсутствия изме-
нения скорости на отрезке времени т; Р2— 1 — Pi — ве-
роятность наличия изменения скорости на отрезке вре-
мени т.
Так как для рассматриваемого процесса х = 0, то
x2='D и формула (1) приобретает вид
R(x) = DPi. (2)
Вероятность появления изменения рассматриваемой
случайной величины на малом интервале времени Ат
может быть принята пропорциональной значению Ат и
равной . Вероятность отсутствия изменения случан-
_ , Ат
нои величины оудет 1-----Вероятность отсутствия
изменения величины на отрезке времени т равна произ-
ведению вероятностей
. § '7Т; ' ВЫЧИСЛЕНИЕ ^КОРРЕЛЯШЮтГЫ -ФУНКЦИЙ.: 9g[
Искомая вероятность может быть найдена как
предел выражения (3) при Дт-> 0:
X _ X
гч И ft Ат\дт Т
Так как Р, (т) = Р, (-т), то в результате получаем кор-
реляционную функцию в виде
—-0,1 1т|
R(r) = De ‘ = 4е
Спектральная плотность [2]
+оо
о / A f п / х -/глт л 2ZO во
5(<о)— J R(t)e dr j + Ю2р ~ [ + 100g)2 •
—оо
300. Решить предыдущую задачу, если известно,
что участки х>0 и х<0 чередуются и изменение
Рис/ 184. График процесса к за- Рис. 185. Последователь-
Даче 300. ность импульсов.
значения всегда сопровождается изменением знака. Гра-
фик такого процесса изображен на рис. 184.
Ответ.
40
, -2-ЧЛ -0.2 |г|
R (т) = De 1 = 4е
е 7 , ТО
S (<0) = -—р
1 -I—— со2 • I + 25<о2
4
301. Определить спектральную плотность последо-
вательности равноотстоящих положительных импульсов,
имеющих одинаковую- ширину и случайную амплитуду
(рис. 185), при следующих исходных данных: период
следования импульсов Г = 0,1 се/с; ширина импульса
282 л СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕ ЫХ С dCTEMAX
[ЗС1
уТ — 0,01 сек, что соответствует скважности у = 0 1-
среднее значение амплитуды импульса х = 20; средне-
квадратичное значение амплитуды импульса |Лх2==хск=
Решение. Представим функцию x(t) в виде суммы
периодической составляющей Х|(0, состоящей из после-
довательности импульсов с постоянной амплитудой, рав-
ной х (рис. 186, а), и случайной составляющей Xz(t)
состоящей из последовательно-
сти импульсов со случайной
амплитудой и средним значени-
ем, равным нулю (рис. 186,6).
Периодическую составляю-
щую разложим в ряд Фурье,
-}-оо . 2glfef
^(0== 2 Cke'~T~, (1)
k~— ОО
где Си — комплексное число.
Амплитуды гармоник
Ak — А-и — |Cfe| —
= | ЪГ sin kjvV | ’ (2)
ной х (рис. 186, а), и
•*/
t,CEK
а)
хг
I] ~Г,сек
, б)
Рис. 186. Составляющие по-
следовательности импульсов.
О
_1
О
что при подстановке исходных данных приводит к ра-
венству
Ak = A_ft = | sin 0,314ft |.
Это дает следующие значения амплитуд гармоник:
А = 2, Аб=1, Л12 = 0,31,
А = 1,98, Л7 = 0,73, Дз = 0,39,
А =1,86, А = 0,46, Л14 = 0,43,
Л3=1,7, Л9 = 0,21, Аз = 0,42,
Л4=1,51, Ао = О, Аб = 0,38,
Л5=1,27, Ai = 0,17, и т. д.
Спектральная плотность для периодической соста-
ляющей (1) может быть записана в виде (см. задачу 292)
?> 4-00
А((0) = 2Я4 У б(ш—^4 (3)
§ 7Л. ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИИ 283
- представляет собой линейчатый спектр. Он изобра-
жен на рис. 187, а, причем площадь импульсной функ-
ции, равная 2л показана условно в виде амплитуды
конечного по высоте импульса.
Рис. 187. Составляющие спектральной
плотности к задаче 301.
Значение амплитуд гармоник (2) может быть также
найдено на основе преобразования Фурье от одиноч-
ного импульса высотой х и продолжительностью уТ.
Изображение Фурье для такого импульса равно
ут
Г I -Jp-layT
Fl Q®) = J xe~lat dt = x-——.
О
Модуль этого выражения
о- • <>>ут
2х sin -
<в
IF, (/со) | =
Амплитуда /г-й гармоники может быть
из формулы (4) для частоты coft подстановкой
(4)
получена
2л/г
03 — —^ - и
284- гл'- i. случайные процессы в лйиецйых-системах [зад
делением полученного значения на период следования Т:
I „ 1. 2лй \ I
л K V I х . .
Ak =--------~-----L = -г- sin /глу
Это выражение совпадает с (2).
Спектральная плотность случайной составляющей
может быть найдена из общего выражения для спект-
ральной плотности случайной величины
S(co)= lim 1 F (/со) |2,
Т0->®^0
которое в рассматриваемом случае превращается в вы-
ражение
S2(co) = у-1 А2(/со) |2,
Где F2(/<o) представляет собой изображение Фурье оди-
ночного импульса, среднеквадратичное значение которого
равно cs=Vx2 — x2. Аналогично формуле (4) можно
записать
1Л (/со) | =
О • аУТ
2g sin —~
со
(5)
• Отсюда- находим спектральную плотность случайной
составляющей
4с2 sin2 —
S2(co) ---------
2' ’ Та2
(6)
Подстановка численных значений дает
с , , 9000 si0,005<о
52(<о)=-----~2-----•
Спектр является непрерывным. Он изображен . па
рис. 187, б. По своей фо(>ме он подобен огибающей
линейчатого спектра, так как значения спектральной
плотности также пропорциональны квадрату модуля
изображения одиночного импульса (4).
302. Спектральная плотность скорости входного
сигнала следящей системы (рис.' 183) может быть
7.1. ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННЫХ .ФУНКЦИЙ . .285
представлена в виде 2TD '*
Ь'| (®) ~ j 4. ю2у2 ' (О
где Da = &ск — средний квадрат скорости. Момент на-
грузки на исполнительной оси постоянен по величине
Ш = Мн const), а знак его меняется вместе с изме-
нением знака скорости исполнительной оси. Считая
приближенно, что знак момента меняется вместе со зна-
ком входной скорости, определить корреляционную функ-
цию для момента нагрузки S2(a), а также взаимные
корреляционные функции для входной скорости и мо-
мента нагрузки S12(e>) и S2l(<o). Считается, что входная
скорость изменяется по закону с нормальным распре-
делением.
Решение. Спектральная плотность момента на-
грузки может быть получена из спектральной плотно-
сти скорости входного сигнала (1), если в ней заменить
средний квадрат скорости на средний квадрат мо-
мента M2 = Mh,
27-Aff,
S2(“) = т+«2Р ‘
Взаимную спектральную плотность можно подсчи-
тать по взаимной корреляционной функции, определяе-
мой как среднее по времени или среднее по множеству
/?12(т)=Нт— + = +
т->°° 27 J,
Вероятность нахождения Q(/ + r) wM(i) в одном интер-
вале (см. задачу 299) равна
I т I
г
а вероятность нахождения в разных интервалах
Р2=1-Р = 1-е ’
При нахождении скорости и момента в разных интер-
валах среднее от их произведения равно нулю. . ,
286 гл. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [303
При нахождении Q и М в одном интервале знак
момента равен знаку скорости. Произведение скорости
на момент будет при этом всегда положительным. При
этом, поскольку величина момента постоянна, момент
можно вынести из-под знака осреднения:
Q (/ + т) М (/) = Мн£ф + т) = МД,
где йс — среднее по модулю значение скорости. Для
нормального распределения
Gc = QcK]/ ~ =0,8QCK.
Таким образом, имеем взаимную корреляционную
функцию
I т| |Т [
=Щ2се г =0,8ЛЩ.ке т,. (2)
Спектральная плотность находится, как изображение
Фурье, из выражения (2):
с / ч 2ПИН£2С 1.67'AfHQcK
12 - 1+ю2Т2- • . • W
Аналогичным образом можно найти, что (т) = /?|2(т)
и S21 (со) = S12 (со).
§ 7.2. Прохождение случайного стационарного сигнала
через линейную систему
&
303. Система слежения за звездами состоит из фото-
элемента, безынерционного усилителя, фильтра (апери-
одического -звена первого порядка) и исполнительного
устройства в виде гироскопа или тахометрического при-
вода (идеального интегрирующего звена). Помеха на
выходе фотоэлемента может быть принята в виде белого
шума со спектральной плотностью S(co) = _/V. Показать,
что среднеквадратичное значение случайной ошибки
системы не зависит от постоянной времени фильтра.
Решение. Передаточная функция разомкнутой
системы имеет вид >
р(1+Тр) ’
s 72 ПРОХОЖДЕНИЕ С УЧАИНО О СИГМА
30-11 s '
где К [сек-1] “ добротность по скорости, Т — постоянная
времени фильтра.
• Передаточная функция замкнутой системы равна
- 1 + Г(р) Тр3 + р + К’
Спектральная плотность ошибки примет вид
Sg (И) = 1 ® (7®) Г (®) = | у (у(в)2+ /ш+/<|2 •
Интегрирование спектральной плотности ошибки по
всем частотам (см. приложение 17) дает средний квад-
рат ошибки
+ 00
Й2 1 f wd(0 - ММ
° — 2л J IТ + /® + К\2 2 -ZX/7V’
—оо
где эквивалентная полоса пропускания белого шума
Как видно из полученных выражений, среднеквад-
ратичная ошибка не зивисит от постоянной времени
фильтра.
304. Для системы слежения за звездами (см. пре-
дыдущую задачу) среднеквадратичное напряжение шума
фотоэлемента Йск = 6 в в полосе частот Af= 10000 гц-
(±5000 гц). Крутизна характеристики фотоэлемента
АфЭ=10 мв/угл. мин. Определить допустимое значение
общего коэффициента усиления (добротности по скоро-
сти Д), при котором среднеквадратичное значение слу-
чайной ошибки не будет превышать 1 угл. мин.
Решение. Представим напряжение шумов фото-
элемента в виде эквивалентного среднеквадратичного
углового сигнала на входе,
бек — — —-—т = 600 угл. мин.
кфЭ 10 10~3 •
вровень белого шума на входе
5П (со) = N = ~ = 36 (угл • мин)2!гц.
288 гл. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ ' {ЗОБ
В задаче 303 было определено, что среднеквадра-
тичное значение ошибки составляет
о = у -2-.
Отсюда находим значение общего коэффициента усиления
К < ~ = — = 0,055 сек'1.
305. Даны передаточные функции разомкнутой' си-
стемы регулирования с астатизмом первого порядка:
1) ^(р) = -^,
3) (Р) = -и Гт Лм Тт Y•
Р(1+ЛР)(1+Л>Р)
Вычислить эквивалентную полосу пропускания белого
шума замкнутой системы, если добротность по скоро-
сти составляет К — 10 сек-1, а постоянные времени
Ti = 0,l сек и Т2 = 0,05 сек.
Ответ.
К 10 -
Г) iV = '<r = T==5 Ч'
м К 10 к
2) Af = ^- = -2- = 5 гц,
= = ТГ 10-0,1 -0,05Т = 7,5 гц-
V rj + TiJ Л 0,1+0,05 )
306. Даны передаточные функции разомкнутой си-
стемы регулирования с астатизмом второго порядка:
W7 (д') — ЛО +ТР).
W W р2(1+?’Р)’
1)
2)
Вычислить эквивалентную полосу пропускания белого
шума замкнутой системы, если добротность по ускоре-
- § 7-2. ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА
289
НИЮ К — 10 саг2, а постоянные
и f = 0,5 сек.
Ответ.
., 1 + Кт2 1 + 10-12
1) Af = —2^ = -2-.Т" =
времени
5,5 гц.
т = 1 сек
*г 1 + Лт2 _ 1 + Ю-12 ,
2) Af— 2(т —Г) 2(1—0,5) 1 гц‘
307. На входе системы регулирования действует
помеха, имеющая спектральную плотность
5п(и) =
Определить коэффициент сглаживания системы, равный
отношению среднеквадратичного значения помехи па
входе к среднеквадратичному значению ошибки '
__ °п
А-сгл >
и среднеквадратичное значение ошибки а. Передаточная
функция разомкнутой системы .
Г(р) = |.
Численные значения коэффициентов:
/( = 0,5 сек-1, ап= 10, Тп = 0,1 сек.
» Ответ.
К™-/ 1 + Я7“/ '+^-Га-4Л
О = -^- = -^-=2,18.
, Ксгл 4,6
308. Решить предыдущую задачу, если передаточная
.функция разомкнутой системы
где Г, = 1 сек.
290 гл. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [80S
Ответ.
тг — т/ 7~п j 1 =, 0’1 । * —
Асгл у 1\ + Т„ КТп V 1 +0,1 0,5 -0,1
= /20Д' = 4,5,
о = -^- = -^-=2,22.
Кстл 4,5
309. На' входе следящей системы действует полез-
ный сигнал, скорость которого изменяется в соответ-
ствии с рис. 183. Спектральная плотность, записанная
для скорости, имеет вид
z.x 277)й
(со) | ю2^2 S
где Dq — QCK — дисперсия скорости. Среднеквадратичное
значение скорости QCK = 2 град/сек. Среднее время про-
должительности одного интервала Т — 1 сек. Определить
среднеквадратичную ошибку, если передаточная функ-
ция разомкнутой системы имеет вид
И7(р) =
’’ p(l + Tip)
Добротность по скорости составляет Д = 25 сек-1, а по-
стоянная времени Т = 0,05 сек.
Решение. Передаточная функция относительно
ошибки равна
го _________1____р (1 +7ip)
J 1 + Г(₽) 7\р* + р + К'
Спектральная плотность ошибки
о sa<°>) 2ТРй(1+о>2Т2)
Se(<o) |Ф(/<о)| щ2 (1 + со2Г) | Т! (/<0)2 +/(В + К р •
Приведем ее к виду, удобному для интегрирования (см.
приложение 17),
о ((Л = 9ТП _______________~ Т21 _________________
® I Т’Г, (у<о)3-+ (Г+-У,) -+(1 -+/</’) /<о-+/С р •
Интегрирование по всем частотам дает средний квадрат
ошибки
e2=27T>aZ3,
ЗЮ]
•§ 7.2. ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА
291
где интеграл
2я
[- 7'f (/«) + 1] da
| 77, (jco)8 + (T + Tt) (/co)2 + (1 + KT) ja + К I2 ’
в соответствии с приложением. 17 равен
г , .. , аой1Ь2
— a2bB + ---------
г_________:___________д3
*3 ~
2a0 («0^3 - ata2)
Значения коэффициентов:
Oo = TT i,
oi = 7' + 7'i,
g2=14-K7’,
o3 = K-
Ьо = О,
bt = - 7'ь
й2= 1>
В результате имеем
6,.-^
г_________аз ________________
J3 2 (а0а3 - a ta2) 2К (Т + Т, + КТ2) '
Окончательно
T + Tt + kt\
Оск
приближенное
ошибки
(1+0°05+2&и?г) = ^°’0068 =0°,082-5'.
выражение для среднеквадратичной
имеет вид
310.
помеха
На входе системы регулирования действует
с корреляционной функцией
/?п (т) = £>пе-411 т 1 (cos р? + j- sin р | т |j
292- ГЛ. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ (ЗИ
и спектральной плотностью
с / \ _ Г) Й Г 20 — со 20 + со ]
SnW 0 [ Ц2 + (СО-0)2 "g2 + (CO + 0)2 ]‘
Численные значения коэффициентов:
Z>u = = 100, р. = 0,4 се/с-1 и. 0=5 сек-1.
Определить коэффициент сглаживания, равный отноше-
нию среднеквадратичного значения помехи на входе
к среднеквадратичной ошибке на выходе системы
Д' — °п
Асгл »
и среднеквадратичную ошибку о. Передаточная функ-
ция разомкнутой системы
Г (/>) = -£,
где добротность системы по скорости К = 0,1 сек-1.
Ответ. Коэффициент сглаживания
м = 02 4- и2 =
С" 1/. , 2нФг + И*) 2И2 ,
1 V . р2К р2
52 + 0,42
=--------, . . - < = 16,7.
5 011/1 I 2'0-4(5г'Ь0’42) 2'0’48
5-0,1 4 52 ,од 52
Среднеквадратичная ошибка
СУп Ю Аг1
о = = -7^=- = 0,6.
Ксгл ‘ 6,7
311. Для аппроксимации корреляционной функции
предыдущей задачи используются две формулы:
/? (т) = De"*11 х 1 cos 0т, (1)
R (т) = £)е-ц 1 т 1 (cos рт + sin 01 т |). (2)
Этим корреляционным функциям соответствуют спек-
тральные плотности:
S121 § 7.2. ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА 293
для формулы (1)
S (со) = [ g2 + (w _ 0)2 + g2 + (Ш + 0)2 ] > (3)
для формулы (2)
S(co)~ р D [ и2 + (с)_р)г + И2 + (ю + 0)2 ]• (4)
Определить дисперсию скорости для формул (1) и (2),
. Ответ. 1) Dfl->oo; 2) Da = (|Д + ₽2)D.
312. На вход системы с передаточной функцией
О, (1)
в момент времени t — 0 поступает случайный центриро-
ванный стационарный сигнал с корреляционной функцией
/?1(т) = О1е^И|. (2)
Определить изменение дисперсии выходной величины
во времени £>2 (/), а также дисперсию выходной вели-
чины в установившемся режиме.
Исходные данные: К =10, 7=10 сек, == 1 и
р = 0,05 сек-1.
Решение. Значение дисперсии на выходе может
быть определено по формуле
t t
D2{t) = [ w (s) ds J w (ц) /?j (i) - s) dr\, (3)
о о
где w (s) и w (Y|) представляют собой функцию веса
системы w (t) при замене t = s и t = тр
Для передаточной функции (1) функция веса будет
w (0 = где а = Т~1 (см. приложение 1). Следо-
вательно,
t t "
£*2 (0 = [ e-as ds J I 1 dr\ =
'о о
e~asds
е-<Ч1е+В(Л-Й4/Г] +
• (4)
294 Гл. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [312
Вычисление интегралов дает при а =/= ц
S
Г — е~№
Г = e-o»ieiHn-s) ±1-----------
1 J 1 р —а ’
о
t
/2 = е-“’1е-вс<1^)^т1 = ~---,
J * а + р
S
t
D, = | e~as (Ц + /2) ds =
0
, n Г 1 p~2at 9p-(a+H)M
= тЗГ7т+т------------T - t 2T2 • (5)
Ll+gr I —pr 1— p27J ' '
В установившемся режиме
n i \ z<2£*i lr\
^(°°)==т+^- (6)
Формула (6) может быть получена также из спек-
тральной плотности входного сигнала
4-00 4-00
$[(«>) = j 7?1(т)е-/“-(1/т= j
— оо — оо
Спектральная плотность выходного сигнала
S2 (о) = | W (/со) |2 S, (со) = -ттгт ^тУ!---^ •
' ’ 1 v ’1 *' ' |(1 +jwT) (p + yw) I2
Интегрирование спектральной плотности S2(co) по
всем частотам дает
4-оо 4~оо
, ч 1 Г о / ч , 1 Г 2№р£>] da
D2(°°) 2„ J S2(c0)rf(0- 2я J |Г(/<й)2 + (1+р7’)рй + и|2 •
— ОО —оо
В соответствии с приложением 17 получаем
При Подстановке числовых значений получаем
D2(t) = 66 + 200е-°-2/ - 266е-°-15/,
7)2(ОО) = 66.
§ 7.3. ОПТИМАЛЬНЫЕ СИСТЕМЫ
295
8141
313. Решить предыдущую задачу, если передаточная
функция системы соответствует идеальному интегри-
рующему звену с передаточной функцией
Г(Р)=^,
где Ki = 0,l сек"1.
Ответ.
DM) = 2K?Di R - = 0,4/ - 8 (1 - в"®-®),
L р Р J
Z)2(oo)—> об.
§ 7.3. Оптимальные системы
314. Передаточная функция ' разомкнутой системы
регулирования имеет вид
W(p) = ^^,
где /С = 100 сек"2 —общий коэффициент усиления разом-
кнутой цепи, ат — постоянная времени корректирующего
устройства. На входе системы действует полезный ре-
bt2
гулярный сигнал вида g = at + —^~, где а = 100 град!сек
и 6=10 град]сек2, и помеха, представляющая собой
белый шум со спектральной плотностью Sn(a>) = .ZV =
= 0,2 град21гц. Определить значение постоянной времени
корректирующего устройства, соответствующее мини-
муму среднеквадратичной ошибки в установившемся
режиме, а также значение среднеквадратичной ошибки.
Решение. Установившееся значение ошибки от
полезного сигнала
хс = (^g + Ц- g = с, (а + bt) + -j-
где Cj и с2 — коэффициенты ошибки. На основании раз-
ложения передаточной функции относительно ошибки
Фх = 1 + (р) = р2 + Ктр+Л
(; ГЛ 7ЛУЧАПНЫ ПРОЦЕССЫ В Л 411 ИНЫХ ИС'-Н'МАХДН
в степенной ряд имеем С[ = 0 и "fr —"д - В результате
регулярная составляющая ошибки
Хс К
ИЛИ
(О
9__ ft2
хс~ /(г •
Средний квадрат случайной ошибки (см. приложение 17)
равен
4- оо
i / I ф <>) I2 АМ(0 ==
K2N.
2л
[— т2 (/га) + 1] do __ (l+/<r2)/V
(/w)2.+ /(t/<0+ К|2 “ 2т ’
а средний квадрат, суммарной ошибки
7г,- .-9 , 72 , (1+^)У
X Лс -Г Лп — -г 2т
Для отыскания минимума последнего выражения
приравняем • нулю первую производную по постоянной
времени корректирующего устройства
2Кт2-(1 +/vt2) = 0,
откуда получаем
т = —— = —=- = 0,1 сек.
I К I 10:)
Среднеквадратичная ошибка определяется из (3):
v = -,/JPl + _1+1«010Л . 0 2 = 1° 41
А<к V НЮ2 + 2-0,1 ’ 1 ’ ’
315. Решить предыдущую задачу, если передаточная
функция разомкнутой системы имеет вид
IV// х К(1+т/0
ру+тР),
где Д’ *= 100 сек'2 и Т = 0,05 сек. '. .
зп| § 7.3 ОПТИМАЛЬНЫЕ СИСТЕМЫ 297
Ответ. :
т= т + "\/т2 + -^ = 0,05 + 1/0705^+0,01 = 0,16 сек.
Среднеквадратичная ошибка
Г ьг , (1+/(T2)2V
Хек = У /<2 + 2 (т - Г)
= 1 / |(Я (1 + Ю°-».162)-0,2? _ , □ о.
У 1002 + 2(0,16-0,05)
316. Решить задачу 314 в предположении, что можно
изменять как значение постоянной времени корректи-
рующего устройства т, так и общий коэффициент уси-
ления /(.
Решение. Дифференцируя выражение (3) в за-
даче 314 по т и по /С и приравнивая частные произвол--
ные нулю, получаем
’=+ “>
-т^ + т-°- <2»
Подставляя (1) в (2) и решая последнее уравнение,
имеем
/<опт=]ХСеК-
Постоянная времени корректирующего звена
т = ZL = = 0,218 сек.
1'К /21
Среднеквадратичная ошибка определяется из (3) за-
дачи 314,
_ 1 / 1()2 (1 + 21 • 0.2188) 0,2 = < о П7
Хек — у 212 + 2-0,218 ’
317. Передаточная функция разомкнутой системы
регулирования имеет вид
298 ГЛ. 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ [317
где /С — общий коэффициент усиления, а Т\ — постоян-
ная времени. Передаточная функция замкнутой системы
равна
1 + Г(р) т^ + р + к
На входе системы действуют помеха в виде белого
шума со спектральной плотностью 5П(«>)==М и полезный
сигнал со спектральной плотностью
Sc( } 1+<о27'2"
Между помехой и полезным сигналом отсутствует кор-
реляция. Исходные данные: 7\ — 0,1 сек, Тс = 20 сек, D =
= 100 град2 и N = 0,01 град2)гц. Определить оптимальное
значение общего коэффициента усиления /<0ПТ) соответ-
ствующее минимуму среднеквадратичной ошибки, и
среднеквадратичную ошибку при К — Кот-
Решение. Составляющая среднего квадрата ошибки,
определяемая помехой (см. приложение 17), равна
+ оо
fl2_ 1 f №WAo _ KN
п 2п J ITHjo^ + jco + KP 2 ' Ш
Составляющая среднего квадрата ошибки, опреде-
ляемая полезным сигналом на входе (см.'приложение 17),
4-сю
fl2 1 f w2(l+w2Tf) 2TCD j
c 2л J | T, (j®)2 + y® + К I2 1 + ^r2
— CO c
4- DO
or n 1 f ________________________[ri - (fo)2] d(S>_____________________=
^^’23 J | TtTc (y®)3 + (Г, + Tc) (j®)2 + (1 + KTc) j<i> + K I2
— oo
D Tt + Tc + KTtTc
ту + тс + кт2
Результирующий средний квадрат ошибки
е2 = 0п + е^=4'- + £»
<2
Tt + Tc + KTJ-'
Т! + тс+кт2
(2)
(3)
3181
.§ 7.3. ОПТИМАЛЬНЫЕ СИСТЕМЫ
299
При минимизации среднеквадратичной ошибки необ-
ходимо приравнять нулю производную от последнего
выражения по коэффициенту усиления. В результате
имеем
N РТС(Т^Т1) р
2 (Г1 + Гс + К7’2)2
Решение последнего уравнения дает оптимальное зне
чение коэффициента усиления
_ Г2Д(Г2-Г2) Гс + Г,
Аонт у NT3 Т2
Определяем численное значение оптимального коэффи-
циента усиления
Г 2-100 (20*-0,1*) _ 20 + 0,1 ~ чо ,
А опт у 0 01 • 203 202 *
Среднеквадратичная ошибка на основе (3) равна
о -1 /30-0,01 , inn 0,1+20.+30-0,1-20 _ По Q
Иск у 2 -+юи 0,1 +20 + 30-20* U ,У'
318. Для предыдущей задачи определить передаточ-
ную функцию системы регулирования, соответствующую
теоретическому минимуму среднеквадратичной ошибки,
и определить значение последней.
Решение. При условии физической реализуемости
системы регулирования искомая частотная передаточная
функция замкнутой системы может быть представлена
в виде
m
Знаменатель (1) определяется из равенства
Ф (/“) ф" (jo) = Sc (а) + Sn (со), (2)
где ф*(/<в) является комплексно сопряженной -ф (/со).
Для нашего случая
о / х „ , 27CD + ?V(1+<о2Г2)
300гл 7. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ СИСТЕМАХ fW
Разложим последнее выражение на комплексно сопря-
женные множители
2T,D + N (1 + со2?2) _ (1+jac»)(l-/асо) г
1 + со2?2 (1 + /?ссо) (1 - /?ссо) '
Отсюда имеем
(3)
где
Далее находим выражение
Sc (w) = 2?СД(1 ~ j?cCo)_= 2?с£> _________1________
ф* (со) (1 + со2?2) \гА (1 — /асо) V Л (1 + /?ссо) (Г — /асо)
Р'азложим последнее выражение иа простые дроби
Sc (со) = 2?СО Г Тс , 1 а 1 1
“ф* (/со) VА L?c + a 1 +/7’сСО ?с + а 1—jacoj
Функция В (/со) определяется членами разложения, соот-
ветствующими полюсам Sc(со), лежащим в верхней
полуплоскости. В результате имеем
D/. . 2?СО ?с 1 /Г\
В = 17Т Т~,— Т~: -т • - (5)
\ /1 7 с 4- ci 1 4~ j7 fCO
Искомая частотная передаточная функция замкну-
той системы (1) равна
ф (/со) = -№- = —с° —Is___________! (6)
ф (;со) А Тс + а 1 + joco •
Определяем численные значения коэффициентов
« = ? С ]/" 2TCD + N = 20 2 • 20 • 100 + 0,01 = 0,032 СеК'
2Г2О 2Г2£» 2Г2О
...ь ____ V ____ С _______ |
. , A[Tc + d)~ (2TcD + N)(Te +a) 2T2fi
Окончательное . выражение для передаточной функции
3181
$ 7.3. .ОПТИМАЛЬНЫЕ СИСТЕМЫ
301
замкнутой 'системы примет вид
®w—гт?>. т
где Т = 0,032 сек. Этой передаточной функции соответ-
ствует передаточная функция разомкнутой системы
W W 1 - Ф (р) Гр ~ р ’ *8>
где К = 4- = 31 сект' — общий коэффициент усиления ра-
зомкнутой системы (добротность по скорости).
Передаточная функция относительно ошибки
Фе(р)=1-Ф(р) = -Г1£_. (9)
Спектральная плотность ошибки.
«»(<») = I фо U®) I2 Sc (®) +1Ф (j®) I2 хп (®) =
7’2соа ‘2ТСР
1 + и2Г2 I 4- со2/2
1 2 Г К. (1ft)
1 + ю2Г2 ' 7
Интегрирование (10) по всем частотам дает средний
квадрат ошибки
+ оо ,
J S.W<to-7^r+4. (Н>
Среднеквадратичная ошибка равна
й ,/ ID . N ,/ 0,032-100 " (Ё01 nOR„
е«= Г ТёТг + 2f = -2(ГГоЖ + тщЖ = 0’56-
ГЛАВА 8
СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
§ 8.1. Построение переходных процессов
319. Определить весовую функцию системы, движе-
ние которой описывается дифференциальным уравнением
a0~ + ($ + bi)x = f(t), (1)
где с0 = 1 сек, = 0,5 и b = 0,2 сек-1, при поступлении
на вход единичной 6-функции = — й) в произ-
вольный момент t = &. Начальное условие х = 0 при t — 0.
Решение. В выражении (1) сделаем подстановку
f (/) = 6 (t — &) и разделим все члены на а0,
I
dx а® + b (t) 60-е)
—тт- 4--:----х =-------• (2) .
• dt а0 а0
или
-g- + P(i)x = Q(<). (3)
Далее находим
= Л (/ _ ^) + (/2 _ е2) = а(1 — &) + р (Р- П
«0 ^а0
§ 8.1. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ 303
Весовая функция
t
WU-O. е)=^” J
О
t
_ e-a («-»)-₽ j . e+a «-»)+₽ (f’-O2) dt. (4)
J «0
При вычислении последнего интервала необходимо
воспользоваться известным свойством б-функции
+ оо
— со
Тогда из формулы (4) имеем
w (t - О, &) = — е"“ <'-<»-₽ . (5)
«0
Подстановка числовых значений дает
w(t-&,&) = е"0-5 <*2-&2>. (6)
320. Для весовой функции предыдущей задачи по-
строить графики:
1) нормальной весовой функции при О'= 2 Сек в виде
w (t — О, О) и в виде w (т, О), где т = t — О,
2) сопряженной весовой функции при £ = 5 сек
в виде w (t — О, О), т. е. в зависимости от смещения О,
и в виде w (0, t — 0), где 0 = t — О — реверс-смещение.
Ответ. 1) Нормальная весовая функция
w(t — О, 0) = g-0,5 (f-2)-o,i (/=-4) ПрИ /^0 = 2 сек.
График изображен на рис. 188, а. Переход к времени
т = t — 0 дает
W (т, О) = g-0.5T-0,lT (г+20) _ g-0,9T-0,lrJ jjpjj -j Q,
График изображен на рис. 188, б.
2) Сопряженная весовая функция
W (t — О, О) = О~и’5 <5-0)-0,l (25-02) _ е0,5 (9--5)+0,1 (Ог-25)
при О t — 5 сек.
304
ГЛ. 8. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[321
График изображен на рис. 188, в.
Переход к реверс-смещению 0 = t — 0 = 5 — & дает
w (0, t — 6) — g-ose+o.' б2 при 0>О.
График изображен на рис. 188, а.
321. Методом последовательных приближений по-
строить переходный процесс в системе, описываемой
дифференциальным уравнением
z/2 у Л у
a0-^2- + ai(t)-^- + anX=-g(t) (I)
при поступлении на вход в момент времени / = О = 1 сек
ступенчатой функции g(t) = gol (t — О). Значения коэф-
фициентов: Со==1 сек2, а{ (t) = (0,9 + 0, 1/) сек, с2 = 0,16
и g0= 1>6. Начальные условия нулевые.
Решение. Замораживаем переменный коэффициент
дифференциального уравнения (1) в момент времени
/ = 0=1 сек. В.результате получаем ах (0) = а°-|- 0,1 = 1 сек.
~ § .8.1 ПОСТРОЕНИЕ ПЕРЕХОДНЫХ- ПР Ц ССОВТад
8г1‘
Уравнение (1) записываем в виде
Go-S' + a<W-S- + Q2X==SrW-O’|T-^- <2)
Первое приближение находится из дифференциаль-
ного уравнения
ас + а‘ + Q2'V| = $)
т = t — &.
Используя преобразование Лапласа, находим изо-
бражение искомой величины
, , = G (р) 1,6 =
1 ? aQp2 + fl] (О') р + я2 р(р2 + р + 0,1б)
_ 1,6_= 10 _ 13,3 3,3
р (р + 0,8) (р + 0,2) р р + 0,2 р + 0,8 '
Переход к оригиналу (см. приложение 1) дает.
х, (т)= 10(1 - 1,33е~°-2х + 0,ЗЗе-°-8т).
Поправка х2(т) находится в результате решения
уравнения
»»-$- +«.(»)> +«V,-----------0,1т^. (4)
Подстановка в (4) числовых значений коэффициентов,
а также найденного первого приближения дает
+ dx^ + 0,16 V2 = 0 027т (e_0>8t _ е^2ху
CLv tlv
Изображение искомой поправки
X =_______0.027 Г 1_____________1 1 =
2; р2 + р + 0,16 L (р + 0,8)2 (р + 0,2)2 J
= 0,027_______________0,027
(р + 0,8)3(р + 0,2) (р+-0,2)3 (р + 0,8) • V ’
Переход к оригиналу можно сделать, воспользовав-
шись интегралом’ свертки. Для этого запишем оригиналы
306 гл. 8. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ [322
следующих изображений:
1 —1 Л-0.8Т
р + 0,8
1 =1 р-0,2т
р + 0,2 • ’
1 =1 21 л-0,8т
(р + 0,8)3 ’ 2
Интеграл свертки
Г т?
х2(т) = 0,027 I • е-0>2 dtj —
о
(\2
- 0,027 ~ е-°>эт‘ • е~°>8 dr, =
о
Гт2 Г 2
= 0,027 J е-°^-°-2х dx1 - 0,027 J е°.6ч-о.8т dT1.
о о
Вычисление интегралов дает
х2 (т) = 0,075 [е~°’2т (т - 0,3т2)— e-°-8i: (т + 0,3т2)].
Таким образом, второе приближение дает
х(т) = л, (т) + х2 (т) = 10 (1 - 1,ЗЗе-°-2т + 0,ЗЗе-°-8т) +
+ 0,075 [е"°*2т (т - 0,3т2) - е-°-8т(т + 0,3т2)].
Сравнение х2(т) и %i(t) показывает, что вычисление
следующей поправки л3(т) не является необходимым.
322. Параметрическая передаточная функция замкну-
той системы регулирования имеет вид
Ф (р, t) = —Т—Атт—• (1)
м ' р + а + bt + ct2 '
Определить переходную функцию системы при посту-
плении входного воздействия g(Z) = gol(O-
в 8.1. ПОСТРОЕНИЕ ПЕРЕ ОДНИ ПРОН С1В 307
32*>J J
Решение. Изображение по Лапласу входной вели-
чины
G(p) = ^-.
Изображение выходной величины равно
у (р t) = Ф (р, 0 • G (р) = -,-т "Ть-ь m • (2)
Зафиксировав в выражении (2) время t — const, на
основании приложения 1 находим оригинал,
У (0 = - 11 - e-(a+w+c/!)q.
. » \ / а 4. bt 4. ct2 1 1
323. Построить графическим путем переходный про-
цесс в системе, описываемой дифференциальным урав-
нением
. ao(O-^- + aiX = fj(x). (I)
-График изменения входного воздействия /,(/) изо
бражен на рис. 189, а. График изменения коэффициента
Рис. 189. Графики к задаче 323.
о0(/) дан на рис. 189, б. Коэффициент at = 2. Начальное
значение х = х0 = 1,5 при t — Q.
Решение. Все члены уравнения (1) разделим на alt
T{t)^ + x = f(t). (2)
Здесь
= И /(0 = -^.
ЗОЯ
ГЛ. в. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
133»
При решении уравнения (2) графическим путем «по-
стоянную» времени Т (/) считаем постоянной на интер-
вале t, t + 'M и равной 7’(^ + 4г)' Ф°РмУла Для реше-
ния в этом случае имеет вид
Рис. 140. Построение переходного процесса к за-
даче 323.
А/ = 0,5 сек. Из точки Е кривой / (/), взятой в середине
первого интервала А/, откладываем по горизонтали от-
резок ЕМ == Т , величина которого берется равной
ординате точки Н кривой Т (t), т. е. тоже в середине
первого интервала А/. Полученная точка М соединяется
прямой линией с заданной начальной точкой процесса А.
В результате получается 'новая точка В искомой кри-
вой х(4). Аналогично берется ордината точки /, отклады-
вается в виде отрезка FN и проводится прямая NB,
дающая новую точку С решения х(1) и т. д.
324Г-'
§ Й2 ОЦГНКА УСТОЙЧИВОСТИ РРГУЛИ В 1ИЯД)
§ 8.2.
Оценка устойчивости и качества регулирования
324. Система регулирования описывается дифферен-
циальным уравнением
а0^- + Щ^ + ^)^- + азУ = Ь^(1). (I)
Значения коэффициентов: ао = О,1 сек3, а{ ~ 4,2 сек2,
а (/) = (72 — 0,10 сек, а3 = 400 и Ьо = 400. Оценить при-
ближенно устойчивость системы, если время работы ее
у — 100 сек.
Решение. Рассмотрим систему с замороженными
коэффициентами при / = 0 и при t — T — 100 сек. В этих
случаях характеристическое уравнение, соответствующее
исходному дифференциальному уравнению (1), будет
0,1р3 + 4,2р2 + 72р + 400 = 0, (2)
0,1р3 + 4,2р2 + 62р + 400 = 0. (3)
Для уравнения (2) находим корни: р1 = 10 сек-1,
р2_3 = ( —16 ± j 12) сек-1. Степень устойчивости ц = | pt j =
= 10 сек-1. Время переходного процесса /п~Зц-1 = 0,3 сек.
Для уравнения (3) корни равны pt = — 25 сек-1,
Р2-з = (~ 8,8 ±/8,7) сек-1. Степень устойчивости т) =
= 8,8 сек-1. Время переходного процесса /п<Зт]-1 =
= 0,34 сек.
За время переходного процесса коэффициент а2(0
изменяется на величину А<22'а0,1 -0,34 = 0,034, что со-
ставляет приблизительно 0,05%. Следовательно, система
может рассматриваться как квазистационарная. Оценка
устойчивости может быть сделана по замороженным
коэффициентам характеристического уравнения. При-
меняя критерий Гурвица, имеем
ata2 (0 > с0с3.
Подстановка числовых значений дает
4,2 (72-0,10 >40.
Последнее неравенство выполняется при любом вре-
мени, лежащем в пределах 0^/^ 100 сек. Следова-
тельно, система устойчива.
310
ГЛ'. 8. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
(3?5.
325. Дана весовая функция квазистационарной си-
стемы
w (/-&, &) = е~а
где б'о = 20 сек, а = 5 сект2, t — текущее время, отсчиты-
ваемое от момента включения системы, О' —момент по-
ступления входного импульса. Определить устойчивость
системы.
Ответ. Нормальная весовая функция затухает и
система является устойчивой в пределах времени
0^^<0о = 20 сек. При />Оо любое малое возмущение
на входе может вызвать неограниченное возрастание
выходной величины.
326. Параметрическая передаточная функция зам-
кнутой системы имеет вид
ф(р, 0 = Атп—72 >
’ p + a + bt + ct2
(1)
где а =10 сек-1, b = 0,1 сек~2 и с = 0,01 сек~3. Опре-
делить коэффициенты ошибки с0(/), сДО и с2(0-
Решение. Находим передаточную функцию зам-
кнутой системы относительно ошибки:
ЧД(Р, 0 = 1 -Ф(р, 0 = • (2)
/ p + a + b/ + ct2
Разлагая последнее выражение в ряд по степени опера-
тора р, получаем
ml л w + c*2 I ар ар2 *
WxVP. О- a + bt + ct2 + (a + bt + ct2)2 (a + bt + ci2)3 • • •
Отсюда "можно определить коэффициенты ошибки
... bt + ci2 _ 0,И+ 0,01/* -
C°'l) a + bt + ct2 10 + 0,k+0,01/2 ’
r if\ _ a_____________ ._____12_______
IV7 (a + bt + ct2)2 (10 + 0,lf + 0,0U2)2 ’
c2(i) _ a 10
2 - (а+Ы + ct2)3 ~ (10+0,k + 0,0ir2)3 ’
327. Объект регулирования совместно с исполни-
тельным органом описывается дифференциальным
V$ 8.2. ОЦЕНКА УСТОЙЧИВОСТИ РЕГУЛИРОВАНИЯ 31!
уравнением
^-(b0+b^x(t), (1)
где р — регулируемая величина, х = g — у — ошибка,
а — входное воздействие,. &0= 100 сект2 и 6, = 0,1 сек-3.
Считая систему квазистационарной, определить необхо-
димые корректирующие устройства, чтобы в пределах
времени работы системы 1000 сек замкнутая си-
стема имела бы показатель колебательности, не превы-
шающий значения Af = l,5.
Задачу решить методом замораживания коэффи-
циентов.
Решение. Передаточная функция исходной разом-
кнутой системы с замороженным коэффициентом равна
= (2)
Л. а, х. представляет собой прямую с наклоном
— 40_йб/дек (рис. 191). Базовая частота л. а. х. <оо=}'Х
Рис. 191. Л. а. х. к задаче 327.
Использовав л. а. х. типа
ие 19), получаем желаемую
разомкнутой системы
2—1 — 2 (см.
передаточную
приложе-
функцию
(р) =
К(1 + Т2р)
р2(1 + гзр)
312
ГЛ. 8. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
Постоянные времени равны
т = 1 1/"
2 а>о г Л-1 — 1 ’
г _ 7'2(7И—1) = 1 J<M(M-1)
2з М+.1 ®в М+1
Передаточная функция корректирующего звена вы-
ражается в виде
W7 (п\__
Г„(р) ~ 1 + 7'3р •
Подстановка исходных значений дает требуемые за-
коны изменения постоянных времени
= ]/ loo + o.ii! ’
= IУ 100 + 0,11 •
При t = 0 значения постоянных времени 7% = 0,173 сек
и 7,3 = 0,0346 сек. При /=1000 сек, 7’2 = б,123 сек и
7’з = 0,0246 сек.
328. Определить передаточную функцию объекта со-
вместно с исполнительным органом по данным преды-
дущей задачи методом замороженных реакций.
Решение.
1. Замораживание весовой функции.
. В уравнении (1) предыдущей задачи необходимо по-
ложить х (t) = д(/ — й). ’
Тогда
t
]'(&0+&1/)6(/-й)1//=/>0 + ЛА (1)
! i
(t — й, й) = J (b0 + bi'b) dt =
= (bo+bi^)K-«) = (&o + M)t- &
Зафиксировав в последнем выражении & = Од = const,
получаем ®0(т) = (&0+Переход к передаточной
,32ft( § 3.2. ОПЁНКА УСТОЙЧИВОСТИ РЕГУЛИРОВАНИЯ 313
функции объекта дает
Г0(р) = L [(&0 + Мо) т] = ". (3)
Эта передаточная функция совпадает с полученным
в задаче 327 выражением (2). Поэтому использование
замороженной весовой функции в данном случае не дает
ничего ,нового по сравнению с методом замороженных
коэффициентов.
2. Замораживание переходной функции.
' В выражении (1) задачи 327 положим х (0 = 1 (t — О).
Тогда, положив t — -& = т, имеем
' . -ч .. т
= j [i0 + bi (О + т)] I (г) ch = &от + /?,Йт + , ’(4)
О
т
у = h0 (/ — &, &) = [ ^от + +.Лр-) ch =
о
__ М* , Мт2 6.,т3
- — + —+ V (5)
Зафиксировав смещение fl =4% = const, получаем за-
£} -^2 Jy 0. ^2
мороженную переходную функцию /?п (т) = Ч—Ну—I-
Ь т3
Ч—g-. Продифференцировав ее' по т, получаем замо-
Ь т2
рожениую весовую функцию ы>0(т) = (i0 + ift%) т Ч—
Передаточная функция объекта
= L [((?0 + | =
*о 4-6,0о , /’| 6,(1Ч-7'ор) /(Л
=----------. (6)
где То = —меняется в пределах от 1000 сек при
^0 = 0 до 2000 сек при Т>0 = 1П00 сек.
ГЛАВА 9
СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ
И С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
§9.1. Системы с временным запаздыванием
329. Структурная схема автоматической системы
имеет вид, показанный на рис. 192. Определить, при
какой величине общего коэффициента усиления разом-
кнутой системы К = k}k2 замкнутая система устойчива
при любых значениях по-
—^У
стоянной'времени Т и вре-
мени запаздывания т.
Ответ. К 1.
330. Для системы авто-
матического ' управления,
структурная схема кото-
Рис. 192. Структурная схема
к задачам 329 и 330.
рой показана на рис. 192, определить критическое время
запаздывания тк. Общий коэффициент усиления разом-
кнутой системы К. = Постоянная времени Т = 0,5 сек.
Решение. Частотная передаточная функция разом-
кнутой системы равна
где 7( = kik2.
Частоту среза юс, при которой а. ф. х. разомкнутой
системы пересекает окружность единичного радиуса, най-
дем из условия
|Г(/Ъс)|=1. 0)
Из уравнения (1) получим
£0с -г •
~ к <9.1. СИСТЕМЫ С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ 815
833J •»
Критическое время запаздывания тк найдем из усло-
вия равенства фазовой частотной характеристики разом-
кнутой системы при частоте <о = <ос величине —л
ф (®с)= — arctg <ос7 — <встк = — л.
Из последнего уравнения находим
л - arctg <*Т л-arctg/№-1 Л1О
Тк = --------------------------Т - 0,18 сек.
331. Передаточная функция разомкнутой системы
автоматического управления имеет вид
где К = 20 сек-1 — общий коэффициент .усиления разом-
кнутой системы, 7 = 0,1 сек — постоянная времени. По-
следовательно в канал управления включается звено
чистого запаздывания, имеющее передаточную функ-
цию е~1р, где т —время запаздывания. Требуется найти
Критическое время запаздывания тк, при котором зам-'
кнутая система автоматического управления находится
на границе устойчивости, и частоту незатухающих коле-
баний <ок.
Ответ, -©к =12,5 сек-1, тк = 0,11 сек.
332. Решить предыдущую задачу, если постоянная
времени 7 = 0.
4 Ответ. <ок = 20 сек~\ тк = 0,78 сек.
333. Передаточная функция разомкнутой системы
имеет вид
1V7/ Ч Ке~ХР
W (Р) =-. .г Ч .
р(1 + Г,р)(1 + Г2р)
С помощью логарифмических частотных характе-
ристик определить критическое время запаздывания тк,
если коэффициент усиления разомкнутой системы
/( = 30 сек-1, постоянные времени. 7t = 0,025 сек и 72 =
== 0,2 сек.
Решение. Асимптотическая л. .а. х. системы при-
ведена на рис. 193. Частота среза разомкнутой системы
316
ГЛ. 9. СИСТЕМЫ С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ
I3SV
<ос = 12,6 сект'. Фазовая частотная характеристика при
частоте со = сос и критическом времени запаздывания тк
Рис. 193. Асимптотическая л. а. х. к задаче 333.
должна пересекать линию "ф= — л. Поэтому
•ф (<ос) = — у — arctg асТ! — arctg асТ 2 — состк = — л.
Отсюда находим
arctg юс7’1-arctg сосЛг .
тк --------------------------= 4,8 • 10-2 сек.
к <ос
334. Определить критическое время запаздывания тк
системы, структурная схема которой приведена на
Рис. 194. Структурная схема к задаче 334.
рис. 194. Общий коэффициент усиления разомкнутой
системы К. = /г^Лз = 5, постоянные времени апериоди-
чёских звеньев = 5 сек и Г2 = 0,4 сек-
Ответ. тк=1,4 сек.
3351 § 9.1. СИСТР^Ы С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ 317
335. Передаточная функция разомкнутой системы
имеет вид
^0(/?) = —Л J. Т2 2Х .
и ' ’ р (1 + Т2р2)
где К = 2 сек-1, Т = 0,1 сек. Для достижения устойчи-
вости системы последовательно в канал управления
вводится звено чистого запаздывания с передаточной
функцией е-тр. Определить, при каких значениях вре-
мени запаздывания т замкнутая система устойчива.
Решение. Результирующая передаточная функция
разомкнутой системы W(р) = W0(p) е~^> = 2) .
Асимптотическая л. а. х. системы приведена на
рис. 195. Замкнутая система будет устойчивой, если
2 7 Тк mln
Рис. 195. Асимптотическая л. а. х. и л. ф. х. к задаче 335.
л. ф. х. пересекает линию ф = — л в диапазоне частот
К + у. Критические значения времени запаздывания тк
находим из следующих уравнений:
2 А^тах= ГС,
Отсюда
Тк max “ 2Д' ” 0,79 сек,
Замкнутая система'.устойчива, если выполняется сле-
дующее неравенство: 0,16 се?с<т<0,79 сек.
т,( min = тг Т = 0,16 сек.
318
ГЛ. 9. СИСТЕМЫ С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ
1336
336. Передаточная функция разомкнутой системы
имеет вид'
ivy/ х ^е~Тр
(Р) т2 2 ,т , , >
Т%> z+7’1p+1
где К — 0,5, Т2 — 1 сек2, Т[ = 0,25 сек.
Определить устойчивость замкнутой системы при сле-
дующих значениях времени запаздывания т: а) т = 0;
б) т = 0,3 сек’, в) т = 2 сек’, г) г = 5 сек.
Ответ: а) Система устойчива; б) система устойчива;
в) система неустойчива; г) система устойчива.
337. Структурная схема автоматической системы при-
ведена на рис. 196. Коэффициенты передачи звеньев
соответственно равны = 1 сек-1, k2 = 0,125, fe3=l. По-
стоянная времени Т — 2 сек. Время запаздывания
Рис. 196. Структурная схема к задаче 337.
т = 0,2 сек. Определить устойчивость системы по крите-
рию Найквиста. Размыкание системы произвести в точке х
(см. рис. 196).
Ответ. Система устойчива.
338. Передаточная функция' разомкнутой системы
с запаздыванием имеет вид
Г(р) =
ка + ^р)
Р2(1 + Т2р)
е~хр,
где 7’1 = 0,5 сек, Т2 = 0,2 сек, т = 0,3 сек.
Определить значения общего коэффициента усиления
разомкнутой системы К, при которых замкнутая система
устойчива. 1
Решение. Фазовая частотная характеристика си-
стемы определяется следующим выражением:
ф (со) =—180°-f-arctg <в7’1 — arctg соТ’г ~ сот, (1)
39fl § 9I- СИСТЕМЫ c ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ 319
приведена на рис. 197. Замкнутая система устойчива,
если л а. х. пересекает линию L = 0 левее точки пере-
сечения ф(<о) линии ф=-^ 180°. В критическом случае
л а х. пересекает линию L = 0 на частоте <о_л. Прово-
дим' асимптотическую л. а. х. так, чтобы она пересекла
Рис. 197. Асимптотическая л. а. х.
и л. ф. х. к задаче 338.
линию £ = 0 на частоте ®_я. Точка пересечения низко-
частотной асимптоты л. а. х. с осью частот равна
УКк = 3,5 сек-1. Отсюда находим, что /Ск=3,52= 12,2 сек-2.
Асимптотическая л. а. х. в точке излома примерно на
3 дб отличается от действительной л. а. х. Поэтому окон-
чательно получаем /Ск = }^2 • 12,2= 17 сек-2. Замкнутая
система устойчива при 0<К<17 сек-2.
339. Передаточная функция, разомкнутой 'системы
имеет вид
Ке-Хр
р(1 + Тр) ’
где К = Ю сек-1, Т = 0,05 сек, т —время запаздывания.
Определить допустимое значение времени запазды-
вания тд, при котором показатель колебательности си-
стемы не превышает Л1=1,1.
Решение, Показатель колебательности системы не
превышает заданного значения М, если выполняется
следующее условие [2]:
Я(Т + т)С
мг + мУм2- 1
2
320 гл. S. СИСТЕМЫ С ВРЕМЕННЫМ 3 ПАЗДЫВАНИЕМ . |Я40
Из неравенства получаем выражение для допусти-
мого времени запаздывания
Л42 + Л4 УЛР — 1 — 2КТ nnQC
Тд =--------2^--------— 0,036 сек.
340. Определить запас устойчивости по фазе и ча-
стоту среза разомкнутой системы при условиях преды-
дущей задачи. Значения коэффициентов: общий коэф-
фициент усиления Д’ = 10 сек-1, Т — 0,05 сек, г = 0,036 сек.
Ответ. Запас устойчивости по фазе р = 42,5°. Частота
среза сос — 10 сек~1.
Рис. 198. Вещественная частотная Рис. 199. Переходная функция
характеристика к задаче 341. к задаче 341.
341. Построить переходную функцию системы, пере-
даточная функция которой имеет вид
' ф(р)=. ^-\ ,
Р + Ке~Хр
где К = 40 сек~\ т= 12,5 • 10 3 сек.
Решение. Амплитудно-фазовая характеристика
системы равна
ф ______ Ке~^‘>х _ К (cos <от — j sin (от)
j(o + Ke~Its>\ ja + Д' (cos сот — j sin (от)
Вещественная частотная характеристика соответ-
ственно равна
Р ((£>) = Re Ф (/со) = • (О
' 7 4 ’ Л7 + (о7 — 2ЛТо sin (от
342р § 9.2. СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 32J
Вещественная частотная характеристика^ построенная
по выражению (1) для К = 40 сект1 и т = 12,5 10~3 сек,
приведена на рис. 198.
По вещественной’ частотной характеристике методом
трапеций построена переходная функция (рис. 199).
§ 9.2. Системы с распределенными параметрами
342. Структурная схема системы автоматического
управления гидротурбиной имеет вид, изображенный на
рис. 200. v, ф и р — соответственно относительные
Рис. 200. Структурная схема системы управ-
ления гидротурбиной.
величины момента нагрузки турбины, момента, разви-
ваемого турбиной, угловой скорости вращения турбины
и перемещения регулирующего органа [8]. Передаточная
функция трубопровода, полученная с учетом волновых
явлений [8], равна
W = '-Whip
1+ythrp '
Передаточная функция турбины №0(р) = -т-^—, пе-
редаточная функция безинерционногорегулятора W0(p) =
— у, 6 = 0,05, Го = 6 сек, й, = 1, у = 0,05. Определить
критическое время запаздывания тк, соответствующее
границе устойчивости системы.
Решение. Передаточная функция разомкнутой си-
стемы равна
UZfnl == fe0 . 1 — 2у th тр _ 1 — 2у th тр
' 6(1 + Тер) ' 14-ythTp ' б (1 4- Тор) (1 4-у th tp)
Характеристическое уравнение замкнутой системы запи-
сывается в виде
- 6(1 4-Г0р)(1 +ythTp)+ 1 -2ythrp = 0.
322
Г СИСТЕМЫ С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ
1343
etp _ е~хР
После замены thro на ———— и несложных пре-
ехр + ехр . 1
образований характеристическое уравнение приведем,
к следующему виду
1 — 2у + (1 + у)6 + (1 + у)67'ор +
4- [1 + 2у + (1 — у) 5 + (1 — v) ЪТор] е~2хр = 0.
Эквивалентная передаточная функция разомкнутой
системы (эквивалентность понимается в смысле тожде-
ственности характеристических уравнений замкнутой
системы) равна
П7 /„)_ »+ЗУ +(1 — V) 6 +(1 — V) r-2rp _
1-2у + (1 + т)б + (1+у)бГор
— 1 46 1 + °’22Р е-2тр
’ 1+0,38р
Эквивалентная частотная передаточная функция ра-
зомкнутой системы примет вид
W (/го) = 1 46 1 + 0,22 е_;2их
М/э(/со)-1,4b 1+038(/<в) е ..
Частота среза, соответствующая модулю (1), равному
единице, равна
(1)
1,462 —1
V 0,382—(0,22-1,46)2 5,3 сек
При т = тк фазовый сдвиг на частоте со = <ос должен
равняться — я. Поэтому
arctg (0,22 • 5,3) - arctg (0,38 • 5,3) - 2 • 5,3тк = - я.
Из последнего уравнения получаем
_ я - arctg (0,22 - 5,3) + arctg (0,38 5,3) _ n 97
тк ‘ о. к о u,zr сек.
2-5,3
343. Найти значение для Критического времени за-
паздывания системы, рассмотренной в предыдущей за-
даче, если
Wo (Р) = тТ» То = Ю сек, б = 0,05, у = 2.
* оР
$ 9.2. СИСТЕМЫ С Р ПРЕД Л ИНЫМИ ПАРАМ РАМИ 323
Ответ.
t>T0 arctg
2 Wy
2у2 — 1
12
344. Определить частоту среза разомкнутой системы
и запас устойчивости по фазе для системы, рассмотрен-
ной в задаче 342. Передаточная функция объекта
%(/>) — 1 + т "р * пеРеДаточная функция приведенного
1 — 2у th то ,
трубопровода wT = 1 + у thrp ’ пеРеДаточная функция
kp (1 + Tip)
регулятора Wp(p)= p(i^/sp) • Значения коэффициен-
тов: коэффициент передачи турбины /го = 2О; постоянная
времени турбины Го = 31,5 сек; время запаздывания
т = 0,95 сек; у = 0,03; коэффициент передачи регуля-
тора kp = 0,77 сек"1; постоянные времени регулятора
7\ = 12,5 сек, Т2 = 0,48 сек.
Ответ. Частота среза разомкнутой системы <ос =»
= 0,6 сек-1, запас устойчивости по фазе и..= 66°.
Рис. 201. Переходный процесс к за-
даче 345.
345. Построить при помощи вещественных частотных
характеристик переходный процесс в системе, рассмо-
тренной в предыдущей задаче, при подаче на вход си-
стемы возмущающего воздействия в виде единичной'
ступенчатой функции.
Ответ. График переходного процесса приведен на -
рис. 201.
ГЛАВА 10
ИМПУЛЬСНЫЕ СИСТЕМЫ
§ 10.1. Дискретные функции и уравнения
импульсных систем
346. Вычислить z-преобразование для функции вре-
мени
/(/) = По + я^ +
определенной для Период дискретности То = 0,1 сек.
Значения коэффициентов: а0 = 1, = 2 сек'1 и а2 — 4 сек"2.
Решение. В соответствий с приложением 2 имеем
г, / ч аог , «i^o* , a2T$z(z + l)
^ (*) = у=Т + 77=17 + . (г - 1—‘
Подстановка числовых значений дает
F _ г л. л. 0>04г(г+1)
г-1 У (г-D8 ' (г-D3 ’
347. Вычислить z-преобразование для функции вре-
мени, изображение Лапласа которой
Решение. Раскладываем изображение на простые
дроби
# . _ KTi
р<У + т\р) р 1 + 7,р '
В соответствии с приложением 2 имеем
. ' ч Kz Kz K(l-d)z
Г1' г-1 z~d (г- 1)(г—d) '
_А'
где rf = e г‘, а Го —период дискретности.
SSOJ
§ 10.1. УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ
325
348. Вычислить z-преобразование для функции вре-
мени, изображение Лапласа которой
£^^ = У(Г+ЛрГ’
Исходные данные: К = 2 сек~\ Г, = 0,1 сек, период ди-
скретности То —0,5 сек.
Ответ.
. ч KTaz KTjZ KT\z z 0,2 0,2
r (ZJ-(г_1)2 г- 1 + 'z — d ~ (z-I)2 z — I ' z — 0,0067 ’
n.
где d = e T' — e~5 = 0,0067.
349. Вычислить z-преобразование функции времени
f(t) — A sin (at = 10 sin (at
в трех случаях:
“ ~ 47? ’
3) =
1 о
Ответ.
' 2) '
3) F(zj = O.
350. Дано z-преобразование дискретной функции
времени
где То —период дискретности. Определить исходную
функцию времени в точках' t = nTQ (п=±0, 1, 2, ...).
Решение. Деление числителя на знаменатель дает
бесконечный ряд (ряд Лорана)
Лг) = «Го(14--| + 4 + ... •
326
ГЛ 10. ИМПУЛЬСНЫЕ СИСТЕМЫ
[351
Отсюда можно получить
f{nT0) = апТ0 = at\t_nTo.
351. Дано z-преобразование дискретной функции
времени
^)=(г-1Л)Тг^Г
Разложением в ряд Лорана
18
16
14
U
. /
-да
да
да
да
Рис. 202. Дискретные функции
времени.
построить исходную функ-
цию времени в точках
t — nT0 (n = 0, 1, 2, ...)
для трех случаев:
1) а— 1, 2) а— 1,8 и
3) а = 0,5.
Ответ. Графики по-
строены на рис. 202.
352. Дано г-преобра-
зование дискретной функ-
ции времени
F № = z2 — 1,5г+ 0^ ' (
Найти исходную ре-
шетчатую функцию вре-
мени разложением на
простые дроби.
Решение. Находим корни уравнения
z2 — 1,5г + 0,5 = 0.
о
Значение корней zt ~ 1 и г2 = 0,5. Далее предста-
вляем Г(г) в виде суммы простых дробей
F = (z—1) (г —0,5) “ 2 (тИГ ~ г - 0,5 ) ’ ^2^
Первое слагаемое в правой части (2) соответствует
оригиналу 1 (пТо), а второе — е~апТ°, причем d = e~aTi1 = z<>
(см. приложение 2). Поэтому можно записать для ори-
гинала
f (пГ0) = 2 [1 (пГ0) - = 2 (г? - г£) = 2 (1 - 0,5").
353. Найти z-преобразование для функции времени
f W = «о + a\t +
3SS1
§ 10.1. УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ
327
определенной при в дискретные моменты времени
t = (п + в) Го. Исходные данные: а0 = 1, щ=2 сек~\
а2 = 3 сек~2, Го=1 сек, г~0,5.
Ответ.
а1^ог , , 2fl2^0Z .
6г
F(z)**-^T'r (z- I)2 z-l -r(z — l)3'r
a2 (1 + 2e) 7'pZ , a2e27pZ 2,75z , 8z
+ (z-l)2 + (z-l) = (z — 1) + (z-l)2 (z — I)»’ ’
354. Найти ^-преобразование функции времени
f (t) = а0 + a{t + a<2t2,
определенной для t 0. Период дискретности То = 1 сек^
и0"=1, at = 1 сек"1 и а2= 1 сек~2.
Решение. В соответствии с приложением 2 нахо*
дим z-преобразование исходной функции для дискрет*,
ных моментов времени nT0 (n = 0, 1, 2, ...):
а0г , а1Г0г , аоФ^+О
F & = ITT + -(ГЛР +.....(^1)8—.
Используя подстановку г — i получаем
Гр (1 - О!2) «27р(1 -гг^) _
2w 4w2 4w3
- I + w J_ I ~ w2 -L ~ w2 _ 1 + 10 4- w2 + w3 '
2w 4w2 4w3 . 4w3
.355. Дано ^-преобразование дискретной функции
времени
F (w) —
ч aTo(l~w2)w
F м =-------W------•
где а = 5 сек~2, а То= 1 сек.
Определить исходную дискретную функцию времени.
п т'х z — 1
Решение. Используя подстановку w =. , на*
ходим г-преобразование функции времени:
F(z) =-----
4
аТдг(г+1)
(z-l)3 *
328
ГЛ to. ИМПУЛЬСНЫЕ СИСТЕМЫ
[35ft
В соответствии с приложением 2 имеем
356. На рис. 203 изображен 'импульсный фильтр.
Импульсный элемент ИЭ генерирует прямоугольные им-
пульсы относительной продолжительности у7о> где у =
=0,05, а период повторения 7'0=1сек. Передаточная
функция непрерывной части
Рис. 203. Импульсный где Ю, а Гр =0,5 сёк.
фильтр к задаче 356. Определить передаточную
функцию фильтра совместно с им-
пульсным элементом, считая, что последовательность
импульсов на выходе импульсного элемента может быть
заменена последовательностью 6-функций.
Решение. Передаточная функция равна
= V7"o 2 w0 = yToZ {w0(kT^. (2)
fe~o
Зтесь w0(kT)~ весовая функция непрерывной части
при замене t = kTa, z = ePT>, a Z {tw0 (kT0)} представляет
z-преобразование весовой функции.
Для рассматриваемой непрерывной части весовая
функци я
<3)
В соответствии с приложением 2 находим
zfA-e~T, 1 = А £_ /ил
(Г, J Г, г-d’ W
_д>
где d = е т>. В результате получаем искомую переда-
точную функцию
................©
После подстановки числовых значений имеем
• Г (г) = вда.:10'1--1— = ' (6):
0,5 z-ё"1 г-0,135
8881
§ 10.1. УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ
329
357. Построить амплитудно-фазовую частотную ха-
рактеристику для импульсного фильтра, приведённого
в предыдущей задаче.
' Решение. В выражении (6) предыдущей задачи
необходимо сделать подстановку z = elaT° - cos <дТ0+
-+/sinro7’o- В результате получается частотная переда-
точная функция фильтра
cos гоГр + j sin юТр
cos w7’0 — 0,135 + j sin v>T0
1
Модуль этого выражения
I W(е/и7'")-|
K1+0,135s-0,27 cos соГр
и фаза
, -r 4. sin wT0
ф = — arctg-------•
т u ь coscoZp —d
А. ф. х. представляет собой окружность (рис. 204).
При го = 0, а также при соТо = 2ил, где п — натуральное
число, модуль и фаза соста-
вляют
Л° = TZTrf = fl о,135 = 1,15
и '
Фо = 0.
При ®7’о = (2п—1)л мо-
дуль и фаза '
711 ~ 1+d = I +0,135 0,88
и
Рис. 204. А. ф. х. к задаче 357-
ф = ± 180°.
Центр окружности смещен вправо от начала коор-'
Динат на величину С = = 0,136, /? = -т-Ц== 1,01..
J 1 — а 1 — а*
358. Найти частотную передаточную функцию им-
пульсного фильтра задачи 356 (см. рис. 203) в зависи-
мости от абсолютной псевдрчастоты.. ; ' • <
гл 10. Импульсные сйс емы
1858
Решение. В передаточной функции (6) задачи 356
перейдем к йУ-преобразованию посредством подстановки
1 + w
z =т-----.
1 — W
В результате имеем
nrr z„A__ уКГо 1 + w
. У^о 1+ w
“ T,(l — d) ' , , 1гТ0 •
' ’ 1 4- w cth
Перейдем к абсолютной псевдочастоте Л = -=г- tg
* о 2
Т
посредством подстановки w
vKT 1+/‘Т’Л
— 7\ (1 ~ d) ' 1 + jTaK ’
Здесь введена эквивалентная постоянная времени
— ~2~"277 • (3)
Подстановка числовых значений дает Та — 0,5 cth 1 —
;«= 0,66 сек. Передаточная функция равна
пут— О-05’10’1 1+/0.5Л _ 1,15(1 +/0,5Л.)
W ~ о,5 (1 - 0,135) ‘ 1 + /0.66Л, 1 + /0.66Л *
359. Решить задачу 356 при условии, что относи-
тельная продолжительность импульса у — 0,5.
Решение. В рассматриваемом случае изображение
Лапласа импульса, генерируемого импульсным элемен-
том при.подаче на его вход единичного сигнала, будет
равно
VTo
f 1 _p—pyTc
Fn (р) = J 1 • е-* dt == .
о
Приведенная передаточная функция непрерывной
части
(Р) = (Р) Fn (р) = р(1 ^Tip) (1 - е-М).
360J
$ ЮЛ. УРАВНЕНИЯ ИМПУЛЬСНЫХ С О ЕМ
331
Дискретная передаточная функция
В соответствии с приложением 2 находим
K(l-d)z К( z zd° \ Krf(rf~v- 1)
(2) (z — 1)(г —rf) z\z— 1 z — d) z — d
(4)
r.
где d — e Г| =0,135, a <7=1—y.
Подстановка числовых значений дает
(5)
из
t То LTZI
Рис. 205. Импульсный
фильтр к задаче 360.
360. Для импульсного фильтра, изображенного на
рис. 205, построить логарифмические амплитудную и
фазовую характеристики. Пере-
даточная функция непрерывной
части
"7«<',’=7(ГГад-
Исходные данные: К — 100 сек-1,
То = 0,05 сек, Ti = 0,2 сек и
у = 0,1. Считать, что последовательность импульсов на
выходе импульсного элемента ИЭ может быть заменена
последовательностью 6-функций.
- Решение. Дискретная передаточная функция им-
пульсного фильтра равна
W (г) = уГ0£ {Wo (р)} = уr0Z { р(1 j?ip) }. (1)
В соответствии с приложением 2 находим
К 1 К КТ, )_
P(l + rip) J-’ I Р 1 + Т,р J
_ к ( г__________z \____К(1 — rf)z
. \ z — I z — d) (z — 1) (z — d) ’
832
ГЛ. 10. ИМПУЛЬСНЫЕ- СИСТЕМЫ
1300
Го
где d = e Ti — е-0-23 = 0,78. Подставляя (2) в (1), имеем
= (3)
Используем подстановку z = ;
W (w) = ... . (4)
2w (1 + w cth j
Переходим к абсолютной псевдочастЬте подстанов-
кой
4 I гг^- \
I *01
т*|1 + л2-/)
W ~ jK (1 + jMTa) •
Рис. 206. Л. а. х. и л. ф. х. к задаче 360.
Подстановка числовых значений дает
w/(iUt= 10(1 + 0.025=^)
ww~ 1мгнбдаг-- {Ь)
Логарифмические амплитудная и фазовая характе-
ристики должны строиться по выражению
. L(Л) = 20 1g| W(jK) | = 201g_10[1+^в£1
' ' ы v /I s х/1+0,21 ГЛ.» —
- , ф(Л)= arg ДГ(/Л)=—90°—arctg 0,217Л.
ад) §. 10.1. УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ 333
Асимптотическая л. а. х. и л. ф. х. построены на
рис. 206.
361. Построить логарифмические амплитудную и фа-
зовые характеристики для импульсного фильтра, изо-
браженного на рис. 205, если передаточная функция
непрерывной части
W° = р(1 + ада + ад ’ (1)
Исходные данные: К.== 10 сек~\ То = 0,1 сек, Т\ = 0,25 сек,
7'2 = 0,01 сёк и у — 0,01. Считать, что последовательность
импульсов на выходе импульсного элемента может быть
заменена последовательностью 6-функций.
Решение. Разложим выражение. (1) на простые
дроби:
К К АГ?
р(1+ад(1 Тад “ р (т.-адд+ад +
кг|
+ (г,-г2)(1 + ад ’
В соответствии с приложением 2 находим дискретную
передаточную функцию
(3>
где ' •
г? -- ' г| Г,
п
= е Г1 . и d2 = е Тг.
Формула (3) может быть представлена в виде
(4)
Используем подстановку 2= ,
»)-тздГ- , ’ г. + Л_4|
2иц 1 + w cth Г*(* d2) I + wcth-^-
\ Л’/ 1 / 1 2 *
334
ГЛ. 10. ИМПУЛЬСНЫЕ СИСТЕМЫ
1361
Перейдем к абсолютной псевдочастоте заменой
w = j -у- А. В результате имеем
г(/л) = уТ0/<(1+/ч^)
1-/Л^
Тг
Так как <Г0 < 27’, и То > 2Тг, то -у- cth —
и ~ 0.
т
Т1г cth ^.^1
Рис. 207. Л. а. х. и л. ф. х. к задаче 361.
При учете этих зависимостей получаем
Г(/л) = у707<(1+А^-)
1-аА
/TTod+m
Г2
1 +
Л>
уЯ [ 1+ /7 то + (JW(727о -
(5)
/7(1+/77,)
Подстановка числовых значений дает
ш _ [1 + /0.004Х-0,015 (/ХИ ~
W jk (1 + /0,25Х) ~
. ~ 1+0.015Х2 (1 + /0.122Х) (1 - /0,Г22Х)
' /7 (1+/0,257) /7.(1+,/0,25Х)
<S 101. УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ 335
863J
* t
Асимптотические л. а. х. и л. ф. х. изображены на
рИС362^7'Импульсной системе регулирования (рис. 208)
^ответствует передаточная функция разомкнутой си-
стемы (см. задачу 360)
.vWl-d)z___________________ (1)
' (г-l)(z-rf) (z- 1) (г-0,78) ’
где д = 100 сек~* 1, То — 0,05 сек, Т{ — 0,2 сек, у = 0,1 и
d==-.e'^ = е-°^=0,78.
Рис. 208. Импульсная система регули-
рования.
Определить передаточную функцию замкнутой си-
стемы и передаточную функцию относительно ошибки.
Ответ. Передаточная функция замкнутой системы
<т> м — -JLM- — yTDK(l-d)z __
l + r(z) (z-l)(z-d) + yT0K(l — d) z
— 7---- °’V?a^nn • (2)
(z — 1) (z — 0,78) 4- 0,1 Iz v ’
Передаточная функция по ошибке
ф м— 1 - (z-l)(z-rf)
1 + IHz) ~ (z-l)(z-d) +уЛЛа-rf)z
(z-l)(z-0,78)
“ (z-l)(z-rf) + 0,Ilz * w
363. Передаточная функция замкнутой импульсной
системы (см. рис. 208)
°-11г
(z-l)(z-0,78) + 0,llz‘
На вход системы поступает ступенчатая функция g(t) —
Sol(t). Найти z-преобразование выходной величины
+(z) и ошибки X(z).
336
ТЛ. 10. ИМПУЛЬСНЫЕ СИСТЕМЫ
|3<и
Решение. Изображение входной величины в соот-
ветствии с приложением 2 будет равно
6(2)-^-.
Изображение выходной вличины
У (х) — Фх (х) G (X) = j) (г _ 0,78)4-0,1 lz] (г- 1)' ’
Изображение ошибки
X (х) = Фл (х) G (х) — [ 1 — Ф (х)] G (х) =
. До (г — 0,78) z
(z-1) (z-0,78)4-0.l lz '
. 364, Найти разностное уравнение, связывающее
входную и выходную величину импульсной системы ре-
гулирования (см. рис. 208).
Передаточная функция замкнутой системы
<7,/ 0,Их
W(г - 1) (z - 0,78) + 0,1 Iz ‘
Решение. Изображения входной и выходной ве-
личин связаны передаточной функцией
У fe) = ф (z) G (х) =____UHfG^x)-------
, - Ф \Z) и (Zj (z- I)(z - 0 78) + 0,1 ь
0,llzG(z) 0,112->6 (2)
z2—1,67x4-0,78 1 — 1,67г-1 + 0,78г-2 "
Перепишем эту формулу в ином виде:
(1 - 1,67х“‘ + 0,78х-2) У (х) = 0,1 lx-‘G (х).
Отсюда может быть получено разностное уравнение
У [Л] - 1.671/ [и - 1] + 0,78// [п - 2] = 0,11g [н - 1 ].
§ 10.2. Устойчивость и качество импульсных систем
365. Передаточная функция замкнутой импульсной
системы регулирования
л,/ V 0,112
Ф («) — _ j 67г 0 78 .
Определить устойчивость системы.
S67J § Ю-2- УСТОЙЧИВОСТЬ И КАЧЕСТВО ИМПУЛЬСНЫХ ' СИСТЕМ 337
Решение, Характеристическое уравнение системы
, 2^- 1,67x4-0,78 = 0.
Находим корни
Z| 2 == 0,835 ± /0,8352 — 0,78 = 0,835 ± /0,292.
Модуль корней
| х(. 2| = /0,8352 4-0.2922 = 0,88 < 1.
Система устойчива.
366. Определить наибольшее значение общего коэф-
фициента усиления для системы импульсного регулиро-
вания,' рассмотренной в 'задаче 362, соответствующее
границе устойчивости.
. , Решение. Характеристическое уравнение системы
может быть получено из формулы (2) задачи 362:
(х - 1) (х - d) 4- уТ0К (1 - d) z .=
= х2-[1 4-d —уГ0/<(1 -d)]x4-d = 0.
Перейдем к ^-преобразованию подстановкой х —
~ 1—В результате получим характеристическое
уравнение в другом виде,
(2.4-2d-да: (1 -d)]w24-2(l-d)w +у70/<(1 -d) = 0.
Условия устойчивости:
22d —у7оК(1 — d) > 0, (1)
d<l, (2)
даС(1 — d)>0. (3)
Критическое значение коэффициента усиления может
быть определено из формулы (1)
К - 2('+rf) =________; = 3240 ,
-кр — уГо (1 - d) 0,1 • 0,05 - 0,22 •
367. Характеристическое уравнение импульсной си-
стемы регулирования
i 5х34-2х24-Зх4-1=0.
3 V №. to. ИМПУЛЬСНЫЕ СИСТЕМЫ [ЗИ
Определить устойчивость системы.
Решение. Используем подстановку z —
Тогда получим
5(1 + г®)3 + 2(1 4- ш)2(1 — iw) +
+ 3(1 + jw)(1 — &>)2 + (1 — &>)3 = 0.
Приведение подобных членов дает
5t®3 + 1 Зг®2 + 11 w + 11 = 0.
Дрименим критерий Гурвица
13- 11 -5- 11=88>0.
Система устойчива.
368. Определить устойчивость системы, характеристи-
ческое уравнение которой
z2 + z2 + z + 1• = 0.
Ответ. Система неустойчива.
369. Передаточная функция замкнутой системы
Ф (z) = г Л’1 , .
' ' г2 — l,5z + 0,6
Определить первые коэффициенты ошибки с0 и
при Z'o = O,'l сек.
Решение. Находим передаточную функцию от-
носительно ошибки:
ФДг)=1-Ф(г)
z2 — 1,5z + 0,5
~ г2 - 1Дг + 0,6 *
Заменяя в последнем выражении z= 1, что соответствует
р = 0, получаем
Со = ФД1) = О.
Для нахождения коэффициента ошибки q продиф-
ференцируем передаточную функцию ФЛ.(е₽Го):
(2Г0г-1,57-0)0,1
dp (z2 —l,5z-|-0,6)2 ‘
3711 § 10.2. УСТОЙЧИВОСТЬ И- КАЧЕСТВО ИМПУЛЬСНЫХ СИСТЕМ 339
При подстановке в последнее выражение, z = 1
получаем
„ _ — 1,5Гр) 0,1 - ~ _ л к срк
q — ц _ + 0>6р Ы о и,о сек.
370. В импульсной системе регулирования коэффи-
циенты ошибки равны со=О, ^=0,01 сек и с2=0,05 сек2.
Определить ошибку в дискретные моменты времени /==
= пТ0 (п — 0, 1, 2, ...) при поступлении на вход Системы
сигнала g(t} — aot + axt2, где а0 = 5 сек~1 ио, = 2 сект2.
Ответ. Значение ошибки в дискретные моменты вре-
мени равно
x(n7’0)=c1g(n7’0)+ >g(nT0) =
— ct (°о + о) + -Ц- • =
= 0,01 (5 + 4п7’0) + 0,05 • 2 = 0,15 + О,О4пТо.
371.. Определить запас устойчивости по модулю и-
по фазе, а также показатель колебательности импульс-
ной системы регулирования, передаточная функция кото-
рой в разомкнутом состоянии приведена в задаче 362
W (г)
Го
где у = 0,1, То = 0,05 сек, К =100 сек’1, d = e ^ =
= е-о.25 _ 0,78, а Тл = 0,2 сек:
Решение. Перейдем к частотной передаточной
функции подстановкой z — , а затем jw = /Z.-y-
(см. задачу 360),
WW~ /Л (1 4-/0.217Л) •
Определим частоту среза для передаточной функ-
ции (1) из равенства
10[1 +0,0252Х|р] (2)
\.р Vl + 0,2172Z2p "
340;""' ГЛ. 10. ИМПУЛЬСНЫЕ СИСТЕМЫ
1372
Приближенное решение (2) дает
А.ср « = 6,8 сек-1.
Запас по фазе для (1) равен
ц = 180° + ф = 90° - arctg 0.217Л.
Запас устойчивости по фазе при Л = Аср равен
= 90° - arctg 0,217 • 6,8 = 34°.
Фазовый сдвиг достигает значения ф= —180° прн
Л-*оо. Поэтому запас устойчивости по модулю
1 _ °’217 ^35
р |Г(/оо)| Ю-0,0252 °0-
Для определения показателя колебательности най-
дем частотную ' передаточную функцию замкнутой
системы
_* 10(1 +0,0252Х2)
Р UM j + г _ 0>2 ] П2 + д + 10 •
Модуль последнего выражения равен
ДЩ^--1^1^0»025^ (3)
/(10- 0,217Z2)2 + X2 ’
Исследование на максимум выражения (3) дает значе-
ние показателя колебательности Лтах = Л1 = 1,56. •
372. На вход импульсной системы с передаточной
функцией в замкнутом состоянии
Ф = г2 - l,3z + 0,4
поступает единичная ступенчатая функция
Построить переходный процесс для выходной вели-
чины у(пТ) и определить время переходного процесса.
Период дискретности 70 = 1 сек.
Решение. Изображение входноц величины равно
0(Z)"7=T! (1)
372] § 10-2. УСТОЙЧИВОСТЬ И КАЧЕСТВО ИМПУЛЬСНЫХ СИСТЕМ 34]
Изображение выходной величины примет вид
У (z) = Ф (z) G (z) = _ jj _ 132 + 0 4) • (2)
Найдем корни характеристического уравнения
z2— l,3z +0,4 = 0. •
Решение дает zt = 0,8 и z2 = 0,5.
Представим выражение (2) в виде
у(2) = —।---------1--£—)
\ г-1 'г —0,8- г —0,5/
Нахождение коэффициентов разложения на простые
дроби дает А = 1, В = — 1,67 и С = 0,67. В результате
имеем
= + <3>
Для приведения (3) к табличному виду (см. при-
ложение 2) положим dt = e~a‘r<i = Zi = 0,8 и 4= е~а*г'° —
= z2 = 0,5. Отсюда находим
О] = -4- In — = 1 0,223 = 0,223 сек”1,
1 о U,o
а2 = ~ In 7^=- = 1 • 0,693 = 0,693 сек”1.
Таблица 1
п —1,67.0,8" 0,67-0,5" у {пТсЛ п —1,67-0,8" 0,67-0,5" У (пТц)
0 -1,67 0,67 0 9 -0,22 0 0,78
1 -1,33 0,33 0 10 -0,18„ 0 0,8 >
2 -1,06 0,16 0,1 11 -0,14 0 0,83
3 -0,85 0,08 0,23 12 -0,11 0 0,89
4 -0,68 0,04 0,36 13 -0,09 0 0,91
5 —0,54 0,02 0,48 14 -0,07 0 0,93
6 -0,43 0,01 . 0,58 15 -0,06 0 0,94
7 —0,35 0 0,65 16 -0,05 0 0,95
8 -0,28 0 0,72
342 ГЛ. 10. ИМПУЛЬСНЫЕ СИСТЕМЫ [87S
t
В соответствии с приложением 2 получаем искомую
дискретную функцию времени
у(пТ0) = 1 — 1,67е~а‘пГ" + 0167е-аг'гГо =
= 1-1,67 г" + 0,67 г" = 1 - 1,67 • 0,8" + 0,67 • 0,5". (4)
Для построения переходного процесса удобно вос-
пользоваться табл. 1.
Вычисление у(пТ0) производилось в таблице до тех
пор, пока ошибка не стала равной 5%. Время переход-
ного процесса составляет при этом tn= 1670= 16 сек.
373. Решить предыдущую задачу разложением изо-
бражения в ряд Лорана.
Решение. Найденное ' изображение выходной ве-
личины (2) разложим в ряд Лорана делением числителя
на знаменатель
П I у I ~з _ о Ч?2 4- I 7г1 — 0 4
о',1г-0,23 +0,17г-*-0,04г-3 |о, 1г-3+0,23г-5+’Ь',36г-4+..;
0,23-0,172-* +0,04г-2
0,23 - 0,53г-* + 0,39г~3 - 0,092г~3
0,36г"1 - 0,35г-2 + 0,092г-3
Коэффициенты при z~n у частного представляют
собой значение выходной величины у{пТ^. Таким об-
разом, при п = 0 и п=1 имеем #(0) = у(То) = О. Далее
получаем ^(27'0) = 0,1, у(ЗТ0) — 0,23, ^(47'0) = 0,36. Про-
должая деление дальше, получим числа, совпадающие
с приведенными в табл. 1.
РАЗДЕЛ II
НЕЛИНЕЙНЫЕ СИСТЕМЫ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ГЛАВА 11
СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ
СИСТЕМ
§ 11.1. Уравнения нелинейных следящих систем i
374. Составить дифференциальные уравнения и струк-
турную схему электромеханической следящей системы,
схема которой изображена на рис. 209. На схеме обо-
значено: -&1, <)2 —углы поворота командной и исполни-
тельной осей, ‘0 = 0'1 “ ^г~ рассогласование (ошибка),
Рис. 209. Электромеханическая следящая система.
ЧЭ — чувствительный элемент (датчик угла рассогласо-
вания), У — линейный усилитель, РУ — релейный усили-
тель, Д —двигатель, Р — редуктор, ТГ — тахогенератор,
РМ — рабочий механизм (объект).
Исходные данные: крутизна статической характери-
стики чувствительного элемента k\ — 1 в/град=57,3 в/рад,
коэффициент усиления линейного усилителя k2 — 2,5,
постоянная времени линейного усилителя Т\ = 0,05 сек,
максимальное напряжение на выходе релейного усилителя
344 ГЛ. II, СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ [374
[73 max = с = 110 в, крутизна статической характери-
, 1 л-2 в • сек
стики тахогенератора я4= 10 - -ад , передаточное от-
ношение редуктора i =1000, скорость холостого хода
двигателя п0 = 6000 об]мин,
3 пусковой момент двигателя
Рис. 210. Статическая
характеристика релейного
усилителя.
А40= 100 Г • см, момент инер-
ции всех вращающихся ча-
стей, приведенный к валу дви-
гателя, J = 0,008 Г • см • сек2.
Влиянием статического момен-
та нагрузки и переходных про-
цессов в цепи якоря двигателя
можно пренебречь. Статичес-
кая характеристика релейного
усилителя изображена —на
рис. 210. Зона нечувствитель
ности b = 0,25 в.
Решение. По заданной принципиальной схеме со-
ставляем дифференциальные уравнения звеньев системы.
1. Уравнение чувствительного элемента
Ui — k\&, & = &[ — ©г,
(i)
где щ —напряжение на выходе чувствительного элемента.
2. Уравнение релейного усилителя
(TiP+l)u2 = k2u, и = и1-щг, (2)
где и2 — напряжение на выходе усилителя, итг — напря-
d
жение тахогенератора, р = .
3. Уравнение релейного усилителя запишем в следую-
щем виде:
u3 = F (u2), (3)
где м3 — напряжение. на выходе усилителя, F(u2) — вели-,
нейная функция, заданная статической характеристикой
(см. рис. 210).
4. Уравнение исполнительного двигателя.
Согласно исходным данным влиянием статического
момента нагрузки и переходных процессов в цепи якоря
двигателя можно пренебречь. Поэтому дифференциальное
в 111. УРАВНЕНИЯ НЕЛИНЕЙНЫХ СЛЕДЯЩИХ СИСТЕМ 345
3741 з
уравнение двигателя (см. гл. 1; можно записать в виде
(Л,Р+l)P^ = fe3«3. • (4)
где #д_ угол поворота вала двигателя, Ты — электроме-
ханическая постоянная времени, ^ — коэффициент пере-
дачи двигателя.
Рис. 211. Структурная схема следящей системы.
Электромеханическая постоянная времени двигателя
(см. гл. 1)
г _ j _ 1 ппо _____л ппе 3,14 • 6000 я ле „рк
Mq J 30Mo 30-100 U,Ub K'
Коэффициент передачи двигателя
6 — Qo — ппч — 3>14 • 6000 . рад
3 max 306/у max 30 110 ’ в • сек
5. Уравнение 'тахогенератора
и„ == (5)
Уравнение редуктора
“&2 = Мд. (6)
где /г5 = —== 0,001 — коэффициент передачи ре-
I lUUv
дуктора.
По уравнениям (1)—(6) составляем структурную схему
системы (рис. 211). Согласно этой схеме дифференциаль-
ное уравнение линейной части системы, записанное от-
носительно входной величины нелинейного звена н2,
имеет Вид
(Лр + 1)(гмр+ 1)рн2 =
= kikz (Тыр + 1) рй, - k2k3\ktk5 + k4p) us. (7)
346 гл. 11. СОСТАВЛЕНИЕ УРАВНЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ (з73
После подстановки численных значений параметров
получим
(0,0025р3 + 0,1р2 + р)и2 =
= (7,14р2 + 143р) «j - (0,143р + 0,82) «3. (8)
Уравнение линейной части системы дополняется
уравнением нелинейного 'звена (3)
и3 = F (м2).
375. Составить дифференциальные уравнения электро-'
механической следящей систе'мы с электромагнитными
муфтами и логическим устройством. На схеме системы
(рис. 212) обозначено: Oj, Ог— углы поворота командной
Рис. 212. Следящая система с электромагнитными муфтами
трення.
и исполнительной осей, •& = &! — О2 — ошибка системы,
ЧЭ — чувствительный элемент, ЛУ — логическое устрой-
ство, ЭМ — электромагнитные муфты, Д — приводной
двигатель, ТГ — тахогенератор, РМ — рабочий механизм.
В этой системе приводной двигатель вращается в од-
ном направлении с постоянной скоростью. Реверсирование
исполнительной оси осуществляется переключением муфт
согласно командам логического устройства. Для по-
строения логического закона управления (рис. 213) ис-
пользуется напряжение щ, пропорциональное ошибке
системы &, и напряжение итт, пропорциональное скорости
вращения исполнительной оси 0-2.
Исходные данные: вращающий Момент приводного
двигателя, приведенный к исполнительной оси, Мо =
= ЮГ- см~, момент инерции всех вращающихся частей,
Йй § 4.1. УРАВНЕНИЯ НЕЛИНЕЙНЫХ СЛЕДЯЩИХ СИСТЕМ 347
приведенный к той же оси, Z = 100 Г • см • сек2-, пара-
метры логического устройства (пересчитанные в угол
рассогласования и угловую скорость) Ь{ = 0,2°, Ь2 —
==0,1 град!сек. Статическим моментом нагрузки и влия-
нием переходных процессов в электромагнитных муфтах
трения можно пренебречь.
Решение. Запишем закон равновесия моментов,
приведейных к исполнительной оси (статическим момен-
том нагрузки пренебрегаем); А
нератор, логическое устройство
и электромагнитные муфты тре- «&=+/
ния, имеет вид
М *= М0Ф (О, &2), (2)
. - „ „ Рис. 213. -Статическая ха-
Где Ф (О, и2)— нелинейный ЛО- рактеристика логического
гический закон, реализуемый устройства,
в управляющем устройстве и
заданный графически на рис. 213. Из уравнений (1)и (2)
и рис. 213 следует
Мо при О< —Ьь &2<Ь2.
— М0 при '&>&[, &2> —1>2, (3)
0 в остальных случаях.
Подставим в уравнения (3) численные значения пара-
метров системы. Получим дифференциальные уравнения
движения системы
0,1 при й < — 0,2°, •©’2 < 0,1 град/'сек,
0,1 при &>0,2°,! О2>— 0,1 град!сек, (4)
0 в остальных случаях.
376. Составить дифференциальные уравнения и струк-
турную схему следящей системы с переменным демпфи-
d^2
dt2
d2ft
dt2 ~
348 ГЛ. II. СОСТАВЛЕНИЕ УРАВНЕНИНЕЛИНЕЙНЫХ СИСТЕМ (37«
рованием (рис. 214). На схеме обозначено: ©ь©2— углы
поворота командной и исполнительной осей,
— ©2— угол рассогласования (ошибка), ЧЭ — чувстви-
тельный элемент (датчик угла рассогласования), РМ —
рабочий механизм, Уь У2— усилители, ТГ\, ТГ2— тахо-
генераторы, Д — двигатель, Р — редуктор.
Рис. 214. Следящая система с переменным демпфированием.
Местная обратная связь в этой системе образуется
тахогенераторами ТГ\ и ТГ2, которые включены после-
довательно и встречно. Разность напряжений этих тахо-
генераторов tz4 — «5 складывается с. напряжением щ,
снимаемым с чувствительного элемента. При большом
угле рассогласования © напряжение и4 > н5, так как ток
в обмотке возбуждения тахогенератора ТГ2 пропорцио-
нален углу ©. Поэтому суммарный сигнал на входе
усилителя У] и2 > «ь что обеспечивает большую ско-
рость нарастания процесса. При малом угле рассогла-
сования «4 < и5 и напряжение на входе усилителя У(
и2 < «ь Поэтому система работает с пониженной ско-
ростью, что исключает перерегулирование. При соста-
влении уравнений системы статическим моментом на-
грузки и влиянием переходных процессов в цепи якоря
двигателя и в обмотке возбуждения тахогенератора ТГ2
можно пренебречь'. Усилители У1 и У2 считаются без-
инерционными.
Решение. Составляем дифференциальные уравне-
ния звеньев системы.
1. Уравнение чувствительного элемента
ux = kft, & = &[ — ©г, (1)
376) § 11.1. УРАВНЕНИЯ нелинейных СЛЕДЯЩИХ СИСТЕМ 349
где k\ — крутизна статической характеристики чувстви-
тельного элемента.
2. Уравнение усилителя У у
и3 — k2u2, и2 = щ + щ — и5, (2)
где и3 — напряжение на выходе усилителя, k2 — коэффи-
циент усиления.
3. Уравнение двигателя
(Тыр + 1) р-&а = k3u3, (3)
где Яд-угол поворота вала двигателя, Т,. и k3— электро-
механическая постоянная времени и коэффициент пере-
дачи двигателя.
Рис. 215. Структурная схема следящей системы с перемен-
ным демпфированием.
4. Уравнение цепи нелинейной обратной связи, со-
стоящей из тахогенератора ТГ2 и усилителя У2,
Нц = &4рМ]Яд, (4)
где ^ — коэффициент пропорциональности.
5. Уравнение тахогенератора Т1\
«5 = (5)
где k5— крутизна статической характеристики тахогене-
ратора.
6. Уравнение редуктора
Я2 = Мд. (6)
где k6 — коэффициент передачи редуктора.
По уравнениям (1) — (6) составляем структурную
схему системы (рис. 215). На этой схеме знаком ixi
350ЛТГ «СТАВЯ НИ У ЛВНЕНИИ НЕЛИНЕЙНЫХ СИСТЕ
обозначено множительное устройство, выполняющее опе-
рацию умножения Двух переменных согласно уравне-
нию (4).
В соответствии со структурной схемой нелинейное
дифференциальное уравнение всей системы имеет вид
ИмР2 + (1 + /г2/г3/г5) р + kxk2k^ О2 “
— k^k^p (&! — Фг) — МАМъ (7)
§ 11.2. Уравнения нелинейных систем стабилизации
377. Составить дифференциальные уравнения и струк-
турную схему системы автоматического регулирования
температуры, схема которой изображена на рис. 216.
Рис. 216. Система автоматического регулиро-
вания температуры.
На схеме обозначено: ОР — объект регулирования, ЧЭ—
чувствительный элемент (мост с термосопротивлением),
РП — поляризованное реле (усилитель), Ддвигатель,
ОБ — обмотки возбуждения двигателя, Р — редуктор,
РО — регулирующий орган (заслонка), ПОС — потенцио-
метр обратной связи.
Исходные данные: объект представляет собой аперио-
дическое звено первого порядка с постоянной времени
Го =1'0 сек, коэффициент передачи объекта и регули-
рующего органа /го=10 срад/рад, коэффициент.передачи
.^1 в ПА УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ СТАБИЛИЗАЦИИ 351
U
чувствительного элемента k{ = 0,25 a-efepad, коэффициент
передачи двигателя k2 == 2 рад/в • сек, передаточное от-
ношение редуктора i = 1000, коэффициент передачи цепи
обратной связи йос = 2,5 а-в/рад. Статическая характе-
ристика поляризованного реле изображена на рис. 217.
Ампер-витки срабатывания реле аи>Ср = 0>5 a-в, макси-
мальное напряжение на выходе релейного усилителя
t/max=U0 в- Влиянием статич'е-
ского момента нагрузки, переход-
ных процессов в обмотках поляри-
зованного реле и постоянными вре-
мени двигателя Тя и Ты можно
пренебречь.
Решение. По заданной прин-
ципиальной схеме составляем диф-
ференциальные уравнения звеньев
системы.
1. Уравнение регулируемого объ-
екта
(Top + \)ft2 = kf®, (1)
где $2 ~~ фактическое значение температуры объекта,
Ф —угол поворота регулирующего органа.
2. Уравнение чувствительного элемента
awi — kfi, •& = &;— ф2, (2)
где — заданное значение температуры объекта, Ф —
ошибка системы.
3. Уравнение релейного усилителя
u-F(aw), aw — awi — awoc, (3)
где F (aw) — нелинейная функция, заданная статической
характеристикой (см. рис. 217).
4. Уравнение двигателя постоянного тока
pa — k2u, (4)
где а —угол поворота вала двигателя.
5. Уравнение редуктора
Ф = /г3а, (5)
где k3= — ~ коэффициент передачи редуктора.
-ашср
Iff
aw^ aw
Рис. 217. Статическая
характеристика поля-
ризованного реле.
352 ГЛ. 11. СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ [378
6. Уравнение цепи обратной связи
aWac = £0Сф. (6)
где аиу0.с — ампер-витки обмотки обратной связи.
.. Структурная схема системы изображена на рис. 218.
Рис. 218. Структурная .схема системы автоматического регу-
лирования температуры.
В соответствии со структурной схемой дифференци-
альное уравнение линейной части системы можно за-
писать в следующем виде:
(Гср + 1) paw = krfr&i - k2k3 [60С (Тор + 1) + kokrlu. (7)
Подставим в уравнение (8) численные значения па-
раметров. Получим
(1 Op2 + р) aw = 0,25pfti - (0,05 р + 0,015) и. (8)
Уравнение линейной части (7) дополняется уравне-
нием нелинейного звена (3)
u = F(aw).
378. Составить дифференциальные уравнения системы
регулирования скорости вращения турбогенератора
(рис. 219). На схеме обозначено: со — отклонение угловой
скорости вращения вала турбогенератора от номиналь-
ного значения, т] — координата положения муфты центро-
бежного механизма, о — перемещение штока золотник-а,
g — перемещение цилиндра гидравлического двигателя и
связанной с ним заслонки.
Исходные данные: объект (турбогенератор) можно
рассматривать как апериодическое звено первого по-
рядка с коэффициентом передачи k0 и постоянной вре-
мени чувствительный элемент представляет собой
3781 § 11.2. УРАВНЕНИЯ НЕЛИНЕ НЫХ СИСТЕМ СТАБИЛИЗАЦИИ 353
апериодическое звено второго порядка с коэффициентом
передачи k\ и постоянными времени 1\ и Т%, k% —
t k3 — , статическая характеристика гидравли-
ческого двигателя задана графиком (рис. 220).
Рис. 220. Статическая
характеристика гидра-
влического двигателя,
Рис. 219. Система регулирования
скорости вращения турбогенера-
тора.
Решение. Запишем дифференциальные уравнения
звеньев системы.
1. Уравнение регулируемого объекта (турбогенер атора)
(Гор+1)® = ^. (1)
2. Уравнение чувствительного элемента (центробеж-
ного механизма)
(Tip + 1)(Т2р + 1)т) = М- (2)
3. Уравнение золотника.
Для составления уравнения золотника зададимся
направлением отсчета всех координат так, как показано
на рис. 219. При произвольном перемещении точек А,
В и С получим '
о = — (3)
4. Уравнение гидравлического двигателя запишем
в следующем виде:
р£=т (4)
354 ГЛ- If. СОСТАВЛЕНИЕ УРАВНЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ (37<|
Где F (о) — нелинейная функция, заданная статической
характеристикой (рис. 220).
По уравнениям (1) —(4) определяем дифференциаль-
ное уравнение линейной части системы
(Тор + 1) (TlP + 1) (Т2р + 1) о = - (k0ktk2 + k3) g. (5)
Это уравнение дополняется уравнением нелинейного
звена (4)
pg = F(o). (6)
379. Составить дифференциальные уравнения системы
автоматического регулирования давления (рис. 221).
Рнс. 221. Система автоматического регулиро-
вания давления.
Рис. 222. Статиче-
ская характери-
стика струйного
усилителя и гид-
равлического дви-
гателя.
На схеме обозначено: 1 — объект; 2 —мембранный изме-
ритель давления (чувствительный элемент); 3 — струй-
ный усилитель; 4 — гидравлический двигатель; 5 — за-
слонка (регулирующий орган).
Исходные данные.
1. Уравнение регулируемого объекта >_
(Тор+ 1)рк = М.
где рк — отклонение давления, <р — угол поворота за-
слонки.
2. Уравнение чувствительного элемента
{Т^р2 + Т2р + 1) с = — klPu.
380] §.И.2. УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ СТАБИЛИЗАЦИИ 355
3. Статическая характеристика струйного усилителя
и гидравлического двигателя изображена на рис. 222.
Ответ. Дифференциальное уравнение линейной части
системы
(ТоР + 1).(7>2 + Т2р + 1) а = -
. Уравнение нелинейного звена
Р Ф = На).
380. Составить дифференциальные уравнения инте-
грирующего привода (рис. 223) при учете нелинейности
Рис. 223. Интегрирующий привод.
типа насыщение в усилителе (рис. 224).'На схеме обо
значено: У — усилитель,
Д — двигатель, ТГ — тахо-
генератор.
Исходные данные: ко-
эффициент передачи дви-
гателя k2 = 4 рад!в • сек,
электромеханическая по-
стоянная времени двига-
теля Тм — 0,1 сек, крути-
зна статической харак-
теристики тахогенератора
kTr = 10~г в сек/рад, мак-
Рис. 224. Статическая характери-
стика усилителя. '
симальное напряжение на выходе усилителя И2тли—
= 120 в, ширина зоны линейности статической харак-
теристики усилителя Ъ — 0,1 в.
Ответ. Дифференциальное уравнение линейной части
системы
(0,1 р + 1)м = (0,1 р + 1 )щ — 0,04 и2.
Уравнение нелинейного звена
и2 = F (и\.
ГЛАВА 12
ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
§ 12.1. Метод фазовых траекторий
381. Исследовать процессы в электромеханической
следящей системе с электромагнитными муфтами трения
и нелинейным логическим устройством (см. рис. 212)
в режиме стабилизации. В качестве исходных данных
принять данные задачи 375.
.Решение. В режиме стабилизации угол поворота
командной оси '8'1 = 0, О2= —О. -Прн этом уравнение
всей системы можно записать в следующем виде (см.
задачу 375):
0,1 при О< — 0,2?, О<0,1 град [сек, (1)
— 0,1 при О > 0,2°, О > — 0,1 град [сек, (2)
0 в остальных случаях., (3)
di2 ~
Найдем уравнение фазовых траекторий для области I
(рис. 225). Для этого введем новые переменные л = 0'
и У = -^~ и уравнение (1) запишем в виде
4Н°,1- (4)
Для исключения времени t разделим это уравнение
dx I—г
на Получим
= (5)
dx у
ИЛИ
у dy—0,1 dx. (6)
8821
§ 12.1. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ
357
Проинтегрировав уравнение (6), получаем уравнение
фазовых траекторий
z/2 = 0,05х + Сь (7)
где Ct — произвольная постоянная.
Уравнение фазовых траекторий для областей II и III
получаются аналогичным образом:
г/2 = — 0,05х + С2 ~ (8)
и
. . . У = С3. (9)
Уравнения (7) и (8) представляют собой уравнения
парабол, симметричных относительно оси х, параметр
у=^>град/сеп
Рис. 225. Фазовые траектории следящей системы к задаче 381.
которых р = 0,025. Уравнение (9) представляет собой
уравнение прямых линий, параллельных оси х. Вид
фазовых траекторий изображен на рис. 225.
Зададимся начальными условиями процесса. Пусть
при? = 0, х = & = 0, у = О' = 0,2 град/сек. По виду фазовой
траектории для заданных начальных отклонений можно
установить, что переходный процесс заканчивается менее,
чем за один период, после чего в системе устанавли-
ваются автоколебания. Амплитуда угловых колебаний
0,26^ и амплитуда колебаний скорости а&=0,1 град/сек
легко определяются по предельному циклу.
., 382. Исследовать процессы в электромеханической
следящей системе с электромагнитными муфтами трения,
358 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [383
рассмотренной в задаче 375, при условии, что вместо не-
линейного логического устройства в системе используется
релейный усилитель. Статическая характеристика F(fi)
этого усилителя изображена на
1^/# рис. 226. Значения параметров ре-
Г лейного усилителя: 6 = 0,2°, с= 1.
Рис. 226. Статическая
характеристика нели-
нейного звена к за-
даче 382.
Ответ. Фазовые траектории си-
стемы представляют собой пара-
болы, уравнения которых
у2 = 0,05х + Сь
у2 = — 0,05х + С2.
Линиями переключения привода
являются прямые ЛВ и CD (рис. 227).
При любых начальных условиях
изображающая точка удаляется от
начала координат. Следовательно, система неустойчива.
383. Исследовать процессы в системе регулирования
Температуры (см. рис. 216) при отключенной местной
Рис. 227. Фазовые траектории следящей системы
к задаче 382.
обратной связи. В качестве исходных данных принять
данные задачи 377.
Решение. В режиме стабилизаций температуры
можно принять й1 = 0, й2= —О. При этом уравнения
W1
$ 12.1. МЕТОД ФАЗОВЫХ ТРАЕКТОРИИ
359
звеньев системы можно записать в следующем виде
(см. задачу 377): 1. Уравнение объекта регулирования (Тор+ 1)е= - £0<р. (1)
2. Уравнение чувствительного элемента awi — kft. (2)
3. Уравнение усилителя (при k0. с — 0) u = F(awi). (3)
4. Уравнение двигателя постоянного тока pa = k2u. (4)
5. Уравнение редуктора <р = k3a. (5)
Учитывая, что ток в обмотке поляризованного реле
пропорционален отклонению температуры О, а скорость
dtp
отклонения регулирующего органа пропорциональна
напряжению и, в качестве входной
величины нелинейного звена (по-
ляризованного реле) можно при-
л. „dtp
нять и, а в качестве выходной —
(рищ 228). На этом рисунке Ь =
ао>ср 0,5 о / dtp \
= ~ь~ °* Ж =2°’ ®°= ПГЛпах =
== ^з^тах=0>22 рад{сек.
В соответствии с уравнением
объекта регулирования (1) и ста-
тической характеристикой нелиней-
ного звена (см. рис. 228), уравне-
ния всей системы можно записать
Рис. 228. Статическая
характеристика нели-
нейного звена к за-
даче 383.
в следующем виде:
(Тор + 1)Ф= - Азд,
(6)
РЧР =
+ <оо при
0 при
— соо при
й> + Ь,
| •&!<&,
&< - ь.
(7)
360 гл. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [383
Решив уравнения (6) и (7) совместно, получйм
(Тор + 1) рй = — koao при + Ь, (8)
(Т ор + 1) = &о®о при &<-Ь, (9)
(Тор+1)рЪ = О при | Ф|<6. (10)
Рассмотрим уравнение (8):
' 0 “I* rff. ( 1 1 )
Введем обозначения х = '&, -^г — У и уравнение (11)
перепишем следующим образом:
То^- + У-~^О. (12)
Для исключения времени из уравнения (12) разде-
лим его н а ~ — у. Получим
dy__ 1 kB(Ot>
... . , dx ~ То Тоу ’
или после разделения переменных
Л—ОЗ)
Проинтегрировав уравнение (13), получим уравнение
фазовых траекторий
х = — Тоу+ 70fe0o)0ln(y+ Z:0®0)+ Ci при х> + 6. (14)
Проделав аналогичные операции с уравнениями (9.)
и (10), получим для них
х = - Тоу — Toko&o\n{y — fe0®0) + С2 при х< - Ь, (15)
х^= — Т0у + С3 при | х | < Ь. (16)
Поставив в уравнения (14) —(16) численные значения,
параметров, получим
х= - 10^ + 221п(2,2 + ^) + С1 при х> + Ь, (17)
х = — 10# — 221п(2,2 — у) + С2 при х< — Ь, (18)
х—— 10//}-С3 при |х|<6. (19)
3841
§_|S.I. МЕТОД ФАЗОВЫХ ТРАЕКТОРИИ
361
- По уравнениям (17) -(19) на рис. 229 построен фазо-
вый портрет всей системы. Там же выделена фазовая
Рис. 229. Фазовые траектории системы регулирова-
ния температуры к задаче 383.
-ъ
о
ъ
Ct)g
траектория, соответствующая начальным условиям: при
/ = 0 •& = 5,7°, 0 = 0. По виду фазовой траектории можно
установить, что процесс в системе
заканчивается немного больше, чем
за один период колебаний. Переход-
ный процесс в системе можй закон-
читься в любой точке отрезка АВ.
384. Исследовать процессы в си-
стеме регулирования температуры,
рассмотренной в задаче 383, при
условии, что поляризованное реле
обладает статической хар актеристи-
ной, изображенной на рис. 230.
Численные значения параметров:
b = 2°, (оо = 0,22 рад [сек.
Ответ. Уравнения фазовых траекторий в области I,
и в области II (рис. 231) следующие:
х = — Юг/ + 221п (2,2+ у) + С[,
Рис. 230. Статическая
характеристика нели-
нейного звена к за-
даче 384.
х — — Юг/ — 22 In (2,2 — у) + С2.
362 гл. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ J38S
Переключение привода происходит на прямых АВ
и CD. В системе при любых начальных условиях уста-
навливаются автоколебания. Амплитуда колебаний тем-
пературы ~ 5°, амплитуда колебаний скорости изме-
нения температуры а*» 1,2 град!сек.
Рис. 231. Фазовые траектории системы регулирования темпе-
• ратуры к задаче 384.
Рис. 232. Система стабилизации ИСЗ и статическая харак-
теристика управляющего устройства к задаче 385.
385. Исследовать устойчивость системы стабилизации
искусственного спутника Земли (ИСЗ), схема которой
изображена на рис. 232 а, б.
§ 12Л. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ
363
Рис. 233. Статическая
характеристика чув-
ствительного элемента
к задаче 385.
1385]
На схеме обозначено: РО — регулируемый объект
1(ИСЗ), ЧЭ\ и ЧЭ2 — чувствительные элементы (датчики
угла рассогласования б и угловой скорости 0), У О — упра-
вляющее устройство (совместно с исполнительным орга-
ном), М — стабилизирующий момент
со стороны исполнительного органа,
И] и «2~напряжения на выходе
чувствительных элементов.
Исходные данные: момент инер-
ции ИСЗ 1 — 5000 Г • см • сек2, мак-
симальное значение стабилизирую-
щего момента Мо — 500 Г • см, коэф-
фициент передачи датчика угла
рассогласования = 1 в/град, коэф-
фициент передачи датчика угловой
скорости k2 = 1 в • сек/град, ширина
зоны нечувствительности управляющего устройства b =
= 0,2 в, ширина зоны нечувствительности ЧЭ2 (рис. 233)
управляю-
среды вра-
«/ = 0,1 град/сек, временное запаздывание в
щем устройстве т = 0,3 сек. Сопротивлением
щению ИСЗ можно пренебречь.
• Решение. Уравнение объекта запишем
J d/2 М.
Уравнение управляющего устройства
М = F (и), (2)
где F (и) — нелинейная функция, заданная'статической
характеристикой (см. рис. 232, б).
Суммарный сигнал на выходе чувствительных эле-
ментов ЧЭ\ и ЧЭ2
u = ui + u2 = ki& + Fi (Oj,
в виде
(1)
(3)
где F (0) — нелинейная функция, статическая характе-
ристика которой изображена на рис. 233, В соответ-
ствии с рис. 233 выражение (3) можно записать в сле-
дующем виде:
и =
ki&
kfl + k2(-& — d)
kfi + k2 (0 + d)
при
при
при
^>d,
b^-d.
(4)
364 гл. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [88В
Переключение исполнительного устройства при от-
сутствии временного запаздывания (t = 0) согласно
Рис. 234. Фазовые траектории системы стабилизации
ИСЗ к задаче 385.
рис. 232, б происходит при и = + b и и= — Ь, или с уче-
том (4)
при | & | d.
b k2(&-d) kt ki ’ b k2 (& — d) fci ki b k2 (& + d) ki ki ’ b k2 (& + d) *1 ki при (6) при й — d. (7)
гр51 § 12.1 МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ 365
Если принять, что в течение времени т движение ИСЗ
происходит с постоянной скоростью, и обозначить х = &,
у=“&, условия переключения исполнительного органа
можно записать в виде
х *+т^ = 0,2 + 0,3Л
х=--^- + тг/ = 0,2-0,3^
при
|y|<d = 0,l, (8)
«-тг-'Ьтгй+'«'-0'3-0’7!'’
*- - £+ту = - О,I -о.7у
х_^_М^ + ,9_0д_0>7й
0,3-0Л
при f/>d=O,l,
О)
при у — d =
= -0,1. (10)
। По формулам (8) —(10) на рис. 234 построены линии
переключения (ломаные ABCD и A'B'C'D'), которые раз-
деляют фазовую плоскость на три области. Согласно (1),
(2) и рис. 232, б уравнения всей системы будут равны
— = — 0,1 для области- Z,
= 0 для области II, (11)
+ -^р- = 0,1 для области III.
После замены х = 0, У — ^ разделим уравнения (11)
на — = у. Получим
у dy = — 0,1 dx для области I,
dy = 0 для области II,
у dy= + 0,1 dx для области III,
366 гл. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ (Ш
откуда после интегрирования найдем уравнения фазо-
вых траекторий
у2 + 0,2х = Cj для области I,
у = С2 для области II,
у2 — 0,2х = С3 для области III.
(12)
Первое и третье уравнения (12) представляют собой
уравнения парабол, оси которых совпадают с осью х.
Второе уравнение (12) есть уравнение прямой. Фазовый
портрет системы изображен на рис. 234. Процесс в си-
стеме является расходящимся при малых начальных
условиях и затухающим при больших начальных усло-
виях. Фазовые траектории сходятся к предельному
циклу, свидетельствующему о наличии в системе авто-
колебаний. Амплитуда угловых колебаний а3 0,3°,
амплитуда колебаний скорости а* «0,14 град) сек.
386. Для системы, структурная схема которой изо-
бражена на рис. 235 а и б, построить фазовый портрет
методом изоклин.
Рис. 235. Структурная схема и статиче-
ская характеристика нелинейной системы
к задаче 386.
Исходные данные: т\=Ъ,Ъсек, 7'2=1 сек, fe=1,
с = 2.
Решение. Согласно структурной схеме уравнения
замкнутой нелинейной сйстемы могут быть записаны1
в следующем виде:
(7'?р2 + 7’2р + 1)х2 = — kc при Х2>0, |
(7’?pZ + Tzp + 1) Х2 = + kc при Х2 < 0. |
s87j § 12.T МЕТОД ФАЗОВЫХ ТРАЕКТОРИИ 367
. dx dxz
Введем обозначения х = х2, У = к одновре-
менно подставим численные значения параметров. По-
лучим
—- = — 2г/— 2х — 4 при х>0,
dy &
— — 2у — 2х + 4 при х < 0.
Для исключения времени поделим уравнения (2) на
= В результате получим
dy 2у + 2х + 4* а 1
-- при х>0,
dy 2у + 2х~4 | <3)
______-------- при х<0. |
Положим в первом уравнении (3) ~ — т, а во вто-
dy
ром — и найдем уравнения изоклин:
2х + 4 п
^=--77+Г при х>0’
2х — 4 (4)
У=~' п + 2 При Х< 0’
По уравнениям (4) для различных значений т и а
строим поле изоклин (рис. 236). Наклон фазовой траек-
тории к осц абсцисс для каждой изоклины на рис. 236
показан отрезками прямых, проведенных соответственно
под углами arctgm и arctg п. Эти отрезки являются
касательными к фазовой траектории.
Как видно из рис. 236, при любых начальных усло-
виях изображающая точка стрёмится к началу коорди-
нат. Следовательно, исследуемая система устойчива.
387. С помощью метода изоклин построить фазовые
траектории и исследовать устойчивость нелинейной си-
стемы, свободное движение которой описывается диф-
ференциальным уравнением
-^г-0,5х^- + х = 0.
at£ 1 ас
368 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 1387
Рис. 236. Изоклины и фазовые траекторий к задаче 386.
й1‘0
Рис. 237. Изоклины и фазовые траектории к задачё 387.
3881 § tZ2/МЕТОД А. М. ЛЯПУНОВА -А. И. ЛУРЬЕ - 369
* dx м
Начальные условия процесса: при t = 0, х = 0, -^-=2,5.
Ответ. Система неустойчива. Уравнение изоклин
X
ц—------—- в
и tn — 0,5x
Фазовые траектории изображены на рис. 237.
§ 12.2. Метод А. М. Ляпунова — А. И. Лурье
388. Исследовать устойчивость нелинейной автома-
тической системы, структурная схема которой изобра-
жена на рис. 238.
Рис. 238. Структурная схема системы к за-
даче 388.
Решение. Согласно структурной схеме система опи-
сывается следующими дифференциальными уравнениями:
Т+ щ = — k&2,
T2$2 + &2 = F(u),
(1)
и = tit — kocfy-
Приведем уравнения (1) к нормальному виду. Для
этого введем обозначения
Ф = Щ,
Получим
П2 = *2. 43 = ^2, О=«> F(ll) = f(o).
I k
Ц| Г] Г) Пзг
П2=—у- И2 + т-/(о)>
1 2 1 2
Пз = П2>
о = т)| - ^осПз-
(2)
370 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [388
Система уравнений (2) совпадает с формой второго
типа (см. п. 6 приложения 23) при « = 3 и «ц = —
11
Д]2 = 0, ^ТЗ = 0, «22 7“ 1 ^23 ~ 0, а31 ~ : 0,
«32=1, «33 = 0, ^1 = 0> = ^3 — 0, «!=!, «2 = 0,
«3 = koc-
Запишем уравнения (2) в канонической форме (см.
приложение 23). Для этого из коэффициентов уравнения
составим определитель
и определим корни характеристического уравнения
D (А.) = О
Ввиду того, что в характеристическом уравнении
имеется один нулевой корень, канонические уравнения
записываются в следующем виде£
х{ = Ip;, + f (а)
Х2 — к2Х2 + / (о),
(4)
6 = £| А'| + р2х2 — rf (о).
Определим постоянные г, и р2:
f ~ (Ci^i + о2й2 + С3Й3) = О,
так как = 0, с2 = 0, Ь3 = 0.
Постоянные р1 и р2 определяются по формулам (п. 10)
приложения 23.
38S.I
§ 12.2. МЕТОД А. М. ЛЯПУНОВА —А. И. ЛУРЬЕ
37.1
Так как в нашем случае с2 = 0, то согласно фор
муле (п. 11) приложения 23 требуется определить только
TV,(Л) и по формуле (п. 12) приложения 23
N1 W ~ ^2^21 (А) ~ ~ Т2
О----—
Л
1 -А
k
Т^'
ДО3|(А) = t>zDS3 (А)-
Определяем D'
(5)
(6)
По формуле (п. 11) приложения 23 находим
>______C\Nj (Л.,1) + сзМз (Ар __ _ kT{
Y1 . D'(M T-x-.Ti’
__ CiNi (А2) + csNз (А2) kT2 + k<x (?г~ 7i)
Ys Р'(Лг)
и определяем
Pl ~ A’lYi у___у i
о _ j ____ I kTz + kpc (T2 — 7i) _
P2 ЛгУг t-2 T2-Ti
Для класса нелинейных систем, к которому при-
надлежит рассматриваемая система, достаточные усло-
вия устойчивости имеют вид (см. приложение 24)
Г2>0 (8)
и
Г2 > — 4О, (9)
где
Г2==4г+лГ = /г + /г0С,
А ' (Р* ~ Рз) — Аг) _ _ 2fe72 + fepc (7г 7[)
U~ 4ХД2 “ 472
Условие (9) приводит к следующему достаточному
условию устойчивости рассматриваемой системы:
^осЛ>^2. СЮ)
372 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [380
389. Исследовать устойчивость нелинейной автомати-
ческой системы, структурная схема которой изображена
на рис. 239.
Рис. 239. Структурная схема системы к задаче 389.
Ответ. Дифференциальные уравнения системы в ка-
нонической форме имеют следующий вид:
х, = Mi + f (о). '
x2 = M2 + f(o),
о = PjX, + 02*2, .
где Х1 = —, Z2 = —4-, а коэффициенты и ₽2 равны
о fe, о (ЪЬ - Т3)
P1 1\Т2 (Tt - Г3) ’ Р2 Т2Т3 (Т3 - 7,) •
Условие устойчивости системы Г2> — 40 (приложе-
ние 24) может быть записано в следующем виде:
kz >
TtT3
T2(Tt + T3)
390. Исследовать устойчивость системы, структурная
схема которой изображена на рис. 240.
Решение. Согласно структурной схеме дифферен-
циальные уравнения системы имеют' следующий вид:
Tiiit + й1 — — kfi,
t> = F (и),
(1)
и = k2Ui + 1г-лщ — /госё.
Преобразуем систему уравнений (1) к канонической
форме, Для этого обозначим
£ = б, о = н, f(a) = /7(u)
§ 12.2. МЕТОД А. М. ЛЯПУНОВА-А. И. ЛУРЬЕ373
и запишем уравнения (1) в виде
, 1 klf
П + Г1 П Ti |>
о — k2r\ + £3f] — £ос£,
/Полученные уравнения (2.) имеют форму (п. 12) при-
ложения 24 при
rt = 3, ai = 7^> rf==7T’ Ct = &3, f = k0.
и равенстве нулю всех остальных коэффициентов.
(2)
Рис. 240. Структурная схема системы к задаче 390.
Определяем корни многочлена
D (А) = А2 + (ЦК = А2 + ~к.
11
Эти корни р авны А] = — у-, А2 = 0.
Коэффициенты р, и & определяем по формулам (п. 17)
приложения 24. Для этого предварительно находим
Д (А) = Со *Ь Ci А =5 &2 *Ь й3А,
D\ (А) = А + cii = А + -уг-,
£)'1(А)=1.
С учетом этих выражений
ь _ Ьз
I тг
71 '
о_______J
Р1
p2 = _d^£_
- Aft-2
374 гл. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 1391
Уравнения системы в канонической форме имеют
вид
= /.j*! + f (о),
%2~ f (О),
О = + $2Х2 — Г.
Достаточные условия устойчивости (1) и (2) прило-
жения 24 в данном случае имеют следующий вид:
Р = К + г>’0
Д1
ИЛИ
г2=-мм;-&з)+£ос>о.
Из этого выражения получим окончательно доста-
точное условие устойчивости в виде
koc> ki(k2Tl — ka) при k2Tt>k3.
§ 12,3. Частотный метод В. М. Попова
391. Структурная схема нелинейной автоматической
системы изображена.на рис. 241. Коэффициент передачи
линейной части системы и нелинейного звена.k = knk№
<4#
Рис. 242. Нелинейная
статическая характери-
стика к задаче 391.
Рис. 241. Структурная
схема системы к за-
даче 391.
условно отнесен к нелинейному звену. Определить, при
каких значениях k система будет абсолютно устойчива,
если характеристика нелинейного звена расположена
в секторе (0, k) (рис. 242),
se)] § 12.3. ЧАСТОТНЫЙ МЕТОД В. М. ПОПОВА 375
Исходные данные: постоянные времени линейной
части системы 7i — 0,5 сек, сек, 7g = 0,1 сек.
Решение. Частотная передаточная функция линей-
ной части системы имеет вид
Г = (1 -Ь/соГ,) <1 + у®Г2) (14-/<оГа) * (1)
Ее вещественная и мнимая части соответственно равны
И (со) = Re Г (/со) =
1 - со2 (TtT2 + 71?3 + ТгТ3)
(1+с^(1+й*)(1 + <
V (со) = Im II" (/со) =
-со(7, + Гг+Г3) + <о37'17'2Г3
,(1фсо2^(1 Wrf)(l+co27i)'
(2)
(3)
Введем некоторые функции
образом:
7/* (®) = Re 1Г (/со) =
(1 + со2??) (1 + co27’D (1 + со2Г2) ’
(4)
V* (со) = со Im W(j(0) =
— со2 (Г, + Г2 + Т3) + со47',7у3
(1 + co2rf)(1 + са2Т’|)(1 -I- со2?"2)'
(5)
По выражениям (4) и (5)
построим характеристику
Г (со) = /(£/’(<о)] (рис. 243)
и через точку I—т~, /0)
£7* (/со) и V’(/co) следующим
Рис. 243. Характеристика
V * (со) = ДР * (со)] к зада-
7 че 391.
проведем прямую Попова
так, чтобы построенная ха-
рактеристика целиком лежала справа от этой прямой.
Согласно рис. 243 -j-
=» 0,08. Поэтому система абсолютно
устойчива для всех нелинейных характеристик, лежащих
376 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [342
в секторе
О < k < 12,5
(6)
и, в частности, для характеристики релейного типа,
изображенной на рис. 242.
Таким образом, достаточное условие абсолютной
устойчивости замкнутой нелинейной системы сводится
в данном случае к выполнению необходимого и доста-
точного условия устойчивости замкнутой линейной си-
стемы, имеющей в разомкнутом состоянии коэффициент
передачи, равный k.
392. Структурная схема нелинейной автоматической
системы изображена на рис. 244. Проверить выполне-
ние достаточного условия абсо-
лютной устойчивости системы при
следующих значениях параметров
системы: Т{—5 сек, Т2 = 1,25 сек,
— 0,5, |2 — 0.05, коэффициент
F(u)
b О
(f*Z£,T,p (1+2£гТгр * Т?рг)
Рис. 244. Структурная схема системы
к задаче 392.
&
Рис. 245. Нелинейная
статическая характери-
стика к задаче 392.
передачи линейной части системы k„ = 4, коэффициент
усиления нелинейного звена &н = у —0,5 (рис. 245).
Решение. Коэффициент передачи разомкнутой си-
стемы
k — kj,kH — 4 • 0,5 = 2
отнесем к нелинейному звену. Тогда частотная переда-
точная функция разомкнутой системы будет равна
~ (1 - ТУ + 2/1,Г,®) (I - + 2/127’2со) ‘
394]
§ 12.3. ЧАСТОТНЫЙ МЕТОД В. М. ПОПОВА
377
Определяем функции
(] - 7?<в2)(| - ф2)-4^27’17>2
t/’ (со) -Re №л(/<о) +
(2)
V* (со) = ® Im Гл (j®) =
-2<o2[(l-7->2)g2T2 + (l.-72(o2)gIT1| -
~ [(1 - 7>2)2 + 4g27>2] [(1 - Г2®2)2 + 4|27’2co21 • W
По выражениям (2) и (3) строим характеристику
у1*(ш) = /[[/*(со)] (рис. 246). На вещественной оси от-
ложим точку с координатами /о). Через эту
точку можно прове-
сти прямую Попова
так, что вся построен-
ная характеристика бу-
дет располагаться спра-
ва от нее. Следова-
тельно, данная система
будет абсолютно устой- i
чивой при заданном
k = 2, если статиче-
У’(ш)
екая 'характеристика Рис. 246. Характеристика V*(©)=•
нелинейного звена це- = f [V * (<»)] к задаче 392.
ликом располагается
в секторе (0, k). Этот сектор заштрихован на рис. 245.
393. Для нелинейной системы, рассмотренной в за-
даче 392, определить граничное значение коэффициента
— ^Л^Н"
Ответ. Граничное значение коэффициента передачи
*-^~3,34.
394. Передаточная функция линейной части системы
= (Г.Р4-1) (Г2р+ 1) •
Определить условия абсолютной устойчивости.
378 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ . ИССЛЕДОВАНИЯ. УСТОЙЧИВОСТИ [зез
Ответ. Характеристика V* (со) — f [U*(со)] целиком рас-
полагается в. нижней полуплоскости. Через точку
/о) при любом 0<А<оо можно провести пря-
мую Попова так, что вся характеристика расположится
правее ее. Поэтому система абсолютно устойчива при
всех k — kjta и для всех нелинейных звеньев, стати-
ческие характеристики которых принадлежат сектору
(О, оо), т. е. располагаются в I и III квадрантах.
§ 12.4. Метод припасовывания
395. Исследовать переходный процесс в системе,
Структурная схема которой изображена на рис. 247, а, б.
Рис. 247. Структурная схема системы и ста-
тическая характеристика нелинейного звена
к задаче 395.
Исходные данные: k = 2 сек~\ b = 0,5, с = 5.
Решение. Согласно структурной схеме дифферен-
циальное уравнение замкнутой нелинейной системы имеет
следующий вид:
х2 + kF (х2) = 0, (1)
где F(x2) — нелинейная функция, заданная статической
характеристикой (см. рис. 247, б), причем
F(x2) = +с] [ при [ при х2' -Ь< > + Ь, Zx2< + Ь, когда х2<0, (2)
F(x2) = -cj ( при 1. при х2< -Ь< z-ь, Zx2< + b, когда х2 > 0. (3)
3951
§ 12.4. Метод гтрипасовыванид
379
Нелинейное уравнение (1) внутри участков (2) и (3)
заменяем двумя- линейными уравнениями;
х2 + &с = 0, (4)
х2 — kc = 0, (5)
или, с учетом численных значений параметров
х2 4* 10 — 0, (6)
х2- 10 = 0. (7)
Решения уравнений (6) и (7) имеют вид
х2= — 10/+ Сь (8)
х2 ~ ю/ ~Ь С2> (9)
где С! и С2 — постоянные интегрирования.
. Для определения постоянной С( на первом участке
процесса зададимся начальными условиями: при t = 0
х2(/) = х2 (0).' Из уравнения (8) находим
Cj ~ Си = Х2(0),
и решение (8) для первого участка окончательно при-
нимает вид
х21=-10/ + х2(0). (10)
Постоянную интегрирования С2 находим из условий
равенства начального значения процесса на втором уча-
стке и конечного значения процесса на первом участке.
При этом учитываем, что скорость на первом участке
х21 = —10 < 0 и согласно (2) переход ко второму участку
происходит при х21 — —Ь — 0,5 в момент времени t = tb
причем из (10)
/,= х2(о) + о,5 , (Ц)
Поэтому из условия припасовывания в точке t =
можно записать
*21 (Л)=—0,5 = x22(/i). (12)
Из уравнения (9) с учетом (12) находим постоян-
ную С2 для второго участка процесса
С2 = С22= -0,5-Ю/j
380 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [Звв
Рис. 248. Кривая переходного
процесса к задаче 395.
и окончательное выражение для решения на втором
участке
х22 = 10(*-О-0Д (13)
На этом участке скорость х22=10>0. Поэтому со-
гласно (3) при х22 = + b в момент t = t2 происходит
переход на третий участок, для которого процесс описы-
вается уравнением (8), но
при новом значении по-
стоянной Ci = С13. Из
уравнений (13)
, 10/1 + 1 Ха (0) + 1,5
‘2 ~ Ю 16 ‘
Условие припасовыва-
ния в точке t = /2 имеет
вид
х22 (^2) — 0,5 = х23 (12), (14)
где х23 означает решение (8) для третьего участка про-
цесса. /
Из уравнения (8) с учетом (14) находим постоян-
ную С1 для третьего участка
С1з = 0,5 + 10/2
и окончательное выражение для решения на этом участке
процесса
*23= — 10(f —/2) + 0,5, />/2. (15)
Дальнейшее йостроение кривой переходного процесса
производится аналогичным образом.
Переходный процесс для двух значений начальных,
условий х2(0) = 0,75 и х2(0) = —0,25 построен на рис. 248.
Как видно из этого рисунка, в системе устанавливаются
автоколебания с амплитудой А — b — 0,5 и частотой
Q =-у-~ 31,4 сек'.
396. Для предыдущей задачи определить амплитуду
и частоту автоколебаний, если
1)6=1 сек~\ 6 = 0,5, с = 5,
2) k = 1 сек~\ b — 0,25, с = 5,
3)6=1 сек~', 6 = 0,25, с =10.
397]
§ 12.4. МЕТОД ПРИПАСОВЫВАНИЯ
,381
Ответ.
1) д = 0,5, й « 15,7 сек-1,
2) Д = 0,25, Й ~ 31,4 сек-1,
3) д= 0,25, Й ~ 62,8 сек-1.
397. Для системы, рассмотренной в задаче 395, найти
условия существования автоколебаний и аналитические
выражения для их частоты и амплитуды.
Решение. Дифференциальное уравнение замкну-
той нелинейной системы (см. рис. 247)
х2 + kF (х2) = 0, (1)
J при х2 > + Ь,
F(x^— + с । При _ Ь<х2< + Ь, когда х2<0, (2)
J при х2 < — Ь,
F(x^ с ( при — b<x2< + b, когда х2>0, (3)
внутри участков (2) и (3) заменяем двумя линейными
дифференциальными уравнениями
х2 + kc = 0, (4)
х2 — kc = 0. (5)
Находим решения уравнений (4) и (5)
x2j ’ kct -Р Cj, (6)
Х22 = kct + С2. (7)
Время t на первом участке условимся отсчитывать
от точки, в которой х21=+6. Тогда начальное условие
для первого участка будет равно
х21 = + b при t = 0.
Используя его, находим постоянную интегрирования
— + Ь. Отсюда на первом участке
х21 = — kct + b. (8)
Для второго участка процесса время t будем отсчи-
тывать от точки, в которой х22 = — Ь. Начальное усло-
вие для второго участка будет
х22 = — Ь при t = 0. (9)
382 ГЛ. 12. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ [397
Чтобы в системе существовало устойчивое периоди-
ческое решение (автоколебания) с периодом Т, необхо-
димо потребовать выполнения единственного условия
(так как рассматривается система первого порядка,
а характеристика F(x2) симметрична относительно на-
чала координат)
Х21 ("2") ~ х22^)' (Ю)
Подставим в (10) значения переменных из (8) и (9).
Получим
/гсТ . , .
(11)
Из (11) находим
~_________________4Ь о_____ 2п __nkc
1 ~ kc ’ 12 “ Т
Амплитуда автоколебаний А определяется как макси-
мальное значение величины x2i, полученной из уравне-
ния (8) в течение полупериода колебаний. Из (8) оче-
видно, что
(12)
^-+b\ = b.
I Л-21 Imax
2
ГЛАВА 13
ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
§ 13.1. Алгебраические способы определения
устойчивости и автоколебаний
398. Исследовать устойчивость состояния равновесия
электромеханической следящей системы, принципиаль-
ная и структурная схемы которой изображены на рис. 209
и 211, при следующих значениях параметров системы:
kx = 1 в/град — 57,3 efpad; k2 = 2,5; k3 — 5,73 рад I в • сек;
А4=0 (скоростная обратная связь отсутствует); й5=0,001;
Тj — 0,05 сек; Тм = 0,05 сек. Статическая характеристика
нелинейного звена изображена на рис. 210. Ширина
зоны нечувствительности & = 0,25e, С7зтах = с= ПО в.
Решение. По структурной схеме (см. рис. 211)
определяем дифференциальное уравнение линейной части
системы (см. задачу 374) при Oj (0 = 0
(Г 1Л/ + (Ti + Ты) р + 1] ри2 = — kik2k3k5u3. (1)
Для нелинейного звена запишем гармонически линеа-
ризованное выражение
»з = [<7 (й) + р] (2)
где согласно приложению 28 для нелинейности
(см. рис. 210)
- =1 • a^b>
384 ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ {898
Подставляя значение и3 из уравнения (2) в уравне-
ние (1), получим линеаризованное уравнение замкнутой
нелинейной системы
[7\Тыр3 + (7\ + Гм). р2 + р + kq (я)] и2 = 0, (4)
где k = kik2k3kz = 0,82 сек"1 — коэффициент передачи ли-
нейной части системы.
Этому дифференциальному уравнению соответствует
характеристическое уравнение
7’17’мр3ч-(7’,1 + 7’м)р2 + р + ^(я) = 0. (5)
Условия существования в уравнении (4) периоди-
ческого решения
и2 = A sin Qt (6)
будем отыскивать с помощью критерия Михайлова.
Для этого в характеристический полином
L (р) - 7\Тыр3 + (7, + ГМ) р2 + р + kq (а) (7)
подставим р = /со, выделим вещественную и мнимую
части и приравняем их нулю:
Х(со, я) = ^(я)-(Г1 + 7’м)со2 = 0, 1
У(со)= со(1 — Т^ТмСО2). J
Из второго уравнения (8) сразу найдем искомую частоту
периодического решения
со = Q = -ZJL_- = - = 20 сек"1. (9)
/ПЛ, /0,05-0,05 v '
Подставим это значение в первое уравнение (8) и
найдем выражение, ' связывающее амплитуду периоди-
ческого решения а = А с параметрами системы
= (10>
.11/1 F К1 11 м
или, после подстановки числовых значений,
4-1Ю Г. № ля е
1----дГ- = 48,8.
398)
§ 13.1. АЛГЕБР ИЧЕСКИЕ СПОСОБЫ
385
Решение этого уравнения дает два значения ампли-
туды А = 0,257 в и А = 2,86 в.
Для исследования устойчивости найденного перио-
дического решения воспользуемся приближенным ана-
литическим условием [25], согласно которому периоди-
ческое решение устойчиво, если выполняется неравенство
(И)
1дХ\* IdY V _ / дУ V / д.
\ да ) \ да / \ да J \ д<
Из выражений (8) находим
дХ k dq (а) _ 4kc 2b2 — а2
да-
да л «3 Va2 — b2 ’ а — ’
«£__-2(7, + 7м)<»,
да
Подставим выражения для частных производных
в (11) и одновременно произведем замену ® = О = ,
Получим условие устойчивости периодического решения
в виде
~ -з)>о
л ааУ а2 — Ь2
ИЛИ
(12)
Следовательно, из двух найденных значений ампли-
туды периодического решения At — 0,257 в и Л2 = 2,86 в
амплитуда А2 соответствует устойчивому периодическому
решению, т. е. является амплитудой автоколебаний.
Определим амплитуду и частоту колебаний исполни-
тельной оси системы. Частота автоколебаний одинакова
для любой переменной системы, в том числе и для
угла А, и равна й = 20 сек-1. Амплитуда колебаний
согласно структурной схеме (см. рис. 211) равна
А) = 7т- = т£ = М4°.
386
ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
13В»
. . Определим зависимость амплитуды и частоты авто-
колебаний от параметров системы. Из выражений (9)
и (10) видно, что частота автоколебаний £2 зависит
только от постоянных времени Т! и Тм, а амплитуда
автоколебаний, кроме того, от коэффициента передачи
линейной части системы k и ширины зоны нечувстви-
тельности нелинейного элемента Ь, причем из (10)
k TtTK(l(a) ’ (13)
Из формулы (13) с учетом (12) получим критическое
значение коэффициента передачи линейной части системы
, _ nb(Tt + Tu)
R«p- 2cTtTM “ v '
Для заданных значений параметров
. _ л • 0.25 (0,05 + 0,05) ~ „ 0057 сек-1
2-110-0.052 ~ О,ии&/ сек .
399. Исследовать следящую систему, рассмотрен-
ную в задаче 398, при наличии скоростной обратной
связи. Коэффициент обратной связи k4 = 10-2 в • сек!рад
(см. рис. 211). Остальные параметры системы остаются
без изменения.
Ответ. Состояние равновесия системы устойчиво.
Автоколебания отсутствуют.
400. Исследовать устойчивость
состояния равновесия системы, стру-
ктурная схема которой изображена
на рис. 249. Если в системе
О
СЧО
—ф
^7
Т/Р*'
• Г,
РЪр Ч)
Рис. 249. Структурная схема системы
К задаче 400.
Рис. 250. Статиче-
ская характеристика
нелинейного звена
к задаче 400.
устанавливаются автоколебания, то определить их ам-
плитуду и частоту для переменной xt. Исходные данные:
7’1=1 сек, 7’2 = 0,01 сек, ^=10, £2 = 5 сек~\ статичс-
§ 1.3.1. АЛГЕБРАИЧЕСКИЕ СПОСОБЫ
387
ская характеристика нелинейного звена изображена на
рис. 250.
Ответ. В системе устанавливаются автоколебания
с амплитудой А » 6,3 и частотой Q = 10 сек~1
%! = 6,3 sin 10/.
401. Найти область устойчивого состояния равно-
весия и область автоколебаний и определить амплитуду
и частоту автоколебаний
для следящей системы,
схема.которой изображена
на рис. 209, при учете не-
линейности типа насыще-
ния в предварительном
усилителе и отсутствии
релейного усилителя и об-
ратной связи по напряже-
нию тахогенератора.
Исходные данные: по-
стоянная времени усили-
теля 7’1 = 0,1 сек, электро-
Рис. 251. Статическая характери-
стика усилителя следящей систе-
мы к задаче 401.
механическая постоянная времени двигателя Г2 = 1 сек,
общий коэффициент передачи линейной части системы
Лл = 20 сек-1, коэффициент передачи чувствительного
элемента А, — 50 в!рад, статическая характеристика уси-
лителя изображена на рис. 251. Исследование провести
для А2= 1 и k2 = 2.
Рис. 252. Структурная схема следящей системы к за-
даче 401.
Решение. Составляем структурную схему системы
(рис. 252). Согласно этой схеме дифференциальное
уравнение линейной части системы при <Ь(0 = 0 запи-
шем в виде
(Ггр+!)/?«!= -/глп2, (1)
где k ....
388
ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
1401
Дифференциальное уравнение нелинейного звена
имеет вид
(Tip+ l)M2 = ^yMb (2)
Коэффициент усиления усилителя ky является не-
линейной функцией, заданной графически (рис. 251).
Поэтому согласно методу гармонической линеаризации
запишем для него гармонически линеаризованное выра-
жение
ky~q(a) + -~^-p, (3)
где коэффициенты гармонической линеаризаций для
характеристики с насыщением имеют значения (см. при-
ложение 28)
q(a) — k2 при а^Ь,
<Да) = -^(агс8Шу + -|-|А--J-) при (4)
. ?'(а) = 0.
Из уравнений (1) —(3) получим линеаризованное
уравнение замкнутой нелинейной системы
[(Г, р + 1) (Т2р + 1) р + k„q (а)]«, = 0, (5)
которому соответствует характеристическое уравнение
Л7’2Р3 + (7’1 + 7’2)р2 + р + М(«) = 0. (6)
Для отыскания условий существования периодиче-
ского решения
«] = A sin Qt (7)
из характеристического полинома после подстановки
р = /<й выделим вещественную и мнимую части и при-
равняем их нулю.;
Х(С0) = М(а) + (Л + 7’2)®2 = 0,
У((о) = (о(1-7’|7’2®2). U
Частота периодического решения находится из вто-
рого уравнения (8)
“,“‘!"7Й"7ЙГ”3,16“'£Л <9)
4011
§ 13.1. АЛГЕБРА11ЧЕ КИЕ П Ь
389
Из первого уравнения (8) с учетом (9) получим фор-
мулу, связывающую ’ амплитуду периодического реше-
ния с параметрами системы
&(arcsta^+|./iT5)=i+Zi. (10)
Для исследования устойчивости периодического реше-
ния найдем частные производные от выражений (8):
' / дХ V _ h дд (А)
\ да ) " дА ’
(^Г=-2О(7’1 + 7’2)=-2^^-=-0,695,
1 ~ ЗТ'Т&2 = 1 - 3 = -2.
Для устойчивости периодического решения (7) требуется.
чтобы выполнялось не-
равенство
(dX\*ldY\*
\ да / \ да /
(12)
\ да) \да) ’ ' '
или, с учетом выраже-
ний (11),
... (13)
Рис. 253. Зависимость коэффици-
ента гармонической линеаризации
от амплитуды колебаний к за-
даче 401.
т. е. частная производная
dq (Л)
—должна быть отри-
цательной.
Для определения знака этой производной по выра-
жению (4) для (?(Л) построим график (рис. 253), со-
гласно которому
при. А>Ь. (14)
300
ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
[401
Следовательно, амплитуда периодического реше-
ния =(7) будет амплитудой автоколебаний лишь при
выполнении условия А >Ь. При А <Ь автоколебания
в системе отсутствуют, что и понятно, так как при этом
согласно рис. 251 нелинейная система превращается
в линейную, которая, как легко показать, устойчива.
Рис. 254. Зависимость изменения
амплитуды и частоты автоколебаний
от параметров системы к задаче 401.
Определим амплитуду автоколебаний. Уравнение (10),
связывающее ее с параметрами системы, является транс-
цендентным. Поэтому для определения амплитуды вос-
пользуемся графоаналитическим методом. Для этого
решим уравнение (10) относительно к — кл1г2:
k =-----------(15)
27’17’2(arcSlnA + ^i/ 1-^)
A
и построим график k = k(AQ) (рис. 254), где Лв = -^ —
амплитуда колебаний исполнительной оси системы (см.
401’1
§ 13.1. АЛГЕБРАИЧЕСКИЕ СПОСОБЫ
391.
рис. 252). Что касается частоты автоколебаний' Q, то
она" остается неизменной для любой переменной- системы
и согласно выражению (9) не зависит oi коэффициента k.
Граничный коэффициент передачи системы &г£) опре-
деляется из выражения (15) при Л = 6 и равен
TiT2 0,1 ч6'
Автоколебания в системе возникают лишь при k > kTB,
Нетрудно убедиться, что граничный коэффициент (16)
Рис. 255. Статическая
характеристика нелиней-
ного звена к задаче 402.
Рис. 256. Зависимости изменения
амплитуды и частоты автоколебаний
от параметров системы к задаче 402.
совпадает с коэффициентом передачи, найденным из
условия границы устойчивости линейной системы. Но,
в отличие от линейной системы, у которой за областью
устойчивости лежит область неустойчивости, в системе
с нелинейностью типа насыщения за областью устой-
чивости лежит область автоколебаний, т. е. устойчивых
периодических колебаний с вполне определенной амп-
литудой и частотой.
На рис. 254 также изображены графики, связываю-
щие амплитуду и частоту автоколебаний с шириной зоны
линейности статической .характеристики нелинейного
звена А при А’2=1.
392 ГЛ. >3. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ (402
Для заданных значений параметров системы по гра-
фику (рис. 254, а) определяем частоту и амплитуду
автоколебаний:
£2 = 3,16 сек~\ 0,022 рад при k2=l;
£2 = 3,16 сек~\ A^^Gfi^pad при /г2 = 2.
402. Найти область устойчивого состояния равнове-
сия и область - автоколебаний для следящей системы,
рассмотренной в задаче 398, если аппроксимированная
статическая характеристика имеет вид, как показано
на рис. 2.55 при 6 = 0,25 в, с = 110 в.
Ответ. Область устойчивости состояния равновесия,
область автоколебаний в зависимости амплитуды и ча-
стоты автоколебаний от коэффициента передачи линей-
ной части системы показаны на рис. 256.
х
§ 13.2. Частотный метод определения автоколебаний
403. Исследовать устойчивость состояния равновесия
нелинейной системы, структурная схема которой изо-
бражена на рис. 257, если заданы параметры линейной
' ~к —
-ъ о
Рис. 257. Структур-
ная схема системы
к задаче 403.
Рис. 258. Статическая
характеристика нели-
нейного звена к за-
даче 403.
части системы k ~ 0,82 сек-1, Т\ = 7’2 — 0,05 сек и стати-
геская характеристика нелинейного звена (рис. 258), для
которой Ь = 0,25, с = ПО.
Решение. Построим амплитудно-фазовую частот-
ную характеристику линейной части системы №д(/©)
4031 § 13.2. ЧАСТОТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ АВТОКОЛЕБАНИЙ 393
и годограф гармонически линеаризованного нелинейного
звена — 2(a) = —
Согласно структурйой схеме частотная передаточная
функция линейной части системы
= /<в(1 + Г,/©) (1+7^©) ’
ее модуль
I (ja) | -----г....Л______
со/О + ЭДО + ф2)
и фаза
ф (<о) = — 90° — arctg , — arctg ®Г2.
После подстановки численных значений параметров
получим
| №л (/©) I = +Qf0025(i)S) . (1)
ф (со) = — 90° — 2 arctg 0,05®. (2)
Задаемся значениями со от 0 до оо и по формулам (1)
и (2) строим амплитудно-фазовую характеристику линей-
ной части системы 1Гл(/<о) (рис. 259).
1m
Рис. 259. Частотные характеристики
линейной- части системы и нелиней-
ного звена к задаче 403.
Гармонически линеаризованная передаточная функ-
ция нелинейного звена согласно приложению 28 равна
30,1 ' ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ (403
Отсюда
— Z (а) =-----!— = - -'W -у-1 г.
' ’ Гн(а) 4с Ca2-fc2
После подстановки численных значений параметров
нелинейного звена получим
- Z (а) = - — > 1 (3)
440 fa2 -0,0625 ’
Задаемся значениями а от а = b = 0,25 до оо и строим
годограф нелинейного звена — Z (а) (рис. 259). В данном
случае этот годограф совпадает с отрицательной веще-
ственной полуосью и имеет две ветви. Минимальное
вначение модуля функции —Z(a)
= 0,0036
достигается при а — b ]/ 2 « 0,352.
Годографы Wn(ja) и — Z(a) пересекаются в двух
точках. Это означает, что уравнение
(/со) = - = — Z (а)
имеет два периодических решения,
х = Д sin 1
х = А2 sin Qt, J
где согласно рис. 259 £2 = 20 сек-1, Д = 0,257, Л2 = 2,86^
Для устойчивости периодического решения требуется,
чтобы амплитудно-фазовая характеристика линейной
части системы И/л(/со) охватывала часть годографа
— Z (а), соответствующую меньшим амплитудам. По-
этому первое из решений (4) является неустойчивым,
а второе — устойчивым. Следовательно, в системе уста-
навливаются автоколебания с амплитудой Л = 2,86 и
частотой £2 = 20 сек-1:-
х = 2,86 sin 20/.
40S1 § 13.2. ЧАСТОТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ АВТОКОЛЕБАНИЙ 395
404. Решить предыдущую задачу, если:
I) k — 2 сек'1, Г1~ 0,05 сек, 7’2 = 0,02 сек, 6 = 0,25,
с — 110;
2)/г = 4 сек-1, Г] = 0,01 сек, 7’2 = 0,08 сек, 6 = 0,25,
с = 110;
3) £ = 0,5 сек-1, 7’> = 0,1 сек, Г2 = 0,01 сек, 6 = 0,5,
с = 110;
4) k = 2 сек-1, Т। = 0,05 сек, Т2 = 0,05 сек, 6 = 0,1,
с =40;
5) k —2 сек'1, Тг — 0,05 сек, Г2 = 0,02 сек, 6 = 0,25,
с = 11.
Ответ.
1) А «4, £>«31,6 сек-1;
2) А ~ 5, й « 35,3 сек'1;
3) Система устойчива, автоколебания отсутствуют;
4) А ~ 2,55, Й « 20 сек-1;
5) Система устойчива, автоколебания отсутствуют.
405. Исследовать устойчивость состояния равновесия
системы, структурная схема которой изображена на
Рис. 261. Статическая
характеристика нелиней-
ного звена к задаче 405.
£1—
Риг. 260. Структур-
ная схема системы
к задаче 405.
рис. 260, если заданы параметры линейной части системы
#1 = 10 сек-1, 7’1 = 0,1 сек и статическая характеристика
нелинейного звена (рис. 261), для которой #1 = 0,1,
#2 = 0,3, £ = tga = 5.
396 ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ 1466
Ответ. Годографы Й7л(/ы) и — 2(д)не пересекаются.
Следовательно, состояние равновесия системы устойчиво,
автоколебания отсутствуют.
406. Исследовать устойчивость состояния равновесия
-электромеханической следящей системы, структурная
схема которой изображена на рис. 211, если заданы
параметры линейных звеньев: fe, = 57,3 в!рад, £2 = 2,5,
k3 — 5,73 рад[в • сек, /г4 = 10“2 в • сек]рад, k5 = 0,001, 7\ =
= 0,05 сек, Ты = 0,05 сек, и статическая характеристика
нелинейного звена (см. рис. 210), для которой & = 0,25 в,
~ 1Ю В.
Решение. По заданной структурной схеме опреде-
лим передаточную функцию линейной части системы
№л(р) и гармонически линеаризованную передаточную
Н.З
Рис. 262. Преобразованная структурная схема
к задаче 406.
, А -
функцию нелинейного звена И7н(а). Для этого структур-
ную схему нелинейной системы представим в виде по-
следовательного соединения нелинейного звена и линей-
ной части системы (рис. 262).
Согласно рис. 262
ну ( гД_ (Л<р-Г Л1Л5) /г(тр+1) z<\
р(г,р+1)(гмр + 1) - р(г,р+1)(гмр+1) ’
где k = k]l:yk:ikr,— коэффициент передачи линейной части
ki
системы, —постоянная времени.
Гармонически линеаризованная передаточная функ-
ция нелинейного звена, имеющего однозначную стати-
4061 § 13.2. ЧАСТОТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ АВТОКОЛЕБАНИЙ „397
ческую характеристику, может быть записана в. виде
^и(а)=9(а), (2)
где <?(«)= <см- приложение 28).
По передаточной функции (1) определяем частотную
передаточную функцию
И7 U + /<от) 0,82(1+0,174/®)
joG + joroa+jceTy j®(l + 0,05jw)2 ’
ее модуль
I tvz /• \I 0,82 К1 + 0,0305м2
I (/®) I - ю (1 + ОД025Ю»)
и фазу
ф(со) = — 90° + arctg 0, 174® — 2 arctg 0,05<э.
(4)
(5)
’ По формулам (4) и (5) строим амплитудно-фазовую
характеристику линейной части
системы (рис. 26Й) и годограф
нелинейного звена
Рнс. 263. Частотные харак-
теристики линейной части
системы и нелинейного звена
к задаче 406.
ла2 1
4с V а2— Ь2
440 Ка2 - 0,0625 !
при значениях амплитуд Ь<
< а<оо. В данном случае этот
годогра*ф совпадает с отрица-
тельной вещественной полу-
осью и имеет две ветви. Минимальное значение мо-
дуля функции — Z (а)
I ~ Z (а) |Ш1П = g ~ 0,0036
у л» a ivy
достигается при а = b ~ 0,352 в.
Как видно из рис. 263, годографы (/со) н — Z (а)
не.имеют общих.точек пересечения. Следовательно, со-
стояние равновесия рассматриваемой системы устойчиво.
398
ГЛ. 13. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
1407
. , 407. Исследовать устойчивость состояния равновесия
нелинейной системы, структурная схема которой изобра-
жена на рис. 264. Параметры линейной части системы:
T^lficeK, 7’2 = 0,9 сек, 7’3= 1,1 сек, ^ = 0,5, £2 = 5,
Рис. 264. Структурная схема системы к' за-
даче 407.
Статическая характеристика нелинейного звена изобра-
жена на рис. 265, где Ь — 1, £3 = 4.
Рис. 266. Частотные характери-
стики линейной части системы
и нелинейного звена к задаче 407.
Рис. .265. Статическая
характеристика нелиней-
ного звена к задаче 407.
Ответ. В системе устанавливаются автоколебания
Xj ~ A sin Qt,
гДе А~ 1,8, Q— 1,7 сек"1. Амплитудно-фазовая характе-
ристика линейной части системы Wn(ja) и годограф
нелинейного звена — Z (а) показаны на рис. 266.
408. Исследовать устойчивость состояния равновесия
нелинейной системы, структурная схема которой изо-
бражена на рис. 267. Параметры линейной части си-
стемы: &i=2, £2=10 сек~\ Т = 0,02 сек, £ = 0.15. Ста-
тическая характеристика нелинейного звена изображена
на рис. 268. ...
409] § 13 2. ЧАСТОТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ АВТОКОЛЕБАНИЙ 399
Ответ. В системе устанавливаются автоколебания
= Asin£2(,
где А ~ 8,5, £2 50 сек"1. Амплитудно-фазовая характе-
ристика линейной части системы И/л(/ы) и годограф
нелинейного звена — Z (а) изображены на рис. 269.
Рис. 267. Структурная схема системы к за-
даче 408.
S.0
#7
Рис. 269. Частотные харак-
теристики линейной части*
системы и нелинейного звена
к задаче 408.
Рис. 268. Статиче-
ская характери-
стика нелинейного
звена к задаче 408.
409. Исследовать устойчивость состояния равновесия
электромеханической следящей системы, рассмотренной
в задаче 406, если статическая характеристика нелиней-
ного звена имеет петлю гистерезиса (рис. 270).
Решение. Согласно структурной схеме (см. рис. 262)
передаточная функция линейной части системы при
исходных данных задачи 406 равна
fe(xp-H) 0,82 (0,174р + 1)
р(Т1р+1){Тар±1) ~ р (0,05р + I)2 ’'
400
ГЛ. 13 ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДО А ИЯ
1409
Частотная передаточная функция нелинейного звена,
имеющего неоднозначную. статическую характеристику,
может быть записана в виде
Wa(a) = q(a) + jq'(a), (2)
где для релейной характеристики с гистерезисной петлей
(рис. 270) в соответствии с приложением 28
Годограф нелинейного звена — Z(a), построенный
по выражению
-Z(a)= - = -^ + /-)> (4)
' ’ Гн(а) 4с \ т а2 1 a J ’ ' ’
изображен на рис. 271. На этом же рисунке построена
амплитудно-фазовая характеристика ' линейной части
и Im
Рис. 270. Статическая
характеристика нели-
нейного звена к за-
даче 409.
Рис. 271. Частотные характери-
стики линейной части системы
и нелинейного звена к задаче 409.
е
системы 1ГЛ (/со), которая полностью совпадает с по-
строенной на рис. 263.
Точка пересечения этих двух кривых определяет
периодическое решение в системе
> «2 = Л§тЙ/, - (5)
41(| §13.2 ЧАСТОТНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ АВТОКОЛЕБАНИЙ 401
где Л ~ 0,73 в, Q « 100 сек~\ Согласно рис. 271 найден-
ное периодическое решение является устойчивым, т. е.
А и Q являются амплитудой и частотой автоколебаний.
410. Исследовать устойчивость состояния равновесия
системы, структурная схема которой изображена на
рис. 272, если задан коэффициент передачи линейной
части системы k= 10 сек~1 и статическая характеристика
нелинейного звена (рис. 273), для которой 6 = 0,5, с = 10.
—д_______Ле
442 - -0,02
o'
7-----^-0.04
(° Wk(ja>)
Рис. 273. Статиче-
ская характери-
стика нелинейного
звена к задаче 410.
Рис. 272. Струк-
турная схема
системы к зада-
че 409.
Рис. 274. Частотные
характеристики линей-
ной части системы
и нелинейного звена
к задаче 410.
Ответ. В системе устанавливаются автоколебания
с амплитудой А = b — 0,5 и частотой Q = 255 сек-1.
Амплитудно-фазовая характеристика линейной части
системы И7я(уи) и годограф нелинейного звена — Z(a)
изображены на рис. 274.
411. Решить ту же задачу, если
1) fe = 2 сек-1, b = 0,5, с = 5;
2) k = 1 сек"1, 6 = 0,25, с = 5;
3) k = 1 сек-1, 6 = 0,5, с = 5.
Ответ.
1) А = 0,5, Й = 25,5 сек-1;
2) А = 0,25, Q = 25,5 сек-1;
3) . . Л = 0,5, П = 63,7 сек-1.-
ГЛАВА 14
ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
§ 14.1. Исследование колебательных переходных
процессов аналитическими методами
412. Для электромеханической . следящей системы,
структурная схема которой изображена на рис. 211,
построить диаграмму качества переходного процесса
по коэффициенту передачи разомкнутой системы k =
•= kik2k3k5 при отключенной местной скоростной обрат-
ной СВЯЗИ (&4 = 0).
Исходные данные: Т( = 0,05 сек, Т^ = сек, ширина
зоны нечувствительности релейного усилителя (см.
рис. 210) b = 1 е, максимальное напряжение на выходе
релейного усилителя t/3raax = c= 100 в.
Решение. Согласно структурной схеме (см. рис. 211)
передаточная функция гармонически линеаризованной
разомкнутой системы равна
Г(р, «)=...Гт" » П)
’ ₽(Л₽ + 1)(Гм₽ + 1)
4с /' 62
где д(а) = — 1/ 1-----— коэффициент гармонической
линеаризации для релейной характеристики с зоной
нечувствительности (см. приложение 28). По передаточ-
ной функции (1) определяем характеристический полином
замкнутой нелинейной системы
D (р, а) = W + (Г, + Ты) р2 + р + kq (а). (2)
Для построения диаграммы качества в полиноме (2)
произведем подстановку р = g + /® (g — показатель за-
тухания). Эту подстановку удобно выполнять путем
ч12] J М. Г.'АНАЛИТИЧЕСКИЕ МЕТОДЫ- 403
разложения полинома £)(р, а) в ряд по степеням /ш
Р (S + 7®)=
-n®+(€)t'“ «»>’+•••• <з>
где индекс g означает, что в выражения для производ-
ных необходимо подставить g вместо р.
Из (2) находим
D ® = TJj* + (Т, + Ти) g +g + kq (о),
Ша=з7^2+2 +1 >
^(-^'к==37'^ + ^ + 7'м)- (4)
3! \ rf₽3/I 1 ы‘ f
Подставим выражения (4) в ряд (3), выделим в последнем
вещественную и мнимую части и приравняем их нулю.
Получим
Х(®, a, g) = TVT^ + (7’1 + Гм) g + 1 + kq (а) -
-[ЗТ^ + ^ + Т^^^О, (5)
У (<о, g) = [37JMg2 + 2 (Л + Тм) g + 1 - Л W] <о = О.
Из уравнений (5) исключим частоту колебаний <о. Для
этого из второго уравнения (5) находим
<o2 = -7—-[37'17'Mg2 + 2(71 + 7'M)g+l]. (6)
Подставим значение со2 в первое уравнение (5).
Получим
Л^3 + (Л + Ум)52 + & + Ма) =
^^[ЗТ^2 + 2(Т\ + ТЫЦ+ 1][37'17'Mg + (r1 + 7'M)I. (7)
Уравнение (7) решаем относительно k. В результате
находим
k ’ W {тк [ЗЛЛХ‘+2 (г'+ 6 +11 х
xiar.r^+tT. + rjbr.T-^-fr. + W-E}, (8)
404
ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
1412
В выражение (8) подставим численные значения
параметров. Получим
к ~ «|^Т (0-046' + ‘-^+ 116 + 30). (9)
Задаемся различными значениями амплитуды коле-
баний а и при выбранных постоянных значениях пока-
Согласио формуле (6) частота колебаний о не зависит
от k й а. Поэтому кривые и = const будут совпадать-
L=-~ 14,2 сек
соответствует автоколебаниям в системе и представляет
собой зависимость амплитуды автоколебаний а»Л от
с кривыми £ = const. Кривая § = 0, и =
коэффициента передачи разомкнутой системы k. Кри-
вые £>0 соответствуют расходящимся колебаниям,
а кривые £< 0 — затухающим колебаниям. Область, ле-
жащая правее пунктирной, прямой, проходящей через
точку k 0,5 сек"\ является областью существования
автоколебаний,. Область расположенная левее этой пря-
414]
. § 143.’АНАЛИТИЧЕСКИЕ МЕТОДЫ
405
мой,, является областью устойчивого равновесного со-
стояния системы.
413. Для системы, рассмотренной в задаче 412, ис-
следовать устойчивость состояния равновесия и опреде-
лить амплитуду А и частоту £2 автоколебании, если
1) k = 0,4 се/с-1;
2) k = 2 сек"1',
3) /г =4 сек"1.
Ответ. Согласно диаграмме качества (см. рис. 275)
имеем
1) состояние равновесия системы устойчиво;
2) А ~8,3°, £2=14,2 се/с"1;
3) А ~ 17°, £2= 14,2 ceiC1.
414. Для системы, рассмотренной в задаче 412,
при k = 2 сек'1 определить время затухания переход-
ного процесса число колебаний m в переходном про-
цессе за время величину перерегулирования ап, если
начальное значение амплитуды колебаний «0=15°.
Решение. Из диаграммы качества переходных
процессов (см. рис. 275) видно, что коэффициент зату-
хания | и частота колебаний ® во время переходного
процесса не остаются постоянными. Выражение для
амплитуды колебаний системы имеет вид
fidt
а = о0е0 ., (1)
где а0 — значение амплитуды колебании, определяемое
начальными условиями. Согласно рис. 275 при k = 2 сек~1
в системе устанавливают автоколебания с амплитудой
А 8,3 град. Из выражения (1) определяем время за-
тухания переходного процесса от амплитуды а0 до
амплитуды А
А
4. [da
J ’
СГ1
где £(а)~ аналитическая зависимость коэффициента
затухания g от амплитуды колебаний а при заданном k.
Зависимость £(п) имеет сложный вид (см. задачу 412)
и поэтому точное вычисление-интеграла (2) затруднено.
(2)
те
ГЛ 14 ОЦЕ1КА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
(414
Время затухания переходного процесса можно оценить
приближенно следующим образом [25]. Грубую оценку
времени производим по формуле
Л
1 . А
-z—1П-----,
Sep
(3)
где gep — среднее значение коэффициента затухания £
на интервале изменения” амплитуды колебаний от а — а!;
(точка ЛГо на рис. 275) до а = А (точка на рис. 275).
Если принять, что в точке Л40 ё —~ 1,5, а в точке AZj
g = 0, то
gcp~-^|±^=-0,75.
Поэтому
~ In 44 ~ 0,79 сек. (4)
— О,/о Id
Для более точного определения времени затухания пе-
реходного процесса разобьем участок A40Afi (рис. 275)
на три отрезка, Л10Л12, М2М3, M3Mt, и определим зна-
чение g внутри каждого отрезка: gi = go= ~ 1,5, g2= — 1,0,
g3 = - 0,5. Тогда
Л
4- In — + -4- In — + 4- In —,
£1 а0 &2 а2 £з «3
(5)
где а2 и а3~ значения амплитуд колебаний в точках
М2 и М3.
Подставим в (5) численные значения параметров.
Получим
, 1 , 14 , 1 , 10 , 1 . 8,3
~ - 1,5 ° 15' + —1,0 П 14 + - 0,5 П 10 0,74 СеК'
Грубую оценку величины перерегулирования произ-
водим по формуле
^ср *
(&ср<о), (6)
I «о I
где gcp и ®ср — средние значения величин g и ® на уча-
стке Л4ОА4Ь «о —начальное значение амплитуды коле-
баний.
41«1
, § 14,1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
407
. /с\ ( 10,2+14,2
По формуле (6) находим [положив <ocp = ———— «.
==12,4 сек'1}
0,75
ап == 15е Я 12'4 ~ 12,4°.
Грубую оценку числа колебаний т за время пере-
ходного процесса производим по формуле
«ср . А
7T-Z—Ш---,
(7)1
откуда
12,4 <8,3 ,
415. Для системы, рассмотренной в задаче 412, про-
извести грубую оценку времени затухания переходного
процесса и числа колебаний за время переходного про-
цесса, если
1) k~2 сек'1, do = 2°;
2) /г = 3 сек'1, а0=15°;
3) k = 3 сек'1, Оо = 4°.
(см. рис. 275)
ti ~ 0,71
ti ~ 0,68
t, — 0,71
Для
имеем
m ~ 2;
ш ~ 1,5;
m ~ 1,6.
характеристика усили-
теля следящей системы
к задаче 416.
сек,
сек,
сек,
электромеханиче-
Ответ. Согласно диаграмме качества переходного про-
цесса
1)
2)
3)
416.
ской следящей системы, струк-
турная схема которой изображена
на рис. 211, построить диаграмму
качества переходного процесса по
коэффициенту передачи разом-
кнутой системы k —ktk2kak5 при
отключенной местной скоростной обратной связи (k4 = 0),
если вместо релейного усилителя применяется усили-
тель с насыщением. Статическая характеристика уси-
лителя изображена на рис. 276.
408
ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
1417
Исходные данные: 7’1 = 0,05 сек, Тм = 0,1 сек, ширина
зоны линейности статической характеристики нелиней-
ного усилителя Ь, — 1 в, коэффициент усиления на ли-
нейном участке fey = tga=100.
Ответ. Диаграмма качества переходного процесса
изображена на рис. 277. Кривые g = const и и — const
совпадают. Границей областей устойчивого состояния
равновесия и автоколебаний является пунктирная пря-
мая, проведенная через точку k 0,3 сек-1.
417. Для системы, структурная схема которой изо-
бражена на рис. 278, построить диаграмму качества пе-
реходного процесса по коэффициенту передачи k.
Исходные данные: /гос = 5, 71 = Та = 0,1 сек, с =10.
Решение. Согласно структурной схеме передаточ-
ная функция линеаризованной нелинейной разомкнутой
системы равна
W й) (Г1Р + 1) [р (Tsp+ 1) + 1г0<Л (а)] ’
417]
§ М.1. АНАЛИТИЧЕСКИЕ МЕТОДЫ.
409
где <Дй) = —— коэффициент гармонической линеариза-
ции для идеальной релейной характеристики (см. при-
ложение 28).
Рис. 278. Структурная схема системы и статическая характеристика
нелинейного звена к задаче 417.
По передаточной функции (1) определяем характе-
ристический полином замкнутой нелинейной системы
Dip, а) = Т^р3 + (Г, + 7’й) р2 +
+ (1 +k0Cq(a)Tl)p + <?(«)(& +Аос). (2)
Полином (2) запишем в виде
D (р,' а) = р3 + Aip2 + Агр + А3, (3)
где ь
. .. Г, + Гг 0,1+0,1
1 TtT2 0,01 ’
А2 = . = 1±°^ое<7(а) _ 100 +
А3 - (fet^e>V(g) e (100fe + 500) q («)
1 \л g U,U1
Для системы третьего порядка, характеристический
полином которой приведен к виду (3), формулы для
коэффициента затухания | и частоты колебаний <о можно
записать в виде [39]
₽ = _ ...~..Л»_________ (4)
6 гИз + оч + г^)2] ’ w
Чтобы £ и й, полученные по этим формулам, определяли
в основном переходный- процесс, должно выполняться
410
ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
Ию
условие
л > । ё |. (6)
Неравенство (6) определяет верхний и нижний пре-
делы для значений g, которые должны подставляться
в формулы (4) и (5).
Рис. 279. Диаграмма качества переходного процесса
к задаче 417.
Подставим в (4) и (5) значения коэффициентов Аь
Л2> Л3, q(a) и полученные уравнения разрешим отно-
сительно k и ®2. Получим
k = 5 +g + 0,157» (10 + 5g + 0,8g2 + 0,04g3),
2 12,7 50ft+ 250 „2
® =--------17m------g.
а 10+ g s
(7)
(8)
Задаемся различными постоянными значениями коэф-
фициента затухания g и по формуле (7) строим кривые
a = a(li) (рис. 279). По формуле (8) строим кривые
<о = const (пунктирные прямые на рис. 279). С меньшей
точностью, но гораздо быстрее эти кривые могут быть
построены по формуле •
4181
• § 14.1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
411
которая получается из (5) при выполнении условия (6).
Из. рис. 279 следует, что на диаграмме, качества пере-
ходных процессов можно выде-
лить две области: область устой-
чивого состояния равновесия при
&<5, где амплитуда колебаний
затухает до нуля, и область авто-
колебаний при Л >5. Эти данные
полностью совпадают с данными,
полученными при исследовании
той же системы точным мето-
Рис. 280. Статическая
характеристика нелиней-
ного звена к задаче 418.
дом Ляпунова — Лурье (см. за-
дачу 388).
418. -Для системы, рассмот-
ренной в задаче 417, построить
диаграмму качества переходного процесса, если нели-
нейное звено (см. рис. 278, а) имеет релейную характе-
ристику с зоной нечувствительности (рис. 280).
Рис. 281. Диаграмма качества переходного процесса
к задаче 418.
Исходные данные те же, что и в задаче 41-7. Ши
рина зоны нечувствительности Ь — 1,0.
412 ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ 141»
Ответ. Диаграмма качества переходного процесса
отображена на рис. 281. Из этой диаграммы видно,
что наличие зоны нечувствительности в релейной харак-
теристике приводит к некоторому расширению области
устойчивого состояния равновесия, соответствующей
k <8,25.
§ 14.2. Исследование колебательных переходных
процессов частотными методами
419. Для системы, структурная схема которой изо-
бражена на рис. 282, определить качество переходного
процесса.
Рис. 282. Структурная схема системы и статическая харак-
теристика нелинейного звена к задаче 419.
Исходные данные: ^^=0,5, Г! = 0,1 сек, 6=1, с = 20.
Решение. Коэффициент затухания £ и частоту
колебаний ® переходного процесса в нелинейной си-
стеме будем отыскивать путем решения гармонически
линеаризованного уравнения
(| + j®) •№„(«)= -1 (1)
или
« + /«>) - - = — Z («), (2)
где (| + /<о) получается из передаточной функции
линейной части системы W„ (р) подстановкой р = £ + /®,
а гармонически линеаризованная передаточная функция
нелинейного звена 1Гн(а) — подстановкой р ~ g + j® в вы-
ражение
. FB(|, а) = ^(а) + ^=1>(а), . (3)
<I#J • § М2. ЧАСТОТНЫЕ МЕТОДЫ 413
врезультате которой получаем
WB(& «) = <7(а) + //(а) = Гн(а). (4)
Уравнение (1) будем решать графически. Для этого
в передаточной, функции линейной части системы
= <5>
произведем подстановку p = g + /co. Получим
W„ + /со) = 7| + /ю)(1 + г1Б + /©7'1)’ ’ (6)
Модуль, этой функции
A (g, (0) = I гл (g + /®) | = . v (7)
yU2 + <o2)[(l + 71g)2+<o2r2]
и фаза
со) =*- arctg-у- arctgyyyj- (8)
Подставим в выражения (7) и (8) приведенные в ис-
ходных данных значения параметров и, задаваясь
различными постоянными значениями показателя зату-
хания g, построим серию кривых W\(g, /®) как функ-
ции от частоты колебаний о при g = const (рис. 283).
На этом же графике нанесем обратную амплитудно-
фазовую характеристику нелинейного звена — Z(a)=>
= -г -g,1 при заданных параметрах звена b и с. Со-
"I! Щ)
гласно приложению 28 для нелинейной характеристики
релейного типа с гистерезисной петлей имеем
Г11(в) = <7(а) + /<7,(«) = ~--|/1—g- (9)
Отсюда
-г<“)--таг=-тг'/1-5'-'5-- (10)
Мнимая часть выражения (10) не зависит от ампли-
туды й. Поэтому годограф —Z(d) представляет собой
прямую, параллельную вещественной оси.
Точки пересечения годографов UMg + /<°) и — Z(a)
определяют решения уравнения (1) при различных
ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ
I4te
значениях g. Для каждого постоянного коэффициента
затухания g по годографу — Z (а) определяем соответст-
вующее значение амплитуды колебаний а, а по годографу
Ц7л (£ + /©)— значение частоты колебаний а. Амплитуду
и частоту периодического решения а = А и о = □ нахо-
дим в точке пересечения годографов ^(g + ya) и — 1 (а)
при g = 0.
Рис. 283. Частотные характеристики линейной части
системы и нелинейного звена к задаче 419.
Согласно рис. 283 при любом k > 0 в системе суще-
ствуют периодические решения, соответствующие авто-
колебанием. При /г = 0,5 находим
А «1,51, П«8 сек1.
Из рис. 283 видно, что периодическое решение с этими
параметрами действительно соответствует автоколеба-
ниям, так как любое увеличение амплитуды колебаний
приводит к g<0, а любое уменьшение ее —к g>0.
Произведем грубую оценку основных качественных
(показателей переходного процесса. Пусть начальное
значение амплитуды колебаний а==д0 = 2. Время пере-
ходного процесса, в течение которого амплитуда коле-
баний уменьшается от значения «с = 2 до значения
4191
§ НХ ЧАСТОТНЫЕ МЕТОДЫ
415
А — 1,51, приближенно оценим по формуле
, 1 , А
•=—In — •
Sep O.Q
(11)
В данном случае А = 1,51, а0 = 2, |ср= —1. Подста-
вим эти значения в (11). Получим
— In = 0,28 сек.
Оценку величины перерегулирования произведем по
формуле
«п ~ а/ , (12)
где а„ —величина перерегулирования, ®ср —среднее
1m
0,04
Рис. 284. Диаграмма качества переходного процесса
к задаче 420.
значение частоты колебаний, которое согласно рис. 283
равно
7 + 8 п г
®ср ~ —2— ~ ‘>5 сек •
Подставим в (12) значения параметров. Найдем
_ 1
«п = 2е " 7-3 =2-0,65=1,3.
416 ГЛ. 14. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ СИСТЕМ [42о
Для грубой оценки числа колебаний за время пере-
ходного процесса воспользуемся формулой
<оср Л 7,5 1,51
т ~ ,П о? ~ -2Л ,П ~2~ ~ °’34-
420. Для системы, рассмотренной в задаче 419, по-
строить диаграмму качества переходного процесса и
определить основные качественные показатели процесса'
если k — 0,2, а остальные параметры такие же, как и
в задаче 419. Начальное значение амплитуды коле-
баний а0 = 2.
Ответ. Диаграмма качества переходного процесса
изображена на рис. 284. Амплитуда и частота автоко-
лебаний соответственно равны
А —1,54, й«4,5.
Время затухания переходного процесса от а0 — 2 до
А = 1,54 /t я* 0,28 сек. Величина перерегулирования
ап ** 0,88. Число колебаний за время переходного про-
цесса m₽sO,I7.
ГЛАВА 15
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
В НЕЛИНЕЙНЫХ СИСТЕМАХ
§ 15.1. Отыскание симметричных одночастотных
вынужденных колебаний графическим методом
421. Определить вынужденные колебания системы,
структурная схема которой изображена на рис. 285,
при синусоидальном внешнем воздействии
= (1)
Исходные данные: k— 10 сек”1, Т\ = 0,1 сек, с =10,
В = 20, ®в= 10 сек-1.
f(t)
Рис. 285. Структурная схема системы и статическая
характеристика нелинейного звена к задаче 421.
Решение. Составим дифференциальное уравнение
замкнутой нелинейной системы. Согласно структурной
'схеме дифференциальное уравнение линейной части си-
стемы имеет вид
(Тхр+ l)px2 = kxi. (2)
•Нелинейное звено может быть описано уравнением
Xi = F(x), (3)
418
ГЛ. 15. НЕЛИНЕЙНЫЕ СИСТЕМЫ
(421
где нелинейная функция F (х) задана статической харак-
теристикой (рис. 285, б).
Подставим (3) в (2) и одновременно учтем, что
x2 = f{f)-x.
Получим
(Лр + 1) рх + kF (х) = (TlP + 1) pf (t). (4)
Решение для установившихся вынужденных колеба-
ний в системе будем искать в форме
х — ав sin (®в/ + ф), (5)
где ав и ф —искомые амплитуда и фаза вынужденных
колебаний.
Уравнение нелинейной системы (4) запишем в виде
Q(p)x + R(p) F(x) —S(p) f (t), (6)
где Q{p) = S (р) = {Т}р + 1) р, R(p) = k. В уравнении (6)
переменную f(t) выразим через переменную х. Для
этого запишем
f(i) = В sin (Hgt = В sin [(сов/ + ф) — ф]. =
= В cos ф sin (юв/+ ф) — В sin ф cos (®в/+ ф). (7)
Из (5) найдем производную
рх = ава>в cos (aBt + ф) (8)
и, подставив (5) и (8) в выражение (7), получим окон-
чательно
= (9)
Подставим значение функции f(i) (9) в уравнение (6).
Получим
[q (р) — S (р) ~ (cos ф - р) | х + R (р) F (х) = 0. (10)
L \ и>в /J
Произведем гармоническую линеаризацию нелинейности
F(x) = q(a)x, (11)
где q (а) = —— коэффициент гармонической линеариза-
ции для идеальной релейной характеристики (см. при-
ложение 28).
K.t. ГРАФИЧЕСКИЙ МЕТОД
419
В выражение (11) вместо амплитуды а подставим
искомую амплитуду вынужденных колебаний ав. Получим
F(x) = <7(aB)x=~x. (12)
Из (10) и (12) получаем характеристическое уравне-
ние для первого приближения
Q(p)-S (р)-^ (cos <р - р) + R (р) q (ав) = 0. (13)
Для отыскания синусоидального решения (5) подста-
вим в (13) р==/ив. Получим
йв Q..(W.+.gy .7(ав) =Ве_/(р> (И)
При получении (14) учтено, что cos <р — / sin <р = e~l(f.
Подставим в (14) выражение для Q(/coB), В(/®в) и
S (/®в), полученные из (6), и значение коэффициента
q(aB) (12):
4с k
ав + . ,, ” . . = .
1®в (1+7i/^в)
(15)
После подстановки численных значений параметров по-
лучим
ав — 6,67- 6,67/ = 20е-/(Р. (16)
На комплексной плоскости (рис.' 286) построим годо-
граф
Z (ав) = ав - 6,67 - 6,67/, (17)
соответствующий левой части уравнения (16), и окруж-
ность радиуса В = 20, соответствующую правой части
того же уравнения. Точка пересечения годографа Z (ав)
и окружности определяет собой решение задачи. По от-
меткам амплитуды ав на годографе Z (ав) находим ампли-
туду вынужденных колебаний в системе ав = Лв = 25,2.
Фазовый сдвиг <р = 20° определяется по дуге окружности.
Следует иметь в виду, что отсчет положительных зна-
чений углов, ф в данном случае производится от поло-
жительной вещественной полуоси по часовой стрелке,
так как в правой части (15) ф’ входит с отрицательным
знаком.
420
ГЛ. 15. НЕЛИНЕЙНЫЕ. СИСТЕМЫ
[422
На рис. 286 видно, что в системе возникают одно-
частотные колебания с частотой ©в=10сек-1 не при
любых значениях амплитуды входного воздействия (1),
а лишь при В>Впор. Для определения порогового зна-
чения амплитуды входного воздействия Впор проведем
окружность, касающуюся годографа Z(aB). Радиус этой
Рис. 286. Графическое построение
для определения вынужденных
колебаний к задаче 421.
окружности и определяет
Впор = 6,67.
422. Для системы,
структурная схема кото-
рой изображена на
рис. 287, определить амп-
литуду Ав и фазу <р выну-
жденных колебаний и
пороговое значение амп-
литуды входного воздей-
ствия.
Исходные данные:
k = 10 сек-1, b = 1, с = 10,
амплитуда и частота вход-
ного воздействия В = 8,
<ов = 20 сек-1. '
Ответ. Уравнение для отыскания амплитуды и фазы
вынужденных колебаний имеет вид
а0-/ • 6,36 I /1 - -у = 8е-/‘Р.
V ав
Графическое построение показано на рис. 288. Согласно
этому рисунку Ав ~ 5, <р = 50°, ВПор=!-.
423. Определить амплитуду и фазу вынужденных ко-
лебаний, в системе, структурная схема которой изобра-
жена на рис. 285, при наличии временного запаздыва-
ния т.
Исходные данные: k= 10 сек'1, Т1 —0,01 сек, т =
= 0,01 сек, с =10,' частота и амплитуда внешнего воз-
действия ©в = 10 сек-1, В = 20.
Решение. Линейная часть системы описывается
дифференциальным уравнением
{Т хр + \) рх2 = kxy
(О
. §-T5 t ГРАФИЧЕСКНП МЕТОД 42T
С учетом временного запаздывания т Уравнение не-
линейного звена запишем в виде
x, = FT(x) = e-^F(x), (2)
где F (х) — нелинейная функция, заданная статической
характеристикой (рис. 285, б).
Рис. 287. Структурная схема системы и статическая харак- -
теристика нелинейного эвена к задаче 422..
Рис. 288. Графическое вострое- Рис. 289. Графическое построение
ние для определения выиу- для определения вынужденных
ждениых колебаний к за- колебаний к задаче 423.
даче 422.
Из (1) и (2) определим дифференциальное уравнение
замкнутой нелинейной системы
(T)p+l)px + /eFI(x) = (T1p+l)p/(/). (3)
, Вынужденные колебания входной величины нелиней-
ного звена х будем искать в виде
х = Л sin (<V + Ч>). И)
422 ГЛ. .15.- -НЕЛИНЕЙНЫЕ СИСТЕМЫ [423
Для отыскания синусоидального решения (4) запишем
выражение
„ Q + R 4 (дч) е~/ТИ>в _ р„-/(р
°в S (Цов) ~ве , (о)
где ав и <р — искомые амплитуда и фаза вынужденных
колебаний, q (ав) == — коэффициент гармонической
линеаризации для идеальной релейной характеристики
а)
Рис. .290. Структурная схема системы и статическая харак-
теристика нелинейного звена к задаче 424.
(см. приложение 28) при а = ав, a Q(jffiB), /?(/а>в) и 5(/<ов)
определяются из уравнения (3).
Согласно уравнению. (3) имеем
Q (jaB) = S (jaB) = /иЕ(1 + Т,/©в),
R G«>B) = k. (6)
Подставим (6) и значение коэффициента q(aB) в (5). По-
лучим
-1ГЮК
ЙЕ + . ?,селу— г == Ве~&. (7)
Е jcoB(l+ 71/<ов) v ’
После подстановки численных значений параметров
и умножения числителя и знаменателя второго слагае-
мого левой части уравнения (7) на сопряженное выра-
жение имеем '
ав - 2,5 - j • 12,3 = 20е_/ч>. (8)
На комплексной плоскости (рис. 289) строим годограф
Z (цв) = ав — 2,5 —j • 12,3
425]
5 15.2 ЧАСТОТНЫЙ МЕТОД
423
и окружность радиуса 20. В точке пересечения по годо-
графу Z (ав) определяем амплитуду вынужденных коле-
баний пв=Л ~ 18,2, а по дуге окружности — фазу ф 38°.
Пороговое значение амплитуды входного воздействия
ВПор-12 3.
424. Для нелинейной системы, структурная схема
которой изображена на рис. 290, определить ампли-
туду Ав и фазу ф вынужденных колебаний.
Исходные данные: k— 10 сек-1, rt = 0,01 сек, Т2 =
= 0,02 сек, Ь — 4, с =10; амплитуда внешнего синусои-
дального воздействия В — 20, частота внешнего воздей-
ствия <ов = Ю сек-1.
Ответ. Ав 21, ф» 35°.
§ 15.2. Отыскание симметричных одночастотных
вынужденных колебаний частотным методом
425. Для нелинейной системы, структурная схема
которой изображена на рис. 285, определить зависимость
амплитуды вынужденных колебаний от амплитуды и
частоты внешнего синусоидального воздействия.
Исходные данные: /?=10сек-1, Г1 = 0,1 сек, с =10.
Решение. По структурной схеме (рис. 285, а) опре-
деляем передаточную функцию гармонически линеари-
зованной замкнутой нелинейной системы
Ф= = l + W„(p)WH(p, а) ' (I>
где Х(р) и F(p)— изображения по Лапласу ошибки си-
стемы x(t) и внешнего синусоидального воздействия f(t),
(р) ~ передаточная функция линейной части системы,
IVjjfp, а)— передаточная функция гармонически линеа-
ризованного нелинейного звена.
Для рассматриваемой системы имеем
Wa(p) = /Лп, (2)
p(fip+ 1) ’ ' ’
Wu(a)~q(a), (3)
где q(a) = — — коэффициент гармонической линеариза-
ции для идеальной релейной статической характеристики
(см. приложение 28).
434
ГЛ. 15. НЕЛИНЕЙНЫЕ системы
1425
Передаточную функцию (1) запишем в виде
Ф = Мд(Р) + №я(а) • (4)
где Мл(р) = -йД-г-обратная передаточная функция ли*
w л \Р)
нейной части системы»
Найдем обратную частотную передаточную функцию
линейной части системы
мд(Н ~ W (5)
и передаточную функцию гармонически линеаризован-
ного нелинейного звена
VFu(o) = — = —, (6)
а на комплексной плоскости tPHC- 291) по формуле (5)
построим обратную амплитудно-фазовую характеристику
1m
2/
Рис. 291. Обратная амплнтудио-фазовая
характеристика линейной части системы
н годограф нелинейного звена к задаче 425.
линейной части системы, а по формуле (6) —годограф
нелинейного звена — №„(«).
По отметкам амплитуды на годографе — IFH(a) опре-
деляем амплитуду вынужденных колебаний ав (точка D
на рис. 291), а по отметкам частоты на годографе
Л1Я (/со) — частоту вынужденных колебаний, равную ча-
стоте внешнего синусоидального воздействия (точка Е
4Ж ' § 15.2. ЧАСТОТН И МЕТ Д 425
на рис. 291). Из (4) находим
дв _ I ф(;а п YI --------1 (/«в) I--- ОЕ
в ав11 |Мл(/<ов)+1Гн(ав)| DE ’
где В — амплитуда внешнего синусоидального воздей-
ствия.
Выражение (7) определяет связь между амплитудой
внешнего воздействия В и амплитудой вынужденных
колебаний ав для любого фиксированного значения ча-
стоты <ов:
В = (8)
Перемещая точку D на рис. 291 при фиксированном
положении точки Е находим зависимость ав{В) при
Рис. 292. Зависимости амплитуды вынужден-
ных колебаний от амплитуды и частоты внеш-
него воздействия к задаче 425.
«в = const (рис. 292), а перемещая точку F при фикси-
рованном положении точки D, находим зависимость
ав(©в) при В — const (пунктирные кривые на рис. 292).
426. Для нелинейной системы, рассмотренной в за-
даче 425, определить зависимость амплитуда вынужден-
ных колебаний ав от амплитуды В и частоты (0в внеш-
него синусоидального воздействия, если передаточная
426
ГЛ.- 15. НЕЛИНЕЙНЫЕ СИСТЕМЫ
Ц2а
функция линейной части системы
= p(TlP+l)(T2P + l) ’
где /г =10 сек-1, Г1 = Г2 = 0,1 сек.
Ответ. Обратная амплитудно-фазовая характеристика
линейной части системы 7Ил(/со) и годограф — 1Г„(а)
!т
7
Рис. 293. Обратная амплитудно-фазовая характеристика линей-
ной части системы и годограф нелинейного звена к задаче 426.
Рис. 294. Зависимости амплитуды вынуж-
денных колебаний от амплитуды и ча-
стоты внешнего воздействия к задаче 426.
изображены на рис. 293. Кривые шЕ = const и В = const
показаны на рис. 294. Частота сов = 10 сек-1, при которой
. JS2 ЧАСТОТНЫЙ МЕТОД
42.7
пороговое значение амплитуды входного синусоидального
воздействия Впор обращается в нуль, равна частоте авто-
колебаний в системе.
427, Определить амплитуду и фазу вынужденных
колебаний скорости вращения электрического двигателя
в нелинейной системе стабилизации, схема которой изо-
бражена на рис. 295. На схеме обозначено: Д —двига-
тель постоянного тока с независимым возбуждением,
Рнс. 295. Система стабилизации скорости вращения элект-
родвигателя к задаче 427.
ТГ — тахогенератор, РУ —релейный усилитель, статиче-
ская характеристика которого изображена на рис. 295, б.
Исходные данные: ширина зоны нечувствительности
релейной характеристики b = 1 в, установившаяся ско-
рость двигателя при максимальном напряжении на вы-
ходе релейного усилителя ыд = ыдтах (рис. 295,6), Qo =
= 625 сек'1, пусковой момент двигателя Мо = 100 Г • см,
момент инерции, приведенный к валу двигателя J =
~ 0,008 Г см • сек2, момент нагрузки на валу двигателя
Л1Н = 0, коэффициент передачи тахогенератора /?тг =
= 0,01 в • сек)рад. На вход системы подается синусои-
дальный входной сигнал
щ (0 = В sin <%/,.
амплитуда которого В = 8 в, а частота <оЕ== 10 сек'1.
Решение. Обычно при исследовании релейный
исполнительный механизм, состоящий из двигателя по-
стоянного тока с независимым возбуждением и реле,
управляющего током якоря, представляется в виде двух
428
ГЛ. 15. нелинейные системы
1427
независимых звеньев. Одно из этих звеньев (двигатель)
является линейным, а другое (релейный усилитель) —
нелинейным. При этом двигатель описывается одним и
тем же дифференциальным уравнением независимо от
положения контактов реле. В действительности же при
разомкнутых контактах реле (—b<u<b) цепь якоря
двигателя разомкнута, и он превращается в обычный
маховик. Если не учитывать момент нагрузки и меха-
нические характеристики двигателя считать линейными,
то при замкнутых контактах реле (и > | Ь |) движение
электродвигателя описывается дифференциальным урав-
нением
+ = О
где Q — угловая скорость вращения двигателя, Зо = ^ ~~
коэффициент наклона механической характеристики.
. При разомкнутых контактах реле дифференциальное
уравнение движения примет вид
Поэтому при исследовании нелинейных систем с релей-
ными исполнительными механизмами двигатель и релей-
ный . усилитель следует рассматривать как одно нели-
нейное звено.
Введем в рассмотренное нормированное значение пе-
редаточной функции гармонически линеаризованного
релейного исполнительного механизма W0(d, jz)
W(d, jz) = ^ W0(d, jz) = ^-q0(d, г) + / ^-q'0(d, z). (3)
В этом выражении d — относительная амплитуда
d = b
z — относительная частота
z = <о7\„ (5)
Ты — постоянная времени двигателя, q0(d, z) и q'0(d, z) —
коэффициенты гармонической линеаризации.
4271
§ 45.2. ЧАСТОТНЫЙ" МЕТОД
429
Аналитические выражения для коэффициентов q0(d, z)
и q'Q(d, z) получаются слишк
удобства расчетов в прнло?
тудно-фазовые характери-
стики нормированной частот-
ной передаточной функции
релейного исполнительного
механизма.
Для определения пара-
метров вынужденных коле-
баний системы составим
сложными. Поэтому для
ии 29 приведены ампли-
Рис 296. Структурная схема
системы стабилизации скоро-
сти вращения электродвигателя
к задаче 427.
структурную схему (рис. 296)
и запишем дифференциальное уравнение замкнутой не-
линейной системы
и + k„F\u, ри) = «j (/), (6)
где
F (и, ри) = q(d, г)и + ри (7)
о
Составим равенство
Q (j<oB) 4- R (/со») [<7 (rfB, zB) + jtf (dB, zB)J R .v
где ав и <p — искомые амплитуда и фаза вынужденных
колебаний, 2в = <двТ'м.
Связь между амплитудой ав и относительной ампли-
тудой вынужденных колебаний устанавливается форму-
лой (4)
В данном частном случае согласно уравнению (6)
имеем
Q (jaB) = S (/со«) = 1, /? (/<ов) = kTr. (10)
Подставим (10) в (8). Получим
ав + kTraB [q(dE,zB) + jq'(du, zB)] = (Il)
Коэффициенты q(dB, zB) и q'(dm zB) определяем по гра-
фикам, приведенным в приложении 29. Для этого пред-
варительно находим
zB = 10 - 0,008 0,5. (1'2)
Trig XUU- .
13Т
ГЛ. 15. НЕЛИНЕЙНЫЕ СИСТЕМЫ
[427
Затем задаемся разными значениями амплитуды аа,
для них по формуле (9) определяем значения отно-
сительной амплитуды dB, по амплитудно-фазовым
Рис. 297. Графическое построение для
определения вынужденных колебаний
к задаче 427.
характеристикам (приложение 29) при гв=0,5 для различ-
ных dB определяем <?0(dB, zB) и q'0(dg, zB) и по выраже-
нию (3) находим
q(dB, zB) = q0(de, zB) = 625q0 (dB, zB),
q'(dB, zB) = -^-q'(dB, ze) = 625^(dB, zB).
(13)
Значения коэффициентов (13) подставляем в (11) и
строим кривую
(^в) ~ “Ь &ТТ^Й [q (^В> 2'н) + jq (</в, ^-вЖ (14)
соответствующую левой части равенства (11) (рис. 297).
Проводим окружность радиуса В = 8 и в точке пересе-
чения ее с кривой Z(aB) находим йв~1,5в, ~ 58°.
Амплитуда вынужденных колебаний угловой скорости
вращения двигателя равна
ГЛАВА 16
ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
ЧЕРЕЗ НЕЛИНЕЙНЫЕ СИСТЕМЫ
§ 16.1. Определение функций и моментов распределения
случайного процесса на выходе нелинейной системы
428. На вход безынерционного усилителя, имеющего
линейную с ограничением статическую характеристику
(рис. 298, а), подается случайный сигнал в виде напря-
жения Mj. Плотность распределения этого сигнала описы-
вается функцией
где щ — среднее значение входного напряжения ии
04 — среднеквадратическое отклонение напряжения tit от
среднего значения щ. В линейной зоне статической
характеристики коэффициент усиления /?=105. В зоне
насыщения выходное напряжение усилителя и2т = 100 в.
Найти и представить в виде графика закон распре-
деления к.’(н2) на выходе усилителя при следующих
исходных данных: среднее значение ?7]==0в, средне-
квадратическое значение 04 = 0,5- 10~3в.
Решение. Так как усилитель безынерционный, то
в линейной зоне и2 =/нц.
Поскольку ko1 = 105 • 0,5 • 10 3 = 50в,. то в этой обла-
сти o2 = kui. Поэтому с учетом того, что tii = 0 в пре-
делах линейности статической. характеристики, закон
распределения выходного напряжения н2 имеет вид
<«(«,)З/М. (2)
432 гл. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ (428
По условиям нормирования функций' распределения
4-оо ' 4~<ю
J J w (и2) du? = 1. (3)
— со —со
Подставляя в последнее
выражение функцию (2),
найдем
2
-« Ц)
f е 2a'i
2л J
-— со
4-сю
=. —I е * 1 = j
V 2л J О2 •
— оо
' Таким образом, в ли-
нейной зоне нормирован-
ные плотности распреде-
ления для относитель-
Рис. 298. Преобразования функ-
ций распределения случайного
сигнала линейным звеном с пасы-
щением при и — 0.
ных переменных z} = п
z2 = — на входе и выходе
°2
одинаковы (рис. 298, б, в).
Протяженность линей-
ной зоны статической ха-
рактеристики усилителя
по оси М] (рис. 298, а) мо-
жет быть определена из
соотношения
«u = -V = -jo5-= Ю в.
Следовательно, ее относительная величина
__ и>л Ю __
о, = 0,5-10-3
Вероятность Р(и2>100 в) появления сигнала и2> 100 в
на выходе усилителя равна нулю, так как более чем 100 в
усилитель дать не может согласно статической харак-
теристике. ...
-42») § 16.1 ОПРЕДЕЛЕНИЕ ФУНКЦИИ И МОМЕНТОВ НА ВЫХОДЕ -433
Вероятность -же Р(м2=100в) появления сигнала
н2= ЮО в, очевидно, равна вероятности Р (м( м1л = 10~3 в).
Поэтому можно записать
Р (и2 = ЮО в) = Р («1 > н,л) = Р (г, > г1л) =
"0’5-Tt;l S~‘b"
При г1л = 2 согласно приложению 31 написанный
интеграл равен 0,477. Поэтому Р (и2= 100 е)=0,5 —0,477 =
= 0,023.
Таким образом, в пределах линейности усилителя
функции w(u2) имеет такое же нормированное распре-
деление, как и ®(М1). На концах интервала линейности
а>(и2=100в) имеет вид дельта-функций с площадью,
равной 0,023 (рис. 298, б и в).
429. Для усилителя предыдущей задачи найти функ-
ции ау(«2) распределения выходного напряжения, если
на его вход подается напряжение иь имеющее случай-
ную величину, распределенную по нормальному закону
(»1~Й1)!
а-(«1) =-р=—е 201 , (1)
V 2л О',
при щ = 0,75 • 10~3 в, Oi = 0,5 • 10~3 в.
Решение. Так же, как и в предыдущем случае,
в линейной области статической характеристики, огра-
ниченной диапазоном — uill<ul<.uill, нормированные
законы распределения w fo) и w (z2) одинаковы. При
этом относительные величины zt и z2 Удобно ввести
в виде
Вероятности появления сигналов |м21>. 100 в равны
нулю. Вероятности же сигналов и2= ± 100 в могут быть
431 ГЛ. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ 142»
определены по формулам
Р (и2 = 100 в) = Р (ы, > «1л) = Р (г, > г;л) =
1 Г
= 0,5 —е 2 dz, (4)
Р(иг = - 100 в>= Р (и, < - и1л) = Р (г, < - г" ) ='
° 1
= 0,5--4= f е~~* dz. (5)
I' 2л J
Подставив в (2) значения йь ы1л и — и1л, найдем
_ Ц1Д - а, _ 1 • 10-3 — 0,75 10~3 _
I 1 _□ ' ~~ О • о *
1Л а, 0,5 10 3
/г ~ Щ ___ ( 1 0,75) • 10 _ _Q -
'*" а1 ~ 0,5 10~3 “ ’ '
Воспользовавшись приложением 31 для модулей | г[л |
Рис. 299. Функция распределения сигнала на вы-
ходе линейного звена.с насыщением при и=^0.
и |г" |, получим следующие значения вероятностей:
Р (и2 = 100 в) = 0,5 - 0,192 = 0,308,
Р (и2 = - 100 в) = 0,5 - 0,494 = 0,006.
Таким образом, на концах интервала линейности
функция w (м2) имеет вид дельта-функций с площадями,
соответственно равными 0,308 и 0,006 (рис. 299).
43l] §..16.1. ОПРЕДЕЛЕНИЕ. ФУНКЦИЙ И МОМЕНТОВ НА ВЫХОДЕ 435
430. Найти функцию распределения ®(н2) выходного
напряжения и2 безынерционного усилителя с релейной ста-
тической характеристикой, изображенной на рис. 300, а,
если на вход его подается напряжение нь случайная
величина которого рас-
пределена так же, как и
в задаче 429. Задачу ре-
шить для двух случаев:
1)
ilt .= 0 в, О| = 2 • 10 3 в;
2)
Й1 = 1,8 - I0’3 в,
о, = 2- Ю-3 в.
Срабатывание релей-
ного усилителя происхо-
дит при напряжении н1п =
= 1,9 10~3 в. Выходное
напряжение zz2m=100 в.
Ответ. В том и дру-
гом случае функция
w (иг) представляет собой
дельта-функции при зна-
чениях z/2 = 0 и zz2= ± 100
дельта-функций, равные вероятностям появления соот-
ветствующего выходного сигнала и2, имеют следующие
иг
0
и.
а)
y\w(u2)tluf
,Р(и2 -<П .
-ЮО -50 0 50 ЮО
е)
Рис. 300. Функция распределения
(б) сигнала на выходе элемента
с идеальной релейной характери*
ст'икой (а).
в (рис. 300, б). Площади этих
величины:
0,658 при н2 = о,
1) p(u2) = 0,171 при и2= ± 100 в,
0 при прочих и2;
0,5019 при и2 — 0,
0,498 при и2 = + 100 в,
2) Р (и2) = 0,0001 при «2= — 100 в,
. 0 при прочих и2.
431. Найти математическое ожидание my(f) и кор-
реляционную функцию Ry(ti, t2) выходной величины y(tj
436 Гл. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ (431
нелинейной системы, структурная схема которой изо-
бражена на рис. 301.
Уравнения, описывающие динамику работы системы,
имеют вид
(Тр + 1)у = F (х), |
x — g — y, J ' '
где нелинейная зависимость F(x) описывается функцией
F (х) = kiX + й2х3. (2)
Входной сигнал g(t) представляет собой стацио-
нарный случайный процесс с нулевым математическим
Рис. 301. Структурная схема нелинейной
системы.
ожиданием (ms=0) и корреляционной функцией
ЗД'. (3)
Моменты более высоких порядков во входном сиг-
нале отсутствуют. Постоянные, входящие в уравнения
(I) — (3), имеют следующие значения: Т = 0,125 сек, kt = 8,
А>2 = 0,4, о? = 6, а =10 сек"1.
Решение. Поскольку нелинейная зависимость (2)
непрерывна и дифференцируема, то для определения
моментов выходной величины y(t) можно воспользо-
ваться ее разложением по моментам входной вели-
чины g(t). Поэтому решение для y(f) будем искать
в виде степенного функционального ряда
оо
!/(/)= 2 Фп(0г”(0. (4)
п==1
Подставляя выражение (4) в (1) и (2) и приравнивая
члены с одинаковой степенью g, получим линейные
дифференциальные уравнения для последовательного
8М1 § 16.1. ОПРЕДЕЛЕНИЕ ФУНКЦИИ И МОМЕНТОВ НА ВЫХОДЕ 437
нахождения необходимых функций <p2Z+i U = О, L 2, ...)
(Тр + l)<P2z+i ~с2м (I — О, 1, 2, ...). (5)
Значения членов с2М, входящих в эти уравнения, для
I == 0 и I = 1 имеют вид: с} = kh
cs = k2 (1 + 3<р, - 3<p2 ~ фЗ). (6)
При заданном виде нелинейности F(g, у) и момен-
тов распределения входного случайного сигнала g(t)
все функцию ф2г+1 (/=1, 2, ...) с четными номерами
равны нулю.
Определив в результате решения системы уравне-
ний (5) функции ф2/+1 (0, можно найти интересующие нас
моменты распределения выходного сигнала y(t) через
моменты входного сигнала g(t). Для этого необходимо
воспользоваться разложением y(t) в ряд (4) по сте-
пеням g(t).
В частности, моменты первого и второго порядков
определяются согласно выражениям
' оо
Шу = S Ф21+1 (О те (t), (7)
/=0 21+1
СО
2 (8)
п, 1=0
где М [g2/+1(O> g2"+1 (^г)1 — соответствующий смешанный
момент распределения входной величины.
Так как по условию задачи, задана только корреля-
ционная функция входного сигнала (момент второго
порядка)
t2) = M [g(tt), g(t2)],
то для решения задачи достаточно определить лишь
функцию Ф1(О- Для этого согласно (5) и (6) необходимо
решить уравнение
(Тр + 1)Ф1 = ^’1.
Решение его дает
- •• : -3')- . .
438 ГЛ. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ [432-
С учетом характера входного сигнала получаем
ту = <Pi (0
RyUi, !I2) = <Pi^i)‘Pi(^)^g(A, *2) =
= fe, (1 — е 7') (1 — е г) =
т — & -1 т у ^~С1 ftz—ti)
. Обозначим т = t2 — Тогда
Я/*!. 4 = fe^(l -е~^)(1
Подставляя значения всех входящих величин, оконча-
тельно найдем
Шу — О,
Ry (Л, т) = 2304 (1 - е-м>) (1-е"8 <т+<>>) е-'Ог.
Таким образом, корреляционная функция выходного
сигнала y(t) зависит не только от интервала т, но и от
начала отсчета по оси времени.
§ 16.2. Расчет нелинейных систем
с помощью статистической линеаризации
432. Методом статистической линеаризации найти
математическое ожидание, дисперсию и корреляционную
функцию на выходе нелинейного безынерционного усили-
теля, если на вход его поступает случайный сигнал щ (/),
имеющий статистические характеристики
mUl(t) = mllt,
(т = t2 — t[).
Статическая характеристика усилителя представлена
на рис. 302. Необходимые для расчета величины име-
ют следующие числовые значения: ти,= 1,6-10~3 в,
cU1=2-10-3 в, Г«1И|= 1 • 10~3 в, ii2m = ЮО в, а = 2 сек~1.
432}
S, 10.2. CIAi it. 1 1 l-.CKAfl ЛИНЕАРИЗАЦИЯ
439
Решение. Согласно методу статистической линеа-
ризации для безынерционного нелинейного звена иско-
мые статистические характеристики выходного напряже-
ния определяются с помощью следующих формул;
= аи,)/пВ1,
оиг = k, (mUl, aUl) ou„
>г)=*" (“«,> ®.М.-
где k0, k\, k" — коэффициенты
зации,
^=т(А;+А1)- (2
Для того чтобы воспользо
ваться коэффициентами стати
стической линеаризации, при
веденными в приложении 30
обозначим
Д 1л == ^2т
статистической линеари-
Рис. 302. Статическая ха-
рактеристика линейного
звена с насыщением.
В соответствии с заданными числовыми значениями
= -^- =
1 «1Л
— =--------= 6,25 • 104,
mUi 1,6-10-3
1.6,
2,
1 «1л
— = —'--°-у=5 104.
% 2-Ю-3
Подставляя эти величины в формулы (П.33)4-(П.35)
приложения 30, получим
k0 « 6,25 • 104 • 0,6 = 3,65 • Ю4,
ftf =5- 104- 0,72 -3,6- 104,
^ = 5. 104 • 0,76 — 3,8 • 104,
=3,7 104.
440 ГЛ. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ [433
. • С учетом этих значений
Ши2 = 58,4е,
&и2 = 74е,
Q = 5328^62,
V,, /2) = 0,152е2.
433. На вход безынерционного электронного трех-
позиционного реле нодается напряжение
«1 «ю «1сл»
где ц10 = 4- 10~3е —постоянная составляющая, м1сл —ста-
ционарная случайная составляющая со спектральной
плотностью
2aD„
S“> = as + ct>* ’
£> =а2 = 25- ЮЛ?2, а = 2 еек~'.
"i “i
Напряжение срабатывания и Отпускания электронного
реле uIcp = ± 2 • 10-3е. Выходное напряжение .реле и2 —
= ± 10 с.
' Применяя метод статистической линеаризации, найти
постоянную составляющую выходного напряжения и20,
его автокорреляционную функцию 7?Us[(^, t2) и взаим-
ную корреляционную функцию и2(^, Л).
Ответ.
«го= 5,4в,
Ru2(tu ^) — 47,7e~2te2,
‘ Ruvu2(ti, ^) = 2,87- 10~2в2.
/
434. Найти математическое ожидание та и диспер-
сию скорости вращения оси двигателя системы, со-
стоящей из безынерционного линейного усилителя, дви-
гателя и тахогенератора с ограниченной линейной
характеристикой. Структурная схема системы представ-
лена на рис. 303. На вход системы подается напряжение
м( (t), представляющее собой сумму постоянного напря-
дай §161 G' ТПСТИЧГСКАЯ ЧПНЕАРИЗАЦИЯ
441
ткения «ю и стационарного случайного процесса с ну-
левым математическим ожиданием (тИ1 = 0) и корреля-
ционной функцией’
R (т) = сг2е-ат fa =12,5 се/с-1)
Коэффициент усиления усилителя по напряжению ky—600.
Рис.' 303. Структурная схема следящей ,
системы с нелинейной обратной связью.
При напряжении ut = 30 в вал двигателя вращается
со_скоростью п = 3000 об/мин, а тахогенератор разви-
вает напряжение нтг = 0,1 в. Электромеханическая по-
стоянная времени двигателя Т — 0,04 сек. Статичес-
кая характеристика тахогенератора имеет вид, пред-
ставленный на рис. 302. Линейная зона характеристики
ограничивается скоростью вращения вала двигателя
3000 об/мин.
Задачу решить для трех значений дисперсии вход-
ного напряжения: о2и =6,25- 10-4в2,25 - 10-4в2,100 • 10~4в2
при «ю = 5 • 10”2в.
Решение. Передаточная функция линейной части
системы
где С(р) = Тр+ 1.
Коэффициент передачи двигателя в соответствии
с заданными условиями задачи имеет значение
. • 2л 3000 • 6,28 _. „ г . picX~i
= Т^ГбО 7....30760- = 10’5 (в • се,е> •
Следовательно, k — 6 • Ю2 •. 10,5 = 6,3 • Ю3 (в • сек)-1.
442 ГЛ. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ [434.
При измерении скорости вращения Q вала двигателя
в padjcen зона линейности статической характерис-
тики тахогенератора равна
Ь — Ил = =314 сек'1.
ои
При этом тахогенератор развивает напряжение птгга =
= 0,1 в.
Можно предполагать, что при заданном виде пере-
даточной функции и нелинейности автоколебания в си-
стеме отсутствуют. Поэтому для решения поставленной
задачи можно применить метод расчета неколебатель-
ных стационарных систем с одной нелинейностью с ис-
пользованием статистической линеаризации.
Согласно приложению 30 для заданной нелинейности
коэффициенты статистической линеаризации вычис-
ляются с помощью следующих формул:
I \ al J \ al /
Для расчета примем
kdma> go)=1(*ч+*;')•
Для вычисления этих статистических коэффициентов
передачи нужно знать mQ и о£2 на выходе двигателя,
которые неизвестны. Поэтому необходимо еще вос-
пользоваться формулами для расчета этих величин.
4341
§ 16.2. СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ
443
Применительно к рассматриваемой схеме можно написать
,*('% + "ю)
ma~C(O) + kko (ma,aa)i
CO
G2=±f ___________*______
a Я J C (/co) + kky (mQ, <ya)
0
(5)
г
SU| (и) da,
(6)
где
С(0) = С(р)р_о,
С (/со) = С (р)Р.1а.
Подставляя значения mu , и1сл, C(p), найдем
_________fe^lO___ /7х
и 1 + kk0 (mQ,Oo) ’ ' J
9 2 f kS au,a
аё = ’JT J 72a2 + [1 + kkt (mQ, oq)]2' ' d(i3' <8)
,o
При написании здесь учтено, что заданной корреля-
ционной функции входного сигнала 7?Ui (т) соответст-
вует спектральная плотность
2аа®
Su (®) = ~гтт •
“i v ' а2 + <о2
Пользуясь приложением 17, находим значение ин-
теграла (8):
' ~ 2
Gfi [1 + kky (niQ, а<>)] [1 + kkt (mQ, ай) + aT] ’
Таким образом, для того чтобы найти значения аа
и та, необходимо решить систему уравнений (7), (8),
используя также уравнения (2)-р(4).
Подставим в уравнения (7) и (9) числовые значе-
ния заданных величин
______________315________ /101
'«и- 1+6,3-103feo(ma, ай) ’
40- 10е
= [1 ± 6,3 • 103й1 (лгй, ай)] [1 + 6,3 • 103й, (та, ай) + 0,5] " <11
444 ГЛ. 16. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ [434
Решение задачи для всех заданных от будем вести
методом последовательных приближений
- 1. aU)=2,5- IO’2 * в.
В качестве первого приближения возьмем значения
коэффициентов /?0 и kt, равные коэффициенту передачи
тахогенератора в линейной зоне:
WD = ы" = = 3,2 КГ4 в • сек.
° 1 о 314
Подставляя эти значения, а также oUj, в (10) и (11),
получим первое приближение:
=105 сек-1, оц” = 48,9 сек1.
Вычислим теперь значения гщ и -ot для следующего
приближения:
m о 105 Оо 48,9
rai = -A = —= 0,333, а1 = -£- = —= 0,156.
1 Ь 31» ’ ’ 1 Ь 315 ’
. Используя формулы (2) —(4), найдем второе прибли-
жение: -
= 3,2 • 10~4 в сек,
= 3,2 • 10-4 в • сек.
Таким образом, второе приближение совпало с пер-
вым. Следовательно, при
а„, = 2,5 - 10"2 в и ию = 5 • 10-2 в
. т.£= 105 сек"1, oQ = 48,9 сек-1
или
/71п= 1000 об!мин, о„ = 566 об/мин.
2. ои, = 5 10 2 в, «ю = 5 • 10-2 в.
В качестве первого приближения берем прежние
значения:
/го” = № = 3,2 Го-4 в сек.
В. результате расчета по формулам (10) и (11) получаем
zziJP= 105 сек~', <т^” = 97,8 сек"'.
4J84J § 16,2. СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ
445
Это соответствует
mW = 0,333, ©<» = 0,312.
Вычисление по формулам (2)—(4) дает
№ = 3,15 • 10"4 в • сек, = 0,94 1О"4 в сек,
/г"(3) = 3,14- 10’4 в-сек, k? = 2,04 • 10“4 в • сек.
Далее в результате расчета находим
mt? — 106 сек ’, = 125,4 сек1.
Расчет по аналогичной методике дает третье при-
ближение:
k(03> = 3,12 • 10~4 в • сек, ki(3> = 1,17- 10~4 в сек,
k"® = 3,05 • 10~4 в • сек, М® = 2,11 • 10"4 в • сек,
та1 = 106 сек1, Ои)== 124,8 сек"1.
Этот результат можно считать окончательным, так
как он мало отличается от второго приближения.
3. <т„, = 0,1 в, н10 = 5- 10*2 в. -
Первое приближение:
4° == — 3,2 • 10"4 в • сек,то = 105 сек~\ = 195 сек"1,
m(i° = 0,333, о?1 = 0,62.
Второе приближение:
= 2,56 • 10"4 в • сек, k(2) = 1,96 • 10"4 в • сек,
та — 123 сек"1,
оЬ2) = 234 сек"1, т? = 0,39, о?1 = 0,744.
Третье приближение
^3) = 2,54 • 10"4 в • сек, = 1,97 10"4 в • сек,
mg’ = 123,4 сек"1, ($’ = 233,9 сек"1.
Это приближение можно считать окончательным,
ак как оно практически не отличается от второго.
446 гл. 16- случайные'процессы в Нелинейных системах изз
435. Найти дисперсию а| угла поворота рамы / во-
круг оси у простейшей гировертикали с маятниковой
коррекцией (рис. 304), если маятник 2 поворачивается
вокруг этой же оси на угол
где —const—математическое ожидание, бел и — слу-
чайная центрированная составляющая с корреляцион-
ной функцией
(т) == ст| е~а <т)-
Маятниковый корректор с усилителем 3 и датчиком
момента 4 имеет нелинейную статическую характери-
стику, представленную на рис. 305. Максимальный
Рис. 304. Гировертикаль с маятни- Рис. 305. Статическая
ковой коррекцией. характеристика маят-
никового корректора.
момент коррекции Л4т=17,5 Г см. Кинетический мо-
мент гироскопа И = 20000 Г-см-сек.
Задачу решить для следующих значений дисперсии
ое = 10,20,30 и 40 угл-мин, т е = 0, а = 0,8 сект1.
Указание. Поскольку структурная схема системы
имеет вид, изображенный на рис. 306, сначала необхо-
димо найти математическое ожидание и дисперсию
ошибки 0' на входе нелинейного элемента. Для этого
4351 § 16.2. СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ 447
используются формулы
C(°)p«ei/]
- С (0) + kk0 (т$, ай) ’ <0
©О
ей = - [ I /ту: vj-ffiz-“Ч Г Se (®)(2)
® и Ji С (j<a) + ук ’ ’ ' '
о
где С (0) = С (р)Р»о — многочлен знаменателя передаточ-
ной функции линейной части (в рассматриваемом слу-
чае С (р) = р), С (/со) = С (р)р^/а, Se (со) — спектральная
Рис. 306. Структурная схема гировертикали
с нелинейной маятниковой коррекцией.
плотность, соответствующая заданной корреляционной
функции Re# (т), k& и k{ — коэффициенты статистической
линеаризации нелинейности (см. рис. 305), которые оп-
ределяются методом последовательных приближений
при решении уравнений (1) й (2) совместно с форму-
лами приложения 30.
После нахождения /?0 и ky математическое ожида-
ние тв и дисперсия определяются по формулам
kkomey
We = C(0) + kko ’
оо
ol — — [I ,; I Se (co) da.
6 л J | C (jto) + ktk I у' ’
0
Ответ.
(угл. мин)2 100 400 900 1600
мин)2 ,94 304 567 849
РАЗДЕЛШ
ОПТИМАЛЬНЫЕ, ЦИФРОВЫЕ,
САМОНАСТРАИВАЮЩИЕСЯ
СИСТЕМЫ И МОДЕЛИРОВАНИЕ
ГЛАВА 17
СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
§ 17.1. Синтез оптимальных систем
с использованием принципа максимума
436. Произвести синтез регулятора, обеспечивающего
оптимальное по быстродействию управление движением
спутника вокруг центра масс по одной из осей. Функ-
циональная схема системы управления представлена на
рис. 307.
Рис. 307. Функциональная схема системы управления угловым
положением спутника.
Момент инерции спутника / = 200 кГ • м • сек2. Ис-
полнительными органами системы управления являются
газовые реактивные двигатели с регулируемой тягой,
развивающие максимальный момент Мт *= 4 кГ • м.
При оптимальном управлении найти время, необходи-
мое для прихода спутника в установившееся нулевое
состояние, если в начальный момент его отклонение
составляло 1°46', а угловая скорость 28,65 град/сек.
Возмущения отсутствуют. Задачу решить, используя
принцип максимума Л. С. Понтрягина.
48в] - 5.17.If ПРИНЦИП.МАКСИМУМА 449
Решение. Уравнения движения спутника при от-
сутствии возмущений имеют вид
г d2® .ж 1
/ di2 М, I
По условию задачи момент М должен быть сформи-
рован так, чтобы спутник переходил из любого откло-
ненного положения в нормально ориентированное за
минимальное время.
Поскольку тяга реактивных исполнительных двига-
телей конечна, то управляющий момент М ограничен
М Л4тах — Мт.
Для решения задачи Преобразуем уравнение (1). Для
d'Q' * ЛТ
этого обозначим х, •=&, х2 = == ф, /г =—Тогда
уравнение (1) запишется в виде
dxt — v dx2 _ , . .
dt ~*2’ dt (2)
где р — нормированная функция управления, модуль ко-
торой | р | 1. Сформируем функцию [2,20]
2
н =5'Ф</Дх1, х2, ц). (з)
Для системы (2)
Н = Ф1^2 + (4)
Максимум этой функции с учетом ограничения (2) на
управляющий сигнал р и обеспечивает оптимальность
системы по быстродействию. Очевидно, что при нало-
женных ограничениях максимум Н имеет место, если уп-
равляющий сигнал р формируется согласно закону [20]
р = sign ф2. (5)
Таким образом, оптимальное по быстродействию
управление будет осуществляться в том случае, если
регулятор будет переключать исполнительное устройство
по релейному закону в соответствии со знаком вспомо-
гательной функции ф2. Для того чтобы найти ф2,
450
ГЛ. 17. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
тж
запишем [20]
dipi_______________________дН „
dt дх, ’
(6)
dt ~~ дх2 Ф1,
Интегрируя эти уравнения, получим
ф1=Ср = ^2 +
где Ci, с2— постоянные интегрирования.
Чтобы наглядно- представить, как происходит пере-
ключение, изобразим процесс движения на фазовой пло-
скости.
Исключим из уравнений (2) dt. При этом для у, =
л= ±1 получим
x2dx2 — ± kdxi,
х2 , . I
-g- = ± kXi + С.
Уравнениям (7) соответствуют параболы, симметричные
относительно оси Xi (рис. 308,а). Спутник придет и бу-
(7)
е)
Рис. 308. Фазовые диаграммы углового движения спутника
• при у±1 (а) и при оптимальном управлении (б).
дет оставаться в исходном положении, если изображаю-
щая точка на фазовой плоскости попадет в начало коорди-
/ d'Q' \
нат (— '0^=0, x2=-^-ss0l. Для этого при произволь-
ном начальном отклонении f>0, 0о изображающая точка М
4i!61;
§ 17.1. ПРИНЦИП МАКСИМУМА
451
должна перейти сначала в точку D (рис. 308, б), а затем
уже по линии переключения АО — в начальную точку..
Переход на траекторию АО достигается изменением
знака управляющей функции р с « — 1» на «+1».
Таким образом, управляющий сигнал р должен
менять знак при выходе изображающей точки на линию
переключения. В соответствии с рис. 308, б
( \
\ dt /п
pW =
+ ! при -^<
и при
I <0,
п
(8)
при -&>
\ dt /п
Уравнение линии переключения находится из выра-
жения (7) и рис. 308, б
= (4?)„ = - /2^0 sign О. (9)
Подставляя числовые значения, получим
Т (4г)„ = “ °’2 siSn (Ю)
Cлeдoвaтeльнoi в регуляторе должно быть устройство,
дифференцирующее ошибку •& по времени и вычисляю-
щее скорость 1-^-1 на линии переключения по фор-
муле (10), а также логическое* устройство, осуществляю-
щее переключение реактивных двигателей на полную
Рис. 309. Функциональная схема оптимального
регулятора.
тягу по закону, выраженному формулами (8). Функцио-
нальная схема регулятора представлена на рис. 309.
452 ГЛ. 17. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
[436
Оптимальное время перехода спутника из заданного
положения в нулевое может быть ‘ определено следую-
щим образом. Из уравнения (2) можно написать'-
dx2 d'b .
-77- =
dt dt
Поэтому db = kp.dt. В результате интегрирования поп-
лутаем
^2-^1 = ^(4—^1)- (П)
Поскольку переход совершается в два этапа и значе-
ния & в начале (-& =-Оь = 28,65 град!сек) и в конце
(-0’2 = 0) заданы, то для вычисления времени на каждом
этапе согласно выражению (11) необходимо найти Ф = 0[
в точке D. Эта точка лежит на пересечении кривых,
описываемых уравнениями
*—" «-It- <|2>
Поэтому
-0] = ± V^k. (13)
с0 определим из начальных условий. Для этого предва-
рительно преобразуем -Оо и -&0 в радианную меру
-Оо — 1° 46' = 0,02 рад, -60 = 28,65 град/сек = 0,5 сек*1.
Тогда для начальных условий имеем
с0 = (0,02)2 + •-= 0,129 рад.
Подстановка с0 и k в (13) дает
А, = /0,129 = 0,345 сек1.
Для расчета необходимо взять знак ( —), так как пере-
ключение происходит в области отрицательных значе-
ний О. Подставляя -О’] в (11), находим время движения
на первом (Д^ = ^ — /0) и втором (Ai2 = ^2 —О участках
д/1==^_/0 = _д__2==___ = 42,3 сек,
Д^2 ^2 Л 0 02 17,3 сек.
Общее время Д/ = Д/( + Д/2 = 59,6 сек.
17.1. ПРИНЦИП МАКСИМУМА
453
437. Спутник, рассмотренный в задаче 436, подвешен
на торсионной подвеске в вакуумной испытательной
камере. Жесткость торсиона равна 2 кГ • м!рад. Силы
сопротивления, пропорциональные скорости вращения •&,
отсутствуют. Спутник сбалансирован и поэтому моменты
от сил тяжести пренебрежимо малы. Найти оптималь-
ный по быстродействию закон управления, уравнение
фазовых траекторий линий переключения и уравнение
для расчета времени движения на участках между пере-
ключениями.
Ответ. Уравнение закона переключения [20]
ц = sign ф2 = sign [Ci sin (0,1/4- с2)];
С] и с2 определяются по начальным условиям.
Фазовые траектории являются эллипсами, описывае-
мыми уравнениями
1 0002 + (ё ±'2)2 = с;
с определяются по начальным условиям.
О
Рис. 310. Фазовая диаграмма оптимального движения
спутника при наличии момента, пропорционального углу
отклонения.
Линия переключения состоит из полуэллипсов, при-
мыкающих к оси О (рис. .310) [20]. Уравнение линии
переключения для n-го полуэллипса
= — У (О — 4п)2 + 4(0 — 4п) sign О . (и = 0, 1, ...).
к.
Уравнение для расчета времени движения изобра-
жающей точки от момента до момента ближайшего
454 ГЛ. 17. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ -УПРАВЛЕНИЯ 1438
переключения t2 равно
— &, = 0,1 с{ [cos (О, Ц + с')—cos (О, Ц + с2)] ± 0,02 (t2—/,).
с' и с' — постоянные для данной траектории, вычислен-
ные по известным значениям & и О в моменты
Логическое устройство должно вырабатывать упра-
вляющие сигналы в соответствии с формулами (8) за-
дачи 436.
438. Найти оптимальный по быстродействию закон
управления электрическим приводом с двигателем неза-
висимого возбуждения,
(рис. 311), уравнения фа-
зовых траекторий и урав-
нение линии переключе-
ния. Суммарный момент
инерции на валу двига-
теля J = 50 Г-см-сек.2. Пу-
сковой момент, развивае-
мый двигателем при иу =
Рис. 311. Электрический привод
с двигателем постоянного тока.
= иут = 30 в, Мв = 0,785 кГ • м_. При этом напряжении
скорость холостого хода йх. х = 3000 об/мин. В качестве
выходной величины рассматривать угол 0 поворота вала
на выходе редуктора, имеющего коэффициент редукции
Лр= Ю-4. Пренебречь индуктивностью цепи якоря. Учесть
ограничение иу^иут — 30 в.
Ответ. Закон управления [20, 28]
Г ( —
р = sign ф2 = sign [ci + с2\1 — е7/].
Уравнение фазовых траекторий
0 = 0О + 0,2 (0о - 0) - 6,28 • 10~3р In .
р. — 3260
Уравнение линии переключения
0П = — [0,2|ё | + 6,28 • 10'3In(1+32|0|)]sign 0.
©о и 0О —начальные значения угла и скорости его из-
менения на рассматриваемом участке оптимального про-
; цесса.
4891
§ 17:2. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 455
§ 17.2. Синтез оптимальных систем
методом динамического программирования
и классического вариационного исчисления
439. Электрический привод с двигателем постоянного
тока независимого возбуждения (рис. 312) нагружен мо-
ментом вязкого трения Л1Н = ^]Й
работает в режиме, при котором
падение напряжения их — i (rR + гя)
на сопротивлении г = гл + гя зна-
чительно больше обратной элек-
тродвижущей силы е = ceQ' Опре-
делить закон управления элек-
тродвигателем, при котором
суммарная энергия потерь, за-
трачиваемая на преодоление мо-
мента вязкого трения и на нагрев,
будет минимальна. Влиянием ин-
дуктивности в цепи якоря прене-
бречь. Момент инерции якоря
с объектом J = 0,2 Г • см -сек2,
коэффициенты пропорционально-
сти двигателя по э. д. с. се — 0,096 в • сек и по моменту
см — 30 Г • см!а, ki = 1'0 Г • ем • сек, гя + гя = 5 ом.
Решение. Уравнение моментов двигателя имеет вид
+ = (1)
большой величины и
Рис. 312. Электрический
привод с двигателем
постоянного тока, на-
груженный моментомвяа-
кого трения. . '
По условиям задачи индуктивность цепи якоря мала.
Поэтому, в соответствии с законом Кирхгофа,
ir + = и0, (2)
откуда следует
Подставляя это выражение в (1), найдем
]
d£i
~dt
Uy / CgCM \
456 ГЛ. I7Z, СИНТЕЗ. ОПТИМАЛЬНЫХ СИСТЕМ „УПРАВЛЕНИЯ М39
Поскольку ——- = 0,52 й,- = 10, пренебрежем
первым членом в скобках. Поэтому приближенно урав-
нение динамики примет вид
1 См
J~dT = ~ kiQ. + — Uy.
Подставив численные значения и упростив, получим
= ЬО. + тиу, (3)
где b = — 50 сек-1, т = 30 в-1 • секг2.
Нам необходимо определить иу как функцию Й.
По условиям задачи двигатель работает в режиме,
при котором сеЙ <С ir. Следовательно, приближенно
(4)
Мощность электрических потерь вычисляется по
формуле.
и2
Рэ = iUy = (5)
Мощность потерь на вязкое трение, если момент Ма
выразить в Г • см, составляет величину
Рм = 9,81‘. 10т5Мп . й-9,81 • Ю’^й2.
Таким образом, минимизируемый функционал, пред-
ставляющий суммарную энергию потерь, имеет вид
оо
7 = J (9,8Ь 10Л1Й2 + yUyj dt.
о
С учетом числовых значений получим
оо
/ = j (a^Va^dt, (6)
о
aj = 0,98.1 • 10-3 dyic • сек-, ' а0 = 0,2 - г- ;
И©9Г § 17.2. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 457
Задачу отыскания оптимального управления, обеспе-
чивающего минимум интеграла (6), будем решать мето-
дом динамического программирования. Тогда для рас-
сматриваемой системы уравнения динамического про-
граммирования запишутся
a,Q2 + а0н2 + (bQ + muj = О,
о । dip „
200»^ + т = О,
где — вспомогательная функция, определяемая урав-
нением
= . Г
dt v' Х^
V — подынтегральная функция ________^Х,___________
минимизируемого функцио- X.
нала. X.
Решив второе уравнение си- Х^
стемы (7), найдем
Рис. 313. Функция оптималь»
дф __ 2д0 ного управления.
"dQ------иУ <8)
т-г ' Йф
Подстановка этого значения в первое уравне-
ние (7) дает
ma0Uy + 2aob£luy — = .0.
В результате решения получаем
иу = — /гй, (9)
где _____
k = — + T/r (A)2 + £l.
т г \т) а0
Используя числовые значения, находим
. 50 50 \2 .0,981 1.0-3 n 1п-з
- 30 + V (зо) + 0,2..X 0,87-10 в. сек.
Таким образом, искомый оптимальный в смысле мини-
мума потерь закон-, управления является линейным
(рис. 313).
458 ГЛ. 17. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ 1440
Следует иметь в виду, что в силу сделанного ранее
допущения се£1 -С ir, полученный закон справедлив в об-
иу
ласти малых значений Q .
се
440. Решить задачу 439 для следующих двух слу-
чаев: а) &1 = 0,1 Г-см-сек, б) гя + гд=100 ом, при не-
изменных остальных исходных данных.
Ответ.
a) k — 0,088 в • сек\
б) /г = 0,442 • 10"4 в • сек.
441. Решить задачу 439, применив классические ва-
риационные методы [2, 20].
Решение. Уравнение динамики системы имеет вид
Ш + mhy.
Необходимо найти закон изменения uv = uu(Q), миними-
зирующий интеграл потерь
' I — | (аД2 + «ому) dt.
о
Для решения поставленной задачи необходимо со-
ставить функцию [2]
//=V+jUf4 (1)
где
akxl + a0u2y
— подынтегральная функция минимизируемого функци-
онала;
2/ = {bftXi + ... + bnixn + tntuy) = 0
— функция, представляющая уравнение первого порядка
по i-й переменной; ^- — произвольный множитель.
4411 § 17.2. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Дифференцируя функцию Н, получаем
п
dH п dH V п
; du °’ du ~2аоиУ
7=1
Отсюда уравнения вариационной задачи имеют вид
-^-= —2j6/iX/ + 2aixi’ 0 = 2^1/^ —2j W/Ay. (3)
7=1 7=1
В рассматриваемом случае
z = — (Ьй -\-тиу) = 0, (4)
У = (Й1Й2 + а0ц2). (5)
На основе (2) и (3), получим
- ЬКг + 2а Д
0 = 2а(1иу — nik-i.
(6)
Решая эту систему относительно переменных и £2,
после исключения функции времени из полученных ре-
шений и* алгебраических преобразований, получим
иу = — kQ,
После подстановки численных значений находим
•: k = 0,87 10-3 в сек.
ГЛАВА 18
СИСТЕМЫ С ЦИФРОВЫМИ ВЫЧИСЛИТЕЛЬНЫМИ
МАШИНАМИ (ЦВМ)
§ 18.1. Передаточные функции систем с ЦВМ
при учете квантования по времени
442. Система регулирования имеет в своем контуре
цифровую вычислительную машину (ЦВМ). Структур-
ная схема системы показана на рис. 314. Найти z—пере-
даточные функции разомкнутой системы в предположе-
нии, что запаздывание в ЦВМ отсутствует и можно
°) б)
Рис. 314. а) Блок-схема системы с ЦВМ; б) эквивалентная
структурная схема.
пренебречь влиянием квантования по уровню, ,т. е.
можно рассматривать линейную задачу.
Передаточная функция непрерывной части
W(p) = (О
' р(1 + Л₽)
Численные значения коэффициентов: общий коэф-
фициент усиления. К =.10 ,сек~\ постоянная времени
71 = 0,05 сек 'и период дискретности ЦВМ Го = 0,1 сек.
442}
§ 18.1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ЦВМ
461
Решение. Передаточная функция W(z) разомкну-
той системы может быть найдена согласно [35, 38]
оо
. W (г) = 2 h (пТ0) z~n = ~~~ F (г), (2)
n=0
где h(nT0) — переходная функция непрерывной части
в дискретные моменты времени (н = О, 1, 2, ...), a F (z)
представляет собой z-предбразование этой функции.
Переходная функция для (1) имеет вид
А(0 = - Г1 (l -е"г>)].
(3)
По таблице z-преобразований находим
лг)-4^-г, (Z'ng-J-
(4)
где d = е т = е"2 = 0,135.
Далее из (2) находим передаточную функцию разомк-
нутой системы _
z — d —
W{z) = К [угу - -Г1(( - -
(z- 1) (z — d)
(5)
z — d
Поскольку переходная функция h{t) является пре-
образованием ~ -
прерывной части W(p), деленной на р, т. е.
то часто используют символическую запись формулы (2)
(6)
Лапласа от передаточной функции не-
BZ(z) = ^4-Z
При этом дискретная передаточная функция может
определяться в следующей последовательности:
К 1
р2 (1 + Tip) J
=K~Z
х Z
— +.-V + ПГ
р Р Р + 4
(7)
462
ГЛ. СИСТЕМЫ С ЦВМ
z-преобразование каждого слагаемого в правой части (7)
нетрудно определить, воспользовавшись таблицей z-npe-
образования (приложение 2),
Г(2)- кiji
А т , т0 , Ту (2- 1)п
- д [-.Л + —г + -
KTofz-d-(2-1)1
-..^-0(2-<0------(8)
Окончательное выражение (8), естественно, совпадает
с (5).
Подстановка численных значений дает
^(г)= (2-W-ir-
Передаточная функция замкнутой системы
0,5682 + 0,297
, W' Z‘ 1 + Г (г) 22 - 0,567г + 0,432 '
443. Решить предыдущую задачу, если передаточная
функция непрерывной части
= Р(1 + 7\/!)(1 + ад ’
Ответ.
, , Г го 7? е-1 2 — 1 - 1
W (г) = /< —®-+—-1—. —-j-+—.—(Л + Г2) ,
1^—1 Ту — Тг z — dy Т^—Ту z — d^ ' 1 J\
Го _А
где dy = е т > и d2 = е Т1.
444. Для системы с ЦВМ (см. рис. 314) определить
дискретные передаточные функции, используя модифи-
цированное z-преобразование.
Передаточная функция непрерывной части
Решение.,
r(z, (1)
446]
§ 18.1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ЦВМ
463
где символ Za означает модифицированное z-преобразо-
вание; о — относительное (безразмерное) время 0^о<1,
означает, что рассматривается смещенная решетчатая
функция для моментов времени t = пТ0 + сТ0.
Обращаясь к таблице модифицированного z-преоб-
разования, получим
W, (2)
где W (г) — дискретная передаточная функция разомк-
нутой системы при о = 0. ,
Окончательно имеем
Ф(г, о)
_ КТВ (pz + I - g)
z—l+KTB •
445. Решить предыдущую задачу, если передаточная
функция непрерывной части
Ответ.
W(z, а) = К, где d = е'
м K[(l-dp)z + dg-d] .
z-d + K-Kd • _
446. Для системы с ЦВМ (см. рис. 314) определить
дискретные передаточные функции разомкнутой системы,
используя z-преобразование и ^-преобразование.
Передаточная функция непрерывной части
IF(p)= •> Л
Р(1 + тУ)
Решение.
z-l ( к ) z-l (.К КТ, 1
B7(z) =---Z „ „-2-г = --Z -5-——U ,
z ( р2(1 + ту) J г ( р2 l + T2lP2
Tt (г — I) Sin-J?- * 1
22 —2z COS-^ + 1
11
464 ..ГЛ. |Я. системыч; IIBM > 1447
Для перехода к ау-преобразованию используем под-
становку' z = , откуда
W'(ay) =
1
tg2 —-
ё 27,
447. Для системы регулирования при учете времен-
ного запаздывания т, вносимого ЦВМ (рис. 315), опре-
делить дискретные передаточные функции разомкнутой
и замкнутой системы.'
Рис. 315. Структурная схема системы с ЦВМ при
учете временного запаздывания.
Передаточная функция непрерывной части
^(р)=^-е-тр,
где т = еТ0 — временное запаздывание, 0<е=С 1, D (z) = 1.
Решение. Дискретная передаточная функция ра-
зомкнутой системы при наличии чистого запаздывания
определяется как
r(z) = ^z4^e-*₽} (1)
inz) = *-W,a)lnpiI0=1_e. (2)
Таким образом, учитывая результат решения за-
дачи 445, получим
IFI(z) = z-1Kr0O2tj.T.o|
448J 5 18.1, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ЦВМ -'465
ИЛИ ‘ : '
z \ _ (z) __ КТ _____' б) 2 + 8_______.
1 + Щг) Л ° z244Kr0(l-e)-l]z + Kr<,e • ( )
448. Для автоматической системы {рис. 316), в ко-
торой ЦВМ осуществляет дискретную коррекцию, опре-
делить передаточные функции разомкнутой и замкнутой
системы.
Рис. 316. Структурная схема цифровой системы
с дискретной коррекцией.
Передаточная функция непрерывной части
№'(р) = -^. (I)
Закон управления, реализуемый ЦВМ, описывается
разностным уравнением вида (см. приложение 23)
и (пТ0) = аох (пТ0) - atx [(п - 1) Го]. (2)
Решение. Дискретная передаточная функция ра-
зомкнутой скорректированной системы —
Гск(г) = Д(г)Г(г), (3)
где
lF/, . Z-I Z-l(W(p)\KT2(Z+l)
W(z)~ г Z[ р J~ г Z[ р3 J 2(z—I)2
— дискретная передаточная функция, соответствующая
приведенной непрерывной части системы;
£)(г)—передаточная функция ЦВМ, выполняющей
роль дискретного корректирующего устройства.
Для определения D(z) проведем г-преобразование
обеих частей равенства (2)
U (z) = (оо - щг"1) X (z). (4)
466 ГЛ. 18- СИСТЕМЫ С ЦВМ [449
Отсюда
- л -л?-'- а°г~а'
U\Z) — X (z) ~а° °12 ~ 2 W
Таким образом, окончательно имеем
(2 + 1)
^к(г)=------------------->
Ф f-л Г«<(г) К^1(г+1)(-^-2-1)
1 + Гск(2) 2г(2_1)2 + Ид1(2 + 1)^г_1)’
§ 18.2. Устойчивость и оценка качества
449. Передаточная функция разомкнутой системы
регулирования с ЦВМ имеет вид , '
W(z) = -^-.
Найти условие устойчивости замкнутой системы и
построить переходный процесс при подаче на вход си-
стемы единичной ступенчатой функции для
Л7'о=1, ЛИ = 0,5 и К7'о=1>5.
Решение. Передаточная функция замкнутой си-
стемы ,
КТВ
2-1 + КГ0 •
Для определения условия устойчивости воспользуемся
алгебраическим критерием устойчивости. Рассмотрим
характеристическое уравнение замкнутой системы
z-I +КТо = О.
Условие устойчивости
/СП <2. (1)
Перейдем к построению переходных процессов путем
разложения изображений входной величины в ряд
Лорана.
4491 § 18.2. УСТОЙЧИВОСТЬ И ОЦЕНКА КАЧЕСТВА 467
Рассмотрим случай КТ0=1. При этом передаточная
функция замкнутой системы будет равна
Ф = г — 1 +КТ0 =~z‘ (2)
Изображение входной величины (см. приложение 13)
7{1(0} = С(г) = т^г./ (3)
Изображение выходной величины
У(г) = Ф(2)С(г) = 1.т^г = т1т. (4)
Разложим последнее выражение в ряд Лорана посреди
ством деления числителя на знаменатель: .
_L__± . _L . _L . _L. цп
г - 1 г + z2 + z3 + zl + ' ' '
Это дает следующие значения функции у на выходе
в дискретные моменты времени: при / = 0 г/ = 0; при
t — To у — 1; при t = 2Ta у— 1; при t = 3TG у= 1 и далее
у=1 при всех значениях t = nT0. График этой функции
изображен на рис. 317 (кривая /).
Рис. 317. Переходные процессы к за-
даче 449.
Между дискретными значениями функции времени
на выходе проведены прямые линии, так как передаточ-
ная функция (1) соответствует идеальному ийтегрирую-
щему звену, переходная функция которого представляет
собой прямую линию.
468
i.'i. s. С1к;п-.мы с ним
W
Аналогичным образом получен ряд Лорана . для
МГо = О,5:
. Г (z) = 0,5 у+ 0,75— + 0,875-^+0,9375-1-+
График переходной функции изображен на рис. 317
(кривая 2).
Для случая Д7о= 1,5 получаем
7(^ = 1,5^ + 0,75^+1,125^ + 0,8375^ + ...
График переходной функции для этого случая изображен
на рис. 317 (кривая 3).
450. Определить, устойчива ли система регулирова-
ния, структурная схема которой соответствует рис. 314.
Передаточная функция непрерывной части
W = р(1+7|Р)(1+Цр) ’
где Д = 2 сек-1, Г! = 0,1 сек, 7’2 = 0,05 сек. Период дис-
кретности То = 0,2 сек.
Ответ. Система устойчива.
.451. Передаточная функция непрерывной части си-
стемы с ЦВМ имеет вид
Г(р) = ^, (1)
где ft = 50 сек-1 — общий коэффициент усиления. Опре-
делить допустимое значение периода дискретности То
для ЦВМ, при котором показатель колебательности
замкнутой системы не будет превышать М = 1,5. Запа-
здывание в ЦВМ равно нулю и влиянием квантования
по уровню можно пренебречь.
Решение. Передаточная функция разомкнутой си-
стемы с ЦВМ может быть найдена согласно
IT(z) = —(2)
' z ( р | z (z — I)2 1 ' f
= (3)
Построим амплитудно-фазовую характеристику ра-
зомкнутой системы по выражению (3). Выполним
4521
§ 18.2. УСТОЙЧИВОСТЬ И ОЦЕНКА' КАЧЕСТВА
469
подстановку
г = е1<йТ° = cos аТ0 + j sin v>T0,
В результате получаем частотную передаточную функцию
КТ0__________
cos (oTD — 1 + j sin <вГо
— J5J.SL. _ ; KTq e+p №То
2 7 2 ё 2 '
Нетрудно видеть, что амплитудно-фазовая характери-
стика представляет собой прямую, параллельную мни-
мой оси и отстоящую от нее на расстоянии (рис. 318).
Для того чтобы показатель колебательности не пре-
вышал заданного значения, амплитудно-фазовая харак-
теристика не должна заходить в окружность, предста-
вляющую собой запретную зону. Она изображена на
рис. 318 пунктиром. От-
сюда получаем условие
Допустимый период дис-
кретности
т 2 м
К М +1 ‘
Для заданных число-
вых значений
1,5
1,5+1 ~
= 0,024 сек.
452. Для системы регулирования, рассмотренной
в задаче 447, определить условия устойчивости и по-
строить область устойчивости в плоскости двух пара-
метров, КТ0 и е,.= -=-.
1 о
Решение. Воспользуемся результатом (4), полу-
ченным в задаче 447. Тогда характеристическое уравне-
ние замкнутой системы можно записать в виде
..... .. . 22 + [/<7?о(1 -4- l]z + KToe.= O
470
ГЛ. 18. СИСТЕМЫ С ЦВМ
[432
ИЛИ
z2 + Az + B — 0, (1)
где
Л = Д7о(1-е)-1,
В = КТог. (2)
Условия устойчивости для уравнений второй степени
имеют вид
Используя
чивости:
1+Л + В>0,
1-Л + В>0,
В<1.
(3)
(2), получим следующие условия устой-
КТ0>0,
KT0(l-2z)<2,
КТог<1.
(4)
Первое условие (4) выполняется тождественно. Со-
вместное рассмотрение двух последних неравенств (4)
Рис. 319. Область устойчи-
вости к задаче 452.
Рис. 320. Область устойчивости
к задаче 453.
дает возможность записать условие устойчивости си-
стемы в окончательном виде так:
2 1 1-2е. если 0<е<.4.,.
кт0 = 1 1 1 —, если 8 ’ 4
Ш1
§ 18.3. СИНТЕЗ СИСТЕМ С ЦВМ
471
Область устойчивости в плоскости параметров КТ0, б,
построенная по уравнению (5), показана на рис. 319.
453. Для системы регулирования, рассмотренной'
в задаче 446, построить область устойчивости в пло-
«т Tq
скости параметров дг0,
Ответ. Область устойчивости в плоскости параметров
показана на рис. 320.
§ 18.3. Синтез систем с ЦВМ
454. Передаточная функция непрерывной части си-
стемы регулирования с ЦВМ имеет вид
r(z,)=Ao_mt (1)
где К = ЮО сек~2 — общий коэффициент усиления разом-
кнутой цепи регулирования, ат — постоянная времени
корректирующего устройства. Определить допустимое
значение периода дискретности То ЦВМ и требуемое
значение постоянной времени корректирующего устрой-
ства, чтобы показатель колебательности не превышал
значения А1=1,3, если запаздывание в ЦВМ равно
нулю, а влиянием квантования по уровню можно пре-
небречь.
Решение. Определим передаточную функцию par
зомкнутой системы совместно с ЦВМ:
W) = -^z{-^} = ^z{^ + -^},. (2)
В соответствии с приложением 13
К 4. 1 - КТ& (Z + 0 J. КТ^Хг (Ъ
Л1рз+р2 J 2(2-I)3 + (2-I)2 ‘ К )
Далее из (2) находим
+ ' <4)
Перейдем к ^-преобразованию, использовав подста-
новку " •
(5)
472
ГЛ. 18. СИСТЕМЫ С ЦВМ
[4&Г
В результате получаем
кт2 (1 + 2 аД (1 - w)
(6)
Получим теперь частотную передаточную функцию
посредством подстановки
№ = ' <7)
где Л представляет собой абсолютную псевдочастоту.
Используя подстановку (7), имеем из (6)
Л?(1 +/7.Т) (1 -/X 4)
-----“W---------(8)
Модуль ^астотной передаточной функции разомкнутой
системы равен
ДУ1 + т2Л21/ 1 + ~ Кг
I (/X) | =----------4г-------1, (9)
а фаза
ф (Л) = — 180° + arctg тХ — arctg , (10)
По выражению (9) на рис. 321 построены л. а. х. По
виду фазовой характеристики (10) этот случай сводится
к л', а. х. типа "2—1—2 (см. приложения 24). В резуль-
тате получаем следующие формулы для расчета; базо-
вая псевдочастота л. а. х. равна
Хо = 10 сек’1,
требуемое значение постоянной времени корректирую-
щего устройства
_ 1 _/ М _ 1 Ез“ по.
т Xor At—I 10 V 1,3-1 0,21 сек,
требуемая протяженность участка л. а. х. с наклоном
20 д131дек
£ _ М + 1__1,3 +.1 7 7.
Л1 - 1 ~ 1,3-1 ~
«551
§ 18.3, СИНТ СИСТЕМ С ЦВМ
473,
допустимое значение периода дискретности
То Т ___________________ 0,21 _— лот п
С 2 Л ~ 7,7 - О’027 Сек'
откуда То ^0,054 сек.
Рис.’ 321. Л. а. х. и л. ф. х. к задаче 454.
455. Произвести расчет следящей системы с аста-
тизмом первого порядка, содержащей в своем контуре
ЦВМ. Исходные данные: максимальная входная ско-
рость Qmax — 20 град [сек; максимальное входное ускоре-
ние етах = 10 град[сек2; максимальная допустимая ошибка
Отах = 4'; непрерывная часть содержит постоянные вре-
мени Тл~- 0,01 сек, 7’2 = 0,002 сек и Ts = 0,001 сек; до-
пустимый показатель колебатёльности М = 1,5; запаз-
дывание в ЦВМ равно нулю. Требуется определить
параметры последовательного корректирующего звена,
включаемого в непрерывную часть, допустимый период
повторения То для ЦВМ и построить переходный про-
цесс при входном воздействии типа единичной ступен-
чатой функции. Влиянием квантования по уровню можно
пренебречь.
Решение. Левее частоты среза л^. а. х. системы
с. ЦВМ; совпадает с л. а. х. непрерывной части, а абсо-
лютная псевдочастота К = (см. задачу 454) совпа-
о
дает с реальной частотой; Поэтому формирование л. а. х
474
ГЛ. 18. СИСТЕМЫ С ЦВМ
- 1455
левее частоты среза можно произвести обычными прие-
мами.
Построим запретную зону для л. а. х. из условий
точности (рис. 322). Контрольная частота
Модуль передаточной функции разомкнутой системы
при Л = ЛК равен
- 202 • 60
I w UM | = -7-^- = = 600 = 55>6 дб‘
По этим данным на рис. 322 построены контрольная
точка Ак и запретная зона, сформированная из прямых
с наклоном 20 дб{дек и 40 дб{дек (наклоны 1 и 2).
Желаемая л. а. х. в низкочастотной области форми-
руется так, чтобы она проходила выше точки Дк на
3 дб, что соответствует увеличению коэффициента уси-
ления в У2 раз. Она состоит из отрезков прямых с на-
клонами 1 — 2—1. В низкочастотной области частотная
функция разомкнутой системы будет
передаточная
иметь вид
К (1 + /Л.т2)
/Л (I
455]
§ СИНТЕЗ СИСТЕМ С ЦВМ
475
Определим параметры желаемой л. а. х. передаточ-
ной функции разомкнутой системы в низкочастотной
части. Базовая частота л. а. х. равна
Ло = ]/-‘^60,= 14,5 сек-1.
Постоянная времени корректирующего звена, форми-
рующая первый излом л. а. х., равна
1 1 о
= =2 сек-
Для получения заданного показателя
ности должно выполняться неравенство
колебатель-
_1_____1_
Т2 Т1
Отсюда получаем минимальное значение
стоянной времени корректирующего звена
второй 1Г0-
0,112 сек.
1
М-1 , 1
М т.
Передаточная функция последовательного корректирую-
щего звена равна
гкз(р) = 4^7 (*1>*2),
и соответствует пассивному звену интегрирующего типа.
Далее определяем необходимое значение общего
коэффициента усиления
К = ]/2 = 1,41 = 420 сек1
г «’так 4
и частоту среза л. а. х.
Лс - AEL = -42°- 0’112 =, 23,5 сек"1.
Т| 2 ’
В соответствии с требованиями к л. а. х. в высоко-
частотной области имеем
476
ГЛ. 18. СИСТЕМЫ С ЦВМ
ТЖ
откуда получаем, допустимое значение периода дискрет-
ности ЦВМ
m О Г 1 Т _ Т' Т* 1 _ '
У°^2ГКГ‘ лГ+Т~У1 у2-/з]-
= 2 • тгхт - °>01 - 0>002 ~ 0,0011 = 0,012 сек.
L 2o,b 1 ,Ь + I J
Переходный процесс при единичном ступенчатом
воздействии изображен на рис. 323.
456. Произвести расчет системы с ЦВМ по исход-
ным данным, приведенным в предыдущей задаче, за
исключением 7\ = 0,05 сек, Т2=
= 0,003 сек, Т3 = 0,001 сек.
Кроме того, в отличие от пре-
дыдущей задачи, задан период
дискретности Го = 0,02 сек.
Требуется определить вид
и параметры последователь-
ного корректирующего устрой-
ства, которое должно быть
введено в непрерывную часть
системы, а также необходимое
значение общего коэффициента усиления К.
Ответ. Общий коэффициент усиления К = 420 сек"1.
В непрерывную часть системы должно быть введено
пассивное интегро-дифференцирующее звено с переда-
точной функцией
Гкз(р) =
(1 + Т2кр) (1 + 7зкр)
(.1 + Ткр) (1 + Т4Кр)
где Г1К — 2 сек, Т%к = 0,12 сек, Тзк — 0,05 сек, Тцк = 0,01 сек.
' 457. Передаточная функция непрерывной части си-
стемы с ЦВМ
W(P) = -^.
Общий коэффициент усиления разомкнутой цепи регу-
лирования К = 1 сек, период дискретности То = 1 сек.
Определить закон управления, реализуемый при по-
мощи ЦВМ (см. рис. 316), который бы обеспечил опти-
мальное в смысле минимума времени протекания про-
458}
§ 18.3. СИНТЕЗ СИСТЕМ' С ЦВМ
477"
цессов регулирование при отработке” ступенчатых воз-
действий, т. е. обеспечил бы системе конечное врёмя;
регулирования.
Решение. Дискретная передаточная функция нё-‘
прерывной части системы
Желаемую передаточную функцию замкнутой системы
возьмем в виде
Ф (г) = 0,5г-1 + 0,5г-2.
При этом переходные процессы в системе будут закан-
чиваться за два периода дискретности
Y (г) = Ф (г) = 0,5г-1 + г'2 + z~3 + ...
Дискретная передаточная функция ЦВМ равна
, , Ф(г) 1 _ г2 —2z+l _ 1—
У 1тФ (г) ‘ Г (Z) г2 - 0,5г - 0,5 — 1 - 0,5z~i - 0,5zr2 ‘
Отсюда закон управления, реализуемый ЦВМ, может
быть записан окончательно в виде рекуррентного соот-
ношения
и (пТ0) = х (пТ0) — 2х [(« — 1) Го] +
+ х [(п - 2) Го] + 0,5ы [(п - 1) Го] + 0,5« [(« -2) Го].
458. Произвести расчет системы с ЦВМ, непрерывная
часть которой имеет те же данные, что и в предыдущей
задаче. Рассчитать дискретное последовательное кор- -
ректирующее устройство D{z) и период дискретности То
таким образом, чтобы обеспечить запас устойчивости,
оцениваемый показателем колебательности, не менее,
чем М 1,5.
Решение. Произведем расчет методом логарифми-
ческих частотных характеристик.
Дискретная частотная передаточная функция исход-
ной нескорректированной системы равна
Г(А)= (О
478
ГЛ. 18. СИСТЕМЫ С ЦВМ
[458
Желаемую дискретную передаточную функцию возьмем
в виде
Д(1 + Ат) (1 - /X
^ж(А) =------, V т Л7 , (2)
(А)2(1 + Л-^)
где ;
1/ т?—г = 1,73 сек,
— Хо г М — 1 ’ ’
Ло — Vft = 1 сек~1,
т 1 , Г Л4(Л4- 1) п -
7о<Хо]/ M+1 0,5 сек,
-у-= 0,25 сек.
Передаточная функция дискретного корректирующего
устройства примет вид
л (ал — = 1
ww 1 + /лП.’ (3)
Соотретствующие логарифмические частотные характе-
ристики построены на рис. 324.
Рис. 324. Логарифмические частотные
характеристики к задаче 458.
Перейдем к «-преобразованию, используя подстановку
Л , 2т \ 2т
ти=D (")=------------------*0+
459] § 18.3. СИНТЕЗ СИСТЕМ С ЦВМ 479
где
откуда закон управления, реализуемый при помощи
ЦВМ, имеет вид >
u(nTo) = box(nTo)-^blx[(n— 1)Т0], ‘ (5)
т. е. используется управление по отклонению и первой
разности (см. приложение 23).
459. Рассчитать дискретное последовательное кор-
ректирующее устройство D(z) и период дискретности То
из условия получения необходимого запаса устойчивости
системы. Система с ЦВМ имеет передаточную функцию
непрерывной части вида
где /< = 90; Т2=10 сек2. Требуемый показатель колеба-
тельности М 1,5.
Ответ. D(z) = b0+biZ~l, где Ь0 = 4, Ьг= —3, То =
*= 0,166 сек.
ГЛАВА 19
ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ
СИСТЕМЫ
§ 19.1. Составление структурных схем экстремальных
и самонастраивающихся систем и исследование
их устойчивости
460. Найти передаточную функцию и составить
структурную схему системы автоматической подстройки
частоты, изображенной на рис. 325. Система должна
подстраивать колебательный контур, состоящий из ин-
дуктивности L и суммарной емкости С — С] + С20, в ре-
зонанс с входным сигналом иу (t) = wOmSin 2nfot. Под-
стройка контура в резонанс осуществляется изменением
величины переменной емкости Cj е помощью двигателя
постоянного тока Д\. Поиск резонанса обеспечивается
синхронным детектированием входного сигнала с по-
мощью синхронного детектора СД и переменного кон-
денсатора С2 малой емкости, величина которой изме-
няется по закону С2 = С2о+C2msin(0ii вращением его
пластин двигателем Д2 с постоянной угловой скоростью
«и. Опорное напряжение частоты «и на синхронный де-
тектор подается с генератора ГОН, приводимого во
вращение двигателем Д2.
С резонансного контура сигнал подается на безынер-
ционный усилитель с коэффициентом усиления ky, на
выходе которого имеется выпрямитель и фильтр Ф\,
настроенный на частоту сигнала «и, с коэффициентом
усиления /2ф1 и полосой пропускания Afi = 1000 гц. По-
сле синхронного детектора СД также имеется фильтр Фг
с коэффициентом усиления &ф2 и полосой пропускания
ад]§ 19.1. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ 481
Д/г = 20 гц. Фильтры Ф\ и Ф2 являются апериодиче-
скими звеньями первого порядка.
Поиск экстремума осуществляется следующим обра-
зом. При расстройке резонансного контура на выходе
синхронного детектора воз-
никает сигнал, пропорцио-
<> и dtiotn
нальныи производной ,
После сглаживания фильт-,
ром Ф2 он поступает на
двигатель, вследствие чего
емкость С\ изменяется до тех
пор, пока производная
не станет равной ну-
лю. Это положение и будет
соответствовать резонансу.
Исходные данные для
расчета передаточных, функ-
ций; R =103 ом, Сю= 400 пф,
L = 0,5 гн, fo— 104 гц, С2=
= 100 + 50 sin о>1/ пф, ко-
эффициенты передачи
фиЛЬТрОВ kqi = k$2 = 0,8,
действующее значение вход-
Рис. 325. Система автоматиче-
ской подстройки частоты.
кого напряжения Ui = ^~= 100 в. Двигатель Д раз-
вивает 3000 об/мин при напряжении 30 в. Редуктор
(Ред) имеет коэффициент передачи /гред = 10~3. Ем-
кость конденсатора G меняется на 80 пф при повороте
его пластин на Г рад. Входное сопротивление усилителя
считать равным бесконечности.
Решение. Структурная схема и передаточная функ-
ция данной системы могут быть представлены в двух
вариантах в зависимости от выбора регулируемых ве-
личин. В качестве последних могут быть приняты ча-
стота входного сигнала f0 или емкость резонансного
контура С = Ci + С2о.' Рассмотрим оба варианта.
Если за регулируемую величину принять частоту
«о = 2л/0, то структурная схема системы будет иметь
482 ГЛ. 19. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВ. СИСТЕМЫ (460
вид, представленный на. рис. 326. Передаточные функ-
ции входящих в систему элементов определяются сле-
дующим образом.
1. (р) = (ру- ~ передаточная функция, характе-
ризующая, как изменяется действующее напряжение
Рис. 326. Структурная схема автоматической системы подст-
ройки частоты с регулируемой величиной соо.
на выходе резонансного контура «2 при изменении ча<
стоты сигнала f0. Будем ее искать в предположении,
что сам контур является безынерционным звеном, так
как работа происходит вблизи резонансной частоты.
Фаза несущей частоты f0 не играет существенной роли
ввиду наличия выпрямителя. С учетом этих допущений
из схемы включения контура (см. рис. 325) следует
Г Т Ul I гк (®) I / ] \
+ Г’
где zK(to)=?7~2<йо*'—г-— сопротивление резонансного кон-
{a0CL -1)
тура. Учитывая это, получим
U2 = tZi -7=^= в. (2)
)/я2(^С-1)2 + <^2
Отсюда
При резонансе = 1 эта производная равна нулю.
При отклонениях частоты со0 от резонансной, зави-
симость 4^" от со в общем случае нелинейная. Поэтому
C/COq j
460] § 19.1. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ 483
передаточная функция W^tiCp) в общем случае может
быть представлена в виде
^к1(р)==*к1(®)- (4)
Если частота входного сигнала отклонится на ±10%
от f0 — 104 гц, то
1 — 5,7 -10 7 в • сек при f = fo+O,lfo,
&К1 (®) = j i ° при
1 7,5 • 10 7 в • сек при f = fo-O,lfo.
2. Wy(p) = ky — передаточная функция усилителя.
3. ^Ф1 (Р) — Ttp + ^— передаточная функция первого
фильтра. Постоянная времени
Tl = ~ 3.14 • 1000 == 3>2 • 10 сек-
'4. ^ф2(р)~~у2рФ^. 1—передаточная функция второго
фильтра, где
n&f2 ~ 3,14-20 =^>016 сек.
5- = — передаТ0Чнаяф^нк*
ция двигателя, где
h — » — п?. х.л — 3000-3,14 __. q с ] -
дв—' 14.x. “ 60-t/x.x. — бо-зо — ,и>ов сек >
Тдв — 0,04 сек.
6- IFpejJp) = &Ред — передаточная функция редуктора,
^ред== Ю •
7. IFC (р) = —передаточная функция, характе-
ризующая изменение емкости Ci при повороте его оси.
В соответствии с заданием, эта характеристика ли-
нейна. Крутизна характеристики
k= 80-^ = 8 • 10-11 ф.
с пад
484 ГЛ. 19. экстремальные и САМОНАСТРАИВ. СИСТЕМЫ (4®9
Г, ГО7 / \ ДОп (р) ,
8. 1кк2(р) = дё, (р) передаточная функция, характе-
ризующая изменение резонансной частоты при измене-
нии емкости С[. Для того чтобы определить ее при до-
пущениях, сделанных в пункте «1», продифференцируем
выражение (2) по С. В результате получим
aCi и' [^2(i _o2£c)2 + w^2]s/a в (р'
(5)
Разделив (5) на (3), найдем
дюо _ £мо
ф~1 • сек *.
(9)
Следовательно, считая контур безынерционным, получим
WK2(p)^kK2(&).
Если задающая частота f0 меняется в пределах ±10%
от /о = 104 гц, то
= \ Ю10 * * 13 ф~1 • сек~1.
Таким образом, передаточная функция системы в ра.
зомкнутом состоянии имеет вид
4 | (“) Мф 14 АЛеЛА 2 (“)
W^P>- р(Г,р+1)(7’2р+1)(ГдВр+1) •
Подставляя числовые значения для частот f0, f0 + 0,1 f0
и fo~O,lfo, получим
f = f0, Й4(Р) = О, (8)
ч 2,28- 1оАу
f - fo + 0,1 fo, wa(p)~ .10-4p + j) (0>016p + I) (0 04p + ’
(9)
10 ’ °’ “ p(3,2-10"4p + l)(0,016p + l)(0,04p+l)‘
(10)
Найдем теперь передаточную функцию, если в ка-
честве регулируемой величины рассматривается ем-
кость Сь
4S°1 § ’ЗЛ. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ 485
Структурная схема такой системы имеет вид, пред-
ставленный на рис. 327. Входящие в эту систему пере-
даточные функции Wy(p), W^dp), WRB(p), Wj^lp) и
Wc(p) точно такие же, как и в предыдущем случае.
Рис. 327. Структурная схема автоматической системы подстройки
частоты с регулируемой величиной Сь
Передаточная функция WK(р) = характери-
зует нарастание напряжения U2 на выходе резонанс-
ного контура при изменении емкости С. При сделан-
ных ранее замечаниях о характере выпрямления сиг-
нала на выходе усилителя можно считать, что
Гк(р) = М«>), (И)
где kK(ю) — коэффициент, вычисляемый по формуле (5).
В случае настройки контура в резонанс kK (со) = 0.
При f = /o + O,lfo *к(со) = — 4,2 • 107 в!ф,
при f — fa — О,9/о ^к(со) = +3,6 • 107 в/ф.
Таким образом, передаточная функция разомкнутой
системы, охваченной обратной связью, имеет следующие
значения:
при / = /0 Гс(р) = 0, (12)
(! при f = f0 + Q,lf0 Wc(p) =
=____________-2,28-ЮЛУ____________
(3,2 • 10~4р + 1) (0,016р + 1) (0,04р + 1) ’ k '
•!йри f = fo-O,lfo U7c(p) =
= —_____________2,08'ky___________. (14)
• (3,2 • 10“4p + 1) (0,016p + 1) (0,04p + 1)
486
ГЛ 19 ЭКСТРЕМАЛЬНЫЕ И С МОН ТР ИВ И ТЕМЫ
[«I
Как видно из выражений (9), (10), (13) и (14), пере-
даточные функции не зависят от выбора регулируемой
величины. Формально это вытекает из того, что
kK 1 (®) • kK 2 (to) = = kK («>) = в/ф.
Перед замкнутым контуром системы необходимо
включить элемент, характеризующий изменение вели-
чины емкости при резонансе от частоты f0 входного
сигнала. Он может быть представлен безынерционным
звеном с коэффициентом передачи
*к(®)
дС ~ l + a2LC
да 0 £<йо
ф • сек.
При /0 и f0 ±10% величина
(®) =
1,34 • 10"14 ф • сек
1,62 • 10"14 ф • сек
1,92 • 10'14 ф • сек
при f = fo + O,lfo,
при f = fo,
при / = fo —О>1.Ло-
461. Составить структурную схему и определить пе-
редаточную функцию самонастраивающейся системы
Рис. 328. Автоматическая самонастраивающаяся система построе-
ния вектора по двум составляющим.
построения вектора по двум составляющим (рис.. 328).
Составляющие вектора задаются в виде переменных
напряжений Ux и Uy, прикладываемых к обмоткам ста-
4вН § 19I. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ
487
тора’ синусно-косинусного трансформатора (СКВТ). Мо-
дуль построенного вектора представляется напряжением
где &чэ =— коэффициент трансформации СКВТ. Угол
а поворота ротора определяет положение вектора U2
в системе координат X, Y. Поворот ротора на угол а
осуществляется следящей системой, состоящей из уси-
лителя с автоматической регулировкой усиления, дви-
гателя и редуктора.
Самонастройка заключается в поддержании постоян-
ного''напряжения U3 на входе в усилитель при одном
и том же рассогласовании Да в широком диапазоне
изменения напряжения Ut. Усилитель является апериоди-
ческим звеном, двигатель представляется в виде произ-
ведения интегрирующего и апериодического звеньев.
Рис. 329. Структурная схема автоматической самонастраиваю-
щейся системы построения вектора по двум составляющим.
Ответ. Структурная схема изображена на рис. 329.
Без автоматической регулировки усиления передаточная
функция системы имеет вид
F (р) = - —т-гу,
' Р(7уР + 1) (7двР+ О
где- Zj ру&у&двАф.
Если, подавая напряжение U2. на автоматический
регулятор усиления, сделать коэффициент его передачи
488 ’ ' гл. 19. ЭКСТРЕМАЛЬНЫЕ Н САМОНАСТРАИВ. СИСТЕМЫ 1*62
fe ' равным -р—, то получим
W ~ р(Гур+1)(ГдВр+1) '
где k^k,l9k'vykyk№kv.
462. В системе,' рассмотренной в задаче 460, опре-
делить коэффициент усиления ky усилителя, обеспечи-
вающий устойчивость управления в пределах отклоне-
ния частоты fQ на ±20%.
Ответ. fey< 1,71 • 107.
463. В системе, рассмотренной в задаче 461, найти
значение коэффициента k' , обеспечивающего устойчи-
вую работу системы при следующих исходных данных:
fe43 = 0,5, = 104, k№ = 12 в-1 • сек\ fep = 1,3 • 10-3, Ту =
= 0,025 сек, Где = 0,045 сек.
Ответ. fepy<0,8.
464. Найти передаточную функцию Ф(р) замкнутой
самонастраивающейся системы с эталонным филь-
тром Ф0(р), структурная схема которой изображена
Рис. 330. Структурная схема самонастраивающейся
системы с эталонным фильтром.
на рис. 330. Определить, будет ли система устойчива
при следующих числовых значениях, входящих в пере-
даточйые функции величин fel)l = fe2 = fe1 = 1, fe3= 100сек-1,
'7'ф = 0,04 сек, Т1 — 0,001 сек, = сек.
«61 $ 19.2. КАЧЕСТВО СИСТЕМ ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ 489
Ответ.
. ^2^1 (ТфР + О + ^ф&3&2 (^iP 4" 1)
~ (7фР+ •) [.Р (Пр + 1)(^2р+ l)+k3k2 (Тгр+ 1) -i- fe,fe2] ’
Если учесть, что k3 много больше других членов, то
можно записать
ф(р)-тДт = Фо(р)-
При заданных значениях величин система устойчива.
465. Система, рассмотренная в предыдущей задаче,
предназначена для сохранения качества регулирования
при изменении передаточной функции выходного эле-
мента \W(p) = —1,1 и значений входящих в нее
\ Р V 2Р Т Ы /
величин. Определить, при каком предельном значе-
нии k2 система будет устойчива. Для сравнения найти
также предельный коэффициент k'2 в случае отсутствия
контура самонастройки (£3 = £ф = 0).
Ответ. /г2<2140 сек-1, А, <1005 сек-1.
§ 19.2. Качество систем экстремального управления,
466. В системе автоматической подстройки частоты,
структурная схема которой представлена на рис. 327,
найти переходный процесс, пренебрегая постоянными
времени фильтров Т\ и Т2. При расчете принять следую-
щие значения входящих величин Гдв = 0,04 сек, £дв =
= 10,5 в-1 • сек-1, 6ф1 = &ф2 = 0,8, ky = 107, £ред = 10-3,
kc = 8 • 10-11 ф. Коэффициент £к(ы) рассчитать по фор-
муле
R2L^(l-b^CL)
kK (со)
dU2
дС
U1------*-w~~:—и •>"' ч/9 в1Ф>
l[R2(l-u*CL) 2]3/2
при R = 1000 ом, Ui= 100 в, С = 500пф, £ = 0,5 гн,
fo0 = 2эт/0 = 6,28 • 103 сек-1.
Начальное отклонение от резонансной частоты со-
ставляет 0,2 <о0 при частоте <о0, равной резонансной ча-
стоте. Внешние возмущения отсутствуют. Начальная
скорость изменения частоты равна нулю.
490 гл. 19. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВ. СИСТЕМЫ [Ж
Решение. Структурная схема системы при сделан-
ных допущениях имеет вид, представленный на рис. 331.
Здесь
~ ^ф1^ф2^у^с^дв^ред 5,35 *10 Ф!в,
Дифференциальные уравнения системы имеют вид
Р (ТмР + 1) Су = kU2,
U2 ~ (®) (Сд Су).
Разрешая эту систему, получим
Гдв-^- + ^ = ^к(<В)(Сд-Су). (1)
Так как при заданных числовых значениях вблизи
«- dU 2
резонанса первый член знаменателя производной
Рис. 331. Структурная схема упрощенной автомати-
ческой системы подстройки частоты.
значительно меньше второго, то можно написать
В формуле (1) Су представляет собой суммарную
емкость Су = Со + С2.' Для исследования же устойчивости
важно знать отклонение ее от резонансного значения
Со — —. Учитывая это, можно записать
kK (<о) = —т—
(2)
-^c0+c2)l]=u^c2.
Подставляя это в уравнение (1), получим
Тдв + kU^CyC2 = kU^[CRC2.
487] § 19.2. КАЧЕСТВО СИСТЕМ ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ 491
Малость отклонений С2 от резонанса позволяет ли-
неаризовать это уравнение по С2:
Т + kV^0CaC2 = ш^сйсл.
Подставляя числовые значения, получим
0,04 + 2>13С2 = 2,13СД.
Корни характеристического уравнения
р-!, 2 = 12,5 ± / /28У = — 12,5 ± /5,3.
Следовательно, общее решение
С2 = П1е(~12>5+/'5-3) f + £>2е(-12-5-/5-з) f. (3)
Для нахождения постоянных интегрирования найдем,
как изменится емкость С при изменении частоты ю
на 20% ю0.
Воспользуемся для этого выражением (2), считая,
что изменение частоты го должно компенсироваться из-
менением емкости. В соответствии с этим можно за-
писать
[1 - (го0 + Дго)2 ед = [1-го2 (Со + ДС) £].
Отсюда следует
ДС = 2 —Дю.
«о
Если Ди = О,2юо, то ДС = О,4Со = 200 пф.
Подставляя начальные условия С2о = 200 пф и С2о=О
в (3), получим
С2 = 200 [1 - e"12-5f (cos 5,3/ + 2,36 sin 5,3 /)].
467. Найти переходный процесс в экстремальной
системе стабилизации угловым положением спутника,
блок-схема которой изображена на рис. 332.
Уравнения, описывающие динамику работы системы,
следующие:
1. Уравнение спутника
j dt2 ш.
492. . ГЛ. Ts.. ЭКСТРЕМАЛЬНЫЕ. И С AM ОПА СТР А ИВ. СИСТЕМЫ [468.
. , 2. Уравнение стабилизирующего двигателя с махо-
виком
М = kuU2.
3. Уравнение логического звена
=/г2^1 sign.
4. Уравнение экстремальной характеристики
= — kfi2.
Исходные данные для расчета: J = 100 кГ • м • сек2,
ki — 60 elpad2, k2 = 100, kM = 0,01 кГ м • в-1, начальные
отклонения 0q=10°, 0о=15 град jсек.
3
Спутник
9
Сиороапт
гироскоп
Управляе-
мый —у
усилитель “г
Двигатели
-махабик //
Рис. 332. Блок-схема экстремальной системы стабилизации
спутника..
‘ Указание. Общее уравнение линеаризовать в точке
0= 15°.
Ответ. 0 = 29° sin (0,56/ + 20° 30').
468. Найти переходный процесс и построить его фа-
зовый портрет в системе, рассмотренной в задаче 467,
если уравнение логического звена имеет вид
— k2Uf sign 6 — /г30,
ka = 4,3 • 103 в • сек. Остальные исходные данные и допу-
щения принять равными приведенным в задаче 467.
Ответ. 0 - 29°<?-°-№ sin (0,558/ + 20° 30').
Фазовый портрет изображен на рис. 333.
469. Определить потери на поиск в системе автома-
тической подстройки частоты, рассмотренной в задаче
460] § 19.2. КАЧЕСТВО СИСТЕМ ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ 493
460. В основу исследования положить структурную
схему, изображенную на рис. 326. За исходные данные
для расчета принять: ky = 107, /гф1 = /гф2 = 0,8, £ред = 10“3,
kc = 8 • 10-11 ф, k.B = 10,5 в-1 • сек-1, Гдв = 0,04 сек, Гф2 =
= 0,016 сек, Тф1 = 3,2 • 10~3 сек, R =1000 ом, С] = 400 пф,
С% — С20 + C2m sin ~ Ю0 + 50 sin 40^ пф, L = 0,5 гц,
<оо = 6,28- 103 сек-1.
Рис. 333. Фазовый портрет переходного
процесса стабилизации, углового положе-
ния спутника.
Решение. Под потерями на поиск понимается
средняя ошибка x(t), возникающая в'экстремальной
системе в установившемся режиме, в результате поиско-
вого движения. Если F (у) представляет собой функцио-
нальную зависимость, характеризующую экстремальные
свойства некоторого элемента при изменении регули-
руемой величины у, то потери на поиск
-j=.--тг 1 d2F 2/Д
F — F3 = • -т-5- X (г),
э 2 dy2 4 ”
где Еэ — экстремальное значение.
При синусоидальном поиске с амплитудой
Рассмотрим потери на поиск, принимая за регулируе-
мую величину емкость Сд = + С\. Применительно
к этому потери на поиск
-494 тл. 19. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВ. СИСТЕМЫ [4В9
где k = kyk^! /гф 2 kuJipkc = 5,35 • 10-6 ф/в — общий коэф-
фициент передачи без резонансного контура с переда-
точной функцией Ц7к2 (р) = — kKz (®о).
о » л, л.
Вторую производную найдем дифференцирова-
9U
нием выражения приведенного в задаче 460,
д2У
дС2 =
UtRVAl* {-[Р2 (1 - co2CL)2 + to2L2]3/2 + ЗР2 (1 - co2CL)g [Р2 (1 - co2CL)2 + соЧ,2]1 Z2}
L/?= (1 - a2CL)2 + co2L2P
{-[P2 (1 - <o2CL)2 + co2L21 + 3R2 (1 - co2CL)2}
[P2(1-co2CU2 + <l>2£2]5/2
Расчет по этой формуле дает
-g- = 4.1(F в/ф*. (2)
Амплитуду ошибки ДС можно найти по формуле
lm ~ I Фх (7®) 1(0=0>' Czm = | 1 Ц? " km, (3)
где
W (/<о) =--7=---4-j'i rrK2 ^п'Гт-ZTtI ПРИ Р = /®1«
и ’ Р(ГДвР+1)(Гф1р+1)(Гф2Р+1) | Г Г J 4
Следовательно,
J (М kQ, = [(фо? + 1) (ф<0? + 1) (72ф2<0? +1)]1/2 X
х {[^к2(°>о) + Лш/ф^фг0! — (^ДВ + Тф! + Тфг)°1]2 +
+ I1 - (Т-двУф, + Гда7ф2 + Гф^)]2}-"2.
Подставляя числовые значения с линеаризацией члена
kK2 (too) в точке, соответствующей отклонению емкости С
на 25 пф от резонансной (на половине амплитуды С2т),
получим
I Фх О) ко = 0,98.
i л \з / 'со®(0| J
Подставляя это выражение в (3), имеем
ДС1т = 0,98С2т = 0,98 • 50 = 49 пф = 4,9 • 10-11 ф.
470] § 19.2. КАЧЕСТВО СИСТЕМ ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ 495
Таким образом, потери на поиск по емкости равны
г г - 1 ЪдЧ] {дс'т>2 -
Ьд Ьдо — к дС2 • 2 —
= i 5,35 • 1СГ6 • 4 • 105 • (4,9)2 • I О-22 = 1,28 • 10-21 ф.
470. На вход следящей системы, изображенной
на рис. 334, поступает управляющий сигнал ug(f) и
Рис. 334. Следящая система, самонастраивающаяся на минимум
квадратичной ошибки.
случайная помеха ип (/), представляющая «белый шум»
со спектральной плотностью Sn(со) = N = const. Система
самонастройки, воздействующая на коэффициенты уси-
ления усилителей в цепи якоря (/гу1) и в цепи возбужде.
ния (/гу2) двигателя Д, обеспечивает минимум общей
квадратической ошибки на выходе. Необходимо опреде-
лить функциональные зависимости коэффициентов уси-
ления kyi и ky2 от скорости изменения входного сигнала
при установившемся режиме работы и изобразить струк-
турную схему с самонастройкой. Коэффициент демпфи-
рования системы § должен быть равен 0,5.
Система уравнений, описывающих динамику работы
системы без самонастройки, имеет вид
496 ГЛ. T9. ЭКСТРЕМАЛЬНЫЕ И САМОПАСТРАИВ. СИСТЕМЫ '470'
Числовые данные для расчета: 7 = 0,2 Г •см • сек2,
см = 70 Г • см[а, г = 2 ом, ив = 30в, /гр=10-4, /гЛвт =
= 0,5 ejzpad, N = 0,01 в2.
Решение. После приведения подобных членов и
упрощения уравнений получим передаточную функцию
системы в разомкнутом состоянии
т Jr _ °-4
смив/гу2 2Ю/гу2 СеК’
kyikpkflBt -5 kyl
k =—г------= 9,6 • 10 -г— сек *.
Яу2Ив ЙУ2
Передаточная функция замкнутой системы
тельно ошибки равна -
ф.(р) = —
р(Тр+1) + 1г
Передаточная функция замкнутой системы
ф(р) = 7-;—у---------------------•
тр2 + тр+1
где
(1)
относи-
(2)
(3)
Поскольку коэффициент демпфирования задан, то
т=2?/т- <4>
Управляющий сигнал ug(t) = ut и помеха wn(Z) некор-
релированы. Поэтому квадратичная ошибка e„ = Sg + en»
где — квадрат ошибки от управляющего сигнала ug(t)
и г2 — дисперсия на выходе от помехи.
С помощью коэффициентов ошибок в типовых режи-
мах находим
г/2
о II
Дисперсия от помехи
4-00
Ед = 2JT / । ф (/“) I2 (га) da =
— оо
4-00
1 [ __________N_________ , Nk
2л J I Т ,, 1 , а ЙЮ = -2-.
“°0 I ~k *
470] § 19.2. КАЧЕСТВО СИСТЕМ ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ 497
Следовательно,
„ «2 №
р2 J----
. “ й2 2
Дифференцируя
условие минимума
[ 2п2йу2
:2-'гу2
ii%2 , Nkyl 9,6 • IO-5
= (9,6- 10-5)2feyi +~ 2^ 1
это выражение по /гу1 и /гу2, получим
квадратичной ошибки
N 9,6 10'
(*У1-М = 0. (5)
L (9,6 • 10~5)2/гу1 2Л22
Второе уравнение для определения /гу1 и /гу2 полу-
чается из (4) в результате подстановки значения k и
возведения в квадрат
Q С IЛ-5 fy71 _ 1 _ См“Аг2
’ kyi 4£2Г 4£2Л- ’
После подстановки численных значений получаем
(6)
' 9,6 • 10 -^—= 5250/гу9.
«У2
В результате совместного решения уравнений (5)
и (6) находим заданные функциональные зависимости
“s
°) б)
Рис. 335. Структурные схемы самонастраивающейся системы:
а) с измерителем скорости входного сигнала; б) с измерителем ско-
рости входного сигнала и спектральной плотности шумов.
сек,
оптимальных значений коэффициентов /гу"т и /гу2т от ско-
рости изменения входного сигнала
/гу2т = 1,4 • Ю~3й2/3
/гу1Т= 107й4/3. .
(7)
(8)
498 ГЛ. 19. ЭКСТРЕМ Е И САМО АС АИВ.СТЕМЫ[475
Таким образом, для оптимального регулирования
с минимумом квадратичной ошибки е? при заданной
спектральной плотности N помехи в виде «белого» шума
и переменной скорости й входного сигнала, экстремаль-
ная система должна содержать измерительное устрой-
ство й и автоматические регуляторы усиления в усили-
телях J7! и У2, реализующие зависимости (7) и (8). Струк-
турная схема такой системы представлена на рис. 335, а.
Если измеряется и спектральная плотность N шумов,
то оптимальные коэффициенты усиления и &у2Т
дрлжны регулироваться в соответствии с выражениями
А$т = 3,02- 10“4~ ,
3/“ “Г”
Структурная схема системы представлена на рис. 335, б.
ГЛАВА 20
СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ
АВТОМАТИЧЕСКИХ СИСТЕМ НА НЕПРЕРЫВНЫХ
ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
§ 20.1. Составление схем для моделирования элементов
автоматических систем на электронных
вычислительных машинах
- ’ 471. Составить схему модели двигателя постоянного
тока с независимым возбуждением, если параметры якоря:
индуктивность La = 0,1 гн, сопротивление Rr — 10 ом; ско-
рость холостого хода при ивх = 24 в пх. х = 3600 об]мин,
пусковой момент Мп = 2 кГ • см, момент инерции
7 = 1,06 • Ю 3 кГ • см • сек и напряжение входного ’сиг-
нала нвх 24 в. В качестве выходной величины двига-
теля принять угловую скорость й. Влиянием сил сухого
трения пренебречь; не учитывать индуктивность и вну-
треннее сопротивление оконечного каскада усилителя,
питающего двигатель.
Решение. Воспользуемся уравнением двигателя
(TRTMpz + Тыр + 1) Q (0 = Мвх (t), (1)
полученным в задаче 15. Найдем постоянные времени
TR, Ты и коэффициент передачи /гд. Тя = LrRr — 0,1 • 10 =
= 0,01 сек;
Qx. X = япх, х30"‘ = 3,14 • 3600 • 30-1 = 377 сек"1;
Т}„ = JQx. хМп1 = 1,06 • 10~3 • 377 • 2~‘ = 0,2 сек;
kR = Йх. х («вх)'1 = 377 • 24’1 = 15,7 в"1. сек1.
500 " ГЛ. 20. СОСТАВЛЕНИЕ СХЕМЩЛЯ МОДЕЛИРОВАНИЯ
[47 <
Подставляя найденные параметры в (1), получим урав-
нение движения двигателя
(0,002р2 + 0,2р + l)Q(/)= 15,7ztBX(/). (2)
Дифференциальное уравнение (2) принадлежит апе-
риодическому звену второго порядка, схема модели
которого приведена в приложении 33.
Для перехода к переменным модели воспользуемся
уравнениями преобразования переменных:
£i(/) — таи2,
- иЪх^) = тии1,
t = mttM,
(3)
где — масштаб представления угловой скорости дви-
гателя в модели в виде напряжения и2; ст,, — масштаб-
ный коэффициент представления входной величины дви-
гателя ипх в виде входной величины модели иъ —мас-
штаб времени, tu — независимая переменная модели (или
машинное время) и / — натуральное время.
Выберем натуральный масштаб времени, т. е. mt = 1.
Для большинства операционных усилителей непрерыв-
ных вычислительных машин линейный диапазон изме-
нения напряжений равен ± 100 в. Поэтому при решении
задачи выходные напряжения операционных усилителей
не должны превышать 100 в. Однако меньшая погреш-
ность решения обеспечивается, когда моделирование
происходит при наибольшем допустимом уровне напря-
жений, что также необходимо учитывать при выборе
масштабных коэффициентов модели. Исходя из этого,
выбираем
О 477
т'-! Доо~ Too = 3,77 в~1 рад ' сек~1'
и 24 (4)
= »ВХ max. = Л 24
100 100 ’ •
Для перехода к машинным переменным подставим
(3) в (1), в результате чего получим уравнение модели
в общем виде
(Т^ар2 + Тар+1)и2Ц) = кА-^щЩ (5)
472] . § 20.1. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ 501
ИЛИ
(0,002р2 + 0,2р + 1) и2 (/) = и, (/). (6)
Для определения числовых значений сопротивлений
и емкостей резисторов и конденсаторов модели, вос-
пользуемся’ формулами приложения 33, откуда следует
* = = 1, = _0 02 сек2,
А]/<б
Ti = = 0,2 сек.
При выборе 7?! = 7?3 = 100 ком, R2 = 20 ком, Т?4 = 7?6=
= 1 мом, R5—10kom и Ci = C2=1 мкф схема модели
(п. 5 приложения 33) будет соответствовать двигателю
постоянного тока с независимым возбуждением с пара-
метрами, заданными в условии задачи.
472. Составить схему модели двигателя постоянного
тока с независимым возбуждением и с параметрами^
Рис. 336. Схема модели двигателя.
заданными в условии предыдущей задачи, но в каче-
стве выходной величины принять не скорость Q, а угол
поворота вала двигателя а. Влиянием сил сухого тре-
нйя пренебречь.
' Ответ. См. рис. 336, где ma = k"1 • ma = 3,77 в-1 • рад—
масштабный коэффициент по углу а. Здесь k = 1 сект1 —
коэффициент передачи интегратора.
Б02
ГЛ. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ
1473
473. Составить схему модели двигателя с независи-
мым возбуждением по условиям задачи 471, но с учетом
влияния момента нагрузки от сил сухого трения А1н =
= М„ sign £2 (рис., 337, б), причем М°н = 0,4 кГ • см.
а)
Рис. 337. Схема модели к задаче 473.
Решение. Составим уравнение равновесия напря-
жений цепи якоря
ивх = ^я + Ая^ + се£2 (1)
и уравнение равновесия моментов на валу двигателя
J = М — ЛГн = см1‘я -Мн sign £2. (2)
Решив их совместно относительно угловой скорости £2,
получим уравнение движения двигателя с учетом мо-
мента нагрузки Ми
(ТяТмр2+Тмр+ 1) Q =/гд«вх — ймМн sign й, (3)
1 X • ^Х X п
где лд = — = —-х—, лм =---= —— = 6—коэффициенты
ее Увх сесЫ Мп
передачи двигателя по напряжению (ka) и по моменту
нагрузки (feM). Коэффициенты сы, ся, р, Тя, Ты опреде-
лены в задаче 15. '
Моделирование статической характеристики сухого
трения (рис. 337, б) производится по схеме п. 2 прило-
жения 34. При этом величина напряжения £/3= С/4= £/н
473J § 20.1. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ 503
подбирается такой, чтобы диоды были надежно закрыты.
Выберем (7п = 20 в. Тогда масштабный коэффициент
0,4
ты = = -эд- = 0,02 кГ -см-в Ч (4)
Для перехода к машинным переменным восполь-
зуемся масштабными коэффициентами, полученными
в задаче 471, та, ти (mt — 1) и коэффициентом тм (4).
После замены переменных уравнение (3) принимает вид
(ТяТыр2 + Тмр + 1) м2(0 = kux (f) - kxUn sign u2, (5)
где k = k = 15 7 • -O’24- = 1 k,—k — 377 • --’°- = 1
где R Ra 1»,/ 3 77 1, R\ RM 2 3>77 1.
Подставив числовые значения в (5), получим уравне-
ние модели
(0,002р2.+ 0,2р + 1) и2 (/) = W] (/} — 20 sign и2. (6)
Уравнение (6) отличается от уравнения (6) задачи 471
дополнительным нелинейным членом 20 sign и2, который
реализуется с помощью схемы, изображенной в пп. 1, 2
приложения 34 при R0 = <x>. При этом из уравнений (3)
и (6) видно, что действие момента от сил сухого трения
'равносильно действию нелинейной отрицательной обрат-
ной связи. Поэтому схема модели, отображающая диф-
ференциальное уравнение движения двигателя с неза-
висимым возбуждением с учетом момента от сил сухого
трения принимает вид, изображенный на рис. 337, а.
Уравнение модели, записанное с помощью параметров
схемы рис. 337, а, принимает вид
(-^ С,С2р2 + Ctp + 1)u2(f) =
= ^Ul(t)-^URsi^u2(t), (7)
Л1«6
где R8 = 100 ком, а величины сопротивлений и емкостей
резисторов Ri~ R6 и конденсаторов Сь С2 получены
в задаче 471. Сопротивление резистора R7 (рис. 337, а),
не вошедшее в уравнение (7), может иметь произволь-
ное конечное значение,- но на порядок или несколько
порядков превосходящее прямые сопротивления диодов
и введенных сопротивлений потенциометров (см. п. 2
приложения 34), включенных в обратную связь опера-
ционного усилителя.
474. Составить в общем виде схему модели двига-
теля с независимым возбуждением с учетом момента
нагрузки от сил сухого трения Ми=°Мх sign Q (рис. 337, б),
если влиянием электромагнитной постоянной времени
цепи якоря Тя можно пренебречь. Выходной величиной
принять угловую скорость вращения вала й, а вход-
ной — напряжение ивх, подаваемое на обмотку якоря..
Все переменные и параметры двигателя с независимым
возбуждением определены в предыдущих задачах.
Решение. Уравнение движения двигателя в машин-
ных переменных (см. предыдущую задачу) при Тя = О
принимает вид
(Тир + 1) и2 (0 = ka щ (/) - ku UK sign и2 (t).
гпа та
Схема модели двигателя, согласно полученному урав-
нению, приведена на рис. 338. Параметры модели
Рис. 338. Схема модели, двигателя к задаче 474.
(сопротивления резисторов /ф — R6 и емкость конденса-
тора С) определяются на основании следующих формул:
г,. 'j' R$Rt> г к ми R&Rg /у
ma> R2R3~ ы'та-
Все масштабные коэффициенты определены при реше-
нии предыдущих задач.
475. Найти уравнение модели, схема которой пред-
ставлена на рис. 339, где напряжение обратной связи «3
47в| § 201- МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ 505
Рис. 339. Схема модели к за-
даче 475.
(2) и преобразований полу-
«21 (р) 1 ' '
является частью, выходного напряжения и2 и снимается
с помощью потенциометра (блока делителя напряже-
ния) Р3; Zo(p), z^p) —операторные сопротивления.
Решение. Отношение переменного сопротивле-
ния 7?„, с которого снимается напряжение и3, к сопро-
тивлению 7?3, -ф- = а, назы- 4^
АЗ
вают коэффициентом дели-
теля напряжения’ Тогда
и3 = аи2.
Уравнение модели
и2 =
(2)
После подстановки (1) в
чим искомое уравнение
Г 7—. 1- 1 1 149 (0
L az0 (р) J - ' '
476. Составить схему модели гидравлического испол-
нительного устройства (рис. 2, а), дифференциальное
уравнение и передаточная функция которого получены
в задаче 2. Параметры гидравлического исполнитель-
ного устройства следующие: ft] =50 сек’1, a=14cjw,
6 = 7 см, С] = 0,05 кГ слГ1 сек, с2 = 0,5 кГ • см"1, с3 =
= 2 кГ • см~{ • сек.
Решение. Найдем постоянные времени и коэффи-
циенты передачи (см. задачу 2):
ft2 = —= =0,667, ft3 = - *= ~ = 0,5,
2 a+b 14 + 7 ’ ’ 6 а 14 ’ ’
. с3 2. . .
ft4 = — = 7пг '=4 сек,
4 с.2 0,5
ktk2 50-0,667- п оо -1
l+ktk3kt .1+50-0,5-4 ’
7’о.е=^=4г = °'1С^
^тп^ = тш4г4-0’001^- _
ft
50S гл. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ (4Тв
Выражение передаточной функции гидравлического
исполнительного устройства
F (р) = -^4 = k (T°i ср+.'} , (1)
Х(р) р(Гр + 1)
где У(р) изображение выходной величины — перемеще-
ния заслонки у, Х(р)— изображение входной величи-
ны — перемещения муфты к.
Представим передаточную функцию (1) в виде про-
изведения
W(p) = Wi(p)W2(p), (2)
И7 (п\_ (Тоср 4" 1) ру _ Y (р) _ I
Гр+)...(3)
На основании передаточной функции IV'i(p) запишем
дифференциальное уравнение
(Тр + 1) у (0 = k (Тоср + 1) х (t), (4)
где y(t) = py = ^. Умножим обе части уравнения (4)
на Гос и к левой части прибавим Ту— Ту
Ту —Ту-}- (ТТоср + T0C)y==k (Тоср 4- 1) Тосх,
(Гос — Г) у + (Тоср + 1) Ту = k (Тоср + 1.) Тосх,
^ОС 1
1ТОС т
y — k т X ТосР + j у.
Но k~~ — kxk2, — Тогда
»=^--етМ- <5>
Для перехода к машинным переменным (щ, и2) вос-
пользуемся масштабными коэффициентами (см. за-
дачу 471),
у — т6и2, х — тхщ, t = mt=\. (6)
Подставив (6) в (5), получим
' (7)
476] § 20.1. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ 507
<
На основании дифференциального уравнения (7) со-
ставляем схему модели (рис. 340), уравнение которой
имеет вад
2 /?, 1 Д2Я3(СЯ5р+1) “2-
Из сравнения уравнений (7) и (8) находим
ф- = kik2 = —50 • 0,667,
Rt ту ту
^~=klk3ki = 50 • 0,5 - 4 = 100,
А2АЗ
СТ?5 = Л>с = 0,1 сек.
(9)
Выбрав масштабные коэффициенты m^ = 66,7 см-в"1'-
•сек"1, тж=10 см-в"1, получим
: А = ^£.50.0,667 = -^ 50- 0,667 = 5. (Ю)
На основании соотношений (9) и (10) выбираем
7?! = 20 ком, R2 = 7?з = 10 ком, R4 = Т?5 = 100 ком, С =
— 1 мкф.
Рис. 340. Схема модели к задаче 476.
Подсоединив к выходу схемы модели, изображен-,
ной на рис. 340, интегратор (п. 8 приложения 33) с ко-
эффициентом передачи k5 = 1 сек"1, получим искомую
508 гл. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ 1477
' I - •: • . - • • : • ' - • :
схему модели гидравлического исполнительного устрой-
ства.
477. Составить дифференциальное уравнение модели,
схема которой изображена на рис. 341, где 7? — потен-
циометры, представляющие собой однотипные блоки де-
лителей напряжения с коэффициентами аь а2 (см. за-
дачу 475). Выходной величиной принять напряжение
н4, а входной — Up
Рис. 341. Схема модели к задаче 477.
Решение. Обозначим выходные напряжения каж-
дого операционного усилителя (щ — u5). Составим
систему уравнений х
U2~-RA^+~RT+~R;-h' (1)
«3=(2)
<3\
(4)
Исключим переменные u2, и3, и5. Для этого выразим
и3 через щ из уравнения ^3) и . подставим в уравнения
4801
§ 20.1. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ
509
(2) и (4). В результате получим
«2 = С1С27?27?зР2«4 + С2 ри4, и5 = С2 рщ.
Кв
Подставив полученные выражения для и2 и «5 в урав-
нение (1) и сделав преобразования, получим 'искомое
дифференциальное уравнение модели
(аор2 + щр + а2) и4 (0 = - Ьощ (0,
г> с п п „ ________г- ( RiRb , \ „ О|/?т
где «0 — С,1Ся/?2/?3, °1-С2(-^- + —а2--^-,
478. Найти установившееся значение выходной ве-
личины и4(/) модели, схема которой изображена на
рис. 341, а дифференциальное уравнение получено в
предыдущей задаче, если входная величина U[(t) =
= 10- 1(0 в, Rt = 1 мом, /?6= 100 ком, «1 = 0,425.
Ответ. и2(оо)= —2,36 в.
479. Составить схему модели идеального интегриру-
ющего звена с передаточной функцией W (р) = , k =
= 14 сек"1.
Решение. Это звено набирается по схеме рис. 342.
Составленное уравнение мо-
дели (см. решение зада- ___|С___
чи 477) „
Рис. 342. Схема модели иде-
ального интегрирующего звена.
Пусть С = 1 мкф и R = 0,02
мом, тогда а = kRC —
= 14-0,02- 1 = 0,28.
480. Составить схему модели апериодического звена
первого порядка с передаточной функцией W (р) =
й = 29, Г = 0.24 сек.
Тр+ 1 ’
610 гл. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ [4S1
Решение. Схема модели изображена на рис. 343.
Составленное уравнение модели (см. решение задачи
477) имеет вид
/ /?2С . \ _ RsRfdz
\ а, Р+1)и^ Rln3ai ui>
откуда
'Г R 2^ 1 R zR 4^2 /1 \
Т = -^Г> k~ 0)
Соотношения (1) позволяют выбрать параметры
схемы на рис. 343: J?i = /?2 = 0,1 мом, 7?3 = 0,02 мом,
Т?4=1 мом, С=1 мкф, aj = 0,417, а2 = 0,242.
Рис. 343. Схема модели апериодического звена пер-
вого порядка.
481. Составить схему модели апериодического звена
первого порядка с передаточной функцией W (р) =
= -^4-г> k = 0,83, 7 = 9 сек.
Гр + 1
Ответ. Схема модели изображена на рис. 343; =
= Т?2 = Кз — 1 МОМ, /?4 = 0,1 МОМ, С=1 мкф, «1 = 0,111,
«2 = 0,92 (см. задачу 480).
482. Составить схему модели консервативного звена
с передаточной функцией W (р) = /г = 7, 7 =
= 0,34 сек.
Решение. Схема модели изображена на рис. 344.
Составленное уравнение модели (см. решение задачи 477)
483]
§ 20.1. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ
511
имеет вид
(ад^а.Р2+j)^2(0 = _ (о
откуда
Г Psa2 Rl
Соотношения (2) позволяют выбрать параметры схемы
на рис. 344: = Т?4 = О, I мом, R2 — Ra — Rs= 1 мом,
С2 = (?! = ! мкф, 01 = 0,700, а2 = 0,863.
Рис. 344. Схема модели консервативного звена.
483. Составить схему модели консервативного звена
с передаточной функцией W(p) = /2^4. i > 6—1, Г =
= 0,007 сек.
Решение. Схема модели изображена на рис. 344
(см. задачу 482). Так как угловая частота свободных
колебаний g = у- = ^ -у- = 143 сек-1 большая, то темп
решения задачи необходимо замедлить, т. е. выбрать
масштаб времени mt < 1. Для перехода от натурального
времени t к машинному R, и обратно служит выражение
t =
При этом 'в уравнении модели (1) предыдущей задачи
вместо натурального времени t будет машинное время
. „ d
а вместо символа производной р = -^- — символ произ'
водной Рм=-^-.
512 ГЛ- 20, СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ ИМ
Тогда, подставив в уравнение модели (1) предыду-
щей задачи
d
получим
т2р, + ! \ 2 (/м) = _ М (и>
\ <\5а2 /
откуда ________
Z’ = mzl/r £=-—*- (п
У fl6a2 ’ Ъ
Так как k = 1, то выбираем /?] = /?2 = 1 мом, cq = 1, т. е.
в схеме рис. 344 можно отключить делитель напряже-
ния cq. Для выбора масштаба времени из первого вы-
ражения (1) найдем
____( mt \2 R2R3R4C1C2
“2 \ Т J R5 ‘
Так как коэффициент а2 должен быть меньше единицы,
то при /?5 = /?2—1 мом и Ci==C2=l мкф выражение
Рис. 345. Схема модели колебательного звена или апе-
риодического звена второго порядка.
(2) позволяет выбрать tnt = 0,1, /?3 — 0,1 мом, R4 = 0,02 мом,
а2 = 0,408 или же m( = 0,01, R3 = 0,1 мом, /?4=1 мом,
а2 — 0,204.
484. Составить схему модели колебательного звена
с передаточной функцией W (р) = у2р2 +2^Гр+'1 ’
Т = 0,167 сек, | = 0,56.
4861
§ 20.2. МОДЕЛИРОВАНИЕ УРАВНЕНИЙ СИСТЕМ
513
Решение. Схема модели изображена на рис. 345.
Составленное уравнение модели (см. решение задачи 477)
имеет вид
(R2R3R5CiC2 о a3R3R3RsCi aiRs
р + р + 1) “2 “ rT и"
откуда находим
т - /" RiR^Rfifi^ £ а3Т , o-iRz /п
r = V—k = ~RT-
Соотношения (1) позволяют выбрать параметры схе-
мы на рис. 345: 7?1 = 7?3 == 0,1 мом, R2 = R6=
= 1 мом, Ct = С2 = 1 мкф, cq = 0,800, eg, = 0,371, «з = 0,670.
485. Составить схему модели апериодического звена
второго порядка с передаточной функцией
T^+hp+'i ’ & = 2’14’ fe==4’3’ Т=1>2 сек-
Ответ. Схема модели изображена на рис. 345; /?] =
= /?4 = 0,1 мом, R2 = 7?з = Т?5 = Re = 1 мом, С1 = С2~ 1мкф,
cq = 0,214, ct2 = 0,695, 03 = 0,357 (см. предыдущую задачу).
§ 20.2. Составление схем для моделирования
дифференциальных уравнений и автоматических систем
на электронных вычислительных машинах
486. Составить схему модели для решения линей-
ного дифференциального уравнения
(«оР5 + «1Р4 + «2Р3 + «зР2 + «4Р + а5) у (0 = bog (0
в натуральном масштабе времени и при нулевых на-
чальных условиях.
Решение. Преобразуем переменные y(t) и g(t)
исходного уравнения в соответствующие переменные
модели с помощью формул
у = тущ,
g = mgu.
(1)
514
ГЛ. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ
I486
Подставив (1) в исходное уравнение, получим
(а0р5 + щр4 + а2р3 + а3р2 + а4р + а5) и5 (/) = Ьои (/). (2)
•Пу
Разрешим уравнение (2) относительно старшей про-
изводной
Р5и5 (0 = - ~ Р4«5 ~ ~ Р2иь ~^Ри5~^-ч5 +
UQ UQ UQ UQ UQ
те Ьо
+ 7Г-Ги^- <3>
fily CLq
По уравнению (3) составляем схему модели (рис. 346).-
Схема модели составляется на основании следующего.
Рис. 346. Схема модели к задаче 486.
Согласно уравнению (3) высшая (пятая). производная
переменной и5 равна сумме членов, пропорциональных
низшим производным и самой переменной и5, взятых
с обратными знаками, и входной величине и. Предпо-
ложим, что в точке б или в точке суммирования всех
переменных имеем высшую производную (p5w5). Тогда,
включив последовательно интеграторы 1—5, на выхо-
дах последних будем получать напряжения, пропорци-
ональные соответствующим низшим производным и
самой переменной. Учитывая, что операционные усили-
тели изменяют знак входного сигнала, необходимо
включить сумматор 6 для изменения знака напряжений,
пропорциональных положительным производным (р3п5
486]
§ 20.2. МОДЕЛИРОВАНИЕ УРАВНЕНИЙ СИСТЕМ
515
и ри5), снимаемых с четных (2 и 4) интеграторов.
Интегратор 1 одновременно выполняет и функцию
суммирования.
Для определения параметров модели (сопротивлений
резисторов Ri—Rw и емкостей конденсаторов Cj — С5)
найдем уравнение модели. Для этого составим систе-
му уравнений:
,. =___t ( И , «5 ~ , «3 , ие Ut\
1 С1Р \«, R10 R8 я8 )’
_ 1 ut
“2 С2р R2 ’
,, =___!_ дз_
4 С4р R< ’
1 И4
“5~ C5p~RT'
Решив систему уравнений (4) относительно искомой
переменной и5, получим уравнение модели в виде
(С 1C2C3C4C5RSR2R3R4R5P5 + C^CqC^CsRzRsRaRsP4 +
+ ^^С3С4С^М5р* + С4С5/?4Р5р2 +
-->*(<). <5)
Минус в правой части уравнения (5) появился в виду
того, что при моделировании использовано нечетное
число операционных усилителей (пять), включенных в
прямую цепь. Чтобы уравнение (5) полностью соответ-
ствовало исходному,, входную величину —напряжение
и — следует подать на вход модели через инвертор, схе-
ма которого приведена в приложении 33.
Сравнив коэффициенты при переменных и их
производных уравнения (5) с соответствующими
516
ГЛ. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ
1487
— a2,
коэффициентами уравнения (2), получим
Rs Rl2
Rg Rs
C4C5R4R5 ~ a3i
Rs R12 <> П _ „
~jR7 ~fy~ C5/'5 — °4’
Rs _ ms .
~Б~ — “о-
Л| Шу
После выбора -масштабных коэффициентов, уравне-
ния (6) позволяют (произвольным образом) выбрать па-
раметры модели при известных значениях коэффициен-
тов исходного уравнения.
487. Как изменятся параметры модели на рис. 346,
если дифференциальное уравнение из условия предыду-
щей задачи решать в измененном масштабе времени,
т. е. решать в замедленном или ускоренном темпе?
Решение. Для перехода от натурального времени
t к машинному tM и обратно служит уравнение
t = mtta, (1)
где tnt — масштаб времени. При mt > 1 темп решения
задачи ускоренный, а при mt <_ 1 — замедленный.
При выборе mt #= 1 темп протекания процессов в
модели должен отличаться от темпа процессов, описы-
ваемых исходным дифференциальным уравнением, т. е.
в уравнении модели (5) предыдущей задачи вместо на-
турального времени t будет машинное время £м, а вме-
v d v
сто символа производной р = ----символ производной
_ d
р,л dtM •
488]
§ 20.2. МОДЕЛИРОВАНИЕ УРАВНЕНИЙ СИСТЕМ
517
Тогда, подставив в уравнение (5) предыдущей задачи
d
получим
(Cfi^Cfi.R.R^R^m^ + C&C&R^R^rn'p* +
*" ~R^~ ^3^4^5^3^4^5mtP3 + ~R^ ^4^5^4^5mtP2 +.-
+ -g- С^т(р + и5 (U = и (Q.
Из сравнения коэффициентов при переменных и их
производных полученного уравнения с соответствующи-
ми коэффициентами уравнения (2) предыдущей задачи
имеем
~ a0mt5 ,
С2С3С4С^R^R^R^R^ = aImt4 ,
Re ^3^4^й^3^4^5 ~ a2mt 3 ’
С4 С&^4^5 = a3mt2 ’ (2)
_Rs_ R = a tn~l
Rg R7 CSKS a4mt ’
Rn 5'
Rs ___mg
Ri my °'
Из полученных соотношений видно, что при реше-
нии задачи в замедленном темпе (mt< 1) величины
сопротивлений резисторов Ri — Ri2 и емкостей конденса-
торов Cj — С5 модели на рис. 346 необходимо увеличи-
вать, а при ускоренном темпе уменьшать.
488. Составить в общем виде схему модели следя-
щей системы, принципиальная и структурная схемы
которой изображены на рис. 22, а параметры и уравне-
ния отдельных звеньев заданы в условии задачи 38.
Решение. Воспользуемся передаточными функци-
ями отдельных звеньев и структурной схемой следящей
системы из решения задачи 38.
518
ГЛ. 20. СОСТАВЛЕНИЕ СХЕМ ДЛЯ МОДЕЛИРОВАНИЯ
[488
Преобразуем структурную схему следящей системы
(рис. 22,6). Перенесем сумматор / на вход предыдуще-
го звена и преобразуем два последних звена прямой
цепи, в результате чего получим структурную схему,
приведенную на рис. 347, а.
Рис. 347. Структурная схема (а) и схема модели (б) следящей
системы.
В этой следящей системе выделим три физические
величины: угол поворота, момент нагрузки и напряже-
ние. Масштабы для времени mt и для напряжения та
примем равными единице. Масштабы по углу и момен-
ту будем выбирать из соотношений
Мн шмин,
# = той.
(1)
Для перехода от структурной схемы следящей сис-
темы (рис. 347, а) к схеме модели воспользуемся мо-
делями элементов структурных схем автоматических
систем (приложение 33). В результате замены элемен-
тов структурной схемы (рис. 347, а) соответствующими
490]
§ 20.2. МОДЕЛИРОВАНИЕ УРАВНЕНИИ СИСТЕМ
519
элементами модели (приложение 33) получим схему моде-
ли следящей системы (рис. 347, б). На основании приня-
тых масштабов обозначим на схеме модели соответствую-
щие структурной схеме следящей системы величины
напряжений
• 1 л 1 „
U. =-----О., и2 =-------$2>
1 1 «о 2
tz3=tz, «"=«",
ин — m
шм
un == —— pa. (2)
5 ‘ ’
Согласно формулам приложения 33 находим
= -g- = fe2, С^7 = ТУ, -g- = fc3,
(3)
C2R$ —Тк,
Ra ГПМ kj
R5 ’
1 _ h
C3R< RS’
При известных числовых значениях параметров сле-
дящей системы и при выборе масштабных коэффициен-
тов формулы (3) позволяют выбрать параметры модели
(сопротивления резисторов — R9 и емкости конденса-
торов С| —С3), при этом изменением величины масштаб-
ных коэффициентов в допустимых пределах облегчается
задача выбора параметров модели.
489. Составить уравнение модели, изображенной на
рис. 347, б относительно выходной величины и2 по вход-
ным ц* и ип, с учетом масштабных коэффициентов, при-
нятых при решении предыдущей задачи.
Ответ.
Г(С,/?7р+ 1)(С2/?8р + 1)р + а-*6*7*8 1 М2(О =
L A1K2A3U8A4J
“ «ТОГ “W “ (СЛр + 1) «.(0-
490. Составить в общем виде схему модели релейной
следящей системы, отличающейся от следящей системы,
схема которой изображена на рис. 22, тем, что вместо
линейного усилителя взят релейный со статической ха-
рактеристикой, приведенной на рис. 348, а. Параметры
и уравнения всех остальных линейных звеньев заданы
в условии задачи 38.
Рис. 348. Статическая характеристика (а) и схема модели (6) к за-
даче 490.
Рис. 349. Схема модели к задаче 491.
j] § 20.2. МОДЕЛИРОВАНИЕ УРАВНЕНИЙ СИСТЕМ 521.
Ответ. Схема модели релейной следящей системы
представлена на рис. 348, б. Схема модели релейного
усилителя взята из приложения 34, при этом принято
Из = Щ = t/з, = Un = U°. Выбор масштабных коэффи-
циентов и параметров линейных элементов модели при-
веден в решении предыдущей задачи.
491. Составить в общем виде схему модели нели-
нейной следящей системы, отличающейся от следя-
щей системы, схема которой изображена на рис. 22,
тем, что вместо линейного усилителя взят релейный со
статической характеристикой, изображенной на рис.
348, а. Кроме того, необходимо учесть приведенный
к валу двигателя следящей системы момент нагрузки
от сил сухого трения (Л4Н = sign 12; см. рис. 337, б).
Параметры и уравнения линейных звеньев заданы в'
условии задачи 38.
Ответ. Схема модели нелинейной следящей системы
с релейным усилителем и с учетом влияния момента
нагрузки от сил сухого трения представлена на рис. 349.
См. задачи 474 и 490.
ПРИЛОЖЕНИЯ
1. Изображения по Лапласу и Карсону — Хевисайду
_ функций времени
Таблица ПЛ
। № п. п. 1 Оригинал Изображение Лапласа Изображение Карсона — Хевисайда
1 । (0 2. р- 1
2 1п И1 и!
pn+1 р"
3 1 Р
р + а р + а
4 а 1 1
р (р + а) р + а
5 e-aZ _ g-|3t 1 Р
р — а (р + а)(р + Р) (р + а) (р + р)
6 (б-а) е-а'-(б~Р)е~р< р + б Р (Р + б)
Р — а (р + а) (р + Р) (р+а) (р + Р)
7 1 Ре~аг - ае~& ар ар (а — р) 1 1
Р (р + а) (р + Р) (р + а) (р + р)
8 б б-а а/ р + б р + б
«Р 1 а(а-р) 1 р(р + а) (р + Р) (р + а) (р + Р)
. б“Р г*
Р(р-а)
1J ПРИЛОЖЕНИЕ B23
Продолжение табл. П.1
1 ‘В ‘В зх | Оригинал . \ - Изображение Ла пласа Изображение Карсона — Хевисайда
9 sin At 1 p
p2 + A2 P2 + A2
10 51п (Х< + ф) л p + t> P(p+6)
P2 + № P2 + A2
ф = arctg -g-
11 4- e~yt sin At л 1 P
(p+v)2 + № (p+V)2 + ^2
p + 6 P (p + 6)
12 4-F(6-Y)2+ А2Х л
(p + Y)2 + № (p + v)2 + ^2
X sin (At + ф)
, t Л
13 v arc+ 6_v 1 +—7..1-- V 1 1
у2 + A2 A V y2 + A2 P[(P + Y)2 + ^2] (p + v)2 + №
X e-vf sin (At — ф)
ф = arctg
14 a + J x p + 6 p + 6
V2 + A2 aKy2 + A2 X V (6 — у)2 + A2 e-vf sin (At + ip) p[(p + v)2 + ^2] (p + v)2+*2
1 J h 1 ф = arctg 6_v arctg
2. z-преобразования функций времени
Таблица П.2
№ п. п. Оригинал f W Преобразование Лапласа Рл (р) «-преобразование F (г) Модифицированное «-преобразование F (г, О)
1 - 1 (О 1 Z Z
р z-Л z-l
2 t 1 Zq2!
Р2 (г-1)2 (Z-l)2 1 z-l
3 !< 1 7’6г(г+1) Tlz _ (l + 2o)^z _ (aT0)2z
р3 2 (г-1)3 (z-l)3 1 2 (z-l)2 1 2 (Z-l)
4 e~at 1 2 и Р~аТо ..
р + а z-d,dC z — d -
5 а ^-t)z -аТ» z zdP
р(р + а) (z-l) (z-d)-’ z — 1 z — d
6 sin р/ Р zsin РТО z2 sin орт0 + z sin 6pr0 _ z2-2zcos PTO + 1 ’ ° 1 °
р2 + Р2 z2 — 2z cos РГО + 1
7 cos р/ Р z2 — г cos PT,, z2 cos opTo — z cos брТо
р2 + р^ z2 — 2z cos PT + 1 z2 - 2z cos PTO + 1
8 ' e~at sin р/ ₽ z d sin рГо .a ( z sin oPTo + d sin 6PTO \
(р + а)3 + р2 z2 — 2z d cos pT0 + d2 \ z2 - 2zrf cos PTO + d2 j
9 e~at cos р/ р + а z2 — zd cos pr0 (, z cos oPT0 — d cos 6pTо \
(р + а)2 + р2 z2 — 2z d cos [}'Г0 + d2 t z2 - 2zd cos pT0 + d2; J
ПРИЛОЖЕНИЕ
4) ПРИЛОЖЕНИЕ 625
3. Нормированная логарифмическая частотная фазовая
Характеристика апериодического звена первого порядка (рис, 350)
4. Нормированные логарифмические амплитудная и фазовая
характеристики колебательного звена (рис. 351а и рис. 3516)
Рис. 351а.
526
IIP JlUAtHML
*5
5. Отклонение асимптотической л. а. х. колебательного звена
от точной (рис. 352)
Рис. 352.
ПРИЛОЖЕНИЕ
527
6. Критерий устойчивости Гурвица
Линейная САУ, характеристический многочлен, который равен
D (р) -аор" + ajp"-1 + а2рп~2 + ... + an-tP2 + ап-2р + ап
я а0 > 0, устойчива, если положительны п главных определителей
матрицы
at 1 аз ' as ... ? • a « 0 0
flo аг I at a a a : • • • 0 0
0 at аз ... i • * • 0 0
0 CLq fl2 I « • « j • • • 0 0
a a a . • • • • • • • 0 0
0 0 0 . * * * • • • an~t 0
0 0 0 • • • a a • an-i an
Д1 -1 al I >0,
Аз
«1
Яо
О
as а5
д2 а4
d а3
01 fl3 «5 ... 0
«О a2 a4 ... 0
An-i = 0 at a3 ... 0
0 «0 a2 ... 0
0 О 0 ,. *
Ал“ ап • Дл-i > О-
Последнее выражение сводится к неравенству ап > 0, так как
предыдущий определитель > 0.
Частные случаи критерия устойчивости Гурвица
1) 7)(р) —Дор + яр
' Условия устойчивости а0 > 0, aj > 0.
2) D (p)«=aop2 + a,p + a2.
Условия устойчивости а0 > 0, > 0, а2 > 0.
3) D (р) - а0р3 + atp2 + а2р + а3.
Условия устойчивости
а0 >0, Я| > 0, а2 >0, а3 > 0, ага2 — а0а3 > 0.
4) D (р) “ Сор’ + aiP3 + а2р'г + а3р + а4.
528
ПРИЛОЖЕНИЕ
Условия устойчивости .
ае > 0, at > 0, а2 >0, а3> О, at > О,
о3 (а^ — <?0о3) — > 0.
5) D (р) = сор5 + а1р4+«,р3 + аар2 + «)/7 + а5.
Условия устойчивости
<10 > 0, Cj>0, а2 > 0, а3 > 0, с., > 0, ' «5 > О,
«1«2 - ава3 > О,
(а^ - с0«3) (о;!о4 — «Ms) - («!«+ — Ms)’ > 0.
6) D (р) = а0р6 + а,р5 + + с3р3 + atp2 + аър + а6.
Условия устойчивости
<7 0 > 0, 01 > 0, а2 > 0, а3 > 0, at > 0, а5 > 0, ав > О,
П-3 (OiOg — ОцОд) <l\ (Oia,| О0П5) > О,
(«1«2 - “о"з) ["5 <а4й3 - «2«б) + й6 .(2бг1°5 - 4)] +
. + (0|«4 - о0о5) [«|йзаб “ а5 (aia4 ~ «о0»)] “ а1яа > °”
7. Диаграмма Вышнеградского с линиями равного затухания
в процентах за один период (рис. 353)
ПРИЛОЖЕНИЕ
529
8. Диаграмма Вышпеградского с линиями равной
нормированной степени устойчивости /гй = h (рис. 354)
У «з
9. Эквивалентные начальные условия в системе регулирования
после воздействия па нее единичной ступенчатой функции
Дифференциальное уравнение системы
(а^ + а.р"-’+ ... +an)y(l)^(bopm + blP,n~l + ... +
где У (0 — выходная величина, g (/) — входное воздействие; y_fl>
У-о< Д-0-начальные условия, имеющие место непосредственно
перед приложением единичной ступенчатой функции; j7+H. ...
^’’-начальные условия, имеющие место непосредственно
530
приложение
110
после приложения единичной ступенчатой фунинии:
и и' = »/ ' ,.<n-m-l) (п-т-П
У+о У-О' У+о У-0' ••• У+о У-о I
,.(п-т) _ (п-т) , Ье .
У+0 -У-JO +~ •*>
“о
' = „(п-m+D 4- Al . 1 _ °1 Г,/п-т) _ ,/n-m)]
0+0 У-О + ав 1 Яо Р+0 У-о ь
у%~1)=№>~т) - у%~т)] - • • .
10. Решения однородных дифференциальных уравнений первого,
второго и третьего порядков
Таблица П.3
1 Порядок | уравнения Вещественные корни Комплексные корни
1 х = хое-а‘< -1 -
2 х =X1e“°it + Аге~а^ __ + Оо G-2 “ С-1 я а^ + »0 /12 — ’— СЦ “ О>2 х = (В cos М + С sin М) е~^ В ^х0 „ VXq+CIq с л
3 х—А1е~а^ + Азе~а^ + Л3е~аз< д at °2q3y0 (й2 + Сз) Ор + Ер ‘ (Иа-а^саз-а.) __ СЬ1€1з>70 + (tt| + ttj) ti0 + g0 2 (а, - aj (аэ - аа) . _ СЧСзХф + (Ctj + Oj) ti0 4* Ео (dj — а3) (а2 — с3) t х = Ле~а^ + (В cos М + С sin М) е~^ . _ (V2 + А2) X» + 2vt>0 + е0 (Т-а^ + Х2 а, (С, - 2у) х0 + 2уо0 - е„ (У-счГ + Ь2 ai(*.2-y2 + vai) х0+ (а2- V2 + ?-2) о0 л ЦУ-а^ + Л2! . (а, - у) е0 АЦу-а.у+М
Примеч а н и е. Здесь а,, с^, Оз — абсолютные значения вещественных
некратных корней, у и А —абсолютные значения вещественной и мнимой частей
комплексных корней, лс — начальное значение исследуемой функции, ^o = JC/(0)
и £0 — к" (0) — начальные значения скорости и ускорении изменения исследуемой
функции.
12] ПРИЛОЖЕНИЕ S31
11. Номограмма для построения вещественной частотной
характеристики замкнутой системы по амплитудно-фазовой
характеристике разомкнутой системы
(вещественная круговая диаграмма) (рис. 355) ' -
12. Кривые для определения времени переходного процесса
и перерегулирования по коэффициенту наклона трапецеидальной
вещественной частотной характеристики (рис. 356)
Рис. 356.-
632
приложение
gis
13. Кривые для определения времени переходного процесса
И перерегулирования для вещественной частотной характеристики,
имеющей максимум (рис. 357)
Запт т> фазе
Рис. 358.
ПРИЛОЖЕНИЕ
533
1»1
IS. Номограмма для построения вещественной частотной
характеристики по заданным качественным показателям (рис. 359)
Рис. 359.
534
ПРИЛОЖЕНИЕ
п«
16. Нахождение квадратичной интегральной оценки
то
О
где х = у — уж — отклонение регулируемой величины от установив-
шегося значения у^.
Изображение регулируемой величины по Лапласу представ-
ляется в виде
У (0) = + • • + bmpm 1
Р,=‘ fi0 + fitp+ ... +anp" р
(и > т).
Тогда интегральная оценка может быть вычислена из выражения
/=—(В0Д0+ BjA1 + ... + Bmb,m — 2bBbi&).
2<ZqA
Определитель Д находится следующим образом:
а0 — а2 а4 —ае ... О
О «1 — а3 as ... О
д_ 0 —а0 аг —а^ ... О
О 0 — at а3 ... О
О 0 0 0 ... an-i
Av (v = 0, 1,..., т) — определитель, получающийся из Д заменой
(v + l)-ro столбца столбцом
а1г ав, 0,.... 0.
Коэффициенты Ву .... Вт вычисляются следующим образом:
В0 = ^о>
Bj я bt — 2feg&2,
Bk = bk ~ 2bk-ibk+i + ••• +2 (“О4 bob2k,
18]
ПРИЛОЖЕНИЕ
535
17. Формулы для интегрирования спектральной плотности
Искомый интегра'л представляется в виде
/ =_L f
п 2 л J Л (/св) Л (-/со)
— ОО
где
А (/®) = а0 (/®)" + а, (/®)"-1 + ... + ап,
G (/®) = b0 (/со)2"-2 + Ь, (у®)2""1 + ... + Ьп-,.
Многочлен G (/®) содержит только четные степени /со. Многочлен
A (j®) должен иметь корни в верхней полуплоскости, что соответ*
ствует устойчивой системе.
Для п = 1
+«>
/ = * f _ Ьо
1 2л J | o0Jw + о, |2 2а0о,*
f —оо
Для п = 2
/ = 1 f [ftp (/®)2 + 6,] с/® _ ° а2
2 2л J | а0(/®)2 + о,/® + о2|2 2о0а, *
— ОО
Для п = 3
= 1 f [60 (jaY + 6, (ja)2 + b2] da
3 2 л J |а0(/®)3 + а1(/®)2 + а2/® + оз|2 =
— CO
—a2b0 + aobi —
ca_________._______a3
2a0 (aaaa — a^)
Для n = 4
+ oo
= 1 f [60 (/m)6 + b, (jaY + b2 (io)2 + b3l da
4 2л J |a0 (ja)4 + «i (io)3 + a2 (ja)2 + a3ja + a412
— oa
60 (—fita4 + a2a3) —00036,+a0a]fc2 + (aoa3 — o,a2)
-------------------------------:------£1-------------
200(0001+0^04-0,0203) •
18. Нормированные стандартные передаточные функции
разомкнутой системы
Передаточные функции для различных степеней и дифферен-
циального уравнения приведены в табл- П.4.
S3.6:
ПРИЛОЖЕНИЕ
Степень
астатизма
№(р)
(«в-
*
Таблица П.4
р2 + 1,4юор
_____«>о
ря + 2©0р2 + 2©jjp
_______________«>о
рл + 2,6©Gp3 + 3,4©Gp2 + 2,6© Gp
2,5©0р -}- ©д.
6,3©Gp + ©д
р3 + 5,1©0р2
2
12®др + ©д
р4 + 7,2©др® + 16©др2
18©дР + го®
р5 + 9ш0р4 + 29©др3 + 38©др2
25©др + ©д
р^ НюдР^ 4- 43©др4 + 8Э©др3 4“ 73®4р2
ад-
ПРИЛОЖЕНИЕ’
537'
13'них введен параметр ю0> определяющий быстродействие си-
стемы. Переходные характеристики, соответствующие этим переда-
точным функциям, приведены на рис. 360. Перерегулирование о %
приведено в таблице. .
Рис. 360. Переходные характеристики, соответствующие стандарт-
ным передаточным функциям.
Рис. 361. Переходные функции для типовых л. а. х. симметричного
вида. - - - - -
Б38
ПРИЛОЖЕ1 И
[Го
19. Типовые л. а. х., соответствующие
М — показатель колебательности. Для типовых симметричных
w
ПРИЛОЖЕНИЕ
539
заданному запасу устойчивости
н ы е л. а. х.
Т а б л и ц а П.5
Тип л. а. х. Базовая частота Ча- стота среза
? I 1 1 № 1 СО V T0Tt КТ, тот1
1-2-1-2-3... ,/~к V г» кт, Tt
2-1-2-3... У К КТ,
Постоянные времени в области
средних и высоких частот
связь с базовой связь с частотой
частотой Среза
7 - 1 1/ М т > 1 . м
12 ffij М-1 2 «е М - 1
' ^Ti<
1 ум (м-i) 1 м
' <й0 М + 1 М + 1
.. tn + 1 Т,
л. а. х. оп равен М =------где m =---------
Ш — I
i-3
Таблица П.6 §
Несимметричные л. а. х.
айна&СЯл&ш
п
. Приведенная здесь формула для 2 Г, является приближенной; она дает .достаточную точность пра
" . . . Z=1
Л1 1,3. Эта' формула становится точной при М — 1 и любом п, либо при п— 1 и любом Л1.
ПРИЛОЖЕНИЕ
641
, 20. Нормированные кривые переходных процессов
для типовых л. а. х.
А. Кривые переходных процессов при входном воздействии
в виде ступенчатой функции g (t) = g0 • 1 (/).
1) Случай симметричных л. а. х. (приложение 19, табл. П.5),
рис. 361.
Кривые рассчитаны для л. а. х. типа 2—1—2, но с большой
точностью отображают переходные процессы в случае всех типов
л. а. х., приведенных в табл. П.5.'
2) Случай несимметричных л. а. х. (приложение 19, табл. П.6),
рис. 362.
Рис. 362. Переходные процессы для типо-
вых л. а. х. несимметричного вида.
Кривые рассчитаны для л. а. х. типа 1—2, но практически при-
годны для л. а. х. всех типов, приведенных в табл. П.6.
Б. Кривые ошибки воспроизведения линейного задающего
воздействия g (I) = at • 1 (/)
1) Случай симметричных л. а. х. (приложение 19, табл. П.5)
рис, 363.
Кривые рассчитаны для л. а. х. типа 2—1—2, но практически
пригодны и для л. а. х. остальных типов, приведенных в табл. П.5).
2) Случай несимметричных л. а. х. (приложение 19, табл. П.6),
рис. 364.
Кривые рассчитаны для л. а. х. типа 1—2, но практически
пригодны и для л. а. х.' остальных типов, приведенных в табл. П.6.
S42
ПРИЛОЖЕНИЕ
ш
21. Корректирующие звенья
Схема корректирующего звена Передаточная функция корректирующего звена Г,
С, и, У1 о 1 4- Т,р С° 1 + Г,Р’ fliC,
и, к 1 + Т,р С° 1 + Лр R,Ct
’ * S А >=ЬП L ’ L 1 ~F ТгР 1 + г.Р
.( я У r * + r^P с° 1 + Лр <^О^+7г2КО+7г2^+ + Wfljfl.,) с2х X (^+«0+«l)-1
644
ПРИЛОЖЕНИЕ
Схема корректирующего Передаточная функция
• звена корректирующего звена
22. Корректирующее звено переменного
Схема ’
Передаточные функции звена
Мойное Т - образное збено
Параметрическая
17г Л (р>
V, В(р) ’
тле
Л (р) ~ ТiTi'l iP* +
-I-1\ (S2 + ТУ р? + (Т. + 5.) р + I.
S,=R,C3 5г-КгС3
В (p)«7’I?’»7ip?-l-7’1 (Ss-|-7’,)pI+
+ 7’2(7’1+S1+Ts)p’+
4-(r1+S|+r2-l-rs+SjJ P + l„
По огибающей
U, (/й) I + Т./й
tr^/й) -о 1 + г/й
Mi
П:РИЛ<ЭЖЕ1.ЩЕ
545
Продолжение табл. П. 7
«о +"*
/?,С,/?2Са К,) 4- У?^С,С2
R0 + «l + ^
тока (двойное .Т-образное звено)
Таблица П. 8
Связь между параметрическими
постоянными времени и постоя»?
нымк времени по огибающей
Условии осуществимости звена
%Гдх+2х + <у;
' ’ 2М‘-°о)
4 -
т7л“
а « »„
646 ПР ЖЕНИН
Рис. 364. Ошибка воспроизведения линейного закона для типовых
л. а. х. несимметричного вида.
23]
ПРИЛОЖЕНИЕ
64,7
Таблица П;9
Выбор параметров звена
2,5 5.0 7,5 10 15 20 - 30 40 50 60 оо
ширина полосы частот. гц ч- - 2.5 “ 5,0 - 7,5 - 10 ± 15 +Jh - 20 ~ 30 _ 40 - 50 ~ 60 резонирует
а 0,758 0.553 0,486 0,453 0,420 0,403 0,386 0,378 0,374 0,370 0.353
со 0.226 0,110 0,077 0,052 0,034 0,025 9,016 0,012 0,009 0,008 0
При составлении этой таблицы принято, что Ct = Сг — CS = C.
Коэффициент передачи на несущей частоте Go. Сопротивления под-
считываются по формулам
2<онаС ’
R -- 1
3 Ц>ИСГ2’
Несущая частота <aH = 2nfH.
23. Приведение дифференциальных уравнений
к канонической форме
А. Для уравнений нелинейной системы n-го порядка, заданных
в нормальной форме
41 = «ii4t + «1242 + ••• + «ьл-14п-1 +&!?>
42 = «2141 + «2242 + ••• + «2. Л-14п-1 + ^2?»
4 л-1 = ап-ь 141 + «п-2, г4г + ••• + «п-ь п-14п-1 + ^п-1£>
cr = cIi]i +с242+' ... + сп-14п-1 ~ri,
каноническая форма записи имеет следующий вид:
X, = kixl + f(c),
хг = А,2Х2 + f (о),
Хц—1 ~ ^n—1^п "Ь f (о),
д = р,х, + ₽2х2 + ... + -г/ (о), (х„=а),
(П.1)
(П-2)
где X], х2,xn-it а = хп — канонические переменные.
Б$8...
ПРИЛОЖЕНИЕ
[23
Для перехода к каноническим уравнениям (П.2) необходимо,
а) вычислить определитель
а11 012*
fl21* О22 — ^>*
, £>(Х) =
ai- п-1
a2t П-1
(П.3)
On—1, |> Яп-Ь 2»
Оп-1* п-1 X
б)
^-1. ?<2>
: в)
ВЫЧИСЛИТЬ
• • •> ^п-ь
вычислить
₽/ =
корни характеристического уравнения Д (X) = О,
коэффициенты ft по формулам
С1Л\ (Xf) + с2Л/2 (X/) + ... + сп^п-| (X;)
D'(k) . '
Выражения Л'/г (X) получаются из определителя D (X)
меной k-ro столбца па столбец
(П.4)
(П.3) за-
bi
Ьг
(П.5)
^и-г
Выражение . D' (Л) представляет собой производную .от D (X) по X.
Б. Для уравнений нелинейной системы n-го порядка, заданных
в нормальной форме
;• .' Ф = O||T)t + о121]2 + ... + ащЦп + bAf (о),
’'l2 = o2lT)I + o22'q2+ ... + a2nrin + ЬгЦо),
= вщПг+ ОпгЧг + • + «пгеПп + bnf; (о).
;а = С|Т]1+сгт|,+ ... +спт)„
канонические' уравнения относительно переменных х\,
принимают вид
; Xi = Xjx, + f (о)
: • .г2 = Х2л;2 + / (о) .
(П-6)
*2. * ••* Хп
(П.7)
Хп *^пХп | (о)
гДс ^-'1, Х2,'.. ., Х,| — корпи характеристического многочлена D (X).
* • о J | ;Х, П|2,
021* о22 — X,
О(Х) =
о in
Й2П
• • » . апп X
Оц|* Оп2,
и 1 Если в уравнении D (Л) = 0 имеется нулевой корень, например
= О, то канонические уравнения для системы уравнений (П.6)
23]
ПРИЛОЖЕНИЕ
заданных
(П.12)
записываются в форме, совпадающей с (П.2)
*1 = Л,*! + f (о),
*2 = К2х2 4- f (ff),
/ * ............................................ (П.8)
%n—l = ^n—ixn-i 4" f (o),
a = PvCi 4-02*2 + • •• + 0n*,7 — rf (a), (o=x«).
Но здесь
r = ~(cibi + c2b2 + ... +спЬц), (П.9)
где
п
Рь = —XmP = ~^k V ci (^ = 1. 2,..., n). (П.10)
AMI U
В формуле (П.10)
NkW=%biDlkm, (П.П)
где Djk (X) обозначает алгебраическое дополнение элемента 1-й
строки и fc-го столбца определителя D (X).
В. Для уравнений нелинейной системы n-го порядка,
в виде
^(л-i) +д|Т1("-2) + ... + ач_р] = — d%,
а = соп + с’«п + г2’)+ + Сп-гЪ(п~2> - f6-
канонические уравнения записываются в виде
А = АГХ1 + { (о),
Аа = К2х2 + f (о),
Хп—1 ~ ^'П—1ХП—1 + f (°).
6 = 01*1 +02*2+ ... +0n-1X(I-l-r)(o),
где Х|, Х2, .... X,г_( — корни многочлена
О (X) = X"-1 4“ GjXn~2 -р сс2^^ 4- ... 4- Яп—>>
В формуле (П.15)
А (X) = с© + CjX 4-1’2^2 + ... 4~ Сп~^п 2» |
Д'(Х)=-^О(Х). I
1*Л
(ПЛЗ)
(П.14)
(П.15)
(П.16)
f
559
ПРИЛОЖЕНИЕ
[24
Если в многочлене. (П.14) имеется один нулевой, корень, напри-
мер, Лп_1 = 0, то в выражении (ПЛЗ)
A(^fe)
₽Л= ~d
(fe = l, 2, .... п-2),
(П.17)
“Л-2
где
П1(Л) = Л"-2 + а1Хи->+ ... +а„.
24. Достаточные условия устойчивости' нелинейных систем
второго, третьего и четвертого порядков
Считаем, что нелинейная система содержит одно нелинейное
ввело, статическая характеристика которого .имеет любую форму,
но она обязательно однозначная, нечетная и симметричная относи-
тельно начала координат.
Производная от функции Ляпунова будет знакоопределенной
для систем третьего порядка, уравнения которых приводятся
к канонической форме (П.2), (П.8) или (ПЛЗ);
для систем четвертого порядка, уравнения которых приводятся
к той же форТче (П.2) или (П.13), но при наличии одного нулевого
корня в уравнении £>(А) = 0;
для систем четвертого порядка с уравнениями типа (П.2), (П.8)
или (ПЛЗ) без нулевого корня,- но при условии, что одному из
вещественных корней уравнения D (Z) = 0 соответствует отрица-
тельная постоянная Р; .
при выполнении условий
Г > 0 при 0- > — -р (П.18)
Г>2/^¥-/2 при (П.19)
где
Г2 = Т- + т- + '', (П.20)
А = ^(^-M24-(P,-fe) (Л, — Л2)
4Л,Л2 • 111 >
Для систем второго порядка, уравнения которых приводятся-
к- форме (П.7), справедливы условия (П.18) и (П.19) при г = 0, если
в формулах (П.20) и (П.21) заменить р, н р2 на yt и у2.
12S
ПРИЛОЖЕНИЕ
551.
25. Переход от л. а. х. вида 20 1g 11 4- W (/®) | к л. а. х.
вида 20 1g | W (/«) | (рис. 365, 366, 367)
Рис. 365.
6И
прилижьниь
Рис. 366.
25]
ПРИЛОЖЕНИЕ
553
Рис. 367.
554
ПРИЛОЖЕНИЕ
[26
26. Типовые л. а. х. систем с ЦВ!Ц
Выбор или Лс производится в соответствии с требованиями, предъявляе
26]
ПРИЛОЖЕНИЕ
555
при учете квантования по времени
мыми к точности или быстродействию системы е ЦВМ.
Таблица П.11
27. Типовые последовательные дискретные корректирующие звенья
№ п.п. Наименование звена Передаточная функция непре- рывного аналога 1Г (р) Дискретная передаточная функция D (г) Частотная передаточная функция । Переходная характеристика
1 Дифферен- цирующее \+Тр « V/ 1 м а N V о а о II I ii ~ - ф г 1 + г» Й Й ф / а j & г
2 Аналог пассивного дифферен- цирующего г 1 + Tip ° 1+Т2р С -I*. G° Т, ’ т,>т2 z — a z—b 0< а < 1, 0 < 6 < 1, а> b 1 + /т,Я, 1 -а 0 1 + /т2Х ’ и 1 - b ’ 1 + с TQ т0 Т* 1 - а 2 ’ “ 1 - 5 2 / If * 4 ’ *
3 Интегри- рующее k _ 1 Р ~ Тр а Z — 1 1-/4 а 2 Tq /^ р| 1*^гТ
556 ПРИЛОЖЕНИЕ
4 Изодром- ное 1+ 1 1 + Гр + N 1 » 1—* а 1 + jtZ / т f—*г1 J J.
4 Тр Тр Го /А. ЧМ) Тв
5 Аналог пассивного интегри- рующего 1 + Т2р I+TW 1\>т2 (1 + a) z + 1 — я (l + 6)z+l-6 а > 1, b > 1, - а < b t + /тгй, = Тр + 2тг -1 + ]ту‘к ’ и Тв +'2Т{ ’ Т — -г — а^с Т1“ 2 Т2“ 2 / 1 —4 ГТ !
^0 1 1 / 1 А А
6 Интегро- дифферен- нируюшее 1 + + Тр 7 Р az г — 1 Z— 1 Z а < 1 а-Ч- jdT^k + (,+т ) A aw / 1н~Г" t ..... -t^
/ТрЛ ( 1 + /^й)-
#1
i л , 2 . <вТ0 ' . 2ш 2 z— 1 1. В таблице использована псевдочастота л = z~- тв ь 2 Го Го z+ 1 2. Переходные характеристики построены для дискретного фильтра с Запдминанием на период повторения.
ПРИЛОЖЕНИЕ 557
28. Коэффициенты гармонической линеаризации основных нелинейных характеристик Таблица П.12
№ н.п. Статические характеристики нелинейного звена 4(a) д'(а)
1 Идеальная '&2 релейная tb_ 4с зга 0
0 X,
ПРИЛОЖЕНИЕ
»
Релейная о зоной иеугеспгеаяютмат
при Ъ
О
№ Статические характеристики
н.п. нелинейного звена
С зоной нечувствительности
и насыщением
K=tga
С зоной нечувствительности
без насыщения
q iai
прн a~^b2
Продолжение табл. П.12
зиняжо^иад
8
Типа люфта или зазпра
k
я
-z- + arcsin
при а 6
9
С насыщением
и гистерезисной петлей
&2
г'
k Г . с + kb , . с — kb
— arcsin —----1- arcsin —--h
я L ka ka
, c + kb f, (c + kf+ ,
+—^~V 1—iW~ +
c~kb -.P, (c — kb)2 ]
T ka V k2a2 J
c + kb
при a --------—
be
яа2
c + kb
при --------—
ПРИЛОЖЕНИЕ
10
4F
ЯП
v — амплитуда скорости
0
Б62
ПРИЛОЖЕНИЕ
I2B.
29. Нормированные амплитудно-фазовые частотные
характеристики релейных исполнительных механизмов
Релейный исполнительный механизм, состоящий из реле и дви-
гателя постоянного тока с независимым возбуждением (рис. 368, а),
рассматривается как одно нелинейное звено автоматической системы.
Рис. 368. Релейный исполнительный механизм.
Статическая характеристика реле изображена на рис. 368,6. Гар-
монически линеаризованная нормированная передаточная' функция’
релейного исполнительного механизма
Го (d, jz) = q0 (d, z) + jq'o (d, z),
где d — ~ — относительная амплитуда, г = <йТM — относительная ча-
стота, Тм — электромеханическая постоянная времени двигателя.
Нормированные амплитудно-фазовые характеристики построены
на рис. 369 и. 370 для различных значений коэффициента у, учиты-
вающего влияние статического момента нагрузки Л4И
Y = 1
Мн
Мо’
где Мо — пусковой момент двигателя.
На рис. 369 пунктиром показаны нормированные амплитудно-
фазовые характеристики, полученные в результате перемножения
нормированной гармонически линеаризованной передаточной, фуяк-
ции реле (см. приложение 28)
1/1-^
и нормированной амплитудно-фазовой характеристики двигателя
остоянного тока с независимым возбуждением
^(/2)=-, * .
" 1 1 + jZ
Сравнение этих характеристик показывает, что при небольших
значениях относительной амплитуды (d < 10) раздельное рассмот-
ение реле и двигателя является недопустимым.
ПРИЛОЖЕНИЕ
Рнс. 369. Нормированные а. ф. х. для случая Мя
Рис. 370. Нормированные а. ф. х. для случая Мн=/=0.
ПРИЛОЖЕНИЕ
565
30. Коэффициенты статистической линеаризации
некоторых типовых нелинейностей
Если на вход нелинейного звена со статической характеристи-
кой y = F(x) действует сигнал, представляющий собой случайный
процесс
х (/) = П1х (0 + Х° (О,
где тх(1) — его математическое ожидание, х° (1)—случайная центри-
рованная составляющая, то процесс на выходе нелинейного звена
приближенно может быть представлен в виде
У (0 =“ 1^тх U) + kax° (f). .
При заданной одномерной плотности вероятности w (х)' коэф-
фициенты статистической линеаризации k0 и fca вычисляются по
формулам
4-00
Г F (тх + х°) w (х) dx + F (тх)
m,J
— ----: = —----!----------------------,--
J xw (х) dx
—-ОО
1
4-00
f F (тх 4- х°) xw (х) dx
= RxU (0) _
2 Rx (0) +~
x2 w (x) dx
— oo
Ниже приводятся значения этих коэффициентов и их графики
для некоторых типовых нелинейностей при действии нормально»,
распределенного входного сигнала, имеющего нормированную плот*
иость вероятности
Z2'
ПРИЛОЖЕЙЙЕ
Рис. 371. Графики,для идеальной релейной характеристики.
80]
ПРИЛОЖЕНИЕ
567
Рис. 372. Графики для однозначной релейной характеристики с 30'
ной нечувствительности.
568
ПРИЛОЖЕНИЕ
ts®
в интеграл -вероятности
1) Идеальная релейная характеристика (рис. 371, а)
*0 = _£_2ф(-^), (П.22)
тх \ )
ki = JL Г 1 _ 4ф2 (^)Т/2, (П.23)
Чг L \
. - с —2
2~ Ох
(П.24)
Графики коэффициентов приведены на рис. 371,6, в'.
2) Однозначная релейная характеристика с зоной нечувстеи-
.тельности (рис. 372, а):
Графики коэффициентов приведены на рис, 372, б, в, е.
ПРИЛОЖЕНИЕ
.559
3) Релейная характеристика с гистерезисом (рис. 373).: ;: ...
Коэффициенты fe0 и определяются соответственно форму-
лами (П.25) н (П.27)
4) Неоднозначная релейная характеристика с зоной нечувст-
вительности (рис. 374)
5) Линейная характеристика с насыщением (рис. 375, а)
kB = -М (.1 + «ц) Ф (- d - "’*) Ф(-Цг^) +'
Г 1 ( l+m' Y __L 1
+ —f'-le 2 ' °' ' — е 2 ' °* ' J }, (П.ЗЗ)
У 2л J
Графики коэффициентов представлены • Иа рис? 375, б, в, е.
$
Рис. 376.
sij
ПРИЛОЖЕНИЕ
571
,. 6) Линейная характеристика с зоной нечувствительности
(рис. 376)
31. Нормированный интеграл плотности вероятности
нормального закона распределения
Значении функции Ф(и)
Таблица ПЛЗ
и Ф(и) и Ф(и) и Ф(и) и Ф(и)
0,00 0,000 0,66 0,245 1,32 0,407 1,98 0,476
0,02 0,008 0,68 0,252 1,34 0,410 2,00 0,477
0,04 0,016 0,70 0,258 1,36 0,413 2,04 0,479
0,06 0,024 0,72 0,264 1,38 0,416 2,08 0,481
0,08 0,032 0,74 0,270 1,40 0,419 2,12 0,483
672
•ПРИЛОЖРИИЕ
. |S1
Продолжение табл. ПЛЗ
и Ф (и) и ф (и) и и (Ф) | и Ф<«)
0,10. 0,040 0,76 0,276 1,42 0,422 ' 2,16 0,485
0,12 0,048 0,78 0,282 1,44 0,425 2,20 0,486
0,14 0,056 0,80 0,288 1,46 0,428 2,24 0,488
0,16 ’ 0,064 0,82 0,294 1,48 0,431 2,28 0,489
0,18 0,071 0,84 0,300 1,50 0,433 2,32 .0,490
0,20 0,079 0,86 0,305 1,52 0,436 2,36 0,491
0,22 0,087 0,88 0,311 1,54 0,438 2,40 0,492
0,24 0,095 0,90 ' 0,316 1,56 0,441 2,44 0,493
0,26 0,103 0,92 0,321 1,58 0,443 2,48 0,493
0,28 0,110 0,94 0,326 1,60 0,445 2,52 0,494
0,30 0,118 0.96 0,332 1,62 0,447 2,56 0,495
0,32 0,126 0,98 0,337 1,64 0,450 2,60 0,495
0,34 0,133 1,00 0,341 1,66 0,452 2,64 0,496
0,36 0,141 1,02 0,346 1,68 0,454 2,68 0,496
0,38 0,148 1,04 0,351 1,70 0,455 2,72 0,497
0,40 0,155 1,06 0,355 1,72 0,457 2,76 0,497
0,42 0,163 1,08 0,360 1,74 0,459 2,80 0,497
0,44 0,170 1,10 0,364 1,76 0,461 2,84 0,498
0,46 0,177 1,12 0,369 1,78 0,463 2,88 0,498
0,48 0,184 1,14. 0,373 1,80 0,464 2,92 0,498
0,50 0,192 1,16 0,377 1,82 0,466 2,96 0,499
0,52 0,199 1,18 0,381 1,84 0,467 3,00 0,499
0,54 0,205 1,20 0,385 1,86 0,469 3,20 0,4993
.0,56 0,212 1,22 0,389 1,88 0,470 3,40 0,4997
0,58 0,219 1,24 0,393 1,90 0,471 3,60 0,49984
82) ‘ -ПРИЛОЖЕНИЕ . 573 Продолжение табл. П.13
и Ф(и) и Ф(и) ' и Ф (и) и Ф («)
0,60 0,62 0,64 0,226 0,232 0,239 1,26 1,28 1,30 0,396 0,400 0,403 1,92 . 1,94 . 1,96 0,473 . 0,474 0,475 3,80 4,00 4,50 5,00 0,49993 0,49997 0,499997 0,49999997
32. Нормированная плотность вероятности закона распределения Значения функции w (z) = J е У 2эт нормального 2. Таблица . П.14
.. 0 2 3 4 5 - 6' 7 8 9'
0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 0,399 391 368 333 290 0,242 194 150 111 079 0,054 036 022 014 008 004 399 390 367 331 287 240 192 148 109 078 053 035 022 013 008 004 399 389 365 329 285 237 189 146 107 076 052 034. 021 013 008 004 399 389 364 327 283 235 187 144 106 075 051 033 021 013 007 004 399 $88 362 325 280 232 185 142 104 073 050 033 020 012 007 004 398. 387 360 323 278 230 183 139 102 072 049 032 020 012 007 004 398 386 359 321 276 228 180 137 101 071 048 031 019 012 007 004 398 385 357 319 273 225 178 135 099 069 047 030 019 011 007 004 398 384 356 317 271 223 176 133 097 068 046 030 018 011 006 00.4 397 383 354 314 269 220 174 132 096 067 045 029 018, 011 006 003
33. Моделирование элементов структурных схем автоматических систем на операционных усилителях
Таблица П.15
тэт
№ п.п. Название элемента Модель элемента Передаточная функция или уравнение элемента
1 Сумматор и. ГГ7Н “г* А. ип» EZH X 4J АН Т НН. X п un+l == Rq У ui i=*L
2 ' Инвертор p «2='—^-«1 =—«!. #0 = #l
3 Безынерционное зве- но У/ ,Jl_ X , , Rp R — " rj Al
ПРИЛОЖЕНИЕ
Апериодическое зве-
но первого порядка
См. также рис. 343
Апериодическое зве-
но второго порядка
См. также рис. 345
k
Ri
g
Пр)
k
Tp + l’
T = RBG
k
^(Р)°Г2„2 7rp . i
тгР +1 iP + 1
ПРИЛОЖЕНИЕ
R,R,
RiRe
<p R4R2R3Ci n*r
11 ~ —#5^6—’ 7 1 27 2’
№ Е. П. Название элемента
6 Колебательное звено
7 - Консервативное звено ч
8 Идеальное интегри- рующее звено (ин- тегратор)
Модель элемента
Схема совпадает со схемой набора
апериодического звена второго
порядка (позиция 5). См. также
рис. 34?, 345
Продолжение табл. П.15
Передаточная функция или уравнение
элемента
Т2р2 + ‘£>Тр+1 ’
R4R3 т —Л/ R4R2R3C
RiRe ’ V R6
1 .. Л RiRzRsCr
2 J/ 7ф?6С2 >6<
h
rW=WTT’“
b - ft4^3 T — T fft^gfts^ 1^2
RiRGr V ft6
R5 = 00 (отключено), | = 0.
ПРИЛОЖЕНИЕ
k 1
^(p) = 7.^-7c-
9' Инерционное инте- грирующее звено
10 Изодромное звено
k
ь 1П 1А2
g
w (р) = А -ь ki = ALLLZpL,
Ec'r-₽’c
ПРИЛОЖЕНИЕ
Примечание. Апериодическое звено второго порядка можно получить с помощью двух после-
довательно соединенных моделей апериодического звена первого порядка.
ПРИЛОЖЕНИЕ
34. Моделирование нелинейных статических характеристик на операционных усилителях
Таблица П.16
2
Статическая
характеристика
Схема, моделирующая статическую
характеристику
Уравнение или аналитическая запись
статической характеристики
Линейная
с ограничением
нли насыще-
ннем
Идеальная
релейная
—kult
—U3 при
“2= U
ku-i,---“=Cui^0,
R
Т, U<
Ut прн Ui =С--—,
ПРИ 'добр=°°; Гдпр> Г3 И Г4</?1.
ПРИЛОЖЕНИЕ:
Ro = °°> 'добр = /дпр, Гэ Н r4 < Ri
№
п. п.
Статическая
характеристика
Схема, моделирующая статическую
характеристику
3
Линейная
с зоной не-
чувствитель-
ности
4
Релейная с зо-
ной не чувстви-
тельности
Продолжение табл. П.16
Уравнение или аналитическая запись
статической характеристики
( ~k («1 - ut) при «1 > Uit
«2 = •>. k_(ut + £7S) при и, < — U3l.
I О, —U3 < щ < U4.
k “ ПрИ Гдобр~р0; гдпр» г3 И /?>•
—Us при U1> l/4,
U6 при w, C —U3,
О, —U3 U\ *C U4.
58') : ПРИЛОЖЕНИЕ
Гдобр- ~ 0>
Г3> Г4> И <6 < ^0-
—1/3 при «1 - Ui < ОД du,
-U4 при Uj > 0, j ПРИ di. .?* °’
U4 при щ + U4 > 0,1 dUl
—Us при u, + U4 < 0 J ПРИ dt <
U'2
k (щ — t/4) при - > 0,
k{Ul + Us) при ^-<0,
const при — U4^-^- — Us
b = C1^° ’
awiiaxovndij
582
ПРИЛОЖЕНИЕ
135
35. Таблица
И 0,0 С,05 0.10 .0,15 0,20 0,25 С.30 0,35 0.40 0,45
0,0 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
. 0,158 0,165 0,176 0,184 0,192 0,199 0,207 0,215 0,223 0,231
1,0 0,310 0,326 0,340 0,356 j 0,371 0,386 0,401 0,417 0,432 0,447
1,5 0,449 0,469 0,494 0,516 '0,538 0,560 0,580 0,603 0,617 0,646
2,0 0,572 0,597 0,628 0,655 0,683 0,709 0,733 0,7^1 0,786 0,810
2,5 0,674 0,705 0,739 0,771 0,802 0.833 0,861 0,891 0,916 0,943
3,0 0,755 0,790 0,828 0,863 0,896 0,928 0,958 0,987 1,013 1,038
3,5 0,814 0,853 0,892 0,928 0,963 0,994 1,024 1,050 1,074 1,095
4,0 0,857 0,896 0,938 0,974 1,008 1,039 1,060 1,090 1,107 1,124
4,5 0,883 0,923 0,960 0,997 1,029 1,057 1,080 1,100 1,115 1,129
5,0 0,896 0,936 0,978 1,012 1,042. 1,067 1,087 1,103 1,112 1,117
5,5 0,900 0,940 0,986 1,019 , 1,046 1,067 1,083 1,093 1,095 1,097
Q&, 0,904 0,943 0,982 1013 1,037 1,054 1,065 1,070 1,068 1,062
6,5 0,904 0,942 0,980 1,009 1,030 1,043 1,050 1,04^ 1,043 1,033
7,0 0,904 0,944 0,979 1,006 1,024 1,035 1,037 1,033 1,023 1,009
7,5 0,907 0,945 0,980 1,006 -1,019 1,025 1,025 1,017 1,005 0,989
8,0 0,910 0,951 0,985 1,008 1,020 1,024 1,021 1,012 0,995 0,981
8,5 0,918 0,956 0,989 1,010 1,021 1,022 1,018 1,007 0,992 0,277
9,0 0,924 0,965 0,997 1,016 1,025 1,025 1,018 1,006 0,992 0,978
9,5 0,932 0,972 1,004 1,022 1,029 1,027 1,019 1,006 0,993 0,982
10,0 0,939 0,978 1,009 1,025 1,031 1,027 1,019 1,006 0,993 0,987
10,5 0,946 0,985 1,013 1,028 1,033 1,028 1,017 1,005 0,993 0,991
11,0 0,947 0,988 1,015 1,029 1,031 1,025 1,014 1,002 0,993 0,991
11,5 0,949 0,988 1,016 1,027 1,028 1,021 1,010 0,999 0,991 0,989
12,0 0,950 0,988 1,015 1,025 1,024 1,015 1,004 0,994 6,988 0,987
12,5 0,950 0,989 1,013 1,022 1,019 1,010 0,999 0,990 0,986 0,986
13,0 0,950 0,989 1,012 1,019 1,015 1,005 0,994 0,986 0,985 0,987
13,5 0,950 0,990, 1,011 1,017 1,011 1,000 0,990. 0,983 0,984 . 0,988
351
ПРИЛОЖЕНИЕ
583
'ИКЦИЙ л (70)
-v/? Таблица П.17
Г 0,50 0,55 0,60 0,65 0,70 6,75 0,80 0,85 С,90 0,95 1,00
0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,240 0,248 0,255 0,259 0,267 0,275 0,282 0,290 0,297 0,304 0,314
0,461 0,476 0,490 0,505 0,519 0,534 0,547 0,562 0,575 0,593 0,603
0,665 0,685 0,706 0,722 0,740 0,758 0,776' 0,794 0,813 0,832 0,844
0,833 0,856 0,878 0,899 0,919 0,938 0,956 0,974 0,986 1,003 1,020
0,967 0,985 1,010 1,031 1,042 1,060 1,078 1,098 1,113 1,125 1,133
1,061 1,082 1,100 1,117 1,130 1,142 1,154 1,164 1,172 1,176 1,178
1,115 1,132 1,145 1,158 1,161 1,166 1,171 1,174 1,175 1,175 1,175
-1,142 1,152 1,158 1,159 1,160 1,161 1,156 1,149 1,141 1,131 1,118
1,138 1,134 1,134 1,138 1,132 1,127 1,111 1,099 1,085 1,071 1,053
1,118 1,115 1,107 1,098 1,084 1,069 1,053 1,037 1,019 1,001 0,986
1,092 1,083 1,070 1,050 1,032 1,016 0,994 0,979 0,962 0,951 0,932
1£51 1,037 1,021 1,003 0,984 0,966 0,949 0,934 0,922 0,914 0,906
1,018 1,001 0,982 0,965 0,948 0,936 0,920 0,910 0,903 0,903 0,905
0,993 0,975 0,957 0,941 0,927 0,917 0,911 0,908 0,909 0,915 0,925
0,974 0,958 0,944 0,926 0,922 0,911 0,920 0,927 0,934 0,946 0,958
0,966 0,951 0,941 0,935 0,932 0,936 0,944 0,955 0,970 0,986 1,004
0,966 0,949 0,944 0,948 0,951 0,958 0,974 0,990 1,006 1,023 1,041
0,970 0,960 0,961 0,966 0,976 0,990 1,006 1,023 1,039 1,053 1,061
0,975 0,972 0,980 0,987 1,000 1,015 1,033 1,048 1,059 1,066 1,066
0,982 0,985 0,993 1,006 1,020 1,036 1,049 1,059 1,063 1,062 1,056
0,987 0,996 1,007 1,017 1,033 1,046 1,054 1,058 1,055 1,048 1,033
0,993 1,002 1,014 1,027 1,039 1,047 1,048 1,044 1,034 1,021 1,005
0,997 1,006 1,017 1,029 1,037 1,043 1,034 1,024 1,010 0,994 0,977
4997 1,006 1,019 1,026 1,027 1,025 1,015 1,000 0,984 0,969 0,958
0,997 1,006 1,018 1,019 1,017 1,010 0,995 0,979 0,965 0,954 0,949
0,997 1,006 1„014 1(012 1,005 0,993 0,980 0,964 0,955 0,950 0,955
0,998 1,006 1,010 1,005 0,995 0,982 0,968 0,958 0,954 0,958 0,970
966*0 Z66*0 300*1 WO* I 666‘0 866*0 666*0 ZOO* I SOO* I SZ6‘0 0*98
966*0 866*0 800*1 WO* I 666*0 866*0 666*0 800*1 800*1 SZ6*0 8*93
966*0 000*1 WO* I 800*1 666*0 866*0 000'1 800*1 800*1 SZ6‘0 0*83'
,Z66f0: 100*1 900*1 800*1 666*0 966*0 000*1 600*1 SOO* I SZ6‘0 S‘f-3
Z66*0 500*1 Z00*l 800*1 666*0 966'0 100*1 010*1 SOO‘l SZ6‘0 0*1-3
866*0 800*1 800*1 WO* I 866*0 966*0 300*1 010*1 SOO* I SZ6‘0 8*85
666*0 800*1 ZOO* I WO* I Z66‘0 966*0 300*1 ПО* I SOO* I H6‘0 0*83
666’0 WO* I 900'1 300*1 866*0 966*0 300*1 110* I 3OO‘l ez6*o 8*33
000*1 WO* I 800*1 000*1 866*0 866*0 300*1 110*1 3OO‘I IZ6‘0 0*33
100’ I W0‘l WO* I 666*0 366*0 866*0 800*1 HO* I 300*1 696*0 8*13
100*1 WO* I 800'I Z66‘0 366*0 W6‘0 800*1 110*1 300*1 896*0 0*13
100*1 WO'l 300*1 966*0 166*0 W6*0 WO* I 310*1 300*1 896*0 8*03
500*1 SOO* I 100*1 866*0 166*0 866*0 800*1 810* I 000*1 Z96‘0 0*08
WO* I 800*1 100*1 866*0 166*0 966*0 900*1 1-10*1 000*1 Z96‘0 8*61
900* Г 900*1 100*1 866*0 366*0 866*0 800*1 SIO‘I 000*1 Z96‘0 0*61
600*1 ZOO*! 100*1 866*0 W6‘0 100*1 600*1 SlO‘l 100*1 996’0 8*81
ою'г 800*1 ICO* I 866*0 866*0 300*1 110*1 810* I 300'1 996*0 0*81
010‘f 900*1 866*0 W6*0 866*0 800*1 310*1 810*1 300*1 996*0 S'ZI-
010*1 800*1 Z66*0 W6*0 866*0 800*1 810*1 910*1 100*1 896*0 O‘Z‘I
600*1 300'1 866*0 866'0 866*0 800*1 1-10*1 910*1 666*0 1-96'0 8*91
ZOO‘1 866*0 366*0 166*0 866*0 900*1 t-10‘1 810*1 Z66‘0 196*0 0*91
WO* I 966*0 886*0 686*0 866*0 900*1 ИО* I t-10‘1 866*0 686*0 8‘8-Г
000*1 166*0 Z86*o" 886*0 866*0' ZOO* I f'lO'l 510*1 866*0 986*0. 0*8-1
966*0 886*0 886*0 Z86‘0 966*0 800*1 810*1 310*1 066*0 f-86‘0 8*1-1
166*0 886*0 886*0 886*0 Z66*0 600*1 910*1 I 10* I 686*0 386'0 0*M-.
f Sfr’o’ Ofr’O . se'o oe*o ss'o OS ‘0 SI'O OI‘O so1 о 0‘0 И
яинаЖок-йЛ t \
ад ПРИЛОЖЕНИЕ§85
Продолжение табл. П.17
0.50 0.55 0,60 0,65 0.70 0,75 0,80 0,85 0,90 0.95 1.00
1,000 1,006 1,008 0,999 0,987 0,974 0,965 0,961 0,965 0,976 0,990
1,002 1,006 1,005 0,994 0,983 0,970 0,969 0,971 0,981 0,997 1,010
1,005 1,007 1,002 0,993 0,983 0,976 0,978 0,987 1,001 1,017 1,030
1,008 1,007 1,001 0,993 0,985 0,984 0,991 1,003 1,019 1,032 1,040
1,011 1,008 1,001 0,994 0,990 0,993 1,003 1,018 1,031 1,039 1,039
1,0И 1,008 1,001 0‘,996 0,995 1,001 1,014 1,027 1,036 1,038 1,028
1,012 1,007 0,999 0,997 0,999 1,008 1,020 1,030 1,032 1,027 1,012
1,009 1,005 0,997 0,998 1 002 1,012 1,023 1,027 1,023 1,013 0 988
1,008 1,002 0,997 0,998 1,004 1,014 1,020 1,018 1,008 0,993 0,979
1,006 0,999 0,995 0,998 1,003 1,012 1,014 1,007 0,993 0,978 0,969
' 1,001 0,995 0,993 0;997 1,004 1,009 1,006 0,995 0,981 0,969 0,967
0,998 . 0,992 0,992 0,996 1,003 1,005 0,998 0,985 0,973 0,967 0,973
0,996 0,991 0,992 0,995 1.W3 1,001 0,991 0,979 0,972 0,974 0,985
0,995 0,991 0,994 0,996 1,001 0,996 0,986 0,976 0,974 0,990 1.Р01
0,995 0,993 0,997 0,996 0,999 0,993 0,983 0,975 0,981 1,002 1,016
0,996 0,995 1,000 0,995 0,998 0,992 0,986 0,988 0,997 1,013 1,024
. 0,996 0,996 1,000 0,997 0,997 0,991 0,991 0,997 1,012 1,024 1,029
0,997 1,000 1,004 1,000 0,996 0,992 0,998 1,008 1,022 1,028 1,026
0,998 1,001 1,006 1,001 0,997 0,994 1,002 1,015 1,025 1,027 1,016
0,999 1,002 1,007 1,002 0,998 0,997 1,007 1,017 1,023 1,023 1,002
1,000 1,002 1,008 1,003 0,999 1,000 1,008 1,017 1,015 1,012 0,988
1,000 1,002 1,006 1,003 1,000 1,002 1,008 1,014 1,005 0,995 0,979
1,000 1,002 1,004 1,003 1,001 1,003 1,005 1,008 0,991 0,985 0,975
1,000 1,002 1,002 1,002 1,002 1,004 1,004 1,001 0,986 0,978 0,977
1,000 1,002 1,000 1,001 1,002 1,004 • 1,002 0,987 0,984 0,977 0,983
ЛИТЕРАТУРА
. . 1. Анисв нов В. И., Вавилов А. А., Фатеев А. В.,
Сборник примеров и задан по лиирйной теории автоматического
регулирования. Госэнергоиздат,. 1959.
2. Бесекерский В. А., Попов Е. П., Теория систем
автоматического регулирования, «Наука», 1966. 1
3. Б есекерскнй В. А., Востоков С. Б., Це й тли и Я.
Электромеханические сглаживающие устройства, «Судострое-
ние», 1964.
4. Б е с е к е р с к и й В. А., О р л о в В. П., По л о н с к а я Л. В,,
Федоров С. М., Проектирование следящих систем малой мощ-
ности, Судпромгиз, 1958.
5. Б е с е к е р с к и й В. А., Ф а б р и к а и т Е. А., Динамический
синтез систем гироскопической стабилизации, «Судостроение», 1968.
6. Васильев Д. В., Митрофанов Б. А. и др,,• Проекти-
рование и расчет следящих систем, «Судостроение», 1964.
7. В а с и ль ев Д. В., Ч у и ч В. Г., Системы автоматического
управления, «Высшая школа», 1967.
8. Воронов А. А., Основы теории автоматического управле-
ния, части 1 и 2, «Энергия», 1966. «
9. Джеймс X., Ник о ль с Н., Филлипс Р., Теория сле-
дящих систем, ГИИЛ, 1953.
. 10. Егоров К. В., Основы теории автоматического регули-
рования, «Энергия», 1967. , .
11. Ивахненко А. Г., Техническая кибернетика, ГИТЛ УСС'Р,
1959.
12. Казаков И. Е., Доступов Б. Г., Статистическая ди-
намика нелинейных автоматических систем, Физматгиз, 1962.
13. К а з а м а р о в А. А., П а л а т и и к А. Т., Роднянский Л. О.,
Динамика двумерных систем автоматического регулирования
«Наука», 1967.
14. Коган Б. Я-, Электронные моделирующие устройства,
Физматгиз, 1963.
15. Красовский А. А., Поспелов Г. С., Основы авто-
матики и технической кибернетики, ГЭИ, 1961.
16. Ку зин Л. Т., Расчет и проектирование дискретных систем-
управления, Машгиз, 1962,
17. Кузовков Н. Т., Теория автоматического регулирова-
ния, основанная :на частотных методах, Оборонгиз, 1960.
18. Летов А. М., Устойчивость нелинейных регулируекШх
систем, Гостехиздат, 1955.
19. Лурье А. И., Некоторые нелинейные задачи теории авто-
матического регулирования, Гостехиздат, 1951.
JIMI ЕРАТУРА
587
20. Павлов А. А., Синтез релейных систем оптимальных по
быстродействию, «Наука», 1966.
21. Первозванский А; А., Случайные процессы в нели-
нейных автоматических системах, Физматгиз, 1962.
22. Под ред. Петрова Б. Н., Автоматическая оптимизация
управляемых систем, ИЛ, 1960.
23. Попов Е. П„ Динамика систем автоматического пегчли-
рования, ГИТТЛ, 1954. _ р у,,1И
24. Попов Е. П„ Автоматическое регулирование и управле-
ние, Физматгиз, 1962.
25. Попов Е. П., П а л ь т о в И. П., Приближенные методы
исследования нелинейных автоматических систем, Физматгиз, 1960.
26. Пугачев В. С., Теорий случайных функций и ее приме-
нение к задачам автоматического управления, Физматгиз, 1960.
27. Пупков К. А., Статистический расчет нелинейных систем
автоматического управления, «Машиностроение», 1965.
28. Скворцов С. В., Синтез корректирующих устройств
судовых следящих систем, «Судостроение», 1968.
29. Солодов А. В., Линейные системы автоматического
управления с переменными параметрами, Физматгиз, 1962.
30. Солодовников В. В., Статистическая динамика ли-
нейных систем автоматического управления, Физматгиз, 1960.
31. Солодовников В. В., Топчеев Ю. И., Крути-
ков а Г. В., Частотный метод- построения переходных процессов:
с приложением таблиц и номограмм, Гостехиздат, 1955.
32. Под ред. Солодовникова В. В., Техническая кибер-
нетика, книги 1 и 2, Теория автоматического регулирования,
«Машиностроение», 1967.
33. Т р а к с е л Дж. Дж., Синтез систем автоматического регу-
лирования, Машгиз, 1959.
34. Под ред. Траксела Дж. Дж., Справочная книга по
технике автоматического регулирования, ГЭИ, 1962.
35. Т у Ю. Т., Цифровые и импульсные системы автоматичес-
кого управления, «Машиностроение», 1964.
36. Фатеев А. В., Основы линейной теории автоматического
регулирования, Госэнергоиздат, 1954.
37. Ф е л ь д б а у м А. А., Вычислительные устройства в авто-
матических системах, Физматгиз, 1959.
38. Федоров С. М., Литвинов А. П., Автоматические
системы с цифровыми управляющими машинами, «Энергия», 1965.
39. Хлыпало Е. И., Нелинейные системы автоматического
регулирования, «Энергия», 1967.
40. Цыпкин Я. 3., Теория линейных импульсных систем,
Физматгиз, 1963.
41. Цянь Сюэ-сень, Техническая кибернетика, ИЛ, 1956.
42. Честнат Г., Майер Р., Проектирование и расчет сле-
дящих систем и систем регулирования, части 1 и 2, ГЭИ, 1959.
43. Шаталов А. С., Структурные методы в теории управ-
лении и электроавтоматике, Госэнергоиздат, 1962.