ЗАДАЧНИК
по теории
автоматического

ЗАДАЧНИК
ПО ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Под редакцией доктора техн. наук,
профессора А. С. ШАТАЛОВА
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ
Допущено Министерством высшего
и среднего специального образования
СССР в качестве учебного пособия
для студентов высших технических
учебных заведений
э
МОСКВА «ЭНЕРГИЯ» 1979

ББК 32.965
3-15
УДК 681.5.011(075.8)
Задачник по теории автоматического управлеп.^х:
3-15 Учеб. пособие для вузов/ Андреев Н. И., Василь¬
ев С. К., Захаров В. Н. и др.; Под ред. А. С. Ша¬
талова.— 2-е изд., перераб. и доп.— М.: Энергия,
1979. — 544 с., с ил.
В пер.: 1 р. 20 к.
Задачник предназначен для практического закрепления вопросов,
излагаемых в учебниках по теории автоматического управления. Кни¬
га содержит задачи, ответы и решения типовых для каждого раздела
задач, справочные таблицы, графики и номограммы. Тематика задач
полностью согласована с новым учебным пособием по заданному
курсу. По сравнению с первым изданием (1971 г.) добавлена значи¬
тельная часть задач, посвященных новым темам, ранее не освещав¬
шимся в курсе. Расширены разделы, содержащие методы оптимиза¬
ции и кибернетические методы.
Задачник рассчитан на студентов вузов, специализирующихся
в области автоматического управления.
^ 30501-310	ББК	32.965
3 	 140-79.	1502000000
051(01)-79	6Ф6.5
Николай Ильич Андреев, Станислав Константинович Васильев,
Виктор Николаевич Захаров, Михаил Михайлович Коротенин,
Николай Семенович Лепилов, Сергей Тимофеевич Павлов,
Александр Степанович Шаталов
Задачник по теории автоматического управления
Рецензент Б. К. Чемоданов
Редактор Н. А. Медведева
Переплет художника С. Н. Орлова
Технический редактор О. Д. Кузнецова
Корректор Г. А. Полонская
ИБ № 2016
Сдано в набор 22.11.78	Подписано в печать 14.06.79	Т-09884
Формат 84X1 ОЗ^зл Бумага типографская № 2 Гарн. шрифта литературная
Печать высокая	Уел.	печ.	л.	28,56	Уч.-изд.	л.	26,84
Тираж 21 000 экз.	Заказ	903	Цена	1	р.	20	к.
Издательство «Энергия», 113114, Москва, М-114, Шлюзовая наб., 10
Московская типография № 10 Союзполиграфпрома при Государствен¬
ном комитете СССР по делам издательств, полиграфии и книжной
торговли. 113114, Москва, М-114, Шлюзовая наб., 10
© Издательство «Энергия», 1979 г.

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Основное содержание задачника сохранено,
поскольку оно опиралось на установившиеся
учебные программы по теории автоматическо¬
го управления (ТАУ). Однако за истекшие
7 лет после первого издания вышел ряд учеб¬
ников и учебных пособий по ТАУ, поэтому
авторы внесли определенные добавления
в текст задачника. Наиболее близок стиль по¬
строения задач и принятые обозначения
к учебному пособию «Теория автоматического
управления» под редакцией А. С. Шаталова
(М., «Высшая школа», 1977), при написании
которого имелось в виду использовать новое
издание задачника в учебном процессе. Авто¬
ры старались исправить все недочеты первого
издания и надеются, что вновь возникшие за¬
мечания будут сообщены читателями в адрес
редакции, за что авторы им заранее благо¬
дарны.
Редактор

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В существующих задачниках по теории автоматиче¬
ского управления [2, 4, 7, 13, 18] практически отраба¬
тываются уже ставшие традиционными методы расчета
элементов и систем автоматического управления, осве¬
щенные в учебной и научно-технической литературе.
Однако в последнее время написан ряд монографий
[1, 3, 8, 15, 19, 26], в которых излагаются дополнитель¬
ные, в ряде случаев более эффективные и достаточно
простые для включения в учебный процесс и инженерную
практику расчетные приемы и методы анализа и син¬
теза.
При составлении данного задачника авторы наряду
с учетом традиционного материала использовали также
указанную выше литературу, отражающую точку зрения
авторов на ряд прикладных вопросов автоматического
управления.
Расположение материала в задачнике преследует
цель обеспечения последовательного практического осво¬
ения основных вопросов теории автоматического управ¬
ления (ТАУ). Современные курсы ТАУ насыщены мате¬
матическим содержанием: это составление уравнений си¬
стем и звеньев, их преобразование и т. д. Но вид урав¬
нений и их порядок существенно зависят от того, какую
область частот охватывает математическая модель явле¬
ния. Поэтому в первых разделах задачника рассматри¬
вается частотный состав сигнала, а также на ряде при¬
меров закрепляются далеко не простые понятия ступен¬
чатой и импульсных функций.
Для анализа процессов во временной области предло¬
жен ряд задач, закрепляющих навыки в практическом
решении матричных уравнений систем и составлении ма¬
тричных уравнений сигналов. Однако центральное место
занимают задачи, направленные на усвоение оператор¬
ных и частотных методов.
4

Как отметил еще акад. А. А. Андронов, операторные
методы являются азбукой теории регулирования, и хотя
они просты по своей основе, то в применении, например,
к дискретной модуляции со сложным формирователем
меандры или модуляции ключом длительного контакта и
в других случаях приводят к большому числу новых со¬
отношений, для которых каждый раз пришлось бы соз¬
давать отдельные таблицы соответствий.
Поэтому в задачнике на ряде примеров поясняется
методика Я-преобразоваиий функций и их изображений,
позволяющая все практические приложения операторно¬
го метода и метода преобразования Фурье свести в еди¬
ную наглядную систему [3, 26].
В задачнике, как и в некоторой другой литературе по
ТАУ [3, 15], не ставилась цель обособить нестационар¬
ные линейные системы от стационарных. Напротив, по¬
добраны задачи, иллюстрирующие общность ряда мето¬
дов анализа: матричного, операторного, близость оценки
начальных значений и т. п.
Первые три главы задачника охватывают в необхо¬
димой последовательности основные проблемы анализа и
синтеза аналоговых линейных систем. Любая более
сложная система неизбежно содержит линейную анало¬
говую часть или при ее анализе используется метод ли¬
неаризации, поэтому в указанных первых главах собра¬
но наибольшее число задач. В этих главах на примерах
линейных аналоговых систем рассмотрены основные
проблемы и последовательность развития задач управ¬
ления. Поэтому для систем другого рода оказалось до¬
статочным рассмотреть только специфические для них
примеры.
В гл. 4, где рассматриваются задачи по дискретным
системам, основное внимание обращено на задачи, ил¬
люстрирующие специфические режимы ключа, требую¬
щие применения аппарата зональных модифицированных
^-передаточных функций. Большое внимание уделено
разработке задач, способствующих внедрению нового
перспективного метода параметров состояний.
Задачи гл. 5 по нелинейным системам тщательно от¬
бирались для охвата современного состояния вопроса,
^яд элементарных задач подобран для показа принци¬
па расчета нелинейных оптимальных систем.
Статистические методы расчета собраны в гл. 6, хотя
они в равной степени могли бы быть распределены и по
5

остальным главам, поскольку детерминистские методы
расчета являются частным случаем статистических рас¬
четов. Однако концентрация материала сделала более
естественным переход от простых задач к сложным и по¬
могла разработке новых наглядных задач:
по непосредственной и статистической линеаризации
для анализа и синтеза нелинейных систем;
по определению оптимальных аналоговых и дискрет¬
ных систем по сложным критериям, частным случаем
которых является минимум среднеквадратичной ошибки.
Задачи по вопросам технической кибернетики, со¬
бранные в гл. 7, следует рассматривать как обзорный
материал, так как существующая степень практического
использования технических решений дает еще мало дан¬
ных для цифровых расчетов, приемлемых для задачника.
Все задачи имеют ответы. Основные задачи имеют
решения и пояснения, способствующие систематической
проработке материала в рекомендуемой последователь¬
ности.
Задачник предназначен для самостоятельной работы
над курсом ТАУ студентами очного и заочного обучения,
а также инженерами и научно-техническими работни¬
ками.
Для удобства самостоятельной работы в книге вве¬
дены три изолированные части:
текст задач (подготовленный читатель может решать
часть из них, не обращаясь к ответам);
ответы и решения;
приложения в виде таблиц преобразований, таблиц
специальных функций и номограмм.
Нумерация задач принята трехразрядная: глава, па¬
раграф, порядковый номер внутри параграфа. Например,
1-3-5 означает 1-я глава, 3-й параграф, задача № 5.
В ответах впереди добавляется цифра 0, т. е. для того
же примера будет 01-3-5.
Сквозная нумерация рисунков отсутствует, они рас¬
пределены по соответствующим задачам (1-3-5) или от¬
ветам (01-3-5).
Между авторами материал распределен следующим
образом: А. С. Шаталов — основной материал гл. 1»
гл. 2, § 3-2, § 4-1, задачи 4-2-8, 6-1-20, 6-1-21, приложе¬
ния; С. Т. Павлов —§ 1-7, 1-8, гл. 3; В. Н. Захаров-^
гл. 4; Н. С. Лепилов — гл. 5, задача 1-8-15; Н. И. Андре¬
ев, С. К. Васильев — гл. 6; М. М. Коротенин — гл. 7.

Часть первая
ЗАДАЧИ
Глава первая
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
АНАЛОГОВЫМИ СТАЦИОНАРНЫМИ
И НЕСТАЦИОНАРНЫМИ ЗВЕНЬЯМИ
1-1. ЗАДАНИЕ ТИПОВЫХ ВХОДНЫХ СИГНАЛОВ
В АНАЛОГОВОЙ И ЧАСТОТНОЙ ФОРМАХ
1-1-1. Для изображенного на рис. 1-1-1 прямоуголь-
ного вещественного спектра ограниченной полосы соо и
единичной высоты p*((o) = l:
а) определить соответствующий этому спектру про¬
цесс Xi[t)\
б) построить график процесса и вычислить его пло¬
щадь;
рх(со)
со
-соо
COq
в) определить зависи¬
мость времени первого
перехода процесса через
нуль Т\ (величины, об¬
ратной быстродействию)
от ширины полосы спек¬
тра и построить график
этой зависимости;
г) установить предель¬
ный процесс, которому эквивалентен X\[t) при бесконеч¬
ном расширении полосы ±соо-
1-1-2. Для процесса, заданного в виде нормированной
функции интегрального синуса
t
dt,
Рис. 1-1-1.
V ГА 2 с; 4-	2	Г	sin	со
Si«^=—]—г
график которого дан на рис. 1-1-2, найти соответствую¬
щий ему частотный спектр и построить его график.
7

Рис. 1-1-2.
Определить процесс,
эквивалентный лг2[/) при
бесконечном расширении
ПОЛОСЫ dzCDo*
1-1-3. По известному
мнимому частотному
спектру единичной функ¬
ции %2(со) =—I/o найти
спектры:	импульса 8[i)
его производных ем.
8[f], а также спектры ли¬
нейной М[/) и квадра-
t ^
ТИЧНОЙ	функций.
1-1-4. Для процесса с вещественными и мнимыми па¬
раметрами, записанного в форме комплексной экспонен¬
циальной функции
е (f, т], Q, ср) = exp [*qf -f / (Qt -f 9)],
найти преобразование Фурье по переменной t:E(jсо, г],
Q, ф) при г|<0. Далее, применяя ^-преобразования в ви¬
де операций выделения вещественной (Re) и мнимой
(1ш) частей, а также полагая отдельные параметры рав¬
ными нулю, найти все возможные виды производных
процессов и соответствующих им спектров в пределах
заданных видов Я-преобразования.
1-1-5. К полученным в предыдущем примере соотно¬
шениям между процессами и спектрами применить до¬
полнительные Я-преобразования в виде операций диф¬
ференцирования по параметру г\ (д/дц) и этим методом
определить спектры процессов:
а) te*f;
б) £-е«;
\ tk
в> кГ’
г)	te4<sin(Q/-l-<p).
1-1-6. Определить спектр амплитудно-модулированно-
го сигнала
x[t) —sin (1 ^—|—ф1) sin (-'Яг^Н-'Фг)
методом подбора необходимого Я-преобразования.

1-1-7. Входной процесс задан в виде произведения
смещенного импульса 6Ю—0] при 0=2 с и его произ¬
водных по времени на непрерывный нестационарный ко¬
эффициент
6(0 = sin у
Найти следующие произведения, характеризующие
интенсивность и дифференцирующие свойства импульса:
а) njoNWK-G];
б) пгм=б(оч*-е];
в) пло=$(*) 8 р-:®].
1-1-8. Дана непрерывная функция b(t)= 5e2t. Найти
следующие интегралы, характеризующие фильтрующие
свойства импульса:
а) М0= J 6(0 6^ — 0]
о
б) M0=J b(t)8[t — b]dt;
о
в) Рз (0 = J b{t)b[t-b\dt
о
при 0=7 с.
1-2. СОСТАВЛЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ЗВЕНЬЕВ
1-2-1. Дано дифференциальное уравнение для систе¬
мы управления (в классической форме записи) относи-
юшей? ?Т?неСТН?Й (выходной) У и заданной (управля-
щей) х функции независимого аргумента (времени) t:
ап(t)t/W(t)... -\-a0(t)y(t) =
=bm{t)x(m)(t)-\- ... -j-60(0x(0.
ренциальных
линейных операторов.
9

1-2-2. Дифференциальное уравнение для системы управления
в классической форме записи имеет вид:
Дп0<п)(Ч+ • • • +а0y{t)=bmX(m)(t)-\- , . . -|~b0X(t).
Записать данное уравнение в операторной форме при нулевых
начальных условиях.
1-2-3. Определить размерность коэффициентов при производных
в следующих уравнениях системы управления, заданных в различ¬
ных формах:
(T2p+l)Uv(p) = {Tlp+l)Ux(p);
(atp2+aip+4 )Uy(p) = (bjp-Hl )Ux(p);
Ci У (i) + У (t) =dzx (t) + dtx (t)+x(t):
(2	= (th
1-2-4. Дано дифференциальное уравнение, описывающее плоское
вращательное движение самолета:
я2 (0	+	(0j	+	«о	(0	0	= МО * + ьо (О 0с + мв,
где a2(t) = d2—c2t— коэффициент момента инерции; ai(t) =
f=k2(t—C\)2-\-d\ — коэффициент тушащего момента; a0(t)=ko(t—
—c0)2+do — коэффициент аэродинамического стабилизирующего мо¬
мента; b0(t) =a0(t); bi(t)=lit+hi — коэффициент момента рулей;
тъ — возмущающий момент.
Рис. 1-2-4.
Физический смысл углов 0, 0С и б виден из рис. 1-2-4. Записать
данное уравнение в перечисленных в задаче 1-2-1 формах.
1-2-5. Даны в общей форме дифференциальные уравнения сле¬
дующих звеньев с постоянными параметрами:
aiy+aoy = boX — апериодического;
aQy=biX+bQx — форсирующего первого порядка;
10

агу + а^у+аъу — ЬцХ — колебательного;
С12У+сюу = Ьох — резонансного;
a0y = b2X + biX-\rboX — форсирующего второго порядка;
aoy = bix — дифференцирующего;
aiy+my = bix — реального дифференцирующего;
а\у = Ьох — интегрирующего.
Записать заданные уравнения в алгебраизованной и оператор¬
ной формах.
1-2-6. По заданному дифференциальному уравнению
звена ci2y-\-aiy-\-aoy=:boX-\-bix получить дифференциаль¬
ные уравнения:
а) для полной импульсной характеристики;
б) для приведенной импульсной характеристики;
в) для перехода от приведенной импульсной характе¬
ристики к полной.
1-2-7. Дана желаемая приведенная импульсная ха¬
рактеристика звена с постоянными параметрами (стаци¬
онарного) в.виде
g [0 — ~Yzq e~zt s in £3/,
где о = Е/71; Q = -^r-]/l—£2 при условной постоянной
времени Г=0,1 с и относительном коэффициенте затуха¬
ния |=0,6.
Составить дифференциальное уравнение звена для
приведенной импульсной характеристики и для переход¬
ной характеристики при заданном коэффициенте усиле¬
ния k=\0.
1-2-8. Для звена с переменными параметрами (неста¬
ционарного) составить дифференциальное уравнение, ре¬
шением которого является приведенная импульсная ха¬
рактеристика вида
где о=2 с-1; £3=6 с-1.
Записать уравнение для момента подачи импульса
to, заданного в буквенной форме, и для конкретного чис¬
лового значения /0=Ю с.
1-2-9. Составить уравнение цепи, приведенной на рис.
11

1-2-10. Составить дифференциальное уравнение цепи,
приведенной на рис. 1-2-10.
1-2-11. Составить дифференциальное уравнение для
условий передачи напряжений контуром, приведенным на
рис. 1-2-11.
1-2-12. Усилитель постоянного тока с большим коэф¬
фициентом усиления охвачен отрицательной обратной
связью, как показано на рис. 1-2-12.
Составить дифференциальное уравнение усилителя
постоянного тока, если:
а) в обратной связи усилителя включен параллель¬
ный контур Ro.cC;
б) в обратной связи усилителя включен только кон¬
денсатор С (/?о.с=0);
в) в обратной связи усилителя включен только рези¬
стор Ro.c (С=0).
1-2-13. Составить дифференциальное уравнение, опи-
Рис. 1-2-11.
Рис. 1-2-12.
R
Рис. 1-2-13.
сывающее передаточные свойства схемы, приведенной на.
рис. 1-2-13.

1-2-14. Составить дифференциальные уравнения для условий
передачи напряжения контурами, приведенными на рис. 1-2-14.
Rt
0Ч=Л-
и*
0-
иа
а)
-г С2
 0
“я
.0—
я
в)
“0
Яф
Рис. 1-2-14.
1-2-15. Составить дифференциальное уравнение для схемы, при¬
веденной на рис. 1-2-14,а, если выход нагружен резистором Ra.
1-2-16. Составить дифференциальные уравнения для схем, при¬
веденных на рис. 1-2-16.
иг
0-
LCl
а)
0—
(?)
П “у
  -0
Рис. 1-2-16.
13

1-2-17. Составить дифференциальное уравнение фильтра низкой
частоты, изображенного на рис. 1-2-17.
Рис. 1-2-17.	Рис.	1-2-18.
1-2-18. Для электродвигателя постоянного тока с независимым
возбуждением (рис. 1-2-18) составить уравнение, связывающее на¬
пряжение, приложенное к якорю, с углом поворота выходного вала,
пренебрегая несовпадением между противо-э. д. с. и приложенным
напряжением.
1-2-19. Составить дифференциальное уравнение, устанавливаю¬
щее зависимость между током управляющего реле и углом поворота
вала руля электрогидравлической рулевой машины, изображенной'
на рис. 1-2-19, где / — управляющее реле; 2, 3 — золотниковые
поршни; 4 — рабочий поршень; 5 — рал руля.
От насоса
При подаче управляющего сигнала поворачивается якорь управ¬
ляющего реле и золотниковые поршни перераспределяют значения
дроссельных сечений. Вследствие этого в рабочем цилиндре обра¬
зуется перепад давления, что вызывает перемещение поршня. Дви¬
жение поршня преобразуется в поворот выходного вала рулевой
машины.
1-2-20. Принципиальное устройство гидравлического двигателя
поступательного движения показано на рис. 1-2-20, где 1 — золот¬
ник; 2 — рабочий цилиндр, 3 — поршень. Гидросмесь под некоторым
давлением поступает от насоса в полость / или II рабочего ци¬
14

линдра й производит перемещение поршня. Управление движением
поршня осуществляется путем перемещения поршня золотника,
который перекрывает входные отверстия в полости цилиндра / или //.
Составить дифференциальное уравнение гидравлического двига¬
теля. При этом внешней нагрузкой и массой поршня пренебречь.
Считать, что скорость v прохождения жидкости через отверстие
постоянна.
\ v
1-2-21. Двухстепенной интегрирующий гироскоп изображен на
рис. 1-12-21. При вращении основания гироскопа вокруг входной оси
(оси чувствительности) с угловой скоростью (Оу возникает гироско¬
пический момент Мг = Н(ду, под действием которого гироскоп по¬
ворачивается вокруг выходной оси х, чему противодействует
демпфер, создающий момент M^=ka)x = h^.
Составить дифференциальное уравнение интегрирующего гиро¬
скопа.
1-2-22. Составить дифференциальное уравнение для электрогид-
равлической рулевой машины, изображенной на рис. !1-2-19, при
условии, что момент инерции подвижных частей рулевой машины
мал.
1-2-23. Составить дифференциальное уравнение электрической
рулевой машины постоянного тока с независимым возбуждением
(рис. 1-2-23).
Для упрощения решения пренебречь моментом сопротивления,
складывающимся из моментов трения в редукторе Ред демпфирую¬
щего и шарнирного, и не учитывать влияние индуктивности в об-
I тке якоря.
Рис. 1-2-23.
Рис. 1-2-24.
15

1-2-24. Составить дифференциальное уравнение магнитоэлектри¬
ческого чувствительного элемента, изображенного на рис. 1-2-24,
если входной величиной считать подводимое к обмотке напряжение
их, а выходной величиной о,— угол поворота рамки. Моментами
трения в опорах подвижной системы пренебречь.
1-2-25. Составить дифференциальное уравнение дифференциру¬
ющего трансформатора (рис. 1-2-25) на холостом ходу при малом
сопротивлении источника.
1-2-26. Составить линеаризованное, дифференциальное уравнение
угольного регулятора напряжения, конструкция подвижной системы
которого изображена на рис. 1 -(2-26,а и графики изменения момен¬
та— на рис. 1-2-26,6.
Рис. 1-2-27.
1-2-27. Составить диффе¬
ренциальное уравнение одно-
тактного магнитного усилителя
(рис. 1-2-27) с положительной
обратной связью и выходом на
активную нагрузку. При со¬
ставлении уравнения считать,
что магнитная цепь при малых
отклонениях имеет линейные
характеристики, и пренебречь
переходными процессами в ра¬
бочих обмотках переменного
тока.
16

1-2-28. оаписать дифференциальное уравнение стаци¬
онарного колебательного звена в матричной форме при
отсутствии входного воздействия (однородная форма
уравнении) для режима последействия от ненулевых на¬
чальных условий у (0_) =ух (0_) =2; у (0) =у2 (0_) =
5с. Использовать обозначения и значения пара¬
метров, принятые в задаче 1-2-7.
1-2-29. Для нестационарного звена, рассмотренного
в примере 1-2-8, написать матрицу коэффициентов, со¬
ответствующую нормальной системе уравнений Коши.
1-3. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ И ИМПУЛЬСНЫХ
ХАРАКТЕРИСТИК
1-3-1. Определить переходную и импульсную характе¬
ристики усилительного y(t)=5x(t) и запаздывающего
y3(t)==5x(t—3) звеньев.
1-3-2. Определить переходную и импульсную характе¬
ристики апериодического звена, заданного уравнением
У\~У х для Т=2 с и й=20. Найти момент времени
при котором импульсная характеристика будет иметь
значение ад (Т) =0,5, а переходная характеристика h(t) =
—19.
1-3-3. Определить переходную и импульсную характе-
ристики апериодического неустойчивого звена, уравнение
которого задано в виде
Ту—y=kx.
1-3-4. Определить переходную и импульсную харак¬
теристики интегрирующего звена, уравнение которого
задано в виде
Ty=kx.
1-3-5. Определить переходную и импульсную характе¬
ристики дифференцирующего звена, уравнение которого
задано в виде
У=Тх.
1-3-6. Определить переходную и импульсную харак¬
теристики форсирующего звена первого порядка, имею-
щего уравнение, заданное в виде
2—903
y=k (х-\-Т х).
17

i-3-7. Определить переходную и импульсную характе¬
ристики реального дифференцирующего звена, заданно¬
го в задаче 1-2-11.
1-3-8. Определить переходную и импульсную характе¬
ристики форсирующего звена второго порядка, уравне¬
ние которого задано в виде
у = k (х + %Тх + Т2х).
1-3-9. Определить переходную и импульсную харак¬
теристики колебательного звена, уравнение которого за¬
дано в виде
Т2у 2 с,Т у-f y — kx.
1-3-10. Определить переходную и импульсную харак¬
теристики резонансного звена, уравнение которого зада¬
но в виде
ад о
1-3-11. Определить переходную и импульсную харак¬
теристики неустойчивого колебательного звена, уравне¬
ние которого задано в виде
T2y — 2tTy-\-y = kx.
1-3-12. Определить переходную и импульсную харак¬
теристики системы, состоящей из двух последовательно
соединенных интегрирующих звеньев (T2y=kx).
1-3-13. Определить переходную и импульсную харак¬
теристики нестационарного звена, заданного уравнением
для произвольного момента задания входного процесса
0 и для значения а=2 с-1.
1-3-14. Для предыдущей задачи применить приблй'
женный метод «замораживания» коэффициентов в точке
^о=г0о=5 с и найти приведенную импульсную характер*1'
стику g[0-
18

Сравнить решения задач 1-3-13 и 1-3-14 в точке t=
=6 с.
п
1-3-15. Для стационарного уравнения 2 Я/*/(,)=л; при
/=о
я=6[т] дано решение в виде приведенной импульсной
характеристики g(t). Используя это решение, определить
полную импульсную характеристику w[т) для уравнения
п
/=0
имеющего ту же левую часть и более сложную правую.
п
1-3-16. Для нестационарного уравнения 2 ai^)y{^—
/=о
—0, 0)=л;(/—0) при х=8[/—0] дано решение g[t—0, 0)
в виде приведенной нестационарной импульсной харак¬
теристики. Перейти от нее к полной импульсной харак¬
теристике, если правая часть усложнена и имеет вид:
/7(0=М0* + М (t)x.
После получения решения в общем виде применить
его к условиям задачи 1-3-13, полагая 60(/)=2+3£;
bi(t) = \0t2\ b2(t)=8-\-t2 при 0i=5 с.
1-3-17. Для колебательного звена, рассмотренного
в задаче 1-2-28, рассчитать матрицу нормированных им¬
пульсных характеристик, используя формулу матричного
экспоненциала [28]. Пояснить роль каждого элемента
матрицы нормированных импульсных характеристик и
сопоставить полную импульсную характеристику коле¬
бательного звена, полученную в задаче 1-3-9, с соответ¬
ствующим элементом матрицы.
1-3-18. Записать матрицу параметрических нормиро¬
ванных импульсных характеристик для нестационарного
звена второго порядка, заданного уравнениями в моди¬
фицированной форме Коши, с матрицей коэффициентов,
определенной в решении задачи 1-2-29. Воспользоваться
формулой для матрицанта [6].
19

1-4. АНАЛИЗ ПРОХОЖДЕНИЯ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ ЗВЕНЬЯ ВО ВРЕМЕННОЙ ОБЛАСТИ
1-4-1. Даны импульсная характеристика апериодиче-
1 т~
ского звена w\t) = -j- е	и входной сигнал x=Vt (У=;
=const). Требуется определить выходной процесс y(t)
при (0_) =0.
1-4-2. Для апериодического звена найти реакцию на
входной сигнал x\t)—aP-1 [/), используя непосредствен¬
но заданное его дифференциальное уравнение в норми¬
рованной форме:
й9+-гУ[0=т-110.
1-4-3. Для колебательного звена, заданного уравнени¬
ями в модифицированной форме Коши, приведенными
в задаче 1-3-17, найти расширенную матрицу реакций на
входной сигнал, заданный функцией
x\t) = (co-fci/) 117).
1-4-4. Дан входной сигнал x = Aent sin	дейст¬
вующий на звено второго порядка, заданное уравнениями
в модифицированной форме Коши с матрицей коэффици¬
ентов В = 0 ' 1	. Требуется:
а1' а2 I
а) составить расширенную за счет входного сигнала
матрицу коэффициентов [28];
б) записать связь между соответствующими элемен¬
тами матрицы gih (без получения решения) и реакцией
в общей форме;
в) подставить значения параметров А=5 ед., tj=
=2 с-1, Q=5 с-1, ф=30°.
1-4-5. Нестационарное звено задано импульсной харак¬
теристикой вида w [t, 6) = -у е~~° (*“9). Входной сигнал
описывается линейной функцией с произвольным смещени¬
ем 5:
x=V[t-t).	(Н
а)	Найти общее выражение для значения реакций
звена в заданный момент времени tB (момент наблюде-’
20

ния) в зависимости от продолжительности действия (ра¬
бочего интервала) 0 для входного процесса заданной
формы (1).
б) Определить численные значения реакции для за¬
данных: момента наблюдения /н—10 с, момента задания
входного процесса 1=2 с, скорости V—3 ед/с, показателя
затухания а=0,4 с-1.
в) Дагь графические пояснения используемых разре¬
зов рельефа импульсной характеристики нестационарно¬
го звена.
1-5. АНАЛИЗ ЛИНЕЙНЫХ ЗВЕНЬЕВ НА ОСНОВЕ МЕТОДА
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1-5-1. Дифференциальные уравнения предварительно
невозбужденных звеньев с постоянными параметрами
даны в задаче 1-2-5. Найти соответствующие им пере¬
даточные функции (ПФ) [28].
1-5-2. Определить ПФ цепи, изображенной на рис.
1-2-10.
1-5-3. Определить ПФ цепи, приведенной на рис.
1-2-11.
1-5-4. Определить ПФ усилителя постоянного тока по
данным задачи 1-2-12.
1-5-5. Определить ПФ безынерционного электродви¬
гателя с независимым возбуждением по данным задачи
1-2-18.
1-5-6. Определить ПФ гидравлического двигателя по¬
ступательного движения по данным задачи 1-2-20.
1-5-7. Определить ПФ интегрирующего гироскопа по
данным задачи 1-2-21.
1-5-8. Определить ПФ схем, приведенных на рис.
1-2-14.
1-5-9. Определить ПФ схем, приведенных на рис.
1-2-16.
1-5-10. Определить ПФ фильтра, приведенного на
рис. 1-2-17.
1-5-11. Определить ПФ гидравлической рулевой ма¬
шины по данным задачи 1-2-19.
1-5-12. Определить ПФ электрической рулевой маши¬
ны постоянного тока с независимым возбуждением по
данным задачи 1-2-23.
1-5-1#3. Определить ПФ магнитоэлектрического чувст¬
вительного элемента по данным задачи 1-2-24.
21

1-5-14. Определить ПФ дифференцирующего транс¬
форматора, изображенного на рис- 1-2-25.
1-5-15. Определить ПФ угольного регулятора напря¬
жения по данным задачи 1-2-26.
1-5-16. Определить ПФ корректирующей цепи в усло¬
виях питания от генератора напряжения (рис. 1-5-16,а) и
генератора тока (рис. 1-5-16,6).
Рис. 1-5-16.
1-5-17. Импульсная характеристика звена w[t) —
=0,0125e_1-25t. Найти ПФ.
2
1-5-18. Импульсная'характеристика звена ш [г1) =у- ет.
Найти ПФ.
1-5-19. Импульсная характеристика звена"! w\t) =
=4t
8 И
т'~т'.е т'
т\
fe],
Найти ПФ.
1-5-20. Импульсная характеристика звена ’ w [f) =
=-^-sinQA Найти ПФ.|
1-5-21. Импульсная характеристика звена w[t) =
=100е—o>3t sin 0,4^.
1-5-22. Импульсная характеристика системы автома¬
тического управления ш[^)=5е-2(+10е_5(. Найти ПФ.
1-5-23. Импульсная характеристика САУ a>[f)='J^5f+
+ 10 sin (At -f -J-) j • 1 [t). Найти ПФ.
1-5-24. Дана переходная характеристика 'h[t) =
_15е-°,5£. j Найти ПФ.
1-5-25. Дана переходная характеристика звена
h[t)= 0,1 (e°>2t—1) • 1 [/). Найти ПФ-
22

1-5-26. Импульсная характеристика системы уравне¬
ния w[t)= 0у02(е-°^—е-^). Найти ПФ.
1-5-27. Импульсная характеристика системы управле-
обходимого Я-преобразования.
1-5-28. Импульсная характеристика ш[/) =0,01 Най¬
ти ПФ.
1-5-29. Дана переходная характеристика Л[/) = 1[>/) +
—J— 1 Oe—Xsin (10/-|-jt/6) . Найти ПФ системы.
1-5-30. Составить операторное уравнение апериодиче¬
ского звена, возбужденного управляющим сигналом и
начальными условиями, и дать его структуру [25].
1-5-31. Составить операторное уравнение колебатель¬
ного звена, возбужденного управляющим сигналом и на¬
чальными условиями, и дать его структуру.
1-5-32. Найти изображение^ функции t2e~l[ методом под¬
бора необходимого преобразования по параметру Я=— о.
1-5-33, Найти изображение функции
1-5-34. Записать в операторной форме нестационар¬
ное уравнение (‘5-x-bt)y-\-y-\-(2-\-3t)y=kx.
1-5-35. Написать в операторной форме уравнение (1-f-
+2*+3/*) у + (2 + Ы) 'у + (4 + 3/) у + (5 + 0 у =
1-5-36. Записать в операторной форме уравнение, дан¬
ное в условии задачи 1-2-4.
1-5-37. Используя метод баланса парциальных изо¬
бражений [25], найти реакцию линейной системы на
смещенный импульс, если система задана уравнением
второго порядка с линейно меняющимися коэффициен¬
тами ty+(2+ I0t)y+ (10 + 29^)г/=(10 + 29£)6[£—0] при
смещении 0=2 с.
1-5-38. По таблице коэффициентов (см. приложе¬
ние 3) для уравнения (l-f-2^+3/2) */+(2+3^)#-f~(l +
-\-2t)y-\-(2-{-t)y—l [t) составить уравнения балансов
изображений, содержащих начальные значения реакции.
1-5-39. Пользуясь таблицей в приложении 3, найти
начальные значения переходной характеристики колеба¬
ния
Найти ПФ методом подбора не
L{e jttcosQt}.
23

тельного звена /г[0), /г[0), /г[0) для £=0,8; Т=2; k—\ и
ее представление в форме ряда.
1-5-40. Найти начальное значение процесса и его про¬
изводных по изображению
Х{р)—- Зр + 2
2р2+4р+ Г
1-5-41. Найти начальный участок переходной харак¬
теристики для звена с ПФ
w (п)=—
w КР) р2 + 4р + ! •
1-5-42. На вход колебательного звена с ПФ
W (v) =	-
w \У)	т*р*+2^Тр+1
подается управляющий сигнал х=3Написать изо¬
бражения вынужденного и собственного компонентов
выходного процесса.
1-5-43. В колебательном звене с ПФ
W(P):
'Гу+2£7>+ !
начальные условия у(0-)=5, у(0_)=2 с-1 и управляю¬
щий сигнал x=3t. Написать изображение выходного про¬
цесса.
1-5-44. На вход реального форсирующего звена с ПФ
W(p) = - ..fe(r^ + 1)
W W	T3p2+	2%Ttp+ 1
подан входной сигнал x[t)=3tz. Определить в форме ря¬
дов методом непрерывного деления:
а) компоненты вынужденного движения в реакции
звена при следующих численных значениях параметров:
£=10; 7"i=0,5 с; Т=5 с; £=0,1;
б) начальный участок процесса.
1-5-45. Для звена, рассмотренного в задаче 1-5-44, за¬
даны помимо входного процесса х—Ъt3 дополнительные
начальные условия z/(0-)==50, г/(0_)=10.
а) Определить начальный участок общей реакции от
воздействия и режима последействия (ликвидации на¬
чальных условий).
б) Сопоставить сложные условия возбуждения звена
с условиями, полученными в предыдущей задаче.
24

1-5-46. Применить общую формулу обратного преоб¬
разования Лапласа, основанную на теореме разложения
и двух типах преобразования — дифференцирования по
параметру X и выделении мнимой части [28], к изобра¬
жению
Y(ri\ =	(2/7+10)10*
Р3 (Р + 2)2 К/7 + З)2 + 42]3 [(/7 + 0,5)2+ 52]2'
1-5-47. На входе нестационарного звена, заданного
параметрической импульсной характеристикой вида
w* V>') = -}-е~”
(см. задачу 1-4-5), действу¬
ет процесс, изображенный
на рис. 1-5-47. Найти реак¬
цию на выходе звена в за¬
данный момент наблюдения 0
/=10 с. (Плавный график
входного процесса заменить	Рис.	1-5-47.
отрезками прямых линий.)
1-5-48. Для нестационарного звена, заданного уравне¬
нием
(0 У + «1 (0 У + а, (0 у = b1(t)x-\- b, (0 +
определить первое приближение параметрической ПФ.
1-6. АНАЛИЗ НЕПРЕРЫВНЫХ ПРОЦЕССОВ НА ОСНОВЕ
МЕТОДА г-ПРЕОБРАЗОВАНИЯ
1-6-1. Для экспоненциальной функции x=e~4t:
а) подобрать интервал дискретности Г0, при котором
ступенчатое описание функции по дискретным точкам не
приводит к погрешности, большей 5% начального значе¬
ния;
б) определить интервал дискретности Гл, при кото¬
ром линейная интерполяция значений функции в середи¬
не промежутков между дискретными точками не превы¬
сит 1 % начального значения;
в) найти z-преобразование выборки дискретных зна¬
чений непрерывного процесса;
г) осуществить обратное ^-преобразование.
1-6-2. Определить, пользуясь исходными соотношени¬
ями приложения 4, 2-изображение X[z] ступенчатой
функции x[t)= 5* 1 [/).
25

1-6-3. Найти 2-изображение косинусоидально изменя¬
ющейся функции x[t) = 2 cos5^.
1-6-4. Найти 2-изображение линейной функции x[t) =
=3t.
1-6-5. Найти г-изображение квадратичной функции
Х® = 7Ж-
1-6-6. Найти 2-изображение синусоиды я[/)=8 sin 2t.
1-6-7. Найти 2-изображение функции x[t)=te~2t.
1-6-8. Дана функция x[t)=e~2t sin 6t. Найти ее 2-изо¬
бражение Х[г\.
1-6-9. Непрерывная функция задана ее изображением
по Лапласу:
у ( п\ 	100
КР)~ Р(Р + *)2 [(/>-3)* + 5Л“
Перейти к 2-изображению и рассчитать процесс в дис¬
кретных точках для Г0=0,8 с.
1-6-10. Для нормированных импульсных характери¬
стик, заданных матрицей решений в виде
,,v II cos Qt 2-1 sin Qt ||
g ^	II — Q sin Q/	cos 2/ H’
определить матрицу 2-изображений универсальным ма¬
тричным методом, поясненным в приложении 17, задав¬
шись интервалом дискретности, соответствующим прира¬
щению аргумента гармонических функций
■QA/=jt/6=30°.
1-6-11. Процесс гармонических затухающих колеба¬
ний
х (t) — £-:r/'sin (Q t -f- <p)
задан своими параметрами a=2 с-1 и Q в общем виде,
а также начальными значениями
х (0)="sin 9 = 1^3/2; х(0) = — a sin у Q cos 9 =
= 0f5Q —/ЯГ.
Определить 2-изображение процесса универсальным
матричным методом, использованным в предыдущей за¬
даче, при том же интервале дискретности £27о=я/6.
1-6-12. Найти 2-изображение функции x(t)=i3/3!,
пользуясь универсальным матричным методом.
26

1-7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
1-7-1. Построить частотные характеристики:	комплексную —
W(jсо), амплитудную — А (со), фазовую ср(со), действительную G(co),
мнимую В (со)—для следующих элементарных звеньев первого
порядка:
а) усилительного с коэффициентом передачи £у = 2;
б)^запаздывающего с^ПФ k3e~p*s при &3 = 1,5; т3 = 1 с;
в) дифференцирующего с ПФ 7р при 7 = 0,5 с;
г) интегрирующего с ПФ k-i/p при /г_1 = 1 с-1;
д) форсирующего с ПФ &ф(1 + 7р) при 6ф = 2; 7 = 0,5 с;
е) апериодического с ПФ &а/(7р+1) при &а=3; 7 = 0,2 с;
ж) апериодического неустойчивого с ПФ &а.н/(7р—1) при
kz.н=3; 7=0,2 с.
1-7-2. Построить частотные характеристики элементарных звень¬
ев второго порядка:
а) форсирующего с ПФ /еф (1 + 2£тр+т2р2) при &ф = 2,5; £ = 0,5;
т=0,5 с;
б) колебательного с ПФ &/(72р2-г2£7р+1) при /г=2,5; £=0,5;
7 = 0,5 с;
в) резонансного с ПФ &p/(p2 + Q2) при &р=2,6; П=2 с-1;
г) колебательного неустойчивого с ПФ k/(T2p2—2£7р-Н) при
£=2,5; £=0,5; 7=0,5 с.
1-7-3. Построить комплексную частотную характеристику (ЧХ)
звена с ПФ W(p)=k/p2 при £=4.
1-7-4. Для реального форсирующего звена, схема которого изо¬
бражена на рис. 1-2-16,6, построить ЧХ при следующих параметрах
схемы: /^ = 40 кОм; г =10 кОм; Ci = 2,5 мкФ.
1-7-5. Построить ЧХ систем, имеющих ПФ вида
45р + 120
а) W (р) — р3 + 4рг_Юр ;
15л + 40
б)	Тр-
1-7-6. Построить ЧХ систем, имеющих ПФ вида
a)	W (р) = (0>2р+ 1) (0,5/?-+- 1) (Зр— 1);
б)	V (p)-(0 2jD+i) (0.5/,+1) (р- 1) •
1-7-7. Построить ЧХ системы, имеющей ПФ вида
8
W (Р) = (1 +80/?) (1 + 12р) *
1-7-8. Передаточная функция разомкнутой системы (рис. 1-7-8,а)
имеет вид:
туг / ч	ко	(Гр.сР	+	1)
{Р) ~ цтлр + 1) (Го.ер + 1) + k2k3T0Xp] (74р2 + р) •
27

Построить ЧХ разомкнутой	(рис. 1-7-8, а) и замкнутой
(рис. 1-7-8,6) систем, а также амплитудную, вещественную и мни¬
мую частотные характеристики замкнутой системы при следующих
числовых значениях параметров:	=250; Го.с = 0,3; Тз = 0,05 с;
&26з = 50; 7’4 = 0,1 с.
Рис. 1-7-8.
1-7-9. Построить ЧХ, соответствующие следующим ПФ:
10 + 5/?
a)	W (р) — Qt2p-\- 1 »
10 + 5»
1-7-10. Построить ЧХ, соответствующую ПФ
k + kT р
W (Р) = Г2ръ + 2фр+ 1 ’
при значениях параметров, приведенных в табл. 1-7-1.
Таблица 1-7-1
Вариант
Параметр
Ограничения на параметры
к
k'
г* ]
а
1
0,5
4
2
kT2>2k'%T\ k’<2k%T
б
1
0,5
0,25
2
kT2<2k’%T; k’<2 ftT
в
1,0
1,2
2,0
1,0
kT2>2k'lT\ fc'>2tiff
г
1
5
2,0
2
kT2<2k'lT; k'>2k%T
28

1-7-11. Передаточные функции разомкнутых систем имеют вид:
я, И7 ,„ч	50(1+0,15/?)
a)	W(p) — р2 (j + 0,05р) >
200 (1 +0,15/;).
)	~,р*	(1 -f- 0,05/7) •
\w,\	200 (1 + 0,2р)2
в) ^ (р) — ^ (1 + 0,04/?) ;
Г) W {Р) = (1 + 0,5/>)^(1	0,1/?)*
д) W (р) --= ^_ j _|_о,2/? + 0,01/?2)(1 +0,05/?);
е) № (р)  	5(1 + 0,03р)
е; w КР) (—1+ 0,2/?+ 0,01/?2) (1+0,05/?) (1 +0,006/?) •
Построить соответствующие заданным ПФ частотные характе¬
ристики.
1-7-12. По ПФ разомкнутых систем
TW /	50
W (р) = (Ю0/?2 + 4/; + 1) (5/7 + 1)
и
50
W № = (Ю0/?2 — 4/? + 1) (5/?+ 1)
построить с помощью шаблонов логарифмические частотные харак¬
теристики (ЛЧХ), комплексные частотные характеристики (ЧХ) на
полулогарифмической комплексной плоскости (строить эти харак¬
теристики целесообразно на одном бланке для обеих систем) и годо¬
графы вектора 1^(/со).
1-7-13. По ПФ разомкнутой системы
, .	Ма&А (TiP + 1)
w (р)-р (Т,р + 1) (Тгр + 1) (Т4р +1) >
где ki=0,97; Тi—20 с; k2=4,0; Т2 =0,25 с; й3=0,75; Г3=0,05 с;
&4 = 5,0; Г4 = 7,0 с, построить амплитудную (методом асимптот) и
фазовую логарифмические частотные характеристики.
1-7-14. По ПФ разомкнутой системы
40/7
W(p)
(7V2 + 2i;7>+l) (TlP+l)
где Го = 0,25 с; £ = 0,7; Ti = 0,5 с, построить амплитудную (методом
асимптот) и фазовую логарифмические частотные характеристики.
е~рт
1-7-15. Для W {р) — Y~+T~p Рассчитать н построить ЧХ, если
х = 0,04 с; Г = 0,01 с.
29

Рис. 1-7-17.
1-7-18. По ПФ разомкнутой системы
50 (0,1/>+ 1)
1-7-16. Для
W(p) =
__	1	+	0,25/1
(1 + 0,02/7) (1 +0,016р) е~°'025р
построить амплитудную и фазовую Ча^
стотные характеристики.
1-7-17. Используя G, В-номограмму
(см. приложение 7), построить ЛЧХ дЛя
согласно-параллельной схемы [24], изо¬
браженной на рис. 1-7-17.
W(p)
■ (100/7= — 4/7+1) (5/7+1) (0,0004/72+0,02/7+1) (0,025/7+1)
построить:
а) с помощью шаблонов ЛЧХ;
б) ЧХ на полулогарифмической комплексной плоскости.
1-7-19. Для разомкнутой системы, имеющей ПФ вида
.	(.Т2Р+	о
/7 <TiP + 1) (Тгр + 1) (7> + 1) »
где &i/e2&3&4=|£ = 40; 71 = 0,2 с; 72 = 0,0125 с; 7з = 0,05 с; 74 =
= 0,015 с; построить ЛЧХ.
1-7-20. Построить ЛЧХ разомкнутой системы, ПФ которой
имеет вид:
w.	(Т\р^	+ 2%1Т1р+\)(\-Тгр)
W(P)~* р (Тзр + 1} (Т^рг + 2^TiP + 1) (7=6/7= + »
+ 2%ьТъР + 1) (Т\р* + 2^Т,р + 1)
где 7i = 0,19 с; gi=0,06; 72=0,025 с; Г3=0,009 с; Г4= 1,0 с;
g4 = 0,6; Г5=0,194 с; 15 = 0,13; Ге=0,06 с; 1в=0,93; 6=0,5.
1-7-21. По ЛЧХ, полученным в 1-7-19, построить ам¬
плитудную и фазовую частотные характеристики замкну¬
той системы. Для построения указанных характеристик
использовать Ф-номограмму (см. приложение 8).
1-7-22. Построить АЧХ и ФЧХ по предварительно полученным
годографам для правой и левой частей уравнения системы [14J.
если ее ПФ имеет вид:
W(p)
Р(Р)
’ Q (р)
£-0,02 р
1 + 0,02 р
при допущении, что
оп 2 — 0,02/?
/р-0,02р	 1
е —2 + 0,02/7
30

1-8. ЧАСТОТНЫЕ СПЕКТРЫ ВЫХОДНЫХ ПРОЦЕССОВ
1-8-1. Определить регулярную и нерегулярную части
процесса на выходе звена с ПФ вида
W(p)
  ft2Р2 Н~ Ьгр -f- Ь0
азР3 + а2р* + а1Р + а0 »
если на входе действует управляющий сигнал, изменяю¬
щийся по линейному закону
1-8-2. Определить импульсную характеристику систе¬
мы и построить ее график по заданной на рис. 1-8-2 ве¬
щественной частотной характеристике G(со).
Б (и)
Рис. 1-8-2.
б (со)
Рис. 1-8-3.
НСО; COi
Рис. 1-8-4.
1-8-3. Определить импульсную характеристику систе¬
мы, если вещественная частотная характеристика имеет
вид треугольника, примыкающего к оси ординат
(рис. 1-8-3).
1-8-4. Определить импульсную характеристику по ве¬
щественной частотной характеристике системы, задан¬
ной в виде трапеции, примыкающей к оси ординат
(рис. 1-8-4).
1-8-5. Определить импульсную характеристику систе¬
мы по вещественной частотной характеристике, задан¬
ной в виде трапецеидальной полоски, не примыкающей
к оси ординат (рис. 1-8-5).
Ш
п
COi	СО	у
Рис. 1-8-5.
31

1-8-6. Вещественная характеристика системы управ,
ления имеет вид, изображенный на рис. 1-8-6. Данную
вещественную характеристику разбить на трапецеидаль.
ные и треугольные элементарные спектры.
1-8-7. Трапецеидальная вещественная характеристика
имеет полосу «>,—12 с“\ излом шх = 6	с'1 и высоту
Р/ = 4. Выписать из таблицы А -функций соответствую,
щую переходную функцию.
1-8-8. Построить переходную характеристику для сле¬
дящей системы, имеющей ПФ разомкнутой цепи
Wfrfi—	180	000	(0,2/7+	1)
— 7,2-10-5/?в|+[0,0182/?5 +[3,85/?4 + 308/73 + 724/?2"+600/?’
при единичном ступенчатом воздействии и нулевых на¬
чальных условиях.
1-8-9. Оценить погрешность построения переходной
характеристики в предыдущей задаче для моментов вре¬
мени t=1 с; 10 с.
1-8-10. По заданной на рис. 1-8-10 вещественной ча¬
стотной характеристике G(со) определить реакцию си¬
стемы на единичное ступенчатое воздействие при нуле¬
вых начальных условиях.
1-8-11. По вещественной частотной характеристике
G(cо) системы регулирования (рис. 1-8-11) построить
кривую переходного процесса h[t) при управляющем
воздействии x[t)=a-l[t), нулевых начальных условиях
и а=1,1.
32

1-8-12. Построить графики переходных характеристик
Ш) замкнутых систем при нулевых начальных услови¬
ях по заданным ПФ разомкнутых систем:
5 (0,03р + 1)
а) W (Р) = (0,01 р2 + 0,2/7 — 1) (0,05/7+ 1) (0,006/?+ 1);
ч	k(Ttp+ 1)	500 (0,03/7+ 1)
б) К(Р>:
р(Т,р+\)(Тгр+\) — /7 (0,1/7 + 1) (0,006/7+ 1)'
1-8-13. Пользуясь методом трапецеидальных частот¬
ных характеристик, построить переходную характеристи¬
ку по вещественной частотной характеристике, изобра¬
женной на рис. 1-8-13.
Рис. 1-8-13.
Рис. 1-8-14.
1-8-14. Построить переходную характеристику по ве¬
щественной частотной характеристике G(a>), приведен¬
ной на рис. 1-8-14, пользуясь методом разбиения харак¬
теристики G (а) на треугольники.
1-8-15. На вход системы, изображенной на рис. 1-8-15,а,
действует сигнал £ (() — e~zt при t > 0. Построить гра-
Модулятор
хЦ)
2
а)
Ш
1 cos U)Ht
x(t)
Демодулятор
Рис. 1-8-15.
3—903
33

фики сигналов на выходе модулятора x(t) и демодуЛя,
тора y{t), а также спектры процессов в точках
[Процесс модуляции и демодуляции представить как
умножение на функцию несущей частоты coscoH^ (рис
1-8-15,б).] Численные значения параметров: а=2 с-п
сон=600 с-1.
1-9. БАЗОВЫЕ ХАРАКТЕРИСТИКИ
1-9-1. Для звена с ПФ, полученной в задаче 1-5-3,
определить базовую характеристику в форме изображе¬
ний и оригиналов, разложенных на компоненты.
1-9-2. Найти реакцию апериодического звена на вход¬
ной сигнал вида x(t)—at2 методом преобразования ба¬
зовой характеристики, полученной в предыдущей задаче.
1-9-3. Определить вектор базовых характеристик для
звена, заданного системой уравнений в форме Коши
второго порядка У\—Уъ У2=х, следующими тремя мето¬
дами:
а) матричным методом путем пересчета нормирован¬
ных импульсных характеристик в базовые;
б) методом разложения в матричный ряд Тейлора
для расширенной системы уравнений;
в) методом преобразования Лапласа.
1-10. НАЧАЛЬНЫЕ УСЛОВИЯ И НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
1-10-1. Для однородного дифференциального уравне¬
ния, записанного в алгебраизованной форме {D2Jr
—|—Q2) г/=0, установить кохмплекс начальных условий для
получения решения в форме гармонических колебаний
у—A sin (Ш-fф) с заданными амплитудой и фазой.
Воспользоваться преобразованием Лапласа и прове¬
рить по предельным теоремам совпадение начальных
значений £=0+ с начальными условиями t=0_.
1-10-2. Для неоднородного дифференциального урав¬
нения
(£>2+Q2)«/=x	(О
найти форму воздействия x(t), обеспечивающего совпа¬
дение возбужденного компонента при нулевых началь¬
ных условиях со свободным компонентом, полученным
в предыдущей задаче.
34

1-10-3. Определить приращение начальных значений
по отношению к начальным условиям для звена с ПФ
W(p)= ■■■■;■ I п.,
Р + 2 9
заданным в общем виде, при возбуждении его ступенча¬
тым сигналом x=a-l[t).
1-10-4. Для предыдущей задачи определить прираще¬
ние начальных значений, если начальные условия зада¬
ны как г/(0_)=0,5 и г/ (0_) =0,75 с-1, а воздействие име¬
ет импульсный характер х=36|7].
1-10-5. Для условий задачи 1-5-39 воспользоваться
общим выражением для начальных значений всех про¬
изводных переходной функции колебательного звена и
решить численный пример для £=4, £=0,8, Т—2, поль¬
зуясь методом переменных состояний (матричным мето¬
дом).
1-10-6. Для условий задачи 1-5-37 найти начальные
значения процесса и его производных в нестационарной
системе, 'пользуясь методом переменных состояний.
Глава вторая
ТОПОЛОГИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
2-1. ОБЩИЕ ПРАВИЛА И ОГРАНИЧЕНИЯ
2-1-1. Для структурной схемы, показанной на рис.
2-1-1:
а)	осуществить перенос линии обратной связи —Т^р
(блок 7) со звена 2 на звено 5, используя правило пере¬
носа узла через узел и через звенья по ходу сигнала,
3*
Рис. 2-1-1.
35

а также переноса сумматора через сумматор и звенья
против направления сигнала;
б)	отметить в новой схеме те промежуточные звенья
у которых изменился режим работы.	’
2-1-2. Для структурной схемы, показанной на рИс
2-1-2:
а)	осуществить перенос параллельной (форсирую,
щей) связи —T'jp (блок 7) со звена 2 на звено 5, приме*
няя соответствующие правила переноса;
Рис. 2-1-2.
б)	оценить условия эквивалентности заданной и пре¬
образованной схем по режимам промежуточных звеньев.
2-1-3. Для структурной схемы, показанной на рис.
2-1-3 (структура апериодического звена), применить пра¬
вило инверсии к обоим элементам схемы (k/Tp, —l/k) и
оценить условия эквивалентности полученной и заданной
структур.
Рис. 2-1-3.	Рис.	2-1-4.
2-1-4. Колебательное звено W0.c(p) включено в цепь
отрицательной обратной связи, охватывающей усили¬
тельное звено, как показано на рис. 2-1-4. Найти обшу10
ПФ схемы, а также ее предел при неограниченном уве¬
личении коэффициента усиления (при глубокой отрица¬
тельной обратной связи).
36

2-1-5. Электронный усилитель имеет ЛАЧХ, показан¬
ную на рис. 2-1-5, где ^(0)=20 дБ; (ос=Ю00 с-1; S(oo) =
_—20 дБ/дек. В схеме он дополнительно охвачен жест¬
кой положительной обратной связью k0,с=0,2. Найти
подходящее описание передаточных свойств усилителя
(ПФ) для случая сверхкритической жесткой обратной
связи, т. е. k0.c>\/k(0).
ДБ
20
10
0
40
-20
Ш)
—^
К
1
(Ос
\
О)
| | X
С— 7П пЫЛаи Л
О Си ди/иек -тsr-
.. . . 1. 1 \ ,
ДБ
го
1(со)
0>ci! X
О)
-20
-40
-60
...
\ \ i
Чсэ1

\сз
\со
Iх
Рис. 2-1-5.
Рис. 2-1-6.
2-1-6. Асимптотическая ЛАЧХ усилителя, показанная
на рис. 2-1-6, имеет &(0) = 10; coci = 100 с-1; 0С2=8ОО с-1
и наклоны в высокочастотной области, соответственно
—20 и —40 дБ/дек. Подобрать подходящее описание ПФ
усилителя для случая охвата его гибкой положительной
обратной связью k0,c(p) =0,01/7.
2-2. ПРЕОБРАЗОВАНИЕ СТРУКТУР ЗВЕНЬЕВ И СИСТЕМ
2-2-1. Усилительное звено с ПФ W—kn охвачено жесткой об¬
ратной связью (рис. 2-2-1). Определить коэффициент усиления к
эквивалентного звена при значениях kn и k0.c, заданных
в табл. 2-2-1.
Таблица 2-2-1
Параметр
Варианты
1
2
3 1 4
5
6 | 7
8
kn
10
10
10
10
10
10
10
30
^о.с
0,01
0,09
0,099
0,2
1
10
20
100
Знак обрат¬
ной связи
+
+
+
+
—
—
—
—

Рис. 2-2-1.	Рис.	2-2-2.
2-2-2. Усилительное звено с ПФ W = ka охв'ачено гибкой обрат¬
ной связью (рис. 2-2-2). Определить ПФ схемы при числовых зна¬
чениях параметров, приведенных в табл. 2-2-2.
Т а б л и ц а 2-2-2
Параметр
Вариант
1
2
3
4
г,
10
10
1000
1000
500
Т
1
1
1
2
2
Знак обратной связи
+
—
. —
—
—
2-2-3. На усилительное звено с Г1Ф W=kn наложена обратная
связь через интегрирующее звено (рис. 2-2-3). Найти выражение
ПФ схемы при числовых значениях параметров, указанных
в табл. 2-2-3.
Таблица 2-2-3
Вариант
араметр
1 i
I
3 !
4
5
6
К
10
100
10
100
1000
10 000
т
0,5
0,5 |
0,5
2,0
2,0
2,0
Знак обратной связи
+
—
—
—
—
Рис. 2-2-3.
38
Рис. 2-2-4.

2-2-4. Дифференцирующее звено с Г1Ф W(p)=Tp охвачено
жесткой обратной связью (рис. 2-2-4). Найти выражение ПФ схемы
при числовых значениях параметров, приведенных в табл. 2-2-4.
Т а б л и ц а 2-2-4
Параметр
Вариант
1
2
3 ! 4
т
0,5
1
1
1
^о. с
10
10
10
■ 20
Знак обратной связи
+
+
—
—
2-2-5. Дифференцирующее звено с ПФ, равной Тр, охвачено
гибкой обратной связью (рис. 2-2-5) Т0.ср. Найти выражение ПФ
схемы при числовых значениях параметров, приведенных в табл. 2-2-5.
Таблица 2-2-5
Параметр
Вариант
1 | 2 | 3
4 | 5 | 6
1
т
1
2
1
10
100
1000
То.с
0,5
1
1
2
0,5
1
Знак обратной связи
+
+
—
—
—
—
Х(р)
гр
Лр) *fP>r
Тр
То.ср
к
\
Р
Y(p)
Рис. 2-2-5.
Рис. 2-2-6.
2-2-6. Найти общее выражение ПФ дифференцирующего звена,
охваченного интегрирующей обратной связью (рис. 2-2-6), и рассчи¬
тать ее числовые значения при значениях параметров, приведенных
в табл. 2-2-6.
39

Т а б л и ц а 2-2-6
Параметр
Вариант ‘
1
2
3
4
5
е
т
1
1
0,5
0,5
1
1
~^9
k
10
0,9
1,98
1,998
—10
Знак обратной связи
+
+
+
’ +
—
2-2-7. Найти общее выражение ПФ
интегрирующего звена, охваченного жест¬
кой обратной связью (рис. 2-2-7).
2-2-8. Найти общее выражение ПФ
интегрирующего звена при наложении
на него обратной связи по производной
(рис. 2-2-8,а) и интегралу (рис. 2-2-8,б).	Рис.	2-2-7.
Рис. 2-2-8.
2-2-9. Апериодическое звено с ПФ W (р) =&/(7р+1) охвачено
жесткой обратной связью (рис. 2-2-9). Определить ПФ схемы при
числовых значениях параметров, приведенных в табл. 2-2-7.
Таблица 2-2-7
Вариант
Параметр
1
2
3
4
5
6
7
8
k
10
10
10
10
0,1
10
10
10
Т
2
2
2
2
2
2
2
1
^о.с
0
10
100
10
5
0,05
0,1
0,1
Знак обрат¬
ной связи
4€
+
—
—
+
+
+
+
+

Рис. 2-2-9.
Рис. 2-2-10.
2-2-10. Найти выражение ПФ апериодического звена, охвачен¬
ного гибкой обратной связью (рис. 2-2-10), и рассчитать ее число¬
вые значения при значениях параметров, приведенных в табл. 2-2-8.
Таблица 2-2-8
Параметр
Вариант
1
2
3
4
5
К
10
10
100
100
100
т
0,5
0,5
1,0
2,0
3,0
т
J О.с
1,0
1,0
1,0
2,0
2,5
Знак обратной связи
+
—
—
+
+
нятто2^!,!* Найти обЩее выражение ПФ апериодического звена при
(рис 2-2 П)На Н6Г0 ратиой связи через интегрирующее звено
х(р) к
~\JEL
I	kc.c
Y(p)
Рис. 2-2-11.
колебательного звена в операторной
^	^	) (р)—(р). Отразить его внутреннюю
структуру различными возможными схемами.
заданий™ DP!oC4HTaobo4iHoCJIOBbIe значения ПФ колебательного звена,
обратными *	’ охваченн°го жесткой k0,c и гибкой Т0 со
в табл 2 2 9	’	При значениях параметров, приведенных
41

Таблица 2-2-9
Параметр
Вариант
1
о
3
4
к
10
10
10
10
2,0
г
5
5
. 5
5
о
£
0,5
0,5
0,5
0,5
0,5
ко,с
1
2
0,5
0,1
0,2
То.с
1
0,5
1
0,5
0,5
Знак обратной связи
—
—
+
+
+
2-2-14. Дана многоконтурная структурная схема си¬
стемы управления (рис. 2-2-14). Требуется свернуть
структурную схему и определить ПФ системы методом
структурных преобразований и по топологической фор¬
муле.
Рис. 2-2-14.
2-2-15. Сверните изображенную на рис. 2-2-15 струк¬
турную схему системы управления и определите ее ПФ
аналитическим методом.
Рис. 2-2-15.
2-2-16. Сверните изображенную на рис. 2-2-16 струк¬
турную схему системы управления и определите ПФ за-
42

ой системы по основному каналу и ПФ ошибки,
мкну1
если
]V, (Р) = ~Г	1	»	'*^2	(Z7)	:
ЛЯ+1 ’
W'(P) = r!f‘
т»р+ i ’
WAp) = T-f-
Ко
.	.	 ну/7)	|	1
Wj(p) 1 >-<5)—I
-ED*
Рис. 2-2-16.
2-2-17. Определить ПФ замкнутой системы управле¬
ния изображенной на рис. 2-2-17, если k\—2\ *2=100;
/г3=Ю0; *4=2,5 1/с; Г3=0,05 с; Г4=0,07 с; Го.с=0,2 с.
Х(р)
ЪР+f
Т'.сР
(Tfyjj+Op
У (р)
Te.c-p-i
-РЬ
Рис. 2-2-17.
2-2-18. Сверните изображенную на рис. 2-2-18 струк
турную схему системы управления и определите П<1
ошибки системы при
*\(/>) = А-; WAp) k'
'ТгР ’
WAp) = -- к3
3 УР) Тгр +
WAP)
РгР + 1 ’
ТгР
Рис. 2-2-18.
43

2-2-19. Сверните структурную схему системы управ¬
ления (рис. 2-2-19) и определите ее ПФ.
WiQ(p) -
W7(p) ■
Х(р)
-Jx
wt(p)
Wp)\*
W2(p)
w4(p) ■
wsm h-eH w‘lp>
Yip)
Wg(p)
Рис. 2-2-19.
2-2-20. Произвести структурные преобразования трехлучевых
прямых схем (рис. 2-2-20,а—г) так, чтобы после преобразования
остались фиксированными три точки: два входа и один выход или
один вход и два выхода.
Xfp)
w,(p)
Х2(р)
*i(p)
W,(p)
х2(р)
W2(p)
W4(p)
Ф
Y(p) X(p)
_	  V,(p)
—Wjffp)
W2(p)
a)
WP>
Wj(p)
w2(p)
VJh(p)
6)
-e-
Y(p) X(p)
W3(p)
Wp)
VIt{p)
уг(р)
6)
Y,(p)
W,lp)
w^fp)
Yz(p)
г)
Рис. 2-2-20.
2-2-21. Произвести аналогичные задаче 2-2-20 структурные пре¬
образования трехлучевых перекрестных схем, изображенных на
рис. 2-2-21,а-?.
44

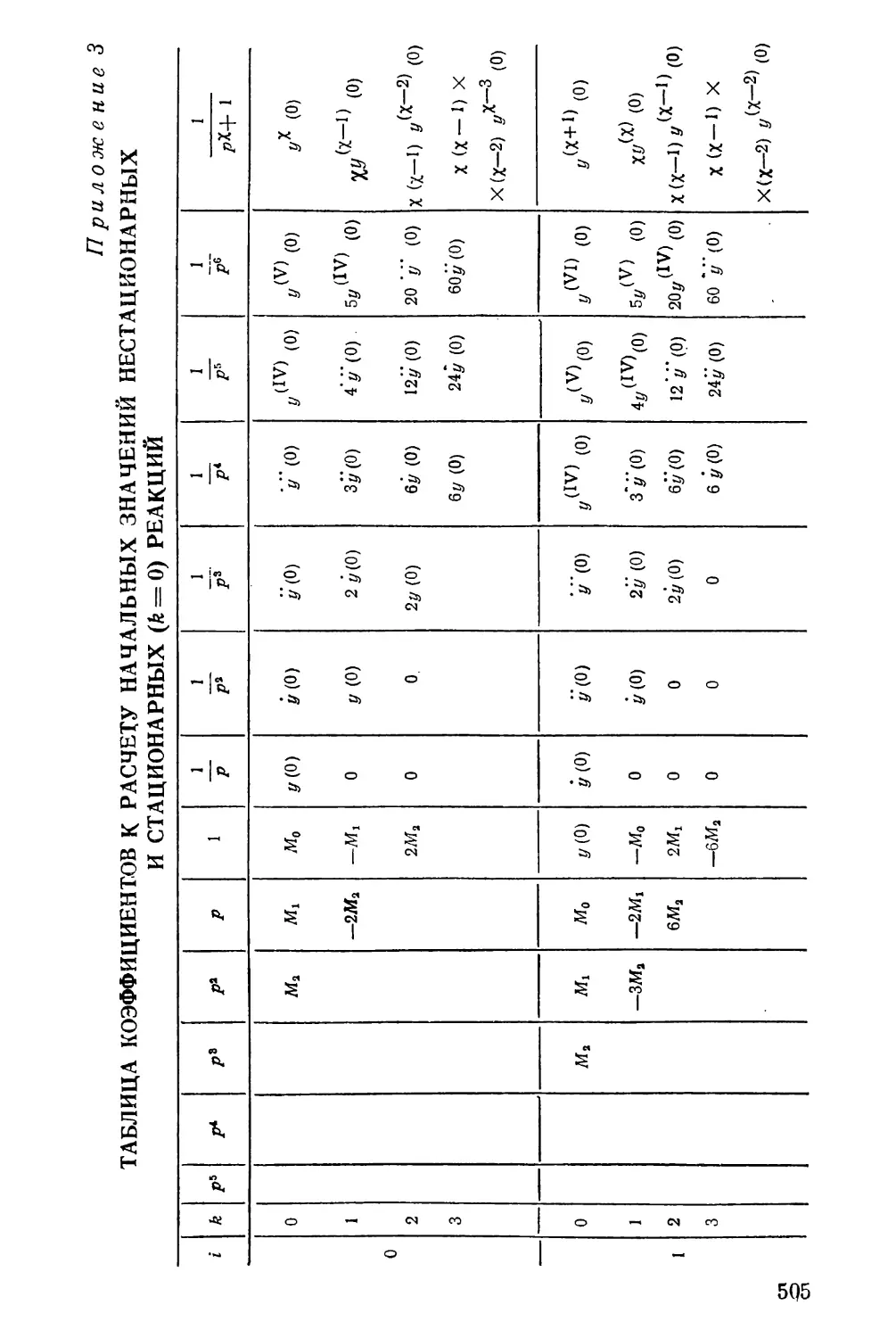
Рис. 2-2-21.
обпДп^о?’ ^Роизвести аналогичные задаче 2-2-20 структурные пре-
изо6пя^р!ИЯ тРехлУчевых перекрестных схем с обратными связями,
изображенных на рис. 2-2-22.
45

2-2-23. Произвести аналогичные задаче 2-2-19 структурные п„
образования многолучевой схемы, изображенной на рис. 2-2-23.
Xz(p)
Х,(р),
Wf(p)
W2tp)
ws(p)
W3(p)
X7(p)
Wfy(p)
I xs(p) xs(p) 1 '
Хц(р)
Yfp)
Рис. 2-2-23.
2-2-24. Построить структурную схему для апериоди¬
ческого звена с ненулевыми начальными условиями
у(0_)ф0, используя решение задачи 01-5-30.
2-2-25. Построить структурную схему для колебатель¬
ного звена с ненулевыми начальными условиями:
у(0_)Ф0] у(0-)=т^0, используя решение задачи 1-5-31.
2-2-26. Построить структуру во временной области по
заданному алгебраизованному уравнению
(T*D*+2lTD+\)y(t)=k{\+TxD)x(t).
2-2-27. Дифференциальное уравнение системы с пере¬
менными коэффициентами дано в виде
а. (0 У{т (0 + «з (0 "у (t)+а, it) у (t) + а, (t) у (t) +
+ а. (0 у it) = Ь, (t) x(t) + К Ц) х (0+6, it) x it) + b„ Ц) x it).
По заданному уравнению построить нестационарную
структуру.
2-2-28. Для системы, заданной в 2-2-27, построить
структуру, соответствующую сопряженным уравнениям
с реверсированным аргументом, решением которых явля¬
ется параметрическая импульсная характеристика
[28].
46

2-3 СТРУКТУРНЫЙ АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
2-3-1. По заданной на рис. 2-3-1 электрической схеме
работающей на усилитель с высокоомным входом,
построить ее структуру и определить ПФ по напряже¬
нию.
0—*—i
LZ>
*/
UX
F
-Х-0
а*
Ut
Of
11-
J
Us
*5
Re UY=US
Рис. 2-3-1.
Рис. 2-3-2.
2-3-2. Электрическая схема фильтра представлена на
рис. 2-3-2. Построить его структурную схему и опреде¬
лить ПФ для холостого хода.
2-3-3. Для активной схемы с усилителем, показанной
на рис. 2-3-3, построить структурную схему, используя
для входного контура режим генератора напряжения,
а для контура обратной связи режим генератора тока.
I II J ли
гвм(р)
Щр)
У(Р)
Рис. 2-3-3.
Рис. 2-3-4.
2-3-4. По заданной на рис. 2-3-4 электрической схеме
оставить структурную схему, отражающую взаимосвя-
За МежДу переменными U, I, £ в операторной форме для
данных параметров цепи: проводимости нагрузки У и
Утреннего сопротивления источника ZBH.
47

2-4. ГРАФЫ
2-4-1. По структурной схеме, приведенной на рйс
2-4-1 и являющейся развитием схемы на рис. 2-2-19, За
f счет введения дополнительных звеньев Км, К\2, К\г п К
построить граф системы и определить ПФ от сигнал-
Х(р) к реакции Y(p).
Wf(p)
У(р)
К12(р)
W7(p)
Ww(p)
I	—\w*ip)
Wj(p)	w2(p)	-+*-*Wj(p)
W3(p)	Wfy(p)
W5(p)
w6(p)
Wg(p)
K1u(p)
Yip)
Рис. 2-4-1.
2-4-2. Методами теории графов определить ПФ систе¬
мы, рассматриваемой в задаче 2-2-19, непосредственно
по структурной схеме рис. 2-2-19, без дополнительных
построений.
2-4-3. По заданной ПФ вида
*(Р) =
biP+bQ
<*гР3+ а2р2 + ахр + а0
построить детализированный граф, иллюстрирующий
преобразования сигнала при формировании импульсной
характеристики системы, и показать на нем общие пра¬
вила для получения ПФ графа.
2-4-4. По заданной в нормальной форме неоднородной
системе уравнений четвертого порядка

построить графы в преобразованной по Лапласу и гиб¬
ридной формах, определить ПФ вида W(p)=Yi(p)/X(p)
и сопоставить ее коэффициенты с коэффициентами си¬
стемы (а).
2-4-5. По заданным коэффициентам ПФ вида
/7—1
2 м
W(p)= ‘-°п_г-
Рп+2 ajpi
i=o
определить коэффициенты ввода воздействия в нормаль¬
ную форму уравнений сс^, приведенную в предыдущей
задаче. Решение получить для п—4 и в общем виде, ис¬
пользуя метод обращения матриц.
2-4-6.^ Провести сопоставление коэффициентов неод¬
нородной системы уравнений задачи 2-4-4 и ПФ в зада¬
че 2-4-5 методом переноса ребер графа к общей верши¬
не г/4.
2-5. ТОПОЛОГИЧЕСКИЕ И БЛОЧНЫЕ ПРЕОБРАЗОВАНИЯ
МАТРИЦ И ОПРЕДЕЛИТЕЛЕЙ
2-5-1. Для многоконтурной системы управления со¬
ставлены уравнения ее элементов и связей между ними,
в результате чего получена система из шести уравнений
относительно координат Yi, Y2, ..., Уб, определитель ко¬
торой имеет вид:
^11
0
0
^14
0
*1.
W 21
^22
^23
0
0
0
0
^32
^33
0
0
0
^41
0
0
W
44
0
0
0
0
^53
0
^55
0
0
0
0
^0 5
где элементами Wik могут быть числа (коэффициенты
передачи) или ПФ. Требуется:
а)	раскрыть определитель, используя топологические
свойства контуров, построенных непосредственно на ма¬
трице коэффициентов, которой соответствует заданный
определитель;
4—903
49

б)	проверить знаки получаемых при этом элементов
путем подсчета числа инверсий в перестановке индексов
коэффициентов, образующих произведения.
2-5-2. Для системы управления, рассмотренной в пре¬
дыдущей задаче, замещенный определитель, учитываю¬
щий условия ввода воздействия Ка\Х, задан в следую¬
щей форме:
0
0
0
^14
0
TFi.
0
U722
1^23
0
0
0
0
^32
^33
0
0
0
*41
0
0
^4*
0
0
0
0
^53
0
^5в
0
0
0
0
^6.
Требуется:
а) по замещенному определителю установить задан¬
ные условия ввода воздействия и съема реакции;
б) на матрице (определителе) системы, приведенной
в задаче 2-5-1, построить прямые пути прохождения сиг¬
нала и несвязанные контуры, использовав их для рас¬
крытия замещенного определителя топологическим мето¬
дом;
в) проверить знаки получаемых в п. «б» произведе¬
ний, содержащих прямые пути;
г) определить ПФ системы для установленных усло¬
вий входа и выхода.
2-5-3. Для электрического фильтра, рассмотренного
в задаче 2-3-2, требуется составить структурную схему,
удобную для последующего топологического анализа, и
определить ПФ фильтра, пользуясь топологическим кон¬
турным методом.
2-5-4. Для электрической схе¬
мы на рис. 2-5-4, считая перемен¬
ной состояния напряжение на
конденсаторе щ, составить пер¬
вичные уравнения цепи, расши-
;* рив их за счет уравнения сигнала
u0=expXt в дифференциальной
форме. Решение уравнений про¬
вести в матричной форме, сохра¬
няя информацию о переменных
«о, щ и i2 до конца решения, по-
Рис. 2-5-4.	ЛОЖИВ	Ио(0)=1 В, 11\ (0_) =1 В.
50

Глава третья
АНАЛИЗ И ОСНОВЫ СИНТЕЗА ЛИНЕЙНЫХ
СИСТЕМ НЕПРЕРЫВНОГО УПРАВЛЕНИЯ
3-1. ТОЧНОСТЬ ВЫНУЖДЕННОГО движения
СТАЦИОНАРНЫХ СИСТЕМ (С ПОСТОЯННЫМИ
ПАРАМЕТРАМИ)
3-1-1. Определить ошибку преобразования управляю¬
щего сигнала реальным дифференцирующим звеном
с ПФ Ф(Р) =	при	эталонной	ПФ	фэ(р)=тр,	если
на вход звена подано входное воздействие:
а) x[/) = l[f);
б) x[t)=vt-\[t)-,
в) =	[t).
3-1-2. Преобразование входного сигнала задано в фор¬
ме упреждения (форсирования) по эталонной формуле
Фэ(р) =0,02 (1+0,9/?), а реализуется оно реальным фор-
сирующим звеном первого порядка, имеющим ПФ
Определить ошибку преобразования.
3-1-3. Определить ошибку преобразования управляю¬
щего сигнала, обусловленную отличием реальной ПФ от
эталонной Фэ (p)=kmp и действием возмущения £(£),
для схемы, структура которой дана на рис. 3-1-3.
3-1-4. Определить ошибку преобразования управля¬
ющего сигнала реальным форсирующим звеном с ПФ
nwn)_ 0,02(1 +0,9/7)
'Г/	П	1	Г»	1
0, 1/7+1
Y
Рис. 3-1-3.
4*
51

при эталонной Фэ(р)—к(1-\-21Тр-\-Т2р2) и числовых зна-
чениях параметров &=0,05; Г=0,5 с; £=0,8; 7\=0,02 с*
72=0,05 с.
3-1-5. Определить необходимый коэффициент усиле¬
ния прямого тракта системы с астатизмом первого по¬
рядка, если допустимая ошибка вынужденного движения
1^1 =0,001 рад, а максимальная скорость яМакс=
=0,6 рад/с.
3-1-6. Определить необходимый коэффициент усиле¬
ния по ускорению для системы с астатизмом второго по¬
рядка, если допустимая ошибка вынужденного движе¬
ния |	=0,06°, а максимальное ускорение х=6°/с2.
3-1-7. Определить коэффициент передачи полезного
сигнала и коэффициент влияния возмущений для усили¬
теля постоянного тока с отрицательной обратной связью.
Структурная схема усилителя представлена на рис.
3-1-7, где приняты следующие обозначения: Ux — вход-
Рис. 3-1-7.
ной сигнал, задаваемый на сетку усилителя через вход¬
ное сопротивление /у, Л<Уа— нестабильность анодного
источника питания; At/др— дрейф напряжения на сетке
лампы из-за эксплуатационных изменений внутренних
свойств лампы (эмиссии); AUCM — нестабильность на¬
пряжения сеточного смещения; AUR — падение напряже¬
ния от тока нагрузки; k — коэффициент усиления уси¬
лителя; Uу—-выходное напряжение; А— ошибки, обу¬
словленные влиянием возмущений; г0 — сопротивление
обратной связи; г2 — сопротивление утечки (положить
Г 2 ^оо).
52

3-1-8. Определить требуемый статический коэффици¬
ент усиления усилителя с отрицательной обратной
связью, если допустимая статическая ошибка |£о| =
=0,002 В, а максимальное выходное напряжение
^у.макс=120 В.
3-1-9. Определить ошибку (рассогласование) следя¬
щей системы, имеющей ПФ ошибки
% (Р)
р^±4р_±2_
~р2 + 9р + 32’
при синусоидальном изменении входной величины с ча¬
стотой соа=0,2 с-1 и единичной амплитудой.
3-1-10. Определить коэффициенты ошибки вынужден¬
ного движения замкнутых систем управления, если ПФ
разомкнутых систем даны в виде
2,24/7+ 1
a) w;xp) =
6 ywM(p) =
р4 + 3,64 /?3 + 3,5 /?2 + 2,99/?’
5/? -}- 30
Р2 + 4/? + 2
3-1-11. Определить установившуюся ошибку следя¬
щей системы, структурная схема которой изображена на
рис. 3-1-11, при действии на нее входного сигнала вида
НО
и постоянного возмущающего воздействия Мв, прило¬
женного к валу двигателя.
Рис. 3-1-11.
3-1-12. В условиях задачи 3-1-11 определить устано¬
вившуюся ошибку системы при действии постоянного
входного сигнала q-\[t) и постоянного возмущения Мв,
если £п=1,5 В/рад; &д=1; &к=0,6; &у=500 мА/В; &дв=
= 1 (г-см)/мА; Г!=0,025 с; 7"=0,015 с; Гдв=0,1 с.
53

3-1-13. Определить порядок астатизма следящей си¬
стемы с ЭМУ по управляющему воздействию и по в0з.
мущению и установившуюся ошибку при воздействии ца
систему постоянного входного сигнала и постоянного
возмущения, структурная схема которой представлена на
рис. 3-1-13, где йг-т — передаточное число от грубого
к точному отсчету; kc — передаточный коэффициент
сельсинов датчика и приемника; &у_д — коэффициент
усиления усилителя-демодулятора; Yy — проводимость
управляющей обмотки ЭМУ; S. —крутизна нара-
у ч
стания э. д. с. в короткозамкнутой обмотке якоря по то¬
ку в управляющей обмотке; Yq — эквивалентная прово¬
димость для поперечной цепи якоря; S, _Е крутизна
* d
нарастания э. д. с. в продольной цепи якоря по току
в короткозамкнутой обмотке якоря; Y—суммарная экви¬
валентная проводимость для цепи ЭМУ, двигателя и со¬
единительных проводов; ki-м — коэффициент, связываю¬
щий ток с вращающим моментом; k9_E —коэффициент,
связывающий частоту вращения с противо-э. д. с. двига¬
теля; ftp — коэффициент передачи редуктора.
3-1-14. Определить установившуюся ошибку системы,
заданной з задаче 3-1-13, при воздействии на нее линей¬
но изменяющегося входного сигнала (pt) и постоянного
возмущения Мв.
3-1-15. Определить коэффициенты ошибки вынужден¬
ного движения и значение установившейся ошибки (рас¬
согласования) следящей системы, заданной уравнением
5 -10-*^+ 15- 10-3^f +% +	100*.
если ее скорость движения Q=10°/c.
54

3-1-16. Определить ошибку вынужденного движения,
выразив ее в функции выходной величины следящей си¬
стемы, структурная схема которой представлена на рис.
3-1-16, с параметрами Г=0,5 с; /e_i=10 с-1.
Х(п)
Jl±
р
-ed-
Рис. 3-1-16.
3-1-17. Определить ошибку вынужденного движения
в функции выходной величины следящей системы, за¬
данной в задаче 3-1-16, если между входом и выходом
введена положительная обратная связь с ПФ (оис
3-1-17):
H(P) = kirP'-
3-1-18. Определить ПФ корректирующего контура
К(р), обеспечивающего получение инвариантной по от¬
ношению к управляющему воздействию системы задан¬
ной структуры (рис. 3-1-18), где
kr _ Tfccfey _ jjY^rSf YqSj	—	м
Wt (/?) = .	У	я	d	1	.
(P)-
TyP + 1) (Tqp + 1) ITp + 1)
ITp + i)
[Jp (Tp + 1) + kQ_EYkf_M] p
Рис. 3-1-18.
3-1-19. Определить ПФ корректирующего контура
К{р) для схемы, изображенной на рис. 3-1-19, обеспечи¬
55

вающего получение системы, инвариантной к возмуще,
нию (инвариантность по Щипанову).
Рис. 3-1-19.
3-1-20. Определить (методом В. С. Кулебакина) ПФ
дополнительного контура, обеспечивающего инвариант¬
ность заданной системы компаундирования, структурная
схема которой изображена на рис. 3-1-20.
Компаундирование электрических машин осуществ¬
ляется путем наложения на их полюсы наряду с парал¬
лельными последовательных обмоток возбуждения.
В этих случаях возбуждение автоматически изменяется
при изменении нагрузки машины и компенсирует паде¬
ние напряжения от тока нагрузки. Как видно из схемы
на рис. 3-1-20, действие последовательной обмотки струк¬
турно эквивалентно регулированию по возмущению
(/нагр) с подачей через дополнительный контур WK ком¬
пенсирующего воздействия, упреждающего ввод возму¬
щения.
-7
Рис. 3-1-20.	Рис.	3-1-21.
3-1-21. Для системы заданной направленным графом
(рис. 3-1-21) определить ПФ компенсирующего звена?
56

обеспечивающего инвариантность системы по отношению
к действующему возмущению, если
3-2. ТОЧНОСТЬ НЕСТАЦИОНАРНЫХ ЛИНЕЙНЫХ СИСТЕМ
3-2-1. Нестационарная следящая система задана об¬
щим уравнением вида
(О Н--1», (О У + 1\ (t) у + р, (t)y = и, (t)x-\-u0 (t) х.
Составить уравнение для ошибки слежения.
3-2-2. Дана нестационарная система управления, за-
м кнута я стандартной единичной отрицательной обратной
связью, показанная на рис. 3-2-2. Уравнение, устанавли¬
вающее связь между входом и реакцией разомкнутой си¬
стемы, имеет вид:
О* (О У + % (0 У+v 1 (О У + V, (о г/ = «, (0 х„-\- и, (*) л:,.
Составить уравнение для ошибки слежения.
3-2-3. Определить в первом приближении параметри¬
ческую передаточную функцию ППФ по уравнению свя¬
зи между воздействием х и ошибкой £
Найти частное значение ППФ для момента наблюде¬
ния /=10 с.
3-2-4. Для уравнения, составленного относительно
ошибки, 5£+(2/+20)£-|-137£=2л: найти операторным ме¬
тодом по формуле первого приближения полную реак¬
цию в момент времени /=20 с от линейно нарастающего
воздействия х=5 (/—0Х), действующего:
а) начиная с 10-й секунды (0^=10 с);
б) начиная с 19-й секунды (0^=19 с).
разомкнутая
система
У
Рис. 3-2-2.
(5/г + 3t -f 2)'t -f- (41 -f 1) C+ (21* + f + 3)C +
+ (f* + 2f+l): = (2f+l);c.
57

3-2-5. Для условий предыдущей задачи найти Прц
ближенное значение ошибки в заданный момент набпю!
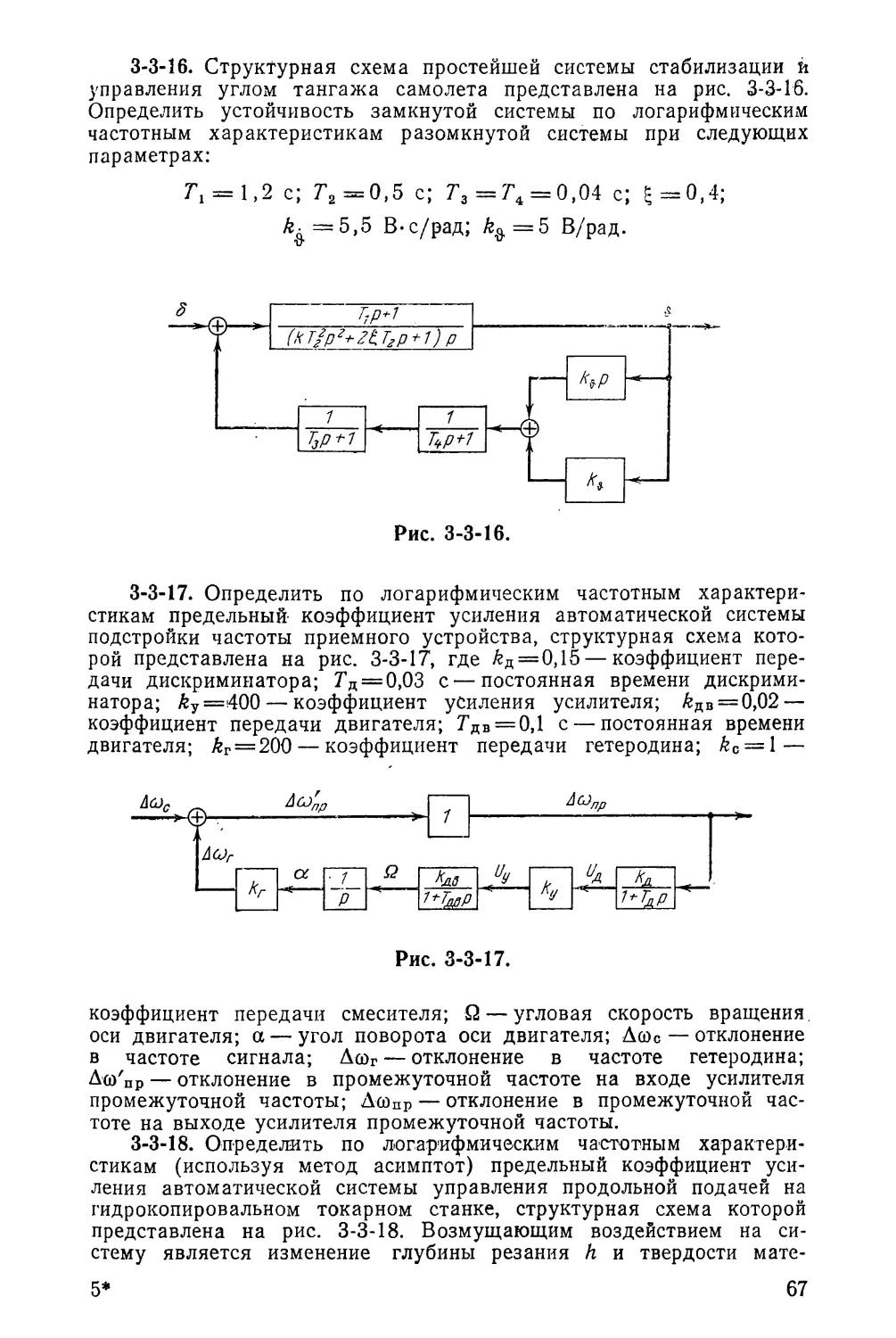
дения /=20 с по формуле вынужденного движения.
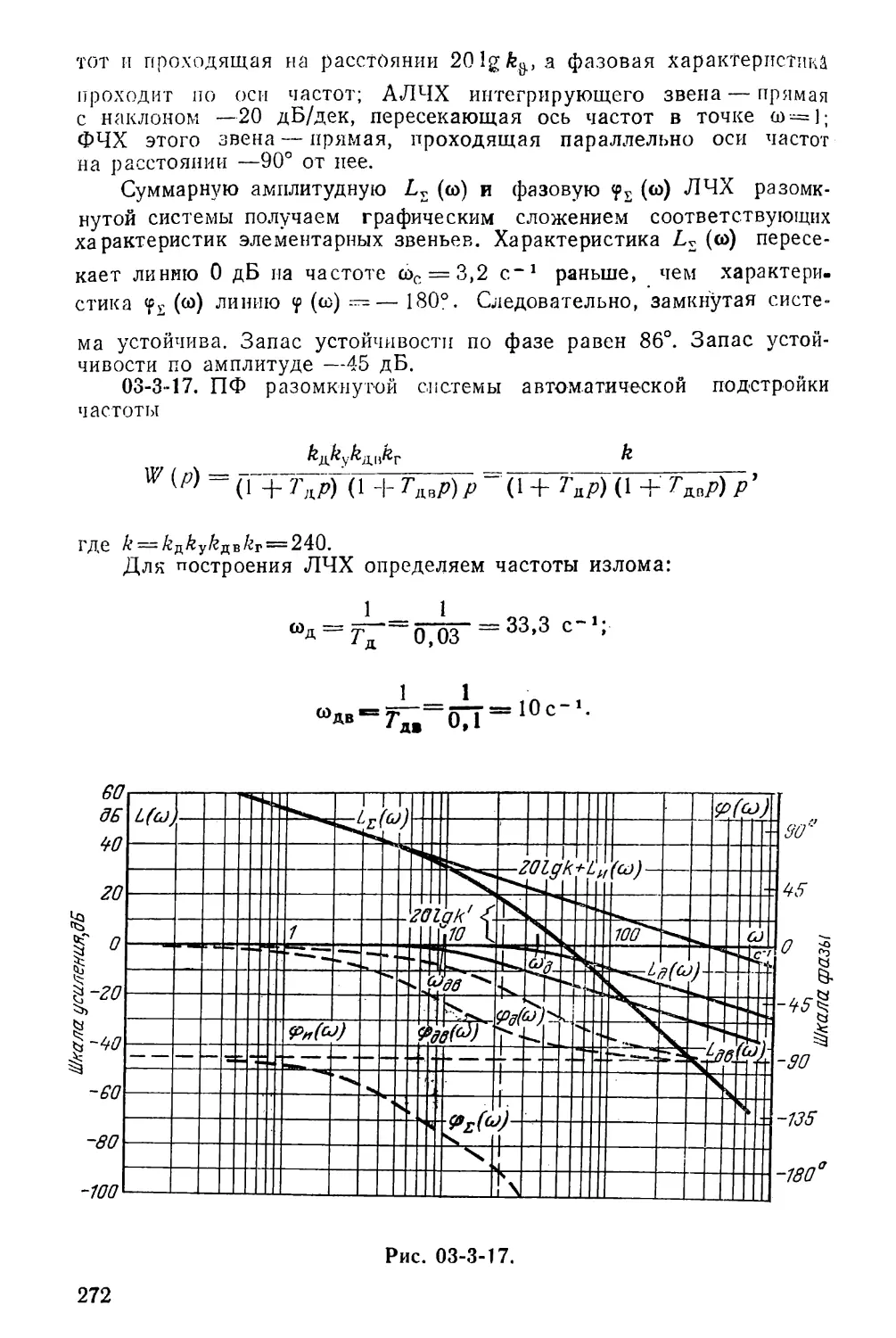
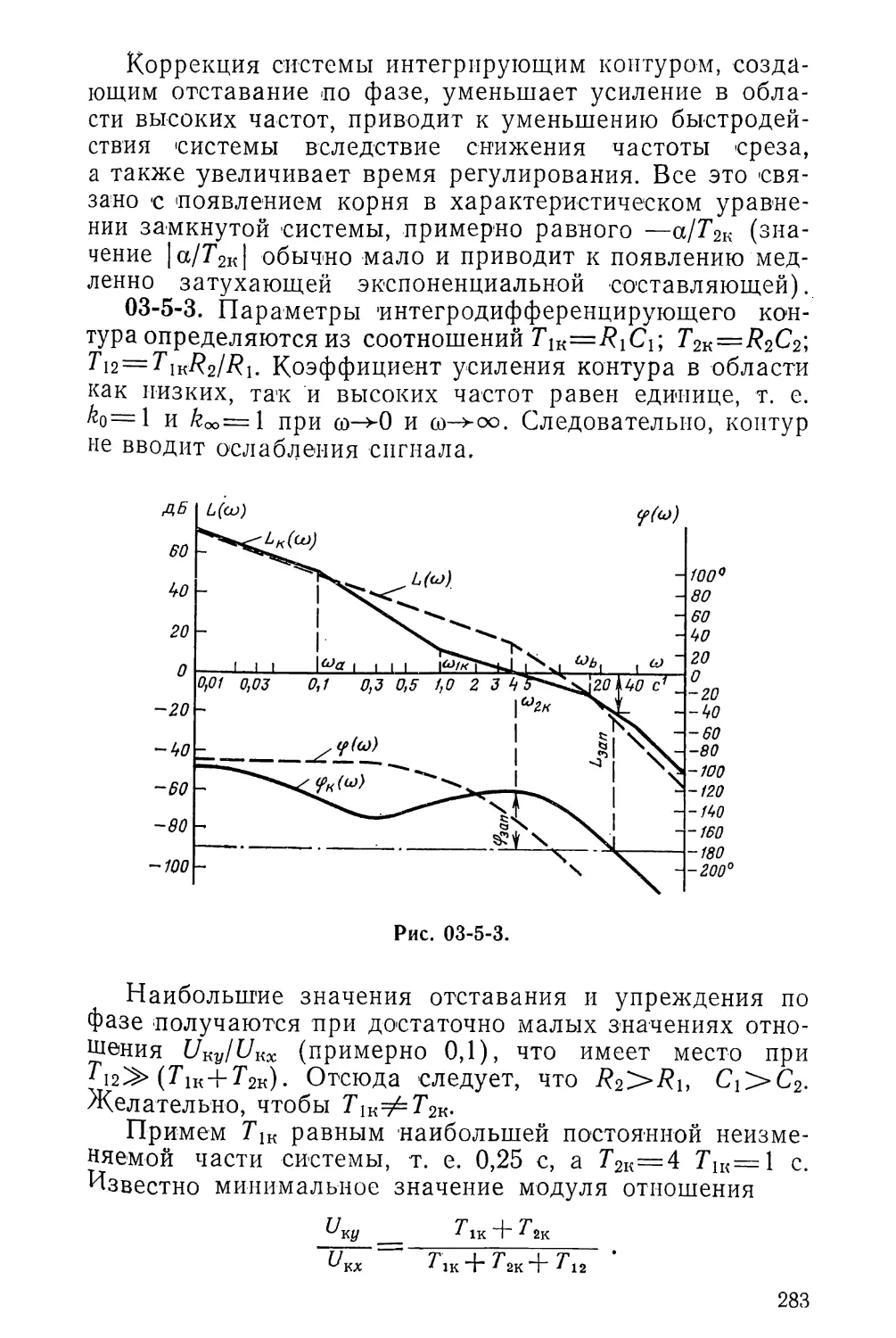
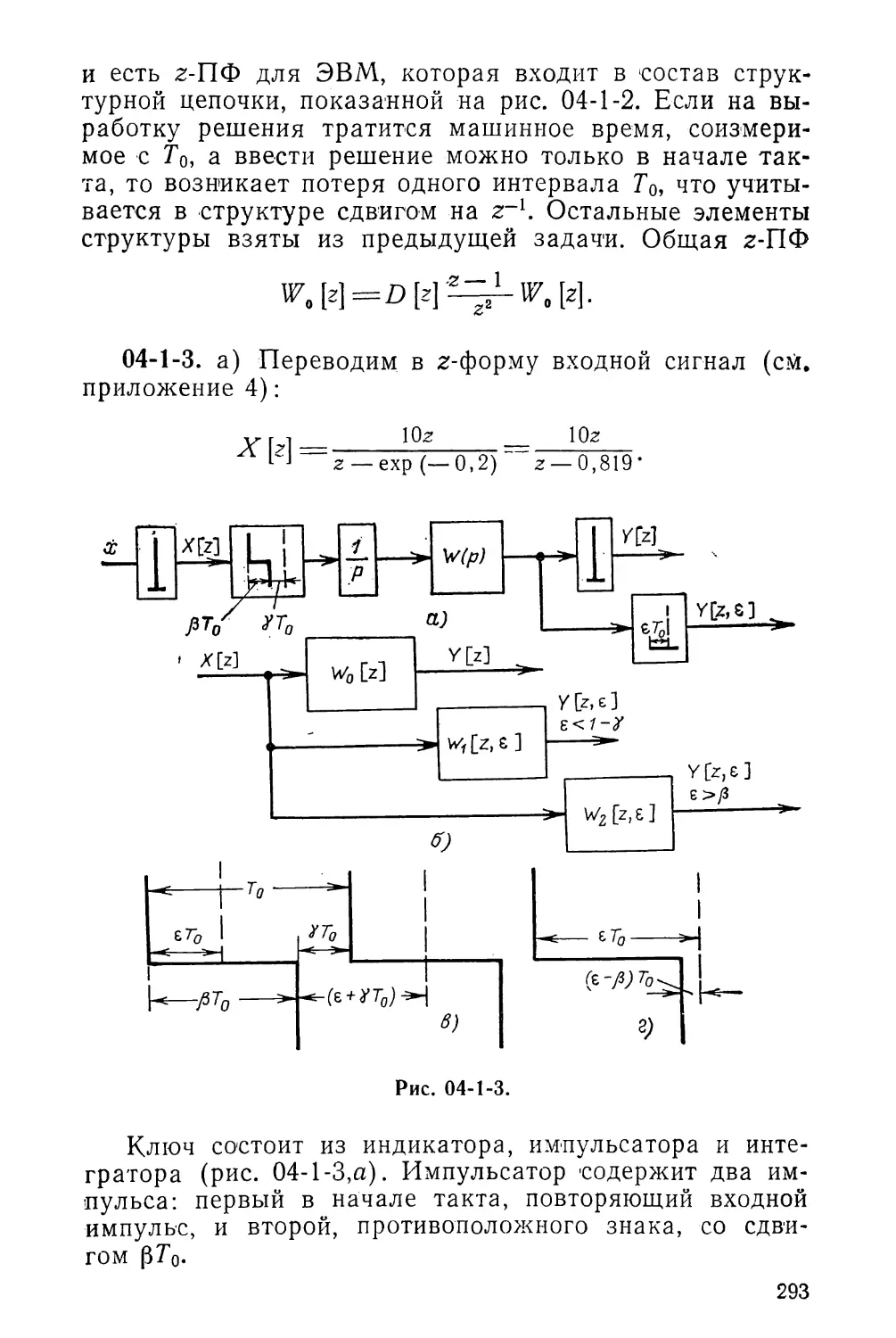
3-3. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ
3-3-1. Оценить по Вышнеградскому, устойчива ли за.
мкнутая система с ПФ разомкнутой системы
w (р) =	 3~р	+	1°
КР) Q (Р)	0,1 /73 + 0,2р2+ 0,5р + 1 ’
3-3-2. Дано характеристическое уравнение замкнутой
системы 0,1р3+17/?2+800р+50 000=0. Установить устой¬
чивость системы по Вышнеградскому.
3-3-3. Проверить устойчивость замкнутой системы,
если ПФ разомкнутой системы
Г (/>)=-; ^+п-.
р2 (5р + 1)
3-3-4. Характеристический полином замкнутой систе-,
мы М(р)=р4+2р3+/?2+10р+20. Проверить систему на
устойчивость.
3-3-5. Определить устойчивость по Гурвицу системы
с характеристическим полиномом
М(р) =/+3/+10+-2/+5.
3-3-6. Определить по Гурвицу, устойчива ли замкну¬
тая система с ПФ прямого тракта
w (р) = —5р + 20
р3+2р* + Зр+1-
3-3-7. Оценить устойчивость по Раусу для системы
с характеристическим полиномом М (р)=0,104р7+
+0,33рв+5,5р5+15,5/+25р3+25р2+19,7+9,5.
3-3-8. Оценить по Раусу и Гурвицу устойчивость сле¬
дящей системы с характеристическим полиномом
М (р) =0,0039+0,35+ 2,05р2+1,135/7+3.
3-3-9. Даны две взаимосвязанные системы, общая
структурная схема которых имеет вид, изображенный из
58

■рис. 3-3-9, где
cosy; 6 = sin у; с = — sin у; rf = cosy;
ТТ5,
Определить условия устойчивости системы с учетом
взаимосвязей.
Рис. 3-3-9.
3-3-10. Определить предельный коэффициент усиле¬
ния для статической системы, принципиальная электри¬
ческая и структурная схемы которой представлены на
рис. 3-3-10, где Тз—0,2 с; Г2=0,1 с; ^=0,05 с.
Обратная связь
:>с
Выход
Рис. 3-3-10.
59

3-3-11. Определить предельный коэффициент уСИл
ния для астатической системы, принципиальная электпи'
ческая и структурная схемы которой даны на рис 3-3 ii
где 7^0,005 с; Т2=0,2 с.
-1
,1
к/
кг
kj
Р
^ ч!/^
Х(р)
TfP + f
Т2р+1
У(Р>
Рис. 3-3-11.
3-3-12. Для систем с ПФ прямого тракта
a )W(p) = -
ю
(0,2/7+ 1) (0,5/> + 1) (3/7— 1)’
б)	W (/?) 	 50(0Д/>	+
(100/J2 —-4/7+1) (Ър + 1) (0,0004/>2 +
+ 1)
+ 0,02р+ 1) (0,025р+1)	•
+J
J=0
L 1
1 .
cj=Zc~1 ~
\ i
и
8
Л-1
CJ = 7C~1\
V
0=0,11 t
-80
-60
cj=0,15Q
-40
cj=0,w\
-20
cj=0,3c'\
jo=0.1
ъСО=0,09
\и=0,077
6)
60

Комплексные частотные характеристики разомкну¬
тых систем изображены на рис. 3-3-12,а и б соответст¬
венно.
Определить, устойчивы ли замкнутые системы.
3-3-13. Для замкнутой системы
четвертого порядка (п=4) вид
годографа Михайлова изображен
на рис. 3-3-13. Каково располо¬
жение корней характеристическо¬
го полинома?
3-3-14. По критерию Найкви-
ста определить устойчивость за¬
мкнутых систем, если для их ра¬
зомкнутых частей заданы годо¬
графы
“7«">= Щ-
и указано расположение полюсов. Эти данные приведе¬
ны в табл. 3-3-1, где i — число корней характеристиче¬
ского уравнения разомкнутой системы, расположенных
на мнимой оси (нейтральных); г — число корней харак¬
теристического уравнения разомкнутой части, располо¬
женных в правой половине комплексной плоскости (пра¬
вых); v — порядок астатизма по управляющему воздей¬
ствию.
3-3-15. Построить структурную схему и определить устойчивость
замкнутой системы стабилизации крена самолета, заданной следую¬
щей системой дифференциальных уравнений:
d2y	dy
Jxx~^T + Мхя --ц = Af6<>..+ AfBT
— уравнение моментов относительно продольной оси самолета;
Ть Ь + 5 = kbIy — уравнение рулевого привода; /у = kyUn — уравнение
усилителя;
^=£и(Упр—у)=^иАу — уравнение	измерительного элемента,
где Jxx — момент инерции самолета; Мх2 — коэффициент тушащего
момента; — коэффициент управляющего момента; Мв^—возму¬
щающий момент; у— угол крена или вращения; б — угол отклоне¬
ния руля; /у — управляющий ток, поступающий на рулевую машину
из усилительного устройства; kb—коэффициент передачи рулевой
машины; Un — напряжение, снимаемое с потенциометра гироскопа
положения; &и — коэффициент передачи измерительного элемента;
Упр — программное значение угла крена.
Параметры системы:	JXx/Mхя = ^У= 13 " с; Mb/MxQ = k^ =
=60 с-1; &5=0,01 рад/мА; Тъ = 0,5 с; ky = 10 мА/В; &и=14 В/рад.
61
У
Рис. 3-3-13.

Таблица 3.3.,
Вид АФХ разомкнутой системы
М+У
1 (я)а0
ю>=0

Продолжение табл. 3-3

64

Продолжение табл. 3-3-1

Продолжение табл. 3 ^
Вид АФХ разомкнутой системы
66

3-3-16. Структурная схема простейшей системы стабилизации и
управления углом тангажа самолета представлена на рис. 3-3-16.
Определить устойчивость замкнутой системы по логарифмическим
частотным характеристикам разомкнутой системы при следующих
параметрах:
7\ = 1,2 с; 7^2 =0,5 с; Тг = 74 = 0,04 с; ^ = 0,4;
* £ — 515 В-с/рад; ^=5 В/рад.
Рис. 3-3-16.
3-3-17. Определить по логарифмическим частотным характери¬
стикам предельный коэффициент усиления автоматической системы
подстройки частоты приемного устройства, структурная схема кото¬
рой представлена на рис. 3-3-17, где £д = 0,15— коэффициент пере¬
дачи дискриминатора; Гд = 0,03 с — постоянная времени дискрими¬
натора; £у=400 — коэффициент усиления усилителя; £дв = 0,02 —
коэффициент передачи двигателя; Гдв = 0,1 с — постоянная времени
двигателя; £г = 200 — коэффициент передачи гетеродина; kc = l—
Рис. 3-3-17.
коэффициент передачи смесителя; Q — угловая скорость вращения,
оси двигателя; а — угол поворота оси двигателя; Дсос — отклонение
в частоте сигнала; Дсог — отклонение в частоте гетеродина;
Асо'пр — отклонение в промежуточной частоте на входе усилителя
промежуточной частоты; ЛсоПр — отклонение в промежуточной час¬
тоте на выходе усилителя промежуточной частоты.
3-3-18. Определить по логарифмическим частотным характери¬
стикам (используя метод асимптот) предельный коэффициент уси¬
ления автоматической системы управления продольной подачей на
гидрокопировальном токарном станке, структурная схема которой
представлена на рис. 3-3-18. Возмущающим воздействием на си¬
стему является изменение глубины резания h и твердости мате¬
5*
67

риала заготовки Нъ, Это возмущение преобразуется процессом
резания во входное значение силы резания APZbx=APz(Ii) . Выход,
ным параметром системы является приращение подачи AS, преоб!
разуемое в процессе резания в выходное значение силы АР2ВЬ1 '
=А Pz(S).
Рис. 3-3-18.
Датчиком в данной системе управления служит главный дви-
гатель станка, на вход которого поступает значение APz(h)—APZ(S),
а на выходе возникает изменение тока питания А/ обмотки двига¬
теля, в одну из фаз которого включается первичная обмотка транс¬
форматора тока .(коэффициенты kit кг). Всякое изменение мощности
резания приводит к приращению выходного напряжения трансфор¬
матора тока АС/, пропорционального /г3, которое после усиления
управляет работой электрогидравлического преобразователя (ЭГП)
с ПФ
w
И'эг.п- \+ТГр>
который установлен на сливе гидромотора суппорта станка с ПФ
AS
^гм — AQ =k'°'
Приращение напряжения на ЭГП вызывает изменение продоль¬
ной подачи и соответствующее ей изменение силы резания APZ(S)
в сторону компенсации возникшего отклонения. Процесс резания
приближенно представляется ПФ
AP^{S)— ke
AS 1 + Трр
Параметры системы: Гд = 0,08 с; Гг = 0,06 с; Гр = 0,09 с.
3-4. КАЧЕСТВО ЛИНЕЙНЫХ СИСТЕМ
НЕПРЕРЫВНОГО УПРАВЛЕНИЯ
3-4-1. Оценить динамическое качество системы регу¬
лирования напряжения, описываемой уравнением
[(7г/Н-1) (Тур-\-1) (T1<'3pJrl)-)rk\AUy(p)=kAUx(p) путем
полного построения переходной характеристики и опре¬
деления по ней времени регулирования tv, перерегулиро¬
вания б, периода колебаний Т и числа полуволн N за
68

время затухания процесса. Параметры системы имеют
следующие значения: 7\=0,4 с; Ту=0,04 с; Ткз—0,1 с;
/г= 12.
3-4-2. Определить приближенные значения перерегу¬
лирования и времени регулирования по вещественной
частотной характеристике замкнутой системы, изобра¬
женной на рис. 1-8-11, и сравнить их с результатами за¬
дачи 1-8-11.
3-4-3. Определить приближенные значения перерегу¬
лирования и времени регулирования по вещественной
частотной характеристике С((о) замкнутой системы, изо¬
браженной на рис. 3-4-3.
Рис. 3-4-3.
, 6(Ь>)
t
т
CJ
*)
6Ы)
±
° б)
Рис. 3-4-4.
+
0>г
3-4-4. Система имеет вещественные частотные харак¬
теристики, изображенные на рис. 3-4-4, с численными
значениями, заданными в табл. 3-4-1. Определить отно-
Таблица 3-4-1
Вариант
а
б
° +
6)Х
Wi
w2
1,0
1,0
1,0
0,1
0,8
1,6
1,2
2,0
1,0
0,2
1,2
2,4
сительное перерегулирование и время достижения пере¬
ходной характеристикой первого максимума.
3-4-5. Определить относительное перерегулирование и
время достижения переходной характеристикой первого
максимума, если вещественная частотная характеристи¬
ка системы задана рис. 3-4-5 и табл. 3-4-2.
69

Таблица l3-4-2
G+
G _
0(0)
<°а
1,2
0,2
1,0
1,4
1,1
0,15
1,0
2,5
1,5
0,3
1,0
3,0
3-4-6. Определить аналитическим способом частоту
собственных демпфированных колебаний сос и относи¬
тельный коэффициент затухания для замкнутой системы,
если ПФ разомкнутой системы
=Р(Тр+\У
для Т=0,2 с и k—3, 5, 8.
3-4-7. Определить число полуволн N за время регули¬
рования и перерегулирование б для системы, заданной
в 3-4-6.
3-4-8. Определить интегральный квадратичный кри¬
терий сближения для интегрирующего привода, реаль¬
ная ПФ которого (b(p)=k/p(Tp-\-l), а эталонная
Фэ (p)=k/p.
3-4-9. Определить интегральный квадратичный крите¬
рий сближения для системы, имеющей реальную ПФ
0(p)=k(T2p-[-l)l{Tip-\-l)t а эталонную Фэ(р) =к/(Т\Р^
+ 1)*
3-4-10. Выбрать электромеханическую постоянную
времени Гдв двигателя постоянного тока, структурная
схема которого без учета нагрузки изображена на рйс;
3-4-10, исходя из минимума интегральной квадратичной
оценки и полагая коэффициент усиления двигателя по
70

скорости /Слв=1 и собственную частоту соо=1 с”1. На
рис. 3-4-10 обозначено:	£дв— входное напряжение
(управляющий входной сигнал); RH и Ln — сопротивле¬
ние и индуктивность якорной цепи; сЕ и см — коэффи¬
циенты по э. д. с. и моменту; J — суммарный момент
инерции ротора с приведенной инерционной нагрузкой;
Q — угловая скорость (выходной сигнал).
Рис. 3-4-10.
3-4-11. Определить квадратичную интегральную оцен¬
ку регулируемого привода с тиристорным преобразова¬
телем, стоуктурная схема которого изображена на рис.
3-4-11.
Ев£
Кп
Едб
Код
Q
	^
1+ТпР
■Кг '
ТмТэр3+Тир+1
“1
!
	J
Рис. 3-4-11.
3-5. СИНТЕЗ ОБЩЕЙ СТРУКТУРЫ СИСТЕМЫ УПРАВЛЕНИЯ
И КОРРЕКТИРУЮЩИХ ЦЕПЕЙ
3-5-1. Определить параметры форсирующего звена
первого порядка (рис. 3-5-1,б), включенного в систему
стабилизации, структурная схема которой изображена
на рис. 3-5-1,а, по каскадной (последовательной) схеме,
обеспечивающего запас по фазе не менее 30° и запас по
усилению —(10-^-12) дБ. Параметры неизменяемой ча¬
сти системы с дополнительно включенным усилителем,
обеспечивающим заданную точность в области низких
частот, имеют следующие числовые значения: k\kykjj=
=40; Гд=0,25 с; Гу=0,0625 с. Уменьшение усиления, вы¬
званное введением форсирующего звена, скомпенсиро¬
вать увеличением коэффициента усиления в (J?i+/?2)/#i
71

раз путем введения дополнительного усилительного кас¬
када. Постоянную времени, входящую в числитель Пф
корректирующего устройства, выбрать равной наибодь-
шей постоянной времени неизменяемой части системы'
т. е. Г1к=0,25 с.	'	’
ия
0—
а)
-СГ>
-0
■О
я2
б)
“У
Of
0“
6)
Рис. 3-5-1.
3-5-2. Определить параметры интегрирующего конту¬
ра (рис. 3-5-1,в), включенного последовательно в систе¬
му, заданную в задаче 3-5-1, и обеспечивающего запас
устойчивости по фазе 50-И300 и запас устойчивости по
амплитуде порядка —(30-НЮ) дБ.
Выбор параметров интегрирующего контура произ¬
водить по стандартным ЛАЧХ разомкнутой системы.
Построить ЛЧХ скорректированной системы и дать
оценку каскадной коррекции системы контуром, создаю¬
щим отставание по фазе.
3-5-3. Осуществить стабилизацию системы, заданной
в задаче 3-5-1, и обеспечить за¬
пас устойчивости по фазе 50—
60° и запас устойчивости по ам¬
плитуде— (30--40) дБ путем ка¬
скадного включения интегродиф-
ференцирующего контура (рис-
3-5-3), действие которого в обла¬
сти низких частот аналогично
Действию интегрирующего конту¬
ра, а в области высоких частот-—
Рис. 3-5-3,	дифференцирующего	контура.
72

Для интегродифференцирующего контура, принцйнй-»
альиая электрическая схема которого дана на рис. 3-5-3,
имеем:
WK (р) =	(т™р	+	*)	(Г2ХР+	1)
Т1КТ2кР2 + |^1 К+ Т 2К+
Р+ 1
При выборе параметров контура рекомендуется при¬
нять Г1к=0,25 с, т. е. равной наибольшей постоянной
времени неизменяемой части системы, a 712k=47,ik=1 с.
Отношение U^y/U^x^.0,1. Выбор параметров корректиру¬
ющего контура производить частотными методами.
3-5-4. Неизменяемая часть синтезируемой системы
имеет ПФ
wQ(p) шш
’ РФЛР'А- 1) (0,003^+ 1) •
Требуется выбрать корректирующее устройство, обес*
печивающее получение следующих характеристик каче¬
ства замкнутой системы:
1) система должна обладать астатизмом первого по¬
рядка;
2) коэффициенты ошибок по скорости и ускорению не
должны превышать: с\ =0,004 с; с2=0,02 с2;
3) длительность переходного процесса /рег не долж¬
на превышать 0,5 с при ступенчатом воздействии, рав¬
ном 0,20 рад;
4) относительное перерегулирование б в переходном
процессе не должно превышать 30%.
Глава четвертая
ДИСКРЕТНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ
УПРАВЛЕНИЯ
Перед решением задач гл. 4 следует ознакомиться
с решением задач § 1-6.
4-1. ОПЕРАТОРНОЕ ОПИСАНИЕ ПРОЦЕССОВ
В ДИСКРЕТНЫХ СИСТЕМАХ
4-1-1. Для изображенной на рис. 4-1-1,а схемы пере¬
хода от аналоговой формы сигнала к дискретной АД и
обратно ДА деформация сигнала показана на рис.
4-1-1,б.
73

Полагая входной сигнал синусоидальным
*о=5 sin (0,1/+л/6),
интервал дискретности 7о=0,8 с и ПФ управляемой ли¬
нейной системы
а)	операторные (в г-форме) описание и структуру
преобразований сигнала АД и ДА;
б) реакцию системы в г-форме;
в) реакцию системы в общей интерполированной
г-форме и для конкретного значения е=0,5.
4-1-2. Включенная в канал дискретного сигнала ЭВМ
реализует алгоритм
'П \nTo\=u2h) [nTo\-\-Ui^ [(п—l)7Y|-j-
-\-iiog [(п—2)Го]—t>iT) [(п—1)Го]—UoT] [(п—2)Го],
т. е. по задержанным в оперативной памяти со сдвигом
на один и два такта данным о дискретных значениях
процессов £ [kT0] и r\ [kT0] вычисляет результат т] [пТо]
в текущем такте.
Используя канал дискретного сигнала и состав си¬
стемы управления, рассмотренные в предыдущем при¬
мере, определить общую г-ПФ с включением цифровой
найти:
Канал
дискретного Г.
сигнала _ |
Рис. 4-1-1.
ЭВМ.
74

4-1-3. Ключ мгновенного контакта с последующим
формирователем прямоугольной меандры заданной
скважности (3=0,2 включен на вход линейной системы
с ПФ
^	=	(р	+ 2) (р + 4) (рИС’	а)•
Входной сигнал, заданный в виде экспоненты *(/)==
=10ехр (—0,1/) и деформированный ключом хп(/), по¬
казан на рис. 4-1-3,6. Требуется:
а) дать операторное описание и структуру ключа
с формирователем;
б) получить 2-изображение реакции линейной систе¬
мы при Го=2 с;
в) определить зональное [3] модифицированное 2-
изображение реакции.
Рис. 4-1-3.	Рис. 4-1-4.
4-1-4. Ключ мгновенного контакта с формирователем
треугольной меандры деформирует входной процесс со¬
гласно рис. 4-1-4. Требуется составить структуру ключа.
4-1-5. Ключ мгновенного контакта с формирователем
трапецеидальной меандры коммутирует входной сигнал,
заданный функцией x(/)=0,l/e-'°>4i. Линейная система
имеет W(p) = \j(р-\-\). Характеристики меандры (рис.
4-1-5 )заданы по зонам в табл. 4-1-1.
Заданный интервал дискретности Г0=0,5 с.
Требуется:
а) составить структуру и ПФ ключа;
б) определить реакцию системы в 2-форме;
в) определить реакцию системы в зонально-модифи¬
цированной 2-форме.
75

Таблица 4-1. |
Зона
Граница
Крутизна
1
(0—0,1) т.
h
о
см
2
о
г
О
сл
о
0
3
(0,5-0,7) Т,
—Юс-1
4
/-N
О
Vi
О
0 (пауза)
Х(р)
Xrt(p)
Wfp)
а)
S
s
1
i
I
1
X
До
6)
Рис. 4-1-6.
4-1-6. Ключ продолжительного контакта периодиче¬
ски замыкает цепь с периодом повторения Г0=1 с и от¬
носительной продолжительностью включения (3=0,7. Со¬
став цепи ключа показан на рис. 4-1-6,а. Для входного
процесса ;Д*)=20*ехр (—0,1 )■*+(),5 sin 10* условия пре¬
образования его ключом показаны ка рис. 4-1-6,6. Тре¬
буется:
а) написать операторное представление процесса по¬
сле ключа Xй (р) (Я-представление) [26];
б) определить общее выражение для реакции на вы¬
ходе.
4-2. АНАЛИЗ И СИНТЕЗ ОДНОКОНТУРНЫХ
ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ
4-2-1. Для одноконтурной системы с ЭВМ в контуре
управления (рис. 4-2-1) с параметрами Я[г]=£д—
W(p)=ko/p; /г0=0,5 с-1 определить, при каких значениях
периода дискретности система устойчива; найти период
76

дискретности, при котором переходный процесс закан¬
чивается за один шаг; определить установившуюся
ошибку (£уст) для входного сигнала x(t)=bo-{-bit9 где
60=2; Ь 1=0,5 с-1.
Указание. Эффектом квантования по уровню и запазды¬
ванием в ЭВМ пренебречь.
Рис. 4-2-1.
4-2-2. Дана система регулирования с ЭВМ в контуре
управления (рис. 4-2-1), где W(р) =kolр2, &0=2,5 с-1;
Г0=0,2 с.
Оценить устойчивость системы для следующих слу¬
чаев:
а)	£>[г]=/гд;
«о
где йд=10; а=:0,7; 6=0,5.
Указание. Эффектом квантования сигналов по уровню и
запаздыванием в ЭВМ пренебречь. Для случая а) построить годо¬
граф корней характеристического уравнения и по его виду оценить
структурную устойчивость системы. Для случая б) применить
алгебраический критерий устойчивости путем последовательного
деления характеристического полинома на обратный.
4-2-3. Дана дискретная система управления, струк¬
турная схема которой приводится на рис. 4-2-3. Числен¬
ные-значения коэффициентов и периода дискретности
равны: /гi=2 с-1; й2=0,4 с-1; £3=5; Г0=0,1 с. Переда-
x(t)
к1
кг.
АД
D[z}
ДА
~Р
Т
Р
'y(t)
Рис. 4-2-3.
77

точная функция ЭВМ D[z\—kд=50. Оценить устойчи-
вость системы и построить переходный процесс.
Указание. Для оценки устойчивости вычислить корни ха¬
рактеристического уравнения. Переходный процесс построить по
дискретным точкам путем деления полинома числителя г-изобра¬
жения процесса на полином знаменателя.
4-2-4. Для дискретной системы с ЭВМ из задачи
4-2-2, п. «б» необходимо: а) построить логарифмические
псевдочастотные характеристики, определить псевдоча¬
стоту среза, запасы устойчивости по амплитуде и фазе;
б)	определить влияние на устойчивость системы за¬
держки в вычислении управляющего сигнала на один
шаг дискретности хз—То.
Указание. Для построения псевдочастотных характеристик
использовать подстановку г= (1	—w).
4-2-5. Произвести синтез дискретной системы, пока¬
занной на рис. 4-2-1, где W(p)—ko/p2, исходя из следую¬
щих условий:
1) переходный процесс должен заканчиваться за три
шага дискретности;
2) система должна иметь астатизм второго порядка
по отношению к входному полезному сигналу.
Проверить полученное решение путем построения пе¬
реходного процесса и определить величину перерегули¬
рования.
4-2-6. Для дискретной системы, приведенной на рис.
4-2-1, где W(р)=1/(T2ip—l); Т 1=2,5 с; Т0=0,2 с, необ¬
ходимо:
а) определить параметры г-ПФ ЭВМ для случая
J-'v Г VI ' 1	1 “-	^
D[A=K j + bz~i
при условии, что установившаяся ошибка при действии
постоянного единичного входного сигнала не превышает
0,05;
б) построить логарифмические псевдочастотные ха¬
рактеристики (ЛПЧХ) и определить запасы устойчиво¬
сти системы по фазе и амплитуде.
4-2-7. Задан объект регулирования (см. условие за¬
дачи 4-2-2). Определить D[z] для случая &о=2,5 с-1;
Т0=0,2 с с учетом дополнительного условия, что при вы¬
числении управляющего сигнала имеет место запазды¬
вание тз—0,1 с.
78

У Казани е. Для построения ЛПЧХ с учетом запаздывания
применить модифицированное 2-преобразование. С целью обеспече¬
ния устойчивости ввести 2-ПФ корректирующего контура первого
порядка вида
_ . п ,	1	— аг~1
И =йд 1 + bz-> '
4-2-8. Для воздействия F (р), приложенного к анало¬
говой части дискретной системы и отделенного от дис¬
кретизатора аналоговым звеном с ПФ W(p), найти ошиб¬
ку воспроизведения в форме ряда с коэффициентами
ошибки, рассчитанными для производных заданного (не
эквивалентного!) воздействия, если ПФ от дискретизато¬
ра до точки съема ошибки в дискретной форме задана
как
ф \7у	^	23 — 1,5г2 -f 0,5
С 12з—г*+ 0,52+ 0,15 *
В ходе решения воспользоваться эквивалентными
формами дискретного изображения по Лапласу и z-изо-
бражения, помещенными в приложении 17. Ответ полу¬
чить в общей форме и для частных значений
F(p)=L{a+frt+YF}- W(p) = 1.
4-3. СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ ПО МЕТОДУ
ПАРАМЕТРОВ СОСТОЯНИЯ
4-3-1. Дана двухконтурная дискретная система (рис.
4-3-1). Требуется:
а) определить уравнение параметров состояния;
б) определить оптимальные значения коэффициентов
ап и 012 алгоритма для выработки управляющих воз¬
действий, исходя из критерия минимума числа шагов
в переходном процессе;
в) построить кривые переходных процессов для слу¬
чая
г/Ц0]=1 и г/2[0]=0.
Рис. 4-3-1.
Рис. 4-3-2.
79

4-3-2. Дана трехкоитурная дискретная система (рис. 4-3-2).
Требуется:
а) определить оптимальные значения коэффициентов Он, at2
и ai3, исходя из критерия минимума числа шагов в переходном
процессе;
б) построить кривые переходных процессов для Т— 1с;	2
при начальных условиях */i[0]=0; г/2 [0] = 0; г/з [0] = 1.
4-3-3. Дана дискретная система (рис. 4-3-3). Требу¬
ется:
а) определить аналитические выражения для опти¬
мальных значений коэффициентов оц, 012 в зависимости
от коэффициента соо и периода Г, исходя из критерия
минимума числа шагов;
б) определить значения Г, при которых эти коэффи¬
циенты дают отрицательные обратные связи.
4-3-4. Решить задачу 4-3-3 для случая., когда об¬
ратная связь через коэффициент со2о положительна.
4-3-5. Для дискретной системы, показанной на рис.
4-3-5, определить аналитические выражения для опти¬
мальных значений коэффициентов Оц и 012, исходя из
условия минимума числа шагов, и определить их числен¬
ные значения при bi2=0,25; £>22=0,5; <*21=2 и 7=1 с.
4-3-6. Объект регулирования задан системой диффе¬
ренциальных уравнений
Определить аналитические выражения для коэффи¬
циентов алгоритма управления ац(7) и cri2(7), исходя
из критерия минимума числа шагов в переходном про¬
цессе, и вычислить их численные значения при Ьц=0,3 и
Рис. 4-3-3.
Рис. 4-3-5.
У\——Ьц^/i+l -^2+0-Wf,
У2—0-У\-\-0-У2-\-1 'Ul-
7=0,5 с.
3Q

4-3-7. Для системы, показанной на рис. 4-3-1, найти'
K0P£!L хаРактеРистического уравнения при условии, что
™мт!Щ1еН1Ы аи 11 °12 Наадены’ ИСХОДЯ из критерия ми¬
нимума числа шагов дискретности в переходном процес¬
се, для расчетного периода дискретности Т= 1 с а дей¬
ствительный период Т0=ХТ=0,5Т.	’
4 3 8. Пусть для системы рис. 4-3-1 выбран следую¬
щий алгоритм управления при полной информации оп—
=1|о“,г(Я12!| где a"„=10; a"12=4,48 и TWO,224 с. Опре¬
делить U\z\ — передаточную функцию ЭВМ для случая
когда имеет место неполная информация о выходных
координатах, а именно отсутствует датчик выходной ко¬
ординаты ^2- Проверить полученный результат путем по¬
строения ЛПЧХ и определения запасов устойчивости по
амплитуде и фазе.
Указание. Для решения этой задачи приравнять матшшы
значении импульсных характеристик замкнутой системы при непол¬
ной и полной информации и из этого условия определить коэсЬ*и
циенты дискретного корректирующего контура пеЕо порядка^ пой
™сго н,лн
4 3 9. Для дискретной системы рис. 4-3-2 задана ма¬
трица алгоритма управления an=||crn по11 i2on nil	гле
<Яп=5; аП‘г=7;2- °и1з=3,34. Период дискретности 7W
—u,d с и о 12— 1. Необходимо определить алгоритмы уп¬
равления для двух случаев неполной информации:
а) при отсутствии датчика выходной координаты уа'
б) при отсутствии датчика выходной координаты yl
Указание. Для определенности решения поставленной за¬
дачи принять для: а) a"u=0 и б) с^^О.б.
л мм1?’ Да.Но .тСТЛМа^ автома™ческого управления
с ЭВМ (рис. 4-3-10). Необходимо определить алгоритмы
идентификации неизвест¬
ного возмущения f2 и не
измеряемой датчиком вы¬
ходной координаты у2.
Период дискретности Т.
Указание. На началь¬
ном участке процесса иденти¬
фикации протяженностью в два
шага дискретности принять
?2[0] =/2[Г]=const.	рис	4_3_j0i
6—903
81

Глава пятая
АНАЛИЗ И СИНТЕЗ НЕЛИНЕЙНЫХ СИСТЕМ
5-1. ТИПОВЫЕ НЕЛИНЕЙНОСТИ И ИХ ХАРАКТЕРИСТИКИ
5-1-1. Определить комплексный гармонический коэф¬
фициент передачи J(А) для нелинейного элемента, ста¬
тическая характеристика которого имеет зону насыще¬
ния (рис. 5-1-1).
-т-4*
‘I
У~Г(Х)
X
W	{	*-
ly=F(X,1
* Cl
LF
Рис. 5-1-1.	Рис.	5-1-2.
5-1-2. Получить выражение для коэффициента передачи нели¬
нейного элемента /(А), статическая характеристика которого пред¬
ставляет релейную характеристику с зоной нечувствительности
(рис. 5-1-2).
5-1-3. Определить комплексный гармонический коэф¬
фициент передачи J(А) для нели-
r,y=F(x) нейного элемента, статическая ха-
-т—— рактеристика которого представля-
ет релейную характеристику с пет-
k	лей	гистерезиса	(рис.	5-1-3).
Построить годограф J (А) при
а=1 и 4&1/я=1.
Рис. 5-1-3.
5-2. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ
5-2-1. Построить фазовый портрет для точки, которая
совершает гармонические колебания по закону х=
=А sin соt.
5-2-2. Для релейной системы, схема которой изобра¬
жена на рис. 5-2-2,а, построить траекторию изображаю¬
щей точки на фазовой плоскости. Релейная характери¬
стика F(x) с зоной нечувствительности и петлей гисте¬
резиса представлена на рис. 5-2-2,б.
82

Уравнения звеньев: *=—х2; X2=kx\\ Х\=F(x).
Параметры звеньев: k=l; a1=1; a2=2; 6=1.
Начальные условия: x(0)=5; x(0)=0.
F(x)
ГГ
*♦
X1
-7
iF(x)
-a2-ar
I я
a)
Рис. 5-2-2.
5-2-3. Для нелинейной системы, схема которой изо¬
бражена на рис. 5-2-3, построить фазовый портрет и ис¬
следовать устойчивость и качество переходных процес¬
сов. Статическая характеристика нелинейного элемента
представляет релейную характеристику с зоной нечувст¬
вительности (см. рис. 5-1-2). Параметры звеньев: Т=
—Ю с; Ь—2; а=1. Для начальных условий х(0)=5;
х(0)=2 построить фазовую траекторию изображающей
точки.
—г
*г
р(Тр + 1)
-ED-
Рис. 5-2-3.
5-2-4. Для системы, структурная схема которой изо¬
бражена на рис. 5-2-3, построить фазовый портрет мето¬
дом изоклин. Параметры звеньев: 7=5 с; Ь=3; а=0,5.
5-3. МЕТОД ПРИПАСОВЫВАНИЯ
5-3-1. Исследовать переходный процесс в системе,
структурная схема которой изображена на рис. 5-3-1,а.
Статическая характеристика нелинейного элемента пред¬
ставляет релейную характеристику (рис. 5-3-1,6). Пара¬
метры звеньев: Ь=2; &i=0,01; k2=l; &з=1; k^=5.
6*
83

Начальные условия: ла(0)—0,01; х2(0)=0.
F(x)
-*Г“
*2
Кг
\F(x)
X
= к,.
р
Р
а)
б)
Рис. 5-3-1.
5-3-2. Построить графики переходных процессов для нелинейной
системы, структурная схема которой изображена на рис. 5-3-2.
Статическая характеристика нелинейного элемента представляет
релейную характеристику с зоной нечувствительности (см.
рис. 5-1-2). Параметры звеньев: а=1; Ъ = 2; Т—10 с; к—\. На¬
чальные условия: х(0)=5; х(0)=0.
F(x)
Х1 .
р(тр+1)
Рис. 5-3-2.
5-4. ИССЛЕДОВАНИЕ РЕЛЕЙНОЙ СИСТЕМЫ
ПО МЕТОДУ Я. 3. ЦЫПКИНА
5-4-1. Определить частоту автоколебаний в релейной
системе (рис. 5-4-1) с помощью частотной характеристи¬
ки релейной системы. Решение произвести с графическим
представлением годографа этой характеристики на ком¬
плексной плоскости по методу Я. 3. Цыпкина. Релейная
характеристика с петлей гистерезиса представлена на
рис. 5-1-3, причем яа/4Ь=0,5.
Ш-
-ЕЕЬ
Рис. 5-4-1.
Рис. 5-4-2.
5-4-2. Определить частоту автоколебаний в релейной системе,
представленной на рис. 5-4-2, с помощью частотной характеристики
84

релейной системы. Решение произвести с графическим представле¬
нием годографа этой характеристики на комплексной плоскости
по методу Я. 3. Цыпкина. Релейная характеристика с петлей гисте¬
резиса представлена на рис. 5-1-3. Параметры системы: &=10;
Тi = l с; 712 = 0,5 с; яа/46 = 2.
5-5. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
АВТОКОЛЕБАНИЙ НЕЛИНЕЙНЫХ СИСТЕМ
ПРИ УСЛОВИИ ФИЛЬТРАЦИИ ВЫСШИХ ГАРМОНИК
5-5-1. В системе стабилизации неуравновешенного ги¬
роскопа (рис. 5-5-1,а) определить методом баланса ве¬
щественных и мнимых характеристик наличие автоколе¬
баний (устойчивого предельного цикла). При наличии
автоколебаний определить амплитуду Лп и частоту авто¬
колебаний соп.
Движение гироскопа описывается системой уравне¬
ний
где /10=19,б-10-5 кг-м2 — момент инерции относительно
оси внешней рамки системы гиромотор плюс внешняя
рамка; Во—9,8* 10-5 кг-м2 — момент инерции гиромотора
относительно оси внутренней рамки; Н=9,8Х
XI О-2 кг-м2/с— кинетический момент гироскопа;
Л'^.дОР)—момент стабилизирующего двигателя; MBYL —
внешний момент (в данном случае он равен нулю); а —
угол поворота гироскопа относительно оси внешней рам¬
ки; (3 — угол поворота гироскопа относительно оси внут¬
ренней рамки; /га=19,6-10-5 кгм2/с — коэффициент
а) стабилизации •
Рис. 5-5-1.
Л,а -f- лаа -[-Щ — — А1С Л ф);
"К — На — Мт,
85

вязкого трения; /г0=9,8-1О~5 кг*м2/с— коэффициент
вязкого трения.
Момент стабилизирующего двигателя есть нелиней¬
ная функция р, представленная на рис. 5-5-1,б, при
m0=4,9-10”3 Н-м.
5-5-2. В нелинейной системе, структурная схема ко¬
торой представлена на рис. 5-5-2,а, определить методом
баланса вещественных и мнимых характеристик наличие
автоколебаний. При наличии автоколебаний определить
F(X)
«опсвав
X3-F(X,
X
б)
Рис. 5-5-2.
их амплитуду Лп и частоту соп, т. е. определить парамет¬
ры предельного цикла. Определить степень подавления
второй и третьей гармоник линейной частью системы.
Характеристика нелинейного элемента F (х) представле¬
на на рис. 5-5-2,б.
Численные значения параметров системы: k\=2\ k2=
—5; k0.c=l\ с= 1; 71=0,01 с; Г2=0,1 с.
5-5-3. В системе стабилизации неуравновешенного ги¬
роскопа (рис. 5-5-1,я), используя частотный метод, опре¬
делить наличие автоколебаний. При наличии автоколе¬
баний определить амплитуду Ап и частоту соп автоколе¬
баний.
Уравнения движения гироскопа:
А0а -f- пая -|- Яр = — МСшЯ (Р)>
Д>Р + Л9Р — На = Мт,
где
Я = 9,8-10-2 кгм2/с; Д= 19,6-Ю~‘ кгм2;
В0 = 9,8-10"‘ кг м2; па= 19,6• 10"‘ кг-м2/с;
/»„"== 9,8-10"' кг-м2/с; т, = 4,9 • 10":2 Н м.
86

Момент стабилизирующего двигателя Мс.д(§) есть
нелинейная функция р, представленная на рис. 5-5-1,б.
Структурная схема системы приведена на рис. 5-5-3. При
исследовании принять Мвн=0.
Рис. 5-5-3.
в 5-5-4. Для нелинейной следящей системы со схемой, представлен¬
ной на рис. 5-5-4,а, используя частотный метод, определить пара¬
метры предельного цикла Апi, coni на выходе следящей системы,
если заданы уравнения и параметры звеньев.
Уравнения усилителя и датчика рассогласований:
Т2Х 3 + Хз=&2Х2‘}
Х2=Хпх—Х\,
где Т2«=0,1 с; &2 = 3000 мА/рад.
Р(х)
б)
тт
Рис. 5-5-4.
Уравнение привода с учетом нагрузки:
Txxx-\-xi=F(x),
где Тi=l с — постоянная времени. Привод обладает нелинейной
характеристикой типа насыщения (рис. 5-5-4,б), 6=10 мА; k± =
= 0,01 рад/(мА-с).
Уравнение обратной связи:
Х’4 = ^О.С-^'1>
где &о..с = 60 мА-с/рад— коэффициент передачи.
87

5-6. МЕТОД ВИБРАЦИОННОЙ ЛИНЕАРИЗАЦИЙ
5-6-1. На входе нелинейной системы, схема которой
представлена на рис. 5-6-1, действует управляющее воз¬
действие, изменяющееся по синусоидальному закону
xY=B sin QB*.
Нелинейный элемент имеет симметричную релейную
характеристику F(х) =с sign х (см. рис.’5-5-2,б).
Численные значения параметров системы: 71—0,01 с;
Т2=0,1 с; kl=2; /е2=5; Л0.с=1; с= 1; QB=30 С"1.
F(x)
-t
ЧР+1
■Zj Г
\р(тгр+1>
Xif.
ED-
Рис. 5-6-1.
Методом вибрационной линеаризации определить ам¬
плитуду синусоидальных колебаний 5, при которой бу¬
дет происходить принудительная синхронизация, т. е.
автоколебания в нелинейной системе «срываются» и си¬
стема переходит на колебания с вынужденной частотой
QB, и закон изменения сигнала на входе нелинейного эле¬
мента.
5-6-2. Для системы, структурная схема которой изо¬
бражена на рис. 5-6-2, определить:
1)	амплитуду автоколебаний Ап на входе нелинейно¬
го элемента и частоту автоколебаний соп;
Fix)
*1
kl
X
h*
•1Ig
*2
)—■
Tffi+1
Н
р(Тгр+1)
*3
Рис. 5-6-2.
2) зависимость между медленно изменяющимися
входной и выходной величинами нелинейного элемента,
т. е. функцию смещения
3) установившуюся ошибку системы

Управляющее воздействие изменяется по закону
Уравнение релейной характеристики F(x)—c sign х
(см. рис. 5-5-2,б).
Численные значения параметров системы: Т{=0 1 с*
Т2~0,2 с; к\— 2; ^2=5; &з=0,01; с=0,5; с0=2.
5-7. СИНТЕЗ ОПТИМАЛЬНЫХ НЕЛИНЕЙНЫХ СИСТЕМ
5-7-1. Используя принцип максимума для объекта,
описываемого уравнением kx=u, определить алгоритм
оптимального управления, который обеспечивает перевод
объекта из начального состояния *(0)=0, х(0)=0 в ко¬
нечное состояние х(Т)=\у х(Т) = 0 за минимальное вре¬
мя Т. Определить число переключений и моменты пере¬
ключений. Построить кривые управления u(t), коорди¬
нат x(\t), x(t) и фазовую траекторию изменения коор¬
динат x(t), x(t) объекта. На управляющее воздействие
наложено ограничение |и|<[/Макс. Параметры системы:
*=2; Uuакс-0,5.
5-7-2. Определить 'моменты переключений и построить графики
управления u(t), координат x(t), x(t) и фазовую траекторию изме¬
нения координат x(t)t x(t) для объекта, описываемого уравнением
kx=u, при следующих начальном и конечном состояниях: х(0) = 1;
*(0) =0,5; х(Т)= 0; х(Т)=0. На управляющее воздействие нало¬
жено ограничение |и\^ С/Макс. - Параметры системы:	k = 2\
^макс = 3.
5-7-3. Используя принцип максимума для объекта, описываемого
уравнением
Т ix+x=ku,
определить алгоритм оптимального управления, который обеспечи¬
вает перевод объекта из начального состояния х(0)=0, i(0)=0
в конечное состояние х(Т) = 1, i(T)=0 за минимальное время Т.
На управляющее воздействие наложено ограничение |м|^С/Макс.
Определить число переключений, моменты переключений и построить
графики управления u(t) и координат x(t), x(t). Параметры си¬
стемы: 7*1 = 0,1 с; k—\\ ^/Макс —10.
5-7-4. Используя принцип максимума для объекта,
который описывается уравнением первого порядка х=
=—ах-\-и, подобрать такое управление и на участке 0<
</<Г, чтобы обеспечить минимум критерия
т
Q= 4-[(*■ + «■) <*.
О
Время движения системы Т. Начальное значение вы¬
ходной величины *(0)=х°. На управляющее воздействие
и дополнительные ограничения не наложены.

Глава шестая
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ
6-1. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ, ПОДВЕРЖЕННЫХ
СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
6-1-1. На входе усилительного звена действует слу¬
чайная функция X(t) с известным математическим ожи¬
данием mx(t) и корреляционной функцией Kx(tu h). Тре¬
буется найти математическое ожидание и корреляцион¬
ную функцию выходной случайной функции Y(t), если
коэффициент усиления k=8.
6-1-2. Определить корреляционную функцию Ky{t\, t2)
на выходе дифференцирующего звена Тр, если корреля¬
ционная функция входного сигнала X
Кх (tt, Q = Кх (h -12) =	,
а Т= 1 с.
6-1-3. Для дифференцирующего звена определить
корреляционную функцию случайной функции Z (t) на:
его выходе, если входная случайная функция X(t) име¬
ет корреляционную функцию вида
гг /,	,	ч	  .	' COS (0 (t, — t2)
Кх (ь> *i) — 0 X
6-1-4. Случайная функция X(t) имеет математическое
ожидание tnx(t) и корреляционную функцию	t2).
Найти математическое ожидание и корреляционную
функцию Y(t), если
Y(f)=[X(t)e-*dt.
о
6-1-5. На вход дифференцирующего звена поступает
случайная функция X(i) с математическим ожиданием
mx(t)=A slnt и корреляционной функцией
Kx(t»U = 2e-0Mi>-U)\
Определить математическое ожидание и дисперсию
выходной случайной функции.
6-1-6. Найти математическое ожидание mv(t) и дис¬
персию Dv на выходе апериодического звена, если на
да

входе с момента U действует возмущение, представляю¬
щее собой стационарную случайную функцию с матема¬
тическим ожиданием mx=const и корреляционной функ¬
цией
кх (t, t’) = КХ (t — t') = De~a]	>.
6-1-7. Найти дисперсию выходной переменной RC-
фильтра, который описывается линейным дифференци¬
альным уравнением T0Y(t)JrY(t)=X(t), где T0=RC=
=0,5 с — постоянная времени. На вход системы начиная
с момента £=0 действует белый шум с постоянной ин¬
тенсивностью с2.
6-1-8. На вход нестационарного звена с импульсной
характеристикой
w[t, т) =
1 О
действует нестационарная случайная функция с матема¬
тическим ожиданием
mx(t)—ar\-axt
и корреляционной функцией
Кх (t, t') = Dxei{t+t,)~'.
Определить математическое ожидание и дисперсию
выходного сигнала Y(t).
6-1-9. На вход следящей системы радиолокатора
(рис. 6-1-9) поступает полезный сигнал X(t), представ¬
ляющий собой случайную стацио¬
нарную функцию с известными I z(t)
значениями математического X(t)\ v(t)
ожидания mx(t)=mXo= const и ———
корреляционной функции
Kx(t) = Dxe~a^= 2е~и.	Р‘
Сигнал помехи (шум радиолокатора) представляет
собой стационарную случайную функцию Z(t) с нулевым
математическим ожиданием и корреляционной функцией
Kz (i) = Dze~a^ = 3e~2W.
Помеха и полезный сигнал взаимно не коррелиро-
ваны.
91

Импульсная характеристика следящей системы ра¬
диолокатора соответствует импульсной характеристике
апериодического звена
Требуется определить вероятностные характеристики
ошибки системы: математическое ожидание ошибки щ и
дисперсию ошибки Dv если известно, что система долж¬
на производить фильтрацию полезного сигнала, т. е. иде¬
альный оператор системы L— 1.
6-1-10. На вход линейной динамической системы регулирования,
которая описывается ПФ W (р) = (bip + b0) / (aip+ao) поступает
случайная функция помехи Z(t) с корреляционной функцией
Определить дисперсию ошибки системы, если полезный сигнал
равен нулю (см. рис. 6-1-9).
6-1-11. На входе фильтра с W(р) ='&/(Тр+1) действует входной
сигнал в виде белого шума со спектральной плотностью 5х(со) =
= 1,2-10~4 В2-с. Определить постоянную времени Т> при которой
СКО на выходе фильтра не будет превосходить ау^0,1 В.
6-1-12. Корреляционная функция случайной функции
Х(1) описывается кусочно-линейной функцией
Найти спектральную плотность этой случайной функ¬
ции.
6-1-13. Для стационарного случайного процесса со
спектральной плотностью Sx(a))=N в полосе частот от
—о)п до +о)п вычислить дисперсию Dx и найти корреля¬
ционную функцию Кх (т).
6-1-14. Корреляционная функция сигнала Х{1) равна:
Найти спектральную плотность.
6-1-15. Найти спектральную плотность случайной
функции X(t)y если ее корреляционная функция пред¬
ставляет собой затухающую по экспоненте косинусоиду
w (х) = 0,95уе_т< = 0,19е~0’2'
Кг (х) = С2<? с I Т I
КДх) =
при I х | < Х0;
при M>V
Кх (х) — Dxe~
Кх (x) = D^_"|x| COSco„t.
92

6-1-16. Лилейная система описывается уравнением вида
ai?(t) +aoY(t) =biX(t) +b0X(t).
Случайная функция X(t), действующая на входе системы, имеет
корреляционную функцию Кх(т) = Ц*£“а\
Найти дисперсию сигнала ка выходе системы.
6-1-17. На вход апериодического звена, описываемого
уравнением T0Y(t) + Y(t) =kX (t), поступает стационар¬
ный сигнал в виде белого шума со спектральной плот¬
ностью Sx=const.
Найти дисперсию сигнала на выходе звена.
6-1-18. Ошибка акселерометра, измеряющего ускоре¬
ние самолета, определяется уравнением
d~ijr1 + 2А -d-^p- + пХ (0 - n'gY (f),
где /г=0,б 1/с; п=6,28 1/с; £=9,81 м/с2 — .постоянные
величины, определяемые параметрами самолета.
Угол у(/)—стационарная случайная функция, кор¬
реляционная функция которой задана выражением
Кт (t) — Ае~аw j^cos p-t -f- -j- sin p | ■
= 3 ■ 10 -	[cos 5t + 0,12 sin 5111],
гдеЛ = 3-10-4 — дисперсия сигнала; a=0,6 — параметр,
характеризующий нерегулярность сигнала y{t)\ р=5 —
преобладающая частота колебаний.
Определить дисперсию ошибки £(/) при установив¬
шемся режиме работы акселерометра.
6-1-19. Определить дисперсию ошибки скорости само¬
лета Dv, найденную путем интегрирования показаний
акселерометра (см. задачу 6-1-18), при условии, что до¬
бавочные ошибки при интегрировании не возникают,
а время работы акселерометра составляет 60 мин.
6-1-20. На линейную систему, заданную ПФ,
W (и) — E0.5p-f ,l
W(-P>— 0,25^+lp+l
действует стационарный случайный сигнал со спектраль¬
ной плотностью, записанной в форме квадрата модуля
частотной характеристики формирующего фильтра
sx (со) = t±L
х 4 7 /со -j- 2
возбужденного белым шумом единичного уровня.
93

Найти аналитическое выражение для корреляцион¬
ной функции и подсчитать дисперсию выходного сигна¬
ла, применяя метод прямого и обратного преобразова¬
ния Лапласа и справочную таблицу приложения 14, при
6=1,25 и 6=0,6.
6-1-21. Для спектральной плотности, полученной на
выходе системы в задаче 6-1-20, определить только зна¬
чение дисперсии при £=1,25, воспользовавшись табли¬
цей приложения 14 и формулами пересчета коэффи¬
циентов.
6-1-22. На следящую систему радиолокатора со
структурной схемой, приве-
z(pj	денной	на рис. 6-1-22, дей¬
ствует полезный сигнал
G (t) =
т. е. координата цели изме¬
няется с постоянной ско-
Рис. 6-1-22.	ростью	с\ в течение рас¬
сматриваемого интервала
времени. Входная помеха Z(t) представляет собой бе¬
лый шум с корреляционной функцией
Kz{x) = S06[t],
где So — интенсивность белого шума.
Определить дисперсию суммарной ошибки следящей
системы.
6-1-23. На вход следящей системы поступает полез¬
ный сигнал в виде стационарного случайного процесса
с нулевым математическим ожиданием и со спектраль¬
ной плотностью
о / \   2 CVZ
Sx П 7 + coV' *
а также помеха в виде белого шума со спектральной
плотностью Sf (со) =N. Система задана своей ПФ
г»
где Г=0,05 с; т=10 с; а= 100 град2; N=0,01 град2-Гц~1.
Определить значение коэффициента усиления прямой
цепи, обеспечивающее минимум среднеквадратической
ошибки, т. е. /г=&0, и значение ошибки при k=kQ.
tIELis
т
IXZ1
р(тр+1) г
у
94

6-2. АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ, ПОДВЕРЖЕННЫХ
СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
6-2-1. Нелинейная система описывается дифференци¬
альным уравнением
p(f) = i-y2(f)+*(f)=/0', X),
где X(t) —стационарная случайная функция времени
с математическим ожиданием, равным нулю, и корреля¬
ционной функцией вида
KA') = Dxe~*".
Найти математическое ожидание и дисперсию выход¬
ной случайной функции У(/), если известно, что в мо¬
мент времени t=0 выходная переменная системы равна
единице.
6-2-2. Поведение нелинейной системы описывается
уравнением
г (0 = 2 —(t) + X(t),
где X(t) —стационарная случайная функция времени
типа «белый шум» с математическим ожиданием
тх — —1 и корреляционной функцией Кх(%—ti) =
=DX8 (т—ti).
Найти математическое ожидание и дисперсию вели¬
чины 7(f), если в момент времени £=0 У(0)=2.
6-2-3. Система управления представляет собой апе¬
риодическое звено, охваченное отрицательной обратной
связью, включающей в себя нелинейное звено с кубиче¬
ской характеристикой. Поведение системы описывается
уравнением 0,2У (/) + 7 (t) =3 [X (t) —2 У3 (t) ].	Входной
сигнал X(t) представляет собой стационарную случай¬
ную функцию типа «белый шум» с нулевым математи¬
ческим ожиданием- и корреляционной функцией Кх{%) =
= 56 (т). Считаем, что в момент времени ^=0 выходная
величина системы равна единице.
Найти математическое ожидание и дисперсию выход¬
ного сигнала 7 (t).
6-2-4. Определить математическое ожидание и дис¬
персию. выходной координаты нелинейной системы 7,
представленной на рис. 6-2-4. Аналитический вид нели¬
нейности X—SY2, Изменение Y(t) по времени опи¬
95

Рис. 6-2-4.
сывается дифференциаль¬
ным уравнением dY(t)/dt=
— 1—V-Y2. Предположим,
что процесс каждый раз на-
чинается при нулевых на¬
чальных условиях, а коэф¬
фициент усиления множи¬
тельного звена 5 является
случайной величиной v,
подчиненной закону равно¬
мерной плотности вероятности на отрезке [—1 /2; +1/2];
Pfowf1 ПРИ — 1/2<о<1/2;
(О при | v |> 1/2.
6-2-5. Найти эквивалентные коэффициенты усиления
К ^i(1> > &i<2) Для нелинейного элемента типа квадратор
Y = X2 при нормальном законе распределения случайной
функции на входе X (t) = mx-{-X (t).
6-2-6. [Определить статистические коэффициенты k„,
k ,(I) , при тех же условиях, что и в задаче 6-2-5, но'
для нелинейного элемента Y (t) = X3 (t).
6-2-7. Найти эквивалентный линейный оператор нели¬
нейной цепи, если на вход системы поступает случайная
о	о
функция X(t)=mx+X(t), где m*=const, a X(t)— ста¬
ционарный белый шум, имеющий корреляционную функ¬
цию Кх{х) =2я506(т); здесь S0 — уровень спектральной
плотности белого шума. Взаимная корреляционная
функция входного сигнала X(t) и выходного К(£)
Кух(') = Ае-а".
6-2-8. Вычислить статистические коэффициенты уси¬
ления &0, &,(1) и k\2) для /нелинейности, представленной на
рис.® 6-2-8.
Рис. 6-2-8.
96
Рис. 6-2-9,

6-2-9. Дана нелинейная разомкнутая система
(рис. 6-2-9). Входной сигнал представляет собой случай¬
ную функцию с корреляционной функцией
где а2х=9 с~2; (3 = 0,01 с-1 и математическим ожиданием
тх= 1.
Пользуясь методом статистической линеаризации,
найти математическое ожидание и дисперсию выходного
сигнала У при заданных значениях параметпов а=5;
6=10; k = 2; 7 = 0,1 с.
6-2-10. Следящая система состоит из исполнительного
устройства с ПФ
и управляющего им реле с идеальной характеристикой
в прямой цепи (рис. 6-2-10), замкнутых единичной отри¬
цательной обратной связью.
Входной полезный сигнал представляет собой линей¬
ную функцию времени mx=Oo + ait.
Помеха—стационарная случайная функция с нуле¬
вым математическим ожиданием, корреляционная функ¬
ция и спектральная плотность которой определяется
формулами
Определить математическое ожидание и среднеквад¬
ратическое отклонение выходной переменной У, если
&=2,5; 7=1 с; а= 15; Ь = а0 = а1 = 1; сг*=0,2.
6-2-11. Определить математическое ожидание и дис¬
персию выходного сигнала У гироскопической системы
гировертикали с нелинейным корректирующим устройст¬
вом релейного типа, подверженной действию случайной
7—903	97
Рис. 6-2 10.
К, (.) = О,*-1’1; S, и =	^5.

стационарной составляющей Z с корреляционной функ¬
цией
и математическим ожиданием mz=const=c.
z
-=Р
■ш-
Рис. 6-2-11.
Система описывается уравнениями
?=k<p(X):
X=Z—Y;
q>(X)=L sign X.
Структурная схема системы может быть представле¬
на в виде схемы, приведенной на рис. 6-2-11.
6-2-12. На вход нелинейной следящей системы по¬
ступает стационарный случайный сигнал с постоянным
математическим ожиданием тх=0,05 В со спектральной
плотностью случайной составляющей
о / \	2aD*
Sx (со) = —г- 2“
х v 7 a2 + со2
при D*=0,0025 В2 и а=12,5 с-1.
Структурная схема системы представлена на
рис. 6-2-12.
Рис. 6-2-12.
Известно, что £i=600; Т=0,04 с; &2=10,5 В-с-1;
а = 314 с"1; 6 = 0,1 В.
Определить математическое ожидание и дисперсию
на входе нелинейного звена my, Dy.
9а

6-3. GiltИМАЯЬНЫЁ СИСТЕМЫ ПО CtATHCfЙЧЕСКИМ
КРИТЕРИЯМ
6-3-1. Иа вход линейной системы управлений
(рис. 6-3-1) с импульсной характеристикой w(т) посту¬
пают независимые полезный сигнал X(t) и помеха
Z(t)\ H(t)—желаемый выходной сигнал; F(t)—реаль¬
ный выходной сигнал; £(/) —ошибка системы; L —ли¬
нейный оператор системы; Y(t)—суммарный входной
сигнал.
Рис. 6-3-1.
Определить оптимальную импульсную характеристи¬
ку фильтрующей системы управления Wq(x)9 обеспечи¬
вающей минимум дисперсии ошибки Dv если известно,
что корреляционные функции равны:
Кх(*) = 3<Г2М; Кг(*)= 2е~м .
Найти минимальное значение дисперсии ошибки.
6-3-2. Определить оптимальную систему экстраполи¬
рования по минимуму дисперсии ошибки и минимум
дисперсии ошибки DlMm 9 если (см. рис. 6-3-1) корреля¬
ционная функция полезного сигнала
Кх Ь) — Аге~л,м = 2е-3|т';
корреляционная функция помехи
Kg(x) = Bte-*,u = e-'x] ;
корреляционная функция входа в систему Ку{т) =
= Кх(х) + Kz(x) ; выход системы H(t)=X(t + tB), где
tB—время экстраполяции.
6-3-3. Для системы управления (см. условие задачи
6-3-1) определить оптимальную импульсную характери¬
стику wq(x) и дисперсию DeMHH если система должна
7*
99

производить упреждение полезного сигнала ‘Я(1)> f. ^
желаемый выходной сигнал H(t) — X(t + TQ), где Тъ~1
время экстраполяции.
6-3-4. На вход системы управления действуют стаци¬
онарный полезный сигнал с корреляционной функцией
f(x (х) = Ъе~2'^ и помеха в виде белого шума /С2(х)=8(х).
Определить оптимальную линейную систему по крите¬
рию минимума дисперсии ошибки, учитывая, что мате¬
матические ожидания mx=mz — 0, a H(t)=X(t). Время
наблюдения Т= оо.
6-3-5. Определить оптимальную Г1Ф линейной систе¬
мы управления, обеспечивающей минимум дисперсии
ошибки и производящей фильтрацию полезного сигнала
вида X(t) =aQ + ait, причем значения случайных коэффи¬
циентов а0 и а\ неизвестны.
Помеха имеет корреляционную функцию Кг (1) =
6-3-6. На вход системы управления (см. рис. 6-3-1)
поступает полезный сигнал X(t) — G0 + G[ty причем коэф¬
фициенты G0> 1 и Gi>l —большие числа.
Помеха — белый шум с корреляционной функцией
/(2(т)=6(т). Время переходного процесса Т— 1 с. Систе¬
ма производит фильтрацию полезного сигнала.
Необходимо, чтобы выполнялись дополнительные
условия:
коэффициенты разложения желаемого сигнала Я(/)С0 =
Случайная составляющая полезного сигнала X(t)= 0.
Определить оптимальную импульсную характеристику
системы, синтезируемой по критерию минимума дисперсии
ошибки Dv и минимальную дисперсию ошибки £>Сшш.
6-3-7. Для системы, заданной в задаче 6-3-6, за ис¬
ключением того, что Gi= 1, т. е. скорость полезного сиг¬
нала ограничена, определить оптимальную импульсную
характеристику системы, созданной по критерию мини¬
мума среднеквадратической ошибки (при ненулевом
математическом ожидании ошибки), а также минималь¬
ное'значение суммарной ошибки.
L
=1; С1=0.
о

6-3-8. flycfb на входе системы имеется полезный сй'Г-
нал X(t) = Go+G\tt причем G0 — велико, a G\ — l.
• Помеха Z(t)—белый шум с корреляционной фуню
цией Кг (т) =6 (т).
Дополнительное условие, накладываемое на импульс¬
ную характеристику (условие астатизма системы):
1
w (ъ) d^ — 1#
У
Система производит фильтрацию сигнала X(t) при
времени регулирования 7=1 с.
Требуется определить оптимальную импульсную ха¬
рактеристику, синтезируемую по критерию максимума
вероятности невыхода ошибки из заданных малых до¬
пусков ±с.
6-3-9. Полезный сигнал системы представляет собой регулярный
сигнал с нулевой случайной составляющей X(t) = Go + Git, где
коэффициент G\~\/V'2Qi G0> 1.
Помеха Z представляет собой центрированную случайную функ¬
цию, подчиненную нормальному закону распределения с корреля¬
ционной функцией
**( т)=й-1Ч
В этом случае а=1. Система должна производить экстраполя¬
цию полезного сигнала, т. с. желаемый выход системы
Н (t) =X{t-\-to) = Go + бы (/ + ГЭ),
где 71э = 6 с — время экстраполяции. Время регулирования системы
Т = 3 с.
Определить оптимальную астатическую систему управления пер¬
вого порядка по критерию максимума вероятности невыхода ошиб¬
ки системы из заданных малых пределов ±с. Произвести сравнение
по точности систем, синтезируемых по данному критерию и по кри¬
терию минимума второго начального момента, с учетом дополни¬
тельного условия
т
J w (т) dz — 1.
o'
6-3-10. На вход системы поступает нестационарный
полезный сигнал с математическим ожиданием mx(t) =
^Co + CV, причем С0^>1. Помеха задана в виде стацио¬
нарного белого шума Д\(т)=*6(т). Желаемый выходной
сигнал //(/) =Х(1 + Т0).
Определить оптимальные импульсные характеристики
^о(т) по критериям среднеквадратической ошибки и
максимума вероятности невыхода ошибки из заданных
101

Допусков при Ci = 1; TQ~3 с; £ = 3; f—i с. Дать срав¬
нение по точности системы управления для выбранных
критериев.
6-3-11. На вход системы управления (рис. 6-3-11) по¬
ступает полезный сигнал вида
X{t)=a0t + alt2l21
где а0= 150 град/с и а\ = 20 град/с2. Помеха представ¬
ляет собой белый шум со спектральной плотностью
SZ(®)=N=0,1 град2/Гц.
Z
1+Тнр
* к
-/
Рис. 6-3-11.
Определить значение постоянной времени корректи¬
рующего устройства Гк, соответствующее минимуму
среднеквадратической ошибки в установившемся режи¬
ме, а также минимальное значение среднеквадратиче¬
ской ошибки, если известно, что коэффициент усиления
k =150 1/с2.
6-3-12. Решить задачу (см. у словие^Г задачи 6-3-11),
если ПФ~ разомкнутой системы W (р)=	при
Т = 0,05 с.
6-3-13. Найти оптимальные значения постоянной вре¬
мени корректирующего устройства Тк и коэффициента
усиления системы k, а также соответствующее им значе¬
ние минимальной среднеквадратической ошибки системы
управления на рис. 6-3-11. Входные сигналы аналогичны
сигналам из условий задачи 6-3-11 при />=100 1/с2;
ао=ЮО град/с; а2 = 10 град/с2; N = 0,2 град2/Гц.
6-3-14. На вход системы управления (рис. 6-3-14)
поступает полезный сигнал со спектральной плотностью
с ч 2rQDx
Sx(w) i ш27'2с •
Помеха представляет собой белый шум со спектраль¬
ной плотностью 5z(co) =7V = 0,01 град2/Гц. Помеха и по-
102

лезный сигнал не коррелированы. Найти оптимальное
значение коэффициента усиления А0пт для системы
управления, обеспечивающей минимум среднеквадрати¬
ческой ошибки, а также значение среднеквадратической
ошибки при k = konT.
.ЛВ±1
Рис. 6-3-14.
6-3-15. На вход системы заданной структуры дейст¬
вует полезный сигнал X(t) в виде случайной функции,
с нулевым математическим ожиданием и с корреляци¬
онной функцией
*,(') = 3<r2N.
Помеха — белый шум с корреляционной функцией
Кг{ Т)=8(Т).
Сигналы X(t) и Z(t) не коррелированы, т. е.
M[XZ\=О, следовательно, Ку{т) = Кх(т) +Kz{r). Же¬
лаемый выходной сигнал Н (t) = X(t), т. е. система пред¬
назначена для копирования полезного сигнала. Отсюда
взаимная корреляционная функция Кун(х) =Кх{г).
Требуется определить оптимальным образом с ис¬
пользованием метода наискорейшего спуска параметры
системы управления q\ = k и q2 — T, если известно, что
система представляет собой апериодическое звено с им¬
пульсной характеристикой
Ю(,)=Ав-^.
За критерий оптимальности взять минимум диспер¬
сии ошибки.
6-3-16. На вход линейной стационарной системы дей¬
ствует сигнал Y (см. рис. 6-3-1), представляющий собой
сумму полезного сигнала X(t) и помехи Z(t). Полезный
сигнал имеет вид: X(t)=X0 + X{t, где Х0 — случайная
величина с очень большим начальным моментом второго
порядка; Х\—случайная величина, распределенная по
закону равной вероятности в диапазоне от —q{ до +q\.
103

Полезный сигнал не коррелирован с помехой, слу-
чайные величины Х0 и Х\ не коррелированы между со¬
бой.
Помеха распределена по нормальному закону со
следующими характеристиками: математическое ожида¬
ние mz=M[Z] = 0, корреляционная функция/(2(т)—-в""111.
Система предназначена для экстраполирования по¬
лезного сигнала, т. е. Н (t) =X(t + 7\>).	•
Определить оптимальную систему, обладающую аста-
тизмом не ниже первого порядка, приняв в качестве
критерия вероятность невыхода ошибки системы из за¬
данных малых допусков ±с} и значение согласующего
множителя, отвечающее максимуму вероятности.
6-3-17. Пусть полезный сигнал нелинейной системы
X(t) представляет собой случайную величину V, кото¬
рая может принимать три значения с равными вероят¬
ностями: -\-с\ 0; —с. Тогда плотность вероятности пара¬
метров
Uf (и) — ” (и — с) ~Ь ® (и) Н~ ^ (и ~Ь с)] •
Помеха представляет собой стационарную случайную
функцию с корреляционной функцией
Кг (x) = D2e-“h|.
Время переходного процесса равно Г.
Желаемая выходная величина
H(t)=x(t, U)=kU,
где к — постоянный коэффициент.
Он р е д ел и т ь он т им а л ь н ы й о п е р а т о р н ел и н е й н о й си -
стемы в классе всех возможных операторов.
6-3-18. Определить оптимальный фильтр Калмана—Бью си для
системы, описываемой уравнением
dX (t) _
dt
где помеха u(t) задана в виде белого шума с корреляционной
функцией вида
Kn(ty t)=Su(0)6(/—т).
Входной сигнал фильтра представляет аддитивную смесь Z(t)~
= X(t)+n(t), где n(t)—стационарный случайный процесс типа
«белый шум» с корреляционной функцией
Kn(t, т) =$п (О)б(^—т).
104

6-3-19. Входной векторный сигнал X многомерной системы,
наблюдаемой на отрезке времени (t—/о), определяется формулой
X = bG + U,
где Ь = 1—матрица коэффициентов, G — векторный полезный сиг¬
нал, описываемый матричным дифференциальным уравнением вида
dG
w = aG + V.
Считаем, что матрица коэффициентов а = 0 и векторный белый
ШуМ V = 0, т. е. G(/) = G(/o) принимает значения
{	1	с	вероятностью	0,5;
° (*•) = { 1
\ — 1с вероятностью 0,5.
U — случайная функция вида «белый шум», подчиняющаяся
нормальному закону распределения, причем математическое ожида¬
ние ее равно нулю, а корреляционная функция Kv(t, т)=гб(^—т).
Критерий оптимальной системы [1]
/0 = ^ + 0^21 (1)
где Di — дисперсия составляющей ошибки системы £i, подчиненной
биномиальному закону распределения; — дисперсия составляю¬
щей ошибки системы £г, подчиненной нормальному закону распре¬
деления.
Определить оптимальную систему (найти фильтр Калмана —
Бьюси) при заданных начальных условиях по приведенному крите¬
рию (1).
6-3-20. Для условий задачи 6-3-19, считая a — const, V = 0,
имеем
G (/) =0 (t0) еа
Определить оптимальный фильтр Калмана—Бьюси по приведен¬
ному критерию:
/, = D1 + D10*.
6-4. ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ,
ПОДВЕРЖЕННЫХ СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
6-4-1. На вход копирующей дискретной системы дей¬
ствует сигнал, представляющий собой сумму полезного
сигнала и помехи (рис. 6-4-1).
Полезный сигнал Х(п + г) является многочленом вто¬
рой степени от времени. Помеха Z(n+e)—случайная
стационарная функция с корреляционной функцией вида
"р”т=0’
у 0 при тф 0.
Найти импульсную характеристику оптимальной
дискретной системы при времени переходного процесса
105

П + 8=2, минимальную дисперсию выходной величины
при значениях коэффициентов ошибки Do=Di — D2=Q.
Определить минимальное значение дисперсии ошибки
^мин»
Х(п+е)
Z(n+e) lY(n + e)
—*-©-
-V(tr+ £)
-H(r/+s) £(n+e)


w (n+e)
F(ti+e)
Рис. 6-4-1.
6-4-2. На вход импульсной системы (рис. 6-4-1) дей¬
ствует полезный сигнал Х(п + &) =Х0 + Х\ (п + г) +Х2(п+
+ е)2, причем коэффициенты Х0 и Х\ могут принимать
очень большие значения, а Х2 представляет собой слу¬
чайную величину с заданным начальным моментом вто¬
рого порядка ii2=tn2x+Dx. Помеха задана стационарной
случайной функцией с нулевым математическим ожида'-
нием и с корреляционной функцией
^w=(*I-np""'T00;
{ 0 при тф 0.
Сигналы Х(п + г) и Z(n + s) не коррелированы между
собой. Система копирующая.
Определить импульсную характеристику дискретной
системы, обеспечивающую минимум среднеквадратиче¬
ской ошибки.
6-4-3. Расчетная схема соответствует рис. 6-4-1 и
условиям задачи 6-4-2. Коэффициент *2 —известная ве¬
личина.
Определить оптимальную импульсную характеристи¬
ку линейной дискретной системы, обеспечивающую мак¬
симум вероятности невыхода ошибки системы из задан¬
ных малых допусков.
6-4-4. Пусть математическое ожидание полезного
сигнала измерителя представляет собой многочлен от
времени
N
Sknk'
*=Э
106

причем значения случайных коэффициентов неиз¬
вестны.
Помеха задана случайной составляющей с корреля¬
ционной функцией вида
Кг [л] = е-“|п|.
Сигналы X(t) и Z(t) взаимно не коррелированы.
Определить оптимальную импульсную характеристи¬
ку дискретного фильтра по минимуму среднеквадрати¬
ческой ошибки.
6-4-5. Для условия задачи 6-4-4 записать оптималь¬
ный алгоритм дискретного фильтра с использованием
z-преобразования для случая N=\.
6-5. ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
6-5-1. На вход следящей системы управления посту¬
пают полезный сигнал Х(£) =а sin G>0f и помеха Z(t)y
имеющая нормальный закон распределения с нулевым
математическим ожиданием и со среднеквадратическим
значением <jz=0,2 В. Амплитуда полезного сигнала,
подлежащая обнаружению, ^ = 0,4 В.
Произведены два замера суммарного входного сиг¬
нала Y(t) системы Y(t)=X(t)-+Z(t) в дискретные мо¬
менты времени tx = T0/4: и t2 = 3T0/4f где Г0=2я/со0—Тх
[Tj — период сигнала X(t)], и получены значения
y1==0,3B; x(t\) —a sin (ot\ = ci\\
У2 = —0,2 В; x(t2)—asmcdt2 = —ci{.
Предполагается, что сигнал X(t) зависит от одного
параметра а, который может принимать лишь два воз¬
можных значения а0 и с априорными вероятностями
Р0 и Р\ соответственно:
а_(ао — ® при Р0 = 0,5;
! а, = 0,4 В при Pt = 0,5.
Найти апостериорные вероятности значений я0 и а{.
6-5-2. Для условия задачи 6-5-1 определить значение
коэффициента правдоподобия Л (У) и определить, какое
значение а наиболее правдоподобно.
6-5-3. В системе оптимального по Нейману—Пирсону
обнаружения определена вероятность ложной тревоги
(вероятность ошибки первого рода) а=0,05. Априорные
107

вероятности значений а0 и равны Я0 = Я1 = 0,5. Вели¬
чина p = £G/S0 = 5, где параметр £0— интеграл от квад¬
рата сигнала X(t), который называют энергией сигнала;
S0 — спектральная плотность шума Z(t) [22].
Требуется найти значение вероятности ложного отбоя
Р и общую безусловную вероятность ошибки Q.
6-5-4. Полезный сигнал системы управления пред¬
ставляет собой высокочастотное синусоидальное колеба¬
ние X(/) =ci[ sin о)о/ с периодом Г0=2я/соо-
Считаем, что время наблюдения Т— 70/г, где п — це¬
лое число.
Пусть а,\ = 1 мВ, спектральная плотность шума Z(i)
S0 = 0,2 мВ2*с.
Каков должен быть период наблюдения Г, чтобы при
Ро=Р\ вероятность безусловной ошибки Q была рав¬
на 0,01%?
6-5-5. Для системы оптимального обнаружения по
Котельникову при Р0 = Р1 = 0,5 известно, что р =
= £0/50 = 5.
Спектральная плотность шума S0 = 0,2 мВ2. Время
наблюдения Т = 2 с.
Найти амплитуду а{ синусоидального сигнала Лг(^) =
— а\ sin о)0£
6-5-6. Входная помеха имеет спектральную плотность
S0 = 0,2 мВ2-с. Априорные вероятности значений а0 и
а\ P0=Pi=0,5. Безусловная вероятность ложной тревоги
б’0=Р0а = 0,025.
Рис. 6-5-в.
Схема (рис., 6-5-6) имеет следующие параметры:
*o=104; 7^=0,1 с; ^=0,01 1/В.
Рассчитать по Нейману—-Пирсону напряжение порога
системы оптимального обнаружения со случайной на¬
чальной фазой.
108

6-5-7. Входной полезный сигнал представлен в виде
X(t) =ах sin (Hot. Время наблюдения 7=2 с^>70, где
70=2л/о)0 — период синусоиды.
Найти^ среднее значение параметра acv=-M [а] при
относительной погрешности а*ОТ11=а*/аср= 1°/,, где о* =
= VS„/ev — абсолютная среднеквадратическая погреш¬
ность; здесь е0—удельная энергия сигнала X(t).
Глава седьмая
КИБЕРНЕТИЧЕСКИЕ АВТОМАТИЧЕСКИЕ
СИСТЕМЫ УПРАВЛЕНИЯ
7-1. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
7-1-1. На рис. 7-1-1 изображена линия связи с актив¬
ным сопротивлением R и переменной нагрузкой /?н. На¬
пряжение [/, приложенное к линии, при изменении
нагрузки не меняется. Параметры схемы: /?= 10 Ом,
[/=400 В, Rn = 2-7-20 Ом.
Определить характеристику передачи энергии по ли¬
нии при изменении полезной нагрузки, г. е. зависимость
мощности, выделяемой в нагрузке, от изменения сопро¬
тивления нагрузки P = f{Rn).
Рис. 7-1-1.
Рис. 7-1-2.
7-1-2. Известно, что не все объекты управления мож¬
но описать аналитически, поэтому экстремальные ха¬
рактеристики приходится снимать экспериментально, на¬
пример к. п. д. различных машин и установок и т. д. При
этом, если для анализа движения экстремальных систем
требуется аналитическое выражение экстремальной ха¬
рактеристики, необходимо аппроксимировать экстре¬
мальные характеристики аналитическими зависимостями.
109

Практикой установлено, что большинство экстремаль¬
ных характеристик аппроксимируется параболами.
Определить аппроксимирующую функцию второго по¬
рядка для части экстремальной характеристики объекта,
заданной в виде табл. 7-1-1,
Таблица 7-1-1
X
1
3.
5
7
9
<Р=/ (X)
1
3
5
4
3
7-1-3. На рис. 7-1-2 представлена непрерывная экстре¬
мальная система, где ИМ—исполнительный механизм;
W — объект регулирования; РЛУ — релейное логическое
устройство. Объект управления безынерционный, а его
статическая характеристика описывается уравнением
y = —kx2 = —2x2.
Рис. 7-13.
Параметры системы: v — скорость изменения входной
величины; т — время выхода в экстремальную область;
Аг/=8%—зона поиска на выходе; А = 4 — начальное
рассогласование; Т = 2 с — период автоколебаний; Р —
потери на поиск.
Определить качественные показатели экстремальной
системы.
7-1-4. Экстремальный объект управления состоит из
двух последовательно соединенных звеньев W\ и W2
(рис. 7-1-3), дифференциальные уравнения которых
имеют вид:
х\ — —Кх2\
т4-+
110

Уравнение исполнительного механизма ИМ
dx
~ЗГ
= ±v.
Численные значения параметров системы:	/С=2;
Т—0,5 с; v—l 1/с. При ^=0 х0= — 1, у0=—2. Зона не¬
чувствительности прибора, измеряющего отклонение от
экстремума, Дун=0,1	(РЛУ — релейное логическое
устройство).
У1
Z
и
> г
Уг
1
~У1макс
i
М0(р)
Iы\(р)
*1
-fL>
(л)
Т
Щ{р)
Уг ,
и\
и
1
А
+ У1
Щ(р)
У/
(л)
U
Рис. 7-1-4.
Определить фазовую траекторию экстремальной си¬
стемы и параметры предельного цикла, предполагая, что
она работает по принципу запоминания экстремума.
7-1-5. Экстремальный объект управления состоит из
двух инерционных звеньев, описываемых уравнениями
г,
т*тг+У'=к*у>
где 7" 1 = 100 с; 7"2 = 10 с; /Сi = 2; К2—\.	-
111

Передаточные функции этих звеньев:
'И'М^Т.Г+Т''	=
Между инерционными звеньями включено нелинейное
звено с.экстремальной характеристикой
y=—Kx2i.
Второе нелинейное звено, управляющее исполнитель¬
ным механизмом и выявляющее отклонение значения
выходной величины от экстремума, представим в виде
эквивалентного реле с характеристикой, приведенной
на рис. 7-1-4,а. Зона чувствительности Д=0,5 ед.
Исполнительный механизм (интегрирующий) описы¬
вается уравнением
dx/dt=K*U,
где /Сз=0,001 1/с; Ub=Kr, здесь /Сн=Ю0 ед.
Структурная схема экстремальной системы показана
на рис. 7-1-4,6. Определить методом гармонического ба¬
ланса параметры предельного цикла: период, амплитуду
автоколебаний и потери на поиск.
7-1-6. По условиям задачи 7-1-5 определить параметры предель¬
ного цикла с помощью комплексных частотных характеристик (ме¬
тод Гольдфарба).
7-1-7. Для экстремальной системы, работающей по принципу
запоминания экстремума, задачи 7-1-4 рассчитать и построить пере-
хедный процесс по выходной координате.
7-2. СИСТЕМЫ, НАСТРАИВАЮЩИЕСЯ НА ЭТАЛОН
7-2-1. На рис. 7-2-1,а приведена схема реализации
замкнутой системы самонастройки на эталон. Переда¬
точная функция объекта Wo(p) изменяется под воздей¬
ствием различных факторов внешней среды и отклоняет¬
ся от ее оптимального вида. С помощью изменения пара¬
метров оптимального корректирующего устройства ОКУ
можно сохранить передаточную функцию системы близ¬
кой к оптимальной. Будем считать, что замкнутая си¬
стема является колебательным звеном. В этом случае
ее структурная схема приобретает вид схемы на
рис. 7-2-1,6. Этой схеме соответствует ПФ вида
ф(п)=1Ж=	}
X (р) Тгр! + Ч%Тр + 1 •
112

Х(р)\~
-/
ОКУ
WQ(p)
ИУ
а)
ВУ
у(р)
Y/p)
В качестве эталонной
динамической характери¬
стики принят коэффициент
х=А\—Л 2,	характеризую¬
щий затухание колебаний
выходной величины, где
А\ — амплитуда первой по¬
луволны /-го периода; Л2 —
амплитуда второй полувол¬
ны i-го периода. Будем счи¬
тать эталонной системой
систему, находящуюся на
границе устойчивости, у ко¬
торой Л 1=Л2, т. е. коэффи¬
циент х равен нулю.
Будем считать также, что
исполнительное устройство
является интегрирующим
звеном с коэффициентом уси¬
ления —k\k>0\. Исполнительное устройство ИУ цепи
самонастройки изменяет коэффициент £ (регулируемым
параметром X здесь является коэффициент |). Это изме¬
нение можно производить, например, путем изменения
одного из сомножителей, подводимых к множительному
звену. Выходом этого звена является величина £.
Определить состав вычислительного устройства по¬
казателя качества, если оно определяет, значение х и
подает ее на вход исполнительного устройства, которое
в соответствии с этим значением по некоторому закону
изменяет коэффициент £ регулятора.
7-2-2. На рис. 7-2-2 приведена структурная схема си¬
стемы с замкнутыми цепями настройки корректирую¬
щего ^ устройства, где W\(p)—ПФ корректирующего
устройства; W2{p)—ПФ объекта регулирования; ВО —
вычислитель отклонений.
Пусть заданная опти¬
мальная ПФ замкнутой
системы получается при
ПФ двух основных звень¬
ев, т. е.
Рис. 7-2-2.
8—903
ф ( п\  ^1» if) ^20 (Р)
• w —i +wl9(p)wii (ру
(1)
113

где Wl0(p) — оптимальная ПФ корректирующего устрой*
ства; W2o(p) —оптимальная ПФ объекта регулирования.
Определить зависимость между вариацией ПФ АФ,
которая обеспечивает достаточную малость отклонений
ДФ при имеющихся отклонениях AW2y и построить струк¬
турную схему, обеспечивающую стабильность ПФ.
7-2-3. Найти ПФ Ф(р) замкнутой самонастраиваю¬
щейся системы с эталонным фильтром
-	/	V
Лр)= Up+\ ’
структурная схема которой изображена на рис. 7-2-3,
при *ф=1; *i = 5; *2 = 2; *3=200 с-1; Гф = 0,05 с; Т{ =
= 0,005 с; Т2=0,1 с.
Рис. 7-2-3.
7-2-4. В качестве одного из принципов самонастрой¬
ки можно применить самонастройку по косвенным пока¬
зателям динамических свойств. Так, по переходной ха¬
рактеристике системы (рис. 7-2-4,а), фиксируя количество
Рис. 7-2-4.
ее переходов через нуль за заданный промежуток вре¬
мени т, можно получить информацию о колебательности
характеристик. Об интенсивности затухания процессов
114

в системе можно судить по числу переходов переходной
характеристики системы через новые нулевые оси, кото¬
рые получаются путем подачи постоянных смещений Uu
U2 и Т. Д.
На основе изложенного выше принципа (самона¬
стройка по косвенным показателям динамических
свойств) построена самонастраивающаяся система
(рис. 7-2-4,б), где 1 — объект регулирования; 2 — ис¬
полнительный элемент; 3— корректирующий элемент;
4 — блок переменных коэффициентов; 5 — элемент срав¬
нения; 6 — исполнительный элемент контура самона¬
стройки; 7 — счетчик импульсов; 8 — сумматор.
Пусть оптимальному коэффициенту демпфирования
(затухания) £=0,35 соответствует число перемен знаков,
равное трем.
Указанные по структурной схеме операторы DA, DB
и Dc имеют следующий вид:
Da — Т2Ар2 + 2 IaTaP + 1;
5в = Т2вр2 Л-2£>вТ ср +1;
Ос = Г2сР2+2£сГсР+1.
Требуется определить диапазон изменения kx и раз¬
рядность счетчика, если при самонастройке ставится
условие неизменности собственной частоты системы
(0ц= 1/Гопт- Параметры системы следующие:	Г0Пт	=
= 0,021 с; Ti = 0,033 с; Г2 = 0,045 с; Г3 = 0,2 с; Тс =
=-0,0139 с; £с = 0,7; Тл = 0,033 с; £Л = 0,72; ГБ = 0,083 с;
£/>=0,72; &л=2-103.
7-2-5. Самонастройку по косвенной оценке колеба¬
тельности переходных процессов и интенсивности их за¬
тухания можно осуществлять также с помощью частот¬
ных фильтров. На рис. 7-2-5,а дана структурная схема
8*
Рис. 7-2-5.
115

самонастраивающейся системы с частотными фильтрами,
где 1 — объект; 2 — регулятор; 3 — элемент сравнения;
4—фильтр низких частот; 5— фильтр высоких частот;
б, 7 — выпрямители; 8 — элемент сравнения; 9 — испол¬
нительный элемент.
Если общий коэффициент усиления системы kkx из¬
меняется за счет k, то, воздействуя на kx, можно восста¬
новить его и тем самым восстановить динамические
свойства системы.
6 ряде случаев простейших систем, объект которых
имеет ПФ вида
W^ = TlP(Ttp+l) >
корневой годограф имеет вид, представленный на
рис. 7-2-5,б. Будем считать, что оптимальный процесс
по колебательности (а>п) и интенсивности затухания (£п)
достигается при kkx=\ и соп=1 (рис. 7-2-5,б). Тогда при
изменении произведения kkx в сторону увеличения
(kkx>\) наблюдается увеличение собственной частоты,
а при (kkx<C\) происходит уменьшение частоты. Следо¬
вательно, изменение частоты может быть использовано
для самонастройки. Однако при этом нужно обеспечить
заданное протекание частотных характеристик системы.
Для решения поставленной задачи используются частот¬
ные фильтры.
Определить частотные характеристики фильтров так,
чтобы система с заданной структурой осуществляла
самонастройку в диапазоне (0.,2-:-9)А*, где k* — опти¬
мальное значение при ступенчатом изменении входного
сигнала на величину г== 10, если 7^0,2 с; Т2 = 5 с. При
расчетах принять, что наименьшее значение амплитуды
сигнала на входе исполнительного элемента А = 3.
7-2-6. На рис. 7-2-6 показана структурная схема сле¬
дящей системы, на вход которой поступают не коррели¬
рованные между собой регулярный полезный сигнал
G = vt и случайная помеха Z типа «белый шум» с авто¬
корреляционной функцией вида /G(t) =а26(т), причем
а2=600 см2/с~2. Коэффициент демпфирования системы
^==0,5. Момент инерции / — 0,02 г-см-с-2. Работа систе¬
мы обеспечивается при входной скорости и^бОО см/с,
а минимально допустимое отношение сигнал/помеха для
измерителя скорости должно быть yfel = 0,5.
Вследствие того что скорость входного сигнала изме¬
няется, для получений минимума суммарной среднеквад¬
116

ратической ошибки требуется подстраивать динамиче¬
ские параметры следящей системы — коэффициент уси¬
ления k и коэффициент вязкого трения F. Требуется
определить постоянную времени измерителя скорости и
функциональные зависимости связей для настройки ко¬
эффициентов k и F из условия минимума среднего квад¬
рата ошибки.
 к __
1	Li
L
щр)
Щр)
Г
Рис. 7-2-6.
Рис. 7-2-7.
7-2-7.	На	рис.	7-2-7	приведена сгруктур.ная	схема	системы
с разомкнутыми цепями настройки корректирующих устройств, где
Wi(p)—ПФ последовательного корректирующего устройства;
NL (р)—ПФ	исполнительной части системы, изменяющаяся	под
действием внешних возмущений.
Внешние возмущения характеризуются функциями fi, ..., fn,
которые измеряются специальными устройствами с передаточными
коэффициентами Ки . •Кп, воздействующими на корректирующие
устройства. Для компенсации изменений ПФ W2 (р) эти же возму¬
щения подводятся через соответствующие измерители к корректи¬
рующему устройству с целыо изменения его ПФ W\(p) таким обра¬
зом, чтобы ПФ замкнутой системы оставалась неизменной:
Ч	_ J!j_(£LW±I£L_	/п
Ф(р)	- I+ir, (p)Wt(p) •	(1)
Пусть условие Wi (р) W2(p) — const выполняется, a Wi (р)
изменяется по следующему закону:
г ,	^.0 (Р)	(Р)
w^p)= W7U) *	()
где Wi0(p) и Wzo(p) —оптимальные ПФ для некоторого начального
состояния системы.
Определить оптимальные параметры корректирующего контура
с помощью ЛЧХ в области частоты среза разомкнутой системы
для управления перегрузкой летательного аппарата, если сила тя¬
жести отсутствует, а ПФ корректирующего звена имеет вид:
ш ( \	1 ^	т ^ т
(р) —	\ +Тр *	1 •""*
Коэффициенты усиления разомкнутой системы
KiK2 = KioK2o = const.	(3)
117

7-3. МАТРИЧНЫЕ ИГРЫ И ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
7-3-1. Игроки А и В одновременно и независимо друг
от друга записывают каждый одно из трех чисел: 1/2
или 3. Если сумма написанных чисел четная, то В пла¬
тит А эту сумму в единицах выигрыша, если она нечет¬
ная, то, наоборот, А платит В эту сумму. Требуется
проанализировать игру, составить ее матрицу и найти
решение.
7-3-2. Два игрока А и В должны выбрать одно из
чисел 1, 2, 3, 4. Если число, выбранное одним из партне¬
ров, на 1 единицу больше числа, выбранного другим, то
первый партнер платит второму 3 единицы выигрыша.
Если же игрок выбрал число, большее по крайней мере
на 2 единицы, чем число, выбранное противником, то он
платит партнеру 4 единицы выигрыша. В случае равного
выбора игра заканчивается вничью. Определить платеж¬
ную матрицу этой игры.
7-3-3. Игроки выбирают целые числа от 1 до т. Если первый
выбрал у, а второй г, то первый получает у—г единиц выигрыша,
если	и	платит	y	+	z	единиц	выигрыша,	если y<z. Записать
матрицу выигрыша А = \\ац\\т,п. Рассмотреть случай, когда т = 4
и т = 5.
7-3-4. Спортивный клуб А располагает тремя вари¬
антами состава команд Аи А2 и А3. Клуб В также рас¬
полагает тремя вариантами Ви В2 и В3. Подавая заявку
на участие в соревновании, ни один из клубов не знает,
какой состав изберет противник. Вероятности выигрыша
клуба А при различных вариантах составов команд
(примерно, из опыта прошлых встреч) заданы матрицей
(табл. 7-3-4).
Таблица 7-3-4
в
л
Вг
В3
Л
0,8
0,2
0,4
Л2
0,4
0,5
0,6
А3
0,1
0,7
0,3
Найти, с какой частотой клубы должны выставлять
каждый из составов во встречах друг с другом, чтобы
добиться наибольшего в среднем числа побед.
118

7-3-5. Определить наименьшее значение линейной
нкции Ф = 5х\—10х2 + 7х3—Зх4 на множестве неотри¬
цательных решений системы уравнений
+Хг + 7хз + 2х4=7/2;
—2х\—Х2 + Зх3 + 3x4=3/2 ;
2х 1 + 2x2 + 8x3 + Х4=4.
7-3-6. Определить среди неотрицательных решений
системы неравенств
—20xi + 12х2—15х3^60;
xi + 2x2—Зх3<6;
3xi + 6x2 + 4x3<g: 12;
—20х 1—15х2 + Зх3 <: 60;
10xi + 5x2—2х3^ 10;	\
6xj + 7x2 + 42хз^^42
такое решение, при котором линейная форма
Ф = Х 1 +Х2 +Х3
достигает своего наименьшего значения.
7-3-7. Дана функция выгоды M=3xi + 4x2.
Требуется решить задачу линейного программирова¬
ния для условий Xi+X2^6; 2xi-f-4x2^21, причем х^О;
х2>0.

Часть вторая
РЕШЕНИЯ
Глава первая
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
АНАЛОГОВЫМИ СТАЦИОНАРНЫМИ
И НЕСТАЦИОНАРНЫМИ ЗВЕНЬЯМИ
01-1. ЗАДАНИЕ ТИПОВЫХ ВХОДНЫХ СИГНАЛОВ
В АНАЛОГОВОЙ И ЧАСТОТНОЙ ФОРМАХ
01-1-1. а) Применим для вещественного спектра фор¬
мулу обратного косинус-преобразования Фурье с огра¬
ниченным верхним пределом интегрирования
о>0
[0 = —- J Рх И COS wtdu).
о
Подставляя рх(со) = 1, получаем:
2 sin сo0t
t
б)	При построении графика (рис. 01-1-1,а) началь¬
ную точку находим путем предельного перехода:
1 ’ t^o * t *
Площадь графика определяется интегрированием:
-rswT-
0 0 0
Ответ получен в виде интегрального синуса, для ко¬
торого из таблиц приложения 9 (последний столбец)
имеем Si(0) =0, Si(oo) =я/2. Следовательно, S=l-
120

в) Время первого перехода графика через нуль равно
полупериоду синусоиды, который найдем из соотноше¬
ния (0о^1 = л или 7"! = jt/coo; кривая, иллюстрирующая эту
зависимость, построена на рис. 01-1-1,6.
г) При бесконечном расширении полосы ю0 процесс
хх [t) эквивалентен единичномуJ импульсу lim хг [t) = 5 [t].
UJ0-)>CO
Рис. 01-1-1.
01-1-2. Перейдем в определенном интеграле, задан¬
ном в условии, от переменной t к со:
(О0
X, (t) = — Г — sin wtdaв;
г х 7	71	)	СО
о
результат интегрирования от этого не изменится. Сопо¬
ставляя полученную формулу
с обратным синус-преобразо¬
ванием Фурье, находим, что
стоящий под знаком интеграла
первый сомножитель является
мнимым спектром с обратным
знаком и с ограниченной по¬
лосой ±0)0, т. е. х2(со)=—1/со
(—(1)о<со<со0) (рис. 01-1-2).
При бесконечном расшире¬
нии полосы спектра соответ¬
ствующий процесс сближает¬
ся с единичной функцией
lim х2 [0=1 [0, имеющей спектр
10°-*°о
(МНИМЫЙ) х2 (to) =— 1 /со.
01-1-3. На основе примененного в предыдущей задаче
предельного перехода имеем:
оо
1\п\ х2 [/) = 1 [0 = Г	sin arfdw.	(1)
(.Од-ьпа	J
!?1

Для интеграла (1) / является параметром, по кото¬
рому под значком интеграла можно проводить такие ли¬
нейные преобразования, как дифференцирование и ин¬
тегрирование.
Дифференцируя обе части приведенной формулы по/,
получаем:
оо
lim Xj [f) = 6 [/] = — f l cos wtdw.	(2)
Wq—^oo	71	J
0
Сомножитель перед косинусом рДсо):^! представ¬
ляет вещественный спектр импульса, а вся полученная
формула (2) является обратным косинус-преобразова¬
нием Фурье. Повторно дифференцируя, находим спектр
функции 6[/] как коэффициент при —sin со/. Интегриро¬
вание по / (1) под знаком интеграла дает:
00
*•11*)-=-§- j* ( sir) cos wtdw,
0
где (—1/со2)—вещественный спектр процесса /*1[/).
Повторное интегрирование дает возможность опреде-
/2
лить спектр процесса 1 [/). Ответы на задание, полу¬
ченные по формулам предельного перехода (соо-^^о),
помещены в табл. 01-1-1.
Таблица 01-1-1
Процесс
X 10
5 Ш
b[t]
b[t]
I [О
м 10
4- 1 m
2!
Вещественный
спектр
р(со)
— со2
0
1
0
1
со2
0
Мнимый спектр
х(ю)
0
со
0
_ 1
со
0
1
со3
Комплексный
спектр
X(jcо)
(/со)2
/со
1
(/со)-1
(/со)-2
(/со)-3
123

0i-l-4. Ё формуле прямого преобразования Фурье
запишем мнимую частоту в векторном обозначении:
У СО = (О.
(1)
Тогда
Е (ш, 7], £2, <р) = J ехр [(к] -)- у£2 — со) t -|- /^>]
Л = -=
ехр (if)
со — 7) - ;2
(2)
Далее, применив заданную операцию Im (...) к ком¬
плексной экспоненциальной функции и к ее спектру, по¬
лучим:
Im {ехр [у -j- j (Qt -f <р)]} = ev sin (Qt -f <j>);
exP Of) ) Q cos + (w — ^l) sin у
(со — 7])2 -f. 22
lm
f exp (yy) I
i w —7] — ya j—
(3)
После обратной замены векторного обозначения на
мнимую частоту согласно формуле (1) получаем спектр
процесса в виде
2 cos <р — т) sin <р + /ю sin'<p
7j2 _|_ 22 — со2 — /2сот]
2	(т)2 + 22 — со2) cos <р — т) (т]2 -f 22 -f- со2) sin ?	.
—	со4	+ 2 (7]2 — а2) со2 4- (7)2 4- 22)2
•	.	22со cos<р — со (т)2 — 22 4-со2) siпу	...
1	со'1 + 2 (г]2 — 22) со2 4- (т]2 4- Й2)2"-	^	'
Если применить к комплексной экспоненциальной
функции и ее спектру (2) другую заданную операцию
Re (...)> а также положить ф=0, то вместо (3) по¬
лучим:
Re [ехр (T\t-f-jQt)] = е*1 cos £2/;
Re [ =
L<0 — 7|-
-jQ
to — ч
(5)
123

После обратной замены (1) для процесса (5) опре¬
деляем спектр:
 	 — л (лг + 8г + ь>г) L
Т)2 + Q2 — (о2 -i /2V]со to4 + 2 (I)2 — й2) со2 + (г,2 + Й2)2 “
+ j	p-vj2	(о2) со
“ ' <о4 -I- 2 (Г)2 — й2) со2 + (г,2 + й2)2	•	к	’
Полагая в соответствиях (3) — (6) отдельные пара¬
метры равными нулю, получаем дополнительные спек¬
тры процессов:
»/ 1 — 7) т
^	'	/(О	—	7]	7]2	-J- О)2	*	7]2	+	(О2	’	'	'
sin(a+T)^	=4^+1^: «
eosQ^-^;'"	(9)
Все соответствия, полученные подобным образом для
заданных преобразований подынтегральной функции и
ее спектра в (2), записаны в табл. 01-1-2, являющиеся
дополнением к приложению 1.
Таблица 01-1-2
Параметры,
приравнива¬
емые нулю
X
(-►) = Re (...)
X (-*) = Im (...)
Функция
Комплексный спектр
Функция
Комплексный спектр
7) — 0
cos (2^+
+ у)
—2 si п<р+/со cos у
22 —со2
sin (2/-f-
+ ¥)
2 cos <р-|-/со sin <f
22 —со2
¥ = 0
tf^cos Ш
/(0 — 7)
e^sin Йt
2
(/<*> — 7))2 + 22
(/«> — 7))24-
Л --- 0 j
cos 2/
/со
sin 2f
2
¥ — 0 J
22 —со2
22 —со2
й = 0 \
¥=0 f
1
/(0—7)
0
0
124

01-1-5. Применив к обеим частям соотЁетстбйя (?)
из предыдущей задачи заданную операцию Х(->) =
=д/<Эг), получим:
а) te**—	—-Пу- 27)(0 -
'	и<й—'Ц)2	(7)2 + (О2)2	^	J (f-f (О2)2 •
б) Применив эту же операцию k раз, получим:
fk^t ^ k\  ^	+	!	С*)	+	/<«>)*+ *
(/(О 	 7])/^+1	(7)2 + (02)’^ + 1 ’
в) Полагая т) = 0, из „6“ получаем:
И ^	(;о))/г+	1	’
г) Применяя преобразование Х(->)=д/дг] к реше¬
ниям (3) предыдущей задачи, получаем:
ter{t sin (Of J_	22 и°>—‘4) cos У+f(/<° — ^ — Q2isin У
П1-Г~г™ *	[(/со	—	-yj)*	H-	a*]2
01-1-6. Заданное произведение гармонических функ¬
ций можно получить из комплексной экспоненциальной
функции, последовательно применяя следующие подста¬
новки и операции X(-^)=Im:
sin (£},/ -|- <р,) sin + срг) = Im | {Im exp [(/Q, -f- Д) t -f-
+/?. + ?*]} -	\ = X (—) exp [/ (Qt -j- ?)],
2г = /2г )
т. e. в комплексной экспоненте производится замена
^2=/QiН-Q2, ф=/ф1+фг. Затем выделяется мнимая часть,
осуществляются подстановки ф2=/ф2, Йг=/Йг и снова
выделяется мнимая часть. Совокупность этих операций
и есть искомое преобразование комплексной экспонен¬
циальной функции при т|=0, т. е. Х(->-) [28].
Применим найденное преобразование к спектру ком¬
плексной экспоненциальной функции, определенному
в задаче 1-1-4:
Im ехР (/?1 + Уа) _ (to —2г) sin у, 4-St cosy,
«-2а —/2,	—	(w-Q^	+	Q*,
(?г = /'Рг. ^s = A);
125

1(£sln?,+S, cosy,) COS <Ps + 62 siny, sinf„ ““	*
— /[S2sin y, cosy2 —■ (tosiny, + 2, cosy,) sin<p2] ( _
(S-A)*+e*,	)'
2w22 [(eTsiny, + 2, cosy,) cosy2 -j- 22siny, siny2] —
— (to2 -{- 22, — 22„) [22 sin y, coS y2 — (tosin y,+2, cos ¥i) s*n У2]
—	1(2,	+	22)2 + й2] [(2,-22)2 + w2j	1
(ш==/св);
|(2,+22)2—со2] [— (2,—22) sin (y,-y2)+/<o cos (у,—y2)]-
—[(2,—22)2—to2][—(2, +22) sin (y,-y2)+/w cos (у,+уг)1 .
X ^“) =	2 [(2, + 22)2 - <o2j [(2, - 22)2 - o>2]
(1)
Примечание. Заданный процесс можно также
представить в виде суммы
x[l) = -j- {cos [(Q, — Q2) t + ?, — 9г] — cos	+
+ f. + 'iP2l}.
где для каждого слагаемого переход к спектру может
быть произведен по формуле (8) из задачи 01-1-4.
С учетом примечания имеем:
vr s.  1 Г — (2, — 22)sin(y,— у2)+ /<0cos (у, — y2) i
— -(2, —22)2 —(о2	1
, — (2, + 22) sin (у, + Уз) + У” cos (у, + у2) ~[
Ч"	(2, + 22)2 — о)2	J*
После приведения к общему знаменателю можс1
быть получена формула (1).
01-1-7.
а)	Используем зависимость [Л. 26]
8(f)6[/—0]=&(0)6[f—0].	(1)
Следовательно,
П, [^] = sin-^-/8 [t — 2] = sin -£81*-2] = 0,58[*-2].
126

б) Применим к (1) операцию дифференцирования по
параметру 0 с изменением знака:
-6(o{-^4'-ei}=W[f-0] =
= --^-0(О)8[*-О]}.	(2)
где
Следовательно,
[0 = -	{	sin	-f2- 68 р - 6] }0=2=
” {“~тгcos ~тт68 р - 01 + sin -12 98 Р - 01)'9_2=
= 0,55 [t — 2]-^-«К-2]-
в) Повторно продифференцируем по —б формулу (2):
6 (О S р _ 6]=-^г	(0)	6	р	—	6]}.
Следовательно,
пз Щ =6(6) 5 р — 0] — 26(6) 5 \t — 6] +6(6) 6 р — 6].
Поскольку 6(6) = sin -2 = 0,5; 6(6) =	cos х
Х2=^-; ^(0) = -(тгУ5*п^--2 = ^-. то
П3 й == 0,55 [* — 6] — 0,4525 [t — 6] -f 0,03445 [t — 6].
01-1-8.
СО
a)	J 6 (t) 6 [/ — б] dt = 6 (6) 1 [/ — 6),	(1)
о
или р, [0 = 5gu 1 \t — 7) = 6015 10*1 [t — 7),
127

Далее обе части (1) дифференцируем по — 0:
б)
°^b(t)’b{t — 9] dt = b(b)b\t — 0] — 6(0)1 [t — б):
О
pt \l) = 5е'*Ь [t- 7] - 10еи 1 [t - 7) =
= 6015-103 {8 [t— 7] — 2-1 [t — 7)};
в)
J b ф) 5 p — 0] dt — b (6) 5 \t — 0] — 2b (0) 5 [t — 0J —f—
о
b (0) 1 [t 0);
p3 [t) = 5eI4S [t — 7] + 20<?14S p — 7] + 20<?’4 -1 p — 7) =
= 6015 • 109 {6 p — 7] — 45 p — 7] + 4 • 1 [i — 7)}.
01-2. СОСТАВЛЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ЗВЕНЬЕВ
01-2-1. Алгебраизованная форма записи:
[an(t)Dn+ ... +a0(t)]y(t) =
= [bm(t)D™ + ... +b0(t)]x(t),
где D=d/di.
Свернутая алгебраизованная форма:
Г sw °*]у (°=Is bi{t) Di] (#) •
L=o j L/=o J
Форма записи с использованием обозначений алге-
браизованных дифференциальных полиномов:
a(t, D)y(t)=b(t, D)x(t).
01-2-2.
(апрп+ ...+ao)Y(p) = (bmpm+ ... +b0)X(p).
01-2-3.
[Г,]=с; [Г2]=с; [at] = c; |W| = c2; [61] =с;
[ci]=c; [d,]=c; [rf2]=c2; [а//«о]=с*; [Pj/P„]=c^.
01-2-4. Алгебраизованная форма записи:
[а2(<)£>Ч“|(рО-Ьао(О]0(О=61(Об(/)-4-6р(/)вс(/)-4-тв

{(d2 - c,t) D2 + [ft, (t - c)2 + dx) D + fe0 (< - c,)* + do} 0 (0 =
= (<?,/ + A,) 8 (0 + [fe, (/ - c,)*d,] 9C (0 + «»•
Свернутая алгебраизованная форма:
(t) 8 (t) + 6„ (0 0C (<) + «V
Форма записи с использованием обозначений АДП:
a(t, D)Q(t)=bl(t)6(t)+b0(t)Qc(t)+mB.
01-2-5.
Алгебраизованная форма	Операторная форма
(axD + а0) у (t) = b0x (/);	(ахр + а0) Y (р) = Ь0Х (р);
а0у (0 = (b,D + ь0) х (/);	aQY (р) = (Ьхр + b0) X (р);
(<z2D2 + a,D + а0) у (t) -= bQx (t);	(а^+ад+ао) Т (р) =- М'
(a2D2 + 6i0) I/ (/) = Ь0х (t);	(a2p2 + а0) Y (р) =	(р);
ад(0 = (b2D2 + bxD + Ьо) x{i)\	a0Y (p) = (b2/?2 + b,p +	b0)	* (p);
ад (0 = b,Dx (0 ;	a0Y (p) = b,/?A (/?);
(a,D + a0) г/ (0 = bxDx (0 ;	(axp + a0) Y (p) = 6,/bY	(p)	I
fllDy (0 = b0x (t).	axpY (p) = b0X (p).
01-2-6. а) Для полной импульсной характеристики
в заданном уравнении полагаем jc(/)=6[tf]. Тогда у(0 —
=w[i) и уравнение принимает вид:
a2w [0 + axw [0 + a0w [*) = 60S [t] + ЬгЬ [*].
б) Приводим всю правую часть заданного уравнения
к одной функции, обозначаемой П (t)=box(t)+bix(t), и
полагаем П(t)=8[t]. Решение его называется приве¬
денной импульсной характеристикой g[t), уравнение
для которой принимает вид:
а2g [0 + aig [0 + аоg [0 — 8 W •
в) Связь между приведенной и полной импульсны¬
ми характеристиками
w[t)=b0g[t)+big[t).
01-2-7. По заданной приведенной импульсной харак¬
теристике
9—903
129

устанавливаем, что ее начальное значение g(0+)=0,
благодаря чему первая производная от импульсной ха¬
рактеристики содержит только два слагаемых:
g [0 = — °g [0 + -JT cos Qt-
Для удобства записи результатов последующего диф¬
ференцирования вводим обозначение
/ [t) =	е~3t cos Qt
или
f[t)=g[t)+<yg[t).	(1)
При определении второй производной от импульсной
характеристики учитываем ненулевое начальное значе¬
ние первой производной g[0+) = l /Т2, поэтому в резуль¬
тате дифференцирования помимо непрерывных произ¬
водных функций появится импульсная составляющая,
а все выражение для второй производной примет вид:
g 10 = — °g [0 — Qtg [0 — °f [0 + g 1°)8 M-
Заменяем f[t) выражением (1), что дает
g [0;+ 2og'[0 + (о2+Q 2)g [0=—5 [t].	(2)
Чтобы получить в правой части уравнения импульс
с единичным коэффициентом, умножаем все члены урав¬
нения (2) на Т2 и заменяем коэффициенты согласно
данным в условии соотношениям:
аГ= ± г = ЯГ; (о2 + Q2) Г2 = Я2 + (1 - Я2) = 1,
что дает
T*g[t) +2Z,Tg[t) +g[t)=8[t].
После подстановки численных значений имеем:
0,01£[0+0,12£[О+£[*)=8[*].
Для переходной характеристики имеем уравнение
с буквенными обозначениями коэффициентов:
T2fi[t) +2%T4i[t) +h[t)=k-l[t)
или с числовыми коэффициентами:
0,01/ф) +0,12й[0 +А[0=10-.ф).
130

01-2-8. Для заданной импульсной характеристики
освобождаемся в знаменателе от текущего аргумента т
путем умножения обеих частей уравнения на двучлен
(/о+т), что дает:
(К “Ь Х) g К Z)=~Q~e Jt S^n
Производим однократное дифференцирование по х:
8 [*о» т)+ (t9 + т) g [tQ9 z) = — 0 (К + т) g I to’ z)J^re Zt cos
(1)
Повторное дифференцирование по x дает:
2g [tQ, x) -j- (t0 -J- x) g [tQi x) = — о {g [^0, x)
+ (f. + T) S' [^o> x)} — (^o + T) ft» T) —
— 0£~"JT COS Qx -|- 6 [x],
где появление импульса вызвано единичным скачком функ¬
ции е~~°* cosQt. Подставляя значение е~'1 cosQt из урав¬
нения (1), получаем:
(^o + t)g‘[t, /о)+2[1+ g(/o + t) ]g[T, U) +
+ [ (а2 + Q2) (/о+т) + 2а] г[т, /о) =6 [т].
Для а=2 с-1 и £2=6 c_J имеем:
(^o + t)g[T, ^о) +2[1 + 2(/0 + т)]§'[т, U) +
+ [40 (/о+т) + 4] g[т, to) =6 [/]
и для конкретного значения /0=Ю с
(10+t)g[T, 10) + (42 + 4т)^[т, 10) +
+ (404 + 40t)g[t, 10)=б[т].
01-2-9. uy = kux9 где k =
01-2-10. ТйуА-иу=их, где T=RC.
01-2-11. THy + Uy=kux, где T,= (/?i + /?2) С; k=CRt.
01-2-12. На основании закона Кирхгофа для точки А,
пренебрегая сеточными токами, имеем:
i 1=12 + 13*	(1)
9*	131

^cei	iix	4	. ^сет
tt— 3-	==	-3—.	/,—■
л* я, •— /?0-с	я0	c
t‘ ^-C^L.
а) Подставляя значения токов в уравнение (1), По,
лучаем:
uyRo.fi -\-иу	wa-	(2)
или
—kux=Tiiy + Uy,
где k=R0.clRx\ T=Ro.cC.
б) Если из контура обратной связи исключить ре¬
зистор Ro.c, т. е. Ro.c-+°°, то из уравнения (2) получим:
lim (йуС + uy/R0C) = — ux/Rx; uyCRx = ux
Ro.c*°°
ИЛИ
Тйу—Ux, где T—RXC.
в) Из уравнения (2) имеем:
uy——kux, где k—Ro.clRx-
01-2-13.
duu
ТЧГ+ии = ки*
где
Ri
01-2-14.
a)
где
6)
R+R, • R+R, *
day	dux
T\ ~~4J~ Л' uy = T 1 ~dJ~	Uxi
T\ — (R\ -j- Rz) C2; T2 = R2C2;
duy	( dux	\
T2 dt + иj, = * (Г, dt + uxJ >
132

т — Р Г • Т Г ^ (^2 "Ь ^») и
Ki^i, 2	1	/?	JL.	А»	_!_ Q » « — ;
e)
d*Uu
-v	duy
^1^2	+	(^1	+	^2	+	^/-2)	+	Uy	=
d2uK
dux
— 7 1^2 сц2 + (7\ + ^2)
где
г)
7\ —^i6\; 7^2 —^2p2\
duy
dux
ТТФ ^2. + (T + 7ф + ЯфС) -п- + Uy = /гГ —тг>
где
/г =
01-2-15.
где
а)
где
б)
где
в)
т -^L 1 „ _ Ь (т i*“*-4-	^
1 dt ~гиУ '~	\	2	dt	~*~их)'
г, = (я, + /?„ “*“/?2) Сг’ 7'2 = ^2с2: л = /?i +н^н
01-2-16.
_<Ц/,	Л/*_
1 dt ^иу—‘ i df »
T’i =''iC1;
<b*v_.f ЯЛ	dux	.
1 dt V1 + /•, )uy~l 1 d<
Л =RiC\;
d2Uy	da„
Т,Г* ~dt~ + (Гз +	-Щ-	+	Uy	=
= *[^2^+(7-1+Г2)-§^ + Ыл.
133

Постоянные коэффициенты k, 'Л, Т2, Т$ и 1\ находятся из
Соотношений Ti~RiCi\ T2=R?.Cz\ T3'l\=--kTiT2\
V	;2	J	X	'l	/	J
г)
d2iiy	iliiy
Г?Тл-^-+(Т3 + ТА) — + Utl -
т\Т:
Постоянные коэффициенты уравнения связаны с параметрами
схемы следующими соотношениями:
ТiTz = kiRiC 1R2C2', ТзТb — kkiRiCiRzCz’y.
Тi + т,= к, (R.C, + Л,С, + /?2С2);
7"з -f- ТА =	+ RiC2 + kR2C2);
r\ ,	rz	 T	{Г	±
kx
Oi-2-17.
Ri + rx
d2u.
k =
R2	r 2	T \ Г 2
duu
1 lTc сit2 +TC (It ~^uy—kux
где
TL — L/R9; Tq — RsC\ R3 — R2 -j-
RqR,
; k =
Ri
Ri+R0
^0 +
При R2<^R0 и /?! > Rq Tl = L/R0; Гс = /?0С.
При R2^>Ro и Ri^>R0 Tl = L/R2; Tc=R.2C и k=L
01-2-18. В -'определенном диапазоне угловая скорость Q--kU,
но Q=d-a/dti где а — угол поворота якоря. Поэтому da/dt=kU или
т J
0
Udt, где Т = \/k.
01-2-19. Уравнение моментов электрогидравлической рулевой
машины в упрощенном линеаризованном виде обычно представляет¬
ся как
Jb -f- kvb + kn§ = kMix,
где / — приведенный момент инерции подвижных частей рулевой
машины и нагрузки; kv — коэффициент скоростного сопротивления;
kn — коэффициент позиционного (шарнирного) момента; /ем — коэф¬
фициент моментной характеристики рулевой машины; 6 — угол
поворота вала рулевой машины; ix — входной ток управляющего
реле.
134

01-2-20. Используя условия непрерывности струи жидкости, по¬
лучаем:
F w= vbx'
где b — ширина отверстия; х — перемещение золотника; v — ско¬
рость жидкости в сечении ЬХх; у— перемещение поршня; dy/dt —
скорость перемещения поршня; F — площадь поршня; Fdy/dt —
секундный объем масла, поступившего в полость цилиндра.
Так как v = const, то dy/dx = kx или
y = k xdt, где k = vb/F.
01-2-21. В установившемся состоянии МД = МГ, т. е.
Н
h<x)x = Ныу, откуда со* = р = — <оу,
а угол поворота гиродвигателя вокруг выходной оси
Н .
fjdt.
01-2-22. &v6 + /en6 = kMix (физический смысл коэффициентов см.
в 01-2-19).
01-2-23. Уравнение моментов двигателя
d2o-
где / — приведенный к валу руля момент инерции якоря двигателя,
редуктора и всех связанных с ним вращающихся частей; а — угол
поворота руля; ХМ — алгебраическая сумма вращающего момента
двигателя и моментов сопротивления.
С учетом заданных допущений уравнение моментов запишется
в виде
d2 а
J	^дв*	(0
Момент двигателя Мдв является функцией входного напряже¬
ния их и угловой частоты вращения (a = da/dt. При условии линей¬
ности механической характеристики будем иметь:
х
M™=~Ra #7“’
где и кЕ — коэффициенты пропорциональности по току и э. д. с.;
Rn — сопротивление цепи обмотки якоря.
Решая совместно уравнения (1) и (2), получаем:
d2a	kikp с[а kj

R4J
где Тм =т-г электромеханическая постоянная времени двигателя;
RjRe
kм = //&£ — коэффициент усиления.
01-2-24. Уравнение моментов движения рамки
d2 а
где / — момент инерции рамки; а — угол поворота рамки; =
= Л4Э—Л4П; М0 — электромагнитный вращающий момент;. Ми — мо¬
мент, создаваемый пружиной.
Так как магнитный поток Ф, создаваемый магнитом, постоянен,
то Ma = kil.
При движении рамки в магнитном поле Ф в ней образуется
э. д. с. e=<kEda/dt.
Ток в рамке i=(ux—e)/JR, где R— сопротивление рамки. Ин¬
дуктивностью рамки пренебрегаем.
Тогда
1	da. ,
= kj £) Uх	^ ~~dt'	= ^аа*
Подставляя последние два выражения в уравнение моментов,
окончательно получаем:
г d2a da
14tr+h ЧГ+к*а== kva*'
где
h — kikElR\ ku = kilR.
01-2-25. Пренебрегая рассеянием, получаем:
для первичной цепи
т di1 I о •
L1 ^ + R1l1 — It-х»
вторичное напряжение иу пропорционально э. д. с. первичной
обмотки:
w2 di,
аУ — w, L1 dt ■
Решая совместно оба уравнения относительно иу и их, по¬
лучаем:
d“y ,	dux
Т dt +l,v = kT dt ’
где
k = wz/wu T — Li/Ri.
01-2-26. Уравнение динамического равновесия подвижной системы
Я+мв.т(ё) + лие)=Л1(Л 0).	(И
где Мв.т(0)—момент вязкого трения; Мп(0)—момент противо¬
действия пружины; М(1, 0)—управляющий момент, создаваемый

электромагнитом. (Управляющий момент зависит от тока I И зазо¬
ра 6. Так как имеет место зависимость 6о—8 = //tg(0—0о), то можно
записать, что управляющий момент зависит от тока I и угла по¬
ворота рычага 0.)
Для малых отклонений приращение момента электромагнита
/дМ\	ГдМ\
Ш (/, 0) = f дЛ	+ ( дв \l=u А0 = s„_МД/ + s,_MLb.
4	' 0=0О	4	'	0=0о
Момент вязкого трения
Л^в.т (0) = s20 + s2 (0)2 -f- . . . ^
что дает хорошее приближение при малых скоростях движения.
Для малых отклонений приращение момента пружины
ЛМп = ('ж)в^во лв==ш
Если в уравнении (1) заменить текущие значения переменных
суммой их установившихся значений и приращений
/=/0 + Д7; 0=0О + Д0; 9 = Д0; 0*= А9,
вычесть уравнение статики и учесть выражения для малых откло¬
нений, то получим:
/Д0 + 5д__^Д0 + kAQ =Sj_MAI -f- s0_^jA0.
После приведения подобных членов окончательно получаем:
7Д0 + 5Я_МА'9 + " sq-m) А0 = si-mА/*
01-2-27.
n
nr, dAuH	«п
T -jfi- + Auv = 2j kxiAuxi,
/=1
n
где T = 2 Ti	суммарная постоянная времени обмоток управления
/=1
cwyi (wyi +kiW0'C)
усилителя; У t —	—	—постоянная времени i-й обмот¬
ки управления;, uxi — входное напряжение на i-й обмотке управле¬
ния; ki коэффициент передачи по i-й обмотке; ryi и wyi — сопро¬
тивление и число витков i-й обмотки; до0.с — число витков обмотки
обратной связи; с — коэффициент, зависящий от конструктивных
параметров.	^J
01-2-28. Для учета только последействия от ненуле¬
вых начальных условий используется однородное урав¬
нение, составленное относительно переменной у, полу¬
ченное из формулы (2) в решении задачи 1-2-7: *
у + 2ау+ {o2+Q2)y=0.	(1)
137

Ввод заданных начальных условий в уравнение про¬
изводится при переходе к неоднородной форме Коши:
//,=0 + £/г -Ь (0_) 6 [*];	i (2)
уг = —■ (о2 ~f~^2) Ух 2оуг -)-у2 (0.) 6 [/]»	/
где наряду с обычными обозначениями у:=Уи У У%>
г/2=у [при замене у суммой второго и третьего членов
с обратными знаками в исходном уравнении (1)] в си¬
стему уравнений вводятся импульсы с масштабами, рав¬
ными соответствующим начальным условиям.
Поскольку в зоне	интегрирование	систе¬
мы (2) можно вести для каждого уравнения независи¬
мо, после окончания интегрирования к моменту времени
0+ начальные решения неоднородной системы уравне¬
ний (2) будут соответствовать заданным начальным
условиям, так как интегрирование единичных импульсов
дает единичные функции.
Таким образом, для дальнейших преобразовании
исходной должна служить система уравнений (2). По¬
скольку преобразования сводятся по заданию к записи
уравнений в матричной форме, достаточно ввести сле¬
дующие обозначения:
матрица коэффициентов
В = =
Ьц Ь12
Ь21 Ь22
- (°2 + ^2)
вектор начальных условий
Y (0_) =
1
-2о
0 1
-100 —12
г/i (о-)

Уг (0-)
2
—5
вектор реакции, т. е. режима последействия,
вЛ*)
у (*) =
Уг (t)
С учетом принятых обозначений система уравне¬
ний (2) приобретает следующую форму:
Y(f) = BY(/) + Y(0_)8[f].
01-2-29. Переписываем уравнение, являющееся реше¬
нием задачи 1-2-8, в нормированной форме:
H-((^pr+2o)£+[(°2 + Q2> + <. + '
S--
1
t о + т:
Ш
138

Для правой части полученной формулы используем
зависимость (1) из решения задачи 01-1-7. Тогда
ё'-
‘2°у g -
(«■+£y+i7T7)5+isH-	(i)
Используем стандартные для формы Коши обозна¬
чения:
g 1 — o + gv
g2 = g-
(2)
В последнем уравнении правую часть заменяем со¬
гласно формуле (1) и получаем:
2<з
t о
ёг-
Т" 2°) ё
W
. (3)
\t> + z 1	62	1	tо
Коэффициенты в правых частях уравнений (2) и (3)
образуют искомую матрицу:
0 1
В(^ *о) =
■Q2 +
2а
tQ + т
-(
+ 2а
После подстановки численных значений коэффициен¬
тов рассматриваемая матрица принимает вид:
0 1
4 \ /	2
| у 40 10+ %) [ 4 10 + т
В(Т, 10) =
01-3. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ И ИМПУЛЬСНЫХ
ХАРАКТЕРИСТИК
01-3-1. Переходные характеристики звеньев:
усилительного h (t) =5 • 117);
запаздывающего /г3[/') =5• 1 [/—3).
Импульсные характеристики звеньев:
усилительного w [/) =56 [/];
запаздывающего ш3[/) =56 [/—3].
01-3-2. Дл- получения переходной и импульсной ха¬
рактеристик апериодического звена необходимо решить
его дифференциальное уравнение соответственно при
x[t)=l[t) И *Г)=6[Ц
139

Характеристическое уравнение апериодического зве¬
на и его корень имеют вид:
Гг]+1=0; ц——1/Г.
Общий вид решения уравнения
h=k + Ce~i/T.
При /=0 /1=0. Следовательно, С——k.
Тогда переходная характеристика звена h=k( 1 —
—e~t/T). При подстановке численных значений &=20 и
Г=2 с получим h—20(1—e^°’5t).
Импульсная характеристика
dh k —t/т
1Г=-Ге
или при подстановке численных значений
ш[/) = 10е~°’5г.
При t=Qc—3T соответственно получим: /г[ЗГ)=19;
«([ЗОггОД
01-3-3. Переходная характеристика h[t)=k[et/T—\].
Импульсная характеристика = etlT .
01-3-4. Переходная характеристику h\t) — -^-t. Им¬
пульсная характеристика w [f)= -jr-1 [£).
01-3-5. Переходная характеристика h[i)—Td[t]. Им¬
пульсная характеристика гс>|7)=7’б[/].
01-3-6. Переходная характеристика h[t)=k{\[i) +
+ 7’6В]}. Импульсная характеристика ш[/)=/г{б[г] +
+ T6[t]}.
01-3-7. Переходная характеристика h\t) — -^-e~tlT.
Импульсная характеристика w	[/] — ~ е_//7|.
01-3-8. Переходная характеристика h[t)=k{\(t) +
+ 2 |Гб[/]+Рб[^]}. Импульсная характеристика ш[/) =
г=л{вв] и ■+г*в ВЛ-
но

01-3-9. Для определения переходной характеристики
колебательного звена его дифференциальное уравнение
записываем в виде
T2fi+2%Th+h—k- \ [/).	(1)
Общее решение уравнения (1):
-S-*-
h = k + Ce Т sin^/l—P-f	(2)
Задавшись начальными условиями h( 0+)=0 и
/г(0+)=0 и подставив их в (2), получим 0=k + С sin ф,
откуда С-—й/sin <р.
Если уравнение (2) продифференцировать и подста¬
вить в него /г(0+) =0, то получим:
0 = — Е sin <j> -J- ]/1 — £2 cos <р,
откуда
tg ср —	~	—; sin ^р = |/" 1—S2; cos<p = S.
Окончательное выражение для переходной характе¬
ристики

h[t) = k |Y— у - -1-е Т sin УI — Е2 -f- arccos ;jj.
Если продифференцировать h[t), то получим им¬
пульсную характеристику в виде
w [t) =	/	 е Т sin 4- V~\ — £2*
11 т /1 — ъ?	т	Y
01-3-10. Переходная характеристика h[t)=k[ 1—
—cos coo/). Импульсная характеристика а;[■/)=&(*)<)sincoof.
01-3-11. Переходная характеристика
* ±
h [/) = k [ 1 + y==^ e T sin^-VT — ?2 + arccos .
Импульсная характеристика
^ -L
TVT=r?e T
141

k tz
01-3-12. Переходная характеристика h [t) =-тг уг. Им-
k
пульсная характеристика w [t)= -frt'l [t).
01-3-13. Решение уравнения с переменными парамет¬
рами. является функцией двух переменных: момента при¬
ложения воздействия 0 и приращения времени^ т=t 0,
отсчитываемого от момента приложения воздействия.
В связи с этим в заданном уравнении следует поло¬
жить t=0+т и переписать его в виде
где y=dy/dx.
Приводим уравнение к нормированной форме:
Для переходной характеристики то же уравнение
имеет вид:
Так как при т = 0 h — 0, то С = —I/о. Тогда
(0 + т)«/+ [1 + о(0 + т)]г/=%,
его решение:
— Га (т) drс
h — е J
где
а(')~ё~ТТ+о;	(х)dx==ln (® + х) + 0-t;
Следовательно,

Переходя снова к аргументу t, получаем:
I _
h[t — 0, в)-
at
Для определения импульсной характеристики приме¬
няем формулу [28]
wlt-д, 0)=	6),
что дает
w\t — 0, б)= j
или
е~"	<?_2t
W[i, 6)=-
01-3-14. Заданное уравнение с замороженными коэф¬
фициентами будет иметь вид:
0£ Ь) + (1+<?9) § Ь) = б [т]
или
5£[т) + И*[т)=6[т],
т. е.
£[т)+2,2£(т)=0,26[г],
откуда
ёЪ) = 0,2е~2-2\
В точке ^=6 с имеем х=i—0=6—5=1 с, следова¬
тельно, g[l)=0,2e-2'2=0,0221.
Для предыдущего примера получаем:
£[х, 0) = ёГ [ 1; 5) = -^1=4-°’135 = 0’0225-
01-3-15.
W [/) =&0g (0 + big (t) + b2g (t).
01-3-16. Правая часть заданного уравнения после
подстановки x=§[t—0] принимает вид:
Я[*-0) = М0)8[*-0]--^{МО)8[*-0]} +
. д2
-{ft, (в) 6 [t -6]}.
дЬ2
143

Используя, так же как и в решении задачи 1-1-8,
правомочность дифференцирования по параметру 0 для
левой и правой частей интегродифференциальных урав¬
нений, получаем:
w[i-b, b)=b'(b)g[t-b, 6)~^-{M6)g[*-0, б)} +
+-|г{М0)£['-в> т•
Для заданных функций и числовых значений пара¬
метров имеем:
w
р — е, 8) = (2 + 36) -ехр -J>1
{
100
2 ехр [—я (t — 8)]
t
2ч ехр [—« (t — в)]
t
}+
}
ИЛИ
W
[/_5,5)=-р-^-~2<) [2_—[— 3• 5 — 20• 5 — 2-105' +
+ 2 + 2-2-5-2+(8 + 5*)4] = —^ехр(10—2f)-l [/—5).
01-3-17. Применяем для решения рекомендованный
в условии метод, согласно которому
g = eB< = E + B*+B'|-+B’-£+...
(1)
Здесь
1 о
о 1
— единичная матрица;
В=
о 1
_(0» + 28) —2а
—матрица коэффициентов, полу¬
ченная в 01-2-28.
Для удобства записи последующих произведений ма¬
триц обозначим:
C^ + ^srrX2.
(2)
144

Тогда
B2 =
В’ =
0 1
0 1
—x2 —2a
—x2 —2a
—x2 —2a
2ax2 4a2—x2
—x2 —2a
0 1
2ax2 4a2—x2
2ax2 4a2—x2
—x2 —2a
x4 — 4a2x2 4a2x2 — 8a3
Суммируя элементы ряда (1), получаем:
£ll &12
&21 ^22
1 —
Х2^
2!
2з*!-5г+...
—хЧ + 2ж-£-+(х‘ — 4oV) -',г+ ...
2!
3!
t — 2а -^Т+ (4о2 — Х2)4г+ • •
3!
1 — 2с f + (4о2 — х2) (W — 8с3)
3!
где gu (/) —реакция по первой фазовой координате, вы¬
званная начальным условием £/(0_)=j/i(0_) = 1; g&it) —
реакция по первой фазовой координате, вызванная на¬
чальным условием у(0_)=г/2(0_) = 1; g2i(t) — реакция по
второй фазовой координате — скорости, вызванная на¬
чальным условием */i(0_)=l; g2z(t) — реакция по ско¬
рости, вызванная начальным условием у2(0_) = 1.
Сопоставлять с полной импульсной характеристикой
колебательного звена следует gi2(t) —реакцию по основ¬
ной координате y=tj\ (первый индекс) на единичный
импульс, заданный в правой части второго — основного
уравнения (второй индекс).
Выпишем из матрицы исследуемый элемент, восста¬
новив согласно (2) первоначальные обозначения пара¬
метров:
gtt [0 t — of.+ (Зо2 — &) Д—. . .
Правая часть этой функции представляет произведе¬
ние рядов
■ sinQf = f-
Q2^3
3!
аН2
21
5!
o*t3
3!
10—9Q3
145

Следовательно,
g.t [*)=-§- e~at sinQi-
01-3-18. Рекомендуемая для решения форма матрй-
цанта:
t	t	г t
g=E + jB(/)d< + jB(Q: jB(#)df. dt + ...
t о	to	L*o	_
Интеграл от матрицы коэффициентов равен матрице,
составленной из проинтегрированных элементов, т. е.
1 0
0 1
0 1
E=
B =
4 „ 2
a n — A
40 10+x 10+t
>, /)*=!
—40т —
0 x
4 In (1 + 0, lx) — 4x— 2 In (1 +0,
Число последующих интегрирований зависит от же¬
лаемой степени приближения.
01-4. АНАЛИЗ ПРОХОЖДЕНИЯ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ ЗВЕНЬЯ ВО ВРЕМЕННОЙ ОБЛАСТИ
01-4-1. w [х) = ш [t)t=z=jr- е ; x(t—*) = V-(t — 4).
Выражения импульсной характеристики и входного
сигнала подставим в уравнение интегральной связи:
* * т
V
у Г
о	0
t 1	t
г (t) = j* ДО [x) X [t — x) d* = -jr j* (t — ■*) £ T d% —
0
te T dt —jr- J x£ T dv —
v_
т
Tte
T—r[ 1—<
= V
t — T
146

01-4-2. По известной формуле
y(f) = e	|	j	Т	-y-df	+	cj,
т. е.
y(t) = e Т j-f- f еТ ЛЙ + с). =
_ JL	—
= е г •[a(27’* + 2Tf + *Vr +С
\
При *=0'у(0)=0, следовательно, С=—2аД откуда
У (t)=a
2Т2 1
Г1-,
+ 2Tt *2+]
01-4-3. Вводим для матричного описания входного
сигнала дополнительные обозначения:
х3=х; х3=х4 + с0б[/]; x4=0 + Ci6[/].
Решением.этих уравнений является заданная функ¬
ция сигнала
Хз-(со~{- с it) 1 [/].
Эта функция вводится в правую часть второго урав¬
нения колебательного звена в форме Коши. Система
уравнений звена совместно с уравнениями, формирую¬
щими сигнал, при едином обозначении переменных при¬
нимает вид:
vi=o + Хо "Ь 0 + 0 -Ь xi (0_) б [i]
Х'?=— (о'2+ £22) Xi—2сгх2 Н~Хз + 0 + Х2 (0_) б [/];
Хз=0 0 -j- 0 Н- х4 -|- с0б [/] \
х4==0 + 0 + 0 + 0 + йб[/].
Решение этой системы уравнений в виде матричного
экспоненциала совпадает по форме с рядом, приведен¬
ным в решении задачи 1-3-17, но входящие в него мат¬
рицы, в том числе единичная и матрица коэффициентов,
имеют размерность 4X4:
В =
0
1
0
0
	X2
—2а
1
0
0
0
0
1
0
0
0
0
147

где xl = o' + Q';
Вг =
0
1
0 0
0
1
0
0
—X2
—2a
1 0
-X2
—2a
1
0
0
0
0 1
0
0
0
1
0
0
0 0
0
0
0
0
—X2
—2a
1
0
2a x2
4a2—x2
2a
1
=,
И T.
Д.
0
0
0
0
0
0
0
0
Следовательно,
8 =
(	,	\	Л 2з<2 ,	\
И — 2! +• • •]	[t— 2! + • • ■)
хЧ + 2ах2 -|р + . . . j |l —4zt + (4а3 — х3)-^- + ,
О
О
2а^2
2!
gu
£l2
£13
£u
—
£21
£22
£23
£24
0
0
£33
£34
0
0
0
£44
Функции, заключенные в скобках, представлены на¬
чальными членами бесконечных рядов; функции, относя¬
щиеся ко входному сигналу, помещенные в двух нижних
строках, даны в замкнутой форме.
Искомая реакция колебательного звена представляет
суперпозицию нормированных импульсных характери¬
стик вида [Л. 27]
y(t) =Cogi3 (t) + Cigi4 (t) =g (t) \\OOc0cl ||t.
01-4-4. Для входного сигнала определяем его на¬
чальные значения:
х(0+) ==А sin ф;
д: (0+) == А sin (Qt -f- ф) -f- Qevt cos (Qt -j- ф)]^==в=
= A (y sin ф -f- Q cos <[>),
148

По таблице, данной в приложении 1, находим матри¬
цу коэффициентов для входного сигнала:
Ь»
Ьз4
_
0 1
^43
Ь44
—х2 2у]
где x2=ri2+<Q2=4 + 25=29.
а)	По заданной матрице коэффициентов звена и мат¬
рице коэффициентов, необходимых для формирования
сигнала, с учетом коэффициента связи матриц Ь2з—1
составляем расширенную матрицу:
0
1
0
0
ai
«2
1
0
0
0
0
1
0
0
—X2
2т,
После определения В2, В3 и т. д. находшм решение:
gu
§ 1 2
gl3
§14
§21
§22
§23
§24
£31
§32
§33
§34
§41
§42
§43
§44
б) Общая форма для искомой реакции звена:
у=Л{5тф£13[/) + (г) sinip + Q cos*i|3)gi4[/)}.
в) С учетом заданных значений имеем:
у = 5 |o,5g13	+	5	j	gu [f) | •
01-4-5. Для определения реакции нестационарного
звена в установленный момент наблюдения tn при вход¬
ном процессе, показанном на рис. 01-4-5,а и характери¬
зуемом определенным смещением g, используется фор¬
мула
е
у (t, 0) = [ да, [/, X,) Л (9 — X,) dx„
о
где т*—in—t — аргумент (переменная интегрирования),
определяющий удаление (по времени) текущих ординат
графика процесса от момента наблюдения; 0=/н—g —
продолжительность действия входного процесса (рабо¬
чий интервал);	т*)	— согласно рис. 01-4-5,6 пара-
149

метрическая импульсная
характеристика, в которой
первый аргумент фиксиро¬
ван и стал параметром, а
второй аргумент (перемен-
t ная интегрирования) харак-
“ теризует удаление момента
приложения импульса от мо¬
мента наблюдения; y(t, 6)
реакция в заданный момент
наблюдения от входного
процесса	установленной
формы с продолжитель¬
ностью рабочего интерва¬
ла 0.
Таким образом, связь
между заданной нестацио¬
нарной и параметрической
импульсными характеристи¬
ками определяется указан¬
ными ниже подстановками:
[+ ч) = W К> 9)1,=/н	= w Кн. к — '*)■
6=^, T.V.
а)	Для заданной фоомы процесса х(6—т*) =
=У(в—т.).
Для заданной нестационарной импульсной характе¬
ристики
^■?{ 1^н»	х*)	i	^
Следовательно,
1 — <?-J0 >
■	—	i	,
0 J
у (t, 0) = j’-у- e (9 — *,)	=	-j-	(0
0
б) Подстановка заданных чисел дает:
0=10—2=8 с;
!/(Ю.8) = |г(8-Ц+)*1.7-
в) На рис. 01-4-5,6 показан рельеф нестационарной
импульсной характеристики w[t, ©) в пределах, огра-
150

ничейных условиями задачи t^\—2 с, 0>2 с. Для оцен¬
ки ‘протекания процесса во времени используются, сече¬
ния рельефа плоскостями, параллельными координатной
плоскости tOw.
Для получения параметрической импульсной харак¬
теристики w*[t, т) используются сечения рельефа пло¬
скостями, параллельными координатной плоскости QOw.
На рисунке заштриховано сечение рельефа для /=10 с
и показаны параллельные сечения для других времен
наблюдения.
01,г5. АНАЛИЗ ЛИНЕЙНЫХ ЗВЕНЬЕВ НА ОСНОВЕ МЕТОДА
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
01-5-1. Для апериодического звена W(p)=k/(Tp+ 1),
где r=ai/a0; k=bolaQ.
Для форсирующего звена первого порядка W(p) =
=±k(l + Тр), где k=bo/ao; T=bijbo.
Для колебательного звена
w (р) — Т2р2 + 2iTp +
где
k
где
  ^0	.	гр	и/ а2 •	£	  #1
ао	V	aQ	2V	а0а2
Для резонансного звена
W (Р)— pi + Qt »
k=^-\	Q=l/
о2	V	а2
Для форсирующего звена второго порядка
W(p)=k(l+2tTp + T2p*),
где
—	Ьг
Qn	f	On
2 V Ь„Ьг
Для дифференцирующего звена W(p)=Tp, где Т=
=bi/an.
151

Для реального дифференцирующего звена W(p) —
=Tip{Tzp+\), где Ti—bija0; r2=ai/Oo-
Для интегрирующего звена W(p)=k/p, где *=bi./ao-
01-5-2.
w (p}~ux(P) — \тр+1) ’ где T = RC-
01-5-3.
V w=W)=W7T»' где k = CR" 7' = («. + R.)C'
01-5-4.
а)
W(P) = —Wjr+i)-’ где k='^T'
T = R0.£-
б)
^(i»)=l/(7»> гДе T = RXC\
в)
W(p) = — k, где k - Ro c/Rx.
01-5-5.
W(p) = a(p)/U(p) = ][Tp, где Г=1/6.
01-5-6.
W(p) = Y(p)IX(p) = k/p, где * = o&/F.
01-5-7.
01-5-8.
а)
^(P)= }r^+l} » где Г, = («, + /?,) С,; T, = RtC,;
б)
где Tl=RlCl',
'P 	/-»	(Pi	+	R>)	f,	 Pi
* 'Rt + Rt + R,; Ri + Ri + R,;

в)
т (i\— Т^Р‘ + (Т, + Тг)р + \
w W т>тгр* + (Г, + Г2 + RxCt) р + 1 >
где	Г,	= ад,
Г (/>)=-	——'
Т'Г^р'1 + (7’ + 7'ф -j- Ref) р + 1	»
где
01-5-9.
а)
W(P)=-fJ+T. где Тх = г,С,;
б)
=	Г‘Р+1-о	,	где	Т^ВД;
TlP + i + A-
в)
и/ /  и (I Ч~ Л A1) (I Ч~	__р	у	п /-> .
w(p)—k (i + r3p) (1+г4р) ’ Где 1
Tt = RtCt; ТгТ=-кТ,Тг-,
r,+r.=*[r(i + A.)+r,(i + -£-+i)]
г)
TJ7 /,-л ь (' + Т\Р) (1 + Т2р)
(1 +Т3р) (1 + Т4р) >
где
TxTt = £ Д С,Я 2С2; Т3Т4 = kkxRfixR&i
Тг Тг — А, (Я,С, -(- -R,C2 -f-i?2C2);
7,. + T4=ft1(/?IcI+/?1c2 + ft/?1cI); ^=-^ртг

U1-5-1U.
W(p)- TJcp2 + ?cP + , , где Tl—R9
f   D П. U   p I *.*.	U	^1
ic —гсэо, ix3 —«2-г	+	^ , «—	+
01-5-11.
A(P)
01-5-12
где
01-5-13.
где
h (p)
J p2 + kfjp + kn
J) — a{p)

’ Ux{p)
(Tup + 1) P 9
k — 1
t 	 RnJ
kE
> M kjkE •
kv
11 г о i r i 1. У
и  klkE , u	ki
h	R '	kv ~-	R
01-5-14.
w (P)=7i+T Г- ™e *=-5Г. Г=4г-
01-5-15.
W (n\ A0 (Z7) __	^/-M	.
А/ (/?)	//?2 +	+ кл — Sq—m
01-5-16. При питании от генератора напряжения
(рис. 1-5-16,а) общее сопротивление схемы будет:
Z(p)=R + Zi(p),
где
I /р\	!	= R' + Ri
^ , i	№+я2)б>+1	•
р+ ~r7+W
154

Передаточная функция корректирующей цейй
^ПЬ|Х (р)  (р)	^2	_
Uнх. (Р)	R + Zy (р) Rx -)- R2
_	R2
R (Rj + R2) Cp + R +	+	R2
При питании от генератора тока (рис. 1-5-16,6) ПФ
схемы имеет размерность сопротивления
Цщх (Р)
h (Р)
01-5-17.
01-5-18.
01-5-19.
01-5-20.
01-5-21.
(Р)
R2
w (р)~
W(p)
W(p)
Ri + R2 ~~ (Ri + R2) Ср +
1
80/J-1- 100	*
k
ТР— 1 ■
_ к (1 + 7»
Rip +
W{p) =
w {р) —
р* + Q2
160
01-5-22.
W{p) =
4/>г +2,4/7+ 1	•
10	  15/7	+	45
/7+2	/7+5	/?2	+	7/7 + 10	•
01-5-23.
w{t)~ 5-|- 10 ^sin4£ coscos 4^ sin-
X 1 [t) = [5 + 5 У2 sin At + 5 У 2 cos At] • 1 [7);
5	20 V2 5 V"2p
X
W(p)
p ~ p2 + 16	1	ps	+16
_ 12,17/72 + 28,28/7 + 81,6
—	(/72+16)/7
155

01-5-24»
цг __k_ -i j г
h[t) = -7r е
Дифференцируя начальную функцию h[t) с учетом
начального фронта /i(0+), получаем импульсную харак¬
теристику:
®[0=15{бй—
Перейдя к изображению по Лапласу, найдем:
w (п) = —^Е	=	30	Р....
w \Р) тР+1	2р+1
(см. также другой способ в решении задачи 1-5-25).
01-5-25. Изображение переходной характеристики
1
0,1
01-5-26.
Р — 0,2 р )	(5p—\)pf
W(p) = pH(p)=-s^rr.
—0,06
W(p):
(2р+ 1) (5р + 1)
01-5-27. Первый способ. Заменяем —1/3 = Я и
полагаем исходной функцией е (t, Я) = е л и дополнитель
ным сомножителем t\(t) = t. Тогда из приложения 2
W
3
Применяя это преобразование к изображению исход¬
ной функции, умноженной на заданный коэффициент
0,1, получаем:
0,1
W(p) = 0,1
д	1
дХ р — X
__	0,1
Р + з
i_— (р-ХУ
з
0,9
(3/>+1)2	*
156

Ё т о р о й способ. Находим изображение по Лапла¬
су для исходной функции:
/
Р + ч
3/? + 1
Используя из приложения 2 четвертый столбец чет¬
вертой строки, находим:
д 3	0,9
W(p) = - 0,1
01-5-28.
(Зд+1)2 •
W(p)=-
др 3/)+1
0,01
Р1 •
01-5-29. Согласно приложению 2 имеем:
1
Н(р):
■+10
10 cos -*-+(/? + 5) sin -Т-
(/? + 5)* + ю«
6 /?2 + 121,6/?+ 125
— (р*+10/?+125)р 5
6/?^+121,6/?+ 125
W{p) = pH(p) =
р2 + 10/?+ 125
01-5-30. Операторное уравнение для реакции звена
при заданных условиях его возбуждения (Tp+\)Y(p) =
=kX (р) + Ту (0_), откуда
rw=T+rA'w+
Варианты структурной схемы для этого случая даны на
рис. 01-5-30.
Рис. 01-5-30.
157

(7’2р2 + 2|Тр -Ь 1) У (р) ~/гХ (р) +
+ (21Т+ Т*р) у (0_) + ТЧ) (0-) •
СтруктУРа звена дана на рис. 01-5-31.
Рис. 01-5-31.
01-5-32.
L{a{t)x[t)}=?;
я(0 = <*; x[t) = e*‘\
Хи» = Це-‘) = 7Х-.
Из приложения 2	для	f4(/)=/2	(четвертая строка)
находим	X (—>-)	(четвертый	столбец)	при т = 2,	= —а:
L{^e~J4=
1	‘ (р + °)
01-5-33. ft(f) = te~4,t\ х [1) = cosQl.
По приложению 2 для данного fz(t) находим:
d у , I ч_ d — (р + з)
" 'dp	Л	dp (р +	а)М-22 "
_	(р+а)2-^2	.
Ю-Ь°)2 + £Т ’
L {е 1 cos Ш} =	а)1	Q2j2	•
01-5-34.
(З/?2 + р + 2) У (р) - ^ Ц5р2 + 3] У (р)} = kX (р).
158

01-5-35.
(,р3 + 2р2 + 4р + 5) Y (р) - JL [(2р> + 3/ + 3р +
+ 1)У(/>)] +-^[3p3Y(p)] = X(p).
01-5-36.
[,d2p2 + (cf, + б.с2,) /> + d0 -j- k,c\] 6 (p) +~§f W*P* +
-f- 2kpip-{-2k0c0) 0 (/?)] +-^r	® (i°)] =
= ^A (p) —jjp \?A (p)] H~ Ao + Kc\) 6c (p)
-Jf t2Vo9c (/?)] —	IMc (p)} + тъ (p).
01-5-37. За начало отсчета времени принимаем мо¬
мент приложения входного воздействия, где т=0. Тогда
уравнение запишется в виде
(2 ■+ т) у+ (22 + 1 От) у+ (68 + 29т) у=688 [т].	(1)
Для решения составим расчетную табл. 01-5-1,
в ячейках которой запишем произведение констант не¬
стационарных коэффициентов уравнения (1) аци где
а20=2; «21= 1; аю-=22; ац=11; а00=68; a0i = 29, на значе¬
ния коэффициентов при начальных значениях реакций,
данных в приложении 3. В первой строке таблицы стар¬
шей производной является #(0), поэтому у(0) и все
моменты Mi равны пулю.
Решение уравнений балансов парциальных изображе¬
ний [25] записано в последней графе табл. 01-5-1. По
полученным начальным значениям производных на осно¬
вании формулы
записываем решение в виде степенного ряда
(2)
.159

Тевая часть уравнения
160

Левая часть уравнения
1 1—903
161

Этот ряд можно свернуть:
У Iх' 2)~"2^Рс_ е~Г)Х sin 2т-
Перейдя к основному отсчету времени, получим:
y\t — 2,2) = 11 «Г5[t~2) sin2 (t — 2).
Ряд (2) можно также получить в форме матриппита
(см. задачу 1-3-18).
01-5-38. Для решения составим расчетную
табл. 01-5-2, в ячейках которой запишем произведения
констант нестационарных коэффициентов уравнения аи:
на коэффициенты при начальных значениях функций,
помещенных в приложении 3.
Так как в первой строке таблицы старшей производ¬
ной является у(0), все младшие производные у{0), т/(0)
и само значение у(0) равны нулю.
01-5-39. Для систем с постоянными параметрами кон¬
станты коэффициентов суть аг-0, т. е. в таблице приложе¬
ния 3 используются только строки /г = 0. Составляем рас¬
четную табл. 01-5-3 для реакции звена, входящей в опе¬
раторное уравнение (4р2+3,2/?+ 1)Я(Р)=11р.
Таблица 01-5-3
Правая часть
уравнения Г! (р)
Левая часть уравнения
Решение уравнения
баланса
а0= 1,
/ = 0
Оу = 3,2,
i = 1
а2 = 4,
i = 2
ь р-1


4 а (о)
h (0) = 0,25
0 .р-г
—
3,26(0)
4 А (0)
сл
о
1
II
О
1
МО)
3,2 6(0)
4 h<IV) (0)
A*IV>(0) =0,098
1
о
6( 0)
3,2 6(IV)(0)
4/t(V) (0)
ft<V) (0) = — 0,02!
Используя данные последней графы табл. 01-5-3, по¬
лучаем переходную функцию в виде ряда
К [0 = 0,25	 0,2	-Ц-+	0,098
— 0,028-^—(-...
102

Если ряд свернуть, то получим:
h[t) = 1 — ~q~E s’n “t- arccos 0,8).
01-5-40.
хф) = 1ЫрХ(р) = \т ДДД, =4-
* (0) = lim [p2X (p) — px (О)] = lim
p->oo
p-*QO
3'S
;lim
p-> oo
—8/r2 —3/;
4/>2 + 8/?+ 2
-- — 2;
x (0) = lim \p3X (p) — p2x (0) — px (0)] --^-=3,25.
/7—>00
Другой способ см. в решении задачи 1-5-41.
01-5-41.
H(p) = ±-W(p)
 £■
/?3 + 4/?2 + /?
Производим непрерывное деление числителя на зна¬
менатель:
Р3 + 4/7г + р
р-2 — 2р-3 + 7р-*—...
-р + 2
1 + 4 + /Г1
— 2 — р-1
— 2 — 8/?~1 — 2р~2
7р~' + 2р-2
Частное от деления представим в виде ряда, в кото¬
ром коэффициенты при отрицательных степенях р рав¬
ны начальным значениям процесса и его производных:
_1	2	7
р2	рг * /74
, Л(0)
А (0) , к (0)
МО)
• р3 I р' л-
где h(0)=0; Л(0)=1; Й(0)=—2; А(0)=7 и т. д.
Переходя от изображений к оригиналам, получаем:
Ч0 = *-г2+М3----
11*
163

01-5-42.
г„<я=з[^+^)-=»(*-НР>
бств
iP) =
tV i — i2
VT=J>
/ -z + jVi-z2 \
cos у
+ (p + T-)
T
sin <?
/I
X
'Kr=T*
• V
?•
Для X (p) — 3/ p2 имеем:
X	L
- j=бгге2 — зr2 -f- /бег2 //1'
* (
-s + / Ki — i2
Тогда
J 1=зг.
X
X
у	(	л __	3^7-
' собств \/v J/"j
VT=r? , (	J_)	.
 ^	 cos	у -+- ^p + 71 J sin у
X'
4
i - S2
J12
2£ К i — E2
где <p=«rctg -	,
01-5-43.
(7>* + 2S7> + 1) Y;(p) =	4-	(2ЕГ	-f-	7»	5	+	2Г2;
36 + 5/;2 (2£Г + Г2/?) + 27’2/X
(1TV4- 2*7> + ])>
01-5-44. Изображение выходного процесса при задан¬
ных числовых значениях параметров
56 (Л/Н- U-3!
К (/7) = Ц7 (р) X (р) --
150
— рл ■ ■ 25р‘ + Р + 1
(Г*р‘ + 2ЦГр+ I) р*
р -f- 2
(I)
а) Для определения компонентов вынужденного дви¬
жения следует отделить в изображении (1) сомножи¬
тель 150/р4, переставить порядок членов в полиномах
1G4

числителя и знаменателя оставшейся части изображения
и произвести непрерывное деление с ограниченным (N=
=4) числом шагов, что дает [28]:
2 + р
2 + 2/7 + 50/72
— р — 50/;2
— р — р2 — 25 рг
_ 49/г + 25р3
— 49р2 — 49/;3 ■
1+ /7+25/7*
р— 49/>2 + 74/73 +
1225//1
+ 74 р3 + 1225р*
Сопоставляя частное с разложением ПФ в ряд Мак-
лорена по степеням р
Г" (0)
W(0) + W' (0)р
IW'" (0)
2!
Р'+
3!
р3 — 2 — р — 49/?2-f-74/?3,
видим, что произведение частного на отделенный сомно¬
житель 150/р4 дает как раз изображение вынужденного
движения
^ьын(Р)
= 150
150
/74
_2_
/7*
(2 — р — 49 /?2 —|— 74 /?3) =
1	49	^	74
Р Р‘
откуда легко перейти к оригиналу
У,т (О = 150		g— 49* + 74) 1 [*).
б) Для определения начального участка процесса
следует произвести непрерывное деление числителя на
знаменатель всего изображения (1) при обычном рас¬
положении членов в полиномах, что дает:
/7+2
р + “25" ^
25
40
25
49
25
49
25/;6 + ръ + /74
1 _г _49_
25 Р ° + 625 Р~
74
(25)3
49
25 + 625 р ' + '625
166

Умножая частное на опущенный коэффициент 150,
получаем изображение начального участка:
т, / \	^ -5 1 6-49 _6 Гб.74 _7 .
^нач (Р)	®Р ~Ъ 25 Р 1	(25)2	Р
Переходим к оригиналу:
».,W = 6-5-+."-75-g—0,714-+...	(2)
01-5-45. Вначале определим общее изображение для
сложной выходной реакции. Для этого к изображению
процессов, полученному в предыдущем примере, следует
прибавить изображение режима последействия. Запи¬
шем его сначала в общем зиде применительно к задан¬
ному знаменателю ПФ звена:
у (п)=
поел \Р) 25рг + р+\	•
Поделим числитель на знаменатель, осуществив два
шага непрерывного деления:
р Во
В,р + 0,04В,
25/Д + р + 1
0,04б,д-1 + 0,04 (В0 — 0,04fij) рг =
В,- 0,04В,	=Цу(0)+у(0)1],
и приравняем начальные значения процесса последейст¬
вия заданным начальным условиям: 0,04Bi=50; В\=
1250; 0,04(В0—0,04Bi)=10; В0=300. Следовательно:
у {»\	50 (25 д + 6)
1 поел \Р>— 25дг + р + 1	’
Yln\A-Y (и\	5°!3(д+2)	+ дМ25д + 6)]	_
у (ЙТ *пкл(Р)—	р4 (25рг + р+ 1)
  50 (25р5 + б/?4 + З/?2 + 6)	/j\
—	25/?6	+	/?б	+ /?4
Теперь перейдем к ответу на вопросы условия.
166

а)	Осуществляем непрерывное деление числителя (1)
на знаменатель:
25/?б+6р4+0+0+3/?+6
25 р*+ р*+ръ.
25 р6+/?5+/?4
р^+О^р-2—0,048/7_3 —
—0,0061/?“4 + 0,122/?-5 +
+ 0,235/?~6 +	•
5 /?*—/?»
5/74+0,2/73+0,2 /72
—1,2/73—0,2/;2+3/;
— 1 ,2 /73—0,048/;2—0,048 р
—0,152/;2+3,048/7+6
—О, \ Ъ2р2—0,006р—0,006
3,054/;+6,006
3,054/;+0,122+0,122/7-1
5,884—0Л22/7-1
Умножая частное на коэффициент 50, получаем изо¬
бражение начального участка, от которого переходим
к оригиналу:
ут [0= (50;+ 10/ - 2,4 + -0,3 + +
+ 6,l++ll,75 + ..Vl[Q.
б)	Сопоставление с начальным участком процесса,
полученным в решении задачи 1-5-44, показывает, что
несмотря на введенные дополнительные начальные
условия у(0_)=50 и у(0_) = 10, входящие в ряд (2),
благодаря затуханию собственного движения старшие
члены рядов в обоих примерах сближаются.
01-5-46. Вводим буквенные обозначения параметров.
Полюсы ПФ:
тц=0, т]2=—2, т]з + /Пз=—3 + /4,
г| 4 + jQ 4=—0,5 + /5.
Кратность полюсов: r4 + 1 =3, r2 +1 =2, р3+1=3, р4 +
+ 1=2. Изображения процесса с вычеркнутыми кратны¬
ми двучленами (—i—) и трехчленами ( = k = ):
“л/_/ ч	(2/7+	10).	Ю4

Y(P)=-
°Пр>
(2/7+ 10) -10'
Тогда [28]
У</>)= j]
Xlm
/73 (/7 + 2)2 [(/7 + 0,5)2 + 52J2
(2p + 10) • IQ4
p'(p + 2)2 Цр + 3)2 + 42]з •
4
1	(V	Y	(Д)
r! ^Y)r	P	 7]
~k=
+E{,+
ft=3 V
’F’li
1+1V _ у +
<?<■>	<+■'	cop+J	(p— vj—/s)
P=P&
8=ffi.
}■
•о
Если теперь обратить внимание только на члены фор¬
мулы (1), содержащие комплексную переменную /Л т°
на основании исходных соотношений, помещенных в при¬
ложении 2, от изображений нетрудно перейти к оригина¬
лам (вещественной и комплексной экспонентам), а сам
характер преобразований остается для временной обла¬
сти тот же (1), что и для изображений.
Таким образом,
У V) = 4-	(0)	Г	+Т7(0)	t	+1г	(0)]	1	[/)	+
—2—
+ '[ У (—2)t+ Y'(—2)]<?'2+-Im
/	3-4
{\(/2-4)«
у (— 3 -j- /4)
2-
(/5М)4 I Г (-3 + /4)Н- Г (-3+/4)] +
+ =У= (- 3 + /4) t* + 2 УГ(- 3 + /4) t +
+ У'7 (— 3 + /4) } <?<-3+'ч>'| +
+ 1т | {7/2+4 Y °-5 + /5)
(/2-5)*
=У (-0,5 +
+ /0,5)/+ У7(— 0,5+/5)]}е«"*>е+/6> #| •
168

При определении производных Y можно заменить
операцию ^ = (—l)z с последующей подстановкой
р=ъ или p=nk-{-iak.
01 “5-47. Определяем параметрическую ПФ по задан¬
ной параметрической весовой функции, имея в виду, что
t==const:
W(l. s) = -L J e-"e-"i, -1^.
0
Заменяем, как указано в условии, реальный график
суммой полубесконечных прямых, показанных на
рис. 01-5-47. Каждый из частных процессов имеет свою
Рис. 01-5-47.
крутизну Vi и свой рабочий интервал 0г- до момента на¬
блюдения /=10 с. Поэтому рабочий интервал следует
положить переменным © и для Хв =vS найти изобра¬
жение
169

Тогда параметрическое изображение реакций
s) — Wi(t, s)X(s)= f(, + g)-p--
Переход к области второго временного аргумента
(рабочего интервала 0) производится на основе обрат¬
ного преобразования Лапласа:
»,<<. 9)=-f [^«-’в + ^-9-^] 1|9).
Имея оригинал, охватывающий все возможные зна¬
чения ©, нетрудно им 'воспользоваться для конкретных
значений в,, полученных при аппроксимации заданного
входного процесса линейными графиками
4
У*
=	0*)	или	^(10)	=	ix
/—О
>>).
\	i=0	i=0	i=0	/
01-5-48. Согласно [28]
1
2,0-Dy bj(t)
w, (t, s) =
l=o
2
У (s-DY ai(t)
/=o
b, (<)s —b, (Q —MO
; a2(0 s2 — [2a2 (0—(0! s+ a2 (0 — a. (0 + M<) '
01-6. АНАЛИЗ НЕПРЕРЫВНЫХ ПРОЦЕССОВ НА ОСНОВЕ
МЕТОДА г-ПРЕОБРАЗОВАНИЯ
01-6-1. а) Наибольшая крутизна заданной функции
наблюдается в точке t=0, где х(0)—	4е_4<|(=о=	4.
Начальное значение функции х(0) = 1. Задаваясь
ехр (—4Г0) =0,95, находим по таблицам 47^0=0,051, от¬
куда Т0—0,051 /4=0,013 с.
б)^При~значении функции на первом шаге| ехр (— 4Тл)
линейная интерполяция для середины отрезка TJ2 дает
1J- ехр (— 4Т_л) ^ а фактическое значение функции в сере¬
170

дине отрезка составляет ехр(—2ТЛ). Приравнивая раз-
ность заданной погрешности ехр^~~ 4^ — ехр(—27^)=
^=0,05, получаем уравнение ехр(—4Тл)— 2ехр(—2Тл)-{~
-|— 0,9 = Отрешение которого имеет вид: ехр(—2ТЛ) =
= 1 — l/0,1 = 0,684. По таблице находим 2Тл = 0,38 с;
Г, = 0,19 с.
■в) ^-изображением непрерывного процесса называет¬
ся изображение по Лапласу последовательности импуль¬
сов € интервалом Г0, модулированных по интенсивности
заданной огибающей x[t).
Во временной области последовательность импульсов
обозначается значком решетки _L, т. е.
_L е* = 18 [t] +Л [t — Г.] -f-е2г)Т°Ь [t — 2Г0| +...	(1)
При переходе к изображению по Лапласу преобразо¬
ваниям подвергаются только импульсы L{b\t — kTJ\ —
 JLT	 JL	Т	Г)
= е 0F = z , где осуществлена замена: е оР — г.
Тогда г-изображение последовательности (1) со¬
ставит:
Е [z] = 1 + Л-1 + (Л-1 f + (Л-1 f +... =
1	Z	Z
1 _ e^T°z~x ~~ z —	~~z~	exp(—	4Г0)	•
(2)
r) Обратное г-преобразование осуществляется путем
непрерывного деления числителя дроби (2) на ее зна¬
менатель. Предварительно надо перейти к числовым зна¬
чениям. Задаемся То—0,2 с. Тогда ехр(—4*0,2) =0,45 и
Е[г\ —	Непрерывное	деление	дает:
z
z—0,45
г z — 0,45
0,45
0,45—0,2022“1
1I+0.45Z-1 + 0,202г“2;;+
+ 0,091z3 + ...
o,202z-!
0,202Z-1 —0,091
В частном имеем ряд 1 + ОДбг-1 + 0,202г~2 +
+0,091г~3-|- ... =е°+е“0>8г-1+е-1’6г~24н?-2’4г3 + .. • Коэф-
171

фициенты полученного ряда ехр (—4kT0) являются ре¬
зультатом обратного z-преобразования и содержат ин¬
формацию об оригинале в дискретных точках /гТ0.
Примечания:
1. Особенность ^-преобразований непрерывных про¬
цессов состоит в свободе выбора интервала Т0 по усло¬
виям точности отображения или по другим соображе¬
ниям. Для дискретных процессов, рассмотренных в гл. 4,
интервал Т0 задан конструкцией ключа.
2. Изображение (2) включено в исходное соотноше¬
ние для z-изображений экспоненциальных функций, по¬
мещенных в приложение 4. Из исходных соотношений
на основе ^-преобразований могут быть получены 2-изо¬
бражения остальных функций.
01-6-2.
X [г] — 2 Re г _ ехр (у-5Го)
2 z (z — cos 5Т0)
z2 — 2z cos 5Г0 + Г
01-6-4.
01-6-5.
|-5.
77'У (г + 1)
2 (г — I)5
01-6-6.
X [г] — 8 1т г _ ехр (J-27.oj
82 sin 2ТQ
z2 — 2z cos 2T0 + 1 *
01-6-7.
X И = [■
дч\ z — exp у(Го
d	z
T0z exp (— 2T0)
[z —exp (— 2Ta)\2'
01-6-8.
s* — 2z exp (— 27e) cos 6T0 + exp'(— 4T,) ’
2
X\z] = Im л _ exp [	2 + /6) 7'ci =
z exp (— 2ГД) slri 6Г0
172

01-6-9. Для получения г-изображения необходимо
разложить заданную сложную дробь на элементарные:
у-/\	 100 I |	(3	|	iuu	|с	|
КР>— ТЩ\ -ДИ -3)2 + 52] (р-ч) /j “f"
+ 1ш[
-2
100
5 (3 + /5) (5 + /5)2 (pi— 3 — /5)
Далее элементарные изображения -следует выразить
в г-форме и провести первый этап дифференцирования
по промежуточным аргументам во втором члене, что
дает:
vwyy.  0,735г  100 Г д 	z	1	,
г*—J1	2~^50 ~dv\ z — ехр (у(Г0)	*”
4—‘ г ( д	100	\	I
z ехр ( 2Г0) ydri	[ (?) - 3)* + 52] f 1=_2 ^
+ 1ш-	22
5/(3+ /5) (г-'ехр[(3 + /5)Г0]} •
Проведем отдельно некоторые преобразования:
д
дт) г — ехр (т)7’„)
0,8zexp(—1,6)   0,16z
7]=—2 [г-ехр (-1,6)]* (г-0,2)»
fa	100	)	_	100	(50	+ 20)	„
) дг, [(т,_3)= +5») /ч=_2 —' ■	(-2-50)»	—	V’/>
т г (3 — /5) (г — 11 cos 4 + / 11 sin 4)
85/ [ (V— 11 cos 4)2 + (11 sin 4)2|
_T^Refz (3 — /5) (z — 7,3 + /8,34)] _	z(3z—19,3)
85 (г2— 14,5z + 121)	85	(z2 — 14,5z + 121) ’
Таким образом,
Л ,  0,735z	0,16z	0,7г	r(0,03z — 0,2)
z— 1	(г — 0,2)2'	z —0,2	z2—14,5z+121 —
. 0,005+ + 0,18z« — 1,51 z3 + 45, 3z2 + 6z
Д — f) (z —o,2)2 (z~f+5z"+l2T)	'
Для расчета значений процесса в дискретных точках
t=kT0=0,8/с (k=0, 1, 2, ...) достаточно произвести де¬
ление
0,005zs+ 0,18z4 — l,51z*+ 45,3z* + 6z
+ —;15.9z4+ M2z3~ 176z2 —54z—5 “
«= — О.ООб + ОДЗг-'Д-..,
173

Тогда по коэффициентам ряда находим:	л(0)	=
= — 0,005, x(TJ = 0,23 и т. д.
01-6-10. Полагая Q7’0 = it/6, имеем 71, —it/6Q.
Матрица решений для этого интервала
ё(П) =
COS •
1 sin ■
— 2 sin -тг- cos -pr-
o	о
Уз
0,5
2
2
2
Уз
~ 2
2
Согласно приложению 17 переход к г-форме осущест¬
вляем по формуле
Уз 0,5
G [zj=z[zE — g(T0)]-' = z
“ 2
2
~2~
2
Уз
(1)
Определитель этой матрицы
det [гЕ - g (Г.)] = (г - J/3/2)2 + 1 /4 = г2 -
— КЗг+1=Д[(г).
Следовательно,
0[г] =
0,5г
\ I
2Д (г)
Д (г)
2 0,5г
г (z — V3/2)
А (г)
Д (г)
(2)
Результат (2) получен без привлечения каких-либо
таблиц [исключительно по процедуре (1)]. Каждая
ячейка (2) может быть проверена по приложению 4.
01-6-11. Матричная форма записи гармонических за¬
тухающих колебаний приведена в шестой строке прило¬
жения 1. Полагая согласно условию г\=—а=—2 х=Хи
х=х2 и используя заданные начальные условия, полу¬
чаем описание исследуемого процесса в пространстве
174

(двумерном) фазовых координат;
sin Q,te~ot
(cos Qt + o2 1 sin 2/) /? jt}
(a2 + 22) sin Qte~jt
Q
Q
cos Ш — с sin Qt
о—?*
X
*1 (°)
*2 (0)
x
(i)
При переходе к г-изображению в правой части (1)
^-преобразованию подвергается только матрица норми¬
рованных импульсных характеристик, а масштабирова¬
ние начальными значениями остается тем же и в обла¬
сти z-изображений. Подготовим значения импульсных
характеристик для t=T0:
g(T„) =
Тогда
^-+Вг‘ \а-*°
( 90—1
V
29~1 +
Q
-2 Т0
0,59~1 с
Vr3
-2 Г0
и~2Т°
— z
0[г]=г[гЕ-в(Гв)]“1 =
Х'-+2-1)^2Г“	0,52
1 1 й~2 То
-2 Г„
-1	1	27-с
(2)
Находим
det [ггЕ - g (Г,)] =(г— V3/2e~2Tf - е~4Т°/П2 +
+ (£Г2 + 1/4) е~4Г° = г2 — |/3 *?_2Г° + е~4Т° = Д (г).
Согласно (1) и (2) получаем:
4 (г)
IV 3
г — V 2
X, [г]
X и
- Q-'
) <?-2г°
2 \
X
Кз
X
2
0,52 —
X
175

или
Хг№
:Д(2) \
Уз
-Й
1
-2 Г0
-f (0.5Й — ]/3)0,5Й_1е-2Г<
I 0,5(У3 22 — 2^1
/	- - К-1	•
+
,-2Г„
)Лз г.-“2Г° + <?"~4Го
Результат можно сопоставить с таблицей приложе¬
ния 4. Универсальный метод удобен для машинного спо¬
соба перехода к z-изображениям, когда g(T0) вы¬
числяется, например, в форме рядов, что не требует
определения- корней характеристических полиномов из
условия det[piE—В] =0 или полюсов дробно-рациональ¬
ных изображений по Лапласу.
01-6-12. Система уравнений для заданной функции
Xi==X2,y Х2—Х3, Х3—Х&, Х4—б	.
Отсюда определяются матрицы коэффициентов и ре¬
шений:
В:
t2
p
0
1
0
0
1
t
2
6
0
0
1
0
t2
0
0
0
1
; g(0 =
0
1
t
2
0
0
0
0
0
0
1
t
0
0
0
Запишем промежуточное выражение для характери¬
стической матрицы:
|*E-g (7.) || =
— T2 о
—;7’30
2—1
-r0
2
6
— T\
0
z — 1
-T0
2
0
0
z— 1
-T0
0
0
0
z — 1
(1)
Ее определитель det||zE—g(7’o)!l = (2—l)4.
В матрице обратной (1) ячейка С]4[г] будет содер¬
жать z-изображение заданной функции. Поэтому вычис-
176

лим не всю обратную матрицу, а только эту ячейку
одним из приведенных ниже способов:
*,[*] =
'-т„
.z ad,4 i| siE — g' (70) |p ad4, |j zE — g (Г„) |i
det || zE — g (f„) |i
det || zE — j
— T* —'Г*
1
G
(2-
n-*_ T*z (z2 + 4z+ 1)
'	(z	—	l)4
01-7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
01-7-1. Частотные характеристики звеньев первого порядка изо¬
бражены на рис. 01-7-1.
01-7-2. Частотные характеристики звеньев второго порядка изо¬
бражены на рис. 01-7-2.
01-7-3. Комплексная частотная характеристика двойного интегри¬
рующего звена изображена на рис. 01-7-3.
01-7-4. Комплексная частотная характеристика заданного фор¬
сирующего звена изображена на рис. 01-7-4.
01-7-5. Комплексные частотные характеристики систем с задан¬
ными ПФ изображены на рис. 01-7-5.
01-7-6. Комплексные частотные характеристики с заданными ПФ
систем изображены на рис. 01-7-6.
01-7-7. Комплексная частотная характеристика заданной систе¬
мы изображена на рис. 01-7-7.
01-7-8.
11 Geo2 + 3788
W	0 ^ 00000225<о° + 2,35coJ + 2 35w2 + 1 +
, .	0,1(о4 — 771о>2 — 250
+ ' со (0,00000225со° + 2,35м1 + 235<o2+i) •
Комплексная характеристика разомкнутой системы изображена
на рис. 01-7-8,а, замкнутой — на рис. 01-7-8,6, амплитудная — на
рис. 01-7-8,в, а вещественная и мнимая частотные характеристики
замкнутой системы даны соответственно на рис. 01-7-8,2 ид.
01-7-9. Комплексная характеристика для случая а изображена
на рис. 01-7-9 сплошной линией, а для случая б — пунктирной.
01-7-10. Комплексные частотные характеристики системы в соот¬
ветствии с заданными числовыми значениями параметров изобра¬
жены на рис. 01-7-10.
01-7-11. Комплексные частотные характеристики заданных
разомкнутых систем изображены на рис. 01-7-11.
01-7-12. Сопрягающие частоты coi=0,l с-1, (о2 = 0,2 с-1. Коэф¬
фициент затухания £ = 0,12.
С помощью шаблонов строим амплитудные логарифмические и
фазовые частотные характеристики каждого из двух звеньев. Скла¬
дывая графически, получаем суммарные частотные характеристики.
12—903	17 7

Рис. 01-7-Г.
178

Рис. 01-7-3.
о, г о, и о,б о,я
Риг 01-7-4
12*
Рис. 01-7-5.
179

Рис. 01-7-6.
. oj ~100 с~1
J/z и & а +
^ ! IT
■'<?>-5# 4
Рсо—2
- -2 /
-и
I!
1
А ^
/л
Рис. 01-7-7.
180

Рис. 01-7-9.
Рис. 01-7-10.
Рис.. 01-7-1Ь
181

со=0,10 4
120 °	110°	100°	30°	80°	70°	SO
50°
-1500
Рис. 01-7-12.

Для системы управления (1), состоящей из статических устойчивых
звеньев, — рис. 01-7-12,а, для системы управления (2), содержащей
неустойчивое-звено второго порядка, — рис. 01-7-12,6.
Используя полученные логарифмические характеристики, для
каждой из заданных двух систем управления легко построить ЧХ
на полулогарифмической комплексной плоскости (рис. 01 -7-12,г).
Годографы W(j(в) построены на рис. 01-7-12,6.
01-7-13. Из ПФ видно, что асимптотическая логарифмическая
амплитудно-частотная характеристика (ЛАЧХ) имеет четыре из¬
лома в точках: оси = 1/7"± = 0,05 с-1; 02=1/72 = 4 с-1; 0з=1/7з =
= 20 с-1; сс>4 = 1/7^4 = 0,143 с-1. Построение ЛАЧХ надо начинать
с интегрирующего звена.
Для этого линейку с наклоном —20 дБ/дек накладывают на
сетку так, чтобы она проходила через точку 0 дБ и со = 1 с-1. Но
так как в ПФ входит усилительное звено /г=i/г2/гз/е4 = 3,64, то
линейку перемещают вверх, параллельно самой себе, на высоту,
равную 20 lg 3,64=11,2 дБ, и проводят прямую линию с наклоном
—20 дБ/дек до точки L(со) =37 дБ и со± = 0,05 с-1. Второй участок
начинается на частоте 0^0,05 с-1, заканчивается на частоте
04 = 0,143 с-1 и проходит с нулевым наклоном на высоте 37 дБ.
Последующие участки, соответствующие апериодическим звеньям,
претерпевают изломы на частотах 02 = 4 с-1, 0з = 2О с-1.
ДБ
-L(co)
cp(co)_
135°
90
90
20
-
4
, -i
Ь5
Q
i
|
n
-20
QJ,
LOtf
to2 1
U
-95
-90
1
! V
-90
-60
"
Ц> (to)
.L_ ... 1
©Si 1
1
l 1 V
1 1 ^
_K...... .
~135
-180°
о о, 1	То	то
Рис. 01-7-13.
Общая ЛАЧХ системы представлена на рис. 01-7-13. Фазовая
частотная характеристика строится по точкам, которые определяют¬
ся достаточно быстро по формуле
/ ч	71 I ,	®	Ю	to	to
¥ (®) = - — + arctg -g-jjg - arctg	_	arctg r -arctg ^.
01-7-14. Асимптотическая ЛАЧХ имеет два излома в точках
©1 = 2 с-1 и 0о = 4 с-1. Фазовая частотная характеристика строится
по точкам, которые определяются по формуле
.	.	71	0,280
fH=y- arctg — б,'б4«« ~ arct& °’5 “•
183

Обе характеристики представлены на рис. 01-7-14.
С;1	1,0	10
Рис, 01-7-14.
'юос'1
01-7-15. Вещественная и мнимая составляющие ЧХ определяю г
ся по формулам
' cos сот — 7'со sin сот
О (со) = -
В (со) =
1 + о>2Г2
sin сот + 7'со cos сот
1 + со2Г2
Фазовая частотная характеристика определяется по формуле
sin сот -(- 7'со cos сот
V (<*>) = cos сот — Т со sin сот *
Комплексная частотная характеристика представлена на
рис. 01-7-1 Г>.
01-7-16. Амплитудная и фазовая частотные характеристики за¬
данной системы построены на рис. 01-7-16.
01-7-17. На G, В-номопрамму (рис. 01-7-17,о) 'наносим ЧХ апе¬
риодического (а) и дифференцирующего (д) звеньев, логарифмиче¬
ские характеристики которых приведены на рис. 01-7-17,а. Задав-
184

Рис. 01-7-17.
18Л

L(w)
(f(o))
90°
4.5
0
-4.5
-90
-135
—180
130°	120°	110°	100°	30°	800	70°	GO0
70°
1 80

шись частотой сок, на рис. 01-7-17,6 находим на кривых изолиний
Ga(ci)it) и ^а(сок), Сд(о)к) и Вл(о)к), затем производим суммиро¬
вание:
О (0)к) = ^а (о)к)4-^д (^к) ;
В (&>к)=^а ((Ок)-|-5д (С0к) •
По найденным G(coK) и	В(сок) на этом же бланке
(рис. 01-7-17,6) находим соответствующую точку ЧХ системы. Для
этой точки считываем амплитуду	Ах(0) в децибелах и фазу<рх(<о)
в градусах, которые наносим	на логарифмическую бумагу
(рис. 01-7-17,а).
01-7-18. При построении ЛЧХ разделяем заданную ПФ на сле¬
дующие элементарные звенья:
1) неустойчивое звено второго порядка
(р) = 50/ (100р2—4р+1);
2) апериодическое звено
^,(р)=1/(5р+1);
3) колебательное звено
W3 (р) = 1 / (0,0004р2 + 0,02/7 +1);
4) апериодическое звено
W,(p) = 1/(0,025/7+1);
5) форсирующее звено первого порядка
№5(р)=0,1/7+1.
Сопрягающие частоты равны: coi = 0,1 с-1; 02 = 0,2 с-1; 03 =
= 50 с-1; 0)4 = 40 с-1; о)5=10 с-1.
Амплитудные логарифмические характеристики на рис. 01-7-18,а
даны сплошными линиями, а фазовые — пунктирными.
Частотная характеристика на полулогарифмической комплексной
плоскости представлена на рис. 01-7-18,6.
01-7-19. Построение ЛАЧХ осуществлялось методом асимптот.
При этом предварительно были определены сопрягающие частоты:
0)1 = 1 /7Л = 5 с-1; 0)2= 1/7"2 = 8 с-1; 03=1/Г3 = 2О с-*; со4=1 /Г4 =
= 66,6 с-1.
Так как для усилительного звена L(co) =20 lg £ = 20 lg 11,48 =
= 32 дБ прямая проходит с нулевым наклоном, а для интегриру¬
ющего звена логарифмическая амплитудная характеристика пред¬
ставляет собой прямую, имеющую наклон —20 дБ/дек и проходя¬
щую через точку L(co)=0; со = 1 с-1, то через точку L(о))=32 дБ
и о)=1 с-1 проводим прямую линию с наклоном —20 дБ/дек до
частоты о) = 5 с-1. В точке со = coi находится сопрягающая частота
апериодического звена с постоянной времени 7\=1/5 с, поэтому
в интервале частот от coi до <Ог проводим прямую с наклоном
—40 дБ/дек. В точке (о = о)2 = 8 с-1 находится сопрягающая час¬
тота форсирующего звена первого порядка с постоянной времени
Т2=1/8 с. Поэтому в интервале частот от 02 = 8 с-1 до ш3=20 с-1
наклон характеристики уменьшается на +20 дБ/дек и прямая пой¬
дет с наклоном —20 дБ/дек.
187

В точке со = соз=20 с-1 находится сопрягающая частота апе¬
риодического звена с постоянной времени Тз = 20 с-1, поэтому
в интервале частот от ©з=20 с-1 до 04 = 66,6 с-1 прямая снова
пойдет с наклоном —40 дБ/дек. В точке 0 = 66,6 с-1 находится
сопрягающая частота апериодического звена с постоянной времени
У4= 1 /66,6 с, поэтому в интервале частот от 04=66,6 с-1 до 0=00
Рис. 01-7-19.
наклон характеристики увеличится на —20 дБ/дек и прямая пойдет
с наклоном —60 дБ/дек. Фазовая характеристика определяется по
формуле
<Р (со) = —	—	arctg	ыТ1	-+-	arctg	с*>7\, — arctg 10Т3 — arctg ы7\.
Обе характеристики представлены на рис. 01-7-19.
01-7-20. Логарифмическая амплитудная частотная характеристика
САУ на рис. 01-7-20 строилась методом асимптот. Фазовая харак-
Рис. 01-7-20.
188

теристика получена путем сложения ординат фазовых характеристик
отдельных звеньев. Фазо-частотные характеристики звеньев на
рис. 01-7-20 нарисованы пунктирными линиями и обозначены циф¬
рами 1—7.
01-7-21. Наносим на Ф-номограмму, изображенную
на рис. 01-7-21,а, ЧХ разомкнутой системы. При этом
значения L(co) и ф(о>) для разомкнутой системы берем
из JI4X, изображенных на рис. 01-7-19. На Ф-номограм-
ме для получения соответствующих точек АФХ по оси
абсцисс откладываем ср(со) в градусах, а по оси ординат
L(co) .в децибелах. В точках пересечения АФХ с кривы¬
ми, идущими вверх, считываем для замкнутой системы
значения L(со), а с кривыми, идущими вниз, — значения
<р(ю).
Полученные значения амплитуды и фазы для замкну-
той системы сводим в табл. 01-7-1.
Таблица 01-7-1
ш,
с-1
Z.(to), дБ
Ф (<о),
град
А (ш)
to, с 1
L (со),
дп
ф (о>),
град
А (со)
1 ,3
+0,06
—2
1,007
24
+9
— 135
2,818
4
+0,32
—6
1,038
32
+ 1
— 180
1,122
6
+0,75
--8
1 ,09
40
—8
— 198
0,39
8
+ 1,5
— 17
1 ,189
50
— 12
—208
0,25
10
+2,2
—22
1,288
80
—25
—238
0,057
20
+9
—60
2,818
Значения амплитуды в децибелах переводим в обыч¬
ные числа и по полученным значениям строим ампли¬
тудную и фазовую характеристики замкнутой системы,
которые приведены на рис. 01-7-21,6.
01-7-22. Уравнение спектров в комплексной форме будет иметь
вид:
. (2—0,0004со2 + /0,Обсо) У (/со) = (3,6—/0,036со) *(/©).
Годографы для правой Р(/со) и левой Q (/со) частей уравнения
изображены на рис. 01-7-22,а. Проведя из начала координат на
годографы для правой и левой частей уравнения векторы Р (/©,•)
и Q (/со?:) в точки, соответствующие одной и той же частоте сог-,
определяем амплитуду вынужденных колебаний по формуле
Л/ ч |Я
Л<^)=а| ОМ)
где а — амплитуда входного синусоидального возмущения.
Сдвиг фаз ф(о)г) равен разности углов а (со*) и Р(сог). Частот¬
ные характеристики системы изображены на рис. 01-7-22,б.
189

а)
Рис. 01-7-21
(а).
190

Рис. 01-7-21 (б).
Рис. 01-7-22.
01-8. ЧАСТОТНЫЕ СПЕКТРЫ ВЫХОДНЫХ ПРОЦЕССОВ
01-8-1. Изображение выходного процесса
у (.л __	Ьгрг	-f- b,p -f- b0
Р2 (ЯгР3 + агР2 + ахр + а„)
Нерегулярная часть (изображение вынужденного
движения) [25]:
bp |	bpdi
УЛР) =
<**рг
а о Р

Регулярная часть (изображение собственного движе¬
ния) Ус(р) определяется как остаток изображения вы¬
ходного процесса после отделения нерегулярной части:
у i ч  Ь2р2 + М + Ь„	Ь0	а0Ь, — Ь0а, _
с ^ '	р2 (агрг + а.гр2 + а,/; + а0)	а0/?2	а2,,/)
а, (Ьоа,—а0Ь,) 12+ |Д2 (ЬрД1—a0&i) —аса3Ьп! р .
а2о (а3 Д3 -г азРг + я, /О + я,,)	'
,_а, (b.Pt — a0b|) — а0а2Ь0 + a20ba
я2о («зД3 + я2.я? + <ир + а0)
В области оригиналов
GO
{/„(/,)} +A j‘Re ус (/,„) cos О)/ flfco =
о
оо
= a-bl~A~- ПО+-^^ + 4- j*6у ^ cosdw’
о
где G;j (со) —вещественный спектр собственного движе¬
ния.
01-8-2. Импульсная характеристика системы (рис.
01-8-2), соответствующая прямоугольной вещественной
частотной характеристике (см. также задачу 1-1-2):
w ГЛ __ 2/-„со„ sin<0|)<
I ’	7Z	СО^	‘
Рис. 01-8-2.
01-8-3.
Г;<0;
со,/
Т~
192

01-8-4.
w [/)
01-8-5.
. “г (1 + *) t , “/ (1 — x) *
/. 1 ч sln о sin T
 ' i<*i (1 +«)	f	2
n	(0,-	(1 + x) t	to I	(1*-*) t ■
2 2
w
0 = 4- sin	cos	sin	+
_1_ ri — r2 -.-..to, +<02y o;„t02—(0, ^
^ (to2 — со,) t2	2	2	/•
01-8-6. Заданная вещественная характеристика может
быть разбита на 3 следующие элементарные трапеции
(рис. 01-8-6,а): О'ГЗ/;	с	высотами	—	(0'2')\
+ {4'2'); —{04') или на шесть следующих треугольни-
13—903
193

ков (рис. 01-8-6,6): 4'3'4; 1'2'2- 5'06; 1Г0'1\ 5'4'5\ 2Г3'3
с значениями высот треугольников: -\-{4'3')\ —(
— (05'); +(4'5'); +(0'Г); —(2'3').
01-8-7. На основании приложения 9 составляем
табл. 01-8-1 при v = f/<Di = //12 и >с=6/12 = 0,5.
Таблица 01-8-1
V
0,0
0,5
1,0
1,5
2,0
2,5
3,0
4,5
6,5
К [V)
A[v)
0
0
0,240
0,960
0,461
1,64
0,665
2,66
0,833
3,33
0,967
3,87
1,061
4,25
1,138
4,55
1,018
4,08
V
7,0
7,5
10
14
17
19
21
24
оо
К И
h [vj
0,993
3,97
0,974
3,90
0,982
3,93
1,000
4,000
1,012
4,06
0,998
3,99
0,995
3,98
1,00
4,000
1,000
4,000
01-8-8.
W (/со) =G (со) +}В (со),
где
С( V	656а>4	—	114,5- 105со2 — 13,1* 108
W	5,2-10“ 9со10 — 2,06-10~ 3со8 + 4,22со6+	*
+ 38 690со4 + 544- 105со2 + 36-104
Вещественная частотная характеристика замкнутой
системы
ft ((п\  6 (со) [1 + 6 (со)] + В2 (со)
• '	[1	+	6 (со)]2 + В2 (со)
Значения G( со), В (со) и Go (со) при различных со све¬
дены в табл. 01-8-2.
Таблица 01-8-2
СО, с“ 1
G( со)
В(со)
ОоН
со, с 1
G (со)
В (со)
G0(u>)
0
—3639
— ОО
1
8
—0,56
—0,45
—0,092
2
—6,2
—2,18
1,16
10
—0,42 -
—0,341
—0,277
3
—2,87
— 1,35
1,35
15
—0,27
—0,235
—0,22
4
— 1,7
—0,98
1,458
20
—0,205
—0,116
—0,203
5
— 1,15
—0,76
1,25
100
—0,006
—0,012
—0,005
194

По данным таблицы на рис. 01-8-8,а построена ве¬
щественная частотная характеристика замкнутой систе¬
мы. Она разбивается на пять элементарных трапецеи¬
дальных характеристик со следующими параметрами:
1) G0 = 0,48; со0=4 с-1; (od=l с-1;	=0,25;
2) Go = 1,48; (о0=7,74 с-1; cod=4,4 с-1; % = 0,57;
3) G0 = 0,62; (0о=8,5 С"1; (od=7,75 с-1; и=0,91;
4) G0=0,11; со0 = 10,5 с-1; (od=8,5 с-1; х=0,81;
5) G0 = 0,31; соо=32 с"1; <od=13 с-1; и = 0,406.
Из таблицы йх-функций выписываем значения ht для
каждой трапецеидальной характеристики, определяем
Hi(t) =Gihi[t) и сводим в табл. 01-8-3. Кривые пере-
13*	195

Трапеция 1
Трапеция 2
Трапе
э= —0,48; ш
о=4 с
х=0,25
G0=l,
СО
6
II
^0
75 с"1; х:
=0,57
Go=0,2; <*0=
1
Л» [“0
/.с
я, [О
* 1
Л. 10 1
Л с |
И At)
' 1
/13 И)
1
—0,386
0,25
—0,185
0,5
0,248
0,07
0,376
0,5
0,297
2
0,703
0,50
—0,34
1,0
0,476
0,13
0,705
1
0,575
3
0,928
0,75
—0,445
1,5
0,685
0,19
1,015
2
0,986
5
1,067
1,25
—0,51
2,5
0,985
0,32
1,46
3,5
1,175 ,
6
1,054
1,50
—0,505
3,0
1,082
0,40
1,605
4
1 г 141
7
1,035
1,75
—0,496
3,5
1,132
0,45
1,68
5
1,019
8
1,024
2,00
—0,491
4,0
1,152
0,52
1,71
6
0,922
10
1 ,027
2,50
—0,492
4,5
1,134
0,58
1,68
7
0,909
—

5,0
1 ,115
0,65
1,65
8
0,970




5,5
1,083
0,71
1,6
9
1 ,039




6,0
1 ,037
0,78
1,53
10
1,063


6,5
1,01
0,84
1,486
13
0,955


7,0
0,975
0,90
1,44
15
1,001



10,0
0,985
1,29
1,45
20
0,972
—
—
—
—
12,0
1,006
1,55
1,49
1-
1 ' '
ходных характеристик Я*(0 всех элементарных трапе¬
ций и суммарного переходного процесса построены на
рис. 01-8-8,6.
01-8-9. Строим график погрешности (рис. 01-8-9) -ку¬
сочно-линейной аппроксимации вещественной характери¬
стики, изображенной на рис. 01-8-8,а. В формуле для
погрешности [25]
= j A Re X (/<*>) cos Ы d<*> — j*
2 AG (со)
со
о
COS wt
Рис. 01-8-9.
интегрирование заменяем суммированием произведении
площадей Si под кривой AG на участке постоянного зна-
196

Таблица 01-8-3
Трапеция 4
<?о=0,П; а'0= 10,5 с-i; х =0,81
Л41П t> с H,[t)
Трапеция 5
G0=—31; cd0=s=32 с"1; х=0,406
Л5 [О t* с
Я5[0
0,06
0,12
0,24
0,41
0,47
0,59
0,71
0,82
1,00
1,06
1,18
1,53
1,77
2,36
0,059
0,115
0,197
0,235
0,228
0,204
0,184
0,182
0,194
0,207
0,212
0,191
0,2
0,5
1,0
2.5
4.0
5.0
6.0
7.0
8.5
10.5
14.0
17.5
21
24
0,282
0,547
1,084
1,156
1.053
0,949
0,911
0,974
1.054
0,965
1,023
0,987
i ,008
0,05
0,10
0,24
0,38
0,47
0,57
0,67
0,81
1,0
1,33
1,67
2,0
2,28
0,031
0,06
0,1195
0,127
0,116
0,104
0,1
0,107
0,116
0,106
0,113
0,091
0,11
1
2
3
8
И
14
18
21
24
26
0,432
0,786
1,013
0,995
0,993
0,985
1,01
1,001
0,997
0,996
0,03
0,06
0,09
0,25
0,34
0,44
0,56
0,66
0,75
0,81
—0,134
—0,244
—0,314
—0,308
—0,307
—0,305'
—О,314
—0,31
—0,309
—0,309
ка погрешности на средние значения функции cosg+g)
на этом участке, т. е.
’
(О
Значения площадей S* и частот определяем по
рис. 01-8-9 и сводим в табл. 01-8-4.
Таблица 01-8-4
иМ* площади
параметр
1
2
3
4
5
6 1
7
8 1
9
10
Sit MM2
36
«г—4
21
4
— 16
210
—36
—14
40
—т2000
Ю;> С'1
0,9
2,2
3,4
4,35
5,0
6,8
9,1
10,9
15,0
59
Далее для площадей Si, указанных в таблице, с уче<
том масштаба площади (10_3) получим:
1)	для 1 с
6 =
36
cos 0,9
cos 2,2
0,9
— 16
cos 5
210
2,2
cos 6,8
■21
+ 40
cos 15
15
6,8
-2000
-36
cos 3,4 * -
”17? I"
cos9,1	_
4 cos 4,35
4,35
cos 10,9	|
cos 59
59~
9,1 A* 10,9
J 10"*= 11,5-10-*;
197

2) для ^ = 10 с
2 /O~cos9 i , cos 22	, O1cos34 .	. cos 43,5
S==— (36-CT+4XT+21 М- + 4-й5
_ i6 cos50_ + 2Ю «*|8. _ 36 C-^i- - 14 ^-+
_j_40cos_^0	2000	10“3	=	—	11,9-.10~3.
01-8-10. Кривая Go (со) приближенно заменяется че¬
тырьмя элементарными трапециями, показанными на
рис. 01-8-10,а. Параметры трапеций: частота среза соо,
коэффициент наклона x=cod/coo и высота G* —сведены
в табл. 01-8-5.
Таблица 01 -8-5
Параметр]
№ трапеции
1
2
3
4
к
0,62
0,31
0,46
0,70
со0, с-1
16
5,5
61,5
28,5
Со
1,62
—0,09
—0,24
—0,29
Далее воспользуемся таблицами |л?)-функций. Так
как таблицы hx(v) рассчитаны для единичной трапеции
с Go=l и соо=1 с-1, то при построении переходного про¬
цесса для каждой трапеции будем пользоваться форму¬
лой
hi[t) = Gih[v/соо).
Строим графики hi[t), ki\t), hz[t) и h^[t). Склады¬
вая ординаты этих кривых, получаем (рис. 01-8-10,6)
суммарную кривую h\t) переходной функции в заданной
системе.
В случае неединичного ступенчатого воздействия
x[t)=b-l[t) ординаты кривой h[t) следует умножить
на Ь.
01-8-11. Заданная вещественная характеристика G(co)
заменяется двумя трапециями: 1) п=0,78; соо=79 с-1;
198

G0=0,69; 2) x=0,84; a0=95 c_1; G0=0,2. Построеннный
график h\t) изображен на рис. 01-8-11.
01-8-12. Графики переходных характеристик систем
изображены на рис. 01-8-12.
01-8-13. Переходная характеристика приведена на
рис. 01-8-13.
о
-Ofi
О 0,02	0,06
Рис. 01-8-11.
199

01-8-14. Парциальные
процессы, соответствующие
треугольным составляющим
частотного спектра, и пере¬
ходная функция системы
изображены на рис. 01-8-14.
lL_ Вещественная частотная ха-
с рактеристика разбивалась
на четыре треугольника (см.
рис. 1-8-14), параметры ко¬
торых сведены в табл.
01-8-6.
Таблица 01-8-6
Параметр
№ треугольника
1
2
3
4
G
1,7
0,26
—0,66
—0,63
й>0. С"1
8
8
20
1,5
Рис. 01-8-14.
01-8-15. Удобно решать задачу, перейдя к изображе¬
ниям сигналов по Лапласу. Изображение входного сиг¬
нала имеет вид:
Е(р) = Ь{е-11Щ = ^Гд.	(1)
После прохождения через косинусный модулятор сиг¬
нал преобразуется к виду
X (/>) = Re {Е (р+К)} = „/+. V .	(2)
Изображение сигнала на выходе демодулятора свя¬
зано с изображением на входе схемы следующей зави¬
симостью:
[У (р) = IT Е С7) +4- Re iE (р + /2<»в)} •
После подстановки Е (р) из формулы (1) получим:
1 I Р +а
у w=4-
200
Р + ° 1 (р + о)2 + 4а>2
;]• <3>

Из выражений (2) и (3) имеем:
х (t) = e~ai cos <oHt\
y(t) — 4r [e~7t + е~°( cos 2wJ]
или
x (t) = e~* cos 6001;	(4)
У (0 = -§- [^'2' -\-е~г* cos 1200*].	(5)
На	рис.	01-8-15,a приведены кривые процессов	x(t)
и y(t). В задаче 1-1-4 получены составляющие спектра
функции	е	5, которая является входным	сигналом,
в виде
Мю)=5г^;	(6>
=	х,н=^.	(?)
На рис. 01-8-15,6 построены кривые составляющих
спектра на входе модулятора.
Выражение спектра на выходе модулятора согласно
формуле (2) имеет вид:
X (fa) =	°	+/(0	__	+	|
(а + fa)2 + С02н	(«*в+в1^».)1 + 4вЧ#»“Г
1 1соа
(С02н — Д2 — СО2) со
(со2н + д2 — ш2) 2 + 402(02
ИЛИ
р, (со) 1=	(600г + 4 + со2) 2
г*' >	(6002	+ 4 — со2)2 + 16со2 ’	(8)
.. / \	(6002 — 4 — со2) со
2 ((D)	(6002 + 4 — со2)2 + 1 бсо2 •
По формулам (8) и (9) на рис. 01-8-15,в строим
кривые вещественной pi мнимой составляющих спектра
на выходе модулятора.
Выражение спектра на выходе демодулятора соглас¬
но формуле (3) имеет вид:
У — — Г q ~~ fo I q (S2 + °2 + ш2) + /ш (^2 — а2 — (02)
W /	9	1^102+02“	(22	+	G	2	 СО2)	2	4^2
(10)
2
при Й = 2(ВН.
201

0;2ррэ«*>)-. М3 (со)
202

Перепишем формулу (10) иначе:
У(Н=-^[Е(Н + У,(М],	(11)
где Е (/со)— спектр сигнала на входе модулятора. Тогда
Y (Ы=	8 <S2 + °2 + ”*)	_|_	; <о (22 - »2 - со2)
(22 -f- о2 — о>2) 2 -f- 4о2со2 I (22 -j- а2 — to2)2 — 4а2со2 2
откуда
p3(io)z=-i-[—  L2 (12002 + 4 + ы2)	1	_12.
r3W 2 [w2 + 4~(120D2 +4 — со2)2 + 1 бсо2J’	у^
К, (to) = — Г-~М -I <о (12002-4 —(О2) 1	3
,у/	2 [со2 + 4	(12002 + 4 — to2)2 + 16(o2J *	1	'
По формулам (12) и (13) на рис. 01-8-15,г строим
кривые составляющих спектра на выходе демодулятора.
01-9. БАЗОВЫЕ ХАРАКТЕРИСТИКИ
01-9-1. Сорласно определению [28] входной сигнал
имеет стандартную экспоненциальную форму ext*rl [{р—Я).
Изображение базовой характеристики будет:
Б(р, X)=-±—W(p) = -
Р ^	(7/7+ 1) (р — А)
Разложение на компоненты дает:
k/T	k/T
(р-\	р-\-	\/Т	)’
(Р + Х/П (р — X)	Х+1/Г^р-Х Р+1/Т
6{t, Я)=-у^р [ехрЯ/ — ехр(— t/T)].
01-9-2. Находим выражение заданного сигнала через
базовый:
•*^=(а1&ехРЯ'Х=о’
т. е. согласно [28] и приложению 2
203

Тогда
где
,(о=*(->«<<. ч={^[гттг(ехр"-
— ехр	ф j) j |}_о =VU" + 2 U'V' + UV",
~u . r fr 	ITtr^_
> U 	 IT\	1	П2	>	U	I
u=
2aT2k
'71+1 ’	(71+1)*	’	~	(71	+	1)»	*
V = expA(— exp(—t/T); V' = texpXt; V" = t* exp Xt.
В результате получаем:
y(t):
ak
'71 + 1
[(
f
2 tT
2 T*
(71 + 1)	1	(71+1)
r)«
xp Xt ■
27'2
(71 + l)2 eXp !v'
x=o
= ak[f — 2П + 2Г2 — 2Г*ехр (“T")]-
01-9-3. а) Для заданных двух уравнений звена
f/i = o + #*;	1
у 2 = 0 —J— 0 —а: /
У i =
У*
составляем матрицу коэффициентов
О 1
В =
о о
и получаем решение относительно нормированных им¬
пульсных характеристик:
g(0 = ехр (В/) = Е+|]В*4=
*=1
■—
1 0
+
0 1
t =
1 *
0 1
0 0
0 1
Ряд имеет ограниченное число членов, так как Bft=0
при А>1. Для расчета вектора базовых характеристик
используем предложенную нами формулу [30]:
6(t, Я) =
fft (t, X)
бъ (/. X)
: (В — ЕЯ)-1 [g (t) — £ е хр'Я7]
(1)
204

Обозначим В—ЕА,=Л и определим обратную ей
матрицу:
Л‘1 = (В—ЕЯ)'
—X	1
О — X
J
" X
О —
1
X2
1
X
I ad£/A* |
(2)
где A,2=det(В—ЕЯ) —det А и ad^A — адъюнкты транспо¬
нированной матрицы. Подставляя полученные матрицы
в (1), определяем:
б (f, Я):
Л-1 X-2
О X-1
1 — exp Xt t	О
О 1 — exp Xt 1
ехрЛ* — 1
t
Л2
X
exp Xt — 1
X
(3)
б) Вводя для возбуждающего сигнала уравнение
уо=%у0—х, образуем расширенную систему уравнений:
Но= ^Уо "Ь 0 -]- 0;
р, = 0 + 0 -fp2;
#2 = У а “Ь О “Ь О
содержащую расншренную матрицу коэффициентов
X
0
0
0
0
X
0
1

1
0
0
А
в
где А= j —вектор ввода возбуждающего сигнала.
205

По расширенной матрице коэффициентов найдем чле¬
ны матричного ряда Тейлора:
Е =
1
0
0
и
0
0
0
1
0
; В t =
0
0
t
9
0
1
t
0
0
R2 JL =
2!
>•
то
го
2! ^
0
см
О
N
0
см
2!
0
ъж=
3!
в k\ k\
(Xt)3 о О
It3 О О
ХН3 О О
(Xt)k О О
xk-4k О о
хк-чк о о
Суммируя по одноименным ячейкам элементы приве¬
денных выше матриц и дополняя получаемые ряды до
экспоненциальных рядов, находим:
й(0=
ехр Xt 0 0
Уо 0
ехр Xt — 1 t
X2 х 1
(;> Л) g(0
(4)
ехр X* — 1 П1
X
б г (*. X)
Для возбуждения звена начальной экспоненциальной
функцией вектор начальных условий будет иметь вид.
поэтому
Б (О, Я) =
Б(*. Я) = g (О
206

Последняя операция выделяет первый столбец в (4),
в котором нижние две строки совпадают с (3).
в) Уравнение g(t) = Bg(t) преобразуем по Лапласу при
начальных условиях, соответствующих формированию
нормированных импульсных характеристик:	g(0)=E.
Тогда
pG (р, Я) — Е = В G (/?, Я)
или
_	_	_	р	—	к	о	О
G(/7, Я) = [Ер — В]-!= о	р-1
[—10/7
|[ ad;/ [Ё/> —В]т ||
Р2 (/> — *)
Вычисляя адъюнкты транспонированной матрицы и
производя деление во всех ячейках на det[E/?—В] =
=р2(р—Я), получаем:
1
G(p, Я) =
 -г 0	0
Р — к
1 _1	1_
р2(р — к) д р2
1 1
— о —
Р
р{р — к)
Х{р)
Б, (р, к)
Б2 (Р> к)
0
О(д)
(5)
В ячейках содержится изображение всех функций,
полученных выше в п. «а» и «б».
Первый столбец (5) содержит изображение входного
сигнала и базовых функций. Они также могут быть
получены как изображение (1)
Б (р, Я) = (В - ЕЯ)-1 [G (р) - ЕА. (6)
Используя результаты (2) и (5), получаем:
б(А Я) =
_l_ _1_
к к2
0 X
1
1
р — к р
0
 1_
Р2
1 1
р — к
1 ( 1
1 ^
1—ъ
Д!
I
1
Р;
1 \рг
1 ( 1
К [р — х
р)
(7)
207

01-10. НАЧАЛЬНЫЕ УСЛОВИЯ И НАЧАЛЬНЫЕ ЗНАЧЕНИЯ
01-10-1. Преобразуем заданное уравнение по Лапла¬
су с учетом ненулевых начальных условий
01-10-2. Переносим в (1) из предыдущей задачи чле¬
ны с отрицательным знаком в правую часть и заменяем
их требуемыми начальными значениями:
(p2+Q2) У(/?)=г/(0+) +py(0+)=AQ cos ф+/?Л sin ф.
Переходим к форме алгебраизованного дифференци¬
ального уравнения:
(D2 -{- Q2) у (t) — AQ cos <р8 [t] -(- A sin <р 8 [t].
Следовательно,
х (it) = А {П cos	[t] -j- sin <p*3 [/]}.
01-10-3. Записываем сумму возбужденного и свобод¬
ного компонентов:
(р‘ + й2) Y (р) - у (0_) - ру (0.) = 0,	(1)
откуда
Так как
/?sin <р + 2 cos
*
т*- sin (Qt -j- <р),
то
#(0_) = Ж2со$ср, //(0_) = i4siny.
Проверка результата:
у (0+) = lim Y (р) = lim
У (0+) = Нш \рхУ{р)-рУ(0)] =
р sin f = AQ cos <f.
— p (p2 -I- 22) "Г	p*	+
e , у (0-) +/»/ (0-)
g+ piy (0.) + ргу (0-)
P2 + 22
208

Находим начальные значения:
y(0+) = \mpY (р) = у(0_);
,,-,0
у (0+) = lim \p*Y (р) — ру (0+)] = у(0_);
/7->0
I/' (0+) = 1 im \ргУ (р) — ргу (0+) — ру (0+)] = а.
р-*0
Таким образом, для младших производных [*/(0+)„
г/(0+)] начальные значения при ступенчатом возбужде¬
нии совпадают с соответствующими начальными усло¬
виями, а для старших производных начальные значения-
формируются независимо и их величины в то же время
служат и приращениями по отношению к нулевым на¬
чальным условиям по этим производным.
01-10-4.
_	3	■	0,5/7	+	0,75
1 '	р* -L- Q* I р2 _[_ Q2 »
У (0+) = 0,5; у[(0+) = 3,75; jj (0+) = -0,5&*
и т. д.
В этой задаче приращения начинаются с первой про¬
изводной:
А//(0) =3,75—0,75=3 и т. д.
01-10-5. Из решения задачи 01-5-39 заимствуем изо¬
бражение исследуемой переходной характеристики:
Н (р) =0,25 (рз + 0,8р2 + 0,25p)-J.
Будем считать, что возбуждение этой реакции про¬
изводится ступенчатой функцией
i. (0 = 0,258 [0;
gt (0) = 0,25
в звене с ПФ № (р) = (р2+0,8/? +0,25)-1.
Уравнение ступенчатой функции (1) дополняем урав¬
нениями для нормированных импульсных характеристик
звена
8i~gY>	|	(2)-
g« = g,—0,25g, — 0,8gt.J
14—903	209-
(1)'

По (1) и (2) составляем матрицу коэффициентов
расширенной системы уравнений В и вектор начальных
условий h(0), соответствующий подаче на вход предва¬
рительно не возбужденного звена ступенчатой функции,
т. е.
В =
0
0
0
0,25
0
0
1
; ь (0) =
0
1
—0,25 -
-0,8
0
(3)
где h(0) —начальные условия для расширенного векто¬
ра состояния, в первой строке которого содержится
входной сигнал, во второй строке — переходная харак¬
теристика звена, в третьей строке — ее производная.
Начальные значения расширенного вектора переход¬
ной характеристики определяются по формуле
h<*> (0) = B*h(0).	(4)
Для k=l имеем:
0	0	о
0	0	1	0=0;	(5)
1	—0,25	—0,
h(0) =
для k — 2
h(0) =
ДЛЯ k = 3
о	о
0	1
—0,25 —(У,?
0,25
0
0
=
0
0
0,25
0,25
0
0
=
0,25
0
—0,2
(6)
0
0
0
3
0,25
0
h(0) =
0
0
1
0
=
—0,2
• (7)
i
-0,25
—0,8
0
—0,0975
Вторые строки векторов (3), (5) — (7) повторяют ре¬
шения, содержащиеся в табл. 01-5-3. Третьи строки от¬
ражают те же производные с увеличенным на единицу
порядком.
01-10-6. Заданное в 1-5-37 нестационарное уравнение
нормируем относительно старшей производной:
»+(^^+10)»+(10//+29)у=(10//+29)6[/-2].
Вводим переменные состояния, связанные однород¬
ными уравнениями
У\=Уг\ Уг=—(10// + 29)f/i—(2//+ 10)у2
210

при компонентах вектора начальных условий для мо¬
мента U=2 с:
yi(2)=0; y2(2) = (10/f + 29)6[f—2] = (10/2 + 29)«[/—
—2], т. е. г/2 (2) =34, откуда
У(2) =
о
34
(1)
Матрица коэффициентов будет нестационарной:
О	1
— (Ю/ / + 29) -(2Д+10)
B(f) =
Определим значения матрицы нестационарных коэф¬
фициентов и ее производных в момент приложения
импульса:
В (2) =
0 1
-34 —11
в (0 =
о
2-10
*3
о
2-2
" /3
в (2) =
; В (2) =
0 0
2,5 0,5
0 0
—2,5 —0,5
И Т. Д.
Для матрицы нормированных импульсных характери¬
стик начальные значения в момент приложения импуль¬
са to=2 с определяются по методу А. С. Шаталова как
0"+,,«.)=[(ж+аТг)'в
(2)
где d/dt, d/dto — селективные (адресованные к функци¬
ям в со' или g (t0) символы дифференцирования по вре¬
мени d/dt), а начальные значения производных вектора
составляют:
y<ft>(fo)=g(ft)(*o)y(<o).	(3)
Применим формулы (2) и (3) для заданного случая.
Для k=0, g(2)=E имеем:
g (2) = В (2) g (2) = j	0	1
—34 —11
поэтому
y(2) = g(2)y(2) =
14*
0 1
0
34
^-34 —11
34
—374
(4)
211

Для 6=1 имеем:
g(0=B(2)g(2) + B(2)g(2) =
_
0
0
+
0 1
2
—34
—И
2,5
0,5
—34 —11
376,5
87,5
шоэтому
У (2) =
—34 —11
0
—374
376,5 87,5
34
' 2975
И т. д. (5)
Первые строки векторов (1),	(3)	— (5) совпадают
с соответствующими производными в момент времени
to=2 с, помещенными в табл. 01-5-1, а вторые строки
•с производными, порядок которых увеличен на единицу.
Глава вторая
ТОПОЛОГИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
02-1. ОБЩИЕ ПРАВИЛА И ОГРАНИЧЕНИЯ
02-1-1. После заданного переноса звено займет новое
место, показанное на рис. 02-1-1, связь станет уже не
-обратной, а согласно-параллельной, звено приобретает
.-новую ПФ Ws{p)y определенную ниже.
Рис. 02-М.
а)	На вход звена W8(p) вместо прежнего сигнала
:go.c поступает новый сигнал W3(p)Wit(p)l0X. Реакция
звена Ws(p), чтобы достигнуть первоначальной величи¬
ны Цо.с на входе звена 2, должна быть предварительно
поделена на ПФ звеньев 6 и 7, т. е. Цо.с/ [Wi(p)WG(p)].
Поэтому
ш (и\ — !	1	^ (п\ „ J	!	— Т1 (Т6 Р + 1)
w*yP) — Wi{p) WAp) wi\P)wt(p) W,(p)	МзМ6(7>+0-
212

Правило. При переносе концов ветви — узла по
ходу сигнала и сумматора против хода сигнала — в пре¬
образуемую .ветвь вносятся инверсные ПФ пройденных
звеньев, т. е. ее ПФ делится на ПФ этих звеньев. Про¬
цедура переноса узла через узел и сумматора через сум¬
матор очевидна.
б) Звенья 1 и 6 в новом режиме должны дополни¬
тельно пропускать сигналы ir)o.clW 1 и rj0.c/^i^6, чего не
было в исходной структуре. Неэквивалентные звенья на
рис. 02-1-1 заштрихованы. Режимы остальных звеньев
и вся преобразованная схема эквивалентны заданным.
02-1-2. а) Правило. При переносе концевых участ¬
ков отдельной ветви через звенья (узла против хода сиг¬
нала, а сумматора — по направлению сигнала) ПФ вет¬
ви умножается на ПФ пройденных звеньев:
W' (р) =	(Р)	(Р) W, (Р) гз (р) 1Г4 (р) =
 	 ^’\k.\kAkST1	 .-V
<Г\р* + 2ф1Р)(Т%р+\у	W
Заданная согласно-параллельная цепь, как видно из
рис. 02-1-2, превратилась в отрицательную обратную
связь. Но при переносе узла через сумматор действует
правило дублирования (расщепления) ветви с ее звенья¬
ми, так как после переноса надо учитывать вход как по
X, так и по Х0шС. Дополнительно к этому при переносе
сумматора через узел ветвь опять дублируется для вво¬
да слагаемых как на выход У, так и в цепь обратной
связи Уо.с. Следовательно, надо формиоовать ПФ: от Хос
к Уо.с— Ws{p)\ от Хо.с к У—W9(p); от X к У0.с—Wi0(p);
от X к Y—Wu(p).
Первая функция после дальнейшего переноса сумма¬
тора и узла ко входу и выходу звена 5 трансформиру¬
ется в W8(p), определяемую выражением (1). Осталь¬
ные функции определяются идентично:
WM=«',.(p)=w,M =	,2)
а их расположение показано на рис. 02-1-2.
б)	Произвольное число ответвлений в узлах не ме¬
няет сигналов в ответвлениях, что соответствует прин¬
ципу однонаправленности (жесткости) структурной схе¬
мы. Сумматоры же вносят дополнительные сигналы. По¬
скольку полная эквивалентность наступает после
213

сумматора на входе звена 5, предыдущие звенья 3, 4
находятся в неэквивалентных условиях (на рис. 02-1-2
они заштрихованы). Режимы остальных первоначальных
звеньев и вся преобразованная схема в целом эквива¬
лентны заданным.
02-1-3. а) На основании правила инверсии ПФ пря-
мой цепи и обратной связи меняются местами и заме-
няются инверсными. Результат показан на рис. 02-1-3,#.
Для заданной и преобразованной структур ПФ схемы
составляет:
k/Tp 	 k
1 + 1 / Тр — \+Тр ’
т. е. схемы по передаточным -свойствам эквивалентны.
б)	По возможностям ввода начальных условий схе¬
мы неэквивалентны. Действительно, в исходную схему
начальное условие вводится на вход в форме импульса
L- y(0-)8[t], сразу интегрируется с масштабом k/T
и в форме сигнала г/(0_)1[/), фиксированного памятью
интегратора на его выходе, возбуждает схему.
В преобразованной схеме на рис. 02-1-3,а интегри¬
рующих звеньев нет и начальные условия подобным
образом ввести нельзя. Эквивалентной по вводу на¬
чальных условий будет схема на рис. 02-1-3,6, где до¬
214

бавлено интегрирующее звено, на которое подается
*/(0_)6[i], а результат интегрирования вводится в кон¬
тур на его выходе.
Указание. Все структурные преобразования, свя¬
занные с ликвидацией интегрирующих звеньев и сокра¬
щением полиномов от р в знаменателе ПФ при умноже¬
нии на пропорциональные полиномы, вводимые в числи¬
теле, нарушают стандартные принципы ввода начальных
условий: при сокращении операторных членов знамена¬
телей должны одновременно создаваться разомкнутые
входные цепи, содержащие сокращенные звенья или
в преобразованной форме интегрирующие звенья.
02-1-4. При конечном усилении
При к —сю
т. е. общая ПФ схемы равна инверсии от ПФ звена,
находящегося в цепи отрицательной обратной связи.
02-1-5. Если принять WY=kr=lO, что справедливо
для диапазона частот 0—1000 с-1, то ПФ схемы фор¬
мально составит:
Результат не имеет физического смысла, так как схе¬
ма, в которой сигналы в прямой цепи и цепи обратной
связи положительны, не может изменять знак входного
сигнала. Составляем ПФ с охватом частот за 1000 с-1:
т у/ (г)\ 	Ч	г	-г"	г	~	4
w КР)— \ kWo c {р)	Т2р2+	21Тр+ 1+ kko.c'
k	 к(Т*р'	+	2фр+\)
10
10.
1—2
Wy(P) =
к
10
0,001/?+ 1 *
Тогда
ю
■ w.(py=
0,001/?+ 1
10
2
0,001/7—1 ’
1 — 0,001/?+ 1
215

Получено неустойчивое апериодическое звено со
структурой, показанной на рис. 02-1-5.
Вывод. Переход коэффициента усиления по петле
положительной обратной связи за критическое значение
kyko.c>\ требует уточнения динамической схемы усиле¬
ния, т. е. учета малых постоянных времени.
Рис. 02-1-5.	Рис.	02-1-6.
02-1-6. В зависимости от охватываемой полосы частот
можно получать следующие ПФ усилителя и схемы
(табл. 02-1-1):
Т а б л и ц а 02-1-1
(D, с-1
wy (Р)
W (р)
0—100
10
10
0,1 р— 1
(V
3
ж
л
0—800
10
10
Я
<1>
Си
0,01 /7+1
0,09 /7—1
О)
0— свыше
103
10
10
(0,01 /?+1) (0,00125 /7+1)
125 -10-7 /72—0,089 /7+1
Из табл. 02-1-1 видно, что для первых двух полос
частот усилителя получаются физически нереальные пе¬
редаточные функции системы в целом (знак — при всех
положительных ПФ элементов). Последняя ПФ второго
порядка, учитывающая наиболее широкую область ча¬
стот, имеет физический смысл. После охвата усилителя
обратной связью +0,01/? получаем неустойчивое звено
второго порядка, структура которого показана на
рис. 02-1-6.
Вывод. При положительных обратных связях по
производным требуется учитывать, определяя ПФ схемы*
также малые постоянные времени усилителя.
216

02-2. ПРЕОБРАЗОВАНИЯ СТРУКТУР ЗВЕНЬЕВ И СИСТЕМ
02-2-1. Решение приведено в табл. 02-2-1.
Таблица 02-2-1
Пара¬
Вариант
метр
I
2
3
I
1 5
G
7
8
k
11,1
100
1000
Формула неприменима
(см. решение 02-1-5)
0,91
0,01
0,05
0,01
02-2-2. Решение приведено в табл. 02-2-2.
Таблица 02-2-2
ПФ
Вариант
1
2
3
4
5
W(p)
См. задачу 2-1-6
10
Ю/Ч-1
1

р
1
"2/7
1
"2/7
02-2-3. Решение приведено в табл. 02-2-3.
Таблица 02-2-3
ПФ
Вариант
1
2
3
4
5
6
W(p)
0,5 р
0,5/?
0,5 р
2/7
2/7
2/7
0,05 /7—1
0,005 р—1
0,05 /7+1
0,02 /?+1
02-2-4. Решение приведено в табл. 02-2-4.
Таблица 02-2-4
ПФ
Вариант
1 1 2 I 3
4
W(p)
02-2-5
Формула неприменима (см. 02-1-6)
. Решение приведено в табл. 02-2-5.
Р
Р
10 /7+1
Таблиц
20 /7+1
а 02-2-5
ОФП
Вариант
1 2 | 3
4
5
6
W(p)
Не реализуемы
Р
10 р
100 р
1
'Х,
р
1+ Р2
1+20 р2
1+50 р2
217

02-2-6. Решение приведено в табл. 02-2-6.
Таблица 02-2-6
Параметр
Вариант
1
2
3
4
5
6
kT
10
0,9
0,99
0,999
— 10
-0,9
W{p)
Нереализуема
10 р
50 р
500 р
1
11 /7
0,52 р
02-2-7. Для положительной обратной связи
W+ (р) = -- ' °'с	.
Р~1
Для отрицательной обратной связи
*-{р)=	•
kko.c Р + 1
02-2-8.
а)
f*W = W7(V<1);
J-W = W7-
TV7 / ч	knp
^ + I/7) — п2 ь ь
Р   ^П^О.С
02-2-9. Решение приведено в табл. 02-2-7.
Таблица 02-2-7
ПФ
Вариант
1
2
3
4
5
6
7
8
W(p)
10
0,1
0,01
0,1
0,2
20
5
12-
2р+\
0,02 /7+1
0,02 /7+1
0,02 /7—1
4/7+1
4/7+1
Z7
р •
02-2-10.
Г W=^^.±U/'+l •
218

Результаты (расчетов сведены в табл. 02-2-8.
Таблица 02-2-8
ПФ
Вариант
1
2
3
4
5
W(p)
Формула неприменима
(см. 2-1-6)
10
100
100
100
15 р+1
200 р+1
50 р+1
Структура звена при ТфТ0.с и Г = Г0.С дана на рис. 02-2-10.
Рис. 02-2-10.
02-2-11.
Pik о..
w± (Р)=~Т
kkn
-(Тр+\)р+1
02-2-12. Запишем уравнение звена в трех условно разрешенных
относительно У(р) формах:
а)
Y (Р) = [kX (р) - 2фрУ (р) - Y (р)];
в)
7 w = Wp [kX (р) ~~ Т2р2у {р)~ 7 (/?)];
У(р) =bX(p)-2\TpY(p)-T*p*Y{p).
По этим уравнениям строим структурные схемы рис. 02-2-12,а—в.
Стандартный ввод начальных условий допускают только схема на
рис. 02-2-12,а и полученная из нее при переносе узла через звено
1/Гр схема рис. 02-2-12,г.
219

Рис. 02-2-12.
02-2-13. Значения ПФ замкнутой обратной связью схемы при¬
ведены в табл. 02-2-9.
Таблица 02-2-9
Вид об¬
Вариант
ратной
2
связи
1
3
4
5
10
10
10
2
2
Vc
25 р* + й р+ 11
25 /7*4-5 р+21
25 />* + 5 p—s4
Р (5 /4-1)
25 р»4-5 /?4-оЗ
Го.с Р
10
10
10
10
1.0
25 ръ+\Ър+\
25 /7*4-10 р+ 1
25 /7*—5 р+1
25 /7* 4-1
25 /7*4-4 /;4-1
02-2-14.	1)	Методом	свертывания схемы (рис.
02-2-14,а) нужно предварительно произвести перенос
таких элементов схемы, как сумматор или узел, через
звено н сторону совмещения их с одноименными элемен¬
тами (узел с узлом или сумматор с сумматором). При
этом возможно несколько вариантов:
а) перенос сумматора 1 через звено W(р) по ходу
сигнала (рис. 02-2-14,а);
б) перенос сумматора 2 через звено W\{p) против
хода сигнала (рис. 02-2-14,е);
в) перенос узла 3 через звено W3(p) по ходу сигнала
(рис. 02-2-14,ж), так что узел 3 совмещается с узлом 4\
г) перенос узла 4 через звено W(р) против хода сиг¬
нала (рис. 02-2-14,3).
В любом случае мы получим многоконтурную схему
с отрицательными неперекрестными связями. В дальней¬
шем свертывание следует вести, начиная с внутреннего
220

Х(р)
Xip)
Wp)
X
W2(p) U/jlp)
1+W1(p)Wz(p)Wii(p)
v(p)
-W§(p)
Q)
W2 ip) Ia/j (p)
Yip)
W‘(p) >■
1+Ц(р) w2(p) wjp)+w2ip} Wj(p) wstp)
г)
УЛр)
W,(p)W2(p>W3(p)
Y(p)
1+Wi ip) Wz (pj W4 (p) +^2 ip) W3 (p) W5ip)
X(p)
w{(p)
W2(p)
w3(p)
-w5(p)
-wh(p)
Ж)
jvjM
V(£>
X(p) i 	 2
T'Wf(p) —-Ф-" >■ Wz(p)	У
*—-W5(p)	w3(p)	-J
3)
w3(p)
Y(p>
Рис. 02-2-14.
22 Г

контура обратной связи, как это показано (для случая
«а») на рис. 02-2-14,а—д.
Передаточная функция системы
Передаточную функцию можно определить сразу по
схемам рис. 02-2-14,е—з, не производя дальнейшего
свертывания (аналогично рис. 02-2-14,а—д).-
Производить в изображенной на рис. 02-2-14,а схеме
перенос сумматора 2 через звено Wz{p) или узла 3 че¬
рез звено W(р) и сумматора 2 против хода сигнала не¬
целесообразно, так как при любом из указанных пере¬
носов требуется вводить дополнительные дублирующие
звенья.
2)	Топологическим методом передаточную функцию
рекомендуется определять по формуле Мезона [12]
в модификации, использующей разложение по контурам:
Входящие в суммы числителя и знаменателя (2) ве¬
личины контуров, их парные произведения и триады
имеют топологические ограничения:
в знаменателе исключаются (полагаются равными
нулю) произведения и триады для контуров, имеющих
общие элементы участка цепи;
в числителе, кроме того, суммируемые величины, про¬
изведения и триады берутся для контуров, изолирован¬
ных от выбранного прямого пути, т. е. не имеющие и
с ним общих элементов.
Определяем контуры на структурной схеме
и прямой путь от X к У, содержащий 2 звена, /" 1=Ц^Г2
С учетом топологических ограничений для рассматри¬
ваемой схемы
ф (р)=
(к)	U,	к)	(/,	к,	I)
L1=—IFiWW4; L2=—W2W3W5
(3)
что совпадает с (1).
222

02-2-15. Используем обозначение промежуточного
сигнала Z и записываем уравнения двух сумматоров:
Wb{p)Y+Z=[Wl(p) + W3{p)]X-
Y-Wz(p)Z=Wi{p)W,{p)X.
Разрешаем систему уравнений относительно
Y(p):
Y(P) =
W, + Ws 1
wtwt —wt
W, 1
1 -wt
Х(Р)>
отсюда
W(p)--
Y (р)	(p)Wi (р) + [W (р)+ W, (р)] W2	(р)
zxjp)~	i+wt(p)W*(p)
02-2-16. Начинать свертывание целесообразно с пере¬
носа первого (входного) сумматора через последова¬
тельно соединенные звенья Wi(р) и W2(р) и совмещения
этого сумматора со вторым. В этом случае получим
Рис. 02-2-16.
структурную схему, изображенную на рис. 02-2-16,а.
В дальнейшем производится свертывание, как показано
на рис. 02-2-16,6 и в.
Передаточная функция замкнутой системы
а, /_ч _ m(p)Wt (p)+Wi(p)] W3 (р)
^КР)— l+Wi {р) Wi {р) ц/з {р)
223

Если подставить значения ПФ элементарных звеньев,
'то получим Ф(/?)=1. Передаточная функция «вход —
ошибка» Фс {р) = 1 — Ф (/?) = 0.
02-2-17. Передаточная функция системы составляет:
ф , ч 	 ktk2k3k4	(Тр.сР+1)
W — (То.сР + 1)	+	1) (Т4р + 1 )р + к2кгТо с X •
X (ТАр + 1) /?2 + WA (ТохР + 1)
При подстановке численных значений
Ф / Ч	500	(0,2/;-!- 1)
®\Р) — (0,2/7 + 1) (0,05/?+ 1) (0,07/?+ 1) /?+ 20 (0,07/? +
+ 1) р1 + 500 (0,2/?+ 1)
02-2-18. Начинать свертывание целесообразно с пере¬
носа первого сумматора через звено W3{p) по ходу сиг¬
нала (рис. 02-2-18,а), затем производится свертывание,
как показано на рис. 02-2-18,6 и в.
Рис. 02-2-18.
Передаточная функция ошибки
ф fn\	TJJsP'	+	TJtP*
С \Р)	(Тър + 1) (Г2р + 1) Тгр + klk2kz
02-2-19. Этапы преобразования структурной схемы
для устранения перекрестных связей показаны на
рис. 02-2-19. От схемы на рис. 02-2-19,2 переходим к схе¬
ме рис. 02-2-19,(5 с укрупненными блоками, по которой
ш (гЛ	W,W2W9	[W,WAWb	+	W4]
w KP) ~ 1— W2W3W± [^8+,\^8U76r7r9+ WbW'Wl0] —■
- r6 [W4W6W9 + w.w.w,
524

X(p)  и 1
Ws<p)-
wz(p) *- w3tp)
Wp)
w7(p)
Wjipn j
a;
V/»
W10(p)
Wa(p)
W2(p)W3(p)
—П ^ ^	-	WP)
-r^i \шГ\
-t 1 , 11 ■	, I ,	,	Y(p)
-	Щр)	-*>►	Ws<p) ■»-€>*- Wsip) —
ff>
Wjtp)
|KaWh
W2(p)Wjlp)
^j(P)
W5fp) ®-^-
щр)
в)
Wg(p)
Yfp)
AT//;
■ ^
w8(p)*
W2jp)W3(p)
\Wp>
w7tp)	■	w7(p)w9ip)\
' w3ip)wHip)\\ r|	w3(p)
*- ws(p)	w6(p)	■
Yfp)
Wgjp)
г)
w2(p) w-(p)
Щ
Щр)
W2(p)W3(p)W4(p)
r+Kj (p) w3<p) whip) wB(p)
W5tp)+ —
WP)
Wpp)Wu(p)
W3(p)Wg(p)
W3(p)+Ws(p)W7(p) Wg(p)
Yfp)
d)
ws(p)
W2tp)Wjtp)
■Wo<P>
Рис. 02-2-19.
15—903
225

02-2-20. На рис. 2-2-20 нет замкнутых контуров (А = 0), поэтому
в топологическую формулу (2) из задачи 02-2-14 подставляем
только прямые пути:
схема а: для Ф1 (р) = Y(р)/Xi(р) r\ = W3(p)\
для Ф2(р) = У(р)Да(р) ri = WiW3i r2=Wit
r3=w,tw2\
схема б: для Ф3(р) = У2(р)/Х(р) r'i=U74, r'2=W2W^
r3=WlWs;
для Ф^(р)=У2(р)/X(p)rl=W3\
Рис. 02-2-20.
схема в: Г\ — W3f r2=W3W2, А = ^4, r2=WiW3)
r3=WiW3W3',
схема г: r\~W3, r/2=W2W3, Гi=W ь, r2=WiW3, r3—WiW2\V?,.
Результаты преобразования заданных структур показаны на
рис. 02-2-20.
02-2-21. Преобразованные структурные схемы приведены на
рис. 02-2-21.
226
Рис. 02-2-21.

02-2-22. При рассмотрении прохождения сигнала Xi полагаем
равным нулю Х2 и одновременно из структурной схемы исключаем
сумматор для ввода второго воздействия. После этого структурная
схема преобразуется согласно рис. 02-2-22,-а—г. Аналогичные преоб¬
разования для сигнала Х2 при Ai = 0 дают структуру на
рис. 02-2-22Д Используя принцип суперпозиции, получаем структур¬
ную схему рис. 02-2-22,ет Для заданной структуры на рис. 2-2-22,6
преобразованная структурная схема дана на рис. 02-2-22,ж.
Рис. 02-2-22.
15*	227

Топологические признаки:
схема а:	контур Li = WiW2WsWi, и прямые пути от Xi
к У: Л = №3, r2=W3W2Wt и от 12 к У: /^ = №4, r2=W2W3Wi
позволяют сразу перейти к схеме на рис. 02-2-22,е.
схема б: контур Li=WW2WW4 и прямые пути к Yi Г\= Ws,
r2=WtW2Wz и к У2 Л = №4, r2=W3WiWit соответствуют схеме
на рис. .02-2-2,ж.
02-2-23. Общая для всех лучей часть ПФ свернутой схемы от¬
ражает один контур L\ и Л = 1, т. е.
1
w (р) = 1 _ г, о?) r2 (р> w, (р) w4 (P)wt (р) wt (р) •
Добавочные сомножители, образуемые из ПФ звеньев, распо¬
ложенных между входом для каждого воздействия и общим вы-
ходом, показаны на рис. 02-2-23 в виде отдельных блоков.
Рис. 02-2-23.
02-2-24. По операторной формуле, приведенной в ре¬
шении задачи 01-5-20, непосредственно строим структур-
ную схему, показанную на рис. 02-2-24,а и состоящую из
двух самостоятельных каналов. Вынося в используемой
формуле общие сомножители за скобки, получаем:
Y(p) = [Ty(Q.) + kX(p)]
Структурная схема показана на рис. 02-2-24,6.
228

Оставляя в левой части исходной формулы только
член TpY(p) и получая далее условное решение относи¬
тельно У(р) вида
У <Р) -=-у [-Г "YW —-Т 7 W +-У (°-)]>
строим по нему детализированную структурную схему,
показанную на рис. 02-2-24,в. В этой схеме ввод началь¬
ного условия производится непосредственно на входном
сумматоре с дополнительным коэффициентом Т или без
него на входе интегратора как изображения импульсов
(см. рис. 02-2-26).
Рис. 02-2-24.
02-2-25. По ПФ, полученной в задаче 1-5-31, с учетом
начальных условий строим структурную схему на
рис. 02-2-25,а. Если общий множитель для трех каналов
вынести в отдельный блок, то получится структура, по¬
казанная на рис. 02-2-25,6. Детализированная структур¬
ная схема, получаемая, как и в предыдущей задаче,
при переходе к условному решению, показана на
рис. 02-2-25,в. Начальные условия могут быть введены
на входной сумматор (после звена к) с теми же коэф¬
фициентами, что и в схеме на рис. 02-2-25,6, или пере¬
несены на входы интеграторов. Тогда согласно струк¬
турным правилам переноса коэффициенты при началь¬
ных условиях станут единичными.
229

Рис. 02-2-25.
02-2-26. Во временной области структура заданного
уравнения показана на рис. 02-2-26. Для стационарных
систем временная структурная схема совпадает с опе¬
раторной структурой, но все величины и операции запи¬
саны для временной области в форме оригиналов.
02-2-27. Запишем заданное уравнение в условно раз-
решенной относительно старшей производной реакции
форме:
D*y (0	(0	D3	+	Ьг	(t)D>	+	bx	(t)	D	+	ЬМ х (t) -
—\[at (0 Dz + аг (t) D2 + a, (f) D + a, (0] у (/)}•	(1)
230

-dn(t)
231
Рис. 02-2-28.

На структурной схеме, показанной на рис. 02-2-27,
для старшей производной входной величины построим
цепочку из трех дифференциаторов, а для перехода от
старшей производной реакции непосредственно к реше¬
нию введем последовательное четырехкратное интегри¬
рование. Тогда на входной части схемы легко найти про¬
изводные воздействия (выходы дифференциаторов) и
реакции (входы интеграторов) и по ним сформировать
дополнительные контуры схем в соответствии с форму¬
лой
у(0=I Щ ^ {к {t) D’x {t)+Ьг {t) х (0+b'(t) х {t) +
+ Ь. (0 X (0 - [Л, (0 у (0 + а2 (0 У (t) + Л, (0 у (0 +
+ (2)
02-2-28. Сопряженные уравнения с реверсированным
аргументом имеют вид [28];
К (t - ') g* У, *] + £ К (t -х)	(t, х)]+
+^Г [я2 V — т) «?* О *)] + К (* — х) (Ь х)] +
+ «,(*—')**(*. х) == 8 [х];	(1)
w* (t> х) = ^т- & (f —х) £* (г1, т)] +^r \b, (t — x) gm (t, x)] +
Iй' ^ x)l + b° V —x) О
Уравнение (1) получается из заданного путем пере¬
хода к однородному уравнению, применения операции
дифференцирования к произведениям приведенной им¬
пульсной характеристики у* на коэффициенты и ревер¬
сирования аргумента в функциях, описывающих коэффи¬
циенты t->t—т. Уравнение (2) для перехода от приве¬
денной импульсной характеристики к полной w*
строится по правой части заданного уравнения также
при переходе к дифференцированию произведений и ре¬
версе аргумента.
Реверсно-сопряженная структура, соответствующая
уравнениям (1),	(2), построена на рис. 02-2-28
путем следующих преобразований исходной структуры
(рис. 02-2-27): перемены местами входа и выхода, заме¬
232

ны сумматоров узлами, а узлов — сумматорами, измене¬
ния направлений всех сигналов и реверса аргумента.
Текущим аргументом, по которому осуществляется диф¬
ференцирование и интегрирование и обусловливается
нестационарность коэффициентов, становится т.
Другой путь построения реверсно-сопряженной струк¬
туры основан на переходе в уравнении (1) к условному
решению относительно старшей производной произведе¬
ния а4(/—т)g*(t, т) и построению по нему правой части
структуры. Левая часть структуры формируется непо¬
средственно по уравнению (2).
02-3. СТРУКТУРНЫЙ АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
02-3-1. Построение структурной схемы, соответствую¬
щей заданной электрической цепи поэтапно, представ¬
лено на рис. 02-3-1,а—в.
а)	Намечаются линии для изображений входной
Ux(p) и выходной Uy{p) величин.
Рис. 02-3-1.
Как разность этих напряжений формируется напря¬
жение, действующее на зажимах конденсатора Ci и ре¬
зистора включенных параллельно:
Ui (p)=Ux(p)-Uy(p).	(1)
Для этого на структурной схеме вводится сумматор,
к которому подводятся напряжения Ux(p) и —Uy(p).
233

б)	По напряжению Ui(p) и проводимостям парал¬
лельных ветвей l/Ru Cip находятся токи ветвей и их
сумма:
в)	По току h(p) определяются падения напряжения,
создаваемые им на последовательно включенных эле¬
ментах 1 /С2р, /?2» и их сумма:
Поскольку полученное напряжение является выход¬
ным напряжением схемы, свободная линия Uy(p) на
последнем этапе соединяется с выходом предыдущих
звеньев.
По структурной схеме определяется ПФ контура:
 	IRxCrf+ViRjCiP	+	l)
RXR2C 2pz +	^1^2	~Ь	^2^2)	Р ~г 1
02-3-2. Структурная схема фильтра показана на
рис. 02-3-2,а. Этапы ее построения даны укрупненно.
1.	Чтобы получить в виде простых разностей напря¬
жения на входных элементах фильтра, следует на струк¬
турной схеме ввести в виде свободных линий напряже-
имя и6(р)[—и6(р)] и Ua(p)[—Va(p)]. На рис. 02-3-2,6
показан этот этап построения структурной схемы и
условия получения необходимых разностей:	Ui(p) =
'=и0{р)—и3{р) и ик{р)=и0{р)—11ъ{р) на сумматорах
2. Умножая полученные разности на проводимости
Сф и 1 /Ri, для чего в структурной схеме введены звенья
проводимостей, получаем на их выводах токи h(p),
h(p)-
3. Далее для наращивания структурной схемы тре¬
буется структурно отобразить распределение токов. За¬
даемся свободной линией токов h(p) +h(p) [оба из них
определяются одним напряжением £Мр)], показанной
(3)
1 и 2.
234

на рис. 02-3-2,6, и, вводя в структурную схему сумма¬
тор 5, получаем на нем ток Is(p)=h(p) — [h(p) +h(p) ]•
4.	Умножая ток 1з(р) на сопротивление резистора R6>
для чего на структурной схеме вводится звено Яз, полу¬
чаем на входе звена напряжение t/3(p). Оно использу¬
ется, во-первых, для ликвидации свободной линии —
U3(p)y т. е. для включения ее в замкнутый контур, и,
во-вторых, на сумматоре 4 формируется необходимое
дальше разностное напряжение U5(p)—U3(p) — Ue(p).
5. Напряжение U5(p) достаточно умножить на сумму
проводимостей С2р + 1//?5, для чего на структурной схеме
введены два параллельных звена проводимостей и сум¬
матор 5, на выходе которого получается суммарный ток
h(p)+h(p), используемый прежде всего для ликвида¬
ции свободной линии токов, т. е. для включения линии
h(p) +h(p) 'В замкнутую схему.
6. Последним этапом является получение тока h{p)
на сумматоре 6: /6(-р)=/4(р) + [/2(р) + h(p)] и умноже¬
ние его на сопротивление резистора R6i что дает напря¬
жение и6(р)=Я61б(р)) позволяющее ликвидировать по¬
235

следнюю свободную линию, т. е. окончательно замкнуть
схему. Общая ПФ схемы от U0 к UG
т\7 / „\ Ь%Р2 + bip + b0
(Р)	ct2p* + alP + a0 ’
где
О (Ь+ '}■
«.=«.C, + S.(Ci + CJ \^ + l)+R,C,g-;
&2 = R3RSC1C,\
b =^~ (— 4-l\-
• R* \R, ^ )’
bi=£ACi+KA{Ct + Cj;
b2 = R3R££2 = a2.
02-3-3. Работа усилителя постоянного тока с отри-
дательной обратной связью при больших коэффициентах
усиления прямой цепи проходит при весьма малых на¬
пряжениях на входе первого каскада (АС/—5-0). Прене¬
брегая этим напряжением в расчете внешних контуров,
получаем входной ток
Л (р) = U (р) + 1с (р) = (/- -НР*р) и* (р) о>
и условия для построения’по формуле (1) начального
участка структурной схемы на рис. 02-3-3.
Рис. 02-3-3.
Так как сеточная цепь усилителя тока не потребляет,
то он полностью будет протекать по цепи обратной свя¬
зи, создавая на резисторе R2 падение напряжения:
U2(p)=R2Ii(p).	(2)
Учитывая, что точка 1 электрической схемы (см.
рис. 2-3-3) имеет потенциал земли, то это же напряже-
236

ние вызовет протекание через конденсатор С2 подпиты¬
вающего тока I2(p)=C2pU2(p).
Суммарный ток 13(р)=11(р) +12(р) создает на рези¬
сторе Ra падение напряжения
U3(P)=RMP)-	(3)
Суммируя напряжения (2) и (3), получаем выходное
напряжение усилителя и заканчиваем построение струк¬
турной схемы
Uy(p)=U2(p)+U3(p).	(4)
Сворачивая структурную схему, получаем ПФ усили¬
теля:
W{p)=W)=(R'+R>+клс*р) Q-+CiP) ■ (5)
02-3-4. Согласно условию задан источник э. д. с. Е(р),
а на структурной схеме требуется показать линии тока
1(р) и напряжения на нагрузке U (р), что и сделано на
рис. 02-3-4. Для получения разности U—E—/ZBH на
структурной схеме введена отрицательная обратная
связь через звено ZBH(p).
Таким образом, сопротивление источника питания на
структуре учитывается дополнительным контуром отри¬
цательной обратной связи, охватывающей звено прово¬
димости нагрузки. По структурной схеме получаем:
Пр)	Y(p)	_	1
Е (р) - 1 + Y (р) Zm (р) Zm (р) + Z (р) ’
^ (Р) _	1	—	z	(Р)
Е (р)	1	+Y(p)Z^P)	Z(p)	+	Zm(p)	‘
237

02-4. ГРАФЫ
02-4-1. Построение структурной схемы обычно начи¬
нается е задания системы уравнений (формализации) и
перехода к условно разрешенной форме. Эти этапы тре¬
буются и при построении графа. Однако поскольку
в условии задана непосредственно структурная схема,
уже опирающаяся на предварительные этапы, то граф
Рис. 02-4-1.
просто копирует существенную часть структурной схемы
в более компактной форме, как показано на рис. 02-4-1,а.
Компактность рисунка достигается: вынесением записи
ПФ звеньев непосредственно на линии, менее рельефным
и однотипным показом узлов и сумматоров, использова¬
нием дуговых линий.
Для получения функции передачи графа следует на
рис. 02-4-1 наметить все комбинации замкнутых конту¬
ров Lu и прямых путей передачи сигнала Гк.
238

На рис. 02-4-1,6 показаны шесть различных контуров
с ПФ:
с	U=W2WzWkWb-
L%= W2 W ~W13 W1 (i /\ 12;
L3=WkW5W6W9-
U=W2W3 Г4 W5 WeKis Wl0Ki2]
Li=W2W7WeWeWtWa;
Ьб—WioKu.
Два возможных прямых пути графа, показанные на
рис. 02-4-1,в имеют ПФ:
ri=Wl WiWaWiWaWeKu;
r^WiWzWjW tKu.
Применяя формулу (2) из задачи 02-2-14 для рас¬
сматриваемого графа, получаем:
ф/„\=	Л (1 - £6) + АО + Lt)	 ,j.
1 — (Li + £2 + i3+ £ф + Ь6-Ь Lt) + L6 (Lt -(- L3 + i5)
или после подстановки ПФ контуров и путей
W/u'W. + ^7) (1 -
w ~ 1 - [HWT, (W'a +	+	w2wswlcKl2Ku	(W,	+	•
+	+	wjrw, +	+
+ WWP.) + W*WtWtWt] K„wi0
(2)
02-4-2. На заданной структурной схеме намечаем
замкнутые контуры, так же, как это проводилось в пре¬
дыдущей задаче по графу. Передаточные функции кон¬
туров:
Li=W2WsWtWa;
L^WsWjWeWu;
L3=WiW5WeW9;
U=W2W3WtWsW6W10-,
U=W2W1W,W9W!lW8.
Точно так же по заданной структурной схеме наме¬
чаем прямые пути:
r^WiWzWaWiWsWe;
rz=WiWiW1Wa.
239

Так как все контуры при любой парной комбинации
имеют общие элементы, то парные произведения и триа¬
ды в формуле передачи отсутствуют. Нет также в схеме
автономных контуров, не связанных с прямыми путями.
Поэтому ПФ для данной структуры имеет вид:
Ф = | - (L, + Ц+Ц + Li+L<)'
Подставляя ПФ контуров и путей, получаем:
	Wtw,w,	(W,W<WB	+ W7)
~~ 1 — WtWtWt (WiW7W,l+ W3) — W3WtW10 x •
X (W3WtWs + W,) - W,W3W3W3
Этот же результат следует из предыдущей задачи
при замене в формуле (2): /Cu=0, /Ci2=Ai3=Ki4= 1.
02-4-3. Полагаем в заданной ПФ числитель равным
1 и записываем операторное уравнение для приведенной
импульсной характеристики:
(a3p3+a2p2+aip+ao)G(p)=l.
Рис. 02-4-3.
Переходим к условно разрешенной форме и по ней
на рис. 02-4-3 строим нижнюю часть графа:
0 М = I1 +	а~а' Р~~ а*р^ G(^l-
Используя числитель заданной ПФ, устанавливаем
связь между приведенной и полной импульсными харак¬
теристиками в операторной форме Ф(р) = (Ь\р+Ьо) G(p)
и достраиваем на том же рисунке верхнюю часть графа.
240

Для проверки функции передачи графа по общим;
правилам находим ПФ контуров
Lj =	CL^Ct/^	р \
Lt = — aji~xp-*\
3
L%= й0а3 р
и прямых путей
Л = «3 lbiP~*>
Г2 = а~хЬ,р-\
Поскольку нет контуров, автономных по отношению
друг к другу, и путям, то передаточная функция имеет
вид:
Ф (п) = г' +
^КР) 1 _(L1 + L2 + L3)*
Подставляя ПФ контуров и путей, получаем:
ф(п)—	ь'Р-*±ь*р:1
W а3 + а2р~ 1 + ахр-2 + а0р~3 •
После преобразований получаем ПФ, заданную
в условии.
02-4-4. Намечаем на стволе графа вершины для вы¬
ходной переменной ух и для производных — переменных
СОСТОЯНИЯ Уг (*=1, 2, 3, 4). По стволу связь между
Рис. 02-4-4.
смежными переменными осуществляется через интегри¬
рующие звенья, изображаемые на рис. 02-4-4,а как р~1у
что соответствует условному решению каждого уравне¬
ния системы (а). Чтобы в вершинах графа получить
все слагаемые, из правой части уравнений (а) вводим
16—903
241

вершину графа для воздействия х и от нее проводим
ребра с весами a j (/= 1, 2, 3, 4), а также образуем дугу
а0 и дуги с весами —a^fp (k=\, 2, 3). Построение графа
закончено.
Топологические признаки построенного графа:
A==cxi/p; Г2=а2/р2; А=аз/Р3; A=ct4/P4;
L1=—а3/р;L2=—а2/р2; L3=—ailp, U=—a0lp.
Устанавливаем общий вид искомой ПФ:
4
2	-	Л (L> +	+	La)	-	Л	(£, + l2) - r3L,
F(/>)=^	;	•	0)
i-2 ч
/=i
После подстановки значений A, А и умножения
числителя и знаменателя ПФ на р4, получаем:
РзД3 Ч~ РгР2 Ч~ PiР ~Ь Ро
W(p)--
(2)
где
Р, = <Х,; Рг = а2 Ч- ai<2ai ®t=a3 + aia3+a2a3'.
Р, = «4+ * А + а2«2 + * А-
В общем виде можно записать:
Ро
И, До Д3 1
1«.|
р.
д2 д3 1 0
а..
р2
аг 1 0 0
аз
Рз
10 0 0
а4
(3)
(4)
р = || а/01| а,	(5)
где ||а/0||—обозначение полученной выше треугольной
матрицы.
На рис. 02-4-4,6 в вершинах графа совмещены пе¬
ременные состояния и их производные, отделенные сим¬
волом интегрирования и обозначенные точками. Такой
граф называется гибридным. Он наиболее экономичен
в начертании и для отображения систем ^дифференци¬
альных уравнений, заданных в нормальной форме. Для
этой цели всем коэффициентам уравнений приданы двой¬
ные индексы, соответствующие концу и началу ребра
(дуги) графа. Кроме того, в коэффициентах учтено из-
242

менение знака, что потребовало введения нового обозна¬
чения &4г=—а%-1 (/=1, 2, 3, 4).
В сложных гибридных графах полностью все связи
можно не рисовать, отображая их отдельно прилагаемой:
матрицей коэффициентов В. Для рассматриваемой за¬
дачи
В:
02-4-5. Из выражения (5) предыдущей задачи для;
общего случая получаем:
а=||а/0|Мр.
Из выражения (4) имеем:
0
1
0
0
0
0
1
0
0
0
0
1
ь41
Ь.12
^43
Ь44
CL\ CLi
а3 1
а3 1	0
1	0	0
_1
10 0 0
Поскольку det||a/0|| = l и \\а/0) 1!т=||а/0||, обращение
матрицы сводится к вычислению для каждой ячейки;
алгебраических дополнений (адъюнктов), т. е.
ООО	1
|| а/0 11-=
0
1
а2 1 |
а2 а3
а3 0|
а3 1
Следовательно,
а\
а3
1
01
а2
1
ах
а2
а3
а 2
1
0
—
CL2
«3
0
—
а2
1
я3
0
0
03
1
0
аг
1
0
1 —а.
0
1
—а3
а2,— а9
а! — 2 а2а3+ а23
г 2	азРз
Pi—	+ (а2з— а2) рз
• (а2 — а23) (32 — (а, — 2а2а3 + а23) \
16*
243'

02-4-6. Ввод входной переменной х через коэффици¬
енты щ более подробно показан на рис. 02-4-6 для ком¬
понента ci2*. Вследствие переноса этого компонента в вер¬
шину г/4 появляются согласно рис. 2-4-4,а три слагаемых:
агр2* — инверсируются ПФ прямого пути;
—сteP2(—а3/р)=а2Дзр* — изменяется	при переносе
знак в ребре а3;
—агр(—аг/р)— а2а2* — изменяется при переносе знак
з ребре аг.
р-1	\у2	р'1
-аг	2%
р Т Р
Рис. 02-4-6.
Коэффициенты при ргх, рх, х, т. е. ае, аеЯз, агйг. вхо¬
дят в состав коэффициентов Рг, Pi. рэ. описываемых фор¬
мулами (3) в задаче 02-4-4.
Точно так же переносятся остальные щх, дополняя
:pft до значений, указанных в (3) для задачи 02-4-4.
02-5. ТОПОЛОГИЧЕСКИЕ И БЛОЧНЫЕ ПРЕОБРАЗОВАНИЯ
МАТРИЦ И ОПРЕДЕЛИТЕЛЕЙ
02-5-1. Все топологические построения производим
непосредственно на матрице коэффициентов, для чего
строим ее на рис. 02-5-1 со следующими упрощениями
по сравнению с заданием: вместо нулевых коэффициен¬
тов оставляем пустые ячейки, а в заполненных ячейках
вместо коэффициентов (или ПФ) записываем только
их индексы:
ik==Wlk.	(1)
а)	Построение замкнутых контуров Li, Lz, L3, L4 на
матрице производим по следующим правилам:
244

обходим контуры против часовой стрелки с обяза¬
тельным чередованием диагональных и недиагональных
коэффициентов;
из каждой строки и. столбца матрицы в контур вклю¬
чаем только по одному недиагональному коэффициенту,
исключаемые же коэф¬
фициенты, пересекае¬
мые линией контура,
обводим дугами;
по условиям замы¬
кания контура число
входящих в него диа¬
гональных элементов
должно быть равным
числу недиагональных
элементов.
Контуры на матри¬
це эквивалентны кон¬
турам на структурной
схеме [25], построен¬
ной по уравнениям,
приведенным к условно
разрешенной форме,
коэффициенты которых заключены в матрице, содержа¬
щей инверсные диагональные коэффициенты с обратным
знаком, т. е.
9kk'==-\fWhk.	(2)
Для раскрытия определителя топологическим контур¬
ным методом предлагается формула
А=Д(1—+	—2LfLftL/+ • . .)>	(3)
содержащая Д— диагональный элемент определителя,
ПФ одиночных контуров Lh пары, триады и другие про¬
изведения ПФ контуров, не имеющих общих элементов,
как и в задаче 2-4-1. Для заданной матрицы согласно
рис. 02-4-4 имеем:
■Д
[1 - S ^
£,= 16-
Ls=14
L4 = 56 • ”55” ■ 65 • ”66
JI = WttWnW»WjruW„-,
”1 1” •21•”22”•32 ”33”•53•”55”•65
14-”11” 41 ”44”;
”66"-
Ls = 23-”22” 32 ”33'
(4)
(5)
(6)
245

Перемножая члены формулы (4) с учетом (5) и (6),
а также обозначений (1) и (2), получаем:
A=WuW22W33W44W55W66—WuiWtiWsiWuWbsWes—
—WuWaiWaiWnWssWee—WnWsiW^WuWssWee—
—Г,, W22W33Wi,W56We5+ WnW2b «7з2Г41 H755ir66 +
+ Г ,4^22^33^4,1^56^65+ ^1,^23^32^^66^65—
-^4^23^32^41^56^65.	(?)
б) Этот же результат мог быть получен по известной
формуле, охватывающей все комбинации перемножае¬
мых элементов:
i = Z(-l)X),V3,,X...X«V	(8)
в которой для определения знака следует выписать пе¬
рестановку П из вторых индексов в сомножителях (8),
т. е.
IJ=qu #2, <7з> <74,	<7б>	(9)
и подсчитать число инверсий И в перестановке (9).
Проверим таким путем знаки у пятого и седьмого
слагаемых в формуле (7). Запишем перестановку #5=^
= 1, 2, 3, 4, 6, 5 и число содержащихся в ней инверсий
#5=0 + 0+0 + 0+1=1, где каждое слагаемое равно чис¬
лу стоящих справа и меньших по значению индексов
в перестановке. Поскольку #5 — нечетное, то знак пя¬
того слагаемого «—». Для перестановки П7=4, 2, 3, 1,
6, 5 имеем #5=3+1 + 1+0+1=6, т. е. число инверсий
четное и знак седьмого слагаемого « + ».
02-5-2. а) Замещенный столбец в определителе ука¬
зывает, относительно какой переменной находится реше¬
ние. В задании в определителе замещен первый столбец
и, следовательно, искомая реакция Y\. Строка, в кото¬
рой располагается коэффициент /Си, указывает номер
уравнения, в которое вводится воздействие. Согласно
заданию /Си расположен в четвертой строке, следова¬
тельно, воздействие вводится в четвертое уравнение.
б)	На рис. 02-5-2 помещена матрица системы та же,
что и на рис. 02-5-1, и на ней намечен прямой путь
Г\="АА" • 14 •"! 1",	(10)
246

состоящий из диагонального элемента четвертой строки
и последующих отрезков, принадлежащих контуру L2,
которые при движении по направлению обхода контура
приводят путь к диагональному элементу «11», принад¬
лежащему первому столбцу.
Для раскрытия замещенного определителя с исполь¬
зованием топологических свойств прямых путей и конту¬
ров исходной матрицы коэффициентов предлагается сле¬
дующая формула:
а*«=-/сд[2г/l-S +
[ (k) V />
- 2 LjL^+J
(j, i, e)
(")
где исключаются все контуры, связанные общими эле¬
ментами не только между собой, но и с прямыми путя¬
ми. [Знак — у коэффи¬
циента К определен	Г/
условиями согласова-	г
ния со знаком форму-	j	11	/
лы (2).]
Согласно рис. 02-5-2	|	zi
прямой путь на матри-	|
де возможен только
один;
независимыми
ЯВЛЯЮТСЯ ТОЛЬКО КОН- кЧ1 . 4/
туры L3 и L4, а потому
формула (11) приобре¬
тает вид:
Д к = -КмДуГх[\- 1
— (L34-L4) +L3L4].
(12)
Подставляя значе¬
ния сомножителей из
формул (5), (6) и (10) и учитывая обозначения (1) и
(2), получаем:
Д/~—/С41 • Д • "44"-14-"11" "(1 —23• "22"• 32 • "33"—
—56."55"*65-"66" + 23*"22"*32*"33"*56*"55"-65*"66") =
=/(41 ^14 ( W22WZzWbbWm~W2ZW,2WbbW„-
-W22 ^33^56^5+ 1^23^32^56^65) .	(13)
247

в) Проверяем знак первого слагаемого формулы (13)
tt^i4^22^33^4i^55^66. В перестановке Пi=4, 2, 3, 1, 5, 6
число инверсий И\—3 +1 + 1 +0 + 0=5. Согласно формуле
(8) в силу нечетности Их имеем знак —. Для четверто¬
го слагаемого Л4=4, 2, 3, 1, 6, 5, откуда Я4=3+1 + 1 +
-/-0+1=6. Благодаря четности имеем знак + .
г) Искомая ПФ
Ф/ЛЧ У\ (Р) _ Д& по формуле (13)
Хь (/?)— А по формуле (7) '	v	;
02-5-3. Структурная схема для полного и наглядного
учета всех контуров получена на рис. 02-5-3 путем не¬
которой деформации рис. 02-3-2 и разделения линий
формирования токов /2 и /5.
Рис. 02-5-3.
Основной прямой путь
л = 27 Я. 27^6	C1(C2jd*	(15)
отображает получение тока по разности напряжений
после умножения ее на проводимость, а затем по сумме
248

токов — путем умножения ее на сопротивление и т. д.
Поэтому обязательно на структурной схеме чередование
проводимостей и сопротивлений.
Второй прямой путь
(16)
отличается от первого только участком 1 /R5 вместо па¬
раллельного С2р.
Третий прямой путь
(17)
наиболее прост, так как не содержит операций форми¬
рования промежуточных напряжений.
Схема содержит восемь контуров:
L, = — Rfi,p\ L2 = — R3C2p;
Lt = -RtCtfr,
L. — -
*L.
R*
I — Иь.
4 Rs •
r   RsR«CzP T   RzRfi.P
7— R„ :	8—	«5
(18)
ния:
He связанные* контуры образуют следующие произведе-
R*R.clP
R*
KW-
R-Л
"ЯЛ
r j  j т R^RiPiP
— з^б—	p	.
(19)
Среди прямых путей только Г3 не имеет общих эле¬
ментов с контурами Lb L2, L6, поэтому функция пере¬
дачи для данной структурной схемы имеет вид:
иАр) _
у о (р)
+ Г2 + Г3 (^1 + ^2 +
•	2	^	^3	+	^б)	+	^2	^4	+	^б)	+	(^3	+	£4)	^6
(О
249

После подстановки значений (18), (19) и ряда сокра.
щений результат совпадает с решением задачи 02-3-2
02-5-4. Уравнение для узла >(< (см. рис. 2-5-4) будет
uljR1-{-Cul — i2. Уравнение для контура, содержащего
конденсатор и источник: Uo=(Ro+JR2)i2 + U\- Уравнение
для базового сигнала в дифференциальной форме
=%щ. Переписываем эти три уравнения в матричной
форме, перенося производные и переменную г2 в левую
часть, а функции состояния, к которым отнесем их и
г/0,— в правую часть:
(1)
Первичную квадратную матрицу обозначим q; в ее
состав входит блок
С -1
0 R
В состав прямоугольной матрицы из правой части (1)
входят блоки
1
0
0
uQ
II Х
0
0
с
—1
ах
1 °
Y,
0
0
R
%
II 1
—1
Y> =
■1/Я,:
U =
а0
«1
0
—у,
; Q =
1
—1
1 0
и
X
0
0 q
i2
1
Q
что позволяет уравнение (1) записать в блочной форме:
U.	(2)
Для перехода к нормальной форме Коши определяем
обратные матрицы:
i-li0,-
,4	.	С	—	1
где detq =
и А
250
ji
i
с
R 1
0 С
j detq,
=RC = (R<>+Ri)C.

Умножив (1) или (2) на q
Uо
Ог
iч
получим:
1 0 0
X 0
и,
0 1/С’ 1/RC
0—Y
*
О
О
1—1
и,
X 0
и.
l/RC — (R, + R)/RRlC
1 /R -1 /R
(3)
Третья строка в выражении (3) имеет самостоятель¬
ное решение для i2=(t/0—U\)jR, если определены пере¬
менные состояния из уравнений
и0 = X о и0
и,	1	IRC	—з	t/,	к	'
где
а =	^ ~Ь *.
(Rz + R„) R,C
Решение (4) в форме матричного экспоненциала
	 	 " *7):
ехр Xt	О
[ехр Xt — ехр (— at)]/RC (X + о) ехр (—at)
"(5)
В (5) сохранена информация о входном сигнале gn,
о базовой характеристике — вынужденном компоненте
напряжения на конденсаторе got и свободном компонен¬
те разряда конденсатора g22> что требовалось в условии.
40{t) 0
4t,i)g(t)
Г лав а третья
АНАЛИЗ И ОСНОВЫ СИНТЕЗА ЛИНЕЙНЫХ
СИСТЕМ НЕПРЕРЫВНОГО УПРАВЛЕНИЯ
03-1. точность вынужденного движения
СТАЦИОНАРНЫХ СИСТЕМ (С постоянными
ПАРАМЕТРАМИ)
03-1-1. Общее выражение для ошибки преобразова¬
ния определяется в виде ряда
С (0 = фс (0) д: (0 + Ф'с (0) X (0 +	X (0 +
Фс
3!
X(f)-
Фг (0)
4!
251

Функция передачи ошибки (р) определяется как раз¬
ность между фактической и эталонной [ПФ:
<■>
Производные от ПФ ошибки при р=0 наиболее
просто находить по формуле непрерывного деления
обращенных полиномов числителя и знаменателя П)'
— тТ р2
— мТ р2— тТ2ръ
1 +Тр
т(—Тр2+Т2р3— Т3р*+ ...)
 тТ2рг
тТ2ръ+пгТг рА
 — тТър4
— тТгр4 — тТАр6
тТАрь
Поскольку
m (- Трг + Гр3 — Гр4 + ...) = <М°) + ® V (0) Р +
. Ф^' (0)	фГ(0) , , фГ (0)	,
Н	2!—Р 	3!—Р	4!	Р
то, приравнивая коэффициенты при одинаковых степенях
р, получаем:	Фс (0) — 0; Ф'с (0) = 0; Ф"с (0) = — ЪпГ\
Ф'" (0) = 6шГ; Ф<1У) (0) = — 24тТ3 ...
Тогда
С (t) = _т {Тх (0 - Гх (0;+ ?VIV) (0 - • ••} ■
В случаях «а» и «б» все высшие производные x(t),
x(t) и т. д. равны нулю, поэтому £(0=0. Для случая «в»
x(t)=xPv’>(t) = ... =0, но £(t)=a.
Следовательно, Z,(t)=—amT.
03-1-2. Значения ПФ ошибки и ее производных вбли¬
зи точки р=0:
Фс(0) = 0; Ф\ф) = — 0,002;
Ф"( (0) = — 0,0032;	(0)	=	+	0,00096	...
Ошибка преобразования управляющего сигнала ре¬
альным форсирующим звеном представится в виде ряда
I (t) =—0,002* (t) —0,016x (0 +0,00016* (f) — . • •
252

03-1-3. Реальная ПФ системы
ф/д)_ wW-= к.!ПЕ
^\р)—х +W(p) (T + km)p+l >
а эталонная Г1Ф дифференцирующего звена Фэ(р) —
=kmp.
Тогда ПФ ошибки
ф ip)=	kmp=-pJT	+	b”)p
с \г/ у*	р+\	^	(Т	+ km) р + 1
Производные от ПФ ошибки при р=0, получаемые
путем деления обращенных полиномов числителя и зна¬
менателя:
Фс (0) = 0; Ф'с (0) - 0; Ф"с (0) = — 2km (Г + km);
Ф"'с(0)=6 km(T + kmy.
Фактическая ПФ системы по возмущению
тр
Ф п(Р)
<? + km)p + l >
а желаемая функция влияния равна нулю. Тогда коэф¬
фициенты ошибки по возмущению равны:
Фв(0)=0; Ф'в(0)=т; Ф"в(0)=—2m(T+km);
Ф"'в(0)=6т(7Ч-*т)2...
Следовательно, суммарная ошибка
СЕ (t) = — km (Гkm) х (t) -\-km(T -)- km)*x(t) —...
... m5 (0 — m (T -|-km) l(t)-\-m(T-\- km)* £ (0-(-...
03-1-4. Передаточная функция ошибки и ее произ¬
водные вблизи точки р=0:
фс (0) = 0; Ф'с(0) = -й(Г1 + Г,);
Ф”с (0) = - 2ft [(TtTt + 257Т, + 2\ТТ2) - (7\+ Г,)2] и т. д.
Ошибка преобразования относительно эталонного
форсирования определяется в виде ряда
m=-k{Tl+Ta)x[t)-k[(TlT2+2lTTl+
+2|7Т2) -(Тг+ЪУ2] х
Для нашего случая £(0=—0,0035а:(t)—0,026x(t) —...
253

-1'
03-1-5. Коэффициент усиления прямого тракта k.
= 600 с-'. Полученный коэффициент име-
х	0.6
. Лмакс
| е, |	0,001	'
>ет физический смысл коэффициента усиления по скоро¬
сти (см. размерность).
03-1-6. Коэффициент усиления по ускорению
х	6
и 	 *макс	 __ JQQ с-2.
03-1-7. Коэффициент передачи полезного сигнала
в соответствии со схемой на рис. 3-1-7
иу
Ф — —
• иг
-Г (Г0Г> + f«r! + Г^*) + Г,Гг
При большом коэффициенте усиления Ф0^—Го/г\-
Влияние возмущений учитывается коэффициентами
'нестабильности анодного питания, влияния дрейфа сет¬
ки лампы, влияния дрейфа напряжения смещения и влия¬
ния тока нагрузки.
Коэффициент влияния нестабильности анодного пи¬
тания
ф 	 «1	_	Г0Г, + Г0Г2 + гхг2
'	Г0гх	+	гвг2	+	г,г2	(\+k)	*
При большом коэффициенте усиления
ф  r0rl+r0r2 + гхг2
1	rxr2k
Если пренебречь проводимостью 1 /г2, то <Di^(/vr
~\-ri)jrxk.
Коэффициент влияния дрейфа сетки лампы
Ф,=
е2 	 Г0Г1 ГиГ2 Г\Г2
Ар ~~д~ (rQrl r0r2-\- rxr2) r,r2
При большом коэффициенте усиления
ф 	   Г0Г1	Н~	Г0г2	4~ Г1Г2
2 r г
I if 2
При большом сопротивлении г2 Фг^—(ro+ri)/ri-
254

Коэффициент влияния дрейфа напряжения смещения
совпадает с коэффициентом передачи полезного сигнала
Ф = ——— = Ф
At'cM
Коэффициент влияния тока нагрузки 1тгр
03-1-8.
Ф. = -> *	=——R. — R Ф
JHarp	''а'нагр
Щ макс	120
У- К	:	60	ООО.
'0,002
03-1-9. Принужденный компонент ошибки gnp при гар¬
моническом управляющем воздействии je=Jtasin<Da/ пред¬
ставляет собою также гармоническую функцию
£Пр (0 = xaAt (юа) cos [«+ + 9е К)]»
где Ле((ва) и 9, (»а) — относительные значения амплитуды
и фазы, соответствующие ПФ ошибки Фс (/«*>) при данной
0) = 0)а» определяемой выражением
Ф (im) =	64i+	2й)8	+	со* .	5<о» + 110т
'	1024+17а>2 + со4 ' > 1024,+ 17<о2 + <о4 '
При Хл = 1 И ша = 0,2 С-1
фс (/*)««-, = G К) + JB К) = 0,062 + /0,00018;
А (ша) = 0,062; tg 9, К) = 0,0029;
9, К) = arctg 0,0029=0° 10'; «уст= 0,062 cos (0,2/+ 0,0029).
03-1-10. Передаточные функции для ошибки, или так
называемые относительные ПФ систем [251, будут иметь
вид:
а)
б)
ф (г)—	1	  3,64+	+ 3,5+ + 2,99р
С	1	+	Ц7	(р)	^4+	3+4++	3,5++	5,23р+ 1 ’
J р2 4- 4р + 2
1 +W(P) Р2+Ър + 32*
Значения коэффициентов ошибки:
а)	Соо=0; С01=2,99 с; С02=—12,14 с2...
б) С00=1 /16; Сох=55/512 с; С02=—15/6384 с2.
255

03-1-11. Свертывая схему, получаем ПФ разомкнутой
системы:
W (п\ — k 1
W (Р,~~ Т\врЦТр+1) ’
-где k—kukAkKkyk№.
Передаточная функция ошибки
(1) /nv 		1	Рг	(Тр+\)Т\а
<(Р) ~~ 1 + w {Р)~~ Т\вр\{Тр + 1) + k (TlP + 1) •
Передаточная функция влияния возмущения
Wm(p)	ТР +1
ФСМ \Р)	{-L.W (р) —Т\вР2 (Тр + 1) + k(TlP -г 1) ’
где WRB(p)=l/T\Bp*.
Ошибка в передаче управляющего сигнала
SvcT = liin Р\ (Р) Qx (р) = T\Bqlk.
р-* о
Ошибка от возмущающего воздействия
С = Urn р х фсм (р) мв (р) = MJk-
р-> о
03-1-12. Используя результаты решения	задачи
3-1-11, получаем:
С1уст = 1Ш1/7ФС(^) “7=0;
p-+Q	*
C«vct=lim Ра\м (Р)\М*Р = MJk — 0,0022МВ;
р-* о
£уст=0,0022Мв.
03-1-13. Для удобства свертывания схемы перенесем
сумматор 2 по ходу сигнала и	совместим его	с суммато¬
ром 3 (см. рис. 3-1-13), после	чего получим:
для ошибки
— У ,	(^УР ~1~ ') УчР ^ Ур	Р	Р .
Фс № = kyp+ 1) (ТЧР + 1) Up (Тр + 1)+ k9_Ek,_MY\р+'
+ kr _ Tkcky _	EqSiq—BdYyV4Y
для возмущения
	feP	(Гр	+	О (ТуР + 0 (тдР + *)
ФСМ (Р) == (Typ+l) (Tqp + 1) [Ip (Тр+ 1) + kB_Ek,_MY\ р + ‘
+.ftr _ jkjty - n,kr_MkpSl_E^Sj^_E^YyYtlY
256

Следовательно, по управляющему воздействию систе¬
ма является астатической первого порядка, а по возму¬
щению — статической.
При Х(р)=Хо/р, М(р)=М0/р
Сет = lim р [Фс (р) X (р) -f Фш (р) Ма {р)\ =
р->0
 	М_ъ
Лг-т^с^у-дkf—M^r —Е ^1 —еУу^чУ
У Ч Я a
так как первое слагаемое равно нулю.
03-1-14. Ошибка в передаче управляющего сигнала
SiycT = litn р^г (р) X (рУ—
У I \rf \У/ и ъ Ь Ь ?	9	V	V
р^>0	4	Яг-тЛсЛу_д«р>/	__Е	—Е ,* Уг Ч
У я ч a
Ошибка от возмущающего воздействия
С2 == lim рФт (р) Мв (р) =
р-¥ 0
Мя
kr..Tkcky_ Ji1_MS[^_E^SI^_EYyYqY •
03-1-15. ПФ замкнутой системы
ПФ ошибки
Ф (п) —	152
уР' 0,00005/?* + 0,015 рг + /» + 100'
ф ,	  0.00005/»3	+ 0,015/»* + р
^{Р)— о,00005/»3 + 0,015/»г+/» + 100
Коэффициенты ошибки
Сох=0,01 с и С02=0,00005 с2.
Установившаяся ошибка
0ycT=CoiQ=O,Ol •10=0,1°=6'.
03-1-16. Для разомкнутой системы
й_,	_	10
W(p)
р(Тр+ 1)	р (0,5/» +	1)
Инверсная Г1Ф разомкнутой системы
УЛР) = Щ^ =;0,05/>* + 0,1/>.
17 —903	257

Ошибка x0(t) вынужденного движения в функции
выходной величины определяется выражением [25]
■*. (О = - С (t)=(0) у (0 + < (0) у (0 + М. у’до +...
Применяя эту формулу, получаем:
— £ (0 — ' У ~Ь	If/“К 0,Обу.
03-1-17. Преобразуем схему на рис. 3-1-17 к другому
виду — рис. 03-1-17. Общая ПФ прямой цепи в этом слу¬
чае W2(p)—k-ilp=\0lp.
Инверсная ПФ разомкнутой системы W2il (p)=p/k-1-
Рис. 03-1-17.
Ошибка вынужденного движения —t,(t)—y/k-i=0,\y.
Из полученного выражения видно, что в системе отсут¬
ствует ошибка от ускорения и старших производных вы¬
ходного процесса.
03-1-18. После переноса сумматора 2 на рис. 3-1-18
в точку А получим структурную схему системы, изобра¬
женную на рис. 03-1-18. Для получения инвариантной по
К(Р) ~
ШР)
Х(р)
й Т
Чр)
w2(p)
Уф)
-Бо¬
рис. 03-1-18.
отношению к управляющему воздействию системы необ¬
ходимо, чтобы ПФ ошибки
с {Р) — ф w	1 — 1 +Wt (р) W2 (р)
была равна нулю.
258

Отсюда получаем Г1Ф корректирующего контура:
LT / \   1		 UР Р + ^) + k^—E^kI—M\ Р .
А W — W2(P)-	kp(TP	+	\)
03-1-19. Инвариантность системы к возмущению I бу¬
дет обеспечиваться при равенстве нулю функции влия¬
ния:
ф (р) = Ш !	=1	1	-K(p)WAp)	_	_п.
в{/>	1(Р)~ l+w (р)	1	- К (р) W2 (р) + Г, (р) Г2 (р)
Отсюда система будет инвариантной к возмущению
при условии, если K(p) = l/W2(p)=0tl (0,5/?+1).
03-1-20. Условие инвариантности можно записать
в виде
—	=	—/игрЯя. откуда Wk(p)=RJSiw_e.
03-1-21. В соответствии с принципом двухканальности
акад. Б. Н. Петрова условие инвариантности запишется:
в виде
*(р) о^+т = -ЧрЖ(рУ,
отсюда ПФ корректирующего контура
/С(р)=-2/(0,6р+1).
03-2. ТОЧНОСТЬ НЕСТАЦИОНАРНЫХ ЛИНЕЙНЫХ СИСТЕМ
03-2-1. Ошибка слежения Z=y—х, откуда
У=х+£.	(1)
Подставляя выражение для у в левую часть задан¬
ного уравнения и преобразовывая его, получаем:
ъ (0Т(0 + !х2 (0 С(0 + w (0	+ i^o (0 С (0 =
= — К (0 ■*+МО •*+ М (0 — “i (0] '•* + К (0 — “о (ОМ
03-2-2. Подставляя зависимость (1) из решения преды¬
дущей задачи в левую часть заданного уравнения, а так¬
же имея в виду, что для заданной стандартной структу¬
ры схемный разбаланс равен по значению и обратен по
знаку ошибке слежения, т. е. х0=—£, получаем:
Уз (0 С+у2 (0 С + К (0 + МО] с + К (0 + «о (0] с =
= — [у, (0 х + у2 (0 х + у 1 (0 jc+у0 (0 л].
17*	259

03-2-3. Согласно общей формуле (28]
т
2 (s-Wbjit)
IF, (t, s)== ^	.
2 (s-Dyai(t)
i—0
Для рассматриваемого уравнения
Ш U с)	— ~	2*	+ 1
1 ' 9 '	(s3 — 3s2D2— D3) (5/2-|- 3/-|- 2) -j-	(s2 — 2sD+
+ D2) (At .4.	1) + (s - D) (2t2+ t +	3)ГЬЛ+.* +	1
ИЛИ
Wx s) =	t	_j_	25)7+7i::rS	*
Для /=10 с
Wx (10, S) 532s* — 268s2 + 235s + 70 ‘
03-2-4.	Находим	параметрическую	передаточную
функцию:
Wl	5^ ^ "5s2 + (s — D) (2/ + 20) + 137	”
2
5ss + (2f + 20)s+ 135	•
Изображение несмещенного воздействия X(s)=5/s2
Изображение параметрической реакции
^ (j. ^	 ю
<• \1> -V — S2 [5s2 + J2t + 20) s +1357' ’
которое для /=20 с будет составлять:
L /20	  -	2/27	24/272 i
— si(s>+ 12s+ 27) —" s2	s'
2/54 __ 2/486
s + 3 s + 9 *
Находим оригинал для произвольного рабочего ИИ'
тервала:
£(/, 0) =0,0740—0,033+0,037 exp (—30) —
—0,004 ехр(—90).
260

фактические рабочие интервалы и реакции в момент
времени /=20 с:
а) 01=20—10=10 с;
£(20,10) =0,74—0,033=0,7;
б) 02=20—19 = 1 с;
■5(20, 1) =0,074—0,033+0,037-0,05=0,043.
03-2-5. Используем из предыдущей задачи значение
Ц7,(/, s) для /=20 с:
Wу (20, s) = 5s2 + 42s + 135 ,
Непрерывное деление числителя на обращенный зна¬
менатель дает:
135 + 42s 5sa
2
"2-1-0,62s -1- 0,074s2
— 0,62s —0,074s2"
0,0148 —0,0046s...
По виду частного устанавливаем, что 20, 0) =
=0,0148; W'i (20, 0)=—0,0046. Отсюда в точке 0=
=20—19=1 с
5 (20,1) =0,0148* (1) -f-0,0046i (1).
Поскольку из предыдущей задачи *(0)=50, то для
0=1 имеем*(1) =5,£(1) =5. Поэтому£(20,1) =0,0148Х
Х5—0,0046-5=0,074—0,023=0,051. Легко заметить ана¬
логию с решением стационарной задачи 03-1-1.
03-3. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ
03-3-1. Для замкнутой системы ф(р)=Ц7(р)/(1 +
+W(p)). Так как IV(р) —Р (р) /Q (р), то Ф(р) =
=Р(р) I (P(p)+Q(p)).
Характеристический полином замкнутой системы
M(p)=P(p)-\-Q(p) равен сумме полиномов знаменате¬
ля и числителя ПФ разомкнутой системы:
Л4(р)=0,1р3+0,2р2 + 0,5р+1+Зр+10=
=0,1рЗ+0,2р2+3,5р+11.
Применяя критерий устойчивости Вышнеградского
(являющийся частным случаем критерия Гурвица), при
положительности всех коэффициентов а0>0; Н|>0; ао>
>0; п3>0 получаем: aia2—0,2-3,5=0,7; a0as=0,l-lf=
261

= 1,1; т. е. а1а2<аоаз. Следовательно, система неустой¬
чива.
03-3-2. аха2 = 17-800= 13 600; а0а3 = 0,1 -50 000=5000;
aia2>aoa3. Система устойчива.
03-3-3. Система устойчива.
03-3-4. Составим по правилу Гурвица матрицу из ко¬
эффициентов уравнения
2
1
0
0
10
1
2
1
0
20
10
1
0
0
0
20
из которой получим определители:
2 1
Д, = 2>0; Д2 =
10 1
= 2— 10 = — 8<0.
Система неустойчива и определять Д3 не имеет
смысла.
03-3-5. Из коэффициентов уравнения получается мат¬
рица
3	10	0
2 ю з 1
0 5 2 10
0 0 0 5
Для систем четвертого порядка достаточно проверки
положительности коэффициентов и предпоследнего
(третьего порядка) диагонального определителя
3 1 о
2 10 3
0 5 2
= 2 (30 — 2) — 5 (9 — 0) = 11.
Поскольку Дз>0, система устойчива.
03-3-6. Система неустойчива.
03-3-7. Вычисления по критерию Рауса удобно запи¬
сать в виде табл. 03-3-1.
Для заданной системы таблица Рауса будет иметь
вид табл. 03-3-2.
Поскольку коэффициенты первого столбца положи¬
тельны, система устойчива.
262

Т а б л и ц а 03-3-1
Параметры
а7
а г.
я3
Ol
ав
а,
а2
ао
Г°- а.
Си =
= аь— г0а4
сгг =
= А53 ■ Г q(Z2
*33 —
= а1— г0а0
t
ll
0
*18
*14 =
= а4е—г1с23
С24 =
= d2 Г1С33
C3i =
= й о /*1*4 3
С44— ^iC53
Г2=^
С14
С15 ~
==С23 /*2С24
*25 =
=*3 3 /*2*34
*35 =
=*43 /*2*44
*4 5 =*44 /*2*54
. . .
. . .
. . .
. . .
. . .
Таблица 03-3-2
Параметры
а7—0,104
а5=5,5
fz3—2d
а,= 19,7
ав=0,33
а4= 15,5
а2=25
а0=Э,5
/*0=0,315
0,6
17,1
16,7
0
/*1=0,55
6,0
15,8
9,5
0
/*2=0,1
15,52
15,75
0
0
/*3=0,386
9,7
9,5
0
0
/*4=1,6
0,55
0
0
0
г5=0
9,5
0
0
0
03-3-8. Для заданной характеристическим полиномом
следящей системы таблица Рауса будет иметь вид
табл. 03-3-3.
Из таблицы видно, что коэффициенты первого столб¬
ца положительны. Следовательно, система устойчива.
Для оценки устойчивости по критерию Гурвица из
коэффициентов характеристического полинома составим
матрицу:
0,35
0,0039
0
0
1,135
2,05
0,35
0,0039
0
3
1,35
2,05
0
0
0
3
263

У я б л и ц а 03-3-3
Параметры
rn=a4=0,0039
£2,=aa=2,05
Сз1=«о=3
rla=as=0,35
1,135
! Сяа=0
/•,=.£-.*0,001
1
—flj т =a 2,049
cS3=&9 — V qC32 = 3
О
11
1
o3
ri =~ = 0,174
C13
о 14—— г jCjj = 0,603
C24=C|5	Г iC33 = 0
с34 =■ 0
Ci«
гг — c =3,4
14
Cl 5 = C23 	г2^24 — 3 ^
<j„ = 0
С35 *= ®
Предпоследний диагональный определитель этой мат¬
рицы
0,35
0,0039
0
Дз =
1,135
2,05
0,35
0
3
1,135
= 1,135(2,05*0,35—1,135*0,0039)—3(0,35*0,35—0)«»
^0,445>0.
Поскольку коэффициенты характеристического поли¬
нома и предпоследний диагональный определитель Дз
положительны, система устойчива.
Сравнивая два критерия, с помощью которых оцени¬
валась устойчивость следящей системы, имеющей харак¬
теристическое уравнение четвертого порядка, видим, что
критерий Гурвица требует меньшего объема вычисли¬
тельных работ.
03-3-9. Для исследования на устойчивость линии вход¬
ных и выходных величин могут быть исключены, и схема
примет вид, изображенный на рис. 03-3-9. На основании
правил свертывания структурных схем получим следую¬
щие ПФ местных замкнутых контуров системы по на¬
правлению сигнала, действующего в общем контуре:
Л .	— Wx (р)	  —	ft
Фх \Р) —Х+ aWx (/7) —	р (Гр _|_ 1) ) + k COS Y	;
I - Wy (p)		—ft
фу (P) =, \\+ 'dWy(pY~ P {Tp+ D + k cos Y
264

Общая ПФ разомкнутой системы с отрицательной
обратной связью будет иметь вид:
W(p) = - ЬсФх (р) - рФу (р) =
k2 sin2 y
0 Q'p + 1) + k cos Y] [p (Гр + 1) + Л cos
k2 sin2 y
= TFQT+ 1) + * cos Yj2~ •
Рис. 03-3-9.
Независимо от входа и выхода в замкнутой системе
характеристический полином один и тот же:
M(p)=P(p)-]-Q (р)=Рр4+27р3+ (2Tk cosy+1)р2 +
+ 2kcos yp+k2eos2y + k2 sin2Y=Pp4+27p3+
+ (2Tk cosy+l)p2+p2& cosy+/(2.
Составим матрицу коэффициентов по Гурвицу в виде
табл. 03-3-4.
Таблица 03-3-4
2 Т
2 k cos Y
0
0
Т2
2 Tk cos Y + i
k2
0
0
2 T
2 k cos y'
0
0
Y 2
2Tk cos Y + 1
k2
Если изменение угла у ограничено в пределах перво¬
го и четвертого квадрантов, то все коэффициенты харак¬
теристического уравнения положительны.
265

= 4&2T2 cos2 у
Определим условия положительности предпоследнего
диагонального определителя, составленного из
табл. 03-3-4:
2Т 2 cos у	0
Дз = Т2 277jcosy+1	k2
0	271	2/г cos y
4kT cos у — 4k2T2 = 4kT [cos y — kT (1 — cos2 y)] .
Условие Аз>0 сводится к неравенству
kT<:	1	-	<0SY
•sinY^gY 1 — cos2y*
Это и есть условие устойчивости.
03-3-10. Для разомкнутой системы
тw (п\ —Ае1	-	-
Q(P) “ (0,05/? + l) (0,ip+ l) (0,2/?+ 1) ’
где k=kik$k3.
Характеристический полином замкнутой системы
M(p)=P(p)+Q(p) =
=0,001 p3+0,035p2+0,35p-f-1 +k.
Условие устойчивости по Вышнеградскому:
0,01225>0,001(1+А:).
Предельное значение коэффициента усиления опреде¬
лится из условия нахождения системы на границе устой¬
чивости:
и 	 0,01225	, , . qc
*пред'	0,001
03-3-11. Для разомкнутой системы
w/, ,	k	_Р (р)
W(P>— р (0,005+ 1) (0,2/? + 1) Q(p) •
Характеристический полином замкнутой САУ
7W(p)=P(p)+Q(p) =
=0,001 р3+0,205р2+p+k.
Условие устойчивости по Вышнеградскому: 0,205>
>0,001А
Предельное значение коэффициента усиления опреде¬
лится из условия нахождения системы на границе устой¬
чивости:
6пред=0,205/0,001=205.
266

03-3-12. Замкнутая система будет устойчива, если при
изменении частоты от нуля до бесконечности N-вектор
(вектор Найквиста) имеет угол поворота (измеряемый
целым числом квадрантов), равный сумме числа ней¬
тральных корней (i) и удвоенного числа правых корней
(2г) характеристического уравнения разомкнутой систе¬
мы [25]:
<Рл'уст=='1“(1' + 2г)-
а) Как видно из рис. 3-3-12,а, ф^=я. Так как для
заданной системы г=0 и г=1, то
?WycT==_i“(0 + 2) = 1t-
Система устойчива.
б) Из ПФ прямого тракта определяем i—0; г=2;
9Nyct = -Y -4 = 2*.
Как видно из рис. 3-3-12,6, фдг=0, а следовательно,
система неустойчива.
03-3-13. Угол поворота фМ годографа Михайлова для
характеристик системы управления с нейтральными ну¬
лями равен сумме углов фч+фг (угол до касательной-j--
4~Угол после касательной [25]: фМ=ф1-)-ф2=180о.
Используем формулу для определения угла поворота
М-вектора
9 м = (п ^гм *м)•
Поскольку годограф при частоте сог проходит через
начало координат, т. е. вектор Михайлова обращается
в нуль, характеристический полином имеет пару мнимых
сопряженных корней ±/сог (напомним, что мнимые кор¬
ни относятся к классу нейтральных).
Других нейтральных корней характеристический по¬
лином не содержит, так как годограф проходит через
начало координат только один раз. Следовательно, iM—
=2. Подставляя это значение в формулу для угла пово¬
рота: 2=4—2гм—2, получаем /*м=0, т. е. остальные два
корня полинома — левые (расположены в левой полови¬
не комплексной плоскости). Такая система находится на
границе устойчивости.
03-3-14. Ответы см. в табл. 03-3-5.
267

Таблица 03-3-5
№
варианта
Ответ
Л’->
варианта
ФЛГ
Ответ
1
тс
°т
Устойчива
16
7Г
-~3 2“
Неустойчива
2
тс
~42
Неустойчива
17
тс
+5т-
Устойчива
3
7С
+2Т
Устойчива
18
ГС
-3Т
Неустойчива
4
	2 —
z 2
Неустойчива
19
тс
+1т
Устойчива
5
тс
+22
Устойчива
20
Неустойчива
6
7С
21Г
Неустойчива
21
тс
+5Т
Устойчива
7
, я
+4Т
Устойчива
22
тс
3 ТГ
Неустойчива'
8
—4^
2
Неустойчива
23
тс
+5-2-
Устойчива
9
тс
+4Т
Устойчива
24
тс
“~3Т
Неустойчива
10
тс
~4Т
Неустойчива
25
тс
+2т
Устойчива
11
7С
+6~2
Устойчива
26
тс
"2Т
Неустойчива
12
13
""6 2
Неустойчива
27
ГС
+2 Т
Устойчива
7С
1 ТГ
Устойчива
28
ГС
—2Т
Неустойчива
14
тс
-Зт
Неустойчива
29
+6Т
Устойчива
15
+5т
Устойчива
30
-«т
Неустойчива
268

Продолжение табл. 03-3-5
Mb
варианта
*N
Ответ
Mb
варианта
Ответ
31
тс
+61
Устойчива
40
7С
Неустойчива
32
7С
6 "2
Неустойчива
41
ТС
+3Т
Устойчива
33
ТС
+6Т
Устойчива
42
ТС
~~Т
Неустойчива.
34
Неустойчива
43
тс
+7Т
Устойчива
35 '
+6_2
Устойчива
44
5-
2
Неустойчива
36
-т
Неустойчива
45
тс
+7Т
Устойчива
37
7С
+Зт
Устойчива
46
тс
-5Т
Неустойчива
38
тс
~~~2
Неустойчива
47
тс
+7Т
Устойчива
39
ТС
+ 3 -гг
Неустойчива
48
-5Т
Неустойчива
03-3-15. Запишем заданные уравнения в операторной форме:
(Т^р +\)pT(p) = k^A (р) + Мя = М/0;
{ГЬР+ 1) А (р) = feB/y (рУ,
h (р) —kyUu(p);
Un(p) =Аи[ГПр(р)—Г (р) ] = kaAT(p).
Передаточные функции звеньев

™ , ГУ W
w^P'> = un(P) =V
W* № = ДГ (p) =
Структурная схема системы будет иметь вид, показанный ра
рис. 03-3-15,а.
Свернем структурную схему между сумматорами 1 и 2 и полу,
чим упрощенную структурную схему, изображенную на рис. 03-3-15,6
Un
L
Ар
Tpp+f
а)
-/
(Тгр+1) р
v^a(p)
I Мв
X-
Wf(p)
“ED-
Л
т
?70
Рис. 03-3-15.

Передаточная функция разомкнутой системы
w Ip) = Wa (р) Wl (Р) = w, (р) Wг (р)	(Р) Wt (р) к, =
к
~{Тьр+\)(Г,р+\)>
где k = k^kyk^ = 84; 20 lg k = 38,5 дБ.
Сопрягающие частоты: со^ = 1/7^= 1/13 = 0,08 с-1;	= 7^
=оТ5=2 с_’-
На рис. 03-3-15,в тонкими сплошными линиями представлены
ЛАЧХ отдельных звеньев. Фазовые характеристики звеньев пред¬
ставлены тонкими штриховыми линиями. Жирной сплошной линией
представлена суммарная амплитудная характеристика, а жирной
штриховой линией — фазовая характеристика разомкнутой системы.
Эти характеристики позволяют сделать вывод, что исследуемая си¬
стема неустойчива (отсутствует запас по фазе).
03-3-16. Передаточная функция разомкнутой системы
h(TlP+\)(TlP+\)
WM=p(kT*tp*+ 2Ч,Тгр+ 1) (7>+ 1) (riP f 1)’
где Тъ = k^/k$= 1,1с.
По полученной ПФ с помощью шаблонов на рис. 03-3-16 строим
амплитудные и фазовые логарифмические частотные характеристики
(ЛЧХ) форсирующих, апериодических и колебательного звеньев.
Амплитудная логарифмическая частотная характеристика
(АЛЧХ) для усилительного звена — прямая, параллельная оси час-
¥(<*>)
90°
Ь9
О
-45
-90
■180°
Рис. 03-3-16.
271

тот и проходящая на расстоянии 20\gk^y а фазовая характеристика
проходит по оси частот; АЛЧХ интегрирующего звена — прямая
с наклоном —20 дБ/дек, пересекающая ось частот в точке со •-= ];
ФЧХ этого звена — прямая, проходящая параллельно оси частот
на расстоянии —90° от нее.
Суммарную амплитудную Lz (со) и фазовую <рЕ (со) ЛЧХ разомк¬
нутой системы получаем графическим сложением соответствующих
характеристик элементарных звеньев. Характеристика LE (со) пересе¬
кает линию 0 дБ на частоте сос = 3,2 с.”1 раньше, чем характери¬
стика <рЕ (со) линию <j> (со) ——180°. Следовательно, замкнутая систе¬
ма устойчива. Запас устойчивости по фазе равен 86°. Запас устой¬
чивости по амплитуде —45 дБ.
03-3-17. ПФ разомкнутой системы автоматической подстройки
частоты
kyjiykдл&г	^
№7(/Э) = (Т+ТД>Г(| +тмр)р = (1 + тар) (1 + тавр) р ’
где к = k^kykftв== 240.
Для построения ЛЧХ определяем частоты излома:
“д = тГ=о,оз =33'3 с-1;
“яв*=^»=о7Т:= 10с_1'
272
Рис. 03-3-17.

Амплитудные и фазовые частотные характеристики апериодиче¬
ских звеньев строим с помощью шаблонов. Амплитудная логарифми¬
ческая частотная характеристика для усилительного и интегрирую¬
щего звеньев — прямая с наклоном —20 дБ/дек, проходящая через
точку с координатами 201g& = 47,6 дБ и со = 1 с-1. Фазовая харак¬
теристика интегрирующего звена — прямая, параллельная оси частот
и проходящая на расстоянии —90° от нее. Фазовая характеристика
усилительного звена проходит по оси частот. Все построенные час¬
тотные характеристики звеньев приведены на рис. 03 3-17.
Суммарную амплитудную Lz (со) и фазовую <fr (со) JI4X разомкну¬
той системы получаем графическим сложением соответствующих ха¬
рактеристик элементарных звеньев.
Характеристика Ls (со) пересекает линию 0 дБ на более высоких
частотах, чем характеристика (со) пересекает линию — 180®, сле¬
довательно, система неустойчива.
Чтобы система находилась на границе колебательной устойчи¬
вости, необходимо амплитудную логарифмическую характеристику
опустить б низ на 201g/e'=17 дБ:
кр = 47,6—17 = 30,6 дБ;
1	30,6
l£ ^кр— 20 — 1>53.
Отсюда критический коэффициент системы kKP = 33,88.
03-3-18. Система управления продольной подачей состоит из по¬
следовательного соединения трех апериодических звеньев. Для по-
18—903
Рис. 03-3-18.
273

строения асимптотической логарифмической амплитудной частотной
характеристики определяем частоты излома:
=7д_“!и>08 = 12,5 с_1;
1 1
а)г = г7“оЖ = 16’6ь с :
1 1
“р = 7'р	0,09	—	11 с •
Асимптотическая^амплитудная ^характеристика^системы Ьъ (со) до
наименьшей частоты излома соР = 11 с-1 будет прямая линия с нуле¬
вым наклоном, проходящая по оси частот; после частоты сор до
частоты (Од — прямая с наклоном —20 дБ/дек; после частоты сод
до частоты о)г — прямая с наклоном —40 дБ/дек. Наконец, после
частоты (ог до со—>-.оо имеем прямую с наклоном —60 дБ/дек. Гра¬
фики функций фд(со), фг((о) и фр(со) строим с помощью шаблона.
Суммарную фазовую характеристику (со) получаем графическим
сложением функций фд (со), фг(оо) и фр(со).
Замкнутая система устойчива, так как амплитудная ^характери¬
стика системы Lz (со) пересекает линию 0 дБ на более низких часто- *
тах, чем фазовая характеристика ^ (со) линию — 180°С._]
Предельный коэффициент усиления разомкнутой системы опре¬
деляется из условия нахождения системы на колебательной границе
устойчивости. Это определяется путем поднятия амплитудной харак¬
теристики вверх на 201 g£c, так чтобы она пересекала линию 0 дБ
при частоте <±>с, когда (со) будет пересекать линию —180°. Из
рис. 03-3-18 видно, что 201g£c = 13 дБ; lg £с = 13/20 = 0,65. По
таблицам десятичных логарифмов находим искомое число £0 = 4/467.
03-4. КАЧЕСТВО ЛИНЕЙНЫХ СИСТЕМ
НЕПРЕРЫВНОГО УПРАВЛЕНИЯ
03-4-1. Уравнение системы при скачкообразном изме¬
нении входного воздействия AUx(p) — l/p в операторной
форме:	(a3p3+a2p2+aiP+ao)	&Uy(p)	=kAUx(p)	=12//?,
где а3=0,0016; а2 = 0,06; ai =0,54; а0=13; k = 12.
Воспользовавшись численным методом отыскания
корней характеристического уравнения a3p3+a2/?2+ai/?+
4~а0=0, путем последовательных приближений получим:
Pi=—34,5 с-1; Р2,з——1,5±/15,3 с-1.
274

На основании теоремы разложения решение заданно¬
го уравнения будет иметь вид:
ШуЦ):
Р( 0)
(2(0) р
кер'{
'С? p(Pi)
+ S PiQ' (л)
i=l
aQp
kePit
a3Pi(p — Pi) (p— Рг)~<*зPi (P — Рз) (P — Pz)
		kePit
'a3p3 {p —	(p —Pi)	’
+
где P(0)—значение полинома правой части уравнения
при р=0; Q(0)—значение полинома левой части урав¬
нения при р=0; Q'(pi) —
производная от Q(p) при
Р=Ри P(pi) —значение
Р{р) При p=Pi.
Подставляя значения
«о, аь а2, а3, к в послед¬
нее выражение, полу¬
чаем:
Af/+/) =0,925—
—0,165е-34’5*—е1>**Х
X (0,76 cos 15,3/ +
+0,44 sin 15,3/), />0.
График
рис. 03-4-1.
По графику определяем следующие показатели ка¬
чества:
/р=1,57 с; 6=59%; 7=0,4 с; N=8.
03-4-2. По вещественной частотной характеристике
определяем интервал существенных частот о)с=100 с-'.
Тогда ориентировочное время регулирования я/сос</Р<
<4я/сос, или 0,0314 с</р<0,126 с. Перерегулирование
6< 18%'.
Уточним полученные значения по приложению 16. По
рис. 1-8-11 определяем коэффициент наклона веществен¬
ной частотной характеристики х=60/90=0,67. По кри¬
вым приложения 16 получим: 6 = 17% и /р=9/90 = 0,1 с.
Полученные результаты достаточно близко совпадают
с /р и 6, получаемыми по переходной характеристике,
изображенной на рис. 01-8-11.
переходной характеристики приведен на
275

03-4-3. Максимальное значение G (со) <0,1, поэтому
высокочастотную часть характеристики можно отбросить.
В этом случае перерегулирование будем определять по
формуле
я  1 » 18(?.-_макс • Gq (0)^   1,18*1,08—1  п 07R
<?0(0)	1	—0,27о,
т. е. 6% =27,5%..
Время регулирования /р>я/сос=3,14/78=0,0403 с.
По кривым приложения 16 получаем:
8= 20%; fp = -^-
: 0,105 с.
03-4-4. В случае горизонтальности вещественной час-i
тотной характеристики, постоянной по знаку (см.
рис. 3-4-4,а), перерегулирование не может превышать
18% и может быть приближенно определено по формуле
Для знакопеременной вещественной частотной харак¬
теристики (рис. 3-4-4,б) необходимо пользоваться фор¬
мулой
8* <0,18 + 0,277^-.
Результаты вычислений сведены в табл. 03-4-1.
Таблица 03-4-1
Вариант
а
fj
К, %
t , с
1 макс’
5*. %
t .с
1 макс'
18
3,14
Менее 21
3,9
18
1,57
Менее 23,5
2,6
орсмл ДОС! пЛ\СПИЛ
. обоих случаях ПО формуле t\ макс—Jt/(01.
03-4-5. При решении используем формулы
•.<М*А~И.277-з-
7.(0)
t = ——
Чмакс ю •
(0)
1;
276

Результаты расчетов сведены в табл. 03-4-2.
Таблица 03-4-2	Таблица	03-4-3
5*. %
t , с
1 макс’
Менее 46
2,2
Менее 33
1,26
Менее 85
1,05
V С"1
Е
2,95
0,645
4,325
0,5
5,8
0,396
Таблица 03-4-4
k
N
»*. %
3
г
Менее 1
Менее
10
О
о
^ 1
Менее
15
о
^2
Менее
25
03-4-6. Частота собственных недемпфированных (сво¬
бодных) колебаний определяется по формуле
где ®о частота собственных демпфированных колеба¬
нии; а, коэффициенты характеристического уравнения
Относительный коэффициент затухания определяется
по формуле
S=-
'(2Yа2а0 *
Результаты сведены в табл. 03-4-3.
03-4-7. Число полуволн за время регулирования Л
определяется по формуле
JT- 1-1,
а б* — по графику, показан¬
ному на рис. 03-4-7. Результа¬
ты расчета сведены в табл.
03-4-4.

03-4-8.
ОО
о
к	к	Г	кТ
р(Тр + 1) р—	~Тр+1	’
00
о
03-4-9.
Г _ k4\
27\	•
03-4-10. Свертывая структурную схему, изображен¬
ную на рис. 3-4-10, получаем:
где £дв=1/се=1 — коэффициент усиления двигателя по
скорости; Tu—JRh/ceCm — электромеханическая постоян¬
ная времени двигателя; T^—LajRa— электрическая по¬
стоянная якорной цепи двигателя.
Так как по условию ш0 — 1 /|/ТэТм = 1 и &дв= 1, ПФ
запишется в виде
где &о=1; «2=1; а\=Тм; а0=0.
В данном случае пг=п—2=0 и квадратичная интег¬
ральная оценка определяется по формуле [Ю]
Эту ПФ можно переписать в ином виде:
Ф (п) —
КР) ТэТмр* + Тмр+\ >
<*2Р2 + <*iP + а0 ’
В0А0
2а2 о А »
где
а0 о>2
'О ах
278

или
. ТЛгН. д8 < : 7'V—М
2 Ты 1 дТм —	2Т\
Полагая д12/дТм=0, находим Гм=1.
03-4-11. В соответствии со схемой 3-4-11 ПФ тирис¬
торного привода запишется в виде
ф (/?)=,
knkji
^мТ'ъТ'пР3 + ('1\ТЭ + ТМТп) р1 -f (7'м + Т„)р -|- knkAnk, + 1
 	bo
а>рг + агр* + а,р-\-ао >
где Ь„ = какАК- а, ;= 1 + кпкАВкт; а, = Тм + Тп;
«2 = Гм(П + ^п); а3 = ТмТэГп.
Квадратичная интегральная оценка
/   ^0^0
*» О 	 г
2а20А >
где В0 = Ь\ = к\к\в-,
Д =
ДВ>
—й2 о
0 <Zj —а3
0 — а0 а9
= во(а,л* — <*.«,) =
= 7’м	+	ТмТа	+	Т%)	+	(Тм	-	Тэ)	кАВктТиТпкп	+
д.=
+ (?\
—
КА
а, —
а2
0
а0
ах
— Яз
0 —
а0
а2
= а\аг — +++ + а„а\ =
= (Гм+Гэ) Г2МГЭ+ (ТМ+ЗТВ) Р„7-п+
“I-(ЗУм I Тп) ТшТ^и.~\~(Тм Тэ)клвктТмТ\ка+
+ (Тп+Тэ^мТэк^К.
03-5. СИНТЕЗ ОБЩЕЙ СТРУКТУРЫ СИСТЕМЫ УПРАВЛЕНИЯ
И КОРРЕКТИРУЮЩИХ ЦЕПЕЙ
03-5-1. Передаточная функция неизменяемой части
системы
40
W № — д(0,25д+ 1) (0.0625/7+1)
279

По полученной ПФ некоррелированной части систе¬
мы строим ЛАЧХ Lo(co) и ФЧХ фо(со) (рис. 03-5-1). He-
корректированная система неустойчива, так как харак¬
теристика Lo(co) пересекает ось 0 дБ позднее, нежели
фо(б>) пересекает ось —180°. Передаточная функция и
параметры контура, создающего упреждение по фазе
(рис. 3-5-1,6), определяются из соотношений
Рис. 03-5-1.
Этот ЛС-контур является реальным пассивным фор¬
сирующим звеном первого порядка. Такой контур, как
известно, осуществляет опережение по фазе в определен¬
ной полосе частот. Максимум положительного фазового
сдвига получается при частоте о)Макс=]/'а/7'1к, соответ¬
ствующей середине наклонного участка ЛАЧХ, и опре¬
деляется из выражения
. а — 1
?шкс = arcsm
Амплитудная характеристика контуром смещается
в направлении положительного приращения усиления
(вверх).
280

Выбрав параметры дифференцирующего контура так,
чтобы постоянная времени Tik—R2C равнялась наиболь¬
шей постоянной времени нескорректированной части сис¬
темы, т. е. 7^=0,25 с, а отношение #i//?i+/?2 = ^2k/7,ik
возможно меньшим (примерно 0,1—0,05), что позволяет
получить необходимое смещение по фазе, получим:
у«М = °,<оХ++,-
Потерю усиления, вызываемую введением корректи¬
рующего контура в области низких частот, компенсируем
увеличением коэффициента усиления системы в
-M?2)/#i раз, что даст общий коэффициент усиления
40& + Ф =800.
*'1
Передаточная функция скорректированной системы
в разомкнутом состоянии будет иметь вид:
гиг / \	 40
УР) р (0,0625/?+!) (0,0125/? + 1)'
В соответствии с ПФ строим ЛЧХ скорректированной
системы 1д(ю) и фд (со) и определяем полученные запасы
по фазе и амплитуде. Они удовлетворяют требуемым.
Заметим, что в области низких частот JIAX скорректи¬
рованной системы совпадает с JIAX неизменяемой части,
т. е. ослабления сигнала не происходит, а в области вы¬
соких частот эти JIAX параллельны. При выборе пара¬
метров корректирующего контура Т\к и а следует стре¬
миться, чтобы частота среза неизменяемой части систе¬
мы оказалась между сопрягающими частотами coiK=
~VTik и (i)2k=1/7'2k, новая частота среза скорректиро¬
ванной системы пришлась бы примерно на середину до¬
статочно длинного участка JIAX, имеющего наклон
в этой области — 20 дБ/дек. Следует, однако, помнить,
что увеличение коэффициента усиления в области высо¬
ких частот, обусловленное последовательным дифферен¬
цирующим контуром, может быть нежелательным вслед¬
ствие увеличения уровня помех.
03-5-2. Определим параметры интегрирующего кон¬
тура (см. рис. 3-5-1,в) так, чтобы получить необходимые
запасы по фазе и амплитуде и обеспечить высокое уси¬
281

ление в области низких частот. Передаточная функция
контура имеет вид:
где
Тж = я А, Т№= (Я, + RJ С, = Л +	Т1к=аТ1К.
Коэффициент усиления этого контура в области низ¬
ких частот k0=l (при о)->0 контур не вводит ослабле¬
ния сигнала), а в области высоких частот kco = TiK/T2K=
= R\/(R1+R2) *
Интегрирующий контур, характеристики которого
изображены на рис. 03-5-2, вызывает в определенной по¬
лосе частот отставание по фазе и смещает в сторону
уменьшения усиления (вниз) амплитудную характери¬
стику на а. Постоянные времени контуров Т\к и Т2к сле¬
дует выбирать так, чтобы сопрягающие частоты шц{ =
= 1 /Г1к и (д2к=1/Т2к были расположены слева, на доста¬
точном удалении от частоты среза стабилизируемой си¬
стемы, а смещение результирующей амплитудной харак¬
теристики — в сторону уменьшения усиления (вниз)
обеспечивало бы достаточный запас по фазе в области
нового значения частоты среза. Из указанных соображе¬
ний выбираем а= (R\+i?2)/#i~20, a TiK=4 с.
Это дает дополнительное отставание по фазе в обла¬
сти новой частоты среза примерно 5—6°. Так как Т2к =
= аТ1к—80 с, то все параметры корректирующего кон¬
тура определены. Построенные частотные характеристи¬
ки Ln((o) и фи(со) скорректированной системы (см.
рис. 03-5-1) позволяют сделать заключение о том, что
поставленные в задаче требования удовлетворяются.
282

Коррекция системы интегрирующим контуром, созда¬
ющим отставание по фазе, уменьшает усиление в обла¬
сти высоких частот, приводит к уменьшению быстродей¬
ствия 'системы вследствие снижения частоты среза,
а также увеличивает время регулирования. Все это свя¬
зано с появлением корня в характеристическом уравне¬
нии замкнутой системы, примерно равного —а/Т2к (зна¬
чение |а/Г2к| обычно мало и приводит к появлению мед¬
ленно затухающей экспоненциальной составляющей).
03-5-3. Параметры интегродифференцирующего кон¬
тура определяются из соотношений TiK=RlCu T2k=R2C2;
T\2 = TWR2/Rl. Коэффициент усиления контура в области
как низких, тан и высоких частот равен единице, т. е.
6о=1 и 600=1 при о)->0 и со-^оо. Следовательно, контур
не вводит ослабления сигнала.
ДБ
60
ho
20
о
-20
-ho
-60
-80
-100
Рис. 03-5-3.
Наибольшие значения отставания и упреждения по
фазе получаются при достаточно малых значениях отно¬
шения ику/и
кх (примерно 0,1), что имеет место при
^i2> {Tik + T2k). Отсюда следует, что R2>Ru Ci>C2.
Желательно, чтобы Т\^ФТ2к.
Примем Г1к равным наибольшей постоянной неизме¬
няемой части системы, т. е. 0,25 с, а Т2к—4 TlK= 1 с.
Известно минимальное значение модуля отношения
у   Т1К “Ь Т%к
Укх	4"	^2К	“Ь	^12
283

Приняв 7,12=9Г2к, получим UKy/UKX = Q,l2l, что удо¬
влетворяет заданным требованиям.
При выбранных значениях параметров ПФ коррек¬
тирующего устройства
ш /лч = (/7+ 1) (0,25/7+ 1)
(10/?+ 1) (0,025/7 + 1)-
Тогда Г1Ф скорректированной системы в разомкнутом
состоянии
W (р) =	40	(р+
кр> р (10/7 + 1) (0,0625/7 + 1) (0,025/7 + 1) •
Характеристики нескорректированной системы приве¬
дены на рис. 03-5-3 штриховыми линиями. Там же
сплошными линиями приведены характеристики скоррек¬
тированной системы, которая устойчива. Запас по фазе
и амплитуде удовлетворяет заданным требованиям.
При стабилизации неустойчивой системы необходимо
параметры интегродифференцирующего контура выби¬
рать так, чтобы частоты соа и опк располагались возмож¬
но дальше слева от частоты среза неизменяемой части
системы, а частота среза пришлась бы примерно по¬
середине между частотами о)2к и соь. Частоты соа и соь
определяются из соотношений
  [6*2 (Ri + R2) + 6*i^l] 	+		4СгС2Я^2 .
Юа —	2С,С2ЯЛ>
„ _ [С2 (Rt + R2) + С Л] + V'lC^ + 'RJ+C&r-^CM
b —	2ClCtRlRi
Применение интегродифференцирующего контура по¬
зволяет увеличить усиление в области низких частот и
расширить частотную характеристику до более высоких
частот за счет упреждающей части контура. Во многих
случаях такой контур позволяет получить лучшие харак¬
теристики качества системы, чем простые контуры.
03-5-4. В отличие от предыдущих задач здесь тре¬
буется выбрать последовательное корректирующее
устройство, обеспечивающее не только стабилизацию
системы, но и получение определенных характеристик
качества.
Требуется по заданным показателям качества систе¬
мы построить желаемую ЛАХ, определить ПФ коррек¬
тирующего устройства, выбрать схему корректирующего
устройства и определить параметры его элементов.
284

flo заданной ПФ W0 (р) строим ЛАХ неизменяемой
части системы. Для построения желаемой ЛАХ восполь¬
зуемся ЗаВИСИМОСТЯМИ 6макс^^1 (Смаке) И ^ыакс==
J=f2(^MaHc), приведенными на рис. 03-5-4,а. По заданно¬
му значению относительного перерегулирования 6Макс=
=30%, пользуясь кривой 6макс=ЫСмаке), находим
jMaKC=l,25 (максимум вещественной частотной харак¬
теристики замкнутой системы). По найденному Смакс и
зл
ь)с
2п
и>с
0—J	С Ь
г)
Рис. 03-5-4.
285

заданному /макс При ПОМОЩИ Кривой /макс —/2 (Смаке)
определяем частоту среза сос, так как ордината кривой
/макс = ЫСмаке) равна kn/о)с и в то же время определяет
заданное значение /макс- Следовательно, о)с = ^я//макс~
~3,2л/0,5=20 рад/с.
Для построения желаемой JIAX через точку сос =
= 20 рад/с на оси частот проводим прямую с наклоном
—20 дБ/дек, которая и будет среднечастотной асимпто¬
той желаемой ЛАХ (рис. 03-5-4,в). Для 'сопряжения
среднечастотного участка с низкочастотным и высоко¬
частотным участками желаемой ЛАХ необходимо опре¬
делить сопрягающие частоты со2 и со3.
Интервалы частот оз2—сос и оос—'со3 должны лежать
в пределах 0,2—0,9 дек. Более точное определение ин¬
тервалов указанных частот производят или о помощью
обычной номограммы для определения G(co) по харак¬
теристикам разомкнутой -системы, или с помощью вспо¬
могательных графиков (рис. 03-5-4,6). При применении
номограммы (см. приложение 10) на ней ограничивают
прямоугольником область, в которой расположены кри¬
вые GMaKc=l,25 и GMHH=GMaKc—1=0,25. Одна -из сторон
полученного прямоугольника дает 2LAU а другая 2уь
Асимптота среднего участка желаемой ЛАХ должна
удовлетворять неравенству
(о) 3^ L\.
Сопряжение среднего участка желаемой ЛАХ с низ¬
кочастотным и высокочастотным участками должно про¬
изводиться так, чтобы при L\^Lm (оо)^0 и О^Аж(оо)^
^—Li избыток фазы был бы не меньше уч.
В данной задаче по кривой на рис. 03-5-4,6 получаем
Li= ±li5 дБ и у! = 42°.
Выбирая в качестве желаемой ЛАХ первого типа для
астатической системы, совмещаем низкочастотный учас¬
ток желаемой ЛАХ с ЛАХ неизменяемой части системы
(рис. 03-5-4,в). В качестве первой сопрягающей частоты
берем частоту он, удовлетворяющую условию coi ~
^ С1/С2=0,004/0,02 = 0,2 ст1.
Сопряжение низкочастотного и среднечастотного
участков ЛАХ должно производиться асимптотой с на¬
клоном —40 дБ/дек. Придавая при coi = 0,2 с-1 наклон
желаемой ЛАХ —40 дБ/дек, находим частоту со2 =
= 3,33 с-1, соответствующую точке пересечения средне¬
частотного участка желаемой ЛАХ с низкочастотным
участком.
286

При этой частоте имеем Li = 15 дБ, что свидетель¬
ствует о правильности решения. (Можно было бы, зная
Li, определить частоту со2 и через точку с координатами
со2, L\ провести прямую с наклоном —40 дБ/дек до пере¬
сечения с низкочастотным участком. Это позволило бы
определить частоту coj.) Высокочастотную асимптоту же¬
лаемой ЛАХ проведем через точку с координатами
—L\ и со3 параллельно асимптоте ЛАХ неизменяемой
части системы в данной области. Построенная желае¬
мая ЛАХ определяет ПФ разомкнутой скорректирован¬
ной системы в виде
W (p) = W (/}) =	300 (0,3р -И)
*ж\Р) w КР) р(5р+ 1) (0,01/7 + 1)(0.003;? + 1)
Для корректирующего устройства ПФ определяется
из соотношения
П7 (п\ WX(P) (0,3/, + 1) (0,1/7 + 1)
wKKP)—WAp) —(5/7+1)(0i01p+ ,) •
Она может быть определена из ЛАХ, получаемой пу¬
тем вычитания из желаемой ЛАХ логарифмической ха¬
рактеристики неизменяемой части. По W(p) строим
фазо-частотную характеристику скорректированной си¬
стемы и проверяем соблюдение условия, что в области
—15 дБ^Аж(со)^15 дБ избыток фазы должен быть
примерно 40°. В рассмотренной задаче эти условия
соблюдены, что обеспечивает получение требуемых ха¬
рактеристик качества системы.
По виду полученных ОФП и ЛАХ корректирующего
устройства выбираем схему корректирующего контура,
приведенную на рис. 3-5-4,г. В общем виде ПФ такого
контура имеет вид:
где
W (п\ (Ь кР + 1) (Т’гАР + 1) '
kW_ ГЛ;Л'!- 1) (Т’р-'- 1)	>
riK = R,C,; 7SK = (ffs»-fK,)Cs; k0=h
7ГТМУГ:
2 a	.	'2	a
b — V b2 — 4a ’ b b + Vb*
■ 4a
287

В соответствии с желаемой JIAX корректирующего
контура требуется обеспечить:
1/Га=0,2 с-1; 1/Г1к=3,33 с-1; 1/Г2к= 10 с"1;
1/Г6=100 с-1; 20 \gkoo = —3,2 дБ; £оо = 7,
или
Та:== 5 с; 7ik=0,3 с; Т2к0,1 с; Ть = 0,01 с.
Задаваясь емкостью Ci = 10 мкФ (емкость С\ вы¬
бирается обычно достаточно большой), определяем со¬
противление резистора R\ = 0,3/10=20 кОм.
Сопротивление резистора R3 определяется из соотно¬
шения
где ai — TJT 1К=*16,65; a2=T2rJTb = 10; Rs= 15,35-30 =
=460 кОм.
Так как
^2^3	 а1	К2	  ft	Д
*l(*I + *,)	“1	’
ТО
=	—	о,4д,	кОм;
с.=тйтгг~0'21 мкф'
Таким образом, схема и все параметры корректиру¬
ющего контура определены.
Глава четвертая
ДИСКРЕТНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ
УПРАВЛЕНИЯ
04-1. ОПЕРАТОРНОЕ ОПИСАНИЕ ПРОЦЕССОВ
В ДИСКРЕТНЫХ СИСТЕМАХ
04-1-1. Для всех поставленных в условии вопросов
потребуется знание 2-изображения входного процесса.
По таблице 2-изображекий (см. приложение 4) находим:
v г Л z2 sin 2fsiri о — <р) : к
л lz\ —	z?~^\2z\cosQTо +1
288

Подставляя заданные значения <р = я/6; £2 = 0,1 с-1;
f0=0,8 с, получаем:
у г j  2, 5z2 — 2,15z
Л lZl ~~ z*— 1,992 + 1 ’
а)	Преобразование ЛД переводит аналоговый сигнал
в последовательность импульсов. Индикация процесса
происходит только в начале каждого такта. На
рис. 04-1-1,а показано условное обозначение импульсного
индикатора-дискретизатора.
АД
ДА
lb* Vi
W(p)
Индикатор (дискретизатор)
в начале
такта
Дискретизатор /	Интегратор
Импульсный,
дифференциатор
1
а)
еГ0\
X[z]
Z-1
W0[Z]
Индикатор
Yfe] (дискретизатор)
Z
смещенный
\
/
w0[z](1-z-i)
Щ[г,е]
6)
Рис. 04-1-1.
Преобразование ДА содержит операции размножения
импульсов и интегрирования, для которых на рис. 04-1-1,а
предусмотрены соответствующие элементы: импульсный
дифференциатор-импульсатор и интегратор.
Импульсатор по одному входному импульсу выраба¬
тывает два таких же импульса разных знаков в начале
и конце такта. Первый импульс запускает интегратор,
который формирует ступеньку в процессе x(t). Второй
импульс прекращает интегрирование и снимает на ин¬
теграторе начальные для следующего такта условия.
Преобразования последовательности импульсов, содер¬
жащиеся в X[z], импульсатором записываются в виде
где 1—первое слагаемое в левой части — отображает
сохранение знака и амплитуды импульсов в начале каж¬
19—903
289

дого такта, а слагаемое — z~l характеризует сдвиг им¬
пульса к концу такта и изменение его знака. В струк¬
турной форме, показанной на рис. 04-1-1,6, роль преоб¬
разователя (1) отраж-ена первым звеном; интегратор
включается в состав ПФ последующей линейной си¬
стемы.
б)	По объединенной (с интегратором ДА преобразо¬
вателя) ПФ системы находим ПФ в 2-форме, называе¬
мую 2-ПФ. Для этого разлагаем ПФ на компоненты:
уу (р) —*(Р) -	2	(0,5/7	+	!)
Р Р2{р + Ъ)[(р+ l)2 + 0,04j —
_ 0,64	1	,12	0,03	■	т	0,43	+	/0,25
Р2	Р	Р+ 3 * Шр+1— У 0,2 *
Для каждого слагаемого по приложению 4 переходим
к г-изображению:
Ш f 1  0,64Г0z	1,122	0,03z	,
w*[z\— (2 — l)2	2 — 1	2 — ехр(-ЗГ0) '
4-г Im 	0,43 + /0,25
* z - exp [Го (— 1 + У о, 2) J •
Подставляя Т0 = 0,8 с, получаем:
К [г] -	[г] +	[г] + Wt [г] + Г. [г] = 4+р—
1.12Z	0,03z	,	г	 0,43	+ /0,25	^
г-1 г —0,091 ~	111	z — 0,45 (0,987 + /0,159) * К )
Отдельно преобразуем четвертое слагаемое:
uy r^i Im (0,43 + /0,25) (z— 0,44 + /0,071) 	 0,25z— 0,08
4Н—	(г — 0,44)2 + (0,071)2	—	z2	—	0,89z+0,2*
Приведя все члены суммы (2) к общему знаменате¬
лю, получим:
iw г 1	 (	0, 9z* + 1, 3z3 — 0,33z2 + 0,43z — 0,03) z
0 W _	(z— l)2 (22 — 0,091) (z2 — 0,89z + 0,2)	*
Совместно с импульсатором 2-ПФ цепи имеет вид:
z 1 ту/ Г 1	 — 0, 9z4 + 1, 3z3 — 0,33z3 + 0,43z — 0,03j
z в N —	(2	— 1) (2 — 0,091) (z2 — 0,89z + 0,2)	•
290

Наконец, г-изображение выходного процесса
У'И==^117.ИЛ-И =
(—0,9г4 + 1,3.г3 — 0,ЗЗ22 + 0,432 — 0,03) (2,5г —2,15) г
■—	(2Г— 1) (г—0,091) (г2 — 0,892 + 0,2) (г2 — 1,992 + 1) " •
Непрерывное деление числителя на знаменатель дает
возможность перейти к ряду по отрицательным степе¬
ням г; коэффициенты ряда — суть значения реакции
y(t) в дискретных точках t==kT0.
в)	Передаточные свойства дискретной схемы опреде¬
ляются только для воздействия и реакции в дискретных
точках, соответствующих всегда началу очередного так¬
та, что отображается одинаковыми индикаторами на
входе и выходе схемы (верхний канал), показанной на
рис. 04-1-1,а. Для изучения свойств реакции в промежу¬
точных точках на выходе индикация точек процесса про¬
исходит импульсом опроса, смещенным на желаемую
часть интервала дискретности еГ0, что на рис. 04-1-1,а
отражено наличием смещенного индикатора. Так как
к моменту опроса любая из экспоненциальных функций,
входящих в описание реакции непосредственно или под
знаком ^-преобразования, изменит свой масштаб на ве¬
личину ехр [еГ0(г|+/Й)], этот масштаб следует ввести
в г-изображение. Кроме того, в интерполированном
г-изображении, изменяя величину е, одновременно услов¬
но сдвигают начало отсчета, чтобы избежать потери
такта.
Перейдем к почленному определению интерполиро¬
ванных г-изображений слагаемых формулы (2), начиная
с последнего:
WA [г, в] = Im
(0,43 + /0,025) [(г — 0,44) +/0,071 ] X
Хехр (—0,8г + /0,1бе)
г2 —0,892 +0,2
(0,432 — 0,207) <?-°’8е siп 0,16г +
+ (0,252 — 0,08) <Г~0’88 cos0,16г
г2 — 0,892 + 0,2
При 8 = 0,5
[г; 0,5]
2 • 0,03 ехр (— 3sТо)  2 • 0,03 ехр (— 2, 4г)
2 — 0,091	2	— 0,091
2 — 0,091
19*
291

При е = 0,5
тг/ г п п	0,0009z
Г3[г; 0,5] =
Для первых слагаемых непосредственно из приложе¬
ния 4 имеем:
Wt[z,,] = Wt[z; 0,5] ==~~у_;
П7 Г, _1	 0,51	[(1	—	е)	(2	—	1)	+	1]	_	0,51	[(1-е)	2=	+ez]
Wl[Z> SJ~	(Z	—	l)2	—
Wl[z; 0,5]= °'2(5Дг1 + г) ■
Суммируя элементы
W01]z, e] = Wx [г, e] + W2 [г, e] + Wz [г9 г] + WA [z, e];
W0[z; 0,5] = Wv[z; 0,5] + W2fc 0,5] +
+ Wz[z; 0,5]+№4[z; 0,5]
и умножая на г-изображения импульсатора и входного
процесса, получаем интерполированное изображение
реакции:
Г[г,*]=Х[г]г-=±ЧГ.[г,*}.
Получение г-изображений иллюстрируется рис. 04-1-1,6
для обычной (верхний канал) и интерполированной
(нижний канал) форм.
04-1-2. Переносим в заданном дискретном уравнении
г]	в левую часть, переходим к г-изображениям т)[z] и
Рис. 04-1-2.
£[г], а сдвиги на один или два такта, имеющиеся в алго¬
ритме, обозначаем соответствующей степенью г-1 и г-2:
Г) [г] +1>1Т] [г] z-'+v 0r) [г] z2 = и2\ [z] +
+ Ы1Ц2] z~l + Uoi[z] zr2.
Отношение
т) [z] u2 + uxz~l + uQz~2 a2z2 + uxz + un
6И
1 + vxz~l + V0z-2
22 VlZ Vo
= D[z]
292

и есть 2-ПФ для ЭВМ, которая входит в состав струк¬
турной цепочки, показанной на рис. 04-1-2. Если на вы¬
работку решения тратится машинное время, соизмери¬
мое с Т0, а ввести решение можно только в начале так¬
та, то возникает потеря одного интервала 70, что учиты¬
вается в структуре сдвигом на z~l. Остальные элементы
структуры взяты из предыдущей задачи. Общая z-ПФ
ИМ*] =D[z\^-W,[z\.
04-1-3. а) Переводим в z-форму входной сигнал (ей.
приложение 4):
Х[г] =
\0z
10 г
z — ехр (—0,2) z — 0,819*
Рис. 04-1-3.
Ключ состоит из индикатора, импульсатора и инте¬
гратора (рис. 04-1-3,а). Импульсатор содержит два им¬
пульса: первый в начале такта, повторяющий входной
импульс, и второй, противоположного знака, со сдви¬
гом |ЗТ0.
293

б) Объединенная с интегратором ключа ПФ
(рис. 04-1-3,6)
•ум , \   2	в__	0,25   0,5 I 0,25	.	-
wo(p) — -p(p + 2) (/7 + 4)	У уу-Г-уу- ^
Первый импульс импульсатора возбуждает звенья,
соответствующие компонентам выражения (1), вызывая
элементарные реакции в виде их весовых функций, от
которых обычным путем можно перейти к z-изображе¬
ниям. Второй импульс импульсатора вызовет реакции
в виде тех же элементарных экспоненциальных функций,
но они к моменту индикации изменят масштаб на коэф¬
фициент ехр (угцТо), будут иметь обратный знак и сдвиг
на один такт, учитываемый сомножителем z_1- Таким об¬
разом, каждая элементарная z-ПФ будет иметь вид дроби
W, (г) = z ~ ехР (Y+t	(2)
1' '	z — ехр y\iT о >
являющейся разностью обычного и умноженного на z_1
интерполированного изображений для функции ехр(т]^)_
при у=г и Tii = 0, У]2=— 2, г]3=—4.
Для рассматриваемой суммы (1) получим:
wz 	0,25	(z	—	1)	‘	0,5 [z — ехр (—0,8)]
^•Н— z_i	z	— ехр (— 4)	‘
, 0,25 [з — ехр (— 1,6)] п 0q 0,5 (з — 0,225)
1 z— exp (-8)	U,Z° z — 0,0183 “Г
L 0,25г — 0,055 __	0,048г + 0,00008
' z — 0,000335	(3 — 0,0183) (з —0,00035) •
в) При изучении реакции внутри такта аппарат ин¬
терполированных z-изображений оказывается недоста¬
точным, так как требуется дополнительно учитывать
расположение импульса опроса по зонам импульсатора,
что отображается зональным интерполированным изо¬
бражением.
Для получения зонально-интерполированного изобра¬
жения реакции для зоны г<Р обратимся к рис. 04-1-3,з.
От первого импульса импульсатора импульс опроса от¬
стоит на интервал &Т0 и в z-изображение экспоненты (2)
вносится масштаб ехр(еГ0т]). От второго импульса, рас¬
положенного позже импульса опроса, реакцию можно
индицировать только в следующем такте при расстоянии
до импульса опроса (е + у)Дк Следовательно, в масштаб
294

войдет коэффициент ехр[;(е + у)л^о] и потеря такта
учтется сомножителем z~l. Для 2-ПФ (2) это дает:
w /г\ _ ехрсГ07]->2-1ехр[(в +у) 7>]] ^
' '	z — ехр т]Т0
При е = 0,5 из (1) получаем:
XV7 14- (л к 1	0,25 (г 1)	0,5 [ехр (	2) г — ехр (—5,2)]	»
Wt[z, U,o]_^—1	_____
■	0,25 [ехр (— 4) z — ехр (—10,4)]
'	z	—	ехр	(— 8)
0,41z — 0,002G7 , 0,0462 — 0,00001
0,25-
2 — 0,0183	1	2	—	0,00035
Для зоны е>р следует пользоваться рис. 04-1-3,г, от¬
куда видно, что индикация производится после обоих
импульсов импульсатора, поэтому импульс опроса учтет
без потери такта обе 'составляющие реакции, но с раз¬
ными масштабами, определяемыми расстояниями до им¬
пульса опроса гТ0 и (е—13)Г0.
Для экспоненты в общем виде получаем г-ПФ
w /х _ ехр еТ0т) — ехр (в — t) ч)Г0 ^
г — ехр^Гф
При е = 0,9
W \у О Q1 О 0)5 [ехр (—3,6) — ехр (	0>4)]
[г, и,У] — и	2 — 0,0183
,0,25 [ехр (—7,2)—ехр (—0,8)]	0,322
— г	2 — 0,00035	2	—	0,0183
0,112 2	0,2U2	+ 0,000l2
z _ 0,00035 — (2 —0,0183) (2— 0,00035) •
Компактная запись зонально-интерполированной ре¬
акции может быть дана единой формулой
Y [г, е] = X [г] [W'	^
1ЧГ2[г>6]е>р,
но фактически она содержит две отдельные строки по
зонам:
Yi = XWx и Y2=XW2.
04-1-4. Треугольную меандру представляем в виде
суммы трех полубесконечных смещенных линейных
функций, как показано на рис. 04-1-4,а. Наклон первой
функции определяется отношением единичной высоты
295

треугольника (фактическая высота вносится умножением
на Х[г]) к половине основания:
5 —	2
Fo *
Крутизна второй наклонной в 2 раза больше и отри¬
цательна (чтобы создать
симметричный спад графи¬
ка):
4
Fo '
Крутизна третьей линии
снова
2
Fo
е>
Рис. 04-1-4.
чтобы на участке размыка¬
ния ключа (скважности)
суммарный процесс оказал¬
ся равным нулю.
В состав ключа вводим
импульсатор из трех им¬
пульсов:
с общим
за которым следует двукратный интегратор
масштабом импульсов 2/(3Т0р2.
Интеграторы с масштабом войдут в объединенную
ПФ, а импульсаторы послужат для формирования из
объединенной ПФ трех компонентов, входящих в общую
z-ПФ (рис. 04-1-4,6).
04-1-5. Переходим к z-изображению входного про¬
цесса:
д	z	I
*[21=0,1-3	т	,
11	дг\ z — ехр т}Г0 |yj=—0,4
0, \zT0 exp (—0,2)
Ьз=—о,
]г0=о,5
0,04z
— [z — ехр (— 0,2)]2 (г — 0,82)2 *
а)	Фигура меандры представляется суммой четырех
наклонных прямых с крутизнами Si = 20 с-1, S2 =
= —20 с-1, S3 = —10 с-1, S4= + 10 с-1.
Относя общий сомножитель 10 к двукратному ин¬
тегратору 10/р2, получаем форму импульсатора:
26 [t] —26 [t—0,05]—б [t—0,25] + 6 [t—0,35].
296

Структура ключа показана на рис. 04-1-5,а.
б)	Преобразуем объединенную ПФ:
Перейдя к z-ПФ, получим три компонента:
-та-*.И=[-|г^'.,гр,,4н.-
z — 1	2	—	ехр	(— 1 )
w\+w\+w\.	(1)
12
10
1-2 1-1 '
а)
Р2
Рис. 04-1-5.
Присоединим теперь к полученной г-ПФ передаточ¬
ные свойства импульсатора, вводя в каждый элемент
суммы (1) четыре слагаемых:
-п+.И =
__Г д 2z — 2 ехр (0,45т)) — ехр (0,25-^) + ехр (0,15т,) ~[
дц	г	—ехрО.бт)	J4=0
2г—2— 1 + 1 _._2г—2ехр(—0,45)—ехр (— 0,25)+ехр(—0,15)
z —1	г	—	0,368
(2— 1)(— 2.0,45 —0,25 + 0,15) + (2z+2— 1 + 1)0,5
— (2- 1)*
_ 0 .	22— 1,195 _	—1,93
z —0,368	г—0,368	•
297

Следовательно, г-изображение реакции
ун	0,4-19,3	_	7,24	^
И (г—0,82)2 (г —0,368) “ (г — 0,082)2 (г — 0,368) *
в)	Для зонального интерполированного изображения
требуется рассчитать масштабы компонентов по рас¬
стоянию до импульса опроса от каждого импульса им-
пульсатора. На рис. 04-1-5,6 эти расстояния (временные
интервалы) показаны для положения импульса опроса
в первой зоне, т. е. впереди трех импульсов им-пульсато¬
ра (е<0,1). Запишем по данным рисунка одно послед¬
нее слагаемое из формулы (1) в интерполированной
форме:
2с exp (— 0,5s) — 2 exp [— (s + 0,9) 0,5] —
— exp !(2 + 0,5) 0,5] + exp [(e -f- 0,3) 0,5]
=	z — 0,368	‘
Для второй зоны 0,1<Св<0,5 расположение импульса
опроса показано на рис. 04-1-5,в. Интерполированная
г-Г1Ф для второй зоны
2с {ехр (— 0,5:) — ехр [(г — 1) 0,5]} —
1	™. ,	, -ехр [-(* + 0,5)0,5J+ехр [-(*+0,3)0,5]
-jQ- W г [г> s]—	2—0,368
Для третьей зоны, где 0,5<[е<;0,7,
г (2ехр (— 0,5:) — 2ехр [— (* — 0,1) 0,5j —
.	—ехр	[—(* — 0,5) 0,5'} +ехр [(* + 0,3) 0,5]
"КГ f2’ 4 =	г	—	0,368
Для четвертой зоны, где 0,7<е<1,
г {2 ехр (— 0,5s) — 2ехр [(е — 0,1) 0,5] +
1	ТГ771	+ ехр [(s — 0,5) 0,5] — ех.р [(е — 0,7) 0,5]
~[(Г	*1*’ S1	2—-0,368
04-1-6. а) Для экспоненциальной функции x1 = erit,
содержащейся во входном процессе, можно получить
П-представление в виде суммы бесконечного числа сме¬
щенных экспоненциальных функций с изменяющимся
знаком. Как показано на рис. 04-1-6, экспоненты с поло¬
жительным знаком имеют смещения на целое число так¬
298

тов, а отрицательные экспоненты имеют смещение на
долю такта рГ0 плюс целое число тактов. Преобразуя
сумму функций на рис. 04-1-6 по Лапласу, для экспо¬
нент получим единое известное изображение, а сумми¬
роваться будут произведения масштабов на операторы
смещения ехр(—kT0p) или ехр[— (р + Л)Т0р]. Беря мас¬
штабы из рисунка, получаем:
( со
1
£П (р)=J] ехР W* to — />)] — ехР [рт. (v — р)\ X
л=0
оо
Xjexp \kTt{n — p)\
k=0
'CXp{(fl+2)TQ7j\
'ezp[(fl + f)T04\
-e-p(pT07])
Рис. 04-1-6.
Суммируя входящие в предыдущую формулу гео¬
метрические прогрессии, находим:
рп / Ч _	1	—	ехр [(7) — р) рг„]
(Р — Ч) [1 — ехр (т) — р) r„i •
Аналогично для синусоидальной функции
£п __ jjm 1 — ехр [(/to — р) рГр]
(Р — /“) [1 — ехр (/» — р) Г0]
(1)
(2)
Теперь входной процесс представим в Я-преобразо-
ванной форме:
л (0 = 20—ехр (V)	+	0,51ш ехр (/ТОО-
п=—0.1
299

Тогда изображение его П-представления будет иметь
вид:
уп/„ч -on д i 1 — ехр [(Y) — р) рг0] ]	I
А	dv	\	(Р-DU-ехр to-р) Г' Ь=0-М^
+ 0,5Im,-1-^pri(/1°-^1 ..J
'	(р—	/10) [1 — ехр (/10 — р)\
(Р + °> 1) (ехр [- (р + 0,1)]} — 0,3 ехр [— \ ,7(р 0,1)] -
— O.Sexp [—0,7 (р + 0,1)] + 1 — ехр [—0,7 (р + 0,1)] —
	—ехр	[—	(/?+ 0,1)] + ехр [— 1,7 fp + 0,1)]	.	_L
—	(/?.+	О,	I)2	(1 — ехр [—	(р -|- О, I)]}2
р [0,55 ехр (— р) -(- 0,14 ехр (— 1,7р) — 0,66 ехр (— 0,7р)] +
+ 10 [1 + ехр (— 1,7р) — 0,84 ехр (— р) — 0,75 ехр (— 0,7^)]
'	(р2 + ЮО) [1 — 1,68 ехр (— р) + ехр (— 2р)}	’
б)	Изображение реакции на выходе системы полу¬
чаем обычным путем:
Y(p)=X*(p)W(p).
Из-за затруднений в аналитических преобразованиях
операторов смещения ехр(—kp) анализ удобнее вести
в области спектров, т. е.
Y(/со) =Хп(/со) W(/со).
04-2. АНАЛИЗ И СИНТЕЗ ОДНОКОНТУРНЫХ
ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ
04-2-1. Для ответа на первый вопрос вначале опре¬
делим z-ПФ разомкнутой системы []3]:
w и=кк о - г ■)■з [-/г}.
Функция передачи замкнутой системы
л Г 1 W[z] _ kRk0T0z-1
ф12] — l+W[z] 1 + (МД"о— 1) г-1 •
Из 'последнего выражения следует, что данная
дискретная система устойчива при условии |&д&оТ0 11 <
<1, так как в этом случае корень характеристического
уравнения расположен внутри круга единичного радиуса.
Из последнего условия имеем:
Го<С 2/йдйо = 0,4 с.
300

Для того чтобы переходный процесс заканчивался за
один шаг дискретности, необходимо, чтобы полюс Ф[г]
был равен нулю. Это условие выполняется в том -случае,
если £д&о7о= 1. Следовательно,
Tt = ~Tk~==0,2 с.
КдК j
Определим установившуюся ошибку системы. Внача¬
ле найдем г-ПФ ошибки:
Ф Ы= !	=	2 ~1
сН 1 +W[z]	1	+	(Мо7'о—	Ог-1	*
Согласно теореме об установившемся значении полу¬
чим:
Суст = lim С [АТ,] = lim - ф [г] X [г].
k-*oo	Z	-*	1	2
Поставив в эту формулу г-изображение входного
сигнала
после преобразований получим:
ьуст =:Ь 1 /	=	0,1.
04-2-2. а) Вначале определим г-ПФ разомкнутой
системы:
Г, И = *А (I - г-) 3 {-!-}= 4*	.
где k*=kRk0T20/2, и найдем г-ПФ замкнутой системы:
Ф[ф
Wt[z] __	k*z~l	(1	+	z->)
1+-W\ [z] l +	—	2)2-'	+	(й*+l)z-2 •
Характеристическое уравнение замкнутой системы
имеет вид:
г2 + (k*—2) г+k* + 1=0.
Корни характеристического уравнения определяются
равенством
21>г = — ± -!-]/£*(£*_ 8).
Годограф корней при изменении к* от 0 до оо при¬
водится на рис. 04-2-2, откуда следует, что данная
301

дискретная система струк¬
турно неустойчива, так как
ветви годографа при любых
значениях k* находятся вне
круга единичного радиуса.
б)	Для данного случая
2-ПФ имеет вид:
Рис. 04-2-2.
(1 — аг-1) (1 +Z-1)
(1 + bz~ *) (1 — г- •)*
Следовательно, г-ПФ замкнутой системы
Характеристический полином этой функции передачи
М [jz] = z3 + (k* + b—2) z2+
+ [&*(1—a) + (1—2 b)]z + b—k*a.
=0,15 + 0,15 z—z2 + z3.
Для определения устойчивости системы разделим ха¬
рактеристический полином iWiflz] на соответствующий
ему обратный mi[z] = l—z + 0,15 z2 + 0,15z3, который по¬
лучается путем перестановки коэффициентов, в резуль¬
тате получим:
0,15 + 0,15z — z2 + z3	1	1	—	г	+	0,15г2 + 0,15г3
0,15 — 0,15z + 0,0225z2 + 0,0225z3 |0,15 + • • •
0,3.г — 1,0225z2 + 0,9775.г3
Остаток от деления умножим на z_1 и получим вто¬
рой полином следующего вида:
Образуем второй обратный полином tn2{z\ =0,9775—
—1,0225z + 0,3 z2 и снова разделим полином М2[г] на
m2[z]:
После подстановки значений /гд=10; /го = 2,5 с
Г0=0,2 с; а=0,7; Ь = 0,5 получим &*=0,5 и M\[z\ =
М2 [г] =0,3—1,0225 г + 0,9775 z2.
0,3— l,0225z + 0,9775z2 0,9775— 1,0225z+0,3z2
0,3 —0,314z + 0,092z2	0,307+	.	.	.
708г" + 0,885z2 -
302

Снова умножим остаток от деления на z~l и обра¬
зуем третью 'пару полиномов: М3[г] =—0,708 + 0,885 г и
/п3[г] =0,885—0,708 г.
Снова разделим Л43[г] на /?г3[1г]:
— 0,708 + 0,8852
— 0,708 + 0,5672
0,3182
0,885 — 0,7082
— о,
Поскольку все частные от деления по модулю меньше
единицы, то согласно критерию Джури [26] данная-
дискретная система устойчива.
04-2-3. Определим ПФ объекта, для чего свернем
внутренний контур обратной связи:
W (п) =	^
Р(Р + Ш •
Найдем г-ПФ разомкнутой	системы
W [г] = ЩЬ. (1	_ г-1)	3 [-.	А =
LJ Лз	1	\p2(P + kMf
k*z~ 1 (1	+ Рг-1)
— (1-z-i) (1-аг-) >
где
а*   ^nHz (T’o + 7эа — 7 э) > р Тэ — пТэ — Т0а
Г0
Г 71	1
« = .	.;T,=,W.
Функция передачи замкнутой системы
ф Ы =	k*z-'(l+?z-')
М 1 + (k*— 1 — a) z-1 + (ft*? +а) г-2 ’
Характеристическое уравнение системы
z2 + (А*—1—a)z+ (А*§+«) =0.
Подстановка численных значений /г*=0,147; § = 0,72;
а = 0,368 дает z2 — 1,221г+0,474=0.
Корни этого уравнения Zi)2=0,615±0,316/ находятся
внутри единичного круга, так как |zi,2|=0,69. Следова¬
тельно, данная система устойчива.
303

+
I
N
+ c
I
N
CX|
cn
0
+
1
N
+
8
I
N
+
- +
+ =
I
N
CM
О
+
I
N
Ю
о
++ +
+ +
05
CD
О
I
N
05
Tt«
(M
О
+
d d
I I
M N
CD CD
О CM
. CO
+ J
I 7
N Ы
t> Г"-
О о
I I
<s T
8 N
~ CO
0
+ °~
I*
N ,
05 *
rf N
CM CD
- 05
и
1	7
N 1
CM N
CO CM
''f CO
« Tt<
О -
О
N
t'-
CO
CO
I I
Tf CD
О О
CM CM
+ +
*M N
CD 00
CD LO
I I
o o
0
7 +
см »
1
£ м
CO LO
" ID
+
+
I »
N I
CM N
© 4f
О О
см
I I
I I
CM N
CM CM
05 05
О О
I
N
CO
05
^ 7
« cS
'•l «2
+
+
I »
CM I
CO N
—I CM
CM CO
cm"
i i
N M
Tf Tf
О О
I 1
N 7
CO 1
05 N
rf CO
- CO
+
+
I *-
Ю (.
4 4
—Г см
i i
CM N
ь- Г"-
о о
I
M
CO
CO
ID
05 Q
N |
S3 7
Ю I
©" 05
+ -
7 +
CM 00
h- I
OL CM
CO ID
I I
I I
N N
ID ID
CM CM
CM
ID
I ~
M *
CO N
CO 05
ID 00
o" —
+ +
в» 05
I I
M N
CD LO
OO
CO ^
5-Г cm"
I I
tM N
CO CO
LO
CM
ID
I -
N I
t"- M
CM C50
ID CO
О —Г
+ +
I
I
IM IM
t"- CM
ID CD
CO ^
~-h CM
I I
IM M
05 05
О о
I
N
LO
CM
Ю
+
I
IM
CO
ID
CO
+
I
CM
304

Для определения переходного процесса найдем его
г-изображение:
и и=ф м агм=,+(Д, _k;z^+х
Х-г^тг.
После подстановки численных значений коэффициен¬
тов получим:
 	0,1472"1 -(- 0,106z-2
1 — 2,2212"' + l,695z"2 — 0,4742"* •
Разделив числитель на знаменатель, получим Н\г\,
приведенную на стр. 304.
В установившемся режиме имеем:
Кст [^«l = lim h [kTt\= lim
k-tco	z-*l
H[z} = 1.
Взяв обратное z-преобразование от частного, полу¬
ченного в результате деления, найдем:
h[kT0] = 0 + 0,1475 (^—Г0) +
+ 0,4326 (i—2T0) +0,7116 (4—ЗТ0) +1
+ 0,926(*—47’0) + 1,046 (*—5Го) +
+1,1076 (/—6Г0) + 1Д256 (t—7T0) +'
+1,1136 (t—8T0) +1,1096 (*—ЭГо) +
-f-1,1056 — 1070)+1,1028(г— ПТ0)+ ... +16(f—ооГ0).
Кривая переходного процесса приводится на
рис. 04-2-3.
04-2-4. а) Передаточная функция разомкнутой си¬
стемы
W Ы =- **г-‘(!-«-■) (1+2-)
и '	(1	+	62-’) (1 — г-1)2	>
20—903	305

2
Подставив z={\+w)j(\—w), получим:
w(w) — k (1 + ^-(1-Ji
W(dD) — n (\+T2w)w*	’
где
* fe* (1 — a) < rp __  1 -j- я rp   1 — 6
* — 2(1 + Ь) ;	1—	Г^Г’	y2—J-qrr
Рис. 04-2-4.
Подстановка численных значений коэффициентов
дает &=0,05; 7"х = 5,67; Г2=0,333. Следовательно, псев¬
дочастоты, соответствующие частотам сопряжения,
равны:
v, = 1 /	0,224; v2= 1 /Т, = 0,176;
v3=1/7’2=3; v4=1.
Учитывая, что звено (1—w) имеет фазовую псевдо-
частотную характеристику, изменяющуюся от 0 до —90°,
после замены w на /v построим с помощью шаблона
апериодического звена амплитудную и фазовую псевдо-
частотные характеристики (рис. 04-2-4), откуда частота
среза для данной системы vcp=0,34; запас по амплитуде
А3ап= — Ю дБ; запас по фазе т]зап=35°.
б)	Для определения влияния на устойчивость систе¬
мы задержки в вычислении управляющего сигнала на
ЗОб

один шаг дискретности необходимо г-ПФ разомкнутой
системы умножить дополнительно на z~K После подста¬
новки z—(1 + ш)/(1—w) получим:
w* (т\ _ fe(l + 7» (1 — ц>) (1 —tt>)
' '	(1 + T2w) w2 (1 + ^)
Следовательно, фазовая частотная характеристика,,
которая приведена на рис. 04-2-4, изменится (пунктир¬
ная линия на рис. 04-2-4). Как следует из рис. 04-2-4,.
в этом случае система близка к границе устойчивости.
04-2-5. Поскольку переходный процесс должен закан¬
чиваться за три шага дискретности, то желаемая г-ПФ'
замкнутой системы должна иметь вид:
ФоМ =z=Alz-1+A2z~2+A 3z~3 .
Согласно второму условию система должна иметь
астатизм второго порядка, поэтому г-ПФ ошибки долж¬
на иметь следующий вид:
Л м , Л г , (г — I)2 1В*гг + В*2)
фс И =1 — ф. и = -— z*~ — •
Определив. г-ПФ разомкнутой системы для данного:
объекта без учета г-ПФ ЭВМ, получим:
W [г] — к (г + 1}
(г-\у >
где k = k0T2о/2.
Следовательно, г-ПФ разомкнутой системы с учетом
искомой D[z] ЭВМ будет иметь вид:
Исходя из запрета сокращения нулей, лежащих на
границе и вне единичного круга, представим Ф0[г] в сле¬
дующем виде:
ф = (~ + 0 (A*\Z + A*z)
Так как Фе[г] и W0[z] связаны соотношением

Для определения искомых коэффициентов Л*ь Л*2,
В* 1 и В*2 используем соотношение
фс И = 1 — Ф. [г],
которое приводится к виду
(г— 1)г(£*,г+Д*г) _ ,	(2+1) (Л*,г + А*г)
23 _ 1	?	,
откуда будем иметь четыре уравнения для определения
четырех неизвестных:
5*1 = 1;
Л*1=2Б*]—В*2;
А*1+А*г=2В*2—В*1;
А*2 = —В*2.
Решая эту систему уравнений, получаем А*4 = 5/4;
•<4*2=—3/4; 5*! = 1; В*2=3/4. Следовательно,
0 Ы = —Р.бг-1)
и\А\ 4/С (1 + 0,75г-1) •
Определим переходный процесс и найдем перерегу¬
лирование. Изображение переходного процесса будет
иметь вид:
Z	-Тг*+-2~г	Г
Н №= ф. И фг= 	5^	•
Деление полинома числителя на полином знамена¬
теля дает:

Переходный процесс будет иметь вид, показанный на
рис. 04-2-5. Кривая переходного процесса имеет макси¬
мум, равный двум единицам, который достигается при
tm= 1то -j- -g-7^ ^ . Следовательно, перерегулирование
составляет 100%.
2,0
1,5
1,0
0,5
h(t> /'Pxt
5 t |
— *
I
_L_
7_
V'
0 T0 im2T0 3T0	4	Tq
Рис. 04-2-5.
04-2-6. Определим z-ФП разомкнутой системы:
U7. [г] =D [г] W [г] =D [г] (1 -г'1) 3
XV7	и	(!— az~l) (ch(Qoro— 1) (г + 1)
woiz\ —	(1+&2-1)	(,г2__2zeh co0r0+	1) ’
где С00= 1/Г1.
Подставив численные значения соо и То, получим:
tw г ]  0,128/гд (1 az 1) (z 0
• W	—1165) (z— 0,606)
Исходя из условия допустимого сокращения полюса
21 = 0,606, положим а = 0,606, тогда 6 = 0,303 и W0(z)
примет вид:
0,128Mz+ О
(z + 0,303) (2—1,65)*
Определим значение &д, исходя из условия требуемой
точности в установившемся режиме. Найдем выражение
для установившейся ошибки:
lim С [&Т0] = 1 im ^=2- Ф(. [г] _JL_ = Фс [1].
k-+0O	z->	1
Так как Фс[,г] = 1/(1 + №0|>]) и по условию задачи
Ф; [1] = о ,05, то из формулы для W0[z\ при г=1
получим 6Д=66. -
309

о) Определим запасы устойчивости системы по
ЛПЧХ. Произведем в W0[z] подстановку z=( 1 +
+ w)/(l-w);
К N
20
(0,58ш + 1) (4,1 w — 1)
Псевдочастоты сопряжения равны vi = 1,88 и v? =
= 0,244.
Логарифмические псевдочастогные характеристики
показаны на рис. 04-2-6, откуда следует, что запас устой¬
чивости по фазе фзап=35°.
Рис. 04-2-6.
04-2-7. Найдем модифицированное ^-преобразование
для ПФ данного объекта:
Г1[г,в] = А.(1-г-*)3|-1-} =
V2
' е2
2.+ 1 ,
г
to
2
N
1
1
7
где е=1—хз/Т—0,5. Приведя выражение для Wi [z, е]
к виду, удобному для построения ЛПЧХ, получим:
к,Тг0,25 (2+ 5,83) (2+ 0,17)
IF, [г, .] =
22 (2— I)2
Подстановка г=(1 + а>)/(1—w) с учетом численных
значений kQ и Т дает:

С целью коррекции ЛПЧХ для обеспечения устой¬
чивости введем ПФ корректирующего контура
г ,	1	+	бег;
°М=г+ш>
где частоты vi и \2 выбраны исходя из требуемых за¬
пасов устойчивости. В результате получим суммарную
ПФ разомкнутой системы следующего вида:
W. [w] = D[w\ Wx [до] =
0,05 (1 + 5w) (1 — w) (1 — 0,71а;) (1 + 0,71до)
^	(Ц+	0,6ш)	(1	+	w)	w2
Рис. 04-2-7.
Характеристики, построенные в соответствии с этой
ПФ, приводятся на рис. 04-2-7, откуда видно, что систе¬
ма устойчива и имеет запас по амплитуде Лзап=—6 дБ
и запас по фазе фзап—30°. Определим z-ПФ корректи¬
рующего контура путем обратной подстановки до =
= (z—l)/(z +1):
U [z\ о,/4 x	'
Таким образом, для данной системы йд=3.74; а =
= 0,66 я 6 = 0,25.
зп

04-2-8. Поскольку воздействие F(p) нельзя отдельно
перевести в z-форму [|можно применять z-преобразова¬
ние только к эквивалентному воздействию Fs(p) =
= F(p)W(р)], то следует функцию передач дискретной
системы задавать в форме, преобразованной по Лапласу.
Согласно приложению 17 дискретная форма преобразо¬
вания Лапласа совпадает с z-формой при замене
^ — *т°р
следовательно,
г3 — 1,5гг + 0,5	~[
ет«Р
ф (ет°Р) = Г г3 1,5гг 4- 0,5	1
>	[	2з_22	+ 0,5гг + 0,15 \2=е
Теперь в выражении для ошибки
Цр) = Р (Р) W (Р) Фс [/оР]} = F{p)V (р)
образуем новую функцию
V(p)=W(p)^ Иг=еГоР}.	(1)
Статический коэффициент ошибки получаем из (1)
при р=0, 2=1:
С =V70) = № (0) ФЛ11 =— L~ .1>5 + °>5	= о
и0 M4L W	C[1J	^	2	1а+ 0>5 + 0>15 V.
Для определения последующих коэффициентов ошиб¬
ки Ck надо дифференцировать (1) по р. Эта процедура
облегчается, если ввести при дифференцировании второго
сомножителя кроме окончательного аргумента р проме¬
жуточный аргумент 2:
dp
дг
(Рф[г]
— ф" р
dp2
г
<*3ф[г]
— ф'" I
Г2 .
в*
dp'
(2)
Тогда при k=\ из (1) получаем:
C'=[tFv (р)]^=Jfw (°)	+T>w (0) ф'с Ш =
— L ПЛ-Ъ- °>65-0,5 —Т0
2 " 1
Tj2 1	7)	0,65	27)	*
312

при k = 2
d*V (p) f дг . „ д d , d2 \	, W(Tl r ,	,
dp*	\f)p2,	(>P\ (>P',dp22J 1	\z\-eTap}'
Поэтому из (2)	f
c-={$'w w ®< i:ч+2 jp w o>) ®, (1| л+
+ Т-.Г'0>)Ф",[1]+Г.«?(ЙФ',[11} и т. д.
Подстановка 2=1 (т. e. ет°р^ при p = 0) проделана
раньше.
Общее выражение для ошибки
00
6=0
Для заданного воздействия в виде полинома второй
степени имеем:
f(t)=a+f>t+yt\
/(f) = p + 2Yf;
f(t) = 2у;
/(0 = 0, далее /<*>(*)= 0 при £>2.
Поэтому
5 (0 = С, (а + pf -f yO + С, (р + Щ + С22у.
Если И7 (р) = 1, то И? (/?) = 0, и общее выражение
для ошибки примет вид:
00
Для заданного полинома сумма (4) имеет конечное
число членов
2
313

04-3. СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ ПО МЕТОДУ
ПАРАМЕТРОВ СОСТОЯНИЯ
04-3-1. Запишем исходные дифференциальные уравне¬
ния объекта в нормальной форме Коши:
У\=0*У\-\-1 •У2+0-М1+0-/2;
у2—0- У1+0-У2+1 'м1+1 *Ь
или в матрично-векторном виде
Y=BY+Aw1+Cf2,
где
Y =
Ух
; в =
0 1
; А
0
; С =
0
Уг
*
D 0
1
1
а) Искомое уравнение параметров состояния имеет
вид:
Y [(А ■+ 1) Т\ = Ф (Г) {Y [ЛТ] + а (Г) и, [кТ] + b (Г)/, [кТ]},
где
Ф(Т) = Ь-'{{Ер-В]-\=т-,
Т
а (О = ([Ф (—х) dz\А;
b (Т) — j [Ф (— X) dx] С.
Подстановка значений матриц А, В и С для данного
примера в последние выражения дает:
ф (T) = L->
: L~ 1
(
р
0
0 1
\
0
р
0 0
1
1
Р Р‘
0 —
Р
ч=Г
1 Т
0 1
а (7) = |
о
ь<г)=|
1 —т
0
,—
-J_ Тг
2 1
0 1
J
1
Т
1 —т
0
2 1
0 1
J
1
Т
314

б)	Для определения оптимальных значений коэффи¬
циентов бц и oi2 алгоритма для выработки управляющих
воздействий вначале найдем фундаментальную матри¬
цу 02.
Так как п=2 и /=1, то минимальное число дискрет¬
ных шагов для перевода объекта из начального состоя¬
ния в конечное равно двум.
Фундаментальная матрица
02=||а(Г); Ф(Г)-1а(Г)||.
Для заданного объекта
1
3
02 =
—72
-тГ2
т
т
Произведем операцию обращения этой матрицы:
1
3
Т2
2Т
	 1
1
7^2
2 Т
Поскольку для замкнутой системы имеет место управ¬
ление по текущей информации о выходных координатах
в каждом шаге, то искомая матрица алгоритма управ¬
ления будет совпадать с первой строкой матрицы G2_1:
0(7):
Таким образом, оц=1 /Т2, ol2=3J2T и алгоритм управ¬
ления имеет вид:
1
3
7*2
2Т
и, \kT\ = —
1
3 1
'fi
2 Т j
Y \kT\.
в)	Найдем переходный процесс для начальных усло¬
вий:
f/i[0]=l; г/2 [0] =0.
При k—0
 1_
7"2	•
ui [0] = -
1 3
1
Т2 2 Т
0
315

Подставив это значение управляющего воздействия
в уравнение параметров состояния, получим:
1 т
1
1
+
	L Т2
2 1
0 1
1
0
Т
Y [71 =
Для k = 1
и, т=-
2
1
Т
»Y [2Т] ==
1 Т
о 1
J- —
Г2 2Г
1
2
Т
+
1
2
П_
" 7
_1_
: J2
_1_
'?2
Кривые переходного процесса приводятся на рис.
04-3-1.
щей.
Рис. 04-3-1.
04-3-2. Порядок решения эрой задачи такой же как и в предыду-
а)	Исходная система дифференциальных уравнений объекта
регулирования имеет вид:
*/i = 0*	+ & 12^/2+0*#з+0* Mi;
i/2 = 0 • г/i + 0 * г/г +1 ‘Уз + О-цц
г/з = 0 * г/i -t- 0 * г/г + 0 - г/з + 1 • Иь
Следовательно,
316
0
Ь\2
0
0
в =
0
0
1
; а =
0
0
0
0
1

Матрицы Ф (Т) и а (Г) уравнения параметров состояния будут
иметь вид:
Ф (Т) =L-]
= L~1
р
0
0
0
^12
0
0
р
0
—
0
0
1
0
0
р
0
0
0
т=Г
1
р
^12
р2
^12
Рг
1
to
J2
b 12—
0
1
р
1
р2
1
-=
0
1
г
0
0
0
0
1
р
т=Г
г
т2
1
т
г
1 — b12z ь12 ~y
0
X bltT*
0 1 —X
dz
0
=
~1ГТ2
0
0 0 1
т
Минимальное число шагов дискретности для перевода выходных
координат объекта из начального состояния в конечное (требуемое)
Ai=nll. Поскольку п = 3 и 1=1, то N=3. Найдем фундаментальную
матрицу для случая N = 3:
G3 = ||а(Г); Ф(7,)-1а(Г); Ф(Г)~2а(Г)Ц.
Д^я определения Ф(Г)-1 и Ф(Т)~2 используем соотношение
Ф(Г) 71 = ф( пТ). В результате получим:
G, =
Матрица алгоритма управления а (Т) определяется как первая
строка матрицы G3 1. Проделав операцию обращения матрицы G3 и
взяв из нее первую строку, получим:
1 , ™
7
19
0
0 ^12^3
— Ь„т*
1 ™
3
5
- — Т2
Т2
—Г Т2
т
т
т
в(Т) =
1 2
11
Ь12Т3 Т2
6 т
Следовательно,
1
2 ^
ап~Ь12Тз у
а12 	 J"! »
°13 =
11
6 Т •
б)	Определим переходные процессы в данной дискретной си¬
стеме. Для Т = 1 с и 612 = 2 ац = 0,5; Oi2 = 2; oi3= 1,833.
317

Для k = 0 при начальных условиях получим:
О
У [0] =	0	;	их	[0]	=	—	||	0,5	2	1,833 [j Y [0] = — 1,833.
После первого дискретного шага имеем:
• (—1,833)1 —
1 2 1
[
0
0,333
Y[rj =
0 1 1
0
+
. —0,5
0 0 1
1
1
1
0,39
0,083
—0,833
Для k = 1
Ul[T} = — I! 0,5	2	1,833	!|
0,39
0,083
—0,833
1,169.
После второго дискретного шага имеем:
Y [2Т] =
1 2 1
(
0,39
0,333
0 1 1
0,083
+
—0,5
X) 0 1
1
—0,833
1
0,11
—0,165
0,336
•(1,169)
Для k = 2 |
и, [2Т\ = — и 0,5 2	1,833||
0,11
—0,165
0,336
= — 0,336.
318

После третьего дискретного шага имеем:
1 2 1
(
0,1
I
0,333
Y [3T] =
0 1 1
—0,
165
-b
—0,5
0 0 1
I
0,336
1
0,006
0
=
0,003
0
0
0
(—0,336)
Ошибки вычислений привели к небольшим погрешностям, но
вектор Y[3r] близок к нулю. Кривые переходных процессов при¬
водятся на рис. 04-3-2.
04-3-3. Система дифференциальных уравнений объек¬
та согласно рис. 4-3-3 имеет вид:
*/i=0-г/1-|-1. г/2+0-ul-\-0-f2\
Ь}2——(02оУ1+0*У2“Ы	*/2-
Следовательно,
B =
0 1
; A =
1 0
и C =
0
—(O20 0
1 1
1
1
Ф (Т) =
а (Т) =
— з\пщТ
cos to0Т
— co0sinw07 cos со0Г
-4- (COS — 1)
w 0
— sinc°o т
Поскольку минимальное число шагов дискретности
для перевода объекта из начального состояния в конеч¬
ное равно двум, то фундаментальная матрица
G*= || а (Г)~, Ф (Т)-’а(Т) || =
(cos — 1)	—	-V	(cos	ш0Т — cos 2ш0Г)
1 . 1
— sinco.r	—■ —-	(sinсо,/ — sin2w07’)
319

Обращение фундаментальной матрицы дает для опре¬
деления коэффициента алгоритма управления следую¬
щую матрицу:
<03.
2sin о>0Г—sin2 2со07'
х
X
—- (sin со0Т — sin2 щТ) -4- (cos (о0Г— cos 2(о0Г)
ю0	ш	б
—-р- sin ШоГ
Ш0
(cos <о0Г — 1)
Следовательно, коэффициенты алгоритма ^правления
011 и 012 для замкнутой дискретной системы определяют¬
ся выражениями:
>2о (sin (о0Г — sin 2и>0Т) _а>20 /
2sin w0T — sin 2ы0Т	4	2
0.1 Ю= —
_ <o0(cos <о0Г — cos 2<о0Т) ^ Юр ^ctgmoT | ctg j
>
°i2	2sinco,7'	—	sin2<o07'
Кривые изменения коэффициентов 0ц(Г) и 012 (Т)
приводятся на рис. 04-3-3, откуда следует, что, исходя из
условия отрицательных обратных связей, диапазон аргу¬
мента cooТ должен лежать в пределах
2пк<^(о0Т2/27i;-l—g-, п — 0, 1, 2, 3...
Следовательно, диапазон изменения Т определяется
соотношением
2пк ^ rp . 2тс | я
/л	ч.	>	/л
Зо>0»
где п=0, 1,2,3...
320

04-3-4. Порядок решения этой задачи аналогичен по¬
рядку решения предыдущей. Матрицы исходной системы
уравнений объекта имеют вид:
в =
0 1
; А =
0
сого о
1
Матрицы уравнения параметров состояния:
1
Ф (Т)= СЪа3*Т ^ShW°7' ;
со0 sh (о0Г	ch со0Т
а (П —
-Г (1 — cb'&J)
<jOqT -
b)0T
Рис. 04-3-4.
Фундаментальная матрица
”■ (ch “ 1)	(сЬ	Ch	2а)о7’)
и2 =
1	1
— sh<o„r — — (sh со0Г — sh 2<в07’)
ш0	со0
Матрица коэффициентов алгоритма управления
“ — (sh со0Т — sh 2сд0Т)	— -у (ch со0Т — ch 2и>0Т)
шо	w	о
Л
— — sh о>0Т
СО()
~г (ch со „Г — 1)
Ю О
21 —903
321

Следовательно, коэффициенты <Тц(!Г) и 0\ъ{Т) за¬
мкнутой системы, оптимальной по минимуму числа ша¬
гов в переходном процессе, определяются выражениями:
. ,т\  «Msi^r-shovO _<■>*„ (л | „c.„t,st0«7'
3м(У)	—	2sh	и>„Т	+	sh'2«„r	4	(^4	~Г	csctl	4	j>
//тт\    Wo(ch оърГ	ch 2u>qT")  f
°ч V 1	—	2shw07’-t-sh2co07’	Г	2
cth
co„7‘
cth шТ
)■
Характер изменения значений сгп и ai2 от cooТ приво¬
дится на рис. 04-3-4, откуда следует, что минимальные
значения о»ц и 012 ограничены значениями сгцмин=со2о и
012мин—©0-
04-3-5. Исходные дифференциальные уравнения объ¬
екта регулирования:
уг = 0 • у1 -(- Ь1гуг -)- 0 • ы,;
г/2 = 0 • г/, — Ьг2у2 -|- a21u,.
Матрицы В и А
в=
0
bi2
|; А=
0
0
	Ь22
а21
Матрицы уравнения параметров состояния:
ф(7) =
1 ^ (1 — е~ЬмТ)
b 22
п	л—ь%%т
а (Г) =
2iL(^r_
.бааГ \
1)
Фундаментальная матрица дискретной системы
0ЛП =
Ьц«» Г.7. , J_ /,	1	1&а27'	+	(1	—	е011') е"
6*.
1Г-(^Г-1)
22-(^r_1}
S22

Следовательно, коэффициенты алгоритма определя¬
ются из выражений
ан(П =
о»(Т)=—
/уЬ^Т
а..Ь127’ (еь»т-1)
ЬггТ + (1 — еЬпТ) еЬмТ
аиТ(еь*т—1)*
Подстановка численных значений й12, Ь22, «21 и Т дает
ац=2,54 и 012=О,676.
04-3-6. Решение этой задачи аналогично предыдущей.
Матрицы В и А определяются выражениями:
в=
-6„ 1
; А =
0
0 0
1
Матрицы уравнения параметров состояния:
Ф (Т) =
а (Т) =
о—ЬцТ
FT (1—-“)
Фундаментальная матрица для двух шагов дискрет¬
ности
02 =
57тГ-57Г (^-,>] FT Г-it'М
т	т
Операция обращения этой матрицы определяет иско¬
мые коэффициенты первой строки сгц(Г) и в\2 (Г):
Iт\	Ь*и
°П (т) =
(ebllT — I)2
т ЬиТ-еь»т (еь“т-1)
T(eb"T-iy
Подстановка численных значений Ьи и Г дает ац=
=3,44 и сг12=2,9.
04-3-7. Как следует из решения задачи 4-3-1, опти¬
мальные значения коэффициентов алгоритма управления
для данного объекта при Т= 1 с равны ац=1/Г2=1 и
(У12=3/27,=1,5. Поскольку Т0ФТ, то уравнение парамет¬
ров состояния имеет вид:
Y [ (Л+1) Го] =Ф (Го) {Y [кТ0] +а (Г0) щ [ЙГ0]},
21*
323

где управляющее воздействие
^[^0]=—a(T)Y[ftr0].
Подстановка этого уравнения в уравнение парамет¬
ров состояния дает:
Y[(&-(-1)7’о] =Ф3(То, Т)У[кТ0],
где
Фз(70, Т)-Ф(То) [Е—а(7'о)0.(О]-
Характеристическое уравнение замкнутой системы
М[z] =det[Ez—Ф3(Го, Г)].
Определим численные значения элементов матрицы
Фг(То,Т).
На основании решения задачи 4-3-1 имеем:
Ф(Г0) =
0 (Г) =
1	0,5
0 1
_L JL
Т2 27'
а (Г0) =
= 11 1, 1,5
—0,125
0,5
Подстановка этих значений в выражение для
Фз(Г0, Т) дает:
0,875 0,3112J
0,5 0,25
Фз (7'.. ТГ~
М
[г] = det |
2 0
0 г
Следовательно, характеристическое уравнение имеет
вид:
0,875 0,3112	1=г*_1)125г	+
—0,5	0,25	)
+ 0,3743.
Корни этого уравнения 21>2=0,5625±0,241/ располо¬
жены внутри единичного круга. Поэтому данная система
устойчива.
04-3-8. Запишем уравнение параметров состояния для
системы с полной информацией в следующем виде:
Y[ (АН-1) Го] =Ф(То) Y[kTo]+Н (Го) Щ [kT0].
Алгоритм управления
и\ [ (&+1) То] ——onY [ (&+1) Т'о] -
Подставив первое уравнение во второе, получим:
щ [ (*+1) Го] =—апФ (То) V[Л7о] -<тпН (Т0)Щ [kT0].
324

Объединив эго уравнение с первым, получим:
Y [(*+1)7',]
Hi [(&-Ь 1) т'о]
Фп.,(7’.) =
= ф"81(Г.)
Y [*Г,]
Я| [»’.]
ф (То)
н (То))
-0ПФ (То)
-о"Н (7.)
где
^Запишем аналогичные выражения для случая непол¬
ной информации с учетом того, что алгоритм управления
первого порядка дает:
V [ (АН-1) Го] =Ф (Го) Y [кТ0] 4- Н (То) щ [kT0];
Ы1 [ (&_г 1) Го] =—<тн! Y [ (k-\-1) Го] — oh2Y [kT о] —tHi[&Г0],
где 0НЬ а112 и СП1 — матрицы коэффициентов алгоритма
управления при неполной информации. После подстанов¬
ки первого уравнения во второе получим:
и, [(*+!) Го] =—{о'\Ф (Го) +oH2}V [*Го] —
-{он.нС^+С-МиД^Го].
Объединив исходное уравнение параметров состоя¬
ния и последнее уравнение, получим следующую зависи¬
мость для случая неполной информации о состоянии
объекта уп
завления:
Y [(* -Ь 1) То.|
и. [(*+ 1)Г,1
= ФН..(Л)
где
Y [*7'0]
[*Г,1
Фн» (Г„)=
Ф(Г.)	Н(7’„)
■ (<ЛФ (Г,) + 0«2} - {он,Н (7"0) + Са,}
Для ооеспечения эквивалентности систем с полной и
неполной информацией должно выполняться условие
ФГ1з1 (Го) =Фнз1 (То),
которое справедливо в том случае, если выполняются ра¬
венства:
0ПФ (Го) —0Н,Ф (Т0) +0Н2;
0”Н(Го)=0«,Н(Го)+Сн1.
Для заданного объекта матрицы Ф(Г0) и Н(Го) име¬
ют вид:
1
Н(Г,) =
Ф(Г„) =
2 Г^о
325

Поскольку выходная координата у2 не замеряется
датчиком, то матрицы crHi и ан2 запишем так:
oHi=IIcr^i 1 01| и а112=11сг//11 0||.
Подстановка этих выражений в исходные • равенства
дает следующую систему уравнений:
CFni 1=СГ,114~0’,/11; 7,0(ТП11“|“^П12=7,оСТ/11;
-Y Т\о\ + г0ап12 = Д- Т\о'„ +.CV
Следовательно,
о'и = °Пц у^~ 0 12;	0	и=	7\~°	12’
Plnp
ф-
J
1+0,5 г1
\
1-ёт°Р
Р
Рис. 04-3-8.
После подстановки численных значений апц=10;
ап12=4,48 и 7’0=0,224 с получим а'ц=30; о"ц=—20,;
£гн1=0,5. Следовательно, алгоритм управления для не¬
полной информации имеет вид:
и\ [ (fe+1) Го] =—ЗОг/i [ (&+1) Г0] +20yi [£Го] —0,5wi [£Г0].
Взяв z-преобразование от левой и правой частей это¬
го уравнения, получим искомую 2-ПФ дискретного кор¬
ректирующего устройства
D\z]
к, [г]
-30
1 — 0,6662-1
И	^	1	+0,52-' •
Структурная схема системы при неполной информа¬
ции приводится на рис. 04-3-8. Построение ЛПЧХ для
разомкнутой системы дает запас по амплитуде Л3ап=
=—6 дБ и запас по фазе фзап=45°.
04-3-9. Решение этой задачи аналогично предыдущей,
а)	Для данного случая имеем:
ан1=||'(т'11а'120|| и crII2=llcr"iicx//i2 0||.
326

Матрицы Ф(Г0) и Н(Г0) для данного объекта, как
это следует из решения задачи 4-3-2, имеют вид:
1
1
То
	 Т2
2 0
0
1
То
0
0
1
Н(Г0) = Ф(7>(Т0) =
 Т з
6 1 0
Т о
Равенство матриц Фпз1(Г0) и <DH3i(r0) дает следую¬
щую систему уравнений относительно искомых коэффи¬
циентов:
стп11=а/п4-а//ц; ToGnu-\-oJl\2=Too/ii-\-o'\2Jro//\2\
± Т\о\ + 7>"12 + о"13 = ■4- Т\о'„ + Т„о'„;
4-	+	-4	7’2о°П-+	7,.Л.=	4-	7>'»+	4-	+	Л-
В последней системе из четырех уравнений имеется
пять неизвестных ст'п, а"ц, a'i2, cr"i2 и снь Так как число
уравнений меньше числа неизвестных, одно неизвестное
можно выбрать произвольно. Следовательно, данная за¬
дача имеет множество решений.
Для определенности возьмем а"ц=0, тогда получим:
Подставив численные значения апц=5; ani2=7,2 и
ап13=4,34 в эти уравнения, получим: ст'ц=5;	a'i2=21,7;
a" 12=—14,5 и сы!=0,65. Таким образом, алгоритм управ¬
ления первого порядка для данного случая имеет вид:
U[ [ (&+1) То] =—5у\ [ (£+1) То]—21,7у2[ (^+1) Го] +
-\-14,5 г/2 [^Го] —0,65^1 [^Го].
327

Следовательно, z-ПФ корректирующего контура име¬
ют вид:
щ [z[	5
D» и
У1 И '	1	+	о.ббг"1	’
21,7(1 —0,67Z-1)
У% [z\	1	0,65г~J
Структурная схема данной системы приводится на
рис. 04-3-9,а.
г0
“ilkTol
V
Од
1
Р
1+0,69z~1
То
1
1+0,5z~1
&
I
I
р-
Р
3,39(1-0,67Z1)
б)	Матрицы а11] и он2 для этого случая имеют вид:
ffHi=lloyii 0 а']3||; он2=11а"ц 0 о'^зН.
Исходя из условия равенства матриц Фн31 (Г0) и
Фп31(7о), для данного случая неполной информации по¬
лучим следующую систему уравнений:
опи=(т' ц-\-о" и; ToOnu-j-ani2=T(i(y'ii;

т 7>"" + ПЛ.+-4- П»'„
"Г ^.ЛгЬ—ТУЛ.Т- ПЛ3=+Т’,а'„ + ?>'„+с",-
в этой системе из четырех уравнений имеется пять
неизвестных. Поэтому один неизвестный коэффициент
можно выбрать произвольно.
Следовательно, решение данной задачи неоднознач-
но. Для определенности выберем сн|===0,5, тогда полу¬
чим после подстановки численных значений коэффици¬
ентов апц=5; ап12—7,2; <тп13==4,34 следующие значения
иекомых ^коэффициентов: а'и=29,2; а"ц=—24,2; о/13=
, 9, а 1з=2,03. Следовательно, алгоритм управления
для данного случая имеет вид:
“i [ (*+1) То] =—29,2^1 [ (к+1) Г0] +24,2yt [кТ0] —
—3,39у3 [ (к+1) То] —2,ОЗу3 [кТ0] — 0,5ы, [кТо].
Из этого выражения следует, что z-ПФ корректиру¬
ющих контуров будут иметь вид:
n ы   29,2j(l —10,832-’)
11 м	1+0,52-*	•
Г) ы    3,39 (1 + 0,б2-‘)
1+0,52-*	•
Структурная схема дискретной системы для данного
случая приводится на рис. 04-3-9Д
04-3-10. Минимальное необходимое число шагов иден¬
тификации на начальном участке определяется по фор-
муле [3J	г
где «--порядок исходного дифференциального уравне
ния объекта, от число измеряемых выходных коорди
нат: | —число неизвестных координат вектора внешни?
возмущений.
Из этой формулы следует, что для одноконтурной си
стемы (m 1) на начальном участке процесса внешни*
возмущения, переменные на каждом шаге дискретности
не могут быть определены (|—1).
329

Почожим что на начальном участке процесса иден¬
тификации /2=const. Тогда число шагов на этом участке
и -^п — т+ |
т
ЧИ.Д '
Поскольку В нашем случае п=2; от—1; 6—1, то
^Шйдем матрицы при известной выходной координате
И
2^2
1
; Фи <Т) =
1
; Н(7) =
!Г
0
0
Т
Аналогично матрицы при неизвестных у2 и ,/2 равны:
Ен:
; Г (Г):
J2
~2
Запишем матрицу Аи1 для двух шагов дискретности:
1
*
О !фи (П|-Еи |Г (П
о
о
.
Аналогично составим матрицу
ъ.
о
О
о
 0J о
рФиТл"1-ФЛП"!е„ j-H (Т)
—1
1
	L Т2
2 7
0
0
0
0
0
т
0
0
0
0
0
0
—1
1
см
к,
i
0
0
0
0
0
—т
Как известно, обобщенный вектор идентифицируемых
j<oopAHHar и В03МУш'ений определяется по формуле
Yh.o6 = L-,0„1Y„.o6.
ЗЗО

Здесь YH.o6=ll«/i[0], yi[T], «i[0], У\[Т], У\[2Т],
— обобщенный вектор измеряемых и известных
координат на двух шагах дискретности; YH.o6=II*/2[0]»
У*[Т], Уг[2Т], /3[0] Г —обобщенный вектор неизмеряе-
мых координат и внешних возмущений.
Следовательно, алгоритм идентификации будет иметь
вид:
X
У2 [0]
3
2 Т
1
2
1
2 т
0
У2 [Т]
1
2 Т
1
2
1
2Т
0
У2 [Щ
1
2 Г
1
2
3
2Т
—1
h [0]
1
р 2
1
Т
1
рг
0
X
[0]
UilTl+Уш [27'] -Ц- в, [Т]
-Т^ [Т]
На последующих шагах дискретности для идентифи¬
кации неизмеряемой координаты y2[kT] и внешнего воз¬
мущения /2[(й—1)Г], k=3, 4, 5 ... воспользуемся фор¬
мулой
YH [(*ш.д + О Т)
Г[(Лш.д+*-1)7’]
для нашего случая имеем:
Рн = -Е„Г (Т) =
Л„ = Ф(Г)-ЕИН (Т) —
YH (&ш.д + i — ОТ1
Yh [(&Ш.Д Ч" 0 Т]
М1 [(&Ш.Д+ *	1)	Т\
о — г*
—1	т
1 Т —1 — Г2
0 1	о	т
331

Так как £шд = 2, то
ККЬш.ь+i) т\=Уш [(2+0 Л;
YH [(^ш.д + *
|| Уг [О + *) 7]
У2 [(1 + О П
р[(К,д+/-1)Л=/.[(1+0Л;
У,[(Ат.д+0Л=^ [(2+0 Л;
[(^ш.л+/: — 1) Л = и\ [О +0 л*
Обращение матрицы Р„ дает:
Р”1^
2
Г
1
2
У 2 "
0
Следовательно, алгоритм идентификации на последу¬
ющих шагах дискретности имеет вид:
у 2 [(2;+ о т]
2
~Т ~"1
1 Г —1 -у- Г2
/. Ц1 + 0 Т\
2
'Р 2 0
Ьч
о
в л
о
X
X
Ух
[(1
+
*) т\ '
У*1
![(1
+
m
Ух
[(2
+
i) r\
«1
[(1
+
i) T]
/= 1, 2, 3
Это выражение определяет алгоритм идентификации
неизмеряемой координаты у2 и неизвестного внешнего
возмущения /2 на третьем и последующих шагах дис¬
кретности.
Глава пятая
АНАЛИЗ И СИНТЕЗ НЕЛИНЕЙНЫХ СИСТЕМ
05-1. ТИПОВЫЕ НЕЛИНЕЙНОСТИ И ИХ ХАРАКТЕРИСТИКИ
05-1-1. Для синусоидального входного сигнала
=А sin (0\t при А>а строим график сигнала на выходе
yz=F(x) (рис. 05-1-1). Так как нелинейность является
однозначной, комплексный коэффициент передачи имеет
только действительную часть, т. е. J(A)—q (А)~В\1А-
332

Определим амплитуду В\ синусной составляющей первой
гармоники на выходе нелинейного элемента, используя
формулу для коэффициента ряда Фурье и кривые из
рис. 05-1-1.
2 тс	П ср
В1 = -i- I* F (A sin ф) sin фйф = ~ j ^ ф -f-
О	*-0
+ j ЙБтфйф = -i- kA^ —-^-sin2^|^ —
ф
— Ь |созф|^2|=-1 ^(p_^dsin2cp + 6cos^, (1)
где
k=b/a; i|?=coi/.	(2)
'со) ,
г "■%
-if ч>
Г| IV
a=fisiny
Д sen p;
Рис. 05-1-1.
На основании рис. 05-1-1 имеем:
sin ср=а/Л; cp=arcsin (а/Л);
cos®=-|/i—(3)
Синус двойного угла выразим через параметр а не¬
линейного элемента и амплитуду сигнала на входе Л:

Используя выражения (2) —(4), равенство (1) мож¬
но записать следующим образом:
Комплексный гармонический коэффициент передачи
нелинейного элемента имеет выражение
05-1-2. Для синусоидального входного сигнала х = А sin он t при
Л>а строим график сигнала на выходе y = F(x) ^ (рис. 05-1-2).
В нашем случае статическая характеристика нелинейного элемента
является однозначной функцией, поэтому комплексный гармониче¬
ский коэффициент передачи имеет только действительную часть
Определим амплитуду синусной составляющей первой гармони¬
ки на выходе нелинейного элемента Вi, используя формулу для
коэффициента ряда Фурье и кривые рис. 05-1-2:
+ kayf 1	(Лагсзт^-Иу^-^)
81 2k (
'м=т=-(
arcsin -j-
J(A) =BJA.
y=F(x) 1У
(1)
Рис. 05-1-2.
о
где Ф=со,1.
На основании рис. 05-1-2 имеем:
а
sin? =
<t
(3)
334

Выражение (1) для коэффициента передачи с учетом рабёнстё
(2) и (3) имеет вид:
'и>=ёг/Л5.
05-1-3. Для синусоидального входного сигнала
x^As\na)it при А>а строим график сигнала на выходе
нелинейного элемента y=F(x) (рис. 05-1-3,а). Опреде¬
лим амплитуды синусной и косинусной составляющих
первой гармоники на выходе нелинейного элемента, ис¬
пользуя формулы для коэффициентов ряда Фурье: .
2тс
2к
в, = ~ \ *вых sin <»,* d (ШЛ = -L j F (A sin <J>) sin cty;
о	о
2тс	2тс
A =	cos	Ш	Jd	(«0,0	=	-Ь	j*	F	(A	sin	ф)	cos	<j>
где
hy=Hx)
\
1
a
^;
! X
«Сэ ^
I
a
,у
-Ч>
9
9
jt
zn
3(А)	а)
a=Asln у>
Рис. 05-1-3.
На основании рис. 05-1-3,а имеем:
1С + Ф	2ic + tp
= j sin^cty j sin ф rf<|» =
CD	« + 9
bx	,	|1t+<f	I	bt	|2*-f<P	4&!
=	  COS	ф	~Г	cos	?	==	—	cos	?•
71	|cp	Л	Я
335

Так как n=Asin<p (рис. 05-1-3,а), то
COS<f>;=]/ 1 —
Итак, амплитуда синусной составляющей определя¬
ется следующим выражением:
в,= ±у.ТГ%.	(1)
Амплитуда косинусной составляющей
тс + ср	2гс + <р
D1 = -^- j' cos4>cty— j cos<}>d<f> = — p-sin^.
<f	я + ф j
Учитывая, что sin ф=a/A (рис. 05-1-3,а), имеем:
A =	(2)
Используя формулы (1) и (2), находим действитель¬
ную и мнимую части комплексного гармонического ко¬
эффициента передачи:
/ л\ ^	t/i я2 •	/о\
Я iA) =	У 1 ~ Ж’	®
(Л) = ^	(4)
Коэффициент передачи
/(А):=яЖ+1я\(А) = ^ У	Ф)
Строим	годограф /(А)	на комплексной плоскости.
Из уравнения (4) имеем:
Аг —	 4abl	,с\
щ' (А) •	(6)
Подставив выражение (6) в (5), получим:
я' И)
q И) + № (А) —	~~	у^—	4нЛ)— а‘ + №	(А) •
336

После приведения подобных и возведения в квадрат
левой и правой частей последнего уравнения получаем:
представляющее собой уравнение окружности в осях
координат q{A), qf (Л) радиуса R=2bi/na~0,5 и цент¬
ром в точке с координатами <70 (Л) =0; ■q'o(A) =
=—2&i/jta=—0,5. Так как q(A)^0, qf(A)^S) [см. вы¬
ражения (3) и (4)], то годограф J(А) представляет
полуокружность
где <7(Л)^0 и <7'(Л)^0 и размещен в четвертом квад¬
ранте. Годограф J(А) изображен на рис. 05-1-3,6.
05-2-1. Для построения фазового портрета определим
производную от координаты х:
Для получения уравнения фазовых траекторий ис¬
ключим время t из уравнений для х и dx/dt. Уравнение
(1)	возведем в квадрат, причем dxjdt обозначим через у:
Уравнение для х также возведем в квадрат и умно¬
жим на (о2:
Произведя сложение левых и правых частей урав¬
нений (2) и (3), получим:
i/М-со2х2==Л 2со2
(!)
Выражению (7) соответствует уравнение
05-2. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ
—7г[^= Лео COS о4.
atL
(i)
у2=А2 со2 cos2 о/.
(2)
со2л:2=Л2о)2 sin2 00/.
О)

Уравнением (4) представлены уравнения фазовых
траекторий изображающей точки [уравнение (4) есть
каноническое уравнение эллипса]. На рис. 05-2-1 пред¬
ставлены кривые изменения координаты х изображаю*
щей точки и скорости y=dx/di в функции времени и
фазовый портрет. Фазовый портрет представляет собой
семейство эллипсов. Каждой фиксированной амплитуде
А соответствует определенный эллипс с полуосями: а=А,
Ь=ыА. Стрелками указано направление движения изо¬
бражающей точки Mi. В верхней половине фазовой пло¬
скости, где dx/dt>0, что означает увеличение х, изо¬
бражающая точка всегда движется слева направо
(в сторону увеличения х). В нижней половине фазовой
плоскости, где dx/dt<0, изображающая точка движется
справа налево. На оси х, разделяющей верхнюю и ниж¬
нюю половины фазовой плоскости, y=dx/dt=0, т. е.
скорость изменения х равна нулю. Следовательно, фазо¬
вая траектория пересекает ось х под прямым углом.
В заключение отметим, что изложенные выше положе¬
ния характерны для любого фазового портрета.
05-2-2. Релейная функция F(x) может иметь три по¬
стоянных значения: Ь, 0 и —Ь.
Имея в виду, что F(x) на отдельных участках по¬
стоянна, введем обозначение
где постоянная к может соответственно принимать зна¬
чения Ь, 0, —Ъ.
Учитывая (1), на основании заданной системы урав¬
нений звеньев условия задачи запишем уравнения си¬
стемы
Рис. 05-2-1.
F(x) =—Х,
(1)
338
x = kv. = xi\ 1
| х | = b [или 0. I
(2)

Интегрирование уравнения (2) при начальных усло¬
виях t—О, х—х0 дает:
х=Хо	(3)
Интегрирование уравнения (3) при /=0; х=х0 дает:
х=х0+xot + Kit212.	(4)
По уравнениям (3) и (4) можно построить, исполь¬
зуя метод припасовывания, по участкам траекторию
изображающей точки.
Рис. 05-2-2.
На каждом участке (где щ не меняет знака) вычис¬
ление х и х производятся по уравнениям (4) и (3) при
соответствующем значении т и при своих начальных
значениях х0 и хц.
Конечные значения х и х каждого предыдущего
участка есть начальные значения х и х каждого после¬
дующего участка.
Для первого участка начальные значения х0 и х0
определяются начальным состоянием системы.
На фазовой плоскости (рис. 05-2-2,а) наносим ли¬
нии переключения и указываем значения xi для различ¬
ных областей плоскости (xi=kx).
При построении используем условия задачи, т. е.
k= 1, ai=l, 6=1, а2=2, и * релейную характеристику
(рис. 5-2-2,б). По уравнениям (3) и (4) на рис. 05-2-2,6
строим траекторию изображающей точки на фазовой
плоскости по участкам,
22* 339

Участок. I. xi — — 1. Начальные условия: л:1о==5
£1о=0. Подставим численные значения в уравнение
(3), (4)	Ия
x — — t) }	...
х=5 —1*!2. \	^
Первое уравнение системы (5) подставим во второе,
получим уравнение траектории — параболы х=5—х2/2
или
х=± V Ю — 2х при 5.	(6)
При двил^нии системы х уменьшается (л^л^о—5),
а уменьшению х соответствует отрицательное значение
производной х,
Следовательно, участок I траектории находится в чет¬
вертом квадранте плоскости и уравнение имеет вид:
х—}^ 10 — 2х при х<5.	(7)
Конечные значения участка /: х=1; х=—2,83.
Участок II. ] х, =0.'^ Начальные [условия: Хд1— 1,
TJ1 == — 2,83.
Уравнение (3) для этого участка представляет пря¬
мую линию
х=х^ = _ 2,83.	(в)
Участок III. х1 = 1. Начальные условия: х10п——2,
X™ =-2,83.
После подстановки численных значений в уравне¬
ния (3), (4) имеем:
х — — 2,83-j-/;	j
<*	(9)
х = — 2— 2,83^-4—.
Из первого уравнения системы (9) получаем:
£=* + 2,83.
340

После подстановки этого выражения во второе урав¬
нение (9) и преобразований имеем:
*2=12 + 2*:
или
х—±У 12~1~2х при х^ — 6.
Конечные значения участка III: * = —1; ;с= |/10.
Участок IV. к, — 0. Начальные условия: XgV =
—•— 1, XqV — }^10. Уравнение (3) для этого участка
представляет собой уравнение прямой линии
х=х™ = ]/Т0.	(10)
Участок V. х,--=■—1. Начальные условия: xv0==2,
■*0=1/То.
После подстановки численных значений в уравнения
(3), (4) имеем:
k=y\Q — t\ ]
,2	(il)
*=2 + ]Л0 t- L j
Из первого уравнения (11) получаем:
t=Y IQ— х.
После подстановки этого выражения во второе урав¬
нение (11) и преобразования имеем:
х— ± Y14— 2х при х<7.
Конечные значения участка V: х--1: х=—)/*12.
Полная фазовая траектория состоит из отрезков пря¬
мых линий и парабол. Система совершает колебания
с увеличивающимися амплитудами отклонения х и ско¬
рости X.
05-2-3. Согласно схеме, приведенной на рис. 5-2-3,
динамические свойства нелинейной системы описывают¬
ся дифференциальным уравнением вида
Ti + x=—<F(x).	(1)

Релейная функция F (х) может иметь три постоянных
значения: Ь, 0 и —Ь.
Запишем уравнение (1) отдельно для каждого из
трех участков:
Тх + х=—b при х^а\	(2)
Тх + х=Ь при	—а;	(3)
Тх + х=0 при \х\<а.	(4)
Таким образом, фазовая плоскость может быть раз¬
бита на три области. Границами этих областей служат
две прямые х=а и х=—а.
Введем обозначение x—dx/dt=y и уравнение (2) пе¬
репишем следующим образом:
Г—Г—Т	(5)
Для исключения времени t из уравнения (5) и раз¬
деления переменных произведем следующие преобразо¬
вания.
Разделим уравнение (5) на y=dx/dt:
du	1	b
при
ИЛИ
откуда
du у + Ь	^
ту
ь + у
dy = dx при х^а.	(6)
Левую часть уравнения (6) преобразуем следующим
образом:
Ту ту + ть — ть _т ть
Ь + у	Ь + у	Ь + у>
поэтому
ТЬ
dx = — Т dyyj—^dy при лЗз-а.	(7)
Проинтегрируем уравнение (7):
X——Ту + ТЬ\п\у + Ь\ +й при х^а,	С8)
342

Проделав аналогичные операции с уравнениями (3)
и (4), получим следующие решения:
х——Ту—ТЪ \п\у—Ь\ +с2 при х^—а;	(9)
х=—Ту + с3 при |.v|<a.	(10)
Итак, фазовая плоскость разбивается на три области.
В области I (рис. 05-2-3,а) справа от граничной прямой
х=а располагается семейство интегральных кривых, по¬
строение которых производится по уравнению (8),
Рис. 05-2-3.
а в области II слева от граничной прямой —а — по
уравнению (9). В области же III между граничными
прямыми х=а и л:=—а траекториями изображающей
точки являются прямые линии, которые строятся по
уравнению (10).
Выбирая соответствующие значения постоянных
интегрирования Ci, i= 1, 2, 3, можно определить фазовую
траекторию, проходящую через любую заданную точку
фазовой плоскости. Поскольку постоянные интегрирова¬
ния входят во все три уравнения в качестве слагаемых,
то достаточно построить фазовую траекторию только
для одного фиксированного значения сг-, например d=0.
Все остальные фазовые траектории определяются путем
343

параллельного переноса построенной траектории вдоль
оси Ох. Подставив в уравнения (8) — (10) численные
значения параметров при .С*=0, получим:
х=—10r/-f-201n|г/—f-2J при х^\\	(11)
*=—10#—201n|#—2\ при *^—1;	(12)
*=—10# при |*| < 1.	(13)
Численные значения координат изображающей точки,
соответствующие уравнению (11) для любого *, пред¬
ставлены в табл. 05-2-1, а уравнению (12)—в табл.
05-2-2.
Таблица ОН-2-1
У
— 10
—5-
—4
—3
—2,5
—2,2
—2
— Г,8
— 1 ,6
— 1,5
X
142
72
53,9
30
11,1
— 12,2
— о:;
— 14,2
—2,32
1,1
У
— 1
—0,5
0
0,5
1
2
3
4
10
15
X
10
13,1
13,9
13,3
12
7,7
2,2
—4,2
—50,3
—93,4
Таблица 05-2?2
У
— 10
—7,5
—5
—3
—2
—1
X
50,3
30
11,1
—2,2
—7,7
— 12
У
1,7
—
1,9
2
2,1
2,5
X
7,08
—
27
со
25
—1J , 1
Г1 родолэ
чсение mat
1л. 05-2
У
—0,5
0
0,5
1
1,2
1.5
X
—13,3
—13,9
—13,1
—10
—7,54
-1,1
У
3
4
5
10
15
—
X
—30
—53,9
—72
—142
—201
—
На рис. 05-2-3,6 представлены фазовые траектории,
соответствующие табл. 05-2-1, а на рис. 05-2-3,в —
табл. 05-2-2.
Фазовый портрет системы получается путем перено¬
са кривых, изображенных на рис. 05-2-3,6 и в вдоль
оси Ох. Он изображен в более крупном масштабе, чем
кривые на рис. 05-2-3,6 и в. При |*|<1 отрезки траек¬
торий получены по уравнению *=—10у + с, где с любое.
344

Переходный процесс в системе при любых начальных'
условиях будет затухающим. Точка М0 соответствует на¬
чальному состоянию системы. Анализ траектории изо¬
бражающей точки для заданных начальных условий по¬
казывает, что процесс в системе заканчивается за два
периода.
Максимальное значение координаты х достигает при¬
близительно 11, а значение скорости в переходном про¬
цессе не превышает начального значения.
05-2-4. Динамические свойства нелинейной системы
описываются следующими уравнениями:
Так как фазовая плоскость может быть разбита на
три области, то необходимо определить уравнения изо¬
клин для каждой области. Найдем уравнение изоклин
для области справа от граничной прямой х=а. Введем
обозначения:
Выражение (5) определяет наклон фазовой траекто¬
рии в данной точке.
Уравнение (1) запишем следующим образом:
Для исключения времени t почленно разделим урав¬
нение (6) на y = dx/dt:
Tx+x=z—b при х^а\
Тх+х=Ь при х^—а;
Тх+.х=0 при |x|<a.
(1)
(2)
(3)
x=dxjdt=y\
dyjdx=N.
(4)
(5)
dy_
dx
J b_
T Ту >
откуда
ъ + у
Ту"-
(7)
Из выражения (7) получаем уравнение изоклин:

Таблица 05-2-3
346

Проделав аналогичные операции с уравнением (2),
получим уравнение изоклин для области слева от гра¬
ничной прямой х=—а в виде
v=-wr+T-	<9)
Изоклины (8) и (9) представляют собой прямые, па¬
раллельные оси Ох и отстоящие от начала координат
на расстояниях, зависящих от величины наклона N при
заданных параметрах системы b и Г. Задаваясь значе¬
ниями N от нуля до бесконечности, получим семейство
изоклин.
Определим уравнение изоклин в области между гра¬
ничными прямыми х=а и х=—а. Запишем уравнение
(3) в виде dy/\dt=—у/Т, откуда
dyldx=—\lT=N.	(10)
Из уравнения (10) следует, что траектории изобра¬
жающей точки в зоне нечувствительности нелинейного
элемента имеют неизменный наклон, равный N=—1/Г.
Танген угла наклона прямых участков составляет ве¬
личину— 1 /Г.
Для построения фазового портрета системы удобнее
вначале выразить параметр N через координату у. Из
уравнений (8) и (9) после подстановки численных зна¬
чений параметров получаем:
N = —	при	х	0,5;	(11)
N =	при д:< — 0,5.	(12)
В табл. 05-2-3 представлены численные значения N
и arctg/V, вычисленные для различных у по формуле
(11), а в табл. 05-2-4 — вычисленные по формуле (12).
Согласно табл. 05-2-3 и 05-2-4 на рис. 05-2-4 прово¬
дим изоклины. На каждой изоклине нанесены линии,
указывающие наклон фазовой траектории arctgA/', когда
она пересекает данную изоклину. Учитывая свойства
фазовых траекторий, для различных положений изобра¬
жающей точки М проводим фазовые траектории так,
чтобы при пересечении соответствующей изоклины на¬
клон фазовой траектории к оси абсцисс был равен
347

arctg N. Для построения участка траектории между
двумя соседними изоклинами Ni и N2 из точки М0 прово¬
дим две прямые с наклонами arctg N1 и arctg N2 в на¬
правлении изоклины N2. Так как траектория в точке Л[0
имеет наклон arctg JVi, а следующую изоклину должна
пересекать с наклоном arctg N2t то она должна лежать
внутри угла, образованного указанными прямыми. Прн-
Рис. 05-2-4.
ближенно можно считать, что точка М\. пересечения тра¬
екторией изоклины N2 находится на середине отрезка
последней, отсекаемого этими прямыми. Из точки Мi
таким же образом проводим две прямые с наклонами
arctg N2 и arctg N3 и получаем точку М2 фазовой тра¬
ектории и т. д. Выбирая другие начальные точки, строим
другие траектории и получаем фазовый портрет.
В области между граничными прямыми х=а и
=—а при а=0,25 наклон фазовых траекторий опреде¬
ляется из выражения
arctg A/=arctg (—О.,2)	Пв'.
348

05-3. МЕТОД ПРИПАСОВЫВАНИЯ
05-3-1. Согласно структурной схеме, изображенной
на рис. 5-3-1, нелинейной системе соответствует следую¬
щая система дифференциальных уравнений:
В зависимости от знака координаты х система нели¬
нейных уравнений (1), описывающая движение системы,
распадается иа две линейные системы:
при х<0
Постоянные и с2 определяются из начальных усло¬
вий. Подставляя значения х2 из уравнений (4),	(5)
в первые уравнения систем (2), (3) и интегрируя урав¬
нения, получаем:
Уравнения (4)—(7) являются уравнениями искомого
переходного процесса. Для построения переходного про¬
цесса необходимо использовать уравнения (4), (6) при
х<0 и уравнения (5), (7) при х>0. Начальное движе¬
ние системы определяется знаком координаты х.
x2 = ktF(x);
X = &4х, -)- k3X2.
(1)
(2)
при х> 0
(3)
Произведем интегрирование систем (2) и (3):
x2=kibt+Ci при л:<0;
х2=—kibt + c2 при х>0.
(4)
(5)
t2
= k2k2b —\- k2cxt + с3 при х < 0;	(6)
х, = — kxk2b ~ + k2c2t + с4 при х > 0.	(7)
349

Подставим численные значения параметров системы !
и начальные условия в третье уравнение системы (1);
a;(0)=£4*i(0) +£3*2(0) =0,05.	!
Так как л: (0) >0, то для построения переходного про- |
цесса на первом участке используем уравнения (5)
и (7).
Из уравнений (5) и (7) для заданных начальных
условий определим постоянные с2 и с4:
с2=х2(0)=0; c4=*i (0) =0,01.
Таким образом, уравнения для построения переход¬
ного процесса после подстановки численных значений
будут иметь вид:
*2=— 0,02^; (8)
JC1=—0,01Y2 4-0,01.	(9)
Движение системы по уравнениям (8) и (9) будет
продолжаться до тех пор, пока координата * не изме¬
нит знак. При х=0, соответствующем моменту времени
t=tu произойдет замена уравнений движения.
Значение 11 определяется из условия
X—kikXi + kzX2=0	(10)
или после подстановки в уравнение (10) Xi и х2 из
уравнений (8) и (9) и численных значений коэффициен¬
тов k3y £4 имеем:
5(—0,0П21 + 0,01)— 0,02^=0,
откуда ti=0,82 с.
Определим значения *1 и х2 в конце первого этапа
переходного процесса:
Xi(ti) =—0,01 t\ + 0,01 =0,00328;	(11)
X2(tt)=—0,02tt=—0,0164.	(12)
Начальные значения функций *1 (t) и x2(t) для вто¬
рого этапа будут равняться их конечным значениям для
первого этапа.
Для удобства на втором этапе переходного процесса
будем вести отсчет времени от нуля.
Подставляя начальные условия (11) и (12) в урав¬
нения (6) и (4) и полагая в последних t—0, находим
с3=0,00328, с±=—0,0164.
350

Уравнения для второго этапа переходного процесса
принимают вид:
*! = 0,01 /2—0,0164/+0,00328;	(13)
я2=0,02/—0,0164.	(14)
Подставляя выражения (13) и (14) в третье уравне¬
ние системы (1) и приравнивая его нулю, находим мо¬
мент переключения t=h:
5(0,01/22—0,0164/2+0,00328)+0,02/2—0,0164=0,
откуда /2=1,24 с.
Подставляя в уравнения (13) и (14) значение време¬
ни /=/2, получаем значение функций х\ (/) и xz(t) на
конце второго этапа переходного процесса, которые
являются начальными значениями для третьего этапа:
х± (/2) =—0,00168; *2 (/2) =0,0084.
На участке /ь /2 координата Х\ согласно уравнению
(13) изменяется по параболе. Момент времени, при ко¬
тором *i достигает экстремума, определим, приравнивая
кулю производную *1, которая получается путем диф¬
ференцирования уравнения (13):
*1=0,02/—0,0164=0,
откуда /'Э2=0,82 с.
Учитывая, что длительность первого участка равна
/1=0,82 с, получаем /a2=/i + /'02=1,64 с. Из уравнения
(13) получаем *1 (/э2)=—0,0034.
Дальнейшее построение переходного процесса произ¬
водим в таком же порядке. Кривые переходного процес¬
са системы изображены на рис. 05-3-1.
351

Численные значения координат х1у x2j faxi для
характерных моментов времени представлены
в табл. 05-3-1.
Таблица 05-3-1
Коорди¬
наты
i = 0
/, - 0,82 с
*8f = IfG4c
t* = 2,06 с
t3 = 2,5 с
Xi
0,01
0,00328
—0,0034
—0,00168
0,00008
k,x,
0,05
0,0164
—0,017
—о; 0084
0,0004
х2
0
—0,0164
0
0,0084
—0,0004
Из приведенных кривых переходного процесса следу¬
ет, что процесс в системе затухающий.
05-3-2. На основании структурной схемы запишем дифференци¬
альное уравнение системы, которое имеет вид:
Т x-\-x——kF (х).	(1)
Нелинейная функция F(х) имеет три постоянных значения:
Запишем уравнение (1) отдельно для каждого из трех участков:
Tx-\-x=—kb при х^а\	.(2)
Tx+x=kb при —а-,	(3)
Тх-\-х — 0 при \х\<а.	(4)
Уравнениям (2) — (4) соответствуют следующие решения:
-L,
х ~ с\ 4 с2е —kbt при х ^ а;	(5)
7
• ~Г t
х с3 -4- c^c ~f~ kbt при	— а\	(б)
1 *
откуда
% — сс 4- с5е т при \ х\ <Са,	(7)
1		t
х — — -у- с2е — kb при хcl,	(8)
х = —-у-с4е т -\-kb при х ^— а;	(9)
1	т	t
1	-4	*
X — — ji
при I X I <а.	(10)
352

Первый участок переходного процесса на основании заданных
начальных условий определяется уравнениями (5) и (8).
Таким образом, постоянные Ci и с2 определяются из начальных
условий при / = 0; л:(0) = 5; х(0)=0.
При этих условиях из уравнения (8) имеем:
сг — —kbT; Сг = — 20.
Разрешая уравнение (5) относительно с1у получаем:
d=x(0)—с2\ ci = 25.
После подстановки в уравнения (5) и (8) численных значений
параметров системы и постоянных ct и с2 уравнения для координат
системы х и х на первом участке окончательно примут вид:
x = 25-^20e-°>lt—21 при х>1;	(И)
х=2е~°>и~2 при х^\.	(12)
Время переходного процесса ti, соответствующее равенству
л = а= 1, определяется из уравнения
1 =25 — 20е~°’и' — 2<,
или
I0<?~°’1/l= 12 — /1в	(13)
Уравнение (13) решим графическим способом. На рис. 05-3-2,а
изображены графики левой и правой частей уравнения (13). Точка
пересечения графиков дает значение времени ti = 7 с. Значение
координаты х в момент врёмени ti из уравнения (12)
х(^) =2е-о.»—2 =—1,007^—1.
23—903	353

Начальные значения функций x(t) и x(t) для второго участка
переходного процесса будут равняться конечным значениям для
первого участка. Определим постоянные с5 и св из условия «сшива¬
ния» в точке t=t 1. Для удобства на втором участке переходного
процесса отсчет времени будем вести от нуля.
Из уравнения (10) имеем:
Ce = —Tx(ti)\ с6= 10.
Из уравнения (7) получаем значение постоянной
c5=x(t 1) —се; съ= 1—10=—9-.
После подстановки в уравнения (7) и (10) численных значений
параметров системы и постоянных с5 и сб получаем уравнения для
координат х и х на втором участке:
х=—9—ИОе-0’1*;	(И)
х=—е-°>и.	(15)
Определим момент времени /2, соответствующий границе второ¬
го и третьего участков. Полагая в уравнении (14) х = —а = — 1,
получаем:
е-°.и2==0,8,
откуда /г=2,25 с.
Значение координаты х в момент времени t2 определяется из
уравнения (15):
i (tz) = —е~°-1 '2'25 = —0,798.
Начальные значения функций x(t) и x(t) для третьего участка
будут равны конечным значениям для второго участка. Определим
постоянные с3 и с4 из условия «сшивания» решения в точке / = /2.
На третьем участке отсчет времени также буДем вести от нуля.
Из уравнения (9) имеем:
crk = T[kb—х(/2)] =27,98.
Из уравнения (6) получаем:
c3 = x(t2) —— —28,98.
Уравнения для координат х и х для третьего участка после
подстановки численных значений параметров в уравнения (6) и (9)
принимают вид:
* = —28,98 + 27,98е-°’" +2/;	(16)
х = —2,798е-°’1* + 2.	(17)
Полагая в уравнении (16) х = —а — — 1, определяем момент
времени /3, который соответствует границе третьего и четвертого
участков
— 1 = — 28,98+ 27,98е~°’,/з + 2*3.
откуда
27,98е-°'Из= 27,98 — 2/.,.	(18)
354

Уравнение (18) решим графическим способом. На рис. 05-3*2,6
изображены графики левой и правой частей уравнения (18). Точка
пересечения графиков дает значение времени = 7,1 с.. Значение
координаты х в момент времени t3 определяем из уравнения (17):
x(t2) =—2,798е-°-7* + 2 = 0,625.
Экстремальное значение координаты x(t) на третьем участке
соответствует моменту времени t3з, при котором я(/)=0. Из урав¬
нения (17) получаем:
0 = — 2,798с-0’Иэз -f-2,
откуда tdз = 3,25 с. На основании уравнения (16) имеем:
x(tas) =—28,98 + 27,98е“°'325+2'3,25 = —2,3.
Дальнейшее построение графиков x(t) и x(t) переходного про¬
цесса, которые представлены на рис. 05-3-2,в, производится анало¬
гичным образом. Численные значения координат х и х для харак¬
терных моментов времени представлены в табл. 05-3-2.
Таблица 05-3-2
Номер участка
Время от начала
участка, с
Время от на¬
чала коорди¬
нат, с
X
X
0
.0
5
0
1
2
2
4,6
—0,36
1
4
4
3,6
—0,66
t\ = 7
7
1
—1
1
8
0,05
—0,905
2
2
9
—0,83
—0,817
t2 =2,25
9,25
— 1
—0,778
2
11,25
—2,03
—0,29
Q
t3 з = 3,25
12,5
—2,3
0
О
4
13,25
—2,23
0,129
*з = 7,1
16,35
— 1
0,625
А
2
18,35
0,13
0,512
ft
/4 = 3,9
20,25
1
0,424
К
t3b = 1,9
22,15
1,44
0
о
tb = 4
24,25
1
—0,37
2
26,25
0,34
—0,304
6
4
28,25
—0,22
—0,248
00
32,05
— 1
—0,17
23*
355

05-4. ИССЛЕДОВАНИЕ РЕЛЕЙНОЙ СИСТЕМЫ
ПО МЕТОДУ Я. 3. ЦЫПКИНА
05-4-1. Строим АФХ линейной части системы:
W(M=W(P)p^ =
1
-z=z G ( о) -J-/5 (^)'
1 + со2 J СО + (О2
Результаты расчетов сведены в табл. 05-4-1.
Т а б л и ц а 05-4-
(О
0
0,1
0,2
0,4
0,5
0,6
G
—1
—0,99
—0,96
—0,86
—0,8
—0,73
В
—10
—4,8
—2,2
— 1,6
— 1,2
со
1
1,4
1,8
2
3
со
G
—0,5
—0,34
—0,24
—0,2
—0,1
0
В
—0,5
—0,24
—0,13
—0,1
—0.033
0
На основании табл. 05-4-1 на рис. 05-4-1 построена
АФХ линейной части системы.
Re \Jfjcon>\
oj = 0jZ
Рис. 05-4-1.
Частотная характеристика релейной системы связана
с частотной характеристикой линейной части следую¬
щей зависимостью:
= Г (/.)+£ G[(2m-f- 1Н+/|] —2ДТ1)<й1> (D
/71+1	1П-\-	1
где /(/о)) —частотная характеристика релейной системы.
356

Используя выражение (1), на рис. 05-4-1 по точкам
строим годограф /(/со). Подробно покажем построение
точки годографа / (/со) для частоты an=0,2 с-1, т. е. век¬
тора J(/coi) . К вектору W (/соi) прибавляем вектор
W* (/Зсо,) = G (3<о,) + / ~в (Зсо,),
где 3©1=0,6 с-1.
К полученной сумме прибавляем вектор
W* (/5(0,) = G (бш,) + / -L В (5ш,).
Процесс, суммирования производим до тех пор, пока
слагаемые существенно изменяют суммарный вектор:
J{jm)=W (/ол) + W* (/3coi) +
+ W* (/5coi) + W* (/7 со i) + ...
Аналогичным образом строим другие точки годо¬
графа /(/со).
Частота автоколебания <оп определяется точкой пере¬
сечения годографа /(/со) с прямой — яа/46, параллель¬
ной действительной оси. Из рис. 05-4-1 найдем (оп=1 с-1.
Условие переключения в нужную сторону (сущест¬
вования автоколебаний)
Щ J 04) | < ~ h' (0),
где
h'(0)^L~'[W(p)\t=t.
Так как
i- prcrtl =i-	-1 —
TO
A' (0)= 1 — e~‘ \ ,=o = 0.
Так как
Re|J(/cou) |=—0,75<0
(см. рис. 05-4-1), то в релейной системе существуют
автоколебания, частота которых шп=1 с-1.
357

05-4-2. Ч a-сто иная характеристика релейной системы /(/со) свя¬
зана с частотной характеристикой линейной части системы W(j®)
следующей зависимостью:
/ (/со) = W (/со) + ^ G [(2т + 1)<о] + / ^ В [(22ИЛ4
В [(2от + 1) И
т+1	т+1
На рис. 05-4-2 построены АФХ линейной части системы
W (/со) = W (р)р=/(0 = О (со) + /Я (со).
и частотная характеристика релейной системы /(/со).
ю о
I I I I"Г I I гт
'oj=5c~1	}
-со=Ч	/
& р	у
1
W(joj)	ojf~ 0,5 с~‘
Частота автоколебания соп определяется точкой пересечения го¬
дографа /(/со) с прямой — тга/46, параллельной действительной оси.
Из рис. 05-4-2 находим соп = 4,3 с”1.
. Условие существования автоколебаний определяется следующей
зависимостью:
где
h’ (0)5= L-' W(p)]i=
{Т\р-\- 1) (Ttp+ 1)
т2-т,
— e
-ki-
h’ (0) — js_ti
Так как Re | J (/con) 1 = —1,1 <0 (см. рис. 05-4-2), то в релейной
системе существуют автоколебания, частота которых соп = 4,3 с
358

05-5. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
АВТОКОЛЕБАНИЙ НЕЛИНЕЙНЫХ СИСТЕМ
ПРИ УСЛОВИИ ФИЛЬТРАЦИИ ВЫСШИХ ГАРМОНИК
05-5-1. Приведем систему уравнений, описывающих
движение гироскопа к одному уравнению с переменной
р. Определяя из второго уравнения а и а и подставляя
их в первое уравнение, получаем:
АД>Р“1~ (А>га3 Ч-Д>па) Р“Ь(папвнг) ^с.дф) +
+'пМва.	(1)
Так как nji -4. Н*, то пренебрегаем папв по сравне¬
нию с Н\ Введя символ дифференцирования D = d$fdt,
получим:
[ДДИ*-ИАоП^ B'tiJD’+H’D] р= -НМС,д ф)+ паМш. (2)
Исследуем колебания гироскопа при подключенном
стабилизирующем двигателе и отсутствии внешнего мо¬
мента, т. е. МВн=0':
ИДП3 + (A^ + B.nJD’ + H'D] $ = -нмс,д(р).	(3)
Периодическое решение ищем в виде (3=4 sin Ш.
Уравнение нелинейно изменяющегося момента Л4С.Д от
р заменим соотношением
Mc.R=qi(A)fi=4m0filnA,	(4)
т е. произведем гармоническую линеаризацию нелиней¬
ного элемента.
Подставляя (4) в (3), получаем линеаризованное
уравнение системы:
рДП3 + (Лпа + В0ла)Ог+Я2П + ^-] (3 = 0.
Характеристическое уравнение системы имеет вид:
А0В„Р3 +	В„па) р* + Н*р + ^ = 0.
359

Заменим p—jсоп и выделим вещественную и мнимую
части:
Равенствами (5) представлен баланс вещественных и
мнимых частей. Устойчивость периодического решения
(предельного цикла) проверим, используя аналитиче¬
ский критерий, основанный на критерии Михайлова.
В системах не выше четвертого порядка для устой¬
чивости предельного цикла требуется, во-первых, чтобы
выполнялось неравенство
во-вторых, все коэффициенты характеристического урав¬
нения должны быть положительны. В решаемой задаче
второе условие выполняется.
Индекс «п» при производных означает, что после
взятия производных необходимо подставить значения
амплитуды и частоты предельного цикла (для периоди¬
ческого решения) а=Ап, со=соп* После замены в харак¬
теристическом уравнении р=/со получаем выражения
для вещественной и мнимой частей АФХ линеаризован¬
ной системы:
Определив соответствующие производные, получим:
(5)
G (а, со) = ^ - (Л«0 + В„па) со*;
В (а, о))=Я2о—ЛоЯосо2.
(аг)„ = - 2(ЛП, + В.^»П<°;
Из второго уравнения (5) получаем
t - Н*
т* 	 •
to*  	 _	•
• ® П— А/)в0 ’
(6)
360

поэтому
(
§) =-2Я"<0;
/ п
dG \ /дВ \	/дО\ /дВ\ _
да )п (да )п Ц )п [да )а~
8т0Н3^ л
' nAK ">U-
критерий устойчивости выполняется, т. е. незатухаю¬
щие колебания существуют.
*3
Чт (р)
НЭ
Рис. 05-5-2.
Частота автоколебаний
Н	9,8.10-2
<о„
VА„Ва	У~ 19,6 -10 — 5-9,8 -10—6
= 705 с'
Подставляя выражение (6) в первое уравнение (5),
получаем формулу для определения амплитуды автоко¬
лебаний:
л 	 4т0А0В0
' ъН (А„п9 +В0па)
4-4,9-10-19,6-10-5-9,8-10-*
3-14.9,8.10-2 (19,6.10-'.9,8.10-« + 9,8.10-М9,6.10-«)—
= 0,0318 рад.
05-5-2. Структурную схему системы на рис. 5-5-2,а
свертываем к виду, представленному на рис. 05-5-2, где
НЭ нелинейный элемент, а ПФ линейной части имеет
вид:
W*(p)= p(tJ+1) (Й°-с + Т^+ 1 ) =
__ &2^0.сПР Ч” ^2 (^1 “Ь k0 с)
P{TlP+i)(T2p+\) ■
(1)
Произведем гармоническую линеаризацию нелиней¬
ного элемента. Комплексный гармонический коэффициент
361

передачи нелинейного элемента имеет только действи¬
тельную часть:
/ (A)=q (А) =4с/яЛ,	(2)
где А — амплитуда колебаний на входе нелинейного
звена.
Линеаризованная разомкнутая система имеет ком¬
плексный коэффициент передачи
№(/<о, A)=Wa{j®)q(A).-
Предельный цикл реальной системы соответствует
границе устойчивости линеаризованной системы, т. е.
Щ/а>ш Лп)=-1
или
Wa(j(oa)q(An)=-l.	(3)
От амплитудно-фазового баланса [формула (3)] пе¬
реходим к балансу вещественных и мнимых характери¬
стик. Представим комплексный коэффициент передачи
линейной части системы в виде отношения полиномов:
w (jm)==vihп)
Баланс вещественных и мнимых характеристик за¬
пишется в виде
G (Ат шп) = Re V 04) + q (An) Re U 04) = 0;	J	(4)
В (A„, (Dn) = ImV 04) + q (4) Im U (bn) = 0,	J
где
и (/сOn) = (ki + k0.c)kz + jksJlo.cTKOn;
R(/con)=—to2n(Ti + T2) +}(con TiT2(o3n);
Re U (/o)n) = (^i+^o.c)^2;
Re V(/<on)=—4>za(Ti+T2)-,
Im U (/con) =k2k0.cTiton;
Im V (jean) =con—TiT2oi3n-
Подставляя значения вещественных и мнимых со¬
ставляющих, а также уравнение (2) в уравнения (4),
получаем:
G 04п, шп) = — “2п (Т1 + г2)+^ (*»+ ko.c) *.=00
. N	М5)
В (Ап, «=(l + ГМ, “п - т,ту„ =0. J
362

Из первого уравнения (5) находим:
2  4е -f~ ^о.с) ^2	/6)
ш«— *Л(Д+72) •	V
Из второго уравнения (5) с учетом (6) получаем:
• + ТАК, ^-ЯЖТтл <6' + *■>■•>*•=«•
откуда
.	4cft27’1 (Г,^!—7’1fe0-c)	,rn
Лп—	И(Г, + Г2)	•	V	;
Подставив (7) в (6), получим:
г	kl + ко
П 7, (ГА-ГЛ.С) •
Для нашего случая амплитуда автоколебаний
„ „	4.1.5-0,01	(0,1-2 — 0,01-1) 	0	11*
п—	3,14	(0,01,+0,1)	’	’
частота автоколебаний
Шп 1^0,01(0,1-2*2о,ЙП-1)	39,6	С	•
Устойчивость предельного цикла проверим, исполь¬
зуя аналитический критерий.
Для устойчивости предельного цикла требуется, во-
первых, чтобы выполнялось неравенство
(£).(£№(£).>*
во-вторых, все коэффициенты характеристического урав¬
нения должны быть положительны (исследуется система
третьего порядка):
G (а, ®) = - «• (Г, + Тг) +	(Л, +-Л0.С) Аг;
В (а» = (l + Г,А2*0 с	(В — Т.Г2Ш*.
363

Определив соответствующие производные, получим:
/22Д — - 4с( fei + feo-c) К
\^а )п	пАгп	;
(£)„=-2».<Г.+П);
(<№ \ _	4сГЛуссоп
\да )а	пА\	;
, I 4c7’1fe2fe0 с	2
(^Jn— 1 +		ЗГ^Ш
fdG_\ fдВ_\	/сЮ\ (дВ\ „Г 4-1(2 + 1)51 w
VajnV*Vn Wnldajn I	3,14.0,11* J A
x (l + iIhi;;,'1 - 3 0,01, о, 1 • 39,6* ) -
— [—2-39,6 (0,01 + 0,1)] (-4- ЬО’ОЬ^-З9’6 j =3110.
На основании структурной схемы, изображенной на
рис. 05-5-2, и выражений (1) и (2) характеристическое
уравнение системы преобразуем к виду
Т%Тгр° + (7\ + Т3) р> + (l + 1^- йЛ.с7\) Р +
+S-(*i + *o.c) *. = 0.
Все коэффициенты характеристического уравнения
положительны. Критерий устойчивости выполняется,
т. е. существует устойчивый предельный цикл.
Определим * степень подавления третьей гармоники
линейной частью системы. На выходе нелинейного эле¬
мента (см. рис. 5-5-2,б) действуют только нечетные гар¬
моники.
На основании уравнения (1) модуль комплексного
коэффициента передачи линейной части имеет выраже¬
ние
, „	+	feo	с)**'.	+	(*.*о.с',<»)■
|ли Л to V( 1	+	У	,)»	«о*	'
364

Коэффициент передачи первой гармоники с частотой
(1)=0)п
*ГЧ*(Ы1=з§!5Х
чх|/	(2+	1)25г	+	(5-1-0,01 -39,6)»	_пло.
(1 — 39,62-0,012-0,12)2 + (0,01+0,1)2.39,62
Коэффициент передачи третьей гармоники с частотой
<в=Зсоп
C=i^«3*")i=3-keX
чх!/"	(2+ 1)252 +(5-1.0,01-3-39,6)2	л m
xXf (1 — 9-39>62*0,012-0, l2)2 + (0,01 -f 0,1)2-9-39,62 и’
Отношение коэффициентов передачи для третьей и пер¬
вой гармоник составляет К(3)//С(1)=0,01 /0,085 = 0,118. Та-
Л ‘ Л
ким образом, амплитуда третьей гармоники на входе
нелинейного элемента составляет всего лишь 11,8%
амплитуды первой гармоники.
05-5-3. Структурную схему на рис. 5-5-3 свернем
к виду, представленному на рис. 05-5-3,а. Линейная
часть системы имеет ПФ вида
w»(Pb
р (г2р2 + 2х^;+ 1)>
где
Н* + плп& ’	—	Я2	+	/#г3 ’
Ал„ + В0па
Я2+папв •
Так как пая#<^Я*, то пренебрегаем яая3 по сравне¬
нию с Н\
Строим частотные характеристики линейной части
"«(р):
k = (9,8Ло~2^*~ = 10 с^кг' м'); к = 20 дБ;
,	19,6-10“*-9,8-10—•
 . = 9.1 о — •
(9,840-*)*	*
365

Линейная часть системы состоит из усилительного,
интегрирующего и колебательного звеньев.
90*
ДБ
- U0
0
<3
- 20
*•
* -90
- 0
%Г180
--20
-270
--U0
L((jo)
vyЯр)
У
НЗ
-1\
а)
/з
-bJ
ШУ
100
б)
Д[
' \<рМ
\ j
-2700
Рис. 05-5-3.
Параметры колебательного звена
К ^ = v‘p* + 2ztp+ V
tz=l,4M0-3 с; |=0,00141; &>с=1 /т=706 с-1.
Частотные характеристики линейной части системы
представлены йа рис. 05-5-3,6. При построении харак-
376

терйстики колебательного звена используем шаблон.
Для контроля определим значение пика амплитудной
характеристики на сопрягающей частоте юс.
Логарифмическая амплитудная частотная ' характе¬
ристика колебательного звена
К И = - 20 lg К(1-«о*х*)* + (2^Г*.
Значение амплитуды на сопрягающей частоте сос
LK (ос) =—201g 2g=—201g 2 - 0,0014=51,2 дБ.
На рис. 05-5-3,6 L(cо)—логарифмическая амплитуд¬
но-частотная характеристика; ф(со) —фазовая частотная
характеристика.
Строим характеристики нелинейного элемента.
Для нелинейного элемента (см. рис. 5-5-1,б) ком¬
плексный гармонический коэффициент передачи имеет
только действительную часть:
] (А) —q (А) =4то / пА.
Для построения характеристик составляем табл. 05-5-1.
Характеристики нелинейного элемента приведены на
рис. 05-5-3,в.
Таблица 05-5-1
А, рад
Я (А)
(н-м)/рад
1
Я (А)
рад/(н-м)
20 lg q (А),
ДБ
201еТТл)’
ДБ
0,0001
6,23-10
1 ,.6-10“ 2
35,9
—35,9
0,001
6,23
1,6-Ю-1
15,9
. —15,9
0,01
6,23-10~1
1,6
—4,1
4,1
0,1
6,23-10-2
1,6-10
—24,1
24,1
1,0
6,23-10“3
1,6-Ю2
—44,1
44,1
На рис. 05-5-3,г построены АФХ линейной части
(/со) и характеристика нелинейного элемента —
1 lq(A), пересчитанные в логарифмический масштаб, на
логарифмической концентрической сетке.
Точка пересечения характеристик линейной части
№л(/со) и нелинейного элемента—\jq(A) дает парамет¬
ры предельного цикла.
Из рис. 05-5-3,в и г определяем:
©п=706 с-1; Лп=0,03 рад.
05-5-4. Схеме, представленной на рис. 5-5-4,а, соответствует
структурная схема на рис. 05-5-4,а. Структурную схему системы
367

(рис. 05-5-4,а) свертываем к виду, представленному на рис. 05-5-4,(
полагая хВх=0, где
Гл {р) = {тфГ\ + ko cP) T(f!p + i) =
__ к0 СТ2р2 -\-[ko cp -j- k2	z2p2	-J-	2t-f- 1
P(TiP + 1) (T2p+ 1) = *p(TlP+ 1) (T2p+ 1) ;
O ^O.c ^
2^.
fe0.
//.?
%(я)
0,01
-
1
-0,005
У- -з*- —
'~к
~
i
i А 1
О
йп
UO МА
г)
мл(/<о)
Jay=0,1c~1
-90 \d)
Рис. 05-5-4.
Строим на рис. 05-5-4,в частотные характеристики линейной
части системы с передаточной функцией Wn(p), используя основной
логарифмический бланк.
Линейная часть состоит из усилительного, двух апериодических,
интегрирующего и форсирующего звеньев второго порядка.
Параметры элементарных звеньев:
368

коэффициент передачи усилительного звена
£2 = 3000 мА/рад; 201g£2 = 69,5 дБ;
сопрягающие частоты апериодических звеньев
i(Dcl=l/ri=l с"1; сос2= 1/Г2= 10 с-1
параметры форсирующего звена второго порядка:
постоянная времени
1Гk0.с гг, л/50-0,1
т== V ~тг	3000	=4,Ы0-2 с;
сопрягающая частота
(ос = 1/т='24,5 с-1;
коэффициент затухания
t _-*°*£.=	55	о 9
k2-2z	3000*2*4,1 • 10“2	и^‘
На рис. 05-5-4,6 L(со)—логарифмическая амплитудно-частотная
характеристика; ф(со)—фазо-частотная характеристика.
Строим характеристики нелинейного элемента.
Для нелинейного элемента (рис. 5-5-4,б) комплексный гармони¬
ческий коэффициент передачи имеет вид:
, , .	/	b	Ъ	-ш	/	иГ\
J (A) =q (А) = — (arcsin	\	1	—	jr)	при	А^Ь;
q(A)=ki при Acby
где А — амплитуда первой гармоники на входе нелинейного эле¬
мента.
Для построения характеристик составляем табл. 05-5-2.
Таблица 05-5-2
А, мА
щ (А), рад/(мА-с)
71ту мА-с/рад
0—10
0,01
100
40
20
0,0053
190
45,6
30
0,00405
247
47,9
50
0,00256
390
51,8
100
0,00127
780
57,9
200
0,00064
1570
64
Характеристики нелинейного элемента приведены на рис. 05-5-4,2.
На рис. 05-5-4,6 построены АФХ линейной части Wn (/со) * и
характеристика нелинейного элемента — 1 /q(A), пересчитанная
в логарифмическом масштабе, на комплексной плоскости.
То^ка пересечения характеристик линейной части (/со) и
нелинейного элемента l/q(A) дает параметры предельного цикла
Из рис. 05-5-4,6—о определяем:
011 = 3,7 с-1; Ап=19 мА,
где Ап — амплитуда автоколебаний на входе нелинейного элемента.

Амплитуда автоколебаний на выходе следящей системы Aai
определяется формулой
Aui=AuQ(Ап) |Ki(j(On) |;
Kt (/c°n) = М,(7\/4гИ):
I K.i 04) I = ^	l+coy’2, = 3/7 / 1 + 3,72-1	= 0,07 c-
Из	рис.	05-5-4,г	q(Au) =0,0058 рад/(мА-с). Окончательно
имеем:
Aat = 19-0,0058-0,07 = 0,0077 рад;
(Оп1 —С)п —3,7 с Ц
05-6. МЕТОД ВИБРАЦИОННОЙ ЛИНЕАРИЗАЦИИ
05-6-1. Исследуемая система, представленная на
рис. 5-6-1, описывается дифференциальным уравнением
(TiD+1) (T2D+\)Dx+ {k0.oTiD +
+ki + k0.c) k2F (х) =ki(T2D+1 )Dxy.	(1)
Вынужденные колебания для переменной х, т. е. сиг¬
нала на входе нелинейного элемента, ищем как первое
приближение в виде
jc=4Bsin(£W+<p)	(2)
с заданной частотой внешнего воздействия йв- Неиз¬
вестными являются амплитуда Ав и сдвиг фазы ф. Вы¬
разим величину ху через х:
Ху=В sin йвt=B sin[ (Йв^+ф) ф] =
=В cos ф sin	(йв*+ф) —В sin ф cos (йв£+ ф).	(3)
Из уравнения (2)
5т(йвЙ-ф)=*/Лв;
cos (QBi+ф) =DxIЛвйв', (D=d/dt).
С учетом полученных выражений уравнение (3) при¬
нимает вид:
ху = £ (cos 9-х - Sin ?	.	(4)
Гармоническая	линеаризация нелинейного	элемента
F(x)=qiX;	(5)
^!=4с/яЛв-	(6)
370

Перепишем уравнение системы (1) с учетом (4)
и (6):
(TtD + 1) (TJD + 1) Dx + (k0 CT,£> + kx + k0J Kq,x +
+	1)D (sin<p-g^- —cos<^.*=0.	(7)
Характеристическое уравнение системы
+ (Г, + 7\) />■ + (1 + rAU) P +
+	+	K.c) K4x +	^ (T,/? + 1) P ^sin f -gj P — COS <p) =
= 0.	(8)
Для отыскания периодического решения с заданной
частотой подставим в характеристическое уравнение (8)
р=/QB и выделим вещественную и мнимую части:
G = (К + Л0.е) А*/, - (Г, + Т2) Й2В +
(ТЯ cos <Р — sin <р) = 0;
В = (1 + 7\* А.с<7,) QB - TJ2Q\ -
_	р^ sin ^	cos J = Q
Лв
(9)
Системой (9) представлен баланс вещественных и
мнимых частей.
Первое уравнение системы (9) умножим на — Г2ЙВ
и сложим оба уравнения почленно:
r2QBfe<7i (^1 + ^0. с) + £2В + Tik2k0'CqiQB +
+ T.Q'.'IT, + Г2) - 7,7^,, -	722fi3
COS (p —
- "X^Я cos9=0.
С учетом уравнения (6) после преобразований полу¬
чаем:
где
— itkji cos 9 = Е — ъАв
Р 	(^2^1	+	Т2k0 с 	 71	с)
Т\&в+1
_4-1-5(0,1-2 + 0, Ь.1_0,0Ы) л,
0 !2. 3Q2 + !	—и,Об.
(10)
24*
371

чим:
Второе уравнение системы (9) умножим на T%Qв и
сложим оба уравнения почленно:
(kx -f- Л0.с)	^2^*в +	2k2k0CQ2l,ql — (7\ -f- Т2) Q2n
- 7,7*.Q\ - ■Q„ sin ? -	7,2Qs„	sin	?	=	0.
С учетом уравнения (6) после преобразований полу-
rc£,Bsin9 = tf — МпАв,	(И)
где
тт _ 4ckz (£, -f- k„ с + 7’i7’2ft0.c2*B)
п~	QB(1+P^B)	=
 4-1 -5 (2 + 1 +0,01-0, М-302) _П0д.
30.(1 + 0,12-302)	—и,^0,
Af=7iQB=0,01 -30=0,3.
Возведя уравнения (10) и (11) в квадрат и сложив
почленно, получим квадратное уравнение
(1 + Af2) я2Л2в—2 (Е + НМ)пАв+Е2+
+ H2—n2k\B2=0,
из которого находим амплитуду вынужденных колебаний
„ Е + НМ'+ V(E + НМ)* — (1 + М*){Ег+Нг—
Ав—	л	(1	+	Мг)
(12)
Поделив уравнение (11) на уравнение (10), найдем
сдвиг фазы
Н — МпАв	/. о\
arctg' Е_пЛв-.	(13)
Амплитуда Ав по своему смыслу есть вещественная
положительная величина. Поэтому будем считать, что
искомое решение для вынужденных колебаний в форме
(2) существует (другими словами, происходит принуди¬
тельная синхронизация) в том случае, если ^формула
(12) дает по крайней мере один вещественный положи¬
тельный ответ для Ав.
На основании этого, учитывая, что
£+#М=0,58 + 0,26-0,3=0,658>0,
372

пор '
лучаем условие принудительной синхронизации (за-
атывания):
{Е+НМ)2^ (1 -\-М)2(Е2-\-Н2—n2k2\B2).
После преобразований (делим обе части неравенства
1+7W2, далее вычитаем Е2 + Н2 и, наконец, умножаем
— 1) получаем:
("~у.	(14)
Захватывание происходит в случае, если амплитуда
внешнего воздействия превосходит некоторое поро-
зое значение Вдор, определяемое формулой (14), кото-
г зависит от соотношения параметров системы и от
зчения задаваемой извне частоты QB и находится по
рмуле
/•(0,26-0,56-0-3)^ , , ,п_,
У (1 + AT2) я2£2, У (1 + 0,32)3,142.22	’	Ш	•
Принимаем В=0,1. По уравнению (12) определяем
плитуду на входе нелинейного элемента
, _ 0,58 + 0,26-0,3 ±У(0,58+ 0,26-0,3)4— "
в	3,14(1	+0,32)	*
— (1 +0 , 32) (0,562 + 0,262 — 3,142-4.Q,I2)	0	,658	+	0,58.
3+2	’
АВ1 =0,362; Лв/= 0,023.
Исследуем устойчивость вынужденных колебаний, так
к получилось два решения.
В нашем случае мы должны исследовать уравнение
(T1D+l)(T2D+l)Dx+(k0.cT1D +
+ &i + &о.с) kzF (х) =0.	(15)
Составим линеаризованное дифференциальное урав-
зие в малых отклонениях от исследуемого решения.
Введем переменную х=х*+Лх,
где
x*=i4Bsin QBt.
Уравнение (15) в малых отклонениях от периодиче-
зго режима (уравнение в вариациях)
(T1D+1)(7’,D+1)DA+ +
+ KcT,D -f- ^о.с) К (ззг) Ьх=0,	(16)
373

где звездочкой (здесь и далее) обозначена подстановка
х=х*. Частная производная представляет собой перио¬
дический коэффициент.
Применим приближенный способ, который состоит
в замене периодических коэффициентов постоянными,
равными их среднему значению за период.
Уравнение (16) заменим уравнением с постоянными
коэффициентами
С учетом (18), сдвинув пределы интегрирования на
—я/2, получаем усредненный за период коэффициент
Производная dF/dx согласно рис. 05-6-1 есть импульс
площадью 2с при х=0. Следовательно, подынтегральная
функция везде равна нулю, кроме точки х=0, где
YА2в—х2=Ав и, как величина, имеющая постоянное
значение, выносится за знак интеграла.
Интеграл от оставшегося выражения (dF jdx)dx даст
площадь под кривой dF/dx, равную 2с. Следовательно,
усредненное за период значение периодического коэф¬
фициента
х=2 с/пАв.	(19)
Подставив это значение в уравнение (17), напишем
характеристическое уравнение линеаризованной си¬
стемы:
(TiD+l) (TzD+ l)DAx+ (k0.cTiD +
+ ki + k0'C) &2%ДЛГ=0,
(17)
где
2тс
О
Так как x = ABsinty, то dx[dty = AB cos ф=)/С42в — х\
откуда
(18)
тс
2
А
2
Т\Т2р3+ (Ti-\-T2)p2+ (1 + к2к0.сТ\к) р +
+ (Й! + Йо.с)^2Х=0.
374

Условие устойчивости по критерию Вышнеградского:
(+ + 7г) (1 +&2&0.СТix) —ТiT2^4% (ki + &о.с) >0.
или с учетом (19)
пАъ{Т\ + Тг) +2cTikz{Tik0.c—T^k i) >0.
Проверяем устойчивость для ABi = 0,362;
3,14-0,362 (0,01+0,1)+2-1 -0,01-5(0,0Ы— 0,1-2) =
=1,23>0.
Вынужденные колебания устойчивы.
\ F 1
аг
Q
- -
1 Ux
X
X
^ О
~
-с
Рис. 05-6-1.
Проверяем устойчивость для Ав2=0,023:
3,14-0,023 (0,01+ 0,1)+2-1-0,01 X
X 5 (0,01 -1 —0,1 • 2) =—0,011 < 0.
Вынужденные колебания неустойчивы, следователь¬
но, Ав=Лв1=0,362.
По уравнению (13) определяем сдвиг фазы:
.	,	Н	—	MtzAr
Ф = — arctg —р—_
■ кАв
, 0,26-0,3-3,14.0,362	,	А	,
arctg 0,58-3,14-0,362	" аг(+?0>143.
05-6-2.. Согласно структурной схеме, изображенной
на рис. 5-6-2, система описывается следующим уравне¬
нием:
D(TiD+ 1) (7+D + 1).к+ {\ + k^D)kik%F(х)—
=D{Trf)+\)kiXy.	(1)
Произведем гармоническую линеаризацию нелиней¬
ного элемента. Входную величину нелинейного звена-
представим в виде
х=х°+х*,	(2)
375

где х°—постоянная составляющая, а
x*=Ausin Ont.
(3)
Считаем, что через нелинейное звено проходит толь¬
ко постоянная составляющая и первая гармоника (имея
в виду, что высшие гармоники не пропускаются линей¬
ной частью системы), т. е.:
F(x)=F°+qix*,	(4)
где F°, qi — коэффициенты ряда Фурье. Величина
2тс
F* = j F (л:0 -j- i4„sin <|>)
Ф = шп*-
Х2 - F(X)
Л-2у
Я+2у
J	I
л 2л
2С0 ~—А sin у	а)
f	F°=	Ф(Х°)
Согласно рис. 05-6-2, а
F° = x\ =
(тс —2у)с — (тс + 2у) с __ 2ус
2тс-	тс	*
где х°2 — постоянная составляющая х2.
Учитывая, что х°=—Лдэшу, получаем:
„2с	.	х°
F.= — arcsin-^.
(5)
376

Величина
2л:
q>=i IF	"4n sin ^sin ^ ~
о
*—T	2lt+T
=^? J sin^t—4 j sin^ = ^nCOSY.
7	TC T
Выразив cos 7 через я0 и Лп
/"j fxQ у
с»*Т=|/ ‘-(tJ.
окончательно получим:
<6>
Определим амплитуду и частоту автоколебаний.
Уравнение (1) с учетом выражений (2) и (4) и за¬
кона управляющего сигнала имеет вид:
D(TxD+l) (T2D+1) (xQ+x*)+k{k2(k3D+l) (F°+
+ (fix*) =k\D. (T2D +1) Cot.	(7)
Уравнение (7) представим в виде двух уравнений
Для периодической и постоянной составляющих:
D {T.D + 1) (T2D + 1) ** + kik2 (ksD + 1) qiX*=0;	(8)
k^=c0.	•	(9)
Уравнение (8) является линейным. Решение этого
Уравнения представляет гармонические колебания с по¬
стоянной амплитудой. С точки зрения устойчивости это
означает, что система находится на границе устойчиво¬
сти. Используем критерий Михайлова.
Характеристическое уравнение системы имеет вид:
Т\Т2РЪ+ (Т1 + Т2) Р2+ ( 1 +&l&2&3<7l)/? + &i&2*7i=0.
Заменим р=/(оп и выделим вещественную и мнимую
части:
TiT2{—/ооп)3— (Т1 + Т2) С02п+
+ (1 +&1&2^3<7i) /сОп+&1^2*71=0»
0=	+	п=0;	}
377

Исключая qi, находим частоту автоколебаний
(И)
... 2
п ТгТ2~к3(Т, + Тгу
Для нашего конкретного случая
“n=V^" 0,1-0,2 — 0,01(0,1+0,2) = 7,68 С *•
Частота <вп не зависит от значения смещения и,
следовательно, от значения управляющего воздействия.
Для определения амплитуды автоколебаний подста¬
вим в первое из уравнений (10) выражение qi из (6)
и <о2п из (11):
откуда
kk-^-Л/ \ (—V 	Т±+1*
кАпу (Д ) =7’,7'2 - k3 (7\ + Г2
л	4k,k2c (Т гТ 2	k3T,	к3Тй) m ,/|	( х°	/1	г)-\
л" -	М77+Л)	У	W	*	{	)
Обозначим.
л   4kjk2с {ТЛТ2 — k?T 1 k3T2)	✓	t	о\
Лп.с—	*(7\	+	7\>)	'	[	}
— амплитуда автоколебаний при отсутствии смещения
(при л:°=0).
Преобразуем выражение (12) с учетом (13):
* А
(Лп.с
Умножив последнее уравнение на (Лп/Лп.с)2 , полу¬
чим:
т-т'+ш'=°-
Это — биквадратное уравнение, из которого получаем
зависимость амплитуды автоколебаний от смещения:
378

Полученное выражение запишем в виде
4,=4,с cos-f,	(15)
где
2х°	/1п\
а = arcsin —А—.	(16)
-^п.с
Выражения (14) и (15) представляют зависимость
амплитуды автоколебаний от смещения
..Определим функцию смещения, используя выражения
(5), (15) и (16).
Из выражения (16) имеем:
sin а=2ж°/Лп.с; х°/Атс— (sin а)/2.
Из выражения (15) Лп.с=Лп/соз(а/2), поэтому
х°_= (з1па)/2	(1
Ап cos (а/2)	4	'	7	4	7
Подставим (16) и (17) в выражение (5):
ро  _2с_ а с	с	 2х°
■arcsin sin-тr=— а = —arcsin-
2 П	7Z	Лпх	‘
Для 0<|лв|<4.с/2
F*—— arcsin .	(18)
Я	п.с	'	'
На рис. 05-6-2,6 приведена кривая функции смеще¬
ния. При х°=Аи.с/2 имеем:
arcsin (2х°/Ап.с)=л/2 и F°=c/2.
^Подставим выражение (18) в уравнение для постоян¬
ной составляющей (9):
и с .	2х°
я2 — arcsin —= са
2 7Z	лп
откуда
<19>
Подставив численные значения, получим:
г.__ 4-2-5-0,5(0,1-0,2—0,01-0,1 —0,01-0,2)	2к п 1ЛС
2-3,14(0,1+0,2)	Sm5-0,5	0,lUb.
379

Сравнивая (19) о (16), видим, что для искусственно
введенной величины а можно записать следующее вы¬
ражение:
k«c '
(20)
Используя соотношения (13), (15) и (20), оконча¬
тельно определяем амплитуду автоколебаний:
4= Ль с COS -j-
или
л   4klk2c(T1T2 kzTx k3T2) тиc0	/oi\
л"— WT+rj	C0Sli^F-	{Zl)
Для нашего случая
д _ 4.2-5-0,5(0,1*0.2 — 0,01 «0,1 — 0,01*0,2) ... 2п
3~ 14 ф, 1 +0,2)	C0S	'-2.5-0,5" ~"
= 0,108.
Амплитуда колебаний зависит не только от парамет¬
ров системы, но и от скорости изменения управляющего
воздействия со. Амплитуда автоколебаний лежит в пре¬
делах Ап.с^Ап^О. Автоколебания существуют до тех
пор, пока управляющее воздействие удовлетворяет усло¬
вию
0< | c0/k2c | <1,
так как для положительного значения косинуса аргу¬
мент должен изменяться в пределах от я/2 до —я/2.
Определим установившееся значение ошибки системы
f^lycT-
Выразим переменную Xi через *, которая уже из¬
вестна. На основании структурной схемы системы (см.
рис. 5-6-2) имеем:
Xi (Т iD + 1) xfkt.	(22)
Учитывая, что х=х°+х*, перепишем уравнение (22)
в виде
*1==>(7\D+1) (*» + **) =
~(TtD+l)x* + ±x\	(23)
380

В соответствии с видом правой части установившееся
решение этого уравнения надо искать в виде
*1уст=*°1+**1,	(24)
где x°i — постоянная составляющая; x*i — периодическая
составляющая.
Подставив (24) в (23), получаем два уравнения для
отыскания указанных величин:
х*'=тгх''	W
х*-±(ГХ+1)х*.	(26)
Подставив численные значения параметров в урав¬
нение (25), получим: x°i=0,5-0,106=0,053.
Уравнение (26) перепишем в изображениях Лапласа:
Х*1(р) = ^г(Г1р+1)Х*(р).
Заменим p=jсоп и определим комплексный коэффи¬
циент передачи:
К (/(О =	=. h—
Х\(р)	1	+ /шп7-,-
Модуль комплексного коэффициента передачи
1*</Шп)1 V 1+Ш2п7'21
Так как х*=Ап sin соп£, то амплитуда автоколебаний
переменной xi запишется следующим образом:
л 	 +	AaV 1 + со2пГ2,	/971
ш — I ка <оп) | — si ’	(27>
т. е.
Am = ^ V1 + 7,68° • 0,01 = 0,068.
2
Таким образом, установившаяся ошибка системы
имеет следующее выражение:
*iycT=*0i+24iii sin (опt,	(28)
где x°i=0,053; ЛП1=0,068; о)п==7,68 с-1.
381

05-7. СИНТЕЗ ОПТИМАЛЬНЫХ НЕЛИНЕЙНЫХ СИСТЕМ
05-7-1. Для того чтобы привести уравнение, описы¬
вающее объект, к нормальному виду, введем фазовые
координаты:
х=хц х=х2.	(1)
Движение объекта с учетом (1) будет описываться
системой уравнений
А-1 ==	== /l > I	(2)
xt = ku = f2. j
Запишем гамильтониан
я=2 ti//.
<=1
где	фг	и	fi — координаты векторов ф и f.	В	дополне¬
ние	к	системе	(2)	составим систему уравнений	для
вспомогательных переменных ф,, где i— 1, 2, используя
следующую зависимость:
= - V	i= 1. 2.
dt	lj	dXi
i=i
Учитывая (2), получаем:
Г^Ф +^-ф,1=0;	(4)
Л	[	дхг	*1 * дхх *2J
дФ:
rVi
-л-	<5)
Решение уравнений (4) и (5) имеет вид:
tyi=Ci\ \|?2=С2—City	(6)
где ci и с2 — постоянные интегрирования.
Выражение для гамильтониана (3) принимает вид:
+'ф2/2==^1«^2"Ь C2^U	Ciktlt.	(7)
В	выражении (7) рассмотрим член,	зависящий от
управления:	, ч
H*={czk—cikt)u.	(8)
382

Так как при оптимальном управлении гамильтониан
// принимает максимальное положительное значение, то
слагаемое Я* должно быть всегда положительным и
наибольшим.
Это будет, если алгоритм оптимального управления
имеет вид:
U (t) =(т[/макс>	(9)
где
a=sign (c2k—Cikt).	(10)
Оптимальное управление u(t) является кусочно-по¬
стоянной функцией, принимающей значения ±ЯМакс> и
имеет не более двух интервалов постоянства, так как
линейная функция сф—С\М меняет знак не более одного
раза.
Решение уравнения, описывающего заданный объект,
на интервале управления при u=+U
макс имеет вид:
X (0 = [
t
о
U,
:(0 = J[c, + %<l<]^ = c4+^
\ (И)
макс /2
2k
О <t<tl9
где U — продолжительность первого участка; с3, с4 — по¬
стоянные интегрирования.
Используя начальные условия, определяем постоян¬
ные интегрирования:
•*(0) = с3 = 0; \	П9у
•*(0) = с4 = 0. }
-Для момента времени ti координаты х и х соответ¬
ственно равны:

На втором участке управления (после переключения
управления) при и=— t/макс координаты х и х опреде-
ляются следующими соотношениями:
1
+ х (tt) = x{Q -	{t-	/,);
tx<t<tv tt=T.
(H)
Для момента времени /2 = ^ — прихода системы в ко¬
нечное состояние х(Т)= 1, х(Т)—0— справедливы сле¬
дующие уравнения:
Х&2) = * (Q - -%*- (*, - О - 0;
•*- (О — (О “1“ (О О"
£/„
(15)
Подставляя численные значения параметров системы
в выражения (11), (13) с учетом (12), имеем:
jt(f)=0,25f;
д: (0 — 0,125/*;
О <*<*,;
x(t1)=0,25t1; 1
c(O=0.125/,I. /
(16)
(17)
После подстановки численных значений параметров
в выражения (14), (15) с учетом (17) получаем:
x(t) = 0,5*,— 0,25/;
х (0 = 0,5ft, — 0,25/*, — 0,125/2;
^^ ^2»
2/,==/.; )
0t5f,ft —0,25**,—0,125f\=l. /
(18)
(19)
384

Из выражения (19) определяем моменты переклю¬
чения:
/1==2 с; fe=4 с.
Выражения (18) для координат движения системы
на втором участке управления с учетом значений мо¬
ментов переключения принимают вид:
х (*) = 1 — 0,25*;
x(t) = — 1-И — 0,125*г;	(20)
На основании выражений (16) и (20) на рис. 05-7-1,а
представлены кривые оптимальных процессов в системе.
Kx(t,) 1
6)
Рис. 05-7-1.
Переходим к построению фазовой траектории изме¬
нения координат x(t) и x{t).
Для получения уравнения фазовой траектории на
первом участке управления из системы (16) исключим
время t:
(21)
x(t) = 2x‘(ty,
0 <*<*,.
Выражение (21) представляет уравнение параболы
с вершиной в начале координат (см. рис. 06-7-1,6). Дви¬
жение изображающей точки происходит по верхней вет-
25—903	335

ви параболы до точки переключения. Координаты точки
переключения получаются из системы (17) при /i=2 с
и соответственно равны: a;(/i)=0,5; x(ti) = 0,5.
Уравнение фазовой траектории на втором участке
управления получается после исключения времени t из
системы (20):
Выражение (22) представляет уравнение параболы
с вершиной на оси х с координатой х=1 (рис. 05-7-1,в).
Парабола (22) отличается от параболы (21) противо¬
положным направлением ветвей.
Фазовая траектория изменения координат x(t), x(t)
объекта представлена на рис. 05-7-1,г. Начальное со¬
стояние объекта соответствует точке Мо, переключение
управления происходит в точке Ми а конечное состояние
объекта отражает точка Мг.
05-7-2. Алгоритм .оптимального управления .независимо от зна-
чений начальных условий аналогичен алгоритму, полученному в за¬
даче 5-7-1, так как уравнения объекта одинаковые, и имеет вид:
На первом участке управления при и = — Х/Макс координаты х
и х определяются выражениями:
Используя начальные условия, определяем постоянные интегри¬
рования:
Подставив численные значения параметров и постоянных инте¬
грирования в выражение (2>‘, получим:
(22)
u(t) ='<т£/макс,
o=sign (czk—Cikt).
(1)
где
(2)
x(0)'=c3 =0,5;
х (0) =	=	1.
(3)
*(/) ="0,5 —' !,5<;
х (/) = I -’г 0,5( — 0,75<г;
(4)
386

Для момента времени О координаты х и х соответственно
(эавны:
* (Л) = 0.5 —1,5/,;	\	^
х(/,)= 1 + 0,5*,— 0,75*2,.
На втором участке управления при и=им&ке координаты х и х
определяются следующими выражениями:
*(<) = х (*,)
^макс
x(t) = x (М + X (/о (/ - U) +	(t - t,Y;
(6)
Подставляя численные значения параметров системы в выра¬
жения (6) с учетом (5), получаем:
*(/) =0,5— 30 + 1,5/;
*(/) = 1 +0,5/ +0,75/2 — 3/!/+ 1,5/2ь
О ^ ^ /г»
(7)
Для момента времени /2 прихода системы в конечное состояние
справедливы следующие уравнения:
ic(/2)=0,5-3/1 + l,5/2=0;	|
х (/2) = 1 + 0,5/2 + 0,75/22 — 3/,/2 + 1,5/2!= 0. J
Из выражения (8) определяем моменты переключения:
/i = l,185 с; /2=2,037 с.	(9)
Выражение	(7) для движения- системы	на	втором	участке
управления с учетом (9) принимает вид:
*(/) =3,056+ 1,5/;	1
х (/) = 3,1 — 3,056/ + 0,75/2;	>	(10)
/i ^ f ^ О*	J
На основании выражений (4) и (10) на рис.	05-7-2,а представ¬
лены графики оптимальных процессов в системе.
Уравнение фазовой траектории на первом участке управления
получается после исключения времени / из системы (4):
*(/) = 1,084—0,333 *2(/).	(11)
Уравнение (11) представляет уравнение параболы с вершиной
на оси х с координатой х= 1,084.
Координаты точки переключения определяем из системы (5)
при /i = l,185 с:
*(/0=0,54; x(/i) = —1,28.
Исключив время / из системы (10), получим уравнение фазовой
траектории на втором участке управления:
х(/)=0,333 x2(t).	(12)
25*	387

Выражение (12) представляет уравнение параболы с вершиной
в начале координат и отличается от параболы (11) направлением
ветвей.
Фазовая траектория изменения координат x(t), x(t) объекта
представлена на рис. 05-7-2,6. Начальное состояние объекта соот¬
ветствует точке Моу переключение управления происходит в точ¬
ке М1, а конечное состояние объекта отражает точка Мг.
Рис. 05-7-2.
05-7-3. Введем фазовые координаты
X = Xt; Х = Х2.	(1)
Движение объекта согласно (1) будет описываться системой
уравнений вида:
х1 = Х2 — fi ]
х2 — ~~Т\~	^2)	=	^2*
Запишем гамильтониан
2
я=Е фл.	(3)
1=1
где ф» и fi— координаты векторов ф и f.
В дополнение к системе (2) составим систему уравнений
для вспомогательных переменных фь i—l, 2, используя зависимость
/=1
388

Учитывая (2), получаем:
i*!__ _ Г_#!_ 1 . Л* г
dt [ (Ъс, 1 дх, 2
<*Фа \J>fi ,	,	_д[,
dt '
Г Of, ,	_dh_	I	Ф,
[ дхг ф‘ + дхг Фг J = —ф<+ т1
) и (5) имеет вид:
Фх=Сх;	1
= с,7’1 + c2et/T', J
= 0;	(4)
(5)
Решение уравнений (4) и (5) имеет вид:
Фх =с,;
Фх
(6).
гДе Ci и Сг ■— постоянные интегрирования.
Выражение для гамильтониана (3) принимает вид:
t
н = ^fi + ^fi=clx2 + (cl +~Y^e Tl j(te + x2).
(7)
В выражении (7) рассмотрим член, зависящий от управле¬
ния и:
Н* — (^с1k +	е ?х ^ и.
(8)
Так как при оптимальном управлении гамильтониан Я прини¬
мает максимальное положительное значение, то слагаемое Я*
Должно быть всегда положительным и наибольшим. Это будет, если
алгоритм оптимального управления имеет вид:
ll(t) =аЯМакс,	(9)
где
= sign ^C,fe +	£г/Г‘^	.
(10)
с k
Функция Cifc+'-jF—е^Тг при любых ^'значениях с, и с2 меняет
знак не более одного раза на отрезке времени управления Т. Таким
образом, оптимальное управление u(t) является кусочно-постоянной
Функцией, которая принимает значение ±Ямакс и имеет не более
Двух интервалов постоянства знака.
Решение уравнения, описывающего движение объекта на ин¬
тервале управления при u=UMAKс, имеет вид:
X (0 = с3 + cjrt{Tl;
* (0 — c3 + c3t — cJ3e~tlTi;	}	(11)
где Cs=kUмакс’, ti — продолжительность первого участка; а, —
постоянные интегрирования.
389

Используя начальные условия, определяем постоянные интегри¬
рования:
х (0) = с3 + с4 = 0;	|	^2^
*(0)>
Из системы (1'2) находим:
С4 = —^^макс|	(13)
С$ =—kT 1 t/макс*	(1^)
Для момента времени координаты i и * соответственно
равны:
# (Л) = ^макс 0 е ^	|
х (h) = ft t/макс (*t -Tt + Tie-‘''r').	j
На втором участке управления при и=—UMакс координаты х
и х определяются следующими соотношениями:
X (0 = с, + с,е-‘'т';	1
x(t)=c, + ctt-c,T1e-t'T4 *	(1б)
t2=T,	J
где Ca=—kUKBLKC\ с7 и с8 — постоянные интегрирования.
Используя конечные условия управления, определяем постоян¬
ные интегрирования:
х(1г)=с, + с,е~1‘1т'= о;	1	(1?)
х (*,) = с8 + с,h — c1T1e~h/Ti = 1 •	/
Из системы (17) определяем:
c,=kUmKCe1^;	(18)
С8 = l-bkUnSLKC ( 1 ^2 ) •	(19)
Для определения моментов переключения ti и U приравниваем
выражение (15) решению системы (16) для момента времени ti.
X (f,) =kUu акс (1	=	ft t/макс	- 1);
х (/,) = ftt/макс (*. - Л +	=
= 1 + ftt/макс (7, + *, + <i - 7*1*(<*г~',> /Г‘) •
После преобразований получаем:
2е^-е{^- 1=0;
2/, _	-	-л,-!	27-, + Т 1e~t,^Tl (1 + е^г') = 0^	(20)
1	2	Ломакс
390

Подставляя численные значения параметров системы, имеем:
2еш> e10t> — 1 =0;	)
2t^	<0,3	+	(1	+<?Ша) =0.	/
Пз первого уравнения системы (21) определяем:
(21)
еша =2el0tl — 1.
(22)
После подстановки выражения (22) во второе уравнение (21)
получаем:
h = 2ti-0,\.	(23)
Рис. 05-7-3.
Подставим зависимость (23) в уравнение (22):
0,3679e20,l’+ 1 = 2e,0i' .
(24)
Момент времени t\ определим графическим способом. На
рис. 05-7-3,а построены кривые функций ф1 = 0,3679е20*-И и ф2 =
=2eiot (табл. 05-7-1). Точка пересечения функций qpi и ф2 соот-
Таблица 0-57-1
U с
0,13
0,14
0,15
,0* 16
0,17
0,18
0,19
Ь
5,95
7,04
8,38
10,01
12,0
14,45
17,43
Ъ
7,34
8,11
8,96
9,9
10,94
12,1
13,37
ветствует моменту времени ^ = 0,159 с.
Из выражения (23) определяем момент переключения /2 =
= 0,218 с.
Построим кривые оптимального управления и переходного про¬
цесса для координат x(t) и x(t) системы.
391

л—^£?Внения Движения системы (11) на интервале времени
при подстановке численных значений параметров системы
н постоянных интегрирования имеют вид:
Уравнения движения системы (16) на интервале времени
при подстановке численных значений параметров системы
и постоянных интегрирования имеют вид:
По уравнениям (25) и (26) вычисляем значения координат х
и х, которые сводим в табл. 05-7-2. На основании этой таблицы на
рис. 5-7-3,б представлены кривые оптимальных процессов в системе.
Таблица 05-7-2
t, С
0
0,04
0,08
10,12
0,159
0,18
0,2
0,218
X
0
0,07
0,25
0,5
0,79
0,92
0,985
1
X
0
3,3
5,5
6,99
7,96
4,66
1,95 *
0
05-7-4. Имеем уравнение объекта х=—ах+и и кри¬
терий оптимальности Q = —Г (л:8 -f-ux)dt.
Введем новую переменную х — вектор с координа¬
тами
(25)
(26)
о
x1(t)=x(t);
г
Я (0=4-j£\
о
причем £о(0)=0.
Тогда получим систему уравнений:

причем
Q=xo{T)— mill.
Задача минимума критерия Q сводится к минимуму
конечного значения хо (■/); значение jci (0) =лс° задано.
Запишем гамильтониан
я=2 М.
<=0
где ft — координаты векторов т1>, f, т. е.
н = Ф./. + Ф./»= f. -2“ (*!. + «’) + Ф. (— ах, + н).	(2)
Составим уравнения для вспомогательных перемен¬
ных г|)0 и ipi. Координата \j>o всегда равна минус единице
[20], т. е.
фо(0=— l=const,	(3)
поэтому
dtyoldt=0-,	(4)
(5)
« ах,	ах, ах,
Граничные условия:
начальные для х
х, (0) = х\
х0 (0) = 0;
конечные значения гр*: у нас задача со свободным
концом траектории, т. е. х(Т) не задано, поэтому
фо(Г)=-1;	(7)
Ч»1(Г)=0.	(8)
Наряду с основной системой уравнений (1) решаем
относительно вектора г|э сопряженную систему уравне¬
ний (4), (5).
Управляющее воздействие и нужно подобрать в каж¬
дый момент времени так, чтобы максимизировать Я.
Перепишем уравнение (2) с учетом (3):
Я =	^ (^2i 4“и*) “Ь (— ахг 4" и)•
393
(б)

Приравнивая дН/ди=0, находим оптимальное управ¬
ление и*:
да.	1	Т1	(9)
и* = <{>,.
В уравнение объекта (второе уравнение системы (1)).
вместо и подставив Цн и, переписав уравнение (5) с уче¬
том (3), приходим к системе уравнений:
тг = —
(10)
dt
Граничные условия для системы (10) согласно (6)
и (8) имеют вид:
£l(0)=x°, xt>i(T)=0.	(П)
Линейные уравнения (10) решаются при условии
'*ПДля нахождения общего решения уравнения (10)
необходимо решить алгебраическое характеристическое
уравнение
— а^-К 1 _ _ а2+Х* —1 = 0.
Корни характеристического уравнения Я1>8= ± ]/а2-{-1.
Обозначим Я = ]/#24“1*
Система частных решений (10) имеет вид:
(0 —	.4“ сг& t |	^12)
Необходимо найти постоянные си с2, du dz. Гранич¬
ные условия (11) принимают вид:
£i(0)=ci + c2=x0;	(18)
ф1(Г) = й1вм, + ^-хг = 0.	(14)
Продифференцируем первое уравнение системы (12):
=	(15)
394

Определим значение производной при t=О, учитывая
(10) и (11):
foi (О
dt
t=o
= схХ — £2Я = — axt (0) -J-	(0)	—	&x	Ф1	(0)•
Из второго уравнения системы (12)
^i(0)=rfi + ^2»	(16)
поэтому
с{К—с2Х=—CLX°+d\ + d2.	(17)
Продифференцируем второе уравнение системы (12):
d^-=-.d1Xe'kt-dM-xt.	(18)
Определим значение производной при /,=0, учитывая
(10), (И) и (16):
= dxX — d2X = хх (0) -{- а$г (0) = х* 4- а (dx + d2),
ai t=o
откуда получаем:
dx%—d2K=x°+'a(di + d2).	(19)
Из выражений (13), (14), (17) и (19) находим по¬
стоянные с\, c2f du d2, в частности,
<    .
1	(Х-а) + (Л + а)*2ХГ’
х°^2ХГ
а,=
(Л — а) + (Л + а) *2ХГ
Из уравнений (9) и (12) определяем оптимальный
закон управления в функции времени:
“ {t) = (X -а) + (Л + а) е2ХГ ~ (X - а) + (X + а) е** =
  х° (е— e2vre~xt)
— (X — а) + {X + а) е2ХТ ’
Определив коэффициенты с\ и с2, используя первое
Уравнение (12), находим x\(t). Далее, исключив время t
из «*(*) и *,(*), получим закон управления м*=м*(х)
в функции выходной величины х=х\.
395

Г лава шестая
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ
06-1. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ, ПОДВЕРЖЕННЫХ
СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
06-1-1. По определению
my (t)=l К (0}; ку (g g=L{t')L{U) {Кх (g g},
где L — линейный оператор. Поэтому получим:
mv{t)=8mx(t), а Kv(h, t2)=64Kx(tu t2).
06-1-2. Корреляционная функция
= 2ae-a('1-/a)a — 4a2 (Y, — g2	=
= 2a [1 - 2a (f, - g2J e~a{t'-h)'Ky (*, - Q.
06-1-3. По определению no z(f) = dx{t)[dt
is (i / \  d*Kx(tu t2)
ИЛИ
kz (g g=o%{t' +	+ * cos со g — g.
08-1-4. Известно, что Y (t) — L {A' (()}; my g =L{/Wj.(/)}
и Ky(t„ Q = L«')L(h) {Kx(tu g}.
Поэтому
t
w? (t)=j	(*)
K„ (g g = j* j’ K* (*„ x.) e~'le-"d^dzt.
06-1-5. Выход звена Y(t) связан с воздействием X(t)
оператором дифференцирования, т. е. Y(t)=dX(t)/dt.
396

Применяя общие правила, получаем:
ти (t) = d (t) [dt — A cost',
^) = 2е-0’5(^),[1-(/а-О,Ь
Значения дисперсии определяются при
Dy{t)=Dy=2.
06-1-6. Для линейной системы
t
Шу (t) = j W (t, x) /Я* (x) rfx.
*0
При	г)=^е-^Т
значение математического ожидания
t
bm ..
™"	j
to
Дисперсия определяется из равенства
t t
°У (0 = /С, (/, о = J f t» (/, х) да (/, ,')	(х,	х')	-rfxrft'	=
to to
t t	t—T	x'
to t0
Разобьем интервал интегрирования по переменной т'
на две части [70, т] и [т, /]. Это позволит освободиться
от знака модуля показателя при е и получить таблич¬
ные интегралы вида
kzD —т~ С С “7“	*(*—“*')
Dy(t)=k-£-e Т )\)е т	Л'+
to *0
-^-(Ф^+р+^гтН.
897

06-1-7. Импульсная характеристика звена
_ tzl
w(t, %) = ^-е т°.
1 О
Корреляционная функция «белого шума» имеет вид:
Кх(т, т')=с2б(т—т').
Подставим найденные значения w(t, т) и /С*(т> т')
в известное выражение для дисперсии выходного сиг¬
нала:
t t
Dy (t) = f f w (it, x) W (t, x') Kx (t, x') dxdx' ==
о 0
= c2( 1—0-
06-1-8. Значение математического ожидания
*
му (t) = у- j в г° (я, -|- й,х) б?х = й0 -)- aJ (t — Т9)
о
_ <_
— (а0 — aj'^e т°.
Дисперсия определяется как
D '	- 2<~rT~T' +2(т+т')-|т-1>1
.0 о
“(l+27.)[l + (a + P)7’0]	(1 — 27’,)* + 7’*0	’
06-1-9. Ошибка, формируемая по схеме рис. 06-1-9,
равна:	где	H(i)— желаемая выход¬
ная величина; L=1 — условие фильтрации. По опреде¬
лению значение математического ожидания ошибки
равно:

Так как значения математических ожиданий желае¬
мой выходной величины и суммарного входного сигнала
системы равны математическому ожиданию полезного
сигнала, можно окончательно записать:
тяс (0=0,19 j mxe-''udi — mx =
=0’19m-.(oL2-1)=°.7(4.-
Дисперсия ошибки определяется из формулы
оо ор
DK = j J w (x) w (Я) Ky (* — Я) dtdl —
— 2 j w (x) Khx (*) di -f Dh.
Для нахождения дисперсии Dc необходимо определить:
коэффициент взаимной корреляции между желаемой
выходной величиной и полезным сигналом
W = К*	СО = 2е-|т|;
дисперсию желаемого сигнала, учитывая при этом,
Что L=l; Dh=Dx=2;
корреляционную функцию полного входного сигнала
системы
Kv(x)=Kx(r)+Kz( т).
399

Подставив найденные значения в выражение для
дисперсии ошибки, найдем:
Д. = 0,04 J J [2в~‘	1	+	Зе~21	']	X
X e^le~^dx,dxt — 0,38 J 2еч 1 }e~°-2'dx + Dx.
Разобьем один интеграл на два:
J в—1	'е~14	dx,	=	j е~а ы~ъ) е~” dx, +
-f
•»»
Окончательно получим:
В^.о 19	0,19Дг_ 0,380^I—D 4 25.
с Y (“1 + Y) Y («2 + Y) “1 + Ч
06-1-10. Определив с помощью преобразования Лапласа весовую
функцию системы а>(т) по формуле
t t
(0 = J J v) Ox) w Ы Кг 0,х2) <*т,л2,
о о
вычислим значение дисперсии ошибки (см. задачу 6-1-8):
р   g2	й\Ь2о -{- Ь2хО>оС
£	ага0	й^с -J- &q
06-1-11. Используя известную формулу, запишем:
ОО	00
с/со   4 Sx
1 Г	2	Sx	Г	di
Dv = — J I w (H*SX (co)rfco	j	-j-p
• ы*Тг 2T
0 0
Окончательно получим:

06-1-12. Спектральную плотность определим, исполь¬
зуя интеграл Фурье:
■"о
ОО
s* (“) — 2 J К.х (х) cos (uxrfx = 2Dx J ^1 cos <•>xdx =
SL|(1-^r)d(sina,,)=-vs
^0	-j
+ jsin mxd-l.J=^.(l — COSO)X,).
06-1-13. По определению
+00	+"п
D* =1^	J	Nd<o	=	^^f
—00	—<o„
П
или Dx=NAf, где Д/=Асо/2я — полоса частот в герцах.
Корреляционная функция может быть определена
с помощью интеграла Фурье:
1 г	1011
(х) = — j Sx (ш) COS (Dido) = -i- J N COS (DTfifu) =
0	0
N .
=—Sinewy.
ftx
06-1-14. Спектральная плотность
S,H=	e-^	= Dx T<ra,,,-/“Vx.
—00	—00
ратуРе°браЗУеМ показатель ^епени к полному квад-
_	00	__ /	/о>	\	1
5, (®) = Д«е 4“* J е Г+ 2* ) dx = 3^* e“ КГ
Тогда
to* оо
так как интеграл в этом выражении равен ]/и/а.
26-903	'	401

06-1-15. По определению
Sx (ш) —— J Dxea *т' cos ш„хе~
Запишем функцию cos шот в комплексном виде:
е/“ох I е-1^
cos «Jax   ь
Тогда
ОС
S* («>)= + j е“а 11	(е,Ш4’	+
с/х.
После интегрирования
$х (®) = « [ а2 + (со, —со)2	а2 + ^Шо + ш)2 } —
_ 2а	<*2	+	со2,	+	со2
' (а2 + со2, + со2)2 — 4со 2,<о2*
06-1-16. Находим спектральную плотность входного 'Сигнала X(t)
оо
Г	•	2Dv-a
s* Н = )КХ (X) в-1“ rfx =	.
—ОО
По уравнению системы в операторной форме
(alp+a0)Y (р) = (bip+bo)X(p)
находим:
_ , ,	+	Ьо	.	_ /; ч _ Ь1/СО+ Ьр
Ф ^ — агр + а, ’ ф ^ ^	а,/со + а, *
Тогда
Ь2,со2 + Ь2 о
1ф (/®)12 = <+ + +-7 •
Спектральная плотность выходного сигнала Y(t)
2Dxa (62,w2 + b\)
Sy (со) = Sx (со) 1 ф (/со) |2 = (a2iC02 + a2o) (a2 _|_ Ш2) •
Дисперсия сигнала на выходе
1	2Dxa	Г	bW	+	b20
^ = 2тГ J ^ ^= 2гс J (а2!со2 + а20) (а2 + со2)
dec.
—00
402

Полученный интеграл можно вычислить путем разложения
подынтегрального выражения на простейшие дроби с привлечением
приложения 13 при п—2. Так,
/.=
1
2п
[Во (/(О)2 + В,]
-Во
IА (/о»)2 +	+	а2	|г
АА
do =
2А0Л!
— В0А2 -f- А0ВХ
2А0А1А2
Поскольку
Во = —b2i\ Bi = b2o\ Ao = ai\ =	■^2==^oct,
окончательно имеем:
2Dxoc (ia0ab21 + axb20)
Dtl = -
2aQalo. (04 a + a0)
(aib20 + gpocb2!)
a0ai (aja + a0)
Кроме того, вычисление интеграла можно заменить преобразо¬
ваниями в частотной области, предложенными А. С. Шаталовым
[26J. Определяем АФЧХ формирующего фильтра №ф(/со) из
условия
a -f- /со
2 Dxa
a2 -f- со2 >
откуда
-у 	2 Dya
k = К2Dxa ; Ц7ф (/со)
а + /ш •
Перемножим частотные характеристики фильтра и системы:
V2DX* (bjсо + &„)
Фш (/») =
К2Dj,a (61/со + &0)
(<х + /со) (а,/со + <х0)
PiP + Pq
ai (/“)2 + (“«1 + ао) (/“) + аа0 ^гР* + l-’-iP + Р-о
Р=/®
Шумовую дисперсию в этом случае находим по общей формуле
[26], переписав ее для системы второго порядка
2y0t;2 —t;2j p,2
^2o P-o
2Dxa I J2'
_ 1 A
ai
о h*i p*2
2*2 L
1 0 P*o
1 CSI
1
+ aQ
0
ax
aa0
или
Вщ 	 Dy	:
■2Dxa
b* i»o0 + Pi b*o
Окончательно имеем:
26*
Dy =
2a,aa0 (aa, + a„) •
fit (ЬУРр + Pibao)
e,a0 (aaj + a0)	•
403

06-1-17. Найдем частотную характеристику звена
Ф (im) =	-
U '	1	+Г,/<о-
Спектральная плотность выходной величины системы
S/H = 1Ф» Г 5, («) =	.
Дисперсия выходного сигнала Y(t)
GO
= V j rrfe d(0=4г arctS
oo
о
27\,
06-1-18. Поскольку ошибка £(/) стационарна, ее спек¬
тральная плотность определяется равенством
<v 7	|	—со2+2/г/со+л2 [2'
Спектральная плотность ST (со) находится по заданной
функции корреляции:
5 (со)= Г e-l“K(i)d% =	2Ла (а2 -f- Р2)	_
7J	К	—	а2 — р2)2 + 4а2со2
—00
2Ла (а2 + р2)
со* + 2<02 (а2 — р2) + (а2 + р2)2 •
Дисперсию D^ вычислим с учетом приложения 13:
00
= i (»)*> =
—00
=;	Дал*	(а2 -(- р2) g*
[(Pi - Р)2 + («. ~ «)2] [(Р, - Р)2 + («, - а)2] А
Х [(Р. ~ Р)2 + («. + »)2] [(Pi + Р)2 + (а, + а)2] *
((Р2 - Р2. + «2 + «2,)! + 4 (<**Р*1 - 2а2а2, - 2а2,р2, + 02,р2 + «*,) ,
'Ч	«, («2, + Р2.)	т*
_1_(Р21 — Р2 + «2, + »2)2 + 4 (а2,Р2 - 2а\а - 2а2Р2 + а2Р2, + а*) \
^	а(а‘ + ?2)	|.
где а, =/г = 0,6 1/с; ^ = у пг — /г2 = 6,26 1/с.
404

Подставив числовые данные, окончательно получим:
Dc = 0,1 м2/с\
Аналогичный результат можно получить, применив методику
расчета А. С. Шаталова. Для этого, используя полученное значение
для спектральной плотности 5т (со), находим ЧХ формирующего
линейного фильтра из тождества
1^ф(/»)12=5т («).
Обозначим:
5
W<b М = р* + 7hp + 7]„ •
Тогда
2Ла (а2 + Р)
со4 + 2со2 (а2 — р2) + (а2 + р2)2 »
(/»)* + 4i (/V0 4- 4»
откуда получаем:
?0=К2«у1 (а2 + р2);
4*о = (**-И*)*! 4*1 =2 (а2 — Р) +2У)0; 1), =2а.
Окончательно ЧХ формирующего фильтра имеет вид:
_	У2«А(«* + У)
И'ф U<*>) —	_|_ 2а (/со) + (а* + р*)	’
а ПФ
w	К 24а (а2 + Р2)
Мф{р) — р2^_2ар + (а2 + р2) ‘
Передаточная функция экселерометра
n}g
Ф (Р) = р2 + 2hp + л2 •
На основе формулы каскадной связи получим:
f,	n2g	К 24а (а2 + Р2)
Ф (Р) Фф КР) ~(рх + 2hp + л2) (р> + 2ар + а2р2)
+ НчР* +	+	|Aiр.+ Цо ’
где
0„ = л2£ К2Ла(а2 + р2);	^	=	л2	(а*	+	J2);
р.1 = 2 [h (а2 + Р2) + ап2]; н-г = а2 + Р2 + Л2 + 4ал;
к-. = «(<* +л); м-* = 1.
405

Выписываем общую формулу для шумовой дисперсии системы
четвертого порядка при vi = v2 = 0:
Dc =
О
о
*
А
о
0 Иг ^3 И*
0 Но Hi Иг
-ц20 0 0 р,0
V20 (НгНз Н1И4)
Из Н4 ^ ^
2но (И1Н2Н3 — НоН2з — H2iH4)
Hi Н2 Нз Н4
о Но Hi Иг
0 0 0 р,0
=0,1 и2/с*
06-1-19. Найдем значение корреляционной функции
по спектральной плотности 5с(оо):
оо	/
(т) = j е/“',5с ((о) dm ■= 2Аа (а2 + p2) J-jLe-“14 cos ^ +
—QO	^
_|—^1_ е “* 1 х I cos -
ft — д(а2 + Р2) _« Ц|у
2а (а2 + Р2)	^
6i — (“2i + P2i) Л—«114
x(cos^+f ,inpM)+ ЪЖп е~“""Х
X^cos p.T-f-g-sin p.hljj
где коэффициенты а, aly b, Ъ\ определяются по прило¬
жению 13. Ошибка скорости определяется как
6
а дисперсия ошибки скорости подсчитывается из равен¬
ства [18]
D„ — 2 Г (Г — -с)	(т)	dt
при переходе к новой переменной интегрирования.
406

Так как	и	2'^>i/ai, то верхний предел в йй-
теграле заменим оо. Тогда, учитывая табличные значе¬
ния интегралов
| е— (Г - т) cospxcfc = tt2^p2 (аТ + -^y) Ъ
j e-aT (Г - т) sin ptrfx =	/рт’ _ _M_ \ %
о
pr
a2 + p2 ’
а также условие задачи, окончательно имеем:
Р.= 4АГ(.■+(!■) [-^+	] = 1.46 М-/С-.
06-1-20. Спектральная плотность на выходе линейной
системы
S,(со) =5*(со) | W(/со) |*=| №*(/©) I*.
где Wx(ja))—ЧХ линейной системы, объединенной
с формирующим фильтром. Вместо объединенной ЧХ
запишем объединенную ПФ системы и фильтра:
Wx(p)=W(p)<b(p),
где для фильтра
Ф (Р) — Р±±..
р + 2>
следовательно,
W (п) = -	- '-р-4~1 Р + 1 —
0,25^ + ip + l р + 2
 	0,5 р2 + 1,5р + 1
0,25рг + (0,5 + £) р2 + (1 + 2|)	р + 2
,  bzp2 ~Ь Ь\Р ~Ь Ь0
а3р3 + а2р2 + alp + aQ	•
Для такой ПФ и соответствующей ей спектральной
плотности 5у(со) изображение корреляционной функции
Дано в третьей строке таблицы приложения 14. Числен¬
ные значения коэффициентов
bo—l;	6i=l,5;	£2=0,5;
1) для £=1,25 а0=2; ai=3,5; a2=l,75; a3=0,25;
2) для £ = 0,6 a0=2; ai=2,2; aa=l,l; a3 = 0,25;
407

Далее расчеты будем вести отдельно для каждого
значения £.
1) 6=1,25:
КЛР) =
2-3,5.0,5г+ 1,75-0,25-12 —2-0,25 (2.1,05— 1,52) , „
 1_	2(3,5.1,75	—	2.0,25)	Р	+
2	0,25/73	+ 1 ,75/72 +
,	2-1,75-1,52 + (2-0,5 — 1,75- 1)а	1	I2
	 11,25	.	—Р	+	—	^
+ 3,5р + 2
_ 0,5/72 + 1,51/? -И 1 _	0,5/Р2 + 1 »51/> + 1	_
Р3 + 7/72 + 14/?+ 8	(/7+ 2) (/7+1) (/7+4)
_ 0,01	0,003 ■	0,93
~~ р + 2	/7+1"*"/> + 4‘
От изображений переходим к оригиналу:
tf3(t) =0,01 ехр (—2т)—0,03ехр (—т)+0,5 ехр (—4т).
Дисперсия выходного сигнала Dy=Ky(0)=0,5.
2) |=0,6:
к, 	1	1.04/72	+0,704/7 + 1
Ъ г\Р)— 2 2(0,25/73 +1 ,1/72 + 2,2/7+ 2)
1.Q4/72 + 0,704/7 + 1	_	l,04p2 + Q,70y + 1
— р* + 4,4/72 + 8,8/) -j- 8	_ (/7 + 2) |/7+ 1,2 —/1 ,6 |2
_ 1,17	1 т— /1.01 +/2,87	1	\
/7 + 2	16	^ 0,8 + /1,6 /7+1,2 — /1,6 J '
При переходе от изображений к оригиналу получаем:
К'г (*) = 1,17ехр(— 2-с) — bjlm{exp[(— 1,2-f
+ /1,6) / + /0,13]}
или
К! 8 (т) = 1,17 ехр (—2т)—1,06 ехр (—1,2т) sin (1,6т+0,13).
Дисперсия выходного сигнала
Dy=K's (0) =1,17— 1,05 sin 70,5=1,04.
06-1-21. Произведем расчет коэффициентов по фор¬
мулам, указанным в приложении 13, для «=3:
Аз-h—cth,

т. е.
Ло=Яз=0>25; A i=ci2==l ,75 j
A2=cl i=3,5; Л3=а0=2;
^.-*==(— 1)‘-вГб-*_т—2 k+2 (-1 )\+А-{-Х
L	k-t-2=0
т. e.
B0— (—1)2 [bh] =0,52=0,25;
^1=(—1) [В2!—262&o]=—1,52 + 2.0,5.1=—1,25;
B2=62o=1.
Согласно приложению 13 имеем:
/ = _ -1 =
3	— 2А0 (Л0Л3 — Л,Л2)
0,25-1,75
— 3,5-0-,25 — 0,25-1,25 — ^ у2 -
=	2-0,25	(0,25.2— 1,75.3,5)	=	°’5,
что совпадает со значением дисперсии, полученным
в задаче 6-1-20 для £=1,25.
06-1-22. Поскольку следящая система стационарна
и входные сигналы некоррелированы, то дисперсия сум¬
марной ошибки будет складываться как
DC = D, -\-D„
где D\—дисперсия ошибки отработки полезного сигна¬
ла; D2 — дисперсия выходного сигнала помехи.
Известно, что ошибка отработки полезного сигнала
следящей системы определяется формулой
tn(t) = YII(t)-G(t)=<k0G(t)+klG'(t)1
где &0=Ф(0) — 1;	&1=Ф'(0) — соответственно коэффи¬
циенты ошибки но положению и по скорости.
Согласно структурной схеме
ф ^ = Тр* + Р + Ь ■
Продифференцировав полученное выражение, запишем:
Ф'(„) = Щр±У)_
(Tp* + p + ky
409

Положив в ПФ Ф(р) и Ф'(р) р—0, находим:
ФД5)=1; Ф'(0)=—1 jk или &0=0; ki=—1/й;
Окончательно ошибка отработки полезного сигнала
•я(0 = —=
Дисперсия
Dt = ~pDc,
где Dc — дисперсия скорости изменения полезного сиг¬
нала С\.
Дисперсия отработки помехи на выходе следящей
системы определяется по известной формуле
D,=^ ? | ф О») !■ S Л») ^^ 11	Г
о	о
Значение D2 получено с учетом, что 5z(o))=5o.
Согласно приложению 13 для п=2 находим:
Л** _
п 	50fe2	Л 0 S0k
2 п 2А0ЛХ	2тс
Так как в нашем случае Во=0; В\=\\ Л0=Т; А 1=1,
то окончательно для дисперсии суммарной ошибки мож¬
но записать:
D, = 0, + Z>, = |H-fj.
Анализ полученного результата позволяет сделать
следующий вывод: чтобы уменьшить дисперсию суммар¬
ной ошибки, необходимо в составляющей ошибке от
полезного сигнала увеличивать коэффициент передачи
следящей системы &, а в составляющей помехи необхо¬
димо значение коэффициента передачи системы умень¬
шать.
06-1-23. Для линейной следящей системы можно за¬
писать, что ошибка от полезного сигнала и помехи опре¬
деляется как дисперсия
E2=E2f + E%,	(1)

i составляющая дисперсии ошибки от полезного сйг-
та равна:
Для определения экстремума коэффициента k необ-
щшо взять производную по k от выражения (2) и
иравнять ее нулю:
Подставив числовые значения, находим_&0=43,9 с-1.
>дставив k0 в уравнение (2), находим £=0,32 град.
6-2. АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ, ПОДВЕРЖЕННЫХ
СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
06-2-1. Известно, что нелинейное уравнение, подоб-
е заданному, можно представить приближенно, ис-
льзуя метод непосредственной линеаризации, в виде
ух уравнений: нелинейного относительно математиче-
их ожиданий сигналов
е / — известная нелинейная функция, и линейного от-
юительно центрированных составляющих:
Учитывая начальные условия и проинтегрировав по¬
денное уравнение, определим значение математиче-
;ого ожидания ту=\.
~р2 	Q (Т: -f Z -f- kTx)
Х	T + z + kv\	У
доставляющая дисперсии ошибки от помехи
>дставив исходные данные в (1) , имеем:
Р2_ kN , a(T + z + kTz)
п — 2	‘	T	+	z	+	№	*
(2)
N ах (х2 — Т2)
2	(T+x +	kx2)2
'да получим:
411

Подставив значение ту=\ в уравнение для случай¬
ной составляющей, после интегрирования его получим:
У (0 = j e~2{t-z]X(x)dx.
Используя уравнение для дисперсии, запишем:
Dy (0 — J j* е~2(2<“'х_т '>f(x (х — х') dxcLx’ -----
=-т\[	e~2’d°.
о
Подставим в полученное уравнение значение корре¬
ляционной функции Кх(о) и произведем интегрирование:
п /л_А« а-2-(а + 2)Г« + 4г1*+21'
uv\l> 2	а2 — 4
06-2-2. Запишем уравнение для нахождения матема¬
тического ожидания ту:
=^	5“ w у "Г шх = 2	пг2у	1 = 1 j- тп у
Интеграл полученного уравнения, обращающийся при
/=0 в единицу, тождественно равен двум. Таким обра¬
зом, mv=2.
Случайная центрированная составляющая выходной
величины определяется из уравнения
dI^- = -^rnyY(f)+X(t).
Подставим полученный ранее результат ту=2 и про¬
интегрируем:
?(0=j е~и~Т>Х(-х) dx.
412

Поскольку относительно центрированных случайных
функций уравнение линейно, то дисперсия Dy(t) опре¬
деляется из уравнения
06-2-3. Линеаризовав исходное уравнение путем раз¬
ложения нелинейной функции в ряд Тейлора в окрест¬
ности точки туу получим уравнения математического
ожидания и центрированных случайных функций вы¬
ходной переменной системы:
Проинтегрировав первое уравнение при заданных на¬
чальных условиях, найдем ту как функцию времени /.
Поскольку интеграл решения при /=0 равен единице,
то ту=\.
Второе уравнение запишем в виде
06-2-4. При заданном законе распределения P(v)
математическое ожидание величины v mv=0.
t t
— Dx f fe {t x)e {t — %^dzd\ = (\ — e *)DX.
Tmy-\-my = k (mx — am* y)\
T-^Y(t) + V+3ka)Y (0 = kX (0;
0
Для дисперсии справедливо уравнение
413

Дисперсия определяется из следующего равенства:
©о	+1/2
Dv= §(v — mvyP(v)dv= f vMdv = 0,083.
—oo	—i/2
Интегрируя уравнение системы при начальном усло¬
вии Y(0) =0, путем сравнения с исходным уравнением
получаем:
t
У (t) = j (1 _ Y‘V) dt=t — u2	.
0
Отсюда можно найти выражение для математиче¬
ского ожидания и дисперсии выходного сигнала Y(t):
-1/2
+1/2
D„ = at — m\= f (t—^-Xdv —
-Г/2
_ /Л _i_ Л*-Л- Л_ Л j- fY
(36	2160	24	^	36	^	V
06-2-5. Статистическая характеристика нелинейного
безынерционного элемента ту, как известно, равна:
mv=M [X2] =т2х + а2х,
тогда
k0=ту/тх=тх + о2х/тх;
k{" = ±V2o\ + Am\.
В данной задаче, учитывая гауссовское распределе¬
ние случайной функции X(t)y для отыскания коэффи¬
циента k\ необходимо продифференцировать функцию
Шу по тх [8]:
А,(2) = dmy[dmx — 2тх.
06-2-6. Функция ту равна начальному моменту
третьего порядка случайной величины X:
ту—М [X3] =М [ (1+т*)3] =т3х+3 тхо2х.
414

Коэффициент
fc(2)	!	2 /\г I	I	о^1/2
1 =J/ *5;==0	4“	6	e*x+9	e*,J •
Дифференцированием функции ту по тх полу¬
чим [8]:
k(2\=dmy Idmx=3 (т2х+о2х) ■
Коэффициент
k0=mvl тх—/п2ж+3 а2ж.
06-2-7. При действии на входе нелинейной системы
белого шума коэффициент k\ определяется по фор¬
муле [9]
^(0) а
1— 2nS„ ~ 2л50‘
Рис. 06-2-7.
Импульсная характеристика системы при действии
белого шума на входе определяется как
а ее ПФ
ОО
Ф(p)=^w(х) e~Iaxdx =	.
о
Коэффициент k„ = ту[тха..
Структурная схема может быть представлена в виде рис. 06-2-7.
Параметры линейной инерционной цепи первого порядка зависят
от математического ожидания тх и уровня спектральной плотности
входного сигнала So,

06-2-8. Учитывая, что нелинейность нечетная, нахо¬
дим статистический коэффициент усиления по матема¬
тическому ожиданию входного сигнала:
——СО
о
Заменив переменные х—mx—tax, получим:
ГПу
V2n
f
J
7*дг
—00
2b
mx
где	—	известная	в	теории вероятности функция,
таблица значений которой представлена в приложе*
нии 12.
Для определения* значений коэффициента’£,(1) и k\2)
применяем соответствующие формулы и, производя ту же
замену переменных, находим:
1-4ф,(^-):
Полученные соотношения для коэффициентов k0, k}2* совпа¬
дают с соотношениями, найденными И. Е. Казаковым для типичных
нелинейных элементов при нормальном законе распределения вход¬
ной переменной (см. приложение 11).
416

06-2-9. Используя приложение 11, находим значение
статистического коэффициента ко для указанной нели¬
нейности:
{о+-о • (Ч?-) - <> - -о • (*=?•)+
1	/	l+/??i	\2	1	/	1—Ш j
+
где /ni=/n*/a; Gi=ax/a.
Значение математического ожидания сигнала на вы¬
ходе определяется согласно формуле для установивше¬
гося режима [9]:
ту= щгт* = к1 |(1 + "г.)ф
[1 (1+т, \г	1 ( 1-т. у -■ .
.“■( ■>)_. »( - )]}.
Импульсная характеристика линейной части аперио¬
дического звена
j -jr- ё~х,Т при Я > 0;
w [Я) = ) т
Г
0 при Я < 0.
Используя это равенство, запишем выражение для
корреляционной функции выходного сигнала Ку(т), при¬
меняя критерий аппроксимации [9]:
00 00
Ky(i) = k\ J с?Я J ш (Я) ОУ (ЯО (т: -(- Я — X')dX' =
—00 —00
00 оо	Х + Х'
= k\ jdX^e “ <r^+x-v, dv =
0 0
lft9t 'p Гл* —		э(т+х—X')
=k .-Ц&- \dx\\ e r	dX’	+
0 n
oo
+ 1
0 v 0
oo X+X
—	-Э (X'—X—X)
e T	dX’
t + X
27—903	417

Окончательно
00 Г	"I
М,)=*£Ц	|л.
о Ц2 — т2
Из полученного уравнения при т=0 находим диспер*
сию
п fe'lfe2 g2
иу— т$+ 1 ха
Конкретные значения k\ находятся с использованием
таблиц Ф-функций (см. приложение 12) при заданных
параметрах нелинейного звена.
Для системы с учетом заданных параметров имеем.
m\ = mx\a= 1/5; ai = a*/a = 3/5;
k,=-j- 4 [° (2>+ф (l>33)i=!’95-
Дисперсия на выходе
k*tk г 3,94-2  , r „-г
У 7"Р+1	°*	0,1-0,01	+	1	’
06-2-10. Перестроим структурную схему так, чтобы
выходом системы был входной сигнал нелинейного зве¬
на V (рис. 06-2-10,а).
Запишем ПФ линеаризованной системы (рис. 06-2-10,0,
в)	по полезному сигналу Фш и по помехе ФЛ (р):
ф {рл	рУр+J)
W™(P)— p(rp+i) + ki)k >
Ф tp\ =	р(Тр+1)	..
p(Tp+\) + kkt ■
Математическое ожидание входного сигнала нели-
нейного звена [8];
_ Фуп (0)
kk0 (mv, ov)
Дисперсия
J.	(!)
= _D*a_ r_ 7-»0-Ю)«-(/ю)«
»	тс	J	l(«	+	j<0) {jсо (Г/со + 1) + kki}\* UW-
—oo
418

Используя приложение 13, получаем окончательно:
п п 1 + [а +	/о\
А = a + kk, + оУГ •	W
я
X
к
р(Тр+1)
д=
а)
mv
)		—
к
р(Тр+1)
ко
&
0
V
) —
к
р(тр\1)
’ *>
ft
г;
Рис. 06-2-10.
Статистические коэффициенты усиления для идеаль¬
ной релейной характеристики &0 и k\ определяются из
приложения 11:
2 Ь
mv
Ф
т-
(3)
27*
419

Подставив значение для k0 в уравнение (1), по¬
лучим:
Используя таблицу Ф-функций (см. приложение 12),
построим прямую 1 на рис. 06-2-10,г, удовлетворяющую
уравнению для ф=(т„/<х,,) при известных значениях
параметров k, Ъ, Т, ао, а\, а, ах.	,
Для совместного решения уравнений (1) и (2) неоо-
ходимо значение коэффициента k\ из уравнения (3)
подставить в уравнение для Dv (2), в результате чего
получим [8]:
Задаваясь рядом значений mv, определяем значе¬
ния ог„ и строим кривую 2. Точка пересечения кривых
определит значения mv и av, удовлетворяющие уравне¬
ниям (1) и (2). По значениям mv—0,282 и <х„=0,538
находим значения &о=1,431 и &i=l,475. Чтобы найти
математическое ожидание и дисперсию выходного сиг¬
нала Y(t), запишем ПФ по полезному сигналу и помехе:
а (1 -|- аТ) m
rTi { \
фуп \Р) = р(Тр+ 1)+J№, ;
Тогда математическое ожидание
420
ту (0 = а» +	—	0,721	-(-1,

а дисперсия
Du
  Dxak2k2i f*	diо
У	к	^	[(a	-f-	/со)	{/со	(T/со + 1) + fc£i}|2
РлЕМ! +^)
a + kkx + «2Г
= 0,01.
Среднеквадратичное значение af/=0,l.
06-2-11. Применив метод статистической линеариза¬
ции, найдем:
'	«2	R
тх =■
kk0(mx,*x) ’	*	?	+	/^i	a.v)
При mz=c тх=0.
Статистические коэффициенты передачи с учетом то¬
го, что тх=0:
М°> ст*) =26;
/Л Ч 2 + У2ъ Ъ 0,98%
k, (0, ах) = лГ— — —— .
1V х/	2У2п	х	°х
Если теперь найденные значения для &i(0, cr*) под¬
ставить в выражение для о2х, то получим алгебраиче¬
ское уравнение второй степени относительно ах.
2 , 0,898kaxb	2 п.
0х Н	р	0	z = U’
0,898bk ш 0,8982L2k2 I Г
* —	20 “Г	4(i2	12
Искомые значения математического ожидания и дис¬
персий отклонения гировертикали равны:
ту=тг
и
2	°2zki(0,°x)k	a2z-Q,898bk
0 у	0 + М°.°х)*	(Ь*+0,8986/Г
Задаваясь значениями параметра гировертикали k,
az, b и р, можно подсчитать значения o>V
06-2-12. Определяем передаточную функцию линей¬
ной части следящей системы W(р) =k\k21 (Тр + \) =
=Л/(7> + 1), где /е=100• 10,5=6300 В-с"1.
Поскольку линейная часть представляет апериодиче¬
ское звено, а нелинейное звено нелинейность типа на-
421

сыщение, то система в целом стационарная, неколеба¬
тельная, и ее можно рассчитать, используя метод ста-
тистической линеаризации [4].
Согласно приложению 11 коэффициенты статистиче¬
ской линеаризации для заданного вида нелинейности
вычисляются по формулам:
где mi—myja\ a\=ayja.
Считаем, что статистический коэффициент k\ в функ¬
ции от неизвестных ту и ау можно получить по формуле
Чтобы подсчитать статистические коэффициенты, не¬
обходимо знать ту и су, которые в свою очередь неиз¬
вестны, поэтому запишем выражения для ту и Dy> ис¬
пользуя ПФ следящей системы:
(ту> °у) — (^i(I) + *i(2) )/2-
ту (Тр+\) + ft-fto К, 5</) р=о
kmx
(4)
СС
А
у
О
00
2
Г	^	Dxa	d
J 742©2 [1 + kki (mtJ, Оу)i2 а2 + со2
п
О
422

Используя приложение 13, находим значение инте-
грала (5):
г)	   /g\
Uy~^[ 1 + 66, (illy ,Qy)\ [1+66, (my, oy) + ol\
Для определения неизвестных oy и my необходимо
решать систему уравнений (4) и (6) совместно
с (1) —(3).
Подставив исходные данные, запишем (4) и (6)
в виде
т 	 315	 ф
тУ — 1 + 63006о (ту, *у) 9	v	1
Г)	40» Ю6Ду	/gj
иу— [1 + 63006, (ту, с^)] [1 + 63006, (ту,*у) + 0,5] *
Для решения системы (7), (8) воспользуемся мето¬
дом последовательных приближений. В качестве первого
приближения примем &0 и k\ равными коэффициентам
передачи нелинейного звена в линейной зоне, т. е.
601=fen=b/a=3,2-10-4 В*с.
Подставив эти значения в систему (7), (8), опреде¬
лим первое приближение для искомых вероятностных
характеристик myi=l05 с-1; сгу1=97,8 с-1.
Найденные значения первого приближения ту\
и ву\ используем для определения mn=m2/i/a=0,333;
€Ti 1=0^2/!/a=0,312.
Подставив эти значения в формулы (1) — (3), най¬
дем второе приближение коэффициентов статистической
линеаризации:
£02 = 3,1410-4 В-с; к™ ^0,94-10-4 В с; к® =
= 3,15-10~4 В с; =	)/2 = 2,05-10'4 В с.
Используем их в формулах (7), (8) и найдем вто¬
рое приближение искомых характеристик: ту2=106 с-1,
0^=124,8 с"1.
Повторяя принятую методику расчета, можно под¬
считать третье приближение коэффициентов:	&оз=
=3,12*10-4 В*с, ^13=2-10-10—4 В-с и соответствующие
им Шуз= 106 с-1 и 0^3=124,8 с-1.
Так как третье приближение дает такой же резуль¬
тат, как и второе, то будем использовать численные
значения второго приближения, поэтому окончательно
запишем mZJ=106 с-1; Dy=156,2* 102 с-2.
423

06-3. ОПТИМАЛЬНЫЕ СИСТЕМЫ ПО СТАТИСТИЧЕСКИМ
КРИТЕРИЯМ
06-3-1. Оптимальную импульсную характеристику
найдем в виде
0У„ (х) =	+ D,8 [х].
Требуется определить ее параметры D0, Dь d\.
Уравнение Колмогорова — Винера для нахождения
импульсной характеристики в данном случае -имеет вид:
j К у (х — Я) wt (Я) dX — Kyh (х) — 0; 0 < X < ОО.
о
По условию задачи синтезируется фильтрующая си¬
стема, т. е. H(t)—X(t) и L=1. Следовательно,
Ку (х) = 3в“2|х| + 2е-и;
Ку„(?) = Кх (x) = 3e-2W.
Подставим значения корреляционных функций и
искомой импульсной характеристики в уравнение Кол¬
могорова — Винера:
J [3<?“2	+	2<Г|х~Х1} [D,e~dl} + D.8 (Я)] dX — Зе~2'=0.
о
Преобразуем его к виду
X	ОО
1
+ 2е _1х~Х| ] De8 (Я) dX -j- j [Зе_2(Х_х) + 2е-(Х_х) ] Dte~dlldX—
_3е~2х = 0.
Выполнив элементарные операции интегрирования,
получим:
3£>,б-2т . (2_d.) т п ,	2/у~т /е(>-*)т _ j) _(_
2 — di (е	’	^	1—d,
+ (3<Г2х + 2е-х)	+
■f _2£i£l	_ Зе_2х = 0.
1 + d,
424
[3e-2(x-X) _^_2g-(x-X) ] Dxe~di dX + J [3e_2'x_ l-f

Приравняв коэффициенты при функциях е
нулю, получим:
3 D\ I	I	3Dj	1	2Dt	 n.
2+ dj ' 1 —d,	2	—	dx	'	1	+dx	*
,—dit	—2*t
3D,
2 —d,
2D,
■ 3D, — 3=0;
-Т=г, -r2D. = 0-
Из первого уравнения получаем:
3(1 — d2,) -f- (4 — d2,) = 0; rf, = + K7/2.
Берем значение корня di>0, так как оно соответст¬
вует устойчивой системе.
Рис. 06-3-1.
Из двух других уравнений получим Do=0,68; D\=
=—0,22.
Окончательно импульсную характеристику запишем
в виде
ю, (т) = — 0,22е~1 '32х + 0,686 [х].
Соответствующая ей ПФ имеет вид:
0,22
W (р) = 0,68 ■
Р+ 1,32 '
Ей соответствует структурная схема на рис. 06-3-1,
Минимальное значение дисперсии ошибки
^мин(X) *,„(*)* = 3 + ^ - 3 • 0,68= 1,15.
о
425

06-3-2. Для решения этой задачи используем инте¬
гральное уравнение Колмогорова — Винера:
о
при 0<т<оо, где Wo(K) —оптимальная импульсная ха¬
рактеристика.
Представим а>о(т) в виде следующей суммы:
т. е. как сумму экспонент и импульса, где N=tn + l—1 —
число слагаемых; т — число слагаемых полезного сиг¬
нала; I — число слагаемых помехи. В нашем примере
А=1 + 1 — 1 - 1 •
Тогда искомая оптимальная функция определяется
в виде
Из условия задачи видно, что А\= 2; Bi=l; di—3;
Ра¬
спределим взаимную корреляционную функцию вход¬
ного и выходного сигналов KVh(т). Из условия задачи
можем записать равенство
Подставляя равенство (3) в формулу (1), получаем
уравнение
т
(1)
(2)
ш0 {z) = D1e~dl'+Dt& (х).
Kvh(U,tt) = M\H K,)T(g],
откуда
8|<,-/,+у=_2в-3М-<9|.
так как т>0, t3>0, можно записать:
(3)

Чтобы избавиться от модуля, представим первый
член /* в формуле (4) в виде двух интегралов:
/* = J (2е~3(т~^ +	)	[£,<Г‘/Д	+	А,8(х)] dX +
О
+ j (2<r3(X-,,-f е“(7‘-т))	А.5	(х)]	ах	=	2е~3('+‘а)
Ф)
Используя фильтрующие свойства импульса, форму¬
лу (5) можно переписать в следующем виде:
I*= j* (2<Г3(Т-Х) + е-(,-Х)) D.e-^dX -f
О
+j (2e~3(l~T) + e~a~J)) D,e~d,x dX + D, (2е_3т -f О =
= 2e~3('+i;>) .	(6)
Обозначим первый член суммы через /ь второй-
через /2.
Определяя отдельно каждый член, получим:
/. = j (2е“3(^ + е-(т_7>) ) D,e~dlXdX =
+
2D,	3T+(3-rf,)X
3—tf,
D,	Л—и-(1—
1-rf,
 	2£)1	o—rflX 	 2Di	—	3T	,	D,	_rf,t
3 — d,
P.
1 — dx
3 — rf.
1-rf.
-t ( 2D' -{- D' \
— e Г з-d, T i-rf, J
2D,	-3t	D,	—i.
3 — rf, e ~ 1 — d, 6	’
427

/, = J (2<г3 (X_T) + ё~ (Х~Т)) £>, e~d'x dX=
— (3 + d,)
    2D,	—	dtt
Pi -+х-(1+Л)Х f
(1+rf.)	J	“
e ->-_l_	D■	e-d‘T /	2£>i
3 + d,	^	1+d,	—	I	3+d
Подставляя выражение для /i и /2 в формулу (4),
получаем:
т*  .—dit Г 2D, j	D I 2D, | Di "I
[ 3 — d, “l — d, ~3 + d, I i + d, J
2Dl ■ e~^ -	e~"	+	D°	(2е_3т+О -
3 —d,
— 2e 3('+g = 0.
(7)
Для выполнения тождества (7) необходимо, чтобы,
коэффициенты при функциях е~й^ , е_3т, е~' равнялись
нулю, т. е. необходимо выполнение следующих трех ра¬
венств:
2D,
Ог
2D,
Ог
3 —d, 1	1	—d, 1 3 + d, 1 1+d,
2D,
= 0;
/
3 — d, 1	0
Di
 Qi
2D„ — 2e э=0;
1 —d, —0
или соответственно
2 (3 + d,) + 2 (3 — d,)
+
(8)
1 — d2,
откуда di=l,46;
9 — d\
X~d\*X~dl =12—12^, + 18 —2^г, = 0,
| pi  n. 0,46D0
1 — 1,46 о	1,54
D0 = e
—3/
428

Из двух последних равенств имеем:
D, = — DJ0,46; 0, = 0,460,; 0.3D, + 0. = в“*Ч
откуда
 q ±	 о	f-
D, = 0,78e »;£>, = — 0, ЗЗе э.
Подставляя в формулу (2) значения коэффициентов,
получаем:
w,, (х) = — 0,ЗЗе_(1'4бх+3<э) +0,78е_3<э8 (х).
Оптимальная ПФ
Wt(p) = 0,78-3t^°^Q..	(9)
Рис. 06-3-2.
Структурная схема системы показана на рис. 06-3-2.
Из выражения (9) имеем:
—з t
Й, = 0,78Г3Ч Й2 = ^46^; 7’2 = 1Тг = 0,69.
Минимум дисперсии ошибки
£>Смин = 2— J 2<r3x[0,33<T3V,'46x + 0,78^8 (х)] dz =
= 2—Ив-3*».
При U = 0 DCMHH = 0,89; при *э ■= оо 0Ыт = 2.
06-3-3. Решение уравнения Колмогорова—Винера
имеет вид:
ю, (х) = 0,22<Г2ЧгМ2х + 0,68е~2Г®8 к%).
429

Минимальное значение дисперсии ошибки в этом
случае
^мин = 3- 1,85Г4\
06-3-4. Спектральная плотность входного сигнала
в систему
s,c>=s,(»)+s,(.)=-S±5-.
Представим суммарный входной сигнал Y(i) в си¬
стему в виде единичного белого шума Y'{t). Для этого
определим ПФ звена W\(p), с выхода которого поступал
бы сигнал в виде белого шума.
Представим спектральную плотность Sv(co) в виде
4 + /®
S«V>- 2 + W
Передаточная функция [1]
WAP)
’=Iф (/«*)!*-
2 + р
Ф (Р)	4	+р	■
Взаимная спектральная плотность
S,A(«o) = SJt(«o)=33Ti-i.
Для определения оптимальной передаточной функции
используем равенство in
К» М=4г
Подынтегральная функция
Syh. (“)	4	2	—	/to	  2
  2_ {_}
ф (— /со) 0 4 + (й2 4 — /со j ^0) — 2/ ш + 4/
^Учитывая, что полюс второй дроби — 4/ лежит в ниж¬
ней полуплоскости, окончательно получаем:
(/“) = [ф (_/со) ] ф(/<0) =4 + /ш •
Искомая оптимальная ПФ имеет вид:
0,5
Wt(p) о,25д+1
430

06-3-5. Импульсная характеристика оптимальной си¬
стемы
wi(x) = A-MIf + C18(x) + D18(*-n, 0<*<Т.
Неизвестные коэффициенты весовой функции Ао, Аь
Сь D\ определяются с использованием необходимого
условия, накладываемого на импульсную характери¬
стику:
j ку (х — Я) W, (Я) dl - Kyk (х) = 0.
о
Подставим заданные значения в исходное уравнение
J	[А	+	Ах + С,8	(х) + D,S (х - Т)] dx = т, + у А
о
где yo> Yi — неопределенные множители Лагранжа.
Представляя полученный интеграл в виде суммы четы¬
рех интегралов и учитывая, что	1 и (%)di=
6	о
= 0, получаем систему линейных алгебраических
уравнений:
аА0 + (а Т + 1) Л1—o?D\ = 0;
а Л о—А\—a2Ci = 0;
AT + ^ + C. + D^ 0;
-^-+^- + D,T = 0,
откуда получаем искомые параметры импульсной ха¬
рактеристики:
.	4а	(аЧг + 3о.Т + 3)
Л°	(**7’г + 6а7’+12)(а7’ +	2) '
Д	6а2
агТ2 + 6аТ+12	’
2(2а27’2 + 9а7’+12)
(а*7, + 6а7’+ 12) (аТ + 2) >
2аГ («Г + 3)
— (а2Г2 + 6а7'+ 12) («Г+ 2) •
431

Окончательно можно записать:
т
Ф. (Р) = J И», (т) e-p'di =^(1_ е~рТ) +
+-ТГ (т-‘-Г- Г‘~,Т ) +:с, + D,e-'T.
При 7=1 с, а=2 с имеем:
Л0=0,93; Л!=0,85; Ci=0,69; />,=0,25;
-	—	Те~рт ) + 0,69 -f 0,2Ьё~рТ.
06-3-6. Условие, необходимое для определения опти¬
мальной импульсной характеристики:
Т	m
$Ky(*-X)W'(X)d,-Kyll(t)+2 Yit< = 0, 0<*<7.
0	/=,	о
Так как по условию задачи Ку(х) = /С2(т) = 6(т), то
KVh(x) =0, Kxz{x) =0, а, следовательно,
1
|8(х —Я)^0(Я)йЯ + То + Т1т = 0» 0<х<7\
о
Найдем решение полученного уравнения, учитывая
фильтрующее свойство б-функции:
о>о(т) +уо+угг=0.
Таким образом, оптимальная импульсная характери¬
стика
^0 (т) =—Yo—YiT,
где уо и Yi — неизвестные множители Лагранжа, кото¬
рые находятся из дополнительных условий, накладывае¬
мых на импульсную характеристику системы:
1
f (—т.—т.’)*=1;
о
1
f *(— Т. — 4t%)d\=°>
о
432

откуда
Yo = —4; у\ — 6.
Итак, искомая импульсная характеристика
w0( т) =4—6т.
Минимальная дисперсия ошибки, отвечающая вы¬
бранной импульсной характеристике,
Ленин = лА - J *<//. W	W * - 2 Ъ i x‘w°(z) dz =
О	1=0 о
= 41 — 6-0 = 4.
06-3-7. Общее выражение необходимого условия для
дао(т) запишется в виде
| [*„ (*-*) + а'т'тп (Л) dx - VW -
0
m—1
_(_ 1Гт!02тСтх-+ 2 Т^=0, 0<t<7\
i=0
Учитывая начальные условия, перепишем это урав¬
нение в виде
1
| [8 (х — Я) - j- хЯ] w0 (Я) dX -|— у0 = 0.
о
Учитывая вид входного сигнала X(t), считаем, что
искомая импульсная характеристика системы может
быть представлена как
^0 (т) =go + gl'X,
где неизвестные коэффициенты g0, gx можно определить
из уравнений:
1
j [8 (х— Я) -[- хЯ] [go + gi*] я?Я-[-Я0 = 0;
о
^o + To + ^"^~g'o + g,i + '^-g,i ^ = 0;
л+т.=0;4"Л+^‘ + 4"^‘==0»
28-903	433-

откуда
So Y* Si 3 To*
Неизвестный множитель Лагранжа y0 определим из
дополнительного условия, накладываемого на оптималь¬
ную импульсную характеристику:
I
Y. + 'l-rv') d%=\,
к-
т. е. —Yo + 3 Yo/16= 1, откуда у0= —16/13.
В результате подстановки получим:
/ ч 16	6
Минимальное значение ошибки на выходе системы
управления
— Yo j W° (Х) dx==~W
06-3-8. Необходимое условие для w0(r) в данной
задаче запишется следующим образом [jl]:
1
Ю\ f иа;в(Я)£/Я + дав(т) +ув = 0> 0<т<1.	(1)
о
Оптимальная импульсная характеристика
(ть 0) = go + glT.
Значения go и g\ можно определить, приравняв нулю
коэффициенты при т°=1 и при т1=т в левой части ис¬
ходного тождества (1) и учитывая условие астатизма
системы:
 л 1 + 0£2i/3 .	—	90/^2 	\
So — 4 4+0GVF’ S1 —4 + 6G2i/3 .
При Gx = 1 величины m\ и как функции от неиз¬
вестного параметра б имеют следующий вид:
4	.	п —4 4 + 29/3 + 979
mC (4+е/З)2 ’ t	|4 + 9/3)2 *
434

Подсчитываем производные от критерия
У 2я£с
по функционалам т\ и D<.
2с	е~'п^	!2Dx~
дР 	с
<>т\	V 2 яИ3/2
дЯ 	 с	/	1	/гегс	\	_ш>с	/2£)с
^>с Гй ^ / d\12	J	е
Найдем оптимальное значение неопределенного пара¬
метра е0 [1]:
_ дР/дт\	1	4	+	290/3	-f	02о/9
* dP/dD^ — 1 — m\/D^ ~ 3 + 290/3 + 920/9
или
4еэ.+462«+2-ге«-4=0'
откуда 0о=1,25.
Окончательно импульсная характеристика оу0(т),
соответствующая максимуму принятого критерия, за¬
пишется следующим образом:
w° (т) = wQ (т, 0О) = 1,28 + 0,57 т.
06-3-9. Оптимальную систему находим в классе астатических
систем первого порядка. Это означает, что на класс допустимых
импульсных характеристик накладывается дополнительное условие
Т
j* w (т) dz = 1,	(1)
о
что гарантирует конечное значение математического ожидания ошиб¬
ки. Запишем уравнение Эйлера для отыскания ш0(т) [1]:
т	т
G\x j Xw0 (X) dX + 9 J	(x) dx + Gyox + Yo + 0-	(2)
0 0
В данном случае искомая импульсная характеристика имеет
вид [1]:
^о(т) =go+£iT+£06[T] +£i6[t—Т].	(3)
Подставив (3) в (2) и затем, приравняв коэффициенты при функ¬
циях е°, е~~ат, еах нулю, получим четыре линейные алгебраические
уравнения, которые вместе с уравнением (1) позволяют определить
пять неизвестных параметров go, g 1, Во, Вi, у0. При фиксированных
28*	435

исходных данных, приведенных в условии задачи, параметры go, gu
Во, В1 определяются как известные функции согласующего пара¬
метра 0. Следовательно, и импульсная характеристика Шо(т) опре¬
деляется как известная функция т и параметра 0, т. е. ДОо(т) =
= ш0(т, 0).
Квадрат математического ожидания и дисперсия ошибки систе¬
мы могут быть также выражены через параметр 0 по формулам:
\ (0) = G2! £ j* zw (т, 0) dz + *]
т'	  1	1	  2’
(0 + 0,24)2 >
о
Т т
О,402 + О,190 + О,б9
Dc (0) — ^ ^ в ^ I w0 (х, 0) w0 (Л, 0) dzdK — ■	Q	24)2
о о
[здесь дана’’уточненная по сравнению с [1] формула для D^ (0)].
Рис. 06-3-9.
Задаваясь различными значениями параметра 0, вычисляем
<критерий
т\ (0)
2с	~2Dj; (0)
Р(9) = у*щщ е
Деление на число Р(1) позволяет нормировать кривую Р(0)
и сделать ее более наглядной (рис. 06-3-9).
Значение 0о, соответствующее максимуму функции Р(0) (или
Р(0)/Р(1)), в данном случае равно 0,43.
Оптимальная система, определенная по максимуму Р, в данном
случае обеспечивает прирост критерия по сравнению с оптимальной
системой, определенной по минимуму среднеквадратической ошибки,
на 26%, т. е.
Я(9р)-Я( 1)
Р( 1)
= 0,26.
Такой же выигрыш будет и в случае, если коэффициент G±
считать не постоянной известной величиной, а случайной, прини¬
мающей значения + 1/1/20 и —\/V~20	с вероятностью р=1/2 и
<7=1/2.
466

В 3T0i\i случае все вычисления останутся прежними, только
вместо квадрата математического ожидания тследует писать
означающую дисперсию ошибки системы, вызванную разбросом слу¬
чайной величины Gx.
Следует отметить, что исходные данные в задаче выбраны спе¬
циально такими, чтобы выигрыш в критерии Р был существенным
при переходе от w0(x, 1) к w°(r) =w0(t, 0о). При других исходных
данных этот выигрыш может быть малым, а иногда и несуществен¬
ным. Однако нужно иметь в виду тот факт, что переход от системы
с импульсной характеристикой ш0(т, 1) к системе с импульсной
характеристикой до°(т)=ДОо(т, 0о) связан не с усложнением системы,
а лишь с изменением параметров этой системы, что обычно легко
осуществимо.
06-3-10. По известным формулам [1] определим ма¬
тематическое ожидание и дисперсию ошибки с учетом
т
дополнительного условия астатизма j* w(t)cLi = 1:
о
т
m^ — mf — mh = j* tny (t — т) w (т) dt — mh =
J j ww (x,) O' W d\dit -f 2Тэ Х2ЬУ (xs) dx2 -f- T\
.0 0 0
T T
= Д> + [ | w(x,—t,)dt,rfx2—
6 0
-2 \w{,)Kyh(i)d,.
0
Определим значение оптимальной импульсной харак¬
теристики, синтезируемой по критерию минимума вто-
>рого начального момента Гс = Д. -f-tn2^
т г
ГС = j \w (xi) w W [Ку (x, — tt) + C\vJ d\d\ —
0 0
T
2 j* ay (X2) [Kyh (X2) - C27>2 L Y] dx2 + Dh + C\T\ - T,
0
(1)
где у —множитель Лагранжа, определяемый из допол¬
нительного условия.
437

Оптимальную импульсную характеристику ш, по мини¬
муму Г,, можно определить из интегрального уравнения
Колмогорова — Винера, которое в нашем случае имеет
вид [1]:
j (О [Ку (\ — S) + С2,х,т2]	—	Куь	(т2)	+
О
+ С21Г9х2-А = 0, 0<т2<Т,	(2)
где А=—у/2; Ку(х) =Kz{x) = &6(т); /Сул(т)=0.
Используя фильтрующее свойство импульса и рас¬
крыв интеграл в уравнении (2), получаем:
да0(х2) = Л-(Я + й1х2),	(3)
где
dl = — С2, ^ j ч,®, (т,)	-)-	7\,	^.
Подставим выражение (3) в интегральное уравнение
(2)	и проинтегрируем:
-J- С2,	т2	J	+
_Я = 0, 0<т2<7\
Приравняв нулю коэффициент при Т2, получим одно
уравнение для определения неизвестных параметров X
и d\\
d■+С2> (4-яг + тгd3') ]+с*'т*=°-	(4>
Другое уравнение получим, подставив (3) в условие
астатичности системы:
^-(ЯГ + Л_Й17’*) = 1.	(5)
Из уравнений (4) и (5) можно определить X и dx.
Для конкретных исходных данных задачи Я=4,70;
di = — 3,4!.
438

Оптимальная импульсная характеристика оконча¬
тельно определяется как
я>0(т) = 1,57—1,14т.
Вычисляем значение оптимальной импульсной харак¬
теристики по критерию максимума вероятности:
mV
P = -L=- е~ W	(6)
У 2nD
Используя метод согласующего множителя [il], за¬
пишем интегральное уравнение для нахождения ^о(т):
j ЩУ{\ —	№\t\i2	—	i=
О
= 0, 0<т2<7.	(7)
Решение уравнения (7) дает:
WQ (X, 0) :
36 + 229
429
36+Q	36 + 0	*
Определим значения т2с и в функции от параметра
т5
15876
С (36+ 6)2 ’
44402 + 2169 +
(36+ Э)2
Задаваясь различными значениями 0, составим таб¬
лицу (табл. 06-3-10) для нахождения 0О, обеспечиваю-
Та блица 06-3-10
6
0
1
4
5
6
7
8
10
«с (9)
12,1
11,6
9,92
9,44
8,9
8,58
8,2
7
Dc( 8)
2
3,32
7,41
9,55
11,8
13,6
17,6
24
Р(0)
0,035
0,037
0,077
0,080
0,080
0,078
0,076
0,071
Щего максимум вероятности Лмакс- Окончательно имеем:
Р(е0)=0,08; 0о = 5,25.
Оптимальная импульсная характеристика
w*(t)=Wo(%, 0о) =3,67—5,35т.
439

Подсчитываем выигрыш в критерии Р при переходе
от ш0(т, 1) к w°(т):
Р(%)-Р( 1) _i 1С
Р( 1)	— 1,1 *
В данном варианте при переходе от wo(rt 1) к ш°(т)=дуо(т, 0о)
получился больший выигрыш в критерии Р. При других исходных
данных этот выигрыш может быть и малым.
Многочисленные расчеты И. М. Демьянова показали, что при
различных комбинациях значений параметров k, а, Т, Тэ зави¬
симость
АР _ГЯ(61) —Я(1)
Р( 1)	Р(	1)
и функция аргумента Р(1) имеет монотонно убывающий характер.
При Р(1)>0,5 выигрыш в критерии ЛР/Р( 1) очень мал (меньше
1%), при Р(1)«0,5 этот выигрыш составляет примерно 1%, при
Р(1)<0,5 выигрыш критерия может достигать больших значений
(нескольких процентов и десятков процентов).
Если Ci — случайная величина, принимающая значения
с вероятностью р= 1/2 и —с с вероятностью *7=1/2, то критерий Р,
определяемый формулой (6) с точностью до несущественного по¬
стоянного множителя, также имеет смысл вероятности невыхода
ошибки системы из заданных малых допусков.
06-3-11. Передаточная функция разомкнутой системы
управления имеет вид:
W(p)=±SL±t^eL.
замкнутая система обладает астатизмом второго по¬
рядка.
Установившееся значение ошибки воспроизведения
полезного сигнала
Cx=*-X=-%-av
где сг — коэффициент ошибки.
Разложим ПФ по ошибке
фс (/?)= р* + kTpK + k
в степенной ряд и найдем с2=2/k. Ошибка воспроизве¬
дения полезного сигнала
tx=ai/k.
440

Дисперсия ошибки системы из-за действия помехи
определяется как
№ Г Н Т\ (/со)2 +1] dmr-(l+ ^2к) м
(j<o)* + kTKj«> + k\* и	2Тк
Квадрат суммарной среднеквадратической ошибки
гг гг I Г) 	 fl2i I П + kT\) N
* ”Т“ С k2 1 WK '
Найдем минимальное значение £2, для чего прирав¬
няем нулю производную £2 по Тк:
2kT2K—(l+,kT2K)=0.
Искомое время 7’к= 1/^fe =0,082 с. При этом мини¬
мальная ^ошибка Смин = [/	-f- Dc = 1,13 град.
06-3-12. Время 7’к=7’-|-У~Тг-\-1 /ft = 0,06 при сред¬
неквадратичной ошибке
' = /¥^^^=2.23 град.
06-3-13. Продифференцировав выражения для сред¬
неквадратичной ошибки по Тк и k и приравняв их нулю,
получим два условия минимума:
Т — 1	2а2. | TVN	п
к KF * fe3onT + 2 —и’
откуда легко найти k0BT = 2l 1/с2.
Постоянная времени корректирующего устройства
7„.ОПТ = 0,218 с.
Суммарная среднеквадратическая ошибка Е==
= 1,07 град.
06-3-14. Передаточная функция замкнутой системы
управления
Г(р) + 1	+	^	+	•
441

Используя приложение 13, найдем среднеквадратич¬
ную ошибку воспроизведения полезного сигнала:
ОС-
п — 1	Г +ь>57~г.)	2ГСРХ	.
2п	J	| гж (/»)■ + /» + *!■ 1 + <о27’гс
—00
= D
Т, + Тс + kT,Tc
Л + Д + кТ\ ■
Составляющая среднеквадратической ошибки от по¬
мехи
k2N	,	kN
2т. j I Г, (/«)* + /« + * I* dw '	-
—00
Суммарная среднеквадратическая ошибка
T2 Т2 Л- Т2 — kN . п7'1 + 7,с + kTjTc
+	2	'	х	Тг+Тс	+	kT2c •
Оптимальное значение коэффициента усиления опре¬
деляется из равенства
,	. /2РЯ<Рс^Т\Г	+ _ор 1/с.
опт J/	N7'3£	Ts	с	ои 1/с.
При йОПт = 30 1/с ошибка £2=0,9 град.
06-3-15. Для данной системы импульсная характери¬
стика имеет вид:
У	ч	2
Дисперсия ошибки
ОО 00
Рс = Г Г [3<Г211+> | —J— S (х — Я)] ~~ e~'/q*	e~V4'dxdX -
^	Яг	Яг
О О
эо
-2* Я\ „—'til
Яг
442

Вычислим производные от функции F по парамет¬
рам qi и ^
dF ^ дР^  q, — 2д2 (3-4?1) . oF
&7, dq,	<7г(1+2?2)	’	dqt	dq2
4<7i (2?, — 3)	(1 + 4^2) [?г2 (1 + 8<7a) — 12<7,<7г]
— 2(72 (1 + 2(72 ) 2?гг (1 -)- 2<72)г '
Зададимся первым приближением параметров <7п = 1
И
Первое приближение критерия Fi=/?(1,1) =2,5.
Производные от критерия по параметрам, соответст¬
вующим первому приближению: dFjdq1=dD:tldqi = 1 и
dF/dq2 = 1,6.
Значение вспомогательного параметра v, определим
из условия минимума p.i(vi) [1]:
(l + v)2 ri+8M + 4-v)|-l2(l + v)(l + 4-v)
fc(v) = —f i—Tf 1	r~\	+
2(i+xOI.1+2(1+^v ).
+ 3.
Графический способ определения минимума fii(v)
дает vi = —0,3.
Вычислим значения второго приближения парамет¬
ров q! и q2:
<7,2= 1—0,3=0,7; <722=1—0,3 -i-^0,95.
Второе приближение критерия F2 = F (0,7; 0,95) —
= 2,21.
Разность между вторым и первым приближениями
критерия F2—Fi = —0,29.
Повторяем цикл. Частные производные для второго
приближения d/7<3<7i = 0,13; dF/dq2 = 0,39. Вспомогатель¬
ный параметр v2=—1,7.
Третье приближение: ^13=0,7—0,13-1,7 = 0,48;
<72з=0,95—0,39-1,7=0,28;
Г3=Г(0,48; 0,28) =2,04;
F3-F2 = 0,17.
Разность еще велика.
443

Четвертое приближение:	<7u=0,50;	q2	4=0,25;	/ч=
=F(0,5; 0,25) =2,01; Г4—Г3=—0,03.
Дальнейшие вычисления можно не делать.
06-3-16. Запишем приближенную формулу для опре¬
деления вероятности [1]:
ущ;
р=р<1'|<с>=7Щвг | exp(_®t/ с"
Где j) —дисперсия составляющей ошибки Sj, вызванной
случайной составляющей полезного сигнала: D^ Дис“
персия составляющей ошибки С„ вызванной действием
помехи.
Дисперсия £>Ci определяется по формуле [1]
г г
j тЦУ (т) dz -f Тэ
о
где Di — дисперсия случайной величины Х\.
Дисперсия DCa определяется по формуле
т т
DJ Кг (*с — Я) до (х) до (Я) dxc/Л.
о б
Произведя подстановку У = -	, запишем выраже-
V D\x
ние вероятности
Р=Р(|С|<с) = р^=уя- |	ехр {-4-}*.	(1)
Полученная формула удобна при вычислениях, так как ПР^
ставляет собой табличную Ф (и)-функцию (см. приложение 1 Ь
Далее необходимо, как и в задаче 6-3-9, записать приведенный
функционал, введя согласующий множитель 0.
Решение данной задачи почти полностью аналогично решению за¬
дачи 6-3-9. Вместо т\ здесь используется D^. Для	и по¬
лучаем зависимости от параметра 0 [1]:
* 2,802	О,402 + О,190 + О,69
Dh (®) = (0 + 0,24)»"’ °С,	=	(0	+ 0,24)»
444

Импульсная характеристика определяется в таком же виде,
как и в задаче 6-3-9. Для определения значения параметра 0 = 0о
подставляем выражения для дисперсий D^ и D^ в формулу (1)
и находим максимум вероятности Р = Р2(0) как функции пара¬
метра 0. Этому максимуму соответствует значение параметра
0о=О,44.
Относительный выигрыш вероятности при переходе от импульс¬
ной характеристики а>о(т, 1) к импульсной характеристике
до0(т, 0)44) составляет:
Р (0)44) Р (1)
Р(\)	0,08.
06-3-17. Решение задачи необходимо начинать с опре¬
деления оптимальной импульсной характеристики А\{х)
по интегральному уравнению [Я]:
т
| Пге-аИ_Х|Л, (Д.) ей = 1.	(1)
0
Решение этого уравнения согласно общему представ¬
лению импульсной характеристики для данной задачи
можно представить в виде
(т) =#o + #iS (т) +#26 (т—^) •	(2)
Коэффициенты а0, аь а2 определяются путем подста¬
новки (2) в (1), интегрирования полученного выраже¬
ния в пределах от 0 до Г и приравнивания в найденном
тождестве нулю коэффициентов при функциях 1, е~~а\ еах»
Окончательно получим:
»
1-е«т
Т=Ге2лТ 2Dz
06-3-18. Оптимальный фильтр представляет собой систему с об¬
ратной связью и описывается векторным дифференциальным урав¬
нением вида [28]
= Q (t, t) [Z (t) - H (t) X (<)] + A (/)'X (<),	U>
гДе X(/)—процесс на выходе оптимального фильтра; Q(/, t) —
матрица переменных коэффициентов.
В нашем случае А=—1/Г; Н= 1; G= 1/Г. Тогда уравнение
(О запишется
dX (t)	_	_
= Q (f, t) [Z (t) _ X (t)] _ X (t) (1/Г),
где Q(^, 2f)=E(O/5n(0).
445

Уравнение для дисперсии ошибки
ЩИ—АЕ(() _L_
dt
'Su{ 0)
Е2 (0+"7rSe(0).
Введем систему уравнений
dv\
^1 + Su (0) Т2 ; —тг ;
dv2 _ vx , v2
dt т ит-вп /-в . dt ~ sn (0) + Т ■
Матрица коэффициентов, обозначаемая F, имеет вид:
” у’	(0)
F =
1
Sn( 0)
Учитывая стационарность матрицы А, переходную матрицу
Т(г, ^о) можно представить как
Т{t, to)=T(t—/0)=Т(x)=L_1{||pE—F||-1}.
Положив = 0, найдем матрицу
(2)
7+7’ — $u (0)
II pE F || =
1 1
s„(0) P- T
обратная матрица определяется как
!| />Е — F Н ~1 = -
Р2 + Y2
P— h'T
S„(0)
1/5,г (0)
p+ 1 /Т
(3)
где у = V1 — Su (0) Sn (0).
Если найти обратное преобразование Лапласа от обратной
матрицы (3) и подставить в (2), то можно записать значение для
дисперсии ошибки, что при / = 0 определяется так:
 2 	V1 + S„ (0)/S„ (0) ch Y t + sh -it
C 9*Kl+S^0)/S,a0)chY*+[l+0,5Su(0)/S„(0)]shY*
Искомый коэффициент оптимального фильтра, изменяемый во
времени, определяется выражением
Q (t. t)
1 Su(0) у I -S„(0)/SB(0)chY< + sh r(t)
2T Sn ('0) ch ft -)- [1 -f- 0,56u (0 )/Sn (0)] sh уt
06-3-19. Оптимальная оценка Go определяется в данной задаче
уравнением
G0 + h r02 G0 (t0) = 0,
dt
rb2
446

где h находится как решение уравнения
r02 h2> h Уо) = 1*
Уравнение Риккати для h можно свести к линейному уравне¬
нию, откуда легко получить уравнение для Я:
г82
h
t — t0 + rG2 *
Оценка определяется уравнением
dGp _	1	1
dt t — t0 + rb*u°'T~t — t0 + rb2A'
Пользуясь уравнением, определяющим оптимальную оценку Gо,
можно найти формулы, вычисляющие дисперсии D\ и D2.
Составляющая ошибки £i определяется формулой
t
С G
?1 = J	+	dx—G-
to
Дисперсия этой составляющей ошибки
G2
Dl = W-tt)irV+ I]2 •
Составляющую ошибки £2 можно найти по формуле
t
-j-
и
<« + /-92 dz’
Дисперсия этой составляющей ошибки
t—U
d2 = -
г 82
I ( J* +1)
В качестве критерия сравнения систем примем
2с
'=тта9
Ы)-
Этот критерий имеет смысл вероятности того, что ошибка си¬
стемы находится в пределах —c^£ = £i +где с — малая по¬
ложительная величина. Значение критерия / зависит от отношения
£*i/^2, которое определяется по формуле
Рх _ гб4
D2 ~t — tQ *
447

Введем переменную b=r/(t—10) и определим значение 02 = Q2q
соответствующее экстремуму критерия I. Это значение равно [\j
•	^	-9V
D, (0%)
РТ+46 —
2 Ь
Получим конкретные значения отношения /(02о)//(1) при раз¬
личных исходных данных, т. е. при различных значениях Ь, исполь¬
зуя формулы
1	1	/V0)
Д1С) = (1/6 Н- 1)2 ’	=	6	(1/6 + I)2 ’ D2 (1) — Ь;
(V1 — 46 — А2	ль
Di (0%) =^1 + 46^7J • Dz (02«) = (|/[ +46+ J)S '
Dt (02о)	(КТ+1б—1)г
Di (02о)	46
Задаваясь значениями b и используя таблицу Ф-функций (приг
^ожение 12), можно получить при b = 0,3; 1,0; 2,0; 3,0; 10,0 значения
/ (02о) //(1) = 1,0; 1,4; 1,9; 5,6, 12 соответственно.
Как видно, с ростом b выигрыш критерия / при переходе от
■оптимальной системы, определенной по критерию минимума средне¬
квадратической ошибки (0=1), к оптимальной системе, определен¬
ной по максимуму критерия /(02о), также растет.
06-3-20. Оптимальная оценка G0 определяется уравнением
dG о
■	—	h	^02	^	@о	+	h	rg2	X; G0 (t0) = 0,
dt
где h определяется как решение уравнения
dh	1
df = 2ah	r02 h2; h (/0) = 1
в виде
2 arQ2
h = ■
1 + exp [— 2a (t — t0)] (2a/*62 — 1) *
Оценка находится уравнением
dG0 f  	2a 	|
dt \a 1 + exp [— 2a (t — <„)] (2ar02 — 1) /	°	+
2 a
X.
1 + exp [— 2a (< — <„)] (2ar02 — 1)
448

Этой оценке соответствует импульсная характеристика оптималь¬
ного фильтра Калмана—Бьюси:
,,	.	ехр	[а (/ + *)]
w 'г> х> — [ехр (2at) — ехр (2at„)] 2а + г02 '
Значение в2, равное оптимальному 02о, определяется с помощью
формулы
fl2 П+y-i
9 0 —	2,и	9
где
2 аг
Р* ~ ~~e2at с*1 to '
06-4. ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ,
ПОДВЕРЖЕННЫХ СЛУЧАЙНЫМ ВОЗДЕЙСТВИЯМ
06-4-1. Поскольку Н(п + &) =Х(п + г), то веса при
разложении Н(п + &) в ряд определяются [1] как Со=1,
С\ = г, с2 — г2/2.
Оптимальная импульсная характеристика находится
из уравнения и]
2 *.('—0 wo (* ~Ье) "Ь 2 т о < /< iV,
1=о	5=0
откуда
**•«»• (0 + в) ч- Y* = 0:	)
(1 + s) -j- То + Ti + Т2 —' 0; J
k\w, (2 + e) + To -f 2y, + 4Ts = 0. I
Система (1) позволяет получить импульсную харак¬
теристику в зависимости от множителей Лагранжа:
То	^
(1)
ю.(0 + в) =
®о(1 + е):
ш0(2 + 6) = -
U2 f
К о
То + Т. + у2
k\ ’
То + 2у, + 4уг
k\
(2)
)
Если подставить (2) в формулу для определения у0,
Vi, Y2 [1]:
N
S lZ + То- Tt У г) = SI (— l)s (Ds -f Cs),
1=0
29—903
449

то получим систему уравнении:
Го + Yi +'Ya Г» + 2Yi + 4г2 	..
ft2.	ft»,	—	lt
Yo
k\
Yo + Yi + Ya О Yo + 2y, + 4y2 .
k\	*	k\
Yo + Yi + Ya Л Yo + 2Yi + 4y2
k\	*	k\
:8S;
Решив полученную систему относительно уоо, ую,
Уго и подставив эти значения в импульсную характери¬
стику, окончательно получим:
ш0 (0 + е) = 1,0 +1,5е + в2;
Wo (1 + е) = —2е—2е2;
о>о(2 + е) =0,5е + е2;
да0(« + е)=0 при п>2.
Оптимальная импульсная характеристика представ¬
лена на рис. 06-4-1.
Минимальное значение дисперсии ошибки
-	=	(1.0 + 1,58 4- s2) + (1,5 + 6,5s + 6s2) 8 +
+ 2(0,5 + 3,0е + 3,Os2) е2.
06-4-2. Учитывая конкретные условия для определе¬
ния Wo, можно записать систему уравнений:
6>e(0 + s) + To = 0;
k\w0(l +s) + y0 + Ti — e(s+ 1)р2 = 0;
k\w% (2 + e) + 4[x2 [wt [0 + 8) + шД 1 + 8)+
+ 4а», [2 + e)] + у, + 2Tl — 4eV? = 0,
450
(1)

Из системы (1) можно легко получить:
ш.<0+«) = —jfc-;
/1 I -1 --Yo — Yi + e(l + e)P-2...
(1 + s) = w0
(8[х2 — ft20) Yo + 2 (2H-2 — k\) Yi +
ш I 4	+	4.[вУ0	+	|*.(Ч-«)]»»
ш«—(^+s)—	fe2„(fe2.+16m-2)
(2)
Для нахождения параметров уо и yi запишем еще
Два дополнительных уравнения:
-Y2
е(1 + е)р,2 — То — Yi I
U2	I
k\ “	ft2
_l(8(x2 — k\) y« + 2 (2y.2 — k\) Y, + 4s [efe20 +jx2(l+^)]^2
“	fe2.(fe20+	I6p-2)
= 1;
Yo I в (1 + e)p.2 — Yo— Yi I
"Р7"Г	k\	T
(8p,2 — fe2o) Yo + 2 (2y.2 - k\) Y, +
I 0	+ 4e [efc20+ p.2 (1 + s)] p,2
fe2o (fe2o + 16h-,)
(3)
Уравнения (2) и (3) позволяют найти пять неизвест¬
ных ny0(0 + e), o>o(l + e), ау0(2 + е), у0, уь
ОБ-4-3. Система имеет математическое ожидание ошиб¬
ки т^=£0 и центрированную составляющую С°, подчинен¬
ную нормальному закону распределения. Критерий зави¬
сит от /п2с и Dv так как
2с ехр {—m2r/DЛ
Р(\Ц<с)-
[1]:
Y 2*	У D(
Приведенный функционал /9 можно представить в виде
29*
/в — бт2,. -f- Dv
451

Учитывая, что [1]:
пг\ =
2 *2^(*+®)—е2
./=о
АП
— £20 XI W* ~Ь 6)»
/=0
(1)
функционал / можно записать в следующем виде:
/« = I
' 2
2/2ш(/ + з)-в2
.А=0
+	^2(/	+	е).
1=0
(2)
Начальные условия, накладываемые на импульсную
характеристику,
2ш(/ + е)-1=0;
/=о
2
^ IW (/-ft)—8=0.
/=0
Определение условного минимума функционала /
можно свести к определению безусловного минимума
функционала
I'q — Iq ~Ь 2^ ТлРл-
к=0
Система относительно w0 имеет вид:
k2oW0(0 + е) +7о = 0;
k20w0(l +е) +70 + 71—© (е + 1) 0/п2х = О;
б'оОАо (2 + е) + 40ш2ос [w0 (0 + е) + Wo (1 + е) +
+ 4w0 (2 + е) ]'—7о + 271—4 e2Qm2x = 0.
Дополнительно можно получить еще два уравнения:
То , е (1 +е) т\в — То — Yi _1
к2 о
*20
(8/Л*Л0 - к2§) То + 2 (2/,2^9 - k2o) Yi + Я i_ 1.
"Т"	£20	(fe2o+	16^9)	—	А’
То
(1 +е) т2х$ — То — Ti
+
к2 о 1	к20	1
(SmVJ _ £20) то + 2 (2/п2х — /г20) Y, + R
к2о (Л21 + 16т2Л0)
е,
452

где
£ = 4s \sk\ + m\6 (1 + s)] m\.
В результате можно определить /г2^ (0) и D^ (0) в функции па¬
раметра 0, представить их в значение критерия и получить значе¬
ние 0 = 0о, соответствующее максимальному значению вероятности
Рмакс по известной методике [п. определив, таким образом, пара¬
метры оптимальной импульсной характеристики.
06-4-4. С учетом ограничения, накладываемого на им¬
пульсную характеристику, исходное интегральное урав¬
нение для дискретной системы запишется в виде
N	г
2	N К у [п — т] — Кну [л] + 2	Y/л'=0, (0<n<N), (1)
где N — время наблюдения входного сигнала; у * — не¬
определенные множители Лагранжа.
Применяя метод неопределенных коэффициентов [1],
искомую оптимальную функцию для данной задачи
можно записать в виде
*>Лп] ==Л()-\- Сх8 [j^] +Z)i6 \ti—Л/].
В результате решения уравнения (1) для случая
г—2, подставляя исходные данные и учитывая началь¬
ные условия, получаем систему линейных алгебраиче¬
ских уравнений для определения параметров оптималь¬
ной импульсной характеристики А0, Аи Clf Dx:
Решив систему (2), найдем искомые параметры им¬
пульсной характеристики
л~ /«гш I о-лг I о\
яЛ0 -(- (&N 1) Л, — а!£), = 0;
аД, — Л, — а 2Cj : 0;
(2)
«W! + 6№* + 12 ’
2 (2«2УУ2 + 9aN + 12)
(3)
1	(а2//2	+	6aN + 12) (aN + 2) ’
2аN (aN + 3)
1 (aiN2 + QaN + 12) (aN + 2) '
)
453

06-4-5. Используя полученные в задаче 6-4-4 значения
коэффициентов оптимальной импульсной характеристики
(3), запишем с помощью г-преобразования выражение
для оптимального алгоритма дискретного фильтра
Отсюда, разделив числитель и знаменатель на г3,
Ф [г] запишем так:
по определению
У [z] (63+b2Z-4- f>iZ-2)=*(z) {а3+а2г~1 +
+ aiz~2+a0z^3).
Окончательно алгоритм оптимального фильтра имеет
У[п]=а3Х[п] +а2Х[п—1] + а,Х[«—2] +
+ аоХ[п—3]—Ь2У[п—1]—b\Y[n—2].
06-5. ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИИ
06-5-1. Вычислим условные плотности вероятности
Р(У|ао) и Р(У|а1) при &=2:
Ф„ [Z] = Д + Ах	+	С,г*	+	Dtz~N	=
аэ.г3 + а2г2 + fliZ + До
Ь323	b^z2,	-|-	b\Z	Ь0	f
al — AQ-\-Cl — 2D,;	6,— 1;
a0 = D,	*V==0.
я3 + CL2Z~1 + a\Z~2 + a0z~3
bz + Ь2г~1 + bxz~2
вид:
454

По формуле Бейеса определим значение апостериор¬
ной вероятности:
Р(п m	яыжгы	-
^	1	г)	—	р	(в1)	р (у I а,)+Я (а„) я (У I Я»)
ехр
Г У\ + У*« 1
1	2°2г	I
I	«*, + Л| , I	(</.—e2.) + (i/2 + a,)21
ехр|	2^|+ехр|	^	/
0,196	0,27.
0,196 + 0,536
Значение апостериорной вероятности
Р(й1| У)=1—Р(а0| Y)=1—0,27=0,73.
06-5-2. По определению
д /ул 7,, (gi)  Я0Р (fli | У)	0,5*0,73	— о 74	1
Л(Г,~ТК)	Р,Р (л„1У)	— 0,5-0,27	1-
Следовательно, наличие сигнала а=а\ более вероят¬
но, чем наличие сигнала а=а0=0.
06-5-3. По формуле для вероятности ложной тревоги
находим [22]:
Ф|	+JS,		а = _|	0Л5	=	о	45
VEt
По таблице Ф-функций (см. приложение 12) нахо¬
дим для Ф=0,45 значение аргумента 1,65, т. е.
1 и I
In h -f- no
0 =1,65 или In h = 1,19.
VE-t.
Искомое значение вероятности ошибки второго рода

Общая безусловная вероятность ошибки Q=poa-f
+Pi (3=0,165.
06-5-4. Искомое значение периода наблюдения т
можно найти, используя формулу для энергии сигна¬
ла Eq. Согласно определению энергия сигнала [22]
г.
Е0 = at1n J sin’ %t dt =
о
To
г С f 1 — cos 2<о0/ \ ,. s 1 T a2xT
=a*,n I g—°-\dt = a\n — T' =
0
Известно, что p=E0/S0) поэтому p=a2\T/2S0. Значе¬
ние же р, кроме того, можно найти, если использовать
формулу для общей безусловной вероятности ошибки
«=4—ф (-£-)•
предварительно представив значение
^=/f=w=1'59Kf-
Поскольку значение Q задано, можно найти, используя
приложение 12, Ур = 7,3. А так как ]/Лр=7,3=1,59]/Т',
то Т = 22 с.
06-5-5. Так как по определению Ур = УТ (см.
решение задачи 6-5-4), то
=	1	мВ.
06-5-6. Из рис. 6-5-6 результирующие сигналы с вы¬
ходов множительных звеньев равны:
Ui=Uo cos сdt=k0X (t) cos (о/;
u'i=u'о sin &t—k0X(/) sin со/.
После прохождения сигналом интегрирующего звена
с постоянной времени интегрирования Тс сигналы опре-
456

деляются как
1 С	1	г
иг = у- \ u1dt = Y~ I К* (0 cosmf dt',
О	о
т	т
и'г — у- J u\dt = у- J k„X (t) sin arf d/.
б	о
Выходные напряжения квадраторов:
«.=м<о,==т5г-
=тг
- т	-1	2
J AT (f) cos erf df I ;
-о	J
И»
Lo
sinurfd^lj
Полагая a=a°i, условие для напряжений можно за¬
писать [22]:
С	I	^	•'с	f	*
~s\ 1Ж и% 4" 5*7 *7*»7 ы * > л*
или
^з [ ^ з ^ ^пор	т'г
7 с
Прежде всего найдем:
/ij/=/i3520=So(ln ро—In с0) =0,6 • 10-3 В2-с2.
Окончательно
hyk\kt 0,6-10-3-0,01 (Ю«)2 R
ипор тгс ~	(0, I)2
06-5-7. Удельная энергия сигнала
т	т
ев = j [/ (<)]2 dt = Г sin* (oj dt — Tj 2.
о	о
Среднеквадратичная погрешность
о* = VSJe. = Y2S.IT = У2 • 0,2/2 = 0,447 мВ.
Так как о*/аСр=0,01, то acp=a*/0,01=45 мВ.
457

Глава севьМа Я
КИБЕРНЕТИЧЕСКИЕ АВТОМАТИЧЕСКИЕ
СИСТЕМЫ УПРАВЛЕНИЯ
07-1. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
07-1-1. Мощность, выделяемая на нагрузке,
иг
«№.+*)• •
(1)
Определим, при каком значении Rs мощность имеет
максимум, для чего возьмем частную производную по
/?н от выражения (1) и приравняем нулю:
ар_ц»(/г-/гн)
dRn (R + Rh)2
это справедливо при R=RH.
(2)
Рис. 07-1-1.
Таким образом, мощность в нагрузке будет макси¬
мальной при равенстве сопротивлений нагрузки и ли¬
нии.
Строим теперь зависимость P=f(RH), сводя расчеты
в табл. 07-1-1.
Таблица 07-1-1
i?H> 0м
2
4
6
8
10
12
14
16
18
20
Р, кВт
2,2
3,26
3,75
3,95
4
3,96
3,89
3,78
3,68
2,0
По данным табл. 07-1-1 строим экстремальную ха¬
рактеристику, представленную на рис. 07-1-1.
458

07-1-2. В качестве аппроксимирующей функции выбе¬
рем интерполяционный многочлен Лагранжа:
ю /ry_f (х \ (*-*0 (*-*») ... (X — хя)—I
<р (X)—t[X0) (Хо_Х1)(х0 —Х2) ... (Хо —ХЛ)“
[ г у \ (X —• Х0) (X Х2) (х Хл) I
~~(Xj — Х0) (Xi — ^2) • • • i%i' ЭС/г)
I f /.- \	—	*о) (* — х') •" Xn-i)	/П
^	(Хп	— ^о) (Я — ^1) • • • (Хп ~~’ %п -1) *
Для указанных в табл. 7-1-1 значений имеем:
. ч	, (х —3) (х —5) (х— 7) (х — 9)	,
<fW	(1 —	3) (1 — 5) (1—7) (1—9)	~
I о	(х—1)	(х —5)	(х —7)	(х —9)	■
"Г°	(3—1)	(3 — 5)	(3—7)	(3 — 9)	~
. _	(х—1)	(х —3)	(х —7)	(х —9)	|
-1-°	(5-1)	(5-3)	(5-7)	(5-9)	"Г"
I А (X— 1)	(х— 3) (х —5) (х —9) _|_
'	(7—1)	(7 — 3) (7 —5) (7 —9)	'
+ 3
(х— 1) (х —3) (х —5) (х —7)
(9-1) (9-3) (9-5) (9-7)
_ х4 — 24х3 + 206xs — 744х + 945 ,
—	384	"Г
, х4 — 22х3 + 164хг — 459х + 35 ,
'	(— 32)
, с х4 — 20х3 + 130х2 — ЗООх + 189 ,
+ 5	64	+
, х4— 18х3 + 104хг — 222х + 135 .
'	(— 96)	'
■ х4 — 16х3 + 86хг — 176х — 105
'	128
Поскольку в условии задана аппроксимирующая
функция второго порядка, то, отбрасывая члены, содер*
жащие х4 и х3, получаем:
...	5 ,	109	. 185.
?(■*)	12 х	48 Х~^~ 96 *
459

07-1-3. Так как управляющее воздействие изменяется
с постоянной скоростью, то
У=—k (vt)2.	(1)
Находим v, используя заданный период автоколеба¬
ний и зону поиска на выходе, учитывая при этом движе¬
ние только до момента переключения:
-Д(/ = ^Ьг(4г)г.	(2)
откуда
— tV'?-	<3>
Подставляя численные значения, получаем:
0=1 ■ |/^=0,2 1/с.
Время выхода в экстремальную область определяет¬
ся согласно [И]:
, = 4 0-1^).	(4)
ИЛИ
х=_±(1_ ^0^8)= 14,4 с.
Потери на поиск
Р=Ау/3;	(5)
или
Р=0,08/3=0,0266.
Таблица 07-1-2
±Х
0
0,2
0,4
0,6
0,8
1
1,2
1,4
0
0,08
0,32
0,72
1,28
2
2,88
3,92
±*
1,6
1,8
2
2,2
2,4
2,6
2,8
3
5,12
6,48
8
9,68
11,52
13,52
15,68
18
460

07-1-4. Используя уравне¬
ние первого звена, построим
экстремальную характеристи¬
ку, сведя расчеты в табл.
07-1-2. Экстремальная зависи¬
мость x\—f(x) показана на
рис. 07-1-2.
Далее необходимо полу¬
чить уравнение фазовой траек¬
тории, характеризующей в каж¬
дый момент состояние объекта.
Для этого запишем дифферен¬
циальное уравнение связи
объекта, подставив значение
Х\ из уравнения первого звена
во второе:
ТЖ + У = ~Кхг-	0)
-0,8 -Д4
0 0,t+ 0,8
1 1 •1 ' 1 V*
2
1 1 l 1
** / °)6/
/ /°’а
\
/ /1l°
\
/ / 1'2
\
/ / 1)£f
\
j / U 6
У
1 / ^ 1,8
JJCf=f(x) \
l/y=F(z) 1
YL
?
i:
I
II
Х!’У \
Рис. 07-1-2.
Решим
dy/dt:
это уравнение относительно производной
dy 	(
dt
Кх2-у)
(2)
Однако для решения уравнения (1) необходимо знать
производную dyldx. Для этого разделим числитель и
знаменатель на dt. Используя выражение (2) и уравне¬
ние исполнительного механизма, можно записать:
ЁН— dyjdt_ 1  .  „ 2	 /оч
dx dx/dt —±vT I Ax	У>-	W
Проведя некоторые преобразования, получим:
W±W»=:±W-J?-	(4)
Для удобства решения введем следующие обозна¬
чения:
1/vT—b, KlvT—bi.	(5)
С учетом (5) выражение (2) имеет вид:
Ш±ЬУ^±ЬХ-
Знак перед коэффициентами b и Ь\ определяется на¬
чальными условиями.
461

Если изображающая точка находится слева от
экстремума и движется в положительном направлении,
то значение скорости при этом положительное и знак
перед коэффициентами b « + », а перед Ъ\ «—».
Если изображающая точка находится справа от
экстремума и движется в отрицательном направлении,
то значение скорости отрицательное и знаки коэффи¬
циентов меняются на противоположные.
В нашем случае начальная точка находится слева от
экстремума, поэтому уравнение для первого интервала
запишется так:
*kr + by = -bix\	(6)
Решение этого уравнения имеет вид [11]:
У =	bdx [ j - Ьгх'<? ш dx + с] =
= е-ь* |_ ьх Jx*ebxdx + с] .	(7)
Стоящий в скобках интеграл табличный, поэтому-
можно записать [11]:
у = ~ Ц-S	(Ьх- 1) + Се-Ь*.	(8)
После замены коэффициентов b и Ь\ параметрами
системы получаем следующее решение:
у = —К (х —vTf — Kv*T -f Ce~x/vT.	(9)
Постоянную интегрирования определяем из началь¬
ных условий при Х—Хо и у=Уо-
Подстановка начальных условий в уравнение (9)
дает:
г/о = — К (х„ - vT)* - Kv'T* + Ce~x°/vT,
п у0 + К (х0 — vT)2 + Kv2T2	. , m
откуда	С = -^2_Г—- ^ x0/vT 	•	0°)
Подставляя значение С в выражение (9), получаем:
у = - К (х - у7У - Kv'T* + [г/, + К (*. - vT)' +
+ Kv'T*] e-{x-x°),vT.	(11)
462

После подстановки начальных условий и численных
значений параметров получим:
1/ = — 2 (jc — 0,5)2 — 0,5-4-3^-2	(12)
Построим отрезок фазовой траектории на первом ин¬
тервале, меняя х в уравнении (12) от значения х=—1
до того значения, при котором функция у будет отли¬
чаться от достигнутого максимального значения в мень¬
шую сторону на значение зоны нечувствительности, т. е.
У=Умамс—Л#н- Расчеты сводим в табл. 07-1-3. По дан¬
ным таблицы строим фазовую траекторию на первом
участке (см. рис. 07-1-2).
Определим момент переключения. Из таблицы вид¬
но, что максимальное значение умакс=—0,35. Переклю¬
чение произойдет в тот момент, когда у уменьшится на
значение зоны нечувствительности, т. е. станет равным
У=Ум&кс—Аун=—0,44. Этому значению соответствует
*=0,65. В результате вычислений получили точку 1
с координатами х10=0,65, у\о=—0,44.
В этой точке произойдет переключение сигнала
управления с +и на —v, и координата х начнет теперь
уменьшаться с постоянной скоростью. При этом знаки
перед коэффициентами b и Ь\ в уравнении (5) поменя¬
ются на противоположные и дифференциальное урав¬
нение, описывающее движение на втором участке, при¬
мет вид:
или
dy
dx
— Ьу — Ьххг.	(14)
Решение уравнения (14) будет следующим [11]:
у = — К(х-{- vT)s — Kv2r + [</„ + К (х„ + vT)* +
+ К^Тг\ е {х~х'о) /оТ.	(15)
После подстановки численных значений параметров
и начальных условий г/ю=—0,44 и Хю=0,65 получим:
у=—2 (х+0,5)2—0,5 + 2,69е2х~1’3.	(16)
Меняя х в уравнении (16) от значения 0,65 до значе¬
ния, при котором вновь достигнутый максимум умень-
463

Таблица 07-1-3
сч
со
ю
(О
о
о
CN
ю
СП
о
"
о
о
о
о
1
7
о
1
со
о
СП
00
со
оо
о
о
о
СО
СО
еГ
о
о
о
о
1
о
1
о
1
ю
1-
т
СЧ
ю
ю
ю
со
о
сч
ГГ
"Л4
Л’
СО
о
о
о
LO
'Л4
о*
+
о
о
о
о
1
о
1
о
1
л
01
сч
сч
се
о
1—1
о
о
Ю
"Л1
о
+
о
о
о
о
1
о
1
о
1
со
ь-
сч
сч
ю
о
о
о
Ю
со
+
о
о
о
о
1
о
I
о
1
л
сч
ю
00
--4
л
сч
LO
ю
О
о
о
о
о
1
1
о
1
сч
сч
сч
Ч*1
со
СП
оо
со
сч
о
1
о
о
о
7
сч
1
7
ю
ю
сч
сч
1Л
сс
л
со
сч
л
СП
ю
о
1
о
сч
1
сч~
1
7
|>-
СП
00
00
с-
00
со
о
со
со
00
оо
?
о
СО
со
1
со
1
7
LO
см
ю
1
со
ю
сч
сч
л
1
1
1
ю
см
о
1
V
ю
J.
-
Ю4
о
1
см
X—ч
т
+
ю
о
1
о
СЧ
1
CN
1
н.
1
1
1
Си
£
сч
со
1
сч
1
h-
о
л
Ef
К
ч
VO
оо
о
об ць
со Л
о о
I I
со
ю
С-1
ю
сч
о
1
. о
о
1
о
1
00
00
со
■л
ю
о
1
о
о
1
о
1
ю
00
сч
сч
о
1
1
о
о
1
LO
оо
со
со
СО
л
о
7
о
1
СП
ю
СП
ю
LO
о
сч
1
о
1
LO
СП
л
ю
со
со
1—1
л
о
сч
со
1
о
1
CU
О)
СО
ю
о
I
см
Ю4
o'
+
н
464

шится на значение зоны нечувствительности Аг/н=0,1,
получим второй участок фазовой траектории. Расчеты
сводим в табл. 07-1-4.
На рис. 07-1-2 показан второй участок фазовой траек¬
тории. Учитывая зону нечувствительности Аун, получа¬
ем точку 2 с координатами у2о=—0,3 и х2о=—0,6. В этой
точке происходит смена знака управления с —v на +v.
Следующий участок фазовой траектории описывается
таким же уравнением, как и первый, но с другими зна¬
чениями координат уо и xq.
После подстановки значений параметров и начальных
условий получаем выражение для фазовой траектории
на третьем участке
у=—2 (*—0,5)2—0,5 + 2fi2er<**u Я.	(17)
Результаты расчетов сводим в табл. 07-1-5.
Таблица 07-1-5
X
—0,6
—0,4
—0,2
0
+ 0,2
+ 0,4
+ 0,6
2,62е (2*+1 »2)
2,62
1,75
1,17
0,746
0,524
0,354
0,236
—2 (*—0,5)1 — О.П
—2,02
-2,12
— 1,48
—1
—0,68
—0,52
—0,52
У
—0,3
—0,37
—0,31
—0,25
—0,16
—0,17
—0,28
На рис. 07-1-2 показан третий участок фазовой траек¬
тории. В конце движения получим точку 3 с координата¬
ми узо——0,23 и Хзо=0,5.
Уравнение, описывающее фазовую траекторию на
участке 4, имеет вид:
у=—2 (* + 0,5) 2—0,5 + 0,276s*-1.	(18)
Дальнейшее построение фазовой траектории приво¬
дит к предельному циклу. Значение * будет изменяться
в пределах ±0,5, а уравнение, описывающее фазовую
траекторию, при положительном v будет иметь вид:
у=—2 (*—0,5) 2—0,5 + 2,25в-(2*+о,	(19)
а при отрицательном v
у=—2 (*+0,5)2—0.5 + 2,256s*-1.	(20)
По предельному циклу можно определить показате¬
ли качества экстремальной системы. Зона поиска на вхо¬
де будет определяться значениями * в крайних точках,
т. е. *=±0,5.
30—903
465

Зона поиска на выходе определяется разностью Ау=^
==^/макс	15.
Потери на поиск определяются как разность
Умакс—у ср. а г/ср является горизонтальной осью симме¬
трии предельного цикла. В нашем случае Р—Ум&кс—
—Уср—0,08.
Период автоколебаний определяется по формуле
7=2Хмакс I и,	(21)
Т'е’	7=2 -0,5/1=1 с.
07-1-5. Условие существования автоколебаний
в замкнутой экстремальной системе:
Г,(/»/2)Г(Л)Г1(У»)Г(^=
=R, (./2) R(A) R, HR (A.) e1 «*■«•<,+••+«.’ =,,
где
(yco 12) =№0 (/со /2) U7'i (/© /2).
Чтобы использовать условие существования автоко¬
лебаний, необходимо провести гармоническую линеари¬
зацию нелинейных звеньев.
В экстремальной системе частота колебаний на вы¬
ходе объекта в 2 раза больше частоты на входе. Поэто¬
му можно применить метод гармонического баланса
в общем виде, т. е. производить гармоническую линеари¬
зацию нелинейных элементов не по основной гармонике
входного сигнала, а по кратным гармоникам,^ содержа¬
щимся в выходном сигнале каждого нелинейного эле¬
мента.
Для звена W(A{) найдем коэффициент гармониче¬
ской линеаризации при (о=2соь где coi — частота вход¬
ного сигнала.
Для звена W(A2) найдем коэффициенты гармониче¬
ской линеаризации при (di=cd/2. За основную частоту
примем частоту на выходе объекта, т. е. со и все фазо¬
вые соотношения нужно учитывать в масштабе ча¬
стоты (О.
Определим выражение для эквивалентного комплекс¬
ного коэффициента передачи нелинейно! о элемеьпа
W (ЛЛ!
Ф=(о*/2,
466

где
0F(Atsin?) sin2<fdf
0
— коэффициент гармонической линеаризации, характе¬
ризующий отношение амплитуды синфазной составляю¬
щей второй гармоники на выходе звена W(А\) к ампли¬
туде синусоидальных колебаний на входе звена W(Ai):
— коэффициент гармонической линеаризации, характе¬
ризующий отношение амплитуды квадратурной состав¬
ляющей второй гармоники на выходе звена W'(A\)
к амплитуде синусоидальных колебаний на входе.
За начало отсчета фаз принят момент перехода вход¬
ного сигнала через нуль в сторону возрастающих зна¬
чений. Определим выходную величину первого нели¬
нейного звена.
F(x)=—Kx2-.=—x\
где x=i4isin(p, /С=1.
Следовательно,
F (Ai sincp) =—А21 sin2 (p.
Подставляя F(Aisincp) в выражение для G(A\) и
В(А\), а затем интегрируя, получаем:
3 №f F(A'sin ^ cos 2(pd?
0
0
j" sin3 cp cos <f> df = 0;
j" sin3 cp cos <p df = 0;
о
ТЕ
В (Л,) = -т- Д ^ sin2 <p cos 2<p dtp —	;
0
R (A) = V[Q (Д)]2 + [В (Л,)]2'=
467

тогда
W(A,) = dl.eln/2.
Определим коэффициенты гармонической линеариза¬
ции для звена W(A2) (см. рис. 7-1-4,б). Нелинейный
элемент представляет собой последовательное соедине¬
ние релейного элемента с зоной нечувствительности и
специального нелинейного элемента (шаговый искатель,
триггер со счетным входом). Сигнал на выходе звена
W(A2) появляется каждый раз, когда входной сигнал
изменится в сторону уменьшения от максимального свое¬
го значения на значение Л- Поэтому частота выходного
сигнала в 2 раза меньше входного, это необходимо
учесть при определении коэффициентов гармонической
линеаризации.
Запишем комплексный коэффициент передачи для
второго нелинейного элемента
W(A2)=G(A2)+jB(A2).
Для определения G(A2) и В(А2) обратимся
к рис. 7-1-4,б, в. Входные колебания имеют частоту о>
и амплитуду А2. Выходные колебания прямоугольной
формы имеют амплитуду U—Kn, частоту *о/2 и сдвиг
фазы а. Поэтому выражения для G(A2) и В{А2) будут
иметь следующий вид (см. рис. 7-1-4,в):
n-f-a
1 С „	. <р ,	4 Кп • a
sir J KaSm~Tdc?==^ATsmT;
 ТС —|— ОС
it-f-a
^	l	ТУ'	V	J	®
J *«C0SiH?=;^rC0STr-
—тс-{-a
За начало отсчета примем момент перехода входного
сигнала через нуль в сторону возрастающих значений.
Тогда имеем:
где отсчет фазовых углов ведется в масштабе частоты
со/2. В масштабе частоты со получим:
G (Л)
В (А)
468

так как
—	a	—arcsin
(о .	.	А	—	Л2
Запишем выражение для частотных характеристик
линейных звеньев в комплексной форме:
Г,
■о*)-
-2/(f+-rctgfT.)
4К
ш Ут^сй2 + 4
,V7 /, \	—/ arctg шГ,
И/ о (/со) =	-	-----	£
2 VJ '	Vt\<&	+	1
Частотные характеристики звеньев, включенных до
звена W(A\), рассматриваются при частоте со/2, фазо¬
вые углы этих звеньев удваиваются, так как за основную
частоту принята частота на выходе звена W(Ai), т. е. (о.
Частотные характеристики звеньев, включенных пос¬
ле звена W(A2), рассматриваются при частоте со.
Условие, при котором в релейной экспериментальной
системе существуют автоколебания:
W(A{) W\ (/о/2) W(A2) Г2(/ю)=1.	(1)
Рассмотрим аналитический способ определения ча¬
стоты и амплитуды автоколебаний. Подставив в уравне¬
ние (1) выражения для сомножителей, получим:
SKzKnK,K2	v
V<*2T*X + 4 V<*2T\ + 1 A
—f(—^-4-a-f 2 arctg Тг + arctg шгЛ
Хаг»	'•	(2)
Определим по рис. 7-1-4,5 значение
ЖгКиК,
At = A2\W(As)\\w(i^-
и подставим в уравнение (2):
128	ifo	.
С	1,
(<о2Гэ, + 4) Уы2Т22 +
где
% = -s- — а — 2 arctg 4- Т — arctg «Т,.
469

Запишем баланс амплитуд
тк\к\к\кг
vljitW (ш27’21 + 4) Уч?Тгг + 1
и баланс фаз
= 1	(3)
Д — а2
То — 0.	(4)
Определим А2 из условия баланса фаз:
 а — arctg Т, — arctg wTt = 0;
 arcsin —j-2— 2 arctg Г, — arctg	- 0;
: cos Г 2 arctg Tj -|- arctg a>T2 j = cos (2(3 -)- y) =
__	1 — tg 2P tg Y -	4	—	vPT*!	—	4a>2TtT2
Kl + tg2 2(i К1 -f tg2 y (4 + сo2T\) V1 + &T\ ’
где
(3 = arctgу = arctg <оТг.
В результате имеем:
А —	^
2	1	+	cos (2р + Y)
= Л	{A	+	tfT\)V\	+	tfT\	 „
(4 + <о2Г2,) V1 + и*Т*г + 4 —<ъ\Т\ — 4«>27’17’2 *	'	'
Подставив значение Л2 в уравнение (3), после пре¬
образований получим:
128№Щ^_
я2Д
_	to2?2,	(<о2Г2,	+ 4)2	1)	(6)
(4 + и2?2,) V1 + <о2Г22 + 4 — ш27'21 — 4со27'17’2 '	1
Обозначим левую часть уравнения (6) через С/Д,
где С — параметр предельного цикла.
Решаем уравнение (6) графически (рис. 07-1-3):
С __	<о27’21	((оаГ21	+ 4)2 (ш2Г22 + 1)
Д _ (4 + ш2?2,) V1 + <о2Г22 + 4 — ю2Р, — 4ш27’1Г2 ’
С 12SK\K\K\KJ\ _ 128-10-М04-4.Ы0* __ 0
Д—	Я2Д	3,142 - 0,5	—	AD-1U.
470

Следовательнб, значение cofi=3,5, Частота автоколеба-
ний
<о=3,5 / 7"1=3,5 /100=0,035 1/с.
Амплитуда автоколебаний
А	(4+12,2)^1+0,12	_ .
2	’	16,21^	1,12	+	4	—	12,2	—	0,49
Рис. 07-1-3.
Потери на поиск
р=А | г (А) 11 Г, (/со/2) 11 wm I =	.
Учитывая соотношение (6) и значение параметра С
(рис. 07-1-3), получим:
С	_ 1,3.103
соТ\ (со27'21 + 4)	12,2-16,2
07-1-6. Как известно, по методу Гольдфарба строится комплекс¬
ная ЧХ линейной части системы W\ (j&/2) W2 (/со) и обратная харак¬
теристика нелинейных звеньев \/W(Ai)W(A2) . Точка пересечения
двух годографов определяет наличие автоколебаний и их параметры.
Наличие двух нелинейных элементов усложняет решение. Пре¬
образуем выражение для условия существования автоколебаний
W(Ai)Wi (/со/2) W2 (jv/W (А 2) = 1,
где (см. рис. 7-1-4,6, в и решение задачи 7-1-5)
А _/тс/2   K3A2W (Л2) I / со

Но
2 к,кн
= U7,
От
-Н*)1
Найдем произведение модуля Wi(j®/2) на саму передаточную
функцию:
К'тЭК/т)-
-|'-0T)lh-0T)|^(f*",,fr,L
-['■0-г)Г-
Таким образом, подставляя в условие существование авто¬
колебаний выражение для W(Ai) и заменяя произведение
| Wi(j<ti/2) | Wi(jto/2), получаем уравнение для определения автоко¬
лебаний:
Обозначим левую часть уравнения через	тогда
w» (/“)
472

На рис. 07-1-4 построены комплексная ЧХ
V» (/«)	(/'	Т-)]2^	(/«)еН2
и обратная характеристика нелинейного элемента 1/И7(Лг):
4Кн I (78-”а)
1
пАо —/ I75-*)
^(Л)	4*н
где
а = arcsin ■
Д — А
Следовательно,
г (Л)=4/^7	^г2	~ ~ •А«)*—пд—л,)] •
Из полученного уравнения определяются значения мнимой и
действительной частей характеристики 1 /W(A2). Точка пересечения
ИМ/со) и 1/№(Л2) определяет со = 0,035 1/с и Л2=1,0, что совпа¬
дает с результатами, полученными аналитическим способом.
Данные по расчету W9(ia) сведены в табл. 07-1-6.
Таблица 07-1-6
СО
0
0,01
0,015
0,02
0,025
0,03
0,035
0,04
R
аз
2
0,7
0,3
0,15
0,075
0,045
0,02'
у, град
90
— 162
—180
—203
—225
—240
—245
—26(
Построение 1/№(Л2) произведено согласно табл. 07-1-7.
Таблица 07-1-7
Л
0,25
0,5
1,0
2,0
4,0
6,0
8,0
Jm
—0,002
0
0,004
0,012
0,028
0,043
0,059
Re
0
—0,004
—0,007
—0,011
—0,0154
—0,0194
—0,022
07-1-7. С учетом того, что координата х изменяется с постоянной
скоростью (x = vt), также с учетом координаты в начальный момент
движения, дифференциальное уравнение связи объекта запишется
следующим образом:
Т ~сЦ + у ~ ~~ К + vt)*’
(1)
473

Преобразуем это уравнение к виду, удобному для интегриро¬
вания:
dy , 1	К
dt~^~T У —— Т (х°	VT)2'
Введем обозначения
1 /Г = 6; KIT = bi.
Уравнение (2) с учетом (3) примет вид:
■^Г + by = —b1(x,o + vT)*i
(2)
(3)
(4)
Применяя метод решения дифференциального уравнения с по*
f bdt
мощью интегрирующего множителя tx=eJ , получаем:
у = е~^ш [- b, j (х„ + vty e^dt + с] = —-
2x0vbx	biV2	in	,	2&!
b2
(5)
Для упрощения дальнейших преобразований подставим в урав¬
нение (5) взятые из решения задачи 7-1-5 численные значения
параметров:
у=— 2t2+6t—5 + Ce~2t.	(6)
Определим С, исходя из начальных условий. При /=0, у(0) =
= у0 = —2, следовательно, —2=»—5+С, откуда С=3.
Таким образом, на первом участке движение описывается
уравнением
у=— 2t* + 6t—5 + 3<?-2*.	(7)
Значение t в момент переключения определяется, как и в пре¬
дыдущей задаче, по значению уы&кс—Ауш. Момент, когда у умень¬
шится на Л*/н = 0,1, соответствует моменту переключения. Меняя t
от нуля до значения, соответствующего точке переключения, полу¬
чаем изменение у во времени на первом участке. Расчету сводим
в табл. 07-1-8,
474

Таблица Q7-1-&
о
(N
ю
ю
^1,
со
о
05
Ь-
7
см"
о
1
о
00
00
ф
00
со
00
о
оо
00
*
»—1
о
г-н
о
о
т—1
о
1
1
1
см
см
ф
СО
см
СО
о
о
05
05
1
о
7
1
00
см
00
Ф
ф
ф
ю
со
о
00
00
1
00
о
1
t"-
00
СМ
см
см
со
ф
ф
о
t"-
1
ь-
о
1
о
ф
г-
ф
СО
со
1
о
1
со
о
1
00
00
00
со
оо
см
ф
00
о
о
ф
со
1
ю
о
1
см '
см
со
05
со
ю
со
о"
о
со
ю
1
ф
7
ю
см
ю
ф
СО
ф
СО
Ю
о
_1
см
ю
со
см
1
1
1
00
t'-
см
о
см
о
см
00
о
см
ю
1
со
7
ю
см
о
со
о
1
со
1
«*«» I
СО
СО ^
см
!=Г
S
ч
\о
I
со
со
+
со
ф	*—«
-Г о
I
см см
,-Г о
см
ю
со
I
О со
~ o'
00
со
оо
см
СО
о
со
00
со
ю
ф см
о —Г
5р
со
см
о
см
о
см
см
О со
1>
см
о	Ф
СО	—•
о - о
см	со
О)
СО
см
1
ф
05
со
ф
см
со
см
о
о
I
СО	Ф	СМ
СО	Ф	ф	о
I	I
о
со
о
о
LO
со
Ф~
+
о
со
475

Процесс на первом участке показан на рис. 07-1-5. В то? мо¬
мент, когда у станет ^равным г/макс—Аув, произойдет переключение
управляющего воздействия. Уравнение, описывающее дальнейшее
движение, будет иметь вид:
dy
-Ш-+Ьу=—Ь1 (х„ — vt)*=— 6, (х\-2x0vt + v4*).	(8)
Решая уравнение (8) с помощью интегрирующего множителя,
имеем:
- Ь.а
у = е	•]
j (х\ - 2x0vt,+ v*n J ш + С] = - ■+
2x0vb1	v2bt	2 х)2Ьл
+—— (М-1)- — t2+-^r- (bt-l)+Ce~bi. (9)
После подстановки численных значений коэффициентов и зна¬
чения хо = 0,65 (см. решение задачи 7-1-5) в момент переключения
имеем:
у = —2/2 + 4,6/—3,14+Се~*К	(10)
Определим С из условия, что при /=0, уо =—0,45. Тогда
—0,45 = — 3,14 + С, откуда С = 2,69. Окончательно имеем:
у = —2/2 + 4,6/—3,14+2,69е-2<.	(11)
Так же как и на первом участке, меняя / от нуля до значения,
соответствующего точке переключения, получим изменение у во
времени на втором участке. Расчеты сводим в табл. 07-1-9.
Продолжая указанные решения до тех пор, пока коэффициенты
решения дифференциального уравнения не будут одинаковыми, по¬
лучаем предельный цикл. Переходный процесс выхода на экстремум
и автоколебания показаны на рис. 07-1-5.
По переходному процессу можно определить время выхода на
предельный цикл. В нашем случае оно составляет 3,1 с.
07-2. СИСТЕМЫ, НАСТРАИВАЮЩИЕСЯ НА ЭТАЛОН
07-2-1. Закон изменения | должен обеспечить умень¬
шение х, если х>0 и, наоборот, увеличение х, если х<
<0. Значение х выразим через коэффициенты Т и на¬
чальную скорость изменения выходной величины. Для
этого напишем выражения для выходной величины у
при у(0)=0] у(0)=Уо [1]:
Т У0	(	£ Л t
у ^	ехр	V	sin~	У1 — **• (О
На протяжении первого периода нет корректирующе¬
го сигнала, т. е. х=0. Через период Т этот сигнал будет
выработан, и его можно определить по формуле [1]
476

После каждого периода значение сигнала определя¬
ется по этой же формуле, но скорость у0 следует брать
равной скорости изменения выходной величины в начале
каждого периода. Из выражения (2) видно, что чем
больше амплитуда колебаний, тем больше значение
сигнала ус.
Так как исполнительное устройство является инте¬
грирующим звеном, то коэффициент £ будет определять¬
ся по формуле [1]:
где £0— начальное значение коэффициента затухания;
ti — конец i-ro периода колебаний системы; уц — сигнал
к в i-м периоде колебаний; t—t\ изменяется от 0 при t=
=ti до ti+1—ti при t—ti+u ti+1—ti — период колебаний
системы при текущем значении коэффициента затухания
£ (так как £^0, то tw—ti^T).
Вычислительное устройство показателя качества
должно включать выпрямители и устройства, запоми¬
нающие амплитуду. Кроме того, должно быть коммути¬
рующее устройство, позволяющее сохранять в течение
периода значения Ai и Л2 (и их разность) и сбрасывать
значения А\ и А2 прежнего периода.
07-2-2. Обозначим изменения ПФ вследствие измене¬
ния внешних условий следующим образом:
=т Wlt (Р) wtt (р) + W20 (р) AWt (ft) + W„ (р) ДWt (/>) +
п
ф(р)=ф0(р) + ДФ(р);
\Vl(p)=Wl0(p)+AWl(p)-,
^2 (Р) —1^20 (р) “Ь Д (р) •
(1)
(2)
(3)
Из формулы
(4)
следует
(5)
Фо (р) + Аф (Р)
[W„ (р) + д г, (р)]	(р)\	=
1— Фо (р) — ДФ (/')
+ ДГ, (р) Д1Г/2 (Р).
(6)
477

Так как приращения ДФ(р) имеют малые значения,
можно записать:
Фо (р) + Аф (р)	ф„ (р)	.	Аф	(р)	_
1-фв-Дф(/>)	1—Фо(р) [1 — Фо(р)]2
- wu (Р) Г20 (р) + iF20 (р) ДГ, (р) + 1Г10 (р) AW, (р).	(7)
Учитывая, что
■ -few =W-‘<P>W»№-
можно записать:
И -У(W ^ {р) АГ* {р)+Wu{р) AW?2 {р)• (8)
Задача сводится к установлению такой связи между
AW\(p) и ДФ(р), которая обеспечила бы достаточную
малость отклонений ДФ(р) при имеющихся оклонениях
AW2(p), а также могла бы быть практически реализо¬
вана.
Наиболее простой реализацией является пропорцио¬
нальная зависимость между приращением ПФ AW\{p) и
изменением ПФ замкнутой системы.
Пусть
№ЛР)=-Т^т^т.	<9>
где £=const.
Тогда, подставляя выражение (9) в (8), получаем:
(р) =' **,. (Р) Wl;	—А^ & -
1 — Фо (р) “Ь [ 1 — Фо (Р)]“
_	(Р)	[1-Ф.	(р)1	ди72	(10)
kWto (Р) + 1_ф0 (р)
Если коэффициент k достаточно велик, то изменения
ДФ(р) ПФ замкнутой системы, вызванные изменением
AW2(p), малы.
Изменение ПФ корректирующего устройства Дй^р)
эквивалентно введению дополнительного сигнала
Z = AWt (р) (Хвх - *вых) = k	(Хвх	-	Хвык),	(11)
478

приложенного к выходу корректирующего устройства
W\о {р) (рис. 07-2-2,а). Так как ■Хвых=:::Ф(р)^вх> то
A ТР. (Р) (*вх - *вых) - -	[^вх	- Ф (Р) ^вх] =
= - МФ (р) Хвх = — k [Ф (р) - Ф0 (/?)] *вх =
= -к[Хаьл-Ф(р)Х„Ь.	(12)
Таким образом, изменение
"М/>) = -т=|^Д®И
эквивалентно введению на выходе корректирующего
устройства с неизменны¬
ми параметрами допол¬
нительного	сигнала
&[^вых Фо(р)^вх]* ЭТОТ
сигнал может быть легко
сформирован посредством
дополнительных связей в
системе и использования
эталонной ПФ Фо(р) (рис.
07-2-2,6). Проверим, обе¬
спечивает ли рассмо¬
тренная схема определен¬
ную стабильность переда¬
точных свойств, несмотря
на изменение ПФ объекта.
Свертывая схему,	Рис.	07-2-2.
представленную на рис.
07-2-2,6, можно найти, что ПФ замкнутой системы с ука¬
занными дополнительными связями имеет вид:
ф/лЧ_ УюУ, + ЦР,Фо
1 + W10W2 + kW2 •
Wjr
vi-г
^ вы X
ir
а)
Если значение k достаточно велико (но устойчивость
замкнутой системы обеспечивается), то Ф(р)^Фо(р).
07-2-3. Преобразуем структурную схему, представлен¬
ную на рис. 7-2-3, к виду, удобному для свертывания
(рис. 07-2-3).
479

Преобразуем вначале согласно-параллельные звенья.
Передаточная функция звеньев будет иметь вид:
Мз I ki
ТфР+ 1 TlP+ 1 —
 ^ф^з	(Т’зР ~f" 1) + ^1 (Тф/7 +1)	..
(7ф/>+1) {ТгР+ 1)	( }
Свернем	часть	схемы с обратными связями, после
чего ПФ этой части примет вид:
117 (п\ —	*2	(ТгР	+	1)	__	/о\
р(Тгр+	о	(7>+ 1) +fe2fe3 (rlP+ i):+k2k,	■	W
Рис. 07-2-3.
Тогда ПФ системы
Ф (/?) =
(ТфД + 1) +	(т, д + 1)
“ (^’+0[д(Л/'+1)(7>+1)+*зМТ1/>+1)+/гЛ] • ''
Подставляя значения коэффициентов и постоянных
времени, получаем:
Ф(р)-	2,5^	+	401
* \У>— 0,000025/>4 + 0,00575/>3 + 0,255/>2 + 23,1/7 + 402 •
Это выражение можно упростить, если учесть, что /г3
много больше других членов. В результате имеем:
т. е.
Ф № ^ 0,05/? + 1 •
4?0

07-2-4. Для решения этого примера применим метод
корневого годографа. Построим корневой годограф, ко¬
торый является геометрическим местом полюсов ПФ си¬
стемы при изменении коэффициента kx (рис. 07-2-4);
Рау Рв, Рс — полюсы ПФ системы.
Из рисунка видно, что реакция системы определяется
главным образом полюсами исполнительного элемента.
Отределим разрядность
счетчика для подсчета
числа переходов. Соглас¬
но условию собственная
частота должна быть не¬
изменной, известно также
оптимальное значение ко¬
эффициента демпфирова¬
ния £опТ- Найдем при этом
требуемую частоту, кото¬
рая определяется как мо¬
дуль вектора корневого
годографа, проведенного
в точку оптимального ре¬
шения, а демпфирова¬
ние — как косинус угла
этого вектора с отрица¬
тельной вещественной по¬
луосью. Радиусом, рав¬
ным 1/Гопт, проводим дугу до точки касания с корневым
годографом. Этим определим диапазон изменения kx=
=8,95-^-17,05 и £с=0,22^-0,557.
Так как между количеством перемен знаков ср пере¬
ходной характеристики системы и коэффициентом демп¬
фирования имеется обратно пропорциональная связь
[4]
Ф=а Цсу	0)
после подстановки в выражение (1) находим иско¬
мый диапазон изменения Ф, т. е. ф0пт=^/£онт- Так как
согласно условию ф0пт=3; |Опт=0,35, то а=1,05. Тогда
согласно (1)
ф1=1,05/0,557=1,8^2; ф2=1,05/0,22=4,5-^5.
Таким образом, для подсчета числа переходов доста¬
точно иметь трехразрядный двоичный счетчик. Переда-
Рис. 07-2-4.
31—903
481

точная функция разомкнутой системы
tw / ч _ k*kA + Т*Р) О + Т*Р) О + 7»
(р)	dadbdc	•	W
Согласно условиям построения годографа значение
ПФ в точке Pi годографа
ш v К ABC	/оч
w (р) DEFGHI’	^
где K=kJzA\ А, й, С — длины векторов, проведенных
в точку Pi; D, £, Р, G, Я, / — длины векторов, прове¬
денных из полюсов в эту же точку.
Учитывая масштаб построения, находим, что Р\—
=Р2—48, после чего подсчитываем числитель ПФ (2)
(1 + 0,033-48) (1+ 0,045-48) (1+0,2-48) =86,6
и знаменатель
DA(р) =7,41; DB (Я =22,76; Dc (Я =2,386.
Подставляя численные значения длин векторов в вы¬
ражение (2), определяем:
, _	86,6	27.96-20.62.36*53 _ .	lf)4
1	7,41.22,76-2,386	40-40.46
Аналогично для второй точки (P2=Pi по условию
построения)
и	86,6	4Ы08.28-70.39-57_ о .о im
7,41-22,76-2,386	52.50*47	—	0,4Z1U.
Так как &А=2-103 и kx=kjkA, то £*i=8,95; kx2=
= 17,05.
07-2-5. По данной структурной схеме определим ча¬
стотные логарифмические характеристики	системы.
Отношение передаточной функции ошибки к входному
сигналу
Тг

Так как по условию Y(p)=r[p, то окончательно
Имеем:
(2)
где
Р/ , N (\+TtP)
с(Р>-~Т+1Щтр+т*р* •
АТ гТ' ■ Р 1 э/ г'
М = Ж; * = -тУ Т№х ' У kkx
(3)
После подстановки численных значений строим
АФЧХ (рис. 07-2-5) для трех значений kkx=0,2; 1; 9
(кривые 1—3).
ДБ
L(co)
40
~ к кх=0,2
3
20
п
кк* = / ч,
и
ккх=9 7 £
-20
%
/ *=/0
-ко
V
J
Рис. 07-2-5.
По условию самонастройки kkx—\ и частота ©п—
=1 С"1.
Выберем фильтры
Лр)
Тогда
кфТфр ,
Тф1 Р + 1
(Р) = т^ГрТ'
где
. . ^ф ('Г2ф/,г +!2^ф1^фр\-\-1)
Ф.экв \Р) — т%рг + 2?ф2Тфр + 1	’
е  I /" А[я . /т.2  у . 6 __ ^	^	Ф1
?Ф1 — у Тфг ’ у ь *1 ф»> * ф*
(4)
(5)
(6)
(7)
Амплитудная логарифмическая характеристика кон¬
тура самонастройки имеет вид кривой 4, показанной на
рисунке пунктиром. Постоянные времени фильтров
31*	483

должны быть выбраны так, чтобы они преобразовывали
входной сигнал ошибки в соответствии с кривой 5. При
этом на частоте соп=1 с-1 и в ее малой окрестности вы¬
ходной сигнал фильтра не воспринимался бы исполни¬
тельным элементом, зато при больших и меньших
частотах, напротив, он поступал бы с усилением, доста¬
точным для привода исполнительного контура самона¬
стройки. Подбор требуемых значений |фь |ф2, /еф выпол¬
няем графически, поскольку поправки на значения ко¬
эффициентов демпфирования £ задаются кривыми (см.
приложение 6).
Условие работоспособности системы [4]
где 6i(|), 62 (^ф 1)—соответственно поправки на значе¬
ния коэффициентов демпфирования; А\ — амплитуда
сигнала на выходе системы; А — амплитуда сигнала на
входе исполнительного элемента.
Для заданного значения А— 3
и из уравнения
20 lg 2 +14—20 lg &ф—62 (Ы =20 lg 3
найдем &ф=0,1; Гф1=0,2 с и Гф2=5 с.
07-2-6. Учитывая некорректированность полезного
сигнала и помехи, определяем средний квадрат суммар¬
ной ошибки [4]:
где £2а — квадрат ошибки смещения; С22—средний квадрат
ошибки, обусловленный наличием помехи; со0 = |//с/У —
частота незатухающих колебаний системы; S — коэффи
диент демпфирования.
201gA>201gAb
При со=соп
20 lg А=20 IgN+b (I) -20 lg кф-б2 (Ы,
Тогда из уравнений (7)
484

Из условия d'Lfjdсо0=0 определим значение частоты
о *о—0,188п2/3, при котором средний квадрат ошибки
имеет минимум. Следовательно, при переменной скоро¬
сти полезного сигнала v изменяется и оптимальная ча¬
стота (о*0. Оптимальные коэффициенты связей, которые
показывают, как следует изменять коэффициент усиле¬
ния и коэффициент вязкого трения для получения
£2мин, соответственно равны [4]:
^опт — ш V — 0,0007 1у4/3;	1
Гопт = 2Ц/ = 0,00376у2/3. J
Рис. 07-2-6.
Постоянная времени измерителя скорости определяет¬
ся по формуле [4]
T=(96k2la2/v2)^.
При i;=600 м/с, 7=0,342 с.
Структурная схема самонастраивающейся следящей
системы, построенная согласно выражению (2) в зависи¬
мости от входного сигнала (переменной скорости п),
изображена на рис. 07-2-6, где 1 — объект управления;
2 — элемент сравнения; 3 — измеритель скорости; 4,
5 — фильтры.
07-2-7. Если не учитывать силы тяжести летательного аппарата,
то при продольном движении нормальное ускорение зависит от
угла отклонения руля и приближенно определяется уравнением
колебательного звена:
(р2 + 2ha>0p + со2о) еи=г /Св&,	(1)
где со2о — квадрат частоты собственных колебаний летательного
аппарата; 2/ко0 — коэффициент, характеризующий степень демпфи¬
рования; 8ц — нормальное ускорение; КЁ —- коэффициент эффектив¬
ности руля; б — угол отклонения руля.
485

Коэффициенты уравнения (1) меняют свои значения в зависи¬
мости от высоты, скорости полета, запаса горючего, упругих дефор¬
маций корпуса и других фактов. Для определенности возьмем
наиболее важные факторы — скорость полета ч и плотность возду¬
ха р. Пусть перегрузка летательного аппарата измеряется безынер¬
ционным акселерометром. Исполнительное устройство — безынерци¬
онный рулевой привод.
Рис. 07-2-7.
Квадрат частоты собственных колебаний летательного аппарата
принимается приближенно пропорциональным скоростному напору:
со2о~р^2.
Коэффициент демпфирования пропорционален скорости:
2/коо»ри.
Коэффициент эффективности руля
К% » fv* =рп2й>20,
откуда
рп2 = Ке/со20 = К,.
Рис. 07-2-8.
На основании уравнения (3) условия задачи находим:
КгК2 = К2Ке/ О)2 о = К 2^v2 = К = const ^
Корректирующее звено имеет коэффициент усиления Кг, значе¬
ние которого должно изменяться обратно пропорционально скорост¬
ному напору: Кг ~ К/ри2.
486

Структурная схема рассматриваемой системы управления пере¬
грузкой с последовательным корректирующим устройством пред¬
ставлена на рис. 07-2-7. Желаемая логарифмическая характеристика
разомкнутой системы, соответствующая максимальному скоростному
напору, представлена на рис. 07-2-8.
Рассматриваемая характеристика имеет нулевой наклон при
©<©о; наклон —40 дБ/дек при ©>©о; наклон —20 дБ/дек при
l/7i^co^ 1/Г2. Приведенная характеристика может быть принята
за основу для определения самонастройки корректирующего устрой¬
ства, так как она отвечает предъявляемым требованиям по качеству
переходного процесса. При этом необходи-	„
мо потребовать от системы самонастройки,	1	,
чтобы изменения значений р и v не умень-	I	L-—I
шали участка характеристики с наклоном ^	|	,	д
асимптоты —20 дБ/дек. Полагаем, что ча-	'
отота ореза соср задана, тогда на основа- у	^	|	|	у
нии уравнения (!) условия задачи в окре¬
стности частоты среза в первом ириближе-; ^	2	^
нии должно удовлетворяться равенство 0	~	*	0
*	igi^.(/®)i+igi^(/(o)i=	Рис 07.2.9
-=lg|VPio(/e)F*o(/®)l.	(2)
где (/со) И7го(/со)—оптимальная постоянная АФХ разомкнутой
системы в области частоты среза.
При выполнении равенства (2) требуемая стабильность харак¬
теристики системы может быть достигнута изменением первой со¬
прягаемой частоты асимптоты корректирующего устройства coi =
= 1/7Y Значение coi находится из условия
201g /С—40(1 g	lg 0о) =20(lg ©ср—lg ©i),
откуда /C(©o/©i)2 = ©cp/©i или ©i = /C©2o/©cpжри2.
Эти соотношения можно реализовать с помощью дифференци¬
рующего четырехполюсника, который приведен на рис. 07-2-9.
Параметры четырехполюсника, который является корректирую¬
щим устройством рассматриваемой системы, определяются из соот¬
ношений
Uq — tRC —[- Uq\
(3)
Умножая правую и левую части второго уравнения системы (3)
на R, получаем:
dac
и = K\U,q -f- RC -jj- у	(4)
где Ki=R/(R-{-Ri)^pv2 — коэффициент усиления корректирующего
устройства.
На основании уравнения (4) находим:
ис- не Judt — не
487

Подставляя значение Uc - в первое уравнение системы (3),
получаем:
If*	С
а0 = и -j- . j udt — RC~ I ^
или
du0 _ da	1__ K,
dt dt ~г RC Ll— RC U°-
Умножим правую и левую части уравнения на RC и перенесем
член, содержащий множитель U0 в левую часть:
dun	da
RC-^ + K^RC-ft + u.
Умножим и разделим первый член левой части 'уравнения на
R+Ri:
du0	R + Ri ^	^ n/r, da	t	/еч
dt	R + R1 RC	+ К'110 — RC dt	+ к-	^ ^
Учитывая, что (R+Ri)C — Ti — постоянная времени корректи¬
рующего устройства, RC = T — постоянная времени корректирую¬
щего устройства, выражение (5) можно переписать в следующем.
виде:
(Tip-\-1)Kitio= {Tp-\-\)ti'
Передаточная функция дифференцирующего четырехполюсника
.	*,(1+7»
(Р) =	1	+Тр	•
Изменение постоянных времени 7\ и 71 может быть достигнуто
с помощью переменного сопротивления резистора R, корректирую¬
щего устройства, чем и будет осуществляться самонастройка при
воздействии возмущающих факторов.
Значения параметров корректирующего устройства определяют¬
ся по формуле
где б — относительная ошибка, значение которой задается. Если
Ri/R^ 10-г-12, то Ki=RI(R+Ri) =0,091-^0,0762.
Подставляя указанные значения в (6), находим T = RC. За¬
даваясь значением С, находим значение R = T/C. Значение Ri
определяется по формуле
Ri=R(l-Ki)IKt.
Зная параметры корректирующего устройства R, Ri и С, можно
определить постоянную времени
Ti=(R + Ri)C.
488

07-3. МАТРИЧНЫЕ ИГРЫ И ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
07-3-1. Игра состоит из двух ходов; оба — личные.
У нас А три стратегии: А\ — писать 1; Л2— писать 2;
As — писать 3. У противника В тоже три стратегии.
Игра представляет собой игру 3X3 с матрицей
(табл. 07-3-1).
Таблица 07-3-1
А
в
Вг
А,
Вг
л,
2
—3
4
А
—3
4
—5
а
4
—5
6
Таблица 07-3-2
А
в
В1
в.2
Вг
А
7
2
9
А
2
9
0
А
9
0
11
Очевидно, на любую выбранную нами стратегию про¬
тивник может ответить наихудшим для нас образом.
Действительно, если мы выберем, например, стратегию
Ль противник на нее будет отвечать стратегией В2, на
стратегию Л2 — стратегией Б3, на стратегию Л3 — страте¬
гией В2.
Таким образом, любой выбор определенной стратегии
неизбежно приведет нас к проигрышу. Решение этой за¬
дачи состоит в следующем.
Чтобы сделать все ац неотрицательными, прибавим
ко всем элементам матрицы число L=5; получим матри¬
цу (табл. 07-3-2).
При этом цена игры увеличилась на 5, а решение не
изменилось. Определим оптимальную стратегию 6*А.
Для этого запишем сначала условия среднего выигрыша:
7е1 + 261 + Я,>1; \
2?j -j- 9£2 -j- 0 ^ 1;	/	(1)
9^ + 0+Шз^ Ь J
где !i=pi/v; g2=p2/v; g3=p3/v; здесь v —цена игры;
pi — частота использования i-R стратегии.
Чтобы избавиться от знаков неравенства, введем
фиктивные переменные z2) z3, которые превращают
489

неравенства (1) в равенства. Тогда условие (1) перепи¬
шется в виде
Необходимо сделать ее как можно меньше. Если все
три стратегии В являются «полезными», то все три фик¬
тивные переменные z\, z2, z3 обратятся в нуль (т. е. вы¬
игрыш, равный цене игры v, будет достигаться при каж¬
дой стратегии Bj). Но мы не можем утверждать, что все
три стратегии являются «полезными». Чтобы доказать
это, попытаемся выразить форму Ф через фиктивные пе¬
ременные Zu z2, z3 и, приравняв их нулю, посмотрим,
будет ли иметь минимум величина (3).
Для этого разрешим уравнения (2) относительно
in h> 5з (т. е. выразим |ь |2, |з через фиктивные пере¬
менные zь z2, z3):
В выражении (5) коэффициенты при всех z положи¬
тельны, значит, любое увеличение zu z2, z3 сверх нуля
может привести только к увеличению формы Ф. Следо¬
вательно, значениями Zi, z2r z3, обращающими форму (5)
в минимум, будут zi=z2=z3=0. Отсюда следует, что ми¬
нимальное значение формы Ф=1 /v=l/5, откуда цена
игры v=5.
Подставляя нулевые значения zu z2, z3 в уравнения
(4), получаем |,=1/20; |2=1/10; |3=1/20 или, умножая
их на V, pi = l/4; р2 = 1/2; р3=1/4.
7?1 + 2?, + 96>-г1 = 1; j
2е1 + 9?, + 0-г1=1;
—[— 0 —|— Ш, — г3= 1. I
(2)
Линейная форма имеет вид:
Ф=|1 + £г+£з-
(3)
Складывая |2 и £3, получаем:
ф 20 г> 10 г* 20 г*’
(5)
490

Таким образом, оптимальная стратегия А имеет вид:
(6)
Ах А2 А3
1/4 1/2 1/4
т. е. в одной четверти всех случаев мы должны писать
цифру 1, в половине случаев 2 и в остальной чет¬
верти 3.
Зная цену игры v=5, можно найти оптимальную
стратегию противника В:
ф* ___	.	(7)
В <7l	<72	<7з
Для этого воспользуемся нашими любыми двумя
«полезными» стратегиями (например, А2 и Л3) и напи¬
шем уравнения согласно табл. 07-3-2:
2^1 + 9^72=5;
9^1 +11 (1—<72—?i)=5,
где qi—частота использования 7-й стратегии противни¬
ка, откуда
<71=^7з=1/4; <72=1/2.
Оптимальная стратегия противника В будет такой
же, как у А:
6*Д=
(8)
| В1	*3
1/4 1/2 1/4
Возвращаясь к первоначальной непреобразованной
игре, получим цену исходной игры v0=0. Следователь¬
но, оптимальные стратегии обеих сторон обеспечивают
средний выигрыш, равный нулю, т. е. игра в одинаковой
мере выгодна или невыгодна для обеих сторон
07-3-2. Матрица А=
п>
элемент ац которой ра-
вен значению выигрыша первого игрока (величине про¬
игрыша второго игрока) при условии, что он выбрал
чистую стратегию с номером i, а его противник чистую
стратегию с номером /, называется платежной матри¬
цей. В этой задаче каждый игрок располагает четырьмя
чистыми стратегиями е{(г'=1, 2, 3, 4).
Элементы матрицы игры
О)
Яц
а\г
Ац
flu
аг\
агг
<7*i
««s
а»2
flu
«14
<24j
а*г
flu
044
491

определяются формулами
3, если
4, если
• 3, если
•4, если
ач =
= /-1;
</-2;
=/ +1;
==* j -j- 2;
(2)
О, если i = }.
Например, ai3—4, так как 1^3—2; ан==4, так как
1^4—2, и т. д. Таким образом,
А =
Необходимо заметить, что игра симметричная.
07-3-3. Каждый игрок в данном случае располагает пятью
чистыми стратегиями еД i= 1, 2, 3, 4, 5). Элементы матрицы игры
А= |15,5 определяются формулами:
0
3
4
4
—3
0
3
4
—4
—3
0
3
—4
—4
—3 0
если i ^\\
если i </.
(и
Для т — Ъу например, аи=1-
=—1—3=—4; а32=3—2=1 и т. д.:
0 —3 —4 —5 —6
1	0—5—6 —7
А =	2	1	0—7—8
3210—9
4	3	2	1	0
Аналогично для т — 4 имеем:
0—3—4 —5
А =
0 —5 —6
1	0	—7
2 1 0
-1=0; ai2 =—1—2 = —3; 013 =
Таблица 07-3-3
д
в
Вг
В2
£3
А
8
2
4
А
4
5
6
А
1
7
3
07-3-4. Нижняя цена игры 0,4; верхняя 0,6. Решение
ищем в области смешанных стратегий. Чтобы не иметь
дело с дробями, умножим все элементы матрицы на 10;
при этом цена игры увеличится в 10 раз, а решение не
изменится. Получим матрицу (табл. 07-3-3).
492

Условие среднего выигрыша имеет вид:
85, —|— 4S2 —?3 — гх — 1;	\
2?i	5£2 —7?3—г2 = 1;	j	0)
«, + 6^ + 3^-г4=1, J
где	а	условие	минимума	формы
Ф=11+52+‘£з=тт.	(2)
Проверяем, все ли три стратегии противника являют¬
ся «полезными». В качестве гипотезы сначала предпола¬
гаем, что фиктивные переменные zly z2, z3=0 и для про¬
верки решаем уравнения (1) относительно gi, g2, Ъ'-
откуда
t  _10_ , _27_	,	_6_ 23^ .
1	Тяв I	“Г	ьяв^2	136^»
136 1 136^ 1 136 2	136
t __12 __22	_Lii •
136	136	136	‘ 1362Гз*	w)
_8	, _8_	,	_32_	32
136+ 136 ^ + 136 г2	136^’
)
откуда
136Ф=30+ 132?! + 18z2—51г3.	(4)
Формула (4) показывает, что увеличение переменных
Z\ и г2 по сравнению с предполагаемым значением нуль
может только увеличить Ф, тогда как увеличение z3 мо¬
жет уменьшить Ф. Однако увеличение г3 надо произво¬
дить осторожно, чтобы величины gb g2, £з, зависящие
от z3f не стали отрицательными. Поэтому положим
в правых частях системы (3) значения zi=0 и 22=0,
а значение z3 будем увеличивать до допустимых преде¬
лов (пока какая-нибудь из величин g2, g3 не обратит¬
ся в нуль). Из второго равенства (3) видно, что увели¬
чение z3 «безопасно» для величины g2— она только уве¬
личивается. Что касается величин gi и g3, то здесь уве¬
личение z3 возможно только до некоторого предела. Зна¬
чение gi=0 при 2з=10/23; значение |3=0 раньше, уже
при z3=1 /4. Следовательно, давая z3 его максимально
допустимое значение 1/4, мы при этом обратим в нуль
величину g3. Чтобы проверить, обращается ли в мини¬
мум форма Ф при 2i=0, z2=0, g3=0, выразим остальные
(не равные нулю) переменные через предположительно
равные нулю Z\, z2, g3.
493

Решая	уравнение	(1) относительно	£ь	£2 и 2з> по¬
лучаем:
t —_1__|	5_г	1_г I 21	р .
.49	‘	49	3	49	»	32	4з’
32 1 32 1	32	2	~	32
р _А _1_Аг
2	32	32	1 ^ 32 2	32	3’
 _8	|	8_	,	136	.
Z?	32	' 32 Zl~i~Z‘	32 3‘
(5)
Составляя форму, получаем:
32Ф=7 + Зг1 + 4г2+£з.	(6>
Из (6) видно, что любое увеличение значений Zi, г2„
£з сверх их предполагаемых нулевых значений можетг
только увеличить форму Ф. Следовательно, решение
игры найдено, оно определяется значениями Zi=z2—%$
=0; из уравнений (5) получаем:
£1=1 /32; £2=3/16; 23=1/4.
Подставляя в формулу (6) значение 21=22=£з=0. на¬
ходим цену игры V, зная, что v=l/Ф [5]: 32Ф — 7 —
=32/v; отсюда v=32/7.
Оптимальная стратегия
6*,=‘||Л Аг II.
Ц 1/7 6/7 II
«Полезные» стратегии (составы Л4 и Л2) должны
применяться с частотами 1/7 и 6/7; состав Лз не должен
применяться. Чтобы найти оптимальную стратегию про¬
тивника, в общем случае можно поступить так: изменить
знак выигрыша на обратный, прибавить к элементам
матрицы постоянную величину L, чтобы сделать их не¬
отрицательными, и решить задачу за противника так же,
как мы решали ее за себя. Однако то обстоятельство,
что нам известна цена игры v, несколько упрощает зада¬
чу. К тому же в данном конкретном случае задача до¬
полнительно упрощается тем, что в решении участвуют
только две «полезные» стратегии противника Bi и В2
(так как значение г$ф0, то при стратегии В3 цена игры
не достигается). Выбирая любую «полезную» стратегию
клуба А, например Ль можно найти частоты q 1 и qz-
Для этого напишем уравнение согласно табл, 7-3-4, зная,
ЧТО (72=1—
8^ + 2 (1—qi) =32/7,
494

где v=32/7 — цена игры. Тогда #1=3/7; #2=4/7. Опти¬
мальная стратегия противника
Вх В2
3/7 4/7
т. е. противник не должен пользоваться составом В3,
а составы Bi и В2 применять с частотами 3/7 и 4/7.
Помня о том, что все элементы умножались на .10, и
возвращаясь к первоначальной матрице, определим
истинную цену игры:
v = -у-: 10 = 0,457.
Это значит, что при большом числе встреч число
побед клуба А составит 0,457 всех встреч.
07-3-5. Произведем тождественные преобразования
системы:
0 = 	(хх -J- х2 -f- 7хъ -f- 2xJ;
0 = ~2	(— 2хг — х2 -j- З*3 -[“ 3*4);
0 = 4 — (2-х^ 4"~ 2*2 -j- 8jc3 4- Х4).
(1)
За разрешающий элемент возьмем х2 в третьем урав¬
нении системы (1). Решая это уравнение относительно
х2, получаем:
*2=2—(*1 + 4*3+ *4/2).	(2)
Подставляя выражение для х2 в первое и второе
уравнения системы (1), получаем
0 = 3/2— (—2*14-3*з4-Зл;4/2);
0 = 7/ 2 — (— хг 4- 7хг 4- 7xt
ад; 1
С./2). ]
(3)
За разрешающий элемент системы (3) возьмем х3.
Решая первое уравнение системы (3) относительно х3,
получаем:
*3=1/2— (—2*i/3+1*4/2).	(4)
Подставляя выражение для *3 в уравнение (2) и во
второе уравнение системы (3), получаем:
х2— — 11*^/3 —J— Зх4/2;
0= — Плг./З.
(5)
495

Из второго уравнения системы (5) следует, что *i=0,
Учитывая это, уравнения (4) и (5) принимают вид:
л:3 = 1/2— lxJ2\
xt — 2>xJ2.
(6)
Подставляя выражение для Xi—х3 из систем (5) и
(6)	в выражение для формы в условии задачи, полу¬
чаем:
Ф=7/2—43х*/2.	(7)
За разрешающий элемент системы (6) возьмем
Из первого уравнения системы (6) находим:
х4=1 — (2х3).
(8)
Подставляя xt в выражения для х2 системы (6) и
(7), получаем:
х2 — 3/2 — Зл:3;
Ф = — 18 +43х
У
(9)
Из системы уравнений (9) видно, что наименьшее
значение линейной формы Фмии=—18; при этом *1=0;
лгз=0; х4=1; лс2=1 /2.
07-3-6. Заданную систему неравенств путем введения
дополнительных переменных г/,- сводим к системе урав¬
нений:
г/, — 60 — (— 20л:, + 12л:2 — 15л:3);
Hi— 6 —(л:, + 2л:2—Зл:3);
Уз — 12 — (Зл:, + 6х2 — 4л:3);
г/4 = 60 — (— 20л:, — 15л:2 —{— Зл:3);
0 = 10 — (Юл:, + 5л:2 — 2л:3 — г/5);
0 = 42 — (6л:, + 7л:2 + 42л:3 — у,).
(1)
За разрешающий элемент системы (1) возьмем х3
и найдем его из шестого уравнения:
(2)
496

Подставляя выражение для х-л в остальные уравнения
системы (1), получаем новую систему уравнений:
У1	' ^	!	7	1	"Т-	6	2	42	]
Ух
Уг
\
= »_ ел
Г 1U I 5	3	\
у— •*! + ~2~	~42У°)	'
/17	,32	,	4	\
•—	^	+	-6“*2+ -42 У*]!
= 57-^^,- “-4г.4-ЛН.
У* = 57
I 7
*^2 до ^/в } >
42 у :
п	ю	/72	-	16	2	\
О	12	f 7	^ ~1~ 3	*^2	42	У& ^5у *
)
За разрешающий элемент системы (3) возьмем xi9
который определим из пятого уравнения:
(3)
_ _7	/14_	7_	1_ Л
Xl б	\27 Х*	72 У*	216У*)'
(4)
Подставляя Xi в выражение (2) для х3 и в систему
уравнений (3), получаем новую систему:
 J> /_5_	, _1_	5_	\
Х* 6	^ 54 Хг ' 72 У*	216 У*);
Уз з
У,
^"54	1512
27
/220	,	17
 -*з + "yo" У5 '
125
72 У5
и —	_ 665
^	g	I 54	2	Г
_-7j	/95_	_ _Ш_ и \
У2	3	(27Х2	72 У5	216	У*	j	*
J7
72
161
Q/л 5	/	265
80—- —■*»■
1512 У°)'
35
143	  дь	ч
~72 У6 ~ T5l2 ] ■
(5)
Согласно уравнениям (2) и (4) одним из неотрица¬
тельных решений системы заданных неравенств является
решение a:i=7/6; х2=0; *3=5/6.
Выразим теперь линейную форму через дополнитель¬
ные переменные, подставив в заданное выражение урав¬
нения (2) и (4):
Ф 2 ( 18 ^ 12 Уь 36
\
32—903
497

Как видно из последнего выражения, дальнейшее
уменьшение линейной формы в области неотрицатель¬
ных значений переменных невозможно, так как все дру¬
гие решения системы не ведут к увеличению формы. По¬
этому первое решение системы (1) ^ = 7/6; х2=0\ х3 =
=5/6 явилось оптимальным, а соответствующее значе¬
ние линейной формы Фмин=2.
07-3-7.	Определим	координаты	первого	участка	по¬
иска.	Для	этого	введем некоторую	фиктивную	перемен¬
ную £. Потребуем, чтобы значения Xi и х2 в выражении
функции выгоды были равны:
xl = 3Z\ )
*;=«)	<■>
Подставляя значения ^ и ^ в неравенство ограни¬
чений выражения (1) условия задачи, получаем:
71 <6; )
22? <21.}	^
Убеждаемся, что при возрастании £ первым нарушает¬
ся верхнее неравенство при g=|1==6/7.
Таким образом, координаты конца первого участка
поиска согласно выражению (1) будут равны:
л:11=3|1=18/7; *21=4^=24/7.	(3)
Для определения координат конца второго участка
исключим переменную х2 из выражения функции вы¬
годы. Используя выражение функции выгоды и первое
неравенство заданной в условии задачи системы, состав¬
ляем следующую систему уравнений:
М = Зхх -f-, 4*2;
§ = хх-\- х2>
откуда
М=24—Xi.	(5)
Введем новую фиктивную переменную для второго
участка ц. С учетом (3) и второго уравнения системы
(4) запишем:
хг=18/7	73;	|
х2 = 24/7 Д- т]- J
Значения *1 и х2 для второго участка из системы (6)
подставим во второе неравенство системы, заданной
в условии задачи:
}	(4)
498

2-^-2т1 + 4^- + 4т)<21>
откуда г]^15/14, чтобы удовлетворить заданной функ¬
ции выгоды. Следовательно, координаты конца второго
участка поиска
**=18/7—15/14=3/2;
*22=24/7+ 15/14=9/2.
Полученные координаты конца второго участка поис¬
ка являются решением задачи линейного программиро¬
вания, т. е. соответствуют наибольшему в пределах об¬
ласти ограничений значению функции выгоды М. Для
того чтобы убедиться в этом, согласно общей методике
определим направления третьего участка. Исключая *2
из выражений
М=3*i + 4*2j
21=2*1 + 4*2,
получаем:
M=Xi + 211
*2=21/4—Xil 2.
Таким образом, координаты третьего участка будут
равны:
*i=*i2+£=3 / 2 + £;
*2=9/2—1/2.
Подставляя последнее выражение в первое неравен¬
ство заданной системы, находим 6+£/2^6 и убеждаем¬
ся, что оно выполняется только при |=0, т. е. в точке
конца второго участка поиска. Это и указывает на то,
что *12, *22 являются решениями задачи.
32*

Часть третья
ПРИЛОЖЕНИЯ
500

   Продолжение приложения 1
ft П/п. Заданные функции Матрицы коэффициентов Начальные значения Матрицы нормированных реакций
tlfl
"а
- ся
ся
ся
с
ся
01
с
^|OJ
а
с
*00
I
а
СЛ
О
СЯ
Д
*сО
s="|ca
+
oi
to
о
о
ся
ся
+
CQ
F”
СЯ
ti
00 w
о ?-
о ^
СЯ ,
^ +
CJ
I
0Q
э-
С
F"
СМ
•О *0
►о
+
F-
СЯ
ся
+
м
Я"
и
+
oq
э-
+
3
с
+
с
F*
э-
+
501

<N
a О
* fee
^ о
^ н
« td
2 3
^3
; к
ж
Ш *_«
>» 5
e? К
О ш
с g
- о
в ж
Ж н
ж о
ш о
*?и
8й
on ja
5 в
Q w
в S
аё
>>
a*
<
ж
ж
н
v2>
T
s—"
>C
ъ
8.
]<	w
Си	^
X	О
,<U,	W*
-J	*.
-J
X
H
t
*
*
X
Ч-'
£ >2?
?T
+
F
I
+
F
+
<2?
'w'
>N
s N
+
■k
и
p-
2b
*
Ml'
>2;
s N_.
<Tb I F
^bg
tr
g
'H'g
502

Получение изображений функций и их произведений из исходных соотношений
503

Получение изображений функций и их произведений из исходных соотношений
Сч
з
*>
о
С
«Ski
У
Ж
§
О
X
§
3
>г
х
х
я-
чз
гС
2,
X
+
см
а
+
в
+
СМ
+
м СЧ
+
+
см
а
+
см
+
с
сч
'+
в
+
см
см
ОП_
+
+
N
I»
I
QJ
Он
X
в 9-
|Т |1Г
Is 1о-
X
+
CM
в
I
CM
3
CM
CO-
+ >"
CM	1
5— CM
+ T
ем -f“
qq. 1
I ем
I «
CM	.
I +
I c*.
+ -j-
см 4
CO.
+
'a
I
cm
+
C2Q-
i
+
02.00.
"I" I
+ +
p'p
1 +
CTL.
+
t5,
+
M
I a
<v
oi
01
в
+
a
G
X ^
^ +
+ &
"a .5
"—' GO
•s x
504

Приложение 3
ТАБЛИЦА КОЭФФИЦИЕНТОВ К РАСЧЕТУ НАЧАЛЬНЫХ ЗНАЧЕНИЙ НЕСТАЦИОНАРНЫХ
И СТАЦИОНАРНЫХ (6 = 0) РЕАКЦИЙ
I +xd
I
2 ©
~ § Т *7
О X — X
*Г Т ^ 1 !
CS) X —. X СМ
a I х i
х X
о о
— С' v см
2- =- I Х
- е * с- -5
+ X й: |
£5 ^ ~ >* см
* к L - к
х X
~ \%
§ 5 £ о
> ^ :й> :=s>
С- tj, ’о
** & § в
2 S 2 ^
> ^ ^ ^
^ 1? § s
° о о S
> :=>
" \* - «
2 § о
> & :»>
% > э s
-г*.
2 о О g
. ^ СО5 СО ^3)
со
€ о §
> ‘-г* ,iS>
~ « 1 со со
а» w
~ \%
О о
<м а>
см
2 § О
:=> •«“ •»
~\ъ.
о о о
• J3) й)
§ € о о
•ft) • С3>
2-0 0
Й>
о
• а, ооо
-
«£ § S
■' j ot
g S 1
* 1^|
ft.
J_- if
О ^ 4-7
5 7 1
"ft.
СI
* f
ft.
s?
Оч
•Si
о —' СМ со
О — СМ со
о
505

Продолжение приложения 3
— +
X
о]
О о X 1
—' — ^ ГГ
(М — ~ ^
+ + — 1
>< х | Ь' 7
^ =5 х х х
X X
о х
_ 5*
о ё + ё
w ^ X |
со ^ й> X
~>< £ *7 ГХ
^ 3 1 1
* X х
> X
-к
2- ^ ©! 2*
~ ~ >
^ Ч, * -
^ Ю CM CD
О S' o' 0,
а § • > Е
> с ^ а>
^ ^ о О
SS) ю CD
е о §
> W • ^
5»> ч? О!
о g о 2,
я 5 > ~
Ч > 2 |
~ к
o'
S sT § s
^ W ю
О о О ^
. —IX о
*м ^ ^
> - ~ :&>
'“■’’ 5fi U) •
й) СО CD CD
~к
ё § о
> I2» :а> °
w <М <N
Э)
о о
gW > § о
а> ^
« <М
-к
o' o'
' ^ О О
! 5s> : ^
o' ^
—Г" 0,
г> . ^ О О
W^>
~1*<
o'
ООО
: =з>
О
О О О
! =*>
-
— £ © 5
S а» ^ 3
•а, 1 « 1
о § g sf
:* 7 с^ 7
«5.
§ 5 5 1
* 7 1 1
ё S jg- 1
. _ :s> •<; см
=3) | CO |
«ч
§ If 5"
^ 1 -
О Я
ё 3? £ §
* 1 2 |
* f
- и
^ 1
1 § «4
*
S?
с%
5
^ ю
* 1
5?
•ft*
О —. <N СО
О СМ СО
-
<м
СО
506

Пра лож е ни е
ТАБЛИЦА ДЛЯ ПЕРЕХОДА ОТ НАЧАЛЬНЫХ ФУНКЦИЙ К ИХ ИЗОБРАЖЕНИЯМ ПО ЛАПЛАСУ
И К ^-ИЗОБРАЖЕНИЯМ
<8
СП
К
N
8
I
£
л
V
<0
V
О
.ц.
N
К
N
К
+
N
СМ
Л.
*
я
1=3
я
I
N
с»
7
+
3
N
N
к
*
+ !
ы
СО
+
CD
+ '
(о
N CD
N I
+ :
-9
+
а
N
507

Начальная функция ^^Лаштасу6 П° 2-изображение Интерполированное 2-изображение
*
У
*
f-ч
¥
Г
1
1
¥
N
ем
f^""4
**to>
1
fa)
9
I
+
1
1
1
|
к.
|
?
{4
*3
'—"
а
1
1
<м
?
К
1
м
*>
К.
N
+
Т
I
N
14
сз
I
ем
К
03
03
+
' F*--
03
к
03
+
03
О
+
03
ем
ем
03
03
+
+
CJ
Cv]
сз
оз
+
ем
а
I
I
03
С
03
ся
508

Изображение по
Начальная функция Лапласу 2-изображение Интерполированное г-изображение
I
f-ч
*С>
I
Т
<ъ
I
Со4
о
I
I
ьг
S'
К
(О
+
	I
<5о
<3
I
+
СЯ
?
<53
+
к
оз
<5>
+
03
k.
т
<^>
N
csi
К
оз
оз
+
Я-N
СЯ
к,
т
N
(N
ад
I
I
N
а
I
<ъ
т
<53
I
s
I
Q
{-«
<з
I
<ъ
в
S**
а
I
I
F-,
03
С
к
а
7
+
к
OS
со
о
о
f-M
<50
N
СМ
03
к,
т
+
03
F-.
т
в
+
03
еч
СМ
СЯ
СЯ
+
в
+
см
"54
+
см
а4
+
El,
+
Е»,
El.
' "
I
<5о
"а
+
СЯ
С
сз
I
03
со
О
509

Приложение 5
ТАБЛИЦА ПЕРЕХОДА ОТ ДЕЦИБЕЛОВ К ПРЯМЫМ
ОТНОШЕНИЯМ
Цеци-
5елы
Отно¬
шение
Деци¬
белы
Отно¬
шение
Деци¬
белы
Отно¬
шение
Деци¬
белы
Отно¬
шение
Деци-
белы
Отно¬
шение
0,0
1,000
4,4
1,660
8,8
2,754
13,2
4,571
17,6
7,586
0,1
1,012
4,5
1,679
8,9
2,786
13,3
4,624
17,7
7,674
0,2
1,023
4,6
1,698
9,0
2,818
13,4
4,677'
17,8
7,762
0,3
1,035
4,7
1,718
9,1
2,851
13,5
4,732
17,9
7,852
0,4
1,047
4,8
1,738
9,2
2,884
13,6
4,786
18,0
7,943
0,5
1,059
4,9
1,758
9,3
3,917
13,7
4,842
18,1
8,035
0,6
1,072
5,0
1,778
. 9,4
2,951
13,8
4,898
18,2
8,128
0,7
1,084
5,1
1,779
9,5
2,985
13,9
4,955
18,3
8,222
0,8
1,096
г,2
1,820
9,6
3,020
14,0
5,012
18,4
8,318
0,9
1,109
5,3
1,841
9,7
3,055
14,1
5,070
18,5
8,414
1,0
1,122
5,4
1,862
9,8
3,090
14,2
5,129
18,6
8,511
М
1,135
5,5
1,884
9,9
3,126
14,3
5,188
18,7
8,610
1,2
1,148
5,6
1,905
10,0
3,162
14,4
5,248
18,8
8,710
1,3
1,161
5,7
1,908
10,1
3,199
14,5
5,309
18,9
8,811
1,4
1,175
5,8
1,950
10,2
3,236
14,6
5,370
19,0
8,913
1,5
1,189
5,9
1,972
10,3
3,373
14,7
5,433
19,1
9,016
1,6
1,202
6,0
1,995
10,4
3,311
14,8
5,495
19,2
9,120
1,7
1,216
6,1
2,018
10,5
3,350
14,9
5,559
19,3
9,226
1,8
1,230
6,2
2,042
10,6
3,388
15,0
5,623
19,4
9,333;
1,9
1,245
6,3
2,065
10,7
3,428
15,1
5,689
19,5
9,441
2,0
1,259
6,4
2,089
10,8
3,467
15,2
5,754
19,6
9,550
2,1
1,274
6,6
2,113
10,9
3,508
15,3
5,821
19,7
9,661
2,2
1,288
6,6
2,138
11,0
3,548
15,4
5,888
19,8
9,772
2,3
1,303
6,7
2,163
11,1
3,589
15,5
5,957
19,9
9,886
2,4
1,318
6,8
2,188
11,2
3,631
15,6
6,026
20,0
10,000
2,5
1,334
6,9
2,213
11,3
3,673
15,7
6,095
10
3,162
2,6
1,349
7,0
2,239
11,4
3,715
15,8
6,166
20
10
2,7
1,365
7,1
2^,265
11,5
3,758
15,9
6,237
30
31,62
2,8
1,380
7,2
2,291
11,6
3,802
16,0
6,310
40
100
2,9
1,396
7,3
2,317
11,7
3,846
16,1
6,383
50
316,2
3,0
1,413
7,4
2,344
11,8
3,890
16,2
6,457
60
1000
3,1
1,429
7,5
2,371
11,9
3,936
16,3
6,531
70
3,162-103
3,2
1,445
7,6
2,399
12,0
3,981
16,4
6,607
80
104
3,3
1,462
7,7
2,427
12,1
4,027
16,5
6,683
90
3,162-104
3,4
1,479
7,8
2,455
12,2
4,074
16,6
6,761
100
105
3,5
1,496
7,9
2,483
12,3
4,121
16,7
6,839
110
3,162 - 10s
3,6
1,514
8,0
2,512
12,4
4,169
16,8
6,918
120
106
3,7
1,531
8,1
1,541
12,5
4,217
16,9
6,998
130
3,162-106
3,8
1,549
8,2
2,570
12,6
4,266
17,0
7,079
140
107
3,9
1,567
8,3
2,600
12,7
4,315
17,1
7,161
4,0
1,585
8,4-
2,630
12,8
4,365
17,2
7,244
4,1
1,603
8,5
2,661
12,9
4,416
17,3
7,328
4,2
1,622
8,6
2,692
13,0
4,467
17,4
7,413
4,3
1,641
8,7
2,723
1
13,1
4,519
17,5
7,499
510

Приложение 6
ДАННЫЕ ДЛЯ КОРРЕКЦИИ АСИМПТОТИЧЕСКИХ ЛАХ
КОЛЕБАТЕЛЬНОГО ЗВЕНА
ДБ
16
14
12
10
8
6
4
О
-2
-4
-S

Прило ою ение 7
НОМОГРАММА ДЛЯ ПЕРЕХОДА ОТ ЛОГАРИФМИЧЕСКОЙ
АМПЛИТУДНО-ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
К ВЕЩЕСТВЕННОЙ И МНИМОЙ ЧАСТОТНЫМ
ХАРАКТЕРИСТИКАМ (G, В-НОМОГРАММА)
/а\-*
512

Приложение 8
НОМОГРАММА ЗАМЫКАНИЯ (Ф-НОМОГРАММА)
со-1,дс~1
33—903
51 3

у
£
о
а
6*,
t;
и
>>
аз
я
и
«
3
аз
я
<
CQ
О
О*
S
S3
0-
о
я
5Я Я
я к
=*5
к ?
>> р<
А ^
^ щ
£s
я я
*? с-
<
я
я
ш 5
е ^
«.S
я о
=1
я
я
>ь
е
с
я
я
ч
я
с
н
LO
О*
о оо о to со ю cn) см сч i.o со t- —1 io oo — о
О^ЬООЮООООСОЮСО-1 ОО СО О N Ю Ю ^
ОСЧ ^ CDOOOiO —1^.-4^000010)0)0)
ООООООО— — — — — — — —OOOO
0,50
OO — lOCOr		 Ю (N 00 00 (M '—i 00 COCD CD
O^OOCOOO-TfCO—OLO —i CO N Ю CD
ОСЧ^СООООО— — — — ООООООО
oooooo — — — — — — — — ©ooo
0,45
1
O-NCDOrOCOLO't^bNMCOCriCTl-N
OCO,t,t-^fOC)M(N-a)(£iCOOOOO!)N
О (M ^ CD CO Q О О — — — О О О О О О О
О^О^ОООО — — — — — — —— — — ООО
о
о*
О СО СМ N О N СО rt< N 1C (М ю со СО СО Ю Ю (М
О <М СО — 00 — — Г-- О — — О С.О С\1 О О О
OC'I’ttDNfflOO - — — ООООООО
о о О О О о — — — — — — — — — — о о
0,35
OlONCO-i-tDOOOrOCOO'aiCOMNN.
O'— - 0с0ф00ю0)000)к^го--0
OOl'tOhOOQOO - — ООООООО
ООООООО — — —— —— —— — — —
0,30
О N - Tf - OJ ОО Tt< О О N СО Ю о МО - ОО
ОООСПОООЮСЧС£ЗОООООООЮСОСМСМ —
осч^юооооооооооооооо
o' о o' о о о о" — — — — — — — — — —
0,25
OC^CDOCDCOOO^CnNNN'tcOimO^O]
OOOOCDOCOOqOCOLOCDCDLO^COCNCSIC^
О - fOiONOOOOIOOOOOOOOO о
О О*4 о о" о* о** о о* — — — — — — — — — —
0,20
O(M-00C0C4t0C000CT)OjCDNO^a)O-
О О) NCOOOOO)CDOCM't'tCOCO(N — (NCM
О — СОЮООООООООООООО о о о
о о о" о” о о~ О*4 О*4 — — — — — — — — — —
о*
0^00 1-0 — COOO^N(MO)COOiCDCDOOO
OOOlO-lOSCDCS|SO)---aOOO-
О — rOiOCOSQOOiOiOOOOOOOOO
o' о о о о" о о о o' о — — — — — — — —
оГо
ОСОО^ СООООСЧООООООООООЮО
ONTfaiCNicOOlCncOCDNOOOOOONOOOOOO
о — оо^ог^ооооооооооооо©
o' о" o' о*~ o' o' o' o' o' o' о о о" o' о" o" o' о~
о
ОЮСОО)Ь>ЬОСОСОСО(БОСЧСО^Ю-0
O(DC^(D(^O(j)l00l(Mc0^Tf^^^L0L0
O-CO'tlONNOOOOCDQOOGlOiOiOiCn
o'
о о o' о o’" o' o' о o' о" o' o' о o~ o' o' o~ о
о
о
OOOOOKM^lCCONCOCDOTf^inNOOO
ОСО-^ЬМОООЮОООООООО--
O-CO'tlOtDNNOOOOOOOIQOOJOJaiO)
o~ о о o' о о o' о" о* o' о о о о о" о о о~
оюоюоюоюоюоюоюоюою
О О — — О) CS СО СО ’’ф' ^ Ю 1C Ю СО N 00 оо
514

Относительные значения сопрягающей частоты
о
а
=1.
с
а;
I
•&
§
СОСОТЮООСПСОоО О <35 ''Т' СМ LO >— <Ф сЬ
  C5,T(NON'^Cv5irjiOlO(£)(M(M,f-sn
О^ФСОСОЬООО)Ь0Ю^^^^ЮЮ со
o' o' o' -Г	Л	Л	_T	r-S	r-Г	Л	Л	Л	л	_T
f°-S!tN(NOco^^,:t,W'H^ioico
I 05 t>- 'Ф (N Ю О О о O' о о о о о о о о
ооооооооооооооооо
о
о
СХ
Сз
ОО »—| Ю LO О t>- О 05	-—I	со СО СО т3-1 LO ^ ^
^^52L2£?^000'-,a^(>*';J<coo5C4 cno5
—< 05 00 CD тГ С\1 О —< ,—'СМ «—| —' О О О	о
оооооооооосГсГооо'сГо
Sz^c^^^c0l"'r^r~'l000c0C)<:^)CSil^)o^f
O’ СО СОООО —' —' —'-00)05050)0)0)00
ОООО —■ —	< —1—н —' о	о	о	о	о	o'	^
О^СО(МГОО(£Ю^’—| '—•	’—1	О	СО	Ю	СО	CD	СО
oocDcooc^r-t^-coh-oioc^Oi—■	^	со	од
О СО Ю СО О —■ ’—■	—1	< О О	05	О)	05	05	О)	05	О
о о о о —
о о о о о о
О N Ю СО О Ю С-) ю
OOiNrHOOONN
О СМ Ю ОО 05 —<1—' —<
о" О 0~ О О —~ rS
-iiooiMMcoaj'too
TCO^0CNOOCONO
*—'000505050505 05 0
’—' ’—1 ’—1 o' o' о" o' o~ o' —Г
22с^^^0т,,т},а1®,ч^т*,оооьюо
O05(D05N05CDN,t05C0NC0-'O(Nli5ffi
ОСМЮГ-050’—' —'^0 005050505050505
о о о о о
—.г-н,—,0000000
0(MScOD'T,t-HCD
ООО^^ЮООЮЬЮ
ocmidi>.050 — — —
о о" о" о" о —Г —Г —Г
LOD'^C^-hCM'TN
О 05 С3> 05 05 050505
—1 —« о о о" О о о" ©-
OlO^0000NWC0^t405(D(D(DN^<D00
ОЬ-СОЮСОСО^СОСОСМСО —, щ СО - r-ч СО Ю
ОСЧЮО-050^—'00050)05050505
о О О о о о
ON05ODOO-'OCS|Tf(MTj'00N(N(N-H
2 CD ’—■	,—'ЮСОСОСОСОООСООО^(М(МСОЮ
OCv']lON050-'-rt^o0050)05050505
о о о о о
— о о о о о о
О О) LQ W О О N ОС) 05 ОО СО О СО CD CD LO OO
OLOOiMDCO^iOlOCODlOO't’^CNCO *'tl
OlMinNQOO^-' —< —1 О О О 05 05 05 05 05
о о о о о
-н-н-^ООООО
О	ю	О	CD	ОО
О	Ю	05	О	о
О	СЧ	'Ф	N	ОО
о	о	о	о	o'
О О ю 00
—* О ^ ю
О -—1 '—|
О I'— СМ СО LO Tt1 ^
‘000505050505
’—,	'	1—,	о o' о o' сГ
о ^ in о ю о ю о ю о ю о ю о ю о ш
О О ■—' « O') (М w D 't -г ю Ю CD CD N N ОО* oo"
33!
515

Относительные значения сопрягающей частоты *
£
о
а
с*.
с
О)
а
а
о
Ъ
о
«а
С2
ос^ю©счсос£>©со©о©Г"-1>-ооооь-юоа©
0NOO(DOOOOOOOOOOOOOOOOT
05010)010000000000000000)
О О О О ^ -н* гн" ^ J ^ J	J J J J -Ч О
ОЮСЧЬССЬ.ЬЬЬООО(МЮОО^гнС^СГ)СОЮ
NN00 000505G)Qa)0)0000^^-00 0
0)05 0^0)0^0 0)0 05 ООО О ООО О ООО
о оооо o' о о о о — — — — — — —' —' — —
OOfMN'-H-'ONCDNOO'^aDO'tNQOOOO)
NOOOOO)0)OOOOOOOCOOO)C)0000'H-H'-'0
00)00)0)00)0)0)0)0)00000000 0
сГ сГ О О О О О О О О О О ,-н,——
С^СОСОСОСО—I 00 СО Ю ^ Ю ОО -1 со ОО (М Ю 0 QO N
ООООООООООООООООООООООООО
оооооооооооооооо Оооо
©00©0~©00©00©©00 — — — — —
CDCDCDWCNO'^OCDCOCOlONOOOOlONOO — —
ООООООООООООООООООООООООО
000000)00)00)0)00)0)0)00)0)00
JJ^JJoooooooocoooo^^
ооооь^о^о^оооьооо —со^^юю
^^^.H^^OOOOOOCOOOOOOOOCIOO
ооооооооо ооооооооооо
J	J J J J J О* О	О О О О О О О' о	о о о
1Г., Г*- f- 00 Ю —■ ЮОЮО^ОЮЮЮЮЮЮЮ^
— — ООЬСООООООООО
50000000000000000000
~ ^-Г —Г *-Г —ГГ	—н о о © о о о о о о о
ё
ЮО-СО'НОО'ТОЮ-ОООМДОЮЮО^-
C^(NCOCO«(N01---00 000 00000
о о о о о о о о о о о о о о о о о о о ©^
— — — — ©~
C£)(NlOOOONW(NOSOin,t'T^'^HCOCN—О
— СОСЧСМСЧХМСЧСО - —' — — О* ZL
о о о о о о о ооооооооооооо
S^OCOlOOlOCO(N--(M(N,tin(£)OlOlClO
ОООооооооооооооооооо
ЮСЧООЮОООООООООООСОЮ^-О — С^С^ —
0SNOOOOOOOOOOOOOOOOOOOOOOOO
ОООООООООООООООО—1ООО
оооооооооооооооо————
^(NO0NOOOOO(NT0O)-^W®00
^СОСО^т)<т1-1СЮЮЮЮЮЮЮ(О<О(О0(О(О
оооооооооооооооооооо
оооооооооооооооооооо
оюоюоюоюоюоюоюоюоюою
О)" О)" О О* — — CN (N СО СО	Ю	Ю	CD	CD	N	N	ОО	со
516

штельные значения сопрягающей частоты х
о
3
сх
с;
а
CD^fOOOOOOCDLOC4)OCOCO—'ООСч —1 СО О '—' b-
СОГ^ЮЮ1"--СООООСч)1ПО^СОСО’—<ОСОСОСЧ)
СО СО СО СО Ю Ю Ю't ^ Ю Ю Ю СО СО СО СО Ю LO СО Ю
СО I СО Ь- ОО СО О! I .'ФЮ'^СО I I со со СЧ) I
О о О О О О О о CD О О О О о О О ООО о
О^ООООО^ООООО,—,^-,0000^-,
ОщОООООсоООООО^соООООсо
о
о
Сх
С5
СО 00 Tf О СО LO О С4) О '—I СО СО 00 со СО CD СЧ) оо
^ОЮОООЬ^ЮСОО^СОч)*^ ^ Ю Ю ^	11
оооооооооооооооооооо
оо"оооооооооооооооооо
'COCOCOLOO-OOOLOOOOOOOOOC4IOOOO
СО СО Ю СО О t— LO	Ю О 1 СО ^ СО СЧ1	»—i	ОО Ь— СО
ОООООООООООООООООООО
- О О ОО О О ’—' ’
СОСОООО — ^O^OOOCOt^t^CNIOOOt^-COCOOO
ЮСОСОтгМО)СОЮЮЮ>О^СОСОСОМ«-<0)ч
оооооооооооооооооооо
J J ^ J J о О О О С О О	^	о	о
ООСОЮ^О^ЮЮ^Ю'—1 '—'О-—' СО С4) СО ОО СО
СО Ю СО Ю СО -•ООСОЮЮСОООО’—' COCOCOCN о о
оооооооооооооооооооо
_	_	о	о	о~о	о~о~	—'	—' —.	—I	г-.о
COOOOOO^'tOO'tOO-.-'NrOOONONOON
(М^ЮЮ'ФСМОЬСОЮСО^ООО—(NCOW-hO
оооооооооооооооооооо
<m-hOOOOQO’
COCCOWOO^inLOOOOlOOOO’^OO^OCOO't
О СО ^ Ю СО ■—1 о оо СО СО СО t"- О О | Сч) О СЧ) г-н
ОООООООООООООООООООО
< '—>’—1 ’—1 О О О О О О О ’—I’—I’—I’—I'—>т
OlOCDCOSCOlOOCO(M^O0rfcO-'OOC')T(M
O’-'CO^'t'^^-'OOONNNQPOOO-^--'
ооооо
U1 I’J Т Т CN '—I U) ии Г' Is- Г' (
ооооооооооооо»
« — ОО^ООООО*
СОООСООГ^^Г-1_ОЮГ-СОСЭЮОЮОСЧ)^СО
Is» О СЧ) СО СО СО СЧ) »—I О О 00 00 00 00 О СО О О О О
ОООООООООООООООООООО
о — —	©о	ооооо
СО NCDNNOCDOC41 Ю О'^СОСО'^ГСОГ^-ОООООО
СОООО—СЧ)СЧ)СЧ)^—,00000000000
оооооооооооооооооооо
о о —. *-« ~	~-Г	Л	о	о"	о	о"	o'	о	о”	о	о"	о"
T^ocor^tv.o.eo^oaoioc'j-.o-.ot'-t^io
S2222rr’H-,'H'HC)Ooooooooo
о о о о оооооооооооооооо
ООО—Н’—I— ^нт-н^-i^T-H^-ir—1^0000
оюоюоюоюоюоюоюоюоюою
О О О О —^CSJC4)cOCO^^lOLOCDCDl^-lN-00 00
517

Относительные значения сопрягающей частоты
о
ПЭ
о
С*.
ю
СМ
.
со
ю
СО
о
		,
см
см
см
см
см
СМ о
1Л
05
05
05
05
СП
СП
05
о
о
о
о
о
о
о
о о
ю
СП
05
05
05
СП
05
СП
о
о
о
о
о
о
о
о о
о
О
о
о
о
о
о
о
		(
00
СО
ю
ю
СО
СО
п-
сзо
СП
о
о
о
о
о о
о
СП
СП
СП
05
05
СП
СП
СП
СП
о
о
о
о
о о
о*
о
СП
СП
СП
05
05
СП
СП
СП
05
о
о
о
о
о о
’ '
О
о
о
о
о
о
о
о
о
' '
со
см
О
05
СП
00
00
t"-.
СО
со
СО О
■*£
о
О
о
о
о
о
СП
СП
СП
05
05
СП
05
05
СП Q
о
о
о
о
о
о
о
СП
05
05
СП
05
СП
05
СП
сп <5
CD
o'
o'
О*4
о
o'
о
о
о —~
о
со
со
ю
■ф
ф
ф
ф
ф
со
со
см
о
оо
г- о
о
о
о
о
о
о
О'
о
о
о
о
о
о
СП
05 о
о
о
о
о
о
о
о
о
о
о
о
о
о
СП
05 о
—'
—'
—'
—1
—*
о"
со
1C
см
со
ф
ю
СО
f"-
оо
г-
СО
ф
со
см о
СО
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
с
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
—■
—1
—
—1
—
о
Ю
ю
LO
со
t'-
05
о
см
ф
ф
ю
ю
ю
ф
"Ф о
со
СП
05
СП
05
05
05
о
о
о
о
о
о
о
о
о о
сГ
СП
05
05
С'.
05
СП
о
о
о
о
о
о
о
о
о о
o'
o'
о
о"
o'
о
—1
~-
ю
СМ
см
см
со
ю
со
00
05
05
СП
05
05 О
CJ
СП
СП
СП
05
05
СП
СП
05
СП
05
СП
СП
05
05
05 о
о'
СП
СП
СП
СП
СП
СП
05
05
СП
СП
05
СП
05
СП
о, о
о
о
о
о
о
о
о
о
о
о
о
о
о
о"
О
о
00
СО
ю
ф
ф
LO
ю
СО
СО
СО
СО
СО
ю
ю
ю о
<м
СП
СП
05
СП
СП
СП
СП
05
05
СП
СП
СП
СП
СП
СП О
о*
СП
СП
05
СП
СП
05
05
05
СП
СП
СП
05
СП
СП
05 о
о
о
о
о
о
СО¬
о
о
о
о
о
о
о
о
о
ю
00
со
ю
ф
со
СО
см
см
см
см
о
о
СП
05 О
О
о
о
о
о
о
о
о
О'
о
о
о-
о
05
СП о
о*
о
о
о
о
о
о
о
со
о
о
о
о
о
05
05 о
•ч
’ 1
’ '
1
’ '
’ '
1—1
1—1
о
о —•
о
LO
со
см
о
о
СП
00
ОО
t> О
pH
о
о
о
о о
о
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
•ч
,_н
’ 1
'~~1
’ 1
LC
о
о
о
см
см
см
см
см
ю
ю
ю
ю
ю
ю
ю о
сэ
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о^
о
о
о
о
о
о
о
о
о
о
о
о о
•ч
’—'
’—|
т~"
1
1—(
h-
IN.
00
00
СП
?СО
ф
ю
ю
ю
ю
ю
ю о
о
СО
со
СО
СО
со
•со
h-
h-
Г"-
г-
h-
Q
“
05
СП
СП
05
05
05
СП
L°5
05
05
СП
05
СП
СП
СП о
■ fc -
о
о"
о
о
о
со
' о
‘О
о
о
' о
о
о
‘ о
o' —Г
о
ю
о
ю
о
ю
о
ю
о
ю
о
ю
о
ю
о
* •*’ р
05
05
о
о
,—1
см
см
со
' со
If
ф
ю
LO
со о
см
СМ
см
см
см
см
см
см
СМ
см
см
см
см
518

Относительные значения сопрягающей частоты
O')
о
а
а
ж
о
о>
о
Ч
№ О) ОО IM Ю -н СО О Ю Ю Ю О	Oi	N
-i(N^N(J)-h-i^05N10c0i0C0^O
ЮЮЮЮЮОСОСОЮЮЮЮЮЮЮЮ
I — CS (N СЧ I	|	—	СМ	—	—	I	I	I
о £5 2 2 2 о 2 о ° о о о о о о
о о о о z; о
CD О' о О О LO о ^
о- о о
о о сГ о"
00 —I со Ю О CV) О - N (М О0 |М Ю Ю О
ОСО^^^СМО(МСО-ФГОСОО-Н(М
ОООООООООООООООО
000000000000 0-00
(DcOLO^^'tOi^triMOOQiONOO
IONOOO ^(N(N(M^OOONNNOO^
ООО О О О О' о о о о о о о о о
о
о
ООО
«00-000
О	N	П-	о	N	СО ^ 00 N « С1	ю	Ю	ОО	N	О
Ю	Ю	N	О	О	1C\)(MCS)CM—I	О	ОО	N	N	О
О	О	О	О	О	О О О О О О	О	О	О	О	О
О о о о
—•000-0
—< СО C\l	—iS(M(NiOCOiniO^(0^0
OONNNOOO-H(M(N(N^OOOOOOO
о о о о о о о о о о о о о о о о
о” o' о~ о" о”
о —«
— — о о о —
Г'-ЮООЮОСГ'-.ООЮС'-^-^ОО’—I S о
OOOSNSOOOO^-H^^O'OOOO
оооооооооооооооо
г-Г © о о" о о" о" — — — _Г	Г _ о —
CDOO^tDrOCD^OOMNOOOOlO^C^IO
оооооооооооооооооооо
0-0000000 о о о о о о о о
— ооооооо
О Ю — СО СО (N —'CM^f N О (N со ^ ^ О
ОООООООООООООООО
оооооооооооооооо
—• —«0000-000
Tj*COCO-HOOON0NOOOO-i(N(NO
оооооооооооооооо
оооооооооооооооо
ооооооо—•
N 0 Ю DIO
о о о о ,го
о о о о
Ю N
О jO О
О jO о
о — см СО СО СО СМ —| ^
ооооооооо
0000000 0-0
СО CV] (М ^ N О О
оооооооо
о о о о о о о о
N ОО 0 -Ф
о о о о
о о о о
о о
о о
о о
00 0-00 — — — — -*
о ю о ю о ю о Ю О LO
оооо — — (МС^СОСО^^ЮЮсО
--h(N(NW^(N<N(NW<NC4(N<N(N
О LO о LO о
Г Ю Ю 0 8
Г) 19

П р и л о ж с ни с 10
НОМОГРАММА ЗАМЫКАНИЯ С ВЫДЕЛЕНИЕМ
ВЕЩЕСТВЕННОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
ЗАМКНУТОЙ СИСТЕМЫ УПРАВЛЕНИЯ G0(м)

ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЗВЕНЬЕВ

Статическая характеристика Коэффициенты гармонической линеаризации
«К
^
X
Си
с
eh
«h
+
а Г
о
V/
...	ч
«	Ч
V	а
Ч
—	а
сГ	I
II	£
5S>	Л*
Q
!\
х
X
*сГ
о
+
х^
«ее
<яН
с
ъ
t-H
<я
+
в |сч
I
«ее I к
«р:
I
а|^
5 К
см
+
О
А
о о
V Л
а
+
JX
-ее
II
X
"а
I
х^
«ее
а
+
^Х
«е»
t
2
а
I
«е»
522

523

•0*
•e
£
В
S.
о
о V
A *
X ^
о
o' о V
Л II *
X X ^
-сГ o' I
II II II
й) :s>
ч
«к
о
А
Я
Си
В
в
А
х
*о
II
а
V/
X
ч
о
»С>
I
ц
624

л\
К
си
с
а
А
S
а*
с
V
А
и
Он
с
+
Q f<
I
V
+
л\
к
Си
о
л
• X
а
А
о
V
• X
а
а I
I У!
Л\ *
^ .о
О
л V
Л . х
*	I	X
а	V/	V/	j	V/
»? I- 5 f
о	I	л" О
II	II	II	!|	II
=Sj	^	^	^	55>
V/ л
х х
о" -о
II II
^	=51
525

626
+(1— mi) e

z™\4 'M- V l^+l
см
527

Статистические коэффициенты усиления I в формулах введены обозначения: mt^=	——;	о, = ——;	Ф (х)
528

а
tus
+->
ii
X
I.
e
X
*3
<M
I
+
IT
+
+ »"
СЧ
I
Й
+
Hi
-h
+
J.
+
iL
-i°*
i
x
.a
S
*oe
X
• н
К X
■ H
к
8<-
H
+
• X £
£ I
X I
, H *
IqV
^ +
ebH
• *
cT
e
X
\ \
34—903
529

— I<N
n
if
0*|3
и
•8-
•8*
+
X
E
+
cT
Q
e
+
Q
X
•	X
•	H
V
Q
X
><
Q
+
<s
о
i
X
X
.4
• X
Q
+
н
■ н
Q
sH
+
X
+
532

+
q4
a
i
x
l£
С
Ь»
+
CM
+
633

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ Ф (а);=
С5.
ft г
Iк
ICM
CO
00
о
СП
о
о
о
о
СП
о
00
1-
ю
ф
см
о
oo
о
см
ф
1"-
о
СО
ф
СО
00
о
см
ф
со
00
CO
г-
t"-
Г"-
00
00
00
00
оо
СП
СП
о
СП
<я
e
CO
СО
со
со
СО
со
со
СО
СО
со
со
ОО
СО
СО
со
со
cT
о
о
о
о"
о"
o'
о*
о
о
о"
о
о
о
o'
о
CM
со
ф
LO
со
г*-
00
о
о
см
со
ф
LO
СО
3
см
см
см
см
см
см
см
см
—
—
to
о
ю
о
СО
г-
_
ю
00
ф
СП
,
со
ю
ф
СО
00
CO
со
00
о
СО
LO
I'-
СП
см
ф
со
CO
со
со
СО
ф
ф
ф
ф
ю
ю
1.0
ю
ю
СО
со
со
ф
CO
со
со
со
со
со
со
СО
СО
СО
СО. СО
со
со
со
со
о
o'
о
о
o'
О*4
о"
о
CD
о
о
о
о”
o'
o'
о
О
г-
оо
СП
о
_
см
СО
ф
LO
со
п-
СО
СП
о
_
3
cn
о
о
СП
о
о
о
о
о
о
о
о
о
о
o~
о*
о
о"
—
—
—
—
—
—
о
о
t'-
ю
со
_
оо
со
со
СП
СО
СМ
00
ф
СП
oo
со
со
СП
см
ю
о
со
ю
оо
со
со
00
oo
о
СП
о
о
о
о
о
см
см
см
см
e
CM
см
см
см
см
со
СО
со
со
со
со
со
со
СО
СО
СО
cT
o'
о"
о
о
о
о
o'
о
о
o'
о
о
o'
о
CD
о
		,
см
со
ф
ю
со
t>-
00
СП
о
	,
см
СО
ф
1.0
00
00
00
00
оо
00
00
00
00
оо
СП
СП
СП
о
СП
СП
о
о
о"
о
o'
о
о"
о
о
о"
o'
о
o'
о
о
o'
о
см
ф
СО
t"-
о
о
_
см
СО
СО
ф
ф
ф
со
С'1
'—-
00
СМ
ю
00
ф
ОО
ф
о
со
со
СП
см
LO
CO
Ф
ф
ф
ю
ю
ю
о
со
со
г*-
1^
Г--
00
ОО
e
CM
см
см
см
см
см
см
см
см
см
см
см
см
см
см
см
о
о"1
О*4
о
о"
о"
о"
CD
o'
o'
о
о
о
о
о
о
Ф
ю
ico
ь-
00
СП
о
,
см
со
ф
ю
со
00
СП
3
CO
со
к
со
СО
со
h-
tn
t'-
tn
t"-
o'
о
о
о
о"
о
о
о~
о~
°~
о~
о
о
o'
о
Ф
о
ю
о
1.0
СП
ф
оо
СО
о
ф
ф
•Ч+*
г-
LO
оо
ю
оо
см
U0
СП
см
ю
СП
см
ю
CO
оо
о
СП
СП
о
о
о
см
см
см
со
СО
e
С 1
см
см
см
см
см
см
см
см
см
СМ
о
o'
о
о"
o'
о
о
о
о"
о"
о"
о
о
о
o'
CD
oo
о
о
, ,
см
СО
ф
ю
СО
N-
00
СП
о
,
см
со
3
Ф
ф
ю
ю
ю
ю
ю
ю
LO
ю
ю
LO
со
со
со
СО
o'
o'
о
о
о"
о
о
CD
о
o'
o'
о
о"
о
CD
о
LO
со
оо
со
СО
о
г-
ф
_
оо
ф
о
со
см
ОО
Ю
о
со
со
о
ф
00
1.0
СП
см
со
о
со
г-
о
CM
см
со
со
ф
ф
ф
1.0
IO
ю
со
со
1'-
|-
00
■0*
'—1
1—4
—1
'
1
>—•
1
1
o"
o'
o'
o'
о
о
CD
о
о"
о
CD
О*4
о"
о
о
о
CM
со
ф
ю
СО
t".
со
СП
о
1
см
со
ф
LO
со
3
CO
со
СО
со
со
со
со
со
ф
ф
ф
ф
ф
ф
ф
ф
о
о
CD
о"
о"
o'
о"
о
о
о"
о
CD
o'
о
CD
o’
о
ю
Ф
со
со
см
о
00
г-.
СО
ф
со
,
СП
г-
-—»
со
ю
СП
со
1"-
ф
оо
см
со
о
ф
1-
3
со
СО
t'-
1'-'-
оо
00
СП
СП
СП
о
о
см
6*
о
о
о
о
о
о
о
о
о
о
o'
о*
о"
о"
o'
о
о*
о
о"
о
o'
о
o'
o'
о"
о
со
1-
00
о
о
_
см
со
ф
ю
со
ь-
00
СП
о
,
3
*—•
см
см
С-1
см
см
см
см
см
см
см
со
со
o'
о
o'
о
o'
о
o'
о
o'
o'
о
о
о
о
о
о
о
о
о
о
СП
СП
СП
СП
О)
00
00
00
tn
Г--
со
о
ф
00
о
со
СП
СО
tn
ю
СП
со
ю
СП
о
о
о
см
см
см
СО
СО
со
ф
ф
ю
ю
ю
■&
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
o'
о
о
о
o'
о
о
о~
о"
о
CD
о~
<£
CD
o'
о
1
см
со
ф
ю
СО
г^
оо
СП
о
1
см
со
ф
LO
3
о
о
о
о
о
о
о
о
о
о
т—1
1
1
1
1
о
о"
о"
о
о
о"
о"
CD
о
о
о"
о"
o'
o'
o'
o'
534

Продолжена с п рало ж.
LD

D
ф
со
O'
©
©
©
СП
о
с-1
Ф
©
CD
CD
со
D
00
©
©
©
©
O'
O'
ОС
ОО
00
00
ОС
ОС
00
05
СП
СП
©
©
©
©
©
©
СП
СП
05
СП
СП
05
05
СП
05
05
©
©
©
©
е
Ф
ф
ф
ф
ф
ф
ф
Ф
Ф
ф
ф
ф
ф
ф
ф
ф
О
о
о
о
о
о
о
О
О
о
о
о
о
©
©
©
ф
CD
00
о
см
ф
CD
00
о
О
о
о
о
О
о
©
а
00
00
00
СП
05
СП
СП
СП
©
см
ф
CD
00
о
Ю
о
СМ
см
см"
см"
см
см"
см
см
со
со"
со
СО
СО
ф
ф"
ю
__
ю
00
СО
CD
05
_
СО
ю
Г'
СП
_
СО
ф
©
Ф
ф
ф
©
ю
©
©
CD
CD
CD
CD
CD
O'
O'
о-
©
СП
СП
СП
СП
05
05
05
05
СП
05
СП
CD
©
©
©
л
ф
ф
ф
ф
ф'
ф
ф
Ф
Ф
ф
ф
ф
ф
ф
ф
tf
о
о
о
о
о
о
о
О
О
о
о
о
о
о
о
©
СМ
ф
CD
00
о
см
ф
CD
00
о
С<!
ф
СО
00
о
см
3
©
ю
©
LO
CD
CD
CD
CD
CD
O'
O'
о-
O'
00
оо
См"
см
см"
см"
см"
СМ
см"
CM
см"
см
см
см"
см
см
см
см"
00
©

O'
СО
ОО
Ф
СП
СО
00
см
O'
• ^
ф
оо
CD
CD
О'-
ОО
ОО
05
СП
О
О
*—<
см
см
СО
СО
СП
00
00
00
00
00
ОО
00
05
СП
05
05
05
©
©
©
©
Л
ф
Ф
ф
ф
ф
Ф
Ф
Ф
ф
ф
Ф
ф
ф
ф
ф
ф
о
о
о
о
о
О
О
О
о
о
О
о
©
о
о
©
о
см
ф
CD
00
о
см
ф
CD
00
о ■
см
ф
D
00
о
3
см
см
см
см
СМ
СО
со
со
СО
.со
ф
ф
ф
ф
ф
ю
СМ
см
см"
см
см"
см"
см
см"
см"
см"
см
см
см"
см"
см
см"
00
ф
о
CD
O'
см
СО
СО
со
см
_
о
00
ю
ф
СО
Ф
LO
©
CD
CD
O'
00
СП
о
см
со
СО
ф
©
O'
O'
O'
O'
O'
O'
о-
1"-
о-
00
00
°р
00
оо
00
оо
*6>
ф
Ф
ф
ф
ф
Ф
ф
Ф
ф
ф
ф
ф
• ф
ф
ф
ф
о
o'
о"
о
о"
О
о"
О
о
о
о
о"
о"
о"
о"
о"
ф
©
CD
O'
00
05
о
см
ф
CD
00
о
см
ф
D
оо
3
©
о
СП
СП
05
СП
о
о
о
о
О
—
—1
—
—
см
см
см
см"
см
см
см
см
см"
см
©
со
СП
CD
Ф
	,
00
CD
со
о
D
со
©
D
см
см
со
ф
ф
©
CD
O'
O'
00
о
о
см
со
CD
CD
CD
CD
CD
CD
CD
CD
CD
CQ
O'
о-
С'-
O'
_
Ф
Ф
Ф
Ф
Ф
Ф
ф
Ф
Ф
ф
ф
ф
ф
ф
ф
&
О
О
О
о
О
О
о
О
О'
о
о
о
©
о
©
©
ОО
о
О
,
СМ
СО
ф
LO
со
O'
00
05
©
1
см
со
3
о-
O'
00
00
00
00
°о
00
оо
00
00
ОО
©
©
©
—
—
—
ф -
ф
LO
©
ю
©
©
ю
ф
ф
СО
см
©
оо
©
O'
00
О
о
см
со
ф
LO
CD
оо
©
©
о
Ф
Ф
ф
©
©
LO
©
LO
ю
LO
ю
ю
LO
ю
©
©
А
Ф
Ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
■W
О
О
о
о
о
о
о
о
о
о
©
о
©
©
о
©
<м
СО
ф
©
CD
O'
00
05
О
1
см
со
ф
LO
©
O'
3
CD
CD
CD
CD
©_
CD
CD
CD
O'
O'
O'
O'
о-
O'
~н
—11
—'
—
—•
*-
—•
—
©
О
СМ
05
см
©
O'
о
см
ф
D
00
©
см
СО
CD
1>-
СП
о
СО
ф
ю
O'
00
СП
о
см
ф
ю
©
см
см
см
СО
СО
СО
со
СО
со
со
СО
ф
ф
ф
ф
ф
ф
А
ф
Ф
ф
Ф
Ф
Ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
Xf
о
О
о
О
О
О
о
о
О
о
о
о
©
©
©
©
©
©
CD
O'
00
05
о
,
см
со
ф
ю
со
O'
оо
©
©
а
ф
Ф
ф
ф
Ф
LO
©
LO
LO
ю
ю
ю
ю
ю
ю
©
©
•*
•>
*
•*
т—|
,—1
’ '
4—1
’ 1
O'
©
см
СП
CD
см
05
ю
Г''
см
O'
см
O'
см
©

CD
СО
ф
CD
00
05
СО
ф
D
O'
©
©
см
со
©
СП
О
о
о
©
о
О
см
см
см
см
А
СО
Ф
Ф
ф
ф
ф
Ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
ф
V
О
О
о
о
о
о
О
о
©-
О'
о
©
©
О
©~
©
©"
00
СП
о
СМ
со
Ф
LO
D
O'
00
©
о
см
со
ф
а
см
см
СО
со
СО
со
СО
со
со
со
СО
СО
ф
ф
ф
ф
ф
•*
^-1
*“4
—1
535

Приложение 13
ФОРМУЛЫ ДЛЯ ИНТЕГРАЛОВ ОТ ДРОБНО¬
РАЦИОНАЛЬНЫХ ФУНКЦИИ
+00
/ -J- I 8п (/<■>)
" “ 2Я j hn (/со) hn (-/со) сы-
—00
где //„ (/со) = Л„ (/со)" + /1, (/со)«-1 + ... + Ап\
gn (/со) = В, (/со)2"'2 + В, (/со)2"-* + ... + B„_j.
При п = 1
+оо
.	1 i Д0	В0
- 2« J |Л/со+А\2	-2i40i41	;
при n — 2
+00
-ij-
I A>/W+A I2
£0 (/(0)2+ Д,
-До
При /2=3
Mo (/w)2+ AJiO+At\
+00
du>
2A0A1
 L f	[^0	(/CO)^	+	(/CO)3	+ ^ll	da	_
2n ) |Л(/(0)» + Л (э)4 AA»+AI* ~
—00
л40АД2
— A2B0 + AqBx —
2yl0
Общая формула
/* =
(- l)n+1 Nn
2A0 Dn f
где
Dn =
<*»
d\% •
• • d\n
d2X
d22 .
• * ^2/1
dn\
^Л2 •
• • dnn
I ^mr — Arfmr—^ (tl <^2m — Г <0)e
a Nn — определитель, полученный из Dn заменой элементов первого
столбца величинами До, Дь ..Д-i.
Формулы перехода от коэффициентов операторных функций
передачи а, b к коэффициентам дробно-рациональных функций
Л, Д:
An—k==:Q’h\
i=k—\
Вп-*-с=(-1)*6гй + 2	2	(-Ч'М.*-!-
О или 2Л+1— п
536

Приложение I 4
ТАБЛИЦА ДЛЯ ОПРЕДЕЛЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
НА ВЫХОДЕ СИСТЕМЫ, ЗАДАННОЙ ТИПОВОЙ 1.Ф,
ВОЗБУЖДЕННОЙ БЕЛЫМ ШУМОМ ЕДИНИЧНОЙ
ИНТЕНСИВНОСТИ
Вид ПФ
Изображение по Лапласу корреляционной
функции
Ьо
К i /А ' 6Va°
a,p-j-a0
_ 2 агр + а0
(р) =
biP+b0
а0621 +а2&2о
1 а0а, р +
*!i
~ йгР2 + Л\Р + «о
242 W 2 а2р2 + а3р + а„
w3 (р) =
ЬгРг+ Ь,р+ Ь0
1 ,г_ _ ,, ,
а3р3 + агр2 +
+ а,р-\-а0
а0(а,а2-а0а3)
+ a2a3b2o — а„а3 (2b0b2 — b2,)] p2 X
X [a0a262i + (а„62 — а26„)2] p} +
1 “ a0
К-з(Р) 2 а3р3 -f- а->р2 -f- а,р+а0
^ (Р) =
Ь;Р’ + Ь2р2 + Ь,р+
"Ь Ьо
а4р*+а Зр3+а2р2 +
+а,/)+а0
*4 (Р) -
[ Ь2о {a0a3ai — а2а3а4 + а^2.,) —
—622а0а1а4+Ьг3(а20а3—а„а,а2) +
+ 26,Ь3а0а,а4] р3 + [620 (ага23 —
—	а,а3а,) +621а0а23+Ь22а0а,а5+
1 + 623а0а2, — 2Ь0Ь2а0а23 —
—2&i63aoai<»3] Р2— !ft2o (a0a,a4 +
+ а„а2а3 — аг2а3) + Ь23 (а,а4 —
—	а2а3) а„ — Ь22аг0а3—b23a20«i+
+ 2b0b2(a2a3 — а,а4) а0 +
+ 2bib-,a2l,ala3al] р j
! . Ь2о
1 а,а2а3 — а2^ — а0а23 а0
~ 2 а4р4 + а3/>3 + а2/?2 + а,/? + а0
537

ПРИЛОЖЕНИЕ 15
ЗАВИСИМОСТЬ ВРЕМЕНИ РЕГУЛИРОВАНИЯ
И ПЕРЕРЕГУЛИРОВАНИЯ ОТ ЗНАЧЕНИЯ МАКСИМУМА
ВЕЩЕСТВЕННОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
ПРИЛОЖЕНИЕ 16
ЗАВИСИМОСТЬ ВРЕМЕНИ РЕГУЛИРОВАНИЯ
И ПЕРЕРЕГУЛИРОВАНИЯ ОТ КОЭФФИЦИЕНТА НАКЛОНА
ТРАПЕЦЕИДАЛЬНОЙ ВЕЩЕСТВЕННОЙ ЧАСТОТНОЙ
ХАРАКТЕРИСТИКИ
538

ПРИЛОЖЕНИЕ I'
ОБОЗНАЧЕНИЯ ФУНКЦИЙ В ОБЛАСТИ АРГУМЕНТОВ t, р, г
И ОПЕРАТОРОВ ПЕРЕВОДА ИЗ ОДНОЙ ОБЛАСТИ В ДРУГУЮ

СПИСОК ЛИТЕРАТУРЫ
1. Андреев Н. И. Корреляционная теория статистически опти¬
мальных систем. М.: Наука, (1966.
2. Анисимов В. И., Вавилов А. А., Фатеев А. В. Сборник при¬
меров и задач по линейной теории автоматического регулирования.
М.—Л.: Госэнергоиздат, 1959.
3. Барковский В. В., Захаров В. Н., Шаталов А. С. Методы
синтеза систем управления. М.: Машиностроение, 1969.
4. Сборник задач по теории автоматического регулирования. М.:
Наука, 1963. В. А. Бесекерский и др.
5. Вентцель Е. С. Элементы теории игр. М.: Физматгиз, 1959.
6. Гантмахер Ф. Р. Теория матриц. М.: Наука, 1967.
7. Заславский Ю. Л. Сборник задач по линейному программи¬
рованию. М.: Наука, 1969.
8. Казаков И. Е., Доступов Б. Г. Статистическая динамика не¬
линейных автоматических систем. М.: Физматгиз, 1962.
9. Казаков И. Е. Статистические методы проектирования систем
управления. М.: Машиностроение, 1969.
10. Красовский А. А., Поспелов Г. С. Основы автоматики и тех¬
нической кибернетики. М.—Л.: Госэнергоиздат, 1962.
11. Лэнинг Д. X., Бэттиин Р. Т. Случайные процессы в задачах
автоматического управления. М.: Физматгиз, 1960.
12. Мезон С., Циммерман Г. Электронные цепи, сигналы и си¬
стемы. М.: Изд-во иностр. лит., 1963.
13. Сборник задач и примеров по теории автоматического регу¬
лирования. М.: Высшая школа, 1969./ В. А. Олейников, Н. С. Зотов,
А. М. Пришвин, Н. В. Соловьев.
14. Павлов С. Т. Построение частотных характеристик для САР,
обладающих постоянным запаздыванием. — «Доклады АН СССР»
1956, т. 107, № 1, с. 79—80.
15. Современные методы проектирования систем автоматического
управления. М.: Машиностроение, 1967./ Б. Н. Петров и др.
16. Попов Е. П., Пальтов И. П. Приближенные методы иссле¬
дования нелинейных автоматических систем. М.: Физматгиз, 1960.
17. Пугачев В. С. Теория случайных функций и ее применение
к задачам автоматического управления. М.: Физматгиз, 1962.
18. Сборник задач по теории вероятностей, математической ста¬
тистике и теории случайных функций./ Под ред. А. А. Свешникова.
М.: Наука, 1965.
19. Теория автоматического управления. Кн. 3, ч. 1. Техническая
кибернетика./ Под ред. В. В. Солодовникова. М.: Машиностроение,
1967.	v
20. Солодовников В. В. Статистическая динамика систем авто¬
матического управления. М.: Физматгиз, 1962.
540

21. Фельдбаум А. А. Основы теории автоматических систем. М.:
Физматгиз, 1963.
22. Теоретические основы связи и управления. М.: Физматгиз,
1963./ А. А. Фельдбаум, А. А. Дудыкин и др.
23. Хлыпало Е. И. Нелинейные системы автоматического регули¬
рования. М.: Энергия, 1967.
24. Цыпкин Я. 3. Теория релейных систем автоматического регу¬
лирования. М.: Физматгиз, 1955.
25. Шаталов А. С. Структурные методы в теории управления и
электроавтоматике. М.—Л.: Госэнергоиздат, 1962
26. Шаталов А. С. Преобразование сигналов и изображающих
их функций обобщенными линейными системами автоматического
управления. М.—Л.: Энергия, 1965.
27. Шаталов А. С., Топчиев Ю. И., Кондратьев В. С. Летатель
ные аппараты как объекты управления. М.: Машиностроение, 1972.
28. Теория автоматического управления. М.: Высшая школа,
1977/ Под ред. А. С. Шаталова.
29. Топчиев Ю. И., Цыплаков А. П. Задачник по теории авто¬
матического управления. М.: Машиностроение, 1977.
30. Шаталов А. С. Блочно-матричная форма расширенных урав¬
нений состояния линейных электрических цепей.—Электричество,
1978, № 12, с. 47—54.

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию	о
Предисловие к первому изданию	4
ЧАСТЬ ПЕРВАЯ
ЗАДАЧИ
Глава первая. Линейные преобразования сигналов ана¬
логовыми стационарными и нестационарными звеньями	7
1-1. Задание типовых входных сигналов в аналоговой и
частотной формах	 7
1-2. Составление линейных дифференциальных уравне¬
ний звеньев 	 9
1-3. Определение переходных и импульсных характеристик	17
1 -4. Анализ прохождения сигналов через линейные звенья
во временной области	20
1-5. Анализ линейных звеньев на основе метода преобра¬
зования Лапласа	21
1-6. Анализ непрерывных процессов на основе метода
г-преобразования 	 25
1-7. Частотные характеристики	27
1-8. Частотные спектры выходных процессов ....	31
1-9. Базовые характеристики	34
1-10. Начальные условия и начальные значения ....	34
Глава вторая. Топологические методы анализа	35
2-1. Общие правила и ограничения	35
2-2. Преобразование структур звеньев и систем ...	37
2-3. Структурный анализ электрических цепей ....	47
2-4. Графы	48
2-5. Топологические и блочные преобразования матриц и
определителей 	 49
Глава третья. Анализ и основы синтеза линейных систем
непрерывного управления ...	51
3-1. Точность вынужденного движения стационарных си¬
стем (с постоянными параметрами)	51
3-2. Точность нестационарных линейных систем ...	57
3-3. Асимптотическая устойчивость	58
3-4. Качество линейных систем непрерывного управления	68
3-5. Синтез общей структуры системы управления и кор¬
ректирующих цепей	 71
542

Глава четвертая. Дискретные автоматические системы
управления  	73
4-1. Операторное описание процессов в дискретных си¬
стемах 	73
4-2. Анализ и синтез одноконтурных дискретных систем
управления	76
4-3. Синтез дискретных систем по методу параметров со¬
стояния 	79
Глава пятая. Анализ и синтез нелинейных систем	82
5-1. Типовые нелинейности и их характеристики ...	82
5-2. Метод фазовых траекторий	  82
5-3. Метод припасовывания	83
5-4. Исследование релейной системы по методу Я. 3. Цып-
кина	  84
5-5. Приближенные методы исследования автоколебаний
нелинейных систем при условии фильтрации высших
гармоник	85
5-6. Метод вибрационной линеаризации	88
5-7. Синтез оптимальных нелинейных систем .	.	89
Глава шестая. Статистические методы исследования авто¬
матических систем управления	90
6-1. Анализ линейных систем, подверженных случайным
воздействиям	90
6-2. Анализ нелинейных систем, подверженных случайным
воздействиям	95
6-3. Оптимальные системы по статистическим критериям	99
6-4. Исследование линейных дискретных систем, подвер¬
женных случайным воздействиям	105
6-5. Элементы теории статистических решений .	.	.	.	107
Глава седьмая. Кибернетические автоматические системы
управления	 ....	109
7-1. Системы экстремального регулирования ....	109
7-2. Системы, настраивающиеся на эталон	112
7-3. Матричные игры и задачи линейного программирова¬
ния 	118
ЧАСТЬ В Т О Р А я
РЕШЕНИЯ
Глава первая. Линейные преобразования сигналов ана¬
логовыми стационарными и нестационарными	звеньями 120
01-1. Задание типовых входных сигналов в аналоговой и
частотной формах	120
01-2. Составление линейных дифференциальных уравнений
звеньев	128
01-3. Определение переходных и импульсных характеристик 139
01-4. Анализ прохождения сигналов через линейные звенья
во временной области .	...	146

01-5. Анализ линейных звеньев на основе метода преобра¬
зования Лапласа	151
01-6. Анализ непрерывных процессов на основе метода
2-преобразования	 ...	170
01-7. Частотные	характеристики	177
01-8. Частотные	спектры выходных процессов .	.	.	.	191
01-9. Базовые характеристики	203
01-10. Начальные	условия и начальные значения ....	208
Глава вторая.	Топологические методы анализа	212
02-1. Общие правила и ограничения	 .212
02-2. Преобразования структур звеньев и систем	.	217
02-3. Структурный анализ электрических цепей	.	.	.	233
02-4. Графы	238
02-5. Топологические и блочные преобразования матриц
и определителей	 .	244
Глава третья. Анализ и основы синтеза линейных систем
непрерывного управления	 251
03-1. Точность вынужденного движения стационарных си¬
стем (с постоянными параметрами)	....	251
03-2. Точность нестационарных линейных систем	.	.	.	259
03-3. Асимптотическая устойчивость	261
03-4. Качество линейных систем непрерывного	управления	274
03-5. Синтез общей структуры системы управления и кор¬
ректирующих цепей	  279
Глава четвертая. Дискретные автоматические системы
управления  	288
04-1. Операторное описание процессов в дискретных систе¬
мах 	288
04-2. Анализ и синтез одноконтурных дискретных систем
управления	300
04-3. Синтез дискретных систем по методу параметров со¬
стояния 	 314
Глава пятая. Анализ и синтез нелинейных	систем	332
05-1. Типовые нелинейности и их характеристики	.	.	332
05-2. Метод фазовых траекторий	 337
05-3. Метод припасовывания	349
05-4. Исследование релейной системы по методу Я. 3. Цып-
кина	356
05-5. Приближенные методы исследования автоколебаний
нелинейных систем при условии фильтрации	высших
гармоник	359
05-6. Метод вибрационной линеаризации	370
05-7. Синтез оптимальных нелинейных систем	....	382
Глава шестая. Статистические методы исследования авто¬
матических систем управления	 396
06-1. Анализ линейных систем, подверженных случайным
воздействиям	  396
544

06-2. Анализ нелинейных систем, подверженных случайным
воздействиям
06-3. Оптимальные системы по статистическим критериям
06-4. Исследование линейных дискретных систем, подвер¬
женных случайным воздействиям
06-5. Элементы теории статистических решений
Глава седьмая. Кибернетические автоматические системы
управления
07-1. Системы экстремального регулирования .
07-2. Системы, настраивающиеся на эталон
07-3. Матричные игры и задачи линейного программирова¬
ния
ЧАСТЬ ТРЕТЬЯ
ПРИЛОЖЕНИЯ
1. Таблица матриц коэффициентов уравнений второго по¬
рядка для воспроизведения воздействий в виде заданных
функций
2. Таблица изображений по Лапласу функций и их произве¬
дений, полученных методом преобразования по парамет¬
ру X исходных соотношений
3. Таблица коэффициентов к расчету начальных значений не¬
стационарных и стационарных (£ = 0) реакций
4. Таблица для перехода от начальных функций к их изо¬
бражениям по Лапласу и к 2-изображениям .
5. Таблица перехода от децибелов к прямым отношениям .
6. Данные для коррекции асимптотических ЛАХ колебатель¬
ного звена
7. Номограмма для перехода от логарифмической амплитуд¬
но-фазовой частотной характеристики к вещественной и
мнимой частотным характеристикам (G, 5-номограмма) .
8. Номограмма замыкания (Ф-номограмма)
9. Таблица hx-функций и специальных функций (нормиро¬
ванный синус, его квадрат и интегральный синус)
10. Номограмма замыкания с выделением вещественной ча¬
стотной характеристики замкнутой системы управления
Сто (со)
11. Характеристики нелинейных звеньев
12.
13. Формулы для интегралов от дробно-рациональных функций
14. Таблица для определения корреляционных функций на
выходе системы, заданной типовой ПФ, возбужденной бе¬
лым шумом единичной интенсивности
15. Зависимость времени регулирования и перерегулирования
от значения максимума вещественной частотной характе¬
ристики
16. Зависимость времени регулирования и перерегулирования
от коэффициента	наклона трапецеидальной	вещественной
частотной характеристики
17. Обозначения функций	в области аргументов	t, р,	z	и	опе¬
раторов перевода	из	одной области в другую	«	.
Список литературы,	 	.	,	,
Таблица значений функции Ф (и) —у ==- ^
2
411
424
449
454
458
458
476
489
500
502
505
507
510
511
512
513
514
520
521
534
536
537
538
538
539
54Q